diff --git "a/6_1_backpropagation_neuron_manual_calculation.ipynb" "b/6_1_backpropagation_neuron_manual_calculation.ipynb"
new file mode 100644--- /dev/null
+++ "b/6_1_backpropagation_neuron_manual_calculation.ipynb"
@@ -0,0 +1,2521 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "jtRAdDVT6jf2"
+ },
+ "outputs": [],
+ "source": [
+ "class Value:\n",
+ "\n",
+ " def __init__(self, data, _children=(), _op='', label=''):\n",
+ " self.data = data\n",
+ " self.grad = 0.0\n",
+ " self._prev = set(_children)\n",
+ " self._op = _op\n",
+ " self.label = label\n",
+ "\n",
+ "\n",
+ " def __repr__(self): # This basically allows us to print nicer looking expressions for the final output\n",
+ " return f\"Value(data={self.data})\"\n",
+ "\n",
+ " def __add__(self, other):\n",
+ " out = Value(self.data + other.data, (self, other), '+')\n",
+ " return out\n",
+ "\n",
+ " def __mul__(self, other):\n",
+ " out = Value(self.data * other.data, (self, other), '*')\n",
+ " return out"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "AIP2sPDm6Los",
+ "outputId": "8e1d5665-fc27-4ddb-95ac-a9cf53f25d51"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "Value(data=-8.0)"
+ ]
+ },
+ "execution_count": 21,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "a = Value(2.0, label='a')\n",
+ "b = Value(-3.0, label='b')\n",
+ "c = Value(10.0, label='c')\n",
+ "e = a*b; e.label='e'\n",
+ "d= e + c; d.label='d'\n",
+ "f = Value(-2.0, label='f')\n",
+ "L = d*f; L.label='L'\n",
+ "L"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {
+ "id": "T0rN8d146jvF"
+ },
+ "outputs": [],
+ "source": [
+ "from graphviz import Digraph\n",
+ "\n",
+ "def trace(root):\n",
+ " #Builds a set of all nodes and edges in a graph\n",
+ " nodes, edges = set(), set()\n",
+ " def build(v):\n",
+ " if v not in nodes:\n",
+ " nodes.add(v)\n",
+ " for child in v._prev:\n",
+ " edges.add((child, v))\n",
+ " build(child)\n",
+ " build(root)\n",
+ " return nodes, edges\n",
+ "\n",
+ "def draw_dot(root):\n",
+ " dot = Digraph(format='svg', graph_attr={'rankdir': 'LR'}) #LR == Left to Right\n",
+ "\n",
+ " nodes, edges = trace(root)\n",
+ " for n in nodes:\n",
+ " uid = str(id(n))\n",
+ " #For any value in the graph, create a rectangular ('record') node for it\n",
+ " dot.node(name = uid, label = \"{ %s | data %.4f | grad %.4f }\" % ( n.label, n.data, n.grad), shape='record')\n",
+ " if n._op:\n",
+ " #If this value is a result of some operation, then create an op node for it\n",
+ " dot.node(name = uid + n._op, label=n._op)\n",
+ " #and connect this node to it\n",
+ " dot.edge(uid + n._op, uid)\n",
+ "\n",
+ " for n1, n2 in edges:\n",
+ " #Connect n1 to the node of n2\n",
+ " dot.edge(str(id(n1)), str(id(n2)) + n2._op)\n",
+ "\n",
+ " return dot"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 247
+ },
+ "id": "k7wjwrfo6nUl",
+ "outputId": "d78c4618-6574-49f9-8e80-f2faa8dad69a"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/svg+xml": [
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 7,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw_dot(L)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "bcJ3Q97AutNy"
+ },
+ "source": [
+ "------------------"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "wFLtnVu1uuaz"
+ },
+ "source": [
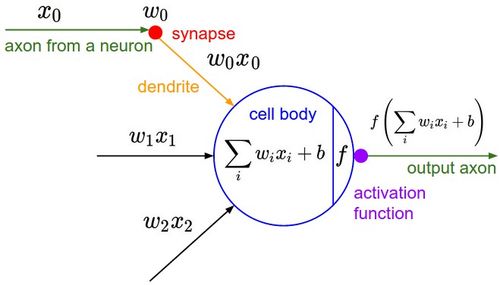
+ "### **Implementing the Neuron Mathematical Mode**"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "VhRE8DEMu3Qb"
+ },
+ "source": [
+ ""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "3rGi-UXPu0lq"
+ },
+ "outputs": [],
+ "source": [
+ "#Inputs x1, x2 of the neuron\n",
+ "x1 = Value(2.0, label='x1')\n",
+ "x2 = Value(0.0, label='x2')\n",
+ "\n",
+ "#Weights w1, w2 of the neuron - The synaptic values\n",
+ "w1 = Value(-3.0, label='w1')\n",
+ "w2 = Value(1.0, label='w2')\n",
+ "\n",
+ "#The bias of the neuron\n",
+ "b = Value(6.7, label='b')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "RQHJZ77FvRz-"
+ },
+ "outputs": [],
+ "source": [
+ "x1w1 = x1*w1; x1w1.label = 'x1*w1'\n",
+ "x2w2 = x2*w2; x2w2.label = 'x2*w2'\n",
+ "\n",
+ "#The summation\n",
+ "x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1*w1 + x2*w2'"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "i33UWc5Yvh5e"
+ },
+ "outputs": [],
+ "source": [
+ "#n is basically the cell body, but without the activation function\n",
+ "n = x1w1x2w2 + b; n.label = 'n'"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 322
+ },
+ "id": "aj871Eg0wVW_",
+ "outputId": "d4b424e3-0b7b-4857-b250-91b4e1b43626"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/svg+xml": [
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 6,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw_dot(n)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "TrUjY3Xrw0TP"
+ },
+ "source": [
+ "Now, we have to get the output i.e. by having the dot product with the activation function.\n",
+ "\n",
+ "So we have to implement the tanh function"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "fd6oiWGaxEIb"
+ },
+ "source": [
+ "Now, tanh is a hyperbolic expression. So it doesnt just contain +, -, it also has exponetials. So we have to create that function first in our Value object.\n",
+ "\n",
+ " \n",
+ "\n",
+ "\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "hAXPXTquy8KN"
+ },
+ "source": [
+ "So now, lets update our Value object"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {
+ "id": "JlYxBvFK0AjA"
+ },
+ "outputs": [],
+ "source": [
+ "import math"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {
+ "id": "4XPxg_t3wl35"
+ },
+ "outputs": [],
+ "source": [
+ "class Value:\n",
+ "\n",
+ " def __init__(self, data, _children=(), _op='', label=''):\n",
+ " self.data = data\n",
+ " self.grad = 0.0\n",
+ " self._prev = set(_children)\n",
+ " self._op = _op\n",
+ " self.label = label\n",
+ "\n",
+ "\n",
+ " def __repr__(self): # This basically allows us to print nicer looking expressions for the final output\n",
+ " return f\"Value(data={self.data})\"\n",
+ "\n",
+ " def __add__(self, other):\n",
+ " out = Value(self.data + other.data, (self, other), '+')\n",
+ " return out\n",
+ "\n",
+ " def __mul__(self, other):\n",
+ " out = Value(self.data * other.data, (self, other), '*')\n",
+ " return out\n",
+ "\n",
+ " def tanh(self):\n",
+ " x = self.data\n",
+ " t = (math.exp(2*x) - 1)/(math.exp(2*x) + 1)\n",
+ " out = Value(t, (self, ), 'tanh')\n",
+ " return out"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {
+ "id": "S3HaLbW_zvne"
+ },
+ "outputs": [],
+ "source": [
+ "#Inputs x1, x2 of the neuron\n",
+ "x1 = Value(2.0, label='x1')\n",
+ "x2 = Value(0.0, label='x2')\n",
+ "\n",
+ "#Weights w1, w2 of the neuron - The synaptic values\n",
+ "w1 = Value(-3.0, label='w1')\n",
+ "w2 = Value(1.0, label='w2')\n",
+ "\n",
+ "#The bias of the neuron\n",
+ "b = Value(6.7, label='b')\n",
+ "\n",
+ "x1w1 = x1*w1; x1w1.label = 'x1*w1'\n",
+ "x2w2 = x2*w2; x2w2.label = 'x2*w2'\n",
+ "\n",
+ "#The summation\n",
+ "x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1*w1 + x2*w2'"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "UuUWxrHQzzYG"
+ },
+ "outputs": [],
+ "source": [
+ "#n is basically the cell body, but without the activation function\n",
+ "n = x1w1x2w2 + b; n.label = 'n'\n",
+ "\n",
+ "#Now we pass n to the activation function\n",
+ "\n",
+ "o = n.tanh(); o.label = 'o'"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 322
+ },
+ "id": "j8zlrUnLz8F4",
+ "outputId": "9ea436d3-3701-4bb8-9fad-7dd9e14cbbe9"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/svg+xml": [
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 11,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw_dot(o)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "wMbP3alD0QYV"
+ },
+ "source": [
+ "We have recieved that output. So now, tanh is our little 'micrograd supported' node here, as an operation :)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "fLfUZz_C6gHv"
+ },
+ "source": [
+ "------------------"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "VGDr6YAm6yA5"
+ },
+ "source": [
+ "We'll be doing the manual backpropagation calculation now"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 30,
+ "metadata": {
+ "id": "bYaK0R-x6grf"
+ },
+ "outputs": [],
+ "source": [
+ "x1 = Value(0.0, label='x1')\n",
+ "x2 = Value(2.0, label='x2')\n",
+ "\n",
+ "w1 = Value(1.0, label='w1')\n",
+ "w2 = Value(-3.0, label='w2')\n",
+ "\n",
+ "b = Value(6.8813735870195432, label='b') #We've set this specific value for calculation purposes. Normally, if you increase this value, the final ouput will close to one.\n",
+ "\n",
+ "x1w1 = x1*w1; x1w1.label = 'x1*w1'\n",
+ "x2w2 = x2*w2; x2w2.label = 'x2*w2'\n",
+ "\n",
+ "x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1*w1 + x2*w2'\n",
+ "\n",
+ "n = x1w1x2w2 + b; n.label = 'n'\n",
+ "o = n.tanh(); o.label = 'o'"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "tj_JGsC77yro"
+ },
+ "source": [
+ "First we know the derivative of o wrt o will be 1, so"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 31,
+ "metadata": {
+ "id": "2lWNxVNE7G3b"
+ },
+ "outputs": [],
+ "source": [
+ "o.grad = 1.0"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 32,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 322
+ },
+ "id": "GgVziDS-7Dcb",
+ "outputId": "65b65dff-d91d-45bc-94ca-6d16e47334f9"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/svg+xml": [
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 32,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw_dot(o)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "VF7cB0Ta7xHh"
+ },
+ "source": [
+ "Now, for do/dn we need to find the derivative through tanh\n",
+ "\\\n",
+ "we know, 0 = tanh(n)\n",
+ "\\\n",
+ "so what will be do/dn\n",
+ "\n",
+ " \n",
+ "\n",
+ "We'll refer the derivatives of tanh (3rd equation) \\\n",
+ "\n",
+ "\n",
+ " \n",
+ "\n",
+ "We will use the first one in that, i.e. 1 - tan^2 x\n",
+ "\\\n",
+ "So basically, \\\n",
+ "=> o = tanh(n) \\\n",
+ "=> do/dn = 1 - tanh(n) ** 2 \\\n",
+ "=> do/dn = 1 - o ** 2\n",
+ "\n",
+ " \n",
+ "\n",
+ "Now this is broken down to a simpler equation which our Value object can perform."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 33,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "CH5LIM0t7XKo",
+ "outputId": "dda95015-4812-4783-96e4-b296e154944a"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "0.4999999999999999"
+ ]
+ },
+ "execution_count": 33,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "1 - (o.data**2)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Xx-dCYXy-EJh"
+ },
+ "source": [
+ "So, it is coming to 0.5 approx"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 34,
+ "metadata": {
+ "id": "Ij0k87Xp9xhy"
+ },
+ "outputs": [],
+ "source": [
+ "n.grad = 0.5"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 35,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 322
+ },
+ "id": "uUgJDWNg-KuG",
+ "outputId": "eea1f42f-dd5a-4be1-f9f1-627fd38f7209"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/svg+xml": [
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 35,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw_dot(o)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "RHIE47QY-ive"
+ },
+ "source": [
+ "Here, we know from previous example that, if it is an addition operation, then the derivative just comes as 1. So here the gradient value of n will itself channel out to its child nodes."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 36,
+ "metadata": {
+ "id": "0TZ4A59h-N9T"
+ },
+ "outputs": [],
+ "source": [
+ "b.grad = 0.5\n",
+ "x1w1x2w2.grad = 0.5"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 37,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 322
+ },
+ "id": "qw-hpdrF-10v",
+ "outputId": "3afda472-65f3-427b-e00f-583c2a0acf05"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/svg+xml": [
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 37,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw_dot(o)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Qvm-W5kA_tSF"
+ },
+ "source": [
+ "Continuing, same we have the '+' operation again. So the grad value of x1w1x2w2 flows onto its child nodes"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 38,
+ "metadata": {
+ "id": "HLyMUTtl-3_7"
+ },
+ "outputs": [],
+ "source": [
+ "x1w1.grad = 0.5\n",
+ "x2w2.grad = 0.5"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 39,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 322
+ },
+ "id": "6C-Mz0kV__oW",
+ "outputId": "0bb5d36d-998b-4b2d-b3df-7ee2293eadbd"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/svg+xml": [
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 39,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw_dot(o)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "cx_0IOPYADNI"
+ },
+ "source": [
+ "Now, its the product '*' (We have already seen how it interchanges the values) \\\n",
+ "So\\\n",
+ "x1 = w1 * x1w1.grad => 1.0 * 0.5 = 0.5 \\\n",
+ "w1 = x1 * x1w1.grad => 0.0 * 0.5 = 0.0\n",
+ "\n",
+ " \n",
+ "\n",
+ "x2 = w2 * x2w2.grad => -3.0 * 0.5 = -1.5\\\n",
+ "w2 = x2 * x2w2.grad => 2.0 * 0.5 = 1.0"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 40,
+ "metadata": {
+ "id": "F0gWiL0rABYo"
+ },
+ "outputs": [],
+ "source": [
+ "x1.grad = 0.5\n",
+ "w1.grad = 0.0\n",
+ "x2.grad = -1.5\n",
+ "w2.grad = 1.0"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 41,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 322
+ },
+ "id": "XeB29tXnBft-",
+ "outputId": "c73f8176-0910-4f00-d7c9-a29e9180ef6f"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/svg+xml": [
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 41,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw_dot(o)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "*P.S. I have edited this file from my local system, I have modified the above cells to the correct value (x1.grad), so in the above node x1, the grad value should display 0.5 not 1.0*"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "s66hkAeJCP64"
+ },
+ "source": [
+ "-----------"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "0L1FyQHhCQk4"
+ },
+ "source": [
+ "**Now, here the weights play a huge rule in reducing the loss function value in the end. Therefore, he we can get to know by changing which 'w' we can affect the final output.** \\\n",
+ "\\\n",
+ "**In this case, w1 has no effect on this neuron's output, as it's gradient is 0** \\\n",
+ "\\\n",
+ "**So, in this example, only 'w2' has an effect.** \\\n",
+ "\\\n",
+ "Therefore, my modifying the value of 'w2' and increasing the bias, we can squash the tanh function and get the final output to flat out to 1."
+ ]
+ }
+ ],
+ "metadata": {
+ "colab": {
+ "provenance": []
+ },
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ },
+ "language_info": {
+ "name": "python"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 0
+}