question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
serialize-and-deserialize-bst | Serialize & Deserialize BST & BT | serialize-deserialize-bst-bt-by-rocket_g-in4x | https://leetcode.com/problems/serialize-and-deserialize-binary-tree/\nhttps://leetcode.com/problems/serialize-and-deserialize-bst/\n\nIn my opinion, although th | rocket_ggy | NORMAL | 2021-01-24T18:43:41.969603+00:00 | 2021-01-24T18:43:41.969643+00:00 | 149 | false | https://leetcode.com/problems/serialize-and-deserialize-binary-tree/\nhttps://leetcode.com/problems/serialize-and-deserialize-bst/\n\nIn my opinion, although the first one is marked as hard, it is actually easier than the second one. Because for the second one, you need to utilize the binary search tree property and make the tree COMPACT as required by the problem. By compact it means you can\'t append "null" values to indicate tree structure. Instead, you need to utilize bst properties to get tree structure.\n\nSolution for BST:\n```\npublic class Codec {\n int index = 0;\n // Encodes a tree to a single string.\n public String serialize(TreeNode root) {\n if (root == null) {\n return "";\n }\n \n //post order traveral: left, right, root\n StringBuilder sb = new StringBuilder();\n \n //left \n String left = serialize(root.left);\n if (left.length() > 0) {\n sb.append(left).append(",");\n }\n \n //right\n String right = serialize(root.right);\n if (right.length() > 0) {\n sb.append(right).append(",");\n }\n \n //root\n sb.append(root.val).append(",");\n\n String result = sb.substring(0, sb.length() - 1).toString();\n return result;\n }\n\n // Decodes your encoded data to tree.\n public TreeNode deserialize(String data) {\n if (data.length() <= 0) {\n return null;\n }\n String[] array = data.split(",");\n index = array.length - 1;\n return helper(array, Integer.MIN_VALUE, Integer.MAX_VALUE);\n }\n \n public TreeNode helper(String[] array, int lower, int upper){\n if (index < 0) {\n return null;\n }\n int num = Integer.valueOf(array[index]);\n if (num < lower || num > upper) {\n return null;\n }\n index--;\n TreeNode root = new TreeNode(num);\n root.right = helper(array, num, upper);\n root.left = helper(array, lower, num);\n return root;\n }\n}\n```\n\nSolution for BT (Not this problem):\n```\npublic class Codec {\n int index = 0;\n // Encodes a tree to a single string.\n public String serialize(TreeNode root) {\n if (root == null) {\n return "null";\n }\n \n StringBuilder sb = new StringBuilder();\n \n //preorder traversal\n sb.append(root.val)\n .append(",")\n .append(serialize(root.left))\n .append(",")\n .append(serialize(root.right));\n\n return sb.toString();\n }\n\n // Decodes your encoded data to tree.\n public TreeNode deserialize(String data) {\n String[] array = data.split(",");\n return helper(array);\n }\n \n public TreeNode helper(String[] array){\n if (array[index].equals("null")) {\n index++;\n return null;\n }\n TreeNode root = new TreeNode(Integer.valueOf(array[index++]));\n root.left = helper(array);\n root.right = helper(array);\n return root;\n }\n}\n``` | 2 | 0 | [] | 0 |
serialize-and-deserialize-bst | Simple Python Solution | faster than 98.16% | Detailed Comments | Easy to Understand | simple-python-solution-faster-than-9816-hioxw | \n# O(n) time and space complexity for both serialization and \n# deserialization\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(s | mad-coder | NORMAL | 2021-01-05T11:37:49.768581+00:00 | 2021-01-05T11:41:25.477463+00:00 | 96 | false | ```\n# O(n) time and space complexity for both serialization and \n# deserialization\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n def serialize(self, root: TreeNode) -> str:\n """Encodes a tree to a single string.\n """\n # if we see a None\n if not root:\n return "-1"\n # Otherwise we serialize root, roo.left and root.right\n # preorder traversal\n return str(root.val) + ","+self.serialize(root.left) + "," + self.serialize(root.right)\n \n\n def deserialize(self, data: str) -> TreeNode:\n """Decodes your encoded data to tree.\n """\n # from preorder list to tree\n def helper(dq): \n # using the dq we deserialize one by one\n value = dq.popleft()\n # if we see -1, means we need to form null node\n if value == -1:\n return None\n # form the actual node\n node = TreeNode(value)\n # form node\'s left\n node.left = helper(dq)\n # form node\'s right\n node.right = helper(dq)\n \n return node\n \n # at first get the node integer vals from the serial of \n # the tree \n #print(data)\n data = map(int,data.split(","))\n # form a deque needed to deserialize\n dq = deque(data)\n # we call helper with the deque list\n return helper(dq)\n \n \n\n# Your Codec object will be instantiated and called as such:\n# Your Codec object will be instantiated and called as such:\n# ser = Codec()\n# deser = Codec()\n# tree = ser.serialize(root)\n# ans = deser.deserialize(tree)\n# return ans\n```\nRuntime: 64 ms, faster than 98.16% of Python3 online submissions for Serialize and Deserialize BST. | 2 | 0 | [] | 0 |
serialize-and-deserialize-bst | Its funny we can cheat like this | its-funny-we-can-cheat-like-this-by-bcb9-q57w | \nvar last *TreeNode \n\ntype Codec struct {\n}\n\nfunc Constructor() Codec {\n return Codec{}\n}\n\n// Serializes a tree to a single string.\nfunc (this *Co | bcb98801xx | NORMAL | 2020-12-05T07:31:15.166406+00:00 | 2020-12-05T07:31:15.166448+00:00 | 132 | false | ```\nvar last *TreeNode \n\ntype Codec struct {\n}\n\nfunc Constructor() Codec {\n return Codec{}\n}\n\n// Serializes a tree to a single string.\nfunc (this *Codec) serialize(root *TreeNode) string {\n last = root\n return ""\n}\n\n// Deserializes your encoded data to tree.\nfunc (this *Codec) deserialize(data string) *TreeNode { \n return last\n}\n``` | 2 | 0 | [] | 1 |
serialize-and-deserialize-bst | C++ Just preorder traversal which gives unique BST structure. No delimiter | c-just-preorder-traversal-which-gives-un-sccl | Preorder uniquely determines stucture of a BST. Just construct a BST by feeding elements from a preorder array.\n2. Used 4 chars per integer element by seriali | bddata | NORMAL | 2020-10-10T05:25:00.207760+00:00 | 2020-10-10T05:33:52.111151+00:00 | 132 | false | 1. Preorder uniquely determines stucture of a BST. Just construct a BST by feeding elements from a preorder array.\n2. Used 4 chars per integer element by serializing binary representation. No need of a delimiter while deserializing.\n3. Complexity serializiation(preorder) : O(n)\n4. Complexity dserializiation(constructing binary tree): O(nlogn) (average case)\n```\nclass Codec {\npublic:\n\n // Encodes a tree to a single string.\n void postOrder(TreeNode* root, string& res){\n if(!root)\n return;\n vector<char> buf(sizeof(int), 0);\n memcpy(buf.data(), &(root->val), sizeof(int));\n for(auto c:buf)\n res.push_back(c);\n postOrder(root->left, res);\n postOrder(root->right, res);\n \n }\n string serialize(TreeNode* root) {\n string res;\n postOrder(root, res);\n return res;\n }\n\n TreeNode* deserialize(int elem, TreeNode* root){\n if(!root)\n return new TreeNode(elem);\n if(root->val > elem)\n root->left = deserialize(elem, root->left);\n else\n root->right = deserialize(elem, root->right); \n return root;\n\n }\n // Decodes your encoded data to tree.\n TreeNode* deserialize(string data) {\n int i = 0;\n TreeNode* root = nullptr;\n while(i< data.size()){\n int elem = 0;\n memcpy(&elem, &data[i], sizeof(int));\n i+=sizeof(int);\n root = deserialize(elem, root);\n }\n return root;\n }\n``` | 2 | 0 | [] | 0 |
serialize-and-deserialize-bst | [C++] Serialize in Preorder (Small String), Deserialize using Preorder & Implied Inorder | c-serialize-in-preorder-small-string-des-ddtw | Brief Explanation\n Serialize the BST in preorder.\n Deserialize the preorder from string.\n Sort preorder to get inorder.\n (Inorder of BST is sorted) \uD83D\u | amanmehara | NORMAL | 2020-10-10T04:59:29.850492+00:00 | 2020-10-10T04:59:29.850523+00:00 | 100 | false | **Brief Explanation**\n* Serialize the BST in preorder.\n* Deserialize the preorder from string.\n* Sort preorder to get inorder.\n *(Inorder of BST is sorted)* \uD83D\uDE00\n* Now generate the BST from Inorder and Preorder traversal.\n\n***problem now reduced to***\nhttps://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/\n\n```\nclass Codec {\npublic:\n\n // Encodes a tree to a single string.\n string serialize(TreeNode* root) {\n stringstream stream;\n serialize(root, stream);\n return stream.str();\n }\n\n // Decodes your encoded data to tree.\n TreeNode* deserialize(string data) {\n stringstream stream(data);\n deque<int> preorder(istream_iterator<int>{stream}, istream_iterator<int>());\n deque<int> inorder = preorder;\n sort(inorder.begin(), inorder.end());\n return deserialize(preorder, inorder, -1);\n }\n \nprivate:\n void serialize(TreeNode* node, stringstream& stream) {\n if (!node) {\n return;\n }\n stream << node->val << " ";\n serialize(node->left, stream);\n serialize(node->right, stream);\n }\n \n TreeNode* deserialize(deque<int>& preorder, deque<int>& inorder, int stop) {\n if (preorder.empty()) {\n return nullptr;\n }\n \n if (inorder.front() == stop) {\n inorder.pop_front();\n return nullptr;\n }\n \n TreeNode* node = new TreeNode(preorder.front());\n preorder.pop_front();\n node->left = deserialize(preorder, inorder, node->val);\n node->right = deserialize(preorder, inorder, stop);\n return node;\n }\n};\n``` | 2 | 1 | [] | 0 |
serialize-and-deserialize-bst | Serialize and Deserialize BST Explained | O(n) | Beats 98.41% 32ms | Queue | CPP | serialize-and-deserialize-bst-explained-6y43k | Here I have used pre-order traversal (root left right) to both serialize and deserialize the tree.\n\n## Serialize:\nThe main idea is when you are at any node o | soham0_0 | NORMAL | 2020-10-10T03:46:33.985673+00:00 | 2020-10-10T04:08:06.197030+00:00 | 90 | false | ### Here I have used pre-order traversal (root left right) to both serialize and deserialize the tree.\n\n## **Serialize:**\nThe main idea is when you are at any node of the tree, append its value to the string and push its children to the queue and continue till the queue is empty.\n\n**Things to note:** \n- Have a look at the constraints, directly appending to the string will only let you handle values within 7 bit range (char). So you have to devise some other way of appending to it correctly.\n- Here I have conveted the int to string using to_string() method and stored them space seperated.\n\n## **Deserialize:**\nThe idea for deserialization is similar to that of serialize, if the root is null, initialize the tree and push the children of root in the queue. Then pop nodes out from queue and keep putting data to the tree and its children to the queue until the string exhausts. \n\n**Things to note:**\n- You have to make sure you extract data from the string correctly in the format that you stored data in it.\n- Here I used strtok() method to extract data from " " seperated string and atoi() method to convert the char* to int and put the value in the tree.\n\n\n```c++\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\nclass Codec {\npublic:\n\n // Encodes a tree to a single string.\n string serialize(TreeNode* root) {\n if(root == NULL) return "";\n string ans = "";\n queue<TreeNode*> q;\n q.push(root);\n while(!q.empty()){\n TreeNode *temp = q.front(); q.pop();\n if(temp != NULL) {\n ans+=to_string(temp->val) + " ";\n q.push(temp->left);\n q.push(temp->right);\n }\n else ans+="null ";\n }\n return ans;\n }\n\n // Decodes your encoded data to tree.\n TreeNode* deserialize(string data) {\n // reverse(data.begin(), data.end());\n queue<TreeNode*> q;\n TreeNode *ans=NULL;\n char *dat = new char [data.size() + 1];\n strcpy(dat, data.c_str());\n char *token = strtok(dat, " ");\n while(token!=NULL){\n // cout << atoi(token) << endl; token = strtok(NULL, " ");\n if(ans==NULL){\n ans = new TreeNode(atoi(token));\n token = strtok(NULL, " ");\n q.push(ans);\n }else{\n TreeNode *temp = q.front(); q.pop();\n if(strcmp(token, "null")) {temp->left = new TreeNode(atoi(token));\n q.push(temp->left);}\n token = strtok(NULL, " ");\n if(token==NULL) break;\n if(strcmp(token, "null")) {temp->right = new TreeNode(atoi(token));\n q.push(temp->right);}\n token = strtok(NULL, " ");\n }\n }\n return ans;\n }\n};\n\n// Your Codec object will be instantiated and called as such:\n// Codec* ser = new Codec();\n// Codec* deser = new Codec();\n// string tree = ser->serialize(root);\n// TreeNode* ans = deser->deserialize(tree);\n// return ans;\n``` | 2 | 0 | [] | 0 |
serialize-and-deserialize-bst | Super Easssssyyyyyyyyyyyyy answer in C language | super-easssssyyyyyyyyyyyyy-answer-in-c-l-awbc | \nstruct TreeNode temp;\nchar serialize(struct TreeNode root) {\n temp=root;\n return "abcd";\n}\n\n/ Decodes your encoded data to tree. /\nstruct TreeNod | user3434r | NORMAL | 2020-10-09T16:51:46.746596+00:00 | 2020-10-09T16:54:46.505842+00:00 | 105 | false | \nstruct TreeNode *temp;\nchar* serialize(struct TreeNode* root) {\n temp=root;\n return "abcd";\n}\n\n/** Decodes your encoded data to tree. */\nstruct TreeNode* deserialize(char* data) {\n \n return temp;\n} | 2 | 3 | [] | 2 |
serialize-and-deserialize-bst | Swift - beat 100% | swift-beat-100-by-buburino-fqvl | \nclass Codec {\n // Encodes a tree to a single string.\n func serialize(_ root: TreeNode?) -> String {\n var arr = [String]()\n serialize(r | Buburino | NORMAL | 2020-10-09T14:55:24.552128+00:00 | 2020-10-09T14:55:24.552161+00:00 | 108 | false | ```\nclass Codec {\n // Encodes a tree to a single string.\n func serialize(_ root: TreeNode?) -> String {\n var arr = [String]()\n serialize(root, &arr)\n return arr.joined(separator: ",")\n }\n \n func serialize(_ root: TreeNode?, _ arr: inout [String]) { \n guard let root = root else{\n return\n }\n arr.append("\\(root.val)")\n serialize(root.left, &arr)\n serialize(root.right, &arr)\n }\n \n // Decodes your encoded data to tree.\n func deserialize(_ data: String) -> TreeNode? {\n guard data != "" else{\n return nil\n }\n \n let arr = data.components(separatedBy:",")\n var index = 0\n return deserialize(arr, &index, Int.min, Int.max)\n }\n \n func deserialize(_ arr: [String], _ index: inout Int, _ minVal: Int, _ maxVal: Int) -> TreeNode? {\n guard index < arr.count, let val = Int(arr[index]) else{\n return nil\n }\n \n if val < minVal || val > maxVal{\n return nil\n }\n \n let node = TreeNode(val)\n index += 1\n \n node.left = deserialize(arr, &index, minVal, val)\n node.right = deserialize(arr, &index, val, maxVal)\n \n return node\n }\n}\n```\n | 2 | 0 | [] | 0 |
serialize-and-deserialize-bst | Java | faster than 99.97% | HashMap | java-faster-than-9997-hashmap-by-sagar_2-c5o8 | \npublic class Codec {\n \n \n private void inorder(TreeNode root, StringBuilder sb)\n {\n if(root==null) return;\n \n sb.a | sagar_2_3 | NORMAL | 2020-10-09T09:09:42.886029+00:00 | 2020-10-10T14:27:12.681202+00:00 | 150 | false | ```\npublic class Codec {\n \n \n private void inorder(TreeNode root, StringBuilder sb)\n {\n if(root==null) return;\n \n sb.append(String.valueOf(root.val)); \n sb.append(" ");\n inorder(root.left,sb);\n inorder(root.right,sb);\n }\n\n public String serialize(TreeNode root) {\n if(root==null) return ""; \n StringBuilder sb = new StringBuilder();\n inorder(root, sb);\n \n return sb.toString().trim();\n }\n\n public TreeNode construct(TreeNode root, int val)\n {\n \n if(root==null) return new TreeNode(val);\n \n if(root.val>val)\n root.left = construct(root.left, val);\n else\n root.right = construct(root.right, val);\n\n return root;\n \n }\n public TreeNode deserialize(String data) {\n if(data=="") return null;\n String[] a = data.split(" ");\n TreeNode root=null;\n \n for(String str : a)\n {\n root = construct(root, Integer.parseInt(str));\n }\n \n return root;\n }\n}\n\n\n``` | 2 | 2 | [] | 2 |
serialize-and-deserialize-bst | C++ | Serialize and De-serialize BST | a simple approach | c-serialize-and-de-serialize-bst-a-simpl-akur | \nclass Codec {\npublic:\n\n string serialize(TreeNode* root) {\n string s="";\n if(root) {\n s += to_string(root->val)+\'.\';\n | sanganak_abhiyanta | NORMAL | 2020-10-09T07:50:14.466644+00:00 | 2020-10-09T09:58:15.747156+00:00 | 94 | false | ```\nclass Codec {\npublic:\n\n string serialize(TreeNode* root) {\n string s="";\n if(root) {\n s += to_string(root->val)+\'.\';\n s += serialize(root->left) + serialize(root->right);\n }\n return s;\n }\n\n TreeNode * insert(TreeNode *root, int val) {\n if(not root) return new TreeNode(val);\n if(val < root->val) root->left = insert(root->left, val);\n else root->right = insert(root->right, val);\n return root;\n }\n\n TreeNode* deserialize(string data) {\n TreeNode *root = nullptr;\n for(int i = 0; i<data.length(); i++) {\n int val = 0;\n while(data[i] != \'.\') \n val = val*10 + data[i++] - \'0\';\n root = insert(root, val);\n }\n return root;\n }\n};\n```\n\n## Example\n```\n 2\n / \\\n1 3\n\nSerialize using Preorded traversal. string : "2.1.3."\nDe-serialize by standard insertion in a BST process \n```\n | 2 | 2 | [] | 0 |
serialize-and-deserialize-bst | Very simple Python solution using 2 approaches - preorder postorder | very-simple-python-solution-using-2-appr-pv6g | \n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# s | vharshal1994 | NORMAL | 2020-08-21T08:40:33.933385+00:00 | 2020-08-21T08:40:33.933427+00:00 | 74 | false | ```\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n\n # Logic: Serialize the tree into pre-order traversal and store it as a string. Deserialize this pre order traversal by popping out the first item from this string.\n \n def serialize(self, root):\n """Encodes a tree to a single string.\n \n :type root: TreeNode\n :rtype: str\n """\n res = []\n def preorder(node):\n if not node:\n return\n res.append(str(node.val))\n preorder(node.left)\n preorder(node.right) \n \n preorder(root)\n return " ".join(res)\n \n\n def deserialize(self, data):\n """Decodes your encoded data to tree.\n \n :type data: str\n :rtype: TreeNode\n """\n def read_from_preorder_array(queue, low, high):\n if not queue:\n return None\n if low < int(queue[0]) < high:\n node = TreeNode(int(queue.popleft())) \n node.left = read_from_preorder_array(queue, low, node.val)\n node.right = read_from_preorder_array(queue, node.val, high)\n return node\n else:\n return None\n \n if not data:\n return None\n queue = collections.deque(data.split(" "))\n return read_from_preorder_array(queue, -sys.maxint, sys.maxint)\n \n\n# Your Codec object will be instantiated and called as such:\n# codec = Codec()\n# codec.deserialize(codec.serialize(root))\n\n\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Codec:\n # Logic: Serialize the tree into post-order traversal and store it as a string. Deserialize this post order traversal by popping out the last item from this string.\n \n def serialize(self, root):\n """Encodes a tree to a single string.\n \n :type root: TreeNode\n :rtype: str\n """\n res = []\n def postorder_traversal(node):\n if not node:\n return\n postorder_traversal(node.left)\n postorder_traversal(node.right)\n res.append(str(node.val))\n \n postorder_traversal(root)\n # print res\n return " ".join(res)\n \n\n def deserialize(self, data):\n """Decodes your encoded data to tree.\n \n :type data: str\n :rtype: TreeNode\n """\n def construct_tree_from_post_order(res, low, high):\n if not res:\n return None\n if low < int(res[-1]) < high:\n val = int(res.pop())\n node = TreeNode(val)\n node.right = construct_tree_from_post_order(res, val, high)\n node.left = construct_tree_from_post_order(res, low, val)\n return node\n else:\n return None\n \n if not data:\n return None\n res = data.split(" ")\n return construct_tree_from_post_order(res, -sys.maxint, sys.maxint)\n \n\n# Your Codec object will be instantiated and called as such:\n# codec = Codec()\n# codec.deserialize(codec.serialize(root))\n``` | 2 | 1 | [] | 0 |
serialize-and-deserialize-bst | Level-order traversal also works! | level-order-traversal-also-works-by-jazo-ty9y | We can use a queue to do a BFS, and encode the values in the order of nodes visited during BFS.\n\nWhen decoding, just insert the values back in that order with | jazonjiao | NORMAL | 2020-07-24T21:34:09.482401+00:00 | 2020-07-24T21:34:09.482439+00:00 | 252 | false | We can use a queue to do a BFS, and encode the values in the order of nodes visited during BFS.\n\nWhen decoding, just insert the values back in that order with BST insertion, building the tree level by level. \n\nThe time complexity for reconstruction is O(n*log(n)), though, slightly worse than O(n) best case.\n\n```\nclass Codec:\n def serialize(self, root: TreeNode) -> str:\n if not root:\n return \'\'\n ans = []\n q = collections.deque([root])\n while q: # BFS\n node = q.popleft()\n ans.append(node.val)\n if node.left:\n q.append(node.left)\n if node.right:\n q.append(node.right)\n return \',\'.join([str(v) for v in ans[::-1]]) # reverse order so that when decoding, popping from the back takes O(1)\n\n def deserialize(self, data: str) -> TreeNode:\n if not data:\n return None\n data = [int(s) for s in data.split(\',\')]\n root = TreeNode(data.pop())\n \n def insert(node, v):\n left = True if v < node.val else False\n if left:\n if not node.left:\n node.left = TreeNode(v)\n else:\n insert(node.left, v) # recursively insert\n else:\n if not node.right:\n node.right = TreeNode(v)\n else:\n insert(node.right, v) # recursively insert\n \n while data:\n insert(root, data.pop()) # insert the value into the tree\n \n return root\n``` | 2 | 0 | ['Python'] | 0 |
count-nodes-equal-to-average-of-subtree | Easy C++ code || Optimization from O(n^2) to O(n) | easy-c-code-optimization-from-on2-to-on-e2tl3 | Solving by brute force,\n\nWe iterate to each and every node by using any traversal (preorder, postorder, inorder). I used preorder. \nFrom each and every node | venkatasaitanish | NORMAL | 2022-05-08T04:01:29.304064+00:00 | 2022-05-08T04:26:02.822199+00:00 | 12,303 | false | Solving by brute force,\n\nWe iterate to each and every node by using any traversal (preorder, postorder, inorder). I used preorder. \nFrom each and every node we calculate sum of its subtree nodes and also maintain a cnt variable to store the no. of nodes, so that we can calculate average.\nIf average is equal to value of the root, we increment the ans.\n**Time complexity : O(n^2)**\n\n```\nclass Solution {\npublic:\n int ans = 0;\n int sum(TreeNode* root, int& cnt){\n if(root==NULL) return 0;\n cnt++;\n int left = sum(root->left,cnt);\n int right = sum(root->right,cnt);\n return (root->val + left + right);\n }\n void solve(TreeNode* root){\n if(root==NULL) return;\n int cnt = 0;\n int avg = (sum(root,cnt))/cnt;\n if(avg==root->val) ans++;\n solve(root->left);\n solve(root->right);\n }\n int averageOfSubtree(TreeNode* root) {\n ans = 0;\n solve(root);\n return ans;\n }\n};\n```\n\n**Optimization: **\n\nBefore we calculated the sum for every sub tree.\nHere we do a postorder traversal, we will calculate the sum of nodes in left sub tree and cnt of nodes in left subtree , as well as for right subtree and use this to root.\n**Time complexity: O(n)**\n```\nclass Solution {\npublic:\n int ans = 0;\n pair<int,int> solve(TreeNode* root){\n if(root==NULL) return {0,0};\n \n auto left = solve(root->left);\n int l_sum = left.first; // sum of nodes present in left sub tree\n int l_cnt = left.second; // no. of nodes present in left sub tree\n \n auto right = solve(root->right);\n int r_sum = right.first; // sum of nodes present in right sub tree\n int r_cnt = right.second; // no. of nodes present in left sub tree\n \n int sum = root->val + l_sum + r_sum;\n int cnt = l_cnt + r_cnt + 1;\n \n if(root->val == sum/cnt) ans++;\n return {sum,cnt};\n }\n int averageOfSubtree(TreeNode* root) {\n solve(root);\n return ans;\n }\n};\n``` | 120 | 2 | ['Recursion'] | 15 |
count-nodes-equal-to-average-of-subtree | 🚀 100% || DFS || Explained Intuition🚀 | 100-dfs-explained-intuition-by-mohamedma-82sg | Problem Description\n\nGiven the root of a binary tree. The task is to determine the number of nodes in the tree whose value matches the floored average of all | MohamedMamdouh20 | NORMAL | 2023-11-02T01:58:23.477327+00:00 | 2023-11-02T13:56:50.168467+00:00 | 10,265 | false | # Problem Description\n\nGiven the **root** of a binary tree. The task is to determine the **number** of nodes in the tree whose value **matches** the floored **average** of all the values within their respective **subtrees**. In other words, you need to count the nodes where the node\'s value is equal to the integer average of all values in its subtree.\n\n- Here\'s some additional information to keep in mind:\n\n - The **average** of a set of elements is calculated by **summing** those elements and **dividing** the sum by the **number** of elements.\n - A **subtree** of a given node **includes** the node **itself** and all of its **descendant** nodes.\n\nThe **goal** is to find the count of nodes in the binary tree that **meet** this condition.\n\n- **Constraints:**\n - The number of nodes in the tree is in the range `[1, 1000]`.\n - `0 <= Node.val <= 1000`.\n \n---\n\n\n# Intuition\n\nHello there,\uD83D\uDE04\n\nLet\'s look\uD83D\uDC40 at today\'s problem.\nIn today\'s problem, We have a **tree**\uD83C\uDF32 and each node in it have a value and for each node we have to check if its value is **equal** to the average of values in its **subtree**. If so, calculate number of nodes with this description.\uD83E\uDD28\n\nBut before that what is a **subtree** of a node ?\uD83E\uDD14\nA subtree in general is a part of a tree\uD83C\uDF32 but for a specific node the subtree is the part of the tree that containing all of its children and descnedants going down to the **leaves**.\uD83C\uDF43\nlet\'s see an example.\n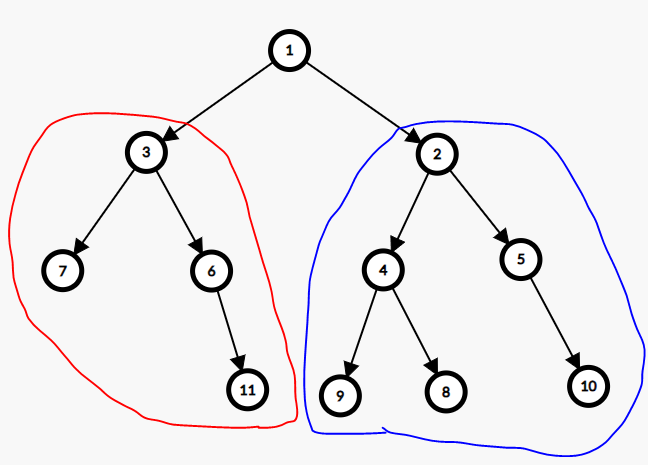\n\nHere the subtree of `node 2` is the part with **blue** color. the subtree of `node 3` is the part with **red** color and also we can consider the **whole tree** as a subtree for `node 1`.\n\nNow how we get the values and number of nodes for all of the node subtree?\uD83E\uDD14\nI will pretend that I didn\'t say the algorithm in the title.\uD83D\uDE02\nWe can do it with a simple algorithm that **traverses** the tree and there is no simpler tha **DFS**, Our hero today\uD83E\uDDB8\u200D\u2642\uFE0F.\n\n- And since any **tree**:\n - has only **one** **root**.\n - **doesn\'t** have **loops**.\n \nThen we can apply **DFS** at the only **root** of the tree and without concerning about the loops.\nThe **DFS** Function of any node will **check** for all nodes in its subtree that meet our requirements and return the number of nodes in its subtree and the sum of values for its subtree.\uD83D\uDCAA\n\n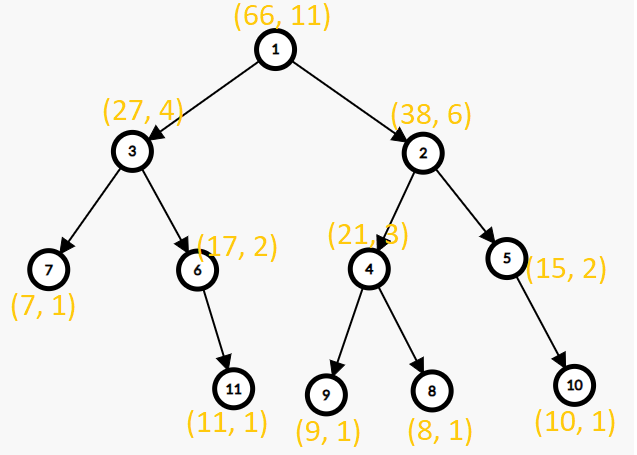\nThis is an example how our DFS will look like for each node since it will return `(sum of values of subtree, number of nodes)`.\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n\n# Approach\n1. Initialize an integer variable `matchingSubtreeCount` to keep track of subtrees with matching averages.\n2. Create a Depth-First Search **DFS** function `calculateSubtreeValues` that takes a `currentNode` as input and returns a pair of integers. These integers represent:\n - The **sum** of values within the current subtree.\n - The **number** of nodes within the current subtree.\n3. In the `calculateSubtreeValues` function:\n - **Base Case**: check if the `currentNode` is null. If it is, return `{0, 0}`, signifying that both the sum and number of nodes are zero for a null node.\n - The **sum** of values in the current subtree is the **sum** of values in the left and right subtrees **plus** the value of the `currentNode` and The **number** of nodes is **number** of nodes in the left and right subtrees then **increment** it by 1 for the `currentNode`.\n - **Increment** the `matchingSubtreeCount` if the current node\'s value matches the average of its subtree.\n - **Return** a pair of values `{sumOfValues, numberOfNodes}` representing the calculated values for the current subtree.\n11. In the main function, perform **DFS** from the root then return `matchingSubtreeCount` after traversing over all the nodes.\n\n\n# Complexity\n- **Time complexity:**$O(N)$\nSince the DFS **traverse** over all the nodes of the tree then the complexity is `O(N)` where `N` is the number of nodes within the tree.\n- **Space complexity:**$O(N)$\nSince the DFS is a **recursive** call and it reserves a **memory stack frame** for each call so the **maximum** number of calls it can make in the same time is `N` calls so complexity is `O(N)`;\n\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int matchingSubtreeCount = 0; // Initialize the count of subtrees with matching averages.\n\n // A Depth-First Search (DFS) function and returns a pair of values:\n // - The sum of values within the current subtree.\n // - The number of nodes within the current subtree.\n pair<int, int> calculateSubtreeValues(TreeNode* currentNode) {\n if (currentNode == nullptr)\n return {0, 0}; // Base case: Return 0 for both sum and number of nodes if the node is null.\n\n // Recursively calculate values for the left and right subtrees.\n auto leftSubtree = calculateSubtreeValues(currentNode->left);\n auto rightSubtree = calculateSubtreeValues(currentNode->right);\n\n // Calculate the sum of values and the number of nodes in the current subtree.\n int sumOfValues = leftSubtree.first + rightSubtree.first + currentNode->val;\n int numberOfNodes = leftSubtree.second + rightSubtree.second + 1;\n\n // Check if the current node\'s value matches the average of its subtree.\n if (sumOfValues / numberOfNodes == currentNode->val)\n matchingSubtreeCount++; \n\n return {sumOfValues, numberOfNodes}; // Return the calculated values for the current subtree.\n }\n\n int averageOfSubtree(TreeNode* root) {\n calculateSubtreeValues(root); // Start the DFS from the root node.\n return matchingSubtreeCount; \n }\n};\n```\n```Java []\nclass Solution {\n private int matchingSubtreeCount = 0; // Initialize the count of subtrees with matching averages.\n\n // A Depth-First Search (DFS) function that returns an array of two values:\n // - The sum of values within the current subtree.\n // - The number of nodes within the current subtree.\n private int[] calculateSubtreeValues(TreeNode currentNode) {\n if (currentNode == null)\n return new int[]{0, 0}; // Base case: Return 0 for both sum and number of nodes if the node is null.\n\n // Recursively calculate values for the left and right subtrees.\n int[] leftSubtree = calculateSubtreeValues(currentNode.left);\n int[] rightSubtree = calculateSubtreeValues(currentNode.right);\n\n // Calculate the sum of values and the number of nodes in the current subtree.\n int sumOfValues = leftSubtree[0] + rightSubtree[0] + currentNode.val;\n int numberOfNodes = leftSubtree[1] + rightSubtree[1] + 1;\n\n // Check if the current node\'s value matches the average of its subtree.\n if (sumOfValues / numberOfNodes == currentNode.val)\n matchingSubtreeCount++;\n\n return new int[]{sumOfValues, numberOfNodes}; // Return the calculated values for the current subtree.\n }\n\n public int averageOfSubtree(TreeNode root) {\n calculateSubtreeValues(root); // Start the DFS from the root node.\n return matchingSubtreeCount; \n }\n}\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.matchingSubtreeCount = 0 # Initialize the count of subtrees with matching averages.\n\n # A Depth-First Search (DFS) function that returns a tuple of two values:\n # - The sum of values within the current subtree.\n # - The number of nodes within the current subtree.\n def calculateSubtreeValues(self, currentNode):\n if currentNode is None:\n return 0, 0 # Base case: Return 0 for both sum and number of nodes if the node is None.\n\n # Recursively calculate values for the left and right subtrees.\n leftSubtree = self.calculateSubtreeValues(currentNode.left)\n rightSubtree = self.calculateSubtreeValues(currentNode.right)\n\n # Calculate the sum of values and the number of nodes in the current subtree.\n sumOfValues = leftSubtree [0] + rightSubtree[0] + currentNode.val\n numberOfNodes = leftSubtree [1] + rightSubtree[1] + 1\n\n # Check if the current node\'s value matches the average of its subtree.\n if sumOfValues // numberOfNodes == currentNode.val:\n self.matchingSubtreeCount += 1\n\n return sumOfValues , numberOfNodes # Return the calculated values for the current subtree.\n\n\n def averageOfSubtree(self, root):\n self.calculateSubtreeValues(root) # Start the DFS from the root node.\n return self.matchingSubtreeCount \n\n```\n\n\n\n | 101 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'Python', 'C++', 'Java', 'Python3'] | 7 |
count-nodes-equal-to-average-of-subtree | ✅ 89.45% Post-order traversal | 8945-post-order-traversal-by-vanamsen-vlhn | Intuition\nThe problem asks us to count the number of nodes where the node\'s value is equal to the average of its subtree (including itself). To calculate the | vanAmsen | NORMAL | 2023-11-02T00:23:06.946547+00:00 | 2023-11-02T01:28:37.042905+00:00 | 15,404 | false | # Intuition\nThe problem asks us to count the number of nodes where the node\'s value is equal to the average of its subtree (including itself). To calculate the average, we need the sum and count of nodes in the subtree. Our first thought could be to traverse the tree and, for every node, calculate the sum and count of nodes in its subtree and then check if the average matches the node\'s value. However, this would lead to recalculating the sum and count for overlapping subtrees, resulting in a time complexity of $O(n^2)$. Instead, we can optimize our approach to calculate the sum and count while traversing the tree in a single pass.\n\n# Live Coding & More\nhttps://youtu.be/vCD1hGT5e8M?si=JfZ7YX5_VMeOETIa\n\n# Approach\n\nTo solve the problem, we employ a post-order traversal approach. In post-order traversal, the tree is traversed in such a way that we first explore the left subtree, then the right subtree, and finally the node itself. This method is particularly suitable for this problem because, to determine the average value of a subtree rooted at a node, we need information from its left and right subtrees first. \n\n## Base Case\nOur recursive function\'s first duty is to identify if it has reached a leaf node, i.e., a node that doesn\'t have children. If the node being processed is `None`, it indicates that it\'s a leaf, and as such, we return both a sum and count of 0. This is because, for non-existent children of leaf nodes, there\'s no value to add or count to increment.\n\n## Recursive Logic\n\nFor every node in the tree, we perform the following steps:\n\n1. **Left Subtree Processing**:\n We recursively calculate the sum and count of nodes for the left child of the current node. This gives us the total value of all nodes and the number of nodes in the left subtree.\n\n2. **Right Subtree Processing**:\n Similarly, we recursively calculate the sum and count of nodes for the right child of the current node. This provides the total value of all nodes and the number of nodes in the right subtree.\n\n3. **Current Node\'s Subtree Calculation**:\n - **Sum**: To calculate the sum of the values in the subtree rooted at the current node, we add the node\'s own value to the sums from the left and right subtrees. \n - **Count**: The count of nodes in the subtree rooted at the current node is found by adding 1 (for the current node itself) to the counts from the left and right subtrees.\n \n4. **Average Comparison**:\n We check if the average of the subtree rooted at the current node matches the node\'s value. The average is calculated by performing integer division of the sum by the count. If they match, it indicates that the node\'s value is indeed the average of its subtree, and we increment our result counter.\n\n5. **Return Values**:\n Finally, for the benefit of the parent node in the recursive chain, we return the current node\'s subtree sum and count. This ensures that as the recursion unwinds, each parent node gets the aggregate values of its children and can perform its own calculations.\n\nBy following this approach, the algorithm efficiently traverses the tree, calculating and checking averages in one pass, without needing to revisit nodes or perform redundant calculations.\n\n# Complexity\n- **Time complexity**: $O(n)$. We perform a single traversal of the tree, visiting each node exactly once.\n- **Space complexity**: $O(h)$, where $h$ is the height of the tree. This accounts for the space used by the call stack during the recursive traversal.\n\n\n# Code\n``` Python []\nclass Solution:\n def averageOfSubtree(self, root: TreeNode) -> int:\n result = 0\n\n def traverse(node):\n nonlocal result\n \n if not node:\n return 0, 0\n \n left_sum, left_count = traverse(node.left)\n right_sum, right_count = traverse(node.right)\n \n curr_sum = node.val + left_sum + right_sum\n curr_count = 1 + left_count + right_count\n \n if curr_sum // curr_count == node.val:\n result += 1\n \n return curr_sum, curr_count\n \n traverse(root)\n return result\n```\n``` C++ []\nclass Solution {\npublic:\n int averageOfSubtree(TreeNode* root) {\n int result = 0;\n traverse(root, result);\n return result;\n }\n\nprivate:\n pair<int, int> traverse(TreeNode* node, int& result) {\n if (!node) return {0, 0};\n \n auto [left_sum, left_count] = traverse(node->left, result);\n auto [right_sum, right_count] = traverse(node->right, result);\n \n int curr_sum = node->val + left_sum + right_sum;\n int curr_count = 1 + left_count + right_count;\n \n if (curr_sum / curr_count == node->val) result++;\n \n return {curr_sum, curr_count};\n }\n};\n```\n``` Java []\nclass Solution {\n public int averageOfSubtree(TreeNode root) {\n int[] result = new int[1];\n traverse(root, result);\n return result[0];\n }\n\n private int[] traverse(TreeNode node, int[] result) {\n if (node == null) return new int[]{0, 0};\n \n int[] left = traverse(node.left, result);\n int[] right = traverse(node.right, result);\n \n int currSum = node.val + left[0] + right[0];\n int currCount = 1 + left[1] + right[1];\n \n if (currSum / currCount == node.val) result[0]++;\n \n return new int[]{currSum, currCount};\n }\n}\n```\n``` Go []\nfunc averageOfSubtree(root *TreeNode) int {\n result := 0\n traverse(root, &result)\n return result\n}\n\nfunc traverse(node *TreeNode, result *int) (int, int) {\n if node == nil {\n return 0, 0\n }\n \n leftSum, leftCount := traverse(node.Left, result)\n rightSum, rightCount := traverse(node.Right, result)\n \n currSum := node.Val + leftSum + rightSum\n currCount := 1 + leftCount + rightCount\n \n if currSum / currCount == node.Val {\n *result++\n }\n \n return currSum, currCount\n}\n```\n``` Rust []\nuse std::rc::Rc;\nuse std::cell::RefCell;\nimpl Solution {\n pub fn average_of_subtree(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {\n fn traverse(node: Option<Rc<RefCell<TreeNode>>>, result: &mut i32) -> (i32, i32) {\n if let Some(n) = node {\n let n = n.borrow();\n let (left_sum, left_count) = traverse(n.left.clone(), result);\n let (right_sum, right_count) = traverse(n.right.clone(), result);\n \n let curr_sum = n.val + left_sum + right_sum;\n let curr_count = 1 + left_count + right_count;\n \n if curr_sum / curr_count == n.val {\n *result += 1;\n }\n \n (curr_sum, curr_count)\n } else {\n (0, 0)\n }\n }\n \n let mut result = 0;\n traverse(root, &mut result);\n result\n }\n}\n```\n``` JavaScript []\nvar averageOfSubtree = function(root) {\n let result = 0;\n \n const traverse = node => {\n if (!node) return [0, 0];\n \n const [leftSum, leftCount] = traverse(node.left);\n const [rightSum, rightCount] = traverse(node.right);\n \n const currSum = node.val + leftSum + rightSum;\n const currCount = 1 + leftCount + rightCount;\n \n if (Math.floor(currSum / currCount) === node.val) result++;\n \n return [currSum, currCount];\n };\n \n traverse(root);\n return result;\n};\n```\n``` PHP []\nclass Solution {\n\n /**\n * @param TreeNode $root\n * @return Integer\n */\n function averageOfSubtree($root) {\n $result = 0;\n $this->traverse($root, $result);\n return $result;\n }\n \n function traverse($node, &$result) {\n if ($node === null) return [0, 0];\n \n list($leftSum, $leftCount) = $this->traverse($node->left, $result);\n list($rightSum, $rightCount) = $this->traverse($node->right, $result);\n \n $currSum = $node->val + $leftSum + $rightSum;\n $currCount = 1 + $leftCount + $rightCount;\n \n if (intval($currSum / $currCount) == $node->val) $result++;\n \n return [$currSum, $currCount];\n }\n}\n```\n``` C# []\npublic class Solution {\n public int AverageOfSubtree(TreeNode root) {\n int result = 0;\n Traverse(root, ref result);\n return result;\n }\n\n private (int, int) Traverse(TreeNode node, ref int result) {\n if (node == null) return (0, 0);\n \n var (leftSum, leftCount) = Traverse(node.left, ref result);\n var (rightSum, rightCount) = Traverse(node.right, ref result);\n \n int currSum = node.val + leftSum + rightSum;\n int currCount = 1 + leftCount + rightCount;\n \n if (currSum / currCount == node.val) result++;\n \n return (currSum, currCount);\n }\n}\n```\n\n# Performance\n\n| Language | Execution Time (ms) | Memory Usage |\n|------------|---------------------|--------------|\n| Java | 0 | 43.2 MB |\n| Rust | 2 | 2.3 MB |\n| C++ | 4 | 12.5 MB |\n| Go | 5 | 4.3 MB |\n| PHP | 17 | 19.8 MB |\n| Python3 | 44 | 17.8 MB |\n| JavaScript | 74 | 47.6 MB |\n| C# | 76 | 40.2 MB |\n\n\n\n\n# What We Learned\nThis problem teaches us the importance of optimizing our approach to avoid recalculating values for overlapping subtrees. By using a post-order traversal, we can calculate the sum and count for each subtree in a single pass, significantly improving the time complexity from $O(n^2)$ to $O(n)$. It also emphasizes the utility of using a nonlocal variable to keep track of the result during recursive traversal. | 77 | 1 | ['Tree', 'PHP', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'JavaScript', 'C#'] | 11 |
count-nodes-equal-to-average-of-subtree | Java | DFS | java-dfs-by-vishnuvs-xph6 | \nclass Solution {\n int res = 0;\n public int averageOfSubtree(TreeNode root) {\n dfs(root);\n return res;\n }\n \n private int[] | vishnuvs | NORMAL | 2022-05-08T04:06:07.287922+00:00 | 2022-05-08T04:06:07.287955+00:00 | 6,858 | false | ```\nclass Solution {\n int res = 0;\n public int averageOfSubtree(TreeNode root) {\n dfs(root);\n return res;\n }\n \n private int[] dfs(TreeNode node) {\n if(node == null) {\n return new int[] {0,0};\n }\n \n int[] left = dfs(node.left);\n int[] right = dfs(node.right);\n \n int currSum = left[0] + right[0] + node.val;\n int currCount = left[1] + right[1] + 1;\n \n if(currSum / currCount == node.val) {\n res++;\n }\n \n return new int[] {currSum, currCount};\n }\n}\n``` | 67 | 2 | ['Depth-First Search', 'Java'] | 12 |
count-nodes-equal-to-average-of-subtree | Sum, Count, Match | sum-count-match-by-votrubac-0qly | Our dfs function returns the sum and count of nodes, and the number of matching nodes.\n\nC++\ncpp\narray<int, 3> dfs(TreeNode* n) {\n if (n == nullptr)\n | votrubac | NORMAL | 2022-05-08T04:04:54.187732+00:00 | 2022-05-08T04:44:13.469333+00:00 | 3,967 | false | Our `dfs` function returns the sum and count of nodes, and the number of matching nodes.\n\n**C++**\n```cpp\narray<int, 3> dfs(TreeNode* n) {\n if (n == nullptr)\n return {0, 0, 0};\n auto p1 = dfs(n->left), p2 = dfs(n->right);\n int sum = p1[0] + p2[0] + n->val, count = 1 + p1[1] + p2[1];\n return {sum, count, p1[2] + p2[2] + (n->val == sum / count)};\n}\nint averageOfSubtree(TreeNode* root) {\n return dfs(root)[2];\n}\n``` | 51 | 1 | [] | 8 |
count-nodes-equal-to-average-of-subtree | 【Video】Give me 8 minutes - How we think about a solution - Why we use postorder traversal? | video-give-me-8-minutes-how-we-think-abo-cpzc | Intuition\nCalculate subtree of left and right child frist\n\n---\n\n# Solution Video\n\nhttps://youtu.be/MV6NpUXCfUU\n\n\u25A0 Timeline of the video\n0:05 Whic | niits | NORMAL | 2023-11-02T04:08:39.804495+00:00 | 2023-11-03T16:42:58.969668+00:00 | 1,761 | false | # Intuition\nCalculate subtree of left and right child frist\n\n---\n\n# Solution Video\n\nhttps://youtu.be/MV6NpUXCfUU\n\n\u25A0 Timeline of the video\n`0:05` Which traversal do you use for this question?\n`1:55` How do you calculate information you need?\n`3:34` How to write Inorder, Preorder, Postorder\n`4:16` Coding\n`7:50` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,919\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n# Approach\n\n### How we think about a solution.\n\nFirst of all, we know that we have to traverse the tree and have 3 well known traversal.\n\nTo be honest, I asked you about the same question in the yesterday\'s post. lol\n\n---\n\n\u25A0 Question\n\nWhich traversal do you use?\n\n---\n\nThinking time...\n\n... \uD83D\uDE29\n\n... \uD83D\uDE0F\n\n... \uD83D\uDE06\n\n... \uD83D\uDE04\n\nMy answer is postorder\n\n---\n\n\u2B50\uFE0F Points\n\nThe reason why we choose postorder traversal is that it processes child nodes (left and right subtrees) first to calculate the subtree\'s sum, number of nodes and number of results, then uses that information to check the condition at the parent node.\n\nTo calculate that information of a subtree including a parent, it is necessary to use information from the child nodes. That\'s why the left and right subtrees should be processed first.\n\nWhen we have\n```\n 5\n / \\\n 6 7\n\n```\n\nthe order of postorder process should be 6, 7 and 5.\n\nSo, we have information of subtree of 6 and information of subtree of 7, then finally we can calculate information of subtree of 5 which is including 6 and 7. \n\n---\n\n- How do you calculate information we need?\n\nTo get result, we need `total sum` and `total number of nodes` because we calculate average of each subtree. This is not complicated. just\n\n##### Total Sum\n---\n`sum of left subtree` + `sum of right subtree` + `current value`\n\n---\n##### Number of nodes\n---\n\n\n`number of nodes from left` + `number of nodes from right` + 1\n\n`+1` is for a current node\n\n---\n\nEasy!\n\nThen every time we calculate number of results with this condition\n\n##### Number of results\n---\n\n\u2B50\uFE0F Points\n\nres += `(node.val == total_sum // total_count)`\n\n---\n\n---\n\n\u25A0 Python Tips\n\nAbout calculation of number of results\n\nIn Python, `True` is equivalent to the integer `1`, and `False` is equivalent to the integer `0`. This is based on implicit conversion between Python\'s boolean type (`bool`) and integer type (`int`). Here are some examples:\n\n```python []\nbool_true = True\nint_one = 1\n\nbool_false = False\nint_zero = 0\n\n# True and 1 are equivalent\nprint(bool_true == int_one) # True\n\n# False and 0 are equivalent\nprint(bool_false == int_zero) # True\n```\n\nAs a result, if a condition is `True`, it is considered as satisfied and is treated as the integer `1`. The result is then added to the variable `res`, which counts the number of nodes that meet the condition.\n\nThat is just pretentious coding style. lol\nIt\'s the same as\n\n```Python []\nres += (node.val == total_sum // total_count)\n\u2193\nif node.val == total_sum // total_count:\n res += 1\n```\n\n---\n\n- How to write inorder, preorder, postorder\n\nAcutually, I wrote the same contents yesterday, but knowing how to write inorder, preorder, and postorder traversals might be helpful for other problems as well.\n\n```python []\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\ndef inorder(root):\n if not root:\n return []\n result = []\n result += inorder(root.left)\n result.append(root.val)\n result += inorder(root.right)\n return result\n\ndef preorder(root):\n if not root:\n return []\n result = []\n result.append(root.val)\n result += preorder(root.left)\n result += preorder(root.right)\n return result\n\ndef postorder(root):\n if not root:\n return []\n result = []\n result += postorder(root.left)\n result += postorder(root.right)\n result.append(root.val)\n return result\n```\n\nLet\'s focus on `result.append(root.val)` in each function.\n\n---\n\n\u2B50\uFE0F Points\n\nFor `Inorder`, we do something `between left and right`.\nFor `Preorder`, we do something `before left and right`.\nFor `Postorder`, we do something `after left and right`.\n\n---\n\nWe use `postorder` this time, so do the key point above after left and right.\n\nYou can compare `postorder` with `inorder` by yesterday\'s daily coding challenge. I put yesterday\'s video and post at bottom of the post.\n\nLet\'s see a real algorithm!\n\n### Algorithm Overview:\n\nThe algorithm calculates the number of nodes in a binary tree where the value of the node is equal to the average value of its subtree. It uses a post-order traversal to process the tree nodes.\n\n### Detailed Explanation:\n\n1. Initialize a variable `res` to 0. This variable will be used to keep track of the count of nodes that meet the specified condition.\n\n2. Define a recursive function `postorder(node)` that takes a `node` as an argument.\n\n3. Inside the `postorder` function:\n - Check if the current `node` is `None`, indicating an empty subtree or a leaf node. If it is, return a tuple `(0, 0)` representing the sum and number of nodes in the subtree.\n\n - Recursively call the `postorder` function on the left child of the current node and store the result in the `left` variable.\n\n - Recursively call the `postorder` function on the right child of the current node and store the result in the `right` variable.\n\n - Use a `nonlocal` statement to access and update the `res` variable in the outer scope. This variable keeps track of the count of nodes that meet the condition.\n\n - Calculate the `total_sum` as the sum of the values of the current node, the left subtree, and the right subtree: `total_sum = left[0] + right[0] + node.val`.\n\n - Calculate the `total_count` as the count of nodes in the current subtree: `total_count = 1 + left[1] + right[1]`.\n\n - Increment the `res` variable when the condition `node.val == total_sum // total_count` is true. This condition checks if the current node\'s value is equal to the average value of its subtree.\n\n - Return a tuple `(total_sum, total_count)` representing the updated sum and count for the current subtree.\n\n4. Call the `postorder(root)` function on the root of the binary tree to initiate the post-order traversal and accumulate the count of nodes that meet the condition in the `res` variable.\n\n5. Return the final value of `res`, which represents the count of nodes in the binary tree where the value of the node is equal to the average value of its subtree.\n\nThe code uses a post-order traversal to process the subtrees before processing the current node, which is essential for correctly computing the average values of subtrees.\n\n# Complexity\n- Time complexity: $$O(N)$$\nN is the number of nodes in the binary tree. This is because the code visits each node exactly once during the post-order traversal, and the work done at each node is constant.\n\n- Space complexity: $$O(N)$$\nThis space is used for the recursive call stack during the post-order traversal. In the worst case, if the binary tree is skewed and unbalanced, the space complexity can be O(N). \n\n```python []\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n res = 0\n\n def postorder(node):\n if not node:\n return (0, 0) # sum, number of nodes\n \n left = postorder(node.left)\n right = postorder(node.right)\n\n nonlocal res\n\n total_sum = left[0] + right[0] + node.val\n total_count = 1 + left[1] + right[1]\n res += (node.val == total_sum // total_count)\n\n return (total_sum, total_count)\n \n postorder(root)\n\n return res\n```\n```javascript []\nvar averageOfSubtree = function(root) {\n var res = 0;\n\n var postorder = function(node) {\n if (!node) {\n return [0, 0]; // sum, number of nodes\n }\n\n var left = postorder(node.left);\n var right = postorder(node.right);\n\n var totalSum = left[0] + right[0] + node.val;\n var totalCount = 1 + left[1] + right[1];\n res += node.val === Math.floor(totalSum / totalCount);\n\n return [totalSum, totalCount];\n };\n\n postorder(root);\n\n return res;\n};\n```\n```java []\nclass Solution {\n private int res = 0; \n\n public int averageOfSubtree(TreeNode root) {\n postorder(root);\n return res; \n }\n\n private int[] postorder(TreeNode node) {\n if (node == null) {\n return new int[]{0, 0}; // sum, number of nodes\n }\n\n int[] left = postorder(node.left);\n int[] right = postorder(node.right);\n\n int totalSum = left[0] + right[0] + node.val;\n int totalCount = 1 + left[1] + right[1];\n res += (node.val == totalSum / totalCount ? 1 : 0);\n\n return new int[]{totalSum, totalCount};\n } \n}\n```\n```C++ []\nclass Solution {\n int res = 0;\n\npublic:\n int averageOfSubtree(TreeNode* root) {\n postorder(root);\n return res;\n }\n\n pair<int, int> postorder(TreeNode* node) {\n if (!node) {\n return {0, 0}; // sum, number of nodes\n }\n\n auto left = postorder(node->left);\n auto right = postorder(node->right);\n\n int totalSum = left.first + right.first + node->val;\n int totalCount = 1 + left.second + right.second;\n res += (node->val == totalSum / totalCount);\n\n return {totalSum, totalCount};\n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/build-an-array-with-stack-operations/solutions/4244407/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/MCYiEw2zvNw\n\n\u25A0 Timeline of the video\n\n`0:04` Basic idea to solve this question\n`1:04` How do you operate each number from the steam of integers?\n`3:34` What operation we need for the two patterns\n`5:17` Coding\n`6:37` Time Complexity and Space Complexity\n\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/find-mode-in-binary-search-tree/solutions/4233557/video-give-me-5-minutes-how-we-think-about-a-solution-why-do-we-use-inorder-traversal/\n\nvideo\nhttps://youtu.be/0i1Ze62pTuU\n\n\u25A0 Timeline of the video\n`0:04` Which traversal do you use for this question?\n`0:34` Properties of a Binary Search Tree\n`1:31` Key point of my solution code\n`3:09` How to write Inorder, Preorder, Postorder\n`4:08` Coding\n`7:13` Time Complexity and Space Complexity\n\n\n\n\n | 46 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 5 |
count-nodes-equal-to-average-of-subtree | c++ solution|| O(N) || 100.00% faster | c-solution-on-10000-faster-by-deleted_us-lsjj | So I am calling at every node and asking total sum and total number of node including that node itself so every subtree will return total sum of tree and total | deleted_user | NORMAL | 2022-05-08T04:57:06.875106+00:00 | 2022-05-08T05:09:03.614378+00:00 | 4,196 | false | So I am calling at every node and asking total sum and total number of node including that node itself so every subtree will return total sum of tree and total number of node. gobal variable will keep updating.\n```\nint count=0;\npair<int,int> valueSum(TreeNode* root){\n\tif(root==NULL) return {0,0};\n\tauto left=valueSum(root->left);\n\tauto right=valueSum(root->right);\n\tint sum=(left.first+right.first+root->val);\n\tint n=(left.second+right.second+1); \n\tcount+=((sum/n)==root->val);\n\treturn {sum,n};\n}\nint averageOfSubtree(TreeNode* root) {\n\tauto p1=valueSum(root);\n\treturn count;\n}\n``` | 37 | 0 | ['Recursion', 'C'] | 4 |
count-nodes-equal-to-average-of-subtree | Python | DFS | Easy to Understand | python-dfs-easy-to-understand-by-mikey98-yt75 | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def init(self, val=0, left=None, right=None):\n# self.val = val\n# self.left | Mikey98 | NORMAL | 2022-05-08T04:29:58.904131+00:00 | 2022-05-08T04:30:15.307935+00:00 | 3,347 | false | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n result = 0\n\t\t\n def traverse(node):\n nonlocal result\n \n if not node:\n return 0, 0\n \n left_sum, left_count = traverse(node.left)\n right_sum, right_count = traverse(node.right)\n \n s = node.val + left_sum + right_sum\n c = 1 + left_count + right_count\n \n if s // c == node.val:\n result += 1\n \n return s, c\n \n traverse(root)\n \n return result\n \n \n | 24 | 0 | ['Depth-First Search', 'Python', 'Python3'] | 6 |
count-nodes-equal-to-average-of-subtree | CPP | Short and Simple | O(n) Time | DFS | O(1) Space | cpp-short-and-simple-on-time-dfs-o1-spac-ybha | \nclass Solution {\npublic:\n pair<int,int> func(TreeNode* root,int &ans){\n if(!root)return {0,0};\n auto p1=func(root->left,ans);\n au | amirkpatna | NORMAL | 2022-05-08T04:07:10.469526+00:00 | 2022-05-08T04:08:53.692214+00:00 | 1,874 | false | ```\nclass Solution {\npublic:\n pair<int,int> func(TreeNode* root,int &ans){\n if(!root)return {0,0};\n auto p1=func(root->left,ans);\n auto p2=func(root->right,ans);\n int avg=(root->val+p1.first+p2.first)/(p1.second+p2.second+1);\n if(avg==root->val)ans++;\n return {root->val+p1.first+p2.first,p1.second+p2.second+1};\n }\n int averageOfSubtree(TreeNode* root) {\n int ans=0;\n func(root,ans);\n return ans;\n }\n};\n``` | 18 | 1 | ['Tree', 'C++'] | 2 |
count-nodes-equal-to-average-of-subtree | Javascript Clean Solution | javascript-clean-solution-by-mertnacak-b1oh | \nvar averageOfSubtree = function (root) {\n let ans = 0;\n function dfs(node) {\n if (node === null) return [0, 0];\n let [leftSum, leftCou | mertnacak | NORMAL | 2022-05-08T06:51:44.949626+00:00 | 2022-05-08T06:51:44.949663+00:00 | 626 | false | ```\nvar averageOfSubtree = function (root) {\n let ans = 0;\n function dfs(node) {\n if (node === null) return [0, 0];\n let [leftSum, leftCount] = dfs(node.left);\n let [rightSum, rightCount] = dfs(node.right);\n\n let sum = leftSum + rightSum + node.val;\n let count = leftCount + rightCount + 1;\n if (Math.floor(sum / count) === node.val) ans++;\n return [sum, count];\n }\n\n dfs(root);\n\n return ans;\n};\n``` | 14 | 0 | ['Depth-First Search', 'JavaScript'] | 2 |
count-nodes-equal-to-average-of-subtree | 👨💻 Simple C++ Solution | Explained in Comments ✏️ | O(n) Solution | simple-c-solution-explained-in-comments-otlr9 | Approach: \nThe approach involves a recursive function, calculateSubtreeSum, that calculates the sum of values and the number of nodes in a subtree. It does thi | saurav_1928 | NORMAL | 2023-11-02T03:40:15.038270+00:00 | 2023-11-02T03:40:51.070481+00:00 | 1,453 | false | # Approach: \nThe approach involves a recursive function, calculateSubtreeSum, that calculates the sum of values and the number of nodes in a subtree. It does this by visiting each node in a bottom-up manner. If a node satisfies the condition (its value equals the average), it increments the count. The averageOfSubtree function initiates this process and returns the final count.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1), No extra space is used , except for recursive stack space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode* left;\n * TreeNode* right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int count = 0; // Initialize a variable to count valid subtrees.\n\n // A helper function to calculate the sum and count of valid subtrees.\n pair<int, int> solve(TreeNode* root) {\n // If the node is null, return 0 for both sum and count.\n if (root == nullptr) return {0, 0}; \n int subtreeSum = root->val; // Initialize the sum with the current node\'s value.\n int subtreeNodeCount = 1; // Initialize the node count with 1 for the current node.\n\n // Recursively calculate the sum and node count for the left and right subtrees.\n pair<int, int> leftSubtree = solve(root->left);\n pair<int, int> rightSubtree = solve(root->right);\n\n // Update the sum and node count with values from left and right subtrees.\n subtreeSum += leftSubtree.first + rightSubtree.first;\n subtreeNodeCount += leftSubtree.second + rightSubtree.second;\n\n // Check if the current node satisfies the condition (value is equal to the average).\n if (root->val == (subtreeSum / subtreeNodeCount)) {\n count++; // Increment the count if the condition is met.\n }\n\n return {subtreeSum, subtreeNodeCount};\n }\n\n int averageOfSubtree(TreeNode* root) {\n pair<int, int> result = solve(root); // Calculate the sum and count.\n return count; // Return the count of valid subtrees.\n }\n};\n\n``` | 12 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 1 |
count-nodes-equal-to-average-of-subtree | ✅ Easiest Possible Approach with Video Explanation✅ Beats 100% ✅ Fastest Too | easiest-possible-approach-with-video-exp-lx7y | \n\n\n# YouTube Video Explanation:\n\nhttps://youtu.be/XGFLJ7HWSPE\n\n\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making | millenium103 | NORMAL | 2023-11-02T05:33:53.862375+00:00 | 2023-11-02T05:33:53.862397+00:00 | 1,166 | false | \n\n\n# YouTube Video Explanation:\n\n[https://youtu.be/XGFLJ7HWSPE](https://youtu.be/XGFLJ7HWSPE)\n\n**\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making complex concepts easy to understand.**\n\nSubscribe Link: https://www.youtube.com/@leetlogics/?sub_confirmation=1\n\n*Subscribe Goal: 200 Subscribers*\n*Current Subscribers: 172*\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to count the number of nodes in a binary tree where the value of the node is equal to the average of the values in its subtree. We need to traverse the tree and keep track of the sum and count of values in the subtree to calculate the average.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We perform a Depth-First Search (DFS) traversal of the binary tree.\n2. For each node, we recursively calculate the sum and count of values in its left and right subtrees.\n3. We then compute the sum and count of values in the current subtree (including the current node).\n4. If the current node\'s value is equal to the computed average, we increment the result.\n5. We return the sum and count of the current subtree to the parent node.\n\n# Complexity\n- Time Complexity: O(N) - We visit each node once during the DFS traversal.\n- Space Complexity: O(H) - In the worst case, the space complexity is O(H), where H is the height of the binary tree, due to the recursion stack.\n\n# Code\n## Java\n```\nclass Solution {\n int result = 0;\n\n public int averageOfSubtree(TreeNode root) {\n dfs(root);\n return result;\n }\n\n private int[] dfs(TreeNode node) {\n if (node == null) {\n return new int[]{0, 0};\n }\n\n int[] left = dfs(node.left);\n int[] right = dfs(node.right);\n\n int currentSum = left[0] + right[0] + node.val;\n int currentCount = left[1] + right[1] + 1;\n\n if (currentSum / currentCount == node.val) {\n result++;\n }\n\n return new int[]{currentSum, currentCount};\n }\n}\n```\n## C++\n```\nclass Solution {\npublic:\n int result = 0;\n\n int averageOfSubtree(TreeNode* root) {\n dfs(root);\n return result;\n }\n\n vector<int> dfs(TreeNode* node) {\n if (!node) {\n return {0, 0};\n }\n\n vector<int> left = dfs(node->left);\n vector<int> right = dfs(node->right);\n\n int currentSum = left[0] + right[0] + node->val;\n int currentCount = left[1] + right[1] + 1;\n\n if (currentSum / currentCount == node->val) {\n result++;\n }\n\n return {currentSum, currentCount};\n }\n};\n```\n## Python\n```\nclass Solution(object):\n def __init__(self):\n self.result = 0\n\n def averageOfSubtree(self, root):\n self.dfs(root)\n return self.result\n\n def dfs(self, node):\n if not node:\n return [0, 0]\n\n left = self.dfs(node.left)\n right = self.dfs(node.right)\n\n currentSum = left[0] + right[0] + node.val\n currentCount = left[1] + right[1] + 1\n\n if currentSum // currentCount == node.val:\n self.result += 1\n\n return [currentSum, currentCount]\n \n```\n## JavaScript\n```\nvar averageOfSubtree = function(root) {\n let result = 0;\n\n const dfs = (node) => {\n if (!node) {\n return [0, 0];\n }\n\n const left = dfs(node.left);\n const right = dfs(node.right);\n\n const currentSum = left[0] + right[0] + node.val;\n const currentCount = left[1] + right[1] + 1;\n\n if (Math.floor(currentSum / currentCount) === node.val) {\n result++;\n }\n\n return [currentSum, currentCount];\n };\n\n dfs(root);\n return result;\n};\n```\n\n\n\n\n\n\n\n | 11 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
count-nodes-equal-to-average-of-subtree | C++ Solution O(n) complexity , Easy solution : ) | c-solution-on-complexity-easy-solution-b-ahq3 | \n# O(n) Solution\n \n\n# Code\n\n\nclass Solution {\npublic:\n pair<int,int> avgCount(TreeNode* root,int &count){\n if(root==NULL){\n retu | ganeshdarshan18 | NORMAL | 2023-11-02T04:27:33.930844+00:00 | 2023-11-02T04:27:33.930869+00:00 | 379 | false | \n# $$O(n)$$ Solution\n \n\n# Code\n```\n\nclass Solution {\npublic:\n pair<int,int> avgCount(TreeNode* root,int &count){\n if(root==NULL){\n return {0,0};\n }\n pair<int,int> lh = avgCount(root->left,count);\n pair<int,int> rh= avgCount(root->right,count);\n\n int sum = lh.first + rh.first + root->val ;\n int ele = lh.second +rh.second + 1;\n\n if(sum/ele==root->val) count++;\n return {sum,ele};\n }\n int averageOfSubtree(TreeNode* root) {\n int count = 0;\n pair<int,int> cnt = avgCount(root,count);\n return count;\n }\n};\n``` | 11 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | ✅ Beats 90.78% 🔥 || DFS 🚀 || Easiest Explanation 💡 | beats-9078-dfs-easiest-explanation-by-go-8n6l | \n\n# Intuition:\nHere we are using DFS to traverse the tree and for each node we are calculating the sum of the subtree and the count of the nodes in the subtr | Gourav-2002 | NORMAL | 2023-11-02T01:58:30.294932+00:00 | 2023-11-02T01:58:30.294949+00:00 | 958 | false | \n\n# Intuition:\n**Here we are using DFS to traverse the tree and for each node we are calculating the sum of the subtree and the count of the nodes in the subtree. If the average of the subtree is equal to the value of the node then we increment the result by 1. We are using a global variable to store the result.**\n\n# Approach: DFS\n1. Initialize the result to 0.\n2. Define a function dfs which takes a node as an argument.\n3. If the node is None then return 0,0.\n4. Call the dfs function recursively on the left and right subtree and store the sum and count of the nodes.\n5. Calculate the sum and count of the current node by adding the value of the node with the sum and count of the left and right subtree.\n6. If the average of the subtree is equal to the value of the node then increment the result by 1.\n7. Return the sum and count of the current node.\n8. Call the dfs function on the root node.\n9. Return the result.\n\n# Complexity Analysis:\n- Time Complexity: **O(N)**, where N is the number of nodes in the tree.\n- Space Complexity: **O(H)**, where H is the height of the tree.\n# Code\n``` Python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n result=0\n\n def dfs(node):\n nonlocal result\n if not node:\n return 0,0\n leftSum,leftCount=dfs(node.left)\n rightSum,rightCount=dfs(node.right)\n curr_sum=node.val+leftSum+rightSum\n curr_count=1+leftCount+rightCount\n if curr_sum//curr_count==node.val:\n result+=1\n return curr_sum,curr_count\n \n dfs(root)\n return result \n```\n``` Java []\n/**\n * Definition for a binary tree node.\n * class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\n\nclass Solution {\n int result = 0;\n \n public int averageOfSubtree(TreeNode root) {\n dfs(root);\n return result;\n }\n\n private int[] dfs(TreeNode node) {\n if (node == null) {\n return new int[]{0, 0};\n }\n\n int[] left = dfs(node.left);\n int[] right = dfs(node.right);\n\n int sum = left[0] + right[0] + node.val;\n int count = left[1] + right[1] + 1;\n\n if (sum / count == node.val) {\n result++;\n }\n\n return new int[]{sum, count};\n }\n}\n```\n``` C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode* left;\n * TreeNode* right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int val) : val(val), left(nullptr), right(nullptr) {}\n * TreeNode(int val, TreeNode* left, TreeNode* right) : val(val), left(left), right(right) {}\n * };\n */\n\nclass Solution {\nprivate:\n int result = 0;\n \npublic:\n int averageOfSubtree(TreeNode* root) {\n dfs(root);\n return result;\n }\n\n vector<int> dfs(TreeNode* node) {\n if (node == nullptr) {\n return {0, 0};\n }\n\n vector<int> left = dfs(node->left);\n vector<int> right = dfs(node->right);\n\n int sum = left[0] + right[0] + node->val;\n int count = left[1] + right[1] + 1;\n\n if (sum / count == node->val) {\n result++;\n }\n\n return {sum, count};\n }\n};\n```\n\n | 11 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++', 'Java', 'Python3'] | 0 |
count-nodes-equal-to-average-of-subtree | Java | Postorder + Suffix sum | java-postorder-suffix-sum-by-surajthapli-3kkp | Do postorder traversal (Left - Right - Root)\n root will contain sum of its subtree + root.val\n If root original val == root.val / count, then increment answer | surajthapliyal | NORMAL | 2022-05-08T04:14:51.932047+00:00 | 2022-05-08T04:24:04.568894+00:00 | 1,222 | false | * Do **postorder** traversal (Left - Right - Root)\n* `root` will contain sum of its subtree + `root.val`\n* If root original val == `root.val / count`, then increment answer\n* return pair of **root.val** (sum of its subtree) and **count** (number of nodes in it subtree)\n```\nclass Solution {\n\n public int averageOfSubtree(TreeNode root) {\n ans = 0;\n solve(root, 0);\n return ans;\n }\n\n int ans = 0;\n\n private int[] solve(TreeNode root, int count) {\n if (root == null) {\n return new int[] { 0, 0 };\n }\n int left[] = solve(root.left, count);\n int right[] = solve(root.right, count);\n int temp = root.val;\n root.val += (left[0] + right[0]);\n count = (left[1] + right[1]) + 1;\n if (temp == (root.val / count)) ans++; \n return new int[] { root.val, count };\n }\n}\n```\n | 11 | 0 | [] | 3 |
count-nodes-equal-to-average-of-subtree | C++ postOrder, inOrder, preOrder transversal->0ms beats 100% | c-postorder-inorder-preorder-transversal-d5vk | Intuition\n Describe your first thoughts on how to solve this problem. \nQuite standard problem for binary trees.\nUsing postOrder, inOrder, preOrder transversa | anwendeng | NORMAL | 2023-11-02T01:39:19.904623+00:00 | 2023-11-02T10:32:25.021074+00:00 | 2,698 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nQuite standard problem for binary trees.\nUsing postOrder, inOrder, preOrder transversal to solve the problem.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBe careful with the definition of average!\n```\nFor the node with value 5: The average of its subtree is \n(5 + 6) / 2 = 11 / 2 = 5.\n```\nUsing the similar idea from @Sergei, the optimized code does not use the pair<int, int>, insteadly uses an unsigned long long, using first 32-bit part for n the number of nodes in subtree , the second 32-bits part for sum of the node values in subtree.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$ + system stack for recursion\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\n using int2=pair<int, int>;\npublic:\n int count=0;\n int2 preOrder(TreeNode* node){\n if (node==NULL) return {0, 0};\n int sum=node->val, i=1;\n auto [sumL, iL]=preOrder(node->left);\n auto [sumR, iR]=preOrder(node->right);\n sum+=(sumL+sumR);\n i+=(iL+iR);\n if (sum/i==node->val) count++;\n // cout<<node->val<<" n="<<i<<" sum="<<sum<<endl;\n return {sum, i};\n }\n\n int2 postOrder(TreeNode* node){\n if (node==NULL) return {0, 0};\n auto [sumL, iL]=postOrder(node->left);\n auto [sumR, iR]=postOrder(node->right);\n int sum=node->val, i=1;\n sum+=(sumL+sumR);\n i+=(iL+iR);\n if (sum/i==node->val) count++;\n // cout<<node->val<<" n="<<i<<" sum="<<sum<<endl;\n return {sum, i};\n }\n\n int2 inOrder(TreeNode* node){\n if (node==NULL) return {0, 0};\n auto [sumL, iL]=inOrder(node->left);\n int sum=node->val, i=1;\n auto [sumR, iR]=inOrder(node->right);\n sum+=(sumL+sumR);\n i+=(iL+iR);\n if (sum/i==node->val) count++;\n // cout<<node->val<<" n="<<i<<" sum="<<sum<<endl;\n return {sum, i};\n }\n\n int averageOfSubtree(TreeNode* root) {\n inOrder(root);\n return count;\n }\n};\n```\n# Code runs 0ms & beats 100%\n```\n#pragma GCC optimize ("O3")\nclass Solution {\npublic:\n signed count=0;\n signed long long inOrder(TreeNode* node){\n if (node==NULL) return 0;\n signed long long sum_n_L=inOrder(node->left);\n signed long long sum_n=node->val+(1L<<32);\n signed long long sum_n_R=inOrder(node->right);\n sum_n+=sum_n_L+sum_n_R;\n if ((sum_n&0xffffffff)/(sum_n>>32 )==node->val) count++;\n // cout<<node->val<<" n="<<i<<" sum="<<sum<<endl;\n return sum_n;\n }\n\n int averageOfSubtree(TreeNode* root) {\n inOrder(root);\n return count;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 10 | 1 | ['Recursion', 'Binary Tree', 'C++'] | 2 |
count-nodes-equal-to-average-of-subtree | C++ Solution | Simple Recursion | c-solution-simple-recursion-by-tejasmn-2lea | \n\nclass Solution {\npublic: \n int count(TreeNode* root)\n {\n //if tree is empty\n if(root==NULL) return 0;\n \n //if tr | tejasmn | NORMAL | 2022-05-08T06:49:50.113059+00:00 | 2022-05-08T06:51:49.679798+00:00 | 911 | false | \n```\nclass Solution {\npublic: \n int count(TreeNode* root)\n {\n //if tree is empty\n if(root==NULL) return 0;\n \n //if tree has single node/leaf node\n if(root->left==NULL && root->right==NULL) return 1; \n \n return 1 + count(root->left) + count(root->right);\n }\n \n \n int sum(TreeNode* root)\n {\n //if tree is empty\n if(root==NULL) return 0;\n \n return root->val + sum(root->left) + sum(root->right);\n }\n \n int averageOfSubtree(TreeNode* root) {\n \n //if tree is empty\n if(root==NULL) return 0;\n \n //if tree has single node/leaf node\n if(root->left==NULL && root->right==NULL) return 1;\n \n //return value or Boolean condition(1 or 0) + rec(root->left) + rec(root->right)\n return (sum(root)/count(root)==root->val) + averageOfSubtree(root->left) + averageOfSubtree(root->right);\n\n }\n};\n```\n | 9 | 0 | ['Recursion', 'C'] | 1 |
count-nodes-equal-to-average-of-subtree | O(N) time || C++/ Java | on-time-c-java-by-xxvvpp-j0w6 | Get Sum and Count from left and right subtree Upfront for O(N) total time.\n# C++\n int averageOfSubtree(TreeNode root) {\n int cnt=0;\n helper | xxvvpp | NORMAL | 2022-05-08T04:09:53.069298+00:00 | 2022-05-08T06:40:47.254451+00:00 | 1,254 | false | Get **Sum** and **Count** from left and right subtree **Upfront for O(N) total time**.\n# C++\n int averageOfSubtree(TreeNode* root) {\n int cnt=0;\n helper(root,cnt);\n return cnt;\n }\n \n pair<int,int> helper(TreeNode* root,int &cnt){\n if(!root) return {0,0};\n pair<int,int> l= helper(root->left,cnt); //sum and count of nodes in left subtree with single call\n pair<int,int> r= helper(root->right,cnt); //sum and count of nodes in right subtree with single call\n int sum= l.first+r.first+root->val; //compute new sum \n int count= l.second+r.second+1; //compute new count of nodes\n if(sum/count==root->val) cnt++; //check if it is candidate or not\n return {sum,count}; \n }\n\t\n# Java\n //user defined data-type\n\tclass data{\n int first,second;\n data(int x,int y){ first=x; second=y; }\n }\n \n public int averageOfSubtree(TreeNode root) {\n int[] cnt= new int[1];\n helper(root,cnt);\n return cnt[0];\n }\n \n data helper(TreeNode root,int[] cnt){\n if(root==null) return new data(0,0);\n data l= helper(root.left,cnt); //sum and count of nodes in left subtree with single call\n data r= helper(root.right,cnt); //sum and count of nodes in right subtree with single call\n int sum= l.first+r.first+root.val; //get sum of subtree\n int count= l.second+r.second+1; //get count of nodes in this subtree\n if(sum/count==root.val) cnt[0]++; //check if it is candidate or not\n return new data(sum,count); \n }\n\t\n**Time** - O(N)\n**Space** - O(1) ignoring Recursion space | 9 | 1 | ['C', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Python | DFS(Preorder Traversal) | python-dfspreorder-traversal-by-thezhund-jzyu | Our goal is to iterate each and every node by using any kind of traversal technique (preorder, postorder, inorder). (I have used preorder here), \n\nFor every n | thezhund | NORMAL | 2022-05-08T05:01:33.896599+00:00 | 2022-05-08T05:01:33.896638+00:00 | 1,601 | false | Our goal is to iterate each and every node by using any kind of traversal technique (preorder, postorder, inorder). (I have used preorder here), \n\nFor every node, we calculate the sum of its subtree nodes and keep a variable to store the no. of nodes, \nso that we can calculate average by total sum/ total nodes.\n\nIf our average is equal to value of the root, we increment the count.\n\nVideo explanation: https://youtu.be/y_3TlyzIRbk\n\nCode:\n\n\n```\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n \n \n def calculate_average(root):\n if root:\n self.summ+=root.val\n self.nodecount+=1\n calculate_average(root.left)\n calculate_average(root.right)\n \n \n def calculate_for_each_node(root):\n if root:\n self.summ = 0\n self.nodecount = 0\n calculate_average(root)\n if ((self.summ)//(self.nodecount)) == root.val:\n self.count+=1 \n calculate_for_each_node(root.left)\n calculate_for_each_node(root.right)\n \n \n self.count = 0\n calculate_for_each_node(root) \n return self.count\n\n``` | 8 | 0 | ['Recursion', 'Python'] | 2 |
count-nodes-equal-to-average-of-subtree | Easy C++ Code With Explaination | easy-c-code-with-explaination-by-baibhav-5dki | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nThe below function is a | baibhavsingh07 | NORMAL | 2023-11-02T05:51:40.995650+00:00 | 2023-11-02T05:51:40.995675+00:00 | 435 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe below function is a recursive function that calculates and returns the number of nodes in the subtree rooted at a given TreeNode. It does this by traversing the left and right subtrees and adding 1 for the current node.\n\nThe solve function is the main recursive function for solving the problem. It takes two parameters: a reference to a TreeNode pointer and a reference to an integer ans (which will store the count of valid subtrees). This function is used to traverse the binary tree.\n\na. If the current node is null (i.e., there is no subtree to process), it returns 0.\n\nb. It recursively calls solve on the left and right subtrees and stores the result in variable s.\n\nc. It calculates the number of nodes in the current subtree (including the current node) by calling the below function and stores it in variable c.\n\nd. It adds the value of the current node to the s.\n\ne. It checks if the average of the subtree (sum of node values divided by the number of nodes) is equal to the value of the root node. If it is, it increments the ans.\n\nf. Finally, it returns s, which is the sum of values in the current subtree.\n\n# Complexity\n- Time complexity:O(n*height) = O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n\n\n int below(TreeNode* root){\n if(!root)\n return 0;\n\n return 1+below(root->left)+below(root->right);\n } \n\n int solve(TreeNode* &root,int &ans){\n if(!root){\n return 0;\n }\n\n int s=0;\n s+=solve(root->left,ans);\n // c=0;\n s+=solve(root->right,ans);\n\n int c = below(root);\n\n s+=root->val;\n\n if(s/c == root->val){\n ans++;\n }\n return s;\n }\n\n\n int averageOfSubtree(TreeNode* root) {\n if(!root)\n return 0;\n\n int ans=0;\n solve(root,ans);\n\n return ans;\n }\n};\n``` | 7 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 1 |
count-nodes-equal-to-average-of-subtree | 🏆C++ || DFS (easy approach) | c-dfs-easy-approach-by-chiikuu-d468 | Code\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : | CHIIKUU | NORMAL | 2023-06-23T17:33:43.233719+00:00 | 2023-06-23T17:39:38.083525+00:00 | 454 | false | # Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int s(TreeNode* root,int &v){\n if(root==NULL)return 0;\n v++;\n return root->val + s(root->right,v) + s(root->left,v);\n }\n int ct=0;\n int averageOfSubtree(TreeNode* root) {\n if(root==NULL)return 0;\n int v=0;\n int x = s(root,v);\n if(root->val == (x/v))ct++;\n averageOfSubtree(root->right);\n averageOfSubtree(root->left);\n return ct;\n }\n};\n```\n\n | 7 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 1 |
count-nodes-equal-to-average-of-subtree | Use pair | use-pair-by-yadivyanshu-tsy8 | \n# Code\n\nclass Solution {\npublic:\n int cnt = 0;\n\n pair<int, int> f(TreeNode* root) {\n if(!root)return {0, 0};\n auto lsum = f(root-> | yadivyanshu | NORMAL | 2023-03-31T18:31:13.859259+00:00 | 2023-03-31T18:31:13.859295+00:00 | 264 | false | \n# Code\n```\nclass Solution {\npublic:\n int cnt = 0;\n\n pair<int, int> f(TreeNode* root) {\n if(!root)return {0, 0};\n auto lsum = f(root->left);\n auto rsum = f(root->right);\n\n int sum = (lsum.first + rsum.first + root->val);\n int c = lsum.second + rsum.second + 1;\n int avg = sum / c;\n if(avg == root->val)cnt++;\n return {sum, c};\n }\n\n int averageOfSubtree(TreeNode* root) {\n f(root);\n return cnt;\n }\n};\n``` | 7 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | Easy | C++ | O(N) fast | easy-c-on-fast-by-ayushkaushk-705v | The naive approach is to iterate over the tree using any traversal and checking for each node the average of subtree.\n\nThe Optimal approach will be bottom up | ayushkaushk | NORMAL | 2022-05-08T10:33:03.619337+00:00 | 2022-05-08T10:33:03.619361+00:00 | 375 | false | **The naive approach is to iterate over the tree using any traversal and checking for each node the average of subtree.**\n\n**The Optimal approach will be bottom up approach and returning count and sum of nodes in subtree using pair c++**\n\n```\nclass Solution {\npublic:\n pair<int,int> iterate(TreeNode *root,int &ans)\n {\n if(!root)return {0,0};\n\t\t\n pair<int,int>left=iterate(root->left,ans);\n pair<int,int>right=iterate(root->right,ans);\n\t\t\n int count=left.first+right.first+1;\n int sum=left.second+right.second+root->val;\n\t\t\n if(root->val==sum/count){\n ans=ans+1;\n }\n\t\t\n return {count,sum};\n\n }\n\t\n int averageOfSubtree(TreeNode* root) \n\t{\n int ans=0; \n iterate(root,ans);\n return ans;\n }\n};\n``` | 7 | 0 | [] | 2 |
count-nodes-equal-to-average-of-subtree | Java Readable Code | 100.00% faster | java-readable-code-10000-faster-by-anoth-sjsp | \nclass Solution {\n \n public class NodeInfo{\n int sum;\n int size;\n public NodeInfo(int sum , int size){\n this.sum = | anothercoderr | NORMAL | 2022-05-08T06:08:35.352781+00:00 | 2022-05-08T06:40:16.426158+00:00 | 402 | false | ```\nclass Solution {\n \n public class NodeInfo{\n int sum;\n int size;\n public NodeInfo(int sum , int size){\n this.sum = sum;\n this.size = size;\n }\n }\n \n int ans = 0;\n \n public int averageOfSubtree(TreeNode root) \n {\n dfs(root);\n return ans;\n }\n \n public NodeInfo dfs(TreeNode node){\n if(node == null)\n return new NodeInfo(0,0);\n \n NodeInfo left = dfs(node.left);\n NodeInfo right = dfs(node.right);\n \n int currentSum = node.val + left.sum + right.sum;\n int currentSize = 1 + left.size + right.size;\n \n if(currentSum / currentSize == node.val)\n ans++;\n \n return new NodeInfo(currentSum , currentSize);\n }\n}\n``` | 7 | 0 | ['Depth-First Search', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | [Python3] post-order dfs | python3-post-order-dfs-by-ye15-efgo | Please pull this commit for solutions of weekly 292. \n\n\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n \n | ye15 | NORMAL | 2022-05-08T04:04:24.506641+00:00 | 2022-05-09T05:45:56.995580+00:00 | 842 | false | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/9aa0edb0815f3e0a75a47808e1690ca424f169e5) for solutions of weekly 292. \n\n```\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n \n def fn(node): \n nonlocal ans\n if not node: return 0, 0 \n ls, ln = fn(node.left)\n rs, rn = fn(node.right)\n s = node.val + ls + rs\n n = 1 + ln + rn\n if s//n == node.val: ans += 1\n return s, n\n \n ans = 0 \n fn(root)\n return ans \n```\n\nAdded iterative implementation \n```\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n ans = 0 \n mp = {None: (0, 0)}\n node, stack = root, []\n prev = None\n while node or stack: \n if node: \n stack.append(node)\n node = node.left \n else: \n node = stack[-1]\n if node.right and node.right != prev: node = node.right\n else: \n stack.pop()\n ls, lc = mp[node.left]\n rs, rc = mp[node.right]\n sm, cnt = ls + node.val + rs, lc + 1 + rc\n mp[node] = (sm, cnt)\n if sm//cnt == node.val: ans += 1\n prev = node \n node = None\n return ans \n``` | 7 | 0 | ['Python3'] | 0 |
count-nodes-equal-to-average-of-subtree | Post Order Traversal C++ Recursion O(n) | post-order-traversal-c-recursion-on-by-g-kt54 | Each call will return sum of it\'s right and left subtree along with its node count, then the root will will handle the remaining calculations.\n\nclass Solutio | gurdeepsingh574574 | NORMAL | 2022-05-08T04:02:43.509441+00:00 | 2022-05-08T04:02:43.509476+00:00 | 456 | false | Each call will return sum of it\'s right and left subtree along with its node count, then the root will will handle the remaining calculations.\n```\nclass Solution {\npublic:\n int averageOfSubtree(TreeNode* root) {\n int count = 0;\n pot(root,count);\n return count;\n }\n \n vector<int> pot(TreeNode* root, int &count){\n if(root == NULL) return {0,0};\n \n vector<int> av1 = pot(root->left,count);\n vector<int> av2 = pot(root->right,count);\n \n if((av1[0]+av2[0]+root->val)/(av1[1]+av2[1]+1) == root->val)\n count++;\n \n return {av1[0]+av2[0]+root->val,av1[1]+av2[1]+1};\n }\n};\n``` | 7 | 1 | ['Recursion', 'Binary Tree'] | 0 |
count-nodes-equal-to-average-of-subtree | C++ || Easy Solution || Explanation With Comments || Using BFS | c-easy-solution-explanation-with-comment-q9y9 | Please Upvote If It Helps\n\n\nclass Solution {\npublic:\n // this function will calculate the sum for the current element subtree\n void average(TreeNode | mayanksamadhiya12345 | NORMAL | 2022-05-08T09:06:46.924691+00:00 | 2022-05-08T09:06:46.924719+00:00 | 547 | false | **Please Upvote If It Helps**\n\n```\nclass Solution {\npublic:\n // this function will calculate the sum for the current element subtree\n void average(TreeNode* node, int& ans)\n {\n int sum=0; // it will calculate the subtree sum for current node#\n int cnt=0; // it will store the number of values that are present in subtree\n \n // pushing current node to the queue\n queue<TreeNode*> q;\n q.push(node);\n \n // BFS\n while(!q.empty())\n {\n int s = q.size();\n \n // iterating over q size\n for(int i=0;i<s;i++)\n {\n // extracting the queue\'s front element\n TreeNode* nod = q.front();\n q.pop();\n \n // after taking the elemets , add that val into the sum and incraese the value\'s cnt by 1\n sum += nod->val;\n cnt++;\n \n // check for current node left and right\n if(nod->left)\n q.push(nod->left);\n if(nod->right)\n q.push(nod->right);\n }\n }\n if(sum/cnt==node->val)\n ans++;\n }\n \n // this function will make sure to iterate all the nodes\n int averageOfSubtree(TreeNode* root) \n {\n // we have to traversal all the given tree and for each node we have to traverse it\'s own subtree\n // so we can use both BFS & DFS here \n // so we will solve this problem by using BFS \n \n int ans = 0;\n queue<TreeNode*> q;\n q.push(root);\n \n // BFS\n while(!q.empty())\n {\n // extracting the size of the queue\n int s = q.size();\n \n // now check for the elements that avaliable in queue\n for(int i=0;i<s;i++)\n {\n // taking out the front element\n TreeNode* node = q.front();\n q.pop();\n \n // call the function for current node and calculate its avg\n average(node,ans);\n \n // after counting the avg\'s chech there is left or right available \n if(node->left)\n q.push(node->left);\n if(node->right)\n q.push(node->right);\n }\n }\n return ans;\n }\n};\n``` | 6 | 0 | ['Tree', 'Breadth-First Search'] | 1 |
count-nodes-equal-to-average-of-subtree | 🚀 Beats 100% | Easy To Understand 🚀🔥 | beats-100-easy-to-understand-by-sanket_d-e2ar | Intuition\n\n\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- T | The_Eternal_Soul | NORMAL | 2023-11-02T03:35:55.317105+00:00 | 2023-11-02T03:35:55.317132+00:00 | 1,275 | false | # Intuition\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int ans = 0;\n\n pair<int,int> postorder(TreeNode* &root,int sum,int count)\n {\n if(root == 0) return {0,0};\n\n auto l = postorder(root->left,sum,count);\n auto r = postorder(root->right,sum,count);\n\n sum = l.first + root->val + r.first;\n count = l.second + 1 + r.second;\n\n if(sum / count == root->val) ans++;\n return {sum,count};\n }\n\n int averageOfSubtree(TreeNode* root) {\n postorder(root,0,0);\n return ans;\n }\n};\n``` | 5 | 0 | ['Tree', 'C', 'Binary Tree', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
count-nodes-equal-to-average-of-subtree | Java Easy Approach | Beats 98% | java-easy-approach-beats-98-by-chourasia-i10o | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | chourasiaavinash80 | NORMAL | 2023-01-12T15:14:40.369368+00:00 | 2023-01-16T09:59:41.920356+00:00 | 545 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\npublic class Pair{\n int f,s;\n Pair(int f, int s){\n this.f = f;\n this.s = s;\n }\n}\n\nclass Solution {\n\n int count;\n public int averageOfSubtree(TreeNode root) {\n count = 0;\n isAverageBT(root);\n return count;\n }\n\n public Pair isAverageBT(TreeNode root){\n if(root==null){\n return new Pair(0,0);\n }\n Pair left = isAverageBT(root.left);\n Pair right = isAverageBT(root.right);\n int sum = root.val + left.f + right.f;\n int number = 1 + left.s + right.s;\n if(sum/number == root.val){\n count++;\n } \n return new Pair(sum,number);\n }\n\n}\n```\n\nPlease Upvote the solution. | 5 | 0 | ['Math', 'Tree', 'Depth-First Search', 'Binary Tree', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Explanation which you are searching for!! | explanation-which-you-are-searching-for-yqbz8 | \nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n self.cnt=0\n def dfs(node):\n if not node:return | neelmehta0086 | NORMAL | 2022-06-03T09:12:43.829432+00:00 | 2022-06-03T09:12:43.829456+00:00 | 168 | false | ```\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n self.cnt=0\n def dfs(node):\n if not node:return [0,0]\n \n x,cntx=dfs(node.left)\n y,cnty=dfs(node.right)\n if node.val==(x+y+node.val)//(cntx+cnty+1):\n self.cnt+=1\n return [node.val+x+y,cntx+cnty+1]\n \n dfs(root)\n return self.cnt\n``` | 5 | 0 | [] | 0 |
count-nodes-equal-to-average-of-subtree | Decorated Python | decorated-python-by-stefanpochmann-lhis | Using a decorator that turns a function evaluating a single node into a function that sums that evaluation over the whole subtree, and uses caching for overall | stefanpochmann | NORMAL | 2022-05-09T00:20:55.157433+00:00 | 2022-05-09T02:55:55.861053+00:00 | 454 | false | Using a decorator that turns a function evaluating a single node into a function that sums that evaluation over the whole subtree, and uses caching for overall O(n) time.\n```\ndef subtree(f):\n @cache\n def g(root):\n return f(root) + g(root.left) + g(root.right) if root else 0\n return g\n\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n\n @subtree\n def sum(root):\n return root.val\n\n @subtree\n def number(root):\n return 1\n\n @subtree\n def equals_average(root):\n return root.val == sum(root) // number(root)\n \n return equals_average(root)\n``` | 5 | 0 | ['Python'] | 2 |
count-nodes-equal-to-average-of-subtree | C++ || DFS || with Explanation | c-dfs-with-explanation-by-amartyasurve-dtbb | \nclass Solution {\npublic:\n \n pair<int,int> path(TreeNode* root)\n\t\t//this function is used to calculate the sum of subtree and the number of | amartyasurve | NORMAL | 2022-05-08T06:15:19.731476+00:00 | 2022-05-08T06:15:19.731507+00:00 | 304 | false | ```\nclass Solution {\npublic:\n \n pair<int,int> path(TreeNode* root)\n\t\t//this function is used to calculate the sum of subtree and the number of nodes in subtree\n {\n if(!root)return {0,0};\n pair<int,int> lh=path(root->left);\n pair<int,int> rh=path(root->right);\n return {root->val+lh.first+rh.first,1+lh.second+rh.second};\n //root->val+lh.first+rh.first --->sum of subtree\n //1+lh.second+rh.second---->number of nodes;\n }\n \n void inorder(TreeNode* root,int &cnt){\n if(!root)return;\n pair<int,int> x=path(root);//pair of sum and count of nodes\n if(root->val==(x.first/x.second))//(x.first/x.second)-->calculating avg\n {cnt++;}//if avg==root->val then increment the count\n inorder(root->left,cnt);\n inorder(root->right,cnt);\n return;\n \n }\n \n int averageOfSubtree(TreeNode* root) {\n if(!root)return 0;\n int cnt=0;\n inorder(root,cnt);\n return cnt;\n }\n};\n``` | 5 | 0 | ['Tree', 'Depth-First Search', 'Recursion', 'Binary Tree'] | 2 |
count-nodes-equal-to-average-of-subtree | C++ | 2 Approaches | BFS | DFS | Easy to understand | c-2-approaches-bfs-dfs-easy-to-understan-p14c | Please upvote it you find this solution helpful:)\nApproach-1: Use Level Order traversal / BFS\n\nclass Solution {\npublic:\n \n \n //use level order t | Yash2arma | NORMAL | 2022-05-08T04:15:43.385180+00:00 | 2022-05-08T04:56:36.027863+00:00 | 591 | false | **Please upvote it you find this solution helpful:)**\n**Approach-1: Use Level Order traversal / BFS**\n```\nclass Solution {\npublic:\n \n \n //use level order traversal and check whether average of the subtree is equal to the node value, if it is increase the res by 1.\n void help(TreeNode* node, int &res)\n {\n int sum=0, cnt=0;\n \n queue<TreeNode*> q;\n q.push(node);\n while(!q.empty())\n {\n int n = q.size();\n for(int i=0; i<n; i++)\n {\n TreeNode* nod = q.front();\n q.pop();\n sum += nod->val;\n cnt++;\n if(nod->left) q.push(nod->left);\n if(nod->right) q.push(nod->right);\n }\n }\n if(sum/cnt == node->val) //if average equals to the node value increase res by 1.\n res++;\n }\n \n //use level order traversal and calling the function help for each node\n int averageOfSubtree(TreeNode* root) \n {\n int res=0;\n queue<TreeNode*> q;\n q.push(root);\n while(!q.empty())\n {\n int n = q.size();\n for(int i=0; i<n; i++)\n {\n TreeNode* node = q.front();\n q.pop();\n help(node, res);\n if(node->left) q.push(node->left);\n if(node->right) q.push(node->right);\n }\n }\n return res; \n }\n};\n```\n\n**Approach-2: Use DFS**\n```\nclass Solution {\npublic:\n pair<int, int> dfs(TreeNode* node, int &cnt) \n {\n if (!node)\n return {0, 0};\n\n auto left_subtree = dfs(node->left, cnt);\n auto right_subtree = dfs(node->right, cnt);\n\n int sum = left_subtree.first + right_subtree.first + node->val;\n int count = 1 + left_subtree.second + right_subtree.second;\n\n if(sum/count == node->val)\n cnt++; //if average equals to node value, increase the count\n\n return {sum, count};\n }\n\n int averageOfSubtree(TreeNode* root) \n {\n int cnt=0;\n dfs(root, cnt);\n return cnt;\n } \n};\n``` | 5 | 0 | ['Breadth-First Search', 'C', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | Java solution by traversal a tree. | java-solution-by-traversal-a-tree-by-yas-si4t | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yash_jadaun | NORMAL | 2023-11-02T11:27:46.239866+00:00 | 2023-11-02T11:27:46.239898+00:00 | 230 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n class Pair{\n int sum;\n int num;\n Pair(int sum,int num){\n this.sum=sum;\n this.num=num;\n }\n }\n int count=0;\n public Pair sol(TreeNode root){\n if(root==null)return new Pair(0,0);\n Pair left= sol(root.left);\n Pair right=sol(root.right);\n int sum1=root.val+left.sum+right.sum;\n int num1=1+left.num+ right.num;\n \n if(root.val==sum1/num1)count++;\n return new Pair(sum1,num1);\n }\n public int averageOfSubtree(TreeNode root) {\n Pair left= sol(root);\n return count;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Simple & Algorithmic Solution : | simple-algorithmic-solution-by-niketh_12-rbcf | Algorithm : \n> ### Calculate the sum and count of the left subtree and also right subtree and store them in a Pair object.\n\n> ### Calculate the avg using th | niketh_1234 | NORMAL | 2023-11-02T05:33:03.108527+00:00 | 2023-11-02T05:33:03.108551+00:00 | 61 | false | # Algorithm : \n> ### *Calculate the sum and count of the left subtree and also right subtree and store them in a Pair object.*\n\n> ### *Calculate the avg using the sum\'s and count\'s from left and right subtrees and check if the avg equals to the root\'s data if equal then increase the ans, Now you can return a new Pair object with the left subtree\'s sum and right subtree\'s and add root\'s and also we need to have total count.* \n\n# Code\n```java []\nclass Pair\n{\n int count = 0,sum = 0;\n Pair(int count,int sum)\n {\n this.count = count;\n this.sum = sum;\n }\n}\nclass Solution {\n private int ans = 0;\n private Pair function(TreeNode root)\n {\n if(root == null)\n return new Pair(0,0);\n Pair left = function(root.left);\n Pair right = function(root.right);\n int totalSum = left.sum+right.sum+root.val;\n int totalCount = left.count+right.count+1;\n int avg = (int)Math.round(totalSum/totalCount);\n if(avg == root.val)\n ans+=1;\n return new Pair(totalCount,totalSum); \n }\n public int averageOfSubtree(TreeNode root) {\n function(root);\n return ans;\n }\n}\n``` | 4 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++', 'Java', 'Python3'] | 0 |
count-nodes-equal-to-average-of-subtree | Python3 Solution | python3-solution-by-motaharozzaman1996-9t3y | \n\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.l | Motaharozzaman1996 | NORMAL | 2023-11-02T01:59:59.882977+00:00 | 2023-11-02T01:59:59.883003+00:00 | 374 | false | \n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n ans=0\n def traverse(node):\n if node is None:\n return (0,0)\n left=traverse(node.left)\n right=traverse(node.right)\n total=left[0]+right[0]+node.val\n count=left[1]+right[1]+1\n if total//count==node.val:\n nonlocal ans\n ans+=1\n return (total,count)\n traverse(root)\n return ans \n``` | 4 | 0 | ['Python', 'Python3'] | 1 |
count-nodes-equal-to-average-of-subtree | 🔥💥 Simple C++ Solution Using Recursion 💥🔥 | simple-c-solution-using-recursion-by-ekn-gv40 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves working with a binary tree and finding the number of subtrees in w | eknath_mali_002 | NORMAL | 2023-11-02T01:57:52.848721+00:00 | 2023-11-02T01:57:52.848746+00:00 | 511 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves working with a binary tree and finding the number of subtrees in which the `average of values in the subtree` is equal to the value of the `root` of that subtree.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Define a recursive function `countNodes` to `count the number of nodes in a subtree`.\n2. Define another recursive function `totalSum` to calculate the `total sum of values in a subtree`.\n3. In the averageOfSubtree function, for each node:\n - Calculate the `sum of values` in the current subtree.\n - Calculate the `total number of nodes` in the current subtree.\n - Calculate the `average` of values in the current subtree.\n - If the average is equal to the value of the current node, increment a `counter`.\n - Recursively call averageOfSubtree on the left and right subtrees.\n4. Finally, return the counter, which represents the` number of subtrees that meet the condition`.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(h)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n \nint countNodes(TreeNode*root){\n if(!root) return 0;\n return 1 + countNodes(root->left)+ countNodes(root->right);\n}\n\nint totalSum(TreeNode*root){\n if(!root) return 0;\n return root->val + totalSum(root->left) + totalSum(root->right);\n}\n int averageOfSubtree(TreeNode* root) {\n if(!root) return 0;\n int sum = root->val + totalSum(root->left) + totalSum(root->right);\n int totalNodes = 1 + countNodes(root->left) + countNodes(root->right);\n \n int avg = floor(sum/totalNodes);\n if(avg==root->val) {\n return 1 + averageOfSubtree(root->left) + averageOfSubtree(root->right);\n }\n return averageOfSubtree(root->left) + averageOfSubtree(root->right);\n\n }\n};\n``` | 4 | 0 | ['Tree', 'Depth-First Search', 'Recursion', 'Binary Tree', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | O(N) Solution || Simple✅ || Easy to Understand ✅|| beat 100%✅ | on-solution-simple-easy-to-understand-be-138b | \n\n# Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(N)\n Add your space complexity here, e.g. O(n) \n | thesaurabhmhaske | NORMAL | 2023-02-19T09:13:26.036491+00:00 | 2023-02-19T09:13:26.036547+00:00 | 557 | false | \n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n pair<int,int> solve(TreeNode* root, int &cnt){\n if(root==NULL){\n return make_pair(0,0);\n }\n pair<int,int> left = solve(root->left, cnt);\n pair<int,int> right = solve(root->right, cnt);\n \n pair<int,int>ans;\n ans.first = root->val + left.first + right.first;\n ans.second = left.second + right.second + 1;\n int num = ans.first / ans.second;\n if(num==root->val) cnt++;\n return ans;\n }\n int averageOfSubtree(TreeNode* root) {\n int cnt=0;\n pair<int,int>p = solve(root,cnt);\n return cnt;\n }\n};\n``` | 4 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | ✅ [Java/C++] 100% Solution using Depth-First Search (Count Nodes Equal to Average of Subtree) | javac-100-solution-using-depth-first-sea-mvxz | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co | arnavsharma2711 | NORMAL | 2023-01-25T10:43:02.292714+00:00 | 2023-01-25T10:43:02.292750+00:00 | 1,045 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int cnt = 0;\n pair<int,int> solve(TreeNode* root)\n {\n if(root == NULL)\n return {0,0};\n auto left = solve(root->left);\n auto right = solve(root->right);\n int sum = left.first + right.first + root->val;\n int nodes = left.second + right.second + 1;\n if(sum/nodes == root->val)\n cnt++;\n return {sum,nodes};\n }\n int averageOfSubtree(TreeNode* root) {\n solve(root);\n return cnt;\n }\n};\n```\n```Java []\nclass Solution {\n int cnt = 0;\n int[] solve(TreeNode root)\n {\n if(root == null)\n return new int[]{0,0};\n int[] left = solve(root.left);\n int[] right = solve(root.right);\n int sum = left[0] + right[0] + root.val;\n int nodes = left[1] + right[1] + 1;\n if(sum/nodes == root.val)\n cnt++;\n return new int[]{sum, nodes};\n }\n public int averageOfSubtree(TreeNode root) {\n solve(root);\n return cnt;\n }\n}\n``` | 4 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | EASIEST JAVA SOLUTION EVER !!! ( Brute Force Approach and Better Pair Approach) 2 Approaches !!! | easiest-java-solution-ever-brute-force-a-bnu3 | Intuition\n- The Brute Approach is very Intuitive.\n- For every node we get the sum of it\'s left substree + sum of it\'s right subtree + value of itself divide | trinityhunter1 | NORMAL | 2023-01-11T01:22:14.885780+00:00 | 2023-01-11T01:22:14.885824+00:00 | 442 | false | # Intuition\n- **The Brute Approach is very Intuitive.**\n- **For every node we get the sum of it\'s left substree + sum of it\'s right subtree + value of itself divided by total numbe rof nodes.**\n\n# Approach\n**Brute Force Approach**\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n\n public static int numOfNodes(TreeNode node){\n\n if(node == null){\n return 0;\n }\n\n return numOfNodes(node.left) + numOfNodes(node.right) + 1;\n\n }\n\n public static int getSum(TreeNode node){\n\n if(node == null){\n return 0;\n }\n\n return getSum(node.left) + getSum(node.right) + node.val;\n\n }\n\n public static void helper(TreeNode node){\n\n if(node == null){\n return;\n }\n\n int sum = getSum(node.left) + getSum(node.right) + node.val;\n int n = numOfNodes(node.left) + numOfNodes(node.right) + 1;\n\n if(n!=0 && (node.val == (sum/n))){\n ans++;\n }\n\n helper(node.left);\n helper(node.right);\n\n }\n\n public static int ans;\n\n public int averageOfSubtree(TreeNode root) {\n\n ans = 0;\n \n helper(root);\n\n return ans;\n\n }\n\n}\n```\n\n\n# Intuition\n- **Creating a new class Pair.**\n- **This will allow us to get the sum of the substree as well as the number of nodes simultaneously.**\n\n# Approach\n**Better Pair Approach**\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\n\nclass Pair{\n\n int sum;\n\n int nodes;\n\n Pair(int sum, int nodes){\n this.sum = sum;\n this.nodes = nodes;\n }\n\n}\n\nclass Solution {\n\n public static Pair helper(TreeNode node){\n\n if(node == null){\n return new Pair(0, 0);\n }\n\n Pair left = helper(node.left);\n\n Pair right = helper(node.right);\n\n int totalSum = left.sum + right.sum + node.val;\n\n int num = left.nodes + right.nodes + 1;\n\n if(num != 0 && (totalSum/num) == node.val){\n ans++;\n }\n\n return new Pair(totalSum, num);\n\n }\n\n public static int ans;\n\n public int averageOfSubtree(TreeNode root) {\n \n ans = 0;\n\n helper(root);\n\n return ans;\n\n }\n\n}\n``` | 4 | 0 | ['Java'] | 1 |
count-nodes-equal-to-average-of-subtree | BhagvadGeeta Solution which is a Raambaan(Panacea) | bhagvadgeeta-solution-which-is-a-raambaa-eggo | Intuition\n Describe your first thoughts on how to solve this problem. \nI dont have any particular thoughts about this problem\nIt just came from my heart and | Abhishek_Singh_Vishen | NORMAL | 2022-12-13T06:54:34.878684+00:00 | 2022-12-13T06:54:34.878708+00:00 | 418 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI dont have any particular thoughts about this problem\nIt just came from my heart and eternal source of Lord krishna\nGod is carrying my chariot\nYou know who I am.\nMost importantly you know who he is.\nDo you understand?\nGOD IS CARRYING MY CHARIOT\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is that \nFirst you traverse til the leftmost node and then rightmost node\nand return the sum of subnodes in 0th index and number of nodes in 1st index\n\nWhen you completed both the traversals you add the 0th index of both the list and find the average of the sum of subnodes per number of subnodes which should be equal to the value of the root\nif it does then we will increment the counter (ctr) \nAt the end we will return the counter(ctr)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(2*n)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def __init__(self):\n self.ctr=0\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n def recur(root):\n if root is None:\n return [0,0]\n list1=recur(root.left)\n list2=recur(root.right)\n sub_node_sum=list1[0]+list2[0]+root.val\n sub_node_count=list1[1]+list2[1]+1\n if((int(sub_node_sum/sub_node_count))==root.val):\n print(root.val)\n self.ctr+=1\n return [sub_node_sum,sub_node_count]\n recur(root)\n return self.ctr\n``` | 4 | 0 | ['Python3'] | 0 |
count-nodes-equal-to-average-of-subtree | Java Clean DFS | java-clean-dfs-by-fllght-0pln | java\nprivate int averageEqualsValueNodes = 0;\n\n public int averageOfSubtree(TreeNode root) {\n sumAndCount(root);\n return averageEqualsValu | FLlGHT | NORMAL | 2022-05-08T07:38:06.620428+00:00 | 2022-05-08T07:38:06.620459+00:00 | 483 | false | ```java\nprivate int averageEqualsValueNodes = 0;\n\n public int averageOfSubtree(TreeNode root) {\n sumAndCount(root);\n return averageEqualsValueNodes;\n }\n\n\n private SumAndCount sumAndCount(TreeNode node) {\n if (node == null) return new SumAndCount(0, 0);\n\n SumAndCount left = sumAndCount(node.left);\n SumAndCount right = sumAndCount(node.right);\n\n int sum = left.sum() + right.sum() + node.val;\n int count = left.count() + right.count() + 1;\n\n if (sum / count == node.val)\n averageEqualsValueNodes++;\n\n return new SumAndCount(sum, count);\n }\n\n private record SumAndCount(int sum, int count) {}\n``` | 4 | 0 | ['Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Python Straightforward recursion | python-straightforward-recursion-by-jstm-o01t | \nclass Solution:\n \n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n self.count = 0\n def recursion(node):\n if | JSTM2022 | NORMAL | 2022-05-08T04:18:45.768972+00:00 | 2022-05-08T04:19:05.488732+00:00 | 192 | false | ```\nclass Solution:\n \n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n self.count = 0\n def recursion(node):\n if node == None:\n return [0, 0]\n val = node.val\n left = recursion(node.left)\n right = recursion(node.right)\n left_val, left_num = left[0], left[1]\n right_val, right_num = right[0], right[1]\n val += left_val\n val += right_val\n if node.val == val // (left_num + right_num + 1):\n self.count += 1\n return [val, left_num + right_num + 1]\n recursion(root)\n return self.count\n``` | 4 | 1 | ['Python'] | 0 |
count-nodes-equal-to-average-of-subtree | Java using Helper Function | java-using-helper-function-by-aditya_jai-2fsi | \n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n | Aditya_jain_2584550188 | NORMAL | 2022-05-08T04:09:49.035029+00:00 | 2022-05-08T04:09:49.035106+00:00 | 290 | false | ```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n \tstatic int count = 0;\n\n\tpublic static int averageOfSubtree(TreeNode root) {\n\t\tcount = 0;\n\t\thelper(root);\n\t\treturn count;\n\t}\n\n\tpublic static int helper(TreeNode root) {\n\t\tif (root == null)\n\t\t\treturn 0;\n\n\t\tint left = helper(root.left);\n\t\tint right = helper(root.right);\n\n\t\tint sum = root.val;\n\t\tif (root.left != null) {\n\t\t\tsum += root.left.val;\n\t\t}\n\t\tif (root.right != null) {\n\t\t\tsum += root.right.val;\n\t\t}\n\t\tif (sum / (left + right + 1) == root.val) {\n\t\t\tcount++;\n\t\t}\n\t\troot.val = sum;\n\t\treturn left + right + 1;\n\t}\n}\n``` | 4 | 0 | ['Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Easy C++ || Using Pair || Reuse the sum and count of SubTrees | easy-c-using-pair-reuse-the-sum-and-coun-ucsa | ```\nclass Solution {\npublic:\n \n int ans = 0;\n \n pair getAverageSubTree(TreeNode root, int currSum, int count)\n {\n if(root == NULL) | Kasturi13 | NORMAL | 2022-05-08T04:00:57.269883+00:00 | 2022-05-08T04:01:31.990503+00:00 | 386 | false | ```\nclass Solution {\npublic:\n \n int ans = 0;\n \n pair<int,int> getAverageSubTree(TreeNode* root, int currSum, int count)\n {\n if(root == NULL) return {0,0};\n \n pair<int,int> left = getAverageSubTree(root -> left, currSum, count);\n pair<int,int> right = getAverageSubTree(root -> right, currSum, count);\n \n currSum += root -> val + left.first + right.first;\n count += left.second + right.second + 1;\n \n if((currSum/count) == root -> val) ans++;\n return {currSum, count};\n }\n \n int averageOfSubtree(TreeNode* root) \n {\n getAverageSubTree(root, 0, 0);\n return ans;\n }\n};\n | 4 | 0 | [] | 1 |
count-nodes-equal-to-average-of-subtree | Very easy solution python, python3 | very-easy-solution-python-python3-by-jai-gk1e | Very easy soln\n\n# Code\n\nclass Solution:\n def averageOfSubtree(self, root: TreeNode) -> int:\n res=[0]\n def dfs(node):\n if not | jaiGurudevCode | NORMAL | 2023-12-10T07:01:26.904716+00:00 | 2023-12-10T07:01:26.904741+00:00 | 28 | false | # Very easy soln\n\n# Code\n```\nclass Solution:\n def averageOfSubtree(self, root: TreeNode) -> int:\n res=[0]\n def dfs(node):\n if not node: return 0,0\n ls,lc=dfs(node.left)\n rs,rc=dfs(node.right)\n s=ls+rs+node.val\n c=1+rc+lc\n if s//c==node.val: res[0]+=1\n return s,c\n dfs(root)\n return res[0]\n``` | 3 | 0 | ['Python', 'Python3'] | 0 |
count-nodes-equal-to-average-of-subtree | Easy solution using C++ | easy-solution-using-c-by-truongtamthanh2-goun | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n- Post order traversal\ | truongtamthanh2004 | NORMAL | 2023-11-29T07:27:30.840748+00:00 | 2023-11-29T07:27:30.840768+00:00 | 242 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Post order traversal\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int count = 0;\n int countNodeValue(TreeNode* root)\n {\n if (!root) return 0;\n return root->val + countNodeValue(root->left) + countNodeValue(root->right);\n }\n int countNode(TreeNode* root)\n {\n if (!root) return 0;\n return 1 + countNode(root->left) + countNode(root->right);\n }\n void NLR(TreeNode* root)\n {\n if (!root) return;\n if (floor(countNodeValue(root) / countNode(root)) == root->val) count++;\n NLR(root->left);\n NLR(root->right);\n }\n int averageOfSubtree(TreeNode* root) {\n // if (!root) return 0;\n // int sum = root->val + countNodeValue(root->left) + countNodeValue(root->right);\n // int nodes = 1 + countNode(root->left) + countNode(root->right);\n // int avg = floor(sum / nodes);\n // if (avg == root->val) return 1 + averageOfSubtree(root->left) + averageOfSubtree(root->right);\n // return averageOfSubtree(root->left) + averageOfSubtree(root->right);\n NLR(root);\n return count;\n }\n};\n\n``` | 3 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | Detailed Dry Run of DFS on Trees!! 😸 | detailed-dry-run-of-dfs-on-trees-by-yash-xtde | Intuition\n\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nDFS \n\n# Complexity\ | yashaswisingh47 | NORMAL | 2023-11-11T03:32:21.816006+00:00 | 2023-11-11T03:32:21.816035+00:00 | 266 | false | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDFS \n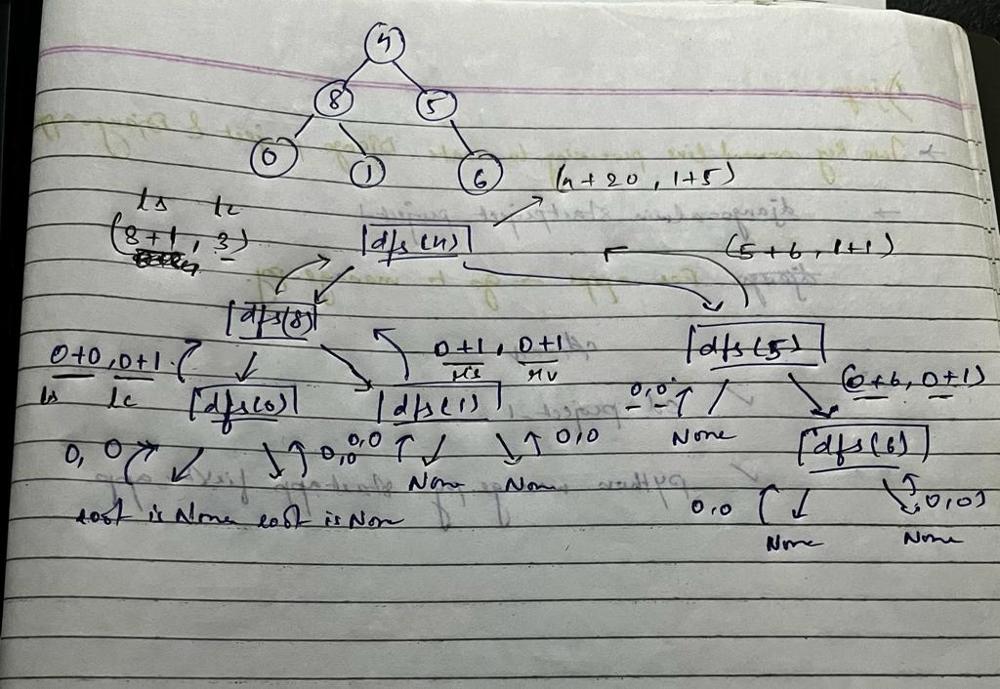\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n count = 0\n def dfs(root):\n nonlocal count\n if not root:\n return 0,0 \n ls , lc = dfs(root.left)\n rs , rc = dfs(root.right)\n if root.val == (root.val + ls + rs) // (lc + rc + 1) : count += 1 \n return root.val + ls + rs , lc + rc + 1\n dfs(root)\n return count\n``` | 3 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'Python3'] | 0 |
count-nodes-equal-to-average-of-subtree | EASY C++ Solution | easy-c-solution-by-2005115-zbgj | \n# Approach\nThe provided code is for a C++ class named Solution, which seems to be related to binary trees. The primary function in this class, averageOfSubtr | 2005115 | NORMAL | 2023-11-02T18:36:26.933885+00:00 | 2023-11-02T18:36:26.933912+00:00 | 1,217 | false | \n# Approach\nThe provided code is for a C++ class named `Solution`, which seems to be related to binary trees. The primary function in this class, `averageOfSubtree`, calculates the number of nodes in a binary tree where the value of the node is equal to the average value of its subtree. Here\'s an approach to understanding how this code works:\n\n1. The `count` function is a recursive helper function that takes a `TreeNode*` (representing the root of a subtree) and a reference to an integer `nodecount` (used to count the nodes meeting the condition).\n\n2. Inside the `count` function, the base case checks if the `root` is `NULL`, which represents an empty subtree. In this case, it returns a pair `{0, 0}`, indicating that the sum and total element count of the subtree are both zero.\n\n3. If the `root` is not `NULL`, it recursively calls the `count` function on the left and right subtrees (`lh` and `rh`), and it calculates the sum of values in the subtree (`sum`) and the total element count in the subtree (`totalele`).\n\n4. It checks if the average of the subtree (calculated as `sum / totalele`) is equal to the value of the current node (`root->val`). If it is, the `nodecount` is incremented.\n\n5. The `count` function returns a pair `{sum, totalele}` representing the sum and total element count for the current subtree.\n\n6. The `averageOfSubtree` function is the entry point. It initializes a variable `cnt` to zero and then calls the `count` function, passing the root of the entire tree and the `cnt` variable as a reference.\n\n7. Finally, the `averageOfSubtree` function returns the value of `cnt`, which contains the count of nodes that meet the condition of having an average value equal to the node\'s value.\n\nThis code recursively traverses the binary tree, counting the nodes that meet the specified condition and returns the count of such nodes.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npair<int,int> count(TreeNode* root, int& nodecount)\n{\n if(root == NULL)\n {\n return {0,0};\n }\n auto lh = count(root->left,nodecount);\n auto rh = count(root->right,nodecount);\n\n int sum = lh.first + rh.first + root->val;\n int totalele = lh.second + rh.second + 1;\n\n if(sum/totalele == root->val)\n {\n nodecount++;\n }\n return {sum,totalele};\n}\npublic:\n int averageOfSubtree(TreeNode* root) {\n int cnt = 0;\n count(root,cnt); \n return cnt;\n }\n};\n``` | 3 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 1 |
count-nodes-equal-to-average-of-subtree | ✅☑[C++/Java/Python/JavaScript] || DFS || EXPLAINED🔥 | cjavapythonjavascript-dfs-explained-by-m-w0jj | PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n1. Public Member Variables:\n\n- int count: This variable is used to keep t | MarkSPhilip31 | NORMAL | 2023-11-02T16:44:58.531546+00:00 | 2023-11-02T16:53:02.404148+00:00 | 69 | false | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n1. **Public Member Variables:**\n\n- `int count`: This variable is used to keep track of the count of subtrees that satisfy the condition.\n1. **postOrder Function:**\n\n - The `postOrder` function takes a pointer to a TreeNode, `root`, as an argument.\n - It follows a post-order traversal approach, which means it first processes the left and right subtrees before processing the current node.\n - The function returns a pair of integers, where the first element of the pair represents the sum of all nodes in the subtree, and the second element represents the count of nodes in the subtree.\n - If the input `root` is `NULL` (i.e., there\'s no node), it returns {0, 0} as the base case.\n - The function recursively calls itself on the left and right subtrees and stores the results in the `left` and `right` variables.\n - It calculates `nodeSum` as the sum of values in the left subtree, right subtree, and the value of the current node.\n - It calculates `nodeCount` as the count of nodes in the left subtree, right subtree, plus 1 for the current node.\n - If the average of the subtree, calculated as `nodeSum / nodeCount`, is equal to the value of the current node (`root->val`), it increments the `count` variable to indicate that this subtree meets the condition.\n - The function then returns the pair {nodeSum, nodeCount}.\n1. **averageOfSubtree Function:**\n\n - The `averageOfSubtree` function takes a TreeNode pointer, `root`, as its argument.\n - It\'s the main entry point for the user, and it will be used to start the process.\n - It calls the `postOrder` function to traverse the binary tree rooted at `root` and count the subtrees that satisfy the condition.\n - Finally, it returns the count of such subtrees as the result.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int count = 0;\n \n pair<int, int> postOrder(TreeNode* root) {\n if (root == NULL) {\n return {0, 0};\n }\n \n // First iterate over left and right subtrees.\n pair<int, int> left = postOrder(root->left);\n pair<int, int> right = postOrder(root->right);\n \n int nodeSum = left.first + right.first + root->val;\n int nodeCount = left.second + right.second + 1;\n\n // Check if the average of the subtree is equal to the node value.\n if (root->val == nodeSum / (nodeCount)) {\n count++;\n }\n \n // Return the sum of nodes and the count in the subtree.\n return {nodeSum, nodeCount};\n }\n \n int averageOfSubtree(TreeNode* root) {\n postOrder(root);\n return count;\n }\n};\n\n\n```\n```C []\n#include <stdlib.h> // For NULL definition\n\nstruct TreeNode {\n int val;\n struct TreeNode* left;\n struct TreeNode* right;\n};\n\nstruct Pair {\n int first;\n int second;\n};\n\nint count = 0;\n\nstruct Pair postOrder(struct TreeNode* root) {\n struct Pair result = {0, 0};\n\n if (root == NULL) {\n return result;\n }\n\n // First iterate over left and right subtrees.\n struct Pair left = postOrder(root->left);\n struct Pair right = postOrder(root->right);\n\n int nodeSum = left.first + right.first + root->val;\n int nodeCount = left.second + right.second + 1;\n\n // Check if the average of the subtree is equal to the node value.\n if (root->val == nodeSum / nodeCount) {\n count++;\n }\n\n // Update the result and return it.\n result.first = nodeSum;\n result.second = nodeCount;\n return result;\n}\n\nint averageOfSubtree(struct TreeNode* root) {\n postOrder(root);\n return count;\n}\n\n\n\n\n```\n```Java []\nclass TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n TreeNode(int x) {\n val = x;\n }\n}\n\npublic class Solution {\n private int count = 0;\n\n public int averageOfSubtree(TreeNode root) {\n postOrder(root);\n return count;\n }\n\n private Pair<Integer, Integer> postOrder(TreeNode root) {\n if (root == null) {\n return new Pair<>(0, 0);\n }\n\n Pair<Integer, Integer> left = postOrder(root.left);\n Pair<Integer, Integer> right = postOrder(root.right);\n\n int nodeSum = left.getKey() + right.getKey() + root.val;\n int nodeCount = left.getValue() + right.getValue() + 1;\n\n if (root.val == nodeSum / nodeCount) {\n count++;\n }\n\n return new Pair<>(nodeSum, nodeCount);\n }\n}\n\n\n\n```\n```python3 []\nclass TreeNode:\n def __init__(self, x):\n self.val = x\n self.left = None\n self.right = None\n\nclass Solution:\n def __init__(self):\n self.count = 0\n\n def postOrder(self, root):\n if root is None:\n return 0, 0\n\n left_sum, left_count = self.postOrder(root.left)\n right_sum, right_count = self.postOrder(root.right)\n\n node_sum = left_sum + right_sum + root.val\n node_count = left_count + right_count + 1\n\n if root.val == node_sum // node_count:\n self.count += 1\n\n return node_sum, node_count\n\n def averageOfSubtree(self, root):\n self.postOrder(root)\n return self.count\n\n\n```\n\n```javascript []\nclass TreeNode {\n constructor(val) {\n this.val = val;\n this.left = this.right = null;\n }\n}\n\nclass Solution {\n constructor() {\n this.count = 0;\n }\n\n postOrder(root) {\n if (root === null) {\n return [0, 0];\n }\n\n const [leftSum, leftCount] = this.postOrder(root.left);\n const [rightSum, rightCount] = this.postOrder(root.right);\n\n const nodeSum = leftSum + rightSum + root.val;\n const nodeCount = leftCount + rightCount + 1;\n\n if (root.val === Math.floor(nodeSum / nodeCount)) {\n this.count++;\n }\n\n return [nodeSum, nodeCount];\n }\n\n averageOfSubtree(root) {\n this.postOrder(root);\n return this.count;\n }\n}\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 3 | 0 | ['Tree', 'Depth-First Search', 'C', 'Binary Tree', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
count-nodes-equal-to-average-of-subtree | EASY TO UNDERSTAND-DFS_APPROACH-with Explanation---BEATS 100% | easy-to-understand-dfs_approach-with-exp-o444 | Intuition\n Describe your first thoughts on how to solve this problem. \nStore the details of the subtrees like number of child nodes and the sum of all the val | lolugucharansai_v | NORMAL | 2023-11-02T15:07:08.870173+00:00 | 2023-11-02T15:28:22.642320+00:00 | 16 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nStore the details of the subtrees like number of child nodes and the sum of all the values child nodes for each node in a hashmap and use dfs to solve the problem.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N) N=number of nodes in the graph.\nfor traversing all the nodes in the graph.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\n int result; // Counter to store the number of nodes meeting the condition.\n\n // Helper function to perform DFS and calculate subtree sum and count.\n pair<int, int> dfs(TreeNode* root, unordered_map<TreeNode*, pair<int, int>>& subtreeInfo) {\n if (!root) {\n return {0, 0};\n }\n \n int sum = root->val;\n int count = 1;\n \n auto leftInfo = dfs(root->left, subtreeInfo);\n auto rightInfo = dfs(root->right, subtreeInfo);\n \n sum += leftInfo.first + rightInfo.first;\n count += leftInfo.second + rightInfo.second;\n \n // Calculate the average for the current subtree rooted at \'root\'.\n int average = sum / count;\n \n // Update the global result if the current node\'s value matches the average.\n if (root->val == average) {\n result++;\n }\n \n // Store the sum and count of the current subtree in the map.\n subtreeInfo[root] = {sum, count};\n \n return {sum, count};\n }\n\npublic:\n int averageOfSubtree(TreeNode* root) {\n result = 0;\n unordered_map<TreeNode*, pair<int, int>> subtreeInfo;\n \n dfs(root, subtreeInfo);\n \n return result;\n }\n};\n\n\n\n```\n\n\n | 3 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | A solution | a-solution-by-nurliaidin-bgkq | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Nurliaidin | NORMAL | 2023-11-02T08:42:28.894066+00:00 | 2023-11-02T08:42:28.894093+00:00 | 102 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n void inOrder(TreeNode* list, int& res) {\n if(list==nullptr) return;\n inOrder(list->left, res);\n int tempSum = 0;\n int counter = 0;\n mergerFun(list, res, tempSum, counter);\n if((list->val) == tempSum/counter) res++;\n\n inOrder(list->right, res);\n }\n void mergerFun(TreeNode* list, int& res, int& tempSum, int& counter) {\n if(list==nullptr) return;\n mergerFun(list->left, res, tempSum, counter);\n \n tempSum += list->val;\n counter++;\n\n mergerFun(list->right, res, tempSum, counter);\n }\n int averageOfSubtree(TreeNode* root) {\n int res = 0;\n inOrder(root, res);\n return res;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | simplest DFS Solution 100% beats🔥 | simplest-dfs-solution-100-beats-by-rajku-8e4k | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rajkushwaha809 | NORMAL | 2023-08-14T18:33:21.004216+00:00 | 2023-08-14T18:33:21.004238+00:00 | 436 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Pair{\n int getKey;\n int getValue;\n public Pair(int a,int b){\n this.getKey=a;\n this.getValue=b;\n }\n}\nclass Solution {\n int count;\n public int averageOfSubtree(TreeNode root) {\n solve(root);\n return count;\n }\n public Pair solve(TreeNode root){\n if(root==null) {\n Pair p = new Pair(0,0);\n return p;\n }\n Pair left1 = solve(root.left);\n Pair right1 = solve(root.right);\n int n= left1.getValue+right1.getValue+1;\n int sum=root.val+left1.getKey+right1.getKey;\n int avg = sum/n;\n if(avg==root.val) count++;\n return new Pair(sum,n);\n }\n}\n``` | 3 | 0 | ['Depth-First Search', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | C++ || DFS ✅ || Easiest Approach 🔥|| No extra computation💡 | c-dfs-easiest-approach-no-extra-computat-8jaj | \nIf you learn/found something new please upvote \uD83D\uDC4D\n\n\n---\n# Code\n\nclass Solution {\n int dfs(TreeNode* root, int &sum, int &count){\n | UjjwalAgrawal | NORMAL | 2023-01-04T11:14:25.707108+00:00 | 2023-01-04T11:14:25.707149+00:00 | 559 | false | ```\nIf you learn/found something new please upvote \uD83D\uDC4D\n```\n\n---\n# Code\n```\nclass Solution {\n int dfs(TreeNode* root, int &sum, int &count){\n if(root == NULL){\n sum = 0, count = 0;\n return 0;\n }\n\n int sum1 = 0, count1 = 0, sum2 = 0, count2 = 0;\n int ans1 = dfs(root->left, sum1, count1);\n int ans2 = dfs(root->right, sum2, count2);\n\n int ans = ans1+ans2;\n sum = sum1+sum2+root->val;\n count = count1+count2+1;\n int avg = (sum/(double)count);\n\n if(avg == root->val)\n ans++;\n\n return ans;\n }\npublic:\n int averageOfSubtree(TreeNode* root) {\n int sum, count;\n\n return dfs(root, sum, count);\n }\n};\n``` | 3 | 0 | ['Depth-First Search', 'Binary Tree', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | Java | 1ms | Beats 99% runtime| Recursive Approach | java-1ms-beats-99-runtime-recursive-appr-skn6 | Intuition\n Describe your first thoughts on how to solve this problem. \nIn general, average of values = (sum of all values / total no of values).\nIn order to | anjali_asolkar | NORMAL | 2022-10-11T08:06:32.376961+00:00 | 2022-10-11T08:09:31.462678+00:00 | 584 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn general, average of values = (sum of all values / total no of values).\nIn order to find the average of subtree for a certain TreeNode, we need to find the sum of all nodes in its left subtree, sum of all nodes in its right subtree, and the total number of nodes in both left and right subtree. This information will be enough to check the condition for the given node.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe create a function that returns an array with 2 integers in it.\nint[ ] arr = {`sum of all nodes in subtree`, `number of nodes in subtree`}\nFor every TreeNode we also check the condition whether the value of the node is equal to the average of the values in its subtree. If the condition is true, we increment the `ans` variable, which was initialised to 0.\n\n# Code\n```\nclass Solution {\n int ans = 0;\n\n public int averageOfSubtree(TreeNode root) {\n subtreeSum(root);\n return ans;\n }\n\n // function to calculate sum of all nodes in subtree\n private int[] subtreeSum(TreeNode root){\n // base condition\n if(root == null)\n return new int[]{0, 0};\n\n // for leaf nodes\n if(root.left == null && root.right == null){ \n ans++;\n return new int[]{root.val, 1};\n }\n\n int[] leftSum = subtreeSum(root.left);\n int[] rightSum = subtreeSum(root.right);\n if((leftSum[0] + rightSum[0] + root.val) / (leftSum[1] + rightSum[1] + 1) == root.val)\n ans++;\n\n return new int[] {(leftSum[0] + rightSum[0] + root.val), (leftSum[1] + rightSum[1] + 1)};\n }\n}\n``` | 3 | 0 | ['Depth-First Search', 'Recursion', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | C++ || O(n) || Easy and fast | c-on-easy-and-fast-by-ayesha1112-3uo6 | \n\n\nclass Solution {\n\npublic:\n\n int ans =0;\n\t\n pair solve(TreeNode root){\n\t\n if(!root) return {0,0};\n\t\t\n auto lh = solve(roo | ayesha1112 | NORMAL | 2022-07-16T04:51:50.629589+00:00 | 2022-07-16T04:52:58.355451+00:00 | 81 | false | \n\n\nclass Solution {\n\npublic:\n\n int ans =0;\n\t\n pair<int,int> solve(TreeNode* root){\n\t\n if(!root) return {0,0};\n\t\t\n auto lh = solve(root->left);\n auto rh = solve(root->right);\n \n int sum = lh.first + rh.first + root->val;\n int n = lh.second + rh.second + 1;\n \n if(sum / n == root->val)ans++;\n \n return {sum,n};\n }\n int averageOfSubtree(TreeNode* root) {\n solve(root);\n return ans;\n }\n}; | 3 | 0 | [] | 0 |
count-nodes-equal-to-average-of-subtree | PostOrder | DFS | Python | postorder-dfs-python-by-hamzaissa14-9juv | \nclass Solution(object):\n def averageOfSubtree(self, root):\n self.count = 0\n def dfs(root):\n if root is None: return 0, 0 \n | HamzaIssa14 | NORMAL | 2022-06-03T11:52:44.186534+00:00 | 2022-06-03T11:52:44.186565+00:00 | 258 | false | ```\nclass Solution(object):\n def averageOfSubtree(self, root):\n self.count = 0\n def dfs(root):\n if root is None: return 0, 0 \n \n leftSum, leftCount = dfs(root.left)\n rightSum, rightCount = dfs(root.right)\n \n current_sum = root.val + leftSum + rightSum\n current_count = 1 + leftCount + rightCount\n \n if root.val == current_sum/current_count:\n self.count += 1\n return current_sum, current_count\n dfs(root)\n return self.count\n \n``` | 3 | 0 | ['Depth-First Search', 'Python'] | 2 |
count-nodes-equal-to-average-of-subtree | javascript DFS post-order recursive solution and BFS iterative solution | javascript-dfs-post-order-recursive-solu-g4n4 | Here I would like to share the DFS approach first, BFS approach (not so elegant but intuitive and can be considered as brute force) will follow after. Please up | leet-do-it | NORMAL | 2022-05-08T07:17:50.073691+00:00 | 2022-05-08T07:17:50.073716+00:00 | 258 | false | Here I would like to share the DFS approach first, BFS approach (*not so elegant but intuitive and can be considered as brute force*) will follow after. Please upvote if it is helpful :)\nThe idea is to traverse through the tree and do something at the node (via a ```traverse(node)``` function + checking the average of the subtree). Hence carrying out a post-order depth-first traversal seems to be logically here (as we have to traverse all before comparing the average).\nHowever, we need to specifying the output of the recursive function, as we need to use the sum of all nodes in the subtree (left and right each) as well as the nodes count, we have to return it for further usage. Finally using closures concept, we can put this ```traverse(node)``` function inside our main function and set ```count``` to track whenever a node (and its subtree) satisfy the required condition.\nBelow is the implementation of DFS approach.\n```\nvar averageOfSubtree = function(root) {\n let count = 0;\n \n function traverse(node) {\n if (node === null) {\n return [0, 0];\n }\n\n let [sumLeft, countLeft] = traverse(node.left);\n let [sumRight, countRight] = traverse(node.right);\n\n if (Math.floor((sumLeft + sumRight + node.val) / (countLeft + countRight + 1)) === node.val) {\n count++;\n }\n\n return [sumLeft + sumRight + node.val, countLeft + countRight + 1];\n }\n \n traverse(root);\n \n return count;\n};\n```\n\nFor BFS, it is intuitive that we want to traverse through the tree, going to all nodes level by level, at each node, we will determine if it is a ```valid``` node satisfying the required condition. \nHence, we can use BFS two times, one is to just traverse the tree, and the other is to traverse the subtree of the node being traversed and checking the condition.\nBelow is the BFS approach implementation. This algorithm is not optimal but it offers another perspective and fun view for dealing with trees :)\n```\nvar averageOfSubtree = function(root) {\n let count = 0;\n\t\n let queue = [];\n if (root === null) return 0;\n queue.push(root);\n while (queue.length) {\n let node = queue.shift();\n if (isValid(node)) {\n count++;\n }\n if (node.left !== null) {\n queue.push(node.left);\n }\n if (node.right !== null) {\n queue.push(node.right);\n }\n }\n return count;\n};\n\nvar isValid = function(node) {\n let sum = 0;\n let count = 0;\n\t\n\tlet queue = [];\n if (node === null) return false;\n queue.push(node);\n \n while (queue.length) {\n let node = queue.shift();\n sum += node.val;\n count++;\n if (node.left !== null) {\n queue.push(node.left);\n }\n if (node.right !== null) {\n queue.push(node.right);\n }\n }\n if (Math.floor(sum / count) === node.val) return true;\n return false;\n}\n``` | 3 | 0 | ['Depth-First Search', 'Breadth-First Search', 'JavaScript'] | 1 |
count-nodes-equal-to-average-of-subtree | Python | DFS | No Global Variable | python-dfs-no-global-variable-by-avuvos-47jn | for each node, we want his left and right subtree sum, number of nodes in that subtree, and number of "good" nodes in that subtree. once we have that informatio | Avuvos | NORMAL | 2022-05-08T06:31:25.378653+00:00 | 2022-05-08T06:31:25.378689+00:00 | 220 | false | for each node, we want his left and right subtree sum, number of nodes in that subtree, and number of "good" nodes in that subtree. once we have that information, we can calculate the result for the root and simply return it.\nour result is the sum of good nodes on left, good nodes on right, and +1 if the current node is also a good node.\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfSubtree(self, root: Optional[TreeNode]) -> int:\n def dfs(node): \n if not node:\n return 0, 0, 0\n \n #give me sum, count and num of good nodes in the subtree\n ls, lc, rl = dfs(node.left) \n rs, rc, rr = dfs(node.right)\n \n res = 0\n if (ls + rs + node.val) // (lc + rc + 1) == node.val:\n res += 1\n\t\t\t\t\n return ls + rs + node.val, lc + rc + 1, res + rl + rr\n return dfs(root)[2]\n``` | 3 | 0 | ['Depth-First Search', 'Python'] | 1 |
count-nodes-equal-to-average-of-subtree | c++ solution using pair O(N) time | c-solution-using-pair-on-time-by-dilipsu-hnbj | \nclass Solution {\npublic:\n pair<int,int>find(TreeNode*root,int&sum)\n {\n if(root==NULL)\n {\n //first sum of subtree\n | dilipsuthar17 | NORMAL | 2022-05-08T04:02:41.512870+00:00 | 2022-05-08T16:04:49.074496+00:00 | 330 | false | ```\nclass Solution {\npublic:\n pair<int,int>find(TreeNode*root,int&sum)\n {\n if(root==NULL)\n {\n //first sum of subtree\n // second size of subtree\n return {0,0};\n }\n auto left=find(root->left,sum);\n auto right=find(root->right,sum);\n int sum_of_subtree=root->val+left.first+right.first;\n int size_of_subtree=1+left.second+right.second;\n if((sum_of_subtree)/(size_of_subtree)==root->val)\n {\n sum++;\n }\n return {sum_of_subtree,size_of_subtree};\n }\n int averageOfSubtree(TreeNode* root) \n {\n int sum=0;\n find(root,sum);\n return sum;\n }\n};\n``` | 3 | 0 | ['C', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | 💢☠💫Easiest👾Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅C#✅💥🔥💫Explained☠💥🔥 Beats 100 | easiestfaster-lesser-cpython3javacpython-dcry | Intuition\n\n\n\n\n\n\n Describe your first thoughts on how to solve this problem. \njavascript []\n//JavaScript Code\n/**\n * Definition for a binary tree node | Edwards310 | NORMAL | 2024-08-24T17:24:05.331003+00:00 | 2024-08-24T17:24:05.331024+00:00 | 106 | false | # Intuition\n\n\n\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n```javascript []\n//JavaScript Code\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n */\n/**\n * @param {TreeNode} root\n * @return {number}\n */\n/*\nclass Pair{\n constructor(son, count){\n this.son = son;\n this.count = count;\n }\n}\nvar res = 0\ndfs = (root) =>{\n if(root === undefined)\n return new Pair(0, 0)\n const l = dfs(root.left)\n const r = dfs(root.right)\n \n let sum = root.val + l.son + r.son\n let height = 1 + l.count + r.count\n \n if(Math.floor(sum / height) === root.val)\n res++\n \n return new Pair(sum, height)\n}\n*/\nvar averageOfSubtree = function(root) {\n function traverse(node) {\n if (!node) \n return {count: 0, sum: 0, result: 0};\n\n let left = traverse(node.left);\n let right = traverse(node.right);\n\n\n const curr = {count: 1 + left.count + right.count, sum: node.val + left.sum + right.sum, result: left.result + right.result};\n\n if (Math.floor(curr.sum / curr.count) === node.val)\n curr.result = (curr.result || 0) + 1;\n \n return curr;\n }\n\n const {result} = traverse(root);\n return result;\n};\n```\n```C++ []\n//C++ Code\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),\n * right(right) {}\n * };\n */\nclass Solution {\n int cnt = 0;\n int sum;\n\nprivate:\n int sumOfNodes(TreeNode* root) {\n if (!root)\n return 0;\n\n sum += root->val;\n sumOfNodes(root->left);\n sumOfNodes(root->right);\n\n return sum;\n }\n int heightOfNodes(TreeNode* root) {\n if (!root)\n return 0;\n int l = heightOfNodes(root->left);\n int r = heightOfNodes(root->right);\n return l + r + 1;\n }\n\npublic:\n int averageOfSubtree(TreeNode* root) {\n if (!root)\n return 0;\n sum = 0;\n int s = sumOfNodes(root);\n int h = heightOfNodes(root);\n if ((sum / h) == root->val)\n ++cnt;\n \n averageOfSubtree(root->left);\n averageOfSubtree(root->right);\n\n //cout << s << endl;\n //cout << height << endl;\n return cnt;\n }\n};\n```\n```Python3 []\n#Python3 Code\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def averageOfSubtree(self, root: TreeNode) -> int:\n ans = 0\n def helper(node, sun, height):\n nonlocal ans\n if not node:\n return (0, 0)\n \n Left = helper(node.left , sun, height)\n Right = helper(node.right, sun, height)\n \n sun = Left[0] + Right[0] + node.val\n height = 1 + Left[1] + Right[1]\n \n if sun // height == node.val:\n ans += 1\n return (sun, height)\n \n helper(root, 0, 0)\n return ans\n```\n```Java []\n//Java Code\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n int cnt = 0;\n private int sumOfNodes(TreeNode root){\n if(root == null)\n return 0;\n return root.val + sumOfNodes(root.left) + sumOfNodes(root.right);\n }\n \n private int heightOfNodes(TreeNode root){\n if(root == null)\n return 0;\n \n return 1 + heightOfNodes(root.left) + heightOfNodes(root.right);\n }\n public int averageOfSubtree(TreeNode root) {\n if(root == null)\n return 0;\n\n int s = sumOfNodes(root);\n int h = heightOfNodes(root);\n \n if(s / h == root.val)\n cnt++;\n \n averageOfSubtree(root.left);\n averageOfSubtree(root.right);\n \n return cnt;\n }\n}\n```\n```C []\n//C Code\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * struct TreeNode *left;\n * struct TreeNode *right;\n * };\n */\n\ntypedef struct Pair{\n int son;\n int count;\n}pair;\n\npair* init(int son, int count){\n pair* p = (pair*)malloc(sizeof(pair));\n p->son = son;\n p->count = count;\n return p;\n}\n\npair* dfs(struct TreeNode* root, int* cnt){\n if(!root){\n return init(0, 0);\n }\n \n pair* Left = dfs(root->left, cnt);\n pair* Right = dfs(root->right, cnt);\n \n int sum = root->val + Left->son + Right->son;\n int height = 1 + Left->count + Right->count;\n \n if(root->val == sum / height)\n (*cnt)++;\n \n return init(sum, height);\n}\n\nint averageOfSubtree(struct TreeNode* root) {\n int cnt = 0;\n dfs(root, &cnt);\n return cnt;\n}\n```\n```Python []\n#Python Code\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution(object):\n def averageOfSubtree(self, root):\n """\n :type root: TreeNode\n :rtype: int\n """\n # Helper function for traversal\n def traverse(root, count):\n \n # Base Case\n if not root: return [0,0]\n \n # Traverse left and get the total sum and count of nodes\n leftSum, leftCount = traverse(root.left, count)\n \n # Traverse right\n rightSum, rightCount = traverse(root.right, count)\n \n # Check the condition\n if (leftSum + root.val + rightSum) // (leftCount + 1 + rightCount) == root.val: count[0] += 1\n \n # Return the data for current subtree back\n return [leftSum + root.val + rightSum, leftCount + 1 + rightCount]\n \n \n # To keep track of the count of nodes\n count = [0]\n \n # Call the helper function\n traverse(root, count)\n \n # Return the count of nodes\n return count[0]\n \n```\n```C# []\n//C# Code\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public int val;\n * public TreeNode left;\n * public TreeNode right;\n * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\npublic class Solution {\n public int count = 0;\n\n public (int sum, int count) SumSub(TreeNode root) {\n if (root == null) \n return (0, 0);\n\n var left = SumSub(root.left);\n var right = SumSub(root.right);\n\n int sum = root.val + left.sum + right.sum;\n int totalCount = 1 + left.count + right.count;\n\n if (root.val == sum / totalCount)\n count++;\n return (sum, totalCount);\n }\n\n public int AverageOfSubtree(TreeNode root) {\n SumSub(root);\n return count;\n }\n}\n```\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N) --> C Code\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N) --> C Code\n# Code\n\n | 2 | 0 | ['Tree', 'Depth-First Search', 'C', 'Binary Tree', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 1 |
count-nodes-equal-to-average-of-subtree | Simple Python DFS Solution | simple-python-dfs-solution-by-will_lynas-aqoq | Intuition\nThe problem involves finding and counting the number of subtrees in a binary tree where the average value of the subtree is equal to the value of the | will_lynas | NORMAL | 2023-12-06T10:43:33.248056+00:00 | 2024-01-20T14:30:05.362811+00:00 | 83 | false | # Intuition\nThe problem involves finding and counting the number of subtrees in a binary tree where the average value of the subtree is equal to the value of the root of that subtree.\n\n# Approach\nThe approach taken here is a recursive one. The function `helper` is a recursive function that takes a node as input and returns a tuple `(count, total)`. The `count` represents the number of nodes in the subtree rooted at the given node, and `total` represents the sum of values of all nodes in the subtree.\n\nThe main function initializes a counter `self.count` to 0 and then calls the `helper` function on the root of the tree. The `helper` function is responsible for traversing the tree recursively and updating the count whenever it finds a subtree with the desired property.\n\nThe code efficiently counts the number of subtrees with the specified property by recursively calculating the count and total for each subtree in a bottom-up manner. The use of a tuple `(count, total)` allows the function to propagate necessary information up the recursive call stack efficiently.\n\n# Complexity\n- Time complexity: $$O(n)$$, where n is the number of nodes in the tree. Each node is visited once.\n- Space complexity: $$O(h)$$, where h is the height of the tree. The space complexity is determined by the depth of the recursion stack. In the worst case, for a skewed tree, it could be $$O(n)$$. In a balanced tree, it would be $$O(\\log n)$$.\n\n# Code\n```python\nclass Solution(object):\n def averageOfSubtree(self, root):\n self.count = 0\n \n def helper(node):\n if not node:\n return (0, 0)\n \n left_count, left_total = helper(node.left)\n right_count, right_total = helper(node.right)\n \n count = 1 + left_count + right_count\n total = node.val + left_total + right_total\n \n if node.val == total // count:\n self.count += 1\n \n return (count, total)\n \n helper(root)\n return self.count\n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Recursion', 'Binary Tree', 'Python'] | 0 |
count-nodes-equal-to-average-of-subtree | Beats 100.00%of users with Java || Simple Java Solution || DFS | beats-10000of-users-with-java-simple-jav-qf9q | Approach\n Describe your approach to solving the problem. \nSimply visit each the nodes from bottom to top, get a helper funstion to save and return the number | gyzhao16 | NORMAL | 2023-11-03T11:39:39.704312+00:00 | 2023-11-03T11:39:39.704336+00:00 | 433 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nSimply visit each the nodes from bottom to top, get a helper funstion to save and return the number of nodes and sum of nodes of each subtree, then compare the average with current node val to count the result.\nCan use an int array or Pair as the return type of the helper function.\n\n# Complexity\n- Time complexity: $$O(n)$$ as we visit each node exactly once.\n\n- Space complexity: $$O(n)$$ as $$O(1)$$ space is needed for each node.\n\n# Code\n```\nclass Solution {\n int res = 0;\n\n public int averageOfSubtree(TreeNode root) {\n traverse(root);\n return res;\n }\n\n private int[] traverse(TreeNode root) {\n if (root == null) {\n return null;\n }\n int[] left = traverse(root.left);\n int[] right = traverse(root.right);\n\n int count = 1;\n int sum = root.val;\n if (left != null) {\n count += left[0];\n sum += left[1];\n }\n if (right != null) {\n count += right[0];\n sum += right[1];\n }\n res += root.val == (sum / count) ? 1 : 0;\n return new int[] {count, sum};\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Java | O(n) time | Beats 100% | java-on-time-beats-100-by-nishant7372-bsvs | java []\nclass Solution {\n int ans;\n public int averageOfSubtree(TreeNode root) {\n ans=0;\n traverse(root);\n return ans;\n }\n | nishant7372 | NORMAL | 2023-11-03T02:36:58.204165+00:00 | 2023-11-03T02:37:46.857028+00:00 | 342 | false | ``` java []\nclass Solution {\n int ans;\n public int averageOfSubtree(TreeNode root) {\n ans=0;\n traverse(root);\n return ans;\n }\n \n private int[] traverse(TreeNode root)\n {\n if(root==null)\n return new int[]{0,0};\n int[] left = traverse(root.left);\n int[] right = traverse(root.right);\n int sum = left[0]+right[0]+root.val;\n int cnt = left[1]+right[1]+1;\n if(sum/cnt==root.val){\n ans++;\n }\n return new int[]{sum,cnt};\n }\n}\n``` | 2 | 0 | ['Tree', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Easy Recursive Approach Tackling Modes | ☑️☑️☑️☑️ | easy-recursive-approach-tackling-modes-b-olo5 | Intuition\n\n\n\nUsing Two Helping fucntion one for traversing each node and another for traversing the subtree of each node.\n\n# Approach\nHere Using array in | shivanigam | NORMAL | 2023-11-02T20:19:23.289230+00:00 | 2023-11-02T20:19:23.289255+00:00 | 475 | false | # Intuition\n\n\n\n*Using Two Helping fucntion one for traversing each node and another for traversing the subtree of each node.*\n\n# Approach\nHere Using array instead of integers because they remain instinct \n\n# Complexity\n- Time complexity:\n**O(N)**\n\n- Space complexity:\n**O(N)**\n\n# Code\n```\nclass Solution {\n public int averageOfSubtree(TreeNode root) {\nint count[]={0};\n fn1(root,count);\n return count[0];\n }\n public static void fn1(TreeNode root,int count[]){\n int Arr[]={0,0};\nif(root==null )\nreturn ;\n fn2(root,Arr);\n if((Arr[1]!=0)&&(Arr[0]/Arr[1]==root.val))\n count[0]++;\n fn1(root.left,count);\n fn1(root.right,count);\n }\n public static void fn2(TreeNode root,int Arr[]){\n if(root==null)\n return ;\n Arr[0]=Arr[0]+root.val;\n Arr[1]++;\n \n fn2(root.left,Arr);\n fn2(root.right,Arr); \n }\n}\n\n``` | 2 | 0 | ['Binary Search Tree', 'Recursion', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Simple java Solution (Post Order Traversal) beats 100% in time. | simple-java-solution-post-order-traversa-ow1b | Intuition\nThis is a problem in which we need to find the average at every node. when you think about it what are the things which we need to compute the averag | harsha0770 | NORMAL | 2023-11-02T19:26:19.750121+00:00 | 2023-11-02T19:26:19.750141+00:00 | 126 | false | # Intuition\nThis is a problem in which we need to find the average at every node. when you think about it what are the things which we need to compute the average-> the sum and the total number of elements involved.\nso you have to solve two sub problems which are to find the sum at each node and the number nodes in the given subtree.\n\n# Approach\nwe follow the approch of dividing the bigger problems into smaller chuncks. As we have discussed in the intution we need to solve both the problems. \nwhy dont we solve the two problems at once and also carry forward the results we got so far while doing this.\nSo we consider the left subtree and the right subtree and then consolidate the results which you got from both of them and create a result for the current subtree. this process goes on and on and on... until we reach the main root. then we go back to the main function and return the final answer.\n\n# Complexity\n- Time complexity:\n$$O(n)$$ as we visit each node once. where n is the number of nodes.\n\n- Space complexity:\n$$O(h)$$ this is due to the call stack space. where h is the height of the tree. \n\n# Code\n```\nclass Solution {\n //return array is going to be of size 3\n public int[] helper(TreeNode root){\n if(root==null){\n return new int[3];\n }\n int[] leftRes = helper(root.left);\n int[] rightRes = helper(root.right);\n\n int totalSum = leftRes[0] + rightRes[0] + root.val;\n int totalCount = leftRes[1] + rightRes[1] + 1;\n int currentAverage = totalSum / totalCount;\n int currentResult = currentAverage == root.val?leftRes[2] + rightRes[2] + 1 : leftRes[2] + rightRes[2];\n\n return new int[]{totalSum, totalCount, currentResult};\n }\n public int averageOfSubtree(TreeNode root) {\n int[] res = helper(root);\n return res[2];\n }\n}\n```\n\nplease let me know if there are any room for improvement or if there is any error with the complexities.\nThank you for reading. Happy coding :) | 2 | 0 | ['Java'] | 0 |
count-nodes-equal-to-average-of-subtree | Easiest Approach || C++ || 4ms | easiest-approach-c-4ms-by-tiwarivishnu42-do0v | Intuition\n Describe your first thoughts on how to solve this problem. \nThe Problem is straightforward so we can think of an algorithm by which we can know sum | tiwarivishnu426 | NORMAL | 2023-11-02T17:55:41.600012+00:00 | 2023-11-02T17:56:04.429915+00:00 | 370 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe Problem is straightforward so we can think of an algorithm by which we can know sum of subtree and no. of nodes for every subtree of the given Tree. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n-> We will use post order travesal to traverse the tree and find sum for every subtree.\n-> We will make use of refernce variable so that we can know no. of nodes present in every subtree at each level.\n> We will backtrack and apply codition to get answer .\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic: int ans =0 ;\nint help(TreeNode* root,int &n){\n if(root==NULL){return 0 ;}\n int x =0 ,y =0 ,n1=0,n2=0;\n x = help(root->left,n1) ;\n y = help(root->right,n2) ;\n n+=(n1+n2+1) ;\n if((x+y+root->val)/n == root->val){ans++; }\n // cout<<n<<" "<<"*"<<root->val<<" " ;\n return root->val + x + y;\n}\n int averageOfSubtree(TreeNode* root) {\n ans =0 ; int n =0 ;\n int k = help(root,n) ;\n return ans ;\n\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
count-nodes-equal-to-average-of-subtree | Beats 100% || EASY C++ SOLUTION using recursion | beats-100-easy-c-solution-using-recursio-ood9 | Intuition\n Describe your first thoughts on how to solve this problem. \n \n# Approach\n Describe your approach to solving the problem. \nUse recursion \n# Comp | vardhman_23 | NORMAL | 2023-11-02T17:30:15.726505+00:00 | 2023-11-02T17:30:15.726527+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n \n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse recursion \n# Complexity\n- Time complexity:\n- O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(height of tree)\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\n pair<int,int> solve(TreeNode* root,int& count){\n if(root==NULL){\n return {0,0};\n }\n pair<int,int> left=solve(root->left,count);\n pair<int,int> right=solve(root->right,count);\n int sum= root->val + left.first + right.first;\n int curr_count= 1+ left.second + right.second;\n if(sum / curr_count==root->val){\n count++;\n }\n return {sum,curr_count};\n }\npublic:\n int averageOfSubtree(TreeNode* root) {\n int result=0;\n solve(root,result);\n return result;\n }\n};\n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | My C Solution | 100% | my-c-solution-100-by-ssseanlin-jouv | Code\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * struct TreeNode *left;\n * struct TreeNode *right;\n * };\ | ssseanlin | NORMAL | 2023-11-02T14:08:34.004684+00:00 | 2023-11-02T14:08:34.004715+00:00 | 37 | false | # Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * struct TreeNode *left;\n * struct TreeNode *right;\n * };\n */\nstruct data{\n int tot;\n int cnt;\n};\ntypedef struct data data;\n\ndata postorder(struct TreeNode* root, int* pCnter){\n data rslt;\n rslt.tot = 0;\n rslt.cnt = 0;\n if(!root) return rslt;\n if(root->left){\n data leftData = postorder(root->left,pCnter);\n rslt.tot += leftData.tot;\n rslt.cnt += leftData.cnt;\n }\n if(root->right){\n data rightData = postorder(root->right,pCnter);\n rslt.tot += rightData.tot;\n rslt.cnt += rightData.cnt;\n }\n rslt.tot += root->val;\n rslt.cnt++;\n if(rslt.tot/rslt.cnt == root->val) ++*pCnter;\n return rslt;\n}\n\nint averageOfSubtree(struct TreeNode* root){\n int cnter = 0;\n data rslt = postorder(root,&cnter);\n return cnter;\n}\n``` | 2 | 0 | ['Depth-First Search', 'Recursion', 'C', 'Binary Tree'] | 0 |
count-nodes-equal-to-average-of-subtree | easy and user friendly approach 100% beat | easy-and-user-friendly-approach-100-beat-qr4g | Intuition\n Describe your first thoughts on how to solve this problem. \n\nstep-1 we need to find root.left total sum and root right total sum and root left hei | somaycoder | NORMAL | 2023-11-02T13:47:19.387416+00:00 | 2023-11-02T13:47:19.387485+00:00 | 15 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nstep-1 we need to find root.left total sum and root right total sum and root left height and root right height then simply check if satisfied the given conditon means increment count value other go to the next recursive call\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nstep-1 create a pair function one part will solve sum for left and right and other part solve the height of left and right \nstep-2 recursive call for left part and right part \nstep-3 calculate total sum for left using lh value\nstep-4 calculate total sum for right using rh value\nstep-5 compare thses values and if the condition will satisfied means increment count value \nstep-6 final step return count\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n pair<int,int>f(TreeNode* root,int &cnt){\n if(root == NULL){\n return {0,0};\n }\n auto lh = f(root->left,cnt);\n auto rh = f(root->right,cnt);\n int sum = lh.first+rh.first+root->val;\n int ele = lh.second+rh.second+1;\n if(sum/ele == root->val){\n cnt++;\n }\n return {sum,ele};\n }\n int averageOfSubtree(TreeNode* root) {\n int cnt = 0;\n f(root,cnt);\n return cnt;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | Beats 100%||c++ solution||easy | beats-100c-solutioneasy-by-nitesh-singh-ll3l | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Nitesh-singh | NORMAL | 2023-11-02T08:53:33.722254+00:00 | 2023-11-02T08:53:33.722284+00:00 | 151 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int res = 0;\n\n pair<int,int> porder(TreeNode* &root,int sum,int count)\n {\n if(root == 0) return {0,0};\n\n auto l = porder(root->left,sum,count);\n auto r = porder(root->right,sum,count);\n\n sum = l.first + root->val + r.first;\n count = l.second + 1 + r.second;\n\n if(sum / count == root->val) res++;\n return {sum,count};\n }\n\n int averageOfSubtree(TreeNode* root) {\n porder(root,0,0);\n return res;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
count-nodes-equal-to-average-of-subtree | Clean Code | beat 100% O(n) Solution | clean-code-beat-100-on-solution-by-cs_ii-3g7g | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | cs_iitian | NORMAL | 2023-11-02T08:49:45.496547+00:00 | 2023-11-02T08:52:19.660696+00:00 | 72 | false | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n\n public int averageOfSubtree(TreeNode root) {\n return helper(root)[2];\n }\n\n public int[] helper(TreeNode root) {\n if(root == null) return new int[] {0, 0, 0};\n\n int[] left = helper(root.left);\n int[] right = helper(root.right);\n \n int sum = left[0] + right[0] + root.val;\n int count = left[1] + right[1] + 1;\n \n return new int[] {sum, count, left[2] + right[2] + (sum/count == root.val ? 1 : 0)};\n }\n}\n``` | 2 | 0 | ['Python', 'C++', 'Java', 'Python3'] | 1 |
count-nodes-equal-to-average-of-subtree | Easiest Java Code with Neat Explaination , Beats 100%. | easiest-java-code-with-neat-explaination-38ya | Intuition\n Describe your first thoughts on how to solve this problem. \n DFS\n\n# Approach\n Describe your approach to solving the problem. \n DFS\nThi | Shashank_008 | NORMAL | 2023-11-02T06:06:52.444410+00:00 | 2023-11-02T06:06:52.444433+00:00 | 211 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n DFS\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n DFS\n*This problem is pretty simple , it wants you to calculate the sum of each subtrees and check if their sums Average is equal to root Node.\nWe can easily calculate the sum of subtrees using DFS (Recursion) , but the important thing is to find the number of nodes , so instead of calculating both of them separately i introduced a class called " Pair " , this class stores the data in each subtrees and the number of nodes in each subtree. By having all these information i think it\'s damn easy to calculate the Nodes Equal to Average of Subtree.\nI Hope this helps , an upvote would mean so much to me :)*\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n```\nclass Solution {\n static int count;\n static class Pair{\n int root_val;\n int cnt;\n Pair(int root_val,int cnt){\n this.root_val=root_val;\n this.cnt=cnt;\n }\n }\n public static Pair calc(TreeNode root){\n if(root==null) return new Pair(0,0);\n Pair left=calc(root.left);\n Pair right=calc(root.right);\n int tot_sum=left.root_val+right.root_val+root.val;\n int tot_nodes=left.cnt+right.cnt+1;\n if(tot_sum/tot_nodes==root.val) count++;\n return new Pair(left.root_val+right.root_val+root.val,left.cnt+right.cnt+1);\n }\n public int averageOfSubtree(TreeNode root) {\n count=0;\n calc(root);\n int temp=count;\n count=0;\n return temp;\n }\n}\n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Recursion', 'Binary Tree', 'Java'] | 1 |
count-nodes-equal-to-average-of-subtree | ✅Easy C++ Code || DFS🚀 || Recursion 🔥 | easy-c-code-dfs-recursion-by-riolog-l931 | \nclass Solution {\nint pairs = 0;\nprivate:\n void helpmeValid(TreeNode* root, int &sum ,int &count)\n {\n if (root == NULL) return ;\n T | RIOLOG | NORMAL | 2023-11-02T04:15:26.651612+00:00 | 2023-11-02T04:15:36.418689+00:00 | 7 | false | ```\nclass Solution {\nint pairs = 0;\nprivate:\n void helpmeValid(TreeNode* root, int &sum ,int &count)\n {\n if (root == NULL) return ;\n TreeNode* node = root;\n \n sum = sum + node->val;\n count += 1;\n\n helpmeValid(node->left, sum, count);\n helpmeValid(node->right, sum , count);\n }\n void helpmePairs(TreeNode* root)\n {\n if (root == NULL) return;\n int sum = 0;\n int count = 0;\n \n helpmeValid(root, sum , count);\n if (root->val == sum / count) pairs += 1;\n \n helpmePairs(root->left); \n helpmePairs(root->right);\n }\npublic:\n int averageOfSubtree(TreeNode* root)\n {\n helpmePairs(root);\n return pairs;\n }\n};\n``` | 2 | 0 | ['Math', 'Depth-First Search', 'Recursion', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | Beats 95% simple post order traversal solution c++ | beats-95-simple-post-order-traversal-sol-2wyz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | AdityaxBhatt | NORMAL | 2023-11-02T02:35:41.372061+00:00 | 2023-11-02T02:35:41.372084+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n) stack space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n \n int dfs(TreeNode* r,int *c,int *cc){\n if(r!=NULL){\n int k=(*cc);\n (*cc)++;\n \n \n int a=dfs(r->left,c,cc);\n int b=dfs(r->right,c,cc);\n if((a+b+r->val)/((*cc)-k)==r->val){\n (*c)++;\n }\n return a+b+r->val;\n\n\n }\n return 0;\n \n }\n int averageOfSubtree(TreeNode* r) {\n int cc=0;\n int c=0;\n dfs(r,&c,&cc);\n return c;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | ✅✅Beats 100.00%of users with Java, C++, Python.✅✅ | beats-10000of-users-with-java-c-python-b-1rg6 | java []\nclass Solution {\n private int ans;\n\n public int averageOfSubtree(TreeNode root) {\n ans = 0;\n calculateAverage(root);\n | otabek_kholmirzaev | NORMAL | 2023-11-02T02:22:17.304010+00:00 | 2023-11-02T04:27:33.485744+00:00 | 31 | false | ```java []\nclass Solution {\n private int ans;\n\n public int averageOfSubtree(TreeNode root) {\n ans = 0;\n calculateAverage(root);\n return ans;\n }\n\n private int[] calculateAverage(TreeNode node) {\n if (node == null)\n return new int[]{ 0, 0 }; \n\n int[] leftSubtree = calculateAverage(node.left);\n int[] rightSubtree = calculateAverage(node.right);\n\n int sum = node.val + leftSubtree[0] + rightSubtree[0];\n int count = 1 + leftSubtree[1] + rightSubtree[1];\n\n if (sum / count == node.val) \n ans++;\n\n return new int[]{ sum, count };\n }\n}\n```\n```python []\nclass Solution:\n def __init__(self):\n self.ans = 0\n\n def averageOfSubtree(self, root):\n self.ans = 0\n self.calculate_average(root)\n return self.ans\n\n def calculate_average(self, node):\n if not node:\n return (0, 0)\n\n left_subtree = self.calculate_average(node.left)\n right_subtree = self.calculate_average(node.right)\n\n sum = node.val + left_subtree[0] + right_subtree[0]\n count = 1 + left_subtree[1] + right_subtree[1]\n\n if sum // count == node.val:\n self.ans += 1\n\n return (sum, count)\n```\n```cpp []\nclass Solution {\nprivate:\n int ans;\n\npublic:\n int averageOfSubtree(TreeNode* root) {\n ans = 0;\n calculateAverage(root);\n return ans;\n }\n\n pair<int, int> calculateAverage(TreeNode* node) {\n if (node == nullptr) \n return {0, 0};\n\n pair<int, int> leftSubtree = calculateAverage(node->left);\n pair<int, int> rightSubtree = calculateAverage(node->right);\n\n int sum = node->val + leftSubtree.first + rightSubtree.first;\n int count = 1 + leftSubtree.second + rightSubtree.second;\n \n if (sum / count == node->val)\n ans++;\n\n return {sum, count};\n }\n};\n```\n```csharp []\npublic class Solution {\n private int ans;\n\n public int AverageOfSubtree(TreeNode root) {\n ans = 0;\n CalculateAverage(root);\n return ans;\n }\n\n private (int, int) CalculateAverage(TreeNode node) {\n if (node == null) return (0, 0);\n var leftSubtree = CalculateAverage(node.left);\n var rightSubtree = CalculateAverage(node.right);\n int sum = node.val + leftSubtree.Item1 + rightSubtree.Item1;\n int count = 1 + leftSubtree.Item2 + rightSubtree.Item2;\n if (sum / count == node.val) ans++;\n return (sum, count);\n }\n}\n```\n# Intuition\nTo solve this problem, you can use a recursive function to traverse the binary tree and calculate the average for each subtree. Here\'s a solution for this problem:\n\n# Approach\nThe **AverageOfSubtree** function initializes the **ans** variable to store the result and then calls the **CalculateAverage** function to traverse the tree and calculate the average for each subtree.\n\nThe **CalculateAverage** function is a recursive function that calculates the sum and count of nodes in the subtree rooted at the current node. It then checks whether the current node\'s value is equal to the average of the subtree and increments the **ans** variable accordingly.\n\nThe **ans** variable keeps track of the number of nodes where the value is equal to the average of the values in its subtree.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is **O(N)**, where N is the number of nodes in the binary tree. This is because the algorithm visits each node in the tree once, and the work done at each node is constant.\n\n- Space complexity:\nThe space complexity is **O(H)**, where H is the **height** of the binary tree. In the worst case, where the tree is completely unbalanced and degenerates into a linked list, the height H is equal to the number of nodes N, resulting in **O(N)** space complexity due to the recursive function calls on the call stack.\n\n\n\n | 2 | 0 | ['C#'] | 1 |
count-nodes-equal-to-average-of-subtree | [C++] Depth-First Search with Sum and Count | c-depth-first-search-with-sum-and-count-t3cy8 | Intuition\n Describe your first thoughts on how to solve this problem. \n- Use Depth-First Search\n- Pass the information (sum and count) of each child node to | pepe-the-frog | NORMAL | 2023-11-02T01:39:38.166152+00:00 | 2023-11-02T01:39:38.166172+00:00 | 424 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Use Depth-First Search\n- Pass the information (sum and count) of each child node to its parent node\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- For each node, get the information for children (DFS)\n- Calculate the sum and count of the current node\n- Update the result if matched\n\n# Complexity\n- Time complexity: $$O(n)$$, where `n` is the number of nodes in the binary tree\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(h)$$, where `h` is the height of the binary tree\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n // time/space: O(n)/O(h)\n int averageOfSubtree(TreeNode* root) {\n int result = 0;\n helper(root, result);\n return result;\n }\nprivate:\n pair<int, int> helper(TreeNode* node, int& result) {\n // terminate\n if (node == NULL) return {0, 0};\n\n // recursive\n auto [sum_left, count_left] = helper(node->left, result);\n auto [sum_right, count_right] = helper(node->right, result);\n\n // calculate the sum and count of the current node\n int sum = node->val + sum_left + sum_right;\n int count = 1 + count_left + count_right;\n\n // update the result if matched\n if (node->val == (sum / count)) result++;\n\n return {sum, count};\n }\n};\n``` | 2 | 1 | ['Tree', 'Depth-First Search', 'Recursion', 'Binary Tree', 'C++'] | 1 |
count-nodes-equal-to-average-of-subtree | 🔥POTD 🔥 02/11/23 🔥C++ ✅✅ Binary Tree 💯💯 ⬆⬆⬆ | potd-021123-c-binary-tree-by-sandipan103-1vit | \n# Code\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode( | sandipan103 | NORMAL | 2023-11-02T01:16:21.886161+00:00 | 2023-11-02T01:16:21.886193+00:00 | 3 | false | \n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n pair<int, pair<int, int>> solve(TreeNode* root) {\n if(!root) return {0, {0, 0}};\n pair<int, pair<int, int>> lAns = solve(root->left), rAns = solve(root->right);\n int totalSum = lAns.second.first + rAns.second.first + root->val;\n int totalNode = lAns.second.second + rAns.second.second + 1;\n int ans = lAns.first + rAns.first;\n if(totalSum / totalNode == root->val) ans++;\n return {ans, {totalSum , totalNode}};\n }\n\n int averageOfSubtree(TreeNode* root) {\n return solve(root).first;\n }\n};\n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Recursion', 'Binary Tree', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | 🗓️ Daily LeetCoding Challenge November, Day 2 | daily-leetcoding-challenge-november-day-7hktx | This problem is the Daily LeetCoding Challenge for November, Day 2. Feel free to share anything related to this problem here! You can ask questions, discuss wha | leetcode | OFFICIAL | 2023-11-02T00:00:04.999126+00:00 | 2023-11-02T00:00:04.999158+00:00 | 1,921 | false | This problem is the Daily LeetCoding Challenge for November, Day 2.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/count-nodes-equal-to-average-of-subtree/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 1 approach in the official solution</summary>
**Approach 1:** Depth First Search (DFS)
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br> | 2 | 0 | [] | 22 |
count-nodes-equal-to-average-of-subtree | Simple solution Using Pair<int,int> | simple-solution-using-pairintint-by-abhi-k5db | Code\n\nclass Solution {\npublic:\nint x=0;\n pair<int,int> count(TreeNode* root){\n if(root==NULL){return {0,0};}\n pair<int,int> lans=count(r | abhijeet5000kumar | NORMAL | 2023-09-08T08:32:13.375246+00:00 | 2023-09-08T08:32:13.375263+00:00 | 111 | false | # Code\n```\nclass Solution {\npublic:\nint x=0;\n pair<int,int> count(TreeNode* root){\n if(root==NULL){return {0,0};}\n pair<int,int> lans=count(root->left);\n pair<int,int> rans=count(root->right);\n pair<int,int> ans;\n ans.first=lans.first+rans.first+root->val;\n ans.second=lans.second+rans.second+1;\n if(ans.first/ans.second==root->val){x++;}\n return ans;\n }\n\n int averageOfSubtree(TreeNode* root) {\n count(root);\n return x;\n }\n};\n``` | 2 | 0 | ['Tree', 'Binary Tree', 'C++'] | 1 |
count-nodes-equal-to-average-of-subtree | Simple C++ Solution | simple-c-solution-by-amitkiet_2024-aee6 | \nclass Solution {\nprivate:\n int noOfNodes(TreeNode* node){\n if(node == NULL){\n return 0;\n }\n \n return 1 + noOf | amitkiet_2024 | NORMAL | 2023-08-01T06:59:46.157387+00:00 | 2023-08-01T06:59:46.157412+00:00 | 251 | false | ```\nclass Solution {\nprivate:\n int noOfNodes(TreeNode* node){\n if(node == NULL){\n return 0;\n }\n \n return 1 + noOfNodes(node -> left) + noOfNodes(node -> right);\n }\n \n int pathsum(TreeNode* node){\n if(node == NULL){\n return 0;\n }\n int lh = pathsum(node -> left);\n int rh = pathsum(node -> right);\n \n return (node -> val) + (lh+rh);\n }\n \n void solve(TreeNode* &node, int &sum){\n \n if(node == NULL) return;\n \n if(pathsum(node) / noOfNodes(node) == (node -> val)){\n cout<<node -> val << " ";\n sum++;\n }\n \n solve(node -> left, sum);\n solve(node -> right, sum);\n \n }\npublic:\n int averageOfSubtree(TreeNode* root) {\n \n int sum = 0;\n solve(root, sum);\n return sum;\n \n }\n};\n\n``` | 2 | 0 | ['Recursion'] | 0 |
count-nodes-equal-to-average-of-subtree | Two Solutions | Brute➡️Optimal - DFS | ✅Clean & Simple CPP Code✅ | two-solutions-bruteoptimal-dfs-clean-sim-f85o | 😊 ~ 𝙒𝙞𝙩𝙝 ❤️ 𝙗𝙮 𝙃𝙞𝙧𝙚𝙣IntuitionHello There Its Easy! Take A Look At The Code And Comments Within It You'll Get It.
Still Have Doubts! Feel Free To Comment, I'll D | hirenjoshi | NORMAL | 2023-07-14T19:42:11.260469+00:00 | 2025-03-01T06:00:13.269277+00:00 | 183 | false | 😊 ~ 𝙒𝙞𝙩𝙝 ❤️ 𝙗𝙮 𝙃𝙞𝙧𝙚𝙣
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
***Hello There Its Easy! Take A Look At The Code And Comments Within It You'll Get It.
Still Have Doubts! Feel Free To Comment, I'll Definitely Reply!***
# Approach
<!-- Describe your approach to solving the problem. -->
***All Accepted :
-> Using DFS (Brute Force)
-> Using DFS (Time Optimized)***
***Note: I'll add comments soon!***
# Complexity
- ***Time complexity: Mentioned with the code***
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- ***Space complexity: Mentioned with the code***
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
**Approach 1 : Using DFS (Brute Force)**
```
class BruteDFS {
int result = 0;
void getSumAndCount(TreeNode* rootNode, int& subtreeSum, int& totalNodes) {
if(rootNode) {
totalNodes++;
subtreeSum += rootNode->val;
getSumAndCount(rootNode->left, subtreeSum, totalNodes);
getSumAndCount(rootNode->right, subtreeSum, totalNodes);
}
}
public:
// O(N*N) & O(H)
int averageOfSubtree(TreeNode* rootNode) {
if(!rootNode)
return 0;
int subtreeSum = 0, totalNodes = 0;
getSumAndCount(rootNode, subtreeSum, totalNodes);
result += (subtreeSum / totalNodes == rootNode->val);
averageOfSubtree(rootNode->left);
averageOfSubtree(rootNode->right);
return result;
}
};
```
**Approach 2 : Using DFS (Time Optimized)**
```
class BottomUpDFS {
public:
// O(N) & O(H)
int averageOfSubtree(TreeNode* rootNode) {
int result = 0;
calcAvgAndUpdateResult(rootNode, result);
return result;
}
private:
std::pair<int, int> calcAvgAndUpdateResult(TreeNode* rootNode, int& result) {
if(!rootNode)
return {0, 0};
auto [sumLeftSubtree, nodesLeft] = calcAvgAndUpdateResult(rootNode->left, result);
auto [sumRightSubtree, nodesRight] = calcAvgAndUpdateResult(rootNode->right, result);
int sumCurrSubtree = sumLeftSubtree + sumRightSubtree + rootNode->val;
int totalNodes = nodesLeft + nodesRight + 1;
result += (sumCurrSubtree / totalNodes == rootNode->val);
return {sumCurrSubtree, totalNodes};
}
};
```
𝗨𝗣𝗩𝗢𝗧𝗘 𝗜𝗙 𝗬𝗢𝗨 𝗟𝗜𝗞𝗘 𝗧𝗛𝗘 𝗦𝗢𝗟𝗨𝗧𝗜𝗢𝗡 👍 | 2 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 2 |
count-nodes-equal-to-average-of-subtree | Simple recursion with memory saving by passing a pair | simple-recursion-with-memory-saving-by-p-j58w | \n# Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n) \n\n# | TechTinkerer | NORMAL | 2023-07-02T13:22:53.074687+00:00 | 2023-07-02T13:23:27.826141+00:00 | 10 | false | \n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n \n pair<int,int> solve(TreeNode * root,int &count){\n if(root==NULL)\n return {0,0};\n \n auto left=solve(root->left,count);\n auto right=solve(root->right,count);\n \n if(((root->val+left.first+right.first)/(1+left.second+right.second))==root->val)\n count+=1;\n \n return {root->val+left.first+right.first,1+left.second+right.second};\n \n }\n int averageOfSubtree(TreeNode* root) {\n \n int count=0;\n \n solve(root,count);\n \n return count;\n \n }\n};\n``` | 2 | 0 | ['Recursion', 'Binary Tree', 'C++'] | 0 |
count-nodes-equal-to-average-of-subtree | C++ solution || O(N) || 100.00% faster and easy | c-solution-on-10000-faster-and-easy-by-h-5x99 | Approach\nRecursion using pair\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n\nclass Solution {\npublic:\n // Used pair to | hello_world121 | NORMAL | 2023-05-31T02:58:22.943805+00:00 | 2023-05-31T02:58:22.943866+00:00 | 7 | false | # Approach\nRecursion using pair\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\npublic:\n // Used pair to store sum and count for every subtree\n typedef pair<int, int> pr;\n pr find(TreeNode* root, int &res) {\n if(!root) return {0, 0};\n pr left = find(root->left, res);\n pr right = find(root->right, res);\n\n int sum = root->val + left.first + right.first;\n int count = left.second+right.second+1; \n if(root->val == sum / count) res++;\n return {sum, count};\n }\n int averageOfSubtree(TreeNode* root) {\n int res = 0; \n find(root, res);\n return res; \n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | Brute force approach, java | brute-force-approach-java-by-adi-07-7vxj | \n\n# Code\n\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * Tre | Adi-07 | NORMAL | 2023-04-20T07:58:32.319865+00:00 | 2023-04-20T07:58:32.319900+00:00 | 347 | false | \n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n int sum=0;\n int count =0;\n int level=0;\n public int averageOfSubtree(TreeNode root) {\n average(root);\n return level;\n }\n public void preorder(TreeNode root)\n {\n if(root==null)\n return ;\n\n sum += root.val;\n count++;\n\n\n preorder(root.left);\n preorder(root.right);\n }\n public void average(TreeNode root)\n {\n if(root==null)\n return;\n\n preorder(root);\n if(sum/count==root.val)\n level++;\n\n sum=0;\n count=0;\n\n average(root.left);\n average(root.right);\n }\n}\n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Java'] | 0 |
count-nodes-equal-to-average-of-subtree | c++||RECURSION | crecursion-by-vishwassrivastava007-caas | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vishwassrivastava007 | NORMAL | 2023-02-12T20:26:54.160210+00:00 | 2023-02-12T20:26:54.160248+00:00 | 402 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int ans=0;\n pair<int,int> solve(TreeNode *root)\n {\n if(root==NULL)\n {\n pair<int,int>p;\n \n return {0,0};\n }\n \n pair<int,int> left=solve(root->left);\n pair<int,int> right=solve(root->right);\n \n int s=left.first+right.first+root->val;\n int a=left.second+right.second+1;\n \n if(round(s/a)==root->val)\n {\n ans++;\n }\n \n pair<int,int>p1;\n \n \n return {s,a};\n }\n int averageOfSubtree(TreeNode* root) \n {\n solve(root);\n \n return ans;\n }\n\n \n};\n``` | 2 | 0 | ['C++'] | 0 |
count-nodes-equal-to-average-of-subtree | easy-soln | well-explained | easy-soln-well-explained-by-nandini-gang-exs0 | Please upvote if you found helpful\uD83D\uDE0A\n#ReviseWithArsh #6Companies30Days Challenge 2023\nChellenge Company 3: Adobe\nQ9. Count nodes equal to average | nandini-gangrade | NORMAL | 2023-01-17T11:40:17.148242+00:00 | 2023-01-17T11:40:17.148273+00:00 | 422 | false | # Please upvote if you found helpful\uD83D\uDE0A\n***#ReviseWithArsh #6Companies30Days Challenge 2023\nChellenge Company 3: Adobe\nQ9. Count nodes equal to average of Subtree***\n\n# Complexity\n- Time complexity:O(n)\n- Space complexity:O(n)\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\n int dfs(TreeNode* root, int &sum, int &count){\n // Base case: if root is null, return 0 for both sum and count\n if(root==NULL){\n sum=0,count=0;\n return 0;\n }\n // Initialize variables to store sum and count of left and right subtrees\n int sum1 = 0, count1 = 0, sum2 = 0, count2 = 0;\n int ans1 = dfs(root->left, sum1, count1); // Recursively calculate sum and count of left subtree\n int ans2 = dfs(root->right, sum2, count2); // Recursively calculate sum and count of right subtree\n\n int ans = ans1+ans2; // Initialize ans as the total number of subtrees with equal average\n sum = sum1+sum2+root->val; // Calculate sum of current subtree\n count = count1+count2+1; // Calculate count of current subtree\n int avg = (sum/(double)count); // Calculate average of current subtree\n\n // Check if current root\'s value is equal to the average of the subtree\n if(avg == root->val)\n ans++;\n\n return ans;\n}\n\n public:\n int averageOfSubtree(TreeNode* root) {\n int sum, count;\n return dfs(root, sum, count);\n }\n}; \n``` | 2 | 0 | ['C++'] | 1 |
count-nodes-equal-to-average-of-subtree | Easy Approach using Pair & DFS || O(n) | easy-approach-using-pair-dfs-on-by-shris-a79j | \n\n# Code\n\n\nclass Solution {\npublic:\n int ans=0;\n\n pair<int,int>solve(TreeNode*root){\n if(root==NULL)return {0,0};\n\n pair<int,int | Shristha | NORMAL | 2023-01-15T08:54:22.564414+00:00 | 2023-01-15T08:54:22.564445+00:00 | 392 | false | \n\n# Code\n```\n\nclass Solution {\npublic:\n int ans=0;\n\n pair<int,int>solve(TreeNode*root){\n if(root==NULL)return {0,0};\n\n pair<int,int>left=solve(root->left);\n int left_sum=left.first;\n int left_size=left.second;\n\n pair<int,int>right=solve(root->right);\n int right_sum=right.first;\n int right_size=right.second;\n\n int sum=left_sum+right_sum+root->val;\n if(sum/(1+left_size+right_size)==root->val){\n ans++;\n }\n return {sum,(1+left_size+right_size)};\n\n\n }\n int averageOfSubtree(TreeNode* root) {\n solve(root);\n return ans;\n \n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.