question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
properties-graph | BEATS 100% VERY EASY SOLUTION IN C++ | beats-100-very-easy-solution-in-c-by-spi-0l0e | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | spidee180 | NORMAL | 2025-03-24T09:39:15.331173+00:00 | 2025-03-24T09:39:15.331173+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int intersect(vector<int>a ,vector<int>b)
{
vector<int>hash1(101 , 0);
vector<int>hash2(101 , 0);
for(auto x: a)
{
if(!hash1[x]) hash1[x] = 1;
}
for(auto x: b)
{
if(!hash2[x]) hash2[x] = 1;
}
int ans = 0;
for(int i = 0; i<= 100; i++)
{
ans += hash1[i] & hash2[i];
}
return ans;
}
void dfs(vector<vector<int>>& adj , vector<int>&seen , int a)
{
seen[a] = 1;
for(auto x: adj[a])
{
if(!seen[x])
{
dfs(adj , seen , x);
}
}
}
int numberOfComponents(vector<vector<int>>& properties, int k) {
int m = properties.size();
int n = properties[0].size();
vector<vector<int>>graph(m);
for(int i = 0; i<m; i++)
{
for(int j = i + 1; j<m; j++ )
{
if(intersect(properties[i] , properties[j]) >= k)
{
graph[i].push_back(j);
graph[j].push_back(i);
}
}
}
int ans = 0;
vector<int>seen(m , 0);
for(int i=0; i<m; i++)
{
if(!seen[i])
{
ans++;
dfs(graph , seen , i);
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
properties-graph | o(n^2 * m ) - DSU but only union under specific conditions | on2-m-dsu-but-only-union-under-specific-41d0w | IntuitionDSU is great for solving connected component questions but we need to modify this one. we only want to union 2 nodes if and only if there are k similar | codescoop | NORMAL | 2025-03-24T07:08:06.688866+00:00 | 2025-03-24T07:08:06.688866+00:00 | 3 | false | # Intuition
DSU is great for solving connected component questions but we need to modify this one. we only want to union 2 nodes if and only if there are k similar numbers between them. so we have to make sure we have that union logic in there otherwise we will union every node.
# Approach
DSU but modified to union only if there are k similarites between 2 unioned nodes.
# Complexity
- Time complexity:
o(n^2 * m)
- Space complexity:
o(n + m) - > o(n)
# Code
```java []
class DSU {
HashMap<Integer,Integer> rank;
HashMap<Integer,Integer> parent;
public DSU (int n ){
rank = new HashMap<>();
parent = new HashMap<>();
for(int i = 0; i < n; i++){
rank.put(i, 1);
parent.put(i, i);
}
}
public int find(int n) {
if (parent.get(n) != n) {
parent.put(n, find(parent.get(n))); // Path compression
}
return parent.get(n);
}
public void union(int a, int b){
int node1 = find(a);
int node2 = find(b);
if(rank.get(node1) > rank.get(node2)){
parent.put(node2, node1);
rank.put(node1, rank.get(node1)+1);
}
else if(rank.get(node1) < rank.get(node2)){
parent.put(node1, node2);
rank.put(node2, rank.get(node2)+1);
}
else{
parent.put(node2, node1);
rank.put(node1, rank.get(node1)+1);
}
}
}
class Solution {
public int numberOfComponents(int[][] properties, int k) {
DSU dsu = new DSU(properties.length);
for(int i = 0; i < properties.length; i++){
Set<Integer> set1 = new HashSet<>();
for(int x = 0 ; x < properties[i].length; x++){
set1.add(properties[i][x]);
}
for(int j = i + 1; j < properties.length; j++){
Set<Integer> set2 = new HashSet<>();
for(int x = 0 ; x < properties[i].length; x++){
set2.add(properties[j][x]);
}
set2.retainAll(set1);
if(set2.size() >=k)
dsu.union(i, j);
}
}
Set<Integer> set = new HashSet<>();
for (int i = 0; i < properties.length; i++) {
set.add(dsu.find(i));
}
return set.size();
}
}
``` | 0 | 0 | ['Java'] | 0 |
properties-graph | [Go] union-find data structure | go-union-find-data-structure-by-ye15-abtp | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | ye15 | NORMAL | 2025-03-24T01:15:29.552920+00:00 | 2025-03-24T01:15:29.552920+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```golang []
func numberOfComponents(properties [][]int, k int) int {
n := len(properties)
ps := []map[int]struct{}{}
for _, p := range properties {
elem := map[int]struct{}{}
for _, x := range p {
elem[x] = struct{}{}
}
ps = append(ps, elem)
}
parent := make([]int, n)
for i := 0; i < n; i++ {
parent[i] = i
}
var find func(p int) int
find = func(p int) int {
if (p != parent[p]) {
parent[p] = find(parent[p])
}
return parent[p]
}
for i := 0; i < n; i++ {
for j := i+1; j < n; j++ {
cnt := 0
for x, _ := range ps[i] {
if _, ok := ps[j][x]; ok {
cnt++
}
}
if cnt >= k {
parent[find(i)] = find(j)
}
}
}
freq := map[int]int{}
for _, x := range parent {
freq[find(x)]++
}
return len(freq)
}
``` | 0 | 0 | ['Go'] | 0 |
properties-graph | SImple Python Solution using Union Find | simple-python-solution-using-union-find-wzfxf | Intuition
Create the edges list first by going through the number properties array as described.
Solve for the nos of connected Components using the Union Find | reddyvignesh00 | NORMAL | 2025-03-24T01:06:05.077969+00:00 | 2025-03-24T01:06:05.077969+00:00 | 6 | false | # Intuition
1. Create the edges list first by going through the number properties array as described.
2. Solve for the nos of connected Components using the Union Find algorithm based on the edge list same as Problem Number:- **323. Number of Connected Components in an Undirected Graph**
# Approach
# Complexity
- Time complexity:
**O(n^2 * m)** For generating the edges. Union Find due to path compression and union by rank omptimzation take O(1) does for n edges.
- Space complexity:
**O(n^2)**
# Code
```python3 []
class Solution:
def numberOfComponents(self, properties: List[List[int]], k: int) -> int:
def intersect(list1, list2, k) -> bool:
list1 = set(list1)
list2 = set(list2)
return len(list1.intersection(list2)) >= k
edges = []
n = len(properties)
R = len(properties)
for r in range(R):
for c in range(r+1, R):
if intersect(properties[r], properties[c], k): edges.append([r, c])
rank = [1 for i in range(n)]
parent = [i for i in range(n)]
def find(n):
while n != parent[n]:
parent[n] = parent[parent[n]]
n = parent[n]
return n
def union(a, b):
p1, p2 = find(a), find(b)
if p1 == p2: return 0
elif rank[p1] > rank[p2]:
rank[p1] += rank[p2]
parent[p2] = p1
else:
rank[p2] += rank[p1]
parent[p1] = p2
return -1
for a, b in edges:
n += union(a, b)
return n
``` | 0 | 0 | ['Python3'] | 0 |
properties-graph | [C++] Union Find. O(n^3). | c-union-find-on3-by-lovebaonvwu-i2fo | null | lovebaonvwu | NORMAL | 2025-03-24T00:53:24.602139+00:00 | 2025-03-24T00:53:24.602139+00:00 | 4 | false |
```cpp []
class DisjointSet {
public:
DisjointSet(int n) : size(n) {
parents.resize(size);
iota(begin(parents), end(parents), 0);
ranks.assign(size, 0);
}
int Find(int x) {
if (parents[x] != x) {
parents[x] = Find(parents[x]);
}
return parents[x];
}
void Union(int x, int y) {
int px = Find(x);
int py = Find(y);
if (px == py) {
return;
}
if (ranks[px] >= ranks[py]) {
parents[py] = px;
++ranks[px];
} else {
parents[px] = py;
++ranks[py];
}
}
int Components() {
int count = 0;
for (int i = 0; i < size; ++i) {
Find(i);
if (parents[i] == i) {
++count;
}
}
return count;
}
private:
vector<int> parents;
vector<int> ranks;
int size;
};
class Solution {
public:
int numberOfComponents(vector<vector<int>>& properties, int k) {
vector<unordered_set<int>> props;
for (auto p : properties) {
props.push_back(unordered_set(begin(p), end(p)));
}
int n = properties.size();
DisjointSet ds(n);
for (int i = 0; i < n; ++i) {
auto si = props[i];
for (int j = i + 1; j < n; ++j) {
auto sj = props[j];
int cnt = 0;
for (auto x : si) {
if (sj.find(x) != sj.end()) {
++cnt;
}
}
if (cnt >= k) {
ds.Union(i, j);
}
}
}
return ds.Components();
}
};
``` | 0 | 0 | ['C++'] | 0 |
properties-graph | Go solution with union-find | go-solution-with-union-find-by-noname987-i66j | IntuitionGiven that we need to find connected components == use union-find techniqueApproachTo make union work we can do:
sort each property and compare them (t | noname987654 | NORMAL | 2025-03-23T23:50:10.513379+00:00 | 2025-03-23T23:50:10.513379+00:00 | 2 | false | # Intuition
Given that we need to find connected components == use union-find technique
# Approach
To make union work we can do:
- sort each property and compare them (this solution) - less memory
- use dictionary per property to effiniently compare - more memory
Use union find algorithm to connect components and in the end find number of distinct
# Complexity
- Time complexity:
O(E)
- Space complexity:
O(n + E) given that we may have edges from all to all
# Code
```golang []
func numberOfComponents(properties [][]int, k int) int {
for i := 0; i < len(properties); i++ {
sort.Slice(properties[i], func(a, b int) bool {
return properties[i][a] < properties[i][b]
})
}
edges := [][]int{}
for i := 0; i < len(properties)-1; i++ {
for j := i+1; j < len(properties); j++ {
if intersect(properties[i], properties[j], k) {
edges = append(edges, []int{i, j})
}
}
}
comp := make([]int, len(properties))
for i := 0; i < len(comp); i++ {
comp[i] = i
}
for i := 0; i < len(edges); i++ {
f, t := edges[i][0], edges[i][1]
c1 := find(comp, f)
merge(comp, t, c1)
// c2 := find(comp, t)
// comp[c1] = c2
}
d := map[int]bool{}
for i := 0; i < len(comp); i++ {
c := find(comp, i)
d[c] = true
}
return len(d)
}
func find(comp []int, n int) int {
if comp[n] != n {
comp[n] = find(comp, comp[n])
}
return comp[n]
}
func merge(comp []int, comp1, comp2 int) {
for comp[comp1] != comp1 {
comp[comp1], comp1 = comp2, comp[comp1]
}
comp[comp1] = comp2
}
func intersect(a, b []int, k int) bool {
i, j := 0, 0
num := 0
for i < len(a) && j < len(b) {
for i + 1 < len(a) && a[i] == a[i+1] {
i += 1
}
for j + 1 < len(b) && b[j] == b[j+1] {
j += 1
}
if a[i] == b[j] {
num += 1
i += 1
j += 1
} else if a[i] < b[j] {
i += 1
} else {
j += 1
}
if num >= k {
return true
}
}
return false
}
``` | 0 | 0 | ['Go'] | 0 |
properties-graph | Union Find + Bit Manipulation. Time O(n^2), space O(n) | union-find-bit-manipulation-time-on2-spa-6ec4 | null | xxxxkav | NORMAL | 2025-03-23T21:27:18.590500+00:00 | 2025-03-23T21:27:18.590500+00:00 | 1 | false | ```
class UnionFind:
def __init__(self, n: int):
self.parent = [*range(n)]
self.rank = [1] * n
def find(self, x: int) -> int:
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x: int, y: int) -> bool:
x, y = self.find(x), self.find(y)
if x == y:
return False
if self.rank[x] < self.rank[y]:
self.parent[x] = y
else:
self.parent[y] = x
if self.rank[x] == self.rank[y]:
self.rank[x] += 1
return True
class Solution:
def numberOfComponents(self, properties: List[List[int]], k: int) -> int:
masks, n = [], len(properties)
for p in properties:
mask = 0
for num in p:
mask |= 1 << num
masks.append(mask)
ans, uf = n, UnionFind(n)
for u in range(n):
for v in range(u):
if (masks[u] & masks[v]).bit_count() >= k:
ans -= uf.union(u, v)
return ans
``` | 0 | 0 | ['Bit Manipulation', 'Union Find', 'Python3'] | 0 |
properties-graph | 3 Solutions | BFS + DFS + DSU | ☑️Path Compression + Rank & Size Method✅ | 🔥Clean CPP Code🔥 | 3-solutions-bfs-dfs-dsu-path-compression-ue0l | 😊 ~ 𝙒𝙞𝙩𝙝 ❤️ 𝙗𝙮 𝙃𝙞𝙧𝙚𝙣IntuitionHi There! Take A Look At The Code You'll Get It.
Still Have Doubts! Feel Free To Comment, I'll Definitely Reply!ApproachAll Accepte | hirenjoshi | NORMAL | 2025-03-23T18:11:47.950411+00:00 | 2025-03-23T18:32:18.152454+00:00 | 9 | false | 😊 ~ 𝙒𝙞𝙩𝙝 ❤️ 𝙗𝙮 𝙃𝙞𝙧𝙚𝙣
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
***Hi There! Take A Look At The Code You'll Get It.
Still Have Doubts! Feel Free To Comment, I'll Definitely Reply!***
# Approach
<!-- Describe your approach to solving the problem. -->
***All Accepted :
-> Using BFS & DFS
-> Using DSU - Union Find (Path Compression + Rank & Size Method)***
# Complexity
- ***Time complexity: Mentioned with the code***
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- ***Space complexity: Mentioned with the code***
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
**Approach 1 : Using BFS & DFS**
```
class CountComponentsUsingBFSOrDFS {
private:
vector<vector<int>> adjList;
void BFS(int node, vector<bool>& visited) {
queue<int> q;
q.push(node);
visited[node] = true;
while(!q.empty()) {
node = q.front(); q.pop();
for(int neighbor : adjList[node]) {
if(!visited[neighbor]) {
visited[neighbor] = true;
q.push(neighbor);
}
}
}
}
void DFS(int node, vector<bool>& visited) {
visited[node] = true;
for(int neighbor : adjList[node])
if(!visited[neighbor])
DFS(neighbor, visited);
}
private:
int intersect(const unordered_set<int>& nums1, const unordered_set<int>& nums2) {
int commonElements = 0;
for(int num : nums1) commonElements += nums2.count(num);
return commonElements;
}
public:
// O(N*M*M) & O(N*M) : Where N = properties.size(), M = properties[i].size().
int numberOfComponents(vector<vector<int>>& properties, int k) {
int n = properties.size();
adjList.resize(n);
// Recreate the properties so that each properties[i] stores unique values
vector<unordered_set<int>> grid(n);
for(int i = 0; i < n; ++i)
for(int num : properties[i])
grid[i].insert(num);
// Construct the graph
for(int i = 0; i < n; ++i)
for(int j = i+1; j < n; ++j)
if(intersect(grid[i], grid[j]) >= k)
adjList[i].push_back(j),
adjList[j].push_back(i);
// Visit all the components, count the result value
vector<bool> visited(n);
int countComponents = 0;
for(int node = 0; node < n; ++node)
if(!visited[node])
DFS(node, visited),
countComponents++;
return countComponents;
}
};
```
**Approach 2 : Using DSU - Union Find (Path Compression + Rank & Size Method)**
```
class CountComponentsUsingDSU {
private:
vector<int> rank, size, parent;
int findRoot(int node) {
if(parent[node] == node)
return node;
return parent[node] = findRoot(parent[node]);
}
void unionBySize(int u, int v) {
int root_u = findRoot(u);
int root_v = findRoot(v);
if(root_u == root_v)
return;
else if(size[root_u] < size[root_v])
parent[root_u] = root_v,
size[root_v] += size[root_u];
else
parent[root_v] = root_u,
size[root_u] += size[root_v];
}
void unionByRank(int u, int v) {
int root_u = findRoot(u);
int root_v = findRoot(v);
if(root_u == root_v)
return;
else if(rank[root_u] < rank[root_v])
parent[root_u] = root_v;
else if(rank[root_v] < rank[root_u])
parent[root_v] = root_u;
else
parent[root_v] = root_u,
rank[root_u]++;
}
private:
int intersect(const unordered_set<int>& nums1, const unordered_set<int>& nums2) {
int commonElements = 0;
for(int num : nums1) commonElements += nums2.count(num);
return commonElements;
}
public:
// O(N*M*M) & O(N*M) : Where N = properties.size(), M = properties[i].size().
int numberOfComponents(vector<vector<int>>& properties, int k) {
int n = properties.size();
// Initialize DSU buffers
rank.resize(n);
size.resize(n, 1);
parent.resize(n, -1);
for(int node = 0; node < n; ++node)
parent[node] = node;
// Recreate the properties so that each properties[i] stores unique values
vector<unordered_set<int>> grid(n);
for(int i = 0; i < n; ++i)
for(int num : properties[i])
grid[i].insert(num);
// Construct the graph edges
vector<vector<int>> edges;
for(int i = 0; i < n; ++i)
for(int j = i+1; j < n; ++j)
if(intersect(grid[i], grid[j]) >= k)
edges.push_back({i, j});
// Hit DSU, build the components
for(auto& edge : edges) {
int u = edge[0];
int v = edge[1];
unionBySize(u, v);
}
// Mark root nodes of each component, count the result value
vector<bool> isRootOfAnyComponent(n);
int countComponents = 0;
for(int node = 0; node < n; ++node)
isRootOfAnyComponent[findRoot(node)] = true,
countComponents += isRootOfAnyComponent[node];
return countComponents;
}
};
```
𝗨𝗣𝗩𝗢𝗧𝗘 𝗜𝗙 𝗬𝗢𝗨 𝗟𝗜𝗞𝗘 𝗧𝗛𝗘 𝗦𝗢𝗟𝗨𝗧𝗜𝗢𝗡 👍 | 0 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Graph', 'Matrix', 'C++'] | 0 |
properties-graph | Easy DSU Approach | easy-dsu-approach-by-22147407-qq44 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | 22147407 | NORMAL | 2025-03-23T17:32:42.857006+00:00 | 2025-03-23T17:32:42.857006+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int>parent,rank;
void init(int n){
parent.resize(n+1);
rank.resize(n+1);
for(int i=0;i<parent.size();i++)parent[i]=i;
}
int find(int u){
if(u==parent[u])return u;
return parent[u]=find(parent[u]);
}
void unionbyrank(int u,int v){
int up=find(u);
int uv=find(v);
parent[uv]=up;
}
bool can(unordered_set<int>&a,unordered_set<int>&b,int k){
int cnt=0;
for(auto i:a){
if(b.find(i)!=b.end())cnt++;
if(cnt==k)return 1;
}return 0;
}
int numberOfComponents(vector<vector<int>>& properties, int k) {
init(properties.size());
vector<unordered_set<int>>st(properties.size());
for(int i=0;i<properties.size();i++){
unordered_set<int>sp;
for(auto j:properties[i])sp.insert(j);
st[i]=sp;
}
for(int i=0;i<properties.size();i++){
for(int j=0;j<i;j++){
if(i==j)continue;
if(can(st[i],st[j],k)){
unionbyrank(i,j);
}
}
}
unordered_set<int>st2;
for(int i=0;i<properties.size();i++){
st2.insert(find(i));
}return st2.size();
}
};
``` | 0 | 0 | ['Union Find', 'Graph', 'Ordered Set', 'C++'] | 0 |
properties-graph | DFS+Map brute force solution | dfsmap-brute-force-solution-by-codewithd-pb0o | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | codewithdubey | NORMAL | 2025-03-23T17:02:31.622397+00:00 | 2025-03-23T17:02:31.622397+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int intersect(vector<int>& vtr1, vector<int>& vtr2) {
unordered_set<int> set1(vtr1.begin(), vtr1.end());
int count = 0;
for (int num : vtr2) {
if (set1.count(num)) {
count++;
set1.erase(num);
}
}
return count;
}
void dfs(int node, map<int, vector<int>>& m, vector<int>& vis) {
vis[node] = 1;
for (auto it : m[node]) {
if (!vis[it]) {
dfs(it, m, vis);
}
}
}
int numberOfComponents(vector<vector<int>>& properties, int k) {
map<int, vector<int>> m;
int n = properties.size();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int val = intersect(properties[i], properties[j]);
if (val >= k) {
m[i].push_back(j);
m[j].push_back(i);
}
}
}
int cnt = 0;
vector<int> vis(n, 0);
for (int i = 0; i < n; i++) {
if (!vis[i]) {
cnt++;
dfs(i, m, vis);
}
}
return cnt;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Fastest (100%) || Short & Concise || Easiest to Understand | fastest-100-short-concise-easiest-to-und-yrt2 | Intuition\nIt\'s like picking the tastiest ramen bowls from a buffet, starting with the yummiest, within a limit, ensuring each bowl adds to your overall satisf | gameboey | NORMAL | 2024-05-09T00:28:04.569649+00:00 | 2024-05-09T16:30:10.644768+00:00 | 26,899 | false | # Intuition\nIt\'s like picking the tastiest ramen bowls from a buffet, starting with the yummiest, within a limit, ensuring each bowl adds to your overall satisfaction!\n\n# Approach\n\nSo, the problem aims to maximize the total happiness gained by selecting the happiest bowls of ramen within the given budget (`k`). It\'s all about enjoying the most happiness while savoring some tasty ramen! Let\'s break down the approach used in the code with Yuji Itadori\'s style:\n\n1. **Sorting the Happiness Bowls**: Just like picking the most delicious ramen bowls, we sort the bowls of happiness in descending order. This way, we can start with the happiest ones first!\n\n2. **Eating the Yummiest Bowls**: With a limited number of bowls we can eat (`k`), we start devouring the yummiest ones! Each time we eat a bowl, we check if it makes us even happier. If it does, we enjoy it; otherwise, we skip it.\n\n3. **Adjusting Happiness Levels**: As we eat the bowls, we also adjust the happiness levels of the remaining bowls. We subtract 1 from their happiness, but only if they were initially positive.\n\n4. **Summing Up the Joy**: After finishing our ramen feast, we sum up all the happiness from the bowls we\'ve eaten. That\'s our total joy!\n\nSo, it\'s all about picking the most happiness-packed bowls within our limit and making sure each bowl we eat adds to our overall joy. Just like enjoying a hearty ramen meal!\n\n\n\n**Dry - Run :**\nLet\'s go through the dry run for the given example:\n\n```\nInput: happiness = [1, 2, 3], k = 2\n```\n\n**Step 1:** Sort the `happiness` array in descending order.\n\n```\nhappiness = [3, 2, 1]\n```\n\n**Step 2:** Initialize variables.\n\n```cpp\ni = 0\nres = 0\n```\n\n**Step 3:** Enter the loop toselect `k` children.\n\n```cpp\nwhile(k--) {\n // k = 2\n happiness[i] = max(happiness[i] - i, 0);\n // happiness[0] = max(3 - 0, 0) = 3\n\n res += happiness[i++];\n // res = 0 + 3 = 3\n // i = 1\n\n // k = 1\n happiness[i] = max(happiness[i] - i, 0);\n // happiness[1] = max(2 - 1, 0) = 1\n\n res += happiness[i++];\n // res = 3 + 1 = 4\n // i = 2\n}\n```\n\nSince `k` is now 0, the loop terminates.\n\n**Step 4:** Return the result.\n\n```cpp\nreturn res; // Returns 4\n```\n\nSo, the maximum sum of happiness values by selecting 2 children is 4, which is achieved by:\n\n1. Selecting the child with the maximum happiness value of 3. The remaining happiness values become `[0, 1]`.\n2. Selecting the child with the happiness value of 1. The remaining happiness value becomes `[0]`.\n\nThe sum of the happiness values of the selected children is 3 + 1 = 4, as mentioned in the explanation.\n\n# Complexity\n- Time complexity: O(nlogn + min(k, n))\n\n- Space complexity: O(1)\n\n# Code\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);\n sort(begin(happiness), end(happiness), greater<int>());\n int i = 0;\n long long res = 0;\n\n while(k--) {\n happiness[i] = max(happiness[i] - i, 0);\n res += happiness[i++];\n }\n\n return res;\n }\n};\n```\n```java []\npublic class Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n long res = 0;\n int n = happiness.length, j = 0;\n\n for (int i = n - 1; i >= n - k; --i) {\n happiness[i] = Math.max(happiness[i] - j++, 0);\n res += happiness[i];\n }\n\n return res;\n }\n}\n```\n```python []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n i = 0\n res = 0\n\n while k > 0:\n happiness[i] = max(happiness[i] - i, 0)\n res += happiness[i]\n i += 1\n k -= 1\n\n return res\n```\n```javascript []\n/**\n * @param {number[]} happiness\n * @param {number} k\n * @return {number}\n */\nvar maximumHappinessSum = function(happiness, k) {\n happiness.sort((a, b) => b - a);\n let i = 0;\n let res = 0;\n\n while (k > 0 && i < happiness.length) {\n happiness[i] = Math.max(happiness[i] - i, 0);\n res += happiness[i];\n i++;\n k--;\n }\n\n return res;\n};\n```\n\n | 112 | 11 | ['Array', 'Greedy', 'Sorting', 'C++', 'Java', 'Python3', 'JavaScript'] | 32 |
maximize-happiness-of-selected-children | 💯Faster✅💯Lesser✅2 Methods🧠Detailed Approach🎯Greedy🔥Heap🔥Python🐍Java☕C++😎 | fasterlesser2-methodsdetailed-approachgr-3sc3 | \uD83D\uDE80 Hi, I\'m Mohammed Raziullah Ansari, and I\'m excited to share 2 ways to solve this question with detailed explanation of each approach:\n\n# \uD83C | Mohammed_Raziullah_Ansari | NORMAL | 2024-05-09T01:11:47.124510+00:00 | 2024-05-09T01:23:32.484038+00:00 | 6,801 | false | # \uD83D\uDE80 Hi, I\'m [Mohammed Raziullah Ansari](https://leetcode.com/Mohammed_Raziullah_Ansari/), and I\'m excited to share 2 ways to solve this question with detailed explanation of each approach:\n\n# \uD83C\uDFAFProblem Explaination: \nYou are given an array `happiness` representing the happiness values of n children standing in a queue, and a positive integer k representing the number of turns you can select children.\n\nIn each turn, you select one child from the queue. When a child is selected, the happiness value of all children who have not been selected decreases by 1, but only if their happiness value is currently positive.\n\nYour task is to maximize the sum of the happiness values of the selected children by strategically choosing which children to select in each turn.\n\n### \uD83D\uDCE5Input:\n- `happiness`: An array of length n representing the happiness values of n children.\n- `k`: A positive integer representing the number of turns you can select children.\n\n### \uD83D\uDCE4Output:\n- Return an integer representing the maximum sum of the happiness values of the selected children.\n\n# \uD83D\uDD0D Methods To Solve This Problem:\nI\'ll be covering two different methods to solve this problem:\n1. Greedy Method\n2. Using Priority Queue\n\n# 1\uFE0F\u20E3 Greedy Method: \n\n### \uD83E\uDDE0Intuition:\nThe objective is to maximize the total happiness sum by selecting children with the highest happiness values. A logical strategy is to prioritize choosing children with the highest happiness values first, considering that the happiness of unselected children decreases over time.\n\nBy selecting children with the highest happiness values initially, we ensure that we capture the maximum happiness before it potentially decreases. This greedy approach aims to maximize short-term happiness gains by locking in the largest happiness scores early on.\n\nTo justify the optimality of this greedy approach, let\'s assume there exists an optimal solution where, for a given turn, the selected child\'s happiness value is not the ith largest in the array. If we swap this selected child with one of the higher happiness values, we would inevitably increase the total happiness sum. Therefore, the greedy approach of selecting the top k happiness scores from the array guarantees the highest possible total happiness sum.\n\nIn summary, adopting a greedy strategy to select the k children with the highest happiness values from the given array maximizes the overall happiness sum, as it captures the most significant happiness gains upfront.\n\n### \uD83D\uDCDADetailed Approach:\n1. **Sort the List in Descending Order:** To efficiently select the children with the highest happiness values, we sort the list of happiness values in descending order.\n\n2. **Initialize Variables:** Initialize `total_happiness_sum` to keep track of the sum of happiness values of the selected children. Initialize `turns` to keep track of the number of turns taken.\n\n3. **Iterate for K Turns:** We iterate for k turns, where in each turn, we:\n - Access the happiness value of the child at index i (where i ranges from 0 to k-1 due to sorting).\n - Decrement the happiness value by the number of turns taken so far. This accounts for the decrement in happiness for all unselected children.\n - Add the adjusted happiness value to `total_happiness_sum`. Ensure that negative happiness values are not considered by taking the maximum of 0 and the computed value.\n - Increment the `turns` variable to prepare for the next iteration.\n\n4. **Return Total Happiness Sum:** After k turns, return the total happiness sum, which represents the maximum sum of happiness values achievable by selecting k children.\n\n<!-- # Complexity\n- \u23F1\uFE0F Time Complexity: `O(n)` where n is the number of pairs in the list.\n -->\n<!-- - \uD83D\uDE80 Space Complexity: `O(n)` for the HashSet. -->\n\n# Code\uD83D\uDC68\uD83C\uDFFB\u200D\uD83D\uDCBB:\n```Python []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n # Sort in descending order\n happiness.sort(reverse=True)\n\n total_happiness_sum = 0\n turns = 0\n\n # Calculate the maximum happiness sum\n for i in range(k):\n # Adjust happiness and ensure it\'s not negative\n total_happiness_sum += max(happiness[i] - turns, 0)\n\n # Increment turns for the next iteration\n turns += 1\n\n return total_happiness_sum\n```\n```Java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n int happinessSize = happiness.length;\n \n // Convert the array to an Integer array for sorting in descending order\n Integer[] happinessArray = new Integer[happinessSize];\n for(int i = 0; i < happinessSize; i++) {\n happinessArray[i] = happiness[i];\n }\n \n Arrays.sort(happinessArray, Collections.reverseOrder());\n\n long totalHappinessSum = 0;\n int turns = 0;\n \n // Calculate the maximum happiness sum\n for(int i = 0; i < k; i++) {\n // Adjust happiness and ensure it\'s not negative\n totalHappinessSum += Math.max(happinessArray[i] - turns, 0); \n\n // Increment turns for the next iteration\n turns++; \n }\n \n return totalHappinessSum;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n // Sort in descending order\n sort(happiness.begin(), happiness.end(), greater<int>());\n \n long long totalHappinessSum = 0;\n int turns = 0;\n \n // Calculate the maximum happiness sum\n for(int i = 0; i < k; i++) {\n // Adjust happiness and ensure it\'s not negative\n totalHappinessSum += max(happiness[i] - turns, 0); \n\n // Increment turns for the next iteration\n turns++; \n }\n \n return totalHappinessSum;\n }\n};\n```\n\n# 2\uFE0F\u20E3 Using Priority Queue:\n### \uD83E\uDDE0Intuition:\nIn our problem, maximizing total happiness relies on selecting the largest available element at each turn. This makes the choice of data structure crucial, and the max heap is particularly well-suited for this purpose. With a max heap, the largest element is always at the top, ensuring efficient access in alignment with our greedy algorithm\'s strategy of selecting the highest happiness value available at each turn.\n\nThe approach begins by constructing a max heap using all values from the happiness array. Then, for each of the k turns, we remove the maximum value from the heap. This ensures that we\'re consistently selecting the child with the highest happiness value at each turn. \n\nAfter removal, we adjust this value by subtracting the number of turns completed so far. This adjustment accounts for the decrease in happiness of the children who haven\'t been selected yet. Finally, we add this adjusted value to our total happiness sum.\n\nBy retaining its greedy nature through selecting the largest happiness values at each step, the utilization of the heap data structure significantly enhances efficiency compared to alternative methods like sorting the happiness array that we did in first approach. \n\n### \uD83D\uDCDADetailed Approach:\n1. **Convert the List to a Max Heap:** To efficiently select the children with the highest happiness values, we can use a max heap. However, Python\'s default heap implementation is a min heap. So, we convert the list into a max heap by inverting the happiness values (multiply each value by -1).\n \n2. **Initialize Variables:** Initialize `total_happiness_sum` to keep track of the sum of happiness values of the selected children. Initialize `turns` to keep track of the number of turns taken.\n\n3. **Iterate for K Turns:** We iterate for k turns, where in each turn, we:\n - Pop the top element from the max heap. Since we inverted the happiness values initially, popping from the heap gives us the child with the highest original happiness value.\n - Decrement the happiness value by the number of turns taken so far. This accounts for the decrement in happiness for all unselected children.\n - Add the happiness value to `total_happiness_sum`. Ensure that negative happiness values are not considered by taking the maximum of 0 and the computed value.\n - Increment the `turns` variable to prepare for the next iteration.\n\n4. **Return Total Happiness Sum:** After k turns, return the total happiness sum, which represents the maximum sum of happiness values achievable by selecting k children.\n\n\n<!-- # Complexity\n- \u23F1\uFE0F Time Complexity: `O(n)` where n is the number of pairs in the list.\n\n- \uD83D\uDE80 Space Complexity: `O(n)` for the two lists. -->\n\n# Code\uD83D\uDC69\uD83C\uDFFB\u200D\uD83D\uDCBB:\n```Python []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n # Convert the list into a max heap by inverting the happiness values \n # Python\'s default heap data structure is a min heap\n max_heap = [-h for h in happiness]\n heapq.heapify(max_heap)\n \n total_happiness_sum = 0\n turns = 0\n\n for i in range(k):\n # Invert again to get the original value\n total_happiness_sum += max(-heapq.heappop(max_heap) - turns, 0)\n\n # Increment turns for the next iteration\n turns += 1\n \n return total_happiness_sum\n```\n```Java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n // Create a max heap using PriorityQueue with a custom comparator\n PriorityQueue<Integer> pq = new PriorityQueue<>(Comparator.reverseOrder());\n\n // Add all elements to the priority queue\n for (int h : happiness) {\n pq.add(h);\n }\n\n long totalHappinessSum = 0;\n int turns = 0;\n\n for (int i = 0; i < k; i++) {\n // Add the current highest value to the total happiness sum and remove it from the max heap \n totalHappinessSum += Math.max(pq.poll() - turns, 0);\n\n // Increment turns for the next iteration\n turns++;\n }\n\n return totalHappinessSum;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n // Max heap by default\n priority_queue<int> pq; \n\n // Push all the happiness values into the priority queue\n for(const auto& h: happiness)\n pq.push(h); \n\n long long totalHappinessSum = 0;\n int turns = 0;\n\n for(int i = 0; i < k; i++) {\n // Add the current highest value to the total happiness sum\n totalHappinessSum += max(pq.top() - turns, 0);\n\n // Remove the highest value after using it\n pq.pop(); \n\n // Increment turns for the next iteration\n turns++; \n }\n\n return totalHappinessSum;\n }\n};\n```\n\n# \uD83D\uDCA1 I invite you to check out [my profile](https://leetcode.com/Mohammed_Raziullah_Ansari/) for detailed explanations and code for each method. Happy coding and learning! \uD83D\uDCDA | 54 | 5 | ['Array', 'Greedy', 'Sorting', 'C++', 'Java', 'Python3'] | 12 |
maximize-happiness-of-selected-children | 👏Beats 97.44% of users with Java🎉|| ⏩Fastest 2 Approaches💯||✅Easy & Well Explained Solution🔥💥 | beats-9744-of-users-with-java-fastest-2-8dknx | Intuition\nGiven an array of happiness levels, decrement elements up to a limit, find the maximum sum of positive happiness values among top \'k\' elements.\n\n | Rutvik_Jasani | NORMAL | 2024-05-09T03:16:34.561027+00:00 | 2024-05-09T03:16:34.561066+00:00 | 4,477 | false | # Intuition\nGiven an array of happiness levels, decrement elements up to a limit, find the maximum sum of positive happiness values among top \'k\' elements.\n\n# I Think This Can Help You(For Proof Click on the Image)\n[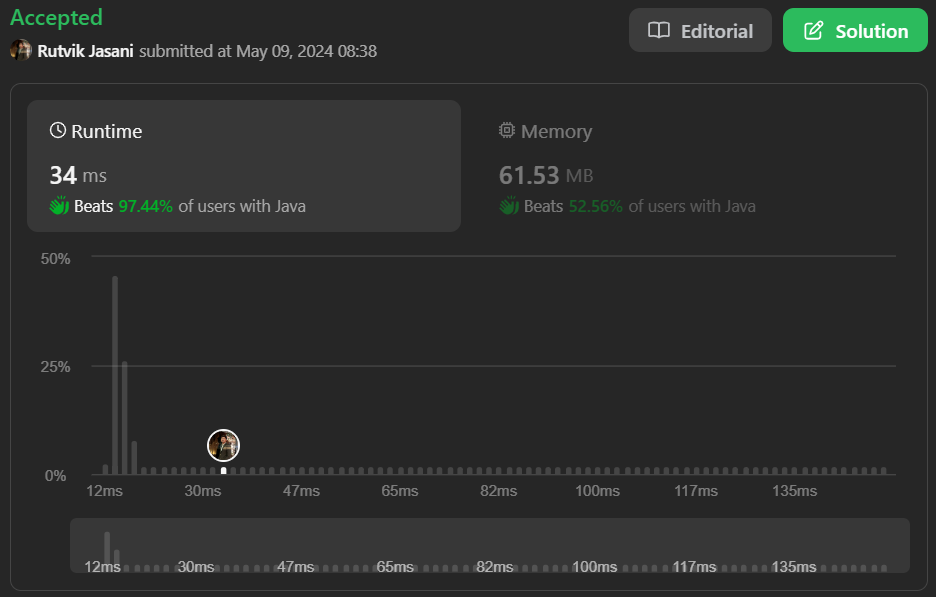](https://leetcode.com/problems/maximize-happiness-of-selected-children/submissions/1253152217/?envType=daily-question&envId=2024-05-09)\n\n\n# Approach\n## Approach 1:\n1. **Sort the Array**: Initially, the array of happiness is sorted in ascending order. This is done to ensure that we start with the highest happiness values.\n\n```java\nArrays.sort(happiness);\n```\n\n2. **Initialize Variables**: \n - `dec`: This variable is used to keep track of the number of decrements made.\n - `max`: This variable stores the maximum sum of happiness.\n - `value`: This variable represents the current value of happiness after decrementing.\n\n```java\nint dec = 0;\nlong max = 0;\nint value = 0;\n```\n\n3. **Iterate through the Sorted Array Backwards**: We iterate through the sorted array from the end towards the beginning, considering the top `k` elements.\n\n```java\nfor (int i = happiness.length - 1; i >= happiness.length - k; i--) {\n // Code block inside loop\n}\n```\n\n4. **Decrement and Calculate Happiness**:\n - `value = happiness[i] - dec;`: Calculate the current happiness value after decrementing it based on the `dec` value.\n - `dec++`: Increment the decrement counter for the next iteration.\n - Check if the decremented value is greater than 0, if yes, add it to the `max` variable.\n\n```java\nvalue = happiness[i] - dec;\ndec++;\nif (value > 0) {\n max += value;\n}\n```\n\n5. **Return the Maximum Sum of Happiness**: Finally, return the calculated maximum sum of happiness.\n\n```java\nreturn max;\n```\n## Approach 2:\n1. **Sort the Array**:\n - Sort the array of happiness in ascending order.\n\n```java\nArrays.sort(happiness);\n```\n\n2. **Initialize Variables**:\n - `dec`: Counter to keep track of the number of decrements.\n - `n`: Length of the happiness array.\n - `ans`: Variable to store the maximum sum of happiness.\n\n```java\nint dec = 0, n = happiness.length;\nlong ans = 0;\n```\n\n3. **Iterate through the Sorted Array Backwards**:\n - Iterate through the sorted array starting from the end and consider the top `k` elements.\n\n```java\nfor (int i = n - 1; i >= n - k; i--) {\n // Code block inside loop\n}\n```\n\n4. **Decrement and Calculate Happiness**:\n - Calculate the current happiness value after decrementing it based on the `dec` value.\n - Add the decremented happiness to `ans` only if it\'s greater than 0.\n\n```java\nans += Math.max(0, happiness[i] - dec);\ndec++;\n```\n\n5. **Return the Maximum Sum of Happiness**:\n - Return the calculated maximum sum of happiness stored in `ans`.\n\n```java\nreturn ans;\n```\n\n# Complexity\n- Time complexity:\nApproach 1: O(n log n)\nApproach 2: O(n log n)\n\n- Space complexity:\nApproach 1: O(1)\nApproach 2: O(1)\n\n# Code\n## Approach 1:\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n int dec = 0;\n long max=0;\n int value=0;\n for(int i=happiness.length-1;i>=happiness.length-k;i--){\n value = happiness[i]-dec;\n dec++;\n if(value>0)\n {\n max += value;\n }\n }\n return max;\n }\n}\n```\n## Approach 2:\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n int dec = 0,n=happiness.length;\n long ans=0;\n for(int i=n-1;i>=n-k;i--){\n ans += Math.max(0,happiness[i]-dec);\n dec++;\n }\n return ans;\n }\n}\n```\n\n\n | 39 | 2 | ['Array', 'Greedy', 'Sorting', 'Java'] | 11 |
maximize-happiness-of-selected-children | ✅ 100% | ✅ Super Easy & Clean Code | ✅ All 3 Approaches | ✅ Made Coding Fun | 100-super-easy-clean-code-all-3-approach-tfl9 | Approach 1 : Reverse Sort\n\n# Intuition\nReverse sort the happiness array and make a variable to keep the sum of the max happiness. Now go through the first k | arib21 | NORMAL | 2024-05-09T01:38:04.273358+00:00 | 2024-05-09T06:08:19.878201+00:00 | 2,793 | false | # Approach 1 : Reverse Sort\n\n# Intuition\nReverse sort the happiness array and make a variable to keep the sum of the max happiness. Now go through the first k elements and each time it will be deducted by i, (i= 0, 1, ... k-1).\n\n# Complexity\n- Time complexity:\nn be the length of the happiness array.\n$$O(nlogn)$$\n\n- Space complexity:\n n be the length of the happiness array.\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n \n int n = happiness.length;\n List<Integer> happinessList = new ArrayList<>();\n \n for (int i = 0 ; i < n ; i++) happinessList.add(happiness[i]);\n \n Collections.sort(happinessList, (a, b) -> (b - a));\n \n long maxHappiness = 0;\n \n for (int i = 0 ; i < k ; i++) {\n maxHappiness += Math.max(happinessList.get(i)-i, 0);\n }\n \n return maxHappiness;\n }\n}\n```\n\n# Approach 2 : Priority Queue (Max Heap)\n\n# Intuition\nCreate a max heap by using priority queue and make a variable to keep the sum of the max happiness. Now go through the first k elements and each time it will be deducted by i, (i= 0, 1, ... k-1).\n\n# Complexity\n- Time complexity:\nn be the length of the happiness array.\n$$O(nlogn + klogn)$$, building priority queue takes nlogn and each iteration we are popping one element which taken logk so for k element klogk\n\n- Space complexity:\n n be the length of the happiness array.\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n \n int n = happiness.length;\n PriorityQueue<Integer> maxheap = new PriorityQueue<>((x, y) -> (y-x));\n \n for (int i = 0 ; i < n ; i++) maxheap.add(happiness[i]);\n \n long maxHappiness = 0;\n \n for (int i = 0 ; i < k ; i++) {\n maxHappiness += Math.max(maxheap.poll()-i, 0);\n }\n \n return maxHappiness;\n }\n}\n```\n\n# Approach 3 : Sort\n\n# Intuition\nSort the happiness array and make a variable to keep the sum of the max happiness. Now go through the last k elements and each time it will be deducted by itr, (itr= 0, 1, ... k-1).\n\n# Complexity\n- Time complexity:\nn be the length of the happiness array.\n$$O(nlogn)$$\n\n- Space complexity:\n n be the length of the happiness array.\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n\n int n = happiness.length;\n Arrays.sort(happiness);\n\n int itr = 0, updatedValue = 0;\n \n long maxHappiness = 0; \n \n for(int i = n-1 ; i >= n-k ; i--)\n {\n updatedValue = happiness[i] - itr;\n \n if(updatedValue > 0)\n {\n maxHappiness += updatedValue;\n }\n \n itr++;\n }\n \n return maxHappiness;\n }\n}\n```\n\n# Submission Screenshot : \n\n\n\n | 31 | 1 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Java'] | 16 |
maximize-happiness-of-selected-children | Sort->partial_sort->maxHeap->radix Sort||82ms Beats 99.98% | sort-partial_sort-maxheap-radix-sort82ms-o207 | Intuition\n Describe your first thoughts on how to solve this problem. \nSeveral months ago, this question is solved by Greedy with max heap which is similar to | anwendeng | NORMAL | 2024-05-09T01:42:43.764738+00:00 | 2024-05-09T12:36:29.247595+00:00 | 1,344 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSeveral months ago, this question is solved by Greedy with max heap which is similar to 1 of solution in editoial.\nPut some more approaches in different ways; otherwise there is no need to post my solutions. For what? Against so heavy competitions promoted by many fake accounts? That will be a joke.\n\n4th method uses radix sort with 512 buckets which is the fastest one\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind the k largest elements using a Greedy algorithm\n1. Method 1 uses std::sort in default ordering which is much faster than sort with the reverse ordering.\n2. Method 2 uses partial_sort (C++20). The TC is reduced, but time not.\n3. Method 3 uses heap(priority_queue) which outperforms the std::sort with reverse ordering but slower than std::sort in default ordering\n4. Method 4 uses radix sort which is the fastest one.\n5. Python 1-line code is provided using sorted function with reverse=True.\nFor comparision the performance of C++ codes are listed in the following table\n\n|Method|Elapsed time|Beats|Memory|\n|---|---|---|---|\n|sort+reverse order|187ms|26.73%|108.92MB|\n|sort+ascending order|98ms|99.63%|107.18MB|\n|partial sort|158ms|67.75%|107.09MB|\n|priority_queue(max heap)|128ms|98.92%|111.30MB|\n|radix sort|82ms|99.98%|133.60MB|\n# Remark \nThe C++ sort are optimized for the default ordering; using reverse order the elapsed time is almost the twice. priority_queue method has less TC but is not so fast like sort+ascending order. The method using radix sort needs the most memory, say probably 30% more; that is a trade-off between space & time.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(k+n\\log n)\\to O(n+k\\log(n))$$\nradix sort: $O(n+k+512)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\nradix sort: $O(512)$\n# C++ using std::sort in default ordering||98ms Beats 99.63%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n const int n=happiness.size();\n sort( happiness.begin(), happiness.end());\n \n long long sum=0;\n for(int i=0; i<k; i++){\n long long x=max(0, happiness[n-1-i]-i);\n // cout<<x<<endl;\n sum+=x;\n }\n \n return sum;\n \n }\n};\n\n```\n# Code using partial_sort\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n const int n=happiness.size();\n partial_sort( happiness.begin(), happiness.begin()+k, happiness.end(), greater<>());\n \n long long sum=0;\n for(int i=0; i<k; i++){\n long long x=max(0, happiness[i]-i);\n // cout<<x<<endl;\n sum+=x;\n }\n \n return sum;\n \n }\n};\n\n```\n# Code using priority_queue||128ms Beats 98.92%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n int n=happiness.size();\n priority_queue<int> pq(happiness.begin(), happiness.end());//maxheap\n long long sum=0;\n for(int i=0; i<k; i++){\n long long x=max(0, pq.top()-i);\n // cout<<x<<endl;\n pq.pop();\n sum+=x;\n }\n \n return sum;\n \n }\n};\n\n```\n# C++ using radix sort|82ms Beats 99.98%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n vector<int> bucket[512];\n void radix_sort(vector<int>& nums) {\n // 1st round\n for (int x : nums)\n bucket[x&511].push_back(x);\n int i = 0;\n for (auto &B : bucket) {\n for (auto v : B)\n nums[i++] = v;\n B.clear();\n }\n // 2nd round\n for (int x : nums)\n bucket[(x>>9)&511].push_back(x);\n i=0;\n for (auto &B : bucket) {\n for (auto v : B)\n nums[i++] = v;\n B.clear();\n }\n // 3rd round\n for (int x : nums)\n bucket[x>>18].push_back(x);\n i=0;\n for (auto &B : bucket) {\n for (auto v : B)\n nums[i++] = v;\n // B.clear();\n }\n }\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n const int n=happiness.size();\n radix_sort( happiness);\n \n long long sum=0;\n for(int i=0; i<k; i++){\n long long x=max(0, happiness[n-1-i]-i);\n // cout<<x<<endl;\n sum+=x;\n }\n \n return sum;\n \n }\n};\n\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Python 1-liner using sorted with reverse=True\n```\nclass Solution:\n def maximumHappinessSum(self, h: List[int], k: int) -> int:\n return sum(max(0, x - i) for i, x in enumerate(sorted(h, reverse=True)[:k]))\n\n```\n | 28 | 0 | ['Greedy', 'Sorting', 'Heap (Priority Queue)', 'C++', 'Python3'] | 8 |
maximize-happiness-of-selected-children | 🔥 🔥 🔥 Easy to understand | 💯 ✅ | In 4 languages 🔥 🔥 🔥 | easy-to-understand-in-4-languages-by-bha-01xl | Intuition\n- The function maximizes happiness by selecting elements from a sorted list, taking into account diminishing returns as more elements are selected. I | bhanu_bhakta | NORMAL | 2024-05-09T00:32:09.382150+00:00 | 2024-05-09T05:31:32.262789+00:00 | 2,321 | false | # Intuition\n- The function maximizes happiness by selecting elements from a sorted list, taking into account diminishing returns as more elements are selected. It uses a strategy where high-value elements have a priority, ensuring that selections early on contribute the most happiness before penalties increase.\n\n# Approach\n- **Sort the List:** Start by sorting the happiness list in descending order to prioritize higher values for early selection.\n- **Initialization:** Set up counters for the number of selections (selected) and the total happiness score (happinessScore).\n- **Iterate with Condition:** For each happiness value, add to the score only if it\'s positive after subtracting the selection count, stopping if k elements are selected.\n- **Return the Result:** After processing up to k elements or exhausting the list, return the accumulated happiness score.\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(1)\n\n# Code\n```Python []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n happinessScore = 0\n\n for turn, score in enumerate(happiness):\n if k == turn:\n return happinessScore\n happinessScore += max(0, score - turn)\n\n return happinessScore\n```\n```Java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n // Sort the array in ascending order\n Arrays.sort(happiness);\n\n // Reverse the array to get descending order\n reverseArray(happiness);\n\n int selected = 0;\n long happinessScore = 0; // Changed to \'long\' to handle larger sums\n\n // Iterate over the sorted happiness values\n for (int score : happiness) {\n if (selected == k) {\n break; // Stop if \'k\' elements have been selected\n }\n // Calculate and add the adjusted happiness value if it\'s positive\n happinessScore += Math.max(0, score - selected);\n selected++;\n }\n\n return happinessScore;\n }\n\n // Helper method to reverse the array\n private void reverseArray(int[] array) {\n for (int i = 0, j = array.length - 1; i < j; i++, j--) {\n int temp = array[i];\n array[i] = array[j];\n array[j] = temp;\n }\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n // Sort the vector in ascending order\n std::sort(happiness.begin(), happiness.end());\n\n // Reverse the vector to get descending order\n std::reverse(happiness.begin(), happiness.end());\n\n int selected = 0;\n long long happinessScore = 0; // Use long long to handle larger sums\n\n // Iterate over the sorted happiness values\n for (int score : happiness) {\n if (selected == k) {\n break; // Stop if \'k\' elements have been selected\n }\n // Calculate and add the adjusted happiness value if it\'s positive\n happinessScore += std::max(0, score - selected);\n selected++;\n }\n\n return happinessScore;\n }\n};\n```\n```Javascript []\n/**\n * @param {number[]} happiness\n * @param {number} k\n * @return {number}\n */\nvar maximumHappinessSum = function (happiness, k) {\n // Sort the array in descending order using sort and a comparison function\n happiness.sort((a, b) => b - a);\n\n let selected = 0;\n let happinessScore = 0;\n\n // Iterate over the sorted happiness values\n for (let score of happiness) {\n if (selected === k) {\n break; // Stop if \'k\' elements have been selected\n }\n // Calculate and add the adjusted happiness value if it\'s positive\n happinessScore += Math.max(0, score - selected);\n selected++;\n }\n\n return happinessScore;\n};\n```\n\n**Please Upvote**\n\n\n | 25 | 4 | ['Array', 'Greedy', 'Sorting', 'C++', 'Java', 'Python3', 'JavaScript'] | 8 |
maximize-happiness-of-selected-children | Easy Video Solution 🔥 || Greedy || Simple Sorting + Count ✅ | easy-video-solution-greedy-simple-sortin-75ds | Intuition\n Describe your first thoughts on how to solve this problem. \nSort the array and dry run few scenarios\n\n\nEasy Video Explanation\n\nhttps://youtu.b | ayushnemmaniwar12 | NORMAL | 2024-03-10T04:04:39.333620+00:00 | 2024-03-10T05:39:34.368039+00:00 | 2,014 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSort the array and dry run few scenarios\n\n\n***Easy Video Explanation***\n\nhttps://youtu.be/8F2paPNQdpo\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N*log(N))\n \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n \n\n# Code\n\n\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& v, int k) {\n sort(v.begin(),v.end());\n long long ans = 0;\n int n=v.size()-1;\n int c=0;\n while(n>=0 && k>0) {\n if(v[n]-c>=0)\n ans=ans+v[n]-c;\n else\n break;\n c++;\n n--;\n k--;\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def maximumHappinessSum(self, v, k):\n v.sort()\n ans = 0\n n = len(v) - 1\n c = 0\n while n >= 0 and k > 0:\n if v[n] - c >= 0:\n ans += v[n] - c\n else:\n break\n c += 1\n n -= 1\n k -= 1\n return ans\n\n```\n```Java []\nimport java.util.Arrays;\n\npublic class Solution {\n public long maximumHappinessSum(int[] v, int k) {\n Arrays.sort(v);\n long ans = 0;\n int n = v.length - 1;\n int c = 0;\n while (n >= 0 && k > 0) {\n if (v[n] - c >= 0) {\n ans += v[n] - c;\n } else {\n break;\n }\n c++;\n n--;\n k--;\n }\n return ans;\n }\n}\n\n\n```\n\n# ***If you like the solution Please Upvote and subscribe to my youtube channel***\n***It Motivates me to record more videos***\n\n*Thank you* \uD83D\uDE00 | 17 | 2 | ['Sorting', 'Counting', 'C++', 'Java', 'Python3'] | 8 |
maximize-happiness-of-selected-children | Python 3 || 6 lines, sort and iterate || T/S: 91% / 64% | python-3-6-lines-sort-and-iterate-ts-91-warxq | \nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n \n happiness.sort(reverse=True)\n \n fo | Spaulding_ | NORMAL | 2024-03-10T04:32:22.885095+00:00 | 2024-06-12T05:04:04.376118+00:00 | 518 | false | ```\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n \n happiness.sort(reverse=True)\n \n for i in range(k):\n\n extra = happiness[i] - i\n if extra <= 0: return ans\n ans+= extra\n\n return ans\n```\n[https://leetcode.com/problems/maximize-happiness-of-selected-children/submissions/1285576262/](https://leetcode.com/problems/maximize-happiness-of-selected-children/submissions/1285576262/)\n\nI could be wrong, but I think that time complexity is *O*(*N*log*N*) and space complexity is *O*(*N*), in which *N* ~ `len(nums)`. | 13 | 0 | ['Python3'] | 5 |
maximize-happiness-of-selected-children | 🚀 Sort + Greedy || Explained Intuition 🚀 | sort-greedy-explained-intuition-by-moham-kuzt | Problem Description\n\nGiven an array happiness of length n representing the happiness values of n children standing in a queue, and a positive integer k, choos | MohamedMamdouh20 | NORMAL | 2024-05-09T02:28:33.287503+00:00 | 2024-05-09T03:26:19.959950+00:00 | 1,260 | false | # Problem Description\n\nGiven an array `happiness` of length `n` representing the happiness values of `n` children standing in a queue, and a positive integer `k`, choose `k` children from the queue in `k` turns. During each turn, selecting a child decreases the happiness value of all children not yet chosen by `1`. However, happiness values cannot become **negative**. Return the maximum sum of happiness values among the selected children.\n\nEx: `happiness` = [1,2,3], `k` = 2\nOutput: 4\nExplanation: Select 2 children as follows:\n1. Pick the child with happiness value 3. Remaining happiness values: [0,1].\n2. Pick the child with happiness value 1. Remaining happiness values: [0].\nSum of selected children\'s happiness values: 3 + 1 = 4.\n\n---\n\n# Intuition\n\nHi there, \uD83D\uDE04\n\nLet\'s dive\uD83E\uDD3F deep into our today\'s problem.\nIn today\'s problem, we have array of happiness indicates each child\'s happiness\uD83D\uDE04\uD83D\uDE14 in it and we have to choose `k` children in `k` turns (rounds).\nBUT we have to **max** the sum of those happiness.\uD83D\uDCC8\n\nHow can we do that ?\uD83E\uDD14\nlet\'s give you some hint.... now, we have to choose `k` children and `max` their sum so what we can do?\nYes, we can **sort** !\uD83E\uDD29\nwe can **sort** the children and choose the **maximum** `k` ones -we can use any other method to get the maximum `k` ones like using a **heap** but sort is my favorite\uD83D\uDE02-.\n\nwhat we can do in a nutshell is to **sort** those happiness `ascending` or `descending` you can use both -C++ and Python solutions are descending and Java solution in ascending-\nthen for each round we choose the (highest current happiness - past rounds till now).\n\nsince all happiness are **decreased** by `1` each round other than selected ones till now then when we choose a happiness in a round we will **decrease** from it the number of past round that we didn\'t select it in.\n\nand finally, we have our answer which is the sum of all selected happiness.\uD83D\uDE03\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n---\n\n# Approach\n\n1. **Sort** the happiness values in `non-increasing` order.\n2. Initialize a variable `total` to store the total happiness sum.\n3. Iterate `k` times:\n a. Calculate the happiness contribution of the current child in this turn by subtracting the turn number from their happiness value. If the result is **negative**, set it to `0`.\n b. Add the calculated happiness contribution to the `total`.\n4. Return the `total` happiness sum.\n\n---\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n // Sort the happiness values in non-increasing order\n sort(happiness.rbegin(), happiness.rend());\n\n long long total = 0;\n for (int turn = 0; turn < k; ++turn) {\n // Calculate the happiness contribution of the current child in this turn\n // since his happinness has been decreased for all of the past rounds\n long long current = max(happiness[turn] - turn, 0);\n // Accumulate the happiness contribution\n total+= current;\n }\n return total;\n }\n};\n```\n```Java []\npublic class Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n // Sort the happiness values in non-increasing order\n Arrays.sort(happiness);\n\n long total = 0;\n for (int turn = happiness.length; happiness.length - turn < k; --turn) {\n // Calculate the happiness contribution of the current child in this turn\n // since his happiness has been decreased for all of the past rounds\n long current = Math.max(happiness[turn - 1] - (happiness.length - turn), 0);\n // Accumulate the happiness contribution\n total += current;\n }\n return total;\n }\n}\n```\n```Python []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n # Sort the happiness values in non-increasing order\n happiness.sort(reverse=True)\n\n total = 0\n for turn in range(k):\n # Calculate the happiness contribution of the current child in this turn\n # since his happiness has been decreased for all of the past rounds\n current = max(happiness[turn] - turn, 0)\n # Accumulate the happiness contribution\n total += current\n \n return total\n```\n\n\n\n | 11 | 1 | ['Greedy', 'Sorting', 'Python', 'C++', 'Java', 'Python3'] | 6 |
maximize-happiness-of-selected-children | One line solution. Beats 90% | one-line-solution-beats-90-by-movsar-lhsh | python\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n\n ans = 0\n | movsar | NORMAL | 2024-05-09T01:23:29.175175+00:00 | 2024-05-09T01:32:01.980134+00:00 | 492 | false | ```python\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n\n ans = 0\n for i in range(k):\n ans += max(0, happiness[i] - i)\n\n return ans\n```\n\n```python\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n return sum(max(0, h - i) for i, h in enumerate(sorted(happiness, reverse=True)[:k]))\n``` | 9 | 0 | ['Sorting', 'Python3'] | 1 |
maximize-happiness-of-selected-children | Truly Optimal O(N) Time: Quick Select + Counting Sort | truly-optimal-on-time-quick-select-count-pjy5 | Intuition\n### Observation 1: How to quantify happiness :)\nIf we have selected k children, their total happiness is \n\n$\sum_{i = 0}^{k-1} max(0, \text{select | aylup | NORMAL | 2024-06-22T21:41:26.132078+00:00 | 2024-08-18T19:24:20.416463+00:00 | 65 | false | # Intuition\n### Observation 1: How to quantify happiness :)\nIf we have selected k children, their total happiness is \n\n$\\sum_{i = 0}^{k-1} max(0, \\text{selectedChildren}[i]- i)$\n\nWith this formula, we see that we can just select topK children in sorted order and arrive at our solution.\n\n$ans = \\sum_{i = 0}^{k-1} max(0, \\text{reverseSortedChildren}[i]- i)$\n\nSince we have to sort, this runs in the worst case $O(n\\log(n))$.\n\nHowever, with a few more observations we can see that we can do better.\n\n### Observation 2: When order doesn\'t matter (QuickSelect)\nIf all of the selected $k$ children have a $\\text{happiness} \\geq k$, their total happiness is \n\n$\\sum_{i = 0}^{k-1} (\\text{selectedChildren}[i]- i)$\n\nThis is because $(\\text{selectedChildren}[i] - i)$ will never be less than $1$ since $(i \\lt k \\leq \\text{selectedChildren}[i])$. Because of this, we can decouple:\n\n$\\sum_{i = 0}^{k-1} \\text{selectedChildren}[i] - \\sum_{i = 0}^{k-1} i$\n\nThis shows that the order we choose them doesn\'t matter.\n\nThus, if we take the $\\text{count\\_geq\\_k}$ of children with $\\text{happiness} \\geq k$, and see that $\\text{count\\_geq\\_k} \\geq k$, then we just take the topK happiest children in any order.\n\n$\\text{ans} = \\sum_{i = 0}^{k-1} (\\text{topKHappiest}[i] - i)$\n\nSince order doesn\'t matter, we can partition the $\\text{topKHappiest}$ using the $O(n)$ algorithm $\\text{quickselect}$. Technically, worst case performance is $O(n^2)$, but if we absolutely care about theoretical complexity we could use the $\\text{median of medians}$ algorithm to guarantee $O(n)$ performance. In the example below, I just choose a random pivot for simplicity.\n\n### Observation 3: When order does matter (CountingSort)\n\nSo what about the case where the $\\text{count\\_geq\\_k} \\lt k$?\n\nThis means all children with $\\text{happiness} \\geq k$ should automatically be included in our set and it doesn\'t matter which order we choose them.\n\nThe remaining children to be selected have $\\text{happiness} \\lt k$, which means the order we choose them does matter. However, since they are bounded by $k$, we can $\\text{counting sort}$ them in $O(k)$ which at worst is $O(n)$.\n\n# Complexity\n- Time complexity: $O(n)$\n\n- Space complexity: $O(n)$\n\n# Code\n```cpp\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n int geq_k_count = 0, n = happiness.size();\n for (int x : happiness) {\n geq_k_count += x >= k;\n }\n\n if (geq_k_count >= k) {\n auto start = happiness.begin();\n std::nth_element(start, start + n - k, happiness.end());\n long long ans = 0;\n for (int i = 0; i < k; ++i) {\n ans += happiness[n - i - 1] - i;\n }\n return ans;\n }\n\n long long ans = 0, picked = 0;\n std::vector<int> count(k);\n for (int x : happiness) {\n if (x < k) {\n ++count[x];\n } else {\n ans += x - picked++;\n }\n }\n\n for (int i = k - 1; i >= picked; --i) {\n while (i >= picked && count[i]--) {\n ans += i - picked++;\n }\n }\n return ans;\n }\n};\n``` | 7 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | ✅✅Fastest 💯💯|| Simplest 🧠🧠 || Greedy | fastest-simplest-greedy-by-thecodealpha-2p2a | Thanks for dropping by\uD83D\uDC4B, I hope it helps :) \n\n# Intuition \uD83D\uDC31\u200D\uD83C\uDFCD\n Describe your first thoughts on how to solve this proble | TheCodeAlpha | NORMAL | 2024-05-09T08:59:53.572054+00:00 | 2024-05-09T09:08:31.185412+00:00 | 153 | false | ## Thanks for dropping by\uD83D\uDC4B, I hope it helps :) \n\n# Intuition \uD83D\uDC31\u200D\uD83C\uDFCD\n<!-- Describe your first thoughts on how to solve this problem. -->\n### Sochne\uD83E\uDDE0 ka hi khel hai saara, aur jab iss question\uD83E\uDD14 ko dekha aur socha toh samaj aaya ki isme aisa kuch aisa istemaal ho raha jo meri zindagi mai nahi hora --- sahi samjhe aap _Sorting_\n### Ab sawal\uD83D\uDCDD ko medium bola hai toh thoda mushkil lagna aam baat hai, magar ek baar tum iss solution\uD83C\uDFAF ko padh loge toh tum paaoge ki mushkil tha nahi par jo shuru mai dar aa gaya mann\uD83E\uDDE0 mai usne karne nahi diya bs\n\n# Approach \uD83D\uDCA1\n<!-- Describe your approach to solving the problem. -->\n### Ab zindagi sorted nahi hai par iss question ko niptane ke liye hum sorting use karenge. \n### Ek baar question ko tameez se padh\uD83D\uDCDA loge toh ek jordaar\uD83D\uDD25 baat samaj aayegi ki, apne ko toh keval K bacho ki khushiyaan\uD83D\uDE01 jodni hai (Relate karna band karo, ki placement mai bhi K bacho ko hi Khushi mili aur tumhara number `K+1` tha, Khair choro, magar Anmol bhi buri ladki nahi hai....)\n### Ab dhyaan\uD83D\uDE07 bhatakna nahi chahiye, kyuki K bache pehle hi aage \uD83C\uDFC3\u200D\u2642\uFE0F chal rahe hain, aur inko hi pakad ke hum iss sawal ko iski manjil\uD83D\uDEE3 tak le jaana hai\n### Humko karna hai Happiness\uD83D\uDE01 Maximise, toh maximum ke liye humko chahiye sabse badi values. Yaha pe tum samaj gye ki sort karna padega khushiyon ko....\n`(Leetcode Giving life lessons through question, samjho...)`\n##### Ab chadta hua\uD83D\uDCC8 (ascending) ya girta hua\uD83D\uDCC9 (descending) sort tumhari marji hai, magar karna toh hai( Priority queue based solution bhi chahiye ho toh bta dena comments mai, iss question ke liye mujhe laga nahi ki maamla complex\uD83E\uDDE0 karne ki need hai, so nahi daal raha hu, kyuki mudda hai solve krna kamse kamse lafdo mai)\n\n#### Ab koi khush hoga toh usko barabar karne ke liye prakriti kisi ko toh dukh degi hi, yahi bola hai question mai ki ek bache ki Khushiya jodne ke baad baaki bache huye bacho ki khushiyan kam hongi (har dukh pe relate mat kiya karo, agle kisi question mai tum hi select hoge, bas kaam krte jao, aur mere solution ko upvote karke, meri Dua lo) Dua Lipa mat socho bhyii, maana sunder hai\uD83D\uDC95\n\n### Ab kiski kitni khushiyan kam hongi\uD83D\uDE22 iske liye hum ek `happinessReduced` variable ko bharte rahenge. Jab bhi kisi khusiyan jod di jayengi tab tab iss dukh ke garhe \uD83D\uDDD1(garhe ka icon ni mila) ko bhardenge hum, Dukh hai par seh lenge....\n\n### Aur jab bhi kisi ki khushiyaan jodni hogi toh dekh lenge ki kya vo dukh ke garhe se jyada hai ya nahi, \n- Agar haan\u2705, toh dono ke difference ko total khushiyon mai jod denge, aur dukh ka garha bharkar aage badhenge\n- Agar nahi\u274C toh fir hum dhundna hi band kar denge, kyuki iska matlab ab dukh khushiyo se bada ho gaya hai, aur loop mai bane rehna bilkul vesa hi hoga jese tum the uski wapsi ki yaad mai ho jaate ho....(__Ekdum Faltu__)\n\n# Algorithm \uD83D\uDC69\u200D\uD83D\uDCBB\n\n### Ek sawal ke nazariye baatein ho gyi kaafi ab maine sprite pee li hai, isiliye no bakwaas\n\n#### Samasya Ka Vivaran - Sawal Ek nazar\uD83D\uDC53 mai\n\n#### Di gayi hai ek integer array `happiness` aur ek integer `k` , aapko apne total khushi ki sum ko adhik se adhik banana hai.\n\n#### Aapko jyada se jyada `k` elements ko array se lena hai aur kam se kam khushi ghatane ki anumati hai. Ek element ki khushi ko 0 tak ghataaya ja sakta hai, lekin 0 se kam nahi, kyuki jo khushi kisi pe hai hi nahi, usko kese hi koi le sakta hai.\n\n#### `maximumHappinessSum` function ko implement karna hai, jo jyada se jyada `k` elements ko istemaal karne ke baad adhik se adhik khushi ke sum ko vaapas kare.\n\n\n1. **Happiness values ko ascending order mein sort karo.**\n2. **Sort ki gayi happiness values ko reverse order mein traverse karo.**\n - **Agar vartaman Khushiya dukh se kam ho toh, total khushiya ko vaapas karo.**\n - **Anytha Vartaman khushi mai dukh ghata kar, total Khushiyo mein jodo.**\n - **Dukh ko badhao.**\n3. **Total adhikatam khushi ke sum ko vaapas karo.**\n\n\n# Complexity \uD83C\uDFCB\uFE0F\u200D\u2640\uFE0F\n- Time complexity: $$O(N * Log(N))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n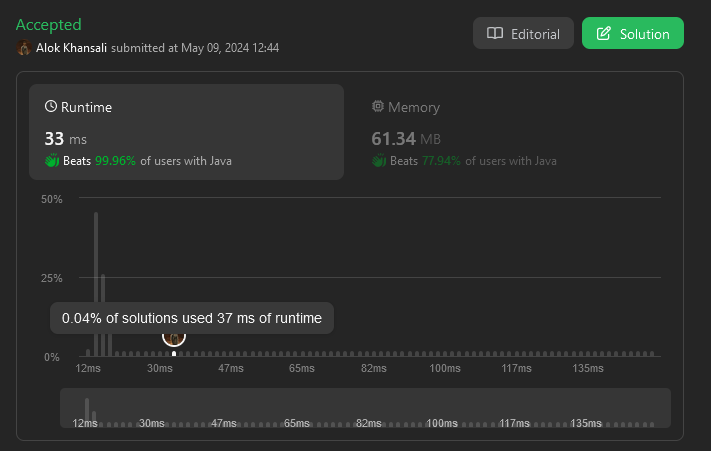\n\n\n# Code\uD83D\uDCBB\n```java []\nclass Solution\n{\npublic\n long maximumHappinessSum(int[] happiness, int k)\n {\n Arrays.sort(happiness); // Sort the happiness values in ascending order\n long totalHappiness = 0, happinessReduced = 0;\n int len = happiness.length;\n\n // Traverse the sorted happiness values in reverse order\n for (int i = len - 1; k > 0; i--, k--)\n {\n // If reducing the happiness value by the current track value makes it non-positive, return the total happiness\n if (happiness[i] - happinessReduced <= 0)\n return totalHappiness;\n totalHappiness += happiness[i] - happinessReduced; // Add the current maximum happiness value to the total\n happinessReduced++; // Increment the track value\n }\n\n return totalHappiness; // Return the total maximum happiness sum\n }\n}\n```\n```cpp []\nclass Solution\n{\npublic:\n long long maximumHappinessSum(vector<int> &happiness, int k)\n {\n sort(happiness.begin(), happiness.end()); // Sort the happiness values in ascending order\n long long totalHappiness = 0, happinessReduced = 0, len = happiness.size();\n\n // Traverse the sorted happiness values in reverse order\n for (int i = len - 1; k > 0; i--, k--)\n {\n // If reducing the happiness value by the current track value makes it non-positive, return the total happiness\n if (happiness[i] - happinessReduced <= 0)\n return totalHappiness;\n totalHappiness += happiness[i] - happinessReduced; // Add the current maximum happiness value to the total\n happinessReduced++; // Increment the track value\n }\n\n return totalHappiness; // Return the total maximum happiness sum\n }\n};\n```\n```python3 []\nfrom typing import List\n\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n # Sort the happiness values in ascending order\n happiness.sort()\n\n total_happiness = 0 # Variable to store the total happiness sum\n happiness_reduced = 0 # Variable to store the amount of happiness reduced\n length = len(happiness) # Get the length of the happiness list\n i = length - 1 # Start from the last element of the sorted happiness list\n\n # Traverse the sorted happiness values in reverse order for \'k\' iterations\n for _ in range(k):\n # If reducing the happiness value by the current track value makes it non-positive,\n # it means we\'ve reached the minimum possible happiness, so we return the total happiness\n if happiness[i] - happiness_reduced <= 0:\n return total_happiness\n \n # Add the current maximum happiness value (after reducing) to the total happiness sum\n total_happiness += happiness[i] - happiness_reduced\n \n # Increment the track value as we reduce happiness for the next iteration\n happiness_reduced += 1\n \n # Move to the next element in the sorted happiness list\n i -= 1\n\n # Return the total maximum happiness sum\n return total_happiness\n\n```\n\n\n\n | 7 | 0 | ['Array', 'Greedy', 'Sorting', 'C++', 'Java', 'Python3'] | 1 |
maximize-happiness-of-selected-children | Simple and straight forward solution, just sort and it's over, beats 94% :) | simple-and-straight-forward-solution-jus-cn1k | Intuition\nJust think of selecting the maximum element from the happiness array, in each iteration of k, until k becomes 0.\n\n# Approach\nFirst, we sort this l | as828 | NORMAL | 2024-05-09T05:06:50.494207+00:00 | 2024-05-09T05:06:50.494237+00:00 | 118 | false | # Intuition\nJust think of selecting the maximum element from the happiness array, in each iteration of k, until k becomes 0.\n\n# Approach\nFirst, we sort this list from lowest to highest happiness. Then, we start from the happiest person and gradually subtract a counter from their happiness, moving towards less happy people. We keep track of how much happiness we\'ve accumulated in a variable called \'happy\' and we will accumulate only if the happiness[i]-counter is positive so that no negative value gets accumulated. This continues until we\'ve made \'k\' iterations. Finally, we return the total accumulated happiness.\n\n# Complexity\n- Time complexity: O(nlogn) for sorting + O(k) for k turns \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n sort(happiness.begin(), happiness.end());\n long long happy = 0;\n long long counter = 0;\n long long i = (happiness.size()-1);\n while(k>0)\n { \n //Ensuring that no negative value get accumulated\n if(happiness[i]-counter > 0) \n happy += (happiness[i] - counter);\n i--;\n counter++;\n k--;\n }\n return happy;\n }\n};\n``` | 7 | 0 | ['C++'] | 3 |
maximize-happiness-of-selected-children | Python | Easy | python-easy-by-khosiyat-a3gw | see the Successfully Accepted Submission\n\n# Code\n\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happines | Khosiyat | NORMAL | 2024-05-09T05:00:44.557275+00:00 | 2024-05-09T05:00:44.557312+00:00 | 226 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/maximize-happiness-of-selected-children/submissions/1253228363/?envType=daily-question&envId=2024-05-09)\n\n# Code\n```\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n indx = 0\n totalHappinessSum = 0\n\n while k > 0:\n happiness[indx] = max(happiness[indx] - indx, 0)\n totalHappinessSum += happiness[indx]\n indx += 1\n k -= 1\n\n return totalHappinessSum\n```\n | 7 | 1 | ['Python3'] | 2 |
maximize-happiness-of-selected-children | [Python3] Sort + Heap + Take Sum - Simple Solution | python3-sort-heap-take-sum-simple-soluti-8xe5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dolong2110 | NORMAL | 2024-03-10T04:44:26.572029+00:00 | 2024-05-09T06:21:01.737418+00:00 | 268 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n##### 1. Sort\n```\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n res = 0\n for i in range(k):\n res += max(0, happiness[i] - i)\n return res\n```\n- Time complexity: $$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n\n\n##### 2. Heap\n```\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n for i in range(len(happiness)): happiness[i] = -happiness[i]\n heapq.heapify(happiness)\n res = 0\n for i in range(k):\n res += max(0, -heapq.heappop(happiness) - i)\n return res\n```\n- Time complexity: $$O(N + klog(N))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n\n##### 3. Pythonic 1-line\n\n```\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n return sum(max(0, h - i) for i, h in enumerate(sorted(happiness, reverse=True)[:k]))\n```\n\n- Time complexity: $$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$ | 7 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Python3'] | 6 |
maximize-happiness-of-selected-children | 🔥Easy C++ Solution With Full Explaination || Beats 100 || Using Sorting | easy-c-solution-with-full-explaination-b-xxuk | \n\n### Intuition:\nThe problem involves selecting children from a queue to maximize the sum of their happiness values. Each time a child is selected, the happi | vanshwari | NORMAL | 2024-03-10T04:10:03.392457+00:00 | 2024-04-03T05:54:09.012961+00:00 | 922 | false | \n\n### Intuition:\nThe problem involves selecting children from a queue to maximize the sum of their happiness values. Each time a child is selected, the happiness of all unselected children decreases by 1.\n\n### Approach:\n1. **Sort the Happiness Values**: Sort the happiness values in non-increasing order to prioritize selecting children with higher happiness values.\n2. **Iterate Through the Sorted Values**: Iterate through the sorted happiness values.\n - For each happiness value, if it is greater than the index (position) of the child in the sorted order and there are still turns left (k > 0), select the child.\n - Increment the answer by the difference between the happiness value and the index.\n - Decrease the number of turns available (k) after selecting a child.\n3. **Return the Maximum Happiness Sum**: Return the maximum sum of happiness achieved by selecting children.\n\n### Complexity:\n- **Time Complexity**: \n - Sorting the happiness values takes O(n log n) time, where n is the number of children.\n - The loop iterates through the sorted happiness values, taking O(n) time.\n - Overall, the time complexity is O(n log n).\n- **Space Complexity**: \n - The space complexity is O(1) as the algorithm only uses a constant amount of extra space.\n\n### Code:\n```cpp\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& hap, int k) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n long long ans = 0;\n sort(hap.begin(), hap.end(), greater<int>());\n int n = hap.size();\n for(int i = 0; i < n; i++) {\n if(hap[i] <= i) break;\n if(k == 0) break;\n ans += hap[i] - i;\n k--;\n }\n return ans;\n }\n};\n``` | 7 | 0 | ['Sorting', 'C++'] | 8 |
maximize-happiness-of-selected-children | C# Solution for Maximise Happiness of Selected Children Problem | c-solution-for-maximise-happiness-of-sel-8iia | Intuition\n Describe your first thoughts on how to solve this problem. \nThe solution aims to maximize the total sum of happiness values by selecting children i | Aman_Raj_Sinha | NORMAL | 2024-05-09T03:29:05.461621+00:00 | 2024-05-09T03:29:05.461659+00:00 | 251 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe solution aims to maximize the total sum of happiness values by selecting children in each round based on their happiness values. It iterates through the sorted array and selects the maximum happiness value that hasn\u2019t been fully selected yet.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tSort the happiness array in descending order to prioritize selecting children with higher happiness values first.\n2.\tIterate through the sorted array for each selection round (up to k rounds or the length of the array).\n3.\tFor each round, pick the ith biggest happiness score and subtract the number of rounds passed from it. If the result is positive, add it to the total sum of happiness and increment the rounds.\n4.\tReturn the total sum of happiness achieved.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tSorting the array takes O(nlogn) time.\n\u2022\tThe iteration through the array for each selection round takes O(n) time.\n\u2022\tOverall, the time complexity is O(nlogn), dominated by the sorting operation.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) as the algorithm uses only a constant amount of extra space for variables regardless of the input size.\n\n# Code\n```\npublic class Solution {\n public long MaximumHappinessSum(int[] happiness, int k) {\n Array.Sort(happiness, (a, b) => b - a); // Sort in descending order\n \n int rounds = 0;\n long totalHappySum = 0;\n \n for (int i = 0; i < k && i < happiness.Length; i++) {\n int selected = happiness[i] - rounds;\n if (selected > 0) {\n totalHappySum += selected;\n rounds++;\n }\n }\n \n return totalHappySum;\n }\n}\n``` | 6 | 0 | ['C#'] | 2 |
maximize-happiness-of-selected-children | Easy | Sorting | Just follow the steps of code | Generic Code | Beat 100% | Refer code | | easy-sorting-just-follow-the-steps-of-co-3zxw | \n\n# Code\n\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happ, int k) {\n\n sort(happ.begin() , happ.end());\n\n in | YASH_SHARMA_ | NORMAL | 2024-05-09T02:32:38.823572+00:00 | 2024-05-09T02:32:38.823601+00:00 | 476 | false | \n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happ, int k) {\n\n sort(happ.begin() , happ.end());\n\n int times = 0;\n\n int n = happ.size();\n int index = n-1;\n long long sum = 0;\n\n for(int i = 1 ; i <= k ; i++)\n {\n int curr_val = happ[index] - times;\n\n if(curr_val <= 0)\n {\n break;\n }\n else\n {\n sum += curr_val;\n }\n\n index--;\n times++;\n }\n\n return sum;\n }\n};\n``` | 6 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | 🔥🔥Beats 99%✅Simple and Easy💯🔥Detailed Explanation🔥Sorting & Greedy🔥[Python, Java, C++ & JS] | beats-99simple-and-easydetailed-explanat-g3lj | \nSubmission link: Python, Java, C++ & JavaScript\n\n## \uD83C\uDFAF Problem Explanation:\nGiven an array happiness and a positive integer k, we need to select | Saketh3011 | NORMAL | 2024-05-09T00:35:51.858645+00:00 | 2024-05-09T01:38:53.589960+00:00 | 473 | false | \nSubmission link: [Python](https://leetcode.com/problems/maximize-happiness-of-selected-children/submissions/1253079848?envType=daily-question&envId=2024-05-09), [Java](https://leetcode.com/problems/maximize-happiness-of-selected-children/submissions/1253081148?envType=daily-question&envId=2024-05-09), [C++](https://leetcode.com/problems/maximize-happiness-of-selected-children/submissions/1253082953?envType=daily-question&envId=2024-05-09) & [JavaScript](https://leetcode.com/problems/maximize-happiness-of-selected-children/submissions/1253083482?envType=daily-question&envId=2024-05-09)\n\n## \uD83C\uDFAF Problem Explanation:\nGiven an array `happiness` and a positive integer `k`, we need to select `k` children from `n` children standing in a queue, where each child has a happiness value `happiness[i]`. In each turn, selecting a child decreases the happiness value of all unselected children by 1. We are to maximize the sum of the happiness values of the selected children.\n\n## \uD83E\uDD14 Intuition:\nTo maximize the sum of happiness values, we should select children with the highest happiness values first. Sorting the `happiness` array in descending order allows us to select the highest happiness values first. And `decrement` value `happiness` for every iteration greedily.\n\n## \uD83E\uDDE0 Approach:\n1. Sort the `happiness` array in descending order.\n2. Initialize variables `decrement` and `result` to 0.\n3. While `k > 0` and the happiness value of the current child minus its index is greater than 0:\n - Add the happiness value of the current child minus its index to the `result`.\n - Decrement `k` and increment `decrement`.\n4. Return the `result`.\n\n## \u2699\uFE0F Dry Run:\n- Input: happiness = [1, 1, 1, 1], k = 2\n- Sorted happiness array: [1, 1, 1, 1]\n- decrement = 0, result = 0\n - k = 2, happiness[0] - 0 = 1 > 0\n - Add 1 to result: result = 1\n - Decrement k: k = 1\n - Increment decrement: decrement = 1\n - k = 1, happiness[1] - 1 = 0 not > 0\n- Return result: 1\n\n# \uD83D\uDCD2 Complexity:\n- \u23F0 Time complexity: $$O(nlog(n))$$, nlog(n) for sorting and O(k) for iteration\n- \uD83E\uDDFA Space complexity: $$O(1)$$\n\n\n# Code\n``` python []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse = True)\n decrement, result = 0, 0\n while (k > 0 and happiness[decrement]-decrement > 0):\n result += happiness[decrement]-decrement\n k, decrement = k-1, decrement+1\n return result\n```\n``` java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n long result = 0;\n int n = happiness.length, decrement = 0;\n while (k > 0 && happiness[n - 1 - decrement] - decrement > 0) {\n result += happiness[n - 1 - decrement] - decrement;\n k--;\n decrement++;\n }\n return result;\n }\n}\n```\n``` cpp []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n sort(happiness.begin(), happiness.end(), greater<int>());\n long long result = 0;\n int decrement = 0;\n while (k > 0 && happiness[decrement] - decrement > 0) {\n result += happiness[decrement] - decrement;\n k--;\n decrement++;\n }\n return result;\n }\n};\n```\n``` javascript []\nvar maximumHappinessSum = function(happiness, k) {\n happiness.sort((a, b) => b - a);\n let result = 0;\n let decrement = 0;\n while (k > 0 && happiness[decrement] - decrement > 0) {\n result += happiness[decrement] - decrement;\n k--;\n decrement++;\n }\n return result;\n}\n```\n\n\n---\n# Please consider giving an Upvote!\n | 6 | 0 | ['Greedy', 'Sorting', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 2 |
maximize-happiness-of-selected-children | Java | Greedy | 5 lines | Clean code | java-greedy-5-lines-clean-code-by-judgem-oz9c | Complexity\n- Time complexity: O(n * log(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(log(n)) used by the sorting algorithm\n Add yo | judgementdey | NORMAL | 2024-05-09T00:22:18.839557+00:00 | 2024-05-09T00:24:07.066631+00:00 | 591 | false | # Complexity\n- Time complexity: $$O(n * log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(log(n))$$ used by the sorting algorithm\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n var ans = 0L;\n Arrays.sort(happiness);\n\n for (var i=0; i<k; i++)\n ans += Math.max(happiness[happiness.length - 1 - i] - i, 0);\n \n return ans;\n }\n}\n```\nIf you like my solution, please upvote it! | 6 | 1 | ['Array', 'Greedy', 'Sorting', 'Java'] | 3 |
maximize-happiness-of-selected-children | Sort and take sum | sort-and-take-sum-by-kreakemp-2h2o | \n\n# Code\n\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long ans = 0;\n sort(happiness. | kreakEmp | NORMAL | 2024-03-10T04:11:52.350877+00:00 | 2024-03-10T04:19:48.308899+00:00 | 1,517 | false | \n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long ans = 0;\n sort(happiness.begin(), happiness.end());\n for(int i = happiness.size() - 1, j = 0; i >= 0 && k > 0; --i, j++, k--){\n if(happiness[i] - j > 0) ans += happiness[i] - j;\n } \n return ans;\n }\n};\n```\n\n---\n\n\n<b>Here is an article of my last interview experience - A Journey to FAANG Company, I recomand you to go through this to know which all resources I have used & how I cracked interview at Amazon:\nhttps://leetcode.com/discuss/interview-experience/3171859/Journey-to-a-FAANG-Company-Amazon-or-SDE2-(L5)-or-Bangalore-or-Oct-2022-Accepted\n\n--- | 6 | 0 | ['C++'] | 7 |
maximize-happiness-of-selected-children | 2 Easy Intuitive Solutions ✅ | 2-easy-intuitive-solutions-by-gurmankd-428g | \n\n---\n# USING SORTING \u25FD\uFE0F\u25AB\uFE0F\u25AA\n\n---\n\n\n## Intuition\n Describe your first thoughts on how to solve this problem. \nSince we aim to | gurmankd | NORMAL | 2024-05-09T05:39:29.481765+00:00 | 2024-05-09T05:39:29.481786+00:00 | 8 | false | \n\n---\n# USING SORTING \u25FD\uFE0F\u25AB\uFE0F\u25AA\n\n---\n\n\n## Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince we aim to maximize the happiness sum, it\'s intuitive to start by selecting children with higher happiness values. Sorting the array in decreasing order of happiness allows us to prioritize selecting children with higher happiness values first.\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem can be approached **GREEDILY**. We want to maximize the happiness sum, so we should select children with higher happiness values first. **Sorting the array in decreasing order of happiness** accomplishes this. Then, we iterate through the sorted array, starting from the highest happiness value. In each iteration, we select a child and decrease the happiness of the remaining children accordingly.\n\n## Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nSorting the array takes $$O(nlogn)$$ time, where $$n$$ is the number of children. The subsequent iteration takes $$O(k)$$ time. Thus, the overall time complexity is $$O(nlogn+k)$$.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is $$O(1)$$ since we only use a constant amount of extra space.\n\n## Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long maxSum = 0;\n\n // sort in decreasing order\n sort(happiness.begin(), happiness.end(), greater<int>());\n\n // select the first child\n maxSum += max(0, happiness[0]);\n\n // iterate through the remaining children\n for (int i = 1; i < k; ++i) {\n if (happiness[i] - i > 0)\n maxSum += happiness[i] - i;\n }\n\n return maxSum;\n }\n};\n```\n\n---\n\n# USING PRIORITY QUEUE (MAX-HEAP) \n\n## Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe use of a **max-heap (priority queue)** is intuitive because it allows us to efficiently select the children with the highest happiness values first. By maintaining a max-heap, we can always extract the child with the maximum happiness value in constant time.\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\n1. We initialize a max-heap (`priority_queue`) and insert all the happiness values into it. Since it\'s a max-heap, the top element will always be the child with the highest happiness value.\n2. We iterate `k` times, representing the number of turns we can select children. In each iteration:\n - We extract the top element (child with the highest happiness value) from the priority queue.\n - We calculate the happiness value of the selected child, considering the happiness of previously selected children. Since we want to maximize the sum of happiness values, we take the maximum of the current happiness value minus the number of previously selected children (to account for the decrease in happiness of remaining children) and 0 (to ensure we don\'t add negative values to the sum).\n - We update the `answer` by adding the calculated happiness value.\n - We increment the `counter` to track the number of selected children.\n3. Finally, we return the maximum happiness sum obtained by selecting k children.\n\n\n## Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nBuilding the priority queue takes $$O(nlogn)$$ time, where $$n$$ is the number of children. Each of the k iterations takes$$ O(logn)$$ time to extract the maximum element from the priority queue. Thus, the overall time complexity is $$O(nlogn+klogn)$$.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is $$O(n)$$ to store the priority queue.\n\n## Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long ans = 0;\n\n int count = 0;\n\n priority_queue<int> pq; // max-heap\n\n for(int &hap : happiness){\n pq.push(hap);\n }\n\n for(int i = 0 ; i < k; i++){\n int hap = pq.top();\n pq.pop();\n\n ans += max(hap-count, 0);\n\n count++;\n }\n return ans;\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | 💯JAVA Solution Explained in HINDI | java-solution-explained-in-hindi-by-the_-ldbu | https://youtu.be/Nsl32H-VYLM\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote | The_elite | NORMAL | 2024-05-09T05:23:16.436248+00:00 | 2024-05-09T05:23:16.436290+00:00 | 139 | false | https://youtu.be/Nsl32H-VYLM\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\n# Subscribe :- [ReelCoding](https://www.youtube.com/@reelcoding?sub_confirmation=1)\n\nSubscribe Goal:- 400\nCurrent Subscriber:- 355\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n long ans = 0, dec = 0;\n Arrays.sort(happiness);\n\n for (int i = happiness.length - 1; i >= happiness.length - k; i--) {\n ans += Math.max(0, happiness[i] - dec);\n dec++;\n }\n\n return ans;\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
maximize-happiness-of-selected-children | heap sort||basic c++code | heap-sortbasic-ccode-by-sujalgupta09-or74 | \n\n# Code\n\nclass Solution {\npublic:\n long long maximumHappinessSum(std::vector<int>& happiness, int k) {\n std::sort(happiness.begin(), happine | sujalgupta09 | NORMAL | 2024-05-09T02:29:36.795184+00:00 | 2024-05-09T02:29:36.795211+00:00 | 453 | false | \n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(std::vector<int>& happiness, int k) {\n std::sort(happiness.begin(), happiness.end(), std::greater<int>());\n\n std::vector<bool> selected(happiness.size(), false);\n\n long long ans = 0;\n int count = 0;\n\n for (int i = 0; i < happiness.size(); ++i) {\n if (!selected[i]) {\n ans += std::max(0, happiness[i] - count);\n ++count;\n selected[i] = true;\n\n if (count >= k) {\n break;\n }\n }\n }\n\n return ans;\n }\n};\n``` | 5 | 0 | ['C++'] | 1 |
maximize-happiness-of-selected-children | Detailed Explanation😴|| Priority Queue + Greedy + Sort || O(n.logn) + O(k.logn)🔥 | detailed-explanation-priority-queue-gree-w0bb | Intuition (Approch: MaxHeap + Greedy)\nGiven our problem\'s requirement to maximize total happiness by selecting the largest element available at each turn, the | rohit_gupta1819 | NORMAL | 2024-05-09T02:03:15.139085+00:00 | 2024-05-09T02:03:15.139107+00:00 | 392 | false | # Intuition (Approch: MaxHeap + Greedy)\nGiven our problem\'s requirement to maximize total happiness by selecting the largest element available at each turn, the selection of an appropriate data structure holds significant importance. The max heap data structure proves to be exceptionally suitable for this scenario. By arranging all happiness scores into a max heap, we guarantee that the largest element consistently resides at the top, ensuring swift accessibility. This attribute seamlessly complements the strategy of our greedy algorithm, which aims to choose the highest happiness value attainable at each iteration.\n\nInitially, we construct a max heap utilizing the values from the happiness array. Subsequently, for each of the k turns, we extract the maximum value from the heap. Following this, we modify this value by subtracting the number of completed turns. This adjustment compensates for the diminishing happiness of the remaining unselected children. Ultimately, we incorporate this adjusted value into our cumulative happiness tally.\n\nBy retaining its inherent greedy approach of selecting the highest happiness values sequentially, the employment of a heap data structure markedly enhances efficiency in contrast to sorting the happiness array.\n\n# Complexity\n- Time complexity: O(n.logn) + O(k.logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n int turns = 0, n = happiness.length;\n long happinessSum = 0;\n Integer[] happinessArray = new Integer[n];\n for(int i = 0; i < n; i++) {\n happinessArray[i] = happiness[i];\n }\n Arrays.sort(happinessArray, Collections.reverseOrder());\n for(int i = 0; i < k; i++){\n happinessSum += Math.max(happinessArray[i] - turns, 0);\n turns++;\n }\n\n return happinessSum;\n }\n}\n```\n---\n\n | 5 | 0 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Java'] | 4 |
maximize-happiness-of-selected-children | [Rust] Small optimization: quickselect the top k rather than sorting all | rust-small-optimization-quickselect-the-4my7n | Intuition\nIf there were no penalty, we would select the k happiest children to maximize the score.\n\nWith the penalty...we still pick the k happiest children, | tiedyedvortex | NORMAL | 2024-05-09T00:37:11.956662+00:00 | 2024-05-09T00:37:11.956688+00:00 | 63 | false | # Intuition\nIf there were no penalty, we would select the k happiest children to maximize the score.\n\nWith the penalty...we still pick the k happiest children, because the penalty doesn\'t change based on which children we select.\n\n# Approach\nInstead of sorting all of happiness, we can sort the top k happiest children; when k is much smaller than n this is more efficient.\n\nRust has a builtin for `slice::select_nth_unstable(&mut self, i)` which partitions a slice so that elements (0..i) are less than or equal to element i, and elements (i+1..) are all greater than element i, returning a tuple of (&mut s[0..i], &mut s[i], &mut s[i+1..]) after the shuffle. This uses a pattern-defeating quicksort and is O(n) according to the docs.\n\nWe care about this last section, so we need to have i = (n-k-1) so that the lengths of elements in the tuple are (n-k-1, 1, k). However, in the event than k == n or k == n-1, this would cause a panic, so in that case we just sort the entire vec.\n\n# Complexity\n- Time complexity: O(n + k log k). The partition operation is O(n), and then we sort the top k. For small k this is essentially linear; for large k this is essentially log-linear.\n\n- Space complexity: O(1) if we partition and sort happiness in-place.\n\n# Code\n```\nuse std::collections::BinaryHeap;\nuse std::cmp::Reverse;\nimpl Solution {\n pub fn maximum_happiness_sum(mut happiness: Vec<i32>, k: i32) -> i64 {\n let n = happiness.len();\n let k = k as usize;\n let top_k = if k + 1 < happiness.len() {\n happiness.select_nth_unstable(n - k - 1).2\n } else {\n happiness.as_mut_slice()\n };\n top_k.sort_unstable();\n\n (0..).zip(top_k.iter().copied().rev())\n .take_while(|&(penalty, unpenalized)| penalty < unpenalized)\n .take(k as usize)\n .map(|(penalty, unpenalized)| (unpenalized - penalty) as i64)\n .sum()\n }\n}\n``` | 5 | 0 | ['Rust'] | 1 |
maximize-happiness-of-selected-children | [Python3] 2 line solution || sort + greedy || 822ms / 43.50mb || beats 100% | python3-2-line-solution-sort-greedy-822m-6t4n | python3 []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse = True)\n return sum | yourick | NORMAL | 2024-03-10T09:01:29.472734+00:00 | 2024-03-10T12:05:52.380178+00:00 | 174 | false | ```python3 []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse = True)\n return sum(max(h-i, 0) for i, h in enumerate(happiness[:k]))\n```\n\n##### For me this problem is similar to [274. H-Index](https://leetcode.com/problems/h-index/description/)\n```python3 []\nclass Solution:\n def hIndex(self, citations: List[int]) -> int:\n return sum(n >= i for i, n in enumerate(sorted(citations, reverse=True), start=1))\n``` | 5 | 0 | ['Sorting', 'Python', 'Python3'] | 1 |
maximize-happiness-of-selected-children | Priority_queue max heap vs min heap | priority_queue-max-heap-vs-min-heap-by-a-jp9c | Intuition\n Describe your first thoughts on how to solve this problem. \nUse a max heap(priority_queue) to solve.\n 2nd approach uses a min heap.\n# Approach\n | anwendeng | NORMAL | 2024-03-10T04:54:41.708259+00:00 | 2024-05-09T01:49:22.067873+00:00 | 324 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse a max heap(priority_queue) to solve.\n 2nd approach uses a min heap.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind the k largest elements using a max heap\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n+k\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n int n=happiness.size();\n priority_queue<int> pq(happiness.begin(), happiness.end());//maxheap\n long long sum=0;\n for(int i=0; i<k; i++){\n long long x=max(0, pq.top()-i);\n // cout<<x<<endl;\n pq.pop();\n sum+=x;\n }\n \n return sum;\n \n }\n};\n\n```\n# C++ using min heap\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n int n=happiness.size();\n priority_queue<int, vector<int>, greater<int>> pq(happiness.begin(), happiness.begin()+k);//minheap\n for(int i=k; i<n; i++){\n pq.push(happiness[i]);\n pq.pop();\n }\n long long sum=0;\n for(int i=k-1; i>=0; i--){\n long long x=max(0, pq.top()-i);\n // cout<<x<<endl;\n pq.pop();\n sum+=x;\n }\n return sum;\n \n }\n};\n``` | 5 | 0 | ['Heap (Priority Queue)', 'C++'] | 1 |
maximize-happiness-of-selected-children | Beats 100% | Java, C++, Python, Javascript| Less Code ✅✅ | beats-100-java-c-python-javascript-less-3opkd | Please Upvote \u2705\u2705\nans: A long variable initialized to 0 to store the maximum happiness sum.\nmin: An integer variable initialized to 0 to keep track o | Ikapoor123 | NORMAL | 2024-03-10T04:14:14.549619+00:00 | 2024-03-10T04:49:22.068217+00:00 | 604 | false | # Please Upvote \u2705\u2705\nans: A long variable initialized to 0 to store the maximum happiness sum.\nmin: An integer variable initialized to 0 to keep track of the minimum happiness given so far.\n\n- The happiness array is sorted in descending order using Arrays.sort(happiness). This ensures that people with higher happiness levels get prioritized.\n\n- The code iterates through the happiness array in reverse order (from highest happiness to lowest) using a for loop starting from i = happiness.length - 1.\n- The loop continues as long as i is greater than or equal to 0 and k (remaining people to be happy) is greater than 0.\n- Inside the loop, for each person (happiness[i]), the difference between their happiness and the min happiness given so far is calculated. This represents the additional happiness gained by giving happiness to this person.\n- If the happiness gain (happiness[i] - min) is positive (meaning the person gets happier), it\'s added to the ans (total happiness sum).\nThe min happiness is then incremented by 1 to account for the happiness given to the current person.\n- After iterating through all relevant elements, the function returns the ans (maximum happiness sum achievable).\n\n# Please Upvote\u2705\u2705\n# Code\n``` java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n long ans = 0;\n int min = 0;\n \n Arrays.sort(happiness);\n \n for(int i=happiness.length-1;i>=0 && k>0;i--){\n \n k--;\n if(min<happiness[i])\n ans+=happiness[i]-min;\n min++;\n }\n return ans;\n }\n}\n```\n```javascript []\n\nvar maximumHappinessSum = function(happiness, k) {\n happiness.sort((a, b) => b - a);\n\n let ans = 0;\n let minHappiness = 0;\n\n for (let i = 0; i < happiness.length && k > 0; i++) {\n if (minHappiness < happiness[i]) {\n ans += happiness[i] - minHappiness;\n }\n minHappiness++;\n k--;\n }\n\n return ans;\n};\n```\n```python []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n ans = 0\n min_happiness = 0\n\n \n happiness.sort(reverse=True)\n\n for i in range(len(happiness)):\n if i >= k:\n break\n\n \n happiness_gain = happiness[i] - min_happiness\n\n \n ans += happiness_gain\n\n min_happiness += 1\n\n return ans\n```\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long ans = 0;\n int minHappiness = 0;\n\n \n sort(happiness.begin(), happiness.end(), std::greater<int>());\n\n for (int i = 0; i < k; i++) {\n if (minHappiness < happiness[i]) {\n ans += happiness[i] - minHappiness;\n }\n minHappiness++;\n }\n\n return ans;\n }\n};\n```\n# Just\n\n\n | 5 | 1 | ['Array', 'C', 'Sorting', 'C++', 'Java', 'Go', 'Python3', 'Kotlin', 'JavaScript', 'C#'] | 2 |
maximize-happiness-of-selected-children | 100% | 100-by-sarvajnya_18-gej7 | Complexity\n- Time complexity: O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n | sarvajnya_18 | NORMAL | 2024-03-10T04:04:45.055060+00:00 | 2024-08-02T13:15:01.782605+00:00 | 467 | false | # Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n s = 0\n for i in range(k):\n s += max(0, happiness[i]-i)\n return s\n``` | 5 | 0 | ['Math', 'Sorting', 'Python3'] | 4 |
maximize-happiness-of-selected-children | Solution | solution-by-yash1hingu-ijzc | Intuition\nThe problem is asking to maximize the sum of happiness by choosing k elements from the given array. The happiness of an athlete decreases by 1 for ea | yash1hingu | NORMAL | 2024-05-09T16:52:40.266067+00:00 | 2024-05-09T16:52:40.266102+00:00 | 43 | false | # Intuition\nThe problem is asking to maximize the sum of happiness by choosing `k` elements from the given array. The happiness of an athlete decreases by 1 for each athlete that has a higher score. So, we need to choose the `k` largest elements from the array to maximize the sum.\n\n# Approach\n- We first sort the array in ascending order.\n- Then, we iterate from the end of the array (which contains the largest elements) towards the beginning.\n- For each element, we check if subtracting the current rank (`j`) from the happiness score will result in a non-positive number or if we have already chosen `k` elements. If either of these conditions is true, we break the loop.\n- Otherwise, we add the adjusted happiness score (happiness score minus rank) to the total sum and increment the rank.\n\n# Complexity\n- Time complexity: The time complexity is $$O(n \\log n)$$ due to the sorting operation, where `n` is the length of the input array.\n- Space complexity: The space complexity is $$O(1)$$ as we are not using any additional space that scales with the input size.\n\n# Code\nThe provided code correctly implements the described approach. Here it is again for reference:\n\n```java\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n long ans = 0;\n int j = 0;\n int n = happiness.length;\n Arrays.sort(happiness);\n for(int i=n-1;i>=0;i--){\n if(happiness[i]-j <= 0 || j==k){\n break;\n }\n ans = ans + (happiness[i]-j);\n j++;\n }\n\n return ans;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
maximize-happiness-of-selected-children | Greedy Approach with explanation | greedy-approach-with-explanation-by-anup-i6sh | Intuition\n- We can greedily pick child with maximum happiness\n- After n pass happiness of childrens decreases by n so if we are picking children at xth time h | anupsingh556 | NORMAL | 2024-05-09T05:15:53.819793+00:00 | 2024-05-09T05:15:53.819820+00:00 | 436 | false | # Intuition\n- We can greedily pick child with maximum happiness\n- After `n` pass happiness of childrens decreases by `n` so if we are picking children at xth time his net happiness will be $$h[x]-x$$\n- We can sort the array and can pick all children who will have positive net happiness \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Sort array in descending order\n- Start picking children from 0th index and add its net happiness in result\n- break the iteration if net happiness if false or we have reached our quota of n students\n# Complexity\n- Time complexity: O(nlogn)\n - O(nlogn) for sorting array\n - O(n) for linear traversal and getting result\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Constant Space no extra space needed\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n sort(h.begin(), h.end(), greater<int>());\n int i=0;\n long long res = 0l;\n while(i<h.size() && i<k) {\n if(h[i]<=i)break;\n res = res + h[i] - i;\n i++;\n }\n return res;\n }\n};\n```\n```go []\nfunc maximumHappinessSum(h []int, k int) int64 {\n sort.Slice(h, func(i, j int) bool {\n return h[i] > h[j]\n })\n\n var res int64 = 0\n for i := 0; i < len(h) && i < k; i++ {\n if h[i] <= i {\n break\n }\n res += int64(h[i] - i)\n }\n return res \n}\n```\n```python []\nclass Solution(object):\n def maximumHappinessSum(self, h, k):\n h.sort(reverse=True)\n res = 0\n for i in range(min(len(h), k)):\n if h[i] <= i:\n break\n res += h[i] - i\n return res\n \n```\n | 4 | 0 | ['Greedy', 'Python', 'C++', 'Go'] | 2 |
maximize-happiness-of-selected-children | Beats 100% || 79ms || Explained Approach || C++ || Java || Python | beats-100-79ms-explained-approach-c-java-eovv | Intuition\n Describe your first thoughts on how to solve this problem. \nWe need to select k children with the maximum happiness value. Therefore, sorting the h | AKJ5196 | NORMAL | 2024-04-09T05:58:40.902316+00:00 | 2024-04-09T05:58:40.902349+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to select k children with the maximum happiness value. Therefore, sorting the happiness vector in non-increasing order seems like a reasonable approach.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the happiness vector in non-increasing order.\n```\nsort(happiness.begin(), happiness.end(), greater<int>());\n```\n2. Initialize sum(long long) which will store the maximum happiness value.\n```\nlong long sum = 0;\n```\n3. Iterate k times over the sorted happiness vector. Remember to decrement the happiness of every other happiness value.\n```\nhappiness[i] = max(0, happiness[i]-i);\nsum += happiness[i];\n```\n# Complexity\n- Time complexity: O(nlog(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);\n sort(happiness.begin(), happiness.end(), greater<int>());\n long long sum = 0;\n for(int i = 0; i < k; i++) {\n happiness[i] = max(0, happiness[i]-i);\n sum += happiness[i];\n }\n return sum;\n }\n};\n```\n```Java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n long sum = 0;\n for (int i = happiness.length - 1; i >= happiness.length - k; i--) {\n happiness[i] = Math.max(0, happiness[i] - (happiness.length - 1 - i));\n sum += happiness[i];\n }\n return sum;\n }\n}\n```\n```Python []\nfrom typing import List\n\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True) \n total_sum = 0\n for i in range(k):\n happiness[i] = max(0, happiness[i] - i) \n total_sum += happiness[i] \n return total_sum \n\n``` | 4 | 0 | ['Array', 'Greedy', 'Sorting', 'C++', 'Java', 'Python3'] | 0 |
maximize-happiness-of-selected-children | Simple approach in JS - beat 100% | simple-approach-in-js-beat-100-by-dhnbro-bx3r | Approach\n Describe your approach to solving the problem. \n- Sorting array in non-ascending order.\n- Iterating through the Sorted Array\n- Calculating the Max | dhnbroken | NORMAL | 2024-03-11T08:04:46.025843+00:00 | 2024-03-11T08:04:46.025875+00:00 | 94 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n- Sorting array in non-ascending order.\n- Iterating through the Sorted Array\n- Calculating the Maximum Happiness Sum, The contribution is calculated by subtracting the index of the child from its happiness value.\n- Handling Non-positive Happiness Values by Math.max\n- Returning the Maximum Happiness Sum\n\n# Complexity\n- Time complexity: O(n log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} happiness\n * @param {number} k\n * @return {number}\n */\nvar maximumHappinessSum = function (happiness = [], k = 0) {\n happiness.sort((a, b) => b - a);\n let max = 0;\n\n for (let i = 0; i < k; i++) {\n max += happiness[i] - i <= 0 ? 0 : happiness[i] - i;\n }\n\n return max;\n};\n``` | 4 | 0 | ['JavaScript'] | 0 |
maximize-happiness-of-selected-children | 🔥Today's Contest Sol | ✅️Beats 100% ✅️| Easy C++ | Full Explanation🔥 | todays-contest-sol-beats-100-easy-c-full-0hau | Intuition\n\n Describe your first thoughts on how to solve this problem. \nWe prioritize selecting children with higher happiness values initially to maximize t | vipulbhardwaj279 | NORMAL | 2024-03-10T04:34:56.957268+00:00 | 2024-03-10T04:47:45.205822+00:00 | 279 | false | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe prioritize selecting children with higher happiness values initially to maximize the sum of happiness. Then we decrement the happiness value of each selected child by its index, ensuring it remains positive, to maximize the overall happiness sum.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the happiness array in non-increasing order.\n2. Initialize the sum of happiness, ans, to 0.\n3. Iterate k times:\n a. Decrement the happiness value of the current child by its index (starting from 0) or set it to 0 if negative.\n b. Add the updated happiness value to ans.\n4. Return ans.\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Please UPVOTE if you like it : )\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n \n sort(h.begin(),h.end(),greater<int>());\n \n int i=0;\n long long ans=0;\n while(k--){\n h[i]=max(h[i]-i,0);\n ans+=h[i];\n i++;\n }\n return ans;\n }\n};\n```\n\n | 4 | 0 | ['C++'] | 5 |
maximize-happiness-of-selected-children | Beats 100% 💯 || 0ms ✅ || 3 line solution 🔥 || Shortest and Very Easy to understand for beginners | beats-100-0ms-3-line-solution-shortest-a-udzx | Code\n\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n sort(h.begin(), h.end(), greater<int>());\n long l | soukarja | NORMAL | 2024-03-10T04:13:36.690992+00:00 | 2024-03-10T04:13:36.691026+00:00 | 92 | false | # Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n sort(h.begin(), h.end(), greater<int>());\n long long tot = 0, c = 0;\n while (k--) if (h[c] - c > 0) tot += h[c] - c; c++;\n return tot;\n }\n};\n```\n\n | 4 | 0 | ['C', 'Python', 'C++', 'Java', 'Python3', 'C#'] | 1 |
maximize-happiness-of-selected-children | Sorting + Greedy solution | sorting-greedy-solution-by-drgavrikov-3ivb | Approach\n Describe your approach to solving the problem. \nTo achieve the maximum sum from $K$ elements of the array, we sort it in descending order and select | drgavrikov | NORMAL | 2024-05-09T19:29:08.040551+00:00 | 2024-06-02T07:51:43.724628+00:00 | 9 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nTo achieve the maximum sum from $K$ elements of the array, we sort it in descending order and select the first $K$ members.\n\nWe subtract the value of the step from the value at that position in the array at each step. If the current value becomes less than zero, we terminate the loop.\n\n# Complexity\n- Time complexity: $O(N * log N)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$ additional space\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n static long long maximumHappinessSum(std::vector<int> &happiness, int k) {\n std::sort(happiness.begin(), happiness.end(), greater<int>());\n long long result = 0;\n for (size_t step = 0; step < k; step++) {\n int value = happiness[step] - static_cast<int>(step);\n if (value < 0) break;\n result += value;\n }\n return result;\n }\n};\n\n```\n\nMost of my solutions are in [C++](https://github.com/drgavrikov/leetcode-cpp) and [Kotlin](https://github.com/drgavrikov/leetcode-jvm) on my [Github](https://github.com/drgavrikov). | 3 | 0 | ['Sorting', 'C++'] | 0 |
maximize-happiness-of-selected-children | Simple Sorting || Implementation | simple-sorting-implementation-by-ashish_-cqof | Maximize-Happiness-Of-Selected-Children\n\n# Code\n\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n long long an | Ashish_Ujjwal | NORMAL | 2024-05-09T12:12:41.925682+00:00 | 2024-05-09T12:12:41.925711+00:00 | 5 | false | # Maximize-Happiness-Of-Selected-Children\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n long long ans = 0;\n sort(h.rbegin(), h.rend());\n int i = 0, m = 0;\n while(k--){\n if(h[i] - m < 0) break;\n else ans += h[i] - m;\n i++;\n m++;\n }\n return ans;\n }\n};\n```\n\n | 3 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Beats 99.97% Time⌛🔥 99.10% Space💾🔥| Python, C++ 💻 | Clear Explanation📗 | beats-9997-time-9910-space-python-c-clea-2vr6 | Beats 99.97% Time\u231B\uD83D\uDD25 99.10% Space\uD83D\uDCBE\uD83D\uDD25| Python, C++ \uD83D\uDCBB | Clear Explanation\uD83D\uDCD7\n\n## 1. Proof\n\n### 1.1. Py | kcp_1410 | NORMAL | 2024-05-09T10:55:40.990768+00:00 | 2024-05-09T10:55:40.990802+00:00 | 18 | false | # Beats 99.97% Time\u231B\uD83D\uDD25 99.10% Space\uD83D\uDCBE\uD83D\uDD25| Python, C++ \uD83D\uDCBB | Clear Explanation\uD83D\uDCD7\n\n## 1. Proof\n\n### 1.1. Python3\n\n\n### 1.2. C++\n\n\n\n## 2. Algorithms\n- Sorting\n- Greedy\n\n## 3. Code (with explanation each line)\n```python3 []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n res = 0 # Result\n cur_k = k # Current k after each pick\n happiness.sort() # Top of stack contains max happiness\n \n while cur_k > 0: # While budget is enough for picking (each iteration indicates each pick)\n pick = happiness.pop() # Greedy: always pick top of stack for max happiness\n picked = k - cur_k # Number of times we\'ve picked, and also the amount of happiness to subtract from the current pick\n if pick > picked: # Ensure the current pick will still be positive after subtracting from it\n res += (pick - picked) # Add the positive subtracted happiness to result\n else: # After subtracting, if happiness is still <= 0 even though we tried to be greedy, that means there\'s nothing more to add to result\n break\n cur_k -= 1 # -1 turn of picking\n \n return res # Result\n```\n\n```cpp []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long int res = 0;\n long long int pick = 0, picked = 0;\n int cur_k = k;\n sort(happiness.begin(), happiness.end());\n\n while (cur_k > 0) {\n pick = happiness.back(); // Greedy: get top of stack\n happiness.pop_back(); // Pop top of stack\n picked = k - cur_k;\n if (pick > picked) {\n res += (pick - picked);\n }\n else {\n break;\n }\n cur_k--;\n }\n return res;\n }\n};\n```\n\n## 4. Complexity\n- Time complexity: $$O(k)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n### Upvote if you find this solution helpful, thank you \uD83E\uDD0D | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'C++', 'Python3'] | 0 |
maximize-happiness-of-selected-children | ✅ One Line Solution | one-line-solution-by-mikposp-g798 | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1\nTime complexity: O(nlog(k)). Space co | MikPosp | NORMAL | 2024-05-09T10:17:03.199299+00:00 | 2024-05-09T10:19:56.937575+00:00 | 349 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1\nTime complexity: $$O(n*log(k))$$. Space complexity: $$O(k)$$.\n```\nclass Solution:\n def maximumHappinessSum(self, a: List[int], k: int) -> int:\n return sum(max(0,v-i) for i,v in enumerate(nlargest(k,a)))\n```\n\n# Code #2.1\nTime complexity: $$O(n*log(k))$$. Space complexity: $$O(k)$$.\n```\nclass Solution:\n def maximumHappinessSum(self, a: List[int], k: int) -> int:\n return sum(v-i for i,v in takewhile(lambda q:lt(*q),enumerate(nlargest(k,a))))\n```\n\n# Code #2.2\nTime complexity: $$O(n*log(k))$$. Space complexity: $$O(k)$$.\n```\nclass Solution:\n def maximumHappinessSum(self, a: List[int], k: int) -> int:\n return -sum(starmap(sub,takewhile(lambda q:lt(*q),enumerate(nlargest(k,a)))))\n``` | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Python', 'Python3'] | 1 |
maximize-happiness-of-selected-children | ✅Easy✨||C++|| Beats 100% || With Explanation || | easyc-beats-100-with-explanation-by-olak-ek26 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves selecting children from a queue to maximize the sum of their happi | olakade33 | NORMAL | 2024-05-09T08:11:27.480605+00:00 | 2024-05-09T08:11:27.480636+00:00 | 92 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves selecting children from a queue to maximize the sum of their happiness values. Each time a child is selected, the happiness of all unselected children decreases by 1.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the Happiness Values: Sort the happiness values in non-increasing order to prioritize selecting children with higher happiness values.\n2. Iterate Through the Sorted Values: Iterate through the sorted happiness values.\n. For each happiness value, if it is greater than the index (position) of the child in the sorted order and there are still turns left (k > 0), select the child.\n. Increment the answer by the difference between the happiness value and the index.\n. Decrease the number of turns available (k) after selecting a child.\n3. Return the Maximum Happiness Sum: Return the maximum sum of happiness achieved by selecting children.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n. Sorting the happiness values takes O(n log n) time, where n is the number of children.\n. The loop iterates through the sorted happiness values, taking O(n) time.\n. Overall, the time complexity is O(n log n).\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) as the algorithm only uses a constant amount of extra space.\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& hap, int k) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n long long ans = 0;\n sort(hap.begin(), hap.end(), greater<int>());\n int n = hap.size();\n for(int i = 0; i < n; i++) {\n if(hap[i] <= i) break;\n if(k == 0) break;\n ans += hap[i] - i;\n k--;\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | 👏😻🙈Beats 97.44% of users with Java🎉||✅ one line (for loop) code || 💯🔥💥 | beats-9744-of-users-with-java-one-line-f-mb0d | SCREENSHORT\n\n\n# Intuition\nWe need max happiness and after selecting one dec all by one ... Hence select the one and sec by dec 1 and so one. \n\n>It\'s too | Prakhar-002 | NORMAL | 2024-05-09T05:51:40.478312+00:00 | 2024-05-09T05:51:40.478342+00:00 | 43 | false | # SCREENSHORT\n\n\n# Intuition\nWe need max happiness and after selecting one dec all by one ... Hence select the one and sec by dec 1 and so one. \n\n>It\'s too easy just follow the steps.\n---\n\n\n# Approach\nWe will add and check max of selected and 0 hence we\'ll get our ans.\n\n1. ### Initialize variables Dec, Ans, n\n\n ```\n int dec = 0;\n int n = happiness.length;\n long ans = 0;\n ```\n2. ### First **sort** the array \n\n ```\n Arrays.sort(happiness);\n ```\n3. ### Apply a for loop in decrement order and upto **n - k** \n \n ```\n for (int i = n - 1; i >= n - k; i--) {\n //loop One line body\n }\n ```\n4. ### Write one line code here that is **max of happ[i] and 0** \n \n ```\n ans += Math.max(0, happiness[i] - dec); \n dec++; \n \n ```\n > Do not write dec++ in the same line it will dec our speed.\n\n ```\n // Do not write like this...\n ans += Math.max(0, happiness[i] - dec++); \n \n ```\n5. ### Return res \uD83D\uDE01\uD83D\uDE01\n\n---\n\n\n# Complexity\n- Time complexity: $O(nlogn)$\n\n- Space complexity: $O(1)$\n\n---\n\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n int dec = 0;\n int n = happiness.length;\n long ans = 0;\n for (int i = n - 1; i >= n - k; i--) {\n ans += Math.max(0, happiness[i] - dec);\n dec++;\n }\n return ans;\n }\n}\n``` | 3 | 0 | ['Greedy', 'Sorting', 'Java'] | 1 |
maximize-happiness-of-selected-children | ✅✅97.44% with Java🔥Beginner Friendly🔥Simple Logic🔥Easy Explanation🔥 | 9744-with-javabeginner-friendlysimple-lo-dib1 | \n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nWe have to maximize the happiness of selected children. From the name itself, we | Pratik-Shrivastava | NORMAL | 2024-05-09T05:47:15.847257+00:00 | 2024-05-09T05:47:15.847282+00:00 | 74 | false | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe have to `maximize` the happiness of selected children. From the name itself, we can conclude that it is a `Greedy Problem`.\nNo need to fear from the name, as the explaination will be easy\uD83D\uDE09.\n\nBut we have to keep the following points in the mind:\n\n 1. We have to select k children with maximum happiness.\n 2. If we select a child, then we cannot reselect it again.\n 3. Each time we select a child, happiness of other\n children decrease by 1.\n 4. Happiness of a child cannot go below 0.\nAfter keeping these points in mind, we are ready to understand the approach of this question.\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can follow the below steps to approach this problems:\n\n Step-1: Sort the array.\n Step-2: Create a variable max_happiness that store our answer.\n Step-3: Create a variable minus_meter that check how much happiness\n we have to substract from the current child.\n Step-4: Iterate over the array from last to first index untill k\n selections are made.\n Step-5: For each child, calculate happiness and add it to answer.\nFinally, return the `max_happiness.`\n\n# Explanation\n$$Step1: $$ We sort the array as we want maximum happiness in each iteration.\n$$Step2: $$ The answer is updated in each iteration so we need a variable to store it.\n$$Step3: $$ In each iteration, we will select a child with maximun happiness but the\nhappiness of other children will decrease by 1. \nSo, we can say that,\n \n`After 1st iteration: happiness of rest children decreased by a total of 1.`\n`After 2nd iteration: happiness of rest children decreased by a total of 2.`\n`After 3rd iteration: happiness of rest children decreased by a total of 3.`\nand so on.\nSo, we need a variable minus_meter to store how much value we need to subtract from each child to find the current_max_happiness.\n\n$$Step4: $$ We iterate from last index as the array is sorted in non-decreasing order(ascending order), so the maximum happiness will be at the last.\n\n $$Step5: $$ We will calculate the current_max_happiness by subtracting the minus_meter and also checking it does not go negative. And then we add in maximum_happiness.\n\nFinally, we will the return the maximum_happines.\n\n\n# Complexity\n- Time complexity: $$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe actual time to complete the program is O(NlogN) (sorting time) + O(N) (Loop time).\nSo, the time complexity becomes O(NlogN).\nWe, are not using any external space so, space complexity is O(1).\n\n\n\n# Code\n\n```java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n\n // Step-1 \n Arrays.sort(happiness);\n\n // Step-2\n long max_happiness = 0;\n\n // Step-3\n int minus_meter = 0;\n\n // Step-4\n for(int i = happiness.length-1; i >= 0 && k > 0; i--)\n {\n // Step-5\n int current_max_happiness = happiness[i] - minus_meter;\n if(current_max_happiness < 0)\n {\n current_max_happiness = 0;\n }\n max_happiness += current_max_happiness;\n\n // Increment minus_meter in each iteration.\n minus_meter++;\n\n // Derement k after each selection.\n k--;\n }\n\n return max_happiness; \n }\n}\n```\nTerms and Conditions:\nIt beat 97% in the first attempt, but when I submitted it again, it only beat 51%. I don\'t know why it happened. That\'s why I am mentioning it here.\nPlease notice the top picture - it took 34 ms in first attempt.\nNow it is taking 35 ms. The difference of 1 ms can create such a huge difference. | 3 | 0 | ['Greedy', 'Java'] | 2 |
maximize-happiness-of-selected-children | 💯✅🔥Easy Java Solution|| 34 ms ||≧◠‿◠≦✌ | easy-java-solution-34-ms-_-by-suyalneera-auyr | Intuition\n Describe your first thoughts on how to solve this problem. \nThe approach taken in the code aims to maximize the total happiness sum by iteratively | suyalneeraj09 | NORMAL | 2024-05-09T00:33:56.123518+00:00 | 2024-05-09T00:33:56.123565+00:00 | 81 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe approach taken in the code aims to maximize the total happiness sum by iteratively reducing the happiness values of the highest elements in the sorted array. By subtracting a decreasing amount from each element, the code attempts to distribute the reductions in a way that maximizes the overall happiness sum.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe given code sorts the array of happiness values in ascending order. It then iterates over the sorted array from the end towards the beginning, adjusting each happiness value by subtracting a decreasing amount based on its position in the sorted array. The adjusted happiness values are summed up to calculate the maximum happiness sum achievable after applying the adjustments.\n# Complexity\n- Time complexity: O(n log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n int n = happiness.length;\n long res = 0;\n \n for (int i = n - 1; k > 0; i--) {\n happiness[i] = Math.max(happiness[i] - (n - 1 - i), 0);\n res += happiness[i];\n k--;\n }\n \n return res;\n }\n}\n```\n\n | 3 | 0 | ['Array', 'Greedy', 'Java'] | 1 |
maximize-happiness-of-selected-children | Easy Solution | beats 100 % | Explanation | easy-solution-beats-100-explanation-by-k-zbk6 | Approach\n Describe your approach to solving the problem. \nGreedy\n# Complexity\n- Time complexity:O(n) n = len(happiness) + n log n\n Add your time complexity | kmuhammadjon | NORMAL | 2024-04-22T11:25:32.852181+00:00 | 2024-04-22T11:25:32.852210+00:00 | 55 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy\n# Complexity\n- Time complexity:O(n) n = len(happiness) + n log n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc maximumHappinessSum(happiness []int, k int) int64 {\n // sorting in reverse order and we greedily start from\n // biggest group\n sort.Slice(happiness, func(i, j int) bool{\n return happiness[i] > happiness[j]\n })\n // actually you can decrese even if t cause negative number\n // and greedy approach still suits \n totalHappiness := 0 \n for i := 0; i < k ; i++{\n if happiness[i] - i > 0{\n // substracting i cuz it is cost to come to that point\n totalHappiness += happiness[i] - i\n }\n }\n\n return int64(totalHappiness)\n}\n``` | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'Go'] | 1 |
maximize-happiness-of-selected-children | Easy java Solution | easy-java-solution-by-1asthakhushi1-bfun | \n\n# Code\n\nclass Solution {\n public long maximumHappinessSum(int[] hap, int k) {\n Arrays.sort(hap);\n long ans=hap[hap.length-1];\n | 1asthakhushi1 | NORMAL | 2024-03-10T04:04:33.794368+00:00 | 2024-03-10T04:10:51.958684+00:00 | 523 | false | \n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] hap, int k) {\n Arrays.sort(hap);\n long ans=hap[hap.length-1];\n k--;\n int count=1;\n for(int i=hap.length-2;i>=0;i--){\n if(k>0){\n if(hap[i]-count<=0){\n ans+=0;\n break;\n }\n else\n ans+=hap[i]-count;\n count++;\n k--;\n }\n }\n return ans;\n }\n}\n``` | 3 | 0 | ['Array', 'Sorting', 'Java'] | 3 |
maximize-happiness-of-selected-children | C++ 100% faster| Priority Queue | Easy Step By Step Explanation | c-100-faster-priority-queue-easy-step-by-aybo | Intuition\n - The key challenge in maximizing the total happiness of selected children lies in strategically choosing children to minimize the overall "happin | VYOM_GOYAL | NORMAL | 2024-03-10T04:02:31.954709+00:00 | 2024-03-10T04:18:06.723111+00:00 | 322 | false | # Intuition\n - The key challenge in maximizing the total happiness of selected children lies in strategically choosing children to minimize the overall "happiness loss" caused by their selection. Since happiness values decrease after each pick, selecting children with the highest initial happiness first minimizes this loss.\n\n# Approach\n - We\'ll leverage a priority queue (PQ) to efficiently select children with the highest happiness values.\n\n - **Prioritize Happiness:** Iterate through the happiness array and insert each happiness value into the priority queue (PQ). The PQ acts as a max-heap, ensuring that the children with the highest happiness are at the top.\n\n - **Select and Accumulate Happiness:**\n - Initialize a variable sum to store the total happiness of selected children.\n - Use a loop to iterate k times (number of selections):\n - Extract the maximum happiness value (top) from the PQ.\n - Since happiness decreases by cnt (number of selections made so far) for remaining children, subtract cnt from top to get the actual happiness gained by selecting this child.\n - If top is still positive (happiness gain exists), add it to the sum.\n - Decrement cnt to account for the happiness decrease on the next selection.\n - Remove (pop) the selected child from the PQ.\n\n# Complexity\n- Time complexity: **O(n * log n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: **O(n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n \n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n priority_queue<int> pq; \n\n for (int h : happiness) {\n pq.push(h);\n }\n\n long long sum = 0;\n int cnt = 0;\n while (k--) {\n int top = pq.top()-cnt;\n pq.pop();\n if(top>0){\n sum+=top;\n }\n cnt++;\n }\n\n return sum;\n }\n};\n\n```\n\n\n | 3 | 0 | ['Array', 'Heap (Priority Queue)', 'C++'] | 3 |
maximize-happiness-of-selected-children | maximize-happiness-of-selected-children 🚀Hard to catch 💯Medium Solution🫡cpp | maximize-happiness-of-selected-children-nppvf | \n\n\n# Code\n\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n sort(h.begin(),h.end());\n long long int s | Saiyam_Dubey_ | NORMAL | 2024-05-11T09:28:16.997801+00:00 | 2024-05-11T09:28:16.997831+00:00 | 2 | false | \n\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n sort(h.begin(),h.end());\n long long int sum=0;\n long long int l=0;\n // int mini = h[0];\n for(int i=h.size()-1,j=0;i>=0,j<k;i--,j++){\n if(h[i]<l){\n long long int add = 0;\n l++;\n sum = sum + add;\n }\n else{\n long long int add = h[i]-l;\n l++;\n sum = sum + add;\n // mini--;\n }\n }\n return sum;\n }\n};\n```\n\n\n | 2 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Happiest solution || Beginner | happiest-solution-beginner-by-pratik_she-p7nj | Intuition\nThe problem seems to involve finding the maximum sum of happiness among a given set of people, where each person\'s happiness is represented by an el | Pratik_Shelke | NORMAL | 2024-05-09T13:39:32.320036+00:00 | 2024-05-09T13:39:32.320064+00:00 | 0 | false | # Intuition\nThe problem seems to involve finding the maximum sum of happiness among a given set of people, where each person\'s happiness is represented by an element in the array. We need to select a subset of size k from the array such that the total happiness sum is maximized.\n\n# Approach\nOne possible approach is to sort the array in ascending order, indicating that the least happy people are at the beginning. Then, iterate through the sorted array from the end (most happy people) and adjust their happiness based on their position in the sorted array. Specifically, for each person, we subtract their current happiness by the number of people with higher happiness levels than them. This adjustment ensures that people with higher happiness contribute more to the total sum. We continue this process until we have selected k people or exhausted the array.\n\n# Complexity\n- Time complexity:\n $$O(nlogn)$$ \n\n- Space complexity:\n $$O(1)$$ \n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n int n=happiness.length;\n int i=n-1;\n long max=0;\n while(k>0 && i>=0)\n { \n max+=Math.max(0,happiness[i]-(n-i-1));\n i--;\n k--; \n \n }\n return max; \n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Java'] | 2 |
maximize-happiness-of-selected-children | Just cant understand why this question is marked medium | just-cant-understand-why-this-question-i-kjm0 | \n\n# Complexity\n- Time complexity:O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your space complexity here, e.g. O(n) | TechTinkerer | NORMAL | 2024-05-09T10:58:50.070951+00:00 | 2024-05-09T10:58:50.070979+00:00 | 8 | false | \n\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long \nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n sort(happiness.begin(),happiness.end(),greater<int>());\n int j=0;\n ll ans=0;\n for(int i=0;i<k;i++){\n\n ans+=((happiness[j]>=i)?(happiness[j]-i):0);\n j++;\n }\n\n return ans;\n }\n};\n``` | 2 | 0 | ['Sorting', 'Heap (Priority Queue)', 'C++'] | 0 |
maximize-happiness-of-selected-children | [C++] 2 lines with std::partial_sort and std::accumulate | c-2-lines-with-stdpartial_sort-and-stdac-7j33 | Intuition\nsort the k largest elements in decreasing order, then sum the values minus n with n starting at 0 and being incremented at each iteration of the sum. | user2670f | NORMAL | 2024-05-09T10:29:19.787337+00:00 | 2024-05-09T10:30:02.016057+00:00 | 37 | false | # Intuition\nsort the k largest elements in decreasing order, then sum the values minus `n` with `n` starting at `0` and being incremented at each iteration of the sum.\n\n# Approach\nUse STL. Note that in order to save a line, I declared the variable `n` in the capture clause of the lambda, which requires the lambda to be non `const`. Lambdas being `const` by default, the keyword is `mutable`.\n\n\n# Complexity\n- Time complexity: $$O(n log(k))$$\n- Space complexity: $$O(1)$$\n\n\n# Code\n```cpp\nlong long maximumHappinessSum(vector<int>& happ, int k) {\n partial_sort(happ.begin(), happ.begin()+k, happ.end(), greater<int>());\n return accumulate(happ.begin(), happ.begin()+k, (long long)0, [n=0](long long a, int b)mutable{return a + max(0, b-n++);});\n}\n``` | 2 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | ✅Easiest Solution🔥||Beat 97.44%🔥||Beginner Friendly✅🔥 | easiest-solutionbeat-9744beginner-friend-pux1 | Intuition\nSorting: The code begins by sorting the array happiness in ascending order using Arrays.sort(happiness);. This step ensures that the array is in asce | siddhesh11p | NORMAL | 2024-05-09T10:08:10.025426+00:00 | 2024-05-09T10:08:44.083304+00:00 | 13 | false | # Intuition\nSorting: The code begins by sorting the array happiness in ascending order using Arrays.sort(happiness);. This step ensures that the array is in ascending order, making it easier to calculate the maximum happiness sum later.\n\nCalculating Maximum Happiness Sum:\nThe algorithm initializes max to 0 to keep track of the maximum happiness sum.\nIt sets n as the length of the happiness array and i as the index pointing to the last element of the sorted array (n - 1).\nThe while loop continues until k becomes 0 or i goes below 0.\nInside the loop, it checks if i is greater than or equal to 0.\nIf true, it calculates the maximum between 0 and happiness[i] - (n - i - 1) and adds this value to max.\nIt then decrements i and k by 1 in each iteration.\n\nReturning Maximum Happiness Sum: \nAfter the loop finishes, the algorithm returns the final value of max, which represents the maximum happiness sum after subtracting k largest elements from the sorted array.\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n $$O(1)$$\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n\n Arrays.sort(happiness);\n long max = 0;\n int n = happiness.length;\n int i = n-1;\n\n while(k>0 && i>=0)\n {\n if(i>=0)\n {\n \n max += Math.max(0, happiness[i] - (n - i-1 ));\n i--;\n k--;\n\n }\n }\n return max;\n }\n}\n\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'Java'] | 1 |
maximize-happiness-of-selected-children | BEATS 100% SIMPLE DART solution with EXPLANATION | beats-100-simple-dart-solution-with-expl-2d0u | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires us to select k children from a queue such that the sum of their ha | Mohamed_Sadeck | NORMAL | 2024-05-09T10:06:46.834153+00:00 | 2024-05-09T10:06:46.834186+00:00 | 16 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to select k children from a queue such that the sum of their happiness values is maximized. Each time a child is selected, the happiness value of all the unselected children decreases by 1. To maximize the sum of happiness values, we should always select the child with the highest current happiness value.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to first sort the happiness values in descending order. Then, iterate over the sorted happiness values. For each happiness value, check if it minus the number of already taken children is greater than 0. If it is, add it to the sum and increment the number of taken children. If it\'s not, return the sum. Continue this process until all k children have been taken or there are no more children left.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(n log n), where n is the number of children. This is because we are sorting the happiness values, which takes O(n log n) time.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1), as we are not using any additional space that scales with the input size. The variables `taken`, `ans`, and `i` use constant space.\n# Code\n```\nclass Solution {\n int maximumHappinessSum(List<int> happiness, int k) {\n // Initialize the number of taken children and the sum of happiness values\n int taken = 0;\n int ans=0;\n int i=0;\n\n // Sort the happiness values in descending order\n happiness.sort((a,b)=>b.compareTo(a));\n\n // Iterate over the sorted happiness values\n while(taken<k && i<happiness.length){\n // If the current happiness value minus the number of taken children is less than or equal to 0, return the sum\n if(happiness[i]-taken <= 0) return ans;\n\n // Add the current happiness value minus the number of taken children to the sum\n ans+=happiness[i]-taken;\n\n // Increment the number of taken children\n taken++;\n\n // Move to the next happiness value\n i++;\n }\n\n // Return the sum of happiness values\n return ans;\n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'Dart'] | 0 |
maximize-happiness-of-selected-children | Simple Java Greedy solution beats 97% | O(nlogn) time and O(n) Space | simple-java-greedy-solution-beats-97-onl-vlpe | Intuition\nA pretty standard Greedy problem. Just be greedy for the child with the maximum leftover happiness from among the not selected ones.\n\n# Approach\n1 | ayushprakash1912 | NORMAL | 2024-05-09T09:59:10.166438+00:00 | 2024-05-09T09:59:10.166475+00:00 | 20 | false | # Intuition\nA pretty standard Greedy problem. Just be greedy for the child with the maximum leftover happiness from among the not selected ones.\n\n# Approach\n1. Sort the array.\n2. Iterate the array in descending order and the happiness value from the top k values while subtracting the number of elements already selected before the element.\n3. Return the sum.\n\n# Complexity\n- Time complexity:\nO(nlogn) // merge sort\n\n- Space complexity:\nO(n) // merge sort\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n\n Arrays.sort(happiness);\n long sum = 0;\n\n for (int i = happiness.length - 1, j = 0; i >= 0 && j < k; i--, j++) {\n sum = sum + Math.max(0, happiness[i] - j);\n }\n\n return sum;\n }\n}\n``` | 2 | 0 | ['Greedy', 'Sorting', 'Java'] | 0 |
maximize-happiness-of-selected-children | easy to understand || Beginer friendly || Fastest (100%) || Short & Concise | easy-to-understand-beginer-friendly-fast-ht25 | Intuition\nThe intuition behind the provided code seems to be finding the maximum possible sum of happiness that can be achieved by selecting a certain number o | utkarsh_the_co | NORMAL | 2024-05-09T09:58:19.029165+00:00 | 2024-05-09T09:58:19.029195+00:00 | 18 | false | # Intuition\nThe intuition behind the provided code seems to be finding the maximum possible sum of happiness that can be achieved by selecting a certain number of participants under given constraints.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1)Sorting the happiness vector: The function sorts the happiness vector in non-increasing order using std::sort with greater<int>(). This step ensures that the highest happiness values come first.\n\n2)Handling the case when k is 1: If k is equal to 1, the function selects the highest happiness value and returns it. This is done to handle the special case when only one participant can be chosen.\n\n3)Iterating through the sorted happiness vector: After handling the case when k is 1, the function iterates through the sorted happiness vector while there are still participants (k > 0) and updates the total happiness sum a.\n\n4)Calculating the contribution of each participant: For each participant, the function calculates their contribution to the total happiness sum. The contribution of the current participant (happiness[i]) is decreased by s, which represents the number of previously selected participants.\n\n5)Updating the total happiness sum and indices: The function updates the total happiness sum a by adding the contribution of the current participant (happiness[i] - s). It also increments i to move to the next participant, decrements k to track the remaining participants to be selected, and increments s to account for the selected participant.\n\n6)Returning the total happiness sum: Finally, the function returns the total happiness sum a, which represents the maximum sum of happiness that can be achieved by selecting k participants following the given rules.\n\n# Complexity\n- Time complexity:\n O(n log n) \n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long a=0;\n int n=happiness.size();\n sort(happiness.begin(),happiness.end(),greater<int>());\n int i=0;\n if(k==1)\n {\n a+=happiness[i];\n return a;\n }\n int s = 0;\n while(k>0)\n {\n if(happiness[i]-s<=0)\n {\n \n return a;\n }\n a+= happiness[i]-s;\n i++;\n k--;\n s++;\n \n }\n return a;\n }\n};\n``` | 2 | 0 | ['Array', 'Sorting', 'C++'] | 0 |
maximize-happiness-of-selected-children | Very easy and short | very-easy-and-short-by-buts-bqqx | \n\n# Intuition Behind the Approach:\n\nBy prioritizing children with the highest initial happiness, the algorithm ensures you capture the maximum benefit early | buts | NORMAL | 2024-05-09T09:15:09.985057+00:00 | 2024-05-09T09:15:09.985088+00:00 | 38 | false | \n\n# Intuition Behind the Approach:\n\nBy prioritizing children with the highest initial happiness, the algorithm ensures you capture the maximum benefit early on. The -i adjustment compensates for the happiness decrease of unselected children, reflecting the dynamic nature of happiness values throughout the selection process.\n\n# Complexity\n- Time complexity:\n$$O(n*log(n))$$ \n\n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nfunc maximumHappinessSum(happiness []int, k int) int64 {\n\n sort.Slice(happiness, func(i, j int) bool {\n return happiness[i] > happiness[j]\n })\n\n ans := int64(0)\n for i:=0; i<k; i++ {\n ans += max(int64(0),int64(happiness[i] - i))\n }\n\n return ans\n}\n``` | 2 | 0 | ['Sorting', 'Go'] | 0 |
maximize-happiness-of-selected-children | FAST 100% | MEMORY EFFICIENT | GREEDY - BEGINNERS | fast-100-memory-efficient-greedy-beginne-wpkk | Intuition\n\nThe goal is to optimize the overall happiness score by picking children with the greatest happiness levels. A sensible tactic is to give preference | ovchi | NORMAL | 2024-05-09T06:55:03.735052+00:00 | 2024-05-09T11:11:20.690262+00:00 | 30 | false | # Intuition\n\nThe goal is to optimize the overall happiness score by picking children with the greatest happiness levels. A sensible tactic is to give preference to those children with the highest happiness ratings initially, given that the happiness of those not chosen diminishes over time.\n\nBy prioritizing children with the highest happiness ratings from the start, we secure the highest possible happiness sum before it possibly diminishes. This method focuses on maximizing immediate happiness gains by securing the highest happiness scores early in the process.\n\n# Complexity\n- Time complexity:$$O(n*log(n))$$ -->\n\n- Space complexity:$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n long long ans=0;\n sort(h.begin(),h.end(),greater<int>());\n for(int i=0; i<k; i++){\n ans+=max(h[i]-i,0);\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Greedy', 'Sorting', 'C++', 'Java'] | 0 |
maximize-happiness-of-selected-children | Greedy Selection | C++ | Java | greedy-selection-c-java-by-lazy_potato-zkoz | Intuition, approach, and complexity disucussed in video solution in detail.\nhttps://youtu.be/0VlhZFs0WLE\n# Code\nC++\n\nclass Solution {\npublic:\n long lo | Lazy_Potato_ | NORMAL | 2024-05-09T06:34:34.939586+00:00 | 2024-05-09T06:34:34.939618+00:00 | 66 | false | # Intuition, approach, and complexity disucussed in video solution in detail.\nhttps://youtu.be/0VlhZFs0WLE\n# Code\nC++\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n sort(happiness.begin(), happiness.end());\n long long dec = 0, hapSum = 0, indx = happiness.size()-1;\n while(k-->0){\n hapSum += max(0ll, happiness[indx--] - (dec++));\n }\n return hapSum;\n }\n};\n```\nJava\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n long dec = 0, hapSum = 0;\n int indx = happiness.length-1;\n while(k-->0){\n hapSum += Math.max(0l, happiness[indx--] - (dec++));\n }\n return hapSum;\n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'C++', 'Java'] | 1 |
maximize-happiness-of-selected-children | 🔥maxHeap - Beginner Friendly Code | Clean Code | C++ | | maxheap-beginner-friendly-code-clean-cod-v8ab | Code\n\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n priority_queue<int, vector<int>> maxHeap;\n | Antim_Sankalp | NORMAL | 2024-05-09T06:32:22.800550+00:00 | 2024-05-09T06:32:22.800603+00:00 | 17 | false | # Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n priority_queue<int, vector<int>> maxHeap;\n for (auto x: happiness)\n {\n maxHeap.push(x);\n }\n\n long long decr = 0;\n long long res = 0;\n while (!maxHeap.empty() && k--)\n {\n int curr = maxHeap.top();\n maxHeap.pop();\n\n if (curr - decr > 0)\n {\n res += curr - decr;\n }\n else\n {\n break;\n }\n\n decr++;\n }\n\n return res;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Simple C++ Solution using MaxHeap | No BS | simple-c-solution-using-maxheap-no-bs-by-ahrk | Intuition\n##### To maximize the sum of happiness, it\'s intuitive to select the k highest values from the given array of happiness. \n\n# Approach\nThe approac | quagmire8 | NORMAL | 2024-05-09T05:16:16.000199+00:00 | 2024-05-09T05:16:16.000223+00:00 | 4 | false | # Intuition\n##### To maximize the sum of happiness, it\'s intuitive to select the k highest values from the given array of happiness. \n\n# Approach\nThe approach is to use a max heap (priority queue) to efficiently find the k maximum values from the array. First, we push all the elements of the array into the max heap. Then, we extract the k maximum values from the heap and calculate the sum of happiness by subtracting the index of each value from its corresponding happiness value, ensuring that the resulting happiness is not negative. Finally, we return the total sum of happiness.\n\n# Complexity\n- Time complexity: \n - Pushing all elements into the priority queue takes O(n log n) time, where n is the size of the `happiness` array.\n - Extracting the k maximum values takes O(k log n) time.\n - Overall time complexity: O((n + k) log n), or O(n log n) if k is constant.\n- Space complexity: \n - The space complexity is O(n) due to the priority queue storing all elements of the `happiness` array.\n\n# Code\n```cpp\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n \n // we can be greedy here and find the k maximums first.\n // for that we can use a maxheap\n\n priority_queue<int> maxHeap;\n\n // push all the elements of the array into the priority queue\n for(int num : happiness) maxHeap.push(num);\n\n // extract the k maximums\n long long ans = 0, i = 0;\n while(k--){\n // the happiness can never be less than 0 so we are taking care of that\n ans += (maxHeap.top() - i > 0) ? maxHeap.top() - i : 0;\n maxHeap.pop();\n i++;\n }\n\n return ans;\n }\n};\n | 2 | 0 | ['Array', 'Greedy', 'Heap (Priority Queue)', 'C++'] | 0 |
maximize-happiness-of-selected-children | O(n) ✔|| EASY APPROACH ✔|| PLEASE UPVOTE😊|| | on-easy-approach-please-upvote-by-kaal_e-hngg | \n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nHere\'s an explanation of the al | KAAL_El | NORMAL | 2024-05-09T04:20:32.986908+00:00 | 2024-05-09T04:20:32.986927+00:00 | 63 | false | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere\'s an explanation of the algorithm\'s intuition:\n\n1. **Sort the happiness values**: The algorithm begins by sorting the given happiness values in non-increasing order. This step ensures that we start with the highest happiness values, which allows us to maximize the total happiness sum.\n\n2. **Iterate over the first k elements**: We iterate over the first k elements of the sorted happiness values. These are the elements we are allowed to reduce to zero.\n\n3. **Accumulate total happiness**: For each element in the iteration, we accumulate its happiness value to the total happiness sum (`count`). If an element has a non-positive value (h[i] <= 0), it means it won\'t contribute to the total happiness, so we return the current total happiness.\n\n4. **Reduce subsequent elements**: For each element in the iteration, we reduce the next element\'s happiness value by the index of the current element plus one (i+1). This step ensures that we decrease the next element\'s value by the number of elements already processed, as per the problem\'s constraint.\n\n5. **Return the total happiness sum**: After iterating over the first k elements and adjusting subsequent elements\' values, we return the total happiness sum accumulated during the process.\n\nOverall, the algorithm prioritizes maximizing the total happiness sum by starting with the highest happiness values and reducing subsequent values strategically based on the number of already processed elements. This ensures that we meet the constraint of reducing only the first k elements and maximize the total happiness sum.\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& h, int k) {\n sort(h.rbegin(), h.rend());\n long long count = 0;\n int i = 0;\n while (i < k) {\n if (h[i] <= 0) return count;\n count += h[i];\n if (i + 1 < h.size()) {\n h[i + 1] -= (i + 1);\n }\n i++;\n }\n return count;\n }\n};\n\n```\n\n | 2 | 0 | ['C++'] | 1 |
maximize-happiness-of-selected-children | 🏆💢💯 Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅💥🔥💫Explained☠💥🔥 Beats 💯 | faster-lesser-cpython3javacpythonexplain-csyv | Intuition\n\n\n\n\n\nC++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long cnt = 0;\n | Edwards310 | NORMAL | 2024-05-09T04:06:54.892050+00:00 | 2024-05-09T04:06:54.892088+00:00 | 53 | false | # Intuition\n\n\n\n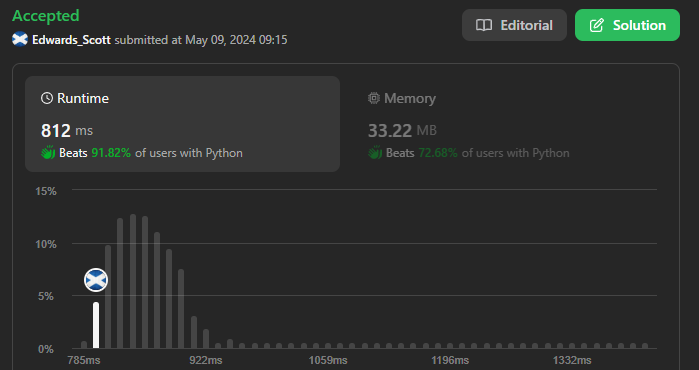\n\n```C++ []\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long cnt = 0;\n sort(happiness.begin(), happiness.end(), greater<int>());\n cnt = (long long)happiness[0];\n for (int i = 1; i < k and happiness[i] - i > 0; ++i)\n cnt += (long long)happiness[i] - i;\n return cnt;\n }\n};\n```\n```python3 []\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n cnt = 0\n happiness.sort(reverse = True)\n cnt = happiness[0]\n for i in range(1, k):\n if happiness[i] - i <= 0:\n break\n cnt += happiness[i] - i\n return cnt\n```\n```C []\nint cmp(const void *a, const int *b){\n return *((int*)b) - *((int*)a);\n }\nlong long maximumHappinessSum(int* happiness, int happinessSize, int k) {\n long long int cnt = 0;\n qsort(happiness, happinessSize, sizeof(int), cmp);\n cnt = (long long)happiness[0];\n for(int i = 1; i < k && (happiness[i] - i) > 0; ++i)\n cnt += (long long)happiness[i] - i;\n return cnt;\n}\n```\n```Java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n long cnt = 0;\n Integer[] happy = new Integer[happiness.length];\n for (int i = 0; i < happiness.length; i++)\n happy[i] = happiness[i];\n Arrays.sort(happy, Collections.reverseOrder());\n cnt = (long) happy[0];\n for (int i = 1; i < k && (happy[i] - i) > 0; i++)\n cnt += (long) happy[i] - i;\n return cnt;\n }\n}\n```\n```python []\nclass Solution(object):\n def maximumHappinessSum(self, happiness, k):\n """\n :type happiness: List[int]\n :type k: int\n :rtype: int\n """\n h = sorted(happiness, reverse = True)\n res = 0\n for i in range(k):\n if h[i] <= i:\n return res\n res += h[i] - i\n return res\n```\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nint cmp(const void *a, const int *b){\n return *((int*)b) - *((int*)a);\n }\nlong long maximumHappinessSum(int* happiness, int happinessSize, int k) {\n long long int cnt = 0;\n qsort(happiness, happinessSize, sizeof(int), cmp);\n cnt = (long long)happiness[0];\n for(int i = 1; i < k && (happiness[i] - i) > 0; ++i)\n cnt += (long long)happiness[i] - i;\n return cnt;\n}\n```\n# Please upvote if it\'s useful for you..\n\n | 2 | 0 | ['Array', 'Greedy', 'C', 'Sorting', 'Python', 'C++', 'Java', 'Python3'] | 3 |
maximize-happiness-of-selected-children | O(k) Fast solution | ok-fast-solution-by-ishaanagrawal-rpnf | \n\n# Approach\n Describe your approach to solving the problem. \nSort the array in descending order. After every pick from the array, all values in the array r | ishaanagrawal | NORMAL | 2024-05-09T04:02:44.144731+00:00 | 2024-05-09T04:02:44.144763+00:00 | 9 | false | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSort the array in descending order. After every pick from the array, all values in the array reduce by 1. So after n picks, total decrement in every value is n. \n\n# Complexity\n- Time complexity: O(k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);\n sort(happiness.begin(), happiness.end(), greater<int>());\n long long ans = 0;\n int x = 0;\n for (int i = 0; i < k; i++) {\n x = happiness[i];\n x = x - i;\n if (x >= 0) {\n ans += x;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Very Simple Code | very-simple-code-by-abulabura-u346 | # Intuition \n\n\n\n\n\n# Complexity\n- Time complexity:O(n \cdot \log n)\n\n\n- Space complexity:O(\log n)\n(the worse-case of the sort() function in c++ is | abulabura | NORMAL | 2024-05-09T04:01:12.484844+00:00 | 2024-05-09T04:01:12.484880+00:00 | 46 | false | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(n \\cdot \\log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(\\log n)$$\n(the worse-case of the sort() function in c++ is $$O(\\log n)$$.)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long res = 0;\n sort(happiness.begin(), happiness.end(), greater<int>());\n for (int i = 0; i < k; i++)\n res += max(happiness[i] - i, 0);\n return res;\n }\n};\n``` | 2 | 0 | ['Greedy', 'Sorting', 'C++'] | 1 |
maximize-happiness-of-selected-children | Easy Cpp Solution | easy-cpp-solution-by-pratham_2521-a8ju | \n# Code\n\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& arr, int k) {\n long long sum= 0 , diff=0 ; \n sort(arr.begi | Pratham_2521 | NORMAL | 2024-05-09T03:54:15.000389+00:00 | 2024-05-09T03:54:15.000419+00:00 | 52 | false | \n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& arr, int k) {\n long long sum= 0 , diff=0 ; \n sort(arr.begin() , arr.end(),greater<int>());\n int n = arr.size();\n for(int i=0 ; i<k ; i++)\n {\n if(arr[i] > diff)\n {\n sum += arr[i] - diff;\n }\n diff++;\n }\n return sum;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
maximize-happiness-of-selected-children | ✅✔️Easy Peasy Solution ✈️✈️✈️ | easy-peasy-solution-by-ajay_1134-m91i | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ajay_1134 | NORMAL | 2024-05-09T03:40:34.154421+00:00 | 2024-05-09T03:40:34.154439+00:00 | 24 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& arr, int k) {\n int n = arr.size();\n long long ans = 0;\n sort(arr.begin(),arr.end(),greater<int>());\n int x = 0;\n for(int i=0; i<k; i++) {\n arr[i] = max(0,arr[i]-x);\n x++;\n }\n for(int i=0; i<k; i++) ans += arr[i];\n return ans;\n }\n};\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 0 |
maximize-happiness-of-selected-children | 2 solutions Heap && sorting || Easy Intuitive C++ Solution 💯 | 2-solutions-heap-sorting-easy-intuitive-nh92h | Intuition\n\nThe problem seems to revolve around maximizing the happiness sum under certain constraints. By observing the provided code, it seems like the algor | _Rishabh_96 | NORMAL | 2024-05-09T02:42:55.403083+00:00 | 2024-05-09T02:42:55.403113+00:00 | 37 | false | # Intuition\n\nThe problem seems to revolve around maximizing the happiness sum under certain constraints. By observing the provided code, it seems like the algorithm is prioritizing higher values of happiness to maximize the sum.\n\n# Approach\n\n1. **Priority Queue**: The algorithm utilizes a priority queue to efficiently access the highest happiness values. This allows it to greedily select the highest happiness values first.\n2. **Iteration**: The algorithm iterates `k` times to select the top `k` happiness values from the priority queue.\n3. **Happiness Sum Calculation**: For each iteration, it calculates the difference between the top happiness value and the counter. This difference is added to the happiness sum.\n4. **Counter Update**: The counter is incremented after each iteration to ensure that each subsequent iteration selects the next highest happiness value.\n5. **Break Condition**: The iteration stops if either `k` becomes 0 or the top happiness value becomes less than or equal to the counter.\n\n# Complexity\n\n- **Time Complexity**: The time complexity of building the priority queue is O(nlogn), where n is the size of the input happiness vector. The iteration runs for at most `k` times, each time involving operations like pushing and popping from the priority queue, which take O(logn) time. Therefore, the overall time complexity is O((n + k)logn).\n- **Space Complexity**: The space complexity is O(n) to store the priority queue. No additional space is used in the algorithm.\n\n\n# Code\n# Using Priority Queue\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n \n priority_queue<int> pq;\n long long counter = 0, happysum = 0;\n\n for(auto it: happiness){\n pq.push(it);\n }\n\n while(k--){\n\n if(pq.top() - counter <= 0){\n break ;\n }\n\n happysum += pq.top() - counter;\n counter++;\n pq.pop();\n\n }\n\n return happysum ;\n\n }\n};\n```\n# Using Sorting\n\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n sort(begin(happiness), end(happiness), greater<int>());\n int i = 0;\n long long res = 0;\n\n while(k--) {\n happiness[i] = max(happiness[i] - i, 0);\n res += happiness[i++];\n }\n\n return res;\n }\n};\n``` | 2 | 0 | ['Sorting', 'Heap (Priority Queue)', 'C++'] | 1 |
maximize-happiness-of-selected-children | Kotlin - Greedy only 6 lines. Simple and Short | kotlin-greedy-only-6-lines-simple-and-sh-p9hr | Code\n\nclass Solution {\n fun maximumHappinessSum(happiness: IntArray, k: Int): Long {\n happiness.sortDescending()\n var result = 0L\n | namanh11611 | NORMAL | 2024-05-09T02:42:55.380948+00:00 | 2024-05-09T02:42:55.380983+00:00 | 42 | false | # Code\n```\nclass Solution {\n fun maximumHappinessSum(happiness: IntArray, k: Int): Long {\n happiness.sortDescending()\n var result = 0L\n for (i in 0 until k) {\n if (happiness[i] > i) result += happiness[i] - i\n }\n return result\n }\n}\n``` | 2 | 0 | ['Kotlin'] | 0 |
maximize-happiness-of-selected-children | Easy C++ Sorting Solution | Beats 100 ✅💯 | easy-c-sorting-solution-beats-100-by-sho-nlpv | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves selecting elements from the array to maximize the sum of happiness | shobhitkushwaha1406 | NORMAL | 2024-05-09T02:34:01.299074+00:00 | 2024-05-09T02:34:01.299105+00:00 | 40 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves selecting elements from the array to maximize the sum of happiness while adhering to the constraint of selecting at most k elements. To maximize the sum, it\'s intuitive to start by selecting the elements with the highest happiness values.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the happiness array in non-decreasing order.\n2. Reverse the sorted array to have the elements in non-increasing order (highest happiness values first).\n3. Initialize a variable count to keep track of the number of elements selected.\n4. Initialize a variable ans to keep track of the sum of happiness.\nIterate through the sorted array:\n5. Subtract the current count from the happiness value of the current element.\n6. If the resulting happiness value is positive, increment count, add the adjusted happiness value to ans, and continue.\n7. If the resulting happiness value is non-positive, break the loop.\n8. If count reaches k, break the loop.\n9. Return the final value of ans as the maximum happiness sum.\n# Complexity\n- Time complexity: O(nlogn) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n int count=0;\n sort(happiness.begin(),happiness.end());\n reverse(happiness.begin(),happiness.end());\n long long ans=0;\n for(int i=0;i<happiness.size();i++){\n happiness[i]-=count;\n if(happiness[i]>0){\n count++;\n ans+=happiness[i];\n }\n else break;\n if(count==k)break;\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Easy Java Solution | Detailed Approach | easy-java-solution-detailed-approach-by-850n9 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves maximizing the sum of happiness by selecting elements from an arra | Rudra_Rajawat | NORMAL | 2024-05-09T02:28:40.829834+00:00 | 2024-05-09T02:28:40.829869+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves maximizing the sum of happiness by selecting elements from an array within a limited selection constraint. One intuitive approach could be to sort the array and then greedily select the top \'k\' elements that contribute positively to the happiness sum.\n\n---\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSort the \'happiness\' array in ascending order.\nInitialize variables sum to store the total happiness sum and count to keep track of the number of elements selected.\nIterate over the last \'k\' elements of the sorted array.\nFor each element, check if selecting it would result in a positive increase in happiness (i.e., if the difference between the element\'s happiness and count is positive).\nIf positive, add this difference to sum, increment count by 1, and continue to the next iteration.\nOnce \'k\' elements are selected or no more elements meet the condition for selection, return the total sum of happiness (sum).\n\n---\n\n\n# Complexity\n\nTime complexity:\n<!-- Add your time complexity here, e.g. $$O(n \\log n)$$ --> \nThe time complexity is O(n log n) due to the sorting step, where \'n\' is the length of the happiness array.\n\nSpace complexity:\n<!-- Add your space complexity here, e.g. $$O(1)$$ --> \nThe space complexity is O(1) since only a constant amount of extra space is used regardless of the size of the input array.\n# Code\n```java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n long sum = 0;\n int count = 0;\n int n = happiness.length;\n Arrays.sort(happiness);\n for(int i=0;i<k;i++){\n if(happiness[n-1-i]-count>0){\n sum += happiness[n-1-i]-count;\n count++;\n }\n }\n return sum;\n }\n}\n```\n\n\n | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'Java'] | 0 |
maximize-happiness-of-selected-children | [C++] Greedy with Simulation | c-greedy-with-simulation-by-awesome-bug-cuzr | Intuition\n Describe your first thoughts on how to solve this problem. \n- Greedy\n - Select the k largest values in happiness\n- Simulation\n - Simulate the | pepe-the-frog | NORMAL | 2024-05-09T01:15:53.552906+00:00 | 2024-05-09T01:15:53.552954+00:00 | 21 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Greedy\n - Select the `k` largest values in `happiness`\n- Simulation\n - Simulate the selection process\n - Increase the `unhappy` value for each round\n - Accumulate the sum by `max(0, happiness[i] - unhappy)` \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- sort the children by their happiness\n- greedy on happiness but decremented by the `unhappy`\n\n# Complexity\n- Time complexity: $$O(n\\times\\log{n})$$ for sorting\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(\\log{n})$$ for sorting\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // time/space: O(nlogn)/O(logn)\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n // sort the children by their happiness\n sort(happiness.begin(), happiness.end(), greater<int>());\n \n // greedy on happiness but decremented by the `unhappy`\n long long sum = 0LL;\n for (int i = 0, unhappy = 0; i < k; i++, unhappy++) {\n sum += max(0, happiness[i] - unhappy);\n }\n return sum;\n }\n};\n``` | 2 | 0 | ['Greedy', 'Sorting', 'Simulation', 'C++'] | 0 |
maximize-happiness-of-selected-children | Beats 97% || EASY and straight to the point. | beats-97-easy-and-straight-to-the-point-kiku8 | Intuition\n Describe your first thoughts on how to solve this problem. \n# UPVOTE PPL.\n# Approach\n Describe your approach to solving the problem. \n\n\n1. Sor | Abhishekkant135 | NORMAL | 2024-05-09T00:58:39.507301+00:00 | 2024-05-09T00:58:39.507332+00:00 | 87 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n# UPVOTE PPL.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n1. **Sorting Happiness Scores:**\n - `Arrays.sort(happiness)`: Sorts the `happiness` array in descending order. This ensures that people with higher happiness scores are considered first for seat assignments.\n\n2. **Initializing Variables:**\n - `int count = 0`: Initializes a variable `count` to keep track of the number of seats assigned so far (out of `k`).\n - `long ans = 0`: Initializes a variable `ans` to store the total happiness sum.\n\n3. **Iterating and Calculating Happiness:**\n - `while (count != k)`: The loop iterates until `k` seats are assigned.\n - `int value = happiness[happiness.length - 1 - count] - count`: This line calculates the happiness contribution for the current person being considered.\n - `happiness[happiness.length - 1 - count]`: Accesses the happiness score of the person at the `count`th position from the end of the sorted `happiness` array (since it\'s sorted descendingly).\n - `- count`: Subtracts the current seat number (`count`) from the happiness score. This penalty represents the unhappiness caused by not assigning a consecutive seat.\n - `if (value > 0)`: Checks if the calculated happiness contribution (`value`) is positive.\n - If positive (`value > 0`), it means there\'s still happiness to be gained by assigning this person a seat, even after considering the penalty.\n - `ans += happiness[happiness.length - 1 - count] - count`: Adds the happiness contribution (`value`) to the total happiness sum (`ans`).\n - `count++`: Increments the `count` to move on to the next person (considering the next seat).\n\n4. **Returning the Maximum Happiness Sum:**\n - `return ans`: After iterating and assigning seats to `k` people, the function returns the final `ans`, which represents the maximum achievable happiness sum considering the happiness scores and seat assignment penalties.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(NLOGN)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n```python []\nclass Solution:\n def maximumHappinessSum(self, happiness, k):\n happiness.sort()\n count = 0\n ans = 0\n while count != k:\n value = happiness[-1 - count] - count\n if value > 0:\n ans += happiness[-1 - count] - count\n count += 1\n return ans\n\n```\n\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n int count=0;\n long ans=0;\n while(count!=k){\n int value=happiness[happiness.length-1-count]-count;\n if(value>0){\n ans+=happiness[happiness.length-1-count]-count;\n }\n count++;\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Python', 'Java'] | 1 |
maximize-happiness-of-selected-children | Kotlin "oneliner" | kotlin-oneliner-by-anton-pogonets-d3j6 | Complexity\n- Time complexity: O(n*log(n))\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\n fun maximumHappinessSum(happiness: IntArray, k: Int) =\n | anton-pogonets | NORMAL | 2024-05-09T00:21:07.419977+00:00 | 2024-05-09T00:21:07.420006+00:00 | 17 | false | # Complexity\n- Time complexity: $$O(n*log(n))$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\n fun maximumHappinessSum(happiness: IntArray, k: Int) =\n happiness.sortedDescending().asSequence().withIndex()\n .take(k)\n .map { it.value.toLong() - it.index }\n .takeWhile { it > 0 }\n .sum()\n}\n``` | 2 | 0 | ['Kotlin'] | 0 |
maximize-happiness-of-selected-children | Fast and Easy Python solution 769 ms, beats 96% | fast-and-easy-python-solution-769-ms-bea-paoa | ```\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n ans = 0\n fo | ANiSh684 | NORMAL | 2024-05-09T00:13:28.914420+00:00 | 2024-05-09T00:27:33.377654+00:00 | 25 | false | ```\nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n happiness.sort(reverse=True)\n ans = 0\n for i in range(k):\n if happiness[i]-i > 0:\n ans += happiness[i]-i\n return ans | 2 | 0 | ['Python', 'Python3'] | 0 |
maximize-happiness-of-selected-children | Java Solution | Easy to Understand | Beginner Friendly | java-solution-easy-to-understand-beginne-3f60 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind this algorithm is to select the children with higher happiness val | amritgg2002 | NORMAL | 2024-03-10T19:49:41.346232+00:00 | 2024-03-10T19:49:41.346259+00:00 | 23 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this algorithm is to select the children with higher happiness values first to maximize the sum. The algorithm iterates through the sorted array of happiness values in descending order, selecting children and decrementing the happiness of the remaining unselected children in each turn.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) Sort the array of happiness values in ascending order.\n\n2) Initialize a variable j to point to the last element of the sorted array.\n\n3) Initialize variables cnt and ans to keep track of the count of selected children and the maximum sum of happiness values, respectively.\n\n4) Iterate through the sorted array from the end, selecting children and updating the ans until either all k children are selected or the remaining happiness becomes non-positive.\n\n5) Return the final ans.\n\n# Complexity\n- Time complexity: **O(n log n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n int len = happiness.length;\n int j = len - 1;\n if (k <= 0)\n return 0;\n Arrays.sort(happiness);\n int cnt = 0;\n long ans = 0;\n while (j >= 0 && k > 0) {\n if (happiness[j] - cnt <= 0)\n break;\n ans += (happiness[j] - cnt);\n cnt++;\n j--;\n k--;\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Array', 'Sorting', 'Java'] | 1 |
maximize-happiness-of-selected-children | sorting || explained with example || c++ | sorting-explained-with-example-c-by-sufe-xbta | Intuition\n Describe your first thoughts on how to solve this problem. \nHow to think about this problem?\n step 1: soting, because we have to maximize happi | sufee_sahin | NORMAL | 2024-03-10T04:17:26.579050+00:00 | 2024-03-10T04:17:26.579084+00:00 | 93 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nHow to think about this problem?\n step 1: soting, because we have to maximize happiness\n step2 : only take care of all those values which are greater than 0.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n 1. Sort the array in reverse order\n 2. take a sum varible to calculate happiness\n 3. run a while loop till k holds\n 4. rather than modifyng the array maintain a count varible to check what would be the happiness to remaining chilrdren.\n 5. because in every iteration remaing happiness decreases by 1\n 6. Example :\n arr = [1,2,3,4,5] k = 4\n after soting = 5,4,3,2,1\nAs k is greater than 0 always so take start sum = H[0] (that is 5);\n k = k-1 = 3\n for i = 1 and k = 3 \n sum = 5 + 4-count = 5 + 3 ( as happiness would have decreased by 1 for\n all)\n for i = 2 and k = 2 \n sum = 9 - (3-2) ( we have again decreased remaing happiness by 1)\n for i = 3 and = 3\n H[3] = 2- count \n = 2 -3 \n = -1;\n the loop will break because if happness of index arr[3] will become negaive.\n7. return the sum value \n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& H, int k) {\n sort(H.rbegin(),H.rend());\n long long sum = H[0];\n int i=1;\n int count = 0;\n k = k-1;\n while(k-- && i<H.size()){\n count++;\n if(H[i]-count > 0){\n sum += H[i] - count;\n }\n else{\n break;\n }\n i++;\n }\n return sum;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Simple and Short | Sorting/Heap | 2 Solutions | simple-and-short-sortingheap-2-solutions-bs0v | \nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n long ans = 0;\n int minus = 0 | spats7 | NORMAL | 2024-03-10T04:15:01.474114+00:00 | 2024-03-11T03:45:05.144677+00:00 | 181 | false | ```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n long ans = 0;\n int minus = 0;\n int i = happiness.length - 1;\n while(minus < k){\n ans += Math.max(happiness[i] - minus, 0);\n minus++;\n i--;\n }\n return ans;\n }\n}\n```\n---\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n PriorityQueue<Integer> heap = new PriorityQueue<>();\n \n for(int happy : happiness){\n heap.add(happy);\n if(heap.size() > k)\n heap.poll();\n }\n long ans = 0;\n while(k > 0){\n ans += Math.max(heap.poll() - (k-1), 0);\n k--;\n }\n return ans;\n }\n}\n\n | 2 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Java'] | 2 |
maximize-happiness-of-selected-children | C++| Easy to understand | O(n logn) | c-easy-to-understand-on-logn-by-di_b-jt5z | Intuition\nStart from the highest happiness, and keep on adding it to the result.\n\n# Approach\n1. Sort the array in decreasing order of happiness\n2. Iterate | di_b | NORMAL | 2024-03-10T04:12:43.736447+00:00 | 2024-03-10T04:12:43.736469+00:00 | 114 | false | # Intuition\nStart from the highest happiness, and keep on adding it to the result.\n\n# Approach\n1. Sort the array in decreasing order of happiness\n2. Iterate over the array and keep on adding the current happiness into the result. As we cannot have negative happiness, add 0, if the happiness is becoming negative.\n3. Current happiness is happiness - the iteration we are in.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n sort(happiness.rbegin(), happiness.rend());\n long long res = 0;\n for(int i = 0; i < k; ++i)\n {\n res += max(happiness[i] - i, 0);\n }\n return res;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Python max Heap | python-max-heap-by-hizinberg-k67s | Intuition\nTo maximize happiness, we want to prioritize placing the happiest people in the grid.\nA max-heap allows us to efficiently access the person with the | hizinberg | NORMAL | 2024-03-10T04:06:29.634396+00:00 | 2024-03-10T04:06:29.634430+00:00 | 44 | false | # Intuition\nTo maximize happiness, we want to prioritize placing the happiest people in the grid.\nA max-heap allows us to efficiently access the person with the highest happiness at any point.\n\n# Approach\nMax-Heap Construction: We convert the happiness list into a max-heap using heapq._heapify_max(we can insert negative numbers instead). This ensures the element with the highest happiness is at the root.\nGreedy Placement: We iterate through a loop (k times):\nWe pop the element with the highest happiness (tem) from the max-heap using heapq._heappop_max.\nWe check if placing this person would still allow for k neighbors (including themselves).\nIf tem - count >= 0 (enough neighbors available):\nAdd the happiness (tem) to the total (ans).\nIncrement the counter (count) for the placed person and their neighbors.\nIf not enough neighbors, we can\'t place this person effectively and move on.\nWe repeat until k people are placed.\n\n# Complexity\n- Time complexity:\nO(n log n) due to creating the max-heap (heapify) and repeated pops/maximum extractions (heappop_max).\n\n- Space complexity:\nO(1) as we use constant extra space for variables.\n\n# Code\n```\nimport heapq as hq \nclass Solution:\n def maximumHappinessSum(self, happiness: List[int], k: int) -> int:\n count=0\n ans=0\n hq._heapify_max(happiness)\n while k:\n tem=heapq._heappop_max(happiness)\n if tem-count>=0:\n ans+=tem-count\n count+=1\n k-=1\n return ans\n \n``` | 2 | 0 | ['Python3'] | 1 |
maximize-happiness-of-selected-children | ✅ Java Solution | Easy to understand | java-solution-easy-to-understand-by-hars-q4gy | CODE\nJava []\npublic long maximumHappinessSum(int[] happiness, int k) {\n\tArrays.sort(happiness);\n\n\tint turn = k, n=happiness.length, i=n-1;\n\tlong res=0; | Harsh__005 | NORMAL | 2024-03-10T04:03:01.985818+00:00 | 2024-03-10T04:03:01.985856+00:00 | 244 | false | ## **CODE**\n```Java []\npublic long maximumHappinessSum(int[] happiness, int k) {\n\tArrays.sort(happiness);\n\n\tint turn = k, n=happiness.length, i=n-1;\n\tlong res=0;\n\twhile(i>=0 && turn > 0){\n\t\tif(k-turn >= happiness[i]) break;\n\n\t\tres += happiness[i--];\n\t\tres -= (k-turn);\n\t\tturn--;\n\t}\n\treturn res;\n}\n``` | 2 | 0 | ['Sorting', 'Java'] | 2 |
maximize-happiness-of-selected-children | Easy Python Solution | easy-python-solution-by-_suraj__007-8dw5 | Code\n\nclass Solution:\n def maximumHappinessSum(self, h: List[int], k: int) -> int:\n count = 0\n g = 0\n h.sort()\n for i in r | _suraj__007 | NORMAL | 2024-03-10T04:02:22.500170+00:00 | 2024-03-10T04:02:22.500202+00:00 | 34 | false | # Code\n```\nclass Solution:\n def maximumHappinessSum(self, h: List[int], k: int) -> int:\n count = 0\n g = 0\n h.sort()\n for i in range(len(h)-1,-1,-1):\n if k==0:\n break\n else:\n k-=1\n a = h[i] - g\n if a>=0:\n count+=h[i] - g\n g+=1\n else:\n count+=0\n g+=1\n return count\n \n \n \n``` | 2 | 0 | ['Python3'] | 0 |
maximize-happiness-of-selected-children | Priority Queue Solution | Full Explanation | priority-queue-solution-full-explanation-laew | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires finding the maximum possible sum of happiness after performing k o | nidhiii_ | NORMAL | 2024-03-10T04:02:10.775815+00:00 | 2024-03-10T04:07:08.114315+00:00 | 140 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the maximum possible sum of happiness after performing k operations. Each operation involves selecting the topmost happiness value from the given vector and subtracting a decreasing value from it. \n\nTo maximize the sum of happiness, we want to select the highest happiness values possible and minimize the amount subtracted from them.\n\nThis can be done using priority queue to find maximum happiness, and a variable `curr_sub` which tracks the subtraction that needs to be done from remaining elements. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize variables `curr_sub` to keep track of the current subtraction that is needed and `max_happ`` to store the maximum happiness.\n- Create a priority queue to store the elements.\n- Insert all elements into the priority queue.\n- Iterate while there are remaining operations to perform (k > 0), and there are still elements in the priority queue, and the top element subtracted by `curr_sub` is still valid.\n- Inside the loop:\n - Calculate the current sum by applying the current modifier to the top element of the priority queue.\n - Add this current sum to the total sum.\n - Remove the top element from the priority queue.\n - Decrement curr_sub as now 1 needs to be subtracted from happiness of all children.\n - Decrease the remaining operations (k) by 1.\n- Return the maximum sum obtained.\n\n# Complexity\n- Time complexity: O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumHappinessSum(vector<int>& happiness, int k) {\n long long int curr_sub = 0, max_happ = 0;\n \n priority_queue<int>pq;\n for(int h:happiness){\n pq.push(h);\n }\n \n while(k>0 and pq.size()>0 and pq.top() + curr_sub >= 0) {\n int curr_happ = pq.top() + curr_sub;\n max_happ += curr_happ;\n pq.pop();\n curr_sub -= 1;\n k--;\n }\n return max_happ;\n }\n};\n``` | 2 | 0 | ['C++'] | 2 |
maximize-happiness-of-selected-children | Super Simple Easy to understand JAVA SOLUTION!!!! | super-simple-easy-to-understand-java-sol-2jjg | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | raj_karthik | NORMAL | 2025-03-15T06:12:54.750013+00:00 | 2025-03-15T06:12:54.750013+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maximumHappinessSum(int[] happiness, int k) {
Arrays.sort(happiness);
int reduction = 0;
long ans = 0;
int n = happiness.length -1;
while( n>= 0 && k > 0){
int toadd= happiness[n] - reduction;
if(toadd >= 0){
ans += toadd;
}
reduction++;
n--;
k--;
}
return ans;
}
}
``` | 1 | 0 | ['Greedy', 'Java'] | 0 |
maximize-happiness-of-selected-children | Easiest c++ solution 87ms beats 97.95% solve by sorting | easiest-c-solution-87ms-beats-9795-solve-iz5n | IntuitionApproachComplexity
Time complexity: O(nlgn)
Space complexity: O(n)
Code | albert0909 | NORMAL | 2025-03-14T06:23:18.252824+00:00 | 2025-03-14T06:23:18.252824+00:00 | 25 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(nlgn)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long maximumHappinessSum(vector<int>& happiness, int k) {
sort(happiness.begin(), happiness.end(), greater<int>());
long long mx = 0;
for(int i = 0;i < k;i++){
if(happiness[i] - i > 0) mx += happiness[i] - i;
else return mx;
}
return mx;
}
};
auto init = []()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
return 'c';
}();
``` | 1 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 0 |
maximize-happiness-of-selected-children | C# | c-by-adchoudhary-6bzm | Code | adchoudhary | NORMAL | 2025-02-26T04:12:26.277841+00:00 | 2025-02-26T04:12:26.277841+00:00 | 3 | false | # Code
```csharp []
public class Solution {
public long MaximumHappinessSum(int[] happiness, int k) {
happiness = happiness.OrderByDescending(x => x).ToArray();
long sum = 0;
int decrease = 0;
for (int i = 0; i < k; i++)
{
if(happiness[i] - decrease > 0)
sum += happiness[i] - decrease;
decrease++;
}
return sum;
}
}
``` | 1 | 0 | ['C#'] | 0 |
maximize-happiness-of-selected-children | C++ || Super Easy || Beats 100% | c-super-easy-beats-100-by-samritsingh7-6ute | IntuitionThe problem requires maximizing the sum of happiness levels. Observing the input, the key insight is that the happiness levels are reduced linearly (by | samritsingh7 | NORMAL | 2025-02-02T10:37:35.166692+00:00 | 2025-02-02T10:37:35.166692+00:00 | 15 | false | # Intuition
The problem requires maximizing the sum of happiness levels. Observing the input, the key insight is that the happiness levels are reduced linearly (by their index). Sorting and then selecting the top k adjusted happiness values ensures the sum is maximized.
# Approach
1. Sort the happiness levels in descending order.
2. Subtract the index from each happiness value to account for the diminishing factor as per the problem's requirements.
3. Start from the largest adjusted happiness value and add them to the result until you reach the k limit or encounter a non-positive value.
# Complexity
- Time complexity:$$O(nlogn)$$
- Space complexity:$$O(1)$$
# Code
```cpp []
class Solution {
public:
long long maximumHappinessSum(vector<int>& happiness, int k) {
sort( happiness.begin(), happiness.end(), greater<int>() );
for( int i = 0; i < happiness.size(); i++ )
happiness[i] = happiness[i] - i;
int i = 0;
long long ans = 0;
while( k && happiness[i] > 0 ){
ans += happiness[i];
k--;
i++;
}
return ans;
}
};
``` | 1 | 0 | ['C++'] | 0 |
maximize-happiness-of-selected-children | Partial sort for top K numbers | partial-sort-for-top-k-numbers-by-yashwa-n9qj | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | yashwanthreddi | NORMAL | 2025-01-22T17:21:51.816483+00:00 | 2025-01-22T17:21:51.816483+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long maximumHappinessSum(vector<int>& happiness, int k) {
partial_sort(happiness.begin(), happiness.begin() + k, happiness.end(), greater<int>());
long long sum = 0;
for(int i = 0; i < k; i++) {
sum += max(0, happiness[i] - i);
if(happiness[i] - i<0)
sum;
}
return sum;
}
};
``` | 1 | 0 | ['Greedy', 'C++'] | 0 |
maximize-happiness-of-selected-children | Java - Solution | java-solution-by-dsuryaprakash89-3edk | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dsuryaprakash89 | NORMAL | 2024-12-06T16:05:58.695254+00:00 | 2024-12-06T16:05:58.695292+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n long count=0;\n //take a pq and add all of them into pq till k while adding add num - p where p is from 1 to k\n PriorityQueue<Integer> pq = new PriorityQueue<>((a,b)->b-a);\n for(int i=0;i<happiness.length;i++){\n pq.add(happiness[i]);\n }\n int p=0;\n for(int i=0;i<k;i++){\n count+=Math.max(pq.poll()-p,0);\n p++;\n }\n return count;\n }\n}\n``` | 1 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'Java'] | 0 |
maximize-happiness-of-selected-children | Easy | Java | Beats 97% | With comments for explanation | easy-java-beats-97-with-comments-for-exp-sw28 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | saiyam3 | NORMAL | 2024-10-10T10:07:42.392719+00:00 | 2024-10-10T10:07:42.392745+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- O(n log n) -->\n\n- Space complexity:\n<!-- O(1) -->\n\n# Code\n```java []\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n Arrays.sort(happiness);\n long res=0;\n\n int n = happiness.length;\n int count = n; //To determine if we are adding happiness count for the first time\n int i = 1; //To decrease the happiness count dynamically\n\n if(k==0) //if k==0 then return 0\n return res;\n\n //To run the loop k times \n while(k>0 && n>=0) { \n //if happiness becomes less or equal to 0 then stop the loop\n if(happiness[n-1] == 0)\n return res;\n else {\n //for first addition to res\n if(count == n) \n res += happiness[n-1];\n //for addition alongwith decreasing the happiness number by 1 each time\n else if(happiness[n-1] - i > 0){\n res += happiness[n-1] - i;\n i++;\n } else {\n return res;\n }\n n--;\n }\n k--; //decreasing k by 1 \n }\n return res;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
maximize-happiness-of-selected-children | Detailed Explanation😴|| Priority Queue + Greedy + Sort || O(n.logn) + O(k.logn)🔥 | detailed-explanation-priority-queue-gree-jwwf | \n\n# Code\n\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n int n = happiness.length;\n long sum=0;\n I | Ankit1317 | NORMAL | 2024-07-31T05:22:33.363196+00:00 | 2024-07-31T05:22:33.363232+00:00 | 1 | false | \n\n# Code\n```\nclass Solution {\n public long maximumHappinessSum(int[] happiness, int k) {\n int n = happiness.length;\n long sum=0;\n Integer [] happinessArray = new Integer[n];\n for(int i = 0; i < n; i++) {\n happinessArray[i] = happiness[i];\n }\n Arrays.sort(happinessArray,Collections.reverseOrder());\n for(int i=0;i<k;i++){\n if(happinessArray[i]-i<=0){\n sum = sum + 0;\n }\n else { \n sum = sum + happinessArray[i]-i;\n }\n }\n return sum;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.