question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-maximum-factor-score-of-array | Java Solution | java-solution-by-dheeraj_2602-cfad | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Dheeraj_2602 | NORMAL | 2024-10-27T17:18:41.901359+00:00 | 2024-10-27T17:18:41.901389+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n^2)\n- Space complexity:\nO(1)\n# Code\n```java []\nclass Solution {\n public long maxScore(int[] nums) {\n if (nums.length == 1) {\n return (long) nums[0] * nums[0];\n }\n long ans = score(nums, -1);\n for (int i = 0; i < nums.length; i++) {\n ans = Math.max(ans, score(nums, i));\n }\n return ans;\n }\n\n long score(int[] nums, int skip) {\n long lcm = skip != 0 ? nums[0] : nums[1];\n long gcd = skip != 0 ? nums[0] : nums[1];\n for (int i = 0; i < nums.length; i++) {\n if (i == skip) {\n continue;\n }\n gcd = GCD(gcd, nums[i]);\n lcm = LCM(lcm, nums[i]);\n }\n return lcm * gcd;\n }\n\n long GCD(long a, long b) {\n while (b != 0) {\n long temp = b;\n b = a % b;\n a = temp;\n }\n return a;\n }\n\n long LCM(long a, long b) {\n return (a / GCD(a, b)) * b;\n }\n}\n\n``` | 0 | 0 | ['Java'] | 0 |
find-the-maximum-factor-score-of-array | 100x speed-up of prevailing "7ms" (fastest) solution | 100x-speed-up-of-prevailing-7ms-fastest-yf53e | Intuition\n\nReuse the prime_factors_t c++ class which I attempted (and developed) in another problem\n\nGCD and LCM calculations are as simple as bitwise AND a | jrmwng | NORMAL | 2024-10-27T16:43:09.521416+00:00 | 2024-10-27T16:43:09.521450+00:00 | 13 | false | # Intuition\n\nReuse the `prime_factors_t` c++ class which I attempted (and developed) in another problem\n\nGCD and LCM calculations are as simple as bitwise AND and bitwise OR respectively in the `prime_factors_t` representation.\n\n# Approach\n\nUse the Excel file which I used in the development of `prime_factors_t` to initialize the `prime_factors_t::g_astCONST` variable and the `prime_factors_t::g_aauPRIME_NUMBER` variable, tailored for this problem.\n\nPossible values of `nums[i]` are finite (only 31). The `prime_factors_t` representations of numbers 1 to 30 are constructed at compile-time (use `constexpr`). Then using look-up table approach to convert `nums[i]` into `prime_factors_t` representation.\n\nUse the "traverse left-to-right" and "traverse right-to-left" pattern that draw my attention recently in another problem.\n\nCombine the results of "left-to-right" and "right-to-left" to obtain the `n + 1` candidates. The for-loop of this procedure is auto-vectorized.\n\nReturn the maximum score among the candidates.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n long long maxScore(vector<int>& nums);\n};\n\n\n\tstruct prime_factors_t : std::tuple<uint32_t>\n\t{\n\t\tusing tuple_t = std::tuple<uint32_t>;\n\n\t\tusing number_t = std::uint64_t;\n\t\tusing encode_t = std::uint32_t; // encoded form\n\n\t\tstruct const_t\n\t\t{\n\t\t\tencode_t uBit0;\n\t\t\tencode_t uMask;\n\t\t};\n\t\tconstexpr static const_t const g_astCONST[]\n\t\t{\n\t\t\t{(1u << 0),(15u << 0)},//2\n\t\t\t{(1u << 4),(7u << 4)},//3\n\t\t\t{(1u << 7),(3u << 7)},//5\n\t\t\t{(1u << 9),(1u << 9)},//7\n\t\t\t{(1u << 10),(1u << 10)},//11\n\t\t\t{(1u << 11),(1u << 11)},//13\n\t\t\t{(1u << 12),(1u << 12)},//17\n\t\t\t{(1u << 13),(1u << 13)},//19\n\t\t\t{(1u << 14),(1u << 14)},//23\n\t\t\t{(1u << 15),(1u << 15)},//29\n\t\t};\n\n\t\tconstexpr static number_t const g_aauPRIME_NUMBER[][4]\n\t\t{\n\t\t\t{2,4,8,16},\n\t\t\t{3,9,27,0},\n\t\t\t{5,25,0,0},\n\t\t\t{7,0,0,0},\n\t\t\t{11,0,0,0},\n\t\t\t{13,0,0,0},\n\t\t\t{17,0,0,0},\n\t\t\t{19,0,0,0},\n\t\t\t{23,0,0,0},\n\t\t\t{29,0,0,0},\n\t\t};\n\n\t\tconstexpr prime_factors_t() = default;\n\t\tconstexpr prime_factors_t(tuple_t&& that)\n\t\t\t: tuple_t(std::move(that))\n\t\t{\n\t\t}\n//\t\tusing tuple_t::tuple;\n\n\t\tconstexpr static std::tuple<encode_t, number_t> encode(number_t uNumber, size_t const zuStart, size_t const zuEnd, encode_t ulPrimeFactors)\n\t\t{\n\t\t\tfor (size_t i = zuStart; i < zuEnd && 1u < uNumber; ++i)\n\t\t\t{\n\t\t\t\tnumber_t const uPrimeNumber = g_aauPRIME_NUMBER[i][0];\n\n\t\t\t\tfor (encode_t uBit = g_astCONST[i].uBit0; uNumber % uPrimeNumber == 0; uNumber /= uPrimeNumber, uBit <<= 1)\n\t\t\t\t{\n\t\t\t\t\tulPrimeFactors |= uBit;\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn{ ulPrimeFactors, uNumber };\n\t\t}\n\n\t\tconstexpr prime_factors_t(number_t uNumber)\n\t\t\t: tuple_t(std::get<0>(encode(uNumber >> std::countr_zero(uNumber), 1u, 10u, (1u << std::countr_zero(uNumber)) - 1u)))\n\t\t{\n\t\t}\n\n\t\tconstexpr static number_t decode(encode_t const ulPrimeFactors, size_t const zuStart, size_t const zuEnd, number_t uFactors)\n\t\t{\n\t\t\tfor (size_t i = zuStart; i < zuEnd && ulPrimeFactors >= g_astCONST[i].uBit0; ++i)\n\t\t\t{\n\t\t\t\tencode_t const uBits = ulPrimeFactors & g_astCONST[i].uMask;\n\n\t\t\t\tif (uBits)\n\t\t\t\t{\n\t\t\t\t\tuFactors *= g_aauPRIME_NUMBER[i][std::popcount(uBits) - 1u];\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn uFactors;\n\t\t}\n\t\t//constexpr static number_t decode(encode_t ulPrimeFactors, size_t const zuStart, number_t uFactors)\n\t\t//{\n\t\t//\twhile (ulPrimeFactors)\n\t\t//\t{\n\t\t//\t\tsize_t const zuIndex0 = zuStart + std::countr_zero(ulPrimeFactors) / 2u;\n\n\t\t//\t\tunsigned const uIndex1 = std::popcount(encode_t(ulPrimeFactors & g_astCONST[zuIndex0].uMask)) - 1u;\n\n\t\t//\t\tulPrimeFactors &= ~g_astCONST[zuIndex0].uMask;\n\n\t\t//\t\tuFactors *= g_aauPRIME_NUMBER[zuIndex0][uIndex1];\n\t\t//\t}\n\t\t//\treturn uFactors;\n\t\t//}\n\n\t\tconstexpr operator number_t () const\n\t\t{\n\t\t\treturn decode(std::get<encode_t>(*this), 1u, 10u, 1u) << std::popcount(encode_t(std::get<encode_t>(*this) & g_astCONST[0].uMask));\n\t\t}\n\t};\n\tprime_factors_t gcd(prime_factors_t const& lhs, prime_factors_t const& rhs)\n\t{\n\t\treturn{ prime_factors_t::tuple_t(std::get<0>(lhs) & std::get<0>(rhs)) };\n\t}\n\tprime_factors_t lcm(prime_factors_t const& lhs, prime_factors_t const& rhs)\n\t{\n\t\treturn{ prime_factors_t::tuple_t(std::get<0>(lhs) | std::get<0>(rhs)) };\n\t}\n\n\n\nlong long Solution::maxScore(vector<int>& nums)\n{\n\tsize_t const n = nums.size();\n\tif (n == 0) return 0ll;\n\n\t// 1. prime factors representation of `nums`\n\tconstexpr static prime_factors_t aPrimeFactors[31]{ 1,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30 };\n\n\t// 2. left-to-right and right-to-left pattern\n\tstd::vector<prime_factors_t> vPrimeFactors_lcm_left;\n\tstd::vector<prime_factors_t> vPrimeFactors_gcd_left;\n\tstd::vector<prime_factors_t> vPrimeFactors_lcm_right;\n\tstd::vector<prime_factors_t> vPrimeFactors_gcd_right;\n\tvPrimeFactors_lcm_left.resize(n);\n\tvPrimeFactors_gcd_left.resize(n);\n\tvPrimeFactors_lcm_right.resize(n);\n\tvPrimeFactors_gcd_right.resize(n);\n\tvPrimeFactors_lcm_left.front() = aPrimeFactors[nums.front()];\n\tvPrimeFactors_gcd_left.front() = aPrimeFactors[nums.front()];\n\tvPrimeFactors_lcm_right.back() = aPrimeFactors[nums.back()];\n\tvPrimeFactors_gcd_right.back() = aPrimeFactors[nums.back()];\n\tfor (size_t i = 1, j = n - 2; i < n; ++i, --j)\n\t{\n\t\tvPrimeFactors_lcm_left[i] = lcm(vPrimeFactors_lcm_left[i - 1], aPrimeFactors[nums[i]]);\n\t\tvPrimeFactors_gcd_left[i] = gcd(vPrimeFactors_gcd_left[i - 1], aPrimeFactors[nums[i]]);\n\t\tvPrimeFactors_lcm_right[j] = lcm(vPrimeFactors_lcm_right[j + 1], aPrimeFactors[nums[j]]);\n\t\tvPrimeFactors_gcd_right[j] = gcd(vPrimeFactors_gcd_right[j + 1], aPrimeFactors[nums[j]]);\n\t}\n\n\t// 3. combine "left-to-right" and "right-to-left" results\n\tstd::vector<prime_factors_t> vCandidate_lcm;\n\tstd::vector<prime_factors_t> vCandidate_gcd;\n\tvCandidate_lcm.resize(1 + n);\n\tvCandidate_gcd.resize(1 + n);\n\tvCandidate_lcm[0] = vPrimeFactors_lcm_right.front();\n\tvCandidate_gcd[0] = vPrimeFactors_gcd_right.front();\n\tif (1 < n)\n\t{\n\t\tvCandidate_lcm[1] = *(vPrimeFactors_lcm_right.begin() + 1);\n\t\tvCandidate_gcd[1] = *(vPrimeFactors_gcd_right.begin() + 1);\n\n\t\tprime_factors_t const* __restrict pstPrimeFactors_lcm_left = vPrimeFactors_lcm_left.data();\n\t\tprime_factors_t const* __restrict pstPrimeFactors_gcd_left = vPrimeFactors_gcd_left.data();\n\t\tprime_factors_t const* __restrict pstPrimeFactors_lcm_right = vPrimeFactors_lcm_right.data() + 2;\n\t\tprime_factors_t const* __restrict pstPrimeFactors_gcd_right = vPrimeFactors_gcd_right.data() + 2;\n\t\tprime_factors_t* __restrict pstPrimeFactors_lcm = vCandidate_lcm.data() + 2;\n\t\tprime_factors_t* __restrict pstPrimeFactors_gcd = vCandidate_gcd.data() + 2;\n\n\t\tfor (size_t i = 0, i_end = n - 2; i < i_end; ++i) // info C5001: loop vectorized\n\t\t{\n\t\t\t//pstPrimeFactors_lcm[i] = lcm(pstPrimeFactors_lcm_left[i], pstPrimeFactors_lcm_right[i]);\n\t\t\t//pstPrimeFactors_gcd[i] = gcd(pstPrimeFactors_gcd_left[i], pstPrimeFactors_gcd_right[i]);\n\t\t\tstd::get<prime_factors_t::encode_t>(pstPrimeFactors_lcm[i]) = std::get<prime_factors_t::encode_t>(pstPrimeFactors_lcm_left[i]) | std::get<prime_factors_t::encode_t>(pstPrimeFactors_lcm_right[i]);\n\t\t\tstd::get<prime_factors_t::encode_t>(pstPrimeFactors_gcd[i]) = std::get<prime_factors_t::encode_t>(pstPrimeFactors_gcd_left[i]) & std::get<prime_factors_t::encode_t>(pstPrimeFactors_gcd_right[i]);\n\t\t}\n\t\tvCandidate_lcm.back() = *(vPrimeFactors_lcm_left.rbegin() + 1);\n\t\tvCandidate_gcd.back() = *(vPrimeFactors_gcd_left.rbegin() + 1);\n\t}\n\n\t// 4. calculate scores\n\tuint64_t uMaxScore = 0;\n\tfor (size_t i = 0, i_end = 1 + n; i < i_end; ++i)\n\t{\n\t\tuint64_t const uGCD = vCandidate_gcd[i];\n\t\tuint64_t const uLCM = vCandidate_lcm[i];\n\n\t\tuMaxScore = std::max(uMaxScore, (uGCD * uLCM));\n\t}\n\n\treturn (long long)(uMaxScore);\n}\n\n#include <iostream>\nstatic auto _______ = []() {\n // turn off sync\n std::ios::sync_with_stdio(false);\n // untie in/out streams\n std::cin.tie(nullptr);\n return 0;\n}();\n\n``` | 0 | 0 | ['Bit Manipulation', 'Bitmask', 'C++'] | 0 |
find-the-maximum-factor-score-of-array | Brute Force solution! | brute-force-solution-by-chiragbellara-mi2u | Intuition\nWe get the product of every possible removal, and compare them.\n\n# Approach\nInitialize the maximum value as the product of the lcm and gcd of the | ChiragBellara | NORMAL | 2024-10-27T15:40:21.597085+00:00 | 2024-10-27T15:40:21.597122+00:00 | 11 | false | # Intuition\nWe get the product of every possible removal, and compare them.\n\n# Approach\nInitialize the maximum value as the product of the lcm and gcd of the entire nums list, as that will be the possible value when no number is removed from the list.\nThen simply iterate over the list and remove every number and check if the lcm * gcd of the list without this number is greater than the current maximum value.\nReturn the final value of the maximum.\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n if len(nums) == 1:\n return nums[0] ** 2\n\n if len(nums) == 0:\n return 0\n\n score = math.gcd(*nums) * math.lcm(*nums)\n for i in range(len(nums)):\n changedList = nums[:i] + nums[i + 1 :]\n score = max(score, math.gcd(*changedList) * math.lcm(*changedList))\n\n return score\n\n``` | 0 | 0 | ['Array', 'Python3'] | 0 |
find-the-maximum-factor-score-of-array | Simple Java Solution | Beats 100% | simple-java-solution-beats-100-by-nithin-i3gv | \n\n# Code\njava []\nclass Solution {\n long gcd(long a, long b) \n { \n return b == 0 ? a: gcd(b, a % b); \n }\n\n long lcm(int[] arr, | nithin_1217 | NORMAL | 2024-10-27T15:25:00.739425+00:00 | 2024-10-27T15:25:00.739457+00:00 | 15 | false | \n\n# Code\n```java []\nclass Solution {\n long gcd(long a, long b) \n { \n return b == 0 ? a: gcd(b, a % b); \n }\n\n long lcm(int[] arr, int idx, int r)\n {\n if (idx == arr.length - 1){\n if(idx == r) return 1;\n return arr[idx];\n }\n if(r == idx){\n idx += 1;\n }\n if (idx == arr.length - 1){\n return arr[idx];\n }\n long a = arr[idx];\n long b = lcm(arr, idx+1, r);\n return (a*b/gcd(a,b)); \n }\n public long maxScore(int[] nums) {\n long lcm = 0, gcd = 0, prod = 0;\n int n = nums.length;\n gcd = nums[0];\n for (int element: nums){\n gcd = gcd(gcd, element);\n\n if(gcd == 1)\n {\n break;\n }\n }\n lcm = lcm(nums,0,-1);\n prod = gcd*lcm;\n for(int i=0;i<n;i++){\n gcd = i == n-1 ? nums[0] : nums[i+1];\n for(int j=0;j<n;j++){\n if(j == i)continue;\n gcd = gcd(gcd,nums[j]);\n }\n lcm = lcm(nums,0,i);\n prod = Math.max(gcd*lcm,prod);\n } \n return prod;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
find-the-maximum-factor-score-of-array | Python3 solution faster than 100% | python3-solution-faster-than-100-by-subh-g6qd | \nimport math\nclass Solution:\n def maxScore(self,nums: list[int]) -> int:\n def product(array):\n if len(array)!=0:\n lcm | elixlamp | NORMAL | 2024-10-27T15:20:20.069814+00:00 | 2024-10-27T15:21:35.645323+00:00 | 26 | false | ```\nimport math\nclass Solution:\n def maxScore(self,nums: list[int]) -> int:\n def product(array):\n if len(array)!=0:\n lcm = array[0]\n gcd = array[0]\n for x in range(len(array)):\n lcm = max(math.lcm(array[x],lcm),lcm)\n gcd = min(math.gcd(array[x],gcd),gcd)\n return lcm*gcd \n maximum = 0\n if len(nums)>0:\n nums.sort()\n regularmax = product(nums)\n if len(nums)==1:\n return regularmax\n for x in range(len(nums)):\n arr = nums[:x] + nums[x+1:]\n maximum = max(maximum,product(arr))\n \n return max(maximum,regularmax)\n else:\n return 1\n``` | 0 | 0 | ['Python', 'Python3'] | 0 |
find-the-maximum-factor-score-of-array | Simple Python solution || 100% faster | simple-python-solution-100-faster-by-chi-y5gg | Code\npython3 []\nimport math\n\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n if len(nums) == 1:\n return nums[0]**2\n | chiragnayak10 | NORMAL | 2024-10-27T14:33:14.793566+00:00 | 2024-10-27T14:33:14.793590+00:00 | 2 | false | # Code\n```python3 []\nimport math\n\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n if len(nums) == 1:\n return nums[0]**2\n max_score = 0\n\n for i in range(-1,len(nums)):\n if i == 0:\n start = 1\n gcd_value = nums[1]\n lcm_value = nums[1]\n else:\n start = 0\n gcd_value = nums[0]\n lcm_value = nums[0]\n\n for j in range(start, len(nums)):\n if j == i:\n continue\n gcd_value = math.gcd(gcd_value, nums[j])\n lcm_value = (lcm_value * nums[j]) // math.gcd(lcm_value, nums[j])\n\n max_score = max(max_score, gcd_value * lcm_value)\n\n return max_score\n\n \n``` | 0 | 0 | ['Python3'] | 0 |
find-the-maximum-factor-score-of-array | Brute Force | brute-force-by-trifecta_of_reality-g7tu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | trifecta_of_reality | NORMAL | 2024-10-27T14:27:05.339924+00:00 | 2024-10-27T14:27:05.339961+00:00 | 16 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n\n\nclass Solution {\npublic:\n long long gcd(long long a, long long b)\n {\n if(b>a)\n swap(a,b);\n if(b==0)\n return a;\n return gcd(a%b, b);\n \n }\n long long calculate_max_factor(vector<int>& arr, int idx)\n {\n long long lcm = arr[0];\n long long hcf = arr[0];\n long long gc = arr[0];\n int n = arr.size();\n if(idx == 0)\n {\n lcm = arr[1];\n hcf = arr[1];\n gc = arr[1];\n }\n for(int i=0;i<n;i++)\n {\n if(i == idx)\n continue;\n hcf = gcd(lcm, arr[i]);\n lcm = (lcm * arr[i])/hcf;\n gc = gcd(gc, arr[i]);\n }\n return lcm * gc;\n }\n long long maxScore(vector<int>& arr) {\n int n = arr.size();\n if(n==1)\n return 1LL * arr[0] * arr[0];\n long long ans = 0;\n ans = calculate_max_factor(arr, -1);\n for(int i=0;i<n;i++)\n {\n ans = max(ans, calculate_max_factor(arr, i));\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
find-the-maximum-factor-score-of-array | c++ solution | c-solution-by-dilipsuthar60-3p9d | \nclass Solution {\npublic:\n long long gcd(long long a,long long b){\n return __gcd(a,b);\n }\n long long lcm(long long a,long long b){\n | dilipsuthar17 | NORMAL | 2024-10-27T13:50:38.202317+00:00 | 2024-10-27T13:50:38.202344+00:00 | 1 | false | ```\nclass Solution {\npublic:\n long long gcd(long long a,long long b){\n return __gcd(a,b);\n }\n long long lcm(long long a,long long b){\n return a*b/gcd(a,b);\n }\n long long maxScore(vector<int>& nums) {\n int n=nums.size();\n if(n==1) return nums[0]*nums[0];\n long long ans=0;\n for(int i=0;i<n;i++){\n long long currGcd=0;\n long long currLcm=0;\n for(int j=0;j<n;j++){\n if(i!=j){\n if(currGcd==0&&currLcm==0){\n currLcm=nums[j];\n currGcd=nums[j];\n }\n else{\n currGcd=gcd(currGcd,nums[j]);\n currLcm=lcm(currLcm,nums[j]);\n }\n }\n }\n ans=max(ans,currLcm*currGcd);\n }\n long long currGcd=0;\n long long currLcm=0;\n for(int i=0;i<n;i++){\n if(i==0){\n currGcd=nums[i];\n currLcm=nums[i];\n }\n else{\n currLcm=lcm(currLcm,nums[i]);\n currGcd=gcd(currGcd,nums[i]);\n }\n }\n return max(ans,currLcm*currGcd);\n }\n};\n``` | 0 | 0 | ['C', 'C++'] | 0 |
find-the-maximum-factor-score-of-array | Rust beginner solution | rust-beginner-solution-by-chenyo-17-ou0f | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | chenyo-17 | NORMAL | 2024-10-27T13:48:27.223287+00:00 | 2024-10-27T13:48:27.223317+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```rust []\nimpl Solution {\n pub fn max_score(nums: Vec<i32>) -> i64 {\n // special case 1\n if nums.is_empty() {\n return 0;\n }\n // precision conversion\n let nums: Vec<i64> = nums.iter().map(|v| *v as i64).collect(); \n // special case 2\n if nums.len() == 1 {\n return nums[0] * nums[0];\n }\n\n // pre-compute the gcd prefix and suffix array\n // time: O(n)\n let n = nums.len();\n // gcd_prefix[i] stores the gcd up to nums[i]\n let mut gcd_prefix = vec![1; n];\n gcd_prefix[0] = nums[0];\n for i in 1..n {\n gcd_prefix[i] = Self::gcd(gcd_prefix[i - 1], nums[i]);\n }\n // gcd_suffix[i] stores the gcd from nums[i] to end\n let mut gcd_suffix = vec![1; n];\n gcd_suffix[n - 1] = nums[n - 1];\n for i in (0..n - 1).rev() {\n gcd_suffix[i] = Self::gcd(gcd_suffix[i + 1], nums[i]);\n }\n\n // precompute lcm prefix and suffix array\n // time: O(n)\n let mut lcm_prefix = vec![1; n];\n // lcm_prefix[i] stores the lcm up to nums[i]\n lcm_prefix[0] = nums[0];\n for i in 1..n {\n lcm_prefix[i] = Self::lcm(lcm_prefix[i - 1], nums[i]);\n }\n // lcm_suffix[i] stores the lcm from nums[i] to end\n let mut lcm_suffix = vec![1; n];\n lcm_suffix[n - 1] = nums[n - 1];\n for i in (0..n - 1).rev() {\n lcm_suffix[i] = Self::lcm(lcm_suffix[i + 1], nums[i]);\n }\n\n // gcd_exclude[i] stores the gcd excluding nums[i]\n // lcm_exclude[i] stores the lcm excluding nums[i]\n let mut gcd_exclude = vec![1; n];\n let mut lcm_exclude = vec![1; n];\n for i in 0..n {\n // corner cases\n if i == 0 {\n gcd_exclude[i] = gcd_suffix[1];\n lcm_exclude[i] = lcm_suffix[1];\n } else if i == n - 1 {\n gcd_exclude[i] = gcd_prefix[n - 2];\n lcm_exclude[i] = lcm_prefix[n - 2];\n } else {\n gcd_exclude[i] = Self::gcd(gcd_prefix[i - 1], gcd_suffix[i + 1]);\n lcm_exclude[i] = Self::lcm(lcm_prefix[i - 1], lcm_suffix[i + 1]);\n }\n }\n\n // start iteration\n // time: O(n) \n // store the score when nothing is removed\n let mut max_score = match gcd_prefix[n - 1] {\n 0 => 0,\n s => lcm_prefix[n - 1].abs() * s,\n };\n for i in 0..n {\n // compute the score when nums[i] is removed\n let new_score = lcm_exclude[i] * gcd_exclude[i];\n max_score = max_score.max(new_score);\n }\n max_score\n }\n\n pub fn gcd(a: i64, b: i64) -> i64 {\n let mut a = a;\n let mut b = b;\n // gcd using euclidean algorithm\n while b != 0 {\n (a, b) = (b, a % b);\n }\n a\n }\n\n pub fn lcm(a: i64, b: i64) -> i64 {\n if a == 0 || b == 0 {\n return 0;\n }\n (a * b).abs() / Self::gcd(a, b)\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
smallest-number-with-all-set-bits | [Java/C++/Python] Different ideas | javacpython-different-ideas-by-lee215-6qce | Explanation\nSolution 1. while loop on res = res * 2 + 1\nSolution 2. Build-in count leading zeros\nSolution 3. Build-in count bit length\n\n# Complexity\nTime | lee215 | NORMAL | 2024-12-01T04:32:41.952130+00:00 | 2024-12-01T12:29:30.946106+00:00 | 1,927 | false | # **Explanation**\nSolution 1. while loop on `res = res * 2 + 1`\nSolution 2. Build-in count leading zeros\nSolution 3. Build-in count bit length\n\n# **Complexity**\nTime `O(logn)`\nSpace `O(1)`\n<br>\n\n**Java**\n```Java\n public int smallestNumber(int n) {\n int res = 1;\n while (res < n)\n res = res * 2 + 1;\n return res;\n }\n```\n```Java\n public int smallestNumber(int n) {\n return -1 >>> Integer.numberOfLeadingZeros(n);\n }\n```\n**C++**\n```C++\n int smallestNumber(int n) {\n return (1 << (32 - __builtin_clz(n))) - 1;\n }\n\n int smallestNumber(int n) {\n return INT_MAX >> __builtin_clz(n) - 1;\n }\n```\n**Python**\n```py [Python3]\n def smallestNumber(self, n: int) -> int:\n return (1 << n.bit_length()) - 1\n``` | 19 | 3 | ['C', 'Python', 'Java'] | 2 |
smallest-number-with-all-set-bits | 🔥 Find the Smallest Number with Only Set Bits 🔢 | find-the-smallest-number-with-only-set-b-8jef | Intuition \uD83D\uDCA1 \n\nThe problem revolves around finding the smallest number greater than or equal to a given number n where the binary representation of | lasheenwael9 | NORMAL | 2024-12-02T04:56:32.750751+00:00 | 2024-12-02T04:56:32.750776+00:00 | 1,265 | false | # Intuition \uD83D\uDCA1 \n\nThe problem revolves around finding the smallest number greater than or equal to a given number `n` where the binary representation of the number contains only `1`s. \n\n1. **Key Insight**: \n - Numbers with only `1`s in their binary representation (e.g., 1, 3, 7, 15) follow the form $$ 2^b - 1 $$, where `b` is the total number of bits. \n - The smallest such number greater than or equal to `n` will have a binary representation of all set bits and at least `b` bits where $$ b = \\lceil \\log_2(n + 1) \\rceil $$. \n\n2. **Approach**: \n - Determine the number of bits `b` needed to represent `n`. \n - Calculate the result as $$ 2^b - 1 $$.\n\n---\n\n# Approach \uD83D\uDEE0\uFE0F \n\n1. Compute the number of bits `b` using the formula `b = log2(n) + 1`. \n2. Return the value $$ (1 << b) - 1 $$, which represents $$ 2^b - 1 $$ with all bits set. \n\n---\n\n# Complexity \u23F3 \n\n- **Time Complexity**: \n $$ O(1) $$ since the calculations involve constant-time operations. \n\n- **Space Complexity**: \n $$ O(1) $$ as no extra space is used. \n\n---\n\n\n\n# Code \uD83D\uDCBB \n\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n int b = log2(n) + 1; // Calculate the number of bits\n return (1 << b) - 1; // Return 2^b - 1\n }\n};\n```\n\n```java []\nclass Solution {\n public int smallestNumber(int n) {\n int b = (int) (Math.log(n) / Math.log(2)) + 1; // Calculate the number of bits\n return (1 << b) - 1; // Return 2^b - 1\n }\n}\n```\n\n```python []\nclass Solution:\n def smallestNumber(self, n: int) -> int:\n b = n.bit_length() # Calculate the number of bits\n return (1 << b) - 1 # Return 2^b - 1\n```\n\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar smallestNumber = function(n) {\n let b = Math.floor(Math.log2(n)) + 1; // Calculate the number of bits\n return (1 << b) - 1; // Return 2^b - 1\n};\n```\n\n---\n\n# Explanation \uD83D\uDCD8 \n\n## Example \n```plaintext\nInput: n = 6 \nOutput: 7 \n\nExplanation: \n- Binary of 6 = `110` \n- Smallest number with all set bits >= 6 is `111` (7 in decimal). \n\nInput: n = 10 \nOutput: 15 \n\nExplanation: \n- Binary of 10 = `1010` \n- Smallest number with all set bits >= 10 is `1111` (15 in decimal). \n```\n\n---\n\n# Takeaway \uD83D\uDE80 \n\nThis problem showcases how mathematical properties of binary numbers simplify implementation! If this helped, **drop a \uD83D\uDC4D and share the love! \uD83D\uDC96** \n\n\n | 14 | 0 | ['Bit Manipulation', 'C++', 'Java', 'Python3', 'JavaScript'] | 2 |
smallest-number-with-all-set-bits | 1 less than largest power of 2 greater than n | 1-less-than-largest-power-of-2-greater-t-4hha | Approach\n- - Find the next larget power of 2 i.e. ceil(log2(n+1))\n- Then reurn power of 2 to the number found above and then - 1 to have all bits set.\n\n# Co | kreakEmp | NORMAL | 2024-12-01T05:03:28.355327+00:00 | 2024-12-01T05:08:17.125979+00:00 | 1,327 | false | # Approach\n- - Find the next larget power of 2 i.e. ceil(log2(n+1))\n- Then reurn power of 2 to the number found above and then - 1 to have all bits set.\n\n# Code\n```cpp []\nint smallestNumber(int n) {\n return pow(2, ceil(log2(n+1))) - 1;\n}\n```\n\n\n\n---\n\n\n<b>Here is an article of my interview experience - A Journey to FAANG Company, I recomand you to go through this to know which all resources I have used & how I cracked interview at Amazon:\nhttps://leetcode.com/discuss/interview-experience/3171859/Journey-to-a-FAANG-Company-Amazon-or-SDE2-(L5)-or-Bangalore-or-Oct-2022-Accepted\n\n\n---\n | 9 | 3 | ['C++'] | 2 |
smallest-number-with-all-set-bits | Python3 || 1 line, Count the bits || T/S: 99% / 59% | python3-1-line-count-the-bits-ts-99-59-b-8rgf | This problem is equivalent to: Given a number n, find the greatest integer with the same bit-length. Thus, we determine the bit-length of n and use mathematics | Spaulding_ | NORMAL | 2024-12-01T04:33:52.161899+00:00 | 2024-12-08T02:29:41.488118+00:00 | 363 | false | This problem is equivalent to: *Given a number *n*, find the greatest integer with the same bit-length.* Thus, we determine the bit-length of *n* and use mathematics to complete the task.\n\n```python3 []\nclass Solution:\n def smallestNumber(self, n: int) -> int:\n \n return pow(2, n.bit_length()) - 1\n```\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n return (1 << (32 - __builtin_clz(n))) - 1;\n }\n};\n```\n```java []\nclass Solution {\n\n public int smallestNumber(int n) {\n return (1 << (Integer.SIZE - Integer.\n \n numberOfLeadingZeros(n))) - 1; }\n}\n\n```\nI could be wrong, but I think that time complexity is *O*(log log *N*) and space complexity is *O*(1), *N* ~ `n`.\n\n[https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1473080933/](https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1473080933/) | 8 | 0 | ['C++', 'Java', 'Python3'] | 0 |
smallest-number-with-all-set-bits | One-Liners | one-liners-by-votrubac-bb78 | Two solutions in case you do not want bit manipulations...\n\nC++\ncpp\nint smallestNumber(int n) {\n return pow(2, floor(log2(n) + 1)) - 1;\n}\n\nC++\ncpp\n | votrubac | NORMAL | 2024-12-01T04:47:16.547971+00:00 | 2024-12-01T04:55:43.978155+00:00 | 440 | false | Two solutions in case you do not want bit manipulations...\n\n**C++**\n```cpp\nint smallestNumber(int n) {\n return pow(2, floor(log2(n) + 1)) - 1;\n}\n```\n**C++**\n```cpp\nint sb[10] = {1, 3, 7, 15, 31, 63, 127, 255, 511, 1023};\nint smallestNumber(int n) {\n return *lower_bound(begin(sb), end(sb), n);\n}\n``` | 7 | 2 | [] | 0 |
smallest-number-with-all-set-bits | Intuition + Approach | Power of 2 | T.C ~ O(logn) | intuition-approach-power-of-2-tc-ologn-b-i4y6 | Intuition\n\nIf we subtract 1 from any power of 2 we will get number having all set bits.\n\nExample:-\n\n 2^3 -1 = (8-1) =7 -> binary(111)\n\n## Approach\n | langesicht | NORMAL | 2024-12-01T04:58:38.616360+00:00 | 2024-12-01T10:58:19.250732+00:00 | 504 | false | # Intuition\n\nIf we subtract 1 from any power of 2 we will get number having all set bits.\n\nExample:-\n\n 2^3 -1 = (8-1) =7 -> binary(111)\n\n## Approach\n- Find 1st power of 2 which is greater than or equal to n+1\n- Ans is (Power of 2) -1\n\n For Example:- \n n = 5,\n power of 2 greater than or equal to (n+1 = 6) is 2^3 =8,\n binary representation of (8-1 = 7) --> 111,\n Therefore 7 is ans\n\n\n# Complexity\n- Time complexity: O(logn)\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int powerOf2(int n){\n int p = 1;\n while(p<n){\n p*=2;\n }\n return p;\n }\n public int smallestNumber(int n) {\n int num = powerOf2(n+1);\n return num-1;\n }\n}\n```\n# PLEASE UPVOTE ! THANKS\n.\n.\n\n. | 6 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | bit_ceil 1 line||beats 100% | bit_ceil-1-linebeats-100-by-anwendeng-osy5 | Intuition\n Describe your first thoughts on how to solve this problem. \nUse bit_ceil (C++20). That is the smallest 2 powers greater or equal to n\n# Approach\n | anwendeng | NORMAL | 2024-12-01T05:52:16.568432+00:00 | 2024-12-01T05:57:33.538119+00:00 | 202 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse bit_ceil (C++20). That is the smallest 2 powers greater or equal to n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- If bit_ceil(n)=n, n is a 2 power, return 2*n-1\n- otherwise return bit_ceil(n)-1\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nAt most $O(\\log n)$ maybe $O(32)=O(1)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code||0ms beats 100%\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(unsigned n) {\n return (bit_ceil(n)==n)?(n<<1)-1:bit_ceil(n)-1;\n }\n};\n```\n# Code variant\n```\nclass Solution {\npublic:\n int smallestNumber(unsigned n) {\n return bit_ceil(n+1)-1;\n }\n};\n``` | 5 | 1 | ['Bit Manipulation', 'C++'] | 2 |
smallest-number-with-all-set-bits | [Python, Java, C++, Rust] Elegant & Short | O(1) | Power Of Two | python-java-c-rust-elegant-short-o1-powe-ki9y | Complexity\n- Time complexity: O(1)\n- Space complexity: O(1)\n\n# Code\npython3 []\nclass Solution:\n def smallestNumber(self, n: int) -> int:\n retu | Kyrylo-Ktl | NORMAL | 2024-12-01T10:03:30.276733+00:00 | 2024-12-01T10:13:13.750927+00:00 | 226 | false | # Complexity\n- Time complexity: $$O(1)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```python3 []\nclass Solution:\n def smallestNumber(self, n: int) -> int:\n return (1 << n.bit_length()) - 1\n```\n```java []\nimport java.math.BigInteger;\n\nclass Solution {\n public int smallestNumber(int n) {\n return (1 << BigInteger.valueOf(n).bitLength()) - 1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n return (1 << (32 - __builtin_clz(n))) - 1;\n }\n};\n```\n```Rust []\nimpl Solution {\n pub fn smallest_number(n: i32) -> i32 {\n (1 << (32 - n.leading_zeros())) - 1\n }\n}\n``` | 4 | 0 | ['Python', 'C++', 'Java', 'Python3', 'Rust'] | 0 |
smallest-number-with-all-set-bits | 🔥Beats 100 % 🔥 | Easiest Solution ✔️ | O(1) and O(n) | Bit Manipulation | beats-100-easiest-solution-o1-and-on-bit-j5ty | Intuition\nThe goal is to find the smallest number >= n where all bits in its binary representation are set (e.g., 1, 3, 7, 15, etc.). Starting from n, we check | ntrcxst | NORMAL | 2024-12-01T05:16:25.863480+00:00 | 2024-12-01T05:16:25.863519+00:00 | 138 | false | # Intuition\nThe goal is to find the smallest number `>= n` where all **bits** in its binary representation are set (e.g., 1, 3, 7, 15, etc.). Starting from `n`, we check if the number satisfies the condition `x & (x + 1) == 0`, which is true only if `x` has all **bits set** , binary \n`0111 & 1000 = 0`. If `x` doesn\'t meet this condition, increment it and check again until the condition holds. Once found, return this number as the smallest value meeting the criteria.\n\n# Approach\n`Step 1` **Understanding the Bitwise Condition :**\n- `x & (x + 1) == 0` is true only when `x` has all bits set in its binary representation. For example:\n - 3 (binary 11): `3 & 4 = 0`\n - 7 (binary 111): 7 & 8 = 0\n\n`Step 2` **Iterate and Increment :**\n- Start from n and keep incrementing `x` until the condition is satisfied.\n\n`Step 3` **Return the Result :**\n- Once the condition is met, `x` is guaranteed to be the\n- `smallest number \u2265 n` with all bits set. Return it.\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```java []\nclass Solution \n{\n public int smallestNumber(int n) \n {\n int x = n;\n \n // Step 1: Check if x has all bits set\n while ((x & (x + 1)) != 0) \n { \n x++; // Step 2: Increment x until the condition is met\n }\n \n return x; // Step 3 : Return Smallest Number with All Set Bits \n }\n}\n``` | 4 | 0 | ['Bit Manipulation', 'Bitmask', 'Java'] | 1 |
smallest-number-with-all-set-bits | 💯Very Easy Detailed Solution || 🎯 Beats 100% || 🎯 Two Approaches | very-easy-detailed-solution-beats-100-tw-svn4 | Approach 1: Brute Force\n Describe your approach to solving the problem. \n1. Helper Function check(String str):\n - This method checks if a given binary str | chaturvedialok44 | NORMAL | 2024-12-02T06:06:30.724977+00:00 | 2024-12-02T06:06:30.725006+00:00 | 187 | false | # Approach 1: Brute Force\n<!-- Describe your approach to solving the problem. -->\n1. **Helper Function check(String str):**\n - This method checks if a given binary string contains only the character \'1\'.\n - If it encounters a \'0\' in the string, it returns false; otherwise, it returns true.\n\n2. **Method smallestNumber(int n):**\n - Starts with result = n.\n - Converts the current number (result) to its binary representation using Integer.toBinaryString(result).\n - Uses the check method to verify if the binary representation contains only 1.\n - If true, the loop breaks, and the number is returned.\n - Otherwise, result is incremented, and the process repeats.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O((k-n).log(k))$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(log(k))$\n# Code\n```java []\nclass Solution {\n private boolean check(String str){\n for(char ch : str.toCharArray()){\n if(ch == \'0\'){\n return false;\n }\n }\n return true;\n }\n public int smallestNumber(int n) {\n int result = n;\n while(true){\n if(check(Integer.toBinaryString(result))){\n break;\n }\n else{\n result++;\n }\n }\n return result;\n }\n}\n```\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe numbers with binary representation containing only 1 are powers of 2-1:\nBinary numbers like 1, 11, 111, etc., correspond to 2^1 - 1, 2^2 - 1, 2^3 - 1, and so on.\nPrecompute these values or derive them directly to reduce brute-force iterations. This would result in logarithmic or constant time checks instead of linear iteration.\n# Approach 2: Optimized Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Initialization:**\n - ans is initialized to 1 (binary: 1).\n\n2. **Iterative Multiplication:**\n - The loop multiplies ans by 2 and adds 1 in each iteration. This operation appends a 1 to the binary representation of ans. For example:\n - Start with 1 (binary: 1).\n - Multiply by 2 and add 1: 1\u21923 (binary: 11).\n - Multiply by 2 and add 1: 3\u21927 (binary: 111).\n - Multiply by 2 and add 1: 7\u219215 (binary: 1111).\n\n3. **Loop Termination:**\n - The loop continues until ans is greater than or equal to n. At this point, ans is returned.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(log(n))$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(1)$\n# Code\n```java []\nclass Solution {\n public int smallestNumber(int n) {\n int ans = 1;\n while(ans < n){\n ans = ans*2 + 1;\n }\n return ans;\n }\n}\n``` | 3 | 0 | ['Math', 'String', 'Bit Manipulation', 'String Matching', 'Bitmask', 'Java'] | 2 |
smallest-number-with-all-set-bits | 💢☠💫Easiest👾Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅C#✅💥🔥💫Explained☠💥🔥 Beats 100 | easiestfaster-lesser-cpython3javacpython-vrhi | \n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\n Describe your first thoughts on how to solve this problem. \n- J | Edwards310 | NORMAL | 2024-12-01T09:56:04.251796+00:00 | 2024-12-01T09:56:04.251831+00:00 | 134 | false | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n- ***JavaScript Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467200570\n- ***C++ Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467182393\n- ***Python3 Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467186457\n- ***Java Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467054963\n- ***C Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467188235\n- ***Python Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467185715\n- ***C# Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467200359\n- ***Go Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467235020\n- ***PHP Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467201851\n- ***Dart Code -->*** https://leetcode.com/problems/smallest-number-with-all-set-bits/submissions/1467204071\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(1)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n\n | 3 | 1 | ['C', 'PHP', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#', 'Dart'] | 0 |
smallest-number-with-all-set-bits | [Python3] Math | python3-math-by-ye15-yo9h | Intuition\nCount the number of bits of n and create an all 1 binary. \n\nAnalysis\nTime complexity O(1)\nSpace complexity O(1)\n\nImplemetation\n\nclass Solutio | ye15 | NORMAL | 2024-12-01T04:44:57.321582+00:00 | 2024-12-01T04:47:44.562088+00:00 | 158 | false | **Intuition**\nCount the number of bits of `n` and create an all `1` binary. \n\n**Analysis**\nTime complexity `O(1)`\nSpace complexity `O(1)`\n\n**Implemetation**\n```\nclass Solution:\n def smallestNumber(self, n: int) -> int:\n return (1<<n.bit_length()) - 1\n``` | 3 | 0 | ['Python3'] | 1 |
smallest-number-with-all-set-bits | Easiest Solution💯 || 100% beats | easiest-solution-100-beats-by-aryaman123-8nan | Code | aryaman123 | NORMAL | 2025-03-19T16:05:29.600995+00:00 | 2025-03-19T16:05:29.600995+00:00 | 93 | false |
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int ans = poweroftwo(n+1);
return ans-1;
}
public int poweroftwo(int n){
int p = 1;
while(p<n){
p*=2;
}
return p;
}
}
``` | 2 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | 100% Best Solution | 100-best-solution-by-luffy240605-nckx | IntuitionAll set bits are present in numbers just before the powers of 2 for example 7 just before 8 , 15 just before 16 etc. So we will count the number of bit | luffy240605 | NORMAL | 2025-01-07T01:25:52.241169+00:00 | 2025-01-07T01:27:15.151351+00:00 | 86 | false | # Intuition
All set bits are present in numbers just before the powers of 2 for example 7 just before 8 , 15 just before 16 etc. So we will count the number of bits in the number n(given) and return 2 to the power the number of bits in that number - 1.
# Approach
Initialize count variable and count the number of bits with the help of a while loop and right shifting or dividing number by 2.
# Complexity
- Time complexity:O(logN)
- Space complexity:O(1)
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int num = n , cnt = 0;
while(num){
num = num >> 1;
cnt++;
}
return pow(2,cnt) - 1;
}
};
``` | 2 | 0 | ['C++'] | 1 |
smallest-number-with-all-set-bits | [Swift, C++, Python3] Simplest solution 0ms O(logN) | swift-c-python3-simplest-solution-0ms-ol-fnfn | Intuition\nThe first numbers which contain only set bits are 1, 3, 7, 15, 31.\nSo, each next only set bits number can be calculated as current * 2 + 1.\n\n\n\n\ | evkobak | NORMAL | 2024-12-02T05:13:20.488650+00:00 | 2024-12-02T07:01:06.156742+00:00 | 43 | false | # Intuition\nThe first numbers which contain only set bits are 1, 3, 7, 15, 31.\nSo, each next only set bits number can be calculated as `current * 2 + 1`.\n\n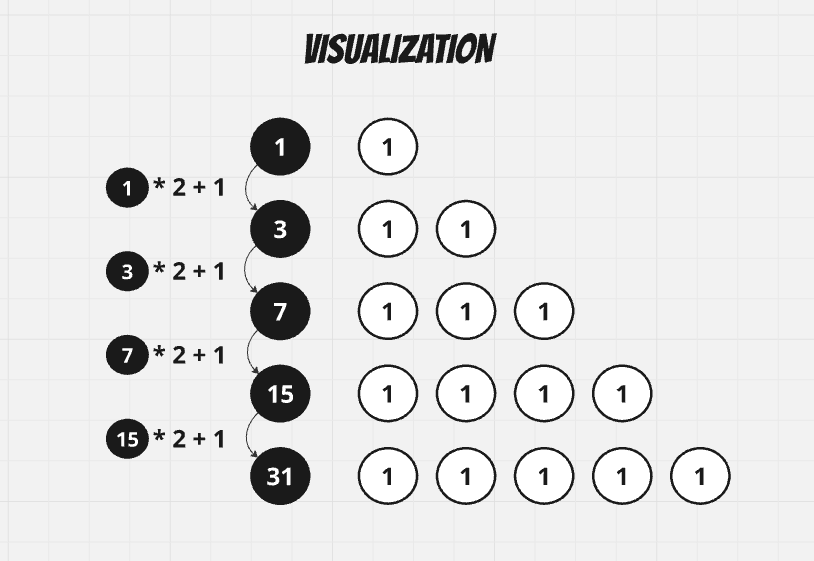\n\n\n# Approach\nWe can start from 1 and calculate next number while our number lesser than n.\n\n# Complexity\n- Time complexity:\nO(logN)\n\n- Space complexity:\nO(1)\n\n\n\n# Swift Code\n```swift []\nclass Solution {\n func smallestNumber(_ n: Int) -> Int {\n var curr = 1\n while curr < n {\n curr = curr * 2 + 1\n }\n return curr\n }\n}\n```\n\n# C++ Code\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n int curr = 1;\n while (curr < n)\n curr = curr * 2 + 1;\n return curr;\n }\n};\n```\n\n# Python3 Code\n```python3 []\nclass Solution:\n def smallestNumber(self, n: int) -> int:\n curr = 1\n while curr < n:\n curr = curr * 2 + 1\n return curr\n```\n | 2 | 0 | ['Swift', 'C++', 'Python3'] | 0 |
smallest-number-with-all-set-bits | Simple and Easy Solution | ✅Beats 100% | C++| Java | Python | JavaScript | simple-and-easy-solution-beats-100-c-jav-e5td | \n\n# \u2B06\uFE0F Upvote if it helps! \u2B06\uFE0F \n## Connect with me on LinkedIn: Bijoy Sing \n\n---\n\n\n## Follow me also on Codeforces: Bijoy Sing\n\n\ | BijoySingh7 | NORMAL | 2024-12-01T05:45:28.738744+00:00 | 2024-12-01T05:47:40.106978+00:00 | 572 | false | \n\n# \u2B06\uFE0F Upvote if it helps! \u2B06\uFE0F \n## Connect with me on LinkedIn: [Bijoy Sing](https://www.linkedin.com/in/bijoy-sing-236a5a1b2/) \n\n---\n\n\n## Follow me also on Codeforces: [Bijoy Sing](https://codeforces.com/profile/BijoySingh7)\n\n\n---\n\n### **Solution in C++, Python, Java, and JavaScript**\n\n```cpp\nclass Solution {\npublic:\n int smallestNumber(int n) {\n int bit = log2(n) + 1; // Calculate the number of bits required\n int ans = (1 << bit) - 1; // Construct the smallest number with all bits set\n return ans;\n }\n};\n```\n\n```python\nclass Solution:\n def smallestNumber(self, n):\n bit = n.bit_length() # Calculate the number of bits required\n ans = (1 << bit) - 1 # Construct the smallest number with all bits set\n return ans\n```\n\n```java\nclass Solution {\n public int smallestNumber(int n) {\n int bit = (int)(Math.log(n) / Math.log(2)) + 1; // Calculate the number of bits required\n int ans = (1 << bit) - 1; // Construct the smallest number with all bits set\n return ans;\n }\n}\n```\n\n```javascript\nclass Solution {\n smallestNumber(n) {\n let bit = Math.floor(Math.log2(n)) + 1; // Calculate the number of bits required\n let ans = (1 << bit) - 1; // Construct the smallest number with all bits set\n return ans;\n }\n}\n```\n\n---\n\n### **Explanation**\nThe goal is to find the smallest integer where all its bits are set to 1, given \\( n \\). \n\n#### Approach:\n1. Calculate the number of bits needed to represent \\( n \\). \n - In C++, Python, JavaScript: Use `log2(n)` and add 1.\n - In Java: Use `Math.log(n) / Math.log(2)` and add 1.\n2. Construct the smallest number with all bits set using bit manipulation: \n \\( (1 << \\text{bit}) - 1 \\). \n This shifts 1 left by `bit` positions, filling it with 1\'s, and subtracts 1 to create the final result.\n\n---\n\n### **Complexity Analysis**\n- **Time Complexity**: \\( O(1) \\) \n All operations (logarithm and bit manipulation) take constant time. \n\n- **Space Complexity**: \\( O(1) \\) \n No additional space is required. \n\n---\n\n### **If you liked the solution, don\'t forget to upvote! \uD83D\uDE0A** | 2 | 0 | ['Bit Manipulation', 'Bitmask', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 2 |
smallest-number-with-all-set-bits | ✅ Simple Java Solution | simple-java-solution-by-harsh__005-57wt | CODE\nJava []\npublic int smallestNumber(int n) {\n\tString str = Integer.toBinaryString(n);\n\tint i=str.length()-1, res = 0;\n\n\twhile(i >= 0) {\n\t\tres += | Harsh__005 | NORMAL | 2024-12-01T05:36:16.680373+00:00 | 2024-12-01T05:36:16.680400+00:00 | 55 | false | ## **CODE**\n```Java []\npublic int smallestNumber(int n) {\n\tString str = Integer.toBinaryString(n);\n\tint i=str.length()-1, res = 0;\n\n\twhile(i >= 0) {\n\t\tres += (1<<i);\n\t\ti--;\n\t}\n\treturn res;\n}\n``` | 2 | 0 | ['Java'] | 1 |
smallest-number-with-all-set-bits | 3370. Smallest Number With All Set Bits | 3370-smallest-number-with-all-set-bits-b-mxkg | Intuition\n\nGenerate string like below:\n0\n01\n011\n0111\n01111\n011111\n\nConvert to decimal\n0\n1\n3\n7\n15\n31\n\nif greater than n, return that converted | pgmreddy | NORMAL | 2024-12-01T05:15:48.081407+00:00 | 2024-12-01T05:24:48.730053+00:00 | 59 | false | # Intuition\n```\nGenerate string like below:\n0\n01\n011\n0111\n01111\n011111\n\nConvert to decimal\n0\n1\n3\n7\n15\n31\n\nif greater than n, return that converted decimal number\n```\n\nor\n```\nn and next to n bit and is 0\n```\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\nvar smallestNumber = function (n) {\n let binaryString = "0";\n while (parseInt(binaryString, 2) < n) {\n binaryString += "1";\n }\n return parseInt(binaryString, 2);\n};\n```\n\n```\nvar smallestNumber = function (n) {\n for (; ; n++) {\n if ((n & (n + 1)) === 0) {\n return n\n }\n }\n}\n```\n | 2 | 0 | ['JavaScript'] | 0 |
smallest-number-with-all-set-bits | Set all bits in n | C++, Python, Java | set-all-bits-in-n-c-python-java-by-not_y-eu9n | Approach\n Describe your approach to solving the problem. \nSet all the bits in n\'s binary representation to 1.\n\nFor the python version, 2^k-1 is a number wi | not_yl3 | NORMAL | 2024-12-01T05:02:18.821899+00:00 | 2024-12-01T20:59:54.003385+00:00 | 188 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nSet all the bits in n\'s binary representation to 1.\n\nFor the python version, $$2^k-1$$ is a number with all `k` set bits.\n# Complexity\n- Time complexity: $$O(log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n for (int bit = 1; bit < n; bit <<= 1)\n n |= bit;\n return n;\n }\n};\n```\n```python []\nclass Solution:\n def smallestNumber(self, n: int) -> int:\n k = 0\n while 1 << k <= n:\n k += 1\n return (1 << k) - 1\n```\n```Java []\nclass Solution {\n public int smallestNumber(int n) {\n int bit = 1;\n while (bit < n)\n bit = (bit << 1) | 1;\n return bit;\n }\n}\n```\n | 2 | 0 | ['Bit Manipulation', 'C', 'Python', 'C++', 'Java', 'Python3'] | 0 |
smallest-number-with-all-set-bits | simple and easy C++ solution | Bitmask | simple-and-easy-c-solution-bitmask-by-sh-5ivk | \n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n###### Let\'s Connect on Linkedin: www.linkedin.com/in/shishirrsiam\n\n\n\n# Code\ncpp []\nclass Solutio | shishirRsiam | NORMAL | 2024-12-01T04:55:12.471249+00:00 | 2024-12-01T04:55:12.471278+00:00 | 102 | false | \n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n###### Let\'s Connect on Linkedin: www.linkedin.com/in/shishirrsiam\n\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) \n {\n bitset<24>bits(n);\n string num, s = bits.to_string();\n\n int idx = s.find(\'1\');\n for(int i = idx; i < 24; i++)\n num += \'1\';\n\n int ans = stoi(num, NULL, 2);\n return ans;\n }\n};\n``` | 2 | 1 | ['Bit Manipulation', 'Bitmask', 'C++'] | 0 |
smallest-number-with-all-set-bits | C code No built-in functions, Only bit manipulation (explained) | c-code-no-built-in-functions-only-bit-ma-muo7 | Code | amiensa | NORMAL | 2025-04-05T22:00:00.105554+00:00 | 2025-04-05T22:00:00.105554+00:00 | 10 | false |
# Code
```c []
int smallestNumber(int n) {
int count = 0; // number of 1's in "n"
int lastone = 0; // refers to last bit with value 1
// in "n" starting from right
int m = n;
for(int i = 1 ; i < 11 ; i++){
if(m & 1){
lastone=i;
count++;
}
m >>= 1;
}
// this line below means we only encounter bits with 1 values
// before reaching the first bit with 0 value
if(lastone==count)return n;
int result = 0;
for(int j = 0 ; j < lastone; j++){
// shift left and set LSB to 1
result = (result << 1) | 1;
}
return result;
}
``` | 1 | 0 | ['Bit Manipulation', 'C'] | 0 |
smallest-number-with-all-set-bits | 100 Beats Solution 🔥|| Java 🎯 | 100-beats-solution-java-by-user8688f-obzg | Approachres * 2 + 1 upto n gives the answerComplexity
Time complexity:O(Log(N))
Space complexity:O(1)
Code | user8688F | NORMAL | 2025-03-22T07:29:25.072332+00:00 | 2025-03-22T07:29:25.072332+00:00 | 29 | false | # Approach
res * 2 + 1 upto n gives the answer
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(Log(N))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->

# Code
```java []
class Solution {
public int smallestNumber(int n) {
int res=1;
while(res<n){
res=res*2+1;
}
return res;
}
}
``` | 1 | 0 | ['Math', 'Java'] | 0 |
smallest-number-with-all-set-bits | 100% Acceptance!✅With Efficient Memory!✅ Very Easy To understand!✅ | 100-acceptancewith-efficient-memory-very-h3uj | IntuitionApproachComplexity
Time complexity:O(n)✅
Space complexity:O(1)✅
Code | velan_m_velan | NORMAL | 2025-03-19T07:55:47.450649+00:00 | 2025-03-19T07:55:47.450649+00:00 | 50 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:$$O(n)$$✅
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(1)$$✅
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int sum=0;
for(int b=0;b<=10;b++){
sum+=pow(2,b);
if(sum>=n)return sum;
}
return -1;
}
};
``` | 1 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Simple Go, no bit manipulation | simple-go-no-bit-manipulation-by-user891-gjbp | ApproachWe need find power of 2 that is bigger than the given number and subtract 1.5 -> 101
next greater number that is a power of 2 is 8
8 -> 1000
subtract 1 | user8912Cp | NORMAL | 2025-03-17T04:06:28.214915+00:00 | 2025-03-17T04:06:28.214915+00:00 | 18 | false | # Approach
We need find power of 2 that is bigger than the given number and subtract 1.
5 -> 101
next greater number that is a power of 2 is 8
8 -> 1000
subtract 1
7 -> 111
Same length as 5 in binary representation, but all bits are ones
# Complexity
- Time complexity:
O(log(n))
- Space complexity:
O(n)
# Code
```golang []
func smallestNumber(n int) int {
result := 1
for result <= n {
result *= 2
}
return result - 1
}
``` | 1 | 0 | ['Go'] | 0 |
smallest-number-with-all-set-bits | ☑️ Finding Smallest Number With All Set Bits. ☑️ | finding-smallest-number-with-all-set-bit-w009 | Code | Abdusalom_16 | NORMAL | 2025-03-15T11:50:46.516379+00:00 | 2025-03-15T11:50:46.516379+00:00 | 19 | false | # Code
```dart []
class Solution {
int smallestNumber(int n) {
while(true){
List<String> conv = n.toRadixString(2).split("");
if(conv.toSet().length == 1 && conv.first == "1"){
return n;
}
n++;
}
return 999;
}
}
``` | 1 | 0 | ['Math', 'Bit Manipulation', 'Dart'] | 0 |
smallest-number-with-all-set-bits | // ONE LINER SOLUTION >- BEATS 100% | one-liner-solution-beats-100-by-fwupexeg-msec | 🧠 Intuition
The goal is to find a pattern related to the highest power of 2 in the given number n. Observing the binary representation of numbers, we notice tha | fWUpExEgyB | NORMAL | 2025-02-27T08:49:50.324449+00:00 | 2025-02-27T08:49:50.324449+00:00 | 53 | false | 🧠 Intuition
The goal is to find a pattern related to the highest power of 2 in the given number n. Observing the binary representation of numbers, we notice that:
The highest power of 2 in n is the most significant set bit.
If we take 2 * highestOneBit(n) - 1, we get a number consisting of all 1s in binary, covering that power of 2.
For example:
n = 5 (binary 101), highest power of 2 = 4 (binary 100), result = 7 (binary 111).
n = 10 (binary 1010), highest power of 2 = 16 (binary 1000), result = 15 (binary 1111).
🔍 Approach
Find the highest power of 2 in n using Integer.highestOneBit(n).
Generate a number with all 1s up to that position using 2 * highestOneBit(n) - 1.
Return the computed result.
⏳ Complexity Analysis
Time Complexity:
O(1)
Integer.highestOneBit(n) runs in constant time as it operates on a fixed 32-bit integer.
Space Complexity:
O(1)
No extra space is used.
💻 Code
java:
class Solution {
public int smallestNumber(int n) {
int nextPower = Integer.highestOneBit(n);
return 2 * nextPower - 1;
}
} | 1 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | EASIEST 2 LINE SOLUTION BEATING 100% IN 0ms | easiest-2-line-solution-beating-100-in-0-ov3w | ApproachTo find the smallest number x greater than or equal to n where x's binary representation consists of only set bits (i.e., all bits are 1), we can utiliz | arshi_bansal | NORMAL | 2025-02-09T07:34:47.579409+00:00 | 2025-02-09T07:34:47.579409+00:00 | 62 | false | # Approach
<!-- Describe your approach to solving the problem. -->
To find the smallest number x greater than or equal to n where x's binary representation consists of only set bits (i.e., all bits are 1), we can utilize the following method:
1. Start with a number of the form 2^k - 1, which in binary is k consecutive set bits (e.g., 3 (11), 7 (111), 15 (1111), etc.).
2. Keep increasing k until 2^k - 1 is greater than or equal to n.
3. Return this number.
# Complexity
- Time complexity: O(log n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int x = 1;
while ((x - 1) < n) {
x <<= 1; // Multiply x by 2
}
return x - 1;
}
}
``` | 1 | 0 | ['Math', 'Bit Manipulation', 'Java'] | 0 |
smallest-number-with-all-set-bits | 0MS 🏆 || 🌟JAVA ☕ | 0ms-java-by-galani_jenis-1x3p | Code | Galani_jenis | NORMAL | 2025-01-29T05:39:29.541636+00:00 | 2025-01-29T05:39:29.541636+00:00 | 58 | false |
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int ans = 1;
while (ans < n)
ans = ans * 2 + 1;
return ans;
}
}
``` | 1 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | "Simple & small" ahh solution | Beats 100%. | simple-small-ahh-solution-beats-100-by-a-6g9s | IntuitionApproach
Find the smallest power of 2 that is strictly greater than n.
Return that power of 2, subtracting 1 as the result.
Complexity
Time complexity: | AnaghaBharadwaj | NORMAL | 2025-01-20T06:04:48.605269+00:00 | 2025-01-20T06:04:48.605269+00:00 | 59 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
1. Find the smallest power of 2 that is strictly greater than n.
2. Return that power of 2, subtracting 1 as the result.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int sol=0;
for(int i=1;i<=n;++i){
if(Math.pow(2,i)>n){
sol =(int)Math.pow(2,i);
break;
}
}
return sol-1;
}
}
``` | 1 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | BEATS 100% WITH 3 LINES OF CODE | beats-100-with-3-lines-of-code-by-yashve-eapv | IntuitionApproachFirst find the number of bits in the number and then return the 2 raise to the power bits -1. If you find any difficulty please refer to my sol | Yashvendra | NORMAL | 2025-01-01T16:45:20.703110+00:00 | 2025-01-01T16:45:20.703110+00:00 | 12 | false | # Intuition
# Approach
First find the number of bits in the number and then return the 2 raise to the power bits -1. If you find any difficulty please refer to my solution.
# Complexity
- Time complexity: O(1).
- Space complexity: O(1).
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int bits = (int) (Math.log(n)/Math.log(2.0));
int x =(int)(Math.pow(2,bits+1));
return x -1;
}
}
``` | 1 | 0 | ['Math', 'Bit Manipulation', 'Java'] | 0 |
smallest-number-with-all-set-bits | 🔥Beats 100 % 🔥 || Easiest Solution ✔️ || JAVA || | beats-100-easiest-solution-java-by-happy-f8bo | IntuitionThe problem revolves around finding the smallest number greater than or equal to a given number n where the binary representation of the number contain | Happy-Singh-Chauhan | NORMAL | 2024-12-24T18:02:26.617969+00:00 | 2024-12-24T18:02:26.617969+00:00 | 38 | false | # Intuition
*The problem revolves around finding the smallest number greater than or equal to a given number n where the binary representation of the number contains only 1s.*
# Approach
1. Determine the number of bits b needed to represent n.
2. Calculate the result as Math.pow(2,b)-1.
# Complexity
- Time complexity:
O(log n)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int count=0;
while(n > 0){
count++;
n=n>>1;
}
return (int)Math.pow(2,count)-1;
}
}
``` | 1 | 0 | ['Math', 'Bit Manipulation', 'Java'] | 0 |
smallest-number-with-all-set-bits | optimal approach: o(logn) | optimal-approach-ologn-by-bhagavanreddy-9ntl | IntuitionApproach :Best approachBy using left shift operatorComplexity
Time complexity:O(LogN)
Space complexity:O(1)
Code | bhagavanreddy | NORMAL | 2024-12-24T15:15:46.384695+00:00 | 2024-12-24T15:15:46.384695+00:00 | 29 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach :Best approach
By using left shift operator
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(LogN)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int pow=1;
while(pow<n){
pow=pow<<1|1 ;
}
return pow;
}
};
``` | 1 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Bit Updation 🔥✅ - Beats 100% | C++ Solution | bit-updation-beats-100-c-solution-by-saj-uoqu | IntuitionStart with the value 1. Now we will keep converting our number from 1 -> 11 -> 111 like this , until it become just greater than the n.Approachwhile th | Sajal0701 | NORMAL | 2024-12-21T13:22:05.892083+00:00 | 2024-12-21T13:22:05.892083+00:00 | 42 | false | # Intuition
Start with the value 1. Now we will keep converting our number from 1 -> 11 -> 111 like this , until it become just greater than the n.
# Approach
while the value of x is lesser than n we will convert right most unset bit to 1.
Simply run a while loop until the value of x is lesser than n. In each iteration left shift the x and take OR with 1 , to set the last bit.
x = x<<1 | 1;
This will give the required answer;
# Complexity
- Time complexity:
$$O(logn)$$ -->
- Space complexity:
$$O(1)$$
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int x = 1;
while(x<n){
x = x << 1 | 1;
}
return x;
}
};
``` | 1 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | ✅ C++ Simple Code ✅ | c-simple-code-by-jagdish9903-liwp | \n\n# Code\ncpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n int ans = log2(n);\n return pow(2, (ans + 1)) - 1; \n }\n};\n | Jagdish9903 | NORMAL | 2024-12-05T07:30:46.303363+00:00 | 2024-12-05T07:30:46.303385+00:00 | 19 | false | \n\n# Code\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n int ans = log2(n);\n return pow(2, (ans + 1)) - 1; \n }\n};\n``` | 1 | 0 | ['Math', 'Bit Manipulation', 'C++'] | 0 |
smallest-number-with-all-set-bits | Used built in function kuch STL ka | used-built-in-function-kuch-stl-ka-by-ye-cz6x | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yesyesem | NORMAL | 2024-12-04T18:54:48.812561+00:00 | 2024-12-04T18:54:48.812597+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\nbool isPowerOfTwo(int n) {\n return n > 0 && __builtin_popcount(n) == 1;\n}\n int smallestNumber(int n) {\n //n > 0 && (n & (n - 1)) == 0;\n // n=n+1;\n\n while(1)\n {\n if(isPowerOfTwo(n+1))\n return n;\n n++;\n }\n return n;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Need to learn bitset conversion binary find_first_not_of() etc need to do STL properly | need-to-learn-bitset-conversion-binary-f-rsw7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yesyesem | NORMAL | 2024-12-04T16:58:18.405964+00:00 | 2024-12-04T16:58:18.405999+00:00 | 15 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n\n while(1)\n {\n string binary = bitset<32>(n).to_string();\n\n binary.erase(0,binary.find_first_not_of(\'0\'));\n\n if(binary.find(\'0\') == string::npos) \n return n;\n else\n n++;\n }\n\n return n;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | C# O(1) solution | c-o1-solution-by-idhammond-hpoe | Approach\nPropagating any set bit to the right by 8 bits then 4 bits, then 2 bits and finally 1 bit, using a shift and or operation, results in all bits to the | idhammond | NORMAL | 2024-12-04T08:08:49.489434+00:00 | 2024-12-04T08:08:49.489479+00:00 | 4 | false | # Approach\nPropagating any set bit to the right by 8 bits then 4 bits, then 2 bits and finally 1 bit, using a shift and or operation, results in all bits to the right of any set bit also getting set.\n\nFor example: `001000000000` -> `001000000010` -> `001000100010` -> `001010101010` -> `001111111111`\n\n# Complexity\n- Time complexity:\n$$O(1)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```csharp []\npublic class Solution {\n public int SmallestNumber(int n) {\n n |= n >> 8;\n n |= n >> 4;\n n |= n >> 2;\n return n | n >> 1;\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
smallest-number-with-all-set-bits | Unique Solution | unique-solution-by-himanshu_gahlot-7qaz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Himanshu_Gahlot | NORMAL | 2024-12-04T04:19:57.723182+00:00 | 2024-12-04T04:19:57.723204+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int smallestNumber(int n) {\n int i=n;\n while(i>=0){\n int bit=Integer.bitCount(i);\n String s=Integer.toBinaryString(i);\n if(bit==s.length())\n return i;\n i++;\n }\n return -1;\n }\n}\n``` | 1 | 0 | ['Bit Manipulation', 'Java'] | 0 |
smallest-number-with-all-set-bits | Simple Solution C# | 0 MS | simple-solution-c-0-ms-by-nyester-iats | Approach\n Describe your approach to solving the problem. \n\n# Code\ncsharp []\npublic class Solution {\n public int SmallestNumber(int n) \n {\n | Nyester | NORMAL | 2024-12-03T11:45:19.966128+00:00 | 2024-12-03T11:45:19.966169+00:00 | 10 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n```csharp []\npublic class Solution {\n public int SmallestNumber(int n) \n {\n // Count the number of bits\n int bits = 0;\n while(n > 0)\n {\n n /= 2;\n bits++;\n } \n int m = 1; \n int sol = 0;\n // Calculate the solution\n for(int i = 1; i <= bits; i ++)\n {\n sol += m;\n m *=2;\n }\n return sol;\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
smallest-number-with-all-set-bits | Binary Manipulation Approach || Python3 | binary-manipulation-approach-python3-by-eind3 | Binary Manipulation Approach:\n\n# Intuition\n- The idea is to find the smallest number that has the same number of bits set to 1 as the binary representation o | lavanyaimmaneni12 | NORMAL | 2024-12-01T18:05:06.418546+00:00 | 2024-12-01T18:05:06.418584+00:00 | 20 | false | # Binary Manipulation Approach:\n\n# Intuition\n- The idea is to find the smallest number that has the same number of bits set to 1 as the binary representation of the given number \\( n \\).\n\n# Approach\n- Convert \\( n \\) to its binary representation.\n- Count the number of bits set to 1.\n- Construct a binary number composed entirely of 1s with the same length.\n- Convert the binary string back to an integer and return it.\n\n# Complexity\n- Time complexity: $$O(\\log n)$$\n- Space complexity: $$O(\\log n)$$\n\n# Code\n```python\nclass Solution:\n def smallestNumber(self, n: int) -> int:\n l = bin(n)[2:] # Convert n to binary and strip the "0b" prefix.\n l = \'1\' * len(l) # Create a binary string of 1s with the same length.\n return int(l, 2) # Convert the binary string back to an integer.\n | 1 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | C bit-shifting | c-bit-shifting-by-michelusa-f0o3 | Set bits, one at a time.\n\n# Code\nc []\nint smallestNumber(int n) {\n int res = 0;\n\n while (n > 0) {\n res = (res << 1) | 1;\n n >>= 1;\ | michelusa | NORMAL | 2024-12-01T11:53:35.169227+00:00 | 2024-12-01T11:53:35.169260+00:00 | 39 | false | Set bits, one at a time.\n\n# Code\n```c []\nint smallestNumber(int n) {\n int res = 0;\n\n while (n > 0) {\n res = (res << 1) | 1;\n n >>= 1;\n }\n\n return res;\n}\n``` | 1 | 0 | ['C'] | 0 |
smallest-number-with-all-set-bits | 🚀 LeetCode Solution: Finding the Greatest Square and the Smallest Number | leetcode-solution-finding-the-greatest-s-zboh | Here\u2019s how your LeetCode solution post could look:\n\n---\n\n### \uD83D\uDE80 LeetCode Solution: Finding the Greatest Square and the Smallest Number\n\n\uD | krishnakanthpathi | NORMAL | 2024-12-01T07:02:02.103897+00:00 | 2024-12-01T07:02:02.103934+00:00 | 20 | false | Here\u2019s how your LeetCode solution post could look:\n\n---\n\n### \uD83D\uDE80 LeetCode Solution: Finding the Greatest Square and the Smallest Number\n\n\uD83D\uDCA1 **Problem Statement**: \nGiven a number `n`, the task is to: \n1. Find the smallest number that is larger than `n` and is a power of 2. \n2. Return the largest number smaller than this power of 2.\n\n---\n\n### \uD83E\uDDF5 **Code Explanation**\n\n```python\nclass Solution:\n def greatestSquare(self, n):\n # Convert number to its binary representation\n cur = bin(n)[2:] # Strips the \'0b\' prefix\n # Create a binary number that\'s just one higher power of 2\n greater = "1" + len(cur) * "0"\n return int(greater, 2) # Convert binary string back to integer\n\n def smallestNumber(self, n: int) -> int:\n # Find the nearest power of 2 that\'s greater than `n`\n nearst = self.greatestSquare(n)\n # Subtract 1 to find the largest number less than `nearst`\n return nearst - 1\n```\n\n---\n\n### \uD83D\uDEE0\uFE0F **Step-by-Step Explanation**\n\n1. **Understanding the Function `greatestSquare`:** \n - Convert the number `n` to its binary representation using `bin(n)`.\n - Skip the `"0b"` prefix using `[2:]`.\n - Append a `"1"` followed by as many `"0"`s as the length of the binary number.\n - Convert this binary string back to a decimal integer to find the nearest power of 2.\n\n \uD83D\uDCDD *Example*: \n For `n = 5` (binary: `101`): \n - Append `"1"` to create `1000`. \n - This corresponds to `8` in decimal.\n\n2. **Understanding the Function `smallestNumber`:** \n - Use `greatestSquare` to find the next power of 2 greater than `n`.\n - Subtract `1` from this number to get the largest number less than that power of 2.\n\n \uD83D\uDCDD *Example*: \n For `n = 5`: \n - Nearest power of 2 = `8`. \n - Subtract `1` \u2192 Result = `7`.\n\n---\n\n### \uD83C\uDF1F **Examples**\n\n#### \uD83D\uDD0D Input: `n = 5` \n- **Step 1:** Binary of 5 is `101`. \n- **Step 2:** Append `"1"` + `"0"` * 3 \u2192 Nearest power of 2 = `8`. \n- **Step 3:** Subtract `1` \u2192 Result = `7`.\n\n#### \uD83D\uDD0D Input: `n = 12` \n- **Step 1:** Binary of 12 is `1100`. \n- **Step 2:** Append `"1"` + `"0"` * 4 \u2192 Nearest power of 2 = `16`. \n- **Step 3:** Subtract `1` \u2192 Result = `15`.\n\n---\n\n### \u26A1 Key Points:\n- This solution works in **O(log(n))**, where `log(n)` comes from binary conversion.\n- Efficient for handling large numbers due to its simplicity in bit manipulation.\n\nHope this helps! \uD83C\uDF1F Keep coding and solving! \uD83D\uDCBB | 1 | 0 | ['Python', 'Python3'] | 0 |
smallest-number-with-all-set-bits | Using Mersenne Numbers | using-mersenne-numbers-by-sapilol-hu4v | \n\n\n# Code\ncpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n int z = 1;\n for (int i = 0; i <= n; i++) {\n z = (1 | LeadingTheAbyss | NORMAL | 2024-12-01T04:36:26.755756+00:00 | 2024-12-01T04:36:26.755781+00:00 | 17 | false | \n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n int z = 1;\n for (int i = 0; i <= n; i++) {\n z = (1 << i);\n if (z > n)\n return z - 1;\n }\n return 0;\n }\n};\n\n``` | 1 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Easy to understand C++ Solution | easy-to-understand-c-solution-by-rajvir_-fqp4 | Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n# Code\ncpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n for(int i | rajvir_singh | NORMAL | 2024-12-01T04:33:26.888809+00:00 | 2024-12-01T04:33:26.888828+00:00 | 109 | false | # Complexity\n- Time complexity: O(1)\n\n- Space complexity: O(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n for(int i = 1; i <= 10; i++){\n int x = pow(2, i) - 1;\n if(x >= n) return x;\n }\n return -1;\n }\n};\n``` | 1 | 0 | ['Bit Manipulation', 'C++'] | 0 |
smallest-number-with-all-set-bits | C++ O(1) Clean 1-Line bit_width | c-o1-clean-1-line-bit_width-by-bramar2-iey7 | Complexity\n- Time complexity: $O(1)$\n\n- Space complexity: $O(1)$\n\n# Code\ncpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n retur | bramar2 | NORMAL | 2024-12-01T04:14:43.991018+00:00 | 2024-12-01T05:56:16.150089+00:00 | 32 | false | # Complexity\n- Time complexity: $O(1)$\n\n- Space complexity: $O(1)$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int smallestNumber(int n) {\n return (1 << bit_width(unsigned(n))) - 1;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Easy C solution 100% 💡 | easy-c-solution-100-by-jossue-05aj | 💡 IntuitionWhen we look at a binary number like 5 = 101, its bitwise complement (within its significant bits) is 2 = 010.
If we perform a bitwise OR between the | Jossue | NORMAL | 2025-04-12T03:57:35.741571+00:00 | 2025-04-12T03:57:35.741571+00:00 | 1 | false | # 💡 Intuition
When we look at a binary number like `5 = 101`, its bitwise complement (within its significant bits) is `2 = 010`.
If we perform a bitwise OR between the number and its complement, we get a result with all bits set:
`5 | 2 = 101 | 010 = 111`.
This idea helps us construct the smallest number greater than or equal to `n` with all bits set starting from the most significant bit.
---
# 🚀 Approach
We build a **mask** with all bits set to `1` until it fully covers the significant bits of `n`.
We shift the mask left and OR it with `1` repeatedly until `~mask & n == 0`, meaning that the mask now covers all bits in `n`.
Finally, we return `n | mask`, which results in the smallest number ≥ `n` with all bits from the highest bit downward set to `1`.
---
# 🧠 Complexity
- **Time complexity:** $$O(\log n)$$
We loop through the number of bits in `n`.
- **Space complexity:** $$O(1)$$
Only a few integer variables are used.
---
# ✅ Code
```c []
int smallestNumber(int n) {
int mask = 0;
while((n & ~mask) != 0){
mask = (mask << 1) | 1;
}
int comp = n ^ mask;
return n | mask;
}
``` | 0 | 0 | ['C'] | 0 |
smallest-number-with-all-set-bits | easiest o(1) java solution (one array and loop) | easiest-o1-java-solution-one-array-and-l-w6qn | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | dpasala | NORMAL | 2025-04-08T19:20:04.739908+00:00 | 2025-04-08T19:20:04.739908+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
if (n == 1) return 1;
int[] arr = new int[]{1, 3, 7, 15, 31, 63, 127, 255, 511, 1023};
for (int i = 1; i < 10; i++) {
if (n == arr[i]) return arr[i];
else if (n > arr[i - 1] && n < arr[i]) return arr[i];
}
return -1;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | One line solution in Kotlin | Math | Logarithm | one-line-solution-in-kotlin-math-logarit-o5me | Code | ahmadali_ok | NORMAL | 2025-04-01T18:18:08.954298+00:00 | 2025-04-01T18:18:08.954298+00:00 | 2 | false |
# Code
```kotlin []
class Solution {
fun smallestNumber(n: Int): Int {
return (2.00.pow(log2(n.toDouble()).toInt().toDouble() + 1.00) - 1.00).toInt()
}
}
``` | 0 | 0 | ['Kotlin'] | 0 |
smallest-number-with-all-set-bits | simple | simple-by-ryuji-zypg | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | ryuji | NORMAL | 2025-03-31T20:02:31.652095+00:00 | 2025-03-31T20:02:31.652095+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```rust []
impl Solution {
pub fn smallest_number(mut n: i32) -> i32 {
let mut count = 0;
while n > 0 {
n /= 2;
count += 1;
}
(0..count).fold(0, |acc, i| acc + 2i32.pow(i))
}
}
``` | 0 | 0 | ['Rust'] | 0 |
smallest-number-with-all-set-bits | Simple Swift Solution | simple-swift-solution-by-felisviridis-1bgz | Code | Felisviridis | NORMAL | 2025-03-28T09:45:36.362757+00:00 | 2025-03-28T09:45:36.362757+00:00 | 1 | false |
# Code
```swift []
class Solution {
func smallestNumber(_ n: Int) -> Int {
var num = 0
while num < n {
num = num << 1 + 1
}
return num
}
}
``` | 0 | 0 | ['Swift'] | 0 |
smallest-number-with-all-set-bits | simplest solution using cpp. | simplest-solution-using-cpp-by-prachi_ja-dv1r | IntuitionApproachComplexity
Time complexity:
O(1)
Space complexity:
O(1)Code | prachi_jadon | NORMAL | 2025-03-25T03:19:42.157769+00:00 | 2025-03-25T03:19:42.157769+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(1)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int ans=1;
while(n!=0)
{
ans=ans*2;
n=n>>1;
}
return ans-1;
}
};
``` | 0 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Something Interesting | something-interesting-by-shakhob-lsh7 | Code | Shakhob | NORMAL | 2025-03-23T01:13:32.592346+00:00 | 2025-03-23T01:13:32.592346+00:00 | 2 | false | # Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
current = n
while True:
if bin(current).count('0') == 1:
return current
current += 1
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Beats 100% | beats-100-by-raji1804-3sc9 | Code | Raji1804 | NORMAL | 2025-03-22T06:10:19.450881+00:00 | 2025-03-22T06:10:19.450881+00:00 | 2 | false |
# Code
```java []
class Solution {
public int smallestNumber(int n) {
double p=0,ans=0;
if(n==1)
return 1;
for(int i=0;i<n;i++)
{
p=Math.pow(2,i);
if(p>n)
{
ans=p-1;
break;
}
}
return (int)ans;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | 0ms JAVA CODE........!!!!!!!!!!!!! | 0ms-java-code-by-devesh_agrawal-svu0 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Devesh_Agrawal | NORMAL | 2025-03-19T14:33:25.881229+00:00 | 2025-03-19T14:33:25.881229+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int x = n;
while ((x & (x + 1)) != 0) {
x++;
}
return x;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | 0ms JAVA CODE........!!!!!!!!!!!!! | 0ms-java-code-by-devesh_agrawal-os5a | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Devesh_Agrawal | NORMAL | 2025-03-19T14:33:24.040483+00:00 | 2025-03-19T14:33:24.040483+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int x = n;
while ((x & (x + 1)) != 0) {
x++;
}
return x;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | Simple Solution by Baby Beginner | simple-solution-by-baby-beginner-by-chan-1mzq | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | chandueddalausa | NORMAL | 2025-03-18T18:10:36.760850+00:00 | 2025-03-18T18:10:36.760850+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
le=len(str(bin(n))[2:])
return(int("1"*le,2))
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | 100% beats | 100-beats-by-kunal_1310-xq5n | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kunal_1310 | NORMAL | 2025-03-17T17:49:01.668679+00:00 | 2025-03-17T17:49:01.668679+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isPower(int n) {
if (n == 1)
return true;
if (n % 2 != 0)
return false;
if (n <= 0)
return false;
while (n > 1) {
if (n % 2 != 0) {
return false;
}
n = n / 2;
}
return true;
}
int smallestNumber(int n) {
if(n==1)return n;
int temp = n;
while(temp>=n){
if (isPower(temp) and temp>=n) {
int x=temp-1;
if(x>=n){
return x;
}
else{
temp++;
}
}
else{
temp++;
}
}
return 0;
}
};
``` | 0 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | SIMPLE C PROGRAM | simple-c-program-by-mr_jaikumar-knby | IntuitionApproachComplexity
Time complexity:0 MS
Space complexity:
Code | Mr_JAIKUMAR | NORMAL | 2025-03-14T05:38:14.846770+00:00 | 2025-03-14T05:38:14.846770+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:0 MS
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
int smallestNumber(int n) {
int jk=0,i=0;
while(n!=0)
{
jk+=pow(2,i);
n=n/2;
i++;
}
return jk;
}
``` | 0 | 0 | ['C'] | 0 |
smallest-number-with-all-set-bits | easy solution | easy-solution-by-owenwu4-tqym | Intuitionuse a loop and play around with the upper bound - n cubed in this caseApproachComplexity
Time complexity:
Space complexity:
Code | owenwu4 | NORMAL | 2025-03-13T21:53:21.360981+00:00 | 2025-03-13T21:53:21.360981+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
use a loop and play around with the upper bound - n cubed in this case
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
for i in range(n, n * n * n):
cur = bin(i)[2:]
if len(set(cur)) == 1 and cur[0] == "1":
return i
return n
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | JAVA | Shift operators | Log N solutions | java-shift-operators-log-n-solutions-by-3nj2p | IntuitionFind the position of leftmost set bit. Leftmost set bit will tell us how many set bits we want.ApproachTo get left most set bit maintain a counter pos | pankajsbagal | NORMAL | 2025-03-12T17:17:11.966283+00:00 | 2025-03-12T17:17:11.966283+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Find the position of leftmost set bit. Leftmost set bit will tell us how many set bits we want.
# Approach
<!-- Describe your approach to solving the problem. -->
To get left most set bit maintain a counter `pos` to count the position of bits.
Shift right by 1 `n>>1` position at a time till given becomes 0. When number becomes 0 we get the position of left most set bit.
Now shift left 1s for `1<<pos` to get power to the base 2 and substract 1 to get all set bits just greater than earlier number `1<<pos - 1`
# Complexity
- Time complexity: O(log(n))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int pos = 0;
while(n!=0) {
pos++;
n = n>>1;
}
return (1<<pos)-1;
}
}
``` | 0 | 0 | ['Math', 'Bit Manipulation', 'Java'] | 0 |
smallest-number-with-all-set-bits | smallest number with all set bits | smallest-number-with-all-set-bits-by-anu-r8yq | Code | AnushaYelleti | NORMAL | 2025-03-12T14:22:09.538125+00:00 | 2025-03-12T14:22:09.538125+00:00 | 1 | false |
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
f=True
ans=0
temp=n
while(f):
b=bin(temp)[2:]
if b.count('1')==len(b):
ans=temp
f=False
temp+=1
return ans
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Python | 1 line | Beats %100 | python-1-line-beats-100-by-isinsarici-dnr9 | Code | isinsarici | NORMAL | 2025-03-11T22:41:14.988261+00:00 | 2025-03-11T22:41:14.988261+00:00 | 2 | false |
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
return int(bin(n)[2:].replace('0', '1'), 2)
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Beats 100% solution. Super easy cpp code. | beats-100-solution-super-easy-cpp-code-b-higl | IntuitionFind the nearest power (p) of 2 which surpasses n. Subtract 1 from the number (p-1);ApproachInitialize count=0;
Run a while loop and divide the number | codestguy | NORMAL | 2025-03-10T12:18:54.578103+00:00 | 2025-03-10T12:18:54.578103+00:00 | 2 | false | # Intuition
Find the nearest power (p) of 2 which surpasses n. Subtract 1 from the number (p-1);
# Approach
Initialize count=0;
Run a while loop and divide the number by 2 till n becomes 0 and count++;
# Complexity
- Time complexity:
O(n).
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int cnt=0;
while(n)
{
n/=2;
cnt++;
}
return (1<<cnt)-1;
}
};
``` | 0 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Simple and Easy Solution with Intuition | ✅Beats 100% | Java | Python 🔥🔥 | simple-and-easy-solution-with-intuition-zdod3 | 🔹 Approach 1: Brute Force (O(logN))IntuitionIterate from num and increment until we find a number where all bits are set.Algorithm
Start with num.
Increment num | sohith_reddy01 | NORMAL | 2025-03-08T19:34:34.862636+00:00 | 2025-03-08T19:40:32.375397+00:00 | 4 | false | ## **🔹 Approach 1: Brute Force (O(logN))**
### **Intuition**
Iterate from `num` and increment until we find a number where **all bits are set**.
### **Algorithm**
1. Start with `num`.
2. Increment `num` until `num & (num + 1) == 0`.
3. Return the result.
### **Implementation**
#### **Java**
```java
class Solution {
public int nearestAllSetBits(int num) {
while ((num & (num + 1)) != 0) {
num++;
}
return num;
}
}
```
#### **Python**
```python
class Solution:
def nearestAllSetBits(self, num: int) -> int:
while (num & (num + 1)) != 0:
num += 1
return num
```
### **Complexity Analysis**
- **Time Complexity:** `O(logN)` – Iterates until reaching a power of `2 - 1`.
- **Space Complexity:** `O(1)` – Uses a single variable.
---
## **🔹 Approach 2: Optimized Bitwise (O(1))**
### **Intuition**
Instead of iterating, leverage bitwise operations:
###### Use this formula:-
##### **Nearest all-1s number = (Next power of 2) - 1**
This works because `2^x - 1` always has all bits set.
### **Algorithm**
1. Find the **next power of 2** of `num`.
2. Subtract `1` to get all bits set.
### **Implementation**
#### **Java**
```java
class Solution {
public int nearestAllSetBits(int num) {
int nextPowerOfTwo = Integer.highestOneBit(num) << 1;
return nextPowerOfTwo - 1;
}
}
```
#### **Python**
```python
class Solution:
def nearestAllSetBits(self, num: int) -> int:
nextPowerOfTwo = 1 << num.bit_length()
return nextPowerOfTwo - 1
```
### **Complexity Analysis**
- **Time Complexity:** `O(1)` – Uses only bitwise operations.
- **Space Complexity:** `O(1)` – No extra memory usage.
---
## **🔍 Comparison Table**
| Approach | Time Complexity | Space Complexity | Key Idea |
|----------|----------------|----------------|----------|
| **Brute Force** | `O(logN)` | `O(1)` | Increment `num` until all bits are `1`. |
| **Bitwise (Optimal)** | `O(1)` | `O(1)` | Use bitwise shifts to compute the result instantly. |
---
## **Conclusion**
- **Brute Force** is simple but inefficient for large numbers.
- **Bitwise Optimization** provides an elegant `O(1)` solution using `Integer.highestOneBit()` or `bit_length()`.
For efficient solutions, **bitwise operations** are the preferred approach. 🚀
---
### ✅ **If you found this explanation helpful, don't forget to upvote!** 🚀

| 0 | 0 | ['Bit Manipulation', 'Bitmask', 'Java', 'Python3'] | 0 |
smallest-number-with-all-set-bits | Without using log | without-using-log-by-nishant15-8y3v | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | nishant15 | NORMAL | 2025-03-08T18:30:48.364081+00:00 | 2025-03-08T18:30:48.364081+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int SmallestNumber(int n)
{
int res = 0;
int j = 0;
for (int i = 1; i <= n; i = i * 2)
{
res += (int)Math.Pow(2, j++);
}
return res;
}
}
``` | 0 | 0 | ['C#'] | 0 |
smallest-number-with-all-set-bits | Optimized simple solution - beats 100%🔥 | optimized-simple-solution-beats-100-by-c-od14 | Complexity
Time complexity: O(1)
Space complexity: O(1)
Code | cyrusjetson | NORMAL | 2025-03-06T05:01:55.445702+00:00 | 2025-03-06T05:01:55.445702+00:00 | 3 | false | # Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int powerr = (int) (Math.log(n) / Math.log(2));
return (int)(Math.pow(2, powerr + 1) - 1);
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | C++ | c-by-nguyenvinhhung2705-fw4y | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kazumin | NORMAL | 2025-03-03T15:32:04.083308+00:00 | 2025-03-03T15:32:04.083308+00:00 | 3 | false | # Intuition
# Approach
# Complexity
- Time complexity:
- Space complexity:
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
n+=1
while((n & n-1) != 0){
n++;
}
return n-1;
}
};
``` | 0 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Elixir solution. | elixir-solution-by-spring555-7blo | IntuitionApproachComplexity
Time complexity: 0ms
Space complexity: 72.15MB
Code | spring555 | NORMAL | 2025-03-02T09:31:13.812577+00:00 | 2025-03-02T09:31:13.812577+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: 0ms
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: 72.15MB
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```elixir []
defmodule Solution do
@spec smallest_number(n :: integer) :: integer
def smallest_number(n) do
smallest_number(n, 1)
end
@spec smallest_number(n :: integer, cur :: integer) :: integer
def smallest_number(n, cur) when cur - 1 < n do
smallest_number(n, cur*2)
end
def smallest_number(_n, cur) do
cur - 1
end
end
``` | 0 | 0 | ['Elixir'] | 0 |
smallest-number-with-all-set-bits | simple log solution | simple-log-solution-by-ishanchauhan79-cnyt | Code | IshanChauhan79 | NORMAL | 2025-02-27T11:02:02.505890+00:00 | 2025-02-27T11:02:02.505890+00:00 | 1 | false |
# Code
```typescript []
function smallestNumber(n: number): number {
const log2 = Math.log2(n + 1);
const log2C = Math.ceil(log2)
return Math.pow(2, log2C) - 1
};
``` | 0 | 0 | ['TypeScript'] | 0 |
smallest-number-with-all-set-bits | Simple js solution | simple-js-solution-by-midhunambadan-jud6 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | midhunambadan | NORMAL | 2025-02-25T12:54:53.307876+00:00 | 2025-02-25T12:54:53.307876+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {number} n
* @return {number}
*/
var smallestNumber = function (n) {
if(n<=1) return n
let x = 1
while (x <= n) {
x = x * 2
}
return x - 1
};
``` | 0 | 0 | ['JavaScript'] | 0 |
smallest-number-with-all-set-bits | Easy Solution | easy-solution-by-kallamswethanareddy-8ohc | Code | kallamswethanareddy | NORMAL | 2025-02-20T16:43:29.488091+00:00 | 2025-02-20T16:43:29.488091+00:00 | 5 | false |
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
x=n
while x>=n:
a=bin(x)[2:]
if '0' in a:
x+=1
if '0' not in a:
return x
break
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Python one-line solution | python-one-line-solution-by-redberry33-bx32 | Code | redberry33 | NORMAL | 2025-02-19T12:52:04.314717+00:00 | 2025-02-19T12:52:04.314717+00:00 | 2 | false |
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
return 2**len(bin(n)[2:]) -1
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | [C++] Simple Solution | c-simple-solution-by-samuel3shin-utqs | Code | Samuel3Shin | NORMAL | 2025-02-18T16:12:28.670617+00:00 | 2025-02-18T16:12:28.670617+00:00 | 3 | false | # Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int cur = 1;
int mult = 2;
while(cur <= n) {
if(cur >= n) return cur;
cur += mult;
mult *= 2;
}
return cur;
}
};
``` | 0 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | 🚀 Smallest Number with Same Binary Length 🔢 | smallest-number-with-same-binary-length-mpxe8 | IntuitionThe goal is to find the smallest possible number that has the same number of binary digits as the given number n.Observations:
The smallest number with | fisherman611 | NORMAL | 2025-02-16T18:28:00.209370+00:00 | 2025-02-16T18:28:00.209370+00:00 | 3 | false | ## Intuition
The goal is to find the smallest possible number that has the same number of binary digits as the given number `n`.
Observations:
1. The smallest number with a given binary length consists of all `1`s in binary representation.
2. Converting `n` to binary helps determine its length.
3. Constructing a new binary number with all `1`s of the same length ensures it is the smallest possible number with that length.
## Approach
1. Convert `n` to its binary representation using `bin(n)[2:]` to remove the `0b` prefix.
2. Determine the length of the binary string.
3. Construct a new binary string consisting entirely of `1`s with the same length.
4. Convert the new binary string back to an integer.
## Complexity
- **Time Complexity**: $$O(\log n)$$
- The binary conversion and string operations take logarithmic time relative to `n`.
- **Space Complexity**: $$O(1)$$
- Only a few integer and string variables are used.
## Code
```python
class Solution:
def smallestNumber(self, n: int) -> int:
# Convert to binary and find its length
binary_string = bin(n)[2:]
# Create the smallest number with the same binary length
return int('1' * len(binary_string), 2)
| 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | EASY SOLUTION BEATS 100% | easy-solution-beats-100-by-lakshmisatvik-jq8s | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | lakshmisatvikasuggula2006 | NORMAL | 2025-02-16T14:29:39.034905+00:00 | 2025-02-16T14:29:39.034905+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
res=bin(n)[2:]
s=''
for i in res:
s+='1'
return int(s,2)
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Typescript ✅ | typescript-by-kay-79-taba | Code | Kay-79 | NORMAL | 2025-02-11T06:15:07.861455+00:00 | 2025-02-11T06:15:07.861455+00:00 | 1 | false | # Code
```typescript []
function smallestNumber(n: number): number {
let bin = n.toString(2).split("");
for (let i = 0; i < bin.length; i++) {
if (bin[i] === "0") bin[i] = "1";
}
return parseInt(bin.join(""), 2);
}
``` | 0 | 0 | ['TypeScript'] | 0 |
smallest-number-with-all-set-bits | C++ solution | c-solution-by-sy7794564-dsa4 | Code | sy7794564 | NORMAL | 2025-02-07T08:30:02.227831+00:00 | 2025-02-07T08:30:02.227831+00:00 | 3 | false |
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int x = 1;
while (x <= n) {
x <<= 1 ;
}
return x-1;
}
};
``` | 0 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | simple C | simple-c-by-hadsid-3ql8 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | hadsid | NORMAL | 2025-02-07T06:46:57.573487+00:00 | 2025-02-07T06:46:57.573487+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
int smallestNumber(int n) {
int k = 0;
while(n)
{
k++;
n >>= 1;
}
return pow(2,k) - 1;
}
``` | 0 | 0 | ['C'] | 0 |
smallest-number-with-all-set-bits | Swift, Beats 100.00%, bit << 1 + | 1 | swift-beats-10000-bit-1-1-by-victor-smk-qq1i | null | Victor-SMK | NORMAL | 2025-02-05T18:06:37.889774+00:00 | 2025-02-05T18:06:37.889774+00:00 | 3 | false |
```swift []
class Solution {
func smallestNumber(_ n: Int) -> Int {
var ans = 1
while ans < n {
ans = ans << 1 | 1
}
return ans
}
}
``` | 0 | 0 | ['Swift'] | 0 |
smallest-number-with-all-set-bits | Smallest Number with All set Bits - python3 | smallest-number-with-all-set-bits-python-gp4v | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | ChaithraDee | NORMAL | 2025-02-01T15:41:29.677792+00:00 | 2025-02-01T15:41:29.677792+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
if n == 1:
return 1
num = 2
for i in range(n):
if 2 ** i - 1 >= n:
return 2 ** i - 1
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Smallest Number with All set Bits - python3 | smallest-number-with-all-set-bits-python-iw9i | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | ChaithraDee | NORMAL | 2025-02-01T15:41:22.606763+00:00 | 2025-02-01T15:41:22.606763+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
if n == 1:
return 1
num = 2
for i in range(n):
if 2 ** i - 1 >= n:
return 2 ** i - 1
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Bit Manipulation | bit-manipulation-by-ivl7sth6io-i5t4 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | iVl7stH6Io | NORMAL | 2025-01-30T21:11:46.486191+00:00 | 2025-01-30T21:11:46.486191+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
ans = 0
while (n):
ans |=1
n >>= 1
ans <<=1
ans >>=1
return ans
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Java two rows solution beats 100% | java-two-rows-solution-beats-100-by-had0-nc96 | IntuitionThere are two ways to solve a problem:
1)Transform to String and search for '0' in a String.
2)Use operator & if all the bits are '1' in bin.ApproachTh | had0uken | NORMAL | 2025-01-27T14:50:27.596300+00:00 | 2025-01-27T14:50:27.596300+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
There are two ways to solve a problem:
1)Transform to String and search for '0' in a String.
2)Use operator & if all the bits are '1' in bin.
# Approach
<!-- Describe your approach to solving the problem. -->
The second way is much faster and quite brief, so we choose it. So we use operator & between n and n(+1). We get 0 only in a case when all bits are '1'. So, we keep iterating n, until we get '0'.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
while ((n&(n+1))!=0)n++;
return n;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | Smallest number with all set bits | smallest-number-with-all-set-bits-by-nib-lrte | Approach2^n-1 has all set bits
case 1:n=3
2^3-1=8-1=7
7 has all set bits "111"Complexity
Time complexity:
O(1)--->100%
Code | NIBISHA | NORMAL | 2025-01-27T13:24:54.724374+00:00 | 2025-01-27T13:24:54.724374+00:00 | 2 | false | # Approach
2^n-1 has all set bits
case 1:n=3
2^3-1=8-1=7
7 has all set bits "111"
# Complexity
- Time complexity:
O(1)--->100%
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
i=0
while(1):
if pow(2,i)-1<n:
i+=1
else:
return pow(2,i)-1
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | easy eye caching java code for beginners!!!!!!!!!!!!!!! | easy-eye-caching-java-code-for-beginners-fyr6 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | CHURCHILL04 | NORMAL | 2025-01-27T03:46:43.286215+00:00 | 2025-01-27T03:46:43.286215+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int ans = 1;
while(ans < n){
ans = ans*2 + 1;
}
return ans;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | 3370. Smallest Number With All Set Bits | 3370-smallest-number-with-all-set-bits-b-8xoh | IntuitionEasy one!Approachwhile loop to count number of bits and returning the result as "2 raised to the power of count"-1.Complexity
Time complexity: O(logN) | SPD-LEGEND | NORMAL | 2025-01-25T06:51:10.647837+00:00 | 2025-01-25T06:51:10.647837+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Easy one!
# Approach
<!-- Describe your approach to solving the problem. -->
while loop to count number of bits and returning the result as "2 raised to the power of count"-1.
# Complexity
- Time complexity: O(logN)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int c = 0;
while(n>0)
{
n/=2;
c++;
}
return (int)Math.pow(2,c)-1;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | 3370. Smallest Number With All Set Bits | 3370-smallest-number-with-all-set-bits-b-57mw | Complexity
Time complexity: O(n)
Space complexity: O(1)
Code | SiriusStella | NORMAL | 2025-01-22T03:21:38.586204+00:00 | 2025-01-22T03:21:38.586204+00:00 | 3 | false | # Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
class Solution(object):
def smallestNumber(self, n):
"""
:type n: int
:rtype: int
"""
if n==1:
return 1
for i in range(n):
if (2**i)-1>=n:
return (2**i)-1
``` | 0 | 0 | ['Python'] | 0 |
smallest-number-with-all-set-bits | simple One-liner 100% java | simple-one-liner-100-java-by-prakharmish-a4ck | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | PrakharMishraEnginner | NORMAL | 2025-01-21T10:11:22.852964+00:00 | 2025-01-21T10:11:22.852964+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int mask = (Integer.highestOneBit(n) << 1) - 1;
return mask;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | The 2^m - 1 Binary Pattern Solution | the-2m-1-binary-pattern-solution-by-mpra-vkxl | IntuitionThe key insight comes from understanding how numbers with all 1's work in binary. When you have a number with m consecutive 1's in binary, it's equal t | mpractice | NORMAL | 2025-01-21T02:51:39.303831+00:00 | 2025-01-21T02:51:39.303831+00:00 | 1 | false | # Intuition
The key insight comes from understanding how numbers with all 1's work in binary. When you have a number with m consecutive 1's in binary, it's equal to 2^m - 1. This is because:
For example with m=4 bits:
1111₂ = 2⁴ - 1 = 16 - 1 = 15₁₀
Breaking this down: 1111₂ = 2³ + 2² + 2¹ + 2⁰ = 8 + 4 + 2 + 1 = 15
So, if we need n 1's in our binary number, we need to find the smallest m where 2^m - 1 will give us a number with at least n 1's.
# Approach
1. First, we need to find how many bits (m) are needed to represent n 1's
* The relationship between n and m is: n ≤ m where 2^(m-1) < n+1 ≤ 2^m
* This can be solved using logarithms: m = ⌈log₂(n+1)⌉
2. Once we have m, our answer will be 2^m - 1
* This creates a binary number with exactly m consecutive 1's
* Which is guaranteed to be the smallest number with at least n 1's
For example, if n = 4:
1. m = ⌈log₂(5)⌉ = 3
2. 2^3 - 1 = 8 - 1 = 7 (111₂)
# Complexity
- Time complexity: $$O(1)$$
* Both logarithm and power operations are constant time
* No loops or iterations needed
- Space complexity: $$O(1)$$
* Only using a constant amount of extra space regardless of input size
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
m = math.ceil(math.log2(n+1))
return int(math.pow(2, m) - 1)
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | 0ms Python | 0ms-python-by-mubina1-blbr | Complexity
Time complexity: O(1)
Space complexity: O(1)
Code | mubina1 | NORMAL | 2025-01-19T14:52:55.232310+00:00 | 2025-01-19T14:52:55.232310+00:00 | 2 | false |
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
a=bin(n).replace('0b', '')
return 2**len(a) - 1
``` | 0 | 0 | ['Python3'] | 0 |
smallest-number-with-all-set-bits | Time Complexity : O( logn ) | Space Complexity : O( 1 ) | time-complexity-o-logn-space-complexity-e3kl5 | Code | Trigun_2005 | NORMAL | 2025-01-18T13:55:54.053781+00:00 | 2025-01-18T13:55:54.053781+00:00 | 3 | false | # Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int result = 0;
while(n > result)
result = result*2 + 1;
return result;
}
};
``` | 0 | 0 | ['C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.