question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
smallest-number-with-all-set-bits | Time Complexity : O( logn ) | Space Complexity : O( 1 ) | time-complexity-o-logn-space-complexity-ifp5f | Code | Trigun_2005 | NORMAL | 2025-01-18T13:55:52.004339+00:00 | 2025-01-18T13:55:52.004339+00:00 | 1 | false | # Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
int result = 0;
while(n > result)
result = result*2 + 1;
return result;
}
};
``` | 0 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | C Solution | c-solution-by-dmpriya-fh9m | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | dmpriya | NORMAL | 2025-01-17T06:46:59.386003+00:00 | 2025-01-17T06:46:59.386003+00:00 | 17 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```c []
int smallestNumber(int n) {
int num = n, temp = 0, count = 0;
while(n > 0){
n = n >> 1;
count++;
}
temp = (1 << count) - 1;
return num | temp;
}
``` | 0 | 0 | ['C'] | 0 |
smallest-number-with-all-set-bits | Beats 100% normal while loop approach | beats-100-normal-while-loop-approach-by-yqy94 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | user2633MX | NORMAL | 2025-01-17T06:24:17.310309+00:00 | 2025-01-17T06:24:17.310309+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int k=n;
int sum=0;
while(n!=0){
sum=sum*10+1;
n=n/2;
}
int num = sum;
int dec_value = 0;
int base = 1;
int temp = num;
while (temp > 0) {
int last_digit = temp % 10;
temp = temp / 10;
dec_value += last_digit * base;
base = base * 2;
}
return dec_value;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | scala oneliner | scala-oneliner-by-vititov-o7nc | null | vititov | NORMAL | 2025-01-16T23:05:11.011343+00:00 | 2025-01-16T23:05:11.011343+00:00 | 2 | false | ```scala []
object Solution {
def smallestNumber(n: Int): Int = (1 << BigInt(n).bitLength)-1
}
``` | 0 | 0 | ['Scala'] | 0 |
smallest-number-with-all-set-bits | one liner | one-liner-by-raviteja_29-alow | Intuitionlongest number possible is the length of the bitsApproachchange all 0s in bits to 1Complexity
Time complexity: O(1)
Space complexity: O(1)
Code | raviteja_29 | NORMAL | 2025-01-16T18:06:56.658429+00:00 | 2025-01-16T18:06:56.658429+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
longest number possible is the length of the bits
# Approach
<!-- Describe your approach to solving the problem. -->
change all 0s in bits to 1
# Complexity
- Time complexity: O(1)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestNumber(self, n: int) -> int:
return int("1"*len(str(bin(n))[2:]),2)
``` | 0 | 0 | ['Math', 'Bit Manipulation', 'Python3'] | 0 |
smallest-number-with-all-set-bits | Easiest soln with 100% beats; | easiest-soln-with-100-beats-by-mamthanag-lb9z | IntuitionApproachTHe idea is simple if n contains a no with all bit set then if we and it with the next no the ans be 0 if its 0 then return n else -1Eg: n=5, | mamthanagaraju1 | NORMAL | 2025-01-16T06:37:16.087934+00:00 | 2025-01-16T06:37:16.087934+00:00 | 13 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
THe idea is simple if n contains a no with all bit set then if we and it with the next no the ans be 0 if its 0 then return n else -1
Eg: n=5,
when n=7 ,n+1=8 so 111&1000 is 0 so ans is 7
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
If u like my soln upvote me
# Code
```cpp []
class Solution {
public:
int smallestNumber(int n) {
while(n!=0){
int i=n;
int a= (i&(i+1));
if(a==0){
return i;
}else{
n++;
}
}
return -1;
}
};
``` | 0 | 0 | ['C++'] | 0 |
smallest-number-with-all-set-bits | Log(n) easy understanding solution | logn-easy-understanding-solution-by-spid-1sbs | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | spidemen | NORMAL | 2025-01-14T00:17:36.079161+00:00 | 2025-01-14T00:17:36.079161+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int smallestNumber(int n) {
// 2 ^ n - 1 >= n --> 2^n >= n + 1
int smallBiger = n + 1;
int digit = 0;
while(smallBiger > 1) {
if (smallBiger % 2 != 0) {
smallBiger += 1;
}
smallBiger = smallBiger / 2;
digit++;
}
return (int)Math.pow(2, digit) - 1;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | Smallest_number_with_all_set_bits solution in java | smallest_number_with_all_set_bits-soluti-8fug | ApproachUse the property of (&) operator which return 1 if both value is one.So for num with setbits num &(num+1) will be 0
explanation:
7 --> 111
8 -- | abi_shree | NORMAL | 2025-01-12T17:02:41.169044+00:00 | 2025-01-12T17:02:41.169044+00:00 | 3 | false |
# Approach
Use the property of (&) operator which return 1 if both value is one.
So for num with setbits num &(num+1) will be 0
>>explanation:
>>> 7 --> 111
>>> 8 --> 1000
>>> 7 & 8 --> 0
```java []
class Solution {
public int smallestNumber(int n) {
int num=n;
while((num & (num+1)) != 0)
{
num++;
}
return num;
}
}
``` | 0 | 0 | ['Java'] | 0 |
smallest-number-with-all-set-bits | 3370 solution in java | 3370-solution-in-java-by-abi_shree-zqpg | ApproachUse the property of (&) operator which return 1 if both value is one.
So for num with setbits num &(num+1) will be 0
explanation:
7 --> 111 | abi_shree | NORMAL | 2025-01-12T16:43:20.530948+00:00 | 2025-01-12T16:43:20.530948+00:00 | 3 | false |
# Approach
Use the property of (&) operator which return 1 if both value is one.
> So for num with setbits num &(num+1) will be 0
>> explanation:
>>> 7 --> 111
>>> 8 --> 1000
>>> 7 & 8 --> 0
# Code
```java []
class Solution {
public int smallestNumber(int n) {
int num = n; // Start with n
while (true) { // Loop until we find the valid number
int temp = num; // Temporary variable to check binary digits
boolean allSet = true; // Flag to check if all bits are set
// Check each bit of the number
while (temp > 0) {
int rem = temp % 2; // Extract the least significant bit
if (rem == 0) { // If any bit is 0, it's not valid
allSet = false;
break;
}
temp /= 2; // Move to the next bit
}
if (allSet) { // If all bits are set, return the number
return num;
}
num++; // Increment the number and check again
}
}
}
``` | 0 | 0 | ['Math', 'Bit Manipulation', 'Java'] | 0 |
populating-next-right-pointers-in-each-node | ✅ [C++/Python/Java] Simple Solution w/ Images & Explanation | BFS + DFS + O(1) Optimized BFS | cpythonjava-simple-solution-w-images-exp-r5nv | We are given a perfect binary tree and we need to populate next pointers in each node of the tree\n\n---\n\n\u2714\uFE0F Solution - I (BFS - Right to Left)\n\nI | archit91 | NORMAL | 2021-12-29T06:23:47.162274+00:00 | 2021-12-29T13:53:54.160080+00:00 | 43,494 | false | We are given a perfect binary tree and we need to populate next pointers in each node of the tree\n\n---\n\n\u2714\uFE0F ***Solution - I (BFS - Right to Left)***\n\nIt\'s important to see that the given tree is a **perfect binary tree**. This means that each node will always have both children and only the last level of nodes will have no children.\n\n<p align=middle><img src=https://assets.leetcode.com/uploads/2019/02/14/116_sample.png width=500 />\n\nNow, we need to populate next pointers of each node with nodes that occur to its immediate right on the same level. This can easily be done with BFS. Since for each node, we require the right node on the same level, we will perform a **right-to-left BFS** instead of the standard left-to-right BFS.\n\nBefore starting the traversal of each level, we would initialize a `rightNode` variable set to NULL. Then, since we are performing right-to-left BFS, we would be starting at rightmost node of each level. We set the next node of `cur` as `rightNode` and update `rightNode = cur`. This would ensure that each node would be assigned its `rightNode` properly while traversing from right to left. \nAlso, if `cur` has a child, we would first push its right child and only then its left child (since we are doing right-to-left BFS). Once BFS is completed (after queue becomes empty), all next node would be populated and we can finally return `root`.\n\nThe process is illustrated below -\n\n<table>\n<tr>\n<td colspan=4>\n<p align=middle>\n<img src=https://assets.leetcode.com/users/images/01e68f51-4905-4f58-b2dd-061aa64c8a91_1640764834.4913242.png width=350 />\n</p>\n</td>\n</tr>\n\n<tr></tr>\n\n<tr>\n<td colspan=4>\n<p align=middle>\n<img src=https://assets.leetcode.com/users/images/e2a49b2c-1493-4e3f-bb36-28b89153bf73_1640768916.6068268.png width=350 />\n<img src=https://assets.leetcode.com/users/images/67ff2271-2b5d-4b5f-8e31-6e14809146ad_1640765277.2783518.png width=350 />\n</p>\n</td>\n\n</tr>\n\n<tr></tr>\n\n<tr>\n<td colspan=4>\n<p align=middle>\n<img src=https://assets.leetcode.com/users/images/e1067d5d-3c94-4efc-b202-f4d18b93a0ac_1640765388.5706594.png width=350 />\n<img src=https://assets.leetcode.com/users/images/d8a07cf0-aa8c-44b9-ab35-98a2e1422d43_1640765420.4366648.png width=350 />\n<img src=https://assets.leetcode.com/users/images/ce1046fb-3212-46a5-b2f7-445ab32df816_1640765451.180103.png width=350 />\n<img src=https://assets.leetcode.com/users/images/bd5a4aff-19fe-4aad-b4e6-5dee5156536f_1640765483.7865818.png width=350 />\n</p>\n\n</tr>\n\n</table>\n\n\n\n\n\n\n\n**C++**\n```cpp\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root) return nullptr;\n queue<Node*> q;\n q.push(root); \n while(size(q)) {\n Node* rightNode = nullptr; // set rightNode to null initially\n for(int i = size(q); i; i--) { // traversing each level\n auto cur = q.front(); q.pop(); // pop a node from current level and,\n cur -> next = rightNode; // set its next pointer to rightNode\n rightNode = cur; // update rightNode as cur for next iteration\n if(cur -> right) // if a child exists\n q.push(cur -> right), // IMP: push right first to do right-to-left BFS\n q.push(cur -> left); // then push left\n }\n }\n return root;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def connect(self, root):\n if not root: return None\n q = deque([root])\n while q:\n rightNode = None\n for _ in range(len(q)):\n cur = q.popleft()\n cur.next, rightNode = rightNode, cur\n if cur.right:\n q.extend([cur.right, cur.left])\n return root\n```\n\n**Java**\n```java\nclass Solution {\n public Node connect(Node root) {\n if(root == null) return null;\n Queue<Node> q = new LinkedList<>();\n q.offer(root);\n while(!q.isEmpty()) {\n Node rightNode = null;\n for(int i = q.size(); i > 0; i--) {\n Node cur = q.poll();\n cur.next = rightNode;\n rightNode = cur;\n if(cur.right != null) {\n q.offer(cur.right);\n q.offer(cur.left);\n }\n }\n }\n return root; \n }\n}\n```\n\n***Time Complexity :*** `O(N)`, where `N` is the number of nodes in the given tree. We only traverse the tree once using BFS which requires `O(N)`.\n***Space Complexity :*** `O(W) = O(N)`, where `W` is the width of given tree. This is required to store the nodes in queue. Since the given tree is a perfect binary tree, its width is given as `W = (N+1)/2 \u2248 O(N)`\n\n\n---\n\n\u2714\uFE0F ***Solution - II (DFS)***\n\nWe can also populate the next pointers recursively using DFS. This is slightly different logic than above but relies on the fact that the given tree is a perfect binary tree.\n\nIn the above solution, we had access to right nodes since we traversed in level-order. But in DFS, once we go to the next level, we cant get access to right node. So, we must update next pointers of the child of each node from the its parent\'s level itself. Thus at each recursive call -\n* If child node exists:\n\t* assign next of left child node as right child node: `root -> left -> next = root -> right`. Note that, if once child exists, the other exists as well.\n\t* assign next of right child node as left child of root\'s next (if root\'s next exists): `root -> right -> next = root -> next -> left`. \n\t**How?** We need right immediate node of right child. This wont exist if current root\'s next node doesnt exists. If next node of current root is present (the next pointer of root would already be populated in above level) , the right immediate node of root\'s right child must be root\'s next\'s left child because if child of root exists, then the child of root\'s next must also exist.\n\n* If child node doesn\'t exist, we have reached the last level, we can directly return since there\'s no child nodes to populate their next pointers\n\nThe process is very similar to the one illustrated in the image below with just the difference that we are traversing with DFS instead of BFS shown below.\n\n```cpp\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root) return nullptr;\n auto L = root -> left, R = root -> right, N = root -> next;\n if(L) {\n L -> next = R; // next of root\'s left is assigned as root\'s right\n if(N) R -> next = N -> left; // next of root\'s right is assigned as root\'s next\'s left (if root\'s next exist)\n connect(L); // recurse left - simple DFS \n connect(R); // recurse right\n }\n return root;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def connect(self, root):\n if not root: return None\n L, R, N = root.left, root.right, root.next\n if L:\n L.next = R\n if N: R.next = N.left\n self.connect(L)\n self.connect(R)\n return root\n```\n\n**Java**\n```java\nclass Solution {\n public Node connect(Node root) {\n if(root == null) return null;\n Node L = root.left, R = root.right, N = root.next;\n if(L != null) {\n L.next = R;\n if(N != null) R.next = N.left;\n connect(L);\n connect(R);\n }\n return root;\n }\n}\n```\n\n***Time Complexity :*** `O(N)`, each node is only traversed once\n***Space Complexity :*** `O(logN)`, required for recursive stack. The maximum depth of recursion is equal to the height of tree which in this case of perfect binary tree is equal to `O(logN)`\n\n---\n\n\u2714\uFE0F ***Solution - III (BFS - Space-Optimized Appraoch)***\n\nThis is a combination of logic of above logics- we will traverse in BFS manner but populate the next pointers of bottom level just as we did in the DFS solution.\n\nUsually standard DFS/BFS takes `O(N)` space, but since we are given the next pointers in each node, we can use them to space-optimize our traversal to `O(1)`. \n* We first populate the next pointers of child nodes of current level. This makes it possible to traverse the next level without using a queue. To populate next pointers of child, the exact same logic as above is used\n* We simply traverse to root\'s left child and repeat the process - traverse current level, fill next pointers of child nodes and then again update `root = root -> left`. So, we are basically performing standard BFS traversal in `O(1)` space by using next pointers to our advantage\n* The process continues till we reach the last level of tree\n\n\nThe process is illustrated in images below -\n\n\n<table>\n <tr>\n <th>Image</th>\n <th>Description</th>\n </tr>\n \n <tr>\n <td><img src=https://assets.leetcode.com/users/images/b681da39-4c99-4e52-8cb8-779583022898_1640761933.124148.png width=500 /></td>\n <td>We start with a perfect binary tree with all next pointers initially NULL</td>\n </tr>\n \n <tr></tr>\n \n <tr>\n <td>\n<img src=https://assets.leetcode.com/users/images/ebbbfada-bd94-4432-ac4b-e0326fc34fd4_1640761979.3636644.png width=500 /></td>\n <td>We start traversal level-by-level, from left to right on each level</br>\n\t\n```cpp\ncur = root\n```\t\n\nEvery iteration, the next pointers of a node\'s child will be updated</br> \n\n```cpp\nif(cur -> left) {\n\tcur -> left -> next = cur -> right;\n\tif(cur -> next) cur -> right -> next = cur -> next -> left;\n}\n```\n\n</td>\n\n </tr>\n \n <tr></tr>\n \n <tr>\n <td><img src=https://assets.leetcode.com/users/images/4935430e-af1b-4fe1-9fc7-c5d35be45b90_1640761999.0506494.png width=500 /></td>\n <td>Move to next level</br>\n\n```cpp\nroot = root -> left\n// next iteration\ncur = root\n```\n\n& repeat:</br>\n\t\n```cpp\nif(cur -> left) {\n\tcur -> left -> next = cur -> right;\n\tif(cur -> next) cur -> right -> next = cur -> next -> left;\n}\n```\n\t\n</td>\n </tr>\n \n <tr></tr>\n \n <tr>\n <td><img src=https://assets.leetcode.com/users/images/9ada5f9e-34f7-4c0b-b513-2bd6ff758cbc_1640762014.5024235.png width=500 /></td>\n <td>Continue the same process with all nodes on current level</br>\n\t\n```cpp\nfor(; cur; cur = cur -> next)\n // ...\n```\n\t\n</td>\n </tr>\n \n <tr></tr>\n \n <tr>\n <td><img src=https://assets.leetcode.com/users/images/8656dc5e-93fb-4260-87a7-a2261171b70d_1640762030.292751.png width=500 /></td>\n <td>No child node exists</br>\n\n```cpp\nif(cur -> left)\n // ...\nelse break\n```\n\nSo, we break here. On the next iteration, root becomes NULL as well and we stop the process.\n</td>\n </tr>\n</table>\n\n\n\n**C++**\n```cpp\nclass Solution {\npublic:\n Node* connect(Node* root) {\n auto head = root;\n for(; root; root = root -> left) \n for(auto cur = root; cur; cur = cur -> next) // traverse each level - it\'s just BFS taking advantage of next pointers \n if(cur -> left) { // update next pointers of children if they exist \n cur -> left -> next = cur -> right;\n if(cur -> next) cur -> right -> next = cur -> next -> left;\n }\n else break; // if no children exist, stop iteration \n \n return head;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def connect(self, root):\n head = root\n while root:\n cur, root = root, root.left\n while cur:\n if cur.left:\n cur.left.next = cur.right\n if cur.next: cur.right.next = cur.next.left\n else: break\n cur = cur.next\n \n return head\n```\n\n**Java**\n```java\nclass Solution {\n public Node connect(Node root) {\n Node head = root;\n for(; root != null; root = root.left) \n for(Node cur = root; cur != null; cur = cur.next) \n if(cur.left != null) {\n cur.left.next = cur.right;\n if(cur.next != null) cur.right.next = cur.next.left;\n } else break;\n \n return head;\n }\n}\n```\n\n***Time Complexity :*** `O(N)`, we only traverse each node once, basically doing a standard BFS.\n***Space Complexity :*** `O(1)`, only constant extra space is being used\n\n\n---\n---\n\n\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, please do comment below \uD83D\uDC47 \n\n---\n--- | 1,013 | 2 | [] | 48 |
populating-next-right-pointers-in-each-node | A simple accepted solution | a-simple-accepted-solution-by-ragepyre-73pv | void connect(TreeLinkNode *root) {\n if (root == NULL) return;\n TreeLinkNode *pre = root;\n TreeLinkNode *cur = NULL;\n while(pre-> | ragepyre | NORMAL | 2014-07-09T15:44:45+00:00 | 2018-10-19T08:48:42.927941+00:00 | 148,030 | false | void connect(TreeLinkNode *root) {\n if (root == NULL) return;\n TreeLinkNode *pre = root;\n TreeLinkNode *cur = NULL;\n while(pre->left) {\n cur = pre;\n while(cur) {\n cur->left->next = cur->right;\n if(cur->next) cur->right->next = cur->next->left;\n cur = cur->next;\n }\n pre = pre->left;\n }\n }\nyou need two additional pointer. | 1,007 | 11 | [] | 93 |
populating-next-right-pointers-in-each-node | Java solution with O(1) memory+ O(n) time | java-solution-with-o1-memory-on-time-by-t66my | \n\n public class Solution {\n public void connect(TreeLinkNode root) {\n TreeLinkNode level_start=root;\n while(level_start!=nu | talent58 | NORMAL | 2014-12-20T21:11:08+00:00 | 2018-10-26T01:51:20.214018+00:00 | 77,186 | false | \n\n public class Solution {\n public void connect(TreeLinkNode root) {\n TreeLinkNode level_start=root;\n while(level_start!=null){\n TreeLinkNode cur=level_start;\n while(cur!=null){\n if(cur.left!=null) cur.left.next=cur.right;\n if(cur.right!=null && cur.next!=null) cur.right.next=cur.next.left;\n \n cur=cur.next;\n }\n level_start=level_start.left;\n }\n }\n } | 577 | 6 | [] | 50 |
populating-next-right-pointers-in-each-node | 7 lines, iterative, real O(1) space | 7-lines-iterative-real-o1-space-by-stefa-loyz | Simply do it level by level, using the next-pointers of the current level to go through the current level and set the next-pointers of the next level.\n\nI say | stefanpochmann | NORMAL | 2015-06-18T20:50:24+00:00 | 2018-10-22T06:54:24.726050+00:00 | 39,165 | false | Simply do it level by level, using the `next`-pointers of the current level to go through the current level and set the `next`-pointers of the next level.\n\nI say "real" O(1) space because of the many recursive solutions ignoring that recursion management needs space.\n\n def connect(self, root):\n while root and root.left:\n next = root.left\n while root:\n root.left.next = root.right\n root.right.next = root.next and root.next.left\n root = root.next\n root = next | 423 | 16 | ['Python'] | 50 |
populating-next-right-pointers-in-each-node | My recursive solution(Java) | my-recursive-solutionjava-by-gnayoaix-xilt | \n public void connect(TreeLinkNode root) {\n if(root == null)\n return;\n \n if(root.left != null){\n root.le | gnayoaix | NORMAL | 2015-04-17T22:09:45+00:00 | 2018-10-23T07:33:20.702260+00:00 | 35,413 | false | \n public void connect(TreeLinkNode root) {\n if(root == null)\n return;\n \n if(root.left != null){\n root.left.next = root.right;\n if(root.next != null)\n root.right.next = root.next.left;\n }\n \n connect(root.left);\n connect(root.right);\n } | 284 | 2 | [] | 32 |
populating-next-right-pointers-in-each-node | My simple non-iterative C++ code with O(1) memory | my-simple-non-iterative-c-code-with-o1-m-abk3 | void connect(TreeLinkNode *root) {\n if(!root)\n return;\n while(root -> left)\n {\n TreeLinkNode *p = root;\n | erudy | NORMAL | 2015-03-03T09:08:30+00:00 | 2018-10-17T05:27:01.699344+00:00 | 24,423 | false | void connect(TreeLinkNode *root) {\n if(!root)\n return;\n while(root -> left)\n {\n TreeLinkNode *p = root;\n while(p)\n {\n p -> left -> next = p -> right;\n if(p -> next)\n p -> right -> next = p -> next -> left;\n p = p -> next;\n }\n root = root -> left;\n }\n } | 202 | 5 | [] | 17 |
populating-next-right-pointers-in-each-node | C++ EASY TO SOLVE || Beginner Friendly with detailed explanations and dry run | c-easy-to-solve-beginner-friendly-with-d-e84d | Behold the legendary battle between Recursive and Interative Approaches \n\nFight!!!\n\nIntuition:-\n We are given a prefect binary tree that means every parent | Cosmic_Phantom | NORMAL | 2021-12-29T03:27:55.387886+00:00 | 2024-08-23T02:29:09.481253+00:00 | 15,621 | false | > # **Behold the legendary battle between Recursive and Interative Approaches** \n***\n***Fight!!!***\n***\n**Intuition:-**\n* We are given a prefect binary tree that means every parent has two children and all the leaves are on the same level . \n* This question is an superior version of binary level order traversal .\n* In level order traversal you will traverse each level of binary tree while outputting the data in that form . So the only difference is that somehow we need to connect the previous levels rightmost node to the next level\'s leftmost node and that\'s it .\n\n**Algorithm:-**\n1. Base case: if the root is null than return null\n2. Now to connect the left subtree of same level with right subtree of that level \n3. The only new line that differentiate from level order traversing is that we need to connect the rightmost node of a level to the leftmost node of the next level.\n4. Now just repeat the steps over and over for every level of tree . \n\n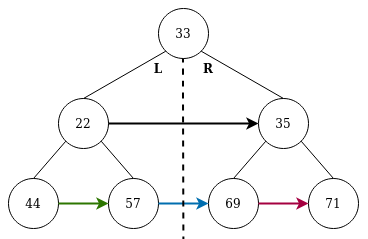 *Image credit goes to @Stargarth*\n\n**We can code this approach by two methods:**\n1. By recursive \n2. Iterative\n<mark>Both solution has time complexity and space complexity as O(n) and O(1) in a virtual manner but if we consider in a true sense than in recursion we use a recursive stack which has some space complexity .<mark>\nSo in a real sense the iterative solution is the best since it has truly O(1) space complexity .\n***\n**Recursive Approach Code:-**\n```\n//Upvote and Comment \n\nclass Solution {\npublic:\nNode* connect(Node* root) {\n //base case\n if(root == NULL) return NULL;\n //connects the left subtree of same level with right subtree of that same level \n if(root->left != NULL) root->left->next = root->right;\n //connect the rightmost node of a level to the leftmost node of the next level.\n if(root->right != NULL && root->next != NULL) root->right->next = root->next->left;\n //recursive calls for left and right subtrees.\n connect(root->left);\n connect(root->right);\n return root;\n }\n};\n```\n***\n**Iterative Approach:-**\nIn iterative approach we will be needing two more pointers named as `curr` and `prev` for linking of left and right nodes\n```\n//Upvote and Comment\n\nclass Solution {\npublic:\n Node* connect(Node* root) {\n //Initialize pointers\n Node *prev = root, *curr;\n while (prev) {\n curr = prev;\n while (curr && curr->left) { \n //connects the left subtree of same level with right subtree of that same level \n curr->left->next = curr->right;\n //connect the rightmost node of a level to the leftmost node of the next level.\n if (curr -> next) curr->right->next = curr->next->left;\n curr = curr->next;\n }\n prev = prev -> left;\n }\n return root;\n }\n};\n```\n | 199 | 11 | ['Recursion', 'C', 'Iterator', 'C++'] | 5 |
populating-next-right-pointers-in-each-node | Python solutions (Recursively, BFS+queue, DFS+stack) | python-solutions-recursively-bfsqueue-df-bcpf | def connect1(self, root):\n if root and root.left and root.right:\n root.left.next = root.right\n if root.next:\n ro | oldcodingfarmer | NORMAL | 2015-07-10T23:25:53+00:00 | 2015-07-10T23:25:53+00:00 | 14,723 | false | def connect1(self, root):\n if root and root.left and root.right:\n root.left.next = root.right\n if root.next:\n root.right.next = root.next.left\n self.connect(root.left)\n self.connect(root.right)\n \n # BFS \n def connect2(self, root):\n if not root:\n return \n queue = [root]\n while queue:\n curr = queue.pop(0)\n if curr.left and curr.right:\n curr.left.next = curr.right\n if curr.next:\n curr.right.next = curr.next.left\n queue.append(curr.left)\n queue.append(curr.right)\n \n # DFS \n def connect(self, root):\n if not root:\n return \n stack = [root]\n while stack:\n curr = stack.pop()\n if curr.left and curr.right:\n curr.left.next = curr.right\n if curr.next:\n curr.right.next = curr.next.left\n stack.append(curr.right)\n stack.append(curr.left) | 150 | 2 | ['Stack', 'Depth-First Search', 'Breadth-First Search', 'Queue', 'Python'] | 17 |
populating-next-right-pointers-in-each-node | Python Solution With Explaintion | python-solution-with-explaintion-by-tyr0-xjwr | I want to share how I come up with this solution with you:\n\nSince we are manipulating tree nodes on the same level, it's easy to come up with\na very standard | tyr034 | NORMAL | 2015-09-21T23:29:40+00:00 | 2018-10-18T10:30:04.965308+00:00 | 15,415 | false | I want to share how I come up with this solution with you:\n\nSince we are manipulating tree nodes on the same level, it's easy to come up with\na very standard BFS solution using queue. But because of next pointer, we actually\ndon't need a queue to store the order of tree nodes at each level, we just use a next\npointer like it's a link list at each level; In addition, we can borrow the idea used in\nthe Binary Tree level order traversal problem, which use cur and next pointer to store \nfirst node at each level; we exchange cur and next every time when cur is the last node\nat each level. \n\n\n class Solution(object):\n def connect(self, root):\n """\n :type root: TreeLinkNode\n :rtype: nothing\n """\n \n if not root:\n return None\n cur = root\n next = root.left\n \n while cur.left :\n cur.left.next = cur.right\n if cur.next:\n cur.right.next = cur.next.left\n cur = cur.next\n else:\n cur = next\n next = cur.left | 136 | 4 | ['Python'] | 7 |
populating-next-right-pointers-in-each-node | C++ Iterative/Recursive | c-iterativerecursive-by-jianchao-li-od4v | Recursive\n\nSimilar to a level-order traversal, even you are not allowed to use a queue, the next pointer provides you with a way to move to the next node in t | jianchao-li | NORMAL | 2015-07-11T09:02:00+00:00 | 2015-07-11T09:02:00+00:00 | 12,734 | false | **Recursive**\n\nSimilar to a level-order traversal, even you are not allowed to use a `queue`, the `next` pointer provides you with a way to move to the next node in the same level.\n\n```cpp\nclass Solution {\npublic:\n Node* connect(Node* root) {\n Node *pre = root, *cur;\n while (pre) {\n cur = pre;\n while (cur && cur -> left) { \n cur -> left -> next = cur -> right;\n if (cur -> next) {\n cur -> right -> next = cur -> next -> left;\n }\n cur = cur -> next;\n }\n pre = pre -> left;\n }\n return root;\n }\n};\n```\n\n**Recursive**\n\nRecursively connect the left and right subtrees.\n\n```cpp\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if (!root) {\n return NULL;\n }\n if (root -> left) {\n root -> left -> next = root -> right;\n if (root -> next) {\n root -> right -> next = root -> next -> left;\n }\n connect(root -> left);\n connect(root -> right);\n }\n return root;\n }\n};\n``` | 131 | 2 | ['Recursion', 'Binary Tree', 'Iterator', 'C++'] | 9 |
populating-next-right-pointers-in-each-node | Java 0ms with visual explanation | java-0ms-with-visual-explanation-by-wils-6bh2 | \n\n\nclass Solution {\n public Node connect(Node root) {\n if(root == null) return null;\n if(root.left != null) root.left.next = root.right;\ | wilsoncursino | NORMAL | 2020-12-07T00:12:47.033875+00:00 | 2020-12-07T00:12:47.033919+00:00 | 6,016 | false | 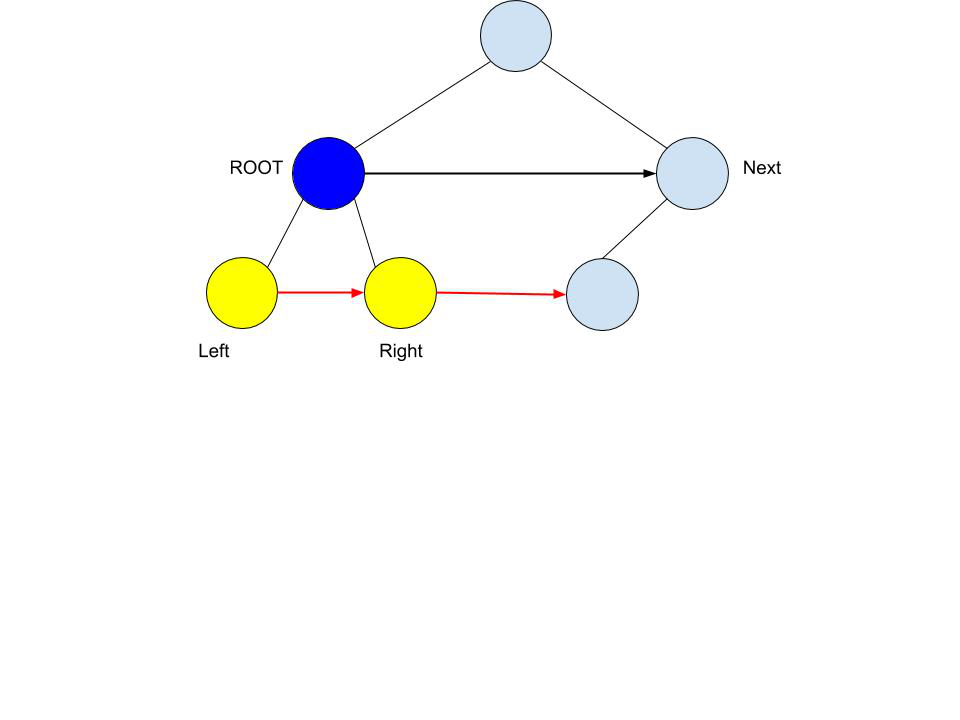\n\n```\nclass Solution {\n public Node connect(Node root) {\n if(root == null) return null;\n if(root.left != null) root.left.next = root.right;\n if(root.right != null && root.next != null) root.right.next = root.next.left;\n connect(root.left);\n connect(root.right);\n return root;\n }\n}\n``` | 129 | 1 | ['Java'] | 16 |
populating-next-right-pointers-in-each-node | C++ || BFS || Iterative || queue | c-bfs-iterative-queue-by-saurav28-l2nm | \n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* left;\n Node* right;\n Node* next;\n\n Node() : val(0), left(NULL), rig | saurav28_ | NORMAL | 2020-11-13T09:48:39.066397+00:00 | 2020-11-13T09:50:03.951228+00:00 | 5,757 | false | ```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* left;\n Node* right;\n Node* next;\n\n Node() : val(0), left(NULL), right(NULL), next(NULL) {}\n\n Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}\n\n Node(int _val, Node* _left, Node* _right, Node* _next)\n : val(_val), left(_left), right(_right), next(_next) {}\n};\n*/\n\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root)return root;\n queue<Node*> q;\n q.push(root);\n while(!q.empty()){\n int n=q.size();\n for(int i=0;i<n;i++){\n Node* x=q.front();\n q.pop();\n if(i!=n-1)x->next=q.front();\n if(x->left)q.push(x->left);\n if(x->right)q.push(x->right);\n }\n }\n return root;\n }\n};\n``` | 76 | 2 | ['Breadth-First Search', 'Queue', 'C', 'C++'] | 6 |
populating-next-right-pointers-in-each-node | ✅ [Python] Two Solutions || BFS and DFS || Image Explanation || Beginner Friendly | python-two-solutions-bfs-and-dfs-image-e-agwc | PLEASE UPVOTE if you like \uD83D\uDE01 If you have any question, feel free to ask. \n Solution 1\n\t Standard BFS with mantaining pre_level and pre_node as the | linfq | NORMAL | 2021-12-29T05:43:06.330243+00:00 | 2021-12-29T07:56:07.689822+00:00 | 6,355 | false | **PLEASE UPVOTE if you like** \uD83D\uDE01 **If you have any question, feel free to ask.** \n* **Solution 1**\n\t* Standard BFS with mantaining `pre_level` and `pre_node` as the previous node in BFS sequence\n\t\t* `level == pre_level` means current `node` is not the first node of `level`, then `pre_node.next = node` and update `pre_node = node`\n\t\t* `else` means `pre_level < level` and `node` is the first node of `level`, then no need to update `pre_node.next`, leave it as `None`, update `pre_node = node` only.\n\t\t* standard BFS, append `node.left` and `node.right` to the queue\n\t```\n\tTime Complexity: O(N)\n\tSpace Complexity: O(N)\n\t```\n\t```\n\tclass Solution(object):\n def connect(self, root):\n if root is None: return None\n dq, pre_level, pre_node = deque([(1, root)]), 0, None\n while dq:\n level, node = dq.popleft()\n if level == pre_level: # current node is not the first node of level\n pre_node.next = node\n pre_node = node\n else: # pre_level < level and node is the first node of level, then no need to update pre_node.next, \n # leave it as None, update pre_node = node only.\n pre_level, pre_node = level, node\n if node.left: # root is a perfect binary tree, once left exists, right must also exist\n dq.append((level + 1, node.left))\n dq.append((level + 1, node.right))\n return root\n\t```\n\n* **Solution 2**\n\t* Recursive DFS, the current root node is responsible for linking the nodes on both sides closest to the central axis for all levels.\n\t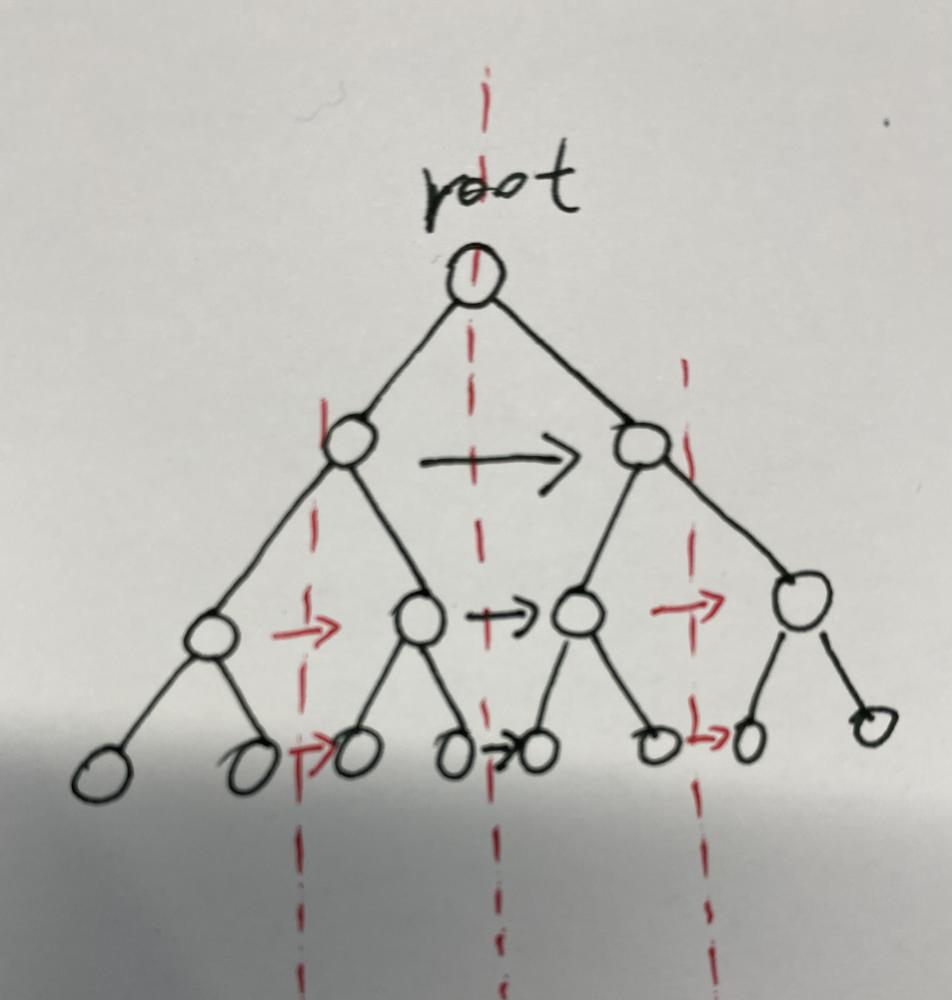\n\n\t\n\t```\n\tTime Complexity: O(N)\n\tSpace Complexity: O(1)\n\t```\n\t```\n\tclass Solution(object):\n def connect(self, root):\n if not root: return root\n if root.left: \n left, right = root.left, root.right\n self.connect(left)\n self.connect(right)\n while left:\n left.next = right\n left, right = left.right, right.left\n return root\n\t```\n\t\n**PLEASE UPVOTE if you like \uD83D\uDE01 If you have any question, feel free to ask.** | 62 | 1 | ['Depth-First Search', 'Breadth-First Search', 'Python'] | 7 |
populating-next-right-pointers-in-each-node | [Python] O(n) time/ O(log n) space recursion, explained | python-on-time-olog-n-space-recursion-ex-hx69 | In this problem we are given that our tree is perfect binary tree, which will help us a lot. Let us use recursion: imagine, that for left and right subtees we a | dbabichev | NORMAL | 2020-11-13T08:55:18.859593+00:00 | 2020-11-13T08:55:18.859631+00:00 | 2,660 | false | In this problem we are given that our tree is perfect binary tree, which will help us a lot. Let us use recursion: imagine, that for left and right subtees we already make all connections, what we need to connect now? See the image and it will become very clear: we need to connect just `O(log n)` pairs now: we go the the left and to the right children. Then from left children we go as right as possible and from right children we go as left as possible.\n\n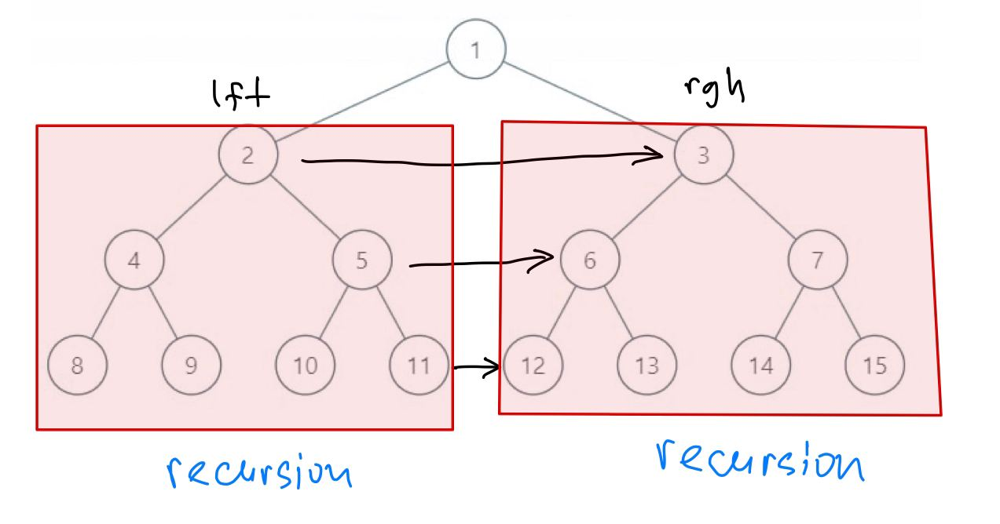\n\n\n**Complexity**: time complexity can be found, using Master theorem: `F(n) = 2*F(n/2) + log n`, from here `F(n) = O(n)`. Space complexity is `O(log n)`, because we use recursion. Note, that space complexity can be reduced to `O(1)`, because we know the structure of our tree!\n\n```\nclass Solution:\n def connect(self, root):\n if not root or not root.left: return root\n \n self.connect(root.left)\n self.connect(root.right)\n \n lft = root.left\n rgh = root.right\n lft.next = rgh\n\n while lft.right: \n lft = lft.right\n rgh = rgh.left\n lft.next = rgh\n \n return root\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 61 | 1 | ['Recursion'] | 4 |
populating-next-right-pointers-in-each-node | Java solution traversing by level without extra space | java-solution-traversing-by-level-withou-k2bu | public class Solution {\n public void connect(TreeLinkNode root) {\n if(root==null) return;\n TreeLinkNode cur = root;\n | upthehell | NORMAL | 2016-05-12T15:07:46+00:00 | 2018-10-17T07:26:09.500360+00:00 | 8,743 | false | public class Solution {\n public void connect(TreeLinkNode root) {\n if(root==null) return;\n TreeLinkNode cur = root;\n TreeLinkNode nextLeftmost = null;\n\n while(cur.left!=null){\n nextLeftmost = cur.left; // save the start of next level\n while(cur!=null){\n cur.left.next=cur.right;\n cur.right.next = cur.next==null? null : cur.next.left;\n cur=cur.next;\n }\n cur=nextLeftmost; // point to next level \n }\n }\n } | 56 | 1 | [] | 3 |
populating-next-right-pointers-in-each-node | 💡JavaScript BFS & DFS Solution | javascript-bfs-dfs-solution-by-aminick-4wwo | The Idea - BFS\n1. BFS using queue\n2. as we are shifing node, connect it to the next in queue\njavascript\nvar connectBFS = function(root) {\n if (root == n | aminick | NORMAL | 2019-11-04T11:37:19.860701+00:00 | 2019-11-04T11:37:19.860736+00:00 | 2,928 | false | #### The Idea - BFS\n1. BFS using queue\n2. as we are shifing node, connect it to the next in queue\n``` javascript\nvar connectBFS = function(root) {\n if (root == null) return root;\n let queue = [root];\n while(queue.length!=0) {\n let next = [];\n while(queue.length!=0) {\n let node = queue.shift();\n node.next = queue[0]||null;\n if (node.left!=null) {\n next.push(node.left);\n next.push(node.right);\n }\n }\n queue = next;\n }\n return root;\n};\n```\n#### The Idea - DFS\n1. pre order scan \n2. set child nodes arrangement before resursion\n``` javascript\nvar connect = function(root) {\n if (root == null || root.left == null) return root;\n root.left.next = root.right;\n root.right.next = root.next ? root.next.left:null;\n connect(root.left);\n connect(root.right);\n return root;\n}\n``` | 44 | 0 | ['JavaScript'] | 5 |
populating-next-right-pointers-in-each-node | BFS || c++ || iterative || explanation || level order traversal | bfs-c-iterative-explanation-level-order-vtl17 | \nBasically this is purely level order travsersal code with slight modification for the root -> next value \n\nYou just have to think 2 things in this question | walkytalkyshubham | NORMAL | 2021-05-06T21:58:00.692069+00:00 | 2022-08-06T16:35:31.773786+00:00 | 2,243 | false | \nBasically this is purely level order travsersal code with slight modification for the root -> next value \n\nYou just have to think 2 things in this question.\n\n1.How to get the last val to NULL ?.\n2.How to get connect with the current node to previous one ?.\n\nIf you are able to find the ans of these two questions mentioned above then you will reach the solution \nalso if you are here to see the solution i would recommend you to pause for a while \nand think about these questions i am sure you willl find the ans otherwise ans \nis just right below you can see anytime you want just give it a though for a whlle.\n\n.\n.\n.\n.\n.\n.\n.\n```\nif(root == NULL) return NULL;\n queue<Node*> q;\n q.push(root);\n while(!q.empty()){\n int size = q.size(); // get size of queue \n for(int i=0 ; i < size ; i++){\n Node* item = q.front(); \n if(size - 1 == i) // checking the last value of the level\n item -> next = NULL; \n \n q.pop();\n \n if(size - 1 != i) // if this is not the last value then previous value will point to next one\n item -> next = q.front(); \n \n if(item -> left != NULL)\n q.push(item -> left);\n if(item -> right != NULL)\n q.push(item -> right);\n }\n } \n return root; \n\t\t\n\n```\n**In an interview there will be a follow up question in which you might be asked to solve this question with recursion so better be prepared for this bomb !!!!**\n```\n\n\nBefore you see the solution as per rituals please please please think of a solution by yourself you might be right or wrong doesn\'t matter you fought hard with the question !!!\n\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n.\n\n Node* connect(Node* root) {\n if(root == NULL) return NULL;\n \n //now part-1 - connect Left node with right node\n if(root->left!=NULL) root->left->next = root->right;\n \n //now part-2 - connect right node with next subtree left node\n if(root->right!=NULL && root->next!=NULL) root->right->next = root->next->left;\n \n //Now do the same job for subtrees\n connect(root->left); \n connect(root->right);\n \n return root; \n // every time return is made, but at last the same root is retured to main\n }\n\n\n*** IF YOU LOVED THE SOLUTION PLEASE CLICK ON THE UPVOTE BUTTON ***\n\n\n\n\t\t | 40 | 0 | ['Breadth-First Search', 'C', 'C++'] | 4 |
populating-next-right-pointers-in-each-node | [Python] 3 approaches - Clean & Concise | python-3-approaches-clean-concise-by-hie-wg1k | \u2714\uFE0F Solution 1: BFS\npython\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if root == None: return None\n\n q = d | hiepit | NORMAL | 2020-02-21T14:53:30.000599+00:00 | 2021-09-08T07:00:39.893987+00:00 | 707 | false | **\u2714\uFE0F Solution 1: BFS**\n```python\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if root == None: return None\n\n q = deque([root])\n while q:\n prev = None\n for _ in range(len(q)):\n curr = q.popleft()\n if prev != None:\n prev.next = curr\n prev = curr\n\n if curr.left != None:\n q.append(curr.left)\n if curr.right != None:\n q.append(curr.right)\n return root\n```\n**Complexity**\n- Time: `O(N)`, where `N` is number of nodes in the Perfect Binary Tree.\n- Space: `O(N/2)`\n\n---\n\n**\u2714\uFE0F Solution 2: DFS**\n```python\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if root == None: return None\n self.connect2Nodes(root.left, root.right)\n self.connect(root.left)\n self.connect(root.right)\n return root\n \n def connect2Nodes(self, root1, root2):\n if root1 == None or root2 == None: return\n root1.next = root2\n self.connect2Nodes(root1.right, root2.left)\n```\n**Complexity**\n- Time: `O(N)`, where `N` is number of nodes in the Perfect Binary Tree.\n- Space: `O(logN)`\n\n---\n\n**\u2714\uFE0F Solution 3: Using previously established next pointers**\n```python\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if root == None: return None\n \n leftMost = root\n while leftMost.left:\n head = leftMost\n leftMost = head.left\n while head:\n head.left.next = head.right\n if head.next != None:\n head.right.next = head.next.left\n head = head.next\n return root\n```\n**Complexity**\n- Time: `O(N)`, where `N` is number of nodes in the Perfect Binary Tree.\n- Space: `O(1)` | 40 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | [Python3] BFS and DFS | python3-bfs-and-dfs-by-zhanweiting-edfj | BFS\n\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, left, right, next):\n self.val = val\n self.left = left\n se | zhanweiting | NORMAL | 2019-09-10T07:45:43.353090+00:00 | 2019-09-10T08:08:34.543883+00:00 | 4,333 | false | * BFS\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, left, right, next):\n self.val = val\n self.left = left\n self.right = right\n self.next = next\n"""\nfrom collections import deque\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n """\n 1 (1)\n 2 (2)-> 3(1)\n 4(4) -> 5(3) -> 6(2) -> 7(1)\n\n"""\n if root == None:\n return None\n q = deque([root])\n while q: # [1] [3,4,5]\n size = len(q) # 1 2\n while size > 0: # > 0\n node = q.popleft() # node =1,2,3\n if size > 1 :# \n node.next = q[0] # 2.next = 3\n size -= 1 # size =1\n \n if node.left: \n q.append(node.left)\n if node.right:\n q.append(node.right)\n return root\n```\n* DFS\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, left, right, next):\n self.val = val\n self.left = left\n self.right = right\n self.next = next\n"""\nfrom collections import deque\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n """\n 1 (1)\n 2 (2)-> 3(1)\n 4(4) -> 5(3) -> 6(2) -> 7(1)\n\n"""\n self.dfs(root)\n return root\n \n ## (1). left child -> right child\n ## (2). right child -> next.left child\n def dfs(self,root):\n if root == None or root.left == None:\n return\n root.left.next = root.right\n if root.next != None: \n root.right.next = root.next.left\n self.dfs(root.left)\n self.dfs(root.right)\n``` | 34 | 0 | ['Breadth-First Search', 'Python', 'Python3'] | 6 |
populating-next-right-pointers-in-each-node | Simple recursive Java solution O(1) space O(n) time | simple-recursive-java-solution-o1-space-61bmi | public void connect(TreeLinkNode root) {\n \n if(root==null) return ;\n \n link(root.left,root.right);\n }\n \n //HELPER FU | zihao_li | NORMAL | 2015-11-02T04:19:41+00:00 | 2015-11-02T04:19:41+00:00 | 5,789 | false | public void connect(TreeLinkNode root) {\n \n if(root==null) return ;\n \n link(root.left,root.right);\n }\n \n //HELPER FUNCTION TO LINK TWO NODES TOGETHER\n public void link(TreeLinkNode left, TreeLinkNode right){\n \n if(left==null && right==null) return ;\n \n left.next = right;\n link(left.left,left.right);\n link(left.right,right.left);\n link(right.left,right.right);\n } | 33 | 1 | ['Recursion', 'Java'] | 7 |
populating-next-right-pointers-in-each-node | Java | Step-by-step Explanation | java-step-by-step-explanation-by-sherrie-91m6 | Please upvote if this helps! Thx :D\n\nclass Solution {\n public Node connect(Node root) {\n if (root == null) return null;\n connectTwoNodes(r | SherrieCao | NORMAL | 2021-12-18T14:03:22.347251+00:00 | 2021-12-18T14:03:22.347281+00:00 | 1,923 | false | ## Please upvote if this helps! Thx :D\n```\nclass Solution {\n public Node connect(Node root) {\n if (root == null) return null;\n connectTwoNodes(root.left, root.right);\n return root;\n }\n \n private void connectTwoNodes(Node n1, Node n2){\n if (n1 == null || n2 == null) return;\n n1.next = n2;\n //Connect two child nodes from the same parent node. \n connectTwoNodes(n1.left, n1.right);\n connectTwoNodes(n2.left, n2.right);\n //Connect two child nodes aside from each other but from different parent nodes . \n connectTwoNodes(n1.right, n2.left);\n } \n}\n``` | 30 | 0 | ['Breadth-First Search', 'Recursion', 'Java'] | 4 |
populating-next-right-pointers-in-each-node | [JAVA] Clean Code, O(N) Time Complexity, 100% Faster Solution | java-clean-code-on-time-complexity-100-f-n0lq | \n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node left;\n public Node right;\n public Node next;\n\n public Node() {} | anii_agrawal | NORMAL | 2020-11-13T08:21:16.461725+00:00 | 2020-11-13T08:23:03.828372+00:00 | 1,245 | false | ```\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node left;\n public Node right;\n public Node next;\n\n public Node() {}\n \n public Node(int _val) {\n val = _val;\n }\n\n public Node(int _val, Node _left, Node _right, Node _next) {\n val = _val;\n left = _left;\n right = _right;\n next = _next;\n }\n};\n*/\n\nclass Solution {\n public Node connect(Node root) {\n \n if (root == null || root.left == null) {\n return root;\n }\n \n root.left.next = root.right;\n if (root.next != null) {\n root.right.next = root.next.left;\n }\n \n connect (root.left);\n connect (root.right);\n \n return root;\n }\n}\n```\n\nPlease help to **UPVOTE** if this post is useful for you.\nIf you have any questions, feel free to comment below.\n**HAPPY CODING :)\nLOVE CODING :)** | 30 | 1 | [] | 6 |
populating-next-right-pointers-in-each-node | C++ short recursive solution, no extra space needed | c-short-recursive-solution-no-extra-spac-mmy6 | Key points:\n Use parent\'s next arrow to find right children\'s next buddy in the neighboring tree.\n In short: root->right->next = root->next->left.\n* Take c | lisongsun | NORMAL | 2021-02-11T00:59:03.200888+00:00 | 2021-02-11T01:00:17.995185+00:00 | 1,043 | false | Key points:\n* Use parent\'s next arrow to find right children\'s next buddy in the neighboring tree.\n* In short: root->right->next = root->next->left.\n* Take care of current level\'s children\'s next arrow problem before move down to children subtree.\n```\n Node* connect(Node* root) {\n if (root) {\n if (root->left) {\n root->left->next = root->right;\n if (root->next)\n root->right->next = root->next->left;\n connect(root->left);\n connect(root->right);\n }\n }\n return root;\n }\n``` | 29 | 1 | ['Recursion', 'C'] | 4 |
populating-next-right-pointers-in-each-node | 🔥 JavaScript : O(1) space, O(n) time 🔥 | javascript-o1-space-on-time-by-akshaymar-ezyx | We iteratively move from each node to the next node, while fixing the next pointers of their children. \n\nvar connect = function(root) {\n let ptr = root;\n | akshaymarch7 | NORMAL | 2020-07-27T12:54:27.369931+00:00 | 2020-07-30T02:37:25.971688+00:00 | 1,333 | false | We iteratively move from each node to the next node, while fixing the next pointers of their children. \n```\nvar connect = function(root) {\n let ptr = root;\n while(root && root.left){\n let temp = root;\n while(temp) {\n temp.left.next = temp.right;\n temp.right.next = temp.next ? temp.next.left : null;\n temp = temp.next;\n }\n root = root.left;\n }\n return ptr;\n}\n``` | 25 | 2 | ['Iterator', 'JavaScript'] | 0 |
populating-next-right-pointers-in-each-node | ✅💯🔥Simple Code🚀📌|| 🔥✔️Easy to understand🎯 || 🎓🧠Beats 100%🔥|| Beginner friendly💀💯 | simple-code-easy-to-understand-beats-100-qta0 | Tuntun Mosi ko Pranam\nSolution tuntun mosi ki photo ke baad hai. Scroll Down\n\n# Code\njava []\n/*\n// Definition for a Node.\nclass Node {\n public int va | atishayj4in | NORMAL | 2024-09-10T18:14:34.415993+00:00 | 2024-09-10T18:14:34.416029+00:00 | 1,663 | false | # Tuntun Mosi ko Pranam\nSolution tuntun mosi ki photo ke baad hai. Scroll Down\n\n# Code\n```java []\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node left;\n public Node right;\n public Node next;\n\n public Node() {}\n \n public Node(int _val) {\n val = _val;\n }\n\n public Node(int _val, Node _left, Node _right, Node _next) {\n val = _val;\n left = _left;\n right = _right;\n next = _next;\n }\n};\n*/\n\nclass Solution {\n public Node connect(Node root) {\n if(root==null){\n return root;\n }\n if(root.left!=null){\n root.left.next=root.right;\n } if(root.right!=null && root.next!=null){\n root.right.next=root.next.left;\n }\n connect(root.left);\n connect(root.right);\n return root;\n }\n}\n```\n | 23 | 1 | ['Linked List', 'Tree', 'Depth-First Search', 'Breadth-First Search', 'C', 'Binary Tree', 'Python', 'C++', 'Java', 'JavaScript'] | 2 |
populating-next-right-pointers-in-each-node | 5 lines C++ simple solution. | 5-lines-c-simple-solution-by-tiny656-t8i9 | class Solution {\n public:\n void connect(TreeLinkNode *root) {\n if (!root) return;\n if (root->left) root->left->next = root-> | tiny656 | NORMAL | 2015-08-09T09:39:30+00:00 | 2015-08-09T09:39:30+00:00 | 2,064 | false | class Solution {\n public:\n void connect(TreeLinkNode *root) {\n if (!root) return;\n if (root->left) root->left->next = root->right;\n if (root->right && root->next) root->right->next = root->next->left;\n connect(root->left);\n connect(root->right);\n }\n }; | 23 | 1 | [] | 0 |
populating-next-right-pointers-in-each-node | Java Solution | Simple BFS Traversal | Very easy iterative solution | java-solution-simple-bfs-traversal-very-zjbnj | \nclass Solution {\n\n public Node connect(Node root) {\n if (root == null) return root;\n Queue<Node> q = new LinkedList<>();\n q.add(r | 1605448777 | NORMAL | 2022-06-24T12:39:04.345875+00:00 | 2022-06-24T12:39:04.345917+00:00 | 1,098 | false | ```\nclass Solution {\n\n public Node connect(Node root) {\n if (root == null) return root;\n Queue<Node> q = new LinkedList<>();\n q.add(root);\n while (!q.isEmpty()) {\n int size = q.size();\n for (int i = 0; i < size; i++) {\n Node curr = q.poll();\n if (curr.left != null) q.add(curr.left);\n if (curr.right != null) q.add(curr.right);\n if (i == size - 1) curr.next = null; else curr.next = q.peek();\n }\n }\n return root;\n }\n}\n``` | 20 | 0 | ['Breadth-First Search', 'Queue', 'Java'] | 1 |
populating-next-right-pointers-in-each-node | Another simple JavaScript solution | another-simple-javascript-solution-by-je-hdsd | Since it's a full binary tree, our job is much simpler, at each node, connects its left and right child, and try to connect the right child with the left child | jeantimex | NORMAL | 2017-10-15T18:34:36.123000+00:00 | 2018-09-13T19:53:39.397636+00:00 | 1,574 | false | Since it's a full binary tree, our job is much simpler, at each node, connects its left and right child, and try to connect the right child with the left child of node's next. A simple preorder traversal should be able to help us solve this problem.\n```\n/**\n * @param {TreeLinkNode} root\n * @return {void} Do not return anything, modify tree in-place instead.\n */\nvar connect = function(root) {\n if (!root || !root.left) { // sanity check\n return;\n }\n \n root.left.next = root.right; // connect left -> right\n root.right.next = root.next ? root.next.left : null; // connect right -> next's left\n \n connect(root.left);\n connect(root.right);\n};\n```\nTime complexity: `O(n)`\nSpace complexity: `O(1)` | 19 | 1 | [] | 1 |
populating-next-right-pointers-in-each-node | Very Easy to understand recursive Method | very-easy-to-understand-recursive-method-8gpm | Simple recursive solution accepted\n\nclass Solution {\npublic:\n \n void solve(Node* l, Node* r){\n \n if(l == NULL || r == NULL) return;\n | rachit7399 | NORMAL | 2020-07-21T16:34:54.296970+00:00 | 2020-07-21T16:34:54.297005+00:00 | 913 | false | Simple recursive solution accepted\n```\nclass Solution {\npublic:\n \n void solve(Node* l, Node* r){\n \n if(l == NULL || r == NULL) return;\n \n l->next = r;\n r->next = NULL;\n \n solve(l->left, l->right);\n solve(l->right, r->left);\n solve(r->left, r->right);\n }\n \n \n Node* connect(Node* root) {\n if(root == NULL) return NULL;\n if(root->left == NULL) return root;\n \n solve(root->left, root->right);\n return root;\n }\n};\n``` | 17 | 0 | ['Recursion', 'C', 'C++'] | 4 |
populating-next-right-pointers-in-each-node | python solution | python-solution-by-pankit-1r7n | \nclass Solution:\n # @param root, a tree link node\n # @return nothing\n def helper(self, left, right):\n if not left or not right:\n | pankit | NORMAL | 2018-07-24T02:42:04.679730+00:00 | 2018-10-11T01:56:10.848397+00:00 | 1,364 | false | ```\nclass Solution:\n # @param root, a tree link node\n # @return nothing\n def helper(self, left, right):\n if not left or not right:\n return\n \n left.next = right\n self.helper(left.right, right.left)\n self.helper(left.left, left.right)\n self.helper(right.left, right.right)\n \n def connect(self, root):\n if not root:\n return\n \n self.helper(root.left, root.right)\n\t``` | 16 | 0 | [] | 2 |
populating-next-right-pointers-in-each-node | Python accepted code | python-accepted-code-by-yasheen-1mv5 | def connect(self, root):\n if not root: return\n while root.left:\n cur = root.left\n prev = None\n while root:\n | yasheen | NORMAL | 2015-08-07T04:18:37+00:00 | 2018-09-18T07:13:08.454507+00:00 | 4,084 | false | def connect(self, root):\n if not root: return\n while root.left:\n cur = root.left\n prev = None\n while root:\n if prev: prev.next = root.left\n root.left.next = root.right\n prev = root.right\n root = root.next\n root = cur | 16 | 0 | [] | 1 |
populating-next-right-pointers-in-each-node | C++ recursive solution | c-recursive-solution-by-cychung-gyxa | \n void connect(TreeLinkNode *root) {\n if(!root) return;\n if(root->left){\n root->left->next = root->right;\n root->rig | cychung | NORMAL | 2017-12-23T05:43:53.078000+00:00 | 2017-12-23T05:43:53.078000+00:00 | 1,003 | false | ```\n void connect(TreeLinkNode *root) {\n if(!root) return;\n if(root->left){\n root->left->next = root->right;\n root->right->next = root->next? root->next->left : NULL;\n }\n connect(root->left);\n connect(root->right);\n }\n``` | 16 | 0 | [] | 2 |
populating-next-right-pointers-in-each-node | Python Solution O(1) and O(n) memory. | python-solution-o1-and-on-memory-by-dars-kofr | \nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n # edge case check\n if not root:\n return None\n \n | darshan_22 | NORMAL | 2020-07-04T15:27:12.675170+00:00 | 2020-07-04T15:27:12.675222+00:00 | 1,663 | false | ```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n # edge case check\n if not root:\n return None\n \n # initialize the queue with root node (for level order traversal)\n queue = collections.deque([root])\n \n # start the traversal\n while queue:\n size = len(queue) # get number of nodes on the current level\n for i in range(size):\n node = queue.popleft() # pop the node\n \n # An important check so that we do not wire the node to the node on the next level.\n if i < size-1:\n node.next = queue[0] # because the right node of the popped node would be the next in the queue. \n \n if node.left:\n queue.append(node.left) \n if node.right:\n queue.append(node.right) \n \n return root\n```\n\nO(1) Memory solution:\n```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n # edge case check\n if not root:\n return None\n \n node = root # create a pointer to the root node\n \n # iterate only until we have a new level (because the connections for Nth level are done when we are at N-1th level)\n while node.left:\n head = node\n while head:\n head.left.next = head.right\n if head.next:\n head.right.next = head.next.left\n \n head = head.next\n \n node = node.left\n\n return root\n``` | 15 | 0 | ['Breadth-First Search', 'Queue', 'Python', 'Python3'] | 2 |
populating-next-right-pointers-in-each-node | JavaScript BFS | javascript-bfs-by-deleted_user-j54q | \nvar connect = function(root) {\n if(!root) return;\n const queue = [root];\n \n while(queue.length) {\n const size = queue.length;\n | deleted_user | NORMAL | 2018-08-03T20:34:17.987521+00:00 | 2018-09-25T23:27:38.217316+00:00 | 1,361 | false | ```\nvar connect = function(root) {\n if(!root) return;\n const queue = [root];\n \n while(queue.length) {\n const size = queue.length;\n const level = queue.slice();\n\n for(let i = 0; i < size; i++) {\n const currentNode = queue.shift();\n currentNode.next = level[i + 1];\n if(currentNode.left) queue.push(currentNode.left);\n if(currentNode.right) queue.push(currentNode.right);\n }\n }\n};\n``` | 15 | 2 | [] | 2 |
populating-next-right-pointers-in-each-node | An iterative java solution | an-iterative-java-solution-by-graceluli-nue7 | public void connect(TreeLinkNode root) {\n \n TreeLinkNode n = root;\n \n while(n != null && n.left != null) {\n TreeLink | graceluli | NORMAL | 2015-11-13T22:57:50+00:00 | 2015-11-13T22:57:50+00:00 | 2,361 | false | public void connect(TreeLinkNode root) {\n \n TreeLinkNode n = root;\n \n while(n != null && n.left != null) {\n TreeLinkNode pre = null;\n \n for(TreeLinkNode p = n; p != null; p = p.next) {\n if(pre != null) pre.next = p.left;\n p.left.next = p.right;\n pre = p.right;\n }\n n = n.left;\n }\n } | 14 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | Python Solution - Recursive Elegant Solution | python-solution-recursive-elegant-soluti-4f3p | I thought that this solution was a little different to the others posted, most of them doing a level order search using the next pointer. However here, I have r | wallahwallah | NORMAL | 2021-12-29T02:56:05.235556+00:00 | 2021-12-30T23:56:17.350705+00:00 | 718 | false | I thought that this solution was a little different to the others posted, most of them doing a level order search using the next pointer. However here, I have recursively split the tree into \'pincer\' segments (this is what I call them because I don\'t know the name), at each level the pair is made up of 1. the right most node of that level in the left node\'s subtree & 2. the left most node of that level in the right node\'s subtree - and then connected node 1 to node 2 at each level.\n\n```\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if not root:\n return\n \n c1, c2 = root.left, root.right\n \n while c1 and c2:\n c1.next = c2\n c1, c2 = c1.right, c2.left\n \n self.connect(root.left)\n self.connect(root.right)\n \n return root\n```\n\t\nThe idea being, that I could simply connect a node\'s left child to it\'s right child, with the only difficulty being to find the \'next\' node of a right child. The \'pincer\' segments help resolve this issue, as the \'next\' node of a right child is simply the other node in that level of the \'pincer\'\n\nI\'m not quite sure the if there is a specific name for this general idea, and would be very appreciative if anyone knows what it is Hope this helps!\n\nEDIT: A diagram illustrating the \'pincer segments\' of each of the first three nodes, and the pointers created by each - in red, blue and green respectively. Note that each node not on the left or right \'boundary\' is visited by two other \'pincer segments\', as is necessary since each node should have a pointer coming in and one coming out.\n\n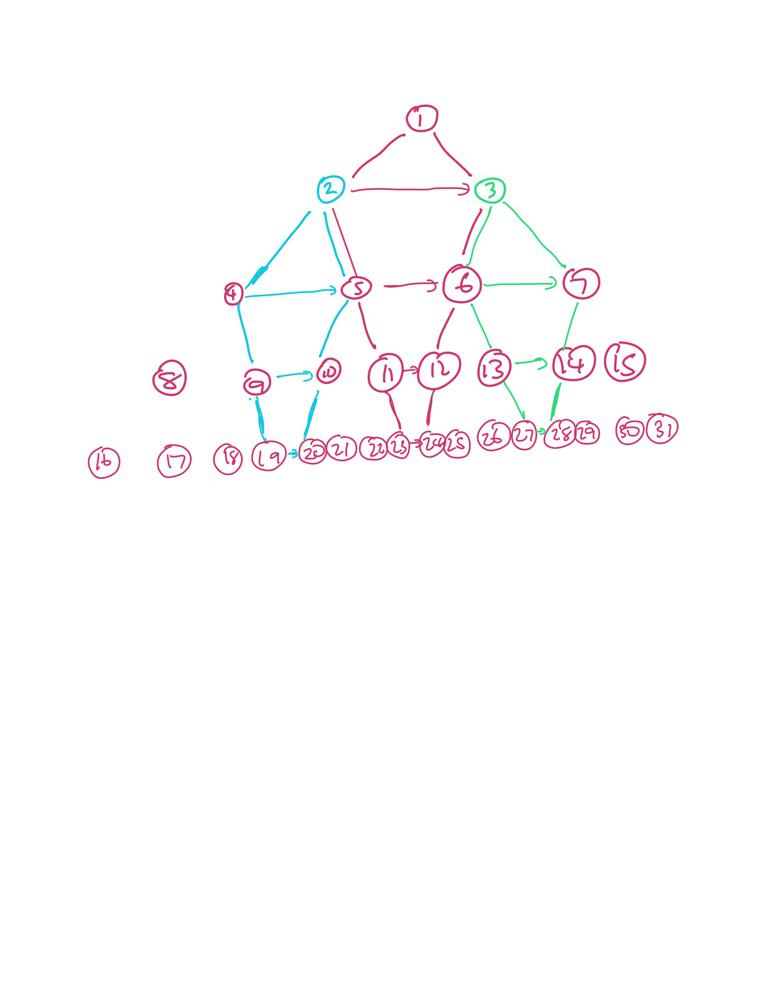 | 13 | 0 | ['Depth-First Search', 'Recursion', 'Python'] | 2 |
populating-next-right-pointers-in-each-node | javascript DFS extremely simple and understandable | javascript-dfs-extremely-simple-and-unde-m5kc | DFS, pass down rightnode\'s left pointer if it exists, otherwise null.\n\nvar connect = function(root, rightNode = null) {\n if (!root) return root;\n \n | anthonysgro1995 | NORMAL | 2021-09-23T04:12:49.659010+00:00 | 2021-09-24T13:54:35.249292+00:00 | 677 | false | DFS, pass down rightnode\'s left pointer if it exists, otherwise null.\n```\nvar connect = function(root, rightNode = null) {\n if (!root) return root;\n \n root.next = rightNode;\n connect(root.left, root.right);\n connect(root.right, rightNode ? rightNode.left : null);\n \n return root;\n};\n``` | 13 | 0 | ['Depth-First Search', 'JavaScript'] | 1 |
populating-next-right-pointers-in-each-node | C++ | [99%, 100% memory] | 5-liner | Recursively crispy AF | c-99-100-memory-5-liner-recursively-cris-zyhk | \nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root and root->left) {\n root->left->next = root->right;\n auto c | s4chin | NORMAL | 2020-11-13T08:42:40.149836+00:00 | 2020-11-13T08:44:01.865598+00:00 | 592 | false | ```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root and root->left) {\n root->left->next = root->right;\n auto c1 = root->left, c2 = root->right;\n while(c1->right) c1->right->next = c2->left, c1 = c1->right, c2 = c2->left;\n root->left = connect(root->left), root->right = connect(root->right);\n }\n return root;\n }\n};\n```\n\nExplanation -\n1. Traverse tree\n2. Make given connections\n3. ???\n4. Profit! | 13 | 3 | [] | 4 |
populating-next-right-pointers-in-each-node | Accepted Java recursive solution | accepted-java-recursive-solution-by-jean-50hb | The recursive solution of my last post, although the space is not O(1) (due to recursion), the solution is still elegant.\n\n public class Solution {\n | jeantimex | NORMAL | 2015-07-04T18:26:09+00:00 | 2015-07-04T18:26:09+00:00 | 1,870 | false | The recursive solution of my last post, although the space is not O(1) (due to recursion), the solution is still elegant.\n\n public class Solution {\n public void connect(TreeLinkNode root) {\n if (root == null) return;\n \n if (root.left != null) {\n root.left.next = root.right;\n }\n \n if (root.right != null) {\n root.right.next = root.next != null ? root.next.left : null;\n }\n \n connect(root.left);\n connect(root.right);\n }\n } | 13 | 1 | ['Java'] | 1 |
populating-next-right-pointers-in-each-node | 5-line 1ms java iterative solution O(n) time O(1) space | 5-line-1ms-java-iterative-solution-on-ti-lxcd | public class Solution {\n public void connect(TreeLinkNode root) {\n if (root == null) { return; }\n for (TreeLinkNode head=root; h | mach7 | NORMAL | 2016-01-19T03:56:35+00:00 | 2016-01-19T03:56:35+00:00 | 2,306 | false | public class Solution {\n public void connect(TreeLinkNode root) {\n if (root == null) { return; }\n for (TreeLinkNode head=root; head.left!=null; head=head.left) {\n for (TreeLinkNode parent=head; parent!=null; parent=parent.next) {\n parent.left.next = parent.right;\n if (parent.next != null) { parent.right.next = parent.next.left; }\n }\n }\n }\n } | 13 | 0 | ['Iterator', 'Java'] | 2 |
populating-next-right-pointers-in-each-node | O(1) space , simple bfs java solution and without recursion | o1-space-simple-bfs-java-solution-and-wi-7kry | Intution: Treating level of tree is as linked list.\n1. From parent level connect children level node as linked list and parent level is already connected so we | deepakkdkk | NORMAL | 2023-06-09T09:47:53.131196+00:00 | 2023-06-09T09:47:53.131234+00:00 | 1,786 | false | Intution: Treating level of tree is as linked list.\n1. From parent level connect children level node as linked list and parent level is already connected so we can move to next node of parent to connect other children node.\n```\nclass Solution {\n public Node connect(Node root) {\n Node head = root;\n for(head = root; head != null;){\n \n if(head.left == null){ // if left is null then it means no children nodes to connect now\n return root;\n }\n Node prev = null;\n Node curr = head; //curr always pointing starting node of every level in starting\n \n while(curr != null){\n \n if(prev != null) // for first node of every level, prev pointing to null\n prev.right.next = curr.left; //connect prev node right to curr left node\n curr.left.next = curr.right; // connect same children nodes of parent \n \n prev = curr; // move prev and curr node to next node\n curr = curr.next;\n }\n head = head.left; // move head to next level\n }\n return root;\n }\n}\n``` | 12 | 0 | ['Breadth-First Search', 'Java'] | 3 |
populating-next-right-pointers-in-each-node | ✔️ 100% Fastest Swift Solution, time: O(n), space: O(1). | 100-fastest-swift-solution-time-on-space-vp8g | \n/**\n * Definition for a Node.\n * public class Node {\n * public var val: Int\n * public var left: Node?\n * public var right: Node?\n *\t publ | sergeyleschev | NORMAL | 2022-04-10T07:08:06.731773+00:00 | 2022-04-10T07:08:06.731805+00:00 | 349 | false | ```\n/**\n * Definition for a Node.\n * public class Node {\n * public var val: Int\n * public var left: Node?\n * public var right: Node?\n *\t public var next: Node?\n * public init(_ val: Int) {\n * self.val = val\n * self.left = nil\n * self.right = nil\n * self.next = nil\n * }\n * }\n */\n\nclass Solution {\n // - Complexity:\n // - time: O(n), where n is the number of nodes in the binary tree.\n // - space: O(1), only constant space is used.\n\n func connect(_ root: Node?) -> Node? {\n var leftMost = root\n\n while leftMost?.left != nil {\n var head = leftMost\n while head != nil {\n head?.left?.next = head?.right\n if let next = head?.next {\n head?.right?.next = next.left\n }\n head = head?.next\n }\n leftMost = leftMost?.left\n }\n\n return root\n }\n\n}\n```\n\nLet me know in comments if you have any doubts. I will be happy to answer.\n\nPlease upvote if you found the solution useful. | 12 | 0 | ['Swift'] | 0 |
populating-next-right-pointers-in-each-node | A concise O(1) space complexity solution | a-concise-o1-space-complexity-solution-b-tqf5 | it fits problem 1 and 2, any comments will be welcome, thanks\n\n void connect(TreeLinkNode root) {\n TreeLinkNode head = root; // the left first node | shichaotan | NORMAL | 2015-01-11T22:17:16+00:00 | 2015-01-11T22:17:16+00:00 | 1,542 | false | it fits problem 1 and 2, any comments will be welcome, thanks\n\n void connect(TreeLinkNode *root) {\n TreeLinkNode *head = root; // the left first node in every level\n TreeLinkNode *cur = NULL; // the current node in the upper level\n TreeLinkNode *pre = NULL; // the prev node in the downer level\n \n while (head) {\n cur = head;\n head = pre = NULL;\n // travel one level in a loop\n while (cur) {\n // left child exist\n if (cur->left) {\n if (pre) pre = pre->next = cur->left;\n else head = pre = cur->left;\n \n }\n // right child exist\n if (cur->right) {\n if (pre) pre = pre->next = cur->right;\n else head = pre = cur->right;\n }\n // next node in the same level\n cur = cur->next;\n }\n }\n } | 12 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | Java recursive and iterative solutions. | java-recursive-and-iterative-solutions-b-bfl7 | \n // dfs iteratively \n public void connect1(TreeLinkNode root) {\n Stack<TreeLinkNode> stack = new Stack<>();\n stack.push(root);\n | oldcodingfarmer | NORMAL | 2016-04-24T16:26:26+00:00 | 2016-04-24T16:26:26+00:00 | 1,897 | false | \n // dfs iteratively \n public void connect1(TreeLinkNode root) {\n Stack<TreeLinkNode> stack = new Stack<>();\n stack.push(root);\n while (!stack.isEmpty()) {\n TreeLinkNode n = stack.pop();\n if (n != null) {\n if (n.right != null) {\n n.left.next = n.right;\n if (n.next != null) {\n n.right.next = n.next.left;\n }\n }\n stack.push(n.right);\n stack.push(n.left);\n }\n }\n }\n \n // bfs iteratively\n public void connect2(TreeLinkNode root) {\n Queue<TreeLinkNode> queue = new LinkedList<>();\n queue.add(root);\n while(!queue.isEmpty()) {\n TreeLinkNode n = queue.poll();\n if (n != null) {\n if (n.right != null) {\n n.left.next = n.right;\n if (n.next != null) {\n n.right.next = n.next.left;\n }\n }\n queue.add(n.left);\n queue.add(n.right);\n }\n }\n }\n \n // dfs recursively\n public void connect(TreeLinkNode root) {\n if (root != null) {\n if (root.right != null) {\n root.left.next = root.right;\n if (root.next != null) {\n root.right.next = root.next.left;\n } \n }\n connect(root.left);\n connect(root.right);\n }\n } | 12 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Recursion', 'Iterator', 'Java'] | 2 |
populating-next-right-pointers-in-each-node | O(n)time/BEATS 99.97% MEMORY/SPEED 0ms MAY 2022 | ontimebeats-9997-memoryspeed-0ms-may-202-666a | \n\n\n(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\nTake care broth | darian-catalin-cucer | NORMAL | 2022-05-15T04:42:54.079149+00:00 | 2022-05-15T04:42:54.079187+00:00 | 1,955 | false | ```\n```\n\n(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, ***please upvote*** this post.)\n***Take care brother, peace, love!***\n\n```\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 38.2MB*** (beats 92.04% / 24.00%).\n* ***Java***\n```\nclass Solution {\n public Node connect(Node root) {\n if(root == null) return null;\n if(root.left != null) root.left.next = root.right;\n if(root.right != null && root.next != null) root.right.next = root.next.left;\n connect(root.left);\n connect(root.right);\n return root;\n }\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***0ms / 7.0MB*** (beats 100.00% / 100.00%).\n* ***C++***\n```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root && root->left != NULL) {\n root->left->next = root->right;\n connect(root->left);\n if(root->next != NULL) root->right->next = root->next->left;\n connect(root->right);\n }\n \n return root;\n }\n};\n```\n\n```\n```\n\n```\n```\n\n\nThe best result for the code below is ***26ms / 12.2MB*** (beats 95.42% / 82.32%).\n* ***Python***\n```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n # edge case check\n if not root:\n return None\n \n node = root # create a pointer to the root node\n \n # iterate only until we have a new level (because the connections for Nth level are done when we are at N-1th level)\n while node.left:\n head = node\n while head:\n head.left.next = head.right\n if head.next:\n head.right.next = head.next.left\n \n head = head.next\n \n node = node.left\n\n return root\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***51ms / 34.2MB*** (beats 100.00% / 84.12%).\n* ***JavaScript***\n```\nvar connect = function(root) {\n let ptr = root;\n while(root && root.left){\n let temp = root;\n while(temp) {\n temp.left.next = temp.right;\n temp.right.next = temp.next ? temp.next.left : null;\n temp = temp.next;\n }\n root = root.left;\n }\n return ptr;\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***68ms / 44.2MB*** (beats 100.00% / 45.25%).\n* ***Kotlin***\n```\nclass Solution {\n fun connect(root: Node?): Node? =\n if (root?.left == null && root?.right == null) root //at bottom of tree \n else root?.apply { //connect next and recurse downwards\n left?.next = right\n right?.next = next?.left\n connect(left)\n connect(right)\n }\n}\n```\n\n```\n```\n\n```\n```\n\nThe best result for the code below is ***12ms / 32.2MB*** (beats 95% / 84%).\n* ***Swift***\n```\nclass Solution {\n // - Complexity:\n // - time: O(n), where n is the number of nodes in the binary tree.\n // - space: O(1), only constant space is used.\n\n func connect(_ root: Node?) -> Node? {\n var leftMost = root\n\n while leftMost?.left != nil {\n var head = leftMost\n while head != nil {\n head?.left?.next = head?.right\n if let next = head?.next {\n head?.right?.next = next.left\n }\n head = head?.next\n }\n leftMost = leftMost?.left\n }\n\n return root\n }\n\n}\n```\n\n```\n```\n\n```\n```\n\n***"Open your eyes. Expect us." - \uD835\uDCD0\uD835\uDCF7\uD835\uDCF8\uD835\uDCF7\uD835\uDD02\uD835\uDCF6\uD835\uDCF8\uD835\uDCFE\uD835\uDCFC*** | 11 | 0 | ['Swift', 'C', 'Python', 'C++', 'Java', 'Python3', 'Kotlin', 'JavaScript'] | 0 |
populating-next-right-pointers-in-each-node | ✅ [C++/Java/Python] | BFS | O(n) Time & O(1) Space | cjavapython-bfs-on-time-o1-space-by-dami-f0y3 | I hope the comments are explicit enough to tell about the iterative BFS approach that is used here.\nTime complexity - O(n)\nSpace complexity - O(1)\n\nC++ \n\n | damian_arado | NORMAL | 2022-04-16T17:08:47.380671+00:00 | 2022-08-11T06:25:19.287605+00:00 | 572 | false | I hope the comments are explicit enough to tell about the iterative BFS approach that is used here.\nTime complexity - O(n)\nSpace complexity - O(1)\n\nC++ \n\n```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root) return root;\n Node* current = root;\n while(current) {\n // this will always be the first node of any level\n Node* level1stNode = current;\n // this runs until we iterate over all the nodes of any level\n while(current) {\n // this links the child nodes (L child -> next = R child) of the same parent node\n if(current->left) {\n current->left->next = current->right;\n }\n // this checks whether there are more nodes towards right at the same level\n if(current->right && current->next) {\n current->right->next = current->next->left;\n }\n // move on the next node of the current level (L -> R)\n current = current->next;\n }\n // move onto the first node of the next level\n current = level1stNode->left;\n }\n return root;\n }\n};\n```\n\nJava\n\n```\nclass Solution {\n public Node connect(Node root) {\n if(root == null) return root;\n Node current = root;\n while(current != null) {\n\t\t\t// this will always be the first node of any level\n Node level1stNode = current;\n\t\t\t// this runs until we iterate over all the nodes of any level\n while(current != null) {\n\t\t\t\t// this links the child nodes (L child -> next = R child) of the same parent node\n if(current.left != null) {\n current.left.next = current.right;\n }\n\t\t\t\t// this checks whether there are more nodes towards right at the same level\n if(current.right != null && current.next != null) {\n current.right.next = current.next.left;\n }\n\t\t\t\t// move on the next node of the current level (L -> R)\n current = current.next;\n }\n\t\t\t// move onto the first node of the next level\n current = level1stNode.left;\n }\n return root;\n }\n}\n```\n\nPython\n\n```\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if not root: return root\n \n self.current = root\n \n while self.current:\n \n # this will always be the first node of any level\n self.level1stNode = self.current\n \n # this runs until we iterate over all the nodes of any level\n while self.current:\n \n # this links the child nodes (L child -> next = R child) of the same parent node\n if self.current.left:\n self.current.left.next = self.current.right\n \n # this checks whether there are more nodes towards right at the same level\n if self.current.right and self.current.next:\n self.current.right.next = self.current.next.left\n \n # move on the next node of the current level (L -> R)\n self.current = self.current.next\n \n # move onto the first node of the next level\n self.current = self.level1stNode.left\n \n return root\n```\n\n\uD83D\uDE80 Thanks for reading. \nAn upvote would be appreciated. ^_^\n | 11 | 0 | ['Breadth-First Search', 'C', 'Iterator', 'Java'] | 0 |
populating-next-right-pointers-in-each-node | 🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏 | beats-super-easy-beginners-by-codewithsp-0jdv | IntuitionThe problem involves connecting all nodes at the same level in a perfect binary tree. Since the tree is perfect (all levels are completely filled), eac | CodeWithSparsh | NORMAL | 2025-01-12T17:08:16.488879+00:00 | 2025-01-12T17:08:16.488879+00:00 | 1,202 | false | 
---
# **Intuition**
The problem involves connecting all nodes at the same level in a perfect binary tree. Since the tree is perfect (all levels are completely filled), each node will have its left child, right child, and potentially a `next` sibling to its immediate right. We can utilize the tree's structure to link these nodes without requiring additional data structures.
---
# **Approach**
1. Start at the root and use a pointer (`leftMost`) to traverse level by level.
2. For each level, traverse the nodes using another pointer (`currNode`).
3. Connect:
- `currNode.left.next` to `currNode.right`.
- If `currNode.next` exists, connect `currNode.right.next` to `currNode.next.left`.
4. Move `leftMost` to the leftmost node of the next level and repeat until all levels are processed.
---
# **Complexity**
- **Time complexity:** $$O(n)$$, where $$n$$ is the number of nodes in the tree. Each node is visited once.
- **Space complexity:** $$O(1)$$, as no additional data structures are used, apart from a few pointers.
---
```java []
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
class Solution {
public Node connect(Node root) {
if (root == null) return null;
Node leftMost = root;
while (leftMost.left != null) {
Node currNode = leftMost;
while (currNode != null) {
currNode.left.next = currNode.right;
if (currNode.next != null) {
currNode.right.next = currNode.next.left;
}
currNode = currNode.next;
}
leftMost = leftMost.left;
}
return root;
}
}
```
```python []
# Definition for a Node.
class Node:
def __init__(self, val=0, left=None, right=None, next=None):
self.val = val
self.left = left
self.right = right
self.next = next
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return None
leftMost = root
while leftMost.left:
currNode = leftMost
while currNode:
currNode.left.next = currNode.right
if currNode.next:
currNode.right.next = currNode.next.left
currNode = currNode.next
leftMost = leftMost.left
return root
```
```cpp []
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(nullptr), right(nullptr), next(nullptr) {}
Node(int _val) : val(_val), left(nullptr), right(nullptr), next(nullptr) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if (!root) return nullptr;
Node* leftMost = root;
while (leftMost->left) {
Node* currNode = leftMost;
while (currNode) {
currNode->left->next = currNode->right;
if (currNode->next) {
currNode->right->next = currNode->next->left;
}
currNode = currNode->next;
}
leftMost = leftMost->left;
}
return root;
}
};
```
```dart []
class Node {
int val;
Node? left;
Node? right;
Node? next;
Node(this.val, [this.left, this.right, this.next]);
}
class Solution {
Node? connect(Node? root) {
if (root == null) return null;
Node? leftMost = root;
while (leftMost!.left != null) {
Node? currNode = leftMost;
while (currNode != null) {
currNode.left!.next = currNode.right;
if (currNode.next != null) {
currNode.right!.next = currNode.next!.left;
}
currNode = currNode.next;
}
leftMost = leftMost.left;
}
return root;
}
}
```
```go []
type Node struct {
Val int
Left *Node
Right *Node
Next *Node
}
func connect(root *Node) *Node {
if root == nil {
return nil
}
leftMost := root
for leftMost.Left != nil {
currNode := leftMost
for currNode != nil {
currNode.Left.Next = currNode.Right
if currNode.Next != nil {
currNode.Right.Next = currNode.Next.Left
}
currNode = currNode.Next
}
leftMost = leftMost.Left
}
return root
}
```
```javascript []
// Definition for a Node.
function Node(val, left, right, next) {
this.val = val === undefined ? 0 : val;
this.left = left === undefined ? null : left;
this.right = right === undefined ? null : right;
this.next = next === undefined ? null : next;
}
var connect = function(root) {
if (!root) return null;
let leftMost = root;
while (leftMost.left) {
let currNode = leftMost;
while (currNode) {
currNode.left.next = currNode.right;
if (currNode.next) {
currNode.right.next = currNode.next.left;
}
currNode = currNode.next;
}
leftMost = leftMost.left;
}
return root;
};
```
---
 {:style='width:250px'} | 10 | 0 | ['Breadth-First Search', 'C', 'Binary Tree', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'Dart'] | 2 |
populating-next-right-pointers-in-each-node | O(n) time and O(1) space Easy Intutive solution for better understanding of recursion | on-time-and-o1-space-easy-intutive-solut-dihl | Intuition\n Describe your first thoughts on how to solve this problem. \nInitially, I considered a bottom-up recursion approach where I would set the next point | Rya-man | NORMAL | 2024-08-27T18:29:16.994985+00:00 | 2024-08-27T18:31:26.949912+00:00 | 1,373 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nInitially, I considered a bottom-up recursion approach where I would set the next pointer during the backtracking step. However, this approach failed when connecting a node on the right to another node on its parent\'s left. This led me to devise a top-down approach, using the `next` pointer of the parent to set the next pointers of the children.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe create a helper function where we pass the node and its parent. The base case is when the node is null. Here\'s the step-by-step process:\n\nIf the node is null, we return immediately.\n\nIf the parent is not null, we set `parent->left->next` to `parent->right`.\n\nIf the parent is not null and parent->next is not null, we set `parent->right->next` to `parent->next->left`.\n\nWe then check if the `root->left` and `root->right` are not null, and recursively call the helper for both the left and right children.\n\n# Complexity\n- Time complexity:\n$$O(n)$$ \n\n- Space complexity:\n$$O(1)$$ if we ignore the recursion stack or else $$O(log(n))$$\n\n# Code\n```cpp []\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* left;\n Node* right;\n Node* next;\n\n Node() : val(0), left(NULL), right(NULL), next(NULL) {}\n\n Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}\n\n Node(int _val, Node* _left, Node* _right, Node* _next)\n : val(_val), left(_left), right(_right), next(_next) {}\n};\n*/\n\nclass Solution {\npublic:\n void helper(Node* root, Node* parent) {\n if (root == NULL)\n return;\n if (parent != NULL)\n parent->left->next = parent->right;\n if (parent != NULL and parent->next != NULL)\n parent->right->next = parent->next->left;\n if (root->left == NULL and root->right == NULL)\n return;\n helper(root->left, root);\n helper(root->right, root);\n }\n Node* connect(Node* root) {\n helper(root, NULL);\n return root;\n }\n};\n```\n``` python3 []\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val: int = 0, left: \'Node\' = None, right: \'Node\' = None, next: \'Node\' = None):\n self.val = val\n self.left = left\n self.right = right\n self.next = next\n"""\n\nclass Solution:\n def helper(self, root: \'Node\', parent: \'Node\') -> None:\n if root is None:\n return\n if parent is not None:\n parent.left.next = parent.right\n if parent is not None and parent.next is not None:\n parent.right.next = parent.next.left\n if root.left is None and root.right is None:\n return\n self.helper(root.left, root)\n self.helper(root.right, root)\n \n def connect(self, root: \'Node\') -> \'Node\':\n self.helper(root, None)\n return root\n\n```\n``` java []\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node left;\n public Node right;\n public Node next;\n\n public Node() {}\n\n public Node(int _val) {\n val = _val;\n }\n\n public Node(int _val, Node _left, Node _right, Node _next) {\n val = _val;\n left = _left;\n right = _right;\n next = _next;\n }\n};\n*/\n\nclass Solution {\n private void helper(Node root, Node parent) {\n if (root == null) return;\n if (parent != null) parent.left.next = parent.right;\n if (parent != null && parent.next != null) parent.right.next = parent.next.left;\n if (root.left == null && root.right == null) return;\n helper(root.left, root);\n helper(root.right, root);\n }\n\n public Node connect(Node root) {\n helper(root, null);\n return root;\n }\n}\n\n\n\n``` | 10 | 0 | ['Linked List', 'Tree', 'C++', 'Java', 'Python3'] | 0 |
populating-next-right-pointers-in-each-node | 2 ms | Easy to Understand | Using Queue | Level Order Traversal | Java | C++ | 2-ms-easy-to-understand-using-queue-leve-c1fj | Intuition\n Describe your first thoughts on how to solve this problem. \nThe approach used here is based on level-order traversal of the tree using a queue. The | yshivhare163 | NORMAL | 2023-06-27T04:26:37.484586+00:00 | 2023-06-27T04:26:37.484616+00:00 | 632 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe approach used here is based on level-order traversal of the tree using a queue. The intuition behind the solution is that by traversing the tree level by level, we can keep track of the next right node for each node in the current level and establish the connections.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nA while loop processes each level. Inside the loop, a for loop iterates through each node, connecting it to the next node in the same level if applicable. Nodes with children are added to the queue for the next level. The process continues until all nodes in the current level are processed.\n\n# Complexity\n- Time complexity: $$O(n)$$ \n (n is number of nodes)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m)$$ \n (m is maximum number of nodes in a level)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n public Node connect(Node root) {\n if (root == null) {\n return null;\n }\n\n Queue<Node> queue = new LinkedList<>();\n queue.add(root);\n\n while (!queue.isEmpty()) {\n int size = queue.size(); // Store the size of the current level\n\n for (int i = 0; i < size; i++) {\n Node node = queue.remove(); // Remove a node from the queue\n\n if (i < size - 1) {\n node.next = queue.peek(); // Set the next pointer to the node at the front of the queue\n }\n\n if (node.left != null) {\n queue.add(node.left); // Add the left child to the queue\n }\n if (node.right != null) {\n queue.add(node.right); // Add the right child to the queue\n }\n }\n }\n\n return root; // Return the modified root node\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if (root == nullptr) return nullptr;\n\n queue<Node*> queue;\n queue.push(root);\n\n while (!queue.empty()) {\n int size = queue.size();\n\n for (int i = 0; i < size; i++) {\n Node* node = queue.front();\n queue.pop();\n\n if (i < size - 1) \n node->next = queue.front();\n \n if (node->left != nullptr) \n queue.push(node->left);\n \n if (node->right != nullptr) \n queue.push(node->right); \n }\n }\n\n return root;\n }\n};\n\n```\nPLease upvote if u found it useful :)\n | 10 | 0 | ['Breadth-First Search', 'Queue', 'Binary Tree', 'C++', 'Java'] | 4 |
populating-next-right-pointers-in-each-node | 0ms || 100% FASTER || JAVA CODE | 0ms-100-faster-java-code-by-raghavdabra-8dtc | \nclass Solution {\n public Node connect(Node root) {\n if(root == null) return null;\n Node left = root.left;\n Node right = root.right | raghavdabra | NORMAL | 2022-10-19T05:26:07.222974+00:00 | 2022-10-19T05:26:07.223017+00:00 | 645 | false | ```\nclass Solution {\n public Node connect(Node root) {\n if(root == null) return null;\n Node left = root.left;\n Node right = root.right;\n while(left != null){\n left.next = right;\n left = left.right;\n right = right.left;\n }\n connect(root.left);\n connect(root.right);\n return root; \n }\n}\n``` | 10 | 0 | ['Java'] | 0 |
populating-next-right-pointers-in-each-node | Share my LOOP JAVA 1MS solution!! Easy understand!! | share-my-loop-java-1ms-solution-easy-und-entl | //Just remember to use result from the last step\n public class Solution {\n public void connect(TreeLinkNode root) {\n if(root==null) retu | herrji | NORMAL | 2016-02-20T08:05:13+00:00 | 2016-02-20T08:05:13+00:00 | 1,709 | false | //Just remember to use result from the last step\n public class Solution {\n public void connect(TreeLinkNode root) {\n if(root==null) return;\n while(root.left!=null){\n TreeLinkNode tmp = root;\n while(tmp!=null){\n tmp.left.next = tmp.right;\n if(tmp.next!=null) tmp.right.next = tmp.next.left;\n tmp = tmp.next;\n }\n root = root.left;\n }\n }\n } | 10 | 2 | ['Java'] | 0 |
populating-next-right-pointers-in-each-node | 📌 C++ || Beats - 97% || Explained Using Level Order Traversal | c-beats-97-explained-using-level-order-t-ocap | Best Solution for Beginners\nWe can solve this using Level order Traversal.\n\n Runtime - 97.14%\uD83D\uDD25 \n\n# Approach\n1. Firstly We will do Level Orde | Luvchaudhary | NORMAL | 2022-12-27T05:22:46.111696+00:00 | 2022-12-27T05:22:46.111739+00:00 | 1,451 | false | # Best Solution for Beginners\nWe can solve this using Level order Traversal.\n\n Runtime - 97.14%\uD83D\uDD25 \n\n# Approach\n1. Firstly We will do Level Order Travesal.\n2. Then at Each Level we will join all nodes present at that Level.\n\n# If you like the solution and understand it then Please Upvote.\u2B06\uFE0F\u2764\uFE0F \n\t* PEACE OUT LUV\u270C\uFE0F*\n\n# Code\n```\n/*\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root == NULL){\n return root;\n }\n queue<Node*>q;\n q.push(root);\n while(!q.empty()){\n int size = q.size();\n vector<Node*>ans;\n for(int i=0; i<size; i++){\n Node* node = q.front();\n q.pop();\n if(node ->left)q.push(node ->left);\n if(node ->right)q.push(node ->right);\n ans.push_back(node);\n }\n for(int i=1; i<ans.size(); i++){\n ans[i-1] ->next = ans[i];\n }\n }\n return root;\n }\n};\n``` | 9 | 0 | ['Linked List', 'Tree', 'Breadth-First Search', 'C++'] | 4 |
populating-next-right-pointers-in-each-node | C++ solutions | c-solutions-by-infox_92-fhgr | \nclass Solution {\npublic:\n Node* connect(Node* root) {\n queue<Node*> q;\n if (root) q.push(root);\n while (q.size()) {\n | Infox_92 | NORMAL | 2022-11-05T03:49:57.942902+00:00 | 2022-11-05T03:49:57.942941+00:00 | 1,112 | false | ```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n queue<Node*> q;\n if (root) q.push(root);\n while (q.size()) {\n int len = q.size();\n Node* curr;\n while (len--) {\n curr = q.front(), q.pop();\n curr->next = len ? q.front():NULL;\n if (curr->left) q.push(curr->left);\n if (curr->right) q.push(curr->right); \n }\n } \n return root;\n }\n};\n\n``` | 9 | 0 | ['C', 'C++'] | 0 |
populating-next-right-pointers-in-each-node | Java BFS and DFS - 4 Solutions | java-bfs-and-dfs-4-solutions-by-aakashde-bv38 | \n\t//DFS\n\t//Time Complexity : O(n), where n is the number of elements in root\n\t//Space Complexity : O(log n), for recursion stack of a perfect BST\n\tpubli | aakashdeo | NORMAL | 2022-02-12T07:33:21.325584+00:00 | 2022-02-12T07:33:59.804504+00:00 | 594 | false | ```\n\t//DFS\n\t//Time Complexity : O(n), where n is the number of elements in root\n\t//Space Complexity : O(log n), for recursion stack of a perfect BST\n\tpublic Node connect(Node root) {\n if(root == null)\n return root;\n dfs(root);\n return root;\n }\n \n private void dfs(Node root) {\n // base\n if(root.left == null)\n return;\n \n root.left.next = root.right;\n dfs(root.left);\n if(root.next != null)\n root.right.next = root.next.left;\n dfs(root.right);\n }\n```\n```\n\t//DFS\n\t//Time Complexity : O(n), where n is the number of elements in root\n\t//Space Complexity : O(log n), for recursion stack of a perfect BST\n\tpublic Node connect1(Node root) {\n if(root == null)\n return root;\n conn(root.left, root.right);\n return root;\n }\n \n private void conn(Node left, Node right) {\n if(left == null)\n return;\n \n left.next = right;\n conn(left.left, left. right);\n conn(left.right, right.left);\n conn(right.left, right.right);\n }\n```\n```\n //BFS\n\t//Time Complexity : O(n), where n is the number of elements in root\n\t//Space Complexity : O(1)\n\tpublic Node connect2(Node root) {\n if(root == null)\n return root;\n \n Node level = root;\n while(level.left != null) {\n Node curr = level;\n while(curr != null) {\n curr.left.next = curr.right;\n if(curr.next != null)\n curr.right.next = curr.next.left;\n curr = curr.next;\n }\n level = level.left;\n }\n return root;\n }\n```\n```\n\t//BFS using Queue\n\t//Time Complexity : O(n), where n is the number of elements in root\n\t//Space Complexity : O(n), for queue\n\tpublic Node connect3(Node root) {\n\t\tif(root == null)\n\t\t\treturn root;\n\t\tQueue<Node> q = new LinkedList<>();\n\t\tq.offer(root);\n\n\t\twhile(!q.isEmpty()) {\n\t\t\tint size = q.size();\n\t\t\tNode prev = q.poll();\n\t\t\tif(prev.left != null) {\n\t\t\t\tq.offer(prev.left);\n\t\t\t\tq.offer(prev.right);\n\t\t\t}\n\t\t\tfor(int i=1; i<size; i++) {\n\t\t\t\tNode curr = q.poll();\n\t\t\t\tprev.next = curr;\n\t\t\t\tif(curr.left != null) {\n\t\t\t\t\tq.offer(curr.left);\n\t\t\t\t\tq.offer(curr.right);\n\t\t\t\t}\n\t\t\t\tprev = curr;\n\t\t\t}\n\t\t}\n\t\treturn root;\n\t} | 9 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Queue', 'Java'] | 0 |
populating-next-right-pointers-in-each-node | Python Simple Solution easy to understand | O(n) and constant Memory | python-simple-solution-easy-to-understan-56xc | \n def helper(self, root, parent=None, isleftChild=True):\n if root is None:\n return None\n \n if parent == None:\n | sathwickreddy | NORMAL | 2021-07-23T16:20:09.368414+00:00 | 2021-08-04T11:38:50.117641+00:00 | 880 | false | ```\n def helper(self, root, parent=None, isleftChild=True):\n if root is None:\n return None\n \n if parent == None:\n #we are at root\n root.next = None\n else:\n #we are at some node other than root\n if isleftChild:\n root.next = parent.right\n else:\n root.next = None\n if parent.next != None:\n root.next = parent.next.left\n \n root.left = self.helper(root.left, root, True)\n root.right = self.helper(root.right, root, False)\n \n return root\n \n def connect(self, root: \'Node\') -> \'Node\':\n return self.helper(root)\n```\nplease upvote ! | 9 | 0 | ['Python', 'C++', 'Java', 'Python3'] | 0 |
populating-next-right-pointers-in-each-node | easy BFS Python 🐍 solution | easy-bfs-python-solution-by-injysarhan-lwzn | \n\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n \n if not root:\n return None\n \n q=collection | injysarhan | NORMAL | 2020-11-14T05:55:02.859691+00:00 | 2020-11-14T05:55:02.859723+00:00 | 925 | false | ```\n\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n \n if not root:\n return None\n \n q=collections.deque()\n \n q.append(root)\n \n while q:\n for i in range(1,len(q)):\n q[i-1].next=q[i]\n q[-1].next=None \n newLevel=deque()\n for node in q:\n if node.left:\n newLevel.append(node.left)\n if node.right:\n newLevel.append(node.right)\n \n q=newLevel\n return root\n``` | 9 | 0 | ['Python', 'Python3'] | 0 |
populating-next-right-pointers-in-each-node | Populating Next Right Pointer in Each Node | C++ | Easy to Understand | populating-next-right-pointer-in-each-no-cqzq | \nclass Solution {\n\npublic:\n Node* connect(Node* root) {\n if(root == NULL || root->left == NULL) return root;\n \n \n if(root | caffeinatedcod3r | NORMAL | 2020-11-13T14:58:38.578370+00:00 | 2020-11-13T15:19:52.572370+00:00 | 323 | false | ```\nclass Solution {\n\npublic:\n Node* connect(Node* root) {\n if(root == NULL || root->left == NULL) return root;\n \n \n if(root->next != NULL){\n root->right->next=root->next->left;\n }\n \n root->left->next = root->right;\n \n connect(root->left);\n connect(root->right);\n \n return root;\n }\n};\n``` | 9 | 0 | ['Recursion', 'C'] | 1 |
populating-next-right-pointers-in-each-node | [Python] Time O(n), Space O(1), Concise Real O(1) Solution | python-time-on-space-o1-concise-real-o1-kqjuz | \nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if (head:=root):\n while (start:=root.left):\n while ro | ztonege | NORMAL | 2020-11-13T11:25:15.508293+00:00 | 2020-11-13T11:25:15.508323+00:00 | 277 | false | ```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if (head:=root):\n while (start:=root.left):\n while root:\n root.left.next = root.right\n root.right.next = root.next.left if root.next else None\n root = root.next\n root = start\n return head\n``` | 9 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | Python, constant space | python-constant-space-by-warmr0bot-6dg2 | Use the already-populated next pointers of the row above to fill the row below:\n\ndef connect(self, root: \'Node\') -> \'Node\':\n\tif not root: return\n\t\n\t | warmr0bot | NORMAL | 2020-11-13T10:06:46.898732+00:00 | 2020-11-13T10:07:03.274431+00:00 | 566 | false | Use the already-populated next pointers of the row above to fill the row below:\n```\ndef connect(self, root: \'Node\') -> \'Node\':\n\tif not root: return\n\t\n\tabove, below = root, root.left\n\twhile below:\n\t\tcur = below\n\t\twhile above:\n\t\t\tif cur == above.left:\n\t\t\t\tcur.next = above.right\n\t\t\t\tabove = above.next\n\t\t\telse:\n\t\t\t\tcur.next = above.left\n\t\t\tcur = cur.next\n\n\t\tabove = below\n\t\tbelow = below.left\n\n\treturn root\n``` | 9 | 0 | ['Python', 'Python3'] | 0 |
populating-next-right-pointers-in-each-node | Go Recursive and Iterative | go-recursive-and-iterative-by-casd82-b4x2 | Recursive:\n\nfunc connect(root *Node) *Node {\n if root == nil {\n return nil\n }\n \n if root.Left != nil {\n root.Left.Next = root. | casd82 | NORMAL | 2020-04-03T05:47:37.109853+00:00 | 2020-04-03T05:55:27.866868+00:00 | 642 | false | Recursive:\n```\nfunc connect(root *Node) *Node {\n if root == nil {\n return nil\n }\n \n if root.Left != nil {\n root.Left.Next = root.Right\n if root.Next != nil {\n root.Right.Next = root.Next.Left\n }\n }\n \n connect(root.Left)\n connect(root.Right)\n \n return root\n}\n```\n\nIterative (BFS with Queue):\n```\nfunc connect(root *Node) *Node {\n if root == nil {\n return nil\n }\n \n type entry struct{\n level int\n node *Node\n }\n \n var queue []entry\n \n var prev *Node\n currLevel := -1\n \n queue = append(queue, entry{level: 0, node: root})\n \n for len(queue) != 0 {\n curr := queue[0]\n queue = queue[1:]\n \n if currLevel != curr.level {\n if prev != nil {\n prev.Next = nil\n }\n currLevel = curr.level\n } else {\n prev.Next = curr.node\n }\n \n prev = curr.node\n \n if curr.node.Left != nil {\n queue = append(queue, entry{level: curr.level+1, node: curr.node.Left})\n }\n \n if curr.node.Right != nil {\n queue = append(queue, entry{level: curr.level+1, node: curr.node.Right})\n }\n }\n \n return root\n}\n``` | 9 | 0 | ['Go'] | 0 |
populating-next-right-pointers-in-each-node | C++ easy recursive solution | c-easy-recursive-solution-by-jtimberlake-enbl | class Solution {\n public:\n void connect(TreeLinkNode *root) {\n if(!root)\n return;\n if(root->left)\n | jtimberlakers | NORMAL | 2015-08-21T03:08:16+00:00 | 2015-08-21T03:08:16+00:00 | 1,031 | false | class Solution {\n public:\n void connect(TreeLinkNode *root) {\n if(!root)\n return;\n if(root->left)\n root->left->next = root->right;\n if(root->next && root->right)\n root->right->next = root->next->left;\n connect(root->left);\n connect(root->right);\n }\n }; | 9 | 1 | [] | 2 |
populating-next-right-pointers-in-each-node | Populating Next Right Pointers in Each Node – BFS Solution in C++ 🚀 | populating-next-right-pointers-in-each-n-clqa | Intuition
The goal is to connect each node to its next right node in a perfect binary tree. If there’s no next right node, it should remain NULL.
This is a clas | Mirin_Mano_M | NORMAL | 2025-02-17T10:27:23.997378+00:00 | 2025-02-17T10:27:23.997378+00:00 | 755 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1) The goal is to connect each node to its next right node in a perfect binary tree. If there’s no next right node, it should remain NULL.
2) This is a classic level-order traversal problem, where we process each level of the tree and connect adjacent nodes at the same level.
3) We can achieve this by using a queue (BFS) to traverse the tree level by level and updating the next pointers.
# Approach
<!-- Describe your approach to solving the problem. -->
1) Handle Edge Case:
i) If the tree is empty (i.e., root == nullptr), return nullptr.
2) Use a Queue for Level-Order Traversal (BFS):
i) Start with the root node and push it to the queue.
ii) Process nodes level by level:
-> For each node, check if it’s the last node in the current level. If not, set its next pointer to the node that comes next in the queue.
-> If the node has left and right children, push them into the queue for processing in the next level.
3) Continue Until the Queue is Empty:
i) The process ensures that all nodes at a level are connected in a chain via their next pointers.
ii) After the entire tree is processed, return the root, which now has all its next pointers correctly set.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Each node is processed once, and each operation inside the loop (push, pop, and next assignment) takes constant time. Hence, the time complexity is O(n), where n is the number of nodes in the tree.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
Each node is processed once, and each operation inside the loop (push, pop, and next assignment) takes constant time. Hence, the time complexity is O(n), where n is the number of nodes in the tree.
# Code
```cpp []
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if(root==nullptr) return {};
queue<Node*> q;
q.push(root);
while(!q.empty()){
int n = q.size();
for(int i=0;i<n;i++){
Node* t = q.front();
q.pop();
if(i!=n-1){
t->next=q.front();
}
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
}
return root;
}
};
```
```Java []
class Solution {
public Node connect(Node root) {
if (root == null) return null;
Queue<Node> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
int n = q.size();
for (int i = 0; i < n; i++) {
Node node = q.poll();
if (i != n - 1) {
node.next = q.peek();
}
if (node.left != null) q.offer(node.left);
if (node.right != null) q.offer(node.right);
}
}
return root;
}
}
``` | 8 | 0 | ['Linked List', 'Tree', 'Breadth-First Search', 'Binary Tree', 'C++', 'Java'] | 0 |
populating-next-right-pointers-in-each-node | Populating Next Right Pointers in Each Node [C++] | populating-next-right-pointers-in-each-n-7b08 | IntuitionThe problem requires us to populate the next pointers in each node of a perfect binary tree. Given the properties of a perfect binary tree, each node h | moveeeax | NORMAL | 2025-01-29T14:24:55.749612+00:00 | 2025-01-29T14:24:55.749612+00:00 | 591 | false | ### Intuition
The problem requires us to populate the `next` pointers in each node of a **perfect binary tree**. Given the properties of a perfect binary tree, each node has either 0 or 2 children, and all leaves are at the same level.
Since each level is **fully populated**, we can use the `next` pointer to traverse each level without needing additional space.
---
### Approach
1. **Start from the Root:** Begin from the leftmost node of the current level.
2. **Iterate Through Nodes on the Current Level:** Use the `next` pointers to traverse through all nodes on the same level.
3. **Connect the Children:**
- Each node's `left->next` should point to `right`.
- If the node has a `next` pointer, then `right->next` should point to the `left` child of the node's `next` neighbor.
4. **Move to the Next Level:** Once we finish a level, move to its leftmost node (which is guaranteed to exist in a perfect binary tree).
5. **Repeat Until All Levels are Processed.**
This approach uses constant **O(1) space** by leveraging the `next` pointers instead of an extra data structure (like a queue in BFS).
---
### Complexity Analysis
- **Time Complexity:**
- We visit each node exactly **once**, and each operation (assigning `next` pointers) is **O(1)**.
- Total complexity is **O(n)**.
- **Space Complexity:**
- Since we are not using extra memory (like a queue or recursion stack), the space complexity is **O(1)**.
---
### Code
```cpp
class Solution {
public:
Node* connect(Node* root) {
if (!root) return nullptr;
Node* leftMost = root;
while (leftMost->left) {
Node* currNode = leftMost;
while (currNode) {
currNode->left->next = currNode->right;
if (currNode->next) {
currNode->right->next = currNode->next->left;
}
currNode = currNode->next;
}
leftMost = leftMost->left;
}
return root;
}
};
```
---
### Explanation of Code
1. **Edge Case:** If the root is `nullptr`, return immediately.
2. **Use `leftMost` to Track the Start of Each Level:**
- Since the tree is perfect, we always have a `leftMost->left` if there is a next level.
3. **Traverse the Current Level Using `next` Pointers:**
- Assign `left->next = right` for each node.
- Assign `right->next = next->left` if the node has a `next` pointer.
4. **Move to the Next Level and Repeat.** | 8 | 0 | ['C++'] | 0 |
populating-next-right-pointers-in-each-node | just 4 lines | very easy for beginners | beats 100% | just-4-lines-very-easy-for-beginners-bea-3pjv | IntuitionIn a perfect binary tree:
All levels are completely filled.
Every parent node has exactly two children.
The goal is to populate the next pointers of ea | sharqawycs | NORMAL | 2025-01-26T15:14:23.689071+00:00 | 2025-01-26T15:14:23.689071+00:00 | 648 | false | # Intuition
In a perfect binary tree:
- All levels are completely filled.
- Every parent node has exactly two children.
The goal is to populate the `next` pointers of each node to point to its immediate right neighbor. If there is no right neighbor, the `next` pointer should point to `null`.
We can take advantage of the tree's perfect structure to recursively connect nodes.
# Approach
1. **Base Case**:
- If the root is `null`, we simply return `null`.
2. **Recursive Connection**:
- Connect the left child of the current node to its right child:
`root.left.next = root.right`
- If the right child has a valid neighbor (via the `next` pointer of the current node), connect it to the left child of that neighbor:
`root.right.next = root.next.left`
- Recursively perform the above steps for the left and right subtrees.
3. **Recursive Traversal**:
- Traverse the tree depth-first, connecting nodes level by level.
# Complexity
- **Time Complexity**:
$$O(n)$$
Each node is visited once, making the traversal linear in the number of nodes.
- **Space Complexity**:
$$O(h)$$
The recursion stack depends on the height of the tree, which is $$O(\log(n))$$ for a perfect binary tree.
# Java Code
```java
class Solution {
public Node connect(Node root) {
// Base case: If the tree is empty, return null
if (root == null) return null;
// Connect the left child to the right child
if (root.left != null) root.left.next = root.right;
// Connect the right child to the left child of the next node, if it exists
if (root.right != null && root.next != null) root.right.next = root.next.left;
// Recursively connect the left and right subtrees
connect(root.left);
connect(root.right);
// Return the root after connections are made
return root;
}
}
```

| 8 | 0 | ['Tree', 'Recursion', 'Binary Tree', 'Java'] | 3 |
populating-next-right-pointers-in-each-node | 🍀Easy BFS 🔥 | | Java 🔥| | Python 🔥| | C++ 🔥 | easy-bfs-java-python-c-by-niketh_1234-u73r | * Extra space but clean code\n---\njava []\nclass Solution {\n public Node connect(Node root) {\n if(root == null)\n return root;\n | niketh_1234 | NORMAL | 2023-06-27T13:00:32.084933+00:00 | 2023-06-27T13:00:32.084966+00:00 | 1,267 | false | # * Extra space but clean code\n---\n```java []\nclass Solution {\n public Node connect(Node root) {\n if(root == null)\n return root;\n Queue<Node> queue = new LinkedList<>();\n queue.add(root);\n while(queue.size() > 0)\n {\n Deque<Node> dq = new ArrayDeque<>();\n int length = queue.size();\n for(int i = 0;i<length;i++)\n {\n Node curr = queue.poll();\n dq.addLast(curr);\n if(curr.left!=null)\n queue.add(curr.left);\n if(curr.right!=null)\n queue.add(curr.right);\n }\n while(dq.size() > 1)\n {\n Node popped = dq.removeFirst();\n popped.next = dq.getFirst();\n }\n Node popped = dq.removeFirst();\n popped.next = null;\n }\n return root;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root == nullptr)\n return root;\n queue<Node*> queue;\n queue.push(root);\n while(queue.size() > 0)\n {\n deque<Node*> dq;\n int length = queue.size();\n for(int i = 0;i<length;i++)\n {\n Node* curr = queue.front();\n queue.pop();\n dq.push_back(curr);\n if(curr->left!=nullptr)\n queue.push(curr->left);\n if(curr->right!=nullptr)\n queue.push(curr->right);\n }\n while(dq.size() > 1)\n {\n Node* popped = dq.front();\n dq.pop_front();\n popped->next = dq.front();\n }\n Node* popped = dq.front();\n dq.pop_front();\n popped->next = nullptr;\n }\n return root;\n }\n};\n```\n```python []\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root:\n return root\n queue = []\n queue.append(root)\n while queue:\n dq = collections.deque()\n length = len(queue)\n for i in range(length):\n curr = queue.pop(0)\n dq.append(curr)\n if curr.left:\n queue.append(curr.left)\n if curr.right:\n queue.append(curr.right)\n while len(dq) > 1:\n popped = dq.popleft()\n popped.next = dq[0]\n popped = dq.popleft()\n popped.next = None\n return root\n```\n---\n>### *Please don\'t forget to upvote if you\'ve liked my solution.* \u2B06\uFE0F\n--- | 8 | 0 | ['Breadth-First Search', 'Python', 'C++', 'Java', 'Python3'] | 0 |
populating-next-right-pointers-in-each-node | ✅C++ || 2 Methods With Logic || BFS Traversal || CLEAN CODE | c-2-methods-with-logic-bfs-traversal-cle-l6mo | Method -1 [Naive Method]\n\n\n\nn==Number of Nodes \nT->O(n) && S->O(n) [For storing all the Nodes after BFS] + O(n/2) [For queue, worst Case as it\'s a Perfect | abhinav_0107 | NORMAL | 2023-01-03T07:38:58.560101+00:00 | 2023-01-03T14:27:29.513254+00:00 | 1,257 | false | ***Method -1 [Naive Method]***\n\n\n\n**n==Number of Nodes \nT->O(n) && S->O(n) [For storing all the Nodes after BFS] + O(n/2) [For queue, worst Case as it\'s a Perfect Binary Tree]**\n\n***Logic -> Level Order Traversal and connect adjacent Nodes!***\n\n\tclass Solution {\n\t\tpublic:\n\t\t\tNode* connect(Node* root) {\n\t\t\t\tif(!root) return NULL;\n\n\t\t\t\tvector<vector<Node*>> lvl;\n\t\t\t\tqueue <Node*> q;\n\t\t\t\tq.push(root);\n\n\t\t\t\twhile(!q.empty()){\n\t\t\t\t\tint size = q.size();\n\t\t\t\t\tvector <Node*> temp;\n\n\t\t\t\t\tfor(int i = 0 ; i < size ; i++){\n\t\t\t\t\t\tNode* node = q.front();\n\t\t\t\t\t\tq.pop();\n\t\t\t\t\t\tif(node -> left) q.push(node -> left);\n\t\t\t\t\t\tif(node -> right) q.push(node -> right);\n\t\t\t\t\t\ttemp.push_back(node);\n\t\t\t\t\t}\n\n\t\t\t\t\ttemp.push_back(NULL);\n\t\t\t\t\tlvl.push_back(temp);\n\t\t\t\t} \n\n\t\t\t\tfor(int i = 0 ; i < lvl.size() ; i++){\n\t\t\t\t\tfor(int j = 0 ; j < lvl[i].size() - 1 ; j++) lvl[i][j] -> next = lvl[i][j + 1];\n\t\t\t\t}\n\n\t\t\t\treturn root;\n\t\t\t}\n\t\t};\n\t\t\n**Method - 2 [Optimized]**\n\n\n\n**n==Number of Nodes\nT->O(n) && S->O(n) [Recursive Stack Space]**\n\n\tclass Solution {\n\tpublic:\n\t\tvoid dfs(Node* l,Node* r){\n\t\t\tif(!l && !r) return;\n\n\t\t\tl -> next = r;\n\t\t\tr -> next = NULL;\n\n\t\t\tdfs(l -> left , l -> right);\n\t\t\tdfs(l -> right , r -> left);\n\t\t\tdfs(r -> left , r -> right);\n\t\t}\n\n\t\tNode* connect(Node* root) {\n\t\t\tif(!root) return NULL;\n\t\t\tdfs(root -> left , root -> right);\n\t\t\treturn root;\n\t\t}\n\t}; | 8 | 0 | ['Breadth-First Search', 'C', 'C++'] | 1 |
populating-next-right-pointers-in-each-node | JAVA| 100% FAST | 0ms | EASY | RECURSION | NODE | java-100-fast-0ms-easy-recursion-node-by-ucay | If you find my solution helpful please upvote it, as it motivates me to post such kind of codes and help the coding community,\nif you have any queries or any i | Narendra_Madireddy | NORMAL | 2022-09-15T00:59:57.243888+00:00 | 2022-09-15T00:59:57.243930+00:00 | 499 | false | If you find my solution helpful please upvote it, as it motivates me to post such kind of codes and help the coding community,\nif you have any queries or any improvements please feel free to comment and share your views.\n\n class Solution {\n public Node connect(Node root) {\n if(root == null){\n return root;\n }\n if(root.left != null) root.left.next = root.right;\n if(root.right != null && root.next != null){\n root.right.next = root.next.left;\n }\n connect(root.left);\n connect (root.right);\n return root;\n }\n } | 8 | 0 | ['Recursion', 'Java'] | 0 |
populating-next-right-pointers-in-each-node | Python with simple recursion + explanation with drawing | python-with-simple-recursion-explanation-gyiq | I divide the code into four part, check out the hashtag. \n#part1: if root is None, we want to just return None.\n#part2: : if cur.left is not None, we want to | dingchiun | NORMAL | 2022-09-05T11:53:11.687600+00:00 | 2022-09-18T07:22:31.346886+00:00 | 462 | false | I divide the code into four part, check out the hashtag. \n`#part1`: if root is None, we want to just return None.\n`#part2:` : if cur.left is not None, we want to build a connection between cur.left and cur.right. See pic:\n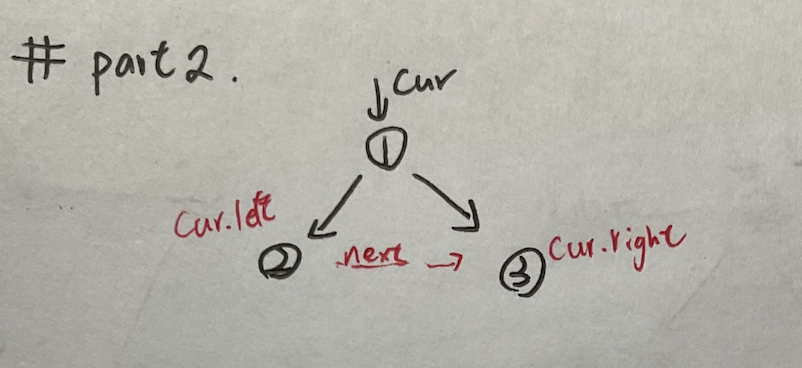\n`#part3`:we want to build connection between node 5 and 6(see pic), if cur.next and cur.left not None.\n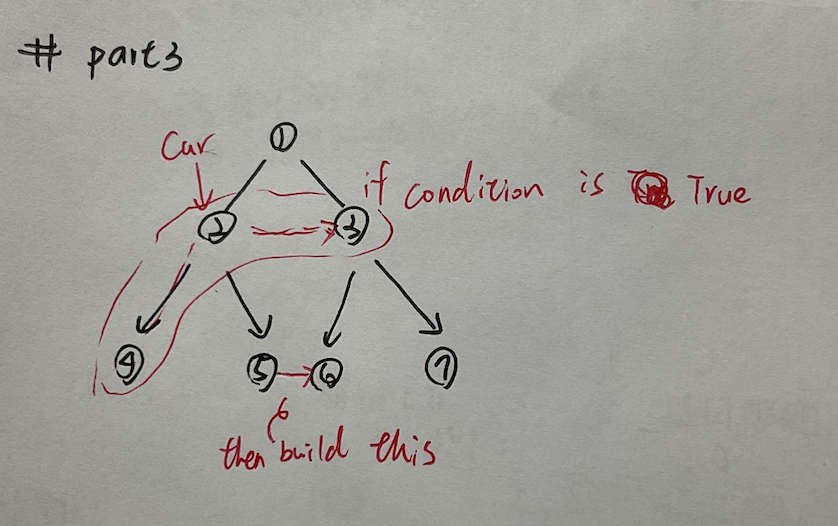\n`#part4` call left node and right node do the same thing\n\nIf this is helpful, don\'t forget give me a star and vote\n\n\n```\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if not root : return None #part1\n def recursion(cur):\n if cur.left: #part2\n cur.left.next = cur.right\n\n if cur.next and cur.left: #part3\n cur.right.next = cur.next.left\n\n recursion(cur.left) if cur.left else None #part4\n recursion(cur.right) if cur.right else None\n \n recursion(root)\n return root\n``` | 8 | 0 | ['Recursion', 'Python'] | 1 |
populating-next-right-pointers-in-each-node | C++ || Efficient || Recursive || Iterative using Queue || 2 solutions || | c-efficient-recursive-iterative-using-qu-xjj3 | If you understand the approach please please upvote!!!\uD83D\uDC4D\nThanks :)\n##### Recursive Approach :-\n Base case: if the root is null than return null\n N | Debajyoti-Shit | NORMAL | 2022-02-16T05:37:38.055150+00:00 | 2022-02-16T05:37:38.055179+00:00 | 519 | false | ##### If you understand the approach please please upvote!!!\uD83D\uDC4D\n***Thanks :)***\n##### Recursive Approach :-\n* Base case: if the root is null than return null\n* Now to connect the left subtree of same level with right subtree of that level\n* The only new line that differentiate from level order traversing is that we need to connect the rightmost node of a level to the leftmost node of the next level.\n* Now just repeat the steps over and over for every level of tree .*\n##### Recursive Code:-\n```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root == NULL) return NULL;\n //connects the left subtree of same level with right subtree of that same level \n if(root->left != NULL) root->left->next = root->right;\n //connect the rightmost node of a level to the leftmost node of the next level.\n if(root->right != NULL && root->next != NULL) root->right->next = root->next->left;\n //recursive calls for left and right subtrees.\n connect(root->left);\n connect(root->right);\n return root;\n }\n};\n```\n\n##### Iterative Approach using Queue(like level-order-traversal):-\n```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root == NULL) return NULL;\n queue<Node*> q;\n q.push(root);\n while(!q.empty()){\n int size = q.size(); // get size of queue \n for(int i=0 ; i < size ; i++){\n Node* item = q.front(); \n if(size - 1 == i) // checking the last value of the level\n item -> next = NULL; \n q.pop();\n \n if(size - 1 != i) // if this is not the last value then previous value will point to next one\n item -> next = q.front(); \n \n if(item -> left != NULL)\n q.push(item -> left);\n if(item -> right != NULL)\n q.push(item -> right);\n }\n } \n return root;\n }\n};\n```\n | 8 | 0 | ['Breadth-First Search', 'Recursion', 'Queue', 'C', 'C++'] | 0 |
populating-next-right-pointers-in-each-node | [JAVA] O(1) Memory Solution (Recursive + Iterative) - Faster than 100% | java-o1-memory-solution-recursive-iterat-myph | 1. Recurisve\n\nclass Solution {\n public Node connect(Node root) {\n if(root == null)\n return root;\n if(root.left != null){\n | Dyanjno123 | NORMAL | 2021-12-29T02:31:31.945808+00:00 | 2022-03-08T02:54:31.309640+00:00 | 769 | false | **1. Recurisve**\n```\nclass Solution {\n public Node connect(Node root) {\n if(root == null)\n return root;\n if(root.left != null){\n if(root.next != null)\n root.right.next = root.next.left;\n else\n root.right.next = null;\n root.left.next = root.right;\n connect(root.left);\n connect(root.right);\n }\n return root;\n }\n}\n```\n\n**2. Iterative**\n```\nclass Solution {\n public Node connect(Node root) {\n Node leftest = root;\n while(leftest != null && leftest.left != null) {\n \tNode curr = leftest;\n \twhile(true) {\n \t\tcurr.left.next = curr.right;\n \t\tif(curr.next != null)\n \t\t\tcurr.right.next = curr.getNextSibling().left;\n \t\telse\n \t\t\tbreak;\n \t}\n \tcurr = curr.left;\n }\n return root;\n }\n}\n``` | 8 | 2 | ['Java'] | 1 |
populating-next-right-pointers-in-each-node | C++ || O(n) time || O(1) space || No recursion space || 0ms || faster than 100% | c-on-time-o1-space-no-recursion-space-0m-a2yr | The idea is to fix the next pointer for child nodes while traversing through parent node. \nOnce you fixed the next pointer then you can traverse this level in | ajaybedre_07 | NORMAL | 2021-09-16T05:58:58.335848+00:00 | 2021-09-18T18:13:31.974822+00:00 | 150 | false | The idea is to fix the next pointer for child nodes while traversing through parent node. \nOnce you fixed the next pointer then you can traverse this level in O(1) space.\n```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root)return root;\n Node* curr=root;\n while(curr->left){\n Node* currLeft=curr->left;\n while(curr){\n curr->left->next=curr->right;\n curr->right->next=curr->next?curr->next->left:NULL;\n curr=curr->next;\n }\n curr=currLeft;\n }\n return root;\n }\n};\n```\nFeel free to ask doubt in comments and please don\'t forget to upvote if you like the solution. | 8 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | python recursion constant space beats 98% short solution | python-recursion-constant-space-beats-98-6h16 | \nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root or not root.left:\n return root\n \n root.le | marriema | NORMAL | 2021-03-18T03:22:30.058767+00:00 | 2021-03-18T03:23:03.443610+00:00 | 451 | false | ```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root or not root.left:\n return root\n \n root.left.next = root.right\n \n if root.next:\n root.right.next = root.next.left\n \n self.connect(root.left)\n self.connect(root.right)\n return root\n``` | 8 | 0 | ['Python', 'Python3'] | 3 |
populating-next-right-pointers-in-each-node | 2 different simple recursion O(n) time beats 100% | 2-different-simple-recursion-on-time-bea-ezu5 | The first solution\'s idea is only on about the fact that root.right.next = root.next.left\n\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\' | truongsinh | NORMAL | 2020-03-31T03:17:45.329682+00:00 | 2020-03-31T03:17:45.329733+00:00 | 518 | false | The first solution\'s idea is only on about the fact that `root.right.next = root.next.left`\n```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root or not root.left:\n return root\n root.left.next = root.right\n if root.next:\n root.right.next = root.next.left\n self.connect(root.left)\n self.connect(root.right)\n return root\n```\n\nThe 2nd solution is as simple as stiching nodes recursively, 3 pairs at a time\n```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root or not root.left:\n return root\n def stich(left, right):\n if not left:\n return\n if left.next:\n # optimize, save huge time\n return\n left.next = right\n stich(left.left, left.right)\n stich(left.right, right.left)\n stich(right.left, right.right)\n stich(root.left, root.right)\n return root\n``` | 8 | 0 | ['Recursion', 'Python'] | 0 |
populating-next-right-pointers-in-each-node | 9-line fast c++ without recursion | 9-line-fast-c-without-recursion-by-mitbb-t2n2 | class Solution {\n public:\n void connect(TreeLinkNode *root) {\n while (root) {\n TreeLinkNode *a = root;\n | mitbbs8080 | NORMAL | 2015-11-03T14:02:36+00:00 | 2015-11-03T14:02:36+00:00 | 548 | false | class Solution {\n public:\n void connect(TreeLinkNode *root) {\n while (root) {\n TreeLinkNode *a = root;\n while (a) {\n if (a->left) {\n a->left->next = a->right;\n if (a->next)\n a->right->next = a->next->left;\n }\n a=a->next;\n }\n root=root->left;\n }\n }\n }; | 8 | 2 | [] | 0 |
populating-next-right-pointers-in-each-node | A simple 0 ms recursive solution without helper function | a-simple-0-ms-recursive-solution-without-lhjx | public void connect(TreeLinkNode root) {\n if (root == null){\n return;\n }\n \n if (root.left != null){\n roo | freelikewind | NORMAL | 2015-12-04T02:11:59+00:00 | 2015-12-04T02:11:59+00:00 | 1,329 | false | public void connect(TreeLinkNode root) {\n if (root == null){\n return;\n }\n \n if (root.left != null){\n root.left.next = root.right;\n if (root.next != null){\n root.right.next = root.next.left;\n }\n }\n \n connect(root.left);\n connect(root.right);\n } | 8 | 1 | ['Java'] | 1 |
populating-next-right-pointers-in-each-node | BFS solution || Explanation || Complexities | bfs-solution-explanation-complexities-by-l3nn | Intuition\nThe goal of this problem is to connect each node at the same level in a perfect binary tree to its immediate neighbor on the right. By establishing t | Anurag_Basuri | NORMAL | 2024-11-02T06:25:26.865113+00:00 | 2024-11-04T13:53:02.457203+00:00 | 1,124 | false | ### Intuition\nThe goal of this problem is to connect each node at the same level in a perfect binary tree to its immediate neighbor on the right. By establishing these connections, each node\u2019s `next` pointer will point to the adjacent node on the same level, or to `None` if it\u2019s the last node in that level. A perfect binary tree allows us to do this efficiently by taking advantage of the tree\'s structure.\n\n### Approach\n1. **Iterate Level by Level**:\n - Start with the root of the tree. Use the `leftmost` pointer to keep track of the leftmost node at each level.\n - For each level, iterate through nodes using their `next` pointers (which have been set in the previous level) to avoid extra space.\n\n2. **Connect Nodes at Each Level**:\n - For each node `current` at a level, connect its `left` child to its `right` child.\n - If `current` has a `next` node, connect `current.right.next` to `current.next.left`. This connects nodes across subtrees.\n\n3. **Move to the Next Level**:\n - After finishing connections for the current level, move `leftmost` down to `leftmost.left` (i.e., the start of the next level).\n\nThis method only uses pointers, without extra data structures like queues or lists, meeting the constant extra space requirement (apart from the implicit stack space if done recursively).\n\n### Complexity\n- **Time Complexity**: \\(O(n)\\), where \\(n\\) is the total number of nodes in the tree. Each node is visited once, and setting the `next` pointers takes constant time for each node.\n- **Space Complexity**: \\(O(1)\\) extra space, since we only use pointers to traverse the tree level by level. Implicit stack space is ignored as per the problem\'s constraints.\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root == NULL) return NULL;\n\n Node* leftmost = root;\n\n while(leftmost->left){\n Node* cur = leftmost;\n\n while(cur){\n cur->left->next = cur->right;\n\n if(cur->next){\n cur->right->next = cur->next->left;\n }\n\n cur = cur->next;\n }\n\n leftmost = leftmost->left;\n }\n\n return root;\n }\n};\n```\n``` python []\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if root is None:\n return None\n\n leftmost = root\n\n while leftmost.left:\n cur = leftmost\n\n while cur:\n cur.left.next = cur.right\n\n if cur.next:\n cur.right.next = cur.next.left\n\n cur = cur.next\n\n leftmost = leftmost.left\n\n return root\n\n``` | 7 | 0 | ['Linked List', 'Tree', 'Breadth-First Search', 'Binary Tree', 'C++', 'Python3'] | 2 |
populating-next-right-pointers-in-each-node | Python 4 Diffrent Solutions | BFS | DFS | python-4-diffrent-solutions-bfs-dfs-by-p-26hp | 1. Iterative BFS | Space:O(n)\n\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if( root == None ):\n return root;\n | paramkumar1 | NORMAL | 2023-03-15T05:48:40.114398+00:00 | 2023-03-15T06:56:10.260409+00:00 | 1,865 | false | # 1. Iterative BFS | Space:O(n)\n```\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if( root == None ):\n return root;\n q = deque();\n q.append(root);\n while( len(q) > 0 ):\n prev = None ;\n size = len(q);\n while(size > 0 ):\n node = q.popleft();\n node.next = prev;\n prev = node;\n if(node.right):q.append(node.right);\n if(node.left):q.append(node.left);\n size -= 1;\n return root;\n```\n\n# 2.Recursive DFS | Space: O(n)\n\n```\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n hmap = defaultdict(list);\n\n def dfs(node,h):\n if( node == None ):\n return;\n else:\n hmap[h].append(node);\n dfs(node.left,h+1);\n dfs(node.right,h+1);\n \n dfs(root,0);\n for key in hmap.keys():\n for i in range(0, len(hmap[key])-1 ):\n hmap[key][i].next = hmap[key][i+1]\n hmap[key][-1].next = None\n return root\n```\n\n# 3.Recusive DFS | Space:O(logn)\n\n```\ndef connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if( root == None ):\n return;\n root.next = None;\n def dfs(node):\n if( node == None or node.left == None ):\n return;\n node.left.next = node.right;\n if(node.next):\n node.right.next =node.next.left;\n dfs(node.left);\n dfs(node.right); \n\n dfs(root);\n return root;\n\n```\n\n# 4. Iterative Optimized BFS or Level order traversal | O(1)\n```\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n prev = root;\n cur = root;\n while(prev):\n cur = prev;\n while( cur ):\n if(cur.left):\n cur.left.next = cur.right;\n if(cur.next):\n cur.right.next = cur.next.left;\n cur = cur.next;\n prev = prev.left;\n\n return root;\n``` | 7 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Python3'] | 2 |
populating-next-right-pointers-in-each-node | Java | Beauty and Easy solution! | Explained & Visualized | O(n) algo, O(1) memo | | java-beauty-and-easy-solution-explained-6xlwh | The task boils down to understanding the structure of the tree and how to traverse it.\nThe solution is that we create a method that contains the right and left | MykolaMurza | NORMAL | 2022-10-28T17:58:33.720257+00:00 | 2022-10-28T18:02:59.348175+00:00 | 507 | false | The task boils down to understanding the structure of the tree and how to traverse it.\nThe solution is that we create a method that **contains the right and left nodes of the same level**.\n1. We connect the left node with the right one using the `next` field.\n2. The **next** left node of the current left one is combined with the **next** right one.\n3. The **next** left node of the current right node is combined with the **next** right node.\n4. And we also take **the next right node of the left one** and combine it with **the left node of the right one**. This is the most difficult step and is the key to solving the problem.\n\n**See the image below!** It turns out that we first connected two nodes and then connected their next level. Moreover, first they combined the "children" of the left, then the "children" of the right, and then they were united.\n\n```java\nclass Solution {\n public static Node connect(Node root) {\n if (root == null || (root.left == null && root.right == null)) return root;\n\n connectNext(root.left, root.right);\n\n return root;\n }\n\n private static void connectNext(Node left, Node right) {\n if (left == null || right == null) return;\n left.next = right; // Step 1 - comments only for the image below!\n\t\t\n connectNext(left.left, left.right); // Step 2\n connectNext(left.right, right.left); // Step 3\n connectNext(right.left, right.right); // Step 4\n }\n}\n```\n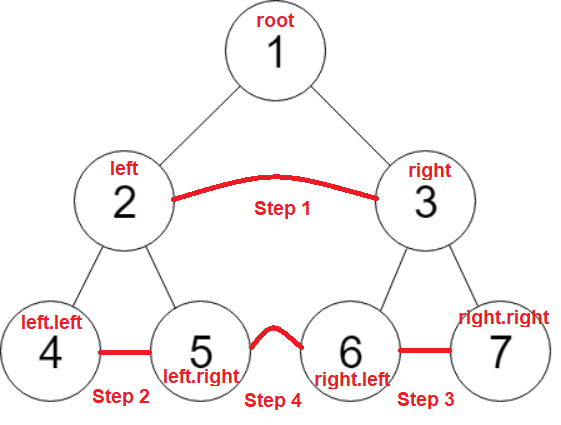\n\n | 7 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Recursion', 'Java'] | 1 |
populating-next-right-pointers-in-each-node | Simple Preorder Traversal | simple-preorder-traversal-by-deepak08-z6du | ```class Solution {\n private void helper(Node root)\n {\n if(root == null)\n return;\n //since it is a leaf node it wont have an | deepak08 | NORMAL | 2021-07-24T19:11:54.641206+00:00 | 2021-07-24T19:11:54.641250+00:00 | 226 | false | ```class Solution {\n private void helper(Node root)\n {\n if(root == null)\n return;\n //since it is a leaf node it wont have any child \n if(root.left == null && root.right == null)\n return;\n //stand on parent and connect left child to right child\n root.left.next = root.right;\n \n //after connecting left child to right , connect parent\'s right child via the next link we created above to left child of adjacent subtree.\n if(root.next != null)\n root.right.next = root.next.left;\n \n helper(root.left);\n helper(root.right);\n }\n public Node connect(Node root) {\n helper(root);\n return root;\n }\n} | 7 | 0 | ['Java'] | 0 |
populating-next-right-pointers-in-each-node | C Easy Iterative Solution | c-easy-iterative-solution-by-yehudisk-9mo6 | \nstruct Node* connect(struct Node* root) {\n\tif (!root)\n return root;\n \n struct Node* ptr_node = root;\n struct Node* first = ptr_node;\n | yehudisk | NORMAL | 2020-11-13T09:42:31.001653+00:00 | 2020-11-13T09:45:18.671719+00:00 | 414 | false | ```\nstruct Node* connect(struct Node* root) {\n\tif (!root)\n return root;\n \n struct Node* ptr_node = root;\n struct Node* first = ptr_node;\n \n while (ptr_node->left) {\n \n while (ptr_node) {\n \n ptr_node->left->next = ptr_node->right;\n \n if (ptr_node->next) {\n ptr_node->right->next = ptr_node->next->left;\n }\n \n ptr_node = ptr_node->next;\n }\n \n first = first->left;\n ptr_node = first;\n }\n \n return root;\n}\n```\n**Like it? please upvote...** | 7 | 0 | ['C', 'Iterator'] | 0 |
populating-next-right-pointers-in-each-node | Java recursive solution 100% - O(N) time / O(1) space / O(N) stack call | java-recursive-solution-100-on-time-o1-s-4rbg | Feel free to discuss Big-O analysis :)\njava\nclass Solution {\n public Node connect(Node root) {\n if (root == null) return null;\n if (root.l | monmonpig | NORMAL | 2020-02-14T10:26:50.991781+00:00 | 2020-02-14T10:27:55.787893+00:00 | 311 | false | Feel free to discuss Big-O analysis :)\n```java\nclass Solution {\n public Node connect(Node root) {\n if (root == null) return null;\n if (root.left != null) root.left.next = root.right;\n if (root.right != null) root.right.next = root.next == null ? null : root.next.left;\n connect(root.left);\n connect(root.right);\n return root;\n }\n}\n``` | 7 | 0 | ['Recursion', 'Java'] | 1 |
populating-next-right-pointers-in-each-node | Python recursive solution | python-recursive-solution-by-he-haitao-h6ii | \u5728\u8FD9\u4E2Arecursion chapter\u5B66\u4E60\u81EA\u5DF1\u609F\u51FA\u6765\u7684\u4E00\u4E2A\u65B9\u6CD5\u3002\n\u4ECEexample\u53EF\u4EE5\u53D1\u73B0\u7ED9\u | he-haitao | NORMAL | 2019-05-13T06:25:00.288923+00:00 | 2019-05-13T07:25:49.548166+00:00 | 715 | false | \u5728\u8FD9\u4E2Arecursion chapter\u5B66\u4E60\u81EA\u5DF1\u609F\u51FA\u6765\u7684\u4E00\u4E2A\u65B9\u6CD5\u3002\n\u4ECEexample\u53EF\u4EE5\u53D1\u73B0\u7ED9\u7684\u89C4\u5F8B\u5C31\u662F\n\u6BCF\u4E2A\u8282\u70B9\uFF08\u975E\u53F6\u5B50\u7ED3\u70B9\uFF09\u5FC5\u6709\u4E24\u4E2A\u5B50\u8282\u70B9\n\u5BF9\u6BCF\u4E00level\u7684\u8282\u70B9\u90FD\u8FDB\u884C\u5982\u4E0B\u64CD\u4F5C\nleft.next = right\nright.next = None\n\u4F46\u662F\u8FD9\u91CC\u53EA\u662F\u8FDE\u63A5\u4E86\u4E24\u4E2A\u8282\u70B9\uFF0C\u4E00\u5C42level\u91CC\u9762\u8282\u70B9\u4E0D\u6B62\u8FD9\u4E48\u591A\uFF0C\u8FD8\u6709\u4E2D\u95F4\u7684\uFF0C\u5C31\u662F\u5DE6\u5B50\u6811\u548C\u53F3\u5B50\u6811\u7684\u4E4B\u95F4\u7684\u5DE6\u5B50\u6811\u7684\u53F3\u8282\u70B9\uFF0C\u548C\u53F3\u5B50\u6811\u7684\u5DE6\u8282\u70B9\u8981\u8FDE\u63A5\u8D77\u6765\uFF0C\u6240\u4EE5\u9012\u5F52\u5199\u4E86\u4E2D\u95F4\u7684\nconnect(left.right,right,left)\n\u867D\u7136\u6700\u540E\u5B9E\u73B0\u4E86\u7A0B\u5E8F\uFF0C\u4F46\u662F\u6539\u8FDB\u7684\u5730\u65B9\u8FD8\u662F\u6709\u5E8F\u591A\n\u5C31\u6BD4\u5982\uFF0C\u8FD9\u4E2Aright.next = None\uFF0C\u8FD9\u91CC\u64CD\u4F5C\u4E86\u591A\u6B21\uFF0C\u5982\u679C\u53EF\u4EE5\u53EA\u8981\u8FDE\u63A5\u4E00\u6B21\u5C31\u8FDE\u4E0A\u7684\u8BDD\u662F\u6700\u597D\u7684\u4E86\u3002\n```\nclass Solution(object):\n def connect(self, root):\n """\n :type root: Node\n :rtype: Node\n """\n if not root:\n return None\n root.next = None\n def connect(left,right):\n if left and right:\n left.next = right\n right.next = None\n connect(left.left,left.right)\n connect(left.right,right.left)\n connect(right.left,right.right)\n connect(root.left,root.right)\n return root\n```\n\u5F88\u660E\u663E\u8FD9\u4E2A\u4E5F\u53EF\u4EE5\u7528BFS\u6765\u505A\uFF0C\u540C\u6837\uFF0C\u4E5F\u662F\u4E4B\u524D\u4ECE\u8BC4\u8BBA\u91CC\u9762\u5B66\u5230\u7684queue\u5B9E\u73B0\u7684BFS\u6765\u89E3\u51B3\u8FD9\u91CC\u7684\u95EE\u9898\n```\nfrom collections import deque\n\nclass Solution(object):\n def connect(self, root):\n """\n :type root: Node\n :rtype: Node\n """\n if not root:\n return None\n root.next = None\n queue = deque([root])\n while queue:\n temp,size=[],len(queue)\n for i in range(size):\n node = queue.popleft()\n if node:\n temp.append(node)\n if node.left and node.right:\n queue.append(node.left)\n queue.append(node.right)\n for index,node in enumerate(temp[:-1]):\n node.next = temp[index+1]\n temp[-1].next = None\n return root\n```\n\u4ECE\u8BC4\u8BBA\u91CC\u9762\u5B66\u5230\u7684\u4E00\u4E2A\u65B9\u6CD5\uFF0C\u786E\u5B9E\uFF0CBFS\u53EF\u4EE5\u4F7F\u7528\uFF0C\u4F46\u662F\u6211\u4EEC\u6CA1\u6709\u5FC5\u8981\u7528\u4E00\u4E2Aqueue\u6765\u5B58\u50A8node\uFF0C\n\u56E0\u4E3Anode\u6709next\u8282\u70B9\uFF0C\u5F53\u6211\u4EEC\u6709\u4E00\u4E2A\u5934\u7ED3\u70B9\u4E4B\u540E\uFF0C\u5C31\u53EF\u4EE5\u50CF\u94FE\u8868\u4E00\u6837\u53BB\u8BBF\u95EE\u4E86\u3002\nreference\uFF1A\nhttps://leetcode.com/problems/populating-next-right-pointers-in-each-node/discuss/37465/Python-Solution-With-Explaintion\n```\nclass Solution(object):\n def connect(self, root):\n """\n :type root: Node\n :rtype: Node\n """\n if not root:\n return None\n cur = root\n nex = cur.left\n while cur.left:\n cur.left.next = cur.right\n if cur.next:\n cur.right.next = cur.next.left\n cur = cur.next\n else:\n cur = nex\n nex = cur.left\n return root\n``` | 7 | 0 | [] | 1 |
populating-next-right-pointers-in-each-node | C# while | c-while-by-bacon-f68w | \npublic class Solution {\n public Node Connect(Node root) {\n var preMostLeft = root;\n while (preMostLeft != null) {\n var cur = p | bacon | NORMAL | 2019-05-05T00:36:19.258288+00:00 | 2019-05-05T00:36:19.258369+00:00 | 584 | false | ```\npublic class Solution {\n public Node Connect(Node root) {\n var preMostLeft = root;\n while (preMostLeft != null) {\n var cur = preMostLeft;\n while (cur != null && cur.left != null) {\n cur.left.next = cur.right;\n if (cur.next != null) {\n cur.right.next = cur.next.left;\n }\n cur = cur.next;\n }\n\n preMostLeft = preMostLeft.left;\n }\n\n return root;\n }\n}\n``` | 7 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | Java/c++/c solutions. Elegant iterative solutions (4 lines) and recursive solutions (5 lines) | javacc-solutions-elegant-iterative-solut-v3gg | C++\n## Recursive\nSetting the next pointer from the parent node makes for a clean solution. The only thing to worry about is how to handle the far right node o | christrompf | NORMAL | 2018-08-25T09:03:33.073515+00:00 | 2022-05-13T05:01:10.025914+00:00 | 457 | false | # **C++**\n## Recursive\nSetting the _next_ pointer from the parent node makes for a clean solution. The only thing to worry about is how to handle the far right node of each level, which doesn\'t have a _next_. This is easy to check for too, just check if the parent node has a _next_ pointer, if it doesn\'t, then you\'re at the far right.\n```cpp\n void connect(TreeLinkNode *root) {\n if (root && root->left) {\n root->left->next = root->right;\n root->right->next = (root->next) ? root->next->left : nullptr;\n connect(root->left);\n connect(root->right);\n }\n }\n```\t\n## Iterative\nSet the _next_ pointer starting from the left of each level, then you can use the _next_ pointer to progress from left to right to complete the level. Once a level is finshed, advance down the left branch and do it again.\n```cpp\n void connect(TreeLinkNode *root) {\n for (; root && root->left; root = root->left) {\n for (TreeLinkNode* pos = root; pos; pos = pos->next) {\n pos->left->next = pos->right;\n pos->right->next = (pos->next) ? pos->next->left : nullptr;\n }\n }\n }\n```\t\n# **Java**\n## Recursive\n```java\n public void connect(TreeLinkNode root) {\n if (null != root && null != root.left) {\n root.left.next = root.right;\n root.right.next = (null != root.next) ? root.next.left : null;\n connect(root.left);\n connect(root.right);\n }\n }\n```\n## Iterative\n```java\n public void connect(TreeLinkNode root) {\n for (; null != root && null != root.left; root = root.left) {\n for (TreeLinkNode pos = root; null != pos; pos = pos.next) {\n pos.left.next = pos.right;\n pos.right.next = (null != pos.next) ? pos.next.left : null;\n }\n }\n }\n```\n# **C**\nSince a c solution would look very much like the c++ solution, I did it slightly differently, but is essentially the same.\n```c\nstruct Node* connect(struct Node* root) {\n if (root) {\n for (struct Node* row_start = root; row_start->left; row_start = row_start->left) {\n struct Node* pos = row_start;\n for (; pos->next; pos = pos->next) {\n pos->left->next = pos->right;\n pos->right->next = pos->next->left;\n }\n pos->left->next = pos->right;\n }\n }\n return root;\n}\n```\n\n**Note that all solutions abuse the fact that the tree is by definition a perfect binary tree. [Solutions that don\'t require perfect tree can be found here](https://leetcode.com/problems/populating-next-right-pointers-in-each-node-ii/discuss/163809/C++-iterative-O(1)-space.-Short-and-easy-to-understand-with-detail.-Bonus-2-line-solution-for-fun)**\n | 7 | 0 | ['C', 'Java'] | 1 |
populating-next-right-pointers-in-each-node | My recursive solution | my-recursive-solution-by-jwang8-8ij2 | void connect(TreeLinkNode *root) {\n if( root == NULL || root->left == NULL && root->right == NULL ) //{} \\ {0}\n {\n return;\n | jwang8 | NORMAL | 2014-07-14T17:30:25+00:00 | 2014-07-14T17:30:25+00:00 | 2,190 | false | void connect(TreeLinkNode *root) {\n if( root == NULL || root->left == NULL && root->right == NULL ) //{} \\ {0}\n {\n return;\n }\n \n TreeLinkNode *p, *q;\n p = root->left;\n q = root->right;\n p->next = q;\n while( p->right != NULL )\n {\n p = p->right;\n q = q->left;\n p->next = q;\n }\n \n connect( root->left );\n connect( root->right );\n } | 7 | 0 | [] | 6 |
populating-next-right-pointers-in-each-node | Simple Iterative solution | simple-iterative-solution-by-1337beef-xnc4 | Populate the levels one by one. curLevel points to node whose children will be linked, nextLevel points to the first node in the next level.\n\n class Soluti | 1337beef | NORMAL | 2014-09-22T15:46:19+00:00 | 2014-09-22T15:46:19+00:00 | 1,154 | false | Populate the levels one by one. curLevel points to node whose children will be linked, nextLevel points to the first node in the next level.\n\n class Solution {\n public:\n void connect(TreeLinkNode *root) {\n if(!root)return;\n TreeLinkNode*curLevel=root,*nextLevel=root->left;\n root->next=NULL;\n while(curLevel->left){\n curLevel->left->next=curLevel->right;\n if (curLevel->next){\n curLevel->right->next = curLevel->next->left;\n curLevel=curLevel->next;\n }\n else {\n curLevel->right->next=NULL;\n curLevel=nextLevel;\n nextLevel=nextLevel->left;\n }\n }\n }\n }; | 7 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | Sharing my Java O(1) extra space code | sharing-my-java-o1-extra-space-code-by-w-yrv6 | public void connect(TreeLinkNode root) {\n TreeLinkNode cur;\n TreeLinkNode nextLevel = root;\n while (nextLevel != null) {\n cu | wzhang84 | NORMAL | 2015-04-05T14:22:09+00:00 | 2015-04-05T14:22:09+00:00 | 952 | false | public void connect(TreeLinkNode root) {\n TreeLinkNode cur;\n TreeLinkNode nextLevel = root;\n while (nextLevel != null) {\n cur = nextLevel;\n // at each level, connects the children nodes\n while (cur != null && \n cur.left != null // checking for leaf nodes\n ) \n {\n cur.left.next = cur.right;\n if (cur.next != null) {\n cur.right.next = cur.next.left;\n }\n cur = cur.next; \n }\n \n nextLevel = nextLevel.left;\n \n }\n } | 7 | 0 | ['Java'] | 0 |
populating-next-right-pointers-in-each-node | Another accepted Java solution | another-accepted-java-solution-by-jeanti-ub16 | Basically, we use the next pointer to help level traversal. No recursion is needed, O(1) constant space, O(n) running time.\n\n public class Solution {\n | jeantimex | NORMAL | 2015-07-04T00:50:28+00:00 | 2015-07-04T00:50:28+00:00 | 644 | false | Basically, we use the next pointer to help level traversal. No recursion is needed, O(1) constant space, O(n) running time.\n\n public class Solution {\n public void connect(TreeLinkNode root) {\n if (root == null) return;\n \n while (root.left != null) {\n TreeLinkNode curr = root;\n \n while (curr != null) {\n curr.left.next = curr.right;\n curr.right.next = curr.next != null ? curr.next.left : null;\n curr = curr.next;\n }\n \n root = root.left;\n }\n }\n } | 7 | 0 | ['Java'] | 0 |
populating-next-right-pointers-in-each-node | Beats 96.94% with step by step explanation, | beats-9694-with-step-by-step-explanation-ar7v | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nThis solution uses a level-order traversal of the binary tree and a queue | Marlen09 | NORMAL | 2023-02-17T04:20:09.620749+00:00 | 2023-02-17T04:20:09.620790+00:00 | 1,486 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution uses a level-order traversal of the binary tree and a queue to keep track of the nodes. For each level, it sets the next pointers of the nodes to the next node in the queue, except for the last node in the level. It then adds the node\'s children to the queue if they exist, and continues with the next level. The function returns the root node of the binary tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def connect(self, root: \'Node\') -> \'Node\':\n if not root:\n return root\n \n # Start with the root node\n queue = [root]\n \n while queue:\n # Get the number of nodes in the current level\n size = len(queue)\n \n # Traverse through the nodes in the current level\n for i in range(size):\n # Get the first node from the queue\n node = queue.pop(0)\n \n # If it\'s not the last node in the level, set its next to the next node in the queue\n if i < size - 1:\n node.next = queue[0]\n \n # Add the node\'s children to the queue if they exist\n if node.left:\n queue.append(node.left)\n if node.right:\n queue.append(node.right)\n \n # Return the root node\n return root\n\n``` | 6 | 0 | ['Tree', 'Depth-First Search', 'Breadth-First Search', 'Python', 'Python3'] | 3 |
populating-next-right-pointers-in-each-node | ✅ [Python, C++,Java]|| Beginner level Solution||100%Faster||Simple-Short-Solution✅ | python-cjava-beginner-level-solution100f-k4su | Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome.\n___\n__\nQ | Anos | NORMAL | 2022-08-14T10:36:01.465570+00:00 | 2022-08-14T10:36:01.465604+00:00 | 442 | false | ***Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome*.**\n___________________\n_________________\n***Q116. Populating Next Right Pointers in Each Node***\n\nYou are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:\n```\nstruct Node {\n int val;\n Node *left;\n Node *right;\n Node *next;\n}\n```\nPopulate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.\nInitially, all next pointers are set to NULL.\n____________________________________________________________________________________________________________________\n\n***Time complexity*** - O(n)\n***Space complexity*** - O(1)\n____________________________________________________________________________________________________________________\n____________________________________________________________________________________________________________________\n\u2705 **Java Code** :\n**Runtime**: 0 ms, faster than 100.00% of Java online submissions for Populating Next Right Pointers in Each Node.\n```\nclass Solution {\n public Node connect(Node root) {\n if(root == null) return root;\n Node current = root;\n while(current != null) {\n Node level1stNode = current;\n while(current != null) \n {\n if(current.left != null) \n current.left.next = current.right;\n if(current.right != null && current.next != null) \n current.right.next = current.next.left;\n\n current = current.next;\n }\n current = level1stNode.left;\n }\n return root;\n }\n}\n```\n**Runtime:** 0ms\n**Memory Usage:** 42.2 MB\n\n____________________________________________________________________________________________________________________\n____________________________________________________________________________________________________________________\n\u2705 **Python Code** :\n\n```\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if not root: return root \n self.current = root\n while self.current:\n self.level1stNode = self.current\n while self.current:\n if self.current.left:\n self.current.left.next = self.current.right\n \n if self.current.right and self.current.next:\n self.current.right.next = self.current.next.left\n \n self.current = self.current.next\n self.current = self.level1stNode.left\n return root\n```\n**Runtime:** 131ms\n**Memory Usage:** 13.8 MB\n\n____________________________________________________________________________________________________________________\n____________________________________________________________________________________________________________________\n\u2705 **C++ Code** :\n\n```\n\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root) return root;\n Node* current = root;\n while(current) {\n Node* level1stNode = current;\n while(current) \n {\n if(current->left)\n current->left->next = current->right;\n if(current->right && current->next)\n current->right->next = current->next->left;\n\n current = current->next;\n }\n current = level1stNode->left;\n }\n return root;\n }\n};\n```\n**Runtime:** 41ms\n**Memory Usage:** 69.7MB\n____________________________________________________________________________________________________________________\n____________________________________________________________________________________________________________________\nIf you like the solution, please upvote \uD83D\uDD3C\nFor any questions, or discussions, comment below. \uD83D\uDC47\uFE0F | 6 | 0 | ['Breadth-First Search', 'C', 'Python', 'Java'] | 0 |
populating-next-right-pointers-in-each-node | C++ || 5 lines code || Very Easy || DFS || Simple || Explanation | c-5-lines-code-very-easy-dfs-simple-expl-z3rc | This solution implements a recursive function - it takes a node, connects the NEXT pointers of it\'s left & right children, and repeats the process for the chil | manoharbanda_ | NORMAL | 2022-03-01T06:56:39.833677+00:00 | 2022-03-01T07:02:29.692019+00:00 | 258 | false | This solution implements a recursive function - it takes a node, connects the NEXT pointers of it\'s left & right children, and repeats the process for the children. So the algorithm is :\nFor each non-leaf node, we do -\n(1) NEXT of Left child is pointed to Right child. Easy.\n(2) NEXT of Right child is pointed to NEXT node in the same level (i.e., parent\'s NEXT\'s left child).\n\nLet\'s consider the below example. Assume we are at the node "2".\n```\n\t\t\t\t 1\nwe are here\t=> 2 -> 3\n\t\t\t 3 4 5 6\n```\n\nSince we\'re at 2, we would already have our NEXT pointer pointing to the node 3 (should have been done at node 1).\nNow, we need to correctly set NEXT pointers of our children, i.e, 3 and 4. We follow the said algorithm here.\nStep 1 : 3\'s NEXT pointer should simply be set to 4.\nStep 2 : We know 4\'s NEXT pointer should now be set to 5. How do we do that? Remember we have 2\'s NEXT set to 3 already? We\'re going to use that to get reference of 3, and then reference of 5 - then we just use it! 4\'s NEXT is set to 2\'s NEXT\'s left, which is 5.\n\nSo the tree now becomes -\n\n```\n\t\t\t\t 1\nwe are here\t=> 2 -> 3\n\t\t\t 3 -> 4 -> 5 6\n```\n\nWe repeat this process until all NEXT nodes are set. \n\nIn case of last node of a level (for ex: 6), we don\'t have NEXT of our parent (3) anyway, so it\'s defaulted to NULL as required already.\nFor leaf nodes, we don\'t have children to set so we return.\n\n\nSolution Code in C++ \n```\nNode* connect(Node* root) {\n\tif(!root || !root->left) return root; // if given empty tree OR root is leaf node\n\troot->left->next = root->right; // making left child\'s next point to right child\n\tif(root->next) root->right->next = root->next->left; // right child\'s next point to its parent\'s next\'s left node\n\troot->left = connect(root->left); // connect all next pointers in left subtree\n\troot->right = connect(root->right); // connect all next pointers in right subtree\n\treturn root;\n}\n```\n\nThanks! Upvote if this helped you! | 6 | 0 | ['Depth-First Search', 'Recursion', 'C'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.