question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
populating-next-right-pointers-in-each-node | Level Order Easy Implementation | level-order-easy-implementation-by-vaibh-xgv9 | \nimport queue\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if root is None:\n return\n m | vaibhavsharma30 | NORMAL | 2022-02-19T17:24:55.144824+00:00 | 2022-02-19T17:25:20.084496+00:00 | 75 | false | ```\nimport queue\nclass Solution:\n def connect(self, root: \'Optional[Node]\') -> \'Optional[Node]\':\n if root is None:\n return\n myqueue=queue.Queue()\n myqueue.put(root)\n myqueue.put(None)\n small=[]\n while myqueue.empty()==False:\n front=myqueue.get()\n if front!=None:\n if front.left!=None:\n myqueue.put(front.left)\n if front.right!=None:\n myqueue.put(front.right)\n small.append(front)\n else:\n if myqueue.empty()==True:\n if len(small)==1:\n front=small[0]\n front.next=None\n else:\n for i in range(len(small)):\n j=i+1\n if j<=len(small)-1:\n small[i].next=small[j]\n if i==len(small)-1:\n small[i].next=None\n break\n else:\n if len(small)==1:\n small[0].next=None\n else:\n for i in range(len(small)):\n j=i+1\n if j<=len(small)-1:\n small[i].next=small[j]\n if i==len(small)-1:\n small[i].next=None\n small=[]\n myqueue.put(None) \n return root\n``` | 6 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | Very easy BFS Solution C++ | Hint for constant Space | very-easy-bfs-solution-c-hint-for-consta-ra7a | Hint for constant space -> is to use the next links that you just created \n\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root == NUL | Preacher001 | NORMAL | 2021-11-28T14:29:59.908584+00:00 | 2021-11-28T14:30:22.087713+00:00 | 286 | false | Hint for constant space -> is to use the next links that you just created \n```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root == NULL) return root;\n queue<Node*> q;\n q.push(root);\n while(!q.empty()){\n int n=q.size();\n int j=0;\n for(int i=0;i<n;i++){\n Node* node = q.front();\n q.pop();\n j++;\n if(j<n){\n Node* x = q.front();\n node->next = x;\n }else{\n node->next = NULL;\n }\n if(node->left) q.push(node->left);\n if(node->right) q.push(node->right);\n \n }\n }\n return root;\n }\n};\n``` | 6 | 0 | ['Breadth-First Search', 'C'] | 1 |
populating-next-right-pointers-in-each-node | 🔥 C++: O(1) space, O(n) time, 7 lines solution 🔥 | c-o1-space-on-time-7-lines-solution-by-d-esli | \n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* left;\n Node* right;\n Node* next;\n\n Node() : val(0), left(NULL), rig | duongdung12a8 | NORMAL | 2021-10-02T01:06:49.801641+00:00 | 2021-10-02T01:06:49.801692+00:00 | 400 | false | ```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* left;\n Node* right;\n Node* next;\n\n Node() : val(0), left(NULL), right(NULL), next(NULL) {}\n\n Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}\n\n Node(int _val, Node* _left, Node* _right, Node* _next)\n : val(_val), left(_left), right(_right), next(_next) {}\n};\n*/\n\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(root && root->left != NULL) {\n root->left->next = root->right;\n connect(root->left);\n if(root->next != NULL) root->right->next = root->next->left;\n connect(root->right);\n }\n \n return root;\n }\n};\n``` | 6 | 0 | ['Recursion', 'C', 'C++'] | 1 |
populating-next-right-pointers-in-each-node | JAVA Solution | 10 lines code | O(n) Time and Constant space | java-solution-10-lines-code-on-time-and-et8bk | Idea here to take advantage of already set values of next. When going to child, parent will already have their next value. We can take advantage of that. This i | arjun8900 | NORMAL | 2021-04-01T04:20:40.975984+00:00 | 2021-04-06T02:54:38.203746+00:00 | 158 | false | Idea here to take advantage of already set values of next. When going to child, parent will already have their next value. We can take advantage of that. This is the minimize solution.\n\n```\npublic Node connect(Node root) {\n if(root == null) return root;\n modify(root);\n \n return root;\n }\n public void modify(Node root){\n if(root.left == null && root.right == null){\n return;\n }\n root.left.next = root.right;\n if(root.next !=null ){\n root.right.next = root.next.left; \n }\n modify(root.left);\n modify(root.right); \n }\n``` | 6 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | [Python] Jump Game III with queue (deque) + visited set | python-jump-game-iii-with-queue-deque-vi-sd9f | BFS to iterate through all indexes connected to starting index. Storing already explored indices allows us to ensure that we only explore each index a single ti | wookiewarlord | NORMAL | 2020-11-29T09:21:58.229884+00:00 | 2020-11-29T09:21:58.229926+00:00 | 293 | false | BFS to iterate through all indexes connected to starting index. Storing already explored indices allows us to ensure that we only explore each index a single time.\n\t\n\tdef canReach(self, arr, start):\n \n q = collections.deque()\n q.append(start)\n visited = set()\n \n while q:\n cur_i = q.popleft()\n \n if arr[cur_i] == 0:\n return True\n \n a, b = cur_i + arr[cur_i], cur_i - arr[cur_i]\n \n if a < len(arr) and a not in visited:\n q.append(a)\n visited.add(a)\n if b >= 0 and b not in visited:\n q.append(b)\n visited.add(b)\n \n return False | 6 | 0 | [] | 0 |
populating-next-right-pointers-in-each-node | C++ || Constant Space || Iterative + Recursive | c-constant-space-iterative-recursive-by-l700c | Iteraitve Solution \n\n\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root || !root->left) return root;\n Node *current = root | rahu | NORMAL | 2020-11-14T10:54:32.741128+00:00 | 2020-11-14T10:54:32.741162+00:00 | 307 | false | Iteraitve Solution \n\n```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root || !root->left) return root;\n Node *current = root;\n while(current->left) {\n Node *temp = current;\n while(current) {\n current->left->next = current->right;\n if(current->next) current->right->next = current->next->left;\n current = current->next;\n }\n current = temp->left;\n }\n return root;\n }\n};\n```\n\nRecursive Solution \n\n```\nclass Solution {\npublic:\n Node* connect(Node* root) {\n if(!root || !root->left) return root;\n root->left->next = root->right;\n if(root->next) root->right->next = root->next->left;\n connect(root->left);\n connect(root->right);\n return root;\n }\n};\n``` | 6 | 0 | ['C', 'C++'] | 0 |
populating-next-right-pointers-in-each-node | 5 Lines Recursive Python Solution🔥🔥🔥 | 5-lines-recursive-python-solution-by-dya-h2q0 | \n\nclass Solution:\n def connect(self, root: \'Node\', next=None) -> \'Node\':\n if root is None: return None\n root.next = next\n self | dyang0829 | NORMAL | 2020-07-30T04:02:42.438231+00:00 | 2020-07-30T04:08:01.636809+00:00 | 391 | false | \n```\nclass Solution:\n def connect(self, root: \'Node\', next=None) -> \'Node\':\n if root is None: return None\n root.next = next\n self.connect(root.left, root.right)\n self.connect(root.right, root.next.left if root.next else None)\n return root\n``` | 6 | 0 | ['Tree', 'Depth-First Search', 'Recursion', 'Python'] | 2 |
populating-next-right-pointers-in-each-node | go (golang): DFS & BFS | go-golang-dfs-bfs-by-mangreen-lu2l | DFS\ngolang\n/**\n * Definition for a Node.\n * type Node struct {\n * Val int\n * Left *Node\n * Right *Node\n * Next *Node\n * }\n */\n\nfunc | mangreen | NORMAL | 2020-05-13T09:55:58.944558+00:00 | 2020-05-13T10:29:26.981517+00:00 | 164 | false | 1. DFS\n```golang\n/**\n * Definition for a Node.\n * type Node struct {\n * Val int\n * Left *Node\n * Right *Node\n * Next *Node\n * }\n */\n\nfunc connect(root *Node) *Node {\n if root == nil {\n return nil\n }\n \n if root.Left != nil {\n root.Left.Next = root.Right\n \n if root.Next != nil {\n root.Right.Next = root.Next.Left\n }\n }\n \n connect(root.Left)\n connect(root.Right)\n \n return root\n}\n```\n2. BFS\n```golang\n/**\n * Definition for a Node.\n * type Node struct {\n * Val int\n * Left *Node\n * Right *Node\n * Next *Node\n * }\n */\n\nfunc connect(root *Node) *Node {\n if root == nil {\n return nil\n }\n \n q := []*Node{ root }\n \n for len(q) > 0 {\n var pre *Node\n \n for _, n := range q {\n q = q[1:]\n \n if pre != nil {\n pre.Next = n\n }\n \n pre = n\n \n if n.Left != nil {\n q = append(q, n.Left)\n }\n \n if n.Right != nil {\n q = append(q, n.Right)\n }\n }\n }\n \n return root\n}\n``` | 6 | 0 | [] | 0 |
k-diff-pairs-in-an-array | Java O(n) solution - one Hashmap, easy to understand | java-on-solution-one-hashmap-easy-to-und-cna6 | \npublic class Solution {\n public int findPairs(int[] nums, int k) {\n if (nums == null || nums.length == 0 || k < 0) return 0;\n \n | tankztc | NORMAL | 2017-03-05T05:31:31.937000+00:00 | 2018-10-21T00:22:27.838050+00:00 | 68,306 | false | ```\npublic class Solution {\n public int findPairs(int[] nums, int k) {\n if (nums == null || nums.length == 0 || k < 0) return 0;\n \n Map<Integer, Integer> map = new HashMap<>();\n int count = 0;\n for (int i : nums) {\n map.put(i, map.getOrDefault(i, 0) + 1);\n }\n \n for (Map.Entry<Integer, Integer> entry : map.entrySet()) {\n if (k == 0) {\n //count how many elements in the array that appear more than twice.\n if (entry.getValue() >= 2) {\n count++;\n } \n } else {\n if (map.containsKey(entry.getKey() + k)) {\n count++;\n }\n }\n }\n \n return count;\n }\n}\n``` | 429 | 6 | [] | 58 |
k-diff-pairs-in-an-array | [Java/Python] Easy Understood Solution | javapython-easy-understood-solution-by-l-e1wq | Explanation\nCount the elements with Counter\nIf k > 0, for each element i, check if i + k exist.\nIf k == 0, for each element i, check if count[i] > 1\n\n\n# E | lee215 | NORMAL | 2017-03-10T13:34:45.483000+00:00 | 2020-08-18T03:14:20.857620+00:00 | 30,731 | false | # **Explanation**\nCount the elements with `Counter`\nIf `k > 0`, for each element `i`, check if `i + k` exist.\nIf `k == 0`, for each element `i`, check if `count[i] > 1`\n<br>\n\n# **Explanation**\nTime `O(N)`\nSpace `O(N)`\n<br>\n\n**Python**\n```py\ndef findPairs(self, nums, k):\n res = 0\n c = collections.Counter(nums)\n for i in c:\n if k > 0 and i + k in c or k == 0 and c[i] > 1:\n res += 1\n return res\n```\nwhich equals to:\n```py\ndef findPairs(self, nums, k):\n c = collections.Counter(nums)\n return sum(k > 0 and i + k in c or k == 0 and c[i] > 1 for i in c)\n```\n\n**Java**\nBy @blackspinner\n```java\n public int findPairs(int[] nums, int k) {\n Map<Integer, Integer> cnt = new HashMap<>();\n for (int x : nums) {\n cnt.put(x, cnt.getOrDefault(x, 0) + 1);\n }\n int res = 0;\n for (int x : cnt.keySet()) {\n if ((k > 0 && cnt.containsKey(x + k)) || (k == 0 && cnt.get(x) > 1)) {\n res++;\n }\n }\n return res;\n }\n``` | 347 | 7 | [] | 51 |
k-diff-pairs-in-an-array | C++ MULTIPLE APPROACHES : MAPS / TWO POINTER | c-multiple-approaches-maps-two-pointer-b-stlo | Hi , This problem is pretty straightforward . Let me explain the problem first. \n##### EXPLANATION : \nThe problem says that we are provided with an array of i | Krypto2_0 | NORMAL | 2022-02-09T01:51:56.404517+00:00 | 2022-02-09T03:22:31.551317+00:00 | 27,122 | false | Hi , This problem is pretty straightforward . Let me explain the problem first. \n##### EXPLANATION : \nThe problem says that we are provided with an array of integers and we have to find out the ***Count of unique pairs*** in the array such that the ***absolute difference of elements of the pair is ==k.***\nMathematically , find the **count of unique pairs ( nums[i], nums[j] )** such that ,\n* *0 <= i < j < nums.length*\n* *|nums[i] - nums[j]| == k*\n\n##### SOLUTION : \nIt is pretty clear that in order to obtain the answer , we have to find all pairs the array which have an absolute difference of \'k\' and then eliminate those which are not unique.\n\nThere are multiple ways to achieve that. \n\n#### 1. USING MAPS : \nWe are aware of the fact that for a pair to be counted as an answer , **both the elements ( x and x+k ) , need to be in the array**. \nSo we simply **create a map and store the frequency** of each element in the map. \nNow we traverse the map and for **each element \'x\'** , we **check if \'x+k\' exists in the map** . If it does , then it means **a unique pair can be formed** and hence, we **increment the answer**. \n##### EDGE CASE : \nThe only edge case is the situation where**k=0**. If k=0 , instead of finding \'x+k\' , we **check if the frequency of \'x\'>1**. If it is , then we**increment the answer** . \nElse , we don\'t **increment the answer , as the frequency of x=1 and hence it can\'t form a pair with itself**.\n\n##### CODE : \n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int,int> a;\n for(int i:nums)\n a[i]++;\n int ans=0;\n for(auto x:a)\n {\n if(k==0)\n { \n if(x.second>1)\n ans++;\n }\n else if(a.find(x.first+k)!=a.end())\n ans++;\n }\n \n return ans;\n }\n};\n```\n**TIME COMPLEXITY : O(N)**\n**SPACE COMPLEXITY : O(N)**\n\n\n#### 2. USING TWO POINTERS : \nWe are aware of the fact that for a pair to be counted as an answer , **both the elements ( x and x+k ) , need to be in the array.** \nIn this approach , **first we sort the array** and maintain 2 pointers. \n* *1st Pointer --> 1st Element of the Pair*\n* *2nd Pointer --> 2nd Element of the Pair*\n\nWe set the 1st pointer at the 0th index and 2nd pointer at the 1st index. Then , \n1. Move the 2nd pointer until **2nd pointer - 1st pointer >=k** . \n2. If the **2nd pointer - 1st pointer ==k** , then **increment the answer and move the 2nd pointer to the next greater element.** \n3. Move the **1st pointer to the next greater element**. \n\nFollow the above procedure until **the 2nd pointer reaches the end of the array**.\n\n##### CODE : \n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n sort(nums.begin(),nums.end());\n int ans=0,i=0,j=1;\n for(i,j;i<nums.size() and j<nums.size();)\n {\n if(i==j or nums[j]-nums[i]<k)\n j++;\n else \n {\n if(nums[j]-nums[i]==k)\n {\n ans++;\n j++;\n for(;j<nums.size();j++)\n if(nums[j]!=nums[j-1])\n break;\n if(j==nums.size())\n return ans;\n j--; \n }\n i++;\n while(i<j and nums[i]==nums[i-1])\n i++;\n }\n }\n return ans;\n }\n};\n```\n**TIME COMPLEXITY : O(NlogN)**\n**SPACE COMPLEXITY : O(1)**\n\n**NOTE : The 2nd approach doesn\'t need to deal with the EDGE CASE mentioned in the 1st approach as , in the 2nd approach after finding a pair , we immediately move to the next greater element.**\n\nIf you found this post helpful , do upvote. \n | 220 | 4 | ['C', 'C++'] | 16 |
k-diff-pairs-in-an-array | An explanation Going from O(NlogN) -> O(N) | an-explanation-going-from-onlogn-on-by-h-3o9b | So, this problem is very similar to a very famous problem Two Sum problem. But a slightly different, there we have to only check wether a pair exists or not whi | hi-malik | NORMAL | 2022-02-09T02:33:40.380577+00:00 | 2022-02-09T02:52:44.499695+00:00 | 11,816 | false | So, this problem is very similar to a very famous problem `Two Sum` problem. But a slightly different, there we have to only check wether a pair exists or not which has 2 sum equals to the target. But here we have to count those such pairs & only consider the unique one.\n\n**Okay, so how we will solve this problem?**\n\n>One of the first idea came in mind that first-of all we sort this array. Let\'s take an example :-\n\n**Input:** nums = [3,1,4,1,5], k = 2\n**Output:** 2\n\nFirst we sort this array & it becomes :- [1,1,3,4,5]. After sorting what we will do is, start from the starting place & check the \'x + k\' exists on to right place or not!\n\n\n\nSo, first we sort the array & then we will look for the binary search. There is a `method in Java library` called **Arrays.binarySearch** & it may be available in `C++ & Python`. In this method we will pass the array [nums], start index [i + 1], end [n] "size of the array" & the value which we have to search [x + k]. If we find that we, then we will store minimum value of \'x\' into a set. Because we need only the **Unique Pair**.\n\nSo, we will get :- **{1,3} & {3,5}** so these are the 2 pairs we will get. \n\n***Let\'s look at the code you will understand more clearly then,***\n\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n Arrays.sort(nums); // sorted the array\n Set<Integer> set = new HashSet<>(); // Declare the HashSet to only consider unique one\'s\n int n = nums.length; // length of the array\n for(int i = 0; i < nums.length - 1; i++){\n // searching for binary index for the no from the i + 1 index to n \n // and check if we are getting nums[i] + k, where nums[i] is our \'x\'\n if(Arrays.binarySearch(nums, i + 1, n, nums[i] + k) > 0){\n set.add(nums[i]);\n }\n }\n return set.size();\n }\n}\n```\n**Time Complexity :-** O(NlogN) + O(N * logN) = O(NlogN) + O(NlogN) = O(2NlogN) = *BigO(NlogN)*\n\n<hr>\n<hr>\n\n> **Now, you we will ask**. Can we further improve it\'s time complexity? **I\'ll say yes. Using HashMap.**\n\nOkay, so considering the same example : nums[3,1,4,1,5]\n\nFirst we will build our HashMap. In Map we will keep the no. as a key & value as a count of occurence\n\n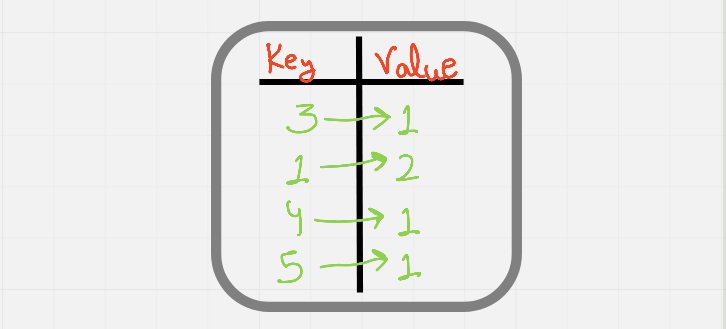\n\nNow, there are 2 cases :-\n1. If k > 0, then in this case we just need to check wether the counter part exists or not. So, if we are iterating \'x + k\' in our map, then we can increment our count\n\n\n2. If k == 0, then we just need to check if x is more then 1 or not [x > 1] in our map.\n\nBut another thing we need to note that here as we iterate from the array after doing counting. Then we will get "1" two times. So, to avoid this instead of iterating over the array, we will iterate over the keyset of this map, which will give us the unique no. i.e. (3,1,4,5).\n\nAlright, so now *I hope approach is clear.*\n\n**Let\'s code it:**\n\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n Map<Integer, Integer> map = new HashMap<>();\n \n for(int num : nums){\n map.put(num, map.getOrDefault(num, 0) + 1);\n }\n int count = 0;\n for(int x : map.keySet()){\n if(k > 0 && map.containsKey(x + k) || k == 0 && map.get(x) > 1) count++;\n }\n return count;\n }\n}\n```\nANALYSIS :-\n* **Time Complexity :-** BigO(N)\n\n* **Space Complexity :-** BigO(N) | 141 | 74 | [] | 17 |
k-diff-pairs-in-an-array | ✅ Well Explained || Two Easy Solutions ✅ | well-explained-two-easy-solutions-by-mah-p1gl | First Approach : Using HashMap\n\n1. First we will create map for counting frequencies of each element in the array.\n2. Now we have 2 cases over here as \n | mahesh340 | NORMAL | 2022-02-09T02:55:22.011249+00:00 | 2022-02-09T07:10:20.726554+00:00 | 23,402 | false | **First Approach : Using HashMap**\n\n1. First we will create map for counting frequencies of each element in the array.\n2. Now we have 2 cases over here as \n -->a) if k == 0 it means we need to count frequency of the same element by using map.get(i) method.\n\t-->b) we need to take counter approach for every element by adding k everytime and check whether that element is present in map or not.\n3. Instead of iterating through array, we will iterate through map.keySet() for getting unique elements.\n\t\n\t\t// O(n) Time Solution\n\t\n\t\tclass Solution {\n\t\t\t\tpublic int findPairs(int[] nums, int k) {\n\t\t\t\t\tMap<Integer, Integer> map = new HashMap();\n\t\t\t\t\tfor (int num : nums)\n\t\t\t\t\t\tmap.put(num, map.getOrDefault(num, 0) + 1);\n\n\t\t\t\t\tint result = 0;\n\t\t\t\t\tfor (int i : map.keySet())\n\t\t\t\t\t\tif (k > 0 && map.containsKey(i + k) || k == 0 && map.get(i) > 1)\n\t\t\t\t\t\t\tresult++;\n\t\t\t\t\treturn result;\n\t\t\t\t}\n\t\t\t}\n\n**Second Approach : Using HashSet**\n\n1. First sort the array.\n2. After that, iterating through loop from first element to the last element.\n3. Using BinarySearch, checked whether (nums[i] + k) is present in the array from index i+1 to n....i.e. if it is present we can take it as for counting approach.\n\t\t\n\t\tArrays.binarySearch(array_name, start_index, end_index, value_for_checking) ==> this method returns index of value which we are searching.\n\t\t\n4. After that just added minimum element to set for getting unique pairs as we know set contains only unique values.\n \n\t\t// O(nlogn) Time Solution\n\n\t\tclass Solution {\n\t\t\tpublic int findPairs(int[] nums, int k) {\n\t\t\t\tSet<Integer> uniquePair = new HashSet();\n\t\t\t\tArrays.sort(nums);\n\t\t\t\tint n = nums.length;\n\n\t\t\t\tfor (int i = 0; i < n - 1; i++)\n\t\t\t\t\tif (Arrays.binarySearch(nums, i + 1, n, nums[i] + k) > 0)\n\t\t\t\t\t\tuniquePair.add(nums[i]);\n\n\t\t\t\treturn uniquePair.size();\n\t\t\t}\n\t\t}\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0\uD83C\uDF38), If you have any question, feel free to ask.** | 132 | 3 | ['Binary Search', 'Sorting', 'Java'] | 12 |
k-diff-pairs-in-an-array | easy java solution, two HashSets O(n) | easy-java-solution-two-hashsets-on-by-lo-x8w1 | \nclass Solution {\n public int findPairs(int[] nums, int k) {\n if (k < 0) return 0;\n Set<Integer> numbers = new HashSet<>();\n Set<In | lolozo | NORMAL | 2018-06-27T04:20:47.129300+00:00 | 2018-06-27T04:20:47.129300+00:00 | 3,127 | false | ```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n if (k < 0) return 0;\n Set<Integer> numbers = new HashSet<>();\n Set<Integer> found = new HashSet<>();\n for (int n : nums) {\n if (numbers.contains(n + k)) found.add(n);\n if (numbers.contains(n - k)) found.add(n - k);\n numbers.add(n);\n }\n return found.size();\n }\n}\n``` | 90 | 1 | [] | 10 |
k-diff-pairs-in-an-array | Two-pointer Approach | two-pointer-approach-by-lixx2100-f98o | The problem is just a variant of 2-sum.\nUpdate: Fixed a bug that can cause integer subtraction overflow.\nUpdate: The code runs in O(n log n) time, using O(1) | lixx2100 | NORMAL | 2017-03-05T07:47:25.627000+00:00 | 2018-10-16T04:42:07.140834+00:00 | 29,917 | false | The problem is just a variant of 2-sum.\n**Update:** Fixed a bug that can cause integer subtraction overflow.\n**Update:** The code runs in `O(n log n)` time, using `O(1)` space.\n\n```java\npublic int findPairs(int[] nums, int k) {\n int ans = 0;\n Arrays.sort(nums);\n for (int i = 0, j = 0; i < nums.length; i++) {\n for (j = Math.max(j, i + 1); j < nums.length && (long) nums[j] - nums[i] < k; j++) ;\n if (j < nums.length && (long) nums[j] - nums[i] == k) ans++;\n while (i + 1 < nums.length && nums[i] == nums[i + 1]) i++;\n }\n return ans;\n}\n``` | 76 | 11 | [] | 19 |
k-diff-pairs-in-an-array | C++ O(N) Time with unordered_map | c-on-time-with-unordered_map-by-lzl12463-dnk0 | See my latest update in repo LeetCode\n\n\n// OJ: https://leetcode.com/problems/k-diff-pairs-in-an-array\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Sp | lzl124631x | NORMAL | 2017-03-06T12:55:01.121000+00:00 | 2022-02-09T09:07:52.544557+00:00 | 10,531 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n```\n// OJ: https://leetcode.com/problems/k-diff-pairs-in-an-array\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(N)\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n if (k < 0) return 0;\n unordered_map<int, int> m;\n for (int n : nums) m[n]++;\n int cnt = 0;\n for (auto p : m) {\n if ((!k && p.second > 1)\n || (k && m.count(p.first + k))) ++cnt;\n }\n return cnt;\n }\n};\n```\n\n---\n\nUpdate 2022/02/08:\n\nBack on 2017/06/06, the constraint of this problem was as follows (You can see the full problem description [here](https://github.com/lzl124631x/LeetCode/commit/8536736d9fb97483cd0875ccb7a7830b30420b24))\n\n>Given an array of integers and an integer **k**, ...\n>**Note:** \n>\n>1. The pairs (i, j) and (j, i) count as the same pair.\n>2. The length of the array won\'t exceed 10,000.\n>3. All the integers in the given input belong to the range: [-1e7, 1e7].\n\nIt didn\'t say that `k >= 0`. That\'s why I added the `k < 0` guard -- just like what we need to do in real world.\n\nNowadays, the constraints on LeetCode are much more detailed and explicit.\n\nIf I write the code today:\n\n```cpp\n// OJ: https://leetcode.com/problems/k-diff-pairs-in-an-array\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(N)\nclass Solution {\npublic:\n int findPairs(vector<int>& A, int k) {\n unordered_map<int, int> m;\n for (int n : A) m[n]++;\n int ans = 0;\n for (auto &[n, cnt] : m) {\n ans += k ? m.count(n - k) : cnt > 1;\n }\n return ans;\n }\n};\n``` | 63 | 1 | [] | 16 |
k-diff-pairs-in-an-array | [Python] O(n) solution, explained | python-on-solution-explained-by-dbabiche-gpcx | Let us just use counter and count frequency of each number in our array. We can have two options:\n\n1. k > 0, it means, that for each unique number i we are as | dbabichev | NORMAL | 2020-10-03T07:28:58.578774+00:00 | 2020-10-03T07:28:58.578809+00:00 | 3,777 | false | Let us just use counter and count frequency of each number in our array. We can have two options:\n\n1. `k > 0`, it means, that for each unique number `i` we are asking if number `i+k` also in table.\n2. `k = 0`, it means, that we are looking for pairs of equal numbers, so just check each frequency.\n\n**Complexity**: time and space complexity is `O(n)`, because we traverse our array twice: first time to create counter and second to find `res`.\n\n```\nclass Solution:\n def findPairs(self, nums, k):\n count = Counter(nums)\n if k > 0:\n res = sum([i + k in count for i in count])\n else:\n res = sum([count[i] > 1 for i in count])\n return res\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 62 | 9 | [] | 5 |
k-diff-pairs-in-an-array | 1-liner in Python, O(n) time | 1-liner-in-python-on-time-by-o_sharp-purd | \n def findPairs(self, nums, k):\n return len(set(nums)&{n+k for n in nums}) if k>0 else sum(v>1 for v in collections.Counter(nums).values()) if k==0 e | o_sharp | NORMAL | 2017-03-05T10:04:11.950000+00:00 | 2018-10-01T02:19:30.865920+00:00 | 18,067 | false | ```\n def findPairs(self, nums, k):\n return len(set(nums)&{n+k for n in nums}) if k>0 else sum(v>1 for v in collections.Counter(nums).values()) if k==0 else 0\n```\nwhich is equivalent to:\n```\n def findPairs(self, nums, k):\n if k>0:\n return len(set(nums)&set(n+k for n in nums))\n elif k==0:\n sum(v>1 for v in collections.Counter(nums).values())\n else:\n return 0\n``` | 61 | 9 | [] | 17 |
k-diff-pairs-in-an-array | [C++] [Java] Clean Code with Explanation [set] [map] | c-java-clean-code-with-explanation-set-m-7su3 | C++\n\nclass Solution {\npublic:\n /**\n * for every number in the array:\n * - if there was a number previously k-diff with it, save the smaller to | alexander | NORMAL | 2017-03-05T04:02:31.343000+00:00 | 2018-10-05T03:12:11.511345+00:00 | 18,832 | false | **C++**\n```\nclass Solution {\npublic:\n /**\n * for every number in the array:\n * - if there was a number previously k-diff with it, save the smaller to a set;\n * - and save the value-index to a map;\n */\n int findPairs(vector<int>& nums, int k) {\n if (k < 0) {\n return 0;\n }\n unordered_set<int> starters;\n unordered_map<int, int> indices;\n for (int i = 0; i < nums.size(); i++) {\n if (indices.count(nums[i] - k)) {\n starters.insert(nums[i] - k);\n }\n if (indices.count(nums[i] + k)) {\n starters.insert(nums[i]);\n }\n\n indices[nums[i]] += 1;\n }\n \n return starters.size();\n }\n};\n```\n**Java**\n```\npublic class Solution {\n public int findPairs(int[] nums, int k) {\n if (k < 0) { return 0; }\n\n Set<Integer> starters = new HashSet<Integer>();\n Set<Integer> uniqs = new HashSet<Integer>();\n for (int i = 0; i < nums.length; i++) {\n if (uniqs.contains(nums[i] - k)) starters.add(nums[i] - k);\n if (uniqs.contains(nums[i] + k)) starters.add(nums[i]);\n uniqs.add(nums[i]);\n }\n\n return starters.size();\n }\n}\n``` | 56 | 1 | [] | 10 |
k-diff-pairs-in-an-array | ✔️ Python O(n) Solution | 98% Faster | Easy Solution | K-diff Pairs in an Array | python-on-solution-98-faster-easy-soluti-sqtp | \uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D\n\nVisit this blog to learn Python tips and techniques and to find a Leetcode solution wit | pniraj657 | NORMAL | 2022-02-09T06:34:27.713867+00:00 | 2023-02-01T05:42:24.115343+00:00 | 6,578 | false | **\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n\nVisit this blog to learn Python tips and techniques and to find a Leetcode solution with an explanation: https://www.python-techs.com/\n\n**Solution:**\n```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n cnt=0\n c=Counter(nums)\n \n if k==0:\n for key,v in c.items():\n if v>1:\n cnt+=1\n else:\n for key,v in c.items():\n if key+k in c:\n cnt+=1\n return cnt\n```\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.**\n | 39 | 3 | ['Python', 'Python3'] | 5 |
k-diff-pairs-in-an-array | C++ super-simple solution O(n), faster than 100% | c-super-simple-solution-on-faster-than-1-v4qf | \nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int, int> map;\n for(auto num:nums)\n map[nu | yehudisk | NORMAL | 2020-10-03T18:42:45.002534+00:00 | 2020-10-03T18:42:45.002576+00:00 | 3,279 | false | ```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int, int> map;\n for(auto num:nums)\n map[num]++;\n \n int res = 0;\n if (k > 0) {\n for(auto a:map)\n if (map.find(a.first+k) != map.end()) \n res++;\n }\n \n else {\n for(auto a:map)\n if (a.second > 1)\n res++;\n }\n \n return res;\n }\n};\n```\n**Like it? please upvote...** | 31 | 3 | ['C'] | 6 |
k-diff-pairs-in-an-array | Java | Easy to understand |Two Approaches | Sorting | HashMap | java-easy-to-understand-two-approaches-s-qznm | Method 1: using sorting and two pointers\n\nclass Solution {\n public int findPairs(int[] nums, int k) {\n Arrays.sort(nums);\n int i=0, j=1, | cyrus18 | NORMAL | 2022-02-09T08:20:51.996610+00:00 | 2022-02-09T08:20:51.996643+00:00 | 3,967 | false | #### **Method 1: using sorting and two pointers**\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n Arrays.sort(nums);\n int i=0, j=1, diff=0, n=nums.length, sum=Integer.MIN_VALUE;\n int count=0;\n while(j<n && i<n-1){\n\t\t // ((nums[i]+nums[j])!=sum) -> this will take care of no repetetion\n\t\t\t//if we found any match, increase i , j by 1\n if(nums[j]-nums[i]==k && (nums[i]+nums[j])!=sum){\n sum=nums[i]+nums[j];\n i++; j++; count++;\n }\n\t\t\t//if diff is smaller than k increase j by 1\n\t\t\telse if((nums[j]-nums[i])<k){\n j++;\n }\n\t\t\t//else case, when diff is greater than k, increase i by 1\n\t\t\telse{\n i++;\n }\n\t\t\t//check if i and j are not same to aoid duplicates\n if(i==j) j++;\n }\n return count;\n }\n}\n```\n**Time Complexity** : O(nlogn) + O(n)\n**Space Complexity** : O(n)\n\n#### **Method 2 : using HashMap**\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n\t // corner cases\n if(nums==null || nums.length==0 || k<0) return 0;\n int count=0;\n Map<Integer, Integer> hash=new HashMap<>();\n\t\t//frequency map\n for(int i:nums)\n hash.put(i, hash.getOrDefault(i, 0)+1);\n for(Map.Entry<Integer, Integer> entry:hash.entrySet())\n\t\t // check if any such pair exist or not\n\t\t\t//in case of k==0 check whether any number having frequency >=2 or not.\n if((hash.containsKey(entry.getKey()+k) && k!=0) || (k==0 && entry.getValue()>1))\n count++;\n return count;\n }\n}\n```\n**Time Complexity** : O(n)\n**Space Complexity** : O(n)\n\n**Don\'t forget to upvote, it inspires me a lot, Thank you!** | 27 | 0 | ['Two Pointers', 'Sorting', 'Binary Tree', 'Java'] | 1 |
k-diff-pairs-in-an-array | Interesting Java Solution/ HashSet Only | interesting-java-solution-hashset-only-b-8vay | Put all numbers n in Hashset S1.\nPut all numbers n+k in HashSet S2.\nThe number of pairs are the intersection of the two Hashsets. Different conditions apply t | wangdi814 | NORMAL | 2017-03-05T15:04:08.049000+00:00 | 2018-10-07T22:09:58.234090+00:00 | 4,270 | false | Put all numbers n in Hashset S1.\nPut all numbers n+k in HashSet S2.\nThe number of pairs are the intersection of the two Hashsets. Different conditions apply to k=0 or k<0.\n\n```\npublic class Solution {\n public int findPairs(int[] nums, int k) {\n \n int ans = 0;\n \n if(k<0) return ans;\n \n Set<Integer> set1 = new HashSet<Integer> ();\n Set<Integer> set2 = new HashSet<Integer> ();\n \n if(k==0){\n for(int n:nums){\n if(!set1.contains(n))\n {set1.add(n);}\n else{\n set1.remove(n);\n if(!set2.contains(n)) ans++;\n set2.add(n);\n }\n }\n }\n else{\n for(int n:nums){\n set1.add(n);\n set2.add(n+k);\n }\n set1.retainAll(set2);\n ans = set1.size();\n }\n \n return ans;\n }\n}\n``` | 24 | 0 | [] | 7 |
k-diff-pairs-in-an-array | [C++] Solution w/ Explanation| Brute force to optimize | Two approaches | c-solution-w-explanation-brute-force-to-7sfxr | Brief note about Question-\n\nWe have to return the number of unique k-diff pairs in the array.\n\nK- diff pair (arr[i], arr[j]) is nothing but basically \n 0 | aryanttripathi | NORMAL | 2022-02-09T06:37:01.306015+00:00 | 2024-08-31T11:25:51.174611+00:00 | 1,639 | false | ***Brief note about Question-***\n\nWe have to ***return the number of unique k-diff pairs in the array.***\n\nK- diff pair (arr[i], arr[j]) is nothing but basically \n* 0 < i < j < arr.size()\n* abs(arr[i] - arr[j]) == k\n______________\n***Solution - I (Accepted)-***\n* We try to implement what the question wants to do, like this is the most basic thing we can do.\n* We traverse from all of the array and find unique pairs where their absoloute difference is k and increment our count.\n* See commented program for explanation.\n```\nTime Complexity --> O(n ^ 2) // where n is the length of the array\nSpace Complexity --> O(n) // as we are using map to store pairs\nIt paases [ 60 / 60] in built test cases\n```\n\n**Code (C++)**\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& arr, int k) {\n int n = arr.size(); // take the size of the array\n int count = 0; // variable to store count\n \n sort(arr.begin(), arr.end()); // sort the array to find unique pairs\n map<pair<int,int>, int> mp; // make a map where key is pair & value if it occurs\n \n for(int i = 0; i < n - 1; i++) // traverse from the whole array\n {\n for(int j = i + 1; j < n; j++)\n {\n if(abs(arr[j] - arr[i]) == k) // if it follows criteria\n {\n // make a pair to find whether it is unique or not\n pair<int,int> p = {arr[i], arr[j]}; \n \n // if this pair not present in the map, then we do the computation\n if(mp.find(p) == mp.end())\n {\n count++; // increment count\n mp[p] = 1; // make its value as 1, saying that now it is present in our map\n }\n }\n }\n }\n return count; // and at last return the count\n }\n};\n```\n__________________\n***Solution - II (Accepted)-***\n* So a question arises can we optimise it.\n* And answer is yes, but how?\n* See, *we have to find number of unique pairs such that their absoloute difference is k.*\n* suppose, **`a - b == k --> a = b + k`**\n* Can\'t we store all the values of array into a map and then `for every value we find value + k`.\n* That\'s all we have to do.\n* see commented code for more explanation.\n```\nTime Complexity --> O(n) // where n is the length of the array\nSpace Complexity --> O(n) // as we are using unordered map to store pairs\nIt paases [ 60 / 60] in built test cases\n```\n**Code (C++)**\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& arr, int k) {\n int n = arr.size(); // take the size of the array\n unordered_map<int, int> mp; // map to store all values of array\n \n for(int i = 0; i < n; i++) //store all values of array into map\n {\n mp[arr[i]]++;\n }\n \n int count = 0; // variable to store the unique pairs\n \n if(k != 0) // if k is not zero\n {\n for(auto it = mp.begin(); it != mp.end(); it++) // traverse in all over the map\n {\n // if value + k is present in map\n if(mp.find(it -> first + k) != mp.end())\n {\n count++; // increment count\n }\n }\n }\n else // see for k = 0, we have to just find all the values greater than 1\n {\n for(auto it = mp.begin(); it != mp.end(); it++)\n {\n if(it -> second > 1)\n {\n count++;\n }\n }\n }\n \n return count; // at last return count\n }\n};\n```\n---\n\n**SOLN - III**\n```\n1) Come back to problem after almost two years.\n2) Solved the same question with set only. \n3) Nothing more about the approach, insert all the elements into the set \nto count only single unique pairs.\n4) But for the case, when k == 0, we need to consider all the elements\nwhose frequency is greater than one. \n5) Also, we don\'t need to bother about their count as it dosen\'t matter.\n6) So, In process of inserting elements into the set, just check if this \nelement already exist into the set that means it\'s frequency is definately \ngoing to be greater than 1, so insert this into left out set.\n7) That\'s it, traverse the set and count the answer.\n8) Easy peasy, anyways, byyye....\n```\n\n***CODE***\n```\nint findPairs(vector<int>& nums, int k) {\n\n set<int> s;\n\n // in case k will be zero,\n // We need to only count those elements whose frequency is\n // greater than 1 \n set<int> leftOutSet; \n\n for(int i: nums) {\n\n if(!s.count(i)) s.insert(i);\n else leftOutSet.insert(i);\n }\n\n int ans = 0;\n for(auto it: s) {\n \n int toFind = it + k;\n if(s.count(toFind)) ans++;\n }\n\n return k == 0 ? leftOutSet.size() : ans;\n }\n};\n\n```\n\n\n***`If u find this useful , please consider to give a upvote!!`*** | 19 | 0 | ['C'] | 1 |
k-diff-pairs-in-an-array | Readable & Simple Python | readable-simple-python-by-terribleprogra-ihxr | O(n) Time.\nO(n) Space.\n\nfrom collections import Counter\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n\t\t#If k is less than 0, | terribleprogrammer | NORMAL | 2019-07-02T00:47:22.378651+00:00 | 2019-07-02T00:47:22.378691+00:00 | 3,180 | false | O(n) Time.\nO(n) Space.\n```\nfrom collections import Counter\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n\t\t#If k is less than 0, then the result is 0 since we are looking fpr pairs with an ABSOLUTE difference of k.\n if k < 0:\n return 0\n \n count = Counter(nums)\n pairs = set([])\n \n for num in count.keys():\n\t\t\t#Special case: If k == 0, then there needs to be at least two occurences of a particular num in nums \n\t\t\t#in order for there to be a pair (num, num).\n if k == 0:\n if count[num] > 1:\n pairs.add((num, num))\n\t\t\t\t\t\n\t\t\t#Regular case: k != 0. Simply check if num + k is a member of the array nums.\n\t\t\t#Insert the pair into the set of pairs (smallerNum, largerNum) so that there are no duplicate pairs.\n else:\n otherNum = num + k\n if otherNum in count:\n pairs.add((num, otherNum) if num <= otherNum else (otherNum, num))\n \n return len(pairs)\n``` | 19 | 0 | ['Ordered Set', 'Python'] | 3 |
k-diff-pairs-in-an-array | O(n) concise solution, C++ | on-concise-solution-c-by-vsmnv-8npa | \nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n if(k < 0) return 0;\n unordered_map<int,int> m;\n for(int i = | vsmnv | NORMAL | 2017-03-05T04:35:57.988000+00:00 | 2017-03-05T04:35:57.988000+00:00 | 7,106 | false | ```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n if(k < 0) return 0;\n unordered_map<int,int> m;\n for(int i = 0; i < nums.size(); ++i)\n ++m[nums[i]];\n int res = 0;\n if(k != 0) {\n for(auto it = m.begin(); it != m.end(); ++it)\n if(m.find(it->first+k) != m.end())\n ++res;\n } else {\n for(auto it = m.begin(); it != m.end(); ++it)\n if(it->second > 1)\n ++res;\n }\n return res;\n }\n};\n``` | 19 | 0 | ['C++'] | 5 |
k-diff-pairs-in-an-array | [C++/Java/Python] Counter - O(N) - Clean & Concise | cjavapython-counter-on-clean-concise-by-8m5gh | Idea\n- Build cnt is a map to map unique numbers and their counts .\n- For each b in cnt: \n\t- If k > 0 and a = b - k exists then we count (a, b) as a k-diff p | hiepit | NORMAL | 2020-10-03T09:14:01.410614+00:00 | 2020-10-03T09:47:43.956816+00:00 | 1,091 | false | **Idea**\n- Build `cnt` is a map to map `unique numbers` and `their counts` .\n- For each `b` in `cnt`: \n\t- If `k > 0` and `a = b - k` exists then we count `(a, b)` as a `k-diff pair`.\n\t- If `k = 0` and `b` appears at least 2 times then we count`(b, b)` as a `k-diff pair`.\n\n**Complexity** \n- Time & Space: O(N)\n\n**Python**\n```python\nclass Solution(object):\n def findPairs(self, nums, k):\n cnt = Counter(nums)\n ans = 0\n for b in cnt:\n if (k > 0 and b - k in cnt) or (k == 0 and cnt[b] >= 2):\n ans += 1\n return ans\n```\n\n**C++**\n```c++\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int, int> cnt;\n for (int x : nums)\n cnt[x] += 1;\n int ans = 0;\n for (auto [b, _] : cnt)\n if ((k > 0 && cnt.count(b - k)) || (k == 0 && cnt[b] >= 2))\n ans += 1;\n return ans;\n }\n};\n```\n\n**Java**\n```java\nclass Solution {\n public int findPairs(int[] nums, int k) {\n HashMap<Integer, Integer> cnt = new HashMap();\n for (int x : nums)\n cnt.put(x, cnt.getOrDefault(x, 0) + 1);\n \n int ans = 0;\n for (int b : cnt.keySet())\n if ((k > 0 && cnt.containsKey(b - k)) || (k == 0 && cnt.get(b) >= 2))\n ans += 1;\n return ans;\n }\n}\n``` | 17 | 7 | [] | 1 |
k-diff-pairs-in-an-array | Java 6ms, Beats 98% Simple 2-Pointer Approach | java-6ms-beats-98-simple-2-pointer-appro-wtve | This is a pretty standard 2 pointer approach with a unique take away when looking at duplicates. One thing that took me a little bit to wrap my head around was | kniffina | NORMAL | 2019-05-24T21:39:05.318382+00:00 | 2019-08-31T14:56:49.918655+00:00 | 3,012 | false | This is a pretty standard 2 pointer approach with a unique take away when looking at duplicates. One thing that took me a little bit to wrap my head around was how we can accurately determine what is a valid answer. I also didn\'t see any posts where they showed this approach so I thought I would share.\n\n\nTo start I think its easier to look at, what IS NOT a valid answer.\n1. If the left pointer has caught up to our right pointer. This is between two different values so if left == right, this will never be a valid answer.\n2. If we have previously used this value to accurately determine that two values compute a valid answer.\n\t* \tFor this problem I used a previous variable and set it whenever we find a value where nums[r] - nums[l] == k. This stops any sort of duplicates from happening.\n3. As mentioned earlier we must also check that nums[r]-nums[l] == k. We use the while loop to get as close as possible for each iteration but we need the final if statement to check accuracy.\n\nHope this helps someone!\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n if(nums == null || nums.length < 1) return 0;\n \n Arrays.sort(nums);\n int l = 0, ans = 0, prev = Integer.MAX_VALUE;\n for(int r = 1; r < nums.length; r++) {\n while(l < r && nums[r] - nums[l] > k) l++;\n \n if(l != r && prev != nums[l] && nums[r] - nums[l] == k) {\n ans++;\n prev = nums[l];\n }\n }\n return ans;\n }\n}\n``` | 17 | 1 | ['Two Pointers', 'Java'] | 2 |
k-diff-pairs-in-an-array | Java O(n) Hashmap One Pass Easy Solution!! | java-on-hashmap-one-pass-easy-solution-b-1g1h | \npublic int findPairs(int[] nums, int k) {\n int count =0;\n HashMap<Integer, Integer> map = new HashMap<>();\n \n for(int i = 0; i | gargeemukherjee | NORMAL | 2021-06-21T13:09:18.675032+00:00 | 2021-06-21T13:09:18.675084+00:00 | 1,650 | false | ```\npublic int findPairs(int[] nums, int k) {\n int count =0;\n HashMap<Integer, Integer> map = new HashMap<>();\n \n for(int i = 0; i < nums.length; i++) {\n if(!map.containsKey(nums[i])) {\n if(map.containsKey(nums[i] + k)) count++;\n if(map.containsKey(nums[i] - k)) count++;\n map.put(nums[i], 1);\n } else if (k == 0) {\n if(map.get(nums[i]) == 1)\n count++;\n map.put(nums[i], map.get(nums[i]) + 1);\n } \n }\n return count;\n }\n``` | 16 | 1 | ['Java'] | 1 |
k-diff-pairs-in-an-array | Python concise O(N) solution using sets, only one pass through the list | python-concise-on-solution-using-sets-on-pcpz | Check whether num + k and num - k are already in the set and also make sure the pair is not already counted. Only goes throught the list one time.\n\nEdit: afte | bindloss | NORMAL | 2019-10-07T20:55:18.545204+00:00 | 2019-10-09T03:32:43.280559+00:00 | 2,313 | false | Check whether num + k and num - k are already in the set and also make sure the pair is not already counted. Only goes throught the list one time.\n\nEdit: after reading other solutions, some memory can be saved by only saving the smallest value between num1 and num2 in pairsSet instead of the sorted tuple.\n```\nclass Solution(object):\n def findPairs(self, nums, k):\n if k < 0: return 0\n numsSet, pairsSet = set(), set()\n for num1 in nums:\n for num2 in [num1 + k, num1 - k]:\n if num2 in numsSet:\n pairsSet.add(tuple(sorted([num1, num2])))\n numsSet.add(num1)\n return len(pairsSet)\n``` | 16 | 0 | ['Python'] | 0 |
k-diff-pairs-in-an-array | Self-explained AC Java Sliding Window | self-explained-ac-java-sliding-window-by-mmn2 | \n public int findPairs(int[] nums, int k) {\n\tif(k<0 || nums.length<=1){\n\t return 0;\n\t}\n\t\t \n Arrays.sort(nums);\n int count = 0;\n | 2010zhouyang | NORMAL | 2017-03-05T04:03:09.438000+00:00 | 2018-09-17T12:12:02.593212+00:00 | 2,888 | false | ```\n public int findPairs(int[] nums, int k) {\n\tif(k<0 || nums.length<=1){\n\t return 0;\n\t}\n\t\t \n Arrays.sort(nums);\n int count = 0;\n int left = 0;\n int right = 1;\n \n while(right<nums.length){\n int firNum = nums[left];\n int secNum = nums[right];\n // If less than k, increase the right index\n if(secNum-firNum<k){\n right++;\n }\n // If larger than k, increase the left index\n else if(secNum - firNum>k){\n left++; \n }\n // If equal, move left and right to next different number\n else{\n count++;\n while(left<nums.length && nums[left]==firNum){\n left++;\n }\n while(right<nums.length && nums[right]==secNum){\n right++;\n }\n \n }\n //left and right should not be the same number\n if(right==left){\n \tright++;\n }\n }\n return count;\n }\n``` | 15 | 1 | [] | 5 |
k-diff-pairs-in-an-array | Best Approach || Easy solution || easy-understanding | best-approach-easy-solution-easy-underst-gwtm | \n//Please upvote,if u like it :)\nint findPairs(vector<int>& nums, int k){\n unordered_map<int,int> mp;\n for(auto it:nums){\n mp[it]+ | 123_tripathi | NORMAL | 2022-02-09T07:38:47.570768+00:00 | 2022-06-17T06:20:55.680187+00:00 | 2,636 | false | ```\n//Please upvote,if u like it :)\nint findPairs(vector<int>& nums, int k){\n unordered_map<int,int> mp;\n for(auto it:nums){\n mp[it]++;\n }\n int ans = 0;\n for(auto it:mp){\n int findd = it.first + k;\n if(mp.find(findd) != mp.end()){\n if(findd == it.first && mp[findd] > 1){\n ans++;\n }else if(findd != it.first){\n ans++;\n }\n }\n }\n return ans;\n }\n//Please upvote,if u like it :)\n``` | 13 | 1 | ['C', 'Ordered Set', 'Python', 'C++', 'Java'] | 1 |
k-diff-pairs-in-an-array | problem with description | problem-with-description-by-endurance-4heu | The question that is being checked for is not the question that is being asked.\n\nThe question being checked for seems to be:\n\nGiven an array of integers num | endurance | NORMAL | 2022-02-09T02:42:19.620304+00:00 | 2022-02-09T06:53:20.816494+00:00 | 439 | false | The question that is being checked for is not the question that is being asked.\n\nThe question being checked for seems to be:\n\n*Given an array of integers nums and an integer k, return the number of unique pairs that are of the form (nums[i], nums[j]) where*\n**nums[i] <= nums[j]\ni != j\nabs(nums[i] - nums[j]) == k**\n\nThe question that is being asked is similar but different:\n\n*Given an array of integers nums and an integer k, return the number of unique pairs that are of the form (nums[i], nums[j]) where*\n**i < j\nabs(nums[i] - nums[j]) == k**\n\nFor all of the examples in the problem description, the two questions give the same answer. Buf for the test case\n```\n[0,3,0]\n3\n```\nthe expected solution is 1, while the answer should be 2, given the actual problem description.\n\nThe pairs for the actual question are (0, 3) and (3, 0)\nThe pair for the checked for question is (0, 3)\n\nFWIW, here\'s a quadratic time brute force literal interpretation of the problem description that gets 2.\n```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n n = len(nums)\n k_diff_pairs = []\n for i in range(n):\n for j in range(n):\n if i < j:\n if abs(nums[i] - nums[j]) == k:\n k_diff_pairs.append((nums[i], nums[j]))\n return len(frozenset(k_diff_pairs))\n```\nAnd here\'s an O(n) time solution\n```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n count = 0\n so_far = dict()\n for num in nums:\n for x in (num - k, num + k):\n if x in so_far:\n if num not in so_far[x]:\n count += 1\n so_far[x].append(num)\n if num not in so_far:\n so_far[num] = []\n return count\n```\nPlease consider updating the problem statement and adding the above test case to the examples.\n\nNote that the above test example is a simplified version of one of the tests used to check a solution, namely\n```\n[1,2,4,4,3,3,0,9,2,3]\n3\n``` | 11 | 0 | [] | 3 |
k-diff-pairs-in-an-array | Python 3, Faster than 99.77%, Dictionary | python-3-faster-than-9977-dictionary-by-qc60h | \n# Faster than 99.77% of Python3 online submissions\n# Memory Usage: 15.6 MB, less than 34.48% of Python3 online submissions\n\nclass Solution:\n def findPa | silvia42 | NORMAL | 2020-10-03T18:25:03.726621+00:00 | 2020-10-03T18:25:03.726667+00:00 | 2,090 | false | ```\n# Faster than 99.77% of Python3 online submissions\n# Memory Usage: 15.6 MB, less than 34.48% of Python3 online submissions\n\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n # return the number of unique pairs\n answ=0\n # create a dictionary: d[x]==nums.count(x)\n d={}\n for x in nums:\n if x in d: d[x]+=1\n else: d[x]=1\n \n if k: # k>0\n answ=sum(x+k in d for x in d.keys())\n else: # k==0\n answ=sum(k>1 for k in d.values())\n \n return answ\n``` | 11 | 0 | ['Python', 'Python3'] | 1 |
k-diff-pairs-in-an-array | C++ O(nlogn) solution without hashmap [detail explanation] | c-onlogn-solution-without-hashmap-detail-uz3m | Sort and then perform two scans in parallel, maintaining a difference as close to k as possible between the two scan positions. In other words, advance the lead | jasperjoe | NORMAL | 2020-02-22T02:20:46.590335+00:00 | 2020-02-22T02:21:20.471520+00:00 | 1,554 | false | Sort and then perform two scans in parallel, maintaining a difference as close to k as possible between the two scan positions. In other words, advance the leading scan when the difference is smaller than k, and advance the lagging scan when the difference is greater. This way we either find a pair or scan through the list and report that no pair exists. Time complexity: O(n log n).\n\t\n\tclass Solution {\n\tpublic:\n\t\tint findPairs(vector<int>& nums, int k) {\n\t\t\tsort(nums.begin(),nums.end());\n\t\t\tint fast=1;\n\t\t\tint slow=0;\n\t\t\tint ans=0;\n\t\t\twhile(slow<nums.size() && fast<nums.size()){\n\t\t\t\tif(nums[fast]-nums[slow]==k){\n\t\t\t\t\tans++;\n\t\t\t\t\tfast++;\n\t\t\t\t\tslow++;\n\t\t\t\t\twhile(fast<nums.size() && nums[fast]==nums[fast-1]){\n\t\t\t\t\t\tfast++;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\telse if(nums[fast]-nums[slow]>k){\n\t\t\t\t\tslow++; \n\t\t\t\t\tif(fast-slow==0){\n\t\t\t\t\t\tfast++;}\n\t\t\t\t}\n\t\t\t\telse{ \n\t\t\t\t\tfast++;\n\t\t\t\t} \n\t\t\t}\n\t\t\treturn ans;\n\n\t\t}\n\t}; | 11 | 1 | ['C', 'Sorting', 'C++'] | 1 |
k-diff-pairs-in-an-array | Beats 99% of Python3(hashmap, no libraries) | beats-99-of-python3hashmap-no-libraries-x9kdh | \nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n d = {}\n cnt = 0\n for i in nums:\n if i not in d: | dxc7528 | NORMAL | 2020-10-03T12:25:58.727970+00:00 | 2020-10-03T12:31:58.050217+00:00 | 457 | false | ```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n d = {}\n cnt = 0\n for i in nums:\n if i not in d:\n d[i] = 1\n else:\n d[i] += 1\n \n if k == 0:\n for i in d.values():\n if i > 1:\n cnt += 1\n else:\n for i in d:\n if k + i in d:\n cnt += 1\n \n return cnt\n``` | 10 | 1 | ['Python'] | 2 |
k-diff-pairs-in-an-array | Java HashMap | java-hashmap-by-hobiter-wp4m | \n public int findPairs(int[] nums, int k) {\n if (k < 0) return 0;\n Map<Integer, Integer> map = new HashMap<>();\n int res = 0;\n | hobiter | NORMAL | 2020-06-07T22:23:42.715418+00:00 | 2020-06-07T22:23:42.715452+00:00 | 825 | false | ```\n public int findPairs(int[] nums, int k) {\n if (k < 0) return 0;\n Map<Integer, Integer> map = new HashMap<>();\n int res = 0;\n for(int i : nums) {\n if (map.containsKey(i)) {\n if (k == 0 && map.get(i) == 1) {\n map.put(i, map.get(i) + 1);\n res++;\n }\n continue;\n }\n res += map.getOrDefault(i + k, 0);\n res += map.getOrDefault(i - k, 0);\n map.put(i, 1);\n }\n return res;\n }\n``` | 10 | 0 | [] | 0 |
k-diff-pairs-in-an-array | JavaScript Solution O(n) Beats 92%R and 100%M using map, easy to understand | javascript-solution-on-beats-92r-and-100-14y5 | \t/*\n\t * @param {number[]} nums\n\t * @param {number} k\n\t * @return {number}\n\t /\n\tvar findPairs = function(nums, k) {\n\t\tif(nums.length === 0 || k < 0 | congweibai | NORMAL | 2019-10-28T11:00:53.224978+00:00 | 2019-10-28T11:00:53.225010+00:00 | 1,671 | false | \t/**\n\t * @param {number[]} nums\n\t * @param {number} k\n\t * @return {number}\n\t */\n\tvar findPairs = function(nums, k) {\n\t\tif(nums.length === 0 || k < 0) return 0\n\t\tlet myMap = new Map(),\n\t\t\tcount = 0\n\t\t//Get wordcount\n\t\tfor(num of nums){\n\t\t\tmyMap.set(num,(myMap.get(num)+1) || 1)\n\t\t}\n\t\t\n\t\t//search solutions\n\t\tmyMap.forEach((value,key) =>{\n\t\t\tif(k === 0){\n\t\t\t\tif(value > 1) count++\n\t\t\t}\n\t\t\telse{\n\t\t\t\tif(myMap.has(key+k)) count++\n\t\t\t}\n\t\t})\n\n\t\treturn count\n\t}; | 10 | 0 | ['JavaScript'] | 1 |
k-diff-pairs-in-an-array | C++ easy solution | c-easy-solution-by-avinash1320-jh65 | \nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n map<pair<int, int>, int> m;\n for(int i=0;i<nums.size();i++){\n | avinash1320 | NORMAL | 2022-02-09T05:08:03.965097+00:00 | 2022-02-09T05:08:03.965125+00:00 | 1,117 | false | ```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n map<pair<int, int>, int> m;\n for(int i=0;i<nums.size();i++){\n for(int j=i+1;j<nums.size();j++){\n if(abs(nums[i]-nums[j])==k and m.find({nums[j], nums[i]})==m.end())\n m[{nums[i], nums[j]}]++;\n }\n }\n return m.size();\n }\n};\n``` | 9 | 1 | ['C', 'C++'] | 1 |
k-diff-pairs-in-an-array | ✅Multiple solutions in C++ with explanations! | multiple-solutions-in-c-with-explanation-4fms | \n> If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistake please let me know. Thank you! | dhruba-datta | NORMAL | 2022-01-11T11:01:25.374916+00:00 | 2022-01-22T17:33:45.878280+00:00 | 913 | false | \n> **If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistake please let me know. Thank you!\u2764\uFE0F**\n> \n\n---\n\n## Explanation:\n\n### Solution 01\n\n- Here we sort the vector to avoid duplicate elements in the set.\n- Take to loops & if the difference is equal to k, push it to set.\n- Calculate the set size in the count variable and return it.\n- **Time complexity:** O(n^2 logn).\n\n### Solution 02\n\n- Here we sort the values and store the element occurrence in the map.\n- If k=0, then the difference of 2 same elements will be equal to 0.\n- If not then we\u2019ll iterate the map & will find if the ***(k-current element)*** is present in the map.\nIf present then we\u2019ll increase count.\n- Also every time we\u2019ll remove the current element from map to avoid repeating elements.\n- **Time complexity:** O(nlogn).\n\n---\n\n## Code:\n\n```cpp\n//Solution 01:\n**class Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n int n= nums.size();\n int count=0;\n sort(nums.begin(), nums.end());\n set<vector<int>>res;\n \n for(int i=0; i<n-1; i++){\n for(int j=i+1; j<n; j++){\n if(abs(nums[i]-nums[j])==k)\n res.insert({nums[i], nums[j]});\n }\n }\n count = res.size();\n return count;\n }\n};**\n\n//Solution 02:\n**class Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n int n= nums.size();\n int count=0, l=0, r=n-1;\n sort(nums.begin(), nums.end());\n unordered_map<int, int>mp;\n \n if(k<0) return 0;\n \n for(auto x: nums)\n mp[x]++;\n\n if(k==0){\n for(auto x:mp){\n if(x.second>1)\n count++;\n }\n }\n else{\n for(auto x:mp){\n x.second--;\n if(mp.count(x.first-k))\n count++;\n x.second++;\n } \n }\n \n return count;\n }\n};**\n```\n\n---\n\n> **Please upvote this solution**\n> | 9 | 0 | ['C', 'Ordered Set', 'C++'] | 2 |
k-diff-pairs-in-an-array | C++ simple soln || Hashing || Beats - 99%, 99% | c-simple-soln-hashing-beats-99-99-by-hel-sit2 | ```\nclass Solution {\npublic:\n int findPairs(vector& nums, int k) {\n unordered_map m;\n for(int x: nums) m[x]++;\n int ans=0;\n | helixpranay31399 | NORMAL | 2020-10-03T18:21:37.907320+00:00 | 2020-10-09T07:49:53.146745+00:00 | 1,014 | false | ```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int,int> m;\n for(int x: nums) m[x]++;\n int ans=0;\n if(k==0)\n {\n for(auto x: m) if(x.second>1) ans++;\n }\n else\n {\n for(auto x: m)\n {\n if(m.count(x.first + k) > 0) ans++; \n }\n }\n return ans;\n }\n}; | 9 | 0 | ['C', 'C++'] | 0 |
k-diff-pairs-in-an-array | JAVA - HashMap Solution / Easy to Understand | java-hashmap-solution-easy-to-understand-h5a9 | \npublic int findPairs(int[] nums, int k) {\n\tif(nums == null || nums.length == 0 || k<0) return 0;\n\tint count = 0;\n\tHashMap<Integer, Integer> hm = new Has | anubhavjindal | NORMAL | 2019-11-17T05:58:24.303783+00:00 | 2019-11-17T05:58:24.303828+00:00 | 781 | false | ```\npublic int findPairs(int[] nums, int k) {\n\tif(nums == null || nums.length == 0 || k<0) return 0;\n\tint count = 0;\n\tHashMap<Integer, Integer> hm = new HashMap<>();\n\tfor(int num : nums) \n\t\thm.put(num, hm.getOrDefault(num, 0)+1);\n\tfor(Map.Entry<Integer, Integer> e : hm.entrySet())\n\t\tif(k==0 && e.getValue()>=2) count++;\n\t\telse if(k!=0 && hm.containsKey(e.getKey()+k)) count++;\n\treturn count;\n}\n``` | 9 | 0 | [] | 0 |
k-diff-pairs-in-an-array | Java, O(n), sets, clean, 7 ms | java-on-sets-clean-7-ms-by-gthor10-bum1 | This problem has two main cases - when k == 0 and all others. The idea is - for number n if there is n + k in the array - pair is possible. We add all numbers f | gthor10 | NORMAL | 2019-09-16T03:33:24.765518+00:00 | 2019-09-16T03:33:24.765565+00:00 | 1,367 | false | This problem has two main cases - when k == 0 and all others. The idea is - for number n if there is n + k in the array - pair is possible. We add all numbers from array to the set, then check for n + k. For k == 0 we need to count how many unqiue numbers repeated 2+ times. For that I use second set - add number that we met for the second time to that second set, then size of that second set will be the result.\n\nO(n) for time - 2 linear scans of the array. O(n) for space - need to store numbers to the set.\n\n```\n public int findPairs(int[] nums, int k) {\n if (k < 0)\n return 0;\n int res = 0;\n Set<Integer> set = new HashSet();\n //if k == 0 we need to count only repeated nums\n //for that we need second set that indicats which num we have\n //count already\n if (k == 0 ) {\n Set<Integer> seen = new HashSet();\n for (int n : nums) {\n //if we met this num before - add it to the second set\n if (set.contains(n)) {\n seen.add(n);\n } else\n set.add(n);\n }\n //size of second set will be the resulting num\n res = seen.size();\n } else {\n //for k > 0 we check if n + k is in the set, this means we have a pair\n for (int n : nums) {\n set.add(n);\n }\n\n for (int n : set) {\n if (set.contains(n + k))\n res++;\n }\n }\n return res;\n }\n``` | 9 | 0 | ['Java'] | 2 |
k-diff-pairs-in-an-array | Using HashMap | Java Code with explaination | using-hashmap-java-code-with-explainatio-faem | If you find it useful do upvote\n\nclass Solution {\n public int findPairs(int[] nums, int k) {\n \n Map<Integer, Integer> map = new HashMap<>( | rizon__kumar | NORMAL | 2022-02-09T05:44:57.685225+00:00 | 2022-02-09T05:45:21.283112+00:00 | 397 | false | If you find it useful do upvote\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n \n Map<Integer, Integer> map = new HashMap<>();\n for(int i = 0; i < nums.length; i++){\n if(map.containsKey(nums[i])){\n // the array element and increament the frequence by 1\n map.put(nums[i], map.get(nums[i]) + 1);\n } else {\n // keep the frequene of current element as 1\n map.put(nums[i], 1);\n }\n }\n int count = 0;\n //create key set\n Set<Integer> set = map.keySet();\n for(int num: set){\n //first check\n if(k > 0 &&map.containsKey(num + k)){\n count++;\n }\n // second check\n if(k==0 && map.get(num) > 1){\n count++;\n }\n }\n return count;\n }\n}\n```\n\n```\nTime Complexity : O(N)\nSpace Complexity : O(N)\n```\n\n**NOTES**\n[(https://github.com/rizonkumar/LeetCode-Notes/blob/bb59b2137e810d07dd1f91470e31e4842bf70fa4/532.pdf)] | 8 | 0 | [] | 1 |
k-diff-pairs-in-an-array | C++ O(n) one pass with unordered_map | c-on-one-pass-with-unordered_map-by-jell-dgfo | ```\nint findPairs(vector& nums, int k) {\n unordered_map mp;\n int ans = 0;\n if(k < 0) return 0;\n for(int num:nums){\n | jellyzhang | NORMAL | 2020-02-24T09:34:58.607799+00:00 | 2020-02-24T09:35:15.462376+00:00 | 568 | false | ```\nint findPairs(vector<int>& nums, int k) {\n unordered_map<int,int> mp;\n int ans = 0;\n if(k < 0) return 0;\n for(int num:nums){\n if(k == 0 && mp[num] == 1){\n ans++;\n }else if(k > 0 && mp[num] == 0){\n ans += mp.count(num - k) + mp.count(num + k);\n }\n mp[num]++;\n }\n return ans;\n \n } | 8 | 0 | ['C++'] | 1 |
k-diff-pairs-in-an-array | Java two pointer solution beats 97% | java-two-pointer-solution-beats-97-by-no-zqtv | The idea is simple. Sort the array first. Then for each number in the array, find if there exists a number satisfy the requirement. Note that right = Math.max(r | notarealname | NORMAL | 2017-04-06T05:31:05.548000+00:00 | 2017-04-06T05:31:05.548000+00:00 | 1,156 | false | The idea is simple. Sort the array first. Then for each number in the array, find if there exists a number satisfy the requirement. Note that ```right = Math.max(right, i + 1)``` can make sure each number in the array is accessed at most twice. So the time complexity is O(nlogn) + O(n) = O(nlogn)\n```\npublic int findPairs(int[] nums, int k) {\n if (nums.length < 2 || k < 0) {\n return 0;\n }\n int count = 0;\n Arrays.sort(nums);\n int right = 0;\n for (int i = 0; i < nums.length; i++) {\n if (i > 0 && nums[i] == nums[i - 1]) {\n continue;\n }\n \n right = Math.max(right, i + 1);\n while (right < nums.length) {\n if (nums[right] - k == nums[i]) {\n count++;\n break;\n } else if (nums[right] - k < nums[i]) {\n right++;\n } else {\n break;\n }\n }\n }\n return count;\n}\n``` | 8 | 0 | [] | 1 |
k-diff-pairs-in-an-array | Easy | Commented | JavaScript hashmap | O(n) solution | easy-commented-javascript-hashmap-on-sol-ecjo | \nvar findPairs = function (nums, k) {\n\tlet map = {}, //Object to store count/frequency of numbers in array\n\t\tcount = 0; //count the desired output/result\ | _kapi1 | NORMAL | 2022-02-09T03:35:24.413155+00:00 | 2022-02-09T03:35:53.126643+00:00 | 1,086 | false | ```\nvar findPairs = function (nums, k) {\n\tlet map = {}, //Object to store count/frequency of numbers in array\n\t\tcount = 0; //count the desired output/result\n\n\t//loop through the array and store the count/frequency in the object\n\tfor (let i = 0; i < nums.length; i++) {\n\t\t/*if num appears for the 1st time them map[nums[i]] will be undefined\n\tand undefined||0 will result in 0 and 0+1 will store 1 as count of that number */\n\t\tmap[nums[i]] = (map[nums[i]] || 0) + 1;\n\t}\n\n\t//loop through keys.In this case keys will be unique as they have the frequency of their occurrences\n\tObject.keys(map).forEach((key) => {\n\t\t/* Now we need to check if target k is 0 or not \n\t\tbecause in case k is 0 then only possible combination to get \n\t\tdifference 0 will be when same num appear twice i.e \n\t\t1-1=0 ,here 1 count has to be 2 in map to get diff 0\n\t\t*/\n\t\tif (k !== 0) {\n\t\t\t/* \n\t\t\tit is given that |a-b|=k\n\t\t\tso a=k+b i.e secondNum=k+key\n\t\t\tSince object stores key as string so we have to typecast it to integer\n\t\t\tand +k is shorthand of parseInt(k)\n\t\t\tso we can write parseInt(k)+parseInt(key) as\n\t\t\t+k + +key (make sure there is space between +/add operator)\n\t\t\t*/\n\t\t\tlet secondNum = +k + +key;\n\t\t\tif (map[secondNum] !== undefined) {\n\t\t\t\tcount++;\n\t\t\t}\n\t\t} else {\n\t\t\t/*So when k is 0 we check is num count is greater or equal\n\t\t\t to 2 because then only we will get difference of these two as 0\n\t\t\t */\n\t\t\tif (map[key] >= 2) count++;\n\t\t}\n\t});\n\treturn count;\n};\n``` | 7 | 0 | ['JavaScript'] | 0 |
k-diff-pairs-in-an-array | Simple java O(n) solution with explaination | simple-java-on-solution-with-explainatio-ct7b | \npublic int findPairs(int[] nums, int k) {\n HashMap<Integer,Integer> map = new HashMap<>();\n int res=0;\n //storing count of all the ele | sameep0108 | NORMAL | 2020-10-08T04:24:13.223834+00:00 | 2020-10-08T04:24:13.223863+00:00 | 1,087 | false | ``` \npublic int findPairs(int[] nums, int k) {\n HashMap<Integer,Integer> map = new HashMap<>();\n int res=0;\n //storing count of all the elements\n for(int i:nums){\n map.put(i,map.getOrDefault(i,0)+1);\n }\n for(int a:map.keySet()){\n if(k!=0){\n //we avoid duplicate by looking for the values (i,j) where i is smaller element eg k=4 (1,3) & (3,1) gives same result but when we are processing 1 we are lloking fr val greater than 1 to form the pair and likewise when we are at 3we are looking for val 3 and above to form the pair\n int b=a+k;\n if(map.containsKey(b)){\n res++;\n }\n }else{\n //processing the key so processing unique values which is occuring twice and diff of it gives 0\n if(map.get(a)>=2)\n res++;\n }\n }\n return res;\n }\n\t``` | 7 | 0 | ['Java'] | 1 |
k-diff-pairs-in-an-array | K diff Pairs | C++ 6 liner solution with explanation | O(nlogn) time | O(1) space | k-diff-pairs-c-6-liner-solution-with-exp-za0h | Upvote this post, if you liked it. Happy Coding :)\n\nApproach : \n1) Sort the nums array.\n2) Loop over the nums array using iterator\n\ta) maintain the previ | sarthakjain1147 | NORMAL | 2020-10-03T16:55:11.650836+00:00 | 2020-10-03T18:35:19.230574+00:00 | 471 | false | <b> Upvote this post, if you liked it. Happy Coding :)</b>\n\nApproach : \n1) Sort the nums array.\n2) Loop over the nums array using iterator\n\ta) maintain the previous value so that we can jump over duplicate values, to make sure that only unique pairs will be counted.\n\tb) perform binary search on elements from the next element (current\'s next element) to last element, to find the value\n\t\twhich can satisfy the pair cond.\n3) return count\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n int prev_val, count = 0;\n sort(nums.begin(), nums.end());\n for(auto it = nums.begin(); it != nums.end(); it++) {\n if(it != nums.begin() and *it == prev_val) continue;\n if(binary_search(it+1, nums.end(), *it + k)) count++;\n prev_val = *it;\n }\n return count;\n }\n};\n```\n\n**I Hope you understood the solution, if you have any doubts regarding the solution or any suggestions to improve the solution,** then feel free to comment down below. | 7 | 1 | [] | 3 |
k-diff-pairs-in-an-array | C++ Solution | One-Pass | Beats 100% | Two-Pointer Approach | c-solution-one-pass-beats-100-two-pointe-so3k | Sort the vector.\nHere 3 cases arise : \n Case - 1 : When nums[j] - nums[i] > k\n\tThe difference between element at j and element at i is greater than required | pikabu | NORMAL | 2020-10-03T09:43:52.626523+00:00 | 2020-10-03T09:43:52.626554+00:00 | 751 | false | Sort the vector.\nHere 3 cases arise : \n* **Case - 1 : When nums[j] - nums[i] > k**\n\tThe difference between element at j and element at i is greater than required, so to reduce it increment i.\n* **Case - 2 : When nums[j] - nums[i] < k**\n\tThe difference between element at j and element at i is lesser than required, so to increase it increment j.\n* **Case - 3 : When nums[j] - nums[i] == k**\n\t Required pair found. Increment ans, and skip similar elements for both i and j.\n\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n \n sort(nums.begin(),nums.end());\n int ans = 0;\n int n = nums.size();\n int i = 0, j = 1;\n while(i<n && j<n){\n if(nums[j] - nums[i] == k && i!=j){\n while(i+1 < n && nums[i+1] == nums[i])\n i++;\n i++;\n while(j+1<n && nums[j+1] == nums[j])\n j++;\n j++;\n ans++;\n }\n else if(nums[j] - nums[i] > k){\n i++;\n }\n else{\n j++;\n }\n }\n return ans;\n }\n};\n``` | 7 | 1 | ['C'] | 3 |
k-diff-pairs-in-an-array | Easy to understand 2 pointer / sliding window approach in python O(1) space, O(nlogn) time | easy-to-understand-2-pointer-sliding-win-dcds | \n def findPairs(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: int\n """\n count = 0\n | leetcoder89 | NORMAL | 2018-07-16T00:43:01.344647+00:00 | 2018-07-16T00:43:01.344647+00:00 | 672 | false | ```\n def findPairs(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: int\n """\n count = 0\n nums.sort()\n \n slow = 0\n fast = 1\n size = len(nums)\n \n while fast < size:\n if nums[fast] - nums[slow] < k: # case 1, diff is less than k\n fast += 1\n elif nums[fast] - nums[slow] > k: # case 2, diff is greater than k\n slow += 1\n else: # case 3, diff is equal to k so increment the count!\n count += 1\n fast += 1\n slow += 1\n \n #Now ignore any duplicates, both slow and fast could be pointing to duplicates\n while slow < size-1 and nums[slow] == nums[slow-1]:\n slow += 1\n \n while fast < size-1 and nums[fast] == nums[fast-1]:\n fast += 1\n \n if fast <= slow: # fast should be atleast one more than slow\n fast = slow + (slow - fast) + 1\n \n return count\n\t\t\t\t\n``` | 7 | 0 | [] | 0 |
k-diff-pairs-in-an-array | Simple Java O(n) with single For-loop & single HashMap | simple-java-on-with-single-for-loop-sing-7xth | Solved it by One For-loop and One HashMap\n```\npublic int findPairs(int[] nums, int k) {\n if(k < 0) return 0;\n Map map = new HashMap();\n int ret = | luckman | NORMAL | 2017-04-24T23:56:32.812000+00:00 | 2018-09-30T00:13:37.001005+00:00 | 1,364 | false | Solved it by One For-loop and One HashMap\n```\npublic int findPairs(int[] nums, int k) {\n if(k < 0) return 0;\n Map<Integer, Boolean> map = new HashMap<Integer, Boolean>();\n int ret = 0;\n for(int n : nums){\n /* if smaller matched value exists */\n if(map.containsKey(n-k) && !map.get(n-k)){\n map.put(n-k,true);\n ret++;\n }\n /* if larger matched value exists */\n if(map.containsKey(n+k) && (!map.containsKey(n) || !map.get(n))){\n map.put(n, true);\n ret++;\n }\n /* if current value has not yet been added*/\n if(!map.containsKey(n)){\n map.put(n, false);\n }\n }\n return ret;\n}\n```` | 7 | 0 | [] | 0 |
k-diff-pairs-in-an-array | c++ using map easy soln | c-using-map-easy-soln-by-klaus04-i0um | \nclass Solution {\npublic:\n int findPairs(vector& nums, int k) {\n \n int n = nums.size();\n mapm; \n for(int i = 0;i1){\ | klaus04 | NORMAL | 2022-02-09T05:13:50.798632+00:00 | 2022-02-09T05:13:50.798681+00:00 | 117 | false | \nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n \n int n = nums.size();\n map<int,int>m; \n for(int i = 0;i<n;i++)\n {\n m[nums[i]]++;\n }\n int sum = 0; \n if(k == 0){\n for(auto i:m){\n if(i.second>1){\n sum++;\n }\n }\n }\n else{\n for(auto i:m){\n if( m.count(i.first + k))\n //if(m.find(i.first + k)!=m.end()) \n {\n sum++;\n }\n }\n }\n return sum;\n \n }\n}; | 6 | 0 | [] | 0 |
k-diff-pairs-in-an-array | Python O(n) solution using hashmap | python-on-solution-using-hashmap-by-bth3-w2sa | ```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n \n hashNums={}\n pairs=set()\n \n for n in n | BTh3 | NORMAL | 2022-02-09T00:33:23.098876+00:00 | 2022-02-09T00:33:23.098908+00:00 | 676 | false | ```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n \n hashNums={}\n pairs=set()\n \n for n in nums: # O(n)\n hashNums[n]=hashNums.get(n,0)+1\n \n if n-k in hashNums:\n pairs.add(tuple(set([n,n-k])))\n \n if n+k in hashNums:\n pairs.add(tuple(set([n,n+k])))\n \n if k==0: # O(n)\n ct=0\n for n,f in hashNums.items():\n ct+=(f>=2)\n return ct\n \n return len(pairs) | 6 | 1 | [] | 0 |
k-diff-pairs-in-an-array | c++ || O(n) - hashing | c-on-hashing-by-wienczyslaw-jtq9 | ```\nclass Solution {\npublic:\n int findPairs(vector& nums, int k) {\n \n unordered_map hash;\n for(int i=0;i1) \n c | wienczyslaw | NORMAL | 2022-02-05T16:13:52.931817+00:00 | 2022-02-05T16:13:52.931853+00:00 | 568 | false | ```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n \n unordered_map<int,int> hash;\n for(int i=0;i<nums.size();i++) hash[nums[i]]++;\n \n int count =0; \n \n for(auto i: hash){\n if(k==0) {\n if(i.second>1) \n count++;\n }\n \n else {\n if (hash.find(i.first - k) != hash.end()) \n count++;\n }\n }\n \n return count;\n \n }\n};\n | 6 | 0 | ['C', 'C++'] | 0 |
k-diff-pairs-in-an-array | Python faster than 93% | python-faster-than-93-by-dh7-ain7 | \nclass Solution:\n def findPairs(self, a: List[int], K: int) -> int:\n s = set(a)\n if K == 0: return sum(1 for x in s if a.count(x) > 1)\n | dh7 | NORMAL | 2020-10-28T20:57:57.413581+00:00 | 2020-10-28T20:57:57.413616+00:00 | 645 | false | ```\nclass Solution:\n def findPairs(self, a: List[int], K: int) -> int:\n s = set(a)\n if K == 0: return sum(1 for x in s if a.count(x) > 1)\n return sum(1 for x in s if x + K in s)\n``` | 6 | 2 | ['Python'] | 1 |
k-diff-pairs-in-an-array | C : 4-lines - simple n short - no built-in Utils/Data Structures, etc | c-4-lines-simple-n-short-no-built-in-uti-l53j | \nint findPairs(int* nums, int numsSize, int k){\n char a[200000] = { 0 }, *m = &a[500];\n for (int i = 0, c = 0, *n = nums ; i < numsSize || (numsSize = | universalcoder12 | NORMAL | 2020-08-27T16:54:04.912456+00:00 | 2020-08-27T21:45:12.268952+00:00 | 355 | false | ```\nint findPairs(int* nums, int numsSize, int k){\n char a[200000] = { 0 }, *m = &a[500];\n for (int i = 0, c = 0, *n = nums ; i < numsSize || (numsSize = c, 0) ; i++)\n for (int j = i, p ; ++j < numsSize ; abs(n[i] - n[j]) == k && !m[p = n[i] + n[j]] ? c += m[p] = 1 : 0);\n return numsSize;\n}\n``` | 6 | 1 | ['C'] | 0 |
k-diff-pairs-in-an-array | 532: Solution with step by step explanation | 532-solution-with-step-by-step-explanati-zy6t | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. First, check if k is less than 0, if yes then return 0.\n2. Create a h | Marlen09 | NORMAL | 2023-03-13T16:49:21.050159+00:00 | 2023-03-13T16:49:21.050201+00:00 | 1,941 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. First, check if k is less than 0, if yes then return 0.\n2. Create a hash table freq to store the frequency of each number in the array.\n3. Iterate through the array nums and for each number, update its frequency in the hash table freq.\n4. Initialize a variable count to 0 to store the count of unique pairs.\n5. Iterate through the keys in the hash table freq and check for each key if there exists a pair with difference k in the hash table.\n6. If k is 0, then increment the count only if the frequency of the number is greater than 1.\n7. If k is not 0, then check if num + k exists in the hash table. If yes, then increment the count.\n8. Return the count of unique pairs.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n if k < 0:\n return 0\n \n # initialize hash table\n freq = {}\n for num in nums:\n freq[num] = freq.get(num, 0) + 1\n \n # iterate through array and find pairs\n count = 0\n for num in freq:\n if k == 0:\n if freq[num] > 1:\n count += 1\n else:\n if num + k in freq:\n count += 1\n \n # return count of unique pairs\n return count\n\n``` | 5 | 0 | ['Array', 'Hash Table', 'Two Pointers', 'Python', 'Python3'] | 1 |
k-diff-pairs-in-an-array | Python 7-line Super Simple and Short Solution | python-7-line-super-simple-and-short-sol-bqk8 | \nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n if (k == 0):\n return len([item for item, count in collections.C | yehudisk | NORMAL | 2021-01-05T19:22:17.183198+00:00 | 2021-01-05T19:22:17.183243+00:00 | 466 | false | ```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n if (k == 0):\n return len([item for item, count in collections.Counter(nums).items() if count > 1])\n \n nums = set(nums)\n res = 0\n for n in nums:\n res += 1 if n-k in nums else 0\n return res\n```\n**Like it? please upvote...** | 5 | 1 | ['Python'] | 0 |
k-diff-pairs-in-an-array | Java O(n) solution with hashmap | java-on-solution-with-hashmap-by-user505-vnw9 | \nclass Solution {\n public int findPairs(int[] nums, int k) {\n int kDiffs = 0;\n Map<Integer, Integer> counter = new HashMap<>();\n \n | user5055f | NORMAL | 2020-10-06T12:31:01.995429+00:00 | 2020-10-06T12:31:01.995474+00:00 | 323 | false | ```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n int kDiffs = 0;\n Map<Integer, Integer> counter = new HashMap<>();\n \n for (int n: nums) {\n int countOfN = counter.getOrDefault(n, 0);\n countOfN++;\n counter.put(n, countOfN);\n \n if (k == 0) {\n if (countOfN == 2) kDiffs++;\n } else if (countOfN == 1) {\n if (counter.containsKey(n - k)) kDiffs++;\n if (counter.containsKey(n + k)) kDiffs++; \n }\n }\n \n return kDiffs;\n }\n}\n\n``` | 5 | 0 | [] | 2 |
k-diff-pairs-in-an-array | C++, self-explanatory one-pass O(n) use hash map | c-self-explanatory-one-pass-on-use-hash-lgefy | cpp\nint findPairs(vector<int>& nums, int k) {;\n unordered_map<int, int> freq;\n int ans = 0;\n for (int n : nums) {\n if (k == 0) {\n | alvin-777 | NORMAL | 2020-10-03T09:18:24.872048+00:00 | 2020-10-03T09:18:24.872081+00:00 | 532 | false | ```cpp\nint findPairs(vector<int>& nums, int k) {;\n unordered_map<int, int> freq;\n int ans = 0;\n for (int n : nums) {\n if (k == 0) {\n if (freq[n] == 1) ++ans; // only count once\n } else if (!freq.count(n)) { // only count when the first time n appears\n if (freq.count(n - k)) ++ans;\n if (freq.count(n + k)) ++ans;\n }\n ++freq[n];\n }\n return ans;\n}\n``` | 5 | 0 | ['C'] | 1 |
k-diff-pairs-in-an-array | [Python] really short and easy, explained | python-really-short-and-easy-explained-b-7gq9 | Let complementary number be a number that is equal to some given number minus k.\nTo form at least one pair for any given number:\n If k is greater than zero, | user9823 | NORMAL | 2020-10-03T08:09:18.559186+00:00 | 2020-10-03T09:50:44.827582+00:00 | 343 | false | Let complementary number be a number that is equal to some given number minus k.\nTo form at least one pair for any given number:\n If k is greater than zero, we only care if count of complementary number is bigger than zero.\n If k is zero, we only care if count of complementary number (that is the current number itself) is bigger than one.\n\nConveniently, both this cases can be expressed with k==0, that will return zero or one.\n\n```\ndef findPairs(self, nums: List[int], k: int) -> int:\n c = collections.Counter(nums)\n return sum(c[n-k] > (k == 0) for n in c)\n``` | 5 | 0 | [] | 1 |
k-diff-pairs-in-an-array | Java O(n) solution with comments | java-on-solution-with-comments-by-nishth-2l2i | class Solution {\n public int findPairs(int[] nums, int k) {\n \n int output=0;\n HashMap hm = new HashMap<>(); \n \n //Stor | nishtha_na | NORMAL | 2020-08-16T11:44:21.715676+00:00 | 2020-08-16T11:47:35.747003+00:00 | 417 | false | class Solution {\n public int findPairs(int[] nums, int k) {\n \n int output=0;\n HashMap <Integer,Integer> hm = new HashMap<>(); \n \n //Storing the frequencies in the hashmpap\n for(int num: nums)\n {\n hm.put(num, hm.getOrDefault(num,0)+1);\n }\n \n \n //Traversing the hashmap\n for (Map.Entry <Integer, Integer> entry: hm.entrySet()) \n {\n int elem = entry.getKey();\n int value = entry.getValue();\n \n \n // finding some other element (elem+ other element=k)\n if(k>0 && hm.containsKey(elem+k))\n output++;\n \n // The number can be paired with itself. Hence, the value should be >1. We don\'t care what value as long as the frequency is greater than one as the question says "k-diff pair".\n else if(k==0 && value >1)\n output++;\n \n }\n return output;\n }\n} | 5 | 0 | [] | 3 |
k-diff-pairs-in-an-array | Python, two pointer, O(nlogn) | python-two-pointer-onlogn-by-clarketm-27f6 | \ndef find_pairs(L: List[int], k: int) -> int:\n """\n K-diff Pairs in an Array\n\n time: O(nlogn)\n space: O(1)\n\n :param List[int] L:\n :pa | clarketm | NORMAL | 2020-04-18T08:06:51.451111+00:00 | 2020-04-18T08:07:43.491408+00:00 | 1,181 | false | ```\ndef find_pairs(L: List[int], k: int) -> int:\n """\n K-diff Pairs in an Array\n\n time: O(nlogn)\n space: O(1)\n\n :param List[int] L:\n :param int k:\n :return int:\n """\n L.sort()\n\n N = len(L)\n\n i = pairs = 0\n j = 1\n\n while j < N:\n if j < N - 1 and L[j] == L[j + 1]:\n j += 1\n\n elif L[j] == L[i] + k:\n pairs += 1\n i += 1\n j += 1\n\n elif L[j] > L[i] + k:\n i += 1\n\n elif L[j] < L[i] + k:\n j += 1\n\n j = max(j, i + 1)\n\n return pairs\n``` | 5 | 0 | ['Two Pointers', 'Python', 'Python3'] | 0 |
k-diff-pairs-in-an-array | JavaScript using object as map | javascript-using-object-as-map-by-shengd-i1qm | \n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar findPairs = function(nums, k) {\n if (!nums.length || k < 0) return 0;\n | shengdade | NORMAL | 2020-02-03T21:25:16.473244+00:00 | 2020-02-03T21:25:16.473277+00:00 | 857 | false | ```\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar findPairs = function(nums, k) {\n if (!nums.length || k < 0) return 0;\n const map = {};\n let counter = 0;\n nums.forEach(n => {\n map[n] = (map[n] || 0) + 1;\n });\n Object.keys(map).forEach(key => {\n if (k === 0) {\n if (map[key] > 1) counter++;\n } else if (map[parseInt(key) + k]) {\n counter++;\n }\n });\n return counter;\n};\n``` | 5 | 0 | ['JavaScript'] | 1 |
k-diff-pairs-in-an-array | 3 java solutions: 1.HashMap without sort; 2.HashMap + sort; 3. Sort + two points | 3-java-solutions-1hashmap-without-sort-2-63qt | HashMap without sort.\nWe define a hashMap. The key element denotes the members of the array. The value has 3 types:\nvalue 1: the key appears once in the array | miaoyao | NORMAL | 2019-12-31T03:33:25.568948+00:00 | 2019-12-31T03:35:52.088854+00:00 | 1,012 | false | 1. HashMap without sort.\nWe define a hashMap. The key element denotes the members of the array. The value has 3 types:\nvalue 1: the key appears once in the array\nvalue 2: the key appears more than once in the array\nvalue 0: the key has been used, this value is used to avoid duplicated pairs.\nWe use a for-loop to initial the hashMap. \nIf k == 0, we just calculate the number which appears more than once in array.\nif k != 0, each number adds k and subtracts k, then using the result to match the map. \n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n if(k<0)return 0;\n Map<Integer,Integer> map = new HashMap<>();\n for(int i = 0; i<nums.length; i++){\n if(map.containsKey(nums[i])){\n map.put(nums[i],2);\n }else{\n map.put(nums[i],1);\n }\n }\n int count = 0;\n if(k==0){\n for(int i = 0; i<nums.length; i++){\n if(map.containsKey(nums[i]) && map.get(nums[i]) > 1){\n count++;\n map.replace(nums[i],0);\n }\n }\n return count;\n }\n for(int i = 0; i<nums.length; i++){\n if(map.containsKey(nums[i] + k) && map.get(nums[i] + k) > 0 && map.get(nums[i]) > 0){\n count++;\n }\n if(map.containsKey(nums[i] - k) && map.get(nums[i] - k) > 0 && map.get(nums[i]) > 0){\n count++;\n }\n map.replace(nums[i],0);\n }\n return count;\n }\n}\n```\n\n2. HashMap + Sort\nThis solution is similar to the first solution. \nWe firstly sort the array, so we don\'t need to consider multiple situations(k==0 or k != 0 ; add or subtract). The sort reduces the complexity of this problem.\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n if(k < 0)return 0;\n Map<Integer, Boolean> map = new HashMap<>();\n int count = 0;\n Arrays.sort(nums);\n for(int i = 0; i < nums.length; i++){\n if(map.containsKey(nums[i]) && map.get(nums[i])){\n count++;\n map.replace(nums[i],false);\n }\n if(!map.containsKey(nums[i] + k)){\n map.put(nums[i] + k, true);\n }\n }\n return count;\n }\n}\n```\n\n3.Sort + Two Points:\nThis solution is based on the ordering of the array.\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n if(k < 0) return 0;\n Arrays.sort(nums);\n int left = 0, right = 1, count = 0;\n while(right < nums.length){\n if(nums[right] - nums[left] > k){\n left++;\n }else if(nums[right] - nums[left] < k || right == left){\n right++;\n }else{\n count++;\n left++;\n right++;\n while(right < nums.length && nums[right] == nums[right - 1]) right++;\n }\n }\n return count;\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
k-diff-pairs-in-an-array | 7 Lines O(n) Python3 (fast and clear and easy understand) | 7-lines-on-python3-fast-and-clear-and-ea-9n7w | make a dictory,and then when k>0 and k==0, we add res :\npython\n def findPairs(self, nums, k):\n\t\tnums.sort()\n res , dic= 0 , {}\n for i in n | macqueen | NORMAL | 2019-10-26T08:48:46.287054+00:00 | 2019-10-26T08:58:09.052157+00:00 | 633 | false | make a dictory,and then when k>0 and k==0, we add res :\n```python\n def findPairs(self, nums, k):\n\t\tnums.sort()\n res , dic= 0 , {}\n for i in nums:\n dic[i] = dic[i]+1 if i in dic else 1\n for i in dic.keys():\n if (i+k in dic and k>0) or (k==0 and dic[i]>1):\n res += 1\n return res \n```\n\nIf this code is not bad , welcome give me a star ,Thanks | 5 | 0 | ['Python3'] | 1 |
k-diff-pairs-in-an-array | Easy to Understand Python Solution using hashmap | easy-to-understand-python-solution-using-hugf | \n def findPairs(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: int\n """\n if k < 0:\n | pgonarkar | NORMAL | 2019-01-30T01:57:53.961368+00:00 | 2019-01-30T01:57:53.961458+00:00 | 416 | false | ```\n def findPairs(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: int\n """\n if k < 0:\n return 0\n hashmap = {}\n count = 0\n for num in nums:\n # check num + k and num - k present in hashmap\n if num not in hashmap: \n if num + k in hashmap:\n count += 1\n if num - k in hashmap:\n count += 1\n hashmap[num] = 1\n else:\n # handling k == 0 condition with by restricting occurances to 1\n if k == 0 and hashmap[num] == 1:\n count += 1\n hashmap[num] += 1\n \n return count\n``` | 5 | 0 | [] | 0 |
k-diff-pairs-in-an-array | Simple Idea O(nlogn) time + O(1) space Java Solution | simple-idea-onlogn-time-o1-space-java-so-ih8m | guess this solution is intuitive.\n\npublic class Solution {\n public int findPairs(int[] nums, int k) {\n if (nums == null || nums.length < 2) return | shevchenko_7 | NORMAL | 2017-03-06T07:40:23.698000+00:00 | 2017-03-06T07:40:23.698000+00:00 | 844 | false | guess this solution is intuitive.\n```\npublic class Solution {\n public int findPairs(int[] nums, int k) {\n if (nums == null || nums.length < 2) return 0;\n int res = 0;\n Arrays.sort(nums);\n for (int i = 0; i < nums.length; i++) {\n if (i > 0 && nums[i] == nums[i - 1]) continue;\n if (helper(nums, i + 1, nums[i] + k)) res++;\n }\n return res;\n }\n private boolean helper(int[] nums, int l, int target) {\n int r = nums.length - 1;\n while (l <= r) {\n int mid = l + (r - l) / 2;\n if (nums[mid] == target) return true;\n if (nums[mid] < target) l = mid + 1;\n else r = mid - 1;\n }\n return false;\n }\n}\n``` | 5 | 0 | [] | 1 |
k-diff-pairs-in-an-array | Short Java Solution, but two HashSets | short-java-solution-but-two-hashsets-by-tgmxi | \npublic class Solution {\n public int findPairs(int[] nums, int k) {\n Arrays.sort(nums);\n Set<Integer> seenNum = new HashSet<>();\n S | shawngao | NORMAL | 2017-03-05T04:15:53.132000+00:00 | 2018-08-19T03:13:39.474564+00:00 | 1,186 | false | ```\npublic class Solution {\n public int findPairs(int[] nums, int k) {\n Arrays.sort(nums);\n Set<Integer> seenNum = new HashSet<>();\n Set<String> seenPair = new HashSet<>();\n int result = 0;\n \n for (int i = 0; i < nums.length; i++) {\n int prev = nums[i] - k;\n if (seenNum.contains(prev) && !seenPair.contains(prev + "," + nums[i])) {\n result++;\n seenPair.add(prev + "," + nums[i]);\n }\n seenNum.add(nums[i]);\n }\n return result;\n }\n}\n``` | 5 | 1 | [] | 1 |
k-diff-pairs-in-an-array | Fastest and Easiest Solution | fastest-and-easiest-solution-by-sbt1999-yhvp | \n# Approach\nInitialization:\n\nseen = {} (an empty HashSet to keep track of numbers we\'ve seen so far)\nuniquePairs = {} (an empty HashSet to store the first | Sbt1999 | NORMAL | 2024-05-25T06:12:45.696647+00:00 | 2024-05-25T06:12:45.696681+00:00 | 721 | false | \n# Approach\nInitialization:\n\nseen = {} (an empty HashSet to keep track of numbers we\'ve seen so far)\nuniquePairs = {} (an empty HashSet to store the first element of each unique pair)\n\n**Iteration 1:**\n\nCurrent number: 3\n\n Check if 3 - 2 = 1 is in seen: false\n Check if 3 + 2 = 5 is in seen: false\n Add 3 to seen: seen = {3}\n\n**Iteration 2:**\n\nCurrent number: 1\n\n Check if 1 - 2 = -1 is in seen: false\n Check if 1 + 2 = 3 is in seen: true\n Add 1 to uniquePairs: uniquePairs = {1}\n Add 1 to seen: seen = {1, 3}\n\n**Iteration 3:**\n\nCurrent number: 4\n\n Check if 4 - 2 = 2 is in seen: false\n Check if 4 + 2 = 6 is in seen: false\n Add 4 to seen: seen = {1, 3, 4}\n\n**Iteration 4:**\n\nCurrent number: 1\n\n Check if 1 - 2 = -1 is in seen: false\n Check if 1 + 2 = 3 is in seen: true\n 1 is already in uniquePairs, so no change.\n Add 1 to seen: seen = {1, 3, 4} (no change as 1 is already present)\n\n\n**Iteration 5:**\n\nCurrent number: 5\n\n Check if 5 - 2 = 3 is in seen: true\n Add 3 to uniquePairs: uniquePairs = {1, 3}\n Check if 5 + 2 = 7 is in seen: false\n Add 5 to seen: seen = {1, 3, 4, 5}\n\n**Final Step:**\n\nThe size of uniquePairs is 2.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n \n if (k < 0) {\n return 0; // Since k is the absolute difference, it can\'t be negative\n }\n\n HashSet<Integer> seen = new HashSet<>();\n HashSet<Integer> uniquePairs = new HashSet<>();\n\n for (int num : nums) {\n if (seen.contains(num - k)) {\n uniquePairs.add(num - k);\n }\n if (seen.contains(num + k)) {\n uniquePairs.add(num);\n }\n seen.add(num);\n }\n\n return uniquePairs.size();\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
k-diff-pairs-in-an-array | Java || very easy || Explanation || Hashmap | java-very-easy-explanation-hashmap-by-ha-aywv | Intuition\nVery easy approach to solve the problem with the help of single loop and hashmap\n\n# Approach\n\n initiate a Map \n enter all elements and its frequ | harshverma2702 | NORMAL | 2023-03-22T18:59:58.490723+00:00 | 2023-03-22T18:59:58.490761+00:00 | 1,312 | false | # Intuition\nVery easy approach to solve the problem with the help of single loop and hashmap\n\n# Approach\n\n* initiate a Map \n* enter all elements and its frequency\n* inside of entry loop of map ,check\n1. if k==0 , it means any element which is occuring more then twice will always have diff ==0 , ex- 1-1=0 , 15-15 =0 ...\n2. else if map contains element + k , then pair++ \n\n# Complexity\n- Time complexity:\no(n)\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n int n =nums.length;\n HashMap<Integer,Integer> map = new HashMap<>();\n for(int i =0;i<n;i++){\n if(map.containsKey(nums[i]))\n map.put(nums[i],map.get(nums[i])+1);\n else\n map.put(nums[i],1);\n }\n int count =0;\n\n for(Map.Entry<Integer,Integer> entry : map.entrySet()){\n int val = entry.getValue();\n int key = entry.getKey();\n\n if(k==0){\n if(val>=2)\n count++;\n }\n\n else if(map.containsKey(key+k))\n count++;\n } \n return count;\n }\n}\n | 4 | 0 | ['Java'] | 0 |
k-diff-pairs-in-an-array | C++ Two-Pointer - T(NlogN) and HashMap - T(N) | c-two-pointer-tnlogn-and-hashmap-tn-by-a-syg7 | TWO-POINTER APPROACH T(NLogN)\n\n1. The approach that I used here is similar to two-sum problem.\n2. In two-sum we select two numbers that sums-up to k, whereas | akshatchaturvedi17 | NORMAL | 2022-02-09T10:20:18.397971+00:00 | 2022-02-09T10:37:20.946878+00:00 | 511 | false | **TWO-POINTER APPROACH T(NLogN)**\n\n1. The approach that I used here is similar to two-sum problem.\n2. In two-sum we select two numbers that sums-up to k, whereas here we have to select two numbers with difference k.\n3. I have used two pointers i & j, in two-sum the we start i from 0 and j from n-1, but here we\'ll start i from 0 and j from 1 because at this point the difference will be minimum b/w nums[i] and nums[j].\n\n**CODE**\n```\nint findPairs(vector<int>& nums, int k) {\n int n = nums.size();\n sort(nums.begin(), nums.end());\n int i=0, j=1, count=0;\n while(j<n){\n if(i==j) j++;\n if(j>n-1) break;\n if(nums[i]+k == nums[j]){\n count++;\n while(j<n and nums[i]+k == nums[j]) j++;\n }else if(nums[i]+k < nums[j]){\n i++;\n }else{\n j++;\n }\n }\n return count;\n }\n```\n\n**HASHMAP APPROACH T(N)**\n\n**CODE**\n```\nint findPairs(vector<int>& nums, int k) {\n unordered_map<int, int> m;\n int c=0;\n for(auto i: nums) m[i]++;\n \n for(int i=0; i<nums.size(); i++){\n if(k!=0){\n if(m[k+nums[i]]>0){\n c++;\n m[k+nums[i]]=0;\n }\n }else{\n if(m[nums[i]]>1) c++;\n m[nums[i]]=0;\n }\n }\n return c;\n }\n``` | 4 | 0 | ['Two Pointers', 'C'] | 0 |
k-diff-pairs-in-an-array | C++ || Simple & Easy Solution|| O(n) || Hashmap | c-simple-easy-solution-on-hashmap-by-nab-h2fa | \n\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n int count =0;\n unordered_map<int,int> mp;\n \n for(i | nabil_jahan | NORMAL | 2022-02-09T04:49:28.364205+00:00 | 2022-03-21T19:53:46.632197+00:00 | 337 | false | \n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n int count =0;\n unordered_map<int,int> mp;\n \n for(int i=0;i<nums.size();i++) mp[nums[i]]++; \n for(auto i: mp){\n if(k==0) {\n if(i.second>1) \n count++;\n }\n else {\n if (mp.find(i.first - k) != mp.end()) \n count++;\n }\n }\n return count;\n \n }\n};\n``` | 4 | 0 | ['C', 'C++'] | 0 |
k-diff-pairs-in-an-array | 💚[C++] 95% Fast and Easy Solution Explained | HASHMAP | c-95-fast-and-easy-solution-explained-ha-7w39 | Welcome to abivilion\'s solution. Kindly Upvote for supporting this article.\n\nSOLUTION\nTC - O(n)\nSC - O(N)\n\n\nclass Solution {\npublic:\n int findPairs | abivilion | NORMAL | 2022-02-09T01:47:08.747598+00:00 | 2022-02-09T01:47:08.747630+00:00 | 555 | false | **Welcome to abivilion\'s solution. Kindly Upvote for supporting this article.**\n\n**SOLUTION**\n**TC - O(n)**\n**SC - O(N)**\n\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n \n unordered_map<int,int>st;\n int count=0;\n \n\t\t//storing in map\n for(auto &it:nums)\n st[it]++;\n\n // if k is 0, then which element FREQUENCY >1 can give 0\n if(k==0) \n {\n for(auto &ko:st) if(ko.second>1) count++;\n \n }\n\n // if k is any other number then ,difference can currentnum+k is present then the pair can give k as a resultant\n // a-b = c\n // a= c+b\n // b =c-a\n else\n for(auto &ki:st)\n {\n if(st.count(ki.first+k)) count++;\n }\n \n return count;\n }\n};\n``` | 4 | 0 | ['C', 'C++'] | 0 |
k-diff-pairs-in-an-array | Binary Search solution [Java] | binary-search-solution-java-by-vaidehi21-o8q0 | \nclass Solution {\n public int findPairs(int[] nums, int k) {\n Arrays.sort(nums);\n int count=0;\n for(int i=0;i<nums.length;i++)\n | vaidehi21 | NORMAL | 2020-10-03T16:18:09.395133+00:00 | 2020-10-03T16:18:09.395166+00:00 | 403 | false | ```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n Arrays.sort(nums);\n int count=0;\n for(int i=0;i<nums.length;i++)\n { \n int low=i+1;\n int high=nums.length-1;\n while(low<=high)\n {\n int mid=low+(high-low)/2;\n if(nums[mid]-nums[i]==k)\n {count++;\n break;\n }else if(nums[mid]-nums[i]>k)\n high=mid-1;\n else\n low=mid+1;\n }\n while(i!=nums.length-1 && nums[i+1]==nums[i])\n i++;\n }\n return count;\n }\n}\n``` | 4 | 0 | ['Binary Tree', 'Java'] | 0 |
k-diff-pairs-in-an-array | Java Soln | 1 pass | O(N)- time and space | java-soln-1-pass-on-time-and-space-by-ap-qq2a | \nclass Solution {\n public int findPairs(int[] nums, int k) {\n HashSet<Integer> set = new HashSet<>();\n\t\tint count = 0;\n\t\t\n\t\tHashSet<Intege | apex2911 | NORMAL | 2020-10-03T10:29:49.626353+00:00 | 2020-10-03T10:30:10.279457+00:00 | 290 | false | ```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n HashSet<Integer> set = new HashSet<>();\n\t\tint count = 0;\n\t\t\n\t\tHashSet<Integer> duplicateset = new HashSet<>();\n\t\t\n\t\t\n\t\tfor (int n : nums) {\n\t\t\tif (set.contains(n)) {\n\t\t\t\tif(k==0 && !duplicateset.contains(n)) {\n\t\t\t\t\tcount++;\n\t\t\t\t\tduplicateset.add(n);\n\t\t\t\t}\n\t\t\t}else {\n\t\t\t\t//check diff of that number exist to find pair. \n\t\t\t\t// It will not count (a,b) and (b,a) as 1 set of number is not added to set yet.\n\t\t\t\tif(k!=0 && set.contains(n-k)) {\n\t\t\t\t\tcount++;\n\t\t\t\t}\n\t\t\t\tif(k!=0 && set.contains(n+k)) {\n\t\t\t\t\tcount++;\n\t\t\t\t}\n\t\t\t\tset.add(n);\n\t\t\t}\n\t\t}\n\t\t\n\t\treturn count;\n }\n}\n``` | 4 | 0 | [] | 0 |
k-diff-pairs-in-an-array | Easy JS Solution | easy-js-solution-by-hbjorbj-t4zp | \nvar findPairs = function(nums, k) {\n if (k < 0) return 0; \n nums = (k === 0) ? nums : Array.from(new Set(nums));\n let m = new Map(), res = 0;\n | hbjorbj | NORMAL | 2020-09-05T13:17:24.019093+00:00 | 2020-09-05T14:18:44.919003+00:00 | 470 | false | ```\nvar findPairs = function(nums, k) {\n if (k < 0) return 0; \n nums = (k === 0) ? nums : Array.from(new Set(nums));\n let m = new Map(), res = 0;\n for (let num of nums) {\n if (m.get(num+k) === 1) res++;\n if (num+k !== num-k && m.get(num-k) === 1) res++;\n m.set(num, m.get(num)+1 || 1);\n }\n return res;\n};\n``` | 4 | 0 | ['JavaScript'] | 1 |
k-diff-pairs-in-an-array | O(N), very easy way by using hashset | on-very-easy-way-by-using-hashset-by-che-5ay2 | \tfrom typing import List\n\n\n\tclass Solution:\n\t\tdef findPairs(self, nums: List[int], k: int) -> int:\n\t\t\tif k < 0:\n\t\t\t\treturn 0\n\n\t\t\tsaw = set | chen_yiming | NORMAL | 2020-05-28T13:53:54.959435+00:00 | 2020-05-28T13:53:54.959485+00:00 | 579 | false | \tfrom typing import List\n\n\n\tclass Solution:\n\t\tdef findPairs(self, nums: List[int], k: int) -> int:\n\t\t\tif k < 0:\n\t\t\t\treturn 0\n\n\t\t\tsaw = set()\n\t\t\tpair = set()\n\n\t\t\tfor num in nums:\n\t\t\t\tif num + k in saw:\n\t\t\t\t\tpair.add((min(num + k, num), max(num + k, num)))\n\n\t\t\t\tif num - k in saw:\n\t\t\t\t\tpair.add((min(num - k, num), max(num - k, num)))\n\n\t\t\t\tsaw.add(num)\n\n\t\t\treturn len(pair)\n | 4 | 0 | ['Python3'] | 0 |
k-diff-pairs-in-an-array | python, reasonably fast (>99.4%), short and readable, explained, different options | python-reasonably-fast-994-short-and-rea-2vqz | Let\'s start with something easy to read:\n\n\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n r = 0\n if k >= 0:\n | rmoskalenko | NORMAL | 2020-03-05T22:40:34.051529+00:00 | 2020-03-06T01:36:18.250310+00:00 | 499 | false | Let\'s start with something easy to read:\n\n```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n r = 0\n if k >= 0:\n c = collections.Counter(nums)\n for i in c:\n if (k==0 and c[i]>1) or (k!=0 and i+k in c):\n r += 1\n return r\n```\n\nSo there are 3 things you need to take care of:\n\n1. The k value is the *absolute* difference, so it has to be a positive number, otherwise we return 0\n2. k==0. this is a special case. let\'s say we have [1,1,1,3,3,3,3,...] the 3x1 will produce 1 pair, 4x3 - another 1. So the logic is every non unique element adds a pair. That is a typical case where collections.Counter can be used.\n3. for all other numbers - we just need to check for every i if i+k is also present.\n\nSo now we are putting it all together.\n\nr is the return value set to 0. If k<0, we return it right away - this is the first case.\nnow we create `c = collections.Counter(nums)` and then as we go through the elements, we check for both cases: where k==0 is i is repeated or if k!=0 (we can use k>0 instead) and i+k is also in c.\n\nSo this program works just fine and it looks readable, but if you want to save a couple lines ... If you look at the main loop, it\'s a combination of a `for` and an `if` and it adds either 1 or nothing. So it could be a good case to use a comprehension instead:\n\n\n```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n c = collections.Counter(nums)\n return 0 if k<0 else sum([ 1 for i in c if (k==0 and c[i]>1) or (k!=0 and i+k in c) ])\n```\n\nThe logic is exactly the same, just different presentation.\n\nAnd if for some reason you don\'t want to use collections, you can replace it with:\n\n```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n #c = collections.Counter(nums) \n c={}\n for i in nums:\n c[i] = c.get(i, 0) + 1 \n return 0 if k<0 else sum([ 1 for i in c if (k==0 and c[i]>1) or (k!=0 and i+k in c) ])\n``` | 4 | 0 | [] | 0 |
k-diff-pairs-in-an-array | Python solution | python-solution-by-rogerfederer-4cuc | \nclass Solution(object):\n def findPairs(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: int\n """ | rogerfederer | NORMAL | 2018-07-04T18:30:02.858940+00:00 | 2018-07-04T18:30:02.858940+00:00 | 998 | false | ```\nclass Solution(object):\n def findPairs(self, nums, k):\n """\n :type nums: List[int]\n :type k: int\n :rtype: int\n """\n if k < 0:\n return 0\n res = 0\n counter = collections.Counter(nums)\n for key in counter:\n if k != 0:\n if key - k in counter:\n res += 1\n else:\n if counter[key] > 1:\n res += 1\n return res\n``` | 4 | 1 | [] | 0 |
k-diff-pairs-in-an-array | ✅3 Method || C++ || Beginner Friendly ||Beat 100% | 3-method-c-beginner-friendly-beat-100-by-dhlh | To solve the problem of finding all unique pairs in an integer array where each pair has a specific difference \( k \), there are several approaches, each with | BhavayGupta2002 | NORMAL | 2024-10-30T12:26:31.758746+00:00 | 2024-10-30T12:26:31.758782+00:00 | 331 | false | To solve the problem of finding all unique pairs in an integer array where each pair has a specific difference \\( k \\), there are several approaches, each with its own complexity and trade-offs. Here\u2019s an overview of the approaches, including the best one:\n\n### 1. **Brute Force Approach**\n- **Idea**: Check all possible pairs in the array and count those that satisfy the condition.\n- **Implementation**:\n ```cpp\n int findPairs(vector<int>& nums, int k) {\n int count = 0;\n int n = nums.size();\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n if (nums[j] - nums[i] == k) {\n count++;\n }\n }\n }\n return count;\n }\n ```\n- **Complexity**: \n - **Time Complexity**: \\( O(n^2) \\) (nested loops)\n - **Space Complexity**: \\( O(1) \\)\n- **Drawback**: Inefficient for large arrays due to quadratic time complexity.\n---\n\n### 2. **Sorting + Two Pointers Approach**\n- **Idea**: Sort the array and use a two-pointer technique to find pairs with the desired difference.\n- **Implementation**:\n ```cpp\n int findPairs(vector<int>& nums, int k) {\n sort(nums.begin(), nums.end());\n int count = 0;\n int n = nums.size();\n int i = 0, j = 1;\n\n while (i < n && j < n) {\n if (i != j && nums[j] - nums[i] == k) {\n count++;\n i++;\n j++;\n // Skip duplicates\n while (i < n && nums[i] == nums[i - 1]) i++;\n while (j < n && j < n && nums[j] == nums[j - 1]) j++;\n } else if (nums[j] - nums[i] < k) {\n j++;\n } else {\n i++;\n if (i == j) j++;\n }\n }\n return count;\n }\n ```\n- **Complexity**: \n - **Time Complexity**: \\( O(n log n) \\) (due to sorting) + \\( O(n) \\) (for the two-pointer traversal)\n - **Space Complexity**: \\( O(1) \\)\n- **Pros**: More efficient than brute force; handles duplicates well.\n- **Cons**: Sorting the array may not be necessary for all applications.\n- ---\n\n### 3. **Hash Set Approach (Optimal Approach)**\n- **Idea**: Use a hash set to track the numbers and count unique pairs with a specific difference.\n- **Implementation**:\n ```cpp\n int findPairs(vector<int>& nums, int k) {\n unordered_set<int> numSet;\n unordered_set<int> seenPairs;\n \n for (int num : nums) {\n numSet.insert(num);\n }\n \n for (int num : numSet) {\n if (numSet.count(num + k)) {\n seenPairs.insert(num);\n }\n }\n \n return seenPairs.size();\n }\n ```\n- **Complexity**: \n - **Time Complexity**: \\( O(n) \\)\n - **Space Complexity**: \\( O(n) \\) (to store unique numbers)\n- **Pros**: Efficient and straightforward; avoids issues with sorting and is easy to implement.\n- **Cons**: Uses additional space for the hash set, though it is considered constant space relative to input. | 3 | 1 | ['Array', 'Hash Table', 'Two Pointers', 'C++'] | 1 |
k-diff-pairs-in-an-array | Brute Force to Functional Programming | Multiple Approaches | brute-force-to-functional-programming-mu-13rx | Solution 1: Brute Force Approach\n\n### Intuition\n- The simplest approach is to check all possible pairs in the array and see if their absolute difference equa | lokeshwar777 | NORMAL | 2024-10-10T17:48:36.925572+00:00 | 2024-10-10T17:48:36.925605+00:00 | 265 | false | ## Solution 1: Brute Force Approach\n\n### Intuition\n- The simplest approach is to check all possible pairs in the array and see if their absolute difference equals $$( k $$).\n\n### Approach\n- Use two nested loops to iterate through the array, check the absolute difference for each pair, and store unique pairs in a set to avoid duplicates.\n\n### Complexity\n- Time complexity: $$O(n^2)$$ \n- Space complexity: $$O(n)$$ (due to the set storing unique pairs)\n\n### Code\n```python3\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n n = len(nums)\n numSet = set()\n\n for i in range(n - 1):\n for j in range(i + 1, n):\n if abs(nums[i] - nums[j]) == k:\n numSet.add((nums[i], nums[j]))\n numSet.add((nums[j], nums[i]))\n\n ans = len(numSet)\n if k != 0:\n ans //= 2\n\n return ans\n```\n\n---\n\n## Solution 2: Two Pointers Approach\n\n### Intuition\n- By sorting the array, we can use two pointers to efficiently find pairs with the desired difference.\n\n### Approach\n- Sort the array and use two pointers to traverse it, adjusting the pointers based on the current difference.\n\n### Complexity\n- Time complexity: $$ O(n\\ log n) $$ (due to sorting)\n- Space complexity: $$ O(1) $$ (in-place sorting)\n\n### Code\n```python3\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n n = len(nums)\n nums.sort()\n ans = 0\n\n i = 0\n j = 1\n while j < n:\n if abs(nums[i] - nums[j]) < k:\n j += 1\n elif abs(nums[i] - nums[j]) > k:\n i += 1\n else:\n ans += 1\n i += 1\n j += 1\n\n while i > 0 and i < n and nums[i - 1] == nums[i]:\n i += 1\n while j > 0 and j < n and nums[j - 1] == nums[j]:\n j += 1\n if i == j:\n j += 1\n\n return ans\n```\n\n---\n\n## Solution 3: Using defaultdict\n\n### Intuition\n- Count the occurrences of each number and check for pairs based on the counts.\n\n### Approach\n- Utilize a `defaultdict` to store counts, then iterate through it to check for pairs.\n\n### Complexity\n- Time complexity: $$ O(n) $$\n- Space complexity: $$ O(m) $$ (where $$ m $$ is the number of unique elements)\n\n### Code\n```python3\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n d = defaultdict(int)\n\n for num in nums:\n d[num] += 1\n\n ans = 0\n for num in d:\n pairExists = k > 0 and num + k in d\n duplicateExists = k == 0 and d[num] > 1\n if pairExists or duplicateExists:\n ans += 1\n\n return ans\n```\n\n---\n\n## Solution 4: Using lambda and reduce\n\n### Intuition\n- Leverage functional programming with `reduce` to compute the count of valid pairs.\n\n### Approach\n- Use `Counter` to count occurrences, then apply `reduce` to sum valid pairs based on conditions.\n\n### Complexity\n- Time complexity: $$ O(n) $$\n- Space complexity: $$ O(m) $$\n\n### Code\n```python3\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n d = Counter(nums)\n\n return reduce(\n lambda x, num: x + ((k > 0 and num + k in d) or (k == 0 and d[num] > 1)),\n d,\n 0,\n )\n```\n\n---\n\n## Solution 5: Using sum\n\n### Intuition\n- A concise way to count valid pairs using a generator expression with `sum`.\n\n### Approach\n- Use `Counter` to count occurrences, then use a generator expression to count valid pairs.\n\n### Complexity\n- Time complexity: $$ O(n) $$\n- Space complexity: $$ O(m) $$\n\n### Code\n```python3\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n d = Counter(nums)\n\n return sum(\n 1 for num in d if (k > 0 and num + k in d) or (k == 0 and d[num] > 1)\n )\n``` | 3 | 0 | ['Hash Table', 'Two Pointers', 'Sorting', 'Python3'] | 0 |
k-diff-pairs-in-an-array | ✅ Beats 99.99% || Two Pointer || K-diff Pairs in an Array | beats-9999-two-pointer-k-diff-pairs-in-a-k9rp | Intuition\nThe code aims to find the number of unique pairs (i, j) in the given vector nums such that the absolute difference between nums[i] and nums[j] is equ | gouravsharma2806 | NORMAL | 2024-01-18T04:56:27.843452+00:00 | 2024-01-18T04:56:27.843493+00:00 | 1,586 | false | # Intuition\nThe code aims to find the number of unique pairs (i, j) in the given vector nums such that the absolute difference between nums[i] and nums[j] is equal to the given integer k.\n\n# Approach\nSort the array nums to make it easier to find pairs with the desired difference.\nUse two pointers (i and j) to traverse the array.\nCalculate the absolute difference diff between nums[i] and nums[j].\nAdjust the pointers based on the value of diff:\nIf diff equals k, insert the pair (nums[i], nums[j]) into a set.\nIf diff is greater than k, move i to the next element.\nIf diff is less than k, move j to the next element.\nAvoid cases where i and j point to the same element.\nReturn the size of the set, which contains unique pairs.\n# Code Explanation:\nThe array nums is sorted to make it easier to find pairs with the desired difference.\nTwo pointers (i and j) are used to traverse the array and find pairs.\nThe set ans is used to store unique pairs with the desired difference.\nThe while loop continues until j reaches the end of the array.\nThe pointers are adjusted based on the absolute difference between nums[i] and nums[j].\nPairs satisfying the condition are added to the set.\nThe final result is the size of the set, indicating the number of unique pairs.\n\n# Complexity\nTime Complexity: O(n log n) - Sorting the array takes O(n log n) time, and the subsequent traversal takes O(n) time.\nSpace Complexity: O(n) - The set (ans) stores unique pairs, and in the worst case, it could store all pairs.\n\n# Code\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n sort(nums.begin(),nums.end());\n set<pair<int,int>> ans;\n\n int i = 0,j=1;\n while(j<nums.size()){\n int diff = nums[j]-nums[i];\n if(diff == k){\n ans.insert({nums[i],nums[j]});\n ++i;\n ++j;\n }\n else if(diff > k ){\n i++;\n }\n else{\n j++;\n }\n if(i == j){\n j++;\n }\n }\n return ans.size();\n }\n};\n``` | 3 | 0 | ['Two Pointers', 'Binary Search', 'Sorting', 'C++'] | 0 |
k-diff-pairs-in-an-array | Unique Solution using Set Nlog(N)!!! | unique-solution-using-set-nlogn-by-aero_-rmg5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | aero_coder | NORMAL | 2023-08-01T09:04:15.957547+00:00 | 2023-09-05T07:19:29.504565+00:00 | 258 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n set<pair<int, int>> st;\n set<int> seen;\n for (int i = 0; i < nums.size(); i++) {\n if (seen.count(nums[i] - k)) {\n st.insert(make_pair(nums[i], nums[i]-k));\n }\n if (seen.count(nums[i] + k)) {\n st.insert(make_pair(nums[i]+k, nums[i] ));\n }\n seen.insert(nums[i]);\n }\n return st.size();\n }\n};\n\n``` | 3 | 0 | ['C++'] | 1 |
k-diff-pairs-in-an-array | Using Binary Search | using-binary-search-by-sithkar-wflh | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. The input nums vecto | Sithkar | NORMAL | 2023-07-29T10:36:14.581851+00:00 | 2023-07-29T10:36:14.581869+00:00 | 1,279 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The input nums vector is sorted in ascending order, just like in the previous solution.\n\n2. The bs function is a binary search function that searches for the value x in the sorted array nums. It returns the index of the element if found, and -1 otherwise. This function will be used to find elements that have a difference of k with the current element at index i.\n\n3. A set ans of pairs is used to store the unique pairs that satisfy the condition of having a difference of k.\n\n4. The code then iterates through the sorted array using a for loop. For each element nums[i], it calls the bs function to find an element with a value of nums[i] + k. If such an element is found (i.e., bs(nums, i+1, nums[i]+k) returns a valid index), it means we have a valid pair, and the pair (nums[i], nums[i]+k) is inserted into the set ans.\n\n5. The function returns the size of the set ans, which represents the count of unique pairs with a difference of k.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlog(n))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n\nint bs(vector<int>&nums,int start, int x){\n int end = nums.size()-1;\n while(start<=end){\n int mid = (start+end)/2;\n if(nums[mid]==x){\n return mid;\n }\n else if(x>nums[mid]){\n start = mid+1;\n }\n else{\n end = mid-1;\n }\n }\n return -1;\n}\n\n\n int findPairs(vector<int>& nums, int k) {\n sort(nums.begin(),nums.end());\n set<pair<int,int>> ans;\n for(int i=0;i<nums.size();i++){\n if(bs(nums,i+1,nums[i]+k)!=-1){\n ans.insert({nums[i],nums[i]+k});\n }\n }\n return ans.size();\n }\n};\n``` | 3 | 0 | ['Binary Search', 'C++'] | 0 |
k-diff-pairs-in-an-array | C++ Solution | c-solution-by-pranto1209-1a0o | Code\n\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int, int> mp;\n for(int x: nums) mp[x]++;\n | pranto1209 | NORMAL | 2023-06-03T10:29:12.049017+00:00 | 2023-06-03T10:29:12.049058+00:00 | 194 | false | # Code\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int, int> mp;\n for(int x: nums) mp[x]++;\n int ans = 0;\n for(auto x: mp) {\n if (k == 0) { \n if(x.second > 1) ans++;\n }\n else if (mp.find(x.first + k) != mp.end()) ans++;\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
k-diff-pairs-in-an-array | Easiest way using Java | easiest-way-using-java-by-us2463035-v6bq | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | us2463035 | NORMAL | 2023-05-01T07:10:22.069884+00:00 | 2023-05-01T07:10:22.069938+00:00 | 973 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n Arrays.sort(nums);\n int count=0;\n for(int i=0;i<nums.length;i++){\n if(i==0 || nums[i]!=nums[i-1]){\n for(int j=i+1;j<nums.length;j++){\n if(Math.abs(nums[i]-nums[j])==k){\n count++;\n break;\n \n }\n }\n }\n }\n return count;\n }\n}\n``` | 3 | 0 | ['Java'] | 1 |
k-diff-pairs-in-an-array | Easy C++ Solution using binary search | easy-c-solution-using-binary-search-by-h-qsqz | \n\n# Code\n\n//TC=O(nlogn)\nclass Solution {\npublic:\nint search(vector<int>& nums,int t,int s){\n int e=nums.size()-1;\n while(s<=e){\n int mid= | Harshit-Vashisth | NORMAL | 2023-03-07T20:32:51.512973+00:00 | 2023-03-09T06:47:53.137342+00:00 | 855 | false | \n\n# Code\n```\n//TC=O(nlogn)\nclass Solution {\npublic:\nint search(vector<int>& nums,int t,int s){\n int e=nums.size()-1;\n while(s<=e){\n int mid=s+(e-s)/2;\n if(nums[mid]==t)\n return mid;\n else if(t>nums[mid])\n s=mid+1;\n else\n e=mid-1;\n }\n return -1;\n}\n int findPairs(vector<int>& nums, int k) {\n sort(nums.begin(),nums.end());\n set<pair<int,int>> ans;\n int i=0;\n for(int i=0;i<nums.size();i++)\n {\n if(search(nums,nums[i]+k,i+1)!=-1)\n ans.insert({nums[i],nums[i]+k});\n }\n return ans.size();\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
k-diff-pairs-in-an-array | Java | Hashmap | java-hashmap-by-aanchal002-h492 | \nclass Solution {\n public int findPairs(int[] nums, int k) {\n HashMap<Integer,Integer> map=new HashMap<>();\n int c=0;\n for(int val: | Aanchal002 | NORMAL | 2022-04-07T17:16:30.987413+00:00 | 2022-04-07T17:16:30.987439+00:00 | 599 | false | ```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n HashMap<Integer,Integer> map=new HashMap<>();\n int c=0;\n for(int val:nums )\n {\n map.put(val,map.getOrDefault(val,0)+1);\n \n }\n for(int i:map.keySet())\n {\n if((k==0 && map.get(i)>1)||(k>0 && map.containsKey(i+k)))\n c++;\n }\n return c;\n }\n}\n``` | 3 | 0 | ['Java'] | 1 |
k-diff-pairs-in-an-array | Python 3 (60ms) | O(n) Counter Hashmap Solution | Easy to Understand | python-3-60ms-on-counter-hashmap-solutio-r1gc | \nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n count = Counter(nums)\n if k > 0:\n return sum([i + k in | MrShobhit | NORMAL | 2022-02-09T14:27:39.076516+00:00 | 2022-02-09T14:27:39.076560+00:00 | 852 | false | ```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n count = Counter(nums)\n if k > 0:\n return sum([i + k in count for i in count])\n else:\n return sum([count[i] > 1 for i in count])\n``` | 3 | 0 | ['Python', 'Python3'] | 1 |
k-diff-pairs-in-an-array | [🔥🔥][JAVA][SIMPLE][EASY][SET][NO SORT]☑️ | javasimpleeasysetno-sort-by-bharathkalya-hu7v | Simplified Clean Coded Solution !\uD83D\uDE00\n\nclass Solution {\n public int findPairs(int[] nums, int k) {\n int pairs = 0, n = nums.length;\n | bharathkalyans | NORMAL | 2022-02-09T12:54:45.618086+00:00 | 2022-02-09T12:55:03.063323+00:00 | 159 | false | Simplified Clean Coded Solution !\uD83D\uDE00\n```\nclass Solution {\n public int findPairs(int[] nums, int k) {\n int pairs = 0, n = nums.length;\n \n HashSet<Integer> set = new HashSet<>();\n HashSet<Integer> repeatedElements = new HashSet<>();\n \n for(int ele : nums){\n if(set.contains(ele)) repeatedElements.add(ele);\n set.add(ele);\n }\n \n // SPECIAL CASE [K == 0]\n if(k == 0) return repeatedElements.size();\n \n // Traversing the SET not the array.\n for(int elementInSet : set)\n if(set.contains(elementInSet + k)) pairs++;\n \n return pairs;\n }\n}\n``` | 3 | 0 | ['Ordered Set', 'Java'] | 0 |
k-diff-pairs-in-an-array | C++ / Python Simple and Clean O(n) Solutions | c-python-simple-and-clean-on-solutions-b-lgt0 | C++:\n\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int, int> map;\n for(auto num:nums)\n | yehudisk | NORMAL | 2022-02-09T08:45:27.341241+00:00 | 2022-02-09T08:45:27.341274+00:00 | 267 | false | **C++:**\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n unordered_map<int, int> map;\n for(auto num:nums)\n map[num]++;\n \n int res = 0;\n if (k > 0) {\n for(auto a:map)\n if (map.find(a.first+k) != map.end()) \n res++;\n }\n \n else {\n for(auto a:map)\n if (a.second > 1)\n res++;\n }\n \n return res;\n }\n};\n```\n**Python:**\n```\nclass Solution:\n def findPairs(self, nums: List[int], k: int) -> int:\n if (k == 0):\n return len([item for item, count in collections.Counter(nums).items() if count > 1])\n \n nums = set(nums)\n res = 0\n for n in nums:\n res += 1 if n-k in nums else 0\n return res\n```\n**Like it? please upvote!** | 3 | 0 | ['C', 'Python'] | 0 |
k-diff-pairs-in-an-array | C++| Two pointers | Lower Bound | nlogn | c-two-pointers-lower-bound-nlogn-by-vaib-itiw | Using two pointer C++ | nlogn :\n\nint findPairs(vector<int>& nums, int k) {\n int ans=0;\n sort(nums.begin(),nums.end());\n int i=0,j=1;\n | vaibhavshekhawat | NORMAL | 2022-02-09T05:39:15.648921+00:00 | 2022-02-09T05:40:43.321381+00:00 | 219 | false | ### Using two pointer C++ | nlogn :\n```\nint findPairs(vector<int>& nums, int k) {\n int ans=0;\n sort(nums.begin(),nums.end());\n int i=0,j=1;\n int n=nums.size();\n while(i<n &&j<n){ \n if(i!=0 && nums[i]==nums[i-1]){i++;continue;}\n if(i==j) {j++;continue;}\n \n int dif=nums[j]-nums[i];\n if(dif==k){i++;ans++;}\n else if(dif<k) j++;\n else i++;\n }\n return ans;\n}\n```\n\n### Using Lower Bound C++ | nlogn :\n```\nint findPairs(vector<int>& nums, int k) {\n int ans=0;\n sort(nums.begin(),nums.end());\n for(auto it=nums.begin();it!=nums.end();it++){ \n if(it!=nums.begin() && *it==*(it-1)) continue; \n auto itr=lower_bound(it+1,nums.end(),k+(*it));\n if(itr==nums.end()) continue;\n if(*itr-*it==k){\n ans++;\n }\n }\n return ans;\n }\n``` | 3 | 0 | ['C'] | 1 |
k-diff-pairs-in-an-array | [Java/Binary Search] Easy to understand | javabinary-search-easy-to-understand-by-uz9hu | Try search for each element because we need to find only unique element so discard those element that have been traversed,\n\nclass Solution \n{\n public int | indiankiller | NORMAL | 2022-02-09T05:04:53.848652+00:00 | 2022-02-09T05:04:53.848699+00:00 | 277 | false | Try search for each element because we need to find only unique element so discard those element that have been traversed,\n```\nclass Solution \n{\n public int findPairs(int[] nums, int k) \n {\n int n = nums.length;\n int count =0;\n Arrays.sort(nums);\n if(k==0)\n {\n int pre = 100000001;\n for(int i=0;i<(n-1);i++)\n {\n if((nums[i]==nums[i+1]) && pre!=nums[i])\n {\n count++;\n }\n pre = nums[i];\n }\n return count;\n }\n int pre = 100000001;\n for(int i=0;i<n;i++)\n {\n if(pre!=nums[i])\n {\n count = count + search(nums,i,k,n-1);\n pre = nums[i]; \n }\n } \n return count;\n }\n public int search(int[] nums,int l,int k,int r)\n {\n int target = nums[l];\n int t = (target+k);\n while(l<=r)\n {\n int mid = (l+r)/2;\n \n if(nums[mid]==t)\n {\n return 1;\n }\n else if(nums[mid]>t)\n {\n r = mid-1;\n }\n else\n {\n l = mid+1;\n }\n \n }\n return 0;\n }\n}\n``` | 3 | 0 | ['Binary Tree', 'Java'] | 0 |
k-diff-pairs-in-an-array | [Python3] Runtime: 58 ms, faster than 99.40% | Memory: 15.6 MB, less than 89.25% | python3-runtime-58-ms-faster-than-9940-m-p4cw | \nclass Solution:\n\tdef findPairs(self, nums: List[int], k: int) -> int:\n\t\tans,check = 0,{}\n\t\tfor i in nums:\n\t\t\tif i not in check:\n\t\t\t\tcheck[i]= | anubhabishere | NORMAL | 2022-02-09T03:35:15.578143+00:00 | 2022-02-09T03:35:15.578181+00:00 | 110 | false | ```\nclass Solution:\n\tdef findPairs(self, nums: List[int], k: int) -> int:\n\t\tans,check = 0,{}\n\t\tfor i in nums:\n\t\t\tif i not in check:\n\t\t\t\tcheck[i]=1\n\t\t\telse:\n\t\t\t\tcheck[i]+=1\n\t\tif k>0:\n\t\t\tfor j in check:\n\t\t\t\tif j+k in check.keys():\n\t\t\t\t\tans+=1\n\t\telse:\n\t\t\tfor j in check:\n\t\t\t\tif check[j]>1:\n\t\t\t\t\tans+=1\n\t\treturn ans\n``` | 3 | 1 | ['Python'] | 0 |
k-diff-pairs-in-an-array | C++ | Easy Understood Solution | map | c-easy-understood-solution-map-by-parth_-kad6 | We need to find pair whose differense is k.\nSo that we can store frequency to map and we will find, whether another key is exist or not whose difference is k.\ | parth_chovatiya | NORMAL | 2022-02-09T02:59:25.624957+00:00 | 2022-02-09T02:59:25.624999+00:00 | 371 | false | We need to find pair whose differense is k.\nSo that we can store frequency to map and we will find, whether another key is exist or not whose difference is k.\nif exist, then we will increment our ans by 1.\n\nLet\'s look at one example.\n**nums = [1,3,5,1,4], k = 2**\n\nNow store frequency to map:\n1-> 2\n3-> 1\n4-> 1\n5-> 1\n\nNow, iterate to map and find key difference of k. If found then increment ans+1.\n\nHere, keys two keys found **(1,3), (3,5)** whose difference is 2. So that **ans = 2**;\n\nWe need to also take care when k=0 given.\nSo that I have just decrement value by 1 and increment value by 1.\n\n```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n int ans = 0;\n map<int,int> mp;\n for(auto &x : nums){\n mp[x]++;\n }\n for(auto &x : mp){\n x.second--;\n if(mp.find(x.first+k) != mp.end() and mp[x.first+k] >= 1)\n ans++;\n x.second++;\n }\n return ans;\n }\n};\n``` | 3 | 0 | [] | 0 |
k-diff-pairs-in-an-array | C++ Two solutions | c-two-solutions-by-brown_wolf_26-ubdv | \nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n // time O(nlgn) space O(1)\n // sort(nums.begin(),nums.end());\n | scorpion_lone_wolf | NORMAL | 2022-01-25T10:31:41.231292+00:00 | 2022-01-25T10:31:41.231332+00:00 | 260 | false | ```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n // time O(nlgn) space O(1)\n // sort(nums.begin(),nums.end());\n // int n=nums.size();\n // int count=0;\n // for(int i=0;i<n;i++){\n // if(i!=0&&nums[i]==nums[i-1])continue;\n // bool res=binary_search(nums.begin()+i+1,nums.end(),nums[i]+k);\n // if(res){\n // count++;\n // } \n // }\n // return count;\n // }\n \n // time O(n) space O(n)\n int n=nums.size();\n int count=0;\n unordered_map<int,int> lookup;\n if(k==0){\n for(int i=0;i<n;i++){\n if(lookup[nums[i]]==1){\n count++;\n } \n lookup[nums[i]] =lookup[nums[i]]+1;\n }\n }else{\n for(int i=0;i<n;i++){\n if(!lookup.count(nums[i])){\n if(lookup.count(nums[i]-k)){\n count++;\n }\n if(lookup.count(nums[i]+k)){\n count++;\n }\n lookup[nums[i]]+=1;\n }\n }\n }\n return count;\n }\n};\n``` | 3 | 0 | ['Binary Tree'] | 0 |
k-diff-pairs-in-an-array | 100% faster || 8 ms || without using map || Worst Case O(n logn) + O(n) | 100-faster-8-ms-without-using-map-worst-9f4o5 | \nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n sort(nums.begin(), nums.end());\n int slow = 0, fast = 1, ans = 0;\n | user0382o | NORMAL | 2021-12-12T17:55:00.121881+00:00 | 2021-12-12T17:55:00.121911+00:00 | 213 | false | ```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n sort(nums.begin(), nums.end());\n int slow = 0, fast = 1, ans = 0;\n while(slow < nums.size() && fast < nums.size()){\n if(nums[fast] - nums[slow] == k){\n slow++;\n fast++;\n ans++;\n while(fast < nums.size() && nums[fast] == nums[fast - 1]) fast++;\n }\n else if(nums[fast] - nums[slow] > k){\n slow++;\n if(fast - slow == 0) fast++;\n }\n else fast++; \n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C', 'Sorting', 'C++'] | 0 |
k-diff-pairs-in-an-array | C++ || Hashmap | c-hashmap-by-yasshpathak-ryxv | \nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n \n int n=nums.size();\n unordered_map<int,int>mymap;\n | yasshpathak | NORMAL | 2021-12-10T13:40:21.785426+00:00 | 2021-12-10T13:40:21.785455+00:00 | 241 | false | ```\nclass Solution {\npublic:\n int findPairs(vector<int>& nums, int k) {\n \n int n=nums.size();\n unordered_map<int,int>mymap;\n int count=0;\n \n \n for(int i=0;i<n;i++){\n mymap[nums[i]]++;\n }\n \n if(k==0){\n for(auto x:mymap){\n if(x.second>1){\n count++;\n }\n }\n return count;\n }\n \n for(auto x:mymap){\n if(mymap.count(x.first-k)){\n count++;\n }\n }\n return count;\n }\n};\n``` | 3 | 0 | ['C'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.