title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Simple Python 🐍 solution using deque (BFS) | employee-importance | 0 | 1 | ```\nclass Solution:\n def getImportance(self, employees: List[\'Employee\'], id: int) -> int:\n emap = {e.id: e for e in employees}\n\n q=deque([id])\n ans=0\n \n while q:\n emp_id=q.popleft()\n ans+=emap[emp_id].importance\n \n for sub in emap[emp_id].subordinates:\n q.append(sub)\n return ans\n \n```\n\nO(N) time and space. | 4 | You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees `employees` where:
* `employees[i].id` is the ID of the `ith` employee.
* `employees[i].importance` is the importance value of the `ith` employee.
* `employees[i].subordinates` is a list of the IDs of the direct subordinates of the `ith` employee.
Given an integer `id` that represents an employee's ID, return _the **total** importance value of this employee and all their direct and indirect subordinates_.
**Example 1:**
**Input:** employees = \[\[1,5,\[2,3\]\],\[2,3,\[\]\],\[3,3,\[\]\]\], id = 1
**Output:** 11
**Explanation:** Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
**Example 2:**
**Input:** employees = \[\[1,2,\[5\]\],\[5,-3,\[\]\]\], id = 5
**Output:** -3
**Explanation:** Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.
**Constraints:**
* `1 <= employees.length <= 2000`
* `1 <= employees[i].id <= 2000`
* All `employees[i].id` are **unique**.
* `-100 <= employees[i].importance <= 100`
* One employee has at most one direct leader and may have several subordinates.
* The IDs in `employees[i].subordinates` are valid IDs. | null |
75% TC and 62% SC easy python solution | employee-importance | 0 | 1 | ```\ndef getImportance(self, employees: List[\'Employee\'], id: int) -> int:\n\td = {j.id:i for i, j in enumerate(employees)}\n\ts = [id]\n\tans = 0\n\twhile(s):\n\t\tcurr = s.pop()\n\t\tans += employees[d[curr]].importance\n\t\tfor child in employees[d[curr]].subordinates: \n\t\t\ts.append(child)\n\treturn ans\n``` | 1 | You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees `employees` where:
* `employees[i].id` is the ID of the `ith` employee.
* `employees[i].importance` is the importance value of the `ith` employee.
* `employees[i].subordinates` is a list of the IDs of the direct subordinates of the `ith` employee.
Given an integer `id` that represents an employee's ID, return _the **total** importance value of this employee and all their direct and indirect subordinates_.
**Example 1:**
**Input:** employees = \[\[1,5,\[2,3\]\],\[2,3,\[\]\],\[3,3,\[\]\]\], id = 1
**Output:** 11
**Explanation:** Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
**Example 2:**
**Input:** employees = \[\[1,2,\[5\]\],\[5,-3,\[\]\]\], id = 5
**Output:** -3
**Explanation:** Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.
**Constraints:**
* `1 <= employees.length <= 2000`
* `1 <= employees[i].id <= 2000`
* All `employees[i].id` are **unique**.
* `-100 <= employees[i].importance <= 100`
* One employee has at most one direct leader and may have several subordinates.
* The IDs in `employees[i].subordinates` are valid IDs. | null |
Solution | employee-importance | 1 | 1 | ```C++ []\nclass Solution {\n void dfs(int id,vector<Employee*> employees, unordered_map<int,int>&mp,int& ans){\n ans += employees[mp[id]]->importance;\n for(auto it:employees[mp[id]]->subordinates)\n dfs(it,employees,mp,ans);\n }\npublic:\n int getImportance(vector<Employee*> employees, int id) {\n int ans = 0,i = 0;\n unordered_map<int,int>IdtoIndex;\n for(auto it:employees)\n IdtoIndex[it->id] = i++; \n dfs(id,employees,IdtoIndex,ans);\n return ans;\n }\n};\n```\n\n```Python3 []\nfrom collections import deque\nclass Solution:\n def getImportance(self, employees: List[\'Employee\'], id: int) -> int:\n \n emp_map = {}\n for emp in employees:\n emp_map[emp.id] = emp\n \n q = deque([emp_map[id]])\n imp = 0\n while len(q)!=0:\n e = q.popleft()\n imp += e.importance\n for subordinate in e.subordinates:\n q.append(emp_map[subordinate])\n return imp\n```\n\n```Java []\nclass Solution {\n Map<Integer, Employee> employeeMap;\n\tpublic int getImportance(List<Employee> employees, int id) {\n\t\tif (employeeMap == null) {\n\t\t\temployeeMap = new HashMap<>();\n\t\t\tfor (Employee emp : employees) {\n\t\t\t\temployeeMap.put(emp.id, emp);\n\t\t\t}\n\t\t}\n\t\tint imp = 0;\n\t\tEmployee emp = employeeMap.get(id);\n\t\timp += emp.importance;\n\t\tif (emp.subordinates.size() > 0) {\n\t\t\tfor (int subId : emp.subordinates) {\n\t\t\t\timp += getImportance(employees, subId);\n\t\t\t}\n\t\t}\n\t\treturn imp;\n\t}\n}\n```\n | 2 | You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees `employees` where:
* `employees[i].id` is the ID of the `ith` employee.
* `employees[i].importance` is the importance value of the `ith` employee.
* `employees[i].subordinates` is a list of the IDs of the direct subordinates of the `ith` employee.
Given an integer `id` that represents an employee's ID, return _the **total** importance value of this employee and all their direct and indirect subordinates_.
**Example 1:**
**Input:** employees = \[\[1,5,\[2,3\]\],\[2,3,\[\]\],\[3,3,\[\]\]\], id = 1
**Output:** 11
**Explanation:** Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
**Example 2:**
**Input:** employees = \[\[1,2,\[5\]\],\[5,-3,\[\]\]\], id = 5
**Output:** -3
**Explanation:** Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.
**Constraints:**
* `1 <= employees.length <= 2000`
* `1 <= employees[i].id <= 2000`
* All `employees[i].id` are **unique**.
* `-100 <= employees[i].importance <= 100`
* One employee has at most one direct leader and may have several subordinates.
* The IDs in `employees[i].subordinates` are valid IDs. | null |
✔ Python3 Solution | DFS | O(n) | employee-importance | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def getImportance(self, employees: List[\'Employee\'], id: int) -> int:\n D = {i.id : e for e, i in enumerate(employees)}\n def dfs(id):\n ans = employees[D[id]].importance\n for i in employees[D[id]].subordinates:\n ans += dfs(i)\n return ans\n return dfs(id)\n``` | 2 | You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees `employees` where:
* `employees[i].id` is the ID of the `ith` employee.
* `employees[i].importance` is the importance value of the `ith` employee.
* `employees[i].subordinates` is a list of the IDs of the direct subordinates of the `ith` employee.
Given an integer `id` that represents an employee's ID, return _the **total** importance value of this employee and all their direct and indirect subordinates_.
**Example 1:**
**Input:** employees = \[\[1,5,\[2,3\]\],\[2,3,\[\]\],\[3,3,\[\]\]\], id = 1
**Output:** 11
**Explanation:** Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
**Example 2:**
**Input:** employees = \[\[1,2,\[5\]\],\[5,-3,\[\]\]\], id = 5
**Output:** -3
**Explanation:** Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.
**Constraints:**
* `1 <= employees.length <= 2000`
* `1 <= employees[i].id <= 2000`
* All `employees[i].id` are **unique**.
* `-100 <= employees[i].importance <= 100`
* One employee has at most one direct leader and may have several subordinates.
* The IDs in `employees[i].subordinates` are valid IDs. | null |
✅ Simple Python DFS Solution | Beats 97% | hashtable | employee-importance | 0 | 1 | 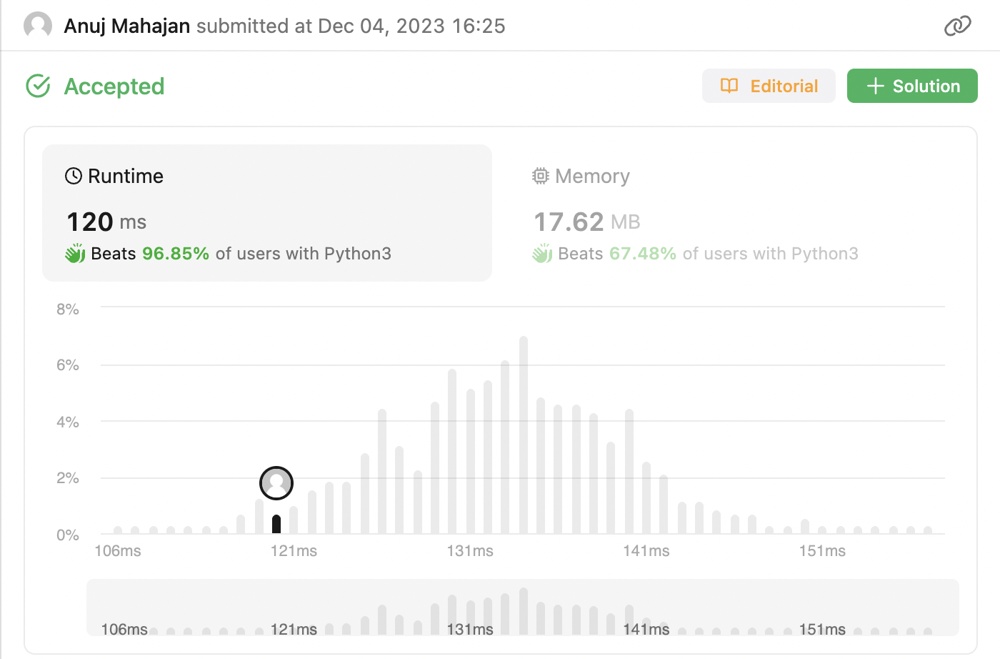\n\n# Code\n```\n"""\n# Definition for Employee.\nclass Employee:\n def __init__(self, id: int, importance: int, subordinates: List[int]):\n self.id = id\n self.importance = importance\n self.subordinates = subordinates\n"""\n\nimport collections\nclass Solution:\n def getImportance(self, employees: List[\'Employee\'], id: int) -> int:\n self.ans = 0\n hashMap = collections.defaultdict(list)\n for val in employees:\n hashMap[val.id].append(val.importance)\n hashMap[val.id].append(val.subordinates)\n \n def dfs(u):\n self.ans += hashMap[u][0]\n for nei in hashMap[u][1]:\n dfs(nei)\n \n dfs(id)\n return self.ans\n \n \n``` | 0 | You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees `employees` where:
* `employees[i].id` is the ID of the `ith` employee.
* `employees[i].importance` is the importance value of the `ith` employee.
* `employees[i].subordinates` is a list of the IDs of the direct subordinates of the `ith` employee.
Given an integer `id` that represents an employee's ID, return _the **total** importance value of this employee and all their direct and indirect subordinates_.
**Example 1:**
**Input:** employees = \[\[1,5,\[2,3\]\],\[2,3,\[\]\],\[3,3,\[\]\]\], id = 1
**Output:** 11
**Explanation:** Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
**Example 2:**
**Input:** employees = \[\[1,2,\[5\]\],\[5,-3,\[\]\]\], id = 5
**Output:** -3
**Explanation:** Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.
**Constraints:**
* `1 <= employees.length <= 2000`
* `1 <= employees[i].id <= 2000`
* All `employees[i].id` are **unique**.
* `-100 <= employees[i].importance <= 100`
* One employee has at most one direct leader and may have several subordinates.
* The IDs in `employees[i].subordinates` are valid IDs. | null |
Solution | stickers-to-spell-word | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minStickers(vector<string>& stickers, string target) {\n constexpr int invalid = -1;\n const int n_stickers = static_cast<int>(stickers.size());\n const int n_target = static_cast<int>(target.size());\n const int n_layouts = (1 << n_target);\n long letter_to_stickers[26] = {};\n int dp[32768];\n \n for (int i_sticker = 0; i_sticker < n_stickers; ++i_sticker)\n for (const char c : stickers[i_sticker])\n letter_to_stickers[c - \'a\'] |= (1L << i_sticker);\n std::memset(dp, invalid, sizeof(dp));\n dp[0] = 0;\n for (int layout = 0; layout < n_layouts; ++layout)\n {\n if (dp[layout] == invalid)\n continue;\n int letter = -1;\n for (int i_target = 0; i_target < n_target; ++i_target)\n {\n if (!((layout >> i_target) & 1)\n && (letter_to_stickers[target[i_target] - \'a\'] != 0))\n {\n letter = target[i_target] - \'a\';\n break;\n }\n }\n if (letter == -1) break;\n for(int i_sticker = 0; i_sticker < n_stickers; ++i_sticker)\n {\n if (((letter_to_stickers[letter] >> i_sticker) & 1) == 0)\n continue;\n int next_layout = layout;\n for (const char c_sticker : stickers[i_sticker])\n {\n for (int i_target = 0; i_target < n_target; ++i_target)\n {\n if ((target[i_target] == c_sticker)\n && (((next_layout >> i_target) & 1) == 0))\n {\n next_layout |= (1 << i_target);\n break;\n }\n }\n }\n dp[next_layout] = (dp[next_layout] == invalid)\n ?(dp[layout] + 1)\n :std::min(dp[next_layout], dp[layout] + 1);\n }\n }\n return dp[n_layouts - 1];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n tcount = Counter(target)\n def getScore(s):\n temp = dict(tcount)\n sdict = defaultdict(int)\n res = 0\n for c in s:\n if c in temp and temp[c] > 0:\n temp[c] -= 1\n res += 1\n sdict[c] += 1\n return (res, sdict)\n stickers = [getScore(s) for s in stickers]\n stickers.sort(key = lambda x: x[0], reverse = True)\n stickers = [x[1] for x in stickers if x[0] > 0]\n opt = [stickers[0]]\n for i in range(1, len(stickers)):\n if opt[-1].keys() == stickers[i].keys() :\n continue\n opt.append(stickers[i])\n stickers = opt[:]\n \n seen = set()\n q = deque([target])\n step = 0\n while q:\n n = len(q)\n step += 1\n for i in range(n):\n cur = q.popleft()\n if cur in seen:\n continue\n seen.add(cur)\n for stick in stickers:\n if cur[0] not in stick:\n continue\n new = str(cur)\n for s in stick:\n new = new.replace(s,\'\', stick[s])\n if new == "":\n return step\n if new not in seen:\n q.append(new)\n return -1\n```\n\n```Java []\nclass Solution {\n private boolean empty(int[] freq) {\n for(int f: freq) if(f > 0) return false;\n return true;\n }\n private String toString(int[] freq) {\n StringBuilder sb = new StringBuilder();\n char c = \'a\';\n for(int f: freq) {\n while(f-- > 0) sb.append(c);\n c++;\n }\n return sb.toString();\n }\n public int minStickers(String[] stickers, String target) {\n int[] targetNaiveCount = new int[26];\n for(char c: target.toCharArray()) targetNaiveCount[c - \'a\']++;\n int[] index = new int[26];\n int N = 0;\n for(int i = 0; i < 26; i++) index[i] = targetNaiveCount[i] > 0 ? N++ : -1;\n int[] targetCount = new int[N];\n int t = 0;\n for(int c: targetNaiveCount) if(c > 0) {\n targetCount[t++] = c;\n }\n int[][] stickersCount = new int[stickers.length][N];\n for(int i = 0; i < stickers.length; i++) {\n for(char c: stickers[i].toCharArray()) {\n int j = index[c - \'a\'];\n if(j >= 0) stickersCount[i][j]++;\n }\n }\n int start = 0;\n for(int i = 0; i < stickers.length; i++) {\n for(int j = start; j < stickers.length; j++) if(j != i) {\n int k = 0;\n while(k < N && stickersCount[i][k] <= stickersCount[j][k]) k++;\n if(k == N) {\n int[] tmp = stickersCount[i];\n stickersCount[i] = stickersCount[start];\n stickersCount[start++] = tmp;\n break;\n }\n }\n }\n Queue<int[]> Q = new LinkedList<>();\n Set<String> visited = new HashSet<>();\n Q.add(targetCount);\n int steps = 0;\n while(!Q.isEmpty()) {\n steps++;\n int size = Q.size();\n while(size-- > 0) {\n int[] freq = Q.poll();\n String cur = toString(freq);\n if(visited.add(cur)) {\n int first = cur.charAt(0) - \'a\';\n for(int i = start; i < stickers.length; i++) if(stickersCount[i][first] != 0) {\n int[] next = freq.clone();\n for(int j = 0; j < N; j++) next[j] = Math.max(next[j] - stickersCount[i][j], 0);\n if(empty(next)) return steps;\n Q.add(next);\n }\n }\n }\n }\n return -1;\n }\n}\n```\n | 1 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Solution | stickers-to-spell-word | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minStickers(vector<string>& stickers, string target) {\n constexpr int invalid = -1;\n const int n_stickers = static_cast<int>(stickers.size());\n const int n_target = static_cast<int>(target.size());\n const int n_layouts = (1 << n_target);\n long letter_to_stickers[26] = {};\n int dp[32768];\n \n for (int i_sticker = 0; i_sticker < n_stickers; ++i_sticker)\n for (const char c : stickers[i_sticker])\n letter_to_stickers[c - \'a\'] |= (1L << i_sticker);\n std::memset(dp, invalid, sizeof(dp));\n dp[0] = 0;\n for (int layout = 0; layout < n_layouts; ++layout)\n {\n if (dp[layout] == invalid)\n continue;\n int letter = -1;\n for (int i_target = 0; i_target < n_target; ++i_target)\n {\n if (!((layout >> i_target) & 1)\n && (letter_to_stickers[target[i_target] - \'a\'] != 0))\n {\n letter = target[i_target] - \'a\';\n break;\n }\n }\n if (letter == -1) break;\n for(int i_sticker = 0; i_sticker < n_stickers; ++i_sticker)\n {\n if (((letter_to_stickers[letter] >> i_sticker) & 1) == 0)\n continue;\n int next_layout = layout;\n for (const char c_sticker : stickers[i_sticker])\n {\n for (int i_target = 0; i_target < n_target; ++i_target)\n {\n if ((target[i_target] == c_sticker)\n && (((next_layout >> i_target) & 1) == 0))\n {\n next_layout |= (1 << i_target);\n break;\n }\n }\n }\n dp[next_layout] = (dp[next_layout] == invalid)\n ?(dp[layout] + 1)\n :std::min(dp[next_layout], dp[layout] + 1);\n }\n }\n return dp[n_layouts - 1];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n tcount = Counter(target)\n def getScore(s):\n temp = dict(tcount)\n sdict = defaultdict(int)\n res = 0\n for c in s:\n if c in temp and temp[c] > 0:\n temp[c] -= 1\n res += 1\n sdict[c] += 1\n return (res, sdict)\n stickers = [getScore(s) for s in stickers]\n stickers.sort(key = lambda x: x[0], reverse = True)\n stickers = [x[1] for x in stickers if x[0] > 0]\n opt = [stickers[0]]\n for i in range(1, len(stickers)):\n if opt[-1].keys() == stickers[i].keys() :\n continue\n opt.append(stickers[i])\n stickers = opt[:]\n \n seen = set()\n q = deque([target])\n step = 0\n while q:\n n = len(q)\n step += 1\n for i in range(n):\n cur = q.popleft()\n if cur in seen:\n continue\n seen.add(cur)\n for stick in stickers:\n if cur[0] not in stick:\n continue\n new = str(cur)\n for s in stick:\n new = new.replace(s,\'\', stick[s])\n if new == "":\n return step\n if new not in seen:\n q.append(new)\n return -1\n```\n\n```Java []\nclass Solution {\n private boolean empty(int[] freq) {\n for(int f: freq) if(f > 0) return false;\n return true;\n }\n private String toString(int[] freq) {\n StringBuilder sb = new StringBuilder();\n char c = \'a\';\n for(int f: freq) {\n while(f-- > 0) sb.append(c);\n c++;\n }\n return sb.toString();\n }\n public int minStickers(String[] stickers, String target) {\n int[] targetNaiveCount = new int[26];\n for(char c: target.toCharArray()) targetNaiveCount[c - \'a\']++;\n int[] index = new int[26];\n int N = 0;\n for(int i = 0; i < 26; i++) index[i] = targetNaiveCount[i] > 0 ? N++ : -1;\n int[] targetCount = new int[N];\n int t = 0;\n for(int c: targetNaiveCount) if(c > 0) {\n targetCount[t++] = c;\n }\n int[][] stickersCount = new int[stickers.length][N];\n for(int i = 0; i < stickers.length; i++) {\n for(char c: stickers[i].toCharArray()) {\n int j = index[c - \'a\'];\n if(j >= 0) stickersCount[i][j]++;\n }\n }\n int start = 0;\n for(int i = 0; i < stickers.length; i++) {\n for(int j = start; j < stickers.length; j++) if(j != i) {\n int k = 0;\n while(k < N && stickersCount[i][k] <= stickersCount[j][k]) k++;\n if(k == N) {\n int[] tmp = stickersCount[i];\n stickersCount[i] = stickersCount[start];\n stickersCount[start++] = tmp;\n break;\n }\n }\n }\n Queue<int[]> Q = new LinkedList<>();\n Set<String> visited = new HashSet<>();\n Q.add(targetCount);\n int steps = 0;\n while(!Q.isEmpty()) {\n steps++;\n int size = Q.size();\n while(size-- > 0) {\n int[] freq = Q.poll();\n String cur = toString(freq);\n if(visited.add(cur)) {\n int first = cur.charAt(0) - \'a\';\n for(int i = start; i < stickers.length; i++) if(stickersCount[i][first] != 0) {\n int[] next = freq.clone();\n for(int j = 0; j < N; j++) next[j] = Math.max(next[j] - stickersCount[i][j], 0);\n if(empty(next)) return steps;\n Q.add(next);\n }\n }\n }\n }\n return -1;\n }\n}\n```\n | 1 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python Accepted DFS + Memo Solution (With Explanation, Easy to Understand) | stickers-to-spell-word | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nDisclaimer: I\'m aware that there are much more optimized solutions for this problem, but I wanted to provide a simple solution for those trying to understand this.\n\nThe main idea behind this solution is that at each point in time, we have two choices; we can either take the current sticker or we can not take the current sticker. \n\n#### Choice 1: Don\'t take the current sticker\nThe first choice is just skipping the current sticker. This means we increment `idx` by 1 and `target` remains the same.\n\n#### Choice 2: Take the current sticker\nIf we take the current sticker (`stickers[idx]`), then we remove all possible letters from the `target` string and recurse with the same list of stickers (e.g., keeping `idx` the same) and add 1 to the result. We only stop trying to take the current sticker when it does not contain any letters in the `target` string.\n\nIn the end, we return the minimum of the different choices we\'ve made. If there is no solution then we `dfs` will return infinity.\n\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n result = self.dfs(stickers, target, 0, {})\n return result if result != float("inf") else -1\n \n def dfs(self, stickers, target, idx, memo):\n # if target is empty then we don\'t need to take any sticker\n if target == "":\n return 0\n # if we\'ve searched through all stickers and haven\'t completed the target\n # then there is no solution\n if idx == len(stickers):\n return float("inf")\n\n # lookup the answer in the cache\n key = (idx, target)\n if key in memo:\n return memo[key]\n \n # choice 1 don\'t take the current sticker\n result = self.dfs(stickers, target, idx+1, memo)\n\n # choice 2 try to take the current sticker\n currentSticker = stickers[idx]\n newTarget = target\n somethingRemoved = False\n for c in currentSticker:\n idxToRemove = newTarget.find(c)\n if idxToRemove != -1:\n newTarget = newTarget[:idxToRemove] + newTarget[idxToRemove+1:]\n somethingRemoved = True\n \n # only try this sticker again if we were able to remove something from\n # the target string\n if somethingRemoved:\n result = min(result, 1 + self.dfs(stickers, newTarget, idx, memo))\n\n # cache the result\n memo[key] = result\n return result\n\n\n``` | 15 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python Accepted DFS + Memo Solution (With Explanation, Easy to Understand) | stickers-to-spell-word | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nDisclaimer: I\'m aware that there are much more optimized solutions for this problem, but I wanted to provide a simple solution for those trying to understand this.\n\nThe main idea behind this solution is that at each point in time, we have two choices; we can either take the current sticker or we can not take the current sticker. \n\n#### Choice 1: Don\'t take the current sticker\nThe first choice is just skipping the current sticker. This means we increment `idx` by 1 and `target` remains the same.\n\n#### Choice 2: Take the current sticker\nIf we take the current sticker (`stickers[idx]`), then we remove all possible letters from the `target` string and recurse with the same list of stickers (e.g., keeping `idx` the same) and add 1 to the result. We only stop trying to take the current sticker when it does not contain any letters in the `target` string.\n\nIn the end, we return the minimum of the different choices we\'ve made. If there is no solution then we `dfs` will return infinity.\n\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n result = self.dfs(stickers, target, 0, {})\n return result if result != float("inf") else -1\n \n def dfs(self, stickers, target, idx, memo):\n # if target is empty then we don\'t need to take any sticker\n if target == "":\n return 0\n # if we\'ve searched through all stickers and haven\'t completed the target\n # then there is no solution\n if idx == len(stickers):\n return float("inf")\n\n # lookup the answer in the cache\n key = (idx, target)\n if key in memo:\n return memo[key]\n \n # choice 1 don\'t take the current sticker\n result = self.dfs(stickers, target, idx+1, memo)\n\n # choice 2 try to take the current sticker\n currentSticker = stickers[idx]\n newTarget = target\n somethingRemoved = False\n for c in currentSticker:\n idxToRemove = newTarget.find(c)\n if idxToRemove != -1:\n newTarget = newTarget[:idxToRemove] + newTarget[idxToRemove+1:]\n somethingRemoved = True\n \n # only try this sticker again if we were able to remove something from\n # the target string\n if somethingRemoved:\n result = min(result, 1 + self.dfs(stickers, newTarget, idx, memo))\n\n # cache the result\n memo[key] = result\n return result\n\n\n``` | 15 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Fast Python solution | stickers-to-spell-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thoughts on how to solve this problem is to use dynamic programming to find the minimum number of stickers needed to spell out the target string.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach I will take is to use dynamic programming to find the minimum number of stickers needed to spell out the target string. I will use a state variable to represent the target string and check if the current state can be reached using a sticker. I will also use a dp array to store the minimum number of stickers needed to reach a certain state. The final answer will be stored in the last element of the dp array.\n# Complexity\n- Time complexity: $$O(2^n * m * l)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(2^n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n n = len(target)\n dp = [-1] * (1 << n)\n dp[0] = 0\n for state in range(1 << n):\n if dp[state] == -1: continue\n for sticker in stickers:\n now = state\n for letter in sticker:\n for i in range(n):\n if (now >> i) & 1: continue\n if target[i] == letter:\n now |= 1 << i\n break\n if dp[now] == -1 or dp[now] > dp[state] + 1:\n dp[now] = dp[state] + 1\n return dp[-1]\n\n``` | 2 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Fast Python solution | stickers-to-spell-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thoughts on how to solve this problem is to use dynamic programming to find the minimum number of stickers needed to spell out the target string.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach I will take is to use dynamic programming to find the minimum number of stickers needed to spell out the target string. I will use a state variable to represent the target string and check if the current state can be reached using a sticker. I will also use a dp array to store the minimum number of stickers needed to reach a certain state. The final answer will be stored in the last element of the dp array.\n# Complexity\n- Time complexity: $$O(2^n * m * l)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(2^n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n n = len(target)\n dp = [-1] * (1 << n)\n dp[0] = 0\n for state in range(1 << n):\n if dp[state] == -1: continue\n for sticker in stickers:\n now = state\n for letter in sticker:\n for i in range(n):\n if (now >> i) & 1: continue\n if target[i] == letter:\n now |= 1 << i\n break\n if dp[now] == -1 or dp[now] > dp[state] + 1:\n dp[now] = dp[state] + 1\n return dp[-1]\n\n``` | 2 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python 3 || 12 lines, dfs || T/S: 75% / 95% | stickers-to-spell-word | 0 | 1 | \n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n\n @lru_cache(None)\n def dfs(target):\n\n if not target: return 0\n tCtr, res = Counter(target), inf\n mn = min(tuple(tCtr), key= lambda x: tCtr[x] )\n\n for sCtr in sCtrs: \n if sCtr[mn] == 0: continue \n nxt = dfs(\'\'.join((tCtr-sCtr).elements()))\n \n if nxt != -1: res = min(res, 1 + nxt)\n \n return -1 if res == inf else res\n\n\n sCtrs = list(filter(lambda s: bool(set(s)\n & set(target)), map(Counter, stickers)))\n \n return dfs(target)\n```\n[https://leetcode.com/problems/stickers-to-spell-word/submissions/1050371803/](http://) | 4 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python 3 || 12 lines, dfs || T/S: 75% / 95% | stickers-to-spell-word | 0 | 1 | \n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n\n @lru_cache(None)\n def dfs(target):\n\n if not target: return 0\n tCtr, res = Counter(target), inf\n mn = min(tuple(tCtr), key= lambda x: tCtr[x] )\n\n for sCtr in sCtrs: \n if sCtr[mn] == 0: continue \n nxt = dfs(\'\'.join((tCtr-sCtr).elements()))\n \n if nxt != -1: res = min(res, 1 + nxt)\n \n return -1 if res == inf else res\n\n\n sCtrs = list(filter(lambda s: bool(set(s)\n & set(target)), map(Counter, stickers)))\n \n return dfs(target)\n```\n[https://leetcode.com/problems/stickers-to-spell-word/submissions/1050371803/](http://) | 4 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
O(2^m * n) time | O(2^m) space | solution explained | stickers-to-spell-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo find the minimum stickers required to spell the target string, we need to find the minimum stickers required for the substrings (subsets).\n\nUse dynamic programming.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- set subsets = total subsets of target string = 2^target string size\n- set dp = a list of size equal to total subsets where dp[i] represents minimum stickers required to spell the ith subset\n- set dp[0] to 0 (no sticker is required to spell an empty string) and rest to -1 \n- create a hashmap to store the target string characters and indices. \n - key = character, value = list of indices of the character occurrences\n - This is to avoid the loop to check if the sticker character is present in the target string\n- loop to traverse all subsets. for each subset i \n - skip if we can\'t reach that subset from the starting subset\n - for each sticker in the stickers list\n - set cur = current subset i\n - for each character in the current sticker\n - if the character is present in the target string\n - if the current subset doesn\'t contain the character (i.e the corresponding bit is not set)\n - add the character to the current subset i.e set the corresponding bit to 1 and break the loop\n - update dp[cur] with the minimum number of required stickers \n- return minimum number of stickers to reach substring n i.e the last value in the dp list\n\n\n# Complexity\n- Time complexity: O(dp list + target_map + loops) \u2192 O(total subsets + target string size + total subsets * stickers * sticker[i]) \u2192 O(2$^m$ + m + 2$^m$ * n * k) \u2192 O(2$^m$ * n * k) \u2192 O(2$^m$ * n) because k <= 10\n - m = target string size\n - n = total stickers\n - k = size of the longest sticker\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(dp list + hashmap) \u2192 O(total subsets + target string size) \u2192 O(2$^m$ + m) \u2192 O(2$^m$)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n subsets = 1 << len(target)\n dp = [-1] * subsets\n dp[0] = 0\n target_map = defaultdict(list)\n for i, c in enumerate(target):\n target_map[c].append(i)\n for i in range(subsets):\n if dp[i] == -1:\n continue\n for sticker in stickers:\n cur = i\n for c in sticker:\n if c in target_map:\n for j in target_map[c]:\n if not (cur >> j & 1):\n cur |= 1 << j \n break\n if dp[cur] == -1 or dp[cur] > dp[i] + 1:\n dp[cur] = dp[i] + 1\n return dp[-1]\n \n``` | 1 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
O(2^m * n) time | O(2^m) space | solution explained | stickers-to-spell-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo find the minimum stickers required to spell the target string, we need to find the minimum stickers required for the substrings (subsets).\n\nUse dynamic programming.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- set subsets = total subsets of target string = 2^target string size\n- set dp = a list of size equal to total subsets where dp[i] represents minimum stickers required to spell the ith subset\n- set dp[0] to 0 (no sticker is required to spell an empty string) and rest to -1 \n- create a hashmap to store the target string characters and indices. \n - key = character, value = list of indices of the character occurrences\n - This is to avoid the loop to check if the sticker character is present in the target string\n- loop to traverse all subsets. for each subset i \n - skip if we can\'t reach that subset from the starting subset\n - for each sticker in the stickers list\n - set cur = current subset i\n - for each character in the current sticker\n - if the character is present in the target string\n - if the current subset doesn\'t contain the character (i.e the corresponding bit is not set)\n - add the character to the current subset i.e set the corresponding bit to 1 and break the loop\n - update dp[cur] with the minimum number of required stickers \n- return minimum number of stickers to reach substring n i.e the last value in the dp list\n\n\n# Complexity\n- Time complexity: O(dp list + target_map + loops) \u2192 O(total subsets + target string size + total subsets * stickers * sticker[i]) \u2192 O(2$^m$ + m + 2$^m$ * n * k) \u2192 O(2$^m$ * n * k) \u2192 O(2$^m$ * n) because k <= 10\n - m = target string size\n - n = total stickers\n - k = size of the longest sticker\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(dp list + hashmap) \u2192 O(total subsets + target string size) \u2192 O(2$^m$ + m) \u2192 O(2$^m$)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n subsets = 1 << len(target)\n dp = [-1] * subsets\n dp[0] = 0\n target_map = defaultdict(list)\n for i, c in enumerate(target):\n target_map[c].append(i)\n for i in range(subsets):\n if dp[i] == -1:\n continue\n for sticker in stickers:\n cur = i\n for c in sticker:\n if c in target_map:\n for j in target_map[c]:\n if not (cur >> j & 1):\n cur |= 1 << j \n break\n if dp[cur] == -1 or dp[cur] > dp[i] + 1:\n dp[cur] = dp[i] + 1\n return dp[-1]\n \n``` | 1 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python with Counter and LRU cache memoization | stickers-to-spell-word | 0 | 1 | # Intuition\nWe can observe that any string target can be reduced into a smaller problem after applying some stickers.\n\nNow, what would be the resulting string given "thehat" if we use the sticker "with"?\n\nWe would remove "th" and the resulting string would be something like "ehat"\n\nOk, now we see that the string got smaller, when do we stop? We stop when we remove every character. That\'s when we have an empty string left.\n\n# Approach\nWhenever we do DFS/ DP (or even BFS), we need to be hyperfocused on the **state** and **choices**. The state is the remaining string we have, the choices are the stickers.\n\nHow do we go from "thehat" => "ehat" when we have sticker "with"? We have to use a counter and take away the characters (This is a easy level question). \n\nNow, we don\'t want our cache to fail identifying "ehat", "haet" etc. So what do you do? You can sort the string for caching.\n\n# Complexity\n$$n$$ is the length of target string\n\n- Time complexity: $$O(nlogn (2^n))$$ - In the worst case we visit every subseqyence of target - each time we will pick out the characters and sort them.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(2^n)$$ - we will store every subsequence of target\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nfrom functools import lru_cache\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n self.sticker_counters = [Counter(sticker) for sticker in stickers]\n target = "".join(sorted(target))\n\n ans = self.dfs(target)\n return -1 if ans == float("inf") else ans\n\n @lru_cache(maxsize=None)\n def dfs(self, remain):\n if remain == "": return 0\n\n remain_counter = Counter(remain)\n min_stickers = float("inf")\n\n for sticker_counter in self.sticker_counters:\n applied_counter = {c: max(count - sticker_counter[c], 0) for c, count in remain_counter.items()}\n applied_counter_s = "".join(sorted([ch * count for ch, count in applied_counter.items()]))\n \n if applied_counter_s != remain:\n num_stickers = 1 + self.dfs(applied_counter_s)\n min_stickers = min(min_stickers, num_stickers)\n \n return min_stickers\n\n\n``` | 2 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python with Counter and LRU cache memoization | stickers-to-spell-word | 0 | 1 | # Intuition\nWe can observe that any string target can be reduced into a smaller problem after applying some stickers.\n\nNow, what would be the resulting string given "thehat" if we use the sticker "with"?\n\nWe would remove "th" and the resulting string would be something like "ehat"\n\nOk, now we see that the string got smaller, when do we stop? We stop when we remove every character. That\'s when we have an empty string left.\n\n# Approach\nWhenever we do DFS/ DP (or even BFS), we need to be hyperfocused on the **state** and **choices**. The state is the remaining string we have, the choices are the stickers.\n\nHow do we go from "thehat" => "ehat" when we have sticker "with"? We have to use a counter and take away the characters (This is a easy level question). \n\nNow, we don\'t want our cache to fail identifying "ehat", "haet" etc. So what do you do? You can sort the string for caching.\n\n# Complexity\n$$n$$ is the length of target string\n\n- Time complexity: $$O(nlogn (2^n))$$ - In the worst case we visit every subseqyence of target - each time we will pick out the characters and sort them.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(2^n)$$ - we will store every subsequence of target\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nfrom functools import lru_cache\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n self.sticker_counters = [Counter(sticker) for sticker in stickers]\n target = "".join(sorted(target))\n\n ans = self.dfs(target)\n return -1 if ans == float("inf") else ans\n\n @lru_cache(maxsize=None)\n def dfs(self, remain):\n if remain == "": return 0\n\n remain_counter = Counter(remain)\n min_stickers = float("inf")\n\n for sticker_counter in self.sticker_counters:\n applied_counter = {c: max(count - sticker_counter[c], 0) for c, count in remain_counter.items()}\n applied_counter_s = "".join(sorted([ch * count for ch, count in applied_counter.items()]))\n \n if applied_counter_s != remain:\n num_stickers = 1 + self.dfs(applied_counter_s)\n min_stickers = min(min_stickers, num_stickers)\n \n return min_stickers\n\n\n``` | 2 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
691: Solution with step by step explanation | stickers-to-spell-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Compute the length of target and create a bitmask maxMask that has a 1 in each position that corresponds to a character in target.\n2. Create a list dp of length maxMask to store the minimum number of stickers required to spell out each bitmask.\n3. Initialize dp[0] to 0, since no stickers are required to spell out the empty string.\n4. Preprocess the stickers list by creating a list stickerCounts of dictionaries that contain the frequency of each character in each sticker.\n5. Iterate over all possible bitmasks mask of target.\n6. If dp[mask] is float(\'inf\'), then skip this mask since it cannot be reached from the starting bitmask.\n7. For each sticker stickerCount in stickerCounts, check if it contains any characters that are needed to fill in the missing characters in mask.\n8. If there are no such characters, then skip this sticker since it cannot help to fill in any missing characters in mask.\n9. Create a new bitmask superMask that represents the state after applying the current sticker to mask.\n10. For each character c in the sticker that matches a character t in target, check if that character is missing from the current bitmask superMask.\n11. If the character is missing, then set the corresponding bit in superMask to 1 to indicate that the character has been added.\n12. If the character appears more than once in the sticker, decrement its frequency counter and continue.\n13. Update the dp array at the new bitmask superMask with the minimum number of stickers required to reach it.\n14. If the final bitmask dp[-1] is still float(\'inf\'), return -1 to indicate that it is impossible to spell out the target string. Otherwise, return dp[-1] as the minimum number of stickers required.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n n = len(target)\n maxMask = 1 << n\n # dp[i] := min # of stickers to spell out i, where i is the bit mask of\n # target.\n dp = [float(\'inf\')] * maxMask\n dp[0] = 0\n \n # Preprocess the stickers to create a mapping of character frequencies\n stickerCounts = []\n for sticker in stickers:\n stickerCounts.append(collections.Counter(sticker))\n \n for mask in range(maxMask):\n if dp[mask] == float(\'inf\'):\n continue\n # Try to expand from `mask` by using each sticker.\n for i, stickerCount in enumerate(stickerCounts):\n # Skip over stickers that do not contain any characters we need\n if not any(c in stickerCount for c in target):\n continue\n superMask = mask\n for c, freq in stickerCount.items():\n for j, t in enumerate(target):\n # Try to apply it on a missing char.\n if c == t and not (superMask >> j & 1):\n superMask |= 1 << j\n freq -= 1\n if freq == 0:\n break\n dp[superMask] = min(dp[superMask], dp[mask] + 1)\n \n return -1 if dp[-1] == float(\'inf\') else dp[-1]\n\n``` | 3 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
691: Solution with step by step explanation | stickers-to-spell-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Compute the length of target and create a bitmask maxMask that has a 1 in each position that corresponds to a character in target.\n2. Create a list dp of length maxMask to store the minimum number of stickers required to spell out each bitmask.\n3. Initialize dp[0] to 0, since no stickers are required to spell out the empty string.\n4. Preprocess the stickers list by creating a list stickerCounts of dictionaries that contain the frequency of each character in each sticker.\n5. Iterate over all possible bitmasks mask of target.\n6. If dp[mask] is float(\'inf\'), then skip this mask since it cannot be reached from the starting bitmask.\n7. For each sticker stickerCount in stickerCounts, check if it contains any characters that are needed to fill in the missing characters in mask.\n8. If there are no such characters, then skip this sticker since it cannot help to fill in any missing characters in mask.\n9. Create a new bitmask superMask that represents the state after applying the current sticker to mask.\n10. For each character c in the sticker that matches a character t in target, check if that character is missing from the current bitmask superMask.\n11. If the character is missing, then set the corresponding bit in superMask to 1 to indicate that the character has been added.\n12. If the character appears more than once in the sticker, decrement its frequency counter and continue.\n13. Update the dp array at the new bitmask superMask with the minimum number of stickers required to reach it.\n14. If the final bitmask dp[-1] is still float(\'inf\'), return -1 to indicate that it is impossible to spell out the target string. Otherwise, return dp[-1] as the minimum number of stickers required.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n n = len(target)\n maxMask = 1 << n\n # dp[i] := min # of stickers to spell out i, where i is the bit mask of\n # target.\n dp = [float(\'inf\')] * maxMask\n dp[0] = 0\n \n # Preprocess the stickers to create a mapping of character frequencies\n stickerCounts = []\n for sticker in stickers:\n stickerCounts.append(collections.Counter(sticker))\n \n for mask in range(maxMask):\n if dp[mask] == float(\'inf\'):\n continue\n # Try to expand from `mask` by using each sticker.\n for i, stickerCount in enumerate(stickerCounts):\n # Skip over stickers that do not contain any characters we need\n if not any(c in stickerCount for c in target):\n continue\n superMask = mask\n for c, freq in stickerCount.items():\n for j, t in enumerate(target):\n # Try to apply it on a missing char.\n if c == t and not (superMask >> j & 1):\n superMask |= 1 << j\n freq -= 1\n if freq == 0:\n break\n dp[superMask] = min(dp[superMask], dp[mask] + 1)\n \n return -1 if dp[-1] == float(\'inf\') else dp[-1]\n\n``` | 3 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python | BFS solution | stickers-to-spell-word | 0 | 1 | I need to say that this is not the fastest or smartes way to solve this problem, however, this is also can be interesting. \nP.S. For those who are interested, the solution is faster than 25% of other solutions. But perhaps it can be optimized a bit.\n\n```\nclass Solution:\n \n @staticmethod\n def substract(c1, c2):\n\t # remove intersection of c1 and c2 from c2 and encode the c1 to string\n remove_keys = []\n result = ""\n for k in c1.keys():\n if k in c2:\n c1[k] -= c2[k]\n if c1[k] <= 0:\n remove_keys.append(k)\n if c1[k] > 0:\n result += k + str(c1[k])\n \n for key in remove_keys:\n c1.pop(key, None)\n return c1, result\n \n def minStickers(self, stickers: List[str], target: str) -> int:\n\t # count all letters in target\n target_count = Counter(target)\n stickers_counter = []\n \n s1 = set(target_count.keys())\n s2 = set()\n \n\t\t# count all letters which are exist in target for every sticker\n for i in range(len(stickers)):\n sticker = stickers[i]\n sticker_counter = defaultdict(int)\n for letter in sticker:\n if letter in target_count:\n sticker_counter[letter] += 1\n stickers_counter.append(sticker_counter)\n s2.update(sticker_counter.keys())\n \n if s2 != s1:\n return -1\n \n total_letters = sum(target_count.values())\n counter = 0\n \n q = deque([target_count])\n visited = set()\n \n\t\t# BFS loop to find the shortest path to get empty target dict\n while q:\n q_size = len(q)\n for _ in range(q_size):\n target_count = q.popleft()\n for sticker in stickers_counter:\n tmp, encoded = self.substract(target_count.copy(), sticker)\n if sum(tmp.values()) == 0:\n return counter+1\n if encoded not in visited:\n q.append(tmp)\n visited.add(encoded)\n counter += 1\n return -1\n\n``` | 1 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python | BFS solution | stickers-to-spell-word | 0 | 1 | I need to say that this is not the fastest or smartes way to solve this problem, however, this is also can be interesting. \nP.S. For those who are interested, the solution is faster than 25% of other solutions. But perhaps it can be optimized a bit.\n\n```\nclass Solution:\n \n @staticmethod\n def substract(c1, c2):\n\t # remove intersection of c1 and c2 from c2 and encode the c1 to string\n remove_keys = []\n result = ""\n for k in c1.keys():\n if k in c2:\n c1[k] -= c2[k]\n if c1[k] <= 0:\n remove_keys.append(k)\n if c1[k] > 0:\n result += k + str(c1[k])\n \n for key in remove_keys:\n c1.pop(key, None)\n return c1, result\n \n def minStickers(self, stickers: List[str], target: str) -> int:\n\t # count all letters in target\n target_count = Counter(target)\n stickers_counter = []\n \n s1 = set(target_count.keys())\n s2 = set()\n \n\t\t# count all letters which are exist in target for every sticker\n for i in range(len(stickers)):\n sticker = stickers[i]\n sticker_counter = defaultdict(int)\n for letter in sticker:\n if letter in target_count:\n sticker_counter[letter] += 1\n stickers_counter.append(sticker_counter)\n s2.update(sticker_counter.keys())\n \n if s2 != s1:\n return -1\n \n total_letters = sum(target_count.values())\n counter = 0\n \n q = deque([target_count])\n visited = set()\n \n\t\t# BFS loop to find the shortest path to get empty target dict\n while q:\n q_size = len(q)\n for _ in range(q_size):\n target_count = q.popleft()\n for sticker in stickers_counter:\n tmp, encoded = self.substract(target_count.copy(), sticker)\n if sum(tmp.values()) == 0:\n return counter+1\n if encoded not in visited:\n q.append(tmp)\n visited.add(encoded)\n counter += 1\n return -1\n\n``` | 1 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
From recursion to memoized | stickers-to-spell-word | 0 | 1 | # Intuition\nTry all stickers.\n\n# Approach 1 (Recursive TLE\'D)\n1. For each sticker, make a counter only for those which have letters that overlap with the target letters. Eg. `target = "hello"` and `stickers = ["help","me"]`. Here `help` overlaps with our target `hello` but `me` does not so we wont make a counter for it.\n2. Now make a DFS call on our target.\n2. Now make a counter for our target.\n3. Then check if the first letter of our target is present in any of the sticker. If it is, then just subtract both the counters. Then form a string from the remaining letters and make another DFS call on it.\n4. Do this till the target is exhausted.\n\n# Complexity\n- Time complexity:\nThis is a tricky one and is difficult to analyze the time complexity perfectly.\nBut we can say the time complexity to be **exponential**.\n\n- Space complexity:\n$$O(N) + O(N)$$ *for recurive stack and new stickers array*\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n\n stickers = [Counter(s) for s in stickers if set(s)&set(target)]\n def generate(target):\n if not target: return 0\n \n target_counter = Counter(target)\n res = float("inf")\n for sticker in stickers:\n if sticker[target[0]] == 0: continue\n tmp = 1 + generate("".join([letter*count for letter,count in (target_counter-sticker).items()]))\n\n res = min(res,tmp)\n return res\n\n res = generate(target)\n return -1 if res == float("inf") else res\n\n```\n\n# Approach 2 (Memoized)\nJust memoize it.\n\n# Complexity\n- Time complexity:\n$$O(N*M)$$ *where N is length of target and M is length of stickers array*\nTake the `target = "abcd"` and `stickers = ["a","b","c","d"]` and see how many times the loop will run to understand the time complexities.\n\n- Space complexity:\n$$O(N*M) + O(N)$$ for DP and recursive stack.\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n\n stickers = [Counter(s) for s in stickers if set(s)&set(target)]\n dp = {}\n def generate(target):\n if not target: return 0\n if target in dp: return dp[target]\n \n target_counter = Counter(target)\n res = float("inf")\n for sticker in stickers:\n if sticker[target[0]] == 0: continue\n tmp = 1 + generate("".join([letter*count for letter,count in (target_counter-sticker).items()]))\n\n res = min(res,tmp)\n dp[target] = res\n return res\n\n res = generate(target)\n return -1 if res == float("inf") else res\n```\n | 5 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
From recursion to memoized | stickers-to-spell-word | 0 | 1 | # Intuition\nTry all stickers.\n\n# Approach 1 (Recursive TLE\'D)\n1. For each sticker, make a counter only for those which have letters that overlap with the target letters. Eg. `target = "hello"` and `stickers = ["help","me"]`. Here `help` overlaps with our target `hello` but `me` does not so we wont make a counter for it.\n2. Now make a DFS call on our target.\n2. Now make a counter for our target.\n3. Then check if the first letter of our target is present in any of the sticker. If it is, then just subtract both the counters. Then form a string from the remaining letters and make another DFS call on it.\n4. Do this till the target is exhausted.\n\n# Complexity\n- Time complexity:\nThis is a tricky one and is difficult to analyze the time complexity perfectly.\nBut we can say the time complexity to be **exponential**.\n\n- Space complexity:\n$$O(N) + O(N)$$ *for recurive stack and new stickers array*\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n\n stickers = [Counter(s) for s in stickers if set(s)&set(target)]\n def generate(target):\n if not target: return 0\n \n target_counter = Counter(target)\n res = float("inf")\n for sticker in stickers:\n if sticker[target[0]] == 0: continue\n tmp = 1 + generate("".join([letter*count for letter,count in (target_counter-sticker).items()]))\n\n res = min(res,tmp)\n return res\n\n res = generate(target)\n return -1 if res == float("inf") else res\n\n```\n\n# Approach 2 (Memoized)\nJust memoize it.\n\n# Complexity\n- Time complexity:\n$$O(N*M)$$ *where N is length of target and M is length of stickers array*\nTake the `target = "abcd"` and `stickers = ["a","b","c","d"]` and see how many times the loop will run to understand the time complexities.\n\n- Space complexity:\n$$O(N*M) + O(N)$$ for DP and recursive stack.\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n\n stickers = [Counter(s) for s in stickers if set(s)&set(target)]\n dp = {}\n def generate(target):\n if not target: return 0\n if target in dp: return dp[target]\n \n target_counter = Counter(target)\n res = float("inf")\n for sticker in stickers:\n if sticker[target[0]] == 0: continue\n tmp = 1 + generate("".join([letter*count for letter,count in (target_counter-sticker).items()]))\n\n res = min(res,tmp)\n dp[target] = res\n return res\n\n res = generate(target)\n return -1 if res == float("inf") else res\n```\n | 5 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python | Easy to Understand | Kinda like coin change problem | stickers-to-spell-word | 0 | 1 | \n# Code\n```\n\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n\n def remove_chars(sticker, target):\n for ch in sticker:\n target = target.replace(ch, \'\', 1)\n return target\n\n memo = {}\n\n def dfs(remaining_target):\n if remaining_target == "":\n return 0\n if remaining_target in memo:\n return memo[remaining_target]\n min_stickers = float("inf")\n\n for sticker in stickers:\n if remaining_target[0] in sticker:\n new_target = remove_chars(sticker, remaining_target)\n res = dfs(new_target)\n min_stickers = min(min_stickers, 1 + res)\n\n memo[remaining_target] = min_stickers\n return memo[remaining_target]\n\n result = dfs(target)\n return result if result != float("inf") else -1\n\n\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Python | Easy to Understand | Kinda like coin change problem | stickers-to-spell-word | 0 | 1 | \n# Code\n```\n\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n\n def remove_chars(sticker, target):\n for ch in sticker:\n target = target.replace(ch, \'\', 1)\n return target\n\n memo = {}\n\n def dfs(remaining_target):\n if remaining_target == "":\n return 0\n if remaining_target in memo:\n return memo[remaining_target]\n min_stickers = float("inf")\n\n for sticker in stickers:\n if remaining_target[0] in sticker:\n new_target = remove_chars(sticker, remaining_target)\n res = dfs(new_target)\n min_stickers = min(min_stickers, 1 + res)\n\n memo[remaining_target] = min_stickers\n return memo[remaining_target]\n\n result = dfs(target)\n return result if result != float("inf") else -1\n\n\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
DP solution | stickers-to-spell-word | 0 | 1 | # Intuition\nAfter using a sticker, we recursively have to decide which sticker to use next until we build the target. We have to try all combinations to find the minimum. Hence DP.\n\n# Approach\nFor each sticker, see how much of target is still left after using it. Recursively call the procedure on this new target.\n\n# Complexity\n- Time complexity: dp is called for every subsequence of target. So O(2^n) where n is the length of the target.\n\n- Space complexity: Each dp call is cached. Hence O(2^n).\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n \n # use the given sticker to remove elements from target. whatever is left of target is returned.\n def match(sticker, target):\n used = set()\n for i, s in enumerate(sticker):\n for j, t in enumerate(target):\n if s == t and j not in used:\n used.add(j)\n break\n res = ""\n for j, t in enumerate(target):\n if j not in used:\n res += t\n return res\n\n @cache\n def dp(target):\n if not target:\n return 0\n res = []\n # try each sticker\n for sticker in stickers:\n new_target = match(sticker, target)\n if len(target) > len(new_target):\n sub = dp(new_target)\n if sub != -1:\n res.append(1 + sub)\n\n if res:\n return min(res)\n else:\n return -1\n\n return dp(target)\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
DP solution | stickers-to-spell-word | 0 | 1 | # Intuition\nAfter using a sticker, we recursively have to decide which sticker to use next until we build the target. We have to try all combinations to find the minimum. Hence DP.\n\n# Approach\nFor each sticker, see how much of target is still left after using it. Recursively call the procedure on this new target.\n\n# Complexity\n- Time complexity: dp is called for every subsequence of target. So O(2^n) where n is the length of the target.\n\n- Space complexity: Each dp call is cached. Hence O(2^n).\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n \n # use the given sticker to remove elements from target. whatever is left of target is returned.\n def match(sticker, target):\n used = set()\n for i, s in enumerate(sticker):\n for j, t in enumerate(target):\n if s == t and j not in used:\n used.add(j)\n break\n res = ""\n for j, t in enumerate(target):\n if j not in used:\n res += t\n return res\n\n @cache\n def dp(target):\n if not target:\n return 0\n res = []\n # try each sticker\n for sticker in stickers:\n new_target = match(sticker, target)\n if len(target) > len(new_target):\n sub = dp(new_target)\n if sub != -1:\n res.append(1 + sub)\n\n if res:\n return min(res)\n else:\n return -1\n\n return dp(target)\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Using DFS to explore each sticker subtraction to remove first letter from target | stickers-to-spell-word | 0 | 1 | # Code\n```\nclass Solution:\n # https://leetcode.com/problems/stickers-to-spell-word/solutions/233915/python-12-lines-solution/\n def minStickers(self, stickers: List[str], target: str) -> int:\n counts = [Counter(s) for s in stickers]\n # T = O(N * W * N) - N is letters in target and S = number of stickers and N for creating next target\n # S = O(N) for stack and O(kW) for counters \n @lru_cache(None)\n def dfs(target):\n if not target: \n return 0\n\n targetCount = collections.Counter(target)\n ans = math.inf\n for count in counts:\n # choose a sticker only if it is able to eliminate \n # first character of target (to reduce search space)\n if target[0] not in count:\n continue \n # counters will only reduce count of letters present in \n # targetCount and will set count to 0 if Count has more \n # of those letters\n remaining = targetCount - count\n # convert the remaining letters back to word\n letters = [ s * c for s, c in remaining.items() ]\n letters.sort()\n nextTarget = "".join(letters)\n # explore how many stickers will be needed for new target\n ans = min(ans, dfs(nextTarget))\n # ans will be 1 sticker used before + remaining ans\n return 1 + ans\n\n ans = dfs(target)\n return ans if ans != math.inf else -1\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
Using DFS to explore each sticker subtraction to remove first letter from target | stickers-to-spell-word | 0 | 1 | # Code\n```\nclass Solution:\n # https://leetcode.com/problems/stickers-to-spell-word/solutions/233915/python-12-lines-solution/\n def minStickers(self, stickers: List[str], target: str) -> int:\n counts = [Counter(s) for s in stickers]\n # T = O(N * W * N) - N is letters in target and S = number of stickers and N for creating next target\n # S = O(N) for stack and O(kW) for counters \n @lru_cache(None)\n def dfs(target):\n if not target: \n return 0\n\n targetCount = collections.Counter(target)\n ans = math.inf\n for count in counts:\n # choose a sticker only if it is able to eliminate \n # first character of target (to reduce search space)\n if target[0] not in count:\n continue \n # counters will only reduce count of letters present in \n # targetCount and will set count to 0 if Count has more \n # of those letters\n remaining = targetCount - count\n # convert the remaining letters back to word\n letters = [ s * c for s, c in remaining.items() ]\n letters.sort()\n nextTarget = "".join(letters)\n # explore how many stickers will be needed for new target\n ans = min(ans, dfs(nextTarget))\n # ans will be 1 sticker used before + remaining ans\n return 1 + ans\n\n ans = dfs(target)\n return ans if ans != math.inf else -1\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
inspired by other's solution | stickers-to-spell-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n stickers_chars = [[0] * 26 for _ in range(len(stickers))]\n for i in range(len(stickers)):\n for ch in stickers[i]:\n stickers_chars[i][ ord(ch) - ord(\'a\') ] += 1\n\n mapper = {}\n mapper[""] = 0\n\n def dfs(target):\n if target in mapper:\n return mapper[target]\n \n ans = 2**31 - 1\n stickers_length = len(stickers_chars)\n target_cnt = [0] * 26\n for ch in target:\n target_cnt[ ord(ch) - ord(\'a\') ] += 1\n\n for i in range(stickers_length):\n # to avoid infinite loop, if current sticker has no available char, skip\n if stickers_chars[i][ ord(target[0]) - ord(\'a\') ] == 0:\n continue\n\n # build next str\n next_str = \'\'\n for j in range(26):\n if target_cnt[j] > 0:\n for k in range(max(0, target_cnt[j] - stickers_chars[i][j])):\n next_str += chr(ord(\'a\') + j)\n \n tmp_ans = dfs(next_str)\n # meaning we able to make target to ""\n if tmp_ans != -1: \n # we keep updating ans to min \n # we increase by 1, meaning current sticker offered chars make current target string to null\n ans = min(ans, tmp_ans + 1) \n \n mapper[target] = -1 if ans == 2**31 - 1 else ans\n return mapper[target]\n\n return dfs(target)\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
inspired by other's solution | stickers-to-spell-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n stickers_chars = [[0] * 26 for _ in range(len(stickers))]\n for i in range(len(stickers)):\n for ch in stickers[i]:\n stickers_chars[i][ ord(ch) - ord(\'a\') ] += 1\n\n mapper = {}\n mapper[""] = 0\n\n def dfs(target):\n if target in mapper:\n return mapper[target]\n \n ans = 2**31 - 1\n stickers_length = len(stickers_chars)\n target_cnt = [0] * 26\n for ch in target:\n target_cnt[ ord(ch) - ord(\'a\') ] += 1\n\n for i in range(stickers_length):\n # to avoid infinite loop, if current sticker has no available char, skip\n if stickers_chars[i][ ord(target[0]) - ord(\'a\') ] == 0:\n continue\n\n # build next str\n next_str = \'\'\n for j in range(26):\n if target_cnt[j] > 0:\n for k in range(max(0, target_cnt[j] - stickers_chars[i][j])):\n next_str += chr(ord(\'a\') + j)\n \n tmp_ans = dfs(next_str)\n # meaning we able to make target to ""\n if tmp_ans != -1: \n # we keep updating ans to min \n # we increase by 1, meaning current sticker offered chars make current target string to null\n ans = min(ans, tmp_ans + 1) \n \n mapper[target] = -1 if ans == 2**31 - 1 else ans\n return mapper[target]\n\n return dfs(target)\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
I want to discuss how to improve the time complexity of my solution to avoid timeout in the last 3. | stickers-to-spell-word | 0 | 1 | # Intuition\nThe idea is to turn strings into counters so that each counter stores the number of each letters in the string.\n\nFor some letters in the target string, we can only find one sticker that has that letter, so these can be handled first.\n\nThen for the rest of the string, I am doing BFS so that once a solution is found, it is guaranteed to be the best one.\n\nI just don\'t know how to improve my code to make it pass the last 3 cases. One direction could be avoiding duplicated states?\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n tcount = Counter(target)\n def getScore(s):\n temp = dict(tcount)\n sdict = defaultdict(int)\n res = 0\n for c in s:\n if c in temp and temp[c] > 0:\n temp[c] -= 1\n res += 1\n sdict[c] += 1\n return (res, sdict)\n stickers = [getScore(s) for s in stickers]\n stickers.sort(key = lambda x: x[0], reverse = True)\n stickers = [x[1] for x in stickers if x[0] > 0]\n opt = [stickers[0]]\n for i in range(1, len(stickers)):\n if opt[-1].keys() == stickers[i].keys() :\n continue\n opt.append(stickers[i])\n stickers = opt[:]\n \n seen = set()\n q = deque([target])\n step = 0\n while q:\n n = len(q)\n step += 1\n for i in range(n):\n cur = q.popleft()\n if cur in seen:\n continue\n seen.add(cur)\n for stick in stickers:\n if cur[0] not in stick:\n continue\n new = str(cur)\n for s in stick:\n new = new.replace(s,\'\', stick[s])\n if new == "":\n return step\n if new not in seen:\n q.append(new)\n return -1\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
I want to discuss how to improve the time complexity of my solution to avoid timeout in the last 3. | stickers-to-spell-word | 0 | 1 | # Intuition\nThe idea is to turn strings into counters so that each counter stores the number of each letters in the string.\n\nFor some letters in the target string, we can only find one sticker that has that letter, so these can be handled first.\n\nThen for the rest of the string, I am doing BFS so that once a solution is found, it is guaranteed to be the best one.\n\nI just don\'t know how to improve my code to make it pass the last 3 cases. One direction could be avoiding duplicated states?\n\n# Code\n```\nclass Solution:\n def minStickers(self, stickers: List[str], target: str) -> int:\n tcount = Counter(target)\n def getScore(s):\n temp = dict(tcount)\n sdict = defaultdict(int)\n res = 0\n for c in s:\n if c in temp and temp[c] > 0:\n temp[c] -= 1\n res += 1\n sdict[c] += 1\n return (res, sdict)\n stickers = [getScore(s) for s in stickers]\n stickers.sort(key = lambda x: x[0], reverse = True)\n stickers = [x[1] for x in stickers if x[0] > 0]\n opt = [stickers[0]]\n for i in range(1, len(stickers)):\n if opt[-1].keys() == stickers[i].keys() :\n continue\n opt.append(stickers[i])\n stickers = opt[:]\n \n seen = set()\n q = deque([target])\n step = 0\n while q:\n n = len(q)\n step += 1\n for i in range(n):\n cur = q.popleft()\n if cur in seen:\n continue\n seen.add(cur)\n for stick in stickers:\n if cur[0] not in stick:\n continue\n new = str(cur)\n for s in stick:\n new = new.replace(s,\'\', stick[s])\n if new == "":\n return step\n if new not in seen:\n q.append(new)\n return -1\n``` | 0 | We are given `n` different types of `stickers`. Each sticker has a lowercase English word on it.
You would like to spell out the given string `target` by cutting individual letters from your collection of stickers and rearranging them. You can use each sticker more than once if you want, and you have infinite quantities of each sticker.
Return _the minimum number of stickers that you need to spell out_ `target`. If the task is impossible, return `-1`.
**Note:** In all test cases, all words were chosen randomly from the `1000` most common US English words, and `target` was chosen as a concatenation of two random words.
**Example 1:**
**Input:** stickers = \[ "with ", "example ", "science "\], target = "thehat "
**Output:** 3
**Explanation:**
We can use 2 "with " stickers, and 1 "example " sticker.
After cutting and rearrange the letters of those stickers, we can form the target "thehat ".
Also, this is the minimum number of stickers necessary to form the target string.
**Example 2:**
**Input:** stickers = \[ "notice ", "possible "\], target = "basicbasic "
**Output:** -1
Explanation:
We cannot form the target "basicbasic " from cutting letters from the given stickers.
**Constraints:**
* `n == stickers.length`
* `1 <= n <= 50`
* `1 <= stickers[i].length <= 10`
* `1 <= target.length <= 15`
* `stickers[i]` and `target` consist of lowercase English letters. | We want to perform an exhaustive search, but we need to speed it up based on the input data being random.
For all stickers, we can ignore any letters that are not in the target word.
When our candidate answer won't be smaller than an answer we have already found, we can stop searching this path.
When a sticker dominates another, we shouldn't include the dominated sticker in our sticker collection. [Here, we say a sticker `A` dominates `B` if `A.count(letter) >= B.count(letter)` for all letters.] |
python3, collections.Counter() and sort list with a tuple as key | top-k-frequent-words | 0 | 1 | **Solution 1: Counter() and sort()** \nhttps://leetcode.com/submissions/detail/875157545/\nRuntime: **57 ms**, faster than 88.57% of Python3 online submissions for Top K Frequent Words. \nMemory Usage: 13.9 MB, less than 94.23% of Python3 online submissions for Top K Frequent Words. \n```\nclass Solution:\n def topKFrequent(self, words: List[str], k: int) -> List[str]:\n l = [(v,k) for k,v in Counter(words).items()]\n l.sort(key=lambda x:(-x[0], x[1]))\n return [w for f,w in l[:k]]\n```\n\n**Solution 2: naive dictionary** \nhttps://leetcode.com/submissions/detail/825652552/ \n110 / 110 test cases passed. \nStatus: Accepted \nRuntime: **96 ms** \nMemory Usage: 13.8 MB \n```\nclass Solution(object):\n def topKFrequent(self, words, k):\n """\n :type words: List[str]\n :type k: int\n :rtype: List[str]\n """\n d = {}\n for word in set(words):\n n = words.count(word)\n if n in d:\n d[n].append(word)\n else:\n d[n] = [word]\n \n res = [] \n for n in sorted(d, reverse=True):\n l = d[n]\n l.sort()\n if len(l)<k-len(res):\n res += l\n else:\n res += l[:k-len(res)]\n break\n return res\n``` | 3 | Given an array of strings `words` and an integer `k`, return _the_ `k` _most frequent strings_.
Return the answer **sorted** by **the frequency** from highest to lowest. Sort the words with the same frequency by their **lexicographical order**.
**Example 1:**
**Input:** words = \[ "i ", "love ", "leetcode ", "i ", "love ", "coding "\], k = 2
**Output:** \[ "i ", "love "\]
**Explanation:** "i " and "love " are the two most frequent words.
Note that "i " comes before "love " due to a lower alphabetical order.
**Example 2:**
**Input:** words = \[ "the ", "day ", "is ", "sunny ", "the ", "the ", "the ", "sunny ", "is ", "is "\], k = 4
**Output:** \[ "the ", "is ", "sunny ", "day "\]
**Explanation:** "the ", "is ", "sunny " and "day " are the four most frequent words, with the number of occurrence being 4, 3, 2 and 1 respectively.
**Constraints:**
* `1 <= words.length <= 500`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* `k` is in the range `[1, The number of **unique** words[i]]`
**Follow-up:** Could you solve it in `O(n log(k))` time and `O(n)` extra space? | null |
Python | 1 line Solution | Easy to Understand | top-k-frequent-words | 0 | 1 | # One Line\n```\nclass Solution:\n def topKFrequent(self, words: List[str], k: int) -> List[str]:\n return [x[0] for x in sorted(Counter(words).items(), key=lambda x:(-x[1], x[0]))][0:k]\n```\n\n# Three Lines (more understandable)\n```\nfrom collections import Counter\n\nclass Solution:\n def topKFrequent(self, words: List[str], k: int) -> List[str]:\n words_dict = Counter(words)\n sorted_dict = [x[0] for x in sorted(words_dict.items(), key=lambda x:(-x[1], x[0]))]\n return sorted_dict[0:k]\n```\n\n\n | 1 | Given an array of strings `words` and an integer `k`, return _the_ `k` _most frequent strings_.
Return the answer **sorted** by **the frequency** from highest to lowest. Sort the words with the same frequency by their **lexicographical order**.
**Example 1:**
**Input:** words = \[ "i ", "love ", "leetcode ", "i ", "love ", "coding "\], k = 2
**Output:** \[ "i ", "love "\]
**Explanation:** "i " and "love " are the two most frequent words.
Note that "i " comes before "love " due to a lower alphabetical order.
**Example 2:**
**Input:** words = \[ "the ", "day ", "is ", "sunny ", "the ", "the ", "the ", "sunny ", "is ", "is "\], k = 4
**Output:** \[ "the ", "is ", "sunny ", "day "\]
**Explanation:** "the ", "is ", "sunny " and "day " are the four most frequent words, with the number of occurrence being 4, 3, 2 and 1 respectively.
**Constraints:**
* `1 <= words.length <= 500`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* `k` is in the range `[1, The number of **unique** words[i]]`
**Follow-up:** Could you solve it in `O(n log(k))` time and `O(n)` extra space? | null |
Top K Frequent Words | top-k-frequent-words | 0 | 1 | Arranging count of each word and returning ***k*** words\n\n# Steps \n - Getting Unique Words in list: words: List[str]\n - Creating Dictionary dict initialized with key as unique list and value as 0 \n - Traversing through list: words: List[str] and counting # of words and storing in Dictionary dict\n - Sorting Dict by value in descending order\n - Lexicographically Sort the words with same count and append key of dict in list output\n - Return first k values in list\n\n# Code\n```\nfrom collections import OrderedDict\n\n# sort x and returning it\ndef mySort(x):\n x.sort()\n return x\n\nclass Solution:\n def topKFrequent(self, words: List[str], k: int) -> List[str]:\n # get unique words from list\n uniqueWords = tuple(words);\n \n dict = {}\n # initializing dict = 0\n for i in uniqueWords :\n dict[i] = 0 ;\n\n # counting no of words\n for i in words:\n dict[i] += 1 ; \n\n # sorting dict in decending order\n dict = {key: value for key, value in sorted(dict.items(), key=lambda item: item[1] , reverse = True ) }\n\n keys = list(dict.keys())\n values = list(dict.values())\n i , j = 0 , 0 \n output = []\n\n # sorting the words with same count Lexicographically\n while i != len(values) and j != len(values):\n if( values[i] == values[j] ):\n j += 1\n else:\n output = output + mySort(keys[i:j]) \n i = j\n output = output + mySort(keys[i:j]) \n \n return output[0:k] \n``` | 1 | Given an array of strings `words` and an integer `k`, return _the_ `k` _most frequent strings_.
Return the answer **sorted** by **the frequency** from highest to lowest. Sort the words with the same frequency by their **lexicographical order**.
**Example 1:**
**Input:** words = \[ "i ", "love ", "leetcode ", "i ", "love ", "coding "\], k = 2
**Output:** \[ "i ", "love "\]
**Explanation:** "i " and "love " are the two most frequent words.
Note that "i " comes before "love " due to a lower alphabetical order.
**Example 2:**
**Input:** words = \[ "the ", "day ", "is ", "sunny ", "the ", "the ", "the ", "sunny ", "is ", "is "\], k = 4
**Output:** \[ "the ", "is ", "sunny ", "day "\]
**Explanation:** "the ", "is ", "sunny " and "day " are the four most frequent words, with the number of occurrence being 4, 3, 2 and 1 respectively.
**Constraints:**
* `1 <= words.length <= 500`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* `k` is in the range `[1, The number of **unique** words[i]]`
**Follow-up:** Could you solve it in `O(n log(k))` time and `O(n)` extra space? | null |
Short and sweet solution. Beats 97% space, 82% time | top-k-frequent-words | 0 | 1 | ```\nclass Solution:\n def topKFrequent(self, words: List[str], k: int) -> List[str]:\n d = {}\n for word in words:\n d[word] = d.get(word, 0) + 1\n \n res = sorted(d, key=lambda word: (-d[word], word))\n return res[:k]\n```\nIf it helped or you learned a new way, kindly upvote. Thanks :) | 4 | Given an array of strings `words` and an integer `k`, return _the_ `k` _most frequent strings_.
Return the answer **sorted** by **the frequency** from highest to lowest. Sort the words with the same frequency by their **lexicographical order**.
**Example 1:**
**Input:** words = \[ "i ", "love ", "leetcode ", "i ", "love ", "coding "\], k = 2
**Output:** \[ "i ", "love "\]
**Explanation:** "i " and "love " are the two most frequent words.
Note that "i " comes before "love " due to a lower alphabetical order.
**Example 2:**
**Input:** words = \[ "the ", "day ", "is ", "sunny ", "the ", "the ", "the ", "sunny ", "is ", "is "\], k = 4
**Output:** \[ "the ", "is ", "sunny ", "day "\]
**Explanation:** "the ", "is ", "sunny " and "day " are the four most frequent words, with the number of occurrence being 4, 3, 2 and 1 respectively.
**Constraints:**
* `1 <= words.length <= 500`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* `k` is in the range `[1, The number of **unique** words[i]]`
**Follow-up:** Could you solve it in `O(n log(k))` time and `O(n)` extra space? | null |
Correct time complexity: O(n log(k)) | top-k-frequent-words | 0 | 1 | # Complexity\n- Time complexity: `O(n log(k))`\n\n- Space complexity: `O(k)`\n\n# Code\n```py\nclass HeapWord:\n def __init__(self, word):\n self.word = word\n\n def __gt__(self, other):\n return self.word < other.word\n \n def __repr__(self):\n return self.word\n\n\nclass Solution:\n def topKFrequent(self, words: List[str], k: int) -> List[str]:\n minheap = []\n\n for w, freq in Counter(words).items():\n w = HeapWord(w)\n heapq.heappush(minheap, (freq, w))\n while len(minheap) > k:\n heapq.heappop(minheap)\n\n maxheap = [(-freq, w.word) for freq, w in minheap]\n heapq.heapify(maxheap)\n\n res = []\n while len(res) != k:\n res.append(heapq.heappop(maxheap)[1])\n\n return res\n\n``` | 0 | Given an array of strings `words` and an integer `k`, return _the_ `k` _most frequent strings_.
Return the answer **sorted** by **the frequency** from highest to lowest. Sort the words with the same frequency by their **lexicographical order**.
**Example 1:**
**Input:** words = \[ "i ", "love ", "leetcode ", "i ", "love ", "coding "\], k = 2
**Output:** \[ "i ", "love "\]
**Explanation:** "i " and "love " are the two most frequent words.
Note that "i " comes before "love " due to a lower alphabetical order.
**Example 2:**
**Input:** words = \[ "the ", "day ", "is ", "sunny ", "the ", "the ", "the ", "sunny ", "is ", "is "\], k = 4
**Output:** \[ "the ", "is ", "sunny ", "day "\]
**Explanation:** "the ", "is ", "sunny " and "day " are the four most frequent words, with the number of occurrence being 4, 3, 2 and 1 respectively.
**Constraints:**
* `1 <= words.length <= 500`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* `k` is in the range `[1, The number of **unique** words[i]]`
**Follow-up:** Could you solve it in `O(n log(k))` time and `O(n)` extra space? | null |
No Need to explain.py | top-k-frequent-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOnly this line confuse you:\nlet me expain \nl.sort(key=lambda x: (-x[0], x[1]))\n\nI use -x[0] because it sort the list in decending order and x[1] is used to sort in lexicographical order.\nBoth perimeter work simultaneously. That Gives the output..\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def topKFrequent(self, words: List[str], k: int) -> List[str]:\n l = []\n ans = []\n for i in set(words):\n l.append([words.count(i), i])\n l.sort(key=lambda x: (-x[0], x[1]))\n\n for i in range(k):\n ans.append(l[i][1])\n\n return ans\n\n```\n\n**Please UPVOTE if you like ::::)))))**\n | 1 | Given an array of strings `words` and an integer `k`, return _the_ `k` _most frequent strings_.
Return the answer **sorted** by **the frequency** from highest to lowest. Sort the words with the same frequency by their **lexicographical order**.
**Example 1:**
**Input:** words = \[ "i ", "love ", "leetcode ", "i ", "love ", "coding "\], k = 2
**Output:** \[ "i ", "love "\]
**Explanation:** "i " and "love " are the two most frequent words.
Note that "i " comes before "love " due to a lower alphabetical order.
**Example 2:**
**Input:** words = \[ "the ", "day ", "is ", "sunny ", "the ", "the ", "the ", "sunny ", "is ", "is "\], k = 4
**Output:** \[ "the ", "is ", "sunny ", "day "\]
**Explanation:** "the ", "is ", "sunny " and "day " are the four most frequent words, with the number of occurrence being 4, 3, 2 and 1 respectively.
**Constraints:**
* `1 <= words.length <= 500`
* `1 <= words[i].length <= 10`
* `words[i]` consists of lowercase English letters.
* `k` is in the range `[1, The number of **unique** words[i]]`
**Follow-up:** Could you solve it in `O(n log(k))` time and `O(n)` extra space? | null |
python3 code | binary-number-with-alternating-bits | 0 | 1 | # Intuition\nThe function first converts n to its binary representation using the built-in bin() function, and then converts the resulting binary string to a regular string. It then extracts two substrings from this string, one containing all the even-indexed bits and the other containing all the odd-indexed bits.\n\nFinally, the function checks if both substrings contain only one type of bit (i.e., all 0s or all 1s), and returns True if this is the case, indicating that the bits are alternating. Otherwise, it returns False.\n\nOverall, this function provides a simple and efficient way to check if an integer has \n\n# Approach\nThe approach for the above code is to first convert the input integer n to its binary representation using the bin() function. The resulting binary string is then converted to a regular string.\n\nNext, the function extracts two substrings from this string, one containing all the even-indexed bits and the other containing all the odd-indexed bits. This is done using Python\'s built-in string slicing syntax, which allows you to extract a substring by specifying a start index, an end index, and a step size.\n\nAfter extracting the two substrings, the function checks if both substrings contain only one type of bit (i.e., all 0s or all 1s), and returns True if this is the case, indicating that the bits are alternating. Otherwise, it returns False.\n\nOverall, this approach is relatively straightforward and efficient, as it involves only simple string manipulations and set operations.\n# Complexity\n- Time complexity:\nO(logn)\n\n- Space complexity:\nO(logn)\n# Code\n```\nclass Solution:\n def hasAlternatingBits(self, n: int) -> bool:\n d = bin(n)[2:]\n s = str(d)\n u = s[::2]\n g = s[1::2]\n if(n==1 or n==0):\n return True\n if(set(u)== {\'0\'} and set(g)=={\'1\'}) or (set(u)== {\'1\'} and set(g)=={\'0\'}) :\n return True\n else:\n return False\n \n \n``` | 1 | Given a positive integer, check whether it has alternating bits: namely, if two adjacent bits will always have different values.
**Example 1:**
**Input:** n = 5
**Output:** true
**Explanation:** The binary representation of 5 is: 101
**Example 2:**
**Input:** n = 7
**Output:** false
**Explanation:** The binary representation of 7 is: 111.
**Example 3:**
**Input:** n = 11
**Output:** false
**Explanation:** The binary representation of 11 is: 1011.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Solution | binary-number-with-alternating-bits | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool hasAlternatingBits(int n) {\n int pre = n&0x1;\n n>>=1; \n while(n!=0)\n {\n if((n&0x1) == pre)\n return false;\n \n pre = n&0x1;\n n>>=1;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def hasAlternatingBits(self, n: int) -> bool:\n bits = bin(n)\n return "00" not in bits and "11" not in bits\n```\n\n```Java []\nclass Solution {\n public boolean hasAlternatingBits(int n) {\n while(n!=0){\n int a=(n&1);\n n>>=1;\n int b=(n&1);\n if(a==b)\n return false;\n }\n return true;\n }\n}\n```\n | 2 | Given a positive integer, check whether it has alternating bits: namely, if two adjacent bits will always have different values.
**Example 1:**
**Input:** n = 5
**Output:** true
**Explanation:** The binary representation of 5 is: 101
**Example 2:**
**Input:** n = 7
**Output:** false
**Explanation:** The binary representation of 7 is: 111.
**Example 3:**
**Input:** n = 11
**Output:** false
**Explanation:** The binary representation of 11 is: 1011.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Easy Solution | Java | Python | binary-number-with-alternating-bits | 1 | 1 | # Python\n```\nclass Solution:\n def hasAlternatingBits(self, n: int) -> bool:\n num = str(bin(n).split(\'b\')[1])\n prev = num[0]\n for i in range(1, len(num)):\n if num[i] == prev:\n return False\n prev = num[i] \n return True\n```\n# Java\n```\nclass Solution {\n public boolean hasAlternatingBits(int n) {\n String s = Integer.toBinaryString(n);\n char prev = s.charAt(0);\n for(int i=1; i<s.length(); i++) {\n int x = Character.compare(prev, s.charAt(i));\n System.out.println(x);\n if(x == 0) {\n return false;\n } \n prev = s.charAt(i);\n }\n return true;\n }\n}\n```\nDo upvote if you like the Solution :) | 2 | Given a positive integer, check whether it has alternating bits: namely, if two adjacent bits will always have different values.
**Example 1:**
**Input:** n = 5
**Output:** true
**Explanation:** The binary representation of 5 is: 101
**Example 2:**
**Input:** n = 7
**Output:** false
**Explanation:** The binary representation of 7 is: 111.
**Example 3:**
**Input:** n = 11
**Output:** false
**Explanation:** The binary representation of 11 is: 1011.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
693: Space 91.89%, Solution with step by step explanation | binary-number-with-alternating-bits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Convert the input integer n to its binary representation using the built-in bin() function. This will return a string of 0s and 1s representing the binary representation of n.\n\n2. Iterate over the binary string from index 0 to the second to last character. For each pair of adjacent characters, check if they are the same. If they are, return False because the bits are not alternating.\n\n3. If the loop completes without returning False, then all the bits are alternating and we can return True.\n\n# Complexity\n- Time complexity:\nO(log n)\n\n- Space complexity:\nO(log n)\n\n# Code\n```\nclass Solution:\n def hasAlternatingBits(self, n: int) -> bool:\n # Step 1: Convert the integer to binary representation\n binary = bin(n)[2:]\n \n # Step 2: Check whether the binary representation has alternating bits\n for i in range(len(binary)-1):\n if binary[i] == binary[i+1]:\n return False\n \n # Step 3: Return True if the binary representation has alternating bits, False otherwise\n return True\n\n``` | 4 | Given a positive integer, check whether it has alternating bits: namely, if two adjacent bits will always have different values.
**Example 1:**
**Input:** n = 5
**Output:** true
**Explanation:** The binary representation of 5 is: 101
**Example 2:**
**Input:** n = 7
**Output:** false
**Explanation:** The binary representation of 7 is: 111.
**Example 3:**
**Input:** n = 11
**Output:** false
**Explanation:** The binary representation of 11 is: 1011.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
2 O(1) UNIQUE SOLUTION WITH EXPLANATION | binary-number-with-alternating-bits | 0 | 1 | \n\n## Approach 1\n- ``` 0x55555555 ``` = 1010101010101010101010101010101 (32 bits)\n- The Q asked if n = ```...101``` or ```...1010``` which is literally a part of ```0x55555555```. \n```\nSuppose n = 21 = 10101 which has 5 digits\nNow lets extract last 5 digits from 0x55555555, 10101\n 1 0 1 0 1\n (^) 1 0 1 0 1\n _________________\n 0 0 0 0 0 = 0\n n = 10 = 1010 which has 4 digits\n 0x55555555 == ...1010101, first extract last 5 digits (10101)\n and now do right shift by 1 and we get 1010 which is 10 = 1010 \n```\n- How can we find out the total digits of a decimal number? ``` log2(n)+1 ```\n- How to extract n number digits from 0x55555555 ?\n```\n Suppose n = 21 = 10101 which has 5 digits\nSo we need five 1 at the last and then by & operation we get the value\n.... 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1\n (&) 1 1 1 1 1\n_______________________________________________________\n0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1\nNow we got 10101 which is we wanted to extract! \n```\n- How to get those ```11111```? By ```100000-1=11111```. So at first we need to ``` right shift 1 by total_digits+1 ```, then do ```-1```. FOR EVEN NUMBER : WE NEED TO ``` right shift 1 by total_digits+2 ``` AS THE LAST BIANRY DIGIT IS 0 AND SUPPOSE WE EXTRACTED ```10101``` BUT WE NEED ```1010```,SO JUST DO ```10101 >> 1``` AND GET ```1010```.\n#### C++\n```\nclass Solution \n{\npublic:\n bool hasAlternatingBits(int n) \n {\n int t = (n&1)^1, bits = int(log2(n))+1, total = t+bits;\n int a = (0x55555555 & ((1LL<<total)-1) )>>t;\n return (n^a)==0;\n }\n};\n```\n#### Python\n```\nclass Solution:\n def hasAlternatingBits(self, n: int) -> bool:\n t, bits = (n & 1) ^ 1, int(math.log2(n)) + 1\n total = t + bits\n a = (0x55555555 & ((1 << total) - 1)) >> t\n return (n^a) == 0\n```\n## Approach 2\n```\n 42 = 1 0 1 0 1 0\n (^) 1 1 1 1 1 1 \n ________________\n 0 1 0 1 0 1 = 21 (42/2=21)\n\n 21 = 1 0 1 0 1 \n (^) 1 1 1 1 1\n ______________\n 0 1 0 1 0 = 10 (21/2=10)\n\n \'IF AND ONLY IF THE PATTERN IS ..10101 OR ..1010\' \'THEN\n n ^ (n digits 1) = THE HALF OF N\'\n\n IN MORE EASY WAY : \n IF N = 1 0 1 0 1 \n THEN 0 1 0 1 0 = HALF OF N\n\n IF N = 1 0 1 0\n THEN 0 1 0 1 = HALF OF N \n```\n#### C++\n```\nclass Solution \n{\npublic:\n bool hasAlternatingBits(int n) \n {\n int mid = n>>1, bit = log2(n)+1, p = n ^ (1LL<<bit)-1;\n return p==mid;\n }\n};\n```\n#### Python\n```\nclass Solution:\n def hasAlternatingBits(self, n: int) -> bool:\n mid, bits = n>>1, int(log2(n))+1\n p = n ^ (1<<bits)-1\n return p==mid\n```\n- Time complexity : O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n### If you find my solution helpful plz upvote | 3 | Given a positive integer, check whether it has alternating bits: namely, if two adjacent bits will always have different values.
**Example 1:**
**Input:** n = 5
**Output:** true
**Explanation:** The binary representation of 5 is: 101
**Example 2:**
**Input:** n = 7
**Output:** false
**Explanation:** The binary representation of 7 is: 111.
**Example 3:**
**Input:** n = 11
**Output:** false
**Explanation:** The binary representation of 11 is: 1011.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Simplest one-liner Python | binary-number-with-alternating-bits | 0 | 1 | \n# Code\n```\nclass Solution:\n def hasAlternatingBits(self, n: int) -> bool:\n return \'11\' not in bin(n) and \'00\' not in bin(n)\n``` | 3 | Given a positive integer, check whether it has alternating bits: namely, if two adjacent bits will always have different values.
**Example 1:**
**Input:** n = 5
**Output:** true
**Explanation:** The binary representation of 5 is: 101
**Example 2:**
**Input:** n = 7
**Output:** false
**Explanation:** The binary representation of 7 is: 111.
**Example 3:**
**Input:** n = 11
**Output:** false
**Explanation:** The binary representation of 11 is: 1011.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Python 3 | binary-number-with-alternating-bits | 0 | 1 | \n# Complexity\n- Time complexity: O(n logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def hasAlternatingBits(self, n: int) -> bool:\n a = list(str(bin(n)[2:]))\n for i in range(len(a)- 1) :\n if a[i] == a[i + 1] :\n return False\n return True\n``` | 2 | Given a positive integer, check whether it has alternating bits: namely, if two adjacent bits will always have different values.
**Example 1:**
**Input:** n = 5
**Output:** true
**Explanation:** The binary representation of 5 is: 101
**Example 2:**
**Input:** n = 7
**Output:** false
**Explanation:** The binary representation of 7 is: 111.
**Example 3:**
**Input:** n = 11
**Output:** false
**Explanation:** The binary representation of 11 is: 1011.
**Constraints:**
* `1 <= n <= 231 - 1` | null |
Binbin's another phenomenal idea | max-area-of-island | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxAreaOfIsland(self, grid: List[List[int]]) -> int:\n rows = len(grid)\n columns = len(grid[0])\n def dfs(row,col):\n if row < 0 or row >= rows or col < 0 or col >= columns or grid[row][col] ==0:\n return \n grid[row][col] = 0\n a[0] += 1\n dfs(row-1,col)\n dfs(row+1,col)\n dfs(row,col-1)\n dfs(row,col+1)\n return a[0]\n MAX=0 \n for row in range(rows):\n for col in range(columns):\n if grid[row][col] == 1:\n a=[0]\n A=dfs(row,col)\n MAX=max(A,MAX)\n \n return MAX\n\n``` | 1 | You are given an `m x n` binary matrix `grid`. An island is a group of `1`'s (representing land) connected **4-directionally** (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The **area** of an island is the number of cells with a value `1` in the island.
Return _the maximum **area** of an island in_ `grid`. If there is no island, return `0`.
**Example 1:**
**Input:** grid = \[\[0,0,1,0,0,0,0,1,0,0,0,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,1,1,0,1,0,0,0,0,0,0,0,0\],\[0,1,0,0,1,1,0,0,1,0,1,0,0\],\[0,1,0,0,1,1,0,0,1,1,1,0,0\],\[0,0,0,0,0,0,0,0,0,0,1,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,0,0,0,0,0,0,1,1,0,0,0,0\]\]
**Output:** 6
**Explanation:** The answer is not 11, because the island must be connected 4-directionally.
**Example 2:**
**Input:** grid = \[\[0,0,0,0,0,0,0,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `grid[i][j]` is either `0` or `1`. | null |
Python Iterative Solution | max-area-of-island | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want to traverse through the grid until we find some non-visited land. When we find some land, we want to call bfs to find all the neighboring land and calculate the area of the island. Every node that is visited can be added to a visited set so that it\'s not checked again while traversing our grid.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe are using an iterative BFS approach using a queue. A set can also be used to keep track of our visited nodes. This could be helpful if there are any constraints to not modify the input grid.\n\nOur bfs function will return the area of the current island which will then be checked against a MaxArea variable. \n\nVery straight forward code, but feel free to post any questions in the comments\n\n# Complexity\n- Time complexity: O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n- Space complexity: O(n*m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> \n\n# Code\n```\nclass Solution:\n def maxAreaOfIsland(self, grid: List[List[int]]) -> int:\n #best case\n if not grid:\n return 0\n \n #initialize values\n rows, cols = len(grid), len(grid[0])\n visited = set()\n curArea = 0\n maxArea = 0\n \n #define bfs and return current island\'s area\n def bfs(r,c):\n queue = collections.deque()\n area = 1\n queue.append((r,c))\n visited.add((r,c))\n while queue:\n row, col = queue.popleft()\n directions = [\n [1,0], #right\n [-1,0], #left\n [0,1], #up\n [0,-1] #down\n ]\n #check all 4 directions \n for dr, dc in directions:\n r,c = row+dr,col+dc\n if (\n r in range(rows) and\n c in range(cols) and \n grid[r][c] == 1 and\n (r,c) not in visited\n ):\n visited.add((r,c))\n queue.append((r,c))\n area += 1\n return area \n\n\n #main logic\n #traverse the grid and check for any non-visited land. If found, perform bfs to find the island\'s area.\n for r in range(rows):\n for c in range(cols):\n if grid[r][c] == 1 and (r,c) not in visited:\n curArea = bfs(r,c)\n maxArea = max(maxArea, curArea)\n\n return maxArea\n \n``` | 5 | You are given an `m x n` binary matrix `grid`. An island is a group of `1`'s (representing land) connected **4-directionally** (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The **area** of an island is the number of cells with a value `1` in the island.
Return _the maximum **area** of an island in_ `grid`. If there is no island, return `0`.
**Example 1:**
**Input:** grid = \[\[0,0,1,0,0,0,0,1,0,0,0,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,1,1,0,1,0,0,0,0,0,0,0,0\],\[0,1,0,0,1,1,0,0,1,0,1,0,0\],\[0,1,0,0,1,1,0,0,1,1,1,0,0\],\[0,0,0,0,0,0,0,0,0,0,1,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,0,0,0,0,0,0,1,1,0,0,0,0\]\]
**Output:** 6
**Explanation:** The answer is not 11, because the island must be connected 4-directionally.
**Example 2:**
**Input:** grid = \[\[0,0,0,0,0,0,0,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `grid[i][j]` is either `0` or `1`. | null |
Click here if you're confused. | max-area-of-island | 0 | 1 | # Intuition\nTreat adjacent 1s as nodes in a graph that are connected. Each island is a subgraph and islands are disconnected. Traversing such a graph of 1 nodes is equivalent to exploring the island, each node is +1 area.\n\nWe mark already explored 1s as 0 to prevent re-exploring or infinite loops. Our traversal algo. will be recursive DFS and we return +1 for each node and recurse all 4 sides. Invalid grid positions simply return 0, ending that side\'s search and contributing no area.\n\nWe do this for every tile in the grid and update a max_area var to return.\n\n# Complexity\n- Time complexity: $O(n*m)$ where n and m are dims. of grid, need to traverse every tile in grid\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n*m)$ since in worst case the recursive stack is $n*m$ deep when grid is all 1s\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxAreaOfIsland(self, grid: List[List[int]]) -> int:\n n_rows, n_cols = len(grid), len(grid[0])\n\n def dfs(r, c):\n if (not 0 <= r < n_rows\n or not 0 <= c < n_cols\n or grid[r][c] == 0):\n return 0\n\n grid[r][c] = 0\n return 1 + dfs(r+1, c) + dfs(r-1, c) + dfs(r, c+1) + dfs(r, c-1)\n\n # traverse all possible land nodes\n max_area = 0\n for ri in range(n_rows):\n for ci in range(n_cols):\n max_area = max(max_area, dfs(ri, ci))\n return max_area\n\n\n\n``` | 2 | You are given an `m x n` binary matrix `grid`. An island is a group of `1`'s (representing land) connected **4-directionally** (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The **area** of an island is the number of cells with a value `1` in the island.
Return _the maximum **area** of an island in_ `grid`. If there is no island, return `0`.
**Example 1:**
**Input:** grid = \[\[0,0,1,0,0,0,0,1,0,0,0,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,1,1,0,1,0,0,0,0,0,0,0,0\],\[0,1,0,0,1,1,0,0,1,0,1,0,0\],\[0,1,0,0,1,1,0,0,1,1,1,0,0\],\[0,0,0,0,0,0,0,0,0,0,1,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,0,0,0,0,0,0,1,1,0,0,0,0\]\]
**Output:** 6
**Explanation:** The answer is not 11, because the island must be connected 4-directionally.
**Example 2:**
**Input:** grid = \[\[0,0,0,0,0,0,0,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `grid[i][j]` is either `0` or `1`. | null |
Python | Sets | BFS | Iterative | Easy | max-area-of-island | 0 | 1 | \n\n# Complexity\n- Time complexity:\nO($n^2$) where **n** is the total number of `vertices`\n\n- Space complexity:\nO($n$)\n\n# Code\n```\nclass GridType:\n def __init__(self):\n self.land = 1\n self.water = 0\n\nclass Solution:\n def maxAreaOfIsland(self, grid: List[List[int]]) -> int:\n if not grid: return 0\n\n rows, cols = len(grid), len(grid[0])\n visited, max_area = set(), 0\n gridDirections = [[1,0],[-1,0],[0,1],[0,-1]]\n gridType = GridType()\n\n def bfs(row, col):\n area = 0\n queue = collections.deque()\n visited.add((row, col))\n queue.append((row, col))\n area += 1\n\n while queue:\n row, col = queue.popleft()\n\n for dr, dc in gridDirections:\n r, c = row + dr, col + dc\n\n if (r in range(rows) and\n c in range(cols) and \n grid[r][c] == gridType.land and\n (r, c) not in visited):\n queue.append((r,c))\n visited.add((r,c))\n area += 1\n return area\n\n for row in range(rows):\n for col in range(cols):\n if grid[row][col] == gridType.land and (row, col) not in visited:\n max_area = max(max_area, bfs(row, col))\n \n return max_area\n``` | 1 | You are given an `m x n` binary matrix `grid`. An island is a group of `1`'s (representing land) connected **4-directionally** (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The **area** of an island is the number of cells with a value `1` in the island.
Return _the maximum **area** of an island in_ `grid`. If there is no island, return `0`.
**Example 1:**
**Input:** grid = \[\[0,0,1,0,0,0,0,1,0,0,0,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,1,1,0,1,0,0,0,0,0,0,0,0\],\[0,1,0,0,1,1,0,0,1,0,1,0,0\],\[0,1,0,0,1,1,0,0,1,1,1,0,0\],\[0,0,0,0,0,0,0,0,0,0,1,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,0,0,0,0,0,0,1,1,0,0,0,0\]\]
**Output:** 6
**Explanation:** The answer is not 11, because the island must be connected 4-directionally.
**Example 2:**
**Input:** grid = \[\[0,0,0,0,0,0,0,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `grid[i][j]` is either `0` or `1`. | null |
Simple 🐍 solution using DFS algo😎 | max-area-of-island | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxAreaOfIsland(self, grid: List[List[int]]) -> int:\n rows, cols = len(grid), len(grid[0])\n visited = set()\n\n def dfs(r, c):\n if(r<0 or r==rows or c<0 or c==cols or grid[r][c]==0 or (r,c) in visited):\n return 0\n visited.add((r,c))\n return 1+dfs(r-1,c) + dfs(r+1,c) + dfs(r,c-1) +dfs(r,c+1)\n area = 0\n\n for i in range(rows):\n for j in range(cols):\n area = max(area,dfs(i,j))\n return area\n\n \n``` | 2 | You are given an `m x n` binary matrix `grid`. An island is a group of `1`'s (representing land) connected **4-directionally** (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The **area** of an island is the number of cells with a value `1` in the island.
Return _the maximum **area** of an island in_ `grid`. If there is no island, return `0`.
**Example 1:**
**Input:** grid = \[\[0,0,1,0,0,0,0,1,0,0,0,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,1,1,0,1,0,0,0,0,0,0,0,0\],\[0,1,0,0,1,1,0,0,1,0,1,0,0\],\[0,1,0,0,1,1,0,0,1,1,1,0,0\],\[0,0,0,0,0,0,0,0,0,0,1,0,0\],\[0,0,0,0,0,0,0,1,1,1,0,0,0\],\[0,0,0,0,0,0,0,1,1,0,0,0,0\]\]
**Output:** 6
**Explanation:** The answer is not 11, because the island must be connected 4-directionally.
**Example 2:**
**Input:** grid = \[\[0,0,0,0,0,0,0,0\]\]
**Output:** 0
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `grid[i][j]` is either `0` or `1`. | null |
696: Solution with step by step explanation | count-binary-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize variables pre_len, cur_len, and count to 0.\n2. Traverse through the string using a for loop that starts at index 1 and ends at the length of the string.\n3. Check if the current character is the same as the previous character using an if statement.\n4. If the current character is the same as the previous character, increment cur_len.\n5. If the current character is different from the previous character, set pre_len to cur_len and set cur_len to 1.\n6. Check if pre_len is greater than or equal to cur_len using an if statement.\n7. If pre_len is greater than or equal to cur_len, increment count.\n8. Return the total count of valid substrings.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countBinarySubstrings(self, s: str) -> int:\n # Initialize variables\n pre_len = 0\n cur_len = 1\n count = 0\n \n # Traverse through the string\n for i in range(1, len(s)):\n # If the current character is the same as the previous character\n if s[i] == s[i-1]:\n cur_len += 1\n # If the current character is different from the previous character\n else:\n pre_len = cur_len\n cur_len = 1\n \n # If the previous length is greater than or equal to the current length\n # then we have a valid substring\n if pre_len >= cur_len:\n count += 1\n \n # Return the total count of valid substrings\n return count\n\n``` | 8 | Given a binary string `s`, return the number of non-empty substrings that have the same number of `0`'s and `1`'s, and all the `0`'s and all the `1`'s in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.
**Example 1:**
**Input:** s = "00110011 "
**Output:** 6
**Explanation:** There are 6 substrings that have equal number of consecutive 1's and 0's: "0011 ", "01 ", "1100 ", "10 ", "0011 ", and "01 ".
Notice that some of these substrings repeat and are counted the number of times they occur.
Also, "00110011 " is not a valid substring because all the 0's (and 1's) are not grouped together.
**Example 2:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are 4 substrings: "10 ", "01 ", "10 ", "01 " that have equal number of consecutive 1's and 0's.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | How many valid binary substrings exist in "000111", and how many in "11100"? What about "00011100"? |
💣Binary Substrings || 🔥Beats 75%🔥 || 😎Enjoy LeetCode... | count-binary-substrings | 0 | 1 | # KARRAR\n>Counting binary substrings...\n>>Using only MIN built-in function...\n>>>Most optimized...\n>>>>Easily Understand able...\n>>>>>Similar to the original solution...\n- PLEASE UPVOTE...\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach:\n Take three variables as your choice...\n Check the numbers and aperate 0s ans 1s...\n Change the value of count according to itrations...\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity:\n- Time complexity: Beats 75% (162 ms)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Beats 55% (16 MB)\n\n\n\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code:\n```\nclass Solution:\n def countBinarySubstrings(self, s: str) -> int:\n pre= 0\n count= 1\n actual= 0\n\n for i in range(1,len(s)):\n if(s[i]==s[i-1]):\n count+=1\n\n else:\n actual+= min(pre,count)\n pre= count\n count= 1\n\n actual+= min(pre,count)\n\n return actual\n``` | 2 | Given a binary string `s`, return the number of non-empty substrings that have the same number of `0`'s and `1`'s, and all the `0`'s and all the `1`'s in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.
**Example 1:**
**Input:** s = "00110011 "
**Output:** 6
**Explanation:** There are 6 substrings that have equal number of consecutive 1's and 0's: "0011 ", "01 ", "1100 ", "10 ", "0011 ", and "01 ".
Notice that some of these substrings repeat and are counted the number of times they occur.
Also, "00110011 " is not a valid substring because all the 0's (and 1's) are not grouped together.
**Example 2:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are 4 substrings: "10 ", "01 ", "10 ", "01 " that have equal number of consecutive 1's and 0's.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | How many valid binary substrings exist in "000111", and how many in "11100"? What about "00011100"? |
Python | Two Pointer Approach | O(N) Time Complexity | O(1) Space Complexity | count-binary-substrings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> Using two pointer approach \n\n# Approach\n<!-- Describe your approach to solving the problem. --> Two Pointers. I also defined a list with just two elements. I keep the number of 0\'s in our window (defined by using two pointers) in the first index of the list and the number of 1\'s in our window in the second index of the list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(1)\n\n# Code\n```\nclass Solution:\n def countBinarySubstrings(self, s: str) -> int:\n\n # time: O(N)\n # space: O(1)\n\n numb = [0,0]\n ans = 0\n\n p1 = 0\n p2 = 1\n\n numb[int(s[p1])] += 1\n \n\n while p2 < len(s):\n sp2_int = int(s[p2])\n if s[p2] == s[p1]:\n if numb[1-sp2_int] == 0:\n numb[sp2_int] += 1\n p2 += 1\n else:\n sp1_int = int(s[p1])\n while s[p1] == s[p2]:\n numb[sp1_int] -= 1\n p1 += 1\n \n else:\n numb[sp2_int] += 1\n if numb[sp2_int] <= numb[1-sp2_int]:\n ans += 1\n p2 += 1\n\n return ans\n\n``` | 2 | Given a binary string `s`, return the number of non-empty substrings that have the same number of `0`'s and `1`'s, and all the `0`'s and all the `1`'s in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.
**Example 1:**
**Input:** s = "00110011 "
**Output:** 6
**Explanation:** There are 6 substrings that have equal number of consecutive 1's and 0's: "0011 ", "01 ", "1100 ", "10 ", "0011 ", and "01 ".
Notice that some of these substrings repeat and are counted the number of times they occur.
Also, "00110011 " is not a valid substring because all the 0's (and 1's) are not grouped together.
**Example 2:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are 4 substrings: "10 ", "01 ", "10 ", "01 " that have equal number of consecutive 1's and 0's.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | How many valid binary substrings exist in "000111", and how many in "11100"? What about "00011100"? |
Minimal complexity answer (one pass, O(n)), beats 99.9% on time complexity. | count-binary-substrings | 0 | 1 | # Intuition\nSee the approach below, the main intuitive leap is to realize that once the string is arranged in "groups" of consecutive 0\'s and 1\'s, you only need information about the lengths of pairs of consecutive groups to count the number of desired substrings. \n\n# Approach\nFor a consecutive string of 0\'s and 1\'s the number of substrings with an equal number of digits is just the minimum of the number of 0\'s and the minimum of the number of 1\'s. So at each step moving through the array we need only keep track of how many digits we saw in the last consecutive string of the last character read, and how many digits we see in the current consecutive string of the current character. \n\nE.g. in 000111100 we read through and tabulate that there are 3 0\'s, then store that information when we read a 1, we count the number of 1\'s and add min(#previous 0\'s, #1\'s) = 3 to the total number of substrings when we read the next 0. Then we forget about the 3 zeros in the first group and start over again with the role of 0 and 1 reversed after we read the next 0. \n\n# Complexity\n- Time complexity:\nO(n), we read once through the input, at most 4 operations are carried out for each digit in the input.\n\n- Space complexity:\nO(n), all the space comes from the input.\n\n# Code\n```\nclass Solution:\n def countBinarySubstrings(self, s: str) -> int:\n last = -1 #a state variable, keeps track of the digit we saw in the last iteration\n tot = 0 #keeps track of the total\n count = 0 #counts the number of the current character that we have seen consecutively\n lastcount = 0 #keeps track of the count for the last set of instances of the previous character\n for i in s:\n if last != i: #new character\n tot += min(count, lastcount) #add the number of valid substrings to the total\n lastcount = count #store the count\n count = 1 #we have now seen one instance of this new character\n last = i\n else:\n count += 1\n tot += min(count, lastcount) #keep track of what happened with the last iteration\n return tot\n\n\n``` | 2 | Given a binary string `s`, return the number of non-empty substrings that have the same number of `0`'s and `1`'s, and all the `0`'s and all the `1`'s in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.
**Example 1:**
**Input:** s = "00110011 "
**Output:** 6
**Explanation:** There are 6 substrings that have equal number of consecutive 1's and 0's: "0011 ", "01 ", "1100 ", "10 ", "0011 ", and "01 ".
Notice that some of these substrings repeat and are counted the number of times they occur.
Also, "00110011 " is not a valid substring because all the 0's (and 1's) are not grouped together.
**Example 2:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are 4 substrings: "10 ", "01 ", "10 ", "01 " that have equal number of consecutive 1's and 0's.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | How many valid binary substrings exist in "000111", and how many in "11100"? What about "00011100"? |
Solution | count-binary-substrings | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int countBinarySubstrings(string s) {\n char anchor;\n int sums = 0, i = 0, j = 0, numa = 0, total = 0, next = 0;\n\n while (i < s.length()){\n anchor = s[i];\n total = 0;\n\n numa = 1;\n for (j = i + 1; j < s.length(); ++j){\n if (s[j] == anchor) numa++;\n else break;\n }\n next = j;\n int range = j + numa;\n for (; j < range && j < s.length(); ++j){\n if (s[j] != anchor) ++total;\n else break;\n }\n sums += total;\n i = next;\n }\n return sums;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def countBinarySubstrings(self, s: str) -> int:\n res = 0\n pb = 0\n ca = s[0]\n cb = 0\n for c in s:\n if c == ca:\n cb += 1\n else:\n res += pb if pb < cb else cb\n ca = c\n pb = cb\n cb = 1\n return res + (pb if pb < cb else cb)\n```\n\n```Java []\nclass Solution {\n public int countBinarySubstrings(String s) {\n int count = 0;\n char[] arr = s.toCharArray();\n if(arr.length == 0) return 0;\n int currentCount = 1;\n int stateCount = 0;\n char state = arr[0];\n\n for(int i = 1; i<arr.length ; i++){\n if(state==arr[i]) {\n currentCount++;\n if(stateCount>=currentCount) count++;\n }\n else{\n state=arr[i];\n stateCount = currentCount;\n currentCount = 1;\n count++;\n } \n }\n return count;\n }\n}\n```\n | 2 | Given a binary string `s`, return the number of non-empty substrings that have the same number of `0`'s and `1`'s, and all the `0`'s and all the `1`'s in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.
**Example 1:**
**Input:** s = "00110011 "
**Output:** 6
**Explanation:** There are 6 substrings that have equal number of consecutive 1's and 0's: "0011 ", "01 ", "1100 ", "10 ", "0011 ", and "01 ".
Notice that some of these substrings repeat and are counted the number of times they occur.
Also, "00110011 " is not a valid substring because all the 0's (and 1's) are not grouped together.
**Example 2:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are 4 substrings: "10 ", "01 ", "10 ", "01 " that have equal number of consecutive 1's and 0's.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | How many valid binary substrings exist in "000111", and how many in "11100"? What about "00011100"? |
Python/C++/Java/Go O(n) by character grouping [w/ Hint] | count-binary-substrings | 1 | 1 | **Hint**:\n\nbinary substring of equal 0s and 1s is **decided** by the **minimal continuous occurrence** between character groups\n\nExample:\n\nGiven s = **000**11111\n\n0\'s continuous occurrence = 3\n1\'s continuous occurrence = 5\n\nmin(3, 5) = 3\n\nThere are 3 binary substrings of equal 0s and 1s as following:\n\n**0**1\n**00**11\n**000**111\n\n\n---\n\n**Implementation** by character grouping in **Python**:\n\n```\nclass Solution:\n def countBinarySubstrings(self, s: str) -> int:\n \n # previous continuous occurrence, current continuous occurrence\n pre_cont_occ, cur_cont_occ = 0, 1\n \n # counter for binary substrings with equal 0s and 1s\n counter = 0\n \n\t\t# scan each character pair in s\n for idx in range(1, len(s)):\n \n if s[idx] == s[idx-1]:\n \n # update current continuous occurrence\n cur_cont_occ += 1\n \n else:\n # update counter of binary substrings between prevous character group and current character group\n counter += min(pre_cont_occ, cur_cont_occ)\n\n # update previous as current\'s continuous occurrence\n pre_cont_occ = cur_cont_occ\n \n # reset current continuous occurrence to 1\n cur_cont_occ = 1\n \n # update for last time\n counter += min(pre_cont_occ, cur_cont_occ)\n \n return counter\n```\n\n---\n\n**Implementation** by character grouping in **C++**:\n\n```\nclass Solution {\npublic:\n int countBinarySubstrings(string s) {\n \n // previous continuous occurrence, current continuous occurrence\n int pre_cont_occ=0, cur_cont_occ= 1;\n \n // counter for binary substrings with equal 0s and 1s\n int counter = 0;\n \n\t\t// scan each character pair in s\n for( int idx = 1 ; idx < s.length() ; idx++ ){\n \n if( s[idx] == s[idx-1] ){\n \n // update current continuous occurrence\n cur_cont_occ += 1;\n \n }else{\n // update counter of binary substrings between prevous character group and current character group\n counter += min(pre_cont_occ, cur_cont_occ);\n\n // update previous as current\'s continuous occurrence\n pre_cont_occ = cur_cont_occ;\n \n // reset current continuous occurrence to 1\n cur_cont_occ = 1;\n }\n }\n // update for last time\n counter += min(pre_cont_occ, cur_cont_occ);\n \n return counter;\n }\n};\n```\n\n---\n\n**Implementation** by character grouping in **Java**:\n\n```\nclass Solution {\n public int countBinarySubstrings(String s) {\n \n // previous continuous occurrence, current continuous occurrence\n int pre_cont_occ=0, cur_cont_occ= 1;\n \n // counter for binary substrings with equal 0s and 1s\n int counter = 0;\n \n\t\t// scan each character pair in s\n for( int idx = 1 ; idx < s.length() ; idx++ ){\n \n if( s.charAt(idx) == s.charAt(idx-1) ){\n \n // update current continuous occurrence\n cur_cont_occ += 1;\n \n }else{\n // update counter of binary substrings between prevous character group and current character group\n counter += Math.min(pre_cont_occ, cur_cont_occ);\n\n // update previous as current\'s continuous occurrence\n pre_cont_occ = cur_cont_occ;\n \n // reset current continuous occurrence to 1\n cur_cont_occ = 1;\n }\n }\n // update for last time\n counter += Math.min(pre_cont_occ, cur_cont_occ);\n \n return counter;\n }\n}\n```\n\n---\n\n**Implementation** by character grouping in **Go**:\n\n```\n// min function have to be implemented by programmer in Golang\nfunc Min(x, y int)int{\n if x < y{\n return x\n }\n return y\n}\n\nfunc countBinarySubstrings(s string) int {\n \n // previous continuous occurrence, current continuous occurrence\n preContOcc, curContOcc := 0, 1\n \n // counter for binary substrings with equal 0s and 1s\n counter := 0\n \n // scan each character pair in s\n for idx := 1; idx < len(s) ; idx++{\n \n if s[idx] == s[idx-1]{\n \n // update current continuous occurrence\n curContOcc += 1\n \n }else{\n \n // update counter of binary substring between previous character group and current character group\n counter += Min(preContOcc, curContOcc)\n \n // update previous as current\'s continuous occurrence\n preContOcc = curContOcc\n \n // reset current continuous occurrence to 1\n curContOcc = 1\n \n }\n \n }\n \n // update for last time\n counter += Min(preContOcc, curContOcc)\n \n return counter\n \n}\n``` | 16 | Given a binary string `s`, return the number of non-empty substrings that have the same number of `0`'s and `1`'s, and all the `0`'s and all the `1`'s in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.
**Example 1:**
**Input:** s = "00110011 "
**Output:** 6
**Explanation:** There are 6 substrings that have equal number of consecutive 1's and 0's: "0011 ", "01 ", "1100 ", "10 ", "0011 ", and "01 ".
Notice that some of these substrings repeat and are counted the number of times they occur.
Also, "00110011 " is not a valid substring because all the 0's (and 1's) are not grouped together.
**Example 2:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are 4 substrings: "10 ", "01 ", "10 ", "01 " that have equal number of consecutive 1's and 0's.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | How many valid binary substrings exist in "000111", and how many in "11100"? What about "00011100"? |
python 3 || O(n) || O(1) | count-binary-substrings | 0 | 1 | ```\nclass Solution:\n def countBinarySubstrings(self, s: str) -> int:\n prev, cur = 0, 1\n res = 0\n for i in range(1, len(s)):\n if s[i] == s[i - 1]:\n cur += 1\n else:\n prev, cur = cur, 1\n\n if cur <= prev:\n res += 1\n \n return res | 3 | Given a binary string `s`, return the number of non-empty substrings that have the same number of `0`'s and `1`'s, and all the `0`'s and all the `1`'s in these substrings are grouped consecutively.
Substrings that occur multiple times are counted the number of times they occur.
**Example 1:**
**Input:** s = "00110011 "
**Output:** 6
**Explanation:** There are 6 substrings that have equal number of consecutive 1's and 0's: "0011 ", "01 ", "1100 ", "10 ", "0011 ", and "01 ".
Notice that some of these substrings repeat and are counted the number of times they occur.
Also, "00110011 " is not a valid substring because all the 0's (and 1's) are not grouped together.
**Example 2:**
**Input:** s = "10101 "
**Output:** 4
**Explanation:** There are 4 substrings: "10 ", "01 ", "10 ", "01 " that have equal number of consecutive 1's and 0's.
**Constraints:**
* `1 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | How many valid binary substrings exist in "000111", and how many in "11100"? What about "00011100"? |
Solution in Python 3 (beats ~98%) | degree-of-an-array | 0 | 1 | ```\nclass Solution:\n def findShortestSubArray(self, nums: List[int]) -> int:\n \tC = {}\n \tfor i, n in enumerate(nums):\n \t\tif n in C: C[n].append(i)\n \t\telse: C[n] = [i]\n \tM = max([len(i) for i in C.values()])\n \treturn min([i[-1]-i[0] for i in C.values() if len(i) == M]) + 1\n\t\t\n\t\t\n- Junaid Mansuri | 49 | Given a non-empty array of non-negative integers `nums`, the **degree** of this array is defined as the maximum frequency of any one of its elements.
Your task is to find the smallest possible length of a (contiguous) subarray of `nums`, that has the same degree as `nums`.
**Example 1:**
**Input:** nums = \[1,2,2,3,1\]
**Output:** 2
**Explanation:**
The input array has a degree of 2 because both elements 1 and 2 appear twice.
Of the subarrays that have the same degree:
\[1, 2, 2, 3, 1\], \[1, 2, 2, 3\], \[2, 2, 3, 1\], \[1, 2, 2\], \[2, 2, 3\], \[2, 2\]
The shortest length is 2. So return 2.
**Example 2:**
**Input:** nums = \[1,2,2,3,1,4,2\]
**Output:** 6
**Explanation:**
The degree is 3 because the element 2 is repeated 3 times.
So \[2,2,3,1,4,2\] is the shortest subarray, therefore returning 6.
**Constraints:**
* `nums.length` will be between 1 and 50,000.
* `nums[i]` will be an integer between 0 and 49,999. | Say 5 is the only element that occurs the most number of times - for example, nums = [1, 5, 2, 3, 5, 4, 5, 6]. What is the answer? |
Easy Python | One-Pass | 3 Approaches | Top Speed | degree-of-an-array | 0 | 1 | **Easy Python | One-Pass | 3 Approaches | Top Speed**\n\n**A) Classic Version**\n\nTypical algorithm:\n\n1. Group elements by label/value. \n2. Find the highest degree, which is the maximum length of each sub-array per label.\n3. Find the shortest span for each sub-array at maximum degree (this is enough to contain the highest degree).\n\n```\nclass Solution:\n def findShortestSubArray(self, nums):\n # Group indexes by element type\n d = defaultdict(list)\n for i,x in enumerate(nums):\n d[x].append(i)\n #\n # Find highest Degree\n m = max([ len(v) for v in d.values() ])\n #\n # Find shortest span for max. degree\n best = len(nums)\n for v in d.values():\n if len(v)==m:\n best = min(best,v[-1]-v[0]+1)\n return best\n```\n\n**B) One-Pass (Optimization)**\n\nHigh Speed algorithm, it\'s an optimized version inspired by the previous code. We simply discover elements, and track the shortest length of the highest degree that we currently see.\n\n```\nclass Solution:\n def findShortestSubArray(self, nums):\n d = defaultdict(list) # Dictionary with [indexes] where each label appears\n m, best = 1, 1 # m = record degree, best = shortest span (for m)\n for i,x in enumerate(nums):\n d[x].append(i) # Add index to respective sub-array\n L =len(d[x]) # Track length of sub-array at label = x\n if L>m:\n # Initialize new Record\n m = L\n best = i - d[x][0] + 1\n elif L == m:\n # Pick best at highest degree\n best = min( best , i - d[x][0] + 1 )\n return best\n```\n\n**C) Hyper-Optimized (Lower Space Complexity)**\n\nThis Final Approach runs under the same principles outlined for (B), but it only uses O( X ) space complexity, where X is the number of unique labels in "nums". It only tracks the initial position, and the degree of each sub-array with label = x. This makes a lot of sense, since we never needed to use intermediate sub-array values.\n\nI hope you found the code helpful. Cheers,\n\n```\n# Note: This code uses a slightly different nomenclature as before.\nclass Solution:\n def findShortestSubArray(self, nums):\n d = {} # Dictionary with information for each label x = nums[i]\n # Entries have the form d[x] = [i, m] = [beginning_subarray, degree]\n #\n A, best = 1, 1 # A = record degree, best = shortest span (for A)\n #\n for i,x in enumerate(nums):\n if x in d:\n d[x][1] += 1 # Update Degree\n m = d[x][1] # Fetch Degree\n L = i - d[x][0] + 1 # Length sub-array\n else:\n d[x] = [i,1]\n L = m = 1\n if m>A:\n # Initialize new Record\n A,best = m, L\n elif A == m:\n # Pick best at highest degree\n best = min( best , L )\n return best\n``` | 24 | Given a non-empty array of non-negative integers `nums`, the **degree** of this array is defined as the maximum frequency of any one of its elements.
Your task is to find the smallest possible length of a (contiguous) subarray of `nums`, that has the same degree as `nums`.
**Example 1:**
**Input:** nums = \[1,2,2,3,1\]
**Output:** 2
**Explanation:**
The input array has a degree of 2 because both elements 1 and 2 appear twice.
Of the subarrays that have the same degree:
\[1, 2, 2, 3, 1\], \[1, 2, 2, 3\], \[2, 2, 3, 1\], \[1, 2, 2\], \[2, 2, 3\], \[2, 2\]
The shortest length is 2. So return 2.
**Example 2:**
**Input:** nums = \[1,2,2,3,1,4,2\]
**Output:** 6
**Explanation:**
The degree is 3 because the element 2 is repeated 3 times.
So \[2,2,3,1,4,2\] is the shortest subarray, therefore returning 6.
**Constraints:**
* `nums.length` will be between 1 and 50,000.
* `nums[i]` will be an integer between 0 and 49,999. | Say 5 is the only element that occurs the most number of times - for example, nums = [1, 5, 2, 3, 5, 4, 5, 6]. What is the answer? |
Solution | degree-of-an-array | 1 | 1 | ```C++ []\n#include <tuple>\n\nclass Solution {\n struct Info {\n int count;\n int startIdx;\n int endIdx;\n\n void updateEnd(int end) {\n endIdx = end;\n ++count;\n }\n int range() const {\n return endIdx - startIdx + 1;\n }\n };\npublic:\n int findShortestSubArray(vector<int>& nums) {\n unordered_map<int, Info> cache; // num, <count, startIdx, endIdx>\n\n for (int i = 0; i < nums.size(); ++i) {\n if (cache.find(nums[i]) != cache.end()) {\n cache[nums[i]].updateEnd(i);\n }\n else {\n cache[nums[i]] = Info{1, i, i};\n }\n }\n int count = 0;\n int shorted = 0;\n for (auto& [k, v] : cache) {\n if (count < v.count) {\n count = v.count;\n\n shorted = v.range();\n }\n else if (count == v.count) {\n if (shorted > v.range()) {\n shorted = v.range();\n }\n }\n }\n return shorted;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findShortestSubArray(self, nums: List[int]) -> int:\n f = collections.Counter(nums)\n d = max(f.values())\n if d == 1:\n return(1)\n nums_f = [n for n in f if f[n] == d]\n ans = len(nums)\n for n in nums_f:\n li = nums.index(n)\n ri = len(nums) - nums[::-1].index(n)\n ans = min(ans, ri - li)\n return(ans)\n```\n\n```Java []\nclass Solution {\n public int findShortestSubArray(int[] nums) {\n \n int max = -1;\n for (int i=0; i<nums.length;i++)\n if (nums[i] > max) max = nums[i];\n\n MinMax [] minmax = new MinMax[max + 1];\n int maxfreq = 0;\n for (int i=0; i<nums.length;i++) {\n if (minmax[nums[i]] == null)\n minmax[nums[i]] = new MinMax(i);\n minmax[nums[i]].max = i;\n minmax[nums[i]].count++;\n\n if (minmax[nums[i]].count > maxfreq)\n maxfreq = minmax[nums[i]].count;\n }\n int minarray = Integer.MAX_VALUE;\n for (int i=0; i<minmax.length;i++) {\n if (minmax[i] != null && minmax[i].count == maxfreq)\n minarray = Math.min(minarray, minmax[i].max - minmax[i].min + 1);\n }\n return minarray;\n }\n private class MinMax {\n int count = 0;\n int min = -1;\n int max = -1;\n\n public MinMax(int i) {\n min = i;\n max = i;\n }\n }\n}\n```\n | 3 | Given a non-empty array of non-negative integers `nums`, the **degree** of this array is defined as the maximum frequency of any one of its elements.
Your task is to find the smallest possible length of a (contiguous) subarray of `nums`, that has the same degree as `nums`.
**Example 1:**
**Input:** nums = \[1,2,2,3,1\]
**Output:** 2
**Explanation:**
The input array has a degree of 2 because both elements 1 and 2 appear twice.
Of the subarrays that have the same degree:
\[1, 2, 2, 3, 1\], \[1, 2, 2, 3\], \[2, 2, 3, 1\], \[1, 2, 2\], \[2, 2, 3\], \[2, 2\]
The shortest length is 2. So return 2.
**Example 2:**
**Input:** nums = \[1,2,2,3,1,4,2\]
**Output:** 6
**Explanation:**
The degree is 3 because the element 2 is repeated 3 times.
So \[2,2,3,1,4,2\] is the shortest subarray, therefore returning 6.
**Constraints:**
* `nums.length` will be between 1 and 50,000.
* `nums[i]` will be an integer between 0 and 49,999. | Say 5 is the only element that occurs the most number of times - for example, nums = [1, 5, 2, 3, 5, 4, 5, 6]. What is the answer? |
697: Solution with step by step explanation | degree-of-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize variables:\n- degree to 0\n- degree_nums dictionary to track the frequency of each number in nums\n- left dictionary to track the leftmost index of each number in nums\n- right dictionary to track the rightmost index of each number in nums\n- shortest to the length of nums\n2. Traverse through nums using the enumerate function:\n- If the current number num is not in degree_nums, add it with frequency 1\n- Otherwise, increment the frequency of num in degree_nums\n- Update the degree variable to be the maximum frequency in degree_nums\n- If num is not in left, add it with index i as the leftmost occurrence\n- Update right[num] to the current index i\n3. Iterate over the degree_nums dictionary to find the numbers with frequency equal to degree:\n- For each number num with frequency freq equal to degree, calculate the length of the subarray with num as the degree using right[num] - left[num] + 1\n- Update shortest to the minimum of its current value and the subarray length\n4. Return shortest as the answer\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findShortestSubArray(self, nums: List[int]) -> int:\n # Initialize variables\n degree = 0\n degree_nums = {}\n left = {}\n right = {}\n shortest = len(nums)\n \n # Traverse through the array\n for i, num in enumerate(nums):\n # Update degree and degree_nums\n if num in degree_nums:\n degree_nums[num] += 1\n else:\n degree_nums[num] = 1\n degree = max(degree, degree_nums[num])\n \n # Update left and right\n if num not in left:\n left[num] = i\n right[num] = i\n \n # Find the shortest subarray with degree\n for num, freq in degree_nums.items():\n if freq == degree:\n shortest = min(shortest, right[num] - left[num] + 1)\n \n # Return the shortest subarray length\n return shortest\n``` | 5 | Given a non-empty array of non-negative integers `nums`, the **degree** of this array is defined as the maximum frequency of any one of its elements.
Your task is to find the smallest possible length of a (contiguous) subarray of `nums`, that has the same degree as `nums`.
**Example 1:**
**Input:** nums = \[1,2,2,3,1\]
**Output:** 2
**Explanation:**
The input array has a degree of 2 because both elements 1 and 2 appear twice.
Of the subarrays that have the same degree:
\[1, 2, 2, 3, 1\], \[1, 2, 2, 3\], \[2, 2, 3, 1\], \[1, 2, 2\], \[2, 2, 3\], \[2, 2\]
The shortest length is 2. So return 2.
**Example 2:**
**Input:** nums = \[1,2,2,3,1,4,2\]
**Output:** 6
**Explanation:**
The degree is 3 because the element 2 is repeated 3 times.
So \[2,2,3,1,4,2\] is the shortest subarray, therefore returning 6.
**Constraints:**
* `nums.length` will be between 1 and 50,000.
* `nums[i]` will be an integer between 0 and 49,999. | Say 5 is the only element that occurs the most number of times - for example, nums = [1, 5, 2, 3, 5, 4, 5, 6]. What is the answer? |
Simple Python Solution with explanation - O(n) | degree-of-an-array | 0 | 1 | ```\nclass Solution:\n def findShortestSubArray(self, nums: List[int]) -> int:\n \'\'\'\n step 1: find the degree\n - create a hashmap of a number and value as list of occurance indices\n - the largest indices array in the hashmap gives us the degree\n step 2: find the minimum length subarray with same degree\n - initialize result as length of array\n - for each indices array, if it\'s length equals degree, means it\'s most frequent element\n - this length will be equal to the difference of first occurance and last occurance of most frequent element\n - compare this length with current result and keep the smallest length as result\n - return result + 1 because difference of indices will give us length - 1\n \n \n \'\'\'\n c = defaultdict(list)\n for i, n in enumerate(nums):\n c[n].append(i) \n degree = max([len(x) for x in c.values()])\n \n result = len(nums)\n for indices in c.values():\n if len(indices) == degree:\n result = min(result, indices[-1] - indices[0])\n return result + 1 \n \n \n``` | 14 | Given a non-empty array of non-negative integers `nums`, the **degree** of this array is defined as the maximum frequency of any one of its elements.
Your task is to find the smallest possible length of a (contiguous) subarray of `nums`, that has the same degree as `nums`.
**Example 1:**
**Input:** nums = \[1,2,2,3,1\]
**Output:** 2
**Explanation:**
The input array has a degree of 2 because both elements 1 and 2 appear twice.
Of the subarrays that have the same degree:
\[1, 2, 2, 3, 1\], \[1, 2, 2, 3\], \[2, 2, 3, 1\], \[1, 2, 2\], \[2, 2, 3\], \[2, 2\]
The shortest length is 2. So return 2.
**Example 2:**
**Input:** nums = \[1,2,2,3,1,4,2\]
**Output:** 6
**Explanation:**
The degree is 3 because the element 2 is repeated 3 times.
So \[2,2,3,1,4,2\] is the shortest subarray, therefore returning 6.
**Constraints:**
* `nums.length` will be between 1 and 50,000.
* `nums[i]` will be an integer between 0 and 49,999. | Say 5 is the only element that occurs the most number of times - for example, nums = [1, 5, 2, 3, 5, 4, 5, 6]. What is the answer? |
Backtrack | partition-to-k-equal-sum-subsets | 0 | 1 | \u5176\u5B9E\u6211\u66F4\u80FD\u7406\u89E3\u4ECE\u6570\u5B57\u6765\u770B\uFF0C\u4F46\u662F\u6570\u5B57\u7684\u65F6\u95F4\u8D85\u65F6\u4E86\u3002\u6876\u6709\u70B9\u4E00\u77E5\u534A\u89E3\u7684\u611F\u89C9\n\n# Code\n```\nclass Solution:\n def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:\n memo = {}\n\n def backtrack(k, bucket, nums, start, used, target):\n # \u57FA\u672C case\n if k == 0:\n # \u6240\u6709\u6876\u90FD\u88AB\u88C5\u6EE1\u4E86\uFF0C\u4E14 nums \u5168\u90E8\u7528\u5B8C\n return True\n if bucket == target:\n res = backtrack(k - 1, 0, nums, 0, used, target)\n # \u7F13\u5B58\u7ED3\u679C\n memo[used] = res\n return res\n if used in memo:\n # \u907F\u514D\u5197\u4F59\u8BA1\u7B97\n return memo[used]\n \n for i in range(start, len(nums)):\n if ((used >> i) & 1) == 1:\n # nums[i] \u5DF2\u7ECF\u88AB\u88C5\u5165\u522B\u7684\u6876\u4E2D\n continue\n if nums[i] + bucket > target:\n continue\n used |= 1 << i\n bucket += nums[i]\n if backtrack(k, bucket, nums, i + 1, used, target):\n return True\n used ^= 1 << i\n bucket -= nums[i]\n \n return False\n \n # \u786E\u4FDD k \u4E0D\u5927\u4E8E nums \u7684\u957F\u5EA6\n if k > len(nums):\n return False\n sum_nums = sum(nums)\n if sum_nums % k != 0:\n return False \n used = 0 # \u4F7F\u7528\u4F4D\u56FE\u6280\u5DE7\n target = sum_nums // k # \u6BCF\u4E2A\u6876\u7684\u76EE\u6807\u548C\n # k \u53F7\u6876\u521D\u59CB\u4EC0\u4E48\u90FD\u6CA1\u88C5\uFF0C\u4ECE nums[0] \u5F00\u59CB\u505A\u9009\u62E9\n return backtrack(k, 0, nums, 0, used, target)\n # nums.sort(reverse=True)\n # # \u6392\u9664\u4E00\u4E9B\u57FA\u672C\u60C5\u51B5\n # if k > len(nums):\n # return False\n # # \u5C06\u6240\u6709\u6570\u7684\u548C\u6C42\u51FA\u6765\n # _sum = sum(nums)\n # # \u5982\u679C\u6240\u6709\u6570\u7684\u548C\u4E0D\u80FD\u88AB k \u6574\u9664\uFF0C\u5C31\u4E0D\u7528\u7EE7\u7EED\u4E86\n # if _sum % k != 0:\n # return False\n # # \u6240\u6709\u5206\u51FA\u6765\u7684\u6876\u9700\u8981\u88C5 target \u4E2A\u6570\u5B57\n # target = _sum // k\n # # k \u4E2A\u6876\n # bucket = [0] * k\n # # \u9012\u5F52\u7A77\u4E3E\n\n # return self.backtrack(nums, 0, bucket, target)\n\n # def backtrack(self, nums, index, bucket, target):\n # # \u6240\u6709\u6570\u90FD\u586B\u5B8C\u4E86\uFF0C\u6BCF\u4E2A\u6876\u91CC\u7684\u6570\u5B57\u548C\u90FD\u662F target\n # if index == len(nums):\n # for i in range(len(bucket)):\n # if bucket[i] != target:\n # return False\n # return True\n \n # # \u6BCF\u4E2A\u6876\u90FD\u5C1D\u8BD5\u4E00\u4E0B\n # for i in range(len(bucket)):\n # # \u5982\u679C\u52A0\u8FDB\u53BB\u8FD9\u4E2A\u6570\uFF0C\u8FD9\u4E2A\u6876\u7684\u6570\u5B57\u548C\u5C31\u8D85\u8FC7\u4E86 target\uFF0C\u90A3\u5C31\u4E0D\u80FD\u52A0\u4E86\n # if bucket[i] + nums[index] > target:\n # continue\n # # \u52A0\u8FDB\u53BB\n # bucket[i] += nums[index]\n # # \u5982\u679C\u8FD9\u4E2A\u52A0\u6CD5\u662F\u53EF\u884C\u65B9\u6848\uFF0C\u5C31\u7EE7\u7EED\u9012\u5F52\u4E0B\u53BB\n # if self.backtrack(nums, index + 1, bucket, target):\n # return True\n # # \u52A0\u5B8C\u53C8\u8981\u64A4\u6D88\u52A0\u6CD5\uFF0C\u6062\u590D\u73B0\u573A\uFF0C\u7EE7\u7EED\u5C1D\u8BD5\u522B\u7684\u52A0\u6CD5\n # bucket[i] -= nums[index]\n # # \u65E0\u89E3\uFF0C\u8FD4\u56DE false\n # return False\n``` | 1 | Given an integer array `nums` and an integer `k`, return `true` if it is possible to divide this array into `k` non-empty subsets whose sums are all equal.
**Example 1:**
**Input:** nums = \[4,3,2,3,5,2,1\], k = 4
**Output:** true
**Explanation:** It is possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Constraints:**
* `1 <= k <= nums.length <= 16`
* `1 <= nums[i] <= 104`
* The frequency of each element is in the range `[1, 4]`. | We can figure out what target each subset must sum to. Then, let's recursively search, where at each call to our function, we choose which of k subsets the next value will join. |
Python | 90ms Faster than 92% | 95% Less Memory | partition-to-k-equal-sum-subsets | 0 | 1 | ```\ndef canPartitionKSubsets(self, nums: List[int], k: int) -> bool:\n\ttotal = sum(nums)\n\n\tif total % k:\n\t\treturn False\n\n\treqSum = total // k\n\tsubSets = [0] * k\n\tnums.sort(reverse = True)\n\n\tdef recurse(i):\n\t\tif i == len(nums): \n\t\t\treturn True\n\n\t\tfor j in range(k):\n\t\t\tif subSets[j] + nums[i] <= reqSum:\n\t\t\t\tsubSets[j] += nums[i]\n\n\t\t\t\tif recurse(i + 1):\n\t\t\t\t\treturn True\n\n\t\t\t\tsubSets[j] -= nums[i]\n\n\t\t\t\t# Important line, otherwise function will give TLE\n\t\t\t\tif subSets[j] == 0:\n\t\t\t\t\tbreak\n\n\t\t\t\t"""\n\t\t\t\tExplanation:\n\t\t\t\tIf subSets[j] = 0, it means this is the first time adding values to that subset.\n\t\t\t\tIf the backtrack search fails when adding the values to subSets[j] and subSets[j] remains 0, it will also fail for all subSets from subSets[j+1:].\n\t\t\t\tBecause we are simply going through the previous recursive tree again for a different j+1 position.\n\t\t\t\tSo we can effectively break from the for loop or directly return False.\n\t\t\t\t"""\n\n\t\treturn False\n\n\treturn recurse(0)\n```\n\n\n | 67 | Given an integer array `nums` and an integer `k`, return `true` if it is possible to divide this array into `k` non-empty subsets whose sums are all equal.
**Example 1:**
**Input:** nums = \[4,3,2,3,5,2,1\], k = 4
**Output:** true
**Explanation:** It is possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Constraints:**
* `1 <= k <= nums.length <= 16`
* `1 <= nums[i] <= 104`
* The frequency of each element is in the range `[1, 4]`. | We can figure out what target each subset must sum to. Then, let's recursively search, where at each call to our function, we choose which of k subsets the next value will join. |
Fully explained Backtracking + DFS in Python | partition-to-k-equal-sum-subsets | 0 | 1 | # Intuition\nTo determine if it\'s possible to divide an array into `k` subsets with equal sums, we can use a depth-first search (DFS) approach. The idea is to find `k` subsets that have a sum of `target_sum`, where `target_sum` is equal to the total sum of the array divided by `k`.\n\n# Approach\n1. Calculate the sum of all numbers in the array. If it is not divisible by `k`, return `False` since equal subsets cannot be formed.\n2. Sort the array in descending order. Sorting helps with pruning, allowing us to quickly skip certain numbers during the DFS search.\n3. Create a boolean array, `used`, to keep track of which numbers have been used in the subsets. Initially, all elements are set to `False`.\n4. Implement a recursive DFS function, `dfs`, which takes three parameters:\n - `sub_sets_count`: The number of subsets found so far.\n - `cur_sum`: The sum of the current subset being constructed.\n - `start_index`: The index of the next number to consider in the array.\n5. In the DFS function:\n - If `sub_sets_count` equals `k`, we have found `k` subsets with equal sums, so we return `True`.\n - If `cur_sum` equals `target_sum`, we move to the next subset by making a recursive call with `sub_sets_count + 1`, `0`, and `0` as the updated parameters.\n - Iterate through the remaining numbers in the array, starting from `start_index`:\n - If the current number has already been used or adding it to `cur_sum` exceeds `target_sum`, skip it.\n - Implement the pruning step: If the current number is equal to the previous number and the previous number has not been used, skip the current number. This helps avoid duplicate computation and improves efficiency.\n - Mark the current number as used by setting `used[i]` to `True`.\n - Recursively call `dfs` with the updated `sub_sets_count`, `cur_sum`, and `i + 1`.\n - If the recursive call returns `True`, it means we have found a valid partition, so we can immediately return `True`.\n - Undo the choice of using the current number by setting `used[i]` back to `False`.\n6. If no solution is found from the DFS search, return `False`.\n\n## Complexity\n- Time complexity: The time complexity of the algorithm is O(n * 2^n), where n is the length of the input array. The algorithm explores all possible subsets of the array, and there are 2^n possible subsets. For each subset, the algorithm performs a constant amount of work.\n- Space complexity: The space complexity is O(n), where n is the length of the input array. This includes the space needed for the `used` array and the recursive call stack.\n\n# Code\n```\nclass Solution:\n def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:\n # Calculate the sum of all numbers in the array\n nums_sum = sum(nums)\n # If the sum cannot be evenly divided by k, it is not possible\n if nums_sum % k != 0:\n return False\n\n # Calculate the target sum for each subset\n target_sum = nums_sum // k\n # Sort the array in descending order to optimize pruning\n nums.sort(reverse=True)\n # Keep track of which numbers have been used in subsets\n used = [False] * len(nums)\n\n # Depth-first search function to explore all possible subsets\n def dfs(sub_sets_count, cur_sum, start_index):\n # If we have found k subsets, it is a valid partition\n if sub_sets_count == k:\n return True\n # If the current subset sum matches the target sum, move to the next subset\n if cur_sum == target_sum:\n return dfs(sub_sets_count + 1, 0, 0)\n \n # Iterate through the remaining numbers in the array\n for i in range(start_index, len(nums)):\n # If the number has been used or adding it exceeds the target sum, skip it\n if used[i] or cur_sum + nums[i] > target_sum:\n continue\n \n # Pruning step: if the current number is the same as the previous number\n # and the previous number hasn\'t been used, skip the current number\n if i > start_index and nums[i] == nums[i - 1] and not used[i - 1]:\n continue\n\n # Mark the current number as used\n used[i] = True\n # Recursive call to explore the next number and update the subset sum\n if dfs(sub_sets_count, cur_sum + nums[i], i + 1):\n return True\n # Undo the choice of using the current number and try the next number in the array\n used[i] = False\n\n # If no solution is found, return False\n return False\n\n # Start the depth-first search from the beginning of the array with an empty subset\n return dfs(0, 0, 0)\n\n``` | 1 | Given an integer array `nums` and an integer `k`, return `true` if it is possible to divide this array into `k` non-empty subsets whose sums are all equal.
**Example 1:**
**Input:** nums = \[4,3,2,3,5,2,1\], k = 4
**Output:** true
**Explanation:** It is possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Constraints:**
* `1 <= k <= nums.length <= 16`
* `1 <= nums[i] <= 104`
* The frequency of each element is in the range `[1, 4]`. | We can figure out what target each subset must sum to. Then, let's recursively search, where at each call to our function, we choose which of k subsets the next value will join. |
[Python3] - Two solutions, DP with Bit mask(48ms), DFS+backtracking with detailed explanations | partition-to-k-equal-sum-subsets | 0 | 1 | Very classic question. Most of the answers in Leetcode discuss use DFS+backtracking (see solution2), but we can optimize the solution with DP and bit mask to O(2^N) time. Still exponential time, but faster. Good luck with your interviews and upvote if you found this useful :)\n\n**Explanations:**\n[1]. If input array has length less than k, or if the sum all of elements in array cannot be equally divided into k parts, return False.\n[2]. Sort the array in descending order, to improve run time.\n[3]. If mask == 0, all the elements have been used, and we need to see whether cur is equal to 0. If it is, we have found a way to evenly partition all the elements into k parts.\n[4]. If cur is 0, while mask is not 0, we found an equal subset. But we need to keep doing this until all the number in the array are used (to find k equal subset).\n[5]. Loop through all the "bits", which represents each number in our input array. \n[6]. Check whether the number is unused. A set bit (1) means unused, 0 means used.\n[7]. Use XOR to mark set bit as used (change from 1 to 0)\n[8]. Initialize mask as 11111...., N set bits.\n\n**[Solution 1] - DP + Bit Mask Solution, O(N*2^N) time (optimized)**\n```\nclass Solution:\n def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:\n if len(nums) < k or int(sum(nums)/k) != sum(nums)/k: return False #[1]\n N = len(nums)\n nums.sort(reverse=True) #[2]\n \n def dp(mask, cur, memo): # Top-down DP with memoization\n if mask == 0: return cur == 0 #[3]\n elif cur == 0: return dp(mask, sum(nums)/k, memo) #[4]\n if (mask, cur) not in memo:\n res = False\n for bit in range(N): #[5]\n if mask & (1 << bit): #[6]\n if nums[bit] > cur: continue # Writing this to be more explicit, for easy-understanding\n if dp(mask ^ (1 << bit), cur-nums[bit], memo): #[7]\n res = True\n break\n memo[(mask, cur)] = res\n return memo[(mask, cur)] \n return dp(2**N-1, sum(nums)/k, dict()) #[8]\n```\n\n**[Solution 2] - DFS + Backtracking Solution, O(k^N) time (less optimal)**\n```\nclass Solution:\n def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:\n if len(nums) < k or int(sum(nums)/k) != sum(nums)/k:\n return False\n nums.sort(reverse=True)\n parts = [sum(nums)/k]*k\n return self.dfs(parts, nums, 0)\n \n def dfs(self, parts, nums, idx):\n if idx == len(nums):\n return not sum(parts)\n for i in range(len(parts)):\n if parts[i] >= nums[idx]:\n parts[i] -= nums[idx]\n if self.dfs(parts, nums, idx+1):\n return True\n parts[i] += nums[idx]\n```\n\n**[Solution 3] -- Just for fun, same complexity as Solution 1 but without memo**\n```python\nclass Solution:\n def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:\n if len(nums)<k or sum(nums)/k != int(sum(nums)/k): return False\n N = len(nums)\n \n @cache #In python we are allowed to use decorators to cache our data so memo is not needed to achieve the same result.\n def dp(mask, cur):\n if mask == 0: return cur == 0\n elif cur == 0: return dp(mask, sum(nums)/k)\n for bit in range(len(nums)):\n if mask & (1 << bit):\n if nums[bit] <= cur and dp(mask ^ (1 << bit), cur-nums[bit]):\n return True\n return False\n \n return dp(2**N-1, sum(nums)/k)\n```\n\n**Simlar Problems:**\n\n[LC473-Matchsticks to Square](https://leetcode.com/problems/matchsticks-to-square/)\n[LC416-Partition Equal Subset Sum](https://leetcode.com/problems/partition-equal-subset-sum/) | 36 | Given an integer array `nums` and an integer `k`, return `true` if it is possible to divide this array into `k` non-empty subsets whose sums are all equal.
**Example 1:**
**Input:** nums = \[4,3,2,3,5,2,1\], k = 4
**Output:** true
**Explanation:** It is possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Constraints:**
* `1 <= k <= nums.length <= 16`
* `1 <= nums[i] <= 104`
* The frequency of each element is in the range `[1, 4]`. | We can figure out what target each subset must sum to. Then, let's recursively search, where at each call to our function, we choose which of k subsets the next value will join. |
Solution | partition-to-k-equal-sum-subsets | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int len;\n vector<int> nums;\n vector<bool> st;\n\n bool dfs(int start, int cur, int k) {\n if (!k) return true;\n if (cur == len) return dfs(0, 0, k - 1);\n for (int i = start; i < nums.size(); i ++ ) {\n if (st[i]) continue;\n if (cur + nums[i] <= len) {\n st[i] = true;\n if (dfs(i + 1, cur + nums[i], k)) return true;\n st[i] = false;\n }\n while (i + 1 < nums.size() && nums[i + 1] == nums[i]) i ++ ;\n if (!cur || cur + nums[i] == len) return false;\n }\n return false;\n }\n bool canPartitionKSubsets(vector<int>& _nums, int k) {\n nums = _nums;\n st.resize(nums.size());\n int sum = accumulate(nums.begin(), nums.end(), 0);\n if (sum % k) return false;\n len = sum / k;\n sort(nums.begin(), nums.end(), greater<int>());\n return dfs(0, 0, k);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:\n def backtrack(i, used, cursum):\n if used == DONE:\n return True\n \n for j in range(i, N):\n if used & (1 << j) > 0:\n continue\n if j > 0 and used & (1 << j - 1) == 0 and nums[j] == nums[j - 1]:\n continue\n \n if nums[j] + cursum < target:\n if backtrack(j + 1, used | (1 << j), cursum + nums[j]):\n return True\n elif nums[j] + cursum == target:\n if backtrack(0, used | (1 << j), 0):\n return True\n \n if i == 0:\n break\n return False\n\n total = sum(nums)\n if total % k != 0:\n return False\n target = total // k\n\n nums.sort(reverse=True)\n N = len(nums)\n DONE = (1 << N) - 1\n print(nums)\n return backtrack(0, 0, 0)\n```\n\n```Java []\nclass Solution {\n int[] nums;\n boolean[] st;\n int n, side;\n public boolean canPartitionKSubsets(int[] nums, int k) {\n this.nums = nums;\n n = nums.length;\n st = new boolean[n];\n \n int sum = 0;\n for (int x : nums) sum += x;\n if (sum % k != 0) return false;\n \n side = sum / k;\n \n Arrays.sort(nums);\n reverse();\n \n return dfs(0, 0, k);\n }\n private boolean dfs(int u, int sum, int k) {\n if (k == 0) return true;\n if (sum > side) return false;\n if (sum == side) return dfs(0, 0, k - 1);\n \n for (int i = u; i < n; i++) {\n if (st[i]) continue;\n st[i] = true;\n if (dfs(i + 1, sum + nums[i], k)) return true;\n st[i] = false;\n \n while (i + 1 < n && nums[i + 1] == nums[i]) i++;\n if (u == 0 || sum + nums[u] == side) return false;\n }\n return false;\n }\n private void reverse() {\n int i = 0, j = n - 1;\n while (i < j) {\n int t = nums[i];\n nums[i++] = nums[j];\n nums[j--] = t;\n }\n }\n}\n```\n | 3 | Given an integer array `nums` and an integer `k`, return `true` if it is possible to divide this array into `k` non-empty subsets whose sums are all equal.
**Example 1:**
**Input:** nums = \[4,3,2,3,5,2,1\], k = 4
**Output:** true
**Explanation:** It is possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 3
**Output:** false
**Constraints:**
* `1 <= k <= nums.length <= 16`
* `1 <= nums[i] <= 104`
* The frequency of each element is in the range `[1, 4]`. | We can figure out what target each subset must sum to. Then, let's recursively search, where at each call to our function, we choose which of k subsets the next value will join. |
Solution | falling-squares | 1 | 1 | ```C++ []\n#include <vector>\n#include <algorithm>\n#include <iterator>\n\nstruct SegmentTree {\n\n SegmentTree(int n) : n(n) {\n size = 1;\n while (size < n) {\n size <<= 1;\n }\n tree.resize(2*size);\n lazy.resize(2*size);\n }\n\n void add_range(int l, int r, int h) {\n l += size;\n r += size;\n\n tree[l] = max(tree[l], h);\n tree[r] = max(tree[r], h);\n if (l != r) {\n if (!(l & 1)) {\n lazy[l+1] = max(lazy[l-1], h);\n }\n if (r & 1) {\n lazy[r-1] = max(lazy[r-1], h);\n }\n }\n l >>= 1;\n r >>= 1;\n while (l != r) {\n tree[l] = max(tree[2*l], tree[2*l + 1]);\n tree[r] = max(tree[2*r], tree[2*r + 1]);\n if (l / 2 != r / 2) {\n if (!(l & 1)) {\n lazy[l+1] = max(lazy[l+1], h);\n }\n if (r & 1) {\n lazy[r-1] = max(lazy[r-1], h);\n }\n }\n l >>= 1;\n r >>= 1;\n }\n while (l > 0) {\n tree[l] = max(tree[2*l], tree[2*l + 1]);\n l >>= 1;\n }\n }\n int max_range(int l, int r) {\n l += size;\n r += size;\n\n int max_val = max(tree[l], tree[r]);\n while (l / 2 != r / 2) {\n if (!(l & 1)) {\n max_val = max(tree[l + 1], max_val);\n max_val = max(lazy[l + 1], max_val);\n }\n if (r & 1) {\n max_val = max(tree[r - 1], max_val);\n max_val = max(lazy[r - 1], max_val);\n }\n max_val = max(max_val, lazy[l]);\n max_val = max(max_val, lazy[r]);\n\n l >>= 1;\n r >>= 1;\n }\n max_val = max(max_val, lazy[r]);\n\n while (l / 2 > 0) {\n max_val = max(lazy[l], max_val);\n l >>= 1;\n }\n return max_val;\n }\n int global_max() {\n return max_range(0, n-1);\n }\n int size;\n int n;\n vector<int> tree;\n vector<int> lazy;\n};\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n \n vector<int> points;\n for (const auto& rect: positions) {\n points.push_back(rect[0]);\n points.push_back(rect[0] + rect[1] - 1);\n }\n sort(begin(points), end(points));\n auto new_end = unique(begin(points), end(points));\n points.resize(distance(begin(points), new_end));\n\n SegmentTree st(points.size());\n\n vector<int> results;\n\n int max_height = 0;\n for (const auto& rect: positions) {\n int x_1 = rect[0];\n int x_2 = rect[0] + rect[1] - 1;\n\n int l = distance(begin(points), lower_bound(begin(points), end(points), x_1));\n int r = distance(begin(points), lower_bound(begin(points), end(points), x_2));\n\n int cur_height = st.max_range(l, r);\n int new_height = rect[1] + cur_height;\n max_height = max(new_height, max_height);\n st.add_range(l, r, new_height);\n results.push_back(max_height);\n }\n return results;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n height = [0]\n pos = [0]\n res = []\n max_h = 0\n for left, side in positions:\n i = bisect.bisect_right(pos, left)\n j = bisect.bisect_left(pos, left + side)\n high = max(height[i - 1:j] or [0]) + side\n pos[i:j] = [left, left + side]\n height[i:j] = [high, height[j - 1]]\n max_h = max(max_h, high)\n res.append(max_h)\n return res\n```\n\n```Java []\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions)\n {\n int[] ends = new int[positions.length*2];\n for(int i=0; i<positions.length; i++)\n {\n ends[i*2+0] = positions[i][0];\n ends[i*2+1] = positions[i][0]+positions[i][1];\n }\n Arrays.sort(ends);\n\n int[] ceilings = new int[ends.length-1];\n int maxAll = 0;\n ArrayList<Integer> results = new ArrayList<>();\n for(int i=0; i<positions.length; i++)\n {\n int X = positions[i][0];\n int x = Arrays.binarySearch(ends, X);\n assert x>=0;\n int maxCeiling = 0;\n int Y = X + positions[i][1];\n for(int y=x; ends[y]<Y; y++)\n maxCeiling = Math.max(maxCeiling, ceilings[y]);\n maxCeiling += (Y-X);\n for(int y=x; ends[y]<Y; y++)\n ceilings[y] = maxCeiling;\n maxAll = Math.max(maxAll, maxCeiling);\n results.add(maxAll);\n }\n return results;\n }\n}\n```\n | 2 | There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array `positions` where `positions[i] = [lefti, sideLengthi]` represents the `ith` square with a side length of `sideLengthi` that is dropped with its left edge aligned with X-coordinate `lefti`.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the **height of the current tallest stack of squares**.
Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ `ith` _square_.
**Example 1:**
**Input:** positions = \[\[1,2\],\[2,3\],\[6,1\]\]
**Output:** \[2,5,5\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of \[2, 5, 5\].
**Example 2:**
**Input:** positions = \[\[100,100\],\[200,100\]\]
**Output:** \[100,100\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of \[100, 100\].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
**Constraints:**
* `1 <= positions.length <= 1000`
* `1 <= lefti <= 108`
* `1 <= sideLengthi <= 106` | If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable? |
Python 3 || 9 lines, bisect || T/S: 98% / 91% | falling-squares | 0 | 1 | ```\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n\n def helper(box: List[int])->int:\n\n l, h = box\n r = l + h\n \n i, j = bisect_right(pos, l), bisect_left (pos, r)\n\n res = h + max(hgt[i-1:j], default = 0)\n pos[i:j], hgt[i:j] = [l, r], [res, hgt[j - 1]]\n\n return res\n\n \n hgt, pos, res, mx = [0], [0], [], 0\n \n return accumulate(map(helper, positions), max)\n```\n[https://leetcode.com/problems/falling-squares/submissions/1050437122/](http://)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ `len(positions)`. | 3 | There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array `positions` where `positions[i] = [lefti, sideLengthi]` represents the `ith` square with a side length of `sideLengthi` that is dropped with its left edge aligned with X-coordinate `lefti`.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the **height of the current tallest stack of squares**.
Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ `ith` _square_.
**Example 1:**
**Input:** positions = \[\[1,2\],\[2,3\],\[6,1\]\]
**Output:** \[2,5,5\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of \[2, 5, 5\].
**Example 2:**
**Input:** positions = \[\[100,100\],\[200,100\]\]
**Output:** \[100,100\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of \[100, 100\].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
**Constraints:**
* `1 <= positions.length <= 1000`
* `1 <= lefti <= 108`
* `1 <= sideLengthi <= 106` | If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable? |
LazySegmentTree python3 | falling-squares | 0 | 1 | # Intuition\nLazySegmentTree with max query and set_value to range.\nhttps://cp-algorithms.com/data_structures/segment_tree.html#assignment-on-segments\n# Approach\nWe normalize the points while dividing them into left and right parts.\nusing (point,0) #left and (point,1) #right to handle the "brushing the left/right side of another square" condition.\n# Complexity\n- Time complexity:\n O(n logn)\n\n- Space complexity:\n O(n)\n\n# Code\n```\nclass LazySegmentTree:\n def __init__(self, data, default=0, func=max):\n self._default = default\n self._func = func\n self._len = len(data)\n self._size = 1 << (self._len - 1).bit_length()\n self._lazy = [None] * (2 * self._size)\n self.data = [default] * (2 * self._size)\n self.data[self._size:self._size + self._len] = data\n for i in reversed(range(self._size)):\n self.data[i] = func(self.data[2 * i], self.data[2 * i + 1])\n\n def __len__(self):\n return self._len\n\n def _push(self, idx):\n if self._lazy[idx] is not None:\n self.data[idx * 2] = self.data[idx * 2 + 1] = self._lazy[idx]\n self._lazy[idx * 2] = self._lazy[idx * 2 + 1] = self._lazy[idx]\n self._lazy[idx] = None\n\n def _update(self, idx, tl, tr, l, r, new_val):\n if l > r:\n return\n if l == tl and r == tr:\n self.data[idx] = new_val\n self._lazy[idx] = new_val\n else:\n self._push(idx)\n tm = (tl + tr) // 2\n self._update(idx * 2, tl, tm, l, min(r, tm), new_val)\n self._update(idx * 2 + 1, tm + 1, tr, max(l, tm + 1), r, new_val)\n self.data[idx] = self._func(self.data[idx * 2], self.data[idx * 2 + 1])\n\n def set_value(self, l, r, value):\n self._update(1, 0, self._size - 1, l, r, value)\n\n def _get(self, idx, tl, tr, pos):\n if tl == tr:\n return self.data[idx]\n self._push(idx)\n tm = (tl + tr) // 2\n if pos <= tm:\n return self._get(idx * 2, tl, tm, pos)\n else:\n return self._get(idx * 2 + 1, tm + 1, tr, pos)\n\n def get(self, pos):\n return self._get(1, 0, self._size - 1, pos)\n \n def _query(self, idx, tl, tr, l, r):\n if l > r:\n return -float(\'inf\') # Using negative infinity as the default for max queries\n if l == tl and tr == r:\n return self.data[idx]\n self._push(idx)\n tm = (tl + tr) // 2\n return max(self._query(idx * 2, tl, tm, l, min(r, tm)), \n self._query(idx * 2 + 1, tm + 1, tr, max(l, tm + 1), r))\n\n def query_range(self, l, r):\n return self._query(1, 0, self._size - 1, l, r)\n \n def __repr__(self):\n return "LazySegmentTree({0})".format(self.data)\n \n def __delitem__(self, idx):\n self[idx] = self._default\n\n def __getitem__(self, idx):\n if isinstance(idx, slice):\n start=idx.start\n stop=idx.stop\n else:\n start=idx\n stop=idx+1\n return self.query_range(start,stop)\n\n def __setitem__(self, idx, value):\n if isinstance(idx, slice):\n start=idx.start\n stop=idx.stop\n else:\n start=idx\n stop=idx+1\n self.set_value(start,stop,value)\n\n\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n s=set()\n for x,a in positions:\n s.add((x,0))\n s.add((x,1))\n s.add((x+a,0))\n s.add((x+a,1))\n d={}\n index=0\n for i in sorted(s):\n d[i]=index\n index+=1\n st=LazySegmentTree([0]*len(d),default=0,func=max)\n\n ans=[]\n ma=0\n\n for x,a in positions: \n cur_h = st[d[(x,1)]:d[(x+a,0)]]+a \n st[d[(x,1)]:d[(x+a,0)]]=cur_h\n ma=max(ma,cur_h)\n ans.append(ma)\n return ans\n``` | 0 | There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array `positions` where `positions[i] = [lefti, sideLengthi]` represents the `ith` square with a side length of `sideLengthi` that is dropped with its left edge aligned with X-coordinate `lefti`.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the **height of the current tallest stack of squares**.
Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ `ith` _square_.
**Example 1:**
**Input:** positions = \[\[1,2\],\[2,3\],\[6,1\]\]
**Output:** \[2,5,5\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of \[2, 5, 5\].
**Example 2:**
**Input:** positions = \[\[100,100\],\[200,100\]\]
**Output:** \[100,100\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of \[100, 100\].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
**Constraints:**
* `1 <= positions.length <= 1000`
* `1 <= lefti <= 108`
* `1 <= sideLengthi <= 106` | If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable? |
✅bruet force || python | falling-squares | 0 | 1 | \n# Code\n```\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n ans=[]\n maxi=0\n arr=[]\n n=len(positions)\n for i in range(n):\n ch=0\n l=positions[i][0]\n r=positions[i][0]+positions[i][1]\n for j in range(len(arr)):\n lf=arr[j][0]\n rf=arr[j][1]\n h=arr[j][2]\n if((l>=lf and l<rf) or(r>lf and r<=rf) or (l<=lf and r>=rf)):\n ch=max(ch,h)\n \n ch+=positions[i][1]\n # print(l,r,ch)\n maxi=max(ch,maxi)\n arr.append([l,r,ch])\n ans.append(maxi)\n return ans\n \n# 6>=2 and 2<7\n``` | 0 | There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array `positions` where `positions[i] = [lefti, sideLengthi]` represents the `ith` square with a side length of `sideLengthi` that is dropped with its left edge aligned with X-coordinate `lefti`.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the **height of the current tallest stack of squares**.
Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ `ith` _square_.
**Example 1:**
**Input:** positions = \[\[1,2\],\[2,3\],\[6,1\]\]
**Output:** \[2,5,5\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of \[2, 5, 5\].
**Example 2:**
**Input:** positions = \[\[100,100\],\[200,100\]\]
**Output:** \[100,100\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of \[100, 100\].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
**Constraints:**
* `1 <= positions.length <= 1000`
* `1 <= lefti <= 108`
* `1 <= sideLengthi <= 106` | If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable? |
Short Python O(n^2) | falling-squares | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBecause the size of the input is lower than 1000, we can free ourselves to use an $$O(n^2)$$ algorithm. we see that at any square we only need to look at previous ones, but we have to keep track of the highest each square can reach in another variable (dp) so if we happen to collide with any of previous squares, we get the maximum of the `dp[i]` and the height of square + max of previous ranks.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe define another array called `dp` which is initialized with all zeroes. `dp[i]` stores the height of the `ith` square.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\n def fallingSquares(self, A):\n ans, dp = [], [0] * len(A)\n for i in range(len(A)):\n dp[i] = A[i][1]\n for j in range(i - 1, -1, -1):\n if A[i][0] <= A[j][0] < A[i][0] + A[i][1] or A[j][0] <= A[i][0] < A[j][0] + A[j][1]:\n dp[i] = max(dp[i], A[i][1] + dp[j])\n ans.append(max(dp[i], ans[-1] if ans else 0))\n return ans\n```\n\nA shorter version of this code is to remove `ans` completely and accumulate `dp`\n```\n def fallingSquares(self, A):\n dp = [0] * len(A)\n for i in range(len(A)):\n for j in range(i, -1, -1):\n if A[i][0] <= A[j][0] < A[i][0] + A[i][1] or A[j][0] <= A[i][0] < A[j][0] + A[j][1]:\n dp[i] = max(dp[i], A[i][1] + dp[j])\n return accumulate(dp, func=max)\n``` | 0 | There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array `positions` where `positions[i] = [lefti, sideLengthi]` represents the `ith` square with a side length of `sideLengthi` that is dropped with its left edge aligned with X-coordinate `lefti`.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the **height of the current tallest stack of squares**.
Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ `ith` _square_.
**Example 1:**
**Input:** positions = \[\[1,2\],\[2,3\],\[6,1\]\]
**Output:** \[2,5,5\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of \[2, 5, 5\].
**Example 2:**
**Input:** positions = \[\[100,100\],\[200,100\]\]
**Output:** \[100,100\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of \[100, 100\].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
**Constraints:**
* `1 <= positions.length <= 1000`
* `1 <= lefti <= 108`
* `1 <= sideLengthi <= 106` | If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable? |
Python (Simple Maths) | falling-squares | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fallingSquares(self, positions):\n h = [0]*len(positions)\n\n for i,(l1,s1) in enumerate(positions):\n r1 = l1 + s1\n h[i] += s1\n for j in range(i+1,len(positions)):\n l2,s2 = positions[j]\n r2 = l2 + s2\n if l2 < r1 and r2 > l1:\n h[j] = max(h[j],h[i])\n\n max_val, ans = 0, []\n\n for i in h:\n max_val = max(max_val,i)\n ans.append(max_val)\n\n return ans\n\n\n\n\n\n\n\n\n\n\n\n \n \n``` | 0 | There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array `positions` where `positions[i] = [lefti, sideLengthi]` represents the `ith` square with a side length of `sideLengthi` that is dropped with its left edge aligned with X-coordinate `lefti`.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the **height of the current tallest stack of squares**.
Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ `ith` _square_.
**Example 1:**
**Input:** positions = \[\[1,2\],\[2,3\],\[6,1\]\]
**Output:** \[2,5,5\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of \[2, 5, 5\].
**Example 2:**
**Input:** positions = \[\[100,100\],\[200,100\]\]
**Output:** \[100,100\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of \[100, 100\].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
**Constraints:**
* `1 <= positions.length <= 1000`
* `1 <= lefti <= 108`
* `1 <= sideLengthi <= 106` | If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable? |
699: Solution with step by step explanation | falling-squares | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize an empty list called "heights" to store the heights of each column, and initialize the maximum height to 0.\n2. Initialize an empty list called "ans" to store the answer.\n3. Iterate through each square in the input array:\na. Find the right edge of the current square.\nb. Initialize the height of the current square to 0.\nc. Iterate through the columns that the square will land on.\nd. Check if the column intersects with the square:\nIf the column intersects with the square, update the height of the square to be the maximum of its current height and the height of the intersecting column.\ne. Update the height of the current square to include its side length.\nf. Append the new height range to the list of heights.\ng. Update the maximum height to be the maximum of its current value and the height of the current square.\nh. Append the new maximum height to the answer list.\n4. Return the answer list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n # Initialize an empty list to store the heights of each column\n heights = []\n # Initialize the maximum height to 0\n max_height = 0\n # Initialize an empty list to store the answer\n ans = []\n \n # Iterate through the squares in the input array\n for left, side in positions:\n # Find the right edge of the square\n right = left + side\n # Initialize the height of the current square to 0\n height = 0\n # Iterate through the columns that the square will land on\n for i in range(len(heights)):\n # Check if the column intersects with the square\n if left < heights[i][1] and right > heights[i][0]:\n # If the column intersects with the square, update the height of the square\n height = max(height, heights[i][2])\n # Update the height of the current square\n height += side\n # Append the new height range to the list of heights\n heights.append((left, right, height))\n # Update the maximum height\n max_height = max(max_height, height)\n # Append the new maximum height to the answer\n ans.append(max_height)\n \n return ans\n\n``` | 0 | There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array `positions` where `positions[i] = [lefti, sideLengthi]` represents the `ith` square with a side length of `sideLengthi` that is dropped with its left edge aligned with X-coordinate `lefti`.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the **height of the current tallest stack of squares**.
Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ `ith` _square_.
**Example 1:**
**Input:** positions = \[\[1,2\],\[2,3\],\[6,1\]\]
**Output:** \[2,5,5\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of \[2, 5, 5\].
**Example 2:**
**Input:** positions = \[\[100,100\],\[200,100\]\]
**Output:** \[100,100\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of \[100, 100\].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
**Constraints:**
* `1 <= positions.length <= 1000`
* `1 <= lefti <= 108`
* `1 <= sideLengthi <= 106` | If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable? |
Python Simple Bottom Up DP | falling-squares | 0 | 1 | # Intuition\nFind best from previously computed values, check edges and add on top if valid else continue.\n\n# Approach\nSimple Bottom up DP\n\n# Complexity\n- Time complexity:\nO(N^2)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def fallingSquares(self, arr: List[List[int]]) -> List[int]:\n n=len(arr)\n dp=[0]*n\n ans=[]\n mmax=0\n for i in range(n):\n l=arr[i][0]\n r=l+arr[i][1]\n for j in range(i):\n ll=arr[j][0]\n rr=ll+arr[j][1]\n if r<=ll or rr<=l: continue\n dp[i]=max(dp[i],dp[j]+r-l)\n if not dp[i]:\n dp[i]=arr[i][1]\n mmax=max(mmax,dp[i])\n ans.append(mmax)\n return ans\n\n\n\n``` | 0 | There are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array `positions` where `positions[i] = [lefti, sideLengthi]` represents the `ith` square with a side length of `sideLengthi` that is dropped with its left edge aligned with X-coordinate `lefti`.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands **on the top side of another square** or **on the X-axis**. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the **height of the current tallest stack of squares**.
Return _an integer array_ `ans` _where_ `ans[i]` _represents the height described above after dropping the_ `ith` _square_.
**Example 1:**
**Input:** positions = \[\[1,2\],\[2,3\],\[6,1\]\]
**Output:** \[2,5,5\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 2.
After the second drop, the tallest stack is squares 1 and 2 with a height of 5.
After the third drop, the tallest stack is still squares 1 and 2 with a height of 5.
Thus, we return an answer of \[2, 5, 5\].
**Example 2:**
**Input:** positions = \[\[100,100\],\[200,100\]\]
**Output:** \[100,100\]
**Explanation:**
After the first drop, the tallest stack is square 1 with a height of 100.
After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100.
Thus, we return an answer of \[100, 100\].
Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
**Constraints:**
* `1 <= positions.length <= 1000`
* `1 <= lefti <= 108`
* `1 <= sideLengthi <= 106` | If positions = [[10, 20], [20, 30]], this is the same as [[1, 2], [2, 3]]. Currently, the values of positions are very large. Can you generalize this approach so as to make the values in positions manageable? |
2 approach with great explanation. Beats 84% user. Recursive and Looping | search-in-a-binary-search-tree | 1 | 1 | \n\n# \u2705 \u2B06\uFE0F --- Soln - 1 --- \u2B06 \u267B\uFE0F\n# \uD83E\uDD29 Intuition and Approach - Recursive \uD83E\uDD73\n\nthe searchBST function is a recursive function that searches for a specific target value in a binary search tree (BST). The function starts its search from the root of the BST and traverses down the tree based on the comparison of the target value with the values of nodes. If the target value is found in the tree, the function returns the corresponding TreeNode*, otherwise, it returns NULL to indicate that the target value is not present in the BST.\n\n# Complexity\n- Time complexity: O(log n)\n\n- Space complexity: O(log n)\n\n\n# Code\n```\n\nclass Solution {\npublic:\n TreeNode* searchBST(TreeNode* root, int target) {\n\n if(root->val == target) return root;\n\n //if the target is lesser than the root->val, then \n else if(root->val > target) return searchBST(root->left,target);\n else return searchBST(root->right, target);\n\n // If the root is null (i.e., the tree is empty) or we have reached a leaf node,\n // we cannot find the target in the tree, so we return null.\n if (root == NULL) return NULL;\n\n // If the current node\'s value is equal to the target value,\n // then we have found the node containing the target value, so we return this node.\n if (root->val == target) return root;\n\n // If the target value is lesser than the current node\'s value,\n // we need to search in the left subtree of the current node.\n // So we recursively call the searchBST function with the left child of the current node.\n else if(root->val > target) return searchBST(root->left,target);\n\n // If the target value is greater than the current node\'s value,\n // we need to search in the right subtree of the current node.\n // So we recursively call the searchBST function with the right child of the current node.\n else return searchBST(root->right, target);\n\n \n }\n};\n```\n# \u2B06\uFE0F\u2705--- Soln - 2 --- \uD83E\uDD73\n\n# \uD83E\uDD29 Intuition and Approach \u267B\uFE0F\nwhile loop to traverse the binary search tree iteratively, moving to the left or right subtree based on the comparison of the target value with the values of nodes. If the target value is found in the tree, the function returns the corresponding TreeNode*, otherwise, it returns NULL to indicate that the target value is not present in the BST. \n\n```\n // The loop continues until either the root becomes NULL (end of the tree) or\n // the root\'s value matches the target value.\n while (root != NULL && root->val != target) {\n\n // If the current node\'s value is greater than the target value,\n // move to the left subtree to continue the search.\n if (root->val > target)\n root = root->left;\n\n // If the current node\'s value is lesser than the target value,\n // move to the right subtree to continue the search.\n else\n root = root->right;\n }\n\n // Return the current node (which contains the target value) if found,\n // or NULL if the target value is not present in the BST.\n return root;\n```\n\n | 41 | You are given the `root` of a binary search tree (BST) and an integer `val`.
Find the node in the BST that the node's value equals `val` and return the subtree rooted with that node. If such a node does not exist, return `null`.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 2
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5000]`.
* `1 <= Node.val <= 107`
* `root` is a binary search tree.
* `1 <= val <= 107` | null |
2 approach with great explanation. Beats 84% user. Recursive and Looping | search-in-a-binary-search-tree | 1 | 1 | \n\n# \u2705 \u2B06\uFE0F --- Soln - 1 --- \u2B06 \u267B\uFE0F\n# \uD83E\uDD29 Intuition and Approach - Recursive \uD83E\uDD73\n\nthe searchBST function is a recursive function that searches for a specific target value in a binary search tree (BST). The function starts its search from the root of the BST and traverses down the tree based on the comparison of the target value with the values of nodes. If the target value is found in the tree, the function returns the corresponding TreeNode*, otherwise, it returns NULL to indicate that the target value is not present in the BST.\n\n# Complexity\n- Time complexity: O(log n)\n\n- Space complexity: O(log n)\n\n\n# Code\n```\n\nclass Solution {\npublic:\n TreeNode* searchBST(TreeNode* root, int target) {\n\n if(root->val == target) return root;\n\n //if the target is lesser than the root->val, then \n else if(root->val > target) return searchBST(root->left,target);\n else return searchBST(root->right, target);\n\n // If the root is null (i.e., the tree is empty) or we have reached a leaf node,\n // we cannot find the target in the tree, so we return null.\n if (root == NULL) return NULL;\n\n // If the current node\'s value is equal to the target value,\n // then we have found the node containing the target value, so we return this node.\n if (root->val == target) return root;\n\n // If the target value is lesser than the current node\'s value,\n // we need to search in the left subtree of the current node.\n // So we recursively call the searchBST function with the left child of the current node.\n else if(root->val > target) return searchBST(root->left,target);\n\n // If the target value is greater than the current node\'s value,\n // we need to search in the right subtree of the current node.\n // So we recursively call the searchBST function with the right child of the current node.\n else return searchBST(root->right, target);\n\n \n }\n};\n```\n# \u2B06\uFE0F\u2705--- Soln - 2 --- \uD83E\uDD73\n\n# \uD83E\uDD29 Intuition and Approach \u267B\uFE0F\nwhile loop to traverse the binary search tree iteratively, moving to the left or right subtree based on the comparison of the target value with the values of nodes. If the target value is found in the tree, the function returns the corresponding TreeNode*, otherwise, it returns NULL to indicate that the target value is not present in the BST. \n\n```\n // The loop continues until either the root becomes NULL (end of the tree) or\n // the root\'s value matches the target value.\n while (root != NULL && root->val != target) {\n\n // If the current node\'s value is greater than the target value,\n // move to the left subtree to continue the search.\n if (root->val > target)\n root = root->left;\n\n // If the current node\'s value is lesser than the target value,\n // move to the right subtree to continue the search.\n else\n root = root->right;\n }\n\n // Return the current node (which contains the target value) if found,\n // or NULL if the target value is not present in the BST.\n return root;\n```\n\n | 41 | Given the `root` of a Binary Search Tree (BST), return _the minimum difference between the values of any two different nodes in the tree_.
**Example 1:**
**Input:** root = \[4,2,6,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,0,48,null,null,12,49\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `0 <= Node.val <= 105`
**Note:** This question is the same as 530: [https://leetcode.com/problems/minimum-absolute-difference-in-bst/](https://leetcode.com/problems/minimum-absolute-difference-in-bst/) | null |
Easy to Understand | BFS | search-in-a-binary-search-tree | 0 | 1 | # Intuition\nThis is similar to Level Order Traversal\n\n# Approach\nUsed the Level Order Traversal approach to find the search value leve; by level. if serach val is found just return that node, else return Null. \n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root is None:\n return \n queue = []\n result = []\n queue.append(root)\n while len(queue) > 0:\n node = queue.pop(0)\n if node.val == val:\n return node\n else:\n if node.left is not None:\n queue.append(node.left) \n if node.right is not None:\n queue.append(node.right)\n return \n\n\n\n | 0 | You are given the `root` of a binary search tree (BST) and an integer `val`.
Find the node in the BST that the node's value equals `val` and return the subtree rooted with that node. If such a node does not exist, return `null`.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 2
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5000]`.
* `1 <= Node.val <= 107`
* `root` is a binary search tree.
* `1 <= val <= 107` | null |
Easy to Understand | BFS | search-in-a-binary-search-tree | 0 | 1 | # Intuition\nThis is similar to Level Order Traversal\n\n# Approach\nUsed the Level Order Traversal approach to find the search value leve; by level. if serach val is found just return that node, else return Null. \n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root is None:\n return \n queue = []\n result = []\n queue.append(root)\n while len(queue) > 0:\n node = queue.pop(0)\n if node.val == val:\n return node\n else:\n if node.left is not None:\n queue.append(node.left) \n if node.right is not None:\n queue.append(node.right)\n return \n\n\n\n | 0 | Given the `root` of a Binary Search Tree (BST), return _the minimum difference between the values of any two different nodes in the tree_.
**Example 1:**
**Input:** root = \[4,2,6,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,0,48,null,null,12,49\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `0 <= Node.val <= 105`
**Note:** This question is the same as 530: [https://leetcode.com/problems/minimum-absolute-difference-in-bst/](https://leetcode.com/problems/minimum-absolute-difference-in-bst/) | null |
Solution | search-in-a-binary-search-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* searchBST(TreeNode* root, int val) {\n if(root==NULL) return root;\n if(root->val==val) return root;\n if(root->val>val) return searchBST(root->left,val);\n else return searchBST(root->right,val);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n\n def bst(node):\n if not node:\n return None\n\n if val > node.val:\n return bst(node.right)\n elif val < node.val:\n return bst(node.left)\n else:\n return node\n \n return None\n\n return bst(root)\n```\n\n```Java []\nclass Solution {\n public TreeNode searchBST(TreeNode root, int val) {\n while (root!=null) {\n if (root.val==val) {\n return root;\n } \n else if (root.val<val) {\n root = root.right;\n }\n else {\n root = root.left;\n } \n }\n return null;\n }\n}\n```\n | 4 | You are given the `root` of a binary search tree (BST) and an integer `val`.
Find the node in the BST that the node's value equals `val` and return the subtree rooted with that node. If such a node does not exist, return `null`.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 2
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5000]`.
* `1 <= Node.val <= 107`
* `root` is a binary search tree.
* `1 <= val <= 107` | null |
Solution | search-in-a-binary-search-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* searchBST(TreeNode* root, int val) {\n if(root==NULL) return root;\n if(root->val==val) return root;\n if(root->val>val) return searchBST(root->left,val);\n else return searchBST(root->right,val);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n\n def bst(node):\n if not node:\n return None\n\n if val > node.val:\n return bst(node.right)\n elif val < node.val:\n return bst(node.left)\n else:\n return node\n \n return None\n\n return bst(root)\n```\n\n```Java []\nclass Solution {\n public TreeNode searchBST(TreeNode root, int val) {\n while (root!=null) {\n if (root.val==val) {\n return root;\n } \n else if (root.val<val) {\n root = root.right;\n }\n else {\n root = root.left;\n } \n }\n return null;\n }\n}\n```\n | 4 | Given the `root` of a Binary Search Tree (BST), return _the minimum difference between the values of any two different nodes in the tree_.
**Example 1:**
**Input:** root = \[4,2,6,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,0,48,null,null,12,49\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `0 <= Node.val <= 105`
**Note:** This question is the same as 530: [https://leetcode.com/problems/minimum-absolute-difference-in-bst/](https://leetcode.com/problems/minimum-absolute-difference-in-bst/) | null |
Python beats 90% (Simple iterative approach) | search-in-a-binary-search-tree | 0 | 1 | ```\nstack, subtree = [], None\nwhile True:\n\twhile root:\n\t\tif root.val == val: subtree = root\n\t\tstack.append(root)\n\t\troot = root.left\n\n\tif subtree: return subtree\n\t\n\tif not stack: return None\n\n\troot = stack.pop().right\n``` | 2 | You are given the `root` of a binary search tree (BST) and an integer `val`.
Find the node in the BST that the node's value equals `val` and return the subtree rooted with that node. If such a node does not exist, return `null`.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 2
**Output:** \[2,1,3\]
**Example 2:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 5000]`.
* `1 <= Node.val <= 107`
* `root` is a binary search tree.
* `1 <= val <= 107` | null |
Python beats 90% (Simple iterative approach) | search-in-a-binary-search-tree | 0 | 1 | ```\nstack, subtree = [], None\nwhile True:\n\twhile root:\n\t\tif root.val == val: subtree = root\n\t\tstack.append(root)\n\t\troot = root.left\n\n\tif subtree: return subtree\n\t\n\tif not stack: return None\n\n\troot = stack.pop().right\n``` | 2 | Given the `root` of a Binary Search Tree (BST), return _the minimum difference between the values of any two different nodes in the tree_.
**Example 1:**
**Input:** root = \[4,2,6,1,3\]
**Output:** 1
**Example 2:**
**Input:** root = \[1,0,48,null,null,12,49\]
**Output:** 1
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `0 <= Node.val <= 105`
**Note:** This question is the same as 530: [https://leetcode.com/problems/minimum-absolute-difference-in-bst/](https://leetcode.com/problems/minimum-absolute-difference-in-bst/) | null |
Easy python solution | insert-into-a-binary-search-tree | 0 | 1 | ```\nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n node = TreeNode(val)\n if not root:\n root = node\n return root\n if not root.left and val < root.val:\n root.left = node\n elif not root.right and val > root.val:\n root.right = node\n \n elif val < root.val:\n self.insertIntoBST(root.left, val)\n else:\n self.insertIntoBST(root.right, val)\n \n return root\n``` | 3 | You are given the `root` node of a binary search tree (BST) and a `value` to insert into the tree. Return _the root node of the BST after the insertion_. It is **guaranteed** that the new value does not exist in the original BST.
**Notice** that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return **any of them**.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Explanation:** Another accepted tree is:
**Example 2:**
**Input:** root = \[40,20,60,10,30,50,70\], val = 25
**Output:** \[40,20,60,10,30,50,70,null,null,25\]
**Example 3:**
**Input:** root = \[4,2,7,1,3,null,null,null,null,null,null\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-108 <= Node.val <= 108`
* All the values `Node.val` are **unique**.
* `-108 <= val <= 108`
* It's **guaranteed** that `val` does not exist in the original BST. | null |
Easy python solution | insert-into-a-binary-search-tree | 0 | 1 | ```\nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n node = TreeNode(val)\n if not root:\n root = node\n return root\n if not root.left and val < root.val:\n root.left = node\n elif not root.right and val > root.val:\n root.right = node\n \n elif val < root.val:\n self.insertIntoBST(root.left, val)\n else:\n self.insertIntoBST(root.right, val)\n \n return root\n``` | 3 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
Beginner-friendly || Simple Depth-First Search in Python3 | insert-into-a-binary-search-tree | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a **Binary Search Tree (BST)**\n- and our goal is to **insert** the new value\n\nThere\'re some methods to insert a new value, and all of these representations **will(could?)** be valid.\nWe\'ll focus on the straightforward solution as the next one:\n```\n# For each node define, if the current node value more than target\n# than go to the left, otherwise - to the right subtree.\n# Once you\'ve reached an empty node - this\'s the place of insertion.\n``` \n\n---\n\nIf you haven\'t familiar with the [BST](https://en.wikipedia.org/wiki/Binary_search_tree), follow the link.\n\n# Approach\n1. check if the `root` doesn\'t exist, this could also means that you\'ve reached the place of insertion, so return `TreeNode(val)`\n2. otherwise check, if the `root.val > val` and if it\'s, than go to the `node.left` subtree\n3. otherwise go to the `node.right` subtree\n4. return `root` \n\n# Complexity\n- Time complexity: **O(h)**, in worst-case scenario, we need to traverse down on full height `h`\n\n- Space complexity: **O(h)**, the same, because of recursive call stack\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if not root:\n return TreeNode(val)\n if root.val > val:\n root.left = self.insertIntoBST(root.left, val)\n else:\n root.right = self.insertIntoBST(root.right, val)\n\n return root\n``` | 1 | You are given the `root` node of a binary search tree (BST) and a `value` to insert into the tree. Return _the root node of the BST after the insertion_. It is **guaranteed** that the new value does not exist in the original BST.
**Notice** that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return **any of them**.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Explanation:** Another accepted tree is:
**Example 2:**
**Input:** root = \[40,20,60,10,30,50,70\], val = 25
**Output:** \[40,20,60,10,30,50,70,null,null,25\]
**Example 3:**
**Input:** root = \[4,2,7,1,3,null,null,null,null,null,null\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-108 <= Node.val <= 108`
* All the values `Node.val` are **unique**.
* `-108 <= val <= 108`
* It's **guaranteed** that `val` does not exist in the original BST. | null |
Beginner-friendly || Simple Depth-First Search in Python3 | insert-into-a-binary-search-tree | 0 | 1 | # Intuition\nThe problem description is the following:\n- there\'s a **Binary Search Tree (BST)**\n- and our goal is to **insert** the new value\n\nThere\'re some methods to insert a new value, and all of these representations **will(could?)** be valid.\nWe\'ll focus on the straightforward solution as the next one:\n```\n# For each node define, if the current node value more than target\n# than go to the left, otherwise - to the right subtree.\n# Once you\'ve reached an empty node - this\'s the place of insertion.\n``` \n\n---\n\nIf you haven\'t familiar with the [BST](https://en.wikipedia.org/wiki/Binary_search_tree), follow the link.\n\n# Approach\n1. check if the `root` doesn\'t exist, this could also means that you\'ve reached the place of insertion, so return `TreeNode(val)`\n2. otherwise check, if the `root.val > val` and if it\'s, than go to the `node.left` subtree\n3. otherwise go to the `node.right` subtree\n4. return `root` \n\n# Complexity\n- Time complexity: **O(h)**, in worst-case scenario, we need to traverse down on full height `h`\n\n- Space complexity: **O(h)**, the same, because of recursive call stack\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if not root:\n return TreeNode(val)\n if root.val > val:\n root.left = self.insertIntoBST(root.left, val)\n else:\n root.right = self.insertIntoBST(root.right, val)\n\n return root\n``` | 1 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
✅ Well Detailed Explanation [Java , C++, Python] 🧠 Beats around 100% users. | insert-into-a-binary-search-tree | 1 | 1 | \n\n# \u2705 \u2B06\uFE0F Approach 1 - iterative method \u2B06 \u267B\uFE0F\n\nIn **CPP** or **JAVA** or **PYTHON**, the main difference is nothing. Only have to change 1-2 **word** in **syntax**. Otherwise the whole code and concept will remain same.\n \n```\nWell defined and describeed in code. Please upvote if it helped.\n```\n\n# Complexity\n- Time complexity : O(logn)\n\n- Space complexity : O(logn)\n\n# Code\n```\n if (root == NULL)\n return new TreeNode(val);\n \n // Create a temporary pointer \'temp\' to store the original root node.\n TreeNode* temp = root;\n \n // Start a while loop to find the appropriate position to insert the new value.\n while (root) {\n // If the value to insert (val) is greater than or equal to the current node\'s value, move to the right subtree.\n if (root->val <= val) {\n // If the right child exists, move \'root\' to the right child and continue the loop.\n if (root->right != NULL)\n root = root->right;\n // If the right child is NULL, it means we have found the appropriate place to insert the new value.\n // Create a new node with the given value and set it as the right child of the current node.\n else {\n root->right = new TreeNode(val);\n // Break out of the loop as the insertion is complete.\n break;\n }\n }\n // If the value to insert (val) is less than the current node\'s value, move to the left subtree.\n else {\n // If the left child exists, move \'root\' to the left child and continue the loop.\n if (root->left != NULL)\n root = root->left;\n // If the left child is NULL, it means we have found the appropriate place to insert the new value.\n // Create a new node with the given value and set it as the left child of the current node.\n else {\n root->left = new TreeNode(val);\n // Break out of the loop as the insertion is complete.\n break;\n }\n }\n }\n \n // Return the original root (temp) of the modified tree after the insertion.\n return temp;\n }\n};\n\n\n```\n\n# \u2705 \u2B06\uFE0F Approach 1 - recursive method \u2B06 \u267B\uFE0F \n\n```\nWell defined and describeed in code. Please upvote if it helped.\n```\n\n# Complexity\n- Time complexity : O(logn)\n\n- Space complexity : O(logn)\n\n# Code\n```\n// If the tree is empty, create a new node with the given value and return it as the new root.\n if(root == NULL) return new TreeNode(val);\n\n // Compare the value to insert (val) with the current node\'s value.\n if (val > root->val)\n // If the value to insert is greater than the current node\'s value, recursively insert it into the right subtree.\n root->right = insertIntoBST(root->right, val);\n else\n // If the value to insert is less than or equal to the current node\'s value, recursively insert it into the left subtree.\n root->left = insertIntoBST(root->left, val);\n\n // Return the root of the modified tree after the insertion.\n return root;\n``` | 35 | You are given the `root` node of a binary search tree (BST) and a `value` to insert into the tree. Return _the root node of the BST after the insertion_. It is **guaranteed** that the new value does not exist in the original BST.
**Notice** that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return **any of them**.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Explanation:** Another accepted tree is:
**Example 2:**
**Input:** root = \[40,20,60,10,30,50,70\], val = 25
**Output:** \[40,20,60,10,30,50,70,null,null,25\]
**Example 3:**
**Input:** root = \[4,2,7,1,3,null,null,null,null,null,null\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-108 <= Node.val <= 108`
* All the values `Node.val` are **unique**.
* `-108 <= val <= 108`
* It's **guaranteed** that `val` does not exist in the original BST. | null |
✅ Well Detailed Explanation [Java , C++, Python] 🧠 Beats around 100% users. | insert-into-a-binary-search-tree | 1 | 1 | \n\n# \u2705 \u2B06\uFE0F Approach 1 - iterative method \u2B06 \u267B\uFE0F\n\nIn **CPP** or **JAVA** or **PYTHON**, the main difference is nothing. Only have to change 1-2 **word** in **syntax**. Otherwise the whole code and concept will remain same.\n \n```\nWell defined and describeed in code. Please upvote if it helped.\n```\n\n# Complexity\n- Time complexity : O(logn)\n\n- Space complexity : O(logn)\n\n# Code\n```\n if (root == NULL)\n return new TreeNode(val);\n \n // Create a temporary pointer \'temp\' to store the original root node.\n TreeNode* temp = root;\n \n // Start a while loop to find the appropriate position to insert the new value.\n while (root) {\n // If the value to insert (val) is greater than or equal to the current node\'s value, move to the right subtree.\n if (root->val <= val) {\n // If the right child exists, move \'root\' to the right child and continue the loop.\n if (root->right != NULL)\n root = root->right;\n // If the right child is NULL, it means we have found the appropriate place to insert the new value.\n // Create a new node with the given value and set it as the right child of the current node.\n else {\n root->right = new TreeNode(val);\n // Break out of the loop as the insertion is complete.\n break;\n }\n }\n // If the value to insert (val) is less than the current node\'s value, move to the left subtree.\n else {\n // If the left child exists, move \'root\' to the left child and continue the loop.\n if (root->left != NULL)\n root = root->left;\n // If the left child is NULL, it means we have found the appropriate place to insert the new value.\n // Create a new node with the given value and set it as the left child of the current node.\n else {\n root->left = new TreeNode(val);\n // Break out of the loop as the insertion is complete.\n break;\n }\n }\n }\n \n // Return the original root (temp) of the modified tree after the insertion.\n return temp;\n }\n};\n\n\n```\n\n# \u2705 \u2B06\uFE0F Approach 1 - recursive method \u2B06 \u267B\uFE0F \n\n```\nWell defined and describeed in code. Please upvote if it helped.\n```\n\n# Complexity\n- Time complexity : O(logn)\n\n- Space complexity : O(logn)\n\n# Code\n```\n// If the tree is empty, create a new node with the given value and return it as the new root.\n if(root == NULL) return new TreeNode(val);\n\n // Compare the value to insert (val) with the current node\'s value.\n if (val > root->val)\n // If the value to insert is greater than the current node\'s value, recursively insert it into the right subtree.\n root->right = insertIntoBST(root->right, val);\n else\n // If the value to insert is less than or equal to the current node\'s value, recursively insert it into the left subtree.\n root->left = insertIntoBST(root->left, val);\n\n // Return the root of the modified tree after the insertion.\n return root;\n``` | 35 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
Python || Easy || Iterative || Recursive || Two Solutions | insert-into-a-binary-search-tree | 0 | 1 | **Recursive Solution:**\n```\nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root==None:\n return TreeNode(val)\n else:\n if root.val<val:\n root.right=self.insertIntoBST(root.right,val)\n else:\n root.left=self.insertIntoBST(root.left,val)\n return root\n```\n**Iterarive Solution:**\n``` \nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root==None:\n return TreeNode(val)\n curr=root\n while True:\n if curr.val<val:\n if curr.right==None:\n curr.right=TreeNode(val)\n break\n curr=curr.right\n else:\n if curr.left==None:\n curr.left=TreeNode(val)\n break\n curr=curr.left\n return root\n```\n**An upvote will be encouraging** | 1 | You are given the `root` node of a binary search tree (BST) and a `value` to insert into the tree. Return _the root node of the BST after the insertion_. It is **guaranteed** that the new value does not exist in the original BST.
**Notice** that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return **any of them**.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Explanation:** Another accepted tree is:
**Example 2:**
**Input:** root = \[40,20,60,10,30,50,70\], val = 25
**Output:** \[40,20,60,10,30,50,70,null,null,25\]
**Example 3:**
**Input:** root = \[4,2,7,1,3,null,null,null,null,null,null\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-108 <= Node.val <= 108`
* All the values `Node.val` are **unique**.
* `-108 <= val <= 108`
* It's **guaranteed** that `val` does not exist in the original BST. | null |
Python || Easy || Iterative || Recursive || Two Solutions | insert-into-a-binary-search-tree | 0 | 1 | **Recursive Solution:**\n```\nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root==None:\n return TreeNode(val)\n else:\n if root.val<val:\n root.right=self.insertIntoBST(root.right,val)\n else:\n root.left=self.insertIntoBST(root.left,val)\n return root\n```\n**Iterarive Solution:**\n``` \nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root==None:\n return TreeNode(val)\n curr=root\n while True:\n if curr.val<val:\n if curr.right==None:\n curr.right=TreeNode(val)\n break\n curr=curr.right\n else:\n if curr.left==None:\n curr.left=TreeNode(val)\n break\n curr=curr.left\n return root\n```\n**An upvote will be encouraging** | 1 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
Best and Efficient recursive solution in python 🐍✔✔ | insert-into-a-binary-search-tree | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root == None:\n return TreeNode(val)\n if root.val < val:\n root.right = self.insertIntoBST(root.right,val)\n else:\n root.left = self.insertIntoBST(root.left,val)\n return root\n``` | 2 | You are given the `root` node of a binary search tree (BST) and a `value` to insert into the tree. Return _the root node of the BST after the insertion_. It is **guaranteed** that the new value does not exist in the original BST.
**Notice** that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return **any of them**.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Explanation:** Another accepted tree is:
**Example 2:**
**Input:** root = \[40,20,60,10,30,50,70\], val = 25
**Output:** \[40,20,60,10,30,50,70,null,null,25\]
**Example 3:**
**Input:** root = \[4,2,7,1,3,null,null,null,null,null,null\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-108 <= Node.val <= 108`
* All the values `Node.val` are **unique**.
* `-108 <= val <= 108`
* It's **guaranteed** that `val` does not exist in the original BST. | null |
Best and Efficient recursive solution in python 🐍✔✔ | insert-into-a-binary-search-tree | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root == None:\n return TreeNode(val)\n if root.val < val:\n root.right = self.insertIntoBST(root.right,val)\n else:\n root.left = self.insertIntoBST(root.left,val)\n return root\n``` | 2 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
Solution | insert-into-a-binary-search-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* insertIntoBST(TreeNode* root, int val) {\n if(root==NULL){\n return new TreeNode(val);\n }\n if(val < root->val){\n root->left=insertIntoBST(root->left,val);\n }\n else{\n root->right=insertIntoBST(root->right,val);\n }\n return root;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def insert(self, root, val):\n if not root:\n return TreeNode(val)\n if val <= root.val:\n root.left = self.insert(root.left, val)\n else:\n root.right = self.insert(root.right, val)\n return root\n\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n return self.insert(root, val)\n```\n\n```Java []\nclass Solution {\n public TreeNode insertIntoBST(TreeNode root, int val) {\n if(root == null) return new TreeNode(val);\n if(root.val > val) root.left = insertIntoBST(root.left, val);\n else root.right = insertIntoBST(root.right, val);\n return root;\n }\n}\n```\n | 2 | You are given the `root` node of a binary search tree (BST) and a `value` to insert into the tree. Return _the root node of the BST after the insertion_. It is **guaranteed** that the new value does not exist in the original BST.
**Notice** that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return **any of them**.
**Example 1:**
**Input:** root = \[4,2,7,1,3\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Explanation:** Another accepted tree is:
**Example 2:**
**Input:** root = \[40,20,60,10,30,50,70\], val = 25
**Output:** \[40,20,60,10,30,50,70,null,null,25\]
**Example 3:**
**Input:** root = \[4,2,7,1,3,null,null,null,null,null,null\], val = 5
**Output:** \[4,2,7,1,3,5\]
**Constraints:**
* The number of nodes in the tree will be in the range `[0, 104]`.
* `-108 <= Node.val <= 108`
* All the values `Node.val` are **unique**.
* `-108 <= val <= 108`
* It's **guaranteed** that `val` does not exist in the original BST. | null |
Solution | insert-into-a-binary-search-tree | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* insertIntoBST(TreeNode* root, int val) {\n if(root==NULL){\n return new TreeNode(val);\n }\n if(val < root->val){\n root->left=insertIntoBST(root->left,val);\n }\n else{\n root->right=insertIntoBST(root->right,val);\n }\n return root;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def insert(self, root, val):\n if not root:\n return TreeNode(val)\n if val <= root.val:\n root.left = self.insert(root.left, val)\n else:\n root.right = self.insert(root.right, val)\n return root\n\n def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n return self.insert(root, val)\n```\n\n```Java []\nclass Solution {\n public TreeNode insertIntoBST(TreeNode root, int val) {\n if(root == null) return new TreeNode(val);\n if(root.val > val) root.left = insertIntoBST(root.left, val);\n else root.right = insertIntoBST(root.right, val);\n return root;\n }\n}\n```\n | 2 | Given a string `s`, you can transform every letter individually to be lowercase or uppercase to create another string.
Return _a list of all possible strings we could create_. Return the output in **any order**.
**Example 1:**
**Input:** s = "a1b2 "
**Output:** \[ "a1b2 ", "a1B2 ", "A1b2 ", "A1B2 "\]
**Example 2:**
**Input:** s = "3z4 "
**Output:** \[ "3z4 ", "3Z4 "\]
**Constraints:**
* `1 <= s.length <= 12`
* `s` consists of lowercase English letters, uppercase English letters, and digits. | null |
Solution | kth-largest-element-in-a-stream | 1 | 1 | ```C++ []\nclass KthLargest {\npublic:\nstruct A\n{\nbool operator()(int a, int b)\n{\n return a<b;\n}\n};\n KthLargest(int k, vector<int>& nums) {\n K =k;\n for(int i=0;i<nums.size();i++)\n {\n pq.push(nums[i]);\n }\n while(pq.size() > k)\n pq.pop();\n }\n int add(int val) {\n pq.push(val);\n if(pq.size() > K) \n pq.pop();\n return pq.top();\n }\n priority_queue<int, vector<int>, greater<int>>pq;\n int K;\n};\n```\n\n```Python3 []\nclass KthLargest:\n def __init__(self, k: int, nums: List[int]):\n self.minHeap, self.k = nums, k\n heapq.heapify(self.minHeap)\n\n while len(self.minHeap) > k:\n heapq.heappop(self.minHeap)\n \n def add(self, val: int) -> int:\n heapq.heappush(self.minHeap, val)\n\n if self.k < len(self.minHeap):\n heapq.heappop(self.minHeap)\n\n return self.minHeap[0]\n```\n\n```Java []\nclass KthLargest {\n int [] a;\n int size = 0;\n int k = 0;\n private int left(int i) {\n return i*2;\n }\n private int right(int i) {\n return i*2+1;\n }\n private int parent(int i) {\n return i/2;\n }\n private void swap(int i, int j) {\n int tmp = a[i];\n a[i] = a[j];\n a[j] = tmp;\n }\n private void siftdown(int i) {\n siftdown(i, a.length);\n } \n private void siftdown(int i, int n) {\n while (2*i < n) {\n int j = i;\n if (a[2*i] < a[j]) {\n j = 2*i;\n }\n if (2*i+1<n && a[2*i+1] < a[j]) {\n j = 2*i+1;\n }\n if (i==j) {\n break;\n }\n swap(i, j);\n i=j;\n }\n }\n private void siftup(int i) {\n while (i/2>=1) {\n if (a[i/2] <= a[i]) {\n break;\n }\n swap(i/2, i);\n i = i/2;\n }\n }\n public KthLargest(int k, int[] nums) {\n this.k = k;\n a = new int[k+1];\n heapifyAndInsert(nums);\n }\n private void heapifyAndInsert(int[] nums) {\n size = Math.min(nums.length, k);\n for (int i = 0; i < size; i++) {\n a[i+1] = nums[i];\n }\n int currK = Math.min(nums.length, k);\n for (int i = currK/2; i>=1; i--) {\n siftdown(i, currK+1);\n }\n for (int i = size; i < nums.length; i++) {\n add(nums[i]);\n }\n }\n public int add(int val) {\n if (size == k) {\n if (val > a[1]) { \n a[1] = val; \n siftdown(1);\n }\n } else {\n size++;\n a[size] = val;\n siftup(size);\n }\n return a[1];\n }\n}\n```\n | 2 | Design a class to find the `kth` largest element in a stream. Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
Implement `KthLargest` class:
* `KthLargest(int k, int[] nums)` Initializes the object with the integer `k` and the stream of integers `nums`.
* `int add(int val)` Appends the integer `val` to the stream and returns the element representing the `kth` largest element in the stream.
**Example 1:**
**Input**
\[ "KthLargest ", "add ", "add ", "add ", "add ", "add "\]
\[\[3, \[4, 5, 8, 2\]\], \[3\], \[5\], \[10\], \[9\], \[4\]\]
**Output**
\[null, 4, 5, 5, 8, 8\]
**Explanation**
KthLargest kthLargest = new KthLargest(3, \[4, 5, 8, 2\]);
kthLargest.add(3); // return 4
kthLargest.add(5); // return 5
kthLargest.add(10); // return 5
kthLargest.add(9); // return 8
kthLargest.add(4); // return 8
**Constraints:**
* `1 <= k <= 104`
* `0 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `-104 <= val <= 104`
* At most `104` calls will be made to `add`.
* It is guaranteed that there will be at least `k` elements in the array when you search for the `kth` element. | null |
Solution | kth-largest-element-in-a-stream | 1 | 1 | ```C++ []\nclass KthLargest {\npublic:\nstruct A\n{\nbool operator()(int a, int b)\n{\n return a<b;\n}\n};\n KthLargest(int k, vector<int>& nums) {\n K =k;\n for(int i=0;i<nums.size();i++)\n {\n pq.push(nums[i]);\n }\n while(pq.size() > k)\n pq.pop();\n }\n int add(int val) {\n pq.push(val);\n if(pq.size() > K) \n pq.pop();\n return pq.top();\n }\n priority_queue<int, vector<int>, greater<int>>pq;\n int K;\n};\n```\n\n```Python3 []\nclass KthLargest:\n def __init__(self, k: int, nums: List[int]):\n self.minHeap, self.k = nums, k\n heapq.heapify(self.minHeap)\n\n while len(self.minHeap) > k:\n heapq.heappop(self.minHeap)\n \n def add(self, val: int) -> int:\n heapq.heappush(self.minHeap, val)\n\n if self.k < len(self.minHeap):\n heapq.heappop(self.minHeap)\n\n return self.minHeap[0]\n```\n\n```Java []\nclass KthLargest {\n int [] a;\n int size = 0;\n int k = 0;\n private int left(int i) {\n return i*2;\n }\n private int right(int i) {\n return i*2+1;\n }\n private int parent(int i) {\n return i/2;\n }\n private void swap(int i, int j) {\n int tmp = a[i];\n a[i] = a[j];\n a[j] = tmp;\n }\n private void siftdown(int i) {\n siftdown(i, a.length);\n } \n private void siftdown(int i, int n) {\n while (2*i < n) {\n int j = i;\n if (a[2*i] < a[j]) {\n j = 2*i;\n }\n if (2*i+1<n && a[2*i+1] < a[j]) {\n j = 2*i+1;\n }\n if (i==j) {\n break;\n }\n swap(i, j);\n i=j;\n }\n }\n private void siftup(int i) {\n while (i/2>=1) {\n if (a[i/2] <= a[i]) {\n break;\n }\n swap(i/2, i);\n i = i/2;\n }\n }\n public KthLargest(int k, int[] nums) {\n this.k = k;\n a = new int[k+1];\n heapifyAndInsert(nums);\n }\n private void heapifyAndInsert(int[] nums) {\n size = Math.min(nums.length, k);\n for (int i = 0; i < size; i++) {\n a[i+1] = nums[i];\n }\n int currK = Math.min(nums.length, k);\n for (int i = currK/2; i>=1; i--) {\n siftdown(i, currK+1);\n }\n for (int i = size; i < nums.length; i++) {\n add(nums[i]);\n }\n }\n public int add(int val) {\n if (size == k) {\n if (val > a[1]) { \n a[1] = val; \n siftdown(1);\n }\n } else {\n size++;\n a[size] = val;\n siftup(size);\n }\n return a[1];\n }\n}\n```\n | 2 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | kth-largest-element-in-a-stream | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n\n# Click the Link in my Profile\n\n# Approach:\n\n- Initialize the class with the value of k and an empty data structure to store the k largest elements encountered so far.\n- When adding a new element to the stream, check if the size of the data structure is less than k.\n- If it is less than k, simply add the new element to the data structure.\n- If it is equal to k, compare the new element with the smallest element in the data structure.\n- If the new element is larger, remove the smallest element and add the new element.\n- If the new element is smaller, do not add it to the data structure.\n- Return the smallest element in the data structure, which represents the kth largest element in the stream.\n# Intuition:\n\n- The problem requires finding the kth largest element in a stream of numbers, which means we need to maintain a collection of the k largest elements seen so far.\n- By using a data structure like a min-heap or a priority queue, we can efficiently keep track of the k largest elements while discarding smaller elements.\n- The idea is to store the k largest elements encountered in a way that we can easily access the smallest element among them.\n- Initially, as we add elements to the stream, we fill the data structure until it reaches a size of k. At this point, we have the k largest elements seen so far, with the smallest among them as the root of the min-heap or the top of the priority queue.\n- For every subsequent element, we compare it with the smallest element in the data structure. If the new element is larger, it becomes one of the k largest elements, replacing the smallest element. Otherwise, it is smaller and can be ignored.\n- By always keeping track of the smallest element among the k largest elements, we can efficiently find the kth largest element at any given point.\n\n\n```Python []\nclass KthLargest:\n def __init__(self, k: int, nums: List[int]):\n self.k = k\n self.min_heap = []\n for num in nums:\n self.add(num)\n\n def add(self, val: int) -> int:\n if len(self.min_heap) < self.k:\n heapq.heappush(self.min_heap, val)\n elif val > self.min_heap[0]:\n heapq.heapreplace(self.min_heap, val)\n return self.min_heap[0]\n```\n```Java []\nclass KthLargest {\n private int k;\n private PriorityQueue<Integer> minHeap;\n\n public KthLargest(int k, int[] nums) {\n this.k = k;\n minHeap = new PriorityQueue<>(k);\n for (int num : nums) {\n add(num);\n }\n }\n\n public int add(int val) {\n if (minHeap.size() < k) {\n minHeap.offer(val);\n } else if (val > minHeap.peek()) {\n minHeap.poll();\n minHeap.offer(val);\n }\n return minHeap.peek();\n }\n}\n```\n```C++ []\nclass KthLargest {\nprivate:\n int k;\n std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;\n\npublic:\n KthLargest(int k, vector<int>& nums) {\n this->k = k;\n for (int num : nums) {\n add(num);\n }\n }\n\n int add(int val) {\n if (minHeap.size() < k) {\n minHeap.push(val);\n } else if (val > minHeap.top()) {\n minHeap.pop();\n minHeap.push(val);\n }\n return minHeap.top();\n }\n};\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D\n | 14 | Design a class to find the `kth` largest element in a stream. Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
Implement `KthLargest` class:
* `KthLargest(int k, int[] nums)` Initializes the object with the integer `k` and the stream of integers `nums`.
* `int add(int val)` Appends the integer `val` to the stream and returns the element representing the `kth` largest element in the stream.
**Example 1:**
**Input**
\[ "KthLargest ", "add ", "add ", "add ", "add ", "add "\]
\[\[3, \[4, 5, 8, 2\]\], \[3\], \[5\], \[10\], \[9\], \[4\]\]
**Output**
\[null, 4, 5, 5, 8, 8\]
**Explanation**
KthLargest kthLargest = new KthLargest(3, \[4, 5, 8, 2\]);
kthLargest.add(3); // return 4
kthLargest.add(5); // return 5
kthLargest.add(10); // return 5
kthLargest.add(9); // return 8
kthLargest.add(4); // return 8
**Constraints:**
* `1 <= k <= 104`
* `0 <= nums.length <= 104`
* `-104 <= nums[i] <= 104`
* `-104 <= val <= 104`
* At most `104` calls will be made to `add`.
* It is guaranteed that there will be at least `k` elements in the array when you search for the `kth` element. | null |
Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | kth-largest-element-in-a-stream | 1 | 1 | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n\n# Click the Link in my Profile\n\n# Approach:\n\n- Initialize the class with the value of k and an empty data structure to store the k largest elements encountered so far.\n- When adding a new element to the stream, check if the size of the data structure is less than k.\n- If it is less than k, simply add the new element to the data structure.\n- If it is equal to k, compare the new element with the smallest element in the data structure.\n- If the new element is larger, remove the smallest element and add the new element.\n- If the new element is smaller, do not add it to the data structure.\n- Return the smallest element in the data structure, which represents the kth largest element in the stream.\n# Intuition:\n\n- The problem requires finding the kth largest element in a stream of numbers, which means we need to maintain a collection of the k largest elements seen so far.\n- By using a data structure like a min-heap or a priority queue, we can efficiently keep track of the k largest elements while discarding smaller elements.\n- The idea is to store the k largest elements encountered in a way that we can easily access the smallest element among them.\n- Initially, as we add elements to the stream, we fill the data structure until it reaches a size of k. At this point, we have the k largest elements seen so far, with the smallest among them as the root of the min-heap or the top of the priority queue.\n- For every subsequent element, we compare it with the smallest element in the data structure. If the new element is larger, it becomes one of the k largest elements, replacing the smallest element. Otherwise, it is smaller and can be ignored.\n- By always keeping track of the smallest element among the k largest elements, we can efficiently find the kth largest element at any given point.\n\n\n```Python []\nclass KthLargest:\n def __init__(self, k: int, nums: List[int]):\n self.k = k\n self.min_heap = []\n for num in nums:\n self.add(num)\n\n def add(self, val: int) -> int:\n if len(self.min_heap) < self.k:\n heapq.heappush(self.min_heap, val)\n elif val > self.min_heap[0]:\n heapq.heapreplace(self.min_heap, val)\n return self.min_heap[0]\n```\n```Java []\nclass KthLargest {\n private int k;\n private PriorityQueue<Integer> minHeap;\n\n public KthLargest(int k, int[] nums) {\n this.k = k;\n minHeap = new PriorityQueue<>(k);\n for (int num : nums) {\n add(num);\n }\n }\n\n public int add(int val) {\n if (minHeap.size() < k) {\n minHeap.offer(val);\n } else if (val > minHeap.peek()) {\n minHeap.poll();\n minHeap.offer(val);\n }\n return minHeap.peek();\n }\n}\n```\n```C++ []\nclass KthLargest {\nprivate:\n int k;\n std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;\n\npublic:\n KthLargest(int k, vector<int>& nums) {\n this->k = k;\n for (int num : nums) {\n add(num);\n }\n }\n\n int add(int val) {\n if (minHeap.size() < k) {\n minHeap.push(val);\n } else if (val > minHeap.top()) {\n minHeap.pop();\n minHeap.push(val);\n }\n return minHeap.top();\n }\n};\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D\n | 14 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.