title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python 95.67% faster | Simplest solution with explanation | Beg to Adv | Greedy | broken-calculator | 0 | 1 | ```python\nclass Solution:\n def brokenCalc(self, startValue: int, target: int) -> int:\n res = 0 # taking a counter. \n while target > startValue: # checking if target value is greater then startValue. \n res += 1 # as if target is greater implies we`ll be having atleast one operation. \n if target%2==0:\n target //=2 # in case number is even. \n else:\n target += 1 # in case number odd. \n return res + startValue - target# startValue - target is for (target<=staetValue). \n```\n***Found helpful, Do upvote!!***\n\n | 3 | There is a broken calculator that has the integer `startValue` on its display initially. In one operation, you can:
* multiply the number on display by `2`, or
* subtract `1` from the number on display.
Given two integers `startValue` and `target`, return _the minimum number of operations needed to display_ `target` _on the calculator_.
**Example 1:**
**Input:** startValue = 2, target = 3
**Output:** 2
**Explanation:** Use double operation and then decrement operation {2 -> 4 -> 3}.
**Example 2:**
**Input:** startValue = 5, target = 8
**Output:** 2
**Explanation:** Use decrement and then double {5 -> 4 -> 8}.
**Example 3:**
**Input:** startValue = 3, target = 10
**Output:** 3
**Explanation:** Use double, decrement and double {3 -> 6 -> 5 -> 10}.
**Constraints:**
* `1 <= startValue, target <= 109` | null |
Python 95.67% faster | Simplest solution with explanation | Beg to Adv | Greedy | broken-calculator | 0 | 1 | ```python\nclass Solution:\n def brokenCalc(self, startValue: int, target: int) -> int:\n res = 0 # taking a counter. \n while target > startValue: # checking if target value is greater then startValue. \n res += 1 # as if target is greater implies we`ll be having atleast one operation. \n if target%2==0:\n target //=2 # in case number is even. \n else:\n target += 1 # in case number odd. \n return res + startValue - target# startValue - target is for (target<=staetValue). \n```\n***Found helpful, Do upvote!!***\n\n | 3 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
[Python] O(logn) solution starting from startValue with detailed explanation | broken-calculator | 0 | 1 | ## 991 Broken Calculator\n\n[https://leetcode.com/problems/broken-calculator/](https://leetcode.com/problems/broken-calculator/)\n\nInstead of doing the smart thing and thinking about the problem from the target backwards as explained [here](https://leetcode.com/problems/broken-calculator/discuss/1076042/Python-C%2B%2B-Explanation-with-illustration-why-we-should-work-with-Y-not-X), I chose to tackle the problem from the startValue upwards.\n\nThe general idea is double the startValue until it is greater than target, and it\'s important to note that the optimal solution **always** requires this many doublings.\n\nNow our task is to figure out when to decrease the value so that it minimizes our number of steps.\n\n**Case 1:**\n\n\n\nIn this example, the difference from the number we get after only doubling and the target is 12. We can see that using the decrease operation at differnce times affects the results differently. The effect of reduction on the final number doubles after every doubling. Decreasing 14 to 13 decreases the final result by 8, since there are 3 doublings after the decrease. This corresponds to 2^3, and so the effects of decreases can be calculated by 2 to the power of the number of doublings remaining. Similarly, there are 2 doublings after the deduction from 26 to 25, and that decreases the final result by 2^2.\n\nTherefore, any difference between the number we get from doubling to the target can be broken down into powers of 2, and those powers of 2 then tells us when and how many times to decrease. In this case, the difference of 12 (112-100) can be broken down into 2^3 + 2^2, telling us that we should decrease once with 3 doublings left and once with 2 doublings left.\n\nThe final result would be the number of doubles + the number of decreases.\n\n**Case 2:**\n\n\n\nIn this case we have to decrease before we double. The difference of 12 (28-16) can be made up of 2^3 + 2^2. However we can\'t decrease 3 doublings before the end, since we don\'t double 3 times. In this case, the earlier we can decrease only affects the final result by 4 (2^2) every time. Therefore the difference can still be broken down into powers of 2, but any powers greater than 2^(max doubles) must be broken down into powers no greater than 2^(max doubles). Here we break the difference down into 3*2^2, meaning we decrease 3 times at 2 doublings before the end.\n\n**Case 3:**\n\nThis is the case where the start is greater than the target. In this case the result is simply target - start.\n\ne.g. \nstart = 20, target = 5\nresult = 15 (20-5)\n\n**Implementation:**\n\nBreaking down the difference into powers of 2 is simply converting the int to binary.\n\n```python\ndef brokenCalc(self, startValue: int, target: int) -> int:\n```\nCase 3\n```python\n if startValue>target:\n return startValue - target\n```\n\nCalculate doublings and difference\nx is the value we get if we only apply doubling\n\n```python\n doublings = 0\n x = startValue\n while x < target:\n x *= 2\n doublings += 1\n diff = bin(x-target)[2:] #saves difference as binary representation\n```\n\nFinal result res is the number of doublings and the number of decreases\n```python\n res = doublings\n #Adds decreases that happen **before** doubling\n if diff[:-doublings]:\n res += int(diff[:-doublings],2)\n #Adds decreases that happen **after** first doubling\n if diff[-doublings:]:\n res += sum(int(i) for i in diff[-doublings:])\n return res\n```\n\nTime: O(logn)\n\nSpace: O(1)\n | 3 | There is a broken calculator that has the integer `startValue` on its display initially. In one operation, you can:
* multiply the number on display by `2`, or
* subtract `1` from the number on display.
Given two integers `startValue` and `target`, return _the minimum number of operations needed to display_ `target` _on the calculator_.
**Example 1:**
**Input:** startValue = 2, target = 3
**Output:** 2
**Explanation:** Use double operation and then decrement operation {2 -> 4 -> 3}.
**Example 2:**
**Input:** startValue = 5, target = 8
**Output:** 2
**Explanation:** Use decrement and then double {5 -> 4 -> 8}.
**Example 3:**
**Input:** startValue = 3, target = 10
**Output:** 3
**Explanation:** Use double, decrement and double {3 -> 6 -> 5 -> 10}.
**Constraints:**
* `1 <= startValue, target <= 109` | null |
[Python] O(logn) solution starting from startValue with detailed explanation | broken-calculator | 0 | 1 | ## 991 Broken Calculator\n\n[https://leetcode.com/problems/broken-calculator/](https://leetcode.com/problems/broken-calculator/)\n\nInstead of doing the smart thing and thinking about the problem from the target backwards as explained [here](https://leetcode.com/problems/broken-calculator/discuss/1076042/Python-C%2B%2B-Explanation-with-illustration-why-we-should-work-with-Y-not-X), I chose to tackle the problem from the startValue upwards.\n\nThe general idea is double the startValue until it is greater than target, and it\'s important to note that the optimal solution **always** requires this many doublings.\n\nNow our task is to figure out when to decrease the value so that it minimizes our number of steps.\n\n**Case 1:**\n\n\n\nIn this example, the difference from the number we get after only doubling and the target is 12. We can see that using the decrease operation at differnce times affects the results differently. The effect of reduction on the final number doubles after every doubling. Decreasing 14 to 13 decreases the final result by 8, since there are 3 doublings after the decrease. This corresponds to 2^3, and so the effects of decreases can be calculated by 2 to the power of the number of doublings remaining. Similarly, there are 2 doublings after the deduction from 26 to 25, and that decreases the final result by 2^2.\n\nTherefore, any difference between the number we get from doubling to the target can be broken down into powers of 2, and those powers of 2 then tells us when and how many times to decrease. In this case, the difference of 12 (112-100) can be broken down into 2^3 + 2^2, telling us that we should decrease once with 3 doublings left and once with 2 doublings left.\n\nThe final result would be the number of doubles + the number of decreases.\n\n**Case 2:**\n\n\n\nIn this case we have to decrease before we double. The difference of 12 (28-16) can be made up of 2^3 + 2^2. However we can\'t decrease 3 doublings before the end, since we don\'t double 3 times. In this case, the earlier we can decrease only affects the final result by 4 (2^2) every time. Therefore the difference can still be broken down into powers of 2, but any powers greater than 2^(max doubles) must be broken down into powers no greater than 2^(max doubles). Here we break the difference down into 3*2^2, meaning we decrease 3 times at 2 doublings before the end.\n\n**Case 3:**\n\nThis is the case where the start is greater than the target. In this case the result is simply target - start.\n\ne.g. \nstart = 20, target = 5\nresult = 15 (20-5)\n\n**Implementation:**\n\nBreaking down the difference into powers of 2 is simply converting the int to binary.\n\n```python\ndef brokenCalc(self, startValue: int, target: int) -> int:\n```\nCase 3\n```python\n if startValue>target:\n return startValue - target\n```\n\nCalculate doublings and difference\nx is the value we get if we only apply doubling\n\n```python\n doublings = 0\n x = startValue\n while x < target:\n x *= 2\n doublings += 1\n diff = bin(x-target)[2:] #saves difference as binary representation\n```\n\nFinal result res is the number of doublings and the number of decreases\n```python\n res = doublings\n #Adds decreases that happen **before** doubling\n if diff[:-doublings]:\n res += int(diff[:-doublings],2)\n #Adds decreases that happen **after** first doubling\n if diff[-doublings:]:\n res += sum(int(i) for i in diff[-doublings:])\n return res\n```\n\nTime: O(logn)\n\nSpace: O(1)\n | 3 | There are three stones in different positions on the X-axis. You are given three integers `a`, `b`, and `c`, the positions of the stones.
In one move, you pick up a stone at an endpoint (i.e., either the lowest or highest position stone), and move it to an unoccupied position between those endpoints. Formally, let's say the stones are currently at positions `x`, `y`, and `z` with `x < y < z`. You pick up the stone at either position `x` or position `z`, and move that stone to an integer position `k`, with `x < k < z` and `k != y`.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** a = 1, b = 2, c = 5
**Output:** \[1,2\]
**Explanation:** Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
**Example 2:**
**Input:** a = 4, b = 3, c = 2
**Output:** \[0,0\]
**Explanation:** We cannot make any moves.
**Example 3:**
**Input:** a = 3, b = 5, c = 1
**Output:** \[1,2\]
**Explanation:** Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
**Constraints:**
* `1 <= a, b, c <= 100`
* `a`, `b`, and `c` have different values. | null |
Longest - Shortest | subarrays-with-k-different-integers | 1 | 1 | If the problem talks about continuous subarrays or substrings, the sliding window technique may help solve it in a linear time. Such problems are tricky, though the solution is simple once you get it. No wonder I am seeing such problems in almost every interview!\n\nHere, we will take a look at [Subarrays with K Different Integers](https://leetcode.com/problems/subarrays-with-k-different-integers/) (LeetCode Hard), which appeared on LeetCode [weekly contest #123](https://leetcode.com/contest/weekly-contest-123). You can also master the sliding windows technique with these additional problems:\n- [Longest Substring Without Repeating Characters](https://leetcode.com/problems/longest-substring-without-repeating-characters/)\n- [Longest Substring with At Most Two Distinct Characters](https://leetcode.com/problems/longest-substring-with-at-most-two-distinct-characters/)\n- [Longest Substring with At Most K Distinct Characters](https://leetcode.com/problems/longest-substring-with-at-most-k-distinct-characters/)\n<!--# Problem Description\nGiven an array ```A``` of positive integers, call a (contiguous, not necessarily distinct) subarray of ```A``` good if the number of different integers in that subarray is exactly ```K```. For example, ```[1,2,3,1,2]``` has 3 different integers: 1, 2, and 3.\n\nReturn the number of good subarrays of ```A```.\n### Example\n**Input:** A = [1,2,1,2,3], K = 2\n**Output:** 7\n**Explanation:** Subarrays formed with exactly 2 different integers: [1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].\n# Coding Practice\nTry solving this problem before moving on to the solutions. It is available on LeetCode Online Judge ([Subarrays with K Different Integers](https://leetcode.com/problems/subarrays-with-k-different-integers/)). Also, as you read through a solution, try implementing it yourself.\n\nLeetCode is my favorite destinations for algorithmic problems. It has 987 problems and counting, with test cases to validate the correctness, as well as computational and memory complexity. There is also a large community discussing different approaches, tips and tricks.\n# Brute-Force Solution\nWe can just iterate through each sub-array using two loops and count the good ones. For the inner loop, we use hash set to count unique numbers; if we the set size becomes larger than ```K```, we break from the inner loop.\n```\nint subarraysWithKDistinct(vector<int>& A, int K, int res = 0) {\n for (auto i = 0; i < A.size(); ++i) {\n unordered_set<int> s;\n for (auto j = i; j < A.size() && s.size() <= K; ++j) {\n s.insert(A[j]);\n if (s.size() == K) ++res;\n }\n }\n return res;\n}\n```\n### Complexity Analysis\nThe time complexity of this solution is *O(n * n)*, where *n* is the length of ```A```. This solution is not accepted by the online judge.\n-->\n# Intuition\nFor numbers `l`, `m`, and `r` (`l <= m <= r`), such as:\n- `[l, r]` is the longest subarray with `k` unique numbers, and\n- `[m, r]` is the shortest subarray with `k` unique numbers,\n\nthere are `m - l + 1` good subarrays that end at `r`.\n\nFor example, for `k == 3` and array `[1, 2, 1, 2, 3]`, the longest subarray is `[0, 4]` and shortest - `[2, 4]`. So, we have `2 - 0 + 1 == 3` good subarrays: `[1, 2, 1, 2, 3]`, `[2, 1, 2, 3]` and `[1, 2, 3]`.\n# Linear Solution\nWe can iterate through the array and use three pointers for our sliding window (`[l, m, r]`). The back of the window is always the current position in the array (`r`). The middle of the window (`m`) is moved so that `nums[m]` appear only once in `[m, r]`.\n\nThis ensures that `[m, r]` is the shortest subarray with a given number of unique elements.\n\nTo do that, we keep tabs on how many times each number appears in our window (`cnt`). After we add next number to the back of our window, we try to move `m` as far as possible while maintaining the same number of unique elements.\n\nIf we collected `k` unique numbers, then we found `m - l + 1` good subarrays.\n\nIf our window reached `k + 1` unique numbers, we reduce set `cnt[nums[m]]` to zero (again, that number appears only at `nums[m]`), increment `m` and set `l = m + 1` (because we are starting a new sequence). This process is demonstrated step-by-step for the test case below; `m - l + 1` window is shown as `+1` in the green background.\n```\n[5,7,5,2,3,3,4,1,5,2,7,4,6,2,3,8,4,5,7]\n7\n```\n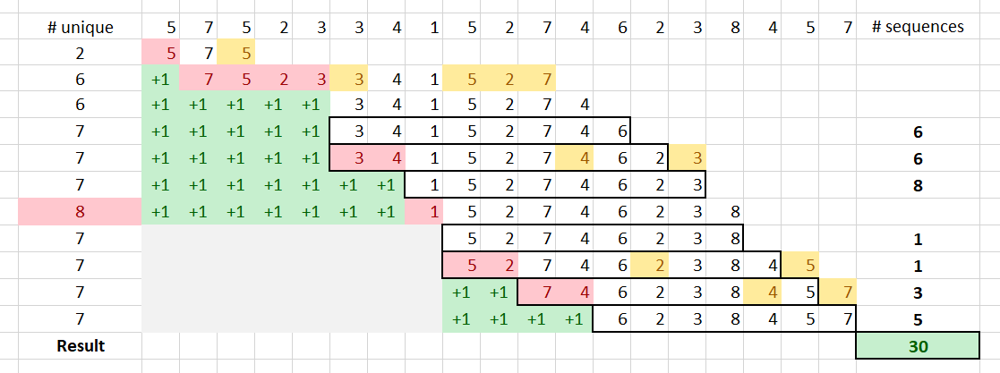\n\n**C++**\n```cpp\nint subarraysWithKDistinct(vector<int>& nums, int k) {\n int cnt[20001] = {}, res = 0, sz = nums.size();\n for (int l = 0, m = 0, r = 0; r < sz; ++r) {\n if (++cnt[nums[r]] == 1)\n if (--k < 0) {\n cnt[nums[m++]] = 0;\n l = m;\n }\n if (k <= 0) {\n while (cnt[nums[m]] > 1)\n --cnt[nums[m++]];\n res += m - l + 1; \n }\n }\n return res;\n} \n```\n**Java**\n```java\npublic int subarraysWithKDistinct(int[] nums, int k) {\n int res = 0, sz = nums.length;\n int[] cnt = new int[sz + 1];\n for (int l = 0, m = 0, r = 0; r < sz; ++r) {\n if (++cnt[nums[r]] == 1)\n if (--k < 0) {\n cnt[nums[m++]] = 0;\n l = m;\n }\n if (k <= 0) {\n while (cnt[nums[m]] > 1)\n --cnt[nums[m++]];\n res += m - l + 1; \n }\n } \n return res;\n}\n```\n**Python 3**\n```python\nclass Solution:\n def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:\n cnt, res, l, m = [0] * (len(nums) + 1), 0, 0, 0\n for n in nums:\n cnt[n] += 1\n if cnt[n] == 1:\n k -= 1\n if (k < 0):\n cnt[nums[m]] = 0\n m += 1\n l = m\n if k <= 0:\n while(cnt[nums[m]] > 1):\n cnt[nums[m]] -= 1\n m += 1\n res += m - l + 1\n return res\n```\n### Complexity Analysis\n- Time Complexity: *O(n)*, where *n* is the length of ```A```.\n- Space Complexity: *O(n)*. | 462 | Given an integer array `nums` and an integer `k`, return _the number of **good subarrays** of_ `nums`.
A **good array** is an array where the number of different integers in that array is exactly `k`.
* For example, `[1,2,3,1,2]` has `3` different integers: `1`, `2`, and `3`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,3\], k = 2
**Output:** 7
**Explanation:** Subarrays formed with exactly 2 different integers: \[1,2\], \[2,1\], \[1,2\], \[2,3\], \[1,2,1\], \[2,1,2\], \[1,2,1,2\]
**Example 2:**
**Input:** nums = \[1,2,1,3,4\], k = 3
**Output:** 3
**Explanation:** Subarrays formed with exactly 3 different integers: \[1,2,1,3\], \[2,1,3\], \[1,3,4\].
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i], k <= nums.length` | null |
Longest - Shortest | subarrays-with-k-different-integers | 1 | 1 | If the problem talks about continuous subarrays or substrings, the sliding window technique may help solve it in a linear time. Such problems are tricky, though the solution is simple once you get it. No wonder I am seeing such problems in almost every interview!\n\nHere, we will take a look at [Subarrays with K Different Integers](https://leetcode.com/problems/subarrays-with-k-different-integers/) (LeetCode Hard), which appeared on LeetCode [weekly contest #123](https://leetcode.com/contest/weekly-contest-123). You can also master the sliding windows technique with these additional problems:\n- [Longest Substring Without Repeating Characters](https://leetcode.com/problems/longest-substring-without-repeating-characters/)\n- [Longest Substring with At Most Two Distinct Characters](https://leetcode.com/problems/longest-substring-with-at-most-two-distinct-characters/)\n- [Longest Substring with At Most K Distinct Characters](https://leetcode.com/problems/longest-substring-with-at-most-k-distinct-characters/)\n<!--# Problem Description\nGiven an array ```A``` of positive integers, call a (contiguous, not necessarily distinct) subarray of ```A``` good if the number of different integers in that subarray is exactly ```K```. For example, ```[1,2,3,1,2]``` has 3 different integers: 1, 2, and 3.\n\nReturn the number of good subarrays of ```A```.\n### Example\n**Input:** A = [1,2,1,2,3], K = 2\n**Output:** 7\n**Explanation:** Subarrays formed with exactly 2 different integers: [1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].\n# Coding Practice\nTry solving this problem before moving on to the solutions. It is available on LeetCode Online Judge ([Subarrays with K Different Integers](https://leetcode.com/problems/subarrays-with-k-different-integers/)). Also, as you read through a solution, try implementing it yourself.\n\nLeetCode is my favorite destinations for algorithmic problems. It has 987 problems and counting, with test cases to validate the correctness, as well as computational and memory complexity. There is also a large community discussing different approaches, tips and tricks.\n# Brute-Force Solution\nWe can just iterate through each sub-array using two loops and count the good ones. For the inner loop, we use hash set to count unique numbers; if we the set size becomes larger than ```K```, we break from the inner loop.\n```\nint subarraysWithKDistinct(vector<int>& A, int K, int res = 0) {\n for (auto i = 0; i < A.size(); ++i) {\n unordered_set<int> s;\n for (auto j = i; j < A.size() && s.size() <= K; ++j) {\n s.insert(A[j]);\n if (s.size() == K) ++res;\n }\n }\n return res;\n}\n```\n### Complexity Analysis\nThe time complexity of this solution is *O(n * n)*, where *n* is the length of ```A```. This solution is not accepted by the online judge.\n-->\n# Intuition\nFor numbers `l`, `m`, and `r` (`l <= m <= r`), such as:\n- `[l, r]` is the longest subarray with `k` unique numbers, and\n- `[m, r]` is the shortest subarray with `k` unique numbers,\n\nthere are `m - l + 1` good subarrays that end at `r`.\n\nFor example, for `k == 3` and array `[1, 2, 1, 2, 3]`, the longest subarray is `[0, 4]` and shortest - `[2, 4]`. So, we have `2 - 0 + 1 == 3` good subarrays: `[1, 2, 1, 2, 3]`, `[2, 1, 2, 3]` and `[1, 2, 3]`.\n# Linear Solution\nWe can iterate through the array and use three pointers for our sliding window (`[l, m, r]`). The back of the window is always the current position in the array (`r`). The middle of the window (`m`) is moved so that `nums[m]` appear only once in `[m, r]`.\n\nThis ensures that `[m, r]` is the shortest subarray with a given number of unique elements.\n\nTo do that, we keep tabs on how many times each number appears in our window (`cnt`). After we add next number to the back of our window, we try to move `m` as far as possible while maintaining the same number of unique elements.\n\nIf we collected `k` unique numbers, then we found `m - l + 1` good subarrays.\n\nIf our window reached `k + 1` unique numbers, we reduce set `cnt[nums[m]]` to zero (again, that number appears only at `nums[m]`), increment `m` and set `l = m + 1` (because we are starting a new sequence). This process is demonstrated step-by-step for the test case below; `m - l + 1` window is shown as `+1` in the green background.\n```\n[5,7,5,2,3,3,4,1,5,2,7,4,6,2,3,8,4,5,7]\n7\n```\n\n\n**C++**\n```cpp\nint subarraysWithKDistinct(vector<int>& nums, int k) {\n int cnt[20001] = {}, res = 0, sz = nums.size();\n for (int l = 0, m = 0, r = 0; r < sz; ++r) {\n if (++cnt[nums[r]] == 1)\n if (--k < 0) {\n cnt[nums[m++]] = 0;\n l = m;\n }\n if (k <= 0) {\n while (cnt[nums[m]] > 1)\n --cnt[nums[m++]];\n res += m - l + 1; \n }\n }\n return res;\n} \n```\n**Java**\n```java\npublic int subarraysWithKDistinct(int[] nums, int k) {\n int res = 0, sz = nums.length;\n int[] cnt = new int[sz + 1];\n for (int l = 0, m = 0, r = 0; r < sz; ++r) {\n if (++cnt[nums[r]] == 1)\n if (--k < 0) {\n cnt[nums[m++]] = 0;\n l = m;\n }\n if (k <= 0) {\n while (cnt[nums[m]] > 1)\n --cnt[nums[m++]];\n res += m - l + 1; \n }\n } \n return res;\n}\n```\n**Python 3**\n```python\nclass Solution:\n def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:\n cnt, res, l, m = [0] * (len(nums) + 1), 0, 0, 0\n for n in nums:\n cnt[n] += 1\n if cnt[n] == 1:\n k -= 1\n if (k < 0):\n cnt[nums[m]] = 0\n m += 1\n l = m\n if k <= 0:\n while(cnt[nums[m]] > 1):\n cnt[nums[m]] -= 1\n m += 1\n res += m - l + 1\n return res\n```\n### Complexity Analysis\n- Time Complexity: *O(n)*, where *n* is the length of ```A```.\n- Space Complexity: *O(n)*. | 462 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
Dictionary Method -With Comments- Beats 79.59% In Runtime | subarrays-with-k-different-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:\n\n count1 = 0\n count2 = 0\n\n left = 0\n right = 0\n\n freq1 = defaultdict(int)\n freq2 = defaultdict(int)\n\n res = 0\n\n for i in range(len(nums)):\n #count frequencies which are greater than k\n if freq1[nums[i]] == 0:\n count1 +=1\n freq1[nums[i]] +=1\n #Count frequencies which are exactly k\n if freq2[nums[i]] == 0:\n count2 +=1\n freq2[nums[i]] +=1\n \n #Checking for count greater than k\n while count1 > k:\n freq1[nums[right]] -=1\n if freq1[nums[right]] == 0:\n count1-=1\n right +=1\n \n #Checking Counts for exact k\n while count2 > k-1:\n freq2[nums[left]] -=1\n if freq2[nums[left]] == 0:\n count2 -=1\n left +=1\n \n res += left - right\n \n return res\n``` | 9 | Given an integer array `nums` and an integer `k`, return _the number of **good subarrays** of_ `nums`.
A **good array** is an array where the number of different integers in that array is exactly `k`.
* For example, `[1,2,3,1,2]` has `3` different integers: `1`, `2`, and `3`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,3\], k = 2
**Output:** 7
**Explanation:** Subarrays formed with exactly 2 different integers: \[1,2\], \[2,1\], \[1,2\], \[2,3\], \[1,2,1\], \[2,1,2\], \[1,2,1,2\]
**Example 2:**
**Input:** nums = \[1,2,1,3,4\], k = 3
**Output:** 3
**Explanation:** Subarrays formed with exactly 3 different integers: \[1,2,1,3\], \[2,1,3\], \[1,3,4\].
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i], k <= nums.length` | null |
Dictionary Method -With Comments- Beats 79.59% In Runtime | subarrays-with-k-different-integers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:\n\n count1 = 0\n count2 = 0\n\n left = 0\n right = 0\n\n freq1 = defaultdict(int)\n freq2 = defaultdict(int)\n\n res = 0\n\n for i in range(len(nums)):\n #count frequencies which are greater than k\n if freq1[nums[i]] == 0:\n count1 +=1\n freq1[nums[i]] +=1\n #Count frequencies which are exactly k\n if freq2[nums[i]] == 0:\n count2 +=1\n freq2[nums[i]] +=1\n \n #Checking for count greater than k\n while count1 > k:\n freq1[nums[right]] -=1\n if freq1[nums[right]] == 0:\n count1-=1\n right +=1\n \n #Checking Counts for exact k\n while count2 > k-1:\n freq2[nums[left]] -=1\n if freq2[nums[left]] == 0:\n count2 -=1\n left +=1\n \n res += left - right\n \n return res\n``` | 9 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
Python Easy Solution | subarrays-with-k-different-integers | 0 | 1 | \n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def atmostk(self,n,k,nums):\n l=0\n r=0\n map=defaultdict(int)\n ans=0\n while r<n:\n map[nums[r]]+=1\n while len(map)>k:\n map[nums[l]]-=1\n if map[nums[l]]==0:\n del map[nums[l]]\n l+=1\n \n ans+=r-l+1\n r+=1\n return ans\n def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:\n return self.atmostk(len(nums),k,nums)-self.atmostk(len(nums),k-1,nums)\n``` | 6 | Given an integer array `nums` and an integer `k`, return _the number of **good subarrays** of_ `nums`.
A **good array** is an array where the number of different integers in that array is exactly `k`.
* For example, `[1,2,3,1,2]` has `3` different integers: `1`, `2`, and `3`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,3\], k = 2
**Output:** 7
**Explanation:** Subarrays formed with exactly 2 different integers: \[1,2\], \[2,1\], \[1,2\], \[2,3\], \[1,2,1\], \[2,1,2\], \[1,2,1,2\]
**Example 2:**
**Input:** nums = \[1,2,1,3,4\], k = 3
**Output:** 3
**Explanation:** Subarrays formed with exactly 3 different integers: \[1,2,1,3\], \[2,1,3\], \[1,3,4\].
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i], k <= nums.length` | null |
Python Easy Solution | subarrays-with-k-different-integers | 0 | 1 | \n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def atmostk(self,n,k,nums):\n l=0\n r=0\n map=defaultdict(int)\n ans=0\n while r<n:\n map[nums[r]]+=1\n while len(map)>k:\n map[nums[l]]-=1\n if map[nums[l]]==0:\n del map[nums[l]]\n l+=1\n \n ans+=r-l+1\n r+=1\n return ans\n def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:\n return self.atmostk(len(nums),k,nums)-self.atmostk(len(nums),k-1,nums)\n``` | 6 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
Solution | subarrays-with-k-different-integers | 1 | 1 | ```C++ []\nclass Solution {\nprivate:\n int atmostk(vector<int>& nums, int k){\n int left = 0;\n int right = 0;\n int count = 0;\n int n = nums.size();\n int freq[20005] = {0};\n while(right < n){\n if(freq[nums[right]]++ == 0){\n k--;\n }\n while(k < 0){\n freq[nums[left]]--;\n if(freq[nums[left]] == 0) k++;\n left++;\n }\n count += right - left + 1;\n right++;\n }\n return count;\n }\npublic:\n int subarraysWithKDistinct(vector<int>& nums, int k) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n return atmostk(nums,k) - atmostk(nums,k-1);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:\n ans = 0\n n = len(nums)\n latest = {}\n unique = 0\n prev = 0\n for i in range(n):\n if nums[i] not in latest:\n unique += 1\n latest[nums[i]] = i\n if unique > k :\n while True:\n if latest[nums[prev]] == prev:\n latest.pop(nums[prev])\n prev += 1\n unique -= 1 \n break\n else:\n prev += 1\n \n if unique == k:\n ans += 1\n tmp = prev\n while True:\n if latest[nums[tmp]] != tmp:\n ans += 1\n tmp += 1\n else:\n break\n return ans\n```\n\n```Java []\nclass Solution {\n public int subarraysWithKDistinct(int[] A, int K) {\n if (A == null || A.length == 0) {\n return 0;\n }\n int count = 0;\n int j = 0;\n int res = 0;\n int prefix = 0;\n int[] arr = new int[A.length + 1];\n for (int value : A) {\n if (arr[value]++ == 0) {\n count++;\n }\n while (count > K) {\n arr[A[j++]]--;\n prefix = 0;\n count--;\n }\n while (arr[A[j]] > 1) {\n prefix++;\n arr[A[j++]]--;\n }\n if (count == K) {\n res += prefix + 1;\n }\n }\n return res;\n }\n}\n```\n | 2 | Given an integer array `nums` and an integer `k`, return _the number of **good subarrays** of_ `nums`.
A **good array** is an array where the number of different integers in that array is exactly `k`.
* For example, `[1,2,3,1,2]` has `3` different integers: `1`, `2`, and `3`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[1,2,1,2,3\], k = 2
**Output:** 7
**Explanation:** Subarrays formed with exactly 2 different integers: \[1,2\], \[2,1\], \[1,2\], \[2,3\], \[1,2,1\], \[2,1,2\], \[1,2,1,2\]
**Example 2:**
**Input:** nums = \[1,2,1,3,4\], k = 3
**Output:** 3
**Explanation:** Subarrays formed with exactly 3 different integers: \[1,2,1,3\], \[2,1,3\], \[1,3,4\].
**Constraints:**
* `1 <= nums.length <= 2 * 104`
* `1 <= nums[i], k <= nums.length` | null |
Solution | subarrays-with-k-different-integers | 1 | 1 | ```C++ []\nclass Solution {\nprivate:\n int atmostk(vector<int>& nums, int k){\n int left = 0;\n int right = 0;\n int count = 0;\n int n = nums.size();\n int freq[20005] = {0};\n while(right < n){\n if(freq[nums[right]]++ == 0){\n k--;\n }\n while(k < 0){\n freq[nums[left]]--;\n if(freq[nums[left]] == 0) k++;\n left++;\n }\n count += right - left + 1;\n right++;\n }\n return count;\n }\npublic:\n int subarraysWithKDistinct(vector<int>& nums, int k) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n return atmostk(nums,k) - atmostk(nums,k-1);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def subarraysWithKDistinct(self, nums: List[int], k: int) -> int:\n ans = 0\n n = len(nums)\n latest = {}\n unique = 0\n prev = 0\n for i in range(n):\n if nums[i] not in latest:\n unique += 1\n latest[nums[i]] = i\n if unique > k :\n while True:\n if latest[nums[prev]] == prev:\n latest.pop(nums[prev])\n prev += 1\n unique -= 1 \n break\n else:\n prev += 1\n \n if unique == k:\n ans += 1\n tmp = prev\n while True:\n if latest[nums[tmp]] != tmp:\n ans += 1\n tmp += 1\n else:\n break\n return ans\n```\n\n```Java []\nclass Solution {\n public int subarraysWithKDistinct(int[] A, int K) {\n if (A == null || A.length == 0) {\n return 0;\n }\n int count = 0;\n int j = 0;\n int res = 0;\n int prefix = 0;\n int[] arr = new int[A.length + 1];\n for (int value : A) {\n if (arr[value]++ == 0) {\n count++;\n }\n while (count > K) {\n arr[A[j++]]--;\n prefix = 0;\n count--;\n }\n while (arr[A[j]] > 1) {\n prefix++;\n arr[A[j++]]--;\n }\n if (count == K) {\n res += prefix + 1;\n }\n }\n return res;\n }\n}\n```\n | 2 | You are given an `m x n` integer matrix `grid`, and three integers `row`, `col`, and `color`. Each value in the grid represents the color of the grid square at that location.
Two squares belong to the same **connected component** if they have the same color and are next to each other in any of the 4 directions.
The **border of a connected component** is all the squares in the connected component that are either **4-directionally** adjacent to a square not in the component, or on the boundary of the grid (the first or last row or column).
You should color the **border** of the **connected component** that contains the square `grid[row][col]` with `color`.
Return _the final grid_.
**Example 1:**
**Input:** grid = \[\[1,1\],\[1,2\]\], row = 0, col = 0, color = 3
**Output:** \[\[3,3\],\[3,2\]\]
**Example 2:**
**Input:** grid = \[\[1,2,2\],\[2,3,2\]\], row = 0, col = 1, color = 3
**Output:** \[\[1,3,3\],\[2,3,3\]\]
**Example 3:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\],\[1,1,1\]\], row = 1, col = 1, color = 2
**Output:** \[\[2,2,2\],\[2,1,2\],\[2,2,2\]\]
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 50`
* `1 <= grid[i][j], color <= 1000`
* `0 <= row < m`
* `0 <= col < n` | null |
✅Python3 33ms🔥🔥 easiest explanation | cousins-in-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Travel by level and storing root of x, y and level will solve this.**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- travel in left to right manner.\n- if current node is None return.\n- if not then if it\'s equals to query then store it\'s parent and level.\n- now next time next query found then compare it\'s parent and level, update anser to true if parent != foundparent and level == foundlevel, else false.\n- that\'s it.\n- return ans.\n\n# Complexity\n- Time complexity: O(H)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(3+stacks of recursion)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:\n levelFound = -1\n ans = False\n foundRoot = -1\n def helper(curr = root, level = 0, par = 0):\n nonlocal levelFound, ans, foundRoot\n if curr:\n if curr.val == x or curr.val == y:\n if levelFound + 1 and foundRoot + 1:\n ans = levelFound == level and foundRoot != par\n return\n else:\n levelFound = level\n foundRoot = par\n helper(curr.left, level + 1, curr.val)\n helper(curr.right, level + 1, curr.val)\n return\n helper()\n return ans\n```\n# Please like and comment below.\n# (\u3063\uFF3E\u25BF\uFF3E)\u06F6\uD83C\uDF78\uD83C\uDF1F\uD83C\uDF7A\u0669(\u02D8\u25E1\u02D8 ) | 4 | Given the `root` of a binary tree with unique values and the values of two different nodes of the tree `x` and `y`, return `true` _if the nodes corresponding to the values_ `x` _and_ `y` _in the tree are **cousins**, or_ `false` _otherwise._
Two nodes of a binary tree are **cousins** if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth `0`, and children of each depth `k` node are at the depth `k + 1`.
**Example 1:**
**Input:** root = \[1,2,3,4\], x = 4, y = 3
**Output:** false
**Example 2:**
**Input:** root = \[1,2,3,null,4,null,5\], x = 5, y = 4
**Output:** true
**Example 3:**
**Input:** root = \[1,2,3,null,4\], x = 2, y = 3
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `1 <= Node.val <= 100`
* Each node has a **unique** value.
* `x != y`
* `x` and `y` are exist in the tree. | null |
✅Python3 33ms🔥🔥 easiest explanation | cousins-in-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Travel by level and storing root of x, y and level will solve this.**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- travel in left to right manner.\n- if current node is None return.\n- if not then if it\'s equals to query then store it\'s parent and level.\n- now next time next query found then compare it\'s parent and level, update anser to true if parent != foundparent and level == foundlevel, else false.\n- that\'s it.\n- return ans.\n\n# Complexity\n- Time complexity: O(H)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(3+stacks of recursion)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:\n levelFound = -1\n ans = False\n foundRoot = -1\n def helper(curr = root, level = 0, par = 0):\n nonlocal levelFound, ans, foundRoot\n if curr:\n if curr.val == x or curr.val == y:\n if levelFound + 1 and foundRoot + 1:\n ans = levelFound == level and foundRoot != par\n return\n else:\n levelFound = level\n foundRoot = par\n helper(curr.left, level + 1, curr.val)\n helper(curr.right, level + 1, curr.val)\n return\n helper()\n return ans\n```\n# Please like and comment below.\n# (\u3063\uFF3E\u25BF\uFF3E)\u06F6\uD83C\uDF78\uD83C\uDF1F\uD83C\uDF7A\u0669(\u02D8\u25E1\u02D8 ) | 4 | You are given two integer arrays `nums1` and `nums2`. We write the integers of `nums1` and `nums2` (in the order they are given) on two separate horizontal lines.
We may draw connecting lines: a straight line connecting two numbers `nums1[i]` and `nums2[j]` such that:
* `nums1[i] == nums2[j]`, and
* the line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
Return _the maximum number of connecting lines we can draw in this way_.
**Example 1:**
**Input:** nums1 = \[1,4,2\], nums2 = \[1,2,4\]
**Output:** 2
**Explanation:** We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1\[1\] = 4 to nums2\[2\] = 4 will intersect the line from nums1\[2\]=2 to nums2\[1\]=2.
**Example 2:**
**Input:** nums1 = \[2,5,1,2,5\], nums2 = \[10,5,2,1,5,2\]
**Output:** 3
**Example 3:**
**Input:** nums1 = \[1,3,7,1,7,5\], nums2 = \[1,9,2,5,1\]
**Output:** 2
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `1 <= nums1[i], nums2[j] <= 2000` | null |
Iterative + Dictionary | cousins-in-binary-tree | 0 | 1 | # Intuition\nThere are two conditions that make nodes X and Y cousins. They are - \n(a) The nodes X and Y should be in the same level of the binary tree.\n(b) Provided that the levels of the nodes X and Y are the same, the parent nodes of X and Y should not be the same.\n\n# Approach\n- Using a dictionary to store the levels of X and Y. Since the dictionary will consist of only two elements, the space complexity is constant.\n- If the dictionary has more than one key, it means that the levels of X and Y are different and you can return False right away in that case.\n- If the dictinary has just one key, it means that the levels of X and Y are the same and you need to ensure that the parents of X and Y are different.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N) - Queue is used.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nfrom collections import deque\n\nclass Solution:\n def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:\n level_map = dict()\n queue = deque()\n queue.append([root, 1, None])\n\n while queue:\n value, level, parent = queue.popleft()\n if value.val == x or value.val == y:\n if level in level_map:\n level_map[level].append([value.val, parent.val])\n else:\n level_map[level] = [[value.val, parent.val if parent != None else None]]\n \n if value.left:\n queue.append([value.left, level+1, value])\n if value.right:\n queue.append([value.right, level+1, value])\n\n if len(level_map.keys()) > 1:\n return False\n else:\n level = level_map.keys()\n for key in level:\n key = int(key)\n if level_map[key][0][1] != level_map[key][1][1]:\n return True\n return False\n \n``` | 1 | Given the `root` of a binary tree with unique values and the values of two different nodes of the tree `x` and `y`, return `true` _if the nodes corresponding to the values_ `x` _and_ `y` _in the tree are **cousins**, or_ `false` _otherwise._
Two nodes of a binary tree are **cousins** if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth `0`, and children of each depth `k` node are at the depth `k + 1`.
**Example 1:**
**Input:** root = \[1,2,3,4\], x = 4, y = 3
**Output:** false
**Example 2:**
**Input:** root = \[1,2,3,null,4,null,5\], x = 5, y = 4
**Output:** true
**Example 3:**
**Input:** root = \[1,2,3,null,4\], x = 2, y = 3
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `1 <= Node.val <= 100`
* Each node has a **unique** value.
* `x != y`
* `x` and `y` are exist in the tree. | null |
Iterative + Dictionary | cousins-in-binary-tree | 0 | 1 | # Intuition\nThere are two conditions that make nodes X and Y cousins. They are - \n(a) The nodes X and Y should be in the same level of the binary tree.\n(b) Provided that the levels of the nodes X and Y are the same, the parent nodes of X and Y should not be the same.\n\n# Approach\n- Using a dictionary to store the levels of X and Y. Since the dictionary will consist of only two elements, the space complexity is constant.\n- If the dictionary has more than one key, it means that the levels of X and Y are different and you can return False right away in that case.\n- If the dictinary has just one key, it means that the levels of X and Y are the same and you need to ensure that the parents of X and Y are different.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N) - Queue is used.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nfrom collections import deque\n\nclass Solution:\n def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:\n level_map = dict()\n queue = deque()\n queue.append([root, 1, None])\n\n while queue:\n value, level, parent = queue.popleft()\n if value.val == x or value.val == y:\n if level in level_map:\n level_map[level].append([value.val, parent.val])\n else:\n level_map[level] = [[value.val, parent.val if parent != None else None]]\n \n if value.left:\n queue.append([value.left, level+1, value])\n if value.right:\n queue.append([value.right, level+1, value])\n\n if len(level_map.keys()) > 1:\n return False\n else:\n level = level_map.keys()\n for key in level:\n key = int(key)\n if level_map[key][0][1] != level_map[key][1][1]:\n return True\n return False\n \n``` | 1 | You are given two integer arrays `nums1` and `nums2`. We write the integers of `nums1` and `nums2` (in the order they are given) on two separate horizontal lines.
We may draw connecting lines: a straight line connecting two numbers `nums1[i]` and `nums2[j]` such that:
* `nums1[i] == nums2[j]`, and
* the line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
Return _the maximum number of connecting lines we can draw in this way_.
**Example 1:**
**Input:** nums1 = \[1,4,2\], nums2 = \[1,2,4\]
**Output:** 2
**Explanation:** We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1\[1\] = 4 to nums2\[2\] = 4 will intersect the line from nums1\[2\]=2 to nums2\[1\]=2.
**Example 2:**
**Input:** nums1 = \[2,5,1,2,5\], nums2 = \[10,5,2,1,5,2\]
**Output:** 3
**Example 3:**
**Input:** nums1 = \[1,3,7,1,7,5\], nums2 = \[1,9,2,5,1\]
**Output:** 2
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `1 <= nums1[i], nums2[j] <= 2000` | null |
Simplest Code to understand with commentssssss!! | cousins-in-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(n)\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(n)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:\n\n def height(node, value, h):\n # Function to find the height of a node with the given value in the binary tree.\n if not node:\n return 0 # If the current node is None, the node was not found; return 0.\n if node.val == value:\n return h # If the current node has the target value, return the height.\n left_height = height(node.left, value, h + 1) # Recursively search in the left subtree.\n if left_height:\n return left_height\n right_height = height(node.right, value, h + 1) # Recursively search in the right subtree.\n if right_height:\n return right_height\n\n def find_parent(node, value):\n # Function to find the parent of a node with the given value in the binary tree.\n if not node:\n return # If the current node is None, the node was not found; return None.\n if (node.left and node.left.val == value) or (node.right and node.right.val == value):\n return node.val # If the child of the current node matches the target value, return the current node\'s value.\n left_parent = find_parent(node.left, value) # Recursively search in the left subtree.\n if left_parent:\n return left_parent\n return find_parent(node.right, value) # Recursively search in the right subtree.\n\n\n x_height, x_parent = height(root, x, 0), find_parent(root, x)\n y_height, y_parent = height(root, y, 0), find_parent(root, y)\n\n # Compare the heights and parents of the two nodes\n if x_height == y_height and x_parent != y_parent:\n return True # The nodes are at the same height and have different parents, so they are cousins.\n else:\n return False # The nodes are not cousins.\n\n``` | 1 | Given the `root` of a binary tree with unique values and the values of two different nodes of the tree `x` and `y`, return `true` _if the nodes corresponding to the values_ `x` _and_ `y` _in the tree are **cousins**, or_ `false` _otherwise._
Two nodes of a binary tree are **cousins** if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth `0`, and children of each depth `k` node are at the depth `k + 1`.
**Example 1:**
**Input:** root = \[1,2,3,4\], x = 4, y = 3
**Output:** false
**Example 2:**
**Input:** root = \[1,2,3,null,4,null,5\], x = 5, y = 4
**Output:** true
**Example 3:**
**Input:** root = \[1,2,3,null,4\], x = 2, y = 3
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `1 <= Node.val <= 100`
* Each node has a **unique** value.
* `x != y`
* `x` and `y` are exist in the tree. | null |
Simplest Code to understand with commentssssss!! | cousins-in-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(n)\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(n)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:\n\n def height(node, value, h):\n # Function to find the height of a node with the given value in the binary tree.\n if not node:\n return 0 # If the current node is None, the node was not found; return 0.\n if node.val == value:\n return h # If the current node has the target value, return the height.\n left_height = height(node.left, value, h + 1) # Recursively search in the left subtree.\n if left_height:\n return left_height\n right_height = height(node.right, value, h + 1) # Recursively search in the right subtree.\n if right_height:\n return right_height\n\n def find_parent(node, value):\n # Function to find the parent of a node with the given value in the binary tree.\n if not node:\n return # If the current node is None, the node was not found; return None.\n if (node.left and node.left.val == value) or (node.right and node.right.val == value):\n return node.val # If the child of the current node matches the target value, return the current node\'s value.\n left_parent = find_parent(node.left, value) # Recursively search in the left subtree.\n if left_parent:\n return left_parent\n return find_parent(node.right, value) # Recursively search in the right subtree.\n\n\n x_height, x_parent = height(root, x, 0), find_parent(root, x)\n y_height, y_parent = height(root, y, 0), find_parent(root, y)\n\n # Compare the heights and parents of the two nodes\n if x_height == y_height and x_parent != y_parent:\n return True # The nodes are at the same height and have different parents, so they are cousins.\n else:\n return False # The nodes are not cousins.\n\n``` | 1 | You are given two integer arrays `nums1` and `nums2`. We write the integers of `nums1` and `nums2` (in the order they are given) on two separate horizontal lines.
We may draw connecting lines: a straight line connecting two numbers `nums1[i]` and `nums2[j]` such that:
* `nums1[i] == nums2[j]`, and
* the line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
Return _the maximum number of connecting lines we can draw in this way_.
**Example 1:**
**Input:** nums1 = \[1,4,2\], nums2 = \[1,2,4\]
**Output:** 2
**Explanation:** We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1\[1\] = 4 to nums2\[2\] = 4 will intersect the line from nums1\[2\]=2 to nums2\[1\]=2.
**Example 2:**
**Input:** nums1 = \[2,5,1,2,5\], nums2 = \[10,5,2,1,5,2\]
**Output:** 3
**Example 3:**
**Input:** nums1 = \[1,3,7,1,7,5\], nums2 = \[1,9,2,5,1\]
**Output:** 2
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `1 <= nums1[i], nums2[j] <= 2000` | null |
BFS solution | cousins-in-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nfrom collections import deque\nclass Solution:\n def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:\n # q madhe parent pan tak\n # BFS use karava lagel\n q=deque()\n # q madhe pahile node jail mag level jail and mag parent jail\n # jasa element bhetel level tak and parent tak eka array madhe\n node1=[]; node2=[]\n q.append([root, 0, -1])\n \n while q:\n node, level, parent = q.popleft()\n\n if node.val==x:\n node1=[level, parent]\n if node.val==y:\n node2=[level, parent]\n\n if node.left:\n q.append([node.left, level+1, node.val])\n if node.right:\n q.append([node.right, level+1, node.val])\n\n if node1[0]==node2[0] and node1[1]!=node2[1]:\n return True\n return False\n``` | 1 | Given the `root` of a binary tree with unique values and the values of two different nodes of the tree `x` and `y`, return `true` _if the nodes corresponding to the values_ `x` _and_ `y` _in the tree are **cousins**, or_ `false` _otherwise._
Two nodes of a binary tree are **cousins** if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth `0`, and children of each depth `k` node are at the depth `k + 1`.
**Example 1:**
**Input:** root = \[1,2,3,4\], x = 4, y = 3
**Output:** false
**Example 2:**
**Input:** root = \[1,2,3,null,4,null,5\], x = 5, y = 4
**Output:** true
**Example 3:**
**Input:** root = \[1,2,3,null,4\], x = 2, y = 3
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `1 <= Node.val <= 100`
* Each node has a **unique** value.
* `x != y`
* `x` and `y` are exist in the tree. | null |
BFS solution | cousins-in-binary-tree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nfrom collections import deque\nclass Solution:\n def isCousins(self, root: Optional[TreeNode], x: int, y: int) -> bool:\n # q madhe parent pan tak\n # BFS use karava lagel\n q=deque()\n # q madhe pahile node jail mag level jail and mag parent jail\n # jasa element bhetel level tak and parent tak eka array madhe\n node1=[]; node2=[]\n q.append([root, 0, -1])\n \n while q:\n node, level, parent = q.popleft()\n\n if node.val==x:\n node1=[level, parent]\n if node.val==y:\n node2=[level, parent]\n\n if node.left:\n q.append([node.left, level+1, node.val])\n if node.right:\n q.append([node.right, level+1, node.val])\n\n if node1[0]==node2[0] and node1[1]!=node2[1]:\n return True\n return False\n``` | 1 | You are given two integer arrays `nums1` and `nums2`. We write the integers of `nums1` and `nums2` (in the order they are given) on two separate horizontal lines.
We may draw connecting lines: a straight line connecting two numbers `nums1[i]` and `nums2[j]` such that:
* `nums1[i] == nums2[j]`, and
* the line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
Return _the maximum number of connecting lines we can draw in this way_.
**Example 1:**
**Input:** nums1 = \[1,4,2\], nums2 = \[1,2,4\]
**Output:** 2
**Explanation:** We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1\[1\] = 4 to nums2\[2\] = 4 will intersect the line from nums1\[2\]=2 to nums2\[1\]=2.
**Example 2:**
**Input:** nums1 = \[2,5,1,2,5\], nums2 = \[10,5,2,1,5,2\]
**Output:** 3
**Example 3:**
**Input:** nums1 = \[1,3,7,1,7,5\], nums2 = \[1,9,2,5,1\]
**Output:** 2
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `1 <= nums1[i], nums2[j] <= 2000` | null |
Python Straight Forward BFS and DFS Solutions | cousins-in-binary-tree | 0 | 1 | Two solutions have the same idea:\n* Iterate the whole tree looking for the target(x and y) - either BFS or DFS\n\t* once found, store `(parent, depth)` as a tuple\n* Compare the parents and depth of two nodes found and get result\n\n**BFS**\n```python\nclass Solution:\n def isCousins(self, root: TreeNode, x: int, y: int) -> bool:\n\t\t# store (parent, depth) tuple\n res = []\n\t\t\n\t\t# bfs\n queue = deque([(root, None, 0)]) \n while queue:\n\t\t\t# minor optimization to stop early if both targets found\n if len(res) == 2:\n break\n node, parent, depth = queue.popleft()\n # if target found\n if node.val == x or node.val == y:\n res.append((parent, depth))\n if node.left:\n queue.append((node.left, node, depth + 1))\n if node.right:\n queue.append((node.right, node, depth + 1))\n\n\t\t# unpack two nodes\n node_x, node_y = res\n\t\t\n\t\t# compare and decide whether two nodes are cousins\t\t\n return node_x[0] != node_y[0] and node_x[1] == node_y[1]\n```\n\n**DFS**\n```python\nclass Solution:\n def isCousins(self, root: TreeNode, x: int, y: int) -> bool:\n\t\t# store (parent, depth) tuple\n\t\tres = [] \n \n\t\t# dfs\n def dfs(node, parent, depth):\n if not node:\n return\n if node.val == x or node.val == y:\n res.append((parent, depth))\n dfs(node.left, node, depth + 1)\n dfs(node.right, node, depth + 1)\n \n dfs(root, None, 0)\n\n\t\t# unpack two nodes found\n node_x, node_y = res \n\t\t\n\t\t# compare and decide whether two nodes are cousins\n return node_x[0] != node_y[0] and node_x[1] == node_y[1]\n``` | 82 | Given the `root` of a binary tree with unique values and the values of two different nodes of the tree `x` and `y`, return `true` _if the nodes corresponding to the values_ `x` _and_ `y` _in the tree are **cousins**, or_ `false` _otherwise._
Two nodes of a binary tree are **cousins** if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth `0`, and children of each depth `k` node are at the depth `k + 1`.
**Example 1:**
**Input:** root = \[1,2,3,4\], x = 4, y = 3
**Output:** false
**Example 2:**
**Input:** root = \[1,2,3,null,4,null,5\], x = 5, y = 4
**Output:** true
**Example 3:**
**Input:** root = \[1,2,3,null,4\], x = 2, y = 3
**Output:** false
**Constraints:**
* The number of nodes in the tree is in the range `[2, 100]`.
* `1 <= Node.val <= 100`
* Each node has a **unique** value.
* `x != y`
* `x` and `y` are exist in the tree. | null |
Python Straight Forward BFS and DFS Solutions | cousins-in-binary-tree | 0 | 1 | Two solutions have the same idea:\n* Iterate the whole tree looking for the target(x and y) - either BFS or DFS\n\t* once found, store `(parent, depth)` as a tuple\n* Compare the parents and depth of two nodes found and get result\n\n**BFS**\n```python\nclass Solution:\n def isCousins(self, root: TreeNode, x: int, y: int) -> bool:\n\t\t# store (parent, depth) tuple\n res = []\n\t\t\n\t\t# bfs\n queue = deque([(root, None, 0)]) \n while queue:\n\t\t\t# minor optimization to stop early if both targets found\n if len(res) == 2:\n break\n node, parent, depth = queue.popleft()\n # if target found\n if node.val == x or node.val == y:\n res.append((parent, depth))\n if node.left:\n queue.append((node.left, node, depth + 1))\n if node.right:\n queue.append((node.right, node, depth + 1))\n\n\t\t# unpack two nodes\n node_x, node_y = res\n\t\t\n\t\t# compare and decide whether two nodes are cousins\t\t\n return node_x[0] != node_y[0] and node_x[1] == node_y[1]\n```\n\n**DFS**\n```python\nclass Solution:\n def isCousins(self, root: TreeNode, x: int, y: int) -> bool:\n\t\t# store (parent, depth) tuple\n\t\tres = [] \n \n\t\t# dfs\n def dfs(node, parent, depth):\n if not node:\n return\n if node.val == x or node.val == y:\n res.append((parent, depth))\n dfs(node.left, node, depth + 1)\n dfs(node.right, node, depth + 1)\n \n dfs(root, None, 0)\n\n\t\t# unpack two nodes found\n node_x, node_y = res \n\t\t\n\t\t# compare and decide whether two nodes are cousins\n return node_x[0] != node_y[0] and node_x[1] == node_y[1]\n``` | 82 | You are given two integer arrays `nums1` and `nums2`. We write the integers of `nums1` and `nums2` (in the order they are given) on two separate horizontal lines.
We may draw connecting lines: a straight line connecting two numbers `nums1[i]` and `nums2[j]` such that:
* `nums1[i] == nums2[j]`, and
* the line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
Return _the maximum number of connecting lines we can draw in this way_.
**Example 1:**
**Input:** nums1 = \[1,4,2\], nums2 = \[1,2,4\]
**Output:** 2
**Explanation:** We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1\[1\] = 4 to nums2\[2\] = 4 will intersect the line from nums1\[2\]=2 to nums2\[1\]=2.
**Example 2:**
**Input:** nums1 = \[2,5,1,2,5\], nums2 = \[10,5,2,1,5,2\]
**Output:** 3
**Example 3:**
**Input:** nums1 = \[1,3,7,1,7,5\], nums2 = \[1,9,2,5,1\]
**Output:** 2
**Constraints:**
* `1 <= nums1.length, nums2.length <= 500`
* `1 <= nums1[i], nums2[j] <= 2000` | null |
Click this if you're confused. | rotting-oranges | 0 | 1 | # Intuition\nAt each minute, we can only convert adjacent fresh oranges to rotten once. This is simply level-by-level BFS traversal. Each level we convert fresh to rotten and increment minutes by 1. Implementing this iteratively, we initialize our queue with all initial rotten oranges, then loop till queue is empty by popping left and appending newly rotten oranges.\n\nNote that we will count an extra minute since last level (all fresh already rotten) still needs to get popped. So we also initialize the count of fresh oranges and subtract this count with each conversion. If number of fresh equal to 0 we exit our loop early. A second use for this count is to return -1 if the count is not 0 after looping.\n\n# Complexity\n- Time complexity: $O(n \\times m)$ since we loop through the whole grid twice.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n \\times m)$ since in worst case our queue could grow to hold a significant portion of the tiles in the grid if a bunch of fresh oranges turn rotten at once\u2014you could imagine a grid where every rotten orange has 4 fresh adjacent and every fresh orange is adjacent to a rotten.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n\n def orangesRotting(self, grid: List[List[int]]) -> int:\n n_rows, n_cols = len(grid), len(grid[0])\n q, n_fresh, n_mins = deque(), 0, 0\n\n # populate with initial rottens\n for r in range(n_rows):\n for c in range(n_cols):\n if grid[r][c] == 1:\n n_fresh += 1\n elif grid[r][c] == 2:\n q.append((r, c))\n\n # BFS\n dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n while n_fresh > 0 and q:\n for _ in range(len(q)): # pop all in level\n r, c = q.popleft()\n\n # convert all adjacent freshes\n for rd, cd in dirs:\n ri, ci = r + rd, c + cd\n if 0 <= ri < n_rows and 0 <= ci < n_cols and grid[ri][ci] == 1:\n grid[ri][ci] = 2\n n_fresh -= 1\n q.append((ri, ci))\n n_mins += 1\n\n return n_mins if n_fresh == 0 else -1\n``` | 1 | You are given an `m x n` `grid` where each cell can have one of three values:
* `0` representing an empty cell,
* `1` representing a fresh orange, or
* `2` representing a rotten orange.
Every minute, any fresh orange that is **4-directionally adjacent** to a rotten orange becomes rotten.
Return _the minimum number of minutes that must elapse until no cell has a fresh orange_. If _this is impossible, return_ `-1`.
**Example 1:**
**Input:** grid = \[\[2,1,1\],\[1,1,0\],\[0,1,1\]\]
**Output:** 4
**Example 2:**
**Input:** grid = \[\[2,1,1\],\[0,1,1\],\[1,0,1\]\]
**Output:** -1
**Explanation:** The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
**Example 3:**
**Input:** grid = \[\[0,2\]\]
**Output:** 0
**Explanation:** Since there are already no fresh oranges at minute 0, the answer is just 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 10`
* `grid[i][j]` is `0`, `1`, or `2`. | null |
Click this if you're confused. | rotting-oranges | 0 | 1 | # Intuition\nAt each minute, we can only convert adjacent fresh oranges to rotten once. This is simply level-by-level BFS traversal. Each level we convert fresh to rotten and increment minutes by 1. Implementing this iteratively, we initialize our queue with all initial rotten oranges, then loop till queue is empty by popping left and appending newly rotten oranges.\n\nNote that we will count an extra minute since last level (all fresh already rotten) still needs to get popped. So we also initialize the count of fresh oranges and subtract this count with each conversion. If number of fresh equal to 0 we exit our loop early. A second use for this count is to return -1 if the count is not 0 after looping.\n\n# Complexity\n- Time complexity: $O(n \\times m)$ since we loop through the whole grid twice.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n \\times m)$ since in worst case our queue could grow to hold a significant portion of the tiles in the grid if a bunch of fresh oranges turn rotten at once\u2014you could imagine a grid where every rotten orange has 4 fresh adjacent and every fresh orange is adjacent to a rotten.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import deque\n\nclass Solution:\n\n def orangesRotting(self, grid: List[List[int]]) -> int:\n n_rows, n_cols = len(grid), len(grid[0])\n q, n_fresh, n_mins = deque(), 0, 0\n\n # populate with initial rottens\n for r in range(n_rows):\n for c in range(n_cols):\n if grid[r][c] == 1:\n n_fresh += 1\n elif grid[r][c] == 2:\n q.append((r, c))\n\n # BFS\n dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n while n_fresh > 0 and q:\n for _ in range(len(q)): # pop all in level\n r, c = q.popleft()\n\n # convert all adjacent freshes\n for rd, cd in dirs:\n ri, ci = r + rd, c + cd\n if 0 <= ri < n_rows and 0 <= ci < n_cols and grid[ri][ci] == 1:\n grid[ri][ci] = 2\n n_fresh -= 1\n q.append((ri, ci))\n n_mins += 1\n\n return n_mins if n_fresh == 0 else -1\n``` | 1 | There is a 1 million by 1 million grid on an XY-plane, and the coordinates of each grid square are `(x, y)`.
We start at the `source = [sx, sy]` square and want to reach the `target = [tx, ty]` square. There is also an array of `blocked` squares, where each `blocked[i] = [xi, yi]` represents a blocked square with coordinates `(xi, yi)`.
Each move, we can walk one square north, east, south, or west if the square is **not** in the array of `blocked` squares. We are also not allowed to walk outside of the grid.
Return `true` _if and only if it is possible to reach the_ `target` _square from the_ `source` _square through a sequence of valid moves_.
**Example 1:**
**Input:** blocked = \[\[0,1\],\[1,0\]\], source = \[0,0\], target = \[0,2\]
**Output:** false
**Explanation:** The target square is inaccessible starting from the source square because we cannot move.
We cannot move north or east because those squares are blocked.
We cannot move south or west because we cannot go outside of the grid.
**Example 2:**
**Input:** blocked = \[\], source = \[0,0\], target = \[999999,999999\]
**Output:** true
**Explanation:** Because there are no blocked cells, it is possible to reach the target square.
**Constraints:**
* `0 <= blocked.length <= 200`
* `blocked[i].length == 2`
* `0 <= xi, yi < 106`
* `source.length == target.length == 2`
* `0 <= sx, sy, tx, ty < 106`
* `source != target`
* It is guaranteed that `source` and `target` are not blocked. | null |
Python Clean & Well Explained (faster than > 90%) | rotting-oranges | 0 | 1 | ```\nfrom collections import deque\n\n# Time complexity: O(rows * cols) -> each cell is visited at least once\n# Space complexity: O(rows * cols) -> in the worst case if all the oranges are rotten they will be added to the queue\n\nclass Solution:\n def orangesRotting(self, grid: List[List[int]]) -> int:\n \n # number of rows\n rows = len(grid)\n if rows == 0: # check if grid is empty\n return -1\n \n # number of columns\n cols = len(grid[0])\n \n # keep track of fresh oranges\n fresh_cnt = 0\n \n # queue with rotten oranges (for BFS)\n rotten = deque()\n \n # visit each cell in the grid\n for r in range(rows):\n for c in range(cols):\n if grid[r][c] == 2:\n # add the rotten orange coordinates to the queue\n rotten.append((r, c))\n elif grid[r][c] == 1:\n # update fresh oranges count\n fresh_cnt += 1\n \n # keep track of minutes passed.\n minutes_passed = 0\n \n # If there are rotten oranges in the queue and there are still fresh oranges in the grid keep looping\n while rotten and fresh_cnt > 0:\n\n # update the number of minutes passed\n # it is safe to update the minutes by 1, since we visit oranges level by level in BFS traversal.\n minutes_passed += 1\n \n # process rotten oranges on the current level\n for _ in range(len(rotten)):\n x, y = rotten.popleft()\n \n # visit all the adjacent cells\n for dx, dy in [(1,0), (-1,0), (0,1), (0,-1)]:\n # calculate the coordinates of the adjacent cell\n xx, yy = x + dx, y + dy\n # ignore the cell if it is out of the grid boundary\n if xx < 0 or xx == rows or yy < 0 or yy == cols:\n continue\n # ignore the cell if it is empty \'0\' or visited before \'2\'\n if grid[xx][yy] == 0 or grid[xx][yy] == 2:\n continue\n \n # update the fresh oranges count\n fresh_cnt -= 1\n \n # mark the current fresh orange as rotten\n grid[xx][yy] = 2\n \n # add the current rotten to the queue\n rotten.append((xx, yy))\n\n \n # return the number of minutes taken to make all the fresh oranges to be rotten\n # return -1 if there are fresh oranges left in the grid (there were no adjacent rotten oranges to make them rotten)\n return minutes_passed if fresh_cnt == 0 else -1\n``` | 811 | You are given an `m x n` `grid` where each cell can have one of three values:
* `0` representing an empty cell,
* `1` representing a fresh orange, or
* `2` representing a rotten orange.
Every minute, any fresh orange that is **4-directionally adjacent** to a rotten orange becomes rotten.
Return _the minimum number of minutes that must elapse until no cell has a fresh orange_. If _this is impossible, return_ `-1`.
**Example 1:**
**Input:** grid = \[\[2,1,1\],\[1,1,0\],\[0,1,1\]\]
**Output:** 4
**Example 2:**
**Input:** grid = \[\[2,1,1\],\[0,1,1\],\[1,0,1\]\]
**Output:** -1
**Explanation:** The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
**Example 3:**
**Input:** grid = \[\[0,2\]\]
**Output:** 0
**Explanation:** Since there are already no fresh oranges at minute 0, the answer is just 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 10`
* `grid[i][j]` is `0`, `1`, or `2`. | null |
Python Clean & Well Explained (faster than > 90%) | rotting-oranges | 0 | 1 | ```\nfrom collections import deque\n\n# Time complexity: O(rows * cols) -> each cell is visited at least once\n# Space complexity: O(rows * cols) -> in the worst case if all the oranges are rotten they will be added to the queue\n\nclass Solution:\n def orangesRotting(self, grid: List[List[int]]) -> int:\n \n # number of rows\n rows = len(grid)\n if rows == 0: # check if grid is empty\n return -1\n \n # number of columns\n cols = len(grid[0])\n \n # keep track of fresh oranges\n fresh_cnt = 0\n \n # queue with rotten oranges (for BFS)\n rotten = deque()\n \n # visit each cell in the grid\n for r in range(rows):\n for c in range(cols):\n if grid[r][c] == 2:\n # add the rotten orange coordinates to the queue\n rotten.append((r, c))\n elif grid[r][c] == 1:\n # update fresh oranges count\n fresh_cnt += 1\n \n # keep track of minutes passed.\n minutes_passed = 0\n \n # If there are rotten oranges in the queue and there are still fresh oranges in the grid keep looping\n while rotten and fresh_cnt > 0:\n\n # update the number of minutes passed\n # it is safe to update the minutes by 1, since we visit oranges level by level in BFS traversal.\n minutes_passed += 1\n \n # process rotten oranges on the current level\n for _ in range(len(rotten)):\n x, y = rotten.popleft()\n \n # visit all the adjacent cells\n for dx, dy in [(1,0), (-1,0), (0,1), (0,-1)]:\n # calculate the coordinates of the adjacent cell\n xx, yy = x + dx, y + dy\n # ignore the cell if it is out of the grid boundary\n if xx < 0 or xx == rows or yy < 0 or yy == cols:\n continue\n # ignore the cell if it is empty \'0\' or visited before \'2\'\n if grid[xx][yy] == 0 or grid[xx][yy] == 2:\n continue\n \n # update the fresh oranges count\n fresh_cnt -= 1\n \n # mark the current fresh orange as rotten\n grid[xx][yy] = 2\n \n # add the current rotten to the queue\n rotten.append((xx, yy))\n\n \n # return the number of minutes taken to make all the fresh oranges to be rotten\n # return -1 if there are fresh oranges left in the grid (there were no adjacent rotten oranges to make them rotten)\n return minutes_passed if fresh_cnt == 0 else -1\n``` | 811 | There is a 1 million by 1 million grid on an XY-plane, and the coordinates of each grid square are `(x, y)`.
We start at the `source = [sx, sy]` square and want to reach the `target = [tx, ty]` square. There is also an array of `blocked` squares, where each `blocked[i] = [xi, yi]` represents a blocked square with coordinates `(xi, yi)`.
Each move, we can walk one square north, east, south, or west if the square is **not** in the array of `blocked` squares. We are also not allowed to walk outside of the grid.
Return `true` _if and only if it is possible to reach the_ `target` _square from the_ `source` _square through a sequence of valid moves_.
**Example 1:**
**Input:** blocked = \[\[0,1\],\[1,0\]\], source = \[0,0\], target = \[0,2\]
**Output:** false
**Explanation:** The target square is inaccessible starting from the source square because we cannot move.
We cannot move north or east because those squares are blocked.
We cannot move south or west because we cannot go outside of the grid.
**Example 2:**
**Input:** blocked = \[\], source = \[0,0\], target = \[999999,999999\]
**Output:** true
**Explanation:** Because there are no blocked cells, it is possible to reach the target square.
**Constraints:**
* `0 <= blocked.length <= 200`
* `blocked[i].length == 2`
* `0 <= xi, yi < 106`
* `source.length == target.length == 2`
* `0 <= sx, sy, tx, ty < 106`
* `source != target`
* It is guaranteed that `source` and `target` are not blocked. | null |
C++ || BFS || Easiest Beginner Friendly Sol || O(n^2) time and O(n^2) space | rotting-oranges | 1 | 1 | # Intuition of this Problem:\nSame type of bfs approach will work as shown in below picture.\n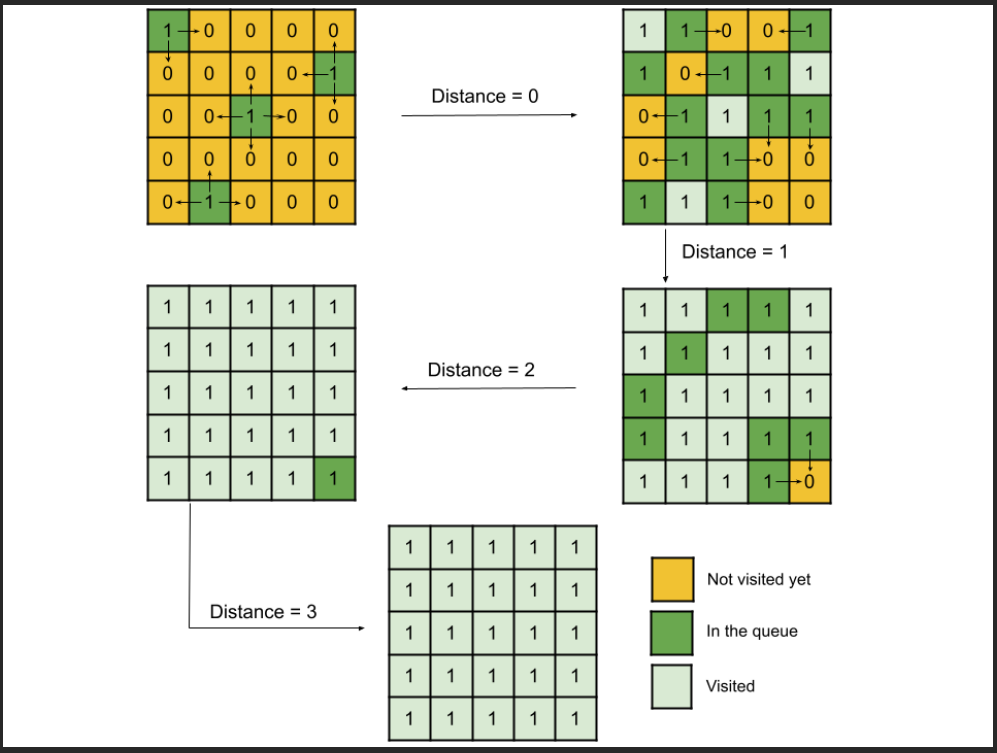\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Create a visited grid to store the state of the cell (fresh, rotten, or empty).\n2. Initialize a queue to store the rotten oranges and count the number of fresh oranges.\n3. Check if there are no fresh oranges, return 0, or if there are no rotten oranges, return -1.\n4. Loop while the queue is not empty.\n - a. Store the size of the queue.\n - b. Loop through the size of the queue.\n - i. Get the front cell of the queue.\n - ii. Check all four directions of the cell to see if there are any fresh oranges.\n - iii. If there is a fresh orange, change its state to rotten and decrement the count of fresh oranges, and push the cell into the queue.\n - c. Increment the minutes.\n1. If there are no fresh oranges, return the minutes.\n2. If there are still fresh oranges, return -1.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int orangesRotting(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n vector<vector<int>> visited = grid;\n //making queue in which we will fill rotten oranges\n queue<pair<int, int>> q;\n int countFreshOrange = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (visited[i][j] == 2) {\n q.push({i, j});\n }\n if (visited[i][j] == 1) {\n countFreshOrange++;\n }\n }\n }\n //q.empty() means there is no rotten orange in the grid and countFreshOrange = 0 means we will rotten the freshoranges in 0 mins\n if (countFreshOrange == 0)\n return 0;\n if (q.empty())\n return -1;\n \n int minutes = -1;\n // we will cover four directions i.e. up, down, left, right\n vector<pair<int, int>> dirs = {{1, 0},{-1, 0},{0, -1},{0, 1}};\n while (!q.empty()) {\n int size = q.size();\n while (size--) {\n auto [x, y] = q.front();\n q.pop();\n for (auto [dx, dy] : dirs) {\n int i = x + dx;\n int j = y + dy;\n if (i >= 0 && i < m && j >= 0 && j < n && visited[i][j] == 1) {\n visited[i][j] = 2;\n countFreshOrange--;\n q.push({i, j});\n }\n }\n }\n minutes++;\n }\n \n if (countFreshOrange == 0)\n return minutes;\n return -1;\n }\n};\n```\n```Java []\nclass Solution {\n public int orangesRotting(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int[][] visited = grid;\n Queue<int[]> q = new LinkedList<>();\n int countFreshOrange = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (visited[i][j] == 2) {\n q.offer(new int[] {i, j});\n }\n if (visited[i][j] == 1) {\n countFreshOrange++;\n }\n }\n }\n if (countFreshOrange == 0)\n return 0;\n if (q.isEmpty())\n return -1;\n \n int minutes = -1;\n int[][] dirs = {{1, 0},{-1, 0},{0, -1},{0, 1}};\n while (!q.isEmpty()) {\n int size = q.size();\n while (size-- > 0) {\n int[] cell = q.poll();\n int x = cell[0];\n int y = cell[1];\n for (int[] dir : dirs) {\n int i = x + dir[0];\n int j = y + dir[1];\n if (i >= 0 && i < m && j >= 0 && j < n && visited[i][j] == 1) {\n visited[i][j] = 2;\n countFreshOrange--;\n q.offer(new int[] {i, j});\n }\n }\n }\n minutes++;\n }\n \n if (countFreshOrange == 0)\n return minutes;\n return -1;\n }\n}\n\n```\n```Python []\nclass Solution:\n def orangesRotting(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n visited = grid\n q = collections.deque()\n countFreshOrange = 0\n for i in range(m):\n for j in range(n):\n if visited[i][j] == 2:\n q.append((i, j))\n if visited[i][j] == 1:\n countFreshOrange += 1\n if countFreshOrange == 0:\n return 0\n if not q:\n return -1\n \n minutes = -1\n dirs = [(1, 0), (-1, 0), (0, -1), (0, 1)]\n while q:\n size = len(q)\n while size > 0:\n x, y = q.popleft()\n size -= 1\n for dx, dy in dirs:\n i, j = x + dx, y + dy\n if 0 <= i < m and 0 <= j < n and visited[i][j] == 1:\n visited[i][j] = 2\n countFreshOrange -= 1\n q.append((i, j))\n minutes += 1\n \n if countFreshOrange == 0:\n return minutes\n return -1\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(m*n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(m*n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Similar Pattern Problems:\n1162. As Far from Land as Possible - https://leetcode.com/problems/as-far-from-land-as-possible/description/\n317. Shortest Distance from All Buildings - https://leetcode.com/problems/shortest-distance-from-all-buildings/description/ | 137 | You are given an `m x n` `grid` where each cell can have one of three values:
* `0` representing an empty cell,
* `1` representing a fresh orange, or
* `2` representing a rotten orange.
Every minute, any fresh orange that is **4-directionally adjacent** to a rotten orange becomes rotten.
Return _the minimum number of minutes that must elapse until no cell has a fresh orange_. If _this is impossible, return_ `-1`.
**Example 1:**
**Input:** grid = \[\[2,1,1\],\[1,1,0\],\[0,1,1\]\]
**Output:** 4
**Example 2:**
**Input:** grid = \[\[2,1,1\],\[0,1,1\],\[1,0,1\]\]
**Output:** -1
**Explanation:** The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
**Example 3:**
**Input:** grid = \[\[0,2\]\]
**Output:** 0
**Explanation:** Since there are already no fresh oranges at minute 0, the answer is just 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 10`
* `grid[i][j]` is `0`, `1`, or `2`. | null |
C++ || BFS || Easiest Beginner Friendly Sol || O(n^2) time and O(n^2) space | rotting-oranges | 1 | 1 | # Intuition of this Problem:\nSame type of bfs approach will work as shown in below picture.\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Create a visited grid to store the state of the cell (fresh, rotten, or empty).\n2. Initialize a queue to store the rotten oranges and count the number of fresh oranges.\n3. Check if there are no fresh oranges, return 0, or if there are no rotten oranges, return -1.\n4. Loop while the queue is not empty.\n - a. Store the size of the queue.\n - b. Loop through the size of the queue.\n - i. Get the front cell of the queue.\n - ii. Check all four directions of the cell to see if there are any fresh oranges.\n - iii. If there is a fresh orange, change its state to rotten and decrement the count of fresh oranges, and push the cell into the queue.\n - c. Increment the minutes.\n1. If there are no fresh oranges, return the minutes.\n2. If there are still fresh oranges, return -1.\n<!-- Describe your approach to solving the problem. -->\n\n# Humble Request:\n- If my solution is helpful to you then please **UPVOTE** my solution, your **UPVOTE** motivates me to post such kind of solution.\n- Please let me know in comments if there is need to do any improvement in my approach, code....anything.\n- **Let\'s connect on** https://www.linkedin.com/in/abhinash-singh-1b851b188\n\n\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int orangesRotting(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n vector<vector<int>> visited = grid;\n //making queue in which we will fill rotten oranges\n queue<pair<int, int>> q;\n int countFreshOrange = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (visited[i][j] == 2) {\n q.push({i, j});\n }\n if (visited[i][j] == 1) {\n countFreshOrange++;\n }\n }\n }\n //q.empty() means there is no rotten orange in the grid and countFreshOrange = 0 means we will rotten the freshoranges in 0 mins\n if (countFreshOrange == 0)\n return 0;\n if (q.empty())\n return -1;\n \n int minutes = -1;\n // we will cover four directions i.e. up, down, left, right\n vector<pair<int, int>> dirs = {{1, 0},{-1, 0},{0, -1},{0, 1}};\n while (!q.empty()) {\n int size = q.size();\n while (size--) {\n auto [x, y] = q.front();\n q.pop();\n for (auto [dx, dy] : dirs) {\n int i = x + dx;\n int j = y + dy;\n if (i >= 0 && i < m && j >= 0 && j < n && visited[i][j] == 1) {\n visited[i][j] = 2;\n countFreshOrange--;\n q.push({i, j});\n }\n }\n }\n minutes++;\n }\n \n if (countFreshOrange == 0)\n return minutes;\n return -1;\n }\n};\n```\n```Java []\nclass Solution {\n public int orangesRotting(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int[][] visited = grid;\n Queue<int[]> q = new LinkedList<>();\n int countFreshOrange = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (visited[i][j] == 2) {\n q.offer(new int[] {i, j});\n }\n if (visited[i][j] == 1) {\n countFreshOrange++;\n }\n }\n }\n if (countFreshOrange == 0)\n return 0;\n if (q.isEmpty())\n return -1;\n \n int minutes = -1;\n int[][] dirs = {{1, 0},{-1, 0},{0, -1},{0, 1}};\n while (!q.isEmpty()) {\n int size = q.size();\n while (size-- > 0) {\n int[] cell = q.poll();\n int x = cell[0];\n int y = cell[1];\n for (int[] dir : dirs) {\n int i = x + dir[0];\n int j = y + dir[1];\n if (i >= 0 && i < m && j >= 0 && j < n && visited[i][j] == 1) {\n visited[i][j] = 2;\n countFreshOrange--;\n q.offer(new int[] {i, j});\n }\n }\n }\n minutes++;\n }\n \n if (countFreshOrange == 0)\n return minutes;\n return -1;\n }\n}\n\n```\n```Python []\nclass Solution:\n def orangesRotting(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n visited = grid\n q = collections.deque()\n countFreshOrange = 0\n for i in range(m):\n for j in range(n):\n if visited[i][j] == 2:\n q.append((i, j))\n if visited[i][j] == 1:\n countFreshOrange += 1\n if countFreshOrange == 0:\n return 0\n if not q:\n return -1\n \n minutes = -1\n dirs = [(1, 0), (-1, 0), (0, -1), (0, 1)]\n while q:\n size = len(q)\n while size > 0:\n x, y = q.popleft()\n size -= 1\n for dx, dy in dirs:\n i, j = x + dx, y + dy\n if 0 <= i < m and 0 <= j < n and visited[i][j] == 1:\n visited[i][j] = 2\n countFreshOrange -= 1\n q.append((i, j))\n minutes += 1\n \n if countFreshOrange == 0:\n return minutes\n return -1\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(m*n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(m*n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Similar Pattern Problems:\n1162. As Far from Land as Possible - https://leetcode.com/problems/as-far-from-land-as-possible/description/\n317. Shortest Distance from All Buildings - https://leetcode.com/problems/shortest-distance-from-all-buildings/description/ | 137 | There is a 1 million by 1 million grid on an XY-plane, and the coordinates of each grid square are `(x, y)`.
We start at the `source = [sx, sy]` square and want to reach the `target = [tx, ty]` square. There is also an array of `blocked` squares, where each `blocked[i] = [xi, yi]` represents a blocked square with coordinates `(xi, yi)`.
Each move, we can walk one square north, east, south, or west if the square is **not** in the array of `blocked` squares. We are also not allowed to walk outside of the grid.
Return `true` _if and only if it is possible to reach the_ `target` _square from the_ `source` _square through a sequence of valid moves_.
**Example 1:**
**Input:** blocked = \[\[0,1\],\[1,0\]\], source = \[0,0\], target = \[0,2\]
**Output:** false
**Explanation:** The target square is inaccessible starting from the source square because we cannot move.
We cannot move north or east because those squares are blocked.
We cannot move south or west because we cannot go outside of the grid.
**Example 2:**
**Input:** blocked = \[\], source = \[0,0\], target = \[999999,999999\]
**Output:** true
**Explanation:** Because there are no blocked cells, it is possible to reach the target square.
**Constraints:**
* `0 <= blocked.length <= 200`
* `blocked[i].length == 2`
* `0 <= xi, yi < 106`
* `source.length == target.length == 2`
* `0 <= sx, sy, tx, ty < 106`
* `source != target`
* It is guaranteed that `source` and `target` are not blocked. | null |
BFS | Iterative | Beats 99.8% | Python | rotting-oranges | 0 | 1 | # Intuition\nThe intuition of the solution is to perform a BFS on the rotten oranges at the same time and increment the counter.\n\nThe neighbors are added only if they are good oranges and their value is set to 2 "rotten".\n# Complexity\n- Time complexity: O(N*M) (BFS visits all the values once)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N*M) (worst case the queue holds all the rotten values)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def orangesRotting(self, grid: List[List[int]]) -> int:\n\n ROWS, COLS = len(grid), len(grid[0])\n q = list() # queue\n count = -1\n\n # Get all rotten oranges\n for i in range(ROWS):\n for j in range(COLS):\n if grid[i][j] == 2:\n q.append([i,j])\n\n\n while q:\n\n tmp = q.copy()\n q.clear()\n\n for i,j in tmp:\n\n if i+1 < ROWS and grid[i+1][j] == 1:\n q.append([i+1, j])\n grid[i+1][j] = 2\n\n if j+1 < COLS and grid[i][j+1] == 1:\n q.append([i, j+1])\n grid[i][j+1] = 2\n\n if i-1 >= 0 and grid[i-1][j] == 1:\n q.append([i-1, j])\n grid[i-1][j] = 2\n\n if j-1 >= 0 and grid[i][j-1] == 1:\n q.append([i, j-1])\n grid[i][j-1] = 2\n\n count += 1\n \n\n for row in grid:\n for col in row:\n if col == 1:\n return -1\n \n\n return count if count >= 0 else 0\n\n\n\n``` | 2 | You are given an `m x n` `grid` where each cell can have one of three values:
* `0` representing an empty cell,
* `1` representing a fresh orange, or
* `2` representing a rotten orange.
Every minute, any fresh orange that is **4-directionally adjacent** to a rotten orange becomes rotten.
Return _the minimum number of minutes that must elapse until no cell has a fresh orange_. If _this is impossible, return_ `-1`.
**Example 1:**
**Input:** grid = \[\[2,1,1\],\[1,1,0\],\[0,1,1\]\]
**Output:** 4
**Example 2:**
**Input:** grid = \[\[2,1,1\],\[0,1,1\],\[1,0,1\]\]
**Output:** -1
**Explanation:** The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
**Example 3:**
**Input:** grid = \[\[0,2\]\]
**Output:** 0
**Explanation:** Since there are already no fresh oranges at minute 0, the answer is just 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 10`
* `grid[i][j]` is `0`, `1`, or `2`. | null |
BFS | Iterative | Beats 99.8% | Python | rotting-oranges | 0 | 1 | # Intuition\nThe intuition of the solution is to perform a BFS on the rotten oranges at the same time and increment the counter.\n\nThe neighbors are added only if they are good oranges and their value is set to 2 "rotten".\n# Complexity\n- Time complexity: O(N*M) (BFS visits all the values once)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N*M) (worst case the queue holds all the rotten values)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def orangesRotting(self, grid: List[List[int]]) -> int:\n\n ROWS, COLS = len(grid), len(grid[0])\n q = list() # queue\n count = -1\n\n # Get all rotten oranges\n for i in range(ROWS):\n for j in range(COLS):\n if grid[i][j] == 2:\n q.append([i,j])\n\n\n while q:\n\n tmp = q.copy()\n q.clear()\n\n for i,j in tmp:\n\n if i+1 < ROWS and grid[i+1][j] == 1:\n q.append([i+1, j])\n grid[i+1][j] = 2\n\n if j+1 < COLS and grid[i][j+1] == 1:\n q.append([i, j+1])\n grid[i][j+1] = 2\n\n if i-1 >= 0 and grid[i-1][j] == 1:\n q.append([i-1, j])\n grid[i-1][j] = 2\n\n if j-1 >= 0 and grid[i][j-1] == 1:\n q.append([i, j-1])\n grid[i][j-1] = 2\n\n count += 1\n \n\n for row in grid:\n for col in row:\n if col == 1:\n return -1\n \n\n return count if count >= 0 else 0\n\n\n\n``` | 2 | There is a 1 million by 1 million grid on an XY-plane, and the coordinates of each grid square are `(x, y)`.
We start at the `source = [sx, sy]` square and want to reach the `target = [tx, ty]` square. There is also an array of `blocked` squares, where each `blocked[i] = [xi, yi]` represents a blocked square with coordinates `(xi, yi)`.
Each move, we can walk one square north, east, south, or west if the square is **not** in the array of `blocked` squares. We are also not allowed to walk outside of the grid.
Return `true` _if and only if it is possible to reach the_ `target` _square from the_ `source` _square through a sequence of valid moves_.
**Example 1:**
**Input:** blocked = \[\[0,1\],\[1,0\]\], source = \[0,0\], target = \[0,2\]
**Output:** false
**Explanation:** The target square is inaccessible starting from the source square because we cannot move.
We cannot move north or east because those squares are blocked.
We cannot move south or west because we cannot go outside of the grid.
**Example 2:**
**Input:** blocked = \[\], source = \[0,0\], target = \[999999,999999\]
**Output:** true
**Explanation:** Because there are no blocked cells, it is possible to reach the target square.
**Constraints:**
* `0 <= blocked.length <= 200`
* `blocked[i].length == 2`
* `0 <= xi, yi < 106`
* `source.length == target.length == 2`
* `0 <= sx, sy, tx, ty < 106`
* `source != target`
* It is guaranteed that `source` and `target` are not blocked. | null |
DFS Solution | Explained in figures | Python | rotting-oranges | 0 | 1 | # Approach\nCreate a 2D array called `rotten_time` that holds the numebr of minutes that a orange will be rotted.\n\n\n<table align="center">\n <tr align="center"><td colspan="5">grid</td></tr>\n <tr>\n <td align="center">1</td>\n <td align="center">1</td>\n <td align="center">1</td>\n <td align="center">1</td>\n <td align="center">2</td>\n </tr>\n <tr>\n <td align="center">2</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">1</td>\n <td align="center">1</td>\n </tr>\n <tr>\n <td align="center">1</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">1</td>\n </tr>\n</table>\n\n* Initiate `rotten_time` array filled with zeros\n<table align="center">\n <tr align="center"><td colspan="5">rotten_time</td></tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n </tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n </tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n </tr>\n</table>\n\n* Execute DFS on all rotten oranges, update the `rotten_time` array and add 1 each level down. Stop if an empty cell or a rotten orange is found.\n* To reduce time, we can stop at these cases:\n * If there is already a less value in the `rotten_time`, that means the reached orange is already rottened from another rottened orange.\n * If another rotten oragne was reached, no need to continue.\n<table align="center">\n <tr align="center"><td colspan="5">rotten_time</td></tr>\n <tr>\n <td align="center" style="background-color: #ffa50010">4</td>\n <td align="center" style="background-color: #ffa50020">3</td>\n <td align="center" style="background-color: #ffa50040">2</td>\n <td align="center" style="background-color: #ffa50060">1</td>\n <td align="center" style="background-color: #ffa50090">0</td>\n </tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center" style="background-color: #ffa50030">2</td>\n <td align="center" style="background-color: #ffa50050">1</td>\n </tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center" style="background-color: #ffa50030">2</td>\n </tr>\n</table>\n\n* While updating the values, if an orange already was rottened, we update the time for the minimum one \n<table align="center">\n <tr align="center"><td colspan="5">rotten_time</td></tr>\n <tr>\n <td align="center" style="background-color: #ffa50060">1</td>\n <td align="center" style="background-color: #ffa50040">2</td>\n <td align="center">2</td>\n <td align="center">1</td>\n <td align="center">0</td>\n </tr>\n <tr>\n <td align="center" style="background-color: #ffa50090">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">2</td>\n <td align="center">1</td>\n </tr>\n <tr>\n <td align="center" style="background-color: #ffa50060">1</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">2</td>\n </tr>\n</table>\n\n* If there are any fresh oranges with no rotten_time, that means that the fruits cannot all be rotted. So `return -1`.\n* Otherwise the **maxiumum number** in the `rotten_time` array indicates the **minimum minutes** that all oranges will be rotted.\n\n# Complexity\n- Time complexity: $$O(mn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(mn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dfs(self, rotten_after, grid, row, col):\n if (col < len(grid[0]) - 1 and grid[row][col + 1] == 1):\n if (rotten_after[row][col + 1] == 0 or rotten_after[row][col + 1] > rotten_after[row][col] + 1):\n rotten_after[row][col + 1] = rotten_after[row][col] + 1\n self.dfs(rotten_after, grid, row, col+1)\n \n if (col > 0 and grid[row][col - 1] == 1):\n if (rotten_after[row][col - 1] == 0 or rotten_after[row][col - 1] > rotten_after[row][col] + 1):\n rotten_after[row][col - 1] = rotten_after[row][col] + 1\n self.dfs(rotten_after, grid, row, col-1)\n \n if (row < len(grid) - 1 and grid[row + 1][col] == 1):\n if (rotten_after[row + 1][col] == 0 or rotten_after[row + 1][col] > rotten_after[row][col] + 1):\n rotten_after[row + 1][col] = rotten_after[row][col] + 1\n self.dfs(rotten_after, grid, row+1, col)\n \n if (row > 0 and grid[row - 1][col] == 1):\n if (rotten_after[row - 1][col] == 0 or rotten_after[row - 1][col] > rotten_after[row][col] + 1):\n rotten_after[row - 1][col] = rotten_after[row][col] + 1\n self.dfs(rotten_after, grid, row-1, col)\n \n def orangesRotting(self, grid: List[List[int]]) -> int:\n # Get rows number\n rows = len(grid)\n if rows == 0:\n return -1\n \n # Get columns number\n cols = len(grid[0])\n\n # Define rotten_after\n rotten_after = [[0] * cols for _ in range(rows)]\n \n # Execute DFS for all rotten oranges\n for row in range(rows):\n for col in range(cols):\n if grid[row][col] == 2:\n self.dfs(rotten_after, grid, row, col)\n\n # Check if there are any fresh oranges left, if so return -1\n for row in range(rows):\n for col in range(cols):\n if grid[row][col] == 1 and rotten_after[row][col] == 0:\n return -1\n\n # Get the maximum time in the rotten_after array\n res = -1\n for row in range(rows):\n for col in range(cols):\n res = max(res, rotten_after[row][col])\n\n return res\n\n\n``` | 1 | You are given an `m x n` `grid` where each cell can have one of three values:
* `0` representing an empty cell,
* `1` representing a fresh orange, or
* `2` representing a rotten orange.
Every minute, any fresh orange that is **4-directionally adjacent** to a rotten orange becomes rotten.
Return _the minimum number of minutes that must elapse until no cell has a fresh orange_. If _this is impossible, return_ `-1`.
**Example 1:**
**Input:** grid = \[\[2,1,1\],\[1,1,0\],\[0,1,1\]\]
**Output:** 4
**Example 2:**
**Input:** grid = \[\[2,1,1\],\[0,1,1\],\[1,0,1\]\]
**Output:** -1
**Explanation:** The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
**Example 3:**
**Input:** grid = \[\[0,2\]\]
**Output:** 0
**Explanation:** Since there are already no fresh oranges at minute 0, the answer is just 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 10`
* `grid[i][j]` is `0`, `1`, or `2`. | null |
DFS Solution | Explained in figures | Python | rotting-oranges | 0 | 1 | # Approach\nCreate a 2D array called `rotten_time` that holds the numebr of minutes that a orange will be rotted.\n\n\n<table align="center">\n <tr align="center"><td colspan="5">grid</td></tr>\n <tr>\n <td align="center">1</td>\n <td align="center">1</td>\n <td align="center">1</td>\n <td align="center">1</td>\n <td align="center">2</td>\n </tr>\n <tr>\n <td align="center">2</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">1</td>\n <td align="center">1</td>\n </tr>\n <tr>\n <td align="center">1</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">1</td>\n </tr>\n</table>\n\n* Initiate `rotten_time` array filled with zeros\n<table align="center">\n <tr align="center"><td colspan="5">rotten_time</td></tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n </tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n </tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n </tr>\n</table>\n\n* Execute DFS on all rotten oranges, update the `rotten_time` array and add 1 each level down. Stop if an empty cell or a rotten orange is found.\n* To reduce time, we can stop at these cases:\n * If there is already a less value in the `rotten_time`, that means the reached orange is already rottened from another rottened orange.\n * If another rotten oragne was reached, no need to continue.\n<table align="center">\n <tr align="center"><td colspan="5">rotten_time</td></tr>\n <tr>\n <td align="center" style="background-color: #ffa50010">4</td>\n <td align="center" style="background-color: #ffa50020">3</td>\n <td align="center" style="background-color: #ffa50040">2</td>\n <td align="center" style="background-color: #ffa50060">1</td>\n <td align="center" style="background-color: #ffa50090">0</td>\n </tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center" style="background-color: #ffa50030">2</td>\n <td align="center" style="background-color: #ffa50050">1</td>\n </tr>\n <tr>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center" style="background-color: #ffa50030">2</td>\n </tr>\n</table>\n\n* While updating the values, if an orange already was rottened, we update the time for the minimum one \n<table align="center">\n <tr align="center"><td colspan="5">rotten_time</td></tr>\n <tr>\n <td align="center" style="background-color: #ffa50060">1</td>\n <td align="center" style="background-color: #ffa50040">2</td>\n <td align="center">2</td>\n <td align="center">1</td>\n <td align="center">0</td>\n </tr>\n <tr>\n <td align="center" style="background-color: #ffa50090">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">2</td>\n <td align="center">1</td>\n </tr>\n <tr>\n <td align="center" style="background-color: #ffa50060">1</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">0</td>\n <td align="center">2</td>\n </tr>\n</table>\n\n* If there are any fresh oranges with no rotten_time, that means that the fruits cannot all be rotted. So `return -1`.\n* Otherwise the **maxiumum number** in the `rotten_time` array indicates the **minimum minutes** that all oranges will be rotted.\n\n# Complexity\n- Time complexity: $$O(mn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(mn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def dfs(self, rotten_after, grid, row, col):\n if (col < len(grid[0]) - 1 and grid[row][col + 1] == 1):\n if (rotten_after[row][col + 1] == 0 or rotten_after[row][col + 1] > rotten_after[row][col] + 1):\n rotten_after[row][col + 1] = rotten_after[row][col] + 1\n self.dfs(rotten_after, grid, row, col+1)\n \n if (col > 0 and grid[row][col - 1] == 1):\n if (rotten_after[row][col - 1] == 0 or rotten_after[row][col - 1] > rotten_after[row][col] + 1):\n rotten_after[row][col - 1] = rotten_after[row][col] + 1\n self.dfs(rotten_after, grid, row, col-1)\n \n if (row < len(grid) - 1 and grid[row + 1][col] == 1):\n if (rotten_after[row + 1][col] == 0 or rotten_after[row + 1][col] > rotten_after[row][col] + 1):\n rotten_after[row + 1][col] = rotten_after[row][col] + 1\n self.dfs(rotten_after, grid, row+1, col)\n \n if (row > 0 and grid[row - 1][col] == 1):\n if (rotten_after[row - 1][col] == 0 or rotten_after[row - 1][col] > rotten_after[row][col] + 1):\n rotten_after[row - 1][col] = rotten_after[row][col] + 1\n self.dfs(rotten_after, grid, row-1, col)\n \n def orangesRotting(self, grid: List[List[int]]) -> int:\n # Get rows number\n rows = len(grid)\n if rows == 0:\n return -1\n \n # Get columns number\n cols = len(grid[0])\n\n # Define rotten_after\n rotten_after = [[0] * cols for _ in range(rows)]\n \n # Execute DFS for all rotten oranges\n for row in range(rows):\n for col in range(cols):\n if grid[row][col] == 2:\n self.dfs(rotten_after, grid, row, col)\n\n # Check if there are any fresh oranges left, if so return -1\n for row in range(rows):\n for col in range(cols):\n if grid[row][col] == 1 and rotten_after[row][col] == 0:\n return -1\n\n # Get the maximum time in the rotten_after array\n res = -1\n for row in range(rows):\n for col in range(cols):\n res = max(res, rotten_after[row][col])\n\n return res\n\n\n``` | 1 | There is a 1 million by 1 million grid on an XY-plane, and the coordinates of each grid square are `(x, y)`.
We start at the `source = [sx, sy]` square and want to reach the `target = [tx, ty]` square. There is also an array of `blocked` squares, where each `blocked[i] = [xi, yi]` represents a blocked square with coordinates `(xi, yi)`.
Each move, we can walk one square north, east, south, or west if the square is **not** in the array of `blocked` squares. We are also not allowed to walk outside of the grid.
Return `true` _if and only if it is possible to reach the_ `target` _square from the_ `source` _square through a sequence of valid moves_.
**Example 1:**
**Input:** blocked = \[\[0,1\],\[1,0\]\], source = \[0,0\], target = \[0,2\]
**Output:** false
**Explanation:** The target square is inaccessible starting from the source square because we cannot move.
We cannot move north or east because those squares are blocked.
We cannot move south or west because we cannot go outside of the grid.
**Example 2:**
**Input:** blocked = \[\], source = \[0,0\], target = \[999999,999999\]
**Output:** true
**Explanation:** Because there are no blocked cells, it is possible to reach the target square.
**Constraints:**
* `0 <= blocked.length <= 200`
* `blocked[i].length == 2`
* `0 <= xi, yi < 106`
* `source.length == target.length == 2`
* `0 <= sx, sy, tx, ty < 106`
* `source != target`
* It is guaranteed that `source` and `target` are not blocked. | null |
✅[Python] Simple and Clean, beats 88%✅ | rotting-oranges | 0 | 1 | ### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n*This is an NFT*\n\n# Intuition\nThe problem asks us to find the minimum number of minutes that must elapse until no cell has a fresh orange. Intuitively, we can think of this problem as a breadth-first search (BFS) problem where we start from all rotten oranges and spread the rot to fresh oranges in all four directions.\n\n# Approach\n1. Create a `deque` called `queue` to store the positions of rotten oranges.\n2. Initialize variables `n` and `m` to the dimensions of the grid.\n3. Initialize variables `count` and `time` to `0` and `-1`, respectively.\n4. Initialize a list `dirs` with the four directions: up, down, left, and right.\n5. Iterate through the grid and for each fresh orange, increment `count` by 1. For each rotten orange, append its position to `queue`.\n6. While `queue` is not empty:\n 1. Create an empty list `rotten`.\n 2. Dequeue all elements from `queue` and append them to `rotten`.\n 3. For each orange in `rotten`, spread the rot to fresh oranges in all four directions. Decrement `count` by 1 for each fresh orange that becomes rotten and append its position to `queue`.\n 4. Increment `time` by 1.\n7. If `count` is 0, return the maximum of `time` and 0. Otherwise, return -1.\n\n# Complexity\n- Time complexity: $$O(nm)$$ where `n` is the number of rows and `m` is the number of columns in the grid.\n- Space complexity: $$O(nm)$$ where `n` is the number of rows and `m` is the number of columns in the grid.\n\n# Code\n```\nclass Solution:\n def orangesRotting(self, grid: List[List[int]]) -> int:\n queue = deque()\n n,m = len(grid),len(grid[0])\n count, time = 0, -1\n dirs = [(1,0),(0,1),(-1,0),(0,-1)]\n for i in range(n):\n for j in range(m):\n if grid[i][j]==1:\n count+=1\n elif grid[i][j]==2:\n queue.append((i,j))\n while len(queue)>0:\n rotten = []\n while len(queue)>0:\n rotten.append(queue.popleft())\n for orange in rotten:\n i,j = orange\n for a,b in dirs:\n new_i, new_j = i+a, j+b\n if 0<=new_i<n and 0<=new_j<m and grid[new_i][new_j]==1:\n count-=1\n grid[new_i][new_j]=2\n queue.append((new_i,new_j))\n time+=1\n if not count:\n return max(time,0)\n else:\n return -1\n``` | 1 | You are given an `m x n` `grid` where each cell can have one of three values:
* `0` representing an empty cell,
* `1` representing a fresh orange, or
* `2` representing a rotten orange.
Every minute, any fresh orange that is **4-directionally adjacent** to a rotten orange becomes rotten.
Return _the minimum number of minutes that must elapse until no cell has a fresh orange_. If _this is impossible, return_ `-1`.
**Example 1:**
**Input:** grid = \[\[2,1,1\],\[1,1,0\],\[0,1,1\]\]
**Output:** 4
**Example 2:**
**Input:** grid = \[\[2,1,1\],\[0,1,1\],\[1,0,1\]\]
**Output:** -1
**Explanation:** The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
**Example 3:**
**Input:** grid = \[\[0,2\]\]
**Output:** 0
**Explanation:** Since there are already no fresh oranges at minute 0, the answer is just 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 10`
* `grid[i][j]` is `0`, `1`, or `2`. | null |
✅[Python] Simple and Clean, beats 88%✅ | rotting-oranges | 0 | 1 | ### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n*This is an NFT*\n\n# Intuition\nThe problem asks us to find the minimum number of minutes that must elapse until no cell has a fresh orange. Intuitively, we can think of this problem as a breadth-first search (BFS) problem where we start from all rotten oranges and spread the rot to fresh oranges in all four directions.\n\n# Approach\n1. Create a `deque` called `queue` to store the positions of rotten oranges.\n2. Initialize variables `n` and `m` to the dimensions of the grid.\n3. Initialize variables `count` and `time` to `0` and `-1`, respectively.\n4. Initialize a list `dirs` with the four directions: up, down, left, and right.\n5. Iterate through the grid and for each fresh orange, increment `count` by 1. For each rotten orange, append its position to `queue`.\n6. While `queue` is not empty:\n 1. Create an empty list `rotten`.\n 2. Dequeue all elements from `queue` and append them to `rotten`.\n 3. For each orange in `rotten`, spread the rot to fresh oranges in all four directions. Decrement `count` by 1 for each fresh orange that becomes rotten and append its position to `queue`.\n 4. Increment `time` by 1.\n7. If `count` is 0, return the maximum of `time` and 0. Otherwise, return -1.\n\n# Complexity\n- Time complexity: $$O(nm)$$ where `n` is the number of rows and `m` is the number of columns in the grid.\n- Space complexity: $$O(nm)$$ where `n` is the number of rows and `m` is the number of columns in the grid.\n\n# Code\n```\nclass Solution:\n def orangesRotting(self, grid: List[List[int]]) -> int:\n queue = deque()\n n,m = len(grid),len(grid[0])\n count, time = 0, -1\n dirs = [(1,0),(0,1),(-1,0),(0,-1)]\n for i in range(n):\n for j in range(m):\n if grid[i][j]==1:\n count+=1\n elif grid[i][j]==2:\n queue.append((i,j))\n while len(queue)>0:\n rotten = []\n while len(queue)>0:\n rotten.append(queue.popleft())\n for orange in rotten:\n i,j = orange\n for a,b in dirs:\n new_i, new_j = i+a, j+b\n if 0<=new_i<n and 0<=new_j<m and grid[new_i][new_j]==1:\n count-=1\n grid[new_i][new_j]=2\n queue.append((new_i,new_j))\n time+=1\n if not count:\n return max(time,0)\n else:\n return -1\n``` | 1 | There is a 1 million by 1 million grid on an XY-plane, and the coordinates of each grid square are `(x, y)`.
We start at the `source = [sx, sy]` square and want to reach the `target = [tx, ty]` square. There is also an array of `blocked` squares, where each `blocked[i] = [xi, yi]` represents a blocked square with coordinates `(xi, yi)`.
Each move, we can walk one square north, east, south, or west if the square is **not** in the array of `blocked` squares. We are also not allowed to walk outside of the grid.
Return `true` _if and only if it is possible to reach the_ `target` _square from the_ `source` _square through a sequence of valid moves_.
**Example 1:**
**Input:** blocked = \[\[0,1\],\[1,0\]\], source = \[0,0\], target = \[0,2\]
**Output:** false
**Explanation:** The target square is inaccessible starting from the source square because we cannot move.
We cannot move north or east because those squares are blocked.
We cannot move south or west because we cannot go outside of the grid.
**Example 2:**
**Input:** blocked = \[\], source = \[0,0\], target = \[999999,999999\]
**Output:** true
**Explanation:** Because there are no blocked cells, it is possible to reach the target square.
**Constraints:**
* `0 <= blocked.length <= 200`
* `blocked[i].length == 2`
* `0 <= xi, yi < 106`
* `source.length == target.length == 2`
* `0 <= sx, sy, tx, ty < 106`
* `source != target`
* It is guaranteed that `source` and `target` are not blocked. | null |
Solution | minimum-number-of-k-consecutive-bit-flips | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minKBitFlips(vector<int>& A, int K) {\n int cur = 0, res = 0, n = A.size();\n for (int i = 0; i < n; ++i) {\n if (i >= K && A[i - K] > 1) {\n cur--;\n A[i - K] -= 2;\n }\n if (cur % 2 == A[i]) {\n if (i + K > n) return -1;\n A[i] += 2;\n cur++;\n res++;\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n n=len(nums)\n x=0\n f=[0]*n\n\n for idx,val in enumerate(nums):\n if idx>=k:\n x^=f[idx-k]\n if x!=val:\n continue\n if k>n-idx:\n return -1\n x^=1\n f[idx]=1\n \n return sum(f)\n```\n\n```Java []\nclass Solution {\n public int minKBitFlips(int[] A, int K) {\n int n = A.length, flipped = 0, res = 0;\n int[] isFlipped = new int[n];\n for (int i = 0; i < A.length; ++i) {\n if (i >= K)\n flipped ^= isFlipped[i - K];\n if (flipped == A[i]) {\n if (i + K > A.length)\n return -1;\n isFlipped[i] = 1;\n flipped ^= 1;\n res++;\n }\n }\n return res;\n }\n}\n```\n | 1 | You are given a binary array `nums` and an integer `k`.
A **k-bit flip** is choosing a **subarray** of length `k` from `nums` and simultaneously changing every `0` in the subarray to `1`, and every `1` in the subarray to `0`.
Return _the minimum number of **k-bit flips** required so that there is no_ `0` _in the array_. If it is not possible, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,1,0\], k = 1
**Output:** 2
**Explanation:** Flip nums\[0\], then flip nums\[2\].
**Example 2:**
**Input:** nums = \[1,1,0\], k = 2
**Output:** -1
**Explanation:** No matter how we flip subarrays of size 2, we cannot make the array become \[1,1,1\].
**Example 3:**
**Input:** nums = \[0,0,0,1,0,1,1,0\], k = 3
**Output:** 3
**Explanation:**
Flip nums\[0\],nums\[1\],nums\[2\]: nums becomes \[1,1,1,1,0,1,1,0\]
Flip nums\[4\],nums\[5\],nums\[6\]: nums becomes \[1,1,1,1,1,0,0,0\]
Flip nums\[5\],nums\[6\],nums\[7\]: nums becomes \[1,1,1,1,1,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= k <= nums.length` | null |
Solution | minimum-number-of-k-consecutive-bit-flips | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int minKBitFlips(vector<int>& A, int K) {\n int cur = 0, res = 0, n = A.size();\n for (int i = 0; i < n; ++i) {\n if (i >= K && A[i - K] > 1) {\n cur--;\n A[i - K] -= 2;\n }\n if (cur % 2 == A[i]) {\n if (i + K > n) return -1;\n A[i] += 2;\n cur++;\n res++;\n }\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n n=len(nums)\n x=0\n f=[0]*n\n\n for idx,val in enumerate(nums):\n if idx>=k:\n x^=f[idx-k]\n if x!=val:\n continue\n if k>n-idx:\n return -1\n x^=1\n f[idx]=1\n \n return sum(f)\n```\n\n```Java []\nclass Solution {\n public int minKBitFlips(int[] A, int K) {\n int n = A.length, flipped = 0, res = 0;\n int[] isFlipped = new int[n];\n for (int i = 0; i < A.length; ++i) {\n if (i >= K)\n flipped ^= isFlipped[i - K];\n if (flipped == A[i]) {\n if (i + K > A.length)\n return -1;\n isFlipped[i] = 1;\n flipped ^= 1;\n res++;\n }\n }\n return res;\n }\n}\n```\n | 1 | Given an array `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return `true` _if these points are a **boomerang**_.
A **boomerang** is a set of three points that are **all distinct** and **not in a straight line**.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,3\],\[3,2\]\]
**Output:** true
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** false
**Constraints:**
* `points.length == 3`
* `points[i].length == 2`
* `0 <= xi, yi <= 100` | null |
Python 3 || 8 lines, accumulate, w/ explanation || T/M: 98% / 100% | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | Here\'s the plan:\n\nAs we iterate`nums`, we want to change zeros to ones and leave ones unchanged. Let\'s call zero the *change-digit* in this case.\n\nWhen we flip digits in the *flip interval*`nums[i:i+k]`, those digits that were initially one are now zero, and or equivalently, if we treat one as the change-digit (call it`toggle`) in the flip-interval we can avoid actually flipping the digits and just keep track of flip-intervals and the current change-digit.\n\nWhat makes it interesting is that when we hit a change-digit in in a flip-interval, we have to switch the change-digit again, and so on until we hit the end of`nums`.\n\nThus, the problem is reduced to counting the number of times the change-digit flips, which we do in`acc`. It\'s much like a`prefix`or`accumulate`structure.\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n\n acc, toggle = [0] * len(nums), 0\n\n for idx, num in enumerate(nums):\n \n if idx >= k: toggle ^= acc[idx -k] # <-- toggle change-digit if we leave a flip interval\n\n if toggle != num: continue # <-- num is not a change digit\n\n if k > len(nums)-idx: return -1 # <-- num is a change digit but we can\'t flip anymore\n\n toggle ^= 1 # <-- num is a change-digit we can flip, so toggle\n acc[idx] = 1 # the change-digit and record it in acc.\n\n return sum(acc) # <-- return the number of flips\n```\n[https://leetcode.com/problems/minimum-number-of-k-consecutive-bit-flips/submissions/885902920/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(N). | 5 | You are given a binary array `nums` and an integer `k`.
A **k-bit flip** is choosing a **subarray** of length `k` from `nums` and simultaneously changing every `0` in the subarray to `1`, and every `1` in the subarray to `0`.
Return _the minimum number of **k-bit flips** required so that there is no_ `0` _in the array_. If it is not possible, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,1,0\], k = 1
**Output:** 2
**Explanation:** Flip nums\[0\], then flip nums\[2\].
**Example 2:**
**Input:** nums = \[1,1,0\], k = 2
**Output:** -1
**Explanation:** No matter how we flip subarrays of size 2, we cannot make the array become \[1,1,1\].
**Example 3:**
**Input:** nums = \[0,0,0,1,0,1,1,0\], k = 3
**Output:** 3
**Explanation:**
Flip nums\[0\],nums\[1\],nums\[2\]: nums becomes \[1,1,1,1,0,1,1,0\]
Flip nums\[4\],nums\[5\],nums\[6\]: nums becomes \[1,1,1,1,1,0,0,0\]
Flip nums\[5\],nums\[6\],nums\[7\]: nums becomes \[1,1,1,1,1,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= k <= nums.length` | null |
Python 3 || 8 lines, accumulate, w/ explanation || T/M: 98% / 100% | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | Here\'s the plan:\n\nAs we iterate`nums`, we want to change zeros to ones and leave ones unchanged. Let\'s call zero the *change-digit* in this case.\n\nWhen we flip digits in the *flip interval*`nums[i:i+k]`, those digits that were initially one are now zero, and or equivalently, if we treat one as the change-digit (call it`toggle`) in the flip-interval we can avoid actually flipping the digits and just keep track of flip-intervals and the current change-digit.\n\nWhat makes it interesting is that when we hit a change-digit in in a flip-interval, we have to switch the change-digit again, and so on until we hit the end of`nums`.\n\nThus, the problem is reduced to counting the number of times the change-digit flips, which we do in`acc`. It\'s much like a`prefix`or`accumulate`structure.\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n\n acc, toggle = [0] * len(nums), 0\n\n for idx, num in enumerate(nums):\n \n if idx >= k: toggle ^= acc[idx -k] # <-- toggle change-digit if we leave a flip interval\n\n if toggle != num: continue # <-- num is not a change digit\n\n if k > len(nums)-idx: return -1 # <-- num is a change digit but we can\'t flip anymore\n\n toggle ^= 1 # <-- num is a change-digit we can flip, so toggle\n acc[idx] = 1 # the change-digit and record it in acc.\n\n return sum(acc) # <-- return the number of flips\n```\n[https://leetcode.com/problems/minimum-number-of-k-consecutive-bit-flips/submissions/885902920/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(N). | 5 | Given an array `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return `true` _if these points are a **boomerang**_.
A **boomerang** is a set of three points that are **all distinct** and **not in a straight line**.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,3\],\[3,2\]\]
**Output:** true
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** false
**Constraints:**
* `points.length == 3`
* `points[i].length == 2`
* `0 <= xi, yi <= 100` | null |
sliding windows + greedy | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n\n\n ans = 0\n current = 0\n flips = [False] * len(nums)\n for i in range(len(nums)):\n if flips[i]:\n current ^=1\n if current ^ nums[i] == 0:\n\n ans += 1\n current ^= 1\n if i + k > len(nums):\n return -1\n if i + k < len(nums):\n flips[i+k] = True \n return ans\n``` | 0 | You are given a binary array `nums` and an integer `k`.
A **k-bit flip** is choosing a **subarray** of length `k` from `nums` and simultaneously changing every `0` in the subarray to `1`, and every `1` in the subarray to `0`.
Return _the minimum number of **k-bit flips** required so that there is no_ `0` _in the array_. If it is not possible, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,1,0\], k = 1
**Output:** 2
**Explanation:** Flip nums\[0\], then flip nums\[2\].
**Example 2:**
**Input:** nums = \[1,1,0\], k = 2
**Output:** -1
**Explanation:** No matter how we flip subarrays of size 2, we cannot make the array become \[1,1,1\].
**Example 3:**
**Input:** nums = \[0,0,0,1,0,1,1,0\], k = 3
**Output:** 3
**Explanation:**
Flip nums\[0\],nums\[1\],nums\[2\]: nums becomes \[1,1,1,1,0,1,1,0\]
Flip nums\[4\],nums\[5\],nums\[6\]: nums becomes \[1,1,1,1,1,0,0,0\]
Flip nums\[5\],nums\[6\],nums\[7\]: nums becomes \[1,1,1,1,1,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= k <= nums.length` | null |
sliding windows + greedy | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n\n\n ans = 0\n current = 0\n flips = [False] * len(nums)\n for i in range(len(nums)):\n if flips[i]:\n current ^=1\n if current ^ nums[i] == 0:\n\n ans += 1\n current ^= 1\n if i + k > len(nums):\n return -1\n if i + k < len(nums):\n flips[i+k] = True \n return ans\n``` | 0 | Given an array `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return `true` _if these points are a **boomerang**_.
A **boomerang** is a set of three points that are **all distinct** and **not in a straight line**.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,3\],\[3,2\]\]
**Output:** true
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** false
**Constraints:**
* `points.length == 3`
* `points[i].length == 2`
* `0 <= xi, yi <= 100` | null |
✅sliding window || prefix || python | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | \n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n n=len(nums)\n ans=0\n arr=[0 for i in range(n)]\n for i in range(n):\n if(i>n-k):\n arr[i]=(arr[i]+arr[i-1])%2\n if((nums[i]==0 and arr[i]==0)or(nums[i]==1 and arr[i]==1)):return -1\n elif(i==0):\n if(nums[i]==0):\n arr[i]+=1\n if(i+k<n):arr[i+k]-=1\n ans+=1\n else:\n arr[i]=(arr[i]+arr[i-1])%2\n if((nums[i]==0 and arr[i]==1)or(nums[i]==1 and arr[i]==0)):continue\n ans+=1\n arr[i]+=1\n if(i+k<n):arr[i+k]-=1\n return ans\n\n\n\n \n``` | 0 | You are given a binary array `nums` and an integer `k`.
A **k-bit flip** is choosing a **subarray** of length `k` from `nums` and simultaneously changing every `0` in the subarray to `1`, and every `1` in the subarray to `0`.
Return _the minimum number of **k-bit flips** required so that there is no_ `0` _in the array_. If it is not possible, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,1,0\], k = 1
**Output:** 2
**Explanation:** Flip nums\[0\], then flip nums\[2\].
**Example 2:**
**Input:** nums = \[1,1,0\], k = 2
**Output:** -1
**Explanation:** No matter how we flip subarrays of size 2, we cannot make the array become \[1,1,1\].
**Example 3:**
**Input:** nums = \[0,0,0,1,0,1,1,0\], k = 3
**Output:** 3
**Explanation:**
Flip nums\[0\],nums\[1\],nums\[2\]: nums becomes \[1,1,1,1,0,1,1,0\]
Flip nums\[4\],nums\[5\],nums\[6\]: nums becomes \[1,1,1,1,1,0,0,0\]
Flip nums\[5\],nums\[6\],nums\[7\]: nums becomes \[1,1,1,1,1,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= k <= nums.length` | null |
✅sliding window || prefix || python | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | \n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n n=len(nums)\n ans=0\n arr=[0 for i in range(n)]\n for i in range(n):\n if(i>n-k):\n arr[i]=(arr[i]+arr[i-1])%2\n if((nums[i]==0 and arr[i]==0)or(nums[i]==1 and arr[i]==1)):return -1\n elif(i==0):\n if(nums[i]==0):\n arr[i]+=1\n if(i+k<n):arr[i+k]-=1\n ans+=1\n else:\n arr[i]=(arr[i]+arr[i-1])%2\n if((nums[i]==0 and arr[i]==1)or(nums[i]==1 and arr[i]==0)):continue\n ans+=1\n arr[i]+=1\n if(i+k<n):arr[i+k]-=1\n return ans\n\n\n\n \n``` | 0 | Given an array `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return `true` _if these points are a **boomerang**_.
A **boomerang** is a set of three points that are **all distinct** and **not in a straight line**.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,3\],\[3,2\]\]
**Output:** true
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** false
**Constraints:**
* `points.length == 3`
* `points[i].length == 2`
* `0 <= xi, yi <= 100` | null |
Python O(n) Solution | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n f = [0] * len(nums)\n psum = 0\n for i in range(len(nums)-k+1):\n if (psum + nums[i])%2 == 0:\n f[i] = 1\n psum += f[i]\n if i-k+1 >= 0:\n psum -= f[i-k+1]\n for i in range(len(nums)-k+1, len(nums)):\n if (psum+nums[i])%2 == 0:\n return -1\n if i-k+1 >= 0:\n psum -= f[i-k+1] \n return sum(f)\n\n``` | 0 | You are given a binary array `nums` and an integer `k`.
A **k-bit flip** is choosing a **subarray** of length `k` from `nums` and simultaneously changing every `0` in the subarray to `1`, and every `1` in the subarray to `0`.
Return _the minimum number of **k-bit flips** required so that there is no_ `0` _in the array_. If it is not possible, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,1,0\], k = 1
**Output:** 2
**Explanation:** Flip nums\[0\], then flip nums\[2\].
**Example 2:**
**Input:** nums = \[1,1,0\], k = 2
**Output:** -1
**Explanation:** No matter how we flip subarrays of size 2, we cannot make the array become \[1,1,1\].
**Example 3:**
**Input:** nums = \[0,0,0,1,0,1,1,0\], k = 3
**Output:** 3
**Explanation:**
Flip nums\[0\],nums\[1\],nums\[2\]: nums becomes \[1,1,1,1,0,1,1,0\]
Flip nums\[4\],nums\[5\],nums\[6\]: nums becomes \[1,1,1,1,1,0,0,0\]
Flip nums\[5\],nums\[6\],nums\[7\]: nums becomes \[1,1,1,1,1,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= k <= nums.length` | null |
Python O(n) Solution | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n f = [0] * len(nums)\n psum = 0\n for i in range(len(nums)-k+1):\n if (psum + nums[i])%2 == 0:\n f[i] = 1\n psum += f[i]\n if i-k+1 >= 0:\n psum -= f[i-k+1]\n for i in range(len(nums)-k+1, len(nums)):\n if (psum+nums[i])%2 == 0:\n return -1\n if i-k+1 >= 0:\n psum -= f[i-k+1] \n return sum(f)\n\n``` | 0 | Given an array `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return `true` _if these points are a **boomerang**_.
A **boomerang** is a set of three points that are **all distinct** and **not in a straight line**.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,3\],\[3,2\]\]
**Output:** true
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** false
**Constraints:**
* `points.length == 3`
* `points[i].length == 2`
* `0 <= xi, yi <= 100` | null |
Python | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n n = len(nums)\n flips = 0\n if nums[0] == 0:\n for i in range(k):\n nums[i] = 1 - nums[i]\n flips += 1\n \n diff = [abs(nums[i+1] - nums[i]) for i in range(n-1)]\n\n for i in range(n-k):\n if diff[i] == 1:\n flips += 1\n \n if i < n-k-1:\n diff[i+k] = 1- diff[i+k]\n \n\n if 1 in diff[n-k:]:\n return -1\n return flips\n\n\n``` | 0 | You are given a binary array `nums` and an integer `k`.
A **k-bit flip** is choosing a **subarray** of length `k` from `nums` and simultaneously changing every `0` in the subarray to `1`, and every `1` in the subarray to `0`.
Return _the minimum number of **k-bit flips** required so that there is no_ `0` _in the array_. If it is not possible, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,1,0\], k = 1
**Output:** 2
**Explanation:** Flip nums\[0\], then flip nums\[2\].
**Example 2:**
**Input:** nums = \[1,1,0\], k = 2
**Output:** -1
**Explanation:** No matter how we flip subarrays of size 2, we cannot make the array become \[1,1,1\].
**Example 3:**
**Input:** nums = \[0,0,0,1,0,1,1,0\], k = 3
**Output:** 3
**Explanation:**
Flip nums\[0\],nums\[1\],nums\[2\]: nums becomes \[1,1,1,1,0,1,1,0\]
Flip nums\[4\],nums\[5\],nums\[6\]: nums becomes \[1,1,1,1,1,0,0,0\]
Flip nums\[5\],nums\[6\],nums\[7\]: nums becomes \[1,1,1,1,1,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= k <= nums.length` | null |
Python | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n n = len(nums)\n flips = 0\n if nums[0] == 0:\n for i in range(k):\n nums[i] = 1 - nums[i]\n flips += 1\n \n diff = [abs(nums[i+1] - nums[i]) for i in range(n-1)]\n\n for i in range(n-k):\n if diff[i] == 1:\n flips += 1\n \n if i < n-k-1:\n diff[i+k] = 1- diff[i+k]\n \n\n if 1 in diff[n-k:]:\n return -1\n return flips\n\n\n``` | 0 | Given an array `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return `true` _if these points are a **boomerang**_.
A **boomerang** is a set of three points that are **all distinct** and **not in a straight line**.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,3\],\[3,2\]\]
**Output:** true
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** false
**Constraints:**
* `points.length == 3`
* `points[i].length == 2`
* `0 <= xi, yi <= 100` | null |
python | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n\n acc, toggle = [0] * len(nums), 0\n\n for idx, num in enumerate(nums):\n \n if idx >= k: toggle ^= acc[idx -k] # <-- toggle change-digit if we leave a flip interval\n\n if toggle != num: continue # <-- num is not a change digit\n\n if k > len(nums)-idx: return -1 # <-- num is a change digit but we can\'t flip anymore\n\n toggle ^= 1 # <-- num is a change-digit we can flip, so toggle\n acc[idx] = 1 # the change-digit and record it in acc.\n\n return sum(acc)\n``` | 0 | You are given a binary array `nums` and an integer `k`.
A **k-bit flip** is choosing a **subarray** of length `k` from `nums` and simultaneously changing every `0` in the subarray to `1`, and every `1` in the subarray to `0`.
Return _the minimum number of **k-bit flips** required so that there is no_ `0` _in the array_. If it is not possible, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,1,0\], k = 1
**Output:** 2
**Explanation:** Flip nums\[0\], then flip nums\[2\].
**Example 2:**
**Input:** nums = \[1,1,0\], k = 2
**Output:** -1
**Explanation:** No matter how we flip subarrays of size 2, we cannot make the array become \[1,1,1\].
**Example 3:**
**Input:** nums = \[0,0,0,1,0,1,1,0\], k = 3
**Output:** 3
**Explanation:**
Flip nums\[0\],nums\[1\],nums\[2\]: nums becomes \[1,1,1,1,0,1,1,0\]
Flip nums\[4\],nums\[5\],nums\[6\]: nums becomes \[1,1,1,1,1,0,0,0\]
Flip nums\[5\],nums\[6\],nums\[7\]: nums becomes \[1,1,1,1,1,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= k <= nums.length` | null |
python | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minKBitFlips(self, nums: List[int], k: int) -> int:\n\n acc, toggle = [0] * len(nums), 0\n\n for idx, num in enumerate(nums):\n \n if idx >= k: toggle ^= acc[idx -k] # <-- toggle change-digit if we leave a flip interval\n\n if toggle != num: continue # <-- num is not a change digit\n\n if k > len(nums)-idx: return -1 # <-- num is a change digit but we can\'t flip anymore\n\n toggle ^= 1 # <-- num is a change-digit we can flip, so toggle\n acc[idx] = 1 # the change-digit and record it in acc.\n\n return sum(acc)\n``` | 0 | Given an array `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return `true` _if these points are a **boomerang**_.
A **boomerang** is a set of three points that are **all distinct** and **not in a straight line**.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,3\],\[3,2\]\]
**Output:** true
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** false
**Constraints:**
* `points.length == 3`
* `points[i].length == 2`
* `0 <= xi, yi <= 100` | null |
Simulation got TLE; so I redefined what is One | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nInstead of toggling `k` elements every time, I chose to toggle `one` and set a reminder to untoggle it `k - 1` steps later.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy \xD7 { Simulation, Bit Manipulation + Toggling `one` }\n\n# Complexity\n| | Gr + Sim | Gr + BitM + Tog |\n|-|:-:|:-:|\n|time|$$O((n-k)k)$$|$$O(n)$$|\n|space|$$O(1)$$|$$O(1)$$|\n\n<!-- - Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nGreedy + Simulation\n\u26A0**TLE**\u2757\n```\nclass Solution:\n def minKBitFlips(self, A: List[int], k: int) -> int:\n n = 0\n for i in range(len(A)-k):\n if A[i] == 0:\n n += 1\n for j in range(i, i+k):\n A[j] ^= 1\n tail = sum(A[-k:])\n if tail == 0:\n return n + 1\n elif tail == k:\n return n\n return -1\n```\n\n\u2193 Greedy + Bit Manipulation + Toggling `one` \u2193\n```\nclass Solution:\n def minKBitFlips(self, A: List[int], k: int) -> int:\n n = 0\n one = 1\n\n t = k - 1\n for i in range(I := len(A)-t):\n if A[i]&1 != one:\n n += 1\n one ^= 1\n A[i+t] |= 2\n if A[i] & 2:\n one ^= 1\n\n for i in range(I, len(A)):\n if A[i]&1 != one:\n return -1\n if A[i] & 2:\n one ^= 1\n\n return n\n``` | 0 | You are given a binary array `nums` and an integer `k`.
A **k-bit flip** is choosing a **subarray** of length `k` from `nums` and simultaneously changing every `0` in the subarray to `1`, and every `1` in the subarray to `0`.
Return _the minimum number of **k-bit flips** required so that there is no_ `0` _in the array_. If it is not possible, return `-1`.
A **subarray** is a **contiguous** part of an array.
**Example 1:**
**Input:** nums = \[0,1,0\], k = 1
**Output:** 2
**Explanation:** Flip nums\[0\], then flip nums\[2\].
**Example 2:**
**Input:** nums = \[1,1,0\], k = 2
**Output:** -1
**Explanation:** No matter how we flip subarrays of size 2, we cannot make the array become \[1,1,1\].
**Example 3:**
**Input:** nums = \[0,0,0,1,0,1,1,0\], k = 3
**Output:** 3
**Explanation:**
Flip nums\[0\],nums\[1\],nums\[2\]: nums becomes \[1,1,1,1,0,1,1,0\]
Flip nums\[4\],nums\[5\],nums\[6\]: nums becomes \[1,1,1,1,1,0,0,0\]
Flip nums\[5\],nums\[6\],nums\[7\]: nums becomes \[1,1,1,1,1,1,1,1\]
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= k <= nums.length` | null |
Simulation got TLE; so I redefined what is One | minimum-number-of-k-consecutive-bit-flips | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nInstead of toggling `k` elements every time, I chose to toggle `one` and set a reminder to untoggle it `k - 1` steps later.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy \xD7 { Simulation, Bit Manipulation + Toggling `one` }\n\n# Complexity\n| | Gr + Sim | Gr + BitM + Tog |\n|-|:-:|:-:|\n|time|$$O((n-k)k)$$|$$O(n)$$|\n|space|$$O(1)$$|$$O(1)$$|\n\n<!-- - Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nGreedy + Simulation\n\u26A0**TLE**\u2757\n```\nclass Solution:\n def minKBitFlips(self, A: List[int], k: int) -> int:\n n = 0\n for i in range(len(A)-k):\n if A[i] == 0:\n n += 1\n for j in range(i, i+k):\n A[j] ^= 1\n tail = sum(A[-k:])\n if tail == 0:\n return n + 1\n elif tail == k:\n return n\n return -1\n```\n\n\u2193 Greedy + Bit Manipulation + Toggling `one` \u2193\n```\nclass Solution:\n def minKBitFlips(self, A: List[int], k: int) -> int:\n n = 0\n one = 1\n\n t = k - 1\n for i in range(I := len(A)-t):\n if A[i]&1 != one:\n n += 1\n one ^= 1\n A[i+t] |= 2\n if A[i] & 2:\n one ^= 1\n\n for i in range(I, len(A)):\n if A[i]&1 != one:\n return -1\n if A[i] & 2:\n one ^= 1\n\n return n\n``` | 0 | Given an array `points` where `points[i] = [xi, yi]` represents a point on the **X-Y** plane, return `true` _if these points are a **boomerang**_.
A **boomerang** is a set of three points that are **all distinct** and **not in a straight line**.
**Example 1:**
**Input:** points = \[\[1,1\],\[2,3\],\[3,2\]\]
**Output:** true
**Example 2:**
**Input:** points = \[\[1,1\],\[2,2\],\[3,3\]\]
**Output:** false
**Constraints:**
* `points.length == 3`
* `points[i].length == 2`
* `0 <= xi, yi <= 100` | null |
Solution | number-of-squareful-arrays | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int count=0;\n bool check(int a,int b){\n int temp = sqrt(a+b);\n return ((temp*temp) == (a+b));\n }\n void help(int curr,vector<int> arr){\n if(curr>= arr.size()){\n count++;\n return ;\n }\n for(int i= curr;i<arr.size();i++){\n if(i== curr || arr[i]!= arr[curr]){\n swap(arr[curr],arr[i]);\n if(curr==0 || (curr>0 && check(arr[curr-1],arr[curr]))) help(curr+1,arr);\n }\n }\n }\n int numSquarefulPerms(vector<int>& arr) {\n sort(arr.begin(),arr.end());\n help(0,arr);\n return count;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n ans = 0\n used = [False] * len(nums)\n\n def isSquare(num: int) -> bool:\n root = int(math.sqrt(num))\n return root * root == num\n\n def dfs(path: List[int]) -> None:\n nonlocal ans\n if len(path) > 1 and not isSquare(path[-1] + path[-2]):\n return\n if len(path) == len(nums):\n ans += 1\n return\n\n for i, a in enumerate(nums):\n if used[i]:\n continue\n if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:\n continue\n used[i] = True\n dfs(path + [a])\n used[i] = False\n\n nums.sort()\n dfs([])\n return ans\n```\n\n```Java []\nclass Solution {\n public int numSquarefulPerms(int[] nums) {\n return permutate(nums, 0);\n }\n int permutate(int[] nums, int idx){\n if(idx>=nums.length){\n return 1;\n }\n int sum = 0;\n for(int i=idx; i<nums.length; i++){\n if(!shouldSwap(nums, idx, i)) continue;\n swap(nums, idx, i);\n if(idx==0 || sumSquare(nums, idx)) sum += permutate(nums, idx+1);\n swap(nums, idx, i);\n }\n return sum;\n }\n boolean shouldSwap(int[] nums, int index, int ii){\n for(int i=index; i<ii; i++){\n if(nums[i]==nums[ii]) return false;\n }\n return true;\n }\n void swap(int[] nums, int i, int j){\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n boolean sumSquare(int[] nums, int idx){\n int sq = (int) Math.sqrt(nums[idx] + nums[idx-1]);\n return (sq*sq)==(nums[idx]+nums[idx-1]);\n }\n}\n```\n | 438 | An array is **squareful** if the sum of every pair of adjacent elements is a **perfect square**.
Given an integer array nums, return _the number of permutations of_ `nums` _that are **squareful**_.
Two permutations `perm1` and `perm2` are different if there is some index `i` such that `perm1[i] != perm2[i]`.
**Example 1:**
**Input:** nums = \[1,17,8\]
**Output:** 2
**Explanation:** \[1,8,17\] and \[17,8,1\] are the valid permutations.
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 12`
* `0 <= nums[i] <= 109` | null |
Solution | number-of-squareful-arrays | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int count=0;\n bool check(int a,int b){\n int temp = sqrt(a+b);\n return ((temp*temp) == (a+b));\n }\n void help(int curr,vector<int> arr){\n if(curr>= arr.size()){\n count++;\n return ;\n }\n for(int i= curr;i<arr.size();i++){\n if(i== curr || arr[i]!= arr[curr]){\n swap(arr[curr],arr[i]);\n if(curr==0 || (curr>0 && check(arr[curr-1],arr[curr]))) help(curr+1,arr);\n }\n }\n }\n int numSquarefulPerms(vector<int>& arr) {\n sort(arr.begin(),arr.end());\n help(0,arr);\n return count;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n ans = 0\n used = [False] * len(nums)\n\n def isSquare(num: int) -> bool:\n root = int(math.sqrt(num))\n return root * root == num\n\n def dfs(path: List[int]) -> None:\n nonlocal ans\n if len(path) > 1 and not isSquare(path[-1] + path[-2]):\n return\n if len(path) == len(nums):\n ans += 1\n return\n\n for i, a in enumerate(nums):\n if used[i]:\n continue\n if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:\n continue\n used[i] = True\n dfs(path + [a])\n used[i] = False\n\n nums.sort()\n dfs([])\n return ans\n```\n\n```Java []\nclass Solution {\n public int numSquarefulPerms(int[] nums) {\n return permutate(nums, 0);\n }\n int permutate(int[] nums, int idx){\n if(idx>=nums.length){\n return 1;\n }\n int sum = 0;\n for(int i=idx; i<nums.length; i++){\n if(!shouldSwap(nums, idx, i)) continue;\n swap(nums, idx, i);\n if(idx==0 || sumSquare(nums, idx)) sum += permutate(nums, idx+1);\n swap(nums, idx, i);\n }\n return sum;\n }\n boolean shouldSwap(int[] nums, int index, int ii){\n for(int i=index; i<ii; i++){\n if(nums[i]==nums[ii]) return false;\n }\n return true;\n }\n void swap(int[] nums, int i, int j){\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n boolean sumSquare(int[] nums, int idx){\n int sq = (int) Math.sqrt(nums[idx] + nums[idx-1]);\n return (sq*sq)==(nums[idx]+nums[idx-1]);\n }\n}\n```\n | 438 | Given the `root` of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a _binary search tree_ is a tree that satisfies these constraints:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8\]
**Output:** \[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8\]
**Example 2:**
**Input:** root = \[0,null,1\]
**Output:** \[1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val <= 100`
* All the values in the tree are **unique**.
**Note:** This question is the same as 538: [https://leetcode.com/problems/convert-bst-to-greater-tree/](https://leetcode.com/problems/convert-bst-to-greater-tree/) | null |
Concise solution on python3 | number-of-squareful-arrays | 0 | 1 | \n# Code\n```\nfrom math import sqrt\n\n\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n\n n = len(nums)\n ans = 0\n\n def ps(n):\n root = int(sqrt(n))\n return root * root == n\n \n def go(mask, prev):\n nonlocal ans\n if mask == 2 ** n - 1:\n ans += 1\n return\n\n for i in range(n):\n if mask & (1 << i):\n continue\n # prevent duplicates\n if i > 0 and nums[i] == nums[i-1] and mask & (1 << i-1) == 0:\n continue\n if prev == None or ps(nums[prev] + nums[i]):\n go(mask | (1 << i), i)\n\n\n nums.sort()\n go(0, None)\n return ans\n\n``` | 0 | An array is **squareful** if the sum of every pair of adjacent elements is a **perfect square**.
Given an integer array nums, return _the number of permutations of_ `nums` _that are **squareful**_.
Two permutations `perm1` and `perm2` are different if there is some index `i` such that `perm1[i] != perm2[i]`.
**Example 1:**
**Input:** nums = \[1,17,8\]
**Output:** 2
**Explanation:** \[1,8,17\] and \[17,8,1\] are the valid permutations.
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 12`
* `0 <= nums[i] <= 109` | null |
Concise solution on python3 | number-of-squareful-arrays | 0 | 1 | \n# Code\n```\nfrom math import sqrt\n\n\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n\n n = len(nums)\n ans = 0\n\n def ps(n):\n root = int(sqrt(n))\n return root * root == n\n \n def go(mask, prev):\n nonlocal ans\n if mask == 2 ** n - 1:\n ans += 1\n return\n\n for i in range(n):\n if mask & (1 << i):\n continue\n # prevent duplicates\n if i > 0 and nums[i] == nums[i-1] and mask & (1 << i-1) == 0:\n continue\n if prev == None or ps(nums[prev] + nums[i]):\n go(mask | (1 << i), i)\n\n\n nums.sort()\n go(0, None)\n return ans\n\n``` | 0 | Given the `root` of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a _binary search tree_ is a tree that satisfies these constraints:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8\]
**Output:** \[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8\]
**Example 2:**
**Input:** root = \[0,null,1\]
**Output:** \[1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val <= 100`
* All the values in the tree are **unique**.
**Note:** This question is the same as 538: [https://leetcode.com/problems/convert-bst-to-greater-tree/](https://leetcode.com/problems/convert-bst-to-greater-tree/) | null |
[Python3] Bitmask DP | number-of-squareful-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are a few approaches for this problem:\n1. Backtracking\nGenerate all possible permutations - `O(n!)`\nCheck if a permutation is squareful - `O(n)`\n=> `O(n! * n)`\n2. Backtracking but just generate squareful permutations\n`O(n! * n)` in the worst case, but normally it will be faster than naive backtracking\n3. Dynamic Programming\nAlthough backtracking can pass all the tests in this problem, however, we can optimize more in time complexity.\nLooking at the constraints `1 <= n <= 12` we can think of bitmask.\nLet our dp state includes:\n`i`: the current index we are considering\n`mask`: marks the used indices (including `i`)\nWhen considering `i`, we just care about `j` that `nums[i] + nums[j]` is a perfect square.\nWe continue considering `j` in our `dp` function until all indices have been considered.\n=> O(n^2 * 2 ^ n) time\n=> Space: O(n * 2^n + n)\n\n# Complexity\n- Time complexity: `O(n^2 * 2^n)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n * 2^n + n)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n n = len(nums)\n adj = defaultdict(list)\n for i in range(n):\n for j in range(i + 1, n):\n if math.sqrt(nums[i] + nums[j]) == int(math.sqrt(nums[i] + nums[j])):\n adj[i].append(j)\n adj[j].append(i)\n\n memo = [[-1 for _ in range(1 << n)] for __ in range(n)]\n def dfs(i: int, mask: int) -> int:\n if mask == (1 << n) - 1:\n return 1\n if memo[i][mask] != -1:\n return memo[i][mask]\n\n answer = 0\n for j in adj[i]:\n if (mask >> j) & 1 == 0:\n answer += dfs(j, mask | (1 << j))\n memo[i][mask] = answer\n return memo[i][mask]\n \n answer = sum(dfs(i, 1 << i) for i in range(n))\n for _, freq in Counter(nums).items():\n # Divide duplicated counts in answer\n answer //= math.factorial(freq)\n return answer\n\n\n``` | 0 | An array is **squareful** if the sum of every pair of adjacent elements is a **perfect square**.
Given an integer array nums, return _the number of permutations of_ `nums` _that are **squareful**_.
Two permutations `perm1` and `perm2` are different if there is some index `i` such that `perm1[i] != perm2[i]`.
**Example 1:**
**Input:** nums = \[1,17,8\]
**Output:** 2
**Explanation:** \[1,8,17\] and \[17,8,1\] are the valid permutations.
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 12`
* `0 <= nums[i] <= 109` | null |
[Python3] Bitmask DP | number-of-squareful-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are a few approaches for this problem:\n1. Backtracking\nGenerate all possible permutations - `O(n!)`\nCheck if a permutation is squareful - `O(n)`\n=> `O(n! * n)`\n2. Backtracking but just generate squareful permutations\n`O(n! * n)` in the worst case, but normally it will be faster than naive backtracking\n3. Dynamic Programming\nAlthough backtracking can pass all the tests in this problem, however, we can optimize more in time complexity.\nLooking at the constraints `1 <= n <= 12` we can think of bitmask.\nLet our dp state includes:\n`i`: the current index we are considering\n`mask`: marks the used indices (including `i`)\nWhen considering `i`, we just care about `j` that `nums[i] + nums[j]` is a perfect square.\nWe continue considering `j` in our `dp` function until all indices have been considered.\n=> O(n^2 * 2 ^ n) time\n=> Space: O(n * 2^n + n)\n\n# Complexity\n- Time complexity: `O(n^2 * 2^n)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n * 2^n + n)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n n = len(nums)\n adj = defaultdict(list)\n for i in range(n):\n for j in range(i + 1, n):\n if math.sqrt(nums[i] + nums[j]) == int(math.sqrt(nums[i] + nums[j])):\n adj[i].append(j)\n adj[j].append(i)\n\n memo = [[-1 for _ in range(1 << n)] for __ in range(n)]\n def dfs(i: int, mask: int) -> int:\n if mask == (1 << n) - 1:\n return 1\n if memo[i][mask] != -1:\n return memo[i][mask]\n\n answer = 0\n for j in adj[i]:\n if (mask >> j) & 1 == 0:\n answer += dfs(j, mask | (1 << j))\n memo[i][mask] = answer\n return memo[i][mask]\n \n answer = sum(dfs(i, 1 << i) for i in range(n))\n for _, freq in Counter(nums).items():\n # Divide duplicated counts in answer\n answer //= math.factorial(freq)\n return answer\n\n\n``` | 0 | Given the `root` of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a _binary search tree_ is a tree that satisfies these constraints:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8\]
**Output:** \[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8\]
**Example 2:**
**Input:** root = \[0,null,1\]
**Output:** \[1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val <= 100`
* All the values in the tree are **unique**.
**Note:** This question is the same as 538: [https://leetcode.com/problems/convert-bst-to-greater-tree/](https://leetcode.com/problems/convert-bst-to-greater-tree/) | null |
Fast and clean Python implementation with explaination | number-of-squareful-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBase on the input constraint, we can see it is a backtracking problem\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each position, try different value. I use an dictionary to maintain different value. \n# Complexity\n- Time complexity:\nO(n!)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass NumCounter():\n def __init__(self):\n self._data = {}\n self.total_element = 0\n \n def remove(self, v):\n self._data[v] -= 1\n self.total_element -= 1\n\n def add(self, v):\n if v not in self._data:\n self._data[v] = 0\n self._data[v] += 1\n self.total_element += 1\n\n def get_total_element(self):\n return self.total_element\n\n def values(self):\n list_values = []\n for k, v in self._data.items():\n if v != 0:\n list_values.append(k)\n return list_values\n\n\ndef back_tracking(last_element, nums_counter: NumCounter):\n if nums_counter.get_total_element() == 0:\n return 1\n res = 0\n for v in nums_counter.values():\n if is_perfect_square(last_element + v):\n nums_counter.remove(v)\n res += back_tracking(v, nums_counter)\n nums_counter.add(v)\n return res\n\ndef is_perfect_square(x):\n return int(x**(1/2)) ** 2 == x\n\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n num_counter = NumCounter()\n for i in nums:\n num_counter.add(i)\n res = 0\n for v in num_counter.values():\n num_counter.remove(v)\n res += back_tracking(v, num_counter)\n num_counter.add(v)\n return res\n``` | 0 | An array is **squareful** if the sum of every pair of adjacent elements is a **perfect square**.
Given an integer array nums, return _the number of permutations of_ `nums` _that are **squareful**_.
Two permutations `perm1` and `perm2` are different if there is some index `i` such that `perm1[i] != perm2[i]`.
**Example 1:**
**Input:** nums = \[1,17,8\]
**Output:** 2
**Explanation:** \[1,8,17\] and \[17,8,1\] are the valid permutations.
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 12`
* `0 <= nums[i] <= 109` | null |
Fast and clean Python implementation with explaination | number-of-squareful-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBase on the input constraint, we can see it is a backtracking problem\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each position, try different value. I use an dictionary to maintain different value. \n# Complexity\n- Time complexity:\nO(n!)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass NumCounter():\n def __init__(self):\n self._data = {}\n self.total_element = 0\n \n def remove(self, v):\n self._data[v] -= 1\n self.total_element -= 1\n\n def add(self, v):\n if v not in self._data:\n self._data[v] = 0\n self._data[v] += 1\n self.total_element += 1\n\n def get_total_element(self):\n return self.total_element\n\n def values(self):\n list_values = []\n for k, v in self._data.items():\n if v != 0:\n list_values.append(k)\n return list_values\n\n\ndef back_tracking(last_element, nums_counter: NumCounter):\n if nums_counter.get_total_element() == 0:\n return 1\n res = 0\n for v in nums_counter.values():\n if is_perfect_square(last_element + v):\n nums_counter.remove(v)\n res += back_tracking(v, nums_counter)\n nums_counter.add(v)\n return res\n\ndef is_perfect_square(x):\n return int(x**(1/2)) ** 2 == x\n\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n num_counter = NumCounter()\n for i in nums:\n num_counter.add(i)\n res = 0\n for v in num_counter.values():\n num_counter.remove(v)\n res += back_tracking(v, num_counter)\n num_counter.add(v)\n return res\n``` | 0 | Given the `root` of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a _binary search tree_ is a tree that satisfies these constraints:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8\]
**Output:** \[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8\]
**Example 2:**
**Input:** root = \[0,null,1\]
**Output:** \[1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val <= 100`
* All the values in the tree are **unique**.
**Note:** This question is the same as 538: [https://leetcode.com/problems/convert-bst-to-greater-tree/](https://leetcode.com/problems/convert-bst-to-greater-tree/) | null |
Number of Squareful Arrays | number-of-squareful-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport math\n\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n maxi=2*max(nums)\n i=1\n temp=set()\n while i*i<=maxi:\n temp.add(i*i)\n i+=1\n temp.add(0) \n\n def answer(num):\n if len(num)==1:\n return num[0] in temp\n for i in range(1,len(num)):\n if (num[i]+nums[i-1]) not in temp:\n return False\n return True \n\n seti=set()\n def rec(lis,ind):\n if ind==len(nums):\n if answer(lis):\n \n seti.add(tuple(nums))\n seti.add(tuple(nums))\n return 0\n ans=0 \n for i in range(ind,len(lis)):\n if i==ind or lis[i]!=lis[ind]:\n lis[i],lis[ind]=lis[ind],lis[i]\n if ind==0 or (nums[ind]+nums[ind-1]) in temp:\n ans+=rec(lis,ind+1)\n lis[i],lis[ind]=lis[ind],lis[i]\n return ans \n rec(nums,0)\n return len(seti) \n``` | 0 | An array is **squareful** if the sum of every pair of adjacent elements is a **perfect square**.
Given an integer array nums, return _the number of permutations of_ `nums` _that are **squareful**_.
Two permutations `perm1` and `perm2` are different if there is some index `i` such that `perm1[i] != perm2[i]`.
**Example 1:**
**Input:** nums = \[1,17,8\]
**Output:** 2
**Explanation:** \[1,8,17\] and \[17,8,1\] are the valid permutations.
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 12`
* `0 <= nums[i] <= 109` | null |
Number of Squareful Arrays | number-of-squareful-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport math\n\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n maxi=2*max(nums)\n i=1\n temp=set()\n while i*i<=maxi:\n temp.add(i*i)\n i+=1\n temp.add(0) \n\n def answer(num):\n if len(num)==1:\n return num[0] in temp\n for i in range(1,len(num)):\n if (num[i]+nums[i-1]) not in temp:\n return False\n return True \n\n seti=set()\n def rec(lis,ind):\n if ind==len(nums):\n if answer(lis):\n \n seti.add(tuple(nums))\n seti.add(tuple(nums))\n return 0\n ans=0 \n for i in range(ind,len(lis)):\n if i==ind or lis[i]!=lis[ind]:\n lis[i],lis[ind]=lis[ind],lis[i]\n if ind==0 or (nums[ind]+nums[ind-1]) in temp:\n ans+=rec(lis,ind+1)\n lis[i],lis[ind]=lis[ind],lis[i]\n return ans \n rec(nums,0)\n return len(seti) \n``` | 0 | Given the `root` of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a _binary search tree_ is a tree that satisfies these constraints:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8\]
**Output:** \[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8\]
**Example 2:**
**Input:** root = \[0,null,1\]
**Output:** \[1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val <= 100`
* All the values in the tree are **unique**.
**Note:** This question is the same as 538: [https://leetcode.com/problems/convert-bst-to-greater-tree/](https://leetcode.com/problems/convert-bst-to-greater-tree/) | null |
same as permutationsII | number-of-squareful-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n### 47. Permutations II\n```python\nclass Solution:\n def permuteUnique(self, nums):\n def backtrack(nums, ans, res):\n if not nums:\n res.append(ans[::])\n s = set()\n for i in range(len(nums)):\n if nums[i] in s: continue\n s.add(nums[i])\n ans.append(nums[i])\n backtrack(nums[:i] + nums[i+1:], ans, res)\n ans.pop()\n return res\n return backtrack(nums, [], [])\n```\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- change a bit about the squre conditions, here add if else condition.\n- if not ans: means we need to at least add a number to ans array\n- else: means there is at least a number, then we need to check square pairs, if it is backtrack to the next.\n- self.res give the result.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n!), but it will stop earlier for 2 prunes of tree.\n- 1 prune permutations\n- 2 prune square pairs\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n def isPerfect(n):\n return pow(int(sqrt(n)), 2) == n\n self.res = 0\n def backtrack(nums, ans):\n if not nums:\n self.res += 1\n s = set()\n for i in range(len(nums)):\n if nums[i] in s: continue\n s.add(nums[i])\n if not ans:\n ans.append(nums[i])\n backtrack(nums[:i] + nums[i+1:], ans)\n ans.pop()\n else:\n if isPerfect(ans[-1] + nums[i]):\n ans.append(nums[i])\n backtrack(nums[:i] + nums[i+1:], ans)\n ans.pop()\n backtrack(nums, [])\n return self.res\n``` | 0 | An array is **squareful** if the sum of every pair of adjacent elements is a **perfect square**.
Given an integer array nums, return _the number of permutations of_ `nums` _that are **squareful**_.
Two permutations `perm1` and `perm2` are different if there is some index `i` such that `perm1[i] != perm2[i]`.
**Example 1:**
**Input:** nums = \[1,17,8\]
**Output:** 2
**Explanation:** \[1,8,17\] and \[17,8,1\] are the valid permutations.
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 1
**Constraints:**
* `1 <= nums.length <= 12`
* `0 <= nums[i] <= 109` | null |
same as permutationsII | number-of-squareful-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n### 47. Permutations II\n```python\nclass Solution:\n def permuteUnique(self, nums):\n def backtrack(nums, ans, res):\n if not nums:\n res.append(ans[::])\n s = set()\n for i in range(len(nums)):\n if nums[i] in s: continue\n s.add(nums[i])\n ans.append(nums[i])\n backtrack(nums[:i] + nums[i+1:], ans, res)\n ans.pop()\n return res\n return backtrack(nums, [], [])\n```\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- change a bit about the squre conditions, here add if else condition.\n- if not ans: means we need to at least add a number to ans array\n- else: means there is at least a number, then we need to check square pairs, if it is backtrack to the next.\n- self.res give the result.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n!), but it will stop earlier for 2 prunes of tree.\n- 1 prune permutations\n- 2 prune square pairs\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSquarefulPerms(self, nums: List[int]) -> int:\n def isPerfect(n):\n return pow(int(sqrt(n)), 2) == n\n self.res = 0\n def backtrack(nums, ans):\n if not nums:\n self.res += 1\n s = set()\n for i in range(len(nums)):\n if nums[i] in s: continue\n s.add(nums[i])\n if not ans:\n ans.append(nums[i])\n backtrack(nums[:i] + nums[i+1:], ans)\n ans.pop()\n else:\n if isPerfect(ans[-1] + nums[i]):\n ans.append(nums[i])\n backtrack(nums[:i] + nums[i+1:], ans)\n ans.pop()\n backtrack(nums, [])\n return self.res\n``` | 0 | Given the `root` of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a _binary search tree_ is a tree that satisfies these constraints:
* The left subtree of a node contains only nodes with keys **less than** the node's key.
* The right subtree of a node contains only nodes with keys **greater than** the node's key.
* Both the left and right subtrees must also be binary search trees.
**Example 1:**
**Input:** root = \[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8\]
**Output:** \[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8\]
**Example 2:**
**Input:** root = \[0,null,1\]
**Output:** \[1,null,1\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `0 <= Node.val <= 100`
* All the values in the tree are **unique**.
**Note:** This question is the same as 538: [https://leetcode.com/problems/convert-bst-to-greater-tree/](https://leetcode.com/problems/convert-bst-to-greater-tree/) | null |
Solution | find-the-town-judge | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findJudge(int n, vector<vector<int>>& trust) {\n vector<int> trusting(n+1,0);\n vector<int> trusted(n+1,0);\n\n for(int i=0; i<trust.size();i++){\n trusting[trust[i][0]]++;\n trusted[trust[i][1]]++;\n } \n int ans = -1;\n for(int i=1; i<=n; i++){\n if(trusting[i] == 0 && trusted[i] == n-1){\n ans = i;\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nf=open("user.out",\'w\')\nwhile True:\n try:\n n=int(input())\n trust=input()[2:-2].split(\'],[\')\n trust_him=[1]*(n+1)\n he_trust=[1]*(n+1)\n for i in trust:\n if i==\'\': break\n i,j=map(int, i.split(\',\'))\n trust_him[j]+=1\n he_trust[i]=0\n ans=-1\n for i in range(1,n+1):\n if he_trust[i] and trust_him[i]==n:\n ans= i\n print(ans,file=f)\n except:\n f.close()\n exit(0)\n```\n\n```Java []\nclass Solution {\n public int findJudge(int n, int[][] trust) {\n int indegree[]=new int[n+1];\n \n for(int i=0;i<trust.length;i++)\n {\n indegree[trust[i][1]]++;\n }\n int judge=-1;\n for(int i=1;i<=n;i++)\n {\n if(indegree[i]==n-1)\n {\n judge=i;\n break;\n }\n }\n for(int i=0;i<trust.length;i++)\n {\n if(trust[i][0]==judge)\n return -1;\n }\n return judge; \n }\n}\n``` | 1 | In a town, there are `n` people labeled from `1` to `n`. There is a rumor that one of these people is secretly the town judge.
If the town judge exists, then:
1. The town judge trusts nobody.
2. Everybody (except for the town judge) trusts the town judge.
3. There is exactly one person that satisfies properties **1** and **2**.
You are given an array `trust` where `trust[i] = [ai, bi]` representing that the person labeled `ai` trusts the person labeled `bi`. If a trust relationship does not exist in `trust` array, then such a trust relationship does not exist.
Return _the label of the town judge if the town judge exists and can be identified, or return_ `-1` _otherwise_.
**Example 1:**
**Input:** n = 2, trust = \[\[1,2\]\]
**Output:** 2
**Example 2:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\]\]
**Output:** 3
**Example 3:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\],\[3,1\]\]
**Output:** -1
**Constraints:**
* `1 <= n <= 1000`
* `0 <= trust.length <= 104`
* `trust[i].length == 2`
* All the pairs of `trust` are **unique**.
* `ai != bi`
* `1 <= ai, bi <= n` | null |
Solution | find-the-town-judge | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findJudge(int n, vector<vector<int>>& trust) {\n vector<int> trusting(n+1,0);\n vector<int> trusted(n+1,0);\n\n for(int i=0; i<trust.size();i++){\n trusting[trust[i][0]]++;\n trusted[trust[i][1]]++;\n } \n int ans = -1;\n for(int i=1; i<=n; i++){\n if(trusting[i] == 0 && trusted[i] == n-1){\n ans = i;\n }\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nf=open("user.out",\'w\')\nwhile True:\n try:\n n=int(input())\n trust=input()[2:-2].split(\'],[\')\n trust_him=[1]*(n+1)\n he_trust=[1]*(n+1)\n for i in trust:\n if i==\'\': break\n i,j=map(int, i.split(\',\'))\n trust_him[j]+=1\n he_trust[i]=0\n ans=-1\n for i in range(1,n+1):\n if he_trust[i] and trust_him[i]==n:\n ans= i\n print(ans,file=f)\n except:\n f.close()\n exit(0)\n```\n\n```Java []\nclass Solution {\n public int findJudge(int n, int[][] trust) {\n int indegree[]=new int[n+1];\n \n for(int i=0;i<trust.length;i++)\n {\n indegree[trust[i][1]]++;\n }\n int judge=-1;\n for(int i=1;i<=n;i++)\n {\n if(indegree[i]==n-1)\n {\n judge=i;\n break;\n }\n }\n for(int i=0;i<trust.length;i++)\n {\n if(trust[i][0]==judge)\n return -1;\n }\n return judge; \n }\n}\n``` | 1 | You have a convex `n`\-sided polygon where each vertex has an integer value. You are given an integer array `values` where `values[i]` is the value of the `ith` vertex (i.e., **clockwise order**).
You will **triangulate** the polygon into `n - 2` triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all `n - 2` triangles in the triangulation.
Return _the smallest possible total score that you can achieve with some triangulation of the polygon_.
**Example 1:**
**Input:** values = \[1,2,3\]
**Output:** 6
**Explanation:** The polygon is already triangulated, and the score of the only triangle is 6.
**Example 2:**
**Input:** values = \[3,7,4,5\]
**Output:** 144
**Explanation:** There are two triangulations, with possible scores: 3\*7\*5 + 4\*5\*7 = 245, or 3\*4\*5 + 3\*4\*7 = 144.
The minimum score is 144.
**Example 3:**
**Input:** values = \[1,3,1,4,1,5\]
**Output:** 13
**Explanation:** The minimum score triangulation has score 1\*1\*3 + 1\*1\*4 + 1\*1\*5 + 1\*1\*1 = 13.
**Constraints:**
* `n == values.length`
* `3 <= n <= 50`
* `1 <= values[i] <= 100` | null |
O(N) Super [EASY] PYTHON 3 | find-the-town-judge | 0 | 1 | # Intuition and Approach\nWe have 2 maps, map 1 keeps track of the arrary[i][0] (think of it as **a** ) and we count how many people **a** trusts and map 2 keeps track of array[i][1] (**b**) we count how many times **b** was trusted we know that a --trusts--> b. We want to return those **b**s whose values == n - 1 so we know that b is trusted by all except himself **and** we also to want to make sure b is not a key in map 1\n\nApart from this we also check for some edge cases for example when there is only 1 guy in town so it is evident that we won\'t trust himself and there is no one else to trust him so he a self proclaimed town judge and when there are more than 1 people but we got no trust list which means we don\'t know who trusts who\n\n\n<!-- Describe your approach to solving the problem. -->\n\n\n# Code\n```\nclass Solution:\n def findJudge(self, n: int, trust: List[List[int]]) -> int:\n mp1 = {}\n mp2 = {}\n if n == 1 and len(trust) == 0: return 1\n if n >= 1 and len(trust) == 0:\n return -1\n if n >= 1 and len(trust) == 1:\n return trust[0][1]\n for i in trust:\n if i[0] not in mp1:\n mp1[i[0]] = 1\n if i[0] in mp1:\n mp1[i[0]] += 1\n if i[1] in mp2 and i[1] not in mp1:\n mp2[i[1]] += 1\n if i[1] not in mp2:\n mp2[i[1]] = 1\n for k, v in mp2.items():\n if k not in mp1 and v == n - 1:\n return k\n \n return -1\n \n``` | 1 | In a town, there are `n` people labeled from `1` to `n`. There is a rumor that one of these people is secretly the town judge.
If the town judge exists, then:
1. The town judge trusts nobody.
2. Everybody (except for the town judge) trusts the town judge.
3. There is exactly one person that satisfies properties **1** and **2**.
You are given an array `trust` where `trust[i] = [ai, bi]` representing that the person labeled `ai` trusts the person labeled `bi`. If a trust relationship does not exist in `trust` array, then such a trust relationship does not exist.
Return _the label of the town judge if the town judge exists and can be identified, or return_ `-1` _otherwise_.
**Example 1:**
**Input:** n = 2, trust = \[\[1,2\]\]
**Output:** 2
**Example 2:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\]\]
**Output:** 3
**Example 3:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\],\[3,1\]\]
**Output:** -1
**Constraints:**
* `1 <= n <= 1000`
* `0 <= trust.length <= 104`
* `trust[i].length == 2`
* All the pairs of `trust` are **unique**.
* `ai != bi`
* `1 <= ai, bi <= n` | null |
O(N) Super [EASY] PYTHON 3 | find-the-town-judge | 0 | 1 | # Intuition and Approach\nWe have 2 maps, map 1 keeps track of the arrary[i][0] (think of it as **a** ) and we count how many people **a** trusts and map 2 keeps track of array[i][1] (**b**) we count how many times **b** was trusted we know that a --trusts--> b. We want to return those **b**s whose values == n - 1 so we know that b is trusted by all except himself **and** we also to want to make sure b is not a key in map 1\n\nApart from this we also check for some edge cases for example when there is only 1 guy in town so it is evident that we won\'t trust himself and there is no one else to trust him so he a self proclaimed town judge and when there are more than 1 people but we got no trust list which means we don\'t know who trusts who\n\n\n<!-- Describe your approach to solving the problem. -->\n\n\n# Code\n```\nclass Solution:\n def findJudge(self, n: int, trust: List[List[int]]) -> int:\n mp1 = {}\n mp2 = {}\n if n == 1 and len(trust) == 0: return 1\n if n >= 1 and len(trust) == 0:\n return -1\n if n >= 1 and len(trust) == 1:\n return trust[0][1]\n for i in trust:\n if i[0] not in mp1:\n mp1[i[0]] = 1\n if i[0] in mp1:\n mp1[i[0]] += 1\n if i[1] in mp2 and i[1] not in mp1:\n mp2[i[1]] += 1\n if i[1] not in mp2:\n mp2[i[1]] = 1\n for k, v in mp2.items():\n if k not in mp1 and v == n - 1:\n return k\n \n return -1\n \n``` | 1 | You have a convex `n`\-sided polygon where each vertex has an integer value. You are given an integer array `values` where `values[i]` is the value of the `ith` vertex (i.e., **clockwise order**).
You will **triangulate** the polygon into `n - 2` triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all `n - 2` triangles in the triangulation.
Return _the smallest possible total score that you can achieve with some triangulation of the polygon_.
**Example 1:**
**Input:** values = \[1,2,3\]
**Output:** 6
**Explanation:** The polygon is already triangulated, and the score of the only triangle is 6.
**Example 2:**
**Input:** values = \[3,7,4,5\]
**Output:** 144
**Explanation:** There are two triangulations, with possible scores: 3\*7\*5 + 4\*5\*7 = 245, or 3\*4\*5 + 3\*4\*7 = 144.
The minimum score is 144.
**Example 3:**
**Input:** values = \[1,3,1,4,1,5\]
**Output:** 13
**Explanation:** The minimum score triangulation has score 1\*1\*3 + 1\*1\*4 + 1\*1\*5 + 1\*1\*1 = 13.
**Constraints:**
* `n == values.length`
* `3 <= n <= 50`
* `1 <= values[i] <= 100` | null |
Java | O(N) O(N) | Easy | find-the-town-judge | 1 | 1 | # Intuition\n1. Create a directed graph from ai to bi where trust[i] = [ai, bi].\n2. Find the one node with in-degree as n-1 & out-degree -1.\n3. Also check that there is only one such node as specified in (2).\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\n public int findJudge(int n, int[][] trust) {\n HashMap<Integer, Integer> in = new HashMap<>();\n HashMap<Integer, Integer> out = new HashMap<>();\n for(int[] i:trust){\n in.put(i[1], in.getOrDefault(i[1], 0)+1);\n out.put(i[0], out.getOrDefault(i[0], 0)+1);\n }\n int m=-1;\n for(int i=1;i<=n;i++){\n //System.out.println(i+"->"+in.getOrDefault(i, 0)+":"+out.getOrDefault(i, 0));\n if(in.getOrDefault(i, 0)==n-1 && out.getOrDefault(i, 0)==0){\n //System.out.println("Yes");\n if(m==-1) m=i;\n else return -1;\n }\n }\n return m;\n }\n}\n``` | 1 | In a town, there are `n` people labeled from `1` to `n`. There is a rumor that one of these people is secretly the town judge.
If the town judge exists, then:
1. The town judge trusts nobody.
2. Everybody (except for the town judge) trusts the town judge.
3. There is exactly one person that satisfies properties **1** and **2**.
You are given an array `trust` where `trust[i] = [ai, bi]` representing that the person labeled `ai` trusts the person labeled `bi`. If a trust relationship does not exist in `trust` array, then such a trust relationship does not exist.
Return _the label of the town judge if the town judge exists and can be identified, or return_ `-1` _otherwise_.
**Example 1:**
**Input:** n = 2, trust = \[\[1,2\]\]
**Output:** 2
**Example 2:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\]\]
**Output:** 3
**Example 3:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\],\[3,1\]\]
**Output:** -1
**Constraints:**
* `1 <= n <= 1000`
* `0 <= trust.length <= 104`
* `trust[i].length == 2`
* All the pairs of `trust` are **unique**.
* `ai != bi`
* `1 <= ai, bi <= n` | null |
Java | O(N) O(N) | Easy | find-the-town-judge | 1 | 1 | # Intuition\n1. Create a directed graph from ai to bi where trust[i] = [ai, bi].\n2. Find the one node with in-degree as n-1 & out-degree -1.\n3. Also check that there is only one such node as specified in (2).\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\n public int findJudge(int n, int[][] trust) {\n HashMap<Integer, Integer> in = new HashMap<>();\n HashMap<Integer, Integer> out = new HashMap<>();\n for(int[] i:trust){\n in.put(i[1], in.getOrDefault(i[1], 0)+1);\n out.put(i[0], out.getOrDefault(i[0], 0)+1);\n }\n int m=-1;\n for(int i=1;i<=n;i++){\n //System.out.println(i+"->"+in.getOrDefault(i, 0)+":"+out.getOrDefault(i, 0));\n if(in.getOrDefault(i, 0)==n-1 && out.getOrDefault(i, 0)==0){\n //System.out.println("Yes");\n if(m==-1) m=i;\n else return -1;\n }\n }\n return m;\n }\n}\n``` | 1 | You have a convex `n`\-sided polygon where each vertex has an integer value. You are given an integer array `values` where `values[i]` is the value of the `ith` vertex (i.e., **clockwise order**).
You will **triangulate** the polygon into `n - 2` triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all `n - 2` triangles in the triangulation.
Return _the smallest possible total score that you can achieve with some triangulation of the polygon_.
**Example 1:**
**Input:** values = \[1,2,3\]
**Output:** 6
**Explanation:** The polygon is already triangulated, and the score of the only triangle is 6.
**Example 2:**
**Input:** values = \[3,7,4,5\]
**Output:** 144
**Explanation:** There are two triangulations, with possible scores: 3\*7\*5 + 4\*5\*7 = 245, or 3\*4\*5 + 3\*4\*7 = 144.
The minimum score is 144.
**Example 3:**
**Input:** values = \[1,3,1,4,1,5\]
**Output:** 13
**Explanation:** The minimum score triangulation has score 1\*1\*3 + 1\*1\*4 + 1\*1\*5 + 1\*1\*1 = 13.
**Constraints:**
* `n == values.length`
* `3 <= n <= 50`
* `1 <= values[i] <= 100` | null |
Easy Python solution for Beginners in O(n+m) Time Complexity | find-the-town-judge | 0 | 1 | APPROACH 1:\n```\nclass Solution:\n def findJudge(self, n: int, trust: List[List[int]]) -> int:\n # Sum of n terms\n Town_judge = (n*(n+1))//2\n\n # Hash map for storing judge and their trusted judges\n judge_trust = dict()\n\n\n for i in trust:\n judge = i[0]\n if judge not in judge_trust:\n Town_judge -= judge\n judge_trust[judge] = [i[1]]\n else:\n judge_trust[judge].append(i[1])\n\n # All n term judges are trusting any other judges\n # condition 1 not satisfied\n if Town_judge == 0: \n return -1\n\n # check if the judge is being trusted by every other judge in the town\n for i in judge_trust:\n # if the town_judge is not in anyone\'s trusted judges\n # condition 2 not satisfied\n if Town_judge not in judge_trust[i]:\n return -1\n\n return Town_judge if Town_judge<=n else -1\n```\n\nAPPROACH 2:\n```\nclass Solution:\n def findJudge(self, n: int, trust: List[List[int]]) -> int:\n judge_trust = {}\n \n for link in trust:\n p1 = link[0]\n if p1 not in judge_trust:\n judge_trust[p1] = [link[1]]\n else:\n judge_trust[p1].append(link[1])\n\n # To store the count of people who are not being trusted by anyone\n cnt = 0\n for judge in range(1,n+1):\n if judge not in judge_trust:\n town_judge = judge\n cnt+=1\n if cnt>1: # There are more than one people who are satisfying the condition 1 which is not appropriate for the town judge\n return -1\n\n # There is no such people who is not trusting anyone\n if cnt == 0 :\n return -1\n \n #Check if the condition 2 is satisfied by the expected Town Judge who is satisfying the condition 1. \n for link in judge_trust:\n if town_judge not in judge_trust[link]: #Expected Town Judge is not being trusted by everyone\n return -1\n \n #Both Conditions are satisfied by the Town Judge\n return town_judge\n \n``` | 1 | In a town, there are `n` people labeled from `1` to `n`. There is a rumor that one of these people is secretly the town judge.
If the town judge exists, then:
1. The town judge trusts nobody.
2. Everybody (except for the town judge) trusts the town judge.
3. There is exactly one person that satisfies properties **1** and **2**.
You are given an array `trust` where `trust[i] = [ai, bi]` representing that the person labeled `ai` trusts the person labeled `bi`. If a trust relationship does not exist in `trust` array, then such a trust relationship does not exist.
Return _the label of the town judge if the town judge exists and can be identified, or return_ `-1` _otherwise_.
**Example 1:**
**Input:** n = 2, trust = \[\[1,2\]\]
**Output:** 2
**Example 2:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\]\]
**Output:** 3
**Example 3:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\],\[3,1\]\]
**Output:** -1
**Constraints:**
* `1 <= n <= 1000`
* `0 <= trust.length <= 104`
* `trust[i].length == 2`
* All the pairs of `trust` are **unique**.
* `ai != bi`
* `1 <= ai, bi <= n` | null |
Easy Python solution for Beginners in O(n+m) Time Complexity | find-the-town-judge | 0 | 1 | APPROACH 1:\n```\nclass Solution:\n def findJudge(self, n: int, trust: List[List[int]]) -> int:\n # Sum of n terms\n Town_judge = (n*(n+1))//2\n\n # Hash map for storing judge and their trusted judges\n judge_trust = dict()\n\n\n for i in trust:\n judge = i[0]\n if judge not in judge_trust:\n Town_judge -= judge\n judge_trust[judge] = [i[1]]\n else:\n judge_trust[judge].append(i[1])\n\n # All n term judges are trusting any other judges\n # condition 1 not satisfied\n if Town_judge == 0: \n return -1\n\n # check if the judge is being trusted by every other judge in the town\n for i in judge_trust:\n # if the town_judge is not in anyone\'s trusted judges\n # condition 2 not satisfied\n if Town_judge not in judge_trust[i]:\n return -1\n\n return Town_judge if Town_judge<=n else -1\n```\n\nAPPROACH 2:\n```\nclass Solution:\n def findJudge(self, n: int, trust: List[List[int]]) -> int:\n judge_trust = {}\n \n for link in trust:\n p1 = link[0]\n if p1 not in judge_trust:\n judge_trust[p1] = [link[1]]\n else:\n judge_trust[p1].append(link[1])\n\n # To store the count of people who are not being trusted by anyone\n cnt = 0\n for judge in range(1,n+1):\n if judge not in judge_trust:\n town_judge = judge\n cnt+=1\n if cnt>1: # There are more than one people who are satisfying the condition 1 which is not appropriate for the town judge\n return -1\n\n # There is no such people who is not trusting anyone\n if cnt == 0 :\n return -1\n \n #Check if the condition 2 is satisfied by the expected Town Judge who is satisfying the condition 1. \n for link in judge_trust:\n if town_judge not in judge_trust[link]: #Expected Town Judge is not being trusted by everyone\n return -1\n \n #Both Conditions are satisfied by the Town Judge\n return town_judge\n \n``` | 1 | You have a convex `n`\-sided polygon where each vertex has an integer value. You are given an integer array `values` where `values[i]` is the value of the `ith` vertex (i.e., **clockwise order**).
You will **triangulate** the polygon into `n - 2` triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all `n - 2` triangles in the triangulation.
Return _the smallest possible total score that you can achieve with some triangulation of the polygon_.
**Example 1:**
**Input:** values = \[1,2,3\]
**Output:** 6
**Explanation:** The polygon is already triangulated, and the score of the only triangle is 6.
**Example 2:**
**Input:** values = \[3,7,4,5\]
**Output:** 144
**Explanation:** There are two triangulations, with possible scores: 3\*7\*5 + 4\*5\*7 = 245, or 3\*4\*5 + 3\*4\*7 = 144.
The minimum score is 144.
**Example 3:**
**Input:** values = \[1,3,1,4,1,5\]
**Output:** 13
**Explanation:** The minimum score triangulation has score 1\*1\*3 + 1\*1\*4 + 1\*1\*5 + 1\*1\*1 = 13.
**Constraints:**
* `n == values.length`
* `3 <= n <= 50`
* `1 <= values[i] <= 100` | null |
C++ | Easy to understand | find-the-town-judge | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findJudge(int n, vector<vector<int>>& trust) {\n \n vector<int> indeg(n+1,0);\n vector<int> outdeg(n+1,0);\n \n for(int i =0;i<trust.size();i++)\n {\n outdeg[trust[i][0]]++;\n indeg[trust[i][1]]++;\n }\n \n for(int i=1;i<=n;i++)\n {\n if(indeg[i]==n-1 && outdeg[i]==0)\n return i;\n }\n \n return -1;\n \n \n }\n};\n``` | 1 | In a town, there are `n` people labeled from `1` to `n`. There is a rumor that one of these people is secretly the town judge.
If the town judge exists, then:
1. The town judge trusts nobody.
2. Everybody (except for the town judge) trusts the town judge.
3. There is exactly one person that satisfies properties **1** and **2**.
You are given an array `trust` where `trust[i] = [ai, bi]` representing that the person labeled `ai` trusts the person labeled `bi`. If a trust relationship does not exist in `trust` array, then such a trust relationship does not exist.
Return _the label of the town judge if the town judge exists and can be identified, or return_ `-1` _otherwise_.
**Example 1:**
**Input:** n = 2, trust = \[\[1,2\]\]
**Output:** 2
**Example 2:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\]\]
**Output:** 3
**Example 3:**
**Input:** n = 3, trust = \[\[1,3\],\[2,3\],\[3,1\]\]
**Output:** -1
**Constraints:**
* `1 <= n <= 1000`
* `0 <= trust.length <= 104`
* `trust[i].length == 2`
* All the pairs of `trust` are **unique**.
* `ai != bi`
* `1 <= ai, bi <= n` | null |
C++ | Easy to understand | find-the-town-judge | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findJudge(int n, vector<vector<int>>& trust) {\n \n vector<int> indeg(n+1,0);\n vector<int> outdeg(n+1,0);\n \n for(int i =0;i<trust.size();i++)\n {\n outdeg[trust[i][0]]++;\n indeg[trust[i][1]]++;\n }\n \n for(int i=1;i<=n;i++)\n {\n if(indeg[i]==n-1 && outdeg[i]==0)\n return i;\n }\n \n return -1;\n \n \n }\n};\n``` | 1 | You have a convex `n`\-sided polygon where each vertex has an integer value. You are given an integer array `values` where `values[i]` is the value of the `ith` vertex (i.e., **clockwise order**).
You will **triangulate** the polygon into `n - 2` triangles. For each triangle, the value of that triangle is the product of the values of its vertices, and the total score of the triangulation is the sum of these values over all `n - 2` triangles in the triangulation.
Return _the smallest possible total score that you can achieve with some triangulation of the polygon_.
**Example 1:**
**Input:** values = \[1,2,3\]
**Output:** 6
**Explanation:** The polygon is already triangulated, and the score of the only triangle is 6.
**Example 2:**
**Input:** values = \[3,7,4,5\]
**Output:** 144
**Explanation:** There are two triangulations, with possible scores: 3\*7\*5 + 4\*5\*7 = 245, or 3\*4\*5 + 3\*4\*7 = 144.
The minimum score is 144.
**Example 3:**
**Input:** values = \[1,3,1,4,1,5\]
**Output:** 13
**Explanation:** The minimum score triangulation has score 1\*1\*3 + 1\*1\*4 + 1\*1\*5 + 1\*1\*1 = 13.
**Constraints:**
* `n == values.length`
* `3 <= n <= 50`
* `1 <= values[i] <= 100` | null |
Solution | maximum-binary-tree-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* check(vector<int>&nums,int s,int e){\n stack<TreeNode*> st;\n\n for(int i=s;i<=e;i++){\n TreeNode* node=new TreeNode( nums[i]);\n while(!st.empty() && nums[i]>st.top()->val){\n node->left=st.top();\n st.pop();\n }\n if(!st.empty()) st.top()->right=node;\n st.push(node);\n }\n while(st.size()>1) st.pop();\n return st.top();\n }\n void see(vector<int>&ans,TreeNode* root){\n if(!root) return ;\n see(ans,root->left);\n ans.push_back(root->val);\n see(ans,root->right);\n return;\n }\n TreeNode* insertIntoMaxTree(TreeNode* root, int val) {\n vector<int> ans;\n see(ans,root);\n ans.push_back(val);\n return check(ans,0,ans.size()-1);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root and root.val > val:\n root.right = self.insertIntoMaxTree(root.right, val)\n return root\n node = TreeNode(val)\n node.left = root\n return node\n```\n\n```Java []\nclass Solution {\n TreeNode solve(TreeNode root,int val){\n if(root == null){\n return new TreeNode(val);\n }\n if(root.val < val){\n TreeNode node = new TreeNode(val);\n node.left = root;\n return node;\n }\n root.right = solve(root.right,val);\n return root;\n }\n public TreeNode insertIntoMaxTree(TreeNode root, int val) {\n return solve(root,val);\n }\n}\n``` | 2 | A **maximum tree** is a tree where every node has a value greater than any other value in its subtree.
You are given the `root` of a maximum binary tree and an integer `val`.
Just as in the [previous problem](https://leetcode.com/problems/maximum-binary-tree/), the given tree was constructed from a list `a` (`root = Construct(a)`) recursively with the following `Construct(a)` routine:
* If `a` is empty, return `null`.
* Otherwise, let `a[i]` be the largest element of `a`. Create a `root` node with the value `a[i]`.
* The left child of `root` will be `Construct([a[0], a[1], ..., a[i - 1]])`.
* The right child of `root` will be `Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]])`.
* Return `root`.
Note that we were not given `a` directly, only a root node `root = Construct(a)`.
Suppose `b` is a copy of `a` with the value `val` appended to it. It is guaranteed that `b` has unique values.
Return `Construct(b)`.
**Example 1:**
**Input:** root = \[4,1,3,null,null,2\], val = 5
**Output:** \[5,4,null,1,3,null,null,2\]
**Explanation:** a = \[1,4,2,3\], b = \[1,4,2,3,5\]
**Example 2:**
**Input:** root = \[5,2,4,null,1\], val = 3
**Output:** \[5,2,4,null,1,null,3\]
**Explanation:** a = \[2,1,5,4\], b = \[2,1,5,4,3\]
**Example 3:**
**Input:** root = \[5,2,3,null,1\], val = 4
**Output:** \[5,2,4,null,1,3\]
**Explanation:** a = \[2,1,5,3\], b = \[2,1,5,3,4\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `1 <= Node.val <= 100`
* All the values of the tree are **unique**.
* `1 <= val <= 100` | null |
Solution | maximum-binary-tree-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n TreeNode* check(vector<int>&nums,int s,int e){\n stack<TreeNode*> st;\n\n for(int i=s;i<=e;i++){\n TreeNode* node=new TreeNode( nums[i]);\n while(!st.empty() && nums[i]>st.top()->val){\n node->left=st.top();\n st.pop();\n }\n if(!st.empty()) st.top()->right=node;\n st.push(node);\n }\n while(st.size()>1) st.pop();\n return st.top();\n }\n void see(vector<int>&ans,TreeNode* root){\n if(!root) return ;\n see(ans,root->left);\n ans.push_back(root->val);\n see(ans,root->right);\n return;\n }\n TreeNode* insertIntoMaxTree(TreeNode* root, int val) {\n vector<int> ans;\n see(ans,root);\n ans.push_back(val);\n return check(ans,0,ans.size()-1);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n if root and root.val > val:\n root.right = self.insertIntoMaxTree(root.right, val)\n return root\n node = TreeNode(val)\n node.left = root\n return node\n```\n\n```Java []\nclass Solution {\n TreeNode solve(TreeNode root,int val){\n if(root == null){\n return new TreeNode(val);\n }\n if(root.val < val){\n TreeNode node = new TreeNode(val);\n node.left = root;\n return node;\n }\n root.right = solve(root.right,val);\n return root;\n }\n public TreeNode insertIntoMaxTree(TreeNode root, int val) {\n return solve(root,val);\n }\n}\n``` | 2 | There are some stones in different positions on the X-axis. You are given an integer array `stones`, the positions of the stones.
Call a stone an **endpoint stone** if it has the smallest or largest position. In one move, you pick up an **endpoint stone** and move it to an unoccupied position so that it is no longer an **endpoint stone**.
* In particular, if the stones are at say, `stones = [1,2,5]`, you cannot move the endpoint stone at position `5`, since moving it to any position (such as `0`, or `3`) will still keep that stone as an endpoint stone.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** stones = \[7,4,9\]
**Output:** \[1,2\]
**Explanation:** We can move 4 -> 8 for one move to finish the game.
Or, we can move 9 -> 5, 4 -> 6 for two moves to finish the game.
**Example 2:**
**Input:** stones = \[6,5,4,3,10\]
**Output:** \[2,3\]
**Explanation:** We can move 3 -> 8 then 10 -> 7 to finish the game.
Or, we can move 3 -> 7, 4 -> 8, 5 -> 9 to finish the game.
Notice we cannot move 10 -> 2 to finish the game, because that would be an illegal move.
**Constraints:**
* `3 <= stones.length <= 104`
* `1 <= stones[i] <= 109`
* All the values of `stones` are **unique**. | null |
✅ Beats 100% | Very easy to understand | Inserting a Node into a Maximum Binary Tree | maximum-binary-tree-ii | 0 | 1 | # Intuition\nWe need to insert a new node with a value `val` into a maximum binary tree. One way we can do it is to traverse the tree recursively comparing the value of the current node with `val` to determine the appropriate placement of the new node.\n\n# Approach\n1. Create a new ndoe with the value `val`.\n2. If the root is `None`, return the new node as the root of the tree.\n3. If the value of the root is less than `val`, make the new node the new root and set the current root as its left child.\n4. Otherwise, recursively insert the new node into the right subtree of the current root.\n5. Return the modified root.\n\n# Complexity\n- Time complexity:\nThe time complexity of this approach is O(n), where n is the number of nodes in the maximum binary tree. In the worst case, we may need to traverse all the nodes in the tree.\n\n- Space complexity:\nThe space complexity is O(n) as well, considering the recursive function calls that can go up to the maximum depth of the tree.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n new_node = TreeNode(val)\n \n if root is None:\n return new_node\n \n if root.val < val:\n new_node.left = root\n return new_node\n \n root.right = self.insertIntoMaxTree(root.right, val)\n return root\n``` | 0 | A **maximum tree** is a tree where every node has a value greater than any other value in its subtree.
You are given the `root` of a maximum binary tree and an integer `val`.
Just as in the [previous problem](https://leetcode.com/problems/maximum-binary-tree/), the given tree was constructed from a list `a` (`root = Construct(a)`) recursively with the following `Construct(a)` routine:
* If `a` is empty, return `null`.
* Otherwise, let `a[i]` be the largest element of `a`. Create a `root` node with the value `a[i]`.
* The left child of `root` will be `Construct([a[0], a[1], ..., a[i - 1]])`.
* The right child of `root` will be `Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]])`.
* Return `root`.
Note that we were not given `a` directly, only a root node `root = Construct(a)`.
Suppose `b` is a copy of `a` with the value `val` appended to it. It is guaranteed that `b` has unique values.
Return `Construct(b)`.
**Example 1:**
**Input:** root = \[4,1,3,null,null,2\], val = 5
**Output:** \[5,4,null,1,3,null,null,2\]
**Explanation:** a = \[1,4,2,3\], b = \[1,4,2,3,5\]
**Example 2:**
**Input:** root = \[5,2,4,null,1\], val = 3
**Output:** \[5,2,4,null,1,null,3\]
**Explanation:** a = \[2,1,5,4\], b = \[2,1,5,4,3\]
**Example 3:**
**Input:** root = \[5,2,3,null,1\], val = 4
**Output:** \[5,2,4,null,1,3\]
**Explanation:** a = \[2,1,5,3\], b = \[2,1,5,3,4\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `1 <= Node.val <= 100`
* All the values of the tree are **unique**.
* `1 <= val <= 100` | null |
✅ Beats 100% | Very easy to understand | Inserting a Node into a Maximum Binary Tree | maximum-binary-tree-ii | 0 | 1 | # Intuition\nWe need to insert a new node with a value `val` into a maximum binary tree. One way we can do it is to traverse the tree recursively comparing the value of the current node with `val` to determine the appropriate placement of the new node.\n\n# Approach\n1. Create a new ndoe with the value `val`.\n2. If the root is `None`, return the new node as the root of the tree.\n3. If the value of the root is less than `val`, make the new node the new root and set the current root as its left child.\n4. Otherwise, recursively insert the new node into the right subtree of the current root.\n5. Return the modified root.\n\n# Complexity\n- Time complexity:\nThe time complexity of this approach is O(n), where n is the number of nodes in the maximum binary tree. In the worst case, we may need to traverse all the nodes in the tree.\n\n- Space complexity:\nThe space complexity is O(n) as well, considering the recursive function calls that can go up to the maximum depth of the tree.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n new_node = TreeNode(val)\n \n if root is None:\n return new_node\n \n if root.val < val:\n new_node.left = root\n return new_node\n \n root.right = self.insertIntoMaxTree(root.right, val)\n return root\n``` | 0 | There are some stones in different positions on the X-axis. You are given an integer array `stones`, the positions of the stones.
Call a stone an **endpoint stone** if it has the smallest or largest position. In one move, you pick up an **endpoint stone** and move it to an unoccupied position so that it is no longer an **endpoint stone**.
* In particular, if the stones are at say, `stones = [1,2,5]`, you cannot move the endpoint stone at position `5`, since moving it to any position (such as `0`, or `3`) will still keep that stone as an endpoint stone.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** stones = \[7,4,9\]
**Output:** \[1,2\]
**Explanation:** We can move 4 -> 8 for one move to finish the game.
Or, we can move 9 -> 5, 4 -> 6 for two moves to finish the game.
**Example 2:**
**Input:** stones = \[6,5,4,3,10\]
**Output:** \[2,3\]
**Explanation:** We can move 3 -> 8 then 10 -> 7 to finish the game.
Or, we can move 3 -> 7, 4 -> 8, 5 -> 9 to finish the game.
Notice we cannot move 10 -> 2 to finish the game, because that would be an illegal move.
**Constraints:**
* `3 <= stones.length <= 104`
* `1 <= stones[i] <= 109`
* All the values of `stones` are **unique**. | null |
[Python3] Using 654. Maximum Binary Tree Solution | maximum-binary-tree-ii | 0 | 1 | # Code\n```\nclass Solution:\n def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n self.lst = []\n def dfs(root):\n if not root:\n return \n dfs(root.left)\n self.lst.append(root.val)\n dfs(root.right)\n dfs(root)\n self.lst.append(val)\n\n def build(nums, l, r):\n if l>=r: return None\n maxIdx = l\n maxVal = nums[l]\n for i in range(l, r):\n if nums[i]>maxVal:\n maxVal = nums[i]\n maxIdx = i\n root = TreeNode(maxVal)\n root.left = build(nums, l, maxIdx)\n root.right = build(nums, maxIdx+1, r)\n return root\n\n return build(self.lst, 0, len(self.lst))\n``` | 0 | A **maximum tree** is a tree where every node has a value greater than any other value in its subtree.
You are given the `root` of a maximum binary tree and an integer `val`.
Just as in the [previous problem](https://leetcode.com/problems/maximum-binary-tree/), the given tree was constructed from a list `a` (`root = Construct(a)`) recursively with the following `Construct(a)` routine:
* If `a` is empty, return `null`.
* Otherwise, let `a[i]` be the largest element of `a`. Create a `root` node with the value `a[i]`.
* The left child of `root` will be `Construct([a[0], a[1], ..., a[i - 1]])`.
* The right child of `root` will be `Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]])`.
* Return `root`.
Note that we were not given `a` directly, only a root node `root = Construct(a)`.
Suppose `b` is a copy of `a` with the value `val` appended to it. It is guaranteed that `b` has unique values.
Return `Construct(b)`.
**Example 1:**
**Input:** root = \[4,1,3,null,null,2\], val = 5
**Output:** \[5,4,null,1,3,null,null,2\]
**Explanation:** a = \[1,4,2,3\], b = \[1,4,2,3,5\]
**Example 2:**
**Input:** root = \[5,2,4,null,1\], val = 3
**Output:** \[5,2,4,null,1,null,3\]
**Explanation:** a = \[2,1,5,4\], b = \[2,1,5,4,3\]
**Example 3:**
**Input:** root = \[5,2,3,null,1\], val = 4
**Output:** \[5,2,4,null,1,3\]
**Explanation:** a = \[2,1,5,3\], b = \[2,1,5,3,4\]
**Constraints:**
* The number of nodes in the tree is in the range `[1, 100]`.
* `1 <= Node.val <= 100`
* All the values of the tree are **unique**.
* `1 <= val <= 100` | null |
[Python3] Using 654. Maximum Binary Tree Solution | maximum-binary-tree-ii | 0 | 1 | # Code\n```\nclass Solution:\n def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:\n self.lst = []\n def dfs(root):\n if not root:\n return \n dfs(root.left)\n self.lst.append(root.val)\n dfs(root.right)\n dfs(root)\n self.lst.append(val)\n\n def build(nums, l, r):\n if l>=r: return None\n maxIdx = l\n maxVal = nums[l]\n for i in range(l, r):\n if nums[i]>maxVal:\n maxVal = nums[i]\n maxIdx = i\n root = TreeNode(maxVal)\n root.left = build(nums, l, maxIdx)\n root.right = build(nums, maxIdx+1, r)\n return root\n\n return build(self.lst, 0, len(self.lst))\n``` | 0 | There are some stones in different positions on the X-axis. You are given an integer array `stones`, the positions of the stones.
Call a stone an **endpoint stone** if it has the smallest or largest position. In one move, you pick up an **endpoint stone** and move it to an unoccupied position so that it is no longer an **endpoint stone**.
* In particular, if the stones are at say, `stones = [1,2,5]`, you cannot move the endpoint stone at position `5`, since moving it to any position (such as `0`, or `3`) will still keep that stone as an endpoint stone.
The game ends when you cannot make any more moves (i.e., the stones are in three consecutive positions).
Return _an integer array_ `answer` _of length_ `2` _where_:
* `answer[0]` _is the minimum number of moves you can play, and_
* `answer[1]` _is the maximum number of moves you can play_.
**Example 1:**
**Input:** stones = \[7,4,9\]
**Output:** \[1,2\]
**Explanation:** We can move 4 -> 8 for one move to finish the game.
Or, we can move 9 -> 5, 4 -> 6 for two moves to finish the game.
**Example 2:**
**Input:** stones = \[6,5,4,3,10\]
**Output:** \[2,3\]
**Explanation:** We can move 3 -> 8 then 10 -> 7 to finish the game.
Or, we can move 3 -> 7, 4 -> 8, 5 -> 9 to finish the game.
Notice we cannot move 10 -> 2 to finish the game, because that would be an illegal move.
**Constraints:**
* `3 <= stones.length <= 104`
* `1 <= stones[i] <= 109`
* All the values of `stones` are **unique**. | null |
Solution | available-captures-for-rook | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numRookCaptures(vector<vector<char>>& board) {\n static vector<pair<int, int>> directions{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};\n\n int r = -1, c = -1;\n for (int i = 0; i < 8 && r == -1; ++i) {\n for (int j = 0; j < 8; ++j) {\n if (board[i][j] == \'R\') {\n tie(r, c) = make_pair(i, j);\n break;\n }\n }\n }\n int result = 0;\n for (const auto& d : directions) {\n int nr, nc;\n tie(nr, nc) = make_pair(r + d.first, c + d.second);\n while (0 <= nr && nr < 8 && 0 <= nc && nc < 8) {\n if (board[nr][nc] == \'p\') {\n ++result;\n }\n if (board[nr][nc] != \'.\') {\n break;\n }\n tie(nr, nc) = make_pair(nr + d.first, nc + d.second);\n }\n }\n return result;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n rook = None\n while rook is None:\n for i in range(8):\n for j in range(8):\n if board[i][j] == \'R\':\n rook = (i, j)\n break\n \n available_captures = 0\n for i in range(rook[0] - 1, -1, -1):\n if board[i][rook[1]] == \'p\':\n available_captures += 1\n break\n elif board[i][rook[1]] == \'B\':\n break\n for i in range(rook[0] + 1, 8):\n if board[i][rook[1]] == \'p\':\n available_captures += 1\n break\n elif board[i][rook[1]] == \'B\':\n break\n for j in range(rook[1] - 1, -1, -1):\n if board[rook[0]][j] == \'p\':\n available_captures += 1\n break\n elif board[rook[0]][j] == \'B\':\n break\n for j in range(rook[1] + 1, 8):\n if board[rook[0]][j] == \'p\':\n available_captures += 1\n break\n elif board[rook[0]][j] == \'B\':\n break\n return available_captures\n```\n\n```Java []\nclass Solution {\n public int numRookCaptures(char[][] board) {\n int ii=0,jj=0;\n for(int i=0;i<8;i++){\n for(int j=0;j<8;j++){\n if(board[i][j]==\'R\'){\n ii=i;\n jj=j;\n break;\n }\n }\n }\n int count=0;\n for(int i=ii;i>=0;i--){\n if(board[i][jj]==\'p\'){\n count++;\n break;\n }\n else if(board[i][jj]==\'B\')\n break;\n }\n for(int i=ii;i<8;i++){\n if(board[i][jj]==\'p\'){\n count++;\n break;\n }\n else if(board[i][jj]==\'B\')\n break;\n }\n for(int j=jj;j<8;j++){\n if(board[ii][j]==\'p\'){\n count++;\n break;\n }\n else if(board[ii][j]==\'B\')\n break;\n }\n for(int j=jj;j>=0;j--){\n if(board[ii][j]==\'p\'){\n count++;\n break;\n }\n else if(board[ii][j]==\'B\')\n break;\n }\n return count;\n }\n}\n``` | 1 | On an `8 x 8` chessboard, there is **exactly one** white rook `'R'` and some number of white bishops `'B'`, black pawns `'p'`, and empty squares `'.'`.
When the rook moves, it chooses one of four cardinal directions (north, east, south, or west), then moves in that direction until it chooses to stop, reaches the edge of the board, captures a black pawn, or is blocked by a white bishop. A rook is considered **attacking** a pawn if the rook can capture the pawn on the rook's turn. The **number of available captures** for the white rook is the number of pawns that the rook is **attacking**.
Return _the **number of available captures** for the white rook_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "R ", ". ", ". ", ". ", "p "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** In this example, the rook is attacking all the pawns.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "B ", "R ", "B ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 0
**Explanation:** The bishops are blocking the rook from attacking any of the pawns.
**Example 3:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ "p ", "p ", ". ", "R ", ". ", "p ", "B ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** The rook is attacking the pawns at positions b5, d6, and f5.
**Constraints:**
* `board.length == 8`
* `board[i].length == 8`
* `board[i][j]` is either `'R'`, `'.'`, `'B'`, or `'p'`
* There is exactly one cell with `board[i][j] == 'R'` | null |
Solution | available-captures-for-rook | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int numRookCaptures(vector<vector<char>>& board) {\n static vector<pair<int, int>> directions{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};\n\n int r = -1, c = -1;\n for (int i = 0; i < 8 && r == -1; ++i) {\n for (int j = 0; j < 8; ++j) {\n if (board[i][j] == \'R\') {\n tie(r, c) = make_pair(i, j);\n break;\n }\n }\n }\n int result = 0;\n for (const auto& d : directions) {\n int nr, nc;\n tie(nr, nc) = make_pair(r + d.first, c + d.second);\n while (0 <= nr && nr < 8 && 0 <= nc && nc < 8) {\n if (board[nr][nc] == \'p\') {\n ++result;\n }\n if (board[nr][nc] != \'.\') {\n break;\n }\n tie(nr, nc) = make_pair(nr + d.first, nc + d.second);\n }\n }\n return result;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n rook = None\n while rook is None:\n for i in range(8):\n for j in range(8):\n if board[i][j] == \'R\':\n rook = (i, j)\n break\n \n available_captures = 0\n for i in range(rook[0] - 1, -1, -1):\n if board[i][rook[1]] == \'p\':\n available_captures += 1\n break\n elif board[i][rook[1]] == \'B\':\n break\n for i in range(rook[0] + 1, 8):\n if board[i][rook[1]] == \'p\':\n available_captures += 1\n break\n elif board[i][rook[1]] == \'B\':\n break\n for j in range(rook[1] - 1, -1, -1):\n if board[rook[0]][j] == \'p\':\n available_captures += 1\n break\n elif board[rook[0]][j] == \'B\':\n break\n for j in range(rook[1] + 1, 8):\n if board[rook[0]][j] == \'p\':\n available_captures += 1\n break\n elif board[rook[0]][j] == \'B\':\n break\n return available_captures\n```\n\n```Java []\nclass Solution {\n public int numRookCaptures(char[][] board) {\n int ii=0,jj=0;\n for(int i=0;i<8;i++){\n for(int j=0;j<8;j++){\n if(board[i][j]==\'R\'){\n ii=i;\n jj=j;\n break;\n }\n }\n }\n int count=0;\n for(int i=ii;i>=0;i--){\n if(board[i][jj]==\'p\'){\n count++;\n break;\n }\n else if(board[i][jj]==\'B\')\n break;\n }\n for(int i=ii;i<8;i++){\n if(board[i][jj]==\'p\'){\n count++;\n break;\n }\n else if(board[i][jj]==\'B\')\n break;\n }\n for(int j=jj;j<8;j++){\n if(board[ii][j]==\'p\'){\n count++;\n break;\n }\n else if(board[ii][j]==\'B\')\n break;\n }\n for(int j=jj;j>=0;j--){\n if(board[ii][j]==\'p\'){\n count++;\n break;\n }\n else if(board[ii][j]==\'B\')\n break;\n }\n return count;\n }\n}\n``` | 1 | On an infinite plane, a robot initially stands at `(0, 0)` and faces north. Note that:
* The **north direction** is the positive direction of the y-axis.
* The **south direction** is the negative direction of the y-axis.
* The **east direction** is the positive direction of the x-axis.
* The **west direction** is the negative direction of the x-axis.
The robot can receive one of three instructions:
* `"G "`: go straight 1 unit.
* `"L "`: turn 90 degrees to the left (i.e., anti-clockwise direction).
* `"R "`: turn 90 degrees to the right (i.e., clockwise direction).
The robot performs the `instructions` given in order, and repeats them forever.
Return `true` if and only if there exists a circle in the plane such that the robot never leaves the circle.
**Example 1:**
**Input:** instructions = "GGLLGG "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: South.
"G ": move one step. Position: (0, 1). Direction: South.
"G ": move one step. Position: (0, 0). Direction: South.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (0, 2) --> (0, 1) --> (0, 0).
Based on that, we return true.
**Example 2:**
**Input:** instructions = "GG "
**Output:** false
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
Repeating the instructions, keeps advancing in the north direction and does not go into cycles.
Based on that, we return false.
**Example 3:**
**Input:** instructions = "GL "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 1). Direction: West.
"G ": move one step. Position: (-1, 1). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 1). Direction: South.
"G ": move one step. Position: (-1, 0). Direction: South.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 0). Direction: East.
"G ": move one step. Position: (0, 0). Direction: East.
"L ": turn 90 degrees anti-clockwise. Position: (0, 0). Direction: North.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (-1, 1) --> (-1, 0) --> (0, 0).
Based on that, we return true.
**Constraints:**
* `1 <= instructions.length <= 100`
* `instructions[i]` is `'G'`, `'L'` or, `'R'`. | null |
✅ Beats 98.87% solutions,✅ Easy to understand Python Code with explanation by ✅ BOLT CODING ✅ | available-captures-for-rook | 0 | 1 | # Explanation:\nFirst we try to find the position of Rook.\nOnce we get that we already know that Rook always attacks in straight line i.e. Rows or Columns (not diagonals). So rather than traversing through the whole list we will only traverse through the rows and columns where Rook can attack. So we right 4 different for loops to traverse through rows and columns.\n\n# Complexity\n- **Time complexity**: O(n^2) : As in worst case scenario the ROOK might be at position (7, 7)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n idx = []\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] == \'R\':\n idx = [i, j]\n break\n x, y = idx[0], idx[1]\n count = 0\n for i in range(x-1, -1, -1):\n if board[i][y] == \'p\':\n count+=1\n break\n elif board[i][y] == \'B\':\n break\n \n for i in range(x+1, 8):\n if board[i][y] == \'p\':\n count+=1\n break\n elif board[i][y] == \'B\':\n break\n\n for i in range(y-1, -1, -1):\n if board[x][i] == \'p\':\n count+=1\n break\n elif board[x][i] == \'B\':\n break\n \n for i in range(y+1, 8):\n if board[x][i] == \'p\':\n count+=1\n break\n elif board[x][i] == \'B\':\n break\n return count\n\n```\n\n# Learning\nTo understand problems in simpler ways, need help with projects, want to learn coding from scratch, work on resume level projects, learn data science ...................\n\nSubscribe to Bolt Coding Channel - https://www.youtube.com/@boltcoding | 1 | On an `8 x 8` chessboard, there is **exactly one** white rook `'R'` and some number of white bishops `'B'`, black pawns `'p'`, and empty squares `'.'`.
When the rook moves, it chooses one of four cardinal directions (north, east, south, or west), then moves in that direction until it chooses to stop, reaches the edge of the board, captures a black pawn, or is blocked by a white bishop. A rook is considered **attacking** a pawn if the rook can capture the pawn on the rook's turn. The **number of available captures** for the white rook is the number of pawns that the rook is **attacking**.
Return _the **number of available captures** for the white rook_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "R ", ". ", ". ", ". ", "p "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** In this example, the rook is attacking all the pawns.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "B ", "R ", "B ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 0
**Explanation:** The bishops are blocking the rook from attacking any of the pawns.
**Example 3:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ "p ", "p ", ". ", "R ", ". ", "p ", "B ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** The rook is attacking the pawns at positions b5, d6, and f5.
**Constraints:**
* `board.length == 8`
* `board[i].length == 8`
* `board[i][j]` is either `'R'`, `'.'`, `'B'`, or `'p'`
* There is exactly one cell with `board[i][j] == 'R'` | null |
✅ Beats 98.87% solutions,✅ Easy to understand Python Code with explanation by ✅ BOLT CODING ✅ | available-captures-for-rook | 0 | 1 | # Explanation:\nFirst we try to find the position of Rook.\nOnce we get that we already know that Rook always attacks in straight line i.e. Rows or Columns (not diagonals). So rather than traversing through the whole list we will only traverse through the rows and columns where Rook can attack. So we right 4 different for loops to traverse through rows and columns.\n\n# Complexity\n- **Time complexity**: O(n^2) : As in worst case scenario the ROOK might be at position (7, 7)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n idx = []\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] == \'R\':\n idx = [i, j]\n break\n x, y = idx[0], idx[1]\n count = 0\n for i in range(x-1, -1, -1):\n if board[i][y] == \'p\':\n count+=1\n break\n elif board[i][y] == \'B\':\n break\n \n for i in range(x+1, 8):\n if board[i][y] == \'p\':\n count+=1\n break\n elif board[i][y] == \'B\':\n break\n\n for i in range(y-1, -1, -1):\n if board[x][i] == \'p\':\n count+=1\n break\n elif board[x][i] == \'B\':\n break\n \n for i in range(y+1, 8):\n if board[x][i] == \'p\':\n count+=1\n break\n elif board[x][i] == \'B\':\n break\n return count\n\n```\n\n# Learning\nTo understand problems in simpler ways, need help with projects, want to learn coding from scratch, work on resume level projects, learn data science ...................\n\nSubscribe to Bolt Coding Channel - https://www.youtube.com/@boltcoding | 1 | On an infinite plane, a robot initially stands at `(0, 0)` and faces north. Note that:
* The **north direction** is the positive direction of the y-axis.
* The **south direction** is the negative direction of the y-axis.
* The **east direction** is the positive direction of the x-axis.
* The **west direction** is the negative direction of the x-axis.
The robot can receive one of three instructions:
* `"G "`: go straight 1 unit.
* `"L "`: turn 90 degrees to the left (i.e., anti-clockwise direction).
* `"R "`: turn 90 degrees to the right (i.e., clockwise direction).
The robot performs the `instructions` given in order, and repeats them forever.
Return `true` if and only if there exists a circle in the plane such that the robot never leaves the circle.
**Example 1:**
**Input:** instructions = "GGLLGG "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: South.
"G ": move one step. Position: (0, 1). Direction: South.
"G ": move one step. Position: (0, 0). Direction: South.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (0, 2) --> (0, 1) --> (0, 0).
Based on that, we return true.
**Example 2:**
**Input:** instructions = "GG "
**Output:** false
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
Repeating the instructions, keeps advancing in the north direction and does not go into cycles.
Based on that, we return false.
**Example 3:**
**Input:** instructions = "GL "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 1). Direction: West.
"G ": move one step. Position: (-1, 1). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 1). Direction: South.
"G ": move one step. Position: (-1, 0). Direction: South.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 0). Direction: East.
"G ": move one step. Position: (0, 0). Direction: East.
"L ": turn 90 degrees anti-clockwise. Position: (0, 0). Direction: North.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (-1, 1) --> (-1, 0) --> (0, 0).
Based on that, we return true.
**Constraints:**
* `1 <= instructions.length <= 100`
* `instructions[i]` is `'G'`, `'L'` or, `'R'`. | null |
Python 3. Not the shortest but Neat and Easy to Understand | available-captures-for-rook | 0 | 1 | The idea is to find the Rook location and then start looking at 4 directions to find nearest piece. Check if the nearest piece is friend or foe using `isupper()`, `islower()`. \nRuntime varies from 48 ms (14%) to 32 ms (96%) so i guess it\'s good enough. Anyways, the most important thing is it\'s easy to understand\n```python\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n \n def check_direction(R,C,direction):\n if direction=="right":\n for col in range(C+1,8): # increasing col \n if board[R][col].islower():return 1\n if board[R][col].isupper():return 0\n if direction=="left":\n for col in range(C-1,-1,-1): # decreasing col \n if board[R][col].islower():return 1\n if board[R][col].isupper():return 0\n if direction=="down":\n for row in range(R+1,8): # increasing row\n if board[row][C].islower():return 1\n if board[row][C].isupper():return 0\n if direction=="up": \n for row in range(R-1,-1,-1): # decreasing col \n if board[row][C].islower():return 1\n if board[row][C].isupper():return 0\n return 0 # we reach the edge (nothing was found)\n \n for row in range(8):\n for col in range(8):\n if board[row][col]=="R":\n\t\t\t\t\t# sum all directions up\n return sum([check_direction(row,col,"right"),\n check_direction(row,col,"left"),\n check_direction(row,col,"up"),\n check_direction(row,col,"down")])\n``` | 9 | On an `8 x 8` chessboard, there is **exactly one** white rook `'R'` and some number of white bishops `'B'`, black pawns `'p'`, and empty squares `'.'`.
When the rook moves, it chooses one of four cardinal directions (north, east, south, or west), then moves in that direction until it chooses to stop, reaches the edge of the board, captures a black pawn, or is blocked by a white bishop. A rook is considered **attacking** a pawn if the rook can capture the pawn on the rook's turn. The **number of available captures** for the white rook is the number of pawns that the rook is **attacking**.
Return _the **number of available captures** for the white rook_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "R ", ". ", ". ", ". ", "p "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** In this example, the rook is attacking all the pawns.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "B ", "R ", "B ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 0
**Explanation:** The bishops are blocking the rook from attacking any of the pawns.
**Example 3:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ "p ", "p ", ". ", "R ", ". ", "p ", "B ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** The rook is attacking the pawns at positions b5, d6, and f5.
**Constraints:**
* `board.length == 8`
* `board[i].length == 8`
* `board[i][j]` is either `'R'`, `'.'`, `'B'`, or `'p'`
* There is exactly one cell with `board[i][j] == 'R'` | null |
Python 3. Not the shortest but Neat and Easy to Understand | available-captures-for-rook | 0 | 1 | The idea is to find the Rook location and then start looking at 4 directions to find nearest piece. Check if the nearest piece is friend or foe using `isupper()`, `islower()`. \nRuntime varies from 48 ms (14%) to 32 ms (96%) so i guess it\'s good enough. Anyways, the most important thing is it\'s easy to understand\n```python\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n \n def check_direction(R,C,direction):\n if direction=="right":\n for col in range(C+1,8): # increasing col \n if board[R][col].islower():return 1\n if board[R][col].isupper():return 0\n if direction=="left":\n for col in range(C-1,-1,-1): # decreasing col \n if board[R][col].islower():return 1\n if board[R][col].isupper():return 0\n if direction=="down":\n for row in range(R+1,8): # increasing row\n if board[row][C].islower():return 1\n if board[row][C].isupper():return 0\n if direction=="up": \n for row in range(R-1,-1,-1): # decreasing col \n if board[row][C].islower():return 1\n if board[row][C].isupper():return 0\n return 0 # we reach the edge (nothing was found)\n \n for row in range(8):\n for col in range(8):\n if board[row][col]=="R":\n\t\t\t\t\t# sum all directions up\n return sum([check_direction(row,col,"right"),\n check_direction(row,col,"left"),\n check_direction(row,col,"up"),\n check_direction(row,col,"down")])\n``` | 9 | On an infinite plane, a robot initially stands at `(0, 0)` and faces north. Note that:
* The **north direction** is the positive direction of the y-axis.
* The **south direction** is the negative direction of the y-axis.
* The **east direction** is the positive direction of the x-axis.
* The **west direction** is the negative direction of the x-axis.
The robot can receive one of three instructions:
* `"G "`: go straight 1 unit.
* `"L "`: turn 90 degrees to the left (i.e., anti-clockwise direction).
* `"R "`: turn 90 degrees to the right (i.e., clockwise direction).
The robot performs the `instructions` given in order, and repeats them forever.
Return `true` if and only if there exists a circle in the plane such that the robot never leaves the circle.
**Example 1:**
**Input:** instructions = "GGLLGG "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: South.
"G ": move one step. Position: (0, 1). Direction: South.
"G ": move one step. Position: (0, 0). Direction: South.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (0, 2) --> (0, 1) --> (0, 0).
Based on that, we return true.
**Example 2:**
**Input:** instructions = "GG "
**Output:** false
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
Repeating the instructions, keeps advancing in the north direction and does not go into cycles.
Based on that, we return false.
**Example 3:**
**Input:** instructions = "GL "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 1). Direction: West.
"G ": move one step. Position: (-1, 1). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 1). Direction: South.
"G ": move one step. Position: (-1, 0). Direction: South.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 0). Direction: East.
"G ": move one step. Position: (0, 0). Direction: East.
"L ": turn 90 degrees anti-clockwise. Position: (0, 0). Direction: North.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (-1, 1) --> (-1, 0) --> (0, 0).
Based on that, we return true.
**Constraints:**
* `1 <= instructions.length <= 100`
* `instructions[i]` is `'G'`, `'L'` or, `'R'`. | null |
🐍🐍🐍 Solution in 3 lines 🐍🐍🐍 with explanation | available-captures-for-rook | 0 | 1 | # Code\n```\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n # dictionary with coordinate {row:column in matrix(board)} of \'Rock\' \n d = {i:x.index(\'R\') for i, x in enumerate(board) if \'R\' in x}\n # making list of 2 string without \'.\', first - row of \'Rock\', second - column of \'Rock\'\n l = [(\'\'.join(board[key]).replace(\'.\',\'\'), \'\'.join([x[d[key]] for x in board]).replace(\'.\',\'\')) for key in d][0]\n # in result we have tuple of 2 strings for expamle (\'pRp\',\'Rp\')\n # sum of list comprehensions with structure if else: (if else)\n return sum([2 if x in l[0] and x in l[1] else 1 if x in l[0] or x in l[1] else 0 for x in [\'Rp\',\'pR\']])\n\n \n```\n\nIf my decision looks like piece of sh#t feel free to say me about it in comments=) | 0 | On an `8 x 8` chessboard, there is **exactly one** white rook `'R'` and some number of white bishops `'B'`, black pawns `'p'`, and empty squares `'.'`.
When the rook moves, it chooses one of four cardinal directions (north, east, south, or west), then moves in that direction until it chooses to stop, reaches the edge of the board, captures a black pawn, or is blocked by a white bishop. A rook is considered **attacking** a pawn if the rook can capture the pawn on the rook's turn. The **number of available captures** for the white rook is the number of pawns that the rook is **attacking**.
Return _the **number of available captures** for the white rook_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "R ", ". ", ". ", ". ", "p "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** In this example, the rook is attacking all the pawns.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "B ", "R ", "B ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 0
**Explanation:** The bishops are blocking the rook from attacking any of the pawns.
**Example 3:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ "p ", "p ", ". ", "R ", ". ", "p ", "B ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** The rook is attacking the pawns at positions b5, d6, and f5.
**Constraints:**
* `board.length == 8`
* `board[i].length == 8`
* `board[i][j]` is either `'R'`, `'.'`, `'B'`, or `'p'`
* There is exactly one cell with `board[i][j] == 'R'` | null |
🐍🐍🐍 Solution in 3 lines 🐍🐍🐍 with explanation | available-captures-for-rook | 0 | 1 | # Code\n```\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n # dictionary with coordinate {row:column in matrix(board)} of \'Rock\' \n d = {i:x.index(\'R\') for i, x in enumerate(board) if \'R\' in x}\n # making list of 2 string without \'.\', first - row of \'Rock\', second - column of \'Rock\'\n l = [(\'\'.join(board[key]).replace(\'.\',\'\'), \'\'.join([x[d[key]] for x in board]).replace(\'.\',\'\')) for key in d][0]\n # in result we have tuple of 2 strings for expamle (\'pRp\',\'Rp\')\n # sum of list comprehensions with structure if else: (if else)\n return sum([2 if x in l[0] and x in l[1] else 1 if x in l[0] or x in l[1] else 0 for x in [\'Rp\',\'pR\']])\n\n \n```\n\nIf my decision looks like piece of sh#t feel free to say me about it in comments=) | 0 | On an infinite plane, a robot initially stands at `(0, 0)` and faces north. Note that:
* The **north direction** is the positive direction of the y-axis.
* The **south direction** is the negative direction of the y-axis.
* The **east direction** is the positive direction of the x-axis.
* The **west direction** is the negative direction of the x-axis.
The robot can receive one of three instructions:
* `"G "`: go straight 1 unit.
* `"L "`: turn 90 degrees to the left (i.e., anti-clockwise direction).
* `"R "`: turn 90 degrees to the right (i.e., clockwise direction).
The robot performs the `instructions` given in order, and repeats them forever.
Return `true` if and only if there exists a circle in the plane such that the robot never leaves the circle.
**Example 1:**
**Input:** instructions = "GGLLGG "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: South.
"G ": move one step. Position: (0, 1). Direction: South.
"G ": move one step. Position: (0, 0). Direction: South.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (0, 2) --> (0, 1) --> (0, 0).
Based on that, we return true.
**Example 2:**
**Input:** instructions = "GG "
**Output:** false
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
Repeating the instructions, keeps advancing in the north direction and does not go into cycles.
Based on that, we return false.
**Example 3:**
**Input:** instructions = "GL "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 1). Direction: West.
"G ": move one step. Position: (-1, 1). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 1). Direction: South.
"G ": move one step. Position: (-1, 0). Direction: South.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 0). Direction: East.
"G ": move one step. Position: (0, 0). Direction: East.
"L ": turn 90 degrees anti-clockwise. Position: (0, 0). Direction: North.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (-1, 1) --> (-1, 0) --> (0, 0).
Based on that, we return true.
**Constraints:**
* `1 <= instructions.length <= 100`
* `instructions[i]` is `'G'`, `'L'` or, `'R'`. | null |
Best Approach using 2 while loops | available-captures-for-rook | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n# Complexity\n- Time complexity:\n- O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n row,col = 0,0\n for i in range(len(board)):\n for j in range(len(board[i])):\n if board[i][j] == "R":\n row = i\n col = j\n break\n i,j = 1,1\n p,r=0,0\n count = 0\n while((int(col-i)>=0 or int(col+j)<8)):\n if(int(col-i)>=0 and p!=1):\n if board[row][col-i]=="p":\n count+=1\n p=1\n \n if board[row][col-i]=="B":\n p=1\n \n i+=1\n if(int(col+j)<8 and r!=1):\n if board[row][col+j]=="p":\n count+=1\n r=1\n \n if board[row][col+j]=="B":\n r=1\n \n j+=1\n k,l=1,1\n o,t=0,0\n while(int(row-k)>=0 or int(row+l)<8):\n if(int(row-k)>=0 and o!=1):\n if board[row-k][col]=="p":\n count+=1\n o=1\n if board[row-k][col]=="B":\n o=1\n \n k+=1\n if(int(row+l)<8 and t!=1):\n if board[row+l][col]=="p":\n count+=1\n t=1\n if board[row+l][col]=="B":\n t=1\n l+=1\n return count\n \n\n\n \n``` | 0 | On an `8 x 8` chessboard, there is **exactly one** white rook `'R'` and some number of white bishops `'B'`, black pawns `'p'`, and empty squares `'.'`.
When the rook moves, it chooses one of four cardinal directions (north, east, south, or west), then moves in that direction until it chooses to stop, reaches the edge of the board, captures a black pawn, or is blocked by a white bishop. A rook is considered **attacking** a pawn if the rook can capture the pawn on the rook's turn. The **number of available captures** for the white rook is the number of pawns that the rook is **attacking**.
Return _the **number of available captures** for the white rook_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "R ", ". ", ". ", ". ", "p "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** In this example, the rook is attacking all the pawns.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "B ", "R ", "B ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 0
**Explanation:** The bishops are blocking the rook from attacking any of the pawns.
**Example 3:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ "p ", "p ", ". ", "R ", ". ", "p ", "B ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** The rook is attacking the pawns at positions b5, d6, and f5.
**Constraints:**
* `board.length == 8`
* `board[i].length == 8`
* `board[i][j]` is either `'R'`, `'.'`, `'B'`, or `'p'`
* There is exactly one cell with `board[i][j] == 'R'` | null |
Best Approach using 2 while loops | available-captures-for-rook | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n# Complexity\n- Time complexity:\n- O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n row,col = 0,0\n for i in range(len(board)):\n for j in range(len(board[i])):\n if board[i][j] == "R":\n row = i\n col = j\n break\n i,j = 1,1\n p,r=0,0\n count = 0\n while((int(col-i)>=0 or int(col+j)<8)):\n if(int(col-i)>=0 and p!=1):\n if board[row][col-i]=="p":\n count+=1\n p=1\n \n if board[row][col-i]=="B":\n p=1\n \n i+=1\n if(int(col+j)<8 and r!=1):\n if board[row][col+j]=="p":\n count+=1\n r=1\n \n if board[row][col+j]=="B":\n r=1\n \n j+=1\n k,l=1,1\n o,t=0,0\n while(int(row-k)>=0 or int(row+l)<8):\n if(int(row-k)>=0 and o!=1):\n if board[row-k][col]=="p":\n count+=1\n o=1\n if board[row-k][col]=="B":\n o=1\n \n k+=1\n if(int(row+l)<8 and t!=1):\n if board[row+l][col]=="p":\n count+=1\n t=1\n if board[row+l][col]=="B":\n t=1\n l+=1\n return count\n \n\n\n \n``` | 0 | On an infinite plane, a robot initially stands at `(0, 0)` and faces north. Note that:
* The **north direction** is the positive direction of the y-axis.
* The **south direction** is the negative direction of the y-axis.
* The **east direction** is the positive direction of the x-axis.
* The **west direction** is the negative direction of the x-axis.
The robot can receive one of three instructions:
* `"G "`: go straight 1 unit.
* `"L "`: turn 90 degrees to the left (i.e., anti-clockwise direction).
* `"R "`: turn 90 degrees to the right (i.e., clockwise direction).
The robot performs the `instructions` given in order, and repeats them forever.
Return `true` if and only if there exists a circle in the plane such that the robot never leaves the circle.
**Example 1:**
**Input:** instructions = "GGLLGG "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: South.
"G ": move one step. Position: (0, 1). Direction: South.
"G ": move one step. Position: (0, 0). Direction: South.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (0, 2) --> (0, 1) --> (0, 0).
Based on that, we return true.
**Example 2:**
**Input:** instructions = "GG "
**Output:** false
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
Repeating the instructions, keeps advancing in the north direction and does not go into cycles.
Based on that, we return false.
**Example 3:**
**Input:** instructions = "GL "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 1). Direction: West.
"G ": move one step. Position: (-1, 1). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 1). Direction: South.
"G ": move one step. Position: (-1, 0). Direction: South.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 0). Direction: East.
"G ": move one step. Position: (0, 0). Direction: East.
"L ": turn 90 degrees anti-clockwise. Position: (0, 0). Direction: North.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (-1, 1) --> (-1, 0) --> (0, 0).
Based on that, we return true.
**Constraints:**
* `1 <= instructions.length <= 100`
* `instructions[i]` is `'G'`, `'L'` or, `'R'`. | null |
Python solution - Regex | available-captures-for-rook | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nif the pattern shows as "p\\.*R" or \'R\\.*p\' then the Rook captures the pawn.\nCheck the row and column separatively.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n### -- check east and west direction -->\n l=\'\'.join(list(*[board[i] for i in range(8) if \'R\' in board[i]]))\n ans=0\n if re.findall(\'p\\.*R\',l):\n ans+=1\n if re.findall(\'R\\.*p\',l):\n ans+=1\n### -- check north and south direction -->\n board=list(zip(*board))\n l=\'\'.join(list(*[board[i] for i in range(8) if \'R\' in board[i]]))\n if re.findall(\'p\\.*R\',l):\n ans+=1\n if re.findall(\'R\\.*p\',l):\n ans+=1\n return(ans)\n \n``` | 0 | On an `8 x 8` chessboard, there is **exactly one** white rook `'R'` and some number of white bishops `'B'`, black pawns `'p'`, and empty squares `'.'`.
When the rook moves, it chooses one of four cardinal directions (north, east, south, or west), then moves in that direction until it chooses to stop, reaches the edge of the board, captures a black pawn, or is blocked by a white bishop. A rook is considered **attacking** a pawn if the rook can capture the pawn on the rook's turn. The **number of available captures** for the white rook is the number of pawns that the rook is **attacking**.
Return _the **number of available captures** for the white rook_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "R ", ". ", ". ", ". ", "p "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** In this example, the rook is attacking all the pawns.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "B ", "R ", "B ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "B ", "p ", "p ", ". ", ". "\],\[ ". ", "p ", "p ", "p ", "p ", "p ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 0
**Explanation:** The bishops are blocking the rook from attacking any of the pawns.
**Example 3:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ "p ", "p ", ". ", "R ", ". ", "p ", "B ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "p ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\]\]
**Output:** 3
**Explanation:** The rook is attacking the pawns at positions b5, d6, and f5.
**Constraints:**
* `board.length == 8`
* `board[i].length == 8`
* `board[i][j]` is either `'R'`, `'.'`, `'B'`, or `'p'`
* There is exactly one cell with `board[i][j] == 'R'` | null |
Python solution - Regex | available-captures-for-rook | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nif the pattern shows as "p\\.*R" or \'R\\.*p\' then the Rook captures the pawn.\nCheck the row and column separatively.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numRookCaptures(self, board: List[List[str]]) -> int:\n### -- check east and west direction -->\n l=\'\'.join(list(*[board[i] for i in range(8) if \'R\' in board[i]]))\n ans=0\n if re.findall(\'p\\.*R\',l):\n ans+=1\n if re.findall(\'R\\.*p\',l):\n ans+=1\n### -- check north and south direction -->\n board=list(zip(*board))\n l=\'\'.join(list(*[board[i] for i in range(8) if \'R\' in board[i]]))\n if re.findall(\'p\\.*R\',l):\n ans+=1\n if re.findall(\'R\\.*p\',l):\n ans+=1\n return(ans)\n \n``` | 0 | On an infinite plane, a robot initially stands at `(0, 0)` and faces north. Note that:
* The **north direction** is the positive direction of the y-axis.
* The **south direction** is the negative direction of the y-axis.
* The **east direction** is the positive direction of the x-axis.
* The **west direction** is the negative direction of the x-axis.
The robot can receive one of three instructions:
* `"G "`: go straight 1 unit.
* `"L "`: turn 90 degrees to the left (i.e., anti-clockwise direction).
* `"R "`: turn 90 degrees to the right (i.e., clockwise direction).
The robot performs the `instructions` given in order, and repeats them forever.
Return `true` if and only if there exists a circle in the plane such that the robot never leaves the circle.
**Example 1:**
**Input:** instructions = "GGLLGG "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (0, 2). Direction: South.
"G ": move one step. Position: (0, 1). Direction: South.
"G ": move one step. Position: (0, 0). Direction: South.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (0, 2) --> (0, 1) --> (0, 0).
Based on that, we return true.
**Example 2:**
**Input:** instructions = "GG "
**Output:** false
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"G ": move one step. Position: (0, 2). Direction: North.
Repeating the instructions, keeps advancing in the north direction and does not go into cycles.
Based on that, we return false.
**Example 3:**
**Input:** instructions = "GL "
**Output:** true
**Explanation:** The robot is initially at (0, 0) facing the north direction.
"G ": move one step. Position: (0, 1). Direction: North.
"L ": turn 90 degrees anti-clockwise. Position: (0, 1). Direction: West.
"G ": move one step. Position: (-1, 1). Direction: West.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 1). Direction: South.
"G ": move one step. Position: (-1, 0). Direction: South.
"L ": turn 90 degrees anti-clockwise. Position: (-1, 0). Direction: East.
"G ": move one step. Position: (0, 0). Direction: East.
"L ": turn 90 degrees anti-clockwise. Position: (0, 0). Direction: North.
Repeating the instructions, the robot goes into the cycle: (0, 0) --> (0, 1) --> (-1, 1) --> (-1, 0) --> (0, 0).
Based on that, we return true.
**Constraints:**
* `1 <= instructions.length <= 100`
* `instructions[i]` is `'G'`, `'L'` or, `'R'`. | null |
Python (Simple DP) | minimum-cost-to-merge-stones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mergeStones(self, stones, k):\n n = len(stones)\n\n if (n-1)%(k-1): return -1\n\n ans = [0]\n\n for i in range(n):\n ans.append(ans[-1] + stones[i])\n\n @lru_cache(None)\n def dfs(lo,hi):\n if hi-lo+1 < k:\n return 0\n\n res = min(dfs(lo,i) + dfs(i+1,hi) for i in range(lo,hi,k-1))\n\n if (hi-lo)%(k-1) == 0:\n res += ans[hi+1] - ans[lo]\n\n return res\n\n return dfs(0,n-1)\n\n\n\n\n\n\n``` | 1 | There are `n` piles of `stones` arranged in a row. The `ith` pile has `stones[i]` stones.
A move consists of merging exactly `k` **consecutive** piles into one pile, and the cost of this move is equal to the total number of stones in these `k` piles.
Return _the minimum cost to merge all piles of stones into one pile_. If it is impossible, return `-1`.
**Example 1:**
**Input:** stones = \[3,2,4,1\], k = 2
**Output:** 20
**Explanation:** We start with \[3, 2, 4, 1\].
We merge \[3, 2\] for a cost of 5, and we are left with \[5, 4, 1\].
We merge \[4, 1\] for a cost of 5, and we are left with \[5, 5\].
We merge \[5, 5\] for a cost of 10, and we are left with \[10\].
The total cost was 20, and this is the minimum possible.
**Example 2:**
**Input:** stones = \[3,2,4,1\], k = 3
**Output:** -1
**Explanation:** After any merge operation, there are 2 piles left, and we can't merge anymore. So the task is impossible.
**Example 3:**
**Input:** stones = \[3,5,1,2,6\], k = 3
**Output:** 25
**Explanation:** We start with \[3, 5, 1, 2, 6\].
We merge \[5, 1, 2\] for a cost of 8, and we are left with \[3, 8, 6\].
We merge \[3, 8, 6\] for a cost of 17, and we are left with \[17\].
The total cost was 25, and this is the minimum possible.
**Constraints:**
* `n == stones.length`
* `1 <= n <= 30`
* `1 <= stones[i] <= 100`
* `2 <= k <= 30` | null |
Python (Simple DP) | minimum-cost-to-merge-stones | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mergeStones(self, stones, k):\n n = len(stones)\n\n if (n-1)%(k-1): return -1\n\n ans = [0]\n\n for i in range(n):\n ans.append(ans[-1] + stones[i])\n\n @lru_cache(None)\n def dfs(lo,hi):\n if hi-lo+1 < k:\n return 0\n\n res = min(dfs(lo,i) + dfs(i+1,hi) for i in range(lo,hi,k-1))\n\n if (hi-lo)%(k-1) == 0:\n res += ans[hi+1] - ans[lo]\n\n return res\n\n return dfs(0,n-1)\n\n\n\n\n\n\n``` | 1 | You have `n` gardens, labeled from `1` to `n`, and an array `paths` where `paths[i] = [xi, yi]` describes a bidirectional path between garden `xi` to garden `yi`. In each garden, you want to plant one of 4 types of flowers.
All gardens have **at most 3** paths coming into or leaving it.
Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.
Return _**any** such a choice as an array_ `answer`_, where_ `answer[i]` _is the type of flower planted in the_ `(i+1)th` _garden. The flower types are denoted_ `1`_,_ `2`_,_ `3`_, or_ `4`_. It is guaranteed an answer exists._
**Example 1:**
**Input:** n = 3, paths = \[\[1,2\],\[2,3\],\[3,1\]\]
**Output:** \[1,2,3\]
**Explanation:**
Gardens 1 and 2 have different types.
Gardens 2 and 3 have different types.
Gardens 3 and 1 have different types.
Hence, \[1,2,3\] is a valid answer. Other valid answers include \[1,2,4\], \[1,4,2\], and \[3,2,1\].
**Example 2:**
**Input:** n = 4, paths = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,1,2\]
**Example 3:**
**Input:** n = 4, paths = \[\[1,2\],\[2,3\],\[3,4\],\[4,1\],\[1,3\],\[2,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `1 <= n <= 104`
* `0 <= paths.length <= 2 * 104`
* `paths[i].length == 2`
* `1 <= xi, yi <= n`
* `xi != yi`
* Every garden has **at most 3** paths coming into or leaving it. | null |
Why DP solution splits (K-1) AND a bonus problem (bottom-up) | minimum-cost-to-merge-stones | 0 | 1 | This took me weeks of intermittent thinking to arrive to! Hoping it would help someone.\nFirst, it\'s a good idea to glean some info from a book and other posts:\n- This problem is almost the same as Matrix-Chain Multiplication in [Cormen](https://edutechlearners.com/download/Introduction_to_algorithms-3rd%20Edition.pdf) ch. 15.2. Except, here K could be any number. For Matrix-Chain Multiplication, K is 2.\n- [Post 1](https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/247657/JAVA-Bottom-Up-%2B-Top-Down-DP-With-Explaination) - starts explaining well, but the later DP code is unnecessarily complicated with 3D DP array.\n- [Post 2](https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/675912/DP-code-decoded-for-non-experts-like-me) - particularly good explanation\n\nMy code and notes:\n```\ndef mergeStones(stones: List[int], K: int):\n N = len(stones)\n if (N-1) % (K-1) != 0:\n return -1\n accum = [0] + list(itertools.accumulate(stones))\n\n dp = [[0]*N for _ in range(N)]\n for l in range(K, N+1):\n for i in range(N-l+1):\n j = i+l-1\n if l > K:\n dp[i][j] = min([dp[i][t] + dp[t+1][j] for t in range(i,j,K-1)])\n if (l-1)%(K-1) == 0:\n dp[i][j] += accum[j+1] - accum[i]\n\n return dp[0][N-1]\n```\n- `dp[i][j]` calculates the min cost of merging stone piles `i..j` to the smallest number of piles possible [1..K) for the subarray [i,j]. We solve subproblems of varying lengths L starting at i\'s=0..len(stones)-L+1 (for each L)\n- When number of stone piles in [i,j] interval L< K, there\'s no merging and no cost: `dp[i][j] = 0`. We might as well start the for-loop with L = K.\n- When number of stone piles in [i,j] interval L> K, we calculate the [i,j] merge cost by splitting [i,j] at (K-1) intervals. This works, because we have already solved all possible subprobs. of smaller L. It does not make sense to split [i,j] anywhere else besides (K-1), because, otherwise, the min merge cost will be calculated redundantly or, worse, incorrectly. \n**E.g.** intermediate subarray `[1,4,3,3,2]`, `K=4`. Splitting `1,4 - 3,3,2` will produce a min merging cost of 0 or no merging (WRONG). Instead, we want to be splitting in such a way that the merges result in the minimum number of piles for the subarray (2 here). That\'s what we are minimizing: the cost of possible merges to the smallest subproblem (with least piles).\nThe only way to produce valid merges are to split one-pile-mergeable subproblems from one of the subarray sides. It does not matter from which side, as long as we are consistent. The side does not matter because we are going through all possible very-last-merge combinations: 1,2,..,K-1 piles at arrays end + remaining piles (adding to K total). Best to verify this by working out all steps for `[1,4,3,3,2]` with K=4 or 3. \n- When numb. of stone piles in `[i,j]` is such that `(j-i+1)%(K-1) == 0`, we add all the stone piles in stones[i, j] to the "base" merge cost, because the base cost is only for merging to K piles (1 on the left and K-1 piles on the right). We still need to merge K to 1 pile to get the intermediate pile value or the final result.\n\n**Bonus: output the merge sequence**\n*Inspired by Matrix-Chain Multiplication problem*\n```\ndef mergeStones(stones: List[int], K: int):\n N = len(stones)\n if (N-1) % (K-1) != 0:\n return -1\n\n def get_trace(trace_arr,i,j,end=False):\n l = j - i + 1\n if l <= K:\n return str([stones[t] for t in range(i,j+1)])\n t = trace_arr[i][j]\n return (\'<\' if (l-1)%(K-1) == 0 else \'\') + get_trace(trace_arr,i,t) + get_trace(trace_arr,t+1,j) + (\'>\' if (l-1)%(K-1) == 0 else \'\')\n\n accum = [0] + list(itertools.accumulate(stones))\n\n dp = [[0]*N for _ in range(N)]\n trace = [[0]*N for _ in range(N)]\n for l in range(K, N+1):\n for i in range(N-l+1):\n j = i+l-1\n if l > K:\n min_t = min([t for t in range(i,j,K-1)], key=lambda t: dp[i][t] + dp[t+1][j])\n trace[i][j] = min_t\n dp[i][j] = dp[i][min_t] + dp[min_t+1][j]\n if (l-1)%(K-1) == 0:\n dp[i][j] += accum[j+1] - accum[i]\n\n print(get_trace(trace,0,N-1))\n return dp[0][N-1]\n```\n\nFinally, lots of thanks to [@lee215](https://leetcode.com/lee215) for such an interesting problem! | 18 | There are `n` piles of `stones` arranged in a row. The `ith` pile has `stones[i]` stones.
A move consists of merging exactly `k` **consecutive** piles into one pile, and the cost of this move is equal to the total number of stones in these `k` piles.
Return _the minimum cost to merge all piles of stones into one pile_. If it is impossible, return `-1`.
**Example 1:**
**Input:** stones = \[3,2,4,1\], k = 2
**Output:** 20
**Explanation:** We start with \[3, 2, 4, 1\].
We merge \[3, 2\] for a cost of 5, and we are left with \[5, 4, 1\].
We merge \[4, 1\] for a cost of 5, and we are left with \[5, 5\].
We merge \[5, 5\] for a cost of 10, and we are left with \[10\].
The total cost was 20, and this is the minimum possible.
**Example 2:**
**Input:** stones = \[3,2,4,1\], k = 3
**Output:** -1
**Explanation:** After any merge operation, there are 2 piles left, and we can't merge anymore. So the task is impossible.
**Example 3:**
**Input:** stones = \[3,5,1,2,6\], k = 3
**Output:** 25
**Explanation:** We start with \[3, 5, 1, 2, 6\].
We merge \[5, 1, 2\] for a cost of 8, and we are left with \[3, 8, 6\].
We merge \[3, 8, 6\] for a cost of 17, and we are left with \[17\].
The total cost was 25, and this is the minimum possible.
**Constraints:**
* `n == stones.length`
* `1 <= n <= 30`
* `1 <= stones[i] <= 100`
* `2 <= k <= 30` | null |
Why DP solution splits (K-1) AND a bonus problem (bottom-up) | minimum-cost-to-merge-stones | 0 | 1 | This took me weeks of intermittent thinking to arrive to! Hoping it would help someone.\nFirst, it\'s a good idea to glean some info from a book and other posts:\n- This problem is almost the same as Matrix-Chain Multiplication in [Cormen](https://edutechlearners.com/download/Introduction_to_algorithms-3rd%20Edition.pdf) ch. 15.2. Except, here K could be any number. For Matrix-Chain Multiplication, K is 2.\n- [Post 1](https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/247657/JAVA-Bottom-Up-%2B-Top-Down-DP-With-Explaination) - starts explaining well, but the later DP code is unnecessarily complicated with 3D DP array.\n- [Post 2](https://leetcode.com/problems/minimum-cost-to-merge-stones/discuss/675912/DP-code-decoded-for-non-experts-like-me) - particularly good explanation\n\nMy code and notes:\n```\ndef mergeStones(stones: List[int], K: int):\n N = len(stones)\n if (N-1) % (K-1) != 0:\n return -1\n accum = [0] + list(itertools.accumulate(stones))\n\n dp = [[0]*N for _ in range(N)]\n for l in range(K, N+1):\n for i in range(N-l+1):\n j = i+l-1\n if l > K:\n dp[i][j] = min([dp[i][t] + dp[t+1][j] for t in range(i,j,K-1)])\n if (l-1)%(K-1) == 0:\n dp[i][j] += accum[j+1] - accum[i]\n\n return dp[0][N-1]\n```\n- `dp[i][j]` calculates the min cost of merging stone piles `i..j` to the smallest number of piles possible [1..K) for the subarray [i,j]. We solve subproblems of varying lengths L starting at i\'s=0..len(stones)-L+1 (for each L)\n- When number of stone piles in [i,j] interval L< K, there\'s no merging and no cost: `dp[i][j] = 0`. We might as well start the for-loop with L = K.\n- When number of stone piles in [i,j] interval L> K, we calculate the [i,j] merge cost by splitting [i,j] at (K-1) intervals. This works, because we have already solved all possible subprobs. of smaller L. It does not make sense to split [i,j] anywhere else besides (K-1), because, otherwise, the min merge cost will be calculated redundantly or, worse, incorrectly. \n**E.g.** intermediate subarray `[1,4,3,3,2]`, `K=4`. Splitting `1,4 - 3,3,2` will produce a min merging cost of 0 or no merging (WRONG). Instead, we want to be splitting in such a way that the merges result in the minimum number of piles for the subarray (2 here). That\'s what we are minimizing: the cost of possible merges to the smallest subproblem (with least piles).\nThe only way to produce valid merges are to split one-pile-mergeable subproblems from one of the subarray sides. It does not matter from which side, as long as we are consistent. The side does not matter because we are going through all possible very-last-merge combinations: 1,2,..,K-1 piles at arrays end + remaining piles (adding to K total). Best to verify this by working out all steps for `[1,4,3,3,2]` with K=4 or 3. \n- When numb. of stone piles in `[i,j]` is such that `(j-i+1)%(K-1) == 0`, we add all the stone piles in stones[i, j] to the "base" merge cost, because the base cost is only for merging to K piles (1 on the left and K-1 piles on the right). We still need to merge K to 1 pile to get the intermediate pile value or the final result.\n\n**Bonus: output the merge sequence**\n*Inspired by Matrix-Chain Multiplication problem*\n```\ndef mergeStones(stones: List[int], K: int):\n N = len(stones)\n if (N-1) % (K-1) != 0:\n return -1\n\n def get_trace(trace_arr,i,j,end=False):\n l = j - i + 1\n if l <= K:\n return str([stones[t] for t in range(i,j+1)])\n t = trace_arr[i][j]\n return (\'<\' if (l-1)%(K-1) == 0 else \'\') + get_trace(trace_arr,i,t) + get_trace(trace_arr,t+1,j) + (\'>\' if (l-1)%(K-1) == 0 else \'\')\n\n accum = [0] + list(itertools.accumulate(stones))\n\n dp = [[0]*N for _ in range(N)]\n trace = [[0]*N for _ in range(N)]\n for l in range(K, N+1):\n for i in range(N-l+1):\n j = i+l-1\n if l > K:\n min_t = min([t for t in range(i,j,K-1)], key=lambda t: dp[i][t] + dp[t+1][j])\n trace[i][j] = min_t\n dp[i][j] = dp[i][min_t] + dp[min_t+1][j]\n if (l-1)%(K-1) == 0:\n dp[i][j] += accum[j+1] - accum[i]\n\n print(get_trace(trace,0,N-1))\n return dp[0][N-1]\n```\n\nFinally, lots of thanks to [@lee215](https://leetcode.com/lee215) for such an interesting problem! | 18 | You have `n` gardens, labeled from `1` to `n`, and an array `paths` where `paths[i] = [xi, yi]` describes a bidirectional path between garden `xi` to garden `yi`. In each garden, you want to plant one of 4 types of flowers.
All gardens have **at most 3** paths coming into or leaving it.
Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.
Return _**any** such a choice as an array_ `answer`_, where_ `answer[i]` _is the type of flower planted in the_ `(i+1)th` _garden. The flower types are denoted_ `1`_,_ `2`_,_ `3`_, or_ `4`_. It is guaranteed an answer exists._
**Example 1:**
**Input:** n = 3, paths = \[\[1,2\],\[2,3\],\[3,1\]\]
**Output:** \[1,2,3\]
**Explanation:**
Gardens 1 and 2 have different types.
Gardens 2 and 3 have different types.
Gardens 3 and 1 have different types.
Hence, \[1,2,3\] is a valid answer. Other valid answers include \[1,2,4\], \[1,4,2\], and \[3,2,1\].
**Example 2:**
**Input:** n = 4, paths = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,1,2\]
**Example 3:**
**Input:** n = 4, paths = \[\[1,2\],\[2,3\],\[3,4\],\[4,1\],\[1,3\],\[2,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `1 <= n <= 104`
* `0 <= paths.length <= 2 * 104`
* `paths[i].length == 2`
* `1 <= xi, yi <= n`
* `xi != yi`
* Every garden has **at most 3** paths coming into or leaving it. | null |
Solution | minimum-cost-to-merge-stones | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int find(int i, int j, vector<int>& prefix, int pile, vector<vector<int>>& dp) {\n if(i >= j) return 0;\n if(dp[i][j] != -1) return dp[i][j];\n int ans = INT_MAX;\n for(int k = i; k < j; k += pile-1) {\n int sum = find(i, k, prefix, pile, dp) + find(k+1, j, prefix, pile,dp);\n ans = min(ans, sum);\n }\n if((j-i) % (pile-1) == 0) \n ans += prefix[j+1] - prefix[i];\n return dp[i][j] = ans;\n }\n int mergeStones(vector<int>& stones, int k) {\n int n = stones.size();\n vector<vector<int>> dp(n+1, vector<int>(n+1, -1));\n if((n-1) % (k-1) != 0) return -1;\n vector<int> prefix;\n prefix.push_back(stones[0]);\n for(int i = 0; i < stones.size(); i++)\n prefix.push_back(prefix.back() + stones[i]);\n return find(0, n-1, prefix, k, dp);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def mergeStones(self, stones: List[int], k: int) -> int:\n n = len(stones)\n if (n - 1) % (k - 1):\n return -1\n prefix = [0] * (n + 1)\n for i in range(n):\n prefix[i + 1] = prefix[i] + stones[i]\n @lru_cache(None)\n def dp(i, j):\n if j - i + 1 < k:\n return 0\n result = min(dp(i, mid) + dp(mid + 1, j) for mid in range(i, j, k - 1))\n if (j - i) % (k - 1) == 0:\n result += prefix[j + 1] - prefix[i]\n return result\n return dp(0, n - 1)\n```\n\n```Java []\nclass Solution {\n int prefix[];\n public int mergeStones(int[] stones, int k) {\n int n=stones.length;\n if((n-1)%(k-1) != 0) return -1;\n prefix=new int[stones.length+1];\n prefix[0]=0;\n int sum=0;\n for(int i=0;i<stones.length;i++){\n sum+=stones[i];\n prefix[i+1]=sum;\n }\n int dp[][]=new int[stones.length][stones.length];\n for(int i=0;i<dp.length;i++){\n for(int j=0;j<dp[0].length;j++){\n dp[i][j]=-1;\n }\n }\n return check(prefix,k,0,stones.length-1,dp);\n }\n public int check(int[] prefix,int k,int i,int j,int dp[][]){\n if(i>=j){\n return 0;\n }\n if(dp[i][j]!=-1){\n return dp[i][j];\n }\n int min=Integer.MAX_VALUE;\n for(int t=i;t<j;t=t+k-1){\n int min1=check(prefix,k,i,t,dp)+check(prefix,k,t+1,j,dp);\n min=Math.min(min,min1);\n }\n if((j-i)%(k-1)==0){\n min+=prefix[j+1]-prefix[i];\n }\n dp[i][j]=min;\n return min;\n }\n}\nclass Solution0 {\n public int mergeStones(int[] stones, int K) {\n int n = stones.length;\n if ((n - 1) % (K - 1) > 0) return -1;\n\n int[] prefix = new int[n+1];\n for (int i = 0; i < n; i++)\n prefix[i + 1] = prefix[i] + stones[i];\n\n int[][] dp = new int[n][n];\n for (int m = K; m <= n; ++m)\n for (int i = 0; i + m <= n; ++i) {\n int j = i + m - 1;\n dp[i][j] = Integer.MAX_VALUE;\n for (int mid = i; mid < j; mid += K - 1)\n dp[i][j] = Math.min(dp[i][j], dp[i][mid] + dp[mid + 1][j]);\n if ((j - i) % (K - 1) == 0)\n dp[i][j] += prefix[j + 1] - prefix[i];\n }\n return dp[0][n - 1];\n }\n}\n``` | 2 | There are `n` piles of `stones` arranged in a row. The `ith` pile has `stones[i]` stones.
A move consists of merging exactly `k` **consecutive** piles into one pile, and the cost of this move is equal to the total number of stones in these `k` piles.
Return _the minimum cost to merge all piles of stones into one pile_. If it is impossible, return `-1`.
**Example 1:**
**Input:** stones = \[3,2,4,1\], k = 2
**Output:** 20
**Explanation:** We start with \[3, 2, 4, 1\].
We merge \[3, 2\] for a cost of 5, and we are left with \[5, 4, 1\].
We merge \[4, 1\] for a cost of 5, and we are left with \[5, 5\].
We merge \[5, 5\] for a cost of 10, and we are left with \[10\].
The total cost was 20, and this is the minimum possible.
**Example 2:**
**Input:** stones = \[3,2,4,1\], k = 3
**Output:** -1
**Explanation:** After any merge operation, there are 2 piles left, and we can't merge anymore. So the task is impossible.
**Example 3:**
**Input:** stones = \[3,5,1,2,6\], k = 3
**Output:** 25
**Explanation:** We start with \[3, 5, 1, 2, 6\].
We merge \[5, 1, 2\] for a cost of 8, and we are left with \[3, 8, 6\].
We merge \[3, 8, 6\] for a cost of 17, and we are left with \[17\].
The total cost was 25, and this is the minimum possible.
**Constraints:**
* `n == stones.length`
* `1 <= n <= 30`
* `1 <= stones[i] <= 100`
* `2 <= k <= 30` | null |
Solution | minimum-cost-to-merge-stones | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int find(int i, int j, vector<int>& prefix, int pile, vector<vector<int>>& dp) {\n if(i >= j) return 0;\n if(dp[i][j] != -1) return dp[i][j];\n int ans = INT_MAX;\n for(int k = i; k < j; k += pile-1) {\n int sum = find(i, k, prefix, pile, dp) + find(k+1, j, prefix, pile,dp);\n ans = min(ans, sum);\n }\n if((j-i) % (pile-1) == 0) \n ans += prefix[j+1] - prefix[i];\n return dp[i][j] = ans;\n }\n int mergeStones(vector<int>& stones, int k) {\n int n = stones.size();\n vector<vector<int>> dp(n+1, vector<int>(n+1, -1));\n if((n-1) % (k-1) != 0) return -1;\n vector<int> prefix;\n prefix.push_back(stones[0]);\n for(int i = 0; i < stones.size(); i++)\n prefix.push_back(prefix.back() + stones[i]);\n return find(0, n-1, prefix, k, dp);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def mergeStones(self, stones: List[int], k: int) -> int:\n n = len(stones)\n if (n - 1) % (k - 1):\n return -1\n prefix = [0] * (n + 1)\n for i in range(n):\n prefix[i + 1] = prefix[i] + stones[i]\n @lru_cache(None)\n def dp(i, j):\n if j - i + 1 < k:\n return 0\n result = min(dp(i, mid) + dp(mid + 1, j) for mid in range(i, j, k - 1))\n if (j - i) % (k - 1) == 0:\n result += prefix[j + 1] - prefix[i]\n return result\n return dp(0, n - 1)\n```\n\n```Java []\nclass Solution {\n int prefix[];\n public int mergeStones(int[] stones, int k) {\n int n=stones.length;\n if((n-1)%(k-1) != 0) return -1;\n prefix=new int[stones.length+1];\n prefix[0]=0;\n int sum=0;\n for(int i=0;i<stones.length;i++){\n sum+=stones[i];\n prefix[i+1]=sum;\n }\n int dp[][]=new int[stones.length][stones.length];\n for(int i=0;i<dp.length;i++){\n for(int j=0;j<dp[0].length;j++){\n dp[i][j]=-1;\n }\n }\n return check(prefix,k,0,stones.length-1,dp);\n }\n public int check(int[] prefix,int k,int i,int j,int dp[][]){\n if(i>=j){\n return 0;\n }\n if(dp[i][j]!=-1){\n return dp[i][j];\n }\n int min=Integer.MAX_VALUE;\n for(int t=i;t<j;t=t+k-1){\n int min1=check(prefix,k,i,t,dp)+check(prefix,k,t+1,j,dp);\n min=Math.min(min,min1);\n }\n if((j-i)%(k-1)==0){\n min+=prefix[j+1]-prefix[i];\n }\n dp[i][j]=min;\n return min;\n }\n}\nclass Solution0 {\n public int mergeStones(int[] stones, int K) {\n int n = stones.length;\n if ((n - 1) % (K - 1) > 0) return -1;\n\n int[] prefix = new int[n+1];\n for (int i = 0; i < n; i++)\n prefix[i + 1] = prefix[i] + stones[i];\n\n int[][] dp = new int[n][n];\n for (int m = K; m <= n; ++m)\n for (int i = 0; i + m <= n; ++i) {\n int j = i + m - 1;\n dp[i][j] = Integer.MAX_VALUE;\n for (int mid = i; mid < j; mid += K - 1)\n dp[i][j] = Math.min(dp[i][j], dp[i][mid] + dp[mid + 1][j]);\n if ((j - i) % (K - 1) == 0)\n dp[i][j] += prefix[j + 1] - prefix[i];\n }\n return dp[0][n - 1];\n }\n}\n``` | 2 | You have `n` gardens, labeled from `1` to `n`, and an array `paths` where `paths[i] = [xi, yi]` describes a bidirectional path between garden `xi` to garden `yi`. In each garden, you want to plant one of 4 types of flowers.
All gardens have **at most 3** paths coming into or leaving it.
Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.
Return _**any** such a choice as an array_ `answer`_, where_ `answer[i]` _is the type of flower planted in the_ `(i+1)th` _garden. The flower types are denoted_ `1`_,_ `2`_,_ `3`_, or_ `4`_. It is guaranteed an answer exists._
**Example 1:**
**Input:** n = 3, paths = \[\[1,2\],\[2,3\],\[3,1\]\]
**Output:** \[1,2,3\]
**Explanation:**
Gardens 1 and 2 have different types.
Gardens 2 and 3 have different types.
Gardens 3 and 1 have different types.
Hence, \[1,2,3\] is a valid answer. Other valid answers include \[1,2,4\], \[1,4,2\], and \[3,2,1\].
**Example 2:**
**Input:** n = 4, paths = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,1,2\]
**Example 3:**
**Input:** n = 4, paths = \[\[1,2\],\[2,3\],\[3,4\],\[4,1\],\[1,3\],\[2,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `1 <= n <= 104`
* `0 <= paths.length <= 2 * 104`
* `paths[i].length == 2`
* `1 <= xi, yi <= n`
* `xi != yi`
* Every garden has **at most 3** paths coming into or leaving it. | null |
Python 3: Short Top-Down DFS, More Comments Than Code | minimum-cost-to-merge-stones | 0 | 1 | **If anyone has questions, I\'ll try to answer. Just leave a comment below! Please upvote if you find this helpful - takes a lot of time to write these.**\n\nHere\'s yet another top-down DFS solution. It\'s very similar to [@cappuccinuo\'s solution](https://leetcode.com/problems/minimum-cost-to-merge-stones/solutions/247657/JAVA-Bottom-Up-+-Top-Down-DP-With-Explaination/) because that\'s the one that helped me the most.\n\nI think top-down DFS is a LOT simpler than the DP solutions without sacrificing any speed. Basically it\'s easier to reason about the problem one step at a time (as top-down DFS generally lets you do) than to have to worry about how to fill in the DP table in the right order. Much more interview friendly.\n\nAnyway, check out the code for details. Here are the core ideas:\n* we start with indices `0..N-1` in `N` piles, where `N` is the length of the stones/piles arrays\n* our goal is to "compress" or "k-merge" these `N` piles into just 1 pile at the end\n* so we want the cost to get `0..N-1` merged into 1 pile: `cost(l=0, r=N-1, p=1)`\n\nThe `cost` function is the top-down DFS function. This is a hard problem because the intuition for getting the DP is difficult. But here it is:\n* for `cost(l, l, p)`, we have just 1 index. We can\'t make _more_ groups than there are indices because we can\'t split piles. Only merge them in groups of k.\n * so if p == 1, then the answer is 0: we have 1 index, 1 group to form. No k-merges are needed. So 0 cost.\n * if p > 1, it\'s impossible. so we return `IMPOSSIBLE=float(\'+inf\')`\n * the "inf trick" is nice in Python because `inf` plus anything is `inf` again. The same is true in other languages, but Python being weakly typed lets you return either an int of `inf` easily; in a strictly typed language you\'d have to return a float everywhere\n* for `cost(l, r, 1)`, if r > l, there is only one way to get 1 pile: start with `k` piles, and k-merge them into 1 pile. So we first get the cost of making those `k` piles, `cost(l, r, k)`, then the cost to merge them: the sum of `l..r`\n* for `cost(l, r, p>1)`, this is the hardest part. We need to consider ALL ways of grouping `l..r` into `p` groups. Which is hard. But there\'s a trick: I call it the "left-most-first" trick. This shows up in a couple of the other very hard DP questions. The idea is this\n * we want to make `p` piles. All possible ways of doing means\n * trying all possible ranges of indices to merge into piles `1 .. p`\n * for each of those `p` piles, trying all possible merge patterns\n * fortunately there\'s a trick: "left-most-first." The idea: there is always a left-most subarray\n * so in this subproblem we focus on forming the left-most group in all possible ways: `cost(l, ?, 1)`. We handle the rest of the elements with `cost(?, r, p-1)`. Recursively that subproblem will handle the remaining `p-1` groups to make\n * the left-most pile can be formed from `1` index, or `1+(k-1)` indices (then 1 k-merge), or `1+2*(k-1)` indices (then 2 k-merges), etc.\n * so we can iterate over the number of indices we k-merge into the left-most group. This considers ALL the possible numbers of indices we can k-merge to form the left-most group. By calling `cost(l, l+L-1, 1)`, we let the `cost` method deal with considering up with all possible k-merge patterns to form that 1 pile\n * for each iteration, we handle the remaining right elements with `cost(l+L, r, p-1)` to form the remaining `p-1` piles.\n * That right subproblem will start with splitting off the _next_ left-most subarray, and consider all possible numbers of indices and k-merges to form them into a new group. Same logic as before!\n * each of those iterations will recurse on the remaining right elements, which will consider all possible numbers and k-merges of the third-to-left group. And so on\n * so in the end we indeed explore every possible number of indices to k-merge into piles 1, 2, .., p. And for each of those numbers of indices, all possible merge patterns. Hooray for recursion!\n\n## Parting Thoughts\n\nThe left-most-first trick is an advanced DP concept IMO. This is just a very hard problem because the top-down DFS/DP variables are not clear. Usually they are - a knapsack-like problem, etc. But in this case there are several alternatives. And none of them, without a LOT of careful thought (and even cheating by looking at other solutions!) lead to an obvious answer.\n\n# Code\n```\nclass Solution:\n def mergeStones(self, piles: List[int], k: int) -> int:\n P = len(piles)\n\n if (P-1)%(k-1):\n return -1\n\n # Considered reverse DP but not very promising in the end. Darn.\n\n # I had an earlier basic top-down DFS solution too but it gave TLE.\n\n # TOP-DOWN DP, gleaned from https://leetcode.com/problems/minimum-cost-to-merge-stones/solutions/247657/JAVA-Bottom-Up-+-Top-Down-DP-With-Explaination/\n\n c = 0\n cs = [] # cumulative sum of piles\n for p in piles:\n c += p\n cs.append(c)\n\n IMPOSSIBLE = float(\'inf\')\n\n def acc(i: int, j: int) -> int:\n return cs[j] - (cs[i-1] if i else 0)\n\n @cache\n def cost(l: int, r: int, p: int) -> int:\n """Returns the cost to compress original indices l..r into p piles."""\n\n if l == r:\n # single index base case: forming 1 group from 1 index is free\n # we should only get here if p is 1, but we check just in case\n return 0 if p == 1 else IMPOSSIBLE\n\n if p == 1:\n # l != r so there are multiple elements in this range\n # to get p==1 groups, we must originally have k groups,\n # then k-merge them to get 1.\n\n # so we compute the cost to get k groups from l..r, cost(...)\n # and then add the cost to k-merge those groups: the sum of l..r\n return cost(l, r, k) + acc(l, r)\n\n # For p > 1 groups we need the minimum cost to form those p groups from l..r\n # Trick: without loss of generality, there is a first (left-most) group.\n # We can form that left-most group from\n # the left-most L = 1 index, l\n # the left-most L = 1+(k-1) indices and doing 1 k-merge\n # the left-most L = 1+2*(k-1) indices and doing 2 k-merges\n # ............. L = 1+m*(k-1) .............................\n # Then when we recurse on the remaining R=r-l+1-L elements (the remaining right subarray),\n # that subproblem will split off the next-left-most group and try all indices that go in\n # that group. And so on.\n\n # We know we can\'t make more than numIndices groups. So the upper bound\n # for L is set by making sure R = r-l+1-L is at least p-1. Solving\n # for L gives the upper bound in the range used here:\n best = IMPOSSIBLE\n for L in range(1, r-l-p+3, k-1):\n best = min(best, cost(l, l+L-1, 1) + cost(l+L, r, p-1))\n\n return best\n\n return cost(0, P-1, 1)\n``` | 0 | There are `n` piles of `stones` arranged in a row. The `ith` pile has `stones[i]` stones.
A move consists of merging exactly `k` **consecutive** piles into one pile, and the cost of this move is equal to the total number of stones in these `k` piles.
Return _the minimum cost to merge all piles of stones into one pile_. If it is impossible, return `-1`.
**Example 1:**
**Input:** stones = \[3,2,4,1\], k = 2
**Output:** 20
**Explanation:** We start with \[3, 2, 4, 1\].
We merge \[3, 2\] for a cost of 5, and we are left with \[5, 4, 1\].
We merge \[4, 1\] for a cost of 5, and we are left with \[5, 5\].
We merge \[5, 5\] for a cost of 10, and we are left with \[10\].
The total cost was 20, and this is the minimum possible.
**Example 2:**
**Input:** stones = \[3,2,4,1\], k = 3
**Output:** -1
**Explanation:** After any merge operation, there are 2 piles left, and we can't merge anymore. So the task is impossible.
**Example 3:**
**Input:** stones = \[3,5,1,2,6\], k = 3
**Output:** 25
**Explanation:** We start with \[3, 5, 1, 2, 6\].
We merge \[5, 1, 2\] for a cost of 8, and we are left with \[3, 8, 6\].
We merge \[3, 8, 6\] for a cost of 17, and we are left with \[17\].
The total cost was 25, and this is the minimum possible.
**Constraints:**
* `n == stones.length`
* `1 <= n <= 30`
* `1 <= stones[i] <= 100`
* `2 <= k <= 30` | null |
Python 3: Short Top-Down DFS, More Comments Than Code | minimum-cost-to-merge-stones | 0 | 1 | **If anyone has questions, I\'ll try to answer. Just leave a comment below! Please upvote if you find this helpful - takes a lot of time to write these.**\n\nHere\'s yet another top-down DFS solution. It\'s very similar to [@cappuccinuo\'s solution](https://leetcode.com/problems/minimum-cost-to-merge-stones/solutions/247657/JAVA-Bottom-Up-+-Top-Down-DP-With-Explaination/) because that\'s the one that helped me the most.\n\nI think top-down DFS is a LOT simpler than the DP solutions without sacrificing any speed. Basically it\'s easier to reason about the problem one step at a time (as top-down DFS generally lets you do) than to have to worry about how to fill in the DP table in the right order. Much more interview friendly.\n\nAnyway, check out the code for details. Here are the core ideas:\n* we start with indices `0..N-1` in `N` piles, where `N` is the length of the stones/piles arrays\n* our goal is to "compress" or "k-merge" these `N` piles into just 1 pile at the end\n* so we want the cost to get `0..N-1` merged into 1 pile: `cost(l=0, r=N-1, p=1)`\n\nThe `cost` function is the top-down DFS function. This is a hard problem because the intuition for getting the DP is difficult. But here it is:\n* for `cost(l, l, p)`, we have just 1 index. We can\'t make _more_ groups than there are indices because we can\'t split piles. Only merge them in groups of k.\n * so if p == 1, then the answer is 0: we have 1 index, 1 group to form. No k-merges are needed. So 0 cost.\n * if p > 1, it\'s impossible. so we return `IMPOSSIBLE=float(\'+inf\')`\n * the "inf trick" is nice in Python because `inf` plus anything is `inf` again. The same is true in other languages, but Python being weakly typed lets you return either an int of `inf` easily; in a strictly typed language you\'d have to return a float everywhere\n* for `cost(l, r, 1)`, if r > l, there is only one way to get 1 pile: start with `k` piles, and k-merge them into 1 pile. So we first get the cost of making those `k` piles, `cost(l, r, k)`, then the cost to merge them: the sum of `l..r`\n* for `cost(l, r, p>1)`, this is the hardest part. We need to consider ALL ways of grouping `l..r` into `p` groups. Which is hard. But there\'s a trick: I call it the "left-most-first" trick. This shows up in a couple of the other very hard DP questions. The idea is this\n * we want to make `p` piles. All possible ways of doing means\n * trying all possible ranges of indices to merge into piles `1 .. p`\n * for each of those `p` piles, trying all possible merge patterns\n * fortunately there\'s a trick: "left-most-first." The idea: there is always a left-most subarray\n * so in this subproblem we focus on forming the left-most group in all possible ways: `cost(l, ?, 1)`. We handle the rest of the elements with `cost(?, r, p-1)`. Recursively that subproblem will handle the remaining `p-1` groups to make\n * the left-most pile can be formed from `1` index, or `1+(k-1)` indices (then 1 k-merge), or `1+2*(k-1)` indices (then 2 k-merges), etc.\n * so we can iterate over the number of indices we k-merge into the left-most group. This considers ALL the possible numbers of indices we can k-merge to form the left-most group. By calling `cost(l, l+L-1, 1)`, we let the `cost` method deal with considering up with all possible k-merge patterns to form that 1 pile\n * for each iteration, we handle the remaining right elements with `cost(l+L, r, p-1)` to form the remaining `p-1` piles.\n * That right subproblem will start with splitting off the _next_ left-most subarray, and consider all possible numbers of indices and k-merges to form them into a new group. Same logic as before!\n * each of those iterations will recurse on the remaining right elements, which will consider all possible numbers and k-merges of the third-to-left group. And so on\n * so in the end we indeed explore every possible number of indices to k-merge into piles 1, 2, .., p. And for each of those numbers of indices, all possible merge patterns. Hooray for recursion!\n\n## Parting Thoughts\n\nThe left-most-first trick is an advanced DP concept IMO. This is just a very hard problem because the top-down DFS/DP variables are not clear. Usually they are - a knapsack-like problem, etc. But in this case there are several alternatives. And none of them, without a LOT of careful thought (and even cheating by looking at other solutions!) lead to an obvious answer.\n\n# Code\n```\nclass Solution:\n def mergeStones(self, piles: List[int], k: int) -> int:\n P = len(piles)\n\n if (P-1)%(k-1):\n return -1\n\n # Considered reverse DP but not very promising in the end. Darn.\n\n # I had an earlier basic top-down DFS solution too but it gave TLE.\n\n # TOP-DOWN DP, gleaned from https://leetcode.com/problems/minimum-cost-to-merge-stones/solutions/247657/JAVA-Bottom-Up-+-Top-Down-DP-With-Explaination/\n\n c = 0\n cs = [] # cumulative sum of piles\n for p in piles:\n c += p\n cs.append(c)\n\n IMPOSSIBLE = float(\'inf\')\n\n def acc(i: int, j: int) -> int:\n return cs[j] - (cs[i-1] if i else 0)\n\n @cache\n def cost(l: int, r: int, p: int) -> int:\n """Returns the cost to compress original indices l..r into p piles."""\n\n if l == r:\n # single index base case: forming 1 group from 1 index is free\n # we should only get here if p is 1, but we check just in case\n return 0 if p == 1 else IMPOSSIBLE\n\n if p == 1:\n # l != r so there are multiple elements in this range\n # to get p==1 groups, we must originally have k groups,\n # then k-merge them to get 1.\n\n # so we compute the cost to get k groups from l..r, cost(...)\n # and then add the cost to k-merge those groups: the sum of l..r\n return cost(l, r, k) + acc(l, r)\n\n # For p > 1 groups we need the minimum cost to form those p groups from l..r\n # Trick: without loss of generality, there is a first (left-most) group.\n # We can form that left-most group from\n # the left-most L = 1 index, l\n # the left-most L = 1+(k-1) indices and doing 1 k-merge\n # the left-most L = 1+2*(k-1) indices and doing 2 k-merges\n # ............. L = 1+m*(k-1) .............................\n # Then when we recurse on the remaining R=r-l+1-L elements (the remaining right subarray),\n # that subproblem will split off the next-left-most group and try all indices that go in\n # that group. And so on.\n\n # We know we can\'t make more than numIndices groups. So the upper bound\n # for L is set by making sure R = r-l+1-L is at least p-1. Solving\n # for L gives the upper bound in the range used here:\n best = IMPOSSIBLE\n for L in range(1, r-l-p+3, k-1):\n best = min(best, cost(l, l+L-1, 1) + cost(l+L, r, p-1))\n\n return best\n\n return cost(0, P-1, 1)\n``` | 0 | You have `n` gardens, labeled from `1` to `n`, and an array `paths` where `paths[i] = [xi, yi]` describes a bidirectional path between garden `xi` to garden `yi`. In each garden, you want to plant one of 4 types of flowers.
All gardens have **at most 3** paths coming into or leaving it.
Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.
Return _**any** such a choice as an array_ `answer`_, where_ `answer[i]` _is the type of flower planted in the_ `(i+1)th` _garden. The flower types are denoted_ `1`_,_ `2`_,_ `3`_, or_ `4`_. It is guaranteed an answer exists._
**Example 1:**
**Input:** n = 3, paths = \[\[1,2\],\[2,3\],\[3,1\]\]
**Output:** \[1,2,3\]
**Explanation:**
Gardens 1 and 2 have different types.
Gardens 2 and 3 have different types.
Gardens 3 and 1 have different types.
Hence, \[1,2,3\] is a valid answer. Other valid answers include \[1,2,4\], \[1,4,2\], and \[3,2,1\].
**Example 2:**
**Input:** n = 4, paths = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,1,2\]
**Example 3:**
**Input:** n = 4, paths = \[\[1,2\],\[2,3\],\[3,4\],\[4,1\],\[1,3\],\[2,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `1 <= n <= 104`
* `0 <= paths.length <= 2 * 104`
* `paths[i].length == 2`
* `1 <= xi, yi <= n`
* `xi != yi`
* Every garden has **at most 3** paths coming into or leaving it. | null |
DP | minimum-cost-to-merge-stones | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n<!-- # Complexity\n- Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mergeStones(self, stones: List[int], k: int) -> int:\n \n @cache\n def rec(i, j):\n # This function will find the min cost to merge stones from [i, j] inclusive.\n \n # If the length of the window is less than k, then we don\'t need any cost to merge them\n if j - i + 1 < k: return 0\n\n min_val = float(\'inf\')\n\n # Finding the left and right sub-problem using the mid values\n # we are increasing the mid with "k-1" values so that the left and right sub problems become valid\n # if k = 3\n # | 0, 1 | 2, 3 | 4, 5 | 6, 7 | 8, 9 |\n\n for mid in range(i, j, k - 1):\n min_val = min(min_val, rec(i, mid) + rec(mid + 1, j))\n\n # If the current subarray is the proper array according to the question, then add the window sum to it; \n # We are adding this because min_val stores the cost for merging the stones in the above stages\n # This is getting add because of the merging of current state.\n\n if (j - i) % (k - 1) == 0:\n min_val += prefix[j + 1] - prefix[i]\n\n return min_val\n\n # Checking whether we can solve the problem or not.\n n = len(stones)\n if (n - k) % (k - 1) != 0: return -1\n\n prefix = [0] * (n + 1)\n for i in range(n):\n prefix[i + 1] = prefix[i] + stones[i]\n\n return rec(0, n - 1)\n``` | 0 | There are `n` piles of `stones` arranged in a row. The `ith` pile has `stones[i]` stones.
A move consists of merging exactly `k` **consecutive** piles into one pile, and the cost of this move is equal to the total number of stones in these `k` piles.
Return _the minimum cost to merge all piles of stones into one pile_. If it is impossible, return `-1`.
**Example 1:**
**Input:** stones = \[3,2,4,1\], k = 2
**Output:** 20
**Explanation:** We start with \[3, 2, 4, 1\].
We merge \[3, 2\] for a cost of 5, and we are left with \[5, 4, 1\].
We merge \[4, 1\] for a cost of 5, and we are left with \[5, 5\].
We merge \[5, 5\] for a cost of 10, and we are left with \[10\].
The total cost was 20, and this is the minimum possible.
**Example 2:**
**Input:** stones = \[3,2,4,1\], k = 3
**Output:** -1
**Explanation:** After any merge operation, there are 2 piles left, and we can't merge anymore. So the task is impossible.
**Example 3:**
**Input:** stones = \[3,5,1,2,6\], k = 3
**Output:** 25
**Explanation:** We start with \[3, 5, 1, 2, 6\].
We merge \[5, 1, 2\] for a cost of 8, and we are left with \[3, 8, 6\].
We merge \[3, 8, 6\] for a cost of 17, and we are left with \[17\].
The total cost was 25, and this is the minimum possible.
**Constraints:**
* `n == stones.length`
* `1 <= n <= 30`
* `1 <= stones[i] <= 100`
* `2 <= k <= 30` | null |
DP | minimum-cost-to-merge-stones | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n<!-- # Complexity\n- Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mergeStones(self, stones: List[int], k: int) -> int:\n \n @cache\n def rec(i, j):\n # This function will find the min cost to merge stones from [i, j] inclusive.\n \n # If the length of the window is less than k, then we don\'t need any cost to merge them\n if j - i + 1 < k: return 0\n\n min_val = float(\'inf\')\n\n # Finding the left and right sub-problem using the mid values\n # we are increasing the mid with "k-1" values so that the left and right sub problems become valid\n # if k = 3\n # | 0, 1 | 2, 3 | 4, 5 | 6, 7 | 8, 9 |\n\n for mid in range(i, j, k - 1):\n min_val = min(min_val, rec(i, mid) + rec(mid + 1, j))\n\n # If the current subarray is the proper array according to the question, then add the window sum to it; \n # We are adding this because min_val stores the cost for merging the stones in the above stages\n # This is getting add because of the merging of current state.\n\n if (j - i) % (k - 1) == 0:\n min_val += prefix[j + 1] - prefix[i]\n\n return min_val\n\n # Checking whether we can solve the problem or not.\n n = len(stones)\n if (n - k) % (k - 1) != 0: return -1\n\n prefix = [0] * (n + 1)\n for i in range(n):\n prefix[i + 1] = prefix[i] + stones[i]\n\n return rec(0, n - 1)\n``` | 0 | You have `n` gardens, labeled from `1` to `n`, and an array `paths` where `paths[i] = [xi, yi]` describes a bidirectional path between garden `xi` to garden `yi`. In each garden, you want to plant one of 4 types of flowers.
All gardens have **at most 3** paths coming into or leaving it.
Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.
Return _**any** such a choice as an array_ `answer`_, where_ `answer[i]` _is the type of flower planted in the_ `(i+1)th` _garden. The flower types are denoted_ `1`_,_ `2`_,_ `3`_, or_ `4`_. It is guaranteed an answer exists._
**Example 1:**
**Input:** n = 3, paths = \[\[1,2\],\[2,3\],\[3,1\]\]
**Output:** \[1,2,3\]
**Explanation:**
Gardens 1 and 2 have different types.
Gardens 2 and 3 have different types.
Gardens 3 and 1 have different types.
Hence, \[1,2,3\] is a valid answer. Other valid answers include \[1,2,4\], \[1,4,2\], and \[3,2,1\].
**Example 2:**
**Input:** n = 4, paths = \[\[1,2\],\[3,4\]\]
**Output:** \[1,2,1,2\]
**Example 3:**
**Input:** n = 4, paths = \[\[1,2\],\[2,3\],\[3,4\],\[4,1\],\[1,3\],\[2,4\]\]
**Output:** \[1,2,3,4\]
**Constraints:**
* `1 <= n <= 104`
* `0 <= paths.length <= 2 * 104`
* `paths[i].length == 2`
* `1 <= xi, yi <= n`
* `xi != yi`
* Every garden has **at most 3** paths coming into or leaving it. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.