Unnamed: 0
int64 0
269
| challenge_id
int64 104
5.95k
| challenge_slug
stringlengths 4
38
| challenge_name
stringlengths 5
57
| challenge_body
stringlengths 9
4.55k
⌀ | challenge_kind
stringclasses 2
values | challenge_preview
stringlengths 9
300
⌀ | challenge_category
stringclasses 2
values | challenge_created_at
stringdate 2013-01-04 20:28:56
2015-01-19 21:40:20
| challenge_updated_at
stringdate 2016-09-01 16:22:55
2022-09-02 10:36:47
| python3_template
stringlengths 2
303
⌀ | python3_template_head
stringclasses 2
values | python3_template_tail
stringclasses 52
values | problem_statement
stringlengths 9
4.55k
| difficulty
float64 0.4
0.6
| allowed_languages
stringclasses 28
values | input_format
stringlengths 1
987
⌀ | output_format
stringlengths 1
1.92k
⌀ | sample_input
stringlengths 1
284
⌀ | sample_output
stringclasses 52
values | difficulty_tag
stringclasses 1
value | editorial_title
stringclasses 32
values | editorial_content
stringclasses 32
values | editorial_draft
float64 0
0
⌀ | editorial_slug
stringclasses 32
values | editorial_published_at
stringdate 2013-03-04 16:26:12
2014-04-24 18:24:07
⌀ | editorial_statistics
stringclasses 45
values | editorial_created_at
stringdate 2013-03-04 16:26:12
2015-01-19 21:44:31
| editorial_updated_at
stringdate 2016-05-12 23:56:02
2020-09-08 16:59:12
| editorial_solution_kind
stringclasses 2
values | editorial_solution_code
stringlengths 2
13k
| editorial_solution_language
stringclasses 1
value | editorial_solution_created_at
stringdate 2016-04-24 02:02:11
2016-04-24 02:03:27
| editorial_solution_updated_at
stringdate 2016-04-24 02:02:11
2020-09-08 16:59:12
| language
stringclasses 7
values |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
0
| 337
|
randomsumexpected
|
Random Sum - Expected Sum
|
Given an a list D of N integers, and an integer T, two numbers L and R are randomly chosen such that 0 ≤ L ≤ R < N.
What is the expected sum of the subarray {d[L]...d[R]} given that (sum{d[L],...d[R]} <= T)?
**Input Format:**
The first line will contain two numbers: N and T. N lines follow, each containing one number from list D.
**Output Format:**
Output one number P, the expected sum of D[L]...D[R] upto 9 decimal places.
**Constraints:**
1 <= N < 100000
0 <= D[i] < 10^7
0 < T <= 10^9
**Sample Input:**
<pre>
5 10
4
5
3
7
1
</pre>
**Sample Output:**
<pre>6.111111111</pre>
**Explaination**
[4],[5],[3],[7],[1],[4,5],[5,3],[3,7],[7,1] subarrays satisfy the property.
4 + 5 + 3 + 7 + 1 + 9 + 8 + 10 + 8 = 55
55/9 = 6.11111111
|
code
|
What is the expected sum of a randomly chosen range of numbers?
|
ai
|
2013-01-29T20:58:30
|
2016-09-09T09:28:39
| null | null | null |
Given an a list D of N integers, and an integer T, two numbers L and R are randomly chosen such that 0 ≤ L ≤ R < N.
What is the expected sum of the subarray {d[L]...d[R]} given that (sum{d[L],...d[R]} <= T)?
**Input Format:**
The first line will contain two numbers: N and T. N lines follow, each containing one number from list D.
**Output Format:**
Output one number P, the expected sum of D[L]...D[R] upto 9 decimal places.
**Constraints:**
1 <= N < 100000
0 <= D[i] < 10^7
0 < T <= 10^9
**Sample Input:**
<pre>
5 10
4
5
3
7
1
</pre>
**Sample Output:**
<pre>6.111111111</pre>
**Explaination**
[4],[5],[3],[7],[1],[4,5],[5,3],[3,7],[7,1] subarrays satisfy the property.
4 + 5 + 3 + 7 + 1 + 9 + 8 + 10 + 8 = 55
55/9 = 6.11111111
| 0.495261
|
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
|
Random Sum - Expected Sum Solution by <a href ="https://www.hackerrank.com/sidsgr88">Siddharth Bora</a>
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><h3>Random Sum - Expected Sum</h3>
<p><strong>Idea:</strong> Two-Pointer</p>
<p><strong>Short Explanation:</strong>
You are expected to have the read the solution to Random Sum problem as the two-pointer idea is carried forward from that.
The problem asks us to give the expected sum of the arrays that have been found in the previous problem. This can be done maintaing a cumulative sum and a cumulative of cumulative sum and keeping a total sum that is updated as we calculate the count moving the two pointers as in the previous problem.</p>
<p><strong>Long Explanation:</strong>
We pre-calculate two arrays. Firstly a cumulative sum and then a cumulative of cumulative sum. The first of these gives the sum of number from the starting to a particular index. The second gives us the sum of all the sequences that start at index 0 and end at indices from 0 to i basically the ith value will be ele0 + (ele0 + ele 1) +...+ (ele0+..+elei) where elex is the xth element in the array.
Now since we need the sum of all the sequences that sum to <= T, we augment the previous question (Random Sum) solution to find the total sum too. Basically whenever we have an l,r we can calculate the sum of all sequences starting at l and ending at indices between l and r(left end inclusive) by
cumcumsum[r-1]-((l>0)?cumcumsum[l-1]:0)-(r-l)*((l>0)?cumsum[l-1]:0);
where cumcumsum is the cumulative of cumulative sum array and cumsum is the cumulative sum array. Here we are subtracting all cumulative sums less than l and also subtracting the portion of cumcumsum[r-1] which extends to the left of l namely the third term. This gives us the cumulative sum and finally we simply have to divide this by the previous answer to get the expected value.</p>
<p><strong>Language : C++</strong></p>
<pre><code>using namespace std;
#include <cmath>
#include <cstdio>
#include <list>
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <string>
#include <vector>
#include <iostream>
#include <sstream>
#include <algorithm>
#define all(c) (c).begin(),(c).end()
#define tr(c,i) for(typeof((c).begin()) i = (c).begin(); i != (c).end(); i++)
typedef long long ll;
typedef pair<int,int> pii;
#define FOR(i,n) for (int i = 0; i < n; i++)
#define SZ(x) ((int)x.size())
#define PB push_back
#define MP make_pair
#define sf(x) scanf("%d",&x)
#define pf(x) printf("%d\n",x)
#define split(str) {vs.clear();istringstream ss(str);while(ss>>(str))vs.push_back(str);}
#define PI 3.141592653589793
int main()
{
ll count=0;
ll count2=0;
int n,t;
sf(n);sf(t);
ll sum=0;
int l=0;
int r=-1;
vector<int> v;
while(n--)
{
int a;
sf(a);
v.PB(a);
}
vector<ll> cumsum;
FOR(i,v.size())
cumsum.PB(v[i]);
for(int i=1;i<v.size();i++)
cumsum[i]+=cumsum[i-1];
vector<ll> cumcumsum;
FOR(i,v.size())
cumcumsum.PB(cumsum[i]);
for(int i=1;i<v.size();i++)
cumcumsum[i]+=cumcumsum[i-1];
// FOR(i,v.size())
// cout<<cumcumsum[i]<<endl;
while(l<v.size())
{
//cout<<r<<" "<<(r<v.size())<<" "<<(sum<=t)<<endl;
while(r<(int)v.size() && sum<=t)
{
//cout<<"hello"<<endl;
//count2+=cumsum[r];
r++;
if(r<v.size())
{
sum+=v[r];
}
}
if(r-l>0)
{ count+=r-l;
//cout<<r<<" "<<l<<endl;
count2+=cumcumsum[r-1]-((l>0)?cumcumsum[l-1]:0)-(r-l)*((l>0)?cumsum[l-1]:0);
}
sum-=v[l];
l++;
}
//cout<<count2<<endl;
//cout<<count<<endl;
double ans=count2*1.0/count;
printf("%.9lf\n",ans);
}
</code></pre>
| 0
|
randexpsum
|
2013-03-04T16:26:12
|
{"contest_participation":6014,"challenge_submissions":421,"successful_submissions":210}
|
2013-03-04T16:26:12
|
2016-05-13T00:04:48
|
tester
|
using namespace std;
#include <cmath>
#include <cstdio>
#include <list>
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <string>
#include <vector>
#include <iostream>
#include <sstream>
#include <algorithm>
#define all(c) (c).begin(),(c).end()
#define tr(c,i) for(typeof((c).begin()) i = (c).begin(); i != (c).end(); i++)
typedef long long ll;
typedef pair<int,int> pii;
#define FOR(i,n) for (int i = 0; i < n; i++)
#define SZ(x) ((int)x.size())
#define PB push_back
#define MP make_pair
#define sf(x) scanf("%d",&x)
#define pf(x) printf("%d\n",x)
#define split(str) {vs.clear();istringstream ss(str);while(ss>>(str))vs.push_back(str);}
#define PI 3.141592653589793
int main()
{
ll count=0;
ll count2=0;
int n,t;
sf(n);sf(t);
ll sum=0;
int l=0;
int r=-1;
vector<int> v;
while(n--)
{
int a;
sf(a);
v.PB(a);
}
vector<ll> cumsum;
FOR(i,v.size())
cumsum.PB(v[i]);
for(int i=1;i<v.size();i++)
cumsum[i]+=cumsum[i-1];
vector<ll> cumcumsum;
FOR(i,v.size())
cumcumsum.PB(cumsum[i]);
for(int i=1;i<v.size();i++)
cumcumsum[i]+=cumcumsum[i-1];
// FOR(i,v.size())
// cout<<cumcumsum[i]<<endl;
while(l<v.size())
{
//cout<<r<<" "<<(r<v.size())<<" "<<(sum<=t)<<endl;
while(r<(int)v.size() && sum<=t)
{
//cout<<"hello"<<endl;
//count2+=cumsum[r];
r++;
if(r<v.size())
{
sum+=v[r];
}
}
if(r-l>0)
{ count+=r-l;
//cout<<r<<" "<<l<<endl;
count2+=cumcumsum[r-1]-((l>0)?cumcumsum[l-1]:0)-(r-l)*((l>0)?cumsum[l-1]:0);
}
sum-=v[l];
l++;
}
//cout<<count2<<endl;
//cout<<count<<endl;
double ans=count2*1.0/count;
printf("%.9lf\n",ans);
}
|
not-set
|
2016-04-24T02:02:11
|
2016-04-24T02:02:11
|
C++
|
1
| 556
|
n-puzzle
|
N Puzzle
|
N Puzzle is a sliding blocks game that takes place on a k * k grid with ((k * k) - 1) tiles each numbered from 1 to N. Your task is to reposition the tiles to their proper order.
**Input Format**
The first line of the input contains an integer k, the size of the square grid. k * k lines follow each line containing an integer I on the tile starting from the top left to bottom right. The empty cell is represented by the number 0.
N = (k * k) -1
0 <= I <= N
**Constraints**
3 <= k <= 5
**Output Format**
The first line contains an integer, M, the number of moves your algorithm has taken to solve the N-Puzzle. M lines follow. Each line indicating the movement of the empty cell (0).
A grid is considered solved if it is of the following configuration.
0 1 2
3 4 5
6 7 8
**Sample Input**
3
0
3
8
4
1
7
2
6
5
**Sample Output**
70
RIGHT
DOWN
...
...
...
**Explanation**
The board given as input is
0 3 8
4 1 7
2 6 5
After RIGHT, the board's configuration is
3 0 8
4 1 7
2 6 5
**Task**
Print all the moves made from the given configuration to
the final solved board configuration.
**Scoring**
On successfully solving the puzzle, your score will be k * k.
|
game
|
N Puzzle is a sliding blocks game that takes place on a k * k grid with (k * k) - 1 tiles each numbered from 1 to N. Place the tiles in their proper order using minimum number of moves.
|
ai
|
2013-04-06T14:13:29
|
2022-08-31T18:04:25
| null | null | null |
N Puzzle is a sliding blocks game that takes place on a k * k grid with ((k * k) - 1) tiles each numbered from 1 to N. Your task is to reposition the tiles to their proper order.
**Input Format**
The first line of the input contains an integer k, the size of the square grid. k * k lines follow each line containing an integer I on the tile starting from the top left to bottom right. The empty cell is represented by the number 0.
N = (k * k) -1
0 <= I <= N
**Constraints**
3 <= k <= 5
**Output Format**
The first line contains an integer, M, the number of moves your algorithm has taken to solve the N-Puzzle. M lines follow. Each line indicating the movement of the empty cell (0).
A grid is considered solved if it is of the following configuration.
0 1 2
3 4 5
6 7 8
**Sample Input**
3
0
3
8
4
1
7
2
6
5
**Sample Output**
70
RIGHT
DOWN
...
...
...
**Explanation**
The board given as input is
0 3 8
4 1 7
2 6 5
After RIGHT, the board's configuration is
3 0 8
4 1 7
2 6 5
**Task**
Print all the moves made from the given configuration to
the final solved board configuration.
**Scoring**
On successfully solving the puzzle, your score will be k * k.
| 0.456522
|
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","tcl","typescript","visualbasic","kotlin","pypy3","swift"]
| null | null | null | null |
Hard
|
May 20-20 Hack Editorial: N - Puzzle
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong><a href="https://www.hackerrank.com/contests/may13/challenges/n-puzzle">N Puzzle</a></strong></p>
<p>N Puzzle is a sliding blocks game that takes place on a k * k grid with k * k - 1 tiles
each numbered from 1 to N. Your task is to reposition the tiles in their proper order</p>
<p><strong>Difficulty Level</strong></p>
<p>Medium ( Implementation heavy )</p>
<p><strong>Problem Setter</strong></p>
<p><a href="https://www.hackerrank.com/dheeraj">Dheeraj M R</a></p>
<p><strong>Required Knowledge</strong></p>
<p>A* algorithm</p>
<p><strong>Approach</strong></p>
<p>N-Puzzle is a classic 1 player game that teaches the basics of heuristics in arriving at
solutions in Artificial Intelligence. </p>
<p>Let us consider for the sake of simplicity, N = 8</p>
<p>The final configuration of an 8 - puzzle will look like</p>
<pre><code>0 1 2
3 4 5
6 7 8
</code></pre>
<p><a href="https://www.hackerrank.com/challenges/pacman-astar">A*</a> algorithm talks about a cost function
and a heuristic. </p>
<p>cost = heuristic_cost + #of steps taken to reach the current state.</p>
<p>the tiles are numbered. For a given unsolved 8 - puzzle configuration say</p>
<pre><code>0 3 8
4 1 7
2 6 5
</code></pre>
<p>We use 2 heuristics for every state and at every iteration</p>
<p>1 such heuristic is </p>
<p>h1 => The number of misplaced tiles.</p>
<p>In the above example, the number of misplaced tiles are 8</p>
<p>2<sup>nd</sup> heuristic we use is</p>
<p>h2 => The manahattan distance between a tile's original position to its current position.</p>
<p>In the above example, the manhattan distance for all tiles are as follows</p>
<p>a<sub>b</sub> => where a is the manhattan distance of tile <em>b</em>.</p>
<p>h2 = 2<sub>3</sub> + 2<sub>8</sub> + 1<sub>4</sub> + 1<sub>1</sub> + 2<sub>7</sub> + 4<sub>2</sub> + 1<sub>6</sub> + 1<sub>5</sub></p>
<p>h2 = 14</p>
<p>Given 2 heuristics, it is always advised to use the maximum as the maximum never underestimates the cost to reach the
required end state ( initial configuration of 8 Puzzle )</p>
<p>If it took 10 moves to reach the current state as shown above, then the cost function of a given state of N - puzzle</p>
<p>is given as </p>
<pre><code>cost = max( h1, h2 ) + 10
cost = max( 14, 8 ) + 10 = 24
</code></pre>
<p>We can then implement a priority queue and record each of possible moves from a given initial state of the board
and then pop the state with the lowest cost function. This procedure is guaranteed to give us a solution.</p>
<p><strong>Problem Setter's code: C++</strong></p>
<p><a href="https://gist.github.com/dheerajrav/5748717">here</a></p>
| 0
|
may-2020-editorial-npuzzle
|
2013-06-10T13:14:35
|
{"contest_participation":3663,"challenge_submissions":135,"successful_submissions":0}
|
2013-06-10T13:14:35
|
2016-05-13T00:04:45
|
setter
|
#include<iostream>
#include<vector>
#include<queue>
#include<set>
#include<map>
#include<algorithm>
#define INRANGE(i, a, b) (i >= a && i < b)
using namespace std;
class SlidingBlock
{
public:
vector < int > disc;
int n;
int cost;
int empty_slot;
vector< string > record_move;
SlidingBlock();
SlidingBlock( int );
SlidingBlock( vector < int >, vector < string > );
vector < string > getMove();
void makeMove( const string move = string() );
bool solved();
vector < SlidingBlock > branches();
void setCost();
void print();
void readBlock();
bool operator< ( const SlidingBlock& ) const;
bool operator> ( const SlidingBlock& ) const;
};
SlidingBlock::SlidingBlock()
{
SlidingBlock( 3 );
}
SlidingBlock::SlidingBlock( int size )
{
n = size;
}
void SlidingBlock::readBlock()
{
int temp;
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < n; j++ )
{
cin >> temp;
disc.push_back( temp );
}
}
int pos = std::abs( std::distance( find( disc.begin(), disc.end(), 0 ), disc.begin()) );
empty_slot = pos;
setCost();
}
SlidingBlock::SlidingBlock( vector < int > node, vector < string > moves )
{
disc.clear();
n = ( int )sqrt( node.size() );
for( int i = 0; i < ( int )node.size(); ++i )
{
disc.push_back( node[ i ] );
if( node[ i ] == 0 )
empty_slot = i;
}
for( int i = 0; i < moves.size(); i++ )
record_move.push_back( moves[ i ] );
setCost();
}
void SlidingBlock::setCost()
{
int h1 = 0 , h2 = 0;
//setting heuristic 1 => number of misplaced blocks
//setting heuristic 2 => distance of the node to its block
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < n; j++ )
{
int val = disc[ n * i + j ];
if( val != n * i + j && val != 0 )
{
h1 += 1;
int exp_pos_x = ( val ) / n;
int exp_pos_y = ( val ) % n;
h2 += abs( i - exp_pos_x ) + abs( j - exp_pos_y );
}
}
}
cost = max( h1, h2) + this->record_move.size();
}
vector < string > SlidingBlock::getMove()
{
vector < string > movements;
if( empty_slot/n > 0 )
movements.push_back( "UP" );
if( empty_slot%n > 0 )
movements.push_back( "LEFT" );
if( empty_slot/n < n - 1 )
movements.push_back( "DOWN" );
if( empty_slot%n < n - 1 )
movements.push_back( "RIGHT" );
return movements;
}
void SlidingBlock::makeMove( string move )
{
if( move.empty() )
{
vector < string > moves = getMove();
int rand_point_index = rand() % moves.size();
makeMove( moves[ rand_point_index ] );
}
else
{
record_move.push_back( move );
int temp = empty_slot;
if( move.compare("UP") == 0 )
empty_slot -= n;
if( move.compare("DOWN") == 0 )
empty_slot += n;
if( move.compare("LEFT") == 0 )
empty_slot -= 1;
if( move.compare("RIGHT") == 0 )
empty_slot += 1;
swap( disc[ temp ], disc[ empty_slot ] );
}
setCost();
}
bool SlidingBlock::solved()
{
bool answer = true;
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < n; j++ )
{
answer &= disc[ n * i + j ] == ( n * i + j );
}
}
return answer;
}
vector < SlidingBlock > SlidingBlock::branches()
{
vector < string > moves = getMove();
vector < SlidingBlock > valid_branches;
for( int i = 0; i < ( int )moves.size(); ++i )
{
valid_branches.push_back( SlidingBlock( disc , record_move ) );
valid_branches[ i ].makeMove( moves[ i ] );
}
return valid_branches;
}
void SlidingBlock::print()
{
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < n; j++ )
{
cout << disc[ n*i + j ] << " ";
}
cout << endl;
}
}
bool SlidingBlock::operator< ( const SlidingBlock& node ) const
{
for( int i = 0; i < ( int )node.disc.size(); i++ )
{
if( node.disc[ i ] < this->disc[ i ] )
{
return true;
}
else if( node.disc[ i ] > this->disc[ i ] )
{
return false;
}
else
{
continue;
}
}
return false;
}
bool SlidingBlock::operator> ( const SlidingBlock& node ) const
{
for( int i = 0; i < ( int )node.disc.size(); i++ )
{
if( node.disc[ i ] > this->disc[ i ] )
{
return true;
}
else if( node.disc[ i ] < this->disc[ i ] )
{
return false;
}
else
{
continue;
}
}
return false;
}
struct OrderByCost
{
bool operator() ( const SlidingBlock &a, const SlidingBlock &b ) const
{
return a.cost >= b.cost;
}
};
class Search
{
public:
SlidingBlock start;
priority_queue< SlidingBlock, vector < SlidingBlock >, OrderByCost > pq;
set< SlidingBlock > explored;
vector < SlidingBlock > expanded;
Search( int n )
{
start = SlidingBlock( n );
start.readBlock();
searchAndPrint();
}
void searchAndPrint()
{
pushNode( start );
SlidingBlock node = SlidingBlock( start.disc, start.record_move );
setExplored( node );
while( !node.solved() )
{
node = getNextNode();
expanded.push_back( node );
vector < SlidingBlock > valid_branches = node.branches();
//Iterate over neighbors
for( int i = 0; i < ( int ) valid_branches.size(); i++ )
{
if( !isExplored( valid_branches[ i ] ) )
{
pushNode( valid_branches[ i ] );
setExplored( node );
}
}
}
cout << node.record_move.size() << endl;
for( auto i = node.record_move.begin(); i != node.record_move.end(); ++i )
cout << *i << endl;
}
void pushNode( SlidingBlock node )
{
pq.push( node );
}
void setExplored( SlidingBlock node )
{
explored.insert( node );
}
bool isExplored( SlidingBlock node )
{
return explored.count( node ) > 0;
}
SlidingBlock getNextNode()
{
SlidingBlock node = pq.top();
pq.pop();
return node;
}
};
int main()
{
set< SlidingBlock > explored;
int n;
cin >> n;
Search *game = new Search( n );
}
|
not-set
|
2016-04-24T02:02:11
|
2016-04-24T02:02:11
|
C++
|
2
| 746
|
game-of-throne-ii
|
Game Of Thrones - II
|
This follows from [Game of Thrones - I](https://www.hackerrank.com/contests/july13/challenges/game-of-thrones).
Now that the king knows how to find out whether a given word has an [anagram](https://en.wikipedia.org/wiki/Anagram) which is a [palindrome](http://en.wikipedia.org/wiki/Palindrome) or not, he encounters another challenge. He realizes that there can be more than one palindrome anagrams for a given word. Can you help him find out how many palindrome anagrams are possible for a given word ?
The king has many words. For each given word, he needs to find out the number of palindrome anagrams of the string. As the number of anagrams can be large, the king needs the number of anagrams % (10<sup>9</sup>+ 7).
**Input format :**<br>
A single line which contains the input string<br>
**Output format :**
A single line which contains the number of anagram strings which are palindrome % (10<sup>9</sup> + 7).
**Constraints :**
1<=length of string <= 10^5
Each character of the string is a lowercase alphabet.
Each test case has at least 1 anagram which is a palindrome.
**Sample Input 01 :**
aaabbbb
**Sample Output 01 :**
3
**Explanation :**
Three palindrome permutations of the given string are abbabba , bbaaabb and bababab.
**Sample Input 02 :**
cdcdcdcdeeeef
**Sample Output 02 :**
90
|
code
|
Can you help the king find the number of ways his door can be unlocked?
|
ai
|
2013-07-02T17:07:43
|
2022-09-02T09:54:54
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts STRING s as parameter.
#
def solve(s):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
s = input()
result = solve(s)
fptr.write(str(result) + '\n')
fptr.close()
|
This follows from [Game of Thrones - I](https://www.hackerrank.com/contests/july13/challenges/game-of-thrones).
Now that the king knows how to find out whether a given word has an [anagram](https://en.wikipedia.org/wiki/Anagram) which is a [palindrome](http://en.wikipedia.org/wiki/Palindrome) or not, he encounters another challenge. He realizes that there can be more than one palindrome anagrams for a given word. Can you help him find out how many palindrome anagrams are possible for a given word ?
The king has many words. For each given word, he needs to find out the number of palindrome anagrams of the string. As the number of anagrams can be large, the king needs the number of anagrams % (10<sup>9</sup>+ 7).
**Input format :**<br>
A single line which contains the input string<br>
**Output format :**
A single line which contains the number of anagram strings which are palindrome % (10<sup>9</sup> + 7).
**Constraints :**
1<=length of string <= 10^5
Each character of the string is a lowercase alphabet.
Each test case has at least 1 anagram which is a palindrome.
**Sample Input 01 :**
aaabbbb
**Sample Output 01 :**
3
**Explanation :**
Three palindrome permutations of the given string are abbabba , bbaaabb and bababab.
**Sample Input 02 :**
cdcdcdcdeeeef
**Sample Output 02 :**
90
| 0.501678
|
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
|
20/20 Hack July Editorial: Game of Thrones - 2
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/july13/challenges/game-of-throne-ii">Game Of Thrones - II</a> </p>
<p><strong>Problem:</strong> Given a string such that at least one of anagram of string is palindrome. Tell how many anagram of given string will be palindrome.</p>
<p><strong>Difficulty level:</strong> Easy <br>
<strong>Required Knowledge:</strong> Permutations, Modular Inverse <br>
<strong>Time Complexity:</strong> O(N) </p>
<p><strong>Approach:</strong> Given a string tell how many anagram of given string will be palindrome. So we can consider a sub-string which we can get by taking half of number of each character. length of this sub-string will L/2 where L is length of original string. we can get permutation of given string then we can concatenate the reverse of given half. so get anagram of given string which will be palindrome.So, we can use following <a href="http://www.regentsprep.org/Regents/math/ALGEBRA/APR2/LpermRep.htm">formula</a> to get number of permutation of given first half. </p>
<p>So , as answer can be very huge . But as in question we are asked for number of permutations which are palindrome % 10^9+7 and we know 10^9 + 7 is a prime number . So, we can get it using modular inverse techniques.</p>
<p><strong>Problem Setter's code:</strong></p>
<pre><code>#!/usr/bin/py
from collections import Counter
mod = 10**9 + 7
def hasPalindrome(word):
x = Counter(word)
count = 0
for i in x:
if x[i]%2!=0:
count += 1
if count > 1:
return False
else:
return True
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b == 0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
word = raw_input()
assert 1 <= len(word) <= 10**5
assert hasPalindrome(word) == True
counter = Counter(word)
denominator = 1
numerator = 0
for i in counter:
numerator += counter[i]/2
denominator = ((denominator%mod)*(getfactmod(counter[i]/2)%mod))%mod
numerator = getfactmod(numerator)
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
</code></pre>
<p><strong>Tester's code:</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
int t;
const long long mod = 1000000007;
long long pow(long long osn){
long long res = 1, tmp = osn;
int m = int(mod - 2);
while(m){
if(m % 2){
res = (res * tmp) % mod;
--m;
}
m >>= 1;
tmp = (tmp * tmp) % mod;
}
return res;
}
long long fact(int num){
long long res(1), curp(num);
while(curp)res = (res * curp--) % mod;
return res;
}
int obr(){
int num[256];
memset(num, 0, sizeof(num));
char s[1001];
cin>>s;
int n = strlen(s);
for(int i = 0; i < n; ++i)++num[s[i]];
for(int i=0 ; i<256 ; i++)
num[i] = num[i]/2;
n = n/2;
long long res = fact(n);
for(int i = 'a'; i <= 'z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
for(int i = 'A'; i <= 'Z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
int topr = int(res);
printf("%d\n", topr);
return 0;
}
int main(){
t = 1;
for(int i = 0; i < t; ++i)
obr();
return 0;
}
</code></pre>
| 0
|
july-2020-editorial-game-of-thrones-ii
|
2013-07-22T04:35:37
|
{"contest_participation":4325,"challenge_submissions":1181,"successful_submissions":695}
|
2013-07-22T04:35:37
|
2016-12-02T19:33:05
|
setter
|
###Python 2
```python
#!/usr/bin/py
from collections import Counter
mod = 10**9 + 7
def hasPalindrome(word):
x = Counter(word)
count = 0
for i in x:
if x[i]%2!=0:
count += 1
if count > 1:
return False
else:
return True
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b == 0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
word = raw_input()
assert 1 <= len(word) <= 10**5
assert hasPalindrome(word) == True
counter = Counter(word)
denominator = 1
numerator = 0
for i in counter:
numerator += counter[i]/2
denominator = ((denominator%mod)*(getfactmod(counter[i]/2)%mod))%mod
numerator = getfactmod(numerator)
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
```
|
not-set
|
2016-04-24T02:02:12
|
2016-07-23T18:36:16
|
Python
|
3
| 746
|
game-of-throne-ii
|
Game Of Thrones - II
|
This follows from [Game of Thrones - I](https://www.hackerrank.com/contests/july13/challenges/game-of-thrones).
Now that the king knows how to find out whether a given word has an [anagram](https://en.wikipedia.org/wiki/Anagram) which is a [palindrome](http://en.wikipedia.org/wiki/Palindrome) or not, he encounters another challenge. He realizes that there can be more than one palindrome anagrams for a given word. Can you help him find out how many palindrome anagrams are possible for a given word ?
The king has many words. For each given word, he needs to find out the number of palindrome anagrams of the string. As the number of anagrams can be large, the king needs the number of anagrams % (10<sup>9</sup>+ 7).
**Input format :**<br>
A single line which contains the input string<br>
**Output format :**
A single line which contains the number of anagram strings which are palindrome % (10<sup>9</sup> + 7).
**Constraints :**
1<=length of string <= 10^5
Each character of the string is a lowercase alphabet.
Each test case has at least 1 anagram which is a palindrome.
**Sample Input 01 :**
aaabbbb
**Sample Output 01 :**
3
**Explanation :**
Three palindrome permutations of the given string are abbabba , bbaaabb and bababab.
**Sample Input 02 :**
cdcdcdcdeeeef
**Sample Output 02 :**
90
|
code
|
Can you help the king find the number of ways his door can be unlocked?
|
ai
|
2013-07-02T17:07:43
|
2022-09-02T09:54:54
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts STRING s as parameter.
#
def solve(s):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
s = input()
result = solve(s)
fptr.write(str(result) + '\n')
fptr.close()
|
This follows from [Game of Thrones - I](https://www.hackerrank.com/contests/july13/challenges/game-of-thrones).
Now that the king knows how to find out whether a given word has an [anagram](https://en.wikipedia.org/wiki/Anagram) which is a [palindrome](http://en.wikipedia.org/wiki/Palindrome) or not, he encounters another challenge. He realizes that there can be more than one palindrome anagrams for a given word. Can you help him find out how many palindrome anagrams are possible for a given word ?
The king has many words. For each given word, he needs to find out the number of palindrome anagrams of the string. As the number of anagrams can be large, the king needs the number of anagrams % (10<sup>9</sup>+ 7).
**Input format :**<br>
A single line which contains the input string<br>
**Output format :**
A single line which contains the number of anagram strings which are palindrome % (10<sup>9</sup> + 7).
**Constraints :**
1<=length of string <= 10^5
Each character of the string is a lowercase alphabet.
Each test case has at least 1 anagram which is a palindrome.
**Sample Input 01 :**
aaabbbb
**Sample Output 01 :**
3
**Explanation :**
Three palindrome permutations of the given string are abbabba , bbaaabb and bababab.
**Sample Input 02 :**
cdcdcdcdeeeef
**Sample Output 02 :**
90
| 0.501678
|
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
|
20/20 Hack July Editorial: Game of Thrones - 2
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/july13/challenges/game-of-throne-ii">Game Of Thrones - II</a> </p>
<p><strong>Problem:</strong> Given a string such that at least one of anagram of string is palindrome. Tell how many anagram of given string will be palindrome.</p>
<p><strong>Difficulty level:</strong> Easy <br>
<strong>Required Knowledge:</strong> Permutations, Modular Inverse <br>
<strong>Time Complexity:</strong> O(N) </p>
<p><strong>Approach:</strong> Given a string tell how many anagram of given string will be palindrome. So we can consider a sub-string which we can get by taking half of number of each character. length of this sub-string will L/2 where L is length of original string. we can get permutation of given string then we can concatenate the reverse of given half. so get anagram of given string which will be palindrome.So, we can use following <a href="http://www.regentsprep.org/Regents/math/ALGEBRA/APR2/LpermRep.htm">formula</a> to get number of permutation of given first half. </p>
<p>So , as answer can be very huge . But as in question we are asked for number of permutations which are palindrome % 10^9+7 and we know 10^9 + 7 is a prime number . So, we can get it using modular inverse techniques.</p>
<p><strong>Problem Setter's code:</strong></p>
<pre><code>#!/usr/bin/py
from collections import Counter
mod = 10**9 + 7
def hasPalindrome(word):
x = Counter(word)
count = 0
for i in x:
if x[i]%2!=0:
count += 1
if count > 1:
return False
else:
return True
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b == 0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
word = raw_input()
assert 1 <= len(word) <= 10**5
assert hasPalindrome(word) == True
counter = Counter(word)
denominator = 1
numerator = 0
for i in counter:
numerator += counter[i]/2
denominator = ((denominator%mod)*(getfactmod(counter[i]/2)%mod))%mod
numerator = getfactmod(numerator)
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
</code></pre>
<p><strong>Tester's code:</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
int t;
const long long mod = 1000000007;
long long pow(long long osn){
long long res = 1, tmp = osn;
int m = int(mod - 2);
while(m){
if(m % 2){
res = (res * tmp) % mod;
--m;
}
m >>= 1;
tmp = (tmp * tmp) % mod;
}
return res;
}
long long fact(int num){
long long res(1), curp(num);
while(curp)res = (res * curp--) % mod;
return res;
}
int obr(){
int num[256];
memset(num, 0, sizeof(num));
char s[1001];
cin>>s;
int n = strlen(s);
for(int i = 0; i < n; ++i)++num[s[i]];
for(int i=0 ; i<256 ; i++)
num[i] = num[i]/2;
n = n/2;
long long res = fact(n);
for(int i = 'a'; i <= 'z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
for(int i = 'A'; i <= 'Z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
int topr = int(res);
printf("%d\n", topr);
return 0;
}
int main(){
t = 1;
for(int i = 0; i < t; ++i)
obr();
return 0;
}
</code></pre>
| 0
|
july-2020-editorial-game-of-thrones-ii
|
2013-07-22T04:35:37
|
{"contest_participation":4325,"challenge_submissions":1181,"successful_submissions":695}
|
2013-07-22T04:35:37
|
2016-12-02T19:33:05
|
tester
|
###C++
```cpp
#include <cstdio>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
int t;
const long long mod = 1000000007;
long long pow(long long osn){
long long res = 1, tmp = osn;
int m = int(mod - 2);
while(m){
if(m % 2){
res = (res * tmp) % mod;
--m;
}
m >>= 1;
tmp = (tmp * tmp) % mod;
}
return res;
}
long long fact(int num){
long long res(1), curp(num);
while(curp)res = (res * curp--) % mod;
return res;
}
int obr(){
int num[256];
memset(num, 0, sizeof(num));
char s[1001];
cin>>s;
int n = strlen(s);
for(int i = 0; i < n; ++i)++num[s[i]];
for(int i=0 ; i<256 ; i++)
num[i] = num[i]/2;
n = n/2;
long long res = fact(n);
for(int i = 'a'; i <= 'z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
for(int i = 'A'; i <= 'Z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
int topr = int(res);
printf("%d\n", topr);
return 0;
}
int main(){
t = 1;
for(int i = 0; i < t; ++i)
obr();
return 0;
}
```
|
not-set
|
2016-04-24T02:02:12
|
2016-07-23T18:36:38
|
C++
|
4
| 791
|
kth-ancestor
|
Kth Ancestor
|
A tree of P nodes is an un-directed connected graph having P-1 edges. Let us denote R as the root node. If A is a node such that it is at a distance of L from R, and B is a node such that it is at at distance of L+1 from
R and A is connected to B, then we call A as the parent of B.
Similarly, if A is at a distance of L from R and B is at a distance of L+K from R and there is a path of length K from A to B, then we call A as the K<sup>th</sup> parent of B.
Susan likes to play with graphs and Tree data structure is one of her favorites. She has designed a problem and wants to know if anyone can solve it. Sometimes she adds or removes a leaf node. Your task is to figure out the K-th parent of a node at any instant.
**Input Format**
The first line contain an integer T denoting the number of test-cases. T test cases follow. First line of each test case contains an integer P, the number of nodes in the tree.
P lines follows each containing two integers X and Y separated by a single space denoting Y as the parent of X. if Y is 0, then X is the root node of the tree. (0 is for namesake and is not in the tree).
The next line contains an integer Q, the number of queries.
Q lines follow each containing a query.
+ 0 Y X : X is added as a new leaf node whose parent is Y
+ 1 X : This tells that leaf node X is removed from the tree
+ 2 X K : In this query output the K<sup>th</sup> parent of X
**Note**
Each node index is any number between 1 and 10<sup>5</sup> i.e., a tree with a single node can have its root indexed as 10<sup>5</sup>
**Output Format**
For each query of type 2, output the K<sup>th</sup> parent of X. If K<sup>th</sup> parent doesn't exist, output 0 and if the node doesn't exist, output 0.
**Constraints**
1<=T<=3
1<=P<=10<sup>5</sup>
1<=Q<=10<sup>5</sup>
1<=X<=10<sup>5</sup>
0<=Y<=10<sup>5</sup>
1<=K<=10<sup>5</sup>
**Sample Input**
2
7
2 0
5 2
3 5
7 5
9 8
8 2
6 8
10
0 5 15
2 15 2
1 3
0 15 20
0 20 13
2 13 4
2 13 3
2 6 10
2 11 1
2 9 1
1
10000 0
3
0 10000 4
1 4
2 4 1
**Sample Output**
2
2
5
0
0
8
0
**Explanation**
There are 2 test cases. The first test case has 7 nodes with 2 as its root. There are 10 queries
+ 0 5 15 -> 15 is added as a leaf node to 5.
+ 2 15 2 -> 2nd parent of 15 is 15->5->2 is 2.
+ 1 3 -> leaf node 3 is removed from the tree.
+ 0 15 20 -> 20 is added as a leaf node to 15.
+ 0 20 13 -> 13 is added as a leaf node to 20.
+ 2 13 4 -> 4th parent of 13 is 2.
+ 2 13 3 -> 3rd parent of 13 is 5.
+ 2 6 10 -> there is no 10th parent of 6 and hence 0.
+ 2 11 1 -> 11 is not a node in the tree, hence 0.
+ 2 9 1 -> 9's parent is 8.
the second testcase has a tree with only 1 node (100000).
+ 0 10000 4 -> 4 is added as a leaf node to 10000.
+ 1 4 -> 4 is removed.
+ 2 4 1 -> as 4 is already removed, answer is 0.
|
code
|
Figure out the K-th parent of a node at any instant.
|
ai
|
2013-08-01T18:06:31
|
2022-08-31T08:14:29
| null | null | null |
A tree of $P$ nodes is an un-directed connected graph having $P-1$ edges. Let us denote $R$ as the root node. If $A$ is a node such that it is at a distance of $L$ from $R$, and $B$ is a node such that it is at at distance of $L+1$ from
$R$ and $A$ is connected to $B$, then we call $A$ as the parent of $B$.
Similarly, if $A$ is at a distance of $L$ from $R$ and $B$ is at a distance of $L+K$ from $R$ and there is a path of length $K$ from $A$ to $B$, then we call $A$ as the $K$<sup>th</sup> parent of $B$.
Susan likes to play with graphs and Tree data structure is one of her favorites. She has designed a problem and wants to know if anyone can solve it. Sometimes she adds or removes a leaf node. Your task is to figure out the $K$<sup>th</sup> parent of a node at any instant.
| 0.435294
|
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
The first line contain an integer $T$ denoting the number of test cases. $T$ test cases follow. First line of each test case contains an integer $P$, the number of nodes in the tree.
$P$ lines follows each containing two integers $X$ and $Y$ separated by a single space denoting $Y$ as the parent of $X$. If $Y$ is $0$, then X is the root node of the tree. ($0$ is for namesake and is not in the tree).
The next line contains an integer $Q$, the number of queries.
$Q$ lines follow each containing a query.
+ $0$ $Y$ $X$ : $X$ is added as a new leaf node whose parent is $Y$ . $X$ is not in the tree while $Y$ is in.
+ $1$ $X$ : This tells that leaf node $X$ is removed from the tree. $X$ is a leaf in the tree.
+ $2$ $X$ $K$ : In this query output the $K$<sup>th</sup> parent of $X$ . $X$ is a node in the tree.
**Note**
+ Each node index is any number between 1 and 10<sup>5</sup> i.e., a tree with a single node can have its root indexed as 10<sup>5</sup>
|
For each query of type $2$, output the $K$<sup>th</sup> parent of $X$. If $K$<sup>th</sup> parent doesn't exist, output $0$ and if the node doesn't exist, output $0$.
|
2
7
2 0
5 2
3 5
7 5
9 8
8 2
6 8
10
0 5 15
2 15 2
1 3
0 15 20
0 20 13
2 13 4
2 13 3
2 6 10
2 11 1
2 9 1
1
10000 0
3
0 10000 4
1 4
2 4 1
|
2
2
5
0
0
8
0
|
Hard
|
Kth Parent : August 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem Statement</strong></p>
<p>Susan needs to find the k<sup>th</sup> parent of a node in the tree.</p>
<p><strong>Difficulty level</strong> Medium</p>
<p><strong>Required Knowledge</strong> Trees, Binary Logic</p>
<p><strong>Time Complexity</strong> O(NlogN)</p>
<p><strong>Approach</strong></p>
<p>The naive approach for this problem is very obvious. Just store the parent of each node and find the k<sup>th</sup> parent by finding parent of each parent. But as the number of queries are large, this approach in the worst case (example: tree having only two leaf nodes) exceeds time limit.</p>
<p>The pick of the problem is that, instead of storing the parent of every node, we store all 2<sup>i</sup>th parent of a node i.e. 2<sup>0</sup>th , 2<sup>1</sup>st, 2<sup>2</sup>th ... parent for each node. </p>
<p>Now for finding k<sup>th</sup> parent of a node A, </p>
<p>Let, <br>
k = (b<sub>l-1</sub>b<sub>l-2</sub>....b<sub>0</sub>) in binary representation be a l-bit number k. </p>
<p>So k = b<sub>0</sub> + b<sub>1</sub> * 2<sup>1</sup> + ... + b<sub>l-2</sub> * 2<sup>l-2</sup> + b<sub>l-1</sub> * 2<sup>l-1</sup> </p>
<p>Let s bits of these l bits are 1, p1,p2,...ps be indices at which bit value is 1. <br>
k = 2<sup>p1</sup> + 2<sup>p2</sup> + ... + 2<sup>ps</sup> </p>
<p>Using above distribution of k, we can find kth node by following procedure. <br>
A1 = 2<sup>p1</sup>th parent of A <br>
A2 = 2<sup>p2</sup>th parent of A1, implies 2<sup>p1</sup>th + 2<sup>p2</sup>th parent of A <br>
A3 = 2<sup>p3</sup>th parent of A2 which will also be 2<sup>p1</sup>th + 2<sup>p2</sup>th + 2<sup>p3</sup>th parent of A. </p>
<p>Similarly <br>
As = 2<sup>ps</sup>th parent of As-1 and also 2<sup>p1</sup>th+2<sup>p2</sup>th .... 2<sup>ps</sup>th parent of A i.e. k<sup>th</sup> parent of A.</p>
<p>So it takes only s summations for finding k<sup>th</sup> parent. Since s is the number of bits in k.
So this process takes O(s) = O(log k) time;</p>
<p>Now the problem is how to find 2<sup>i</sup> parents of each node?</p>
<p>Let parent[i][j] be 2<sup>j</sup>th parent of node i.
Initially we know parent[i][0] i.e. first parent of all the nodes.</p>
<p>For j>0</p>
<pre><code>parent[i][j] = 2^jth parent of i
= (2^j-1th + 2^j-1th) parent of i
= 2^j-1th parent of (2^j-1th parent of i)
= 2^j-1th parent of parent[i][j-1]
= parent[parent[i][j-1][j-1]
</code></pre>
<p>The pseudo code is as follows</p>
<pre><code>for i from 1 to n
parent[i][0] = parent of i
for i from 1 to n
for j from 1 to m
parent[i][j] = parent[parent[i][j-1]][j-1]
</code></pre>
<p>In above code, m is the maximum value j can attain. In worst case, the highest value of parent a node can have is n-1. </p>
<p>2^m<=n-1
m = O(log n)</p>
<p>Hence above process takes O(n log n) time as well as O(n log n) space.</p>
<p><strong>Problem Setter's code</strong> </p>
<pre><code>//shashwat001
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <queue>
#include <stack>
#include <map>
#include <utility>
#include <algorithm>
#include <cassert>
using namespace std;
#define INF 2147483647
#define LINF 9223372036854775807
#define mp make_pair
#define pb push_back
typedef long long int lli;
typedef pair<int,int> pi;
int p[100000][40]={{0}};
int a[100005],isnode[100005];
int main ()
{
int q,ch,x,y,t;
scanf("%d",&t);
assert(t>=1 && t<=3);
while(t--)
{
memset(p,0,sizeof(p));
memset(isnode,0,sizeof(isnode));
int i,n,j;
scanf("%d",&n);
assert(n>=1 && n<=100000);
for(i = 0;i < n;i++)
{
scanf("%d %d",&x,&y);
assert(x>=1 && x<=100000);
assert(y>=0 && y<=100000);
a[i] = x;
if(y!=0)
assert(isnode[y]==1);
assert(isnode[x]==0);
isnode[x] = 1;
p[x][0] = y;
}
int lgn = (int)(log(n)/log(2))+1;
for(j = 1;j<=lgn;j++)
{
for(i = 0;i < n;i++)
{
p[a[i]][j] = p[p[a[i]][j-1]][j-1];
}
}
scanf("%d",&q);
assert(q>0 && q<=100000);
for(i = 0;i < q;i++)
{
scanf("%d",&ch);
assert(ch>=0 && ch<=2);
if(ch == 0) //Add an edge
{
scanf("%d %d",&x,&y);
assert(y>=1 && y<=100000);
assert(x>=1 && x<=100000);
assert(isnode[x]==1);
assert(isnode[y]==0);
isnode[y] = 1;
p[y][0] = x;
j = 0;
while(p[y][j]!=0)
{
p[y][j+1] = p[p[y][j]][j];
j++;
}
while(j<=lgn)
{
p[y][j] = 0;
j++;
}
}
else if(ch == 1) //Remove an edge
{
scanf("%d",&x);
assert(x>=1 && x<=100000);
assert(isnode[x]==1);
isnode[x] = 0;
for(j = 0;j <= lgn;j++)
{
p[x][j] = 0;
}
}
else
{
scanf("%d %d",&x,&y);
assert(x>=1 && x<=100000);
assert(y>=1 && y<=100000);
j = 0;
while(y>0)
{
if(y&1)
x = p[x][j];
y = y>>1;
j++;
}
printf("%d\n",x);
}
}
}
return 0;
}
</code></pre>
| 0
|
aug-2020-editorial-kth-parent
|
2013-08-13T08:25:00
|
{"contest_participation":3656,"challenge_submissions":458,"successful_submissions":180}
|
2013-08-13T08:25:00
|
2016-12-02T15:06:47
|
setter
|
###C++
```cpp
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <queue>
#include <stack>
#include <map>
#include <utility>
#include <algorithm>
#include <cassert>
using namespace std;
#define INF 2147483647
#define LINF 9223372036854775807
#define mp make_pair
#define pb push_back
typedef long long int lli;
typedef pair<int,int> pi;
int p[100000][40]={{0}};
int a[100005],isnode[100005];
int main ()
{
int q,ch,x,y,t;
scanf("%d",&t);
assert(t>=1 && t<=3);
while(t--)
{
memset(p,0,sizeof(p));
memset(isnode,0,sizeof(isnode));
int i,n,j;
scanf("%d",&n);
assert(n>=1 && n<=100000);
for(i = 0;i < n;i++)
{
scanf("%d %d",&x,&y);
assert(x>=1 && x<=100000);
assert(y>=0 && y<=100000);
a[i] = x;
if(y!=0)
assert(isnode[y]==1);
assert(isnode[x]==0);
isnode[x] = 1;
p[x][0] = y;
}
int lgn = (int)(log(n)/log(2))+1;
for(j = 1;j<=lgn;j++)
{
for(i = 0;i < n;i++)
{
p[a[i]][j] = p[p[a[i]][j-1]][j-1];
}
}
scanf("%d",&q);
assert(q>0 && q<=100000);
for(i = 0;i < q;i++)
{
scanf("%d",&ch);
assert(ch>=0 && ch<=2);
if(ch == 0) //Add an edge
{
scanf("%d %d",&x,&y);
assert(y>=1 && y<=100000);
assert(x>=1 && x<=100000);
assert(isnode[x]==1);
assert(isnode[y]==0);
isnode[y] = 1;
p[y][0] = x;
j = 0;
while(p[y][j]!=0)
{
p[y][j+1] = p[p[y][j]][j];
j++;
}
while(j<=lgn)
{
p[y][j] = 0;
j++;
}
}
else if(ch == 1) //Remove an edge
{
scanf("%d",&x);
assert(x>=1 && x<=100000);
assert(isnode[x]==1);
isnode[x] = 0;
for(j = 0;j <= lgn;j++)
{
p[x][j] = 0;
}
}
else
{
scanf("%d %d",&x,&y);
assert(x>=1 && x<=100000);
assert(y>=1 && y<=100000);
j = 0;
while(y>0)
{
if(y&1)
x = p[x][j];
y = y>>1;
j++;
}
printf("%d\n",x);
}
}
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:12
|
2016-07-23T13:56:04
|
C++
|
5
| 803
|
help-mike
|
Help Mike
|
Harvey Specter has agreed to take Mike Ross to a meeting filled with brilliant scientists at NSA Headquarters. But, as always, it's not going to be easy for Mike. He has to solve a puzzle given by Harvey.
Harvey gives two numbers N and K and defines a set A.<br>
*A = { x : x is a [natural number](https://en.wikipedia.org/wiki/Natural_number) ≤ N }*
(i.e), A = {1,2,3,4,5,6,...., N}
Mike has to find the total number of pairs of elements A[i] and A[j] belonging to the given set, such that, i < j and their sum is divisible by K<br>
**Input Format**
An integer T followed by T lines, each containing a pair of space separated integers N and K.
**Output Format**
T integers on separate lines. Each integer denotes the answer corresponding to that test case.
**Constraints**
1<=T<=100
K<=N<=10<sup>9</sup>
1<=K<=10000
**Sample Input**
2
10 4
7 3
**Sample Output**
10
7
**Explanation**
For the 1<sup>st</sup> test case, there are 10 pairs whose sum is divisible by 4.
(1,3), (1,7), (2,6), (2,10), (3,5), (3,9), (4,8), (5,7), (6,10) and (7,9)
For the 2<sup>nd</sup> test case, there are 7 pairs whose sum is divisible by 3.
(1,2), (1,5), (2,4), (2,7), (3,6), (4,5) and (5,7)
|
code
|
Help Mike attend the NSA meeting
|
ai
|
2013-08-13T09:29:32
|
2022-09-02T09:54:27
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER k
#
def solve(n, k):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
k = int(first_multiple_input[1])
result = solve(n, k)
fptr.write(str(result) + '\n')
fptr.close()
|
Harvey Specter has agreed to take Mike Ross to a meeting filled with brilliant scientists at NSA Headquarters. But, as always, it's not going to be easy for Mike. He has to solve a puzzle given by Harvey.
Harvey gives two numbers N and K and defines a set A.<br>
*A = { x : x is a [natural number](https://en.wikipedia.org/wiki/Natural_number) ≤ N }*
(i.e), A = {1,2,3,4,5,6,...., N}
Mike has to find the total number of pairs of elements A[i] and A[j] belonging to the given set, such that, i < j and their sum is divisible by K<br>
**Input Format**
An integer T followed by T lines, each containing a pair of space separated integers N and K.
**Output Format**
T integers on separate lines. Each integer denotes the answer corresponding to that test case.
**Constraints**
1<=T<=100
K<=N<=10<sup>9</sup>
1<=K<=10000
**Sample Input**
2
10 4
7 3
**Sample Output**
10
7
**Explanation**
For the 1<sup>st</sup> test case, there are 10 pairs whose sum is divisible by 4.
(1,3), (1,7), (2,6), (2,10), (3,5), (3,9), (4,8), (5,7), (6,10) and (7,9)
For the 2<sup>nd</sup> test case, there are 7 pairs whose sum is divisible by 3.
(1,2), (1,5), (2,4), (2,7), (3,6), (4,5) and (5,7)
| 0.579365
|
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
|
Help Mike - Sept 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem Statement</strong></p>
<p>Help Mike in finding the total number of pairs of elements A[i] and A[j] belonging to the given set such that i < j and their sum is divisible by K</p>
<p><strong>Difficulty Level</strong> Easy-Medium</p>
<p><strong>Required knowledge</strong> : Basic Hashing , Maths</p>
<p><strong>Time complexity</strong> : O(K) , O(1) will be accepted . O(N/K) or O(N) will go for TLE(time limit exceeded) under given time constraints.</p>
<p><strong>Approach</strong> :</p>
<p>To solve the problem in O(K) time limit, we can create an array rem[K]. The array rem[i] will store the number of integers in the set A, such that on dividing by K, you get i as the remainder. rem[i] can be calculated in O(1) time.
rem[i] = (N-i)/K;</p>
<p>Now, the sum of two integers is divisible by K if:</p>
<ul>
<li>Both numbers are divisible by K and such selection can be made in rem[0](rem[0]-1)/2 ways.</li>
<li>On dividing first number by K, reminder is p then on dividing second number K, reminder must be K-p . i.e. number of ways can be rem[p]*rem[K-p] where p can belong to 0 to K/2.</li>
<li>K is even and on dividing both numbers, the reminder is K/2 i.e. rem[K/2]*(rem[K/2]-1)/2 .</li>
</ul>
<p>We can sum up all these possibilities to get the required output.</p>
<p><strong>Problem Setter's code:</strong></p>
<pre><code>#include<bits/stdc++.h>
using namespace std;
#define print(p) cout<<p<<endl;
int main()
{
int T;
long long int N,K,i;
cin>>T;
while(T--)
{
cin>>N>>K;
long long int arr[K];
arr[0] = N/K;
for(i=1 ; i< K ; i++)
arr[i] = (int)(N-i)/K + 1;
if(K%2!=0)
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< (float)K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
cout<<sum<<endl;
}
else
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
sum = sum + (arr[K/2]*(arr[K/2] - 1))/2;
cout<<sum<<endl;
}
}
return 0;
}
</code></pre>
<p><strong>Problem Tester's Code</strong></p>
<pre><code>#!/usr/bin/py
import math
T = input()
1 <= T <= 100
for t in range(T):
N, K = map(int, raw_input().strip().split(" "))
assert 1 <= N <= 10**9
assert 1 <= K <= 10**4
assert K <= N
n_by_k = math.floor(N/K)
n_mod_k = N%K
count_less_than_k = K/2 if K % 2 == 1 else (K - 1)/2
sum = count_less_than_k*n_by_k
summation_limit = n_by_k - 1
sum += K*(summation_limit*(summation_limit + 1))/2
sum += (summation_limit+1)*(n_mod_k)
if n_mod_k > 0:
extra = n_mod_k - count_less_than_k
if K%2==0:
extra -= 1
sum += extra if extra > 0 else 0
print int(sum)
</code></pre>
| 0
|
sep-2020-editorial-help-mike
|
2013-09-16T13:48:37
|
{"contest_participation":3240,"challenge_submissions":1167,"successful_submissions":494}
|
2013-09-16T13:48:37
|
2016-12-03T12:59:31
|
setter
|
###C++
```cpp
#include<bits/stdc++.h>
using namespace std;
#define print(p) cout<<p<<endl;
int main()
{
int T;
long long int N,K,i;
cin>>T;
while(T--)
{
cin>>N>>K;
long long int arr[K];
arr[0] = N/K;
for(i=1 ; i< K ; i++)
arr[i] = (int)(N-i)/K + 1;
if(K%2!=0)
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< (float)K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
cout<<sum<<endl;
}
else
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
sum = sum + (arr[K/2]*(arr[K/2] - 1))/2;
cout<<sum<<endl;
}
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T17:46:38
|
C++
|
6
| 803
|
help-mike
|
Help Mike
|
Harvey Specter has agreed to take Mike Ross to a meeting filled with brilliant scientists at NSA Headquarters. But, as always, it's not going to be easy for Mike. He has to solve a puzzle given by Harvey.
Harvey gives two numbers N and K and defines a set A.<br>
*A = { x : x is a [natural number](https://en.wikipedia.org/wiki/Natural_number) ≤ N }*
(i.e), A = {1,2,3,4,5,6,...., N}
Mike has to find the total number of pairs of elements A[i] and A[j] belonging to the given set, such that, i < j and their sum is divisible by K<br>
**Input Format**
An integer T followed by T lines, each containing a pair of space separated integers N and K.
**Output Format**
T integers on separate lines. Each integer denotes the answer corresponding to that test case.
**Constraints**
1<=T<=100
K<=N<=10<sup>9</sup>
1<=K<=10000
**Sample Input**
2
10 4
7 3
**Sample Output**
10
7
**Explanation**
For the 1<sup>st</sup> test case, there are 10 pairs whose sum is divisible by 4.
(1,3), (1,7), (2,6), (2,10), (3,5), (3,9), (4,8), (5,7), (6,10) and (7,9)
For the 2<sup>nd</sup> test case, there are 7 pairs whose sum is divisible by 3.
(1,2), (1,5), (2,4), (2,7), (3,6), (4,5) and (5,7)
|
code
|
Help Mike attend the NSA meeting
|
ai
|
2013-08-13T09:29:32
|
2022-09-02T09:54:27
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER k
#
def solve(n, k):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
k = int(first_multiple_input[1])
result = solve(n, k)
fptr.write(str(result) + '\n')
fptr.close()
|
Harvey Specter has agreed to take Mike Ross to a meeting filled with brilliant scientists at NSA Headquarters. But, as always, it's not going to be easy for Mike. He has to solve a puzzle given by Harvey.
Harvey gives two numbers N and K and defines a set A.<br>
*A = { x : x is a [natural number](https://en.wikipedia.org/wiki/Natural_number) ≤ N }*
(i.e), A = {1,2,3,4,5,6,...., N}
Mike has to find the total number of pairs of elements A[i] and A[j] belonging to the given set, such that, i < j and their sum is divisible by K<br>
**Input Format**
An integer T followed by T lines, each containing a pair of space separated integers N and K.
**Output Format**
T integers on separate lines. Each integer denotes the answer corresponding to that test case.
**Constraints**
1<=T<=100
K<=N<=10<sup>9</sup>
1<=K<=10000
**Sample Input**
2
10 4
7 3
**Sample Output**
10
7
**Explanation**
For the 1<sup>st</sup> test case, there are 10 pairs whose sum is divisible by 4.
(1,3), (1,7), (2,6), (2,10), (3,5), (3,9), (4,8), (5,7), (6,10) and (7,9)
For the 2<sup>nd</sup> test case, there are 7 pairs whose sum is divisible by 3.
(1,2), (1,5), (2,4), (2,7), (3,6), (4,5) and (5,7)
| 0.579365
|
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
|
Help Mike - Sept 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem Statement</strong></p>
<p>Help Mike in finding the total number of pairs of elements A[i] and A[j] belonging to the given set such that i < j and their sum is divisible by K</p>
<p><strong>Difficulty Level</strong> Easy-Medium</p>
<p><strong>Required knowledge</strong> : Basic Hashing , Maths</p>
<p><strong>Time complexity</strong> : O(K) , O(1) will be accepted . O(N/K) or O(N) will go for TLE(time limit exceeded) under given time constraints.</p>
<p><strong>Approach</strong> :</p>
<p>To solve the problem in O(K) time limit, we can create an array rem[K]. The array rem[i] will store the number of integers in the set A, such that on dividing by K, you get i as the remainder. rem[i] can be calculated in O(1) time.
rem[i] = (N-i)/K;</p>
<p>Now, the sum of two integers is divisible by K if:</p>
<ul>
<li>Both numbers are divisible by K and such selection can be made in rem[0](rem[0]-1)/2 ways.</li>
<li>On dividing first number by K, reminder is p then on dividing second number K, reminder must be K-p . i.e. number of ways can be rem[p]*rem[K-p] where p can belong to 0 to K/2.</li>
<li>K is even and on dividing both numbers, the reminder is K/2 i.e. rem[K/2]*(rem[K/2]-1)/2 .</li>
</ul>
<p>We can sum up all these possibilities to get the required output.</p>
<p><strong>Problem Setter's code:</strong></p>
<pre><code>#include<bits/stdc++.h>
using namespace std;
#define print(p) cout<<p<<endl;
int main()
{
int T;
long long int N,K,i;
cin>>T;
while(T--)
{
cin>>N>>K;
long long int arr[K];
arr[0] = N/K;
for(i=1 ; i< K ; i++)
arr[i] = (int)(N-i)/K + 1;
if(K%2!=0)
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< (float)K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
cout<<sum<<endl;
}
else
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
sum = sum + (arr[K/2]*(arr[K/2] - 1))/2;
cout<<sum<<endl;
}
}
return 0;
}
</code></pre>
<p><strong>Problem Tester's Code</strong></p>
<pre><code>#!/usr/bin/py
import math
T = input()
1 <= T <= 100
for t in range(T):
N, K = map(int, raw_input().strip().split(" "))
assert 1 <= N <= 10**9
assert 1 <= K <= 10**4
assert K <= N
n_by_k = math.floor(N/K)
n_mod_k = N%K
count_less_than_k = K/2 if K % 2 == 1 else (K - 1)/2
sum = count_less_than_k*n_by_k
summation_limit = n_by_k - 1
sum += K*(summation_limit*(summation_limit + 1))/2
sum += (summation_limit+1)*(n_mod_k)
if n_mod_k > 0:
extra = n_mod_k - count_less_than_k
if K%2==0:
extra -= 1
sum += extra if extra > 0 else 0
print int(sum)
</code></pre>
| 0
|
sep-2020-editorial-help-mike
|
2013-09-16T13:48:37
|
{"contest_participation":3240,"challenge_submissions":1167,"successful_submissions":494}
|
2013-09-16T13:48:37
|
2016-12-03T12:59:31
|
tester
|
###Python 2
```python
#!/usr/bin/py
import math
T = input()
1 <= T <= 100
for t in range(T):
N, K = map(int, raw_input().strip().split(" "))
assert 1 <= N <= 10**9
assert 1 <= K <= 10**4
assert K <= N
n_by_k = math.floor(N/K)
n_mod_k = N%K
count_less_than_k = K/2 if K % 2 == 1 else (K - 1)/2
sum = count_less_than_k*n_by_k
summation_limit = n_by_k - 1
sum += K*(summation_limit*(summation_limit + 1))/2
sum += (summation_limit+1)*(n_mod_k)
if n_mod_k > 0:
extra = n_mod_k - count_less_than_k
if K%2==0:
extra -= 1
sum += extra if extra > 0 else 0
print int(sum)
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T17:46:49
|
Python
|
7
| 800
|
chocolate-game
|
Chocolate Game
|
Laurel and Hardy have N piles of chocolates with each pile containing some number of chocolates. The piles are arranged from left to right in a non decreasing order based on the number of chocolates in each pile. They play the following game.
For every continuous subsequence of chocolate piles (at least 2 piles form a subsequence), you choose one of the piles and remove at least one chocolate from it. It should be noted that, on removal, the non-decreasing order of the chocolate piles must be maintained. The last person to make a valid move wins.
Suppose, Laurel plays first always. In how many of the continuous subsequences of chocolate piles will he win, if a game is played?
**Input Format**
The first line contains an integer N denoting the number of piles. The next line contains the number of chocolates in each pile, arranged from left to right and separated by a single space between them.
**Output Format**
A single integer denoting the number of continuous subsequences of chocolate piles in which Laurel will win.
**Constraints**
2 <= n <= 100000
1 <= d[i] <= 1,000,000,000
**Sample Input**
5
1 1 2 2 3
**Sample Output**
5
**Explanation**
Of the 10 continuous-sub-sequence of chocolate piles,
Laurel loses in [1,1], [1,1,2], [1,1,2,2], [1,2,2,3], [2,2] and
wins in [1,1,2,2,3], [1,2], [1,2,2], [2,2,3] and [2,3] and hence 5.
|
code
|
Count continuous sub-sequences for winning Chocolate Game.
|
ai
|
2013-08-09T20:02:16
|
2022-08-31T08:15:06
|
#
# Complete the 'chocolateGame' function below.
#
# The function is expected to return an INTEGER.
# The function accepts INTEGER_ARRAY arr as parameter.
#
def chocolateGame(arr):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
arr_count = int(input().strip())
arr = list(map(int, input().rstrip().split()))
result = chocolateGame(arr)
fptr.write(str(result) + '\n')
fptr.close()
|
Laurel and Hardy have $n$ piles of chocolates with each pile containing some number of chocolates. The piles are arranged from left to right in a non decreasing order based on the number of chocolates in each pile. They play the following game.
For every continuous subsequence of chocolate piles (at least 2 piles form a subsequence), Laurel and Hardy will play game on this subsequence of chocolate piles, Laurel plays first, and they play in turn. In one move, the player can choose one of the piles and remove at least one chocolate from it, but the non-decreasing order of the chocolate piles must be maintained. The last person to make a valid move wins.
How many continuous subsequences of chocolate piles will Laurel win if both of them play optimally? The number of chocolates of each pile will be recovered after the game ends for each subsequences.
| 0.487805
|
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains an integer $n$ denoting the number of piles.
The second line contains the number of chocolates in each pile, arranged from left to right and separated by a single space between them.
|
A single integer denoting the number of continuous subsequences of chocolate piles in which Laurel will win.
|
5
1 1 2 2 3
|
5
|
Hard
|
2020 September Editorial: Chocolate Game
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p>This is a challenging problem. In case of any queries beyond the scope of this editorial, contact our problem setter, WanBo: [email protected] </p>
<p>Let us start by simplifying this problem:
Given d[], can you win if you play first? </p>
<pre><code>d[0] <= d[1] <= ... <= d[n-1]
</code></pre>
<p>Transform d[] to another array a[] using the following transformation: <br>
a[i] = d[i+1] - d[i] </p>
<p>So from the array d[] we get a new array a[]: <br>
d[0], d[1], ... d[n-1] <br>
d[1] - d[0], d[2] - d[1], ..., d[n-1] - d[n-2] </p>
<pre><code>a[i] = d[i + 1] - d[i]
a[i - 1] = d[i] - d[i - 1]
</code></pre>
<p>If we remove x from d[i]: <br>
d[i] -= x ==> a[i] += x and a[i - 1] -= x
==> we remove x from the a[i - 1] and add it to a[i] </p>
<p>This is a classic staircase NIM game.
a[] with N elements is a win state
<==> 0 != xorsum{a[i] | 0 <= i < N and (N - i) % 2 == 1} </p>
<p>Naive solution to the original problem:</p>
for(i = 0; i + 1
<p>We transform this to: <br>
==></p>
<p>for(i = 0; i < n; i++)
for(j = i + 1; j < n; j++) {
xor = 0
for(k = j; k >= i; k -= 2) xor ^= d[k]
if(xor != 0) res++
}</p>
<p>==> The inner for(k = j; k >= i; k -= 2) can be easily optimized by maintain the xor prefix sum of odd position and even position separately. O(n^3) ==> O(n^2) </p>
<p>==>
We can find the number of losing states.
How many y exist such that x xor y == 0 for a given x? </p>
<p><==> Find the number of elements equals to x.
We can define a data structure to optimize this to O(n logn).
This need enough analysis and careful coding, but it is not the hardest part of this challenge. <br>
<br></p>
<h3>C++ Solution</h3>
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define LL long long
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr "#b": "void PV(T a, T b) {while(a != b)cout inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
templateinline bool chmax(T &a, T b) {return a v(d + i, d + j + 1);
for(int k = (int) v.size() - 1; k > 0; k--) v[k] -= v[k - 1];
reverse(ALL(v));
int xr = 0;
for(int k = 0; k 0) res++;
}
P(i);
}
return res;
}
map M;
LL solve() {
LL res = 0;
{
M.clear();
M[0] = 1;
int xr = 0;
for(int i = n - 1; i >= 0; i -= 2) {
int t = d[i];
if(i > 0) t = d[i] - d[i - 1];
res += M[xr ^ d[i]];
if(i > 0) res += M[xr ^ t];
xr ^= t;
M[xr]++;
}
}
{
M.clear();
M[0] = 1;
int xr = 0;
for(int i = n - 2; i >= 0; i -= 2) {
int t = d[i];
if(i > 0) t = d[i] - d[i - 1];
res += M[xr ^ d[i]];
if(i > 0) res += M[xr ^ t];
xr ^= t;
M[xr]++;
}
}
res = (LL) n * (n - 1) / 2 - res;
return res;
}
int main() {
ios_base::sync_with_stdio(0);
cin >> N;
assert(1 > d[i];
assert(1 = d[i - 1]);
n = N;
//LL res1 = brute();
LL res2 = solve();
cout
| 0
|
chocolate-game
|
2013-09-24T09:33:08
|
{"contest_participation":3240,"challenge_submissions":230,"successful_submissions":51}
|
2013-09-24T09:33:08
|
2016-07-23T16:18:17
|
setter
|
###C++
```cpp
#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<x<<"]\n";
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n";
#define P2(x,y) cerr<<"["#x" = "<<x<<", "#y" = "<<y<<"]\n";
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define mp make_pair
#define pb push_back
template<class T>void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T>inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T>inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
const int inf = 0x3f3f3f3f;
const int mod = int(1e9) + 7;
int N, n;
int d[100010];
int s[100010];
int s1[100010];
int s2[100010];
LL brute() {
LL res = 0;
for(int i = 0; i < n; i++) {
for(int j = i + 1; j < n; j++) {
vector<int> v(d + i, d + j + 1);
for(int k = (int) v.size() - 1; k > 0; k--) v[k] -= v[k - 1];
reverse(ALL(v));
int xr = 0;
for(int k = 0; k < v.size(); k += 2) xr ^= v[k];
if(xr > 0) res++;
}
P(i);
}
return res;
}
map<int, int> M;
LL solve() {
LL res = 0;
{
M.clear();
M[0] = 1;
int xr = 0;
for(int i = n - 1; i >= 0; i -= 2) {
int t = d[i];
if(i > 0) t = d[i] - d[i - 1];
res += M[xr ^ d[i]];
if(i > 0) res += M[xr ^ t];
xr ^= t;
M[xr]++;
}
}
{
M.clear();
M[0] = 1;
int xr = 0;
for(int i = n - 2; i >= 0; i -= 2) {
int t = d[i];
if(i > 0) t = d[i] - d[i - 1];
res += M[xr ^ d[i]];
if(i > 0) res += M[xr ^ t];
xr ^= t;
M[xr]++;
}
}
res = (LL) n * (n - 1) / 2 - res;
return res;
}
int main() {
ios_base::sync_with_stdio(0);
cin >> N;
assert(1 <= N && N <= 100000);
for(int i = 0; i < N; i++) {
cin >> d[i];
assert(1 <= d[i] && d[i] <= 1000000000);
}
for(int i = 1; i < N; i++) assert(d[i] >= d[i - 1]);
n = N;
//LL res1 = brute();
LL res2 = solve();
cout << res2 << endl;
//P2(res1, res2);
//assert(res1 == res2);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T16:18:18
|
C++
|
8
| 836
|
sherlock-puzzle
|
Sherlock Puzzle
|
Sherlock Holmes is bored to death as there aren't any interesting cases to solve. Dr Watson finding it impossible to be around Sherlock goes out to get some fresh air. Just as he lays his feet out of the door, he is thrown right back into his house by the explosion in front of his apartment. The metropolitan police arrive at the scene a few minutes later. They search the place thoroughly for any evidence that could throw some light on the event that unfolded. Unable to get any clues, they call Sherlock for help. After repeated persuasion by Mycroft Holmes and Dr Watson, Sherlock agrees to look at the crime scene.
Sherlock walks into the apartment, the walls are all black and dripping wet as the fire was recently extinguished. With his skills, he observes, deduces and eliminates the impossible. What's left after it is a simple puzzle left by an evil computer genius and the future Arch Nemesis of Sherlock, Jim Moriarty.
Given a binary string (**S**) which contains '0's and '1's and an integer **K**,
find the length (**L**) of the longest contiguous subsequence of (S * K) such that twice the number of zeroes is <= thrice the number of ones (2 * #0s <= 3 * #1s) in that sequence.
S * K is defined as follows:
S * 1 = S
S * K = S + S * (K - 1)
**Input Format**
The first (and only) line contains an integer K and the binary string S separated by a single space.
**Constraints**
1 <= |S| <= 1,000,000
1 <= K <= 1,000,000
**Output Format**
A single integer L - the answer to the test case
**Sample Input**
2 00010
**Sample Output**
2
**Explanation**
S * K = 0001000010
"1" and "10" meet the requirement that 2 * #0 <= 3 * #1
The longest one is "10", length = 2.
|
code
|
Help Sherlock get close to his Arch Nemesis, Jim Moriarty.
|
ai
|
2013-08-24T15:49:01
|
2022-09-02T09:54:36
| null | null | null |
Sherlock Holmes is bored to death as there aren't any interesting cases to solve. Dr Watson finding it impossible to be around Sherlock goes out to get some fresh air. Just as he lays his feet out of the door, he is thrown right back into his house by the explosion in front of his apartment. The metropolitan police arrive at the scene a few minutes later. They search the place thoroughly for any evidence that could throw some light on the event that unfolded. Unable to get any clues, they call Sherlock for help. After repeated persuasion by Mycroft Holmes and Dr Watson, Sherlock agrees to look at the crime scene.
Sherlock walks into the apartment, the walls are all black and dripping wet as the fire was recently extinguished. With his skills, he observes, deduces and eliminates the impossible. What's left after it is a simple puzzle left by an evil computer genius and the future Arch Nemesis of Sherlock, Jim Moriarty.
Given a binary string (**S**) which contains '0's and '1's and an integer **K**,
find the length (**L**) of the longest contiguous subsequence of (S * K) such that twice the number of zeroes is <= thrice the number of ones (2 * #0s <= 3 * #1s) in that sequence.
S * K is defined as follows:
S * 1 = S
S * K = S + S * (K - 1)
**Input Format**
The first (and only) line contains an integer K and the binary string S separated by a single space.
**Constraints**
1 <= |S| <= 1,000,000
1 <= K <= 1,000,000
**Output Format**
A single integer L - the answer to the test case
**Sample Input**
2 00010
**Sample Output**
2
**Explanation**
S * K = 0001000010
"1" and "10" meet the requirement that 2 * #0 <= 3 * #1
The longest one is "10", length = 2.
| 0.567568
|
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
2020 September Editorial: Sherlock Puzzle
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p>For any more queries, beyond the scope of this editorial, feel free to contact our problem setter WanBo: [email protected] </p>
<p>What is the longest contiguous sub-sequence of (S * K) with (2 * number of zeroes <= 3 * number of ones)?
Let replace '0' by -2 and '1' by 3: </p>
<p>Then we need to find the longest sub-string such that the sum[i, j] >= 0. </p>
<p><strong>1)</strong> If sum(S) >= 0, answer = len(S) * K</p>
<p><strong>2)</strong> If S == 1, how can we find the answer? <br>
p[i] = S[0] + S[1] + ... + S[i]
sum[i, j] = p[j + 1] - p[i] <br>
==> For every i, we just need to find the largest j that p[j] >= p[i]. </p>
<p><strong>How do we accelerate the search?</strong> <br>
n can be as large as 10^6 so we need to find the j for every i at least O(log n). But p[i] is not ordered, and because of this we can not use binary search directly. </p>
<pre><code>If rmax[k] = max{p[i] | k <= i < n}
==> rmax[0] >= rmax[1] >= ... >= rmax[n - 1]
</code></pre>
<p>Then for every i, we just need to find the largest k that rmax[k] >= p[i]. We can solve it by binary search. We can solve this sub-problem O(nlogn). </p>
<p>Now, can we optimize O(nlogn) to O(n)? <br>
Observe that when you find a best interval (i0,j0) and want to find a better (i1,j1) with i1 > i0, there must be p[i1] < p[i0] and j1 > j0 (An exercise to the reader - Why?). Therefore, you increment the value of i until you find smaller value of p[i], and then increase j until rmax[j + 1] < p[i]. We will increase i, j at most 2 * n times, so that we can solve it linearly. </p>
<p><strong>3)</strong> If S > 1, how do we solve this problem? <br>
If the longest subsequence is a substring of S, then we can solve it as S == 1. Else we need to maximize the length of suffix(S) + S * i + prefix(S) <br>
suffix(S)_1 + S * i + prefix(S)_1 >= suffix(S)_2 + S * j + prefix(S)_2 <br>
S + S * i + S > S * j ==> i >= j - 1. <br>
Obviously, i >= j - 1, so the best i will be the (largest_i) or (largest_i - 1). </p>
<p>How do we calculate the largest_i? </p>
<pre><code>T = sum(suffix(S) + prefix(S))
largest_i = -T / sum(S)
</code></pre>
<p>We can set the i to largest_i and largest_i - 1, and choose the best answer. </p>
<p>If we set i = x: <br>
T + S * x >= 0 ==> T >= -S * x. </p>
<p><strong>What we need to solve is:</strong> <br>
What's the longest suffix(S) + prefix(S) that sum of this should be >= -S * x </p>
<p>==> sub-problem: <br>
S[i, ..., n - 1] + S[0, ..., j] >= threshold
What the maximal n - i + (j + 1)? </p>
<p>For suffix(S): <br>
If rsum[i] = sum[i, n - 1] <br>
If i0 < i1 and rsum[i0] >= rsum[i1], then i1 can not be the best choice. <br>
We can maintain a monotonous sequence of suffix that:
(i0, rsum[i0]) (i1, rsum[i1]) ... <br>
i0 < i1 < ... <br>
sum[i0] < sum[i1] < ... </p>
<p>For prefix(S): <br>
If lsum[i] = sum[0, i] <br>
If i0 < i1 and lsum[i0] <= lsum[i1], then i0 can not be the best choice. <br>
We can maintain a monotonous sequence of suffix that:
(i0, lsum[i0]) (i1, lsum[i1]) ... <br>
i0 < i1 < ... <br>
sum[i0] > sum[i1] > ... </p>
<p>==> <br>
Given A[] and B[], A is increasing, B is decreasing, for every A[i], how to find the largest j that B[j] >= T - A[i].
This can be solve in O(n) like the method described in the case when K == 1. (exercise) </p>
<h3>C++ Solution from the Problem Setter, WanBo </h3>
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
typedef vector VI;
typedef pair PII;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr "#b": " void PV(T a, T b) {while(a != b)cout inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template inline bool chmax(T &a, T b) {return a L, R;
for(int i = n - 1; i >= 0; i--) {
while(!L.empty() && sL[i] >= L.back().x) L.pop_back();
L.pb(mp(sL[i], n - i));
}
for(int i = 0; i = R.back().x) R.pop_back();
R.pb(mp(sR[i], i + 1));
}
int res = 0;
for(int i = 0; i = least) chmax(res, L[i].y);
for(int i = 0; i = least) chmax(res, R[i].y);
int l = 0, r = (int) R.size() - 1;
while(l = 0) {
while(r >= 0 && L[l].x + R[r].x = 0) chmax(res, L[l].y + R[r].y);
l++;
}
return res;
}
int p[N];
int rmax[N];
LL solve() {
for(int i = 0; i = 0; i--) rmax[i] = max(rmax[i + 1], p[i]);
int mx = 0;
int l = 0;
int r = 0;
for(int i = 0; i = p[l]) continue;
int rr = -1;
while(r = 0) {
rr = r - i;
r++;
}
r--;
int len = rr;
if(mx pt(S.length() + 1, 0);
LL res = 0;
for(int i = 0; i = 0 && chmax(res, (LL)(j - i + 1))) {
pi = i, pj = j;
}
}
return res;
}
int main() {
cin >> K >> s;
n = s.length();
for(int i = 0; i = 0) {
res = (LL) n * K;
} else {
int tot = 0;
{
int mx = 0;
for(int i = n - 1; i >= 0; i--) {
sL[i] = sL[i + 1] + d[i];
chmax(mx, sL[i]);
}
tot += mx;
}
{
int mx = 0;
for(int i = 0; i 0) sR[i] = sR[i - 1] + d[i];
else sR[i] = d[i];
chmax(mx, sR[i]);
}
tot += mx;
}
if(K >= 2) {
LL T = min(K - 2, tot / abs(score));
res += n * T;
// P(res);
res += crossMid(-score * T);
chmax(res, solve());
} else {
res = solve();
}
}
cout
| 0
|
sep2020-sherlock-puzzle
|
2013-09-24T09:42:06
|
{"contest_participation":3240,"challenge_submissions":292,"successful_submissions":72}
|
2013-09-24T09:42:06
|
2016-07-23T17:59:56
|
setter
|
###C++
```cpp
#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int, int> PII;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<x<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<x<<", "#y" = "<<y<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define FOR(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define uni(v) sort(ALL(v)), v.resize(unique(ALL(v)) - v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n"); cout.flush();}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
const int inf = 0x3f3f3f3f;
const int mod = int(1e9) + 7;
const int N = 1111111;
string s;
int K;
int n;
int c0, c1;
int score;
int d[N];
int sL[N];
int sR[N];
int crossMid(int least) {
vector<PII> L, R;
for(int i = n - 1; i >= 0; i--) {
while(!L.empty() && sL[i] >= L.back().x) L.pop_back();
L.pb(mp(sL[i], n - i));
}
for(int i = 0; i < n; i++) {
while(!R.empty() && sR[i] >= R.back().x) R.pop_back();
R.pb(mp(sR[i], i + 1));
}
int res = 0;
for(int i = 0; i < L.size(); i++) if(L[i].x >= least) chmax(res, L[i].y);
for(int i = 0; i < R.size(); i++) if(R[i].x >= least) chmax(res, R[i].y);
int l = 0, r = (int) R.size() - 1;
while(l < L.size() && r >= 0) {
while(r >= 0 && L[l].x + R[r].x < least) r--;
if(r >= 0) chmax(res, L[l].y + R[r].y);
l++;
}
return res;
}
int p[N];
int rmax[N];
LL solve() {
for(int i = 0; i < n; i++) p[i + 1] = sR[i];
rmax[n] = p[n];
for(int i = n - 1; i >= 0; i--) rmax[i] = max(rmax[i + 1], p[i]);
int mx = 0;
int l = 0;
int r = 0;
for(int i = 0; i < n; i++) {
if(i != 0 && p[i] >= p[l]) continue;
int rr = -1;
while(r <= n && rmax[r] - p[i] >= 0) {
rr = r - i;
r++;
}
r--;
int len = rr;
if(mx <= len) {
mx = len;
l = i;
}
}
return mx;
}
LL brute() {
string S;
for(int i = 0; i < K; i++) S += s;
vector<int> pt(S.length() + 1, 0);
LL res = 0;
for(int i = 0; i < S.length(); i++) pt[i + 1] = pt[i] + d[i % n];
int pi = -1, pj = -1;
for(int i = 0; i < S.length(); i++)
for(int j = i; j < S.length(); j++) {
LL sc = pt[j + 1] - pt[i];
if(sc >= 0 && chmax(res, (LL)(j - i + 1))) {
pi = i, pj = j;
}
}
return res;
}
int main() {
cin >> K >> s;
n = s.length();
for(int i = 0; i < n; i++) {
if(s[i] == '0') {
c0++;
d[i] = -2;
} else {
c1++;
d[i] = 3;
}
score += d[i];
}
//P(score);
LL res = 0;
if(score >= 0) {
res = (LL) n * K;
} else {
int tot = 0;
{
int mx = 0;
for(int i = n - 1; i >= 0; i--) {
sL[i] = sL[i + 1] + d[i];
chmax(mx, sL[i]);
}
tot += mx;
}
{
int mx = 0;
for(int i = 0; i < n; i++) {
if(i > 0) sR[i] = sR[i - 1] + d[i];
else sR[i] = d[i];
chmax(mx, sR[i]);
}
tot += mx;
}
if(K >= 2) {
LL T = min(K - 2, tot / abs(score));
res += n * T;
// P(res);
res += crossMid(-score * T);
chmax(res, solve());
} else {
res = solve();
}
}
cout << res << endl;
//P(brute());
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T17:59:56
|
C++
|
9
| 1,049
|
angry-children-2
|
Angry Children 2
|
Bill Gates is on one of his philanthropic journeys to a village in Utopia. He has **N** packets of candies and would like to distribute one packet to each of the **K** children in the village (each packet may contain different number of candies). To avoid a fight between the children, he would like to pick **K** out of **N** packets such that the unfairness is minimized.
Suppose the **K** packets have (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>,....x<sub>k</sub>) candies in them, where x<sub>i</sub> denotes the number of candies in the i<sup>th</sup> packet, then we define *unfairness* as

where \|a\| denotes the absolute value of a.
**Input Format**
The first line contains an integer N.
The second line contains an integer K.
N lines follow each integer containing the candy in the i<sup>th</sup> packet.
**Output Format**
A single integer which will be minimum unfairness.
**Constraints**
2<=N<=10<sup>5</sup>
2<=K<=N
0<= number of candies in each packet <=10<sup>9</sup>
**Sample Input #00**
7
3
10
100
300
200
1000
20
30
**Sample Output #00**
40
**Explanation #00**
Bill Gates will choose packets having 10, 20 and 30 candies.So unfairness will be \|10-20\| + \|20-30\| + \|10-30\| = 40. We can verify that it will be minimum in this way.
**Sample Input #01**
10
4
1
2
3
4
10
20
30
40
100
200
**Sample Output #01**
10
**Explanation #01**
Bill Gates will choose 4 packets having 1,2,3 and 4 candies. So, unfairness will be \|1-2\| + \|1-3\| + \|1-4\| + \|2-3\| + \|2-4\| + \|3-4\| = 10
|
code
|
Select K elements from N elements such that the sum absolute value of differences of adjacent elements is minimized
|
ai
|
2013-10-08T12:22:10
|
2022-08-31T08:14:42
|
#
# Complete the 'angryChildren' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER k
# 2. INTEGER_ARRAY packets
#
def angryChildren(k, packets):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
k = int(input().strip())
packets = []
for _ in range(n):
packets_item = int(input().strip())
packets.append(packets_item)
result = angryChildren(k, packets)
fptr.write(str(result) + '\n')
fptr.close()
|
Bill Gates is on one of his philanthropic journeys to a village in Utopia. He has brought a box of packets of candies and would like to distribute one packet to each of the children. Each of the packets contains a number of candies. He wants to minimize the cumulative difference in the number of candies in the packets he hands out. This is called the *unfairness sum*. Determine the minimum unfairness sum achievable.
For example, he brings $n = 7$ packets where the number of candies is $packets = [3,3,4,5,7,9,10]$. There are $k = 3$ children. The minimum difference between all packets can be had with $3, 3, 4$ from indices $0, 1$ and $2$. We must get the difference in the following pairs: $\{(0,1),(0,2),(1,2)\}$. We calculate the *unfairness sum* as:
```
packets candies
0 3 indices difference result
1 3 (0,1),(0,2) |3-3| + |3-4| 1
2 4 (1,2) |3-4| 1
Total = 2
```
**Function Description**
Complete the *angryChildren* function in the editor below. It should return an integer that represents the minimum unfairness sum achievable.
angryChildren has the following parameter(s):
- *k*: an integer that represents the number of children
- *packets*: an array of integers that represent the number of candies in each packet
| 0.532895
|
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains an integer $n$.
The second line contains an integer $k$.
Each of the next $n$ lines contains an integer $packets[i]$.
|
A single integer representing the minimum achievable unfairness sum.
**Sample Input 0**
7
3
10
100
300
200
1000
20
30
**Sample Output 0**
40
**Explanation 0**
Bill Gates will choose packets having 10, 20 and 30 candies. The unfairness sum is $|10-20| + |20-30| + |10-30| = 40$.
**Sample Input 1**
10
4
1
2
3
4
10
20
30
40
100
200
**Sample Output 1**
10
**Explanation 1**
Bill Gates will choose 4 packets having 1,2,3 and 4 candies. The unfairness sum i $|1-2| + |1-3| + |1-4| + |2-3| + |2-4| + |3-4| = 10$.
|
Hard
|
Angry Children 2 : Oct 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/oct13/challenges/angry-children-2">Angry Children 2</a></p>
<p>Choose K out of N elements of an array, following the given constraints. Read the complete problem statement <a href="https://www.hackerrank.com/contests/oct13/challenges/angry-children-2">here</a> </p>
<p><strong>Difficulty Level</strong></p>
<p>Medium</p>
<p><strong>Required Knowledge</strong></p>
<p>Sorting, Easy Dynammic Progamming</p>
<p><strong>Time Complexity</strong></p>
<p>O(NlogN)</p>
<p><strong>Approach</strong></p>
<p>In this problem, we are given a list of N numbers out of which K numbers are to be chosen such that the anger coefficient is minimized. </p>
<p>Let us define D as the anger-coefficient of chosen K numbers.</p>
<p>First, we claim that k such numbers can only be obtained if we sort the list and chose k contiguous numbers. This can easily be proved. Suppose we choose numbers X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>,....X<sub>r</sub>, X<sub>r+1</sub>,....,X<sub>K</sub> (all are in increasing order but not continuous in the sorted list) i.e. there exists a number p which lies between X<sub>r</sub> and X<sub>r+1</sub>.Now, if we include p and drop X<sub>1</sub>, our anger coefficient will decrease by an amount = </p>
<p>( |X<sub>1</sub> - X<sub>2</sub>| + |X<sub>1</sub> - X<sub>3</sub>| + .... + |X<sub>1</sub> - X<sub>K</sub>| ) - ( |p - X<sub>2</sub>| + |p - X<sub>3</sub>| + .... + |p - X<sub>K</sub>| )</p>
<p>which is certainly positive. This shows that the solution will consist of k continues elements of the sorted list. Now there exists (N-K+1) such sets of elements. The problem can be redefined as to find the minimum of the D obtained from all these sets. </p>
<p>First, we sort the list in increasing order: X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>,....X<sub>K</sub>,X<sub>K+1</sub>,....,X<sub>N</sub>. The next step is to find the value of D for the first K elements i.e. from X<sub>1</sub> to X<sub>K</sub>. suppose we have calculated D for first i elements. when we include X<sub>i+1</sub>, the value of D increases by ( |X<sub>i+1</sub> - X<sub>1</sub>| + |X<sub>i+1</sub> - X<sub>2</sub>| +....+ |X<sub>i+1</sub> - X<sub>i</sub>| ), which in turn is equal to ( i*X<sub>K</sub> - (X<sub>1</sub> + X<sub>2</sub> + ....+X<sub>i</sub>) ). We just need to store the sum of current elements and repeat the step for i = 1 to k-1.</p>
<p>Now that we have the solution for X<sub>1</sub> to X<sub>K</sub>, we would want to calculate the same for X<sub>2</sub> to X<sub>K+1</sub>. This can be done in O(1) time.</p>
<p>New anger coefficient = old anger coefficient + ( |X<sub>K+1</sub> - X<sub>2</sub>| + |X<sub>K+1</sub> - X<sub>3</sub>| + .... + |X<sub>K+1</sub> - X<sub>K</sub>| ) - ( |X<sub>1</sub> - X<sub>2</sub>| + |X<sub>1</sub> - X<sub>3</sub>| + .... + |X<sub>1</sub> - X<sub>K</sub>| ). This can be written in the following form:</p>
<p>New anger coefficient = old anger coefficient + K.(X<sub>K</sub> - X<sub>1</sub>) - K.(X<sub>1</sub> + X<sub>2</sub> +....+X<sub>K</sub>) + ( X<sub>1</sub> - X<sub>K</sub>)</p>
<p>At every point we just need to update the sum of the K elements, calculate the new anger co-efficient and update the minimum value of the same. </p>
<p><strong>Setter's Code</strong> :</p>
<pre><code>n = input()
k = input()
assert 1 <= n <= 10**5
assert 1 <= k <= n
lis = []
for i in range(n):
lis.append(input())
lis.sort()
sum_lis = []
for i in lis:
assert 0 <= i <= 10**9
val = 1-k
answer = 0
sum_lis.append(lis[0])
for i in range(1,n):
sum_lis.append(sum_lis[i-1]+lis[i])
for i in range(k):
answer += val*lis[i]
val += 2
final_answer = answer
for i in range(k,n):
new_answer = answer + (k-1)*lis[i] + (k-1)*lis[i-k] - 2*(sum_lis[i-1]-sum_lis[i-k])
final_answer = min(new_answer, final_answer)
answer = new_answer
print final_answer
</code></pre>
<p><strong>Tester's Code</strong> :</p>
<pre><code>#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<assert.h>
using namespace std;
#define Max_N 100001
typedef long long int ll;
long long int sum[Max_N];
int N,K,input[Max_N];
ll min(ll a,ll b)
{
if(a>b) return b;
else return a;
}
int main()
{
int val;
scanf("%d%d",&N,&K);
assert(1<=N && N<=100000);
assert(1<=K && K<=N);
for(int i=1;i<=N;i++)
{
scanf("%d",&input[i]);
assert(0<=input[i] && input[i]<=1000000000);
}
input[0]=0;
sort(input+1,input+N+1);
sum[0]=0;
for(int i=1;i<=N;i++) sum[i]=input[i]+sum[i-1];
val=1-K;
ll answer=0,compare,previous;
for(int i=1;i<=K;i++){
answer+=(ll)val*input[i];
val+=2;
}
//printf("%lld is answeer\n",answer);
previous=answer;
for(int i=K+1;i<=N;i++){
compare=(ll)(K-1)*input[i];
compare=previous + (ll)(K-1)*input[i] + (ll)(K-1)*input[i-K]-(ll)2*(sum[i-1]-sum[i-K]);
answer=min(answer,compare);
previous=compare;
}
printf("%lld\n",answer);
return 0;
}
</code></pre>
| 0
|
oct-2020-angry-children-ii
|
2013-10-29T06:01:32
|
{"contest_participation":7868,"challenge_submissions":2266,"successful_submissions":1120}
|
2013-10-29T06:01:32
|
2018-05-14T17:07:47
|
setter
|
###Python 2
```python
n = input()
k = input()
assert 1 <= n <= 10**5
assert 1 <= k <= n
lis = []
for i in range(n):
lis.append(input())
lis.sort()
sum_lis = []
for i in lis:
assert 0 <= i <= 10**9
val = 1-k
answer = 0
sum_lis.append(lis[0])
for i in range(1,n):
sum_lis.append(sum_lis[i-1]+lis[i])
for i in range(k):
answer += val*lis[i]
val += 2
final_answer = answer
for i in range(k,n):
new_answer = answer + (k-1)*lis[i] + (k-1)*lis[i-k] - 2*(sum_lis[i-1]-sum_lis[i-k])
final_answer = min(new_answer, final_answer)
answer = new_answer
print final_answer
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T14:51:01
|
Python
|
||
10
| 1,049
|
angry-children-2
|
Angry Children 2
|
Bill Gates is on one of his philanthropic journeys to a village in Utopia. He has **N** packets of candies and would like to distribute one packet to each of the **K** children in the village (each packet may contain different number of candies). To avoid a fight between the children, he would like to pick **K** out of **N** packets such that the unfairness is minimized.
Suppose the **K** packets have (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>,....x<sub>k</sub>) candies in them, where x<sub>i</sub> denotes the number of candies in the i<sup>th</sup> packet, then we define *unfairness* as

where \|a\| denotes the absolute value of a.
**Input Format**
The first line contains an integer N.
The second line contains an integer K.
N lines follow each integer containing the candy in the i<sup>th</sup> packet.
**Output Format**
A single integer which will be minimum unfairness.
**Constraints**
2<=N<=10<sup>5</sup>
2<=K<=N
0<= number of candies in each packet <=10<sup>9</sup>
**Sample Input #00**
7
3
10
100
300
200
1000
20
30
**Sample Output #00**
40
**Explanation #00**
Bill Gates will choose packets having 10, 20 and 30 candies.So unfairness will be \|10-20\| + \|20-30\| + \|10-30\| = 40. We can verify that it will be minimum in this way.
**Sample Input #01**
10
4
1
2
3
4
10
20
30
40
100
200
**Sample Output #01**
10
**Explanation #01**
Bill Gates will choose 4 packets having 1,2,3 and 4 candies. So, unfairness will be \|1-2\| + \|1-3\| + \|1-4\| + \|2-3\| + \|2-4\| + \|3-4\| = 10
|
code
|
Select K elements from N elements such that the sum absolute value of differences of adjacent elements is minimized
|
ai
|
2013-10-08T12:22:10
|
2022-08-31T08:14:42
|
#
# Complete the 'angryChildren' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER k
# 2. INTEGER_ARRAY packets
#
def angryChildren(k, packets):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
k = int(input().strip())
packets = []
for _ in range(n):
packets_item = int(input().strip())
packets.append(packets_item)
result = angryChildren(k, packets)
fptr.write(str(result) + '\n')
fptr.close()
|
Bill Gates is on one of his philanthropic journeys to a village in Utopia. He has brought a box of packets of candies and would like to distribute one packet to each of the children. Each of the packets contains a number of candies. He wants to minimize the cumulative difference in the number of candies in the packets he hands out. This is called the *unfairness sum*. Determine the minimum unfairness sum achievable.
For example, he brings $n = 7$ packets where the number of candies is $packets = [3,3,4,5,7,9,10]$. There are $k = 3$ children. The minimum difference between all packets can be had with $3, 3, 4$ from indices $0, 1$ and $2$. We must get the difference in the following pairs: $\{(0,1),(0,2),(1,2)\}$. We calculate the *unfairness sum* as:
```
packets candies
0 3 indices difference result
1 3 (0,1),(0,2) |3-3| + |3-4| 1
2 4 (1,2) |3-4| 1
Total = 2
```
**Function Description**
Complete the *angryChildren* function in the editor below. It should return an integer that represents the minimum unfairness sum achievable.
angryChildren has the following parameter(s):
- *k*: an integer that represents the number of children
- *packets*: an array of integers that represent the number of candies in each packet
| 0.532895
|
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains an integer $n$.
The second line contains an integer $k$.
Each of the next $n$ lines contains an integer $packets[i]$.
|
A single integer representing the minimum achievable unfairness sum.
**Sample Input 0**
7
3
10
100
300
200
1000
20
30
**Sample Output 0**
40
**Explanation 0**
Bill Gates will choose packets having 10, 20 and 30 candies. The unfairness sum is $|10-20| + |20-30| + |10-30| = 40$.
**Sample Input 1**
10
4
1
2
3
4
10
20
30
40
100
200
**Sample Output 1**
10
**Explanation 1**
Bill Gates will choose 4 packets having 1,2,3 and 4 candies. The unfairness sum i $|1-2| + |1-3| + |1-4| + |2-3| + |2-4| + |3-4| = 10$.
|
Hard
|
Angry Children 2 : Oct 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/oct13/challenges/angry-children-2">Angry Children 2</a></p>
<p>Choose K out of N elements of an array, following the given constraints. Read the complete problem statement <a href="https://www.hackerrank.com/contests/oct13/challenges/angry-children-2">here</a> </p>
<p><strong>Difficulty Level</strong></p>
<p>Medium</p>
<p><strong>Required Knowledge</strong></p>
<p>Sorting, Easy Dynammic Progamming</p>
<p><strong>Time Complexity</strong></p>
<p>O(NlogN)</p>
<p><strong>Approach</strong></p>
<p>In this problem, we are given a list of N numbers out of which K numbers are to be chosen such that the anger coefficient is minimized. </p>
<p>Let us define D as the anger-coefficient of chosen K numbers.</p>
<p>First, we claim that k such numbers can only be obtained if we sort the list and chose k contiguous numbers. This can easily be proved. Suppose we choose numbers X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>,....X<sub>r</sub>, X<sub>r+1</sub>,....,X<sub>K</sub> (all are in increasing order but not continuous in the sorted list) i.e. there exists a number p which lies between X<sub>r</sub> and X<sub>r+1</sub>.Now, if we include p and drop X<sub>1</sub>, our anger coefficient will decrease by an amount = </p>
<p>( |X<sub>1</sub> - X<sub>2</sub>| + |X<sub>1</sub> - X<sub>3</sub>| + .... + |X<sub>1</sub> - X<sub>K</sub>| ) - ( |p - X<sub>2</sub>| + |p - X<sub>3</sub>| + .... + |p - X<sub>K</sub>| )</p>
<p>which is certainly positive. This shows that the solution will consist of k continues elements of the sorted list. Now there exists (N-K+1) such sets of elements. The problem can be redefined as to find the minimum of the D obtained from all these sets. </p>
<p>First, we sort the list in increasing order: X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>,....X<sub>K</sub>,X<sub>K+1</sub>,....,X<sub>N</sub>. The next step is to find the value of D for the first K elements i.e. from X<sub>1</sub> to X<sub>K</sub>. suppose we have calculated D for first i elements. when we include X<sub>i+1</sub>, the value of D increases by ( |X<sub>i+1</sub> - X<sub>1</sub>| + |X<sub>i+1</sub> - X<sub>2</sub>| +....+ |X<sub>i+1</sub> - X<sub>i</sub>| ), which in turn is equal to ( i*X<sub>K</sub> - (X<sub>1</sub> + X<sub>2</sub> + ....+X<sub>i</sub>) ). We just need to store the sum of current elements and repeat the step for i = 1 to k-1.</p>
<p>Now that we have the solution for X<sub>1</sub> to X<sub>K</sub>, we would want to calculate the same for X<sub>2</sub> to X<sub>K+1</sub>. This can be done in O(1) time.</p>
<p>New anger coefficient = old anger coefficient + ( |X<sub>K+1</sub> - X<sub>2</sub>| + |X<sub>K+1</sub> - X<sub>3</sub>| + .... + |X<sub>K+1</sub> - X<sub>K</sub>| ) - ( |X<sub>1</sub> - X<sub>2</sub>| + |X<sub>1</sub> - X<sub>3</sub>| + .... + |X<sub>1</sub> - X<sub>K</sub>| ). This can be written in the following form:</p>
<p>New anger coefficient = old anger coefficient + K.(X<sub>K</sub> - X<sub>1</sub>) - K.(X<sub>1</sub> + X<sub>2</sub> +....+X<sub>K</sub>) + ( X<sub>1</sub> - X<sub>K</sub>)</p>
<p>At every point we just need to update the sum of the K elements, calculate the new anger co-efficient and update the minimum value of the same. </p>
<p><strong>Setter's Code</strong> :</p>
<pre><code>n = input()
k = input()
assert 1 <= n <= 10**5
assert 1 <= k <= n
lis = []
for i in range(n):
lis.append(input())
lis.sort()
sum_lis = []
for i in lis:
assert 0 <= i <= 10**9
val = 1-k
answer = 0
sum_lis.append(lis[0])
for i in range(1,n):
sum_lis.append(sum_lis[i-1]+lis[i])
for i in range(k):
answer += val*lis[i]
val += 2
final_answer = answer
for i in range(k,n):
new_answer = answer + (k-1)*lis[i] + (k-1)*lis[i-k] - 2*(sum_lis[i-1]-sum_lis[i-k])
final_answer = min(new_answer, final_answer)
answer = new_answer
print final_answer
</code></pre>
<p><strong>Tester's Code</strong> :</p>
<pre><code>#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<assert.h>
using namespace std;
#define Max_N 100001
typedef long long int ll;
long long int sum[Max_N];
int N,K,input[Max_N];
ll min(ll a,ll b)
{
if(a>b) return b;
else return a;
}
int main()
{
int val;
scanf("%d%d",&N,&K);
assert(1<=N && N<=100000);
assert(1<=K && K<=N);
for(int i=1;i<=N;i++)
{
scanf("%d",&input[i]);
assert(0<=input[i] && input[i]<=1000000000);
}
input[0]=0;
sort(input+1,input+N+1);
sum[0]=0;
for(int i=1;i<=N;i++) sum[i]=input[i]+sum[i-1];
val=1-K;
ll answer=0,compare,previous;
for(int i=1;i<=K;i++){
answer+=(ll)val*input[i];
val+=2;
}
//printf("%lld is answeer\n",answer);
previous=answer;
for(int i=K+1;i<=N;i++){
compare=(ll)(K-1)*input[i];
compare=previous + (ll)(K-1)*input[i] + (ll)(K-1)*input[i-K]-(ll)2*(sum[i-1]-sum[i-K]);
answer=min(answer,compare);
previous=compare;
}
printf("%lld\n",answer);
return 0;
}
</code></pre>
| 0
|
oct-2020-angry-children-ii
|
2013-10-29T06:01:32
|
{"contest_participation":7868,"challenge_submissions":2266,"successful_submissions":1120}
|
2013-10-29T06:01:32
|
2018-05-14T17:07:47
|
tester
|
###C++
```cpp
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<assert.h>
using namespace std;
#define Max_N 100001
typedef long long int ll;
long long int sum[Max_N];
int N,K,input[Max_N];
ll min(ll a,ll b)
{
if(a>b) return b;
else return a;
}
int main()
{
int val;
scanf("%d%d",&N,&K);
assert(1<=N && N<=100000);
assert(1<=K && K<=N);
for(int i=1;i<=N;i++)
{
scanf("%d",&input[i]);
assert(0<=input[i] && input[i]<=1000000000);
}
input[0]=0;
sort(input+1,input+N+1);
sum[0]=0;
for(int i=1;i<=N;i++) sum[i]=input[i]+sum[i-1];
val=1-K;
ll answer=0,compare,previous;
for(int i=1;i<=K;i++){
answer+=(ll)val*input[i];
val+=2;
}
//printf("%lld is answeer\n",answer);
previous=answer;
for(int i=K+1;i<=N;i++){
compare=(ll)(K-1)*input[i];
compare=previous + (ll)(K-1)*input[i] + (ll)(K-1)*input[i-K]-(ll)2*(sum[i-1]-sum[i-K]);
answer=min(answer,compare);
previous=compare;
}
printf("%lld\n",answer);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T14:51:25
|
C++
|
||
11
| 1,084
|
period
|
Period
|
You are given 2 integers **a** and **b**. Let a number be defined as . As we know  will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define
 (where x an integer)<br /><br /> and the operation  on AC number as:

This problem is to find the smallest positive integer **n**, such that:

We call the integer **n** as period. You are given **a**, **b** and **m**. Can you figure out the period?
**Input Format**
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.
**Output Format**
Output the Period if it exists, otherwise output "-1" (quotes only for reference)
**Constraints**
1 ≤ T ≤ 300
5 ≤ m ≤ 10<sup>7</sup>
0 ≤ a, b < m
**Sample Input #00**
4
0 0 13
1 0 7
3 0 10007
1 1 19
**Sample Output #00**
-1
1
5003
18
**Explanation #00**
For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.
|
code
|
Can you find the period?
|
ai
|
2013-10-16T05:50:59
|
2022-09-02T09:54:45
| null | null | null |
You are given 2 integers **a** and **b**. Let a number be defined as
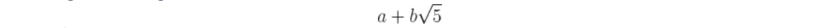. As we know 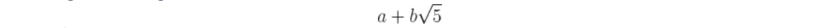 will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define
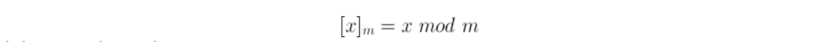 (where x an integer)<br /><br /> and the operation  on AC number as:
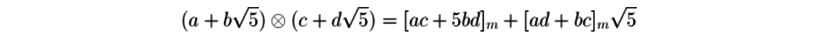
This problem is to find the smallest positive integer **n**, such that:

We call the integer **n** as period. You are given **a**, **b** and **m**. Can you figure out the period?
**Input Format**
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.
**Output Format**
Output the Period if it exists, otherwise output "-1" (quotes only for reference)
**Constraints**
1 ≤ T ≤ 300
5 ≤ m ≤ 10<sup>7</sup>
0 ≤ a, b < m
**Sample Input #00**
4
0 0 13
1 0 7
3 0 10007
1 1 19
**Sample Output #00**
-1
1
5003
18
**Explanation #00**
For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.
| 0.564516
|
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
|
Hard
|
Period : Oct 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem</strong> <a href="https://www.hackerrank.com/contests/oct13/challenges/period">Period</a></p>
<p><strong>Difficulty</strong> : Medium-Hard</p>
<p><strong>Required Knowledge</strong> : Group Theory, Euler's Criterion, Lagrange's theorem</p>
<p><strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/AekdyCoin">AekDy Coin</a></p>
<p><strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/cpcs">Cao Peng</a></p>
<p><strong>Approach</strong></p>
<p>For one given P, the AC number <img src="https://hr-filepicker.s3.amazonaws.com/period1.png" alt="image1" title=""> that satisfies 0 ≤ a,b < p
and a<sup>2</sup> ≅ 5b<sup>2</sup>(mod P) have th property:</p>
<p>Suppose, </p>
<p>∀n ∈ Z<sup>+</sup>, <br>
(a + b√5)<sup>n</sup> = c + d√5</p>
<p>Then we have c<sup>2</sup> = 5d<sup>2</sup>(mod P) <br>
Quite obvious by mathematical induction.
So if a<sup>2</sup> ≅5b<sup>2</sup>(mod P), we could not find the Period since the expected result AC number is with c=1 and d = 0.</p>
<p>So for the remaindering AC number, we have a<sup>2</sup>≠5b<sup>2</sup>(mod P) <br>
If 5 is one quadratic residue modulo P, then we can find (P-1)<sup>2</sup> such unique AC number satisfy. a<sup>2</sup>≠5b<sup>2</sup>(mod P) </p>
<p>Proof:</p>
<p>If 5 is one quadratic residue modulo P , then for the <a href="https://en.wikipedia.org/wiki/Primitive_root_modulo_n">primitive root</a> <strong>g</strong>, we have </p>
<p>g<sup>2k</sup> ≅5(mod P) the AC number such that a<sup>2</sup>≅5b<sup>2</sup>(mod P) must satisfy:</p>
<p>g<sup>2I(a)</sup>≅g<sup>2k</sup>g<sup>2I(b)</sup>(mod P), which means </p>
<p>2I(a)≅2(k+I(b))(mod P - 1), there are totally 2(P-1) AC number that satisfy that condition. (which means they also satisfy </p>
<p>a<sup>2</sup>≅5b<sup>2</sup>(mod P), but don't forget 0 + 0√5, so there are </p>
<p>P<sup>2</sup> - 2(P-1) - 1 = (P-1)<sup>2</sup> AC numbers such that a<sup>2</sup>≠5b<sup>2</sup>(mod P) </p>
<p>If 5 is not one quadratic residue modulo P, then we can find P<sup>2</sup> - 1 = (P-1)(P+1) such unique AC number satisfies, </p>
<p>a<sup>2</sup>≠5b<sup>2</sup>(mod P), because only one AC number o + 0√5 satisfies, </p>
<p>a<sup>2</sup>≅5b<sup>2</sup>(mod P) </p>
<p>We can use <a href="https://en.wikipedia.org/wiki/Euler%27s_criterion">Euler's Criterion</a> to judge whether 5 is one quadratic residue modulo P in O(logP) time.
The identity element in this group is 1.
However there are other 2 properties that guarantee it is a group. I will ignore the proof here.</p>
<p>Finally, base one [Lagrange's Theorem)(<a href="http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)">http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)</a>) we have
Period C, where C is the number of AC number satisfies
a<sup>2</sup>≠5b<sup>2</sup>(mod P). Simple brute force will work. </p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include<iostream>
#include<queue>
#include<cstdio>
#include<cmath>
#include<string>
#include<vector>
#include<algorithm>
#include<stack>
#include<cstring>
#include<map>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define pb push_back
#define mp make_pair
bool isPrime(int n) {
if(n==1)return 0;
for(int i =2; i * i <= n; ++ i) if( n % i == 0 ) return 0;
return 1;
}
inline LL MOD(LL a, LL b) {a%=b; return a<0?a+b:a;}
LL powmod(LL a, LL b, LL c){
LL ret = 1%c; a%=c;
while(b){
if(b&1)ret=ret*a%c;
a=a*a%c;
b>>=1;
}
return ret;
}
// P is one prime number
LL inv( LL a, LL p) {return powmod( a, p - 2, p ) ; }
LL P;
class Element {
public:
LL a, b;
// a + b Sqrt(5)
Element(){}
Element(LL _a, LL _b) :a(_a),b(_b){}
Element operator+(const Element e) {
return Element(MOD(a + e.a , P),MOD(b + e.b , P));
}
Element operator*(const Element e) {
return Element(MOD(a*e.a + b*e.b * 5, P),MOD(a*e.b+b*e.a, P));
}
Element operator^(LL k){
if(k==0) return Element(1,0);
--k;
Element ret = *this, a = *this;
while(k){
if(k&1) ret= ret * a ;
a = a * a;
k >>= 1;
}
return ret;
}
Element inverse(){
if(!a&&!b) return *this;
if(b == 0) {
return Element(inv(a, P) , 0 );
}
if(a == 0) {
return Element(0, inv(5*b%P, P));
}
LL iv = inv( MOD(-b,P) , P );
LL x, y;
y = inv( iv * (a*a%P) % P + b*5 , P );
x = (iv * a % P * y) % P;
return Element( x, y) ;
}
bool isZ(){
return !a && !b;
}
bool isE(){
return a == 1 && b == 0;
}
bool operator<(const Element e) const {
if(a == e.a) return b < e.b;
return a < e.a;
}
void rand_gen(){
do{a = rand()%P; b= rand()%P;}while(0);
}
void out(){
cout << a <<" " << b << endl;
}
};
// a + b Sqrt(5)
LL circle( Element a ) {
Element b =a;
LL c = 1;
while( ! a.isE( )) {
a = a * b;
++ c;
//a.out();
if(a.a == b.a && a.b == b.b) {
return - 1;
}
}
return c;
}
bool isRes(LL a, LL P ){
return powmod(a, (P-1)/2, P) == 1;
}
LL my_solution(Element e , LL P) {
LL a = e.a, b = e.b;
if(MOD(a*a-5*b*b,P)==0) return -1;
LL n = P*P,ans;
if(isRes(5,P)) {
n = n - 2*P+1;
}else -- n;
ans = n;
for(LL i = 1; i*i <= n; ++ i) if(n%i == 0) {
if( (Element(a,b) ^(i)).isE() )
ans = min(ans, i );
if( (Element(a,b) ^(n/i)).isE() )
ans = min(ans, n/i );
}
return ans;
}
void dp(){
while( true ) {
P = rand()%1000 + 6;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
LL my_ans = my_solution(e, P);
LL bf = circle(e) ;
static int cas = 0; ++ cas;
if(my_ans == bf) {
cout <<"correct @" << cas <<" ans = " << my_ans<< endl;
}else {
cout <<"error"<<endl;
cout << P << endl;
e.out();
return;
}
}
}
Element rand_one_bad(LL P) {
for (LL a = 1; a < P; ++a)
for (LL b = 1; b < P; ++b) {
if (MOD(a * a - 5 * b * b, P) == 0) {
return Element(a, b);
}
}
return Element(0,0);
}
void gen(int x ){
char in[] = "input00.in";
in[6]='0'+x;
freopen(in,"w", stdout);
int T = (x+1)*10;
int LIMIT[] = {100, 10000, 1e6,1e6};
cout << T << endl;
while(T --) {
P = rand()% (int)LIMIT[x/3] + 13;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
if( P < 1e4 && isRes(5,P) && rand()%2 == 0) {
e = rand_one_bad(P);
}
cout << e.a <<" " << e.b <<" " << P << endl;
}
}
void run(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
freopen(out,"w", stdout);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
}
void _cmp_with_bf(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
int T ,cas = 0;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
LL my = my_solution( Element(a,b), P) ;
LL bf = circle( Element(a,b) ) ;
if(my != bf) {
cout <<"SB"<<endl;
cout << a <<" " << b <<" " << P << endl;
cout <<my <<" " << bf << endl;
exit(0);
}
cout <<"correct @" << x <<" case " << cas ++ << endl;
}
}
int main() {
srand( time( NULL )) ;
// for(int i = 0; i < 10;++i) gen(i);
// for(int i = 0; i < 10; ++ i) run(i);
// for(int i=0;i<10;++i) _cmp_with_bf(i);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int mul(ll x,ll y,int p) {
return x * y % p;
}
int powermod(ll x,ll y,int p) { //x ^ y mod p
if (x == 0) {
return 0;
}
if (y == 0) {
return 1;
}
if (y & 1) {
return mul(powermod(x, y ^ 1, p), x, p);
}
x = powermod(x, y >> 1, p);
return mul(x, x, p);
}
pair<int,int> help(int a,int b,ll x,int p) { // (a + b * sqrt(5)) ^ n mod p
if (x == 0) {
return make_pair(1, 0);
}
pair<int,int> A, B;
if (x & 1) {
A = help(a, b, x - 1, p);
B = make_pair(a, b);
}
else {
A = B = help(a, b, x >> 1, p);
}
a = mul(A.first, B.first, p) + mul(5, mul(A.second,B.second, p), p);
if (a >= p) {
a -= p;
}
b = mul(A.first, B.second, p) + mul(A.second , B.first, p);
if (b >= p) {
b -= p;
}
return make_pair(a, b);
}
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int z;
for (scanf("%d",&z);z;--z) {
int a,b,p;
ll x;
scanf("%d%d%d",&a,&b,&p);
if (mul(a,a,p) == mul(mul(b,b,p),5,p)) {
puts("-1");
continue;
}
else if (powermod(5, p >> 1, p) == 1) {
x = p - 1;
x *= (p - 1);
}
else {
x = p;
x *= x;
--x;
}
ll answer = -1;
pair<int,int> temp;
for (ll i = 1; i * i <= x; ++i) {
if (x % i) {
continue;
}
if ((answer < 0) || (i < answer)) {
temp = help(a,b,i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = i;
}
}
if ((answer < 0) || (x / i < answer)) {
temp = help(a,b,x / i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = x / i;
}
}
}
printf("%lld\n",answer);
}
return 0;
}
</code></pre>
| 0
|
oct-2020-editorial-period
|
2013-10-29T06:13:09
|
{"contest_participation":7868,"challenge_submissions":564,"successful_submissions":106}
|
2013-10-29T06:13:09
|
2016-07-23T18:18:41
|
setter
|
###C++
```cpp
#include<iostream>
#include<queue>
#include<cstdio>
#include<cmath>
#include<string>
#include<vector>
#include<algorithm>
#include<stack>
#include<cstring>
#include<map>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define pb push_back
#define mp make_pair
bool isPrime(int n) {
if(n==1)return 0;
for(int i =2; i * i <= n; ++ i) if( n % i == 0 ) return 0;
return 1;
}
inline LL MOD(LL a, LL b) {a%=b; return a<0?a+b:a;}
LL powmod(LL a, LL b, LL c){
LL ret = 1%c; a%=c;
while(b){
if(b&1)ret=ret*a%c;
a=a*a%c;
b>>=1;
}
return ret;
}
// P is one prime number
LL inv( LL a, LL p) {return powmod( a, p - 2, p ) ; }
LL P;
class Element {
public:
LL a, b;
// a + b Sqrt(5)
Element(){}
Element(LL _a, LL _b) :a(_a),b(_b){}
Element operator+(const Element e) {
return Element(MOD(a + e.a , P),MOD(b + e.b , P));
}
Element operator*(const Element e) {
return Element(MOD(a*e.a + b*e.b * 5, P),MOD(a*e.b+b*e.a, P));
}
Element operator^(LL k){
if(k==0) return Element(1,0);
--k;
Element ret = *this, a = *this;
while(k){
if(k&1) ret= ret * a ;
a = a * a;
k >>= 1;
}
return ret;
}
Element inverse(){
if(!a&&!b) return *this;
if(b == 0) {
return Element(inv(a, P) , 0 );
}
if(a == 0) {
return Element(0, inv(5*b%P, P));
}
LL iv = inv( MOD(-b,P) , P );
LL x, y;
y = inv( iv * (a*a%P) % P + b*5 , P );
x = (iv * a % P * y) % P;
return Element( x, y) ;
}
bool isZ(){
return !a && !b;
}
bool isE(){
return a == 1 && b == 0;
}
bool operator<(const Element e) const {
if(a == e.a) return b < e.b;
return a < e.a;
}
void rand_gen(){
do{a = rand()%P; b= rand()%P;}while(0);
}
void out(){
cout << a <<" " << b << endl;
}
};
// a + b Sqrt(5)
LL circle( Element a ) {
Element b =a;
LL c = 1;
while( ! a.isE( )) {
a = a * b;
++ c;
//a.out();
if(a.a == b.a && a.b == b.b) {
return - 1;
}
}
return c;
}
bool isRes(LL a, LL P ){
return powmod(a, (P-1)/2, P) == 1;
}
LL my_solution(Element e , LL P) {
LL a = e.a, b = e.b;
if(MOD(a*a-5*b*b,P)==0) return -1;
LL n = P*P,ans;
if(isRes(5,P)) {
n = n - 2*P+1;
}else -- n;
ans = n;
for(LL i = 1; i*i <= n; ++ i) if(n%i == 0) {
if( (Element(a,b) ^(i)).isE() )
ans = min(ans, i );
if( (Element(a,b) ^(n/i)).isE() )
ans = min(ans, n/i );
}
return ans;
}
void dp(){
while( true ) {
P = rand()%1000 + 6;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
LL my_ans = my_solution(e, P);
LL bf = circle(e) ;
static int cas = 0; ++ cas;
if(my_ans == bf) {
cout <<"correct @" << cas <<" ans = " << my_ans<< endl;
}else {
cout <<"error"<<endl;
cout << P << endl;
e.out();
return;
}
}
}
Element rand_one_bad(LL P) {
for (LL a = 1; a < P; ++a)
for (LL b = 1; b < P; ++b) {
if (MOD(a * a - 5 * b * b, P) == 0) {
return Element(a, b);
}
}
return Element(0,0);
}
void gen(int x ){
char in[] = "input00.in";
in[6]='0'+x;
freopen(in,"w", stdout);
int T = (x+1)*10;
int LIMIT[] = {100, 10000, 1e6,1e6};
cout << T << endl;
while(T --) {
P = rand()% (int)LIMIT[x/3] + 13;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
if( P < 1e4 && isRes(5,P) && rand()%2 == 0) {
e = rand_one_bad(P);
}
cout << e.a <<" " << e.b <<" " << P << endl;
}
}
void run(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
freopen(out,"w", stdout);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
}
void _cmp_with_bf(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
int T ,cas = 0;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
LL my = my_solution( Element(a,b), P) ;
LL bf = circle( Element(a,b) ) ;
if(my != bf) {
cout <<"SB"<<endl;
cout << a <<" " << b <<" " << P << endl;
cout <<my <<" " << bf << endl;
exit(0);
}
cout <<"correct @" << x <<" case " << cas ++ << endl;
}
}
int main() {
srand( time( NULL )) ;
// for(int i = 0; i < 10;++i) gen(i);
// for(int i = 0; i < 10; ++ i) run(i);
// for(int i=0;i<10;++i) _cmp_with_bf(i);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T18:18:32
|
C++
|
||||
12
| 1,084
|
period
|
Period
|
You are given 2 integers **a** and **b**. Let a number be defined as . As we know  will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define
 (where x an integer)<br /><br /> and the operation  on AC number as:

This problem is to find the smallest positive integer **n**, such that:

We call the integer **n** as period. You are given **a**, **b** and **m**. Can you figure out the period?
**Input Format**
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.
**Output Format**
Output the Period if it exists, otherwise output "-1" (quotes only for reference)
**Constraints**
1 ≤ T ≤ 300
5 ≤ m ≤ 10<sup>7</sup>
0 ≤ a, b < m
**Sample Input #00**
4
0 0 13
1 0 7
3 0 10007
1 1 19
**Sample Output #00**
-1
1
5003
18
**Explanation #00**
For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.
|
code
|
Can you find the period?
|
ai
|
2013-10-16T05:50:59
|
2022-09-02T09:54:45
| null | null | null |
You are given 2 integers **a** and **b**. Let a number be defined as
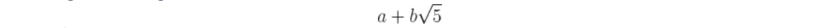. As we know 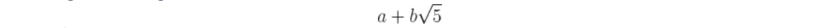 will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define
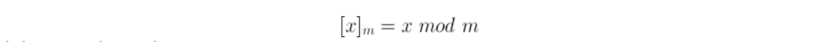 (where x an integer)<br /><br /> and the operation  on AC number as:
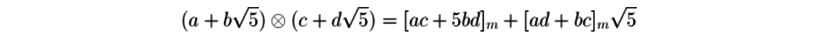
This problem is to find the smallest positive integer **n**, such that:

We call the integer **n** as period. You are given **a**, **b** and **m**. Can you figure out the period?
**Input Format**
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.
**Output Format**
Output the Period if it exists, otherwise output "-1" (quotes only for reference)
**Constraints**
1 ≤ T ≤ 300
5 ≤ m ≤ 10<sup>7</sup>
0 ≤ a, b < m
**Sample Input #00**
4
0 0 13
1 0 7
3 0 10007
1 1 19
**Sample Output #00**
-1
1
5003
18
**Explanation #00**
For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.
| 0.564516
|
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
|
Hard
|
Period : Oct 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem</strong> <a href="https://www.hackerrank.com/contests/oct13/challenges/period">Period</a></p>
<p><strong>Difficulty</strong> : Medium-Hard</p>
<p><strong>Required Knowledge</strong> : Group Theory, Euler's Criterion, Lagrange's theorem</p>
<p><strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/AekdyCoin">AekDy Coin</a></p>
<p><strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/cpcs">Cao Peng</a></p>
<p><strong>Approach</strong></p>
<p>For one given P, the AC number <img src="https://hr-filepicker.s3.amazonaws.com/period1.png" alt="image1" title=""> that satisfies 0 ≤ a,b < p
and a<sup>2</sup> ≅ 5b<sup>2</sup>(mod P) have th property:</p>
<p>Suppose, </p>
<p>∀n ∈ Z<sup>+</sup>, <br>
(a + b√5)<sup>n</sup> = c + d√5</p>
<p>Then we have c<sup>2</sup> = 5d<sup>2</sup>(mod P) <br>
Quite obvious by mathematical induction.
So if a<sup>2</sup> ≅5b<sup>2</sup>(mod P), we could not find the Period since the expected result AC number is with c=1 and d = 0.</p>
<p>So for the remaindering AC number, we have a<sup>2</sup>≠5b<sup>2</sup>(mod P) <br>
If 5 is one quadratic residue modulo P, then we can find (P-1)<sup>2</sup> such unique AC number satisfy. a<sup>2</sup>≠5b<sup>2</sup>(mod P) </p>
<p>Proof:</p>
<p>If 5 is one quadratic residue modulo P , then for the <a href="https://en.wikipedia.org/wiki/Primitive_root_modulo_n">primitive root</a> <strong>g</strong>, we have </p>
<p>g<sup>2k</sup> ≅5(mod P) the AC number such that a<sup>2</sup>≅5b<sup>2</sup>(mod P) must satisfy:</p>
<p>g<sup>2I(a)</sup>≅g<sup>2k</sup>g<sup>2I(b)</sup>(mod P), which means </p>
<p>2I(a)≅2(k+I(b))(mod P - 1), there are totally 2(P-1) AC number that satisfy that condition. (which means they also satisfy </p>
<p>a<sup>2</sup>≅5b<sup>2</sup>(mod P), but don't forget 0 + 0√5, so there are </p>
<p>P<sup>2</sup> - 2(P-1) - 1 = (P-1)<sup>2</sup> AC numbers such that a<sup>2</sup>≠5b<sup>2</sup>(mod P) </p>
<p>If 5 is not one quadratic residue modulo P, then we can find P<sup>2</sup> - 1 = (P-1)(P+1) such unique AC number satisfies, </p>
<p>a<sup>2</sup>≠5b<sup>2</sup>(mod P), because only one AC number o + 0√5 satisfies, </p>
<p>a<sup>2</sup>≅5b<sup>2</sup>(mod P) </p>
<p>We can use <a href="https://en.wikipedia.org/wiki/Euler%27s_criterion">Euler's Criterion</a> to judge whether 5 is one quadratic residue modulo P in O(logP) time.
The identity element in this group is 1.
However there are other 2 properties that guarantee it is a group. I will ignore the proof here.</p>
<p>Finally, base one [Lagrange's Theorem)(<a href="http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)">http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)</a>) we have
Period C, where C is the number of AC number satisfies
a<sup>2</sup>≠5b<sup>2</sup>(mod P). Simple brute force will work. </p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include<iostream>
#include<queue>
#include<cstdio>
#include<cmath>
#include<string>
#include<vector>
#include<algorithm>
#include<stack>
#include<cstring>
#include<map>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define pb push_back
#define mp make_pair
bool isPrime(int n) {
if(n==1)return 0;
for(int i =2; i * i <= n; ++ i) if( n % i == 0 ) return 0;
return 1;
}
inline LL MOD(LL a, LL b) {a%=b; return a<0?a+b:a;}
LL powmod(LL a, LL b, LL c){
LL ret = 1%c; a%=c;
while(b){
if(b&1)ret=ret*a%c;
a=a*a%c;
b>>=1;
}
return ret;
}
// P is one prime number
LL inv( LL a, LL p) {return powmod( a, p - 2, p ) ; }
LL P;
class Element {
public:
LL a, b;
// a + b Sqrt(5)
Element(){}
Element(LL _a, LL _b) :a(_a),b(_b){}
Element operator+(const Element e) {
return Element(MOD(a + e.a , P),MOD(b + e.b , P));
}
Element operator*(const Element e) {
return Element(MOD(a*e.a + b*e.b * 5, P),MOD(a*e.b+b*e.a, P));
}
Element operator^(LL k){
if(k==0) return Element(1,0);
--k;
Element ret = *this, a = *this;
while(k){
if(k&1) ret= ret * a ;
a = a * a;
k >>= 1;
}
return ret;
}
Element inverse(){
if(!a&&!b) return *this;
if(b == 0) {
return Element(inv(a, P) , 0 );
}
if(a == 0) {
return Element(0, inv(5*b%P, P));
}
LL iv = inv( MOD(-b,P) , P );
LL x, y;
y = inv( iv * (a*a%P) % P + b*5 , P );
x = (iv * a % P * y) % P;
return Element( x, y) ;
}
bool isZ(){
return !a && !b;
}
bool isE(){
return a == 1 && b == 0;
}
bool operator<(const Element e) const {
if(a == e.a) return b < e.b;
return a < e.a;
}
void rand_gen(){
do{a = rand()%P; b= rand()%P;}while(0);
}
void out(){
cout << a <<" " << b << endl;
}
};
// a + b Sqrt(5)
LL circle( Element a ) {
Element b =a;
LL c = 1;
while( ! a.isE( )) {
a = a * b;
++ c;
//a.out();
if(a.a == b.a && a.b == b.b) {
return - 1;
}
}
return c;
}
bool isRes(LL a, LL P ){
return powmod(a, (P-1)/2, P) == 1;
}
LL my_solution(Element e , LL P) {
LL a = e.a, b = e.b;
if(MOD(a*a-5*b*b,P)==0) return -1;
LL n = P*P,ans;
if(isRes(5,P)) {
n = n - 2*P+1;
}else -- n;
ans = n;
for(LL i = 1; i*i <= n; ++ i) if(n%i == 0) {
if( (Element(a,b) ^(i)).isE() )
ans = min(ans, i );
if( (Element(a,b) ^(n/i)).isE() )
ans = min(ans, n/i );
}
return ans;
}
void dp(){
while( true ) {
P = rand()%1000 + 6;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
LL my_ans = my_solution(e, P);
LL bf = circle(e) ;
static int cas = 0; ++ cas;
if(my_ans == bf) {
cout <<"correct @" << cas <<" ans = " << my_ans<< endl;
}else {
cout <<"error"<<endl;
cout << P << endl;
e.out();
return;
}
}
}
Element rand_one_bad(LL P) {
for (LL a = 1; a < P; ++a)
for (LL b = 1; b < P; ++b) {
if (MOD(a * a - 5 * b * b, P) == 0) {
return Element(a, b);
}
}
return Element(0,0);
}
void gen(int x ){
char in[] = "input00.in";
in[6]='0'+x;
freopen(in,"w", stdout);
int T = (x+1)*10;
int LIMIT[] = {100, 10000, 1e6,1e6};
cout << T << endl;
while(T --) {
P = rand()% (int)LIMIT[x/3] + 13;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
if( P < 1e4 && isRes(5,P) && rand()%2 == 0) {
e = rand_one_bad(P);
}
cout << e.a <<" " << e.b <<" " << P << endl;
}
}
void run(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
freopen(out,"w", stdout);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
}
void _cmp_with_bf(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
int T ,cas = 0;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
LL my = my_solution( Element(a,b), P) ;
LL bf = circle( Element(a,b) ) ;
if(my != bf) {
cout <<"SB"<<endl;
cout << a <<" " << b <<" " << P << endl;
cout <<my <<" " << bf << endl;
exit(0);
}
cout <<"correct @" << x <<" case " << cas ++ << endl;
}
}
int main() {
srand( time( NULL )) ;
// for(int i = 0; i < 10;++i) gen(i);
// for(int i = 0; i < 10; ++ i) run(i);
// for(int i=0;i<10;++i) _cmp_with_bf(i);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int mul(ll x,ll y,int p) {
return x * y % p;
}
int powermod(ll x,ll y,int p) { //x ^ y mod p
if (x == 0) {
return 0;
}
if (y == 0) {
return 1;
}
if (y & 1) {
return mul(powermod(x, y ^ 1, p), x, p);
}
x = powermod(x, y >> 1, p);
return mul(x, x, p);
}
pair<int,int> help(int a,int b,ll x,int p) { // (a + b * sqrt(5)) ^ n mod p
if (x == 0) {
return make_pair(1, 0);
}
pair<int,int> A, B;
if (x & 1) {
A = help(a, b, x - 1, p);
B = make_pair(a, b);
}
else {
A = B = help(a, b, x >> 1, p);
}
a = mul(A.first, B.first, p) + mul(5, mul(A.second,B.second, p), p);
if (a >= p) {
a -= p;
}
b = mul(A.first, B.second, p) + mul(A.second , B.first, p);
if (b >= p) {
b -= p;
}
return make_pair(a, b);
}
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int z;
for (scanf("%d",&z);z;--z) {
int a,b,p;
ll x;
scanf("%d%d%d",&a,&b,&p);
if (mul(a,a,p) == mul(mul(b,b,p),5,p)) {
puts("-1");
continue;
}
else if (powermod(5, p >> 1, p) == 1) {
x = p - 1;
x *= (p - 1);
}
else {
x = p;
x *= x;
--x;
}
ll answer = -1;
pair<int,int> temp;
for (ll i = 1; i * i <= x; ++i) {
if (x % i) {
continue;
}
if ((answer < 0) || (i < answer)) {
temp = help(a,b,i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = i;
}
}
if ((answer < 0) || (x / i < answer)) {
temp = help(a,b,x / i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = x / i;
}
}
}
printf("%lld\n",answer);
}
return 0;
}
</code></pre>
| 0
|
oct-2020-editorial-period
|
2013-10-29T06:13:09
|
{"contest_participation":7868,"challenge_submissions":564,"successful_submissions":106}
|
2013-10-29T06:13:09
|
2016-07-23T18:18:41
|
tester
|
###C++
```cpp
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int mul(ll x,ll y,int p) {
return x * y % p;
}
int powermod(ll x,ll y,int p) { //x ^ y mod p
if (x == 0) {
return 0;
}
if (y == 0) {
return 1;
}
if (y & 1) {
return mul(powermod(x, y ^ 1, p), x, p);
}
x = powermod(x, y >> 1, p);
return mul(x, x, p);
}
pair<int,int> help(int a,int b,ll x,int p) { // (a + b * sqrt(5)) ^ n mod p
if (x == 0) {
return make_pair(1, 0);
}
pair<int,int> A, B;
if (x & 1) {
A = help(a, b, x - 1, p);
B = make_pair(a, b);
}
else {
A = B = help(a, b, x >> 1, p);
}
a = mul(A.first, B.first, p) + mul(5, mul(A.second,B.second, p), p);
if (a >= p) {
a -= p;
}
b = mul(A.first, B.second, p) + mul(A.second , B.first, p);
if (b >= p) {
b -= p;
}
return make_pair(a, b);
}
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int z;
for (scanf("%d",&z);z;--z) {
int a,b,p;
ll x;
scanf("%d%d%d",&a,&b,&p);
if (mul(a,a,p) == mul(mul(b,b,p),5,p)) {
puts("-1");
continue;
}
else if (powermod(5, p >> 1, p) == 1) {
x = p - 1;
x *= (p - 1);
}
else {
x = p;
x *= x;
--x;
}
ll answer = -1;
pair<int,int> temp;
for (ll i = 1; i * i <= x; ++i) {
if (x % i) {
continue;
}
if ((answer < 0) || (i < answer)) {
temp = help(a,b,i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = i;
}
}
if ((answer < 0) || (x / i < answer)) {
temp = help(a,b,x / i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = x / i;
}
}
}
printf("%lld\n",answer);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T18:18:41
|
C++
|
End of preview. Expand
in Data Studio
| Field | Type† | What it contains |
|---|---|---|
challenge_id |
integer | Unique numeric identifier for the coding challenge |
challenge_slug |
string | URL-friendly slug used in challenge links |
challenge_name |
string | Human-readable challenge title |
challenge_body |
string | Full challenge description (HTML/Markdown) including input/output, examples, etc. |
challenge_kind |
string | High-level content type (e.g., code, game) |
challenge_preview |
string | One-sentence teaser shown in listings |
challenge_category |
string | Top-level category such as ai, algorithms, databases |
challenge_created_at |
ISO 8601 string | When the challenge was first created |
challenge_updated_at |
ISO 8601 string | Most-recent metadata update time |
python3_template |
string (nullable) | Complete Python 3 starter code supplied to users |
python3_template_head |
string (nullable) | Header portion of the Python 3 template |
python3_template_tail |
string (nullable) | Footer portion of the Python 3 template |
problem_statement |
string | Canonical statement (often plain-text version of challenge_body) |
difficulty |
float | Continuous difficulty score in [0, 1] |
allowed_languages |
JSON string | Array of language identifiers permitted for submissions |
input_format |
string (nullable) | “Input Format” section verbatim |
output_format |
string (nullable) | “Output Format” section verbatim |
sample_input |
string (nullable) | Example stdin for the challenge |
sample_output |
string (nullable) | Expected stdout for the sample input |
difficulty_tag |
string | Discrete label (Easy, Medium, Hard) |
editorial_title |
string | Title of the official editorial article |
editorial_content |
string | Full HTML body of the editorial |
editorial_draft |
boolean (0/1) | 1 if editorial is still a draft |
editorial_slug |
string | URL-friendly slug for the editorial |
editorial_published_at |
ISO 8601 string | Publication timestamp of the editorial |
editorial_statistics |
JSON string | Engagement stats (participation, submissions, success rate) |
editorial_created_at |
ISO 8601 string | Editorial first-save timestamp |
editorial_updated_at |
ISO 8601 string | Last editorial edit time |
editorial_solution_kind |
string | Tag for reference solution (e.g., tester, reference) |
editorial_solution_code |
string | Full reference solution source code |
editorial_solution_language |
string | Language of the reference solution |
editorial_solution_created_at |
ISO 8601 string | Creation time of the reference solution |
editorial_solution_updated_at |
ISO 8601 string | Last update time of the reference solution |
language |
string | Detected programming language for this row |
- Downloads last month
- 36