Unnamed: 0
int64 0
269
| challenge_id
int64 104
5.95k
| challenge_slug
stringlengths 4
38
| challenge_name
stringlengths 5
57
| challenge_body
stringlengths 9
4.55k
⌀ | challenge_kind
stringclasses 2
values | challenge_preview
stringlengths 9
300
⌀ | challenge_category
stringclasses 2
values | challenge_created_at
stringdate 2013-01-04 20:28:56
2015-01-19 21:40:20
| challenge_updated_at
stringdate 2016-09-01 16:22:55
2022-09-02 10:36:47
| python3_template
stringlengths 2
303
⌀ | python3_template_head
stringclasses 2
values | python3_template_tail
stringclasses 52
values | problem_statement
stringlengths 9
4.55k
| difficulty
float64 0.4
0.6
| allowed_languages
stringclasses 28
values | input_format
stringlengths 1
987
⌀ | output_format
stringlengths 1
1.92k
⌀ | sample_input
stringlengths 1
284
⌀ | sample_output
stringclasses 52
values | difficulty_tag
stringclasses 1
value | editorial_title
stringclasses 32
values | editorial_content
stringclasses 32
values | editorial_draft
float64 0
0
⌀ | editorial_slug
stringclasses 32
values | editorial_published_at
stringdate 2013-03-04 16:26:12
2014-04-24 18:24:07
⌀ | editorial_statistics
stringclasses 45
values | editorial_created_at
stringdate 2013-03-04 16:26:12
2015-01-19 21:44:31
| editorial_updated_at
stringdate 2016-05-12 23:56:02
2020-09-08 16:59:12
| editorial_solution_kind
stringclasses 2
values | editorial_solution_code
stringlengths 2
13k
| editorial_solution_language
stringclasses 1
value | editorial_solution_created_at
stringdate 2016-04-24 02:02:11
2016-04-24 02:03:27
| editorial_solution_updated_at
stringdate 2016-04-24 02:02:11
2020-09-08 16:59:12
| language
stringclasses 7
values |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
0 | 337 |
randomsumexpected
|
Random Sum - Expected Sum
|
Given an a list D of N integers, and an integer T, two numbers L and R are randomly chosen such that 0 ≤ L ≤ R < N.
What is the expected sum of the subarray {d[L]...d[R]} given that (sum{d[L],...d[R]} <= T)?
**Input Format:**
The first line will contain two numbers: N and T. N lines follow, each containing one number from list D.
**Output Format:**
Output one number P, the expected sum of D[L]...D[R] upto 9 decimal places.
**Constraints:**
1 <= N < 100000
0 <= D[i] < 10^7
0 < T <= 10^9
**Sample Input:**
<pre>
5 10
4
5
3
7
1
</pre>
**Sample Output:**
<pre>6.111111111</pre>
**Explaination**
[4],[5],[3],[7],[1],[4,5],[5,3],[3,7],[7,1] subarrays satisfy the property.
4 + 5 + 3 + 7 + 1 + 9 + 8 + 10 + 8 = 55
55/9 = 6.11111111
|
code
|
What is the expected sum of a randomly chosen range of numbers?
|
ai
|
2013-01-29T20:58:30
|
2016-09-09T09:28:39
| null | null | null |
Given an a list D of N integers, and an integer T, two numbers L and R are randomly chosen such that 0 ≤ L ≤ R < N.
What is the expected sum of the subarray {d[L]...d[R]} given that (sum{d[L],...d[R]} <= T)?
**Input Format:**
The first line will contain two numbers: N and T. N lines follow, each containing one number from list D.
**Output Format:**
Output one number P, the expected sum of D[L]...D[R] upto 9 decimal places.
**Constraints:**
1 <= N < 100000
0 <= D[i] < 10^7
0 < T <= 10^9
**Sample Input:**
<pre>
5 10
4
5
3
7
1
</pre>
**Sample Output:**
<pre>6.111111111</pre>
**Explaination**
[4],[5],[3],[7],[1],[4,5],[5,3],[3,7],[7,1] subarrays satisfy the property.
4 + 5 + 3 + 7 + 1 + 9 + 8 + 10 + 8 = 55
55/9 = 6.11111111
| 0.495261 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
|
Random Sum - Expected Sum Solution by <a href ="https://www.hackerrank.com/sidsgr88">Siddharth Bora</a>
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><h3>Random Sum - Expected Sum</h3>
<p><strong>Idea:</strong> Two-Pointer</p>
<p><strong>Short Explanation:</strong>
You are expected to have the read the solution to Random Sum problem as the two-pointer idea is carried forward from that.
The problem asks us to give the expected sum of the arrays that have been found in the previous problem. This can be done maintaing a cumulative sum and a cumulative of cumulative sum and keeping a total sum that is updated as we calculate the count moving the two pointers as in the previous problem.</p>
<p><strong>Long Explanation:</strong>
We pre-calculate two arrays. Firstly a cumulative sum and then a cumulative of cumulative sum. The first of these gives the sum of number from the starting to a particular index. The second gives us the sum of all the sequences that start at index 0 and end at indices from 0 to i basically the ith value will be ele0 + (ele0 + ele 1) +...+ (ele0+..+elei) where elex is the xth element in the array.
Now since we need the sum of all the sequences that sum to <= T, we augment the previous question (Random Sum) solution to find the total sum too. Basically whenever we have an l,r we can calculate the sum of all sequences starting at l and ending at indices between l and r(left end inclusive) by
cumcumsum[r-1]-((l>0)?cumcumsum[l-1]:0)-(r-l)*((l>0)?cumsum[l-1]:0);
where cumcumsum is the cumulative of cumulative sum array and cumsum is the cumulative sum array. Here we are subtracting all cumulative sums less than l and also subtracting the portion of cumcumsum[r-1] which extends to the left of l namely the third term. This gives us the cumulative sum and finally we simply have to divide this by the previous answer to get the expected value.</p>
<p><strong>Language : C++</strong></p>
<pre><code>using namespace std;
#include <cmath>
#include <cstdio>
#include <list>
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <string>
#include <vector>
#include <iostream>
#include <sstream>
#include <algorithm>
#define all(c) (c).begin(),(c).end()
#define tr(c,i) for(typeof((c).begin()) i = (c).begin(); i != (c).end(); i++)
typedef long long ll;
typedef pair<int,int> pii;
#define FOR(i,n) for (int i = 0; i < n; i++)
#define SZ(x) ((int)x.size())
#define PB push_back
#define MP make_pair
#define sf(x) scanf("%d",&x)
#define pf(x) printf("%d\n",x)
#define split(str) {vs.clear();istringstream ss(str);while(ss>>(str))vs.push_back(str);}
#define PI 3.141592653589793
int main()
{
ll count=0;
ll count2=0;
int n,t;
sf(n);sf(t);
ll sum=0;
int l=0;
int r=-1;
vector<int> v;
while(n--)
{
int a;
sf(a);
v.PB(a);
}
vector<ll> cumsum;
FOR(i,v.size())
cumsum.PB(v[i]);
for(int i=1;i<v.size();i++)
cumsum[i]+=cumsum[i-1];
vector<ll> cumcumsum;
FOR(i,v.size())
cumcumsum.PB(cumsum[i]);
for(int i=1;i<v.size();i++)
cumcumsum[i]+=cumcumsum[i-1];
// FOR(i,v.size())
// cout<<cumcumsum[i]<<endl;
while(l<v.size())
{
//cout<<r<<" "<<(r<v.size())<<" "<<(sum<=t)<<endl;
while(r<(int)v.size() && sum<=t)
{
//cout<<"hello"<<endl;
//count2+=cumsum[r];
r++;
if(r<v.size())
{
sum+=v[r];
}
}
if(r-l>0)
{ count+=r-l;
//cout<<r<<" "<<l<<endl;
count2+=cumcumsum[r-1]-((l>0)?cumcumsum[l-1]:0)-(r-l)*((l>0)?cumsum[l-1]:0);
}
sum-=v[l];
l++;
}
//cout<<count2<<endl;
//cout<<count<<endl;
double ans=count2*1.0/count;
printf("%.9lf\n",ans);
}
</code></pre>
| 0 |
randexpsum
|
2013-03-04T16:26:12
|
{"contest_participation":6014,"challenge_submissions":421,"successful_submissions":210}
|
2013-03-04T16:26:12
|
2016-05-13T00:04:48
|
tester
|
using namespace std;
#include <cmath>
#include <cstdio>
#include <list>
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <string>
#include <vector>
#include <iostream>
#include <sstream>
#include <algorithm>
#define all(c) (c).begin(),(c).end()
#define tr(c,i) for(typeof((c).begin()) i = (c).begin(); i != (c).end(); i++)
typedef long long ll;
typedef pair<int,int> pii;
#define FOR(i,n) for (int i = 0; i < n; i++)
#define SZ(x) ((int)x.size())
#define PB push_back
#define MP make_pair
#define sf(x) scanf("%d",&x)
#define pf(x) printf("%d\n",x)
#define split(str) {vs.clear();istringstream ss(str);while(ss>>(str))vs.push_back(str);}
#define PI 3.141592653589793
int main()
{
ll count=0;
ll count2=0;
int n,t;
sf(n);sf(t);
ll sum=0;
int l=0;
int r=-1;
vector<int> v;
while(n--)
{
int a;
sf(a);
v.PB(a);
}
vector<ll> cumsum;
FOR(i,v.size())
cumsum.PB(v[i]);
for(int i=1;i<v.size();i++)
cumsum[i]+=cumsum[i-1];
vector<ll> cumcumsum;
FOR(i,v.size())
cumcumsum.PB(cumsum[i]);
for(int i=1;i<v.size();i++)
cumcumsum[i]+=cumcumsum[i-1];
// FOR(i,v.size())
// cout<<cumcumsum[i]<<endl;
while(l<v.size())
{
//cout<<r<<" "<<(r<v.size())<<" "<<(sum<=t)<<endl;
while(r<(int)v.size() && sum<=t)
{
//cout<<"hello"<<endl;
//count2+=cumsum[r];
r++;
if(r<v.size())
{
sum+=v[r];
}
}
if(r-l>0)
{ count+=r-l;
//cout<<r<<" "<<l<<endl;
count2+=cumcumsum[r-1]-((l>0)?cumcumsum[l-1]:0)-(r-l)*((l>0)?cumsum[l-1]:0);
}
sum-=v[l];
l++;
}
//cout<<count2<<endl;
//cout<<count<<endl;
double ans=count2*1.0/count;
printf("%.9lf\n",ans);
}
|
not-set
|
2016-04-24T02:02:11
|
2016-04-24T02:02:11
|
C++
|
1 | 556 |
n-puzzle
|
N Puzzle
|
N Puzzle is a sliding blocks game that takes place on a k * k grid with ((k * k) - 1) tiles each numbered from 1 to N. Your task is to reposition the tiles to their proper order.
**Input Format**
The first line of the input contains an integer k, the size of the square grid. k * k lines follow each line containing an integer I on the tile starting from the top left to bottom right. The empty cell is represented by the number 0.
N = (k * k) -1
0 <= I <= N
**Constraints**
3 <= k <= 5
**Output Format**
The first line contains an integer, M, the number of moves your algorithm has taken to solve the N-Puzzle. M lines follow. Each line indicating the movement of the empty cell (0).
A grid is considered solved if it is of the following configuration.
0 1 2
3 4 5
6 7 8
**Sample Input**
3
0
3
8
4
1
7
2
6
5
**Sample Output**
70
RIGHT
DOWN
...
...
...
**Explanation**
The board given as input is
0 3 8
4 1 7
2 6 5
After RIGHT, the board's configuration is
3 0 8
4 1 7
2 6 5
**Task**
Print all the moves made from the given configuration to
the final solved board configuration.
**Scoring**
On successfully solving the puzzle, your score will be k * k.
|
game
|
N Puzzle is a sliding blocks game that takes place on a k * k grid with (k * k) - 1 tiles each numbered from 1 to N. Place the tiles in their proper order using minimum number of moves.
|
ai
|
2013-04-06T14:13:29
|
2022-08-31T18:04:25
| null | null | null |
N Puzzle is a sliding blocks game that takes place on a k * k grid with ((k * k) - 1) tiles each numbered from 1 to N. Your task is to reposition the tiles to their proper order.
**Input Format**
The first line of the input contains an integer k, the size of the square grid. k * k lines follow each line containing an integer I on the tile starting from the top left to bottom right. The empty cell is represented by the number 0.
N = (k * k) -1
0 <= I <= N
**Constraints**
3 <= k <= 5
**Output Format**
The first line contains an integer, M, the number of moves your algorithm has taken to solve the N-Puzzle. M lines follow. Each line indicating the movement of the empty cell (0).
A grid is considered solved if it is of the following configuration.
0 1 2
3 4 5
6 7 8
**Sample Input**
3
0
3
8
4
1
7
2
6
5
**Sample Output**
70
RIGHT
DOWN
...
...
...
**Explanation**
The board given as input is
0 3 8
4 1 7
2 6 5
After RIGHT, the board's configuration is
3 0 8
4 1 7
2 6 5
**Task**
Print all the moves made from the given configuration to
the final solved board configuration.
**Scoring**
On successfully solving the puzzle, your score will be k * k.
| 0.456522 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","tcl","typescript","visualbasic","kotlin","pypy3","swift"]
| null | null | null | null |
Hard
|
May 20-20 Hack Editorial: N - Puzzle
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong><a href="https://www.hackerrank.com/contests/may13/challenges/n-puzzle">N Puzzle</a></strong></p>
<p>N Puzzle is a sliding blocks game that takes place on a k * k grid with k * k - 1 tiles
each numbered from 1 to N. Your task is to reposition the tiles in their proper order</p>
<p><strong>Difficulty Level</strong></p>
<p>Medium ( Implementation heavy )</p>
<p><strong>Problem Setter</strong></p>
<p><a href="https://www.hackerrank.com/dheeraj">Dheeraj M R</a></p>
<p><strong>Required Knowledge</strong></p>
<p>A* algorithm</p>
<p><strong>Approach</strong></p>
<p>N-Puzzle is a classic 1 player game that teaches the basics of heuristics in arriving at
solutions in Artificial Intelligence. </p>
<p>Let us consider for the sake of simplicity, N = 8</p>
<p>The final configuration of an 8 - puzzle will look like</p>
<pre><code>0 1 2
3 4 5
6 7 8
</code></pre>
<p><a href="https://www.hackerrank.com/challenges/pacman-astar">A*</a> algorithm talks about a cost function
and a heuristic. </p>
<p>cost = heuristic_cost + #of steps taken to reach the current state.</p>
<p>the tiles are numbered. For a given unsolved 8 - puzzle configuration say</p>
<pre><code>0 3 8
4 1 7
2 6 5
</code></pre>
<p>We use 2 heuristics for every state and at every iteration</p>
<p>1 such heuristic is </p>
<p>h1 => The number of misplaced tiles.</p>
<p>In the above example, the number of misplaced tiles are 8</p>
<p>2<sup>nd</sup> heuristic we use is</p>
<p>h2 => The manahattan distance between a tile's original position to its current position.</p>
<p>In the above example, the manhattan distance for all tiles are as follows</p>
<p>a<sub>b</sub> => where a is the manhattan distance of tile <em>b</em>.</p>
<p>h2 = 2<sub>3</sub> + 2<sub>8</sub> + 1<sub>4</sub> + 1<sub>1</sub> + 2<sub>7</sub> + 4<sub>2</sub> + 1<sub>6</sub> + 1<sub>5</sub></p>
<p>h2 = 14</p>
<p>Given 2 heuristics, it is always advised to use the maximum as the maximum never underestimates the cost to reach the
required end state ( initial configuration of 8 Puzzle )</p>
<p>If it took 10 moves to reach the current state as shown above, then the cost function of a given state of N - puzzle</p>
<p>is given as </p>
<pre><code>cost = max( h1, h2 ) + 10
cost = max( 14, 8 ) + 10 = 24
</code></pre>
<p>We can then implement a priority queue and record each of possible moves from a given initial state of the board
and then pop the state with the lowest cost function. This procedure is guaranteed to give us a solution.</p>
<p><strong>Problem Setter's code: C++</strong></p>
<p><a href="https://gist.github.com/dheerajrav/5748717">here</a></p>
| 0 |
may-2020-editorial-npuzzle
|
2013-06-10T13:14:35
|
{"contest_participation":3663,"challenge_submissions":135,"successful_submissions":0}
|
2013-06-10T13:14:35
|
2016-05-13T00:04:45
|
setter
|
#include<iostream>
#include<vector>
#include<queue>
#include<set>
#include<map>
#include<algorithm>
#define INRANGE(i, a, b) (i >= a && i < b)
using namespace std;
class SlidingBlock
{
public:
vector < int > disc;
int n;
int cost;
int empty_slot;
vector< string > record_move;
SlidingBlock();
SlidingBlock( int );
SlidingBlock( vector < int >, vector < string > );
vector < string > getMove();
void makeMove( const string move = string() );
bool solved();
vector < SlidingBlock > branches();
void setCost();
void print();
void readBlock();
bool operator< ( const SlidingBlock& ) const;
bool operator> ( const SlidingBlock& ) const;
};
SlidingBlock::SlidingBlock()
{
SlidingBlock( 3 );
}
SlidingBlock::SlidingBlock( int size )
{
n = size;
}
void SlidingBlock::readBlock()
{
int temp;
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < n; j++ )
{
cin >> temp;
disc.push_back( temp );
}
}
int pos = std::abs( std::distance( find( disc.begin(), disc.end(), 0 ), disc.begin()) );
empty_slot = pos;
setCost();
}
SlidingBlock::SlidingBlock( vector < int > node, vector < string > moves )
{
disc.clear();
n = ( int )sqrt( node.size() );
for( int i = 0; i < ( int )node.size(); ++i )
{
disc.push_back( node[ i ] );
if( node[ i ] == 0 )
empty_slot = i;
}
for( int i = 0; i < moves.size(); i++ )
record_move.push_back( moves[ i ] );
setCost();
}
void SlidingBlock::setCost()
{
int h1 = 0 , h2 = 0;
//setting heuristic 1 => number of misplaced blocks
//setting heuristic 2 => distance of the node to its block
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < n; j++ )
{
int val = disc[ n * i + j ];
if( val != n * i + j && val != 0 )
{
h1 += 1;
int exp_pos_x = ( val ) / n;
int exp_pos_y = ( val ) % n;
h2 += abs( i - exp_pos_x ) + abs( j - exp_pos_y );
}
}
}
cost = max( h1, h2) + this->record_move.size();
}
vector < string > SlidingBlock::getMove()
{
vector < string > movements;
if( empty_slot/n > 0 )
movements.push_back( "UP" );
if( empty_slot%n > 0 )
movements.push_back( "LEFT" );
if( empty_slot/n < n - 1 )
movements.push_back( "DOWN" );
if( empty_slot%n < n - 1 )
movements.push_back( "RIGHT" );
return movements;
}
void SlidingBlock::makeMove( string move )
{
if( move.empty() )
{
vector < string > moves = getMove();
int rand_point_index = rand() % moves.size();
makeMove( moves[ rand_point_index ] );
}
else
{
record_move.push_back( move );
int temp = empty_slot;
if( move.compare("UP") == 0 )
empty_slot -= n;
if( move.compare("DOWN") == 0 )
empty_slot += n;
if( move.compare("LEFT") == 0 )
empty_slot -= 1;
if( move.compare("RIGHT") == 0 )
empty_slot += 1;
swap( disc[ temp ], disc[ empty_slot ] );
}
setCost();
}
bool SlidingBlock::solved()
{
bool answer = true;
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < n; j++ )
{
answer &= disc[ n * i + j ] == ( n * i + j );
}
}
return answer;
}
vector < SlidingBlock > SlidingBlock::branches()
{
vector < string > moves = getMove();
vector < SlidingBlock > valid_branches;
for( int i = 0; i < ( int )moves.size(); ++i )
{
valid_branches.push_back( SlidingBlock( disc , record_move ) );
valid_branches[ i ].makeMove( moves[ i ] );
}
return valid_branches;
}
void SlidingBlock::print()
{
for( int i = 0; i < n; i++ )
{
for( int j = 0; j < n; j++ )
{
cout << disc[ n*i + j ] << " ";
}
cout << endl;
}
}
bool SlidingBlock::operator< ( const SlidingBlock& node ) const
{
for( int i = 0; i < ( int )node.disc.size(); i++ )
{
if( node.disc[ i ] < this->disc[ i ] )
{
return true;
}
else if( node.disc[ i ] > this->disc[ i ] )
{
return false;
}
else
{
continue;
}
}
return false;
}
bool SlidingBlock::operator> ( const SlidingBlock& node ) const
{
for( int i = 0; i < ( int )node.disc.size(); i++ )
{
if( node.disc[ i ] > this->disc[ i ] )
{
return true;
}
else if( node.disc[ i ] < this->disc[ i ] )
{
return false;
}
else
{
continue;
}
}
return false;
}
struct OrderByCost
{
bool operator() ( const SlidingBlock &a, const SlidingBlock &b ) const
{
return a.cost >= b.cost;
}
};
class Search
{
public:
SlidingBlock start;
priority_queue< SlidingBlock, vector < SlidingBlock >, OrderByCost > pq;
set< SlidingBlock > explored;
vector < SlidingBlock > expanded;
Search( int n )
{
start = SlidingBlock( n );
start.readBlock();
searchAndPrint();
}
void searchAndPrint()
{
pushNode( start );
SlidingBlock node = SlidingBlock( start.disc, start.record_move );
setExplored( node );
while( !node.solved() )
{
node = getNextNode();
expanded.push_back( node );
vector < SlidingBlock > valid_branches = node.branches();
//Iterate over neighbors
for( int i = 0; i < ( int ) valid_branches.size(); i++ )
{
if( !isExplored( valid_branches[ i ] ) )
{
pushNode( valid_branches[ i ] );
setExplored( node );
}
}
}
cout << node.record_move.size() << endl;
for( auto i = node.record_move.begin(); i != node.record_move.end(); ++i )
cout << *i << endl;
}
void pushNode( SlidingBlock node )
{
pq.push( node );
}
void setExplored( SlidingBlock node )
{
explored.insert( node );
}
bool isExplored( SlidingBlock node )
{
return explored.count( node ) > 0;
}
SlidingBlock getNextNode()
{
SlidingBlock node = pq.top();
pq.pop();
return node;
}
};
int main()
{
set< SlidingBlock > explored;
int n;
cin >> n;
Search *game = new Search( n );
}
|
not-set
|
2016-04-24T02:02:11
|
2016-04-24T02:02:11
|
C++
|
2 | 746 |
game-of-throne-ii
|
Game Of Thrones - II
|
This follows from [Game of Thrones - I](https://www.hackerrank.com/contests/july13/challenges/game-of-thrones).
Now that the king knows how to find out whether a given word has an [anagram](https://en.wikipedia.org/wiki/Anagram) which is a [palindrome](http://en.wikipedia.org/wiki/Palindrome) or not, he encounters another challenge. He realizes that there can be more than one palindrome anagrams for a given word. Can you help him find out how many palindrome anagrams are possible for a given word ?
The king has many words. For each given word, he needs to find out the number of palindrome anagrams of the string. As the number of anagrams can be large, the king needs the number of anagrams % (10<sup>9</sup>+ 7).
**Input format :**<br>
A single line which contains the input string<br>
**Output format :**
A single line which contains the number of anagram strings which are palindrome % (10<sup>9</sup> + 7).
**Constraints :**
1<=length of string <= 10^5
Each character of the string is a lowercase alphabet.
Each test case has at least 1 anagram which is a palindrome.
**Sample Input 01 :**
aaabbbb
**Sample Output 01 :**
3
**Explanation :**
Three palindrome permutations of the given string are abbabba , bbaaabb and bababab.
**Sample Input 02 :**
cdcdcdcdeeeef
**Sample Output 02 :**
90
|
code
|
Can you help the king find the number of ways his door can be unlocked?
|
ai
|
2013-07-02T17:07:43
|
2022-09-02T09:54:54
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts STRING s as parameter.
#
def solve(s):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
s = input()
result = solve(s)
fptr.write(str(result) + '\n')
fptr.close()
|
This follows from [Game of Thrones - I](https://www.hackerrank.com/contests/july13/challenges/game-of-thrones).
Now that the king knows how to find out whether a given word has an [anagram](https://en.wikipedia.org/wiki/Anagram) which is a [palindrome](http://en.wikipedia.org/wiki/Palindrome) or not, he encounters another challenge. He realizes that there can be more than one palindrome anagrams for a given word. Can you help him find out how many palindrome anagrams are possible for a given word ?
The king has many words. For each given word, he needs to find out the number of palindrome anagrams of the string. As the number of anagrams can be large, the king needs the number of anagrams % (10<sup>9</sup>+ 7).
**Input format :**<br>
A single line which contains the input string<br>
**Output format :**
A single line which contains the number of anagram strings which are palindrome % (10<sup>9</sup> + 7).
**Constraints :**
1<=length of string <= 10^5
Each character of the string is a lowercase alphabet.
Each test case has at least 1 anagram which is a palindrome.
**Sample Input 01 :**
aaabbbb
**Sample Output 01 :**
3
**Explanation :**
Three palindrome permutations of the given string are abbabba , bbaaabb and bababab.
**Sample Input 02 :**
cdcdcdcdeeeef
**Sample Output 02 :**
90
| 0.501678 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
|
20/20 Hack July Editorial: Game of Thrones - 2
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/july13/challenges/game-of-throne-ii">Game Of Thrones - II</a> </p>
<p><strong>Problem:</strong> Given a string such that at least one of anagram of string is palindrome. Tell how many anagram of given string will be palindrome.</p>
<p><strong>Difficulty level:</strong> Easy <br>
<strong>Required Knowledge:</strong> Permutations, Modular Inverse <br>
<strong>Time Complexity:</strong> O(N) </p>
<p><strong>Approach:</strong> Given a string tell how many anagram of given string will be palindrome. So we can consider a sub-string which we can get by taking half of number of each character. length of this sub-string will L/2 where L is length of original string. we can get permutation of given string then we can concatenate the reverse of given half. so get anagram of given string which will be palindrome.So, we can use following <a href="http://www.regentsprep.org/Regents/math/ALGEBRA/APR2/LpermRep.htm">formula</a> to get number of permutation of given first half. </p>
<p>So , as answer can be very huge . But as in question we are asked for number of permutations which are palindrome % 10^9+7 and we know 10^9 + 7 is a prime number . So, we can get it using modular inverse techniques.</p>
<p><strong>Problem Setter's code:</strong></p>
<pre><code>#!/usr/bin/py
from collections import Counter
mod = 10**9 + 7
def hasPalindrome(word):
x = Counter(word)
count = 0
for i in x:
if x[i]%2!=0:
count += 1
if count > 1:
return False
else:
return True
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b == 0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
word = raw_input()
assert 1 <= len(word) <= 10**5
assert hasPalindrome(word) == True
counter = Counter(word)
denominator = 1
numerator = 0
for i in counter:
numerator += counter[i]/2
denominator = ((denominator%mod)*(getfactmod(counter[i]/2)%mod))%mod
numerator = getfactmod(numerator)
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
</code></pre>
<p><strong>Tester's code:</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
int t;
const long long mod = 1000000007;
long long pow(long long osn){
long long res = 1, tmp = osn;
int m = int(mod - 2);
while(m){
if(m % 2){
res = (res * tmp) % mod;
--m;
}
m >>= 1;
tmp = (tmp * tmp) % mod;
}
return res;
}
long long fact(int num){
long long res(1), curp(num);
while(curp)res = (res * curp--) % mod;
return res;
}
int obr(){
int num[256];
memset(num, 0, sizeof(num));
char s[1001];
cin>>s;
int n = strlen(s);
for(int i = 0; i < n; ++i)++num[s[i]];
for(int i=0 ; i<256 ; i++)
num[i] = num[i]/2;
n = n/2;
long long res = fact(n);
for(int i = 'a'; i <= 'z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
for(int i = 'A'; i <= 'Z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
int topr = int(res);
printf("%d\n", topr);
return 0;
}
int main(){
t = 1;
for(int i = 0; i < t; ++i)
obr();
return 0;
}
</code></pre>
| 0 |
july-2020-editorial-game-of-thrones-ii
|
2013-07-22T04:35:37
|
{"contest_participation":4325,"challenge_submissions":1181,"successful_submissions":695}
|
2013-07-22T04:35:37
|
2016-12-02T19:33:05
|
setter
|
###Python 2
```python
#!/usr/bin/py
from collections import Counter
mod = 10**9 + 7
def hasPalindrome(word):
x = Counter(word)
count = 0
for i in x:
if x[i]%2!=0:
count += 1
if count > 1:
return False
else:
return True
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b == 0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
word = raw_input()
assert 1 <= len(word) <= 10**5
assert hasPalindrome(word) == True
counter = Counter(word)
denominator = 1
numerator = 0
for i in counter:
numerator += counter[i]/2
denominator = ((denominator%mod)*(getfactmod(counter[i]/2)%mod))%mod
numerator = getfactmod(numerator)
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
```
|
not-set
|
2016-04-24T02:02:12
|
2016-07-23T18:36:16
|
Python
|
3 | 746 |
game-of-throne-ii
|
Game Of Thrones - II
|
This follows from [Game of Thrones - I](https://www.hackerrank.com/contests/july13/challenges/game-of-thrones).
Now that the king knows how to find out whether a given word has an [anagram](https://en.wikipedia.org/wiki/Anagram) which is a [palindrome](http://en.wikipedia.org/wiki/Palindrome) or not, he encounters another challenge. He realizes that there can be more than one palindrome anagrams for a given word. Can you help him find out how many palindrome anagrams are possible for a given word ?
The king has many words. For each given word, he needs to find out the number of palindrome anagrams of the string. As the number of anagrams can be large, the king needs the number of anagrams % (10<sup>9</sup>+ 7).
**Input format :**<br>
A single line which contains the input string<br>
**Output format :**
A single line which contains the number of anagram strings which are palindrome % (10<sup>9</sup> + 7).
**Constraints :**
1<=length of string <= 10^5
Each character of the string is a lowercase alphabet.
Each test case has at least 1 anagram which is a palindrome.
**Sample Input 01 :**
aaabbbb
**Sample Output 01 :**
3
**Explanation :**
Three palindrome permutations of the given string are abbabba , bbaaabb and bababab.
**Sample Input 02 :**
cdcdcdcdeeeef
**Sample Output 02 :**
90
|
code
|
Can you help the king find the number of ways his door can be unlocked?
|
ai
|
2013-07-02T17:07:43
|
2022-09-02T09:54:54
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts STRING s as parameter.
#
def solve(s):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
s = input()
result = solve(s)
fptr.write(str(result) + '\n')
fptr.close()
|
This follows from [Game of Thrones - I](https://www.hackerrank.com/contests/july13/challenges/game-of-thrones).
Now that the king knows how to find out whether a given word has an [anagram](https://en.wikipedia.org/wiki/Anagram) which is a [palindrome](http://en.wikipedia.org/wiki/Palindrome) or not, he encounters another challenge. He realizes that there can be more than one palindrome anagrams for a given word. Can you help him find out how many palindrome anagrams are possible for a given word ?
The king has many words. For each given word, he needs to find out the number of palindrome anagrams of the string. As the number of anagrams can be large, the king needs the number of anagrams % (10<sup>9</sup>+ 7).
**Input format :**<br>
A single line which contains the input string<br>
**Output format :**
A single line which contains the number of anagram strings which are palindrome % (10<sup>9</sup> + 7).
**Constraints :**
1<=length of string <= 10^5
Each character of the string is a lowercase alphabet.
Each test case has at least 1 anagram which is a palindrome.
**Sample Input 01 :**
aaabbbb
**Sample Output 01 :**
3
**Explanation :**
Three palindrome permutations of the given string are abbabba , bbaaabb and bababab.
**Sample Input 02 :**
cdcdcdcdeeeef
**Sample Output 02 :**
90
| 0.501678 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
|
20/20 Hack July Editorial: Game of Thrones - 2
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/july13/challenges/game-of-throne-ii">Game Of Thrones - II</a> </p>
<p><strong>Problem:</strong> Given a string such that at least one of anagram of string is palindrome. Tell how many anagram of given string will be palindrome.</p>
<p><strong>Difficulty level:</strong> Easy <br>
<strong>Required Knowledge:</strong> Permutations, Modular Inverse <br>
<strong>Time Complexity:</strong> O(N) </p>
<p><strong>Approach:</strong> Given a string tell how many anagram of given string will be palindrome. So we can consider a sub-string which we can get by taking half of number of each character. length of this sub-string will L/2 where L is length of original string. we can get permutation of given string then we can concatenate the reverse of given half. so get anagram of given string which will be palindrome.So, we can use following <a href="http://www.regentsprep.org/Regents/math/ALGEBRA/APR2/LpermRep.htm">formula</a> to get number of permutation of given first half. </p>
<p>So , as answer can be very huge . But as in question we are asked for number of permutations which are palindrome % 10^9+7 and we know 10^9 + 7 is a prime number . So, we can get it using modular inverse techniques.</p>
<p><strong>Problem Setter's code:</strong></p>
<pre><code>#!/usr/bin/py
from collections import Counter
mod = 10**9 + 7
def hasPalindrome(word):
x = Counter(word)
count = 0
for i in x:
if x[i]%2!=0:
count += 1
if count > 1:
return False
else:
return True
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b == 0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
word = raw_input()
assert 1 <= len(word) <= 10**5
assert hasPalindrome(word) == True
counter = Counter(word)
denominator = 1
numerator = 0
for i in counter:
numerator += counter[i]/2
denominator = ((denominator%mod)*(getfactmod(counter[i]/2)%mod))%mod
numerator = getfactmod(numerator)
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
</code></pre>
<p><strong>Tester's code:</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
int t;
const long long mod = 1000000007;
long long pow(long long osn){
long long res = 1, tmp = osn;
int m = int(mod - 2);
while(m){
if(m % 2){
res = (res * tmp) % mod;
--m;
}
m >>= 1;
tmp = (tmp * tmp) % mod;
}
return res;
}
long long fact(int num){
long long res(1), curp(num);
while(curp)res = (res * curp--) % mod;
return res;
}
int obr(){
int num[256];
memset(num, 0, sizeof(num));
char s[1001];
cin>>s;
int n = strlen(s);
for(int i = 0; i < n; ++i)++num[s[i]];
for(int i=0 ; i<256 ; i++)
num[i] = num[i]/2;
n = n/2;
long long res = fact(n);
for(int i = 'a'; i <= 'z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
for(int i = 'A'; i <= 'Z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
int topr = int(res);
printf("%d\n", topr);
return 0;
}
int main(){
t = 1;
for(int i = 0; i < t; ++i)
obr();
return 0;
}
</code></pre>
| 0 |
july-2020-editorial-game-of-thrones-ii
|
2013-07-22T04:35:37
|
{"contest_participation":4325,"challenge_submissions":1181,"successful_submissions":695}
|
2013-07-22T04:35:37
|
2016-12-02T19:33:05
|
tester
|
###C++
```cpp
#include <cstdio>
#include <cstring>
#include <bits/stdc++.h>
using namespace std;
int t;
const long long mod = 1000000007;
long long pow(long long osn){
long long res = 1, tmp = osn;
int m = int(mod - 2);
while(m){
if(m % 2){
res = (res * tmp) % mod;
--m;
}
m >>= 1;
tmp = (tmp * tmp) % mod;
}
return res;
}
long long fact(int num){
long long res(1), curp(num);
while(curp)res = (res * curp--) % mod;
return res;
}
int obr(){
int num[256];
memset(num, 0, sizeof(num));
char s[1001];
cin>>s;
int n = strlen(s);
for(int i = 0; i < n; ++i)++num[s[i]];
for(int i=0 ; i<256 ; i++)
num[i] = num[i]/2;
n = n/2;
long long res = fact(n);
for(int i = 'a'; i <= 'z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
for(int i = 'A'; i <= 'Z'; ++i)
if(num[i])res = (res * pow(fact(num[i]))) % mod;
int topr = int(res);
printf("%d\n", topr);
return 0;
}
int main(){
t = 1;
for(int i = 0; i < t; ++i)
obr();
return 0;
}
```
|
not-set
|
2016-04-24T02:02:12
|
2016-07-23T18:36:38
|
C++
|
4 | 791 |
kth-ancestor
|
Kth Ancestor
|
A tree of P nodes is an un-directed connected graph having P-1 edges. Let us denote R as the root node. If A is a node such that it is at a distance of L from R, and B is a node such that it is at at distance of L+1 from
R and A is connected to B, then we call A as the parent of B.
Similarly, if A is at a distance of L from R and B is at a distance of L+K from R and there is a path of length K from A to B, then we call A as the K<sup>th</sup> parent of B.
Susan likes to play with graphs and Tree data structure is one of her favorites. She has designed a problem and wants to know if anyone can solve it. Sometimes she adds or removes a leaf node. Your task is to figure out the K-th parent of a node at any instant.
**Input Format**
The first line contain an integer T denoting the number of test-cases. T test cases follow. First line of each test case contains an integer P, the number of nodes in the tree.
P lines follows each containing two integers X and Y separated by a single space denoting Y as the parent of X. if Y is 0, then X is the root node of the tree. (0 is for namesake and is not in the tree).
The next line contains an integer Q, the number of queries.
Q lines follow each containing a query.
+ 0 Y X : X is added as a new leaf node whose parent is Y
+ 1 X : This tells that leaf node X is removed from the tree
+ 2 X K : In this query output the K<sup>th</sup> parent of X
**Note**
Each node index is any number between 1 and 10<sup>5</sup> i.e., a tree with a single node can have its root indexed as 10<sup>5</sup>
**Output Format**
For each query of type 2, output the K<sup>th</sup> parent of X. If K<sup>th</sup> parent doesn't exist, output 0 and if the node doesn't exist, output 0.
**Constraints**
1<=T<=3
1<=P<=10<sup>5</sup>
1<=Q<=10<sup>5</sup>
1<=X<=10<sup>5</sup>
0<=Y<=10<sup>5</sup>
1<=K<=10<sup>5</sup>
**Sample Input**
2
7
2 0
5 2
3 5
7 5
9 8
8 2
6 8
10
0 5 15
2 15 2
1 3
0 15 20
0 20 13
2 13 4
2 13 3
2 6 10
2 11 1
2 9 1
1
10000 0
3
0 10000 4
1 4
2 4 1
**Sample Output**
2
2
5
0
0
8
0
**Explanation**
There are 2 test cases. The first test case has 7 nodes with 2 as its root. There are 10 queries
+ 0 5 15 -> 15 is added as a leaf node to 5.
+ 2 15 2 -> 2nd parent of 15 is 15->5->2 is 2.
+ 1 3 -> leaf node 3 is removed from the tree.
+ 0 15 20 -> 20 is added as a leaf node to 15.
+ 0 20 13 -> 13 is added as a leaf node to 20.
+ 2 13 4 -> 4th parent of 13 is 2.
+ 2 13 3 -> 3rd parent of 13 is 5.
+ 2 6 10 -> there is no 10th parent of 6 and hence 0.
+ 2 11 1 -> 11 is not a node in the tree, hence 0.
+ 2 9 1 -> 9's parent is 8.
the second testcase has a tree with only 1 node (100000).
+ 0 10000 4 -> 4 is added as a leaf node to 10000.
+ 1 4 -> 4 is removed.
+ 2 4 1 -> as 4 is already removed, answer is 0.
|
code
|
Figure out the K-th parent of a node at any instant.
|
ai
|
2013-08-01T18:06:31
|
2022-08-31T08:14:29
| null | null | null |
A tree of $P$ nodes is an un-directed connected graph having $P-1$ edges. Let us denote $R$ as the root node. If $A$ is a node such that it is at a distance of $L$ from $R$, and $B$ is a node such that it is at at distance of $L+1$ from
$R$ and $A$ is connected to $B$, then we call $A$ as the parent of $B$.
Similarly, if $A$ is at a distance of $L$ from $R$ and $B$ is at a distance of $L+K$ from $R$ and there is a path of length $K$ from $A$ to $B$, then we call $A$ as the $K$<sup>th</sup> parent of $B$.
Susan likes to play with graphs and Tree data structure is one of her favorites. She has designed a problem and wants to know if anyone can solve it. Sometimes she adds or removes a leaf node. Your task is to figure out the $K$<sup>th</sup> parent of a node at any instant.
| 0.435294 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
The first line contain an integer $T$ denoting the number of test cases. $T$ test cases follow. First line of each test case contains an integer $P$, the number of nodes in the tree.
$P$ lines follows each containing two integers $X$ and $Y$ separated by a single space denoting $Y$ as the parent of $X$. If $Y$ is $0$, then X is the root node of the tree. ($0$ is for namesake and is not in the tree).
The next line contains an integer $Q$, the number of queries.
$Q$ lines follow each containing a query.
+ $0$ $Y$ $X$ : $X$ is added as a new leaf node whose parent is $Y$ . $X$ is not in the tree while $Y$ is in.
+ $1$ $X$ : This tells that leaf node $X$ is removed from the tree. $X$ is a leaf in the tree.
+ $2$ $X$ $K$ : In this query output the $K$<sup>th</sup> parent of $X$ . $X$ is a node in the tree.
**Note**
+ Each node index is any number between 1 and 10<sup>5</sup> i.e., a tree with a single node can have its root indexed as 10<sup>5</sup>
|
For each query of type $2$, output the $K$<sup>th</sup> parent of $X$. If $K$<sup>th</sup> parent doesn't exist, output $0$ and if the node doesn't exist, output $0$.
|
2
7
2 0
5 2
3 5
7 5
9 8
8 2
6 8
10
0 5 15
2 15 2
1 3
0 15 20
0 20 13
2 13 4
2 13 3
2 6 10
2 11 1
2 9 1
1
10000 0
3
0 10000 4
1 4
2 4 1
|
2
2
5
0
0
8
0
|
Hard
|
Kth Parent : August 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem Statement</strong></p>
<p>Susan needs to find the k<sup>th</sup> parent of a node in the tree.</p>
<p><strong>Difficulty level</strong> Medium</p>
<p><strong>Required Knowledge</strong> Trees, Binary Logic</p>
<p><strong>Time Complexity</strong> O(NlogN)</p>
<p><strong>Approach</strong></p>
<p>The naive approach for this problem is very obvious. Just store the parent of each node and find the k<sup>th</sup> parent by finding parent of each parent. But as the number of queries are large, this approach in the worst case (example: tree having only two leaf nodes) exceeds time limit.</p>
<p>The pick of the problem is that, instead of storing the parent of every node, we store all 2<sup>i</sup>th parent of a node i.e. 2<sup>0</sup>th , 2<sup>1</sup>st, 2<sup>2</sup>th ... parent for each node. </p>
<p>Now for finding k<sup>th</sup> parent of a node A, </p>
<p>Let, <br>
k = (b<sub>l-1</sub>b<sub>l-2</sub>....b<sub>0</sub>) in binary representation be a l-bit number k. </p>
<p>So k = b<sub>0</sub> + b<sub>1</sub> * 2<sup>1</sup> + ... + b<sub>l-2</sub> * 2<sup>l-2</sup> + b<sub>l-1</sub> * 2<sup>l-1</sup> </p>
<p>Let s bits of these l bits are 1, p1,p2,...ps be indices at which bit value is 1. <br>
k = 2<sup>p1</sup> + 2<sup>p2</sup> + ... + 2<sup>ps</sup> </p>
<p>Using above distribution of k, we can find kth node by following procedure. <br>
A1 = 2<sup>p1</sup>th parent of A <br>
A2 = 2<sup>p2</sup>th parent of A1, implies 2<sup>p1</sup>th + 2<sup>p2</sup>th parent of A <br>
A3 = 2<sup>p3</sup>th parent of A2 which will also be 2<sup>p1</sup>th + 2<sup>p2</sup>th + 2<sup>p3</sup>th parent of A. </p>
<p>Similarly <br>
As = 2<sup>ps</sup>th parent of As-1 and also 2<sup>p1</sup>th+2<sup>p2</sup>th .... 2<sup>ps</sup>th parent of A i.e. k<sup>th</sup> parent of A.</p>
<p>So it takes only s summations for finding k<sup>th</sup> parent. Since s is the number of bits in k.
So this process takes O(s) = O(log k) time;</p>
<p>Now the problem is how to find 2<sup>i</sup> parents of each node?</p>
<p>Let parent[i][j] be 2<sup>j</sup>th parent of node i.
Initially we know parent[i][0] i.e. first parent of all the nodes.</p>
<p>For j>0</p>
<pre><code>parent[i][j] = 2^jth parent of i
= (2^j-1th + 2^j-1th) parent of i
= 2^j-1th parent of (2^j-1th parent of i)
= 2^j-1th parent of parent[i][j-1]
= parent[parent[i][j-1][j-1]
</code></pre>
<p>The pseudo code is as follows</p>
<pre><code>for i from 1 to n
parent[i][0] = parent of i
for i from 1 to n
for j from 1 to m
parent[i][j] = parent[parent[i][j-1]][j-1]
</code></pre>
<p>In above code, m is the maximum value j can attain. In worst case, the highest value of parent a node can have is n-1. </p>
<p>2^m<=n-1
m = O(log n)</p>
<p>Hence above process takes O(n log n) time as well as O(n log n) space.</p>
<p><strong>Problem Setter's code</strong> </p>
<pre><code>//shashwat001
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <queue>
#include <stack>
#include <map>
#include <utility>
#include <algorithm>
#include <cassert>
using namespace std;
#define INF 2147483647
#define LINF 9223372036854775807
#define mp make_pair
#define pb push_back
typedef long long int lli;
typedef pair<int,int> pi;
int p[100000][40]={{0}};
int a[100005],isnode[100005];
int main ()
{
int q,ch,x,y,t;
scanf("%d",&t);
assert(t>=1 && t<=3);
while(t--)
{
memset(p,0,sizeof(p));
memset(isnode,0,sizeof(isnode));
int i,n,j;
scanf("%d",&n);
assert(n>=1 && n<=100000);
for(i = 0;i < n;i++)
{
scanf("%d %d",&x,&y);
assert(x>=1 && x<=100000);
assert(y>=0 && y<=100000);
a[i] = x;
if(y!=0)
assert(isnode[y]==1);
assert(isnode[x]==0);
isnode[x] = 1;
p[x][0] = y;
}
int lgn = (int)(log(n)/log(2))+1;
for(j = 1;j<=lgn;j++)
{
for(i = 0;i < n;i++)
{
p[a[i]][j] = p[p[a[i]][j-1]][j-1];
}
}
scanf("%d",&q);
assert(q>0 && q<=100000);
for(i = 0;i < q;i++)
{
scanf("%d",&ch);
assert(ch>=0 && ch<=2);
if(ch == 0) //Add an edge
{
scanf("%d %d",&x,&y);
assert(y>=1 && y<=100000);
assert(x>=1 && x<=100000);
assert(isnode[x]==1);
assert(isnode[y]==0);
isnode[y] = 1;
p[y][0] = x;
j = 0;
while(p[y][j]!=0)
{
p[y][j+1] = p[p[y][j]][j];
j++;
}
while(j<=lgn)
{
p[y][j] = 0;
j++;
}
}
else if(ch == 1) //Remove an edge
{
scanf("%d",&x);
assert(x>=1 && x<=100000);
assert(isnode[x]==1);
isnode[x] = 0;
for(j = 0;j <= lgn;j++)
{
p[x][j] = 0;
}
}
else
{
scanf("%d %d",&x,&y);
assert(x>=1 && x<=100000);
assert(y>=1 && y<=100000);
j = 0;
while(y>0)
{
if(y&1)
x = p[x][j];
y = y>>1;
j++;
}
printf("%d\n",x);
}
}
}
return 0;
}
</code></pre>
| 0 |
aug-2020-editorial-kth-parent
|
2013-08-13T08:25:00
|
{"contest_participation":3656,"challenge_submissions":458,"successful_submissions":180}
|
2013-08-13T08:25:00
|
2016-12-02T15:06:47
|
setter
|
###C++
```cpp
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <queue>
#include <stack>
#include <map>
#include <utility>
#include <algorithm>
#include <cassert>
using namespace std;
#define INF 2147483647
#define LINF 9223372036854775807
#define mp make_pair
#define pb push_back
typedef long long int lli;
typedef pair<int,int> pi;
int p[100000][40]={{0}};
int a[100005],isnode[100005];
int main ()
{
int q,ch,x,y,t;
scanf("%d",&t);
assert(t>=1 && t<=3);
while(t--)
{
memset(p,0,sizeof(p));
memset(isnode,0,sizeof(isnode));
int i,n,j;
scanf("%d",&n);
assert(n>=1 && n<=100000);
for(i = 0;i < n;i++)
{
scanf("%d %d",&x,&y);
assert(x>=1 && x<=100000);
assert(y>=0 && y<=100000);
a[i] = x;
if(y!=0)
assert(isnode[y]==1);
assert(isnode[x]==0);
isnode[x] = 1;
p[x][0] = y;
}
int lgn = (int)(log(n)/log(2))+1;
for(j = 1;j<=lgn;j++)
{
for(i = 0;i < n;i++)
{
p[a[i]][j] = p[p[a[i]][j-1]][j-1];
}
}
scanf("%d",&q);
assert(q>0 && q<=100000);
for(i = 0;i < q;i++)
{
scanf("%d",&ch);
assert(ch>=0 && ch<=2);
if(ch == 0) //Add an edge
{
scanf("%d %d",&x,&y);
assert(y>=1 && y<=100000);
assert(x>=1 && x<=100000);
assert(isnode[x]==1);
assert(isnode[y]==0);
isnode[y] = 1;
p[y][0] = x;
j = 0;
while(p[y][j]!=0)
{
p[y][j+1] = p[p[y][j]][j];
j++;
}
while(j<=lgn)
{
p[y][j] = 0;
j++;
}
}
else if(ch == 1) //Remove an edge
{
scanf("%d",&x);
assert(x>=1 && x<=100000);
assert(isnode[x]==1);
isnode[x] = 0;
for(j = 0;j <= lgn;j++)
{
p[x][j] = 0;
}
}
else
{
scanf("%d %d",&x,&y);
assert(x>=1 && x<=100000);
assert(y>=1 && y<=100000);
j = 0;
while(y>0)
{
if(y&1)
x = p[x][j];
y = y>>1;
j++;
}
printf("%d\n",x);
}
}
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:12
|
2016-07-23T13:56:04
|
C++
|
5 | 803 |
help-mike
|
Help Mike
|
Harvey Specter has agreed to take Mike Ross to a meeting filled with brilliant scientists at NSA Headquarters. But, as always, it's not going to be easy for Mike. He has to solve a puzzle given by Harvey.
Harvey gives two numbers N and K and defines a set A.<br>
*A = { x : x is a [natural number](https://en.wikipedia.org/wiki/Natural_number) ≤ N }*
(i.e), A = {1,2,3,4,5,6,...., N}
Mike has to find the total number of pairs of elements A[i] and A[j] belonging to the given set, such that, i < j and their sum is divisible by K<br>
**Input Format**
An integer T followed by T lines, each containing a pair of space separated integers N and K.
**Output Format**
T integers on separate lines. Each integer denotes the answer corresponding to that test case.
**Constraints**
1<=T<=100
K<=N<=10<sup>9</sup>
1<=K<=10000
**Sample Input**
2
10 4
7 3
**Sample Output**
10
7
**Explanation**
For the 1<sup>st</sup> test case, there are 10 pairs whose sum is divisible by 4.
(1,3), (1,7), (2,6), (2,10), (3,5), (3,9), (4,8), (5,7), (6,10) and (7,9)
For the 2<sup>nd</sup> test case, there are 7 pairs whose sum is divisible by 3.
(1,2), (1,5), (2,4), (2,7), (3,6), (4,5) and (5,7)
|
code
|
Help Mike attend the NSA meeting
|
ai
|
2013-08-13T09:29:32
|
2022-09-02T09:54:27
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER k
#
def solve(n, k):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
k = int(first_multiple_input[1])
result = solve(n, k)
fptr.write(str(result) + '\n')
fptr.close()
|
Harvey Specter has agreed to take Mike Ross to a meeting filled with brilliant scientists at NSA Headquarters. But, as always, it's not going to be easy for Mike. He has to solve a puzzle given by Harvey.
Harvey gives two numbers N and K and defines a set A.<br>
*A = { x : x is a [natural number](https://en.wikipedia.org/wiki/Natural_number) ≤ N }*
(i.e), A = {1,2,3,4,5,6,...., N}
Mike has to find the total number of pairs of elements A[i] and A[j] belonging to the given set, such that, i < j and their sum is divisible by K<br>
**Input Format**
An integer T followed by T lines, each containing a pair of space separated integers N and K.
**Output Format**
T integers on separate lines. Each integer denotes the answer corresponding to that test case.
**Constraints**
1<=T<=100
K<=N<=10<sup>9</sup>
1<=K<=10000
**Sample Input**
2
10 4
7 3
**Sample Output**
10
7
**Explanation**
For the 1<sup>st</sup> test case, there are 10 pairs whose sum is divisible by 4.
(1,3), (1,7), (2,6), (2,10), (3,5), (3,9), (4,8), (5,7), (6,10) and (7,9)
For the 2<sup>nd</sup> test case, there are 7 pairs whose sum is divisible by 3.
(1,2), (1,5), (2,4), (2,7), (3,6), (4,5) and (5,7)
| 0.579365 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
|
Help Mike - Sept 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem Statement</strong></p>
<p>Help Mike in finding the total number of pairs of elements A[i] and A[j] belonging to the given set such that i < j and their sum is divisible by K</p>
<p><strong>Difficulty Level</strong> Easy-Medium</p>
<p><strong>Required knowledge</strong> : Basic Hashing , Maths</p>
<p><strong>Time complexity</strong> : O(K) , O(1) will be accepted . O(N/K) or O(N) will go for TLE(time limit exceeded) under given time constraints.</p>
<p><strong>Approach</strong> :</p>
<p>To solve the problem in O(K) time limit, we can create an array rem[K]. The array rem[i] will store the number of integers in the set A, such that on dividing by K, you get i as the remainder. rem[i] can be calculated in O(1) time.
rem[i] = (N-i)/K;</p>
<p>Now, the sum of two integers is divisible by K if:</p>
<ul>
<li>Both numbers are divisible by K and such selection can be made in rem[0](rem[0]-1)/2 ways.</li>
<li>On dividing first number by K, reminder is p then on dividing second number K, reminder must be K-p . i.e. number of ways can be rem[p]*rem[K-p] where p can belong to 0 to K/2.</li>
<li>K is even and on dividing both numbers, the reminder is K/2 i.e. rem[K/2]*(rem[K/2]-1)/2 .</li>
</ul>
<p>We can sum up all these possibilities to get the required output.</p>
<p><strong>Problem Setter's code:</strong></p>
<pre><code>#include<bits/stdc++.h>
using namespace std;
#define print(p) cout<<p<<endl;
int main()
{
int T;
long long int N,K,i;
cin>>T;
while(T--)
{
cin>>N>>K;
long long int arr[K];
arr[0] = N/K;
for(i=1 ; i< K ; i++)
arr[i] = (int)(N-i)/K + 1;
if(K%2!=0)
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< (float)K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
cout<<sum<<endl;
}
else
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
sum = sum + (arr[K/2]*(arr[K/2] - 1))/2;
cout<<sum<<endl;
}
}
return 0;
}
</code></pre>
<p><strong>Problem Tester's Code</strong></p>
<pre><code>#!/usr/bin/py
import math
T = input()
1 <= T <= 100
for t in range(T):
N, K = map(int, raw_input().strip().split(" "))
assert 1 <= N <= 10**9
assert 1 <= K <= 10**4
assert K <= N
n_by_k = math.floor(N/K)
n_mod_k = N%K
count_less_than_k = K/2 if K % 2 == 1 else (K - 1)/2
sum = count_less_than_k*n_by_k
summation_limit = n_by_k - 1
sum += K*(summation_limit*(summation_limit + 1))/2
sum += (summation_limit+1)*(n_mod_k)
if n_mod_k > 0:
extra = n_mod_k - count_less_than_k
if K%2==0:
extra -= 1
sum += extra if extra > 0 else 0
print int(sum)
</code></pre>
| 0 |
sep-2020-editorial-help-mike
|
2013-09-16T13:48:37
|
{"contest_participation":3240,"challenge_submissions":1167,"successful_submissions":494}
|
2013-09-16T13:48:37
|
2016-12-03T12:59:31
|
setter
|
###C++
```cpp
#include<bits/stdc++.h>
using namespace std;
#define print(p) cout<<p<<endl;
int main()
{
int T;
long long int N,K,i;
cin>>T;
while(T--)
{
cin>>N>>K;
long long int arr[K];
arr[0] = N/K;
for(i=1 ; i< K ; i++)
arr[i] = (int)(N-i)/K + 1;
if(K%2!=0)
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< (float)K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
cout<<sum<<endl;
}
else
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
sum = sum + (arr[K/2]*(arr[K/2] - 1))/2;
cout<<sum<<endl;
}
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T17:46:38
|
C++
|
6 | 803 |
help-mike
|
Help Mike
|
Harvey Specter has agreed to take Mike Ross to a meeting filled with brilliant scientists at NSA Headquarters. But, as always, it's not going to be easy for Mike. He has to solve a puzzle given by Harvey.
Harvey gives two numbers N and K and defines a set A.<br>
*A = { x : x is a [natural number](https://en.wikipedia.org/wiki/Natural_number) ≤ N }*
(i.e), A = {1,2,3,4,5,6,...., N}
Mike has to find the total number of pairs of elements A[i] and A[j] belonging to the given set, such that, i < j and their sum is divisible by K<br>
**Input Format**
An integer T followed by T lines, each containing a pair of space separated integers N and K.
**Output Format**
T integers on separate lines. Each integer denotes the answer corresponding to that test case.
**Constraints**
1<=T<=100
K<=N<=10<sup>9</sup>
1<=K<=10000
**Sample Input**
2
10 4
7 3
**Sample Output**
10
7
**Explanation**
For the 1<sup>st</sup> test case, there are 10 pairs whose sum is divisible by 4.
(1,3), (1,7), (2,6), (2,10), (3,5), (3,9), (4,8), (5,7), (6,10) and (7,9)
For the 2<sup>nd</sup> test case, there are 7 pairs whose sum is divisible by 3.
(1,2), (1,5), (2,4), (2,7), (3,6), (4,5) and (5,7)
|
code
|
Help Mike attend the NSA meeting
|
ai
|
2013-08-13T09:29:32
|
2022-09-02T09:54:27
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER k
#
def solve(n, k):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
k = int(first_multiple_input[1])
result = solve(n, k)
fptr.write(str(result) + '\n')
fptr.close()
|
Harvey Specter has agreed to take Mike Ross to a meeting filled with brilliant scientists at NSA Headquarters. But, as always, it's not going to be easy for Mike. He has to solve a puzzle given by Harvey.
Harvey gives two numbers N and K and defines a set A.<br>
*A = { x : x is a [natural number](https://en.wikipedia.org/wiki/Natural_number) ≤ N }*
(i.e), A = {1,2,3,4,5,6,...., N}
Mike has to find the total number of pairs of elements A[i] and A[j] belonging to the given set, such that, i < j and their sum is divisible by K<br>
**Input Format**
An integer T followed by T lines, each containing a pair of space separated integers N and K.
**Output Format**
T integers on separate lines. Each integer denotes the answer corresponding to that test case.
**Constraints**
1<=T<=100
K<=N<=10<sup>9</sup>
1<=K<=10000
**Sample Input**
2
10 4
7 3
**Sample Output**
10
7
**Explanation**
For the 1<sup>st</sup> test case, there are 10 pairs whose sum is divisible by 4.
(1,3), (1,7), (2,6), (2,10), (3,5), (3,9), (4,8), (5,7), (6,10) and (7,9)
For the 2<sup>nd</sup> test case, there are 7 pairs whose sum is divisible by 3.
(1,2), (1,5), (2,4), (2,7), (3,6), (4,5) and (5,7)
| 0.579365 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
|
Help Mike - Sept 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem Statement</strong></p>
<p>Help Mike in finding the total number of pairs of elements A[i] and A[j] belonging to the given set such that i < j and their sum is divisible by K</p>
<p><strong>Difficulty Level</strong> Easy-Medium</p>
<p><strong>Required knowledge</strong> : Basic Hashing , Maths</p>
<p><strong>Time complexity</strong> : O(K) , O(1) will be accepted . O(N/K) or O(N) will go for TLE(time limit exceeded) under given time constraints.</p>
<p><strong>Approach</strong> :</p>
<p>To solve the problem in O(K) time limit, we can create an array rem[K]. The array rem[i] will store the number of integers in the set A, such that on dividing by K, you get i as the remainder. rem[i] can be calculated in O(1) time.
rem[i] = (N-i)/K;</p>
<p>Now, the sum of two integers is divisible by K if:</p>
<ul>
<li>Both numbers are divisible by K and such selection can be made in rem[0](rem[0]-1)/2 ways.</li>
<li>On dividing first number by K, reminder is p then on dividing second number K, reminder must be K-p . i.e. number of ways can be rem[p]*rem[K-p] where p can belong to 0 to K/2.</li>
<li>K is even and on dividing both numbers, the reminder is K/2 i.e. rem[K/2]*(rem[K/2]-1)/2 .</li>
</ul>
<p>We can sum up all these possibilities to get the required output.</p>
<p><strong>Problem Setter's code:</strong></p>
<pre><code>#include<bits/stdc++.h>
using namespace std;
#define print(p) cout<<p<<endl;
int main()
{
int T;
long long int N,K,i;
cin>>T;
while(T--)
{
cin>>N>>K;
long long int arr[K];
arr[0] = N/K;
for(i=1 ; i< K ; i++)
arr[i] = (int)(N-i)/K + 1;
if(K%2!=0)
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< (float)K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
cout<<sum<<endl;
}
else
{
long long int sum = 0;
sum = sum + (arr[0]*(arr[0] - 1))/2;
for(i=1 ; i< K/2 ; i++)
{
sum = sum + arr[i]*arr[K-i];
}
sum = sum + (arr[K/2]*(arr[K/2] - 1))/2;
cout<<sum<<endl;
}
}
return 0;
}
</code></pre>
<p><strong>Problem Tester's Code</strong></p>
<pre><code>#!/usr/bin/py
import math
T = input()
1 <= T <= 100
for t in range(T):
N, K = map(int, raw_input().strip().split(" "))
assert 1 <= N <= 10**9
assert 1 <= K <= 10**4
assert K <= N
n_by_k = math.floor(N/K)
n_mod_k = N%K
count_less_than_k = K/2 if K % 2 == 1 else (K - 1)/2
sum = count_less_than_k*n_by_k
summation_limit = n_by_k - 1
sum += K*(summation_limit*(summation_limit + 1))/2
sum += (summation_limit+1)*(n_mod_k)
if n_mod_k > 0:
extra = n_mod_k - count_less_than_k
if K%2==0:
extra -= 1
sum += extra if extra > 0 else 0
print int(sum)
</code></pre>
| 0 |
sep-2020-editorial-help-mike
|
2013-09-16T13:48:37
|
{"contest_participation":3240,"challenge_submissions":1167,"successful_submissions":494}
|
2013-09-16T13:48:37
|
2016-12-03T12:59:31
|
tester
|
###Python 2
```python
#!/usr/bin/py
import math
T = input()
1 <= T <= 100
for t in range(T):
N, K = map(int, raw_input().strip().split(" "))
assert 1 <= N <= 10**9
assert 1 <= K <= 10**4
assert K <= N
n_by_k = math.floor(N/K)
n_mod_k = N%K
count_less_than_k = K/2 if K % 2 == 1 else (K - 1)/2
sum = count_less_than_k*n_by_k
summation_limit = n_by_k - 1
sum += K*(summation_limit*(summation_limit + 1))/2
sum += (summation_limit+1)*(n_mod_k)
if n_mod_k > 0:
extra = n_mod_k - count_less_than_k
if K%2==0:
extra -= 1
sum += extra if extra > 0 else 0
print int(sum)
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T17:46:49
|
Python
|
7 | 800 |
chocolate-game
|
Chocolate Game
|
Laurel and Hardy have N piles of chocolates with each pile containing some number of chocolates. The piles are arranged from left to right in a non decreasing order based on the number of chocolates in each pile. They play the following game.
For every continuous subsequence of chocolate piles (at least 2 piles form a subsequence), you choose one of the piles and remove at least one chocolate from it. It should be noted that, on removal, the non-decreasing order of the chocolate piles must be maintained. The last person to make a valid move wins.
Suppose, Laurel plays first always. In how many of the continuous subsequences of chocolate piles will he win, if a game is played?
**Input Format**
The first line contains an integer N denoting the number of piles. The next line contains the number of chocolates in each pile, arranged from left to right and separated by a single space between them.
**Output Format**
A single integer denoting the number of continuous subsequences of chocolate piles in which Laurel will win.
**Constraints**
2 <= n <= 100000
1 <= d[i] <= 1,000,000,000
**Sample Input**
5
1 1 2 2 3
**Sample Output**
5
**Explanation**
Of the 10 continuous-sub-sequence of chocolate piles,
Laurel loses in [1,1], [1,1,2], [1,1,2,2], [1,2,2,3], [2,2] and
wins in [1,1,2,2,3], [1,2], [1,2,2], [2,2,3] and [2,3] and hence 5.
|
code
|
Count continuous sub-sequences for winning Chocolate Game.
|
ai
|
2013-08-09T20:02:16
|
2022-08-31T08:15:06
|
#
# Complete the 'chocolateGame' function below.
#
# The function is expected to return an INTEGER.
# The function accepts INTEGER_ARRAY arr as parameter.
#
def chocolateGame(arr):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
arr_count = int(input().strip())
arr = list(map(int, input().rstrip().split()))
result = chocolateGame(arr)
fptr.write(str(result) + '\n')
fptr.close()
|
Laurel and Hardy have $n$ piles of chocolates with each pile containing some number of chocolates. The piles are arranged from left to right in a non decreasing order based on the number of chocolates in each pile. They play the following game.
For every continuous subsequence of chocolate piles (at least 2 piles form a subsequence), Laurel and Hardy will play game on this subsequence of chocolate piles, Laurel plays first, and they play in turn. In one move, the player can choose one of the piles and remove at least one chocolate from it, but the non-decreasing order of the chocolate piles must be maintained. The last person to make a valid move wins.
How many continuous subsequences of chocolate piles will Laurel win if both of them play optimally? The number of chocolates of each pile will be recovered after the game ends for each subsequences.
| 0.487805 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains an integer $n$ denoting the number of piles.
The second line contains the number of chocolates in each pile, arranged from left to right and separated by a single space between them.
|
A single integer denoting the number of continuous subsequences of chocolate piles in which Laurel will win.
|
5
1 1 2 2 3
|
5
|
Hard
|
2020 September Editorial: Chocolate Game
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p>This is a challenging problem. In case of any queries beyond the scope of this editorial, contact our problem setter, WanBo: [email protected] </p>
<p>Let us start by simplifying this problem:
Given d[], can you win if you play first? </p>
<pre><code>d[0] <= d[1] <= ... <= d[n-1]
</code></pre>
<p>Transform d[] to another array a[] using the following transformation: <br>
a[i] = d[i+1] - d[i] </p>
<p>So from the array d[] we get a new array a[]: <br>
d[0], d[1], ... d[n-1] <br>
d[1] - d[0], d[2] - d[1], ..., d[n-1] - d[n-2] </p>
<pre><code>a[i] = d[i + 1] - d[i]
a[i - 1] = d[i] - d[i - 1]
</code></pre>
<p>If we remove x from d[i]: <br>
d[i] -= x ==> a[i] += x and a[i - 1] -= x
==> we remove x from the a[i - 1] and add it to a[i] </p>
<p>This is a classic staircase NIM game.
a[] with N elements is a win state
<==> 0 != xorsum{a[i] | 0 <= i < N and (N - i) % 2 == 1} </p>
<p>Naive solution to the original problem:</p>
for(i = 0; i + 1
<p>We transform this to: <br>
==></p>
<p>for(i = 0; i < n; i++)
for(j = i + 1; j < n; j++) {
xor = 0
for(k = j; k >= i; k -= 2) xor ^= d[k]
if(xor != 0) res++
}</p>
<p>==> The inner for(k = j; k >= i; k -= 2) can be easily optimized by maintain the xor prefix sum of odd position and even position separately. O(n^3) ==> O(n^2) </p>
<p>==>
We can find the number of losing states.
How many y exist such that x xor y == 0 for a given x? </p>
<p><==> Find the number of elements equals to x.
We can define a data structure to optimize this to O(n logn).
This need enough analysis and careful coding, but it is not the hardest part of this challenge. <br>
<br></p>
<h3>C++ Solution</h3>
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define LL long long
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr "#b": "void PV(T a, T b) {while(a != b)cout inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
templateinline bool chmax(T &a, T b) {return a v(d + i, d + j + 1);
for(int k = (int) v.size() - 1; k > 0; k--) v[k] -= v[k - 1];
reverse(ALL(v));
int xr = 0;
for(int k = 0; k 0) res++;
}
P(i);
}
return res;
}
map M;
LL solve() {
LL res = 0;
{
M.clear();
M[0] = 1;
int xr = 0;
for(int i = n - 1; i >= 0; i -= 2) {
int t = d[i];
if(i > 0) t = d[i] - d[i - 1];
res += M[xr ^ d[i]];
if(i > 0) res += M[xr ^ t];
xr ^= t;
M[xr]++;
}
}
{
M.clear();
M[0] = 1;
int xr = 0;
for(int i = n - 2; i >= 0; i -= 2) {
int t = d[i];
if(i > 0) t = d[i] - d[i - 1];
res += M[xr ^ d[i]];
if(i > 0) res += M[xr ^ t];
xr ^= t;
M[xr]++;
}
}
res = (LL) n * (n - 1) / 2 - res;
return res;
}
int main() {
ios_base::sync_with_stdio(0);
cin >> N;
assert(1 > d[i];
assert(1 = d[i - 1]);
n = N;
//LL res1 = brute();
LL res2 = solve();
cout
| 0 |
chocolate-game
|
2013-09-24T09:33:08
|
{"contest_participation":3240,"challenge_submissions":230,"successful_submissions":51}
|
2013-09-24T09:33:08
|
2016-07-23T16:18:17
|
setter
|
###C++
```cpp
#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<x<<"]\n";
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n";
#define P2(x,y) cerr<<"["#x" = "<<x<<", "#y" = "<<y<<"]\n";
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define mp make_pair
#define pb push_back
template<class T>void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T>inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T>inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
const int inf = 0x3f3f3f3f;
const int mod = int(1e9) + 7;
int N, n;
int d[100010];
int s[100010];
int s1[100010];
int s2[100010];
LL brute() {
LL res = 0;
for(int i = 0; i < n; i++) {
for(int j = i + 1; j < n; j++) {
vector<int> v(d + i, d + j + 1);
for(int k = (int) v.size() - 1; k > 0; k--) v[k] -= v[k - 1];
reverse(ALL(v));
int xr = 0;
for(int k = 0; k < v.size(); k += 2) xr ^= v[k];
if(xr > 0) res++;
}
P(i);
}
return res;
}
map<int, int> M;
LL solve() {
LL res = 0;
{
M.clear();
M[0] = 1;
int xr = 0;
for(int i = n - 1; i >= 0; i -= 2) {
int t = d[i];
if(i > 0) t = d[i] - d[i - 1];
res += M[xr ^ d[i]];
if(i > 0) res += M[xr ^ t];
xr ^= t;
M[xr]++;
}
}
{
M.clear();
M[0] = 1;
int xr = 0;
for(int i = n - 2; i >= 0; i -= 2) {
int t = d[i];
if(i > 0) t = d[i] - d[i - 1];
res += M[xr ^ d[i]];
if(i > 0) res += M[xr ^ t];
xr ^= t;
M[xr]++;
}
}
res = (LL) n * (n - 1) / 2 - res;
return res;
}
int main() {
ios_base::sync_with_stdio(0);
cin >> N;
assert(1 <= N && N <= 100000);
for(int i = 0; i < N; i++) {
cin >> d[i];
assert(1 <= d[i] && d[i] <= 1000000000);
}
for(int i = 1; i < N; i++) assert(d[i] >= d[i - 1]);
n = N;
//LL res1 = brute();
LL res2 = solve();
cout << res2 << endl;
//P2(res1, res2);
//assert(res1 == res2);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T16:18:18
|
C++
|
8 | 836 |
sherlock-puzzle
|
Sherlock Puzzle
|
Sherlock Holmes is bored to death as there aren't any interesting cases to solve. Dr Watson finding it impossible to be around Sherlock goes out to get some fresh air. Just as he lays his feet out of the door, he is thrown right back into his house by the explosion in front of his apartment. The metropolitan police arrive at the scene a few minutes later. They search the place thoroughly for any evidence that could throw some light on the event that unfolded. Unable to get any clues, they call Sherlock for help. After repeated persuasion by Mycroft Holmes and Dr Watson, Sherlock agrees to look at the crime scene.
Sherlock walks into the apartment, the walls are all black and dripping wet as the fire was recently extinguished. With his skills, he observes, deduces and eliminates the impossible. What's left after it is a simple puzzle left by an evil computer genius and the future Arch Nemesis of Sherlock, Jim Moriarty.
Given a binary string (**S**) which contains '0's and '1's and an integer **K**,
find the length (**L**) of the longest contiguous subsequence of (S * K) such that twice the number of zeroes is <= thrice the number of ones (2 * #0s <= 3 * #1s) in that sequence.
S * K is defined as follows:
S * 1 = S
S * K = S + S * (K - 1)
**Input Format**
The first (and only) line contains an integer K and the binary string S separated by a single space.
**Constraints**
1 <= |S| <= 1,000,000
1 <= K <= 1,000,000
**Output Format**
A single integer L - the answer to the test case
**Sample Input**
2 00010
**Sample Output**
2
**Explanation**
S * K = 0001000010
"1" and "10" meet the requirement that 2 * #0 <= 3 * #1
The longest one is "10", length = 2.
|
code
|
Help Sherlock get close to his Arch Nemesis, Jim Moriarty.
|
ai
|
2013-08-24T15:49:01
|
2022-09-02T09:54:36
| null | null | null |
Sherlock Holmes is bored to death as there aren't any interesting cases to solve. Dr Watson finding it impossible to be around Sherlock goes out to get some fresh air. Just as he lays his feet out of the door, he is thrown right back into his house by the explosion in front of his apartment. The metropolitan police arrive at the scene a few minutes later. They search the place thoroughly for any evidence that could throw some light on the event that unfolded. Unable to get any clues, they call Sherlock for help. After repeated persuasion by Mycroft Holmes and Dr Watson, Sherlock agrees to look at the crime scene.
Sherlock walks into the apartment, the walls are all black and dripping wet as the fire was recently extinguished. With his skills, he observes, deduces and eliminates the impossible. What's left after it is a simple puzzle left by an evil computer genius and the future Arch Nemesis of Sherlock, Jim Moriarty.
Given a binary string (**S**) which contains '0's and '1's and an integer **K**,
find the length (**L**) of the longest contiguous subsequence of (S * K) such that twice the number of zeroes is <= thrice the number of ones (2 * #0s <= 3 * #1s) in that sequence.
S * K is defined as follows:
S * 1 = S
S * K = S + S * (K - 1)
**Input Format**
The first (and only) line contains an integer K and the binary string S separated by a single space.
**Constraints**
1 <= |S| <= 1,000,000
1 <= K <= 1,000,000
**Output Format**
A single integer L - the answer to the test case
**Sample Input**
2 00010
**Sample Output**
2
**Explanation**
S * K = 0001000010
"1" and "10" meet the requirement that 2 * #0 <= 3 * #1
The longest one is "10", length = 2.
| 0.567568 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
2020 September Editorial: Sherlock Puzzle
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p>For any more queries, beyond the scope of this editorial, feel free to contact our problem setter WanBo: [email protected] </p>
<p>What is the longest contiguous sub-sequence of (S * K) with (2 * number of zeroes <= 3 * number of ones)?
Let replace '0' by -2 and '1' by 3: </p>
<p>Then we need to find the longest sub-string such that the sum[i, j] >= 0. </p>
<p><strong>1)</strong> If sum(S) >= 0, answer = len(S) * K</p>
<p><strong>2)</strong> If S == 1, how can we find the answer? <br>
p[i] = S[0] + S[1] + ... + S[i]
sum[i, j] = p[j + 1] - p[i] <br>
==> For every i, we just need to find the largest j that p[j] >= p[i]. </p>
<p><strong>How do we accelerate the search?</strong> <br>
n can be as large as 10^6 so we need to find the j for every i at least O(log n). But p[i] is not ordered, and because of this we can not use binary search directly. </p>
<pre><code>If rmax[k] = max{p[i] | k <= i < n}
==> rmax[0] >= rmax[1] >= ... >= rmax[n - 1]
</code></pre>
<p>Then for every i, we just need to find the largest k that rmax[k] >= p[i]. We can solve it by binary search. We can solve this sub-problem O(nlogn). </p>
<p>Now, can we optimize O(nlogn) to O(n)? <br>
Observe that when you find a best interval (i0,j0) and want to find a better (i1,j1) with i1 > i0, there must be p[i1] < p[i0] and j1 > j0 (An exercise to the reader - Why?). Therefore, you increment the value of i until you find smaller value of p[i], and then increase j until rmax[j + 1] < p[i]. We will increase i, j at most 2 * n times, so that we can solve it linearly. </p>
<p><strong>3)</strong> If S > 1, how do we solve this problem? <br>
If the longest subsequence is a substring of S, then we can solve it as S == 1. Else we need to maximize the length of suffix(S) + S * i + prefix(S) <br>
suffix(S)_1 + S * i + prefix(S)_1 >= suffix(S)_2 + S * j + prefix(S)_2 <br>
S + S * i + S > S * j ==> i >= j - 1. <br>
Obviously, i >= j - 1, so the best i will be the (largest_i) or (largest_i - 1). </p>
<p>How do we calculate the largest_i? </p>
<pre><code>T = sum(suffix(S) + prefix(S))
largest_i = -T / sum(S)
</code></pre>
<p>We can set the i to largest_i and largest_i - 1, and choose the best answer. </p>
<p>If we set i = x: <br>
T + S * x >= 0 ==> T >= -S * x. </p>
<p><strong>What we need to solve is:</strong> <br>
What's the longest suffix(S) + prefix(S) that sum of this should be >= -S * x </p>
<p>==> sub-problem: <br>
S[i, ..., n - 1] + S[0, ..., j] >= threshold
What the maximal n - i + (j + 1)? </p>
<p>For suffix(S): <br>
If rsum[i] = sum[i, n - 1] <br>
If i0 < i1 and rsum[i0] >= rsum[i1], then i1 can not be the best choice. <br>
We can maintain a monotonous sequence of suffix that:
(i0, rsum[i0]) (i1, rsum[i1]) ... <br>
i0 < i1 < ... <br>
sum[i0] < sum[i1] < ... </p>
<p>For prefix(S): <br>
If lsum[i] = sum[0, i] <br>
If i0 < i1 and lsum[i0] <= lsum[i1], then i0 can not be the best choice. <br>
We can maintain a monotonous sequence of suffix that:
(i0, lsum[i0]) (i1, lsum[i1]) ... <br>
i0 < i1 < ... <br>
sum[i0] > sum[i1] > ... </p>
<p>==> <br>
Given A[] and B[], A is increasing, B is decreasing, for every A[i], how to find the largest j that B[j] >= T - A[i].
This can be solve in O(n) like the method described in the case when K == 1. (exercise) </p>
<h3>C++ Solution from the Problem Setter, WanBo </h3>
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
typedef vector VI;
typedef pair PII;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr "#b": " void PV(T a, T b) {while(a != b)cout inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template inline bool chmax(T &a, T b) {return a L, R;
for(int i = n - 1; i >= 0; i--) {
while(!L.empty() && sL[i] >= L.back().x) L.pop_back();
L.pb(mp(sL[i], n - i));
}
for(int i = 0; i = R.back().x) R.pop_back();
R.pb(mp(sR[i], i + 1));
}
int res = 0;
for(int i = 0; i = least) chmax(res, L[i].y);
for(int i = 0; i = least) chmax(res, R[i].y);
int l = 0, r = (int) R.size() - 1;
while(l = 0) {
while(r >= 0 && L[l].x + R[r].x = 0) chmax(res, L[l].y + R[r].y);
l++;
}
return res;
}
int p[N];
int rmax[N];
LL solve() {
for(int i = 0; i = 0; i--) rmax[i] = max(rmax[i + 1], p[i]);
int mx = 0;
int l = 0;
int r = 0;
for(int i = 0; i = p[l]) continue;
int rr = -1;
while(r = 0) {
rr = r - i;
r++;
}
r--;
int len = rr;
if(mx pt(S.length() + 1, 0);
LL res = 0;
for(int i = 0; i = 0 && chmax(res, (LL)(j - i + 1))) {
pi = i, pj = j;
}
}
return res;
}
int main() {
cin >> K >> s;
n = s.length();
for(int i = 0; i = 0) {
res = (LL) n * K;
} else {
int tot = 0;
{
int mx = 0;
for(int i = n - 1; i >= 0; i--) {
sL[i] = sL[i + 1] + d[i];
chmax(mx, sL[i]);
}
tot += mx;
}
{
int mx = 0;
for(int i = 0; i 0) sR[i] = sR[i - 1] + d[i];
else sR[i] = d[i];
chmax(mx, sR[i]);
}
tot += mx;
}
if(K >= 2) {
LL T = min(K - 2, tot / abs(score));
res += n * T;
// P(res);
res += crossMid(-score * T);
chmax(res, solve());
} else {
res = solve();
}
}
cout
| 0 |
sep2020-sherlock-puzzle
|
2013-09-24T09:42:06
|
{"contest_participation":3240,"challenge_submissions":292,"successful_submissions":72}
|
2013-09-24T09:42:06
|
2016-07-23T17:59:56
|
setter
|
###C++
```cpp
#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <sstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int, int> PII;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<x<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<x<<", "#y" = "<<y<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define FOR(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define uni(v) sort(ALL(v)), v.resize(unique(ALL(v)) - v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n"); cout.flush();}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
const int inf = 0x3f3f3f3f;
const int mod = int(1e9) + 7;
const int N = 1111111;
string s;
int K;
int n;
int c0, c1;
int score;
int d[N];
int sL[N];
int sR[N];
int crossMid(int least) {
vector<PII> L, R;
for(int i = n - 1; i >= 0; i--) {
while(!L.empty() && sL[i] >= L.back().x) L.pop_back();
L.pb(mp(sL[i], n - i));
}
for(int i = 0; i < n; i++) {
while(!R.empty() && sR[i] >= R.back().x) R.pop_back();
R.pb(mp(sR[i], i + 1));
}
int res = 0;
for(int i = 0; i < L.size(); i++) if(L[i].x >= least) chmax(res, L[i].y);
for(int i = 0; i < R.size(); i++) if(R[i].x >= least) chmax(res, R[i].y);
int l = 0, r = (int) R.size() - 1;
while(l < L.size() && r >= 0) {
while(r >= 0 && L[l].x + R[r].x < least) r--;
if(r >= 0) chmax(res, L[l].y + R[r].y);
l++;
}
return res;
}
int p[N];
int rmax[N];
LL solve() {
for(int i = 0; i < n; i++) p[i + 1] = sR[i];
rmax[n] = p[n];
for(int i = n - 1; i >= 0; i--) rmax[i] = max(rmax[i + 1], p[i]);
int mx = 0;
int l = 0;
int r = 0;
for(int i = 0; i < n; i++) {
if(i != 0 && p[i] >= p[l]) continue;
int rr = -1;
while(r <= n && rmax[r] - p[i] >= 0) {
rr = r - i;
r++;
}
r--;
int len = rr;
if(mx <= len) {
mx = len;
l = i;
}
}
return mx;
}
LL brute() {
string S;
for(int i = 0; i < K; i++) S += s;
vector<int> pt(S.length() + 1, 0);
LL res = 0;
for(int i = 0; i < S.length(); i++) pt[i + 1] = pt[i] + d[i % n];
int pi = -1, pj = -1;
for(int i = 0; i < S.length(); i++)
for(int j = i; j < S.length(); j++) {
LL sc = pt[j + 1] - pt[i];
if(sc >= 0 && chmax(res, (LL)(j - i + 1))) {
pi = i, pj = j;
}
}
return res;
}
int main() {
cin >> K >> s;
n = s.length();
for(int i = 0; i < n; i++) {
if(s[i] == '0') {
c0++;
d[i] = -2;
} else {
c1++;
d[i] = 3;
}
score += d[i];
}
//P(score);
LL res = 0;
if(score >= 0) {
res = (LL) n * K;
} else {
int tot = 0;
{
int mx = 0;
for(int i = n - 1; i >= 0; i--) {
sL[i] = sL[i + 1] + d[i];
chmax(mx, sL[i]);
}
tot += mx;
}
{
int mx = 0;
for(int i = 0; i < n; i++) {
if(i > 0) sR[i] = sR[i - 1] + d[i];
else sR[i] = d[i];
chmax(mx, sR[i]);
}
tot += mx;
}
if(K >= 2) {
LL T = min(K - 2, tot / abs(score));
res += n * T;
// P(res);
res += crossMid(-score * T);
chmax(res, solve());
} else {
res = solve();
}
}
cout << res << endl;
//P(brute());
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T17:59:56
|
C++
|
9 | 1,049 |
angry-children-2
|
Angry Children 2
|
Bill Gates is on one of his philanthropic journeys to a village in Utopia. He has **N** packets of candies and would like to distribute one packet to each of the **K** children in the village (each packet may contain different number of candies). To avoid a fight between the children, he would like to pick **K** out of **N** packets such that the unfairness is minimized.
Suppose the **K** packets have (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>,....x<sub>k</sub>) candies in them, where x<sub>i</sub> denotes the number of candies in the i<sup>th</sup> packet, then we define *unfairness* as

where \|a\| denotes the absolute value of a.
**Input Format**
The first line contains an integer N.
The second line contains an integer K.
N lines follow each integer containing the candy in the i<sup>th</sup> packet.
**Output Format**
A single integer which will be minimum unfairness.
**Constraints**
2<=N<=10<sup>5</sup>
2<=K<=N
0<= number of candies in each packet <=10<sup>9</sup>
**Sample Input #00**
7
3
10
100
300
200
1000
20
30
**Sample Output #00**
40
**Explanation #00**
Bill Gates will choose packets having 10, 20 and 30 candies.So unfairness will be \|10-20\| + \|20-30\| + \|10-30\| = 40. We can verify that it will be minimum in this way.
**Sample Input #01**
10
4
1
2
3
4
10
20
30
40
100
200
**Sample Output #01**
10
**Explanation #01**
Bill Gates will choose 4 packets having 1,2,3 and 4 candies. So, unfairness will be \|1-2\| + \|1-3\| + \|1-4\| + \|2-3\| + \|2-4\| + \|3-4\| = 10
|
code
|
Select K elements from N elements such that the sum absolute value of differences of adjacent elements is minimized
|
ai
|
2013-10-08T12:22:10
|
2022-08-31T08:14:42
|
#
# Complete the 'angryChildren' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER k
# 2. INTEGER_ARRAY packets
#
def angryChildren(k, packets):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
k = int(input().strip())
packets = []
for _ in range(n):
packets_item = int(input().strip())
packets.append(packets_item)
result = angryChildren(k, packets)
fptr.write(str(result) + '\n')
fptr.close()
|
Bill Gates is on one of his philanthropic journeys to a village in Utopia. He has brought a box of packets of candies and would like to distribute one packet to each of the children. Each of the packets contains a number of candies. He wants to minimize the cumulative difference in the number of candies in the packets he hands out. This is called the *unfairness sum*. Determine the minimum unfairness sum achievable.
For example, he brings $n = 7$ packets where the number of candies is $packets = [3,3,4,5,7,9,10]$. There are $k = 3$ children. The minimum difference between all packets can be had with $3, 3, 4$ from indices $0, 1$ and $2$. We must get the difference in the following pairs: $\{(0,1),(0,2),(1,2)\}$. We calculate the *unfairness sum* as:
```
packets candies
0 3 indices difference result
1 3 (0,1),(0,2) |3-3| + |3-4| 1
2 4 (1,2) |3-4| 1
Total = 2
```
**Function Description**
Complete the *angryChildren* function in the editor below. It should return an integer that represents the minimum unfairness sum achievable.
angryChildren has the following parameter(s):
- *k*: an integer that represents the number of children
- *packets*: an array of integers that represent the number of candies in each packet
| 0.532895 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains an integer $n$.
The second line contains an integer $k$.
Each of the next $n$ lines contains an integer $packets[i]$.
|
A single integer representing the minimum achievable unfairness sum.
**Sample Input 0**
7
3
10
100
300
200
1000
20
30
**Sample Output 0**
40
**Explanation 0**
Bill Gates will choose packets having 10, 20 and 30 candies. The unfairness sum is $|10-20| + |20-30| + |10-30| = 40$.
**Sample Input 1**
10
4
1
2
3
4
10
20
30
40
100
200
**Sample Output 1**
10
**Explanation 1**
Bill Gates will choose 4 packets having 1,2,3 and 4 candies. The unfairness sum i $|1-2| + |1-3| + |1-4| + |2-3| + |2-4| + |3-4| = 10$.
|
Hard
|
Angry Children 2 : Oct 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/oct13/challenges/angry-children-2">Angry Children 2</a></p>
<p>Choose K out of N elements of an array, following the given constraints. Read the complete problem statement <a href="https://www.hackerrank.com/contests/oct13/challenges/angry-children-2">here</a> </p>
<p><strong>Difficulty Level</strong></p>
<p>Medium</p>
<p><strong>Required Knowledge</strong></p>
<p>Sorting, Easy Dynammic Progamming</p>
<p><strong>Time Complexity</strong></p>
<p>O(NlogN)</p>
<p><strong>Approach</strong></p>
<p>In this problem, we are given a list of N numbers out of which K numbers are to be chosen such that the anger coefficient is minimized. </p>
<p>Let us define D as the anger-coefficient of chosen K numbers.</p>
<p>First, we claim that k such numbers can only be obtained if we sort the list and chose k contiguous numbers. This can easily be proved. Suppose we choose numbers X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>,....X<sub>r</sub>, X<sub>r+1</sub>,....,X<sub>K</sub> (all are in increasing order but not continuous in the sorted list) i.e. there exists a number p which lies between X<sub>r</sub> and X<sub>r+1</sub>.Now, if we include p and drop X<sub>1</sub>, our anger coefficient will decrease by an amount = </p>
<p>( |X<sub>1</sub> - X<sub>2</sub>| + |X<sub>1</sub> - X<sub>3</sub>| + .... + |X<sub>1</sub> - X<sub>K</sub>| ) - ( |p - X<sub>2</sub>| + |p - X<sub>3</sub>| + .... + |p - X<sub>K</sub>| )</p>
<p>which is certainly positive. This shows that the solution will consist of k continues elements of the sorted list. Now there exists (N-K+1) such sets of elements. The problem can be redefined as to find the minimum of the D obtained from all these sets. </p>
<p>First, we sort the list in increasing order: X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>,....X<sub>K</sub>,X<sub>K+1</sub>,....,X<sub>N</sub>. The next step is to find the value of D for the first K elements i.e. from X<sub>1</sub> to X<sub>K</sub>. suppose we have calculated D for first i elements. when we include X<sub>i+1</sub>, the value of D increases by ( |X<sub>i+1</sub> - X<sub>1</sub>| + |X<sub>i+1</sub> - X<sub>2</sub>| +....+ |X<sub>i+1</sub> - X<sub>i</sub>| ), which in turn is equal to ( i*X<sub>K</sub> - (X<sub>1</sub> + X<sub>2</sub> + ....+X<sub>i</sub>) ). We just need to store the sum of current elements and repeat the step for i = 1 to k-1.</p>
<p>Now that we have the solution for X<sub>1</sub> to X<sub>K</sub>, we would want to calculate the same for X<sub>2</sub> to X<sub>K+1</sub>. This can be done in O(1) time.</p>
<p>New anger coefficient = old anger coefficient + ( |X<sub>K+1</sub> - X<sub>2</sub>| + |X<sub>K+1</sub> - X<sub>3</sub>| + .... + |X<sub>K+1</sub> - X<sub>K</sub>| ) - ( |X<sub>1</sub> - X<sub>2</sub>| + |X<sub>1</sub> - X<sub>3</sub>| + .... + |X<sub>1</sub> - X<sub>K</sub>| ). This can be written in the following form:</p>
<p>New anger coefficient = old anger coefficient + K.(X<sub>K</sub> - X<sub>1</sub>) - K.(X<sub>1</sub> + X<sub>2</sub> +....+X<sub>K</sub>) + ( X<sub>1</sub> - X<sub>K</sub>)</p>
<p>At every point we just need to update the sum of the K elements, calculate the new anger co-efficient and update the minimum value of the same. </p>
<p><strong>Setter's Code</strong> :</p>
<pre><code>n = input()
k = input()
assert 1 <= n <= 10**5
assert 1 <= k <= n
lis = []
for i in range(n):
lis.append(input())
lis.sort()
sum_lis = []
for i in lis:
assert 0 <= i <= 10**9
val = 1-k
answer = 0
sum_lis.append(lis[0])
for i in range(1,n):
sum_lis.append(sum_lis[i-1]+lis[i])
for i in range(k):
answer += val*lis[i]
val += 2
final_answer = answer
for i in range(k,n):
new_answer = answer + (k-1)*lis[i] + (k-1)*lis[i-k] - 2*(sum_lis[i-1]-sum_lis[i-k])
final_answer = min(new_answer, final_answer)
answer = new_answer
print final_answer
</code></pre>
<p><strong>Tester's Code</strong> :</p>
<pre><code>#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<assert.h>
using namespace std;
#define Max_N 100001
typedef long long int ll;
long long int sum[Max_N];
int N,K,input[Max_N];
ll min(ll a,ll b)
{
if(a>b) return b;
else return a;
}
int main()
{
int val;
scanf("%d%d",&N,&K);
assert(1<=N && N<=100000);
assert(1<=K && K<=N);
for(int i=1;i<=N;i++)
{
scanf("%d",&input[i]);
assert(0<=input[i] && input[i]<=1000000000);
}
input[0]=0;
sort(input+1,input+N+1);
sum[0]=0;
for(int i=1;i<=N;i++) sum[i]=input[i]+sum[i-1];
val=1-K;
ll answer=0,compare,previous;
for(int i=1;i<=K;i++){
answer+=(ll)val*input[i];
val+=2;
}
//printf("%lld is answeer\n",answer);
previous=answer;
for(int i=K+1;i<=N;i++){
compare=(ll)(K-1)*input[i];
compare=previous + (ll)(K-1)*input[i] + (ll)(K-1)*input[i-K]-(ll)2*(sum[i-1]-sum[i-K]);
answer=min(answer,compare);
previous=compare;
}
printf("%lld\n",answer);
return 0;
}
</code></pre>
| 0 |
oct-2020-angry-children-ii
|
2013-10-29T06:01:32
|
{"contest_participation":7868,"challenge_submissions":2266,"successful_submissions":1120}
|
2013-10-29T06:01:32
|
2018-05-14T17:07:47
|
setter
|
###Python 2
```python
n = input()
k = input()
assert 1 <= n <= 10**5
assert 1 <= k <= n
lis = []
for i in range(n):
lis.append(input())
lis.sort()
sum_lis = []
for i in lis:
assert 0 <= i <= 10**9
val = 1-k
answer = 0
sum_lis.append(lis[0])
for i in range(1,n):
sum_lis.append(sum_lis[i-1]+lis[i])
for i in range(k):
answer += val*lis[i]
val += 2
final_answer = answer
for i in range(k,n):
new_answer = answer + (k-1)*lis[i] + (k-1)*lis[i-k] - 2*(sum_lis[i-1]-sum_lis[i-k])
final_answer = min(new_answer, final_answer)
answer = new_answer
print final_answer
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T14:51:01
|
Python
|
||
10 | 1,049 |
angry-children-2
|
Angry Children 2
|
Bill Gates is on one of his philanthropic journeys to a village in Utopia. He has **N** packets of candies and would like to distribute one packet to each of the **K** children in the village (each packet may contain different number of candies). To avoid a fight between the children, he would like to pick **K** out of **N** packets such that the unfairness is minimized.
Suppose the **K** packets have (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>,....x<sub>k</sub>) candies in them, where x<sub>i</sub> denotes the number of candies in the i<sup>th</sup> packet, then we define *unfairness* as

where \|a\| denotes the absolute value of a.
**Input Format**
The first line contains an integer N.
The second line contains an integer K.
N lines follow each integer containing the candy in the i<sup>th</sup> packet.
**Output Format**
A single integer which will be minimum unfairness.
**Constraints**
2<=N<=10<sup>5</sup>
2<=K<=N
0<= number of candies in each packet <=10<sup>9</sup>
**Sample Input #00**
7
3
10
100
300
200
1000
20
30
**Sample Output #00**
40
**Explanation #00**
Bill Gates will choose packets having 10, 20 and 30 candies.So unfairness will be \|10-20\| + \|20-30\| + \|10-30\| = 40. We can verify that it will be minimum in this way.
**Sample Input #01**
10
4
1
2
3
4
10
20
30
40
100
200
**Sample Output #01**
10
**Explanation #01**
Bill Gates will choose 4 packets having 1,2,3 and 4 candies. So, unfairness will be \|1-2\| + \|1-3\| + \|1-4\| + \|2-3\| + \|2-4\| + \|3-4\| = 10
|
code
|
Select K elements from N elements such that the sum absolute value of differences of adjacent elements is minimized
|
ai
|
2013-10-08T12:22:10
|
2022-08-31T08:14:42
|
#
# Complete the 'angryChildren' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER k
# 2. INTEGER_ARRAY packets
#
def angryChildren(k, packets):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
k = int(input().strip())
packets = []
for _ in range(n):
packets_item = int(input().strip())
packets.append(packets_item)
result = angryChildren(k, packets)
fptr.write(str(result) + '\n')
fptr.close()
|
Bill Gates is on one of his philanthropic journeys to a village in Utopia. He has brought a box of packets of candies and would like to distribute one packet to each of the children. Each of the packets contains a number of candies. He wants to minimize the cumulative difference in the number of candies in the packets he hands out. This is called the *unfairness sum*. Determine the minimum unfairness sum achievable.
For example, he brings $n = 7$ packets where the number of candies is $packets = [3,3,4,5,7,9,10]$. There are $k = 3$ children. The minimum difference between all packets can be had with $3, 3, 4$ from indices $0, 1$ and $2$. We must get the difference in the following pairs: $\{(0,1),(0,2),(1,2)\}$. We calculate the *unfairness sum* as:
```
packets candies
0 3 indices difference result
1 3 (0,1),(0,2) |3-3| + |3-4| 1
2 4 (1,2) |3-4| 1
Total = 2
```
**Function Description**
Complete the *angryChildren* function in the editor below. It should return an integer that represents the minimum unfairness sum achievable.
angryChildren has the following parameter(s):
- *k*: an integer that represents the number of children
- *packets*: an array of integers that represent the number of candies in each packet
| 0.532895 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains an integer $n$.
The second line contains an integer $k$.
Each of the next $n$ lines contains an integer $packets[i]$.
|
A single integer representing the minimum achievable unfairness sum.
**Sample Input 0**
7
3
10
100
300
200
1000
20
30
**Sample Output 0**
40
**Explanation 0**
Bill Gates will choose packets having 10, 20 and 30 candies. The unfairness sum is $|10-20| + |20-30| + |10-30| = 40$.
**Sample Input 1**
10
4
1
2
3
4
10
20
30
40
100
200
**Sample Output 1**
10
**Explanation 1**
Bill Gates will choose 4 packets having 1,2,3 and 4 candies. The unfairness sum i $|1-2| + |1-3| + |1-4| + |2-3| + |2-4| + |3-4| = 10$.
|
Hard
|
Angry Children 2 : Oct 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/oct13/challenges/angry-children-2">Angry Children 2</a></p>
<p>Choose K out of N elements of an array, following the given constraints. Read the complete problem statement <a href="https://www.hackerrank.com/contests/oct13/challenges/angry-children-2">here</a> </p>
<p><strong>Difficulty Level</strong></p>
<p>Medium</p>
<p><strong>Required Knowledge</strong></p>
<p>Sorting, Easy Dynammic Progamming</p>
<p><strong>Time Complexity</strong></p>
<p>O(NlogN)</p>
<p><strong>Approach</strong></p>
<p>In this problem, we are given a list of N numbers out of which K numbers are to be chosen such that the anger coefficient is minimized. </p>
<p>Let us define D as the anger-coefficient of chosen K numbers.</p>
<p>First, we claim that k such numbers can only be obtained if we sort the list and chose k contiguous numbers. This can easily be proved. Suppose we choose numbers X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>,....X<sub>r</sub>, X<sub>r+1</sub>,....,X<sub>K</sub> (all are in increasing order but not continuous in the sorted list) i.e. there exists a number p which lies between X<sub>r</sub> and X<sub>r+1</sub>.Now, if we include p and drop X<sub>1</sub>, our anger coefficient will decrease by an amount = </p>
<p>( |X<sub>1</sub> - X<sub>2</sub>| + |X<sub>1</sub> - X<sub>3</sub>| + .... + |X<sub>1</sub> - X<sub>K</sub>| ) - ( |p - X<sub>2</sub>| + |p - X<sub>3</sub>| + .... + |p - X<sub>K</sub>| )</p>
<p>which is certainly positive. This shows that the solution will consist of k continues elements of the sorted list. Now there exists (N-K+1) such sets of elements. The problem can be redefined as to find the minimum of the D obtained from all these sets. </p>
<p>First, we sort the list in increasing order: X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>,....X<sub>K</sub>,X<sub>K+1</sub>,....,X<sub>N</sub>. The next step is to find the value of D for the first K elements i.e. from X<sub>1</sub> to X<sub>K</sub>. suppose we have calculated D for first i elements. when we include X<sub>i+1</sub>, the value of D increases by ( |X<sub>i+1</sub> - X<sub>1</sub>| + |X<sub>i+1</sub> - X<sub>2</sub>| +....+ |X<sub>i+1</sub> - X<sub>i</sub>| ), which in turn is equal to ( i*X<sub>K</sub> - (X<sub>1</sub> + X<sub>2</sub> + ....+X<sub>i</sub>) ). We just need to store the sum of current elements and repeat the step for i = 1 to k-1.</p>
<p>Now that we have the solution for X<sub>1</sub> to X<sub>K</sub>, we would want to calculate the same for X<sub>2</sub> to X<sub>K+1</sub>. This can be done in O(1) time.</p>
<p>New anger coefficient = old anger coefficient + ( |X<sub>K+1</sub> - X<sub>2</sub>| + |X<sub>K+1</sub> - X<sub>3</sub>| + .... + |X<sub>K+1</sub> - X<sub>K</sub>| ) - ( |X<sub>1</sub> - X<sub>2</sub>| + |X<sub>1</sub> - X<sub>3</sub>| + .... + |X<sub>1</sub> - X<sub>K</sub>| ). This can be written in the following form:</p>
<p>New anger coefficient = old anger coefficient + K.(X<sub>K</sub> - X<sub>1</sub>) - K.(X<sub>1</sub> + X<sub>2</sub> +....+X<sub>K</sub>) + ( X<sub>1</sub> - X<sub>K</sub>)</p>
<p>At every point we just need to update the sum of the K elements, calculate the new anger co-efficient and update the minimum value of the same. </p>
<p><strong>Setter's Code</strong> :</p>
<pre><code>n = input()
k = input()
assert 1 <= n <= 10**5
assert 1 <= k <= n
lis = []
for i in range(n):
lis.append(input())
lis.sort()
sum_lis = []
for i in lis:
assert 0 <= i <= 10**9
val = 1-k
answer = 0
sum_lis.append(lis[0])
for i in range(1,n):
sum_lis.append(sum_lis[i-1]+lis[i])
for i in range(k):
answer += val*lis[i]
val += 2
final_answer = answer
for i in range(k,n):
new_answer = answer + (k-1)*lis[i] + (k-1)*lis[i-k] - 2*(sum_lis[i-1]-sum_lis[i-k])
final_answer = min(new_answer, final_answer)
answer = new_answer
print final_answer
</code></pre>
<p><strong>Tester's Code</strong> :</p>
<pre><code>#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<assert.h>
using namespace std;
#define Max_N 100001
typedef long long int ll;
long long int sum[Max_N];
int N,K,input[Max_N];
ll min(ll a,ll b)
{
if(a>b) return b;
else return a;
}
int main()
{
int val;
scanf("%d%d",&N,&K);
assert(1<=N && N<=100000);
assert(1<=K && K<=N);
for(int i=1;i<=N;i++)
{
scanf("%d",&input[i]);
assert(0<=input[i] && input[i]<=1000000000);
}
input[0]=0;
sort(input+1,input+N+1);
sum[0]=0;
for(int i=1;i<=N;i++) sum[i]=input[i]+sum[i-1];
val=1-K;
ll answer=0,compare,previous;
for(int i=1;i<=K;i++){
answer+=(ll)val*input[i];
val+=2;
}
//printf("%lld is answeer\n",answer);
previous=answer;
for(int i=K+1;i<=N;i++){
compare=(ll)(K-1)*input[i];
compare=previous + (ll)(K-1)*input[i] + (ll)(K-1)*input[i-K]-(ll)2*(sum[i-1]-sum[i-K]);
answer=min(answer,compare);
previous=compare;
}
printf("%lld\n",answer);
return 0;
}
</code></pre>
| 0 |
oct-2020-angry-children-ii
|
2013-10-29T06:01:32
|
{"contest_participation":7868,"challenge_submissions":2266,"successful_submissions":1120}
|
2013-10-29T06:01:32
|
2018-05-14T17:07:47
|
tester
|
###C++
```cpp
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<assert.h>
using namespace std;
#define Max_N 100001
typedef long long int ll;
long long int sum[Max_N];
int N,K,input[Max_N];
ll min(ll a,ll b)
{
if(a>b) return b;
else return a;
}
int main()
{
int val;
scanf("%d%d",&N,&K);
assert(1<=N && N<=100000);
assert(1<=K && K<=N);
for(int i=1;i<=N;i++)
{
scanf("%d",&input[i]);
assert(0<=input[i] && input[i]<=1000000000);
}
input[0]=0;
sort(input+1,input+N+1);
sum[0]=0;
for(int i=1;i<=N;i++) sum[i]=input[i]+sum[i-1];
val=1-K;
ll answer=0,compare,previous;
for(int i=1;i<=K;i++){
answer+=(ll)val*input[i];
val+=2;
}
//printf("%lld is answeer\n",answer);
previous=answer;
for(int i=K+1;i<=N;i++){
compare=(ll)(K-1)*input[i];
compare=previous + (ll)(K-1)*input[i] + (ll)(K-1)*input[i-K]-(ll)2*(sum[i-1]-sum[i-K]);
answer=min(answer,compare);
previous=compare;
}
printf("%lld\n",answer);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T14:51:25
|
C++
|
||
11 | 1,084 |
period
|
Period
|
You are given 2 integers **a** and **b**. Let a number be defined as . As we know  will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define
 (where x an integer)<br /><br /> and the operation  on AC number as:

This problem is to find the smallest positive integer **n**, such that:

We call the integer **n** as period. You are given **a**, **b** and **m**. Can you figure out the period?
**Input Format**
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.
**Output Format**
Output the Period if it exists, otherwise output "-1" (quotes only for reference)
**Constraints**
1 ≤ T ≤ 300
5 ≤ m ≤ 10<sup>7</sup>
0 ≤ a, b < m
**Sample Input #00**
4
0 0 13
1 0 7
3 0 10007
1 1 19
**Sample Output #00**
-1
1
5003
18
**Explanation #00**
For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.
|
code
|
Can you find the period?
|
ai
|
2013-10-16T05:50:59
|
2022-09-02T09:54:45
| null | null | null |
You are given 2 integers **a** and **b**. Let a number be defined as
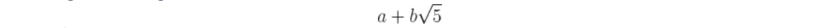. As we know 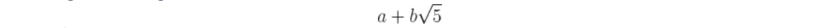 will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define
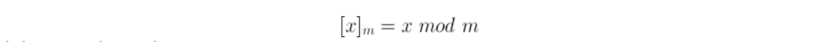 (where x an integer)<br /><br /> and the operation  on AC number as:
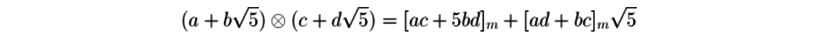
This problem is to find the smallest positive integer **n**, such that:

We call the integer **n** as period. You are given **a**, **b** and **m**. Can you figure out the period?
**Input Format**
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.
**Output Format**
Output the Period if it exists, otherwise output "-1" (quotes only for reference)
**Constraints**
1 ≤ T ≤ 300
5 ≤ m ≤ 10<sup>7</sup>
0 ≤ a, b < m
**Sample Input #00**
4
0 0 13
1 0 7
3 0 10007
1 1 19
**Sample Output #00**
-1
1
5003
18
**Explanation #00**
For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.
| 0.564516 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
|
Hard
|
Period : Oct 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem</strong> <a href="https://www.hackerrank.com/contests/oct13/challenges/period">Period</a></p>
<p><strong>Difficulty</strong> : Medium-Hard</p>
<p><strong>Required Knowledge</strong> : Group Theory, Euler's Criterion, Lagrange's theorem</p>
<p><strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/AekdyCoin">AekDy Coin</a></p>
<p><strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/cpcs">Cao Peng</a></p>
<p><strong>Approach</strong></p>
<p>For one given P, the AC number <img src="https://hr-filepicker.s3.amazonaws.com/period1.png" alt="image1" title=""> that satisfies 0 ≤ a,b < p
and a<sup>2</sup> ≅ 5b<sup>2</sup>(mod P) have th property:</p>
<p>Suppose, </p>
<p>∀n ∈ Z<sup>+</sup>, <br>
(a + b√5)<sup>n</sup> = c + d√5</p>
<p>Then we have c<sup>2</sup> = 5d<sup>2</sup>(mod P) <br>
Quite obvious by mathematical induction.
So if a<sup>2</sup> ≅5b<sup>2</sup>(mod P), we could not find the Period since the expected result AC number is with c=1 and d = 0.</p>
<p>So for the remaindering AC number, we have a<sup>2</sup>≠5b<sup>2</sup>(mod P) <br>
If 5 is one quadratic residue modulo P, then we can find (P-1)<sup>2</sup> such unique AC number satisfy. a<sup>2</sup>≠5b<sup>2</sup>(mod P) </p>
<p>Proof:</p>
<p>If 5 is one quadratic residue modulo P , then for the <a href="https://en.wikipedia.org/wiki/Primitive_root_modulo_n">primitive root</a> <strong>g</strong>, we have </p>
<p>g<sup>2k</sup> ≅5(mod P) the AC number such that a<sup>2</sup>≅5b<sup>2</sup>(mod P) must satisfy:</p>
<p>g<sup>2I(a)</sup>≅g<sup>2k</sup>g<sup>2I(b)</sup>(mod P), which means </p>
<p>2I(a)≅2(k+I(b))(mod P - 1), there are totally 2(P-1) AC number that satisfy that condition. (which means they also satisfy </p>
<p>a<sup>2</sup>≅5b<sup>2</sup>(mod P), but don't forget 0 + 0√5, so there are </p>
<p>P<sup>2</sup> - 2(P-1) - 1 = (P-1)<sup>2</sup> AC numbers such that a<sup>2</sup>≠5b<sup>2</sup>(mod P) </p>
<p>If 5 is not one quadratic residue modulo P, then we can find P<sup>2</sup> - 1 = (P-1)(P+1) such unique AC number satisfies, </p>
<p>a<sup>2</sup>≠5b<sup>2</sup>(mod P), because only one AC number o + 0√5 satisfies, </p>
<p>a<sup>2</sup>≅5b<sup>2</sup>(mod P) </p>
<p>We can use <a href="https://en.wikipedia.org/wiki/Euler%27s_criterion">Euler's Criterion</a> to judge whether 5 is one quadratic residue modulo P in O(logP) time.
The identity element in this group is 1.
However there are other 2 properties that guarantee it is a group. I will ignore the proof here.</p>
<p>Finally, base one [Lagrange's Theorem)(<a href="http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)">http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)</a>) we have
Period C, where C is the number of AC number satisfies
a<sup>2</sup>≠5b<sup>2</sup>(mod P). Simple brute force will work. </p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include<iostream>
#include<queue>
#include<cstdio>
#include<cmath>
#include<string>
#include<vector>
#include<algorithm>
#include<stack>
#include<cstring>
#include<map>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define pb push_back
#define mp make_pair
bool isPrime(int n) {
if(n==1)return 0;
for(int i =2; i * i <= n; ++ i) if( n % i == 0 ) return 0;
return 1;
}
inline LL MOD(LL a, LL b) {a%=b; return a<0?a+b:a;}
LL powmod(LL a, LL b, LL c){
LL ret = 1%c; a%=c;
while(b){
if(b&1)ret=ret*a%c;
a=a*a%c;
b>>=1;
}
return ret;
}
// P is one prime number
LL inv( LL a, LL p) {return powmod( a, p - 2, p ) ; }
LL P;
class Element {
public:
LL a, b;
// a + b Sqrt(5)
Element(){}
Element(LL _a, LL _b) :a(_a),b(_b){}
Element operator+(const Element e) {
return Element(MOD(a + e.a , P),MOD(b + e.b , P));
}
Element operator*(const Element e) {
return Element(MOD(a*e.a + b*e.b * 5, P),MOD(a*e.b+b*e.a, P));
}
Element operator^(LL k){
if(k==0) return Element(1,0);
--k;
Element ret = *this, a = *this;
while(k){
if(k&1) ret= ret * a ;
a = a * a;
k >>= 1;
}
return ret;
}
Element inverse(){
if(!a&&!b) return *this;
if(b == 0) {
return Element(inv(a, P) , 0 );
}
if(a == 0) {
return Element(0, inv(5*b%P, P));
}
LL iv = inv( MOD(-b,P) , P );
LL x, y;
y = inv( iv * (a*a%P) % P + b*5 , P );
x = (iv * a % P * y) % P;
return Element( x, y) ;
}
bool isZ(){
return !a && !b;
}
bool isE(){
return a == 1 && b == 0;
}
bool operator<(const Element e) const {
if(a == e.a) return b < e.b;
return a < e.a;
}
void rand_gen(){
do{a = rand()%P; b= rand()%P;}while(0);
}
void out(){
cout << a <<" " << b << endl;
}
};
// a + b Sqrt(5)
LL circle( Element a ) {
Element b =a;
LL c = 1;
while( ! a.isE( )) {
a = a * b;
++ c;
//a.out();
if(a.a == b.a && a.b == b.b) {
return - 1;
}
}
return c;
}
bool isRes(LL a, LL P ){
return powmod(a, (P-1)/2, P) == 1;
}
LL my_solution(Element e , LL P) {
LL a = e.a, b = e.b;
if(MOD(a*a-5*b*b,P)==0) return -1;
LL n = P*P,ans;
if(isRes(5,P)) {
n = n - 2*P+1;
}else -- n;
ans = n;
for(LL i = 1; i*i <= n; ++ i) if(n%i == 0) {
if( (Element(a,b) ^(i)).isE() )
ans = min(ans, i );
if( (Element(a,b) ^(n/i)).isE() )
ans = min(ans, n/i );
}
return ans;
}
void dp(){
while( true ) {
P = rand()%1000 + 6;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
LL my_ans = my_solution(e, P);
LL bf = circle(e) ;
static int cas = 0; ++ cas;
if(my_ans == bf) {
cout <<"correct @" << cas <<" ans = " << my_ans<< endl;
}else {
cout <<"error"<<endl;
cout << P << endl;
e.out();
return;
}
}
}
Element rand_one_bad(LL P) {
for (LL a = 1; a < P; ++a)
for (LL b = 1; b < P; ++b) {
if (MOD(a * a - 5 * b * b, P) == 0) {
return Element(a, b);
}
}
return Element(0,0);
}
void gen(int x ){
char in[] = "input00.in";
in[6]='0'+x;
freopen(in,"w", stdout);
int T = (x+1)*10;
int LIMIT[] = {100, 10000, 1e6,1e6};
cout << T << endl;
while(T --) {
P = rand()% (int)LIMIT[x/3] + 13;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
if( P < 1e4 && isRes(5,P) && rand()%2 == 0) {
e = rand_one_bad(P);
}
cout << e.a <<" " << e.b <<" " << P << endl;
}
}
void run(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
freopen(out,"w", stdout);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
}
void _cmp_with_bf(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
int T ,cas = 0;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
LL my = my_solution( Element(a,b), P) ;
LL bf = circle( Element(a,b) ) ;
if(my != bf) {
cout <<"SB"<<endl;
cout << a <<" " << b <<" " << P << endl;
cout <<my <<" " << bf << endl;
exit(0);
}
cout <<"correct @" << x <<" case " << cas ++ << endl;
}
}
int main() {
srand( time( NULL )) ;
// for(int i = 0; i < 10;++i) gen(i);
// for(int i = 0; i < 10; ++ i) run(i);
// for(int i=0;i<10;++i) _cmp_with_bf(i);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int mul(ll x,ll y,int p) {
return x * y % p;
}
int powermod(ll x,ll y,int p) { //x ^ y mod p
if (x == 0) {
return 0;
}
if (y == 0) {
return 1;
}
if (y & 1) {
return mul(powermod(x, y ^ 1, p), x, p);
}
x = powermod(x, y >> 1, p);
return mul(x, x, p);
}
pair<int,int> help(int a,int b,ll x,int p) { // (a + b * sqrt(5)) ^ n mod p
if (x == 0) {
return make_pair(1, 0);
}
pair<int,int> A, B;
if (x & 1) {
A = help(a, b, x - 1, p);
B = make_pair(a, b);
}
else {
A = B = help(a, b, x >> 1, p);
}
a = mul(A.first, B.first, p) + mul(5, mul(A.second,B.second, p), p);
if (a >= p) {
a -= p;
}
b = mul(A.first, B.second, p) + mul(A.second , B.first, p);
if (b >= p) {
b -= p;
}
return make_pair(a, b);
}
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int z;
for (scanf("%d",&z);z;--z) {
int a,b,p;
ll x;
scanf("%d%d%d",&a,&b,&p);
if (mul(a,a,p) == mul(mul(b,b,p),5,p)) {
puts("-1");
continue;
}
else if (powermod(5, p >> 1, p) == 1) {
x = p - 1;
x *= (p - 1);
}
else {
x = p;
x *= x;
--x;
}
ll answer = -1;
pair<int,int> temp;
for (ll i = 1; i * i <= x; ++i) {
if (x % i) {
continue;
}
if ((answer < 0) || (i < answer)) {
temp = help(a,b,i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = i;
}
}
if ((answer < 0) || (x / i < answer)) {
temp = help(a,b,x / i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = x / i;
}
}
}
printf("%lld\n",answer);
}
return 0;
}
</code></pre>
| 0 |
oct-2020-editorial-period
|
2013-10-29T06:13:09
|
{"contest_participation":7868,"challenge_submissions":564,"successful_submissions":106}
|
2013-10-29T06:13:09
|
2016-07-23T18:18:41
|
setter
|
###C++
```cpp
#include<iostream>
#include<queue>
#include<cstdio>
#include<cmath>
#include<string>
#include<vector>
#include<algorithm>
#include<stack>
#include<cstring>
#include<map>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define pb push_back
#define mp make_pair
bool isPrime(int n) {
if(n==1)return 0;
for(int i =2; i * i <= n; ++ i) if( n % i == 0 ) return 0;
return 1;
}
inline LL MOD(LL a, LL b) {a%=b; return a<0?a+b:a;}
LL powmod(LL a, LL b, LL c){
LL ret = 1%c; a%=c;
while(b){
if(b&1)ret=ret*a%c;
a=a*a%c;
b>>=1;
}
return ret;
}
// P is one prime number
LL inv( LL a, LL p) {return powmod( a, p - 2, p ) ; }
LL P;
class Element {
public:
LL a, b;
// a + b Sqrt(5)
Element(){}
Element(LL _a, LL _b) :a(_a),b(_b){}
Element operator+(const Element e) {
return Element(MOD(a + e.a , P),MOD(b + e.b , P));
}
Element operator*(const Element e) {
return Element(MOD(a*e.a + b*e.b * 5, P),MOD(a*e.b+b*e.a, P));
}
Element operator^(LL k){
if(k==0) return Element(1,0);
--k;
Element ret = *this, a = *this;
while(k){
if(k&1) ret= ret * a ;
a = a * a;
k >>= 1;
}
return ret;
}
Element inverse(){
if(!a&&!b) return *this;
if(b == 0) {
return Element(inv(a, P) , 0 );
}
if(a == 0) {
return Element(0, inv(5*b%P, P));
}
LL iv = inv( MOD(-b,P) , P );
LL x, y;
y = inv( iv * (a*a%P) % P + b*5 , P );
x = (iv * a % P * y) % P;
return Element( x, y) ;
}
bool isZ(){
return !a && !b;
}
bool isE(){
return a == 1 && b == 0;
}
bool operator<(const Element e) const {
if(a == e.a) return b < e.b;
return a < e.a;
}
void rand_gen(){
do{a = rand()%P; b= rand()%P;}while(0);
}
void out(){
cout << a <<" " << b << endl;
}
};
// a + b Sqrt(5)
LL circle( Element a ) {
Element b =a;
LL c = 1;
while( ! a.isE( )) {
a = a * b;
++ c;
//a.out();
if(a.a == b.a && a.b == b.b) {
return - 1;
}
}
return c;
}
bool isRes(LL a, LL P ){
return powmod(a, (P-1)/2, P) == 1;
}
LL my_solution(Element e , LL P) {
LL a = e.a, b = e.b;
if(MOD(a*a-5*b*b,P)==0) return -1;
LL n = P*P,ans;
if(isRes(5,P)) {
n = n - 2*P+1;
}else -- n;
ans = n;
for(LL i = 1; i*i <= n; ++ i) if(n%i == 0) {
if( (Element(a,b) ^(i)).isE() )
ans = min(ans, i );
if( (Element(a,b) ^(n/i)).isE() )
ans = min(ans, n/i );
}
return ans;
}
void dp(){
while( true ) {
P = rand()%1000 + 6;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
LL my_ans = my_solution(e, P);
LL bf = circle(e) ;
static int cas = 0; ++ cas;
if(my_ans == bf) {
cout <<"correct @" << cas <<" ans = " << my_ans<< endl;
}else {
cout <<"error"<<endl;
cout << P << endl;
e.out();
return;
}
}
}
Element rand_one_bad(LL P) {
for (LL a = 1; a < P; ++a)
for (LL b = 1; b < P; ++b) {
if (MOD(a * a - 5 * b * b, P) == 0) {
return Element(a, b);
}
}
return Element(0,0);
}
void gen(int x ){
char in[] = "input00.in";
in[6]='0'+x;
freopen(in,"w", stdout);
int T = (x+1)*10;
int LIMIT[] = {100, 10000, 1e6,1e6};
cout << T << endl;
while(T --) {
P = rand()% (int)LIMIT[x/3] + 13;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
if( P < 1e4 && isRes(5,P) && rand()%2 == 0) {
e = rand_one_bad(P);
}
cout << e.a <<" " << e.b <<" " << P << endl;
}
}
void run(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
freopen(out,"w", stdout);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
}
void _cmp_with_bf(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
int T ,cas = 0;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
LL my = my_solution( Element(a,b), P) ;
LL bf = circle( Element(a,b) ) ;
if(my != bf) {
cout <<"SB"<<endl;
cout << a <<" " << b <<" " << P << endl;
cout <<my <<" " << bf << endl;
exit(0);
}
cout <<"correct @" << x <<" case " << cas ++ << endl;
}
}
int main() {
srand( time( NULL )) ;
// for(int i = 0; i < 10;++i) gen(i);
// for(int i = 0; i < 10; ++ i) run(i);
// for(int i=0;i<10;++i) _cmp_with_bf(i);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T18:18:32
|
C++
|
||||
12 | 1,084 |
period
|
Period
|
You are given 2 integers **a** and **b**. Let a number be defined as . As we know  will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define
 (where x an integer)<br /><br /> and the operation  on AC number as:

This problem is to find the smallest positive integer **n**, such that:

We call the integer **n** as period. You are given **a**, **b** and **m**. Can you figure out the period?
**Input Format**
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.
**Output Format**
Output the Period if it exists, otherwise output "-1" (quotes only for reference)
**Constraints**
1 ≤ T ≤ 300
5 ≤ m ≤ 10<sup>7</sup>
0 ≤ a, b < m
**Sample Input #00**
4
0 0 13
1 0 7
3 0 10007
1 1 19
**Sample Output #00**
-1
1
5003
18
**Explanation #00**
For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.
|
code
|
Can you find the period?
|
ai
|
2013-10-16T05:50:59
|
2022-09-02T09:54:45
| null | null | null |
You are given 2 integers **a** and **b**. Let a number be defined as
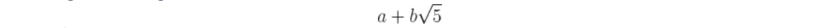. As we know 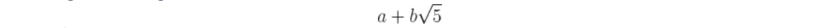 will be an irrational number when b is non-zero. In this problem, we call it the AC number. We define
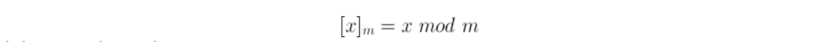 (where x an integer)<br /><br /> and the operation  on AC number as:
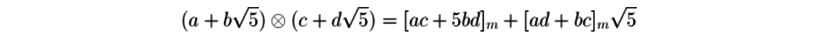
This problem is to find the smallest positive integer **n**, such that:

We call the integer **n** as period. You are given **a**, **b** and **m**. Can you figure out the period?
**Input Format**
The first line of the input contains a single integer T denoting the number of test-cases.
T lines follow, each containing 3 integers - a, b and m separated by a single space.
**Output Format**
Output the Period if it exists, otherwise output "-1" (quotes only for reference)
**Constraints**
1 ≤ T ≤ 300
5 ≤ m ≤ 10<sup>7</sup>
0 ≤ a, b < m
**Sample Input #00**
4
0 0 13
1 0 7
3 0 10007
1 1 19
**Sample Output #00**
-1
1
5003
18
**Explanation #00**
For the 1st test-case, no amount of operation ⊗ on a = 0, b = 0 gives 1 on the RHS. Hence the answer is -1.
When a = 1, b = 0, we have 1 for n = 1.
On repeated operations, the third and the fourth testcases sum to 1 for n = 5003 and n = 18 respectively.
| 0.564516 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
|
Hard
|
Period : Oct 2020 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem</strong> <a href="https://www.hackerrank.com/contests/oct13/challenges/period">Period</a></p>
<p><strong>Difficulty</strong> : Medium-Hard</p>
<p><strong>Required Knowledge</strong> : Group Theory, Euler's Criterion, Lagrange's theorem</p>
<p><strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/AekdyCoin">AekDy Coin</a></p>
<p><strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/cpcs">Cao Peng</a></p>
<p><strong>Approach</strong></p>
<p>For one given P, the AC number <img src="https://hr-filepicker.s3.amazonaws.com/period1.png" alt="image1" title=""> that satisfies 0 ≤ a,b < p
and a<sup>2</sup> ≅ 5b<sup>2</sup>(mod P) have th property:</p>
<p>Suppose, </p>
<p>∀n ∈ Z<sup>+</sup>, <br>
(a + b√5)<sup>n</sup> = c + d√5</p>
<p>Then we have c<sup>2</sup> = 5d<sup>2</sup>(mod P) <br>
Quite obvious by mathematical induction.
So if a<sup>2</sup> ≅5b<sup>2</sup>(mod P), we could not find the Period since the expected result AC number is with c=1 and d = 0.</p>
<p>So for the remaindering AC number, we have a<sup>2</sup>≠5b<sup>2</sup>(mod P) <br>
If 5 is one quadratic residue modulo P, then we can find (P-1)<sup>2</sup> such unique AC number satisfy. a<sup>2</sup>≠5b<sup>2</sup>(mod P) </p>
<p>Proof:</p>
<p>If 5 is one quadratic residue modulo P , then for the <a href="https://en.wikipedia.org/wiki/Primitive_root_modulo_n">primitive root</a> <strong>g</strong>, we have </p>
<p>g<sup>2k</sup> ≅5(mod P) the AC number such that a<sup>2</sup>≅5b<sup>2</sup>(mod P) must satisfy:</p>
<p>g<sup>2I(a)</sup>≅g<sup>2k</sup>g<sup>2I(b)</sup>(mod P), which means </p>
<p>2I(a)≅2(k+I(b))(mod P - 1), there are totally 2(P-1) AC number that satisfy that condition. (which means they also satisfy </p>
<p>a<sup>2</sup>≅5b<sup>2</sup>(mod P), but don't forget 0 + 0√5, so there are </p>
<p>P<sup>2</sup> - 2(P-1) - 1 = (P-1)<sup>2</sup> AC numbers such that a<sup>2</sup>≠5b<sup>2</sup>(mod P) </p>
<p>If 5 is not one quadratic residue modulo P, then we can find P<sup>2</sup> - 1 = (P-1)(P+1) such unique AC number satisfies, </p>
<p>a<sup>2</sup>≠5b<sup>2</sup>(mod P), because only one AC number o + 0√5 satisfies, </p>
<p>a<sup>2</sup>≅5b<sup>2</sup>(mod P) </p>
<p>We can use <a href="https://en.wikipedia.org/wiki/Euler%27s_criterion">Euler's Criterion</a> to judge whether 5 is one quadratic residue modulo P in O(logP) time.
The identity element in this group is 1.
However there are other 2 properties that guarantee it is a group. I will ignore the proof here.</p>
<p>Finally, base one [Lagrange's Theorem)(<a href="http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)">http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)</a>) we have
Period C, where C is the number of AC number satisfies
a<sup>2</sup>≠5b<sup>2</sup>(mod P). Simple brute force will work. </p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include<iostream>
#include<queue>
#include<cstdio>
#include<cmath>
#include<string>
#include<vector>
#include<algorithm>
#include<stack>
#include<cstring>
#include<map>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define pb push_back
#define mp make_pair
bool isPrime(int n) {
if(n==1)return 0;
for(int i =2; i * i <= n; ++ i) if( n % i == 0 ) return 0;
return 1;
}
inline LL MOD(LL a, LL b) {a%=b; return a<0?a+b:a;}
LL powmod(LL a, LL b, LL c){
LL ret = 1%c; a%=c;
while(b){
if(b&1)ret=ret*a%c;
a=a*a%c;
b>>=1;
}
return ret;
}
// P is one prime number
LL inv( LL a, LL p) {return powmod( a, p - 2, p ) ; }
LL P;
class Element {
public:
LL a, b;
// a + b Sqrt(5)
Element(){}
Element(LL _a, LL _b) :a(_a),b(_b){}
Element operator+(const Element e) {
return Element(MOD(a + e.a , P),MOD(b + e.b , P));
}
Element operator*(const Element e) {
return Element(MOD(a*e.a + b*e.b * 5, P),MOD(a*e.b+b*e.a, P));
}
Element operator^(LL k){
if(k==0) return Element(1,0);
--k;
Element ret = *this, a = *this;
while(k){
if(k&1) ret= ret * a ;
a = a * a;
k >>= 1;
}
return ret;
}
Element inverse(){
if(!a&&!b) return *this;
if(b == 0) {
return Element(inv(a, P) , 0 );
}
if(a == 0) {
return Element(0, inv(5*b%P, P));
}
LL iv = inv( MOD(-b,P) , P );
LL x, y;
y = inv( iv * (a*a%P) % P + b*5 , P );
x = (iv * a % P * y) % P;
return Element( x, y) ;
}
bool isZ(){
return !a && !b;
}
bool isE(){
return a == 1 && b == 0;
}
bool operator<(const Element e) const {
if(a == e.a) return b < e.b;
return a < e.a;
}
void rand_gen(){
do{a = rand()%P; b= rand()%P;}while(0);
}
void out(){
cout << a <<" " << b << endl;
}
};
// a + b Sqrt(5)
LL circle( Element a ) {
Element b =a;
LL c = 1;
while( ! a.isE( )) {
a = a * b;
++ c;
//a.out();
if(a.a == b.a && a.b == b.b) {
return - 1;
}
}
return c;
}
bool isRes(LL a, LL P ){
return powmod(a, (P-1)/2, P) == 1;
}
LL my_solution(Element e , LL P) {
LL a = e.a, b = e.b;
if(MOD(a*a-5*b*b,P)==0) return -1;
LL n = P*P,ans;
if(isRes(5,P)) {
n = n - 2*P+1;
}else -- n;
ans = n;
for(LL i = 1; i*i <= n; ++ i) if(n%i == 0) {
if( (Element(a,b) ^(i)).isE() )
ans = min(ans, i );
if( (Element(a,b) ^(n/i)).isE() )
ans = min(ans, n/i );
}
return ans;
}
void dp(){
while( true ) {
P = rand()%1000 + 6;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
LL my_ans = my_solution(e, P);
LL bf = circle(e) ;
static int cas = 0; ++ cas;
if(my_ans == bf) {
cout <<"correct @" << cas <<" ans = " << my_ans<< endl;
}else {
cout <<"error"<<endl;
cout << P << endl;
e.out();
return;
}
}
}
Element rand_one_bad(LL P) {
for (LL a = 1; a < P; ++a)
for (LL b = 1; b < P; ++b) {
if (MOD(a * a - 5 * b * b, P) == 0) {
return Element(a, b);
}
}
return Element(0,0);
}
void gen(int x ){
char in[] = "input00.in";
in[6]='0'+x;
freopen(in,"w", stdout);
int T = (x+1)*10;
int LIMIT[] = {100, 10000, 1e6,1e6};
cout << T << endl;
while(T --) {
P = rand()% (int)LIMIT[x/3] + 13;
while(!isPrime(P)) ++ P;
Element e; e.rand_gen();
if( P < 1e4 && isRes(5,P) && rand()%2 == 0) {
e = rand_one_bad(P);
}
cout << e.a <<" " << e.b <<" " << P << endl;
}
}
void run(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
freopen(out,"w", stdout);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
}
void _cmp_with_bf(int x ){
char in[] = "input00.in";
char out[] = "output01.out";
in[6]='0'+x;
out[7]='0'+x;
freopen(in,"r",stdin);
int T ,cas = 0;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
LL my = my_solution( Element(a,b), P) ;
LL bf = circle( Element(a,b) ) ;
if(my != bf) {
cout <<"SB"<<endl;
cout << a <<" " << b <<" " << P << endl;
cout <<my <<" " << bf << endl;
exit(0);
}
cout <<"correct @" << x <<" case " << cas ++ << endl;
}
}
int main() {
srand( time( NULL )) ;
// for(int i = 0; i < 10;++i) gen(i);
// for(int i = 0; i < 10; ++ i) run(i);
// for(int i=0;i<10;++i) _cmp_with_bf(i);
int T ;
cin >> T;
while(T --) {
LL a, b; cin >> a >> b >> P;
if(!isPrime(P) || P <= 5 || a >= P || b >= P || a < 0 || b < 0) {
cerr <<"SB" << endl;
exit(0);
}
cout << my_solution( Element(a,b), P) << endl;
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int mul(ll x,ll y,int p) {
return x * y % p;
}
int powermod(ll x,ll y,int p) { //x ^ y mod p
if (x == 0) {
return 0;
}
if (y == 0) {
return 1;
}
if (y & 1) {
return mul(powermod(x, y ^ 1, p), x, p);
}
x = powermod(x, y >> 1, p);
return mul(x, x, p);
}
pair<int,int> help(int a,int b,ll x,int p) { // (a + b * sqrt(5)) ^ n mod p
if (x == 0) {
return make_pair(1, 0);
}
pair<int,int> A, B;
if (x & 1) {
A = help(a, b, x - 1, p);
B = make_pair(a, b);
}
else {
A = B = help(a, b, x >> 1, p);
}
a = mul(A.first, B.first, p) + mul(5, mul(A.second,B.second, p), p);
if (a >= p) {
a -= p;
}
b = mul(A.first, B.second, p) + mul(A.second , B.first, p);
if (b >= p) {
b -= p;
}
return make_pair(a, b);
}
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int z;
for (scanf("%d",&z);z;--z) {
int a,b,p;
ll x;
scanf("%d%d%d",&a,&b,&p);
if (mul(a,a,p) == mul(mul(b,b,p),5,p)) {
puts("-1");
continue;
}
else if (powermod(5, p >> 1, p) == 1) {
x = p - 1;
x *= (p - 1);
}
else {
x = p;
x *= x;
--x;
}
ll answer = -1;
pair<int,int> temp;
for (ll i = 1; i * i <= x; ++i) {
if (x % i) {
continue;
}
if ((answer < 0) || (i < answer)) {
temp = help(a,b,i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = i;
}
}
if ((answer < 0) || (x / i < answer)) {
temp = help(a,b,x / i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = x / i;
}
}
}
printf("%lld\n",answer);
}
return 0;
}
</code></pre>
| 0 |
oct-2020-editorial-period
|
2013-10-29T06:13:09
|
{"contest_participation":7868,"challenge_submissions":564,"successful_submissions":106}
|
2013-10-29T06:13:09
|
2016-07-23T18:18:41
|
tester
|
###C++
```cpp
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
int mul(ll x,ll y,int p) {
return x * y % p;
}
int powermod(ll x,ll y,int p) { //x ^ y mod p
if (x == 0) {
return 0;
}
if (y == 0) {
return 1;
}
if (y & 1) {
return mul(powermod(x, y ^ 1, p), x, p);
}
x = powermod(x, y >> 1, p);
return mul(x, x, p);
}
pair<int,int> help(int a,int b,ll x,int p) { // (a + b * sqrt(5)) ^ n mod p
if (x == 0) {
return make_pair(1, 0);
}
pair<int,int> A, B;
if (x & 1) {
A = help(a, b, x - 1, p);
B = make_pair(a, b);
}
else {
A = B = help(a, b, x >> 1, p);
}
a = mul(A.first, B.first, p) + mul(5, mul(A.second,B.second, p), p);
if (a >= p) {
a -= p;
}
b = mul(A.first, B.second, p) + mul(A.second , B.first, p);
if (b >= p) {
b -= p;
}
return make_pair(a, b);
}
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int z;
for (scanf("%d",&z);z;--z) {
int a,b,p;
ll x;
scanf("%d%d%d",&a,&b,&p);
if (mul(a,a,p) == mul(mul(b,b,p),5,p)) {
puts("-1");
continue;
}
else if (powermod(5, p >> 1, p) == 1) {
x = p - 1;
x *= (p - 1);
}
else {
x = p;
x *= x;
--x;
}
ll answer = -1;
pair<int,int> temp;
for (ll i = 1; i * i <= x; ++i) {
if (x % i) {
continue;
}
if ((answer < 0) || (i < answer)) {
temp = help(a,b,i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = i;
}
}
if ((answer < 0) || (x / i < answer)) {
temp = help(a,b,x / i,p);
if ((temp.first == 1) && (temp.second == 0)) {
answer = x / i;
}
}
}
printf("%lld\n",answer);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T18:18:41
|
C++
|
||||
13 | 1,090 |
missile-defend
|
HackerX
|
**Update:** A slight modification in the problem statement (see below)
Evil Nation A is angry and plans to launch **N** guided-missiles at the peaceful Nation B in an attempt to wipe out all of Nation B's people. Nation A's missile _i_ will arrive in nation B at time t<sub>i</sub>. Missile _i_ communicates with its headquarters by unique radio signals with a frequency equal to f<sub>i</sub>. Can you help the peaceful Nation B survive by building a defensive system that will stop the missiles dead in the sky?
**Defensive system:**
The only way to defend Nation B from the attacking missile is by counter attacking them with a _hackerX_ missile. You have a lot of _hackerX_ missiles and each one of them has its own radio frequency. An individual _hackerX_ missile can destroy Evil Nation A’s attacking missile if the radio frequency of both of the missiles match. Each _hackerX_ missile can be used an indefinite number of times. Its invincible and doesn't get destroyed in the collision.
The good news is you can adjust the frequency of the _hackerX_ missile to match the evil missiles' frequency. When changing the _hackerX_ missile's initial frequency fA to the new defending frequency fB, you will need \|fB - fA\| units of time to do.
<strike>Each _hackerX_ missile can only destroy one of Nation A's missile at a time. So if two evil missiles with same frequency arrive at the same time, you need at least two _hackerX_ missiles with the same frequency as the evil missiles to avoid damage.</strike>
If two evil missles with same frequency arrive at the same time, we can destroy them both with one _hackerX_ missile. You can set the frequency of a _hackerX_ missile to any value when its fired.
What is the minimum number of _hackerX_ missiles you must launch to keep Nation B safe?
**Input Format:**
The first line contains a single integer **N** denoting the number of missiles.
This is followed by **N** lines each containing two integers t<sub>i</sub> and f<sub>i</sub> denoting the time & frequency of the i<sup>th</sup> missile.
**Output Format:**
A single integer denoting the minimum number of _hackerX_ missiles you need to defend the nation.
**Constraints:**
1 <= N <= 100000
0 <= t<sub>i</sub> <= 100000
0 <= f<sub>i</sub> <= 100000
t<sub>1</sub> <= t<sub>2</sub> <= ... <= t<sub>N</sub>
**Sample Input #00**
4
1 1
2 2
3 1
5 1
**Sample Output #00**
1
**Explanation #00**
A _HackerX_ missile is launched at t = 1 with a frequency f = 1, and destroys the first missile. It re-tunes its frequency to f = 2 in 1 unit of time, and destroys the missile that is going to hit Nation B at t = 2. It re-tunes its frequency back to 1 in 1 unit of time and destroys the missile that is going to hit the nation at t = 3. It is relaunched at t = 5 with f = 1 and destroys the missile that is going to hit nation B at t = 5. Hence, you need only 1 _HackerX_ to protect nation B.
**Sample Input #01**
4
1 1
2 3
3 1
5 1
**Sample Output #01**
2
**Explanation #01**
Destroy 1 missile at t = 1, f = 1. now at t = 2, there is a missile with frequency 3. The launched missile takes 2 units of time to destroy this, hence we need a new hackerX missile to destroy this one. The first hackerX missile can destroy the 3rd missile which has the same frequency as itself. The same hackerX missile destroys the missile that is hitting its city at t = 5. Thus, we need atleast 2 hackerX missiles.
|
code
|
Find the minimum number of hackerX missiles you must launch to keep Nation B safe.
|
ai
|
2013-10-16T17:50:34
|
2022-08-31T08:14:32
|
#
# Complete the 'missileDefend' function below.
#
# The function is expected to return an INTEGER.
# The function accepts 2D_INTEGER_ARRAY missiles as parameter.
#
def missileDefend(missiles):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
missiles = []
for _ in range(n):
missiles.append(list(map(int, input().rstrip().split())))
result = missileDefend(missiles)
fptr.write(str(result) + '\n')
fptr.close()
|
**Update:** A slight modification in the problem statement (see below)
Evil Nation A is angry and plans to launch **N** guided-missiles at the peaceful Nation B in an attempt to wipe out all of Nation B's people. Nation A's missile _i_ will arrive in nation B at time t<sub>i</sub>. Missile _i_ communicates with its headquarters by unique radio signals with a frequency equal to f<sub>i</sub>. Can you help the peaceful Nation B survive by building a defensive system that will stop the missiles dead in the sky?
**Defensive system:**
The only way to defend Nation B from the attacking missile is by counter attacking them with a _hackerX_ missile. You have a lot of _hackerX_ missiles and each one of them has its own radio frequency. An individual _hackerX_ missile can destroy Evil Nation A’s attacking missile if the radio frequency of both of the missiles match. Each _hackerX_ missile can be used an indefinite number of times. Its invincible and doesn't get destroyed in the collision.
The good news is you can adjust the frequency of the _hackerX_ missile to match the evil missiles' frequency. When changing the _hackerX_ missile's initial frequency fA to the new defending frequency fB, you will need \|fB - fA\| units of time to do.
<strike>Each _hackerX_ missile can only destroy one of Nation A's missile at a time. So if two evil missiles with same frequency arrive at the same time, you need at least two _hackerX_ missiles with the same frequency as the evil missiles to avoid damage.</strike>
If two evil missles with same frequency arrive at the same time, we can destroy them both with one _hackerX_ missile. You can set the frequency of a _hackerX_ missile to any value when its fired.
What is the minimum number of _hackerX_ missiles you must launch to keep Nation B safe?
**Input Format:**
The first line contains a single integer **N** denoting the number of missiles.
This is followed by **N** lines each containing two integers t<sub>i</sub> and f<sub>i</sub> denoting the time & frequency of the i<sup>th</sup> missile.
**Output Format:**
A single integer denoting the minimum number of _hackerX_ missiles you need to defend the nation.
**Constraints:**
1 <= N <= 100000
0 <= t<sub>i</sub> <= 100000
0 <= f<sub>i</sub> <= 100000
t<sub>1</sub> <= t<sub>2</sub> <= ... <= t<sub>N</sub>
**Sample Input #00**
4
1 1
2 2
3 1
5 1
**Sample Output #00**
1
**Explanation #00**
A _HackerX_ missile is launched at t = 1 with a frequency f = 1, and destroys the first missile. It re-tunes its frequency to f = 2 in 1 unit of time, and destroys the missile that is going to hit Nation B at t = 2. It re-tunes its frequency back to 1 in 1 unit of time and destroys the missile that is going to hit the nation at t = 3. It is relaunched at t = 5 with f = 1 and destroys the missile that is going to hit nation B at t = 5. Hence, you need only 1 _HackerX_ to protect nation B.
**Sample Input #01**
4
1 1
2 3
3 1
5 1
**Sample Output #01**
2
**Explanation #01**
Destroy 1 missile at t = 1, f = 1. now at t = 2, there is a missile with frequency 3. The launched missile takes 2 units of time to destroy this, hence we need a new hackerX missile to destroy this one. The first hackerX missile can destroy the 3rd missile which has the same frequency as itself. The same hackerX missile destroys the missile that is hitting its city at t = 5. Thus, we need atleast 2 hackerX missiles.
| 0.538462 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
| null | null | null | null |
Hard
|
hackerX : Oct 20/20 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem</strong>: <a href="https://www.hackerrank.com/contests/oct13/challenges/missile-defend">hackerX</a></p>
<p><strong>Difficulty</strong>: Medium-Hard</p>
<p><strong>Required Knowledge</strong>: Minimum Path cover, Dilworth's theorem</p>
<p><strong>Problem Setter</strong>: <a href="https://www.hackerrank.com/wanbo">Wanbo</a></p>
<p><strong>Problem Tester</strong>: <a href="https://www.hackerrank.com/cpcs">Cao Peng</a>, <a href="https://www.hackerrank.com/khongor">Khongor</a></p>
<p><strong>Approach</strong></p>
<p>What's the requirement if one hackerX missiles can defend both (ti, fi) and (tj, fj) when ti <= tj? </p>
<p>tj - ti >= \|fi - fj\| (because you just need \|fi - fj\| units time to change the frequency from fi to fj,
so you can defend tj after defend ti by this hackerX missiles if you need.
So if we regard every coming missiles (ti, fi) as an vertex i, and if tj - ti >= \|fi - fj\| then we add an edge from i to j,
this edge indicates that one hackerX can defend the j<sup>th</sup> missile after defending the i<sup>th</sup> missile. </p>
<p>So the solution for this challenge seems obvious, we just need to find the "Minimum Path Cover"(Can be changed to MaxFlow problem) of this graph. </p>
<p>But n can be as large as 100000, and there are at most O(n<sup>2</sup>) edges, even generating the graph will get TLE, we need to optimize our solution. </p>
<p>We haven't taken advantage of the particularity of this graph in the previous analysis, we just look this as a more general problem.</p>
<p>tj - ti >= \|fi - fj\|
<==>
If fi < fj, tj - ti >= fj - fi ==> ti - fi <= tj - fj ==> Ai <= Aj (Ai = ti - fi)
If fi >= fj, tj - ti >= fi - fj ==> ti + fi <= tj + fj ==> Bi <= Bj (Bi = ti + fi)</p>
<p>Can we remove some constraints?</p>
<ol>
<li>ti <= tj</li>
<li>If fi < fj, Ai <= Aj ==> Ai + 2 * fi <= Aj + 2 * fj ==> Bi <= Bj</li>
<li>If fi >= fj, Bi <= Bj ==> Bi - 2 * fi <= Bj - 2 * fj ==> Ai <= Aj</li>
</ol>
<p>We can combine 2) with 3) to "Ai <= Aj && Bi <= Bj"
Ai + Bi <= Aj + Bj ==> ti <= tj ==> ti <= tj can be removed. </p>
<p>==></p>
<p>edge(i->j) <==> Ai <= Aj && Bi <= Bj</p>
<p>We need to find the minimum path cover in the graph which edge(i->j) <==> Ai <= Aj && Bi <= Bj. </p>
<p>According to <a href="https://en.wikipedia.org/wiki/Dilworth%27s_theorem">Dilworth's theorem</a>, the minimum path cover in this graph is equal to the longest anti-chain.
So we just need to choose a maximum vertexes subset from the graph, where any of two do not have an edge.
1. Sort the (Ai, Bi) by the first key value Ai, if Ai == Aj, then smaller Bi comes first.
2. The longest decreasing subsequence of Bi will be the answer.(This is a very classic question that can be solved by O(nlgn).</p>
<p><strong>Problem Setter Code</strong>:</p>
<pre><code>#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <iomanip>
#include <sstream>
#include <fstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
typedef vector<int> VI;
typedef vector<LL> VL;
typedef vector<PII> VPII;
typedef vector<PLL> VPLL;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<(x)<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<(x)<<", "#y" = "<<(y)<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define FOR(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define rep(i, n) for(int i = 0; i < n; i++)
#define UN(v) sort(ALL(v)), v.resize(unique(ALL(v))-v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
template<class T> string tostring(T x, int len = 0) {stringstream ss; ss << x; string r = ss.str(); if(r.length() < len) r = string(len - r.length(), '0') + r; return r;}
template<class T> void convert(string x, T& r) {stringstream ss(x); ss >> r;}
template<class A, class B> ostream& operator<<(ostream &o, pair<A, B> t) {o << "(" << t.x << ", " << t.y << ")"; return o;}
const int inf = 0x3f3f3f3f;
const int mod = int(1e9) + 7;
const int N = 111111;
int t[N], f[N];
int d[N];
int n;
int LIS(VI v) {
fill(d, d + n, 1);
for(int i = 0; i < n; i++)
for(int j = 0; j < i; j++)
if(v[i] > v[j]) chmax(d[i], d[j] + 1);
int res = 0;
for(int i = 0; i < n; i++) chmax(res, d[i]);
return res;
}
int LIS1(VI v) {
MM(d, 0x3f);
d[1] = v[0];
for(int i = 1; i < v.size(); i++) {
int t = upper_bound(d + 1, d + N, v[i]) - d;
if(t != 1 && d[t - 1] >= v[i]) continue;
d[t] = v[i];
}
int res = 0;
for(int i = 1; i < N; i++) if(d[i] != inf) res = i;
return res;
}
int main() {
cin >> n;
for(int i = 0; i < n; i++) cin >> t[i] >> f[i];
for(int i = 1; i < n; i++) assert(t[i] >= t[i - 1]);
VI v;
VPII vp;
for(int i = 0; i < n; i++) vp.pb(mp(t[i] - f[i], t[i] + f[i]));
sort(ALL(vp));
for(int i = 0; i < n; i++) v.pb(vp[i].second);
reverse(ALL(v));
//PV(ALL(v));
cout << LIS1(v) << endl;
//P2(LIS1(v), LIS(v));
//assert(LIS1(v) == LIS(v));
return 0;
}
</code></pre>
<p><strong>Problem Tester Code</strong>:</p>
<pre><code>#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
pair<int,int> a[100005];
set<int> have;
int main() {
int n;
scanf("%d",&n);
for (int i = 0; i < n; ++i) {
int x,y;
scanf("%d%d",&x,&y);
a[i] = make_pair(x + y,x - y);
}
sort(a, a + n);
for (int i = 0; i < n; ++i) {
//printf("%d %d\n",a[i].first,a[i].second);
set<int>::iterator t = have.lower_bound(a[i].second);
if ((t != have.end()) && (*t == a[i].second)) {
continue;
}
if (t != have.begin()) {
have.erase(--t);
}
have.insert(a[i].second);
}
printf("%d\n",have.size());
return 0;
}
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <utility>
using namespace std;
#define Pair pair<int, int>
#define MAX 100000
Pair v[MAX];
int a[MAX];
int dp[MAX + 1];
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
int x, y;
scanf("%d%d", &x, &y);
v[i] = make_pair(x - y, x + y);
}
sort(v, v + n);
for (int i = 0; i < n; i++)
a[i] = v[n - i - 1].second;
int r = 1;
dp[1] = a[0];
for (int i = 1; i < n; i++) {
int low = 1, high = r;
if (a[i] <= dp[1]) {
dp[1] = a[i];
continue;
}
while (low < high) {
int mid = (low + high + 1) / 2;
if (dp[mid] >= a[i])
high = mid - 1;
else
low = mid;
}
if (low == r) r++;
dp[low + 1] = a[i];
}
cout << r << endl;
return 0;
}
</code></pre>
| 0 |
oct-2020-editorial-hackerx
|
2013-10-30T05:56:08
|
{"contest_participation":7868,"challenge_submissions":955,"successful_submissions":110}
|
2013-10-30T05:56:08
|
2016-07-23T14:05:03
|
setter
|
###C++
```cpp
#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <iomanip>
#include <sstream>
#include <fstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
typedef vector<int> VI;
typedef vector<LL> VL;
typedef vector<PII> VPII;
typedef vector<PLL> VPLL;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<(x)<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<(x)<<", "#y" = "<<(y)<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define FOR(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define rep(i, n) for(int i = 0; i < n; i++)
#define UN(v) sort(ALL(v)), v.resize(unique(ALL(v))-v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
template<class T> string tostring(T x, int len = 0) {stringstream ss; ss << x; string r = ss.str(); if(r.length() < len) r = string(len - r.length(), '0') + r; return r;}
template<class T> void convert(string x, T& r) {stringstream ss(x); ss >> r;}
template<class A, class B> ostream& operator<<(ostream &o, pair<A, B> t) {o << "(" << t.x << ", " << t.y << ")"; return o;}
const int inf = 0x3f3f3f3f;
const int mod = int(1e9) + 7;
const int N = 111111;
int t[N], f[N];
int d[N];
int n;
int LIS(VI v) {
fill(d, d + n, 1);
for(int i = 0; i < n; i++)
for(int j = 0; j < i; j++)
if(v[i] > v[j]) chmax(d[i], d[j] + 1);
int res = 0;
for(int i = 0; i < n; i++) chmax(res, d[i]);
return res;
}
int LIS1(VI v) {
MM(d, 0x3f);
d[1] = v[0];
for(int i = 1; i < v.size(); i++) {
int t = upper_bound(d + 1, d + N, v[i]) - d;
if(t != 1 && d[t - 1] >= v[i]) continue;
d[t] = v[i];
}
int res = 0;
for(int i = 1; i < N; i++) if(d[i] != inf) res = i;
return res;
}
int main() {
cin >> n;
for(int i = 0; i < n; i++) cin >> t[i] >> f[i];
for(int i = 1; i < n; i++) assert(t[i] >= t[i - 1]);
VI v;
VPII vp;
for(int i = 0; i < n; i++) vp.pb(mp(t[i] - f[i], t[i] + f[i]));
sort(ALL(vp));
for(int i = 0; i < n; i++) v.pb(vp[i].second);
reverse(ALL(v));
//PV(ALL(v));
cout << LIS1(v) << endl;
//P2(LIS1(v), LIS(v));
//assert(LIS1(v) == LIS(v));
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T14:04:43
|
C++
|
14 | 1,090 |
missile-defend
|
HackerX
|
**Update:** A slight modification in the problem statement (see below)
Evil Nation A is angry and plans to launch **N** guided-missiles at the peaceful Nation B in an attempt to wipe out all of Nation B's people. Nation A's missile _i_ will arrive in nation B at time t<sub>i</sub>. Missile _i_ communicates with its headquarters by unique radio signals with a frequency equal to f<sub>i</sub>. Can you help the peaceful Nation B survive by building a defensive system that will stop the missiles dead in the sky?
**Defensive system:**
The only way to defend Nation B from the attacking missile is by counter attacking them with a _hackerX_ missile. You have a lot of _hackerX_ missiles and each one of them has its own radio frequency. An individual _hackerX_ missile can destroy Evil Nation A’s attacking missile if the radio frequency of both of the missiles match. Each _hackerX_ missile can be used an indefinite number of times. Its invincible and doesn't get destroyed in the collision.
The good news is you can adjust the frequency of the _hackerX_ missile to match the evil missiles' frequency. When changing the _hackerX_ missile's initial frequency fA to the new defending frequency fB, you will need \|fB - fA\| units of time to do.
<strike>Each _hackerX_ missile can only destroy one of Nation A's missile at a time. So if two evil missiles with same frequency arrive at the same time, you need at least two _hackerX_ missiles with the same frequency as the evil missiles to avoid damage.</strike>
If two evil missles with same frequency arrive at the same time, we can destroy them both with one _hackerX_ missile. You can set the frequency of a _hackerX_ missile to any value when its fired.
What is the minimum number of _hackerX_ missiles you must launch to keep Nation B safe?
**Input Format:**
The first line contains a single integer **N** denoting the number of missiles.
This is followed by **N** lines each containing two integers t<sub>i</sub> and f<sub>i</sub> denoting the time & frequency of the i<sup>th</sup> missile.
**Output Format:**
A single integer denoting the minimum number of _hackerX_ missiles you need to defend the nation.
**Constraints:**
1 <= N <= 100000
0 <= t<sub>i</sub> <= 100000
0 <= f<sub>i</sub> <= 100000
t<sub>1</sub> <= t<sub>2</sub> <= ... <= t<sub>N</sub>
**Sample Input #00**
4
1 1
2 2
3 1
5 1
**Sample Output #00**
1
**Explanation #00**
A _HackerX_ missile is launched at t = 1 with a frequency f = 1, and destroys the first missile. It re-tunes its frequency to f = 2 in 1 unit of time, and destroys the missile that is going to hit Nation B at t = 2. It re-tunes its frequency back to 1 in 1 unit of time and destroys the missile that is going to hit the nation at t = 3. It is relaunched at t = 5 with f = 1 and destroys the missile that is going to hit nation B at t = 5. Hence, you need only 1 _HackerX_ to protect nation B.
**Sample Input #01**
4
1 1
2 3
3 1
5 1
**Sample Output #01**
2
**Explanation #01**
Destroy 1 missile at t = 1, f = 1. now at t = 2, there is a missile with frequency 3. The launched missile takes 2 units of time to destroy this, hence we need a new hackerX missile to destroy this one. The first hackerX missile can destroy the 3rd missile which has the same frequency as itself. The same hackerX missile destroys the missile that is hitting its city at t = 5. Thus, we need atleast 2 hackerX missiles.
|
code
|
Find the minimum number of hackerX missiles you must launch to keep Nation B safe.
|
ai
|
2013-10-16T17:50:34
|
2022-08-31T08:14:32
|
#
# Complete the 'missileDefend' function below.
#
# The function is expected to return an INTEGER.
# The function accepts 2D_INTEGER_ARRAY missiles as parameter.
#
def missileDefend(missiles):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
missiles = []
for _ in range(n):
missiles.append(list(map(int, input().rstrip().split())))
result = missileDefend(missiles)
fptr.write(str(result) + '\n')
fptr.close()
|
**Update:** A slight modification in the problem statement (see below)
Evil Nation A is angry and plans to launch **N** guided-missiles at the peaceful Nation B in an attempt to wipe out all of Nation B's people. Nation A's missile _i_ will arrive in nation B at time t<sub>i</sub>. Missile _i_ communicates with its headquarters by unique radio signals with a frequency equal to f<sub>i</sub>. Can you help the peaceful Nation B survive by building a defensive system that will stop the missiles dead in the sky?
**Defensive system:**
The only way to defend Nation B from the attacking missile is by counter attacking them with a _hackerX_ missile. You have a lot of _hackerX_ missiles and each one of them has its own radio frequency. An individual _hackerX_ missile can destroy Evil Nation A’s attacking missile if the radio frequency of both of the missiles match. Each _hackerX_ missile can be used an indefinite number of times. Its invincible and doesn't get destroyed in the collision.
The good news is you can adjust the frequency of the _hackerX_ missile to match the evil missiles' frequency. When changing the _hackerX_ missile's initial frequency fA to the new defending frequency fB, you will need \|fB - fA\| units of time to do.
<strike>Each _hackerX_ missile can only destroy one of Nation A's missile at a time. So if two evil missiles with same frequency arrive at the same time, you need at least two _hackerX_ missiles with the same frequency as the evil missiles to avoid damage.</strike>
If two evil missles with same frequency arrive at the same time, we can destroy them both with one _hackerX_ missile. You can set the frequency of a _hackerX_ missile to any value when its fired.
What is the minimum number of _hackerX_ missiles you must launch to keep Nation B safe?
**Input Format:**
The first line contains a single integer **N** denoting the number of missiles.
This is followed by **N** lines each containing two integers t<sub>i</sub> and f<sub>i</sub> denoting the time & frequency of the i<sup>th</sup> missile.
**Output Format:**
A single integer denoting the minimum number of _hackerX_ missiles you need to defend the nation.
**Constraints:**
1 <= N <= 100000
0 <= t<sub>i</sub> <= 100000
0 <= f<sub>i</sub> <= 100000
t<sub>1</sub> <= t<sub>2</sub> <= ... <= t<sub>N</sub>
**Sample Input #00**
4
1 1
2 2
3 1
5 1
**Sample Output #00**
1
**Explanation #00**
A _HackerX_ missile is launched at t = 1 with a frequency f = 1, and destroys the first missile. It re-tunes its frequency to f = 2 in 1 unit of time, and destroys the missile that is going to hit Nation B at t = 2. It re-tunes its frequency back to 1 in 1 unit of time and destroys the missile that is going to hit the nation at t = 3. It is relaunched at t = 5 with f = 1 and destroys the missile that is going to hit nation B at t = 5. Hence, you need only 1 _HackerX_ to protect nation B.
**Sample Input #01**
4
1 1
2 3
3 1
5 1
**Sample Output #01**
2
**Explanation #01**
Destroy 1 missile at t = 1, f = 1. now at t = 2, there is a missile with frequency 3. The launched missile takes 2 units of time to destroy this, hence we need a new hackerX missile to destroy this one. The first hackerX missile can destroy the 3rd missile which has the same frequency as itself. The same hackerX missile destroys the missile that is hitting its city at t = 5. Thus, we need atleast 2 hackerX missiles.
| 0.538462 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
| null | null | null | null |
Hard
|
hackerX : Oct 20/20 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem</strong>: <a href="https://www.hackerrank.com/contests/oct13/challenges/missile-defend">hackerX</a></p>
<p><strong>Difficulty</strong>: Medium-Hard</p>
<p><strong>Required Knowledge</strong>: Minimum Path cover, Dilworth's theorem</p>
<p><strong>Problem Setter</strong>: <a href="https://www.hackerrank.com/wanbo">Wanbo</a></p>
<p><strong>Problem Tester</strong>: <a href="https://www.hackerrank.com/cpcs">Cao Peng</a>, <a href="https://www.hackerrank.com/khongor">Khongor</a></p>
<p><strong>Approach</strong></p>
<p>What's the requirement if one hackerX missiles can defend both (ti, fi) and (tj, fj) when ti <= tj? </p>
<p>tj - ti >= \|fi - fj\| (because you just need \|fi - fj\| units time to change the frequency from fi to fj,
so you can defend tj after defend ti by this hackerX missiles if you need.
So if we regard every coming missiles (ti, fi) as an vertex i, and if tj - ti >= \|fi - fj\| then we add an edge from i to j,
this edge indicates that one hackerX can defend the j<sup>th</sup> missile after defending the i<sup>th</sup> missile. </p>
<p>So the solution for this challenge seems obvious, we just need to find the "Minimum Path Cover"(Can be changed to MaxFlow problem) of this graph. </p>
<p>But n can be as large as 100000, and there are at most O(n<sup>2</sup>) edges, even generating the graph will get TLE, we need to optimize our solution. </p>
<p>We haven't taken advantage of the particularity of this graph in the previous analysis, we just look this as a more general problem.</p>
<p>tj - ti >= \|fi - fj\|
<==>
If fi < fj, tj - ti >= fj - fi ==> ti - fi <= tj - fj ==> Ai <= Aj (Ai = ti - fi)
If fi >= fj, tj - ti >= fi - fj ==> ti + fi <= tj + fj ==> Bi <= Bj (Bi = ti + fi)</p>
<p>Can we remove some constraints?</p>
<ol>
<li>ti <= tj</li>
<li>If fi < fj, Ai <= Aj ==> Ai + 2 * fi <= Aj + 2 * fj ==> Bi <= Bj</li>
<li>If fi >= fj, Bi <= Bj ==> Bi - 2 * fi <= Bj - 2 * fj ==> Ai <= Aj</li>
</ol>
<p>We can combine 2) with 3) to "Ai <= Aj && Bi <= Bj"
Ai + Bi <= Aj + Bj ==> ti <= tj ==> ti <= tj can be removed. </p>
<p>==></p>
<p>edge(i->j) <==> Ai <= Aj && Bi <= Bj</p>
<p>We need to find the minimum path cover in the graph which edge(i->j) <==> Ai <= Aj && Bi <= Bj. </p>
<p>According to <a href="https://en.wikipedia.org/wiki/Dilworth%27s_theorem">Dilworth's theorem</a>, the minimum path cover in this graph is equal to the longest anti-chain.
So we just need to choose a maximum vertexes subset from the graph, where any of two do not have an edge.
1. Sort the (Ai, Bi) by the first key value Ai, if Ai == Aj, then smaller Bi comes first.
2. The longest decreasing subsequence of Bi will be the answer.(This is a very classic question that can be solved by O(nlgn).</p>
<p><strong>Problem Setter Code</strong>:</p>
<pre><code>#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <iomanip>
#include <sstream>
#include <fstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
typedef vector<int> VI;
typedef vector<LL> VL;
typedef vector<PII> VPII;
typedef vector<PLL> VPLL;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<(x)<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<(x)<<", "#y" = "<<(y)<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define FOR(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define rep(i, n) for(int i = 0; i < n; i++)
#define UN(v) sort(ALL(v)), v.resize(unique(ALL(v))-v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
template<class T> string tostring(T x, int len = 0) {stringstream ss; ss << x; string r = ss.str(); if(r.length() < len) r = string(len - r.length(), '0') + r; return r;}
template<class T> void convert(string x, T& r) {stringstream ss(x); ss >> r;}
template<class A, class B> ostream& operator<<(ostream &o, pair<A, B> t) {o << "(" << t.x << ", " << t.y << ")"; return o;}
const int inf = 0x3f3f3f3f;
const int mod = int(1e9) + 7;
const int N = 111111;
int t[N], f[N];
int d[N];
int n;
int LIS(VI v) {
fill(d, d + n, 1);
for(int i = 0; i < n; i++)
for(int j = 0; j < i; j++)
if(v[i] > v[j]) chmax(d[i], d[j] + 1);
int res = 0;
for(int i = 0; i < n; i++) chmax(res, d[i]);
return res;
}
int LIS1(VI v) {
MM(d, 0x3f);
d[1] = v[0];
for(int i = 1; i < v.size(); i++) {
int t = upper_bound(d + 1, d + N, v[i]) - d;
if(t != 1 && d[t - 1] >= v[i]) continue;
d[t] = v[i];
}
int res = 0;
for(int i = 1; i < N; i++) if(d[i] != inf) res = i;
return res;
}
int main() {
cin >> n;
for(int i = 0; i < n; i++) cin >> t[i] >> f[i];
for(int i = 1; i < n; i++) assert(t[i] >= t[i - 1]);
VI v;
VPII vp;
for(int i = 0; i < n; i++) vp.pb(mp(t[i] - f[i], t[i] + f[i]));
sort(ALL(vp));
for(int i = 0; i < n; i++) v.pb(vp[i].second);
reverse(ALL(v));
//PV(ALL(v));
cout << LIS1(v) << endl;
//P2(LIS1(v), LIS(v));
//assert(LIS1(v) == LIS(v));
return 0;
}
</code></pre>
<p><strong>Problem Tester Code</strong>:</p>
<pre><code>#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
pair<int,int> a[100005];
set<int> have;
int main() {
int n;
scanf("%d",&n);
for (int i = 0; i < n; ++i) {
int x,y;
scanf("%d%d",&x,&y);
a[i] = make_pair(x + y,x - y);
}
sort(a, a + n);
for (int i = 0; i < n; ++i) {
//printf("%d %d\n",a[i].first,a[i].second);
set<int>::iterator t = have.lower_bound(a[i].second);
if ((t != have.end()) && (*t == a[i].second)) {
continue;
}
if (t != have.begin()) {
have.erase(--t);
}
have.insert(a[i].second);
}
printf("%d\n",have.size());
return 0;
}
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <utility>
using namespace std;
#define Pair pair<int, int>
#define MAX 100000
Pair v[MAX];
int a[MAX];
int dp[MAX + 1];
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
int x, y;
scanf("%d%d", &x, &y);
v[i] = make_pair(x - y, x + y);
}
sort(v, v + n);
for (int i = 0; i < n; i++)
a[i] = v[n - i - 1].second;
int r = 1;
dp[1] = a[0];
for (int i = 1; i < n; i++) {
int low = 1, high = r;
if (a[i] <= dp[1]) {
dp[1] = a[i];
continue;
}
while (low < high) {
int mid = (low + high + 1) / 2;
if (dp[mid] >= a[i])
high = mid - 1;
else
low = mid;
}
if (low == r) r++;
dp[low + 1] = a[i];
}
cout << r << endl;
return 0;
}
</code></pre>
| 0 |
oct-2020-editorial-hackerx
|
2013-10-30T05:56:08
|
{"contest_participation":7868,"challenge_submissions":955,"successful_submissions":110}
|
2013-10-30T05:56:08
|
2016-07-23T14:05:03
|
tester
|
###C++
```cpp
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
pair<int,int> a[100005];
set<int> have;
int main() {
int n;
scanf("%d",&n);
for (int i = 0; i < n; ++i) {
int x,y;
scanf("%d%d",&x,&y);
a[i] = make_pair(x + y,x - y);
}
sort(a, a + n);
for (int i = 0; i < n; ++i) {
//printf("%d %d\n",a[i].first,a[i].second);
set<int>::iterator t = have.lower_bound(a[i].second);
if ((t != have.end()) && (*t == a[i].second)) {
continue;
}
if (t != have.begin()) {
have.erase(--t);
}
have.insert(a[i].second);
}
printf("%d\n",have.size());
return 0;
}
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <utility>
using namespace std;
#define Pair pair<int, int>
#define MAX 100000
Pair v[MAX];
int a[MAX];
int dp[MAX + 1];
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
int x, y;
scanf("%d%d", &x, &y);
v[i] = make_pair(x - y, x + y);
}
sort(v, v + n);
for (int i = 0; i < n; i++)
a[i] = v[n - i - 1].second;
int r = 1;
dp[1] = a[0];
for (int i = 1; i < n; i++) {
int low = 1, high = r;
if (a[i] <= dp[1]) {
dp[1] = a[i];
continue;
}
while (low < high) {
int mid = (low + high + 1) / 2;
if (dp[mid] >= a[i])
high = mid - 1;
else
low = mid;
}
if (low == r) r++;
dp[low + 1] = a[i];
}
cout << r << endl;
return 0;
}
```
|
not-set
|
2016-04-24T02:02:13
|
2016-07-23T14:05:04
|
C++
|
15 | 1,042 |
flip
|
Find The Operations
|
You are given a square grid of size N, with rows numbered from 0 to N - 1 starting from the top and columns numbered from 0 to N - 1 starting from the left.
A cell (u, v) refers to the cell that is on the u<sup>th</sup> row and the v<sup>th</sup> column. Each cell contains an integer - 0 or 1. You can pick any cell and flip the number in all the cells (including the picked cell) within the Manhattan distance D from the picked cell. A flip here means changing the number from 0 to 1 and vice-versa. The manhattan distance from the cell (u, v) to the cell (x, y) is equal to $|u - x| + |v - y|$ where $|i|$ is the absolute value of i.
Your mission is to change all values in the grid to zero without using more than N×N flips.
**Input Format**
The first line of the input contains two integers N and D separated by a single space.
Each line in the next N lines contains N integers separated by a single space which are either 0 or 1. the i<sub>th</sub> number on the j<sub>th</sub> line is the number on the cell (i - 1, j - 1) of the grid.
**Constraints**
1 ≤ N ≤ 20
0 ≤ D ≤ 40
**Output Format**
If there is no solution, your output should contain exactly a single string "Impossible" (without quotes). If a solution exists, print out the string "Possible" (without quotes) in the first line of your output. In the second line, print out an integer M which represent the number of operations that you need. Each line in the next M lines should contain a pair of integers separated by a single space representing the cell that you picked for the corresponding operation. Note that if there is more than one solution you can pick any one of them.
**Sample Input:#00**
3 1
0 1 0
1 1 1
0 1 0
**Sample Output:#00**
Possible
1
1 1
**Sample Input:#01**
3 2
1 0 1
1 1 0
0 0 0
**Sample Output:#01**
Impossible
**Explanation**
In the first testcase, we can perform the first operation in the center cell, this will flip all the elements to 0 within 1 manhattan distance.
In the second testcase, we cannot make it an all 0 matrix under 9 moves. Hence, Impossible.
|
code
|
Let's try to modify a 0-1 grid.
|
ai
|
2013-10-07T10:39:47
|
2022-09-02T09:54:42
| null | null | null |
You are given a square grid of size N, with rows numbered from 0 to N - 1 starting from the top and columns numbered from 0 to N - 1 starting from the left.
A cell (u, v) refers to the cell that is on the u<sup>th</sup> row and the v<sup>th</sup> column. Each cell contains an integer - 0 or 1. You can pick any cell and flip the number in all the cells (including the picked cell) within the Manhattan distance D from the picked cell. A flip here means changing the number from 0 to 1 and vice-versa. The manhattan distance from the cell (u, v) to the cell (x, y) is equal to $|u - x| + |v - y|$ where $|i|$ is the absolute value of i.
Your mission is to change all values in the grid to zero without using more than N×N flips.
**Input Format**
The first line of the input contains two integers N and D separated by a single space.
Each line in the next N lines contains N integers separated by a single space which are either 0 or 1. the i<sub>th</sub> number on the j<sub>th</sub> line is the number on the cell (i - 1, j - 1) of the grid.
**Constraints**
1 ≤ N ≤ 20
0 ≤ D ≤ 40
**Output Format**
If there is no solution, your output should contain exactly a single string "Impossible" (without quotes). If a solution exists, print out the string "Possible" (without quotes) in the first line of your output. In the second line, print out an integer M which represent the number of operations that you need. Each line in the next M lines should contain a pair of integers separated by a single space representing the cell that you picked for the corresponding operation. Note that if there is more than one solution you can pick any one of them.
**Sample Input:#00**
3 1
0 1 0
1 1 1
0 1 0
**Sample Output:#00**
Possible
1
1 1
**Sample Input:#01**
3 2
1 0 1
1 1 0
0 0 0
**Sample Output:#01**
Impossible
**Explanation**
In the first testcase, we can perform the first operation in the center cell, this will flip all the elements to 0 within 1 manhattan distance.
In the second testcase, we cannot make it an all 0 matrix under 9 moves. Hence, Impossible.
| 0.5 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
Find The Operations : Nov 20/20 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/nov13/challenges/FLIP">Find The Operations</a> <br>
Let's try to modify a 0-1 grid. Problem statement <a href="https://www.hackerrank.com/contests/nov13/challenges/FLIP">here</a>. </p>
<p><strong>Difficulty Level</strong></p>
<p>Medium-Hard</p>
<p><strong>Required Knowledge</strong></p>
<p>Gaussian Elimination, Linear Algebra</p>
<p><strong>Time Complexity</strong></p>
<p>O(N^2) for each test case</p>
<p><strong>Problem Setter</strong> <br>
<a href="https://www.hackerrank.com/tuananhnb93">Tran Dang Tuan Anh</a> </p>
<p><strong>Problem Tester</strong> <br>
<a href="https://www.hackerrank.com/cpcs">Peng Cao</a></p>
<p><strong>Approach</strong>
Given N and D <br>
and initial matrix given is M[N][N]. <br>
Construct Matrices A[NXN][NXN] and B[NXN]. Such as <br>
For all A [i][j] i be the index for each value in M, and A[i][j] = 1 if j lies in the given "D" Manhattan distance from i. </p>
<p>Hence we get the A[][] matrix that contains the information of all the j values that will be flipped, for corresponding i. </p>
<p>And we fill B[i] with initial values of all i in M[N][N]</p>
<p>Now we know that each element will be flipped only once. It can have a value 0 or 1 initially. So we try to solve by <a href="http://en.wikipedia.org/wiki/Gaussian_elimination">Gaussian Elimination</a> equation Ax=B but instead of subtraction we take ^(XOR) as we don't have to deal with -ve values. </p>
<p>If B[i] ==1 and corresponding all the j's in A[i][j] are 0. It is Impossible to solve. <br>
Also when B[i]== 1 and diagonal A[i][i] =0 we can not flip the value hence Impossible to solve. <br>
For all other cases it is Possible and in the end we are left with a diagonal matrix and the result matrix B. Corresponding to the state where all Elements are 0.</p>
<p>After that we simply count the elements in B[NXN] array and for each index in B (index/N, index%N) is the required index.</p>
<p><strong>Setter's Code</strong> :</p>
<pre><code>#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <string>
#include <memory.h>
#include <sstream>
#include <complex>
#include <cassert>
#define REP(i,n) for(int i = 0, _n = (n); i < _n; i++)
#define REPD(i,n) for(int i = (n) - 1; i >= 0; i--)
#define FOR(i,a,b) for (int i = (a), _b = (b); i <= _b; i++)
#define FORD(i,a,b) for (int i = (a), _b = (b); i >= _b; i--)
#define FORN(i,a,b) for(int i=a;i<b;i++)
#define FOREACH(it,c) for (__typeof((c).begin()) it=(c).begin();it!=(c).end();it++)
#define RESET(c,x) memset (c, x, sizeof (c))
#define PI acos(-1)
#define sqr(x) ((x) * (x))
#define PB push_back
#define MP make_pair
#define F first
#define S second
#define Aint(c) (c).begin(), (c).end()
#define SIZE(c) (c).size()
#define DEBUG(x) { cerr << #x << " = " << x << endl; }
#define PR(a,n) {cerr<<#a<<" = "; FOR(_,1,n) cerr << a[_] << ' '; cerr <<endl;}
#define PR0(a,n) {cerr<<#a<<" = ";REP(_,n) cerr << a[_] << ' '; cerr << endl;}
#define LL long long
#define maxn 24
using namespace std;
int Gauss(int n, int a[][maxn * maxn], int b[]) {
for (int i = 0; i < n; i++) {
int row = -1;
for (int j = i; j < n; j++)
if (a[j][i]) {
row = j;
break;
}
if (row == -1) continue;
if (!a[i][i])
for (int j = 0; j <= n; j++)
a[i][j] ^= a[row][j];
for (int k = i; k < n; k++)
if (k != i && a[k][i] == 1) {
for (int j = 0; j <= n; j++)
a[k][j] ^= a[i][j];
}
}
for (int i = 0; i < n; i++)
if (a[i][n]) {
int ok = 0;
for (int j = 0; j < n; j++)
if (a[i][j]) {
ok = 1;
break;
}
if (!ok) return 0;
}
for (int i = n - 1; i >= 0; i--) {
if (a[i][i] == 0 && a[i][n] == 1) return 0;
if (a[i][i] == 0) b[i] = 0;
else b[i] = a[i][n];
if (b[i])
for (int j = i - 1; j >= 0; j--)
if (a[j][i] == 1) a[j][n] ^= 1;
}
return 1;
}
int n, d, g[maxn][maxn], a[maxn * maxn][maxn * maxn], root[maxn * maxn];
int main() {
cin >> n >> d;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> g[i][j];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
int row = i * n + j;
a[row][n * n] = g[i][j];
for (int x = 0; x < n; x++)
for (int y = 0; y < n; y++)
if (abs(x - i) + abs(y - j) <= d) {
// cerr << x * n + y << endl;
a[row][x * n + y] = 1;
}
}
int res = Gauss(n * n, a, root);
if (!res) cout << "Impossible" << endl;
else {
cout << "Possible" << endl;
int cnt = 0;
for (int i = 0; i < n * n; i++)
cnt += root[i];
cout << cnt << endl;
for (int i = 0; i < n * n; i++)
if (root[i]) cout << i / n << " " << i % n << endl;
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 402;
int a[N][N],b[N];
vector<int> result;
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int n, d,i,j,k;
scanf("%d%d",&n,&d);
for (i = 0; i < n; ++i) {
for (j = 0; j < n; ++j) {
scanf("%d",b + i * n + j);
for (int x = max(i - d, 0); (x < n) && (x <= i + d); ++x) {
int dd = x - i;
if (dd < 0) {
dd = -dd;
}
dd = d - dd;
for (int y = max(j - dd, 0); (y < n) && (y <= j + dd); ++y) {
a[i * n + j][x * n + y] = 1;
}
}
}
}
int m = n * n;
for (i = 0; i < m; ++i) {
for (j = i; j < m; ++j) {
if (a[j][i]) {
break;
}
}
if (j < m) {
if (j != i) {
// exchange row j and row i
for (k = 0; k < m; ++k) {
int t = a[j][k];
a[j][k] = a[i][k];
a[i][k] = t;
}
k = b[i];
b[i] = b[j];
b[j] = k;
}
for (j = i + 1; j < m; ++j) {
if (a[j][i]) {
for (int k = i; k < m; ++k) {
a[j][k] ^= a[i][k];
}
b[j] ^= b[i];
}
}
}
}
for (i = m - 1; i >= 0; --i) {
for (j = i + 1; j < m; ++j) {
b[i] ^= (a[i][j] & b[j]);
}
if ((a[i][i] == 0) && (b[i] != 0)) {
break;
}
if (b[i]) {
result.push_back(i);
}
}
if (i < 0) {
puts("Possible");
printf("%d\n",result.size());
for (int i = 0; i < result.size(); ++i) {
printf("%d %d\n",result[i] / n, result[i] % n);
}
}
else {
puts("Impossible");
}
return 0;
}
</code></pre>
| 0 |
nov-2020-editorial-find-the-operations
|
2013-11-27T06:59:25
|
{"contest_participation":3343,"challenge_submissions":160,"successful_submissions":76}
|
2013-11-27T06:59:25
|
2016-12-08T11:34:28
|
setter
|
###C++
```cpp
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <string>
#include <memory.h>
#include <sstream>
#include <complex>
#include <cassert>
#define REP(i,n) for(int i = 0, _n = (n); i < _n; i++)
#define REPD(i,n) for(int i = (n) - 1; i >= 0; i--)
#define FOR(i,a,b) for (int i = (a), _b = (b); i <= _b; i++)
#define FORD(i,a,b) for (int i = (a), _b = (b); i >= _b; i--)
#define FORN(i,a,b) for(int i=a;i<b;i++)
#define FOREACH(it,c) for (__typeof((c).begin()) it=(c).begin();it!=(c).end();it++)
#define RESET(c,x) memset (c, x, sizeof (c))
#define PI acos(-1)
#define sqr(x) ((x) * (x))
#define PB push_back
#define MP make_pair
#define F first
#define S second
#define Aint(c) (c).begin(), (c).end()
#define SIZE(c) (c).size()
#define DEBUG(x) { cerr << #x << " = " << x << endl; }
#define PR(a,n) {cerr<<#a<<" = "; FOR(_,1,n) cerr << a[_] << ' '; cerr <<endl;}
#define PR0(a,n) {cerr<<#a<<" = ";REP(_,n) cerr << a[_] << ' '; cerr << endl;}
#define LL long long
#define maxn 24
using namespace std;
int Gauss(int n, int a[][maxn * maxn], int b[]) {
for (int i = 0; i < n; i++) {
int row = -1;
for (int j = i; j < n; j++)
if (a[j][i]) {
row = j;
break;
}
if (row == -1) continue;
if (!a[i][i])
for (int j = 0; j <= n; j++)
a[i][j] ^= a[row][j];
for (int k = i; k < n; k++)
if (k != i && a[k][i] == 1) {
for (int j = 0; j <= n; j++)
a[k][j] ^= a[i][j];
}
}
for (int i = 0; i < n; i++)
if (a[i][n]) {
int ok = 0;
for (int j = 0; j < n; j++)
if (a[i][j]) {
ok = 1;
break;
}
if (!ok) return 0;
}
for (int i = n - 1; i >= 0; i--) {
if (a[i][i] == 0 && a[i][n] == 1) return 0;
if (a[i][i] == 0) b[i] = 0;
else b[i] = a[i][n];
if (b[i])
for (int j = i - 1; j >= 0; j--)
if (a[j][i] == 1) a[j][n] ^= 1;
}
return 1;
}
int n, d, g[maxn][maxn], a[maxn * maxn][maxn * maxn], root[maxn * maxn];
int main() {
cin >> n >> d;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> g[i][j];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
int row = i * n + j;
a[row][n * n] = g[i][j];
for (int x = 0; x < n; x++)
for (int y = 0; y < n; y++)
if (abs(x - i) + abs(y - j) <= d) {
// cerr << x * n + y << endl;
a[row][x * n + y] = 1;
}
}
int res = Gauss(n * n, a, root);
if (!res) cout << "Impossible" << endl;
else {
cout << "Possible" << endl;
int cnt = 0;
for (int i = 0; i < n * n; i++)
cnt += root[i];
cout << cnt << endl;
for (int i = 0; i < n * n; i++)
if (root[i]) cout << i / n << " " << i % n << endl;
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:14
|
2016-07-23T18:03:16
|
C++
|
16 | 1,042 |
flip
|
Find The Operations
|
You are given a square grid of size N, with rows numbered from 0 to N - 1 starting from the top and columns numbered from 0 to N - 1 starting from the left.
A cell (u, v) refers to the cell that is on the u<sup>th</sup> row and the v<sup>th</sup> column. Each cell contains an integer - 0 or 1. You can pick any cell and flip the number in all the cells (including the picked cell) within the Manhattan distance D from the picked cell. A flip here means changing the number from 0 to 1 and vice-versa. The manhattan distance from the cell (u, v) to the cell (x, y) is equal to $|u - x| + |v - y|$ where $|i|$ is the absolute value of i.
Your mission is to change all values in the grid to zero without using more than N×N flips.
**Input Format**
The first line of the input contains two integers N and D separated by a single space.
Each line in the next N lines contains N integers separated by a single space which are either 0 or 1. the i<sub>th</sub> number on the j<sub>th</sub> line is the number on the cell (i - 1, j - 1) of the grid.
**Constraints**
1 ≤ N ≤ 20
0 ≤ D ≤ 40
**Output Format**
If there is no solution, your output should contain exactly a single string "Impossible" (without quotes). If a solution exists, print out the string "Possible" (without quotes) in the first line of your output. In the second line, print out an integer M which represent the number of operations that you need. Each line in the next M lines should contain a pair of integers separated by a single space representing the cell that you picked for the corresponding operation. Note that if there is more than one solution you can pick any one of them.
**Sample Input:#00**
3 1
0 1 0
1 1 1
0 1 0
**Sample Output:#00**
Possible
1
1 1
**Sample Input:#01**
3 2
1 0 1
1 1 0
0 0 0
**Sample Output:#01**
Impossible
**Explanation**
In the first testcase, we can perform the first operation in the center cell, this will flip all the elements to 0 within 1 manhattan distance.
In the second testcase, we cannot make it an all 0 matrix under 9 moves. Hence, Impossible.
|
code
|
Let's try to modify a 0-1 grid.
|
ai
|
2013-10-07T10:39:47
|
2022-09-02T09:54:42
| null | null | null |
You are given a square grid of size N, with rows numbered from 0 to N - 1 starting from the top and columns numbered from 0 to N - 1 starting from the left.
A cell (u, v) refers to the cell that is on the u<sup>th</sup> row and the v<sup>th</sup> column. Each cell contains an integer - 0 or 1. You can pick any cell and flip the number in all the cells (including the picked cell) within the Manhattan distance D from the picked cell. A flip here means changing the number from 0 to 1 and vice-versa. The manhattan distance from the cell (u, v) to the cell (x, y) is equal to $|u - x| + |v - y|$ where $|i|$ is the absolute value of i.
Your mission is to change all values in the grid to zero without using more than N×N flips.
**Input Format**
The first line of the input contains two integers N and D separated by a single space.
Each line in the next N lines contains N integers separated by a single space which are either 0 or 1. the i<sub>th</sub> number on the j<sub>th</sub> line is the number on the cell (i - 1, j - 1) of the grid.
**Constraints**
1 ≤ N ≤ 20
0 ≤ D ≤ 40
**Output Format**
If there is no solution, your output should contain exactly a single string "Impossible" (without quotes). If a solution exists, print out the string "Possible" (without quotes) in the first line of your output. In the second line, print out an integer M which represent the number of operations that you need. Each line in the next M lines should contain a pair of integers separated by a single space representing the cell that you picked for the corresponding operation. Note that if there is more than one solution you can pick any one of them.
**Sample Input:#00**
3 1
0 1 0
1 1 1
0 1 0
**Sample Output:#00**
Possible
1
1 1
**Sample Input:#01**
3 2
1 0 1
1 1 0
0 0 0
**Sample Output:#01**
Impossible
**Explanation**
In the first testcase, we can perform the first operation in the center cell, this will flip all the elements to 0 within 1 manhattan distance.
In the second testcase, we cannot make it an all 0 matrix under 9 moves. Hence, Impossible.
| 0.5 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
Find The Operations : Nov 20/20 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/nov13/challenges/FLIP">Find The Operations</a> <br>
Let's try to modify a 0-1 grid. Problem statement <a href="https://www.hackerrank.com/contests/nov13/challenges/FLIP">here</a>. </p>
<p><strong>Difficulty Level</strong></p>
<p>Medium-Hard</p>
<p><strong>Required Knowledge</strong></p>
<p>Gaussian Elimination, Linear Algebra</p>
<p><strong>Time Complexity</strong></p>
<p>O(N^2) for each test case</p>
<p><strong>Problem Setter</strong> <br>
<a href="https://www.hackerrank.com/tuananhnb93">Tran Dang Tuan Anh</a> </p>
<p><strong>Problem Tester</strong> <br>
<a href="https://www.hackerrank.com/cpcs">Peng Cao</a></p>
<p><strong>Approach</strong>
Given N and D <br>
and initial matrix given is M[N][N]. <br>
Construct Matrices A[NXN][NXN] and B[NXN]. Such as <br>
For all A [i][j] i be the index for each value in M, and A[i][j] = 1 if j lies in the given "D" Manhattan distance from i. </p>
<p>Hence we get the A[][] matrix that contains the information of all the j values that will be flipped, for corresponding i. </p>
<p>And we fill B[i] with initial values of all i in M[N][N]</p>
<p>Now we know that each element will be flipped only once. It can have a value 0 or 1 initially. So we try to solve by <a href="http://en.wikipedia.org/wiki/Gaussian_elimination">Gaussian Elimination</a> equation Ax=B but instead of subtraction we take ^(XOR) as we don't have to deal with -ve values. </p>
<p>If B[i] ==1 and corresponding all the j's in A[i][j] are 0. It is Impossible to solve. <br>
Also when B[i]== 1 and diagonal A[i][i] =0 we can not flip the value hence Impossible to solve. <br>
For all other cases it is Possible and in the end we are left with a diagonal matrix and the result matrix B. Corresponding to the state where all Elements are 0.</p>
<p>After that we simply count the elements in B[NXN] array and for each index in B (index/N, index%N) is the required index.</p>
<p><strong>Setter's Code</strong> :</p>
<pre><code>#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <string>
#include <memory.h>
#include <sstream>
#include <complex>
#include <cassert>
#define REP(i,n) for(int i = 0, _n = (n); i < _n; i++)
#define REPD(i,n) for(int i = (n) - 1; i >= 0; i--)
#define FOR(i,a,b) for (int i = (a), _b = (b); i <= _b; i++)
#define FORD(i,a,b) for (int i = (a), _b = (b); i >= _b; i--)
#define FORN(i,a,b) for(int i=a;i<b;i++)
#define FOREACH(it,c) for (__typeof((c).begin()) it=(c).begin();it!=(c).end();it++)
#define RESET(c,x) memset (c, x, sizeof (c))
#define PI acos(-1)
#define sqr(x) ((x) * (x))
#define PB push_back
#define MP make_pair
#define F first
#define S second
#define Aint(c) (c).begin(), (c).end()
#define SIZE(c) (c).size()
#define DEBUG(x) { cerr << #x << " = " << x << endl; }
#define PR(a,n) {cerr<<#a<<" = "; FOR(_,1,n) cerr << a[_] << ' '; cerr <<endl;}
#define PR0(a,n) {cerr<<#a<<" = ";REP(_,n) cerr << a[_] << ' '; cerr << endl;}
#define LL long long
#define maxn 24
using namespace std;
int Gauss(int n, int a[][maxn * maxn], int b[]) {
for (int i = 0; i < n; i++) {
int row = -1;
for (int j = i; j < n; j++)
if (a[j][i]) {
row = j;
break;
}
if (row == -1) continue;
if (!a[i][i])
for (int j = 0; j <= n; j++)
a[i][j] ^= a[row][j];
for (int k = i; k < n; k++)
if (k != i && a[k][i] == 1) {
for (int j = 0; j <= n; j++)
a[k][j] ^= a[i][j];
}
}
for (int i = 0; i < n; i++)
if (a[i][n]) {
int ok = 0;
for (int j = 0; j < n; j++)
if (a[i][j]) {
ok = 1;
break;
}
if (!ok) return 0;
}
for (int i = n - 1; i >= 0; i--) {
if (a[i][i] == 0 && a[i][n] == 1) return 0;
if (a[i][i] == 0) b[i] = 0;
else b[i] = a[i][n];
if (b[i])
for (int j = i - 1; j >= 0; j--)
if (a[j][i] == 1) a[j][n] ^= 1;
}
return 1;
}
int n, d, g[maxn][maxn], a[maxn * maxn][maxn * maxn], root[maxn * maxn];
int main() {
cin >> n >> d;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> g[i][j];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
int row = i * n + j;
a[row][n * n] = g[i][j];
for (int x = 0; x < n; x++)
for (int y = 0; y < n; y++)
if (abs(x - i) + abs(y - j) <= d) {
// cerr << x * n + y << endl;
a[row][x * n + y] = 1;
}
}
int res = Gauss(n * n, a, root);
if (!res) cout << "Impossible" << endl;
else {
cout << "Possible" << endl;
int cnt = 0;
for (int i = 0; i < n * n; i++)
cnt += root[i];
cout << cnt << endl;
for (int i = 0; i < n * n; i++)
if (root[i]) cout << i / n << " " << i % n << endl;
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 402;
int a[N][N],b[N];
vector<int> result;
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int n, d,i,j,k;
scanf("%d%d",&n,&d);
for (i = 0; i < n; ++i) {
for (j = 0; j < n; ++j) {
scanf("%d",b + i * n + j);
for (int x = max(i - d, 0); (x < n) && (x <= i + d); ++x) {
int dd = x - i;
if (dd < 0) {
dd = -dd;
}
dd = d - dd;
for (int y = max(j - dd, 0); (y < n) && (y <= j + dd); ++y) {
a[i * n + j][x * n + y] = 1;
}
}
}
}
int m = n * n;
for (i = 0; i < m; ++i) {
for (j = i; j < m; ++j) {
if (a[j][i]) {
break;
}
}
if (j < m) {
if (j != i) {
// exchange row j and row i
for (k = 0; k < m; ++k) {
int t = a[j][k];
a[j][k] = a[i][k];
a[i][k] = t;
}
k = b[i];
b[i] = b[j];
b[j] = k;
}
for (j = i + 1; j < m; ++j) {
if (a[j][i]) {
for (int k = i; k < m; ++k) {
a[j][k] ^= a[i][k];
}
b[j] ^= b[i];
}
}
}
}
for (i = m - 1; i >= 0; --i) {
for (j = i + 1; j < m; ++j) {
b[i] ^= (a[i][j] & b[j]);
}
if ((a[i][i] == 0) && (b[i] != 0)) {
break;
}
if (b[i]) {
result.push_back(i);
}
}
if (i < 0) {
puts("Possible");
printf("%d\n",result.size());
for (int i = 0; i < result.size(); ++i) {
printf("%d %d\n",result[i] / n, result[i] % n);
}
}
else {
puts("Impossible");
}
return 0;
}
</code></pre>
| 0 |
nov-2020-editorial-find-the-operations
|
2013-11-27T06:59:25
|
{"contest_participation":3343,"challenge_submissions":160,"successful_submissions":76}
|
2013-11-27T06:59:25
|
2016-12-08T11:34:28
|
tester
|
###C++
```cpp
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 402;
int a[N][N],b[N];
vector<int> result;
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int n, d,i,j,k;
scanf("%d%d",&n,&d);
for (i = 0; i < n; ++i) {
for (j = 0; j < n; ++j) {
scanf("%d",b + i * n + j);
for (int x = max(i - d, 0); (x < n) && (x <= i + d); ++x) {
int dd = x - i;
if (dd < 0) {
dd = -dd;
}
dd = d - dd;
for (int y = max(j - dd, 0); (y < n) && (y <= j + dd); ++y) {
a[i * n + j][x * n + y] = 1;
}
}
}
}
int m = n * n;
for (i = 0; i < m; ++i) {
for (j = i; j < m; ++j) {
if (a[j][i]) {
break;
}
}
if (j < m) {
if (j != i) {
// exchange row j and row i
for (k = 0; k < m; ++k) {
int t = a[j][k];
a[j][k] = a[i][k];
a[i][k] = t;
}
k = b[i];
b[i] = b[j];
b[j] = k;
}
for (j = i + 1; j < m; ++j) {
if (a[j][i]) {
for (int k = i; k < m; ++k) {
a[j][k] ^= a[i][k];
}
b[j] ^= b[i];
}
}
}
}
for (i = m - 1; i >= 0; --i) {
for (j = i + 1; j < m; ++j) {
b[i] ^= (a[i][j] & b[j]);
}
if ((a[i][i] == 0) && (b[i] != 0)) {
break;
}
if (b[i]) {
result.push_back(i);
}
}
if (i < 0) {
puts("Possible");
printf("%d\n",result.size());
for (int i = 0; i < result.size(); ++i) {
printf("%d %d\n",result[i] / n, result[i] % n);
}
}
else {
puts("Impossible");
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:14
|
2016-07-23T18:04:21
|
C++
|
17 | 779 |
oil-well
|
Oil Well
|
Mr. Road Runner bought a piece of land in the middle of a desert for a nominal amount. It turns out that the piece of land is now worth millions of dollars as it has an oil reserve under it. Mr. Road Runner contacts the ACME corp to set up the oil wells on his land. Setting up oil wells is a costly affair and the charges of setting up oil wells are as follows.
The rectangular plot bought by Mr. Road Runner is divided into *r* * *c* blocks. Only some blocks are suitable for setting up the oil well and these blocks have been marked. ACME charges nothing for building the first oil well. For every subsequent oil well built, the cost would be the maximum **ACME distance** between the new oil well and the existing oil wells.
If *(x,y)* is the position of the block where a new oil well is setup and *(x1, y1)* is the position of the block of an existing oil well, the *ACME distance* is given by
max(|x-x1|, |y-y1|)
the maximum *ACME distance* is the maximum among all the *ACME distance* between existing oil wells and new wells.
If the distance of any two adjacent blocks (horizontal or vertical) is considered 1 unit, what is the minimum cost *(E)* in units it takes to set up oil wells across all the marked blocks?
**Input format**
The first line of the input contains two space separated integers *r* *c*.
*r* lines follow each containing *c* space separated integers.
1 indicates that the block is suitable for setting up an oil well, whereas 0 isn't.
r c
M11 M12 ... M1c
M21 M22 ... M2c
...
Mr1 Mr2 ... Mrc
**Output format**
Print the minimum value E as the answer.
**Constraints**
1 <= r, c <= 50
**Sample Input #00:**
3 4
1 0 0 0
1 0 0 0
0 0 1 0
**Sample Output #00:**
3
**Explanation:**
(1, 1) (2, 1) (3, 3) are the places where are to be setup.
There are 3! = 6 ways to do it.
(1, 1) (2, 1) (3, 3) ==> cost = 0 + 1 + 2 = 3
(1, 1) (3, 3) (2, 1) ==> cost = 0 + 2 + 2 = 4
(2, 1) (1, 1) (3, 3) ==> cost = 0 + 1 + 2 = 3
(2, 1) (3, 3) (1, 1) ==> cost = 0 + 2 + 2 = 4
(3, 3) (1, 1) (2, 1) ==> cost = 0 + 2 + 2 = 4
(3, 3) (2, 1) (1, 1) ==> cost = 0 + 2 + 2 = 4
So E = 3
|
code
|
Given RxC matrix with 0/1. Rearrange the cells having 1 so that the manhattan disctance sum of adjacent cells in this list is minimal. Fidn the sum
|
ai
|
2013-07-25T18:13:47
|
2022-08-31T08:14:52
|
#
# Complete the 'oilWell' function below.
#
# The function is expected to return an INTEGER.
# The function accepts 2D_INTEGER_ARRAY blocks as parameter.
#
def oilWell(blocks):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
r = int(first_multiple_input[0])
c = int(first_multiple_input[1])
blocks = []
for _ in range(r):
blocks.append(list(map(int, input().rstrip().split())))
result = oilWell(blocks)
fptr.write(str(result) + '\n')
fptr.close()
|
Mr. Road Runner bought a piece of land in the middle of a desert for a nominal amount. It turns out that the piece of land is now worth millions of dollars as it has an oil reserve under it. Mr. Road Runner contacts the ACME corp to set up the oil wells on his land. Setting up oil wells is a costly affair and the charges of setting up oil wells are as follows.
The rectangular plot bought by Mr. Road Runner is divided into *r* * *c* blocks. Only some blocks are suitable for setting up the oil well and these blocks have been marked. ACME charges nothing for building the first oil well. For every subsequent oil well built, the cost would be the maximum **ACME distance** between the new oil well and the existing oil wells.
If *(x,y)* is the position of the block where a new oil well is setup and *(x1, y1)* is the position of the block of an existing oil well, the *ACME distance* is given by
max(|x-x1|, |y-y1|)
the maximum *ACME distance* is the maximum among all the *ACME distance* between existing oil wells and new wells.
If the distance of any two adjacent blocks (horizontal or vertical) is considered 1 unit, what is the minimum cost *(E)* in units it takes to set up oil wells across all the marked blocks?
| 0.547945 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line of the input contains two space separated integers *r* *c*.
*r* lines follow each containing *c* space separated integers.
1 indicates that the block is suitable for setting up an oil well, whereas 0 isn't.
r c
M11 M12 ... M1c
M21 M22 ... M2c
...
Mr1 Mr2 ... Mrc
|
Print the minimum value E as the answer.
|
3 4
1 0 0 0
1 0 0 0
0 0 1 0
|
3
|
Hard
|
November 2020 Editorial: Oil Well
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><h3>A General Idea</h3>
<p>The solution is based on this:
After setting up k points, only the minimal rectangle covering all the existing points is of importance to us. Start with K = 0, 1, 2 .. etc. and progress. </p>
<p><strong>Why is this the case?</strong> </p>
<p>1) For the points inside the rectangle which have not yet been set up, the cost for setting up those is fixed: the sum of the maximum distance between each of them to the edge of the rectangle. </p>
<p>2) For the points outside the rectangle, the maximum distance will only be dependent on the points in this rectangle, because the oil wells inside that rectangle cannot be a a greater distance. </p>
<p>So let us start with this easy Dynamic Programming function, by using the above mentioned rule inductively: </p>
<p>Let F(lx, ly, rx, ry) be the cost of setting up all the oil wells inside rectangle with top-left corner at coordinates (lx, ly) and bottom-right corner at coordinates (rx, ry). </p>
<p>F(lx, ly, rx, ry) = min(F(lx', ly', rx', ry') + cost_of_points_not_set_up) </p>
<p>n <= 50 <br>
The upper bound on the number of points is O(n ^ 2). </p>
<p>There are n ^ 4 states, and we need to enumurate (lx', ly', rx', ry') which will be done O(n ^ 4) times, and we need to calculate the cost which can be done in O(n ^ 2) time, so the total complexity is O(n ^ 10). </p>
<h3>How do we optimize this?></h3>
<p>As we can see, if there are at least one point strictly between (lx, ly, rx, ry) and (lx', ly', rx', ry'), the cost will not be optimal. So, we add the inner points first before expanding the rectangle. </p>
<p>Here is the rule we will enforce:
While adding a new point, the new rectangle can not contain any point which is strictly inside it. </p>
<p>So the choice of (lx', ly', rx', ry') will be restricted. And we can calculate the cost of the new points in O(n). So the complexity can be optimized to O(n ^ 4) * O(n) = O(n ^ 5). </p>
<h3>Solution:</h3>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int inf = 1000000000;
const int N = 52;
int dp[N][N][N][N], a[N][N];
int ab(int x) {
return (x > 0)?x:(-x);
}
int dis(int x1,int y1,int x2,int y2) {
return max(ab(x1 - x2), ab(y1 - y2));
}
int cal(int x,int y,int x1,int y1,int x2, int y2) {
return max(dis(x,y,x1,y1), dis(x,y,x2,y2));
}
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int m, n;
scanf("%d%d",&m,&n);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d",&a[i][j]);
}
}
for (int i = m - 1; i >= 0; --i) {
for (int j = n - 1; j >= 0; --j) {
for (int k = i; k < m; ++k) {
for (int h = (k == i)?(j + 1):j; h < n; ++h) {
dp[i][j][k][h] = inf;
if (i < k) {
int may = dp[i + 1][j][k][h];
for (int y = j; y <= h; ++y) {
if (a[i][y]) {
may += cal(i, y, i + 1, j, k, h);
}
}
dp[i][j][k][h] = min(dp[i][j][k][h], may);
may = dp[i][j][k - 1][h];
for (int y = j; y <= h; ++y) {
if (a[k][y]) {
may += cal(k, y, i ,j, k - 1, h);
}
}
dp[i][j][k][h] = min(dp[i][j][k][h], may);
}
if (j < h) {
int may = dp[i][j + 1][k][h];
for (int x = i; x <= k; ++x) {
if (a[x][j]) {
may += cal(x, j, i, j + 1, k, h);
}
}
dp[i][j][k][h] = min(dp[i][j][k][h], may);
may = dp[i][j][k][h - 1];
for (int x = i; x <= k; ++x) {
if (a[x][h]) {
may += cal(x, h, i, j, k, h - 1);
}
}
dp[i][j][k][h] = min(dp[i][j][k][h], may);
}
}
}
}
}
printf("%d\n",dp[0][0][m - 1][n - 1]);
return 0;
}
</code></pre>
| 0 |
nov2020-oil-well
|
2013-11-27T09:48:45
|
{"contest_participation":3343,"challenge_submissions":405,"successful_submissions":60}
|
2013-11-27T09:48:45
|
2016-07-23T15:04:07
|
setter
|
###C++
```cpp
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int inf = 1000000000;
const int N = 52;
int dp[N][N][N][N], a[N][N];
int ab(int x) {
return (x > 0)?x:(-x);
}
int dis(int x1,int y1,int x2,int y2) {
return max(ab(x1 - x2), ab(y1 - y2));
}
int cal(int x,int y,int x1,int y1,int x2, int y2) {
return max(dis(x,y,x1,y1), dis(x,y,x2,y2));
}
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */
int m, n;
scanf("%d%d",&m,&n);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d",&a[i][j]);
}
}
for (int i = m - 1; i >= 0; --i) {
for (int j = n - 1; j >= 0; --j) {
for (int k = i; k < m; ++k) {
for (int h = (k == i)?(j + 1):j; h < n; ++h) {
dp[i][j][k][h] = inf;
if (i < k) {
int may = dp[i + 1][j][k][h];
for (int y = j; y <= h; ++y) {
if (a[i][y]) {
may += cal(i, y, i + 1, j, k, h);
}
}
dp[i][j][k][h] = min(dp[i][j][k][h], may);
may = dp[i][j][k - 1][h];
for (int y = j; y <= h; ++y) {
if (a[k][y]) {
may += cal(k, y, i ,j, k - 1, h);
}
}
dp[i][j][k][h] = min(dp[i][j][k][h], may);
}
if (j < h) {
int may = dp[i][j + 1][k][h];
for (int x = i; x <= k; ++x) {
if (a[x][j]) {
may += cal(x, j, i, j + 1, k, h);
}
}
dp[i][j][k][h] = min(dp[i][j][k][h], may);
may = dp[i][j][k][h - 1];
for (int x = i; x <= k; ++x) {
if (a[x][h]) {
may += cal(x, h, i, j, k, h - 1);
}
}
dp[i][j][k][h] = min(dp[i][j][k][h], may);
}
}
}
}
}
printf("%d\n",dp[0][0][m - 1][n - 1]);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:14
|
2016-07-23T15:04:07
|
C++
|
18 | 625 |
random
|
Random
|
Given an array 'D' with n elements: d[0], d[1], ..., d[n-1], you can perform the following two steps on the array.
1. Randomly choose two indexes (l, r) with l < r, swap (d[l], d[r])
2. Randomly choose two indexes (l, r) with l < r, reverse (d[l...r]) (both inclusive)
After you perform the first operation **a** times and the second operation **b** times, you randomly choose two indices _l_ & _r_ with _l_ < _r_ and calculate the S = sum(d[l...r]) (both inclusive).
Now, you are to find the expected value of S.
**Input Format**
The first line of the input contains 3 space separated integers - n, a and b.
The next line contains n space separated integers which are the elements of the array *d*.
n a b
d[0] d[1] ... d[n-1]
**Output Format**
Print the expected value of S.
E(S)
**Constraints**
2 <= n <= 1000
1 <= a <= 10<sup>9</sup>
1 <= b <= 10
The answer will be considered correct, if the absolute or relative error doesn't exceed 10<sup>-4</sup>.
**Sample Input #00:**
3 1 1
1 2 3
**Sample Output #00:**
4.666667
**Explanation #00:**
At step 1):
You have three choices:
1. swap(1, 2), 2 1 3
2. swap(1, 3), 3 2 1
3. swap(2, 3), 1 3 2
At step 2):
For every result you have three choices for reversing:
1. [2 1 3] -> [1 2 3] [3 1 2] [2 3 1]
2. [3 2 1] -> [2 3 1] [1 2 3] [3 1 2]
3. [1 3 2] -> [3 1 2] [2 3 1] [1 2 3]
So you have 9 possible arrays with each having a 1/9 probability.
For the last step:
Each of the 9 arrays will have 3 possible sums with equal probability. For [1 2 3], you can get 1+2, 2+3 and 1+2+3.
Since there will be 27 outcome for this input, one can calculate the expected value by finding sum of all 27 S and dividing it by 27.
|
code
|
Expected value of a random sub array?
|
ai
|
2013-04-26T18:31:55
|
2022-09-02T09:55:42
| null | null | null |
Given an array 'D' with n elements: d[0], d[1], ..., d[n-1], you can perform the following two steps on the array.
1. Randomly choose two indexes (l, r) with l < r, swap (d[l], d[r])
2. Randomly choose two indexes (l, r) with l < r, reverse (d[l...r]) (both inclusive)
After you perform the first operation **a** times and the second operation **b** times, you randomly choose two indices _l_ & _r_ with _l_ < _r_ and calculate the S = sum(d[l...r]) (both inclusive).
Now, you are to find the expected value of S.
**Input Format**
The first line of the input contains 3 space separated integers - n, a and b.
The next line contains n space separated integers which are the elements of the array *d*.
n a b
d[0] d[1] ... d[n-1]
**Output Format**
Print the expected value of S.
E(S)
**Constraints**
2 <= n <= 1000
1 <= a <= 10<sup>9</sup>
1 <= b <= 10
The answer will be considered correct, if the absolute or relative error doesn't exceed 10<sup>-4</sup>.
**Sample Input #00:**
3 1 1
1 2 3
**Sample Output #00:**
4.666667
**Explanation #00:**
At step 1):
You have three choices:
1. swap(0, 1), 2 1 3
2. swap(0, 2), 3 2 1
3. swap(1, 2), 1 3 2
At step 2):
For every result you have three choices for reversing:
1. [2 1 3] -> [1 2 3] [3 1 2] [2 3 1]
2. [3 2 1] -> [2 3 1] [1 2 3] [3 1 2]
3. [1 3 2] -> [3 1 2] [2 3 1] [1 2 3]
So you have 9 possible arrays with each having a 1/9 probability.
For the last step:
Each of the 9 arrays will have 3 possible sums with equal probability. For [1 2 3], you can get 1+2, 2+3 and 1+2+3.
Since there will be 27 outcome for this input, one can calculate the expected value by finding sum of all 27 S and dividing it by 27.
| 0.422619 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
|
Hard
|
November 2020 Editorial - Random
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p>Here are the two atomic steps which need to be performed a number of times: </p>
<p>1) Randomly choose two indexes (l, r) with l < r and then swap (d[l], d[r]). <br>
2) Randomly choose two indexes (l, r) with l < r and then reverse (d[l…r]) (both inclusive) </p>
<p>We can calculate these two steps separately, because of the linearity of the expectation, we can calculate the expected array after the first step (repeated <em>a</em> times): (A[0], A[1], ..., A[n - 1]) and use this array as the input of the second step (repeated <em>b</em> times), then we can calculate the final answer based on the output at the end of the second step. </p>
<p><strong>Solution for Step (1), i.e. swapping elements:</strong> </p>
<p>How does one compute the expected value of the element in the i-th position after Step (1)? <br>
Let P(i, j, k) be the possibility that d[i] goes to the j-th position after executing Step (1) k times. </p>
<p>A[i] = P(i, i, n1) * d[i] + sum(P(j, i, n1) * d[j] (i != j)) </p>
<p>// because all the operations are randomly chosen. <br>
P(i, i, k) = P(0, 0, k) <br>
P(j, i, k) = P(0, 1, k) </p>
<p>==> A[i] = P(0, 0, n1) * d[i] + P(0, 1, n1) * (sum - d[i]) </p>
<p>P(0, 1, n1) = P(0, 2, n1) = ... = P(0, n - 1, n1) </p>
<p>and</p>
<p>P(0, 0, n1) + P(0, 1, n1) + ... + P(0, n - 1, n1) = P(0, 0, n1) + (n - 1) * P(0, 1, n1) = 1 </p>
<p>==> P(0, 1, n1) = (1 - P(0, 0, n1)) / (n - 1). </p>
<p>So we only need to calculate P(0, 0, n1). </p>
<p>P(0, 0, k) = P(0, 0, k - 1) * P(unchanged) + P(0, 1, k - 1) * P(swap(0, 1)) + P(0, 2, k - 1) * P(swap(0, 2)) + ... + P(0, n - 1, k - 1) * P(swap(0, n - 1)) </p>
<p>Because P(0, 1, k) = P(0, 2, k) = ... = P(0, n - 1, k), P(swap(0, 1)) = P(swap(0, 2)) = ... = P(swap(0, n - 1)) </p>
<p>//P(swap(0, 1)) = 1 / C(n, 2)
//P(unchanged) + (n - 1) * P(swap(0, 1)) = 1 ==> P(unchanged) = (n - 2) / n. </p>
<p>==> </p>
<p>P(0, 0, k) = P(0, 0, k - 1) * P(unchanged) + P(0, 1, k - 1) * P(swap(0, 1)) * (n - 1)
= P(0, 0, k - 1) * P(unchanged) + (1 - P(0, 0, k - 1)) * P(swap(0, 1))
= a * P(0, 0, k - 1) + b</p>
<p>F[k] = a * F[k - 1] + b</p>
<p>==> F[k] + r = a * (F[k] + r) //geometric progression
==> F[n1] + r = a ^ n1 * (1 + r)
==> F[n1] = a ^ n1 * (1 + r) - r</p>
<p><strong>Solution for Step (2), i.e. reversing elements:</strong> <br>
Because n2 is relatively small, so we can calculate the expected output array after each operation.
A0 A1 ... An-1
The first problem to solve is: after executing one random reverse, what is the expected output?
Similar to the first step, we only need to calculate the P(i, j): the possibility that Ai goes to the jth position. </p>
<p>P(i, j) = number_of_reverse_intervals_swap_(i, j) / C(n, 2) <br>
number_of_reverse_intervals_swap_(i, j) = min(i + 1, n - j). </p>
<h3>Solution:</h3>
<pre><code>#include <map>
#include <set>
#include <list>
#include <cmath>
#include <ctime>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <bitset>
#include <climits>
#include <cstdlib>
#include <cstring>
#include <utility>
#include <sstream>
#include <iostream>
#include <algorithm>
#define sqr(x) ((x)*(x))
#define ABS(x) ((x<0)?(-(x)):(x))
#define eps (1e-13)
#define mp make_pair
#define pb push_back
#define Pair pair<int,int>
#define xx first
#define yy second
#define equal(a,b) (ABS((a)-(b))<eps)
using namespace std;
template<class T> string tostring(T x) { ostringstream out; out<<x; return out.str();}
long long toint(string s) { istringstream in(s); long long x; in>>x; return x; }
int dx[8]={0, 0, 1,-1, 1, 1,-1,-1};
int dy[8]={1,-1, 0, 0,-1, 1,-1, 1};
int kx[8]={1, 1,-1,-1, 2, 2,-2,-2};
int ky[8]={2,-2, 2,-2, 1,-1, 1,-1};
/////////////////////////////////////////////////////////////////////////////////////////////////////
int d[1000], n;
double p1, p2;
#define MAX 2
typedef struct matrix
{
int row,col;
double m[MAX][MAX];
matrix(int r,int c,int k)
{
row=r;
col=c;
for (int i=0;i<r;i++)
for (int j=0;j<c;j++)
m[i][j]=k;
}
matrix(){}
} matrix;
matrix operator *(matrix a,matrix b)
{
matrix c;
double t;
c.row=a.row; c.col=b.col;
for (int i=0;i<c.row;i++)
for (int j=0;j<c.col;j++)
{
t=0;
for (int k=0;k<a.col;k++)
t=(t+a.m[i][k]*b.m[k][j]);
c.m[i][j]=t;
}
return c;
}
matrix pow(matrix a,int k)
{
matrix c;
if (k==1) return a;
c = pow(a, k / 2);
c = c * c;
if (k % 2 == 0) return c;
else return c * a;
}
int ways(int cnt) {
return cnt * (cnt - 1) / 2;
}
void calc(int cnt) {
int tot = ways(n);
matrix m(2, 2, 0);
m.m[0][0] = (tot - n + 1.0) / tot; m.m[0][1] = (n - 1.0) / tot;
m.m[1][0] = 1.0 / tot; m.m[1][1] = (tot - 1.0) / tot;
m = pow(m, cnt);
p1 = m.m[0][0];
p2 = m.m[0][1];
}
double f[1000][1000]; // probability of j'th number being at i'th place after all operations
double g[1000][1000];
double sum1[1000][1001], sum2[1000][1001], sum3[1000][1001];
void calc2(int cnt) {
memset(f, 0, sizeof(f));
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (i == j) f[i][j] = p1;
else f[i][j] = p2 / (n - 1);
for (int iter = 0; iter < cnt; iter++) {
for (int c = 0; c < n; c++) {
sum1[c][0] = sum2[c][0] = sum3[c][0] = 0.0;
for (int i = 0; i < n; i++) {
sum1[c][i + 1] = sum1[c][i] + f[i][c];
sum2[c][i + 1] = sum2[c][i] + f[i][c] * (n - i) / (double) ways(n);
sum3[c][i + 1] = sum3[c][i] + f[i][c] * (i + 1) / (double) ways(n);
}
}
for (int i = 0; i < n; i++) {
for (int k = 0; k < n; k++) {
// same
g[i][k] += f[i][k] * (min(n - 1 - i, i) + ways(i) + ways(n - 1 - i)) / (double) ways(n);
if (n - i - 1 > i) g[i][k] += (sum1[k][n - i] - sum1[k][i + 1]) * (i + 1) / (double) ways(n); // i + 1 .. n - i - 1
if (n - i - 1 < i) g[i][k] += (sum1[k][i] - sum1[k][n - i - 1]) * (n - i) / (double) ways(n); // n - i - 1 .. i - 1
if (i != n - 1) g[i][k] += (sum2[k][n] - sum2[k][max(n - i - 1, i) + 1]); // max(n - i - 1, i)+1 .. n - 1
if (i != 0) g[i][k] += (sum3[k][min(n - i - 1, i)]); // 0 .. min(n - i - 1, i) - 1
}
}
memcpy(f, g, sizeof(g));
memset(g, 0, sizeof(g));
}
}
int main() {
// freopen("random.in", "r", stdin);
int n1, n2;
scanf("%d%d%d", &n, &n1, &n2);
for (int i = 0; i < n; i++)
scanf("%d", &d[i]);
calc(n1);
calc2(n2);
double res = 0.0;
for (int i = 0; i < n; i++) { // place
double p = ((i + 1) * (n - i) - 1.0) / (n * (n - 1) / 2.0);
for (int j = 0; j < n; j++) // number
res += d[j] * f[i][j] * p;
}
printf("%.9lf\n", res);
return 0;
}
</code></pre>
| 0 |
nov2020-random
|
2013-11-27T11:19:54
|
{"contest_participation":3343,"challenge_submissions":129,"successful_submissions":52}
|
2013-11-27T11:19:54
|
2016-07-23T19:18:26
|
setter
|
###C++
```cpp
#include <map>
#include <set>
#include <list>
#include <cmath>
#include <ctime>
#include <stack>
#include <queue>
#include <vector>
#include <cstdio>
#include <string>
#include <bitset>
#include <climits>
#include <cstdlib>
#include <cstring>
#include <utility>
#include <sstream>
#include <iostream>
#include <algorithm>
#define sqr(x) ((x)*(x))
#define ABS(x) ((x<0)?(-(x)):(x))
#define eps (1e-13)
#define mp make_pair
#define pb push_back
#define Pair pair<int,int>
#define xx first
#define yy second
#define equal(a,b) (ABS((a)-(b))<eps)
using namespace std;
template<class T> string tostring(T x) { ostringstream out; out<<x; return out.str();}
long long toint(string s) { istringstream in(s); long long x; in>>x; return x; }
int dx[8]={0, 0, 1,-1, 1, 1,-1,-1};
int dy[8]={1,-1, 0, 0,-1, 1,-1, 1};
int kx[8]={1, 1,-1,-1, 2, 2,-2,-2};
int ky[8]={2,-2, 2,-2, 1,-1, 1,-1};
/////////////////////////////////////////////////////////////////////////////////////////////////////
int d[1000], n;
double p1, p2;
#define MAX 2
typedef struct matrix
{
int row,col;
double m[MAX][MAX];
matrix(int r,int c,int k)
{
row=r;
col=c;
for (int i=0;i<r;i++)
for (int j=0;j<c;j++)
m[i][j]=k;
}
matrix(){}
} matrix;
matrix operator *(matrix a,matrix b)
{
matrix c;
double t;
c.row=a.row; c.col=b.col;
for (int i=0;i<c.row;i++)
for (int j=0;j<c.col;j++)
{
t=0;
for (int k=0;k<a.col;k++)
t=(t+a.m[i][k]*b.m[k][j]);
c.m[i][j]=t;
}
return c;
}
matrix pow(matrix a,int k)
{
matrix c;
if (k==1) return a;
c = pow(a, k / 2);
c = c * c;
if (k % 2 == 0) return c;
else return c * a;
}
int ways(int cnt) {
return cnt * (cnt - 1) / 2;
}
void calc(int cnt) {
int tot = ways(n);
matrix m(2, 2, 0);
m.m[0][0] = (tot - n + 1.0) / tot; m.m[0][1] = (n - 1.0) / tot;
m.m[1][0] = 1.0 / tot; m.m[1][1] = (tot - 1.0) / tot;
m = pow(m, cnt);
p1 = m.m[0][0];
p2 = m.m[0][1];
}
double f[1000][1000]; // probability of j'th number being at i'th place after all operations
double g[1000][1000];
double sum1[1000][1001], sum2[1000][1001], sum3[1000][1001];
void calc2(int cnt) {
memset(f, 0, sizeof(f));
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (i == j) f[i][j] = p1;
else f[i][j] = p2 / (n - 1);
for (int iter = 0; iter < cnt; iter++) {
for (int c = 0; c < n; c++) {
sum1[c][0] = sum2[c][0] = sum3[c][0] = 0.0;
for (int i = 0; i < n; i++) {
sum1[c][i + 1] = sum1[c][i] + f[i][c];
sum2[c][i + 1] = sum2[c][i] + f[i][c] * (n - i) / (double) ways(n);
sum3[c][i + 1] = sum3[c][i] + f[i][c] * (i + 1) / (double) ways(n);
}
}
for (int i = 0; i < n; i++) {
for (int k = 0; k < n; k++) {
// same
g[i][k] += f[i][k] * (min(n - 1 - i, i) + ways(i) + ways(n - 1 - i)) / (double) ways(n);
if (n - i - 1 > i) g[i][k] += (sum1[k][n - i] - sum1[k][i + 1]) * (i + 1) / (double) ways(n); // i + 1 .. n - i - 1
if (n - i - 1 < i) g[i][k] += (sum1[k][i] - sum1[k][n - i - 1]) * (n - i) / (double) ways(n); // n - i - 1 .. i - 1
if (i != n - 1) g[i][k] += (sum2[k][n] - sum2[k][max(n - i - 1, i) + 1]); // max(n - i - 1, i)+1 .. n - 1
if (i != 0) g[i][k] += (sum3[k][min(n - i - 1, i)]); // 0 .. min(n - i - 1, i) - 1
}
}
memcpy(f, g, sizeof(g));
memset(g, 0, sizeof(g));
}
}
int main() {
// freopen("random.in", "r", stdin);
int n1, n2;
scanf("%d%d%d", &n, &n1, &n2);
for (int i = 0; i < n; i++)
scanf("%d", &d[i]);
calc(n1);
calc2(n2);
double res = 0.0;
for (int i = 0; i < n; i++) { // place
double p = ((i + 1) * (n - i) - 1.0) / (n * (n - 1) / 2.0);
for (int j = 0; j < n; j++) // number
res += d[j] * f[i][j] * p;
}
printf("%.9lf\n", res);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:14
|
2016-07-23T19:18:26
|
C++
|
||||
19 | 1,574 |
hacker-country
|
Hacker Country
|
There are *N* cities in the Hacker Country. There is a unique directed road connecting each pair of different cities directly. However, each road has its own cost which you must pay for passing it each time. You are planning to visit the country. Here are the conditions to be satisfied:
+ You can start at any city you'd like to
+ You can pass through as many roads as you can
+ You must pass at least 2 different cities
+ At the end of the trip, you should come back to the city where you started
+ The average cost per road should be minimum
As a top programmer, could you calculate the minimum average cost?
**Input format**
The first line of the input is an integer *N*.
Each of the next *N* lines contains *N* integers separated by a single space. The j<sup>th</sup> integer of the i<sup>th</sup> row denotes the amount you must pay to go from the i<sup>th</sup> city to the j<sup>th</sup> city.
There are no roads that connect a city to itself.
**Constraints**
1 < N <= 500
0 < cost of any road <= 200.
i<sup>th</sup> integer of the i<sup>th</sup> row will always be 0 implying there is no self connecting road.
**Output format**
Output the minimum cost as a rational number p/q. The greatest common divisor of p and q should be 1.
**Sample input**
2
0 1
2 0
**Sample Output**
3/2
**Explanation**
You travel across both the cities with an average cost of (2+1)/2 = 3/2
**Timelimits**
Timelimits for this challenge is given [here](https://www.hackerrank.com/environment)
|
code
|
What is the minimum cost of a road trip in Hacker Country?
|
ai
|
2013-12-20T08:10:24
|
2022-08-31T08:14:32
|
#
# Complete the 'hackerCountry' function below.
#
# The function is expected to return a STRING.
# The function accepts 2D_INTEGER_ARRAY tolls as parameter.
#
def hackerCountry(tolls):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
tolls = []
for _ in range(n):
tolls.append(list(map(int, input().rstrip().split())))
result = hackerCountry(tolls)
fptr.write(result + '\n')
fptr.close()
|
There are *N* cities in *Hacker Country*. Each pair of cities are directly connected by a unique directed road, and each road has its own toll that must be paid every time it is used. You're planning a road trip in *Hacker Country*, and its itinerary must satisfy the following conditions:
+ You can start in any city.
+ You must use $2$ or more different roads (meaning you will visit $2$ or more cities).
+ At the end of your trip, you should be back in your city of origin.
+ The average cost (sum of tolls paid per road traveled) should be minimum.
Can you calculate the *minimum average cost* of a trip in *Hacker Country*?
**Time Limits**
Time limits for this challenge are provided [here](https://www.hackerrank.com/environment).
| 0.533333 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line is an integer, $N$ (number of cities).
The $N$ subsequent lines of $N$ space-separated integers each describe the respective tolls or traveling from city $i$ to city $j$; in other words, the $j^{th}$ integer of the $i^{th}$ line denotes the toll for traveling from city $i$ to city $j$.
**Note:** As there are no roads connecting a city to itself, the $i^{th}$ integer of line $i$ will always be $0$.
**Constraints**
$1 \lt N \leq 500$
$0 \lt toll \ cost \leq 200$
$roads \ traveled \geq 2$
|
Print the *minimum cost* as a rational number $p \ / \ q$ (tolls paid over roads traveled). The *greatest common divisor* of $p$ and $q$ should be $1$.
|
2
0 1
2 0
|
3/2
|
Hard
|
Hacker Country : Codesprint 5 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/codesprint5/challenges/hacker-country">Hacker Country</a></p>
<p><strong>Difficulty Level</strong> : Easy-Hard <br>
<strong>Required Knowledge</strong> : Directed Cycles, minimum mean length <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/cpcs">Cao Peng</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/dsoboliev">Dmytro Soboliev</a></p>
<p><strong>Approach</strong></p>
<p>The approach for this problem is explained <a href="https://hr-filepicker.s3.amazonaws.com/perfect-country.pdf">here</a></p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <cassert>
#include <algorithm>
using namespace std;
const int N = 505;
int d[N][N],a[N][N];
int cmp(const pair<int,int> &a,const pair<int,int> &b) { // a - b
return a.first * b.second - a.second * b.first;
}
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
int main() {
int n;
scanf("%d",&n);
assert((n > 1) && (n <= 500));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d",&a[i][j]);
if (i == j) {
assert(a[i][j] == 0);
}
else {
assert((a[i][j] > 0) && (a[i][j] <= 200));
}
}
}
// d[i + 1][j] = min(d[i][k] + a[k][j])
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
bool mark = false;
for (int k = 0; k < n; ++k) {
if (k != j) {
if (mark) {
d[i + 1][j] = min(d[i + 1][j] , d[i][k] + a[k][j]);
}
else {
mark = true;
d[i + 1][j] = d[i][k] + a[k][j];
}
}
}
}
}
pair<int,int> answer;
// answer = min max (d[n][i] - d[k][i]) / (n - k)
for (int i = 0; i < n; ++i) {
pair<int,int> now = make_pair(d[n][i] - d[0][i], n);
for (int k = 1; k < n; ++k) {
pair<int,int> temp = make_pair(d[n][i] - d[k][i], n - k);
if (cmp(temp, now) > 0) {
now = temp;
}
}
if ((i == 0) || (cmp(now, answer) < 0)) {
answer = now;
}
}
int g = gcd(answer.first, answer.second);
printf("%d/%d\n",answer.first / g, answer.second / g);
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
using namespace std;
const int maxN = 600;
const int inf = 1000000000;
int g[maxN][maxN], d[maxN][maxN];
int n;
long long gcd(long long a, long long b) {
if (a == 0 || b == 0) {
return a + b;
}
if (a > b) {
return gcd(a % b, b);
} else {
return gcd(b % a, a);
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d", &g[i][j]);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < n; ++j) {
int best = inf;
for (int k = 0; k < n; ++k) {
if (j != k) {
best = min(best, d[i - 1][k] + g[k][j]);
}
}
d[i][j] = best;
}
}
long long p = inf, q = 1;
for (int i = 0; i < n; ++i) {
long long a = 0, b = 1;
for (int j = 0; j < n; ++j) {
long long c = d[n][i] - d[j][i];
long long d = n - j;
if (c * b > a * d) {
a = c;
b = d;
}
}
if (a * q < b * p) {
p = a;
q = b;
}
}
long long d = gcd(p, q);
p /= d;
q /= d;
cout << p << "/" << q << endl;
return 0;
}
</code></pre>
| 0 |
codesprint5-hacker-country
|
2014-01-21T11:07:30
|
{"contest_participation":12558,"challenge_submissions":482,"successful_submissions":103}
|
2014-01-21T11:07:30
|
2016-07-23T14:03:54
|
setter
|
###C++
```cpp
#include <cstdio>
#include <cstring>
#include <cassert>
#include <algorithm>
using namespace std;
const int N = 505;
int d[N][N],a[N][N];
int cmp(const pair<int,int> &a,const pair<int,int> &b) { // a - b
return a.first * b.second - a.second * b.first;
}
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
int main() {
int n;
scanf("%d",&n);
assert((n > 1) && (n <= 500));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d",&a[i][j]);
if (i == j) {
assert(a[i][j] == 0);
}
else {
assert((a[i][j] > 0) && (a[i][j] <= 200));
}
}
}
// d[i + 1][j] = min(d[i][k] + a[k][j])
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
bool mark = false;
for (int k = 0; k < n; ++k) {
if (k != j) {
if (mark) {
d[i + 1][j] = min(d[i + 1][j] , d[i][k] + a[k][j]);
}
else {
mark = true;
d[i + 1][j] = d[i][k] + a[k][j];
}
}
}
}
}
pair<int,int> answer;
// answer = min max (d[n][i] - d[k][i]) / (n - k)
for (int i = 0; i < n; ++i) {
pair<int,int> now = make_pair(d[n][i] - d[0][i], n);
for (int k = 1; k < n; ++k) {
pair<int,int> temp = make_pair(d[n][i] - d[k][i], n - k);
if (cmp(temp, now) > 0) {
now = temp;
}
}
if ((i == 0) || (cmp(now, answer) < 0)) {
answer = now;
}
}
int g = gcd(answer.first, answer.second);
printf("%d/%d\n",answer.first / g, answer.second / g);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:15
|
2016-07-23T14:03:41
|
C++
|
20 | 1,574 |
hacker-country
|
Hacker Country
|
There are *N* cities in the Hacker Country. There is a unique directed road connecting each pair of different cities directly. However, each road has its own cost which you must pay for passing it each time. You are planning to visit the country. Here are the conditions to be satisfied:
+ You can start at any city you'd like to
+ You can pass through as many roads as you can
+ You must pass at least 2 different cities
+ At the end of the trip, you should come back to the city where you started
+ The average cost per road should be minimum
As a top programmer, could you calculate the minimum average cost?
**Input format**
The first line of the input is an integer *N*.
Each of the next *N* lines contains *N* integers separated by a single space. The j<sup>th</sup> integer of the i<sup>th</sup> row denotes the amount you must pay to go from the i<sup>th</sup> city to the j<sup>th</sup> city.
There are no roads that connect a city to itself.
**Constraints**
1 < N <= 500
0 < cost of any road <= 200.
i<sup>th</sup> integer of the i<sup>th</sup> row will always be 0 implying there is no self connecting road.
**Output format**
Output the minimum cost as a rational number p/q. The greatest common divisor of p and q should be 1.
**Sample input**
2
0 1
2 0
**Sample Output**
3/2
**Explanation**
You travel across both the cities with an average cost of (2+1)/2 = 3/2
**Timelimits**
Timelimits for this challenge is given [here](https://www.hackerrank.com/environment)
|
code
|
What is the minimum cost of a road trip in Hacker Country?
|
ai
|
2013-12-20T08:10:24
|
2022-08-31T08:14:32
|
#
# Complete the 'hackerCountry' function below.
#
# The function is expected to return a STRING.
# The function accepts 2D_INTEGER_ARRAY tolls as parameter.
#
def hackerCountry(tolls):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
tolls = []
for _ in range(n):
tolls.append(list(map(int, input().rstrip().split())))
result = hackerCountry(tolls)
fptr.write(result + '\n')
fptr.close()
|
There are *N* cities in *Hacker Country*. Each pair of cities are directly connected by a unique directed road, and each road has its own toll that must be paid every time it is used. You're planning a road trip in *Hacker Country*, and its itinerary must satisfy the following conditions:
+ You can start in any city.
+ You must use $2$ or more different roads (meaning you will visit $2$ or more cities).
+ At the end of your trip, you should be back in your city of origin.
+ The average cost (sum of tolls paid per road traveled) should be minimum.
Can you calculate the *minimum average cost* of a trip in *Hacker Country*?
**Time Limits**
Time limits for this challenge are provided [here](https://www.hackerrank.com/environment).
| 0.533333 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line is an integer, $N$ (number of cities).
The $N$ subsequent lines of $N$ space-separated integers each describe the respective tolls or traveling from city $i$ to city $j$; in other words, the $j^{th}$ integer of the $i^{th}$ line denotes the toll for traveling from city $i$ to city $j$.
**Note:** As there are no roads connecting a city to itself, the $i^{th}$ integer of line $i$ will always be $0$.
**Constraints**
$1 \lt N \leq 500$
$0 \lt toll \ cost \leq 200$
$roads \ traveled \geq 2$
|
Print the *minimum cost* as a rational number $p \ / \ q$ (tolls paid over roads traveled). The *greatest common divisor* of $p$ and $q$ should be $1$.
|
2
0 1
2 0
|
3/2
|
Hard
|
Hacker Country : Codesprint 5 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/codesprint5/challenges/hacker-country">Hacker Country</a></p>
<p><strong>Difficulty Level</strong> : Easy-Hard <br>
<strong>Required Knowledge</strong> : Directed Cycles, minimum mean length <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/cpcs">Cao Peng</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/dsoboliev">Dmytro Soboliev</a></p>
<p><strong>Approach</strong></p>
<p>The approach for this problem is explained <a href="https://hr-filepicker.s3.amazonaws.com/perfect-country.pdf">here</a></p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <cassert>
#include <algorithm>
using namespace std;
const int N = 505;
int d[N][N],a[N][N];
int cmp(const pair<int,int> &a,const pair<int,int> &b) { // a - b
return a.first * b.second - a.second * b.first;
}
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
int main() {
int n;
scanf("%d",&n);
assert((n > 1) && (n <= 500));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d",&a[i][j]);
if (i == j) {
assert(a[i][j] == 0);
}
else {
assert((a[i][j] > 0) && (a[i][j] <= 200));
}
}
}
// d[i + 1][j] = min(d[i][k] + a[k][j])
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
bool mark = false;
for (int k = 0; k < n; ++k) {
if (k != j) {
if (mark) {
d[i + 1][j] = min(d[i + 1][j] , d[i][k] + a[k][j]);
}
else {
mark = true;
d[i + 1][j] = d[i][k] + a[k][j];
}
}
}
}
}
pair<int,int> answer;
// answer = min max (d[n][i] - d[k][i]) / (n - k)
for (int i = 0; i < n; ++i) {
pair<int,int> now = make_pair(d[n][i] - d[0][i], n);
for (int k = 1; k < n; ++k) {
pair<int,int> temp = make_pair(d[n][i] - d[k][i], n - k);
if (cmp(temp, now) > 0) {
now = temp;
}
}
if ((i == 0) || (cmp(now, answer) < 0)) {
answer = now;
}
}
int g = gcd(answer.first, answer.second);
printf("%d/%d\n",answer.first / g, answer.second / g);
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
using namespace std;
const int maxN = 600;
const int inf = 1000000000;
int g[maxN][maxN], d[maxN][maxN];
int n;
long long gcd(long long a, long long b) {
if (a == 0 || b == 0) {
return a + b;
}
if (a > b) {
return gcd(a % b, b);
} else {
return gcd(b % a, a);
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d", &g[i][j]);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < n; ++j) {
int best = inf;
for (int k = 0; k < n; ++k) {
if (j != k) {
best = min(best, d[i - 1][k] + g[k][j]);
}
}
d[i][j] = best;
}
}
long long p = inf, q = 1;
for (int i = 0; i < n; ++i) {
long long a = 0, b = 1;
for (int j = 0; j < n; ++j) {
long long c = d[n][i] - d[j][i];
long long d = n - j;
if (c * b > a * d) {
a = c;
b = d;
}
}
if (a * q < b * p) {
p = a;
q = b;
}
}
long long d = gcd(p, q);
p /= d;
q /= d;
cout << p << "/" << q << endl;
return 0;
}
</code></pre>
| 0 |
codesprint5-hacker-country
|
2014-01-21T11:07:30
|
{"contest_participation":12558,"challenge_submissions":482,"successful_submissions":103}
|
2014-01-21T11:07:30
|
2016-07-23T14:03:54
|
tester
|
###C++
```cpp
#include <iostream>
#include <cstdio>
using namespace std;
const int maxN = 600;
const int inf = 1000000000;
int g[maxN][maxN], d[maxN][maxN];
int n;
long long gcd(long long a, long long b) {
if (a == 0 || b == 0) {
return a + b;
}
if (a > b) {
return gcd(a % b, b);
} else {
return gcd(b % a, a);
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
scanf("%d", &g[i][j]);
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < n; ++j) {
int best = inf;
for (int k = 0; k < n; ++k) {
if (j != k) {
best = min(best, d[i - 1][k] + g[k][j]);
}
}
d[i][j] = best;
}
}
long long p = inf, q = 1;
for (int i = 0; i < n; ++i) {
long long a = 0, b = 1;
for (int j = 0; j < n; ++j) {
long long c = d[n][i] - d[j][i];
long long d = n - j;
if (c * b > a * d) {
a = c;
b = d;
}
}
if (a * q < b * p) {
p = a;
q = b;
}
}
long long d = gcd(p, q);
p /= d;
q /= d;
cout << p << "/" << q << endl;
return 0;
}
```
|
not-set
|
2016-04-24T02:02:15
|
2016-07-23T14:03:54
|
C++
|
21 | 1,667 |
matrix-tracing
|
Matrix Tracing
|
A word from the English dictionary is taken and arranged as a matrix. e.g. "MATHEMATICS"
MATHE
ATHEM
THEMA
HEMAT
EMATI
MATIC
ATICS
There are many ways to trace this matrix in a way that helps you construct this word. You start tracing the matrix from the top-left position and at each iteration, you either move RIGHT or DOWN, and ultimately reach the bottom-right of the matrix. It is assured that any such tracing generates the same word. How many such tracings can be possible for a given
word of length m+n-1 written as a matrix of size m * n?
**Input Format**
The first line of input contains an integer T. T test cases follow.
Each test case contains 2 space separated integers m & n (in a new line) indicating that the matrix has m rows and each row has n characters.
**Constraints**
1 <= T <= 10<sup>3</sup>
1 ≤ m,n ≤ 10<sup>6</sup>
**Output Format**
Print the number of ways (S) the word can be traced as explained in the problem statement.
If the number is larger than 10<sup>9</sup>+7,
print `S mod (10^9 + 7)` for each testcase (in a new line).
**Sample Input**
1
2 3
**Sample Output**
3
**Explanation**
Let's consider a word AWAY written as the matrix
AWA
WAY
Here, the word AWAY can be traced in 3 different ways, traversing either RIGHT or DOWN.
AWA
Y
AW
AY
A
WAY
Hence the answer is 3.
**Timelimit**
Time limit for this challenge is given [here](https://www.hackerrank.com/environment)
|
code
|
How many ways can you trace a given matrix? - 30 Points
|
ai
|
2014-01-14T08:25:46
|
2022-09-02T09:54:13
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER m
#
def solve(n, m):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
result = solve(n, m)
fptr.write(str(result) + '\n')
fptr.close()
|
A word from the English dictionary is taken and arranged as a matrix. e.g. "MATHEMATICS"
MATHE
ATHEM
THEMA
HEMAT
EMATI
MATIC
ATICS
There are many ways to trace this matrix in a way that helps you construct this word. You start tracing the matrix from the top-left position and at each iteration, you either move RIGHT or DOWN, and ultimately reach the bottom-right of the matrix. It is assured that any such tracing generates the same word. How many such tracings can be possible for a given
word of length m+n-1 written as a matrix of size m * n?
**Input Format**
The first line of input contains an integer T. T test cases follow.
Each test case contains 2 space separated integers m & n (in a new line) indicating that the matrix has m rows and each row has n characters.
**Constraints**
1 <= T <= 10<sup>3</sup>
1 ≤ m,n ≤ 10<sup>6</sup>
**Output Format**
Print the number of ways (S) the word can be traced as explained in the problem statement.
If the number is larger than 10<sup>9</sup>+7,
print `S mod (10^9 + 7)` for each testcase (in a new line).
**Sample Input**
1
2 3
**Sample Output**
3
**Explanation**
Let's consider a word AWAY written as the matrix
AWA
WAY
Here, the word AWAY can be traced in 3 different ways, traversing either RIGHT or DOWN.
AWA
Y
AW
AY
A
WAY
Hence the answer is 3.
**Timelimit**
Time limit for this challenge is given [here](https://www.hackerrank.com/environment)
| 0.563758 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
|
Matrix Tracing : Codesprint 5 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/codesprint5/challenges/matrix-tracing">Matrix Tracing</a></p>
<p><strong>Difficulty Level</strong> : Easy-Medium <br>
<strong>Required Knowledge</strong> : Combinatorics, Counting, Inverse modulo operation <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/dheeraj">Dheeraj</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/abhiranjan">Abhiranjan</a> </p>
<p><strong>Approach</strong> </p>
<p>Firstly we note that we are given a grid, and only possible ways to reach from top left to bottom right is a DOWN move and RIGHT move. <br>
It can be observed that that from each point there are always a DOWN and LEFT move (if it doesn't go off board). So given m,n in total we have m-1 RIGHT moves and n-1 LEFT moves. And imagine we auto-move RIGHT and just have to choose when to move DOWN. </p>
<p>So from m+n-2 total moves we choose m-1 down moves. Hence total ways comes out to be <sup>m+n-2</sup>C<sub>m-1</sub>. </p>
<p>Another way to look at is m+n-2 total moves where m-1 are of one type and n-1 are of another type </p>
<p>Hence total number of move is: <code>(m+n-2)!/(m-1)!(n-1)!</code></p>
<p>As we have to print ans mod 10<sup>9</sup>+7, answer should go as</p>
<pre><code>moves = (m+n-2)! / (m-1)! (n-1)! % (10^9+7)
= (m+n-2)! * (m-1)!^(-1) * (n-1)!^(-1) % (10^9+7)
</code></pre>
<p>For this we need to separately calculate Numerator and Denominator using modular and inverse modular operation. </p>
<p><strong>Factorial</strong> <br>
To calculate the factorial we use the following property</p>
<pre><code>(a*b) mod m = ((a mod m)*(b mod m)) mod m
</code></pre>
<p>to calculate factorial as </p>
<pre><code>fact(0) = 1
fact(n) = fact(n-1)*n % (10^9+7)
</code></pre>
<p><strong>Inverse</strong> <br>
Fermat's Little theorem says that</p>
<pre><code>a^(p-1) == 1 mod p
where p is prime
gcd(a, p) != 1
</code></pre>
<p>Multiplying both sides by <code>a^(-1)</code>, we get</p>
<pre><code>a^(p-1) * a^(-1) == a^(-1) mod p
a^(p-2) == a^(-1) mod p
a^(-1) == a^(p-2) mod p
</code></pre>
<p><strong>Larger Powers</strong> <br>
For calculating larger powers we use the following property</p>
<pre><code> 1 , m == 0
a^m = (b*b) % p , even m
(b*b*a) % p , odd m
where
b = a^floor(m/2)
</code></pre>
<p>In this way we can calculate <code>a^m</code> in <code>log(m)</code> steps.</p>
<p><strong>Final Solution</strong> </p>
<p>So, we can rewrite our above equation as</p>
<pre><code> moves = (m+n-2)! * (m-1)!^(-1) * (n-1)!^(-1) % (10^9+7)
= (m+n-2)! * (m-1)!^(p-2) * (n-1)!^(p-2) % (10^9+7)
</code></pre>
<p><strong>Setter's Solution</strong> </p>
<pre><code>#!/usr/bin/py
mod = 10**9 + 7
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b==0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
t = input()
assert 1 <= t <= 10**3
for _ in range(t):
a,b = map(int, raw_input().strip().split(' '))
assert 1 <= a <= 10**6
assert 1 <= b <= 10**6
denominator = 1
numerator = 1
for i in range(1, a+b-1):
numerator = ((numerator%mod)*(i%mod))%mod
for i in range(1, a):
denominator = ((denominator%mod)*(i%mod))%mod
for i in range(1, b):
denominator = ((denominator%mod)*(i%mod))%mod
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
</code></pre>
<p><strong>Tester's Solution</strong> </p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
const int sz = 2e6;
const long long mod = 1e9+7;
long long fact[sz];
long long _pow(int a, int b) {
if(b == 0)
return 1ll;
long long ret = _pow(a, b/2);
ret = (ret*ret) % mod;
ret = (ret+mod)% mod;
if(b%2 == 1)
ret = (ret*a) % mod;
ret = (ret+mod)% mod;
assert(ret >= 0);
assert(ret < mod);
return ret;
}
long long inv(int a) {
a%= mod;
a = (a+mod)%mod;
return _pow(a, mod-2);
}
int main()
{
fact[0] = 1;
for(int i = (int)1; i <= (int)sz-1; ++i) {
fact[i] = (fact[i-1]*i) % mod;
}
int test;
scanf("%d", &test);
assert(test >= 1);
assert(test <= 1e3);
while(test--) {
int n, m;
cin >> n >> m;
assert(1 <= n); assert(n <= 1e6);
assert(1 <= m); assert(m <= 1e6);
n--; m--;
long long ans = fact[n+m];
ans = (ans*inv(fact[n])) % mod;
ans = (ans + mod) % mod;
ans = (ans*inv(fact[m])) % mod;
ans = (ans + mod) % mod;
assert(ans >= 0);
assert( ans < mod);
cout << ans << "\n";
}
return 0;
}
</code></pre>
| 0 |
codesprint5-matrix-tracing
|
2014-01-23T06:50:58
|
{"contest_participation":12558,"challenge_submissions":2521,"successful_submissions":1331}
|
2014-01-23T06:50:58
|
2016-07-23T16:33:25
|
setter
|
###Python 2
```python
#!/usr/bin/py
mod = 10**9 + 7
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b==0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
t = input()
assert 1 <= t <= 10**3
for _ in range(t):
a,b = map(int, raw_input().strip().split(' '))
assert 1 <= a <= 10**6
assert 1 <= b <= 10**6
denominator = 1
numerator = 1
for i in range(1, a+b-1):
numerator = ((numerator%mod)*(i%mod))%mod
for i in range(1, a):
denominator = ((denominator%mod)*(i%mod))%mod
for i in range(1, b):
denominator = ((denominator%mod)*(i%mod))%mod
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
```
|
not-set
|
2016-04-24T02:02:15
|
2016-07-23T16:33:12
|
Python
|
||||
22 | 1,667 |
matrix-tracing
|
Matrix Tracing
|
A word from the English dictionary is taken and arranged as a matrix. e.g. "MATHEMATICS"
MATHE
ATHEM
THEMA
HEMAT
EMATI
MATIC
ATICS
There are many ways to trace this matrix in a way that helps you construct this word. You start tracing the matrix from the top-left position and at each iteration, you either move RIGHT or DOWN, and ultimately reach the bottom-right of the matrix. It is assured that any such tracing generates the same word. How many such tracings can be possible for a given
word of length m+n-1 written as a matrix of size m * n?
**Input Format**
The first line of input contains an integer T. T test cases follow.
Each test case contains 2 space separated integers m & n (in a new line) indicating that the matrix has m rows and each row has n characters.
**Constraints**
1 <= T <= 10<sup>3</sup>
1 ≤ m,n ≤ 10<sup>6</sup>
**Output Format**
Print the number of ways (S) the word can be traced as explained in the problem statement.
If the number is larger than 10<sup>9</sup>+7,
print `S mod (10^9 + 7)` for each testcase (in a new line).
**Sample Input**
1
2 3
**Sample Output**
3
**Explanation**
Let's consider a word AWAY written as the matrix
AWA
WAY
Here, the word AWAY can be traced in 3 different ways, traversing either RIGHT or DOWN.
AWA
Y
AW
AY
A
WAY
Hence the answer is 3.
**Timelimit**
Time limit for this challenge is given [here](https://www.hackerrank.com/environment)
|
code
|
How many ways can you trace a given matrix? - 30 Points
|
ai
|
2014-01-14T08:25:46
|
2022-09-02T09:54:13
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER m
#
def solve(n, m):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
result = solve(n, m)
fptr.write(str(result) + '\n')
fptr.close()
|
A word from the English dictionary is taken and arranged as a matrix. e.g. "MATHEMATICS"
MATHE
ATHEM
THEMA
HEMAT
EMATI
MATIC
ATICS
There are many ways to trace this matrix in a way that helps you construct this word. You start tracing the matrix from the top-left position and at each iteration, you either move RIGHT or DOWN, and ultimately reach the bottom-right of the matrix. It is assured that any such tracing generates the same word. How many such tracings can be possible for a given
word of length m+n-1 written as a matrix of size m * n?
**Input Format**
The first line of input contains an integer T. T test cases follow.
Each test case contains 2 space separated integers m & n (in a new line) indicating that the matrix has m rows and each row has n characters.
**Constraints**
1 <= T <= 10<sup>3</sup>
1 ≤ m,n ≤ 10<sup>6</sup>
**Output Format**
Print the number of ways (S) the word can be traced as explained in the problem statement.
If the number is larger than 10<sup>9</sup>+7,
print `S mod (10^9 + 7)` for each testcase (in a new line).
**Sample Input**
1
2 3
**Sample Output**
3
**Explanation**
Let's consider a word AWAY written as the matrix
AWA
WAY
Here, the word AWAY can be traced in 3 different ways, traversing either RIGHT or DOWN.
AWA
Y
AW
AY
A
WAY
Hence the answer is 3.
**Timelimit**
Time limit for this challenge is given [here](https://www.hackerrank.com/environment)
| 0.563758 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
|
Matrix Tracing : Codesprint 5 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/codesprint5/challenges/matrix-tracing">Matrix Tracing</a></p>
<p><strong>Difficulty Level</strong> : Easy-Medium <br>
<strong>Required Knowledge</strong> : Combinatorics, Counting, Inverse modulo operation <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/dheeraj">Dheeraj</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/abhiranjan">Abhiranjan</a> </p>
<p><strong>Approach</strong> </p>
<p>Firstly we note that we are given a grid, and only possible ways to reach from top left to bottom right is a DOWN move and RIGHT move. <br>
It can be observed that that from each point there are always a DOWN and LEFT move (if it doesn't go off board). So given m,n in total we have m-1 RIGHT moves and n-1 LEFT moves. And imagine we auto-move RIGHT and just have to choose when to move DOWN. </p>
<p>So from m+n-2 total moves we choose m-1 down moves. Hence total ways comes out to be <sup>m+n-2</sup>C<sub>m-1</sub>. </p>
<p>Another way to look at is m+n-2 total moves where m-1 are of one type and n-1 are of another type </p>
<p>Hence total number of move is: <code>(m+n-2)!/(m-1)!(n-1)!</code></p>
<p>As we have to print ans mod 10<sup>9</sup>+7, answer should go as</p>
<pre><code>moves = (m+n-2)! / (m-1)! (n-1)! % (10^9+7)
= (m+n-2)! * (m-1)!^(-1) * (n-1)!^(-1) % (10^9+7)
</code></pre>
<p>For this we need to separately calculate Numerator and Denominator using modular and inverse modular operation. </p>
<p><strong>Factorial</strong> <br>
To calculate the factorial we use the following property</p>
<pre><code>(a*b) mod m = ((a mod m)*(b mod m)) mod m
</code></pre>
<p>to calculate factorial as </p>
<pre><code>fact(0) = 1
fact(n) = fact(n-1)*n % (10^9+7)
</code></pre>
<p><strong>Inverse</strong> <br>
Fermat's Little theorem says that</p>
<pre><code>a^(p-1) == 1 mod p
where p is prime
gcd(a, p) != 1
</code></pre>
<p>Multiplying both sides by <code>a^(-1)</code>, we get</p>
<pre><code>a^(p-1) * a^(-1) == a^(-1) mod p
a^(p-2) == a^(-1) mod p
a^(-1) == a^(p-2) mod p
</code></pre>
<p><strong>Larger Powers</strong> <br>
For calculating larger powers we use the following property</p>
<pre><code> 1 , m == 0
a^m = (b*b) % p , even m
(b*b*a) % p , odd m
where
b = a^floor(m/2)
</code></pre>
<p>In this way we can calculate <code>a^m</code> in <code>log(m)</code> steps.</p>
<p><strong>Final Solution</strong> </p>
<p>So, we can rewrite our above equation as</p>
<pre><code> moves = (m+n-2)! * (m-1)!^(-1) * (n-1)!^(-1) % (10^9+7)
= (m+n-2)! * (m-1)!^(p-2) * (n-1)!^(p-2) % (10^9+7)
</code></pre>
<p><strong>Setter's Solution</strong> </p>
<pre><code>#!/usr/bin/py
mod = 10**9 + 7
def getfactmod(b):
val = 1
for i in range(1,b):
val =((val%mod)*((i+1)%mod))%mod
return val
def getpowermod(a,b):
if b==0:
return 1
if b == 1:
return a
temp = getpowermod(a,b/2)
if b%2==0:
return ((temp%mod)**2)%mod
else:
return (a*((temp%mod)**2))%mod
def inversemod(a):
return getpowermod(a,mod-2)
if __name__ == '__main__':
t = input()
assert 1 <= t <= 10**3
for _ in range(t):
a,b = map(int, raw_input().strip().split(' '))
assert 1 <= a <= 10**6
assert 1 <= b <= 10**6
denominator = 1
numerator = 1
for i in range(1, a+b-1):
numerator = ((numerator%mod)*(i%mod))%mod
for i in range(1, a):
denominator = ((denominator%mod)*(i%mod))%mod
for i in range(1, b):
denominator = ((denominator%mod)*(i%mod))%mod
answer = ((numerator%mod)*(inversemod(denominator)%mod))%mod
print answer
</code></pre>
<p><strong>Tester's Solution</strong> </p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
const int sz = 2e6;
const long long mod = 1e9+7;
long long fact[sz];
long long _pow(int a, int b) {
if(b == 0)
return 1ll;
long long ret = _pow(a, b/2);
ret = (ret*ret) % mod;
ret = (ret+mod)% mod;
if(b%2 == 1)
ret = (ret*a) % mod;
ret = (ret+mod)% mod;
assert(ret >= 0);
assert(ret < mod);
return ret;
}
long long inv(int a) {
a%= mod;
a = (a+mod)%mod;
return _pow(a, mod-2);
}
int main()
{
fact[0] = 1;
for(int i = (int)1; i <= (int)sz-1; ++i) {
fact[i] = (fact[i-1]*i) % mod;
}
int test;
scanf("%d", &test);
assert(test >= 1);
assert(test <= 1e3);
while(test--) {
int n, m;
cin >> n >> m;
assert(1 <= n); assert(n <= 1e6);
assert(1 <= m); assert(m <= 1e6);
n--; m--;
long long ans = fact[n+m];
ans = (ans*inv(fact[n])) % mod;
ans = (ans + mod) % mod;
ans = (ans*inv(fact[m])) % mod;
ans = (ans + mod) % mod;
assert(ans >= 0);
assert( ans < mod);
cout << ans << "\n";
}
return 0;
}
</code></pre>
| 0 |
codesprint5-matrix-tracing
|
2014-01-23T06:50:58
|
{"contest_participation":12558,"challenge_submissions":2521,"successful_submissions":1331}
|
2014-01-23T06:50:58
|
2016-07-23T16:33:25
|
tester
|
###C++
```cpp
#include <bits/stdc++.h>
using namespace std;
const int sz = 2e6;
const long long mod = 1e9+7;
long long fact[sz];
long long _pow(int a, int b) {
if(b == 0)
return 1ll;
long long ret = _pow(a, b/2);
ret = (ret*ret) % mod;
ret = (ret+mod)% mod;
if(b%2 == 1)
ret = (ret*a) % mod;
ret = (ret+mod)% mod;
assert(ret >= 0);
assert(ret < mod);
return ret;
}
long long inv(int a) {
a%= mod;
a = (a+mod)%mod;
return _pow(a, mod-2);
}
int main()
{
fact[0] = 1;
for(int i = (int)1; i <= (int)sz-1; ++i) {
fact[i] = (fact[i-1]*i) % mod;
}
int test;
scanf("%d", &test);
assert(test >= 1);
assert(test <= 1e3);
while(test--) {
int n, m;
cin >> n >> m;
assert(1 <= n); assert(n <= 1e6);
assert(1 <= m); assert(m <= 1e6);
n--; m--;
long long ans = fact[n+m];
ans = (ans*inv(fact[n])) % mod;
ans = (ans + mod) % mod;
ans = (ans*inv(fact[m])) % mod;
ans = (ans + mod) % mod;
assert(ans >= 0);
assert( ans < mod);
cout << ans << "\n";
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:15
|
2016-07-23T16:33:25
|
C++
|
||||
23 | 959 |
recalling-early-days-gp-with-trees
|
Recalling Early Days GP with Trees
|
[Chinese Version](https://hr-testcases.s3.amazonaws.com/959/959-chinese.md)<br/>
[Russian Version](https://hr-testcases.s3.amazonaws.com/959/959_rus.md)<br/>
You are given a [tree](http://en.wikipedia.org/wiki/Tree_(graph_theory)) with N nodes and each has a value associated with it. You are given Q queries, each of which is either an update or a retrieval operation.
The **update query** is of the format
i j X
This means you'd have to add a [GP](http://en.wikipedia.org/wiki/Geometric_progression) series to the nodes which lie in the path from node `i` to node `j` (both inclusive) with first term of the GP as `X` on node `i` and the common ratio as `R` (given in the input)
The **retrieval** query is of the format
i j
You need to return the sum of the node values (S) lying in the path from node i to node j modulo 100711433.
**Input Format**
The first line contains two integers (N and R respectively) separated by a space.
In the next N-1 lines, the i<sup>th</sup> line describes the i<sup>th</sup> edge: a line with two integers a b separated by a single space denotes an edge between a, b.
The next line contains 2 space separated integers (U and Q respectively) representing the number of Update and Query operations to follow.
U lines follow. Each of the next U lines contains 3 space separated integers (i,j, and X respectively).
Each of the next Q lines contains 2 space separated integers, i and j respectively.
**Output Format**
It contains exactly Q lines and each line containing the answer of the i<sup>th</sup> query.
**Constraints**
2 <= N <= 100000
2 <= R <= 10<sup>9</sup>
1 <= U <= 100000
1 <= Q <= 100000
1 <= X <= 10
1 <= a, b, i, j <= N
**Sample Input**
6 2
1 2
1 4
2 6
4 5
4 3
2 2
1 6 3
5 3 5
6 4
5 1
**Sample Output**
31
18
**Explanation**
The node values after the first updation becomes :
3 6 0 0 0 12
The node values after second updation becomes :
3 6 20 10 5 12
Answer to Query #1: 12 + 6 + 3 + 10 = 31
Answer to Query #2: 5 + 10 +3 = 18
|
code
|
Answer the queries performed on trees.
|
ai
|
2013-09-25T18:56:57
|
2022-08-31T08:33:17
| null | null | null |
[Chinese Version](https://hr-testcases.s3.amazonaws.com/959/959-chinese.md)<br/>
[Russian Version](https://hr-testcases.s3.amazonaws.com/959/959_rus.md)<br/>
You are given a [tree](http://en.wikipedia.org/wiki/Tree_(graph_theory)) with N nodes and each has a value associated with it. You are given Q queries, each of which is either an update or a retrieval operation.
The **update query** is of the format
i j X
This means you'd have to add a [GP](http://en.wikipedia.org/wiki/Geometric_progression) series to the nodes which lie in the path from node `i` to node `j` (both inclusive) with first term of the GP as `X` on node `i` and the common ratio as `R` (given in the input)
The **retrieval** query is of the format
i j
You need to return the sum of the node values (S) lying in the path from node i to node j modulo 100711433.
**Input Format**
The first line contains two integers (N and R respectively) separated by a space.
In the next N-1 lines, the i<sup>th</sup> line describes the i<sup>th</sup> edge: a line with two integers a b separated by a single space denotes an edge between a, b.
The next line contains 2 space separated integers (U and Q respectively) representing the number of Update and Query operations to follow.
U lines follow. Each of the next U lines contains 3 space separated integers (i,j, and X respectively).
Each of the next Q lines contains 2 space separated integers, i and j respectively.
**Output Format**
It contains exactly Q lines and each line containing the answer of the i<sup>th</sup> query.
**Constraints**
2 <= N <= 100000
2 <= R <= 10<sup>9</sup>
1 <= U <= 100000
1 <= Q <= 100000
1 <= X <= 10
1 <= a, b, i, j <= N
**Sample Input**
6 2
1 2
1 4
2 6
4 5
4 3
2 2
1 6 3
5 3 5
6 4
5 1
**Sample Output**
31
18
**Explanation**
The node values after the first updation becomes :
3 6 0 0 0 12
The node values after second updation becomes :
3 6 20 10 5 12
Answer to Query #1: 12 + 6 + 3 + 10 = 31
Answer to Query #2: 5 + 10 +3 = 18
| 0.409091 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
| null | null | null | null |
Hard
|
Recalling Early Days with GP Trees : 101 Hack January Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101jan14/challenges/recalling-early-days-gp-with-trees">Recalling Early Days with GP Trees</a></p>
<p><strong>Difficulty Level</strong> : Medium-Hard <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/devuy11">Devendra Agarwal</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/wanbo">Wanbo</a> </p>
<p><strong>Approach</strong> </p>
<p><strong>Observations</strong></p>
<ol>
<li><p>The Number 100711433 is a prime number , so that we can find its inverse (except when R is not a multiple of 100711433)</p></li>
<li><p>You need to first tackle all the Updates and then all the Queries.</p></li>
</ol>
<p>Choose any node as root of the tree.</p>
<p>Make 2 arrays Dist_DFSL[] and Dist_DFSR[] for the Tree.</p>
<p><strong>Update Method</strong></p>
<p>i j St</p>
<p>Let anc be the ancestor node of node i and node j.</p>
<p>Add value St in Dist_DFSL[i]</p>
<p>Add -St*power(R,d1+1) in Dist_DFSL[Parent[anc]] where d1 denotes the total number of edges between node i and node anc and power(a,b) denotes a^b mod 100711433</p>
<p>Add -St*power(R,d1) in Dist_DFSR[anc] where d1 denotes the total number of edges between node i and node anc and power(a,b) denotes a^b mod 100711433</p>
<p>Add St*power(R,d1+d2) in Dist_DFSR[j] where d2 represent the total edges in path from ancestor to j.</p>
<p>d1 and d2 can be calculated by precalculating the depth of each node from root.</p>
<p>d1=depth[i]-depth[anc]</p>
<p>d2=depth[j]-depth[anc]</p>
<p>After all Update Queries, we need the final values at each node and to do so ,we run a DFS on the Tree and do the following:</p>
<p>Dist_DFSL[parent]=(Dist_DFSL[parent]+Dist_DFSL[child]*R)%mod</p>
<p>Dist_DFSR[parent]=(Dist_DFSR[parent]+Dist_DFSR[child]*R_inverse)%mod</p>
<p><strong>Note</strong> :: R_Inverse * R = 1 mod (100711433)</p>
<p>Now value at each Node is :</p>
<p>Sum[Node]=Dist_DFSL[Node]+ Dist_DFSR[NOde]</p>
<p>Now, Run a BFS(or DFS) on the graph and store the sum to each Node from the root in Sum[] array.</p>
<p><strong>Answering the Query</strong></p>
<p>i j</p>
<p>Answer= Sum[i] + Sum[j] - Sum[anc] - Sum[Parent[anc]]</p>
<p><strong>NOTE</strong>:Precaution in Calculating R_inv and solving the problem when R is multiple of 100711433</p>
<p><strong>Time Complexity: O( (U+Q) log N)</strong> //computing lca part otherwise everything in O(1) time.</p>
<p><strong>Setter's Solution</strong> </p>
<pre><code>//Author : Devendra Agarwal
#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<vector>
#include<string.h>
using namespace std;
#define MaxN 100001 //Maximum Nodes
typedef long long int ll;
int N,R,level[MaxN],Parent[MaxN],Dist_DFSL[MaxN],Dist_DFSR[MaxN],Root[MaxN][17],Store_Power_R[MaxN],store[MaxN],mod=100711433,R_inv,Sum[MaxN],Queue[MaxN];
vector<int> Graph[MaxN]; //to store graph
/* To calculate the inverse of a number in multiplicative modulo b*/
int inverse(int a,int b) //b>a
{
int Remainder,p0=0,p1=1,pcurr=1,q,m=b;
while(a!=0)
{
Remainder=b%a;
q=b/a;
if(Remainder!=0)
{
pcurr=p0-((ll)p1*(ll)q)%m;
if(pcurr<0)
pcurr+=m;
p0=p1;
p1=pcurr;
}
b=a;
a=Remainder;
}
return pcurr;
}
/*Storing the Parent and height using DFS*/
void DFS(int root)
{
for(vector<int> ::iterator it=Graph[root].begin();it!=Graph[root].end();it++){
if((*it)!=Parent[root]){ //not visiting more than once
level[(*it)]=level[root]+1;
Parent[(*it)]=root;
DFS((*it));
}
}
return;
}
/*Calculating Data necessary for calculating ancestor and some pre-processing for quicker implementation*/
void process()
{
memset(Root,-1,sizeof(Root));
for(int i=1;i<=N;i++) Root[i][0]=Parent[i];
for(int i=1;(1<<i) <= N; i++)
for(int j=1;j<=N;j++)
if(Root[j][i-1]!=-1)
Root[j][i]=Root[Root[j][i-1]][i-1];
store[0]=0;
store[1]=0;
int cmp=2;
for(int i=2;i<=N;i++){
if(cmp>i) store[i]=store[i-1];
else{
store[i]=store[i-1]+1;
cmp<<=1;
}
}
Store_Power_R[0]=1;
for(int i=1;i<=N;i++)
Store_Power_R[i]=((ll)Store_Power_R[i-1]*(ll)R)%mod;
}
/*Returns the lca of two nodes, same implementation as was used in topcoder tutorials*/
int lca(int p,int q) //Fnds the LCA of 2 nodes
{
int temp;
if(level[p]>level[q]){
temp=p;p=q;q=temp;
}
//level[q]>=level[p]
int steps=store[level[q]];
for(int i=steps;i>=0;i--)
if(level[q]-(1<<i) >= level[p])
q=Root[q][i];
if(p==q) return p;
for(int i=steps;i>=0;i--)
if(Root[p][i]!=Root[q][i])
p=Root[p][i],q=Root[q][i];
return Parent[p];
}
/*This Find the Dist_DFSL and Dist_DFSR after all update queries*/
void DFS_new(int root)
{
for(vector<int> ::iterator it=Graph[root].begin();it!=Graph[root].end();it++){
if((*it)!=Parent[root]){ //not visiting more than once
DFS_new((*it));
Dist_DFSL[root]=(Dist_DFSL[root]+((ll)Dist_DFSL[*it]*(ll)R)%mod)%mod; //Updating root from children
Dist_DFSR[root]=(Dist_DFSR[root]+((ll)Dist_DFSR[*it]*(ll)R_inv)%mod)%mod; //Updating root from children
}
}
}
/*This find the Sum[] array*/
void BFS(int root)
{
Queue[0]=root;
int st=0,end=1,node;
while(st<end){
node=Queue[st];
st++;
for(vector<int>::iterator it=Graph[node].begin();it!=Graph[node].end();it++){
if((*it)!=Parent[node]){
Sum[(*it)]=(Sum[(*it)]+Sum[node])%mod;
Queue[end]=(*it);
end++;
}
}
}
}
int main()
{
int x,y,U,Q,anc,ans,St;
scanf("%d%d",&N,&R);
if(R%mod!=0) //Checking the tricky case
R_inv=inverse(R,mod);
else
R_inv=0;
for(int i=1;i<N;i++){
scanf("%d%d",&x,&y);
Graph[x].push_back(y);
Graph[y].push_back(x);
}
level[1]=0;
Parent[1]=0;
DFS(1);
process();
memset(Dist_DFSL,0,sizeof(Dist_DFSL));
memset(Dist_DFSR,0,sizeof(Dist_DFSR));
memset(Sum,0,sizeof(Sum));
scanf("%d%d",&U,&Q);
while(U--){
scanf("%d%d%d",&x,&y,&St);
anc=lca(x,y);
Dist_DFSL[x]=(Dist_DFSL[x]+St)%mod;
Dist_DFSL[Parent[anc]]=(Dist_DFSL[Parent[anc]]-((ll)St*(ll)Store_Power_R[level[x]-level[anc]+1])%mod)%mod;
Dist_DFSR[y]=(Dist_DFSR[y]+((ll)St*(ll)Store_Power_R[level[y]+level[x]-2*level[anc]])%mod)%mod;
Dist_DFSR[anc]=(Dist_DFSR[anc]-((ll)St*(ll)Store_Power_R[level[x]-level[anc]])%mod)%mod;
}
Dist_DFSL[0]=Dist_DFSR[0]=0;
DFS_new(1);
if(R%mod!=0) //Check for the tricky test case
for(int i=1;i<=N;i++) Sum[i]=(Dist_DFSL[i]+Dist_DFSR[i])%mod;
else
for(int i=1;i<=N;i++) Sum[i]=Dist_DFSL[i];
BFS(1);
while(Q--){
scanf("%d%d",&x,&y);
anc=lca(x,y);
ans=(Sum[x]+Sum[y]-Sum[anc]-Sum[Parent[anc]])%mod;
printf("%d\n",(ans+ mod)%mod);
}
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong> </p>
<pre><code>#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <iomanip>
#include <sstream>
#include <fstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
typedef vector<int> VI;
typedef vector<LL> VL;
typedef vector<PII> VPII;
typedef vector<PLL> VPLL;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<(x)<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<(x)<<", "#y" = "<<(y)<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define FOR(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define rep(i, n) for(int i = 0; i < n; i++)
#define UN(v) sort(ALL(v)), v.resize(unique(ALL(v))-v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
template<class T> string tostring(T x, int len = 0) {stringstream ss; ss << x; string r = ss.str(); if(r.length() < len) r = string(len - r.length(), '0') + r; return r;}
template<class T> void convert(string x, T& r) {stringstream ss(x); ss >> r;}
template<class A, class B> ostream& operator<<(ostream &o, pair<A, B> t) {o << "(" << t.x << ", " << t.y << ")"; return o;}
const int inf = 0x3f3f3f3f;
const int mod = 100711433;
const int N = 111111;
const int V = 111111;
vector<int> g[V];
vector<int> chain[V];
int father[V], heavy[V];
int depth[V], size[V];
int chainID[V], top[V];
int tL[V], tR[V];
int w[V];
void DFS(int u) {
size[u] = 1;
for(int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if(v == father[u]) continue;
father[v] = u;
depth[v] = depth[u] + 1;
DFS(v);
size[u] += size[v];
if(heavy[u] == -1 || size[v] > size[heavy[u]]) heavy[u] = v;
}
}
void HLD_DFS(int n) {
MM(heavy, -1);
MM(father, -1);
MM(depth, 0);
DFS(0);
int id = 0;
for(int i = 0; i < n; i++) {
if(father[i] == -1 || heavy[father[i]] != i) {
for(int k = i; k != -1; k = heavy[k]) {
chainID[k] = id;
chain[id].push_back(k);
top[k] = i;
}
id++;
}
}
for(int i = 0; i < id; i++) {
tL[i] = i > 0 ? tR[i - 1] + 1 : 1;
tR[i] = tL[i] + chain[i].size() - 1;
for(int j = 0; j < chain[i].size(); j++) {
w[chain[i][j]] = tL[i] + j;
}
}
}
int LCA(int u, int v) {
while(chainID[u] != chainID[v]) {
if(depth[top[u]] > depth[top[v]]) swap(u, v);
v = father[top[v]];
}
return depth[u] < depth[v] ? u : v;
}
LL exp(LL x, LL n, LL m = ~0ULL >> 1) {
x %= m;
LL r = 1 % m;
while(n) {
if(n & 1) r = r * x % m;
x = x * x % m, n >>= 1;
}
return r;
}
LL inv(int x) {
return exp(x, mod - 2, mod);
}
int n, R;
int iR;
LL q[N];
LL iq[N];
void ADD(int u, int v, int s, int r) {
/*
if(depth[u] > depth[v]) {
int ns;
while(chain[u] != chain[v]) {
int len = top[u] - u + 1;
ns = s * q[top[u] - u + 1] % mod;
add(w[top[u]], w[u], ns * R % mod, iR);
u = top[u] + 1;
}
add(w[v], w[u], ns * R % mod , iR);
} else {
int ns;
swap(u, v);
VPII vp;
while(chain[u] != chain[v]) {
int len = top[u] - u + 1;
ns = s * q[top[u] - u + 1] % mod;
vp.pb(mp(top[u], w[u]));
u = top[u] + 1;
}
add(w[v], w[u], ns * R % mod , iR);
}
*/
}
LL d[N];
int main() {
cin >> n >> R;
for(int i = 0; i < n - 1; i++) {
int u, v;
cin >> u >> v;
u--, v--;
g[u].pb(v);
g[v].pb(u);
}
HLD_DFS(n);
int U, Q;
cin >> U >> Q;
iR = inv(R);
iq[0] = q[0] = 1;
for(int i = 1; i < N; i++) q[i] = q[i - 1] * R % mod;
for(int i = 1; i < N; i++) iq[i] = iq[i - 1] * iR % mod;
while(U--) {
int u, v, s;
cin >> u >> v >> s;
u--, v--;
int x = LCA(u, v);
int t = depth[u] - depth[x];
vector<int> left, right;
while(u != x) {
left.pb(u);
u = father[u];
}
left.pb(x);
while(v != x) {
right.pb(v);
v = father[v];
}
reverse(ALL(right));
for(int i = 0; i < right.size(); i++) left.pb(right[i]);
for(int i = 0; i < left.size(); i++) {
d[left[i]] += s;
s = (LL) s * R % mod;
}
/* ADD(u, x, s, R);
ADD(x, v, s * q[t] % mod, R);
ADD(x, x, -s * q[t] % mod, 1);*/
}
while(Q--) {
int u, v;
cin >> u >> v;
u--, v--;
int x = LCA(u, v);
// LL r = SUM(u) + SUM(v) - 2 * SUM(father[x]);
// r = (r % mod + mod) % mod;
LL r = 0;
while(u != x) {
r += d[u];
u = father[u];
}
r += d[x];
while(v != x) {
r += d[v];
v = father[v];
}
r = (r % mod + mod) % mod;
cout << r << endl;
}
return 0;
}
</code></pre>
| 0 |
101-hack-jan-recalling-early-days-with-gp-trees
|
2014-02-03T12:29:31
|
{"contest_participation":1791,"challenge_submissions":71,"successful_submissions":23}
|
2014-02-03T12:29:31
|
2016-05-13T00:03:45
|
setter
|
//Author : Devendra Agarwal
#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<vector>
#include<string.h>
using namespace std;
#define MaxN 100001 //Maximum Nodes
typedef long long int ll;
int N,R,level[MaxN],Parent[MaxN],Dist_DFSL[MaxN],Dist_DFSR[MaxN],Root[MaxN][17],Store_Power_R[MaxN],store[MaxN],mod=100711433,R_inv,Sum[MaxN],Queue[MaxN];
vector<int> Graph[MaxN]; //to store graph
/* To calculate the inverse of a number in multiplicative modulo b*/
int inverse(int a,int b) //b>a
{
int Remainder,p0=0,p1=1,pcurr=1,q,m=b;
while(a!=0)
{
Remainder=b%a;
q=b/a;
if(Remainder!=0)
{
pcurr=p0-((ll)p1*(ll)q)%m;
if(pcurr<0)
pcurr+=m;
p0=p1;
p1=pcurr;
}
b=a;
a=Remainder;
}
return pcurr;
}
/*Storing the Parent and height using DFS*/
void DFS(int root)
{
for(vector<int> ::iterator it=Graph[root].begin();it!=Graph[root].end();it++){
if((*it)!=Parent[root]){ //not visiting more than once
level[(*it)]=level[root]+1;
Parent[(*it)]=root;
DFS((*it));
}
}
return;
}
/*Calculating Data necessary for calculating ancestor and some pre-processing for quicker implementation*/
void process()
{
memset(Root,-1,sizeof(Root));
for(int i=1;i<=N;i++) Root[i][0]=Parent[i];
for(int i=1;(1<<i) <= N; i++)
for(int j=1;j<=N;j++)
if(Root[j][i-1]!=-1)
Root[j][i]=Root[Root[j][i-1]][i-1];
store[0]=0;
store[1]=0;
int cmp=2;
for(int i=2;i<=N;i++){
if(cmp>i) store[i]=store[i-1];
else{
store[i]=store[i-1]+1;
cmp<<=1;
}
}
Store_Power_R[0]=1;
for(int i=1;i<=N;i++)
Store_Power_R[i]=((ll)Store_Power_R[i-1]*(ll)R)%mod;
}
/*Returns the lca of two nodes, same implementation as was used in topcoder tutorials*/
int lca(int p,int q) //Fnds the LCA of 2 nodes
{
int temp;
if(level[p]>level[q]){
temp=p;p=q;q=temp;
}
//level[q]>=level[p]
int steps=store[level[q]];
for(int i=steps;i>=0;i--)
if(level[q]-(1<<i) >= level[p])
q=Root[q][i];
if(p==q) return p;
for(int i=steps;i>=0;i--)
if(Root[p][i]!=Root[q][i])
p=Root[p][i],q=Root[q][i];
return Parent[p];
}
/*This Find the Dist_DFSL and Dist_DFSR after all update queries*/
void DFS_new(int root)
{
for(vector<int> ::iterator it=Graph[root].begin();it!=Graph[root].end();it++){
if((*it)!=Parent[root]){ //not visiting more than once
DFS_new((*it));
Dist_DFSL[root]=(Dist_DFSL[root]+((ll)Dist_DFSL[*it]*(ll)R)%mod)%mod; //Updating root from children
Dist_DFSR[root]=(Dist_DFSR[root]+((ll)Dist_DFSR[*it]*(ll)R_inv)%mod)%mod; //Updating root from children
}
}
}
/*This find the Sum[] array*/
void BFS(int root)
{
Queue[0]=root;
int st=0,end=1,node;
while(st<end){
node=Queue[st];
st++;
for(vector<int>::iterator it=Graph[node].begin();it!=Graph[node].end();it++){
if((*it)!=Parent[node]){
Sum[(*it)]=(Sum[(*it)]+Sum[node])%mod;
Queue[end]=(*it);
end++;
}
}
}
}
int main()
{
int x,y,U,Q,anc,ans,St;
scanf("%d%d",&N,&R);
if(R%mod!=0) //Checking the tricky case
R_inv=inverse(R,mod);
else
R_inv=0;
for(int i=1;i<N;i++){
scanf("%d%d",&x,&y);
Graph[x].push_back(y);
Graph[y].push_back(x);
}
level[1]=0;
Parent[1]=0;
DFS(1);
process();
memset(Dist_DFSL,0,sizeof(Dist_DFSL));
memset(Dist_DFSR,0,sizeof(Dist_DFSR));
memset(Sum,0,sizeof(Sum));
scanf("%d%d",&U,&Q);
while(U--){
scanf("%d%d%d",&x,&y,&St);
anc=lca(x,y);
Dist_DFSL[x]=(Dist_DFSL[x]+St)%mod;
Dist_DFSL[Parent[anc]]=(Dist_DFSL[Parent[anc]]-((ll)St*(ll)Store_Power_R[level[x]-level[anc]+1])%mod)%mod;
Dist_DFSR[y]=(Dist_DFSR[y]+((ll)St*(ll)Store_Power_R[level[y]+level[x]-2*level[anc]])%mod)%mod;
Dist_DFSR[anc]=(Dist_DFSR[anc]-((ll)St*(ll)Store_Power_R[level[x]-level[anc]])%mod)%mod;
}
Dist_DFSL[0]=Dist_DFSR[0]=0;
DFS_new(1);
if(R%mod!=0) //Check for the tricky test case
for(int i=1;i<=N;i++) Sum[i]=(Dist_DFSL[i]+Dist_DFSR[i])%mod;
else
for(int i=1;i<=N;i++) Sum[i]=Dist_DFSL[i];
BFS(1);
while(Q--){
scanf("%d%d",&x,&y);
anc=lca(x,y);
ans=(Sum[x]+Sum[y]-Sum[anc]-Sum[Parent[anc]])%mod;
printf("%d\n",(ans+ mod)%mod);
}
return 0;
}
|
not-set
|
2016-04-24T02:02:15
|
2016-04-24T02:02:15
|
C++
|
24 | 959 |
recalling-early-days-gp-with-trees
|
Recalling Early Days GP with Trees
|
[Chinese Version](https://hr-testcases.s3.amazonaws.com/959/959-chinese.md)<br/>
[Russian Version](https://hr-testcases.s3.amazonaws.com/959/959_rus.md)<br/>
You are given a [tree](http://en.wikipedia.org/wiki/Tree_(graph_theory)) with N nodes and each has a value associated with it. You are given Q queries, each of which is either an update or a retrieval operation.
The **update query** is of the format
i j X
This means you'd have to add a [GP](http://en.wikipedia.org/wiki/Geometric_progression) series to the nodes which lie in the path from node `i` to node `j` (both inclusive) with first term of the GP as `X` on node `i` and the common ratio as `R` (given in the input)
The **retrieval** query is of the format
i j
You need to return the sum of the node values (S) lying in the path from node i to node j modulo 100711433.
**Input Format**
The first line contains two integers (N and R respectively) separated by a space.
In the next N-1 lines, the i<sup>th</sup> line describes the i<sup>th</sup> edge: a line with two integers a b separated by a single space denotes an edge between a, b.
The next line contains 2 space separated integers (U and Q respectively) representing the number of Update and Query operations to follow.
U lines follow. Each of the next U lines contains 3 space separated integers (i,j, and X respectively).
Each of the next Q lines contains 2 space separated integers, i and j respectively.
**Output Format**
It contains exactly Q lines and each line containing the answer of the i<sup>th</sup> query.
**Constraints**
2 <= N <= 100000
2 <= R <= 10<sup>9</sup>
1 <= U <= 100000
1 <= Q <= 100000
1 <= X <= 10
1 <= a, b, i, j <= N
**Sample Input**
6 2
1 2
1 4
2 6
4 5
4 3
2 2
1 6 3
5 3 5
6 4
5 1
**Sample Output**
31
18
**Explanation**
The node values after the first updation becomes :
3 6 0 0 0 12
The node values after second updation becomes :
3 6 20 10 5 12
Answer to Query #1: 12 + 6 + 3 + 10 = 31
Answer to Query #2: 5 + 10 +3 = 18
|
code
|
Answer the queries performed on trees.
|
ai
|
2013-09-25T18:56:57
|
2022-08-31T08:33:17
| null | null | null |
[Chinese Version](https://hr-testcases.s3.amazonaws.com/959/959-chinese.md)<br/>
[Russian Version](https://hr-testcases.s3.amazonaws.com/959/959_rus.md)<br/>
You are given a [tree](http://en.wikipedia.org/wiki/Tree_(graph_theory)) with N nodes and each has a value associated with it. You are given Q queries, each of which is either an update or a retrieval operation.
The **update query** is of the format
i j X
This means you'd have to add a [GP](http://en.wikipedia.org/wiki/Geometric_progression) series to the nodes which lie in the path from node `i` to node `j` (both inclusive) with first term of the GP as `X` on node `i` and the common ratio as `R` (given in the input)
The **retrieval** query is of the format
i j
You need to return the sum of the node values (S) lying in the path from node i to node j modulo 100711433.
**Input Format**
The first line contains two integers (N and R respectively) separated by a space.
In the next N-1 lines, the i<sup>th</sup> line describes the i<sup>th</sup> edge: a line with two integers a b separated by a single space denotes an edge between a, b.
The next line contains 2 space separated integers (U and Q respectively) representing the number of Update and Query operations to follow.
U lines follow. Each of the next U lines contains 3 space separated integers (i,j, and X respectively).
Each of the next Q lines contains 2 space separated integers, i and j respectively.
**Output Format**
It contains exactly Q lines and each line containing the answer of the i<sup>th</sup> query.
**Constraints**
2 <= N <= 100000
2 <= R <= 10<sup>9</sup>
1 <= U <= 100000
1 <= Q <= 100000
1 <= X <= 10
1 <= a, b, i, j <= N
**Sample Input**
6 2
1 2
1 4
2 6
4 5
4 3
2 2
1 6 3
5 3 5
6 4
5 1
**Sample Output**
31
18
**Explanation**
The node values after the first updation becomes :
3 6 0 0 0 12
The node values after second updation becomes :
3 6 20 10 5 12
Answer to Query #1: 12 + 6 + 3 + 10 = 31
Answer to Query #2: 5 + 10 +3 = 18
| 0.409091 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
| null | null | null | null |
Hard
|
Recalling Early Days with GP Trees : 101 Hack January Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101jan14/challenges/recalling-early-days-gp-with-trees">Recalling Early Days with GP Trees</a></p>
<p><strong>Difficulty Level</strong> : Medium-Hard <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/devuy11">Devendra Agarwal</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/wanbo">Wanbo</a> </p>
<p><strong>Approach</strong> </p>
<p><strong>Observations</strong></p>
<ol>
<li><p>The Number 100711433 is a prime number , so that we can find its inverse (except when R is not a multiple of 100711433)</p></li>
<li><p>You need to first tackle all the Updates and then all the Queries.</p></li>
</ol>
<p>Choose any node as root of the tree.</p>
<p>Make 2 arrays Dist_DFSL[] and Dist_DFSR[] for the Tree.</p>
<p><strong>Update Method</strong></p>
<p>i j St</p>
<p>Let anc be the ancestor node of node i and node j.</p>
<p>Add value St in Dist_DFSL[i]</p>
<p>Add -St*power(R,d1+1) in Dist_DFSL[Parent[anc]] where d1 denotes the total number of edges between node i and node anc and power(a,b) denotes a^b mod 100711433</p>
<p>Add -St*power(R,d1) in Dist_DFSR[anc] where d1 denotes the total number of edges between node i and node anc and power(a,b) denotes a^b mod 100711433</p>
<p>Add St*power(R,d1+d2) in Dist_DFSR[j] where d2 represent the total edges in path from ancestor to j.</p>
<p>d1 and d2 can be calculated by precalculating the depth of each node from root.</p>
<p>d1=depth[i]-depth[anc]</p>
<p>d2=depth[j]-depth[anc]</p>
<p>After all Update Queries, we need the final values at each node and to do so ,we run a DFS on the Tree and do the following:</p>
<p>Dist_DFSL[parent]=(Dist_DFSL[parent]+Dist_DFSL[child]*R)%mod</p>
<p>Dist_DFSR[parent]=(Dist_DFSR[parent]+Dist_DFSR[child]*R_inverse)%mod</p>
<p><strong>Note</strong> :: R_Inverse * R = 1 mod (100711433)</p>
<p>Now value at each Node is :</p>
<p>Sum[Node]=Dist_DFSL[Node]+ Dist_DFSR[NOde]</p>
<p>Now, Run a BFS(or DFS) on the graph and store the sum to each Node from the root in Sum[] array.</p>
<p><strong>Answering the Query</strong></p>
<p>i j</p>
<p>Answer= Sum[i] + Sum[j] - Sum[anc] - Sum[Parent[anc]]</p>
<p><strong>NOTE</strong>:Precaution in Calculating R_inv and solving the problem when R is multiple of 100711433</p>
<p><strong>Time Complexity: O( (U+Q) log N)</strong> //computing lca part otherwise everything in O(1) time.</p>
<p><strong>Setter's Solution</strong> </p>
<pre><code>//Author : Devendra Agarwal
#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<vector>
#include<string.h>
using namespace std;
#define MaxN 100001 //Maximum Nodes
typedef long long int ll;
int N,R,level[MaxN],Parent[MaxN],Dist_DFSL[MaxN],Dist_DFSR[MaxN],Root[MaxN][17],Store_Power_R[MaxN],store[MaxN],mod=100711433,R_inv,Sum[MaxN],Queue[MaxN];
vector<int> Graph[MaxN]; //to store graph
/* To calculate the inverse of a number in multiplicative modulo b*/
int inverse(int a,int b) //b>a
{
int Remainder,p0=0,p1=1,pcurr=1,q,m=b;
while(a!=0)
{
Remainder=b%a;
q=b/a;
if(Remainder!=0)
{
pcurr=p0-((ll)p1*(ll)q)%m;
if(pcurr<0)
pcurr+=m;
p0=p1;
p1=pcurr;
}
b=a;
a=Remainder;
}
return pcurr;
}
/*Storing the Parent and height using DFS*/
void DFS(int root)
{
for(vector<int> ::iterator it=Graph[root].begin();it!=Graph[root].end();it++){
if((*it)!=Parent[root]){ //not visiting more than once
level[(*it)]=level[root]+1;
Parent[(*it)]=root;
DFS((*it));
}
}
return;
}
/*Calculating Data necessary for calculating ancestor and some pre-processing for quicker implementation*/
void process()
{
memset(Root,-1,sizeof(Root));
for(int i=1;i<=N;i++) Root[i][0]=Parent[i];
for(int i=1;(1<<i) <= N; i++)
for(int j=1;j<=N;j++)
if(Root[j][i-1]!=-1)
Root[j][i]=Root[Root[j][i-1]][i-1];
store[0]=0;
store[1]=0;
int cmp=2;
for(int i=2;i<=N;i++){
if(cmp>i) store[i]=store[i-1];
else{
store[i]=store[i-1]+1;
cmp<<=1;
}
}
Store_Power_R[0]=1;
for(int i=1;i<=N;i++)
Store_Power_R[i]=((ll)Store_Power_R[i-1]*(ll)R)%mod;
}
/*Returns the lca of two nodes, same implementation as was used in topcoder tutorials*/
int lca(int p,int q) //Fnds the LCA of 2 nodes
{
int temp;
if(level[p]>level[q]){
temp=p;p=q;q=temp;
}
//level[q]>=level[p]
int steps=store[level[q]];
for(int i=steps;i>=0;i--)
if(level[q]-(1<<i) >= level[p])
q=Root[q][i];
if(p==q) return p;
for(int i=steps;i>=0;i--)
if(Root[p][i]!=Root[q][i])
p=Root[p][i],q=Root[q][i];
return Parent[p];
}
/*This Find the Dist_DFSL and Dist_DFSR after all update queries*/
void DFS_new(int root)
{
for(vector<int> ::iterator it=Graph[root].begin();it!=Graph[root].end();it++){
if((*it)!=Parent[root]){ //not visiting more than once
DFS_new((*it));
Dist_DFSL[root]=(Dist_DFSL[root]+((ll)Dist_DFSL[*it]*(ll)R)%mod)%mod; //Updating root from children
Dist_DFSR[root]=(Dist_DFSR[root]+((ll)Dist_DFSR[*it]*(ll)R_inv)%mod)%mod; //Updating root from children
}
}
}
/*This find the Sum[] array*/
void BFS(int root)
{
Queue[0]=root;
int st=0,end=1,node;
while(st<end){
node=Queue[st];
st++;
for(vector<int>::iterator it=Graph[node].begin();it!=Graph[node].end();it++){
if((*it)!=Parent[node]){
Sum[(*it)]=(Sum[(*it)]+Sum[node])%mod;
Queue[end]=(*it);
end++;
}
}
}
}
int main()
{
int x,y,U,Q,anc,ans,St;
scanf("%d%d",&N,&R);
if(R%mod!=0) //Checking the tricky case
R_inv=inverse(R,mod);
else
R_inv=0;
for(int i=1;i<N;i++){
scanf("%d%d",&x,&y);
Graph[x].push_back(y);
Graph[y].push_back(x);
}
level[1]=0;
Parent[1]=0;
DFS(1);
process();
memset(Dist_DFSL,0,sizeof(Dist_DFSL));
memset(Dist_DFSR,0,sizeof(Dist_DFSR));
memset(Sum,0,sizeof(Sum));
scanf("%d%d",&U,&Q);
while(U--){
scanf("%d%d%d",&x,&y,&St);
anc=lca(x,y);
Dist_DFSL[x]=(Dist_DFSL[x]+St)%mod;
Dist_DFSL[Parent[anc]]=(Dist_DFSL[Parent[anc]]-((ll)St*(ll)Store_Power_R[level[x]-level[anc]+1])%mod)%mod;
Dist_DFSR[y]=(Dist_DFSR[y]+((ll)St*(ll)Store_Power_R[level[y]+level[x]-2*level[anc]])%mod)%mod;
Dist_DFSR[anc]=(Dist_DFSR[anc]-((ll)St*(ll)Store_Power_R[level[x]-level[anc]])%mod)%mod;
}
Dist_DFSL[0]=Dist_DFSR[0]=0;
DFS_new(1);
if(R%mod!=0) //Check for the tricky test case
for(int i=1;i<=N;i++) Sum[i]=(Dist_DFSL[i]+Dist_DFSR[i])%mod;
else
for(int i=1;i<=N;i++) Sum[i]=Dist_DFSL[i];
BFS(1);
while(Q--){
scanf("%d%d",&x,&y);
anc=lca(x,y);
ans=(Sum[x]+Sum[y]-Sum[anc]-Sum[Parent[anc]])%mod;
printf("%d\n",(ans+ mod)%mod);
}
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong> </p>
<pre><code>#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <iomanip>
#include <sstream>
#include <fstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
typedef vector<int> VI;
typedef vector<LL> VL;
typedef vector<PII> VPII;
typedef vector<PLL> VPLL;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<(x)<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<(x)<<", "#y" = "<<(y)<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define FOR(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define rep(i, n) for(int i = 0; i < n; i++)
#define UN(v) sort(ALL(v)), v.resize(unique(ALL(v))-v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
template<class T> string tostring(T x, int len = 0) {stringstream ss; ss << x; string r = ss.str(); if(r.length() < len) r = string(len - r.length(), '0') + r; return r;}
template<class T> void convert(string x, T& r) {stringstream ss(x); ss >> r;}
template<class A, class B> ostream& operator<<(ostream &o, pair<A, B> t) {o << "(" << t.x << ", " << t.y << ")"; return o;}
const int inf = 0x3f3f3f3f;
const int mod = 100711433;
const int N = 111111;
const int V = 111111;
vector<int> g[V];
vector<int> chain[V];
int father[V], heavy[V];
int depth[V], size[V];
int chainID[V], top[V];
int tL[V], tR[V];
int w[V];
void DFS(int u) {
size[u] = 1;
for(int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if(v == father[u]) continue;
father[v] = u;
depth[v] = depth[u] + 1;
DFS(v);
size[u] += size[v];
if(heavy[u] == -1 || size[v] > size[heavy[u]]) heavy[u] = v;
}
}
void HLD_DFS(int n) {
MM(heavy, -1);
MM(father, -1);
MM(depth, 0);
DFS(0);
int id = 0;
for(int i = 0; i < n; i++) {
if(father[i] == -1 || heavy[father[i]] != i) {
for(int k = i; k != -1; k = heavy[k]) {
chainID[k] = id;
chain[id].push_back(k);
top[k] = i;
}
id++;
}
}
for(int i = 0; i < id; i++) {
tL[i] = i > 0 ? tR[i - 1] + 1 : 1;
tR[i] = tL[i] + chain[i].size() - 1;
for(int j = 0; j < chain[i].size(); j++) {
w[chain[i][j]] = tL[i] + j;
}
}
}
int LCA(int u, int v) {
while(chainID[u] != chainID[v]) {
if(depth[top[u]] > depth[top[v]]) swap(u, v);
v = father[top[v]];
}
return depth[u] < depth[v] ? u : v;
}
LL exp(LL x, LL n, LL m = ~0ULL >> 1) {
x %= m;
LL r = 1 % m;
while(n) {
if(n & 1) r = r * x % m;
x = x * x % m, n >>= 1;
}
return r;
}
LL inv(int x) {
return exp(x, mod - 2, mod);
}
int n, R;
int iR;
LL q[N];
LL iq[N];
void ADD(int u, int v, int s, int r) {
/*
if(depth[u] > depth[v]) {
int ns;
while(chain[u] != chain[v]) {
int len = top[u] - u + 1;
ns = s * q[top[u] - u + 1] % mod;
add(w[top[u]], w[u], ns * R % mod, iR);
u = top[u] + 1;
}
add(w[v], w[u], ns * R % mod , iR);
} else {
int ns;
swap(u, v);
VPII vp;
while(chain[u] != chain[v]) {
int len = top[u] - u + 1;
ns = s * q[top[u] - u + 1] % mod;
vp.pb(mp(top[u], w[u]));
u = top[u] + 1;
}
add(w[v], w[u], ns * R % mod , iR);
}
*/
}
LL d[N];
int main() {
cin >> n >> R;
for(int i = 0; i < n - 1; i++) {
int u, v;
cin >> u >> v;
u--, v--;
g[u].pb(v);
g[v].pb(u);
}
HLD_DFS(n);
int U, Q;
cin >> U >> Q;
iR = inv(R);
iq[0] = q[0] = 1;
for(int i = 1; i < N; i++) q[i] = q[i - 1] * R % mod;
for(int i = 1; i < N; i++) iq[i] = iq[i - 1] * iR % mod;
while(U--) {
int u, v, s;
cin >> u >> v >> s;
u--, v--;
int x = LCA(u, v);
int t = depth[u] - depth[x];
vector<int> left, right;
while(u != x) {
left.pb(u);
u = father[u];
}
left.pb(x);
while(v != x) {
right.pb(v);
v = father[v];
}
reverse(ALL(right));
for(int i = 0; i < right.size(); i++) left.pb(right[i]);
for(int i = 0; i < left.size(); i++) {
d[left[i]] += s;
s = (LL) s * R % mod;
}
/* ADD(u, x, s, R);
ADD(x, v, s * q[t] % mod, R);
ADD(x, x, -s * q[t] % mod, 1);*/
}
while(Q--) {
int u, v;
cin >> u >> v;
u--, v--;
int x = LCA(u, v);
// LL r = SUM(u) + SUM(v) - 2 * SUM(father[x]);
// r = (r % mod + mod) % mod;
LL r = 0;
while(u != x) {
r += d[u];
u = father[u];
}
r += d[x];
while(v != x) {
r += d[v];
v = father[v];
}
r = (r % mod + mod) % mod;
cout << r << endl;
}
return 0;
}
</code></pre>
| 0 |
101-hack-jan-recalling-early-days-with-gp-trees
|
2014-02-03T12:29:31
|
{"contest_participation":1791,"challenge_submissions":71,"successful_submissions":23}
|
2014-02-03T12:29:31
|
2016-05-13T00:03:45
|
tester
|
#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <iomanip>
#include <sstream>
#include <fstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
typedef vector<int> VI;
typedef vector<LL> VL;
typedef vector<PII> VPII;
typedef vector<PLL> VPLL;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<(x)<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<(x)<<", "#y" = "<<(y)<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define FOR(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define rep(i, n) for(int i = 0; i < n; i++)
#define UN(v) sort(ALL(v)), v.resize(unique(ALL(v))-v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
template<class T> string tostring(T x, int len = 0) {stringstream ss; ss << x; string r = ss.str(); if(r.length() < len) r = string(len - r.length(), '0') + r; return r;}
template<class T> void convert(string x, T& r) {stringstream ss(x); ss >> r;}
template<class A, class B> ostream& operator<<(ostream &o, pair<A, B> t) {o << "(" << t.x << ", " << t.y << ")"; return o;}
const int inf = 0x3f3f3f3f;
const int mod = 100711433;
const int N = 111111;
const int V = 111111;
vector<int> g[V];
vector<int> chain[V];
int father[V], heavy[V];
int depth[V], size[V];
int chainID[V], top[V];
int tL[V], tR[V];
int w[V];
void DFS(int u) {
size[u] = 1;
for(int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if(v == father[u]) continue;
father[v] = u;
depth[v] = depth[u] + 1;
DFS(v);
size[u] += size[v];
if(heavy[u] == -1 || size[v] > size[heavy[u]]) heavy[u] = v;
}
}
void HLD_DFS(int n) {
MM(heavy, -1);
MM(father, -1);
MM(depth, 0);
DFS(0);
int id = 0;
for(int i = 0; i < n; i++) {
if(father[i] == -1 || heavy[father[i]] != i) {
for(int k = i; k != -1; k = heavy[k]) {
chainID[k] = id;
chain[id].push_back(k);
top[k] = i;
}
id++;
}
}
for(int i = 0; i < id; i++) {
tL[i] = i > 0 ? tR[i - 1] + 1 : 1;
tR[i] = tL[i] + chain[i].size() - 1;
for(int j = 0; j < chain[i].size(); j++) {
w[chain[i][j]] = tL[i] + j;
}
}
}
int LCA(int u, int v) {
while(chainID[u] != chainID[v]) {
if(depth[top[u]] > depth[top[v]]) swap(u, v);
v = father[top[v]];
}
return depth[u] < depth[v] ? u : v;
}
LL exp(LL x, LL n, LL m = ~0ULL >> 1) {
x %= m;
LL r = 1 % m;
while(n) {
if(n & 1) r = r * x % m;
x = x * x % m, n >>= 1;
}
return r;
}
LL inv(int x) {
return exp(x, mod - 2, mod);
}
int n, R;
int iR;
LL q[N];
LL iq[N];
void ADD(int u, int v, int s, int r) {
/*
if(depth[u] > depth[v]) {
int ns;
while(chain[u] != chain[v]) {
int len = top[u] - u + 1;
ns = s * q[top[u] - u + 1] % mod;
add(w[top[u]], w[u], ns * R % mod, iR);
u = top[u] + 1;
}
add(w[v], w[u], ns * R % mod , iR);
} else {
int ns;
swap(u, v);
VPII vp;
while(chain[u] != chain[v]) {
int len = top[u] - u + 1;
ns = s * q[top[u] - u + 1] % mod;
vp.pb(mp(top[u], w[u]));
u = top[u] + 1;
}
add(w[v], w[u], ns * R % mod , iR);
}
*/
}
LL d[N];
int main() {
cin >> n >> R;
for(int i = 0; i < n - 1; i++) {
int u, v;
cin >> u >> v;
u--, v--;
g[u].pb(v);
g[v].pb(u);
}
HLD_DFS(n);
int U, Q;
cin >> U >> Q;
iR = inv(R);
iq[0] = q[0] = 1;
for(int i = 1; i < N; i++) q[i] = q[i - 1] * R % mod;
for(int i = 1; i < N; i++) iq[i] = iq[i - 1] * iR % mod;
while(U--) {
int u, v, s;
cin >> u >> v >> s;
u--, v--;
int x = LCA(u, v);
int t = depth[u] - depth[x];
vector<int> left, right;
while(u != x) {
left.pb(u);
u = father[u];
}
left.pb(x);
while(v != x) {
right.pb(v);
v = father[v];
}
reverse(ALL(right));
for(int i = 0; i < right.size(); i++) left.pb(right[i]);
for(int i = 0; i < left.size(); i++) {
d[left[i]] += s;
s = (LL) s * R % mod;
}
/* ADD(u, x, s, R);
ADD(x, v, s * q[t] % mod, R);
ADD(x, x, -s * q[t] % mod, 1);*/
}
while(Q--) {
int u, v;
cin >> u >> v;
u--, v--;
int x = LCA(u, v);
// LL r = SUM(u) + SUM(v) - 2 * SUM(father[x]);
// r = (r % mod + mod) % mod;
LL r = 0;
while(u != x) {
r += d[u];
u = father[u];
}
r += d[x];
while(v != x) {
r += d[v];
v = father[v];
}
r = (r % mod + mod) % mod;
cout << r << endl;
}
return 0;
}
|
not-set
|
2016-04-24T02:02:15
|
2016-04-24T02:02:15
|
C++
|
25 | 1,058 |
cube-summation
|
Cube Summation
|
[Chinese Version](https://hr-testcases.s3.amazonaws.com/1058/1058-chinese.md)<br/>
[Russian Version](https://hr-testcases.s3.amazonaws.com/1058/1058_rus.md)<br/>
You are given a 3-D Matrix in which each block contains 0 initially. The first block is defined by the coordinate (1,1,1) and the last block is defined by the coordinate (N,N,N). There are two types of queries.
UPDATE x y z W
updates the value of block (x,y,z) to W.
QUERY x1 y1 z1 x2 y2 z2
calculates the sum of the value of blocks whose x coordinate is between x1 and x2 (inclusive), y coordinate between y1 and y2 (inclusive) and z coordinate between z1 and z2 (inclusive).
**Input Format**
The first line contains an integer T, the number of test-cases. T testcases follow.
For each test case, the first line will contain two integers N and M separated by a single space.
N defines the N * N * N matrix.
M defines the number of operations.
The next M lines will contain either
1. UPDATE x y z W
2. QUERY x1 y1 z1 x2 y2 z2
**Output Format**
Print the result for each QUERY.
**Constrains**
1 <= T <= 50
1 <= N <= 100
1 <= M <= 1000
1 <= x1 <= x2 <= N
1 <= y1 <= y2 <= N
1 <= z1 <= z2 <= N
1 <= x,y,z <= N
-10<sup>9</sup> <= W <= 10<sup>9</sup>
**Sample Input**
2
4 5
UPDATE 2 2 2 4
QUERY 1 1 1 3 3 3
UPDATE 1 1 1 23
QUERY 2 2 2 4 4 4
QUERY 1 1 1 3 3 3
2 4
UPDATE 2 2 2 1
QUERY 1 1 1 1 1 1
QUERY 1 1 1 2 2 2
QUERY 2 2 2 2 2 2
**Sample Output**
4
4
27
0
1
1
**Explanation**
First test case, we are given a cube of 4 * 4 * 4 and 5 queries. Initially all the cells (1,1,1) to (4,4,4) are 0.
`UPDATE 2 2 2 4` makes the cell (2,2,2) = 4
`QUERY 1 1 1 3 3 3`. As (2,2,2) is updated to 4 and the rest are all 0. The answer to this query is 4.
`UPDATE 1 1 1 23`. updates the cell (1,1,1) to 23.
`QUERY 2 2 2 4 4 4`. Only the cell (1,1,1) and (2,2,2) are non-zero and (1,1,1) is not between (2,2,2) and (4,4,4). So, the answer is 4.
`QUERY 1 1 1 3 3 3`. 2 cells are non-zero and their sum is 23+4 = 27.
|
code
|
Update and query a 3-d matrix
|
ai
|
2013-10-10T09:07:12
|
2022-08-31T08:33:13
|
#
# Complete the 'cubeSum' function below.
#
# The function is expected to return an INTEGER_ARRAY.
# The function accepts following parameters:
# 1. INTEGER n
# 2. STRING_ARRAY operations
#
def cubeSum(n, operations):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
T = int(input().strip())
for T_itr in range(T):
first_multiple_input = input().rstrip().split()
matSize = int(first_multiple_input[0])
m = int(first_multiple_input[1])
ops = []
for _ in range(m):
ops_item = input()
ops.append(ops_item)
res = cubeSum(matSize, ops)
fptr.write('\n'.join(map(str, res)))
fptr.write('\n')
fptr.close()
|
[Chinese Version](https://hr-testcases.s3.amazonaws.com/1058/1058-chinese.md)<br/>
[Russian Version](https://hr-testcases.s3.amazonaws.com/1058/1058_rus.md)<br/>
Define a 3-D Matrix in which each block contains 0 initially. The first block is defined by the coordinates (1,1,1) and the last block is defined by the coordinates (n,n,n). There are two types of queries.
UPDATE x y z W
Update the value of block (x,y,z) to W.
QUERY x1 y1 z1 x2 y2 z2
Calculate the sum of the values of blocks whose x coordinate is between x1 and x2 (inclusive), y coordinate between y1 and y2 (inclusive) and z coordinate between z1 and z2 (inclusive).
**Function Description**
Complete the *cubeSum* function in the editor below.
*cubeSum* has the following parameters:
- *int n: the dimensions of the 3-d matrix
- *string operations[m]:* the operations to perform
**Returns**
- *int[]:* the results of each `QUERY` operation
**Input Format**
The first line contains an integer $T$, the number of test-cases. $T$ testcases follow.
For each test case, the first line contains two space-separated integers, $n$ and $m$.
$n$ defines the $n\times n\times n$ matrix.
$m$ defines the number of operations.
The next $m$ lines will contain an operation either of these forms:
1. UPDATE x y z W
2. QUERY x1 y1 z1 x2 y2 z2
**Constraints**
$1 \le T \le 50$
$1 \le n \le 100$
$1 \le m \le 1000$
$1 \le x1 \le x2 \le n$
$1 \le y1 \le y2 \le n$
$1 \le z1 \le z2 \le n$
$1 \le x,y,z \le n$
-10<sup>9</sup> \le W \le 10<sup>9</sup>
**Sample Input**
2
4 5
UPDATE 2 2 2 4
QUERY 1 1 1 3 3 3
UPDATE 1 1 1 23
QUERY 2 2 2 4 4 4
QUERY 1 1 1 3 3 3
2 4
UPDATE 2 2 2 1
QUERY 1 1 1 1 1 1
QUERY 1 1 1 2 2 2
QUERY 2 2 2 2 2 2
**Sample Output**
4
4
27
0
1
1
**Explanation**
In the first test case, there is a cube of 4 * 4 * 4 and there are 5 queries. Initially all the cells (1,1,1) to (4,4,4) are 0.
`UPDATE 2 2 2 4` makes the cell (2,2,2) = 4
`QUERY 1 1 1 3 3 3`. As (2,2,2) is updated to 4 and the rest are all 0. The answer to this query is 4.
`UPDATE 1 1 1 23`. updates the cell (1,1,1) to 23.
`QUERY 2 2 2 4 4 4`. Only the cell (1,1,1) and (2,2,2) are non-zero and (1,1,1) is not between (2,2,2) and (4,4,4). So, the answer is 4.
`QUERY 1 1 1 3 3 3`. 2 cells are non-zero and their sum is 23+4 = 27.
| 0.56 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
Hard
|
Cube Summation : 101 Hack January Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101jan14/challenges/cube-summation">Cube Summation</a></p>
<p><strong>Difficulty Level</strong> : Medium <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/stranger9811">Ashok Kumar</a> <br>
<strong>Problem Testers</strong> : <a href="https://www.hackerrank.com/shashank21j">Shashank</a>, <a href="https://www.hackerrank.com/abhiranjan">Abhiranjan</a> <br>
<strong>Required Knowledge</strong> : <a href="https://en.wikipedia.org/wiki/Fenwick_tree">Binary Index Tree</a> </p>
<p><strong>Approach</strong> <br>
This problem is based on <a href="https://en.wikipedia.org/wiki/Fenwick_tree">fenwick trees</a>.
Consider this problem:</p>
<p><strong>A High level explanation of fenwick tree.</strong></p>
<p>Consider this problem:</p>
<p>Given an array(let say A) of size n initialized to zero. In this array only two operations can be performed </p>
<ol>
<li>update x</li>
<li>summation i j</li>
</ol>
<p>using fenwick tree both of these operation be done in O(logn) time.</p>
<p>First we have to construct a new array(let say B). B[i] stores summation of values of A[x] to A[i](here x is some index less than i). Now to get
"summation x y" we have to calculate A[0]+....+A[j] and A[0]+....+A[i].</p>
<p>To get A[0]+....+A[j] we will make use of array B.</p>
<pre><code>sum = 0;
while(j>0) {
sum += B[j];
j -= (j & -j); // consider updated j as x in above explanation.
}
</code></pre>
<p>This while loops takes O(logn) time. Similarly we can perform update operation. </p>
<p>In original problem we have to find summation in 3-dimensions. So we can again use fenwick tree with three dimension. Now summation operation will look like this:</p>
<pre><code> long long y1,x1,sum=0;
while (z>0) {
x1=x;
while(x1>0) {
y1=y;
while(y1>0) {
sum += matrix[x1][y1][z];
y1-= (y1 & -y1);
}
x1 -= (x1 & -x1);
}
z -= (z & -z);
}
return sum;
</code></pre>
<p><strong>Problem Setter's solution</strong></p>
<pre><code>#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long matrix[101][101][101];
void update(long long n,long long x,long long y,long long z,long long val) {
long long y1,x1;
while(z <= n) {
x1 = x;
while(x1 <= n) {
y1 = y;
while(y1 <= n) {
matrix[x1][y1][z] += val;
y1 += (y1 & -y1 );
}
x1 += (x1 & -x1);
}
z += (z & -z);
}
}
long long calculate_sum(long long x,long long y,long long z) {
long long y1,x1,sum=0;
while (z>0) {
x1=x;
while(x1>0) {
y1=y;
while(y1>0) {
sum += matrix[x1][y1][z];
y1-= (y1 & -y1);
}
x1 -= (x1 & -x1);
}
z -= (z & -z);
}
return sum;
}
void process(long long n,long long m) {
long long x,y,z,x0,y0,z0;
long long value1,value2,val;
char command[10];
memset(matrix,0,sizeof(matrix));
while(m--) {
scanf("%s",command);
if(!strcmp(command,"QUERY")) {
scanf("%lld %lld %lld %lld %lld %lld",&x0,&y0,&z0,&x,&y,&z);
value1 = calculate_sum(x,y,z)- calculate_sum(x0-1,y,z)
- calculate_sum(x,y0-1,z) + calculate_sum(x0-1,y0-1,z);
value2 = calculate_sum(x,y,z0-1) - calculate_sum(x0-1,y,z0-1)
- calculate_sum(x,y0-1,z0-1) + calculate_sum(x0-1,y0-1,z0-1);
printf("%lld\n",value1 - value2);
//PrintMatrix(n);
}
if(!strcmp(command,"UPDATE")) {
scanf("%lld %lld %lld %lld",&x,&y,&z,&val);
x0 = x;
y0 = y;
z0 = z ;
value1 = calculate_sum(x,y,z)- calculate_sum(x0-1,y,z)
- calculate_sum(x,y0-1,z) + calculate_sum(x0-1,y0-1,z);
value2 = calculate_sum(x,y,z0-1) - calculate_sum(x0-1,y,z0-1)
- calculate_sum(x,y0-1,z0-1) + calculate_sum(x0-1,y0-1,z0-1);
update(n,x,y,z,val -(value1 - value2 ));
}
}
}
int main() {
long long cases; scanf("%lld",&cases);
while(cases--) {
long long n,m; scanf("%lld %lld",&n,&m);
process(n,m);
}
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong> </p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
const int sz = 111;
long long tree[sz][sz][sz];
void update(int x, int y, int z, long long val) {
int xx = x;
while(xx < sz) {
int yy = y;
while(yy < sz) {
int zz = z;
while(zz < sz) {
tree[xx][yy][zz] += val;
zz += zz & (-zz);
}
yy += yy & (-yy);
}
xx += xx&(-xx);
}
}
long long f(int x, int y, int z) {
long long ret = 0;
int xx = x;
while(xx > 0) {
int yy = y;
while(yy > 0) {
int zz = z;
while(zz > 0) {
ret += tree[xx][yy][zz];
zz -= zz & (-zz);
}
yy -= yy & (-yy);
}
xx -= xx & (-xx);
}
return ret;
}
long long solve(int x1, int y1, int z1, int x2, int y2, int z2){
long long j4 = f(x1-1, y1-1, z1-1);
long long j1 = f(x2, y1-1, z1-1) - j4;
long long j2 = f(x1-1, y2, z1-1) - j4;
long long j3 = f(x1-1, y1-1, z2) - j4;
return f(x2, y2, z2) - f(x2, y1-1, z2) - f(x1-1, y2, z2) - f(x2, y2, z1-1) + 2*j4 + j1 + j2 + j3;
}
int main()
{
int test;
scanf("%d", &test);
assert(test>=1);
assert(test<=50);
while(test--) {
memset(tree, 0, sizeof(tree));
int N, M;
cin >> N >> M;
assert(N>=1);
assert(N<=100);
assert(M>=1);
assert(M<=1000);
string st;
int x1, y1, z1, x2, y2, z2;
long long val;
while(M--) {
cin >> st;
assert(st == "QUERY" || st == "UPDATE");
if(st[0] == 'Q') {
cin >> x1 >> y1 >> z1;
cin >> x2 >> y2 >> z2;
assert(1 <= x1);
assert(x1 <= x2);
assert(x2 <= N);
assert(1 <= y1);
assert(y1 <= y2);
assert(y2 <= N);
assert(1 <= z1);
assert(z1 <= z2);
assert(z2 <= N);
cout << solve(x1, y1, z1, x2, y2, z2) << "\n";
}
else if (st[0] == 'U') {
cin >> x1 >> y1 >> z1 >> val;
assert(1 <= x1); assert(x1 <= N);
assert(1 <= y1); assert(y1 <= N);
assert(1 <= z1); assert(z1 <= N);
assert(-1e9 <= val);
assert(val <= 1e9);
long long existingVal = solve(x1, y1, z1, x1, y1, z1);
update(x1, y1, z1, val-existingVal);
}
}
}
return 0;
}
</code></pre>
<p>Now Time Complexity of update and summation operation will be O((logn)^3). Since we have to reduce each x,y,z coordinate.</p>
| 0 |
101-hack-jan-cube-summation
|
2014-02-05T18:23:32
|
{"contest_participation":1791,"challenge_submissions":401,"successful_submissions":276}
|
2014-02-05T18:23:32
|
2016-05-13T00:03:42
|
setter
|
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long matrix[101][101][101];
void update(long long n,long long x,long long y,long long z,long long val) {
long long y1,x1;
while(z <= n) {
x1 = x;
while(x1 <= n) {
y1 = y;
while(y1 <= n) {
matrix[x1][y1][z] += val;
y1 += (y1 & -y1 );
}
x1 += (x1 & -x1);
}
z += (z & -z);
}
}
long long calculate_sum(long long x,long long y,long long z) {
long long y1,x1,sum=0;
while (z>0) {
x1=x;
while(x1>0) {
y1=y;
while(y1>0) {
sum += matrix[x1][y1][z];
y1-= (y1 & -y1);
}
x1 -= (x1 & -x1);
}
z -= (z & -z);
}
return sum;
}
void process(long long n,long long m) {
long long x,y,z,x0,y0,z0;
long long value1,value2,val;
char command[10];
memset(matrix,0,sizeof(matrix));
while(m--) {
scanf("%s",command);
if(!strcmp(command,"QUERY")) {
scanf("%lld %lld %lld %lld %lld %lld",&x0,&y0,&z0,&x,&y,&z);
value1 = calculate_sum(x,y,z)- calculate_sum(x0-1,y,z)
- calculate_sum(x,y0-1,z) + calculate_sum(x0-1,y0-1,z);
value2 = calculate_sum(x,y,z0-1) - calculate_sum(x0-1,y,z0-1)
- calculate_sum(x,y0-1,z0-1) + calculate_sum(x0-1,y0-1,z0-1);
printf("%lld\n",value1 - value2);
//PrintMatrix(n);
}
if(!strcmp(command,"UPDATE")) {
scanf("%lld %lld %lld %lld",&x,&y,&z,&val);
x0 = x;
y0 = y;
z0 = z ;
value1 = calculate_sum(x,y,z)- calculate_sum(x0-1,y,z)
- calculate_sum(x,y0-1,z) + calculate_sum(x0-1,y0-1,z);
value2 = calculate_sum(x,y,z0-1) - calculate_sum(x0-1,y,z0-1)
- calculate_sum(x,y0-1,z0-1) + calculate_sum(x0-1,y0-1,z0-1);
update(n,x,y,z,val -(value1 - value2 ));
}
}
}
int main() {
long long cases; scanf("%lld",&cases);
while(cases--) {
long long n,m; scanf("%lld %lld",&n,&m);
process(n,m);
}
return 0;
}
|
not-set
|
2016-04-24T02:02:15
|
2016-04-24T02:02:15
|
C++
|
||||
26 | 1,058 |
cube-summation
|
Cube Summation
|
[Chinese Version](https://hr-testcases.s3.amazonaws.com/1058/1058-chinese.md)<br/>
[Russian Version](https://hr-testcases.s3.amazonaws.com/1058/1058_rus.md)<br/>
You are given a 3-D Matrix in which each block contains 0 initially. The first block is defined by the coordinate (1,1,1) and the last block is defined by the coordinate (N,N,N). There are two types of queries.
UPDATE x y z W
updates the value of block (x,y,z) to W.
QUERY x1 y1 z1 x2 y2 z2
calculates the sum of the value of blocks whose x coordinate is between x1 and x2 (inclusive), y coordinate between y1 and y2 (inclusive) and z coordinate between z1 and z2 (inclusive).
**Input Format**
The first line contains an integer T, the number of test-cases. T testcases follow.
For each test case, the first line will contain two integers N and M separated by a single space.
N defines the N * N * N matrix.
M defines the number of operations.
The next M lines will contain either
1. UPDATE x y z W
2. QUERY x1 y1 z1 x2 y2 z2
**Output Format**
Print the result for each QUERY.
**Constrains**
1 <= T <= 50
1 <= N <= 100
1 <= M <= 1000
1 <= x1 <= x2 <= N
1 <= y1 <= y2 <= N
1 <= z1 <= z2 <= N
1 <= x,y,z <= N
-10<sup>9</sup> <= W <= 10<sup>9</sup>
**Sample Input**
2
4 5
UPDATE 2 2 2 4
QUERY 1 1 1 3 3 3
UPDATE 1 1 1 23
QUERY 2 2 2 4 4 4
QUERY 1 1 1 3 3 3
2 4
UPDATE 2 2 2 1
QUERY 1 1 1 1 1 1
QUERY 1 1 1 2 2 2
QUERY 2 2 2 2 2 2
**Sample Output**
4
4
27
0
1
1
**Explanation**
First test case, we are given a cube of 4 * 4 * 4 and 5 queries. Initially all the cells (1,1,1) to (4,4,4) are 0.
`UPDATE 2 2 2 4` makes the cell (2,2,2) = 4
`QUERY 1 1 1 3 3 3`. As (2,2,2) is updated to 4 and the rest are all 0. The answer to this query is 4.
`UPDATE 1 1 1 23`. updates the cell (1,1,1) to 23.
`QUERY 2 2 2 4 4 4`. Only the cell (1,1,1) and (2,2,2) are non-zero and (1,1,1) is not between (2,2,2) and (4,4,4). So, the answer is 4.
`QUERY 1 1 1 3 3 3`. 2 cells are non-zero and their sum is 23+4 = 27.
|
code
|
Update and query a 3-d matrix
|
ai
|
2013-10-10T09:07:12
|
2022-08-31T08:33:13
|
#
# Complete the 'cubeSum' function below.
#
# The function is expected to return an INTEGER_ARRAY.
# The function accepts following parameters:
# 1. INTEGER n
# 2. STRING_ARRAY operations
#
def cubeSum(n, operations):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
T = int(input().strip())
for T_itr in range(T):
first_multiple_input = input().rstrip().split()
matSize = int(first_multiple_input[0])
m = int(first_multiple_input[1])
ops = []
for _ in range(m):
ops_item = input()
ops.append(ops_item)
res = cubeSum(matSize, ops)
fptr.write('\n'.join(map(str, res)))
fptr.write('\n')
fptr.close()
|
[Chinese Version](https://hr-testcases.s3.amazonaws.com/1058/1058-chinese.md)<br/>
[Russian Version](https://hr-testcases.s3.amazonaws.com/1058/1058_rus.md)<br/>
Define a 3-D Matrix in which each block contains 0 initially. The first block is defined by the coordinates (1,1,1) and the last block is defined by the coordinates (n,n,n). There are two types of queries.
UPDATE x y z W
Update the value of block (x,y,z) to W.
QUERY x1 y1 z1 x2 y2 z2
Calculate the sum of the values of blocks whose x coordinate is between x1 and x2 (inclusive), y coordinate between y1 and y2 (inclusive) and z coordinate between z1 and z2 (inclusive).
**Function Description**
Complete the *cubeSum* function in the editor below.
*cubeSum* has the following parameters:
- *int n: the dimensions of the 3-d matrix
- *string operations[m]:* the operations to perform
**Returns**
- *int[]:* the results of each `QUERY` operation
**Input Format**
The first line contains an integer $T$, the number of test-cases. $T$ testcases follow.
For each test case, the first line contains two space-separated integers, $n$ and $m$.
$n$ defines the $n\times n\times n$ matrix.
$m$ defines the number of operations.
The next $m$ lines will contain an operation either of these forms:
1. UPDATE x y z W
2. QUERY x1 y1 z1 x2 y2 z2
**Constraints**
$1 \le T \le 50$
$1 \le n \le 100$
$1 \le m \le 1000$
$1 \le x1 \le x2 \le n$
$1 \le y1 \le y2 \le n$
$1 \le z1 \le z2 \le n$
$1 \le x,y,z \le n$
-10<sup>9</sup> \le W \le 10<sup>9</sup>
**Sample Input**
2
4 5
UPDATE 2 2 2 4
QUERY 1 1 1 3 3 3
UPDATE 1 1 1 23
QUERY 2 2 2 4 4 4
QUERY 1 1 1 3 3 3
2 4
UPDATE 2 2 2 1
QUERY 1 1 1 1 1 1
QUERY 1 1 1 2 2 2
QUERY 2 2 2 2 2 2
**Sample Output**
4
4
27
0
1
1
**Explanation**
In the first test case, there is a cube of 4 * 4 * 4 and there are 5 queries. Initially all the cells (1,1,1) to (4,4,4) are 0.
`UPDATE 2 2 2 4` makes the cell (2,2,2) = 4
`QUERY 1 1 1 3 3 3`. As (2,2,2) is updated to 4 and the rest are all 0. The answer to this query is 4.
`UPDATE 1 1 1 23`. updates the cell (1,1,1) to 23.
`QUERY 2 2 2 4 4 4`. Only the cell (1,1,1) and (2,2,2) are non-zero and (1,1,1) is not between (2,2,2) and (4,4,4). So, the answer is 4.
`QUERY 1 1 1 3 3 3`. 2 cells are non-zero and their sum is 23+4 = 27.
| 0.56 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
Hard
|
Cube Summation : 101 Hack January Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101jan14/challenges/cube-summation">Cube Summation</a></p>
<p><strong>Difficulty Level</strong> : Medium <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/stranger9811">Ashok Kumar</a> <br>
<strong>Problem Testers</strong> : <a href="https://www.hackerrank.com/shashank21j">Shashank</a>, <a href="https://www.hackerrank.com/abhiranjan">Abhiranjan</a> <br>
<strong>Required Knowledge</strong> : <a href="https://en.wikipedia.org/wiki/Fenwick_tree">Binary Index Tree</a> </p>
<p><strong>Approach</strong> <br>
This problem is based on <a href="https://en.wikipedia.org/wiki/Fenwick_tree">fenwick trees</a>.
Consider this problem:</p>
<p><strong>A High level explanation of fenwick tree.</strong></p>
<p>Consider this problem:</p>
<p>Given an array(let say A) of size n initialized to zero. In this array only two operations can be performed </p>
<ol>
<li>update x</li>
<li>summation i j</li>
</ol>
<p>using fenwick tree both of these operation be done in O(logn) time.</p>
<p>First we have to construct a new array(let say B). B[i] stores summation of values of A[x] to A[i](here x is some index less than i). Now to get
"summation x y" we have to calculate A[0]+....+A[j] and A[0]+....+A[i].</p>
<p>To get A[0]+....+A[j] we will make use of array B.</p>
<pre><code>sum = 0;
while(j>0) {
sum += B[j];
j -= (j & -j); // consider updated j as x in above explanation.
}
</code></pre>
<p>This while loops takes O(logn) time. Similarly we can perform update operation. </p>
<p>In original problem we have to find summation in 3-dimensions. So we can again use fenwick tree with three dimension. Now summation operation will look like this:</p>
<pre><code> long long y1,x1,sum=0;
while (z>0) {
x1=x;
while(x1>0) {
y1=y;
while(y1>0) {
sum += matrix[x1][y1][z];
y1-= (y1 & -y1);
}
x1 -= (x1 & -x1);
}
z -= (z & -z);
}
return sum;
</code></pre>
<p><strong>Problem Setter's solution</strong></p>
<pre><code>#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long matrix[101][101][101];
void update(long long n,long long x,long long y,long long z,long long val) {
long long y1,x1;
while(z <= n) {
x1 = x;
while(x1 <= n) {
y1 = y;
while(y1 <= n) {
matrix[x1][y1][z] += val;
y1 += (y1 & -y1 );
}
x1 += (x1 & -x1);
}
z += (z & -z);
}
}
long long calculate_sum(long long x,long long y,long long z) {
long long y1,x1,sum=0;
while (z>0) {
x1=x;
while(x1>0) {
y1=y;
while(y1>0) {
sum += matrix[x1][y1][z];
y1-= (y1 & -y1);
}
x1 -= (x1 & -x1);
}
z -= (z & -z);
}
return sum;
}
void process(long long n,long long m) {
long long x,y,z,x0,y0,z0;
long long value1,value2,val;
char command[10];
memset(matrix,0,sizeof(matrix));
while(m--) {
scanf("%s",command);
if(!strcmp(command,"QUERY")) {
scanf("%lld %lld %lld %lld %lld %lld",&x0,&y0,&z0,&x,&y,&z);
value1 = calculate_sum(x,y,z)- calculate_sum(x0-1,y,z)
- calculate_sum(x,y0-1,z) + calculate_sum(x0-1,y0-1,z);
value2 = calculate_sum(x,y,z0-1) - calculate_sum(x0-1,y,z0-1)
- calculate_sum(x,y0-1,z0-1) + calculate_sum(x0-1,y0-1,z0-1);
printf("%lld\n",value1 - value2);
//PrintMatrix(n);
}
if(!strcmp(command,"UPDATE")) {
scanf("%lld %lld %lld %lld",&x,&y,&z,&val);
x0 = x;
y0 = y;
z0 = z ;
value1 = calculate_sum(x,y,z)- calculate_sum(x0-1,y,z)
- calculate_sum(x,y0-1,z) + calculate_sum(x0-1,y0-1,z);
value2 = calculate_sum(x,y,z0-1) - calculate_sum(x0-1,y,z0-1)
- calculate_sum(x,y0-1,z0-1) + calculate_sum(x0-1,y0-1,z0-1);
update(n,x,y,z,val -(value1 - value2 ));
}
}
}
int main() {
long long cases; scanf("%lld",&cases);
while(cases--) {
long long n,m; scanf("%lld %lld",&n,&m);
process(n,m);
}
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong> </p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
const int sz = 111;
long long tree[sz][sz][sz];
void update(int x, int y, int z, long long val) {
int xx = x;
while(xx < sz) {
int yy = y;
while(yy < sz) {
int zz = z;
while(zz < sz) {
tree[xx][yy][zz] += val;
zz += zz & (-zz);
}
yy += yy & (-yy);
}
xx += xx&(-xx);
}
}
long long f(int x, int y, int z) {
long long ret = 0;
int xx = x;
while(xx > 0) {
int yy = y;
while(yy > 0) {
int zz = z;
while(zz > 0) {
ret += tree[xx][yy][zz];
zz -= zz & (-zz);
}
yy -= yy & (-yy);
}
xx -= xx & (-xx);
}
return ret;
}
long long solve(int x1, int y1, int z1, int x2, int y2, int z2){
long long j4 = f(x1-1, y1-1, z1-1);
long long j1 = f(x2, y1-1, z1-1) - j4;
long long j2 = f(x1-1, y2, z1-1) - j4;
long long j3 = f(x1-1, y1-1, z2) - j4;
return f(x2, y2, z2) - f(x2, y1-1, z2) - f(x1-1, y2, z2) - f(x2, y2, z1-1) + 2*j4 + j1 + j2 + j3;
}
int main()
{
int test;
scanf("%d", &test);
assert(test>=1);
assert(test<=50);
while(test--) {
memset(tree, 0, sizeof(tree));
int N, M;
cin >> N >> M;
assert(N>=1);
assert(N<=100);
assert(M>=1);
assert(M<=1000);
string st;
int x1, y1, z1, x2, y2, z2;
long long val;
while(M--) {
cin >> st;
assert(st == "QUERY" || st == "UPDATE");
if(st[0] == 'Q') {
cin >> x1 >> y1 >> z1;
cin >> x2 >> y2 >> z2;
assert(1 <= x1);
assert(x1 <= x2);
assert(x2 <= N);
assert(1 <= y1);
assert(y1 <= y2);
assert(y2 <= N);
assert(1 <= z1);
assert(z1 <= z2);
assert(z2 <= N);
cout << solve(x1, y1, z1, x2, y2, z2) << "\n";
}
else if (st[0] == 'U') {
cin >> x1 >> y1 >> z1 >> val;
assert(1 <= x1); assert(x1 <= N);
assert(1 <= y1); assert(y1 <= N);
assert(1 <= z1); assert(z1 <= N);
assert(-1e9 <= val);
assert(val <= 1e9);
long long existingVal = solve(x1, y1, z1, x1, y1, z1);
update(x1, y1, z1, val-existingVal);
}
}
}
return 0;
}
</code></pre>
<p>Now Time Complexity of update and summation operation will be O((logn)^3). Since we have to reduce each x,y,z coordinate.</p>
| 0 |
101-hack-jan-cube-summation
|
2014-02-05T18:23:32
|
{"contest_participation":1791,"challenge_submissions":401,"successful_submissions":276}
|
2014-02-05T18:23:32
|
2016-05-13T00:03:42
|
tester
|
#include <bits/stdc++.h>
using namespace std;
const int sz = 111;
long long tree[sz][sz][sz];
void update(int x, int y, int z, long long val) {
int xx = x;
while(xx < sz) {
int yy = y;
while(yy < sz) {
int zz = z;
while(zz < sz) {
tree[xx][yy][zz] += val;
zz += zz & (-zz);
}
yy += yy & (-yy);
}
xx += xx&(-xx);
}
}
long long f(int x, int y, int z) {
long long ret = 0;
int xx = x;
while(xx > 0) {
int yy = y;
while(yy > 0) {
int zz = z;
while(zz > 0) {
ret += tree[xx][yy][zz];
zz -= zz & (-zz);
}
yy -= yy & (-yy);
}
xx -= xx & (-xx);
}
return ret;
}
long long solve(int x1, int y1, int z1, int x2, int y2, int z2){
long long j4 = f(x1-1, y1-1, z1-1);
long long j1 = f(x2, y1-1, z1-1) - j4;
long long j2 = f(x1-1, y2, z1-1) - j4;
long long j3 = f(x1-1, y1-1, z2) - j4;
return f(x2, y2, z2) - f(x2, y1-1, z2) - f(x1-1, y2, z2) - f(x2, y2, z1-1) + 2*j4 + j1 + j2 + j3;
}
int main()
{
int test;
scanf("%d", &test);
assert(test>=1);
assert(test<=50);
while(test--) {
memset(tree, 0, sizeof(tree));
int N, M;
cin >> N >> M;
assert(N>=1);
assert(N<=100);
assert(M>=1);
assert(M<=1000);
string st;
int x1, y1, z1, x2, y2, z2;
long long val;
while(M--) {
cin >> st;
assert(st == "QUERY" || st == "UPDATE");
if(st[0] == 'Q') {
cin >> x1 >> y1 >> z1;
cin >> x2 >> y2 >> z2;
assert(1 <= x1);
assert(x1 <= x2);
assert(x2 <= N);
assert(1 <= y1);
assert(y1 <= y2);
assert(y2 <= N);
assert(1 <= z1);
assert(z1 <= z2);
assert(z2 <= N);
cout << solve(x1, y1, z1, x2, y2, z2) << "\n";
}
else if (st[0] == 'U') {
cin >> x1 >> y1 >> z1 >> val;
assert(1 <= x1); assert(x1 <= N);
assert(1 <= y1); assert(y1 <= N);
assert(1 <= z1); assert(z1 <= N);
assert(-1e9 <= val);
assert(val <= 1e9);
long long existingVal = solve(x1, y1, z1, x1, y1, z1);
update(x1, y1, z1, val-existingVal);
}
}
}
return 0;
}
|
not-set
|
2016-04-24T02:02:15
|
2016-04-24T02:02:15
|
C++
|
||||
27 | 1,543 |
bike-racers
|
Bike Racers
|
[Chinese Version](https://hr-filepicker.s3.amazonaws.com/feb14/chinese/1543-chinese.md)<br/>
[Russian Version](https://hr-filepicker.s3.amazonaws.com/feb-14/russian/1543-russian.md)<br/>
There are _N_ bikers present in a city (shaped as a grid) having _M_ bikes. All the bikers want to participate in the HackerRace competition, but unfortunately only _K_ bikers can be accommodated in the race. Jack is organizing the HackerRace and wants to start the race as soon as possible. He can instruct any biker to move towards any bike in the city. In order to minimize the time to start the race, Jack instructs the bikers in such a way that first _K_ bikes are acquired in the minimum time.
Every biker moves with a unit speed and one bike can be acquired by only one biker. *A biker can proceed in any direction*. Consider distance between bike and bikers as euclidean distance.
Jack would like to know the *square of required time* to start the race as soon as possible.
**Input Format**
The first line contains three integers - N,M,K separated by a single space.
Following N lines will contain N pairs of integers denoting the co-ordinates of N bikers. Each pair of integers is separated by a single space. The next M pairs of lines will denote the co-ordinates of M bikes.
**Output Format**
A single line containing the square of required time.
**Constraints**
1 <= N <= 250
1 <= M <= 250
1 <= K <= min(N,M)
0 <= x<sub>i</sub>,y<sub>i</sub> <= 10<sup>7</sup>
**Sample Input #00:**
3 3 2
0 1
0 2
0 3
100 1
200 2
300 3
**Sample Output #00:**
40000
**Explanation #00:**
There's need for two bikers for the race. The first biker (0,1) will be able to reach the first bike (100,1) in 100 time units. The second biker (0,2) will be able to reach the second bike (200,2) in 200 time units. This is the most optimal solution and will take 200 time units. So output will be 200<sup>2</sup> = 40000.
|
code
|
Calculate the square of the minimum time required to start the bike race.
|
ai
|
2013-12-13T23:10:30
|
2022-08-31T08:14:22
|
#
# Complete the 'bikeRacers' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. 2D_INTEGER_ARRAY bikers
# 2. 2D_INTEGER_ARRAY bikes
#
def bikeRacers(bikers, bikes):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
k = int(first_multiple_input[2])
bikers = []
for _ in range(n):
bikers.append(list(map(int, input().rstrip().split())))
bikes = []
for _ in range(n):
bikes.append(list(map(int, input().rstrip().split())))
result = bikeRacers(bikers, bikes)
fptr.write(str(result) + '\n')
fptr.close()
|
There are $N$ bikers present in a city (shaped as a grid) having $M$ bikes. All the bikers want to participate in the HackerRace competition, but unfortunately only $K$ bikers can be accommodated in the race. Jack is organizing the HackerRace and wants to start the race as soon as possible. He can instruct any biker to move towards any bike in the city. In order to minimize the time to start the race, Jack instructs the bikers in such a way that the first $K$ bikes are acquired in the minimum time.
Every biker moves with a unit speed and one bike can be acquired by only one biker. *A biker can proceed in any direction*. Consider distance between bikes and bikers as Euclidean distance.
Jack would like to know the *square of required time* to start the race as soon as possible.
| 0.406504 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains three integers, $N$, $M$, and $K$, separated by a single space.
The following $N$ lines will contain $N$ pairs of integers denoting the co-ordinates of $N$ bikers. Each pair of integers is separated by a single space. The next $M$ lines will similarly denote the co-ordinates of the $M$ bikes.
|
A single line containing the square of required time.
|
3 3 2
0 1
0 2
0 3
100 1
200 2
300 3
|
40000
|
Hard
|
Bike Racers - 2020 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem</strong> : Tell the time by which K bikers will get bike. Read full problem <a href="https://www.hackerrank.com/contests/feb14/challenges/bike-racers">here</a> </p>
<p><strong>Required Knowledge</strong> : Binary Search, Bipartite Matching . </p>
<p><strong>Time Complexity</strong> : O(K^2 * log(10^14 ) ) </p>
<p><strong>Approach</strong> :</p>
<p>This is a problem for which you have to solve 2 <strong>subproblems</strong>, each subproblem will help you in learning some useful concept.</p>
<p><strong>Subproblem 1</strong> First try to solve a problem, Given N bikes and M bikers and time T, How many bikers (at max) will be get a bike ? while each bikers can have only one bike and one bike can be accommodated by only one biker.<br></p>
<p><strong>Solution</strong> : Make a bipartite graph, Having N node in one partite and having M nove in other partite and connect a node X from first partite to a node Y of second partite iff bike Y is reachable from biker X is given amount of time T.</p>
<p><strong>Value of maxium bipartite matching is the solution of subproblem 1</strong></p>
<p>Now using this subproblem we can check whether in given amount of Time whether K bikers can get bike or not.</p>
<p>Now define a function f in given manner</p>
<p><strong>f(T)</strong> = true if K bikers can get in bike in square_root(T) time.<br>
else false.</p>
<p>as it is very obvious that if <strong>f(T) = true</strong> then <strong>f(T1) = true</strong> for all T1>=T.</p>
<p>and f(0) = false and f(10^16) = true. as all co-ordinates X,Y <= 10^7<br>
Now we can use classical binary search to get the value of exact value of T.</p>
<p><strong>Subproblem 2</strong> : Binary search can solved using the classical method.<br></p>
<pre><code>long long int low = 0;
long long int high = 10000000000000000;
while(low < high)
{
long long int mid = (low + high) / 2;
if( f( mid ) )
{
high = mid;
}
else
{
low = mid+1 ;
}
}
</code></pre>
<p>Which will give the precise value of <strong>Square of Time</strong>.</p>
<p><strong>Setter's code</strong> :</p>
<pre><code>//Hopcraft carp maxium matching algorithm time complexity = E*sqrt(V)
#include<iostream>
#include<cstdlib>
#include <cstdio>
#include <queue>
#include <vector>
#include<bits/stdc++.h>
using namespace std;
#define SET(x) memset(x, -1, sizeof(x))
#define CLR(x) memset(x, 0, sizeof(x))
#define MAX 2001
#define NIL 0
#define INF (1<<28)
int N,M,K;
vector< int > edges[MAX]; // edges of left side
bool visited[MAX];
int Left[MAX], Right[MAX];
long long int dist[MAX][MAX];
bool dfs(int u) {
if(visited[u]) return false;
visited[u] = true;
int len = edges[u].size(), i, v;
for(i=0; i<len; i++) {
v = edges[u][i];
if(Right[v]==-1) {
Right[v] = u, Left[u] = v;
return true;
}
}
for(i=0; i<len; i++) {
v = edges[u][i];
if(dfs(Right[v])) {
Right[v] = u, Left[u] = v;
return true;
}
}
return false;
}
int match() {
SET(Left); // left = -1
SET(Right); // right = -1
int i, ret = 0;
bool done;
do {
done = true;
CLR(visited); // visited = 0
for(i=1; i<=N; i++) {
if(Left[i]==-1 && dfs(i)) {
done = false;
}
}
} while(!done);
for(i=1; i<=N; i++) ret += (Left[i]!=-1);
return ret;
}
bool check ( long long int val)
{
for(int i=1 ; i<=N ; i++)
{
for( int j=1 ; j<=M ; j++)
{
if(dist[i][j] <=val)
{
edges[i].push_back(j);
}
}
}
long long int num_match = match();
for(int i= 1 ; i<= N ; i++)
edges[i].clear();
if(num_match >=K)
return true;
else
return false;
}
int main()
{
cin>>N>>M>>K;
assert(K <= N);
assert(K <= M);
int a,b;
pair<long long int,long long int> P[N+1];
pair<long long int,long long int> Q[M+1];
for(int i=1 ; i<=N; i++)
cin>>P[i].first>>P[i].second;
for(int i=1 ; i<=M ; i++)
cin>>Q[i].first>>Q[i].second;
for(int i=1 ; i<=N ; i++)
{
for(int j=1 ; j<=M ; j++)
{
dist[i][j] = (P[i].first - Q[j].first)*(P[i].first - Q[j].first) + (P[i].second - Q[j].second)*(P[i].second - Q[j].second);
}
}
long long int low = 0;
long long int high = 10000000000000000;
while(low < high)
{
long long int mid = (low + high) / 2;
if( check( mid ) )
{
high = mid;
}
else
{
low = mid+1 ;
}
}
cout<<low<<endl;
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong> :</p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
const int sz = 2000;
long long userX[sz], userY[sz];
long long bikeX[sz], bikeY[sz];
int lt[sz];
int N, M, K;
bool vis[sz];
bool validPath(int userId, int bikerId, long long distanceAllowed) {
long long distX = userX[userId] - bikeX[bikerId];
distX *= distX;
long long distY = userY[userId] - bikeY[bikerId];
distY *= distY;
return distX + distY <= distanceAllowed;
}
bool dfs(int u, long long distanceAllowed) {
if(u == -1)
return true;
if(vis[u])
return false;
vis[u] = true;
for(int i = 0; i < (int)M; ++i) {
int id = lt[i];
if(validPath(u, i, distanceAllowed) && dfs(id, distanceAllowed)) {
lt[i] = u;
return true;
}
}
return false;
}
int matching(long long tm) {
memset(lt, -1, sizeof(lt));
int ret = 0;
for(int i = 0; i < (int)N; ++i) {
memset(vis, 0, sizeof(vis));
if(dfs(i, tm))
ret++;
}
return ret;
}
long long binarySearch(long long l = 0, long long r = 1e17) {
if(l == r)
return l;
long long mid = (l+r)/2;
int match = matching(mid);
return match >= K ? binarySearch(l, mid) : binarySearch(mid+1, r);
}
int main()
{
cin >> N >> M >> K;
assert(1 <= N); assert(N <= sz);
assert(1 <= M); assert(M <= sz);
assert(1 <= K); assert(K <= min(N, M));
for(int i = 0; i < (int)N; ++i) {
cin >> userX[i] >> userY[i];
assert(0 <= userX[i]); assert(userX[i] <= 1e7);
assert(0 <= userY[i]); assert(userY[i] <= 1e7);
}
for(int i = 0; i < (int)M; ++i) {
cin >> bikeX[i] >> bikeY[i];
assert(0 <= bikeX[i]); assert(bikeX[i] <= 1e7);
assert(0 <= bikeY[i]); assert(bikeY[i] <= 1e7);
}
cout << binarySearch() << endl;
return 0;
}
</code></pre>
| 0 |
feb14-bike-racers
|
2014-02-27T05:02:05
|
{"contest_participation":2769,"challenge_submissions":556,"successful_submissions":192}
|
2014-02-27T05:02:05
|
2016-12-02T20:11:31
|
setter
|
###C++
```cpp
//Hopcraft carp maxium matching algorithm time complexity = E*sqrt(V)
#include<iostream>
#include<cstdlib>
#include <cstdio>
#include <queue>
#include <vector>
#include<bits/stdc++.h>
using namespace std;
#define SET(x) memset(x, -1, sizeof(x))
#define CLR(x) memset(x, 0, sizeof(x))
#define MAX 2001
#define NIL 0
#define INF (1<<28)
int N,M,K;
vector< int > edges[MAX]; // edges of left side
bool visited[MAX];
int Left[MAX], Right[MAX];
long long int dist[MAX][MAX];
bool dfs(int u) {
if(visited[u]) return false;
visited[u] = true;
int len = edges[u].size(), i, v;
for(i=0; i<len; i++) {
v = edges[u][i];
if(Right[v]==-1) {
Right[v] = u, Left[u] = v;
return true;
}
}
for(i=0; i<len; i++) {
v = edges[u][i];
if(dfs(Right[v])) {
Right[v] = u, Left[u] = v;
return true;
}
}
return false;
}
int match() {
SET(Left); // left = -1
SET(Right); // right = -1
int i, ret = 0;
bool done;
do {
done = true;
CLR(visited); // visited = 0
for(i=1; i<=N; i++) {
if(Left[i]==-1 && dfs(i)) {
done = false;
}
}
} while(!done);
for(i=1; i<=N; i++) ret += (Left[i]!=-1);
return ret;
}
bool check ( long long int val) {
for(int i=1 ; i<=N ; i++) {
for( int j=1 ; j<=M ; j++) {
if(dist[i][j] <=val) {
edges[i].push_back(j);
}
}
}
long long int num_match = match();
for(int i= 1 ; i<= N ; i++)
edges[i].clear();
if(num_match >=K)
return true;
else
return false;
}
int main() {
cin>>N>>M>>K;
int a,b;
pair<long long int,long long int> P[N+1];
pair<long long int,long long int> Q[M+1];
for(int i=1 ; i<=N; i++)
cin>>P[i].first>>P[i].second;
for(int i=1 ; i<=M ; i++)
cin>>Q[i].first>>Q[i].second;
for(int i=1 ; i<=N ; i++) {
for(int j=1 ; j<=M ; j++) {
dist[i][j] = (P[i].first - Q[j].first)
*(P[i].first - Q[j].first)
+ (P[i].second - Q[j].second)
*(P[i].second - Q[j].second);
}
}
long long int low = 0;
long long int high = 10000000000000000;
while(low < high) {
long long int mid = (low + high) / 2;
if( check( mid ) ) {
high = mid;
} else {
low = mid+1 ;
}
}
cout << low << endl;
return 0;
}
```
|
not-set
|
2016-04-24T02:02:16
|
2016-12-02T20:11:31
|
C++
|
28 | 1,543 |
bike-racers
|
Bike Racers
|
[Chinese Version](https://hr-filepicker.s3.amazonaws.com/feb14/chinese/1543-chinese.md)<br/>
[Russian Version](https://hr-filepicker.s3.amazonaws.com/feb-14/russian/1543-russian.md)<br/>
There are _N_ bikers present in a city (shaped as a grid) having _M_ bikes. All the bikers want to participate in the HackerRace competition, but unfortunately only _K_ bikers can be accommodated in the race. Jack is organizing the HackerRace and wants to start the race as soon as possible. He can instruct any biker to move towards any bike in the city. In order to minimize the time to start the race, Jack instructs the bikers in such a way that first _K_ bikes are acquired in the minimum time.
Every biker moves with a unit speed and one bike can be acquired by only one biker. *A biker can proceed in any direction*. Consider distance between bike and bikers as euclidean distance.
Jack would like to know the *square of required time* to start the race as soon as possible.
**Input Format**
The first line contains three integers - N,M,K separated by a single space.
Following N lines will contain N pairs of integers denoting the co-ordinates of N bikers. Each pair of integers is separated by a single space. The next M pairs of lines will denote the co-ordinates of M bikes.
**Output Format**
A single line containing the square of required time.
**Constraints**
1 <= N <= 250
1 <= M <= 250
1 <= K <= min(N,M)
0 <= x<sub>i</sub>,y<sub>i</sub> <= 10<sup>7</sup>
**Sample Input #00:**
3 3 2
0 1
0 2
0 3
100 1
200 2
300 3
**Sample Output #00:**
40000
**Explanation #00:**
There's need for two bikers for the race. The first biker (0,1) will be able to reach the first bike (100,1) in 100 time units. The second biker (0,2) will be able to reach the second bike (200,2) in 200 time units. This is the most optimal solution and will take 200 time units. So output will be 200<sup>2</sup> = 40000.
|
code
|
Calculate the square of the minimum time required to start the bike race.
|
ai
|
2013-12-13T23:10:30
|
2022-08-31T08:14:22
|
#
# Complete the 'bikeRacers' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. 2D_INTEGER_ARRAY bikers
# 2. 2D_INTEGER_ARRAY bikes
#
def bikeRacers(bikers, bikes):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
k = int(first_multiple_input[2])
bikers = []
for _ in range(n):
bikers.append(list(map(int, input().rstrip().split())))
bikes = []
for _ in range(n):
bikes.append(list(map(int, input().rstrip().split())))
result = bikeRacers(bikers, bikes)
fptr.write(str(result) + '\n')
fptr.close()
|
There are $N$ bikers present in a city (shaped as a grid) having $M$ bikes. All the bikers want to participate in the HackerRace competition, but unfortunately only $K$ bikers can be accommodated in the race. Jack is organizing the HackerRace and wants to start the race as soon as possible. He can instruct any biker to move towards any bike in the city. In order to minimize the time to start the race, Jack instructs the bikers in such a way that the first $K$ bikes are acquired in the minimum time.
Every biker moves with a unit speed and one bike can be acquired by only one biker. *A biker can proceed in any direction*. Consider distance between bikes and bikers as Euclidean distance.
Jack would like to know the *square of required time* to start the race as soon as possible.
| 0.406504 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains three integers, $N$, $M$, and $K$, separated by a single space.
The following $N$ lines will contain $N$ pairs of integers denoting the co-ordinates of $N$ bikers. Each pair of integers is separated by a single space. The next $M$ lines will similarly denote the co-ordinates of the $M$ bikes.
|
A single line containing the square of required time.
|
3 3 2
0 1
0 2
0 3
100 1
200 2
300 3
|
40000
|
Hard
|
Bike Racers - 2020 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Problem</strong> : Tell the time by which K bikers will get bike. Read full problem <a href="https://www.hackerrank.com/contests/feb14/challenges/bike-racers">here</a> </p>
<p><strong>Required Knowledge</strong> : Binary Search, Bipartite Matching . </p>
<p><strong>Time Complexity</strong> : O(K^2 * log(10^14 ) ) </p>
<p><strong>Approach</strong> :</p>
<p>This is a problem for which you have to solve 2 <strong>subproblems</strong>, each subproblem will help you in learning some useful concept.</p>
<p><strong>Subproblem 1</strong> First try to solve a problem, Given N bikes and M bikers and time T, How many bikers (at max) will be get a bike ? while each bikers can have only one bike and one bike can be accommodated by only one biker.<br></p>
<p><strong>Solution</strong> : Make a bipartite graph, Having N node in one partite and having M nove in other partite and connect a node X from first partite to a node Y of second partite iff bike Y is reachable from biker X is given amount of time T.</p>
<p><strong>Value of maxium bipartite matching is the solution of subproblem 1</strong></p>
<p>Now using this subproblem we can check whether in given amount of Time whether K bikers can get bike or not.</p>
<p>Now define a function f in given manner</p>
<p><strong>f(T)</strong> = true if K bikers can get in bike in square_root(T) time.<br>
else false.</p>
<p>as it is very obvious that if <strong>f(T) = true</strong> then <strong>f(T1) = true</strong> for all T1>=T.</p>
<p>and f(0) = false and f(10^16) = true. as all co-ordinates X,Y <= 10^7<br>
Now we can use classical binary search to get the value of exact value of T.</p>
<p><strong>Subproblem 2</strong> : Binary search can solved using the classical method.<br></p>
<pre><code>long long int low = 0;
long long int high = 10000000000000000;
while(low < high)
{
long long int mid = (low + high) / 2;
if( f( mid ) )
{
high = mid;
}
else
{
low = mid+1 ;
}
}
</code></pre>
<p>Which will give the precise value of <strong>Square of Time</strong>.</p>
<p><strong>Setter's code</strong> :</p>
<pre><code>//Hopcraft carp maxium matching algorithm time complexity = E*sqrt(V)
#include<iostream>
#include<cstdlib>
#include <cstdio>
#include <queue>
#include <vector>
#include<bits/stdc++.h>
using namespace std;
#define SET(x) memset(x, -1, sizeof(x))
#define CLR(x) memset(x, 0, sizeof(x))
#define MAX 2001
#define NIL 0
#define INF (1<<28)
int N,M,K;
vector< int > edges[MAX]; // edges of left side
bool visited[MAX];
int Left[MAX], Right[MAX];
long long int dist[MAX][MAX];
bool dfs(int u) {
if(visited[u]) return false;
visited[u] = true;
int len = edges[u].size(), i, v;
for(i=0; i<len; i++) {
v = edges[u][i];
if(Right[v]==-1) {
Right[v] = u, Left[u] = v;
return true;
}
}
for(i=0; i<len; i++) {
v = edges[u][i];
if(dfs(Right[v])) {
Right[v] = u, Left[u] = v;
return true;
}
}
return false;
}
int match() {
SET(Left); // left = -1
SET(Right); // right = -1
int i, ret = 0;
bool done;
do {
done = true;
CLR(visited); // visited = 0
for(i=1; i<=N; i++) {
if(Left[i]==-1 && dfs(i)) {
done = false;
}
}
} while(!done);
for(i=1; i<=N; i++) ret += (Left[i]!=-1);
return ret;
}
bool check ( long long int val)
{
for(int i=1 ; i<=N ; i++)
{
for( int j=1 ; j<=M ; j++)
{
if(dist[i][j] <=val)
{
edges[i].push_back(j);
}
}
}
long long int num_match = match();
for(int i= 1 ; i<= N ; i++)
edges[i].clear();
if(num_match >=K)
return true;
else
return false;
}
int main()
{
cin>>N>>M>>K;
assert(K <= N);
assert(K <= M);
int a,b;
pair<long long int,long long int> P[N+1];
pair<long long int,long long int> Q[M+1];
for(int i=1 ; i<=N; i++)
cin>>P[i].first>>P[i].second;
for(int i=1 ; i<=M ; i++)
cin>>Q[i].first>>Q[i].second;
for(int i=1 ; i<=N ; i++)
{
for(int j=1 ; j<=M ; j++)
{
dist[i][j] = (P[i].first - Q[j].first)*(P[i].first - Q[j].first) + (P[i].second - Q[j].second)*(P[i].second - Q[j].second);
}
}
long long int low = 0;
long long int high = 10000000000000000;
while(low < high)
{
long long int mid = (low + high) / 2;
if( check( mid ) )
{
high = mid;
}
else
{
low = mid+1 ;
}
}
cout<<low<<endl;
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong> :</p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
const int sz = 2000;
long long userX[sz], userY[sz];
long long bikeX[sz], bikeY[sz];
int lt[sz];
int N, M, K;
bool vis[sz];
bool validPath(int userId, int bikerId, long long distanceAllowed) {
long long distX = userX[userId] - bikeX[bikerId];
distX *= distX;
long long distY = userY[userId] - bikeY[bikerId];
distY *= distY;
return distX + distY <= distanceAllowed;
}
bool dfs(int u, long long distanceAllowed) {
if(u == -1)
return true;
if(vis[u])
return false;
vis[u] = true;
for(int i = 0; i < (int)M; ++i) {
int id = lt[i];
if(validPath(u, i, distanceAllowed) && dfs(id, distanceAllowed)) {
lt[i] = u;
return true;
}
}
return false;
}
int matching(long long tm) {
memset(lt, -1, sizeof(lt));
int ret = 0;
for(int i = 0; i < (int)N; ++i) {
memset(vis, 0, sizeof(vis));
if(dfs(i, tm))
ret++;
}
return ret;
}
long long binarySearch(long long l = 0, long long r = 1e17) {
if(l == r)
return l;
long long mid = (l+r)/2;
int match = matching(mid);
return match >= K ? binarySearch(l, mid) : binarySearch(mid+1, r);
}
int main()
{
cin >> N >> M >> K;
assert(1 <= N); assert(N <= sz);
assert(1 <= M); assert(M <= sz);
assert(1 <= K); assert(K <= min(N, M));
for(int i = 0; i < (int)N; ++i) {
cin >> userX[i] >> userY[i];
assert(0 <= userX[i]); assert(userX[i] <= 1e7);
assert(0 <= userY[i]); assert(userY[i] <= 1e7);
}
for(int i = 0; i < (int)M; ++i) {
cin >> bikeX[i] >> bikeY[i];
assert(0 <= bikeX[i]); assert(bikeX[i] <= 1e7);
assert(0 <= bikeY[i]); assert(bikeY[i] <= 1e7);
}
cout << binarySearch() << endl;
return 0;
}
</code></pre>
| 0 |
feb14-bike-racers
|
2014-02-27T05:02:05
|
{"contest_participation":2769,"challenge_submissions":556,"successful_submissions":192}
|
2014-02-27T05:02:05
|
2016-12-02T20:11:31
|
tester
|
###C++
```cpp
#include <bits/stdc++.h>
using namespace std;
const int sz = 2000;
long long userX[sz], userY[sz];
long long bikeX[sz], bikeY[sz];
int lt[sz];
int N, M, K;
bool vis[sz];
bool validPath(int userId, int bikerId, long long distanceAllowed) {
long long distX = userX[userId] - bikeX[bikerId];
distX *= distX;
long long distY = userY[userId] - bikeY[bikerId];
distY *= distY;
return distX + distY <= distanceAllowed;
}
bool dfs(int u, long long distanceAllowed) {
if(u == -1)
return true;
if(vis[u])
return false;
vis[u] = true;
for(int i = 0; i < (int)M; ++i) {
int id = lt[i];
if(validPath(u, i, distanceAllowed) && dfs(id, distanceAllowed)) {
lt[i] = u;
return true;
}
}
return false;
}
int matching(long long tm) {
memset(lt, -1, sizeof(lt));
int ret = 0;
for(int i = 0; i < (int)N; ++i) {
memset(vis, 0, sizeof(vis));
if(dfs(i, tm))
ret++;
}
return ret;
}
long long binarySearch(long long l = 0, long long r = 1e17) {
if(l == r)
return l;
long long mid = (l+r)/2;
int match = matching(mid);
return match >= K ? binarySearch(l, mid) : binarySearch(mid+1, r);
}
int main()
{
cin >> N >> M >> K;
assert(1 <= N); assert(N <= sz);
assert(1 <= M); assert(M <= sz);
assert(1 <= K); assert(K <= min(N, M));
for(int i = 0; i < (int)N; ++i) {
cin >> userX[i] >> userY[i];
assert(0 <= userX[i]); assert(userX[i] <= 1e7);
assert(0 <= userY[i]); assert(userY[i] <= 1e7);
}
for(int i = 0; i < (int)M; ++i) {
cin >> bikeX[i] >> bikeY[i];
assert(0 <= bikeX[i]); assert(bikeX[i] <= 1e7);
assert(0 <= bikeY[i]); assert(bikeY[i] <= 1e7);
}
cout << binarySearch() << endl;
return 0;
}
```
|
not-set
|
2016-04-24T02:02:16
|
2016-07-23T13:49:52
|
C++
|
29 | 1,319 |
board-cutting
|
Cutting Boards
|
[Chinese Version](https://hr-filepicker.s3.amazonaws.com/feb14/chinese/1319-chinese.md)<br/>
[Russian Version](https://hr-filepicker.s3.amazonaws.com/feb-14/russian/1319-russian.md)<br/>
Alice gives a wooden board composed of M X N wooden square pieces to Bob and asks him to find the minimal cost of breaking the board into square wooden pieces.
Bob can cut the board along horizontal and vertical lines, and each cut divides the board in smaller parts. Each cut has a cost depending on whether the cut is made along a horizontal or a vertical line.
Let us denote the costs of cutting it along consecutive vertical lines with x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>n-1</sub>, and the cost of cutting it along horizontal lines with y<sub>1</sub>, y<sub>2</sub>, ..., y<sub>m-1</sub>. If a cut (of cost **c**) is made and it passes through **n** segments, then total cost of this cut will be **n\*c**.
The cost of cutting the whole board into single squares is the sum of the cost of successive cuts used to cut the whole board into square wooden pieces of size *1x1*. Bob should compute the minimal cost of breaking the whole wooden board into squares of size *1x1*.
Bob needs your help to find the minimal cost. Can you help Bob with this challenge?
**Input Format**
A single integer in the first line T, stating the number of test cases. T testcases follow.
For each test case, the first line contains two positive integers M and N separated by a single space.
In the next line, there are integers y<sub>1</sub>, y<sub>2</sub>, ..., y<sub>m-1</sub>, separated by spaces. Following them are integers x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>n-1</sub>, separated by spaces.
**Output Format**
For each test-case, write an integer in separate line which denotes the minimal cost of cutting the whole wooden board into single wooden squares. Since the answer can be very large, output the answer modulo 10<sup>9</sup>+7.
**Constraints**
1 <= T <= 20
2 <= M,N <= 1000000
0 <= x<sub>i</sub> <= 10<sup>9</sup>
0 <= y<sub>i</sub> <= 10<sup>9</sup>
**Sample Input #00**
1
2 2
2
1
**Sample Output #00**
4
**Sample Input #01**
1
6 4
2 1 3 1 4
4 1 2
**Sample Output #01**
42
**Explanation**
*Sample Case #00:*At first, board should be cut horizontally, where y1 = 2, then it should be cut vertically. So total cost will be 2\*1 + 1\*2 = 4.
*Sample Case #01:* We should start cutting using y<sub>5</sub>, x<sub>1</sub>, y<sub>3</sub>, y<sub>1</sub>, x<sub>3</sub>, y<sub>2</sub>, y<sub>4</sub> and x<sub>2</sub>, in order. First cut will be a horizontal one where cost = y5 = 4. Next we will do a vertical cut with x1. Since this cut passes through two segments (created by previous vertical cut), it's total cost will be 2\*x1 = 2\*4. Similarly next horizontal cut (y3) will pass through two segments and will cost 2\*y3 = 2\*3. We can proceed in similar way and get overall cost as 4 + 4\*2 + 3\*2 + 2\*2 + 2\*4 + 1\*3 + 1\*3 + 1\*6 = 42.
|
code
|
Find the minimum cost of breaking down an m x n board into 1 x 1 pieces.
|
ai
|
2013-11-15T11:51:49
|
2022-08-31T08:14:37
|
#
# Complete the 'boardCutting' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER_ARRAY cost_y
# 2. INTEGER_ARRAY cost_x
#
def boardCutting(cost_y, cost_x):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
q = int(input().strip())
for q_itr in range(q):
first_multiple_input = input().rstrip().split()
m = int(first_multiple_input[0])
n = int(first_multiple_input[1])
cost_y = list(map(int, input().rstrip().split()))
cost_x = list(map(int, input().rstrip().split()))
result = boardCutting(cost_y, cost_x)
fptr.write(str(result) + '\n')
fptr.close()
|
Alice gives Bob a board composed of $1 \times 1$ wooden squares and asks him to find the minimum cost of breaking the board back down into its individual squares. To break the board down, Bob must make cuts along its horizontal and vertical lines.
To reduce the board to squares, Bob makes horizontal and vertical cuts across the entire board. Each cut has a given cost, $cost\_y[i]$ or $cost\_x[j]$ for each cut along a row or column across one board, so the cost of a cut must be multiplied by the number of segments it crosses. The cost of cutting the whole board down into $1 \times 1$ squares is the sum of the costs of each successive cut.
Can you help Bob find the minimum cost? The number may be large, so print the value modulo $10^9+7$.
For example, you start with a $2\times 2$ board. There are two cuts to be made at a cost of $cost\_y[1]=3$ for the horizontal and $cost\_x[1]=1$ for the vertical. Your first cut is across $1$ piece, the whole board. You choose to make the horizontal cut between rows $1$ and $2$ for a cost of $1\times 3=3$. The second cuts are vertical through the two smaller boards created in step $1$ between columns $1$ and $2$. Their cost is $2\times 1=2$. The total cost is $3 + 2=5$ and $5\%(10^9+7)=5$.
**Function Description**
Complete the *boardCutting* function in the editor below. It should return an integer.
boardCutting has the following parameter(s):
- *cost_x*: an array of integers, the costs of vertical cuts
- *cost_y*: an array of integers, the costs of horizontal cuts
| 0.5 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
The first line contains an integer $q$, the number of queries.
The following $q$ sets of lines are as follows:
- The first line has two positive space-separated integers $m$ and $n$, the number of rows and columns in the board.
- The second line contains $m-1$ space-separated integers cost_y[i], the cost of a horizontal cut between rows $[i]$ and $[i+1]$ of one board.
- The third line contains $n-1$ space-separated integers cost_x[j], the cost of a vertical cut between columns $[j]$ and $[j+1]$ of one board.
|
For each of the $q$ queries, find the minimum cost ($minCost$) of cutting the board into $1 \times 1$ squares and print the value of $minCost \text{ % } (10^9+7)$.
**Sample Input 0**
1
2 2
2
1
**Sample Output 0**
4
**Explanation 0**
We have a $2 \times 2$ board, with cut costs $cost\_y[1] = 2$ and $cost\_x[1] = 1$. Our first cut is horizontal between $y[1]$ and $y[2]$, because that is the line with the highest cost ($2$). Our second cut is vertical, at $x[1]$. Our first cut has a $totalCost$ of $2$ because we are making a cut with cost $cost\_y[1]=2$ across $1$ segment, the uncut board. The second cut also has a $totalCost$ of $2$ but we are making a cut of cost $cost\_x[1]=1$ across $2$ segments. Our answer is $minCost = ( (2 \times 1) + (1 \times 2) ) \ \% \ (10^9+7) = 4$.
**Sample Input 1**
1
6 4
2 1 3 1 4
4 1 2
**Sample Output 1**
42
**Explanation 1**
Our sequence of cuts is: $y[5]$, $x[1]$, $y[3]$, $y[1]$, $x[3]$, $y[2]$, $y[4]$ and $x[2]$.
*Cut 1:* Horizontal with cost $cost\_y[5] = 4$ across $1$ segment. $totalCost = 4 \times 1 = 4$.
*Cut 2:* Vertical with cost $cost\_x[1] = 4$ across $2$ segments. $totalCost = 4 \times 2 = 8$.
*Cut 3:* Horizontal with cost $cost\_y[3] = 3$ across $2$ segments. $totalCost = 3 \times 2 = 6$.
*Cut 4:* Horizontal with cost $cost\_y[1] = 2$ across $2$ segments. $totalCost = 2 \times 2 = 4$.
*Cut 5:* Vertical with cost $cost\_x[3] = 2$ across $4$ segments. $totalCost = 2 \times 4 = 8$.
*Cut 6:* Horizontal with cost $cost\_y[2] = 1$ across $3$ segments. $totalCost = 1 \times 3 = 3$.
*Cut 7:* Horizontal with cost $cost\_y[4] = 1$ across $3$ segments. $totalCost = 1 \times 3 = 3$.
*Cut 8:* Vertical with cost $cost\_x[2] = 1$ across $6$ segments. $totalCost = 1 \times 6 = 6$.
$totalCost =4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42$. We then print the value of $42 \ \% \ (10^9 + 7)$.
|
Hard
|
Cutting Boards - 2020 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/feb14/challenges/board-cutting">Cutting Boards</a></p>
<p><strong>Difficulty</strong> : Easy-Medium </p>
<p><strong>Required Knowledge</strong> : Greedy Algorithm </p>
<p><strong>Approach</strong> </p>
<p>The board should be broken in square wooden pieces, so that means we have to cut the board along every horizontal and verticle line.The order in which we make the cuts is important here.For minimum cost, sort the lines according to cost in decreasing order. </p>
<p>Let there be a 5x5 board and the cost along horizontal lines be y1,y2,y3,y4,y5 and along verticle lines be x1,x2,x3,x4,x5</p>
<p>Sort the lines according to cost in decreasing order.Let the lines be y4,x3,y5,x2,x1,y1,x4,y2,y3,x5 in decreasing order of cost.</p>
<pre><code>V = number of vertical cuts
H = number of horizontal cuts
</code></pre>
<p>Initially both V and H be zero
minimum_cost=0
Now traverse the lines in sorted order
if the line is horizontal
minimum_cost+=(cost of cut along that particular line)<em>(V+1)
H++
if the line is verticle
minimum_cost+=(cost of cut along that particular line)</em>(H+1)
V++</p>
<p><strong>Setter's Solution</strong></p>
<pre><code>#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
struct arr{
long long int val;
int horv;
};
typedef struct arr arr;
int compare(arr c , arr d){
if(c.val > d.val){
return 1;
}
return 0;
}
arr a[2000020];
int main(){
int tc;
scanf("%d",&tc);
while(tc--){
int n,m;
scanf("%d %d",&m,&n);
int i;
int j=0;
for(i=1;i<m;i++){
scanf("%lld",&a[j].val);
a[j].horv=1; // its a horizontal line
j++;
}
for(i=1;i<n;i++){
scanf("%lld",&a[j].val);
a[j].horv=0; // verticle line
j++;
}
sort(a,a+j,compare);
int v=0;
int h=0;
long long int cost=0;
for(i=0;i<j;i++){
if(a[i].horv==1){ // making cut along horizontal line
cost=(cost+(a[i].val*(v+1))%1000000007)%1000000007;
h++;
}
else if(a[i].horv==0){ // making cut along verticle line
cost=(cost+(a[i].val*(h+1))%1000000007)%1000000007;
v++;
}
}
printf("%lld\n",cost);
}
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong></p>
<pre><code>-- {{{
module Main where
---------------------Import-------------------------
import Data.List
import qualified Data.Map as Map
import qualified Data.Set as Set
import Data.Char
import Data.Int -- Int32, Int64
import System.IO
import Data.Ratio -- x = 5%6
import Data.Bits -- (.&.), (.|.), shiftL...
import Text.Printf -- printf "%0.6f" (1.0)
import Control.Monad
import qualified Data.ByteString.Lazy.Char8 as BS
import qualified Data.Vector as V
import System.Directory
import System.FilePath
-- }}}
main :: IO ()
main = BS.getContents >>= mapM_ print. validate. map readIntegerArray. BS.lines
p :: Integer
p = 10^9+7
validate :: [[Integer]] -> [Integer]
validate ([t]: arr)
| 3 * fromIntegral t /= length arr = error "t /= 3*length arr"
| t < 0 || t > 20 = error "t is out of bound"
| otherwise = parse arr
parse :: [[Integer]] -> [Integer]
parse [] = []
parse ([n, m]: a: b: left)
| n < 0 || n > 10^6 = error "n is out of range"
| m < 0 || m > 10^6 = error "m is out of range"
| fromIntegral n - 1 /= length a = error "n - 1 /= length a"
| fromIntegral m - 1 /= length b = error "m - 1 /= length b"
| any (\x -> x < 0 || x > 10^9) a = error "element of a is out of bound"
| any (\x -> x < 0 || x > 10^9) b = error "element of a is out of bound"
| otherwise = (solve a b): parse left
solve :: [Integer] -> [Integer] -> Integer
solve aa bb = solve1 1 (reverse. sort`$ aa) 1 (reverse. sort $`bb)
where
solve1 :: Integer -> [Integer] -> Integer -> [Integer] -> Integer
solve1 _ [] _ [] = 0
solve1 aCut [] _ (b:brr) = b*aCut + solve1 aCut [] undefined brr
solve1 _ (a:arr) bCut [] = a*bCut + solve1 undefined arr bCut []
solve1 aCut (a:arr) bCut (b:brr)
| a > b = ((a*bCut) `rem` p + solve1 (aCut+1) arr bCut (b:brr)) `rem` p
| otherwise = ((b*aCut) `rem` p + solve1 aCut (a:arr) (bCut+1) brr ) `rem` p
---------------------Input---------------------------- {{{
getInteger = (\(Just (x_yzpqr,_)) -> x_yzpqr). BS.readInteger
getInt = (\(Just (x_yzpqr,_)) -> x_yzpqr). BS.readInt
getIntArray = readIntArray
getIntegerArray = readIntegerArray
readIntArray input_pqr =
case x_yzpqr of
Just (a_yzpqr, xs_pqr) -> a_yzpqr : readIntArray xs_pqr
Nothing -> []
where
x_yzpqr = BS.readInt. BS.dropWhile isSpace $ input_pqr
readIntegerArray input_pqr =
case x_yzpqr of
Nothing -> []
Just (y_zpqr, ys_pqr) -> y_zpqr : readIntegerArray ys_pqr
where
x_yzpqr = BS.readInteger. BS.dropWhile isSpace $ input_pqr
------------------------------------------------------ }}}
</code></pre>
| 0 |
feb14-board-cutting
|
2014-02-27T05:13:32
|
{"contest_participation":2769,"challenge_submissions":927,"successful_submissions":696}
|
2014-02-27T05:13:32
|
2018-04-17T17:56:40
|
setter
|
###C++
```cpp
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
struct arr{
long long int val;
int horv;
};
typedef struct arr arr;
int compare(arr c , arr d){
if(c.val > d.val){
return 1;
}
return 0;
}
arr a[2000020];
int main(){
int tc;
scanf("%d",&tc);
while(tc--){
int n,m;
scanf("%d %d",&m,&n);
int i;
int j=0;
for(i=1;i<m;i++){
scanf("%lld",&a[j].val);
a[j].horv=1; // its a horizontal line
j++;
}
for(i=1;i<n;i++){
scanf("%lld",&a[j].val);
a[j].horv=0; // verticle line
j++;
}
sort(a,a+j,compare);
int v=0;
int h=0;
long long int cost=0;
for(i=0;i<j;i++){
if(a[i].horv==1){ // making cut along horizontal line
cost=(cost+(a[i].val*(v+1))%1000000007)%1000000007;
h++;
}
else if(a[i].horv==0){ // making cut along verticle line
cost=(cost+(a[i].val*(h+1))%1000000007)%1000000007;
v++;
}
}
printf("%lld\n",cost);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:16
|
2016-07-23T14:25:46
|
C++
|
||
30 | 1,319 |
board-cutting
|
Cutting Boards
|
[Chinese Version](https://hr-filepicker.s3.amazonaws.com/feb14/chinese/1319-chinese.md)<br/>
[Russian Version](https://hr-filepicker.s3.amazonaws.com/feb-14/russian/1319-russian.md)<br/>
Alice gives a wooden board composed of M X N wooden square pieces to Bob and asks him to find the minimal cost of breaking the board into square wooden pieces.
Bob can cut the board along horizontal and vertical lines, and each cut divides the board in smaller parts. Each cut has a cost depending on whether the cut is made along a horizontal or a vertical line.
Let us denote the costs of cutting it along consecutive vertical lines with x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>n-1</sub>, and the cost of cutting it along horizontal lines with y<sub>1</sub>, y<sub>2</sub>, ..., y<sub>m-1</sub>. If a cut (of cost **c**) is made and it passes through **n** segments, then total cost of this cut will be **n\*c**.
The cost of cutting the whole board into single squares is the sum of the cost of successive cuts used to cut the whole board into square wooden pieces of size *1x1*. Bob should compute the minimal cost of breaking the whole wooden board into squares of size *1x1*.
Bob needs your help to find the minimal cost. Can you help Bob with this challenge?
**Input Format**
A single integer in the first line T, stating the number of test cases. T testcases follow.
For each test case, the first line contains two positive integers M and N separated by a single space.
In the next line, there are integers y<sub>1</sub>, y<sub>2</sub>, ..., y<sub>m-1</sub>, separated by spaces. Following them are integers x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>n-1</sub>, separated by spaces.
**Output Format**
For each test-case, write an integer in separate line which denotes the minimal cost of cutting the whole wooden board into single wooden squares. Since the answer can be very large, output the answer modulo 10<sup>9</sup>+7.
**Constraints**
1 <= T <= 20
2 <= M,N <= 1000000
0 <= x<sub>i</sub> <= 10<sup>9</sup>
0 <= y<sub>i</sub> <= 10<sup>9</sup>
**Sample Input #00**
1
2 2
2
1
**Sample Output #00**
4
**Sample Input #01**
1
6 4
2 1 3 1 4
4 1 2
**Sample Output #01**
42
**Explanation**
*Sample Case #00:*At first, board should be cut horizontally, where y1 = 2, then it should be cut vertically. So total cost will be 2\*1 + 1\*2 = 4.
*Sample Case #01:* We should start cutting using y<sub>5</sub>, x<sub>1</sub>, y<sub>3</sub>, y<sub>1</sub>, x<sub>3</sub>, y<sub>2</sub>, y<sub>4</sub> and x<sub>2</sub>, in order. First cut will be a horizontal one where cost = y5 = 4. Next we will do a vertical cut with x1. Since this cut passes through two segments (created by previous vertical cut), it's total cost will be 2\*x1 = 2\*4. Similarly next horizontal cut (y3) will pass through two segments and will cost 2\*y3 = 2\*3. We can proceed in similar way and get overall cost as 4 + 4\*2 + 3\*2 + 2\*2 + 2\*4 + 1\*3 + 1\*3 + 1\*6 = 42.
|
code
|
Find the minimum cost of breaking down an m x n board into 1 x 1 pieces.
|
ai
|
2013-11-15T11:51:49
|
2022-08-31T08:14:37
|
#
# Complete the 'boardCutting' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER_ARRAY cost_y
# 2. INTEGER_ARRAY cost_x
#
def boardCutting(cost_y, cost_x):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
q = int(input().strip())
for q_itr in range(q):
first_multiple_input = input().rstrip().split()
m = int(first_multiple_input[0])
n = int(first_multiple_input[1])
cost_y = list(map(int, input().rstrip().split()))
cost_x = list(map(int, input().rstrip().split()))
result = boardCutting(cost_y, cost_x)
fptr.write(str(result) + '\n')
fptr.close()
|
Alice gives Bob a board composed of $1 \times 1$ wooden squares and asks him to find the minimum cost of breaking the board back down into its individual squares. To break the board down, Bob must make cuts along its horizontal and vertical lines.
To reduce the board to squares, Bob makes horizontal and vertical cuts across the entire board. Each cut has a given cost, $cost\_y[i]$ or $cost\_x[j]$ for each cut along a row or column across one board, so the cost of a cut must be multiplied by the number of segments it crosses. The cost of cutting the whole board down into $1 \times 1$ squares is the sum of the costs of each successive cut.
Can you help Bob find the minimum cost? The number may be large, so print the value modulo $10^9+7$.
For example, you start with a $2\times 2$ board. There are two cuts to be made at a cost of $cost\_y[1]=3$ for the horizontal and $cost\_x[1]=1$ for the vertical. Your first cut is across $1$ piece, the whole board. You choose to make the horizontal cut between rows $1$ and $2$ for a cost of $1\times 3=3$. The second cuts are vertical through the two smaller boards created in step $1$ between columns $1$ and $2$. Their cost is $2\times 1=2$. The total cost is $3 + 2=5$ and $5\%(10^9+7)=5$.
**Function Description**
Complete the *boardCutting* function in the editor below. It should return an integer.
boardCutting has the following parameter(s):
- *cost_x*: an array of integers, the costs of vertical cuts
- *cost_y*: an array of integers, the costs of horizontal cuts
| 0.5 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
The first line contains an integer $q$, the number of queries.
The following $q$ sets of lines are as follows:
- The first line has two positive space-separated integers $m$ and $n$, the number of rows and columns in the board.
- The second line contains $m-1$ space-separated integers cost_y[i], the cost of a horizontal cut between rows $[i]$ and $[i+1]$ of one board.
- The third line contains $n-1$ space-separated integers cost_x[j], the cost of a vertical cut between columns $[j]$ and $[j+1]$ of one board.
|
For each of the $q$ queries, find the minimum cost ($minCost$) of cutting the board into $1 \times 1$ squares and print the value of $minCost \text{ % } (10^9+7)$.
**Sample Input 0**
1
2 2
2
1
**Sample Output 0**
4
**Explanation 0**
We have a $2 \times 2$ board, with cut costs $cost\_y[1] = 2$ and $cost\_x[1] = 1$. Our first cut is horizontal between $y[1]$ and $y[2]$, because that is the line with the highest cost ($2$). Our second cut is vertical, at $x[1]$. Our first cut has a $totalCost$ of $2$ because we are making a cut with cost $cost\_y[1]=2$ across $1$ segment, the uncut board. The second cut also has a $totalCost$ of $2$ but we are making a cut of cost $cost\_x[1]=1$ across $2$ segments. Our answer is $minCost = ( (2 \times 1) + (1 \times 2) ) \ \% \ (10^9+7) = 4$.
**Sample Input 1**
1
6 4
2 1 3 1 4
4 1 2
**Sample Output 1**
42
**Explanation 1**
Our sequence of cuts is: $y[5]$, $x[1]$, $y[3]$, $y[1]$, $x[3]$, $y[2]$, $y[4]$ and $x[2]$.
*Cut 1:* Horizontal with cost $cost\_y[5] = 4$ across $1$ segment. $totalCost = 4 \times 1 = 4$.
*Cut 2:* Vertical with cost $cost\_x[1] = 4$ across $2$ segments. $totalCost = 4 \times 2 = 8$.
*Cut 3:* Horizontal with cost $cost\_y[3] = 3$ across $2$ segments. $totalCost = 3 \times 2 = 6$.
*Cut 4:* Horizontal with cost $cost\_y[1] = 2$ across $2$ segments. $totalCost = 2 \times 2 = 4$.
*Cut 5:* Vertical with cost $cost\_x[3] = 2$ across $4$ segments. $totalCost = 2 \times 4 = 8$.
*Cut 6:* Horizontal with cost $cost\_y[2] = 1$ across $3$ segments. $totalCost = 1 \times 3 = 3$.
*Cut 7:* Horizontal with cost $cost\_y[4] = 1$ across $3$ segments. $totalCost = 1 \times 3 = 3$.
*Cut 8:* Vertical with cost $cost\_x[2] = 1$ across $6$ segments. $totalCost = 1 \times 6 = 6$.
$totalCost =4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42$. We then print the value of $42 \ \% \ (10^9 + 7)$.
|
Hard
|
Cutting Boards - 2020 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/feb14/challenges/board-cutting">Cutting Boards</a></p>
<p><strong>Difficulty</strong> : Easy-Medium </p>
<p><strong>Required Knowledge</strong> : Greedy Algorithm </p>
<p><strong>Approach</strong> </p>
<p>The board should be broken in square wooden pieces, so that means we have to cut the board along every horizontal and verticle line.The order in which we make the cuts is important here.For minimum cost, sort the lines according to cost in decreasing order. </p>
<p>Let there be a 5x5 board and the cost along horizontal lines be y1,y2,y3,y4,y5 and along verticle lines be x1,x2,x3,x4,x5</p>
<p>Sort the lines according to cost in decreasing order.Let the lines be y4,x3,y5,x2,x1,y1,x4,y2,y3,x5 in decreasing order of cost.</p>
<pre><code>V = number of vertical cuts
H = number of horizontal cuts
</code></pre>
<p>Initially both V and H be zero
minimum_cost=0
Now traverse the lines in sorted order
if the line is horizontal
minimum_cost+=(cost of cut along that particular line)<em>(V+1)
H++
if the line is verticle
minimum_cost+=(cost of cut along that particular line)</em>(H+1)
V++</p>
<p><strong>Setter's Solution</strong></p>
<pre><code>#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
struct arr{
long long int val;
int horv;
};
typedef struct arr arr;
int compare(arr c , arr d){
if(c.val > d.val){
return 1;
}
return 0;
}
arr a[2000020];
int main(){
int tc;
scanf("%d",&tc);
while(tc--){
int n,m;
scanf("%d %d",&m,&n);
int i;
int j=0;
for(i=1;i<m;i++){
scanf("%lld",&a[j].val);
a[j].horv=1; // its a horizontal line
j++;
}
for(i=1;i<n;i++){
scanf("%lld",&a[j].val);
a[j].horv=0; // verticle line
j++;
}
sort(a,a+j,compare);
int v=0;
int h=0;
long long int cost=0;
for(i=0;i<j;i++){
if(a[i].horv==1){ // making cut along horizontal line
cost=(cost+(a[i].val*(v+1))%1000000007)%1000000007;
h++;
}
else if(a[i].horv==0){ // making cut along verticle line
cost=(cost+(a[i].val*(h+1))%1000000007)%1000000007;
v++;
}
}
printf("%lld\n",cost);
}
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong></p>
<pre><code>-- {{{
module Main where
---------------------Import-------------------------
import Data.List
import qualified Data.Map as Map
import qualified Data.Set as Set
import Data.Char
import Data.Int -- Int32, Int64
import System.IO
import Data.Ratio -- x = 5%6
import Data.Bits -- (.&.), (.|.), shiftL...
import Text.Printf -- printf "%0.6f" (1.0)
import Control.Monad
import qualified Data.ByteString.Lazy.Char8 as BS
import qualified Data.Vector as V
import System.Directory
import System.FilePath
-- }}}
main :: IO ()
main = BS.getContents >>= mapM_ print. validate. map readIntegerArray. BS.lines
p :: Integer
p = 10^9+7
validate :: [[Integer]] -> [Integer]
validate ([t]: arr)
| 3 * fromIntegral t /= length arr = error "t /= 3*length arr"
| t < 0 || t > 20 = error "t is out of bound"
| otherwise = parse arr
parse :: [[Integer]] -> [Integer]
parse [] = []
parse ([n, m]: a: b: left)
| n < 0 || n > 10^6 = error "n is out of range"
| m < 0 || m > 10^6 = error "m is out of range"
| fromIntegral n - 1 /= length a = error "n - 1 /= length a"
| fromIntegral m - 1 /= length b = error "m - 1 /= length b"
| any (\x -> x < 0 || x > 10^9) a = error "element of a is out of bound"
| any (\x -> x < 0 || x > 10^9) b = error "element of a is out of bound"
| otherwise = (solve a b): parse left
solve :: [Integer] -> [Integer] -> Integer
solve aa bb = solve1 1 (reverse. sort`$ aa) 1 (reverse. sort $`bb)
where
solve1 :: Integer -> [Integer] -> Integer -> [Integer] -> Integer
solve1 _ [] _ [] = 0
solve1 aCut [] _ (b:brr) = b*aCut + solve1 aCut [] undefined brr
solve1 _ (a:arr) bCut [] = a*bCut + solve1 undefined arr bCut []
solve1 aCut (a:arr) bCut (b:brr)
| a > b = ((a*bCut) `rem` p + solve1 (aCut+1) arr bCut (b:brr)) `rem` p
| otherwise = ((b*aCut) `rem` p + solve1 aCut (a:arr) (bCut+1) brr ) `rem` p
---------------------Input---------------------------- {{{
getInteger = (\(Just (x_yzpqr,_)) -> x_yzpqr). BS.readInteger
getInt = (\(Just (x_yzpqr,_)) -> x_yzpqr). BS.readInt
getIntArray = readIntArray
getIntegerArray = readIntegerArray
readIntArray input_pqr =
case x_yzpqr of
Just (a_yzpqr, xs_pqr) -> a_yzpqr : readIntArray xs_pqr
Nothing -> []
where
x_yzpqr = BS.readInt. BS.dropWhile isSpace $ input_pqr
readIntegerArray input_pqr =
case x_yzpqr of
Nothing -> []
Just (y_zpqr, ys_pqr) -> y_zpqr : readIntegerArray ys_pqr
where
x_yzpqr = BS.readInteger. BS.dropWhile isSpace $ input_pqr
------------------------------------------------------ }}}
</code></pre>
| 0 |
feb14-board-cutting
|
2014-02-27T05:13:32
|
{"contest_participation":2769,"challenge_submissions":927,"successful_submissions":696}
|
2014-02-27T05:13:32
|
2018-04-17T17:56:40
|
tester
|
###Haskell
```haskell
-- {{{
module Main where
---------------------Import-------------------------
import Data.List
import qualified Data.Map as Map
import qualified Data.Set as Set
import Data.Char
import Data.Int -- Int32, Int64
import System.IO
import Data.Ratio -- x = 5%6
import Data.Bits -- (.&.), (.|.), shiftL...
import Text.Printf -- printf "%0.6f" (1.0)
import Control.Monad
import qualified Data.ByteString.Lazy.Char8 as BS
import qualified Data.Vector as V
import System.Directory
import System.FilePath
-- }}}
main :: IO ()
main = BS.getContents >>= mapM_ print. validate. map readIntegerArray. BS.lines
p :: Integer
p = 10^9+7
validate :: [[Integer]] -> [Integer]
validate ([t]: arr)
| 3 * fromIntegral t /= length arr = error "t /= 3*length arr"
| t < 0 || t > 20 = error "t is out of bound"
| otherwise = parse arr
parse :: [[Integer]] -> [Integer]
parse [] = []
parse ([n, m]: a: b: left)
| n < 0 || n > 10^6 = error "n is out of range"
| m < 0 || m > 10^6 = error "m is out of range"
| fromIntegral n - 1 /= length a = error "n - 1 /= length a"
| fromIntegral m - 1 /= length b = error "m - 1 /= length b"
| any (\x -> x < 0 || x > 10^9) a = error "element of a is out of bound"
| any (\x -> x < 0 || x > 10^9) b = error "element of a is out of bound"
| otherwise = (solve a b): parse left
solve :: [Integer] -> [Integer] -> Integer
solve aa bb = solve1 1 (reverse. sort$ aa) 1 (reverse. sort $bb)
where
solve1 :: Integer -> [Integer] -> Integer -> [Integer] -> Integer
solve1 _ [] _ [] = 0
solve1 aCut [] _ (b:brr) = b*aCut + solve1 aCut [] undefined brr
solve1 _ (a:arr) bCut [] = a*bCut + solve1 undefined arr bCut []
solve1 aCut (a:arr) bCut (b:brr)
| a > b = ((a*bCut) `rem` p + solve1 (aCut+1) arr bCut (b:brr)) `rem` p
| otherwise = ((b*aCut) `rem` p + solve1 aCut (a:arr) (bCut+1) brr ) `rem` p
---------------------Input---------------------------- {{{
getInteger = (\(Just (x_yzpqr,_)) -> x_yzpqr). BS.readInteger
getInt = (\(Just (x_yzpqr,_)) -> x_yzpqr). BS.readInt
getIntArray = readIntArray
getIntegerArray = readIntegerArray
readIntArray input_pqr =
case x_yzpqr of
Just (a_yzpqr, xs_pqr) -> a_yzpqr : readIntArray xs_pqr
Nothing -> []
where
x_yzpqr = BS.readInt. BS.dropWhile isSpace $ input_pqr
readIntegerArray input_pqr =
case x_yzpqr of
Nothing -> []
Just (y_zpqr, ys_pqr) -> y_zpqr : readIntegerArray ys_pqr
where
x_yzpqr = BS.readInteger. BS.dropWhile isSpace $ input_pqr
------------------------------------------------------ }}}
```
|
not-set
|
2016-04-24T02:02:16
|
2016-07-23T14:26:06
|
Python
|
||
31 | 1,857 |
mathematical-expectation
|
Mathematical Expectation
|
[Chinese Version](https://hr-filepicker.s3.amazonaws.com/feb14/chinese/1857-chinese.md)<br/>
[Russian Version](https://hr-filepicker.s3.amazonaws.com/feb-14/russian/1857-russian.md)<br/>
Let's consider a random permutation p<sub>1</sub>, p<sub>2</sub>, ..., p<sub>N</sub> of numbers 1, 2, ..., N and calculate the value F=(X<sub>2</sub>+...+X<sub>N-1</sub>)<sup>K</sup>, where X<sub>i</sub> equals 1 if one of the following two conditions holds: p<sub>i-1</sub> < p<sub>i</sub> > p<sub>i+1</sub> or p<sub>i-1</sub> > p<sub>i</sub> < p<sub>i+1</sub> and X<sub>i</sub> equals 0 otherwise. What is the expected value of F?
**Input Format:**
The first line contains two integers K and N.
**Output Format:**
Print the expected value of F as an irreducible fraction p / q. Follow sample input for more clarification.
**Constraints:**
1000 <= N <= 10<sup>9</sup>
1 <= K <= 5
**Sample input**
1 1000
**Sample Output**
1996 / 3
|
code
|
Expected value of Seyaua's function
|
ai
|
2014-02-06T20:29:14
|
2022-09-02T09:55:42
| null | null | null |
Let's consider a random permutation p<sub>1</sub>, p<sub>2</sub>, ..., p<sub>N</sub> of numbers 1, 2, ..., N and calculate the value F=(X<sub>2</sub>+...+X<sub>N-1</sub>)<sup>K</sup>, where X<sub>i</sub> equals 1 if one of the following two conditions holds: p<sub>i-1</sub> < p<sub>i</sub> > p<sub>i+1</sub> or p<sub>i-1</sub> > p<sub>i</sub> < p<sub>i+1</sub> and X<sub>i</sub> equals 0 otherwise. What is the expected value of F?
**Input Format:**
The first line contains two integers K and N.
**Output Format:**
Print the expected value of F as an irreducible fraction p / q. Follow sample input for more clarification.
**Constraints:**
1000 <= N <= 10<sup>9</sup>
1 <= K <= 5
**Sample input**
1 1000
**Sample Output**
1996 / 3
| 0.586207 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
|
Hard
|
Mathematical Expectation - 2020 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/feb14/challenges/mathematical-expectation">Mathematical Expectation</a> </p>
<p><strong>Difficulty</strong> : Medium-Hard <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/seyaua">Levgen Soboliev</a> </p>
<p><strong>Approach</strong> </p>
<ol>
<li><p>Let's write simple bruteforce solution and generate all answers for small N (N<=20). After that one can observe, that for each K the answer is P_K(N), where P_K is a polynom of K-th power. So, after generating small answer we can interpolate the results and get needed polynom. So, now we obtain a solution where we need to keep just the coefficients of each P_K. Do not forget that the answer can be very big, so we have to use something like BigIntegers.</p></li>
<li><p>We can look at random variable (X_1+X_2+..+X_N)^K open the parentheses and use the linearity of mathematical expectation. In this case we have to work with this variables very careful, because some of them are not independent. This way is much harder than previous, so this is just an idea :) But with this idea one can solve this problem for bigger K.</p></li>
</ol>
<p><strong>Setter's Solution</strong></p>
<pre><code>import java.io.*;
import java.util.*;
import java.math.*;
public class Solution {
public static void main(String[] args) {
new Solution().run();
}
// 1 : +2/3*n^1-4/3*n^0
// 2 : 40*n^2-144*n+131 / 90
// 3 : 280*n^3-1344*n^2+2063*n-1038 / 945
// 4 : 2800*n^4-15680*n^3+28844*n^2-19288*n+4263 / 14175
// 5 : 12320*n^5-73920*n^4+130328*n^3-29568*n^2-64150*n-5124 / 93555
// 6 : 44844800*n^6-269068800*n^5+322081760*n^4+706113408*n^3-1344748912*n^2-329275872*n+957888513 / 510810300
void output(BigInteger num, BigInteger denom) {
BigInteger gcd = num.gcd(denom);
num = num.divide(gcd);
denom = denom.divide(gcd);
System.out.println(num + " / " + denom);
}
void solve(int k, BigInteger n) {
if (k == 1) {
BigInteger num = BigInteger.valueOf(2).multiply(n).subtract(BigInteger.valueOf(4));
BigInteger denom = BigInteger.valueOf(3);
output(num, denom);
} else if (k == 2) {
BigInteger n2 = n.pow(2);
BigInteger num = BigInteger.valueOf(40).multiply(n2).subtract(BigInteger.valueOf(144).multiply(n)).add(BigInteger.valueOf(131));
BigInteger denom = BigInteger.valueOf(90);
output(num, denom);
} else if (k == 3) {
BigInteger n2 = n.pow(2);
BigInteger n3 = n.pow(3);
BigInteger num = BigInteger.valueOf(280).multiply(n3).subtract(BigInteger.valueOf(1344).multiply(n2)).add(BigInteger.valueOf(2063).multiply(n)).subtract(BigInteger.valueOf(1038));
BigInteger denom = BigInteger.valueOf(945);
output(num, denom);
} else if (k == 4) {
BigInteger n2 = n.pow(2);
BigInteger n3 = n.pow(3);
BigInteger n4 = n.pow(4);
BigInteger num = BigInteger.valueOf(2800).multiply(n4).subtract(BigInteger.valueOf(15680).multiply(n3)).add(BigInteger.valueOf(28844).multiply(n2)).subtract(BigInteger.valueOf(19288).multiply(n)).add(BigInteger.valueOf(4263));
BigInteger denom = BigInteger.valueOf(14175);
output(num, denom);
} else if (k == 5) {
BigInteger n2 = n.pow(2);
BigInteger n3 = n.pow(3);
BigInteger n4 = n.pow(4);
BigInteger n5 = n.pow(5);
BigInteger num = BigInteger.valueOf(12320).multiply(n5).subtract(BigInteger.valueOf(73920).multiply(n4)).add(BigInteger.valueOf(130328).multiply(n3)).subtract(BigInteger.valueOf(29568).multiply(n2)).subtract(BigInteger.valueOf(64150).multiply(n)).subtract(BigInteger.valueOf(5124));
BigInteger denom = BigInteger.valueOf(93555);
output(num, denom);
} else if (k == 6) {
BigInteger n2 = n.pow(2);
BigInteger n3 = n.pow(3);
BigInteger n4 = n.pow(4);
BigInteger n5 = n.pow(5);
BigInteger n6 = n.pow(6);
BigInteger num = BigInteger.valueOf(44844800).multiply(n6).subtract(BigInteger.valueOf(269068800).multiply(n5)).add(BigInteger.valueOf(322081760).multiply(n4)).add(BigInteger.valueOf(706113408).multiply(n3)).subtract(BigInteger.valueOf(1344748912).multiply(n2)).subtract(BigInteger.valueOf(329275872).multiply(n)).add(BigInteger.valueOf(957888513));
BigInteger denom = BigInteger.valueOf(510810300);
output(num, denom);
}
}
void run() {
Scanner in = new Scanner(System.in);
int k = in.nextInt();
BigInteger n = in.nextBigInteger();
solve(k, n);
}
}
</code></pre>
| 0 |
feb14-mathematical-expectation
|
2014-03-03T12:02:38
|
{"contest_participation":2769,"challenge_submissions":187,"successful_submissions":38}
|
2014-03-03T12:02:38
|
2016-07-23T19:18:53
|
setter
|
###Java
```java
import java.io.*;
import java.util.*;
import java.math.*;
public class Solution {
public static void main(String[] args) {
new Solution().run();
}
// 1 : +2/3*n^1-4/3*n^0
// 2 : 40*n^2-144*n+131 / 90
// 3 : 280*n^3-1344*n^2+2063*n-1038 / 945
// 4 : 2800*n^4-15680*n^3+28844*n^2-19288*n+4263 / 14175
// 5 : 12320*n^5-73920*n^4+130328*n^3-29568*n^2-64150*n-5124 / 93555
// 6 : 44844800*n^6-269068800*n^5+322081760*n^4+706113408*n^3-1344748912*n^2-329275872*n+957888513 / 510810300
void output(BigInteger num, BigInteger denom) {
BigInteger gcd = num.gcd(denom);
num = num.divide(gcd);
denom = denom.divide(gcd);
System.out.println(num + " / " + denom);
}
void solve(int k, BigInteger n) {
if (k == 1) {
BigInteger num = BigInteger.valueOf(2).multiply(n).subtract(BigInteger.valueOf(4));
BigInteger denom = BigInteger.valueOf(3);
output(num, denom);
} else if (k == 2) {
BigInteger n2 = n.pow(2);
BigInteger num = BigInteger.valueOf(40).multiply(n2).subtract(BigInteger.valueOf(144).multiply(n)).add(BigInteger.valueOf(131));
BigInteger denom = BigInteger.valueOf(90);
output(num, denom);
} else if (k == 3) {
BigInteger n2 = n.pow(2);
BigInteger n3 = n.pow(3);
BigInteger num = BigInteger.valueOf(280).multiply(n3).subtract(BigInteger.valueOf(1344).multiply(n2)).add(BigInteger.valueOf(2063).multiply(n)).subtract(BigInteger.valueOf(1038));
BigInteger denom = BigInteger.valueOf(945);
output(num, denom);
} else if (k == 4) {
BigInteger n2 = n.pow(2);
BigInteger n3 = n.pow(3);
BigInteger n4 = n.pow(4);
BigInteger num = BigInteger.valueOf(2800).multiply(n4).subtract(BigInteger.valueOf(15680).multiply(n3)).add(BigInteger.valueOf(28844).multiply(n2)).subtract(BigInteger.valueOf(19288).multiply(n)).add(BigInteger.valueOf(4263));
BigInteger denom = BigInteger.valueOf(14175);
output(num, denom);
} else if (k == 5) {
BigInteger n2 = n.pow(2);
BigInteger n3 = n.pow(3);
BigInteger n4 = n.pow(4);
BigInteger n5 = n.pow(5);
BigInteger num = BigInteger.valueOf(12320).multiply(n5).subtract(BigInteger.valueOf(73920).multiply(n4)).add(BigInteger.valueOf(130328).multiply(n3)).subtract(BigInteger.valueOf(29568).multiply(n2)).subtract(BigInteger.valueOf(64150).multiply(n)).subtract(BigInteger.valueOf(5124));
BigInteger denom = BigInteger.valueOf(93555);
output(num, denom);
} else if (k == 6) {
BigInteger n2 = n.pow(2);
BigInteger n3 = n.pow(3);
BigInteger n4 = n.pow(4);
BigInteger n5 = n.pow(5);
BigInteger n6 = n.pow(6);
BigInteger num = BigInteger.valueOf(44844800).multiply(n6).subtract(BigInteger.valueOf(269068800).multiply(n5)).add(BigInteger.valueOf(322081760).multiply(n4)).add(BigInteger.valueOf(706113408).multiply(n3)).subtract(BigInteger.valueOf(1344748912).multiply(n2)).subtract(BigInteger.valueOf(329275872).multiply(n)).add(BigInteger.valueOf(957888513));
BigInteger denom = BigInteger.valueOf(510810300);
output(num, denom);
}
}
void run() {
Scanner in = new Scanner(System.in);
int k = in.nextInt();
BigInteger n = in.nextBigInteger();
solve(k, n);
}
}
```
|
not-set
|
2016-04-24T02:02:16
|
2016-07-23T19:18:54
|
Java
|
||||
32 | 1,828 |
isosceles-triangles
|
Isosceles Triangles
|
[Sevenkplus](http://sevenkplus.com/) has a regular polygon. Each vertex of the polygon has a color, either white or black. Sevenkplus wants to count the number of isosceles triangles whose vertices are vertices of the regular polygon and have the same color.
**Input Format**
The first line contains an integer T. T testcases follow.
For each test case, there is only one line, which consists of a 01-string with length >= 3. Number of vertices `n` of the regular polygon equals length of the string. The string represents color of vertices in clockwise order. `0` represents white and `1` represents black.
**Output Format**
For each test case, output one line in the format `Case #t: ans`, where `t` is the case number (starting from 1), and `ans` is the answer.
**Constraints**
Sum of all n in the input <= 10^6.
**Sample Input**
5
001
0001
10001
111010
1101010
**Sample Output**
Case 1: 0
Case 2: 1
Case 3: 1
Case 4: 2
Case 5: 3
**Explanation**
In case 5, indices of vertices of the three monochromatic isosceles triangles are (0,3,5), (1,3,5) and (2,4,6) (assuming indices start from 0).
**Timelimits**
Timelimits for this challenge is given [here](https://www.hackerrank.com/environment)
|
code
|
How many monochromatic isosceles triangles are there?
|
ai
|
2014-02-02T04:29:46
|
2022-09-02T09:55:24
| null | null | null |
[Sevenkplus](http://sevenkplus.com/) has a regular polygon. Each vertex of the polygon has a color, either white or black. Sevenkplus wants to count the number of isosceles triangles whose vertices are vertices of the regular polygon and have the same color.
**Input Format**
The first line contains an integer T. T testcases follow.
For each test case, there is only one line, which consists of a 01-string with length >= 3. Number of vertices `n` of the regular polygon equals length of the string. The string represents color of vertices in clockwise order. `0` represents white and `1` represents black.
**Output Format**
For each test case, output one line in the format `Case #t: ans`, where `t` is the case number (starting from 1), and `ans` is the answer.
**Constraints**
Sum of all n in the input <= 10^6.
**Sample Input**
5
001
0001
10001
111010
1101010
**Sample Output**
Case 1: 0
Case 2: 1
Case 3: 1
Case 4: 2
Case 5: 3
**Explanation**
In case 5, indices of vertices of the three monochromatic isosceles triangles are (0,3,5), (1,3,5) and (2,4,6) (assuming indices start from 0).
**Timelimits**
Timelimits for this challenge is given [here](https://www.hackerrank.com/environment)
| 0.488636 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
Isosceles Triangles - 101 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101feb14/challenges/isosceles-triangles">Isosceles Triangles</a> </p>
<p><strong>Difficulty</strong> : Medium-Hard <br>
<strong>Required Knowledge</strong> : Bichromatic Isosceles Triangles <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/sevenkplus">Yuzhou Gu</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/dsoboliev">Dmytro Soboliev</a> </p>
<p><strong>Approach</strong> </p>
<pre><code># of monochromatic isosceles triangl = # of triangle - # of bichromatic isosceles triangle
</code></pre>
<p>Each bichromatic isosceles triangle has two bichromatic edges, so we only need to count # of bichromatic edges. </p>
<p>Consider a pair (i,j) of vertices with different colors.
Then its contribution to number of bichromatic edges in isosceles triangles is determined by distance between the vertices.
With some analysis we find that this is easy to calculate. </p>
<pre>when n is odd and n%3 != 0:
each pair is in 3 iso tri
when n is odd and n%3 == 0:
each pair, except for O(n) pairs, is in 3 iso tri
when n is even and n%3 != 0:
each pair, except for O(n) of them,
if dis is even, is in 4 iso tri
if dis is odd, is in 2 iso tri
when n is even and n%3 == 0:
each pair, except for O(n) of them,
if dis is even, is in 4 iso tri
if dis is odd, is in 2 iso tri
</pre>
<p><strong>Setter's Solution</strong> </p>
<pre><code>#include <cstdio>
#include <cstring>
#include <cmath>
#include <cassert>
#include <ctime>
#include <set>
#include <map>
#include <vector>
#include <string>
#include <sstream>
#include <numeric>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define N 1000010
char a[N]; int n;
ll ff() {
ll S = 0;
if (n&1) {
S = (ll)n*(n-1)/2;
if (n%3 == 0) S -= n/3*2;
} else {
S = (ll)n*(n/2-1);
if (n%3 == 0) S -= n/3*2;
}
return S;
}
ll gg() {
ll S = 0;
if (n&1) {
int S0 = 0, S1 = 0;
for (int i = 0; i < n; i ++)
if (a[i] == '0') S0 ++;
else S1 ++;
S = (ll) S0*S1*6;
if (n%3 == 0) {
int n1 = n/3, n2 = n1*2;
for (int i = 0; i < n; i ++) {
if (a[i] != a[(i+n1)%n]) S -= 2;
if (a[i] != a[(i+n2)%n]) S -= 2;
}
}
} else {
int S00 = 0, S01 = 0, S10 = 0, S11 = 0;
for (int i = 0; i < n; i += 2)
if (a[i] == '0') S00 ++;
else S01 ++;
for (int i = 1; i < n; i += 2)
if (a[i] == '0') S10 ++;
else S11 ++;
S += (ll)S00*S01*8;
S += (ll)S10*S11*8;
S += (ll)S00*S11*4;
S += (ll)S10*S01*4;
int n1 = n/2;
for (int i = 0; i < n; i ++)
if (a[i] != a[(i+n1)%n]) S -= 2;
if (n%3 == 0) {
int n1 = n/3, n2 = n1*2;
for (int i = 0; i < n; i ++) {
if (a[i] != a[(i+n1)%n]) S -= 2;
if (a[i] != a[(i+n2)%n]) S -= 2;
}
}
}
return S/2;
}
int main() {
int __; scanf("%d", &__);
int _ = 0;
while (scanf("%s", a) != EOF) {
_ ++;
n = strlen(a);
cout << "Case " << _ << ": " << ff()-gg()/2 << endl;
}
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong> </p>
<pre><code>#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string>
#include <ctime>
#include <complex>
#pragma comment (linker, "/STACK:256000000")
using namespace std;
struct base {
double x, y;
base() { x = y = 0;}
base(int x_) { x = x_, y = 0;}
base(double x_) { x = x_, y = 0;}
base(double x, double y): x(x), y(y) {}
double imag() const { return y;}
double real() const { return x;}
void imag(double value) { y = value;}
void real(double value) { x = value;}
base& operator *= (const base& other) { return *this = base(x * other.x - y * other.y, y * other.x + x * other.y);}
base& operator /= (double value) { return *this = base(x / value, y / value);}
base& operator += (const base& other) { return *this = base(x + other.x, y + other.y);}
base& operator -= (const base& other) { return *this = base(x - other.x, y - other.y);}
};
base operator * (const base& a, const base& b) { return base(a.x * b.x - a.y * b.y, a.y * b.x + a.x * b.y);}
base operator * (const base& a, double value) { return base(a.x * value, a.y * value);}
base operator + (const base& a, const base& b) { return base(a.x + b.x, a.y + b.y);}
base operator - (const base& a, const base& b) { return base(a.x - b.x, a.y - b.y);}
base operator / (const base& a, double value) { return base(a.x / value, a.y / value);}
const double pi = 2 * acos(0.);
const int maxC = 4500000;
int rev[maxC];
base na[maxC], nb[maxC];
void shuffle(base* data, int n) {
for (int i = 0; i < n; ++i) {
if (i < rev[i]) {
swap(data[i], data[rev[i]]);
}
}
}
void Step(base* data, int N) {
if (N == 1) return;
Step(data, N / 2);
Step(data + N / 2, N / 2);
base w(cos(2. * pi / N), sin(2. * pi / N));
base cur(1), buf;
for (int i = 0; i < N / 2; ++i, cur *= w) {
buf = cur * data[i + N / 2];
data[i + N / 2] = data[i] - buf;
data[i] += buf;
}
}
void multiply(int a[], int n, int b[], int m, long long res[], int& len) {
int q = n + m;
int sz = 1;
while (sz < q) sz *= 2;
for (int i = 0; i < n; ++i) na[i].x = a[i];
for (int i = 0; i < m; ++i) na[i].y = b[i];
for (int i = n; i < sz; ++i) na[i].x = 0.0;
for (int i = m; i < sz; ++i) na[i].y = 0.0;
for (int i = 0; i < sz; ++i) nb[i] = 0;
int bits = 0;
while ((1 << bits) < sz) ++bits;
for (int i = 0; i < sz; ++i) {
*(rev + i) = 0;
for (int j = 0; j < bits; ++j) {
if (i & (1 << j)) {
*(rev + i) += 1 << (bits - j - 1);
}
}
}
int index = 0;
for (int i = 0;;++i) if ((1 << i) == sz) { index = i; break;}
shuffle(na, sz);
Step(na, sz);
nb[0] = na[0].x * na[0].y;
for (int i = 1; i < sz; ++i) {
base buf1 = na[i], buf2 = base(na[sz - i].x, -na[sz - i].y);
base tx = (buf1 + buf2) / 2.;
base ty = base(0, -1) * (buf1 - buf2) / 2.;
nb[i] = tx * ty;
}
shuffle(nb, sz);
Step(nb, sz);
reverse(nb + 1, nb + sz);
for (int i = 0; i < sz; ++i) {
nb[i] /= (double)(sz);
}
for (int i = 0; i < sz; ++i) {
res[i] = (long long)(nb[i].real() + 0.5);
}
len = sz;
while (len > 1 && res[len - 1] == 0) --len;
}
const int maxL = 1100000;
int c[maxL];
long long res[4 * maxL];
long long resO[4 * maxL];
int ps[maxL];
void buildResO(int c[], int n) {
for (int i = 0; i < 4 * n; ++i) {
resO[i] = 0;
}
for (int i = 0; i < 2 * n; ++i) {
resO[i] = res[i];
}
for (int i = 0; i + 1 < 2 * n; ++i) {
if (i < n) {
resO[i] += (i + 1);
} else {
resO[i] += 2 * n - 1 - i;
}
}
for (int i = 0; i < n; ++i) {
ps[i] = c[i];
if (i > 0) {
ps[i] += ps[i - 1];
}
}
for (int i = 0; i < n; ++i) {
resO[i] -= 2 * ps[i];
}
int current = ps[n - 1];
for (int i = n; i + 1 < 2 * n; ++i) {
current -= c[i - n];
resO[i] -= 2 * current;
}
for (int i = n + n - 1; i >= 0; --i) {
resO[i + n] += resO[i];
}
}
long long getAnswer(int c[], int n) {
int m;
for (int i = 0; i < 4 * n; ++i) {
res[i] = 0;
}
multiply(c, n, c, n, res, m);
buildResO(c, n);
for (int i = n + n - 1; i >= 0; --i) {
res[i + n] += res[i];
}
long long ways = 0LL;
for (int i = 0; i < n; ++i) {
if (c[i] == 1) {
ways += (res[2 * i] + res[2 * (i + n)] - 1LL) / 2LL;
} else {
ways += (resO[2 * i] + resO[2 * (i + n)] - 1LL) / 2LL;
}
}
if (n % 3 == 0) {
for (int i = 0; i < n / 3; ++i) {
if (c[i] == 1 && c[i + n / 3] == 1 && c[i + 2 * n / 3] == 1) {
ways -= 2LL;
}
if (c[i] == 0 && c[i + n / 3] == 0 && c[i + 2 * n / 3] == 0) {
ways -= 2LL;
}
}
}
return ways;
}
char colors[maxL];
void solve(int test) {
scanf("%s", &colors);
int n = strlen(colors);
for (int i = 0; i < n; ++i) {
c[i] = colors[i] - '0';
}
printf("Case %d: %lld\n", test, getAnswer(c, n));
for (int i = 0; i < n; ++i) {
colors[i] = 0;
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int tests;
scanf("%d\n", &tests);
for (int i = 0; i < tests; ++i) {
solve(i + 1);
//cerr << (i + 1) << ": " << clock() << endl;
}
return 0;
}
</code></pre>
| 0 |
101feb14-isosceles-triangles
|
2014-03-03T12:39:18
|
{"contest_participation":1550,"challenge_submissions":54,"successful_submissions":9}
|
2014-03-03T12:39:18
|
2016-07-23T19:10:55
|
setter
|
###C++
```cpp
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cassert>
#include <ctime>
#include <set>
#include <map>
#include <vector>
#include <string>
#include <sstream>
#include <numeric>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define N 1000010
char a[N]; int n;
ll ff() {
ll S = 0;
if (n&1) {
S = (ll)n*(n-1)/2;
if (n%3 == 0) S -= n/3*2;
} else {
S = (ll)n*(n/2-1);
if (n%3 == 0) S -= n/3*2;
}
return S;
}
ll gg() {
ll S = 0;
if (n&1) {
int S0 = 0, S1 = 0;
for (int i = 0; i < n; i ++)
if (a[i] == '0') S0 ++;
else S1 ++;
S = (ll) S0*S1*6;
if (n%3 == 0) {
int n1 = n/3, n2 = n1*2;
for (int i = 0; i < n; i ++) {
if (a[i] != a[(i+n1)%n]) S -= 2;
if (a[i] != a[(i+n2)%n]) S -= 2;
}
}
} else {
int S00 = 0, S01 = 0, S10 = 0, S11 = 0;
for (int i = 0; i < n; i += 2)
if (a[i] == '0') S00 ++;
else S01 ++;
for (int i = 1; i < n; i += 2)
if (a[i] == '0') S10 ++;
else S11 ++;
S += (ll)S00*S01*8;
S += (ll)S10*S11*8;
S += (ll)S00*S11*4;
S += (ll)S10*S01*4;
int n1 = n/2;
for (int i = 0; i < n; i ++)
if (a[i] != a[(i+n1)%n]) S -= 2;
if (n%3 == 0) {
int n1 = n/3, n2 = n1*2;
for (int i = 0; i < n; i ++) {
if (a[i] != a[(i+n1)%n]) S -= 2;
if (a[i] != a[(i+n2)%n]) S -= 2;
}
}
}
return S/2;
}
int main() {
int __; scanf("%d", &__);
int _ = 0;
while (scanf("%s", a) != EOF) {
_ ++;
n = strlen(a);
cout << "Case " << _ << ": " << ff()-gg()/2 << endl;
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:16
|
2016-07-23T19:10:40
|
C++
|
33 | 1,828 |
isosceles-triangles
|
Isosceles Triangles
|
[Sevenkplus](http://sevenkplus.com/) has a regular polygon. Each vertex of the polygon has a color, either white or black. Sevenkplus wants to count the number of isosceles triangles whose vertices are vertices of the regular polygon and have the same color.
**Input Format**
The first line contains an integer T. T testcases follow.
For each test case, there is only one line, which consists of a 01-string with length >= 3. Number of vertices `n` of the regular polygon equals length of the string. The string represents color of vertices in clockwise order. `0` represents white and `1` represents black.
**Output Format**
For each test case, output one line in the format `Case #t: ans`, where `t` is the case number (starting from 1), and `ans` is the answer.
**Constraints**
Sum of all n in the input <= 10^6.
**Sample Input**
5
001
0001
10001
111010
1101010
**Sample Output**
Case 1: 0
Case 2: 1
Case 3: 1
Case 4: 2
Case 5: 3
**Explanation**
In case 5, indices of vertices of the three monochromatic isosceles triangles are (0,3,5), (1,3,5) and (2,4,6) (assuming indices start from 0).
**Timelimits**
Timelimits for this challenge is given [here](https://www.hackerrank.com/environment)
|
code
|
How many monochromatic isosceles triangles are there?
|
ai
|
2014-02-02T04:29:46
|
2022-09-02T09:55:24
| null | null | null |
[Sevenkplus](http://sevenkplus.com/) has a regular polygon. Each vertex of the polygon has a color, either white or black. Sevenkplus wants to count the number of isosceles triangles whose vertices are vertices of the regular polygon and have the same color.
**Input Format**
The first line contains an integer T. T testcases follow.
For each test case, there is only one line, which consists of a 01-string with length >= 3. Number of vertices `n` of the regular polygon equals length of the string. The string represents color of vertices in clockwise order. `0` represents white and `1` represents black.
**Output Format**
For each test case, output one line in the format `Case #t: ans`, where `t` is the case number (starting from 1), and `ans` is the answer.
**Constraints**
Sum of all n in the input <= 10^6.
**Sample Input**
5
001
0001
10001
111010
1101010
**Sample Output**
Case 1: 0
Case 2: 1
Case 3: 1
Case 4: 2
Case 5: 3
**Explanation**
In case 5, indices of vertices of the three monochromatic isosceles triangles are (0,3,5), (1,3,5) and (2,4,6) (assuming indices start from 0).
**Timelimits**
Timelimits for this challenge is given [here](https://www.hackerrank.com/environment)
| 0.488636 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
Isosceles Triangles - 101 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101feb14/challenges/isosceles-triangles">Isosceles Triangles</a> </p>
<p><strong>Difficulty</strong> : Medium-Hard <br>
<strong>Required Knowledge</strong> : Bichromatic Isosceles Triangles <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/sevenkplus">Yuzhou Gu</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/dsoboliev">Dmytro Soboliev</a> </p>
<p><strong>Approach</strong> </p>
<pre><code># of monochromatic isosceles triangl = # of triangle - # of bichromatic isosceles triangle
</code></pre>
<p>Each bichromatic isosceles triangle has two bichromatic edges, so we only need to count # of bichromatic edges. </p>
<p>Consider a pair (i,j) of vertices with different colors.
Then its contribution to number of bichromatic edges in isosceles triangles is determined by distance between the vertices.
With some analysis we find that this is easy to calculate. </p>
<pre>when n is odd and n%3 != 0:
each pair is in 3 iso tri
when n is odd and n%3 == 0:
each pair, except for O(n) pairs, is in 3 iso tri
when n is even and n%3 != 0:
each pair, except for O(n) of them,
if dis is even, is in 4 iso tri
if dis is odd, is in 2 iso tri
when n is even and n%3 == 0:
each pair, except for O(n) of them,
if dis is even, is in 4 iso tri
if dis is odd, is in 2 iso tri
</pre>
<p><strong>Setter's Solution</strong> </p>
<pre><code>#include <cstdio>
#include <cstring>
#include <cmath>
#include <cassert>
#include <ctime>
#include <set>
#include <map>
#include <vector>
#include <string>
#include <sstream>
#include <numeric>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define N 1000010
char a[N]; int n;
ll ff() {
ll S = 0;
if (n&1) {
S = (ll)n*(n-1)/2;
if (n%3 == 0) S -= n/3*2;
} else {
S = (ll)n*(n/2-1);
if (n%3 == 0) S -= n/3*2;
}
return S;
}
ll gg() {
ll S = 0;
if (n&1) {
int S0 = 0, S1 = 0;
for (int i = 0; i < n; i ++)
if (a[i] == '0') S0 ++;
else S1 ++;
S = (ll) S0*S1*6;
if (n%3 == 0) {
int n1 = n/3, n2 = n1*2;
for (int i = 0; i < n; i ++) {
if (a[i] != a[(i+n1)%n]) S -= 2;
if (a[i] != a[(i+n2)%n]) S -= 2;
}
}
} else {
int S00 = 0, S01 = 0, S10 = 0, S11 = 0;
for (int i = 0; i < n; i += 2)
if (a[i] == '0') S00 ++;
else S01 ++;
for (int i = 1; i < n; i += 2)
if (a[i] == '0') S10 ++;
else S11 ++;
S += (ll)S00*S01*8;
S += (ll)S10*S11*8;
S += (ll)S00*S11*4;
S += (ll)S10*S01*4;
int n1 = n/2;
for (int i = 0; i < n; i ++)
if (a[i] != a[(i+n1)%n]) S -= 2;
if (n%3 == 0) {
int n1 = n/3, n2 = n1*2;
for (int i = 0; i < n; i ++) {
if (a[i] != a[(i+n1)%n]) S -= 2;
if (a[i] != a[(i+n2)%n]) S -= 2;
}
}
}
return S/2;
}
int main() {
int __; scanf("%d", &__);
int _ = 0;
while (scanf("%s", a) != EOF) {
_ ++;
n = strlen(a);
cout << "Case " << _ << ": " << ff()-gg()/2 << endl;
}
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong> </p>
<pre><code>#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string>
#include <ctime>
#include <complex>
#pragma comment (linker, "/STACK:256000000")
using namespace std;
struct base {
double x, y;
base() { x = y = 0;}
base(int x_) { x = x_, y = 0;}
base(double x_) { x = x_, y = 0;}
base(double x, double y): x(x), y(y) {}
double imag() const { return y;}
double real() const { return x;}
void imag(double value) { y = value;}
void real(double value) { x = value;}
base& operator *= (const base& other) { return *this = base(x * other.x - y * other.y, y * other.x + x * other.y);}
base& operator /= (double value) { return *this = base(x / value, y / value);}
base& operator += (const base& other) { return *this = base(x + other.x, y + other.y);}
base& operator -= (const base& other) { return *this = base(x - other.x, y - other.y);}
};
base operator * (const base& a, const base& b) { return base(a.x * b.x - a.y * b.y, a.y * b.x + a.x * b.y);}
base operator * (const base& a, double value) { return base(a.x * value, a.y * value);}
base operator + (const base& a, const base& b) { return base(a.x + b.x, a.y + b.y);}
base operator - (const base& a, const base& b) { return base(a.x - b.x, a.y - b.y);}
base operator / (const base& a, double value) { return base(a.x / value, a.y / value);}
const double pi = 2 * acos(0.);
const int maxC = 4500000;
int rev[maxC];
base na[maxC], nb[maxC];
void shuffle(base* data, int n) {
for (int i = 0; i < n; ++i) {
if (i < rev[i]) {
swap(data[i], data[rev[i]]);
}
}
}
void Step(base* data, int N) {
if (N == 1) return;
Step(data, N / 2);
Step(data + N / 2, N / 2);
base w(cos(2. * pi / N), sin(2. * pi / N));
base cur(1), buf;
for (int i = 0; i < N / 2; ++i, cur *= w) {
buf = cur * data[i + N / 2];
data[i + N / 2] = data[i] - buf;
data[i] += buf;
}
}
void multiply(int a[], int n, int b[], int m, long long res[], int& len) {
int q = n + m;
int sz = 1;
while (sz < q) sz *= 2;
for (int i = 0; i < n; ++i) na[i].x = a[i];
for (int i = 0; i < m; ++i) na[i].y = b[i];
for (int i = n; i < sz; ++i) na[i].x = 0.0;
for (int i = m; i < sz; ++i) na[i].y = 0.0;
for (int i = 0; i < sz; ++i) nb[i] = 0;
int bits = 0;
while ((1 << bits) < sz) ++bits;
for (int i = 0; i < sz; ++i) {
*(rev + i) = 0;
for (int j = 0; j < bits; ++j) {
if (i & (1 << j)) {
*(rev + i) += 1 << (bits - j - 1);
}
}
}
int index = 0;
for (int i = 0;;++i) if ((1 << i) == sz) { index = i; break;}
shuffle(na, sz);
Step(na, sz);
nb[0] = na[0].x * na[0].y;
for (int i = 1; i < sz; ++i) {
base buf1 = na[i], buf2 = base(na[sz - i].x, -na[sz - i].y);
base tx = (buf1 + buf2) / 2.;
base ty = base(0, -1) * (buf1 - buf2) / 2.;
nb[i] = tx * ty;
}
shuffle(nb, sz);
Step(nb, sz);
reverse(nb + 1, nb + sz);
for (int i = 0; i < sz; ++i) {
nb[i] /= (double)(sz);
}
for (int i = 0; i < sz; ++i) {
res[i] = (long long)(nb[i].real() + 0.5);
}
len = sz;
while (len > 1 && res[len - 1] == 0) --len;
}
const int maxL = 1100000;
int c[maxL];
long long res[4 * maxL];
long long resO[4 * maxL];
int ps[maxL];
void buildResO(int c[], int n) {
for (int i = 0; i < 4 * n; ++i) {
resO[i] = 0;
}
for (int i = 0; i < 2 * n; ++i) {
resO[i] = res[i];
}
for (int i = 0; i + 1 < 2 * n; ++i) {
if (i < n) {
resO[i] += (i + 1);
} else {
resO[i] += 2 * n - 1 - i;
}
}
for (int i = 0; i < n; ++i) {
ps[i] = c[i];
if (i > 0) {
ps[i] += ps[i - 1];
}
}
for (int i = 0; i < n; ++i) {
resO[i] -= 2 * ps[i];
}
int current = ps[n - 1];
for (int i = n; i + 1 < 2 * n; ++i) {
current -= c[i - n];
resO[i] -= 2 * current;
}
for (int i = n + n - 1; i >= 0; --i) {
resO[i + n] += resO[i];
}
}
long long getAnswer(int c[], int n) {
int m;
for (int i = 0; i < 4 * n; ++i) {
res[i] = 0;
}
multiply(c, n, c, n, res, m);
buildResO(c, n);
for (int i = n + n - 1; i >= 0; --i) {
res[i + n] += res[i];
}
long long ways = 0LL;
for (int i = 0; i < n; ++i) {
if (c[i] == 1) {
ways += (res[2 * i] + res[2 * (i + n)] - 1LL) / 2LL;
} else {
ways += (resO[2 * i] + resO[2 * (i + n)] - 1LL) / 2LL;
}
}
if (n % 3 == 0) {
for (int i = 0; i < n / 3; ++i) {
if (c[i] == 1 && c[i + n / 3] == 1 && c[i + 2 * n / 3] == 1) {
ways -= 2LL;
}
if (c[i] == 0 && c[i + n / 3] == 0 && c[i + 2 * n / 3] == 0) {
ways -= 2LL;
}
}
}
return ways;
}
char colors[maxL];
void solve(int test) {
scanf("%s", &colors);
int n = strlen(colors);
for (int i = 0; i < n; ++i) {
c[i] = colors[i] - '0';
}
printf("Case %d: %lld\n", test, getAnswer(c, n));
for (int i = 0; i < n; ++i) {
colors[i] = 0;
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int tests;
scanf("%d\n", &tests);
for (int i = 0; i < tests; ++i) {
solve(i + 1);
//cerr << (i + 1) << ": " << clock() << endl;
}
return 0;
}
</code></pre>
| 0 |
101feb14-isosceles-triangles
|
2014-03-03T12:39:18
|
{"contest_participation":1550,"challenge_submissions":54,"successful_submissions":9}
|
2014-03-03T12:39:18
|
2016-07-23T19:10:55
|
tester
|
###C++
```cpp
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string>
#include <ctime>
#include <complex>
#pragma comment (linker, "/STACK:256000000")
using namespace std;
struct base {
double x, y;
base() { x = y = 0;}
base(int x_) { x = x_, y = 0;}
base(double x_) { x = x_, y = 0;}
base(double x, double y): x(x), y(y) {}
double imag() const { return y;}
double real() const { return x;}
void imag(double value) { y = value;}
void real(double value) { x = value;}
base& operator *= (const base& other) { return *this = base(x * other.x - y * other.y, y * other.x + x * other.y);}
base& operator /= (double value) { return *this = base(x / value, y / value);}
base& operator += (const base& other) { return *this = base(x + other.x, y + other.y);}
base& operator -= (const base& other) { return *this = base(x - other.x, y - other.y);}
};
base operator * (const base& a, const base& b) { return base(a.x * b.x - a.y * b.y, a.y * b.x + a.x * b.y);}
base operator * (const base& a, double value) { return base(a.x * value, a.y * value);}
base operator + (const base& a, const base& b) { return base(a.x + b.x, a.y + b.y);}
base operator - (const base& a, const base& b) { return base(a.x - b.x, a.y - b.y);}
base operator / (const base& a, double value) { return base(a.x / value, a.y / value);}
const double pi = 2 * acos(0.);
const int maxC = 4500000;
int rev[maxC];
base na[maxC], nb[maxC];
void shuffle(base* data, int n) {
for (int i = 0; i < n; ++i) {
if (i < rev[i]) {
swap(data[i], data[rev[i]]);
}
}
}
void Step(base* data, int N) {
if (N == 1) return;
Step(data, N / 2);
Step(data + N / 2, N / 2);
base w(cos(2. * pi / N), sin(2. * pi / N));
base cur(1), buf;
for (int i = 0; i < N / 2; ++i, cur *= w) {
buf = cur * data[i + N / 2];
data[i + N / 2] = data[i] - buf;
data[i] += buf;
}
}
void multiply(int a[], int n, int b[], int m, long long res[], int& len) {
int q = n + m;
int sz = 1;
while (sz < q) sz *= 2;
for (int i = 0; i < n; ++i) na[i].x = a[i];
for (int i = 0; i < m; ++i) na[i].y = b[i];
for (int i = n; i < sz; ++i) na[i].x = 0.0;
for (int i = m; i < sz; ++i) na[i].y = 0.0;
for (int i = 0; i < sz; ++i) nb[i] = 0;
int bits = 0;
while ((1 << bits) < sz) ++bits;
for (int i = 0; i < sz; ++i) {
*(rev + i) = 0;
for (int j = 0; j < bits; ++j) {
if (i & (1 << j)) {
*(rev + i) += 1 << (bits - j - 1);
}
}
}
int index = 0;
for (int i = 0;;++i) if ((1 << i) == sz) { index = i; break;}
shuffle(na, sz);
Step(na, sz);
nb[0] = na[0].x * na[0].y;
for (int i = 1; i < sz; ++i) {
base buf1 = na[i], buf2 = base(na[sz - i].x, -na[sz - i].y);
base tx = (buf1 + buf2) / 2.;
base ty = base(0, -1) * (buf1 - buf2) / 2.;
nb[i] = tx * ty;
}
shuffle(nb, sz);
Step(nb, sz);
reverse(nb + 1, nb + sz);
for (int i = 0; i < sz; ++i) {
nb[i] /= (double)(sz);
}
for (int i = 0; i < sz; ++i) {
res[i] = (long long)(nb[i].real() + 0.5);
}
len = sz;
while (len > 1 && res[len - 1] == 0) --len;
}
const int maxL = 1100000;
int c[maxL];
long long res[4 * maxL];
long long resO[4 * maxL];
int ps[maxL];
void buildResO(int c[], int n) {
for (int i = 0; i < 4 * n; ++i) {
resO[i] = 0;
}
for (int i = 0; i < 2 * n; ++i) {
resO[i] = res[i];
}
for (int i = 0; i + 1 < 2 * n; ++i) {
if (i < n) {
resO[i] += (i + 1);
} else {
resO[i] += 2 * n - 1 - i;
}
}
for (int i = 0; i < n; ++i) {
ps[i] = c[i];
if (i > 0) {
ps[i] += ps[i - 1];
}
}
for (int i = 0; i < n; ++i) {
resO[i] -= 2 * ps[i];
}
int current = ps[n - 1];
for (int i = n; i + 1 < 2 * n; ++i) {
current -= c[i - n];
resO[i] -= 2 * current;
}
for (int i = n + n - 1; i >= 0; --i) {
resO[i + n] += resO[i];
}
}
long long getAnswer(int c[], int n) {
int m;
for (int i = 0; i < 4 * n; ++i) {
res[i] = 0;
}
multiply(c, n, c, n, res, m);
buildResO(c, n);
for (int i = n + n - 1; i >= 0; --i) {
res[i + n] += res[i];
}
long long ways = 0LL;
for (int i = 0; i < n; ++i) {
if (c[i] == 1) {
ways += (res[2 * i] + res[2 * (i + n)] - 1LL) / 2LL;
} else {
ways += (resO[2 * i] + resO[2 * (i + n)] - 1LL) / 2LL;
}
}
if (n % 3 == 0) {
for (int i = 0; i < n / 3; ++i) {
if (c[i] == 1 && c[i + n / 3] == 1 && c[i + 2 * n / 3] == 1) {
ways -= 2LL;
}
if (c[i] == 0 && c[i + n / 3] == 0 && c[i + 2 * n / 3] == 0) {
ways -= 2LL;
}
}
}
return ways;
}
char colors[maxL];
void solve(int test) {
scanf("%s", &colors);
int n = strlen(colors);
for (int i = 0; i < n; ++i) {
c[i] = colors[i] - '0';
}
printf("Case %d: %lld\n", test, getAnswer(c, n));
for (int i = 0; i < n; ++i) {
colors[i] = 0;
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int tests;
scanf("%d\n", &tests);
for (int i = 0; i < tests; ++i) {
solve(i + 1);
//cerr << (i + 1) << ": " << clock() << endl;
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:16
|
2016-07-23T19:10:55
|
C++
|
34 | 1,071 |
coloring-tree
|
Coloring Tree
|
You are given a tree with **N** nodes with every node being colored. A color is represented by an integer ranging from 1 to 10<sup>9</sup>. Can you find the number of distinct colors available in a subtree rooted at the node **s**?
**Input Format**
The first line contains three space separated integers representing the number of nodes in the tree (**N**), number of queries to answer (**M**) and the root of the tree.
In each of the next N-1 lines, there are two space separated integers(a b) representing an edge from node a to Node b.
N lines follow: N+i<sup>th</sup> line contains the color of the i<sup>th</sup> node.
M lines follow: Each line containg a single integer s.
**Output Format**
Output exactly M lines, each line containing the output of the i<sub>th</sub> query.
**Constraints**
0=< M <= 10<sup>5</sup><br>
1=< N <= 10<sup>5</sup><br>
1=< root <= N<br>
1=< color of the Node <= 10<sup>9</sup><br>
**Example**
**Sample Input**
4 2 1
1 2
2 4
2 3
10
20
20
30
1
2
**Sample Output**
3
2
**Explanation**
Query 1-Subtree rooted at 1 is the entire tree and colors used are 10 20 20 30 , so the answer is 3(10,20 and 30)
Query 2-Subtree rooted at 2 contains color 20 20 30, so the answer is 2(20 and 30)
|
code
|
Given a tree with all nodes colored, find the number of distinct colors rooted at a given node.
|
ai
|
2013-10-12T06:23:17
|
2022-09-02T10:00:36
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER_ARRAY.
# The function accepts following parameters:
# 1. 2D_INTEGER_ARRAY tree
# 2. INTEGER_ARRAY color
# 3. INTEGER_ARRAY s
#
def solve(tree, color, s):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
r = int(first_multiple_input[2])
tree = []
for _ in range(n - 1):
tree.append(list(map(int, input().rstrip().split())))
color = []
for _ in range(n):
color_item = int(input().strip())
color.append(color_item)
s = []
for _ in range(m):
s_item = int(input().strip())
s.append(s_item)
result = solve(tree, color, s)
fptr.write('\n'.join(map(str, result)))
fptr.write('\n')
fptr.close()
|
You are given a tree with **N** nodes with every node being colored. A color is represented by an integer ranging from 1 to 10<sup>9</sup>. Can you find the number of distinct colors available in a subtree rooted at the node **s**?
**Input Format**
The first line contains three space separated integers representing the number of nodes in the tree (**N**), number of queries to answer (**M**) and the root of the tree.
In each of the next N-1 lines, there are two space separated integers(a b) representing an edge from node a to Node b and vice-versa.
N lines follow: N+i<sup>th</sup> line contains the color of the i<sup>th</sup> node.
M lines follow: Each line containg a single integer s.
**Output Format**
Output exactly M lines, each line containing the output of the i<sub>th</sub> query.
**Constraints**
0 <= M <= 10<sup>5</sup><br>
1 <= N <= 10<sup>5</sup><br>
1 <= root <= N<br>
1 <= color of the Node <= 10<sup>9</sup><br>
**Example**
**Sample Input**
4 2 1
1 2
2 4
2 3
10
20
20
30
1
2
**Sample Output**
3
2
**Explanation**
Query 1-Subtree rooted at 1 is the entire tree and colors used are 10 20 20 30 , so the answer is 3(10,20 and 30)
Query 2-Subtree rooted at 2 contains color 20 20 30, so the answer is 2(20 and 30)
| 0.413793 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
|
Coloring Tree - 101 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Difficulty Level</strong> : Medium <br>
<strong>Required Knowledge</strong> : DFS and Segment Trees<br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/devuy11">Devendra Agarwal</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/darkshadows">Lalit Kundu</a> <br></p>
<p>Store the order in which you execute DFS starting from the given root.Now observe that each subtree will correspond to the sub-array of the array formed by DFS. Store the starting and ending position for each subtree in the array.</p>
<p>Now the question reduces to finding the number of distinct value in the sub-array.</p>
<p>Note that atmax 10^5 different colors are used as N<=10^5 ,so store the colors used in the tree and map it to an integer from 1 to 10^5.Now the question is to find number of distinct values in the sub-array given that all the values are from 1 to 10^5.</p>
<p>The result of a query [a, b] is number of integers whose last occurrence in [1, b] is >= a(Last Occurence in [1,b] is in [a,b]).</p>
<p>Let's have two kinds of events: QueryEvent and NumberEvent. First we read whole input and sort all events, the key for QueryEvents are their end (i.e. b for query [a, b]), and for NumberEvents the key is their position in array.</p>
<p>We also have a segment tree which answers the queries of kind: how many elements are at position range [x, y]. Initially the tree is empty.</p>
<p>Then we process events in order:<br>
<strong>a</strong>. When we meet a NumberEvent:<br>
1. If number has occurred before ,then we put 0 in that position of seg tree and update the tree.<br>
2. We put 1 in position of number in the segment tree.<br>
<strong>b</strong>.When we meet a QueryEvent:<br>
- Query the segment tree (for finding number of 1's in the range), and find the answer.<br></p>
<p><strong>Setter's Code</strong> </p>
<pre><code>#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#include<vector>
#include<string.h>
using namespace std;
#define Max_N 1000001
#define INF 1000000000
int N,color[Max_N],root,from,to,counter,parent[Max_N],s,q,search_here[Max_N],highest,last_occurence[Max_N],where,val,ind ,seg[1<<21],power[25],level,answer[Max_N];
vector<int> myvector[Max_N];
struct transfer
{
int start,end;
}Node[Max_N];
typedef struct queries qu;
struct queries
{
int ind ,left,right;
bool operator<(const qu q)const{
return right<q.right;
}
}Q[Max_N];
void DFS(int rooti)
{
Node[rooti].start=counter;
counter++;
while(!myvector[rooti].empty()){
to=myvector[rooti].back();
if(to!=parent[rooti]){
parent[to]=rooti;
DFS(to);
}
myvector[rooti].pop_back();
}
Node[rooti].end=counter-1;
}
int search(int low,int high,int s)
{
int mid=(low+high)>>1;
if(search_here[mid]==s) return mid;
else if(search_here[mid]>s) return search(low,mid-1,s);
else return search(mid+1,high,s);
}
void constant()
{
power[0]=1;
for(int i=1;i<=23;i++) power[i]=power[i-1]<<1;
}
void obtain(int x)
{
int y=x;
level=0;
while(x){
x>>=1;
level++;
}
if(power[level-1]!=y) level++;
}
void update(int pos,int val)
{
seg[pos]=val;
pos=pos>>1;
while(pos){
seg[pos]=seg[pos<<1]+seg[(pos<<1)+1];
pos>>=1;
}
return;
}
int Query(int s,int e,int i,int j,int node)
{
if(i>e || s>j) return 0;
if(s>=i && j>=e) return seg[node];
return (Query(s,((s+e)>>1),i,j,(node<<1))+Query(((s+e)>>1)+1,e,i,j,(node<<1)+1));
}
int main()
{
int v;
scanf("%d%d%d",&N,&q,&root);
//connections
for(int i=1;i<N;i++){
scanf("%d%d",&from,&to);
myvector[from].push_back(to);
myvector[to].push_back(from);
}
counter=1;
parent[root]=root;
DFS(root);
//color of the graph
for(int i=1;i<=N;i++){
scanf("%d",&v);
color[Node[i].start]=v;
search_here[i]=v; //finally i need to sort so no troubles
}
for(int i=0;i<q;i++){
scanf("%d",&s);
Q[i].ind =i;
Q[i].left=Node[s].start;
Q[i].right=Node[s].end;
}
sort(Q,Q+q);
sort(search_here+1,search_here+N+1);
highest=2;
for(int i=2;i<=N;i++){
if(search_here[i]==search_here[highest-1]) continue;
else{
search_here[highest]=search_here[i];
highest++;
}
}
highest--;
where=0;
constant();
obtain(N);
for(int i=0;i<=N;i++) last_occurence[i]=-INF;
memset(seg,0,sizeof(seg));
//search in search_here from 1 to highest ind ed
for(int i=1;i<=N;i++){
val=color[i];
ind =search(1,highest,val);
if(last_occurence[ind ]<0){
last_occurence[ind]=i;
update(power[level-1]+last_occurence[ind]-1,1);
}
else{
update(power[level-1]-1+last_occurence[ind ],0);
last_occurence[ind]=i;
update(power[level-1]-1+last_occurence[ind ],1);
}
while(Q[where].right==i){
answer[Q[where].ind]=Query(1,power[level-1],Q[where].left,Q[where].right,1);
where++;
}
}
for(int i=0;i<q;i++) printf("%d\n",answer[i]);
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong> </p>
<pre><code>/*
Author:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%% LALIT KUNDU %%%%%%%%
%%%%%%%% IIIT HYDERABAD %%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<vector>
#include<cassert>
#include<sstream>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<algorithm>
using namespace std;
#define pb push_back
#define mp make_pair
#define clr(x) x.clear()
#define sz(x) ((int)(x).size())
#define F first
#define S second
#define REP(i,a,b) for(i=a;i<b;i++)
#define rep(i,b) for(i=0;i<b;i++)
#define rep1(i,b) for(i=1;i<=b;i++)
#define mod 1000000007
#define pdn(n) printf("%d\n",n)
#define sl(n) scanf("%d",&n)
#define sd(n) scanf("%d",&n)
#define pn printf("\n")
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<int> VI;
typedef vector<VI> VVI;
typedef long long LL;
#define INF 1000000007
int LMITR[1000009];
map < int ,int > PI;
#define MAX 10000009
int tree[MAX+1]={};
void update(int idx, int val) {
while (idx <= MAX) {
tree[idx] += val;
idx += (idx & -idx);
}
}
int readi(int idx) {
int sum = 0;
while (idx > 0) {
sum +=(int) tree[idx];
idx -= (idx & -idx);
}
return sum;
}
int to[1000005],ar[1000009];
void foo(int n, int q, vector < pair < pair < int,int >, int > > qu)
{
int i;
for(i=n; i>=1; i--)
{
if(PI.count(ar[i])==0)
LMITR[i]=INF;
else LMITR[i]=PI[ar[i]];
PI[ar[i]]=i;
}
PI.clear();
for(i=1; i<=n; i++)
if(PI.count(ar[i])==0)
PI[ar[i]]=1,update(i,1);
sort(qu.begin(),qu.end());
int cur=0,ans[1000007];
for(i=1; i<=n; i++)
{
while(cur<q && qu[cur].F.F==i)
{
ans[qu[cur].S]=readi(qu[cur].F.S);
cur++;
}
if(LMITR[i]!=INF)
update(LMITR[i],1);
if(i==1)
{
if(readi(1))
update(1,-readi(1));
}
else
update(i,readi(i-1)-readi(i));
}
for(i=0; i<q; i++)
printf("%d\n",ans[i]);
}
VI arr[1000009];
int mymap[1000009]={},counter=0,flag[1000009]={},siz[1000009]={};
string str;
int dfs1(int p)
{
flag[p]=1;
if(siz[p]!=-1)return siz[p];
int i,ret=1;
for(i=0; i<arr[p].size(); i++)
if(flag[arr[p][i]]==0)ret+=dfs1(arr[p][i]);
siz[p]=ret;
return ret;
}
void dfs(int p)
{
int j,i;
stack < int > mystack;
mystack.push(p);
flag[p]=1;
while(!mystack.empty())
{
i=mystack.top();
mystack.pop();
mymap[i]=counter;
counter++;
for(int j=0;j<arr[i].size();j++)
{
if(flag[arr[i][j]]==0)
mystack.push(arr[i][j]),flag[arr[i][j]]=1;
}
}
}
int temp[1000009]={};
int main()
{
int n,q,i,j,u,v,root,k;
sl(n),sl(q),sl(root);
root--;
for(i=1; i<n; i++)
{
sl(u),sl(v);
u--,v--;
arr[u].pb(v);
arr[v].pb(u);
}
for(i=0; i<n; i++)
sl(temp[i]);
dfs(root);
memset(siz,-1,sizeof(siz));
memset(flag,0,sizeof(flag));
dfs1(root);
for(i=1; i<=n; i++)
{
ar[mymap[i-1]+1]=temp[i-1];
}
vector < pair < pair < int ,int > , int > > query;
for(i=0; i<q; i++)
{
scanf("%d",&j);
query.pb(mp(mp(mymap[j-1]+1,mymap[j-1]+siz[j-1]),i));
}
foo(n,q,query);
return 0;
}
</code></pre>
| 0 |
101feb14-coloring-tree
|
2014-03-03T16:23:22
|
{"contest_participation":1550,"challenge_submissions":146,"successful_submissions":86}
|
2014-03-03T16:23:22
|
2016-05-13T00:03:32
|
setter
|
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#include<vector>
#include<string.h>
using namespace std;
#define Max_N 1000001
#define INF 1000000000
int N,color[Max_N],root,from,to,counter,parent[Max_N],s,q,search_here[Max_N],highest,last_occurence[Max_N],where,val,ind ,seg[1<<21],power[25],level,answer[Max_N];
vector<int> myvector[Max_N];
struct transfer
{
int start,end;
}Node[Max_N];
typedef struct queries qu;
struct queries
{
int ind ,left,right;
bool operator<(const qu q)const{
return right<q.right;
}
}Q[Max_N];
void DFS(int rooti)
{
Node[rooti].start=counter;
counter++;
while(!myvector[rooti].empty()){
to=myvector[rooti].back();
if(to!=parent[rooti]){
parent[to]=rooti;
DFS(to);
}
myvector[rooti].pop_back();
}
Node[rooti].end=counter-1;
}
int search(int low,int high,int s)
{
int mid=(low+high)>>1;
if(search_here[mid]==s) return mid;
else if(search_here[mid]>s) return search(low,mid-1,s);
else return search(mid+1,high,s);
}
void constant()
{
power[0]=1;
for(int i=1;i<=23;i++) power[i]=power[i-1]<<1;
}
void obtain(int x)
{
int y=x;
level=0;
while(x){
x>>=1;
level++;
}
if(power[level-1]!=y) level++;
}
void update(int pos,int val)
{
seg[pos]=val;
pos=pos>>1;
while(pos){
seg[pos]=seg[pos<<1]+seg[(pos<<1)+1];
pos>>=1;
}
return;
}
int Query(int s,int e,int i,int j,int node)
{
if(i>e || s>j) return 0;
if(s>=i && j>=e) return seg[node];
return (Query(s,((s+e)>>1),i,j,(node<<1))+Query(((s+e)>>1)+1,e,i,j,(node<<1)+1));
}
int main()
{
int v;
scanf("%d%d%d",&N,&q,&root);
//connections
for(int i=1;i<N;i++){
scanf("%d%d",&from,&to);
myvector[from].push_back(to);
myvector[to].push_back(from);
}
counter=1;
parent[root]=root;
DFS(root);
//color of the graph
for(int i=1;i<=N;i++){
scanf("%d",&v);
color[Node[i].start]=v;
search_here[i]=v; //finally i need to sort so no troubles
}
for(int i=0;i<q;i++){
scanf("%d",&s);
Q[i].ind =i;
Q[i].left=Node[s].start;
Q[i].right=Node[s].end;
}
sort(Q,Q+q);
sort(search_here+1,search_here+N+1);
highest=2;
for(int i=2;i<=N;i++){
if(search_here[i]==search_here[highest-1]) continue;
else{
search_here[highest]=search_here[i];
highest++;
}
}
highest--;
where=0;
constant();
obtain(N);
for(int i=0;i<=N;i++) last_occurence[i]=-INF;
memset(seg,0,sizeof(seg));
//search in search_here from 1 to highest ind ed
for(int i=1;i<=N;i++){
val=color[i];
ind =search(1,highest,val);
if(last_occurence[ind ]<0){
last_occurence[ind]=i;
update(power[level-1]+last_occurence[ind]-1,1);
}
else{
update(power[level-1]-1+last_occurence[ind ],0);
last_occurence[ind]=i;
update(power[level-1]-1+last_occurence[ind ],1);
}
while(Q[where].right==i){
answer[Q[where].ind]=Query(1,power[level-1],Q[where].left,Q[where].right,1);
where++;
}
}
for(int i=0;i<q;i++) printf("%d\n",answer[i]);
return 0;
}
|
not-set
|
2016-04-24T02:02:16
|
2016-04-24T02:02:16
|
C++
|
||||
35 | 1,071 |
coloring-tree
|
Coloring Tree
|
You are given a tree with **N** nodes with every node being colored. A color is represented by an integer ranging from 1 to 10<sup>9</sup>. Can you find the number of distinct colors available in a subtree rooted at the node **s**?
**Input Format**
The first line contains three space separated integers representing the number of nodes in the tree (**N**), number of queries to answer (**M**) and the root of the tree.
In each of the next N-1 lines, there are two space separated integers(a b) representing an edge from node a to Node b.
N lines follow: N+i<sup>th</sup> line contains the color of the i<sup>th</sup> node.
M lines follow: Each line containg a single integer s.
**Output Format**
Output exactly M lines, each line containing the output of the i<sub>th</sub> query.
**Constraints**
0=< M <= 10<sup>5</sup><br>
1=< N <= 10<sup>5</sup><br>
1=< root <= N<br>
1=< color of the Node <= 10<sup>9</sup><br>
**Example**
**Sample Input**
4 2 1
1 2
2 4
2 3
10
20
20
30
1
2
**Sample Output**
3
2
**Explanation**
Query 1-Subtree rooted at 1 is the entire tree and colors used are 10 20 20 30 , so the answer is 3(10,20 and 30)
Query 2-Subtree rooted at 2 contains color 20 20 30, so the answer is 2(20 and 30)
|
code
|
Given a tree with all nodes colored, find the number of distinct colors rooted at a given node.
|
ai
|
2013-10-12T06:23:17
|
2022-09-02T10:00:36
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER_ARRAY.
# The function accepts following parameters:
# 1. 2D_INTEGER_ARRAY tree
# 2. INTEGER_ARRAY color
# 3. INTEGER_ARRAY s
#
def solve(tree, color, s):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
r = int(first_multiple_input[2])
tree = []
for _ in range(n - 1):
tree.append(list(map(int, input().rstrip().split())))
color = []
for _ in range(n):
color_item = int(input().strip())
color.append(color_item)
s = []
for _ in range(m):
s_item = int(input().strip())
s.append(s_item)
result = solve(tree, color, s)
fptr.write('\n'.join(map(str, result)))
fptr.write('\n')
fptr.close()
|
You are given a tree with **N** nodes with every node being colored. A color is represented by an integer ranging from 1 to 10<sup>9</sup>. Can you find the number of distinct colors available in a subtree rooted at the node **s**?
**Input Format**
The first line contains three space separated integers representing the number of nodes in the tree (**N**), number of queries to answer (**M**) and the root of the tree.
In each of the next N-1 lines, there are two space separated integers(a b) representing an edge from node a to Node b and vice-versa.
N lines follow: N+i<sup>th</sup> line contains the color of the i<sup>th</sup> node.
M lines follow: Each line containg a single integer s.
**Output Format**
Output exactly M lines, each line containing the output of the i<sub>th</sub> query.
**Constraints**
0 <= M <= 10<sup>5</sup><br>
1 <= N <= 10<sup>5</sup><br>
1 <= root <= N<br>
1 <= color of the Node <= 10<sup>9</sup><br>
**Example**
**Sample Input**
4 2 1
1 2
2 4
2 3
10
20
20
30
1
2
**Sample Output**
3
2
**Explanation**
Query 1-Subtree rooted at 1 is the entire tree and colors used are 10 20 20 30 , so the answer is 3(10,20 and 30)
Query 2-Subtree rooted at 2 contains color 20 20 30, so the answer is 2(20 and 30)
| 0.413793 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
|
Coloring Tree - 101 Hack February Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Difficulty Level</strong> : Medium <br>
<strong>Required Knowledge</strong> : DFS and Segment Trees<br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/devuy11">Devendra Agarwal</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/darkshadows">Lalit Kundu</a> <br></p>
<p>Store the order in which you execute DFS starting from the given root.Now observe that each subtree will correspond to the sub-array of the array formed by DFS. Store the starting and ending position for each subtree in the array.</p>
<p>Now the question reduces to finding the number of distinct value in the sub-array.</p>
<p>Note that atmax 10^5 different colors are used as N<=10^5 ,so store the colors used in the tree and map it to an integer from 1 to 10^5.Now the question is to find number of distinct values in the sub-array given that all the values are from 1 to 10^5.</p>
<p>The result of a query [a, b] is number of integers whose last occurrence in [1, b] is >= a(Last Occurence in [1,b] is in [a,b]).</p>
<p>Let's have two kinds of events: QueryEvent and NumberEvent. First we read whole input and sort all events, the key for QueryEvents are their end (i.e. b for query [a, b]), and for NumberEvents the key is their position in array.</p>
<p>We also have a segment tree which answers the queries of kind: how many elements are at position range [x, y]. Initially the tree is empty.</p>
<p>Then we process events in order:<br>
<strong>a</strong>. When we meet a NumberEvent:<br>
1. If number has occurred before ,then we put 0 in that position of seg tree and update the tree.<br>
2. We put 1 in position of number in the segment tree.<br>
<strong>b</strong>.When we meet a QueryEvent:<br>
- Query the segment tree (for finding number of 1's in the range), and find the answer.<br></p>
<p><strong>Setter's Code</strong> </p>
<pre><code>#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#include<vector>
#include<string.h>
using namespace std;
#define Max_N 1000001
#define INF 1000000000
int N,color[Max_N],root,from,to,counter,parent[Max_N],s,q,search_here[Max_N],highest,last_occurence[Max_N],where,val,ind ,seg[1<<21],power[25],level,answer[Max_N];
vector<int> myvector[Max_N];
struct transfer
{
int start,end;
}Node[Max_N];
typedef struct queries qu;
struct queries
{
int ind ,left,right;
bool operator<(const qu q)const{
return right<q.right;
}
}Q[Max_N];
void DFS(int rooti)
{
Node[rooti].start=counter;
counter++;
while(!myvector[rooti].empty()){
to=myvector[rooti].back();
if(to!=parent[rooti]){
parent[to]=rooti;
DFS(to);
}
myvector[rooti].pop_back();
}
Node[rooti].end=counter-1;
}
int search(int low,int high,int s)
{
int mid=(low+high)>>1;
if(search_here[mid]==s) return mid;
else if(search_here[mid]>s) return search(low,mid-1,s);
else return search(mid+1,high,s);
}
void constant()
{
power[0]=1;
for(int i=1;i<=23;i++) power[i]=power[i-1]<<1;
}
void obtain(int x)
{
int y=x;
level=0;
while(x){
x>>=1;
level++;
}
if(power[level-1]!=y) level++;
}
void update(int pos,int val)
{
seg[pos]=val;
pos=pos>>1;
while(pos){
seg[pos]=seg[pos<<1]+seg[(pos<<1)+1];
pos>>=1;
}
return;
}
int Query(int s,int e,int i,int j,int node)
{
if(i>e || s>j) return 0;
if(s>=i && j>=e) return seg[node];
return (Query(s,((s+e)>>1),i,j,(node<<1))+Query(((s+e)>>1)+1,e,i,j,(node<<1)+1));
}
int main()
{
int v;
scanf("%d%d%d",&N,&q,&root);
//connections
for(int i=1;i<N;i++){
scanf("%d%d",&from,&to);
myvector[from].push_back(to);
myvector[to].push_back(from);
}
counter=1;
parent[root]=root;
DFS(root);
//color of the graph
for(int i=1;i<=N;i++){
scanf("%d",&v);
color[Node[i].start]=v;
search_here[i]=v; //finally i need to sort so no troubles
}
for(int i=0;i<q;i++){
scanf("%d",&s);
Q[i].ind =i;
Q[i].left=Node[s].start;
Q[i].right=Node[s].end;
}
sort(Q,Q+q);
sort(search_here+1,search_here+N+1);
highest=2;
for(int i=2;i<=N;i++){
if(search_here[i]==search_here[highest-1]) continue;
else{
search_here[highest]=search_here[i];
highest++;
}
}
highest--;
where=0;
constant();
obtain(N);
for(int i=0;i<=N;i++) last_occurence[i]=-INF;
memset(seg,0,sizeof(seg));
//search in search_here from 1 to highest ind ed
for(int i=1;i<=N;i++){
val=color[i];
ind =search(1,highest,val);
if(last_occurence[ind ]<0){
last_occurence[ind]=i;
update(power[level-1]+last_occurence[ind]-1,1);
}
else{
update(power[level-1]-1+last_occurence[ind ],0);
last_occurence[ind]=i;
update(power[level-1]-1+last_occurence[ind ],1);
}
while(Q[where].right==i){
answer[Q[where].ind]=Query(1,power[level-1],Q[where].left,Q[where].right,1);
where++;
}
}
for(int i=0;i<q;i++) printf("%d\n",answer[i]);
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong> </p>
<pre><code>/*
Author:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%% LALIT KUNDU %%%%%%%%
%%%%%%%% IIIT HYDERABAD %%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<vector>
#include<cassert>
#include<sstream>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<algorithm>
using namespace std;
#define pb push_back
#define mp make_pair
#define clr(x) x.clear()
#define sz(x) ((int)(x).size())
#define F first
#define S second
#define REP(i,a,b) for(i=a;i<b;i++)
#define rep(i,b) for(i=0;i<b;i++)
#define rep1(i,b) for(i=1;i<=b;i++)
#define mod 1000000007
#define pdn(n) printf("%d\n",n)
#define sl(n) scanf("%d",&n)
#define sd(n) scanf("%d",&n)
#define pn printf("\n")
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<int> VI;
typedef vector<VI> VVI;
typedef long long LL;
#define INF 1000000007
int LMITR[1000009];
map < int ,int > PI;
#define MAX 10000009
int tree[MAX+1]={};
void update(int idx, int val) {
while (idx <= MAX) {
tree[idx] += val;
idx += (idx & -idx);
}
}
int readi(int idx) {
int sum = 0;
while (idx > 0) {
sum +=(int) tree[idx];
idx -= (idx & -idx);
}
return sum;
}
int to[1000005],ar[1000009];
void foo(int n, int q, vector < pair < pair < int,int >, int > > qu)
{
int i;
for(i=n; i>=1; i--)
{
if(PI.count(ar[i])==0)
LMITR[i]=INF;
else LMITR[i]=PI[ar[i]];
PI[ar[i]]=i;
}
PI.clear();
for(i=1; i<=n; i++)
if(PI.count(ar[i])==0)
PI[ar[i]]=1,update(i,1);
sort(qu.begin(),qu.end());
int cur=0,ans[1000007];
for(i=1; i<=n; i++)
{
while(cur<q && qu[cur].F.F==i)
{
ans[qu[cur].S]=readi(qu[cur].F.S);
cur++;
}
if(LMITR[i]!=INF)
update(LMITR[i],1);
if(i==1)
{
if(readi(1))
update(1,-readi(1));
}
else
update(i,readi(i-1)-readi(i));
}
for(i=0; i<q; i++)
printf("%d\n",ans[i]);
}
VI arr[1000009];
int mymap[1000009]={},counter=0,flag[1000009]={},siz[1000009]={};
string str;
int dfs1(int p)
{
flag[p]=1;
if(siz[p]!=-1)return siz[p];
int i,ret=1;
for(i=0; i<arr[p].size(); i++)
if(flag[arr[p][i]]==0)ret+=dfs1(arr[p][i]);
siz[p]=ret;
return ret;
}
void dfs(int p)
{
int j,i;
stack < int > mystack;
mystack.push(p);
flag[p]=1;
while(!mystack.empty())
{
i=mystack.top();
mystack.pop();
mymap[i]=counter;
counter++;
for(int j=0;j<arr[i].size();j++)
{
if(flag[arr[i][j]]==0)
mystack.push(arr[i][j]),flag[arr[i][j]]=1;
}
}
}
int temp[1000009]={};
int main()
{
int n,q,i,j,u,v,root,k;
sl(n),sl(q),sl(root);
root--;
for(i=1; i<n; i++)
{
sl(u),sl(v);
u--,v--;
arr[u].pb(v);
arr[v].pb(u);
}
for(i=0; i<n; i++)
sl(temp[i]);
dfs(root);
memset(siz,-1,sizeof(siz));
memset(flag,0,sizeof(flag));
dfs1(root);
for(i=1; i<=n; i++)
{
ar[mymap[i-1]+1]=temp[i-1];
}
vector < pair < pair < int ,int > , int > > query;
for(i=0; i<q; i++)
{
scanf("%d",&j);
query.pb(mp(mp(mymap[j-1]+1,mymap[j-1]+siz[j-1]),i));
}
foo(n,q,query);
return 0;
}
</code></pre>
| 0 |
101feb14-coloring-tree
|
2014-03-03T16:23:22
|
{"contest_participation":1550,"challenge_submissions":146,"successful_submissions":86}
|
2014-03-03T16:23:22
|
2016-05-13T00:03:32
|
tester
|
/*
Author:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%% LALIT KUNDU %%%%%%%%
%%%%%%%% IIIT HYDERABAD %%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<iostream>
#include<vector>
#include<cassert>
#include<sstream>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<algorithm>
using namespace std;
#define pb push_back
#define mp make_pair
#define clr(x) x.clear()
#define sz(x) ((int)(x).size())
#define F first
#define S second
#define REP(i,a,b) for(i=a;i<b;i++)
#define rep(i,b) for(i=0;i<b;i++)
#define rep1(i,b) for(i=1;i<=b;i++)
#define mod 1000000007
#define pdn(n) printf("%d\n",n)
#define sl(n) scanf("%d",&n)
#define sd(n) scanf("%d",&n)
#define pn printf("\n")
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<int> VI;
typedef vector<VI> VVI;
typedef long long LL;
#define INF 1000000007
int LMITR[1000009];
map < int ,int > PI;
#define MAX 10000009
int tree[MAX+1]={};
void update(int idx, int val) {
while (idx <= MAX) {
tree[idx] += val;
idx += (idx & -idx);
}
}
int readi(int idx) {
int sum = 0;
while (idx > 0) {
sum +=(int) tree[idx];
idx -= (idx & -idx);
}
return sum;
}
int to[1000005],ar[1000009];
void foo(int n, int q, vector < pair < pair < int,int >, int > > qu)
{
int i;
for(i=n; i>=1; i--)
{
if(PI.count(ar[i])==0)
LMITR[i]=INF;
else LMITR[i]=PI[ar[i]];
PI[ar[i]]=i;
}
PI.clear();
for(i=1; i<=n; i++)
if(PI.count(ar[i])==0)
PI[ar[i]]=1,update(i,1);
sort(qu.begin(),qu.end());
int cur=0,ans[1000007];
for(i=1; i<=n; i++)
{
while(cur<q && qu[cur].F.F==i)
{
ans[qu[cur].S]=readi(qu[cur].F.S);
cur++;
}
if(LMITR[i]!=INF)
update(LMITR[i],1);
if(i==1)
{
if(readi(1))
update(1,-readi(1));
}
else
update(i,readi(i-1)-readi(i));
}
for(i=0; i<q; i++)
printf("%d\n",ans[i]);
}
VI arr[1000009];
int mymap[1000009]={},counter=0,flag[1000009]={},siz[1000009]={};
string str;
int dfs1(int p)
{
flag[p]=1;
if(siz[p]!=-1)return siz[p];
int i,ret=1;
for(i=0; i<arr[p].size(); i++)
if(flag[arr[p][i]]==0)ret+=dfs1(arr[p][i]);
siz[p]=ret;
return ret;
}
void dfs(int p)
{
int j,i;
stack < int > mystack;
mystack.push(p);
flag[p]=1;
while(!mystack.empty())
{
i=mystack.top();
mystack.pop();
mymap[i]=counter;
counter++;
for(int j=0;j<arr[i].size();j++)
{
if(flag[arr[i][j]]==0)
mystack.push(arr[i][j]),flag[arr[i][j]]=1;
}
}
}
int temp[1000009]={};
int main()
{
int n,q,i,j,u,v,root,k;
sl(n),sl(q),sl(root);
root--;
for(i=1; i<n; i++)
{
sl(u),sl(v);
u--,v--;
arr[u].pb(v);
arr[v].pb(u);
}
for(i=0; i<n; i++)
sl(temp[i]);
dfs(root);
memset(siz,-1,sizeof(siz));
memset(flag,0,sizeof(flag));
dfs1(root);
for(i=1; i<=n; i++)
{
ar[mymap[i-1]+1]=temp[i-1];
}
vector < pair < pair < int ,int > , int > > query;
for(i=0; i<q; i++)
{
scanf("%d",&j);
query.pb(mp(mp(mymap[j-1]+1,mymap[j-1]+siz[j-1]),i));
}
foo(n,q,query);
return 0;
}
|
not-set
|
2016-04-24T02:02:16
|
2016-04-24T02:02:16
|
C++
|
||||
36 | 1,148 |
xoring-ninja
|
Xoring Ninja
|
Given a list containing N integers, calculate the XOR\_SUM of all the non-empty subsets of the list and print the value of sum % (10<sup>9</sup> + 7).
XOR operation on a list (or a subset of the list) is defined as the XOR of all the elements present in it. <br>
E.g. XOR of list containing elements {A,B,C} = ((A^B)^C), where ^ represents `XOR`.
E.g. XOR\_SUM of list A having three elements {X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>} can be given as follows.<br>
All non-empty subsets will be *{X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>, (X<sub>1</sub>,X<sub>2</sub>), (X<sub>2</sub>,X<sub>3</sub>), (X<sub>1</sub>,X<sub>3</sub>), (X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>)}*
XOR\_SUM(A) = X<sub>1</sub> + X<sub>2</sub> + X<sub>3</sub> + X<sub>1</sub>^X<sub>2</sub> + X<sub>2</sub>^X<sub>3</sub> + X<sub>1</sub>^X<sub>3</sub> + ((X<sub>1</sub>^X<sub>2</sub>)^X<sub>3</sub>)
**Input Format**
An integer T, denoting the number of testcases. 2T lines follow.<br>
Each testcase contains two lines, first line will contains an integer N
followed by second line containing N integers separated by a single space.<br>
**Output Format**
T lines, i<sup>th</sup> line containing the output of the i<sup>th</sup> testcase.<br>
**Constraints**
1 <= T <= 5<br>
1 <= N <= 10<sup>5</sup><br>
0 <= A[i] <= 10<sup>9</sup><br>
**Sample Input #00**
1
3
1 2 3
**Sample Output #00**
12
**Explanation**
The given case will have 7 non-empty subsets whose XOR is given below<br>
1 = 1
2 = 2
3 = 3
1^2 = 3
2^3 = 1
3^1 = 2
1^2^3 = 0
So sum of all such XORs is 12.
|
code
|
Given a list of integers, sum the XORs of all the list's non-empty subsets and mod your answer by 10^9 + 7.
|
ai
|
2013-10-22T17:20:15
|
2022-08-31T08:14:58
|
#
# Complete the 'xoringNinja' function below.
#
# The function is expected to return an INTEGER.
# The function accepts INTEGER_ARRAY arr as parameter.
#
def xoringNinja(arr):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
arr_count = int(input().strip())
arr = list(map(int, input().rstrip().split()))
result = xoringNinja(arr)
fptr.write(str(result) + '\n')
fptr.close()
|
An [XOR](https://en.wikipedia.org/wiki/Exclusive_or) operation on a list is defined here as the *xor* ($\oplus$) of all its elements (e.g.: $XOR(\{A, B, C\}) = A \oplus B \oplus C$).
The $XorSum$ of set $arr$ is defined here as the sum of the $XOR$s of all non-empty subsets of $arr$ known as $arr'$. The set $arr'$ can be expressed as:
$\begin{eqnarray} XorSum(arr) = \sum_{i = 1}^{2^n-1} XOR(arr'_i) = XOR(arr'_1) + XOR(arr'_2) + \dots + XOR(arr'_{2^n-2}) + XOR(arr'_{2^n-1}) \end{eqnarray}$
**For example:** Given set $arr = \{n_1, n_2, n_3\}$
- The set of possible non-empty subsets is: $arr' = \{\{n_1\}, \{n_2\}, \{n_3\}, \{n_1, n_2\}, \{n_1, n_3\}, \{n_2, n_3\}, \{n_1, n_2, n_3\}\}$
- The $XorSum$ of these non-empty subsets is then calculated as follows:
$XorSum(arr)$ = $ n_1 + n_2 + n_3 + (n_1 \oplus n_2) + (n_1 \oplus n_3) + (n_2 \oplus n_3) + (n_1 \oplus n_2 \oplus n_3)$
Given a list of $n$ space-separated integers, determine and print $XorSum\ \%\ (10^9+7)$.
For example, $arr = \{3,4\}$. There are three possible subsets, $arr' = \{\{3\},\{4\},\{3,4\}\}$. The XOR of $arr'[1] = 3$, of $arr'[2] = 4$ and of $arr[3] = 3 \oplus 4 = 7$. The XorSum is the sum of these: $3 + 4 + 7 = 14$ and $14\ \%\ (10^9+7) = 14$.
**Note:** The cardinality of [powerset](https://en.wikipedia.org/wiki/Power_set)$(n)$ is $2^n$, so the set of non-empty subsets of set $arr$ of size $n$ contains $2^n-1$ subsets.
**Function Description**
Complete the *xoringNinja* function in the editor below. It should return an integer that represents the XorSum of the input array, modulo $(10^9+7)$.
xoringNinja has the following parameter(s):
- *arr*: an integer array
| 0.492408 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains an integer $T$, the number of test cases.
Each test case consists of two lines:
- The first line contains an integer $n$, the size of the set $arr$.
- The second line contains $n$ space-separated integers $arr[i]$.
|
For each test case, print its $XorSum\ \%\ (10^9+7)$ on a new line. The $i^{th}$ line should contain the output for the $i^{th}$ test case.
|
1
3
1 2 3
|
12
|
Hard
|
Xoring Ninja 2020 Hack March Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p>Description: We have to find the sum of all subsets in which elements of each subset are XORed together. Fint it <a href="https://www.hackerrank.com/contests/mar14/challenges/xoring-ninja">here</a>.</p>
<p><strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/shashank21j">Shashank Sharma</a></p>
<p><strong>Problem Editorialist</strong> : Tusshar Singh</p>
<p><strong>Time Complexity</strong> : O(N) per test cases.</p>
<p>Solution: Find OR of all the elements and multiply it with 2^(n-1) where n is the total number of elements. This gives us the answer.</p>
<p>Idea: </p>
<p>There will be total 2^n subsets.<br>
If ith bit of any element is set, then that bit will be set in xor of half of the total subsets which is 2^(n-1).<br>
To find out all the set bits in all the numbers we find OR of all the numbers.<br>
Since each set bit appears in half of the total subsets we multiply OR of all numbers with 2^n-1 to get the final result.</p>
<p>Code:</p>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
#define MOD 1000000007
long long int power(long long int n, long long int k)
{
long long int result, pow;
if(k==0)
return 1;
if(n==0)
return 0;
if(n==1)
return 1;
result=n%MOD;
pow=1;
while(pow*2<=k)
{
pow=pow*2;
result=(result*result);
result=result%MOD;
}
if(k-pow!=0)
result=result*power(n, k-pow);
result=result%MOD;
return result;
}
int main() {
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
long long ans=0,temp;
for(int i=0;i<n;i++)
{
cin>>temp;
ans|=temp;
}
ans*=power(2,n-1);
ans%=MOD;
cout<<ans<<"\n";
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong> :</p>
<pre><code>#!/usr/bin
from math import *
t=int(raw_input())
assert(t<=5)
assert(t>=1)
for i in range(0,t):
n=int(raw_input())
assert(n<=10**5)
assert(n>=1)
a=[]
b=[]
for j in range(0,int(log(10**9,2)+1)):
b=[0]*n
a.append(b)
number=map(int, raw_input().split())
for j in range(0,n):
z=number[j]
assert(z>=0)
assert(z<=10**9)
k=0
while(z>0):
a[k][j]=z&1
z>>=1
k+=1
sum1=0
for j in range(0,int(log(10**9,2)+1)):
od=0
for k in range(0,n):
if(a[j][k]==1):
od=1
break
if od!=0:
sum1=(sum1+ 2**(j+n-1))%1000000007
print sum1
</code></pre>
| 0 |
mar14-xoring-ninja
|
2014-03-23T17:52:57
|
{"contest_participation":2080,"challenge_submissions":577,"successful_submissions":438}
|
2014-03-23T17:52:57
|
2018-05-08T18:32:33
|
setter
|
###C++
```cpp
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
#define MOD 1000000007
long long int power(long long int n, long long int k)
{
long long int result, pow;
if(k==0)
return 1;
if(n==0)
return 0;
if(n==1)
return 1;
result=n%MOD;
pow=1;
while(pow*2<=k)
{
pow=pow*2;
result=(result*result);
result=result%MOD;
}
if(k-pow!=0)
result=result*power(n, k-pow);
result=result%MOD;
return result;
}
int main() {
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
long long ans=0,temp;
for(int i=0;i<n;i++)
{
cin>>temp;
ans|=temp;
}
ans*=power(2,n-1);
ans%=MOD;
cout<<ans<<"\n";
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:35
|
2016-07-23T16:10:37
|
C++
|
37 | 1,148 |
xoring-ninja
|
Xoring Ninja
|
Given a list containing N integers, calculate the XOR\_SUM of all the non-empty subsets of the list and print the value of sum % (10<sup>9</sup> + 7).
XOR operation on a list (or a subset of the list) is defined as the XOR of all the elements present in it. <br>
E.g. XOR of list containing elements {A,B,C} = ((A^B)^C), where ^ represents `XOR`.
E.g. XOR\_SUM of list A having three elements {X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>} can be given as follows.<br>
All non-empty subsets will be *{X<sub>1</sub>, X<sub>2</sub>, X<sub>3</sub>, (X<sub>1</sub>,X<sub>2</sub>), (X<sub>2</sub>,X<sub>3</sub>), (X<sub>1</sub>,X<sub>3</sub>), (X<sub>1</sub>,X<sub>2</sub>,X<sub>3</sub>)}*
XOR\_SUM(A) = X<sub>1</sub> + X<sub>2</sub> + X<sub>3</sub> + X<sub>1</sub>^X<sub>2</sub> + X<sub>2</sub>^X<sub>3</sub> + X<sub>1</sub>^X<sub>3</sub> + ((X<sub>1</sub>^X<sub>2</sub>)^X<sub>3</sub>)
**Input Format**
An integer T, denoting the number of testcases. 2T lines follow.<br>
Each testcase contains two lines, first line will contains an integer N
followed by second line containing N integers separated by a single space.<br>
**Output Format**
T lines, i<sup>th</sup> line containing the output of the i<sup>th</sup> testcase.<br>
**Constraints**
1 <= T <= 5<br>
1 <= N <= 10<sup>5</sup><br>
0 <= A[i] <= 10<sup>9</sup><br>
**Sample Input #00**
1
3
1 2 3
**Sample Output #00**
12
**Explanation**
The given case will have 7 non-empty subsets whose XOR is given below<br>
1 = 1
2 = 2
3 = 3
1^2 = 3
2^3 = 1
3^1 = 2
1^2^3 = 0
So sum of all such XORs is 12.
|
code
|
Given a list of integers, sum the XORs of all the list's non-empty subsets and mod your answer by 10^9 + 7.
|
ai
|
2013-10-22T17:20:15
|
2022-08-31T08:14:58
|
#
# Complete the 'xoringNinja' function below.
#
# The function is expected to return an INTEGER.
# The function accepts INTEGER_ARRAY arr as parameter.
#
def xoringNinja(arr):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
arr_count = int(input().strip())
arr = list(map(int, input().rstrip().split()))
result = xoringNinja(arr)
fptr.write(str(result) + '\n')
fptr.close()
|
An [XOR](https://en.wikipedia.org/wiki/Exclusive_or) operation on a list is defined here as the *xor* ($\oplus$) of all its elements (e.g.: $XOR(\{A, B, C\}) = A \oplus B \oplus C$).
The $XorSum$ of set $arr$ is defined here as the sum of the $XOR$s of all non-empty subsets of $arr$ known as $arr'$. The set $arr'$ can be expressed as:
$\begin{eqnarray} XorSum(arr) = \sum_{i = 1}^{2^n-1} XOR(arr'_i) = XOR(arr'_1) + XOR(arr'_2) + \dots + XOR(arr'_{2^n-2}) + XOR(arr'_{2^n-1}) \end{eqnarray}$
**For example:** Given set $arr = \{n_1, n_2, n_3\}$
- The set of possible non-empty subsets is: $arr' = \{\{n_1\}, \{n_2\}, \{n_3\}, \{n_1, n_2\}, \{n_1, n_3\}, \{n_2, n_3\}, \{n_1, n_2, n_3\}\}$
- The $XorSum$ of these non-empty subsets is then calculated as follows:
$XorSum(arr)$ = $ n_1 + n_2 + n_3 + (n_1 \oplus n_2) + (n_1 \oplus n_3) + (n_2 \oplus n_3) + (n_1 \oplus n_2 \oplus n_3)$
Given a list of $n$ space-separated integers, determine and print $XorSum\ \%\ (10^9+7)$.
For example, $arr = \{3,4\}$. There are three possible subsets, $arr' = \{\{3\},\{4\},\{3,4\}\}$. The XOR of $arr'[1] = 3$, of $arr'[2] = 4$ and of $arr[3] = 3 \oplus 4 = 7$. The XorSum is the sum of these: $3 + 4 + 7 = 14$ and $14\ \%\ (10^9+7) = 14$.
**Note:** The cardinality of [powerset](https://en.wikipedia.org/wiki/Power_set)$(n)$ is $2^n$, so the set of non-empty subsets of set $arr$ of size $n$ contains $2^n-1$ subsets.
**Function Description**
Complete the *xoringNinja* function in the editor below. It should return an integer that represents the XorSum of the input array, modulo $(10^9+7)$.
xoringNinja has the following parameter(s):
- *arr*: an integer array
| 0.492408 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains an integer $T$, the number of test cases.
Each test case consists of two lines:
- The first line contains an integer $n$, the size of the set $arr$.
- The second line contains $n$ space-separated integers $arr[i]$.
|
For each test case, print its $XorSum\ \%\ (10^9+7)$ on a new line. The $i^{th}$ line should contain the output for the $i^{th}$ test case.
|
1
3
1 2 3
|
12
|
Hard
|
Xoring Ninja 2020 Hack March Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p>Description: We have to find the sum of all subsets in which elements of each subset are XORed together. Fint it <a href="https://www.hackerrank.com/contests/mar14/challenges/xoring-ninja">here</a>.</p>
<p><strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/shashank21j">Shashank Sharma</a></p>
<p><strong>Problem Editorialist</strong> : Tusshar Singh</p>
<p><strong>Time Complexity</strong> : O(N) per test cases.</p>
<p>Solution: Find OR of all the elements and multiply it with 2^(n-1) where n is the total number of elements. This gives us the answer.</p>
<p>Idea: </p>
<p>There will be total 2^n subsets.<br>
If ith bit of any element is set, then that bit will be set in xor of half of the total subsets which is 2^(n-1).<br>
To find out all the set bits in all the numbers we find OR of all the numbers.<br>
Since each set bit appears in half of the total subsets we multiply OR of all numbers with 2^n-1 to get the final result.</p>
<p>Code:</p>
<pre><code>#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
#define MOD 1000000007
long long int power(long long int n, long long int k)
{
long long int result, pow;
if(k==0)
return 1;
if(n==0)
return 0;
if(n==1)
return 1;
result=n%MOD;
pow=1;
while(pow*2<=k)
{
pow=pow*2;
result=(result*result);
result=result%MOD;
}
if(k-pow!=0)
result=result*power(n, k-pow);
result=result%MOD;
return result;
}
int main() {
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
long long ans=0,temp;
for(int i=0;i<n;i++)
{
cin>>temp;
ans|=temp;
}
ans*=power(2,n-1);
ans%=MOD;
cout<<ans<<"\n";
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong> :</p>
<pre><code>#!/usr/bin
from math import *
t=int(raw_input())
assert(t<=5)
assert(t>=1)
for i in range(0,t):
n=int(raw_input())
assert(n<=10**5)
assert(n>=1)
a=[]
b=[]
for j in range(0,int(log(10**9,2)+1)):
b=[0]*n
a.append(b)
number=map(int, raw_input().split())
for j in range(0,n):
z=number[j]
assert(z>=0)
assert(z<=10**9)
k=0
while(z>0):
a[k][j]=z&1
z>>=1
k+=1
sum1=0
for j in range(0,int(log(10**9,2)+1)):
od=0
for k in range(0,n):
if(a[j][k]==1):
od=1
break
if od!=0:
sum1=(sum1+ 2**(j+n-1))%1000000007
print sum1
</code></pre>
| 0 |
mar14-xoring-ninja
|
2014-03-23T17:52:57
|
{"contest_participation":2080,"challenge_submissions":577,"successful_submissions":438}
|
2014-03-23T17:52:57
|
2018-05-08T18:32:33
|
tester
|
###Python 2
```python
#!/usr/bin
from math import *
t=int(raw_input())
assert(t<=5)
assert(t>=1)
for i in range(0,t):
n=int(raw_input())
assert(n<=10**5)
assert(n>=1)
a=[]
b=[]
for j in range(0,int(log(10**9,2)+1)):
b=[0]*n
a.append(b)
number=map(int, raw_input().split())
for j in range(0,n):
z=number[j]
assert(z>=0)
assert(z<=10**9)
k=0
while(z>0):
a[k][j]=z&1
z>>=1
k+=1
sum1=0
for j in range(0,int(log(10**9,2)+1)):
od=0
for k in range(0,n):
if(a[j][k]==1):
od=1
break
if od!=0:
sum1=(sum1+ 2**(j+n-1))%1000000007
print sum1
```
|
not-set
|
2016-04-24T02:02:35
|
2016-07-23T16:10:46
|
Python
|
38 | 1,767 |
ones-and-twos
|
Ones and Twos
|
You are using at most **A** number of 1s and at most **B** number of 2s. How many different evaluation results are possible when they are formed in an expression containing only addition `+` sign and multiplication `*` sign are allowed?
Note that, multiplication takes precedence over addition.
For example, if **A=2** and **B=2**, then we have the following expressions:
* `1`, `1*1` = 1
* `2`, `1*2`, `1*1*2`, `1+1` = 2
* `1+2`, `1+1*2` = 3
* `2+2`, `2*2`, `1+1+2`, `1*2*2`, `1*1*2*2`, `1*2+1*2`, `1*1*2+2`, `1*2+2` = 4
* `1+2+2`, `1+1*2+2` = 5
* `1+1+2+2`, `1+1+2*2` = 6
So there are 6 unique results that can be formed if A = 2 and B = 2.
**Input Format**
The first line contains the number of test cases T, T testcases follow each in a newline.
Each testcase contains 2 integers A and B separated by a single space.
**Output Format**
Print the number of different evaluations modulo (%) (10<sup>9</sup>+7.)
**Constraints**
1 <= T <= 10<sup>5</sup>
0<=A<=1000000000
0<=B<=1000
**Sample Input**
4
0 0
2 2
0 2
2 0
**Sample Output**
0
6
2
2
**Explanation**
+ When A = 0, B = 0, there are no expressions, hence 0.
+ When A = 2, B = 2, as explained in the problem statement above, expressions leads to 6 possible solutions.
+ When A = 0, B = 2, we have `2`, `2+2` or `2*2`, hence 2.
+ When A = 2, B = 0, we have `1` or `1*1`, `1+1` hence 2.
|
code
|
Using A 1's and B 2's how many different evaluations are possible only by performing addition and multiplication
|
ai
|
2014-01-29T15:42:24
|
2022-08-31T08:14:53
|
#
# Complete the 'onesAndTwos' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER a
# 2. INTEGER b
#
def onesAndTwos(a, b):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
a = int(first_multiple_input[0])
b = int(first_multiple_input[1])
result = onesAndTwos(a, b)
fptr.write(str(result) + '\n')
fptr.close()
|
You are using at most **A** number of 1s and at most **B** number of 2s. How many different evaluation results are possible when they are formed in an expression containing only addition `+` sign and multiplication `*` sign are allowed?
Note that, multiplication takes precedence over addition.
For example, if **A=2** and **B=2**, then we have the following expressions:
* `1`, `1*1` = 1
* `2`, `1*2`, `1*1*2`, `1+1` = 2
* `1+2`, `1+1*2` = 3
* `2+2`, `2*2`, `1+1+2`, `1*2*2`, `1*1*2*2`, `1*2+1*2`, `1*1*2+2`, `1*2+2` = 4
* `1+2+2`, `1+1*2+2` = 5
* `1+1+2+2`, `1+1+2*2` = 6
So there are 6 unique results that can be formed if A = 2 and B = 2.
| 0.545455 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains the number of test cases T, T testcases follow each in a newline.
Each testcase contains 2 integers A and B separated by a single space.
|
Print the number of different evaluations modulo (%) (10<sup>9</sup>+7.)
|
4
0 0
2 2
0 2
2 0
|
0
6
2
2
|
Hard
|
Ones and Twos - 2020 Hack March Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/mar14/challenges/ones-and-twos">Ones and Twos</a> <br>
<strong>Difficulty Level</strong> : Medium-Hard <br>
<strong>Required Knowledge</strong> : DP <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/tmt514">Shang En Huang</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/dsoboliev">Dmytro Soboliev</a> </p>
<p><strong>Solution</strong> </p>
<p>If you are still getting wrong answer but don't know why, please try this test case:</p>
<pre><code> 2
6 14
2 1
</code></pre>
<p>The answer should be </p>
<pre><code> 301
4
</code></pre>
<h3>Part I.</h3>
<p>Let's consider simple cases, say when <strong>A</strong> = 0. In this case, all numbers will be generated by using all 2's. For each integer <strong>X</strong>, consider its binary representation (a<sub>0</sub> + a<sub>1</sub>*2 + a<sub>2</sub>*4+a<sub>3</sub>*8+...). It's not hard to prove you need at least (a<sub>1</sub>*1 + a<sub>2</sub>*2+a<sub>3</sub>*3+...) number of 2's to produce this number.</p>
<p>Hence when given the value of <strong>B</strong> the answer should be:</p>
<blockquote>
<p>The number of ways partitioning <strong>i <= B</strong> into distinct sum of positive integers.</p>
</blockquote>
<p>This can be solved by <strong>O(B<sup>2</sup>)</strong> dynamic programming: Just let <code>dp[i][j]</code> be the number of ways partitioning <code>i</code> into distinct sum of positive integers with last term (highest bit) equal or less than <code>j</code>. So if we consider the state <code>dp[i][j]</code>, into two situations: the last term is <code>j</code> or not. If yes, there are exactly <code>dp[i-j][j-1]</code> ways. Otherwise it would be <code>dp[i][j-1]</code>. Please consider the following code:</p>
<p><strong>Language : C++</strong></p>
<pre><code>for (int j = 0; j <= B; j++) dp[0][j] = 1;
for (int i = 1; i <= B; i++)
for (int j = 1; j <= B; j++)
dp[i][j] = (i>j? dp[i-j][j-1] : 0) + dp[i][j-1];
</code></pre>
<p>Then in the case <strong>A=0</strong>, the solution can be calculated from <code>dp[1][B] + dp[2][B] + ... + dp[B][B]</code>. (Don't forget to mod.)</p>
<h3>Part II: O(T A lg A + B<sup>2</sup>)</h3>
<p>From now on, when we consider an integer, we only consider the representation with fewest 2's.</p>
<p>What if we have some 1's? If using only twos can make a number <strong>X</strong>, then we can build all integers in the ranage <strong>[X, X+A]</strong>. Suppose we have a number <strong>2<sup>K</sup></strong>, where <strong>2A < 2<sup>K</sup></strong>. We split the terms by "Terms less than*<em>2<sup>K</sup></em>* and terms no less than <strong>2<sup>K</sup></strong>". For terms less than <strong>2<sup>K</sup></strong>. We will know that the sum of all parts contributed by 2's will be less than <strong>2<sup>K</sup></strong> (Why?).</p>
<p>Hence, if we choose minimal <strong>K</strong> with <strong>2A < 2<sup>K</sup></strong>, then we can guarantee that the sum of whole part less than <strong>2<sup>K</sup></strong> will still less than <strong>2<sup>K</sup></strong>. (Given the condition that we use least number of 2's.)</p>
<p></p>
<p>For each <strong>t, 0 <= t < 2<sup>K</sup></strong>, let <strong>R[t]</strong> be the least number of 2's which can build <strong>t</strong>. Modify the DP table from part I: <code>dp[i][j]</code> be the number of ways partitioning <code>i</code> into distinct sum of positive integers with last term (highest bit) equal or less than <code>j</code> <em>and with first term (lowest bit) at least <b>K</b></em>.</p>
<pre><code>cpp
for (int j = 0; j <= B; j++) dp[0][j] = 1;
for (int i = 1; i <= B; i++)
for (int j = 1; j <= B; j++)
dp[i][j] = (j>=K && i>j ? dp[i-j][j-1] : 0) + dp[i][j-1];
</code></pre>
<p>In this <strong>t</strong>, the ways to make numbers that modulo <strong>2<sup>K</sup></strong> equals <strong>t</strong> is exactly <code>dp[1][B] + dp[2][B] + ... + dp[B - R[t]][B]</code>. (Please mod.)</p>
<p>We can easily get the relations <code>R[0] = R[1] = ... = R[A] = 0</code>, and for <strong>t > A</strong>,
<strong>R[t]</strong> = min<sub><strong>0 <= j < K</strong></sub>{ <strong>R[t-2<sup>j</sup>] + j</strong> }</p>
<p>In conclusion, for each test case, we can go over each <strong>0 <= t < 2<sup>K</sup></strong>. Then the time complexity is <strong>O(T K 2<sup>K</sup> + B^2) = O(T A lg A + B^2)</strong>.</p>
<h3>Part III: O(T lg A + B^2)</h3>
<p>The remaining parts:</p>
<ol>
<li>calculate <strong>R[0]..R[2<sup>K</sup>-1]</strong> efficiently</li>
<li>calculate the sum <strong>dp[ B-R[i] ][ B-R[i] ]</strong> efficiently</li>
</ol>
<p>In order to solve (2), we need to count "How many <strong>i</strong>'s are there such that <strong>R[i] = r</strong>?" for each <strong>r = 0, 1, ..., 2<sup>K</sup>-1</strong>.</p>
<p>(Maybe not) Surprisingly, we have the following properties:</p>
<p></p>
<blockquote>
<p><strong>Prop</strong>: for any integer no more than <strong>2<sup>K-1</sup></strong>, we only need at most one "2 term".</p>
<p><strong>Prop2</strong>: for any integer in <strong>(2<sup>K-1</sup>, 2<sup>K</sup>)</strong> we use at most two "2 terms".</p>
</blockquote>
<p>Hence we can find the sum with a single loop enumerating from 0 to K-1.</p>
<p>Happy thinking & happy coding :)</p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((int)(c).size())
typedef long long LL;
int MOD = 1e9+7;
int p[33][1005], up[33]={};
void add(int &x, LL v) {
x = (x+v)%MOD;
}
const int MXB = 1000;
void pre(int S) {
if(up[S]) return;
up[S] = 1;
p[S][0] = 1;
for(int l=S;l<=MXB;l++) {
for(int j=MXB;j>=l;j--)
add(p[S][j], p[S][j-l]);
}
for(int j=1;j<=MXB;j++) add(p[S][j], p[S][j-1]);
//printf("build: "); for(int j=0;j<=MXB;j++) printf("%d ", p[S][j]); puts("");
}
void solve() {
int A, B, s;
LL t;
scanf("%d%d", &A, &B);
if (A == 0) {
pre(1);
printf("%d\n", (p[1][B]+MOD-1)%MOD);
return;
}
for(t=2,s=1;t<=A;t*=2,s++);
t *= 2; s++;
pre(s);
//printf("s=%d\n", s);
int ans = 0;
LL last = 0, last2 = t/2+A+1;
for(int u=0;u<s && u<=B;u++) {
LL nxt = min(t, (1LL<<u) + A + (u>0));
LL nxt2 = min(t, (1LL<<u) + A + t/2 + (u>0));
add(ans, (nxt-last)*1LL*p[s][B-u]);
if(u+s-1<=B) add(ans, (nxt2-last2)*1LL*p[s][B-(u+s-1)]);
//printf("u=%d: [%I64d, %I64d) %d; [%I64d, %I64d) \n", u, last, nxt, p[s][B-u], last2, nxt2);
last = nxt;
last2 = nxt2;
}
//printf("nxt=%I64d\n", last);
printf("%d\n", (ans+MOD-1)%MOD);
}
int main(void) {
int T;
scanf("%d", &T);
while(T--) solve();
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <ctime>
#include <set>
#include <cassert>
using namespace std;
const int P = 1000000007;
const int maxN = 1100;
int d[maxN][maxN], s[maxN][maxN];
void precalc() {
d[maxN - 1][0] = 1;
for (int i = maxN - 1; i > 0; --i) {
for (int j = 0; j < maxN; ++j) {
if (d[i][j] == 0) {
continue;
}
d[i - 1][j] += d[i][j];
if (d[i - 1][j] >= P) {
d[i - 1][j] -= P;
}
if (j + (i - 1) < maxN) {
d[i - 1][j + (i - 1)] += d[i][j];
if (d[i - 1][j + (i - 1)] >= P) {
d[i - 1][j + (i - 1)] -= P;
}
}
}
}
for (int i = 0; i < maxN; ++i) {
for (int j = 0; j < maxN; ++j) {
s[i][j] = d[i][j];
if (j > 0) {
s[i][j] += s[i][j - 1];
if (s[i][j] >= P) {
s[i][j] -= P;
}
}
}
}
}
void rec(int left, int position, int current, vector < long long >* numbers) {
if (position == 0) {
numbers->push_back(current);
return ;
}
rec(left, position - 1, current, numbers);
if (left >= position) {
rec(left - position, position - 1, current + (1 << position), numbers);
}
}
long long getWays(int a, int n, int up, long long& no_next) {
vector < long long > numbers;
rec(n, up - 1, 0, &numbers);
sort(numbers.begin(), numbers.end());
long long res = 1;
long long last = 0;
for (int i = 0; i < numbers.size(); ++i) {
if (numbers[i] > last + a) {
res += a;
last = numbers[i];
++res;
} else {
res += numbers[i] - last;
last = numbers[i];
}
}
no_next = (res + a) % P;
long long bound = (1 << up) - 1;
if (bound > last + a) {
res += a;
} else {
res += bound - last;
}
res %= P;
return res;
}
const int maxM = 40;
vector < int > bounds[maxM][maxM];
vector < int > scores[maxM][maxM];
vector < int > add[maxM][maxM];
int up_bound[maxM][maxM];
void prebuild() {
for (int up = 1; up <= 30; ++up) {
for (int n = 1; n <= up; ++n) {
vector < long long > numbers;
rec(n, up - 1, 0, &numbers);
sort(numbers.begin(), numbers.end());
set < long long > diff;
for (int i = 1; i < numbers.size(); ++i) {
if (numbers[i] != numbers[i - 1] + 1) {
diff.insert(numbers[i] - numbers[i - 1] - 1);
}
}
if ((1 << up) - 1 != numbers.back() + 1) {
diff.insert((1 << up) - numbers.back() - 2);
}
for (set < long long > :: iterator it = diff.begin(); it != diff.end(); ++it) {
bounds[up][n].push_back(*it);
scores[up][n].push_back(0);
add[up][n].push_back(0);
}
for (int index = 0; index < bounds[up][n].size(); ++index) {
long long value = bounds[up][n][index];
long long last = 0;
scores[up][n][index] = 1;
for (int i = 0; i < numbers.size(); ++i) {
if (numbers[i] > last + value) {
++add[up][n][index];
++scores[up][n][index];
last = numbers[i];
} else {
scores[up][n][index] += numbers[i] - last;
last = numbers[i];
}
}
++add[up][n][index];
}
up_bound[up][n] = numbers.back();
}
}
}
long long getWaysFast(int a, int n, int up, long long& no_next) {
int index = lower_bound(bounds[up][n].begin(), bounds[up][n].end(), a) - bounds[up][n].begin();
if (index == bounds[up][n].size()) {
no_next = (up_bound[up][n] + a + 1) % P;
return min((1 << up) - 1, up_bound[up][n] + a) + 1;
}
long long score = scores[up][n][index];
score += (long long)(a) * (long long)(add[up][n][index]);
score %= P;
no_next = score;
if (up_bound[up][n] + a > (1 << up) - 1) {
score -= up_bound[up][n] + a - ((1 << up) - 1);
}
return score;
}
void solve() {
int a, b;
scanf("%d%d", &a, &b);
assert(0 <= a && a <= 1e9);
assert(0 <= b && b <= 1e3);
if (a == 0) {
printf("%d\n", (s[1][b] + P - 1) % P);
return ;
}
int up = 0;
for (int i = 1; ; ++i) {
if ((1 << i) > a) {
up = i;
break;
}
}
long long res = 0;
if (b >= up + 5) {
res += (long long)(s[up][b - up - 4]) * (long long)(1 << up);
res %= P;
}
for (int i = (b >= up + 5 ? (b - up - 3) : 0); i < b; ++i) {
int current = d[up][i];
if (current == 0) {
continue;
}
int n = b - i;
long long up_on = d[up][i] - d[up + 1][i];
if (up_on < 0) {
up_on += P;
}
long long up_off = d[up + 1][i];
long long has_next = up_on;
long long no_next = up_off;
if (i + up <= b) {
has_next = (up_on + up_off) % P;
no_next = 0;
}
if (n > up) {
res += has_next * (long long)(1 << up);
res %= P;
res += no_next * (long long)((1 << up) + a);
res %= P;
} else {
long long q;
res += has_next * getWaysFast(a, n, up, q);
res %= P;
res += no_next * q;
res %= P;
}
}
{
res += (long long)(d[up][b]) * (long long)(a + 1);
res %= P;
}
res = (res + P - 1) % P;
printf("%d\n", (int)(res));
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
precalc();
prebuild();
int tests;
scanf("%d", &tests);
assert(1 <= tests && tests <= 1e5);
for (int i = 0; i < tests; ++i) {
solve();
}
return 0;
}
</code></pre>
| 0 |
mar14-ones-and-twos
|
2014-03-27T19:47:34
|
{"contest_participation":2080,"challenge_submissions":137,"successful_submissions":15}
|
2014-03-27T19:47:34
|
2016-07-23T15:23:45
|
setter
|
###C++
```cpp
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((int)(c).size())
typedef long long LL;
int MOD = 1e9+7;
int p[33][1005], up[33]={};
void add(int &x, LL v) {
x = (x+v)%MOD;
}
const int MXB = 1000;
void pre(int S) {
if(up[S]) return;
up[S] = 1;
p[S][0] = 1;
for(int l=S;l<=MXB;l++) {
for(int j=MXB;j>=l;j--)
add(p[S][j], p[S][j-l]);
}
for(int j=1;j<=MXB;j++) add(p[S][j], p[S][j-1]);
//printf("build: "); for(int j=0;j<=MXB;j++) printf("%d ", p[S][j]); puts("");
}
void solve() {
int A, B, s;
LL t;
scanf("%d%d", &A, &B);
if (A == 0) {
pre(1);
printf("%d\n", (p[1][B]+MOD-1)%MOD);
return;
}
for(t=2,s=1;t<=A;t*=2,s++);
t *= 2; s++;
pre(s);
//printf("s=%d\n", s);
int ans = 0;
LL last = 0, last2 = t/2+A+1;
for(int u=0;u<s && u<=B;u++) {
LL nxt = min(t, (1LL<<u) + A + (u>0));
LL nxt2 = min(t, (1LL<<u) + A + t/2 + (u>0));
add(ans, (nxt-last)*1LL*p[s][B-u]);
if(u+s-1<=B) add(ans, (nxt2-last2)*1LL*p[s][B-(u+s-1)]);
//printf("u=%d: [%I64d, %I64d) %d; [%I64d, %I64d) \n", u, last, nxt, p[s][B-u], last2, nxt2);
last = nxt;
last2 = nxt2;
}
//printf("nxt=%I64d\n", last);
printf("%d\n", (ans+MOD-1)%MOD);
}
int main(void) {
int T;
scanf("%d", &T);
while(T--) solve();
return 0;
}
```
|
not-set
|
2016-04-24T02:02:35
|
2016-07-23T15:23:27
|
C++
|
39 | 1,767 |
ones-and-twos
|
Ones and Twos
|
You are using at most **A** number of 1s and at most **B** number of 2s. How many different evaluation results are possible when they are formed in an expression containing only addition `+` sign and multiplication `*` sign are allowed?
Note that, multiplication takes precedence over addition.
For example, if **A=2** and **B=2**, then we have the following expressions:
* `1`, `1*1` = 1
* `2`, `1*2`, `1*1*2`, `1+1` = 2
* `1+2`, `1+1*2` = 3
* `2+2`, `2*2`, `1+1+2`, `1*2*2`, `1*1*2*2`, `1*2+1*2`, `1*1*2+2`, `1*2+2` = 4
* `1+2+2`, `1+1*2+2` = 5
* `1+1+2+2`, `1+1+2*2` = 6
So there are 6 unique results that can be formed if A = 2 and B = 2.
**Input Format**
The first line contains the number of test cases T, T testcases follow each in a newline.
Each testcase contains 2 integers A and B separated by a single space.
**Output Format**
Print the number of different evaluations modulo (%) (10<sup>9</sup>+7.)
**Constraints**
1 <= T <= 10<sup>5</sup>
0<=A<=1000000000
0<=B<=1000
**Sample Input**
4
0 0
2 2
0 2
2 0
**Sample Output**
0
6
2
2
**Explanation**
+ When A = 0, B = 0, there are no expressions, hence 0.
+ When A = 2, B = 2, as explained in the problem statement above, expressions leads to 6 possible solutions.
+ When A = 0, B = 2, we have `2`, `2+2` or `2*2`, hence 2.
+ When A = 2, B = 0, we have `1` or `1*1`, `1+1` hence 2.
|
code
|
Using A 1's and B 2's how many different evaluations are possible only by performing addition and multiplication
|
ai
|
2014-01-29T15:42:24
|
2022-08-31T08:14:53
|
#
# Complete the 'onesAndTwos' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER a
# 2. INTEGER b
#
def onesAndTwos(a, b):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
a = int(first_multiple_input[0])
b = int(first_multiple_input[1])
result = onesAndTwos(a, b)
fptr.write(str(result) + '\n')
fptr.close()
|
You are using at most **A** number of 1s and at most **B** number of 2s. How many different evaluation results are possible when they are formed in an expression containing only addition `+` sign and multiplication `*` sign are allowed?
Note that, multiplication takes precedence over addition.
For example, if **A=2** and **B=2**, then we have the following expressions:
* `1`, `1*1` = 1
* `2`, `1*2`, `1*1*2`, `1+1` = 2
* `1+2`, `1+1*2` = 3
* `2+2`, `2*2`, `1+1+2`, `1*2*2`, `1*1*2*2`, `1*2+1*2`, `1*1*2+2`, `1*2+2` = 4
* `1+2+2`, `1+1*2+2` = 5
* `1+1+2+2`, `1+1+2*2` = 6
So there are 6 unique results that can be formed if A = 2 and B = 2.
| 0.545455 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains the number of test cases T, T testcases follow each in a newline.
Each testcase contains 2 integers A and B separated by a single space.
|
Print the number of different evaluations modulo (%) (10<sup>9</sup>+7.)
|
4
0 0
2 2
0 2
2 0
|
0
6
2
2
|
Hard
|
Ones and Twos - 2020 Hack March Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/mar14/challenges/ones-and-twos">Ones and Twos</a> <br>
<strong>Difficulty Level</strong> : Medium-Hard <br>
<strong>Required Knowledge</strong> : DP <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/tmt514">Shang En Huang</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/dsoboliev">Dmytro Soboliev</a> </p>
<p><strong>Solution</strong> </p>
<p>If you are still getting wrong answer but don't know why, please try this test case:</p>
<pre><code> 2
6 14
2 1
</code></pre>
<p>The answer should be </p>
<pre><code> 301
4
</code></pre>
<h3>Part I.</h3>
<p>Let's consider simple cases, say when <strong>A</strong> = 0. In this case, all numbers will be generated by using all 2's. For each integer <strong>X</strong>, consider its binary representation (a<sub>0</sub> + a<sub>1</sub>*2 + a<sub>2</sub>*4+a<sub>3</sub>*8+...). It's not hard to prove you need at least (a<sub>1</sub>*1 + a<sub>2</sub>*2+a<sub>3</sub>*3+...) number of 2's to produce this number.</p>
<p>Hence when given the value of <strong>B</strong> the answer should be:</p>
<blockquote>
<p>The number of ways partitioning <strong>i <= B</strong> into distinct sum of positive integers.</p>
</blockquote>
<p>This can be solved by <strong>O(B<sup>2</sup>)</strong> dynamic programming: Just let <code>dp[i][j]</code> be the number of ways partitioning <code>i</code> into distinct sum of positive integers with last term (highest bit) equal or less than <code>j</code>. So if we consider the state <code>dp[i][j]</code>, into two situations: the last term is <code>j</code> or not. If yes, there are exactly <code>dp[i-j][j-1]</code> ways. Otherwise it would be <code>dp[i][j-1]</code>. Please consider the following code:</p>
<p><strong>Language : C++</strong></p>
<pre><code>for (int j = 0; j <= B; j++) dp[0][j] = 1;
for (int i = 1; i <= B; i++)
for (int j = 1; j <= B; j++)
dp[i][j] = (i>j? dp[i-j][j-1] : 0) + dp[i][j-1];
</code></pre>
<p>Then in the case <strong>A=0</strong>, the solution can be calculated from <code>dp[1][B] + dp[2][B] + ... + dp[B][B]</code>. (Don't forget to mod.)</p>
<h3>Part II: O(T A lg A + B<sup>2</sup>)</h3>
<p>From now on, when we consider an integer, we only consider the representation with fewest 2's.</p>
<p>What if we have some 1's? If using only twos can make a number <strong>X</strong>, then we can build all integers in the ranage <strong>[X, X+A]</strong>. Suppose we have a number <strong>2<sup>K</sup></strong>, where <strong>2A < 2<sup>K</sup></strong>. We split the terms by "Terms less than*<em>2<sup>K</sup></em>* and terms no less than <strong>2<sup>K</sup></strong>". For terms less than <strong>2<sup>K</sup></strong>. We will know that the sum of all parts contributed by 2's will be less than <strong>2<sup>K</sup></strong> (Why?).</p>
<p>Hence, if we choose minimal <strong>K</strong> with <strong>2A < 2<sup>K</sup></strong>, then we can guarantee that the sum of whole part less than <strong>2<sup>K</sup></strong> will still less than <strong>2<sup>K</sup></strong>. (Given the condition that we use least number of 2's.)</p>
<p></p>
<p>For each <strong>t, 0 <= t < 2<sup>K</sup></strong>, let <strong>R[t]</strong> be the least number of 2's which can build <strong>t</strong>. Modify the DP table from part I: <code>dp[i][j]</code> be the number of ways partitioning <code>i</code> into distinct sum of positive integers with last term (highest bit) equal or less than <code>j</code> <em>and with first term (lowest bit) at least <b>K</b></em>.</p>
<pre><code>cpp
for (int j = 0; j <= B; j++) dp[0][j] = 1;
for (int i = 1; i <= B; i++)
for (int j = 1; j <= B; j++)
dp[i][j] = (j>=K && i>j ? dp[i-j][j-1] : 0) + dp[i][j-1];
</code></pre>
<p>In this <strong>t</strong>, the ways to make numbers that modulo <strong>2<sup>K</sup></strong> equals <strong>t</strong> is exactly <code>dp[1][B] + dp[2][B] + ... + dp[B - R[t]][B]</code>. (Please mod.)</p>
<p>We can easily get the relations <code>R[0] = R[1] = ... = R[A] = 0</code>, and for <strong>t > A</strong>,
<strong>R[t]</strong> = min<sub><strong>0 <= j < K</strong></sub>{ <strong>R[t-2<sup>j</sup>] + j</strong> }</p>
<p>In conclusion, for each test case, we can go over each <strong>0 <= t < 2<sup>K</sup></strong>. Then the time complexity is <strong>O(T K 2<sup>K</sup> + B^2) = O(T A lg A + B^2)</strong>.</p>
<h3>Part III: O(T lg A + B^2)</h3>
<p>The remaining parts:</p>
<ol>
<li>calculate <strong>R[0]..R[2<sup>K</sup>-1]</strong> efficiently</li>
<li>calculate the sum <strong>dp[ B-R[i] ][ B-R[i] ]</strong> efficiently</li>
</ol>
<p>In order to solve (2), we need to count "How many <strong>i</strong>'s are there such that <strong>R[i] = r</strong>?" for each <strong>r = 0, 1, ..., 2<sup>K</sup>-1</strong>.</p>
<p>(Maybe not) Surprisingly, we have the following properties:</p>
<p></p>
<blockquote>
<p><strong>Prop</strong>: for any integer no more than <strong>2<sup>K-1</sup></strong>, we only need at most one "2 term".</p>
<p><strong>Prop2</strong>: for any integer in <strong>(2<sup>K-1</sup>, 2<sup>K</sup>)</strong> we use at most two "2 terms".</p>
</blockquote>
<p>Hence we can find the sum with a single loop enumerating from 0 to K-1.</p>
<p>Happy thinking & happy coding :)</p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((int)(c).size())
typedef long long LL;
int MOD = 1e9+7;
int p[33][1005], up[33]={};
void add(int &x, LL v) {
x = (x+v)%MOD;
}
const int MXB = 1000;
void pre(int S) {
if(up[S]) return;
up[S] = 1;
p[S][0] = 1;
for(int l=S;l<=MXB;l++) {
for(int j=MXB;j>=l;j--)
add(p[S][j], p[S][j-l]);
}
for(int j=1;j<=MXB;j++) add(p[S][j], p[S][j-1]);
//printf("build: "); for(int j=0;j<=MXB;j++) printf("%d ", p[S][j]); puts("");
}
void solve() {
int A, B, s;
LL t;
scanf("%d%d", &A, &B);
if (A == 0) {
pre(1);
printf("%d\n", (p[1][B]+MOD-1)%MOD);
return;
}
for(t=2,s=1;t<=A;t*=2,s++);
t *= 2; s++;
pre(s);
//printf("s=%d\n", s);
int ans = 0;
LL last = 0, last2 = t/2+A+1;
for(int u=0;u<s && u<=B;u++) {
LL nxt = min(t, (1LL<<u) + A + (u>0));
LL nxt2 = min(t, (1LL<<u) + A + t/2 + (u>0));
add(ans, (nxt-last)*1LL*p[s][B-u]);
if(u+s-1<=B) add(ans, (nxt2-last2)*1LL*p[s][B-(u+s-1)]);
//printf("u=%d: [%I64d, %I64d) %d; [%I64d, %I64d) \n", u, last, nxt, p[s][B-u], last2, nxt2);
last = nxt;
last2 = nxt2;
}
//printf("nxt=%I64d\n", last);
printf("%d\n", (ans+MOD-1)%MOD);
}
int main(void) {
int T;
scanf("%d", &T);
while(T--) solve();
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <ctime>
#include <set>
#include <cassert>
using namespace std;
const int P = 1000000007;
const int maxN = 1100;
int d[maxN][maxN], s[maxN][maxN];
void precalc() {
d[maxN - 1][0] = 1;
for (int i = maxN - 1; i > 0; --i) {
for (int j = 0; j < maxN; ++j) {
if (d[i][j] == 0) {
continue;
}
d[i - 1][j] += d[i][j];
if (d[i - 1][j] >= P) {
d[i - 1][j] -= P;
}
if (j + (i - 1) < maxN) {
d[i - 1][j + (i - 1)] += d[i][j];
if (d[i - 1][j + (i - 1)] >= P) {
d[i - 1][j + (i - 1)] -= P;
}
}
}
}
for (int i = 0; i < maxN; ++i) {
for (int j = 0; j < maxN; ++j) {
s[i][j] = d[i][j];
if (j > 0) {
s[i][j] += s[i][j - 1];
if (s[i][j] >= P) {
s[i][j] -= P;
}
}
}
}
}
void rec(int left, int position, int current, vector < long long >* numbers) {
if (position == 0) {
numbers->push_back(current);
return ;
}
rec(left, position - 1, current, numbers);
if (left >= position) {
rec(left - position, position - 1, current + (1 << position), numbers);
}
}
long long getWays(int a, int n, int up, long long& no_next) {
vector < long long > numbers;
rec(n, up - 1, 0, &numbers);
sort(numbers.begin(), numbers.end());
long long res = 1;
long long last = 0;
for (int i = 0; i < numbers.size(); ++i) {
if (numbers[i] > last + a) {
res += a;
last = numbers[i];
++res;
} else {
res += numbers[i] - last;
last = numbers[i];
}
}
no_next = (res + a) % P;
long long bound = (1 << up) - 1;
if (bound > last + a) {
res += a;
} else {
res += bound - last;
}
res %= P;
return res;
}
const int maxM = 40;
vector < int > bounds[maxM][maxM];
vector < int > scores[maxM][maxM];
vector < int > add[maxM][maxM];
int up_bound[maxM][maxM];
void prebuild() {
for (int up = 1; up <= 30; ++up) {
for (int n = 1; n <= up; ++n) {
vector < long long > numbers;
rec(n, up - 1, 0, &numbers);
sort(numbers.begin(), numbers.end());
set < long long > diff;
for (int i = 1; i < numbers.size(); ++i) {
if (numbers[i] != numbers[i - 1] + 1) {
diff.insert(numbers[i] - numbers[i - 1] - 1);
}
}
if ((1 << up) - 1 != numbers.back() + 1) {
diff.insert((1 << up) - numbers.back() - 2);
}
for (set < long long > :: iterator it = diff.begin(); it != diff.end(); ++it) {
bounds[up][n].push_back(*it);
scores[up][n].push_back(0);
add[up][n].push_back(0);
}
for (int index = 0; index < bounds[up][n].size(); ++index) {
long long value = bounds[up][n][index];
long long last = 0;
scores[up][n][index] = 1;
for (int i = 0; i < numbers.size(); ++i) {
if (numbers[i] > last + value) {
++add[up][n][index];
++scores[up][n][index];
last = numbers[i];
} else {
scores[up][n][index] += numbers[i] - last;
last = numbers[i];
}
}
++add[up][n][index];
}
up_bound[up][n] = numbers.back();
}
}
}
long long getWaysFast(int a, int n, int up, long long& no_next) {
int index = lower_bound(bounds[up][n].begin(), bounds[up][n].end(), a) - bounds[up][n].begin();
if (index == bounds[up][n].size()) {
no_next = (up_bound[up][n] + a + 1) % P;
return min((1 << up) - 1, up_bound[up][n] + a) + 1;
}
long long score = scores[up][n][index];
score += (long long)(a) * (long long)(add[up][n][index]);
score %= P;
no_next = score;
if (up_bound[up][n] + a > (1 << up) - 1) {
score -= up_bound[up][n] + a - ((1 << up) - 1);
}
return score;
}
void solve() {
int a, b;
scanf("%d%d", &a, &b);
assert(0 <= a && a <= 1e9);
assert(0 <= b && b <= 1e3);
if (a == 0) {
printf("%d\n", (s[1][b] + P - 1) % P);
return ;
}
int up = 0;
for (int i = 1; ; ++i) {
if ((1 << i) > a) {
up = i;
break;
}
}
long long res = 0;
if (b >= up + 5) {
res += (long long)(s[up][b - up - 4]) * (long long)(1 << up);
res %= P;
}
for (int i = (b >= up + 5 ? (b - up - 3) : 0); i < b; ++i) {
int current = d[up][i];
if (current == 0) {
continue;
}
int n = b - i;
long long up_on = d[up][i] - d[up + 1][i];
if (up_on < 0) {
up_on += P;
}
long long up_off = d[up + 1][i];
long long has_next = up_on;
long long no_next = up_off;
if (i + up <= b) {
has_next = (up_on + up_off) % P;
no_next = 0;
}
if (n > up) {
res += has_next * (long long)(1 << up);
res %= P;
res += no_next * (long long)((1 << up) + a);
res %= P;
} else {
long long q;
res += has_next * getWaysFast(a, n, up, q);
res %= P;
res += no_next * q;
res %= P;
}
}
{
res += (long long)(d[up][b]) * (long long)(a + 1);
res %= P;
}
res = (res + P - 1) % P;
printf("%d\n", (int)(res));
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
precalc();
prebuild();
int tests;
scanf("%d", &tests);
assert(1 <= tests && tests <= 1e5);
for (int i = 0; i < tests; ++i) {
solve();
}
return 0;
}
</code></pre>
| 0 |
mar14-ones-and-twos
|
2014-03-27T19:47:34
|
{"contest_participation":2080,"challenge_submissions":137,"successful_submissions":15}
|
2014-03-27T19:47:34
|
2016-07-23T15:23:45
|
tester
|
###C++
```cpp
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <ctime>
#include <set>
#include <cassert>
using namespace std;
const int P = 1000000007;
const int maxN = 1100;
int d[maxN][maxN], s[maxN][maxN];
void precalc() {
d[maxN - 1][0] = 1;
for (int i = maxN - 1; i > 0; --i) {
for (int j = 0; j < maxN; ++j) {
if (d[i][j] == 0) {
continue;
}
d[i - 1][j] += d[i][j];
if (d[i - 1][j] >= P) {
d[i - 1][j] -= P;
}
if (j + (i - 1) < maxN) {
d[i - 1][j + (i - 1)] += d[i][j];
if (d[i - 1][j + (i - 1)] >= P) {
d[i - 1][j + (i - 1)] -= P;
}
}
}
}
for (int i = 0; i < maxN; ++i) {
for (int j = 0; j < maxN; ++j) {
s[i][j] = d[i][j];
if (j > 0) {
s[i][j] += s[i][j - 1];
if (s[i][j] >= P) {
s[i][j] -= P;
}
}
}
}
}
void rec(int left, int position, int current, vector < long long >* numbers) {
if (position == 0) {
numbers->push_back(current);
return ;
}
rec(left, position - 1, current, numbers);
if (left >= position) {
rec(left - position, position - 1, current + (1 << position), numbers);
}
}
long long getWays(int a, int n, int up, long long& no_next) {
vector < long long > numbers;
rec(n, up - 1, 0, &numbers);
sort(numbers.begin(), numbers.end());
long long res = 1;
long long last = 0;
for (int i = 0; i < numbers.size(); ++i) {
if (numbers[i] > last + a) {
res += a;
last = numbers[i];
++res;
} else {
res += numbers[i] - last;
last = numbers[i];
}
}
no_next = (res + a) % P;
long long bound = (1 << up) - 1;
if (bound > last + a) {
res += a;
} else {
res += bound - last;
}
res %= P;
return res;
}
const int maxM = 40;
vector < int > bounds[maxM][maxM];
vector < int > scores[maxM][maxM];
vector < int > add[maxM][maxM];
int up_bound[maxM][maxM];
void prebuild() {
for (int up = 1; up <= 30; ++up) {
for (int n = 1; n <= up; ++n) {
vector < long long > numbers;
rec(n, up - 1, 0, &numbers);
sort(numbers.begin(), numbers.end());
set < long long > diff;
for (int i = 1; i < numbers.size(); ++i) {
if (numbers[i] != numbers[i - 1] + 1) {
diff.insert(numbers[i] - numbers[i - 1] - 1);
}
}
if ((1 << up) - 1 != numbers.back() + 1) {
diff.insert((1 << up) - numbers.back() - 2);
}
for (set < long long > :: iterator it = diff.begin(); it != diff.end(); ++it) {
bounds[up][n].push_back(*it);
scores[up][n].push_back(0);
add[up][n].push_back(0);
}
for (int index = 0; index < bounds[up][n].size(); ++index) {
long long value = bounds[up][n][index];
long long last = 0;
scores[up][n][index] = 1;
for (int i = 0; i < numbers.size(); ++i) {
if (numbers[i] > last + value) {
++add[up][n][index];
++scores[up][n][index];
last = numbers[i];
} else {
scores[up][n][index] += numbers[i] - last;
last = numbers[i];
}
}
++add[up][n][index];
}
up_bound[up][n] = numbers.back();
}
}
}
long long getWaysFast(int a, int n, int up, long long& no_next) {
int index = lower_bound(bounds[up][n].begin(), bounds[up][n].end(), a) - bounds[up][n].begin();
if (index == bounds[up][n].size()) {
no_next = (up_bound[up][n] + a + 1) % P;
return min((1 << up) - 1, up_bound[up][n] + a) + 1;
}
long long score = scores[up][n][index];
score += (long long)(a) * (long long)(add[up][n][index]);
score %= P;
no_next = score;
if (up_bound[up][n] + a > (1 << up) - 1) {
score -= up_bound[up][n] + a - ((1 << up) - 1);
}
return score;
}
void solve() {
int a, b;
scanf("%d%d", &a, &b);
assert(0 <= a && a <= 1e9);
assert(0 <= b && b <= 1e3);
if (a == 0) {
printf("%d\n", (s[1][b] + P - 1) % P);
return ;
}
int up = 0;
for (int i = 1; ; ++i) {
if ((1 << i) > a) {
up = i;
break;
}
}
long long res = 0;
if (b >= up + 5) {
res += (long long)(s[up][b - up - 4]) * (long long)(1 << up);
res %= P;
}
for (int i = (b >= up + 5 ? (b - up - 3) : 0); i < b; ++i) {
int current = d[up][i];
if (current == 0) {
continue;
}
int n = b - i;
long long up_on = d[up][i] - d[up + 1][i];
if (up_on < 0) {
up_on += P;
}
long long up_off = d[up + 1][i];
long long has_next = up_on;
long long no_next = up_off;
if (i + up <= b) {
has_next = (up_on + up_off) % P;
no_next = 0;
}
if (n > up) {
res += has_next * (long long)(1 << up);
res %= P;
res += no_next * (long long)((1 << up) + a);
res %= P;
} else {
long long q;
res += has_next * getWaysFast(a, n, up, q);
res %= P;
res += no_next * q;
res %= P;
}
}
{
res += (long long)(d[up][b]) * (long long)(a + 1);
res %= P;
}
res = (res + P - 1) % P;
printf("%d\n", (int)(res));
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
precalc();
prebuild();
int tests;
scanf("%d", &tests);
assert(1 <= tests && tests <= 1e5);
for (int i = 0; i < tests; ++i) {
solve();
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:35
|
2016-07-23T15:23:45
|
C++
|
40 | 1,050 |
devu-police
|
Devu Vs Police
|
[Mandarin-Chinese](https://hr-filepicker.s3.amazonaws.com/infinitum-mar14/mandarin/1050-devupolice.md)
[Russian](https://hr-filepicker.s3.amazonaws.com/infinitum-mar14/russian/1050-devupolice.md)
It is holi festival, festival of colors. Devu is having fun playing holi and is throwing balloons with his girlfriend Glynis. Police saw this mischief and tried arresting his girlfriend, Devu being a mathematician asked police not to arrest his girlfriend and instead torture him with brain teaser. Devu was a young engineering fellow and he did not knew that policeman was equally good in mathematics, policeman gave Devu a problem which is as follows:
Let f(n,k) = n<sup>k</sup>
Your aim is to answer f(n1,k1)<sup>f(n2,k2)</sup> % n
Can you help devu and his girlfriend rescue from modern police.
**Input Format**
You are given `T` which is the number of queries to solve.
Each Query consist of 5 space separated integers `n1 k1 n2 k2 n`
**Output Format**
Output contains exactly T lines. i<sup>th</sup> line containing the answer for the i<sup>th</sup> query.
**Constraints**
1 <= T <= 10000
0 <= n1,k1,n2,k2 <= 10<sup>9</sup>
1 <= n <= 10<sup>7</sup>
**Note** The output to 0<sup>0</sup> should be 1.
**Sample Input**
1
2 1 2 2 15
**Sample Output**
1
**Explanation**
f(2,1) = 2
f(2,2) = 4
so answer is 16 mod 15 = 1
[Editorial](https://www.hackerrank.com/blog/infinitum-mar14-devu-police)
|
code
|
Help Devu escape from police
|
ai
|
2013-10-09T04:59:51
|
2022-09-02T09:54:38
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n1
# 2. INTEGER k1
# 3. INTEGER n2
# 4. INTEGER k2
# 5. INTEGER n
#
def solve(n1, k1, n2, k2, n):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n1 = int(first_multiple_input[0])
k1 = int(first_multiple_input[1])
n2 = int(first_multiple_input[2])
k2 = int(first_multiple_input[3])
n = int(first_multiple_input[4])
result = solve(n1, k1, n2, k2, n)
fptr.write(str(result) + '\n')
fptr.close()
|
It is holi festival, festival of colors. Devu is having fun playing holi and is throwing balloons with his girlfriend Glynis. Police saw this mischief and tried arresting his girlfriend, Devu being a mathematician asked police not to arrest his girlfriend and instead torture him with brain teaser. Devu was a young engineering fellow and he did not knew that policeman was equally good in mathematics, policeman gave Devu a problem which is as follows:
Let $f(n,k) = n^k$
Your aim is to answer $f(n_1,k_1)^{f(n_2,k_2)} \bmod n$
Can you help devu and his girlfriend rescue from modern police.
| 0.431818 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
You are given $T$ which is the number of queries to solve.
Each Query consist of 5 space separated integers $n_1,k_1,n_2,k_2,n$
|
Output contains exactly $T$ lines. $i^{\text{th}}$ line containing the answer for the $i^{\text{th}}$ query.
|
1
2 1 2 2 15
|
1
|
Hard
|
Devu Vs Police Infinitum Mar14 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/infinitum-mar14/challenges/devu-police">Problem Statement</a> </p>
<p><strong>Problem Setter</strong> : <a href="http://hackerrank.com/devuy11">Devendra</a> <br>
<strong>Problem Tester</strong> : <a href="http://hackerrank.com/cpcs">Cao Peng</a> <br>
<strong>Required Knowledge</strong>: Chinese Remainder Theorm </p>
<p>The Basic Idea Exploited here is Chinese Remainder Theorom.<br>
let n = p[1]^e[1] * p[2]^e[2] * p[3]^e[3] <em>...</em> p[k]^e[k] where p[i] is prime.<br>
let expr = A[1]^A[2]^A[3] where A[1] = f(n1,k1) , A[2] = n2, A[3] = k2<br>
so, calculating expr mod n is equivalent in calculating<br>
CRT ( expr mod p[1]^e[1] , expr mod p[2]^[e_2] ,......., expr mod p[k]^e[k] )<br>
Now lets see the case when e[i] = 1, then calculating expr mod p[i] is equivalent to A[1]^( A[2]^A[3] mod (p[i] -1 ) ) mod p[i].<br>
Euler Totient Period for p[i] is p[i] - 1.<br>
Now for the case of p[i]^e[i] where e[i]!=1, euler totient period is given by p[i]^e[i] - p[i]^(e[i]-1)<br>
<strong>Note:</strong> :Be carefull with Euler Totient period concept which is valid only if A[1] is coprime to p[i]. It is left as an exercise for the reader to figure it out how to procede then.<br></p>
<p><strong>Solution</strong> by <a href="http://hackerrank.com/cpcs">cpcs</a> </p>
<p>Let a = n1<sup>k1</sup> % n and b = n2<sup>k2</sup>, we need to calculate a^b mod n. We can judge whether a = 0/1 or b = 0,1 first to deal with the special conditions like 0^0, 1^p...etc. <br>
Then we can suppose a > 1 and b > 1. <br>
The solution is based on that although n may not be a prime, the period of the n1<sup>x</sup> % n is phi(n) , where phi is the euler function. <br>
But the starting point of the first period may be starts from phi(n). That means for any y >= phi(n) we have n1<sup>(y)</sup> == n1<sup>(y + phi(n))</sup> (mod n) </p>
<p>So if we found b is smaller enough, namely if b < phi(n), we can directly calculate the result using O(logb) algorithm. Otherwise we have b>=phi(n) then n1<sup>k1</sup> == n1<sup>(b % phi(n) + phi(n))</sup> mod n, so we just calculate n1 <sup>(b % phi(n) + phi(n))</sup> % n. </p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include<stdio.h>
#include<iostream>
#include<string.h>
#include<vector>
#include<assert.h>
using namespace std;
typedef long long int ll;
int sieve_par=3162;
int prime[3162] , array[3162],counter=0;
ll inverse(ll a,ll b) //b>a
{
ll Remainder,p0=0,p1=1,pcurr=1,q,m=b;
while(a!=0)
{
Remainder=b%a;
q=b/a;
if(Remainder!=0)
{
pcurr=p0-(p1*q)%m;
if(pcurr<0)
pcurr+=m;
p0=p1;
p1=pcurr;
}
b=a;
a=Remainder;
}
return pcurr;
}
ll binpow(ll a,ll b,ll mod)
{
ll ans=1;
while(b)
if(b&1){
ans=(ans*a)%mod;
b--;
}
else{
a=(a*a)%mod;
b>>=1;
}
return ans%mod;
}
ll CRT(ll mod[],ll rem[],int t) //t is the number of pairs of rem and mod
{
ll ans = rem[0],m = mod[0];
for(int i = 1;i < t;++i)
{
ll a = inverse(m,mod[i]);
ll b = inverse(mod[i],m);
ans = (ans * b * mod[i] + rem[i] * a * m) % (m * mod[i]);
m *= mod[i];
}
return ans;
}
void sieve()
{
for(int i=1;i<sieve_par;i++)
array[i]=1;
array[0]=0;
int j;
for(int i=2;i<=sieve_par;i++)
{
if(array[i-1]==1)
{
prime[counter]=i;
for(j=i*i;j<=sieve_par;j+=i)
array[j-1]=0;
counter++;
}
}
}
int check(ll a,ll b,ll n)
{
ll ans=1;
while(b)
if(b&1){
ans=ans*a;
if(ans>n) return -1;
b--;
}
else{
a=a*a;
if(a>n) return -1;
b>>=1;
}
return ans;
}
ll solveit(int n1,int k1,int n2,int k2,int m,int p)
{
ll x=1,y=0;
if(n1==0){
if(n2==0 && k2==0 && k1==0) return 1;
if(n2==0 && k2==0 && k1!=0) return 0;
if(k1==0 || n2==0) return 1;
return 0;
}
if(n1 % p == 0 ){
ll ans;
while(n1%p == 0){
n1/=p;
x=x*p;
y++;
}
ans= check(n2,k2,m);
ans= ans* k1*y;
if(ans>=0) ans= check(p,ans,m);
if(ans<0) return 0;
else x= ans;
}
ll a=binpow(n2,k2,m-(m/p));
ll b=binpow(n1,k1,m);
ll c= binpow(b,a,m);
return (c*x)%m;
}
int main()
{
sieve();
int test,n1,n2,n,k1,k2,t;
ll mod[15],rem[15],ans;
//printf("%d is counter\n",counter);
scanf("%d",&test);
assert(test<=10000);
while(test--){
scanf("%d%d%d%d%d",&n1,&k1,&n2,&k2,&n);
assert(n1<=1000000000 && k1<=1000000000 && n2<=1000000000 && k2<=1000000000 && n<=10000000);
assert(n1>=0 && k1>=0 && n2>=0 && k2>=0 && n>=1);
if(n==1){
printf("0\n");
continue;
}
t=0;
for(int i=0;i<counter;i++){
if(n< prime[i]*prime[i]) break;
if(n%prime[i]==0){
mod[t]=1;
while(n%prime[i]==0){
n/=prime[i];
mod[t]*=prime[i];
}
rem[t]=solveit(n1,k1,n2,k2,mod[t],prime[i]);
t++;
}
}
if(n>1){
mod[t]=n;
rem[t]=solveit(n1,k1,n2,k2,mod[t],n);
t++;
}
printf("%lld\n",CRT(mod,rem,t));
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>import java.math.*;
import java.util.*;
public class Solution {
public static long powermod(long x,long y,long M) {
x %= M;
if (y == 0) {
return 1;
}
if (x == 0) {
return 0;
}
long r = 1L;
for (;y > 0; y >>= 1) {
if ((y & 1) > 0) {
r = r * x % M;
}
x = x * x % M;
}
return r;
}
public static long phi(long m) {
long p = 1L;
for (long i = 2L; i * i <= m; ++i) {
if (m % i == 0) {
long j = 1L;
while (m % i == 0) {
m /= i;
j *= i;
}
p *= j - j / i;
}
}
return (m > 1)?(p * (m - 1)):p;
}
public static long cmp(long n,long k,long x) { //n ^ k > x < x = x
long i = 0L, temp = 1L;
while ((i < k) && (temp < x)) {
i++;
temp *= n;
}
if ((i >= k) && (temp <= x)) {
return temp;
}
return -1;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
for (int cases = scanner.nextInt(); cases > 0; cases--) {
long n1 = scanner.nextLong();
long k1 = scanner.nextLong();
long n2 = scanner.nextLong();
long k2 = scanner.nextLong();
long n = scanner.nextLong();
if (n == 1) {
System.out.println(0);
}
else {
long x = powermod(n1,k1,n);
if ((k2 == 0) || (n2 == 1)) {
System.out.println(x);
}
else if (n2 == 0) {
System.out.println(1);
}
else if (x <= 1) {
System.out.println(x);
}
else { // n2 > 1, k2 > 0, x > 1
long p = phi(n);
long y = cmp(n2,k2,p);
System.out.println(powermod(x, (y >= 0)?y:(powermod(n2,k2,p) + p),n));
}
}
}
}
}
</code></pre>
| 0 |
infinitum-mar14-devu-police
|
2014-04-01T21:20:47
|
{"contest_participation":1667,"challenge_submissions":241,"successful_submissions":76}
|
2014-04-01T21:20:47
|
2016-12-09T10:05:33
|
setter
|
###C++
```cpp
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<vector>
#include<assert.h>
using namespace std;
typedef long long int ll;
int sieve_par=3162;
int prime[3162] , array[3162],counter=0;
ll inverse(ll a,ll b) //b>a
{
ll Remainder,p0=0,p1=1,pcurr=1,q,m=b;
while(a!=0)
{
Remainder=b%a;
q=b/a;
if(Remainder!=0)
{
pcurr=p0-(p1*q)%m;
if(pcurr<0)
pcurr+=m;
p0=p1;
p1=pcurr;
}
b=a;
a=Remainder;
}
return pcurr;
}
ll binpow(ll a,ll b,ll mod)
{
ll ans=1;
while(b)
if(b&1){
ans=(ans*a)%mod;
b--;
}
else{
a=(a*a)%mod;
b>>=1;
}
return ans%mod;
}
ll CRT(ll mod[],ll rem[],int t) //t is the number of pairs of rem and mod
{
ll ans = rem[0],m = mod[0];
for(int i = 1;i < t;++i)
{
ll a = inverse(m,mod[i]);
ll b = inverse(mod[i],m);
ans = (ans * b * mod[i] + rem[i] * a * m) % (m * mod[i]);
m *= mod[i];
}
return ans;
}
void sieve()
{
for(int i=1;i<sieve_par;i++)
array[i]=1;
array[0]=0;
int j;
for(int i=2;i<=sieve_par;i++)
{
if(array[i-1]==1)
{
prime[counter]=i;
for(j=i*i;j<=sieve_par;j+=i)
array[j-1]=0;
counter++;
}
}
}
int check(ll a,ll b,ll n)
{
ll ans=1;
while(b)
if(b&1){
ans=ans*a;
if(ans>n) return -1;
b--;
}
else{
a=a*a;
if(a>n) return -1;
b>>=1;
}
return ans;
}
ll solveit(int n1,int k1,int n2,int k2,int m,int p)
{
ll x=1,y=0;
if(n1==0){
if(n2==0 && k2==0 && k1==0) return 1;
if(n2==0 && k2==0 && k1!=0) return 0;
if(k1==0 || n2==0) return 1;
return 0;
}
if(n1 % p == 0 ){
ll ans;
while(n1%p == 0){
n1/=p;
x=x*p;
y++;
}
ans= check(n2,k2,m);
ans= ans* k1*y;
if(ans>=0) ans= check(p,ans,m);
if(ans<0) return 0;
else x= ans;
}
ll a=binpow(n2,k2,m-(m/p));
ll b=binpow(n1,k1,m);
ll c= binpow(b,a,m);
return (c*x)%m;
}
int main()
{
sieve();
int test,n1,n2,n,k1,k2,t;
ll mod[15],rem[15],ans;
//printf("%d is counter\n",counter);
scanf("%d",&test);
assert(test<=10000);
while(test--){
scanf("%d%d%d%d%d",&n1,&k1,&n2,&k2,&n);
assert(n1<=1000000000 && k1<=1000000000 && n2<=1000000000 && k2<=1000000000 && n<=10000000);
assert(n1>=0 && k1>=0 && n2>=0 && k2>=0 && n>=1);
if(n==1){
printf("0\n");
continue;
}
t=0;
for(int i=0;i<counter;i++){
if(n< prime[i]*prime[i]) break;
if(n%prime[i]==0){
mod[t]=1;
while(n%prime[i]==0){
n/=prime[i];
mod[t]*=prime[i];
}
rem[t]=solveit(n1,k1,n2,k2,mod[t],prime[i]);
t++;
}
}
if(n>1){
mod[t]=n;
rem[t]=solveit(n1,k1,n2,k2,mod[t],n);
t++;
}
printf("%lld\n",CRT(mod,rem,t));
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:35
|
2016-07-23T18:01:09
|
C++
|
41 | 1,050 |
devu-police
|
Devu Vs Police
|
[Mandarin-Chinese](https://hr-filepicker.s3.amazonaws.com/infinitum-mar14/mandarin/1050-devupolice.md)
[Russian](https://hr-filepicker.s3.amazonaws.com/infinitum-mar14/russian/1050-devupolice.md)
It is holi festival, festival of colors. Devu is having fun playing holi and is throwing balloons with his girlfriend Glynis. Police saw this mischief and tried arresting his girlfriend, Devu being a mathematician asked police not to arrest his girlfriend and instead torture him with brain teaser. Devu was a young engineering fellow and he did not knew that policeman was equally good in mathematics, policeman gave Devu a problem which is as follows:
Let f(n,k) = n<sup>k</sup>
Your aim is to answer f(n1,k1)<sup>f(n2,k2)</sup> % n
Can you help devu and his girlfriend rescue from modern police.
**Input Format**
You are given `T` which is the number of queries to solve.
Each Query consist of 5 space separated integers `n1 k1 n2 k2 n`
**Output Format**
Output contains exactly T lines. i<sup>th</sup> line containing the answer for the i<sup>th</sup> query.
**Constraints**
1 <= T <= 10000
0 <= n1,k1,n2,k2 <= 10<sup>9</sup>
1 <= n <= 10<sup>7</sup>
**Note** The output to 0<sup>0</sup> should be 1.
**Sample Input**
1
2 1 2 2 15
**Sample Output**
1
**Explanation**
f(2,1) = 2
f(2,2) = 4
so answer is 16 mod 15 = 1
[Editorial](https://www.hackerrank.com/blog/infinitum-mar14-devu-police)
|
code
|
Help Devu escape from police
|
ai
|
2013-10-09T04:59:51
|
2022-09-02T09:54:38
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n1
# 2. INTEGER k1
# 3. INTEGER n2
# 4. INTEGER k2
# 5. INTEGER n
#
def solve(n1, k1, n2, k2, n):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n1 = int(first_multiple_input[0])
k1 = int(first_multiple_input[1])
n2 = int(first_multiple_input[2])
k2 = int(first_multiple_input[3])
n = int(first_multiple_input[4])
result = solve(n1, k1, n2, k2, n)
fptr.write(str(result) + '\n')
fptr.close()
|
It is holi festival, festival of colors. Devu is having fun playing holi and is throwing balloons with his girlfriend Glynis. Police saw this mischief and tried arresting his girlfriend, Devu being a mathematician asked police not to arrest his girlfriend and instead torture him with brain teaser. Devu was a young engineering fellow and he did not knew that policeman was equally good in mathematics, policeman gave Devu a problem which is as follows:
Let $f(n,k) = n^k$
Your aim is to answer $f(n_1,k_1)^{f(n_2,k_2)} \bmod n$
Can you help devu and his girlfriend rescue from modern police.
| 0.431818 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
You are given $T$ which is the number of queries to solve.
Each Query consist of 5 space separated integers $n_1,k_1,n_2,k_2,n$
|
Output contains exactly $T$ lines. $i^{\text{th}}$ line containing the answer for the $i^{\text{th}}$ query.
|
1
2 1 2 2 15
|
1
|
Hard
|
Devu Vs Police Infinitum Mar14 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
.MathJax_SVG_LineBox {display: table!important}
.MathJax_SVG_LineBox span {display: table-cell!important; width: 10000em!important; min-width: 0; max-width: none; padding: 0; border: 0; margin: 0}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/infinitum-mar14/challenges/devu-police">Problem Statement</a> </p>
<p><strong>Problem Setter</strong> : <a href="http://hackerrank.com/devuy11">Devendra</a> <br>
<strong>Problem Tester</strong> : <a href="http://hackerrank.com/cpcs">Cao Peng</a> <br>
<strong>Required Knowledge</strong>: Chinese Remainder Theorm </p>
<p>The Basic Idea Exploited here is Chinese Remainder Theorom.<br>
let n = p[1]^e[1] * p[2]^e[2] * p[3]^e[3] <em>...</em> p[k]^e[k] where p[i] is prime.<br>
let expr = A[1]^A[2]^A[3] where A[1] = f(n1,k1) , A[2] = n2, A[3] = k2<br>
so, calculating expr mod n is equivalent in calculating<br>
CRT ( expr mod p[1]^e[1] , expr mod p[2]^[e_2] ,......., expr mod p[k]^e[k] )<br>
Now lets see the case when e[i] = 1, then calculating expr mod p[i] is equivalent to A[1]^( A[2]^A[3] mod (p[i] -1 ) ) mod p[i].<br>
Euler Totient Period for p[i] is p[i] - 1.<br>
Now for the case of p[i]^e[i] where e[i]!=1, euler totient period is given by p[i]^e[i] - p[i]^(e[i]-1)<br>
<strong>Note:</strong> :Be carefull with Euler Totient period concept which is valid only if A[1] is coprime to p[i]. It is left as an exercise for the reader to figure it out how to procede then.<br></p>
<p><strong>Solution</strong> by <a href="http://hackerrank.com/cpcs">cpcs</a> </p>
<p>Let a = n1<sup>k1</sup> % n and b = n2<sup>k2</sup>, we need to calculate a^b mod n. We can judge whether a = 0/1 or b = 0,1 first to deal with the special conditions like 0^0, 1^p...etc. <br>
Then we can suppose a > 1 and b > 1. <br>
The solution is based on that although n may not be a prime, the period of the n1<sup>x</sup> % n is phi(n) , where phi is the euler function. <br>
But the starting point of the first period may be starts from phi(n). That means for any y >= phi(n) we have n1<sup>(y)</sup> == n1<sup>(y + phi(n))</sup> (mod n) </p>
<p>So if we found b is smaller enough, namely if b < phi(n), we can directly calculate the result using O(logb) algorithm. Otherwise we have b>=phi(n) then n1<sup>k1</sup> == n1<sup>(b % phi(n) + phi(n))</sup> mod n, so we just calculate n1 <sup>(b % phi(n) + phi(n))</sup> % n. </p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include<stdio.h>
#include<iostream>
#include<string.h>
#include<vector>
#include<assert.h>
using namespace std;
typedef long long int ll;
int sieve_par=3162;
int prime[3162] , array[3162],counter=0;
ll inverse(ll a,ll b) //b>a
{
ll Remainder,p0=0,p1=1,pcurr=1,q,m=b;
while(a!=0)
{
Remainder=b%a;
q=b/a;
if(Remainder!=0)
{
pcurr=p0-(p1*q)%m;
if(pcurr<0)
pcurr+=m;
p0=p1;
p1=pcurr;
}
b=a;
a=Remainder;
}
return pcurr;
}
ll binpow(ll a,ll b,ll mod)
{
ll ans=1;
while(b)
if(b&1){
ans=(ans*a)%mod;
b--;
}
else{
a=(a*a)%mod;
b>>=1;
}
return ans%mod;
}
ll CRT(ll mod[],ll rem[],int t) //t is the number of pairs of rem and mod
{
ll ans = rem[0],m = mod[0];
for(int i = 1;i < t;++i)
{
ll a = inverse(m,mod[i]);
ll b = inverse(mod[i],m);
ans = (ans * b * mod[i] + rem[i] * a * m) % (m * mod[i]);
m *= mod[i];
}
return ans;
}
void sieve()
{
for(int i=1;i<sieve_par;i++)
array[i]=1;
array[0]=0;
int j;
for(int i=2;i<=sieve_par;i++)
{
if(array[i-1]==1)
{
prime[counter]=i;
for(j=i*i;j<=sieve_par;j+=i)
array[j-1]=0;
counter++;
}
}
}
int check(ll a,ll b,ll n)
{
ll ans=1;
while(b)
if(b&1){
ans=ans*a;
if(ans>n) return -1;
b--;
}
else{
a=a*a;
if(a>n) return -1;
b>>=1;
}
return ans;
}
ll solveit(int n1,int k1,int n2,int k2,int m,int p)
{
ll x=1,y=0;
if(n1==0){
if(n2==0 && k2==0 && k1==0) return 1;
if(n2==0 && k2==0 && k1!=0) return 0;
if(k1==0 || n2==0) return 1;
return 0;
}
if(n1 % p == 0 ){
ll ans;
while(n1%p == 0){
n1/=p;
x=x*p;
y++;
}
ans= check(n2,k2,m);
ans= ans* k1*y;
if(ans>=0) ans= check(p,ans,m);
if(ans<0) return 0;
else x= ans;
}
ll a=binpow(n2,k2,m-(m/p));
ll b=binpow(n1,k1,m);
ll c= binpow(b,a,m);
return (c*x)%m;
}
int main()
{
sieve();
int test,n1,n2,n,k1,k2,t;
ll mod[15],rem[15],ans;
//printf("%d is counter\n",counter);
scanf("%d",&test);
assert(test<=10000);
while(test--){
scanf("%d%d%d%d%d",&n1,&k1,&n2,&k2,&n);
assert(n1<=1000000000 && k1<=1000000000 && n2<=1000000000 && k2<=1000000000 && n<=10000000);
assert(n1>=0 && k1>=0 && n2>=0 && k2>=0 && n>=1);
if(n==1){
printf("0\n");
continue;
}
t=0;
for(int i=0;i<counter;i++){
if(n< prime[i]*prime[i]) break;
if(n%prime[i]==0){
mod[t]=1;
while(n%prime[i]==0){
n/=prime[i];
mod[t]*=prime[i];
}
rem[t]=solveit(n1,k1,n2,k2,mod[t],prime[i]);
t++;
}
}
if(n>1){
mod[t]=n;
rem[t]=solveit(n1,k1,n2,k2,mod[t],n);
t++;
}
printf("%lld\n",CRT(mod,rem,t));
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>import java.math.*;
import java.util.*;
public class Solution {
public static long powermod(long x,long y,long M) {
x %= M;
if (y == 0) {
return 1;
}
if (x == 0) {
return 0;
}
long r = 1L;
for (;y > 0; y >>= 1) {
if ((y & 1) > 0) {
r = r * x % M;
}
x = x * x % M;
}
return r;
}
public static long phi(long m) {
long p = 1L;
for (long i = 2L; i * i <= m; ++i) {
if (m % i == 0) {
long j = 1L;
while (m % i == 0) {
m /= i;
j *= i;
}
p *= j - j / i;
}
}
return (m > 1)?(p * (m - 1)):p;
}
public static long cmp(long n,long k,long x) { //n ^ k > x < x = x
long i = 0L, temp = 1L;
while ((i < k) && (temp < x)) {
i++;
temp *= n;
}
if ((i >= k) && (temp <= x)) {
return temp;
}
return -1;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
for (int cases = scanner.nextInt(); cases > 0; cases--) {
long n1 = scanner.nextLong();
long k1 = scanner.nextLong();
long n2 = scanner.nextLong();
long k2 = scanner.nextLong();
long n = scanner.nextLong();
if (n == 1) {
System.out.println(0);
}
else {
long x = powermod(n1,k1,n);
if ((k2 == 0) || (n2 == 1)) {
System.out.println(x);
}
else if (n2 == 0) {
System.out.println(1);
}
else if (x <= 1) {
System.out.println(x);
}
else { // n2 > 1, k2 > 0, x > 1
long p = phi(n);
long y = cmp(n2,k2,p);
System.out.println(powermod(x, (y >= 0)?y:(powermod(n2,k2,p) + p),n));
}
}
}
}
}
</code></pre>
| 0 |
infinitum-mar14-devu-police
|
2014-04-01T21:20:47
|
{"contest_participation":1667,"challenge_submissions":241,"successful_submissions":76}
|
2014-04-01T21:20:47
|
2016-12-09T10:05:33
|
tester
|
###Java
```java
import java.math.*;
import java.util.*;
public class Solution {
public static long powermod(long x,long y,long M) {
x %= M;
if (y == 0) {
return 1;
}
if (x == 0) {
return 0;
}
long r = 1L;
for (;y > 0; y >>= 1) {
if ((y & 1) > 0) {
r = r * x % M;
}
x = x * x % M;
}
return r;
}
public static long phi(long m) {
long p = 1L;
for (long i = 2L; i * i <= m; ++i) {
if (m % i == 0) {
long j = 1L;
while (m % i == 0) {
m /= i;
j *= i;
}
p *= j - j / i;
}
}
return (m > 1)?(p * (m - 1)):p;
}
public static long cmp(long n,long k,long x) { //n ^ k > x < x = x
long i = 0L, temp = 1L;
while ((i < k) && (temp < x)) {
i++;
temp *= n;
}
if ((i >= k) && (temp <= x)) {
return temp;
}
return -1;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
for (int cases = scanner.nextInt(); cases > 0; cases--) {
long n1 = scanner.nextLong();
long k1 = scanner.nextLong();
long n2 = scanner.nextLong();
long k2 = scanner.nextLong();
long n = scanner.nextLong();
if (n == 1) {
System.out.println(0);
}
else {
long x = powermod(n1,k1,n);
if ((k2 == 0) || (n2 == 1)) {
System.out.println(x);
}
else if (n2 == 0) {
System.out.println(1);
}
else if (x <= 1) {
System.out.println(x);
}
else { // n2 > 1, k2 > 0, x > 1
long p = phi(n);
long y = cmp(n2,k2,p);
System.out.println(powermod(x, (y >= 0)?y:(powermod(n2,k2,p) + p),n));
}
}
}
}
}
```
|
not-set
|
2016-04-24T02:02:35
|
2016-07-23T18:01:49
|
Java
|
42 | 1,329 |
a-very-special-multiple
|
A Very Special Multiple
|
[Mandarin](http://hr-filepicker.s3.amazonaws.com/infinitum-mar14/mandarin/1329-veryspecialmultiple.md) \| [Russian](http://hr-filepicker.s3.amazonaws.com/infinitum-mar14/russian/1329-veryspecialmultiple.md) \| [Japanese](http://hr-filepicker.s3.amazonaws.com/infinitum-mar14/japanese/1329-veryspecialmultiple.md)
Charlie and Johnny play a game. For every integer _X_ Charlie gives, Johnny has to find the smallest positive integer _Y_, such that X x Y (X multiplied by Y) contains only 4's and 0's and starts with one or more 4's followed by zero or more 0's. (i.e.), 404 is an invalid number but 4400, 440, and 444 are valid numbers.
If _a_ is the number of 4's and _b_ is the number of 0's, can you print the value of (2 x a) + b.
**Input Format**
The first line contains an integer `T`.
`T` lines follow, each line containing the integer `X` as stated above.
**Output Format**
For every X, print the output (2 x a) + b in a newline as stated in the problem statement.
**Constraints**
1 <= T <= 100
1 <= X <= 10<sup>10</sup>
**Sample Input**
3
4
5
80
**Sample Output**
2
3
4
**Explanation**
For the 1<sup>st</sup> test-case, the smallest such multiple of 4 is **4** itself. Hence value of a will be 1 and and value of b will be 0. The required value of (2 x a) + b is 2.
For the 2<sup>nd</sup> test-case, **Y** = 8 and 40 is the minimum such multiple of 5. Hence value of a,b and (2 x a) + b will be 1, 1 and 3 respectively.
[Editorial](https://www.hackerrank.com/blog/infinitum-mar14-a-very-special-multiple)
|
code
|
Find the number of 4's and 0's in the multiple
|
ai
|
2013-11-18T07:44:55
|
2022-09-02T09:54:43
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts LONG_INTEGER x as parameter.
#
def solve(x):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
x = int(input().strip())
result = solve(x)
fptr.write(str(result) + '\n')
fptr.close()
|
Charlie and Johnny play a game. For every integer $X$ Charlie gives, Johnny has to find the smallest positive integer $Y$ such that $X \times Y$ ($X$ multiplied by $Y$) contains only 4s and 0s and starts with one or more 4s followed by zero or more 0s. For example, 404 is an invalid number but 4400, 440, and 444 are valid numbers.
If $a$ is the number of 4s and $b$ is the number of 0s, can you print the value of $(2\times a) + b$?
**Input Format**
The first line of input contains a single integer $T$, the number of test cases.
$T$ lines follow, each line containing the integer $X$ as stated above.
**Output Format**
For every $X$, print the output $(2\times a) + b$ in a newline as stated in the problem statement.
**Constraints**
$1 \le T \le 100$
$1 \le X \le 10^{10}$
**Sample Input**
3
4
5
80
**Sample Output**
2
3
4
**Explanation**
For the 1<sup>st</sup> test case, the smallest such multiple of $4$ is 4 itself. Hence the value of $a$ will be $1$ and and the value of $b$ will be $0$, and the answer is $(2\times a) + b = 2$.
For the 2<sup>nd</sup> test case, $Y = 8$ and 40 is the minimum such multiple of $5$. Hence the values of $a$, $b$ and $(2 \times a) + b$ will be $1$, $1$ and $3$ respectively.
| 0.564103 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
|
A Very Special Multiple Infinitum Mar14 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/infinitum-mar14/challenges/a-very-special-multiple">Problem Statement</a> </p>
<p><strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/shashank21j">Shashank Sharma</a> <br>
<strong>Problem Tester</strong> : <a href="http://hackerrank.com/itsmecoders">Satvik Gupta</a> <br>
<strong>Required Knowledge</strong>: Fermat's Theorm, Sieve of Eratosthenes, Totient Function, Division
<strong>Time Complexity</strong> : O(root(N))</p>
<p><strong>Approach</strong> </p>
<p>The Multiple X*Y can be divided into 4*(1111....00000...) <br>
Now 0's are made up of all multiple of 2/5. </p>
<p>now our multiple (1111...)is rid of all 2,5 hence it is coprime to 10, so Fermat's theorm holds </p>
<p>1111...n times can be written as (10<sup>n</sup> - 1)/9, so </p>
<p><img src="http://hr-blog.s3.amazonaws.com/infinitum-mar14/specialmultiple1.gif" alt="latex" title=""> </p>
<p>hence phi(9x) is a solution but it is not the smallest. <br>
We take the divisors of 9x, minimum of those which solves it is the required number. </p>
<p>but 9x can be a large number. Hence we solve for prime factors of 9x and get solutions s1,s2 etc. We take lcm of those values to get the right answer. </p>
<p>in the end we return 2*a + b</p>
<p><strong>Tester's Code</strong> </p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
ll sieve(ll a[],ll b[],ll n)
{
ll i,k,j;
for(i=0;i<n;i++)
{
a[i]=i,b[i]=0;
}
for (j=2;j*j<n;j++)
{
k=j;
if(a[j]!=0)
{
while(k*j<n)
{
a[k*j]=0;
k=k+1;
}
}
}
i=2;j=0;
while(i<n)
{
if(a[i]!=0)
{
b[j]=a[i];
j++;
}
i++;
}
return j;
}
ll gcd(ll a,ll b)
{
ll d;
a=a>=0?a:-a;
b=b>=0?b:-b;
while(b!=0)
{
d=a%b;
a=b;
b=d;
}
return a;
}
ll abmodP(ll a, ll b,ll mod)
{
ll aprod = a;
ll ans = 0;
while(b > 0) {
if(b & 1) ans = (ans + aprod) % mod;
b = b >> 1;
aprod = (aprod << 1) % mod;
}
return ans;
}
long long int power(long long int a,long long int b,long long int c)//To calculate A^B%C
{
long long int res=1,apower=a;
while(b > 0)
{
if(b%2 == 1)
{
res=abmodP(res,apower,c);
}
apower = abmodP(apower,apower,c);
b=b/2 ;
}
return res%c;
}
ll a[100005],b[100005];
int main()
{
ll n = 100000;
ll k = sieve(a,b,n);
ll t,x;
ll i,j;
scanf("%lld",&t);
while(t--)
{
ll d[20][3];
scanf("%lld",&x);
if(x==0)
cout << 0 << endl;
else if(x==1)
cout << 2 << endl;
else
{
x = x*9;
ll len=0;
for(i=0;b[i]*b[i] <= x && i<k ; i++)
{
ll count=0;
if(x%b[i]==0)
{
ll an1=1;
d[len][0]=b[i];
while(x%b[i]==0)
x=x/b[i],count+=1,an1*=b[i];
d[len][1]=count,d[len][2]=an1;
len+=1;
}
}
if(x!=1)
d[len][0]=x,d[len][1]=1,d[len][2]=x,len=len+1;
ll c2=0,c5=0,c3=0;
if(d[0][0]==2)
c2=d[0][1];
if(d[0][0]==5)
c5=d[0][1];
if(len > 1 && d[1][0]==5)
c5=d[1][1];
if(len > 2 && d[2][0]==5)
c5=d[2][1];
ll y=max(c5,c2-2);
ll e[20];
ll len1=0;
for(i=0;i<len;i++)
{
if(d[i][0]!=2 && d[i][0]!=5)
{
ll a1 = d[i][2]/d[i][0];
a1 = a1 * (d[i][0]-1);
ll min1=a1;
for(j=1;j*j<a1;j++)
{
if(a1%j==0)
{
ll po= power((ll)10,j,d[i][2]);
if(po < 0)
po+=d[i][2];
if(po==1)
min1 = min(j,min1);
else
{
po= power((ll)10,(a1/j),d[i][2]);
if(po < 0)
po+=d[i][2];
if(po==1)
min1 = min(a1/j,min1);
}
}
}
e[len1]=min1;
len1+=1;
}
}
ll lcm = e[0];
for(i=1;i<len1;i++)
{
lcm = (lcm * e[i])/gcd(lcm,e[i]);
}
printf("%lld\n",2*lcm + y);
}
}
return 0;
}
</code></pre>
| 0 |
infinitum-mar14-a-very-special-multiple
|
2014-04-01T21:24:58
|
{"contest_participation":1667,"challenge_submissions":122,"successful_submissions":48}
|
2014-04-01T21:24:58
|
2016-12-02T17:29:23
|
tester
|
###C++
```cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;
ll sieve(ll a[],ll b[],ll n)
{
ll i,k,j;
for(i=0;i<n;i++)
{
a[i]=i,b[i]=0;
}
for (j=2;j*j<n;j++)
{
k=j;
if(a[j]!=0)
{
while(k*j<n)
{
a[k*j]=0;
k=k+1;
}
}
}
i=2;j=0;
while(i<n)
{
if(a[i]!=0)
{
b[j]=a[i];
j++;
}
i++;
}
return j;
}
ll gcd(ll a,ll b)
{
ll d;
a=a>=0?a:-a;
b=b>=0?b:-b;
while(b!=0)
{
d=a%b;
a=b;
b=d;
}
return a;
}
ll abmodP(ll a, ll b,ll mod)
{
ll aprod = a;
ll ans = 0;
while(b > 0) {
if(b & 1) ans = (ans + aprod) % mod;
b = b >> 1;
aprod = (aprod << 1) % mod;
}
return ans;
}
long long int power(long long int a,long long int b,long long int c)//To calculate A^B%C
{
long long int res=1,apower=a;
while(b > 0)
{
if(b%2 == 1)
{
res=abmodP(res,apower,c);
}
apower = abmodP(apower,apower,c);
b=b/2 ;
}
return res%c;
}
ll a[100005],b[100005];
int main()
{
ll n = 100000;
ll k = sieve(a,b,n);
ll t,x;
ll i,j;
scanf("%lld",&t);
while(t--)
{
ll d[20][3];
scanf("%lld",&x);
if(x==0)
cout << 0 << endl;
else if(x==1)
cout << 2 << endl;
else
{
x = x*9;
ll len=0;
for(i=0;b[i]*b[i] <= x && i<k ; i++)
{
ll count=0;
if(x%b[i]==0)
{
ll an1=1;
d[len][0]=b[i];
while(x%b[i]==0)
x=x/b[i],count+=1,an1*=b[i];
d[len][1]=count,d[len][2]=an1;
len+=1;
}
}
if(x!=1)
d[len][0]=x,d[len][1]=1,d[len][2]=x,len=len+1;
ll c2=0,c5=0,c3=0;
if(d[0][0]==2)
c2=d[0][1];
if(d[0][0]==5)
c5=d[0][1];
if(len > 1 && d[1][0]==5)
c5=d[1][1];
if(len > 2 && d[2][0]==5)
c5=d[2][1];
ll y=max(c5,c2-2);
ll e[20];
ll len1=0;
for(i=0;i<len;i++)
{
if(d[i][0]!=2 && d[i][0]!=5)
{
ll a1 = d[i][2]/d[i][0];
a1 = a1 * (d[i][0]-1);
ll min1=a1;
for(j=1;j*j<a1;j++)
{
if(a1%j==0)
{
ll po= power((ll)10,j,d[i][2]);
if(po < 0)
po+=d[i][2];
if(po==1)
min1 = min(j,min1);
else
{
po= power((ll)10,(a1/j),d[i][2]);
if(po < 0)
po+=d[i][2];
if(po==1)
min1 = min(a1/j,min1);
}
}
}
e[len1]=min1;
len1+=1;
}
}
ll lcm = e[0];
for(i=1;i<len1;i++)
{
lcm = (lcm * e[i])/gcd(lcm,e[i]);
}
printf("%lld\n",2*lcm + y);
}
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:35
|
2016-07-23T18:13:45
|
C++
|
||||
43 | 2,152 |
reverse-factorization
|
Reverse Factorization
|
At the time when Pythagoreanism was prevalent, people were also focused on different ways to factorize a number. In one class, Pythagoreas asked his disciples to solve one such problem, _Reverse Factorization_. They were given a set of integer, `A` = _{a<sub>1</sub>, a<sub>2</sub>,..., a<sub>K</sub>}_, and an integer `N`. They need to find the a way to reach `N`, starting from `1`, and at each step multiplying current value by any element of `A`. But soon they realise that there may exist more than one way to reach `N`. So they decided to find a way in which number of states are least. All of sudden they started on this new problem. People solved it and then started shouting their answer. CRAP!!!. There still exists multiple answers. So finally after much consideration, they settled on the lexicographically smallest series among those solutions which contains the least number of states.
For example, if `N = 12` and `A = {2, 3, 4}` then following ways exists
(a) 1 -> 2 -> 4 -> 12
x2 x2 x3
(b) 1 -> 4 -> 12
x4 x3
(c) 1 -> 3 -> 12
x3 x4
Here `(a)` is not the minimal state, as it has 4 states in total. While `(b)` and `(c)` are contenders for answer, both having 3 states, `(c)` is lexicographically smaller than `(b)` so it is the answer. In this case you have to print `1 3 12`. If there exists no way to reach `N` print `-1`.
**Input**
Input contains two lines where first line contains two space separated integer, `N K`, representing the final value to reach and the size of set `A`, respectively. Next line contains `K` space integers representing the set `A` = _{a<sub>1</sub>, a<sub>2</sub>,..., a<sub>K</sub>}_.
**Output**
Print the steps to reach `N` if it exists. Otherwise print `-1`.
**Constraints**
1 ≤ N ≤ 10<sup>9</sup>
1 ≤ K ≤ 20
2 ≤ a<sub>i</sub> ≤ 20, where _i ∈ [1..K]_
a<sub>i</sub> ≠ a<sub>j</sub>, where 1 <= i, j <= K AND _i_ ≠ _j_
**Note:**
* _Lexicographical order:_ If `list1` = _[p<sub>1</sub>, p<sub>2</sub>, ...p<sub>m</sub>]_ and `list2` = _[q<sub>1</sub>, q<sub>2</sub>,...q<sub>n</sub>]_ are two ordered lists, then `list1` is lexicographically smaller than `list2` if any one of the following condition satisfies.
+ _p<sub>i</sub> = q<sub>i</sub>_, for _i_ ∈ [1..m] AND _m < n_.
+ _p<sub>i</sub> = q<sub>i</sub>_, for _i_ ∈ _[1..k]_ AND _k_ < min(_m_, _n_) AND _p<sub>k+1</sub> < q<sub>k+1</sub>_.
* You need to find the _lexigraphically smallest_ series among those solutions which contains the least number of states.
**Sample Input #00**
12 3
2 3 4
**Sample Output #00**
1 3 12
**Sample Input #01**
15 5
2 10 6 9 11
**Sample Output #01**
-1
**Sample Input #02**
72 9
2 4 6 9 3 7 16 10 5
**Sample Output #02**
1 2 8 72
**Explanation**
*Test Case #00:* This is the same case which is explaned above.
*Test Case #01:* Here no way exists so that we can reach `15` starting from `1`.
*Test Case #02:* There are multiple ways to reach `72` using these 8 numbers. Out of which following 6 ways consists of minimal states (4).
States => Multiplication operation
1 9 18 72 => (x9, x2, x4)
1 4 36 72 => (x4, x9, x2)
1 2 8 72 => (x2, x4, x9)
1 2 18 72 => (x2, x9, x4)
1 4 8 72 => (x4, x2, x9)
1 9 36 72 => (x9, x4, x2)
As series `1 2 8 72` is lexicographically smallest, it is the answer.
|
code
|
Find multiples to reach `N`.
|
ai
|
2014-03-17T22:45:59
|
2017-03-10T08:53:18
| null | null | null |
At the time when Pythagoreanism was prevalent, people were also focused on different ways to factorize a number. In one class, Pythagoras asked his disciples to solve one such problem, _Reverse Factorization_. They were given a set of integer, $A = \{a_1, a_2, \cdots, a_K\}$, and an integer $N$. They need to find the a way to reach $N$, starting from $1$, and at each step multiplying current value by any element of $A$. But soon they realised that there may exist more than one way to reach $N$. So they decided to find a way in which number of states are least. All of sudden they started on this new problem. People solved it and then started shouting their answer. CRAP!!!. There still exists multiple answers. So finally after much consideration, they settled on the lexicographically smallest series among those solutions which contains the least number of states.
For example, if $N = 12$ and $A = {2, 3, 4}$ then following ways exists
```
(a) 1 -> 2 -> 4 -> 12
x2 x2 x3
(b) 1 -> 4 -> 12
x4 x3
(c) 1 -> 3 -> 12
x3 x4
```
Here `(a)` is not the minimal state, as it has $4$ states in total. While `(b)` and `(c)` are contenders for answer, both having 3 states, `(c)` is lexicographically smaller than `(b)` so it is the answer. In this case you have to print `1 3 12`. If there exists no way to reach $N$ print `-1`.
| 0.5 |
["haskell","clojure","scala","erlang","sbcl","ocaml","fsharp","racket","elixir"]
|
Input contains two lines where first line contains two space separated integer, $N$ and $K$, representing the final value to reach and the size of set $A$, respectively. Next line contains `K` space integers representing the set $A = \{a_1, a_2, \cdots, a_K\}$.
|
Print the steps to reach $N$ if it exists. Otherwise print `-1`.
|
Hard
|
Reverse Factorization, Functional Programming Contest - March'14
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="/contests/lambda-calculi-mar14/challenges/reverse-factorization">Problem Statement</a> <br>
<strong>Difficulty Level</strong> : Medium-Hard <br>
<strong>Required Knowledge</strong> : Breadth First Search, Simple Maths <br>
<strong>Problem Setter</strong> : <a href="/abhiranjan">Abhiranjan</a> </p>
<p>It was a decoy problem from the author. Initially it appears to be a factorization problem, but when looking closely it became clear that even a simple BFS can be used to solved this problem. Following two properties should help in solving this problem via BFS.</p>
<ol>
<li>Find the solution with minimum number of steps. Elements of set <em>A = {a<sub>1</sub>, a<sub>2</sub>, ..., a<sub>K</sub>}</em> acts as the edge between an integer/node <em>P</em> and _{P*a<sub>1</sub>, P*a<sub>2</sub>, ..., P*a<sub>K</sub>}_</li>
<li>In order to find the lexicographically smallest solution, we need to enqueue smaller element earlier larger element, i.e., sort the elements of set <em>A</em> before multiplying it with the current number in BFS.</li>
</ol>
<p>PS: Implementing queue and BFS can be a tricky task in few languages.</p>
<p>We need to start from <em>1</em> and then multiplying current number with the elements of <em>A</em>. We need to store the parent node of the current node, as it is required to trace the path from <em>1</em> to <em>N</em>.</p>
<p><strong>Setter's Code</strong></p>
<p>*<em>Language : *</em></p>
<pre><code>import Data.List
import qualified Data.Map as Map
data Queue a = Queue {
active :: [a]
, inactive :: [a]
} deriving (Show)
emptyQ :: Queue a
emptyQ = Queue [] []
swapQ :: Queue a -> Queue a
swapQ q = Queue {active = inactive q, inactive = active q}
isEmptyQ :: Queue a -> Bool
isEmptyQ q = null (active q) && null (inactive q)
peekQ :: Queue a -> (a, Queue a)
peekQ q
| isEmptyQ q = error "queue is empty, can't look"
| null. inactive $ q = (head q1, Queue {active = [], inactive = q1})
| otherwise = (head. inactive $ q, q)
where
q1 = reverse. active $ q
popQ :: Queue a -> (a, Queue a)
popQ q = (h, q1 {inactive = tail. inactive $ q1})
where
(h, q1) = peekQ q
enqueue :: a -> Queue a -> Queue a
enqueue x q = q {active = x: active q}
bfs :: Integer -> [Integer] -> Map.Map Integer Integer
bfs n arr1 = snd. bfs1 $ (enqueue 1 emptyQ, Map.empty)
where
arr = sort arr1
bfs1 :: (Queue Integer, Map.Map Integer Integer) -> (Queue Integer, Map.Map Integer Integer)
bfs1 (q, st)
| isEmptyQ q = (q, st)
| otherwise = bfs1 nextState
where
(x, q1) = popQ q
nextState = foldl' foldFunc (q1,st) arr
foldFunc acc@(qq, sst) mul =
let
m = mul*x
in
if (m > n) || Map.member m sst
then acc
else (enqueue m qq, Map.insert m x sst)
tracePath :: Integer -> Map.Map Integer Integer -> Maybe [Integer]
tracePath n mp
| not (Map.member n mp) = Nothing
| otherwise = Just. reverse. traverse $ n
where
traverse 1 = [1]
traverse x = x : traverse (Map.findWithDefault (-1) x mp)
printPath :: Maybe [Integer] -> String
printPath Nothing = show (-1)
printPath (Just arr) = unwords. map show $ arr
main :: IO ()
main = getContents >>= putStrLn. printPath. (\[[n, k], arr] -> tracePath n (bfs n arr)). map (map read. words). lines
</code></pre>
| 0 |
lambda-calculi-mar14-reverse-factorization
|
2014-04-02T19:30:44
|
{"contest_participation":797,"challenge_submissions":56,"successful_submissions":46}
|
2014-04-02T19:30:44
|
2016-05-13T00:03:08
|
setter
|
import Data.List
import qualified Data.Map as Map
data Queue a = Queue {
active :: [a]
, inactive :: [a]
} deriving (Show)
emptyQ :: Queue a
emptyQ = Queue [] []
swapQ :: Queue a -> Queue a
swapQ q = Queue {active = inactive q, inactive = active q}
isEmptyQ :: Queue a -> Bool
isEmptyQ q = null (active q) && null (inactive q)
peekQ :: Queue a -> (a, Queue a)
peekQ q
| isEmptyQ q = error "queue is empty, can't look"
| null. inactive $ q = (head q1, Queue {active = [], inactive = q1})
| otherwise = (head. inactive $ q, q)
where
q1 = reverse. active $ q
popQ :: Queue a -> (a, Queue a)
popQ q = (h, q1 {inactive = tail. inactive $ q1})
where
(h, q1) = peekQ q
enqueue :: a -> Queue a -> Queue a
enqueue x q = q {active = x: active q}
bfs :: Integer -> [Integer] -> Map.Map Integer Integer
bfs n arr1 = snd. bfs1 $ (enqueue 1 emptyQ, Map.empty)
where
arr = sort arr1
bfs1 :: (Queue Integer, Map.Map Integer Integer) -> (Queue Integer, Map.Map Integer Integer)
bfs1 (q, st)
| isEmptyQ q = (q, st)
| otherwise = bfs1 nextState
where
(x, q1) = popQ q
nextState = foldl' foldFunc (q1,st) arr
foldFunc acc@(qq, sst) mul =
let
m = mul*x
in
if (m > n) || Map.member m sst
then acc
else (enqueue m qq, Map.insert m x sst)
tracePath :: Integer -> Map.Map Integer Integer -> Maybe [Integer]
tracePath n mp
| not (Map.member n mp) = Nothing
| otherwise = Just. reverse. traverse $ n
where
traverse 1 = [1]
traverse x = x : traverse (Map.findWithDefault (-1) x mp)
printPath :: Maybe [Integer] -> String
printPath Nothing = show (-1)
printPath (Just arr) = unwords. map show $ arr
main :: IO ()
main = getContents >>= putStrLn. printPath. (\[[n, k], arr] -> tracePath n (bfs n arr)). map (map read. words). lines
|
not-set
|
2016-04-24T02:02:36
|
2016-04-24T02:02:36
|
Python
|
||
44 | 2,176 |
hexagonal-grid
|
Hexagonal Grid
|
You are given a hexagonal grid of size _2xN_. Your task is to construct the grid with _2x1_ dominoes. The dominoes can be arranged in any of the three orientations shown below. To add to the woes, certain cells of the hexogonal grid are blackened i.e., no domino can occupy that cell. Can you construct such a hexagonal grid? The blackened cell and the 3 dominoes are shown in the figure below.

**Input Format**
The first line contains a single integer _T_, the number of testcases.
_T_ testcases follow.
Each testcase contains three lines. The first line of the testcase contains a single integer _N_, size of the hexagonal grid.
The next two lines describe the grid and have _N_ characters each (0 corresponds to cell to be filled with domino and 1 corresponds to blackened cell).
**Output Format**
For each testcase output `YES` if there exists at least one way to fill structure with dominoes and output `NO` otherwise.
**Constraints**
1 ≤ _T_ ≤ 100
1 ≤ _N_ ≤ 10
**Note**
There must be no domino above black cells.
All other cells should have only one domino above it.
**Sample input**
6
6
010000
000010
2
00
00
2
00
10
2
00
01
2
00
11
2
10
00
**Sample Output**
YES
YES
NO
NO
YES
NO
**Explanation**
First testcase in sample input describes grid from the picture.
For second testcase, there are two ways to fill it. Either place two red dominoes horizontally side-by-side or place two yellow dominoes vertically side-by-side.
|
code
|
You are given a hexagonal grid of size 2xN. Your task is to
construct the grid with dominoes of given size.
|
ai
|
2014-03-20T21:45:12
|
2022-08-31T08:14:47
|
#
# Complete the 'hexagonalGrid' function below.
#
# The function is expected to return a STRING.
# The function accepts following parameters:
# 1. STRING a
# 2. STRING b
#
def hexagonalGrid(a, b):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
n = int(input().strip())
a = input()
b = input()
result = hexagonalGrid(a, b)
fptr.write(result + '\n')
fptr.close()
|
You are given a hexagonal grid consisting of two rows, each row consisting of $n$ cells. The cells of the first row are labelled $a_1, a_2, \ldots a_n$ and the cells of the second row are labelled $b_1, b_2, \ldots, b_n$.
For example, for $n = 6$:

(Note that the $b_i$ is connected with $a_{i+1}$.)
Your task is to tile this grid with $2\times 1$ *tiles* that look like the following:

As you can see above, there are three possible orientations in which a tile can be placed.
Your goal is to tile the whole grid such that every cell is covered by a tile, and no two tiles occupy the same cell. To add to the woes, certain cells of the hexagonal grid are *blackened*. No tile must occupy a blackened cell.
Is it possible to tile the grid?
Here's an example. Suppose we want to tile this grid:

Then we can do the tiling as follows:

| 0.5 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains a single integer $t$, the number of test cases.
The first line of each test case contains a single integer $n$ denoting the length of the grid.
The second line contains a binary string of length $n$. The $i^\text{th}$ character describes whether cell $a_i$ is blackened.
The third line contains a binary string of length $n$. The $i^\text{th}$ character describes whether cell $b_i$ is blackened.
A `0` corresponds to an empty cell and a `1` corresponds to blackened cell.
|
For each test case, print `YES` if there exists at least one way to tile the grid, and `NO` otherwise.
|
6
6
010000
000010
2
00
00
2
00
10
2
00
01
2
00
11
2
10
00
|
YES
YES
NO
NO
YES
NO
|
Hard
|
Hexagonal Grid - 101 Hack March Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101mar14/challenges/hexagonal-grid">Hexagonal Grid</a> <br>
<strong>Difficulty Level</strong> : Easy-Medium <br>
<strong>Required Knowledge</strong> : Recursion or DP <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/Seyaua">Seyaua</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/abhiranjan">Abhiranjan Kumar</a> <br></p>
<p><strong>Solution</strong> <br>
There are a lot of ways to solve this problem. The easiest one is to just run a recursion, where in each step we will try to fill just two empty cells. The constraints are very small, so this solution works very fast. As an alternative solution you can write something like dynamic programming by submasks.</p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <vector>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <bitset>
#include <queue>
#pragma comment(linker, "/STACK:256000000")
using namespace std;
const int maxN = 12;
int a[2][maxN];
int n;
bool fnd = false;
bool is_in(int i, int j) {
return (0 <= i && i < 2 && j >= 0 && j < n);
}
int dx[] = {0, 1, 1};
int dy[] = {1, 0, -1};
void rec() {
if (fnd) return;
int change = false;
for (int i = 0; i < 2 && !change && !fnd; ++i) {
for (int j = 0; j < n && !change && !fnd; ++j) {
if (a[i][j] == 0) {
change = true;
for (int k = 0; k < 3 && !fnd; ++k) {
if (is_in(i + dx[k], j + dy[k]) && a[i + dx[k]][j + dy[k]] == 0) {
a[i][j] = 1;
a[i + dx[k]][j + dy[k]] = 1;
rec();
a[i][j] = 0;
a[i + dx[k]][j + dy[k]] = 0;
}
}
}
}
}
if (!change) {
fnd = true;
}
}
void solve() {
scanf("%d", &n);
string s1, s2;
cin >> s1 >> s2;
for (int i = 0; i < n; ++i) {
a[0][i] = s1[i] - '0';
a[1][i] = s2[i] - '0';
}
fnd = false;
rec();
if (fnd) {
cout << "YES" << endl;
} else {
cout << "NO" << endl;
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int t;
scanf("%d", &t);
for (int i = 0; i < t; ++i) {
solve();
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
int a[2][101];
int dp[105][105];
int N;
bool solve(int l, int r) {
if(l == -1 && r == -1)
return 1;
if(l < -1 ||r < -1)
return 0;
if(l < 0 && r >= 0 && a[1][r] == 1)
return solve(l, r-1);
if(r < 0 && l >= 0 && a[0][l] == 1)
return solve(l-1, r);
if(l < 0 || r < 0)
return 0;
int &ret = dp[l][r];
if(ret != -1)
return ret;
ret = 0;
if(a[0][l] == 1)
ret |= solve(l-1, r);
if(a[1][r] == 1)
ret |= solve(l, r-1);
if(l > 0 && a[0][l] == 0 && a[0][l-1] == 0)
ret |= solve(l-2, r);
if(r > 0 && a[1][r] == 0 && a[1][r-1] == 0)
ret |= solve(l, r-2);
if(l == r && a[0][l] == 0 && a[1][r] == 0)
ret |= solve(l-1, r-1);
if(l == r+1 && a[0][l] == 0 && a[1][r] == 0)
ret |= solve(l-1, r-1);
return ret;
}
int main()
{
int t;
scanf("%d", &t);
assert(t >= 1 && t <= 100);
while(t--) {
memset(dp, -1, sizeof(dp));
cin >> N;
assert( N >= 1 && N <= 10);
string st[2];
cin >> st[0] >> st[1];
assert((int)st[0].length() == N);
assert((int)st[1].length() == N);
for(int i = 0; i < (int)N; ++i) {
assert(st[0][i] == '0' || st[0][i] == '1');
assert(st[1][i] == '0' || st[1][i] == '1');
a[0][i] = st[0][i] == '0' ? 0 : 1;
a[1][i] = st[1][i] == '0' ? 0 : 1;
}
cout << (solve(N-1, N-1) == 1 ? "YES" : "NO") << "\n";
}
return 0;
}
</code></pre>
| 0 |
101mar14-hexagonal-grid
|
2014-04-04T08:43:27
|
{"contest_participation":1218,"challenge_submissions":208,"successful_submissions":134}
|
2014-04-04T08:43:27
|
2016-07-23T14:48:42
|
setter
|
###C++
```cpp
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <vector>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <bitset>
#include <queue>
#pragma comment(linker, "/STACK:256000000")
using namespace std;
const int maxN = 12;
int a[2][maxN];
int n;
bool fnd = false;
bool is_in(int i, int j) {
return (0 <= i && i < 2 && j >= 0 && j < n);
}
int dx[] = {0, 1, 1};
int dy[] = {1, 0, -1};
void rec() {
if (fnd) return;
int change = false;
for (int i = 0; i < 2 && !change && !fnd; ++i) {
for (int j = 0; j < n && !change && !fnd; ++j) {
if (a[i][j] == 0) {
change = true;
for (int k = 0; k < 3 && !fnd; ++k) {
if (is_in(i + dx[k], j + dy[k]) && a[i + dx[k]][j + dy[k]] == 0) {
a[i][j] = 1;
a[i + dx[k]][j + dy[k]] = 1;
rec();
a[i][j] = 0;
a[i + dx[k]][j + dy[k]] = 0;
}
}
}
}
}
if (!change) {
fnd = true;
}
}
void solve() {
scanf("%d", &n);
string s1, s2;
cin >> s1 >> s2;
for (int i = 0; i < n; ++i) {
a[0][i] = s1[i] - '0';
a[1][i] = s2[i] - '0';
}
fnd = false;
rec();
if (fnd) {
cout << "YES" << endl;
} else {
cout << "NO" << endl;
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int t;
scanf("%d", &t);
for (int i = 0; i < t; ++i) {
solve();
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T14:48:30
|
C++
|
45 | 2,176 |
hexagonal-grid
|
Hexagonal Grid
|
You are given a hexagonal grid of size _2xN_. Your task is to construct the grid with _2x1_ dominoes. The dominoes can be arranged in any of the three orientations shown below. To add to the woes, certain cells of the hexogonal grid are blackened i.e., no domino can occupy that cell. Can you construct such a hexagonal grid? The blackened cell and the 3 dominoes are shown in the figure below.

**Input Format**
The first line contains a single integer _T_, the number of testcases.
_T_ testcases follow.
Each testcase contains three lines. The first line of the testcase contains a single integer _N_, size of the hexagonal grid.
The next two lines describe the grid and have _N_ characters each (0 corresponds to cell to be filled with domino and 1 corresponds to blackened cell).
**Output Format**
For each testcase output `YES` if there exists at least one way to fill structure with dominoes and output `NO` otherwise.
**Constraints**
1 ≤ _T_ ≤ 100
1 ≤ _N_ ≤ 10
**Note**
There must be no domino above black cells.
All other cells should have only one domino above it.
**Sample input**
6
6
010000
000010
2
00
00
2
00
10
2
00
01
2
00
11
2
10
00
**Sample Output**
YES
YES
NO
NO
YES
NO
**Explanation**
First testcase in sample input describes grid from the picture.
For second testcase, there are two ways to fill it. Either place two red dominoes horizontally side-by-side or place two yellow dominoes vertically side-by-side.
|
code
|
You are given a hexagonal grid of size 2xN. Your task is to
construct the grid with dominoes of given size.
|
ai
|
2014-03-20T21:45:12
|
2022-08-31T08:14:47
|
#
# Complete the 'hexagonalGrid' function below.
#
# The function is expected to return a STRING.
# The function accepts following parameters:
# 1. STRING a
# 2. STRING b
#
def hexagonalGrid(a, b):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
n = int(input().strip())
a = input()
b = input()
result = hexagonalGrid(a, b)
fptr.write(result + '\n')
fptr.close()
|
You are given a hexagonal grid consisting of two rows, each row consisting of $n$ cells. The cells of the first row are labelled $a_1, a_2, \ldots a_n$ and the cells of the second row are labelled $b_1, b_2, \ldots, b_n$.
For example, for $n = 6$:

(Note that the $b_i$ is connected with $a_{i+1}$.)
Your task is to tile this grid with $2\times 1$ *tiles* that look like the following:

As you can see above, there are three possible orientations in which a tile can be placed.
Your goal is to tile the whole grid such that every cell is covered by a tile, and no two tiles occupy the same cell. To add to the woes, certain cells of the hexagonal grid are *blackened*. No tile must occupy a blackened cell.
Is it possible to tile the grid?
Here's an example. Suppose we want to tile this grid:

Then we can do the tiling as follows:

| 0.5 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line contains a single integer $t$, the number of test cases.
The first line of each test case contains a single integer $n$ denoting the length of the grid.
The second line contains a binary string of length $n$. The $i^\text{th}$ character describes whether cell $a_i$ is blackened.
The third line contains a binary string of length $n$. The $i^\text{th}$ character describes whether cell $b_i$ is blackened.
A `0` corresponds to an empty cell and a `1` corresponds to blackened cell.
|
For each test case, print `YES` if there exists at least one way to tile the grid, and `NO` otherwise.
|
6
6
010000
000010
2
00
00
2
00
10
2
00
01
2
00
11
2
10
00
|
YES
YES
NO
NO
YES
NO
|
Hard
|
Hexagonal Grid - 101 Hack March Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101mar14/challenges/hexagonal-grid">Hexagonal Grid</a> <br>
<strong>Difficulty Level</strong> : Easy-Medium <br>
<strong>Required Knowledge</strong> : Recursion or DP <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/Seyaua">Seyaua</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/abhiranjan">Abhiranjan Kumar</a> <br></p>
<p><strong>Solution</strong> <br>
There are a lot of ways to solve this problem. The easiest one is to just run a recursion, where in each step we will try to fill just two empty cells. The constraints are very small, so this solution works very fast. As an alternative solution you can write something like dynamic programming by submasks.</p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <vector>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <bitset>
#include <queue>
#pragma comment(linker, "/STACK:256000000")
using namespace std;
const int maxN = 12;
int a[2][maxN];
int n;
bool fnd = false;
bool is_in(int i, int j) {
return (0 <= i && i < 2 && j >= 0 && j < n);
}
int dx[] = {0, 1, 1};
int dy[] = {1, 0, -1};
void rec() {
if (fnd) return;
int change = false;
for (int i = 0; i < 2 && !change && !fnd; ++i) {
for (int j = 0; j < n && !change && !fnd; ++j) {
if (a[i][j] == 0) {
change = true;
for (int k = 0; k < 3 && !fnd; ++k) {
if (is_in(i + dx[k], j + dy[k]) && a[i + dx[k]][j + dy[k]] == 0) {
a[i][j] = 1;
a[i + dx[k]][j + dy[k]] = 1;
rec();
a[i][j] = 0;
a[i + dx[k]][j + dy[k]] = 0;
}
}
}
}
}
if (!change) {
fnd = true;
}
}
void solve() {
scanf("%d", &n);
string s1, s2;
cin >> s1 >> s2;
for (int i = 0; i < n; ++i) {
a[0][i] = s1[i] - '0';
a[1][i] = s2[i] - '0';
}
fnd = false;
rec();
if (fnd) {
cout << "YES" << endl;
} else {
cout << "NO" << endl;
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int t;
scanf("%d", &t);
for (int i = 0; i < t; ++i) {
solve();
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <bits/stdc++.h>
using namespace std;
int a[2][101];
int dp[105][105];
int N;
bool solve(int l, int r) {
if(l == -1 && r == -1)
return 1;
if(l < -1 ||r < -1)
return 0;
if(l < 0 && r >= 0 && a[1][r] == 1)
return solve(l, r-1);
if(r < 0 && l >= 0 && a[0][l] == 1)
return solve(l-1, r);
if(l < 0 || r < 0)
return 0;
int &ret = dp[l][r];
if(ret != -1)
return ret;
ret = 0;
if(a[0][l] == 1)
ret |= solve(l-1, r);
if(a[1][r] == 1)
ret |= solve(l, r-1);
if(l > 0 && a[0][l] == 0 && a[0][l-1] == 0)
ret |= solve(l-2, r);
if(r > 0 && a[1][r] == 0 && a[1][r-1] == 0)
ret |= solve(l, r-2);
if(l == r && a[0][l] == 0 && a[1][r] == 0)
ret |= solve(l-1, r-1);
if(l == r+1 && a[0][l] == 0 && a[1][r] == 0)
ret |= solve(l-1, r-1);
return ret;
}
int main()
{
int t;
scanf("%d", &t);
assert(t >= 1 && t <= 100);
while(t--) {
memset(dp, -1, sizeof(dp));
cin >> N;
assert( N >= 1 && N <= 10);
string st[2];
cin >> st[0] >> st[1];
assert((int)st[0].length() == N);
assert((int)st[1].length() == N);
for(int i = 0; i < (int)N; ++i) {
assert(st[0][i] == '0' || st[0][i] == '1');
assert(st[1][i] == '0' || st[1][i] == '1');
a[0][i] = st[0][i] == '0' ? 0 : 1;
a[1][i] = st[1][i] == '0' ? 0 : 1;
}
cout << (solve(N-1, N-1) == 1 ? "YES" : "NO") << "\n";
}
return 0;
}
</code></pre>
| 0 |
101mar14-hexagonal-grid
|
2014-04-04T08:43:27
|
{"contest_participation":1218,"challenge_submissions":208,"successful_submissions":134}
|
2014-04-04T08:43:27
|
2016-07-23T14:48:42
|
tester
|
###C++
```cpp
#include <bits/stdc++.h>
using namespace std;
int a[2][101];
int dp[105][105];
int N;
bool solve(int l, int r) {
if(l == -1 && r == -1)
return 1;
if(l < -1 ||r < -1)
return 0;
if(l < 0 && r >= 0 && a[1][r] == 1)
return solve(l, r-1);
if(r < 0 && l >= 0 && a[0][l] == 1)
return solve(l-1, r);
if(l < 0 || r < 0)
return 0;
int &ret = dp[l][r];
if(ret != -1)
return ret;
ret = 0;
if(a[0][l] == 1)
ret |= solve(l-1, r);
if(a[1][r] == 1)
ret |= solve(l, r-1);
if(l > 0 && a[0][l] == 0 && a[0][l-1] == 0)
ret |= solve(l-2, r);
if(r > 0 && a[1][r] == 0 && a[1][r-1] == 0)
ret |= solve(l, r-2);
if(l == r && a[0][l] == 0 && a[1][r] == 0)
ret |= solve(l-1, r-1);
if(l == r+1 && a[0][l] == 0 && a[1][r] == 0)
ret |= solve(l-1, r-1);
return ret;
}
int main()
{
int t;
scanf("%d", &t);
assert(t >= 1 && t <= 100);
while(t--) {
memset(dp, -1, sizeof(dp));
cin >> N;
assert( N >= 1 && N <= 10);
string st[2];
cin >> st[0] >> st[1];
assert((int)st[0].length() == N);
assert((int)st[1].length() == N);
for(int i = 0; i < (int)N; ++i) {
assert(st[0][i] == '0' || st[0][i] == '1');
assert(st[1][i] == '0' || st[1][i] == '1');
a[0][i] = st[0][i] == '0' ? 0 : 1;
a[1][i] = st[1][i] == '0' ? 0 : 1;
}
cout << (solve(N-1, N-1) == 1 ? "YES" : "NO") << "\n";
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T14:48:42
|
C++
|
46 | 2,135 |
count-palindromes
|
Count Palindromes
|
A string is made of only lowercase latin letters (a,b,c,d,.....,z). Can you find the length of the lexicographically smallest string such that it has exactly **K** sub-strings, each of which are palindromes?
**Input Format**
The first line of input contains single integer **T** - the number of testcases.
T lines follow, each containing the integer K.
**Output Format**
Output exactly T lines. Each line should contain single integer - the length of the lexicographically smallest string.
**Constraints:**
1 <= T <= 100
1 <= K <= 10<sup>12</sup>
**Sample input**
2
10
17
**Sample Output**
4
7
**Explanation**
for K = 10, one of the smallest possible strings that satisfies the property is `aaaa`.
All 10 palindromes are
+ a,a,a,a
+ aa, aa, aa
+ aaa, aaa
+ aaaa
**Note**
Two sub-strings with different indices are both counted.
|
code
|
What is the smallest string that contains exactly K palindromes?
|
ai
|
2014-03-15T11:46:14
|
2022-09-02T10:08:05
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts LONG_INTEGER k as parameter.
#
def solve(k):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
k = int(input().strip())
result = solve(k)
fptr.write(str(result) + '\n')
fptr.close()
|
A string is made of only lowercase latin letters (a,b,c,d,.....,z). Can you find the length of the lexicographically smallest string such that it has exactly $K$ sub-strings, each of which are palindromes?
| 0.426829 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
The first line of input contains single integer $T$ - the number of testcases.
T lines follow, each containing the integer $K$.
|
Output exactly $T$ lines. Each line should contain single integer - the length of the lexicographically smallest string.
|
2
10
17
|
4
7
|
Hard
|
Count Palindromes - 101 Hack March Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101mar14/challenges/count-palindromes">Count Palindromes</a> <br>
<strong>Difficulty Level</strong> : Medium-Hard <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/seyaua">Levgen Soboliev</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/tmt514">Shang-En Huang
</a> <br></p>
<p><strong>Solution</strong> </p>
<p>Let the string s has X sub-strings, which are palindromes. Let's look at s+'a'. If it has more than K sub-strings, which are palindromes - let's look at s+'b'. The point is that if we start from empty string in such recursive way we will get the smallest lexicographically string which has exactly K palindromes. So, now we have a solution - just add the smallest possible symbol and maintain the total number of sub-strings which are palindromes no more than K. But this solution is slow. We need some clever observation. At first, if K is big - we will have a lot of 'a' at the beginning of resulting string. More precise we will have exactly S number of 'a' at the beginning of the resulting string, where S * (S + 1) / 2 <= K. So, this part we can make using O(1) time. After that, if the difference Y = K - S * (S + 1) / 2 is big, than we will just add 'b' to resulting string and will have a lot 'a' again. If the difference Y is small, than we can just add the smallest possible symbol and count the number of new sub-strings which are palindromes. In each of this two cases we will get the difference between current number of sub-strings-palindromes less than 1000 and just go with simple recursive procedure to find next symbols.</p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <cmath>
#include <queue>
#include <bitset>
#include <ctime>
#include <string>
#include <cstring>
#pragma comment(linker, "/STACK:256000000")
using namespace std;
const int maxN = 20000;
const int BOUND = 2000;
long long find_limit(long long k) {
long long l = 0, r = 5000000;
long long result = 0;
while (l <= r) {
long long key = (l + r) / 2;
long long total = (key * (key + 1)) / 2;
if (total <= k) {
result = key;
l = key + 1;
} else {
r = key - 1;
}
}
return result;
}
char s[maxN];
void solvebig(long long k) {
int MID = 10000;
long long counta = find_limit(k);
long long total = (counta * (counta + 1)) / 2;
k -= total;
if (k == 0) {
cout << counta << endl;
return;
}
if (k == 1) {
cout << counta + 1 << endl;
return;
}
MID = min(MID, (int)counta);
for (int i = 0; i < MID; ++i) {
s[i] = 'a';
}
int res = counta;
s[MID] = 'b';
--k;
bool addonly_a = true;
for (int i = MID + 1; ; ++i) {
for (char c = 'a'; c <= 'z'; ++c) {
s[i] = c;
if (c != 'a') {
addonly_a = false;
}
long long cur = 0;
if (addonly_a) {
cur = i - MID + 1;
} else {
int bound = min(MID, 2 * (i - MID + 10));
bound = min(bound, i + 1);
for (int j = 1; j <= bound; ++j) {
bool good = true;
for (int k = 0; k < j / 2; ++k) {
if (s[i - k] != s[i - j + 1 + k]) {
good = false;
break;
}
}
if (good) {
++cur;
}
}
}
if (cur == k) {
cout << counta + (i - MID + 1) << endl;
return;
}
if (cur < k) {
k -= cur;
break;
}
}
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output2.txt", "w", stdout);
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
//cerr << i << endl;
long long k;
cin >> k;
solvebig(k);
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>//by tmt514
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <iostream>
#include <cassert>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((int)(c).size())
typedef long long LL;
int main(void) {
int T;
scanf("%d", &T);
assert(1 <= T && T <= 100);
while(T--) {
LL n;
cin >> n;
assert(1 <= n && n <= 1e12);
vector<int> B;
B.push_back(0);
int m=0;
while(n>0) {
++m;
//try 'a'
LL p = m-B.back();
if(SZ(B)>=2) p += (m-B.back() <= B.back()-B[SZ(B)-2]-1);
if(SZ(B)>=3) p += (m-B.back() <= B[SZ(B)-2]-B[SZ(B)-3]-1);
if(p <= n) { n -= p; continue; }
//try 'b'
p = 1;
if(SZ(B)>=2) p += 1;
if(p <= n) { n -= p; B.push_back(m); continue; }
//try 'c' (assert n == 1)
p = 1;
if(p <= n) { n -= p; continue; }
}
printf("%d\n", (int)m);
}
return 0;
}
</code></pre>
| 0 |
101mar14-count-palindromes
|
2014-04-08T07:38:59
|
{"contest_participation":1218,"challenge_submissions":58,"successful_submissions":14}
|
2014-04-08T07:38:58
|
2016-07-23T18:40:52
|
setter
|
###C++
```cpp
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <cmath>
#include <queue>
#include <bitset>
#include <ctime>
#include <string>
#include <cstring>
#pragma comment(linker, "/STACK:256000000")
using namespace std;
const int maxN = 20000;
const int BOUND = 2000;
long long find_limit(long long k) {
long long l = 0, r = 5000000;
long long result = 0;
while (l <= r) {
long long key = (l + r) / 2;
long long total = (key * (key + 1)) / 2;
if (total <= k) {
result = key;
l = key + 1;
} else {
r = key - 1;
}
}
return result;
}
char s[maxN];
void solvebig(long long k) {
int MID = 10000;
long long counta = find_limit(k);
long long total = (counta * (counta + 1)) / 2;
k -= total;
if (k == 0) {
cout << counta << endl;
return;
}
if (k == 1) {
cout << counta + 1 << endl;
return;
}
MID = min(MID, (int)counta);
for (int i = 0; i < MID; ++i) {
s[i] = 'a';
}
int res = counta;
s[MID] = 'b';
--k;
bool addonly_a = true;
for (int i = MID + 1; ; ++i) {
for (char c = 'a'; c <= 'z'; ++c) {
s[i] = c;
if (c != 'a') {
addonly_a = false;
}
long long cur = 0;
if (addonly_a) {
cur = i - MID + 1;
} else {
int bound = min(MID, 2 * (i - MID + 10));
bound = min(bound, i + 1);
for (int j = 1; j <= bound; ++j) {
bool good = true;
for (int k = 0; k < j / 2; ++k) {
if (s[i - k] != s[i - j + 1 + k]) {
good = false;
break;
}
}
if (good) {
++cur;
}
}
}
if (cur == k) {
cout << counta + (i - MID + 1) << endl;
return;
}
if (cur < k) {
k -= cur;
break;
}
}
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output2.txt", "w", stdout);
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
//cerr << i << endl;
long long k;
cin >> k;
solvebig(k);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T18:40:45
|
C++
|
47 | 2,135 |
count-palindromes
|
Count Palindromes
|
A string is made of only lowercase latin letters (a,b,c,d,.....,z). Can you find the length of the lexicographically smallest string such that it has exactly **K** sub-strings, each of which are palindromes?
**Input Format**
The first line of input contains single integer **T** - the number of testcases.
T lines follow, each containing the integer K.
**Output Format**
Output exactly T lines. Each line should contain single integer - the length of the lexicographically smallest string.
**Constraints:**
1 <= T <= 100
1 <= K <= 10<sup>12</sup>
**Sample input**
2
10
17
**Sample Output**
4
7
**Explanation**
for K = 10, one of the smallest possible strings that satisfies the property is `aaaa`.
All 10 palindromes are
+ a,a,a,a
+ aa, aa, aa
+ aaa, aaa
+ aaaa
**Note**
Two sub-strings with different indices are both counted.
|
code
|
What is the smallest string that contains exactly K palindromes?
|
ai
|
2014-03-15T11:46:14
|
2022-09-02T10:08:05
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts LONG_INTEGER k as parameter.
#
def solve(k):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
k = int(input().strip())
result = solve(k)
fptr.write(str(result) + '\n')
fptr.close()
|
A string is made of only lowercase latin letters (a,b,c,d,.....,z). Can you find the length of the lexicographically smallest string such that it has exactly $K$ sub-strings, each of which are palindromes?
| 0.426829 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
The first line of input contains single integer $T$ - the number of testcases.
T lines follow, each containing the integer $K$.
|
Output exactly $T$ lines. Each line should contain single integer - the length of the lexicographically smallest string.
|
2
10
17
|
4
7
|
Hard
|
Count Palindromes - 101 Hack March Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/101mar14/challenges/count-palindromes">Count Palindromes</a> <br>
<strong>Difficulty Level</strong> : Medium-Hard <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/seyaua">Levgen Soboliev</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/tmt514">Shang-En Huang
</a> <br></p>
<p><strong>Solution</strong> </p>
<p>Let the string s has X sub-strings, which are palindromes. Let's look at s+'a'. If it has more than K sub-strings, which are palindromes - let's look at s+'b'. The point is that if we start from empty string in such recursive way we will get the smallest lexicographically string which has exactly K palindromes. So, now we have a solution - just add the smallest possible symbol and maintain the total number of sub-strings which are palindromes no more than K. But this solution is slow. We need some clever observation. At first, if K is big - we will have a lot of 'a' at the beginning of resulting string. More precise we will have exactly S number of 'a' at the beginning of the resulting string, where S * (S + 1) / 2 <= K. So, this part we can make using O(1) time. After that, if the difference Y = K - S * (S + 1) / 2 is big, than we will just add 'b' to resulting string and will have a lot 'a' again. If the difference Y is small, than we can just add the smallest possible symbol and count the number of new sub-strings which are palindromes. In each of this two cases we will get the difference between current number of sub-strings-palindromes less than 1000 and just go with simple recursive procedure to find next symbols.</p>
<p><strong>Setter's Code</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
#include <algorithm>
#include <set>
#include <map>
#include <vector>
#include <cmath>
#include <queue>
#include <bitset>
#include <ctime>
#include <string>
#include <cstring>
#pragma comment(linker, "/STACK:256000000")
using namespace std;
const int maxN = 20000;
const int BOUND = 2000;
long long find_limit(long long k) {
long long l = 0, r = 5000000;
long long result = 0;
while (l <= r) {
long long key = (l + r) / 2;
long long total = (key * (key + 1)) / 2;
if (total <= k) {
result = key;
l = key + 1;
} else {
r = key - 1;
}
}
return result;
}
char s[maxN];
void solvebig(long long k) {
int MID = 10000;
long long counta = find_limit(k);
long long total = (counta * (counta + 1)) / 2;
k -= total;
if (k == 0) {
cout << counta << endl;
return;
}
if (k == 1) {
cout << counta + 1 << endl;
return;
}
MID = min(MID, (int)counta);
for (int i = 0; i < MID; ++i) {
s[i] = 'a';
}
int res = counta;
s[MID] = 'b';
--k;
bool addonly_a = true;
for (int i = MID + 1; ; ++i) {
for (char c = 'a'; c <= 'z'; ++c) {
s[i] = c;
if (c != 'a') {
addonly_a = false;
}
long long cur = 0;
if (addonly_a) {
cur = i - MID + 1;
} else {
int bound = min(MID, 2 * (i - MID + 10));
bound = min(bound, i + 1);
for (int j = 1; j <= bound; ++j) {
bool good = true;
for (int k = 0; k < j / 2; ++k) {
if (s[i - k] != s[i - j + 1 + k]) {
good = false;
break;
}
}
if (good) {
++cur;
}
}
}
if (cur == k) {
cout << counta + (i - MID + 1) << endl;
return;
}
if (cur < k) {
k -= cur;
break;
}
}
}
}
int main() {
//freopen("input.txt", "r", stdin);
//freopen("output2.txt", "w", stdout);
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
//cerr << i << endl;
long long k;
cin >> k;
solvebig(k);
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>//by tmt514
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <iostream>
#include <cassert>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((int)(c).size())
typedef long long LL;
int main(void) {
int T;
scanf("%d", &T);
assert(1 <= T && T <= 100);
while(T--) {
LL n;
cin >> n;
assert(1 <= n && n <= 1e12);
vector<int> B;
B.push_back(0);
int m=0;
while(n>0) {
++m;
//try 'a'
LL p = m-B.back();
if(SZ(B)>=2) p += (m-B.back() <= B.back()-B[SZ(B)-2]-1);
if(SZ(B)>=3) p += (m-B.back() <= B[SZ(B)-2]-B[SZ(B)-3]-1);
if(p <= n) { n -= p; continue; }
//try 'b'
p = 1;
if(SZ(B)>=2) p += 1;
if(p <= n) { n -= p; B.push_back(m); continue; }
//try 'c' (assert n == 1)
p = 1;
if(p <= n) { n -= p; continue; }
}
printf("%d\n", (int)m);
}
return 0;
}
</code></pre>
| 0 |
101mar14-count-palindromes
|
2014-04-08T07:38:59
|
{"contest_participation":1218,"challenge_submissions":58,"successful_submissions":14}
|
2014-04-08T07:38:58
|
2016-07-23T18:40:52
|
tester
|
###C++
```cpp
//by tmt514
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <iostream>
#include <cassert>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((int)(c).size())
typedef long long LL;
int main(void) {
int T;
scanf("%d", &T);
assert(1 <= T && T <= 100);
while(T--) {
LL n;
cin >> n;
assert(1 <= n && n <= 1e12);
vector<int> B;
B.push_back(0);
int m=0;
while(n>0) {
++m;
//try 'a'
LL p = m-B.back();
if(SZ(B)>=2) p += (m-B.back() <= B.back()-B[SZ(B)-2]-1);
if(SZ(B)>=3) p += (m-B.back() <= B[SZ(B)-2]-B[SZ(B)-3]-1);
if(p <= n) { n -= p; continue; }
//try 'b'
p = 1;
if(SZ(B)>=2) p += 1;
if(p <= n) { n -= p; B.push_back(m); continue; }
//try 'c' (assert n == 1)
p = 1;
if(p <= n) { n -= p; continue; }
}
printf("%d\n", (int)m);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T18:40:52
|
C++
|
48 | 1,768 |
the-bouncing-flying-ball
|
The Bouncing Flying Ball
|
Sergey and Chen are locked in a rectangular box of Dimension L\*W\*H. Evil Larry has put a machine which is located at a point inside the box (p,q,r) which starts shooting balls in every direction (dx,dy,dz) where
-N ≤ dx, dy, dz ≤ N except (0, 0, 0)
such that the ball goes through (p, q, r) -> (p + dx, q + dy, r + dz) -> (p + 2dx, q + 2dy, r + 2dz) and so on.
so, a total of (2N + 1)<sup>3</sup> - 1 balls are fired. Sergey is standing at (a,b,c) and Chen is standing at (d,e,f). Provided all the balls follow reflection property and have constant velocity and gravity is not taken into account, can you tell how many balls are caught by Sergey and Chen? Sergey and Chen can catch the ball if it passes through the point at which they are standing.
**Input Format**
The first line contains the number of test cases, T lines follow, each containing a testcase.
Each testcase contains 13 integers in the following order
L W H a b c d e f p q r N
**Output Format**
For each test case please output two integers indicating the number of balls that are caught by Sergey and C, respectively.
**Constraints**
T = 1
1 ≤ L, W, H, a, b, c, d, e, f, p, q, r, N ≤ 50
**Sample Input**
1
3 3 3 1 1 1 1 1 2 2 2 2 1
**Sample Output**
8 4
**Explanation**
Here, L, W, H = (3, 3, 3), Sergey is at (1, 1, 1) and Chen is at (1, 1, 2) and the machine Larry put is at (2, 2, 2).
Balls are thrown at -1 ≤ x, y, z ≤ 1 from (2, 2, 2).
+ (-1, -1, -1): (2, 2, 2)->(1, 1, 1) Sergey
+ (-1, -1, 0): (2, 2, 2)->(1, 1, 2) Chen
+ (-1, -1, 1): (2, 2, 2)->(1, 1, 3)->(0, 0, 2)->(1, 1, 1) Sergey
+ (-1, 0, -1): (2, 2, 2)->(1, 2, 1)->(0, 2, 0)->(1, 2, 1)->(2, 2, 2)->(3, 2, 3)->...
+ (-1, 0, 0): (2, 2, 2)->(1, 2, 2)->(0, 2, 2)->(1, 2, 2)->(2, 2, 2)->(3, 2, 2)->...
+ (-1, 0, 1): (2, 2, 2)->(1, 2, 3)->(0, 2, 2)->(1, 2, 1)->(2, 2, 0)->(3, 2, 1)->...
+ (-1, 1, -1): (2, 2, 2)->(1, 3, 1)->(0, 2, 0)->(1, 1, 1) Sergey
+ (-1, 1, 0): (2, 2, 2)->(1, 3, 2)->(0, 2, 2)->(1, 1, 2) Chen
+ (-1, 1, 1): (2, 2, 2)->(1, 3, 3)->(0, 2, 2)->(1, 1, 1) Sergey
+ (0, *, *): x-coordinate never changed
+ (1, -1, -1): (2, 2, 2)->(3, 1, 1)->(2, 0, 0)->(1, 1, 1) Sergey
+ (1, -1, 0): (2, 2, 2)->(3, 1, 2)->(2, 0, 2)->(1, 1, 2) Chen
+ (1, -1, 1): (2, 2, 2)->(3, 1, 3)->(2, 0, 2)->(1, 1, 1) Sergey
+ (1, 0, -1): (2, 2, 2)->(3, 2, 1)->(2, 2, 0)->(1, 2, 1)->(0, 2, 2)->...
+ (1, 0, 0): (2, 2, 2)->(3, 2, 2)->(2, 2, 2)->(1, 2, 2)->(0, 2, 2)->...
+ (1, 0, 1): (2, 2, 2)->(3, 2, 3)->(2, 2, 2)->(1, 2, 1)->(0, 2, 0)->...
+ (1, 1, -1): (2, 2, 2)->(3, 3, 1)->(2, 2, 0)->(1, 1, 1) Sergey
+ (1, 1, 0): (2, 2, 2)->(3, 3, 2)->(2, 2, 2)->(1, 1, 2) Chen
+ (1, 1, 1): (2, 2, 2)->(3, 3, 3)->(2, 2, 2)->(1, 1, 1) Sergey
|
code
|
Some bouncing balls are flying from a single source in a rectangular box. You are going to count how many balls passes through point A and point B
|
ai
|
2014-01-29T16:38:17
|
2022-09-02T09:54:45
| null | null | null |
Sergey and Chen are locked in a rectangular box of Dimension L\*W\*H. Evil Larry has put a machine which is located at a point inside the box (p,q,r) which starts shooting balls in every direction (dx,dy,dz) where
-N ≤ dx, dy, dz ≤ N except (0, 0, 0)
such that the ball goes through (p, q, r) -> (p + dx, q + dy, r + dz) -> (p + 2dx, q + 2dy, r + 2dz) and so on.
so, a total of (2N + 1)<sup>3</sup> - 1 balls are fired. Sergey is standing at (a,b,c) and Chen is standing at (d,e,f). Provided all the balls follow reflection property and have constant velocity and gravity is not taken into account, can you tell how many balls are caught by Sergey and Chen? Sergey and Chen can catch the ball if it passes through the point at which they are standing.
**Input Format**
The first line contains the number of test cases, T lines follow, each containing a testcase.
Each testcase contains 13 integers in the following order
L W H a b c d e f p q r N
**Output Format**
For each test case please output two integers indicating the number of balls that are caught by Sergey and C, respectively.
**Constraints**
T = 1
1 ≤ L, W, H, a, b, c, d, e, f, p, q, r, N ≤ 50
**Sample Input**
1
3 3 3 1 1 1 1 1 2 2 2 2 1
**Sample Output**
8 4
**Explanation**
Here, L, W, H = (3, 3, 3), Sergey is at (1, 1, 1) and Chen is at (1, 1, 2) and the machine Larry put is at (2, 2, 2).
Balls are thrown at -1 ≤ x, y, z ≤ 1 from (2, 2, 2).
+ (-1, -1, -1): (2, 2, 2)->(1, 1, 1) Sergey
+ (-1, -1, 0): (2, 2, 2)->(1, 1, 2) Chen
+ (-1, -1, 1): (2, 2, 2)->(1, 1, 3)->(0, 0, 2)->(1, 1, 1) Sergey
+ (-1, 0, -1): (2, 2, 2)->(1, 2, 1)->(0, 2, 0)->(1, 2, 1)->(2, 2, 2)->(3, 2, 3)->...
+ (-1, 0, 0): (2, 2, 2)->(1, 2, 2)->(0, 2, 2)->(1, 2, 2)->(2, 2, 2)->(3, 2, 2)->...
+ (-1, 0, 1): (2, 2, 2)->(1, 2, 3)->(0, 2, 2)->(1, 2, 1)->(2, 2, 0)->(3, 2, 1)->...
+ (-1, 1, -1): (2, 2, 2)->(1, 3, 1)->(0, 2, 0)->(1, 1, 1) Sergey
+ (-1, 1, 0): (2, 2, 2)->(1, 3, 2)->(0, 2, 2)->(1, 1, 2) Chen
+ (-1, 1, 1): (2, 2, 2)->(1, 3, 3)->(0, 2, 2)->(1, 1, 1) Sergey
+ (0, *, *): x-coordinate never changed
+ (1, -1, -1): (2, 2, 2)->(3, 1, 1)->(2, 0, 0)->(1, 1, 1) Sergey
+ (1, -1, 0): (2, 2, 2)->(3, 1, 2)->(2, 0, 2)->(1, 1, 2) Chen
+ (1, -1, 1): (2, 2, 2)->(3, 1, 3)->(2, 0, 2)->(1, 1, 1) Sergey
+ (1, 0, -1): (2, 2, 2)->(3, 2, 1)->(2, 2, 0)->(1, 2, 1)->(0, 2, 2)->...
+ (1, 0, 0): (2, 2, 2)->(3, 2, 2)->(2, 2, 2)->(1, 2, 2)->(0, 2, 2)->...
+ (1, 0, 1): (2, 2, 2)->(3, 2, 3)->(2, 2, 2)->(1, 2, 1)->(0, 2, 0)->...
+ (1, 1, -1): (2, 2, 2)->(3, 3, 1)->(2, 2, 0)->(1, 1, 1) Sergey
+ (1, 1, 0): (2, 2, 2)->(3, 3, 2)->(2, 2, 2)->(1, 1, 2) Chen
+ (1, 1, 1): (2, 2, 2)->(3, 3, 3)->(2, 2, 2)->(1, 1, 1) Sergey
| 0.538462 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
The bouncing flying ball - March'14 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/mar14/challenges/the-bouncing-flying-ball">The bouncing flying ball</a> <br>
<strong>Difficulty Level</strong> : Hard <br>
<strong>Required Knowledge</strong> : Chinese Remainder Theorem <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/tmt514">Shang-En Huang</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/sdya">sdya</a> </p>
<p><strong>Approach</strong> </p>
<p>For each direction (dx, dy, dz), the ball is flying through (p, q, r) -> (p+dx, p+dy, p+dz) -> ... as a line segment.
We need to determine whether the ball touches (a, b, c) first or (d, e, f) first. This is equivalent to solve an integral equation using <a href="http://en.wikipedia.org/wiki/Chinese_remainder_theorem">Chinese Remainder Theorem</a>:</p>
<ul>
<li><strong>p</strong> + <strong>t</strong> * (dx / g) = <strong>a</strong> or <strong>-a</strong> (mod <strong>2L</strong>)</li>
<li><strong>q</strong> + <strong>t</strong> * (dy / g) = <strong>b</strong> or <strong>-b</strong> (mod <strong>2W</strong>)</li>
<li><strong>r</strong> + <strong>t</strong> * (dz / g) = <strong>c</strong> or <strong>-c</strong> (mod <strong>2H</strong>)</li>
</ul>
<p>where <strong>g > 0</strong> is the greatest common divisor of (dx, dy, dz). The minimum positive <strong>t > 0</strong> is the variable that we want to know.</p>
<p>There are a few ways to calculate with more efficiency:</p>
<ol>
<li>Use less multiplicity & division. (aka. use less "%" operations) <br>
For example, we can cache the inversion calculation (pre-caculate something like <strong>v<sup>-1</sup></strong> modulo <strong>M</strong>)</li>
<li>For same (dx/g, dy/g, dz/g) directions we can calculate the solution only once, and add the <strong>multiplicity</strong> that Sergey or Chen get.</li>
<li>Calculate the solution to (-dx, -dy, -dz) when calculating (dx, dy, dz)'s solution: when we handling (dx, dy, dz) we are finding minimum <strong>t > 0</strong> that satisfying the equations; but when we handling (-dx, -dy, -dz) we are finding the maximum <strong>t < LCM(2L, 2W, 2H)</strong> that satisfying the <strong>same</strong> equations.</li>
<li>To solve the system of equations above, there is no need to seperate the equation system into 8 system of equations.</li>
</ol>
<p><strong>Setter's Code</strong></p>
<pre><code>/ by tmt514
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
#define FOR(it,c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(x) ((int)(x).size())
int L, W, H, a, b, c, d, e, f, p, q, r, N;
int inv_tbl[105][105], u_inv_tbl[105][105];
int inv(int x, int y, int P, int Q, int R, int S) {
if(y==0) return P;
return inv(y, x%y, R, S, P-R*(x/y), Q-S*(x/y));
}
//cache the inversion results (note that 1 <= M <= 200)
int inv(int x, int M) {
if(!u_inv_tbl[x][M]) {
u_inv_tbl[x][M] = 1;
inv_tbl[x][M] = (inv(x, M, 1, 0, 0, 1)%M+M)%M;
}
return inv_tbl[x][M];
}
int sol[105], qb, qe;
void getsol(int ql, int qr, int &modulo, int u, int x, int p, int M) {
// u + ?x = p or -p (mod) M
// ? = sol (mod) modulo
if (x < 0) { u = -u; x = -x; }
int p1 = ((p-u)%M+M)%M;
int p2 = ((-p-u)%M+M)%M;
int G = __gcd(M, x);
M/=G; x/=G;
int g = __gcd(modulo, M), MM = M / g;
int ret_modulo = modulo * MM;
modulo /= g;
int MMInv = inv(modulo%MM, MM);
if (p1 % G == 0) {
p1 = p1/G * inv(x, M);
for(int it=ql;it<qr;it++) {
int t = sol[it];
// ? = p1 (mod) MM
// ? = t (mod) modulo
if ((p1 - t) % g) continue;
int tmp = ((p1 - t) * MMInv * modulo + t) % ret_modulo;
tmp = (tmp+ret_modulo)%ret_modulo;
sol[qe++] = tmp;
}
}
if (p2 % G == 0) {
p2 = p2/G * inv(x, M);
for(int it=ql;it<qr;it++) {
int t = sol[it];
// ? = p2 (mod) M
// ? = t (mod) modulo
if ((p2 - t) % g) continue;
int tmp = ((p2 - t) * MMInv * modulo + t) % ret_modulo;
tmp = (tmp+ret_modulo)%ret_modulo;
sol[qe++] = tmp;
}
}
qb = qr;
modulo = ret_modulo;
}
void ask(int &min_pos, int &min_neg, int u, int v, int w, int x, int y, int z) {
int modulo = 1;
// initialize the solution queue
sol[0] = 0;
qb = 0, qe = 1;
// p + ?x = u or -u (mod) 2L
// q + ?y = v or -v (mod) 2W
// r + ?z = w or -w (mod) 2H
getsol(qb, qe, modulo, p, x, u, 2*L);
getsol(qb, qe, modulo, q, y, v, 2*W);
getsol(qb, qe, modulo, r, z, w, 2*H);
if (qb == qe) { min_pos = min_neg = -1; return; }
min_pos = *min_element(sol + qb, sol + qe);
min_neg = modulo - *max_element(sol + qb, sol + qe);
}
int muls[105][105][105];
int main(void) {
int T;
scanf("%d", &T);
while(T--) {
scanf("%d%d%d", &L, &W, &H);
scanf("%d%d%d", &a, &b, &c);
scanf("%d%d%d", &d, &e, &f);
scanf("%d%d%d", &p, &q, &r);
scanf("%d", &N);
memset(muls, 0, sizeof(muls));
const int offset = 50;
int cSergey = 0, cChen = 0;
// caculate multiplicity
for(int x=-N;x<=N;x++) for(int y=-N;y<=N;y++) for(int z=-N;z<=N;z++) {
int g = __gcd(abs(x), __gcd(abs(y), abs(z)));
if(g) muls[x/g+offset][y/g+offset][z/g+offset]++;
}
// caculate positive (x, y, z) and negative (-x, -y, -z) at same time
for(int x=0;x<=N;x++) for(int y=-N;y<=N;y++) for(int z=-N;z<=N;z++) {
if((x==0&&y<0) || (x==0 && y==0 && z<0)) continue;
int g = __gcd(abs(x), __gcd(abs(y), abs(z)));
if(!g) continue;
if(g == 1) {
int S_pos, S_neg, C_pos, C_neg;
ask(S_pos, S_neg, a, b, c, x, y, z);
ask(C_pos, C_neg, d, e, f, x, y, z);
int m_pos = muls[x+offset][y+offset][z+offset];
int m_neg = muls[-x+offset][-y+offset][-z+offset];
if(S_pos != -1 && C_pos != -1) (S_pos < C_pos? cSergey+=m_pos: cChen+=m_pos);
else if(S_pos != -1) cSergey+=m_pos;
else if(C_pos != -1) cChen+=m_pos;
if(S_neg != -1 && C_neg != -1) (S_neg < C_neg? cSergey+=m_neg: cChen+=m_neg);
else if(S_neg != -1) cSergey+=m_neg;
else if(C_neg != -1) cChen+=m_neg;
}
}
printf("%d %d\n", cSergey, cChen);
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
#include <cmath>
#include <iostream>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((long long)(c).size())
typedef long long LL;
long long L, W, H, x, y, z, a, b, c, p, q, r, N;
const long long INF = 1000000000000000000LL;
long long gcdtbl[105][10005];
long long gcd3[105][105][105];
long long inv[105][10005];
long long cache[105][105][105];
long long fac[105][105][105][7];
long long gcd(long long a, long long b) {
if (a == 0 || b == 0) {
return a + b;
}
if (a > b) {
return gcd(a % b, b);
} else {
return gcd(b % a, a);
}
}
long long pre() {
for(long long i=0;i<=100;i++) for(long long j=0;j<=10000;j++) gcdtbl[i][j] = gcd(i, j);
for(long long i=0;i<=100;i++) for(long long j=0;j<=100;j++) for(long long k=0;k<=100;k++) gcd3[i][j][k] = gcd(gcd(i, j), k);
for(long long i=2;i<=100;i++) for(long long j=0;j<=10000;j++) if(gcd(i, j) > 1) inv[i][j] = 0;
else for(long long k=0;k<=100;k++) if(j*k%i==1) { inv[i][j] = k; break; }
for(long long i=1;i<=100;i++) for(long long j=1;j<=100;j++) for(long long k=1;k<=100;k++) {
static long long p[15]={64,9,25,49,11,13,17,19,23,29,31,37,41,43,47};
static long long q[15]={2, 3, 5, 7,11,13,17,19,23,29,31,37,41,43,47};
long long t=0;
for(long long l=0;l<15;l++) if(i%q[l]==0 || j%q[l]==0 || k%q[l]==0) fac[i][j][k][t++] = p[l];
}
return 0;
}
long long solve(long long gx, long long gy, long long gz, long long u, long long v, int w) {
//gx * t = u 2L
//gy * t = v 2W
//gz * t = w 2H
long long A = 2*L, B = 2*W, C = 2*H;
long long gA = gcdtbl[A][gx], gB = gcdtbl[B][gy], gC = gcdtbl[C][gz];
if (u % gA || v % gB || w % gC) return INF;
u /= gA; A /= gA; gx /= gA; u = u * inv[A][gx];
v /= gB; B /= gB; gy /= gB; v = v * inv[B][gy];
w /= gC; C /= gC; gz /= gC; w = w * inv[C][gz];
// t = u (mod A)
// t = v (mod B)
// t = w (mod C)
for(long long *it = &fac[A][B][C][0]; *it; it++) {
long long p = *it;
long long pa = gcdtbl[A][p], pb = gcdtbl[B][p], pc = gcdtbl[C][p];
if(pa>=pb&&pa>=pc) { if((u-v)%pb||(u-w)%pc) return INF; else { B/=pb; C/=pc; }}
else if(pb>=pa&&pb>=pc) { if((v-u)%pa||(v-w)%pc) return INF; else { A/=pa; C/=pc; }}
else if(pc>=pa&&pc>=pb) { if((w-u)%pa||(w-v)%pb) return INF; else { A/=pa; B/=pb; }}
}
long long ABC = A*B*C, t = ((v-u)*inv[B][A]*A+u);
t = ((w-t)*inv[C][A*B]*A*B+t);
t = (t%ABC+ABC)%ABC;
return t;
}
long long hit(long long vx, long long vy, long long vz, long long u, long long v, long long w) {
long long tx = gcdtbl[2*L][abs(vx)], ty = gcdtbl[2*W][abs(vy)], tz = gcdtbl[2*H][abs(vz)];
if(((u-p)%tx && (u+p)%tx) || ((v-q)%ty && (v+q)%ty) || ((w-r)%tz && (w+r)%tz)) return INF;
vx = (vx % (2*L) + 2*L) % (2*L);
vy = (vy % (2*W) + 2*W) % (2*W);
vz = (vz % (2*H) + 2*H) % (2*H);
long long t = INF;
for(long long i=0;i<8;i++) t = min(t, solve(vx, vy, vz, (i&1? 4*L-u-p: 2*L+u-p), (i&2? 4*W-v-q: 2*W+v-q), (i&4? 4*H-w-r: 2*H+w-r)));
return t;
}
void solve() {
cin >> L >> W >> H >> x >> y >> z >> a >> b >> c >> p >> q >> r >> N;
//scanf("%d%d%d%d%d%d%d%d%d%d%d%d%d", &L, &W, &H, &x, &y, &z, &a, &b, &c, &p, &q, &r, &N);
long long pi = 0, kel = 0;
memset(cache, 0, sizeof(cache));
for (long long vx = -N; vx <= N; vx++)
for(long long vy = -N; vy <= N; vy++)
for(long long vz = -N; vz <= N; vz++) {
if(vx==0 && vy==0 && vz==0) continue;
long long cx = vx, cy = vy, cz = vz;
long long g = gcd3[abs(cx)][abs(cy)][abs(cz)];
cx /= g; cy /= g; cz /= g;
long long &tmp = cache[cx+50][cy+50][cz+50];
if (tmp) {
if (tmp == 1) ++pi;
if (tmp == 2) ++kel;
continue;
}
long long tp = hit(cx, cy, cz, x, y, z);
long long th = hit(cx, cy, cz, a, b, c);
if (tp < th) ++pi, tmp = 1;
if (tp > th) ++kel, tmp = 2;
if (tp == th) tmp = 3;
}
cout << pi << " " << kel << endl;
//printf("%d %d\n", pi, kel);
static long long cs=0;
//cerr << ++cs << endl;
//fprintf(stderr, "Case #%d: %d %d\n", ++cs, pi, kel);
}
int main(void) {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
long long T;
pre();
cin >> T;
while(T--) solve();
return 0;
}
</code></pre>
| 0 |
mar14-the-bouncing-flying-ball
|
2014-04-15T09:40:26
|
{"contest_participation":2080,"challenge_submissions":74,"successful_submissions":19}
|
2014-04-15T09:40:26
|
2016-07-23T18:17:52
|
setter
|
###C++
```cpp
/ by tmt514
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
#define FOR(it,c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(x) ((int)(x).size())
int L, W, H, a, b, c, d, e, f, p, q, r, N;
int inv_tbl[105][105], u_inv_tbl[105][105];
int inv(int x, int y, int P, int Q, int R, int S) {
if(y==0) return P;
return inv(y, x%y, R, S, P-R*(x/y), Q-S*(x/y));
}
//cache the inversion results (note that 1 <= M <= 200)
int inv(int x, int M) {
if(!u_inv_tbl[x][M]) {
u_inv_tbl[x][M] = 1;
inv_tbl[x][M] = (inv(x, M, 1, 0, 0, 1)%M+M)%M;
}
return inv_tbl[x][M];
}
int sol[105], qb, qe;
void getsol(int ql, int qr, int &modulo, int u, int x, int p, int M) {
// u + ?x = p or -p (mod) M
// ? = sol (mod) modulo
if (x < 0) { u = -u; x = -x; }
int p1 = ((p-u)%M+M)%M;
int p2 = ((-p-u)%M+M)%M;
int G = __gcd(M, x);
M/=G; x/=G;
int g = __gcd(modulo, M), MM = M / g;
int ret_modulo = modulo * MM;
modulo /= g;
int MMInv = inv(modulo%MM, MM);
if (p1 % G == 0) {
p1 = p1/G * inv(x, M);
for(int it=ql;it<qr;it++) {
int t = sol[it];
// ? = p1 (mod) MM
// ? = t (mod) modulo
if ((p1 - t) % g) continue;
int tmp = ((p1 - t) * MMInv * modulo + t) % ret_modulo;
tmp = (tmp+ret_modulo)%ret_modulo;
sol[qe++] = tmp;
}
}
if (p2 % G == 0) {
p2 = p2/G * inv(x, M);
for(int it=ql;it<qr;it++) {
int t = sol[it];
// ? = p2 (mod) M
// ? = t (mod) modulo
if ((p2 - t) % g) continue;
int tmp = ((p2 - t) * MMInv * modulo + t) % ret_modulo;
tmp = (tmp+ret_modulo)%ret_modulo;
sol[qe++] = tmp;
}
}
qb = qr;
modulo = ret_modulo;
}
void ask(int &min_pos, int &min_neg, int u, int v, int w, int x, int y, int z) {
int modulo = 1;
// initialize the solution queue
sol[0] = 0;
qb = 0, qe = 1;
// p + ?x = u or -u (mod) 2L
// q + ?y = v or -v (mod) 2W
// r + ?z = w or -w (mod) 2H
getsol(qb, qe, modulo, p, x, u, 2*L);
getsol(qb, qe, modulo, q, y, v, 2*W);
getsol(qb, qe, modulo, r, z, w, 2*H);
if (qb == qe) { min_pos = min_neg = -1; return; }
min_pos = *min_element(sol + qb, sol + qe);
min_neg = modulo - *max_element(sol + qb, sol + qe);
}
int muls[105][105][105];
int main(void) {
int T;
scanf("%d", &T);
while(T--) {
scanf("%d%d%d", &L, &W, &H);
scanf("%d%d%d", &a, &b, &c);
scanf("%d%d%d", &d, &e, &f);
scanf("%d%d%d", &p, &q, &r);
scanf("%d", &N);
memset(muls, 0, sizeof(muls));
const int offset = 50;
int cSergey = 0, cChen = 0;
// caculate multiplicity
for(int x=-N;x<=N;x++) for(int y=-N;y<=N;y++) for(int z=-N;z<=N;z++) {
int g = __gcd(abs(x), __gcd(abs(y), abs(z)));
if(g) muls[x/g+offset][y/g+offset][z/g+offset]++;
}
// caculate positive (x, y, z) and negative (-x, -y, -z) at same time
for(int x=0;x<=N;x++) for(int y=-N;y<=N;y++) for(int z=-N;z<=N;z++) {
if((x==0&&y<0) || (x==0 && y==0 && z<0)) continue;
int g = __gcd(abs(x), __gcd(abs(y), abs(z)));
if(!g) continue;
if(g == 1) {
int S_pos, S_neg, C_pos, C_neg;
ask(S_pos, S_neg, a, b, c, x, y, z);
ask(C_pos, C_neg, d, e, f, x, y, z);
int m_pos = muls[x+offset][y+offset][z+offset];
int m_neg = muls[-x+offset][-y+offset][-z+offset];
if(S_pos != -1 && C_pos != -1) (S_pos < C_pos? cSergey+=m_pos: cChen+=m_pos);
else if(S_pos != -1) cSergey+=m_pos;
else if(C_pos != -1) cChen+=m_pos;
if(S_neg != -1 && C_neg != -1) (S_neg < C_neg? cSergey+=m_neg: cChen+=m_neg);
else if(S_neg != -1) cSergey+=m_neg;
else if(C_neg != -1) cChen+=m_neg;
}
}
printf("%d %d\n", cSergey, cChen);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T18:17:39
|
C++
|
49 | 1,768 |
the-bouncing-flying-ball
|
The Bouncing Flying Ball
|
Sergey and Chen are locked in a rectangular box of Dimension L\*W\*H. Evil Larry has put a machine which is located at a point inside the box (p,q,r) which starts shooting balls in every direction (dx,dy,dz) where
-N ≤ dx, dy, dz ≤ N except (0, 0, 0)
such that the ball goes through (p, q, r) -> (p + dx, q + dy, r + dz) -> (p + 2dx, q + 2dy, r + 2dz) and so on.
so, a total of (2N + 1)<sup>3</sup> - 1 balls are fired. Sergey is standing at (a,b,c) and Chen is standing at (d,e,f). Provided all the balls follow reflection property and have constant velocity and gravity is not taken into account, can you tell how many balls are caught by Sergey and Chen? Sergey and Chen can catch the ball if it passes through the point at which they are standing.
**Input Format**
The first line contains the number of test cases, T lines follow, each containing a testcase.
Each testcase contains 13 integers in the following order
L W H a b c d e f p q r N
**Output Format**
For each test case please output two integers indicating the number of balls that are caught by Sergey and C, respectively.
**Constraints**
T = 1
1 ≤ L, W, H, a, b, c, d, e, f, p, q, r, N ≤ 50
**Sample Input**
1
3 3 3 1 1 1 1 1 2 2 2 2 1
**Sample Output**
8 4
**Explanation**
Here, L, W, H = (3, 3, 3), Sergey is at (1, 1, 1) and Chen is at (1, 1, 2) and the machine Larry put is at (2, 2, 2).
Balls are thrown at -1 ≤ x, y, z ≤ 1 from (2, 2, 2).
+ (-1, -1, -1): (2, 2, 2)->(1, 1, 1) Sergey
+ (-1, -1, 0): (2, 2, 2)->(1, 1, 2) Chen
+ (-1, -1, 1): (2, 2, 2)->(1, 1, 3)->(0, 0, 2)->(1, 1, 1) Sergey
+ (-1, 0, -1): (2, 2, 2)->(1, 2, 1)->(0, 2, 0)->(1, 2, 1)->(2, 2, 2)->(3, 2, 3)->...
+ (-1, 0, 0): (2, 2, 2)->(1, 2, 2)->(0, 2, 2)->(1, 2, 2)->(2, 2, 2)->(3, 2, 2)->...
+ (-1, 0, 1): (2, 2, 2)->(1, 2, 3)->(0, 2, 2)->(1, 2, 1)->(2, 2, 0)->(3, 2, 1)->...
+ (-1, 1, -1): (2, 2, 2)->(1, 3, 1)->(0, 2, 0)->(1, 1, 1) Sergey
+ (-1, 1, 0): (2, 2, 2)->(1, 3, 2)->(0, 2, 2)->(1, 1, 2) Chen
+ (-1, 1, 1): (2, 2, 2)->(1, 3, 3)->(0, 2, 2)->(1, 1, 1) Sergey
+ (0, *, *): x-coordinate never changed
+ (1, -1, -1): (2, 2, 2)->(3, 1, 1)->(2, 0, 0)->(1, 1, 1) Sergey
+ (1, -1, 0): (2, 2, 2)->(3, 1, 2)->(2, 0, 2)->(1, 1, 2) Chen
+ (1, -1, 1): (2, 2, 2)->(3, 1, 3)->(2, 0, 2)->(1, 1, 1) Sergey
+ (1, 0, -1): (2, 2, 2)->(3, 2, 1)->(2, 2, 0)->(1, 2, 1)->(0, 2, 2)->...
+ (1, 0, 0): (2, 2, 2)->(3, 2, 2)->(2, 2, 2)->(1, 2, 2)->(0, 2, 2)->...
+ (1, 0, 1): (2, 2, 2)->(3, 2, 3)->(2, 2, 2)->(1, 2, 1)->(0, 2, 0)->...
+ (1, 1, -1): (2, 2, 2)->(3, 3, 1)->(2, 2, 0)->(1, 1, 1) Sergey
+ (1, 1, 0): (2, 2, 2)->(3, 3, 2)->(2, 2, 2)->(1, 1, 2) Chen
+ (1, 1, 1): (2, 2, 2)->(3, 3, 3)->(2, 2, 2)->(1, 1, 1) Sergey
|
code
|
Some bouncing balls are flying from a single source in a rectangular box. You are going to count how many balls passes through point A and point B
|
ai
|
2014-01-29T16:38:17
|
2022-09-02T09:54:45
| null | null | null |
Sergey and Chen are locked in a rectangular box of Dimension L\*W\*H. Evil Larry has put a machine which is located at a point inside the box (p,q,r) which starts shooting balls in every direction (dx,dy,dz) where
-N ≤ dx, dy, dz ≤ N except (0, 0, 0)
such that the ball goes through (p, q, r) -> (p + dx, q + dy, r + dz) -> (p + 2dx, q + 2dy, r + 2dz) and so on.
so, a total of (2N + 1)<sup>3</sup> - 1 balls are fired. Sergey is standing at (a,b,c) and Chen is standing at (d,e,f). Provided all the balls follow reflection property and have constant velocity and gravity is not taken into account, can you tell how many balls are caught by Sergey and Chen? Sergey and Chen can catch the ball if it passes through the point at which they are standing.
**Input Format**
The first line contains the number of test cases, T lines follow, each containing a testcase.
Each testcase contains 13 integers in the following order
L W H a b c d e f p q r N
**Output Format**
For each test case please output two integers indicating the number of balls that are caught by Sergey and C, respectively.
**Constraints**
T = 1
1 ≤ L, W, H, a, b, c, d, e, f, p, q, r, N ≤ 50
**Sample Input**
1
3 3 3 1 1 1 1 1 2 2 2 2 1
**Sample Output**
8 4
**Explanation**
Here, L, W, H = (3, 3, 3), Sergey is at (1, 1, 1) and Chen is at (1, 1, 2) and the machine Larry put is at (2, 2, 2).
Balls are thrown at -1 ≤ x, y, z ≤ 1 from (2, 2, 2).
+ (-1, -1, -1): (2, 2, 2)->(1, 1, 1) Sergey
+ (-1, -1, 0): (2, 2, 2)->(1, 1, 2) Chen
+ (-1, -1, 1): (2, 2, 2)->(1, 1, 3)->(0, 0, 2)->(1, 1, 1) Sergey
+ (-1, 0, -1): (2, 2, 2)->(1, 2, 1)->(0, 2, 0)->(1, 2, 1)->(2, 2, 2)->(3, 2, 3)->...
+ (-1, 0, 0): (2, 2, 2)->(1, 2, 2)->(0, 2, 2)->(1, 2, 2)->(2, 2, 2)->(3, 2, 2)->...
+ (-1, 0, 1): (2, 2, 2)->(1, 2, 3)->(0, 2, 2)->(1, 2, 1)->(2, 2, 0)->(3, 2, 1)->...
+ (-1, 1, -1): (2, 2, 2)->(1, 3, 1)->(0, 2, 0)->(1, 1, 1) Sergey
+ (-1, 1, 0): (2, 2, 2)->(1, 3, 2)->(0, 2, 2)->(1, 1, 2) Chen
+ (-1, 1, 1): (2, 2, 2)->(1, 3, 3)->(0, 2, 2)->(1, 1, 1) Sergey
+ (0, *, *): x-coordinate never changed
+ (1, -1, -1): (2, 2, 2)->(3, 1, 1)->(2, 0, 0)->(1, 1, 1) Sergey
+ (1, -1, 0): (2, 2, 2)->(3, 1, 2)->(2, 0, 2)->(1, 1, 2) Chen
+ (1, -1, 1): (2, 2, 2)->(3, 1, 3)->(2, 0, 2)->(1, 1, 1) Sergey
+ (1, 0, -1): (2, 2, 2)->(3, 2, 1)->(2, 2, 0)->(1, 2, 1)->(0, 2, 2)->...
+ (1, 0, 0): (2, 2, 2)->(3, 2, 2)->(2, 2, 2)->(1, 2, 2)->(0, 2, 2)->...
+ (1, 0, 1): (2, 2, 2)->(3, 2, 3)->(2, 2, 2)->(1, 2, 1)->(0, 2, 0)->...
+ (1, 1, -1): (2, 2, 2)->(3, 3, 1)->(2, 2, 0)->(1, 1, 1) Sergey
+ (1, 1, 0): (2, 2, 2)->(3, 3, 2)->(2, 2, 2)->(1, 1, 2) Chen
+ (1, 1, 1): (2, 2, 2)->(3, 3, 3)->(2, 2, 2)->(1, 1, 1) Sergey
| 0.538462 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
The bouncing flying ball - March'14 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><a href="https://www.hackerrank.com/contests/mar14/challenges/the-bouncing-flying-ball">The bouncing flying ball</a> <br>
<strong>Difficulty Level</strong> : Hard <br>
<strong>Required Knowledge</strong> : Chinese Remainder Theorem <br>
<strong>Problem Setter</strong> : <a href="https://www.hackerrank.com/tmt514">Shang-En Huang</a> <br>
<strong>Problem Tester</strong> : <a href="https://www.hackerrank.com/sdya">sdya</a> </p>
<p><strong>Approach</strong> </p>
<p>For each direction (dx, dy, dz), the ball is flying through (p, q, r) -> (p+dx, p+dy, p+dz) -> ... as a line segment.
We need to determine whether the ball touches (a, b, c) first or (d, e, f) first. This is equivalent to solve an integral equation using <a href="http://en.wikipedia.org/wiki/Chinese_remainder_theorem">Chinese Remainder Theorem</a>:</p>
<ul>
<li><strong>p</strong> + <strong>t</strong> * (dx / g) = <strong>a</strong> or <strong>-a</strong> (mod <strong>2L</strong>)</li>
<li><strong>q</strong> + <strong>t</strong> * (dy / g) = <strong>b</strong> or <strong>-b</strong> (mod <strong>2W</strong>)</li>
<li><strong>r</strong> + <strong>t</strong> * (dz / g) = <strong>c</strong> or <strong>-c</strong> (mod <strong>2H</strong>)</li>
</ul>
<p>where <strong>g > 0</strong> is the greatest common divisor of (dx, dy, dz). The minimum positive <strong>t > 0</strong> is the variable that we want to know.</p>
<p>There are a few ways to calculate with more efficiency:</p>
<ol>
<li>Use less multiplicity & division. (aka. use less "%" operations) <br>
For example, we can cache the inversion calculation (pre-caculate something like <strong>v<sup>-1</sup></strong> modulo <strong>M</strong>)</li>
<li>For same (dx/g, dy/g, dz/g) directions we can calculate the solution only once, and add the <strong>multiplicity</strong> that Sergey or Chen get.</li>
<li>Calculate the solution to (-dx, -dy, -dz) when calculating (dx, dy, dz)'s solution: when we handling (dx, dy, dz) we are finding minimum <strong>t > 0</strong> that satisfying the equations; but when we handling (-dx, -dy, -dz) we are finding the maximum <strong>t < LCM(2L, 2W, 2H)</strong> that satisfying the <strong>same</strong> equations.</li>
<li>To solve the system of equations above, there is no need to seperate the equation system into 8 system of equations.</li>
</ol>
<p><strong>Setter's Code</strong></p>
<pre><code>/ by tmt514
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
#define FOR(it,c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(x) ((int)(x).size())
int L, W, H, a, b, c, d, e, f, p, q, r, N;
int inv_tbl[105][105], u_inv_tbl[105][105];
int inv(int x, int y, int P, int Q, int R, int S) {
if(y==0) return P;
return inv(y, x%y, R, S, P-R*(x/y), Q-S*(x/y));
}
//cache the inversion results (note that 1 <= M <= 200)
int inv(int x, int M) {
if(!u_inv_tbl[x][M]) {
u_inv_tbl[x][M] = 1;
inv_tbl[x][M] = (inv(x, M, 1, 0, 0, 1)%M+M)%M;
}
return inv_tbl[x][M];
}
int sol[105], qb, qe;
void getsol(int ql, int qr, int &modulo, int u, int x, int p, int M) {
// u + ?x = p or -p (mod) M
// ? = sol (mod) modulo
if (x < 0) { u = -u; x = -x; }
int p1 = ((p-u)%M+M)%M;
int p2 = ((-p-u)%M+M)%M;
int G = __gcd(M, x);
M/=G; x/=G;
int g = __gcd(modulo, M), MM = M / g;
int ret_modulo = modulo * MM;
modulo /= g;
int MMInv = inv(modulo%MM, MM);
if (p1 % G == 0) {
p1 = p1/G * inv(x, M);
for(int it=ql;it<qr;it++) {
int t = sol[it];
// ? = p1 (mod) MM
// ? = t (mod) modulo
if ((p1 - t) % g) continue;
int tmp = ((p1 - t) * MMInv * modulo + t) % ret_modulo;
tmp = (tmp+ret_modulo)%ret_modulo;
sol[qe++] = tmp;
}
}
if (p2 % G == 0) {
p2 = p2/G * inv(x, M);
for(int it=ql;it<qr;it++) {
int t = sol[it];
// ? = p2 (mod) M
// ? = t (mod) modulo
if ((p2 - t) % g) continue;
int tmp = ((p2 - t) * MMInv * modulo + t) % ret_modulo;
tmp = (tmp+ret_modulo)%ret_modulo;
sol[qe++] = tmp;
}
}
qb = qr;
modulo = ret_modulo;
}
void ask(int &min_pos, int &min_neg, int u, int v, int w, int x, int y, int z) {
int modulo = 1;
// initialize the solution queue
sol[0] = 0;
qb = 0, qe = 1;
// p + ?x = u or -u (mod) 2L
// q + ?y = v or -v (mod) 2W
// r + ?z = w or -w (mod) 2H
getsol(qb, qe, modulo, p, x, u, 2*L);
getsol(qb, qe, modulo, q, y, v, 2*W);
getsol(qb, qe, modulo, r, z, w, 2*H);
if (qb == qe) { min_pos = min_neg = -1; return; }
min_pos = *min_element(sol + qb, sol + qe);
min_neg = modulo - *max_element(sol + qb, sol + qe);
}
int muls[105][105][105];
int main(void) {
int T;
scanf("%d", &T);
while(T--) {
scanf("%d%d%d", &L, &W, &H);
scanf("%d%d%d", &a, &b, &c);
scanf("%d%d%d", &d, &e, &f);
scanf("%d%d%d", &p, &q, &r);
scanf("%d", &N);
memset(muls, 0, sizeof(muls));
const int offset = 50;
int cSergey = 0, cChen = 0;
// caculate multiplicity
for(int x=-N;x<=N;x++) for(int y=-N;y<=N;y++) for(int z=-N;z<=N;z++) {
int g = __gcd(abs(x), __gcd(abs(y), abs(z)));
if(g) muls[x/g+offset][y/g+offset][z/g+offset]++;
}
// caculate positive (x, y, z) and negative (-x, -y, -z) at same time
for(int x=0;x<=N;x++) for(int y=-N;y<=N;y++) for(int z=-N;z<=N;z++) {
if((x==0&&y<0) || (x==0 && y==0 && z<0)) continue;
int g = __gcd(abs(x), __gcd(abs(y), abs(z)));
if(!g) continue;
if(g == 1) {
int S_pos, S_neg, C_pos, C_neg;
ask(S_pos, S_neg, a, b, c, x, y, z);
ask(C_pos, C_neg, d, e, f, x, y, z);
int m_pos = muls[x+offset][y+offset][z+offset];
int m_neg = muls[-x+offset][-y+offset][-z+offset];
if(S_pos != -1 && C_pos != -1) (S_pos < C_pos? cSergey+=m_pos: cChen+=m_pos);
else if(S_pos != -1) cSergey+=m_pos;
else if(C_pos != -1) cChen+=m_pos;
if(S_neg != -1 && C_neg != -1) (S_neg < C_neg? cSergey+=m_neg: cChen+=m_neg);
else if(S_neg != -1) cSergey+=m_neg;
else if(C_neg != -1) cChen+=m_neg;
}
}
printf("%d %d\n", cSergey, cChen);
}
return 0;
}
</code></pre>
<p><strong>Tester's Code</strong></p>
<pre><code>#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
#include <cmath>
#include <iostream>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((long long)(c).size())
typedef long long LL;
long long L, W, H, x, y, z, a, b, c, p, q, r, N;
const long long INF = 1000000000000000000LL;
long long gcdtbl[105][10005];
long long gcd3[105][105][105];
long long inv[105][10005];
long long cache[105][105][105];
long long fac[105][105][105][7];
long long gcd(long long a, long long b) {
if (a == 0 || b == 0) {
return a + b;
}
if (a > b) {
return gcd(a % b, b);
} else {
return gcd(b % a, a);
}
}
long long pre() {
for(long long i=0;i<=100;i++) for(long long j=0;j<=10000;j++) gcdtbl[i][j] = gcd(i, j);
for(long long i=0;i<=100;i++) for(long long j=0;j<=100;j++) for(long long k=0;k<=100;k++) gcd3[i][j][k] = gcd(gcd(i, j), k);
for(long long i=2;i<=100;i++) for(long long j=0;j<=10000;j++) if(gcd(i, j) > 1) inv[i][j] = 0;
else for(long long k=0;k<=100;k++) if(j*k%i==1) { inv[i][j] = k; break; }
for(long long i=1;i<=100;i++) for(long long j=1;j<=100;j++) for(long long k=1;k<=100;k++) {
static long long p[15]={64,9,25,49,11,13,17,19,23,29,31,37,41,43,47};
static long long q[15]={2, 3, 5, 7,11,13,17,19,23,29,31,37,41,43,47};
long long t=0;
for(long long l=0;l<15;l++) if(i%q[l]==0 || j%q[l]==0 || k%q[l]==0) fac[i][j][k][t++] = p[l];
}
return 0;
}
long long solve(long long gx, long long gy, long long gz, long long u, long long v, int w) {
//gx * t = u 2L
//gy * t = v 2W
//gz * t = w 2H
long long A = 2*L, B = 2*W, C = 2*H;
long long gA = gcdtbl[A][gx], gB = gcdtbl[B][gy], gC = gcdtbl[C][gz];
if (u % gA || v % gB || w % gC) return INF;
u /= gA; A /= gA; gx /= gA; u = u * inv[A][gx];
v /= gB; B /= gB; gy /= gB; v = v * inv[B][gy];
w /= gC; C /= gC; gz /= gC; w = w * inv[C][gz];
// t = u (mod A)
// t = v (mod B)
// t = w (mod C)
for(long long *it = &fac[A][B][C][0]; *it; it++) {
long long p = *it;
long long pa = gcdtbl[A][p], pb = gcdtbl[B][p], pc = gcdtbl[C][p];
if(pa>=pb&&pa>=pc) { if((u-v)%pb||(u-w)%pc) return INF; else { B/=pb; C/=pc; }}
else if(pb>=pa&&pb>=pc) { if((v-u)%pa||(v-w)%pc) return INF; else { A/=pa; C/=pc; }}
else if(pc>=pa&&pc>=pb) { if((w-u)%pa||(w-v)%pb) return INF; else { A/=pa; B/=pb; }}
}
long long ABC = A*B*C, t = ((v-u)*inv[B][A]*A+u);
t = ((w-t)*inv[C][A*B]*A*B+t);
t = (t%ABC+ABC)%ABC;
return t;
}
long long hit(long long vx, long long vy, long long vz, long long u, long long v, long long w) {
long long tx = gcdtbl[2*L][abs(vx)], ty = gcdtbl[2*W][abs(vy)], tz = gcdtbl[2*H][abs(vz)];
if(((u-p)%tx && (u+p)%tx) || ((v-q)%ty && (v+q)%ty) || ((w-r)%tz && (w+r)%tz)) return INF;
vx = (vx % (2*L) + 2*L) % (2*L);
vy = (vy % (2*W) + 2*W) % (2*W);
vz = (vz % (2*H) + 2*H) % (2*H);
long long t = INF;
for(long long i=0;i<8;i++) t = min(t, solve(vx, vy, vz, (i&1? 4*L-u-p: 2*L+u-p), (i&2? 4*W-v-q: 2*W+v-q), (i&4? 4*H-w-r: 2*H+w-r)));
return t;
}
void solve() {
cin >> L >> W >> H >> x >> y >> z >> a >> b >> c >> p >> q >> r >> N;
//scanf("%d%d%d%d%d%d%d%d%d%d%d%d%d", &L, &W, &H, &x, &y, &z, &a, &b, &c, &p, &q, &r, &N);
long long pi = 0, kel = 0;
memset(cache, 0, sizeof(cache));
for (long long vx = -N; vx <= N; vx++)
for(long long vy = -N; vy <= N; vy++)
for(long long vz = -N; vz <= N; vz++) {
if(vx==0 && vy==0 && vz==0) continue;
long long cx = vx, cy = vy, cz = vz;
long long g = gcd3[abs(cx)][abs(cy)][abs(cz)];
cx /= g; cy /= g; cz /= g;
long long &tmp = cache[cx+50][cy+50][cz+50];
if (tmp) {
if (tmp == 1) ++pi;
if (tmp == 2) ++kel;
continue;
}
long long tp = hit(cx, cy, cz, x, y, z);
long long th = hit(cx, cy, cz, a, b, c);
if (tp < th) ++pi, tmp = 1;
if (tp > th) ++kel, tmp = 2;
if (tp == th) tmp = 3;
}
cout << pi << " " << kel << endl;
//printf("%d %d\n", pi, kel);
static long long cs=0;
//cerr << ++cs << endl;
//fprintf(stderr, "Case #%d: %d %d\n", ++cs, pi, kel);
}
int main(void) {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
long long T;
pre();
cin >> T;
while(T--) solve();
return 0;
}
</code></pre>
| 0 |
mar14-the-bouncing-flying-ball
|
2014-04-15T09:40:26
|
{"contest_participation":2080,"challenge_submissions":74,"successful_submissions":19}
|
2014-04-15T09:40:26
|
2016-07-23T18:17:52
|
tester
|
###C++
```cpp
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
#include <cmath>
#include <iostream>
using namespace std;
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); it++)
#define SZ(c) ((long long)(c).size())
typedef long long LL;
long long L, W, H, x, y, z, a, b, c, p, q, r, N;
const long long INF = 1000000000000000000LL;
long long gcdtbl[105][10005];
long long gcd3[105][105][105];
long long inv[105][10005];
long long cache[105][105][105];
long long fac[105][105][105][7];
long long gcd(long long a, long long b) {
if (a == 0 || b == 0) {
return a + b;
}
if (a > b) {
return gcd(a % b, b);
} else {
return gcd(b % a, a);
}
}
long long pre() {
for(long long i=0;i<=100;i++) for(long long j=0;j<=10000;j++) gcdtbl[i][j] = gcd(i, j);
for(long long i=0;i<=100;i++) for(long long j=0;j<=100;j++) for(long long k=0;k<=100;k++) gcd3[i][j][k] = gcd(gcd(i, j), k);
for(long long i=2;i<=100;i++) for(long long j=0;j<=10000;j++) if(gcd(i, j) > 1) inv[i][j] = 0;
else for(long long k=0;k<=100;k++) if(j*k%i==1) { inv[i][j] = k; break; }
for(long long i=1;i<=100;i++) for(long long j=1;j<=100;j++) for(long long k=1;k<=100;k++) {
static long long p[15]={64,9,25,49,11,13,17,19,23,29,31,37,41,43,47};
static long long q[15]={2, 3, 5, 7,11,13,17,19,23,29,31,37,41,43,47};
long long t=0;
for(long long l=0;l<15;l++) if(i%q[l]==0 || j%q[l]==0 || k%q[l]==0) fac[i][j][k][t++] = p[l];
}
return 0;
}
long long solve(long long gx, long long gy, long long gz, long long u, long long v, int w) {
//gx * t = u 2L
//gy * t = v 2W
//gz * t = w 2H
long long A = 2*L, B = 2*W, C = 2*H;
long long gA = gcdtbl[A][gx], gB = gcdtbl[B][gy], gC = gcdtbl[C][gz];
if (u % gA || v % gB || w % gC) return INF;
u /= gA; A /= gA; gx /= gA; u = u * inv[A][gx];
v /= gB; B /= gB; gy /= gB; v = v * inv[B][gy];
w /= gC; C /= gC; gz /= gC; w = w * inv[C][gz];
// t = u (mod A)
// t = v (mod B)
// t = w (mod C)
for(long long *it = &fac[A][B][C][0]; *it; it++) {
long long p = *it;
long long pa = gcdtbl[A][p], pb = gcdtbl[B][p], pc = gcdtbl[C][p];
if(pa>=pb&&pa>=pc) { if((u-v)%pb||(u-w)%pc) return INF; else { B/=pb; C/=pc; }}
else if(pb>=pa&&pb>=pc) { if((v-u)%pa||(v-w)%pc) return INF; else { A/=pa; C/=pc; }}
else if(pc>=pa&&pc>=pb) { if((w-u)%pa||(w-v)%pb) return INF; else { A/=pa; B/=pb; }}
}
long long ABC = A*B*C, t = ((v-u)*inv[B][A]*A+u);
t = ((w-t)*inv[C][A*B]*A*B+t);
t = (t%ABC+ABC)%ABC;
return t;
}
long long hit(long long vx, long long vy, long long vz, long long u, long long v, long long w) {
long long tx = gcdtbl[2*L][abs(vx)], ty = gcdtbl[2*W][abs(vy)], tz = gcdtbl[2*H][abs(vz)];
if(((u-p)%tx && (u+p)%tx) || ((v-q)%ty && (v+q)%ty) || ((w-r)%tz && (w+r)%tz)) return INF;
vx = (vx % (2*L) + 2*L) % (2*L);
vy = (vy % (2*W) + 2*W) % (2*W);
vz = (vz % (2*H) + 2*H) % (2*H);
long long t = INF;
for(long long i=0;i<8;i++) t = min(t, solve(vx, vy, vz, (i&1? 4*L-u-p: 2*L+u-p), (i&2? 4*W-v-q: 2*W+v-q), (i&4? 4*H-w-r: 2*H+w-r)));
return t;
}
void solve() {
cin >> L >> W >> H >> x >> y >> z >> a >> b >> c >> p >> q >> r >> N;
//scanf("%d%d%d%d%d%d%d%d%d%d%d%d%d", &L, &W, &H, &x, &y, &z, &a, &b, &c, &p, &q, &r, &N);
long long pi = 0, kel = 0;
memset(cache, 0, sizeof(cache));
for (long long vx = -N; vx <= N; vx++)
for(long long vy = -N; vy <= N; vy++)
for(long long vz = -N; vz <= N; vz++) {
if(vx==0 && vy==0 && vz==0) continue;
long long cx = vx, cy = vy, cz = vz;
long long g = gcd3[abs(cx)][abs(cy)][abs(cz)];
cx /= g; cy /= g; cz /= g;
long long &tmp = cache[cx+50][cy+50][cz+50];
if (tmp) {
if (tmp == 1) ++pi;
if (tmp == 2) ++kel;
continue;
}
long long tp = hit(cx, cy, cz, x, y, z);
long long th = hit(cx, cy, cz, a, b, c);
if (tp < th) ++pi, tmp = 1;
if (tp > th) ++kel, tmp = 2;
if (tp == th) tmp = 3;
}
cout << pi << " " << kel << endl;
//printf("%d %d\n", pi, kel);
static long long cs=0;
//cerr << ++cs << endl;
//fprintf(stderr, "Case #%d: %d %d\n", ++cs, pi, kel);
}
int main(void) {
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
long long T;
pre();
cin >> T;
while(T--) solve();
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T18:17:52
|
C++
|
50 | 486 |
k-balance
|
k-balance number
|
Your task is to calculate the sum (indicated by S) of all the k-balanced integers between [L, R]. An integer is called k-balanced when either of #1 or #2 below holds true.
1. The length of the integer <= k
2. Sum of the first k digits (with no leading zeros) is equal to the sum of the last k digits.
**Input format**
L R k
**Output format**
S % 1000000007
**Constraints**
0 < L <= R < 10^18
0 < k <= 18
**Sample Input**
9 23 1
**Sample Output**
42
**Explanation**
9, 11 and 22 are the only 3 integers between 9 and 23 ( both included ) that are k-balanced. Hence, the answer is 9+11+22=42
|
code
|
Your task is to calculate the sum(indicated by S) of all the k-balanced integers between [L,R].
|
ai
|
2013-03-14T16:03:43
|
2022-09-02T09:55:00
| null | null | null |
Your task is to calculate the sum (indicated by S) of all the k-balanced integers between [L, R]. An integer is called k-balanced when either of #1 or #2 below holds true.
1. The length of the integer <= k
2. Sum of the first k digits (with no leading zeros) is equal to the sum of the last k digits.
**Input format**
L R k
**Output format**
S % 1000000007
**Constraints**
0 < L <= R < 10^18
0 < k <= 18
**Sample Input**
9 23 1
**Sample Output**
42
**Explanation**
9, 11 and 22 are the only 3 integers between 9 and 23 ( both included ) that are k-balanced. Hence, the answer is 9+11+22=42
| 0.526316 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
|
May 20-20 Hack Editorial: K-Balance
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong><a href="https://www.hackerrank.com/contests/may13/challenges/k-blance">K Balance</a></strong></p>
<p>Find the sum of numbers between L and R having either <= K digits or having sum of first K digits equal to sum of last K digits.</p>
<p><strong>Difficulty Level</strong></p>
<p>Hard</p>
<p><strong>Problem Setter</strong></p>
<p><a href="https://www.hackerrank.com/wanbo">Wanbo</a> <br>
Editorial by <a href="https://www.hackerrank.com/piyush006">Piyush</a></p>
<p><strong>Required Knowledge</strong></p>
<p>Combinatorics, Dynamic Programming</p>
<p><strong>Approach</strong></p>
<p>Let's reduce the problem to finding </p>
<pre><code>f(n) = the sum of K-balance numbers <= N
</code></pre>
<p>The answer to the problem will then be </p>
<pre><code>f(r) - f(l-1)
f(N){
// D is the number of digits of N.
D = Digits(N);
ans = 0;
//For numbers with lesser number of digits.
for(I = 1; I < |D|;I++) ans += f(I);
//For numbers with equal number of digits.
ans += Sum(); // what is sum?
}
</code></pre>
<p>We can reduce K if the first K digits overlap with last K digits, so that they don't overlap.
To find Sum() , we can break our sum into sum at individual digit position and then sum it as : </p>
<pre><code>10^(d-1) * S(d-1) + 10^(d-2)*S(d-2) + .. 10^(0) * S(0) // S(i) is the sum of digits at position i
</code></pre>
<p>For finding sum at individual digit position i, we can again break it into as :</p>
<pre><code>0*Count(0) + 1*Count(1) + 2*Count(2) + ... + 9*Count(9) // Count(j) is the count of numbers having digit j at position i.
</code></pre>
<p>So our approach looks like : </p>
<pre><code>Sum()
{
ans = 0;
for(I = 0;I <= |D|;I++){
SumAtI = 0;
for(J=1;J<=9;J++){
SumAtI += J*Count(I , J);
}
ans += SumAtI * 10^(I);
}
}
</code></pre>
<p>Finding Count(p , x) <br>
We have simply fixed the digit at some position 'p' to be 'x' , and we have to find the count of numbers which have digit at position 'p' as 'x'. There have to be |D| - p digits before p , and p - 1 after p that will form a number . Also sum of first K digits should be equal to last K . Another condition is that since the number of digits is equal to |D| , we need to take care of the fact that the number does not exceed N itself. For doing this , we take a function: F(I , State , Sum) . This means that we are at the Ith digit , and State tells us that if all the digits taken before are equal to corresponding digits of N (if true would imply that Ith digit has to be <= Ith digit of N) , Sum stores the sum of digits taken in the first K digits.We will increase sum if Ith digit is in first K digits , decrease if it is in the last K digits , and make no change if it is between .This way if we get 0 sum in the end , that means our number satisfies all conditions.</p>
<pre><code>F(I,state,sum){
//Base Case
if(N == -1) return (Sum == 0);
//If Ith is first digit , we can't take 0 .
//If state variable is true , that means we are in prefix of N , so Ith digit has to be less than Dig[I]
for(J = ((I == |D| - 1) ? 1 : 0) ;J <= (state ? Dig[I] : 9); J++){
//digit is in first K digits.
if(I >= |D| - K)
r += F(I - 1, state && (Dig[I] == J) , sum + J);
//digit is in last K digits.
else if(n < K){
if(sum >= i)
ans += F(I - 1, state && (Dig[I] == J), sum - J);
}
//digit is in between
else ans += F(I - 1, state && (Dig[I] == J), sum);
}
return ans;
}
</code></pre>
<p>Returning to Count(p, x)
We only have the pth digit as x, but depending on starting |D|-p digits , we can have different values of (state,sum) at pth digit, so we will try all such values of (state,sum), and count the total numbers.</p>
<pre><code>Count(p, x){
for(State = 0 ; State <= 1; State ++){
for(Sum = 0; Sum <= (|D| - p)*9 ;Sum++){
ans += [ Numbers With (|D|-p)_Digits And Reach (State,Sum) ] * [ F(p,state,sum) and x as the pth digit] ;
}
}
}
</code></pre>
<p>Finding the count of numbers with \|D\|-P digits and reaching (state,sum) as required can be done either using another recursive function , or using function F itself . This completes our Sum() function . Find(x) function is easy to implement as well if you have understood the basic idea developed above( would be good exercise infact) . It can be also be eliminated, but at the cost of one more variable in the state of function F.</p>
<p><strong>Problem Setter's Code: C++</strong></p>
<p><a href="https://gist.github.com/dheerajrav/5757729">Setter's code</a></p>
<p><strong>Problem Tester's Code: C++</strong></p>
<p><a href="https://www.hackerrank.com/rest/contests/may13/challenges/k-blance/hackers/piyush006/download_solution">Tester's code</a></p>
| 0 |
may-2020-editorial-k-balance
|
2013-06-11T15:00:56
|
{"contest_participation":3663,"challenge_submissions":242,"successful_submissions":69}
|
2013-06-11T15:00:56
|
2016-07-23T18:44:37
|
setter
|
###C++
```cpp
#include<map>
#include<set>
#include<ctime>
#include<cmath>
#include<queue>
#include<stack>
#include<bitset>
#include<vector>
#include<cstdio>
#include<string>
#include<cassert>
#include<cstring>
#include<numeric>
#include<sstream>
#include<iterator>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
#define MM(a,x) memset(a, x, sizeof(a))
#define P(x) cout<<#x<<" = "<<x<<endl;
#define P2(x,y) cout<<#x<<" = "<<x<<", "<<#y<<" = "<<y<<endl;
#define PV(a,n) for(int i=0;i<n;i++) cout<<#a<<"[" << i <<"] = "<<a[i]<<endl;
#define TM(a,b) cout<<#a<<"->"<<#b<<": "<<1.*(b-a)/CLOCKS_PER_SEC<<"s\n";
const LL MD = LL(1e9) + 7;
LL ten[51];
LL p10[51];
LL h(LL m);
LL brute(LL L, LL R, int k) {
LL ret = 0;
for(int i = L; i <= R; i++) {
int s[100], ct;
if(i % 100000000 == 0) P(i);
LL T = i;
ct = 0;
while(T) {
s[ct++] = T % 10;
T /= 10;
}
if(ct < k) {ret += i; continue;}
int sL = 0, sR = 0;
for(int j = 0; j < k; j++) {
sL += s[j];
sR += s[ct - j - 1];
}
if(sL == sR)
ret = (ret + i) % MD;
}
return ret % MD;
}
vector<int> toD(LL n) {
vector<int> r;
while(n) {
r.push_back(n % 10);
n /= 10;
}
reverse(r.begin(), r.end());
return r;
}
LL h(LL m) {
LL L = 1, R = LL(pow(10., (int)m) + 0.5) - 1;
LL t1 = L + R;
LL n = R - L + 1;
if(t1 % 2 == 0) t1 /= 2;
else if(n % 2 == 0) n /= 2;
t1 %= MD;
n %= MD;
LL ret = t1 * n % MD;
return ret;
}
LL g(int cur, int sz, int p[], int k, bool allZero) {
// PV(p, sz);
// P(cur);
LL ret = 0;
int pZero = 0;
for(int i = 0; i < cur; i++) {
if(p[i] == 0) {
pZero = i + 1;
} else {
break;
}
}
vector<int> d;
for(int i = pZero; i < cur; i++) d.push_back(p[i]);
sz -= pZero;
int nsure = d.size(), L, R, M;
if(sz <= k) {
LL sure = 0;
for(int i = 0; i < nsure; i++) {
sure = (10 * sure + d[i]) % MD;
}
int nosure = sz - nsure;
int minus = allZero && (nosure > 0);
ret = (h(nosure) - minus * h(nosure - 1) % MD + (ten[nosure] - minus * ten[nosure - 1]) % MD * ten[nosure] % MD * sure % MD) % MD;
if(ret < 0) ret += MD;
return ret;
}
if(2 * k <= sz) {
M = sz - 2 * k, L = R = k;
} else {
M = 2 * k - sz, L = R = sz - k;
}
LL dL[10][100] = {};
LL X[10][100] = {};
X[0][0] = 1;
for(int i = 1; i <= 9; i++) {
int st = (i == 1 && allZero) ? 1 : 0;
for(int j = 0; j < 100; j++) {
for(int l = st; l <= 9 && l <= j; l++) {
X[i][j] += X[i - 1][j - l];
}
X[i][j] %= MD;
}
}
LL dR[10][100] = {};
LL Y[10][100] = {};
Y[0][0] = 1;
for(int i = 1; i <= 9; i++) {
for(int j = 0; j < 100; j++) {
for(int l = 0; l <= 9 && l <= j; l++) {
Y[i][j] += Y[i - 1][j - l];
}
Y[i][j] %= MD;
}
}
for(int i = 1; i <= 9; i++)
for(int j = 0; j < 100; j++) {
for(int x = i - 1; x >= 0; x--) {
for(int y = (allZero && x == i - 1); y <= 9 && y <= j; y++) {
if(x != i - 1)
dL[i][j] += X[i - 1][j - y] * y % MD * ten[x] % MD;
else
dL[i][j] += Y[i - 1][j - y] * y % MD * ten[x] % MD;
}
}
dL[i][j] %= MD;
}
for(int i = 1; i <= 9; i++)
for(int j = 0; j < 100; j++) {
for(int x = i - 1; x >= 0; x--) {
for(int y = 0; y <= 9 && y <= j; y++) {
dR[i][j] += Y[i - 1][j - y] * y % MD * ten[x] % MD;
}
}
dR[i][j] %= MD;
}
if(nsure < L) {
// cout << "1)" << endl;
int nL = L - nsure;
int sL = 0;
LL sure = 0;
for(int i = 0; i < nsure; i++) {
sure = (10 * sure + d[i]) % MD;
sL += d[i];
}
for(int ds = 0; ds + sL < 100; ds++) {
LL cL = ten[M] * Y[R][ds + sL] % MD;
LL vL = (dL[nL][ds] + X[nL][ds] * sure % MD * ten[nL]) % MD * ten[M + R] % MD;
ret += cL * vL % MD;
LL cM = X[nL][ds] * Y[R][ds + sL] % MD;
LL vM = h(M) * ten[R] % MD;
ret += cM * vM % MD;
LL cR = X[nL][ds] * ten[M];
LL vR = dR[R][ds + sL];
ret += cR * vR % MD;
}
ret %= MD;
} else if(nsure <= L + M) {
// cout << "2)" << endl;
int sL = 0;
int nM = L + M - nsure;
LL vL = 0, vM = 0;
for(int i = 0; i < L; i++) {
sL += d[i];
vL = (10 * vL + d[i]) % MD;
}
for(int i = L; i < nsure; i++) {
vM = (10 * vM + d[i]) % MD;
}
LL cL = ten[nM] * Y[R][sL] % MD;
vL = vL * ten[M + R] % MD;
ret += cL * vL % MD;
LL cM = Y[R][sL] % MD;
vM = vM * ten[nM] % MD;
vM = (h(nM) + vM * ten[nM]) % MD * ten[R] % MD;
ret += cM * vM % MD;
LL cR = ten[nM];
LL vR = dR[R][sL];
ret += cR * vR % MD;
ret %= MD;
} else {
// cout << "3)" << endl;
LL sure = 0;
int sL = 0, sR = 0;
for(int i = 0; i < L; i++) sL += d[i];
for(int i = L + M; i < nsure; i++) sR += d[i];
for(int i = 0; i < nsure; i++) sure = (10 * sure + d[i]) % MD;
int nR = R - (nsure - (L + M));
if(sL >= sR) {
LL cR = Y[nR][sL - sR];
LL vR = dR[nR][sL - sR];
ret += (vR + sure * ten[nR] % MD * cR) % MD;
ret %= MD;
}
}
//P(ret);
//cout << endl;
return ret;
}
void dfs(int cur, vector<int>& D, int p[], int k, bool isEqual, bool allZero, LL & r) {
int sz = (int) D.size();
if(cur == sz) {
if(isEqual) return;
else r += g(cur, D.size(), p, k, allZero);
return;
}
if(isEqual) {
for(int i = 0; i <= D[cur]; i++) {
p[cur] = i;
dfs(cur + 1, D, p, k, i == D[cur], allZero && (i == 0), r);
}
} else {
if(allZero) {
for(int i = cur; i < D.size(); i++) {
r += g(i, D.size(), p, k, 1);
p[i] = 0;
}
} else {
r += g(cur, D.size(), p, k, 0);
}
}
}
//1,2,...,n
LL f(LL n, LL k) {
vector<int> D = toD(n);
LL r = 0;
int p[50] = {};
dfs(0, D, p, k, 1, 1, r);
r %= MD;
return r;
}
int main() {
p10[0] = ten[0] = 1;
for(int i = 1; i < 50; i++) {
p10[i] = 10 * p10[i - 1];
ten[i] = 10 * ten[i - 1] % MD;
}
LL L, R, k;
cin >> L >> R >> k;
assert(L <= R && R < LL(1e18));
LL rL = f(L, k);
LL rR = f(R + 1, k);
// P(rL);
// P(rR);
LL r = (rR - rL + MD) % MD;
cout << r << endl;
//P(brute(L, R, k));
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T18:44:37
|
C++
|
51 | 2,293 |
p-sequences
|
P-sequences
|
We call a sequence of `N` natural numbers (*a*<sub>1</sub>, *a*<sub>2</sub>, ..., *a*<sub>N</sub>) a *P-sequence*, if the product of any two adjacent numbers in it is not greater than *P*. In other words, if a sequence (*a*<sub>1</sub>, *a*<sub>2</sub>, ..., *a*<sub>N</sub>) is a *P-sequence*, then *a*<sub>i</sub> * *a*<sub>i+1</sub> ≤ `P` ∀ 1 ≤ i < N
You are given `N` and `P`. Your task is to find the number of such *P-sequences* of `N` integers modulo 10<sup>9</sup>+7.
**Input Format**
The first line of input consists of `N`
The second line of the input consists of `P`.
**Constraints**
2 ≤ N ≤ 10<sup>3</sup>
1 ≤ P ≤ 10<sup>9</sup>
1 ≤ a<sub>i</sub>
**Output Format**
Output the number of *P-sequences* of `N` integers modulo 10<sup>9</sup>+7.
**Sample Input #00**
2
2
**Sample Output #00**
3
**Explanation #00**
3 such sequences are {1,1},{1,2} and {2,1}
|
code
|
How many sequences of N elements are there if product of two adjacent elements is not greater than P
|
ai
|
2014-03-31T21:26:34
|
2022-08-31T08:14:51
|
#
# Complete the 'pSequences' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER p
#
def pSequences(n, p):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
p = int(input().strip())
result = pSequences(n, p)
fptr.write(str(result) + '\n')
fptr.close()
|
We call a sequence of `N` natural numbers (*a*<sub>1</sub>, *a*<sub>2</sub>, ..., *a*<sub>N</sub>) a *P-sequence*, if the product of any two adjacent numbers in it is not greater than *P*. In other words, if a sequence (*a*<sub>1</sub>, *a*<sub>2</sub>, ..., *a*<sub>N</sub>) is a *P-sequence*, then *a*<sub>i</sub> * *a*<sub>i+1</sub> ≤ `P` ∀ 1 ≤ i < N
You are given `N` and `P`. Your task is to find the number of such *P-sequences* of `N` integers modulo 10<sup>9</sup>+7.
| 0.550562 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line of input consists of `N`
The second line of the input consists of `P`.
|
Output the number of *P-sequences* of `N` integers modulo 10<sup>9</sup>+7.
|
2
2
|
3
|
Hard
|
P-Sequences - Week 1 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Difficulty level</strong> : Medium <br>
<strong>Required knowledge</strong> : Partial sums trick, DP <br>
<strong>Problem setter</strong> : <a href="https://www.hackerrank.com/zxqfd555">Sergey Kulik</a> <br>
<strong>Problem tester</strong> : <a href="https://www.hackerrank.com/dsoboliev">Dmytro Soboliev</a> </p>
<p><strong>Approach</strong></p>
<p>Consider a valid P-sequence of <strong>N</strong> integers: (<strong>a<sub>1</sub></strong>, <strong>a<sub>2</sub></strong>, ..., <strong>a<sub>N</sub></strong>). If you take some <strong>i</strong> (1 <= <strong>i</strong> < <strong>N</strong>) and take a pair (<strong>a<sub>i</sub></strong>, <strong>a<sub>i+1</sub></strong>) from this sequence, at least one of the following statements will be true:</p>
<ul>
<li><strong>a<sub>i</sub></strong> is not greater than the square root (in future, to be short, sqrt) of <strong>P</strong>.</li>
<li><strong>a<sub>i+1</sub></strong> is not greater than the square root of <strong>P</strong>.</li>
</ul>
<p>And this fact gives a rise to the key idea of the solution. Let's have a DP <strong>F(N, R, t)</strong>. The meaning of the DP state is: the number of P-sequences of <strong>N</strong> integer numbers, where:</p>
<ul>
<li>if <strong>t</strong> is false, then <strong>R</strong> is the <strong>N</strong>-th term of a P-sequence.</li>
<li>if <strong>t</strong> is true, then <strong>R</strong> is the maximal possible number that can be the <strong>N+1</strong>-th term of a P-sequence.</li>
</ul>
<p>Basically, false value of <strong>t</strong> corresponds to the above case where <strong>a<sub>i</sub></strong> isn't greater than <strong>sqrt(P)</strong> and true value of <strong>t</strong> corresponds to the case where <strong>a<sub>i</sub></strong> is actually greater than <strong>sqrt(P)</strong>, but <strong>a<sub>i+1</sub></strong> is not greater than <strong>sqrt(P)</strong>.</p>
<p>We have O(<strong>N</strong> * sqrt(<strong>P</strong>)) states here, so we can calculate this DP in affordable time.</p>
<p>When we calculate the DP, we should take care of the initial DP values and about the DP transitions.</p>
<p>The initial DP values are the values of <strong>F(N, R, t)</strong> where <strong>N</strong> is equal to one. Here </p>
<ul>
<li><p><strong>F(1, R, false)</strong> equals to one because <strong>R</strong> is the the only term of a P-sequence sequence here.</p></li>
<li><p><strong>F(1, R, true)</strong> equals to the number of such integers <strong>K</strong> from the range [1; <strong>P</strong>] such that <strong>N</strong> divided by <strong>K</strong> equals to <strong>R</strong>. This number can be obtained by solving the corresponding equation, see the solution for the details.</p></li>
</ul>
<p>When <strong>t</strong> (that means that <strong>a<sub>i+1</sub></strong> is not greater than <strong>sqrt(P)</strong>) is false you should take the sum of the following values in order to get <strong>F(N, R, t)</strong>:</p>
<ul>
<li><p>the sum of <strong>F(N - 1, R', false)</strong>, where <strong>R'</strong> for <strong>R'</strong> from <strong>1</strong> to <strong>sqrt(P)</strong>. This corresponds to the case where the both <strong>a<sub>i</sub></strong> and <strong>a<sub>i+1</sub></strong> are not greater than <strong>sqrt(P)</strong>.</p></li>
<li><p>the sum of <strong>F(N - 1, R', true)</strong>, where <strong>R'</strong> is greater or equal to <strong>R</strong>. This follows derives from the above DP state definition and corresponds to the case when <strong>a<sub>i</sub></strong> is greater than <strong>sqrt(P)</strong> but <strong>a<sub>i+1</sub></strong> is smaller than <strong>sqrt(P)</strong>.</p></li>
</ul>
<p>When we have the true value of <strong>t</strong>, the transition is simpler. Here the value of <strong>F(N, R, t)</strong> equals to the sum of <strong>F(N - 1, R', t)</strong>, where <strong>R'</strong> is not greater than <strong>R</strong> and then multiplied by the amount of such numbers <strong>K</strong> in the range [1; <strong>P</strong>] that <strong>P</strong> divided by <strong>K</strong> is <strong>R</strong>.</p>
<p>Here we're taking a sum of a multiple previously calculated DP states, but using, for example, the partial sums trick, we can do it in O(1).</p>
<p><strong>Setter's solution</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define maxn 1000 + 5
#define max_sqrt_k 32000
#define mod 1000000007
int dp[2][max_sqrt_k][2], n, k, sqrt_k, i, j, t, ret, pref, sum0, sum1, count_lr[max_sqrt_k], le, ri, l, p;
void upd (int &a, int b) {
a += b;
if (a >= mod) a -= mod;
}
int main (int argc, char * const argv[]) {
scanf("%d %d", &n, &k);
while (sqrt_k * sqrt_k < k) ++sqrt_k;
for(i = 1; i <= sqrt_k; i++) dp[1][i][0] = 1;
for(i = 1; i < sqrt_k; i++) {
le = k / (i + 1) + 1;
ri = k / i;
if (ri <= sqrt_k) continue;
le = max(le, sqrt_k + 1);
count_lr[i] = ri - le + 1;
}
for(i = 1; i < sqrt_k; i++) dp[1][i][1] = count_lr[i];
l = 1;
for(i = 2; i <= n; i++) {
p = l;
l ^= 1;
sum0 = sum1 = 0;
for(j = 1; j <= sqrt_k; j++) {
upd(sum0, dp[p][j][0]);
upd(sum1, dp[p][j][1]);
}
t = sqrt_k;
for(j = 1; j <= sqrt_k; j++) {
while (j * t > k) upd(sum0, mod - dp[p][t--][0]);
dp[l][j][0] = sum1 + sum0;
if (dp[l][j][0] >= mod) dp[l][j][0] -= mod;
upd(sum1, mod - dp[p][j][1]);
}
pref = 0;
for(j = 1; j < sqrt_k; j++) {
upd(pref, dp[p][j][0]);
dp[l][j][1] = (count_lr[j] * 1LL * pref) % mod;
}
}
for(j = 1; j <= sqrt_k; j++) {
upd(ret, dp[l][j][0]);
upd(ret, dp[l][j][1]);
}
printf("%d\n", ret);
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong></p>
<pre><code>/*
Solution by sdya (Dmytro Soboliev)
*/
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cassert>
using namespace std;
const int P = 1000000007;
const int maxN = 64000;
vector < int > bounds, ways;
int d[2][maxN], add[maxN];
int buildBounds(int p) {
for (int i = 1; i * i <= p; ++i) {
ways.push_back(i);
bounds.push_back(p / i);
}
int m = bounds.size();
for (int i = 0; i < m; ++i) {
ways.push_back(bounds[m - 1 - i]);
bounds.push_back(ways[m - 1 - i]);
}
return m + m;
}
int main() {
int n, p;
cin >> n >> p;
assert(1 <= n && n <= 1e3);
assert(1 <= p && p <= 1e9);
int m = buildBounds(p);
int u = 0, v = 1;
memset(d[u], 0, sizeof(d[u]));
d[u][m - 1] = 1;
for (int i = 0; i < n; ++i, swap(u, v)) {
int covered = m - 1;
memset(add, 0, sizeof(add));
memset(d[v], 0, sizeof(d[v]));
for (int j = 0; j < m; ++j) {
if (d[u][j] == 0) {
continue;
}
while (covered >= 0 && bounds[covered] <= ways[j]) {
--covered;
}
add[covered + 1] += d[u][j];
if (add[covered + 1] >= P) {
add[covered + 1] -= P;
}
for (int k = covered; k >= 0; --k) {
int right = min(bounds[k], ways[j]);
int left = k == m - 1 ? 1 : bounds[k + 1] + 1;
if (left <= right) {
d[v][k] += (long long)(d[u][j]) * (long long)(right - left + 1) % (long long)(P);
if (d[v][k] >= P) {
d[v][k] -= P;
}
} else {
break;
}
}
}
for (int j = 1; j < m; ++j) {
add[j] += add[j - 1];
if (add[j] >= P) {
add[j] -= P;
}
}
for (int j = 0; j < m; ++j) {
int right = bounds[j];
int left = j == m - 1 ? 1 : bounds[j + 1] + 1;
d[v][j] += (long long)(add[j]) * (long long)(right - left + 1) % (long long)(P);
if (d[v][j] >= P) {
d[v][j] -= P;
}
}
}
long long res = 0;
for (int i = 0; i < m; ++i) {
res += d[u][i];
}
cout << res % P << endl;
return 0;
}
</code></pre>
| 0 |
w1-p-sequences
|
2014-04-24T18:24:07
|
{"contest_participation":2214,"challenge_submissions":260,"successful_submissions":117}
|
2014-04-24T18:24:07
|
2016-07-23T15:27:56
|
setter
|
###C++
```cpp
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define maxn 1000 + 5
#define max_sqrt_k 32000
#define mod 1000000007
int dp[2][max_sqrt_k][2], n, k, sqrt_k, i, j, t, ret, pref, sum0, sum1, count_lr[max_sqrt_k], le, ri, l, p;
void upd (int &a, int b) {
a += b;
if (a >= mod) a -= mod;
}
int main (int argc, char * const argv[]) {
scanf("%d %d", &n, &k);
while (sqrt_k * sqrt_k < k) ++sqrt_k;
for(i = 1; i <= sqrt_k; i++) dp[1][i][0] = 1;
for(i = 1; i < sqrt_k; i++) {
le = k / (i + 1) + 1;
ri = k / i;
if (ri <= sqrt_k) continue;
le = max(le, sqrt_k + 1);
count_lr[i] = ri - le + 1;
}
for(i = 1; i < sqrt_k; i++) dp[1][i][1] = count_lr[i];
l = 1;
for(i = 2; i <= n; i++) {
p = l;
l ^= 1;
sum0 = sum1 = 0;
for(j = 1; j <= sqrt_k; j++) {
upd(sum0, dp[p][j][0]);
upd(sum1, dp[p][j][1]);
}
t = sqrt_k;
for(j = 1; j <= sqrt_k; j++) {
while (j * t > k) upd(sum0, mod - dp[p][t--][0]);
dp[l][j][0] = sum1 + sum0;
if (dp[l][j][0] >= mod) dp[l][j][0] -= mod;
upd(sum1, mod - dp[p][j][1]);
}
pref = 0;
for(j = 1; j < sqrt_k; j++) {
upd(pref, dp[p][j][0]);
dp[l][j][1] = (count_lr[j] * 1LL * pref) % mod;
}
}
for(j = 1; j <= sqrt_k; j++) {
upd(ret, dp[l][j][0]);
upd(ret, dp[l][j][1]);
}
printf("%d\n", ret);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T15:24:00
|
C++
|
52 | 2,293 |
p-sequences
|
P-sequences
|
We call a sequence of `N` natural numbers (*a*<sub>1</sub>, *a*<sub>2</sub>, ..., *a*<sub>N</sub>) a *P-sequence*, if the product of any two adjacent numbers in it is not greater than *P*. In other words, if a sequence (*a*<sub>1</sub>, *a*<sub>2</sub>, ..., *a*<sub>N</sub>) is a *P-sequence*, then *a*<sub>i</sub> * *a*<sub>i+1</sub> ≤ `P` ∀ 1 ≤ i < N
You are given `N` and `P`. Your task is to find the number of such *P-sequences* of `N` integers modulo 10<sup>9</sup>+7.
**Input Format**
The first line of input consists of `N`
The second line of the input consists of `P`.
**Constraints**
2 ≤ N ≤ 10<sup>3</sup>
1 ≤ P ≤ 10<sup>9</sup>
1 ≤ a<sub>i</sub>
**Output Format**
Output the number of *P-sequences* of `N` integers modulo 10<sup>9</sup>+7.
**Sample Input #00**
2
2
**Sample Output #00**
3
**Explanation #00**
3 such sequences are {1,1},{1,2} and {2,1}
|
code
|
How many sequences of N elements are there if product of two adjacent elements is not greater than P
|
ai
|
2014-03-31T21:26:34
|
2022-08-31T08:14:51
|
#
# Complete the 'pSequences' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER p
#
def pSequences(n, p):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
p = int(input().strip())
result = pSequences(n, p)
fptr.write(str(result) + '\n')
fptr.close()
|
We call a sequence of `N` natural numbers (*a*<sub>1</sub>, *a*<sub>2</sub>, ..., *a*<sub>N</sub>) a *P-sequence*, if the product of any two adjacent numbers in it is not greater than *P*. In other words, if a sequence (*a*<sub>1</sub>, *a*<sub>2</sub>, ..., *a*<sub>N</sub>) is a *P-sequence*, then *a*<sub>i</sub> * *a*<sub>i+1</sub> ≤ `P` ∀ 1 ≤ i < N
You are given `N` and `P`. Your task is to find the number of such *P-sequences* of `N` integers modulo 10<sup>9</sup>+7.
| 0.550562 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","r","ruby","rust","scala","swift","typescript"]
|
The first line of input consists of `N`
The second line of the input consists of `P`.
|
Output the number of *P-sequences* of `N` integers modulo 10<sup>9</sup>+7.
|
2
2
|
3
|
Hard
|
P-Sequences - Week 1 Editorial
|
<style id="MathJax_SVG_styles">.MathJax_SVG_Display {text-align: center; margin: 1em 0em; position: relative; display: block!important; text-indent: 0; max-width: none; max-height: none; min-width: 0; min-height: 0; width: 100%}
.MathJax_SVG .MJX-monospace {font-family: monospace}
.MathJax_SVG .MJX-sans-serif {font-family: sans-serif}
.MathJax_SVG {display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 100%; font-size-adjust: none; text-indent: 0; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0; min-height: 0; border: 0; padding: 0; margin: 0}
.MathJax_SVG * {transition: none; -webkit-transition: none; -moz-transition: none; -ms-transition: none; -o-transition: none}
.mjx-svg-href {fill: blue; stroke: blue}
</style><svg style="display: none;"><defs id="MathJax_SVG_glyphs"></defs></svg><p><strong>Difficulty level</strong> : Medium <br>
<strong>Required knowledge</strong> : Partial sums trick, DP <br>
<strong>Problem setter</strong> : <a href="https://www.hackerrank.com/zxqfd555">Sergey Kulik</a> <br>
<strong>Problem tester</strong> : <a href="https://www.hackerrank.com/dsoboliev">Dmytro Soboliev</a> </p>
<p><strong>Approach</strong></p>
<p>Consider a valid P-sequence of <strong>N</strong> integers: (<strong>a<sub>1</sub></strong>, <strong>a<sub>2</sub></strong>, ..., <strong>a<sub>N</sub></strong>). If you take some <strong>i</strong> (1 <= <strong>i</strong> < <strong>N</strong>) and take a pair (<strong>a<sub>i</sub></strong>, <strong>a<sub>i+1</sub></strong>) from this sequence, at least one of the following statements will be true:</p>
<ul>
<li><strong>a<sub>i</sub></strong> is not greater than the square root (in future, to be short, sqrt) of <strong>P</strong>.</li>
<li><strong>a<sub>i+1</sub></strong> is not greater than the square root of <strong>P</strong>.</li>
</ul>
<p>And this fact gives a rise to the key idea of the solution. Let's have a DP <strong>F(N, R, t)</strong>. The meaning of the DP state is: the number of P-sequences of <strong>N</strong> integer numbers, where:</p>
<ul>
<li>if <strong>t</strong> is false, then <strong>R</strong> is the <strong>N</strong>-th term of a P-sequence.</li>
<li>if <strong>t</strong> is true, then <strong>R</strong> is the maximal possible number that can be the <strong>N+1</strong>-th term of a P-sequence.</li>
</ul>
<p>Basically, false value of <strong>t</strong> corresponds to the above case where <strong>a<sub>i</sub></strong> isn't greater than <strong>sqrt(P)</strong> and true value of <strong>t</strong> corresponds to the case where <strong>a<sub>i</sub></strong> is actually greater than <strong>sqrt(P)</strong>, but <strong>a<sub>i+1</sub></strong> is not greater than <strong>sqrt(P)</strong>.</p>
<p>We have O(<strong>N</strong> * sqrt(<strong>P</strong>)) states here, so we can calculate this DP in affordable time.</p>
<p>When we calculate the DP, we should take care of the initial DP values and about the DP transitions.</p>
<p>The initial DP values are the values of <strong>F(N, R, t)</strong> where <strong>N</strong> is equal to one. Here </p>
<ul>
<li><p><strong>F(1, R, false)</strong> equals to one because <strong>R</strong> is the the only term of a P-sequence sequence here.</p></li>
<li><p><strong>F(1, R, true)</strong> equals to the number of such integers <strong>K</strong> from the range [1; <strong>P</strong>] such that <strong>N</strong> divided by <strong>K</strong> equals to <strong>R</strong>. This number can be obtained by solving the corresponding equation, see the solution for the details.</p></li>
</ul>
<p>When <strong>t</strong> (that means that <strong>a<sub>i+1</sub></strong> is not greater than <strong>sqrt(P)</strong>) is false you should take the sum of the following values in order to get <strong>F(N, R, t)</strong>:</p>
<ul>
<li><p>the sum of <strong>F(N - 1, R', false)</strong>, where <strong>R'</strong> for <strong>R'</strong> from <strong>1</strong> to <strong>sqrt(P)</strong>. This corresponds to the case where the both <strong>a<sub>i</sub></strong> and <strong>a<sub>i+1</sub></strong> are not greater than <strong>sqrt(P)</strong>.</p></li>
<li><p>the sum of <strong>F(N - 1, R', true)</strong>, where <strong>R'</strong> is greater or equal to <strong>R</strong>. This follows derives from the above DP state definition and corresponds to the case when <strong>a<sub>i</sub></strong> is greater than <strong>sqrt(P)</strong> but <strong>a<sub>i+1</sub></strong> is smaller than <strong>sqrt(P)</strong>.</p></li>
</ul>
<p>When we have the true value of <strong>t</strong>, the transition is simpler. Here the value of <strong>F(N, R, t)</strong> equals to the sum of <strong>F(N - 1, R', t)</strong>, where <strong>R'</strong> is not greater than <strong>R</strong> and then multiplied by the amount of such numbers <strong>K</strong> in the range [1; <strong>P</strong>] that <strong>P</strong> divided by <strong>K</strong> is <strong>R</strong>.</p>
<p>Here we're taking a sum of a multiple previously calculated DP states, but using, for example, the partial sums trick, we can do it in O(1).</p>
<p><strong>Setter's solution</strong></p>
<pre><code>#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define maxn 1000 + 5
#define max_sqrt_k 32000
#define mod 1000000007
int dp[2][max_sqrt_k][2], n, k, sqrt_k, i, j, t, ret, pref, sum0, sum1, count_lr[max_sqrt_k], le, ri, l, p;
void upd (int &a, int b) {
a += b;
if (a >= mod) a -= mod;
}
int main (int argc, char * const argv[]) {
scanf("%d %d", &n, &k);
while (sqrt_k * sqrt_k < k) ++sqrt_k;
for(i = 1; i <= sqrt_k; i++) dp[1][i][0] = 1;
for(i = 1; i < sqrt_k; i++) {
le = k / (i + 1) + 1;
ri = k / i;
if (ri <= sqrt_k) continue;
le = max(le, sqrt_k + 1);
count_lr[i] = ri - le + 1;
}
for(i = 1; i < sqrt_k; i++) dp[1][i][1] = count_lr[i];
l = 1;
for(i = 2; i <= n; i++) {
p = l;
l ^= 1;
sum0 = sum1 = 0;
for(j = 1; j <= sqrt_k; j++) {
upd(sum0, dp[p][j][0]);
upd(sum1, dp[p][j][1]);
}
t = sqrt_k;
for(j = 1; j <= sqrt_k; j++) {
while (j * t > k) upd(sum0, mod - dp[p][t--][0]);
dp[l][j][0] = sum1 + sum0;
if (dp[l][j][0] >= mod) dp[l][j][0] -= mod;
upd(sum1, mod - dp[p][j][1]);
}
pref = 0;
for(j = 1; j < sqrt_k; j++) {
upd(pref, dp[p][j][0]);
dp[l][j][1] = (count_lr[j] * 1LL * pref) % mod;
}
}
for(j = 1; j <= sqrt_k; j++) {
upd(ret, dp[l][j][0]);
upd(ret, dp[l][j][1]);
}
printf("%d\n", ret);
return 0;
}
</code></pre>
<p><strong>Tester's Solution</strong></p>
<pre><code>/*
Solution by sdya (Dmytro Soboliev)
*/
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cassert>
using namespace std;
const int P = 1000000007;
const int maxN = 64000;
vector < int > bounds, ways;
int d[2][maxN], add[maxN];
int buildBounds(int p) {
for (int i = 1; i * i <= p; ++i) {
ways.push_back(i);
bounds.push_back(p / i);
}
int m = bounds.size();
for (int i = 0; i < m; ++i) {
ways.push_back(bounds[m - 1 - i]);
bounds.push_back(ways[m - 1 - i]);
}
return m + m;
}
int main() {
int n, p;
cin >> n >> p;
assert(1 <= n && n <= 1e3);
assert(1 <= p && p <= 1e9);
int m = buildBounds(p);
int u = 0, v = 1;
memset(d[u], 0, sizeof(d[u]));
d[u][m - 1] = 1;
for (int i = 0; i < n; ++i, swap(u, v)) {
int covered = m - 1;
memset(add, 0, sizeof(add));
memset(d[v], 0, sizeof(d[v]));
for (int j = 0; j < m; ++j) {
if (d[u][j] == 0) {
continue;
}
while (covered >= 0 && bounds[covered] <= ways[j]) {
--covered;
}
add[covered + 1] += d[u][j];
if (add[covered + 1] >= P) {
add[covered + 1] -= P;
}
for (int k = covered; k >= 0; --k) {
int right = min(bounds[k], ways[j]);
int left = k == m - 1 ? 1 : bounds[k + 1] + 1;
if (left <= right) {
d[v][k] += (long long)(d[u][j]) * (long long)(right - left + 1) % (long long)(P);
if (d[v][k] >= P) {
d[v][k] -= P;
}
} else {
break;
}
}
}
for (int j = 1; j < m; ++j) {
add[j] += add[j - 1];
if (add[j] >= P) {
add[j] -= P;
}
}
for (int j = 0; j < m; ++j) {
int right = bounds[j];
int left = j == m - 1 ? 1 : bounds[j + 1] + 1;
d[v][j] += (long long)(add[j]) * (long long)(right - left + 1) % (long long)(P);
if (d[v][j] >= P) {
d[v][j] -= P;
}
}
}
long long res = 0;
for (int i = 0; i < m; ++i) {
res += d[u][i];
}
cout << res % P << endl;
return 0;
}
</code></pre>
| 0 |
w1-p-sequences
|
2014-04-24T18:24:07
|
{"contest_participation":2214,"challenge_submissions":260,"successful_submissions":117}
|
2014-04-24T18:24:07
|
2016-07-23T15:27:56
|
tester
|
###C++
```cpp
/*
Solution by sdya (Dmytro Soboliev)
*/
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cassert>
using namespace std;
const int P = 1000000007;
const int maxN = 64000;
vector < int > bounds, ways;
int d[2][maxN], add[maxN];
int buildBounds(int p) {
for (int i = 1; i * i <= p; ++i) {
ways.push_back(i);
bounds.push_back(p / i);
}
int m = bounds.size();
for (int i = 0; i < m; ++i) {
ways.push_back(bounds[m - 1 - i]);
bounds.push_back(ways[m - 1 - i]);
}
return m + m;
}
int main() {
int n, p;
cin >> n >> p;
assert(1 <= n && n <= 1e3);
assert(1 <= p && p <= 1e9);
int m = buildBounds(p);
int u = 0, v = 1;
memset(d[u], 0, sizeof(d[u]));
d[u][m - 1] = 1;
for (int i = 0; i < n; ++i, swap(u, v)) {
int covered = m - 1;
memset(add, 0, sizeof(add));
memset(d[v], 0, sizeof(d[v]));
for (int j = 0; j < m; ++j) {
if (d[u][j] == 0) {
continue;
}
while (covered >= 0 && bounds[covered] <= ways[j]) {
--covered;
}
add[covered + 1] += d[u][j];
if (add[covered + 1] >= P) {
add[covered + 1] -= P;
}
for (int k = covered; k >= 0; --k) {
int right = min(bounds[k], ways[j]);
int left = k == m - 1 ? 1 : bounds[k + 1] + 1;
if (left <= right) {
d[v][k] += (long long)(d[u][j]) * (long long)(right - left + 1) % (long long)(P);
if (d[v][k] >= P) {
d[v][k] -= P;
}
} else {
break;
}
}
}
for (int j = 1; j < m; ++j) {
add[j] += add[j - 1];
if (add[j] >= P) {
add[j] -= P;
}
}
for (int j = 0; j < m; ++j) {
int right = bounds[j];
int left = j == m - 1 ? 1 : bounds[j + 1] + 1;
d[v][j] += (long long)(add[j]) * (long long)(right - left + 1) % (long long)(P);
if (d[v][j] >= P) {
d[v][j] -= P;
}
}
}
long long res = 0;
for (int i = 0; i < m; ++i) {
res += d[u][i];
}
cout << res % P << endl;
return 0;
}
```
|
not-set
|
2016-04-24T02:02:36
|
2016-07-23T15:27:56
|
C++
|
53 | 2,301 |
manasa-and-factorials
|
Manasa and Factorials
|
Manasa was sulking her way through a boring class when suddenly her teacher singled her out and asked her a question. He gave her a number **n** and Manasa has to come up with the smallest number **m** which contains atleast **n** number of zeros at the end of **m!**. Help Manasa come out of the sticky situation.
**Input Format**
The first line contains an integer _T_ i.e. the number of Test cases.
Next T lines will contain an integer n.
**Output Format**
Print smallest such number m.
**Constraints**
1 ≤ _T_ ≤ 100 <br>
1 ≤ _n_ ≤ 10<sup>16</sup>
**Sample Input**
3
1
2
3
**Sample Output**
5
10
15
**Explanation**
1. As 4! = 24 and 5! = 120, so minimum value of m will be 5.
2. As 9! = 362880 and 10! = 3628800, so minimum value of m will be 10.
3. As 14! = 87178291200 and 15! = 1307674368000, so minimum value of m will be 15.
|
code
|
Think about number of zeros in k!
|
ai
|
2014-04-04T20:18:51
|
2022-09-02T09:54:31
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts LONG_INTEGER n as parameter.
#
def solve(n):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
n = int(input().strip())
result = solve(n)
fptr.write(str(result) + '\n')
fptr.close()
|
Manasa was sulking her way through a boring class when suddenly her teacher singled her out and asked her a question. He gave her a number **n** and Manasa has to come up with the smallest number **m** which contains atleast **n** number of zeros at the end of **m!**. Help Manasa come out of the sticky situation.
**Input Format**
The first line contains an integer _T_ i.e. the number of Test cases.
Next T lines will contain an integer n.
**Output Format**
Print smallest such number m.
**Constraints**
1 ≤ _T_ ≤ 100 <br>
1 ≤ _n_ ≤ 10<sup>16</sup>
**Sample Input**
3
1
2
3
**Sample Output**
5
10
15
**Explanation**
1. As 4! = 24 and 5! = 120, so minimum value of m will be 5.
2. As 9! = 362880 and 10! = 3628800, so minimum value of m will be 10.
3. As 14! = 87178291200 and 15! = 1307674368000, so minimum value of m will be 15.
| 0.487273 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null |
{"contest_participation":1581,"challenge_submissions":287,"successful_submissions":188}
|
2014-04-29T17:15:38
|
2016-12-02T22:59:21
|
setter
|
###C++
```cpp
// Author Amit Pandey
#include<bits/stdc++.h>
using namespace std;
bool check(long long int p, long long int n)
{
long long int temp = p , outp =0, five = 5;
while(five < temp)
{
outp += temp/five;
five = five*5;
// cout<<temp<<" "<<five<<endl;
}
if(outp>= n)
return true;
else
return false;
}
int main()
{
int t;
cin>>t;
while(t--)
{
long long int n;
cin>>n;
if(n==1)
{
cout<<"5"<<endl;
continue;
}
long long int low =2;
long long int high = 100*n;
while(low <high)
{
long long int mid = (low+high)/2;
if(check(mid,n) == true)
high = mid;
else
low = mid+1;
}
cout<<low<<endl;
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:37
|
2016-07-23T17:34:17
|
C++
|
54 | 2,301 |
manasa-and-factorials
|
Manasa and Factorials
|
Manasa was sulking her way through a boring class when suddenly her teacher singled her out and asked her a question. He gave her a number **n** and Manasa has to come up with the smallest number **m** which contains atleast **n** number of zeros at the end of **m!**. Help Manasa come out of the sticky situation.
**Input Format**
The first line contains an integer _T_ i.e. the number of Test cases.
Next T lines will contain an integer n.
**Output Format**
Print smallest such number m.
**Constraints**
1 ≤ _T_ ≤ 100 <br>
1 ≤ _n_ ≤ 10<sup>16</sup>
**Sample Input**
3
1
2
3
**Sample Output**
5
10
15
**Explanation**
1. As 4! = 24 and 5! = 120, so minimum value of m will be 5.
2. As 9! = 362880 and 10! = 3628800, so minimum value of m will be 10.
3. As 14! = 87178291200 and 15! = 1307674368000, so minimum value of m will be 15.
|
code
|
Think about number of zeros in k!
|
ai
|
2014-04-04T20:18:51
|
2022-09-02T09:54:31
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts LONG_INTEGER n as parameter.
#
def solve(n):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
n = int(input().strip())
result = solve(n)
fptr.write(str(result) + '\n')
fptr.close()
|
Manasa was sulking her way through a boring class when suddenly her teacher singled her out and asked her a question. He gave her a number **n** and Manasa has to come up with the smallest number **m** which contains atleast **n** number of zeros at the end of **m!**. Help Manasa come out of the sticky situation.
**Input Format**
The first line contains an integer _T_ i.e. the number of Test cases.
Next T lines will contain an integer n.
**Output Format**
Print smallest such number m.
**Constraints**
1 ≤ _T_ ≤ 100 <br>
1 ≤ _n_ ≤ 10<sup>16</sup>
**Sample Input**
3
1
2
3
**Sample Output**
5
10
15
**Explanation**
1. As 4! = 24 and 5! = 120, so minimum value of m will be 5.
2. As 9! = 362880 and 10! = 3628800, so minimum value of m will be 10.
3. As 14! = 87178291200 and 15! = 1307674368000, so minimum value of m will be 15.
| 0.487273 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null |
{"contest_participation":1581,"challenge_submissions":287,"successful_submissions":188}
|
2014-04-29T17:15:38
|
2016-12-02T22:59:21
|
tester
|
###Python 2
```python
def pcount(p, n):
''' the number of factors p of n! (where p is prime) '''
if n < p:
return 0
return n / p + pcount(p, n / p)
def f(n):
''' Least m such that m! has n trailing zeroes '''
L, R = 0, 5*n
while R - L > 1:
M = L + R >> 1
if pcount(5, M) < n:
L = M
else:
R = M
return R
z = input()
assert 1 <= z <= 100
for cas in xrange(z):
n = input()
assert 1 <= n <= 10**16
print f(n)
```
|
not-set
|
2016-04-24T02:02:37
|
2016-07-23T17:34:26
|
Python
|
55 | 2,298 |
courier-rank
|
Courier Rank
|
CourierRank is a very famous and well established company in the market and well known for transporting products with minimum cost for their customers. Your friend chandu works at CourierRank and is facing a problem these days. You being an excellent programmer and his friend. He asks you to help him with the problem.
Problem requires to deliver N couriers(Assume each courier to be identical) to N locations in the city with two kinds of delivery options:
- A Big Truck: It can carry any number of boxes to any location in the city for cost L dollars.
- A Small Car: It costs R dollars for delivering 1 box to a location 1 unit away.
For the sake of simplicity, Let us assume that:
1) The whole city is located on a single straight road.
2) The distance between consecutive cities is 1 unit.
3) All the couriers are placed exactly 1 unit distance before the first location.
Help your friend chandu, Finding the minimum cost for delivering the couriers.
**Input**
First line of input contains three integers N,L,R seperated by space, Where N is the number of Boxes, L and R are as described above.
Second line of input contains N integers seperated by space which are the locations where ith box needs to be couriered.
**Output**
Output contains a single integer, which the minimum possible cost(in dollars) for delivering all the boxes to their respective locations.
**Constraints**
1<=N<=100
1<=L,R<=100000
1<=location of box <= 10^6
**Sample Input**
5 82456 74095
761 685761 43 138742 8650
**Sample Output**
412280
|
code
| null |
ai
|
2014-04-03T22:55:02
|
2016-09-09T09:42:08
| null | null | null |
CourierRank is a very famous and well established company in the market and well known for transporting products with minimum cost for their customers. Your friend chandu works at CourierRank and is facing a problem these days. You being an excellent programmer and his friend. He asks you to help him with the problem.
Problem requires to deliver N couriers(Assume each courier to be identical) to N locations in the city with two kinds of delivery options:
- A Big Truck: It can carry any number of boxes to any location in the city for cost L dollars.
- A Small Car: It costs R dollars for delivering 1 box to a location 1 unit away.
For the sake of simplicity, Let us assume that:
1) The whole city is located on a single straight road.
2) The distance between consecutive cities is 1 unit.
3) All the couriers are placed exactly 1 unit distance before the first location.
Help your friend chandu, Finding the minimum cost for delivering the couriers.
**Input**
First line of input contains three integers N,L,R seperated by space, Where N is the number of Boxes, L and R are as described above.
Second line of input contains N integers seperated by space which are the locations where ith box needs to be couriered.
**Output**
Output contains a single integer, which the minimum possible cost(in dollars) for delivering all the boxes to their respective locations.
**Constraints**
1<=N<=100
1<=L,R<=100000
1<=location of box <= 10^6
**Sample Input**
5 82456 74095
761 685761 43 138742 8650
**Sample Output**
412280
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-05-01T07:27:59
|
2016-05-13T00:02:45
|
setter
|
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <fstream>
#include <cstdlib>
#include <cassert>
#include <vector>
#include <algorithm>
#include <stack>
#include <set>
#include <map>
#include <math.h>
#include <ctime>
// STL
#define pb push_back
#define LL long long
#define ULL unsigned long long
#define L long
#define VCTP vector<pair<LL,LL> >
#define PII pair<LL,LL>
#define PDD pair<double,double>
#define F first
#define S second
// Useful constants
#define INF (int)1e9
#define EPS 1e-9
// Useful hardware instructions
#define bitcount __builtin_popcount
#define gcd __gcd
// Useful container manipulation / traversal macros
#define forall(i,a,b) for(int i=a;i<b;i++)
#define foreach(v, c) for( typeof( (c).begin()) v = (c).begin(); v != (c).end(); ++v)
#define all(a) a.begin(), a.end()
#define in(a,b) ( (b).find(a) != (b).end())
#define pb push_back
#define fill(a,v) memset(a, v, sizeof a)
#define sz(a) ((int)(a.size()))
#define mp make_pair
// Some common useful functions
#define maX(a,b) ( (a) > (b) ? (a) : (b))
#define miN(a,b) ( (a) < (b) ? (a) : (b))
#define checkbit(n,b) ( (n >> b) & 1)
#define DREP(a) sort(all(a)); a.erase(unique(all(a)),a.end())
#define INDEX(arr,ind) (lower_bound(all(arr),ind)-arr.begin())
#define st_clk double st=clock();
#define end_clk double en=clock();
#define show_time cout<<"\tTIME="<<(en-st)/CLOCKS_PER_SEC<<endl;
#define rd readInt()
#define sc(n) scanf("%d",&n)
#define scst(n) scanf("%s",n)
#define f_in(st) freopen(st,"r",stdin);
#define f_out(st) freopen(st,"w",stdout);
using namespace std;
inline int readInt(){
long int n = 0, c = gc(), f = 1;
while(c != '-' && (c < '0' || c > '9')) c = gc();
if(c == '-') f = -1, c = gc();
while(c >= '0' && c <= '9')
n = (n<<3) + (n<<1) + c - '0', c = gc();
return n * f;
}
/*
Problem can be solved using Dynamic programming. Solution is based on a tricky observation that optimal solution won't ever use truck to deliver
courier to a location where no courier is destined to be.
Reason: Let us say many couriers are taken by truck to position i and none of it was actually destined for there. let x be the couriers that should be moved
forward for their destined location and y be the couriers which should be moved backward for their destined location.
Case I: x > y, then we can use truck to deliver at location i+1 for more optimal result.
Case II: y > x, then we can use truck to deliver at location i-1 for more optimal result.
case III: x == y, then we can use truck to deliver at any of the two locations for more optimal result.
*/
long long dp[102][102];
int findcost(vector<int> bb,int tc,int _lc){
int n = bb.size();
long long ans = 0;
long long lc = _lc;
for(int i=0;i<n;i++) ans+=bb[i]*lc;
sort(bb.begin(),bb.end());
memset(dp,63,sizeof(dp));
for(int i=0;i<n;i++){
dp[i][1] = tc;
for(int j=0;j<i;j++)
dp[i][1] += min(bb[j],bb[i]-bb[j])*lc;
long long t = dp[i][1];
for(int j=i+1;j<n;j++) t+=(bb[j]-bb[i])*lc;
ans = min(ans,t);
for(int j=2;j<=i+1;j++) {
for(int k=0;k<i;k++){
t = dp[k][j-1] + tc;
for(int l=k+1;l<i;l++) t+=min(bb[l]-bb[k],bb[i]-bb[l])*lc;
dp[i][j] = min(dp[i][j],t);
}
t = dp[i][j];
for(int k=i+1;k<n;k++) t+=(bb[k]-bb[i])*lc;
ans = min(ans,t);
}
}
return int(ans);
}
int main()
{
#ifndef ONLINE_JUDGE
f_in("10.in")
f_out("10.out");
#endif
int N,LC,RC;
scanf("%d%d%d",&N,&LC,&RC);
vector<int> boxes;
for(int i=0;i<N;i++) {int temp; scanf("%d",&temp); boxes.push_back(temp); }
printf("%d\n",findcost(boxes,LC,RC));
return 0;
}
|
not-set
|
2016-04-24T02:02:37
|
2016-04-24T02:02:37
|
C++
|
56 | 2,475 |
sherlock-and-permutations
|
Sherlock and Permutations
|
Watson asks Sherlock:
Given a string _S_ of _N_ `0's` and _M_ `1's`, how many unique permutations of this string start with `1`?
Help Sherlock by printing the answer modulo (_10<sup>9</sup>+7_).
**Input Format**
First line contains _T_, the number of test cases.
Each test case consists of _N_ and _M_ separated by a space.
**Output Format**
For each test case, print the answer modulo (_10<sup>9</sup>+7_).
**Constraints**
1 ≤ T ≤ 200
1 ≤ N,M ≤ 1000
**Sample Input**
2
1 1
2 3
**Sample Output**
1
6
**Explanation**
Test1: Out of all unique permutations ie. `01` and `10`, only second permutation satisfies. Hence, output is 1.
Test2: Out of all unique permutations ie. `00111 01011 01101 01110 10011 10101 10110 11001 11010 11100`, only `10011 10101 10110 11001 11010 11100` satisfy. Hence, output is 6.
|
code
|
Help Sherlock in counting permutations.
|
ai
|
2014-05-01T14:02:20
|
2022-09-02T09:54:12
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER m
#
def solve(n, m):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
result = solve(n, m)
fptr.write(str(result) + '\n')
fptr.close()
|
Watson asks Sherlock:
Given a string _S_ of _N_ `0's` and _M_ `1's`, how many unique permutations of this string start with `1`?
Help Sherlock by printing the answer modulo (_10<sup>9</sup>+7_).
**Input Format**
First line contains _T_, the number of test cases.
Each test case consists of _N_ and _M_ separated by a space.
**Output Format**
For each test case, print the answer modulo (_10<sup>9</sup>+7_).
**Constraints**
1 ≤ T ≤ 200
1 ≤ N,M ≤ 1000
**Sample Input**
2
1 1
2 3
**Sample Output**
1
6
**Explanation**
Test1: Out of all unique permutations ie. `01` and `10`, only second permutation satisfies. Hence, output is 1.
Test2: Out of all unique permutations ie. `00111 01011 01101 01110 10011 10101 10110 11001 11010 11100`, only `10011 10101 10110 11001 11010 11100` satisfy. Hence, output is 6.
| 0.598086 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
| null | null | null | null | null |
{"contest_participation":922,"challenge_submissions":417,"successful_submissions":322}
|
2014-05-21T08:40:53
|
2016-12-02T15:01:16
|
setter
|
###C++
```cpp
//Language: C++
//Author: darkshadows(Lalit Kundu)
#include<bits/stdc++.h>
#define assn(n,a,b) assert(n<=b && n>=a)
using namespace std;
typedef long long LL;
#define MOD 1000000007
#define MAX 1000033
LL mpow(LL a, LL n)
{
LL ret=1;
LL b=a;
while(n)
{
if(n&1)ret=(ret*b)%MOD;
b=(b*b)%MOD;
n>>=1;
}
return (LL)ret;
}
LL fac[MAX],inv[MAX];
void precalc()
{
LL i;
fac[0]=1;
inv[0]=1;
fac[1]=1;
inv[1]=1;
for(i=2; i<MAX; i++)
{
fac[i]=(i*fac[i-1])%MOD;
inv[i]=mpow(fac[i],MOD-2);
}
}
LL choose(LL n,LL r)
{
if(n<r)return 0ll;
LL ret1=(inv[r]*inv[n-r])%MOD;
LL ret=(ret1*fac[n])%MOD;
return ret;
}
int main()
{
precalc();
int t;
cin >> t;
assn(t,1,200);
while(t--)
{
LL n,m,t=1ll,ans=1ll;
cin >> m >> n;
assn(n,1,1000);
assn(m,1,1000);
n--;
m+=n;
cout << choose(m,n) << endl;
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:39
|
2016-07-23T16:31:46
|
C++
|
||||
57 | 2,475 |
sherlock-and-permutations
|
Sherlock and Permutations
|
Watson asks Sherlock:
Given a string _S_ of _N_ `0's` and _M_ `1's`, how many unique permutations of this string start with `1`?
Help Sherlock by printing the answer modulo (_10<sup>9</sup>+7_).
**Input Format**
First line contains _T_, the number of test cases.
Each test case consists of _N_ and _M_ separated by a space.
**Output Format**
For each test case, print the answer modulo (_10<sup>9</sup>+7_).
**Constraints**
1 ≤ T ≤ 200
1 ≤ N,M ≤ 1000
**Sample Input**
2
1 1
2 3
**Sample Output**
1
6
**Explanation**
Test1: Out of all unique permutations ie. `01` and `10`, only second permutation satisfies. Hence, output is 1.
Test2: Out of all unique permutations ie. `00111 01011 01101 01110 10011 10101 10110 11001 11010 11100`, only `10011 10101 10110 11001 11010 11100` satisfy. Hence, output is 6.
|
code
|
Help Sherlock in counting permutations.
|
ai
|
2014-05-01T14:02:20
|
2022-09-02T09:54:12
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER m
#
def solve(n, m):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
result = solve(n, m)
fptr.write(str(result) + '\n')
fptr.close()
|
Watson asks Sherlock:
Given a string _S_ of _N_ `0's` and _M_ `1's`, how many unique permutations of this string start with `1`?
Help Sherlock by printing the answer modulo (_10<sup>9</sup>+7_).
**Input Format**
First line contains _T_, the number of test cases.
Each test case consists of _N_ and _M_ separated by a space.
**Output Format**
For each test case, print the answer modulo (_10<sup>9</sup>+7_).
**Constraints**
1 ≤ T ≤ 200
1 ≤ N,M ≤ 1000
**Sample Input**
2
1 1
2 3
**Sample Output**
1
6
**Explanation**
Test1: Out of all unique permutations ie. `01` and `10`, only second permutation satisfies. Hence, output is 1.
Test2: Out of all unique permutations ie. `00111 01011 01101 01110 10011 10101 10110 11001 11010 11100`, only `10011 10101 10110 11001 11010 11100` satisfy. Hence, output is 6.
| 0.598086 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
| null | null | null | null | null |
{"contest_participation":922,"challenge_submissions":417,"successful_submissions":322}
|
2014-05-21T08:40:53
|
2016-12-02T15:01:16
|
tester
|
###C++
```cpp
//Language: C++
//Author: xorfire(R Goutham)
#include <cstdio>
#include <cassert>
int mod = 1000000007, comb[2001][2001];
int main()
{
// Computing Binomial coefficients
for (int i = 0; i <= 2000; i++)
{
comb[i][0] = comb[i][i] = 1;
for (int j = 1; j < i; j++)
{
comb[i][j] = comb[i-1][j] + comb[i-1][j-1];
if (comb[i][j] >= mod) comb[i][j] -= mod;
}
}
int t; scanf("%d", &t);
while (t--)
{
int n, m; scanf("%d%d", &n, &m);
assert(1 <= n and 1 <= m and n + m - 1 <= 2000);
printf("%d\n", comb[n + m - 1][n]);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:39
|
2016-07-23T16:32:55
|
C++
|
||||
58 | 2,462 |
gcd-product
|
GCD Product
|
[Russian](https://hr-filepicker.s3.amazonaws.com/w3/russian/2462-gcd-product.pdf)<br/>
This time your assignment is really simple.
Calculate GCD(1, 1) * GCD(1, 2) * ... * GCD(1, M) * GCD(2, 1) * GCD(2, 2) * ... * GCD(2, M) * ... * GCD(N, 1) * GCD(N, 2) * ... * GCD(N, M).
where GCD is defined as the [Greatest Common Divisor](https://en.wikipedia.org/wiki/Greatest_common_divisor).
**Input Format**
The first and only line contains two space separated integers *N* and *M*.
**Output Format**
Output the required product modulo 10<sup>9</sup>+7.
**Constraints**
1 <= *N*, *M* <= 1.5 * 10<sup>7</sup>
**Sample input:**
<pre>4 4</pre>
**Sample output:**
<pre>96</pre>
**Explanation**
For the above testcase, N = 4, M = 4. So,
GCD(1, 1) * GCD(1, 2) * ...... * GCD(4, 4) = 1 * 1 * 1 * 1 * 1 * 2 * 1 * 2 * 1 * 1 * 3 * 1 * 1 * 2 * 1 * 4 = 96.
|
code
|
Find the product of the Greatest Common Divisors for all the pairs inside a rectangle.
|
ai
|
2014-04-29T10:32:28
|
2022-09-02T09:54:44
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER m
#
def solve(n, m):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
result = solve(n, m)
fptr.write(str(result) + '\n')
fptr.close()
|
This time your assignment is really simple.
Calculate GCD(1, 1) * GCD(1, 2) * ... * GCD(1, M) * GCD(2, 1) * GCD(2, 2) * ... * GCD(2, M) * ... * GCD(N, 1) * GCD(N, 2) * ... * GCD(N, M).
where GCD is defined as the [Greatest Common Divisor](https://en.wikipedia.org/wiki/Greatest_common_divisor).
**Input Format**
The first and only line contains two space separated integers *N* and *M*.
**Output Format**
Output the required product modulo 10<sup>9</sup>+7.
**Constraints**
1 <= *N*, *M* <= 1.5 * 10<sup>7</sup>
**Sample input:**
<pre>4 4</pre>
**Sample output:**
<pre>96</pre>
**Explanation**
For the above testcase, N = 4, M = 4. So,
GCD(1, 1) * GCD(1, 2) * ...... * GCD(4, 4) = 1 * 1 * 1 * 1 * 1 * 2 * 1 * 2 * 1 * 1 * 3 * 1 * 1 * 2 * 1 * 4 = 96.
| 0.426136 |
["c","clojure","cobol","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
| null | null | null | null | null |
{"contest_participation":1475,"challenge_submissions":236,"successful_submissions":103}
|
2014-05-26T14:49:21
|
2016-12-08T09:25:32
|
setter
|
###C++
```cpp
#include <cstdio>
#include <algorithm>
using namespace std;
#define maxn 15000000 + 5
#define mod 1000000007
#define tm Tm
int n, m, i, j, p[maxn], dp[maxn], sf[maxn], sfn, g, tn, tm, ret, pref[maxn], l, c, p1, p2, r, carry;
long long sfm[maxn], t;
int pw (int x, long long p) {
if (!p) return 1;
if (p == 1) return x;
int q = pw(x, p >> 1);
q = (1LL * q * q) % mod;
if (p & 1) q = (1LL * q * x) % mod;
return q;
}
int main (int argc, char * const argv[]) {
scanf("%d %d", &n, &m);
if (n < m) swap(n, m);
for(i = 2; i <= n; i++) if (p[i] == 0) {
j = i;
while (j <= n) {
if (!p[j]) p[j] = i;
j += i;
}
}
for(i = 2; i <= n; i++) {
if (i == p[i]) dp[i] = -1; else
if (p[(i / p[i])] == p[i]) dp[i] = 0; else dp[i] = -1 * dp[i / p[i]];
pref[i] = pref[i - 1] + dp[i];
}
for(i = 1; i <= n; i++) if (dp[i] != 0) {
sf[++sfn] = i;
sfm[sfn] = dp[i];
}
sf[sfn + 1] = m + 1;
ret = 1;
carry = 1, t = 1, tn = tm = -1;
for(g = 2; g <= m; g++) {
if (n / g != tn || m / g != tm) {
ret = (ret * 1LL * pw(carry, t)) % mod;
carry = 1LL;
} else {
carry = (carry * 1LL * g) % mod;
continue;
}
tn = n / g;
tm = m / g;
t = 1LL * tn * tm;
if (g <= 600000) {
l = 1;
while (l <= tm) {
++c;
r = min(min(tn / (p1 = tn / l), tm / (p2 = tm / l)), tm);
t += p1 * 1LL * p2 * (pref[r] - pref[l - 1]);
l = r + 1;
}
} else for(i = 1; sf[i] <= tm; i++) t += sfm[i] * (tn / sf[i]) * (tm / sf[i]);
carry = (1LL * carry * g) % mod;
}
ret = (ret * 1LL * pw(carry, t)) % mod;
printf("%d\n", ret);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:39
|
2016-07-23T18:25:31
|
C++
|
||||
59 | 2,462 |
gcd-product
|
GCD Product
|
[Russian](https://hr-filepicker.s3.amazonaws.com/w3/russian/2462-gcd-product.pdf)<br/>
This time your assignment is really simple.
Calculate GCD(1, 1) * GCD(1, 2) * ... * GCD(1, M) * GCD(2, 1) * GCD(2, 2) * ... * GCD(2, M) * ... * GCD(N, 1) * GCD(N, 2) * ... * GCD(N, M).
where GCD is defined as the [Greatest Common Divisor](https://en.wikipedia.org/wiki/Greatest_common_divisor).
**Input Format**
The first and only line contains two space separated integers *N* and *M*.
**Output Format**
Output the required product modulo 10<sup>9</sup>+7.
**Constraints**
1 <= *N*, *M* <= 1.5 * 10<sup>7</sup>
**Sample input:**
<pre>4 4</pre>
**Sample output:**
<pre>96</pre>
**Explanation**
For the above testcase, N = 4, M = 4. So,
GCD(1, 1) * GCD(1, 2) * ...... * GCD(4, 4) = 1 * 1 * 1 * 1 * 1 * 2 * 1 * 2 * 1 * 1 * 3 * 1 * 1 * 2 * 1 * 4 = 96.
|
code
|
Find the product of the Greatest Common Divisors for all the pairs inside a rectangle.
|
ai
|
2014-04-29T10:32:28
|
2022-09-02T09:54:44
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER m
#
def solve(n, m):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
result = solve(n, m)
fptr.write(str(result) + '\n')
fptr.close()
|
This time your assignment is really simple.
Calculate GCD(1, 1) * GCD(1, 2) * ... * GCD(1, M) * GCD(2, 1) * GCD(2, 2) * ... * GCD(2, M) * ... * GCD(N, 1) * GCD(N, 2) * ... * GCD(N, M).
where GCD is defined as the [Greatest Common Divisor](https://en.wikipedia.org/wiki/Greatest_common_divisor).
**Input Format**
The first and only line contains two space separated integers *N* and *M*.
**Output Format**
Output the required product modulo 10<sup>9</sup>+7.
**Constraints**
1 <= *N*, *M* <= 1.5 * 10<sup>7</sup>
**Sample input:**
<pre>4 4</pre>
**Sample output:**
<pre>96</pre>
**Explanation**
For the above testcase, N = 4, M = 4. So,
GCD(1, 1) * GCD(1, 2) * ...... * GCD(4, 4) = 1 * 1 * 1 * 1 * 1 * 2 * 1 * 2 * 1 * 1 * 3 * 1 * 1 * 2 * 1 * 4 = 96.
| 0.426136 |
["c","clojure","cobol","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
| null | null | null | null | null |
{"contest_participation":1475,"challenge_submissions":236,"successful_submissions":103}
|
2014-05-26T14:49:21
|
2016-12-08T09:25:32
|
tester
|
###C++
```cpp
#include <map>
#include <set>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <vector>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <cassert>
#include <numeric>
#include <iomanip>
#include <sstream>
#include <fstream>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef vector<int> VI;
typedef vector<LL> VL;
typedef vector<PII> VPII;
#define MM(a,x) memset(a,x,sizeof(a));
#define ALL(x) (x).begin(), (x).end()
#define P(x) cerr<<"["#x<<" = "<<(x)<<"]\n"
#define PP(x,i) cerr<<"["#x<<i<<" = "<<x[i]<<"]\n"
#define P2(x,y) cerr<<"["#x" = "<<(x)<<", "#y" = "<<(y)<<"]\n"
#define TM(a,b) cerr<<"["#a" -> "#b": "<<1e3*(b-a)/CLOCKS_PER_SEC<<"ms]\n";
#define UN(v) sort(ALL(v)), v.resize(unique(ALL(v))-v.begin())
#define mp make_pair
#define pb push_back
#define x first
#define y second
struct _ {_() {ios_base::sync_with_stdio(0);}} _;
template<class A, class B> ostream& operator<<(ostream &o, pair<A, B> t) {o << "(" << t.x << ", " << t.y << ")"; return o;}
template<class T> void PV(T a, T b) {while(a != b)cout << *a++, cout << (a != b ? " " : "\n");}
template<class T> inline bool chmin(T &a, T b) {return a > b ? a = b, 1 : 0;}
template<class T> inline bool chmax(T &a, T b) {return a < b ? a = b, 1 : 0;}
template<class T> string tostring(T x, int len = 0) {stringstream ss; ss << x; string r = ss.str(); if(r.length() < len) r = string(len - r.length(), '0') + r; return r;}
template<class T> void convert(string x, T& r) {stringstream ss(x); ss >> r;}
const int inf = 0x3f3f3f3f;
const long long linf = 0x3f3f3f3f3f3f3f3fLL;
const int mod = int(1e9) + 7;
const int N = 15111111;
int n, m;
int F[N];
inline LL exp(LL x, LL n, LL m = mod) {
LL r = 1;
while(n) {
if(n & 1) r = r * x % m;
x = x * x % m, n >>= 1;
}
return r;
}
int main() {
cin >> n >> m;
if(n > m) swap(n, m);
time_t t1 = clock();
for(int i = 1; i < N; i++) F[i] = (LL)(n / i) * (m / i) % (mod - 1);
for(int i = n; i >= 1; i--)
for(int j = i + i; j <= n; j += i) {
F[i] -= F[j];
if(F[i] < 0) F[i] += mod - 1;
}
int res = 1;
for(int i = 1; i <= n; i++) res = res * exp(i, F[i]) % mod;
cout << res << endl;
/*
{
int br = 1;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
br = (LL) br * __gcd(i, j) % mod;
cout << br << endl;
assert(br == res);
}
*/
time_t t2 = clock();
TM(t1, t2);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:39
|
2016-07-23T18:25:38
|
C++
|
||||
60 | 2,560 |
palindrome-test
|
Palindrome Test
|
Palindrome blablabla
Ecrire programme blabla langage blabla
Verifier chaine blabla.
Entrée :
la chaine (String)
Sortie :
booléen
|
code
|
Vérifier que le mot est un palindrome
|
ai
|
2014-05-28T11:15:53
|
2016-09-09T09:43:55
| null | null | null |
Palindrome blablabla
Ecrire programme blabla langage blabla
Verifier chaine blabla.
Entrée :
la chaine (String)
Sortie :
booléen
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-05-28T11:40:26
|
2016-05-13T00:02:19
|
setter
|
hello
|
not-set
|
2016-04-24T02:02:40
|
2016-04-24T02:02:40
|
Unknown
|
61 | 2,560 |
palindrome-test
|
Palindrome Test
|
Palindrome blablabla
Ecrire programme blabla langage blabla
Verifier chaine blabla.
Entrée :
la chaine (String)
Sortie :
booléen
|
code
|
Vérifier que le mot est un palindrome
|
ai
|
2014-05-28T11:15:53
|
2016-09-09T09:43:55
| null | null | null |
Palindrome blablabla
Ecrire programme blabla langage blabla
Verifier chaine blabla.
Entrée :
la chaine (String)
Sortie :
booléen
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-05-28T11:40:26
|
2016-05-13T00:02:19
|
tester
|
Hello tester
|
not-set
|
2016-04-24T02:02:40
|
2016-04-24T02:02:40
|
Unknown
|
62 | 2,491 |
sherlock-and-minimax
|
Sherlock and MiniMax
|
[Русский](https://hr-filepicker.s3.amazonaws.com/101may14/russian/2491-sherlock-and-minimax.pdf) \|
[中文](https://hr-filepicker.s3.amazonaws.com/101may14/chinese/2491-sherlock-and-minimax.pdf)<br/>
Watson gives Sherlock an array _A<sub>1</sub>,A<sub>2</sub>...A<sub>N</sub>_.
He asks him to find an integer _M_ between _P_ and _Q_(both inclusive), such that, _min {|A<sub>i</sub>-M|, 1 ≤ i ≤ N}_ is maximised. If there are multiple solutions, print the smallest one.
**Input Format**
The first line contains _N_. The next line contains space separated _N_ integers, and denote the array _A_. The third line contains two space separated integers denoting _P_ and _Q_.
**Output Format**
In one line, print the required answer.
**Constraints**
1 ≤ N ≤ 10<sup>2</sup>
1 ≤ A<sub>i</sub> ≤ 10<sup>9</sup>
1 ≤ P ≤ Q ≤ 10<sup>9</sup>
**Sample Input**
3
5 8 14
4 9
**Sample Output**
4
**Explanation**
For M = 4,6,7, or 9, the result is 1. Since we have to output the smallest of the multiple solutions, we print 4.
|
code
|
Watson gives Sherlock an array A1,A2...AN. Find an integer M
between P and Q(both inclusive), satistying a condition.
|
ai
|
2014-05-06T18:57:55
|
2022-08-31T08:14:38
|
#
# Complete the 'sherlockAndMinimax' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER_ARRAY arr
# 2. INTEGER p
# 3. INTEGER q
#
def sherlockAndMinimax(arr, p, q):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
arr = list(map(int, input().rstrip().split()))
first_multiple_input = input().rstrip().split()
p = int(first_multiple_input[0])
q = int(first_multiple_input[1])
result = sherlockAndMinimax(arr, p, q)
fptr.write(str(result) + '\n')
fptr.close()
|
Watson gives Sherlock an array of integers. Given the endpoints of an integer range, for all $M$ in that inclusive range, determine the minimum( abs(arr[i]-M) for all $1 \le i \le |arr|$) ). Once that has been determined for all integers in the range, return the $M$ which generated the maximum of those values. If there are multiple $M$'s that result in that value, return the lowest one.
For example, your array $arr = [3,5,7,9]$ and your range is from $p=6$ to $q=8$ inclusive.
```
M |arr[1]-M| |arr[2]-M| |arr[3]-M| |arr[4]-M| Min
6 3 1 1 3 1
7 4 2 0 2 0
8 5 3 1 1 1
```
We look at the `Min` column and see the maximum of those three values is $1$. Two $M$'s result in that answer so we choose the lower value, $6$.
**Function Description**
Complete the *sherlockAndMinimax* function in the editor below. It should return an integer as described.
sherlockAndMinimax has the following parameters:
- *arr*: an array of integers
- *p*: an integer that represents the lowest value of the range for $M$
- *q*: an integer that represents the highest value of the range for $M$
| 0.541436 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
The first line contains an integer $n$, the number of elements in $arr$.
The next line contains $n$ space-separated integers $arr[i]$.
The third line contains two space-separated integers $p$ and $q$, the inclusive endpoints for the range of $M$.
|
Print the value of $M$ on a line.
|
3
5 8 14
4 9
|
4
|
Hard
| null | null | null | null | null |
{"contest_participation":1164,"challenge_submissions":299,"successful_submissions":128}
|
2014-05-30T22:31:21
|
2018-04-17T13:18:01
|
setter
|
###C++
```cpp
#include <bits/stdc++.h>
using namespace std;
int n;
int arr[109];
int A, B;
int answer;
//returns the value to be maximised if M=x
int check( int x )
{
int ret = INT_MAX;
for( int i = 0; i < n; ++i )
ret =min(ret, abs( x- arr[i] ));
return ret;
}
// check is x is within limits and if check(x) is better store the answer
void limits( int x )
{
if( x < A || x > B ) return;
if(check(x) > check(answer)) answer = x;
}
int main()
{
scanf( "%d", &n );
for( int i = 0; i < n; ++i ) scanf( "%d", &arr[i] );
scanf( "%d%d", &A, &B );
answer = A;
// check for A and B
limits( A );
limits( B );
for( int i = 0; i < n; ++i )
for( int j = i+1; j < n; ++j )
{
// check for (A_i + A_j)/2
limits( (arr[i]+arr[j])/2 );
}
printf( "%d\n",answer );
return 0;
}
```
|
not-set
|
2016-04-24T02:02:40
|
2016-07-23T14:21:41
|
C++
|
63 | 2,491 |
sherlock-and-minimax
|
Sherlock and MiniMax
|
[Русский](https://hr-filepicker.s3.amazonaws.com/101may14/russian/2491-sherlock-and-minimax.pdf) \|
[中文](https://hr-filepicker.s3.amazonaws.com/101may14/chinese/2491-sherlock-and-minimax.pdf)<br/>
Watson gives Sherlock an array _A<sub>1</sub>,A<sub>2</sub>...A<sub>N</sub>_.
He asks him to find an integer _M_ between _P_ and _Q_(both inclusive), such that, _min {|A<sub>i</sub>-M|, 1 ≤ i ≤ N}_ is maximised. If there are multiple solutions, print the smallest one.
**Input Format**
The first line contains _N_. The next line contains space separated _N_ integers, and denote the array _A_. The third line contains two space separated integers denoting _P_ and _Q_.
**Output Format**
In one line, print the required answer.
**Constraints**
1 ≤ N ≤ 10<sup>2</sup>
1 ≤ A<sub>i</sub> ≤ 10<sup>9</sup>
1 ≤ P ≤ Q ≤ 10<sup>9</sup>
**Sample Input**
3
5 8 14
4 9
**Sample Output**
4
**Explanation**
For M = 4,6,7, or 9, the result is 1. Since we have to output the smallest of the multiple solutions, we print 4.
|
code
|
Watson gives Sherlock an array A1,A2...AN. Find an integer M
between P and Q(both inclusive), satistying a condition.
|
ai
|
2014-05-06T18:57:55
|
2022-08-31T08:14:38
|
#
# Complete the 'sherlockAndMinimax' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER_ARRAY arr
# 2. INTEGER p
# 3. INTEGER q
#
def sherlockAndMinimax(arr, p, q):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
n = int(input().strip())
arr = list(map(int, input().rstrip().split()))
first_multiple_input = input().rstrip().split()
p = int(first_multiple_input[0])
q = int(first_multiple_input[1])
result = sherlockAndMinimax(arr, p, q)
fptr.write(str(result) + '\n')
fptr.close()
|
Watson gives Sherlock an array of integers. Given the endpoints of an integer range, for all $M$ in that inclusive range, determine the minimum( abs(arr[i]-M) for all $1 \le i \le |arr|$) ). Once that has been determined for all integers in the range, return the $M$ which generated the maximum of those values. If there are multiple $M$'s that result in that value, return the lowest one.
For example, your array $arr = [3,5,7,9]$ and your range is from $p=6$ to $q=8$ inclusive.
```
M |arr[1]-M| |arr[2]-M| |arr[3]-M| |arr[4]-M| Min
6 3 1 1 3 1
7 4 2 0 2 0
8 5 3 1 1 1
```
We look at the `Min` column and see the maximum of those three values is $1$. Two $M$'s result in that answer so we choose the lower value, $6$.
**Function Description**
Complete the *sherlockAndMinimax* function in the editor below. It should return an integer as described.
sherlockAndMinimax has the following parameters:
- *arr*: an array of integers
- *p*: an integer that represents the lowest value of the range for $M$
- *q*: an integer that represents the highest value of the range for $M$
| 0.541436 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
The first line contains an integer $n$, the number of elements in $arr$.
The next line contains $n$ space-separated integers $arr[i]$.
The third line contains two space-separated integers $p$ and $q$, the inclusive endpoints for the range of $M$.
|
Print the value of $M$ on a line.
|
3
5 8 14
4 9
|
4
|
Hard
| null | null | null | null | null |
{"contest_participation":1164,"challenge_submissions":299,"successful_submissions":128}
|
2014-05-30T22:31:21
|
2018-04-17T13:18:01
|
tester
|
###C++
```cpp
//C++ Code
Author Gerald
#ifdef ssu1
#define _GLIBCXX_DEBUG
#endif
#undef NDEBUG
#include <algorithm>
#include <functional>
#include <numeric>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <cstring>
#include <cassert>
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <queue>
#include <bitset>
#include <sstream>
using namespace std;
#define fore(i, l, r) for(int i = (l); i < (r); ++i)
#define forn(i, n) fore(i, 0, n)
#define fori(i, l, r) fore(i, l, (r) + 1)
#define sz(v) int((v).size())
#define all(v) (v).begin(), (v).end()
#define pb push_back
#define mp make_pair
#define X first
#define Y second
#if ( _WIN32 || __WIN32__ )
#define LLD "%I64d"
#else
#define LLD "%lld"
#endif
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
template<typename T> T abs(T a) { return a < 0 ? -a : a; }
template<typename T> T sqr(T a) { return a*a; }
const int INF = (int)1e9;
const ld EPS = 1e-9;
const ld PI = 3.1415926535897932384626433832795;
int readInt(int l, int r){
int x;
if(scanf("%d", &x) != 1){
fprintf(stderr, "Expected int in range [%d, %d], but haven't found!", l, r);
throw;
}
if(!(l <= x && x <= r)){
fprintf(stderr, "Expected int in range [%d, %d], but found %d!", l, r, x);
throw;
}
return x;
}
int f(const vector<int>& a, int m){
int mn = (int)2e9;
forn(i, sz(a)){
mn = min(mn, abs(a[i] - m));
}
return mn;
}
int main(){
#ifdef ssu1
assert(freopen("input.txt", "rt", stdin));
//assert(freopen("output.txt", "wt", stdout));
#endif
int n, p, q;
n = readInt(1, 100);
vector<int> a(n);
forn(i, n)
a[i] = readInt(1, 1000000000);
p = readInt(1, 1000000000);
q = readInt(1, 1000000000);
assert(p <= q);
vector<int> pat;
pat.pb(p);
pat.pb(q);
forn(i, n){
forn(j, n){
int x = (a[i] + a[j]) / 2;
fori(y, x - 1, x + 1){
if(p <= y && y <= q)
pat.pb(y);
}
}
}
sort(all(pat));
int curmx = -1, m = -1;
forn(i, sz(pat)){
if(f(a, pat[i]) > curmx){
curmx = f(a, pat[i]);
m = pat[i];
}
}
printf("%d\n", m);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:40
|
2016-07-23T14:24:58
|
C++
|
64 | 2,413 |
roy-and-alpha-beta-trees
|
Roy and alpha-beta trees
|
[Russian](https://hr-filepicker.s3.amazonaws.com/w4/russian/2413-roy-and-alpha-beta-trees.pdf)<br/>
Roy has taken a liking to the [Binary Search Trees](https://en.wikipedia.org/wiki/Binary_search_tree)(*BST*). He is interested in knowing the number of ways an array *A* of *N* integers can be arranged to form a *BST*. Thus, he tries a few combinations, and notes down the numbers at the odd levels and the numbers at the even levels.
You're given two values, *alpha* and *beta*. Can you calculate the sum of *Liking* of all possible *BST's* that can be formed from an array of *N* integers? *Liking* of each *BST* is defined as follows
(sum of numbers on even levels * alpha) - (sum of numbers on odd levels * beta)
**Note**
+ The root element is at level 0 ( Even )
+ The elements smaller or equal to the parent element are present in the left subtree, elements greater than or equal to the parent element are present in the right subtree. Explained [here](https://www.hackerrank.com/contests/w4/challenges/roy-and-alpha-beta-trees/forum/questions/6070)
If the answer is no less than 10<sup>9</sup> + 9, output the answer % 10<sup>9</sup> + 9.
**Update**
If the answer is less than 0, keep adding 10<sup>9</sup> + 9 until the value turns non negative.
**Input Format**
The first line of input file contains an integer, *T*, denoting the number of test cases to follow.
Each testcase comprises of 3 lines.
The first line contains _N_, the number of integers.
The second line contains two space separated integers, _alpha_ and _beta_.
The third line contains space separated _N integers_, denoting the *i<sub>th</sub>* integer in array *A[i]*.
**Output Format**
Output _T_ lines. Each line contains the answer to its respective test case.
**Constraints**
1 ≤ *T* ≤ 10
1 ≤ *N* ≤ 150
1 ≤ *A[i]* ≤ 10<sup>9</sup>
1 ≤ *alpha,beta* ≤ 10<sup>9</sup>
**Sample Input**
<pre>
4
1
1 1
1
2
1 1
1 2
3
1 1
1 2 3
5
1 1
1 2 3 4 5
</pre>
**Sample Output**
<pre>
1
0
6
54
</pre>
**Explanation**
There are 4 test cases in total.
+ For the first test case, only 1 BST can be formed with `1` as the root node. Hence the *Liking* / sum is 1.
+ For the second test case, we get 2 BSTs of the form, the *Liking* of the first tree is 1 * 1 - 2 * 1 = -1 and 2 * 1 - 1 * 1 = 1, this sums to 0, hence the answer.
<pre>
1 2
\ /
2 1
</pre>
+ For the third test case, we get 5 BSTs. The *Liking* of each of the BST from left to right are 2, -2, 4, 2, 0 which sums to 6 and hence the answer.
<pre>
1 2 3 3 1
\ / \ / / \
2 1 3 1 2 3
\ \ / /
3 2 1 2
</pre>
+ Similarly, for the 4th test case, the answer is 54.
|
code
|
Can you calculate the sum of Liking of all possible BST's that can be formed from an array of N integers.
|
ai
|
2014-04-21T11:02:40
|
2022-09-02T10:00:36
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER alpha
# 2. INTEGER beta
# 3. INTEGER_ARRAY a
#
def solve(alpha, beta, a):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
n = int(input().strip())
first_multiple_input = input().rstrip().split()
alpha = int(first_multiple_input[0])
beta = int(first_multiple_input[1])
a = list(map(int, input().rstrip().split()))
result = solve(alpha, beta, a)
fptr.write(str(result) + '\n')
fptr.close()
|
Roy has taken a liking to the [Binary Search Trees](https://en.wikipedia.org/wiki/Binary_search_tree)(*BST*). He is interested in knowing the number of ways an array $A$ of $N$ integers can be arranged to form a *BST*. Thus, he tries a few combinations, and notes down the numbers at the odd levels and the numbers at the even levels.
You're given two values, *alpha* and *beta*. Can you calculate the sum of *Liking* of all possible *BST's* that can be formed from an array of $N$ integers? *Liking* of each *BST* is defined as follows
(sum of numbers on even levels * alpha) - (sum of numbers on odd levels * beta)
**Note**
+ The root element is at level $0$ ( Even )
+ The elements smaller or equal to the parent element are present in the left subtree, elements greater than or equal to the parent element are present in the right subtree. Explained [here](https://www.hackerrank.com/contests/w4/challenges/roy-and-alpha-beta-trees/forum/questions/6070)
If the answer is no less than $10^9+9$, output the answer % $10^9+9$.
(If the answer is less than $0$, keep adding $10^9+9$ until the value turns non negative.)
**Input Format**
The first line of input file contains an integer, $T$, denoting the number of test cases to follow.
Each testcase comprises of $3$ lines.
The first line contains $N$, the number of integers.
The second line contains two space separated integers, _alpha_ and _beta_.
The third line contains space separated $N$ integers_, denoting the $i^{th}$ integer in array $A[i]$.
**Output Format**
Output $T$ lines. Each line contains the answer to its respective test case.
**Constraints**
$1 \le T \le 10$
$1 \le N \le 150$
$1 \le A[i] \le 10^9$
$1 \le alpha,beta \le 10^{9}$
**Sample Input**
<pre>
4
1
1 1
1
2
1 1
1 2
3
1 1
1 2 3
5
1 1
1 2 3 4 5
</pre>
**Sample Output**
<pre>
1
0
6
54
</pre>
**Explanation**
There are $4$ test cases in total.
+ For the first test case, only $1$ BST can be formed with `1` as the root node. Hence the *Liking* / sum is $1$.
+ For the second test case, we get 2 BSTs of the form, the *Liking* of the first tree is $1 * 1 - 2 * 1 = -1$ and $2 * 1 - 1 * 1 = 1$, this sums to $0$, hence the answer.
<pre>
1 2
\ /
2 1
</pre>
+ For the third test case, we get $5$ BSTs. The *Liking* of each of the BST from left to right are $2, -2, 4, 2, 0$ which sums to $6$ and hence the answer.
<pre>
1 2 3 3 1
\ / \ / / \
2 1 3 1 2 3
\ \ / /
3 2 1 2
</pre>
+ Similarly, for the fourth test case, the answer is $54$.
| 0.578431 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
| null | null | null | null | null |
{"contest_participation":1868,"challenge_submissions":144,"successful_submissions":109}
|
2014-06-01T21:08:38
|
2016-12-02T07:25:09
|
setter
|
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
class ANKBST02_solver {
long go(int lo, int hi, int odd) {
if (lo > hi) {
return 0;
}
if (dp[lo][hi][odd] == -1) {
long ans = 0;
for (int root = lo; root <= hi; root++) {
//consider all BST in left subtree of root
ans += (go(lo, root - 1, 1 -odd) * cnt[hi - root - 1 + 1]) % MOD;
if (ans >= MOD) ans -= MOD;
if (ans < 0) ans += MOD;
//consider all BST in right subtree
ans += (go(root + 1, hi, 1 -odd) * cnt[root - 1 - lo + 1]) % MOD;
if (ans >= MOD) ans -= MOD;
if (ans < 0) ans += MOD;
//totTrees is total number of trees considered
long totTrees = (cnt[hi - root] * cnt[root - lo]) % MOD;
//remember to add the root as many times for each tree
ans += (totTrees * ((mul[odd] * a[root]) % MOD)) % MOD;
if(ans >= MOD) ans -= MOD;
if (ans < 0) ans += MOD;
}
dp[lo][hi][odd] = ans;
}
return dp[lo][hi][odd];
}
public void solve() throws IOException {
cnt = generateCatalan(205, MOD);
cnt[0] = 1;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
PrintWriter pw = new PrintWriter(System.out);
int t = Integer.parseInt(br.readLine());
while (t --> 0) {
int n = Integer.parseInt(br.readLine());
assert(n <= 200);
a = new long[n] ;
mul = new long[2];
int i = 0;
for (StringTokenizer tokenizer = new StringTokenizer(br.readLine()); tokenizer.hasMoreTokens(); ) {
String s = tokenizer.nextToken();
mul[i ++] = Integer.parseInt(s);
}
mul[1] = -mul[1];
i = 0;
for (StringTokenizer tokenizer = new StringTokenizer(br.readLine()); tokenizer.hasMoreTokens(); ) {
String s = tokenizer.nextToken();
a[i ++] = Integer.parseInt(s);
}
assert(i == n);
Arrays.sort(a);
dp = new long[n][n][2];
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
for (int l = 0; l < 2; l++) {
dp[j][k][l] = -1;
}
}
}
pw.println(go(0, n - 1, 0));
}
pw.close();
}
long[] a;
long[][][] dp;
long[] cnt;
long MOD = (int) (1e9 + 9);
long[] mul;
public static long[] generateCatalan(int n, long module) {
long[] inv = generateReverse(n + 2, module);
long[] Catalan = new long[n];
Catalan[1] = 1;
for (int i = 1; i < n - 1; i++) {
Catalan[i + 1] = (((2 * (2 * i + 1) * inv[i + 2]) % module) * Catalan[i]) % module;
}
return Catalan;
}
public static long[] generateReverse(int upTo, long module) {
long[] result = new long[upTo];
if (upTo > 1)
result[1] = 1;
for (int i = 2; i < upTo; i++)
result[i] = (module - module / i * result[((int) (module % i))] % module) % module;
return result;
}
}
public class Solution {
public static void main(String[] args) throws IOException {
new ANKBST02_solver().solve();
}
}
|
not-set
|
2016-04-24T02:02:40
|
2016-04-24T02:02:40
|
Python
|
||||
65 | 2,212 |
rooted-tree
|
Rooted Tree
|
[Русский](https://hr-filepicker.s3.amazonaws.com/101may14/russian/2212-rooted_tree.pdf) \|
[中文](https://hr-filepicker.s3.amazonaws.com/101may14/chinese/2212-rooted_tree.pdf)<br/>
You are given a rooted [tree](http://en.wikipedia.org/wiki/Tree_(graph_theory)) with _N_ nodes and the root of the tree, _R_, is also given. Each node of the tree contains a value, that is initially empty. You have to mantain the tree under two operations:
1. Update Operation
2. Report Operation
**Update Operation**
Each Update Operation begins with the character `U`. Character `U` is followed by 3 integers _T, V and K_. For every node which is the descendent of the node _T_, update it's value by adding _V + d\*K_, where _V_ and _K_ are the parameters of the query and _d_ is the distance of the node from _T_. Note that _V_ is added to node _T_.
**Report Operation**
Each Report Operation begins with the character `Q`. Character `Q` is followed by 2 integers, _A_ and _B_. Output the sum of values of nodes in the path from _A_ to _B_ modulo _(10<sup>9</sup> + 7)_
**Input Format**
The first Line consists of 3 space separated integers, _N E R_, where _N_ is the number of nodes present, _E_ is the total number of queries (update + report), and _R_ is root of the tree.
Each of the next _N-1_ lines contains 2 space separated integers, _X_ and _Y_ (_X_ and _Y_ are connected by an edge).
Thereafter, _E_ lines follows: each line can represent either the Update Operation or the Report Operation.<br>
- _Update Operation_ is of the form : _U T V K_.
- _Report Operation_ is of the form : _Q A B_.
**Output Format**
Output the answer for every given report operation.
**Constraints**
1 ≤ N, E ≤ 10<sup>5</sup>
1 ≤ E ≤ 10<sup>5</sup>
1 ≤ R, X, Y, T, A, B ≤ N
1 ≤ V, K ≤ 10<sup>9</sup>
X ≠ Y
**Sample Input**
7 7 1
1 2
2 3
2 4
2 5
5 6
6 7
U 5 10 2
U 4 5 3
Q 1 7
U 6 7 4
Q 2 7
Q 1 4
Q 2 4
**Sample Output**
36
54
5
5
**Explanation**
- Values of Nodes after `U 5 10 2`: `[0 0 0 0 10 12 14]`.
- Values of Nodes after `U 4 5 3`: `[0 0 0 5 10 12 14]`.
- Sum of the Nodes from 1 to 7: 0 + 0 + 10 + 12 + 14 = 36.
- Values of Nodes after `U 6 7 4`: [0 0 0 5 10 19 25].
- Sum of the Nodes from 2 to 7: 0 + 10 + 19 + 25 = 54.
- Sum of the Nodes from 1 to 4: 0 + 0 + 5 = 5.
- Sum of the Nodes from 2 to 4: 0 + 5 = 5.
|
code
|
Maintain the given tree under Update and Query operations.
|
ai
|
2014-03-23T14:11:05
|
2022-08-31T08:33:19
| null | null | null |
You are given a rooted [tree](http://en.wikipedia.org/wiki/Tree_(graph_theory)) with _N_ nodes and the root of the tree, _R_, is also given. Each node of the tree contains a value, that is initially empty. You have to mantain the tree under two operations:
1. Update Operation
2. Report Operation
**Update Operation**
Each Update Operation begins with the character `U`. Character `U` is followed by 3 integers _T, V and K_. For every node which is the descendent of the node _T_, update it's value by adding _V + d\*K_, where _V_ and _K_ are the parameters of the query and _d_ is the distance of the node from _T_. Note that _V_ is added to node _T_.
**Report Operation**
Each Report Operation begins with the character `Q`. Character `Q` is followed by 2 integers, _A_ and _B_. Output the sum of values of nodes in the path from _A_ to _B_ modulo _(10<sup>9</sup> + 7)_
**Input Format**
The first Line consists of 3 space separated integers, _N E R_, where _N_ is the number of nodes present, _E_ is the total number of queries (update + report), and _R_ is root of the tree.
Each of the next _N-1_ lines contains 2 space separated integers, _X_ and _Y_ (_X_ and _Y_ are connected by an edge).
Thereafter, _E_ lines follows: each line can represent either the Update Operation or the Report Operation.<br>
- _Update Operation_ is of the form : _U T V K_.
- _Report Operation_ is of the form : _Q A B_.
**Output Format**
Output the answer for every given report operation.
**Constraints**
1 ≤ N, E ≤ 10<sup>5</sup>
1 ≤ E ≤ 10<sup>5</sup>
1 ≤ R, X, Y, T, A, B ≤ N
1 ≤ V, K ≤ 10<sup>9</sup>
X ≠ Y
**Sample Input**
7 7 1
1 2
2 3
2 4
2 5
5 6
6 7
U 5 10 2
U 4 5 3
Q 1 7
U 6 7 4
Q 2 7
Q 1 4
Q 2 4
**Sample Output**
36
54
5
5
**Explanation**
- Values of Nodes after `U 5 10 2`: `[0 0 0 0 10 12 14]`.
- Values of Nodes after `U 4 5 3`: `[0 0 0 5 10 12 14]`.
- Sum of the Nodes from 1 to 7: 0 + 0 + 10 + 12 + 14 = 36.
- Values of Nodes after `U 6 7 4`: [0 0 0 5 10 19 25].
- Sum of the Nodes from 2 to 7: 0 + 10 + 19 + 25 = 54.
- Sum of the Nodes from 1 to 4: 0 + 0 + 5 = 5.
- Sum of the Nodes from 2 to 4: 0 + 5 = 5.
| 0.423729 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
Hard
| null | null | null | null | null |
{"contest_participation":1164,"challenge_submissions":30,"successful_submissions":9}
|
2014-06-02T06:04:31
|
2016-12-01T20:38:59
|
setter
|
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<iostream>
#include<string.h>
#include<vector>
#include<set>
#include<map>
#include<utility>
#include<bitset>
#include<queue>
#include<stack>
#include<assert.h>
using namespace std;
#define mod 1000000007
typedef long long int ll;
//Variables required for HL tree
int which[100001],size_sub[100001],parent[100001],depth[100001],seg_size,mapping[100001],counter,skip[100001],N,root,visit[100001],level;
bool hlson[100001];
vector<int> myvector[100001];
const ll inv = 500000004;
int power[25];
void constant()
{
power[0]=1;
for(int i=1;i<=25;i++) power[i]=power[i-1]<<1;
}
int obtain(int x)
{
int l=0,y=x;
while(x!=0){
l++;
x>>=1;
}
if(power[l-1]!=y) l++;
return l;
}
struct node{
ll v,vx,d,dx,xxd;
node(ll a=0,ll b=0,ll c=0,ll e=0, ll f=0){
v=a;
vx=b;
d=c;
dx=e;
xxd=f;
}
node operator + (const node &x)const{
return node( (x.v+v)%mod , (x.vx+vx)%mod , (x.d+d)%mod, (x.dx+dx)%mod , (x.xxd+xxd)%mod );
}
node operator % (int m) const{
return node( v%m , vx%m , d%m , dx%m , xxd%m );
}
}HL[1<<18],freq[100001];
/*********************************FOR FINDING LCA***********************************/
int Root[100001][18],store[100001];
void init()
{
store[0]=0;store[1]=0;store[2]=1;
int cmp=4;
for(int i=3;i<=100000;i++){
if(cmp>i) store[i]=store[i-1];
else{
store[i]=store[i-1]+1;
cmp<<=1;
}
}
}
void process(int N)
{
memset(Root,-1,sizeof(Root));
for(int i=1;i<=N;i++) Root[i][0]=parent[i];
for(int i=1;(1<<i)<=N;i++)
for(int j=1;j<=N;j++)
if(Root[j][i-1]!=-1)
Root[j][i]=Root[Root[j][i-1]][i-1];
}
int lca(int p,int q)
{
int temp;
if(depth[p]>depth[q]) swap(p,q);
int steps=store[depth[q]];
for(int i=steps;i>=0;i--)
if(depth[q]-(1<<i) >= depth[p])
q=Root[q][i];
if(p==q) return p;
for(int i=steps;i>=0;i--){
if(Root[p][i]!=Root[q][i])
p=Root[p][i],q=Root[q][i];
}
return parent[p];
}
/*********************************FOR FINDING LCA***********************************/
/*********************************HL Tree Coding Begins***************************/
void dfs_pre(int root)
{
which[root]=-1;
skip[root]=root; //only purpose is to init it!
size_sub[root]=1;
for(vector<int>::iterator it=myvector[root].begin();it!=myvector[root].end();it++){
if(parent[root]==*it) continue;
parent[*it]=root;
depth[*it]=depth[root]+1;
dfs_pre(*it);
size_sub[root]+=size_sub[*it];
}
for(vector<int>::iterator it=myvector[root].begin();it!=myvector[root].end();it++){
if(parent[root]==*it) continue;
if(size_sub[*it]>size_sub[root]/2){
hlson[*it]=true;
which[root]=*it;
}
else{
hlson[*it]=false;
}
}
}
void dfs_cal(int root)
{
int z;
for(vector<int>::iterator it=myvector[root].begin();it!=myvector[root].end();it++){
if(parent[root]==*it) continue;
if(hlson[*it]){ //heavy node detected
skip[*it]=skip[root];
if(skip[root]==root){
z=*it;
//construction of segment tree begins
while(z!=-1){
mapping[z]=seg_size;
seg_size++;
z=which[z];
}
}
}
dfs_cal(*it);
}
}
void seg_Update(int l)
{
int v;
while(l!=0){
v=(l<<1);
HL[l]=(HL[v]+HL[v+1]);
l>>=1;
}
}
node seg_Query(int l,int r,int i,int j,int nod)
{
int v,mid;
if(j<l || i>r) return node();
if(l>=i && j>=r){
return HL[nod];
}
v=nod<<1;
mid=(l+r)>>1;
return seg_Query(l,mid,i,j,v)+seg_Query(mid+1,r,i,j,v+1);
}
node HL_Update(int x,node v)
{
int ind;
if(hlson[x]){ //Heavy Part
ind=mapping[x]+power[level-1];
HL[ind]=(HL[ind]+v);
seg_Update(ind>>1);
}
}
node fun(ll x,ll v,ll d)
{
x=depth[x];
return ( node( v,v*x,d,d*x,((x*x-x)%mod)*d )%mod );
}
node HL_Query(int i,int j) //from i to j --> j is the ancestor
{
node r;
int end,st;
while(i!=j){
if(hlson[i]){
end=skip[i];
st=i;
i=end;
end=which[i];
if(depth[end]<=depth[j]){
r=r+seg_Query(1,power[level-1],mapping[j]+1,mapping[st]+1,1);
return r;
}
else{ //carry on
r=r+seg_Query(1,power[level-1],mapping[end]+1,mapping[st]+1,1);
}
}
else{
r=r+freq[i];
i=parent[i];
}
}
return ((r+freq[j]));
}
/*********************************HL Tree Coding Ends***************************/
ll part1(node A,ll dep)
{
ll ret1 = ( A.v*(dep+1) - A.vx - A.dx*(dep) + A.xxd*(ll)inv )%mod;
ll ret2 = ( ( A.d*(dep*dep+dep) ) %mod )*(ll)inv ;
return (ret1+ret2)%mod;
}
ll part2(node A,ll a,ll y,ll z) //a-ances , y-left , z-right
{
ll cons = ( a*(y+z-(ll)2*a+(ll)1) + ((y-a)*(y-a+(ll)1))/(ll)2 + ((z-a)*(z-a+(ll)1))/(ll)2 )%mod;
return (( (A.v-A.dx)*(y+z-(ll)2*a+(ll)1) + A.d*(cons) ) %mod);
}
void solve()
{
node A,B,C,D;
char c;
int x,y,anc,Q;
ll s,b,nodes,expr,k,solution;
memset(freq,0,sizeof(freq));
scanf("%d%d%d",&N,&Q,&root);
assert(N<=100000 && N>=1);
assert(Q<=100000 && Q>=1);
assert(root<=N && root>=1);
for(int i=1;i<N;i++){
scanf("%d%d",&x,&y);
assert(x>=1 && x<=N);
assert(y>=1 && y<=N);
assert(x!=y);
myvector[x].push_back(y);
myvector[y].push_back(x);
}
seg_size=0;
parent[root]=root;
depth[root]=0;
dfs_pre(root); //find heavy edges, parent, depth,which[]
process(N);
dfs_cal(root); //construct segment tree;
level=obtain(seg_size);
for(int i=0;i<Q;i++){
scanf(" %c",&c);
if(c=='U'){
scanf("%d%lld%lld",&x,&s,&k);
assert(x>=1 && x<=N);
assert(s>=1 && s<=1000000000);
assert(k>=1 && k<=1000000000);
A=fun(x,s,k);
HL_Update(x,A);
freq[x]= (freq[x] + A) % mod;
}
else{
scanf("%d%d",&x,&y);
assert(x>=1 && x<=N);
assert(y>=1 && y<=N);
anc=lca(x,y);
A=HL_Query(x,anc);
B=HL_Query(y,anc);
solution= part1(A,depth[x]) + part1 ( B, depth[y]) - freq[anc].v;
if(anc!=root){
A = HL_Query(parent[anc],root);
solution = solution + part2(A,depth[anc],depth[x],depth[y]);
}
solution = solution % mod;
if(solution<0) solution+=mod;
printf("%lld\n",solution);
}
}
}
int main()
{
constant();
init();
solve();
return 0;
}
|
not-set
|
2016-04-24T02:02:40
|
2016-04-24T02:02:40
|
C++
|
||||
66 | 2,212 |
rooted-tree
|
Rooted Tree
|
[Русский](https://hr-filepicker.s3.amazonaws.com/101may14/russian/2212-rooted_tree.pdf) \|
[中文](https://hr-filepicker.s3.amazonaws.com/101may14/chinese/2212-rooted_tree.pdf)<br/>
You are given a rooted [tree](http://en.wikipedia.org/wiki/Tree_(graph_theory)) with _N_ nodes and the root of the tree, _R_, is also given. Each node of the tree contains a value, that is initially empty. You have to mantain the tree under two operations:
1. Update Operation
2. Report Operation
**Update Operation**
Each Update Operation begins with the character `U`. Character `U` is followed by 3 integers _T, V and K_. For every node which is the descendent of the node _T_, update it's value by adding _V + d\*K_, where _V_ and _K_ are the parameters of the query and _d_ is the distance of the node from _T_. Note that _V_ is added to node _T_.
**Report Operation**
Each Report Operation begins with the character `Q`. Character `Q` is followed by 2 integers, _A_ and _B_. Output the sum of values of nodes in the path from _A_ to _B_ modulo _(10<sup>9</sup> + 7)_
**Input Format**
The first Line consists of 3 space separated integers, _N E R_, where _N_ is the number of nodes present, _E_ is the total number of queries (update + report), and _R_ is root of the tree.
Each of the next _N-1_ lines contains 2 space separated integers, _X_ and _Y_ (_X_ and _Y_ are connected by an edge).
Thereafter, _E_ lines follows: each line can represent either the Update Operation or the Report Operation.<br>
- _Update Operation_ is of the form : _U T V K_.
- _Report Operation_ is of the form : _Q A B_.
**Output Format**
Output the answer for every given report operation.
**Constraints**
1 ≤ N, E ≤ 10<sup>5</sup>
1 ≤ E ≤ 10<sup>5</sup>
1 ≤ R, X, Y, T, A, B ≤ N
1 ≤ V, K ≤ 10<sup>9</sup>
X ≠ Y
**Sample Input**
7 7 1
1 2
2 3
2 4
2 5
5 6
6 7
U 5 10 2
U 4 5 3
Q 1 7
U 6 7 4
Q 2 7
Q 1 4
Q 2 4
**Sample Output**
36
54
5
5
**Explanation**
- Values of Nodes after `U 5 10 2`: `[0 0 0 0 10 12 14]`.
- Values of Nodes after `U 4 5 3`: `[0 0 0 5 10 12 14]`.
- Sum of the Nodes from 1 to 7: 0 + 0 + 10 + 12 + 14 = 36.
- Values of Nodes after `U 6 7 4`: [0 0 0 5 10 19 25].
- Sum of the Nodes from 2 to 7: 0 + 10 + 19 + 25 = 54.
- Sum of the Nodes from 1 to 4: 0 + 0 + 5 = 5.
- Sum of the Nodes from 2 to 4: 0 + 5 = 5.
|
code
|
Maintain the given tree under Update and Query operations.
|
ai
|
2014-03-23T14:11:05
|
2022-08-31T08:33:19
| null | null | null |
You are given a rooted [tree](http://en.wikipedia.org/wiki/Tree_(graph_theory)) with _N_ nodes and the root of the tree, _R_, is also given. Each node of the tree contains a value, that is initially empty. You have to mantain the tree under two operations:
1. Update Operation
2. Report Operation
**Update Operation**
Each Update Operation begins with the character `U`. Character `U` is followed by 3 integers _T, V and K_. For every node which is the descendent of the node _T_, update it's value by adding _V + d\*K_, where _V_ and _K_ are the parameters of the query and _d_ is the distance of the node from _T_. Note that _V_ is added to node _T_.
**Report Operation**
Each Report Operation begins with the character `Q`. Character `Q` is followed by 2 integers, _A_ and _B_. Output the sum of values of nodes in the path from _A_ to _B_ modulo _(10<sup>9</sup> + 7)_
**Input Format**
The first Line consists of 3 space separated integers, _N E R_, where _N_ is the number of nodes present, _E_ is the total number of queries (update + report), and _R_ is root of the tree.
Each of the next _N-1_ lines contains 2 space separated integers, _X_ and _Y_ (_X_ and _Y_ are connected by an edge).
Thereafter, _E_ lines follows: each line can represent either the Update Operation or the Report Operation.<br>
- _Update Operation_ is of the form : _U T V K_.
- _Report Operation_ is of the form : _Q A B_.
**Output Format**
Output the answer for every given report operation.
**Constraints**
1 ≤ N, E ≤ 10<sup>5</sup>
1 ≤ E ≤ 10<sup>5</sup>
1 ≤ R, X, Y, T, A, B ≤ N
1 ≤ V, K ≤ 10<sup>9</sup>
X ≠ Y
**Sample Input**
7 7 1
1 2
2 3
2 4
2 5
5 6
6 7
U 5 10 2
U 4 5 3
Q 1 7
U 6 7 4
Q 2 7
Q 1 4
Q 2 4
**Sample Output**
36
54
5
5
**Explanation**
- Values of Nodes after `U 5 10 2`: `[0 0 0 0 10 12 14]`.
- Values of Nodes after `U 4 5 3`: `[0 0 0 5 10 12 14]`.
- Sum of the Nodes from 1 to 7: 0 + 0 + 10 + 12 + 14 = 36.
- Values of Nodes after `U 6 7 4`: [0 0 0 5 10 19 25].
- Sum of the Nodes from 2 to 7: 0 + 10 + 19 + 25 = 54.
- Sum of the Nodes from 1 to 4: 0 + 0 + 5 = 5.
- Sum of the Nodes from 2 to 4: 0 + 5 = 5.
| 0.423729 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
Hard
| null | null | null | null | null |
{"contest_participation":1164,"challenge_submissions":30,"successful_submissions":9}
|
2014-06-02T06:04:31
|
2016-12-01T20:38:59
|
tester
|
#ifdef ssu1
#define _GLIBCXX_DEBUG
#endif
#undef NDEBUG
#include <algorithm>
#include <functional>
#include <numeric>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <cstring>
#include <cassert>
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <queue>
#include <bitset>
#include <sstream>
using namespace std;
#define fore(i, l, r) for(int i = (l); i < (r); ++i)
#define forn(i, n) fore(i, 0, n)
#define fori(i, l, r) fore(i, l, (r) + 1)
#define sz(v) int((v).size())
#define all(v) (v).begin(), (v).end()
#define pb push_back
#define mp make_pair
#define X first
#define Y second
#if ( _WIN32 || __WIN32__ )
#define LLD "%I64d"
#else
#define LLD "%lld"
#endif
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
template<typename T> T abs(T a) { return a < 0 ? -a : a; }
template<typename T> T sqr(T a) { return a*a; }
const int INF = (int)1e9;
const ld EPS = 1e-9;
const ld PI = 3.1415926535897932384626433832795;
int readInt(int l, int r){
int x;
if(scanf("%d", &x) != 1){
fprintf(stderr, "Expected int in range [%d, %d], but haven't found!", l, r);
throw;
}
if(!(l <= x && x <= r)){
fprintf(stderr, "Expected int in range [%d, %d], but found %d!", l, r, x);
throw;
}
return x;
}
const int NMAX = 300000;
const int LOG = 20;
const int mod = 1000000000 + 7;
int n, q, root, used[NMAX];
vector<int> g[NMAX];
int dep[NMAX], p[NMAX][LOG], lf[NMAX], rg[NMAX], mul[3][NMAX], timer = 0;
void dfs(int v, int pv){
used[v] = 1;
dep[v] = (v == pv ? 0 : dep[pv] + 1);
lf[v] = rg[v] = timer++;
p[v][0] = pv;
fore(lev, 1, LOG){
p[v][lev] = p[p[v][lev - 1]][lev - 1];
}
forn(i, sz(g[v])){
int u = g[v][i];
if(u == pv)
continue;
dfs(u, v);
rg[v] = rg[u];
}
}
int lca(int a, int b){
if(dep[a] < dep[b])
swap(a, b);
forn(i, LOG){
if((dep[a] - dep[b]) & (1 << i)){
a = p[a][i];
}
}
for(int i = LOG - 1; i >= 0; --i){
if(p[a][i] != p[b][i]){
a = p[a][i];
b = p[b][i];
}
}
if(a != b)
a = p[a][0], b = p[b][0];
assert(a == b);
return a;
}
inline void norm(int& v){
while(v < 0)
v += mod;
while(v >= mod)
v -= mod;
}
int modpow(int a, int b){
int ans = 1 % mod;
while(b){
if(b & 1)
ans = (ans * li(a)) % mod;
a = (a * li(a)) % mod;
b >>= 1;
}
return ans;
}
inline int rev(int a){
return modpow(a, mod - 2);
}
inline int doMod(li v){
return (int)((v % mod + mod) % mod);
}
void upd(int t[NMAX], int i, int v){
for(; i < NMAX; i = (i | (i + 1))){
t[i] += v;
norm(t[i]);
}
}
int sum(int t[NMAX], int r){
int ans = 0;
for(; r >= 0; r = (r & (r + 1)) - 1){
ans += t[r];
norm(ans);
}
return ans;
}
int sum(int t[NMAX], int l, int r){
int ans = sum(t, r) - sum(t, l - 1);
norm(ans);
return ans;
}
int get(int a){
int pw = 1, ans = 0;
forn(i, 3){
ans = (ans + sum(mul[i], 0, lf[a]) * 1LL * pw) % mod;
pw = (pw * 1LL * dep[a]) % mod;
}
return ans;
}
int dist(int a, int b){
int mid = lca(a, b);
int ans = get(a) + get(b) - 2 * get(mid);
norm(ans);
if(mid == root)
ans += get(mid);
else
ans += get(mid) - get(p[mid][0]);
norm(ans);
return ans;
}
void rangeupd(int t[NMAX], int l, int r, int val){
upd(t, l, val);
upd(t, r + 1, doMod(mod - val));
}
void doUpdQuery(int t, int V, int U){
int L = lf[t], R = rg[t], x = V;
rangeupd(mul[0], L, R, doMod((1 - dep[t]) * li(x)));
rangeupd(mul[1], L, R, x);
x = U;
rangeupd(mul[0], L, R, doMod(-(1 - dep[t]) * 1LL * doMod(x * 1LL * dep[t])));
rangeupd(mul[1], L, R, doMod(-x * 1LL * dep[t]));
rangeupd(mul[1], L, R, doMod(-x * 1LL * dep[t] + x));
rangeupd(mul[2], L, R, x);
x = doMod(-x * 1LL * rev(2));
rangeupd(mul[0], L, R, doMod(((dep[t] * 1LL * dep[t] - dep[t]) % mod) * li(x)));
rangeupd(mul[1], L, R, doMod((-2 * dep[t] + 1) * li(x)));
rangeupd(mul[2], L, R, x);
}
int main(){
#ifdef ssu1
assert(freopen("input.txt", "rt", stdin));
//assert(freopen("output.txt", "wt", stdout));
#endif
n = readInt(1, 100000);
q = readInt(1, 100000);
root = readInt(1, n) - 1;
forn(i, n - 1){
int a, b;
a = readInt(1, n) - 1;
b = readInt(1, n) - 1;
g[a].pb(b);
g[b].pb(a);
}
dfs(root, root);
forn(v, n){
assert(used[v]);
}
forn(qi, q){
char type;
assert(scanf(" %c ", &type) == 1);
assert(type == 'Q' || type == 'U');
if(type == 'Q'){
int a, b;
a = readInt(1, n) - 1;
b = readInt(1, n) - 1;
printf("%d\n", dist(a, b));
}else{
int t, v, k;
t = readInt(1, n) - 1;
v = readInt(1, 1000000000);
k = readInt(1, 1000000000);
doUpdQuery(t, v, k);
}
}
return 0;
}
|
not-set
|
2016-04-24T02:02:40
|
2016-04-24T02:02:40
|
C++
|
||||
67 | 2,523 |
easy-sum
|
Easy sum
|
Little Kevin had never heard the word 'Infinitum'. So he asked his mentor to explain the word to him. His mentor knew that 'Infinitum' is a very large number. To show him how big [Infinitum](http://en.wikipedia.org/wiki/Ad_infinitum) can be, his mentor gave him a challenge: to sum the numbers from _1_ up to _N_. The sum started to get really large and was out of `long long int` range. And so the lesson was clear.
Now his mentor introduced him to the concept of *mod* and asked him to retain only the remainder instead of the big number. And then, he gave him a formula to compute:
$$\sum_{i=1}^{N} (i\%m)$$
**Input Format**
The first line contains _T_, the number of test cases.
_T_ lines follow, each containing 2 space separated integers _N m_
**Output Format**
Print the result on new line corresponding to each test case.
**Constraint**
1 ≤ _T_ ≤ 1000
1 ≤ _N_ ≤ 10<sup>9</sup>
1 ≤ _m_ ≤ 10<sup>9</sup>
**Sample Input**
3
10 5
10 3
5 5
**Sample Output**
20
10
10
**Explanation**
Case 1: _N_ = 10 _m_ = 5,
1%5 + 2%5 + 3%5 + 4%5 + 5%5 + 6%5 + 7%5 + 8%5 + 9%5 + 10%5 = 20.
Similar explanation follows for Case 2 and 3.
|
code
|
Find the mod sum
|
ai
|
2014-05-14T04:26:01
|
2022-09-02T09:55:04
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER m
#
def solve(n, m):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
result = solve(n, m)
fptr.write(str(result) + '\n')
fptr.close()
|
Little Kevin had never heard the word 'Infinitum'. So he asked his mentor to explain the word to him. His mentor knew that 'Infinitum' is a very large number. To show him how big [Infinitum](http://en.wikipedia.org/wiki/Ad_infinitum) can be, his mentor gave him a challenge: to sum the numbers from _1_ up to _N_. The sum started to get really large and was out of `long long int` range. And so the lesson was clear.
Now his mentor introduced him to the concept of *mod* and asked him to retain only the remainder instead of the big number. And then, he gave him a formula to compute:
$$\sum_{i=1}^{N} (i\%m)$$
**Input Format**
The first line contains _T_, the number of test cases.
_T_ lines follow, each containing 2 space separated integers _N m_
**Output Format**
Print the result on new line corresponding to each test case.
**Constraint**
1 ≤ _T_ ≤ 1000
1 ≤ _N_ ≤ 10<sup>9</sup>
1 ≤ _m_ ≤ 10<sup>9</sup>
**Sample Input**
3
10 5
10 3
5 5
**Sample Output**
20
10
10
**Explanation**
Case 1: _N_ = 10 _m_ = 5,
1%5 + 2%5 + 3%5 + 4%5 + 5%5 + 6%5 + 7%5 + 8%5 + 9%5 + 10%5 = 20.
Similar explanation follows for Case 2 and 3.
| 0.597523 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null |
{"contest_participation":2021,"challenge_submissions":1071,"successful_submissions":793}
|
2014-06-02T11:02:56
|
2016-12-07T10:25:14
|
setter
|
###Python 2
```python
for _ in range(input()):
N,M = [int(x) for x in raw_input().split()]
k = N%M
print (M-1)*(M)/2*(N/M) + k*(k+1)/2
```
|
not-set
|
2016-04-24T02:02:40
|
2016-07-23T18:55:35
|
Python
|
68 | 2,523 |
easy-sum
|
Easy sum
|
Little Kevin had never heard the word 'Infinitum'. So he asked his mentor to explain the word to him. His mentor knew that 'Infinitum' is a very large number. To show him how big [Infinitum](http://en.wikipedia.org/wiki/Ad_infinitum) can be, his mentor gave him a challenge: to sum the numbers from _1_ up to _N_. The sum started to get really large and was out of `long long int` range. And so the lesson was clear.
Now his mentor introduced him to the concept of *mod* and asked him to retain only the remainder instead of the big number. And then, he gave him a formula to compute:
$$\sum_{i=1}^{N} (i\%m)$$
**Input Format**
The first line contains _T_, the number of test cases.
_T_ lines follow, each containing 2 space separated integers _N m_
**Output Format**
Print the result on new line corresponding to each test case.
**Constraint**
1 ≤ _T_ ≤ 1000
1 ≤ _N_ ≤ 10<sup>9</sup>
1 ≤ _m_ ≤ 10<sup>9</sup>
**Sample Input**
3
10 5
10 3
5 5
**Sample Output**
20
10
10
**Explanation**
Case 1: _N_ = 10 _m_ = 5,
1%5 + 2%5 + 3%5 + 4%5 + 5%5 + 6%5 + 7%5 + 8%5 + 9%5 + 10%5 = 20.
Similar explanation follows for Case 2 and 3.
|
code
|
Find the mod sum
|
ai
|
2014-05-14T04:26:01
|
2022-09-02T09:55:04
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER m
#
def solve(n, m):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
result = solve(n, m)
fptr.write(str(result) + '\n')
fptr.close()
|
Little Kevin had never heard the word 'Infinitum'. So he asked his mentor to explain the word to him. His mentor knew that 'Infinitum' is a very large number. To show him how big [Infinitum](http://en.wikipedia.org/wiki/Ad_infinitum) can be, his mentor gave him a challenge: to sum the numbers from _1_ up to _N_. The sum started to get really large and was out of `long long int` range. And so the lesson was clear.
Now his mentor introduced him to the concept of *mod* and asked him to retain only the remainder instead of the big number. And then, he gave him a formula to compute:
$$\sum_{i=1}^{N} (i\%m)$$
**Input Format**
The first line contains _T_, the number of test cases.
_T_ lines follow, each containing 2 space separated integers _N m_
**Output Format**
Print the result on new line corresponding to each test case.
**Constraint**
1 ≤ _T_ ≤ 1000
1 ≤ _N_ ≤ 10<sup>9</sup>
1 ≤ _m_ ≤ 10<sup>9</sup>
**Sample Input**
3
10 5
10 3
5 5
**Sample Output**
20
10
10
**Explanation**
Case 1: _N_ = 10 _m_ = 5,
1%5 + 2%5 + 3%5 + 4%5 + 5%5 + 6%5 + 7%5 + 8%5 + 9%5 + 10%5 = 20.
Similar explanation follows for Case 2 and 3.
| 0.597523 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null |
{"contest_participation":2021,"challenge_submissions":1071,"successful_submissions":793}
|
2014-06-02T11:02:56
|
2016-12-07T10:25:14
|
tester
|
###Python 2
```python
for c in xrange(input()):print(lambda N,m:N/m*m*(m-1)/2+(N%m*2+1)**2/8)(*map(int,raw_input().split()))
```
|
not-set
|
2016-04-24T02:02:40
|
2016-07-23T18:56:00
|
Python
|
69 | 1,636 |
crush
|
Array Manipulation
|
[Russian](https://hr-filepicker.s3.amazonaws.com/w4/russian/1636-crush.pdf)<br/>
Devendra is on cloud nine after seeing his crush smiling at him in class. At that very moment his professor singles him out and asks him a question. Devendra's mind is all too fuzzy with his crush and her smile to concentrate on anything else. Help him solve the problem :<br>
You are given a list of size N, initialized with zeroes. You have to perform M queries on the list and output the maximum of final values of all the N elements in the list. For every query, you are given three integers a, b and k and you have to add value k to all the elements ranging from index a to b(both inclusive).
**Input Format**
First line will contain two integers _N_ and _M_ separated by a single space.<br>
Next M lines will contain three integers _a_, _b_ and _k_ separated by a single space.<br>
Numbers in list are numbered from _1_ to _N_.
**Output Format**
A single line containing *maximum value in the final list.*
**Constraints**
3 ≤ *N* ≤ 10<sup>7</sup>
1 ≤ *M* ≤ 2 \* 10<sup>5</sup>
1 ≤ *a* ≤ *b* ≤ N
0 ≤ *k* ≤ 10<sup>9</sup>
**Sample Input #00**
5 3
1 2 100
2 5 100
3 4 100
**Sample Output #00**
200
**Explanation**
After first update list will be `100 100 0 0 0`. <br>
After second update list will be `100 200 100 100 100`.<br>
After third update list will be `100 200 200 200 100`.<br>
So the required answer will be 200.
**Note**
The initial testcases are easy and naive solutions might pass. Only efficient solutions can pass the additional testcases.
|
code
|
Perform m operations on an array and print the maximum of the values.
|
ai
|
2014-01-09T11:29:47
|
2022-09-02T09:59:47
|
#
# Complete the 'arrayManipulation' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. 2D_INTEGER_ARRAY queries
#
def arrayManipulation(n, queries):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
queries = []
for _ in range(m):
queries.append(list(map(int, input().rstrip().split())))
result = arrayManipulation(n, queries)
fptr.write(str(result) + '\n')
fptr.close()
|
Starting with a 1-indexed array of zeros and a list of operations, for each operation add a value to each the array element between two given indices, inclusive. Once all operations have been performed, return the maximum value in the array.
**Example**
$n = 10$
$queries = [[1, 5, 3], [4, 8, 7], [6, 9, 1]$
Queries are interpreted as follows:
```
a b k
1 5 3
4 8 7
6 9 1
```
Add the values of $k$ between the indices $a$ and $b$ inclusive:
```
index-> 1 2 3 4 5 6 7 8 9 10
[0,0,0, 0, 0,0,0,0,0, 0]
[3,3,3, 3, 3,0,0,0,0, 0]
[3,3,3,10,10,7,7,7,0, 0]
[3,3,3,10,10,8,8,8,1, 0]
```
The largest value is $10$ after all operations are performed.
**Function Description**
Complete the function *arrayManipulation* in the editor below.
arrayManipulation has the following parameters:
- *int n* - the number of elements in the array
- *int queries[q][3]* - a two dimensional array of queries where each *queries[i]* contains three integers, *a*, *b*, and *k*.
**Returns**
- *int* - the maximum value in the resultant array
| 0.504803 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
The first line contains two space-separated integers $n$ and $m$, the size of the array and the number of operations.
Each of the next $m$ lines contains three space-separated integers $a$, $b$ and $k$, the left index, right index and summand.
|
5 3
1 2 100
2 5 100
3 4 100
|
200
|
Hard
| null | null | null | null | null |
{"contest_participation":1783,"challenge_submissions":658,"successful_submissions":361}
|
2014-06-03T07:16:46
|
2020-09-08T16:59:12
|
setter
|
```cpp
#include <bits/stdc++.h>
using namespace std;
long a[400009];
int main() {
int n;
int m;
cin >> n >> m;
vector < pair < int, int > > v;
for(int a0 = 0; a0 < m; a0++) {
int a;
int b;
int k;
cin >> a >> b >> k;
//storing the query
//this will add k in the prefix sum for index >= a
v.push_back(make_pair(a, k));
//adding -1*k will remove k from the prefix sum for index > b
v.push_back(make_pair(b+1, -1 * k));
}
long mx = 0, sum = 0;
sort(v.begin(), v.end());
for(int i=0 ; i<2*m; i++) {
sum += v[i].second;
mx = max(mx, sum);
}
cout<<mx<<endl;
return 0;
}
```
|
not-set
|
2016-04-24T02:02:40
|
2018-07-18T10:50:18
|
C++
|
|
70 | 1,636 |
crush
|
Array Manipulation
|
[Russian](https://hr-filepicker.s3.amazonaws.com/w4/russian/1636-crush.pdf)<br/>
Devendra is on cloud nine after seeing his crush smiling at him in class. At that very moment his professor singles him out and asks him a question. Devendra's mind is all too fuzzy with his crush and her smile to concentrate on anything else. Help him solve the problem :<br>
You are given a list of size N, initialized with zeroes. You have to perform M queries on the list and output the maximum of final values of all the N elements in the list. For every query, you are given three integers a, b and k and you have to add value k to all the elements ranging from index a to b(both inclusive).
**Input Format**
First line will contain two integers _N_ and _M_ separated by a single space.<br>
Next M lines will contain three integers _a_, _b_ and _k_ separated by a single space.<br>
Numbers in list are numbered from _1_ to _N_.
**Output Format**
A single line containing *maximum value in the final list.*
**Constraints**
3 ≤ *N* ≤ 10<sup>7</sup>
1 ≤ *M* ≤ 2 \* 10<sup>5</sup>
1 ≤ *a* ≤ *b* ≤ N
0 ≤ *k* ≤ 10<sup>9</sup>
**Sample Input #00**
5 3
1 2 100
2 5 100
3 4 100
**Sample Output #00**
200
**Explanation**
After first update list will be `100 100 0 0 0`. <br>
After second update list will be `100 200 100 100 100`.<br>
After third update list will be `100 200 200 200 100`.<br>
So the required answer will be 200.
**Note**
The initial testcases are easy and naive solutions might pass. Only efficient solutions can pass the additional testcases.
|
code
|
Perform m operations on an array and print the maximum of the values.
|
ai
|
2014-01-09T11:29:47
|
2022-09-02T09:59:47
|
#
# Complete the 'arrayManipulation' function below.
#
# The function is expected to return a LONG_INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. 2D_INTEGER_ARRAY queries
#
def arrayManipulation(n, queries):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
m = int(first_multiple_input[1])
queries = []
for _ in range(m):
queries.append(list(map(int, input().rstrip().split())))
result = arrayManipulation(n, queries)
fptr.write(str(result) + '\n')
fptr.close()
|
Starting with a 1-indexed array of zeros and a list of operations, for each operation add a value to each the array element between two given indices, inclusive. Once all operations have been performed, return the maximum value in the array.
**Example**
$n = 10$
$queries = [[1, 5, 3], [4, 8, 7], [6, 9, 1]$
Queries are interpreted as follows:
```
a b k
1 5 3
4 8 7
6 9 1
```
Add the values of $k$ between the indices $a$ and $b$ inclusive:
```
index-> 1 2 3 4 5 6 7 8 9 10
[0,0,0, 0, 0,0,0,0,0, 0]
[3,3,3, 3, 3,0,0,0,0, 0]
[3,3,3,10,10,7,7,7,0, 0]
[3,3,3,10,10,8,8,8,1, 0]
```
The largest value is $10$ after all operations are performed.
**Function Description**
Complete the function *arrayManipulation* in the editor below.
arrayManipulation has the following parameters:
- *int n* - the number of elements in the array
- *int queries[q][3]* - a two dimensional array of queries where each *queries[i]* contains three integers, *a*, *b*, and *k*.
**Returns**
- *int* - the maximum value in the resultant array
| 0.504803 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
The first line contains two space-separated integers $n$ and $m$, the size of the array and the number of operations.
Each of the next $m$ lines contains three space-separated integers $a$, $b$ and $k$, the left index, right index and summand.
|
5 3
1 2 100
2 5 100
3 4 100
|
200
|
Hard
| null | null | null | null | null |
{"contest_participation":1783,"challenge_submissions":658,"successful_submissions":361}
|
2014-06-03T07:16:46
|
2020-09-08T16:59:12
|
tester
|
```python
def arrayManipulation(n, queries):
arr = [0] * (n+1)
# add the value at first index
# subtract the value at last index + 1
for q in queries:
start, end, amt = q
arr[start-1] += amt
arr[end] -= amt
# max value and running sum
mv = -1
running = 0
for a in arr:
running += a
if running > mv:
mv = running
return mv
```
|
not-set
|
2016-04-24T02:02:40
|
2020-09-08T16:59:12
|
Python
|
|
71 | 472 |
print
|
Difficult Printer
|
There are N printers and you have M papers to print. But every paper has a diffculty value (indicated by d[i]), and every printer has an ability value (indicated by a[j]). The printer j can print the paper i, iff a[j] >= d[i].
It takes one second for a printer to print a paper (if it's possible to print that is). Your task is to calculate the minimal seconds (indicated by T) for the printers to print all the papers.
**Input format:**
N M<br>
a[0] a[1] ... a[n-1]<br>
d[0] d[1] ... d[m-1]<br>
**Output format:**
T
**Constraints:**
0 < N, M, a[i], d[i] < 100000
Every testcase assures that the answer is finite.
**Sample Input:**
3 5<br>
7 4 6<br>
1 3 4 6 1<br>
**Sample Output:**
2
**Explanation:**
One possibility.
The printer with ability 7 prints the pages of difficulty 1 first and then difficulty 3 (takes 2s)<br>
The printer with ability 4 prints the pages of difficulty 1 first and then difficulty 4 (takes 2s)<br>
The printer with ability 6 prints the pages of difficulty 6<br>
The maximum amount of pages a printer had was 2, so the answer is 2.
|
code
| null |
ai
|
2013-03-11T17:19:00
|
2016-09-09T09:29:21
| null | null | null |
There are N printers and you have M papers to print. But every paper has a diffculty value (indicated by d[i]), and every printer has an ability value (indicated by a[j]). The printer j can print the paper i, iff a[j] >= d[i].
It takes one second for a printer to print a paper (if it's possible to print that is). Your task is to calculate the minimal seconds (indicated by T) for the printers to print all the papers.
**Input format:**
N M<br>
a[0] a[1] ... a[n-1]<br>
d[0] d[1] ... d[m-1]<br>
**Output format:**
T
**Constraints:**
0 < N, M, a[i], d[i] < 100000
Every testcase assures that the answer is finite.
**Sample Input:**
3 5<br>
7 4 6<br>
1 3 4 6 1<br>
**Sample Output:**
2
**Explanation:**
One possibility.
The printer with ability 7 prints the pages of difficulty 1 first and then difficulty 3 (takes 2s)<br>
The printer with ability 4 prints the pages of difficulty 1 first and then difficulty 4 (takes 2s)<br>
The printer with ability 6 prints the pages of difficulty 6<br>
The maximum amount of pages a printer had was 2, so the answer is 2.
| 0.592 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-03T14:05:30
|
2017-04-13T02:32:24
|
tester
|
#include <bits/stdc++.h>
using namespace std;
int nPrinters, nPapers;
vector <int> a, d;
bool canSolveWithin(int maxTime) {
int printerIdx = 0, paperIdx = 0;
while(printerIdx < nPrinters && paperIdx < nPapers) {
int curTime = 0;
while(paperIdx < nPapers && curTime < maxTime && d[paperIdx] <= a[printerIdx]) {
paperIdx++;
curTime++;
}
printerIdx++;
}
return paperIdx == nPapers;
}
int main()
{
cin >> nPrinters >> nPapers;
int tmp;
for(int i = 0; i < (int)nPrinters; ++i) {
cin >> tmp;
a.push_back(tmp);
}
for(int i = 0; i < (int)nPapers; ++i) {
cin >> tmp;
d.push_back(tmp);
}
sort(a.begin(), a.end());
reverse(a.begin(), a.end());
sort(d.begin(), d.end());
reverse(d.begin(), d.end());
assert(a[0] >= d[0]);
int minTime = 1, maxTime = 1e5;
while(minTime < maxTime) {
int midTime = (minTime + maxTime) / 2;
if(canSolveWithin(midTime))
maxTime = midTime;
else
minTime = midTime+1;
}
cout << minTime << "\n";
return 0;
}
|
not-set
|
2016-04-24T02:02:40
|
2016-04-24T02:02:40
|
C++
|
72 | 2,572 |
gifts
|
Gifts
|
In order to transform her student into the perfect knight, Shaina has given to Koga the best possible gifts for a saint: a bunch of scrolls that contains all ancient techniques discovered by older saints.
Shaina said:
> Listen carefully Koga, here you have all the attack techniques from all the Athena's Saints - Bronze, Silver and Gold Saints - before you. It is your duty to master them all.
Koga said:
> Great! Can I learn them in any order I want to?
Shaina said:
> No my young saint, certain order must be respected, but you can always switch amongst Bronze, Silver and Gold as you wish. Within each type, only outer techniques will make you powerful enough to learn and master inner techniques. If you see the scrolls of a some type as a list, you could never learn from the i-th, if neither (i + 1)-th or (i - 1)-th scroll has been mastered yet. You need at least one of them. In other words, from each type
perspective, learning the techniques is some sort of travel from the outside to inside.
Koga said:
> I understand Shaina. Is there anything else I should know?
Shaina said:
> Actually, there is one more thing: every time you learn a technique, no matter what is its type, you should use one of these stones, respecting the order they
currently have; the stone will increase the power you got from the just learned technique. Basically, the stone multiplies the power of the technique.
Koga said:
> Wait a minute, that means some learning order will get the largest possible overall power. How will I know which technique to learn after each one?
Shaina said:
> Look up inside you Koga and you will find the answer.
Koga is somewhat crazy, but within himself he is a wise saint and should be able to solve the riddle. But could you?
**Input Format**
Input begins with a line containing 3 (B, S, G) integers separated by a single white space, denoting we have B, S, and G bronze, silver and gold scrolls respectively. B + S + G lines follow each one with some integer saying the power of some technique: first B belong to bronze's, next S belong to silver's and last G belong to gold's. Scrolls for each type are arranged in the same order these integers are given in the input. The input ends with B + S + G lines, having each one a single integer describing the multiplication power of some stone. The input order matches the one in which Koga will receive the stones.
**Output Format**
Output just one line with a single integer: the largest possible sum you can get from learning the techniques with the restrictions mentioned above. **Remember that you must pick the outer techniques from each type first and yes, don't forget to properly use the stones :)**
**Constraints**
* 1 <= B, S, G <= 20
* All input numbers are positive.
* The output will always fit in **32 bits signed integer**.
**Sample Input:**
2 2 2
4
1
2
3
5
6
1
2
3
4
5
6
**Sample Output:**
91
**Sample Input:**
4 4 4
10
1
10
9
10
1
10
9
10
1
10
9
1
2
3
4
5
6
7
8
9
10
11
12
**Sample Output:**
648
**Explanation**
In the first test case, we have 4, 1 for bronze, 2, 3 for silver and 5, 6 for gold. On the other hand, stones multipliers are 1, 2, 3, 4, 5, 6. The best possible way to learn the techniques (i.e. the one achieving the largest possible result) is:
* B2 S1 S2 B1 G1 G2 = 1x1 + 2x2 + 3x3 + 4x4 + 5x5 + 6x6 = 91
*Note: For a complete list with all possible ways and their results, click [here](http://pastebin.com/e860K0XZ)*
|
code
|
From these gifts, what's the best you can do?
|
ai
|
2014-06-03T18:11:32
|
2019-07-02T13:58:34
| null | null | null |
Shaina has given to her student, Koga, a bunch of scrolls, some instructions to remember while learning the techniques described in the scrolls, and some stones that will multiply the power of the techniques. The instructions are as follows:
1. He has to master all the Bronze, Silver, and Gold Saints techniques.
2. He cannot learn them in just any random order, but can switch among Bronze, Silver, and Gold. Within each type, only outer techniques will make him powerful enough to learn and master inner techniques. That is, if he sees the scrolls of some type as a list, you could never learn from the $i^{th}$, if neither $(i + 1)^{th}$ nor $(i - 1)^{th}$ scroll has been mastered yet.
3. And lastly, every time he learns a technique, whichever type it is, he has to use one of these stones, respecting the order they currently have.
You have to help him figure out the specific learning order that will get Koga the largest possible overall power.
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
|
Input begins with a line containing three integers, $B$, $S$, and $G$, separated by a single white space, denoting we have $B$, $S$, and $G$ bronze, silver, and gold scrolls, respectively. $B + S + G$ lines follow, each one with some integer saying the power of some technique: first $B$ belong to bronze's, next $S$ belong to silver's and last $G$ belong to gold's. Scrolls for each type are arranged in the same order these integers are given in the input. The input ends with $B + S + G$ lines, each having a single integer describing the multiplication power of some stone. The input order matches the one in which Koga will receive the stones.
**Constraints**
$1 \le B, S, G \le 10$
$1 \le B_i, S_i, G_i \le 10^5$
$1 \le i^{th} stone \le 300$
All input numbers are positive.
|
Output just one line with a single integer: the largest possible sum you can get from learning the techniques with the restrictions mentioned above. **Remember that you must pick the outer techniques from each type first and, yes, don't forget to properly use the stones :)**
The output will always fit in a **32-bit signed integer**.
|
2 2 2
4
1
2
3
5
6
1
2
3
4
5
6
|
91
|
Hard
| null | null | null | null | null | null |
2014-06-03T20:56:00
|
2017-02-12T04:14:52
|
setter
|
//============================================================================
// Name : GIFTS.cpp
// Author : Shaka
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//============================================================================
#include <cstdio>
#include <cassert>
using namespace std;
const int MAXN = 21;
int dp[MAXN][MAXN][MAXN][MAXN][MAXN][MAXN];
int A[MAXN], B[MAXN], C[MAXN];
int weight[MAXN * 3];
int N, M, L;
int solve(int a, int b, int c, int d, int e, int f) {
if (a > b && c > d && e > f) return 0; //no more scrolls to learn
if (!dp[a][b][c][d][e][f]) { //all values are positive, so 0 means unvisited state in the dp
int &rx = dp[a][b][c][d][e][f], tmp;
int wx = weight[(N - 1 + a - b) + (M - 1 + c - d) + (L - 1 + e - f)];
//possible transitions in bronze techniques
if (a <= b) {
tmp = wx * A[a] + solve(a + 1, b, c, d, e, f);
if (tmp > rx) rx = tmp;
}
if (a < b) {
tmp = wx * A[b] + solve(a, b - 1, c, d, e, f);
if (tmp > rx) rx = tmp;
}
//possible transitions in silver techniques
if (c <= d) {
tmp = wx * B[c] + solve(a, b, c + 1, d, e, f);
if (tmp > rx) rx = tmp;
}
if (c < d) {
tmp = wx * B[d] + solve(a, b, c, d - 1, e, f);
if (tmp > rx) rx = tmp;
}
//possible transitions in gold techniques
if (e <= f) {
tmp = wx * C[e] + solve(a, b, c, d, e + 1, f);
if (tmp > rx) rx = tmp;
}
if (e < f) {
tmp = wx * C[f] + solve(a, b, c, d, e, f - 1);
if (tmp > rx) rx = tmp;
}
}
return dp[a][b][c][d][e][f];
}
int main() {
register int i;
scanf("%d%d%d", &N, &M, &L);
for (i = 0; i < N; ++i) scanf("%d", A + i);
for (i = 0; i < M; ++i) scanf("%d", B + i);
for (i = 0; i < L; ++i) scanf("%d", C + i);
for (i = 0; i < N + M + L; ++i) scanf("%d", weight + i);
printf("%d\n", solve(0, N - 1, 0, M - 1, 0, L - 1));
return 0;
}
|
not-set
|
2016-04-24T02:02:40
|
2016-04-24T02:02:40
|
C++
|
73 | 2,561 |
dance-class
|
Dancing in Pairs
|
Bob is a dance teacher and he started dance classes recently. He observes a strange attendance pattern among his students. Initially, there are no students. On day *i*, a new student starts attending the class. The student stops attending the class, if and only if he has attended the class for _i_ consecutive days.
Also, the student resumes attending the class, if and only if he has not attended the class for _i_ consecutive days.
We denote the student who starts coming on day *i* as student *i*.
To mark attendance, `o` denotes present and `x` denotes absent.
For example, the schedule for student 1 from day 1 is as follows:
`oxoxoxoxoxoxoxoxoxox...`
The schedule for the student 3 from day 1 is as follows:
`xxoooxxxoooxxxoooxxx...`
(Student 3 starts attending the class from day 3, and stops attending from day 6, and then starts attending from day 9, and so on. )
The schedule for the student 5 from day 1 is as follows.
`xxxxoooooxxxxxoooooxxxxx...`
Bob wants his students to dance in pairs. However, if the number of students coming on day _i_ is odd, then there will be someone who can't find a partner. So Bob wants to know if the number of students coming on day i is even or odd. We denote the number of students coming on day _i_ as _N(i)_. Please find out whether _N(i)_ is even or odd.
**Input format**
The first line contains an integer, _T_, which denotes the number of test cases.
For each test case, there is an integer _i_
**Output Format**
For each test case, if _N(i)_ is even, then print `even`.
If _N(i)_ is odd, then print one line `odd`.
**Constraints**
1 ≤ *T* ≤ 100
1 ≤ *i* ≤ 10<sup>18</sup>
**Sample Input**
4
1
2
3
4
**Sample Output**
odd
odd
odd
even
**Explanation**
The number of students coming on day 1 is 1: only student #1 attends the class. So N(1)=1 and it is odd.
The number of students coming on day 2 is 1: student #2, so n(2)=1 and it is odd.
The number of students coming on day 3 is 3: student #1, student #2, and student #3. So N(3)=3 and it is odd.
The number of students coming on day 4 is 2: student #3 and student #4. So N(4)=2 and it is even.
|
code
|
Find out if they can dance in pairs?
|
ai
|
2014-05-29T07:35:20
|
2022-09-02T09:54:27
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a STRING.
# The function accepts LONG_INTEGER i as parameter.
#
def solve(i):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
i = int(input().strip())
result = solve(i)
fptr.write(result + '\n')
fptr.close()
|
Bob is a dance teacher and he started dance classes recently. He observes a strange attendance pattern among his students. Initially, there are no students. On day *i*, a new student starts attending the class. The student stops attending the class, if and only if he has attended the class for _i_ consecutive days.
Also, the student resumes attending the class, if and only if he has not attended the class for _i_ consecutive days.
We denote the student who starts coming on day *i* as student *i*.
To mark attendance, `o` denotes present and `x` denotes absent.
For example, the schedule for student 1 from day 1 is as follows:
`oxoxoxoxoxoxoxoxoxox...`
The schedule for the student 3 from day 1 is as follows:
`xxoooxxxoooxxxoooxxx...`
(Student 3 starts attending the class from day 3, and stops attending from day 6, and then starts attending from day 9, and so on. )
The schedule for the student 5 from day 1 is as follows.
`xxxxoooooxxxxxoooooxxxxx...`
Bob wants his students to dance in pairs. However, if the number of students coming on day _i_ is odd, then there will be someone who can't find a partner. So Bob wants to know if the number of students coming on day i is even or odd. We denote the number of students coming on day _i_ as _N(i)_. Please find out whether _N(i)_ is even or odd.
**Input format**
The first line contains an integer, _T_, which denotes the number of test cases.
For each test case, there is an integer _i_
**Output Format**
For each test case, if _N(i)_ is even, then print `even`.
If _N(i)_ is odd, then print one line `odd`.
**Constraints**
1 ≤ *T* ≤ 100
1 ≤ *i* ≤ 10<sup>18</sup>
**Sample Input**
4
1
2
3
4
**Sample Output**
odd
odd
odd
even
**Explanation**
The number of students coming on day 1 is 1: only student #1 attends the class. So N(1)=1 and it is odd.
The number of students coming on day 2 is 1: student #2, so n(2)=1 and it is odd.
The number of students coming on day 3 is 3: student #1, student #2, and student #3. So N(3)=3 and it is odd.
The number of students coming on day 4 is 2: student #3 and student #4. So N(4)=2 and it is even.
| 0.580645 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null |
{"contest_participation":2021,"challenge_submissions":338,"successful_submissions":195}
|
2014-06-09T09:29:38
|
2016-12-03T09:20:56
|
setter
|
###Python 2
```python
import fileinput
n=0
for line in fileinput.input():
t=int(line)
if n>0:
p=1
q=10**9+1
while q-p>=2:
mi=(p+q)/2
if mi**2>t:
q=mi
else:
p=mi
ans=p
if ans%2==1:
print 'odd'
else:
print 'even'
else:
n=int(line)
```
|
not-set
|
2016-04-24T02:02:41
|
2016-07-23T17:55:14
|
Python
|
74 | 2,561 |
dance-class
|
Dancing in Pairs
|
Bob is a dance teacher and he started dance classes recently. He observes a strange attendance pattern among his students. Initially, there are no students. On day *i*, a new student starts attending the class. The student stops attending the class, if and only if he has attended the class for _i_ consecutive days.
Also, the student resumes attending the class, if and only if he has not attended the class for _i_ consecutive days.
We denote the student who starts coming on day *i* as student *i*.
To mark attendance, `o` denotes present and `x` denotes absent.
For example, the schedule for student 1 from day 1 is as follows:
`oxoxoxoxoxoxoxoxoxox...`
The schedule for the student 3 from day 1 is as follows:
`xxoooxxxoooxxxoooxxx...`
(Student 3 starts attending the class from day 3, and stops attending from day 6, and then starts attending from day 9, and so on. )
The schedule for the student 5 from day 1 is as follows.
`xxxxoooooxxxxxoooooxxxxx...`
Bob wants his students to dance in pairs. However, if the number of students coming on day _i_ is odd, then there will be someone who can't find a partner. So Bob wants to know if the number of students coming on day i is even or odd. We denote the number of students coming on day _i_ as _N(i)_. Please find out whether _N(i)_ is even or odd.
**Input format**
The first line contains an integer, _T_, which denotes the number of test cases.
For each test case, there is an integer _i_
**Output Format**
For each test case, if _N(i)_ is even, then print `even`.
If _N(i)_ is odd, then print one line `odd`.
**Constraints**
1 ≤ *T* ≤ 100
1 ≤ *i* ≤ 10<sup>18</sup>
**Sample Input**
4
1
2
3
4
**Sample Output**
odd
odd
odd
even
**Explanation**
The number of students coming on day 1 is 1: only student #1 attends the class. So N(1)=1 and it is odd.
The number of students coming on day 2 is 1: student #2, so n(2)=1 and it is odd.
The number of students coming on day 3 is 3: student #1, student #2, and student #3. So N(3)=3 and it is odd.
The number of students coming on day 4 is 2: student #3 and student #4. So N(4)=2 and it is even.
|
code
|
Find out if they can dance in pairs?
|
ai
|
2014-05-29T07:35:20
|
2022-09-02T09:54:27
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a STRING.
# The function accepts LONG_INTEGER i as parameter.
#
def solve(i):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
i = int(input().strip())
result = solve(i)
fptr.write(result + '\n')
fptr.close()
|
Bob is a dance teacher and he started dance classes recently. He observes a strange attendance pattern among his students. Initially, there are no students. On day *i*, a new student starts attending the class. The student stops attending the class, if and only if he has attended the class for _i_ consecutive days.
Also, the student resumes attending the class, if and only if he has not attended the class for _i_ consecutive days.
We denote the student who starts coming on day *i* as student *i*.
To mark attendance, `o` denotes present and `x` denotes absent.
For example, the schedule for student 1 from day 1 is as follows:
`oxoxoxoxoxoxoxoxoxox...`
The schedule for the student 3 from day 1 is as follows:
`xxoooxxxoooxxxoooxxx...`
(Student 3 starts attending the class from day 3, and stops attending from day 6, and then starts attending from day 9, and so on. )
The schedule for the student 5 from day 1 is as follows.
`xxxxoooooxxxxxoooooxxxxx...`
Bob wants his students to dance in pairs. However, if the number of students coming on day _i_ is odd, then there will be someone who can't find a partner. So Bob wants to know if the number of students coming on day i is even or odd. We denote the number of students coming on day _i_ as _N(i)_. Please find out whether _N(i)_ is even or odd.
**Input format**
The first line contains an integer, _T_, which denotes the number of test cases.
For each test case, there is an integer _i_
**Output Format**
For each test case, if _N(i)_ is even, then print `even`.
If _N(i)_ is odd, then print one line `odd`.
**Constraints**
1 ≤ *T* ≤ 100
1 ≤ *i* ≤ 10<sup>18</sup>
**Sample Input**
4
1
2
3
4
**Sample Output**
odd
odd
odd
even
**Explanation**
The number of students coming on day 1 is 1: only student #1 attends the class. So N(1)=1 and it is odd.
The number of students coming on day 2 is 1: student #2, so n(2)=1 and it is odd.
The number of students coming on day 3 is 3: student #1, student #2, and student #3. So N(3)=3 and it is odd.
The number of students coming on day 4 is 2: student #3 and student #4. So N(4)=2 and it is even.
| 0.580645 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null |
{"contest_participation":2021,"challenge_submissions":338,"successful_submissions":195}
|
2014-06-09T09:29:38
|
2016-12-03T09:20:56
|
tester
|
###Python 2
```python
from decimal import Decimal as D
for cas in range(input()):print["even","odd"][int(D(input()).sqrt())&1]
```
|
not-set
|
2016-04-24T02:02:41
|
2016-07-23T17:55:35
|
Python
|
75 | 2,339 |
permutation-problem
|
Permutation Problem
|
How many n-digit numbers (without leading zeros) are there such that no digit occurs more than k times?
As the count of such n-digit numbers can be very large, print the answer mod (10<sup>9</sup>+7)
**Input Format**
The first line contains an integer, _T_ , the number of test cases. This is followed by _T_ lines each containing 2 space separated integers, _n_ _k_
**Constraints**
_T_ ≤ 100000
1 ≤ _n_ ≤ 1000
1 ≤ _k_ ≤ 10<sup>9</sup>
**Sample Input**
2
2 3
2 1
**Sample Output**
90
81
**Explanation**
Case 1: A number can appear three times. So we have 9 (all except 0) numbers for first digit and 10 numbers for the second digit.
Case 2: A number can appear only once. So we have 9 choices for the first digit and 9(all except the first one) for the second digit.
|
code
|
Find the number of n digit numbers
|
ai
|
2014-04-10T09:15:12
|
2022-09-02T09:54:56
|
#
# Complete the 'solve' function below.
#
# The function is expected to return an INTEGER.
# The function accepts following parameters:
# 1. INTEGER n
# 2. INTEGER k
#
def solve(n, k):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
t = int(input().strip())
for t_itr in range(t):
first_multiple_input = input().rstrip().split()
n = int(first_multiple_input[0])
k = int(first_multiple_input[1])
result = solve(n, k)
fptr.write(str(result) + '\n')
fptr.close()
|
How many n-digit numbers (without leading zeros) are there such that no digit occurs more than k times?
As the count of such n-digit numbers can be very large, print the answer mod (10<sup>9</sup>+7)
**Input Format**
The first line contains an integer, _T_ , the number of test cases. This is followed by _T_ lines each containing 2 space separated integers, _n_ and _k_
**Constraints**
_T_ ≤ 100000
1 ≤ _n_ ≤ 1000
1 ≤ _k_ ≤ 10<sup>9</sup>
**Sample Input**
2
2 3
2 1
**Sample Output**
90
81
**Explanation**
Case 1: A number can appear three times. So we have 9 (all except 0) numbers for first digit and 10 numbers for the second digit.
Case 2: A number can appear only once. So we have 9 choices for the first digit and 9(all except the first one) for the second digit.
| 0.469388 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
|
Hard
| null | null | null | null | null |
{"contest_participation":2021,"challenge_submissions":165,"successful_submissions":54}
|
2014-06-09T09:30:00
|
2016-12-06T19:43:26
|
tester
|
###C++
```cpp
#include <stdio.h>
#include <stdlib.h>
#define mod 1000000007
#define min(a,b) ((a)<(b)?(a):(b))
#define LIM 1000
#define ull unsigned long long
#define _9_10 300000003 // (9/10'ths mod 10^9+7)
ull fac[LIM+1];
ull ifc[LIM+1];
ull **F[11];
int main() {
// precalculate factorials and inverse factorials
fac[0] = ifc[0] = fac[1] = ifc[1] = 1;
for (int i = 2; i <= LIM; i++) { // put the inverses in ifc
ifc[i] = (mod - mod/i) * ifc[mod%i] % mod;
}
for (int i = 2; i <= LIM; i++) { // precalculate fac and ifc
fac[i] = fac[i-1] * i % mod;
ifc[i] = ifc[i-1] * ifc[i] % mod;
}
// precalculate F[d][n][k] = f_d(n,k)
// around 10^2/2 * 600^2/2 < 10000000 operations
for (int d = 0; d <= 10; d++) {
F[d] = (ull**)malloc((LIM+1)*sizeof(ull*));
for (int n = 0; n <= LIM; n++) {
F[d][n] = (ull*)calloc(n+1, sizeof(ull));
for (int k = 0; k <= n; k++) {
if (n == 0) {
F[d][n][k] = 1;
} else if (k == 0 or d == 0) {
F[d][n][k] = 0;
} else {
ull s = 0;
ull pw = 1;
int nn = n;
int nk = k-1;
for (int e = 0; e <= d; e++) {
if (e*k > n) break;
s += fac[d] * ifc[e] % mod * ifc[d-e] % mod * fac[n] % mod * ifc[nn] % mod * pw % mod * F[d-e][nn][min(nn,nk)];
pw = pw * ifc[k] % mod;
nn -= k;
}
F[d][n][k] = s % mod;
}
}
}
}
ull **f = F[10];
int z;
scanf("%d", &z);
for (int cas = 1; cas <= z; cas++) {
int n, k;
scanf("%d%d", &n, &k);
ull ans = f[n][min(n, k)] * _9_10 % mod; // 1/10'ths of the numbers start with zero
printf("%llu\n", ans);
}
}
```
|
not-set
|
2016-04-24T02:02:41
|
2016-07-23T18:38:08
|
C++
|
||||
76 | 2,557 |
kundu-and-tree
|
Kundu and Tree
|
Kundu is true tree lover. Tree is a connected graph having _N_ vertices and _N-1_ edges. Today when he got a tree, he colored each edge with one of either red(`r`) or black(`b`) color. He is interested in knowing how many triplets(a,b,c) of vertices are there , such that, there is atleast one edge having red color on all the three paths i.e. from vertex _a_ to _b_, vertex _b_ to _c_ and vertex _c_ to _a_ . Note that (a,b,c), (b,a,c) and all such permutations will be considered as the same triplet.
If the answer is greater than 10<sup>9</sup> + 7, print the answer modulo (%) 10<sup>9</sup> + 7.
**Input Format**
The first line contains an integer _N_, i.e., the number of vertices in tree.
The next _N-1_ lines represent edges: 2 space separated integers denoting an edge followed by a color of the edge. A color of an edge is denoted by a small letter of English alphabet, and it can be either red(`r`) or black(`b`).
**Output Format**
Print a single number i.e. the number of triplets.
**Constraints**
1 ≤ _N_ ≤ 10<sup>5</sup><br>
A node is numbered between 1 to *N*.
**Sample Input**
5
1 2 b
2 3 r
3 4 r
4 5 b
**Sample Output**
4
**Explanation**
Given tree is something like this.<br>

(2,3,4) is one such triplet because on all paths i.e 2 to 3, 3 to 4 and 2 to 4 there is atleast one edge having red color.<br>
(2,3,5), (1,3,4) and (1,3,5) are other such triplets.
Note that (1,2,3) is NOT a triplet, because the path from 1 to 2 does not have an edge with red color.
|
code
|
Find the number of triplets (a,b,c) such that atleast one edge is colored red on all the three paths.
|
ai
|
2014-05-28T05:49:51
|
2022-08-31T08:33:12
| null | null | null |
Kundu is true tree lover. Tree is a connected graph having _N_ vertices and _N-1_ edges. Today when he got a tree, he colored each edge with one of either red(`r`) or black(`b`) color. He is interested in knowing how many triplets(a,b,c) of vertices are there , such that, there is atleast one edge having red color on all the three paths i.e. from vertex _a_ to _b_, vertex _b_ to _c_ and vertex _c_ to _a_ . Note that (a,b,c), (b,a,c) and all such permutations will be considered as the same triplet.
If the answer is greater than 10<sup>9</sup> + 7, print the answer modulo (%) 10<sup>9</sup> + 7.
**Input Format**
The first line contains an integer _N_, i.e., the number of vertices in tree.
The next _N-1_ lines represent edges: 2 space separated integers denoting an edge followed by a color of the edge. A color of an edge is denoted by a small letter of English alphabet, and it can be either red(`r`) or black(`b`).
**Output Format**
Print a single number i.e. the number of triplets.
**Constraints**
1 ≤ _N_ ≤ 10<sup>5</sup><br>
A node is numbered between 1 to *N*.
**Sample Input**
5
1 2 b
2 3 r
3 4 r
4 5 b
**Sample Output**
4
**Explanation**
Given tree is something like this.<br>

(2,3,4) is one such triplet because on all paths i.e 2 to 3, 3 to 4 and 2 to 4 there is atleast one edge having red color.<br>
(2,3,5), (1,3,4) and (1,3,5) are other such triplets.
Note that (1,2,3) is NOT a triplet, because the path from 1 to 2 does not have an edge with red color.
| 0.465839 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
Hard
| null | null | null | null | null |
{"contest_participation":3,"challenge_submissions":0,"successful_submissions":0}
|
2014-06-12T12:50:12
|
2016-12-02T11:13:36
|
setter
|
#include<bits/stdc++.h>
using namespace std;
#define MOD 1000000007
#define s(a) scanf("%d",&a);
vector<int> edges[100009];
long long int visited[100009];
long long int count1[100009];
long long int B[100009],C[100009],D[100009];
void dfs(int x, int temp)
{
if(visited[x] == 0)
visited[x] = temp;
for(int i = 0 ; i< edges[x].size() ; i++)
{
if(visited[edges[x][i]] == 0)
dfs(edges[x][i],temp);
}
return;
}
int main()
{
int n,i,a,b;
char c;
s(n);
for(i=0 ; i< n -1 ; i++)
{
s(a);
s(b);
cin>>c;
if( c != 'r')
{
edges[a].push_back(b);
edges[b].push_back(a);
}
}
int temp = 1;
for(i=1 ; i<=n ; i++)
{
if(visited[i] == 0)
{
dfs(i,temp);
temp++;
}
}
for(i=1 ; i<= n ; i++)
count1[visited[i]]++;
long long int sum = 0;
B[n-1] = count1[n];
for(i=n-2;i>=0;i--) B[i] = (B[i+1] + count1[i+1])%MOD;
for(i=1;i<n-1;i++) C[i] = (count1[i+1]*B[i+1])%MOD;
D[n-2] = C[n-2];
for(i=n-3;i>=1;i--) D[i] = (D[i+1] + C[i])%MOD;
for(i=0;i<n-2;i++) sum = (sum + count1[i+1]*D[i+1])%MOD;
cout<< ( MOD + sum )%MOD<<endl;
return 0;
}
|
not-set
|
2016-04-24T02:02:41
|
2016-04-24T02:02:41
|
C++
|
||||
77 | 2,557 |
kundu-and-tree
|
Kundu and Tree
|
Kundu is true tree lover. Tree is a connected graph having _N_ vertices and _N-1_ edges. Today when he got a tree, he colored each edge with one of either red(`r`) or black(`b`) color. He is interested in knowing how many triplets(a,b,c) of vertices are there , such that, there is atleast one edge having red color on all the three paths i.e. from vertex _a_ to _b_, vertex _b_ to _c_ and vertex _c_ to _a_ . Note that (a,b,c), (b,a,c) and all such permutations will be considered as the same triplet.
If the answer is greater than 10<sup>9</sup> + 7, print the answer modulo (%) 10<sup>9</sup> + 7.
**Input Format**
The first line contains an integer _N_, i.e., the number of vertices in tree.
The next _N-1_ lines represent edges: 2 space separated integers denoting an edge followed by a color of the edge. A color of an edge is denoted by a small letter of English alphabet, and it can be either red(`r`) or black(`b`).
**Output Format**
Print a single number i.e. the number of triplets.
**Constraints**
1 ≤ _N_ ≤ 10<sup>5</sup><br>
A node is numbered between 1 to *N*.
**Sample Input**
5
1 2 b
2 3 r
3 4 r
4 5 b
**Sample Output**
4
**Explanation**
Given tree is something like this.<br>

(2,3,4) is one such triplet because on all paths i.e 2 to 3, 3 to 4 and 2 to 4 there is atleast one edge having red color.<br>
(2,3,5), (1,3,4) and (1,3,5) are other such triplets.
Note that (1,2,3) is NOT a triplet, because the path from 1 to 2 does not have an edge with red color.
|
code
|
Find the number of triplets (a,b,c) such that atleast one edge is colored red on all the three paths.
|
ai
|
2014-05-28T05:49:51
|
2022-08-31T08:33:12
| null | null | null |
Kundu is true tree lover. Tree is a connected graph having _N_ vertices and _N-1_ edges. Today when he got a tree, he colored each edge with one of either red(`r`) or black(`b`) color. He is interested in knowing how many triplets(a,b,c) of vertices are there , such that, there is atleast one edge having red color on all the three paths i.e. from vertex _a_ to _b_, vertex _b_ to _c_ and vertex _c_ to _a_ . Note that (a,b,c), (b,a,c) and all such permutations will be considered as the same triplet.
If the answer is greater than 10<sup>9</sup> + 7, print the answer modulo (%) 10<sup>9</sup> + 7.
**Input Format**
The first line contains an integer _N_, i.e., the number of vertices in tree.
The next _N-1_ lines represent edges: 2 space separated integers denoting an edge followed by a color of the edge. A color of an edge is denoted by a small letter of English alphabet, and it can be either red(`r`) or black(`b`).
**Output Format**
Print a single number i.e. the number of triplets.
**Constraints**
1 ≤ _N_ ≤ 10<sup>5</sup><br>
A node is numbered between 1 to *N*.
**Sample Input**
5
1 2 b
2 3 r
3 4 r
4 5 b
**Sample Output**
4
**Explanation**
Given tree is something like this.<br>

(2,3,4) is one such triplet because on all paths i.e 2 to 3, 3 to 4 and 2 to 4 there is atleast one edge having red color.<br>
(2,3,5), (1,3,4) and (1,3,5) are other such triplets.
Note that (1,2,3) is NOT a triplet, because the path from 1 to 2 does not have an edge with red color.
| 0.465839 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
Hard
| null | null | null | null | null |
{"contest_participation":3,"challenge_submissions":0,"successful_submissions":0}
|
2014-06-12T12:50:12
|
2016-12-02T11:13:36
|
tester
|
// When I wrote this, only God and I understood what I was doing
// Now, God only knows
#include<bits/stdc++.h>
using namespace std;
#define assn(n,a,b) assert(n<=b && n>=a)
#define pb push_back
typedef vector<int> VI;
typedef long long LL;
#define MOD 1000000007
LL mpow(LL a, LL n)
{LL ret=1;LL b=a;while(n) {if(n&1)
ret=(ret*b)%MOD;b=(b*b)%MOD;n>>=1;}
return (LL)ret;}
VI ar[100005]={};
int flag[100005]={};
int bfs(int node)
{
queue < int > myq;
myq.push(node);
flag[node]=1;
int p,cnt=0;
while(!myq.empty())
{
p=myq.front();
cnt++;
myq.pop();
for(int i=0; i<ar[p].size(); i++)
if(flag[ar[p][i]]==0)flag[ar[p][i]]=1,myq.push(ar[p][i]);
}
return cnt;
}
int main()
{
int n,i,j,u,v;
VI arr;
string s;
cin >> n;
assn(n,1,100000);
for(i=1; i<n; i++)
{
cin >> u >> v >> s;
u--,v--;
if(s[0]!='r')ar[u].pb(v),ar[v].pb(u);
}
for(i=0; i<n; i++)
if(flag[i]==0)arr.pb(bfs(i));
LL ans=0,sum=0;
n=arr.size();
for(i=0; i<n; i++)
ans+=arr[i];
sum=ans;
ans=(ans*ans*ans)%MOD;
for(i=0; i<n; i++)
{
ans-=(arr[i]*arr[i]*arr[i])%MOD;
if(ans<0)ans+=MOD;
}
for(i=0; i<n; i++)
{
ans-=(3*arr[i]*arr[i]*(sum-arr[i]))%MOD;
if(ans<0)ans+=MOD;
}
cout << (ans*mpow(6,MOD-2))%MOD << endl;
return 0;
}
|
not-set
|
2016-04-24T02:02:41
|
2016-04-24T02:02:41
|
Go
|
||||
78 | 104 |
median
|
Median Updates
|
The median of *M* numbers is defined as the middle number after sorting them in order, if *M* is odd. Or it is the average of the middle 2 numbers (again after sorting), if *M* is even. You have an empty number list at first. Then you can add in or remove some number from the list. For each add or remove operation, output the median of numbers in the list.
**Example :**
For a set of *M = 5* numbers *{9, 2, 8, 4, 1}* the median is the third number in sorted set *{1, 2, 4, 8, 9}* which is *4*. Similarly, for a set of *M = 4*, *{5, 2, 10, 4}*, the median is the average of second and the third element in the sorted set *{2, 4, 5, 10}* which is *(4+5)/2 = 4.5*.
**Input:**
The first line is an integer *N* that indicates the number of operations. Each of the next *N* lines is either *a x* or *r x* . *a x* indicates that x is added to the set, and *r x* indicates that x is removed from the set.
**Output:**
For each operation: If the operation is _add_ output the median after adding *x* in a single line. If the operation is _remove_ and the number *x* is not in the list, output *Wrong!* in a single line. If the operation is _remove_ and the number *x* is in the list, output the median after deleting *x* in a single line. (If the result is an integer DO NOT output decimal point. And if the result is a real number , DO NOT output trailing 0s.)
**Note**
If your median is 3.0, print only 3. And if your median is 3.50, print only 3.5. Whenever you need to print the median and the list is empty, print *Wrong!*
**Constraints:**
0 < *N* <= 100,000
For each *a x* or *r x*, *x* will always be an integer which will fit in 32 bit signed integer.
**Sample Input:**
7
r 1
a 1
a 2
a 1
r 1
r 2
r 1
**Sample Output:**
Wrong!
1
1.5
1
1.5
1
Wrong!
**Note:** As evident from the last line of the input, if after remove operation the list becomes empty, you have to print *Wrong!*.
|
code
|
Return the median after each number is added to a list.
|
algorithm
|
2013-01-04T20:28:56
|
2022-08-31T08:33:08
|
#!/bin/python
def median(a,x):
N = int(input())
s = []
x = []
for i in range(0, N):
tmp = input().strip().split(' ')
a, b = [xx for xx in tmp]
s.append(a)
x.append(int(b))
median(s,x)
| null | null |
The median of $M$ numbers is defined as the middle number after sorting them in order if $M$ is odd. Or it is the average of the middle two numbers if $M$ is even. You start with an empty number list. Then, you can add numbers to the list, or remove existing numbers from it. After each add or remove operation, output the median.
**Example:**
For a set of $M = 5$ numbers ${9, 2, 8, 4, 1}$ the median is the third number in the sorted set ${1, 2, 4, 8, 9}$, which is $4$. Similarly, for a set of $M = 4$ numbers, ${5, 2, 10, 4}$, the median is the average of the second and the third element in the sorted set ${2, 4, 5, 10}$, which is $(4+5)/2 = 4.5$.
**Input:**
The first line is an integer, $N$, that indicates the number of operations. Each of the next $N$ lines is either _a x_ or _r x_. _a x_ indicates that $x$ is added to the set, and _r x_ indicates that $x$ is removed from the set.
**Output:**
For each operation: If the operation is _add_, output the median after adding $x$ in a single line. If the operation is _remove_ and the number $x$ is not in the list, output *Wrong!* in a single line. If the operation is _remove_ and the number $x$ is in the list, output the median after deleting $x$ in a single line. (If the result is an integer DO NOT output decimal point. And if the result is a real number, DO NOT output trailing 0s.)
**Note**
If your median is 3.0, print only 3. And if your median is 3.50, print only 3.5. Whenever you need to print the median and the list is empty, print *Wrong!*
**Constraints:**
$0 \lt N \le 10$<sup>$5$</sup>
For each _a x_ or _r x_, $x$ will always be a signed integer (which will fit in 32 bits).
**Sample Input:**
7
r 1
a 1
a 2
a 1
r 1
r 2
r 1
**Sample Output:**
Wrong!
1
1.5
1
1.5
1
Wrong!
**Note:** As evident from the last line of the input, if after remove operation the list becomes empty, you have to print *Wrong!*.
| 0.418014 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
Hard
| null | null | null | null | null | null |
2014-06-16T10:15:13
|
2016-12-01T23:14:40
|
setter
|
#include <cstdio>
#include <set>
#include <cstring>
#include <string>
using namespace std;
multiset<int> s1,s2; //0<=|s1|-|s2|<=1
char s[55];
void gao() {
int a,b;
bool f1,f2;
if (s1.empty()) {
puts("Wrong!");
return;
}
if (s1.size()==s2.size()) {
a=*s1.rbegin();
b=*s2.begin();
f1=a%2;
f2=b%2;
if (f1==f2) {
printf("%.0lf\n",(a*1.+b)/2.);
}
else {
printf("%.1lf\n",(a*1.+b)/2.);
}
}
else {
printf("%d\n",*s1.rbegin());
}
}
void gao1(int x) { //add x
if (s1.empty()) {
s1.insert(x);
}
else if (s1.size()==s2.size()) {
s2.insert(x);
s1.insert(*s2.begin());
s2.erase(s2.begin());
}
else {
s1.insert(x);
s2.insert(*s1.rbegin());
s1.erase(s1.find(*s1.rbegin()));
}
gao();
}
void gao2(int x) {
multiset<int>::iterator t1=s1.find(x),t2=s2.find(x);
if ((t1==s1.end()) && (t2==s2.end())) {
puts("Wrong!");
return;
}
if (s1.size()==s2.size()) {
if (t2!=s2.end()) {
s2.erase(t2);
}
else {
s1.erase(t1);
s1.insert(*s2.begin());
s2.erase(s2.begin());
}
}
else if (t1!=s1.end()) {
s1.erase(t1);
}
else {
s2.erase(t2);
s2.insert(*s1.rbegin());
s1.erase(s1.find(*s1.rbegin()));
}
gao();
}
int main() {
int i,x;
/*s1.clear();
s2.clear();*/
for (scanf("%d",&i);i;--i) {
scanf("%s%d",s,&x);
if (s[0]=='a') {
gao1(x);
}
else {
gao2(x);
}
}
return 0;
}
|
not-set
|
2016-04-24T02:02:41
|
2016-04-24T02:02:41
|
C++
|
||||
79 | 104 |
median
|
Median Updates
|
The median of *M* numbers is defined as the middle number after sorting them in order, if *M* is odd. Or it is the average of the middle 2 numbers (again after sorting), if *M* is even. You have an empty number list at first. Then you can add in or remove some number from the list. For each add or remove operation, output the median of numbers in the list.
**Example :**
For a set of *M = 5* numbers *{9, 2, 8, 4, 1}* the median is the third number in sorted set *{1, 2, 4, 8, 9}* which is *4*. Similarly, for a set of *M = 4*, *{5, 2, 10, 4}*, the median is the average of second and the third element in the sorted set *{2, 4, 5, 10}* which is *(4+5)/2 = 4.5*.
**Input:**
The first line is an integer *N* that indicates the number of operations. Each of the next *N* lines is either *a x* or *r x* . *a x* indicates that x is added to the set, and *r x* indicates that x is removed from the set.
**Output:**
For each operation: If the operation is _add_ output the median after adding *x* in a single line. If the operation is _remove_ and the number *x* is not in the list, output *Wrong!* in a single line. If the operation is _remove_ and the number *x* is in the list, output the median after deleting *x* in a single line. (If the result is an integer DO NOT output decimal point. And if the result is a real number , DO NOT output trailing 0s.)
**Note**
If your median is 3.0, print only 3. And if your median is 3.50, print only 3.5. Whenever you need to print the median and the list is empty, print *Wrong!*
**Constraints:**
0 < *N* <= 100,000
For each *a x* or *r x*, *x* will always be an integer which will fit in 32 bit signed integer.
**Sample Input:**
7
r 1
a 1
a 2
a 1
r 1
r 2
r 1
**Sample Output:**
Wrong!
1
1.5
1
1.5
1
Wrong!
**Note:** As evident from the last line of the input, if after remove operation the list becomes empty, you have to print *Wrong!*.
|
code
|
Return the median after each number is added to a list.
|
algorithm
|
2013-01-04T20:28:56
|
2022-08-31T08:33:08
|
#!/bin/python
def median(a,x):
N = int(input())
s = []
x = []
for i in range(0, N):
tmp = input().strip().split(' ')
a, b = [xx for xx in tmp]
s.append(a)
x.append(int(b))
median(s,x)
| null | null |
The median of $M$ numbers is defined as the middle number after sorting them in order if $M$ is odd. Or it is the average of the middle two numbers if $M$ is even. You start with an empty number list. Then, you can add numbers to the list, or remove existing numbers from it. After each add or remove operation, output the median.
**Example:**
For a set of $M = 5$ numbers ${9, 2, 8, 4, 1}$ the median is the third number in the sorted set ${1, 2, 4, 8, 9}$, which is $4$. Similarly, for a set of $M = 4$ numbers, ${5, 2, 10, 4}$, the median is the average of the second and the third element in the sorted set ${2, 4, 5, 10}$, which is $(4+5)/2 = 4.5$.
**Input:**
The first line is an integer, $N$, that indicates the number of operations. Each of the next $N$ lines is either _a x_ or _r x_. _a x_ indicates that $x$ is added to the set, and _r x_ indicates that $x$ is removed from the set.
**Output:**
For each operation: If the operation is _add_, output the median after adding $x$ in a single line. If the operation is _remove_ and the number $x$ is not in the list, output *Wrong!* in a single line. If the operation is _remove_ and the number $x$ is in the list, output the median after deleting $x$ in a single line. (If the result is an integer DO NOT output decimal point. And if the result is a real number, DO NOT output trailing 0s.)
**Note**
If your median is 3.0, print only 3. And if your median is 3.50, print only 3.5. Whenever you need to print the median and the list is empty, print *Wrong!*
**Constraints:**
$0 \lt N \le 10$<sup>$5$</sup>
For each _a x_ or _r x_, $x$ will always be a signed integer (which will fit in 32 bits).
**Sample Input:**
7
r 1
a 1
a 2
a 1
r 1
r 2
r 1
**Sample Output:**
Wrong!
1
1.5
1
1.5
1
Wrong!
**Note:** As evident from the last line of the input, if after remove operation the list becomes empty, you have to print *Wrong!*.
| 0.418014 |
["ada","bash","c","clojure","coffeescript","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fortran","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","octave","pascal","perl","php","pypy3","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","whitespace"]
|
Hard
| null | null | null | null | null | null |
2014-06-16T10:15:13
|
2016-12-01T23:14:40
|
tester
|
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
typedef pair< int , int > pii;
int main() {
int t;
cin>>t;
char c;
int n;
int insert_counter = 0;
tree < pii , null_type , less<pii> , rb_tree_tag , tree_order_statistics_node_update > T;
for (int i = 0;i<t;i++) {
cin>>c>>n;
if (c == 'r') {
auto it = T.find_by_order( T.order_of_key( {n,-1} ) );
if( it == T.end() || it->first != n ) {
cout<<"Wrong!"<<endl;
continue;
}
else {
T.erase( T.find_by_order( T.order_of_key( {n,-1} ) ) );
}
}
else if (c == 'a') {
T.insert(make_pair(n,insert_counter++));
}
if (T.size()==0) {
cout<<"Wrong!"<<endl;
continue;
}
else if (T.size()%2 == 1) {
cout<<T.find_by_order(T.size()/2)->first<<endl;
}
else {
long long int t1 = T.find_by_order(T.size()/2)->first;
long long int t2 = T.find_by_order(T.size()/2 -1)->first;
long long int temp = t1 + t2;
if (temp == -1) cout<<"-";
cout<<temp/2;
if (temp<0)temp*=-1;
if (temp%2==1) {
cout<<".5";
}
cout<<endl;
}
}
return 0;
}
|
not-set
|
2016-04-24T02:02:41
|
2016-04-24T02:02:41
|
C++
|
||||
80 | 2,581 |
even-odd-query
|
Even Odd Query
|
You are given an array *A* of size *N*. You are also given an integer *Q*. Can you figure out the answer to each of the *Q* queries?
Each query contains 2 integers x and y, and you need to find whether the value find(x,y) is Odd or Even:
find(int x,int y)
{
if(x>y) return 1;
ans = pow(A[x],find(x+1,y))
return ans
}
Note : pow(a,b) = *a<sup>b</sup>*.
**Input Format**
The first line of the input contains an integer *N*.
The next line contains *N* space separated non-negative integers(whole numbers less than or equal to 9).
The line after that contains a positive integer, *Q* , the denotes the number of queries to follow.
*Q* lines follow, each line contains two positive integer *x* and *y* separated by a single space.
**Output Format**
For each query, display 'Even' if the value returned is Even, otherwise display 'Odd'.
**Constraints**
2 ≤ *N* ≤ 10<sup>5</sup>
2 ≤ *Q* ≤ 10<sup>5</sup>
1 ≤ *x,y* ≤ *N*
*x* ≤ *y*
Array is 1-indexed.
*No 2 consecutive entries in the array will be zero.*
**Sample Input**
3
3 2 7
2
1 2
2 3
**Sample Output**
Odd
Even
**Explanation**
find(1,2) = 9, which is Odd
find(2,3) = 128, which is even
|
code
|
Is the number odd or even?
|
ai
|
2014-06-08T11:37:31
|
2022-09-02T09:54:12
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a STRING_ARRAY.
# The function accepts following parameters:
# 1. INTEGER_ARRAY arr
# 2. 2D_INTEGER_ARRAY queries
#
def solve(arr, queries):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
arr_count = int(input().strip())
arr = list(map(int, input().rstrip().split()))
q = int(input().strip())
queries = []
for _ in range(q):
queries.append(list(map(int, input().rstrip().split())))
result = solve(arr, queries)
fptr.write('\n'.join(result))
fptr.write('\n')
fptr.close()
|
You are given an array *A* of size *N*. You are also given an integer *Q*. Can you figure out the answer to each of the *Q* queries?
Each query contains 2 integers x and y, and you need to find whether the value find(x,y) is Odd or Even:
find(int x,int y)
{
if(x>y) return 1;
ans = pow(A[x],find(x+1,y))
return ans
}
Note : pow(a,b) = *a<sup>b</sup>*.
**Input Format**
The first line of the input contains an integer *N*.
The next line contains *N* space separated non-negative integers(whole numbers less than or equal to 9).
The line after that contains a positive integer, *Q* , the denotes the number of queries to follow.
*Q* lines follow, each line contains two positive integer *x* and *y* separated by a single space.
**Output Format**
For each query, display 'Even' if the value returned is Even, otherwise display 'Odd'.
**Constraints**
2 ≤ *N* ≤ 10<sup>5</sup>
2 ≤ *Q* ≤ 10<sup>5</sup>
1 ≤ *x,y* ≤ *N*
*x* ≤ *y*
Array is 1-indexed.
*No 2 consecutive entries in the array will be zero.*
**Sample Input**
3
3 2 7
2
1 2
2 3
**Sample Output**
Odd
Even
**Explanation**
find(1,2) = 9, which is Odd
find(2,3) = 128, which is even
| 0.551471 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null |
{"contest_participation":2182,"challenge_submissions":916,"successful_submissions":579}
|
2014-06-18T06:05:31
|
2016-12-05T12:34:41
|
setter
|
###C++
```cpp
#include<stdio.h>
#include<assert.h>
#define MaxN 100000
int A[MaxN+1];
int main()
{
int N,Q,x,y,last=1,flip;
scanf("%d",&N);
for(int i=1;i<=N;i++){
scanf("%d",&A[i]);
assert(0 <= A[i] && A[i]<=9);
assert(!(last==0 && last==A[i]));
last=A[i];
}
scanf("%d",&Q);
while(Q--){
scanf("%d %d",&x,&y);
assert(x<=y && y<=N && x>=1);
if(x!=y && A[x+1]==0) flip=1;
else flip=0;
if(flip) printf("Odd\n");
else if(A[x]&1) printf("Odd\n");
else printf("Even\n");
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:42
|
2016-07-23T16:31:21
|
C++
|
81 | 2,581 |
even-odd-query
|
Even Odd Query
|
You are given an array *A* of size *N*. You are also given an integer *Q*. Can you figure out the answer to each of the *Q* queries?
Each query contains 2 integers x and y, and you need to find whether the value find(x,y) is Odd or Even:
find(int x,int y)
{
if(x>y) return 1;
ans = pow(A[x],find(x+1,y))
return ans
}
Note : pow(a,b) = *a<sup>b</sup>*.
**Input Format**
The first line of the input contains an integer *N*.
The next line contains *N* space separated non-negative integers(whole numbers less than or equal to 9).
The line after that contains a positive integer, *Q* , the denotes the number of queries to follow.
*Q* lines follow, each line contains two positive integer *x* and *y* separated by a single space.
**Output Format**
For each query, display 'Even' if the value returned is Even, otherwise display 'Odd'.
**Constraints**
2 ≤ *N* ≤ 10<sup>5</sup>
2 ≤ *Q* ≤ 10<sup>5</sup>
1 ≤ *x,y* ≤ *N*
*x* ≤ *y*
Array is 1-indexed.
*No 2 consecutive entries in the array will be zero.*
**Sample Input**
3
3 2 7
2
1 2
2 3
**Sample Output**
Odd
Even
**Explanation**
find(1,2) = 9, which is Odd
find(2,3) = 128, which is even
|
code
|
Is the number odd or even?
|
ai
|
2014-06-08T11:37:31
|
2022-09-02T09:54:12
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a STRING_ARRAY.
# The function accepts following parameters:
# 1. INTEGER_ARRAY arr
# 2. 2D_INTEGER_ARRAY queries
#
def solve(arr, queries):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
arr_count = int(input().strip())
arr = list(map(int, input().rstrip().split()))
q = int(input().strip())
queries = []
for _ in range(q):
queries.append(list(map(int, input().rstrip().split())))
result = solve(arr, queries)
fptr.write('\n'.join(result))
fptr.write('\n')
fptr.close()
|
You are given an array *A* of size *N*. You are also given an integer *Q*. Can you figure out the answer to each of the *Q* queries?
Each query contains 2 integers x and y, and you need to find whether the value find(x,y) is Odd or Even:
find(int x,int y)
{
if(x>y) return 1;
ans = pow(A[x],find(x+1,y))
return ans
}
Note : pow(a,b) = *a<sup>b</sup>*.
**Input Format**
The first line of the input contains an integer *N*.
The next line contains *N* space separated non-negative integers(whole numbers less than or equal to 9).
The line after that contains a positive integer, *Q* , the denotes the number of queries to follow.
*Q* lines follow, each line contains two positive integer *x* and *y* separated by a single space.
**Output Format**
For each query, display 'Even' if the value returned is Even, otherwise display 'Odd'.
**Constraints**
2 ≤ *N* ≤ 10<sup>5</sup>
2 ≤ *Q* ≤ 10<sup>5</sup>
1 ≤ *x,y* ≤ *N*
*x* ≤ *y*
Array is 1-indexed.
*No 2 consecutive entries in the array will be zero.*
**Sample Input**
3
3 2 7
2
1 2
2 3
**Sample Output**
Odd
Even
**Explanation**
find(1,2) = 9, which is Odd
find(2,3) = 128, which is even
| 0.551471 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null |
{"contest_participation":2182,"challenge_submissions":916,"successful_submissions":579}
|
2014-06-18T06:05:31
|
2016-12-05T12:34:41
|
tester
|
###C++
```cpp
#include <bits/stdc++.h>
using namespace std;
int A[100008], N;
int find(int x, int y){
if(A[x]%2) return 1;
if(x == y) return 0;
if(A[x+1] == 0) return 1;
return 0;
}
int main(){
int x,y,Q;
cin >> N;
for(int i = 1; i <= N; i++) cin >> A[i];
cin >> Q;
while(Q--){
cin >> x >> y;
if(find(x,y)) cout << "Odd" << endl;
else cout << "Even" << endl;
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:42
|
2016-07-23T16:31:28
|
C++
|
82 | 3,092 |
reverse-trip-to-jerusalem
|
Reverse Trip to Jerusalem
|
You and your $N-1$ friends recently got tired of playing Trip to Jerusalem (i.e. Musical Chairs). In order to make things interesting again, you decide to invent a new game. And you call it *Reverse Trip to Jerusalem*.
Here's how it works. Instead of arranging the chairs in a circle, the $N$ friends (including you) arrange yourselves in a circle. Then exactly one person in the circle holds the chair.
For the first round, all $N$ of you will be in the circle. The music starts and plays for $C_1$ seconds. Every second, the person holding the chair shall pass it to the person to his left. The person who receives the chair when the music ends is OUT and he/she is not included in the circle in the subsequent rounds. The person to his left then receives the chair. And that's where the chair starts for the second round.
For the $i^\text{th}$ round, $N-i+1$ players remain and the person holding the chair is the person to the left of the most recently outed person. The music starts and plays for $C_i$ seconds. The procedure for passing the chair is the same as the first round. The player who receives the chair when the music ends is OUT.
The person who remains after $N-1$ rounds is the winner.
Of course, you want to win this. It is your dream and you believe that you will survive. The person who initially holds the chair in the first round is Todd. You wish to know where to position yourself in order to win the game.
**Input Format**
The input consists of two lines.
The first line contains a single integer $N$.
The second line contains $N-1$ integers, the $C_i$'s, each separated by single spaces.
**Output Format**
Output a single line describing the winning position. If the winning position is the $P^\text{th}$ position to the left of Todd, then output the integer $P$ (Note that $0 < P < N$). However, if the winning position is Todd's position, print `YOU MUST BE TODD`.
**Constraints**
$1 \le N \le 2\cdot 10^5$
$1 \le C_i \le 2\cdot 10^5$
**Sample Input 1**
5
1 2 2 4
**Sample Output 1**
2
**Sample Input 2**
2
1
**Sample Output 2**
YOU MUST BE TODD
**Explanation**
In the first case, let $P_1$, $P_2$, $P_3$ and $P_4$ be the four persons to Todd's left, in that order. The first round begins with Todd passing the chair to $P_1$, which subsequently outs him (since the music is only 1 second long). The second round starts with $P_2$ holding the chair. The music ends when $P_4$ receives the chair, thus forcing him out of the game. The third round starts with Todd again and stops at $P_3$. The fourth round starts with Todd and ends with Todd and so $P_2$ survives.
In the second case, Todd passes the chair to the other person, the 1-second music stops and that person is out of the game. Hence, the only way to win the game is to become Todd.
|
code
|
Winning in Trip to Jerusalem is so two thousand and late. Winning Reverse Trip to Jerusalem is what matters.
|
ai
|
2014-06-19T02:26:40
|
2018-03-13T12:03:35
| null | null | null |
You and your $N-1$ friends recently got tired of playing Trip to Jerusalem (i.e. Musical Chairs). In order to make things interesting again, you decide to invent a new game. And you call it *Reverse Trip to Jerusalem*.
Here's how it works. Instead of arranging the chairs in a circle, the $N$ friends (including you) arrange yourselves in a circle. Then exactly one person in the circle holds the chair.
For the first round, all $N$ of you will be in the circle. The music starts and plays for $C_1$ seconds. Every second, the person holding the chair shall pass it to the person to his left. The person who receives the chair when the music ends is OUT and he/she is not included in the circle in the subsequent rounds. The person to his left then receives the chair. And that's where the chair starts for the second round.
For the $i^\text{th}$ round, $N-i+1$ players remain and the person holding the chair is the person to the left of the most recently outed person. The music starts and plays for $C_i$ seconds. The procedure for passing the chair is the same as the first round. The player who receives the chair when the music ends is OUT.
The person who remains after $N-1$ rounds is the winner.
Of course, you want to win this. It is your dream and you believe that you will survive. The person who initially holds the chair in the first round is Todd. You wish to know where to position yourself in order to win the game.
**Input Format**
The input consists of two lines.
The first line contains a single integer $N$.
The second line contains $N-1$ integers, the $C_i$'s, each separated by single spaces.
**Output Format**
Output a single line describing the winning position. If the winning position is the $P^\text{th}$ position to the left of Todd, then output the integer $P$ (Note that $0 < P < N$). However, if the winning position is Todd's position, print `YOU MUST BE TODD`.
**Constraints**
$1 \le N \le 2\cdot 10^5$
$1 \le C_i \le 2\cdot 10^5$
*Note:* The time limit is half of the usual time limit.
**Sample Input 1**
5
1 2 2 4
**Sample Output 1**
2
**Sample Input 2**
2
1
**Sample Output 2**
YOU MUST BE TODD
**Explanation**
In the first case, let $P_1$, $P_2$, $P_3$ and $P_4$ be the four persons to Todd's left, in that order. The first round begins with Todd passing the chair to $P_1$, which subsequently outs him (since the music is only 1 second long). The second round starts with $P_2$ holding the chair. The music ends when $P_4$ receives the chair, thus forcing him out of the game. The third round starts with Todd again and stops at $P_3$. The fourth round starts with Todd and ends with Todd and so $P_2$ survives.
In the second case, Todd passes the chair to the other person, the 1-second music stops and that person is out of the game. Hence, the only way to win the game is to become Todd.
| 0.5 |
["c","cpp","java","python3","python","cpp14"]
|
Hard
| null | null | null | null | null |
{"contest_participation":83,"challenge_submissions":12,"successful_submissions":4}
|
2014-06-21T10:01:03
|
2018-02-06T18:33:47
|
setter
|
```cpp
#include <stdio.h>
#include <stdlib.h>
struct tree {
int count; // how many are alive at this tree
int l; // leftmost index
tree *parent;
tree *left;
tree *right;
};
int n;
tree *root;
tree *curr;
tree *leftmost() {
// find the leftmost alive leaf
tree *t = root;
while (t->left) {
if (t->left->count) {
// there are alive leaves on the left. go there
t = t->left;
} else {
t = t->right;
}
}
return t;
}
tree *create(int l, int r) {
// create a tree on range [l,r)
tree *t = (tree*)malloc(sizeof(tree));
t->count = r - l;
t->l = l;
t->parent = 0;
t->left = 0;
t->right = 0;
if (r - l > 1) {
int m = l + r >> 1;
t->left = create(l, m);
t->right = create(m, r);
t->left->parent = t;
t->right->parent = t;
}
return t;
}
void init() {
root = create(0, n);
curr = leftmost();// start at person 0
}
int count_right(tree *t) {
// how many alive leaves are to the right of leaf t?
int ct = 0;
while (t->parent) {
tree *p = t->parent;
if (p->left == t) {
ct += p->right->count;
}
t = p;
}
return ct;
}
void forward(int k) {
// assumes k < root->count
int ct = count_right(curr);
if (k > ct) {
// wrap around
k -= ct + 1;
curr = leftmost();
}
if (k) {
// go up
while (curr->parent) {
tree *p = curr->parent;
if (p->left == curr) {
if (k <= p->right->count) {
curr = p->right;
break;
} else {
k -= p->right->count;
}
}
curr = p;
}
// go down
while (curr->left) {
if (k <= curr->left->count) {
curr = curr->left;
} else {
k -= curr->left->count;
curr = curr->right;
}
}
}
}
void eliminate() {
// eliminate curr
curr->count = 0;
for (tree *p = curr->parent; p; p = p->parent) {
p->count--;
}
// find next alive leaf
forward(1);
}
int main() {
scanf("%d",&n);
init();
for (int i = 0; i < n - 1; ++i) {
int C;
scanf("%d", &C);
forward(C % (n-i)); // move to C'th person
eliminate(); // eliminate
}
if (curr->l == 0) {
printf("YOU MUST BE TODD\n");
} else {
printf("%d\n", curr->l);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:42
|
2018-02-06T17:55:02
|
C++
|
||||
83 | 3,092 |
reverse-trip-to-jerusalem
|
Reverse Trip to Jerusalem
|
You and your $N-1$ friends recently got tired of playing Trip to Jerusalem (i.e. Musical Chairs). In order to make things interesting again, you decide to invent a new game. And you call it *Reverse Trip to Jerusalem*.
Here's how it works. Instead of arranging the chairs in a circle, the $N$ friends (including you) arrange yourselves in a circle. Then exactly one person in the circle holds the chair.
For the first round, all $N$ of you will be in the circle. The music starts and plays for $C_1$ seconds. Every second, the person holding the chair shall pass it to the person to his left. The person who receives the chair when the music ends is OUT and he/she is not included in the circle in the subsequent rounds. The person to his left then receives the chair. And that's where the chair starts for the second round.
For the $i^\text{th}$ round, $N-i+1$ players remain and the person holding the chair is the person to the left of the most recently outed person. The music starts and plays for $C_i$ seconds. The procedure for passing the chair is the same as the first round. The player who receives the chair when the music ends is OUT.
The person who remains after $N-1$ rounds is the winner.
Of course, you want to win this. It is your dream and you believe that you will survive. The person who initially holds the chair in the first round is Todd. You wish to know where to position yourself in order to win the game.
**Input Format**
The input consists of two lines.
The first line contains a single integer $N$.
The second line contains $N-1$ integers, the $C_i$'s, each separated by single spaces.
**Output Format**
Output a single line describing the winning position. If the winning position is the $P^\text{th}$ position to the left of Todd, then output the integer $P$ (Note that $0 < P < N$). However, if the winning position is Todd's position, print `YOU MUST BE TODD`.
**Constraints**
$1 \le N \le 2\cdot 10^5$
$1 \le C_i \le 2\cdot 10^5$
**Sample Input 1**
5
1 2 2 4
**Sample Output 1**
2
**Sample Input 2**
2
1
**Sample Output 2**
YOU MUST BE TODD
**Explanation**
In the first case, let $P_1$, $P_2$, $P_3$ and $P_4$ be the four persons to Todd's left, in that order. The first round begins with Todd passing the chair to $P_1$, which subsequently outs him (since the music is only 1 second long). The second round starts with $P_2$ holding the chair. The music ends when $P_4$ receives the chair, thus forcing him out of the game. The third round starts with Todd again and stops at $P_3$. The fourth round starts with Todd and ends with Todd and so $P_2$ survives.
In the second case, Todd passes the chair to the other person, the 1-second music stops and that person is out of the game. Hence, the only way to win the game is to become Todd.
|
code
|
Winning in Trip to Jerusalem is so two thousand and late. Winning Reverse Trip to Jerusalem is what matters.
|
ai
|
2014-06-19T02:26:40
|
2018-03-13T12:03:35
| null | null | null |
You and your $N-1$ friends recently got tired of playing Trip to Jerusalem (i.e. Musical Chairs). In order to make things interesting again, you decide to invent a new game. And you call it *Reverse Trip to Jerusalem*.
Here's how it works. Instead of arranging the chairs in a circle, the $N$ friends (including you) arrange yourselves in a circle. Then exactly one person in the circle holds the chair.
For the first round, all $N$ of you will be in the circle. The music starts and plays for $C_1$ seconds. Every second, the person holding the chair shall pass it to the person to his left. The person who receives the chair when the music ends is OUT and he/she is not included in the circle in the subsequent rounds. The person to his left then receives the chair. And that's where the chair starts for the second round.
For the $i^\text{th}$ round, $N-i+1$ players remain and the person holding the chair is the person to the left of the most recently outed person. The music starts and plays for $C_i$ seconds. The procedure for passing the chair is the same as the first round. The player who receives the chair when the music ends is OUT.
The person who remains after $N-1$ rounds is the winner.
Of course, you want to win this. It is your dream and you believe that you will survive. The person who initially holds the chair in the first round is Todd. You wish to know where to position yourself in order to win the game.
**Input Format**
The input consists of two lines.
The first line contains a single integer $N$.
The second line contains $N-1$ integers, the $C_i$'s, each separated by single spaces.
**Output Format**
Output a single line describing the winning position. If the winning position is the $P^\text{th}$ position to the left of Todd, then output the integer $P$ (Note that $0 < P < N$). However, if the winning position is Todd's position, print `YOU MUST BE TODD`.
**Constraints**
$1 \le N \le 2\cdot 10^5$
$1 \le C_i \le 2\cdot 10^5$
*Note:* The time limit is half of the usual time limit.
**Sample Input 1**
5
1 2 2 4
**Sample Output 1**
2
**Sample Input 2**
2
1
**Sample Output 2**
YOU MUST BE TODD
**Explanation**
In the first case, let $P_1$, $P_2$, $P_3$ and $P_4$ be the four persons to Todd's left, in that order. The first round begins with Todd passing the chair to $P_1$, which subsequently outs him (since the music is only 1 second long). The second round starts with $P_2$ holding the chair. The music ends when $P_4$ receives the chair, thus forcing him out of the game. The third round starts with Todd again and stops at $P_3$. The fourth round starts with Todd and ends with Todd and so $P_2$ survives.
In the second case, Todd passes the chair to the other person, the 1-second music stops and that person is out of the game. Hence, the only way to win the game is to become Todd.
| 0.5 |
["c","cpp","java","python3","python","cpp14"]
|
Hard
| null | null | null | null | null |
{"contest_participation":83,"challenge_submissions":12,"successful_submissions":4}
|
2014-06-21T10:01:03
|
2018-02-06T18:33:47
|
tester
|
```cpp
#include <cstdio>
#include <cstring>
#include <string>
#include <map>
#include <algorithm>
using namespace std;
int f[200010];
int main() {
int n;
scanf("%d",&n);
for (int i = 0; i + 1 < n; ++i) {
scanf("%d",f + i);
}
int x = 0;
for (int i = 2; i <= n; ++i) {
x = (x + f[n - i] + 1) % i;
}
if (x == 0) {
puts("YOU MUST BE TODD");
}
else {
printf("%d\n",x);
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:42
|
2018-02-06T17:55:02
|
C++
|
||||
84 | 2,579 |
messy-medians
|
Messy Medians
|
Robin is stuck doing a terminally boring data entry job. She has to enter a lot of numeric observations manually and report running medians after each step to her project lead. The task is sufficiently mind-numbing for her to make a lot of entry errors. Fortunately, she has a keen eye and often notices her mistakes. On the other hand, sometimes she makes mistakes while spotting - or correcting - previous mistakes, and so on.
<br>
Your task is to implement a program that will help Robin finish this boring job as soon as possible. The program will accept user input and report a running median for all the observations entered so far. It should also be capable of rolling back to any previous state (including those that were previously rolled back on their own).
**Input Format**
First line contains an integer,*T*, the total number of lines to follow.
<br>
Each of the following *T* lines contains either:
1. a positive integer *N* that will contribute in calculation of the current running median;
2. or a request to roll back to a previous state, which is represented by a negative number between -1 and -*M*, where *M* is the total number of queries executed so far. -1 requests a return to the immediately preceding state (which actually results in no state change), while -*M* requests a return to the state after entering the very first number.
**Output Format**
Output *T* integers, representing current running medians after performing operations on corresponding lines in the input.
**Constraints**
1 ≤ _T_ ≤ 10<sup>5</sup>
1 ≤ _N_ ≤ 10<sup>9</sup>
1 ≤ _M_ ≤ number of queries executed so far.
**Notes**
* You will never be asked to roll back to a non-existent state, or a state for which the running median is not well-defined. In particular, the first line after *T* will always be a positive number.
* You should print out the median after executing each query, including rollbacks.
* For collections with even number of elements we report the smaller of the two candidate medians.
**Sample Input**
10
1
5
-2
3
2
5
4
-7
2
-3
**Sample Output**
1
1
1
1
2
2
3
1
1
3
**Explanation**
(This represents the collection of the numbers tracked after each step, with median in bold.)
Step 1: 1 -> [**1**]
Step 2: 5 -> [**1**, 5]
Step 3: request a return to state after step (3 - 2) = 1 -> [**1**]
Step 4: 3 -> [**1**, 3]
Step 5: 2 -> [1, **2**, 3]
Step 6: 5 -> [1, **2**, 3, 5]
Step 7: 4 -> [1, 2, **3**, 4, 5]
Step 8: request a return to state after step (8 - 7) = 1 -> [**1**]
Step 9: 2 -> [**1**, 2]
Step 10: request a return to state after step (10 - 3) = 7 -> [1, 2, **3**, 4, 5]
---
**Tested by:** [Abhiranjan Kumar](/abhiranjan)
|
code
|
(Add|Remove|getMedian)
|
ai
|
2014-06-05T17:02:31
|
2016-09-01T16:22:55
| null | null | null |
Robin is stuck doing a terminally boring data entry job. She has to enter a lot of numeric observations manually and report running medians after each step to her project lead. The task is sufficiently mind-numbing for her to make a lot of entry errors. Fortunately, she has a keen eye and often notices her mistakes. On the other hand, sometimes she makes mistakes while spotting - or correcting - previous mistakes, and so on.
<br>
Your task is to implement a program that will help Robin finish this boring job as soon as possible. The program will accept user input and report a running median for all the observations entered so far. It should also be capable of rolling back to any previous state (including those that were previously rolled back on their own).
**Input Format**
First line contains an integer,*T*, the total number of lines to follow.
<br>
Each of the following *T* lines contains either:
1. a positive integer *N* that will contribute in calculation of the current running median;
2. or a request to roll back to a previous state, which is represented by a negative number between -1 and -*M*, where *M* is the total number of queries executed so far. -1 requests a return to the immediately preceding state (which actually results in no state change), while -*M* requests a return to the state after entering the very first number.
**Output Format**
Output *T* integers, representing current running medians after performing operations on corresponding lines in the input.
**Constraints**
1 ≤ _T_ ≤ 10<sup>5</sup>
1 ≤ _N_ ≤ 10<sup>9</sup>
1 ≤ _M_ ≤ number of queries executed so far.
**Notes**
* You will never be asked to roll back to a non-existent state, or a state for which the running median is not well-defined. In particular, the first line after *T* will always be a positive number.
* You should print out the median after executing each query, including rollbacks.
* For collections with even number of elements we report the smaller of the two candidate medians.
**Sample Input**
10
1
5
-2
3
2
5
4
-7
2
-3
**Sample Output**
1
1
1
1
2
2
3
1
1
3
**Explanation**
(This represents the collection of the numbers tracked after each step, with median in bold.)
Step 1: 1 -> [**1**]
Step 2: 5 -> [**1**, 5]
Step 3: request a return to state after step (3 - 2) = 1 -> [**1**]
Step 4: 3 -> [**1**, 3]
Step 5: 2 -> [1, **2**, 3]
Step 6: 5 -> [1, **2**, 3, 5]
Step 7: 4 -> [1, 2, **3**, 4, 5]
Step 8: request a return to state after step (8 - 7) = 1 -> [**1**]
Step 9: 2 -> [**1**, 2]
Step 10: request a return to state after step (10 - 3) = 7 -> [1, 2, **3**, 4, 5]
---
**Tested by:** [Abhiranjan Kumar](/abhiranjan)
| 0.574468 |
["haskell","clojure","scala","erlang","sbcl","ocaml","fsharp","racket","elixir"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-23T20:20:45
|
2016-12-07T10:52:12
|
setter
|
object Solution {
class BinomHeap[T](lt: (T, T) => Boolean) {
def min(a: Option[T], b: Option[T]): Option[T] =
(a, b) match {
case (None, None) => None
case (None, _) => b
case (_, None) => a
case (Some(a), Some(b)) =>
if (lt(a, b))
Some(a)
else
Some(b)
}
case class Node(val rank: Int, val x: T, val ts: List[Node]) {
val size = 1 << rank
override def toString =
"Tree (" ++ rank.toString ++ "): " ++ x.toString ++ " [" ++ ((ts map (_.toString)) mkString ", ") ++ "]"
def link(other: Node) = {
require(rank == other.rank)
if (lt(x, other.x))
new Node(rank + 1, x, other :: ts)
else
new Node(rank + 1, other.x, this :: other.ts)
}
}
class Heap(xxmin: => Option[T], val size: Int, val ts: List[Node]) {
lazy val xmin: Option[T] = xxmin
override def toString =
"Heap:\n" ++ ((ts map (x => "\t" ++ x.toString)) mkString "\n") ++ "\n"
def isEmpty = size == 0
def insert(x: T): Heap =
insTree(new Node(0, x, Nil))
def merge(other: Heap) =
new Heap(min(xmin, other.xmin), size + other.size, mergeAux(other).ts)
def deleteMin = {
val (t @ Node(_, x, ts1), h2) = removeMinTree
mkHeap(t.size - 1, ts1.reverse) merge h2
}
private def mkHeap(sz: Int, ts: List[Node]): Heap =
new Heap((new Heap(None, sz, ts)).findMin, sz, ts)
private def findMin = {
val (t, _) = removeMinTree
Some(t.x)
}
@annotation.tailrec
private def insTree(t: Node): Heap =
ts match {
case Nil => new Heap(Some(t.x), size + t.size, List(t))
case t0 :: ts0 =>
if (t.rank < t0.rank)
new Heap(min(Some(t.x), xmin), size + t.size, t :: ts)
else {
require(t.rank == t0.rank)
mkHeap(size - t0.size, ts0) insTree (t link t0)
}
}
private def mergeAux(other: Heap): Heap =
(ts, other.ts) match {
case (_, Nil) => this
case (Nil, _) => other
case (t1 :: ts1, t2 :: ts2) =>
if (t1.rank < t2.rank)
mkHeap(size + other.size, t1 :: (mkHeap(size - t1.size, ts1) mergeAux other).ts)
else if (t2.rank < t1.rank)
mkHeap(size + other.size, t2 :: (mergeAux(mkHeap(other.size - t2.size, ts2))).ts)
else
(mkHeap(size - t1.size, ts1) mergeAux mkHeap(size - t2.size, ts2)) insTree (t1 link t2)
}
private def removeMinTree: (Node, Heap) = {
ts match {
case List(t) => (t, new Heap(None, 0, Nil))
case t :: ts => {
val (t0, h0) = mkHeap(size - t.size, ts).removeMinTree
if (lt(t.x, t0.x))
(t, mkHeap(size - t.size, ts))
else
(t0, mkHeap(t.size + h0.size, t :: h0.ts))
}
case _ => (ts.head, this)
}
}
}
def empty: Heap = new Heap(None, 0, Nil)
}
class RunningMedian(val l: BinomHeap[Int]#Heap, val r: BinomHeap[Int]#Heap) {
require(l.size == r.size || l.size == r.size + 1)
def med = l.xmin
def add(x: Int) = {
if (l.size == 0 || x <= l.xmin.get) {
val nl = l insert x
if (nl.size == r.size + 2) {
val x0 = nl.xmin
val nl0 = nl.deleteMin
new RunningMedian(nl0, r insert x0.get)
}
else
new RunningMedian(nl, r)
}
else {
val nr = r insert x
if (nr.size > l.size) {
val x0 = nr.xmin
val nr0 = nr.deleteMin
new RunningMedian(l insert x0.get, nr0)
}
else
new RunningMedian(l, nr)
}
}
}
@annotation.tailrec
def loop(n: Int, lim: Int, rm: RunningMedian, store: collection.immutable.Vector[RunningMedian]): Unit = {
if (n > lim)
()
else {
val x = readLine.toInt
if (x > 0) {
val rm0 = rm add x
println(rm0.med.get)
loop(n + 1, lim, rm0, store :+ rm0)
}
else {
val rm0 = store(n + x - 1)
println(rm0.med.get)
loop(n + 1, lim, rm0, store :+ rm0)
}
}
}
def main(args: Array[String]) = {
val rm = new RunningMedian(new BinomHeap[Int](_ > _).empty, new BinomHeap[Int](_ < _).empty)
val n = readLine.toInt
loop(1, n, rm, collection.immutable.Vector())
}
}
|
not-set
|
2016-04-24T02:02:43
|
2016-04-24T02:02:43
|
Python
|
85 | 2,579 |
messy-medians
|
Messy Medians
|
Robin is stuck doing a terminally boring data entry job. She has to enter a lot of numeric observations manually and report running medians after each step to her project lead. The task is sufficiently mind-numbing for her to make a lot of entry errors. Fortunately, she has a keen eye and often notices her mistakes. On the other hand, sometimes she makes mistakes while spotting - or correcting - previous mistakes, and so on.
<br>
Your task is to implement a program that will help Robin finish this boring job as soon as possible. The program will accept user input and report a running median for all the observations entered so far. It should also be capable of rolling back to any previous state (including those that were previously rolled back on their own).
**Input Format**
First line contains an integer,*T*, the total number of lines to follow.
<br>
Each of the following *T* lines contains either:
1. a positive integer *N* that will contribute in calculation of the current running median;
2. or a request to roll back to a previous state, which is represented by a negative number between -1 and -*M*, where *M* is the total number of queries executed so far. -1 requests a return to the immediately preceding state (which actually results in no state change), while -*M* requests a return to the state after entering the very first number.
**Output Format**
Output *T* integers, representing current running medians after performing operations on corresponding lines in the input.
**Constraints**
1 ≤ _T_ ≤ 10<sup>5</sup>
1 ≤ _N_ ≤ 10<sup>9</sup>
1 ≤ _M_ ≤ number of queries executed so far.
**Notes**
* You will never be asked to roll back to a non-existent state, or a state for which the running median is not well-defined. In particular, the first line after *T* will always be a positive number.
* You should print out the median after executing each query, including rollbacks.
* For collections with even number of elements we report the smaller of the two candidate medians.
**Sample Input**
10
1
5
-2
3
2
5
4
-7
2
-3
**Sample Output**
1
1
1
1
2
2
3
1
1
3
**Explanation**
(This represents the collection of the numbers tracked after each step, with median in bold.)
Step 1: 1 -> [**1**]
Step 2: 5 -> [**1**, 5]
Step 3: request a return to state after step (3 - 2) = 1 -> [**1**]
Step 4: 3 -> [**1**, 3]
Step 5: 2 -> [1, **2**, 3]
Step 6: 5 -> [1, **2**, 3, 5]
Step 7: 4 -> [1, 2, **3**, 4, 5]
Step 8: request a return to state after step (8 - 7) = 1 -> [**1**]
Step 9: 2 -> [**1**, 2]
Step 10: request a return to state after step (10 - 3) = 7 -> [1, 2, **3**, 4, 5]
---
**Tested by:** [Abhiranjan Kumar](/abhiranjan)
|
code
|
(Add|Remove|getMedian)
|
ai
|
2014-06-05T17:02:31
|
2016-09-01T16:22:55
| null | null | null |
Robin is stuck doing a terminally boring data entry job. She has to enter a lot of numeric observations manually and report running medians after each step to her project lead. The task is sufficiently mind-numbing for her to make a lot of entry errors. Fortunately, she has a keen eye and often notices her mistakes. On the other hand, sometimes she makes mistakes while spotting - or correcting - previous mistakes, and so on.
<br>
Your task is to implement a program that will help Robin finish this boring job as soon as possible. The program will accept user input and report a running median for all the observations entered so far. It should also be capable of rolling back to any previous state (including those that were previously rolled back on their own).
**Input Format**
First line contains an integer,*T*, the total number of lines to follow.
<br>
Each of the following *T* lines contains either:
1. a positive integer *N* that will contribute in calculation of the current running median;
2. or a request to roll back to a previous state, which is represented by a negative number between -1 and -*M*, where *M* is the total number of queries executed so far. -1 requests a return to the immediately preceding state (which actually results in no state change), while -*M* requests a return to the state after entering the very first number.
**Output Format**
Output *T* integers, representing current running medians after performing operations on corresponding lines in the input.
**Constraints**
1 ≤ _T_ ≤ 10<sup>5</sup>
1 ≤ _N_ ≤ 10<sup>9</sup>
1 ≤ _M_ ≤ number of queries executed so far.
**Notes**
* You will never be asked to roll back to a non-existent state, or a state for which the running median is not well-defined. In particular, the first line after *T* will always be a positive number.
* You should print out the median after executing each query, including rollbacks.
* For collections with even number of elements we report the smaller of the two candidate medians.
**Sample Input**
10
1
5
-2
3
2
5
4
-7
2
-3
**Sample Output**
1
1
1
1
2
2
3
1
1
3
**Explanation**
(This represents the collection of the numbers tracked after each step, with median in bold.)
Step 1: 1 -> [**1**]
Step 2: 5 -> [**1**, 5]
Step 3: request a return to state after step (3 - 2) = 1 -> [**1**]
Step 4: 3 -> [**1**, 3]
Step 5: 2 -> [1, **2**, 3]
Step 6: 5 -> [1, **2**, 3, 5]
Step 7: 4 -> [1, 2, **3**, 4, 5]
Step 8: request a return to state after step (8 - 7) = 1 -> [**1**]
Step 9: 2 -> [**1**, 2]
Step 10: request a return to state after step (10 - 3) = 7 -> [1, 2, **3**, 4, 5]
---
**Tested by:** [Abhiranjan Kumar](/abhiranjan)
| 0.574468 |
["haskell","clojure","scala","erlang","sbcl","ocaml","fsharp","racket","elixir"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-23T20:20:45
|
2016-12-07T10:52:12
|
tester
|
**Approach #1**
module Main where
import Data.List
import Data.Char
import qualified Data.Vector as V
import qualified Data.Map as Map
import Text.Printf
data SegmentTree = Leaf {
count :: Int
, index :: Int
}
| Node {
count :: Int
, leftIdx :: Int
, rightIdx :: Int
, leftTree :: SegmentTree
, rightTree :: SegmentTree
}
initialiseTree :: Int -> SegmentTree
initialiseTree = createNode 1
where
createNode l r
| l == r = Leaf 0 l
| otherwise = Node 0 l r (createNode l mid) (createNode (mid+1) r)
where
mid = (l+r) `div` 2
insertNode :: Int -> SegmentTree -> SegmentTree
insertNode val lf@(Leaf cnt idx) = if idx == val then lf{count = cnt+1} else lf
insertNode val nd@(Node cnt lIdx rIdx lTree rTree)
| lIdx <= val && val <= rIdx = nd {count = cnt+1, leftTree = insertNode val lTree, rightTree = insertNode val rTree}
| otherwise = nd
getElements :: Int -> SegmentTree -> Int
getElements val (Leaf cnt idx) = if idx <= val then cnt else 0
getElements val (Node cnt lIdx rIdx lTree rTree)
| lIdx > val = 0
| rIdx < val = cnt
| otherwise = getElements val lTree + getElements val rTree
getMedian :: SegmentTree -> Int
getMedian root = binarySearch (leftIdx root) (rightIdx root)
where
cnt = (count root + 1)`div`2
binarySearch l r
| l == r = l
| getElements mid root >= cnt = binarySearch l mid
| otherwise = binarySearch (mid+1) r
where mid = (l+r+0) `div` 2
main :: IO ()
main = getContents >>= mapM_ print. solve. map read. words
solve (n:arr)
| n /= length arr = error $ "length arr = " ++ show (length arr)
| any (\x -> x == 0 || x > 10^9) arr = error $ "arr = " ++ show arr
| otherwise = map getIdx [ getMedian (trees V.! i) |i <- [1..len]]
where
ans = [ (indAns i, trees V.! i) | i <- [1..len]]
indAns i = getIdx $ getMedian (trees V.! i)
root = initialiseTree. length $ sarr
vArr = V.fromList arr
trees = V.fromList $ root : [ let v = vArr V.! (i - 1) in
if v > 0 then
insertNode (getRIdx v) (trees V.! (i-1))
else trees V.! (i+v)
| i <- [1..len]
]
sarr = map head. group. dropWhile (<= 0). sort $ arr
len = length arr
idx, revIdx :: Map.Map Int Int
revIdx = Map.fromList. zip sarr $ [1..]
idx = Map.fromList. zip [(1::Int)..] $ sarr
getRIdx key = Map.findWithDefault (-1) key revIdx
getIdx key = Map.findWithDefault (-1) key idx
---
**Approach #2**
import qualified Data.Vector as V
import qualified Data.MultiSet as MultiSet
import Text.Printf -- printf "%0.6f" (1.0)
data MSet a = MSet {
mSet :: MultiSet.MultiSet a
, size :: Int
}-- deriving (Show)
instance Show a => Show (MSet a) where
show (MSet st sz) = printf "%d: %s" sz (show.MultiSet.toList $ st)
emptyMSet :: MSet a
emptyMSet = MSet MultiSet.empty 0
insertIntoMSet, deleteFromMSet :: (Show a, Ord a) => a -> MSet a -> MSet a
insertIntoMSet x (MSet st sz) = MSet (MultiSet.insert x st) (sz+1)
deleteFromMSet x (MSet st sz)
| MultiSet.member x st = MSet (MultiSet.delete x st) (sz-1)
| otherwise = error $ printf "member %s not found in set = %s\n" (show x) (show st)
data Container a = Container {
firstSet :: MSet a
, secondSet :: MSet a
}-- deriving (Show)
instance Show a => Show (Container a) where
show (Container fSet sSet) = printf "{%-25s %-25s}" (show fSet) (show sSet)
emptyContainer :: Container Int
emptyContainer = Container emptyMSet emptyMSet
addToContainer :: (Show a, Ord a) => a -> Container a -> Container a
addToContainer x cont
| sz1 + sz2 == 0 = cont { firstSet = insertIntoMSet x fSet }
| sz2 == 0 && x >= mx1 = cont { secondSet = insertIntoMSet x sSet }
| sz2 == 0 && x < mx1 = cont { firstSet = insertIntoMSet x (deleteFromMSet mx1 fSet),
secondSet = insertIntoMSet mx1 sSet }
| sz1 == sz2 && x <= mn2 = cont { firstSet = insertIntoMSet x fSet }
| sz1 == sz2 && x > mn2 = cont { firstSet = insertIntoMSet mn2 fSet,
secondSet = insertIntoMSet x (deleteFromMSet mn2 sSet) }
| sz1 == sz2+1 && x >= mx1 = cont { secondSet = insertIntoMSet x sSet}
| sz1 == sz2+1 && x < mx1 = cont { firstSet = insertIntoMSet x (deleteFromMSet mx1 fSet),
secondSet = insertIntoMSet mx1 sSet}
| otherwise = error $ printf "Error\nfirstSet = %s\nsecondSet = %s\nmx1 = %s, mn2 = %s, x = %s" (show fSet) (show sSet) (show mx1) (show mn2) (show x)
where
sz1 = size. firstSet $ cont
sz2 = size. secondSet $ cont
fSet = firstSet cont
sSet = secondSet cont
mx1 = MultiSet.findMax. mSet $ fSet
mn2 = MultiSet.findMin. mSet $ sSet
getMedian :: (Show a, Ord a) => Container a -> a
getMedian = MultiSet.findMax. mSet. firstSet
main :: IO ()
main = getContents >>= mapM_ (print. getMedian). tail. V.toList. validate. map read. lines
validate (n:a)
| n /= len = error $ printf "n = %d, len = %d\n" n len
| any (\x -> x > 10^9|| x < -n) a = error $ printf "a = %s\n" (show a)
| otherwise = containers
where
len = length a
vArr = V.fromList a
containers1 = scanl (flip addToContainer) emptyContainer a
containers = V.fromList $ emptyContainer : [getContainer i | i <- [1..n]]
getContainer idx
| val >= 0 = addToContainer val (containers V.! (idx-1))
| val < 0 = containers V.! (idx + val)
where
val = vArr V.! (idx-1)
|
not-set
|
2016-04-24T02:02:43
|
2016-04-24T02:02:43
|
Python
|
86 | 3,129 |
world-peace
|
World Peace
|
The Artifact of World Peace was obtained by the evil Pharaoh. He smashed it into pieces and hid them inside a temple. The temple has a very elaborate and confusing floor plan. It contained different rooms. Each room has a trap. Moreover, to go from one room to another, you must pass by a corridor and each of these also has a trap. The Pharaoh suddenly realized he was low on budget because the college tuition fee of his children suddenly increased. Unprepared to sacrifice the future of his children, he decided to not push through with the traps inside the rooms BUT retain the traps in the corridors. Don't be fooled though, it is still very difficult to infiltrate this temple.
You decide that you want to get the pieces of this Sacred Artifact of _World Peace_, put these together to recreate the Artifact of _World Peace_ and then finally obtain millions of dollars by selling it on eBay.
You list down all the known rooms of this temple. Each corridor has a trap and a certain skill level is required to clear this trap. Furthermore, to secure all pieces of the artifact, you realize that you just need to form the safest routes between pairs of rooms.
To summarize, the temple has $R$ known rooms and $C$ corridors. Each corridor connects two rooms and has its corresponding trap. Each trap has a certain _skill level_ $s$ required in order to clear it. If your skill level is below this $s$, you fail the trap and subsequently die a slow, horrible and painful death. After planning, you realize you just have to travel between $P$ pairs of rooms. For each pair of rooms $A$ and $B$, you must select the safest corridors (i.e. the path which requires the lowest skill level) to travel from room $A$ to room $B$. Given these information, you must find out the minimum skill level you must have in order to survive travelling through the corridors which connect each of these pairs of rooms.
**Input Format**
The first line of input contains two integers, the number of rooms $R$ in the temple and the number of corridors $C$ in the temple. The rooms are numbered from $1$ to $R$.
The next $C$ lines each contain three integers: $A$, $B$ and $s$ in that order. This tells us that to survive the corridor connecting room $A$ and room $B$, your skill level must be $s$ or higher.
The next line contains a single integer, $P$. This indicates how many pairs of rooms you must plan a route for.
The next $P$ lines each contain two integers, $A$ and $B$. This tells us that you must plan the safest route between rooms $A$ and $B$.
**Output Format**
Output a single line containing a single integer, $S$, the minimum skill level you must have in order to travel between each of the $P$ pairs of rooms.
If it is impossible to travel between one of the $P$ pairs of rooms, output `MISSION IMPOSSIBLE`.
**Constraints**
$1 \le R \le 10^5$
$1 \le C \le 10^5$
$1 \le P \le 10^5$
$1 \le A, B \le R$
$A \ne B$
$1 \le s \le 10^6$
**Sample Input 1**
8 12
1 2 1
1 4 2
2 3 5
2 4 4
3 4 2
5 2 11
5 2 10
5 6 1
6 8 3
7 6 2
8 7 3
5 8 4
2
1 3
5 8
**Sample Output 1**
3
**Sample Input 2**
3 1
1 3 100
1
1 2
**Sample Output 2**
MISSION IMPOSSIBLE
**Explanation**
The first case corresponds to the following floor plan:

The safest path to travel from room $1$ to room $3$ is going from room $1$ to room $4$ then room $4$ to room $3$. The minimum skill level to safely traverse the corridors connecting these rooms is $2$. The safest path to travel from room $5$ to room $8$ is going from room $5$ to room $6$, then room $7$ and finally room $8$ (or if you're feeling less adventurous, you could skip going to room $7$ and travel from $5$ to $6$ to $8$ instead). The minimum skill level to safely traverse these corridors is $3$. Thus to travel between all $P = 2$ pairs of rooms, one must have a minimum skill level of $3$.
For the second case, there is no way to get from room $1$ to room $2$ regardless of your skill level. How did they get the pieces there? It shall remain a mystery.
|
code
|
How skillful must you be to retrieve The Artifact of World Peace?
|
ai
|
2014-06-22T19:04:22
|
2018-02-06T18:26:45
| null | null | null |
The Artifact of World Peace was obtained by the evil Pharaoh. He smashed it into pieces and hid them inside a temple. The temple has a very elaborate and confusing floor plan. It contained different rooms. Each room has a trap. Moreover, to go from one room to another, you must pass by a corridor and each of these also has a trap. The Pharaoh suddenly realized he was low on budget because the college tuition fee of his children suddenly increased. Unprepared to sacrifice the future of his children, he decided to not push through with the traps inside the rooms BUT retain the traps in the corridors. Don't be fooled though, it is still very difficult to infiltrate this temple.
You decide that you want to get the pieces of this Sacred Artifact of _World Peace_, put these together to recreate the Artifact of _World Peace_ and then finally obtain millions of dollars by selling it on eBay.
You list down all the known rooms of this temple. Each corridor has a trap and a certain skill level is required to clear this trap. Furthermore, to secure all pieces of the artifact, you realize that you just need to form the safest routes between pairs of rooms.
To summarize, the temple has $R$ known rooms and $C$ corridors. Each corridor connects two rooms and has its corresponding trap. Each trap has a certain _skill level_ $s$ required in order to clear it. If your skill level is below this $s$, you fail the trap and subsequently die a slow, horrible and painful death. After planning, you realize you just have to travel between $P$ pairs of rooms. For each pair of rooms $A$ and $B$, you must select the safest corridors (i.e. the path which requires the lowest skill level) to travel from room $A$ to room $B$. Given these information, you must find out the minimum skill level you must have in order to survive travelling through the corridors which connect each of these pairs of rooms.
**Input Format**
The first line of input contains two integers, the number of rooms $R$ in the temple and the number of corridors $C$ in the temple. The rooms are numbered from $1$ to $R$.
The next $C$ lines each contain three integers: $A$, $B$ and $s$ in that order. This tells us that to survive the corridor connecting room $A$ and room $B$, your skill level must be $s$ or higher.
The next line contains a single integer, $P$. This indicates how many pairs of rooms you must plan a route for.
The next $P$ lines each contain two integers, $A$ and $B$. This tells us that you must plan the safest route between rooms $A$ and $B$.
**Output Format**
Output a single line containing a single integer, $S$, the minimum skill level you must have in order to travel between each of the $P$ pairs of rooms.
If it is impossible to travel between one of the $P$ pairs of rooms, output `MISSION IMPOSSIBLE`.
**Constraints**
$1 \le R \le 10^5$
$1 \le C \le 10^5$
$1 \le P \le 10^5$
$1 \le A, B \le R$
$A \ne B$
$1 \le s \le 10^6$
**Sample Input 1**
8 12
1 2 1
1 4 2
2 3 5
2 4 4
3 4 2
5 2 11
5 2 10
5 6 1
6 8 3
7 6 2
8 7 3
5 8 4
2
1 3
5 8
**Sample Output 1**
3
**Sample Input 2**
3 1
1 3 100
1
1 2
**Sample Output 2**
MISSION IMPOSSIBLE
**Explanation**
The first case corresponds to the following floor plan:

The safest path to travel from room $1$ to room $3$ is going from room $1$ to room $4$ then room $4$ to room $3$. The minimum skill level to safely traverse the corridors connecting these rooms is $2$. The safest path to travel from room $5$ to room $8$ is going from room $5$ to room $6$, then room $7$ and finally room $8$ (or if you're feeling less adventurous, you could skip going to room $7$ and travel from $5$ to $6$ to $8$ instead). The minimum skill level to safely traverse these corridors is $3$. Thus to travel between all $P = 2$ pairs of rooms, one must have a minimum skill level of $3$.
For the second case, there is no way to get from room $1$ to room $2$ regardless of your skill level. How did they get the pieces there? It shall remain a mystery.
| 0.5 |
["c","cpp","java","python3","python","cpp14"]
|
Hard
| null | null | null | null | null | null |
2014-06-24T05:03:25
|
2018-02-06T18:32:10
|
setter
|
```cpp
#include <stdio.h>
struct edge {
int a, b, s;
};
int ea[111111];
int eb[111111];
int es[111111];
int pa[111111];
int pb[111111];
int ps[111111];
int r, c, p;
int find(int n) {
return ps[n] < 0 ? n : ps[n] = find(ps[n]);
}
int kaya(int cost) {
for (int i = 0; i < r; i++) ps[i] = -1;
for (int i = 0; i < c; i++) {
if (es[i] > cost) continue;
int fa = find(ea[i]);
int fb = find(eb[i]);
if (fa != fb) {
if (ps[fa] == ps[fb]) ps[fb]--;
if (ps[fa] > ps[fb]) {
ps[fa] = fb;
} else {
ps[fb] = fa;
}
}
}
for (int i = 0; i < p; i++) {
if (find(pa[i]) != find(pb[i])) return 0;
}
return 1;
}
int main() {
scanf("%d%d", &r, &c);
for( int i = 0; i < c; i++) {
int a, b, s;
scanf("%d%d%d", &a, &b, &s);
ea[i] = --a;
eb[i] = --b;
es[i] = s;
}
scanf("%d", &p);
for (int i = 0; i < p; i++) {
int a, b;
scanf("%d%d", &a, &b);
pa[i] = --a;
pb[i] = --b;
}
int L = -1;
int R = 1000001;
if (!kaya(R)) {
printf("MISSION IMPOSSIBLE\n");
} else {
while (R - L > 1) {
int M = L + R >> 1;
(kaya(M) ? R : L) = M;
}
printf("%d\n", R);
}
}
```
|
not-set
|
2016-04-24T02:02:43
|
2018-02-06T18:26:46
|
C++
|
||||
87 | 3,129 |
world-peace
|
World Peace
|
The Artifact of World Peace was obtained by the evil Pharaoh. He smashed it into pieces and hid them inside a temple. The temple has a very elaborate and confusing floor plan. It contained different rooms. Each room has a trap. Moreover, to go from one room to another, you must pass by a corridor and each of these also has a trap. The Pharaoh suddenly realized he was low on budget because the college tuition fee of his children suddenly increased. Unprepared to sacrifice the future of his children, he decided to not push through with the traps inside the rooms BUT retain the traps in the corridors. Don't be fooled though, it is still very difficult to infiltrate this temple.
You decide that you want to get the pieces of this Sacred Artifact of _World Peace_, put these together to recreate the Artifact of _World Peace_ and then finally obtain millions of dollars by selling it on eBay.
You list down all the known rooms of this temple. Each corridor has a trap and a certain skill level is required to clear this trap. Furthermore, to secure all pieces of the artifact, you realize that you just need to form the safest routes between pairs of rooms.
To summarize, the temple has $R$ known rooms and $C$ corridors. Each corridor connects two rooms and has its corresponding trap. Each trap has a certain _skill level_ $s$ required in order to clear it. If your skill level is below this $s$, you fail the trap and subsequently die a slow, horrible and painful death. After planning, you realize you just have to travel between $P$ pairs of rooms. For each pair of rooms $A$ and $B$, you must select the safest corridors (i.e. the path which requires the lowest skill level) to travel from room $A$ to room $B$. Given these information, you must find out the minimum skill level you must have in order to survive travelling through the corridors which connect each of these pairs of rooms.
**Input Format**
The first line of input contains two integers, the number of rooms $R$ in the temple and the number of corridors $C$ in the temple. The rooms are numbered from $1$ to $R$.
The next $C$ lines each contain three integers: $A$, $B$ and $s$ in that order. This tells us that to survive the corridor connecting room $A$ and room $B$, your skill level must be $s$ or higher.
The next line contains a single integer, $P$. This indicates how many pairs of rooms you must plan a route for.
The next $P$ lines each contain two integers, $A$ and $B$. This tells us that you must plan the safest route between rooms $A$ and $B$.
**Output Format**
Output a single line containing a single integer, $S$, the minimum skill level you must have in order to travel between each of the $P$ pairs of rooms.
If it is impossible to travel between one of the $P$ pairs of rooms, output `MISSION IMPOSSIBLE`.
**Constraints**
$1 \le R \le 10^5$
$1 \le C \le 10^5$
$1 \le P \le 10^5$
$1 \le A, B \le R$
$A \ne B$
$1 \le s \le 10^6$
**Sample Input 1**
8 12
1 2 1
1 4 2
2 3 5
2 4 4
3 4 2
5 2 11
5 2 10
5 6 1
6 8 3
7 6 2
8 7 3
5 8 4
2
1 3
5 8
**Sample Output 1**
3
**Sample Input 2**
3 1
1 3 100
1
1 2
**Sample Output 2**
MISSION IMPOSSIBLE
**Explanation**
The first case corresponds to the following floor plan:

The safest path to travel from room $1$ to room $3$ is going from room $1$ to room $4$ then room $4$ to room $3$. The minimum skill level to safely traverse the corridors connecting these rooms is $2$. The safest path to travel from room $5$ to room $8$ is going from room $5$ to room $6$, then room $7$ and finally room $8$ (or if you're feeling less adventurous, you could skip going to room $7$ and travel from $5$ to $6$ to $8$ instead). The minimum skill level to safely traverse these corridors is $3$. Thus to travel between all $P = 2$ pairs of rooms, one must have a minimum skill level of $3$.
For the second case, there is no way to get from room $1$ to room $2$ regardless of your skill level. How did they get the pieces there? It shall remain a mystery.
|
code
|
How skillful must you be to retrieve The Artifact of World Peace?
|
ai
|
2014-06-22T19:04:22
|
2018-02-06T18:26:45
| null | null | null |
The Artifact of World Peace was obtained by the evil Pharaoh. He smashed it into pieces and hid them inside a temple. The temple has a very elaborate and confusing floor plan. It contained different rooms. Each room has a trap. Moreover, to go from one room to another, you must pass by a corridor and each of these also has a trap. The Pharaoh suddenly realized he was low on budget because the college tuition fee of his children suddenly increased. Unprepared to sacrifice the future of his children, he decided to not push through with the traps inside the rooms BUT retain the traps in the corridors. Don't be fooled though, it is still very difficult to infiltrate this temple.
You decide that you want to get the pieces of this Sacred Artifact of _World Peace_, put these together to recreate the Artifact of _World Peace_ and then finally obtain millions of dollars by selling it on eBay.
You list down all the known rooms of this temple. Each corridor has a trap and a certain skill level is required to clear this trap. Furthermore, to secure all pieces of the artifact, you realize that you just need to form the safest routes between pairs of rooms.
To summarize, the temple has $R$ known rooms and $C$ corridors. Each corridor connects two rooms and has its corresponding trap. Each trap has a certain _skill level_ $s$ required in order to clear it. If your skill level is below this $s$, you fail the trap and subsequently die a slow, horrible and painful death. After planning, you realize you just have to travel between $P$ pairs of rooms. For each pair of rooms $A$ and $B$, you must select the safest corridors (i.e. the path which requires the lowest skill level) to travel from room $A$ to room $B$. Given these information, you must find out the minimum skill level you must have in order to survive travelling through the corridors which connect each of these pairs of rooms.
**Input Format**
The first line of input contains two integers, the number of rooms $R$ in the temple and the number of corridors $C$ in the temple. The rooms are numbered from $1$ to $R$.
The next $C$ lines each contain three integers: $A$, $B$ and $s$ in that order. This tells us that to survive the corridor connecting room $A$ and room $B$, your skill level must be $s$ or higher.
The next line contains a single integer, $P$. This indicates how many pairs of rooms you must plan a route for.
The next $P$ lines each contain two integers, $A$ and $B$. This tells us that you must plan the safest route between rooms $A$ and $B$.
**Output Format**
Output a single line containing a single integer, $S$, the minimum skill level you must have in order to travel between each of the $P$ pairs of rooms.
If it is impossible to travel between one of the $P$ pairs of rooms, output `MISSION IMPOSSIBLE`.
**Constraints**
$1 \le R \le 10^5$
$1 \le C \le 10^5$
$1 \le P \le 10^5$
$1 \le A, B \le R$
$A \ne B$
$1 \le s \le 10^6$
**Sample Input 1**
8 12
1 2 1
1 4 2
2 3 5
2 4 4
3 4 2
5 2 11
5 2 10
5 6 1
6 8 3
7 6 2
8 7 3
5 8 4
2
1 3
5 8
**Sample Output 1**
3
**Sample Input 2**
3 1
1 3 100
1
1 2
**Sample Output 2**
MISSION IMPOSSIBLE
**Explanation**
The first case corresponds to the following floor plan:

The safest path to travel from room $1$ to room $3$ is going from room $1$ to room $4$ then room $4$ to room $3$. The minimum skill level to safely traverse the corridors connecting these rooms is $2$. The safest path to travel from room $5$ to room $8$ is going from room $5$ to room $6$, then room $7$ and finally room $8$ (or if you're feeling less adventurous, you could skip going to room $7$ and travel from $5$ to $6$ to $8$ instead). The minimum skill level to safely traverse these corridors is $3$. Thus to travel between all $P = 2$ pairs of rooms, one must have a minimum skill level of $3$.
For the second case, there is no way to get from room $1$ to room $2$ regardless of your skill level. How did they get the pieces there? It shall remain a mystery.
| 0.5 |
["c","cpp","java","python3","python","cpp14"]
|
Hard
| null | null | null | null | null | null |
2014-06-24T05:03:25
|
2018-02-06T18:32:10
|
tester
|
```cpp
#include <cstdio>
#include <cstring>
#include <string>
#include <cassert>
using namespace std;
const int N = 100005;
int f[N],num[N];
struct node {
int x,y,s;
};
node a[N];
pair<int,int> b[N];
int getf(int x) {
return (f[x] == x)?x:(f[x] = getf(f[x]));
}
void make(int x,int y) {
x = getf(x);
y = getf(y);
if (x == y) {
return;
}
if (num[x] < num[y]) {
f[x] = y;
num[y] += num[x];
}
else {
f[y] = x;
num[x] += num[y];
}
}
bool check(int m,int n,int p,int v) {
for (int i = 0; i < n; ++i) {
num[f[i] = i] = 1;
}
for (int i = 0; i < m; ++i) {
if (a[i].s <= v) {
make(a[i].x,a[i].y);
}
}
for (int i = 0; i < p; ++i) {
if (getf(b[i].first) != getf(b[i].second)) {
return false;
}
}
return true;
}
int main() {
int n,m;
scanf("%d%d",&n,&m);
assert((n >= 1) && (n <= 100000));
assert((m >= 1) && (m <= 100000));
int left = 2000000, right = 0;
for (int i = 0; i < m; ++i) {
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].s);
assert((a[i].x >= 1) && (a[i].x <= n));
assert((a[i].y >= 1) && (a[i].y <= n) && (a[i].x != a[i].y));
assert((a[i].s >= 1) && (a[i].s <= 1000000));
--a[i].x;
--a[i].y;
left = min(left, a[i].s);
right = max(right, a[i].s);
}
int p;
scanf("%d",&p);
assert((p >= 1) && (p <= 100000));
for (int i = 0; i < p; ++i) {
scanf("%d%d",&b[i].first,&b[i].second);
assert((b[i].first >= 1) && (b[i].first <= n));
assert((b[i].second >= 1) && (b[i].second <= n) && (b[i].first != b[i].second));
--b[i].first;
--b[i].second;
}
int answer = -1;
while (left <= right) {
int mid =(left + right) >> 1;
if (check(m,n,p,mid)) {
answer = mid;
right = mid - 1;
}
else {
left = mid + 1;
}
}
if (answer >= 0) {
printf("%d\n",answer);
}
else {
puts("MISSION IMPOSSIBLE");
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:43
|
2018-02-06T18:26:46
|
C++
|
||||
88 | 3,152 |
uppals-ego
|
Uppal's Ego
|
Ramu is very good at maths. He always tries to play with different kinds of numbers. This time he has discovered a new type of numbers and has named them **KMH** numbers. According to him, a number **N** is a **KMH** number, if **the sum of its prime divisors is a power of 2** i.e **_(2, 4, 8, ...and so on)._**
**Example:**
**1. 15= 3 X 5**
prime divisors 3,5
sum = 3 + 5 = 8
**2. 3025 = 5<sup>2</sup> X 11<sup>2</sup>**
prime divisors 5,11
sum = 5 + 11 = 16
So **15**, **3025** are some **KMH numbers**.
Uppal is Ramu’s roommate and Ramu challenges him to do a task related to **KMH** numbers. Uppal will be given 2 integers **A,B** and asked to tell **the number of integers between A and B (inclusive) whose "Sum of digits" is a KMH number**. Uppal takes every lose to his ego . So he has asked your help so that he can answer all queries asked by Ramu. Help Uppal so that his ego doesn't get hurt.
**Example**
**44**
sum of digits : 4 + 4 = 8
8 = 2<sup>3</sup>
sum of prime divisors = 2.
So **44** is a number whose sum of digits is a **KMH** number.
###**INPUT FORMAT**
First line contains number of test cases **T**.
Next **T** lines will contain two integers **A** and **B** separated by a space.
###**OUTPUT FORMAT**
Output should contain **T** lines, each conatining answer to Ramu's query explained above.
###**CONSTRAINTS:**
Number of test cases **T**, **1 ≤ T ≤ 100**
**1 ≤ A ≤ B ≤ 10<sup>15</sup>**
###**SAMPLE INPUT**
2
1 10
40 50
###**SAMPLE OUTPUT**
3
2
###**EXPLANATION**
In the first test case **2**, **4** and **8** are the numbers between **1** and **10**.
In the second test case **40** and **44** are the numbers between **40** and **50**.
|
code
|
Help Uppal so that his ego doesn't get hurt.
|
ai
|
2014-06-24T08:08:53
|
2016-09-09T09:47:13
| null | null | null |
Ramu is very good at maths. He always tries to play with different kinds of numbers. This time he has discovered a new type of numbers and has named them **KMH** numbers. According to him, a number **N** is a **KMH** number, if **the sum of its prime divisors is a power of 2** i.e **_(2, 4, 8, ...and so on)._**
**Example:**
**1. 15= 3 X 5**
prime divisors 3,5
sum = 3 + 5 = 8
**2. 3025 = 5<sup>2</sup> X 11<sup>2</sup>**
prime divisors 5,11
sum = 5 + 11 = 16
So **15**, **3025** are some **KMH numbers**.
Uppal is Ramu’s roommate and Ramu challenges him to do a task related to **KMH** numbers. Uppal will be given 2 integers **A,B** and asked to tell **the number of integers between A and B (inclusive) whose "Sum of digits" is a KMH number**. Uppal takes every lose to his ego . So he has asked your help so that he can answer all queries asked by Ramu. Help Uppal so that his ego doesn't get hurt.
**Example**
**44**
sum of digits : 4 + 4 = 8
8 = 2<sup>3</sup>
sum of prime divisors = 2.
So **44** is a number whose sum of digits is a **KMH** number.
###**INPUT FORMAT**
First line contains number of test cases **T**.
Next **T** lines will contain two integers **A** and **B** separated by a space.
###**OUTPUT FORMAT**
Output should contain **T** lines, each conatining answer to Ramu's query explained above.
###**CONSTRAINTS:**
Number of test cases **T**, **1 ≤ T ≤ 100**
**1 ≤ A ≤ B ≤ 10<sup>15</sup>**
###**SAMPLE INPUT**
2
1 10
40 50
###**SAMPLE OUTPUT**
3
2
###**EXPLANATION**
In the first test case **2**, **4** and **8** are the numbers between **1** and **10**.
In the second test case **40** and **44** are the numbers between **40** and **50**.
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","erlang","brainfuck","javascript","go","d","ocaml","pascal","sbcl","python3","groovy","objectivec","fsharp","cobol","visualbasic","lolcode","smalltalk","tcl","whitespace","tsql","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-24T08:24:54
|
2017-11-21T15:46:55
|
setter
|
#include<iostream>
#include<string>
#define LL long long int
#define rep(i,x,n) for(i=x;i<n;i++)
using namespace std;
LL kmh[25],p=0,dp[16][136];
//returns string value of an integer
string convert(LL n)
{
LL i,j,k;
if(n==0)return "0";
string str;
for(i=n;i!=0;i/=10)
{
str=(char)(i%10+48)+str;
}
return str;
}
LL cal(LL n)
{
string str=convert(n);
LL x=0,ans=0,i,j,k,bits,l=str.length();
rep(i,0,l)
{
bits=l-i;
rep(j,0,str[i]-48)
{
rep(k,0,p)
{
if(kmh[k]-x-j>=0)ans+=dp[bits-1][kmh[k]-x-j];
}
}
x+=(str[i]-48);
}
return ans;
}
int main()
{
LL i,j,k,n,t,a,b;
//compute KMH numbers
LL d[136]={0};
for(i=2;i<136;i++)
{
if(!d[i])
{
for(j=i;j<136;j+=i)
d[j]+=i;
}
}
for(i=2;i<136;i++)if((d[i]&(d[i]-1))==0)kmh[p++]=i;
//dp to compute number of integers of x bits with s sum as dp[x][s]
rep(i,0,10)dp[1][i]=1;
dp[0][0]=1;
rep(i,2,16) //bits
{
rep(j,0,136) //sum
{
rep(k,0,10) //setting MSB as k
{
if(j-k>=0)
dp[i][j]+=dp[i-1][j-k];
}
}
}
cin>>t;
while(t--)
{
cin>>a>>b;
cout<<cal(b+1)-cal(a)<<endl;
}
return 0;
}
|
not-set
|
2016-04-24T02:02:43
|
2016-04-24T02:02:43
|
C++
|
89 | 3,098 |
big-balls
|
Big Balls
|
In the jackpot round of a game show, Big Balls, you are given $N$ jackpot balls, each having an integer weight (in grams). Within the time alloted, you may put two balls on opposite sides of a scale in order to determine which ball is heavier. To help you with your task, the host added some extra balls (different from the $N$ jackpot balls) and reveals to you how heavy each of them are (in grams).
At the end of the allotted time, you must guess the weight of each of the $N$ balls. Take note that each of your guesses must be a positive integer. The only catch is that if the sum of your guesses exceeds the actual sum of the weights, you go home with nothing. Knowing this, you reckon that guessing too high at any point is too risky (it would cost you everything), you decide to guess the weight of each ball such that the sum of the weights of your guesses is minimized.
**Input Format**
The first line of input will contain two positive integers, $N$ and $M$, separated by a space.
The next $M$ lines describe the comparisons you were able to do during the time alloted.
With each comparison you gain one of the following information:
* Type A: Ball $X$ is heavier than Ball $Y$.
* Type B: Ball $X$ is lighter than Ball $Y$.
* Type C: Ball $X$ is heavier than the ball weighing $W$ grams.
* Type D: Ball $X$ is lighter than the ball weighing $W$ grams.
The $M$ lines will each contain a letter from $A$ to $D$ representing the statement it describes and two integers. If the statement is of type $A$ or $B$, the two integers will be $X$ and $Y$ (in that order), describing which two balls were compared. If the statement is of type $C$ or $D$, the two integers will be $X$ and $W$ (in that order), giving an upper/lower bound for the weight of ball $X$.
**Output Format**
If it is impossible to make a logical conclusion (i.e. there are contradictions with the statements given), output a single line containing the word `IMPOSSIBLE`.
Otherwise, output $N$ lines, each containing a single integer. The $i^\text{th}$ line should contain your guess (based on the strategy described above) for the weight of Ball $i$.
It is guaranteed that the answer is unique. Note that balls may have the same weights.
**Constraints**
$1 \le N \le 2\cdot 10^5$
$1 \le M \le 2\cdot 10^5$
$1 \le X \le N$
$1 \le Y \le N$
$X \ne Y$
$1 \le W \le 10^9$
**Sample Input 1**
1 1
D 1 1
**Sample Output 1**
IMPOSSIBLE
**Sample Input 2**
5 6
A 2 1
B 1 2
C 3 4
D 4 12
B 5 4
C 1 1
**Sample Output 2**
2
3
5
2
1
**Explanation**
The first case deals with $N = 1$ ball and exactly $M = 1$ statement stating that Ball $1$ is lighter than the ball weighing $1$ gram. Hence its weight must be less than $1$ gram. There is no positive integer less than $1$ and so this setup is impossible.
The second case deals with $N = 5$ balls and $M = 6$ statements which translate as follows:
* Ball 2 is heavier than Ball 1.
* Ball 1 is lighter than Ball 2.
* Ball 3 is heavier than the ball weighing 4 grams.
* Ball 4 is lighter than the ball weighing 12 grams.
* Ball 5 is lighter than Ball 4.
* Ball 1 is heavier than the ball weighing 1 gram.
Since the only lower bound for Ball 1 is the fact that it is heavier than $1$ gram, we should guess $2$ for Ball 1. We shouldn't guess any higher since we might go over the sum. Now, since Ball 2 is heavier than Ball 1, we should guess $3$ for that. And so on.
|
code
|
Guess the weights of the balls from comparisons.
|
ai
|
2014-06-19T03:48:36
|
2016-09-09T09:46:50
| null | null | null |
In the jackpot round of a game show, Big Balls, you are given $N$ jackpot balls, each having an integer weight (in grams). Within the time alloted, you may put two balls on opposite sides of a scale in order to determine which ball is heavier. To help you with your task, the host added some extra balls (different from the $N$ jackpot balls) and reveals to you how heavy each of them are (in grams).
At the end of the allotted time, you must guess the weight of each of the $N$ balls. Take note that each of your guesses must be a positive integer. The only catch is that if the sum of your guesses exceeds the actual sum of the weights, you go home with nothing. Knowing this, you reckon that guessing too high at any point is too risky (it would cost you everything), you decide to guess the weight of each ball such that the sum of the weights of your guesses is minimized.
**Input Format**
The first line of input will contain two positive integers, $N$ and $M$, separated by a space.
The next $M$ lines describe the comparisons you were able to do during the time alloted.
With each comparison you gain one of the following information:
* Type A: Ball $X$ is heavier than Ball $Y$.
* Type B: Ball $X$ is lighter than Ball $Y$.
* Type C: Ball $X$ is heavier than the ball weighing $W$ grams.
* Type D: Ball $X$ is lighter than the ball weighing $W$ grams.
The $M$ lines will each contain a letter from $A$ to $D$ representing the statement it describes and two integers. If the statement is of type $A$ or $B$, the two integers will be $X$ and $Y$ (in that order), describing which two balls were compared. If the statement is of type $C$ or $D$, the two integers will be $X$ and $W$ (in that order), giving an upper/lower bound for the weight of ball $X$.
**Output Format**
If it is impossible to make a logical conclusion (i.e. there are contradictions with the statements given), output a single line containing the word `IMPOSSIBLE`.
Otherwise, output $N$ lines, each containing a single integer. The $i^\text{th}$ line should contain your guess (based on the strategy described above) for the weight of Ball $i$.
It is guaranteed that the answer is unique. Note that balls may have the same weights.
**Constraints**
$1 \le N \le 2\cdot 10^5$
$1 \le M \le 2\cdot 10^5$
$1 \le X \le N$
$1 \le Y \le N$
$X \ne Y$
$1 \le W \le 10^9$
**Sample Input 1**
1 1
D 1 1
**Sample Output 1**
IMPOSSIBLE
**Sample Input 2**
5 6
A 2 1
B 1 2
C 3 4
D 4 12
B 5 4
C 1 1
**Sample Output 2**
2
3
5
2
1
**Explanation**
The first case deals with $N = 1$ ball and exactly $M = 1$ statement stating that Ball $1$ is lighter than the ball weighing $1$ gram. Hence its weight must be less than $1$ gram. There is no positive integer less than $1$ and so this setup is impossible.
The second case deals with $N = 5$ balls and $M = 6$ statements which translate as follows:
* Ball 2 is heavier than Ball 1.
* Ball 1 is lighter than Ball 2.
* Ball 3 is heavier than the ball weighing 4 grams.
* Ball 4 is lighter than the ball weighing 12 grams.
* Ball 5 is lighter than Ball 4.
* Ball 1 is heavier than the ball weighing 1 gram.
Since the only lower bound for Ball 1 is the fact that it is heavier than $1$ gram, we should guess $2$ for Ball 1. We shouldn't guess any higher since we might go over the sum. Now, since Ball 2 is heavier than Ball 1, we should guess $3$ for that. And so on.
| 0.5 |
["c","cpp","java","python3","python","cpp14"]
|
Hard
| null | null | null | null | null | null |
2014-06-24T19:18:31
|
2017-03-17T05:18:04
|
setter
|
#include <stdio.h>
#include <stdlib.h>
#define ll long long
int lower[211111];
int upper[211111];
char cmd[111];
int xs[211111];
int ys[211111];
int *adj[211111];
int adc[211111];
int deg[211111];
int que[211111];
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++) {
lower[i] = 0;
upper[i] = 2111111111;
adc[i] = deg[i] = 0;
}
int c = 0;
for (int i = 0; i < m; i++) {
int x, y;
scanf("%s%d%d", cmd, &x, &y);
x--;
if (*cmd == 'A' or *cmd == 'B') y--;
if (*cmd == 'B') {
*cmd = 'A';
x ^= y, y ^= x, x ^= y;
}
if (*cmd == 'A') {
xs[c] = x;
ys[c] = y;
c++;
adc[y]++;
} else if (*cmd == 'C') {
if (lower[x] < y) lower[x] = y;
} else if (*cmd == 'D') {
if (upper[x] > y) upper[x] = y;
} else {
//assert(0);// shouldn't happen
}
}
for (int i = 0; i < n; i++) {
adj[i] = (int*)malloc(adc[i] * sizeof(int));
adc[i] = 0;
}
for (int i = 0; i < c; i++) {
int x = xs[i];
int y = ys[i];
adj[y][adc[y]++] = x;
deg[x]++;
}
int q = 0;
for (int i = 0; i < n; i++) {
if (!deg[i]) que[q++] = i;
}
int succ = 1;
for (int f = 0; f < q; f++) {
int i = que[f];
if (!(succ = ++lower[i] < upper[i])) break;
for (int nb = 0; nb < adc[i]; nb++) {
int j = adj[i][nb];
if (lower[j] < lower[i]) lower[j] = lower[i];
if (!--deg[j]) que[q++] = j;
}
}
succ &= q == n;
if (succ) {
for (int i = 0; i < n; i++) {
printf("%d\n", lower[i]);
}
} else {
printf("IMPOSSIBLE\n");
}
}
|
not-set
|
2016-04-24T02:02:44
|
2016-04-24T02:02:44
|
C++
|
||||
90 | 3,098 |
big-balls
|
Big Balls
|
In the jackpot round of a game show, Big Balls, you are given $N$ jackpot balls, each having an integer weight (in grams). Within the time alloted, you may put two balls on opposite sides of a scale in order to determine which ball is heavier. To help you with your task, the host added some extra balls (different from the $N$ jackpot balls) and reveals to you how heavy each of them are (in grams).
At the end of the allotted time, you must guess the weight of each of the $N$ balls. Take note that each of your guesses must be a positive integer. The only catch is that if the sum of your guesses exceeds the actual sum of the weights, you go home with nothing. Knowing this, you reckon that guessing too high at any point is too risky (it would cost you everything), you decide to guess the weight of each ball such that the sum of the weights of your guesses is minimized.
**Input Format**
The first line of input will contain two positive integers, $N$ and $M$, separated by a space.
The next $M$ lines describe the comparisons you were able to do during the time alloted.
With each comparison you gain one of the following information:
* Type A: Ball $X$ is heavier than Ball $Y$.
* Type B: Ball $X$ is lighter than Ball $Y$.
* Type C: Ball $X$ is heavier than the ball weighing $W$ grams.
* Type D: Ball $X$ is lighter than the ball weighing $W$ grams.
The $M$ lines will each contain a letter from $A$ to $D$ representing the statement it describes and two integers. If the statement is of type $A$ or $B$, the two integers will be $X$ and $Y$ (in that order), describing which two balls were compared. If the statement is of type $C$ or $D$, the two integers will be $X$ and $W$ (in that order), giving an upper/lower bound for the weight of ball $X$.
**Output Format**
If it is impossible to make a logical conclusion (i.e. there are contradictions with the statements given), output a single line containing the word `IMPOSSIBLE`.
Otherwise, output $N$ lines, each containing a single integer. The $i^\text{th}$ line should contain your guess (based on the strategy described above) for the weight of Ball $i$.
It is guaranteed that the answer is unique. Note that balls may have the same weights.
**Constraints**
$1 \le N \le 2\cdot 10^5$
$1 \le M \le 2\cdot 10^5$
$1 \le X \le N$
$1 \le Y \le N$
$X \ne Y$
$1 \le W \le 10^9$
**Sample Input 1**
1 1
D 1 1
**Sample Output 1**
IMPOSSIBLE
**Sample Input 2**
5 6
A 2 1
B 1 2
C 3 4
D 4 12
B 5 4
C 1 1
**Sample Output 2**
2
3
5
2
1
**Explanation**
The first case deals with $N = 1$ ball and exactly $M = 1$ statement stating that Ball $1$ is lighter than the ball weighing $1$ gram. Hence its weight must be less than $1$ gram. There is no positive integer less than $1$ and so this setup is impossible.
The second case deals with $N = 5$ balls and $M = 6$ statements which translate as follows:
* Ball 2 is heavier than Ball 1.
* Ball 1 is lighter than Ball 2.
* Ball 3 is heavier than the ball weighing 4 grams.
* Ball 4 is lighter than the ball weighing 12 grams.
* Ball 5 is lighter than Ball 4.
* Ball 1 is heavier than the ball weighing 1 gram.
Since the only lower bound for Ball 1 is the fact that it is heavier than $1$ gram, we should guess $2$ for Ball 1. We shouldn't guess any higher since we might go over the sum. Now, since Ball 2 is heavier than Ball 1, we should guess $3$ for that. And so on.
|
code
|
Guess the weights of the balls from comparisons.
|
ai
|
2014-06-19T03:48:36
|
2016-09-09T09:46:50
| null | null | null |
In the jackpot round of a game show, Big Balls, you are given $N$ jackpot balls, each having an integer weight (in grams). Within the time alloted, you may put two balls on opposite sides of a scale in order to determine which ball is heavier. To help you with your task, the host added some extra balls (different from the $N$ jackpot balls) and reveals to you how heavy each of them are (in grams).
At the end of the allotted time, you must guess the weight of each of the $N$ balls. Take note that each of your guesses must be a positive integer. The only catch is that if the sum of your guesses exceeds the actual sum of the weights, you go home with nothing. Knowing this, you reckon that guessing too high at any point is too risky (it would cost you everything), you decide to guess the weight of each ball such that the sum of the weights of your guesses is minimized.
**Input Format**
The first line of input will contain two positive integers, $N$ and $M$, separated by a space.
The next $M$ lines describe the comparisons you were able to do during the time alloted.
With each comparison you gain one of the following information:
* Type A: Ball $X$ is heavier than Ball $Y$.
* Type B: Ball $X$ is lighter than Ball $Y$.
* Type C: Ball $X$ is heavier than the ball weighing $W$ grams.
* Type D: Ball $X$ is lighter than the ball weighing $W$ grams.
The $M$ lines will each contain a letter from $A$ to $D$ representing the statement it describes and two integers. If the statement is of type $A$ or $B$, the two integers will be $X$ and $Y$ (in that order), describing which two balls were compared. If the statement is of type $C$ or $D$, the two integers will be $X$ and $W$ (in that order), giving an upper/lower bound for the weight of ball $X$.
**Output Format**
If it is impossible to make a logical conclusion (i.e. there are contradictions with the statements given), output a single line containing the word `IMPOSSIBLE`.
Otherwise, output $N$ lines, each containing a single integer. The $i^\text{th}$ line should contain your guess (based on the strategy described above) for the weight of Ball $i$.
It is guaranteed that the answer is unique. Note that balls may have the same weights.
**Constraints**
$1 \le N \le 2\cdot 10^5$
$1 \le M \le 2\cdot 10^5$
$1 \le X \le N$
$1 \le Y \le N$
$X \ne Y$
$1 \le W \le 10^9$
**Sample Input 1**
1 1
D 1 1
**Sample Output 1**
IMPOSSIBLE
**Sample Input 2**
5 6
A 2 1
B 1 2
C 3 4
D 4 12
B 5 4
C 1 1
**Sample Output 2**
2
3
5
2
1
**Explanation**
The first case deals with $N = 1$ ball and exactly $M = 1$ statement stating that Ball $1$ is lighter than the ball weighing $1$ gram. Hence its weight must be less than $1$ gram. There is no positive integer less than $1$ and so this setup is impossible.
The second case deals with $N = 5$ balls and $M = 6$ statements which translate as follows:
* Ball 2 is heavier than Ball 1.
* Ball 1 is lighter than Ball 2.
* Ball 3 is heavier than the ball weighing 4 grams.
* Ball 4 is lighter than the ball weighing 12 grams.
* Ball 5 is lighter than Ball 4.
* Ball 1 is heavier than the ball weighing 1 gram.
Since the only lower bound for Ball 1 is the fact that it is heavier than $1$ gram, we should guess $2$ for Ball 1. We shouldn't guess any higher since we might go over the sum. Now, since Ball 2 is heavier than Ball 1, we should guess $3$ for that. And so on.
| 0.5 |
["c","cpp","java","python3","python","cpp14"]
|
Hard
| null | null | null | null | null | null |
2014-06-24T19:18:31
|
2017-03-17T05:18:04
|
tester
|
#include <cstdio>
#include <cstring>
#include <string>
#include <queue>
#include <set>
#include <cassert>
using namespace std;
const int N = 200002;
set<int> con[N];
int ind[N],L[N],G[N],a[N];
char s[5];
queue<int> q;
bool run(int n) {
int m = 0;
for (int i = 0; i < n; ++i) {
if (L[i] - 1 < G[i] + 1) {
return false;
}
//printf("%d %d %d\n",i,L[i],G[i]);
if (ind[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
int x = q.front();
q.pop();
++m;
a[x] = G[x] + 1;
//printf("a[%d] = %d\n",x,a[x]);
for (set<int>::iterator t = con[x].begin(); t != con[x].end(); ++t) {
G[*t] = max(a[x], G[*t]);
if (L[*t] - 1 < G[*t] + 1) {
//puts("haha");
return false;
}
if (--ind[*t] == 0) {
q.push(*t);
}
}
}
//printf("m = %d\n",m);
return (m == n);
}
int main() {
int n,m;
scanf("%d%d",&n,&m);
assert((n >= 1) && (n <= 200000));
assert((m >= 1) && (m <= 200000));
for (int i = 0; i < n; ++i) {
L[i] = 2000000000;
G[i] = 0;
}
for (int i = 0; i < m; ++i) {
int x,y;
scanf("%s%d%d",s,&x,&y);
assert((strcmp(s,"A") == 0) || (strcmp(s,"B") == 0) || (strcmp(s,"C") == 0) || (strcmp(s,"D") == 0));
--x;
switch(s[0]) {
case 'A':
--y;
assert((x >= 0) && (x < n));
assert((y >= 0) && (y < n) && (y != x));
if (con[y].find(x) == con[y].end()) {
con[y].insert(x);
++ind[x];
}
break;
case 'B':
--y;
assert((x >= 0) && (x < n));
assert((y >= 0) && (y < n) && (y != x));
if (con[x].find(y) == con[x].end()) {
con[x].insert(y);
++ind[y];
}
break;
case 'C':
assert((y >= 1) && (y <= 1000000000));
G[x] = max(G[x], y);
break;
case 'D':
assert((y >= 1) && (y <= 1000000000));
L[x] = min(L[x], y);
break;
}
}
if (run(n)) {
for (int i = 0; i < n; ++i) {
printf("%d\n",a[i]);
}
}
else {
puts("IMPOSSIBLE");
}
return 0;
}
|
not-set
|
2016-04-24T02:02:44
|
2016-04-24T02:02:44
|
C++
|
||||
91 | 3,153 |
testing-iii
|
Testing III
|
There are $w$ watermelons. Print YES if it can be divided into two parts, each weighing an even number. Print NO otherwise.
This is identical to the Watermelon challenge on Codeforces.
|
code
|
This problem is easy.
|
ai
|
2014-06-24T19:35:49
|
2016-09-09T09:47:13
| null | null | null |
There are $w$ watermelons. Print YES if it can be divided into two parts, each weighing an even number. Print NO otherwise.
This is identical to the Watermelon challenge on Codeforces.
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-24T19:39:59
|
2016-05-13T00:01:39
|
tester
|
#include <cstdio>
int main(void) {
int n;
scanf("%d", &n);
puts((n >= 4 && n % 2 == 0) ? "YES" : "NO");
return 0;
}
|
not-set
|
2016-04-24T02:02:44
|
2016-04-24T02:02:44
|
C++
|
92 | 3,051 |
connecting-points
|
Connecting points
|
John has his own 3-dimensional space. He currently has $N$ distinct points that belong to this space.
Today John is connecting the points with each other. In each step, he chooses two points and connects them together by drawing a curved line between them. After that he always puts single point somewhere on the curved line. Note that this point initially has 2 connections, and it can be further connected by curve lines with others. Also note that multiple curved-lines can be drawn between each pair of points.
<br>
There is one condition: each point which currently has strictly less than $K$ connections can be used for making new connections again.
<br>
John wants to maximize total number of drawn curve lines. Help him and calculate how many curve lines can John draw. Note that a pair of point can be connected multiple times with different curved lines.
PS: Refer to the explanation/image given below for more clarity.
**Input Format**
The first line contains a single integer $T$, representing the number of test cases to follow. Each of the following $T$ lines (or testcases) contains two integers separated by single space: $N$ - the number of points in three-dimensional space, $K$ - number of maximum connections that can be made for the present testcase.
**Output Format**
For each of the test case, print the count of drawn curve lines, or $-1$ if John will never end connecting the points.
**Constraints**
$1 \le T \le 50$
$1 \le N \le 10^9$
$0 \le K \le 10$
**Sample Input:**
5
7 0
47 1
2 2
2 3
3 10
**Sample Output:**
0
23
2
5
-1
**Explanation**
*Sample Case #00:* Points are not allowed to be connected at all, so no curved-line can be drawn.
*Sample Case #01:* Since only one line can be drawn out of a point, at most 23 pair of points can be joined via curves.
*Sample Case #02:* John connects both points twice. It yields four points two initial and two appended. All points are connected twice.
*Sample Case #03:* Following picture illustrates the process of connecting the points. Orange points with three edges no longer can be connected.

<br>
*Sample Case #04:* John will never stop adding points.
---
**Tested by** [Shang-En Huang](https://www.hackerrank.com/tmt514)
|
code
|
How many curve lines will be drawn?
|
ai
|
2014-06-16T18:38:48
|
2019-07-02T13:58:38
| null | null | null |
John has his own 3-dimensional space. He currently has $N$ distinct points that belong to this space.
Today John is connecting the points with each other. In each step, he chooses two points and connects them together by drawing a curved line between them. After that he always puts single point somewhere on the curved line. Note that this point initially has 2 connections, and it can be further connected by curve lines with others. Also note that multiple curved-lines can be drawn between each pair of points.
<br>
There is one condition: each point which currently has strictly less than $K$ connections can be used for making new connections again.
<br>
John wants to maximize total number of drawn curve lines. Help him and calculate how many curve lines can John draw. Note that a pair of point can be connected multiple times with different curved lines.
PS: Refer to the explanation/image given below for more clarity.
**Input Format**
The first line contains a single integer $T$, representing the number of test cases to follow. Each of the following $T$ lines (or testcases) contains two integers separated by single space: $N$ - the number of points in three-dimensional space, $K$ - number of maximum connections that can be made for the present testcase.
**Output Format**
For each of the test case, print the count of drawn curve lines, or $-1$ if John will never end connecting the points.
**Constraints**
$1 \le T \le 50$
$1 \le N \le 10^9$
$0 \le K \le 10$
**Sample Input:**
5
7 0
47 1
2 2
2 3
3 10
**Sample Output:**
0
23
2
5
-1
**Explanation**
*Sample Case #00:* Points are not allowed to be connected at all, so no curved-line can be drawn.
*Sample Case #01:* Since only one line can be drawn out of a point, at most 23 pair of points can be joined via curves.
*Sample Case #02:* John connects both points twice. It yields four points two initial and two appended. All points are connected twice.
*Sample Case #03:* Following picture illustrates the process of connecting the points. Orange points with three edges no longer can be connected.

<br>
*Sample Case #04:* John will never stop adding points.
---
**Tested by** [Shang-En Huang](https://www.hackerrank.com/tmt514)
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-24T21:08:10
|
2016-05-13T00:01:37
|
setter
|
#include <iostream>
#include <sstream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cctype>
#include <cstring>
#include <vector>
#include <list>
#include <queue>
#include <deque>
#include <stack>
#include <map>
#include <set>
#include <algorithm>
#include <numeric>
using namespace std;
typedef pair<int, int> PII;
typedef vector<int> VI;
#define FOR(i, a, b) for(int i = (a); i < (b); ++i)
#define RFOR(i, a, b) for(int i = (a) - 1; i >= (b); --i)
#define CLEAR(a, b) memset(a, b, sizeof(a))
#define ALL(a) (a).begin(),(a).end()
#define PB push_back
#define MP make_pair
#define MOD 1000000007
#define INF 1000000007
#define y1 agaga
#define ll long long
#define ull unsigned long long
vector<int> V;
int n,k;
int f(int n, int k)
{
if (n == 1 || k == 0) return 0;
if (k == 1) return n / 2;
if (k == 2) return n;
if (k >= 4) return -1;
return -2;
}
int main()
{
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int t;
cin >> t;
while (t--)
{
cin >> n >> k;
if (f(n,k)!=-2)
{
cout << f(n,k) << endl;
continue;
}
cout << (ll)(n)*3-1<< endl;
}
return 0;
}
|
not-set
|
2016-04-24T02:02:44
|
2016-04-24T02:02:44
|
C++
|
93 | 3,051 |
connecting-points
|
Connecting points
|
John has his own 3-dimensional space. He currently has $N$ distinct points that belong to this space.
Today John is connecting the points with each other. In each step, he chooses two points and connects them together by drawing a curved line between them. After that he always puts single point somewhere on the curved line. Note that this point initially has 2 connections, and it can be further connected by curve lines with others. Also note that multiple curved-lines can be drawn between each pair of points.
<br>
There is one condition: each point which currently has strictly less than $K$ connections can be used for making new connections again.
<br>
John wants to maximize total number of drawn curve lines. Help him and calculate how many curve lines can John draw. Note that a pair of point can be connected multiple times with different curved lines.
PS: Refer to the explanation/image given below for more clarity.
**Input Format**
The first line contains a single integer $T$, representing the number of test cases to follow. Each of the following $T$ lines (or testcases) contains two integers separated by single space: $N$ - the number of points in three-dimensional space, $K$ - number of maximum connections that can be made for the present testcase.
**Output Format**
For each of the test case, print the count of drawn curve lines, or $-1$ if John will never end connecting the points.
**Constraints**
$1 \le T \le 50$
$1 \le N \le 10^9$
$0 \le K \le 10$
**Sample Input:**
5
7 0
47 1
2 2
2 3
3 10
**Sample Output:**
0
23
2
5
-1
**Explanation**
*Sample Case #00:* Points are not allowed to be connected at all, so no curved-line can be drawn.
*Sample Case #01:* Since only one line can be drawn out of a point, at most 23 pair of points can be joined via curves.
*Sample Case #02:* John connects both points twice. It yields four points two initial and two appended. All points are connected twice.
*Sample Case #03:* Following picture illustrates the process of connecting the points. Orange points with three edges no longer can be connected.

<br>
*Sample Case #04:* John will never stop adding points.
---
**Tested by** [Shang-En Huang](https://www.hackerrank.com/tmt514)
|
code
|
How many curve lines will be drawn?
|
ai
|
2014-06-16T18:38:48
|
2019-07-02T13:58:38
| null | null | null |
John has his own 3-dimensional space. He currently has $N$ distinct points that belong to this space.
Today John is connecting the points with each other. In each step, he chooses two points and connects them together by drawing a curved line between them. After that he always puts single point somewhere on the curved line. Note that this point initially has 2 connections, and it can be further connected by curve lines with others. Also note that multiple curved-lines can be drawn between each pair of points.
<br>
There is one condition: each point which currently has strictly less than $K$ connections can be used for making new connections again.
<br>
John wants to maximize total number of drawn curve lines. Help him and calculate how many curve lines can John draw. Note that a pair of point can be connected multiple times with different curved lines.
PS: Refer to the explanation/image given below for more clarity.
**Input Format**
The first line contains a single integer $T$, representing the number of test cases to follow. Each of the following $T$ lines (or testcases) contains two integers separated by single space: $N$ - the number of points in three-dimensional space, $K$ - number of maximum connections that can be made for the present testcase.
**Output Format**
For each of the test case, print the count of drawn curve lines, or $-1$ if John will never end connecting the points.
**Constraints**
$1 \le T \le 50$
$1 \le N \le 10^9$
$0 \le K \le 10$
**Sample Input:**
5
7 0
47 1
2 2
2 3
3 10
**Sample Output:**
0
23
2
5
-1
**Explanation**
*Sample Case #00:* Points are not allowed to be connected at all, so no curved-line can be drawn.
*Sample Case #01:* Since only one line can be drawn out of a point, at most 23 pair of points can be joined via curves.
*Sample Case #02:* John connects both points twice. It yields four points two initial and two appended. All points are connected twice.
*Sample Case #03:* Following picture illustrates the process of connecting the points. Orange points with three edges no longer can be connected.

<br>
*Sample Case #04:* John will never stop adding points.
---
**Tested by** [Shang-En Huang](https://www.hackerrank.com/tmt514)
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","go","javascript","erlang","sbcl","d","ocaml","pascal","python3","groovy","objectivec","fsharp","visualbasic","lolcode","smalltalk","tcl","java8","r","racket","rust","swift","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-24T21:08:10
|
2016-05-13T00:01:37
|
tester
|
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
#define SZ(x) ((int)(x).size())
#define FOR(it, c) for(__typeof((c).begin()) it = (c).begin(); it != (c).end(); ++it)
using namespace std;
typedef long long LL;
void solve() {
int n, k;
scanf("%d%d", &n, &k);
if(k == 0) {
printf("0\n");
} else if(k == 1) {
printf("%d\n", n/2);
} else if(k == 2) {
printf("%d\n", n==1? 0: n);
} else if(k == 3) {
printf("%lld\n", n==1? 0LL: n + (2LL*n-1));
} else
puts("-1");
}
int main(void) {
int T;
scanf("%d", &T);
while(T--) solve();
return 0;
}
|
not-set
|
2016-04-24T02:02:44
|
2016-04-24T02:02:44
|
C++
|
94 | 3,097 |
skwishinese
|
Skwishinese
|
The language Skwishinese has its own elegant, albeit complicated, measure for the beauty of a word.
Before we can start describing how to measure it, we must first define a subsequence. Discovered by and named after the famous Skwishinese doctor, Aaron J. Subsequence, a _subsequence_ of a word is another word that can be formed by removing one or more (possibly none) of the letters of that word. For example, `loooo` is a subsequence of `troolooloo`, but `trooooll` and `banana` are not.
Moreover, the _reverse_ of a word is obtained simply by reversing the order of the letters. For example, the reverse of `troolooloo` is `oolooloort`. We denote the reverse of $U$ by $U^R$.
Let $U$ be a Skwishinese word. We can form a nonsensical word, $UU^R$, by _concatenating_ $U$ and its reverse. For example, if $U$ is `loooo`, then $UU^R$ will be `looooooool`.
Now, the _beauty_ of a Skwishinese word $V$ is the length of the shortest word $U$ that is a subsequence of $V$ and such that $V$ is a subsequence of $UU^R$ (the concatenation of $U$ and its reverse).
For example, the beauty of the word `troolooloo` is 6, because 6 is the length of the shortest word $U$ satisfying the above conditions (in this case, $U$ is `troolo`).
**Input Format**
The input consists of exactly two lines.
The first line contains $N$, a positive integer giving the length of the word $V$.
The second line contains $V$ a word in Skwishinese. It is a string consisting only of lowercase letters from the English alphabet.
**Output Format**
Output the beauty of the Skwishinese word $V$.
**Constraints**
$1 \le N \le 400$
$V$ consists only of lowercase letters
**Sample Input**
6
oleleo
**Sample Output**
4
**Explanation**
One such possible $U$ is `oele` (because `oele` is a subsequence of `oleleo`, and `oleleo` is a subsequence of $UU^R$ = `oeleeleo`). Another is `olel`.
It can be shown that this is the shortest possible, so the answer is 4.
|
code
|
Determine how beautiful a Skwishinese word is.
|
ai
|
2014-06-19T03:42:29
|
2018-02-06T18:45:19
| null | null | null |
The language Skwishinese has its own elegant, albeit complicated, measure for the beauty of a word.
Before we can start describing how to measure it, we must first define a subsequence. Discovered by and named after the famous Skwishinese doctor, Aaron J. Subsequence, a _subsequence_ of a word is another word that can be formed by removing one or more (possibly none) of the letters of that word. For example, `loooo` is a subsequence of `troolooloo`, but `trooooll` and `banana` are not.
Moreover, the _reverse_ of a word is obtained simply by reversing the order of the letters. For example, the reverse of `troolooloo` is `oolooloort`. We denote the reverse of $U$ by $U^R$.
Let $U$ be a Skwishinese word. We can form a nonsensical word, $UU^R$, by _concatenating_ $U$ and its reverse. For example, if $U$ is `loooo`, then $UU^R$ will be `looooooool`.
Now, the _beauty_ of a Skwishinese word $V$ is the length of the shortest word $U$ that is a subsequence of $V$ and such that $V$ is a subsequence of $UU^R$ (the concatenation of $U$ and its reverse).
For example, the beauty of the word `troolooloo` is 6, because 6 is the length of the shortest word $U$ satisfying the above conditions (in this case, $U$ is `troolo`).
**Input Format**
The input consists of exactly two lines.
The first line contains $N$, a positive integer giving the length of the word $V$.
The second line contains $V$ a word in Skwishinese. It is a string consisting only of lowercase letters from the English alphabet.
**Output Format**
Output the beauty of the Skwishinese word $V$.
**Constraints**
$1 \le N \le 400$
$V$ consists only of lowercase letters
**Sample Input**
6
oleleo
**Sample Output**
4
**Explanation**
One such possible $U$ is `oele` (because `oele` is a subsequence of `oleleo`, and `oleleo` is a subsequence of $UU^R$ = `oeleeleo`). Another is `olel`.
It can be shown that this is the shortest possible, so the answer is 4.
| 0.5 |
["c","cpp","java","python3","python","cpp14"]
|
Hard
| null | null | null | null | null | null |
2014-06-25T11:28:33
|
2018-02-06T18:45:22
|
setter
|
```cpp
#include <stdio.h>
#define infinity 111111111
int min(int a, int b) {
return a < b ? a : b;
}
char V[411];
int F[411][411][411];
int main() {
int N;
scanf("%d%s", &N, V);
for (int i = N; i >= 0; i--) {
// try on ones and zeroes
for (int j = 0; j < N; j++) {
for (int k = j ? j - 1 : 0; k < N; k++) {
if (j > k) {// empty strjng
F[i][j][k] = 0;
} else if (i >= N) {
F[i][j][k] = infinity;
} else {
int X;
if (V[i] != V[j] and V[i] != V[k]) {
X = 1 + F[i+1][j][k];
} else if (V[i] != V[j] and V[i] == V[k]) {
X = 1 + F[i+1][j][k-1];
} else if (V[i] == V[j] and V[i] != V[k]) {
X = 1 + F[i+1][j+1][k];
} else if (V[i] == V[j] and V[i] == V[k]) {
X = 1 + F[i+1][j+1][k-1];
}
F[i][j][k] = min(F[i+1][j][k], X);
}
}
}
}
printf("%d\n", F[0][0][N-1]);
}
```
|
not-set
|
2016-04-24T02:02:44
|
2018-02-06T18:45:22
|
C++
|
||||
95 | 3,097 |
skwishinese
|
Skwishinese
|
The language Skwishinese has its own elegant, albeit complicated, measure for the beauty of a word.
Before we can start describing how to measure it, we must first define a subsequence. Discovered by and named after the famous Skwishinese doctor, Aaron J. Subsequence, a _subsequence_ of a word is another word that can be formed by removing one or more (possibly none) of the letters of that word. For example, `loooo` is a subsequence of `troolooloo`, but `trooooll` and `banana` are not.
Moreover, the _reverse_ of a word is obtained simply by reversing the order of the letters. For example, the reverse of `troolooloo` is `oolooloort`. We denote the reverse of $U$ by $U^R$.
Let $U$ be a Skwishinese word. We can form a nonsensical word, $UU^R$, by _concatenating_ $U$ and its reverse. For example, if $U$ is `loooo`, then $UU^R$ will be `looooooool`.
Now, the _beauty_ of a Skwishinese word $V$ is the length of the shortest word $U$ that is a subsequence of $V$ and such that $V$ is a subsequence of $UU^R$ (the concatenation of $U$ and its reverse).
For example, the beauty of the word `troolooloo` is 6, because 6 is the length of the shortest word $U$ satisfying the above conditions (in this case, $U$ is `troolo`).
**Input Format**
The input consists of exactly two lines.
The first line contains $N$, a positive integer giving the length of the word $V$.
The second line contains $V$ a word in Skwishinese. It is a string consisting only of lowercase letters from the English alphabet.
**Output Format**
Output the beauty of the Skwishinese word $V$.
**Constraints**
$1 \le N \le 400$
$V$ consists only of lowercase letters
**Sample Input**
6
oleleo
**Sample Output**
4
**Explanation**
One such possible $U$ is `oele` (because `oele` is a subsequence of `oleleo`, and `oleleo` is a subsequence of $UU^R$ = `oeleeleo`). Another is `olel`.
It can be shown that this is the shortest possible, so the answer is 4.
|
code
|
Determine how beautiful a Skwishinese word is.
|
ai
|
2014-06-19T03:42:29
|
2018-02-06T18:45:19
| null | null | null |
The language Skwishinese has its own elegant, albeit complicated, measure for the beauty of a word.
Before we can start describing how to measure it, we must first define a subsequence. Discovered by and named after the famous Skwishinese doctor, Aaron J. Subsequence, a _subsequence_ of a word is another word that can be formed by removing one or more (possibly none) of the letters of that word. For example, `loooo` is a subsequence of `troolooloo`, but `trooooll` and `banana` are not.
Moreover, the _reverse_ of a word is obtained simply by reversing the order of the letters. For example, the reverse of `troolooloo` is `oolooloort`. We denote the reverse of $U$ by $U^R$.
Let $U$ be a Skwishinese word. We can form a nonsensical word, $UU^R$, by _concatenating_ $U$ and its reverse. For example, if $U$ is `loooo`, then $UU^R$ will be `looooooool`.
Now, the _beauty_ of a Skwishinese word $V$ is the length of the shortest word $U$ that is a subsequence of $V$ and such that $V$ is a subsequence of $UU^R$ (the concatenation of $U$ and its reverse).
For example, the beauty of the word `troolooloo` is 6, because 6 is the length of the shortest word $U$ satisfying the above conditions (in this case, $U$ is `troolo`).
**Input Format**
The input consists of exactly two lines.
The first line contains $N$, a positive integer giving the length of the word $V$.
The second line contains $V$ a word in Skwishinese. It is a string consisting only of lowercase letters from the English alphabet.
**Output Format**
Output the beauty of the Skwishinese word $V$.
**Constraints**
$1 \le N \le 400$
$V$ consists only of lowercase letters
**Sample Input**
6
oleleo
**Sample Output**
4
**Explanation**
One such possible $U$ is `oele` (because `oele` is a subsequence of `oleleo`, and `oleleo` is a subsequence of $UU^R$ = `oeleeleo`). Another is `olel`.
It can be shown that this is the shortest possible, so the answer is 4.
| 0.5 |
["c","cpp","java","python3","python","cpp14"]
|
Hard
| null | null | null | null | null | null |
2014-06-25T11:28:33
|
2018-02-06T18:45:22
|
tester
|
```cpp
#include <cstring>
#include <string>
#include <cstdio>
#include <cctype>
#include <cassert>
using namespace std;
char s[402];
int dp[2][402][402];
void better(int &x,int y) {
if ((x < 0) || (x > y)) {
x = y;
}
}
int main() {
memset(dp,0xff,sizeof(dp));
dp[0][0][0] = 0;
int n;
scanf("%d%s",&n,s);
assert((n >= 1) && (n <= 400));
assert(strlen(s) == n);
int answer = n, last = 0;
for (int i = 1; i <= n; ++i) {
assert(islower(s[i - 1]));
int now = i & 1;
memcpy(dp[now], dp[last],sizeof(dp[0]));
for (int j = 0; j < i; ++j) {
for (int k = 0; (k < i) && (j + k < n); ++k) {
if (dp[last][j][k] >= 0) {
int jj = (s[i - 1] == s[j])?(j + 1):j;
int kk = (s[i - 1] == s[n - k - 1])?(k + 1):k;
better(dp[now][jj][kk], dp[last][j][k] + 1);
if (jj + kk >= n) {
answer = min(answer, dp[now][jj][kk]);
}
}
}
}
last = now;;
}
printf("%d\n",answer);
return 0;
}
```
|
not-set
|
2016-04-24T02:02:44
|
2018-02-06T18:45:22
|
C++
|
||||
96 | 3,164 |
net-admin
|
Network administration
|
Like every IT company, the Uplink Corporation has its own network. But, unlike the rest of the companies around the world, Uplink's network is subject to very specific restrictions:
* Any pair of servers within the network should be directly connected by at most 1 link.
* Each link is controlled by some specific network administrator.
* No server has more than 2 links connected to it, that are controlled by the same administrator.
* For easier management, links controlled by some administrator cannot be redundant (this is, removing any link will disconnect some two previously connected servers)
Notice that 2 connected servers might not have any direct link between them. Furthermore, in order to keep the network in a secured status, Uplink directives periodically try to perform some modifications over the network to mislead hackers. The problem is, having such a huge network, they need a software to efficiently simulate the network status after any of such modifications. You have been assigned to write the core section of that software.
Operations performed by the directives are:
* Change the administrator assigned to some particular link.
* Place some number of security devices along a particular link.
Also, given a network administrator, they would like to know how many devices are in the path created by links controlled by that administrator (if any) between 2 servers.
**Input Format**
Input begins with a line containing 4 integers $S, L, A, T$ separated by a single whitespace, denoting the number of servers, links, network administrators and transformations, respectively. $L$ lines follow each one with 3 integers $x, y~(x \lt y)$ and $a_i~(1 \le a_i \le A)$, saying that there is a link between server $x$ and server $y$, and that link is controlled by administrator $a_i$. Initially, network topology fulfills the restrictions described above and there is no security device along any link. Remaining $T$ lines in the input follow one the next formats:
* $1$ $A$ $B$ $a_i$
meaning that link between server $A$ and server $B$ $(A \lt B)$ is requested to be assigned to administrator $a_i$
* $2$ $A$ $B$ $x$
meaning that the number of security devices along the link between server $A$ and server $B$ $(A \lt B)$ will be fixed to $x$, removing any existing devices on this link before the operation. The involved link will always exist.
* $3$ $A$ $B$ $a_i$
meaning that directives want to know the number of security devices placed along the path between server $A$ and server $B$, just considering links controlled by administrator $a_i$.
**Output Format**
For each network transformation in the form $1$ $A$ $B$ $a_i$ you should output:
* "Wrong link" if there is no direct link between server $A$ and server $B$.
* "Already controlled link" if the requested link does exist, but it is already controlled by administrator $a_i$.
* "Server overload" if administrator $a_i$ already controls 2 links connected to one of the involved servers.
* "Network redundancy" if the requested assignment creates no new connection considering just the links controlled by $a_i$.
* "Assignment done" if none of the above conditions holds. In this case, link directly connecting $A$ with $B$ is assigned to $a_i$.
For each network transformation in the form $3$ $A$ $B$ $a_i$ you should output:
* "No connection" if there is no path between the requested servers considering just the links controlled by $a_i$.
* "$D$ security devices placed" where **D** is the number of security devices placed so far on the existing connection between the requested servers considering just the links controlled by $a_i$.
**Constraints**
$1 \le S \le 10^5$
$1 \le L \le 5 \times 10^5$
$1 \le A \le 10^2$
$1 \le T \le 5 \times 10^5$
$1 \le x \le 2000$
**Sample Input:**
4 5 3 15
1 2 1
2 3 1
3 4 2
1 4 2
1 3 3
2 3 4 49
1 1 2 3
2 1 4 64
3 1 4 2
1 1 2 3
3 4 2 3
3 1 3 3
1 1 4 3
3 3 4 2
3 2 4 1
2 1 4 13
2 1 3 21
2 2 3 24
1 2 3 3
1 2 4 3
**Sample Output:**
Assignment done
64 security devices placed
Already controlled link
No connection
0 security devices placed
Server overload
49 security devices placed
No connection
Network redundancy
Wrong link
|
code
|
Given a network administrator, find out how many devices are in the path created by links controlled by that administrator (if any) between 2 servers.
|
ai
|
2014-06-25T22:32:13
|
2022-09-02T10:00:41
|
#
# Complete the 'solve' function below.
#
# The function is expected to return a STRING_ARRAY.
# The function accepts following parameters:
# 1. INTEGER s
# 2. INTEGER a
# 3. 2D_INTEGER_ARRAY links
# 4. 2D_INTEGER_ARRAY queries
#
def solve(s, a, links, queries):
# Write your code here
|
#!/bin/python3
import math
import os
import random
import re
import sys
|
if __name__ == '__main__':
fptr = open(os.environ['OUTPUT_PATH'], 'w')
first_multiple_input = input().rstrip().split()
s = int(first_multiple_input[0])
l = int(first_multiple_input[1])
a = int(first_multiple_input[2])
t = int(first_multiple_input[3])
links = []
for _ in range(l):
links.append(list(map(int, input().rstrip().split())))
queries = []
for _ in range(t):
queries.append(list(map(int, input().rstrip().split())))
result = solve(s, a, links, queries)
fptr.write('\n'.join(result))
fptr.write('\n')
fptr.close()
|
<sub><strong>Time Limits</strong> C:5, Cpp:5, C#:6, Java:8, Php:18, Ruby:20, Python:20, Perl:18, Haskell:10, Scala:14, Javascript:20, Pascal:5</sub>
Like every IT company, the Uplink Corporation has its own network. But, unlike the rest of the companies around the world, Uplink's network is subject to very specific restrictions:
* Any pair of servers within the network should be directly connected by at most 1 link.
* Each link is controlled by some specific network administrator.
* No server has more than 2 links connected to it, that are controlled by the same administrator.
* For easier management, links controlled by some administrator cannot be redundant (this is, removing any link will disconnect some two previously connected servers)
Notice that 2 connected servers might not have any direct link between them. Furthermore, in order to keep the network in a secured status, Uplink directives periodically try to perform some modifications over the network to mislead hackers. The problem is, having such a huge network, they need a software to efficiently simulate the network status after any of such modifications. You have been assigned to write the core section of that software.
Operations performed by the directives are:
* Change the administrator assigned to some particular link.
* Place some number of security devices along a particular link.
Also, given a network administrator, they would like to know how many devices are in the path created by links controlled by that administrator (if any) between 2 servers.
**Input Format**
Input begins with a line containing 4 integers $S, L, A, T$ separated by a single whitespace, denoting the number of servers, links, network administrators and transformations, respectively. $L$ lines follow each one with 3 integers $x, y~(x \lt y)$ and $a_i~(1 \le a_i \le A)$, saying that there is a link between server $x$ and server $y$, and that link is controlled by administrator $a_i$. Initially, network topology fulfills the restrictions described above and there is no security device along any link. Remaining $T$ lines in the input follow one the next formats:
* $1$ $A$ $B$ $a_i$
meaning that link between server $A$ and server $B$ $(A \lt B)$ is requested to be assigned to administrator $a_i$
* $2$ $A$ $B$ $x$
meaning that the number of security devices along the link between server $A$ and server $B$ $(A \lt B)$ will be fixed to $x$, removing any existing devices on this link before the operation. The involved link will always exist.
* $3$ $A$ $B$ $a_i$
meaning that directives want to know the number of security devices placed along the path between server $A$ and server $B$, just considering links controlled by administrator $a_i$.
**Output Format**
For each network transformation in the form $1$ $A$ $B$ $a_i$ you should output:
* "Wrong link" if there is no direct link between server $A$ and server $B$.
* "Already controlled link" if the requested link does exist, but it is already controlled by administrator $a_i$.
* "Server overload" if administrator $a_i$ already controls 2 links connected to one of the involved servers.
* "Network redundancy" if the requested assignment creates no new connection considering just the links controlled by $a_i$.
* "Assignment done" if none of the above conditions holds. In this case, link directly connecting $A$ with $B$ is assigned to $a_i$.
For each network transformation in the form $3$ $A$ $B$ $a_i$ you should output:
* "No connection" if there is no path between the requested servers considering just the links controlled by $a_i$.
* "$D$ security devices placed" where **D** is the number of security devices placed so far on the existing connection between the requested servers considering just the links controlled by $a_i$.
**Constraints**
$1 \le S \le 10^5$
$1 \le L \le 5 \times 10^5$
$1 \le A \le 10^2$
$1 \le T \le 5 \times 10^5$
$1 \le x \le 2000$
**Sample Input:**
4 5 3 15
1 2 1
2 3 1
3 4 2
1 4 2
1 3 3
2 3 4 49
1 1 2 3
2 1 4 64
3 1 4 2
1 1 2 3
3 4 2 3
3 1 3 3
1 1 4 3
3 3 4 2
3 2 4 1
2 1 4 13
2 1 3 21
2 2 3 24
1 2 3 3
1 2 4 3
**Sample Output:**
Assignment done
64 security devices placed
Already controlled link
No connection
0 security devices placed
Server overload
49 security devices placed
No connection
Network redundancy
Wrong link
| 0.416667 |
["c","clojure","cpp","cpp14","cpp20","csharp","erlang","go","haskell","java","java8","java15","javascript","julia","kotlin","lua","objectivec","perl","php","pypy3","python3","ruby","rust","scala","swift","typescript","r"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-25T22:32:35
|
2016-12-03T07:57:19
|
setter
|
//============================================================================
// Name : NETADMIN.cpp
// Author : Shaka
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//============================================================================
#include <cstdio>
#include <algorithm>
#include <map>
using namespace std;
const int MAXSERVER = 8000, MAXADMIN = 100, MAXLINK = 1e5;
struct node {
node *prx, *lft, *rgt;
bool rev;
int sum, fx, size;
node() {
clear();
}
void clear() {
lft = rgt = prx = NULL;
rev = 0;
sum = fx = 0;
size = 1;
}
bool is_root() {
return !prx || (prx->lft != this && prx->rgt != this);
}
};
struct lnk {
node *a, *b;
lnk() {
clear();
}
node *get() {
if (a) return a;
else if (b) return b;
return NULL;
}
node *get_diff(node* x) {
if (a == x) return b;
else if (b == x) return a;
return get();
}
void add(node *x) {
if (!a) a = x;
else if (!b) b = x;
}
void del(node* x) {
if (a == x) a = NULL;
else if (b == x) b = NULL;
}
void clear() {
a = b = NULL;
}
int count() {
return (a != NULL) + (b != NULL);
}
};
typedef pair<int, int> pii;
typedef pair<int, node*> pin;
static void clean_reverse(node *px) {
if (px->rev) {
px->rev = 0;
swap(px->lft, px->rgt);
if (px->lft)
px->lft->rev ^= 1;
if (px->rgt)
px->rgt->rev ^= 1;
}
}
static void fix_size_and_sum(node *px) {
int lsize = px->lft ? px->lft->size : 0;
int rsize = px->rgt ? px->rgt->size : 0;
px->size = lsize + rsize + 1;
int lsum = px->lft ? px->lft->sum : 0;
int rsum = px->rgt ? px->rgt->sum : 0;
px->sum = lsum + rsum + px->fx;
}
void zig(node *p) {
node *q = p->prx, *r = q->prx;
if ((q->lft = p->rgt)) q->lft->prx = q;
p->rgt = q, q->prx = p;
if (((p->prx = r))) {
if (r->lft == q) r->lft = p;
if (r->rgt == q) r->rgt = p;
}
}
void zag(node *p) {
node *q = p->prx, *r = q->prx;
if ((q->rgt = p->lft)) q->rgt->prx = q;
p->lft = q, q->prx = p;
if (((p->prx = r))) {
if (r->lft == q) r->lft = p;
if (r->rgt == q) r->rgt = p;
}
}
lnk table[MAXSERVER][MAXADMIN];
map<pii, pin> ehash;
static void splay(node *px) {
struct node *f, *gf;
while (!px->is_root()) {
f = px->prx;
gf = f->prx;
if (!gf) {
clean_reverse(f);
clean_reverse(px);
if (f->lft == px) zig(px);
else zag(px);
fix_size_and_sum(f);
fix_size_and_sum(px);
} else {
clean_reverse(gf);
clean_reverse(f);
clean_reverse(px);
if (gf->lft == f)
if (f->lft == px) zig(f), zig(px);
else zag(px), zig(px);
else if (f->lft == px) zig(px), zag(px);
else zag(f), zag(px);
fix_size_and_sum(gf);
fix_size_and_sum(f);
fix_size_and_sum(px);
}
}
clean_reverse(px);
}
static void make_last (node *x) {
splay(x);
if (x->rgt) x->rev ^= 1;
}
static void make_first (node *x) {
splay(x);
if (x->lft) x->rev ^= 1;
}
static void add_edge(int a, int b, int i, node *px) {
node *l, *r;
l = table[a][i].get();
if (l) make_last(l);
r = table[b][i].get();
if (r) make_first(r);
px->lft = l;
if (l) l->prx = px;
px->rgt = r;
if (r) r->prx = px;
px->rev = 0;
px->prx = NULL;
fix_size_and_sum(px);
table[a][i].add(px);
table[b][i].add(px);
}
static void del_edge(int a, int b, int x, node *px) {
splay(px);
if (px->lft) px->lft->prx = NULL;
if (px->rgt) px->rgt->prx = NULL;
table[a][x].del(px);
table[b][x].del(px);
px->lft = NULL;
px->rgt = NULL;
px->prx = NULL;
fix_size_and_sum(px);
}
static bool connected(int a, int b, int x) {
node *pa = table[a][x].get(), *pb = table[b][x].get();
if (pa != pb) {
splay(pa), splay(pb);
return pa->prx != NULL;
}
return true;
}
int xrank(node* px) {
splay(px);
return px->lft ? px->lft->size : 0;
}
node* frx[MAXLINK];
int main() {
register int N, M, C, T, i, j, a, b, x, cmd;
scanf("%d%d%d%d", &N, &M, &C, &T);
for (i = 0; i < M; ++i)
frx[i] = new node();
ehash.clear();
pii key;
for (i = 0; i < M; ++i) {
scanf("%d%d%d", &a, &b, &j);
--a, --b, --j;
key = make_pair(a, b);
node *ptx = frx[i];
ehash[key] = make_pair(j + 1, ptx);
add_edge(a, b, j, ptx);
}
node *px, *qx, *tx, *ux;
int rpx, rqx, rtx, rux;
while (T--) {
scanf("%d%d%d%d", &cmd, &a, &b, &i);
--a, --b;
if (cmd == 1) {
--i;
key = make_pair(a, b);
pin& data = ehash[key];
x = data.first;
if (!x) { //not found in edges storage
printf("Wrong link\n");
continue;
}
--x;
if (x == i) { //this cable is already controlled by this admin
printf("Already controlled link\n");
continue;
}
if (table[a][i].count() == 2 || table[b][i].count() == 2) { //at least one of the serves has 2 cables related the new admin
printf("Server overload\n");
continue;
}
if (table[a][i].count() > 0 && table[b][i].count() > 0 && connected(a, b, i)) { //it is possible to get from one of them to the other
printf("Network redundancy\n");
continue;
}
px = data.second; //get the proper node (i.e. the node for edge a <-> b)
del_edge(a, b, x, px);
add_edge(a, b, i, px);
data.first = i + 1; //update the company owning this cable
printf("Assignment done\n");
} else if(cmd == 2) {
key = make_pair(a, b);
pin& data = ehash[key];
px = data.second;
splay(px);
px->fx = i;
fix_size_and_sum(px);
} else {
--i;
if (a > b) swap(a, b);
key = make_pair(a, b);
pin& data = ehash[key];
if (data.second && data.first == i + 1) {
printf("%d security devices placed\n", data.second->fx);
continue;
}
lnk al = table[a][i], bl = table[b][i];
if (al.count() > 0 && bl.count() > 0 && connected(a, b, i)) {
if (al.count() == 1 && bl.count() == 1) { //happy case :)
px = al.get();
make_first(px);
x = px->sum;
} else if (al.count() + bl.count() == 3) { //one is extreme, we need to find the next one
if (al.count() > 1) swap(al, bl);
px = al.get();
make_first(px);
x = px->sum;
qx = bl.a, tx = bl.b;
if (xrank(qx) > xrank(tx)) swap(qx, tx);
splay(qx);
x -= qx->rgt->sum;
} else { //hard case, invoking creativity :)
px = al.a, qx = al.b, tx = bl.a, ux = bl.b;
rpx = xrank(px), rqx = xrank(qx), rtx = xrank(tx), rux = xrank(ux);
if (rpx > rqx) swap(px, qx), swap(rpx, rqx);
if (rtx > rux) swap(tx, ux), swap(rtx, rux);
if (rpx > rtx) swap(px, tx), swap(rpx, rtx), swap(qx, ux), swap(rqx, rux);
/**
* At this point:
* a is to the left and b to the right
* px is the lowest a's edge and qx is the highest a's edge
* tx is the lowest b's edge and ux is the highest b's edge
* */
splay(qx);
x = qx->fx + qx->rgt->sum;
splay(tx);
x -= tx->rgt->sum;
}
printf("%d security devices placed\n", x);
} else printf("No connection\n");
}
}
return 0;
}
|
not-set
|
2016-04-24T02:02:44
|
2016-04-24T02:02:44
|
C++
|
97 | 2,565 |
xor-love
|
XOR love
|
Devendra loves the XOR operation very much which is denoted by $\wedge$ sign in most of the programming languages. He has a list $A$ of $N$ numbers and he wants to know the answers of $M$ queries. Each query will be denoted by three numbers i.e. $K,P,R$ .
For query $K,P \text{ and } R$, he has to print the value of the $KPRsum$ which can be described as given below. As the value of the $KPRsum$ can be large. So, print it modulus $(10^9 + 7)$.
$$ KPRsum = \sum_{i=P}^{R-1} \sum_{j=i+1}^{R} (K \oplus (A[i] \oplus A[j]) )$$
**Input Format**
The first line contains an integer $N$, i.e., the number of the elements in the list. List is numbered from $1$ to $N$.
Next line will contain $N$ space seperated integers.
Third line will contain a number $M$ i.e. number of queries followed by $M$ lines each containing integers $K,P \& R$.
**Output Format**
Print $M$ lines, $i^{th}$ line will be answer of $i^{th}$ query. **Answer will be 0 in case of P=R.**
**Constraints**
$1 \le N \le 10^5$
$1 \le A[i] \le 10^6$
$1 \le M \le 10^5$
$0 \le K \le 10^6$
$1 \le P \le R \le N$
**Sample Input**
3
1 2 3
2
1 1 3
2 1 3
**Sample Output**
5
4
**Explanation**
For first query, it will will be $$(1 \oplus( 1 \oplus 2) ) + (1 \oplus( 1 \oplus 3) ) + (1 \oplus( 2 \oplus 3) ) = 5 $$
|
code
|
Reply to query related to XOR.
|
ai
|
2014-05-30T20:35:04
|
2022-09-02T09:55:10
| null | null | null |
Devendra loves the XOR operation very much which is denoted by $\wedge$ sign in most of the programming languages. He has a list $A$ of $N$ numbers and he wants to know the answers of $M$ queries. Each query will be denoted by three numbers i.e. $K,P,R$ .
For query $K,P \text{ and } R$, he has to print the value of the $KPRsum$ which can be described as given below. As the value of the $KPRsum$ can be large. So, print it modulus $(10^9 + 7)$.
$$ KPRsum = \sum_{i=P}^{R-1} \sum_{j=i+1}^{R} (K \oplus (A[i] \oplus A[j]) )$$
**Input Format**
The first line contains an integer $N$, i.e., the number of the elements in the list. List is numbered from $1$ to $N$.
Next line will contain $N$ space seperated integers.
Third line will contain a number $M$ i.e. number of queries followed by $M$ lines each containing integers $K,P \& R$.
**Output Format**
Print $M$ lines, $i^{th}$ line will be answer of $i^{th}$ query. **Answer will be 0 in case of P=R.**
**Constraints**
$1 \le N \le 10^5$
$1 \le A[i] \le 10^6$
$1 \le M \le 10^5$
$0 \le K \le 10^6$
$1 \le P \le R \le N$
**Sample Input**
3
1 2 3
2
1 1 3
2 1 3
**Sample Output**
5
4
**Explanation**
For first query, it will will be $$(1 \oplus( 1 \oplus 2) ) + (1 \oplus( 1 \oplus 3) ) + (1 \oplus( 2 \oplus 3) ) = 5 $$
| 0.476923 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-26T10:13:36
|
2016-12-06T09:46:26
|
setter
|
###C++
```cpp
#include<stdio.h>
#include<algorithm>
#include<vector>
#include<set>
#include<stdlib.h>
#include<string.h>
#include<utility>
#include<assert.h>
using namespace std;
typedef long long int ll;
int A[100001][31];
int main()
{
ll answer=0,ones,zeros,o,z;
int N,x,pow[31],y,k,M;
pow[0]=1;
for(int i=1;i<31;i++) pow[i]=pow[i-1]<<1;
scanf("%d",&N);
assert(N<=100000 && N>=1);
for(int i=0;i<31;i++) A[0][i]=0;
for(int i=1;i<=N;i++)
{
scanf("%d",&x);
assert(x<=1000000 && x>=1);
for(int j=0;j<31;j++) A[i][j] = A[i-1][j]+((x&pow[j])?1:0);
}
scanf("%d",&M);
assert(M<=10000);
while(M--)
{
answer=0;
scanf("%d",&k);
assert(k>=1 && k<=1000000);
x=0;
y=N;
for(int i=0;i<31;i++){
o=A[y][i]-A[x][i];
z = (y-x) - o;
ones = z*o;
zeros = (z*(z-1) + o*(o-1))/2;
if((k&pow[i])==0)
answer = (answer + (ll)pow[i]*ones);
else
answer = (answer + (ll)pow[i]*zeros);
}
printf("%lld\n",answer%(1000000007));
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:45
|
2016-07-23T18:58:34
|
C++
|
98 | 2,565 |
xor-love
|
XOR love
|
Devendra loves the XOR operation very much which is denoted by $\wedge$ sign in most of the programming languages. He has a list $A$ of $N$ numbers and he wants to know the answers of $M$ queries. Each query will be denoted by three numbers i.e. $K,P,R$ .
For query $K,P \text{ and } R$, he has to print the value of the $KPRsum$ which can be described as given below. As the value of the $KPRsum$ can be large. So, print it modulus $(10^9 + 7)$.
$$ KPRsum = \sum_{i=P}^{R-1} \sum_{j=i+1}^{R} (K \oplus (A[i] \oplus A[j]) )$$
**Input Format**
The first line contains an integer $N$, i.e., the number of the elements in the list. List is numbered from $1$ to $N$.
Next line will contain $N$ space seperated integers.
Third line will contain a number $M$ i.e. number of queries followed by $M$ lines each containing integers $K,P \& R$.
**Output Format**
Print $M$ lines, $i^{th}$ line will be answer of $i^{th}$ query. **Answer will be 0 in case of P=R.**
**Constraints**
$1 \le N \le 10^5$
$1 \le A[i] \le 10^6$
$1 \le M \le 10^5$
$0 \le K \le 10^6$
$1 \le P \le R \le N$
**Sample Input**
3
1 2 3
2
1 1 3
2 1 3
**Sample Output**
5
4
**Explanation**
For first query, it will will be $$(1 \oplus( 1 \oplus 2) ) + (1 \oplus( 1 \oplus 3) ) + (1 \oplus( 2 \oplus 3) ) = 5 $$
|
code
|
Reply to query related to XOR.
|
ai
|
2014-05-30T20:35:04
|
2022-09-02T09:55:10
| null | null | null |
Devendra loves the XOR operation very much which is denoted by $\wedge$ sign in most of the programming languages. He has a list $A$ of $N$ numbers and he wants to know the answers of $M$ queries. Each query will be denoted by three numbers i.e. $K,P,R$ .
For query $K,P \text{ and } R$, he has to print the value of the $KPRsum$ which can be described as given below. As the value of the $KPRsum$ can be large. So, print it modulus $(10^9 + 7)$.
$$ KPRsum = \sum_{i=P}^{R-1} \sum_{j=i+1}^{R} (K \oplus (A[i] \oplus A[j]) )$$
**Input Format**
The first line contains an integer $N$, i.e., the number of the elements in the list. List is numbered from $1$ to $N$.
Next line will contain $N$ space seperated integers.
Third line will contain a number $M$ i.e. number of queries followed by $M$ lines each containing integers $K,P \& R$.
**Output Format**
Print $M$ lines, $i^{th}$ line will be answer of $i^{th}$ query. **Answer will be 0 in case of P=R.**
**Constraints**
$1 \le N \le 10^5$
$1 \le A[i] \le 10^6$
$1 \le M \le 10^5$
$0 \le K \le 10^6$
$1 \le P \le R \le N$
**Sample Input**
3
1 2 3
2
1 1 3
2 1 3
**Sample Output**
5
4
**Explanation**
For first query, it will will be $$(1 \oplus( 1 \oplus 2) ) + (1 \oplus( 1 \oplus 3) ) + (1 \oplus( 2 \oplus 3) ) = 5 $$
| 0.476923 |
["bash","c","clojure","cpp","cpp14","cpp20","csharp","d","elixir","erlang","fsharp","go","groovy","haskell","java","java8","java15","javascript","julia","kotlin","lolcode","lua","objectivec","ocaml","pascal","perl","php","python3","r","racket","ruby","rust","sbcl","scala","smalltalk","swift","tcl","typescript","visualbasic","pypy3"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-26T10:13:36
|
2016-12-06T09:46:26
|
tester
|
###C++
```cpp
#ifdef ssu1
#define _GLIBCXX_DEBUG
#endif
#undef NDEBUG
#include <algorithm>
#include <functional>
#include <numeric>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <cstring>
#include <cassert>
#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <queue>
#include <bitset>
#include <sstream>
using namespace std;
#define fore(i, l, r) for(int i = (l); i < (r); ++i)
#define forn(i, n) fore(i, 0, n)
#define fori(i, l, r) fore(i, l, (r) + 1)
#define sz(v) int((v).size())
#define all(v) (v).begin(), (v).end()
#define pb push_back
#define mp make_pair
#define X first
#define Y second
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
template<typename T> T abs(T a) { return a < 0 ? -a : a; }
template<typename T> T sqr(T a) { return a*a; }
const int INF = (int)1e9;
const ld EPS = 1e-9;
const ld PI = 3.1415926535897932384626433832795;
/*
This is just to check correctness of input
*/
int readInt(int l, int r){
int x;
if(scanf("%d", &x) != 1){
fprintf(stderr, "Expected int in range [%d, %d], but haven't found!", l, r);
throw;
}
if(!(l <= x && x <= r)){
fprintf(stderr, "Expected int in range [%d, %d], but found %d!", l, r, x);
throw;
}
return x;
}
int readInt(int l, int r, string name){
int x;
if(scanf("%d", &x) != 1){
fprintf(stderr, "Expected int %s in range [%d, %d], but haven't found!", name.c_str(), l, r);
throw;
}
if(!(l <= x && x <= r)){
fprintf(stderr, "Expected int %s in range [%d, %d], but found %d!", name.c_str(), l, r, x);
throw;
}
return x;
}
li readLong(li l, li r){
li x;
if(scanf("%lld", &x) != 1){
fprintf(stderr, "Expected long long in range [%lld, %lld], but haven't found!", l, r);
throw;
}
if(!(l <= x && x <= r)){
fprintf(stderr, "Expected long long in range [%lld, %lld], but found %lld!", l, r, x);
throw;
}
return x;
}
li readLong(li l, li r, string name){
li x;
if(scanf("%lld", &x) != 1){
fprintf(stderr, "Expected long long %s in range [%lld, %lld], but haven't found!", name.c_str(), l, r);
throw;
}
if(!(l <= x && x <= r)){
fprintf(stderr, "Expected long long %s in range [%lld, %lld], but found %lld!", name.c_str(), l, r, x);
throw;
}
return x;
}
const ld __EPS__ = 1e-15;
ld readDouble(double l, double r){
double x;
if(scanf("%lf", &x) != 1){
fprintf(stderr, "Expected double in range [%lf, %lf], but haven't found!", l, r);
throw;
}
if(!(l <= x + __EPS__ && x <= r + __EPS__)){
fprintf(stderr, "Expected double in range [%lf, %lf], but found %lf!", l, r, x);
throw;
}
return x;
}
ld readDouble(double l, double r, string name){
double x;
if(scanf("%lf", &x) != 1){
fprintf(stderr, "Expected double %s in range [%lf, %lf], but haven't found!", name.c_str(), l, r);
throw;
}
if(!(l <= x + __EPS__ && x <= r + __EPS__)){
fprintf(stderr, "Expected double %s in range [%lf, %lf], but found %lf!", name.c_str(), l, r, x);
throw;
}
return x;
}
const int LOG = 22;
const int NMAX = 100000;
const int VMAX = 1000000;
int bit(int v, int i){
return (v >> i) & 1;
}
int z[LOG][NMAX], o[LOG][NMAX], n;
void upd(int t[NMAX], int i, int di){
for(; i < n; i = (i | (i + 1)))
t[i] += di;
}
int sum(int t[NMAX], int r){
int ans = 0;
for(; r >= 0; r = (r & (r + 1)) - 1)
ans += t[r];
return ans;
}
int sum(int t[NMAX], int l, int r){
return sum(t, r) - sum(t, l - 1);
}
int main(){
#ifdef ssu1
assert(freopen("input.txt", "rt", stdin));
//assert(freopen("output.txt", "wt", stdout));
#endif
n = readInt(1, NMAX, "n");
forn(i, n){
int cur = readInt(1, VMAX, "a[i]");
forn(j, LOG){
if(bit(cur, j))
upd(o[j], i, 1);
else
upd(z[j], i, 1);
}
}
int m = readInt(1, 100000, "m");
forn(mi, m){
int K, l, r;
K = readInt(0, VMAX);
l = readInt(1, n) - 1;
r = readInt(1, n) - 1;
assert(l <= r);
li ans = 0;
forn(i, LOG){
int cnt[2];
cnt[0] = sum(o[i], l, r);
cnt[1] = sum(z[i], l, r);
// if(i == 0)
// cerr << cnt[0] << " " << cnt[1] << endl;
forn(b1, 2){
forn(b2, b1 + 1){
int result = b1 ^ b2 ^ bit(K, i);
if(result == 0)
continue;
li ways = 0;
if(b1 == b2)
ways = (cnt[b1] * 1LL * (cnt[b1] - 1)) / 2;
else
ways = cnt[b1] * 1LL * cnt[b2];
ans += ways * (1LL << i);
}
}
}
printf("%lld\n", ans % (int(1e9) + 7));
}
return 0;
}
```
|
not-set
|
2016-04-24T02:02:45
|
2016-07-23T18:58:47
|
C++
|
99 | 3,166 |
dcbus
|
Dassu And Business
|
Dassu is very disturbed since the brutal murdur of her pet mosquito. As such, she is unable to concentrate on her studies.
So, she decided to step into business.<br>
She had learnt that she had to deal with **2 type of people - Dealers and Customers**.
There are **N dealers** and **M customers**. Also, there are **P types of products**.
Dealer i provides each item at cost **CP<sub>i</sub>** and has **A<sub>ij</sub>** units of j-th item.
Customer i buys each item at **SP<sub>i</sub>** and requires at the most **B<sub>ij</sub>** units of j-th item.<br>
(If a dealer has X items of some type, it is **not necessary** that you purchase all X items. You can purchase any number of items between **0 to X(both inclusive)** . Similiary, if a customer can buy X products of a type, it is **not necessary** to give him exact X products. Rather you can give him any number of items from **0 to X(both inclusive)** to him, **depending upon your profit** .)
Now she has **R rupees** initially.
She knows that **dealers come in early morning** so as to sell their items as soon as possible.
She also knows that the **customers come in at night** after their office.
<br><br>So what is the **maximum profit that she can make today?** Assume dealers gives no loan.
<br><br>
###INPUT FORMAT
The **First Line** of Input will have 4 Integers - **N, M, P** & **R**.<br>
The **next line** will have **N** integers, the rate of every dealer (CP<sub>i</sub> is the rate at which i-th dealer provides all the products).<br>
The **next line** will have **M** integers, the Selling Price for every customer(SP<sub>i</sub> is the rate at which i-th customer buys all the products).<br>
The **next N lines** will have **P integers each**. It will represent the matrix **A[][]**.<br>
The **next M lines** will have **P integers each**. It will represent the matrix **B[][]**.<br>
###OUTPUT FORMAT
Output a **Single Integer** corresponding to the **maximum profit** Miss Dassu can make today.
###CONSTRAINTS
1<= N,M,P,R <=1000<br>
0<= A<sub>ij</sub>, B<sub>ij</sub>, CP<sub>i</sub>, SP<sub>i</sub> <= 1000<br>
The Sum of all A<sub>ij</sub> will not exceed 1000<br>
The Sum of all B<sub>ij</sub> will not exceed 1000<br>
###EXAMPLE
**INPUT :**
<br><br>
3 2 2 3<br>
1 2 3<br>
4 5<br>
1 2<br>
1 3<br>
2 3<br>
0 2<br>
3 1<br>
<br><br>
**OUTPUT :**
<br><br>
11<br><br>
**EXPLANATION**
<br><br>Dassu has 3 rupees in the begining. She can buy 1 item<sub>1</sub> and 2 item<sub>2</sub> from dealer<sub>1</sub>. The cost will be 1 rupees each, i.e. 3 rupees. She can sell 1 item<sub>1</sub> and 1 item<sub>2</sub> to customer<sub>2</sub> at 5 rupees each, and 1 item<sub>2</sub> to customer<sub>1</sub> at 4 rupees. So she sells them for 14 rupees, making a profit of 11.
|
code
|
Help Dassu make the maximum out of the day.
|
ai
|
2014-06-26T10:16:14
|
2016-09-09T09:47:21
| null | null | null |
Dassu is very disturbed since the brutal murdur of her pet mosquito. As such, she is unable to concentrate on her studies.
So, she decided to step into business.<br>
She had learnt that she had to deal with **2 type of people - Dealers and Customers**.
There are **N dealers** and **M customers**. Also, there are **P types of products**.
Dealer i provides each item at cost **CP<sub>i</sub>** and has **A<sub>ij</sub>** units of j-th item.
Customer i buys each item at **SP<sub>i</sub>** and requires at the most **B<sub>ij</sub>** units of j-th item.<br>
(If a dealer has X items of some type, it is **not necessary** that you purchase all X items. You can purchase any number of items between **0 to X(both inclusive)** . Similiary, if a customer can buy X products of a type, it is **not necessary** to give him exact X products. Rather you can give him any number of items from **0 to X(both inclusive)** to him, **depending upon your profit** .)
Now she has **R rupees** initially.
She knows that **dealers come in early morning** so as to sell their items as soon as possible.
She also knows that the **customers come in at night** after their office.
<br><br>So what is the **maximum profit that she can make today?** Assume dealers gives no loan.
<br><br>
###INPUT FORMAT
The **First Line** of Input will have 4 Integers - **N, M, P** & **R**.<br>
The **next line** will have **N** integers, the rate of every dealer (CP<sub>i</sub> is the rate at which i-th dealer provides all the products).<br>
The **next line** will have **M** integers, the Selling Price for every customer(SP<sub>i</sub> is the rate at which i-th customer buys all the products).<br>
The **next N lines** will have **P integers each**. It will represent the matrix **A[][]**.<br>
The **next M lines** will have **P integers each**. It will represent the matrix **B[][]**.<br>
###OUTPUT FORMAT
Output a **Single Integer** corresponding to the **maximum profit** Miss Dassu can make today.
###CONSTRAINTS
1<= N,M,P,R <=1000<br>
0<= A<sub>ij</sub>, B<sub>ij</sub>, CP<sub>i</sub>, SP<sub>i</sub> <= 1000<br>
The Sum of all A<sub>ij</sub> will not exceed 1000<br>
The Sum of all B<sub>ij</sub> will not exceed 1000<br>
###EXAMPLE
**INPUT :**
<br><br>
3 2 2 3<br>
1 2 3<br>
4 5<br>
1 2<br>
1 3<br>
2 3<br>
0 2<br>
3 1<br>
<br><br>
**OUTPUT :**
<br><br>
11<br><br>
**EXPLANATION**
<br><br>Dassu has 3 rupees in the begining. She can buy 1 item<sub>1</sub> and 2 item<sub>2</sub> from dealer<sub>1</sub>. The cost will be 1 rupees each, i.e. 3 rupees. She can sell 1 item<sub>1</sub> and 1 item<sub>2</sub> to customer<sub>2</sub> at 5 rupees each, and 1 item<sub>2</sub> to customer<sub>1</sub> at 4 rupees. So she sells them for 14 rupees, making a profit of 11.
| 0.5 |
["bash","c","cpp","java","csharp","php","ruby","python","perl","haskell","clojure","scala","lua","erlang","brainfuck","javascript","go","d","ocaml","pascal","sbcl","python3","groovy","objectivec","fsharp","cobol","visualbasic","lolcode","smalltalk","tcl","whitespace","tsql","cpp14"]
| null | null | null | null |
Hard
| null | null | null | null | null | null |
2014-06-27T05:17:03
|
2018-08-14T21:11:55
|
setter
|
<br><br>[CODE](http://ideone.com/z3TwMM)
|
not-set
|
2016-04-24T02:02:45
|
2016-04-24T02:02:45
|
Unknown
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.