question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
range-sum-of-bst
|
my_rangeSumBST
|
my_rangesumbst-by-rinatmambetov-tdvh
|
# Intuition \n\n\n\n\n\n\n\n\n\n\n\n# Code\n\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===u
|
RinatMambetov
|
NORMAL
|
2023-04-27T07:18:24.334173+00:00
|
2023-04-27T07:18:24.334208+00:00
| 391 | false |
<!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n<!-- # Complexity\n- Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n */\n/**\n * @param {TreeNode} root\n * @param {number} low\n * @param {number} high\n * @return {number}\n */\nvar rangeSumBST = function(root, low, high) {\n let sum=0;\n\n if(root){\n sum+=(root.val>=low&&root.val<=high)?root.val:0;\n sum+=rangeSumBST(root.left,low,high);\n sum+=rangeSumBST(root.right,low,high);\n }\n \n return sum;\n};\n```
| 5 | 0 |
['JavaScript']
| 0 |
range-sum-of-bst
|
JAVA 100% Solution (Range Sum of BST)
|
java-100-solution-range-sum-of-bst-by-ar-602r
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
arnavsharma2711
|
NORMAL
|
2022-12-07T13:53:27.720967+00:00
|
2022-12-07T13:53:27.721006+00:00
| 627 | false |
# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int rangeSumBST(TreeNode root, int low, int high) {\n int sum=0;\n if(root==null)\n return sum;\n if(root.val>=low && root.val<=high)\n sum+=root.val;\n \n sum+=rangeSumBST(root.left,low,high);\n sum+=rangeSumBST(root.right,low,high);\n\n return sum;\n }\n}\n```
| 5 | 0 |
['Breadth-First Search', 'Binary Search Tree', 'Recursion', 'Java']
| 0 |
range-sum-of-bst
|
[Java] Runtime: 0ms, faster than 100% || Recursive + Iterative solutions
|
java-runtime-0ms-faster-than-100-recursi-3nap
|
Complexity\n- Time complexity: O(N)\n- Space complexity: O(N)\n\n# Approach\nDepth-First Search\n\n# Code\nRecursive Implementation \n\nclass Solution {\n pr
|
decentos
|
NORMAL
|
2022-12-07T03:06:27.241605+00:00
|
2022-12-07T03:06:27.241645+00:00
| 944 | false |
# Complexity\n- Time complexity: O(N)\n- Space complexity: O(N)\n\n# Approach\nDepth-First Search\n\n# Code\nRecursive Implementation \n```\nclass Solution {\n private int sum = 0;\n public int rangeSumBST(TreeNode root, int low, int high) {\n if (root == null) return sum;\n if (root.val >= low && root.val <= high) sum += root.val;\n if (low < root.val) rangeSumBST(root.left, low, high);\n if (root.val < high) rangeSumBST(root.right, low, high);\n return sum;\n }\n}\n```\n\nIterative Implementation\n```\nclass Solution {\n public int rangeSumBST(TreeNode root, int low, int high) {\n int sum = 0;\n Stack<TreeNode> stack = new Stack<>();\n stack.push(root);\n\n while (!stack.empty()) {\n TreeNode current = stack.pop();\n if (current == null) continue;\n if (current.val >= low && current.val <= high) sum += current.val;\n if (low < current.val) stack.push(current.left);\n if (current.val < high) stack.push(current.right);\n }\n return sum;\n }\n}\n```\n\n\n\n
| 5 | 0 |
['Java']
| 0 |
range-sum-of-bst
|
C++ || Easy to Understand || Explained
|
c-easy-to-understand-explained-by-mohakh-bg8w
|
Intuition\n Describe your first thoughts on how to solve this problem. \nCase-1 : If currVal is in range [>=low && <= high] \n Then traverse both the le
|
mohakharjani
|
NORMAL
|
2022-12-07T00:31:59.556125+00:00
|
2022-12-07T00:33:20.789544+00:00
| 3,122 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Case-1** : If currVal is in range [>=low && <= high] \n Then **traverse both** the left and right subtree\n\n**Case-2 :** If [currVal <= low] \nThen traverse only the right subtree\n\n**Case-3 :** If [currVal >= high]\nThen traverse only the left subtree\n \n\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int solve(TreeNode* curr, int& low, int& high)\n {\n if (curr == NULL) return 0;\n \n int ans = 0;\n bool isInRange = false;\n if (curr->val >= low && curr->val <= high) \n {\n isInRange = true;\n ans += curr->val;\n }\n \n if (isInRange || (curr->val <= low)) ans += solve(curr->right, low, high);\n if (isInRange || (curr->val >= high)) ans += solve(curr->left, low, high);\n return ans;\n }\n int rangeSumBST(TreeNode* root, int low, int high) \n {\n return solve(root, low, high);\n \n }\n};\n```
| 5 | 1 |
['Recursion', 'C', 'C++']
| 0 |
range-sum-of-bst
|
Python Elegant & Short | Recursive | Three lines
|
python-elegant-short-recursive-three-lin-hkht
|
\n def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:\n if root is None:\n return 0\n return self.rangeSum
|
Kyrylo-Ktl
|
NORMAL
|
2022-08-31T10:06:13.382301+00:00
|
2022-08-31T10:06:13.382342+00:00
| 958 | false |
\n def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:\n if root is None:\n return 0\n return self.rangeSumBST(root.left, low, high) + \\\n self.rangeSumBST(root.right, low, high) + \\\n root.val * (low <= root.val <= high)\n
| 5 | 0 |
['Recursion', 'Python', 'Python3']
| 1 |
range-sum-of-bst
|
JAVA short 0ms solution faster than 100% ✅
|
java-short-0ms-solution-faster-than-100-i0bmd
|
Runtime: 0 ms, faster than 100.00% of Java online submissions for Range Sum of BST.\nMemory Usage: 67.1 MB, less than 42.28% of Java online submissions for Rang
|
Z3ROsum
|
NORMAL
|
2022-07-31T23:18:07.889899+00:00
|
2022-07-31T23:18:07.889929+00:00
| 160 | false |
Runtime: 0 ms, faster than 100.00% of Java online submissions for Range Sum of BST.\nMemory Usage: 67.1 MB, less than 42.28% of Java online submissions for Range Sum of BST.\n```\nclass Solution {\n int sum = 0;\n int lo = 0; // low\n int hi = 0; // and high\n public int rangeSumBST(TreeNode root, int low, int high) {\n lo = low;\n hi = high;\n addSum(root);\n return sum;\n }\n \n void addSum(TreeNode root) {\n if (root == null) return;\n if (root.val >= lo && root.val <= hi) { // if the root value is in the range\n sum += root.val; // add to sum\n addSum(root.left); // left\n addSum(root.right); // right\n } else if (root.val < lo) addSum(root.right); // if the root value is too small\n else addSum(root.left); // if the root value is too big\n }\n}\n```
| 5 | 0 |
['Recursion', 'Java']
| 0 |
range-sum-of-bst
|
3 line code lmaooooo.... DFS
|
3-line-code-lmaooooo-dfs-by-astareadytoc-luc7
|
I don\'t think this code requires intiution but for beginner here is the brute force first approach all you need to calculate sum right? so what you could do is
|
astareadytocode
|
NORMAL
|
2021-06-23T16:31:49.806915+00:00
|
2021-06-23T16:31:49.806947+00:00
| 149 | false |
**I don\'t think this code requires intiution but for beginner here is the brute force first approach all you need to calculate sum right? so what you could do is check if your root value is lie b/w the range just add it in your answer and call on your left and right childs and add their answer too return the answer**\n\n\n**since it\'s BST we can improve our logic check if your root->val is greater than high? if yes this means no need to call on right child it will never give you an answer so call on only left now check if root->val is less than low? if yes no need to call on left it won\'t give you an answer so call on right only now if both the cases are not true it means your root value is lie b/w range so add root->val in your answer and call on left and right simple that\'s it bois/girls.......... don\'t forget to upvote \n```\nclass Solution {\npublic:\n int rangeSumBST(TreeNode* root, int low, int high) {\n if(!root)return 0;\n if(root->val>high)return rangeSumBST(root->left, low,high);\n else if(root->val<low)return rangeSumBST(root->right,low,high);\n else return root->val + rangeSumBST(root->left, low,high) + rangeSumBST(root->right,low,high);\n }\n};\n```
| 5 | 2 |
[]
| 0 |
range-sum-of-bst
|
Rust TreeNode implementation could be simplified
|
rust-treenode-implementation-could-be-si-8czw
|
Current TreeNode in rust looks like that \n\npub struct TreeNode {\n pub val: i32,\n pub left: Option<Rc<RefCell<TreeNode>>>,\n pub right: Option<Rc<RefCe
|
zxcq544
|
NORMAL
|
2021-01-11T03:38:00.506730+00:00
|
2021-01-11T03:38:00.506773+00:00
| 201 | false |
Current TreeNode in rust looks like that \n```\npub struct TreeNode {\n pub val: i32,\n pub left: Option<Rc<RefCell<TreeNode>>>,\n pub right: Option<Rc<RefCell<TreeNode>>>,\n }\n ```\n But since each node in tree has only one owner it could be simplified to \n ```\npub struct TreeNode {\n pub val: i32,\n pub left: Option<Box<TreeNode>>,\n pub right: Option<Box<TreeNode>>,\n}\n```\nHow does it help ?\n1. It will work faster since we don\'t do reference counting. So compared to current 12-20 ms we will get better results for rust.\n2. Code to build tree becomes simpler.\n
| 5 | 0 |
['Rust']
| 1 |
range-sum-of-bst
|
[C++/Python] in-order BST traverse
|
cpython-in-order-bst-traverse-by-codeday-emjs
|
\nclass Solution { // DFS: in-order traverse\npublic: // Time/Space Complexity: O(N); O(N)\n int rangeSumBST(TreeNode* root, int low, int high) {\n ve
|
codedayday
|
NORMAL
|
2020-11-15T20:13:16.814497+00:00
|
2022-12-07T04:52:44.865218+00:00
| 401 | false |
```\nclass Solution { // DFS: in-order traverse\npublic: // Time/Space Complexity: O(N); O(N)\n int rangeSumBST(TreeNode* root, int low, int high) {\n vector<int> nums;\n dfs(root, nums);\n int ans = 0;\n for(auto e: nums) \n if(e >= low && e <=high) ans += e;\n return ans;\n }\n \nprivate:\n void dfs(TreeNode* root, vector<int>& nums){\n if(!root) return;\n dfs(root->left, nums);\n nums.push_back(root->val);\n dfs(root->right, nums);\n }\n};\n```\n\nApproach 2(python)\n```\nclass Solution:\n def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:\n \n def dfs(root):\n if root:\n dfs(root.left)\n nums.append(root.val)\n dfs(root.right)\n \n nums=[]\n dfs(root)\n running_sum = list(itertools.accumulate(nums))\n left = max(bisect.bisect_left(nums, low)-1, 0)\n right = min(bisect.bisect_left(nums, high), len(nums) - 1) \n return running_sum[right] - running_sum[left]\n```
| 5 | 0 |
['C++', 'Python3']
| 0 |
range-sum-of-bst
|
[C++] Recursive One-liner Solutions explained, ~100% Time, ~80% Space
|
c-recursive-one-liner-solutions-explaine-vvn0
|
This is a rather straightfoward problem and we might easily solve it calling a helper dfs function to gradually go top-down, from node to node, to solve it.\n\n
|
ajna
|
NORMAL
|
2020-11-15T09:07:09.929155+00:00
|
2020-11-15T12:39:36.970181+00:00
| 452 | false |
This is a rather straightfoward problem and we might easily solve it calling a helper `dfs` function to gradually go top-down, from node to node, to solve it.\n\nI preferred going for an extra bit of challenge and writing directly a recursive one-liner, ignoring the condition that it is a BST, since I found little value in potentially skipping a conditional every time we examine a node, whereas that would have costed much more code complexity.\n\nTo do so, I "hid" the result variable as a fourth optional parameter, defaulted to `0`.\n\nI will then return it when `root == NULL`, ie: we ended up out of the tree; otherwise, I will call recursively our `rangeSumBST` function on both the `left` and `right` branches, with a twist:\n* the call to the `left` branch will keep increasing `res` with the value of the current `root->val`;\n* the call to the `right` branch will every time reset `res` to `0` and compute a sub-sum from scratch.\n\nOnce all the recursive calls will be done, we I will have to just the result of `root->val` plus the sub-sum of everything to the left of it with the sub-sum of whatever is at the right of it :)\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n int rangeSumBST(TreeNode* root, int low, int high, int res = 0) {\n return root ? rangeSumBST(root->left, low, high, res + (root->val >= low && root->val <= high ? root->val : 0)) + rangeSumBST(root->right, low, high) : res;\n }\n};\n```\n\nAnd looking back to the one-liner I wrote in May, one that has some earlier stopping condition, I really struggle to find it worth in terms of extra performances, since it is one more check at each step.\n\nBasically at each iteration we update the upper and lower limit `low` and `high` as we go: going `left` will reduce potentially reduce `high`, while going `right` will have us check if we need to update `low`.\n\nAt the beginning of our code, we are not checking that `root` is not `NULL`, plus the new condition `low <= high`, meaning we already reached a part of the tree that does not matter to us.\n\nFor example, if we started with `low == 10` and `high == 20`, moving `left` after having it a node with value `9` or lower (and thus having updated `high` to that value) would not be meaningul, since by definition any value to its left needs to be smaller in a BST; similarly moving `right` after encountering anything `> 20` should have us halt right there.\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n int rangeSumBST(TreeNode* root, int low, int high) {\n return root && low <= high ? (root->val >= low && root->val <= high ? root->val : 0) + rangeSumBST(root->left, low, min(high, root->val)) + rangeSumBST(root->right, max(root->val, low), high) : 0;\n }\n};\n```\n\nHybrid of the 2 approaches, using also [RedaKerouicha](https://leetcode.com/RedaKerouicha/)\'s suggestion:\n\n```cpp\nclass Solution {\npublic:\n int rangeSumBST(TreeNode* root, const int low, const int high, const int res = 0) {\n return root && low <= high ? rangeSumBST(root->left, low, min(high, root->val), res + (root->val >= low && root->val <= high ? root->val : 0)) + rangeSumBST(root->right, max(root->val, low), high) : res;\n }\n};\n```
| 5 | 2 |
['Depth-First Search', 'Graph', 'C', 'C++']
| 2 |
range-sum-of-bst
|
JS fast and simple solution
|
js-fast-and-simple-solution-by-ahmed_gaa-cdzl
|
\n\njs\nvar rangeSumBST = function(root, L, R) {\n if(!root)return 0 \n let v = (root.val <= R && root.val >= L)? root.val : 0\n return v + rangeSumBS
|
ahmed_gaafer
|
NORMAL
|
2020-04-10T11:54:16.311136+00:00
|
2020-04-10T11:55:26.095676+00:00
| 401 | false |
\n\n```js\nvar rangeSumBST = function(root, L, R) {\n if(!root)return 0 \n let v = (root.val <= R && root.val >= L)? root.val : 0\n return v + rangeSumBST(root.left, L, R) + rangeSumBST(root.right, L, R)\n};\n```
| 5 | 0 |
['Recursion', 'JavaScript']
| 1 |
range-sum-of-bst
|
javascript recursive solution
|
javascript-recursive-solution-by-ruden91-10lu
|
\nconst rangeSumBST = (root, L, R) => {\n\tif (root === null) {\n \t return 0;\n } \n\n return (root.val >= L && root.val <= R ? root.val : 0) + ra
|
ruden91
|
NORMAL
|
2019-05-01T12:49:54.654664+00:00
|
2019-05-01T12:49:54.654721+00:00
| 828 | false |
```\nconst rangeSumBST = (root, L, R) => {\n\tif (root === null) {\n \t return 0;\n } \n\n return (root.val >= L && root.val <= R ? root.val : 0) + rangeSumBST(root.left, L , R) + rangeSumBST(root.right, L , R);\n}\n```
| 5 | 0 |
['Binary Search', 'Recursion', 'Binary Tree', 'JavaScript']
| 2 |
range-sum-of-bst
|
Swift
|
swift-by-dcompet03-17fh
|
\n\nclass Solution {\n func rangeSumBST(_ root: TreeNode?, _ L: Int, _ R: Int) -> Int {\n var sum = 0\n guard let node = root else { return sum
|
dcompet03
|
NORMAL
|
2019-03-22T07:45:25.228467+00:00
|
2019-03-22T07:45:25.228517+00:00
| 613 | false |
\n```\nclass Solution {\n func rangeSumBST(_ root: TreeNode?, _ L: Int, _ R: Int) -> Int {\n var sum = 0\n guard let node = root else { return sum }\n if L <= node.val && node.val <= R {\n sum += node.val\n }\n if L < node.val {\n sum = sum + rangeSumBST(node.left, L, R)\n }\n if node.val < R {\n sum = sum + rangeSumBST(node.right, L, R)\n }\n\n return sum\n }\n}\n```
| 5 | 1 |
[]
| 0 |
range-sum-of-bst
|
[Rust] recursive solution
|
rust-recursive-solution-by-hanaasagi-5hzg
|
\n// Definition for a binary tree node.\n// #[derive(Debug, PartialEq, Eq)]\n// pub struct TreeNode {\n// pub val: i32,\n// pub left: Option<Rc<RefCell<Tree
|
hanaasagi
|
NORMAL
|
2019-01-03T14:32:52.440012+00:00
|
2019-01-03T14:32:52.440056+00:00
| 234 | false |
```\n// Definition for a binary tree node.\n// #[derive(Debug, PartialEq, Eq)]\n// pub struct TreeNode {\n// pub val: i32,\n// pub left: Option<Rc<RefCell<TreeNode>>>,\n// pub right: Option<Rc<RefCell<TreeNode>>>,\n// }\n// \n// impl TreeNode {\n// #[inline]\n// pub fn new(val: i32) -> Self {\n// TreeNode {\n// val,\n// left: None,\n// right: None\n// }\n// }\n// }\nuse std::rc::Rc;\nuse std::cell::RefCell;\nimpl Solution {\n pub fn range_sum_bst(root: Option<Rc<RefCell<TreeNode>>>, l: i32, r: i32) -> i32 {\n if let Some(root) = root {\n let mut sum = 0;\n if l <= root.borrow().val && root.borrow().val <=r {\n sum += root.borrow().val;\n }\n \n if l < root.borrow().val {\n sum += Self::range_sum_bst(root.borrow().left.clone(), l, r);\n }\n \n if r > root.borrow().val {\n sum += Self::range_sum_bst(root.borrow().right.clone(), l, r);\n }\n return sum;\n }\n return 0;\n }\n}\n```
| 5 | 0 |
[]
| 0 |
range-sum-of-bst
|
Simple recursive C++ code beats 100%
|
simple-recursive-c-code-beats-100-by-gop-8jff
|
\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : v
|
gopi_krishna
|
NORMAL
|
2018-11-13T01:02:19.058205+00:00
|
2018-11-13T01:02:19.058246+00:00
| 1,056 | false |
```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\nclass Solution {\npublic:\n int rangeSumBST(TreeNode* root, int L, int R) {\n if (root ==NULL){return 0;}\n else if (root->val > R)\n return rangeSumBST(root->left, L,R);\n else if (root->val < L)\n return rangeSumBST(root->right, L,R);\n else\n return root->val+rangeSumBST(root->left,L,root->val)+rangeSumBST(root->right, root->val,R);\n }\n};\n```
| 5 | 1 |
[]
| 0 |
range-sum-of-bst
|
C++ with Morris inOrder traversal
|
c-with-morris-inorder-traversal-by-feelf-221m
|
\'\'\'\nclass Solution {\npublic:\n \n int inorderTraversal(TreeNode root,int L, int R){\n int sum = 0;\n TreeNode cur = root,pre;\n w
|
feelforthunder
|
NORMAL
|
2018-11-11T04:30:37.628579+00:00
|
2018-11-11T04:30:37.628669+00:00
| 737 | false |
\'\'\'\nclass Solution {\npublic:\n \n int inorderTraversal(TreeNode* root,int L, int R){\n int sum = 0;\n TreeNode *cur = root,*pre;\n while(cur!=nullptr){\n if(cur->left!=nullptr){\n pre = cur->left;\n while(pre->right!=nullptr && pre->right!=cur){\n pre = pre->right;\n }\n if(pre->right==nullptr){\n pre->right = cur;\n cur = cur->left;\n }else{\n if(cur->val>=L && cur->val<=R)\n sum+=cur->val;\n pre->right = nullptr;\n cur = cur->right;\n }\n }else{\n if(cur->val>=L && cur->val<=R)\n sum+=cur->val;\n cur = cur->right;\n }\n }\n return sum;\n }\n int rangeSumBST(TreeNode* root, int L, int R) {\n if(root==nullptr)\n return 0;\n return inorderTraversal(root,L,R);\n }\n};\n\'\'\'\nTime complexity: O(n)\nSpace complexity: O(1)
| 5 | 1 |
[]
| 0 |
range-sum-of-bst
|
✅Using Anonymous as Recursive. Modern, Simple Solution✅
|
using-anonymous-as-recursive-modern-simp-2vv7
|
If you have question, pls, write below. I will answer.\n# Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:
|
husanmusa
|
NORMAL
|
2024-04-09T20:56:06.044456+00:00
|
2024-04-09T20:56:06.044472+00:00
| 276 | false |
If you have question, pls, write below. I will answer.\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc rangeSumBST(root *TreeNode, low int, high int) int {\n\tsum := 0\n\tvar recur func(root *TreeNode)\n\n\trecur = func(root *TreeNode) {\n\t\tif root.Val >= low && root.Val <= high {\n\t\t\tsum += root.Val\n\t\t}\n\t\tif root.Left != nil {\n\t\t\trecur(root.Left)\n\t\t}\n\t\tif root.Right != nil {\n\t\t\trecur(root.Right)\n\t\t}\n\t}\n\trecur(root)\n\n\treturn sum\n}\n\n```
| 4 | 0 |
['Go']
| 3 |
range-sum-of-bst
|
Basic code logic for beginners || 100ms runtime
|
basic-code-logic-for-beginners-100ms-run-ff6f
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nAny Depth first traversal approach (Preorder traversal) \n Describe your
|
deeparasan_31
|
NORMAL
|
2024-01-08T14:59:48.178928+00:00
|
2024-01-08T15:13:24.704170+00:00
| 1,170 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nAny Depth first traversal approach (Preorder traversal) \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(h) //height of the tree\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int sum=0;\n void preorder(TreeNode* root, int low, int high){\n if(root==NULL)\n return;\n if(root->val >=low && root->val <=high)\n sum+=(root->val);\n preorder(root->left,low,high);\n preorder(root->right,low,high);\n }\n\n int rangeSumBST(TreeNode* root,int low,int high) {\n preorder(root,low,high); //preorder traversal \n return sum;\n }\n};\n```
| 4 | 0 |
['C', 'C++']
| 0 |
range-sum-of-bst
|
For Fun :)
|
for-fun-by-yagathorn-adxb
|
\n# Approach\n Describe your approach to solving the problem. \nRecursive Traversal: Use recursion to traverse the tree. It checks each node to see if its value
|
Yagathorn
|
NORMAL
|
2024-01-08T08:29:29.036000+00:00
|
2024-01-08T09:00:14.225827+00:00
| 134 | false |
\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Recursive Traversal**: Use recursion to traverse the tree. It checks each node to see if its value falls within the given range.\n\n**Conditional Summation**: At each node, the solution adds the node\'s value to the sum if the value is between low and high (inclusive).\n\n**Base Case for Recursion**: The recursion stops when a null node is reached, which is a leaf\'s child in the BST.\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(logN)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\n//FAST I/O\n const static auto fast = [] {\n ios_base::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return 0;\n}();\n\nclass Solution {\npublic:\n int rangeSumBST(TreeNode* root, int low, int high) {\n return (root == nullptr) ? 0 : (((root->val <= high && root->val >= low) ? root->val : 0) + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high));\n }\n};\n```\n```C# []\npublic class Solution {\n public int RangeSumBST(TreeNode root, int low, int high) => (root == null) ? 0 : (((root.val <= high && root.val >= low) ? root.val : 0) + RangeSumBST(root.left, low, high) + RangeSumBST(root.right, low, high));\n}\n```\n```Java []\npublic class Solution {\n public int rangeSumBST(TreeNode root, int low, int high) {\n return (root == null) ? 0 : (((root.val <= high && root.val >= low) ? root.val : 0) + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high));\n }\n}\n```\n
| 4 | 0 |
['C++', 'Java', 'C#']
| 0 |
range-sum-of-bst
|
Golang Naive Solution (DFS) and Optimal (DFS+Binary Search Tree Features) | Beats 100%
|
golang-naive-solution-dfs-and-optimal-df-0bmw
|
\n# 1. Naive solution\n\nNaive solution that does not exploit the features of the binary search tree is the usual DFS (alternate traversal of all nodes with sel
|
vltvdnl
|
NORMAL
|
2023-12-25T12:32:09.538218+00:00
|
2024-01-17T14:18:13.682143+00:00
| 198 | false |
\n# 1. Naive solution\n\nNaive solution that does not exploit the features of the binary search tree is the usual DFS (alternate traversal of all nodes with selection of matching nodes according to the condition).\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nfunc rangeSumBST(root *TreeNode, low int, high int) int {\n if root == nil{\n return 0\n }\n\n if root.Val>= low && root.Val<=high{\n return root.Val + rangeSumBST(root.Left, low, high)+rangeSumBST(root.Right, low, high)\n }else{\n return rangeSumBST(root.Left, low, high)+rangeSumBST(root.Right, low, high)\n }\n}\n```\n\n\n# 2. Optimal Solution\n\nSince we are working with a **binary search tree**, we can exploit its **features**.\nIf **node.Val < low** then we may not even consider the part of the tree that lies to the **left of this node**. \nSimilarly, if **node.Val > high** then we may not even consider the part of the tree that lies to the **right of this node**. \nIf node fits the condition **(low<=node.Val<=high)**, then we bypass both the left and right parts, as in the first solution. (adding node.Val to the answer).\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(log(n))$$\n\n# Code\n```\nfunc rangeSumBST(root *TreeNode, low int, high int) int {\n if root == nil{\n return 0\n }\n if root.Val < low{ //the root < left, so we don\'t need to go to the left\n return rangeSumBST(root.Right, low, high)\n }else if root.Val <=high{\n return root.Val + rangeSumBST(root.Left, low, high)+rangeSumBST(root.Right, low, high) // root fits, we go to left and right\n } else{\n return rangeSumBST(root.Left, low, high) //root > high, so we don\'t need to go to the right\n } \n}\n```\n## If you hava any question, feel free to ask. If you like the solution or the explaination, Please UPVOTE!\n
| 4 | 0 |
['Depth-First Search', 'Binary Search Tree', 'Binary Tree', 'Go']
| 2 |
range-sum-of-bst
|
Simple Java Solution
|
simple-java-solution-by-sohaebahmed-3noy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sohaebAhmed
|
NORMAL
|
2023-09-03T04:05:13.243125+00:00
|
2023-09-03T04:05:13.243146+00:00
| 606 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n int sum = 0;\n public int rangeSumBST(TreeNode root, int low, int high) {\n if(root == null) {\n return 0;\n }\n if(root.val >= low && root.val <= high) {\n sum += root.val;\n }\n if(root.val > low) {\n rangeSumBST(root.left, low, high);\n }\n if(root.val < high) {\n rangeSumBST(root.right, low, high);\n }\n return sum;\n }\n}\n```
| 4 | 0 |
['Tree', 'Depth-First Search', 'Binary Search Tree', 'Binary Tree', 'Java']
| 1 |
range-sum-of-bst
|
Python || 97.84% Faster || Explained Line by Line || Recursive Solution
|
python-9784-faster-explained-line-by-lin-gymg
|
\nclass Solution:\n def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:\n\t s = 0 # answer is zero initially\n\t if root: # if
|
pulkit_uppal
|
NORMAL
|
2022-12-07T06:36:42.574851+00:00
|
2022-12-07T06:36:42.574896+00:00
| 431 | false |
```\nclass Solution:\n def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:\n\t s = 0 # answer is zero initially\n\t if root: # if we have a root\n\t\t if low <= root.val <= high: # if in the right range\n\t\t\t s += root.val \n # if the root is in the range [low, high]\n\t\t if low <= root.val: \n\t\t\t s += self.rangeSumBST(root.left,low,high) # add nodes to the left sub tree\n\t\t if root.val <= high: \n\t\t\t s += self.rangeSumBST(root.right,low,high) # add nodes to the right sub tree\n\t return s\n```\n\n**An upvote will be encouraging**
| 4 | 0 |
['Binary Search Tree', 'Recursion', 'Binary Tree', 'Python', 'Python3']
| 1 |
range-sum-of-bst
|
Easy Explained | Recursion | Optimized | 2 line Code | CPP
|
easy-explained-recursion-optimized-2-lin-03yw
|
Approach\nWe are doing regular tree traversal and adding values within [L, R]. Note that in the solution description, we are given BST, however, this solution w
|
bhalerao-2002
|
NORMAL
|
2022-12-07T06:03:59.553532+00:00
|
2022-12-07T06:03:59.553577+00:00
| 849 | false |
# Approach\nWe are doing regular tree traversal and adding values within [L, R]. Note that in the solution description, we are given BST, however, this solution works for any binary tree.\n\n# CPP Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic://Thanks to Bhalerao-2002\nint rangeSumBST(TreeNode* root, int L, int R) {\n if (root == nullptr) return 0;//If tree is not Exist \n return (root->val >= L && root->val <= R ? root->val : 0) +\n rangeSumBST(root->left, L, R)/*For Left Side traversal of BST*/ + rangeSumBST(root->right, L, R)/*For Right Side traversal of BST*/;\n}\n};\n```\n# Upvote If it Helped :)
| 4 | 0 |
['C++']
| 0 |
range-sum-of-bst
|
97.27% fast javascript very easy to understand solution
|
9727-fast-javascript-very-easy-to-unders-2tl8
|
Visit my youtube! Thank you!\nhttps://www.youtube.com/channel/UCkhEaNAOO8tig5NHqqxXIeg\n\n/**\n * Definition for a binary tree node.\n * function TreeNode(val,
|
rlawnsqja850
|
NORMAL
|
2022-12-07T01:23:01.024044+00:00
|
2023-01-09T04:27:25.134650+00:00
| 559 | false |
Visit my youtube! Thank you!\nhttps://www.youtube.com/channel/UCkhEaNAOO8tig5NHqqxXIeg\n```\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n */\n/**\n * @param {TreeNode} root\n * @param {number} low\n * @param {number} high\n * @return {number}\n */\nvar rangeSumBST = function(root, low, high) {\n let sum = 0;\n\n let iterate = (node=root) =>{\n if(!node) return;\n\n iterate(node.left)\n\n if(node.val>=low && node.val<=high) sum += node.val;\n\n iterate(node.right)\n }\n\n iterate()\n return sum;\n};\n```
| 4 | 0 |
['JavaScript']
| 0 |
range-sum-of-bst
|
🗓️ Daily LeetCoding Challenge December, Day 7
|
daily-leetcoding-challenge-december-day-rjaus
|
This problem is the Daily LeetCoding Challenge for December, Day 7. Feel free to share anything related to this problem here! You can ask questions, discuss wha
|
leetcode
|
OFFICIAL
|
2022-12-07T00:00:12.888427+00:00
|
2022-12-07T00:00:12.888466+00:00
| 4,191 | false |
This problem is the Daily LeetCoding Challenge for December, Day 7.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/range-sum-of-bst/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 1 approach in the official solution</summary>
**Approach 1:** Depth First Search
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 4 | 0 |
[]
| 35 |
range-sum-of-bst
|
C++|| Two Solutions|| Recursion and Queue
|
c-two-solutions-recursion-and-queue-by-j-c6g0
|
Apporach 1: \nUsing Inorder Traversal\n\nclass Solution {\npublic:\n int sum=0;\n int rangeSumBST(TreeNode* root, int low, int high) {\n if(root==NU
|
jahnavimahara
|
NORMAL
|
2022-08-02T13:24:53.083921+00:00
|
2022-08-02T18:34:20.216222+00:00
| 121 | false |
Apporach 1: \nUsing Inorder Traversal\n```\nclass Solution {\npublic:\n int sum=0;\n int rangeSumBST(TreeNode* root, int low, int high) {\n if(root==NULL)\n {\n return sum;\n }\n rangeSumBST(root->left,low,high);\n if(root->val>high){\n return sum;\n }\n if(root->val>=low&&root->val<=high)\n {\n sum=sum+root->val;\n }\n rangeSumBST(root->right,low,high);\n return sum;\n }\n};\n```\n\nApproach 2:\nUsing Queue and property of BST:\nExplaination :\n1. Take a Queue data structure and push root to it;\n2. If node->val is in the range then both the subtrees can be in the range so we w\'ll add both left and right child : node->right and node->right to the queue.\n3. If the node->val is lower than (low) ,the left subtree will also be smaller than (low) but there is a possibility that its right child can be in the range , so we\'ll eliminate left subtree and add node->right to the queue.\n4. If the node->val is greater than (high),the rightt subtree will also be greater than (low) ,but there is a possibility that its leftt child can be in the range , so we\'ll eliminate right subtree and add node->right to the queue.\n**CODE**\n```\n int rangeSumBST(TreeNode* root, int low, int high) {\n if(root==NULL)return 0;\n int sum =0;\n queue<TreeNode*>q;\n q.push(root);\n while(!q.empty()){\n TreeNode* node=q.front();\n q.pop();\n if(node->val<low)\n {\n if(node->right!=NULL)q.push(node->right);\n }\n else if(node->val >high && node->left!=NULL){\n q.push(node->left); \n }\n else if(node->val>=low && node->val <=high){\n sum+=(node->val);\n if(node->left!=NULL)q.push(node->left);\n if(node->right!=NULL)q.push(node->right);\n } \n }\n return sum;\n }\n\n```
| 4 | 0 |
['Binary Search Tree', 'Recursion', 'Queue']
| 0 |
range-sum-of-bst
|
Range Sum of BST by using inorder
|
range-sum-of-bst-by-using-inorder-by-ash-cifc
|
\'\'\'\n\nclass Solution {\npublic:\n void inorder(TreeNoderoot, vector&v){\n if(root==NULL) return ;\n inorder(root->left,v);\n v.push_
|
Ashish_49
|
NORMAL
|
2022-07-29T06:24:00.579054+00:00
|
2022-07-29T06:24:00.579125+00:00
| 27 | false |
\'\'\'\n\nclass Solution {\npublic:\n void inorder(TreeNode*root, vector<int>&v){\n if(root==NULL) return ;\n inorder(root->left,v);\n v.push_back(root->val);\n inorder(root->right, v);\n \n }\n int rangeSumBST(TreeNode* root, int low, int high) {\n vector<int>v;\n inorder(root, v);\n int sum=0;\n for(int i=0; i<v.size();i++){\n if(v[i]>=low && v[i]<=high){\n sum+=v[i]; \n }\n }\n return sum;\n }\n}; \'\'\'
| 4 | 0 |
[]
| 0 |
range-sum-of-bst
|
[Python] Recursive + Memory usage less than 93%
|
python-recursive-memory-usage-less-than-pnazt
|
Upvote if it was usefull for you \uD83D\uDE42\n\n```\nclass Solution:\n def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:\n
|
lipatino
|
NORMAL
|
2022-04-13T15:49:13.076463+00:00
|
2022-04-13T15:49:13.076507+00:00
| 260 | false |
Upvote if it was usefull for you \uD83D\uDE42\n\n```\nclass Solution:\n def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:\n suma = 0\n def search(node):\n nonlocal suma\n if node:\n if node.val <= high and node.val >=low:\n suma+=node.val\n search(node.left)\n search(node.right)\n search(root)\n return(suma)
| 4 | 0 |
['Recursion', 'Python']
| 0 |
range-sum-of-bst
|
c++
|
c-by-satyamraj999-u4f7
|
\nclass Solution {\npublic:\n int res=0;\n void fun(TreeNode* root, int low, int high){\n if(root==NULL){\n return;\n }\n
|
satyamraj999
|
NORMAL
|
2021-12-14T16:54:13.994464+00:00
|
2021-12-14T16:54:13.994503+00:00
| 187 | false |
```\nclass Solution {\npublic:\n int res=0;\n void fun(TreeNode* root, int low, int high){\n if(root==NULL){\n return;\n }\n if(root->val<low){\n fun(root->right,low, high);\n }\n if(root->val>=low && root->val<=high){\n res+=root->val;\n fun(root->left,low, high);\n fun(root->right,low, high);\n }\n if(root->val>high){\n fun(root->left,low, high);\n }\n }\n int rangeSumBST(TreeNode* root, int low, int high) {\n fun(root, low, high);\n return res;\n }\n};\n```
| 4 | 0 |
['Recursion', 'C', 'Binary Tree']
| 0 |
range-sum-of-bst
|
C++ Super-Simple and Easy Recursive Solution
|
c-super-simple-and-easy-recursive-soluti-l7xu
|
We iterate through the entire tree.\nFor every node, if its value is within the range, we add it to res.\n\nclass Solution {\npublic:\n void rec(TreeNode* ro
|
yehudisk
|
NORMAL
|
2021-12-14T07:53:08.863922+00:00
|
2021-12-14T07:53:08.863967+00:00
| 351 | false |
We iterate through the entire tree.\nFor every node, if its value is within the range, we add it to `res`.\n```\nclass Solution {\npublic:\n void rec(TreeNode* root, int low, int high) {\n if (!root) return;\n if (root->val <= high && root->val >= low) res += root->val;\n rec(root->left, low, high);\n rec(root->right, low, high);\n }\n \n int rangeSumBST(TreeNode* root, int low, int high) {\n rec(root, low, high);\n return res;\n }\n \nprivate:\n int res = 0;\n};\n```
| 4 | 0 |
['C']
| 0 |
range-sum-of-bst
|
C++ Solution - 91% Faster - Recursion
|
c-solution-91-faster-recursion-by-huzaif-gq9s
|
\t/\n\t * Definition for a binary tree node.\n\t * struct TreeNode {\n\t * int val;\n\t * TreeNode left;\n\t * TreeNode right;\n\t * TreeNode()
|
huzaifamalik47
|
NORMAL
|
2021-08-30T08:58:21.979831+00:00
|
2021-08-30T08:58:50.085450+00:00
| 381 | false |
\t/**\n\t * Definition for a binary tree node.\n\t * struct TreeNode {\n\t * int val;\n\t * TreeNode *left;\n\t * TreeNode *right;\n\t * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n\t * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n\t * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n\t * };\n\t */\n\tclass Solution {\n\tpublic:\n\t\tint sum=0;\n\t\tint rangeSumBST(TreeNode* root, int low, int high) {\n\t\t\tif(root==NULL){\n\t\t\t\treturn 0;\n\t\t\t}\n\t\t\tif(root->val >= low && root->val <= high){\n\t\t\t\tsum+=root->val;\n\t\t\t}\n\t\t\trangeSumBST(root->left,low,high);\n\t\t\trangeSumBST(root->right,low,high);\n\n\t\t\treturn sum;\n\n\n\t\t}\n\n\t};\n\t\n**\tPlease upvote if it helped. **
| 4 | 0 |
['Recursion', 'C']
| 0 |
range-sum-of-bst
|
Easy Recursive Python3 solution faster than 99%
|
easy-recursive-python3-solution-faster-t-0b2b
|
```\nclass Solution:\n def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:\n s = 0\n def explore(root, low, high):\n
|
sevdariklejdi
|
NORMAL
|
2021-08-06T11:00:54.296638+00:00
|
2021-08-06T11:01:26.324447+00:00
| 537 | false |
```\nclass Solution:\n def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:\n s = 0\n def explore(root, low, high):\n nonlocal s\n if low<=root.val<=high:\n s += root.val\n if root.left and low<root.val:\n explore(root.left, low, high)\n if root.right and high>=root.val:\n explore(root.right, low, high)\n explore(root, low, high)\n return s\n\t
| 4 | 0 |
['Recursion', 'Python', 'Python3']
| 0 |
range-sum-of-bst
|
Java & cpp one liner soln (brute force) And Java clean soln using BST
|
java-cpp-one-liner-soln-brute-force-and-zxprl
|
Java:\n\nclass Solution {\n public int rangeSumBST(TreeNode root, int low, int high) {\n \n return (root != null && root.val <= high && root.va
|
samriddhjn
|
NORMAL
|
2021-07-08T13:03:45.598878+00:00
|
2021-07-08T13:03:45.598921+00:00
| 275 | false |
Java:\n```\nclass Solution {\n public int rangeSumBST(TreeNode root, int low, int high) {\n \n return (root != null && root.val <= high && root.val >= low ? root.val : 0) + (root == null ? 0 : rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high));\n }\n}\n```\ncpp:\n```\nclass Solution {\npublic:\n int rangeSumBST(TreeNode* root, int low, int high) {\n\n return (root != NULL && root->val <= high && root->val >= low ? root->val : 0) + (root == NULL ? 0 : rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high));\n }\n};\n```\n\nJava (clean code):\n```\nclass Solution {\n public int rangeSumBST(TreeNode root, int low, int high) {\n \n if (root == null) return 0;\n \n if (root.val >= low && root.val <= high) {\n \n return root.val + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high);\n }\n else if (root.val < low) {\n \n return rangeSumBST(root.right, low, high);\n }\n \n else {\n return rangeSumBST(root.left, low, high);\n }\n }\n}\n```
| 4 | 1 |
['Binary Search', 'Depth-First Search', 'Recursion', 'C', 'C++', 'Java']
| 0 |
range-sum-of-bst
|
Follow Up Question for Interview Preparations
|
follow-up-question-for-interview-prepara-duvl
|
I see that many people got confused by the language of the question, but still this question seems easy.\nIf this question were to appear in a interview, it wil
|
user0904ql
|
NORMAL
|
2020-11-16T05:35:40.373145+00:00
|
2020-11-16T05:35:40.373179+00:00
| 364 | false |
I see that many people got confused by the language of the question, but still this question seems easy.\nIf this question were to appear in a interview, it will be a warm up question and then it will be slightly modified to add complexity.\n\nOne such question - How can we handle if there are multiple queries for getting range sum ? i.e. ```getRangeSumBST(int low, int high)``` is called again and again with different low, high values. \nHow would you optimize? \n\n\n\n
| 4 | 0 |
[]
| 3 |
range-sum-of-bst
|
Simple DFS Solution JAVA
|
simple-dfs-solution-java-by-aoali77-owtn
|
\nclass Solution {\n public int rangeSumBST(TreeNode root, int low, int high) {\n int[] res = new int[1];\n dfs(root, low, high, res);\n
|
aoali77
|
NORMAL
|
2020-11-15T13:33:34.367861+00:00
|
2020-11-15T13:33:34.367900+00:00
| 495 | false |
```\nclass Solution {\n public int rangeSumBST(TreeNode root, int low, int high) {\n int[] res = new int[1];\n dfs(root, low, high, res);\n return res[0];\n }\n private void dfs(TreeNode root, int low, int high, int[] sum){\n if(root == null) return;\n if(root.val <= high && root.val >= low) sum[0] += root.val;\n dfs(root.left, low, high, sum);\n dfs(root.right, low, high, sum);\n }\n}\n```
| 4 | 0 |
['Depth-First Search', 'Java']
| 2 |
range-sum-of-bst
|
C++ Super-Simple Recursive Easiest Sol
|
c-super-simple-recursive-easiest-sol-by-cb5n9
|
\nclass Solution {\npublic:\n void rec(TreeNode* root, int low, int high) {\n if (!root) return;\n if (root->val <= high && root->val >= low) r
|
yehudisk
|
NORMAL
|
2020-11-15T08:18:56.808548+00:00
|
2020-11-15T08:18:56.808588+00:00
| 205 | false |
```\nclass Solution {\npublic:\n void rec(TreeNode* root, int low, int high) {\n if (!root) return;\n if (root->val <= high && root->val >= low) res+=root->val;\n rec(root->left, low, high);\n rec(root->right, low, high);\n }\n int rangeSumBST(TreeNode* root, int low, int high) {\n rec(root, low, high);\n return res;\n }\n \nprivate:\n int res = 0;\n};\n```\n**Like it? please upvote...**
| 4 | 0 |
['C']
| 0 |
number-of-unique-good-subsequences
|
[Java/C++/Python] DP, 4 lines O(N) Time, O(1) Space
|
javacpython-dp-4-lines-on-time-o1-space-oozfr
|
Intuition\nAn easier or harder version of 940. Distinct Subsequences II\n\n\n# Explanation\nthe subsequence 0 is tricky,\nso firstly we only count the case with
|
lee215
|
NORMAL
|
2021-08-29T04:01:00.062321+00:00
|
2021-08-29T04:38:00.154546+00:00
| 12,523 | false |
# **Intuition**\nAn easier or harder version of [940. Distinct Subsequences II](https://leetcode.com/problems/distinct-subsequences-ii/discuss/192017)\n<br>\n\n# **Explanation**\nthe subsequence 0 is tricky,\nso firstly we only count the case without any leading 0\n\nWe count the number of subsequence that ends with 0 and ends with 1.\n\nIf we meed 0,\nwe can append 0 to all existing `ends0 + ends1` subsequences,\nand make up `ends0 + ends1` different subsequences that ends with 0.\nans these subsequences has length >= 2,\nSo `ends0 = ends0 + ends1`.\n\nIf we meed 1, the same,\nwe can append 1 to all existing `ends0 + ends1` subsequence,\nand make up `ends0 + ends1` different subsequence that ends with 1,\nans these subsequences has length >= 2.\nSo `1` is not in them, `ends1 = ends0 + ends1 + 1`.\n\nThe result is `ends1 + ends2`, and don\'t forget about `0`.\nThe final result is `ends1 + ends2 + has0`.\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(1)`\n<br>\n\n**Java**\n```java\n public int numberOfUniqueGoodSubsequences(String binary) {\n int mod = (int)1e9 + 7, ends0 = 0, ends1 = 0, has0 = 0;\n for (int i = 0; i < binary.length(); ++i) {\n if (binary.charAt(i) == \'1\') {\n ends1 = (ends0 + ends1 + 1) % mod;\n } else {\n ends0 = (ends0 + ends1) % mod;\n has0 = 1;\n }\n }\n return (ends0 + ends1 + has0) % mod;\n }\n```\n**C++**\n```cpp\n int numberOfUniqueGoodSubsequences(string binary) {\n int mod = 1e9 + 7, dp[2] = {0, 0};\n for (char& c: binary)\n dp[c - \'0\'] = (dp[0] + dp[1] + c - \'0\') % mod;\n return (dp[0] + dp[1] + (binary.find("0") != string::npos)) % mod;\n }\n```\n**Python**\n```py\n def numberOfUniqueGoodSubsequences(self, b):\n mod = 10**9 + 7\n dp = [0, 0]\n for c in b:\n dp[int(c)] = (sum(dp) + int(c)) % mod\n return (sum(dp) + (\'0\' in b)) % mod\n```\n\nIf you have any questions, feel free to ask. \nIf you like solution and explanations, please **Upvote**!\n
| 351 | 4 |
[]
| 41 |
number-of-unique-good-subsequences
|
DP O(n) | O(1)
|
dp-on-o1-by-votrubac-6scy
|
You just need to go through few examples to figure out the transition formula. Here is an example for "01011001":\n\n\n\nC++\ncpp\nint numberOfUniqueGoodSubsequ
|
votrubac
|
NORMAL
|
2021-08-29T04:58:07.708729+00:00
|
2021-08-29T05:26:35.188959+00:00
| 6,544 | false |
You just need to go through few examples to figure out the transition formula. Here is an example for "01011001":\n\n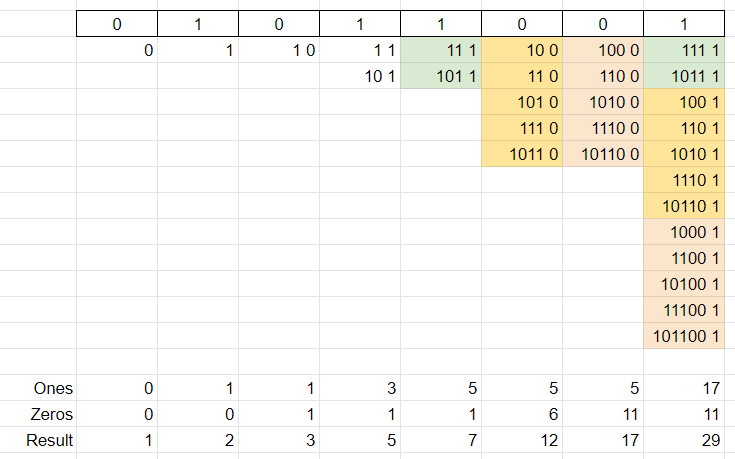\n\n**C++**\n```cpp\nint numberOfUniqueGoodSubsequences(string binary) {\n int mod = 1000000007, zeros = 0, ones = 0;\n for (auto ch : binary)\n if (ch == \'1\')\n ones = (zeros + ones + 1) % mod;\n else\n zeros = (zeros + ones) % mod;\n return (ones + zeros + (zeros || binary[0] == \'0\')) % mod;\n} \n```
| 164 | 4 |
['C']
| 10 |
number-of-unique-good-subsequences
|
C++ Clean DP Solution with Explanation time:O(n) space:O(1)
|
c-clean-dp-solution-with-explanation-tim-qxrq
|
dp[i][j] denote the number of distinct subsequences starting with \'i\' and end with \'j\'\nHere\'s the dp transition:\nCase \'0\':\nIf the current character is
|
felixhuang07
|
NORMAL
|
2021-08-29T04:00:33.658505+00:00
|
2021-08-29T04:01:52.330539+00:00
| 4,361 | false |
```dp[i][j]``` denote the number of distinct subsequences starting with \'i\' and end with \'j\'\nHere\'s the dp transition:\n**Case \'0\':**\nIf the current character is \'0\', since we are counting distinct subsequences and there shouldn\'t be any leading zeros in the subsequences, we set ```dp[0][0] = 1```, ex: string "000000" only have a subsequence \'0\'\n```dp[1][0] = dp[1][0] + dp[1][1]``` because it will be the number of ways that we add a \'0\' to a subsequence starting with \'1\' and ends with either \'0\' or \'1\'\n\n**Case \'1\':**\nIf the current character is \'1\', since we can\'t have leading zeros, ```dp[0][1]``` is always 0 ("0001" is not a valid subsequence)\nThe transition will be ```dp[1][1] = dp[1][0] + dp[1][1] + 1```. As we can see, ```dp[1][0] + dp[1][1]``` part is same as the case ending with zero. Since we append a \'1\' to every subsequence ```dp[1][0]``` and ```dp[1][1]```, we are missing the subsequence "1" with length 1; therefore, we add a one to it.\n\nNote that all calculation above should be done with modulo.\n\nTime Complexity: O(n)\nSpace Complexity: O(1)\n\n```\ntypedef int64_t ll;\n\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string s) {\n const int mod = 1e9 + 7;\n ll dp[2][2] = {};\n for(char c : s) {\n int a = c - \'0\';\n if(a == 0) {\n dp[0][0] = 1;\n dp[1][0] = (dp[1][0] + dp[1][1]) % mod;\n } else {\n dp[1][1] = (dp[1][0] + dp[1][1] + 1) % mod;\n }\n }\n return (dp[0][0] + dp[0][1] + dp[1][0] + dp[1][1]) % mod;\n }\n};\n```\nPlease upvote!
| 103 | 0 |
['Dynamic Programming', 'C']
| 8 |
number-of-unique-good-subsequences
|
Accepted || C++ || DP O(n) || Explanation with Intuition
|
accepted-c-dp-on-explanation-with-intuit-nbia
|
Straight Forward DP.\n\nWhat we need?\n- Number of non empty unique subsequences of the given string, without leading zeroes\n \n\nIntution/Approach.\n -
|
changoi
|
NORMAL
|
2021-08-29T04:01:42.486184+00:00
|
2021-08-31T16:11:06.199981+00:00
| 2,771 | false |
Straight Forward DP.\n\nWhat we need?\n- Number of non empty unique subsequences of the given string, without leading zeroes\n \n```\nIntution/Approach.\n - A valid subsequence will have a \'1\' as MSB\n - Let at index i we have \'1\'. Then, \n - we can take all unique subsequences in [i+1, n-1], \n - add \'1\' to their start, we get new unique subsequences starting with \'1\'\n \n - Why will new generated subsequences be unique?\n - Because we are adding same character to the start of every unique subsequence we have till now. Thus, even though, first character will be \n same, the subsequent part will be unique for each subsequence.\n \n - Are we missing any valid subsequence?\n - Yes.\n - Subsequence "1" . \n - Because, we are adding to \'1\' to every subsequence, this "1" will become "11", \n - Thats why we have to add extra one at each ith index.\n\n\t- Similarly, for index i which have \'0\'\n \n ``` \n\n**DP States.**\n- dp[1][i] = # different good Subsequence with leading ones, in substring [i:n-1]\n- dp[0][i] = #different good Subsequence with leading zeroes, in substring [i:n-1]\n\n\n**DP Transition.**\n- Let\'s say at index i, we have s[i] == \'1\'\n\t- Then, this leading one can be added at the beginning of all subsequences starting with \'0\' and to all subsequences starting at \'1\'.\n\t- As, explained in the intution, whenever we add a character to the beginning, we loose, subsequence "1"\n\t- dp[1][i] = (dp[0][i+1]+dp[1][i+1]+1)\n- Similarily, for the case s[i] == \'0\'\n \n\n**TC** - O(n)\n**SC** - O(n), can be optimised to O(1)\n```\n#define ll long long\nint mod = 1e9 + 7;\n\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string s) {\n int n = s.length(), ans = 0, first = n, zero = 0;\n \n vector<vector<int>> dp(2,vector<int>(n+1, 0)); \n \n for(int i=n-1; i>=0; --i){\n if(s[i]==\'0\') {\n zero = 1;\n dp[0][i] = (1ll*dp[0][i+1] + 1ll + dp[1][i+1])%mod;\n dp[1][i] = dp[1][i+1];\n }\n else {\n dp[1][i] = (1ll*dp[0][i+1] + 1ll + dp[1][i+1])%mod;\n dp[0][i] = dp[0][i+1];\n }\n }\n \n return (dp[1][0] + zero)%mod;\n \n }\n};\n```
| 48 | 1 |
[]
| 10 |
number-of-unique-good-subsequences
|
[Python] 7 lines dp solution, explained
|
python-7-lines-dp-solution-explained-by-b8aut
|
This problem is very similar to problem 940. Distinct Subsequences II, so if you already solved or at least have seen it, it will help a lot. The idea is to use
|
dbabichev
|
NORMAL
|
2021-08-29T04:01:05.105880+00:00
|
2021-08-29T08:00:26.440390+00:00
| 2,391 | false |
This problem is very similar to problem **940. Distinct Subsequences II**, so if you already solved or at least have seen it, it will help a lot. The idea is to use `dp`, where `dp[i]` is number of unique subsequences for string `S[0], ... S[i]` - which do not start with **0** (we will deal with `0` case in the end). Then, each time we add symbol we need to do the following:\n\n1. Imagine that we have `t1, t2, ..., tk` unique subsequences for `i-1`. We also have options `t1 + S[i], t2 + S[i], ..., tk + S[i]`.\n2. However some of strings are the same, exactly for this we keep dictionary `last`: is the last place for each symbol so far. So, we subtract `dp[last[x]]` number of options. \n3. Also if we meet symbol `0` for the first time, we need to subtract `1`.\n\nLet us go through example `S = 111000101` and see what what options we have:\n\n1. `dp[0] = 1`, we have only one option: empty string `""`.\n2. Consider next symbol: `1`, we have `"", 1`, `dp[1] = 2.`\n3. Consider next symbol: `1`. We need to double number of options: we have `4` of them: `"", 1` and `1, 11` but one of them is repetition, it is `dp[last[1]]`, so we have options `"", 1, 11` and `dp[3] = 3`.\n4. Similarly `dp[4] = 4` and we have options `"", 1, 11, 111`.\n5. Now we have element `0` and we meet it for the first time, so we have `"", 1, 11, 111`, `0, 10, 110, 1110`. We need to remove option `0` at the moment, so we have `"", 1, 11, 111, 10, 110, 1110` and `dp[5] = 7`.\n6. Now we have again element `0`. We meet it not for the first time, so we have previous options `"", 1, 11, 111, 10, 110, 1110`, new options are `0, 10, 110, 1110, 100, 1100, 11100`. How many of this options are intersect: it is `10, 110, 1110` and also we need to remove "0", so optoins we are not happy with is `0, 10, 110, 1110`, which is exaclty what we had on step `4` but with added `0`.\n7. I think you understand the logic now and can continue this for the rest of the string: I leave it to you as exercise, put your solutions in comments :)\n\nIn the end we need to deal with `0` case: we need to subtract `-1` for empty set and add `int("0" in S)` to check if we have `0` in our string.\n\n#### Complexity\nTime complexity is `O(n)`, space complexity also `O(n)`.\n\n#### Code\n```python\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, S):\n dp, last = [1], {}\n for i, x in enumerate(S):\n dp.append(dp[-1] * 2)\n dp[-1] -= dp[last[x]] if x in last else int(x == "0")\n dp[-1] = dp[-1] % (10**9 + 7)\n last[x] = i\n\n return dp[-1] - 1 + int("0" in S)\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**
| 44 | 2 |
['Dynamic Programming']
| 4 |
number-of-unique-good-subsequences
|
[Python] Explanation with pictures.
|
python-explanation-with-pictures-by-bake-u8sa
|
Take 1110001 as an example.\nLet\'s count how many new subsequences each digit brings.\n\n\n\n\n\n\nThe code is not concise, please refer to others\'.\n\n\ndef
|
Bakerston
|
NORMAL
|
2021-08-29T04:06:28.154723+00:00
|
2021-08-29T04:34:00.102023+00:00
| 1,279 | false |
Take `1110001` as an example.\nLet\'s count how many **new** subsequences each digit brings.\n\n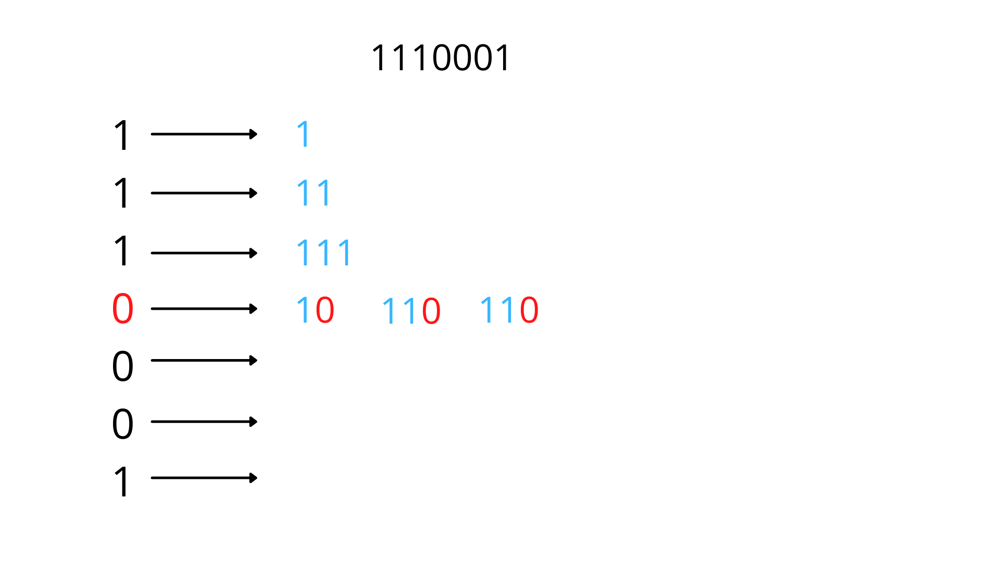\n\n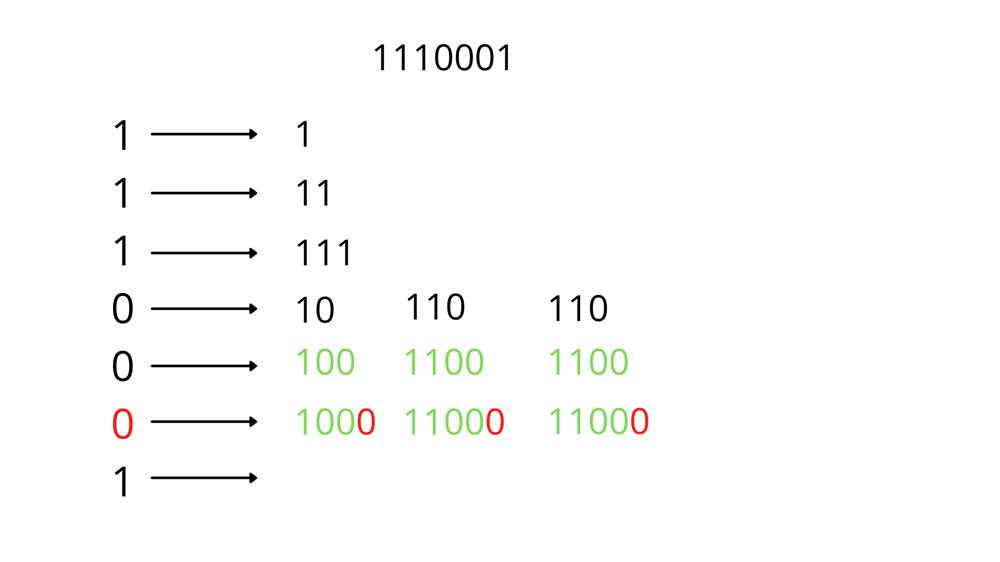\n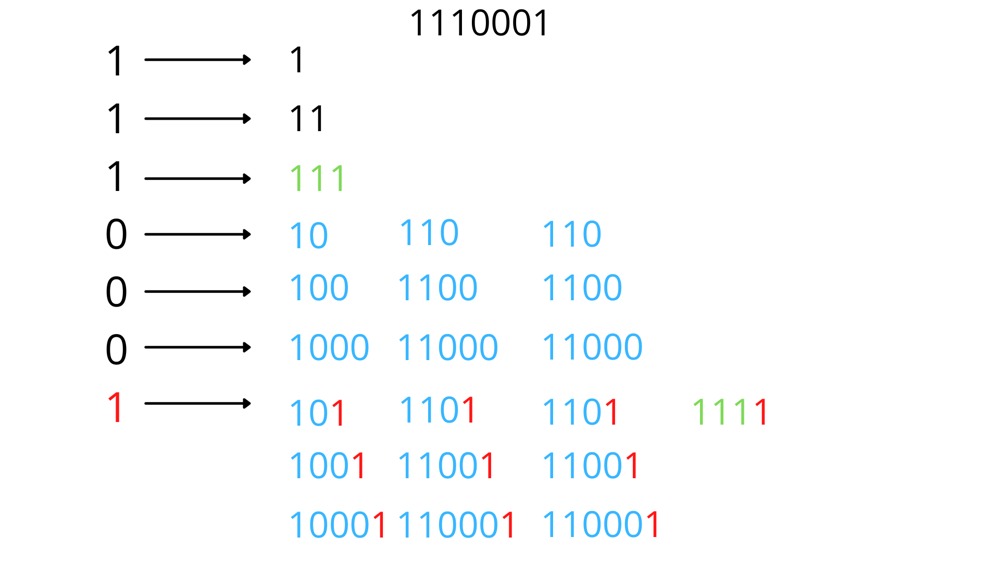\n\nThe code is not concise, please refer to others\'.\n\n```\ndef numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n mod, n = 10 ** 9 + 7, len(binary)\n\n one_idx, zero_idx = binary.find("1"), binary.find("0")\n if zero_idx == -1: return n\n if one_idx == -1: return 1\n\n ans = [0] * n\n ans[one_idx] = 1\n\n for i in range(one_idx + 1, n):\n if binary[i] != binary[i - 1]:\n ans[i] = ans[i - 1]\n j = i - 1\n while j > 0 and binary[j] == binary[j - 1]: \n ans[i] += ans[j - 1]\n j -= 1\n if j > 0: ans[i] += ans[j - 1]\n else:\n ans[i] = ans[i - 1]\n\n return (sum(ans) + 1) % mod\n```\n\n\n
| 24 | 2 |
[]
| 1 |
number-of-unique-good-subsequences
|
✅ C++ Simple DP Solution with comments | Easy to understand
|
c-simple-dp-solution-with-comments-easy-tcbh4
|
INTUTION - Every leading 1 can generate 1 + prev binary strings either ending with 0 or 1.\nEvery 0 can generate prev binary strings ending with 0 and 1.\n\n\nL
|
gaurav31200
|
NORMAL
|
2022-07-14T09:23:55.046387+00:00
|
2022-07-14T14:42:31.597336+00:00
| 1,305 | false |
**INTUTION** - Every leading 1 can generate 1 + prev binary strings either ending with 0 or 1.\nEvery 0 can generate prev binary strings ending with 0 and 1.\n\n```\nLet\'s take an example, 1101 endWithOnes endWithZeroes\nindex 0(1) -> only 1 can be generated. 1 0\nindex 1(1) -> 1,11 can be generated. 2 0\nindex 2(0) -> 1,11 and 10,110 can be generated 2 2\nindex 3(1) -> 1,11,111,101,1101 and 10,110 5 2\n```\n**Ans=** (endWithOnes)**5** + (endWithZeroes)**2** + (for 0 itself)**1** = **8**\n\n\n\n\n\n**C++ Code:**\n```\nint numberOfUniqueGoodSubsequences(string binary) {\n bool hasZero = false;\n int endWithZeroes=0,endWithOnes=0,mod=1e9+7;\n \n for(auto b:binary){\n if(b==\'1\'){\n endWithOnes = (endWithOnes + endWithZeroes + 1)%mod;\n }else{\n hasZero=true;\n endWithZeroes = (endWithOnes + endWithZeroes)%mod;\n }\n }\n \n return (endWithOnes + endWithZeroes + hasZero)%mod;\n }\n```\n**Please Upvote if you like the explaination : )**
| 15 | 0 |
['Dynamic Programming', 'C', 'C++']
| 1 |
number-of-unique-good-subsequences
|
[C++] clean code, DP with O(1) space
|
c-clean-code-dp-with-o1-space-by-wei0155-t14a
|
We can iterate from the last character to the begin and store the previous zeros and ones.\nBecause the good subsequences must start from \'1\' except subsequen
|
wei01555
|
NORMAL
|
2021-08-29T05:33:08.477745+00:00
|
2021-08-29T05:35:51.782060+00:00
| 838 | false |
We can iterate from the last character to the begin and store the previous zeros and ones.\nBecause the good subsequences must start from \'1\' except subsequence \'0\', we can just store current zeros and ones.\nAt the end, number of one will be the number of good subsequences. Besides, we have to check the edge case \'0\'.\n```\nclass Solution {\n int MOD = 1000000007;\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n int zero = 0;\n long long ones = 0;\n long long zeros = 0;\n \n for (int i = binary.size() - 1; i >= 0; --i) {\n if (binary[i] == \'1\') {\n ones = (ones + zeros + 1) % MOD;\n } else {\n zero = 1;\n zeros = (ones + zeros + 1) % MOD;\n }\n }\n return (ones + zero) % MOD;\n }\n};\n```
| 11 | 1 |
['Dynamic Programming', 'C']
| 3 |
number-of-unique-good-subsequences
|
Java || DP || time O(n) || similar to the problem 940
|
java-dp-time-on-similar-to-the-problem-9-achy
|
\nclass Solution {\n public int numberOfUniqueGoodSubsequences(String binary) {\n int initialZeroCount= 0;\n while(initialZeroCount < binary.le
|
achyutav
|
NORMAL
|
2021-12-09T01:52:01.909666+00:00
|
2021-12-09T01:53:06.118335+00:00
| 1,260 | false |
```\nclass Solution {\n public int numberOfUniqueGoodSubsequences(String binary) {\n int initialZeroCount= 0;\n while(initialZeroCount < binary.length() && binary.charAt(initialZeroCount) == \'0\') initialZeroCount++;\n if(initialZeroCount == binary.length()) return 1;\n long[] dp = new long[binary.length()];\n dp[initialZeroCount] = 1;\n int lastOne = 0, lastZero = 0;\n long mod = (long) Math.pow(10, 9)+7;\n for(int i=initialZeroCount+1;i<binary.length();i++){\n int j = binary.charAt(i) == \'1\' ? lastOne : lastZero;\n long dup = j > 0 ? dp[j-1] : 0;\n dp[i] = 2 * dp[i-1] - dup;\n if(dp[i] < 0) dp[i] += mod;\n dp[i] %= mod;\n if(binary.charAt(i) == \'0\') lastZero = i;\n else lastOne = i;\n }\n \n int hasZero = 0;\n if(binary.contains("0")) hasZero = 1;\n \n \n return (int) (dp[binary.length()-1] + hasZero);\n }\n}\n```
| 7 | 1 |
['Dynamic Programming', 'Java']
| 0 |
number-of-unique-good-subsequences
|
[C++] Memorization | Recurssion
|
c-memorization-recurssion-by-askvij-l23q
|
Below is the three obervation we have to see\nThree Observations:\n1. String can\'t start from zero(except only 0), so our string will always start from 1\n2. S
|
askvij
|
NORMAL
|
2021-08-29T04:03:37.706964+00:00
|
2021-08-29T04:03:37.706996+00:00
| 1,306 | false |
Below is the three obervation we have to see\nThree Observations:\n1. String can\'t start from zero(except only 0), so our string will always start from 1\n2. String starting from \'1\' will always cover all the good string which can be formed from any one choosen afer this one . For example "100100" \nAll unique good string starting from 0th position = [1, 10, 100, 11, 101, 1010, 10100, 1001, 10010, 100100, 110, 1100, 1000, 100000]\nAll unique good string starting from 3th position = [1, 10, 100]\nif we see unique good string staring from 0th position covers all unique good string 3rd position i.e we only need to calculate for the first position of \'1\' only\n3. If string contains zero than we can +1 the total string count ( "0" is valid string)\n\nBelow is my contest code\n\n```\nclass Solution {\npublic:\n vector<vector<int>> o_z;\n vector<long long> memo;\n long long MOD = 1e9 + 7;\n long long solve(int pos, int &n) {\n if (pos >= n) return 0;\n long long &ret = memo[pos];\n if (ret != -1) return ret;\n ret = 1; // string ending at this position\n ret +=solve(o_z[pos][0], n); // for next position we can choose zero\n ret %= MOD;\n ret += solve(o_z[pos][1], n); // for next position we can choose one\n return ret % MOD;\n \n \n }\n int numberOfUniqueGoodSubsequences(string binary) {\n int n = binary.size();\n memo.resize(n + 1, -1);\n o_z.resize(n, vector<int>(2, 0));\n o_z[n-1][0] = o_z[n-1][1] = n + 1;\n int last_one = n + 1, last_zero = n + 1;\n if (binary[n-1] == \'0\') last_zero = n - 1;\n else last_one = n - 1;\n for (int i = n - 2; i >= 0; i--) {\n o_z[i][0] = last_zero;\n o_z[i][1] = last_one;\n if (binary[i] == \'0\') last_zero = i;\n else last_one = i;\n }\n long long ret = solve(last_one, n);\n if (last_zero < n) ret += 1;\n return ret % MOD;\n \n }\n};\n```\n\n
| 7 | 1 |
['Recursion', 'Memoization', 'C']
| 3 |
number-of-unique-good-subsequences
|
java simple solution| O(n) with detailed explanation
|
java-simple-solution-on-with-detailed-ex-wb7v
|
Refer: https://www.codingninjas.com/codestudio/library/number-of-unique-good-subsequences\nConsider two variables, say, \u201CendsWithZero\u201D and \u201CendsW
|
KhoonharBilla
|
NORMAL
|
2022-02-06T09:34:00.954298+00:00
|
2022-02-06T09:34:00.954328+00:00
| 687 | false |
Refer: https://www.codingninjas.com/codestudio/library/number-of-unique-good-subsequences\nConsider two variables, say, \u201CendsWithZero\u201D and \u201CendsWithOne\u201D to keep the count of the number of subsequences ending with 0 and 1, respectively.\n\nDefine a flag \u201ChasZero\u201D to check if the given binary string contains \u20180\u2019 or not.\n\nTraverse the binary string and update the values of \u201CendsWithZero\u201D and \u201CendsWithOne\u201D in this manner - \n\nIf the current character is \u20181\u2019, then you can - \n\nAppend it to all the subsequences ending with \u20180\u2019 and ending with \u20181\u2019. In this way, you get the total number of subsequences ending with \u20181\u2019 till now. \n\nOr You chose not to append this \u20181\u2019 to the previous subsequences and consider it a subsequence of a single character, i.e. the subsequence \u20181\u2019, which is also a valid unique good subsequence.\n\nSo, we update endsWithOne as follows:\n\nendsWithOne = endsWithOne + endsWithZero + 1\n\nIf the current character is \u20180\u2019, then -\n\nAppend it to the subsequences ending with \u20180\u2019 and ending with \u20181\u2019. In this way, you get the total number of subsequences ending with \u20180\u2019 till now. \n\nThe subsequence \u20180\u2019 is also valid. But we will not increase the count by one every time we encounter \u20180\u2019. Instead, we will add 1 for this subsequence only once at the end. Why? Shortly, we will see a dry run of this approach which will help you understand the reason behind this.\n\nSo, we update endsWithZero as follows:\n\nendsWithZero = endsWithOne + endsWithZero\n\n \n\nCalculate the total number of unique good subsequences as follows:\n\nnumberOfUniquegoodSubsequences = endsWithOne + endsWithZero + hasZero\n\n\n```\nclass Solution {\n public int numberOfUniqueGoodSubsequences(String binary) {\n // if current char is 1 dp[i] = 2* dp[i-1]\n // if current character is zero dp[i] = 2*(dp[i-1]-1);\n int endsWithOne = 0;\n int endsWithTwo = 0;\n int MOD = 1_000_000_007;\n int hasZero = 0;\n for(int i=0; i<binary.length();i++){\n if(binary.charAt(i)==\'1\'){\n endsWithOne = (endsWithOne + endsWithTwo + 1)%MOD;\n }else{\n hasZero = 1;\n endsWithTwo = (endsWithOne + endsWithTwo)%MOD;\n }\n }\n int ans = (endsWithOne + endsWithTwo + hasZero)%MOD;\n \n return ans;\n }\n}\n```\n
| 5 | 0 |
['Dynamic Programming', 'Java']
| 0 |
number-of-unique-good-subsequences
|
[Python] simple DP solution with thinking process and pattern explanation
|
python-simple-dp-solution-with-thinking-mzdvj
|
I couldn\'t solve this problem during the contest. \nAnd it actually took me quite a while to understand the solutions in the Discussion (but they are very help
|
davidcn21
|
NORMAL
|
2021-08-29T22:56:06.906967+00:00
|
2021-08-31T11:33:17.980434+00:00
| 677 | false |
I couldn\'t solve this problem during the contest. \nAnd it actually took me quite a while to understand the solutions in the Discussion (but they are very helpful!).\nI hope my thinking process in the following can be also helpful to others.\n\nLet\'s use **dp0 & dp1** to represent the number of unique subsequences that end with 0 and 1 respectively.\n\n**- Wrong idea -**\nWhen I derived the DP equation during the contest, I was thinking about sth like **dp1 = 2 * dp1 + dp0 + ...**, where factor **2** comes from the fact that \nwhen we see 1, we can choose to `add` or `not add` 1 to the previous subsequences that end with 1. And the resulting subsequences will all end with 1.\nThis is clearly wrong because subsequences [1, 11] will become [1, 11, 11, 111] where 11 is doubly counted.\n\n**- Pattern in subsequences -**\nAfter reading several solutions, I went through examples and realized I ignored a pattern in the subsequences.\nLet\'s name the two groups of unique subsequences that end with 0 and 1 as **G0 & G1** respectively.\n* In **G1**, for example, if say 110100**111** exists, then 110100**11** and 110100**1** must also exist!\n* In the meantime, in **G0** 110100 must exist.\n\nSo when we iterate over the string and see a "1", we can add it to all of them in **G1** [..., 110100**111**, 110100**11**, 110100**1**, ...] --> [..., 110100**1111**, 110100**111**, 110100**11**, ...], and the orignally last one 110100**1**, which was missing then, can be generated _again_ from **G0** [..., 110100, ...] --> [..., 110100**1**, ...]\n\nAs a result, the new **G1*** has two parts:\n1. subsequences whose length of consecutive "1" in the end `L == 1`. They come from previous **G0**, each adding a "1".\n2. subsequences with `L > 1`, which come from previous **G1**.\n\nThe first part covers all the subsequences with `L == 1` that were previously in **G1**.\n\n\n```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n \n dp0, dp1 = 0, 0 # number of unique subsequences that end with 0 or 1\n for val in binary:\n if val == \'0\':\n if dp0 == 0:\n dp0 = dp1 + 1 # add "0" to dp0 related subsequences group\n else:\n dp0 = (dp0 + dp1) % (10 ** 9 + 7)\n else:\n if dp0 == 0:\n dp1 = dp1 + 1\n else:\n dp1 = (dp0 + dp1) % (10 ** 9 + 7)\n return (dp0 + dp1) % (10 ** 9 + 7)\n```
| 5 | 0 |
[]
| 1 |
number-of-unique-good-subsequences
|
C++ 6 liners concise O(n) time solution beats 100% with explanation
|
c-6-liners-concise-on-time-solution-beat-45ge
|
Idea: remove all prefix 0s first (and ues has zero to check if there are at least one 0s\n1. p0 is the number of unique good subsequences ends with 0\n-> if an
|
eminem18753
|
NORMAL
|
2021-08-29T05:47:43.686168+00:00
|
2021-08-30T00:33:58.338462+00:00
| 762 | false |
Idea: remove all prefix 0s first (and ues has zero to check if there are at least one 0s\n1. p0 is the number of unique good subsequences ends with 0\n-> if an 0 is encountered, it is updated with p0=p0+p1\n-> because the new subsequence can be prefixed by subsequences ended with "0" (eg. p0) or "1" (eg. p1)\n2. p1 is te number of unique good sequences ends with 1\n-> if an 1 is encountered, it is updated with p1=p0+p1+1\n-> because the new subsequence can be prefixed by subsequences ended with "0" (eg. p0) or "1" (eg. p1) or nothing (eg. 1)\n3. if there is a zero, add 1 to the result\n\nNote: no need to add 1 to p0 because the subsequence can not be prefixed by "0" (eg. no need to accumulate forward)\n```\nint numberOfUniqueGoodSubsequences(string& binary) \n{\n\tint n=binary.length(),p0=0,p1=0,d=1000000007;\n\tbool has_zero=false;\n\n\tfor(int i=0;i<n;i++)\n\t\tif(binary[i]==\'0\') has_zero=true,p0=(p0+p1)%d;\n\t\telse p1=(p0+p1+1)%d;\n\n\treturn (p0+p1+has_zero)%d;\n}\n```
| 5 | 0 |
[]
| 2 |
number-of-unique-good-subsequences
|
Python/Go O(n) by DP [w/ Hint]
|
pythongo-on-by-dp-w-hint-by-brianchiang_-0wx3
|
Python O(n) by DP\n\nHint:\n\nDefine\nS0 = the number of good subsequence count ending in 0\nS1 = the number of good subsequence count ending in 1\nF0 = the exi
|
brianchiang_tw
|
NORMAL
|
2021-12-17T14:01:07.879665+00:00
|
2021-12-18T13:44:34.189628+00:00
| 555 | false |
Python O(n) by DP\n\n**Hint**:\n\nDefine\n**S0** = the number of good subsequence count **ending in 0**\n**S1** = the number of good subsequence count **ending in 1**\n**F0** = the **existence flag of 0** in input binary string\n\nDP( i ) computes and return S0, S1, F0 for index i\n\n```\n## Base case :\nif i == -1:\n\t\n\t# Empty string has no good subsequence\n\treturn 0, 0, 0\n```\n\n```\n## General cases:\nif i != -1\n\t\n\tif cut_digit == 1:\n\t\t\n\t\t# current good = ( S0 concate with 1 ) + ( S1 concate with 1 ) + 1 alone\n\t\t# + "1" is allowed because leading 1 is valid by description\n\t\tS1 = S0 + S1 + 1\n\t\tS0 = S0\n\t\t\n\telse:\n\t\t# current good = ( S0 concate with 0 ) + ( S1 concate with 0 ) \n\t\t# + "0" is NOT allowed because leading 0 is invalid by description\n\t\tS0 = S0 + S1\n\t\tS1 = S1\n\t\t\n\t\t# update existence flag of 0\n\t\tF0 = F0 | (1-cur_digit)\n\t\n\treturn S0, S1, F0\n```\n\n---\n\nFinal answer = **S0 + S1 + F0**\n( F0 is for **single "0"** if "0" exists in input binary string )\n\n---\n\n**Implementation** by bottom-up DP in Python:\n\n```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n \n \n # zero_as_last: the count of S0, good sequence ending in 0\n # one_as_last : the count of S1: good sequence ending in 1\n # zero_exist: existence flag of 0 in given binary\n \n dp = {"zero_as_last": 0, "one_as_last": 0, "zero_exist": 0}\n \n for bit in map(int, binary):\n \n if bit:\n # current good = ( S0 concate with 1 ) + ( S1 concate with 1 ) + 1 alone\n # + "1" is allowed because leading 1 is valid by description\n dp["one_as_last"] = dp["zero_as_last"] + dp["one_as_last"] + 1\n \n else:\n # current good = ( S0 concate with 0 ) + ( S1 concate with 0 ) \n # + "0" is NOT allowed because leading 0 is invalid by description\n dp["zero_as_last"] = dp["zero_as_last"] + dp["one_as_last"]\n \n # check the existence of 0\n dp["zero_exist"] |= (1-bit)\n \n \n return sum( dp.values() ) % ( 10**9 + 7 )\n```\n\n---\n\n**Implementaiton** by Bottom-up DP in Golang\n\n```\n\nfunc numberOfUniqueGoodSubsequences(binary string) int {\n \n // Modulo constant, required by description\n const modulo_const int = 1e9 + 7\n \n zero_as_last := 0\n one_as_last := 0\n zero_exist := 0\n \n for _, bitChar := range binary{\n \n \n if bitChar == \'1\'{\n one_as_last = (zero_as_last + one_as_last + 1) % (modulo_const)\n }else{\n zero_as_last = (zero_as_last + one_as_last ) % (modulo_const)\n zero_exist = 1\n }\n \n \n }\n \n return (zero_as_last + one_as_last + zero_exist) % (modulo_const)\n \n}\n```\n\n---\n\n**Implementation** by Top-down DP\n\n```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n \n \n def dp(ending_idx):\n \n if ending_idx == -1:\n \n return 0, 0 ,0\n \n else:\n prev_zero, prev_one, zero_exist = dp(ending_idx-1)\n \n cur_digit = int( binary[ending_idx] )\n \n if cur_digit == 1:\n zero_as_last = prev_zero\n one_as_last = ( (prev_zero + prev_one) + 1 ) % (10**9+7)\n \n else:\n zero_as_last = ( (prev_zero + prev_one) ) % (10**9+7)\n one_as_last = prev_one\n \n zero_exist = zero_exist | (1-cur_digit) \n \n \n return zero_as_last, one_as_last, zero_exist\n \n # -------------------------\n\n return sum( dp( len(binary)-1 ) ) % (10**9+7)\n```\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #940 Distinct Subsequence II](https://leetcode.com/problems/distinct-subsequences-ii/)
| 4 | 0 |
['Dynamic Programming', 'Python', 'Go']
| 0 |
number-of-unique-good-subsequences
|
DP Intuition - visual explanation
|
dp-intuition-visual-explanation-by-tarun-kgl0
|
Consider we have a tree and each node can have two children i.e. you can extend it with 0 or 1. Initially we have a dummy node(x).\n\n1. Process one character a
|
tarun111
|
NORMAL
|
2021-08-29T05:04:29.744201+00:00
|
2021-08-29T05:28:52.902821+00:00
| 1,143 | false |
Consider we have a tree and each node can have two children i.e. you can extend it with 0 or 1. Initially we have a dummy node(x).\n\n1. Process one character at a time\n2. Figure out which all nodes can be extended with current character\n3. Store only the delta at current location\n\nInput: 111001\n\n1. process 1. We only have a dummy node and only one edge can be formed here, so count = 1\n2. process 1. We have one dummy node but it is already extended in previous step. We\'re only left with previous node and we can only extend it. count = 1\n3. process 1. Same as above. count = 1\n4. process 0. This is the first time 0 is coming. We can extend all nodes with 0 since no one has any edge with 0. count = 4\n5. process 0. Previous step extended all previous steps. We can only extend previous step 0 ends. There is only one exception since we can\'t extend 0 prefix. count = 3\n6. process 1. We have 3 characters which need extension. Before this, we already covered everything(find last one\'s occurrence). count = 1+3(we can\'t extend 0)+3 = 7\n7. To get the answer -> add all these counts\n\n**The reason why we\'re not adding to all existing edges is to avoid duplication**\n\n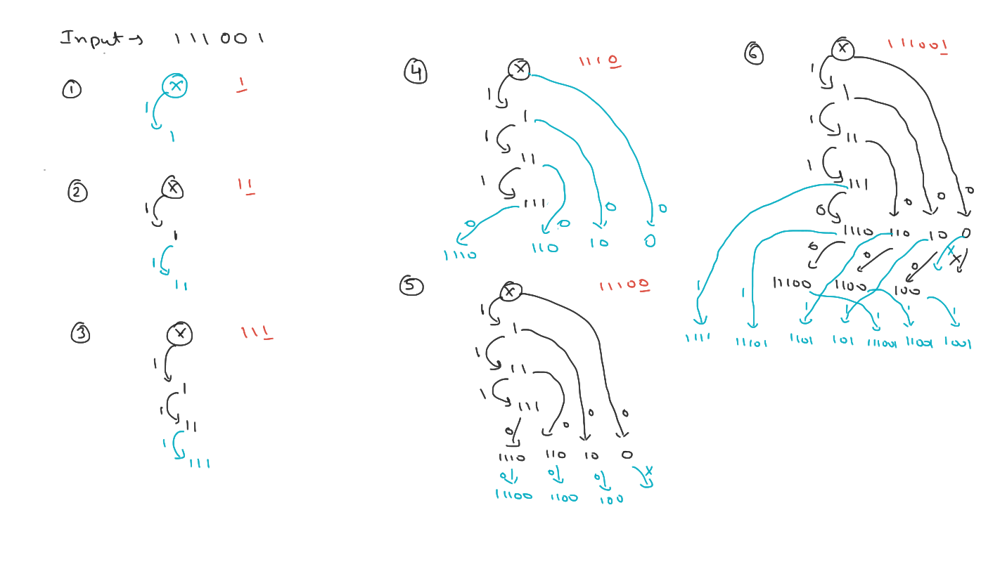\n\n\nTo implement this we have a count array which would contain data of only delta counters which are new by including current character. We try to find the last character which needs some extension and add all delta upto current character. In this process, we need to check about edge case when 0 can be extended.\n\n```\nclass Solution {\n private static final int MOD = 1_000_000_007;\n \n public int numberOfUniqueGoodSubsequences(String binary) {\n int[] count = new int[binary.length()];\n \n int[] occurrence = new int[2];\n int[] lastPosition = new int[] {-1, -1};\n \n int firstZeroLoc = -1;\n \n for (int i = 0; i < binary.length(); i++) {\n int idx = binary.charAt(i) - \'0\';\n if (firstZeroLoc == -1 && binary.charAt(i) == \'0\') {\n firstZeroLoc = i;\n }\n \n if (i == 0) {\n occurrence[idx]++;\n lastPosition[idx] = 0;\n count[0] = 1;\n continue;\n }\n \n long sum = 0;\n \n if (occurrence[idx] == 0) {\n sum++;\n }\n \n int start = Math.max(0, lastPosition[idx]);\n sum += getSum(count, start, i, firstZeroLoc);\n sum %= MOD;\n \n lastPosition[idx] = i;\n occurrence[idx]++;\n count[i] = (int) sum;\n }\n \n long ans = 0;\n for (int i = 0; i < binary.length(); i++) {\n ans += count[i];\n ans %= MOD;\n }\n return (int) ans;\n }\n \n private int getSum(int[] count, int start, int end, int firstZeroLoc) {\n long sum = 0;\n for (int i = start; i < end; i++) {\n if (i == firstZeroLoc) {\n if (count[i] - 1 == 0) {\n sum += MOD;\n } else {\n sum += count[i] - 1;\n }\n\n } else {\n sum += count[i];\n }\n sum %= MOD;\n }\n return (int) sum;\n }\n}\n```
| 4 | 0 |
['Dynamic Programming', 'Java']
| 0 |
number-of-unique-good-subsequences
|
Python - Greedy strategy, use 3 variables. O(n) time O(1) space
|
python-greedy-strategy-use-3-variables-o-94gn
|
Idea:\n\n If we\'re in the middle of processing the string and see a \'1\', no new subsequences are created from old subsequences that we had before the last \'
|
kcsquared
|
NORMAL
|
2021-08-29T04:00:39.980770+00:00
|
2021-08-29T04:27:11.748883+00:00
| 493 | false |
**Idea:**\n\n* If we\'re in the middle of processing the string and see a \'1\', no new subsequences are created from old subsequences that we had **before** the last \'1\'. \n* However, all the new subsequences that were created since the last \'1\' **do create one** new subsequence each.\n* The same is true for \'0\'. So just track these three variables; the only edge case is if there are no zeros or no ones.\n\n\n```python\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n mod = 10 ** 9 + 7\n n = len(binary)\n first_one = binary.find(\'1\')\n if first_one < 0: # If no ones\n return 1\n\n if \'0\' not in binary: # If no zeros\n return n % mod\n\n total = new_since_last_0 = new_since_last_1 = 1\n\n for x in binary[first_one + 1:]: # Start counting after the first 1\n if x == \'1\':\n new_since_last_0 += new_since_last_1\n total += new_since_last_1\n else:\n new_since_last_1 += new_since_last_0\n total += new_since_last_0\n total %= mod\n new_since_last_0 %= mod\n new_since_last_1 %= mod\n\n return (total + 1) % mod # Add 1 for the single zero\n```
| 4 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
TIME O(n) || SPACE O(1) || C++
|
time-on-space-o1-c-by-yash___sharma-h8ez
|
\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n long long int a = 0, b = 0, c = 0, d = 0,mod = 1e9+7;\n /*s
|
yash___sharma_
|
NORMAL
|
2023-03-05T16:32:29.627572+00:00
|
2023-03-05T16:32:29.627614+00:00
| 1,378 | false |
```\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n long long int a = 0, b = 0, c = 0, d = 0,mod = 1e9+7;\n /*strart end end a -> 0..0, b -> 0...1, c -> 1....0, d -> 1.....1*/\n for(auto &i: binary){\n if(i==\'0\'){\n a = 1;\n c = (c+d)%mod;\n }else{\n d = (c+d+1)%mod;\n }\n }\n return (a+b+c+d)%mod;\n }\n};\n```
| 3 | 0 |
['Dynamic Programming', 'C', 'C++']
| 0 |
number-of-unique-good-subsequences
|
C++ Detail explanation
|
c-detail-explanation-by-quangtuaka-jjec
|
When we see that problem, the first solution we appear in our head is using recursion to find the subsequences and we push this string into a map with key => va
|
quangtuaka
|
NORMAL
|
2022-07-28T08:34:49.561061+00:00
|
2022-07-28T08:56:01.883135+00:00
| 648 | false |
When we see that problem, the first solution we appear in our head is using recursion to find the subsequences and we push this string into a map with key => value or tuple to get the unique string. After that we return the size as a result of problem. This solution is nice, it\'s can solve the problem, but the constrain of the problem not allow we to do this easily. \n \n `1 <= binary.length <= 10^5` with this constrain if we using recursion the time complexity is very huge. The solution will be **Time Limit Exceeded**. Because of that, we need another appoard. Let\'s find out better solution with **O(N)** runtime complexity and **O(1)** space complexity.\n \nWe split this problem into smaller problems, the question is "*If I add a new number to a string, how many new subsequences can I have?*"\n\nFind the number of **unique good subsequences** of `binary`. The good subsequences just is the subsequences **without leading zero**. To be easily handle the case zero leading, it\'s better for us when going from last element to first element and now the question became "*If I add a new number to a head of string, how many **unique subsequences** can be create?*".\n\n`binary consists of only \'0\'s and \'1\'s.` depend on that constrain, elements we can add to head of string just be `1` or `0`. \n\n"*How many unique subsequences can be create?*"\nExample: \n- We have a empty string like `""` so our `subsequences` will be `[]`. \n\nBecause each subsequences is **unique**, that mean we just can be add sequences \'1\' and \'0\' only one time. To hadle this we create a flag to mark sequence `1` and `0` had appear or not.\n- `If number == \'1\'`:\n\t- We add a `1` to string. String is `"1"` so `subsequences` become `["1"]` => number of unique subsequences we create be `1`.\n\t- We add new `1` to head of string like `"11"`. `The subsequences` is `["1", "11"]` => number of unique subsequences we create be `1`.\n\t- `...` and so on with string `"1111"`. `The subsequences` is `["1", "11", "111", "1111"]` => number of unique subsequences we create still be `1`.\n\t\tSo we have procedural code: \n\t\t```\n\t\tresult = 0\n\t\tuniqueSubsequence = 0\n\t\tone = true\n\t\t\n\t\tfrom last number to first number: \n\t\t\tif number == \'1\':\n\t\t\t\tif one == true:\n\t\t\t\t\tuniqueSubsequence += 1\n\t\t\t\t\tone = false\n\t\t\t\t\n\t\t\tresult += uniqueSubsequence\n\t\t```\n- `If number == \'0\'`:\n\t- We add a `0` to string. String is `"0"` so `subsequences` become `["0"]` => number of unique subsequences we create be `1`. Simple, right!\n\t- Add a new `0` to a string. String become `"00"` but `subsequences` still `["0"]`, cause good subsequences is not have leading zero except `"0"` so not like `1`, `0` only add new unique subsequences at first time this appear => number of unique subsequences we create be `0`. \n\tOur procedural code become: \n\t\t\n\t\t``` \n\t\tresult = 0\n\t\tuniqueSubsequence = 0\n\t\tone = true\n\t\tzero = true\n\n\t\tfrom last number to first number: \n\t\t\tif number == \'1\':\n\t\t\t\tif one == true:\n\t\t\t\t\tuniqueSubsequence += 1\n\t\t\t\t\tone = false\n\t\t\t\tresult += uniqueSubsequence\n\t\t\t\t\n\t\t\tif number == \'0\':\n\t\t\t\tif zero == true:\n\t\t\t\t\tuniqueSubsequence += 1\n\t\t\t\t\tresult += 1\n\t\t\t\t\tzero = false\n\t\t```\n\n- What if we add `0` to a string `"11"`. The string become "011" and the `sequences` be `["1", "11", "0"]`. Right!\n- And we add a `1` to head of this string. Now string become `"1011"`. So how many subsequences can we create now? \n\t\nHead back to last step when string became `"011"`. Our `sequences` actually be something like `["1", "11", "0", "01", "011"]` , but we have to remove `"01"` and `"011"` cause their are not a good subsequences. When we add a new number `1` to head the `sequences` became `["1", "11", "0", "111" "10" "101", "1011"]` not just `["1", "11", "0", "111", "10"]`. \n\t\nWhat is that mean? That mean when we face a `0` leading we have to track all the **last result** (the path `["1", "11"]`) like the unique subsequence because we will remove all their not good subsequence (the path `["01", "011"]`) in the next step. \n\nLet\'s complete our procedural code:\n``` \nresult = 0\nuniqueSubsequence = 0\none = true\nzero = true\n\nfrom last number to first number: \n\tif number == \'1\':\n\t\tif one == true:\n\t\t\tuniqueSubsequence += 1\n\t\t\tone = false\n\t\tresult += uniqueSubsequence\n\n\tif number == \'0\':\n\t\tuniqueSubsequence += result\n\t\tif zero == true:\n\t\t\tuniqueSubsequence += 1\n\t\t\tresult += 1\n\t\t\tzero = false\n\nreturn result\n```\n\nOk that is everything of this problem! Here is my C++ code:\n```\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n long res = 0,\n unqCase = 0,\n len = binary.length();\n \n bool zero = true,\n one = true;\n \n for (int i = len - 1; i >= 0; --i) {\n if (binary[i] == \'1\') {\n if (one) {\n unqCase++; \n one = false;\n }\n \n res += unqCase;\n } else {\n unqCase += res;\n \n if (zero) {\n unqCase++;\n res++;\n zero = false;\n }\n }\n \n res %= (long) 1e9+7;\n }\n\n return res;\n }\n};\n```\n\n**Conclusion:**\n- Runtime complexity: **O(N)**\n- Space complexity: **O(1)**
| 3 | 0 |
['C', 'C++']
| 1 |
number-of-unique-good-subsequences
|
Python | O(n) solution, think like a Trie, use O(1) space | Visual explanation | 13 lines
|
python-on-solution-think-like-a-trie-use-7pzt
|
This question bugged me for a long time.\nI spent probably 3 hrs working on it.\nI had a solution in place but in reached TLE arround test 30.\nI finally found
|
dotaneli
|
NORMAL
|
2022-02-09T13:59:40.133430+00:00
|
2022-02-09T14:07:31.562262+00:00
| 343 | false |
This question bugged me for a long time.\nI spent probably 3 hrs working on it.\nI had a solution in place but in reached TLE arround test 30.\nI finally found an O(n) time complex. solution with O(1) space complex.\n\nIt hit me that the permuations, the unique permutations, can be represented as a Trie:\n\nLet\'s assume the binary is "1101".\n\n**Step A - add "1"**\nWe now have a possiblity to add 1 zero, and 1 one.\nCounters[0] = 1\nCounters[1] = 1\nLength = 1\n\n\n\n**Step B - add "1"**\nThe additional "1" uses 1 One from our "One" bucket, but also allows a new "One" to be added.\nAfter adding it, we can add 2 zeros, or 1 one. So after adding the 1, our One bucket remains the same, but out zero bucket increase by the size of the One bucket\n\nCounters[0] = 2\nCounters[1] = 1\nLength = 1 + counters[1] = 1 + 1 = 2\n\n\n\n**Step C - add "0"**\nNow let\'s add a zero. Remember that we have a bucket of 2 Zeros, and indeed 2 Zeros we\'ll add.\nAfter that addition, 2 Zero will remain optional, but the number of Ones will increase from 1 to 3.\n\nCounters[0] = 2\nCounters[1] = 3\nLength = 2 + counters[0] = 2 + 2 = 4\n\n\n\n**Step D - add "1"**\nIn this final step, we have a place for 2 Zeros, and 3 Ones. This "One" will use the bucket of 3.\n\nCounters[0] = 5\nCounters[1] = 3\nLength = 4 + counters[1] = 4 + 3 = 7\n\n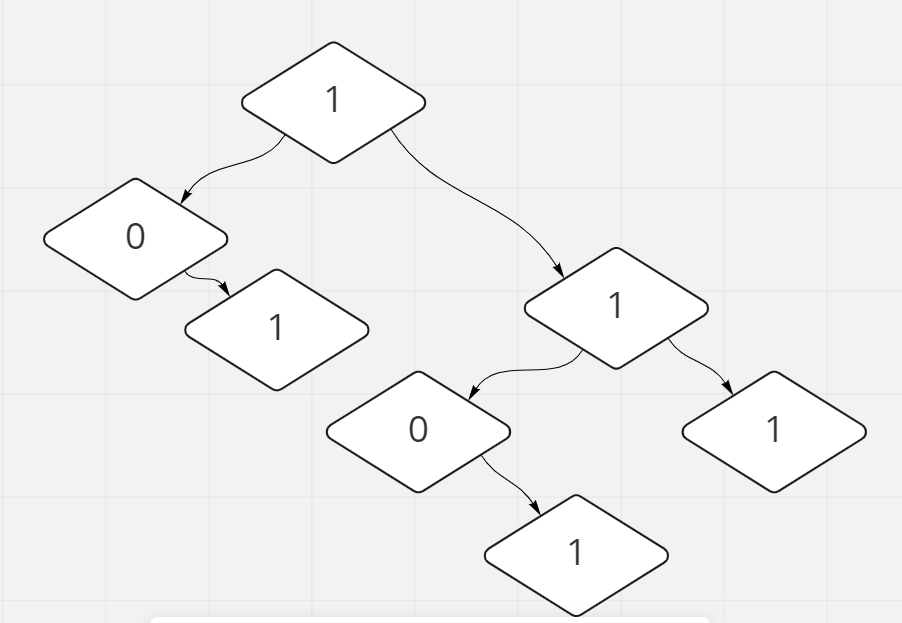\n\n\n**Remember a single "0"**\nIf there\'s a zero anywhere in our string, we\'ll need to remember to carry the single 0.\nsince "1101" has a zero, we\'ll add 1 to our length.\nlength = 7 + 1 = 8\n\nAnswer is indeed 8\n\n\nMy code\n\n```\nclass Solution:\n\tdef numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n\t\ttotal_len = 1\n\t\tif "0" in binary:\n\t\t\ttotal_len = 2\n\n\t\t# Remove left zero trailer, irrelevant\n\t\twhile i<len(binary) and binary[i] == "0": i+=1\n\t\tbinary = binary[i:]\n\n\t\t# Handle zeros only string\n\t\tif i == len(binary): return 1\n\n\t\t# Counters to count how many options to add zeros or ones uniquely exist.\n\t\t# Zeros in counters[0] and Ones in counters[1].\n\t\t# Populate first char manually\n\t\tcounters = [1,1]\n\t\tfor x in range(1,len(binary)):\n\t\t\tchar = binary[x]\n\t\t\tval = int(char)\n\n\t\t\t# Have the current char use all of the possible places to add based on "counters"\n\t\t\ttotal_len += counters[val]\n\t\t\t\n\t\t\t# Don\'t forget that if we used all the "ones", we created new "ones" and "zeros" opportunity\n\t\t\tcounters[abs(1-val)] += counters[val]\n\t\treturn total_len % 1000000007\n```\n\n\n\n
| 3 | 0 |
['Python']
| 0 |
number-of-unique-good-subsequences
|
[Java] - DP - O(N) time, O(1) space - explained
|
java-dp-on-time-o1-space-explained-by-ey-qalu
|
This problem is actually very similar to Distinct Subsequences, with 2 differences:\n1. Valid chars here are only 0 and 1\n2. No leading zeros is allowed\n\nThi
|
Eynav
|
NORMAL
|
2021-12-25T16:53:22.746456+00:00
|
2022-01-13T16:13:26.840529+00:00
| 326 | false |
This problem is actually very similar to [Distinct Subsequences](https://leetcode.com/problems/distinct-subsequences-ii/), with 2 differences:\n1. Valid chars here are only `0` and `1`\n2. No leading zeros is allowed\n\nThis solution is less elegant than [awsome Lee\'s](https://leetcode.com/problems/number-of-unique-good-subsequences/discuss/1431819/JavaC%2B%2BPython-DP-4-lines-O(N)-Time-O(1)-Space), because I kept the idea of needing to count all sub-sequences, regardless of the allowed chars (using an array and not two vars), in order to help following the logic and understand how to conquer this problem.\n\n```\nclass Solution {\n \n private static final int MOD = 1000000007;\n \n public int numberOfUniqueGoodSubsequences(String binary) {\n boolean addZero = false; \n int count = 1; // in the first round we "concat" to the empty binary\n int[] countEndsWith = new int[2]; \n for (int i=0; i<binary.length(); i++) {\n char c = binary.charAt(i);\n int cIndex = c-\'0\';\n int endsWithCCount = count; // all valid sub-binaries + c at the end => same count\n if (c == \'0\') {\n addZero = true;\n // every time c is \'0\', we concat it to "" and get "0" - we wish to count it only once (done in the end)\n endsWithCCount--; \n }\n count = (count + endsWithCCount - countEndsWith[cIndex]) % MOD; // w/out c at the end minus dups (= already end with c)\n count = count < 0 ? count + MOD : count; // may be negative due to MOD\n countEndsWith[cIndex] = endsWithCCount;\n }\n count--; // remove the empty binary\n if (addZero) count++; // add "0"\n return count;\n }\n}\n```
| 3 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
Java DP
|
java-dp-by-mi1-o1tt
|
\nclass Solution {\n int mod = (int) Math.pow(10,9)+7;\n public int numberOfUniqueGoodSubsequences(String binary) {\n if(!binary.contains("1")){\n
|
mi1
|
NORMAL
|
2021-12-08T09:30:40.363765+00:00
|
2021-12-08T09:30:40.363797+00:00
| 195 | false |
```\nclass Solution {\n int mod = (int) Math.pow(10,9)+7;\n public int numberOfUniqueGoodSubsequences(String binary) {\n if(!binary.contains("1")){\n return 1;\n }\n int len = binary.length();\n int[] last = new int[2];\n Arrays.fill(last, -1);\n long[] dp = new long[len];\n int start = binary.indexOf(\'1\') + 1;\n dp[start - 1] = 1;\n for (int i = start; i < binary.length(); i++) {\n int ch = Character.getNumericValue(binary.charAt(i));\n dp[i] = 2 * dp[i - 1];\n dp[i]%=mod;\n if (last[ch] - 1 >= 0) {\n dp[i] -= dp[last[ch] - 1];\n dp[i]+=mod;\n dp[i]%=mod;\n }\n last[ch] = i;\n }\n return (int) dp[len - 1] + (binary.contains("0") ? 1 : 0);\n }\n}\n```
| 3 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
Split sequences ending with 0 and 1 (Algorithm explained)
|
think-sequences-ending-with-0-and-1-well-uawe
|
IntuitionSince its binary string, sub-sequence can only end with '1' or '0'. This can be used to build up our algorithm. Instead of actual squences, we will us
|
dharmendersheshma
|
NORMAL
|
2024-12-26T18:15:17.147458+00:00
|
2024-12-26T18:32:03.949177+00:00
| 151 | false |
# Intuition
Since its binary string, sub-sequence can only end with '1' or '0'. This can be used to build up our algorithm. Instead of actual squences, we will use the infered counts for them.
**Important observation:**
Each append of '1' or '0' to some sequence will create a new unique sequence.
So we will count our sequences for given ith position by taking help from sequences for (i-1)th position.
Lets keep track of two counts, first the count of sequences which ends with 1 (endWith1). And second the count of sequences which ends with 0 (endWith0).
Iterating from left to right in binary string:
1. If we encounter '0' than we can append this 0 to all existing endWith0 and endWith1 sequences. Leading to new endWith0 => endWith0 + endWith1 (As appending 0 in end of different sequences gives different unique strings). We also check if atleast one "0" is encountered, since standalone "0" is valid sequence.
2. If we encounter '1' than we can append this 1 to all existing endWith0 and endWith1 sequences. Leading to new endWith1 => endWith0 + endWith1 + 1 (why this extra 1, read below).
Technically we will always have only one "1" unique sequence and only one "0" unique sequence. But our above calculation logic is bit different for both. Why is that?
Lets see it by example:
**Case 1**:
Lets say string was "111", not adding "1" to strings ending with 1 set, instead will increment total count by one in end.
First '1':
-----> endsWith1: [1]
Second '1':
-----> endsWith1: [11]
Third '1':
-----> endsWith1: [111]
See we have a loss here by the time we reach 3rd '1'. Total count in set is 1 and incrementing by one for sequence "1" equals to 2.
But it should be like below:
First '1':
-----> endsWith1: [1]
Second '1':
-----> endsWith1: [11, 1]
Third '1':
-----> endsWith1: [111, 11, 1]
Total count => 3 (correct answer)
**Note** that "1" is ALWAYS carried forward in the set, not duplicated.
**Case 2**:
Binary string is "100", not adding "0" to strings ending with 0 set, instead will increment total count by one in end.
Pos 0: '1'
-----> endsWith1: [1], endsWith0: []
Pos 1: '0'
-----> endsWith1: [1], endsWith0: [10]
Pos 2: '0'
-----> endsWith1: [1], endsWith0: [100, 10]
Note that "10" in endsWith0 in last iteration came from appending zero to endsWith1 entry of "1")
Total count in set is endsWith1 + endsWith0 counts => 3 and incrementing it by one more for sequence "0" equals to 4. Which is correct answer (1, 100, 10, 0).
Now assume we had followed the approach of 0 appending same as 1 appending from above.
Pos 0: '1'
-----> endsWith1: [1], endsWith0: []
Pos 1: '0'
-----> endsWith1: [1], endsWith0: [10, 0]
Pos 2: '0'
-----> endsWith1: [1], endsWith0: [100, 10, 00, 0]
Total count => endsWith1 + endsWith0 => 5 (WRONG)
See in last iteration we got invalid entry of "00". So we cant follow same approach for both the cases and reason why we separate out one "0" sequence compared to one "1" sequence. Hence why we split 1 ending and 0 ending sequences. Otherwise we could have directly doubled in each iteration (sed lyf!).
I hope above examples fills missing pieces from other solutions.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public int numberOfUniqueGoodSubsequences(String binary) {
int mod = (int) 1e9 + 7;
int endsWithZero = 0;
int endsWithOne = 0;
int seenZero = 0;
for(int i = 0; i < binary.length(); i++) {
if(binary.charAt(i) == '0') {
endsWithZero = (endsWithZero + endsWithOne) % mod;
seenZero = 1;
} else {
endsWithOne = (endsWithZero + endsWithOne + 1) % mod;
}
}
return (endsWithZero + endsWithOne + seenZero) % mod;
}
}
```
| 2 | 0 |
['Java']
| 1 |
number-of-unique-good-subsequences
|
1987. Number of Unique Good Subsequences [Python]
|
1987-number-of-unique-good-subsequences-rypwi
|
\n\npython\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n mod = 10**9 + 7\n dp = [[0, 0] for _ in range(2)]
|
shellpy03
|
NORMAL
|
2023-08-28T21:05:14.199230+00:00
|
2023-08-28T21:05:14.199259+00:00
| 343 | false |
\n\n```python\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n mod = 10**9 + 7\n dp = [[0, 0] for _ in range(2)] # dp[i][j] represents count of subsequences ending at index i with last element j (0 or 1)\n n = len(binary)\n \n for ch in binary:\n if ch == \'0\':\n # For a \'0\', we have two cases:\n # 1. Extend the subsequences ending with \'0\' by one more \'0\'.\n # 2. Extend the subsequences ending with \'1\' by appending this \'0\' to form new subsequences.\n dp[0][0] = 1\n dp[1][0] = (dp[1][0] + dp[1][1]) % mod\n else:\n # For a \'1\', we have one case:\n # Extend the subsequences ending with \'0\' or \'1\' by appending this \'1\' to form new subsequences.\n dp[1][1] = (dp[1][0] + dp[1][1] + 1) % mod\n \n # The answer is the sum of counts of subsequences ending with \'0\' and \'1\',\n # considering all the possibilities.\n result = (dp[0][0] + dp[0][1] + dp[1][0] + dp[1][1]) % mod\n return result\n\n# Create an instance of the Solution class\nsol = Solution()\n\n# Test cases\nprint(sol.numberOfUniqueGoodSubsequences("001")) # Output: 2\nprint(sol.numberOfUniqueGoodSubsequences("11")) # Output: 2\nprint(sol.numberOfUniqueGoodSubsequences("101")) # Output: 5\n```\n\n**Intuition:**\n\nThe algorithm works by maintaining two sets of counts for each index: `dp[i][0]` represents the count of subsequences ending at index `i` with the last element being \'0\', and `dp[i][1]` represents the count of subsequences ending at index `i` with the last element being \'1\'. \n\nWhen a \'0\' is encountered, two possibilities arise:\n1. We can extend the subsequences ending with \'0\' by one more \'0\', and this count is updated in `dp[0][0]`.\n2. We can append this \'0\' to subsequences ending with \'1\', creating new subsequences, and this count is updated in `dp[1][0]`.\n\nWhen a \'1\' is encountered, we can extend the subsequences ending with \'0\' or \'1\' by appending this \'1\' to form new subsequences. This count is updated in `dp[1][1]`.\n\nFinally, the answer is the sum of counts of subsequences ending with \'0\' and \'1\', considering all the possibilities.\n\n**Time Complexity:**\n\nThe algorithm iterates through the binary string once, performing constant time operations for each character. Hence, the time complexity is O(N), where N is the length of the binary string. The space complexity is O(1) since we are using a fixed-size array for dynamic programming.\n\n# Code\n```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n mod = 10**9 + 7\n dp = [[0, 0] for _ in range(2)]\n n = len(binary)\n \n for ch in binary:\n if ch == \'0\':\n dp[0][0] = 1\n dp[1][0] = (dp[1][0] + dp[1][1]) % mod\n else:\n dp[1][1] = (dp[1][0] + dp[1][1] + 1) % mod\n \n return (dp[0][0] + dp[0][1] + dp[1][0] + dp[1][1]) % mod\n```
| 2 | 0 |
['Python3']
| 0 |
number-of-unique-good-subsequences
|
O(N) using unique subsequences II
|
on-using-unique-subsequences-ii-by-lazy1-pkug
|
\n\n\nclass Solution {\npublic:\n int mod = 1e9 + 7;\n\nint numberOfUniqueGoodSubsequences(string s)\n{\n\n unordered_map<char, int> index; //stores updat
|
lazy1234
|
NORMAL
|
2022-08-16T02:24:28.113397+00:00
|
2022-08-16T02:24:28.113435+00:00
| 113 | false |
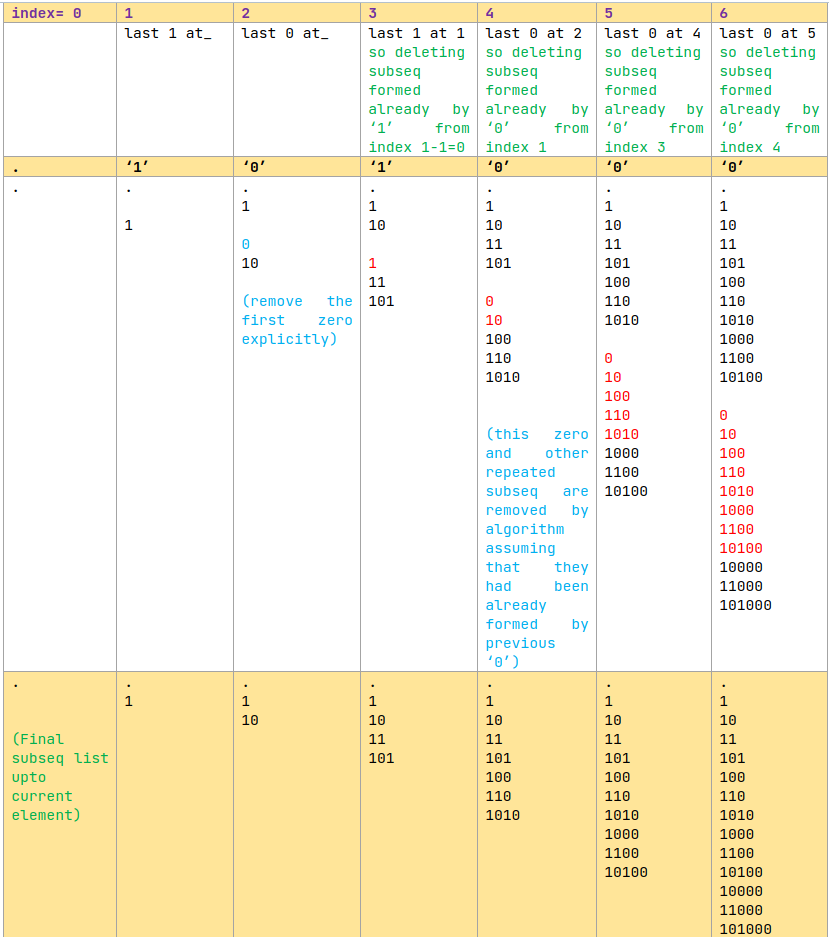\n\n```\nclass Solution {\npublic:\n int mod = 1e9 + 7;\n\nint numberOfUniqueGoodSubsequences(string s)\n{\n\n unordered_map<char, int> index; //stores updated index of current element\n vector<long long> v(s.size() + 1, 0); //stores no. of subsequences\n\n v[0] = 1; // empty subsequence\n\n\t//index of first zero\n int firstZero=-1;\n \n for (int i = 1; i <= s.size(); i++)\n {\n\n\t\t//expected value is twice of previous subsequences by taking current element or rejecting it\n\t\t//suppose subseq-{1,11,111} =3 elements and current item =\'0\' then expected values are \n\t\t//{1,11,111,10,110,1110} = 2*3 =6\n\t\t\n long long expected = (2 * v[i - 1]) % mod;\n\n if (index.find(s[i - 1]) != index.end()) //if item already present\n {\n\t\t\t//subtract the subsequences formed by last current element with its previous element\n\t\t\t//if current element =\'0\' then previous \'0\' has already formed some subsequences with its previous element\n v[i] = expected - v[index[s[i - 1]] - 1];\n }\n else //first apprearance\n {\n v[i] = expected;\n\n\t\t\t//if its first zero then remove that zero to avoid further subsequences starting with 0\n if(s[i-1]==\'0\'){\n v[i]--;\n \n firstZero =i-1;\n }\n }\n\n index[s[i - 1]] = i;\n\n }\n \n while(v[s.size()]<0){\n v[s.size()]+=mod;\n }\n\t\n\t//if a zero is present then add that first zero to final answer \n\t//also remove empty subsequence from answer\n return (firstZero!=-1) ? (v[s.size()])%mod : (v[s.size()-1] ) %mod ;\n}\n \n};\n```
| 2 | 0 |
['Dynamic Programming', 'C']
| 0 |
number-of-unique-good-subsequences
|
C++ Dp solution
|
c-dp-solution-by-uttu_dce-hh6r
|
\nclass Solution {\npublic:\n int mod = 1e9 + 7;\n #define ll long long\n int numberOfUniqueGoodSubsequences(string binary) {\n int len = binary
|
uttu_dce
|
NORMAL
|
2022-02-26T06:22:16.972527+00:00
|
2022-02-26T06:22:16.972571+00:00
| 229 | false |
```\nclass Solution {\npublic:\n int mod = 1e9 + 7;\n #define ll long long\n int numberOfUniqueGoodSubsequences(string binary) {\n int len = binary.length();\n vector<ll> dp(len + 1);\n ll ans = 0;\n \n int last_occ_1 = 0;\n int last_occ_0 = 0;\n \n int i = 0;\n while(binary[i] == \'0\') i++;\n \n i = max(i, 1);\n for(i; i <= len; i++) {\n dp[i] = (2*dp[i - 1]) % mod;\n \n if(binary[i - 1] == \'0\') {\n if(last_occ_0) dp[i]-=dp[last_occ_0 - 1];\n \n last_occ_0 = i;\n } else {\n if(last_occ_1) dp[i]-=dp[last_occ_1- 1];\n else dp[i] = (dp[i] % mod + 1) % mod;\n \n last_occ_1 = i;\n }\n if(dp[i] < 0) dp[i]+=mod;\n }\n \n for(char c : binary) {\n if(c == \'0\') {\n dp[len]++;\n break;\n }\n }\n \n return dp[len];\n }\n};\n```
| 2 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
C++ dynamic programming with state compression 19ms
|
c-dynamic-programming-with-state-compres-nn0d
|
\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n long endswith[2] = {}, mod = 1e9+7;\n \n bool haszer
|
alexunxus
|
NORMAL
|
2022-01-11T08:16:47.514860+00:00
|
2022-01-11T08:16:47.514904+00:00
| 303 | false |
```\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n long endswith[2] = {}, mod = 1e9+7;\n \n bool haszero = false;\n for (char& c: binary) {\n haszero |= (c == \'0\');\n endswith[c-\'0\'] = (endswith[0] + endswith[1] + (c == \'0\'?0L:1L)) % mod;\n }\n return (endswith[0] + endswith[1]) % mod + haszero;\n }\n};\n```
| 2 | 0 |
['Dynamic Programming', 'C']
| 1 |
number-of-unique-good-subsequences
|
C++ DP Solution O(N) Space & O(1) Solutions
|
c-dp-solution-on-space-o1-solutions-by-l-pmcc
|
```\n*O(N) Space \nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n int N = binary.length();\n const int MOD =
|
level7
|
NORMAL
|
2021-12-07T04:53:31.796148+00:00
|
2021-12-07T05:00:00.207340+00:00
| 173 | false |
```\n*****O(N) Space ****\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n int N = binary.length();\n const int MOD = 1e9 + 7;\n vector<int> dp(N+1, 0);\n vector<int> last(2, -1);\n \n dp[0] = 1;\n for(int i = 0; i < N; i++){\n int x = binary[i] - \'0\';\n dp[i+1] = dp[i] * 2 %MOD;\n \n if(last[x] >= 0){\n dp[i+1] = dp[i+1] - dp[last[x]];\n }\n else if(x == 0){\n dp[i+1] -= 1;\n }\n dp[i+1] = dp[i+1] >= 0 ? dp[i+1]%MOD : dp[i+1]+MOD;\n last[x] = i;\n }\n \n dp[N]--;\n \n if(last[0] >= 0){\n dp[N]++;\n }\n \n return dp[N];\n }\n};\n\n*******O(1) Space********\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n int N = binary.length();\n const int MOD = 1e9 + 7;\n vector<int> last(2, -1);\n \n int prev = 1;\n int curr = 0;\n for(int i = 0; i < N; i++){\n int x = binary[i] - \'0\';\n curr = prev * 2 %MOD;\n \n if(last[x] >= 0){\n curr = curr - last[x];\n }\n else if(x == 0){\n curr -= 1;\n }\n curr = curr >= 0 ? curr%MOD : curr+MOD;\n last[x] = prev;\n prev = curr;\n }\n \n curr--;\n \n if(last[0] >= 0){\n curr++;\n }\n \n return curr;\n }\n};
| 2 | 0 |
['C']
| 0 |
number-of-unique-good-subsequences
|
Python O(n) Runtime O(1) Space DP Solution with Explanation
|
python-on-runtime-o1-space-dp-solution-w-evxs
|
\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n # Go through right to left, consider index i in binary\n #
|
zlax
|
NORMAL
|
2021-11-12T08:18:45.560016+00:00
|
2021-11-12T08:18:45.560049+00:00
| 193 | false |
```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n # Go through right to left, consider index i in binary\n # Maintain sequences that end with 0 or 1\n # if val at index i is 0, the new endZero at i is prev endZero + endOne.\n # Can\'t make new sequence with this 0\n # if val at index i is 1, the new endOne at i is prev endZero + endOne + 1 \n # Can start new sequence here as well\n \n endZero, endOne = 0, 0\n hasOne = False\n \n for val in binary:\n if val == \'0\':\n hasOne = True\n endZero = endZero + endOne\n else:\n endOne = endZero + endOne + 1\n \n return (endZero + endOne + hasOne) % (10**9+7)\n```
| 2 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
Simple Solution with DP
|
simple-solution-with-dp-by-aleeg0-lj7f
|
Approach
Create an array in which we will store the number of combinations for the ith element
We find the first element case value is 1, because we don't care
|
Aleeg0
|
NORMAL
|
2025-01-11T11:35:35.718818+00:00
|
2025-01-11T11:35:35.718818+00:00
| 49 | false |
# Approach
1. Create an array in which we will store the number of combinations for the ith element
2. We find the first element case value is 1, because we don't care about the leading zeros (from the condition)
3. The number of combinations of the current element is equal to the number of combinations of the previous element multiplied by <b>2</b>. In code <b><i> 2 * combination[i - 1].</i></b>
<b>Important</b>: This number of combinations includes duplicates.
4. Delete the duplicate for the current number of combinations: the number of duplicates is equal to the number of combinations of the element before the element which have the same value.
<b>For example</b>
if the current element is 1, then the number of duplicates is equal to the number of combinations the element had before the previous 1.
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(N)
# Code
```csharp []
public class Solution {
public int NumberOfUniqueGoodSubsequences(string binary)
{
const long MOD = 1000000007L;
int n = binary.Length;
long[] combinations = new long[n];
int i = 0, j = 0;
while (i < n && binary[i] == '0')
++i;
if (i == n)
return 1;
int last1 = i,
last0 = i > 0 ? i -1 : 0;
combinations[i++] = 1;
for (;i < n; ++i)
{
if (binary[i] == '0')
{
j = last0;
last0 = i;
}
else
{
j = last1;
last1 = i;
}
long dup = j > 0 ? combinations[j - 1] : 0;
combinations[i] = (2 * combinations[i - 1] % MOD - dup + MOD) % MOD;
}
return (int)((combinations[n - 1] + (binary.IndexOf('0') != -1 ? 1L : 0L)) % MOD);
}
}
```
| 1 | 0 |
['C#']
| 0 |
number-of-unique-good-subsequences
|
Easily Provable bottom-up DP in Python, O(n) Time, O(1) Space (With proper explanation)
|
easily-provable-bottom-up-dp-in-python-o-azny
|
Intuition\nWe let dp[i] be the number of unique subsequences starting with binary[i]\n\nObserve that there are 3 disjoint types of subsequences starting with bi
|
BrandonTang89
|
NORMAL
|
2024-07-01T12:58:42.468879+00:00
|
2024-07-01T12:58:42.468910+00:00
| 128 | false |
# Intuition\nWe let `dp[i]` be the number of unique subsequences starting with `binary[i]`\n\nObserve that there are 3 disjoint types of subsequences starting with `binary[i]`\n- The singleton sequence `binary[i]`: type 1\n- Sequences that start with `binary[i]`, with second character `0`: type 2\n- Sequences that stat with `binary[i]`, with second character `1`: type 3\n\nWe let \n- `nZero[i]` be the index of the smallest `j > i` such that `binary[j] = 0`\n- `nOne[i]` be the index of the smallest `j > i` such that `binary[j] = 1`\n\nObserve that\n- The number of type 1 subsequences is always 1\n- The number of type 2 subsequences is `dp[nZero[i]]`\n - This is because if the second character is 0, we can greedily assume that this 0 comes from the **first** 0 on the right of `binary[i]`\n - Consider any constructible subsequence with `binary[i]` as the first digit and a 0 as the second digit. If this 0 came from `binary[k]` where `k > nZero[i]`, we could also construct this same subsequence by keeping the same digits selected but taking `binary[nZero[i]` rather than `binary[k]`\n- The number of type 3 subsequences is `dp[nOne[i]]`\n - With symmetric reasoning\n \nSince the 3 types of subsequences are mutually exclusive and mutually exhaustive:\n```dp[i] = 1 + dp[nZero[i]] + dp[nOne[i]]```\n\nThe answer is then `dp[i]` where `i` is the index of the leftmost 1. We also need to add back 1 if there is a 0 in the array. \n\n# Approach\nThis problem is suitable to be dealt with in a bottom-up manner since if we deal with the list from right to left, we can compute `nZero[i]` and `nOne[i]` on the fly and avoid having to store those arrays separately.\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nMOD = int(1e9+7)\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n n = len(binary)\n nZero = None\n nOne = None\n\n dp = [0 for _ in range(n)]\n for i in range(n-1, -1, -1):\n dp[i] = 1 + (0 if not nZero else a[nZero]) + (0 if not nOne else a[nOne])\n dp[i] %= MOD\n\n if binary[i] == \'0\': nZero = i\n else: nOne = i\n \n ans = 0\n if nOne is not None: ans = dp[nOne] # most significant one\n if nZero is not None: ans += 1\n return ans\n```
| 1 | 0 |
['Dynamic Programming', 'Python3']
| 1 |
number-of-unique-good-subsequences
|
Java | Tabulation | Explained
|
java-tabulation-explained-by-prashant404-fl0q
|
Method 1 \n Every character generates 2x subsequences generated till its previous character because you can either include or exclude this char\n To avoid dupli
|
prashant404
|
NORMAL
|
2023-12-13T14:16:24.742190+00:00
|
2023-12-13T14:16:24.742208+00:00
| 68 | false |
**Method 1** \n* Every character generates 2x subsequences generated till its previous character because you can either include or exclude this char\n* To avoid duplicates, remove the subsequences generated till the char before the previous occurrence of this char because all those subsequences will be generated again by the repeated occurrence of the char\n>T/S: O(n)/O(n), where n = size(s)\n```\nprivate static final int MOD = (int) (1e9 + 7);\n\npublic int distinctSubseqII(String s) {\n\tvar n = s.length();\n\tvar dp = new int[n + 1];\n\tvar lastIndex = new HashMap<Character, Integer>();\n\tdp[0] = 1;\n\n\tfor (var i = 1; i <= n; i++) {\n\t\tvar ch = s.charAt(i - 1);\n\t\tdp[i] = 2 * dp[i - 1] % MOD;\n\n\t\tif (lastIndex.containsKey(ch))\n\t\t\tdp[i] = (dp[i] - dp[lastIndex.get(ch) - 1]) % MOD;\n\n\t\tlastIndex.put(ch, i);\n\t}\n\n\n\tif (--dp[n] < 0)\n\t\tdp[n] += MOD;\n\n\treturn dp[n] % MOD;\n}\n```\n\n**Method 2** \n>T/S: O(n)/O(1)\n```\npublic int distinctSubseqII(String s) {\n\tvar subsEndingAtChar = new HashMap<Character, Integer>(); \n\tvar totalSubs = 1; //Empty string, starting at count 1\n\n\tfor (var i = 0; i < s.length(); i++) {\n\t\tvar ch = s.charAt(i);\n\t\tvar subsEndingHere = 2 * totalSubs - subsEndingAtChar.getOrDefault(ch, 0); \n\t\tsubsEndingAtChar.put(ch, totalSubs);\n\n\t\tif (subsEndingHere < 0)\n\t\t\ttotalSubs = subsEndingHere + MOD;\n\t\telse\n\t\t\ttotalSubs = subsEndingHere % MOD;\n\t}\n\n\tif (--totalSubs < 0)\n\t\ttotalSubs += MOD;\n\n\treturn totalSubs;\n}\n```\n***Please upvote if this helps***
| 1 | 0 |
['Java']
| 0 |
number-of-unique-good-subsequences
|
Generic Solution for DP, can be extended to k different characters.
|
generic-solution-for-dp-can-be-extended-irrep
|
\nclass Solution {\n int mod = (int)1e9 + 7;\n public int numberOfUniqueGoodSubsequences(String binary) {\n int n = binary.length();\n int [
|
namandeept
|
NORMAL
|
2023-09-21T01:46:38.101239+00:00
|
2023-09-21T01:46:38.101262+00:00
| 113 | false |
```\nclass Solution {\n int mod = (int)1e9 + 7;\n public int numberOfUniqueGoodSubsequences(String binary) {\n int n = binary.length();\n int []dp = new int[n + 1];\n\n dp[0] = 1;\n boolean []foundZero = new boolean[n];\n int []last = new int[2];\n Arrays.fill(last, -1);\n Arrays.fill(foundZero, true);\n \n for(int i=0; i<n; i++) {\n if(binary.charAt(i) != \'0\') foundZero[i] = false;\n else break;\n }\n \n for(int i=1; i<=n; i++) {\n int val = binary.charAt(i - 1) - \'0\';\n dp[i] = dp[i-1] * 2 % mod;\n if(val == 0) {\n if(last[0] != -1) {\n dp[i] -= dp[last[0]];\n dp[i]--;\n if(last[0] > 0 && foundZero[last[0] - 1]) {\n dp[i]++;\n }\n }\n }\n else {\n if(i>=2 && foundZero[i-2]) dp[i]--; \n if(last[1] != -1) {\n dp[i] -= dp[last[1]];\n if(last[1] > 0 && foundZero[last[1] - 1]) {\n dp[i] += 1;\n }\n }\n }\n dp[i] %= mod;\n last[val] = (i - 1);\n }\n dp[n]--;\n if(dp[n] < 0) dp[n] += mod;\n return dp[n]; \n }\n}\n```
| 1 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
0(n) Dynamic Programming solution
|
0n-dynamic-programming-solution-by-aryan-g3dz
|
\n\n# Complexity\n- Time complexity:\n0(n)\n- Space complexity:\n0(n)\n# Code\n\nconst int mod = 1e9 + 7;\nint norm(int x) {\n if (x < 0) {\n x += mod
|
ARYAN-PRAKASH
|
NORMAL
|
2023-06-16T08:46:13.755255+00:00
|
2023-06-16T08:46:28.437509+00:00
| 126 | false |
\n\n# Complexity\n- Time complexity:\n0(n)\n- Space complexity:\n0(n)\n# Code\n```\nconst int mod = 1e9 + 7;\nint norm(int x) {\n if (x < 0) {\n x += mod;\n }\n if (x >= mod) {\n x -= mod;\n }\n return x;\n}\ntemplate<class T>\nT power(T a, int b) {\n T res = 1;\n for (; b; b /= 2, a *= a) {\n if (b % 2) {\n res *= a;\n }\n }\n return res;\n}\n\n\nstruct Mint {\n int x;\n Mint(int val = 0) {\n this->x = norm(val);\n }\n int val() const {\n return x;\n }\n // operator overloading \n Mint operator-() const {\n return Mint(norm(mod - x));\n }\n \n Mint &operator*=(const Mint &rhs) {\n x = (x * 1LL * rhs.x) % mod;\n return *this;\n }\n Mint &operator+=(const Mint &rhs) {\n x = norm(x + rhs.x);\n return *this;\n }\n Mint &operator-=(const Mint &rhs) {\n x = norm(x - rhs.x);\n return *this;\n }\n Mint &operator/=(const Mint &rhs) {\n return *this *= rhs.inv();\n }\n friend Mint operator*(const Mint &lhs, const Mint &rhs) {\n Mint res = lhs;\n res *= rhs;\n return res;\n }\n friend Mint operator+(const Mint &lhs, const Mint &rhs) {\n Mint res = lhs;\n res += rhs;\n return res;\n }\n friend Mint operator-(const Mint &lhs, const Mint &rhs) {\n Mint res = lhs;\n res -= rhs;\n return res;\n }\n friend Mint operator/(const Mint &lhs, const Mint &rhs) {\n Mint res = lhs;\n res /= rhs;\n return res;\n }\n \n friend ostream & operator<<(ostream &out, const Mint &c){\n out<<c.x;\n return out;\n }\n\n // important functions\n Mint inv() const {\n assert(x != 0);\n return power(*this, mod - 2);\n }\n \n\n \n\n};\n\nvector<Mint> fact;\nvector<Mint> inv_fact;\n \nvoid gen_fact(int n){\n assert(n >= 1);\n \n fact.resize(n + 1);\n inv_fact.resize(n + 1);\n fact[0] = 1;\n fact[1] = 1;\n\n for(int i = 2;i<=n;i++){\n fact[i] = fact[i - 1] * i;\n inv_fact[i] = fact[i].inv();\n }\n\n}\n\nMint C(int n,int r){\n if(r > n) return 0;\n assert((int) fact.size() > n);\n return fact[n] * Mint(fact[r] * fact[n - r]).inv();\n}\n\nMint P(int n,int r){\n return C(n,r) * fact[r];\n} \n\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string s) {\n int n = (int) s.size();\n \n\n vector<int> pos(2,-1);\n vector<Mint> dp(n + 2);\n for(int i = n - 1;i>=0;i--){\n dp[i] = dp[i + 1] * 2;\n if(pos[s[i] - \'0\'] == -1){\n dp[i] += 1;\n }else{\n dp[i] -= dp[pos[s[i]-\'0\']];\n }\n pos[s[i] - \'0\'] = i + 1;\n }\n\n for(int i = 0;i<n;i++){\n if(s[i] == \'0\'){\n dp[0] -= dp[i + 1];\n break;\n }\n } \n return dp[0].x;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C++']
| 1 |
number-of-unique-good-subsequences
|
[Python] Dynamic Programming with thought process when being asked during interviews
|
python-dynamic-programming-with-thought-pefzf
|
Dynamic Programming\nOnce you see the answer might be very large, 99% of possibility resolving this promble is to use dynamic programming.\nLet\'s simplify the
|
jandk
|
NORMAL
|
2022-11-05T19:37:52.753360+00:00
|
2022-11-05T19:37:52.753406+00:00
| 123 | false |
### Dynamic Programming\nOnce you see the answer might be very large, 99% of possibility resolving this promble is to use dynamic programming.\nLet\'s simplify the question first without considering unique requirement, how to find out the number of good subsequences at index `i` given the number of good subsequences at index `i - 1`. \nWe know that `1` can construct new good subsequences, while `0` doesn\'t. So if index `i` is `1` then the `dp[i] = dp[i - 1] * 2 + 1`. Why? because we can append `1` to each of good subsequence we got from `dp[i - 1]`, as well as the single `1` at index `i`. \n\nOtherwise `dp[i] = dp[i - 1] * 2` for `0` since leading `0` is invalid for good subsequences.\nThen the next step is the difficult part, how about adding unique back?\nNow we have the total number of good subsequences with duplicates, in order to get the unique, we have to remove the duplicate, literally `dp[i] = dp[i] - dup`.\nSo now the problem changes to be how many duplicate subsequences we add by appending `1` or `0`?\nWe can assume there is no dup in `dp[i -1]` and so we can only care about the dup introduced by appending index `i`. Let\'s simpilfy the problem first by considering `1` only since `0` followes the same idea. \nThe intuitive thought is that in order to have dup, the `1` at index `i` can replace the last seen `1` at index `k`. There must be subsequences including `1` at index `k`, and those without index `k`. \nNow we append `1` after those without index `k` as if we didn\'t pick the `1` at index `k` but picked `1` at index `i` instead.\nfor example, `1011` and we are looking at the last `1`, where we have subsequences\n```\n1\n10\n101\n11\n```\nwith `1` and `10` being without the `1` at index 2.\nThen we append `1` at index 3, then `10 + 1= 101, 1 + 1 = 11` which are equal to append `1` at index 2 to `1` and `10`, the number of good subsequences added by appending index 2. \nalright, then what about the last single `1` introduced by index 3? it\'s equals to consider the `1` at index 0. \nFinally, it turns out to be the number of dup is equal to the sum of number of subsequences added by appending each `1` appeared before index `i`.\nSo the transition is \n```\ndp[i] = dp[i] * 2 + 1 - sum(diff[...i] for k in nums if k == 1) when nums[i] == 1\ndp[i] = dp[i] * 2 - sum(diff[...i] for k in nums if k== 0) when nums[i] == 0\n```\n\n```python\ndef numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n\tzero_diff = one_diff = count = 0\n\tfor c in binary:\n\t\tprev, count = count, count * 2\n\t\tif c == \'1\':\n\t\t\tcount += 1 - one_diff\n\t\t\tone_diff += count - prev\n\t\telse: \n\t\t\tcount -= zero_diff\n\t\t\tzero_diff += count - prev\n\t\tcount %= 10 ** 9 + 7 \n\treturn count + int(\'0\' in binary)\n```\n\n*Time Complexity*= **O(N)**\n*Space Complexity*= **O(1)**\n
| 1 | 0 |
['Dynamic Programming', 'Python']
| 0 |
number-of-unique-good-subsequences
|
C++ || dp || Explained solution
|
c-dp-explained-solution-by-rajdeep_nagar-17bx
|
```\n\n/\n\nwe starting with "0" then stop, only one subsequence\n\notherwise on each position we have two choices , either take it or not take it\n\n\nBut how
|
Rajdeep_Nagar
|
NORMAL
|
2022-09-08T11:17:12.094783+00:00
|
2022-09-08T11:17:12.094818+00:00
| 379 | false |
```\n\n/*\n\nwe starting with "0" then stop, only one subsequence\n\notherwise on each position we have two choices , either take it or not take it\n\n\nBut how to avoid duplicates ?\n\n\ndp[i][j]= no of distincnt subsequences starting with (i=0/1) and ends with (j=0/1) or look likes [i...j]\n\nans= dp[0][0]+dp[0][1]+dp[1][0]+dp[1][1]\n\nif s[i]==\'0\'\n\nthen we stick this \'0\' to all subsequences of type [1....0] and [1...1]\n\nso dp[1][0] increases to dp[1][0]+dp[1][1]\n\nalso we can make one subsequence of type "0" (dp[0][0])\n\nso we make dp[0][0]=1\n\n\n(NOTE subsequence of type [0...1] is not valid)\n\nif s[i]==\'1\'\n\nthen we stick this \'1\' to all subsequences of type [1...0] and [1....1] , also we\n\ncan get one new subsequence that is "1"\n\nso dp[1][1] increases to dp[1][0]+dp[1][1]+1\n\n\nans= dp[0][0]+dp[0][1]+dp[1][0]+dp[1][1]\n\n\n*/\n\nint mod=1e9+7;\n\nint dp[2][2];\n\nclass Solution {\npublic:\n int n;\n int numberOfUniqueGoodSubsequences(string binary) {\n \n memset(dp,0,sizeof(dp));\n \n n=binary.size();\n \n for(char ch:binary){\n \n if(ch==\'0\'){\n dp[0][0]=1;\n dp[1][0]=dp[1][0]+dp[1][1];\n dp[1][0]%=mod;\n }\n else{\n dp[1][1]=dp[1][0]+dp[1][1]+1;\n dp[1][1]%=mod;\n }\n }\n \n return (dp[0][0]+dp[0][1]+dp[1][0]+dp[1][1])%mod;\n\n \n }\n};
| 1 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
1987 python
|
1987-python-by-akhil_krish_na-u4jn
|
\tclass Solution:\n\t\tdef numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n\t\t\tans = 1\n\t\t\tif "0" in binary:\n\t\t\t\tans += 1\n\t\t\tmod = int(
|
Akhil_krish_na
|
NORMAL
|
2022-09-08T09:12:52.939250+00:00
|
2022-09-08T09:12:52.939301+00:00
| 272 | false |
\tclass Solution:\n\t\tdef numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n\t\t\tans = 1\n\t\t\tif "0" in binary:\n\t\t\t\tans += 1\n\t\t\tmod = int(1e9+7)\n\t\t\tn = len(binary)\n\t\t\ti = 0\n\t\t\twhile i< n and binary[i] == "0":\n\t\t\t\ti+= 1\n\t\t\tif i == n:\n\t\t\t\treturn 1\n\t\t\tbinary = binary[i:]\n\t\t\ttrie = [1,1]\n\n\t\t\tfor i,v in enumerate(binary[1:]):\n\t\t\t\tval = int(v)\n\t\t\t\tif val == 0:\n\t\t\t\t\ttrie[1] += trie[0]\n\t\t\t\t\ttrie[1] %= mod\n\t\t\t\telse:\n\t\t\t\t\ttrie[0] += trie[1]\n\t\t\t\t\ttrie[0] %= mod\n\n\t\t\t\tans += trie[val]%mod\n\t\t\treturn ans%mod\n\n
| 1 | 0 |
['Dynamic Programming', 'Python']
| 0 |
number-of-unique-good-subsequences
|
✅✅Faster || Easy To Understand || C++ Code
|
faster-easy-to-understand-c-code-by-__kr-yfg7
|
Using Dp\n\n Time Complexity :- O(N)\n\n Space Complexity :- O(1)\n\n\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n
|
__KR_SHANU_IITG
|
NORMAL
|
2022-07-21T04:42:32.999786+00:00
|
2022-07-21T04:42:32.999834+00:00
| 544 | false |
* ***Using Dp***\n\n* ***Time Complexity :- O(N)***\n\n* ***Space Complexity :- O(1)***\n\n```\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n \n int n = binary.size();\n \n long long mod = 1e9 + 7;\n \n // dp[i][j] will tell us no. of subsequence starting with i and ending with j\n \n // dp[0][1] will be always 0, because "01" is invalid\n \n vector<vector<int>> dp(2, vector<int> (2, 0));\n \n for(int i = 0; i < n; i++)\n {\n if(binary[i] == \'0\')\n {\n // no. of subsequence starting with 0 and ending with 0 i.e "0"\n \n dp[0][0] = 1;\n \n // no. of subsequence starting with 1 and ending with 0\n \n dp[1][0] = (dp[1][0] % mod + dp[1][1] % mod) % mod;\n }\n else\n {\n // no. of subsequence starting with 1 and ending with 1\n \n dp[1][1] = (dp[1][0] % mod + dp[1][1] % mod + 1 % mod) % mod;\n }\n }\n \n return (dp[0][0] % mod + dp[1][0] % mod + dp[1][1] % mod) % mod;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C', 'C++']
| 0 |
number-of-unique-good-subsequences
|
DP O(N) time, O(1) space
|
dp-on-time-o1-space-by-diyora13-8xun
|
\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string s) \n {\n int n=s.length(),i=0,mod=1e9+7;\n int ans=1,one=0,zero=-1,
|
diyora13
|
NORMAL
|
2022-05-23T07:05:23.132059+00:00
|
2022-05-23T07:05:23.132087+00:00
| 300 | false |
```\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string s) \n {\n int n=s.length(),i=0,mod=1e9+7;\n int ans=1,one=0,zero=-1,z=0;\n \n while(i<n && s[i]==\'0\') i++,z=1;\n if(i==n) return z;\n \n i++;\n while(i<n)\n {\n int lst=ans;\n ans=(ans*2)%mod;\n \n if(s[i]==\'0\' && zero!=-1) ans=(ans-zero+mod)%mod;\n else if(s[i]==\'1\' && one!=-1) ans=(ans-one+mod)%mod;\n \n if(s[i]==\'1\') one=lst;\n else zero=lst,z=1;\n \n i++;\n }\n return (ans+z)%mod;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C', 'C++']
| 0 |
number-of-unique-good-subsequences
|
[C++] Explained O(n) time, O(1) space DP
|
c-explained-on-time-o1-space-dp-by-tinfu-s0oi
|
Lets use 2 set to represent strings that are awaiting 1 and 0 to create a sub sequence respectively, let\'s call them exp1 and exp0. We also define a variable t
|
tinfu330
|
NORMAL
|
2022-02-17T22:25:06.934008+00:00
|
2022-02-18T04:07:32.939378+00:00
| 369 | false |
Lets use 2 set to represent strings that are awaiting 1 and 0 to create a sub sequence respectively, let\'s call them exp1 and exp0. We also define a variable to check if there is a zero in string as a special case handle, hence the variable (bool) hasZero. Let\'s run through an example "101":\n\nAt the beginning, we are expecting 1 to get our first sub sequence, thus:\nexp0: []\nexp1: [""]\nhasZero = false\nresult: []\n\nat i = 0, the character is \'1\', we add it to the expected 1 set, the incoming 1 has created unique subsequence equal to the size of exp1, so res += exp1.size(), and the new 1 will also be expecting a 0 to form a new subsequence:\nexp0: ["1"]\nexp1: ["1"]\nhasZero = false\nresult: ["1"]\n\nat i = 1, we repeat the previous logic, but use exp0 to replace exp1\nexp0: ["10"]\nexp1: ["1","10"]\nhasZero = true\nres = ["1", "10"]\n\nat i = 2:\nexp0: ["10","11","101"]\nexp1: ["11", "101"]\nhasZero = true;\nres = ["1","10","11","101"]\n\nbecause we have a zero as a unique sub-sequence, so add it to res\nres = ["0","1","10","11","101"]\nres.size() = 5\n\nWe can simply use a count as space optimization if you observe the pattern.\n\n```\nclass Solution {\nprivate:\n const int M = 1e9 + 7;\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n int res = 0;\n bool hasZero = false;\n int exp0 = 0;\n int exp1 = 1;\n \n for (char &eachC : binary) {\n if (eachC == \'1\') {\n res = (res + exp1) % M;\n exp0 = (exp0 + exp1) % M;\n } else {\n hasZero = true;\n res = (res + exp0) % M;\n exp1 = (exp1 + exp0) % M;\n }\n }\n if (hasZero) res = (res + 1) % M;\n return res;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C', 'C++']
| 0 |
number-of-unique-good-subsequences
|
C++, reverse, no. of distinct sub sequences ending at 1
|
c-reverse-no-of-distinct-sub-sequences-e-c693
|
\n\nint numberOfUniqueGoodSubsequences(string binary) {\n unsigned long long dp[2] = {0};\n reverse(binary.begin(), binary.end());\n bool z
|
shubhamchandra01
|
NORMAL
|
2022-01-12T19:02:33.177314+00:00
|
2022-01-12T19:02:33.177362+00:00
| 196 | false |
```\n\nint numberOfUniqueGoodSubsequences(string binary) {\n unsigned long long dp[2] = {0};\n reverse(binary.begin(), binary.end());\n bool zero = false;\n const long long mod = 1e9 + 7;\n for (char &c: binary) {\n dp[c - \'0\'] = dp[0] + dp[1] + 1LL;\n dp[c - \'0\'] %= mod;\n zero = zero || c == \'0\';\n }\n return (dp[1] + zero) % mod;\n }\n\n\n```
| 1 | 0 |
[]
| 1 |
number-of-unique-good-subsequences
|
C++ || DP || O(N)/O(1) || Simple || Notes
|
c-dp-ono1-simple-notes-by-aholtzman-atb0
|
\n// Check if any Zero\n// Find the first 1, start count after the first 1 (The first 1 will be in all the combination other than "0")\n// for every digit multi
|
aholtzman
|
NORMAL
|
2021-12-13T21:52:43.300911+00:00
|
2021-12-14T15:30:57.002588+00:00
| 202 | false |
```\n// Check if any Zero\n// Find the first 1, start count after the first 1 (The first 1 will be in all the combination other than "0")\n// for every digit multiple the number - duplications\n// Duplication - In the case where we remove all the character between identical characters\n// The remove of either produce identical string.\n// Example: "1010---0" => "101----0" identical to "1010----"\n// In this case we have to dedact the count of "1010" (the combinations of "101")\n// add 1 if any 0 for the single "0" case\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n int n = binary.length();\n bool any_zero = (binary.find(\'0\') < n); \n long long count = 0;\n int zeros = 0;\n int ones = 0;\n int i = 0;\n\t\t// Search the first \'1\' - The first \'1\' will be part of all the combination other than single \'0\'\n for (; i<n; i++)\n {\n if (binary[i] == \'1\')\n {\n\t\t\t // count the first \'1\'\n count++;\n i++; \n break;\n }\n }\n // After the first \'1\' treat \'1\' and \'0\' the same way\n for (; i<n; i++)\n {\n char c = binary[i];\n int prev = count;\n if (c == \'0\')\n {\n count = (count*2-zeros) %1000000007;\n zeros = prev;\n }\n else\n {\n count = (count*2-ones) %1000000007;\n ones = prev;\n }\n if (count < 0) count += 1000000007;\n }\n\t\t// add the case of single \'0\'\n if (any_zero)\n count = (count+1) %1000000007;\n\n return count;\n \n }\n};\n```
| 1 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
Nice DP approach in C++
|
nice-dp-approach-in-c-by-trishanku_sarma-00hl
|
class Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n \n int n = binary.length();\n \n long long MOD
|
TRISHANKU_SARMA
|
NORMAL
|
2021-09-25T11:06:58.295989+00:00
|
2021-09-25T11:06:58.296032+00:00
| 333 | false |
class Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n \n int n = binary.length();\n \n long long MOD = 1000000007;\n \n vector< long long > DP( n+1 , 1);\n \n bool leadingZeroes = true;\n bool hasZero = false;\n \n vector< long long >count( 2, 0 );\n \n for( int i = 1 ; i<=n ; i++ ){\n\n long long repeat = count[ binary[i-1] == \'0\' ? 0 : 1 ]; \n \n if(binary[ i-1 ] == \'0\' ){\n hasZero = true;\n repeat ++; \n }\n \n if( leadingZeroes && binary[ i-1 ] == \'0\' ) continue;\n \n if( leadingZeroes && binary[ i-1 ] == \'1\' )\n leadingZeroes = false;\n \n DP[ i ] = ( DP[ i-1 ] * 2 - repeat )%MOD;\n \n if( DP[i] < 0 )\n DP[ i ] += MOD;\n \n count[ binary[i-1] == \'0\' ? 0 : 1 ] += DP[i] - DP[i-1]; \n }\n \n return ( hasZero ? DP[n] : DP[n]-1 )%MOD; \n }\n};\n\n// minus parts ::\n\n// a) no leading zeroes except 0\n// b) unique subsequences\n\n// * 0 0 1 1 0 1 0 1 \n// 1 2 4\n\n// 0 -> 1\n// 1 ->
| 1 | 1 |
[]
| 1 |
number-of-unique-good-subsequences
|
Without DP - Every 0/1 after first 1's doubles total count - Easy to understand
|
without-dp-every-01-after-first-1s-doubl-z4bd
|
If you want to understand another solution this is also very interesting\nhttps://stackoverflow.com/questions/46608552/unique-subsequences-for-a-binary-array\nO
|
amitnsky
|
NORMAL
|
2021-08-30T17:46:06.951533+00:00
|
2021-08-30T17:46:06.951584+00:00
| 268 | false |
If you want to understand another solution this is also very interesting\nhttps://stackoverflow.com/questions/46608552/unique-subsequences-for-a-binary-array\nOriginal paper: https://doi.org/10.1016/j.tcs.2008.08.035 (Read only these two topics: Preliminaries and Counting distinct subsequence)\n\nAlthough none of the codes mentioned there will work, because 1. Code is not correct 2. It is not very specialised to this prblm.\n\nBased on the ideas mentioned there I have implemented my own solution:\n\nSpace `O(1)`\nTime `O(n)`\n\n```c++\n#define MOD 1000000007\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string s) {\n int count = 1, n = s.size(), k=0, zero=0;\n map<char,int> seen;\n \n while(k<n && s[k]==\'0\') k++;\n if(k==n) return 1;\n for(int i=k+1; i<n; i++){\n int temp = count;\n char ch=s[i];\n count = (count*2)%MOD;\n if(seen[ch])\n count -= seen[ch];\n seen[ch] = temp%MOD;\n if(count<0) count += MOD;\n }\n zero = s.find("0")!=string::npos;\n return (count+zero)%MOD;\n }\n};\n```\n\nThanks @lee215\nI was missing few edge cases which I got from your solution.\n\nWill share a detailed explanation of this solution soon.\n\nUpvote if it helped you.
| 1 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
JavaScript Solution
|
javascript-solution-by-stevenkinouye-xks7
|
javascript\nconst MOD = 1000000007;\n\nvar numberOfUniqueGoodSubsequences = function(binary) {\n let endsZero = 0;\n let endsOne = 0;\n let hasZero = 0
|
stevenkinouye
|
NORMAL
|
2021-08-29T21:52:48.354001+00:00
|
2021-08-29T21:52:48.354058+00:00
| 170 | false |
```javascript\nconst MOD = 1000000007;\n\nvar numberOfUniqueGoodSubsequences = function(binary) {\n let endsZero = 0;\n let endsOne = 0;\n let hasZero = 0;\n for (let i = 0; i < binary.length; i++) {\n if (binary[i] === \'1\') {\n endsOne = (endsZero + endsOne + 1) % MOD;\n } else {\n endsZero = (endsZero + endsOne) % MOD;\n hasZero = 1;\n }\n }\n return (endsZero + endsOne + hasZero) % MOD;\n};\n```
| 1 | 0 |
['JavaScript']
| 1 |
number-of-unique-good-subsequences
|
[Python3] bit-mask dp
|
python3-bit-mask-dp-by-ye15-vdj1
|
Please see this commit for solutions of weekly 256.\n\n\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n \n @
|
ye15
|
NORMAL
|
2021-08-29T17:18:18.659167+00:00
|
2021-08-30T04:23:03.618765+00:00
| 275 | false |
Please see this [commit](https://github.com/gaosanyong/leetcode/commit/7abfd85d1a68e375fcc0be60558909fd98b270f3) for solutions of weekly 256.\n\n```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n \n @cache\n def fn(i, mask, v): \n """Return # unique good subsequences starting with 1."""\n if i == len(binary) or not mask: return v\n x = int(binary[i])\n if not mask & (1<<x): return fn(i+1, mask, v)\n return (fn(i+1, 3, 1) + fn(i+1, mask^(1<<x), v)) % 1_000_000_007\n \n return fn(0, 2, 0) + int("0" in binary)\n```\n\nA shorter dp \n```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n f0 = f1 = 0\n for ch in binary: \n if ch == "0": f0 += f1\n else: f1 += f0 + 1\n return (f0 + f1 + int("0" in binary)) % 1_000_000_007\n```
| 1 | 0 |
['Python3']
| 1 |
number-of-unique-good-subsequences
|
[Kotlin] O(n) Time and O(1) Space Solution
|
kotlin-on-time-and-o1-space-solution-by-3j7sw
|
\nclass Solution {\n fun numberOfUniqueGoodSubsequences(binary: String): Int {\n val mod = 1000000007L\n var res = 0L\n val positions =
|
catcatcute
|
NORMAL
|
2021-08-29T07:08:14.907689+00:00
|
2021-08-29T07:08:14.907736+00:00
| 112 | false |
```\nclass Solution {\n fun numberOfUniqueGoodSubsequences(binary: String): Int {\n val mod = 1000000007L\n var res = 0L\n val positions = arrayOf(0L, 1L)\n binary.forEach {\n val bit = it - \'0\'\n val other = (bit + 1) % 2\n res = (res + positions[bit]) % mod\n positions[other] = (positions[other] + positions[bit]) % mod\n }\n if (binary.contains(\'0\')) {\n ++res\n }\n return res.toInt()\n }\n}\n```
| 1 | 0 |
[]
| 0 |
number-of-unique-good-subsequences
|
5 types of nodes in the imaginery Trie + Visualization
|
5-types-of-nodes-in-the-imaginery-trie-v-pudy
|
If we imagine a binary trie tree, there are 5 types of nodes:\n1) The "0" node, the root node of the "0" tree\n2) A node in the "1" tree that has no left child
|
quadpixels
|
NORMAL
|
2021-08-29T04:05:52.951810+00:00
|
2021-08-29T04:26:21.398834+00:00
| 220 | false |
If we imagine a binary trie tree, there are 5 types of nodes:\n1) The "0" node, the root node of the "0" tree\n2) A node in the "1" tree that has no left child or right child (left child means "0", right child means "1")\n3) A node in the "1" tree that has left child but no right child\n4) A node in the "1" tree that has right child but no left child\n5) A node in the "1" tree that has both children\n\nEvery time if we insert into the trie tree:\n* If we have a "0":\n * we create type 1), and also, \n * 2) becomes 3), \n * 4) becomes 5),\n * 4) is gone\n* If we have a "1", then \n * 2) becomes 4), \n * 3) becomes 5), \n * 3) is gone\n\n\nVisualization:\n\n\n\nCode: (1337C0D3 Supportz Emojis so why not use them \uD83D\uDCAA\uD83D\uDE00\uD83C\uDF1A\uD83D\uDE2C\uD83D\uDE2C\uD83D\uDE2C\uD83D\uDCAA\uD83D\uDCAA\n```\nclass Solution {\npublic:\n int \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(int a, int b) {\n return int((long(a)+long(b)) % 1000000007L);\n }\n int numberOfUniqueGoodSubsequences(string binary) {\n bool has0 = false; // does 0 exist?\n bool has1 = false;\n int n00 = 0; // No left child or right child\n int n10 = 0; // has left child, no right child\n int n01 = 0; // has right child, no left child\n int n11 = 0; // has both children\n \n for (char c : binary) {\n if (c == \'0\') {\n has0 = true;\n }\n \n if (has1) {\n int n00_next = 0, n10_next = 0, n11_next = 0, n01_next = 0;\n if (c == \'0\') {\n n00_next = \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n00, n01);\n n10_next = \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n10, n00);\n n11_next = \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n11, n01);\n n01_next = 0;\n } else {\n n00_next = \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n00, n10);\n n01_next = \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n01, n00);\n n11_next = \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n10, n11);\n n10_next = 0;\n }\n n00 = n00_next; n10 = n10_next; n01 = n01_next; n11 = n11_next;\n }\n \n if (c == \'1\') {\n if (has1 == false) {\n has1 = true;\n n00 = 1;\n }\n }\n \n //printf("%d %d %d %d\\n", n00, n01, n10, n11);\n }\n return \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(int(has0), \n \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n00,\n \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n10,\n \uD83D\uDE00\uD83D\uDE00\uD83D\uDE00(n01, n11)\n )\n )\n );\n }\n};\n```
| 1 | 1 |
['Dynamic Programming', 'Trie']
| 0 |
number-of-unique-good-subsequences
|
Python Hard
|
python-hard-by-lucasschnee-0w0i
| null |
lucasschnee
|
NORMAL
|
2025-02-08T03:02:56.314046+00:00
|
2025-02-08T03:03:15.554814+00:00
| 11 | false |
```
class Solution:
def numberOfUniqueGoodSubsequences(self, binary: str) -> int:
MOD = 10 ** 9 + 7
zeroes = 0
ones = 0
for x in binary:
if x == "0":
zeroes += ones
if x == "1":
ones += zeroes + 1
return (ones + zeroes + int("0" in binary)) % MOD
```
| 0 | 0 |
['Python3']
| 0 |
number-of-unique-good-subsequences
|
1987. Number of Unique Good Subsequences
|
1987-number-of-unique-good-subsequences-7fdro
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-16T13:35:18.739979+00:00
|
2025-01-16T13:35:18.739979+00:00
| 11 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int numberOfUniqueGoodSubsequences(String input) {
int constant = (int) 1e9 + 7;
int zeroEnd = 0;
int oneEnd = 0;
int flagZero = 0;
for (int idx = 0; idx < input.length(); idx++) {
if (input.charAt(idx) == '0') {
zeroEnd = (zeroEnd + oneEnd) % constant;
flagZero = 1;
} else {
oneEnd = (zeroEnd + oneEnd + 1) % constant;
}
}
return (zeroEnd + oneEnd + flagZero) % constant;
}
}
```
| 0 | 0 |
['Java']
| 0 |
number-of-unique-good-subsequences
|
Dynamic programming
|
dynamic-programming-by-yadavanuj109-5q4g
|
IntuitionIdea: Divide the problem into subproblems and save the solution of subproblems in array.Let "ugs" be an array which stores the unique good subseq.at ev
|
yadavanuj109
|
NORMAL
|
2025-01-04T05:32:14.995097+00:00
|
2025-01-04T05:32:14.995097+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Idea: Divide the problem into subproblems and save the solution of subproblems in array.
Let "ugs" be an array which stores the unique good subseq.at every index from right.
That means ugs[i] will have unique good subs. starting with binary[i].
# Approach
<!-- Describe your approach to solving the problem. -->
Subproblem => to calculate ugs[i] we have to compare {binary[i], ugs[i +1] }
Equation
ugs[i] = Summation of u[k] where k = {i + 1, i + 2, ... l} & l must be the first index to match binary[i] == binary[l] or l = n - 1
Proof:
if binary[i] == binary[l] for some l then ..
ugs formed with binary[i] must eq. ugs formed with binary[l]
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n)
# Code
```typescript []
function numberOfUniqueGoodSubsequences(binary: string): number {
const mod7 = Math.pow(10,9) + 7;
const ugs = new Array<number>(binary.length);
let sum = 0;
let i = 0;
while (i < binary.length) {
ugs[i] = 0;
if (binary[i] !== "1") {
sum = 1;
i++;
} else break;
}
if (i === binary.length) return 1;
if (binary[binary.length - 1] !== "1") sum = 1;
let l = binary.length - 1;
const charc = binary[l];
while (l > i) {
if (binary[l] === charc) {
ugs[l] = 1;
l--;
} else {
ugs[l] = binary.length - l;
sum = 1;
l--;
break;
}
}
for (let j = l; j > i; j--) {
if (binary[j] !== "1") sum = 1;
let k = j + 1;
let sb = 0;
while (k < binary.length) {
sb += ugs[k];
sb %= mod7;
if (binary[j] === binary[k]) break;
else k++;
}
ugs[j] = sb;
}
return ugs.reduce((prv, curv) => (prv + curv) % mod7, sum + 1);
};
```
| 0 | 0 |
['TypeScript']
| 0 |
number-of-unique-good-subsequences
|
DP, O(n) TC
|
dp-on-tc-by-filinovsky-47c6
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Filinovsky
|
NORMAL
|
2024-11-07T09:10:12.832619+00:00
|
2024-11-07T09:10:12.832667+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n n = len(binary)\n # tab[i][j] contains the number of unique subsequences of suffix[i:]\n # such that the first letter of subsequence is \'j\'\n tab = [[0, 0] for i in range(n)]\n ans = 0 if \'0\' not in set(binary) else 1\n for i in range(n-1, -1, -1):\n res = 0\n if binary[i] != \'0\':\n res += tab[i+1][0] if i < n-1 else 0\n tab[i][0] = tab[i+1][0] if i < n-1 else 0\n res += 1\n tab[i][1] = (tab[i+1][1] if i < n-1 else 0) + res\n ans += res\n else:\n res += tab[i+1][1] if i < n-1 else 0\n tab[i][1] = tab[i+1][1] if i < n-1 else 0\n res += 1\n tab[i][0] = (tab[i+1][0] if i < n-1 else 0) + res\n return ans % (10**9 + 7)\n```
| 0 | 0 |
['Python3']
| 0 |
number-of-unique-good-subsequences
|
Python (Simple DP)
|
python-simple-dp-by-rnotappl-nogg
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rnotappl
|
NORMAL
|
2024-11-01T16:46:32.704485+00:00
|
2024-11-01T16:46:32.704525+00:00
| 15 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary):\n total, count_zero, count_one, mod = 0, 0, 0, 10**9+7\n\n for i in binary:\n if i == "1":\n count_one += count_zero + 1 \n else:\n count_zero += count_one\n\n return (count_zero + count_one + ("0" in binary))%mod\n```
| 0 | 0 |
['Python3']
| 0 |
number-of-unique-good-subsequences
|
1987. Number of Unique Good Subsequences.cpp
|
1987-number-of-unique-good-subsequencesc-j04h
|
Code\n\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n const int MOD = 1\'000\'000\'007; \n long f0 = 0, f1
|
202021ganesh
|
NORMAL
|
2024-10-23T11:34:01.068707+00:00
|
2024-10-23T11:34:01.068726+00:00
| 1 | false |
**Code**\n```\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n const int MOD = 1\'000\'000\'007; \n long f0 = 0, f1 = 0; \n for (auto& ch : binary) {\n if (ch == \'0\') f0 = (f0 + f1) % MOD; \n else f1 = (f0 + f1 + 1) % MOD; \n }\n return (f0 + f1 + (f0 || binary[0] == \'0\')) % MOD; \n }\n};\n```
| 0 | 0 |
['C']
| 0 |
number-of-unique-good-subsequences
|
C# Dynamic Programming Solution
|
c-dynamic-programming-solution-by-getrid-w8ja
|
Intuition\n- Describe your first thoughts on how to solve this problem. Recognize the Need for Dynamic Counting: The first thought is that this problem involve
|
GetRid
|
NORMAL
|
2024-09-17T18:47:53.493673+00:00
|
2024-09-17T18:47:53.493696+00:00
| 4 | false |
# Intuition\n- <!-- Describe your first thoughts on how to solve this problem. -->Recognize the Need for Dynamic Counting: The first thought is that this problem involves counting subsequences, but with specific restrictions (e.g., no leading zeros except for the subsequence "0"). The natural approach is to break the problem down into subsequences that end in \'0\' and those that end in \'1\', because each binary character can either extend existing subsequences or form new ones.\n\n- Handle Leading Zeros Specially: The condition that subsequences cannot have leading zeros (except for "0" itself) suggests that we need to treat subsequences formed by \'1\'s differently from those formed by \'0\'s. This leads to the idea of separating subsequences ending in \'0\' from those ending in \'1\'.\n\n- Accumulate Results with Dynamic Programming: Every time we encounter a \'1\', it can extend all previously formed subsequences and also start new subsequences. Similarly, a \'0\' extends subsequences but only those that already exist, and we handle the special case of the "0" subsequence separately.\n___\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n// subseqEndingIn1 keeps track of subsequences ending in \'1\'. Every time a \'1\' is encountered, we can \n// create new subsequences by appending it to all existing subsequences and also count \'1\' as a subsequence \n// by itself.\n// subseqEndingIn0 keeps track of subsequences ending in \'0\'. Every time a \'0\' is encountered, it extends\n// subsequences that end with \'1\' or \'0\'.\n// hasZero is a flag used to check if there is at least one \'0\'. If there is, we need to account for the \n// valid subsequence "0".\n// Modulo operations ensure that the results do not exceed 1069 + 7.\n___\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(n), where \'n\' is the length of the binary string..\n___\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(1), since we are only using a few variables.\n___\n\n# Code\n```csharp []\npublic class Solution {\n public int NumberOfUniqueGoodSubsequences(string binary) {\n const int MOD = 1000000007;\n long subseqEndingIn0 = 0; // Count of subsequences ending with \'0\'\n long subseqEndingIn1 = 0; // Count of subsequences ending with \'1\'\n bool hasZero = false; // To check if the subsequence "0" should be added\n\n foreach (char c in binary) {\n if (c == \'1\') {\n subseqEndingIn1 = (subseqEndingIn1 + subseqEndingIn0 + 1) % MOD; // New \'1\' can form new subsequences\n } else {\n subseqEndingIn0 = (subseqEndingIn0 + subseqEndingIn1) % MOD; // New \'0\' can extend subsequences\n hasZero = true; // There is at least one \'0\'\n }\n }\n\n long result = (subseqEndingIn0 + subseqEndingIn1) % MOD;\n if (hasZero) {\n result = (result + 1) % MOD; // Add the subsequence "0" if there was at least one \'0\'\n }\n\n return (int)result;\n }\n}\n\n```
| 0 | 0 |
['String', 'Dynamic Programming', 'C#']
| 0 |
number-of-unique-good-subsequences
|
O(n) dp, just reverse iterate
|
on-dp-just-reverse-iterate-by-asherlau-n0jd
|
Intuition\n Describe your first thoughts on how to solve this problem. \nreversly iterate the array, if it is 0, we know, it is invalid, but can contribute to l
|
asherlau
|
NORMAL
|
2024-08-15T03:28:25.902340+00:00
|
2024-08-15T03:28:25.902370+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nreversly iterate the array, if it is 0, we know, it is invalid, but can contribute to later 1\'s subsequences, so we store the amount of ending 0, subsequnces\nif it is 1, we use previous n0 and n1 subsequence and plus 1, because the unique 1 <- s[i], it can be later contribute or as single unique character. \nwe only return the result that start with 1, so return n0, and if there is single 0, we add 1. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimpl Solution {\n pub fn number_of_unique_good_subsequences(binary: String) -> i32 {\n //dp[i][0] <- the number of subsequence start by 0 at i\n //dp[i][1] <- the number of subsequence start by 1 at i\n //dp[i][1] = dp[i + 1][0] + dp[i + 1][1]\n //dp[i][0] = dp[i + 1][0] + dp[i + 1][1]\n let n = binary.len();\n let binary = binary.as_bytes();\n let mut has0 = 0;\n let mut n0 = 0;\n let mut n1 = 0;\n let m = 1e9 as i32 + 7;\n for i in (0..n).rev(){\n if binary[i] == b\'1\'{\n n1 = (n0 + n1 + 1)%m;\n }else{\n n0 = (n0 + n1 + 1)%m;\n has0 = 1;\n }\n }\n return (n1 + has0)%m;\n } \n}\n```
| 0 | 0 |
['Rust']
| 0 |
number-of-unique-good-subsequences
|
Python 3: TC O(N), SC O(1): Simple Code, Complicated Derivation and Proof
|
python-3-tc-on-sc-o1-simple-code-complic-9nwy
|
Intuition\n\nI left all of my thought process and stuff to show you that I did not have an easy time with this one.\n\nEventually I had to peek at @votrubac\'s
|
biggestchungus
|
NORMAL
|
2024-08-14T03:41:28.535972+00:00
|
2024-08-14T03:41:28.535991+00:00
| 4 | false |
# Intuition\n\nI left all of my thought process and stuff to show you that I did *not* have an easy time with this one.\n\nEventually I had to peek at @votrubac\'s solution. Even then I didn\'t really understand it and I had to fumble around with it some more.\n\nIn the end this turns out to be similar to DP, but not quite.\n\n## Uniques Versus Total\n\nThe total number is a lot easier to count with combinatorics. But the *unique* count is *much* more challenging.\n\nUltimately what I wound up doing was going through a complicated example problem, looking at the pattern, and fumbling around until I got something approximately right, then refined it into a solution.\n\nThis is @votrubac\'s approach. It works... if you have lots of time. If you\'re pitched this **in an interview though you don\'t have time to work through a complicated example problem.**\n\n## Interview Approach\n\nMy lesson learned with this problem is that if we need to count uniques, **we need to track the number of new sequences we\'ll get with each character.** This is the DP-like solution.\n\nZeros and ones are mostly symmetric situations except for the no leading zeros thing except for \'0\' itself. So **let\'s ignore a single leading zero for now.** **If there\'s a zero anywhere in the string we can add one at the end.**\n\n## Track What we Want: Numbers of New Subsequences\n\nSuppose we know, for each index, what `a0` and `a1` are; the number of new subsequences we get when appending a 0 or a 1 to all existing subsequences, respectively.\n\n## Let\'s Look at Appending Zeros\n\nNow let\'s look at all unique prefixes `p` where adding a zero results in a new prefix:\n* `p` is unique by assertion\n* `p0` is unique by definition\n\nIf we add another `0` in a row, then for each `p` we\'d have\n* `p`\n* `p0`\n* `p00`\n\nThe number of new sequences is the count of `p`. This continues, so we find that **if we keep appending zeros, then the number of new subsequences doesn\'t change.** That\'s because we only get a new subsequence for the situation were added zero every single time, which is only true for the original subsequences `p` before we started appending zeros.\n\nThe same logic applies for ones.\n\n**So we want to store the number of subsequences `p` where adding a zero creates a new unique subsequence, and same for ones.** We\'ll call those `a0` and `a1`, "added subsequences via 0/1"\n\nNow let\'s suppose we added a one instead. We\'ll add `a1` new subsequences by assumption. For each of those `a1` subsequences `p\'` we\'ll get a new unique subsequence `p\'1`.\n\nHow does this change `a0`? The only new subsequences we added are `p\'1`, so the change is somewhere in 0..`p\'1`. Any other subsequences we could append a 0 to and get a new subsequence are still there.\n\nLet\'s look at the result of adding 0 to each of those `p\'1`. We\'ll get `p\'10`. Are these all unique?\n\nLet\'s do a proof by contradiction. Suppose `p\'10` is NOT unique, that we already had it. To have gotten `p\'10` before though, we\'d have to have seen\n* `p\'` already, otherwise we can\'t have added a `10` later\n* `p\'1` already, otherwise we can\'t have added the last `0`\n\nBut that means we saw `p\'1` already, which is a contradiction because we just said that `p\'` by definition are all the prefixes where adding a `1` is a brand new subsequence.\n\nTherefore we have proven that all the `p\'10` are new subsequences.\n\n## How a0 and a1 Change at Each Index\n\nSo finally we learn that\n* suppose we add `a0` subsequences when we see a `0`, and `a1` if we see a 1\n* if we see a 0, then `a0` doesn\'t change: this is the `p -> p, p0 -> p, p0, p00 -> ...` stuff\n* if we see a 1, then all the new `a1` subsequences of the form `p\'1` will yield a new subsequence `p\'10` if we append a `0`, proved by contradiction. So in addition to the `a0` we had before, we gain `a1` new subsequences\n\nTherefore:\n* when we see a `0`: `a0` doesn\'t change, `a0 += a1`\n* when we see a `1`: `a1` doesn\'t change, `a1 += a0`\n* and `total` increases by `a0` or `a1`, whichever one corresponds to the character we just saw\n\n# Approach\n\nIf there\'s a zero anywhere in the string then we\'ll have one special number that is just "0". It doesn\'t follow the append rules because you can\'t have `00` or `01`.\n\nIf there no zero then we know the answer, it\'s the length because we have `1`, `11`, `111`, etc. One to `len(binary)`.\n\nTherefore we handle `0` separately.\n\nThis means that at the start\n* if we add a `1`, we get one new subsequence: `0 -> 0, 1`\n* if we add a `0`, we get zero new subsequences: `0 -> 0`\n\nThis will make `total` the count of all subsequences starting with a one. Therefore at the end we add `+1` to account for the single binary subsequence of `0` itself.\n\n# Final Thoughts\n\nI think "count the uniques" problems require a different thought process, one similar to DP but not quite the same.\n\nThis is really more similar to the "quick update trick," where you record how values change at each index, then find a fast way to update that in `O(1)`.\n\nIn this case the problem was solved easily in the end (although the derivation and proof are tricky) by recording\n* the number of new subsequences we get when appending a 0\n* the number we get when appending a 1\n\nAnd then updating those.\n\nThis is conceptually a lot easier than the LC hint, which is to use DP. That\'s possible, but I think LC\'s idea is that we can effectively compute `a0` and `a1` as tracked here using the change in uniques we saw the last time we saw each digit. That works, but it\'s kind of ugly and roundabout. It\'s just easier to say "we want to know how `total` changes if we see either digit, and know how `a0` and `a1` change at each element."\n\nThe code is easier this way; many other solutions have more complicated `ans_i - ans_{i-1} + ..` stuff. It\'s mathematically equivalent but this just seems a lot cleaner.\n\n# Complexity\n- Time complexity: linear\n \n- Space complexity: constant\n\n# Code\n```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n # subseq of binary is good if\n # > not empty\n # > no leading zeros (except 0 itself)\n\n # number of unique good subsequences\n\n # subSEQUENCE, not subARRAY\n\n # ways to make a unique subsequence: take the number with length l and append or prepend a digit\n\n # what if we count total unique subsequences then account for leading zeroes later?\n\n # for total subsequences:\n # suppose we have all uniques up to i\n # then we append binary[i]\n \n # ugh, dont\' know if appending will make a new unique\n\n # other idea:\n # starting with one one, or two ones, or three ones, etc. are all unique\n # then we take 1+ zeros\n # etc.\n # these are all unique\n\n # suppose we have uniques split up by prefix, e.g. those starting with 1+ ones and 1+ zeros\n # then when we add a new char, e.g. 1\n # adding 1 one may or may not make a new unique if prepending to zero\n #\n # so this isn\'t a good way to split up the problem\n\n # all possible subsequences: 2**len-1 (nonempty)\n\n # can we count duplicates quickly?\n\n # WAIT: for each stretch of ones and zeros:\n # we can take any number of ones and at least one zero, then continue\n # that "then continue" will return all\n\n # UGH THIS IS HARD\n #\n # Can\'t find the right subproblem, I\'m sure it\'s something like O(1) DP as we proceed but I can\'t get it\n #\n # for 0000000 there\'s only one\n # for 100000 there\'s 1, 10, 100, 100, ... so len + 1 including 0 itself\n # for 101010 there\'s\n # 1, 11, 111\n # 10, 110, 1110\n\n # so let\'s return to number of uniques starting with each number of ones and zeros; anything that\'s 0001... is diff from 001...\n #\n # so if we have u unique combinations starting with a one after some index i\n # then each of the leftZeros\n #\n \n # HINT: number of uniques is the number of unique decimal values, which makes sense\n # each distinct number is a distinct subsequence\n\n # HINT 2: find the answer at each indedx based on the previous indexes\' answers\n\n # so left-to-right DP... which I knew already basically\n\n # if we have a bunch of uniques up to i\n # > if they\'re maximum length thus far, then adding a new digit is a new value\n # > otherwise it might not be\n\n # maybe once again we get all uniques ending with each number of zeros and ones\n # if current digit is one: all uniques ending with zero, plus a 1, is a new unique\n # all uniques ending with one, plus a 1, gets complicated\n # e.g. 1, 11, 111\n # 101, 1001\n # adding a 1 gives 11, 111, 1111 => only the max ones gets larger\n # but 1011, 10011 are uniques too\n #\n # can\'t solve, need to peek at solutions\n\n # votrubac: get transition formula from a nontrivial example, knowing we want O(1) idx-to-idx update\n\n # e.g. 0 0 1 0 1 0 0 1 0\n #\n # 0: 0\n # 0: 0\n # 1: 0, 1 +1 (2)\n # 0: 0, 1, 10 +1 (3)\n # 1: 0, 1, 10, 11, 101 +2 (5)\n # 0: 0, 1, 10, 11, 101, 100, 110, 1010 +3 (8)\n # 0: 0, 1, 10, 11, 101, 100, 110, 1010, 1000, 1100, 10100 +3 (11)\n # 1: 0, 1, 10, 11, 101, 100, 110, 1010, 1000, 1100, 10100, 111, 1011, 1001, 1101, 10101, 10001, 11001, 101001 +8 (19)\n\n\n # something about\n # > get the new sequences we got when we added a 1\n # > if we add another one, we get the same number of new sequences\n # > the new sequences are\n # > all sequences\n # > minus the ones that are the same if we add a 1\n # > the latter is the number we added the first time we saw a 1 in this stretch\n\n # track the number of new sequences we get if we add either digit\n if not any(c == \'0\' for c in binary): return len(binary)\n\n # ignore special case of leading zero to start\n\n BIG = 10**9 + 7\n\n # record the number of new sequences we get if we add a 0 and a 1\n a0 = 0\n a1 = 1\n total = 0\n for c in binary:\n if c == \'0\':\n total = (total + a0) % BIG\n a1 = (a1 + a0) % BIG\n else:\n total = (total + a1) % BIG\n a0 = (a0 + a1) % BIG\n\n return total + 1 # leading zero\n\n # Hokay, lucky guess. Now why?\n\n # if we have a0 prefixes where adding a zero makes a new sequence\n # then we indeed add a zero: for each of those a0 we have p and p0 now\n # then when we add another zero, we get p, p0, p00: only the ones we added a zero to *and were unique* are new uniques with 00\n # that\'s a0 still\n #\n # for each of those p, p0, p00, ...\n # if we add a 1 then all of those p01, p001, etc. are new (?)\n # suppose p01 is NOT new\n # that means we already had a p01 before\n # and before making p01 we must have had p0\n # but we just said that p0 was new\n # therefore this leads to a contradiction\n\n # start with p, prefixes where adding a zero is unique. that means p0 does NOT exist\n # so adding a zero: means we get p, p0 for all p\n # add another zero: we get p, p0, p00 for all p\n # etc: each zero adds a number of sequences equal to p\n #\n # now if we add a 1:\n # suppose we have the count of p\' where p\'1 is new; p\'1 is not among the sequences we have\n # are all the p0 part of p\'?\n # suppose p0 is not part of p\'. that means p01 already exists in p\'\n # for that to be true, we must have had p0 already before seeing an earlier 1\n # that means p0 is part of p\n # but that contradicts the fact that p by definition is a prefix | p0 has not been seen before\n # therefore p01 is new\n # and p001 is new\n # and so on\n```
| 0 | 0 |
['Python3']
| 0 |
number-of-unique-good-subsequences
|
Dynamic Programming Solution - End with 0/1
|
dynamic-programming-solution-end-with-01-5t9p
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind this solution is to use dynamic programming to count the number of
|
orel12
|
NORMAL
|
2024-08-03T06:26:29.475610+00:00
|
2024-08-03T06:26:29.475640+00:00
| 43 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is to use dynamic programming to count the number of unique good subsequences. We can keep track of subsequences ending with \'0\' and \'1\' separately, and build longer subsequences from shorter ones.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We use a vector `dp` of size 2 to store the count of good subsequences:\n - `dp[0]` represents the count of good subsequences ending with \'0\'\n - `dp[1]` represents the count of good subsequences ending with \'1\'\n\n2. We iterate through the binary string:\n - For \'0\', we update `dp[0]` by adding `dp[1]` to it (all good subsequences ending with \'1\' can now end with \'0\')\n - For \'1\', we update `dp[1]` by adding `dp[0]`, `dp[1]`, and 1 (all existing good subsequences plus the new subsequence \'1\')\n\n3. We use a boolean `has_zero` to keep track of whether we\'ve seen a \'0\' in the string.\n\n4. At the end, we return the sum of `dp[0]`, `dp[1]`, and `has_zero` (to account for the "0" subsequence if it exists).\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe algorithm iterates through the input string once, performing constant-time operations for each character.\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe use a fixed-size vector `dp` of size 2 and a boolean variable, which is constant extra space regardless of the input size.\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfUniqueGoodSubsequences(string binary) {\n const int MOD = 1000000007;\n int n = binary.length();\n vector<long long> dp(2, 0);\n bool haszero = false;\n \n for (char c : binary) {\n if (c == \'0\') {\n haszero = true;\n dp[0] = (dp[0] + dp[1]) % MOD;\n } else {\n dp[1] = (dp[0] + dp[1] + 1) % MOD;\n }\n }\n \n return (dp[0] + dp[1] + haszero) % MOD;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
number-of-unique-good-subsequences
|
Basic Java
|
basic-java-by-amitkyadav6993-hcmh
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
amitkyadav6993
|
NORMAL
|
2024-07-29T10:22:34.180718+00:00
|
2024-07-29T10:22:34.180741+00:00
| 10 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private static final int MOD = 1000000007;\n public int numberOfUniqueGoodSubsequences(String binary) {\n\n int n = binary.length();\n int zeroCount = 0, oneCount = 0;\n boolean hasZero = false;\n \n for (int i = 0; i < n; i++) {\n char ch = binary.charAt(i);\n if (ch == \'1\') {\n oneCount = (zeroCount + oneCount + 1) % MOD;\n } else {\n zeroCount = (zeroCount + oneCount) % MOD;\n hasZero = true;\n }\n }\n \n return (oneCount + zeroCount + (hasZero ? 1 : 0)) % MOD;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
number-of-unique-good-subsequences
|
Easy Java Solution
|
easy-java-solution-by-harshkumar_23-qajk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
harshkumar_23
|
NORMAL
|
2024-06-19T01:23:53.822185+00:00
|
2024-06-19T01:23:53.822203+00:00
| 19 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numberOfUniqueGoodSubsequences(String binary) {\n \n int endsWithOne = 0;\n int endsWithTwo = 0;\n int MOD = 1_000_000_007;\n int hasZero = 0;\n for(int i=0; i<binary.length();i++){\n if(binary.charAt(i)==\'1\'){\n endsWithOne = (endsWithOne + endsWithTwo + 1)%MOD;\n }else{\n hasZero = 1;\n endsWithTwo = (endsWithOne + endsWithTwo)%MOD;\n }\n }\n int ans = (endsWithOne + endsWithTwo + hasZero)%MOD;\n \n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
number-of-unique-good-subsequences
|
java dp
|
java-dp-by-mot882000-q1mu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
mot882000
|
NORMAL
|
2024-06-04T03:44:14.319176+00:00
|
2024-06-04T03:44:14.319194+00:00
| 11 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numberOfUniqueGoodSubsequences(String binary) {\n\n // 0 \uC774 lead \uD558\uBA74 \uC548\uB41C\uB2E4. \n // 1. dp[n][2] , 0 \uB610\uB294 1\uB85C \uB05D\uB098\uB294 \uAC12\uC744 \uC800\uC7A5\n \n // 2. \uCD5C\uCD08 1\uC774 \uBC1C\uC0DD\uD558\uAE30 \uC804\uAE4C\uC9C0 dp[i]\uB294 \uAC74\uB108 \uB6F4\uB2E4. \n // 1\uC774 \uBC1C\uC0DD\uD558\uBA74 dp[i][1] \uC5D0 1\uC744 \uB123\uC5B4\uC900\uB2E4. \n \n // 3 .1\uC774 \uBC1C\uC0DD\uD55C \uD6C4\uC5D0\uB294 \n // \uC774\uC804\uC5D0 \uBC1C\uC0DD\uD55C \uAC12\uB4E4\uC744 \uC774\uC6A9\uD574 \uC0C8\uB85C\uC6B4 subsequence\uB97C \uB9CC\uB4E4\uC5B4\uC8FC\uACE0 \uAE30\uC874 \uAC12\uB4E4\uC744 \uC778\uACC4\uD574\uC900\uB2E4. \n // 1) s.charAt(i) == 0 \uC77C \uB54C \n // dp[i][0] += dp[i-1][0]+ dp[i-1][1];\n // dp[i][1] += dp[i-1][1];\n // 2) s.charAt(i) == 1 \uC77C \uB54C \n // dp[i][1] += dp[i-1][0]+ dp[i-1][1]+1;\n // dp[i][0] += dp[i-1][0];\n // \u203B 1\uC740 leading\uC774 \uAC00\uB2A5\uD558\uAE30 \uB54C\uBB38\uC5D0 1 \uD558\uB098\uB9CC \uC788\uB294 sequence\uB97C \uC720\uC9C0\uD558\uAE30 \uC704\uD574 1\uC744 \uB354 \uB354\uD574\uC900\uB2E4. \n\n // 101\n\n // dp[0][] : [] [1] \n\n // dp[1][] : [10] [1]\n\n // dp[2][] : [10] [101 11 1] 0\uC774 \uD558\uB098\uB77C\uB3C4 \uC788\uC5C8\uC73C\uBBC0\uB85C [0] \uD3EC\uD568 \uCD1D 5\uAC1C\n\n // 4. dp[n-1][0]+dp[n-1][1] \uBC18\uD658 \u203B 0\uC774 \uD558\uB098\uB77C\uB3C4 \uBC1C\uC0DD\uD588\uC73C\uBA74 subsequence 0 \uC774 \uD3EC\uD568\uC774 \uB418\uC5B4\uC57C\uD558\uBBC0\uB85C 1\uC744 \uCD94\uAC00\uB85C \uB354\uD574\uC900\uB2E4.\n\n\n\n final int MOD = 1_000_000_007;\n \n int n = binary.length();\n\n // for(int i = 0; i < arr.length; i++) System.out.print(arr[i]+ " ");System.out.println();\n\n long dp[][] = new long[n][2];\n\n if( binary.charAt(0) == \'0\' ) dp[0][0] = 1;\n else dp[0][1] = 1;\n\n long cnt1 = dp[0][1];\n long cnt0 = dp[0][0];\n\n for(int i = 1; i < n; i++) {\n if ( binary.charAt(i) == \'0\' ) cnt0++;\n\n if ( cnt1 == 0 ) {\n if ( binary.charAt(i) == \'1\' ) {\n dp[i][1] = 1;\n cnt1++;\n }\n } else{\n if ( binary.charAt(i) == \'0\' ){\n dp[i][0] += dp[i-1][0]+ dp[i-1][1];\n dp[i][1] += dp[i-1][1];\n } else{\n dp[i][1] += dp[i-1][0]+ dp[i-1][1]+1;\n dp[i][0] += dp[i-1][0];\n }\n \n dp[i][0] %= MOD;\n dp[i][1] %= MOD;\n }\n }\n\n // for(int i = 0; i <dp.length; i++) {\n // System.out.print( "["+ dp[i][0] + " " + dp[i][1]+ "] ");\n // } System.out.println();\n \n long result = dp[n-1][0] + dp[n-1][1];\n result %= MOD;\n if ( cnt0 > 0 && binary.length() > 1) {\n result++;\n result %= MOD;\n }\n\n return (int)result;\n }\n}\n```
| 0 | 0 |
['Dynamic Programming', 'Java']
| 0 |
number-of-unique-good-subsequences
|
[Rust / Elixir] bottom-up DP
|
rust-elixir-bottom-up-dp-by-minamikaze39-6hbz
|
Approach\nIterate the string from right to left, and maintain 3 variables:\nans: Number of unique good subsequences so far, excluding "0".\nsuffix: Number of un
|
Minamikaze392
|
NORMAL
|
2024-05-17T09:43:52.096515+00:00
|
2024-05-17T09:54:04.980589+00:00
| 0 | false |
# Approach\nIterate the string from right to left, and maintain 3 variables:\n`ans`: Number of unique **good** subsequences so far, excluding `"0"`.\n`suffix`: Number of unique subsequences starting with `"0"`, and also including the empty string `""`.\n`has_0`: Records if there is any `"0"` found, so that we can add 1 to the final answer.\n\nCase 1: When a `"1"` is encountered, increase `ans` by `suffix`.\nCase 2: When a `"0"` is encountered, increase `suffix` by `ans + 1`, and also set the `has_0` flag.\n# Why does it work\nWe can guarantee that in Case 1, we can find exactly (`suffix`) new unique **good** subsequences to add to `ans`. Let\'s say when for the 1st time we encounter a `"1"` after `str` is included to `suffix`, we can create `"1str"`, and the 2nd time we can create `"11str"`, 3rd time `"111str"` etc...\n\nSame logic for Case 2, i.e. `"0str"`, `"00str"`, `"000str"` etc..., except that we need to add 1 more which is a new unique subsequence of just `"0"`s, i.e. `"0"`, `"00"`, `"000"` etc...\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```Rust []\nimpl Solution {\n pub fn number_of_unique_good_subsequences(binary: String) -> i32 {\n let mut ans = 0;\n let mut suffix = 1;\n let mut has_0 = 0;\n let large = 1_000_000_007;\n for b in binary.bytes().rev() {\n if b == b\'0\' {\n suffix = (ans + suffix + 1) % large;\n has_0 = 1;\n }\n else {\n ans = (ans + suffix) % large;\n }\n }\n ans + has_0\n }\n}\n```\n```Elixir []\ndefmodule Solution do\n @large 1_000_000_007\n\n @spec number_of_unique_good_subsequences(binary :: String.t) :: integer\n def number_of_unique_good_subsequences(binary) do\n String.to_charlist(binary)\n |> List.foldr({0, 1, 0}, fn\n ?0, {ans, head0, _} -> {ans, rem(head0 + ans + 1, @large), 1}\n ?1, {ans, head0, has_0} -> {rem(ans + head0, @large), head0, has_0}\n end)\n |> then(fn {ans, _, has_0} -> rem(ans + has_0, @large) end)\n end\nend\n```
| 0 | 0 |
['Dynamic Programming', 'Rust', 'Elixir']
| 0 |
number-of-unique-good-subsequences
|
Javascript - DP
|
javascript-dp-by-faustaleonardo-dyk0
|
Code\n\n/**\n * @param {string} binary\n * @return {number}\n */\nvar numberOfUniqueGoodSubsequences = function (binary) {\n let countZero = 0;\n let endsOne
|
faustaleonardo
|
NORMAL
|
2024-05-16T00:04:20.920019+00:00
|
2024-05-16T00:04:20.920039+00:00
| 12 | false |
# Code\n```\n/**\n * @param {string} binary\n * @return {number}\n */\nvar numberOfUniqueGoodSubsequences = function (binary) {\n let countZero = 0;\n let endsOne = 0;\n let endsZero = 0;\n const MOD = 10 ** 9 + 7;\n\n for (const char of binary) {\n if (char === \'1\') {\n endsOne = (endsOne + endsZero + 1) % MOD;\n } else {\n endsZero = (endsOne + endsZero) % MOD;\n countZero = 1;\n }\n }\n\n return (endsOne + endsZero + countZero) % MOD;\n};\n\n```
| 0 | 0 |
['Dynamic Programming', 'JavaScript']
| 0 |
number-of-unique-good-subsequences
|
DP
|
dp-by-rktayal-ymsk
|
\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n dp, has_0, mod = [0, 0], 0, 10**9+7\n for char in binary:\n
|
rktayal
|
NORMAL
|
2024-04-02T05:47:33.332580+00:00
|
2024-04-02T05:47:33.332640+00:00
| 15 | false |
```\nclass Solution:\n def numberOfUniqueGoodSubsequences(self, binary: str) -> int:\n dp, has_0, mod = [0, 0], 0, 10**9+7\n for char in binary:\n if char == \'0\':\n has_0 = 1\n new_val = sum(dp)\n dp[0] = new_val\n else:\n new_val = sum(dp) + 1\n dp[1] = new_val\n return (sum(dp) + has_0) % mod \n```
| 0 | 0 |
['Python3']
| 0 |
number-of-unique-good-subsequences
|
Go solution with Runtime 26 ms Beats 100.00% of users with Go
|
go-solution-with-runtime-26-ms-beats-100-bqa3
|
Approach\n\n1. Initialization: Initialize necessary variables, including count to store the count of unique good subsequences ending at each position, occurrenc
|
pvt2024
|
NORMAL
|
2024-02-08T09:09:57.124066+00:00
|
2024-02-08T09:09:57.124097+00:00
| 5 | false |
# Approach\n\n**1. Initialization:** Initialize necessary variables, including count to store the count of unique good subsequences ending at each position, occurrence to track the occurrences of \'0\'s and \'1\'s, lastPosition to store the last position of \'0\'s and \'1\'s encountered, and firstZeroLoc to track the first occurrence of \'0\' in the binary string.\n\n**2. Main Loop:**\n\n- Iterate over each character in the binary string.\n- Update occurrence, lastPosition, and firstZeroLoc based on the current character.\n- For each character, compute the count of unique good subsequences ending at the current position.\n- Store the count in the count array.\n\n**3. Sum Calculation:**\n\n- After processing all characters, compute the total count of unique good subsequences.\n- Sum up all counts stored in the count array, taking care of the modulo operation to prevent integer overflow.\n\n**4. Return:**\n- Return the total count of unique good subsequences.\n\n# Complexity\n\n- **Time complexity:**\n - The program iterates over each character in the binary string once, resulting in a time complexity of O(N), where N is the length of the binary string.\n - Within each iteration, the program performs constant-time operations.\n - Overall, the time complexity is O(N).\n\n- **Space complexity:**\n - The program uses additional space to store the count array, occurrence, lastPosition, and a few other variables.\n - The space complexity is O(N) to store the count array and O(1) for other variables.\n - Overall, the space complexity is O(N).\n# Code\n```\nconst MOD = 1000000007\n\nfunc numberOfUniqueGoodSubsequences(binary string) int {\n\tcount := make([]int, len(binary))\n\toccurrence := [2]int{0, 0}\n\tlastPosition := [2]int{-1, -1}\n\tfirstZeroLoc := -1\n\n\tfor i, ch := range binary {\n\t\tidx := int(ch - \'0\')\n\t\tif firstZeroLoc == -1 && ch == \'0\' {\n\t\t\tfirstZeroLoc = i\n\t\t}\n\n\t\tif i == 0 {\n\t\t\toccurrence[idx]++\n\t\t\tlastPosition[idx] = 0\n\t\t\tcount[0] = 1\n\t\t\tcontinue\n\t\t}\n\n\t\tvar sum int64 = 0\n\n\t\tif occurrence[idx] == 0 {\n\t\t\tsum++\n\t\t}\n\n\t\tstart := max(0, lastPosition[idx])\n\t\tsum += int64(getSum(count, start, i, firstZeroLoc))\n\t\tsum %= MOD\n\n\t\tlastPosition[idx] = i\n\t\toccurrence[idx]++\n\t\tcount[i] = int(sum)\n\t}\n\n\tvar ans int64 = 0\n\tfor _, c := range count {\n\t\tans += int64(c)\n\t\tans %= MOD\n\t}\n\treturn int(ans)\n}\n\nfunc getSum(count []int, start, end, firstZeroLoc int) int {\n\tvar sum int64 = 0\n\tfor i := start; i < end; i++ {\n\t\tif i == firstZeroLoc {\n\t\t\tif count[i]-1 == 0 {\n\t\t\t\tsum += MOD\n\t\t\t} else {\n\t\t\t\tsum += int64(count[i] - 1)\n\t\t\t}\n\t\t} else {\n\t\t\tsum += int64(count[i])\n\t\t}\n\t\tsum %= MOD\n\t}\n\treturn int(sum)\n}\n\nfunc max(a, b int) int {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\n\n```
| 0 | 0 |
['Go']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.