question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-score-triangulation-of-polygon | Easy Solution With Explanation | BOTTOM UP & TOP BOTTOM | C++ | easy-solution-with-explanation-bottom-up-ahsv | [Please Upvote if it helped you ]\nint the comp function we pass the first and last index (l =0 and r = n-1)\n Now every edge of the polygon will be a side of t | Might_Guy | NORMAL | 2020-04-01T08:00:50.882782+00:00 | 2020-06-28T07:13:05.381237+00:00 | 492 | false | [Please Upvote if it helped you ]\nint the comp function we pass the first and last index (l =0 and r = n-1)\n* Now every edge of the polygon will be a side of the triangles to be made \n* lets take an edge to be made by A[0] ,A[n-1] and a vertex i in between the two\n* By taking i our problem is divided into 2 sub-problems of ( l , i ) & ( i , r ) \n* And for the taken i our ans will be = A[l]*A[r]*A[i] + ans1+ans2; (ans1 and ans2 are ans of the two sub problems) \n* now we have to select the minimum of these answers and return it\n\nNow for DP we see that our function needs start and end index of the array hence we store it in a 2D matrix\n\nTOP BOTTOM:\n```\nclass Solution {\npublic:\n int comp(int l,int r,vector<int>& A,vector<vector<int>>&dp){\n if(dp[l][r]!=0)\n return dp[l][r];\n if(r-l<2)\n return 0;\n if(r-l==2){\n dp[l][r]=A[l]*A[l+1]*A[r];\n return dp[l][r];\n }\n int max_ans =INT_MAX/2;\n for(int i=l+1;i<r;i++){\n int ans1 = comp(l,i,A,dp);\n int ans2 = comp(i,r,A,dp);\n int my = A[l]*A[r]*A[i] + ans1+ans2;\n max_ans = min(max_ans,my);\n }\n dp[l][r]=max_ans;\n return max_ans;\n }\n int minScoreTriangulation(vector<int>& A) {\n int n =A.size();\n if(n<3)\n return 0;\n vector<vector<int>>dp(n,vector<int>(n,0));\n return comp(0,n-1,A,dp);\n \n \n }\n};\n```\n\nBOTTOM UP:\n\n```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& A) {\n int n = A.size();\n vector<vector<int>>dp(n,vector<int>(n,INT_MAX));\n for(int len=1;len<=n;len++){\n for(int start=0;start+len-1<n;start++){\n int end = start+len-1;\n if(len<3){\n dp[start][end]=0;\n continue;\n } \n for(int mid=start+1;mid<end;mid++){\n int pro = A[start]*A[mid]*A[end];\n int can_be = dp[start][mid]+dp[mid][end]+pro;\n dp[start][end] = min(can_be,dp[start][end]);\n \n }\n }\n }\n return dp[0][n-1];\n }\n};\n```\n\nSlight Variation\n\n```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& A) {\n int n = A.size();\n vector<vector<int>>dp(n,vector<int>(n,0));\n for(int len=3;len<=n;len++){\n for(int start=0;start+len-1<n;start++){\n int end = start+len-1;\n dp[start][end] = INT_MAX;\n for(int mid=start+1;mid<end;mid++){\n int pro = A[start]*A[mid]*A[end];\n int can_be = dp[start][mid]+dp[mid][end]+pro;\n dp[start][end] = min(can_be,dp[start][end]);\n \n }\n }\n }\n return dp[0][n-1];\n }\n};\n``` | 4 | 0 | [] | 2 |
minimum-score-triangulation-of-polygon | c++, bottom-up DP , easy to understand | c-bottom-up-dp-easy-to-understand-by-fig-ezlk | \nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& A) {\n int n = A.size();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n | fight_club | NORMAL | 2019-11-21T13:08:09.545998+00:00 | 2019-11-21T13:08:09.546028+00:00 | 505 | false | ```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& A) {\n int n = A.size();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n \n for(int gap = 0; gap < n; gap++){\n for(int i = 0,j=i+gap; i < n,j < n; i++,j++){\n if(gap == 0 || gap == 1){\n dp[i][j] = 0;\n }\n else\n {\n int ans = 1<<30;\n for(int k = i+1; k < j; k++){\n ans = min(ans,A[i]*A[k]*A[j] + dp[i][k] + dp[k][j]);\n \n dp[i][j] = ans;\n }\n }\n \n }\n }\n \n return dp[0][n-1];\n \n }\n};\n``` | 4 | 0 | [] | 0 |
minimum-score-triangulation-of-polygon | recursion and memorisation | recursion-and-memorisation-by-ac1-g9qd | Start with recursion hit the TLE :D\n\n def minScoreTriangulation(self, A: List[int]) -> int:\n def backtrack(start,end):\n res = sys.maxs | ac1 | NORMAL | 2019-05-18T10:10:52.451177+00:00 | 2019-05-18T10:11:46.811706+00:00 | 630 | false | Start with recursion hit the TLE :D\n```\n def minScoreTriangulation(self, A: List[int]) -> int:\n def backtrack(start,end):\n res = sys.maxsize\n if end -start +1< 3:\n return 0\n for i in range(start+1,end):\n res = min(res,backtrack(start,i)+ backtrack(i,end)+ A[start]*A[end]*A[i])\n return res\n return backtrack(0,len(A)-1)\n```\nand use memorisation\n```\nclass Solution:\n def minScoreTriangulation(self, A: List[int]) -> int:\n cache ={}\n def backtrack(start,end):\n res = sys.maxsize\n if end -start +1< 3:\n return 0\n if (start,end) not in cache: \n for i in range(start+1,end):\n res = min(res,backtrack(start,i)+ backtrack(i,end)+ A[start]*A[end]*A[i])\n cache[(start,end)] = res\n return cache[(start,end)]\n return backtrack(0,len(A)-1)\n``` | 4 | 0 | ['Backtracking', 'Memoization', 'Python'] | 1 |
minimum-score-triangulation-of-polygon | Variant of MATRIX CHAIN MULTIPLICATION | DP | DRY RUN attached | variant-of-matrix-chain-multiplication-d-3bx9 | Intuition\nThere are three variable which are used i (start point), j (end point) & k (start -> end). This shows its a variation of MATRIX CHAIN MULTIPLICATION\ | JigarSiddhpura | NORMAL | 2024-07-29T07:36:45.967458+00:00 | 2024-07-29T07:36:45.967490+00:00 | 241 | false | # Intuition\nThere are three variable which are used `i` (start point), `j` (end point) & `k` (start -> end). This shows its a variation of `MATRIX CHAIN MULTIPLICATION`\n\n# Dry Run for [3,7,4,5]\n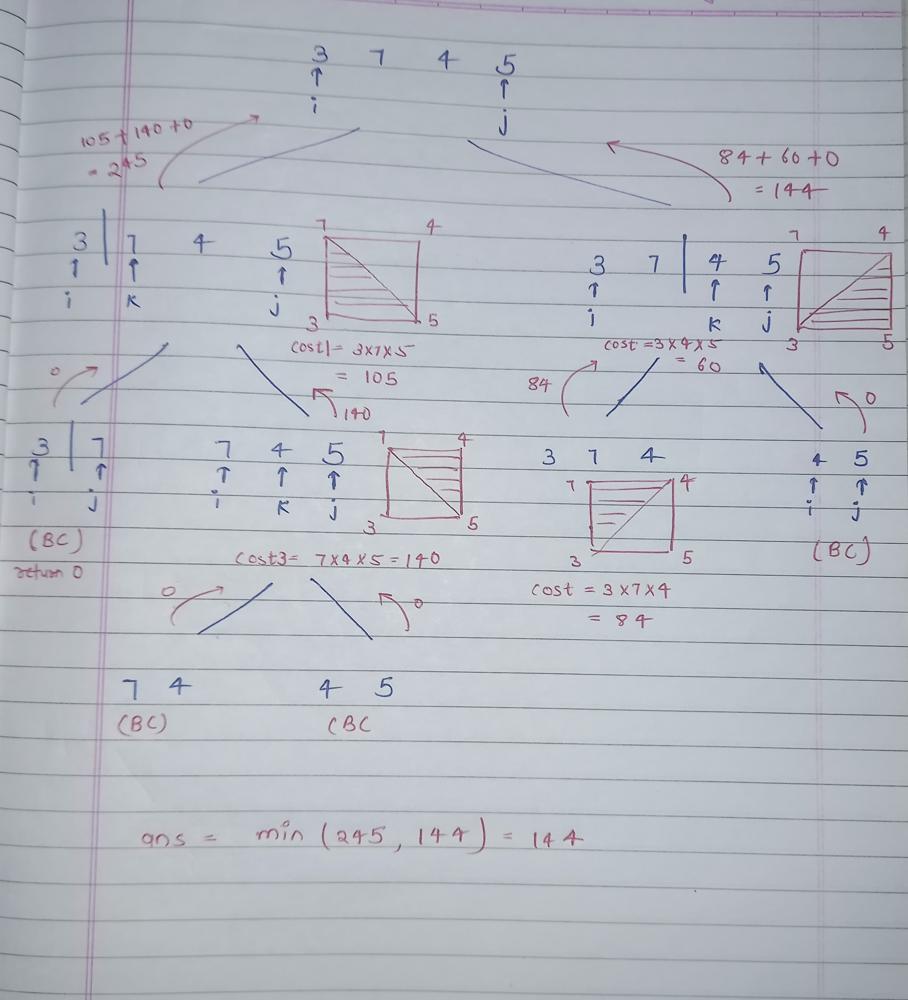\n\n\n# Complexity\n- Time complexity: `O(n^3)`:\n\n O(n) possible values for i\n O(n) possible values for j\n O(n) iterations for k in each subproblem\n\n- Space complexity: `O(n^2)` (2D array)\n\n# Code\n```\nclass Solution {\n // variant of MATRIX CHAIN MULTIPLICATION\n public int minScoreTriangulation(int[] values) {\n int n = values.length;\n int[][] dp = new int[n][n];\n\n Arrays.stream(dp).forEach(row -> Arrays.fill(row, -1));\n return mcm(values, 0, n-1, dp);\n }\n public int mcm(int[] values, int i, int j, int[][] dp) {\n if (i >= j-1) return 0; // no triangle possible with 2 points\n if (dp[i][j] != -1) return dp[i][j];\n\n int minScore = Integer.MAX_VALUE;\n\n for(int k=i+1; k<j; k++) {\n int score = (values[i] * values[j] * values[k]) // current triangle score\n + mcm(values, i, k, dp) // left partition score\n + mcm(values, k, j, dp); // right partition score\n \n minScore = Math.min(minScore, score);\n }\n return dp[i][j] = minScore;\n }\n}\n``` | 3 | 0 | ['Array', 'Dynamic Programming', 'Java'] | 2 |
minimum-score-triangulation-of-polygon | Python || 91.95% Faster || DP || 3 solutions | python-9195-faster-dp-3-solutions-by-pul-k93f | \n#Recursive\n#Time Complexity: Exponential\n#Space Complexity: O(n)\nclass Solution1:\n def minScoreTriangulation(self, values: List[int]) -> int:\n | pulkit_uppal | NORMAL | 2023-09-30T09:13:16.478901+00:00 | 2023-09-30T09:13:16.478925+00:00 | 610 | false | ```\n#Recursive\n#Time Complexity: Exponential\n#Space Complexity: O(n)\nclass Solution1:\n def minScoreTriangulation(self, values: List[int]) -> int:\n def solve(i, j):\n if i+1 == j:\n return 0\n m = float(\'inf\')\n for k in range(i+1, j):\n m = min(m, values[i] * (values[j]*values[k]) + solve(i, k) + solve(k, j))\n return m\n return solve(0, len(values)-1)\n \n#Memoization (Top-Down)\n#Time Complexity: O(n^2)\n#Space Complexity: O(n^2) + O(n)\nclass Solution2:\n def minScoreTriangulation(self, values: List[int]) -> int:\n def solve(i, j):\n if i+1 == j:\n return 0\n if dp[i][j] != -1:\n return dp[i][j]\n m = float(\'inf\')\n for k in range(i+1, j):\n m = min(m, values[i] * (values[j]*values[k]) + solve(i, k) + solve(k, j))\n dp[i][j] = m\n return dp[i][j]\n \n n = len(values)\n dp = [[-1 for j in range(n)] for i in range(n)]\n return solve(0, n-1)\n\n#Tabulation (Bottom-Up)\n#Time Complexity: O(n^2)\n#Space Complexity: O(n^2)\nclass Solution:\n def minScoreTriangulation(self, values: List[int]) -> int:\n n = len(values)\n dp = [[0 for j in range(n)] for i in range(n)]\n for i in range(n-1, -1, -1):\n for j in range(i+2, n):\n m = float(\'inf\')\n for k in range(i+1, j):\n m = min(m, values[i]*values[j]*values[k] + dp[i][k] + dp[k][j])\n dp[i][j] = m\n return dp[0][n-1]\n```\n**An upvote will be encouraging** | 3 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Python', 'Python3'] | 1 |
minimum-score-triangulation-of-polygon | C++ Aditya Verma's Approach ✅✅ | c-aditya-vermas-approach-by-akshay_ar_20-ltk5 | Intuition\n Describe your first thoughts on how to solve this problem. \n- Matrix Chain Multiplication [M C M]\n\n# Approach\n Describe your approach to solving | akshay_AR_2002 | NORMAL | 2023-04-08T19:16:11.638547+00:00 | 2023-04-08T19:16:11.638589+00:00 | 884 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Matrix Chain Multiplication [M C M]\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- First initialize the dynamic programming array \'dp\' with -1. This is done to indicate that a particular subproblem has not been solved yet. It is initialized to -1 since the minimum possible value is always non-negative, and any valid computed result will be greater than or equal to 0.\n\n- The solve() first checks for the base case where the range of indices is less than 2. If the range i >= j, it returns 0 since there are no triangles to be formed.\n\n- It further checks if the subproblem has already been solved by checking if dp[i][j] is not equal to -1. If the value is already computed, it returns the precomputed value.\n\n- If the subproblem has not been solved before, the function iterates over all possible indices k such that i <= k < j.\n\n- It then recursively calls the solve function on the two subproblems i-k and k+1-j and calculates the temporary answer by adding the two subproblems\' answers and the score of the current triangle formed by the vertices i-1, j, and k. The score of the triangle is calculated by multiplying the values at the three vertices.\n\n- Finally, it returns the minimum value of all possible temporary answers and stores it in the dp array.\n\n- solve() memoizes the results by storing the minimum value of each subproblem in the dp array. By storing the already computed results, it avoids the repeated computation of subproblems, reducing the time complexity of the algorithm.\n\n# Complexity\n- Time complexity: O(n^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n int dp[102][102];\n\n int solve(vector <int> &values, int i, int j)\n {\n if(i >= j)\n return 0;\n\n if(dp[i][j] != -1)\n return dp[i][j];\n\n int mini = INT_MAX;\n\n for(int k = i; k < j; k++)\n {\n int tempAns = solve(values, i, k) + solve(values, k+1, j) + values[i-1] * values[j] * values[k];\n mini = min(mini, tempAns);\n } \n\n return dp[i][j] = mini; \n }\n\n int minScoreTriangulation(vector<int>& values) \n {\n int n = values.size();\n memset(dp, -1, sizeof(dp));\n return solve(values, 1, n-1);\n }\n};\n``` | 3 | 0 | ['C++'] | 1 |
minimum-score-triangulation-of-polygon | Minimum Score Triangulation of Polygon similar to matrix chain multiplication problem | minimum-score-triangulation-of-polygon-s-xwwd | \nclass Solution {\npublic:\n int f(int i,int j,vector<int>& values,vector<vector<int>>&dp)\n {\n if(i==j) return 0;\n int mini=1e9;\n | riturajkumar7256 | NORMAL | 2022-07-29T08:13:51.596156+00:00 | 2022-10-13T14:42:55.675906+00:00 | 436 | false | ```\nclass Solution {\npublic:\n int f(int i,int j,vector<int>& values,vector<vector<int>>&dp)\n {\n if(i==j) return 0;\n int mini=1e9;\n if(dp[i][j]!=-1) return dp[i][j];\n \n for(int k=i;k<j;k++)\n {\n int steps=values[i-1]*values[k]*values[j]+f(i,k,values,dp)+f(k+1,j,values,dp);\n mini=min(mini,steps); \n }\n return dp[i][j]=mini;\n }\n int minScoreTriangulation(vector<int>& values) {\n int n=values.size();\n vector<vector<int>>dp(n,vector<int>(n,-1));\n return f(1,n-1,values,dp);\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'C'] | 1 |
minimum-score-triangulation-of-polygon | C++ Explained | MCM variation | c-explained-mcm-variation-by-bit_legion-y9cm | Because we need to check for every possible combination of sides, therefore, we can approach this question by MCM. \n\n\nclass Solution {\npublic:\n \n in | biT_Legion | NORMAL | 2021-06-15T03:58:41.602178+00:00 | 2021-06-15T03:58:41.602221+00:00 | 453 | false | Because we need to check for every possible combination of sides, therefore, we can approach this question by MCM. \n\n```\nclass Solution {\npublic:\n \n int dp[1005][1005];\n \n int MSTP(vector <int> &arr, int i, int j){\n if(i >= j)\n return 0;\n \n if(dp[i][j] != -1)\n return dp[i][j];\n \n int ans = INT_MAX;\n for(int k = i; k<j; k++){\n\n int left = MSTP(arr, i, k);\n int right = MSTP(arr, k+1, j);\n\t\t\t\t\t\t\t\t\t// cost of joining the two parts \n int count = left+right + arr[i-1]*arr[k]*arr[j];\n \n ans = min(ans, count);\n }\n return dp[i][j] = ans;\n }\n \n int minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n \n memset(dp, -1, sizeof(dp));\n \n return MSTP(values, 1, n-1);\n }\n};\n``` | 3 | 1 | ['Dynamic Programming', 'C'] | 0 |
minimum-score-triangulation-of-polygon | Java DP, easy to understand. Just few lines | java-dp-easy-to-understand-just-few-line-e01e | Given vertices [0, n-1]\uFF0Cchoose one of them between 0 & n-1, say vertice i. \n\nThe whole polygon could be splited into 3 parts,\n1. A triangle formed by 3 | ryan7887 | NORMAL | 2021-01-17T03:12:28.462055+00:00 | 2021-01-17T03:12:28.462081+00:00 | 140 | false | Given vertices [0, n-1]\uFF0Cchoose one of them between 0 & n-1, say vertice i. \n\nThe whole polygon could be splited into 3 parts,\n1. A triangle formed by 3 vertices 0, i, n-1\n2. A polygon formed by vertices [0, i]\n3. A polygon formed by vertices [i, n-1]\n\nNow the problem is transformed into "get the minimum value of sum( One triangle + Two sub problems)"\n~~~\nprivate int triangles(int[] A, int lo, int hi) {\n if (hi-lo+1<3) return 0; //less than 3 vertices\n\tint ans = Integer.MAX_VALUE;;\n for (int i=lo+1; i<hi; i++) {\n ans = Math.min(ans, A[lo]*A[i]*A[hi] + triangles(A, lo, i) + triangles(A, i, hi));\n }\n return ans;\n}\n\nreturn triangles(A, 0, A.length-1);\n~~~\n\nFor optimization, all you need to do is add cache into above logic. \n~~~\nclass Solution {\n int[][] memo;\n \n public int minScoreTriangulation(int[] A) {\n memo = new int[A.length][A.length];\n Arrays.stream(memo).forEach(x -> Arrays.fill(x, -1));\n return triangles(A, 0, A.length-1);\n }\n \n private int triangles(int[] A, int lo, int hi) {\n if (hi-lo+1<3) return 0; //less than 3 vertices\n if (memo[lo][hi]>=0) return memo[lo][hi];\n int ans = Integer.MAX_VALUE;;\n for (int i=lo+1; i<hi; i++) {\n ans = Math.min(ans, A[lo]*A[i]*A[hi] + triangles(A, lo, i) + triangles(A, i, hi));\n }\n memo[lo][hi]=ans;\n return ans;\n }\n}\n~~~\n\n | 3 | 0 | [] | 0 |
minimum-score-triangulation-of-polygon | [PYTHON 3] DP | Iterative Solution | python-3-dp-iterative-solution-by-mohame-yf9y | \nclass Solution:\n def minScoreTriangulation(self, A: List[int]) -> int:\n n = len(A)\n dp = [[0 for i in range(n)] for j in range(n)]\n | mohamedimranps | NORMAL | 2020-06-07T15:37:37.032948+00:00 | 2020-06-07T15:37:37.033003+00:00 | 547 | false | ```\nclass Solution:\n def minScoreTriangulation(self, A: List[int]) -> int:\n n = len(A)\n dp = [[0 for i in range(n)] for j in range(n)]\n for k in range(2 , n):\n for i in range(n - k):\n start , end = i , i + k\n dp[start][end] = float("inf")\n for j in range(start + 1 , end):\n dp[start][end] = min(dp[start][end] , dp[start][j] + dp[j][end] + A[start] * A[end] * A[j])\n return dp[0][-1]\n``` | 3 | 0 | ['Dynamic Programming', 'Iterator', 'Python3'] | 1 |
minimum-score-triangulation-of-polygon | Ruby 100%. Explanation. Image. | ruby-100-explanation-image-by-user9697n-8mcd | Leetcode: 1039. Minimum Score Triangulation of Polygon.\n\nThis is a recursive function. To calculate a minimum split into triangle pices we select one edge bet | user9697n | NORMAL | 2020-04-09T17:59:10.804437+00:00 | 2020-04-09T17:59:10.804493+00:00 | 276 | false | #### Leetcode: 1039. Minimum Score Triangulation of Polygon.\n\nThis is a recursive function. To calculate a minimum split into triangle pices we select one **edge** between to vertex (let it be an edge between first and last vertex). And draw all possible triangles with this **edge**. It will be **N-2** triangles, because there are **N-2** vertexes beside first and last one. In this funcion we split the poigon in three sub poligons: **prev poligon**, triange that used this edge, and **future poligion**. \nFor eaxmple if we have 5 vertexes with indices 0, 1, 2, 3, 4, it\'s could be **prev poligon: [0,1,2]**, **triange: [0,2,4]**, **future poligion: [2,3,4]**. Each of this poligons could be send in recursive call, or calculated inplace if it has 3 sides.\n\n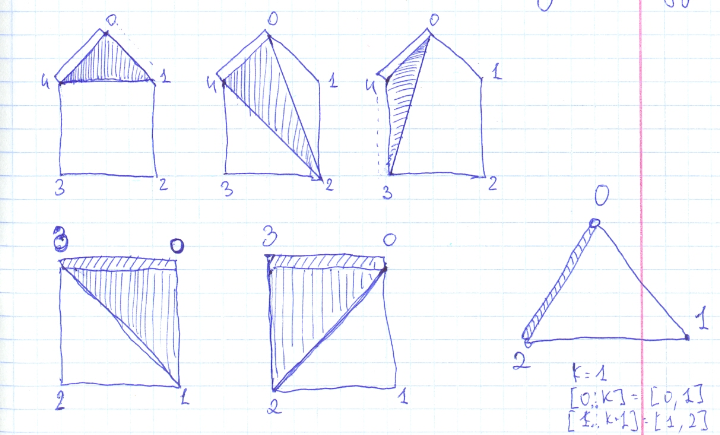\n\n\n```Ruby\n# 1039. Minimum Score Triangulation of Polygon\n# https://leetcode.com/problems/minimum-score-triangulation-of-polygon/\n# Runtime: 84 ms, faster than 100.00% of Ruby online submissions for Minimum Score Triangulation of Polygon.\n# Memory Usage: 9.5 MB, less than 100.00% of Ruby online submissions for Minimum Score Triangulation of Polygon.\n# @param {Integer[]} a\n# @return {Integer}\ndef min_score_triangulation(a)\n @h = Array.new(a.size).map{Array.new(a.size)}\n @a = a\n rec(0,a.size-1)\n \nend\n\ndef rec(first,last)\n size = last - first + 1\n return 0 if 3 > size\n return @a[first+0]*@a[first+1]*@a[first+2] if 3 == size\n return @h[first][last] if @h[first][last]\n min = 1_000_000\n finish = last\n (first+1...finish).each do |k|\n prev_val = rec(first,k)\n cur_val = @a[first] * @a[k] * @a[finish]\n future_val = rec(k,finish)\n total = prev_val+cur_val+future_val\n min = total if total < min\n end\n @h[first][last] = min\n return min\n\nend\n``` | 3 | 0 | ['Ruby'] | 0 |
minimum-score-triangulation-of-polygon | Two Solutions in Python 3 (DP) (Top Down and Bottom Up) | two-solutions-in-python-3-dp-top-down-an-ypgb | DP - Top Down - With Recursion (Slower): (seven lines)\n\nclass Solution:\n def minScoreTriangulation(self, A: List[int]) -> int:\n \tSP, LA = [[0]*50 for | junaidmansuri | NORMAL | 2019-09-27T04:25:42.333075+00:00 | 2019-09-27T05:43:46.093662+00:00 | 1,014 | false | _DP - Top Down - With Recursion (Slower):_ (seven lines)\n```\nclass Solution:\n def minScoreTriangulation(self, A: List[int]) -> int:\n \tSP, LA = [[0]*50 for i in range(50)], len(A)\n \tdef MinPoly(a,b):\n \t\tL, m = b - a + 1, math.inf; \n \t\tif SP[a][b] != 0 or L < 3: return SP[a][b]\n \t\tfor i in range(a+1,b): m = min(m, A[a]*A[i]*A[b] + MinPoly(a,i) + MinPoly(i,b))\n \t\tSP[a][b] = m; return SP[a][b]\n \treturn MinPoly(0,LA-1)\n\t\t\n\t\t\n```\n_DP - Bottom Up - Without Recursion (Faster):_ (six lines)\n```\nclass Solution:\n def minScoreTriangulation(self, A: List[int]) -> int:\n \tSP, L = [[0]*50 for _ in range(50)], len(A)\n \tfor i in range(2,L):\n \t\tfor j in range(L-i):\n \t\t\ts, e, SP[s][e] = j, j + i, math.inf\n \t\t\tfor k in range(s+1,e): SP[s][e] = min(SP[s][e], A[s]*A[k]*A[e] + SP[s][k] + SP[k][e])\n \treturn SP[0][L-1]\n\t\t\n\t\t\n- Junaid Mansuri\n(LeetCode ID)@hotmail.com | 3 | 1 | ['Dynamic Programming', 'Python', 'Python3'] | 0 |
minimum-score-triangulation-of-polygon | java dp | java-dp-by-sumonon-7qx6 | It is always the matter of modeling.\nIn this problem, the key step is that when we take out any triangle from a polygen, the remain parts of the polygen can be | sumonon | NORMAL | 2019-08-06T14:00:06.819978+00:00 | 2019-08-06T14:00:06.820014+00:00 | 183 | false | It is always the matter of modeling.\nIn this problem, the key step is that when we take out any triangle from a polygen, the remain parts of the polygen can be split up to smaller polygen but faces same kind of problems, which constructs subproblems here.\n\nfrom this point, a top-down version that is easier to understand is generated: \nwhen we pick up a triangle, we can just use the same recursion function to both the left and the right part of the rest polygen. And we do this for every triangle to see which one (together with its subproblems) is the smallest.\n\n\nThe bottom-up version may be harder to get over. First we have to compute the product of every triangle that is formed by continous three numbers. This is the base situation for dp. \nAfter that, we gradually increase the current searched polygen size in every loop, and for every current polygen, we compute every product for two edge vertices and one node within. and the dp value for current polygen is the min of these products. here we construct the dp for size k.\nBy this means, we can reach polygen from size 3 to n, and get the min for size n, which is the answer.\n\n\n```\nclass Solution {\n public int minScoreTriangulation(int[] A) {\n int n = A.length, j;\n int[][] dp = new int[n][n];\n for (int d=2;d<n;d++){\n for (int i=0; i+d<n; i++){\n j = i+d;\n dp[i][j] = Integer.MAX_VALUE;\n for (int k=i+1;k<j;k++){\n dp[i][j] = Math.min(dp[i][j], A[i]*A[j]*A[k]+\n dp[i][k]+dp[k][j]);\n }\n }\n }\n return dp[0][n-1];\n }\n}\n``` | 3 | 0 | [] | 0 |
minimum-score-triangulation-of-polygon | Java code inspired by votrubac's solution. | java-code-inspired-by-votrubacs-solution-3xjg | This below solution is just an implementation in java of an awesome solution by votrubac here : https://leetcode.com/problems/minimum-score-triangulation-of-pol | successinvain | NORMAL | 2019-05-07T16:01:13.138001+00:00 | 2019-05-07T16:01:13.138040+00:00 | 303 | false | This below solution is just an implementation in java of an awesome solution by votrubac here : https://leetcode.com/problems/minimum-score-triangulation-of-polygon/discuss/286753/C%2B%2B-with-picture\n```\n//Algorithm:\n//pick a side with i, j vertices, pick an anchor (k) to form a triangle.\n// move the anchor (k) along the remaining vertices and compute\n//a) the current triangle formed by i, j, k\n//b) score for the remaining polygons that could be 1 or 2. 1 where there are no points in between j and k or where there are no points in between i and k.\n//c) memoize the score for polygons.\n\nclass Solution {\n private int[][] dp;\n public int minScoreTriangulation(int[] A) {\n dp = new int[A.length][A.length];\n return minScoreHelper( A, 0, A.length - 1 );\n }\n \n private int minScoreHelper( int[] A, int i, int j ) {\n if ( j == i + 1 ) return 0; // meaning no triangle.\n if ( dp[i][j] != 0 ) return dp[i][j];\n int res = Integer.MAX_VALUE;\n for ( int k = i + 1; k < j; k++ ) {\n int thisTriangleScore = A[i]*A[k]*A[j];\n int leftPolygonScore = minScoreHelper( A, i, k );\n int rightPolygonScore = minScoreHelper( A, k, j );\n res = Math.min( res, thisTriangleScore + leftPolygonScore + rightPolygonScore );\n }\n dp[i][j] = res;\n return res;\n }\n \n}\n``` | 3 | 0 | [] | 0 |
minimum-score-triangulation-of-polygon | [Java] Memoization (Top Down) | java-memoization-top-down-by-ztztzt8888-wq9b | \n\tpublic static int minScoreTriangulation(int[] arr) {\n int len = arr.length;\n int[][] lookup = new int[len][len];\n return minScoreFro | ztztzt8888 | NORMAL | 2019-05-05T04:29:35.256556+00:00 | 2019-05-05T04:29:35.256660+00:00 | 427 | false | ```\n\tpublic static int minScoreTriangulation(int[] arr) {\n int len = arr.length;\n int[][] lookup = new int[len][len];\n return minScoreFromTo(arr, 0, len - 1, lookup);\n }\n\n private static int minScoreFromTo(int[] arr, int from, int to, int[][] lookup) {\n if (from >= to || from + 1 == to) {\n return 0;\n } else {\n if (lookup[from][to] > 0) {\n return lookup[from][to];\n }\n }\n\n int min = Integer.MAX_VALUE;\n\n for (int mid = from + 1; mid < to; mid++) {\n min = Math.min(min, arr[mid]*arr[from]*arr[to]\n + minScoreFromTo(arr, from, mid, lookup) + minScoreFromTo(arr, mid, to, lookup));\n }\n\n lookup[from][to] = min;\n\n return min;\n }\n``` | 3 | 0 | [] | 1 |
minimum-score-triangulation-of-polygon | DP Java | dp-java-by-poorvank-n2e0 | Try all possible combinations.\n\n\nLet Minimum Cost of triangulation of vertices from i to j be min(i, j)\nIf j <= i + 2 Then\n min(i, j) = 0\nElse\n min(i, | poorvank | NORMAL | 2019-05-05T04:03:09.938442+00:00 | 2019-05-05T04:03:09.938487+00:00 | 443 | false | Try all possible combinations.\n\n```\nLet Minimum Cost of triangulation of vertices from i to j be min(i, j)\nIf j <= i + 2 Then\n min(i, j) = 0\nElse\n min(i, j) = Math.min { min(i, k) + min(k, j) + (A[i]*A[j]*A[k]) } i+1<=k<=j-1\n```\n\n```\npublic int minScoreTriangulation(int[] A) {\n int n = A.length;\n if (n < 3) {\n return 0;\n }\n int[][] dp = new int[n][n];\n for (int gap = 0; gap < n; gap++) {\n for (int i = 0, j = gap; j < n; i++, j++) {\n if (j>=i+2) {\n dp[i][j] = Integer.MAX_VALUE;\n for (int k = i+1; k < j; k++) {\n int val = (A[i]*A[j]*A[k])+dp[i][k]+dp[k][j];\n dp[i][j] =Math.min(dp[i][j],val);\n }\n }\n }\n }\n return dp[0][n-1];\n }\n``` | 3 | 1 | [] | 0 |
minimum-score-triangulation-of-polygon | Minimum Score Triangulation of Polygon | minimum-score-triangulation-of-polygon-b-1cxi | Code | Ansh1707 | NORMAL | 2025-03-27T20:12:15.123729+00:00 | 2025-03-27T20:12:15.123729+00:00 | 48 | false |
# Code
```python []
class Solution(object):
def minScoreTriangulation(self, values):
"""
:type values: List[int]
:rtype: int
"""
n = len(values)
dp = [[0] * n for _ in range(n)]
for length in range(2, n):
for i in range(n - length):
j = i + length
dp[i][j] = float('inf')
for k in range(i + 1, j):
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + values[i] * values[k] * values[j])
return dp[0][n-1]
``` | 2 | 0 | ['Array', 'Dynamic Programming', 'Python'] | 0 |
minimum-score-triangulation-of-polygon | Simple C++ Solution | simple-c-solution-by-divyanshu_singh_cs-r3x9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Divyanshu_singh_cs | NORMAL | 2023-07-27T11:10:04.165512+00:00 | 2023-07-27T11:10:04.165535+00:00 | 350 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int solve(vector<int>& values,int i,int j,vector<vector<int>> &dp){\n if(i+1==j){\n return 0;\n }\n if(dp[i][j]!=-1){\n return dp[i][j];\n }\n int ans = INT_MAX;\n for(int k=i+1;k<j;k++){\n ans=min(ans,values[i]*values[j]*values[k]+solve(values,i,k,dp)+ solve(values,k,j,dp));\n }\n dp[i][j]=ans;\n return dp[i][j];\n }\n int minScoreTriangulation(vector<int>& values) {\n int n=values.size();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n return solve(values,0,n-1,dp);\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
minimum-score-triangulation-of-polygon | Recursive, Memoization, Tabulation Approach Java | recursive-memoization-tabulation-approac-elfk | Complexity\n- Time complexity: O(n^3) for tabulation\n\n- Space complexity: O(n^2)\n\n# Code\n\nclass Solution {\n public int minScoreTriangulation(int[] val | athravmehta06 | NORMAL | 2023-04-25T16:34:45.000220+00:00 | 2023-04-25T16:34:45.000276+00:00 | 1,238 | false | # Complexity\n- Time complexity: $$O(n^3)$$ for tabulation\n\n- Space complexity: $$O(n^2)$$\n\n# Code\n```\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int n = values.length;\n // return helperRec(values, 0, n - 1);\n\n int[][] dp = new int[n + 1][n + 1];\n for(int[] row : dp) Arrays.fill(row, -1);\n return helperMem(values, 0, n - 1, dp);\n\n // return helperTab(values);\n }\n \n // RECURSIVE APPROACH\n public int helperRec(int[] values, int i, int j){\n if(i + 1 == j) return 0; // if there are only two nodes then a triangle cannot be obtained.\n int ans = Integer.MAX_VALUE;\n for(int k = i + 1; k < j; k++){\n ans = Math.min(ans, values[i] * values[j] * values[k] + helperRec(values, i, k) + helperRec(values, k, j));\n }\n return ans;\n }\n // MEMOIZATION APPROACH\n public int helperMem(int[] values, int i, int j, int[][] dp){\n if(i + 1 == j) return 0; // if there are only two nodes then a triangle cannot be obtained.\n if(dp[i][j] != -1) return dp[i][j];\n int ans = Integer.MAX_VALUE;\n for(int k = i + 1; k < j; k++){\n ans = Math.min(ans, values[i] * values[j] * values[k] + helperMem(values, i, k, dp) + helperMem(values, k, j, dp));\n }\n return dp[i][j] = ans;\n }\n // TABULATION APPROACH\n public int helperTab(int[] values){\n int x = values.length;\n int[][] dp = new int[x + 1][x + 1];\n\n for(int i = x - 1; i >= 0; i--){\n for(int j = i + 2; j < x; j++){ // i + 2 se isliye start kra h because minimum 3 nodes honi chaiye to 1 and 2 pe triangle nhi bnega\n int ans = Integer.MAX_VALUE;\n for(int k = i + 1; k < j; k++){\n ans = Math.min(ans, values[i] * values[j] * values[k] + dp[i][k] + dp[k][j]);\n }\n dp[i][j] = ans;\n }\n }\n return dp[0][x - 1];\n }\n}\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Java'] | 0 |
minimum-score-triangulation-of-polygon | Minimum Score Triangulation of Polygon(Matrix Multiplication) - Java sol | minimum-score-triangulation-of-polygonma-5lt9 | \n\n# Code\n\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int N = values.length;\n int[][] dp = new int[N][N];\n | whopiyushanand | NORMAL | 2023-02-20T15:18:07.674776+00:00 | 2023-02-20T15:18:07.674819+00:00 | 1,334 | false | \n\n# Code\n```\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int N = values.length;\n int[][] dp = new int[N][N];\n for(int len=2; len<N; len++){\n for(int row=0, col=len; row<N-len; row++, col++){\n dp[row][col] = Integer.MAX_VALUE;\n for(int k=row+1; k<col; k++){\n dp[row][col] = Math.min(dp[row][col], dp[row][k] + dp[k][col] + values[row]*values[k]*values[col]);\n }\n }\n }\n return dp[0][N-1];\n }\n}\n``` | 2 | 0 | ['Dynamic Programming', 'Java'] | 0 |
minimum-score-triangulation-of-polygon | Matrix Chain Multiplication || DP || Memoization | matrix-chain-multiplication-dp-memoizati-w775 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | _shiv_70 | NORMAL | 2023-01-11T11:22:46.154953+00:00 | 2023-01-11T11:23:20.709345+00:00 | 1,320 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(N^3)\n\n- Space complexity:\nO(N*N)+O(N)\n\n# Code\n```\nclass Solution {\npublic:\nint fun(int i,int j,vector<int>& arr, vector<vector<int>> &dp){\n if(i==j) return 0;\n int mini=1e9;\n if(dp[i][j]!=-1) return dp[i][j];\n for(int k=i;k<j;k++){\n int steps=arr[i-1]*arr[k]*arr[j]+fun(i,k,arr,dp)+fun(k+1,j,arr,dp);\n mini=min(mini,steps);\n }\n return dp[i][j]=mini;\n}\n int minScoreTriangulation(vector<int>& arr) {\n int n=arr.size();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n return fun(1,n-1,arr,dp);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Memoization', 'C++'] | 1 |
minimum-score-triangulation-of-polygon | c++ | easy | short | c-easy-short-by-venomhighs7-l6d4 | \n\n# Code\n\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& A) {\n int n = A.size();\n vector<vector<int>> dp(n, vector<int | venomhighs7 | NORMAL | 2022-11-02T04:06:09.419134+00:00 | 2022-11-02T04:06:09.419167+00:00 | 2,143 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& A) {\n int n = A.size();\n vector<vector<int>> dp(n, vector<int>(n));\n for (int j = 2; j < n; ++j) {\n for (int i = j - 2; i >= 0; --i) {\n dp[i][j] = INT_MAX;\n for (int k = i + 1; k < j; ++k)\n dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[j] * A[k]);\n }\n }\n return dp[0][n - 1];\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
minimum-score-triangulation-of-polygon | Java Solutions Recursion,Memoization and Bottom up DP | java-solutions-recursionmemoization-and-naatj | Simple Recusion\n\nclass Solution {\npublic int minScoreTriangulation(int[] values) {\n int n=values.length-1;\n return solve(values,0,n);\n }\ | jaswinder_97 | NORMAL | 2022-10-21T03:50:03.535557+00:00 | 2022-10-21T03:50:03.535602+00:00 | 555 | false | Simple Recusion\n```\nclass Solution {\npublic int minScoreTriangulation(int[] values) {\n int n=values.length-1;\n return solve(values,0,n);\n }\n private int solve(int[] values,int i,int j){\n if(i+1==j) return 0;\n int ans=Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++){\n ans=Math.min(ans,values[i]*values[j]*values[k]+solve(values,i,k)+solve(values,k,j));\n }\n return ans;\n }\n}\n```\nRecursion using Memoization\n\n```\npublic int minScoreTriangulation(int[] values) {\n int n=values.length-1;\n int[][] dp=new int[n+1][n+1];\n for(int i=0;i<=n;i++){\n for(int j=0;j<=n;j++) dp[i][j]=-1;\n }\n return solveMem(values,0,n,dp);\n }\n private int solveMem(int[] values,int i,int j,int[][] dp){\n if(i+1==j) return 0;\n if(dp[i][j]!=-1) return dp[i][j];\n int ans=Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++){\n ans=Math.min(ans,values[i]*values[j]*values[k]+solve(values,i,k,dp)+solve(values,k,j,dp));\n }\n dp[i][j]=ans;\n return dp[i][j];\n }\n```\nBottom up DP\n\n```\npublic int minScoreTriangulation(int[] values) {\n int n=values.length;\n int[][] dp=new int[n][n];\n for(int len=2;len<=n;len++){\n for(int i=0;i<n-len;i++){\n int j=i+len;\n int ans=Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++){\n ans=Math.min(ans,values[i]*values[j]*values[k]+dp[i][k]+dp[k][j]);\n }\n dp[i][j]=ans;\n }\n }\n return dp[0][n-1];\n }\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization'] | 0 |
minimum-score-triangulation-of-polygon | DP Solution in Javascript (Recursion + Dp Memo + Dp tabulation) | dp-solution-in-javascript-recursion-dp-m-9dps | 1. Recursion\n\n\nfunction solveRec(value, i, j) {\n // base case\n if (i + 1 === j) return 0;\n let ans = Number.MAX_VALUE;\n for (let k = i + 1; k < j; k+ | vivekdogra | NORMAL | 2022-08-03T19:29:51.409852+00:00 | 2022-08-03T19:29:51.409891+00:00 | 226 | false | **1. Recursion**\n\n````\nfunction solveRec(value, i, j) {\n // base case\n if (i + 1 === j) return 0;\n let ans = Number.MAX_VALUE;\n for (let k = i + 1; k < j; k++) {\n ans = Math.min(\n ans,\n value[i] * value[j] * value[k] +\n solveRec(value, i, k) +\n solveRec(value, k, j)\n );\n }\n return ans;\n}\nvar minScoreTriangulation = function (values) {\n let n = values.length;\n return solveRec(values, 0, n - 1);\n};\n````\n\n**2. Recursion + memoization (Top down approach)**\n\n````\nfunction solveMem(value, i, j, dp) {\n // base case\n if (i + 1 === j) return 0;\n if (dp[i][j] !== -1) return dp[i][j];\n let ans = Number.MAX_VALUE;\n for (let k = i + 1; k < j; k++) {\n ans = Math.min(\n ans,\n value[i] * value[j] * value[k] +\n solveMem(value, i, k, dp) +\n solveMem(value, k, j, dp)\n );\n }\n dp[i][j] = ans;\n return dp[i][j];\n}\nvar minScoreTriangulation = function (values) {\n let n = values.length;\n let dp = new Array(n).fill(-1).map(() => Array(n).fill(-1));\n return solveMem(values, 0, n - 1, dp);\n};\n````\n\n**3. Bottom up approach (Tabulation)**\n\n```\nfunction solveTab(value) {\n // base case\n let n = value.length;\n let dp = new Array(n).fill(0).map(() => Array(n).fill(0));\n for (let i = n - 1; i >= 0; i--) {\n for (let j = i + 2; j < n; j++) {\n let ans = Number.MAX_VALUE;\n for (let k = i + 1; k < j; k++) {\n ans = Math.min(\n ans,\n value[i] * value[j] * value[k] + dp[i][k] + dp[k][j]\n );\n }\n dp[i][j] = ans;\n }\n }\n\n return dp[0][n - 1];\n}\nvar minScoreTriangulation = function (values) {\n let n = values.length;\n return solveTab(values);\n};\n\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'JavaScript'] | 2 |
minimum-score-triangulation-of-polygon | C++ || Memoization || Tabulation | c-memoization-tabulation-by-tejasdarwai-d40f | Memoization\n\nint solve(vector<int> &values, int i, int j, vector<vector<int>> &dp){\n if(i+1==j){\n return 0;\n }\n if(dp[i][j | TejasDarwai | NORMAL | 2022-07-21T09:08:44.811899+00:00 | 2022-07-21T09:08:44.811955+00:00 | 228 | false | Memoization\n```\nint solve(vector<int> &values, int i, int j, vector<vector<int>> &dp){\n if(i+1==j){\n return 0;\n }\n if(dp[i][j]!=-1){\n return dp[i][j];\n }\n int ans=INT_MAX;\n for(int k=i+1; k<j; k++){\n ans = min(ans, (values[i]*values[j]*values[k])+solve(values, i, k, dp)+solve(values, k,j, dp));\n }\n return dp[i][j] = ans;\n }\n int minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n vector<vector<int>> dp(n+1, vector<int>(n+1, -1));\n return solve(values, 0, n-1, dp);\n }\n```\n\nTabulation\n```\nint minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n vector<vector<int>> dp(n, vector<int>(n, 0));\n for(int i=n-1; i>=0; i--){\n for(int j=i+2; j<n; j++){\n int ans = INT_MAX;\n for(int k=i+1; k<j; k++){\n ans = min(ans, values[i]*values[j]*values[k] + dp[i][k] + dp[k][j]);\n }\n dp[i][j] = ans;\n }\n }\n return dp[0][n-1];\n }\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C'] | 0 |
minimum-score-triangulation-of-polygon | 1039. Minimum Score Triangulation of Polygon | 1039-minimum-score-triangulation-of-poly-j9pe | // This is nothing but matrix chain multiplication .\n\n\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int N = values.length; | Ardhendu_init_ | NORMAL | 2022-07-14T08:11:58.140476+00:00 | 2022-07-14T08:13:54.934841+00:00 | 424 | false | **// This is nothing but matrix chain multiplication .**\n\n```\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int N = values.length;\n int dp [][] = new int [N][N];\n for(int i = 0 ; i < N ; i++){\n for(int j = 0 ; j < N ; j++){\n dp[i][j]= -1;\n }\n }\n return helper(values , 1 , N-1, dp);\n }\n static int helper(int arr[], int i , int j , int dp [][] ){\n if(i >= j ){\n return 0;\n }\n \n if(dp[i][j] != -1 ){\n return dp[i][j];\n }\n int min = Integer.MAX_VALUE;\n for(int k = i ; k <= j-1 ; k++){\n int temp = helper(arr , i , k, dp)+helper(arr , k+1 , j, dp)+ (arr[i-1]*arr[k]*arr[j]);\n min = Math.min(min , temp);\n }\n return dp[i][j]=min;\n }\n}\n``` | 2 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 0 |
minimum-score-triangulation-of-polygon | Matrix Chain Multiplication | Tabulation | matrix-chain-multiplication-tabulation-b-g471 | Same as Matrix Chain Multiplication \n\nclass Solution {\npublic:\n// Time Complexity -> O(N^3) \n// Space Complexity -> O(N^2)\n int minScoreTriangulation(v | _limitlesspragma | NORMAL | 2022-05-30T17:06:06.950631+00:00 | 2022-05-30T17:06:06.950853+00:00 | 156 | false | # ***Same as Matrix Chain Multiplication*** \n```\nclass Solution {\npublic:\n// Time Complexity -> O(N^3) \n// Space Complexity -> O(N^2)\n int minScoreTriangulation(vector<int>& arr) {\n int n=arr.size();\n \n vector<vector<int>> dp(n, vector<int>(n,0));\n \n for(int i=n-2;i>=1;i--){\n for(int j=i+1;j<n;j++){\n dp[i][j]=INT_MAX;\n for(int k=i;k<j;k++){\n dp[i][j] = min(dp[i][j],arr[i-1]*arr[k]*arr[j] + dp[i][k] + dp[k+1][j]);\n }\n }\n }\n return dp[1][n-1];\n }\n};\n``` | 2 | 0 | ['Dynamic Programming'] | 0 |
minimum-score-triangulation-of-polygon | Simple Python DFS with Explanation (12 lines) | simple-python-dfs-with-explanation-12-li-1me5 | the intuition here is that l and r are ALWAYS going to be in a triange\nwe just need to figure out the third point in the triangle\npossible third points are al | jaredlwong | NORMAL | 2022-02-15T04:35:53.269740+00:00 | 2022-02-15T04:35:53.269789+00:00 | 276 | false | the intuition here is that l and r are ALWAYS going to be in a triange\nwe just need to figure out the third point in the triangle\npossible third points are all indices between l and r\n\nonce you draw the lines between l, r and some i between l and r\nyou have two subproblems and one triangle\ntwo subproblems are l to i, and i to r\none triange is the triangle with indices l,r,i\n\nin the case where i=l+1, or i=r-1 we have two established sides of the triangle\nwhen i=l+1 we already have (l,i), (r,l)\nwhen i=r-1 we already have (r-1,r), (r,l)\n \nin the case where l+1 < i < r-1\nimagine the third index is somewhere in the middle of the polygon\nyou can imagine drawing two new lines (l,i) and (i,r)\nthen you have the two subproblems\n\n```\nfrom functools import cache\nclass Solution:\n def minScoreTriangulation(self, values: List[int]) -> int:\n @cache\n def dfs(l, r):\n if r-l+1 < 3:\n return 0\n m = float(\'inf\')\n for i in range(l+1, r):\n m = min(m, dfs(l, i) + dfs(i, r) + values[l]*values[r]*values[i])\n return m\n return dfs(0, len(values)-1)\n``` | 2 | 0 | ['Depth-First Search', 'Python'] | 0 |
minimum-score-triangulation-of-polygon | Aditya Verma approach - recursion memoization - JAVA - | aditya-verma-approach-recursion-memoizat-wkt7 | \nclass Solution {\n int[][] t = new int[51][51];\n public int minScoreTriangulation(int[] values) \n {\n for(int i=0;i<51;i++)\n {\n | siddharth_78 | NORMAL | 2021-08-07T05:24:11.831041+00:00 | 2022-03-31T01:52:56.876975+00:00 | 235 | false | \nclass Solution {\n int[][] t = new int[51][51];\n public int minScoreTriangulation(int[] values) \n {\n for(int i=0;i<51;i++)\n {\n for(int j=0;j<51;j++)\n {\n t[i][j] = -1;\n }\n }\n \n return solve(values,0,values.length - 1);\n }\n \n int solve(int[] values, int i, int j)\n {\n if(i >= j)\n {\n return 0;\n }\n \n if(i+1 == j)\n {\n return 0;\n }\n \n if(t[i][j] != -1)\n {\n return t[i][j];\n }\n \n int min = Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++)\n {\n int temp_ans = solve(values,i,k) + solve(values,k,j) + (values[i] * values[k] * values[j]);\n \n min = Math.min(min,temp_ans);\n }\n \n t[i][j] = min;\n return min;\n }\n} | 2 | 5 | [] | 1 |
minimum-score-triangulation-of-polygon | C++ | dynamic programming | Using gap strategy | c-dynamic-programming-using-gap-strategy-5coj | \nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n vector<vector<int>> dp(n,vector<int>( | armangupta48 | NORMAL | 2021-05-02T23:08:43.751967+00:00 | 2021-05-02T23:08:43.752006+00:00 | 352 | false | ```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n vector<vector<int>> dp(n,vector<int>(n,0));\n for(int g = 0;g<n;g++)\n {\n for(int i = 0,j = g;j<n;i++,j++)\n {\n if(g==0 || g==1)\n {\n dp[i][j] = 0;\n }\n else if(g == 2)\n {\n dp[i][j] = values[i]*values[i+1]*values[j];\n }\n else\n {\n int ans = INT_MAX;\n for(int k = i+1;k<j;k++)\n {\n int trai = values[i]*values[j]*values[k];\n int pleft = dp[i][k];\n int pright = dp[k][j];\n int total = trai+pleft+pright;\n if(total<ans)\n ans = total;\n }\n dp[i][j]=ans;\n }\n }\n }\n return dp[0][n-1];\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'C', 'C++'] | 1 |
minimum-score-triangulation-of-polygon | Java DP | java-dp-by-vardhamank93-vc0p | \nclass Solution {\n public int minScoreTriangulation(int[] A) {\n int[][] dp = new int[A.length][A.length];\n \n for(int g = 0; g < dp. | vardhamank93 | NORMAL | 2020-11-27T09:21:49.638301+00:00 | 2020-11-27T09:21:49.638335+00:00 | 273 | false | ```\nclass Solution {\n public int minScoreTriangulation(int[] A) {\n int[][] dp = new int[A.length][A.length];\n \n for(int g = 0; g < dp.length; g++){\n for(int i = 0,j = g; j < dp[0].length; i++,j++){\n if(g == 0){\n dp[i][j] = 0; // trivial case as no triangle can be formed by 1 points\n }else if(g == 1){\n dp[i][j] = 0; // Same trivial\n }else if(g == 2){\n dp[i][j] = A[i]*A[i+1]*A[i+2]; // Also Trivial as we only have 3 points\n }else{\n int min = Integer.MAX_VALUE;\n for(int k = i+1; k < j; k++){\n int tri = A[i]*A[j]*A[k]; // calclating triangle\n int left = dp[i][k]; // calculating left part\n int right = dp[k][j]; // calculating right part\n \n int total = tri + left + right;\n if(total < min){\n min = total;\n }\n }\n dp[i][j] = min;\n }\n }\n }\n \n return dp[0][A.length - 1];\n }\n}\n``` | 2 | 0 | ['Dynamic Programming', 'Java'] | 0 |
minimum-score-triangulation-of-polygon | 4 ms C++ solution beats 100% of all submissions, top down approach | 4-ms-c-solution-beats-100-of-all-submiss-2p7c | \nint dp[55][55];\nint minScore(vector<int>& A,int n,int i,int j){\n \n if(dp[i][j] != -1) return dp[i][j];\n if(j == 0) j = n-1;\n int res = INT_ | vishalnsit | NORMAL | 2020-06-07T06:06:30.480075+00:00 | 2020-06-07T06:06:30.480122+00:00 | 346 | false | ```\nint dp[55][55];\nint minScore(vector<int>& A,int n,int i,int j){\n \n if(dp[i][j] != -1) return dp[i][j];\n if(j == 0) j = n-1;\n int res = INT_MAX;\n bool loopRun = false;\n for(int k=i+1;k<j;k++){\n loopRun = true;\n int temp = (A[i]*A[j]*A[k]) + minScore(A,n,i,k) + minScore(A,n,k,j);\n if(res > temp) res = temp;\n }\n if(!loopRun) return dp[i][j] = 0;\n return dp[i][j] = res;\n}\n\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& A) {\n int n = A.size();\n for(int i=0;i<=n;i++){\n for(int j=0;j<=n;j++){\n dp[i][j] = -1;\n }\n }\n return minScore(A,n,0,0);\n \n }\n};\n```\n\nPlease upvote if it helps!! | 2 | 0 | ['Dynamic Programming', 'Memoization', 'C'] | 0 |
minimum-score-triangulation-of-polygon | C++ bottom up and memoization solution with explanation | c-bottom-up-and-memoization-solution-wit-5e2d | \n/*\n /*\n https://leetcode.com/problems/minimum-score-triangulation-of-polygon/submissions/\n \n The idea is to take each pair of vertices possibl | cryptx_ | NORMAL | 2020-01-06T06:20:47.449195+00:00 | 2020-01-06T06:40:04.621874+00:00 | 442 | false | ```\n/*\n /*\n https://leetcode.com/problems/minimum-score-triangulation-of-polygon/submissions/\n \n The idea is to take each pair of vertices possible and then with those fixed, find \n a vertex in between such that the polygon on left and right side of it are of min score.\n \n*/\n\nclass Solution {\npublic:\n // TC: O(N^3)\n // SC: O(N^2)\n int minScoreTriangulationTabular(vector<int>& arr) {\n if(arr.empty())\n return 0;\n \n const int N = arr.size();\n // dp(i, j): min triangulation score of polygon with vertices \n // starting from i..j and there is an edge between i and j\n vector<vector<int> > dp(N, vector<int>(N, 0));\n \n // start swiping each vertex using index \'i\' and use the index\n // \'j\' to keep the other end fixed, this i and j edge will then be evaluated\n // with every other vertex in between them by making a triangle with it and checking\n // the score of left and right side of remaining polygon.\n // first vertex\n for(int i = 2; i < N; i++) {\n // second vertex\n for(int j = i - 2; j >= 0; j--) {\n // pick the third vertex in between the endpoints\n for(int k = j + 1; k < i; k++) {\n int curr_area = arr[i] * arr[k] * arr[j]; \n dp[j][i] = min(dp[j][i] == 0 ? INT_MAX : dp[j][i],\n dp[j][k] + curr_area + dp[k][i]);\n }\n }\n }\n return dp[0][N-1];\n }\n \n // using memoization\n // TC: O(N ^ 3)\n // SC: O(N ^ 2)\n int minScoreTriangulationRec(vector<vector<int> >& dp, \n vector<int>& arr, int i, int j) {\n \n if(dp[i][j] == 0)\n // pick a vertex in between and evaulate the triangulation score\n for(int k = i + 1; k < j; k++) {\n int curr_score = arr[i] * arr[k] * arr[j];\n \n dp[i][j] = min(dp[i][j] == 0 ? INT_MAX : dp[i][j],\n minScoreTriangulationRec(dp, arr, i, k) + // left polygon\n curr_score + // curret triangle with (i, k, j) vertices\n minScoreTriangulationRec(dp, arr, k, j)); // right polygon\n } \n \n return dp[i][j];\n }\n \n int minScoreTriangulationRecDriver(vector<int>& arr) {\n if(arr.empty())\n return 0;\n const int N = arr.size();\n vector<vector<int> > dp(N, vector<int>(N, 0));\n \n return minScoreTriangulationRec(dp, arr, 0, N-1); \n }\n \n int minScoreTriangulation(vector<int>& A) {\n //return minScoreTriangulationTabular(A);\n return minScoreTriangulationRecDriver(A);\n }\n};\n``` | 2 | 0 | [] | 0 |
minimum-score-triangulation-of-polygon | c++ memorized DFS solution in O(n^3) complexity | c-memorized-dfs-solution-in-on3-complexi-928h | \nclass Solution {\npublic:\n vector<vector<int>> dp;\n int memorizedDFS(vector<int>& A, int start, int end){\n if(start + 1 == end)\n r | mintyiqingchen | NORMAL | 2019-09-11T08:29:44.244421+00:00 | 2019-10-07T15:57:00.231528+00:00 | 331 | false | ```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n int memorizedDFS(vector<int>& A, int start, int end){\n if(start + 1 == end)\n return 0;\n if(dp[start][end] != -1)\n return dp[start][end];\n \n if(start + 2 == end){\n dp[start][end] = A[start] * A[start+1] * A[end];\n return dp[start][end];\n }\n int j = start + 1;\n int res = INT_MAX;\n while(j != end){\n int a = memorizedDFS(A, start, j) + memorizedDFS(A, j, end) + A[start] * A[j] * A[end];\n res = min(res, a);\n j ++;\n }\n dp[start][end] = res;\n return res;\n }\n int minScoreTriangulation(vector<int>& A) {\n dp = vector<vector<int>>(A.size(), vector<int>(A.size(), -1));\n int res = INT_MAX;\n return memorizedDFS(A, 0, A.size()-1);\n }\n};\n``` | 2 | 0 | [] | 1 |
minimum-score-triangulation-of-polygon | [Java] DP | java-dp-by-peritan-xbg1 | dp[i][j] = min cost for A[i..j]\nbase case: if j - i + 1 == 3 (length == 3), dp[i][j] = A[i]A[i+1]A[i+2]\ndp[i][j] = dp[i][k] + dp[k][j] + A[i]A[j]A[k]\n\nin bo | peritan | NORMAL | 2019-05-05T04:05:37.249794+00:00 | 2019-05-05T05:12:57.973013+00:00 | 237 | false | dp[i][j] = min cost for A[i..j]\nbase case: if j - i + 1 == 3 (length == 3), dp[i][j] = A[i]*A[i+1]*A[i+2]\ndp[i][j] = dp[i][k] + dp[k][j] + A[i]*A[j]*A[k]\n\nin bottom up approach\none key point is we should constructure the answer start from base case\nyou can draw a graph, start from side = 4, when you separate the graph into 2 triangle, you have to know the side = 3 answer beforehand\nsame from side = 5, when you separate the graph into 1 triangle and one side = 4 shape, you have to know the side = 4 answers beforehand\nso we start from side = 3 to side = n, to construct the answer\n\n```\n public int minScoreTriangulation(int[] A) {\n int n = A.length;\n int[][] dp = new int[n][n];\n for (int side = 3; side <= n; side++) {\n for (int i = 0, j = side-1; j < n; i++, j++) {\n if (j - i + 1 == 3) {\n dp[i][j] = A[i] * A[i+1] * A[i+2];\n } else {\n int min = Integer.MAX_VALUE;\n for (int k = i+1; k < j; k++)\n min = Math.min(min, dp[i][k] + dp[k][j] + A[i] * A[j] * A[k]);\n dp[i][j] = min;\n }\n }\n }\n return dp[0][n-1];\n }\n``` | 2 | 1 | [] | 0 |
minimum-score-triangulation-of-polygon | Marvelous memoization :) | marvelous-memoization-by-pradyumnaprahas-uamp | Intuition\n Describe your first thoughts on how to solve this problem. \nFirst come up with a backtracking solution trying all possible combinations then later | PradyumnaPrahas2_2 | NORMAL | 2024-12-03T15:00:33.192661+00:00 | 2024-12-03T15:00:33.192688+00:00 | 25 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst come up with a backtracking solution trying all possible combinations then later optimize using 2d array to avoid repeatitive calculations.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCome up with a backtracking soln, take a pen and paper and draw the tree diagram like this.\n\nEg arr=[1,2,3,4,5] answer=38\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N^3)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N^2)\n# Code\n```java []\nclass Solution {\n public int matrixChainMul(int[] values,int start,int end,int[][] dp){\n if(start+1==end){\n return 0;\n }\n if(dp[start][end]!=0){\n return dp[start][end];\n }\n int res=Integer.MAX_VALUE;\n for(int i=start+1;i<end;i++){\n int left=matrixChainMul(values,start,i,dp);\n int right=matrixChainMul(values,i,end,dp);\n int cur=values[start]*values[i]*values[end];\n res=Math.min(res,left+right+cur);\n }\n dp[start][end]=res;\n return res;\n }\n public int minScoreTriangulation(int[] values) {\n int[][] dp=new int[values.length][values.length];\n return matrixChainMul(values,0,values.length-1,dp);\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Backtracking', 'Java'] | 0 |
minimum-score-triangulation-of-polygon | Best C++ Solution | 0ms, beats 100% | DP | best-c-solution-0ms-beats-100-dp-by-prat-wol9 | Code\ncpp []\nclass Solution {\npublic:\n int solve(vector<int>& v, int i, int j, vector<vector<int>>& dp) {\n if(i+1 == j) return 0;\n\n if(dp | prateek_sen | NORMAL | 2024-10-29T04:34:44.454784+00:00 | 2024-10-29T04:34:44.454809+00:00 | 26 | false | # Code\n```cpp []\nclass Solution {\npublic:\n int solve(vector<int>& v, int i, int j, vector<vector<int>>& dp) {\n if(i+1 == j) return 0;\n\n if(dp[i][j] != -1) return dp[i][j];\n\n int ans = INT_MAX;\n for(int k=i+1; k<j; k++) {\n ans = min(ans, v[i]*v[j]*v[k] + solve(v, k, j, dp) + solve(v, i, k, dp));\n }\n dp[i][j] = ans;\n return dp[i][j];\n }\n\n int minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n vector<vector<int>> dp(n, vector<int>(n, -1));\n int ans = solve(values, 0, n-1, dp);\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-score-triangulation-of-polygon | ✅ One Line Solution | one-line-solution-by-mikposp-khqb | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n \n\nTime complexity: O(n^2). Space complexity: O( | MikPosp | NORMAL | 2024-03-03T11:00:34.523894+00:00 | 2024-03-03T11:00:34.523928+00:00 | 113 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n<!-- -->\n\nTime complexity: $$O(n^2)$$. Space complexity: $$O(n^2)$$\n```\nclass Solution:\n def minScoreTriangulation(self, v: List[int]) -> int:\n return (f:=cache(lambda i,j:j-i>1 and min(f(i,k)+v[i]*v[k]*v[j]+f(k,j) for k in range(i+1,j))))(0,len(v)-1)\n```\n\n(Disclaimer 2: all code above is just a product of fantasy, it is not claimed to be pure impeccable oneliners - please, remind about drawbacks only if you know how to make it better. PEP 8 is violated intentionally) | 1 | 0 | ['Array', 'Dynamic Programming', 'Recursion', 'Memoization', 'Python', 'Python3'] | 0 |
minimum-score-triangulation-of-polygon | Easy solution || using Recursion or Memoization or Tabulation || | easy-solution-using-recursion-or-memoiza-k1av | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | zephyrus17 | NORMAL | 2024-02-03T05:23:26.060221+00:00 | 2024-02-03T05:23:26.060247+00:00 | 365 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint solve(vector<int>& val,int i,int j){\n // base case\n if(i+1==j) return 0;\n\n // for choices for k we have use the loop from i+1 to j-1 choices\n int ans=INT_MAX;\n for(int k=i+1;k<j;k++){\n ans=min(ans,val[i]*val[k]*val[j]+solve(val,i,k)+solve(val,k,j));\n }\n return ans;\n}\n// solve using memoisation \nint solveMemo(vector<int>& val,int i,int j,vector<vector<int>>&dp){\n // base case\n if(i+1==j) return 0;\n if(dp[i][j]!=-1) return dp[i][j];\n // for choices for k we have use the loop from i+1 to j-1 choices\n int ans=INT_MAX;\n for(int k=i+1;k<j;k++){\n ans=min(ans,val[i]*val[k]*val[j]+solveMemo(val,i,k,dp)+solveMemo(val,k,j,dp));\n }\n return dp[i][j]=ans;\n}\n// using tabulation method\nint solveTab(vector<int>& val){\n int n=val.size();\n vector<vector<int>>dp(n,vector<int>(n,0));\n for(int i=n-1;i>=0;i--){\n for(int j=i+2;j<n;j++){\n \n int ans=INT_MAX;\n for(int k=i+1;k<j;k++){\n ans=min(ans,val[i]*val[k]*val[j]+dp[i][k]+dp[k][j]);\n }\n dp[i][j]=ans;\n }\n }\n return dp[0][n-1];\n}\n int minScoreTriangulation(vector<int>& values) {\n // this pattern is called mcm pattern\n // return solve (values,0,values.size()-1);\n \n // int n=values.size();\n // vector<vector<int>>dp(n,vector<int>(n,-1));\n // return solveMemo(values,0,n-1,dp);\n\n // using tabulation method\n return solveTab(values);\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-score-triangulation-of-polygon | Python DP Solution, Faster than 94% | python-dp-solution-faster-than-94-by-div-7pf9 | \n Describe your first thoughts on how to solve this problem. \n\n# Approach\nWe can solve it with Dynamic programming. DP(pos1,pos2) is the minimum cost of tri | Divyanshuyyadav | NORMAL | 2023-09-29T14:00:41.254545+00:00 | 2023-09-29T14:00:41.254578+00:00 | 100 | false | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe can solve it with Dynamic programming. DP(pos1,pos2) is the minimum cost of triangulation of vertices from pos1 to pos2. if (pos2-pos1<2) return 0 means its not possible to get any triangle. Else, we do DP(pos1,pos2)= min(DP(pos1,pos)+ DP(pos,pos2) + Cost(pos1,pos2,pos))) where Cost(pos1,pos2,k) is the cost of choose triangle with vertices (pos1,pos2,pos) and pos go from pos1+1 to pos2-1\n\n\n# Complexity\n- Time complexity: O(n^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minScoreTriangulation(self, values: List[int]) -> int:\n @cache\n def dp(pos1: int, pos2: int) -> int:\n if pos2 - pos1 <= 1:\n return 0\n ans = inf\n for pos in range(pos1 + 1, pos2):\n ans = min(ans, dp(pos1, pos) + dp(pos, pos2) + values[pos1] * values[pos2] * values[pos])\n return ans\n\n return dp(0, len(values) - 1)\n``` | 1 | 0 | ['Python3'] | 0 |
minimum-score-triangulation-of-polygon | dynamic programming - Problem Pattern | Matrix Chain Multiplication || | dynamic-programming-problem-pattern-matr-nazc | Intuition\n Describe your first thoughts on how to solve this problem. \nThis is the child problem of MCM .\n\nProblem Description:\nThe problem involves findin | imsej_al | NORMAL | 2023-08-30T11:39:07.925249+00:00 | 2023-08-30T11:39:07.925278+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is the child problem of MCM .\n\nProblem Description:\nThe problem involves finding the minimum score needed to triangulate a convex polygon formed by a sequence of vertices, where each vertex has an associated value. Triangulation refers to partitioning the polygon into non-overlapping triangles by connecting the vertices with edges.\n\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n^3)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n^2)\n\n# Code\n```\nclass Solution {\n int t[51][51];\n int solve(vector<int>& values,int i,int j){\n if(i >= j) return 0;\n int mn = INT_MAX;\n if(t[i][j] != -1) return t[i][j];\n for(int k = i; k <=j-1; k++){\n int temp = solve(values,i,k) + solve(values,k+1,j) +( values[i-1] * values[k] * values[j]);\n if(temp < mn) mn = temp;\n }\n return t[i][j] = mn;\n }\npublic:\n int minScoreTriangulation(vector<int>& values) {\n memset(t,-1,sizeof(t));\n int j = values.size()-1;\n return solve(values,1,j);\n }\n};\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'Memoization', 'C++'] | 0 |
minimum-score-triangulation-of-polygon | C++ || DP solution || Tabulation method | c-dp-solution-tabulation-method-by-hey_h-2ont | Intuition\nMatrix Chain Multiplication [M C M] . DP solution using tabulation method.\n\n\n\n# Complexity\n- Time complexity:O(n^3)\n Add your time complexity h | Hey_Himanshu | NORMAL | 2023-06-06T14:08:54.595550+00:00 | 2023-06-06T14:08:54.595590+00:00 | 14 | false | # Intuition\nMatrix Chain Multiplication [M C M] . DP solution using tabulation method.\n\n\n\n# Complexity\n- Time complexity:O(n^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\n#include<bits/stdc++.h>\nusing namespace std ;\nclass Solution {\npublic:\n\n \nint solveTab(vector<int> &values){\n int n = values.size();\n vector<vector<int>> dp(n, vector<int> (n,0)) ;\n\n for(int i = n-1 ; i>=0 ; i--){\n for(int j = i+2 ; j<n ; j++){\n int ans =INT_MAX;\n\n for(int k = i+1;k<j ;k++){\n ans = min(ans ,values[i]*values[j]*values[k] + dp[i][k] + dp[k][j] ) ;\n }\n dp[i][j] = ans ;\n \n } \n }\n return dp[0][n-1];\n\n}\n\nint minScoreTriangulation(vector<int> &values)\n{\n return solveTab(values);\n}\n\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Matrix', 'C++'] | 0 |
minimum-score-triangulation-of-polygon | Recursive Triangulation with Dynamic Programming | recursive-triangulation-with-dynamic-pro-mio8 | Intuition\nWe have to recursively form every possible triangles \n\n# Approach\nWe select first index and last index as a base, and the function recursively fin | harsh_reality_ | NORMAL | 2023-06-03T13:16:27.477378+00:00 | 2023-06-03T13:16:27.477423+00:00 | 172 | false | # Intuition\nWe have to recursively form every possible triangles \n\n# Approach\nWe select first index and last index as a base, and the function recursively find the best possible third index\n\n# Complexity\n-Time complexity:\nO(n^3)\n\n-Space complexity:\nO(n^2) + O(n)\n\n# Recursive and Memoized Code \n```\nclass Solution {\n int f(vector<int> &nums, int i, int j, vector<vector<int>> &dp) {\n //if there is no vertex in between \'i\' and \'j\' \n //then no triangles will be formed between them\n if(i + 1 == j)\n return 0;\n \n if(dp[i][j] != -1)\n return dp[i][j];\n \n int mini = INT_MAX;\n //searching for \'k\' between \'i\' and \'j\'\n //so traversing from (i+1) to (j-1)\n for(int k=i+1; k<j; k++) {\n //recursively taking \'i\' and \'k\' as one base and fining third vertex between them\n //similar recursive call for \'k\' and \'j\'\n int score = (nums[i] * nums[j] * nums[k]) + f(nums, i, k, dp) + f(nums, k, j, dp);\n mini = min(mini, score);\n }\n return dp[i][j] = mini;\n }\npublic:\n int minScoreTriangulation(vector<int>& nums) {\n int n = nums.size();\n vector<vector<int>> dp(n+1, vector<int>(n+1, -1));\n \n //selecting the first vertex and last vertex as base and searching for third vertex\n return f(nums, 0, n-1, dp);\n\n }\n};\n```\n# Tabulated Code\n```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& nums) {\n int n = nums.size();\n vector<vector<int>> dp(n+1, vector<int>(n+1, 0));\n \n for(int i=n-1; i>=0; i--) {\n //j starts from (i+2) because there should be atleast one \n //vertex between them to form a traingle and\n //and that\'s why k starts from (i+1) till (j-1)\n for(int j=i+2; j<n; j++) {\n int mini = INT_MAX;\n for(int k=i+1; k<j; k++) {\n int score = (nums[i] * nums[j] * nums[k]) + dp[i][k] + dp[k][j];\n mini = min(mini, score);\n }\n dp[i][j] = mini;\n }\n }\n \n return dp[0][n-1];\n\n }\n};\n\n```\n\n | 1 | 0 | ['Divide and Conquer', 'Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 0 |
minimum-score-triangulation-of-polygon | Beats 100% | Java | Matrix Chain Multiplication | beats-100-java-matrix-chain-multiplicati-02s2 | \n# Complexity\n- Time complexity: n^2\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: n^2\n Add your space complexity here, e.g. O(n) \n\n# | PrashantNegi878 | NORMAL | 2023-04-29T07:38:18.382222+00:00 | 2023-04-29T07:46:15.572022+00:00 | 822 | false | \n# Complexity\n- Time complexity: n^2\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: n^2\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int[][] dp;\n public int minScoreTriangulation(int[] values) {\n int l=values.length;\n dp = new int[l][l];\n for(int[] i : dp) Arrays.fill(i,-1);\n return solve(values,1,l-1); \n }\n\n public int solve(int[] values, int i,int j)\n {\n if(i>=j) return 0;\n if(dp[i][j]!=-1) return dp[i][j];\n int min=Integer.MAX_VALUE;\n for(int k=i;k<j;k++)\n {\n int temp=solve(values,i,k)+solve(values,k+1,j)+\n values[i-1]*values[k]*values[j];\n min=Math.min(min,temp);\n }\n\n return dp[i][j]=min;\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Matrix', 'Java'] | 1 |
minimum-score-triangulation-of-polygon | python super easy dp top down | python-super-easy-dp-top-down-by-harrych-umb9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | harrychen1995 | NORMAL | 2023-01-24T16:01:14.352164+00:00 | 2023-01-24T16:05:58.425111+00:00 | 140 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minScoreTriangulation(self, values: List[int]) -> int:\n\n\n @functools.lru_cache(None)\n def dp(l, r):\n if r-l + 1 == 3:\n return values[l] * values[l+1] * values[l+2]\n if r-l + 1 < 3:\n return 0\n ans = float("inf")\n for i in range(l+1, r):\n ans = min(ans, values[l]*values[i]*values[r] + dp(l, i) + dp(i, r))\n return ans\n return dp(0, len(values)-1)\n\n``` | 1 | 0 | ['Python3'] | 0 |
minimum-score-triangulation-of-polygon | Just a runnable solution | just-a-runnable-solution-by-ssrlive-wh5y | Code\n\nimpl Solution {\n pub fn min_score_triangulation(values: Vec<i32>) -> i32 {\n let n = values.len();\n let mut dp = vec![vec![0; n]; n]; | ssrlive | NORMAL | 2023-01-11T08:00:54.041398+00:00 | 2023-01-11T08:00:54.041440+00:00 | 33 | false | # Code\n```\nimpl Solution {\n pub fn min_score_triangulation(values: Vec<i32>) -> i32 {\n let n = values.len();\n let mut dp = vec![vec![0; n]; n];\n for j in 2..n {\n for i in (0..j - 1).rev() {\n dp[i][j] = i32::MAX;\n for k in i + 1..j {\n dp[i][j] = dp[i][j].min(dp[i][k] + dp[k][j] + values[i] * values[j] * values[k]);\n }\n }\n }\n dp[0][n - 1]\n }\n}\n``` | 1 | 0 | ['Rust'] | 0 |
minimum-score-triangulation-of-polygon | EASY MCM + TABULATION C++ CODE | SHORT & BEATS 90% | easy-mcm-tabulation-c-code-short-beats-9-qj06 | \n\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n O(NNN)\n\n- Space complexity:\n Add your space complexity here, e.g. O(n) \n O(N* | anmolbtw | NORMAL | 2023-01-05T12:59:22.621818+00:00 | 2023-01-05T12:59:22.621864+00:00 | 147 | false | \n\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N*N*N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N*N)\n# Code\n```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& arr) {\n int N=arr.size();\n vector<vector<int>> dp(N,vector<int>(N,-1));\n \n for(int i=1;i<N;i++){\n dp[i][i]=0;\n }\n for(int i=N-1;i>=1;i--){\n for(int j=i+1;j<N;j++){\n int mini=INT_MAX;\n // partioning loop\n for(int k=i;k<=j-1;k++){\n int ans = dp[i][k]+ dp[k+1][j] + arr[i-1]*arr[k]*arr[j];\n mini = min(mini,ans);\n }\n dp[i][j] = mini;\n }\n }\n return dp[1][N-1];\n }\n};\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 0 |
minimum-score-triangulation-of-polygon | EASY MCM C++ IMPLEMENTATION | SHORT AND COMMENTED CODE | easy-mcm-c-implementation-short-and-comm-hex8 | Intuition\n Describe your first thoughts on how to solve this problem. \nJust basic MCM (Matrix chain multiplication) concept implementation.\n\n\n# Complexity\ | anmolbtw | NORMAL | 2023-01-05T12:52:57.979298+00:00 | 2023-01-05T12:52:57.979343+00:00 | 90 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust basic MCM (Matrix chain multiplication) concept implementation.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N*N*N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N*N) + O(N)\n# Code\n```\nclass Solution {\npublic:\n int lol(vector<int>& arr, int i, int j, vector<vector<int>>& dp){\n // base case\n if(i == j) return 0;\n\n if(dp[i][j]!=-1) return dp[i][j];\n\n int mini = INT_MAX;\n\n // MCM partitions\n for(int k = i; k<= j-1; k++){\n int ans = lol(arr,i,k,dp) + lol(arr,k+1,j,dp) + arr[i-1]*arr[k]*arr[j];\n mini = min(mini,ans);\n }\n return dp[i][j]=mini;\n }\n int minScoreTriangulation(vector<int>& arr) {\n int n=arr.size();\n int i=1;\n int j=n-1;\n vector<vector<int>> dp(n,vector<int>(n,-1));\n\n return lol(arr,i,j,dp);\n }\n};\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'C++'] | 0 |
minimum-score-triangulation-of-polygon | Python Simple DP Solution | Faster than 94% | python-simple-dp-solution-faster-than-94-348e | Approach\n Describe your approach to solving the problem. \nWe can solve it with Dynamic programming. DP(pos1,pos2) is the minimum cost of triangulation of vert | hemantdhamija | NORMAL | 2022-12-15T09:46:34.500333+00:00 | 2022-12-15T09:46:34.500375+00:00 | 236 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe can solve it with Dynamic programming. ```DP(pos1,pos2)``` is the minimum cost of triangulation of vertices from pos1 to pos2. ```if (pos2-pos1<2) return 0``` means its not possible to get any triangle. Else, we do ```DP(pos1,pos2)= min(DP(pos1,pos)+ DP(pos,pos2) + Cost(pos1,pos2,pos)))``` where ```Cost(pos1,pos2,k)``` is the cost of choose triangle with vertices ```(pos1,pos2,pos)``` and ```pos``` go from ```pos1+1``` to ```pos2-1```\n\n# Complexity\n- Time complexity: $$O(n^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minScoreTriangulation(self, values: List[int]) -> int:\n @cache\n def dp(pos1: int, pos2: int) -> int:\n if pos2 - pos1 <= 1:\n return 0\n ans = inf\n for pos in range(pos1 + 1, pos2):\n ans = min(ans, dp(pos1, pos) + dp(pos, pos2) + values[pos1] * values[pos2] * values[pos])\n return ans\n\n return dp(0, len(values) - 1)\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'Recursion', 'Python', 'Python3'] | 0 |
minimum-score-triangulation-of-polygon | Java || 3 approaches || Recursion, Memoization, Tabulation || Easy Understanding | java-3-approaches-recursion-memoization-xtrpv | ```\n//RECURSIVE SOLUTION\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int n = values.length;\n return recursion(valu | black_butler | NORMAL | 2022-09-13T17:21:37.083077+00:00 | 2022-09-13T17:21:37.083126+00:00 | 66 | false | ```\n//RECURSIVE SOLUTION\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int n = values.length;\n return recursion(values,0,n-1);\n }\n public int recursion(int[] v,int i,int j)\n {\n if(i+1==j) //if only two vertices are present\n return 0;\n int min = Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++) //we iterate from >i to <j\n {\n min = Math.min(min,v[i]*v[j]*v[k]+recursion(v,i,k)+recursion(v,k,j));\n }\n return min;\n }\n}\n//how do we figure out whether it is a 2D matrix or 1D matrix, check the number of variables changing \n//RECURSION => TABULATION\n\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int n = values.length;\n int[][] dp = new int[n][n];\n for(int[] row:dp)\n Arrays.fill(row,-1);\n return memoization(values,0,n-1,dp);\n }\n public int memoization(int[] v,int i,int j,int[][] dp)\n {\n if(i+1==j) //if only two vertices are present\n return 0;\n if(dp[i][j]!=-1)\n return dp[i][j];\n int min = Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++) //we iterate from >i to <j\n {\n min = Math.min(min,v[i]*v[j]*v[k]+memoization(v,i,k,dp)+memoization(v,k,j,dp));\n }\n dp[i][j]=min;\n return dp[i][j];\n }\n}\n\n//TABULATION - it is the exact opposite of Top Down approach(MEMOIZATION)\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n return tabulation(values);\n }\n public int tabulation(int[] v)\n { \n int n=v.length;\n int[][] dp = new int[n][n];\n //In Top-Down dp we were starting i,j with 0 and n-1 but in Bottom up we are doing a bit different we start i from n-1;\n for(int i=n-1;i>=0;i--)\n {\n for(int j=i+2;j<n;j++) \n//if we start j=i it will be a single pointer and wont form a triangle\n//if we start from j=i+1 it will meet the base condition in memoization and recursion and return 0 so we start from i+2 and iterate till n \n {\n int min = Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++) //we iterate from >i to <j\n {\n min = Math.min(min,(v[i]*v[j]*v[k]+dp[i][k]+dp[k][j]));\n }\n dp[i][j]=min; \n } \n }\n return dp[0][n-1]; //as it bottom up, it is the reverse of top down\n }\n} | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Java'] | 0 |
minimum-score-triangulation-of-polygon | python, dynamic programming solution with explanation | python-dynamic-programming-solution-with-hpl2 | dp[i][j] means min score get from values[i:j+1] -> closed interval[i, j]\ndp[i][j] = (1) + (2) + (3) =min(dp[i][k] + dp[k][j] + values[i] * values[k] * values[j | shun6096tw | NORMAL | 2022-08-26T10:01:06.541128+00:00 | 2022-08-27T08:02:24.049655+00:00 | 101 | false | ```dp[i][j]``` means min score get from ```values[i:j+1]``` -> closed interval```[i, j]```\n```dp[i][j] = (1) + (2) + (3) =min(dp[i][k] + dp[k][j] + values[i] * values[k] * values[j] for k in closed interval [i+1,j-1])```\n```\n j i\n --------------\n\t / \\ | \\\n / \\ (3) | \\\n / \\ | (1) \\\n \\ \\ | /\n\t\\ (2) \\ | /\n\t \\ \\ | /\n\t -------------- \n k\n```\neg. values=```[3,7,4,5,9]```\n<img src="https://latex.codecogs.com/svg.image?\\begin{bmatrix}&space;&&space;3&space;&&space;7&space;&&space;4&space;&&space;5&space;&&space;9&space;\\\\3&space;&&space;0&space;&&space;0&space;&&space;84&space;&&space;144&space;&&space;279&space;\\\\7&space;&&space;0&space;&&space;0&space;&&space;0&space;&&space;140&space;&&space;432&space;\\\\4&space;&&space;0&space;&&space;0&space;&&space;0&space;&&space;0&space;&&space;180&space;\\\\5&space;&&space;0&space;&&space;0&space;&&space;0&space;&&space;0&space;&&space;0&space;\\\\9&space;&&space;0&space;&&space;0&space;&&space;0&space;&&space;0&space;&&space;0&space;\\end{bmatrix}" />\n### iteration\ntc is ```O(len(value)**3)```, sc is ```O(len(value)**2)```\n``` python\nclass Solution:\n def minScoreTriangulation(self, values: List[int]) -> int:\n if len(values) == 3: return values[0] * values[1] * values[2]\n leng = len(values)\n dp = [[0]*leng for _ in range(leng)]\n for i in range(leng-3, -1, -1):\n for j in range(i, leng):\n for k in range(i+1, j):\n if dp[i][j] == 0:\n dp[i][j] = dp[i][k] + dp[k][j] + values[i] * values[k] * values[j]\n else:\n dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + values[i]*values[k]*values[j])\n return dp[0][leng-1]\n```\n\n### dfs\ntc is ```O(len(value)**3)```, sc is ```O(len(value)**2)```\n``` python\nmax_ = 2**31 - 1\nclass Solution:\n def minScoreTriangulation(self, values: List[int]) -> int:\n if len(values) == 3: return values[0] * values[1] * values[2]\n @cache\n def dfs(i, j):\n if j-i <= 1: return 0 # there is no triangle between neighbor\n ans = max_\n for k in range(i+1, j):\n ans = min(ans, dfs(i,k) + dfs(k,j) + values[i] * values[k] * values[j])\n return ans\n return dfs(0, len(values)-1)\n``` | 1 | 0 | ['Dynamic Programming', 'Python'] | 0 |
minimum-score-triangulation-of-polygon | C++ with Dynamic Programing | c-with-dynamic-programing-by-sroy04560-utz9 | \n### 8 ms, faster than 81.81%\n### 7.9 MB, less than 99.32% \n\nclass Solution {\npublic:\n //MCM memorization method\n // assign a matrix -1 initally\n | sroy04560 | NORMAL | 2022-08-15T20:37:44.493978+00:00 | 2022-08-15T20:37:44.494030+00:00 | 196 | false | ```\n### 8 ms, faster than 81.81%\n### 7.9 MB, less than 99.32% \n\nclass Solution {\npublic:\n //MCM memorization method\n // assign a matrix -1 initally\n //then we store value after check that t[i][j]!=-1\n int t[50][51];\n int solve(vector<int>& values,int i,int j ){\n if(i>=j)return 0;\n \n if(t[i][j]!=-1)return t[i][j];\n \n int mn=INT_MAX; \n \n for(int k=i;k<=j-1;k++){\n \n int temp=solve(values,i,k)+solve(values,k+1,j)+\n values[i-1]*values[k]*values[j];\n mn=min(mn,temp);\n \n }\n return t[i][j]=mn;\n }\n \n int minScoreTriangulation(vector<int>& values) {\n memset(t,-1,sizeof(t));\n return solve(values,1,values.size()-1);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization', 'C'] | 0 |
minimum-score-triangulation-of-polygon | C++ | TOP DOWN DP | BOTTOM UP DP | c-top-down-dp-bottom-up-dp-by-sharmaachi-jw5p | TOP DOWN APPROACH\nTime Complexity -> O(N)\nSpace Complexity -> O (N * N)\n\n\tclass Solution {\n\tpublic:\n \n int solveMem(vector &v, int i, int j, vect | sharmaachintya | NORMAL | 2022-07-18T10:56:18.575196+00:00 | 2022-07-18T10:56:18.575243+00:00 | 26 | false | **TOP DOWN APPROACH**\n*Time Complexity ->* O(N)\n*Space Complexity ->* O (N * N)\n\n\tclass Solution {\n\tpublic:\n \n int solveMem(vector<int> &v, int i, int j, vector<vector<int>> &dp)\n {\n // base case\n if (i+1 == j)\n return 0;\n \n if(dp[i][j] != -1)\n return dp[i][j];\n \n int ans = INT_MAX;\n for (int k=i+1;k<j;k++) // We can select any vertices between i+1 and j-1\n {\n ans = min(ans, v[i]*v[j]*v[k] + solveMem(v, i, k, dp) + solveMem(v, k, j, dp));\n }\n dp[i][j] = ans;\n return dp[i][j];\n }\n \n int minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n vector<vector<int>> dp(n, vector<int> (n, -1));\n return solveMem(values, 0, n-1, dp);\n\t\t}\n\t};\n\t\n**BOTTOM UP APPROACH**\n*Time Complexity ->* O(N * N * N)\n*Space Complexity ->* O(N * N)\n\n\tclass Solution {\n\tpublic:\n\t\tint solveTab(vector<int> &v)\n\t\t{\n\t\t\tint n = v.size();\n\t\t\tvector<vector<int>> dp (n, vector<int> (n, 0));\n\n\t\t\tint ans = INT_MAX;\n\n\t\t\tfor (int i=n-1;i>=0;i--)\n\t\t\t{\n\t\t\t\tfor (int j=i+2;j<n;j++)\n\t\t\t\t{\n\t\t\t\t\tint ans = INT_MAX;\n\t\t\t\t\tfor (int k=i+1;k<j;k++)\n\t\t\t\t\t{\n\t\t\t\t\t\tans = min (ans, v[i]*v[j]*v[k] + dp[i][k] + dp[k][j]);\n\t\t\t\t\t}\n\t\t\t\t\tdp[i][j] = ans;\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn dp[0][n-1];\n\t\t}\n\n\t\tint minScoreTriangulation(vector<int>& values) {\n\t\t\treturn solveTab(values);\n\t\t}\n\t}; | 1 | 0 | ['Dynamic Programming'] | 0 |
minimum-score-triangulation-of-polygon | Very Easy clean code | Variation of MCM | very-easy-clean-code-variation-of-mcm-by-hanc | If you have seen Balloon Burst and this problem, not able to find the solution .\nJust read the following pattern carefully .\n\nThese both are the child proble | AjayRajawat01 | NORMAL | 2022-07-15T05:52:14.380382+00:00 | 2022-07-15T05:52:14.380420+00:00 | 55 | false | If you have seen Balloon Burst and this problem, not able to find the solution .\nJust read the following pattern carefully .\n\nThese both are the child problem of MCM .\n\nIf you have seen Balloon Burst and this problem, not able to find the solution .\nJust read the following pattern carefully .\n\nThese both are the child problem of MCM .\n\n```\nclass Solution {\npublic:\n int dp[51][51];\n int solve(vector<int>& values, int i, int j){\n //base case\n if(i>=j) return 0;\n if(dp[i][j]!=-1) return dp[i][j];\n \n int ans = INT_MAX;\n for(int k = i; k<=j-1; k++){\n int temp = solve(values, i, k) + solve(values, k+1, j) + (values[i-1]*values[k]*values[j]) ;\n ans = min(ans,temp);\n }\n return dp[i][j] = ans;\n }\n int minScoreTriangulation(vector<int>& values) {\n memset(dp,-1,sizeof(dp));\n return solve(values, 1 , values.size()-1); \n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-score-triangulation-of-polygon | JAVA|| HARD TO UNDERSTAD CODE | java-hard-to-understad-code-by-ankit1104-1sww | class Solution {\n public int minScoreTriangulation(int[] arr) {\n int n=arr.length;\n int dp[][] = new int[101][101];\n for(int i=0;i<1 | ankit1104 | NORMAL | 2022-06-29T21:07:44.847938+00:00 | 2022-06-29T21:07:44.847970+00:00 | 52 | false | class Solution {\n public int minScoreTriangulation(int[] arr) {\n int n=arr.length;\n int dp[][] = new int[101][101];\n for(int i=0;i<101;i++){\n for(int j=0;j<101;j++){\n dp[i][j]=-1;\n }\n }\n return solve(arr,1,n-1,dp);\n \n }\n public int solve(int[] arr ,int i,int j,int[][]dp){\n if(i>=j){\n return 0;\n \n }\n if(dp[i][j]!=-1){\n return dp[i][j];\n \n }\n int mn= Integer.MAX_VALUE;\n for(int k=i;k<j;k++){\n int tempans = solve(arr,i,k,dp)+solve(arr,k+1,j,dp)+arr[i-1]*arr[k]*arr[j];\n mn=Math.min(mn,tempans);\n }\n dp[i][j]=mn;\n return dp[i][j];\n }\n} | 1 | 0 | [] | 0 |
minimum-score-triangulation-of-polygon | C++✅ || Simple || Memoization code | c-simple-memoization-code-by-prinzeop-xw0c | \nclass Solution {\nprivate:\n\tint helper(vector<int> &nums, int i, int j, vector<vector<int>> &dp) {\n\t\tif (j - i <= 1) return 0; // no triangle\n\t\tif (dp | casperZz | NORMAL | 2022-06-17T18:14:34.978945+00:00 | 2022-06-17T18:14:34.978986+00:00 | 101 | false | ```\nclass Solution {\nprivate:\n\tint helper(vector<int> &nums, int i, int j, vector<vector<int>> &dp) {\n\t\tif (j - i <= 1) return 0; // no triangle\n\t\tif (dp[i][j] != -1) return dp[i][j];\n\t\tint mini = 1e9;\n\t\tfor (int ind = i + 1; ind < j; ++ind) {\n\t\t\tint cost = nums[i] * nums[ind] * nums[j] + helper(nums, i, ind, dp) + helper(nums, ind, j, dp);\n\t\t\tmini = min(mini, cost);\n\t\t}\n\t\treturn dp[i][j] = mini;\n\t}\npublic:\n int minScoreTriangulation(vector<int>& nums) {\n\t\tint n = nums.size();\n\t\tvector<vector<int>> dp(n + 1, vector<int>(n + 1, -1));\n\t\treturn helper(nums, 0, n - 1, dp);\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
minimum-score-triangulation-of-polygon | JavaScript Recursive: 60% time, 46% space | javascript-recursive-60-time-46-space-by-5udp | \nvar minScoreTriangulation = function(values) {\n let dp = Array(values.length).fill().map((i) => Array(values.length).fill(0));\n function dfs(i, j) {\n | hqz3 | NORMAL | 2022-05-29T23:30:04.992116+00:00 | 2022-05-29T23:30:04.992148+00:00 | 126 | false | ```\nvar minScoreTriangulation = function(values) {\n let dp = Array(values.length).fill().map((i) => Array(values.length).fill(0));\n function dfs(i, j) {\n if (dp[i][j]) return dp[i][j];\n if (j - i < 2) return 0;\n let min = Infinity;\n // k forms a triangle with i and j, thus bisecting the array into two parts\n // These two parts become two subproblems that can be solved recursively\n for (let k = i + 1; k < j; k++) {\n let sum = values[i] * values[j] * values[k] + dfs(i, k) + dfs(k, j);\n min = Math.min(min, sum);\n }\n return dp[i][j] = min;\n }\n return dfs(0, values.length - 1);\n};\n``` | 1 | 0 | ['JavaScript'] | 1 |
minimum-score-triangulation-of-polygon | Matrix Chain Multiplication || Easy || C++ || Memoization | matrix-chain-multiplication-easy-c-memoi-0r5v | \nclass Solution {\npublic:\n \n int dp[51][51];\n \n int solve(vector<int>&values, int i, int j)\n {\n if(i>=j)\n return 0;\n | i_m_harsh_shah | NORMAL | 2022-05-28T12:28:38.572971+00:00 | 2022-05-28T12:28:38.573018+00:00 | 130 | false | ```\nclass Solution {\npublic:\n \n int dp[51][51];\n \n int solve(vector<int>&values, int i, int j)\n {\n if(i>=j)\n return 0;\n if(dp[i][j]!=-1)\n return dp[i][j];\n \n int ans = INT_MAX;\n \n for(int k=i;k<=j-1;k++)\n {\n int temp = solve(values,i,k) + solve(values,k+1,j) + values[i-1]*values[j]*values[k];\n \n ans = min(ans,temp);\n }\n dp[i][j] = ans;\n return dp[i][j];\n }\n \n int minScoreTriangulation(vector<int>& values) {\n \n int n = values.size();\n \n int i = 1;\n int j = n-1;\n memset(dp,-1,sizeof(dp));\n return solve(values,i,j);\n \n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 0 |
minimum-score-triangulation-of-polygon | Clean and concise MCM code || Recursion + Memorization || C++ | clean-and-concise-mcm-code-recursion-mem-692n | \nclass Solution {\nprivate:\n int solve(int st,int en,vector<int> &arr,vector<vector<int>> &dp){\n if(st+1 == en) return 0;\n if(dp[st][en] != | _Pinocchio | NORMAL | 2022-05-19T16:09:56.224890+00:00 | 2022-05-19T16:09:56.224934+00:00 | 143 | false | ```\nclass Solution {\nprivate:\n int solve(int st,int en,vector<int> &arr,vector<vector<int>> &dp){\n if(st+1 == en) return 0;\n if(dp[st][en] != -1) return dp[st][en];\n \n int ans = 1e9;\n \n for(int cut=st+1;cut<en;cut++){\n int left = solve(st,cut,arr,dp);\n int right = solve(cut,en,arr,dp);\n int curr = arr[st] * arr[cut] * arr[en];\n \n int curr_res = left + curr + right;\n \n ans = min(ans,curr_res);\n }\n \n return dp[st][en] = ans;\n }\npublic:\n int minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n vector<vector<int>> dp(n,vector<int> (n,-1));\n return solve(0,n-1,values,dp);\n }\n};\n``` | 1 | 0 | ['Recursion', 'Memoization', 'C', 'C++'] | 0 |
minimum-score-triangulation-of-polygon | PYTHON SOL || RECURSION + MEMO || EXPLAINED || WITH PICTURES || | python-sol-recursion-memo-explained-with-yfwz | EXPLAINED\n\nWe need to make n-2 triangles -> For this we need to remove n -3 triangles from polygon\n\nNow a polygon with side say 6 can have multiple ways to | reaper_27 | NORMAL | 2022-05-13T13:03:56.810263+00:00 | 2022-05-13T13:03:56.810294+00:00 | 172 | false | # EXPLAINED\n```\nWe need to make n-2 triangles -> For this we need to remove n -3 triangles from polygon\n\nNow a polygon with side say 6 can have multiple ways to remove triangle ( multiple triangle)\n\nSo here comes DP\nWe try each traingle ony by one\n\n```\n\n\n\n\n\n\n\n\n# CODE\n```\nclass Solution:\n def recursion(self,start,end):\n if start >= end :\n return 0\n \n if self.dp[start][end] != -1 : return self.dp[start][end]\n\n best = float(\'inf\')\n \n for mid in range(start,end):\n tmp = self.recursion(start,mid) + self.recursion(mid+1,end) + \\\n self.values[start-1]*self.values[mid]*self.values[end]\n if tmp < best: best = tmp\n \n self.dp[start][end] = best\n return best\n \n def minScoreTriangulation(self, values: List[int]) -> int:\n n = len(values)\n self.dp = [[-1 for i in range(n)] for j in range(n)]\n self.values = values\n return self.recursion(1,n-1)\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Python', 'Python3'] | 1 |
minimum-score-triangulation-of-polygon | Tabulation || Dynamic Programming | tabulation-dynamic-programming-by-devta1-kj56 | This problem seeks knowledge of Matrix chain multiplication which uses 1 unique pattern of DP that is GAP Strategy, for visualising the problem you need to draw | devta108 | NORMAL | 2022-04-23T10:24:05.742083+00:00 | 2022-04-23T10:25:33.673968+00:00 | 229 | false | This problem seeks knowledge of ***Matrix chain multiplication*** which uses 1 unique pattern of DP that is **GAP Strategy**, for visualising the problem you need to draw all the possible **triangulation** of given polygon, which will be easier if you know about ***catalan numbers*** and it\'s application.\nThen this solution will make sense.\n```\nclass Solution {\n public int minScoreTriangulation(int[] values) {\n int len = values.length;\n int[][] dp = new int[len][len];\n for(int gap = 2;gap<len;gap++){\n \n for(int i=0,j=gap;j<len;i++,j++){\n if(gap==2) dp[i][j] = values[i]*values[i+1]*values[i+2];\n else{\n int min = Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++){\n int base = values[i]*values[j]*values[k];\n int above = dp[i][k];\n int down = dp[k][j];\n int total = base+above+down;\n if(total<min) min = total;\n }\n dp[i][j] = min;\n }\n }\n }\n return dp[0][len-1];\n }\n}\n```\n\nHappy coding, this problem is very intutive and infuses lot of concept at a time, code is not hard but it\'s intution is hard to think,\nthere are problems in leetcode which counts as medium though their solution is above 100 lines of code, they are medium coz they are implementaion based, and this problem is intution based that\'s why it is hard to crack in first go.\nHappy coding\uD83D\uDE0A\uD83D\uDE4F | 1 | 0 | ['Dynamic Programming', 'Java'] | 0 |
minimum-score-triangulation-of-polygon | C++, top-down recursive | c-top-down-recursive-by-cx3129-ikuz | \n\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& values)\n {\n int n=values.size();\n \n vector<vector<int>> ca | cx3129 | NORMAL | 2022-04-21T05:16:39.115354+00:00 | 2022-04-21T05:17:36.797004+00:00 | 117 | false | ```\n\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& values)\n {\n int n=values.size();\n \n vector<vector<int>> cache(n,vector<int>(n,-1));\n return calculate(values, 0, n - 1, cache);\n }\n\n int calculate(vector<int>& values, int from, int to,vector<vector<int>>& cache)\n {\n if (to - from < 2) return 0;\n if (to - from == 2) return values[from] * values[from + 1] * values[from + 2];\n \n if(cache[from][to]>=0) return cache[from][to];\n\n int v1 = values[from];\n int v2 = values[to];\n\n int minProd = INT_MAX;\n\n for (int k = from + 1; k < to; ++k)\n {\n int curProd = v1 * v2 * values[k];\n \n int p1 = calculate(values, from, k, cache);\n int p2 = calculate(values, k, to, cache);\n\n int prod = curProd + p1 + p2;\n \n minProd = min(minProd, prod);\n }\n \n cache[from][to]=minProd;\n return minProd;\n }\n};\n``` | 1 | 0 | [] | 1 |
minimum-score-triangulation-of-polygon | TypeScript/JavaScript Dynamic Programming Solution | typescriptjavascript-dynamic-programming-xljo | \nconst minScoreTriangulation = (values: number[]): number => {\n const dp = new Array(values.length + 1)\n .fill(0)\n .map(() => new Array(values.length | the-technomancer | NORMAL | 2022-04-10T08:18:07.981493+00:00 | 2022-04-10T08:18:07.981531+00:00 | 110 | false | ```\nconst minScoreTriangulation = (values: number[]): number => {\n const dp = new Array(values.length + 1)\n .fill(0)\n .map(() => new Array(values.length + 1).fill(null));\n\n return minScoreTriangulationHelper(values, dp, 0, values.length - 1);\n};\n\nconst minScoreTriangulationHelper = (\n values: number[],\n dp: number[][],\n row: number,\n col: number\n): number => {\n if (col - row <= 1) return 0;\n\n if (dp[row][col] !== null) return dp[row][col];\n\n dp[row][col] = Number.MAX_VALUE;\n\n for (let i = row + 1; i < col; i++) {\n dp[row][col] = Math.min(\n dp[row][col],\n minScoreTriangulationHelper(values, dp, row, i) +\n values[row] * values[i] * values[col] +\n minScoreTriangulationHelper(values, dp, i, col)\n );\n }\n\n return dp[row][col];\n};\n``` | 1 | 0 | ['Dynamic Programming', 'TypeScript', 'JavaScript'] | 0 |
minimum-score-triangulation-of-polygon | c++ || DP || memoization | c-dp-memoization-by-jyotirmayjain_27-qrym | \nclass Solution {\npublic:\n int dp[60][60];\n int mcm(vector<int>&v,int i,int j)\n {\n if(dp[i][j]!=-1)\n return dp[i][j];\n | jyotirmayjain_27 | NORMAL | 2022-04-01T08:09:48.795188+00:00 | 2022-04-01T08:09:48.795221+00:00 | 106 | false | ```\nclass Solution {\npublic:\n int dp[60][60];\n int mcm(vector<int>&v,int i,int j)\n {\n if(dp[i][j]!=-1)\n return dp[i][j];\n int ans=INT_MAX;\n for(int k=i+1;k<j;k++)\n {\n int temp=v[i]*v[k]*v[j]+mcm(v,i,k)+mcm(v,k,j);\n // cout<<temp<<" " << i << " " << j << endl;\n if(ans>temp)\n ans=temp;\n }\n if(ans==INT_MAX)\n return dp[i][j]= 0;\n return dp[i][j]= ans;\n }\n \n int minScoreTriangulation(vector<int>& values) {\n memset(dp,-1,sizeof dp);\n return mcm(values,0,values.size()-1);\n \n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization'] | 0 |
minimum-score-triangulation-of-polygon | PYTHON solution Memoization DP | python-solution-memoization-dp-by-raghav-ub5y | \t#MEMOIZATION\t\n\t\tclass Solution:\n\t\t\tdef minScoreTriangulation(self, arr: List[int]) -> int:\n\t\t\t\tN=len(arr)\n\t\t\t\tdp=[[-1](N+1) for i in range(N | RaghavGupta22 | NORMAL | 2022-02-22T06:26:38.170682+00:00 | 2022-02-22T06:26:38.170725+00:00 | 245 | false | \t#MEMOIZATION\t\n\t\tclass Solution:\n\t\t\tdef minScoreTriangulation(self, arr: List[int]) -> int:\n\t\t\t\tN=len(arr)\n\t\t\t\tdp=[[-1]*(N+1) for i in range(N+1)]\n\t\t\t\tdef solve(i,j):\n\t\t\t\t\tif i>=j:\n\t\t\t\t\t\treturn 0 \n\t\t\t\t\tif dp[i][j]!=-1:\n\t\t\t\t\t\treturn dp[i][j]\n\t\t\t\t\tminn=float(\'inf\')\n\t\t\t\t\tfor k in range(i,j):\n\t\t\t\t\t\tminn=min(minn,solve(i,k)+solve(k+1,j)+(arr[i-1]*arr[k]*arr[j]))\n\t\t\t\t\t\tdp[i][j]=minn\n\t\t\t\t\treturn dp[i][j]\n\n\t\t\t\treturn solve(1,N-1) | 1 | 0 | ['Dynamic Programming', 'Memoization', 'Python'] | 0 |
minimum-score-triangulation-of-polygon | Just Matrix Chain Multiplication 😋!!! | just-matrix-chain-multiplication-by-chan-uk29 | Just observe the test cases and your calculated output and do keep in mind the problem of matrix chain multiplication. You will find that it\'s basically exactl | chandramani_lc | NORMAL | 2022-02-16T06:34:22.494477+00:00 | 2022-02-19T11:54:26.533678+00:00 | 204 | false | Just observe the test cases and your calculated output and do keep in mind the problem of matrix chain multiplication. You will find that it\'s basically exactly the same.\n\n```\nclass Solution {\npublic:\n int dp[51][51];\n \n int help(vector<int>& values, int l, int r)\n {\n if(l >= r)\n return 0;\n \n int res = INT_MAX;\n \n if(dp[l][r] != -1)\n return dp[l][r];\n \n for(int k=l;k<r;k++)\n {\n int tmp = help(values,l,k)+help(values,k+1,r)+values[l-1]*values[k]*values[r];\n res = min(res, tmp);\n }\n \n return dp[l][r] = res;\n }\n \n int minScoreTriangulation(vector<int>& values) {\n int n = values.size();\n \n memset(dp,-1, sizeof(dp));\n \n return help(values, 1, n-1);\n }\n};\n```\n\nTime Complexity : O(n^3)\nSpace Complexity : O(n^2) | 1 | 0 | ['C', 'Matrix', 'C++'] | 0 |
minimum-score-triangulation-of-polygon | C++ RECURSION | MEMOIZATION | CATALAN NUMBERS | c-recursion-memoization-catalan-numbers-dt45l | Simple Recursive Solution with Memoization\n```\nclass Solution {\npublic:\n vector> dp;\n int fun(int i,int j,vector &arr){\n //Base case \n | njcoder | NORMAL | 2022-02-10T06:54:01.504487+00:00 | 2022-02-10T06:54:01.504523+00:00 | 141 | false | **Simple Recursive Solution with Memoization**\n```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n int fun(int i,int j,vector<int> &arr){\n //Base case \n if(j - i <= 1) return 0;\n if(j - i == 2) return arr[i]*arr[i+1]*arr[i+2];\n if(dp[i][j] != -1) return dp[i][j];\n int mini = INT_MAX;\n for(int part = i+1;part < j;part++){\n //Now i - part - j creates a triangle \n int l = fun(i,part,arr);\n int r = fun(part,j,arr);\n \n int ans = arr[i]*arr[j]*arr[part] + l + r;\n mini = min(mini, ans);\n }\n return dp[i][j] = mini;\n }\n \n int minScoreTriangulation(vector<int>& arr) {\n int n = arr.size();\n dp = vector<vector<int>> (n,vector<int> (n,-1));\n return fun(0,n-1,arr); // means we are creating the base of triangle as \n //the values with vertices 0 and n-1\n \n }\n}; | 1 | 0 | ['Recursion', 'Memoization'] | 0 |
minimum-score-triangulation-of-polygon | [python] top down dp with comments | python-top-down-dp-with-comments-by-somb-xtnb | \n"""\n\n1039. Minimum Score Triangulation of Polygon\n\nVery similiar to other problems on DP on intervals (aka MCM). You don\'t particularily need\nthe geomet | somb | NORMAL | 2022-02-08T16:37:01.923598+00:00 | 2022-02-08T16:37:01.923640+00:00 | 139 | false | ```\n"""\n\n1039. Minimum Score Triangulation of Polygon\n\nVery similiar to other problems on DP on intervals (aka MCM). You don\'t particularily need\nthe geometric intuition for this one. \n\nI copy/pasted my soln for Burst Balloons and changed the following things:\nhttps://leetcode.com/problems/burst-balloons/discuss/1755801/python-2-ways-bottom-up-and-top-down-with-comments\n\n\n1. we want to find the minimum insted of maximum so:\nret = 0\nto ret = float(\'inf\')\n\nret = max(ret, prod + dfs(left, last) + dfs(last, right))\nto ret = min(ret, prod + dfs(left, last) + dfs(last, right))\n\n2. change the base case since we need a minimum sized triangle:\n\nif left >= right:\n return 0\n \nto if right - left + 1 < 3:\n return 0\n\n3. no virtual window to account for boundaries. \n\nthe "balloon" we pop is the vertex value we pick, forming the triangle of the other polygonal edges.\n\nComplexity:\n\nIt is O(n^3) for time and O(n^2) for space.\n\n\n\n\n"""\n\n \nimport inspect\n\ndef stack_depth():\n return len(inspect.getouterframes(inspect.currentframe())) - 1\n \n \nclass SolutionDFS:\n def minScoreTriangulation(self, nums: List[int]) -> int: \n @cache\n def dfs(left, right):\n #print("{indent}dfs({left},{right}) called".format(\n # indent=" " * stack_depth(), left=left,right=right))\n \n if right - left + 1 < 3: # equivalent to left + 1 = right \n return 0\n \n ret = float(\'inf\')\n \n for last in range(left + 1, right):\n # remainder: we want to burst all the way to the left/right\n prod = nums[left] * nums[last] * nums[right]\n # note, here last is always skipped in the recursive calls below \n ret = min(ret, prod + dfs(left, last) + dfs(last, right))\n \n return ret\n \n return dfs(0, len(nums) - 1)\n \nSolution = SolutionDFS\n``` | 1 | 0 | ['Dynamic Programming', 'Python'] | 0 |
minimum-score-triangulation-of-polygon | clean and easy c++ solution || 4ms runtime | clean-and-easy-c-solution-4ms-runtime-by-y9xw | \nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& arr) {\n int n = arr.size();\n int dp[n-1][n-1];\n for(int g = 0; g < n-1; g++) | thanoschild | NORMAL | 2022-02-03T06:59:19.676789+00:00 | 2022-02-03T06:59:19.676827+00:00 | 95 | false | ```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& arr) {\n int n = arr.size();\n int dp[n-1][n-1];\n for(int g = 0; g < n-1; g++)\n {\n for(int i=0, j = g; j<n-1; i++, j++)\n {\n if(g == 0)\n dp[i][j] = 0;\n else if(g == 1)\n dp[i][j] = arr[i]*arr[j]*arr[j+1];\n else\n {\n int mincost = INT_MAX;\n for(int k = i; k<j; k++)\n {\n int lc = dp[i][k];\n int rc = dp[k+1][j];\n int mc = arr[i]*arr[k+1]*arr[j+1];\n int tc = lc + rc + mc;\n mincost = min(tc, mincost);\n } \n dp[i][j] = mincost; \n }\n }\n }\n return dp[0][n-2]; \n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'C'] | 0 |
minimum-score-triangulation-of-polygon | c++ simple solution , matrix chain multiplication | c-simple-solution-matrix-chain-multiplic-onjz | \nclass Solution {\npublic:\n int t[51][51];\n int solve(vector<int> & arr , int i , int j){\n if(i>=j){\n return 0;\n }\n | sparsh3435 | NORMAL | 2022-02-02T11:35:58.852625+00:00 | 2022-02-02T11:35:58.852668+00:00 | 76 | false | ```\nclass Solution {\npublic:\n int t[51][51];\n int solve(vector<int> & arr , int i , int j){\n if(i>=j){\n return 0;\n }\n if(t[i][j]!=-1){\n return t[i][j];\n }\n int mn = INT_MAX;\n for(int k = i ; k<j ; k++){\n int temp = solve(arr , i , k)+solve(arr ,k+1 , j) + arr[i-1]*arr[k]*arr[j];\n mn = min(mn , temp);\n }\n \n return t[i][j] = mn;\n }\n int minScoreTriangulation(vector<int>& arr) {\n memset(t , -1 ,sizeof(t));\n int ans = solve(arr , 1 , arr.size()-1);\n return ans;\n }\n};\n``` | 1 | 0 | ['Dynamic Programming'] | 0 |
minimum-score-triangulation-of-polygon | C++ | Gap Strategy | Matrix Chain Multiplication | (Tabulation+Memoization) | c-gap-strategy-matrix-chain-multiplicati-defu | Recursion+Memoization\n\n//TC===>O(n^3)\n//SC====>O(51^2)\nint dp[51][51];\nint solve(int i,int j,vector<int>&values)\n{\n if(j-i<2)return 0; \n \n \n | utsav___gupta | NORMAL | 2022-01-31T06:01:38.615211+00:00 | 2022-01-31T06:22:01.136813+00:00 | 119 | false | **Recursion+Memoization**\n```\n//TC===>O(n^3)\n//SC====>O(51^2)\nint dp[51][51];\nint solve(int i,int j,vector<int>&values)\n{\n if(j-i<2)return 0; \n \n \n if(dp[i][j]!=-1)return dp[i][j];\n int ans=INT_MAX;\n for(int k=i+1;k<j;k++)\n {\n int v1=values[i]*values[j]*values[k];\n int v2=solve(i,k,values)+solve(k,j,values);\n ans=min(ans,v1+v2);\n }\n \n return dp[i][j]=ans;\n \n \n}\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& values)\n {\n int n=values.size();\n memset(dp,-1,sizeof(dp));\n return solve(0,n-1,values);\n \n }\n};\n```\n**Tabulation->**\n```\nclass Solution {\npublic:\n int minScoreTriangulation(vector<int>& values)\n {\n //TC===>O(N^3)\n //SC===>O(N^2)\n int n=values.size();\n int dp[n][n];\n memset(dp,0,sizeof(dp));\n for(int g=2;g<n;g++)\n {\n for(int i=0,j=g;j<n;j++,i++)\n {\n if(g==2)\n {\n dp[i][j]=(values[i]*values[j]*values[i+1]);\n }\n else\n {\n int ans=INT_MAX;\n for(int k=i+1;k<j;k++)\n {\n int v1=values[i]*values[j]*values[k];\n int v2=dp[i][k]+dp[k][j];\n ans=min(ans,v1+v2);\n }\n dp[i][j]=ans;\n }\n }\n }\n \n \n return dp[0][n-1]; \n \n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C'] | 0 |
minimum-score-triangulation-of-polygon | Easy Java DP Solution | easy-java-dp-solution-by-parikshit3097-crec | \nclass Solution {\n public int minScoreTriangulation(int[] arr) {\n if(arr.length ==3){\n return arr[0] * arr[1] * arr[2];\n }\n | parikshit3097 | NORMAL | 2022-01-25T02:16:21.058945+00:00 | 2022-01-25T02:16:21.058981+00:00 | 67 | false | ```\nclass Solution {\n public int minScoreTriangulation(int[] arr) {\n if(arr.length ==3){\n return arr[0] * arr[1] * arr[2];\n }\n int [][]dp = new int[arr.length][arr.length];\n \n for(int gap = 2; gap<arr.length; gap++){\n for(int left=0; left<arr.length-gap; left++){\n int right = left + gap;\n dp[left][right] = Integer.MAX_VALUE;\n for(int i=left + 1; i<right; i++){\n dp[left][right] = Math.min(dp[left][right], dp[left][i] + dp[i][right] + arr[left]*arr[i]*arr[right]);\n }\n }\n }\n \n return dp[0][dp.length-1];\n }\n}\n``` | 1 | 0 | [] | 0 |
minimum-score-triangulation-of-polygon | Same as Matrix Chain Multiplication || Standard Problem || Memoized Code | same-as-matrix-chain-multiplication-stan-9g5g | class Solution {\npublic:\n \n int t[101][101];\n \n int solve(vector& arr, int i, int j)\n {\n //memoized code\n if(i>=j)\n | Sumit4399 | NORMAL | 2021-12-31T16:30:34.777140+00:00 | 2021-12-31T16:30:34.777170+00:00 | 107 | false | class Solution {\npublic:\n \n int t[101][101];\n \n int solve(vector<int>& arr, int i, int j)\n {\n //memoized code\n if(i>=j)\n return 0;\n \n if(t[i][j] != -1)\n return t[i][j];\n \n int mn= INT_MAX;\n for(int k=i; k<j; k++)\n {\n int temp= solve(arr, i, k) + solve(arr, k+1, j) + \n arr[i-1]*arr[k]*arr[j];\n \n if(temp<mn)\n t[i][j]=mn= min(mn, temp);\n }\n \n return t[i][j];\n }\n \n \n int minScoreTriangulation(vector<int>& values) {\n \n memset(t,-1,sizeof(t));\n int i=1; \n int j=values.size()-1;\n return solve(values, i, j);\n }\n}; | 1 | 1 | ['Dynamic Programming', 'C'] | 0 |
minimum-score-triangulation-of-polygon | Most Easy Memo in the Universe | most-easy-memo-in-the-universe-by-mayank-qjxy | I STRONGLY URGE YOU TO SEE THE TABULATION SOLUTION FIRST (IF INDIAN THEN FROM PEPCODING YOUTUBE CHANNEL)\n\n\nclass Solution {\n public int minScoreTriangula | mayank357000 | NORMAL | 2021-12-04T12:31:02.094734+00:00 | 2021-12-04T12:31:02.094761+00:00 | 242 | false | I STRONGLY URGE YOU TO SEE THE TABULATION SOLUTION FIRST (IF INDIAN THEN FROM PEPCODING YOUTUBE CHANNEL)\n\n```\nclass Solution {\n public int minScoreTriangulation(int[] arr) {\n int dp[][]=new int[arr.length][arr.length];\n for(int i=0;i<arr.length;i++)\n {\n Arrays.fill(dp[i],-1);\n }\n return solve(arr,0,arr.length-1,dp);\n }\n \n int solve(int arr[],int i,int j,int dp[][])\n {\n if(j-i<=1)//\n return 0;\n \n if(dp[i][j]!=-1)\n return dp[i][j];\n \n int min=Integer.MAX_VALUE;\n for(int k=i+1;k<j;k++)\n {\n int cost=arr[i]*arr[k]*arr[j]+solve(arr,i,k,dp)+solve(arr,k,j,dp);\n \n min=Math.min(min,cost); \n }\n return dp[i][j]=min;\n }\n \n}\n``` | 1 | 0 | ['Memoization', 'Java'] | 1 |
remove-outermost-parentheses | [Java/C++/Python] Count Opened Parenthesis | javacpython-count-opened-parenthesis-by-p45ye | Intuition\nQuote from @shubhama,\nPrimitive string will have equal number of opened and closed parenthesis.\n\n## Explanation:\nopened count the number of opene | lee215 | NORMAL | 2019-04-07T04:11:05.952839+00:00 | 2019-04-07T04:11:05.952913+00:00 | 57,070 | false | ## **Intuition**\nQuote from @shubhama,\nPrimitive string will have equal number of opened and closed parenthesis.\n\n## **Explanation**:\n`opened` count the number of opened parenthesis.\nAdd every char to the result,\nunless the first left parenthesis,\nand the last right parenthesis.\n\n## **Time Complexity**:\n`O(N)` Time, `O(N)` space\n\n<br>\n\n**Java:**\n```\n public String removeOuterParentheses(String S) {\n StringBuilder s = new StringBuilder();\n int opened = 0;\n for (char c : S.toCharArray()) {\n if (c == \'(\' && opened++ > 0) s.append(c);\n if (c == \')\' && opened-- > 1) s.append(c);\n }\n return s.toString();\n }\n```\n\n**C++:**\n```\n string removeOuterParentheses(string S) {\n string res;\n int opened = 0;\n for (char c : S) {\n if (c == \'(\' && opened++ > 0) res += c;\n if (c == \')\' && opened-- > 1) res += c;\n }\n return res;\n }\n```\n\n**Python:**\n```\n def removeOuterParentheses(self, S):\n res, opened = [], 0\n for c in S:\n if c == \'(\' and opened > 0: res.append(c)\n if c == \')\' and opened > 1: res.append(c)\n opened += 1 if c == \'(\' else -1\n return "".join(res)\n```\n | 781 | 7 | [] | 92 |
remove-outermost-parentheses | Solution | solution-by-deleted_user-9ev5 | C++ []\nclass Solution {\npublic:\n string removeOuterParentheses(string S) {\n string res;\n int opened = 0;\n for (char c : S) {\n | deleted_user | NORMAL | 2023-05-22T07:17:34.191764+00:00 | 2023-05-22T07:47:24.600942+00:00 | 42,627 | false | ```C++ []\nclass Solution {\npublic:\n string removeOuterParentheses(string S) {\n string res;\n int opened = 0;\n for (char c : S) {\n if (c == \'(\' && opened++ > 0) res += c;\n if (c == \')\' && opened-- > 1) res += c;\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def removeOuterParentheses(self, S: str) -> str:\n res, opened = [], 0\n for c in S:\n if c == \'(\' and opened > 0: res.append(c)\n if c == \')\' and opened > 1: res.append(c)\n opened += 1 if c == \'(\' else -1\n \n return "".join(res)\n```\n\n```Java []\nclass Solution {\n public String removeOuterParentheses(String s) {\n int len = s.length();\n if (len <= 2) return "";\n char[] c = s.toCharArray();\n StringBuilder newString = new StringBuilder();\n int open = 1;\n int openLeft = 0;\n for (int i = 1; i < len; i++) {\n if (c[i] == \'(\') {\n open++;\n if (open > 1) newString.append(\'(\');\n }\n else {\n if (open > 1) newString.append(\')\');\n open--;\n }\n }\n return newString.toString();\n }\n}\n``` | 500 | 1 | ['C++', 'Java', 'Python3'] | 13 |
remove-outermost-parentheses | ✅ Beats 100 % || C++ || Easy to Understand || Without Using Stack | beats-100-c-easy-to-understand-without-u-z586 | Intuition\n Describe your first thoughts on how to solve this problem. \nWe need to remove the outermost parentheses from each segment of valid parentheses in t | chitrakshsuri | NORMAL | 2024-06-04T06:32:49.321582+00:00 | 2024-06-04T06:32:49.321603+00:00 | 25,463 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to remove the outermost parentheses from each segment of valid parentheses in the given string. A valid parentheses string is one where every opening parenthesis ( has a matching closing parenthesis ). If we can track how many open and close parentheses we\'ve seen, we can figure out which parentheses are the outermost ones and skip them.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n# **1. Initialize Variables:**\n- \'result\': An empty string to store the final output.\n- balance: A counter to keep track of the balance of parentheses (( increases the balance and ) decreases it).\n\n# **2. Loop Through the String:**\n- Use a for loop to go through each character in the string s.\n- For each character:\n - If it\u2019s an opening parenthesis (:\n - If the balance is more than 0, it means this ( is not an outermost parenthesis, so add it to \'result\'.\n - Increase the balance by 1.\n - If it\u2019s a closing parenthesis ):\n - Decrease the balance by 1.\n - If the balance is more than 0 after decreasing, it means this ) is not an outermost parenthesis, so add it to \'result\'.\n\n# **3. Return the Result:**\n- After processing all characters, the \'result\' string will contain the original string without the outermost parentheses.\n\n# Complexity\n**- Time complexity:**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- The time complexity is O(n), where n is the length of the string s. This is because we go through the string once.\n\n**- Space complexity:**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- The space complexity is O(n), where n is the length of the string s, because the result string might store almost all characters from s.\n\n# Code\n```\nclass Solution {\npublic:\n // Function to remove outermost parentheses of every primitive string in the\n // decomposition of s\n string removeOuterParentheses(string s) {\n string result; // To store the final result\n int balance = 0; // To keep track of the balance of parentheses\n\n // Iterate through each character in the string\n for (int i = 0; i < s.size(); i++) {\n if (s[i] == \'(\') {\n // If balance is greater than 0, it means this \'(\' is not an\n // outermost parenthesis\n if (balance > 0) {\n result += s[i]; // Add the character to the result\n }\n balance++; // Increase the balance for \'(\'\n } else {\n balance--; // Decrease the balance for \')\'\n // If balance is greater than 0, it means this \')\' is not an\n // outermost parenthesis\n if (balance > 0) {\n result += s[i]; // Add the character to the result\n }\n }\n }\n\n return result; // Return the final result after removing outermost\n // parentheses\n }\n};\n```\n\n\nPLEASE UPVOTE IT IF YOU LIKED IT, IT REALLY MOTIVATES :)\n | 380 | 1 | ['C++'] | 6 |
remove-outermost-parentheses | Well Explained Code in JAVA || | well-explained-code-in-java-by-sakshamka-45oe | \n\n# Approach\nThis is a solution to the problem of removing outermost parentheses from a string containing only parentheses.\n\nThe approach used is to keep t | sakshamkaushiik | NORMAL | 2023-02-09T19:11:43.729664+00:00 | 2023-02-09T19:11:43.729710+00:00 | 17,848 | false | \n\n# Approach\nThis is a solution to the problem of removing outermost parentheses from a string containing only parentheses.\n\nThe approach used is to keep track of the parentheses using a stack. Whenever an opening parenthesis is encountered, it is pushed onto the stack. Whenever a closing parenthesis is encountered, the last opening parenthesis is popped from the stack.\n\nIf the stack size is greater than zero after pushing or popping, it means that the parenthesis is not an outer parenthesis, and it is added to the result string. If the stack size is zero, it means that the parenthesis is an outer parenthesis and it is not added to the result string.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(n), where n is the length of the input string. This is because each character in the string is processed once and the push and pop operations on the stack take O(1) time each.\n\n\n\n- Space complexity:\nThe space complexity of this solution is O(n), where n is the length of the input string. This is because the maximum size of the stack is n/2 (if all the parentheses are opening parentheses), and in the worst case, the result string can also have a size of n/2.\n\n# Code\n```\nclass Solution {\n public String removeOuterParentheses(String s) {\n Stack<Character> bracket = new Stack<>();\n StringBuilder sb = new StringBuilder("");\n for(int i=0;i<s.length();i++){\n if(s.charAt(i)==\'(\'){\n if(bracket.size()>0){\n sb.append(s.charAt(i));\n }\n bracket.push(s.charAt(i));\n }else{\n bracket.pop();\n if(bracket.size()>0){\n sb.append(s.charAt(i));\n }\n }\n }\n return sb.toString();\n }\n}\n```\n\n | 246 | 0 | ['Stack', 'Java'] | 6 |
remove-outermost-parentheses | My Java 3ms Straight Forward Solution | Beats 100% | my-java-3ms-straight-forward-solution-be-fnze | \nclass Solution {\n public String removeOuterParentheses(String S) {\n \n StringBuilder sb = new StringBuilder();\n int open=0, close=0 | debdattakunda | NORMAL | 2019-04-07T19:53:33.359919+00:00 | 2019-04-07T19:53:33.359985+00:00 | 13,058 | false | ```\nclass Solution {\n public String removeOuterParentheses(String S) {\n \n StringBuilder sb = new StringBuilder();\n int open=0, close=0, start=0;\n for(int i=0; i<S.length(); i++) {\n if(S.charAt(i) == \'(\') {\n open++;\n } else if(S.charAt(i) == \')\') {\n close++;\n }\n if(open==close) {\n sb.append(S.substring(start+1, i));\n start=i+1;\n }\n }\n return sb.toString();\n }\n}\n``` | 109 | 3 | [] | 15 |
remove-outermost-parentheses | C++ 0ms solution | c-0ms-solution-by-dan0907-62w1 | \nclass Solution {\npublic:\n string removeOuterParentheses(string S) {\n int count = 0;\n std::string str;\n for (char c : S) {\n | dan0907 | NORMAL | 2019-05-10T17:29:30.113941+00:00 | 2019-10-29T13:14:01.405451+00:00 | 10,291 | false | ```\nclass Solution {\npublic:\n string removeOuterParentheses(string S) {\n int count = 0;\n std::string str;\n for (char c : S) {\n if (c == \'(\') {\n if (count++) {\n str += \'(\';\n }\n } else {\n if (--count) {\n str += \')\';\n }\n }\n }\n return str;\n }\n};\n``` | 98 | 1 | ['C'] | 11 |
remove-outermost-parentheses | 💡One Pass | FAANG SDE-1 Interview😯 | one-pass-faang-sde-1-interview-by-aditya-m4il | \nVery Easy Beginner Friendly Solution \uD83D\uDCA1\nDo not use stack to prevent more extra space.\n\n\nPlease do Upvote if it helps :)\n\n\n# Complexity\n- Tim | AdityaBhate | NORMAL | 2022-12-16T06:40:07.118768+00:00 | 2022-12-16T06:40:07.118804+00:00 | 16,202 | false | ```\nVery Easy Beginner Friendly Solution \uD83D\uDCA1\nDo not use stack to prevent more extra space.\n\n\nPlease do Upvote if it helps :)\n```\n\n# Complexity\n- Time complexity: O(n) //One pass\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) //For resultant string\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string removeOuterParentheses(string s) {\n string res;\n int count=0;\n for(int i=0;i<s.size();i++){\n if(s[i]==\'(\' && count==0)\n count++;\n else if(s[i]==\'(\' && count>=1){\n res+=s[i];\n count++;\n } \n else if(s[i]==\')\' && count>1){\n res+=s[i];\n count--;\n }\n else if(s[i]==\')\' && count==1)\n count--;\n }\n return res;\n }\n};\n``` | 85 | 3 | ['String', 'Stack', 'C++', 'Java', 'Python3'] | 7 |
remove-outermost-parentheses | [c++] two solution stack and with out stack(only slight modification in stack sol.) | c-two-solution-stack-and-with-out-stacko-qxfn | please upVote my solution if you like it.\n\nMy first solution is stack based and it consume more memory than with out stack solution in my second solution to e | sanjeev1709912 | NORMAL | 2020-08-28T04:47:50.579025+00:00 | 2020-08-28T04:48:12.549655+00:00 | 4,982 | false | please **upVote** my solution if you like it.\n\nMy first solution is stack based and it consume more memory than with out stack solution in my second solution to elemenate stack from it so please reffer to that also \n\n\n\'\'\'\nclass Solution {\npublic:\n\n string removeOuterParentheses(string S) {\n stack<char>st;\n string ans;\n for(auto a:S)\n {\n if(a==\'(\')\n {\n if(st.size()>0)\n {\n ans+=\'(\';\n }\n st.push(\'(\');\n }\n else\n {\n if(st.size()>1)\n {\n ans+=\')\';\n }\n st.pop();\n }\n }\n return ans;\n }\n};\n\'\'\'\n\nSolution without stack \n\n\'\'\'\nclass Solution {\npublic:\n\n string removeOuterParentheses(string S) {\n int st=0;\n string ans;\n for(auto a:S)\n {\n if(a==\'(\')\n {\n if(st>0)\n {\n ans+=\'(\';\n }\n st++;\n }\n else\n {\n if(st>1)\n {\n ans+=\')\';\n }\n st--;\n }\n }\n return ans;\n }\n};\n\'\'\' | 63 | 0 | ['Stack', 'C'] | 3 |
remove-outermost-parentheses | [Python] Simple O(n) solution - beats 97% | python-simple-on-solution-beats-97-by-ye-5se3 | python\ndef removeOuterParentheses(self, S):\n\tres = []\n\tbalance = 0\n\ti = 0\n\tfor j in range(len(S)):\n\t\tif S[j] == "(":\n\t\t\tbalance += 1\n\t\telif S | yerbola | NORMAL | 2019-05-26T04:59:38.122390+00:00 | 2019-11-02T20:00:13.945787+00:00 | 5,265 | false | ```python\ndef removeOuterParentheses(self, S):\n\tres = []\n\tbalance = 0\n\ti = 0\n\tfor j in range(len(S)):\n\t\tif S[j] == "(":\n\t\t\tbalance += 1\n\t\telif S[j] == ")":\n\t\t\tbalance -= 1\n\t\tif balance == 0:\n\t\t\tres.append(S[i+1:j])\n\t\t\ti = j+1\n\treturn "".join(res)\n``` | 52 | 0 | [] | 10 |
remove-outermost-parentheses | Easy to understand Python with comments | easy-to-understand-python-with-comments-6qskb | Python\nclass Solution:\n def removeOuterParentheses(self, S: str) -> str:\n res = \'\'\n stack = []\n \n # basket is used to sto | cglotr | NORMAL | 2019-06-25T14:34:23.879552+00:00 | 2019-06-29T15:29:58.771041+00:00 | 3,814 | false | ```Python\nclass Solution:\n def removeOuterParentheses(self, S: str) -> str:\n res = \'\'\n stack = []\n \n # basket is used to store previous value\n basket = \'\'\n \n for p in S:\n if p == \'(\':\n stack.append(p)\n else:\n stack.pop()\n basket += p\n \n # if the stack is empty it means we have a valid\n # decomposition. remove the outer parentheses\n # and put it in the result/res. make sure to\n # clean up the basket though!\n if not stack:\n res += basket[1:-1]\n basket = \'\'\n \n return res\n``` | 47 | 0 | ['Stack', 'Python'] | 4 |
remove-outermost-parentheses | [JAVA] beats 98%, simple iterative solution | java-beats-98-simple-iterative-solution-n33eq | \nclass Solution {\n public String removeOuterParentheses(String S) {\n StringBuilder sb = new StringBuilder();\n int counter = 0;\n for | jamsrandorj | NORMAL | 2019-11-13T21:58:11.645114+00:00 | 2019-11-13T21:58:11.645149+00:00 | 3,143 | false | ```\nclass Solution {\n public String removeOuterParentheses(String S) {\n StringBuilder sb = new StringBuilder();\n int counter = 0;\n for(char c : S.toCharArray()){\n if(c == \'(\'){\n if(counter != 0) sb.append(c);\n counter++;\n }\n else{\n counter--;\n if(counter != 0) sb.append(c);\n }\n }\n \n return sb.toString();\n }\n}\n``` | 35 | 1 | ['Java'] | 4 |
remove-outermost-parentheses | Ridiculously Simple JAVA O(n) Solution + Explanation [0ms Beats 100% Time & Memory] | ridiculously-simple-java-on-solution-exp-tmav | Explanation:\nSince the input String only consists of parentheses we don\'t even have to mainatain a Stack. We can simply maintain a counter which is O(1) and k | agrawroh | NORMAL | 2019-04-12T19:20:05.924040+00:00 | 2019-04-12T19:20:05.924136+00:00 | 4,390 | false | **Explanation:**\nSince the input String only consists of parentheses we don\'t even have to mainatain a Stack. We can simply maintain a counter which is O(1) and keep incrementing and decrementing it\'s value based on the opening/closing bracket.\n\n**Algorithm:**\n1. Convert the given input String to a `char` array and start scanning.\n2. Maintain a `sum` counter (Initially 0) and for every following character in the input char array,\n3. When, `(` check whether **sum** is greater than **zero** and if yes, add this char to your String Builder; Also, increment the **sum** by **1** \n4. When, `)` decrement the **sum** by **1** and then, check whether **sum** is greater than **zero** and if yes, add this char to your String Builder;\n5. Return the string from your builder.\n\n**Code:**\n```\npublic String removeOuterParentheses(String S) {\n\tStringBuilder builder = new StringBuilder();\n\tchar[] chr = S.toCharArray();\n\tint sum = 0;\n\tfor (int i = 0; i < chr.length; i++) {\n\t\tif (chr[i] == \'(\') {\n\t\t\tif (sum > 0) { builder.append(chr[i]); }\n\t\t\tsum += 1;\n\t\t} else {\n\t\t\tsum -= 1;\n\t\t\tif (sum > 0) { builder.append(chr[i]); }\n\t\t}\n\t}\n\treturn builder.toString();\n}\n```\n\n**Compressed Version:**\n```\npublic String removeOuterParentheses(String S) {\n\tStringBuilder builder = new StringBuilder();\n\tchar[] chr = S.toCharArray();\n\tint sum = 0;\n\tfor (int i = 0; i < chr.length; i++) {\n\t\tif ((chr[i] == \'(\' && sum++ > 0) || (chr[i] == \')\' && --sum > 0)) {\n\t\t\tbuilder.append(chr[i]);\n\t\t}\n\t}\n\treturn builder.toString();\n}\n``` | 32 | 0 | [] | 4 |
remove-outermost-parentheses | C++ Two pointers | c-two-pointers-by-votrubac-hq23 | Intuition\nWhen the number of open parentheses equals closed, we found a primitive string.\n# Solution\nUse two pointers to track primitive strings; when open = | votrubac | NORMAL | 2019-04-07T04:01:04.880510+00:00 | 2019-04-07T04:01:04.880544+00:00 | 4,220 | false | # Intuition\nWhen the number of ```open``` parentheses equals ```closed```, we found a primitive string.\n# Solution\nUse two pointers to track primitive strings; when ```open == close```, remove outermost parentheses and add the string to the result.\n```\nstring removeOuterParentheses(string S, string res = "") {\n for (auto p1 = 0, p2 = 0, open = 0, close = 0; p2 < S.size(); ++p2) {\n if (S[p2] == \'(\') ++open;\n else ++close;\n if (open == close) {\n res += S.substr(p1 + 1, p2 - p1 - 1);\n p1 = p2 + 1;\n }\n }\n return res;\n}\n```\n# Complexity Analysis\nRuntime: O(n).\nMemory: O(n) to store the result. | 31 | 3 | [] | 4 |
remove-outermost-parentheses | Python - Super Easy - 98% Speed | python-super-easy-98-speed-by-aragorn-8wku | We just need a For-Loop to count the number of Parenthesis open. The "append" operator goes at the center of the expression to avoid including the Outermost Pat | aragorn_ | NORMAL | 2020-04-24T00:48:34.579703+00:00 | 2020-07-01T02:31:33.295675+00:00 | 3,796 | false | We just need a For-Loop to count the number of Parenthesis open. The "append" operator goes at the center of the expression to avoid including the Outermost Patentheses. Cheers,\n\n```\nclass Solution:\n def removeOuterParentheses(self, S: str) -> str:\n popen, result = 0, []\n for x in S:\n if x==\')\':\n popen -= 1\n if popen>0:\n result.append(x)\n if x==\'(\':\n popen += 1\n return \'\'.join(result)\n``` | 30 | 0 | ['Python', 'Python3'] | 2 |
remove-outermost-parentheses | Python solution using stack and maintaining counter | python-solution-using-stack-and-maintain-8bcy | Before I explain any further get this, let\'s say for each "(" you get you put -1 and for each ")" you get you put +1 to the counter varriable and because of th | dubeyaman157 | NORMAL | 2022-10-09T07:50:10.472671+00:00 | 2022-12-25T08:26:21.686114+00:00 | 1,725 | false | # Before I explain any further get this, let\'s say for each "(" you get you put -1 and for each ")" you get you put +1 to the counter varriable and because of that whenever we encounter a valid paranthese our sum will be zero for example for (()())(()) can be decomposed to (()()) + (()) note that for each valid decomposition our sum will be zero. Example (()) -1-1+1+1 ==0 also for (()()) -1-1+1-1+1+1==0 for each time our sum is zero we are looking at a valid decompostion and hence at that moment we take what we have in our stack and remove the outter brackets which is done easily using stack[1:-1] it will exlude the first and last from our stack and we add this value to our answer list and make our stack empty again for future decompistion, we repeat this and return the " ".join(final_answer) here final answer is the list that has all the decompositions with there outter barckets removed. Upvote if you liked the approch. Thanks\n\n\n```\nclass Solution:\n def removeOuterParentheses(self, s: str) -> str:\n stack = []\n final_answer = []\n counter=0\n for val in s:\n stack.append(val)\n if val==\'(\':\n counter+=1\n elif val==\')\':\n counter-=1\n if counter==0:\n final_answer+=stack[1:-1]\n stack=[]\n \n return "".join(final_answer)\n``` | 25 | 0 | ['Stack', 'Python'] | 2 |
remove-outermost-parentheses | ✅Java Simple Solution || ✅Runtime 2ms || ✅ Beats100% | java-simple-solution-runtime-2ms-beats10-m5lq | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ahmedna126 | NORMAL | 2023-08-29T19:41:17.745408+00:00 | 2023-11-07T11:40:55.689863+00:00 | 2,206 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String removeOuterParentheses(String s) {\n int count = 0;\n StringBuilder result = new StringBuilder();\n\n for (char c : s.toCharArray()) {\n if (c == \'(\') {\n if (count != 0) {\n result.append(c);\n }\n count++;\n } else {\n if (count != 1) {\n result.append(c);\n }\n count--;\n }\n }\n\n return result.toString();\n }\n}\n\n```\n\n## For additional problem-solving solutions, you can explore my repository on GitHub: [GitHub Repository](https://github.com/ahmedna126/java_leetcode_challenges)\n\n\n\n | 23 | 0 | ['Java'] | 2 |
remove-outermost-parentheses | C++ stack and without stack solutions. | c-stack-and-without-stack-solutions-by-k-hvf6 | Stack implementation\n\nclass Solution {\npublic:\n string removeOuterParentheses(string s)\n {\n stack<char>sc;\n string ans;\n for( | kfaisal-se | NORMAL | 2021-06-10T10:35:12.857655+00:00 | 2021-06-10T10:35:12.857687+00:00 | 2,968 | false | **Stack implementation**\n```\nclass Solution {\npublic:\n string removeOuterParentheses(string s)\n {\n stack<char>sc;\n string ans;\n for(char i:s)\n {\n if(i == \'(\')\n {\n if(sc.size() > 0)\n {\n ans += i;\n }\n sc.push(i);\n }\n else\n {\n if(sc.size() > 1)\n {\n ans += i;\n }\n sc.pop();\n }\n }\n return ans;\n }\n};\n```\n**Without stack implementation**\n```\nclass Solution {\npublic:\n string removeOuterParentheses(string s)\n {\n int count = 0;\n string ans;\n for(char i:s)\n {\n if(i == \'(\')\n {\n if(count > 0)\n {\n ans += i;\n }\n count++;\n }\n else\n {\n if(count > 1)\n {\n ans += i;\n }\n count--;\n }\n }\n return ans;\n }\n};\n```\n**Like the solution?\nPlease upvote \u30C4** | 23 | 0 | ['Stack', 'C', 'C++'] | 2 |
remove-outermost-parentheses | Javascript solution - 98% faster | javascript-solution-98-faster-by-whiskey-t3pm | \nvar removeOuterParentheses = function(S) {\n let parenthesCount = 0;\n let result = "";\n \n for (const letter of S) {\n if (letter === "(" | whiskey022 | NORMAL | 2019-09-11T08:57:39.284718+00:00 | 2019-09-11T09:01:16.318939+00:00 | 2,705 | false | ```\nvar removeOuterParentheses = function(S) {\n let parenthesCount = 0;\n let result = "";\n \n for (const letter of S) {\n if (letter === "(") {\n if (parenthesCount) {\n result += letter;\n }\n parenthesCount++;\n } else {\n parenthesCount--;\n if (parenthesCount) {\n result += letter;\n }\n }\n }\n \n return result;\n};\n``` | 22 | 0 | ['JavaScript'] | 2 |
remove-outermost-parentheses | Beats 100% 🔥 of users|| JAVA || Without Using Stack || Easy to understand ✅ | beats-100-of-users-java-without-using-st-0n68 | Intuition\n Describe your first thoughts on how to solve this problem. \nRemove the outermost parentheses from each primitive valid parentheses substring by tra | Abhishek_Yadav_leetcode | NORMAL | 2024-09-07T19:56:23.427996+00:00 | 2024-09-08T08:08:02.534349+00:00 | 1,772 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRemove the outermost parentheses from each primitive valid parentheses substring by tracking balance.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1) Initialize: Convert the string to a character array, create a StringBuilder, and initialize a count for balance.\n\n2) Process Characters:\nTraverse from the second character.\nFor each \'(\', increase the balance and add it to the result.\nFor each \')\', add it to the result if balance is greater than 0, then decrease the balance.\n3) Return: Convert the StringBuilder to a string and return it.\n# Complexity\n- Time complexity:\nO(n) \u2014 Each character is processed once.\n- Space complexity:\nO(n) \u2014 Space for the result string.\n\n# Code\n```java []\nclass Solution {\n public String removeOuterParentheses(String s) {\n StringBuilder ans = new StringBuilder();\n char[] a = s.toCharArray();\n int n = a.length;\n int count = 0;\n for (int i = 1; i < n; i++) {\n if (a[i] == \'(\') {\n count++;\n ans.append(\'(\');\n } else {\n if (count == 0) {\n i++;\n } else {\n ans.append(\')\');\n count--;\n }\n }\n }\n return ans.toString();\n }\n}\n\n```\n\n | 19 | 0 | ['Java'] | 2 |
remove-outermost-parentheses | Javascript beats 99.26% easy to understand | javascript-beats-9926-easy-to-understand-abi7 | \nvar removeOuterParentheses = function(S) {\n let result = \'\';\n let open = 0\n for (let i = 0; i < S.length; i++) {\n if (S[i] === \'(\') {\ | careyl96 | NORMAL | 2019-05-29T00:01:24.199522+00:00 | 2019-05-29T00:01:24.199590+00:00 | 1,048 | false | ```\nvar removeOuterParentheses = function(S) {\n let result = \'\';\n let open = 0\n for (let i = 0; i < S.length; i++) {\n if (S[i] === \'(\') {\n if (open > 0) { \n\t\t\t\tresult += \'(\';\n\t\t\t}\n\t\t\topen++;\n } else if (S[i] === \')\') {\n if (open > 1) { \n\t\t\t\tresult += \')\'; \n\t\t\t}\n\t\t\topen--;\n }\n }\n return result;\n};\n``` | 18 | 0 | [] | 0 |
remove-outermost-parentheses | Python3- simple solution 99.8% | python3-simple-solution-998-by-logan_kd-cb6p | \nclass Solution:\n def removeOuterParentheses(self, S: str) -> str:\n res = ""\n count = 0\n first = 0\n for i in range(len(S)): | logan_kd | NORMAL | 2019-10-06T22:58:38.602821+00:00 | 2019-10-06T23:05:49.107911+00:00 | 2,312 | false | ```\nclass Solution:\n def removeOuterParentheses(self, S: str) -> str:\n res = ""\n count = 0\n first = 0\n for i in range(len(S)):\n if S[i] == "(":\n count +=1\n else:\n count -= 1\n \n if(count == 0):\n res +=(S[first+1:i])\n first = i+1\n return res\n``` | 17 | 0 | ['Python', 'Python3'] | 5 |
remove-outermost-parentheses | Shortest Python Solution | shortest-python-solution-by-flowingwater-l1cx | \nclass Solution:\n def removeOuterParentheses(self, S: str) -> str:\n cnt, res = 0, \'\'\n for c in S:\n if c == \')\': cnt -= 1 \ | flowingwater526 | NORMAL | 2019-08-14T06:47:41.356265+00:00 | 2019-08-14T06:47:41.356330+00:00 | 2,852 | false | ```\nclass Solution:\n def removeOuterParentheses(self, S: str) -> str:\n cnt, res = 0, \'\'\n for c in S:\n if c == \')\': cnt -= 1 \n if cnt != 0: res += c \n if c == \'(\': cnt+=1 \n return res\n``` \n | 16 | 0 | ['Python', 'Python3'] | 5 |
remove-outermost-parentheses | ✅☑️ Best C++ 2 Solution Ever || String || Stack || One Stop Solution. | best-c-2-solution-ever-string-stack-one-rq3hx | Intuition\n Describe your first thoughts on how to solve this problem. \nWe can solve this question using Multiple Approaches. (Here I have explained all the po | its_vishal_7575 | NORMAL | 2023-02-16T17:03:13.887148+00:00 | 2023-02-16T17:03:13.887182+00:00 | 2,410 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can solve this question using Multiple Approaches. (Here I have explained all the possible solutions of this problem).\n\n1. Solved using String + Stack.\n2. Solved using String.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can easily understand the all the approaches by seeing the code which is easy to understand with comments.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity is given in code comment.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity is given in code comment.\n\n# Code\n```\n/*\n\n Time Complexity : O(N), Where N is the size of the string(num). Here loop creates the time complexity.\n\n Space complexity : O(N), Stack(store) space.\n\n Solved using String + Stack.\n\n*/\n\n\n/***************************************** Approach 1 *****************************************/\n\nclass Solution {\npublic:\n string removeOuterParentheses(string s) {\n stack<char> store;\n string ans = "";\n for(auto c : s){\n if(c == \'(\'){\n if(store.size() > 0){\n ans += c;\n }\n store.push(c);\n }\n else if(c == \')\'){\n if(store.size() > 1){\n ans += c;\n }\n store.pop();\n }\n }\n return ans;\n }\n};\n\n\n\n\n\n\n/*\n\n Time Complexity : O(N), Where N is the size of the string(num). Here loop creates the time complexity.\n\n Space complexity : O(1), Constant space. Extra space is only allocated for the String(ans), however the\n output does not count towards the space complexity.\n\n Solved using String.\n\n*/\n\n\n/***************************************** Approach 2 *****************************************/\n\nclass Solution {\npublic:\n string removeOuterParentheses(string s) {\n string ans = "";\n int openParentheses = 0;\n for(auto c : s){\n if(c == \'(\'){\n if(openParentheses > 0){\n ans += c;\n }\n openParentheses++;\n }\n else if(c == \')\'){\n if(openParentheses > 1){\n ans += c;\n }\n openParentheses--;\n }\n }\n return ans;\n }\n};\n\n```\n\n***IF YOU LIKE THE SOLUTION THEN PLEASE UPVOTE MY SOLUTION BECAUSE IT GIVES ME MOTIVATION TO REGULARLY POST THE SOLUTION.***\n\n | 15 | 0 | ['String', 'Stack', 'C++'] | 1 |
remove-outermost-parentheses | Easy Solution with Dry Run and Example | easy-solution-with-dry-run-and-example-b-xotj | Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve this, we need to:\n\n1. Traverse the string while keeping track of the number | reaperrrrrr | NORMAL | 2024-08-24T17:02:28.139784+00:00 | 2024-08-24T17:02:28.139809+00:00 | 1,128 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this, we need to:\n\n1. Traverse the string while keeping track of the number of open and close parentheses using a counter.\n \n1. Append the parentheses to the result string only when they are not the outermost ones.\n\n---\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Initialization**:\n\n- Start with an empty result string ans.\n- Use a counter cnt initialized to 0 to keep track of the balance of open and close parentheses.\n\n2. **Traversing the String:**\n\n- Iterate through each character in the string s.\n\n- For each \'(\':\n - If cnt is 0, it indicates this \'(\' is an outer parenthesis, so we increment cnt without adding it to ans.\n - Otherwise, increment cnt and add the parenthesis to ans.\n \n- For each \')\':\n - If cnt is 1, it indicates this \')\' is an outer parenthesis, so we decrement cnt without adding it to ans.\n - Otherwise, decrement cnt and add the parenthesis to ans.\nReturning the Result:\n\nThe string ans now contains the input string s without its outermost parentheses.\n\n---\n\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) -> for ans string which is required!\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n\n# Dry Run\n**Consider the input string s = "(()())(())":**\n\n- The first primitive string is "(()())":\n - The outermost parentheses are removed, resulting in "()()".\n- The second primitive string is "(())":\n - The outermost parentheses are removed, resulting in "()".\n- Concatenate these results to get "()()()".\n\n---\n\n\n# Code\n\n```cpp []\nclass Solution {\npublic:\n string removeOuterParentheses(string s) {\n string ans = "";\n int cnt = 0;\n for(int i=0;i<s.size();i++){\n if(cnt ==0 && s[i]==\'(\') cnt++;\n else if(s[i]==\'(\'){\n cnt++;\n ans+=s[i];\n }\n if(cnt == 1 && s[i]==\')\') cnt--;\n else if(s[i]==\')\'){\n cnt--;\n ans+=s[i];\n }\n }\n return ans; \n }\n};\n```\n\n```javascript []\nfunction removeOuterParentheses(s) {\n let ans = "";\n let cnt = 0;\n\n for (let i = 0; i < s.length; i++) {\n if (cnt === 0 && s[i] === \'(\') {\n cnt++;\n } else if (s[i] === \'(\') {\n cnt++;\n ans += s[i];\n } else if (cnt === 1 && s[i] === \')\') {\n cnt--;\n } else {\n cnt--;\n ans += s[i];\n }\n }\n\n return ans;\n}\n\n```\n```python []\ndef removeOuterParentheses(s: str) -> str:\n ans = ""\n cnt = 0\n\n for char in s:\n if cnt == 0 and char == \'(\':\n cnt += 1\n elif char == \'(\':\n cnt += 1\n ans += char\n elif cnt == 1 and char == \')\':\n cnt -= 1\n else:\n cnt -= 1\n ans += char\n\n return ans\n\n```\n```java []\npublic class Solution {\n public String removeOuterParentheses(String s) {\n StringBuilder ans = new StringBuilder();\n int cnt = 0;\n\n for (int i = 0; i < s.length(); i++) {\n if (cnt == 0 && s.charAt(i) == \'(\') {\n cnt++;\n } else if (s.charAt(i) == \'(\') {\n cnt++;\n ans.append(s.charAt(i));\n } else if (cnt == 1 && s.charAt(i) == \')\') {\n cnt--;\n } else {\n cnt--;\n ans.append(s.charAt(i));\n }\n }\n\n return ans.toString();\n }\n}\n\'\n```\n\n | 13 | 0 | ['String', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
remove-outermost-parentheses | aam admi approach | aam-admi-approach-by-tejaswibhagat-xlfg | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | tejaswibhagat | NORMAL | 2024-04-19T16:09:08.161290+00:00 | 2024-04-19T16:09:08.161315+00:00 | 818 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string removeOuterParentheses(string s) {\n string ans = "";\n int count = 0;\n for(char ch : s){\n if(ch == \'(\' && count == 0)\n count++;\n else if(ch == \'(\' && count>=1){\n ans += ch;\n count++;\n }\n \n else if(ch == \')\' && count >1){\n ans += ch;\n count--;\n }\n else if(ch ==\')\' && count == 1)\n count--;\n\n }\n return ans;\n }\n};\n``` | 13 | 0 | ['C++'] | 2 |
remove-outermost-parentheses | wont get a more straight forward solution than this. | wont-get-a-more-straight-forward-solutio-vlf4 | Intuition\n Describe your first thoughts on how to solve this problem. \nguys please upvote , I work so hard explaining things and you potatoes dont even upvote | Abhishekkant135 | NORMAL | 2024-04-14T19:31:00.969475+00:00 | 2024-04-14T19:31:00.969501+00:00 | 875 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nguys please upvote , I work so hard explaining things and you potatoes dont even upvote the post . SHAME on you. NOW UPVOTE\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n1. **Initializing Variables:**\n - `StringBuilder sb = new StringBuilder("");`: Creates a `StringBuilder` object named `sb` to efficiently build the resulting string.\n - `int count = 0`: Initializes a variable `count` to 0 to keep track of the nesting depth of parentheses encountered while iterating through the string.\n\n2. **Iterating Through the String:**\n - The `for` loop iterates through each character (`s.charAt(i)`) in the `s` string.\n - **Handling Opening Parentheses (\'(\'):**\n - `if (s.charAt(i) == \'(\')`: Checks if the current character is an opening parenthesis.\n - `count++`: Increments the `count` to indicate entering a new level of nesting.\n - `if (count > 1)`: If the current nesting depth (`count`) is greater than 1 (meaning we\'re inside an existing parenthetical group), the character is appended to the `StringBuilder` (`sb.append(s.charAt(i))`) as it\'s not part of the outermost parentheses.\n - **Handling Closing Parentheses (\')\'):**\n - `else`: If the current character is a closing parenthesis.\n - `count--`: Decrements the `count` to indicate exiting a level of nesting.\n - `if (count > 0)`: If the current nesting depth (`count`) is still greater than 0 (meaning we\'re still within a parenthetical group), the character is appended to the `StringBuilder` (`sb.append(s.charAt(i))`) as it\'s not part of the outermost parentheses.\n\n3. **Building the Result:**\n - After iterating through the entire string, the `StringBuilder` `sb` contains the characters that are not part of the outermost parentheses in the original string.\n\n4. **Returning the Result:**\n - `return sb.toString()`: Converts the `StringBuilder` `sb` to a String object and returns it.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- The code iterates through the string once, resulting in a time complexity of O(n), where n is the length of the string `s`.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- The space complexity is O(n) due to the use of the `StringBuilder` object, which creates extra space in proportion to the length of the resulting string. However, this is generally considered more efficient than creating a new String object for each character appended during modification.\n# Code\n```\nclass Solution {\n public String removeOuterParentheses(String s) {\n StringBuilder sb=new StringBuilder("");\n int count=0;\n for(int i=0;i<s.length();i++){\n if(s.charAt(i)==\'(\'){\n count++;\n if(count>1){\n sb.append(s.charAt(i));\n }\n }\n else{\n count--;\n if(count>0){\n sb.append(s.charAt(i));\n }\n }\n }\n return sb.toString();\n }\n}\n``` | 12 | 0 | ['String', 'Java'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.