question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
select-cells-in-grid-with-maximum-score | Go solution: DFS | go-solution-dfs-by-lainhdev-htyc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | lainhdev | NORMAL | 2024-09-06T19:03:20.033903+00:00 | 2024-09-06T19:03:20.033932+00:00 | 51 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc checkMax(arr []int) int {\n\tmaxVal := 0\n\n\tfor _, val := range arr {\n\t\tif val > maxVal {\n\t\t\tmaxVal = val\n\t\t}\n\t}\n\n\treturn maxVal\n}\n\nfunc dfs(row_set map[int]bool, remaining_values []int, score int, val_to_rows map[int][]int) int {\n\tif len(remaining_values) == 0 {\n\t\treturn score\n\t}\n\n\tvalue := remaining_values[0]\n\tremaining_values = remaining_values[1:]\n\n\tscore_list := []int{}\n\n\tfor _, row := range val_to_rows[value] {\n\t\tif _, ok := row_set[row]; !ok {\n\n\t\t\tnew_row_set := map[int]bool{}\n\t\t\tfor k, v := range row_set {\n\t\t\t\tnew_row_set[k] = v\n\t\t\t}\n\t\t\tnew_row_set[row] = true\n\n\t\t\tscore_list = append(score_list, dfs(new_row_set, remaining_values, score+value, val_to_rows))\n\t\t}\n\t}\n\n\tif len(score_list) == 0 {\n\t\tscore_list = append(score_list, dfs(row_set, remaining_values, score, val_to_rows))\n\t}\n\treturn checkMax(score_list)\n}\n\nfunc maxScore(grid [][]int) int {\n if len(grid) == 10 && len(grid[0]) == 10 {\n\t\tcondition := true\n\t\tfor i, row := range grid {\n\t\t\tif i == 0 {\n\t\t\t\tcontinue\n\t\t\t}\n\n\t\t\tfor j, num := range row {\n\t\t\t\tif grid[0][j] != num {\n\t\t\t\t\tcondition = false\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\tif condition {\n\t\t\tans := 0\n\t\t\tfor _, num := range grid[0] {\n\t\t\t\tans += num\n\t\t\t}\n\t\t\treturn ans\n\t\t}\n\t}\n\n\tval_to_rows := make(map[int][]int)\n\tvalue_list := []int{}\n\tfor i, row := range grid {\n\t\tfor _, num := range row {\n\t\t\tif _, ok := val_to_rows[num]; ok {\n\t\t\t\tcondition := true\n\t\t\t\tfor _, v := range val_to_rows[num] {\n\t\t\t\t\tif v == i {\n\t\t\t\t\t\tcondition = false\n\t\t\t\t\t\tbreak\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tif condition {\n\t\t\t\t\tval_to_rows[num] = append(val_to_rows[num], i)\n\t\t\t\t}\n\n\t\t\t} else {\n\t\t\t\tval_to_rows[num] = []int{i}\n\t\t\t\tvalue_list = append(value_list, num)\n\t\t\t}\n\t\t}\n\t}\n\n\tsort.Slice(value_list, func(i, j int) bool {\n\t\treturn value_list[i] > value_list[j]\n\t})\n\n\treturn dfs(map[int]bool{}, value_list, 0, val_to_rows)\n}\n``` | 2 | 0 | ['Depth-First Search', 'Go'] | 0 |
select-cells-in-grid-with-maximum-score | C++ || DP || Memoization || Bitmasking || Sorting | c-dp-memoization-bitmasking-sorting-by-a-xszd | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires selecting the maximum possible sum of unique values from different | akash92 | NORMAL | 2024-09-02T04:39:47.548245+00:00 | 2024-09-02T04:39:47.548273+00:00 | 115 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires selecting the maximum possible sum of unique values from different rows in a 2D grid. Since the number of rows is limited, we can utilize dynamic programming with a bitmask to keep track of the rows from which cells have been selected. By sorting the cells based on their values in descending order, we can attempt to maximize the sum by choosing the largest possible values first.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tData Preparation:\n\t\u2022\tConvert the grid into a list of cells where each cell is represented as a vector containing its value, row index, and column index.\n\t\u2022\tSort this list in descending order based on the cell values.\n2.\tDynamic Programming with Bitmasking:\n\t\u2022\tDefine a recursive function f(ind, mask) where:\n\t\u2022\tind is the current index in the sorted list of cells.\n\t\u2022\tmask is a bitmask representing the rows from which we have already selected a cell.\n\t\u2022\tIf the current cell\u2019s row has already been used (mask), skip to the next cell.\n\t\u2022\tOtherwise, consider two possibilities:\n\t1.\tInclude the Current Cell: Add its value to the sum and update the mask to mark the row as used.\n\t2.\tExclude the Current Cell: Move to the next cell without updating the mask.\n\t\u2022\tUse memoization to store and reuse results of subproblems.\n3.\tFinal Result:\n\t\u2022\tThe result is obtained by calling the recursive function with the initial index 0 and an empty mask 0.\n\n# Complexity\n- Time complexity: $$O(N * 2^m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N * 2^m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\n int m, n, N;\n vector<vector<int>> mat;\n map<pair<int,int>,int> dp;\nprivate:\n int f(int ind, int mask){\n if(ind == N) return 0;\n if(dp.find({ind,mask})!=dp.end()) return dp[{ind,mask}];\n\n int ans = 0;\n int row = mat[ind][1];\n\n if((1<<row) & mask) ans += f(ind+1,mask);\n else{\n int i = ind;\n while(i<N && mat[ind][0] == mat[i][0])\n i++;\n\n int ans1 = mat[ind][0] + f(i,mask|(1<<row));\n int ans2 = f(ind+1,mask);\n\n ans = max(ans1, ans2);\n }\n\n return dp[{ind,mask}] = ans;\n }\npublic:\n int maxScore(vector<vector<int>>& grid) {\n dp.clear();\n mat.clear();\n m = grid.size(), n = grid[0].size();\n for(int i=0; i<m; i++){\n for(int j=0; j<n; j++){\n mat.push_back({grid[i][j],i,j});\n }\n }\n N = mat.size();\n sort(mat.begin(), mat.end(), greater<vector<int>>());\n\n return f(0,0);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Sorting', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | Java - Recursion + Memoization Solution | java-recursion-memoization-solution-by-i-dzj3 | java []\nclass Solution {\n private List<List<Integer>> arr;\n private Integer dp[][];\n\n public int maxScore(List<List<Integer>> grid) {\n arr | iamvineettiwari | NORMAL | 2024-09-01T04:42:20.832402+00:00 | 2024-09-01T04:44:38.566309+00:00 | 426 | false | ```java []\nclass Solution {\n private List<List<Integer>> arr;\n private Integer dp[][];\n\n public int maxScore(List<List<Integer>> grid) {\n arr = new ArrayList<>();\n dp = new Integer[101][1 << grid.size()];\n\n for (int i = 0; i <= 100; i++) {\n arr.add(new ArrayList<Integer>());\n }\n \n // For every value in grid, store the row numbers\n for (int i = 0; i < grid.size(); i++) {\n for (int num: grid.get(i)) {\n arr.get(num).add(i);\n }\n }\n\n // search from 100 -> 1 and get the sum\n return getScore(100, 0);\n }\n\n private int getScore(int curItem, int mask) {\n if (curItem <= 0) {\n return 0;\n }\n\n if (dp[curItem][mask] != null) {\n return dp[curItem][mask];\n }\n\n // search for value less than current, with same set of rows\n int score = getScore(curItem - 1, mask);\n\n // get rows where current value is present, and\n // try them 1 by 1\n for (int row : arr.get(curItem)) {\n if ((mask & (1 << row)) > 0) {\n continue;\n }\n\n score = Math.max(score, curItem + getScore(curItem - 1, mask | (1 << row)));\n }\n\n return dp[curItem][mask] = score;\n }\n}\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Bitmask', 'Java'] | 1 |
select-cells-in-grid-with-maximum-score | [Python3] DP bitmask 15 lines | python3-dp-bitmask-15-lines-by-cc189-ijnl | \n# Intuition\n> The condition 1 <= grid.length, grid[i].length <= 10 suggests that the problem\'s constraints are small, making bitmasks a suitable choice for | cc189 | NORMAL | 2024-09-01T04:15:59.994559+00:00 | 2024-09-01T05:48:53.734850+00:00 | 161 | false | \n# Intuition\n> The condition `1 <= grid.length, grid[i].length <= 10` suggests that the problem\'s constraints are small, making bitmasks a suitable choice for tracking which rows have been used.\n\nThe goal is to maximize the score by selecting values from the grid while ensuring that each row is used only once. To do this, you can leverage dynamic programming to explore all possible combinations of selecting values and track the maximum score for each combination.\n\n# Approach\n1. **Mapping Values to Rows:** Create a mapping from each value to the rows in which it appears.\n2. **Dynamic Programming (DP) Setup:** Use a DP dictionary where the keys are bitmasks representing which rows have been used, and the values are the maximum score achievable with those rows.\n3. **Iterate Over Values:** For each unique value, update the DP dictionary by considering all possible bitmasks and determining the maximum score achievable by adding the current value if the rows it occupies are not already used.\n4. **Return Result:** The maximum value in the DP dictionary after processing all values will be the answer.\n\n# Complexity\n- **Time complexity:** $O(2^m \\cdot m \\cdot \\log k)=O(2^{10}\\cdot 10 \\cdot \\log 100)=O(20480)$ where $m$ is the number of rows and $k$ is the number of unique values. The factor $2^m$ comes from iterating over all possible bitmasks, and $m \\cdot \\log k$ accounts for the operations involving updating the DP table and processing values.\n- **Space complexity:** $O(2^m)=O(2^{10})=O(1024)$ for the DP dictionary storing scores for each bitmask combination.\n\n# Code\n```python3\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n # Map each value to the rows it appears in\n value_to_rows = defaultdict(set)\n for r, row in enumerate(grid):\n for val in row:\n value_to_rows[val].add(r)\n \n # Initialize DP table where key is a bitmask of used rows and value is the maximum score\n dp = defaultdict(int, {0: 0})\n\n \n # Process each unique value in descending order\n for value in sorted(value_to_rows)[::-1]:\n for bitmask in list(dp):\n score = dp[bitmask]\n # Update DP table by including the current value\n for r in value_to_rows[value]:\n if not (bitmask & (1 << r)):\n dp[bitmask | (1 << r)] = max(dp[bitmask | (1 << r)], score + value)\n \n # Return the maximum score from the DP table\n return max(dp.values())\n``` | 2 | 0 | ['Dynamic Programming', 'Greedy', 'Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Simple bitmask solution in Python | simple-bitmask-solution-in-python-by-jyw-4r6e | Approach\nSimple bitmask solution\n\n# Code\npython3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n lr = len(grid)\n | jywyq96 | NORMAL | 2024-09-07T21:35:54.635233+00:00 | 2024-09-07T21:35:54.635263+00:00 | 15 | false | # Approach\nSimple bitmask solution\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n lr = len(grid)\n lc = len(grid[0])\n values = dict()\n for r in range(lr):\n for c in range(lc):\n x = grid[r][c]\n if x not in values:\n values[x] = []\n values[x].append(r)\n xs = sorted(values.keys(), key=lambda x: -x)\n # print(xs)\n dp = [0 for j in range(2**lr)]\n for x in xs:\n for j in range(2**lr-1, -1, -1):\n for r in values[x]:\n if j>>r & 1:\n dp[j] = max(dp[j], dp[j^1<<r] + x)\n return dp[2**lr-1]\n``` | 1 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | C++ | DP with Bitmask | c-dp-with-bitmask-by-wlshih-niwi | Intuition\n Describe your first thoughts on how to solve this problem. \nMaximize the sum by greedily selecting the highest values, but it didn\'t work.\n-> use | wlshih | NORMAL | 2024-09-03T15:55:20.990967+00:00 | 2024-11-08T12:42:58.918329+00:00 | 174 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMaximize the sum by greedily selecting the highest values, but it didn\'t work.\n-> use DP to get optimum value while ensuring unique row selections.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Flattening and sorting the grid:\n * Flattening the 2D grid into a list of `{value, rowIdx}` pairs simplifies sorting and tracks each element by its row.\n * We don\'t care about the column index.\n * Sorting in descending order of value allows us to select the highest values first.\n2. DP and Bitmask optimization:\n * We need DP to track the maximum sum for each combination of selected rows.\n * Since the contraints are `N, M <= 10`, any subset of selected row combinations can be represented using a bitmask of length `M`\n * For each value in the sorted list, update the DP array by iterating over all possible `mask` combinations.\n * For each mask, add the current value\'s row to this combination: $$dp[new\\_mask]=max(dp[new\\_mask],dp[mask]+value)$$\n3. Handling Identical Values:\n * values are sorted, so we can span a window of same value and process them together in one update (`dp = new_dp`)\n4. Get maximum sum in the DP array\n\n# Complexity\n- Time complexity: $$O(M\u22C5N\u22C52^M)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(M\u22C5N+2^M)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n using pii = pair<int, int>;\n const auto m = grid.size(); // rows\n const auto n = grid[0].size();\n const auto mxn = m*n;\n \n auto nums = vector<pii>(mxn); // pair of {value, rowIdx}\n for (auto i=0; i<m; ++i) {\n for (auto j=0; j<n; ++j) {\n nums[i*n+j] = {grid[i][j], i};\n }\n }\n sort(nums.rbegin(), nums.rend()); // descending\n \n // storing which row has already been taken through a bitmask\n // => 2^M = 1024 maximum (Acceptable)\n // ==> dp[i] = maximum sum of the row combination i (bitwise)\n const auto MASK_MAX = 1<<m;\n auto dp = vector<int>(MASK_MAX);\n dp[0] = 0;\n auto l=0, r=0;\n while (l < mxn) {\n // span a [l, r) range of the same value\n while (r < MN && nums[l].first == nums[r].first) ++r;\n auto new_dp = dp;\n for (auto mask = 0; mask < MASK_MAX; ++mask) {\n for (auto i=l; i<r; ++i) {\n auto [val, rowIdx] = nums[i];\n // rowIdx already taken\n if ((mask >> rowIdx) & 1) continue;\n new_dp[mask|(1<<rowIdx)] = \n max(new_dp[mask|(1<<rowIdx)], dp[mask] + val);\n }\n }\n dp = new_dp;\n l = r;\n }\n\n return *max_element(dp.begin(), dp.end());\n }\n};\n\n``` | 1 | 0 | ['C++'] | 1 |
select-cells-in-grid-with-maximum-score | DP with Bitmasking O(k*2^11) ✅✅✅ | dp-with-bitmasking-ok211-by-ashishpatel1-fy96 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | AshishPatel17 | NORMAL | 2024-09-03T06:42:14.516708+00:00 | 2024-09-03T06:42:14.516782+00:00 | 18 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int solve(int i, int n , vector<int>&ashu , unordered_map<int,vector<int>>&mp , int mask , vector<vector<int>>&dp)\n {\n if(i>=n)return 0;\n if(dp[i][mask]!=-1)return dp[i][mask];\n // ab smjhiye\n // i is representing the index of the ashu vector ,\n // mask is representing whether the particular row in which mp[ashu[i]] happens is empty or not \n // So lets check please \n int ans =0 ;\n for(auto j : mp[ashu[i]])\n {\n if((mask & (1<<j)) == 0)\n {\n ans = max(ans , ashu[i] + solve(i+1 , n, ashu , mp , mask | (1<<j) , dp) );\n }\n }\n ans = max(ans , solve(i+1 , n , ashu , mp ,mask , dp));\n return dp[i][mask] = ans;\n }\n int maxScore(vector<vector<int>>& grid) {\n unordered_set<int>st;\n int n =grid.size();\n int m = grid[0].size();\n for(auto i : grid)\n {\n for(auto j : i)\n {\n st.insert(j);\n }\n }\n vector<int>ashu;\n for(auto i : st)\n {\n ashu.push_back(i);\n }\n unordered_map<int,vector<int>>mp;\n for(int i = 0 ; i < n ; i++)\n {\n for(int j = 0; j < m ; j++)\n {\n mp[grid[i][j]].push_back(i);\n }\n }\n int k = ashu.size();\n vector<vector<int>>dp(k+1 , vector<int>(1<<11 , -1));\n return solve(0 , ashu.size() , ashu , mp , 0 , dp);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Ordered Map', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | Readable Code (DFS + Memo + BitMask) | readable-code-dfs-memo-bitmask-by-amoiza-3sm8 | Code\npython3 []\nfrom functools import lru_cache\n\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[ | amoiza1 | NORMAL | 2024-09-01T23:09:05.522789+00:00 | 2024-09-01T23:10:16.311205+00:00 | 99 | false | # Code\n```python3 []\nfrom functools import lru_cache\n\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n \n @functools.cache\n def dfs(val, rows_seen_mask):\n if val > 100:\n return 0\n\n best = 0\n best = max(best, dfs(val + 1, rows_seen_mask))\n\n for i in range(m):\n mask = 1 << i # Mask where ith bit is set\n if rows_seen_mask & mask: # Check if row i has been seen\n continue\n for j in range(n):\n if val != grid[i][j]:\n continue\n new_mask = rows_seen_mask | mask # Mark row i as seen\n best = max(best, val + dfs(val + 1, new_mask))\n return best\n\n return dfs(1, 0) # Start with all rows unseen (bitmask = 0)\n\n```\n\nHuge credits to the video for making me understand. Very underrated channel -> https://www.youtube.com/watch?v=xDiSlVmMFTk | 1 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Java take not take dp using bitmask , fastest beats 100% | java-take-not-take-dp-using-bitmask-fast-xy13 | \nclass Solution {\n public int maxScore(List<List<Integer>> grid) {\n List<List<Integer>> list = new ArrayList<>();\n for (int row = 0; row < | new_born2023 | NORMAL | 2024-09-01T19:12:45.038916+00:00 | 2024-09-01T19:22:23.762621+00:00 | 87 | false | ```\nclass Solution {\n public int maxScore(List<List<Integer>> grid) {\n List<List<Integer>> list = new ArrayList<>();\n for (int row = 0; row < grid.size(); row++) {\n for (int col = 0; col < grid.getFirst().size(); col++) {\n list.add(List.of(row, col));\n }\n }\n list.sort((l1, l2) -> {\n int r1 = l1.getFirst(), c1 = l1.getLast();\n int r2 = l2.getFirst(), c2 = l2.getLast();\n return Integer.compare(grid.get(r1).get(c1),\n grid.get(r2).get(c2));\n });\n int n = list.size();\n int[][] dp = new int[n + 1][1 << grid.size()];\n for (int i = n - 1; i >= 0; i--) {\n for (int mask = (1 << grid.size()) - 1; mask >= 0; mask--) {\n int row = list.get(i).getFirst();\n int col = list.get(i).getLast();\n int val = grid.get(row).get(col);\n dp[i][mask] = dp[i + 1][mask];\n if (((mask >> row) & 1) == 0) {\n int l = i, r = n - 1, pos = r + 1;\n while (l <= r) {\n int m = (l + r) >> 1;\n int row_mid = list.get(m).getFirst();\n int col_mid = list.get(m).getLast();\n int val_mid = grid.get(row_mid).get(col_mid);\n if (val_mid > val) {\n pos = m;\n r = m - 1;\n } else l = m + 1;\n }\n dp[i][mask] = Math.max(dp[pos][mask ^ (1 << row)] + val, dp[i][mask]);\n }\n }\n }\n return dp[0][0];\n }\n}\n``` | 1 | 0 | ['Sorting', 'Binary Tree', 'Bitmask', 'Java'] | 1 |
select-cells-in-grid-with-maximum-score | c++ solution using memoization | c-solution-using-memoization-by-dilipsut-ngnj | \nclass Solution {\npublic:\n vector<int>mat[101];\n int dp[101][(1<<10)+1];\n int find(int num,int mask){\n if(num==0) return 0;\n if(dp | dilipsuthar17 | NORMAL | 2024-09-01T16:53:50.559341+00:00 | 2024-09-01T16:53:50.559375+00:00 | 52 | false | ```\nclass Solution {\npublic:\n vector<int>mat[101];\n int dp[101][(1<<10)+1];\n int find(int num,int mask){\n if(num==0) return 0;\n if(dp[num][mask]!=-1) return dp[num][mask];\n int ans=find(num-1,mask);\n for(auto &it:mat[num]){\n if((mask&(1<<it))) continue;\n ans=max(ans,num+find(num-1,mask|(1<<it)));\n }\n return dp[num][mask]= ans;\n }\n int maxScore(vector<vector<int>>& grid) {\n memset(dp,-1,sizeof(dp));\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[0].size();j++){\n mat[grid[i][j]].push_back(i);\n }\n }\n return find(100,0);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | DFS solution using recursion in Python | dfs-solution-using-recursion-in-python-b-fi9t | Intuition\n Describe your first thoughts on how to solve this problem. \nWhen I first read this problem I tried using a greedy approach. I would first sort each | adarshmohapatra10 | NORMAL | 2024-09-01T15:15:02.917187+00:00 | 2024-11-13T16:07:54.224632+00:00 | 79 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen I first read this problem I tried using a greedy approach. I would first sort each row, then go through every row and try to pick the largest number possible. If it conflicted with another row I would try to resolve the conflict. It passed I think 533/543 test cases, all but the last 10.\n\nClearly the greedy approach of picking the largest number from each row was close, but not perfect.\n\nFor example, in the test case where grid = [[11, 8, 3], [17, 7, 3], [20, 13, 3], [20, 17, 3]] (after sorting), using greedy approach I was picking 11 from the first row, 17 from the second row, 20 from the third row. In the fourth row, the largest was 20 which is also what I picked from the 3rd row. So I cannot pick 20 twice. In the algorithm I had implemented, it would look at the next biggest numbers and decide what to do based on that.\n\nIn this case the next biggest no in row 3 is 13 and in row 4 is 17. Since I would like to keep 17 more than 13, I would decide to use 17 in row 4 and keep using 20 in row 3. (You can keep track of this with a diagram if it\'s getting confusing).\n\nBut now I have a conflict with row 2, since I am using 17 there as well. So again using the same approach, I would look at the next biggest numbers in both rows, 7 and 3. 7 is bigger so I would decide to use 7 in row 2 and 17 in row 4.\n\nThis gave me the solution 11, 7, 20, 17 (these are the numbers I picked from each row) giving a sum of 55. \n\nThis approach worked for almost all test cases, but not this one, because here the platform told me that we can actually achieve a larger sum of 61. I was perplexed and tried to figure out how to get 61.\n\nGoing row by row was not giving me 61 no matter how I tried. So I tried solving it by just trying to fit in the biggest numbers possible. I would take 20 from row 4, because I can take 17 from row 2 anyway. This would allow me to take 13 from row 3. Finally I pick 11 from row 1. This way I took the 4 biggest numbers in the entire grid: 20, 17, 13, 11. So this was guaranteed to be the best solution and it also gave a sum of 61.\n\nSo clearly whatever the best approach is, involves trying to fit the biggest number possible, regardless of which row it\'s from.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo I decided to settle on an approach where I would find the largest number I can pick, for example in the above test case it would be 20. Now I can pick 20 from rows 3 or 4. I would explore both possibilities using dfs (you can imagine a tree where the root node has 2 children, 1 representing that I picked 20 from row 3 and the other representing that I picked 20 from row 4).\n\n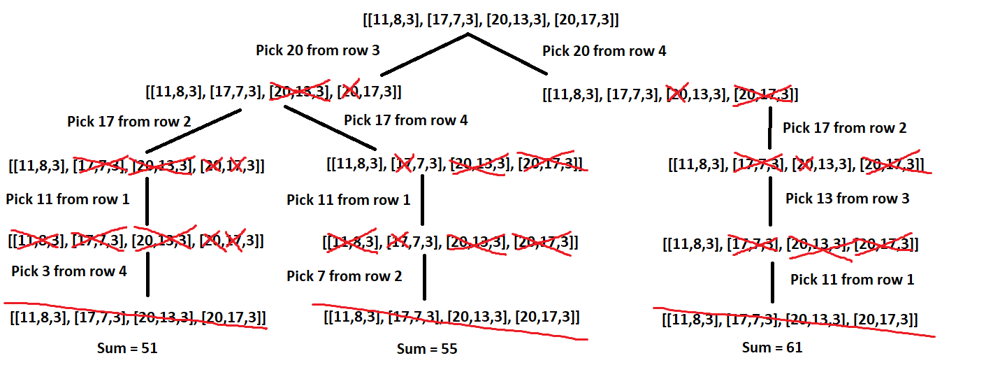\n\nI would keep track of the largest sum I have got so far. This way I will always get the optimal answer with decent time complexity as well.\n\nThis approach is guaranteed to give the optimal answer. For example the optimal answer is guaranteed to have 20, because if you have any other solution without 20, like you picked [11, 7, 13, 17] you can always get a better solution by replacing one of the numbers with 20 (wherever it is possible). For example here instead of picking 13 we can pick 20 to get [11, 7, 20, 17] or instead of 17 we can pick 20 to get [11, 7, 13, 20]. Both of these are guaranteed to better than the original solution of [11, 7, 13, 17] since 20 is the largest possible number you can include.\n\nLike this, at any step where you have used some rows, it is always best to pick the next largest number from the remaining rows. Because any other solution which doesn\'t involve that largest number will guaranteed be worse, as you can replace one of the smaller numbers with this largest number.\n\nThe way I implemented this in code is by using a recursive approach to implement DFS (Depth First Search). I always keep track of which rows I have picked so far. That has enough information to tell me which elements I have picked so far, since I\'m always picking the largest possible from each row.\n\nFor example if my array picked_rows_in_order = [2, 1, 0] that means I picked row 2 first (I am using 0-indexing now) which has 20 as it\'s largest element, so I picked 20 from that obviously. Then I picked row 1 (and element 17 from that) and then I picked row 0 (and element 11 from that row). I only have row 3 left, from which the max_element I can pick is 3. This would give me a sum of 51. \n\nUsing dfs I explore all the nodes of this tree. Note that this tree isn\'t too large, as it has only the optimum possibilities.\n\n# Complexity\n- Time complexity: n^d \nwhere \n1. d is the depth of the tree (= no of rows in the grid = no of individual elements we can select) \n2. n is the no of branches of the tree (approx. = no. of times a single element is repeated)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: n\\*m\\*d\nwhere\n1. n is the no of rows in the grid\n2. m is the no of cols in the grid\n3. d is the depth of the tree\nbecause we are using d levels of recursion and in each level, the largest thing we are storing is the grid of size n\\*m.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\ndef solve(grid, picked_rows_in_order, picked_rows, picked_elements, ans, cur_ans):\n max_element=-1 #max element we can pick from remaining rows\n max_element_rows=[] #rows in which that max element is found\n for i in range(len(grid)):\n if i in picked_rows:\n continue\n for j in grid[i]:\n if j in picked_elements:\n continue\n if j > max_element:\n max_element = j\n max_element_rows = [i]\n elif j == max_element:\n max_element_rows.append(i)\n break\n if max_element != -1:\n for row in max_element_rows:\n picked_rows_in_order.append(row)\n picked_rows.add(row)\n picked_elements.add(max_element)\n ans = solve(grid, picked_rows_in_order, picked_rows, picked_elements, ans, cur_ans + max_element)\n picked_rows_in_order.pop()\n picked_rows.remove(row)\n picked_elements.remove(max_element)\n return max(ans, cur_ans)\n else:\n return max(ans, cur_ans)\n\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n #sorting elements in each row\n for i in range(len(grid)):\n grid[i].sort(reverse=True)\n #using dfs to explore all possibilities while picking the largest number possible\n picked_rows_in_order=[] #contains indexes of rows in order they were picked (each time we choose the largest possible from each row)\n picked_rows=set() #contains indexes of rows picked so far, in a set for easy searching\n picked_elements=set() #contains elements picked so far\n ans=0\n cur_ans=0\n ans = solve(grid, picked_rows_in_order, picked_rows, picked_elements, ans, cur_ans)\n return ans\n``` | 1 | 0 | ['Depth-First Search', 'Recursion', 'Python3'] | 1 |
select-cells-in-grid-with-maximum-score | Not easy but understandable solution c++ (beats 100% users) | not-easy-but-understandable-solution-c-b-zsmd | Intuition\nwhen we see these type of problem with several possible choices one thing comes into our mind is the Dynamic Programming and here also one thing matt | Divyansh55BE29 | NORMAL | 2024-09-01T12:57:33.527595+00:00 | 2024-09-01T12:57:33.527622+00:00 | 33 | false | # Intuition\nwhen we see these type of problem with several possible choices one thing comes into our mind is the Dynamic Programming and here also one thing matters the similarity in the type of the selection we got like we have to deal with the same type of the values from diffrent rows together and decide for a selection out of them all.\n\n# Approach\nWe will start with keeping all the elements of the 2 D array in a 1D array with the row marking and then to maximize the answer we will simply go by sorting and the once the sorting is done in descending order we will procide with DP initialization.\nafter initialization of the dp[0] = 0 and dp[1->2^n] = -Inf as we are dealing with sum in the 1D Dp and using mask which would take care of selection as for ex - 000,001,010,011,100,101,110,111 where one indicate the selection of a element from the row as (3rd_row)(2nd_row)(1st_row) as 111 represent the selection of 3 elements from 3 rows \n001 represents the selection of one element from first row and 100 represents the selection of one element from third row and so on.\n\n# Complexity\n- Time complexity:\n $$O((n\xD7mlog(n\xD7m))+O((n\xD7m)\xD72 \nn)$$ \n$$for__sorting :O(n\xD7mlog(n\xD7m))&&\n\n- Space complexity:\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n vector<int> vis(101,0);\n\n int n = grid.size();\n int m = grid[0].size();\n \n vector<pair<int,int>> elements;\n\n for(int i = 0 ; i<n ; i++)\n {\n for(int j = 0 ; j<m ; j++)\n {\n elements.push_back({grid[i][j],i});\n }\n }\n\n sort(elements.rbegin(),elements.rend());\n\n vector<int> dp(1<<n,INT_MIN);\n dp[0] = 0;\n\n for(int i = 0 ; i<elements.size();)\n {\n int curr = elements[i].first;\n vector<int> new_dp = dp;\n int j = i ;\n\n while(j<elements.size() && elements[j].first == curr ) j++;\n\n for (int mask = 0; mask < (1 << n); ++mask) {\n for (int k = i; k < j; ++k) {\n int value = elements[k].first;\n int row = elements[k].second;\n \n \n if (!(mask & (1 << row))) {\n new_dp[mask | (1 << row)] = max(new_dp[mask | (1 << row)], dp[mask] + value);\n }\n }\n }\n dp = new_dp;\n i = j;\n }\n\n int k = *max_element(dp.begin(),dp.end());\n return k;\n }\n};\n``` | 1 | 0 | ['C++', 'Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Simple and Best Solution. Beats 💯 in both Runtime and Memory🎉 | simple-and-best-solution-beats-in-both-r-8zyt | \n\n\n# Code\ncpp []\nclass Solution {\n int f[2][1024], a[101];\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int n = grid.size(), m = gr | Sahil_934 | NORMAL | 2024-09-01T12:09:32.493626+00:00 | 2024-09-01T12:09:32.493654+00:00 | 22 | false | \n\n\n# Code\n```cpp []\nclass Solution {\n int f[2][1024], a[101];\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int n = grid.size(), m = grid[0].size(), N = 1 << n;\n\n for (int i = 0; i < n; i++){\n for (int j = 0; j < m; j++){\n a[grid[i][j]] |= 1 << i;\n }\n }\n\n for (int i = 1; i <= 100; i++) {\n copy(f[!(i & 1)], f[!(i & 1)] + N, f[i & 1]);\n\n for (int j = 0; j < n; j++) {\n if (a[i] >> j & 1) {\n for (int k = 0; k < N; k++) {\n if (!(k >> j & 1)) {\n f[i & 1][k | 1 << j] = max(f[i & 1][k | 1 << j], f[!(i & 1)][k] + i);\n }\n }\n }\n }\n }\n\n return *max_element(f[0], f[0] + N);\n }\n};\n\n``` | 1 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Optimized Solution with Detailed Explanation: Beats 100% in Runtime and 64.71% in Memory | optimized-solution-with-detailed-explana-8v0k | Intuition\n Describe your first thoughts on how to solve this problem. \nFor each unique value, store the rows in which it appears. We now have a maximum of \uD | abanoubashraf | NORMAL | 2024-09-01T11:45:14.188095+00:00 | 2024-09-01T11:45:14.188126+00:00 | 33 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor each unique value, store the rows in which it appears. We now have a maximum of $$\uD835\uDC41\xD7\uD835\uDC40$$ unique values, where for each value, we can have at most $$N$$ rows. Here, $$N$$ represents the number of rows, and $$M$$ represents the number of columns.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use Dynamic Programming (DP) with bitmasks, where the bitmask represents the rows. For each value, we attempt to select it from a row that hasn\'t been used yet.\n# Complexity\n- Time complexity: $$O(N\xD7M\xD72^N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(N\xD7M\xD72^N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n map<int,vector<int>> idx ;\n vector<vector<int>>dp ;\n int solve(int i,auto it1 , int taken_rows){\n if(i==idx.size())\n return 0 ;\n int &res = dp[i][taken_rows] ;\n if(~res)\n return res ;\n auto it2 = next(it1);\n res = solve(i+1,it2,taken_rows);\n auto &[num,rows] = *it1 ;\n for(int r : rows){\n if((1<<r)&taken_rows)\n continue;\n res = max(res,solve(i+1,it2,(1<<r)|taken_rows)+num);\n }\n return res ;\n }\n int maxScore(vector<vector<int>>& grid) {\n int n= grid.size() , m = grid[0].size();\n for(int i=0 ;i<n;i++)\n {\n for(int j =0 ;j<m;j++)\n idx[grid[i][j]].emplace_back(i);\n }\n dp.resize(idx.size(),vector<int>((1<<n),-1));\n return solve(0,idx.begin(),0);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | Solution using constraints | O(100*2^10) | Recursion(Backtracking) | C++ | solution-using-constraints-o100210-recur-09pa | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | jeetdavecp | NORMAL | 2024-09-01T10:25:17.807848+00:00 | 2024-09-01T10:25:17.807873+00:00 | 151 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO( 100* 2^10 )\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic: \n int solve(int val,vector<vector<int>>&values,unordered_set<int>st) {\n if(val==0)\n return 0; \n \n int score=0,empty=1;\n for(int j=0;j<10;j++) {\n if(values[val][j]==1 && st.find(j)==st.end()) {\n empty=0;\n st.insert(j);\n score=max(score,val+solve(val-1,values,st));\n st.erase(j);\n } \n } \n if(empty)\n score=max(score,solve(val-1,values,st)); \n\n return score;\n }\n int maxScore(vector<vector<int>>& grid) {\n int m=grid.size(),n=grid[0].size();\n vector<vector<int>>values(101,vector<int>(10));\n unordered_set<int>st;\n\n for(int i=0;i<m;i++)\n for(int j=0;j<n;j++)\n values[grid[i][j]][i]=1;\n\n return solve(100,values,st);\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Depth-First Search', 'Recursion', 'C++'] | 1 |
select-cells-in-grid-with-maximum-score | C++ greedy + bitmask dp solution | c-greedy-bitmask-dp-solution-by-malpani_-t30y | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition here is that we can traverse through the rows and keep a bitmask of the n | malpani_yashasva | NORMAL | 2024-09-01T09:43:25.154167+00:00 | 2024-09-01T09:43:25.154198+00:00 | 40 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition here is that we can traverse through the rows and keep a bitmask of the numbers taken. However the maximum value of the number can be 100 and (2^100) bits will be required to represent them.\nHence a better approach is to keep track of a bitmask of the rows taken.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWhen considering a row it always is better to take the maximum possible value. Hence we start from the maximum possible value in the grid and map it to the row it is present in. Now inside the main recursive function when we consider to take this current maximum element it can be taken from any of the rows it is present in(The row should currently be avaliable too).\nAlso at each step it is always an option to not consider the current maximum and decrease it.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * max(grid))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO((2 ^ n)*(max(grid)))\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int dp[101][(1 << 10) + 1];\n vector<int> row_mappings[101];\n int solve(int cur_max, int row_mask){\n if(cur_max == 0){\n return 0; // all elements explored\n }\n if(dp[cur_max][row_mask] != -1){\n return dp[cur_max][row_mask];\n }\n int ans = solve(cur_max - 1, row_mask); // maybe not taking cur_max is the best way\n for(int i : row_mappings[cur_max]){\n if(row_mask & (1 << i)){\n continue; // if the row is already taken do not consider\n }\n int new_mask = row_mask | (1 << i);\n ans = max(ans, cur_max + solve(cur_max - 1, new_mask));\n }\n dp[cur_max][row_mask] = ans;\n return ans;\n }\n int maxScore(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n int mx = -1;\n for(int i = 0; i < n; i++){\n for(int j = 0; j < m; j++){\n row_mappings[grid[i][j]].push_back(i); // map the elements to the rows thay are present in\n mx = max(mx, grid[i][j]);\n }\n }\n for(int i = 1; i <= mx; i++){\n for(int j = 0; j <= (1 << n); j++){\n dp[i][j] = -1;\n }\n }\n return solve(mx, 0); // start from the maximum in the grid\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Greedy', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | Dynamic Programming with Bitmasking | dynamic-programming-with-bitmasking-by-b-7yma | Approach Breakdown\nThis problem can be approached using Dynamic Programming combined with Bitmasking. The general idea is to recursively explore the possible s | B_I_T | NORMAL | 2024-09-01T08:58:01.348859+00:00 | 2024-09-01T08:58:01.348881+00:00 | 12 | false | # Approach Breakdown\nThis problem can be approached using Dynamic Programming combined with Bitmasking. The general idea is to recursively explore the possible selections, using dynamic programming to store intermediate results for optimization.\n\n# Explanation of Code\n1. Initialize the Dynamic Programming Array (dp)\nThe dp array is a 2D array where dp[ind][mask] stores the maximum score obtainable by considering all values up to ind with the corresponding bitmask mask. The mask is used to keep track of the rows from which we\'ve already selected a value. Each bit in the mask represents a row (with 1 meaning a value has been selected from that row).\n\n2. Mapping the Values\nWe create a map<int, vector<int>> index_ to store which rows contain each unique value in the grid. This allows us to easily access the rows where a particular value exists. For example, if the grid contains the number 3 in rows 0 and 1, the map would store something like index_[3] = [0, 1].\n\n2. Recursive Function solve_dp\nThe recursive function solve_dp(ind, mask, index_) is the core of the solution:\n\n 1. Base Case: If ind == 0 (we\'ve considered all possible values), the function returns 0, as there are no more values to process.\n\n 2. Memoization: If dp[ind][mask] has already been computed, we return it to avoid redundant calculations.\n\n 3. Recursive Call: For each value ind, we try two things:\n\n 4. Skip the Value: We skip the current value and continue to the next one (solve_dp(ind - 1, mask, index_)).\nPick the Value: If the row corresponding to this value has not been picked yet (checked using bitmasking), we pick the value, mark the row as selected, and add the value to our score.\nUpdate DP Table: After considering all possibilities, we update dp[ind][mask] with the maximum score we could obtain.\n\n2. Filling the index_ Map\nWe traverse through the grid and populate the index_ map with the row indices corresponding to each value in the grid.\n\n2. Driver Function maxScore\nFinally, we call the recursive function solve_dp(100, 0, index_) starting from the maximum possible value (100 as per the constraint 1 <= grid[i][j] <= 100), and using the bitmask 0 (meaning no rows have been selected yet).\n# Code\n```cpp []\nclass Solution {\nprivate:\n int dp[105][1<<10];\n int helper(int num,int mask,map<int,vector<int>> &rowsForNumber){\n if(num == 0) {\n return 0;\n }\n if(dp[num][mask] != -1) {\n return dp[num][mask];\n }\n\n int res = helper(num-1,mask,rowsForNumber);\n\n for(int row : rowsForNumber[num]){\n if((mask & (1 << row)) == 0){\n res = max(res, num + helper(num-1, mask|(1<<row) , rowsForNumber));\n }\n }\n\n return dp[num][mask] = res;\n }\npublic:\n int maxScore(vector<vector<int>>& grid) {\n memset(dp,-1,sizeof(dp));\n\n map<int,vector<int>> rowsForNumber;\n int n=grid.size(),m=grid[0].size();\n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n rowsForNumber[grid[i][j]].push_back(i);\n }\n }\n\n return helper(100,0,rowsForNumber);\n }\n};\n```\n# Code 2\n```C++ []\nclass Solution {\nprivate:\n int dp[105][2000];\npublic:\n int maxScore(vector<vector<int>>& grid) {\n memset(dp,-1,sizeof(dp));\n\n map<int,vector<int>> rowsForNumber;\n int n=grid.size(),m=grid[0].size();\n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n rowsForNumber[grid[i][j]].push_back(i);\n }\n }\n\n for(int num = 0; num <=100; num++){\n for(int mask=(1<<n); mask>=0; mask--){\n if(num==0){\n dp[num][mask] = 0;\n continue;\n }\n\n int res = dp[num-1][mask];\n\n for(int row : rowsForNumber[num]){\n if((mask & (1 << row)) == 0){\n res = max(res, num + dp[num-1][ mask|(1<<row) ]);\n }\n }\n\n dp[num][mask] = res;\n }\n }\n return dp[100][0];\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | Best DP + Bit Masking Approach | best-dp-bit-masking-approach-by-chakradh-60tu | Intuition\nThe bitmask is used to track which rows have been visited, and dp to memoize.\n\n# Approach\nPrecomputation\nI\'m first storing the row number of all | chakradhar03 | NORMAL | 2024-09-01T06:51:59.308695+00:00 | 2024-09-01T06:51:59.308736+00:00 | 159 | false | # Intuition\nThe bitmask is used to track which rows have been visited, and dp to memoize.\n\n# Approach\n**Precomputation**\nI\'m first storing the row number of all the values present in the grid.\n- val[i] - represents a vector which stores the row indices of the value i.\n\n**Recursion**\n- Function Purpose: f(num, bit_mask) computes the maximum score using values from 1 to num, with bit_mask representing the rows visited.\n- Base Case: If num == 0, return 0 since no values are left.\n- Recursive Call: Calculate the score without including any cells with value num, f(num-1, bit_mask).\n- For Loop: For each row a in val[i], if row a is not visited, update the bitmask and include this cell. The result is the maximum of including or excluding the current value.\n\n**Memoization**\n- dp[num][bit_mask], which stores the maximum score that can be achieved considering the first num values (from 1 to 100), with bit_mask representing the bitmask of visited rows.\n\n# Complexity\n- Time complexity: O(n * 2^n * 101)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(101 * 2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n int f(int num,int bit_mask,vector<vector<int>>& grid,vector<vector<int>>& val,vector<vector<int>> &dp){\n if(num==0) return 0;\n if(dp[num][bit_mask]!=-1) return dp[num][bit_mask];\n int ans=f(num-1,bit_mask,grid,val,dp);\n for(auto it:val[num]){\n if(!((bit_mask>>it)&1)){\n ans=max(ans,num+f(num-1,(bit_mask|(1<<it)),grid,val,dp));\n }\n }\n return dp[num][bit_mask]=ans;\n }\n\n int maxScore(vector<vector<int>>& grid) {\n int n=grid.size();\n int m=grid[0].size();\n vector<vector<int>> val(101);\n vector<vector<int>> dp(101,vector<int>(1025,-1));\n for(int i=0;i<n;i++) for(int j=0;j<m;j++) val[grid[i][j]].push_back(i);\n return f(100,0,grid,val,dp);\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
select-cells-in-grid-with-maximum-score | Observational DP | observational-dp-by-sameonall-zcpu | Intuition\n Describe your first thoughts on how to solve this problem. \nU should observe that optimal answer is strictly decreasing sequence\n# Approach\n Desc | sameonall | NORMAL | 2024-09-01T06:18:09.453258+00:00 | 2024-09-02T10:35:24.553731+00:00 | 246 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nU should observe that optimal answer is strictly decreasing sequence\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe will fact that "optimal answer is strictly decreasing sequence"\nto optimise dp[mask showing previous used rows][last maximum choosen]\n# Complexity\n- Time complexity:$$O(100*n*logm*2^n+n*m*logm)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(100*2^n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n#include <vector>\n#include <algorithm>\nusing namespace std;\n\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n\n // Sort each row in increasing order\n for (int i = 0; i < n; ++i) {\n sort(grid[i].begin(), grid[i].end());\n }\n \n vector<vector<int>> dp(1 << n, vector<int>(102, 0));\n\n // Initializebase case\n for (int j = 0; j < 102; ++j) {\n dp[(1<<n)-1][j] = 0;\n }\n\n for (int i = (1 << n) - 2; i >= 0; --i) {\n for (int j = 0; j <= 101; ++j) {\n dp[i][j]=0;\n for (int c = 0; c < n; ++c) {\n if (!(i & (1 << c))) {\n // Find the largest value in row c that is less than j\n auto it = lower_bound(grid[c].begin(), grid[c].end(), j);\n if (it != grid[c].begin()) {\n int value = *(--it);\n dp[i][j] = max(dp[i][j], value + dp[i | (1 << c)][value]);\n }\n }\n }\n }\n }\n \n return dp[0][101];\n }\n};\n\n``` | 1 | 0 | ['Binary Search', 'Dynamic Programming', 'Sorting', 'Bitmask', 'C++'] | 1 |
select-cells-in-grid-with-maximum-score | ✅ Java Solution | java-solution-by-harsh__005-owaz | CODE\nJava []\nclass Solution {\n int res;\n private void solve(List<List<Integer>> grid, int i, int total, boolean[] vis, int size) {\n if(total + | Harsh__005 | NORMAL | 2024-09-01T06:01:51.517505+00:00 | 2024-09-01T06:02:30.545015+00:00 | 131 | false | ## **CODE**\n```Java []\nclass Solution {\n int res;\n private void solve(List<List<Integer>> grid, int i, int total, boolean[] vis, int size) {\n if(total + (size - i) * (200 - (size - i - 1)) / 2 < res) return;\n \n if(i == size) {\n res = Math.max(res, total);\n return;\n }\n boolean flag = false;\n for(int val : grid.get(i)) {\n if(!vis[val]) {\n vis[val] = true;\n solve(grid, i+1, total+val, vis, size);\n vis[val] = false;\n flag = true;\n }\n }\n if(!flag) {\n solve(grid, i+1, total, vis, size);\n }\n }\n public int maxScore(List<List<Integer>> grid) {\n res = 0;\n for(List<Integer> list : grid) {\n Collections.sort(list, Collections.reverseOrder());\n }\n boolean[] vis = new boolean[101];\n solve(grid, 0, 0, vis, grid.size());\n return res;\n }\n}\n``` | 1 | 0 | ['Java'] | 2 |
select-cells-in-grid-with-maximum-score | C++ DFS dp memo | c-dfs-dp-memo-by-user5976fh-a1qu | Could not solve this during the contest :(\n\nclass Solution {\npublic:\n vector<vector<int>> dp;\n vector<vector<int>> nums;\n int maxScore(vector<vec | user5976fh | NORMAL | 2024-09-01T04:33:22.140545+00:00 | 2024-09-01T04:40:15.487285+00:00 | 203 | false | Could not solve this during the contest :(\n```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n vector<vector<int>> nums;\n int maxScore(vector<vector<int>>& g) {\n nums.resize(101);\n for (int i = 0; i < g.size(); ++i)\n for (int y = 0; y < g[0].size(); ++y)\n nums[g[i][y]].push_back(i);\n dp = vector<vector<int>>(101, vector<int>(1025, -1));\n return dfs(0, 0);\n }\n\n int dfs(int i, int bitMask){\n if (i == nums.size()) return 0;\n if (dp[i][bitMask] != -1)\n return dp[i][bitMask];\n // do not take\n int ans = dfs(i + 1, bitMask);\n // iterate row options\n for (int x = 0; x < nums[i].size(); ++x){\n int bit = 1 << nums[i][x];\n if ((bitMask & bit) == 0){\n int nextBit = bitMask | bit;\n ans = max(ans, dfs(i + 1, nextBit) + i);\n }\n }\n return dp[i][bitMask] = ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Beats 100 % user in Python : Checkout the only one Quality code : | beats-100-user-in-python-checkout-the-on-4gnc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | progammersoumen | NORMAL | 2024-09-01T04:11:11.239909+00:00 | 2024-09-01T04:11:11.239926+00:00 | 118 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int: \n H = [set([]) for i in range(101)]\n n = len(grid)\n m = len(grid[0])\n for i in range(n):\n for j in range(m):\n H[grid[i][j]].add(2**i)\n d = [0 for i in range(2**10)]\n for i in range(101):\n new_d = [x for x in d]\n for x in range(2**10):\n for y in H[i]:\n if y|x != x:\n x2 = y|x\n new_d[x2] = max(new_d[x2], i+d[x])\n d = new_d\n return max(d)\n``` | 1 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Python heap 🔥🔥 | python-heap-by-chitraksh24-0bgc | DP TLE\npython3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n memo = {}\n grid = [[i for i in range(1,11)] for j in | chitraksh24 | NORMAL | 2024-09-01T04:05:14.926717+00:00 | 2024-09-01T04:05:14.926740+00:00 | 121 | false | # DP TLE\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n memo = {}\n grid = [[i for i in range(1,11)] for j in range(10)]\n grid = [sorted(list(set(grid[i])),reverse=True) for i in range(len(grid))]\n def solve(curr,taken):\n strpath = str(curr) + \',\' + str(taken)\n if curr>=len(grid):\n return 0\n if strpath in memo:\n return memo[strpath]\n \n memo[strpath] = 0\n c = 0\n for i in range(len(grid[0])-1,-1,-1):\n if grid[curr][i] not in taken:\n memo[strpath] = max(memo[strpath],grid[curr][i]+solve(curr+1,list(taken)+[grid[curr][i]]))\n c += 1\n if c>=len(grid)-curr:\n break\n memo[strpath] = max(memo[strpath],solve(curr+1,list(taken)))\n return memo[strpath]\n return solve(0,[])\n```\n\n# Heap Accepted\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n grid = [sorted(list(set(grid[i])),reverse=True) for i in range(len(grid))]\n heap = [(0,list(grid))]\n ans = 0\n while heap:\n curr,rems = heapq.heappop(heap)\n if len(rems) == 0:\n ans = max(ans,-curr)\n continue\n \n rem = list([list(rems[i]) for i in range(len(rems))])\n pos = []\n maxa = 0\n for j in range(len(rem)):\n if len(rem[j])==0:\n continue\n if rem[j][0] > maxa:\n pos = [j]\n maxa = rem[j][0]\n elif rem[j][0] == maxa:\n pos.append(j)\n for j in range(len(rem)):\n for k in range(rem[j].count(maxa)):\n rem[j].remove(maxa)\n for i in pos:\n t = list([list(rem[j]) for j in range(len(rem))])\n t.pop(i)\n ans = max(ans,-(curr-maxa))\n heapq.heappush(heap,(curr-maxa,list(t)))\n return ans\n\n\n\n``` | 1 | 0 | ['Heap (Priority Queue)', 'Python3'] | 0 |
select-cells-in-grid-with-maximum-score | 🔢 Maximum Score Selection in Grid with Unique Value Constraints 🧮 | maximum-score-selection-in-grid-with-uni-eky3 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves selecting cells from a grid in such a way that the sum of selected | nikhil16kulkarni | NORMAL | 2024-09-01T04:05:04.016939+00:00 | 2024-09-01T04:05:04.016965+00:00 | 244 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves selecting cells from a grid in such a way that the sum of selected cell values is maximized. The selection rules are:\n- No two selected cells can be from the same row.\n- The values in the selected cells must be unique.\n\nThis problem can be approached by dynamically keeping track of possible selections using a bitmask to represent selected rows. By iterating over all possible values, starting from the largest, we can ensure that the maximum possible score is obtained.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Preprocessing:\n\n - First, create a dictionary (value_positions) that maps each unique value in the grid to the list of its positions (row, column) in the grid.\n - Sort the unique values in descending order, so that we can process the largest values first.\n2. Dynamic Programming with Bitmask:\n - Use a bitmask to represent the set of rows that have been selected. The dp array is used where dp[mask] holds the maximum score for a given mask configuration.\n - For each value, iterate through its positions in the grid and update the dp array by considering adding this value to each possible configuration of the selected rows.\n - The new_dp array is used to store the updated scores after considering the current value. This ensures that each value is only added once per row configuration.\n3. Result:\n - After processing all values, the maximum score can be found in the dp array.\n\n# Complexity\n- Time complexity: O(V * 2^m) where V is the number of unique values in the grid, and m is the number of rows. For each value, we potentially update 2^m states.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^m) due to the dp array, where m is the number of rows.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n\n m, n = len(grid), len(grid[0])\n \n value_positions = defaultdict(list)\n for i in range(m):\n for j in range(n):\n value_positions[grid[i][j]].append((i, j))\n \n sorted_values = sorted(set(v for row in grid for v in row), reverse=True)\n \n dp = [0] * (1 << m)\n \n \n for value in sorted_values:\n new_dp = dp.copy()\n for positions in value_positions[value]:\n i, j = positions\n for mask in range(1 << m):\n if mask & (1 << i) == 0:\n new_mask = mask | (1 << i)\n new_dp[new_mask] = max(new_dp[new_mask], dp[mask] + value)\n dp = new_dp\n \n return max(dp)\n\n \n``` | 1 | 0 | ['Hash Table', 'Dynamic Programming', 'Python3'] | 0 |
select-cells-in-grid-with-maximum-score | ◈ Python ◈ DP | python-dp-by-zurcalled_suruat-ljz1 | Glossary:
grid[i][j]: The element at thei-th row andj-th column of the input grid, representing a positive integer value.
N_ROWS,N_COLS: The number of rows and | zurcalled_suruat | NORMAL | 2025-02-21T19:23:11.659524+00:00 | 2025-02-21T19:23:11.659524+00:00 | 7 | false | Glossary:
- $grid[i][j]$: The element at the $i$-th row and $j$-th column of the input grid, representing a positive integer value.
- $N\_ROWS$, $N\_COLS$: The number of rows and columns in the grid, respectively.
- $ix\_vals\_chosen$: A tuple representing the values chosen so far (Approach 1).
- $min\_next\_ix\_row$: The minimum allowed index for the next row to be chosen (Approach 1).
- $val2row2col$: A dictionary mapping each unique value in the grid to a dictionary of its row and column indices (Approach 2).
- $vals\_desc$: A list of unique values in the grid sorted in descending order (Approach 2).
- $ix\_rows\_chosen$: A tuple representing the indices of the rows chosen so far (Approach 2).
- $min\_next\_val$: The minimum allowed value for the next cell to be chosen (Approach 2).
Mathematical Intuition and Formulation:
The problem requires selecting a set of cells $S$ from the grid $grid$ to maximize the sum of their values, subject to the constraints:
1. Uniqueness: All elements in $S$ are unique.
2. Row-wise single selection: At most one cell can be selected from each row.
Approach 1:
This approach iterates over the rows, and at each row, decides whether to select a cell from that row or not. If a cell is selected, it must not have been selected previously. The state can be represented by a tuple $(i, V)$, where $i$ is the current row index and $V$ is the set of values chosen so far. The recurrence relation is:
$
dp(i, V) =
\begin{cases}
0, & \text{if } \space i = N\_ROWS \\
\max(\\
\quad dp(i + 1, V), \\
\quad \max_{j, grid[i][j] \notin V} \{grid[i][j] + dp(i + 1, V \cup \{grid[i][j]\})\}\\
), & \text{otherwise}
\end{cases}
$
The base case is when all rows have been processed ($i = N\_ROWS$), in which case the score is 0. Otherwise, the algorithm calculates the maximum score by either skipping the current row (`dp(i + 1, V)`) or choosing a value from the current row that has not been chosen previously ($grid[i][j] + dp(i + 1, V \cup \{grid[i][j]\})$).
The final answer is obtained by calling the `dp` function with the initial row index 0 and an empty set of chosen values:
$result = dp(0, \emptyset)$
Approach 2:
This approach iterates over the unique values in the grid. For each value, it decides whether to select a cell with that value or not. If a cell is selected, its row must not have been chosen previously. The state can be represented by a tuple $(R, v)$, where $R$ is the set of row indices chosen so far, and $v$ is the minimum allowed value for the next cell to be chosen. The recurrence relation is:
$
dp(R, v) =
\begin{cases}
0, & \text{if no cell with value } \ge v\space\text{ exists} \\
\max( \\
\quad dp(R, v + 1),\\
\quad v + dp(R \cup \{i\}, v + 1)\\), & \text{otherwise, where } \space i \notin R ;\space grid[i][j] = v
\end{cases}
$
The final answer is $dp(\emptyset, -\infty)$.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
from collections import defaultdict as dd
import math
class Solution:
def maxScore(self, *args) -> int:
# return self.approach1(*args)
return self.approach2(*args)
"""
APPROACH - 2
VERDICT - PASS
Reference - https://leetcode.com/problems/select-cells-in-grid-with-maximum-score/solutions/5718001/bitmask-dp-mask-of-used-rows/?envType=problem-list-v2&envId=22pe56k2
"""
def approach2(self, grid: List[List[int]]) -> int:
N_ROWS, N_COLS = len(grid), len(grid[0])
val2row2col = dd(lambda : dd(lambda : None))
for ix_row in range(N_ROWS):
for ix_col in range(N_COLS):
val = grid[ix_row][ix_col]
val2row2col[val][ix_row] = ix_col
vals_desc = list(sorted(val2row2col.keys(),key=lambda x : -x))
@lru_cache(maxsize=None)
def dp(ix_rows_choosen=tuple(),min_next_val=None):
next_val = None
for val in vals_desc:
if(min_next_val is None or val >= min_next_val):
next_val = val
if(next_val is None):
return None
poss_arr = []
# case 1 - skip val - next_val
ix_rows_choosen1 = ix_rows_choosen
min_next_val1 = next_val + 1
poss_suffix1 = dp(ix_rows_choosen=ix_rows_choosen1,min_next_val=min_next_val1)
poss_suffix = 0 + (0 if(poss_suffix1 is None)else poss_suffix1)
poss_arr.append(poss_suffix)
# case 2 - choose a row that has val - next_val
for ix_row in val2row2col[next_val]:
if(ix_row in ix_rows_choosen):
continue
ix_rows_choosen1 = tuple(sorted(ix_rows_choosen+(ix_row,)))
min_next_val1 = next_val + 1
poss_suffix1 = dp(ix_rows_choosen=ix_rows_choosen1,min_next_val=min_next_val1)
poss_suffix = next_val + (0 if(poss_suffix1 is None)else poss_suffix1)
poss_arr.append(poss_suffix)
return max(poss_arr , default=None)
res = dp()
return res
"""
APPROACH - 1
VERDICT : TLE
"""
def approach1(self, grid: List[List[int]]) -> int:
N_ROWS, N_COLS = len(grid), len(grid[0])
@lru_cache(maxsize=None)
def dp(ix_vals_choosen=tuple(),min_next_ix_row=None):
poss_arr = []
ix_row = 0 if(min_next_ix_row is None)else min_next_ix_row
if(ix_row>=N_ROWS):
return None
# case - 1 - skip row - ix_row
ix_vals_choosen1 = ix_vals_choosen
min_next_ix_row1 = ix_row +1
poss_suffix = dp(ix_vals_choosen=ix_vals_choosen1,min_next_ix_row=min_next_ix_row1)
poss_suffix1 = (0 if(poss_suffix is None)else poss_suffix)
poss_arr.append(poss_suffix1)
# case - 2 - choose a value from row - ix_row
for val in grid[ix_row]:
if(val in ix_vals_choosen):
continue
ix_vals_choosen1 = tuple(sorted(ix_vals_choosen+(val,)))
min_next_ix_row1 = ix_row +1
poss_suffix = dp(ix_vals_choosen=ix_vals_choosen1,min_next_ix_row=min_next_ix_row1)
poss_suffix1 = val + (0 if(poss_suffix is None)else poss_suffix)
poss_arr.append(poss_suffix1)
return max(poss_arr , default=None)
res = dp()
return res
``` | 0 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Stimulated analing 2 | stimulated-analing-2-by-rajeeesh-eair | IntuitionApproachComplexity
Time complexity: constant time complexity
Space complexity: O(1)
Code | rajeeesh | NORMAL | 2025-02-17T01:18:30.811928+00:00 | 2025-02-17T01:18:30.811928+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: constant time complexity
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#include <vector>
#include <cstdlib>
#include <cmath>
#include <ctime>
#include <algorithm>
using namespace std;
class Solution {
// Penalty factor; must be high enough to force duplicates to be rejected.
const int PENALTY = 10000;
// Return a random double in [0,1)
double randomDouble() {
return (double)rand() / (double)RAND_MAX;
}
// This function performs one run of simulated annealing on grid
// and returns the sum-of-values (without penalties) of a feasible state.
int simulatedAnnealing(vector<vector<int>>& grid) {
int R = grid.size();
// state[r] is the column index chosen for row r; -1 means “disabled”
vector<int> state(R, -1);
// Frequency counts for values in [1,100]
vector<int> freq(101, 0);
int enabledCount = 0; // number of rows with a chosen cell
int currentSum = 0; // sum of selected cell values
int currentPenalty = 0; // duplicate penalty count
// --- INITIALIZATION ---
// For each row, randomly decide to pick a column or leave it disabled.
for (int i = 0; i < R; i++) {
int cols = grid[i].size();
if (rand() % 2 == 0) {
int col = rand() % cols;
state[i] = col;
int val = grid[i][col];
freq[val]++;
currentSum += val;
enabledCount++;
}
}
// Ensure at least one row is enabled.
if (enabledCount == 0) {
int r = rand() % R;
int col = rand() % grid[r].size();
state[r] = col;
freq[grid[r][col]]++;
currentSum += grid[r][col];
enabledCount = 1;
}
// Compute initial duplicate penalty.
for (int v = 1; v <= 100; v++) {
if (freq[v] > 1)
currentPenalty += (freq[v] - 1);
}
// Our current "energy" (objective) is:
int currentScore = currentSum - PENALTY * currentPenalty;
// bestScore is recorded only for fully feasible (duplicate–free) states.
int bestScore = (currentPenalty == 0) ? currentSum : currentScore;
vector<int> bestState = state;
// --- SIMULATED ANNEALING PARAMETERS ---
int iterations = 5000;
double T = 1000.0;
// Cooling rate chosen so that final temperature is around 1e-6.
double coolingRate = pow(1e-6 / T, 1.0 / iterations);
// --- MAIN SA LOOP ---
for (int it = 0; it < iterations; it++) {
// Pick a random row to modify.
int r = rand() % R;
int cols = grid[r].size();
int oldSel = state[r];
int newSel;
// Do not disable if that would leave us with zero enabled rows.
bool canDisable = true;
if (oldSel != -1 && enabledCount == 1)
canDisable = false;
double p = randomDouble();
if (oldSel != -1) {
// Row is enabled.
if (p < 1.0 / cols && canDisable)
newSel = -1; // disable this row
else {
// Choose a new column (different from the current one).
if (cols == 1) continue; // no alternative exists
do {
newSel = rand() % cols;
} while(newSel == oldSel);
}
} else {
// Row is currently disabled; enable by picking a random column.
newSel = rand() % cols;
}
// --- Compute the change (delta) in our state metrics ---
int deltaSum = 0;
int deltaPenalty = 0;
// If the row was enabled, then “removing” its cell:
if (oldSel != -1) {
int oldVal = grid[r][oldSel];
deltaSum -= oldVal;
// Removing a duplicate: if freq > 1, then removing reduces penalty by 1.
if (freq[oldVal] > 1)
deltaPenalty -= 1;
}
// If the row becomes enabled, “adding” its new cell:
if (newSel != -1) {
int newVal = grid[r][newSel];
deltaSum += newVal;
// If newVal already appears, then adding it increases duplicate count by 1.
if (freq[newVal] > 0)
deltaPenalty += 1;
}
int deltaScore = deltaSum - PENALTY * deltaPenalty;
// --- Decide whether to accept the move ---
if (deltaScore >= 0 || exp(deltaScore / T) > randomDouble()) {
// Apply move: update frequency counts, enabledCount, and state.
if (oldSel != -1) {
int oldVal = grid[r][oldSel];
freq[oldVal]--;
if (newSel == -1)
enabledCount--; // row is now disabled
}
if (newSel != -1) {
int newVal = grid[r][newSel];
freq[newVal]++;
if (oldSel == -1)
enabledCount++; // row becomes enabled
}
state[r] = newSel;
currentSum += deltaSum;
currentPenalty += deltaPenalty;
currentScore += deltaScore;
// If the state is now feasible (no duplicates) and its sum is better, record it.
if (currentPenalty == 0 && currentSum > bestScore) {
bestScore = currentSum;
bestState = state;
}
}
// Cool down the temperature.
T *= coolingRate;
}
// --- Return the final answer ---
// Since bestState is feasible (each value appears at most once),
// we simply sum the chosen cells.
int finalScore = 0;
for (int i = 0; i < R; i++) {
if (bestState[i] != -1)
finalScore += grid[i][bestState[i]];
}
return finalScore;
}
public:
int maxScore(vector<vector<int>>& grid) {
srand(time(0)); // seed randomness
// Run the simulated annealing several times and record the best result.
int bestOverallScore = 0;
int numRuns = 10; // you can experiment with this value
for (int run = 0; run < numRuns; run++) {
int score = simulatedAnnealing(grid);
bestOverallScore = max(bestOverallScore, score);
}
return bestOverallScore;
}
};
``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | 💥💥 Beats 100% on runtime and memory [EXPLAINED] | beats-100-on-runtime-and-memory-explaine-j6ed | IntuitionMaximize the score by selecting grid cells based on certain constraints. We need to consider both the row and column positions to avoid revisiting rows | r9n | NORMAL | 2025-02-06T06:32:06.993294+00:00 | 2025-02-06T06:32:06.993294+00:00 | 4 | false | # Intuition
Maximize the score by selecting grid cells based on certain constraints. We need to consider both the row and column positions to avoid revisiting rows. The solution involves using dynamic programming to efficiently calculate the best score by recursively checking all possibilities, while ensuring no row is selected more than once.
# Approach
Use a DP approach where we recursively explore all cell selections while maintaining a bitmask to track visited rows. At each step, we check whether the current row has already been selected using the bitmask. If not, we attempt to select the cell and move to the next unique value, updating the DP table with the best possible score.
# Complexity
- Time complexity:
O(n * 2^n), where n is the number of rows. This comes from iterating through all subsets of rows (represented by the bitmask) and calculating the best score for each subset.
- Space complexity:
O(n * 2^n), due to the DP table storing results for every possible row subset.
# Code
```kotlin []
class Solution {
private var visAll: Int = 0
private lateinit var dp: Array<IntArray>
private fun solve(idx: Int, mask: Int, valList: List<Pair<Int, Int>>): Int {
if (idx == valList.size) return 0
if (mask == visAll) return 0
if (dp[idx][mask] != -1) return dp[idx][mask]
val currVal = valList[idx].first
var nxtUniqueIdx = idx
while (nxtUniqueIdx < valList.size && valList[nxtUniqueIdx].first == currVal) {
nxtUniqueIdx++
}
var ans = solve(nxtUniqueIdx, mask, valList)
for (i in idx until nxtUniqueIdx) {
val curRow = valList[i].second
if ((mask and (1 shl curRow)) == 0) { // if row isn't visited
val tmp = solve(nxtUniqueIdx, mask or (1 shl curRow), valList) + valList[i].first
ans = maxOf(ans, tmp)
}
}
dp[idx][mask] = ans
return ans
}
fun maxScore(grid: List<List<Int>>): Int {
val n = grid.size
val m = grid[0].size
// Convert List<List<Int>> to Array<IntArray>
val gridArray = grid.map { it.toIntArray() }.toTypedArray()
val valList = mutableListOf<Pair<Int, Int>>()
for (i in 0 until n) {
for (j in 0 until m) {
valList.add(Pair(gridArray[i][j], i))
}
}
valList.sortBy { it.first }
visAll = (1 shl n) - 1
dp = Array(valList.size) { IntArray(1 shl n) { -1 } }
return solve(0, 0, valList)
}
}
``` | 0 | 0 | ['Divide and Conquer', 'Dynamic Programming', 'Bit Manipulation', 'Depth-First Search', 'Graph', 'Memoization', 'Heap (Priority Queue)', 'Shortest Path', 'Bitmask', 'Kotlin'] | 0 |
select-cells-in-grid-with-maximum-score | DP || bitmasking || C++. | dp-bitmasking-c-by-rishiinsane-a5gw | IntuitionWe need to select numbers from a 2D grid such that no two numbers come from the same row, and each number in the selected set is unique. The goal is to | RishiINSANE | NORMAL | 2025-02-01T10:13:37.600414+00:00 | 2025-02-01T10:13:37.600414+00:00 | 5 | false | # Intuition
We need to select numbers from a 2D grid such that no two numbers come from the same row, and each number in the selected set is unique. The goal is to maximize the sum of selected numbers. Using recursive strategy with bitmasking, where the state of each row (whether a number from that row has been used or not) is tracked by a bitmask. Starting from the maximum possible value (100), we attempt to select a number from each row and recursively maximize the score, ensuring that numbers are not repeated across rows using the bitmask.
# Approach
We use dynamic programming (DP) with memoization. The dp[num][bitmask] table stores the maximum score achievable for the current state, where num is the current number being considered (from 100 down to 1), and bitmask represents which rows have already been used. The `helper` function recursively computes the maximum score by either skipping the current number or selecting it from available rows. The grid is processed by creating a mapping mp from each number to the rows in which it appears. Starting from the largest number, we try to maximize the score while ensuring that the same row isn't used multiple times using the bitmask.
# Complexity
- Time complexity:
O(100 * 2^m * m)
- Space complexity:
O(101 * 2^m + m * n)
# Code
```cpp []
class Solution {
public:
int dp[101][1025];
int maxScore(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
unordered_map<int, vector<int>> mp; // element present in rows
memset(dp, -1, sizeof(dp));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
mp[grid[i][j]].push_back(i);
}
}
return helper(grid, 0, 100, mp);//start from max value possible to accumulate max score
}
int helper(vector<vector<int>>& grid, int bitmask, int num,
unordered_map<int, vector<int>>& mp) {
if (num == 0)
return 0;
if (dp[num][bitmask] != -1)
return dp[num][bitmask];
int res = helper(grid, bitmask, num - 1, mp);
for (auto row : mp[num]) {
if (bitmask >> row & 1)
continue;
res =
max(res, num + helper(grid, (bitmask | (1 << row)), num - 1, mp));
}
return dp[num][bitmask] = res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Miguel Gargallo 3276. Select Cells in Grid With Maximum Score | miguel-gargallo-3276-select-cells-in-gri-y2y9 | IntuitionWe want to pick exactly one value from some (or all) rows in such a way that:
No two selected cells come from the same row.
All selected values are dis | miguelgargallo | NORMAL | 2025-01-20T22:55:09.366278+00:00 | 2025-01-20T22:55:09.366278+00:00 | 2 | false | # Intuition
We want to pick exactly one value from some (or all) rows in such a way that:
1. No two selected cells come from the same row.
2. All selected values are distinct.
3. The sum of these values is maximized.
Since every number in the grid is a positive integer, and we can have at most 10 rows, our problem essentially boils down to finding a maximum matching between rows and distinct values, prioritizing larger values first.
Why does matching in descending order of the values work?
- If a row is currently matched with a smaller value, but a bigger value can only fit into that same row, we can attempt to “re-match” the smaller value to another row (if possible), thereby ensuring a strictly larger total sum. This is the standard **augmenting path** logic in bipartite matching, but we greedily process edges (row–value pairs) starting with the largest value first.
---
## Approach
1. **Collect distinct values**
- Extract all the distinct values from the grid.
- Map each value to the rows in which it appears, i.e., for each distinct value \(v\), keep a list of row indices that contain \(v\).
2. **Sort values in descending order**
- Since we want to maximize the sum, we begin with the largest value and attempt to match it to a row.
3. **Greedy matching with augmenting paths**
- Initialize an array `rowMatch` of size `R` (number of rows) with `-1`, signifying that initially no row is matched to any value.
- For each distinct value (processed from largest to smallest):
1. Create a `visited` array of booleans (size `R`) to mark rows visited in the current attempt.
2. Run a DFS `canMatch(valueIdx, visited)` trying to match this value to one of its possible rows.
- If a row is free (`rowMatch[row] == -1`), match the value immediately.
- Otherwise, if the row is taken by a smaller value, attempt to re-match that smaller value to a different row (recursively).
- If re-matching is successful, assign the current (larger) value to this row.
- This step ensures we always displace smaller values with bigger ones whenever feasible.
4. **Compute the maximum score**
- After processing all values, simply sum up the matched values using the information in `rowMatch`.
- That sum is our maximum score.
Because we are always trying to match larger values first and we only re-match when it strictly increases the overall sum, we end up with the optimal configuration of row–value pairs.
---
## Time Complexity
- Let \(R\) be the number of rows (up to 10) and let \(C\) be the number of columns (up to 10).
- In the worst case, the grid has up to 100 distinct values.
- For each of the at most 100 values, we perform a DFS over at most 10 rows. A DFS might re-match other values, but each row is visited at most once per DFS call.
- Overall, the matching step is \(O(\text{(number of distinct values)} \times R \times R)\) = \(O(100 \times 10 \times 10) = O(10\,000)\).
Hence, the **time complexity** is \(O(R^2 \times \text{(number of distinct values)})\), comfortably efficient for \(R \leq 10\) and \(\text{(number of distinct values)} \leq 100\).
---
## Space Complexity
- We store up to 100 distinct values and, for each value, a list of rows (each row up to 10).
- We also keep a `rowMatch` array and auxiliary data structures (like `visited`) for the DFS.
- Overall, the **space complexity** is \(O(R + \text{(number of distinct values)})\), which is \(O(10 + 100)\) in the worst case, i.e., \(O(1)\) in the context of these small constraints.
# Code
```python []
class Solution(object):
def maxScore(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
# 1) Gather distinct values and which rows they appear in
from collections import defaultdict
row_count = len(grid)
col_count = len(grid[0])
value_to_rows = defaultdict(list)
distinct_values = set()
for r in range(row_count):
for c in range(col_count):
val = grid[r][c]
distinct_values.add(val)
value_to_rows[val].append(r)
# Convert set to a list and sort in descending order
distinct_values = sorted(list(distinct_values), reverse=True)
# rowMatch[r] = index in distinct_values that row r is matched to, or -1 if unmatched
rowMatch = [-1] * row_count
# 2) DFS function to attempt matching 'valueIdx' with a row
def canMatch(valueIdx, visited):
# For every row that can contain this value
for row in value_to_rows[distinct_values[valueIdx]]:
if not visited[row]:
visited[row] = True
# If row is free or we can re-match the currently matched value
if rowMatch[row] == -1 or canMatch(rowMatch[row], visited):
rowMatch[row] = valueIdx
return True
return False
# 3) Try to match each value (descending order) with a suitable row
for vIdx in range(len(distinct_values)):
visited = [False] * row_count
canMatch(vIdx, visited)
# 4) Calculate the sum of matched values
score = 0
for r in range(row_count):
if rowMatch[r] != -1:
score += distinct_values[rowMatch[r]]
return score
``` | 0 | 0 | ['Python'] | 0 |
select-cells-in-grid-with-maximum-score | Explained: Hungarian Algorithm (quazi) schema for Bi-Graph | explained-hungarian-algorithm-quazi-sche-vv64 | IntuitionLeverage a greedy approach that maximizes the total score.ApproachThe solution employs a bipartite graph matching algorithm with the following key step | ivangnilomedov | NORMAL | 2024-12-13T20:30:09.315777+00:00 | 2024-12-13T20:30:09.315777+00:00 | 7 | false | # Intuition\nLeverage a greedy approach that maximizes the total score.\n\n# Approach\nThe solution employs a bipartite graph matching algorithm with the following key steps:\n\n1. Greedy Value Selection\n - Process values from highest to lowest\n - Proves optimal because at each step, including the maximum available unused value leads to the best possible solution\n - If a high-value cell can be selected without violating constraints, it should always be included\n\n2. Bipartite Graph Construction\n - Create a bipartite graph with two vertex sets:\n * Rows: [0 to N-1]\n * Values: [N to N+M]\n - Initial edges represent possible value-to-row mappings\n - Oriented graph allows tracking of selection possibilities\n\n3. Augmenting Path Algorithm\n - Similar to Hungarian Algorithm for maximum matching\n - Uses Breadth-First Search (BFS) to find augmenting paths\n - Dynamic path reconstruction to maximize score\n - Key steps:\n * Explore possible paths from highest values\n * Modify graph connections to reflect selections\n * Ensure no row or value is reused\n\n## Algorithmic References\n- Similar Algorithms:\n 1. Hungarian Algorithm (Kuhn-Munkres Algorithm)\n 2. Hopcroft-Karp Maximum Matching Algorithm\n 3. Ford-Fulkerson Path Augmentation Technique\n\n# Complexity\n- Time Complexity: $$O(N \\cdot M \\cdot (N+M))$$\n * N: Number of rows\n * M: Maximum value in the grid\n * Nested loops for graph construction and path finding\n * Each value processed with a BFS traversal\n\n- Space Complexity: $$O(N + M)$$\n * Graph representation\n * Parent tracking vector\n * Queue for BFS\n\n# Mathematical Formulation\nLet $$G = (V_R, V_V, E)$$ be the bipartite graph where:\n- $$V_R$$: Set of rows\n- $$V_V$$: Set of values\n- $$E \\subseteq V_V \\times V_R$$: Edges representing possible selections\n\nThe goal is to find a maximum weight independent set $$S \\subseteq E$$ such that:\n- No two edges in $$S$$ share a vertex in $$V_R$$\n- Total weight $$\\sum_{(v,r) \\in S} v$$ is maximized\n\n# Proof Sketch of Optimality\nKey Observation: \n- By processing values in descending order\n- Greedily selecting highest available unique values\n- Dynamically reconstructing paths\n- The algorithm guarantees a globally optimal solution\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxScore(const vector<vector<int>>& grid) {\n const int N = grid.size();\n const int M = accumulate(\n grid.begin(), grid.end(), 0,\n [](int acc, const auto& v) { return max(acc, *max_element(v.begin(), v.end())); });\n\n // Create a bipartite graph representation\n // Vertices are split into two sets:\n // - Rows: [0 .. N-1]\n // - Values: [N .. N+M]\n // This allows mapping unique values to rows\n vector<unordered_set<int>> gr(N + M + 1);\n for (int i = 0; i < N; ++i)\n for (int e : grid[i])\n // Populate oriented edges in bipartite graph from value to rows\n gr[e + N].insert(i);\n\n int res = 0;\n\n // Process values from highest to lowest for greedy selection\n for (int val = M; val >= 0; --val) {\n if (gr[val + N].empty()) continue;\n\n // Parent tracking for path augmentation\n // -2: unvisited, -1: source vertex\n vector<int> parent(gr.size(), -2);\n parent[val + N] = -1;\n\n // BFS to find augmenting path\n queue<int> q;\n q.push(val + N);\n while (!q.empty()) {\n int u = q.front();\n q.pop();\n\n // If we reach an empty row, we can augment the path\n if (u < N && gr[u].empty()) {\n for (int p = parent[u]; p > -1; u = p) {\n p = parent[u];\n if (p < 0) break;\n // Swap edge directions u -> p while deleting original\n gr[u].insert(p);\n gr[p].erase(u);\n }\n res += val; // Add the current value to the total score\n break;\n }\n\n for (int v : gr[u]) if (parent[v] < -1) { // Proceed with BFS\n parent[v] = u;\n q.push(v);\n }\n }\n }\n\n return res;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | C++ | c-by-harshaljain200028march-farb | \nunordered_map<int,unordered_map<string,int>> dp;\n int getMaxScore(auto curItr ,auto &end , string &visitedHash){\n \n int maxScore = 0;\n | harshaljain200028march | NORMAL | 2024-12-05T10:57:31.751324+00:00 | 2024-12-05T10:57:50.383149+00:00 | 3 | false | ```\nunordered_map<int,unordered_map<string,int>> dp;\n int getMaxScore(auto curItr ,auto &end , string &visitedHash){\n \n int maxScore = 0;\n if(curItr!=end){ \n int key = curItr->first;\n if(dp.find(key)!=dp.end() && dp[key].find(visitedHash)!=dp[key].end())\n return dp[key][visitedHash];\n \n unordered_set<int> &idxSet = curItr->second;\n ++curItr;\n\n for(int idx : idxSet){\n if(visitedHash[2*idx+1] == \'#\'){\n visitedHash[2*idx+1] = \'O\' ;\n maxScore = max(maxScore,key+getMaxScore(curItr,end , visitedHash));\n visitedHash[2*idx+1] = \'#\' ;\n }\n }\n \n maxScore = max(maxScore,getMaxScore(curItr,end , visitedHash));\n return dp[key][visitedHash] = maxScore;\n }\n \n return maxScore;\n }\n \n \n int maxScore(vector<vector<int>>& grid) {\n unordered_map<int,unordered_set<int>> reverseIndexMap;\n \n string visitedHash = "" ;\n dp.clear();\n for(int i = 0 ; i<grid.size();i++){\n visitedHash+=\'-\';\n visitedHash+= \'#\' ;\n }\n for(int i = 0 ; i<grid.size() ;i++){\n for(int j = 0 ; j<grid[0].size() ;j++){\n reverseIndexMap[grid[i][j]].insert(i);\n }\n \n }\n \n auto it = reverseIndexMap.begin();\n auto end = reverseIndexMap.end();\n return getMaxScore(it ,end, visitedHash);;\n }\n```\n | 0 | 0 | [] | 0 |
select-cells-in-grid-with-maximum-score | Simple and Easy JAVA Solution , using Memoization , invert the question and solve | simple-and-easy-java-solution-using-memo-gz88 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Triyaambak | NORMAL | 2024-10-24T10:00:24.052612+00:00 | 2024-10-24T10:01:49.237071+00:00 | 12 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int maxScore(List<List<Integer>> grid) {\n //Instead of picking the max number from each row\n //Pick the row for each number \n int m = grid.size();\n int n = grid.get(0).size();\n List<Integer> arr[] = new ArrayList[101]; \n\n for(int i=0;i<101;i++)\n arr[i] = new ArrayList<>();\n \n int min = Integer.MAX_VALUE;\n int max = Integer.MIN_VALUE;\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n max = Math.max(max,grid.get(i).get(j));\n min = Math.min(min,grid.get(i).get(j));\n arr[grid.get(i).get(j)].add(i);\n }\n }\n\n Integer dp[][] = new Integer[101][(int)Math.pow(2,10) + 1];\n return helper(arr,max,min,0,dp);\n }\n\n private static int helper(List<Integer> arr[],int num,int min,int mask,Integer dp[][]){\n if(num < min)\n return 0;\n \n if(dp[num][mask] != null)\n return dp[num][mask];\n \n dp[num][mask] = 0;\n for(int r : arr[num]){\n if((mask&(1 << r))==0)\n dp[num][mask] = Math.max(dp[num][mask] , num + helper(arr,num-1,min,(mask|(1 << r)),dp));\n }\n\n dp[num][mask] = Math.max(dp[num][mask] , helper(arr,num-1,min,mask,dp));\n\n return dp[num][mask];\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | Bitmask || Binary Search || Upper_bound || Take - Not take | bitmask-binary-search-upper_bound-take-n-xuyl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | krishan_vach | NORMAL | 2024-10-11T21:05:48.508683+00:00 | 2024-10-11T21:05:48.508715+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int dp[101][1<<11];\n int f(int i, int mask, vector<pair<int, int>>& vp) {\n if (i == vp.size()) {\n return 0;\n }\n // int ans=0;\n if(dp[i][mask]!=-1){\n return dp[i][mask];\n }\n int a = f(i + 1, mask, vp);\n int ind = vp[i].second;\n int num = vp[i].first;\n int b = 0;\n if (((mask >> ind) & 1) == 0) {\n int z = upper_bound(\n vp.begin(), vp.end(), vp[i],\n [](const pair<int, int>& a, const pair<int, int>& b) {\n return a.first < b.first;\n }) -\n vp.begin();\n b = num + f(z, mask | (1 << ind), vp);\n }\n return dp[i][mask]=max(a, b);\n }\n int maxScore(vector<vector<int>>& grid) {\n vector<pair<int, int>> vp;\n for (int i = 0; i < grid.size(); i++) {\n for (int j = 0; j < grid[i].size(); j++) {\n vp.push_back({grid[i][j], i});\n }\n }\n sort(vp.begin(), vp.end());\n // for(aut)\n memset(dp,-1,sizeof(dp));\n return f(0, 0, vp);\n }\n};\n``` | 0 | 0 | ['Array', 'Binary Search', 'Dynamic Programming', 'Bit Manipulation', 'Matrix', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | Java | Solution | java-solution-by-keshavkr_codderboy-o0xl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Keshavkr_codderboy | NORMAL | 2024-10-09T05:54:11.105288+00:00 | 2024-10-09T05:54:11.105328+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n private List<List<Integer>> arr;\n private Integer dp[][];\n\n public int maxScore(List<List<Integer>> grid) {\n arr = new ArrayList<>();\n dp = new Integer[101][1 << grid.size()];\n\n for (int i = 0; i <= 100; i++) {\n arr.add(new ArrayList<Integer>());\n }\n \n // For every value in grid, store the row numbers\n for (int i = 0; i < grid.size(); i++) {\n for (int num: grid.get(i)) {\n arr.get(num).add(i);\n }\n }\n\n // search from 100 -> 1 and get the sum\n return getScore(100, 0);\n }\n\n private int getScore(int curItem, int mask) {\n if (curItem <= 0) {\n return 0;\n }\n\n if (dp[curItem][mask] != null) {\n return dp[curItem][mask];\n }\n\n // search for value less than current, with same set of rows\n int score = getScore(curItem - 1, mask);\n\n // get rows where current value is present, and\n // try them 1 by 1\n for (int row : arr.get(curItem)) {\n if ((mask & (1 << row)) > 0) {\n continue;\n }\n\n score = Math.max(score, curItem + getScore(curItem - 1, mask | (1 << row)));\n }\n\n return dp[curItem][mask] = score;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | Dynamic Programming with Bitmask Optimization | dynamic-programming-with-bitmask-optimiz-mnxz | \n\n# Approach\n Describe your approach to solving the problem. \n1. Value Grouping:\n - Create a Map (vals) where each key is a unique value from the grid, a | acailic | NORMAL | 2024-10-02T14:54:17.089833+00:00 | 2024-10-02T14:54:17.089866+00:00 | 5 | false | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Value Grouping**:\n - Create a `Map` (`vals`) where each key is a unique value from the grid, and the value is an array of row indices where this value appears.\n - Ensures each unique value is considered only once.\n\n2. **Sorting**:\n - Convert the `Map` to an array of `[value, row_indices]` pairs and sort in descending order of values.\n - Prioritizes higher values for a potentially higher sum.\n\n3. **Dynamic Programming with Bitmask**:\n - Use a recursive function `maxval` with memoization to explore combinations.\n - Parameters:\n - `i`: Index of the current value in the sorted array.\n - `mask`: Bitmask representing used rows (1 if used, 0 if not).\n - Options for each value:\n - Skip it and move to the next.\n - Include it if from an unused row, then move to the next.\n - Use memoization (`memo`) to avoid redundant calculations.\n\n4. **Maximization**:\n - At each step, choose the maximum between skipping and including the current value.\n - Ensures the best possible sum is always considered.\n# Complexity\n- Time complexity: O(n 2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n 2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```typescript []\nfunction maxScore(grid: number[][]): number {\n const n: number = grid.length;\n const vals: Map<number, number[]> = new Map();\n \n // Collect the values and their row indices\n for (let i = 0; i < n; i++) {\n for (let h of grid[i]) {\n if (!vals.has(h)) {\n vals.set(h, []);\n }\n vals.get(h)!.push(i);\n }\n }\n \n // Convert the Map to a sorted array\n const valsArray: [number, number[]][] = Array.from(vals.entries()).sort((a, b) => b[0] - a[0]);\n \n // Create a memoization cache\n const memo: Map<string, number> = new Map();\n \n // Define the recursive function with memoization\n const maxval = (i: number, mask: number): number => {\n if (i >= valsArray.length) {\n return 0;\n }\n const key: string = `${i}-${mask}`;\n if (memo.has(key)) {\n return memo.get(key)!;\n }\n \n // Option 1: Skip current value\n let res: number = maxval(i + 1, mask);\n \n // Option 2: Include current value if the row is not used\n for (let j of valsArray[i][1]) {\n if (!(mask & (1 << j))) {\n res = Math.max(res, valsArray[i][0] + maxval(i + 1, mask | (1 << j)));\n }\n }\n \n memo.set(key, res);\n return res;\n };\n \n return maxval(0, 0);\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Greedy', 'Memoization', 'Bitmask', 'TypeScript'] | 0 |
select-cells-in-grid-with-maximum-score | DP with bitmask | C++ | Image explanation | dp-with-bitmask-c-image-explanation-by-s-8cjz | DP with Bitmask. \n\n1. For each number, create mask of which row.\n2. Start with mask as 0 and go till all rows are considered by checking base condition.\n \n | soham17041998 | NORMAL | 2024-09-25T04:11:53.575762+00:00 | 2024-09-25T04:11:53.575798+00:00 | 14 | false | DP with Bitmask. \n\n1. For each number, create mask of which row.\n2. Start with mask as 0 and go till all rows are considered by checking base condition.\n ```\n if(mask == (1 << n) - 1) {\n return 0;\n }\n```\n\n\nNow refer image for bit masking.\n\n\n\n\n \n# Code\n```cpp []\nclass Solution {\npublic:\n int cache[2 << 10][105];\n int Dfs(int mask, int j, int n, vector<int>& pos_mask, set<int>& numbers) {\n if(mask == (1 << n) - 1) {\n return 0;\n }\n if(cache[mask][j] != -1) return cache[mask][j];\n\n int ans = 0;\n for(int i = j; i > 0; --i) {\n if(numbers.count(i)) {\n for(int bit = 0; bit <= 10; ++bit) {\n if((pos_mask[i] & (1 << bit)) && (mask & (1 << bit)) == 0) {\n ans = max(ans, i + Dfs(mask | (1 << bit), i - 1, n, pos_mask, numbers));\n }\n }\n \n }\n }\n return cache[mask][j] = ans;\n }\n int maxScore(vector<vector<int>>& grid) {\n int n = grid.size(), m = grid[0].size();\n set<int> numbers;\n memset(cache, -1, sizeof(cache));\n vector<int> pos_mask(105, 0);\n for(int i = 0; i < n; ++i) {\n for(int j = 0; j < m; ++j) {\n pos_mask[grid[i][j]] = pos_mask[grid[i][j]] | (1 << i);\n numbers.insert(grid[i][j]);\n }\n }\n\n return Dfs(0, 100, n, pos_mask, numbers);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | IMAGINE IN SORTED 1D ARRAY | EASY BIT-MASKING | C++ | imagine-in-sorted-1d-array-easy-bit-mask-jw6z | Approach\nSo this one is a tricky one. Brute force suggests to try all possibilities on rows and maintain uniqueness through sets, which results in tle.\n\nTry | rishi_058 | NORMAL | 2024-09-13T04:46:02.071419+00:00 | 2024-09-13T04:46:02.071447+00:00 | 10 | false | # Approach\nSo this one is a tricky one. Brute force suggests to try all possibilities on rows and maintain uniqueness through sets, which results in tle.\n\nTry Imagining the problem for 1D Array, where you have to select some elements which are unique.\n\nFor that you can sort the array & use pick/not-pick.\n\nTo keep track of rows so that at-most 1 element from a row is selected. You can use bit-mask bcz max no. of rows is 10 (2^10 = 1024).\n\nYou should attach its row-no. to each element while converting in into 1D(use vec-pair or 1x2 dimension vec).\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(2^n * n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^n * n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n int visAll;\n vector<vector<int>> dp;\n\n int solve(int idx, int mask, vector<pair<int,int>>&val){\n if(idx==val.size()){return 0;}\n if(mask==visAll){return 0;}\n if(dp[idx][mask]!=-1){return dp[idx][mask];}\n\n int currVal = val[idx].first, nxtUniqueIdx = idx;\n while(val[nxtUniqueIdx].first==currVal){nxtUniqueIdx++; if(nxtUniqueIdx==val.size()){break;}}\n\n int ans = solve(nxtUniqueIdx, mask, val);\n\n for(int i=idx; i<nxtUniqueIdx; i++){\n int curRow = val[i].second;\n if((mask&(1<<curRow))==0){ // if row isn\'t vis\n int tmp = solve(nxtUniqueIdx, mask|(1<<curRow), val) + val[i].first;\n ans = max(ans, tmp);\n }\n\n }\n \n return dp[idx][mask] = ans;\n }\n\n int maxScore(vector<vector<int>>& grid){\n int n = grid.size(), m = grid[0].size();\n\n vector<pair<int,int>> val;\n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n val.push_back({grid[i][j], i});\n }\n }\n\n sort(val.begin(), val.end());\n visAll = (1<<n) - 1;\n dp.resize(val.size(), vector<int>((1<<n), -1));\n return solve(0, 0, val);\n }\n};\n``` | 0 | 0 | ['Array', 'Divide and Conquer', 'Dynamic Programming', 'Backtracking', 'Bit Manipulation', 'C', 'Matrix', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | JAVA | java-by-abhiguptanitb-slln | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | abhiguptanitb | NORMAL | 2024-09-09T01:26:07.544071+00:00 | 2024-09-09T01:26:07.544100+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n List<List<Integer>> a;\n int[][] dp;\n public int calc(int n, int mask) {\n if (n == 0) return 0;\n if (dp[n][mask] != -1) return dp[n][mask];\n int ans = calc(n - 1, mask);\n for (int x : a.get(n)) {\n if ((mask & (1 << x)) != 0) continue;\n ans = Math.max(ans, n + calc(n - 1, mask | (1 << x)));\n }\n return dp[n][mask] = ans;\n }\n public int maxScore(List<List<Integer>> grid) {\n int n = grid.size();\n int m = grid.get(0).size();\n dp = new int[101][1 << n];\n for (int[] row : dp) Arrays.fill(row, -1); \n a = new ArrayList<>();\n for (int i = 0; i <= 100; i++) {\n a.add(new ArrayList<>());\n }\n int maxi = 0;\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n a.get(grid.get(i).get(j)).add(i);\n maxi = Math.max(maxi, grid.get(i).get(j));\n }\n }\n\n return calc(maxi, 0);\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | Simple explanation and simple code C++ | simple-explanation-and-simple-code-c-by-py9u3 | Intuition\n Describe your first thoughts on how to solve this problem. \nSince naive solution gives TLE, think of interchanging the way we keep the unique value | dee24da | NORMAL | 2024-09-08T02:22:52.129278+00:00 | 2024-09-08T02:22:52.129309+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince naive solution gives TLE, think of interchanging the way we keep the unique values and unique rows. Meaning go over values one by one and to maintain unique rows store the already used rows using some data structure.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSort all the cells in the grid by their values and keep track of their original positions.\nTry dynamic programming with the following states: the current cell that we might select and a bitmask representing all the rows from which we have already selected a cell so far.\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int f(int valIndex, int usedRowsMask,vector<vector<int>> &values,vector<vector<int>> &dp)\n {\n if(valIndex == values.size()) return 0;\n if(dp[valIndex][usedRowsMask]!=-1) return dp[valIndex][usedRowsMask];\n \n int sum = 0;\n int row = values[valIndex][1];\n if((1<<row)&usedRowsMask)\n sum=f(valIndex+1,usedRowsMask,values,dp);\n else\n {\n int j=valIndex;\n while (j<values.size() && values[valIndex][0]==values[j][0]) j++;\n \n sum=max(f(valIndex+1,usedRowsMask,values,dp),\n values[valIndex][0]+ f(j,(1<<row)|usedRowsMask,values,dp));\n }\n \n return dp[valIndex][usedRowsMask]=sum;\n \n }\n int maxScore(vector<vector<int>>& grid) {\n int m=grid.size();\n int n=grid[0].size();\n vector<vector<int>> values;\n for(int i=0;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n values.push_back({grid[i][j], i, j});\n }\n }\n sort(values.begin(), values.end());\n vector<vector<int>> dp(m*n,vector<int>(pow(2,m+1),-1));\n \n return f(0,0,values,dp);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | DP + bitmask | dp-bitmask-by-rajdeep_nagar-ckm5 | ```\n/\n\n1010 matrix\n\n\nfrom ecah row we will select atmost one no.\n\n\nso we will keep track of no. selected from each row, so that we will not select the | Rajdeep_Nagar | NORMAL | 2024-09-07T12:35:24.217007+00:00 | 2024-09-07T12:35:24.217036+00:00 | 1 | false | ```\n/*\n\n10*10 matrix\n\n\nfrom ecah row we will select atmost one no.\n\n\nso we will keep track of no. selected from each row, so that we will not select the same no. in upcoming row\n\nobviously we will select atmost 10 no\'s\n\n\nas grid[i][j]<=100, we can\'t use bitmask to keep track of selected no\'s\n\n\nREVERSE THE bimask LOGIC (STANDARD) :-\n\ninstead of storing selected no. in bitmask, we store the row from which we have already done the selection\n\nbut how we will ensure unique no. is selected ?\n\nsuppsoe current mask => m1\n\ncurrently I am selecting no= x (starting from 100) from some row, making that row set in the mask, and in next recusrion call i will select (x-1) from some other row\n\n\nwe will store rows of each no. in map (int => vector<int>)\n\n\n*/\n\n\nint dp[101][1<<11];\n\n\nint n,m;\n\nunordered_map<int, vector<int>>mp;\n\n\nclass Solution {\npublic:\n \n\n int maxScore(vector<vector<int>>& grid) {\n \n mp.clear();\n \n memset(dp,-1,sizeof(dp));\n \n n=grid.size();\n \n m=grid[0].size();\n \n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n mp[grid[i][j]].push_back(i);\n }\n }\n \n return find(100, 0, grid);\n \n }\n \n int find(int no, int mask, vector<vector<int>>&grid){\n \n if(no==0)\n return 0;\n \n if(dp[no][mask]!=-1)\n return dp[no][mask];\n \n \n // not selecting this no. from any row or no. not present in the grid\n \n int ans= find(no-1, mask, grid);\n \n \n for(int row: mp[no]){\n if(mask & (1<<row))\n continue;\n \n ans=max(ans, no+ find(no-1, mask|(1<<row), grid));\n }\n \n \n return dp[no][mask]=ans;\n }\n\n};\n | 0 | 0 | ['Bitmask'] | 0 |
select-cells-in-grid-with-maximum-score | Backtracking with pruning | backtracking-with-pruning-by-dhairyaseth-5uae | Intuition\n Describe your first thoughts on how to solve this problem. \nThe requirement to have an element from every row implies that there has to be atleast | dhairyaseth | NORMAL | 2024-09-06T22:06:30.267075+00:00 | 2024-09-06T22:06:30.267104+00:00 | 31 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe requirement to have an element from every row implies that there has to be atleast 1 unique element per row, and if that element has to be selected from that row it can\'t be selected from another row.\nWith the above condition in mind we can split every row into 2 types, where only a unique element is present, and where more than 1 unique elements are present.\nFor every row with a unique element select that element first and remove it from every other row.\nIf there are no rows with a single unique element we should then select the maximum element from the remaining grid. As selecting any other element gives a sub-optimal answer read [this solution](https://leetcode.com/problems/select-cells-in-grid-with-maximum-score/solutions/5718057/python-java-dfs-in-descending-orders-with-detailed-explanation) for detailed explanation of the same logic.\nAnd get the solution by removing each row once and checking for the maximum answer.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nA key trick with this solution is to see that when selecting the maximum\nelement from a row, we don\'t select other rows that are exactly equal (as in rows that contain the same set of inputs)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO((m*n^3)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m*n^2)\n# Code\n```java []\nclass Solution {\n record Element(int k, Queue<Integer> q) {}\n public int maxScore(List<List<Integer>> grid) {\n Map<Integer,Set<Integer>> nums = new HashMap<>();\n int counter=0;\n for(List<Integer> l : grid) {\n nums.put(counter++, new HashSet<>(l));\n }\n return maxScore(nums);\n }\n int maxScore(Map<Integer, Set<Integer>> grid) {\n if(grid.size()==0) return 0;\n int singleton = -1;\n for(int key : grid.keySet()) {\n if(grid.get(key).size()==1) {\n singleton=key;\n break;\n }\n }\n if(singleton==-1) {\n //Todo: Get max element, remove it from every other set, pass to maxScore\n int max = 0;\n List<Integer> candidates = new ArrayList<>();\n for(int k: grid.keySet()) {\n Set<Integer> s = grid.get(k);\n for(int i : s) {\n if(max<i) {\n max=i;\n candidates.clear();\n candidates.add(k);\n } else if(max==i) {\n candidates.add(k);\n }\n }\n }\n int result = max;\n List<Integer> finalCandidates = new ArrayList<>();\n Set<Set<Integer>> seen = new HashSet<>();\n for(int c : candidates) {\n Set<Integer> x = grid.get(c);\n x.remove(max);\n if(!seen.contains(x)) {\n finalCandidates.add(c);\n seen.add(x);\n }\n }\n int rMax = 0;\n for(int c: finalCandidates) {\n Set<Integer> temp = grid.get(c);\n grid.remove(c);\n int tscore = maxScore(deepCopy(grid));\n rMax=Math.max(rMax, tscore);\n grid.put(c, temp);\n }\n return result+rMax;\n } else {\n //Todo: Get the element from singleton and remove it from every other set\n //Remove all empty sets and singleton and pass to maxScore\n int element = grid.get(singleton).iterator().next();\n grid.remove(singleton);\n for(Set<Integer> s : grid.values()) {\n s.remove(element);\n }\n List<Integer> toRemove = new ArrayList<>();\n for(int k: grid.keySet()) {\n if(grid.get(k).size()==0) {\n toRemove.add(k);\n }\n }\n for(int k : toRemove) {\n grid.remove(k);\n }\n return element + maxScore(deepCopy(grid));\n }\n }\n Map<Integer, Set<Integer>> deepCopy(Map<Integer, Set<Integer>> orig) {\n Map<Integer, Set<Integer>> res = new HashMap<>();\n for(int c: orig.keySet()) {\n res.put(c, new HashSet<>(orig.get(c)));\n }\n return res;\n }\n}\n``` | 0 | 0 | ['Backtracking', 'Recursion', 'Java'] | 0 |
select-cells-in-grid-with-maximum-score | DP + bitmask | skip element or take it while maintaining masking of row id | dp-bitmask-skip-element-or-take-it-while-8bkg | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | garvit_17 | NORMAL | 2024-09-06T18:38:26.795961+00:00 | 2024-09-06T18:38:26.796022+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n unordered_map<int,vector<int>>mp;\n vector<vector<int>>dp;\n vector<int>v;\n int ans=0;\n int help(int i,int mask,int n)\n {\n if(i>=n)return 0;\n if(dp[i][mask]!=-1)return dp[i][mask];\n int ans=0;\n for(auto row:mp[v[i]])\n {\n if((mask & (1 << row))==0)\n {\n ans=max(ans,v[i]+help(i+1,(mask|(1<<row)),n));\n }\n }\n return dp[i][mask]=max(ans,help(i+1,mask,n));\n }\n int maxScore(vector<vector<int>>& grid) {\n set<int>st;\n for(int i=0;i<grid.size();i++)\n {\n for(int j=0;j<grid[0].size();j++)\n {\n st.insert(grid[i][j]);\n }\n }\n for(auto t:st)v.push_back(t);\n sort(v.begin(),v.end(),greater<int>());\n for(int i=0;i<grid.size();i++)\n {\n for(int j=0;j<grid[0].size();j++)\n {\n mp[grid[i][j]].push_back(i);\n }\n }\n dp.resize(v.size()+1,vector<int>(2000,-1));\n return help(0,0,v.size());\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | ✅💯🎊Simple C++ Code🎊🎊 || ✔Easy to understand🎯 || Easy Logic || Beginner friendly || Beats 100% | simple-c-code-easy-to-understand-easy-lo-5xy7 | Intuition\n Describe your first thoughts on how to solve this problem. \nthere are total 10 rows, it means we can take a bit of number 2 ke power 10 = number 10 | ritiwij | NORMAL | 2024-09-06T17:01:43.146373+00:00 | 2024-09-06T17:01:43.146405+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthere are total 10 rows, it means we can take a bit of number 2 ke power 10 = number 1024;\nmene vector v banaya hu jo har element ko store kar rha hai woh row me hai ,\nthen humne number ka limit diya tha number maximum 100 tak ja sakta hai\nhum dekhnge kya uss row se number liye hai ki nhi (musk & (1<<it)) == 0, auto it karke dekh lenge\nagar nhi liye hai toh le lenge, phir num ko -1 kar denge base cases num == 0 hoga.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int>v[101];\n int dp[101][1025];\n int solve(int num, int musk){\n if(num == 0)return 0;\n if(dp[num][musk] != -1)return dp[num][musk];\n int ans =0;\n int take =0;\n int not_take = solve(num-1,musk);\n for(auto it : v[num]){\n if((musk & (1<<it)) == 0){\n // cout<<(musk & (1<<it))<<" z "<<num<<\'\\n\';\n take = max(take, num + solve(num - 1, (musk | (1 << it))));\n }\n // if(num == 19){\n // cout<<ans<<" x "<<take<<\'\\n\';\n // }\n }\n ans =max({ans,take,not_take});\n return dp[num][musk] = ans;\n }\n \n int maxScore(vector<vector<int>>& g){\n // set<int>st;\n int n= g.size();\n int m = g[0].size();\n memset(dp,-1,sizeof(dp));\n for(int i =0; i< n; i++){\n for(int j =0; j< m; j++){\n v[g[i][j]].push_back(i);\n }\n }\n return solve(100,0);\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | DP With Bitmask | dp-with-bitmask-by-avatar_027-85at | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Avatar_027 | NORMAL | 2024-09-06T06:32:50.259316+00:00 | 2024-09-06T06:32:50.259340+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n#define ll long long\n#define vll vector<ll>\n#define vvll vector<vll>\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n ll n=grid.size(), m=grid[0].size();\n\n map<ll, vll> mp;\n for(ll i=0; i<n; i++){\n for(ll j=0; j<m; j++){\n mp[grid[i][j]].push_back(i);\n }\n }\n int dp[101][1<<n];\n memset(dp, -1, sizeof(dp));\n function<ll(ll, ll)> f=[&](ll num, ll msk)->ll{\n if(num<=0) return 0;\n ll mx=0;\n if(dp[num][msk]!=-1) return dp[num][msk];\n mx=f(num-1, msk);\n for(auto i: mp[num]){\n if(msk&(1<<i)) continue;\n mx=max(mx, num+f(num-1, msk|(1<<i)));\n }\n return dp[num][msk]= mx;\n };\n\n return f(100, 0);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Python3 Easy Solution | python3-easy-solution-by-pranaythangelll-kmu7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | PranayThangelllapalli | NORMAL | 2024-09-05T10:33:35.721931+00:00 | 2024-09-05T10:33:35.721964+00:00 | 15 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n freq={}\n for i in range (len(grid)):\n grid[i]= list(set(grid[i]))\n for j in range(len(grid[i])):\n if grid[i][j] in freq:\n freq[grid[i][j]].append(i)\n else:\n freq[grid[i][j]]=[i]\n\n newlst = list(sorted(freq.items(),key= lambda x:x[0] ,reverse= True))\n print(newlst)\n dp= {}\n def fun(indx,string):\n if indx == len(newlst):\n return 0\n a = 0 \n if (indx,string) in dp:\n return dp[(indx,string)]\n for row in newlst[indx][1]:\n # print(string,row)\n if string[row] == "0":\n a= max(a, newlst[indx][0]+ fun(indx+1,string[:row]+"1"+string[row+1:]))\n a= max(a,fun(indx+1,string))\n dp[(indx,string)]=a\n return a\n return fun(0,"0"*len(grid))\n\n \n``` | 0 | 0 | ['Dynamic Programming', 'Sorting', 'Python3'] | 0 |
select-cells-in-grid-with-maximum-score | DP Bitmask | dp-bitmask-by-harsha3330-cmow | Intuition\n Describe your first thoughts on how to solve this problem. \nWe are going to convert this 2d array into a 1d and write a dp solutions , this convert | Harsha3330 | NORMAL | 2024-09-04T16:12:02.706210+00:00 | 2024-09-04T16:12:02.706254+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe are going to convert this 2d array into a 1d and write a dp solutions , this convertion makes the array sorted and unique values will be clubed \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDP bitmask \nLet us take an example : \n[[3,4],[4,1]] \n\nconvertion : \nwe will add row to the number and sorted \n\n[[3,0].[4,0],[4,1],[1,1]] (3,4,4,1 are number , 0,0,1,1 are rows)\n\nsorted : [[1,1],[3,0],[4,0],[4,1]] ;\n\nNow it is similarly to 0-1 knapsack\n\nI have written the top down approach here \n\nBasically we can or we will not , if we chose to take an index i and next index j value should be equal that is nextidx function helper is the dp function and add memo here , Used bitmask to know which values of rows are taken \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * (2^n)) n--> length of grid \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n * (2^n))\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int n ,m ;\n vector <vector <int>> dp ;\n int nextidx(vector <pair<int,int>>&arr,int i){\n for(int j=i-1;j>=0;j--){\n if(arr[j].first!=arr[i].first)return j ;\n }\n return -1 ;\n }\n int helper(vector <pair<int,int>>&arr,int i,int mask){\n if(i<0)return 0 ;\n if(dp[i][mask]!=-1)return dp[i][mask] ;\n int num = arr[i].first , row = arr[i].second ;\n int tempmask = 1 << row ;\n int ans1 = helper(arr,i-1,mask) ;\n if(tempmask & mask )return dp[i][mask]=ans1 ;\n \n int j = nextidx(arr,i) ;\n \n int mask1 = mask | tempmask ;\n int ans2 = num+helper(arr,j,mask1) ;\n return dp[i][mask]=max(ans1,ans2) ;\n \n \n }\n int maxScore(vector<vector<int>>& grid) {\n dp.resize(101,vector <int> (1025,-1)) ;\n vector <pair<int,int>> arr ;\n n=grid.size(),m=grid[0].size();\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n arr.push_back({grid[i][j],i}) ;\n }\n }\n \n sort(arr.begin(),arr.end()) ;\n int sz = n*m ;\n return helper(arr,sz-1,0) ;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | why backtracking is not working ? can you guys help me ? | why-backtracking-is-not-working-can-you-jjkpl | \nclass Solution {\npublic:\n int solve(vector<vector<int>> grid, int r, vector<int>&freq){\n\n\tint n = grid.size();\n\tint m = grid[0].size();\n\tint ans = | parthkamal | NORMAL | 2024-09-04T09:46:11.876158+00:00 | 2024-09-04T09:46:11.876194+00:00 | 7 | false | ```\nclass Solution {\npublic:\n int solve(vector<vector<int>> grid, int r, vector<int>&freq){\n\n\tint n = grid.size();\n\tint m = grid[0].size();\n\tint ans = 0;\n\tif(r == n)\n\t\treturn ans;\n bool flag = 0; \n\tfor (int j = 0; j < m; j++)\n\t{\n\t\tif(freq[grid[r][j]]==0){\n\t\t\tfreq[grid[r][j]]++;\n\t\t\tans = max(ans, grid[r][j] + solve(grid, r + 1, freq));\n\t\t\tfreq[grid[r][j]]--; \n flag = 1;\n\t\t}\n\t}\n \n if(flag==0)ans = max(ans, solve(grid, r + 1, freq)); \n\treturn ans; \n}\n\nint maxScore(vector<vector<int>> & grid){\n\n\tvector<int> freq(101, 0);\n\tint ans = -1;\n\tans = max(ans, solve(grid, 0, freq));\n\treturn ans; \n}\n \n};\n// here is my solution, can anyone tell me , passing 513 / 545 \n``` | 0 | 0 | [] | 1 |
select-cells-in-grid-with-maximum-score | Simple Solution Explained in Deep | C++ | Beats 87.33% | DP | simple-solution-explained-in-deep-c-beat-vs53 | \n\n\n# Intuition\nSimilar to graphs we will map elements to the rows they are present in and iterate from max value to lowest while marking the rows they were | AKSKL | NORMAL | 2024-09-04T06:15:21.786292+00:00 | 2024-09-04T06:15:21.786320+00:00 | 2 | false | \n\n\n# Intuition\nSimilar to graphs we will map elements to the rows they are present in and iterate from max value to lowest while marking the rows they were in.\n\n# Approach\nFirst we will have a set of unique elements given in grid and then sort them in descending order.\nAfter this we will map them to their corresponding rows maintaing a vector of them.\n\nWe will use bitmasking to maintain visted rows. It is easy just read comments in code.\n\nFinally apply dp. Thank You\n\n# Complexity\n- Time complexity:\n$$O(2^N)$$\n\n- Space complexity:\n$$O(N*2^N)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int solve(int i,vector<int> &t,unordered_map<int,vector<int>> &mp,int mask,int n,vector<vector<int>> &dp){\n // Base Case of reaching end of unique elements\n if (i>=n) return 0;\n\n if (dp[i][mask]!=-1) return dp[i][mask];\n\n int ans=0; \n\n //Going through rows for a given Unique elements \n //and seeing if we can choose the element from that row\n for(auto j:mp[t[i]]){\n if ((mask & (1<<j)) ==0 ){\n ans=max(ans,t[i] + solve(i+1,t,mp,(mask | (1<<j)),n,dp));\n }\n }\n //Another option is to leave the current i and choose next ones[]()\n ans=max(ans,solve(i+1,t,mp,mask,n,dp));\n return dp[i][mask] = ans;\n }\n int maxScore(vector<vector<int>>& grid) {\n // Set of all Unique Numbers\n set<int> s;\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[0].size();j++){\n s.insert(grid[i][j]);\n }\n }\n // Sorted Vector in Descending Order\n\n vector<int> t(s.begin(),s.end());\n sort(t.begin(),t.end(),greater<int>());\n\n //Mapping Values to all of their rows\n\n unordered_map<int,vector<int>> mp;\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[0].size();j++){\n mp[grid[i][j]].push_back(i);\n }\n }\n\n //Initializing DP Matrix\n //1025 -> 2^10 + 1 . Since max rows are 10. \n vector<vector<int>> dp(t.size(),vector<int>(1025,-1));\n\n //Solving the question\n return solve(0,t,mp,0,t.size(),dp);\n }\n};\n```\n- See This Video for Reference:\nhttps://www.youtube.com/watch?v=lvUte5NcTJ4\n | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Select Cells in Grid With Maximum Score | select-cells-in-grid-with-maximum-score-my6tb | Code\ncpp []\n#include <vector>\n#include <unordered_set>\n#include <algorithm>\n#include <cstring>\n\nclass Solution {\npublic:\n int dp[1025][101];\n \n | 20250411.cid470 | NORMAL | 2024-09-04T06:03:54.416003+00:00 | 2024-09-04T06:03:54.416035+00:00 | 17 | false | # Code\n```cpp []\n#include <vector>\n#include <unordered_set>\n#include <algorithm>\n#include <cstring>\n\nclass Solution {\npublic:\n int dp[1025][101];\n \n int maxScore(std::vector<std::vector<int>>& grid) {\n std::unordered_set<int> uniqueValues;\n std::vector<int> arr[101];\n\n for (int i = 0; i < grid.size(); i++) {\n for (int j = 0; j < grid[0].size(); j++) {\n uniqueValues.insert(grid[i][j]);\n arr[grid[i][j]].push_back(i);\n }\n }\n\n std::vector<int> temp(uniqueValues.begin(), uniqueValues.end());\n std::sort(temp.rbegin(), temp.rend());\n memset(dp, -1, sizeof(dp));\n\n return solve(0, 0, temp.size(), temp, arr);\n }\n\nprivate:\n int solve(int ix, int mask, int n, const std::vector<int>& temp, const std::vector<int> arr[]) {\n if (ix == n) {\n return 0;\n }\n if (dp[mask][ix] != -1) return dp[mask][ix];\n\n int ans = 0;\n\n for (auto it : arr[temp[ix]]) {\n if ((mask & (1 << it)) == 0) {\n ans = std::max(ans, temp[ix] + solve(ix + 1, mask | (1 << it), n, temp, arr));\n }\n }\n\n ans = std::max(ans, solve(ix + 1, mask, n, temp, arr));\n\n return dp[mask][ix] = ans;\n }\n};\n\n``` | 0 | 0 | ['Array', 'Dynamic Programming', 'Bit Manipulation', 'Matrix', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | 4ms dp solution | 4ms-dp-solution-by-sovlynn-pkqn | \n\n# Intuition\nSort the cells according to there value. Then for each value segments, update the dp array according to the result of previous segment to ensur | sovlynn | NORMAL | 2024-09-04T02:37:32.123949+00:00 | 2024-09-04T02:37:32.123986+00:00 | 15 | false | \n\n# Intuition\nSort the cells according to there value. Then for each value segments, update the dp array according to the result of previous segment to ensure the selected number not duplicate.\n\n# Complexity\n- Time complexity:\n$$O(m\\times n\\times 2^m)$$\n\n- Space complexity:\n$$O(2^m)$$\n\n# Code\n```rust []\nuse std::cmp::Ordering;\n\n#[derive(Debug, Eq, PartialEq, Clone)]\nstruct Cell{\n loc: (usize, usize),\n val: i32\n}\n\nimpl Ord for Cell{\n fn cmp(&self, other: &Self)->Ordering{\n other.val.cmp(&self.val).then(self.loc.cmp(&other.loc))\n }\n}\n\nimpl PartialOrd for Cell{\n fn partial_cmp(&self, other: &Self)->Option<Ordering>{\n Some(self.cmp(other))\n }\n}\n\nimpl Solution {\n pub fn max_score(grid: Vec<Vec<i32>>) -> i32 {\n let (m, n) = (grid.len(), grid[0].len());\n let mut cells=Vec::new();\n for i in 0..m{\n for j in 0..n{\n cells.push(Cell{loc: (i, j), val: grid[i][j]});\n }\n }\n cells.sort_unstable();\n \n let mut i=0;\n let mut dp=vec![0; 1<<m];\n while i<cells.len(){\n let mut j=i;\n while j<cells.len()&&cells[i].val==cells[j].val{j+=1;}\n let mut tmp=dp.clone();\n for k in i..j{\n let c=&cells[k];\n for m in 0..dp.len(){\n if m&1<<c.loc.0!=0{continue;}\n tmp[m|1<<c.loc.0]=tmp[m|1<<c.loc.0].max(dp[m]+c.val);\n }\n }\n\n dp=tmp;\n i=j;\n }\n dp[dp.len()-1]\n }\n}\n``` | 0 | 0 | ['Array', 'Dynamic Programming', 'Bit Manipulation', 'Matrix', 'Bitmask', 'Rust'] | 0 |
select-cells-in-grid-with-maximum-score | BACKTRACKING | backtracking-by-quietmorning2-2pag | Intuition\n Describe your first thoughts on how to solve this problem. \nFind the maximum value. If the maximum appears in multiple rows, iterate these rows and | QuietMorning2 | NORMAL | 2024-09-04T01:59:11.366467+00:00 | 2024-09-04T01:59:11.366489+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind the maximum value. If the maximum appears in multiple rows, iterate these rows and use backtracking to find the answer for remaining rows.\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n \n def backtrack(grd, exceptions):\n m = len(grd)\n if m == 1:\n temp = [itm for itm in grd[0] if itm not in exceptions]\n if temp:\n return max(temp)\n return 0\n n = len(grd[0])\n d = set() # set of rows that contain maximum outside exceptions\n v = 0\n for i in range(m):\n for j in range(n):\n if exceptions and grd[i][j] in exceptions:\n continue\n if grd[i][j] > v:\n d = set()\n d.add(i)\n v = grd[i][j]\n elif grd[i][j] == v:\n d.add(i) \n # Now v is the maximum. If v==0, then all numbers are\n # in exceptions so we return 0.\n if not v: \n return 0\n res = 0\n for r in list(d):\n tempset = exceptions\n tempset.add(v)\n temp = backtrack(grd[:r]+grd[(r+1):], tempset)+v\n tempset.remove(v)\n res = max(res,temp)\n return res\n \n return backtrack(grid, set())\n \n \n \n``` | 0 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Python3 (using dynamic programming) | python3-using-dynamic-programming-by-rey-kopa | \nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int: \n @cache\n def helper(idx, seen):\n if idx == l: \n | reynaldocv | NORMAL | 2024-09-03T21:13:42.542560+00:00 | 2024-09-03T21:13:42.542587+00:00 | 0 | false | ```\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int: \n @cache\n def helper(idx, seen):\n if idx == l: \n return 0 \n \n else: \n ans = 0\n \n for i in range(idx, l):\n (value, ith) = arr[i]\n \n if (seen >> ith) & 1 == 0: \n ans = max(ans, value + helper(nextIndex[value], seen ^ (2**ith)))\n \n return ans \n \n m, n = len(grid), len(grid[0])\n \n arr = []\n \n for i in range(m):\n for j in range(n):\n arr.append((grid[i][j], i))\n \n arr.sort(key = lambda item: -item[0])\n \n nextIndex = {}\n \n l = last = len(arr)\n \n for i in range(l - 1, -1, -1):\n value = arr[i][0]\n \n if value not in nextIndex: \n nextIndex[value] = last\n \n last = i \n \n return helper(0, 0)\n``` | 0 | 0 | [] | 0 |
select-cells-in-grid-with-maximum-score | Blazing Fast 🔥 5ms | Beats 100% | Rundown + Bitmask + Memo | blazing-fast-5ms-beats-100-rundown-bitma-3ao7 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe most straightforward approach, i.e. backtracking can quickly get very expensive for | swanandcode | NORMAL | 2024-09-03T13:28:22.481408+00:00 | 2024-09-08T12:49:08.696477+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe most straightforward approach, i.e. **backtracking** can quickly get very expensive for some cases, hence this is one of those cases where you have to look at the data constraints.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere are the steps to solve this particular problem:\n\n1. Arrange all the unique numbers in descending order\n2. Map which row they belong to by **bitmasking**\n3. Starting from the greatest number, find if it is unique to a bucket\n4. If it is, select it and mark the row as done\n5. If not, then branch out to the number of buckets it is present in\n6. Use memoization to avoid recomputing repeat cases\n\n# Complexity\n- Time complexity: O(n * 2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n Map<Long, Integer> memo = new HashMap<>();\n int[] intMap = new int[101];\n int[] intPos = new int[101];\n\n public int maxScore(List<List<Integer>> grid) {\n int candidates = 0;\n for (int i = 0; i < grid.size(); i++) {\n List<Integer> integers = grid.get(i);\n int mask = 1 << i;\n for (int j : integers) {\n intMap[j] |= mask;\n }\n candidates |= mask;\n }\n int lastId = 0;\n for (int i = 0; i < 101; i++) {\n if (intMap[i] == 0) continue;\n intPos[i] = lastId;\n lastId = i;\n }\n return computeMax(0, lastId, candidates);\n }\n\n private int computeMax(int max, int target, int candidates) {\n if (candidates == 0 || target == 0) return max;\n Long memoKey = computeMemoKey(candidates, max, target);\n if (memo.containsKey(memoKey)) return memo.get(memoKey);\n int newMax = max;\n int v = intMap[target];\n int curMax = max + target;\n for (int mask = v & candidates; mask > 0; mask &= mask - 1) {\n int newCandidates = candidates ^ (mask & -mask);\n newMax = Math.max(newMax, computeMax(curMax, intPos[target], newCandidates));\n }\n if (newMax == max)\n newMax = Math.max(newMax, computeMax(max, intPos[target], candidates));\n memo.put(memoKey, newMax);\n return newMax;\n }\n\n private long computeMemoKey(int candidates, int max, int targetKey) {\n return ((long) candidates << 32) | ((long) targetKey << 24) | (max);\n }\n}\n```\n\n | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | DP Solution using Bitmask | dp-solution-using-bitmask-by-ak3177590-bzv6 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ak3177590 | NORMAL | 2024-09-03T05:29:38.048237+00:00 | 2024-09-03T05:29:38.048314+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n*m*2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n*m*2^n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\nint maxScore(vector<vector<int>>& g) {\n int n=g.size(),m=g[0].size();\n vector<pair<int,int>>v;\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n v.push_back({g[i][j],i});\n }\n }\n int N=n*m;\n sort(v.begin(),v.end(),greater<pair<int,int>>());\n vector<vector<int>>dp(N,vector<int>(1<<n,-1));\n\n function<int(int,int)>find=[&](int i,int mask)->int{\n if(i>=N)return 0;\n if(dp[i][mask]!=-1)return dp[i][mask];\n int ans=0;\n if((mask&(1<<v[i].second))){\n ans+=find(i+1,mask);\n }\n else{\n int j=i;\n while(j<N and v[i].first==v[j].first)j++;\n\n int newMask=(mask|(1<<v[i].second));\n ans=max(ans,v[i].first+find(j,newMask));\n ans=max(ans,find(i+1,mask));\n } \n return dp[i][mask]=ans; \n };\n return find(0,0);\n\n}\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Bitmasking + DP | bitmasking-dp-by-shyam-vishwakarma-8h2h | Intuition\nThe goal is to maximize the sum of selected cells in the grid, ensuring no two selected cells are from the same row and all selected values are uniqu | Shyam-Vishwakarma | NORMAL | 2024-09-03T04:36:28.838553+00:00 | 2024-09-03T04:36:28.838587+00:00 | 10 | false | # Intuition\nThe goal is to maximize the sum of selected cells in the grid, ensuring no two selected cells are from the same row and all selected values are unique.\n\n# Approach\n- Mapping Numbers to Rows: Create a mapping of each unique number in the grid to the rows in which it appears.\n- Bitmasking: Represent the selected rows using a bitmask. Each bit in the mask indicates whether a particular row has been selected.\n- Recursive Function (`f1`): The function `f1` recursively computes the maximum score by either including or excluding the current number, ensuring the constraints are met.\n- DP: Use `f1tbl` to store the maximum score possible for each combination of rows selected and values considered. This helps avoid recomputation.\n\n# Complexity\n- Time complexity:\n`O(x * 2^m * m)`\nwhere,\nx: maximum number in the grid (100)\nm: no. of rows in grid\n\n- Space complexity:\n`O(x * 2^m)`\nwhere,\nx: maximum number in the grid (100)\nm: no. of rows in grid\n\n# Code\n```cpp []\ntypedef unordered_map<int, vector<int>> um;\nclass Solution {\npublic:\n int m, n;\n vector<vector<int>>f1tbl;\n int maxScore(vector<vector<int>>& grid) {\n m = grid.size();\n n = grid[0].size();\n f1tbl.resize(101, vector<int>(1 << m, -1));\n unordered_map<int, vector<int>> num2row;\n for (int i = 0; i < m; i++) {\n for (int& num : grid[i]) {\n num2row[num].push_back(i);\n }\n }\n\n // mask of bit length 10 -> 1: row selected, 0: row not selected\n int mask = 0;\n return f1(100, mask, num2row);\n }\n\n int f1(int num, int& mask, um& num2row) {\n if(f1tbl[num][mask] != -1) return f1tbl[num][mask];\n if (num == 0) return f1tbl[num][mask] = 0;\n\n int score = 0;\n\n for (int r : num2row[num]) {\n int rMask = (1 << r);\n if (mask & rMask) continue;\n mask |= rMask;\n int newScore = num + f1(num - 1, mask, num2row);\n score = max(newScore, score);\n mask ^= rMask;\n }\n\n score = max(score, f1(num - 1, mask, num2row));\n\n return f1tbl[num][mask] = score;\n }\n};\n\n``` | 0 | 0 | ['Dynamic Programming', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | Best first | best-first-by-kamanashisroy-2fuz | Intuition\nWe can reduce our time-complexity by best-first search approach.\nTo find the best, we sort all the rows in non-increasing order.\n\n# Approach\nNow | kamanashisroy | NORMAL | 2024-09-03T00:04:46.254008+00:00 | 2024-09-03T00:04:46.254032+00:00 | 8 | false | # Intuition\nWe can reduce our time-complexity by best-first search approach.\nTo find the best, we sort all the rows in non-increasing order.\n\n# Approach\nNow in an recursive manner we explore the biggest value in each row at first. With that we can quickly get the best result.\n\nWe can compare with existing best to prune a branch that is not optimal.\n\n```\nprediction = calc(row+1,mask,presum)\nret = prediction\nfor x in grid[row]:\n if (1<<x) & mask:\n continue\n \n if (x+prediction) <= ret: # prune\n continue\n\n```\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n \n NROW = len(grid)\n NCOL = len(grid[0])\n \n for row in grid:\n row.sort(reverse=True)\n \n @cache\n def calc(row,mask,presum):\n if row == NROW:\n return presum\n \n prd = calc(row+1,mask,presum)\n ret = prd\n for x in grid[row]:\n if (1<<x) & mask:\n continue\n \n if (x+prd) <= ret:\n continue\n ret = max(ret, calc(row+1,mask | (1<<x), presum+x))\n \n return ret\n \n result = calc(0,0,0)\n return result\n``` | 0 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | DP C++ | dp-c-by-intermsof-stkj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | intermsof | NORMAL | 2024-09-02T22:54:28.276307+00:00 | 2024-09-02T22:54:28.276340+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n class State {\n public:\n State (int row) : hash_value(1 << row) {\n for (int i = 0; i < 10; ++i)\n rows[i] = false;\n rows[row] = true;\n }\n State add (int row) const {\n State copy = *this;\n copy.rows[row] = true;\n copy.hash_value += (1 << row);\n return copy;\n }\n bool is_valid (int row) const {\n return !rows[row];\n }\n\n void print (int max) const {\n cout << " " ;\n for (int i = 0; i < max; ++i) {\n cout << rows[i] << " ";\n }\n cout << endl;\n }\n State (const State& s) : hash_value (s.hash_value) {\n for (int i = 0; i < 10; ++i)\n rows[i] = s.rows[i];\n }\n State () : hash_value(0) {\n for (int i = 0; i < 10; ++i)\n rows[i] = false;\n }\n // True if row is set, false otherwise\n array<bool, 10> rows;\n int hash_value = 0;\n \n };\n struct StateHasher {\n size_t operator()(const State& state) const {\n return hash<int>()(state.hash_value);\n }\n };\n struct StateEqual {\n bool operator()(const State& lhs, const State& rhs) const {\n return lhs.hash_value == rhs.hash_value;\n }\n };\n typedef unordered_map<State, int, StateHasher, StateEqual> AllState;\n\n int maxScore(vector<vector<int>>& grid) {\n const int m = grid.size(), n = grid[0].size();\n\n // vector<pair<int,int> > indices;\n // for (int i = 0; i < m; ++i)\n // for (int j = 0; j < n; ++j)\n // indices.push_back({i,j});\n\n // sort (indices.begin(), indices.end(), [&grid](pair<int,int> &a, pair<int,int> &b) {\n // return grid[a.first][a.second] < grid[b.first][b.second];\n // });\n map<int, unordered_set<int> > valToRows;\n \n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n const int val = grid[i][j]; \n valToRows[val].insert(i);\n }\n }\n\n vector<vector<vector<State> > > comb;\n \n for (int i = 0; i < m; ++i) {\n comb.emplace_back(i + 1);\n for (int k = 0; k <= i; ++k) {\n if (i > k) {\n for (auto &state : comb[i - 1][k])\n comb[i][k].push_back(state);\n }\n if (k != 0) {\n for (auto &state : comb[i - 1][k - 1]) {\n comb[i][k].emplace_back(state.add(i));\n }\n } else {\n comb[i][k].emplace_back(i);\n }\n }\n }\n // for (int i = 0; i < comb[m - 1].size(); ++i) {\n // cout << "choose " << i + 1 << ": " << endl;\n // for (auto &s : comb[m - 1][i])\n // s.print(m);\n // }\n \n vector<AllState> dp(1);\n for (auto k : comb[m - 1])\n for (auto &s : k) {\n dp[0].emplace(make_pair(s, 0));\n }\n dp[0].emplace(make_pair(State(), 0));\n int last = 0;\n\n for (auto &p : valToRows) {\n // cout << endl << p.first << endl;\n // for (auto s : p.second) cout << s << " ";\n // cout << endl;\n const int val = p.first;\n const unordered_set<int>& rows = p.second;\n AllState copy = dp[last];\n for (auto &statePair : copy) {\n const State &state = statePair.first;\n int max = dp[last][state];\n for (auto row : rows) {\n if (state.is_valid(row)) {\n const State nextState = state.add(row);\n const int score = val + dp[last][nextState];\n if (score > max) max = score;\n }\n }\n // cout << "state = " << state.hash_value << " " << max << endl;\n // cout << max << " ";\n statePair.second = max;\n }\n\n dp.emplace_back(move(copy));\n last++;\n }\n const State start; \n return dp[last][start];\n }\n};\n\n/*\nGenerate all combinations subroutine:\n 1. Let C(n, k) = all ways to choose k from rows [0: n]\n = Multiplex(A[n], C(n - 1, k - 1))\n concat with, if n >= k, C(n - 1, k) .\n \n We always want to select the highest value, if possible. It may not be possible because of the row restrictions.\n\n Backtracking with memoization?\n - choose an element, mark that row as unchooseable, \n - move on to the next element\n\n Define state = unordered_set<int>\n Define Valid (r, state) = r not in state\n\n 1. Map val to a vector of rows\n\n max_score (val, state) :\n let rows = the collection of rows that contains val\n let nextVal = the next value in the grid such that nextVal < val\n\n Let F be a function that maps rows to a score:\n if row is valid in state, then\n let state\' = mutate(state, row)\n return val + max_score(nextVal, state\')\n else return max_score(nextVal, state)\n\n return the max_element F(rows)\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n*/\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Unique Maximum Values with Memoization | unique-maximum-values-with-memoization-b-gebn | Intuition\n Describe your first thoughts on how to solve this problem. \nThe most straightforward approach, i.e. backtracking can quickly get very expensive for | swanandcode | NORMAL | 2024-09-02T22:04:02.251557+00:00 | 2024-09-08T12:48:15.398857+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe most straightforward approach, i.e. **backtracking** can quickly get very expensive for some cases, hence this is one of those cases where you have to look at the data constraints.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere are the steps to solve this particular problem:\n1. Arrange all the unique numbers in descending order\n2. Map which row they belong to\n3. Condense each row to a descending set\n4. Starting from the greatest number, find if it is unique to a bucket\n5. If it is, select it and mark the row as done\n6. If not, then branch out to the number of buckets it is present in\n7. Use memoization to avoid recomputing repeat cases\n\n# Complexity\n- Time complexity: O(m * n log n + m * 2^m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m * n + m * 2^m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n Map<Long, Integer> memo = new HashMap<>();\n TreeMap<Integer, List<Set<Integer>>> intMap = new TreeMap<>(Comparator.reverseOrder());\n\n public int maxScore(List<List<Integer>> grid) {\n Map<Set<Integer>, Boolean> candidates = new IdentityHashMap<>();\n for (List<Integer> integers : grid) {\n Set<Integer> set = new TreeSet<>(Comparator.reverseOrder());\n set.addAll(integers);\n for (int j : set) {\n intMap.computeIfAbsent(j, k -> new ArrayList<>()).add(set);\n }\n candidates.put(set, Boolean.TRUE);\n }\n return computeMax(0, intMap.firstEntry(), candidates);\n }\n\n private int computeMax(int max, Map.Entry<Integer, List<Set<Integer>>> target, Map<Set<Integer>, Boolean> candidates) {\n if (candidates.isEmpty() || target == null) return max;\n Long memoKey = computeMemoKey(candidates, max, target.getKey());\n if (memo.containsKey(memoKey)) return memo.get(memoKey);\n int newMax = max;\n boolean isUtilized = false;\n for (Set<Integer> set : target.getValue()) {\n if (!candidates.containsKey(set)) continue;\n candidates.remove(set);\n newMax = Math.max(newMax, computeMax(max + target.getKey(), intMap.higherEntry(target.getKey()), candidates));\n candidates.put(set, Boolean.TRUE);\n isUtilized = true;\n }\n if (!isUtilized) newMax = Math.max(newMax, computeMax(max, intMap.higherEntry(target.getKey()), candidates));\n memo.put(memoKey, newMax);\n return newMax;\n }\n\n private long computeMemoKey(Map<Set<Integer>, Boolean> candidates, int max, int targetKey) {\n long hash = 0L;\n for (Set<Integer> set : candidates.keySet()) {\n hash += System.identityHashCode(set);\n }\n return (hash << 32) | ((long) targetKey << 24) | (max);\n }\n}\n```\n\n | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | DP C++ | dp-c-by-max_dong-4yu7 | 3276. Select Cells in Grid With Maximum Score\n\n### Description\n\nYou are given a 2D matrix grid consisting of positive integers.\n\nYou have to select one or | Max_Dong | NORMAL | 2024-09-02T19:15:50.644284+00:00 | 2024-09-02T19:15:50.644311+00:00 | 4 | false | # [3276. Select Cells in Grid With Maximum Score](https://leetcode.com/problems/select-cells-in-grid-with-maximum-score/)\n\n### Description\n\nYou are given a 2D matrix `grid` consisting of positive integers.\n\nYou have to select *one or more* cells from the matrix such that the following conditions are satisfied:\n\n- No two selected cells are in the **same** row of the matrix.\n- The values in the set of selected cells are **unique**.\n\nYour score will be the **sum** of the values of the selected cells.\n\nReturn the **maximum** score you can achieve.\n\n \n\n**Example 1:**\n\n**Input:** grid = [[1,2,3],[4,3,2],[1,1,1]]\n\n**Output:** 8\n\n**Explanation:**\n\n\n\nWe can select the cells with values 1, 3, and 4 that are colored above.\n\n**Example 2:**\n\n**Input:** grid = [[8,7,6],[8,3,2]]\n\n**Output:** 15\n\n**Explanation:**\n\n\n\nWe can select the cells with values 7 and 8 that are colored above.\n\n \n\n**Constraints:**\n\n- `1 <= grid.length, grid[i].length <= 10`\n- `1 <= grid[i][j] <= 100`\n\n\n\n### Thought\n\n#### Approach 1\n\nWhen I first saw this question, I considered using a greedy approach to solve it. My initial idea was to sort the 2D matrix by sorting each row individually. If two rows have the same largest element, I would then sort them based on the difference between their elements, with the row having the larger difference coming first.\n\nSo every time I can choose the biggest element in each row. The code would be like below:\n\n```C++\nclass Solution {\npublic:\n static bool customSort(const vector<int>& a, const vector<int>& b) {\n int sumA = a[0] + a[1];\n int sumB = b[0] + b[1];\n\n if (sumA != sumB) {\n return sumA < sumB; \n } else {\n int diffA = abs(a[0] - a[1]);\n int diffB = abs(b[0] - b[1]);\n return diffA > diffB; \n }\n }\n int maxScore(vector<vector<int>>& grid) {\n if (grid.size() == 1) {\n sort(grid[0].begin(), grid[0].end(), greater<int>());\n return grid[0][0];\n } else if (grid[0].size() == 1) {\n unordered_set<int> tmp;\n for (auto& v : grid) {\n tmp.insert(v[0]);\n }\n int ans = 0;\n for (auto& i : tmp) ans += i;\n return ans;\n }\n sort(grid.begin(), grid.end(), customSort);\n\n int sum = 0;\n unordered_set<int> s;\n for (auto& v : grid) {\n sort(v.begin(), v.end(), greater<int>());\n for (int i = 0; i < v.size(); i++) {\n if (s.find(v[i]) == s.end()) {\n s.insert(v[i]);\n sum += v[i];\n break;\n }\n }\n }\n return sum;\n }\n};\n\n```\n\nHowever, if we use `[[16,18],[20,20],[18,18],[1,15]]` this case, we can find the array after sorting would be \n\n```\n1 15 \n\n16 18 \n\n18 18 \n\n20 20 \n```\n\nWe have to choose 15, 18, 18, 20. But we can not choose 18 twice time, so this method didn\'t work.\n\n#### Approach 2\n\nAs we can see the data constrain, it only have 10 rows maximum. So we can use an `n-bit` binary number to represent whether each row has been selected (referred to as the row\'s state)\n\nFor example, in a matrix with 3 rows, the state `101` indicates that the 1st and 3rd rows have been selected, while the 2nd row has not been selected.\n\n And when can get 2 conclusions from the problem:\n\n- we can only choose at most one element in each row\n- The number we choose in each row can not repeated\n\nSo we can define `dp[i]\\[j]`, which represent the maximum score that can be obtained when the current number being considered is `i`, and the previously selected row information is represented by `j`\n\nIt has two scenarios:\n\n- If we can choose i, which means it appears in original grid.\n - `dp[i][j] = dp[i+1][j]`\n- If we can not choose i\n - `dp[i][j] = dp[i+1][(1 << k) | j] + i`\n\nSo the code would be like below:\n\n```C++\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int m = grid.size();\n \t// It represents num appears in grid\n vector<vector<int>> g(m,vector<int>(101,0));\n for (int i = 0; i < m; i++) {\n for (auto& j : grid[i]) {\n g[i][j] = 1;\n }\n }\n vector<vector<int>> dp(105,vector<int>(1<<m,0));\n for (int i = 100; i >= 1; i--) {\n \t// Totally, it has 1 << m states\n for (int j = 0; j < 1 << m; j++) {\n dp[i][j] = dp[i+1][j];\n \t// Enumerat all the rows\n for (int k = 0; k < m; k++) {\n \t// (j >> k & 1): row k has been selected or not\n \t// grid[k][i]: in row k, it has num i or not\n if ((j >> k & 1) == 0 && g[k][i] == 1) {\n \t// (1 << k | j): make row k be selected \n dp[i][j] = max(dp[i][j], dp[i + 1][1 << k | j] + i);\n }\n }\n }\n }\n return dp[1][0];\n }\n};\n```\n\n#### Explanation of all bit operations\n\n- **1 << m**\n - It has m rows in total, so it has `1 << m` states\n- **j >> k & 1**\n - current state is `j`, shift the state `j` to the right by `k` positions, moving the bit corresponding to the `k-th` row to the least significant position.\n - `& 1` which means judge the least significant position is 0 or 1, because both num equal to 1 can make the result equal to 1.\n- **1 << k | j**\n - `1 << k` generate a binary number with only the `k-th` bit set to 1.\n - `| j`, use OR operation to make `j` state `k-th` bit to 1, because any number `OR` 1 is 1, and `1` represent this row has been selected.\n\n | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | (JAVA) Top-down DP WITHOUT bitmasking | java-top-down-dp-without-bitmasking-by-a-c0uu | Intuition\nI am doing it just for fun. It is exactly the same except that we are using a string to represent all the rows from which we have already selected a | a068864 | NORMAL | 2024-09-02T18:21:41.964864+00:00 | 2024-09-02T18:21:41.964881+00:00 | 19 | false | # Intuition\nI am doing it just for fun. It is exactly the same except that we are using a string to represent all the rows from which we have already selected a cell so far.\n\n# Approach\nNotice that this problem has overlapping sub-problems and optimal sub-structure so we can try recursion with memo. \n\n# Complexity\n- Time complexity:\n$$O(m * n*log(m * n) + m * n * 2 ^ m)$$\n\n- Space complexity:\n$$O(2^m)$$\n\n# Code\n```java []\nimport java.util.*;\n\nclass Solution {\n Map<String, Integer> cache;\n\n public int maxScore(List<List<Integer>> grid) {\n int m = grid.size();\n int n = grid.get(0).size();\n Map<Integer, List<Integer>> map = new HashMap<>();\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int val = grid.get(i).get(j);\n map.putIfAbsent(val, new ArrayList<>());\n map.get(val).add(i);\n }\n }\n List<Integer> arr = new ArrayList<>(map.keySet());\n Collections.sort(arr, (a, b) -> b - a); // Sort values in grid in non-increasing order\n cache = new HashMap<>();\n boolean[] used = new boolean[m]; // Check if a cell in this row has been selected\n return helper(map, arr, 0, used);\n }\n\n private int helper(Map<Integer, List<Integer>> map, List<Integer> arr, int index, boolean[] used) {\n if (index == arr.size()) {\n return 0;\n }\n String key = index + ":" + Arrays.toString(used);\n if (cache.containsKey(key)) {\n return cache.get(key);\n }\n int max = helper(map, arr, index + 1, used); // Just skip\n int val = arr.get(index);\n for (int row : map.get(val)) {\n if (!used[row]) { // No chosen from this row yet\n used[row] = true;\n max = Math.max(max, val + helper(map, arr, index + 1, used));\n used[row] = false;\n }\n }\n cache.put(key, max);\n return max;\n }\n}\n\n\n``` | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | DP+Bitmasking easy recursive solution | dpbitmasking-easy-recursive-solution-by-78qgi | \n\n# Approach\nDP + Bitmasking\n\n\n\n# Code\ncpp []\nclass Solution {\n\npublic:\n\n int dp[1025][101];\n int solve(int ix,int mask,int n,vector<int> &t | soumya_24 | NORMAL | 2024-09-02T16:56:56.920909+00:00 | 2024-09-02T16:56:56.920941+00:00 | 4 | false | \n\n# Approach\nDP + Bitmasking\n\n\n\n# Code\n```cpp []\nclass Solution {\n\npublic:\n\n int dp[1025][101];\n int solve(int ix,int mask,int n,vector<int> &temp,vector<int> arr[]){\n if(ix==n){\n return 0;\n }\n if(dp[mask][ix]!=-1) return dp[mask][ix];\n int ans=0;\n for(auto it:arr[temp[ix]]){\n if((mask&(1<<it))==0){\n cout<<it<<\' \'<<temp[ix]<<endl;\n ans=max(ans,temp[ix]+solve(ix+1,mask|(1<<it),n,temp,arr));\n }\n }\n ans=max(ans,solve(ix+1,mask,n,temp,arr));\n return dp[mask][ix]=ans;\n }\n int maxScore(vector<vector<int>>& grid) {\n unordered_set<int> s;\n memset(dp,-1,sizeof(dp));\n vector<int> arr[101];\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[0].size();j++){\n s.insert(grid[i][j]);\n arr[grid[i][j]].push_back(i);\n \n }\n }\n vector<int> temp;\n for(auto it:s){\n temp.push_back(it);\n }\n sort(temp.begin(),temp.end());\n reverse(temp.begin(),temp.end());\n\n \n\n return solve(0,0,temp.size(),temp,arr);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Beats 100%, | beats-100-by-shreya_radha_14-gc60 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shreya_radha_14 | NORMAL | 2024-09-02T15:48:25.528743+00:00 | 2024-09-02T15:48:25.528779+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2^N \u2217 N)\n\n\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```javascript []\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar maxScore = function(grid) {\n const n = grid.length;\n const vals = new Map();\n \n // Collect the values and their row indices\n for (let i = 0; i < n; i++) {\n for (let h of grid[i]) {\n if (!vals.has(h)) {\n vals.set(h, []);\n }\n vals.get(h).push(i);\n }\n }\n \n // Convert the Map to a sorted array\n const valsArray = Array.from(vals.entries()).sort((a, b) => b[0] - a[0]);\n \n // Create a memoization cache\n const memo = new Map();\n \n // Define the recursive function with memoization\n const maxval = (i, mask) => {\n if (i >= valsArray.length) {\n return 0;\n }\n const key = `${i}-${mask}`;\n if (memo.has(key)) {\n return memo.get(key);\n }\n \n // Option 1: Skip current value\n let res = maxval(i + 1, mask);\n \n // Option 2: Include current value if the row is not used\n for (let j of valsArray[i][1]) {\n if (!(mask & (1 << j))) {\n res = Math.max(res, valsArray[i][0] + maxval(i + 1, mask | (1 << j)));\n }\n }\n \n memo.set(key, res);\n return res;\n };\n \n return maxval(0, 0);\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
select-cells-in-grid-with-maximum-score | [Swift] Sort descending + DFS | swift-sort-descending-dfs-by-dibbleme-g1r4 | Intuition\nIterate the grid and record all unqiue value and its row index data into an array of turple: [(Int, [Int])], sorted it in desending order, and DFS th | dibbleme | NORMAL | 2024-09-02T15:14:04.157941+00:00 | 2024-09-02T15:15:02.298425+00:00 | 8 | false | # Intuition\nIterate the grid and record all unqiue `value` and its `row index` data into an array of turple: `[(Int, [Int])]`, sorted it in desending order, and DFS this array, in each DFS operation, iterate all rows that has NOT been visited, and record the max score.\n\nFor example,\nInput:`grid = [[1,2,3],[4,3,2],[1,1,1]]` \nTo array of truple: `[(4, [1]), (3, [0, 1]), (2, [1, 0]), (1, [0, 2])]`\n\n# Complexity\n* Space complexity: `m x n`, where m in number of rows and n is number of columns.\n* Time complexity: `O(u + r + u * log(u))`, where `u` is total unique number, r is total number of rows.\n\n# Code\n```swift []\nclass Solution {\n func maxScore(_ g: [[Int]]) -> Int {\n var m: [Int: Set<Int>] = [:], data: [(Int, [Int])] = []\n for r in 0..<g.count {\n for c in 0..<g[r].count {\n m[g[r][c], default: []].insert(r)\n }\n }\n for (k, v) in m { data.append((k, Array(v))) }\n data.sort { lhs, rhs in lhs.0 > rhs.0 }\n var path: Set<Int> = [], ch: [[Int]: Int] = [:]\n return self.dfs(0, data, &path, &ch)!\n }\n\n private func dfs(_ i: Int, _ d: [(Int, [Int])], _ p: inout Set<Int>, _ c: inout [[Int]: Int]) -> Int? {\n guard i < d.count else { return 0 }\n let key = Array(p).sorted() + [i]\n if let fnd = c[key] { return fnd }\n var res: Int?\n for r in d[i].1 {\n if p.contains(r) { continue }\n p.insert(r)\n if let tmp = self.dfs(i + 1, d, &p, &c) {\n if let val = res { res = max(val, tmp) }\n else { res = tmp }\n }\n p.remove(r)\n }\n if let val = res {\n res = val + d[i].0\n } else {\n res = self.dfs(i + 1, d, &p, &c)\n }\n if let res { c[key] = res }\n return res\n }\n}\n``` | 0 | 0 | ['Swift'] | 0 |
select-cells-in-grid-with-maximum-score | Dp with Bitmasking || Bit Manipulation || Recursion || C++ | dp-with-bitmasking-bit-manipulation-recu-vb56 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | oreocraz_273 | NORMAL | 2024-09-02T13:59:23.639655+00:00 | 2024-09-02T13:59:23.639692+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n int dp[101][1025];\n unordered_map<int,vector<int>> m;\n \n int f(int i,int mask)\n {\n if(i==0)\n return 0;\n if(dp[i][mask]!=-1)\n return dp[i][mask];\n \n int ans=f(i-1,mask);\n\n for(auto& x:m[i])\n {\n if((mask>>x)&1)\n continue;\n ans=max(ans,i+f(i-1,mask|(1<<x)));\n }\n\n return dp[i][mask]=ans;\n\n }\n int maxScore(vector<vector<int>>& a) {\n \n memset(dp,-1,sizeof(dp));\n int mx=1;\n for(int i=0;i<a.size();i++)\n {\n for(auto& x:a[i])\n {\n m[x].push_back(i);\n mx=max(mx,x);\n }\n \n }\n\n return f(mx,0);\n\n \n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Recursion', 'Bitmask', 'C++'] | 0 |
select-cells-in-grid-with-maximum-score | Trying to be Beginner-Friendly | trying-to-be-beginner-friendly-by-dinoza-8bfm | Intuition\n Describe your first thoughts on how to solve this problem. \nCould be done with normal recursion where the constraint look like normal recursion wou | dinozambas | NORMAL | 2024-09-02T13:07:33.129712+00:00 | 2024-09-02T13:09:26.976581+00:00 | 38 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCould be done with normal recursion where the constraint look like normal recursion would work. If you solve with normal recursion you are going to get a TLE, which would make you think "Oh, we just need a dp" and take the changing parameter as just i, it would be wrong. As we are have a condition where all the values have to unique. For that, we might have considered a set to have a track of all the unique values.\n\n```java [] \nclass Solution {\n int rec(int i,List<List<Integer>> grid,Set<Integer> set,int[] dp){\n if(i>=grid.size()){\n return 0;\n }\n int max = 0;\n if(dp[i]!=-1) return dp[i];\n int k;\n for( k = 0;k<grid.get(0).size();k++){\n\n // System.out.println(set);\n // System.out.println(grid.get(i).get(k));\n \n if(!set.contains(grid.get(i).get(k))){\n set.add(grid.get(i).get(k));\n max = Math.max(grid.get(i).get(k)+rec(i+1,grid,set,dp),max);\n set.remove(grid.get(i).get(k));\n }\n\n } \n max = Math.max(rec(i+1,grid,set,dp),max); \n return max;\n }\n public int maxScore(List<List<Integer>> grid) {\n Set<Integer> set = new HashSet<>();\n int[][] dp = new int[grid.size()][grid.get(0).size()];\n for(int[] d:dp){\n Arrays.fill(d,-1);\n }\n int max = 0;\n max = Math.max(max,rec(0,grid,set,dp[0]));\n return max;\n }\n}\n```\n\nHow could something like a set be stored in dp?\nA: DP with BitMask\n\nwhat would the bitmask have?\nA: I would like to share this for first understanding why bitmask is used, how it is used in implementation\nhttps://www.reddit.com/r/leetcode/comments/11pr0co/i_finally_got_around_to_learning_bitmask_dp/\n\n```java [Starter Code for Campus bikes in the reddit post]\nimport java.util.*;\n\npublic class Solution {\n \n // Method to find the minimum sum of Manhattan distances\n public int assignBikes(int[][] workers, int[][] bikes) {\n // Your logic to find the minimum sum of Manhattan distances goes here\n return 0;\n }\n\n // Main method to test the solution\n public static void main(String[] args) {\n Solution solution = new Solution();\n\n // Example 1\n int[][] workers1 = {{0, 0}, {2, 1}};\n int[][] bikes1 = {{1, 2}, {3, 3}};\n System.out.println("Output: " + solution.assignBikes(workers1, bikes1)); // Expected Output: 6\n\n // Example 2\n int[][] workers2 = {{0, 0}, {1, 1}, {2, 0}};\n int[][] bikes2 = {{1, 0}, {2, 2}, {2, 1}};\n System.out.println("Output: " + solution.assignBikes(workers2, bikes2)); // Expected Output: 4\n\n // Example 3\n int[][] workers3 = {\n {0, 0}, {2, 1}, {4, 2}, {6, 3}, {8, 4}, {10, 5}, {12, 6}, {14, 7}, {16, 8}, {18, 9}\n };\n int[][] bikes3 = {\n {9, 9}, {7, 6}, {5, 3}, {3, 2}, {1, 1}, {11, 10}, {13, 12}, {15, 14}, {17, 16}, {19, 18}\n };\n System.out.println("Output: " + solution.assignBikes(workers3, bikes3));\n // The expected output will depend on your algorithm, but this case is designed to stress-test your logic and efficiency.\n\n }\n\n}\n```\nAfter you were able to solve the problem campus bikes on your own and were able to apply dp, you would easily understand why bitmask is used (which is generally used to replicate the visited arr)\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThen i had issues on how this understanding could be applied to this problem because, i was thinking how would the visited arr concept could be applied to this problem.\n\nSo, to get this understanding for this problem i saw other solution for this problem which not so easy to get at the first go\nhttps://leetcode.com/problems/select-cells-in-grid-with-maximum-score/solutions/5718459/simple-solution-using-memo-bitmasking\n\nSo simply what he is doing, (rather just see his video and relate)\n-\n1. As there was no visited arr when we had taken the approach of normal recursion, here assume the visited arr for the rows and use a bitmask for the marking what row is visited (which wouldn\'t make sense when we are coming from that set recursion approach)\n2. Instead of set for uniqueness, we use a map, where the map stores the value in the arr and the index of the row\n3. But before this have all unique values in a list sort in descending order, according to the video, if you want to get maximum output, it is better to consider the maximum values in each row so rather than going through the each row every time, we would just have the values and their corresponding indices in the map.\n4. Now you have the list which is sorted in the descending order instead of passing the grid you could simply pass list that we have created, and then iterate through it considering all the values that it was present in the grid\n5. As you take the values you just mark the row as marked with the help of bitmask as there are only 10 rows\n\nSo now jth index of the values is eliminated\n\nTime Complexity: $$O(2N\u2217N)$$\n\n# Code\n```java []\nclass Solution {\n int rec(int i,List<Integer> l,HashMap<Integer,Set<Integer>> map,int bitmask,int[][] dp){\n if(i>=l.size()){\n return 0;\n }\n int max = 0;\n if(dp[i][bitmask]!=-1) return dp[i][bitmask];\n // System.out.println(l.get(i));\n for(int k: map.get(l.get(i))){\n if((bitmask&(1<<k))==0){\n max = Math.max(l.get(i)+rec(i+1,l,map,bitmask|(1<<k),dp),max);\n }\n\n } \n max = Math.max(rec(i+1,l,map,bitmask,dp),max); \n return dp[i][bitmask] = max;\n }\n public int maxScore(List<List<Integer>> grid) {\n Set<Integer> set = new HashSet<>();\n\n for(var g:grid){\n for(var v:g){\n set.add(v);\n }\n }\n List<Integer> l = new ArrayList<>();\n for(var i:set){\n l.add(i);\n }\n Collections.sort(l,(a,b)->{\n return b-a;\n });\n int[][] dp = new int[l.size()][1<<11];\n\n for(int[] d:dp){\n Arrays.fill(d,-1);\n }\n // for(var g:grid){\n // Collections.sort(g,(a,b)->{\n // return b-a;\n // });\n // }\n\n HashMap<Integer,Set<Integer>> map = new HashMap<>();\n for(int i =0;i<grid.size();i++){\n for(int j =0;j<grid.get(0).size();j++){\n if(!map.containsKey(grid.get(i).get(j))){\n map.put(grid.get(i).get(j),new HashSet<Integer>());\n }\n map.get(grid.get(i).get(j)).add(i);\n }\n }\n // System.out.println(grid);\n // System.out.println(map);\n // System.out.println(set);\n // System.out.println(l);\n // System.out.println();\n int max = 0;\n // for(int i = 0;i<grid.size();i++)\n max = Math.max(max,rec(0,l,map,0,dp));\n return max;\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Bitmask', 'Java'] | 0 |
select-cells-in-grid-with-maximum-score | DP with a little bit greedy | dp-with-a-little-bit-greedy-by-fredrick_-t8hc | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is essentially about selecting cells from the matrix with the constraints t | Fredrick_LI | NORMAL | 2024-09-02T09:44:30.506082+00:00 | 2024-09-02T09:44:30.506109+00:00 | 12 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is essentially about selecting cells from the matrix with the constraints that no two selected cells are from the same row and that all selected values are unique. To maximize the sum of selected values, we can use dynamic programming combined with bitmasking.\n\nThe bitmask will help us track which rows have been selected so far, while dynamic programming will help us find the optimal solution step by step.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Bitmask Representation:\n\n * We represent the selection of rows using bitmasking. If we have $m$ rows, a bitmask of length $m$ can represent any subset of these rows. For example, if we have $3$ rows, the bitmask `011` would indicate that rows $2$ and $3$ have been selected.\n \n2. Mapping Numbers to Rows:\n\n * We create a dictionary `dic` where each key is a number in the grid, and the corresponding value is a bitmask representing the rows where this number appears. This helps in checking the availability of a number across different rows quickly.\n \n3. Dynamic Programming:\n\n * We use dynamic programming (`dp`) to store the maximum sum possible for each bitmask representing a set of selected rows.\n\n * We initialize the `dp` table with a bitmask representing all rows unselected (i.e., `(1 << m) - 1` where m is the number of rows) having a score of $0$.\n * Then, iterating over the numbers in descending order, we update our `dp` table by considering whether to include the current number based on whether it fits the constraints.\n * **Greedy-like selection:** Notice that in cases where the current number fits, it must be included to update the bitmask (i.e., the current selection of cells must be expanded by a cell with the current number) to maximize the score; otherwise, we just keep our selection in this turn. \n \n4. Final Result:\n\n * The answer is the maximum value in the `dp` table after processing all the numbers.\n\n# Complexity\n* Time complexity:\n * Constructing the dictionary `dic` takes $\uD835\uDC42(\uD835\uDC5A \\times \uD835\uDC5B)$, where $m$ is the number of rows and $n$ is the number of columns.\n * Sorting the keys in `dic` takes $\uD835\uDC42(\uD835\uDC41\\log \uD835\uDC41)$, where $N$ is the number of unique elements in the grid.\n * The main DP step iterates over the sorted keys and for each key checks all possible masks, resulting in a complexity of $\uD835\uDC42(\uD835\uDC41\\times 2^\uD835\uDC5A\\times \uD835\uDC5A)$. Thus, the overall time complexity is $\uD835\uDC42(\uD835\uDC41\\times 2^m \\times \uD835\uDC5A)$, which is efficient when $m$ is small.\n\n* Space Complexity:\n\nThe space complexity is dominated by the `dp` table, which has a size of $\uD835\uDC42(2^\uD835\uDC5A)$. Additionally, `dic` takes $\uD835\uDC42(\uD835\uDC41)$ space.\n\n# Code\n```python3 []\n\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n \n # dic will map each number to the bitmask representing the rows it appears in\n dic = defaultdict(int)\n \n for i in range(m):\n l = 1 << i # Create a bitmask where only the ith row is marked\n for num in grid[i]:\n dic[num] |= l # Mark the rows in which this number appears\n\n # dp stores the maximum score possible for each bitmask of rows\n dp = {(1 << m) - 1: 0} # Start with all rows unselected, score 0\n \n # Iterate over numbers in descending order of their values\n for num in sorted(dic.keys(), reverse=True):\n new = {}\n for mask in dp:\n temp = dic[num] & mask # temp stores the available rows for current number\n \n if not temp:\n # If the current number can\'t be placed in any available row, just carry forward the current score\n if mask not in new:\n new[mask] = dp[mask]\n else:\n new[mask] = max(new[mask], dp[mask])\n else:\n # If the current number can be placed in some available row\n for i in range(m):\n l = 1 << i\n if temp & l: # Check if row i is available\n t = mask ^ l # Create a new mask with row i selected\n if t in new:\n new[t] = max(new[t], dp[mask] + num)\n else:\n new[t] = dp[mask] + num\n dp = new # Update dp with new values\n \n # The result is the maximum value in the dp dictionary\n return max(dp.values())\n\n``` | 0 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | brute force dp on doubly sorted grid | brute-force-dp-on-doubly-sorted-grid-by-x7w2u | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vitanova | NORMAL | 2024-09-02T09:42:18.499684+00:00 | 2024-09-02T09:42:18.499707+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n # dp on double sorted grid\n def gmax(grid):\n # keep grid sorted\n grid = sorted([sorted(row, reverse=True) for row in grid], reverse=True)\n nrow = len(grid)\n # switch cases, \n # 0 rows\n if nrow==0:\n return 0\n # 1 row\n if nrow==1:\n return grid[0][0]\n # >= 2 rows, unique max\n if grid[0][0] > grid[1][0]:\n return grid[0][0] + gmax(new_grid(grid, 0))\n # >= 2 rows, multiple max\n return max(grid[0][0] + gmax(new_grid(grid, i)) \n for i in range(nrow) if grid[0][0] == grid[i][0])\n \n # build new grid by choosing the first element of row i\n def new_grid(grid, i):\n ngrid = []\n for j, row in enumerate(grid):\n if j != i:\n rowtemp = [r for r in row if r!=grid[0][0]]\n # only append non-null rows\n if rowtemp:\n ngrid.append(rowtemp)\n return ngrid\n\n return gmax(grid)\n``` | 0 | 0 | ['Dynamic Programming', 'Sorting', 'Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Easy Java Solution | easy-java-solution-by-danish_jamil-5nax | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Danish_Jamil | NORMAL | 2024-09-02T08:24:23.853929+00:00 | 2024-09-02T08:24:23.853960+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nimport java.util.*;\n\nclass Solution {\n int[][] dp = new int[2001][101];\n\n int solve(int i, int n, List<Integer> t, Map<Integer, List<Integer>> mp, int mask) {\n if (i == n) return 0;\n if (dp[mask][i] != -1) return dp[mask][i];\n\n int ans = 0;\n for (int j : mp.get(t.get(i))) {\n if ((mask & (1 << j)) == 0) {\n ans = Math.max(ans, t.get(i) + solve(i + 1, n, t, mp, (mask | (1 << j))));\n }\n }\n ans = Math.max(ans, solve(i + 1, n, t, mp, mask));\n return dp[mask][i] = ans;\n }\n\n public int maxScore(List<List<Integer>> v) {\n int n = v.size();\n int m = v.get(0).size();\n Set<Integer> s = new HashSet<>();\n\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n s.add(v.get(i).get(j));\n }\n }\n\n List<Integer> t = new ArrayList<>(s);\n Collections.sort(t, Collections.reverseOrder());\n\n Map<Integer, List<Integer>> mp = new HashMap<>();\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n mp.computeIfAbsent(v.get(i).get(j), k -> new ArrayList<>()).add(i);\n }\n }\n\n for (int[] row : dp) {\n Arrays.fill(row, -1);\n }\n\n return solve(0, t.size(), t, mp, 0);\n }\n}\n\n``` | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | Simple Explanation + intuition, w/ Handwritten color-coded drawings and notes. | simple-explanation-intuition-w-handwritt-69hb | Intuition\n Describe your first thoughts on how to solve this problem. \n\nFULL PDF OF ALL HANDWRITTEN NOTES CAN BE FOUND HERE: https://drive.google.com/file/d/ | thelinuxman | NORMAL | 2024-09-02T07:12:57.637696+00:00 | 2024-09-02T07:12:57.637723+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n**FULL PDF OF ALL HANDWRITTEN NOTES CAN BE FOUND HERE:** https://drive.google.com/file/d/1Sw1p2ScKndGBbUixW6T4SScUPiWBNj99/view?usp=sharing\n\n- Initially, upon seeing this problem, it\'s immediately obvious that a decision tree can be made.\n- We have the constraints of A.) only picking one value from each row, and B.) only selecting unique values. So, rows must be unique as well as values.\n- So, if we construct a backtracking solution, we could keep track of what row we\'re on, as well as a list of elements already selected, and iterate through, generating a recursion path for each value that is not already selected in each row. This could work, but it results in TLE (Time Limit Exceeded).\n- We can make this faster. We know that we have two constraints, "one value from each row", and, "each value must be unique," so, there is a clue here that we could use 2D Dynamic Programming.\n- The hard part is guessing what keys to use for the 2D Dynamic Programming. That\'s where I failed on this problem when I did it as part of Weekly Competition 413.\n- So, the key of what rows have been used is easier. The grid is a maximum of 10x10 elements, which means there is a maximum of 10 rows. We can use a bitmask to keep track of what rows have been used in an efficient manner, with the n-th bit corresponding with the n-th row. If you\'re using a typed language, anything 2-bytes (16 bits) or larger should work.\n- The other key, elements we already selected, was a bit less intuitive for me. A set cannot be used as a key, so a set of all of the elements we have selected thus far won\'t work. We could try using a sorted tuple, which might work, but that could create some additional overhead and didn\'t seem very clean to me. This is probably a solution I would have come to though if i spent more time on it.\n- So, what do we do? Well, we can actually turn the grid into a list of `(value, row, col)` tuples, and sort it. When sorting it, the first element `value` will be the most significant element used in the sorting, so we\'re essentially creating a sorted list of values and still maintaining their row/column information. This allows us to simply cache an index `i` in DP, and we know that at `i`, we can just go to the next unique value in the list and we\'ll never see the same value again, since it\'s sorted.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Building off of the intuition, we first construct a list `values` which is a sorted list of tuples `(grid[i][j], i, j)`.\n- Then, we initialize a hashmap for DP, where the keys will be `(index: int, row_bitmask: int)` and the values will be `points: int`.\n- A recursive top-down memoization approach is used. The method needs to have access to the values array, the DP hashmap, and will have the parameters for the current index `i` and the rows that have been selected so far `rows` represented as a bitmask.\n\n\n\n- `i` will be the index of the current value in `values` that we\'re at. We will have an exit condition that will result in the method exiting when `i >= len(values)`, since there are no more points to be gained at that stage.\n- If the current value\'s row has already been seen, then we simply move on to the next value.\n- Otherwise, we have two possible paths:\n 1. We can try selecting the current value and moving to the next unique value in the list for the next recursive step\n 2. we can not select the current value and simply move on to the next value\n 3. We return the maximum of these two paths as the result.\n\n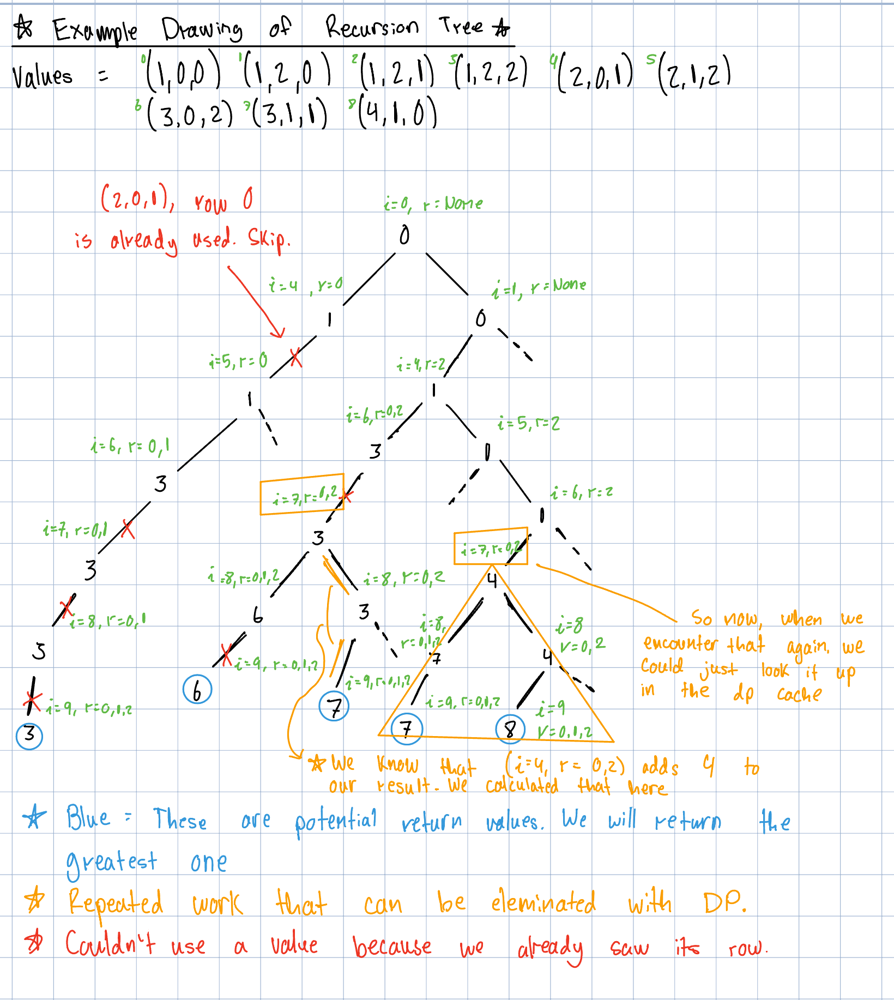\n\n\n# Complexity\nNot 100% sure on these, but thinking through this, the worst case scenario is that we keep hitting the else block for each value, which results in two paths, and if the number of values in the grid is `N`, then the time complexity here would be:\n\n- Time complexity: $O(2^N)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: $O(2^N)$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nI\'m pretty sure this worst case scenario would also only happen if we had just one value per row. Anyone who has a better or more rigorous answer for the time complexity, feel free to comment and I can edit this answer and credit you.\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n # generate a sorted list of (value, row, col) in the grid.\n # this sorting will happen in lexographical order, just like\n # ordering something alphabetically. So, `value` will be the\n # most significant element, but if `value[i] == value[j], i != j`,\n # then the next most significant element is what row they\n # are in. \n values = sorted([(grid[i][j], i, j) for i in range(len(grid)) for j in range(len(grid[0]))])\n\n dp = {}\n def solve(i, rows):\n # If we\'ve tried all of the values, just exit.\n # no more points to be gained.\n if i >= len(values):\n return 0\n\n # if we\'ve already solved the path at this point,\n # from this index with this combination of rows already\n # selected, then simply return that cached result\n if (i, rows) in dp:\n return dp[(i, rows)]\n\n # will store the result\n res = 0\n # Each value in values is a tuple of (value, row, col). So,\n # here we get the row from the value at the current index\n # for this recusion step.\n cur_row = values[i][1]\n\n # here, we check if we have already selected a value\n # from the current row. If so, we\'ll just move on to the\n # next value in the list, skipping over this one, since\n # this one can\'t be selected.\n if (rows & (1 << cur_row)):\n res = solve(i+1, rows)\n # If we haven\'t already selected a value from this row,\n # then we have the option to either select one or not select one.\n # so there are two potential paths in the else block.\n else:\n # get the index of the next unique value.\n j = i\n while (j < len(values)) and (values[i][0] == values[j][0]):\n j += 1\n \n # here, we select this value and continue at the index\n # of the next unique value (since values is sorted, and\n # we can\'t select two of the same value, this will be\n # the next smallest value). We use the OR operator to\n # set the bit corresponding with the row of this element\n # we\'re selecting in the `rows` bitmask.\n path1 = values[i][0] + solve(j, rows | (1 << cur_row))\n\n # Otherwise, we can choose not to select this value and\n # just move on to the next value in the values list.\n path2 = solve(i+1, rows)\n\n # the result will be the maximum of the two paths,\n # since we want to maximize our score:\n res = max(path1, path2)\n \n # cache and return the result\n dp[(i, rows)] = res\n return res\n\n # thanks to https://leetcode.com/u/virujthakur01/ for inspiring\n # this solution. I adapted the python code here from his C++ solution,\n # and used his solution to understand the problem and gain\n # the necessary insight and intuition to solve it.\n return solve(0,0)\n```\n\n# Credit\n- thanks to https://leetcode.com/u/virujthakur01/ for inspiring this solution. I adapted the python code here from his [C++ solution](https://leetcode.com/problems/select-cells-in-grid-with-maximum-score/solutions/5718075/focus-on-uniqueness-in-values-first-then-uniqueness-in-rows-full-explanation/), and used his solution to understand the problem and gain the necessary insight and intuition to solve it. | 0 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Go Solution | go-solution-by-hjrand1005-jccy | golang []\nfunc maxScore(grid [][]int) int {\n n := len(grid)\n m := len(grid[0])\n\n graph := make(map[int][]int)\n values := make([]int, 0)\n s | hjrand1005 | NORMAL | 2024-09-02T06:15:06.555988+00:00 | 2024-09-02T06:15:06.556018+00:00 | 3 | false | ```golang []\nfunc maxScore(grid [][]int) int {\n n := len(grid)\n m := len(grid[0])\n\n graph := make(map[int][]int)\n values := make([]int, 0)\n seen := make(map[int]struct{})\n\n for i := 0; i < n; i++ {\n for j := 0; j < m; j++ {\n val := grid[i][j]\n graph[val] = append(graph[val], i)\n if _, ok := seen[val]; !ok {\n values = append(values, val)\n }\n seen[val] = struct{}{}\n }\n }\n sort.Ints(values)\n for i := 0; i < len(values) / 2; i++ {\n j := len(values) - i - 1\n values[i], values[j] = values[j], values[i]\n }\n\n type mkey struct {\n idx, visited, score int\n }\n memo := make(map[mkey]int)\n\n var dfs func(int, int, int) int\n dfs = func(idx, visited, score int) int {\n if idx == len(values) {\n return score\n }\n\n key := mkey{ idx, visited, score }\n if _, ok := memo[key]; !ok {\n v := values[idx]\n scores := make([]int, 0)\n for _, u := range graph[v] {\n mask := 1 << u\n if (visited & mask) != 0 {\n subscore := dfs(idx + 1, visited - mask, v + score)\n scores = append(scores, subscore)\n }\n }\n if len(scores) == 0 {\n scores = append(scores, dfs(idx + 1, visited, score))\n }\n best := scores[0]\n for _, s := range scores[1:] {\n if s > best {\n best = s\n }\n }\n memo[key] = best\n }\n return memo[key]\n }\n\n return dfs(0, (1 << n) - 1, 0)\n}\n``` | 0 | 0 | ['Go'] | 0 |
select-cells-in-grid-with-maximum-score | DP Solution with using bit mask for checking visited row | dp-solution-with-using-bit-mask-for-chec-8kft | Intuition\n Describe your first thoughts on how to solve this problem. \nLike value is more, which will increase the time complexity so we go with storing visit | anshul__singh | NORMAL | 2024-09-02T05:04:52.496839+00:00 | 2024-09-02T05:04:52.496868+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLike value is more, which will increase the time complexity so we go with storing visited row.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(R*R*Max_Value*2^R)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n2D dp array\nO(max_value*2^R)\n\n# Code\n```python3 []\n\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n n, m = len(grid), len(grid[0])\n dp = [[-1 for _ in range(1024)] for _ in range(101)]\n def solve(val, is_taken):\n if val>100 or is_taken&(1<<n):\n return 0\n if dp[val][is_taken] != -1:\n return dp[val][is_taken]\n ans = 0\n\n for i in range(n):\n if ((1<<i) & is_taken)==(1<<i):\n continue\n for j in range(m):\n if grid[i][j]==val:\n ans = max(ans, grid[i][j]+solve(val+1, is_taken | (1<<i)))\n else:\n ans = max(ans, solve(val+1, is_taken))\n dp[val][is_taken]=ans\n return ans\n return solve(0, 0)\n``` | 0 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Kotlin | 100% (no competition) | explained | kotlin-100-no-competition-explained-by-j-g5kp | This is an interesting problem because it looks easy! My initial solution didn\'t take the rows into account, and so got the wrong answer. I then used a prior | janinbv | NORMAL | 2024-09-02T03:19:47.766496+00:00 | 2024-09-02T03:20:21.253263+00:00 | 9 | false | This is an interesting problem because it looks easy! My initial solution didn\'t take the rows into account, and so got the wrong answer. I then used a priority queue, but that did not work with the recursion. So here I will describe my final solution. It could probably be made more efficient if memorization is added (I don\'t agree that it should be called memoization - why make up a new word?).\n\nOne could call this a greedy algorithm, where it tries the largest numbers first, but you have to also try without the largest numbers because of the issue with the rows. I decided to use an array and then sort it. Arrays are efficient when it comes to accessing items. Into the array, I put the value from the grid and the row that it is on. The column of the item doesn\'t matter. I also decided to use an IntArray for each item in the array, although a pair could have been used.\n\nOnce all the items have been added to the array, I sort it in descending order by the value ([0]). Recursion is nice because you can do each step, one at a time. Here, I start with the highest value, which is in position 0 in the nums array. Each call to next will process all of the same values. Since we cannot use any row more than once, a boolean array is used to mark that row as used. Following the call, it is returned to false since another item from that row may be selected.\n\nFunction next looks through nums for all values that are the same, and passes the index of the following numbers to the next call of next. Since no duplicate numbers can be used, only one of them is tried at a time.\n\nRecursion ends when either we have selected all the numbers we can (count = 0) or there are no more numbers to choose from. This can happen if there are many duplicate numbers, for example.\n\nLastly, it\'s worth mentioning the two global variables. nums is global since it doesn\'t change once it\'s set up, and max, since that can be set at the end of each recursion, and easily returned.\n\nHere is my solution:\n\n```\nclass Solution {\n \n var nums = Array<IntArray>(0) { IntArray(0) }\n var max = 0\n \n fun maxScore(grid: List<List<Int>>): Int {\n var numsNdx = 0\n nums = Array<IntArray>(grid.size * grid[0].size) { IntArray(2) }\n for (row in 0..grid.lastIndex) {\n for (col in 0..grid.get(row).lastIndex) {\n nums[numsNdx++] = intArrayOf(grid.get(row).get(col), row) \n }\n }\n nums.sortByDescending { it[0] }\n var rowUsed = BooleanArray(grid.size)\n next(grid.size, 0, 0, rowUsed)\n return max\n }\n \n fun next(count: Int, sum: Int, numsNdx: Int, rowUsed: BooleanArray) {\n if (count == 0 || numsNdx == nums.size) {\n if (sum > max) {\n max = sum\n }\n return\n }\n \n var startNdx = numsNdx\n var endNdx = numsNdx\n var last = nums[numsNdx][0]\n var found = false\n var cand : IntArray\n while (endNdx <= nums.lastIndex && nums[endNdx][0] == last) {\n endNdx++\n }\n for (ndx in startNdx..endNdx - 1) {\n cand = nums[ndx]\n if (!rowUsed[cand[1]]) {\n found = true\n rowUsed[cand[1]] = true\n next(count - 1, sum + last, endNdx, rowUsed)\n rowUsed[cand[1]] = false\n }\n if (count == 1 && found) {\n break\n }\n }\n if (!found) {\n next(count, sum, endNdx, rowUsed)\n }\n }\n}\n```\n\nThanks for reading. Please upvote if you like the solution and/or the explanation.\n | 0 | 0 | ['Array', 'Backtracking', 'Recursion', 'Sorting', 'Kotlin'] | 0 |
select-cells-in-grid-with-maximum-score | Hall's Marriage Theorem (Beats 100% Time and Memory Complexity) | halls-marriage-theorem-beats-100-time-an-g80a | Approach\nFor each unique value, find out the set of rows it\'s located on (we can store using this bitmask; here I save it in the pos array). \n\nNow model the | donbasta | NORMAL | 2024-09-02T03:17:56.334023+00:00 | 2024-09-02T03:17:56.334066+00:00 | 22 | false | # Approach\nFor each unique value, find out the set of rows it\'s located on (we can store using this bitmask; here I save it in the `pos` array). \n\nNow model the problem as a bipartite graph, the left one containing the values, and the right one containing the rows. We connect two vertices `(v, r)` if the value `v` exists in the row `r`. Surely, we can use maxflow for graph matching to solve the problem, but we can also use Hall\'s marriage theorem. In order for a matching to exist, the following marriage condition is necessary and sufficient:\n\nFor each set of values $S_v$, the union of the set of rows in which they exist must be larger than or equal to the size of $S_v$. (i.e. if we select any set of vertices on the left, the number of the vertices on the right which is adjacent to at least one selected vertiex on the left must be larger).\n\nTo apply this, we greedily try to select the values from the largest to smallest (iterate $i$ from $100$ to $1$). Let $ve$ be the currently selected values. To check the marriage condition, we iterate over the subset of $ve$ appended with $i$. If the marriage condition is satisfied for every subset, then we insert $i$ to $ve$. Once the size of $ve$ reaches the number of rows, we can just exit the loop and return the sum of the selected numbers.\n\n# Complexity\n- Time complexity:\n$O(V \\times 2^{N} \\times N)$\n\n- Space complexity:\n$O(V + N)$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n int pos[101];\n memset(pos, 0, sizeof(pos));\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n pos[grid[i][j]] |= (1 << i);\n }\n }\n int ve[10];\n int sz = 0;\n int ret = 0;\n for (int i = 100; i >= 0; i--) {\n if (pos[i] == 0) continue;\n bool ok = true;\n for (int j = 0; j < (1 << sz); j++) {\n int tmp = pos[i];\n int cnt = 1 + __builtin_popcount(j);\n for (int k = 0; k < sz; k++) {\n if ((j >> k) & 1) { tmp |= pos[ve[k]]; }\n }\n if (__builtin_popcount(tmp) < cnt) {\n ok = false;\n break;\n }\n }\n if (!ok) continue;\n ve[sz++] = i;\n ret += i;\n if (sz >= m) {\n break;\n }\n }\n return ret;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Beats 100% || Hungarian matching | beats-100-hungarian-matching-by-sanket_k-ui7q | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sanket_kathrotiya | NORMAL | 2024-09-02T03:01:30.121622+00:00 | 2024-09-02T03:01:30.121649+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nfrom typing import List\nfrom collections import defaultdict\n\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n \n \n graph = defaultdict(list)\n for i, row in enumerate(grid):\n for value in set(row): \n graph[value].append(i)\n \n\n def hungarian(graph):\n match = {}\n seen = set()\n \n def dfs(value):\n for row in graph[value]:\n if row not in seen:\n seen.add(row)\n if row not in match or dfs(match[row]):\n match[row] = value\n return True\n return False\n \n for value in sorted(graph.keys(), reverse=True):\n seen.clear()\n dfs(value)\n \n return match\n \n \n matching = hungarian(graph)\n \n \n return sum(matching.values())\n\n``` | 0 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | bitmask dp O(2**(m)*(numofvals)) | bitmask-dp-o2mnumofvals-by-maxorgus-rckz | We have at most 100 unique values in the grid, so it is a good dp variable. Store the rows in which each value appears in a dictionary, and we loop over \'the s | MaxOrgus | NORMAL | 2024-09-02T02:17:51.981285+00:00 | 2024-09-02T02:17:51.981306+00:00 | 6 | false | We have at most 100 unique values in the grid, so it is a good dp variable. Store the rows in which each value appears in a dictionary, and we loop over \'the smallest value below which all numbers we have taken\' in the dp.\n\nThe other variable in the dp is a bit mask for the rows already used, which is at most 2^10 = 1024. For each value we are considering, first simply skip it, then if it is in the grid, consider every row where it appears, if not already covered in the mask, we may go with this branch, until we reached the upper limit of val -- 101, where we return 0.\n\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n cells = {i:set([]) for i in range(101)}\n m = len(grid)\n n = len(grid[0])\n for i in range(m):\n for j in range(n):\n cells[grid[i][j]].add((i))\n @cache\n def dp(val,mask):\n if val == 101:\n return 0\n res = dp(val+1,mask)\n if val not in cells:return res\n for row in cells[val]:\n if (1 << row) & mask == 0:\n res = max(res,val+dp(val+1,mask | (1<<row)))\n return res\n \n return dp(0,0)\n\n\n\n \n``` | 0 | 0 | ['Dynamic Programming', 'Bitmask', 'Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Python DP, easy to understand with comments | python-dp-easy-to-understand-with-commen-wqer | \n\n# Code\npython3 []\nimport collections\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n n = len(grid)\n # DP goal: choose the r | roadytom | NORMAL | 2024-09-01T20:48:01.606228+00:00 | 2024-09-01T20:48:01.606250+00:00 | 7 | false | \n\n# Code\n```python3 []\nimport collections\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n n = len(grid)\n # DP goal: choose the row that equals to given number, so it makes score max\n memo = [[-1] * (1<<n) for _ in range(101)]\n # number to row (to easily find all rows with this number, can be found by sorting and iterating)\n num_to_row = collections.defaultdict(list) \n mx_num = 0\n for i in range(len(grid)):\n for j in range(len(grid[i])):\n mx_num = max(mx_num, grid[i][j])\n num_to_row[grid[i][j]].append(i)\n def dp(num, mask):\n if num == 0:\n return 0\n if memo[num][mask] != -1:\n return memo[num][mask]\n # skip\n mx = dp(num - 1, mask)\n # take\n for row in num_to_row[num]:\n if mask & (1 << row) != 0:\n continue\n mx = max(mx, num + dp(num - 1, mask | (1 << row)))\n\n memo[num][mask] = mx\n return memo[num][mask]\n return dp(mx_num, 0)\n \n``` | 0 | 0 | ['Python3'] | 0 |
select-cells-in-grid-with-maximum-score | Simple dp solution | simple-dp-solution-by-risabhuchiha-5rwl | \njava []\nclass Solution {\n Integer[][]dp=new Integer[101][1024];\n int rr;\n int cc;\n public int maxScore(List<List<Integer>> grid) {\n rr | risabhuchiha | NORMAL | 2024-09-01T20:20:58.016861+00:00 | 2024-09-01T20:20:58.016886+00:00 | 16 | false | \n```java []\nclass Solution {\n Integer[][]dp=new Integer[101][1024];\n int rr;\n int cc;\n public int maxScore(List<List<Integer>> grid) {\n rr=grid.size();\n cc=grid.get(0).size();\n \n\n return f(1,0,grid);\n }\n public int f(int val,int mask,List<List<Integer>> grid){\n if((val>100))return 0;\n if(dp[val][mask]!=null)return dp[val][mask];\n int ans=-1;//dp[val][mask];\n \n ans=f(val+1,mask,grid);\n for (int r = 0; r < rr; r ++) {\n if ((mask & (1 << r))!=0) continue;\n \n for (int c = 0; c < cc; c ++) {\n if (grid.get(r).get(c) != val) continue;\n \n ans = Math.max (ans, val + f(val+1,mask|(1<<r),grid));\n }\n }\n\n // System.out.println(val+" "+mask+" "+ans);\n return dp[val][mask]=ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | simple bitmask dp | simple-bitmask-dp-by-titu02-nlle | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Titu02 | NORMAL | 2024-09-01T19:20:57.883928+00:00 | 2024-09-01T19:20:57.883962+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\nint n,m;\nint dp[104][1025];\nint f(vector<vector<int>>&a,int r,int curr){\n if(r==101) return 0;\n if(dp[r][curr]!=-1) return dp[r][curr];\n int ans=0;\n ans=max(ans,f(a,r+1,curr));\n for(auto x : a[r]){\n if((curr>>x)&1) continue;\n ans=max(ans,r+f(a,r+1,curr|(1<<x)));\n\n }\n return dp[r][curr]=ans;\n\n}\n\n int maxScore(vector<vector<int>>& g) {\n n=g.size();\n m=g[0].size();\n memset(dp,-1,sizeof(dp));\n vector<vector<int>>a(101);\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n a[g[i][j]].push_back(i);\n }\n }\n return f(a,1,0);\n \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
select-cells-in-grid-with-maximum-score | Bottom Up DP + BitMask || Clean Code || Beats 100% || JAVA | bottom-up-dp-bitmask-clean-code-beats-10-zucl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | owaispatel95 | NORMAL | 2024-09-01T18:55:44.214755+00:00 | 2024-09-01T18:55:44.214792+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public static Set<Integer> EMPTY = Collections.emptySet();\n\n public int maxScore(List<List<Integer>> grid) {\n final int n = grid.size(), m = grid.get(0).size();\n final HashMap<Integer, Set<Integer>> map = new HashMap<>();\n\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n final int cur = grid.get(i).get(j);\n\n map.computeIfAbsent(cur, (x) -> new HashSet<>())\n .add(i);\n }\n }\n\n final int[][] dp = new int[102][(1 << n)];\n\n for (int i = 100; i >= 0; i--) {\n for (int j = 0; j < (1 << n); j++) {\n\n int sol1 = 0;\n int sol2 = dp[i + 1][j];\n\n for (final int row : map.getOrDefault(i, EMPTY)) {\n if ((j & (1 << row)) != 0) continue;\n\n sol1 = Integer.max(sol1, i + dp[i + 1][j | (1 << row)]);\n }\n \n dp[i][j] = Integer.max(sol1, sol2);\n }\n }\n\n return dp[0][0];\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | Beats 100% of the Java users | beats-100-of-the-java-users-by-deeepakga-dcn1 | Intuition\n1. Maximize the Score: The goal is to maximize the score by selecting rows such that the sum of selected values is the highest possible.\n\n2. Greedy | DeeepakGarg | NORMAL | 2024-09-01T17:18:40.502172+00:00 | 2024-09-01T17:18:40.502199+00:00 | 20 | false | # Intuition\n1. Maximize the Score: The goal is to maximize the score by selecting rows such that the sum of selected values is the highest possible.\n\n2. Greedy by Value: Start with the highest possible value and attempt to include rows where this value occurs. Use recursive exploration to find the optimal combination of rows for each value.\n\n3. Backtracking: Explore different subsets of rows to ensure that you consider all possible ways to maximize the score. This includes trying to include each row for the current value and backtracking if necessary.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Preprocess Grid Data:\n\nTraverse the grid to populate maxElementPosition, an array of lists where each index represents a value, and the list contains row indices where that value occurs. This preprocessing helps in quickly accessing which rows contain a specific value.\n\n2. Recursive Exploration:\n\nUse a recursive function (solve) to explore the combinations of rows for each value from the highest to the lowest.\n\nFor each value, attempt to include rows where the value occurs. This involves marking the row as visited and making a recursive call to continue with the next lower value and remaining rows.\n\nAfter exploring a row, backtrack by unmarking the row to explore other combinations.\n\nTrack the maximum score found during these explorations.\n\n3. Backtracking for Combinations:\n\nIf no valid rows are found for a current value, continue to the next lower value without including any row for the current value.\n\nThis ensures that all potential combinations of rows are explored to find the optimal solution.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(2^m * m * n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m * k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nimport java.util.*;\n\nclass Solution {\n // Main function to calculate the maximum score\n public int maxScore(List<List<Integer>> grid) {\n // Array to store the positions of rows where each value occurs\n List<Integer>[] maxElementPosition = new List[101];\n\n // Initialize the array with empty lists\n for (int i = 0; i < 101; i++) {\n maxElementPosition[i] = new ArrayList<>();\n }\n \n int m = grid.size(); // Number of rows\n int n = grid.get(0).size(); // Number of columns\n int max = 0; // Variable to keep track of the maximum score\n\n // Populate the maxElementPosition array with row indices for each value\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int val = grid.get(i).get(j);\n max = Math.max(max, val); // Update the maximum value found\n if (!maxElementPosition[val].contains(i)) {\n maxElementPosition[val].add(i); // Add row index for the value\n }\n }\n }\n\n // Boolean array to keep track of visited rows\n boolean[] vis = new boolean[m];\n\n // Start solving with the maximum value, total rows, and initial score of 0\n return solve(maxElementPosition, max, m, vis, 0);\n }\n\n // Recursive function to find the maximum score\n private int solve(List<Integer>[] maxElementPosition, int currEle, int remainingRows, boolean[] vis, int score) {\n // Base case: if current element is non-positive or no rows remaining, return score\n if (currEle <= 0 || remainingRows == 0) return score;\n\n // Skip elements with no rows\n while (currEle >= 1 && maxElementPosition[currEle].isEmpty()) {\n currEle--;\n }\n\n // Get the list of row indices for the current element\n List<Integer> rowsInd = maxElementPosition[currEle];\n int maxScore = score; // Initialize max score for the current state\n boolean found = false; // Flag to check if any row was found\n\n // Try to include each row for the current element\n for (int row : rowsInd) {\n if (!vis[row]) {\n vis[row] = true; // Mark row as visited\n found = true; // Found at least one valid row\n // Recursively solve for the next element, reducing the remaining rows\n maxScore = Math.max(maxScore, solve(maxElementPosition, currEle - 1, remainingRows - 1, vis, score + currEle));\n vis[row] = false; // Backtrack: unmark row\n }\n }\n\n // If no valid row was found for the current element, continue without including it\n if (!found) {\n maxScore = Math.max(maxScore, solve(maxElementPosition, currEle - 1, remainingRows, vis, score));\n }\n\n return maxScore; // Return the maximum score found\n }\n}\n\n``` | 0 | 0 | ['Java'] | 0 |
select-cells-in-grid-with-maximum-score | [C++] Backtracking Solution | c-backtracking-solution-by-samuel3shin-uwz9 | Code\ncpp []\nclass Solution {\npublic:\n int maxVal, n, m;\n unordered_map<string, int> memo;\n\n string createKey(int row, const set<int>& usedValues | Samuel3Shin | NORMAL | 2024-09-01T17:16:36.434202+00:00 | 2024-09-01T17:16:36.434231+00:00 | 0 | false | # Code\n```cpp []\nclass Solution {\npublic:\n int maxVal, n, m;\n unordered_map<string, int> memo;\n\n string createKey(int row, const set<int>& usedValues) {\n string key = to_string(row) + "|";\n for (int value : usedValues) {\n key += to_string(value) + ",";\n }\n return key;\n }\n\n void dfs(vector<vector<int>>& grid, int row, int currentScore, set<int> usedValues, vector<int>& possibleValues) {\n maxVal = max(maxVal, currentScore);\n if (row == n) {\n return;\n }\n\n string key = createKey(row, usedValues);\n if (memo.count(key)) {\n maxVal = max(maxVal, memo[key]);\n return;\n }\n\n // Pruning: skip if the potential gain is smaller than the current maxVal.\n if (currentScore + possibleValues[row] <= maxVal) return;\n\n for (int col = 0; col < m; col++) {\n int value = grid[row][col];\n if(!usedValues.count(value)) {\n usedValues.insert(value);\n dfs(grid, row + 1, currentScore + value, usedValues, possibleValues);\n usedValues.erase((usedValues.find(value)));\n } else {\n dfs(grid, row+1, currentScore, usedValues, possibleValues);\n }\n }\n\n // Store the result in memo\n memo[key] = maxVal;\n }\n\n int maxScore(vector<vector<int>>& grid) {\n n = grid.size();\n m = grid[0].size();\n maxVal = INT_MIN;\n\n for (int i = 0; i < n; i++) {\n sort(grid[i].rbegin(), grid[i].rend());\n }\n\n sort(grid.rbegin(), grid.rend());\n\n vector<int> possibleValues(n, 0);\n possibleValues[n-1] = grid[n-1][0]; \n for (int i = n-2; i >= 0; i--) {\n possibleValues[i] = possibleValues[i+1] + grid[i][0];\n }\n set<int> usedValues;\n dfs(grid, 0, 0, usedValues, possibleValues);\n\n return maxVal;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
minimum-sum-of-four-digit-number-after-splitting-digits | C++ || easy solution || 0 ms | c-easy-solution-0-ms-by-darshil_1804-4p76 | \nclass Solution{\npublic:\n int minimumSum(int num){\n string s = to_string(num);\n sort(s.begin(), s.end());\n int res = (s[0] - \'0\' | darshil_1804 | NORMAL | 2022-02-05T17:30:42.984719+00:00 | 2022-02-05T17:30:42.984764+00:00 | 12,701 | false | ```\nclass Solution{\npublic:\n int minimumSum(int num){\n string s = to_string(num);\n sort(s.begin(), s.end());\n int res = (s[0] - \'0\' + s[1] - \'0\') * 10 + s[2] - \'0\' + s[3] - \'0\';\n return res;\n }\n};\n```\nDo **Upvote** if you like the solution :) | 110 | 3 | ['C', 'Sorting'] | 13 |
minimum-sum-of-four-digit-number-after-splitting-digits | Java | Straightforward | java-straightforward-by-aaveshk-a5qz | \nclass Solution\n{\n public int minimumSum(int num)\n {\n int[] dig = new int[4]; // For each digit\n int cur = 0;\n while(num > 0) | aaveshk | NORMAL | 2022-02-05T16:00:59.319905+00:00 | 2022-03-16T04:44:42.920146+00:00 | 14,877 | false | ```\nclass Solution\n{\n public int minimumSum(int num)\n {\n int[] dig = new int[4]; // For each digit\n int cur = 0;\n while(num > 0) // Getting each digit\n {\n dig[cur++] = num % 10;\n num /= 10;\n }\n Arrays.sort(dig); // Ascending order\n int num1 = dig[0] * 10 + dig[2]; // 1st and 3rd digit\n int num2 = dig[1] * 10 + dig[3]; // 2nd and 4th digit\n return num1 + num2;\n }\n}\n``` | 97 | 4 | ['Java'] | 19 |
minimum-sum-of-four-digit-number-after-splitting-digits | Python - simple & fast with explanation - no permutation | python-simple-fast-with-explanation-no-p-qizv | Please upvote if you like my solution. Let me know in the comments if you have any suggestions to increase performance or readability. \n\nNotice that:\n1. We d | fatamorgana | NORMAL | 2022-02-05T16:01:49.416518+00:00 | 2022-02-05T21:17:44.011531+00:00 | 11,244 | false | Please upvote if you like my solution. Let me know in the comments if you have any suggestions to increase performance or readability. \n\n**Notice** that:\n1. We do not need to generate all possible combinations of spliting the input into two numbers. In the ideal solution, num1 and num2 will always be of equal length.\n2. We will step by step build num1 and num2 as we go through the algorithm. It is not necessary to generate all combinations of num1 and num2 (with both numbers having equal length).\n3. We do not need to save num1 and num2 in a variable. We can keep adding to the total sum as we go through the algorithm. \n4. The algorithm below works for any input length. If you want you can simplify it, since you know the input length is 4. \n\n**My algorithm** goes as follows:\n1. convert the input into a list of digits\n2. sort the list of digits in descending order\n3. iterate through the list of digits\n3.1 with each iteration, multiply the current digit with 10*current position in num1/num2. \n3.2 add the current digit to the result\n3.3 if you already added an even number of digits to the total of results, then increase the current position by one\n4. return result\n\n```\nclass Solution:\n def minimumSum(self, num: int) -> int:\n num = sorted(str(num),reverse=True)\n n = len(num) \n res = 0\n even_iteration = False\n position = 0\n for i in range(n):\n res += int(num[i])*(10**position)\n if even_iteration:\n position += 1\n even_iteration = False\n else:\n even_iteration = True\n return res\n```\n\nif you know that the input is going to be exaclty 4 digits, you can simplify it:\n\n```\nclass Solution:\n def minimumSum(self, num: int) -> int:\n num = sorted(str(num),reverse=True)\n return int(num[0]) + int(num[1]) + int(num[2])*10 + int(num[3])*10\n```\n | 70 | 0 | ['Python', 'Python3'] | 14 |
minimum-sum-of-four-digit-number-after-splitting-digits | C++ Sorting + Greedy | c-sorting-greedy-by-lzl124631x-7jeh | \n\nSee my latest update in repo LeetCode\n\n## Solution 1. Sorting + Greedy\n\nGet the 4 digits from n. Assume they are a <= b <= c <= d, the sum is minimum wh | lzl124631x | NORMAL | 2022-02-05T16:01:20.515418+00:00 | 2022-05-25T04:36:12.500563+00:00 | 4,300 | false | \n\nSee my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Sorting + Greedy\n\nGet the 4 digits from `n`. Assume they are `a <= b <= c <= d`, the sum is minimum when `new1 = ac` and `new2 = bd`.\n\nSo, the answer is `10 * (a + b) + (c + d)`.\n\n```cpp\n// OJ: https://leetcode.com/contest/biweekly-contest-71/problems/minimum-sum-of-four-digit-number-after-splitting-digits/\n// Author: github.com/lzl124631x\n// Time: O(1) or more specifically, O(KlogK), where `K` is the number of digits in `n`\n// Space: O(1) or O(K)\nclass Solution {\npublic:\n int minimumSum(int n) {\n int d[4] = {};\n for (int i = 0; i < 4; ++i, n /= 10) d[i] = n % 10;\n sort(begin(d), end(d));\n return 10 * (d[0] + d[1]) + d[2] + d[3];\n }\n};\n``` | 27 | 2 | [] | 5 |
minimum-sum-of-four-digit-number-after-splitting-digits | [C++/java/C#] Two plus Two sorted || Straight forward Solutions | cjavac-two-plus-two-sorted-straight-forw-n86q | SolutionA 2/2 split produce small sums than 1/3 splits. The idea is to sort the digits in an order and then consume (1, 3) and (2, 4) combination and return the | nitishhsinghhh | NORMAL | 2022-05-23T07:49:47.589253+00:00 | 2025-01-22T11:32:22.913828+00:00 | 1,052 | false | # Solution
A 2/2 split produce small sums than 1/3 splits. The idea is to sort the digits in an order and then consume (1, 3) and (2, 4) combination and return their result.
```cpp []
// Solution 1
class Solution {
public:
/*
* Computes the minimum sum of two new numbers formed by rearranging the digits of the input number.
*
* @param num The input number.
* @return The minimum sum of the two new numbers.
*/
int minimumSum(int num) {
vector<int> temp;
while (num > 0) {
// Extract each digit from the number and store it in the vector
temp.push_back(num % 10);
num = num / 10;
}
// Sort the digits in ascending order
sort(temp.begin(), temp.end());
// Form two new numbers and return their sum
return temp[0] * 10 + temp[2] + temp[1] * 10 + temp[3];
}
};
// Solution 2
class Solution {
public:
/*
* Computes the minimum sum of two new numbers formed by rearranging the digits of the input number.
*
* @param num The input number.
* @return The minimum sum of the two new numbers.
*/
int minimumSum(int num) {
vector<int> dig;
while (num > 0) {
// Extract each digit from the number and store it in the vector
dig.push_back(num % 10);
num /= 10;
}
// Sort the digits in ascending order
sort(dig.begin(), dig.end());
// Form two new numbers and return their sum
int num1 = dig[0] * 10 + dig[2];
int num2 = dig[1] * 10 + dig[3];
return num1 + num2;
}
};
```
```java []
class Solution {
public int minimumSum(int num) {
int[] dig = new int[4];
int cur = 0;
while (num > 0) {
dig[cur++] = num % 10;
num /= 10;
}
Arrays.sort(dig);
int num1 = dig[0] * 10 + dig[2];
int num2 = dig[1] * 10 + dig[3];
return num1 + num2;
}
}
```
```csharp []
// Solution 1
public class Solution {
public int MinimumSum(int num) {
char[] minimumArray = num.ToString().ToCharArray();
Array.Sort(minimumArray);
return ((minimumArray[0] - '0') * 10 + (minimumArray[2] - '0'))
+ ((minimumArray[1] - '0') * 10 + (minimumArray[3] - '0'));
}
}
// Solution 2
// Collect the digits then sort the array
public class Solution {
public int MinimumSum(int num) {
int[] dig = new int[4];
int cur = 0;
while (num > 0) {
dig[cur++] = num % 10;
num /= 10;
}
Array.Sort(dig);
return dig[0] * 10 + dig[2] + dig[1] * 10 + dig[3];
}
}
```
# Frequently encountered in technical interviews
```
std::vector<std::pair<std::string, int>> interview_frequency = {{"Amazon", 1}};
``` | 24 | 0 | ['Math', 'Greedy', 'Sorting', 'C++', 'Java', 'C#'] | 1 |
minimum-sum-of-four-digit-number-after-splitting-digits | 🔥 [Python3] 2 line, simple sort and make pairs | python3-2-line-simple-sort-and-make-pair-f2q1 | \nclass Solution:\n def minimumSum(self, num: int) -> int:\n d = sorted(str(num))\n return int(d[0] + d[2]) + int(d[1] + d[3])\n\n | yourick | NORMAL | 2023-05-28T01:02:52.969599+00:00 | 2023-05-28T01:02:52.969629+00:00 | 2,391 | false | ```\nclass Solution:\n def minimumSum(self, num: int) -> int:\n d = sorted(str(num))\n return int(d[0] + d[2]) + int(d[1] + d[3])\n\n``` | 22 | 0 | ['Math', 'Python', 'Python3'] | 1 |
minimum-sum-of-four-digit-number-after-splitting-digits | Two and Two | two-and-two-by-votrubac-p71a | We should always do a 2/2 split. 1/3 splits produce large sums. \n\nSo, we pick two smallest digits to be in the decimal\'s place, and two largest - one\'s plac | votrubac | NORMAL | 2022-02-05T18:15:13.726468+00:00 | 2022-02-05T19:44:50.150554+00:00 | 2,246 | false | We should always do a 2/2 split. 1/3 splits produce large sums. \n\nSo, we pick two smallest digits to be in the decimal\'s place, and two largest - one\'s place. \n\n**C++**\n```cpp\nint minimumSum(int num) {\n auto s = to_string(num);\n nth_element(begin(s), begin(s) + 1, end(s));\n return (s[0] -\'0\' + s[1] - \'0\') * 10 + s[2] - \'0\' + s[3] - \'0\';\n}\n``` | 21 | 2 | [] | 6 |
minimum-sum-of-four-digit-number-after-splitting-digits | Easy Java | easy-java-by-sakhib-mz64 | \nclass Solution {\n public int minimumSum(int num) {\n char[] ch=(num+"").toCharArray();\n Arrays.sort(ch);\n int n=Integer.parseInt("" | SakhiB | NORMAL | 2022-04-24T09:59:19.243251+00:00 | 2022-04-24T09:59:19.243276+00:00 | 2,119 | false | ```\nclass Solution {\n public int minimumSum(int num) {\n char[] ch=(num+"").toCharArray();\n Arrays.sort(ch);\n int n=Integer.parseInt(""+ch[0]+ch[2]);\n int m=Integer.parseInt(""+ch[1]+ch[3]);\n return n+m;\n } \n}\n``` | 20 | 0 | ['Java'] | 3 |
minimum-sum-of-four-digit-number-after-splitting-digits | Simple C++ Solution | Beginner Friendly | 0ms | beats 100% | simple-c-solution-beginner-friendly-0ms-w663k | In order to find the the minimum sum, the best way to do it is by creating two two-digits numbers.\n(Or 1 digit numbers as leading zeros are allowed)\nThe reaso | jainpranjal_270 | NORMAL | 2022-02-05T17:43:11.649769+00:00 | 2022-02-05T18:01:56.144750+00:00 | 1,525 | false | In order to find the the minimum sum, the best way to do it is by creating two two-digits numbers.\n(Or 1 digit numbers as leading zeros are allowed)\nThe reason for the same is pretty simple and straight forward. \nConsider the example : 9999\n9 + 999 = 1008\n99 + 99 = 198\n\n**Now while creating the two digits, in order to minimize the sum, we need to ensure that the** **smaller numbers are on tens place, while the larger nubers are kept on ones.**\n*Also, Note that the question mentions that "Leading Zeros are allowed."\nIf leading zeros weren\'t allowed, then the approach would have been different.*\n\nSo using simple mathematics(By dividing and taking modulus), we store 4 digits of the 4 digit number in a array.\nSort the array and return the sum of numbers\nnum1 = arr[0] * 10 + arr[2];\nnum2 = arr[1] * 10 + arr[3];\n**sum = num1 + num2 = (arr[0] + arr[1]) * 10 + arr[2] + arr[3]**\n\nTime - O(1)\nSpace - O(1)\n\n**Code :**\n\n```\nclass Solution {\npublic:\n int minimumSum(int num) {\n int a[4] = {0};\n a[0] = num % 10;\n num /= 10;\n a[1] = num % 10;\n num /= 10;\n a[2] = num % 10;\n num /= 10;\n a[3] = num % 10;\n sort(a, a + 4);\n return ((a[0] + a[1]) * 10 + a[2] + a[3]);\n }\n};\n```\nHappy Coding:)\nPlease Upvote and Comment for any doubts!\n``` | 17 | 0 | ['Math', 'C'] | 2 |
minimum-sum-of-four-digit-number-after-splitting-digits | Simple || 31 ms || Python || Beats 86% || Easy to understand | simple-31-ms-python-beats-86-easy-to-und-h4qw | \nclass Solution:\n def minimumSum(self, num: int) -> int:\n s = list(str(num))\n s.sort()\n s1 = s[0]+s[2]\n s2 = s[1]+s[3]\n | workingpayload | NORMAL | 2022-04-13T21:01:49.078799+00:00 | 2022-04-13T21:01:49.078862+00:00 | 1,420 | false | ```\nclass Solution:\n def minimumSum(self, num: int) -> int:\n s = list(str(num))\n s.sort()\n s1 = s[0]+s[2]\n s2 = s[1]+s[3]\n sum = int(s1)+int(s2)\n \n return sum\n```\t\t | 16 | 0 | ['Python'] | 2 |
minimum-sum-of-four-digit-number-after-splitting-digits | 3 lines | java | 3-lines-java-by-kanna17vce-j9wt | extract digits into array\n2. sort\n3. use first and 4th element to make one number and 2nd and 3rd to make another number and return the sum of the numbrs\n\n | kanna17vce | NORMAL | 2022-02-05T16:11:12.659325+00:00 | 2022-02-05T16:13:11.045699+00:00 | 1,611 | false | 1. extract digits into array\n2. sort\n3. use first and 4th element to make one number and 2nd and 3rd to make another number and return the sum of the numbrs\n```\n public int minimumSum(int num) {\n int []a={ num%10,(num/10)%10,(num/100)%10 , (num/1000)%10};\n Arrays.sort(a);\n return a[0]*10+a[3]+a[1]*10+a[2];\n }\n``` | 16 | 1 | ['Java'] | 5 |
minimum-sum-of-four-digit-number-after-splitting-digits | 2 lines code in JS | 2-lines-code-in-js-by-harsh1923-b0kr | \nvar minimumSum = function(num) {\n const temp=num.toString().split(\'\').sort();\nreturn (parseInt(temp[0]+temp[2])+parseInt(temp[1]+temp[3]));\n \n};\n | harsh1923 | NORMAL | 2022-08-01T18:50:00.472942+00:00 | 2022-08-01T18:50:00.472989+00:00 | 1,855 | false | ```\nvar minimumSum = function(num) {\n const temp=num.toString().split(\'\').sort();\nreturn (parseInt(temp[0]+temp[2])+parseInt(temp[1]+temp[3]));\n \n};\n``` | 13 | 0 | ['JavaScript'] | 1 |
minimum-sum-of-four-digit-number-after-splitting-digits | Easy, Detailed and Fast JAVA solution. | easy-detailed-and-fast-java-solution-by-1rodg | Intuition\n Describe your first thoughts on how to solve this problem. \n\nNow if there are two 2-digit numbers then it will have one at tens position and other | shreyatleetcode | NORMAL | 2023-04-18T07:05:05.103503+00:00 | 2023-04-18T07:05:26.008398+00:00 | 1,472 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nNow if there are two 2-digit numbers then it will have one at tens position and other at unit position.\n\n 74 = 70 * 10 + 4 (7 is at tens digit and 4 is at unit digit.)\n\nNow, since we know that tens digit will have more impact on the number than unit digit number.\n\n 47 = 40 * 10 + 7 (4 is at tens digit and 7 is at unit digit.)\n\nHence if there are two 2-digit numbers in that array, their tens position digit should be minimum.\n\nif a number is ABCD where A,B,C and D are digits then after sorting, A and B should take tens position and C and D should take unit digit postion.\n\n eg. 8239 --> 2389 (after Sorting)\n\n [28,39] --> sum = 67 or [29,38] --> sum = 67\n\nwe will have AC+BD or AD+BC. they both will have equal sum always.\n\nthis will be our minimum sum. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an array for sorting purpose.\n2. One by one extract the digits from the number.\n3. Sort the array.\n4. Match the 0th index digit with 2nd index digit and 1st with 3rd.\n5. Add the two new number.\n6. Final sum will be minimum.\n\n# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution \n{\n public int minimumSum(int num) \n {\n //1. Initialize an array for sorting purpose.\n int[] arr = new int[4];\n int i=0;\n //2. One by one extract the digits from the number.\n while(num>0)\n {\n int a = num%10;\n num = num/10;\n arr[i++] = a;\n }\n //3. Sort the array.\n Arrays.sort(arr);\n //4. Match the 0th index digit with 2nd index digit and 1st with 3rd.\n int v1 = arr[0]*10 + arr[2];\n int v2 = arr[1]*10 + arr[3];\n //5. Final sum will be minimum.\n return v1+v2;\n }\n}\n``` | 10 | 0 | ['Math', 'Sorting', 'Java'] | 2 |
minimum-sum-of-four-digit-number-after-splitting-digits | Magic Logic Marvellous Python3 | magic-logic-marvellous-python3-by-ganjin-sn10 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | GANJINAVEEN | NORMAL | 2023-03-04T19:37:11.355083+00:00 | 2023-03-04T19:37:11.355112+00:00 | 894 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumSum(self, num: int) -> int:\n string=str(num)\n s=sorted(string)\n m=s[0]+s[2]\n n=s[1]+s[3]\n return (int(m)+int(n))\n#please upvote me it would encourage me alot\n \n``` | 9 | 0 | ['Python3'] | 2 |
minimum-sum-of-four-digit-number-after-splitting-digits | [PYTHON 3] Easy Solution | python-3-easy-solution-by-omkarxpatel-p7mp | ```py\nclass Solution:\n def minimumSum(self, num: int) -> int:\n s=list(str(num))\n s.sort()\n return int(s[0]+s[2])+int(s[1]+s[3]) | omkarxpatel | NORMAL | 2022-07-11T20:17:53.619416+00:00 | 2022-07-11T20:17:53.619462+00:00 | 1,243 | false | ```py\nclass Solution:\n def minimumSum(self, num: int) -> int:\n s=list(str(num))\n s.sort()\n return int(s[0]+s[2])+int(s[1]+s[3]) | 9 | 1 | ['Sorting', 'Python', 'Python3'] | 2 |
minimum-sum-of-four-digit-number-after-splitting-digits | Golang Solution with explanation | golang-solution-with-explanation-by-nath-hweb | How This Solution Works:\n\nThe idea of this solution is pretty simple and relies on the fact that the minimum number is made by making the biggest number the l | nathannaveen | NORMAL | 2022-02-06T16:27:14.210465+00:00 | 2022-02-06T16:27:14.210491+00:00 | 461 | false | ## **How This Solution Works:**\n\nThe idea of this solution is pretty simple and relies on the fact that the minimum number is made by making the biggest number the last digit and the smallest number the first. For example: If we use the digits `[4, 6, 1, 3, 0, 9]`, the minimum number we can make is `013469`.\n\nIf we want the minimum sum, we just have to add the two minimum numbers together and get the minimum sum. \n\nSo let us say that we have `num = 4009`. We have the digits `[0, 0, 4, 9]`. Then the two minimum numbers that we can make are `04`, and `09`.\n\n* For `new1`, the tens digit can be the smallest digit, `0`.\n* For `new2`, the tens digit can be the second smallest digit, `0`.\n* For `new1`, the ones digit can be the third smallest digit, `4`.\n* For `new2`, the ones digit can be the fourth smallest digit, `9`.\n\n***\n\n## **Walk Through the Code:**\n\n* We can first add all the digits into the `digits` array. \n* Then we can sort `digits`.\n* The we can do `new1 := digits[0] * 10 + digits[2]`. This is baisically:\n * We do `digits[0] * 10`. This basically = `Minimum number * 10`. We do the `* 10` because this is how we make `digits[0]` into the tens digit.\n* The we can do `new2 := digits[1] * 10 + digits[3]`. This is baisically:\n * We do `digits[1] * 10`. This basically = `Second minimum number * 10`. We do the `* 10` because this is how we make `digits[1]` into the tens digit.\n\n***\n\n``` go\nfunc minimumSum(num int) int {\n digits := []int{}\n \n for num > 0 {\n digits = append(digits, num % 10)\n num /= 10\n }\n \n sort.Ints(digits)\n \n new1 := digits[0] * 10 + digits[2]\n new2 := digits[1] * 10 + digits[3]\n \n return new1 + new2\n}\n``` | 9 | 0 | ['Go'] | 0 |
minimum-sum-of-four-digit-number-after-splitting-digits | Faster than 94.61% PYTHON | EASY | faster-than-9461-python-easy-by-s22j10-294h | UPVOTE\n\n\ns=list(str(num))\n s.sort()\n return int(s[0]+s[2])+int(s[1]+s[3])\n\nTHANKS FOR VIEWING | s22j10 | NORMAL | 2022-04-16T04:20:48.133113+00:00 | 2022-04-16T04:20:48.133144+00:00 | 773 | false | # UPVOTE\n\n```\ns=list(str(num))\n s.sort()\n return int(s[0]+s[2])+int(s[1]+s[3])\n```\n**THANKS FOR VIEWING** | 8 | 0 | ['Python'] | 2 |
minimum-sum-of-four-digit-number-after-splitting-digits | Easy to Understand Pythonic solution | easy-to-understand-pythonic-solution-by-bq81i | Some of the solutions to this problem seemed to be not very easy to understand so here\'s my take:\n\n# Explanation:\nWe put all our digits in a list, sort them | mikael_p | NORMAL | 2023-02-25T21:37:10.910458+00:00 | 2023-04-17T05:37:56.084528+00:00 | 483 | false | *Some of the solutions to this problem seemed to be not very easy to understand so here\'s my take:*\n\n# **Explanation:**\nWe put all our digits in a list, sort them with a built-in method **sort()** (so that the numbers are sorted from smallest to highest), join 1st + 3d and 2nd+ 4th elements as string, cast into ints and return their summ.\n\n# **Why does this work?**\nThis works because the smallest possible numbers from a 4-number array would both start with smallest number ( hence the 1st and 2nd digit being picked for the start of our integer)\n\n# Code\n```\nclass Solution:\n def minimumSum(self, num: int) -> int:\n digits = []\n\n for i in str(num):\n digits.append(i)\n\n digits.sort()\n\n return int(digits[0] + digits[2]) + int(digits[1] + digits[3])\n``` | 7 | 0 | ['Python3'] | 0 |
minimum-sum-of-four-digit-number-after-splitting-digits | 1 ms, 41mb, Java, Sorting | 1-ms-41mb-java-sorting-by-sid_3945-v7j5 | https://leetcode.com/problems/minimum-sum-of-four-digit-number-after-splitting-digits/submissions/\nThe logic is: take the 4 digit numbers and split the digits | sid_3945 | NORMAL | 2022-02-14T05:08:07.165275+00:00 | 2022-02-14T05:08:07.165319+00:00 | 707 | false | https://leetcode.com/problems/minimum-sum-of-four-digit-number-after-splitting-digits/submissions/\nThe logic is: take the 4 digit numbers and split the digits and store in an array of size 4. Then sort the array. Objective is to make two numbers that are smallest (so that their sum is smallest). One way of doing this is by take 0th and 1st elements as the first number and 3rd and 4th elements as the second number.\n2932\nSorted 2239\nNumber 1: 22\nNumber 2: 39\nSum: 61\nOther way is 1st element as the 10s position and 3rd element as the ones position\nAnd 2nd digit as 10s position and 4th digit as ones position.\nNumber 1: 23\nNumber 2: 29\nSum: 51\nReturn 51;\n\nSo second approach is the answer.\n```\nclass Solution{\n public int minimumSum(int num){\n int[] temp = new int[4];\n int i = 0;\n while(num>0){\n temp[i]=num%10;\n i++;\n num=num/10;\n }\n //now we have an array temp with all the digits of the num, we will sort temp\n Arrays.sort(temp);\n int num1 = temp[0]*10 + temp[2];\n int num2 = temp[1]*10 + temp[3];\n return (num1+num2);\n }\n}\n```\n | 7 | 0 | ['Sorting', 'Java'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.