source
stringclasses 3
values | instruction
stringlengths 23
3.97k
| input
stringclasses 1
value | output
stringlengths 1
3.75k
|
|---|---|---|---|
agentica-org/DeepScaleR-Preview-Dataset
|
Define: For any three-digit natural number $m$, if $m$ satisfies that the tens digit is $1$ greater than the hundreds digit, and the units digit is $1$ greater than the tens digit, then this three-digit number is called an "upward number"; for any three-digit natural number $n$, if $n$ satisfies that the tens digit is $1$ less than the hundreds digit, and the units digit is $1$ less than the tens digit, then this three-digit number is called a "downward number." The multiple of $7$ of an "upward number" $m$ is denoted as $F(m)$, and the multiple of $8$ of a "downward number" $n$ is denoted as $G(n)$. If $\frac{F(m)+G(n)}{18}$ is an integer, then each pair of $m$ and $n$ is called a "seven up eight down number pair." In all "seven up eight down number pairs," the maximum value of $|m-n|$ is ______.
|
531
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A point $(x, y)$ is randomly selected such that $0 \leq x \leq 4$ and $0 \leq y \leq 5$. What is the probability that $x + y \leq 5$? Express your answer as a common fraction.
|
\frac{3}{5}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A digital watch displays time in a 24-hour format showing only hours and minutes. Find the largest possible sum of the digits in the display.
|
24
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A quadrilateral has vertices at $(0,1)$, $(3,4)$, $(4,3)$ and $(3,0)$. Its perimeter can be expressed in the form $a\sqrt2+b\sqrt{10}$ with $a$ and $b$ integers. What is the sum of $a$ and $b$?
|
6
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A certain item has a cost price of $4$ yuan and is sold at a price of $5$ yuan. The merchant is planning to offer a discount on the selling price, but the profit margin must not be less than $10\%$. Find the maximum discount rate that can be offered.
|
12\%
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Evaluate $\sqrt[3]{1+27} \cdot \sqrt[3]{1+\sqrt[3]{27}}$.
|
\sqrt[3]{112}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
For some integer $m$, the polynomial $x^3 - 2011x + m$ has the three integer roots $a$, $b$, and $c$. Find $|a| + |b| + |c|$.
|
98
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Two cylindrical cans have the same volume. The height of one can is triple the height of the other. If the radius of the narrower can is 12 units, how many units are in the length of the radius of the wider can? Express your answer in simplest radical form.
|
12\sqrt{3}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A projection takes $\begin{pmatrix} 1 \\ -2 \end{pmatrix}$ to $\begin{pmatrix} \frac{3}{2} \\ -\frac{3}{2} \end{pmatrix}.$ Which vector does the projection take $\begin{pmatrix} -4 \\ 1 \end{pmatrix}$ to?
|
\begin{pmatrix} -5/2 \\ 5/2 \end{pmatrix}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
For a positive number such as 3.27, 3 is referred to as the integral part of the number and .27 as the decimal part. Find a positive number such that its decimal part, its integral part, and the number itself form a geometric progression.
|
\frac{3 + \sqrt{5}}{2}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
If Ravi shortens the length of one side of a $5 \times 7$ index card by $1$ inch, the card would have an area of $24$ square inches. What is the area of the card in square inches if instead he shortens the length of the other side by $1$ inch?
|
18
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
There are 7 light bulbs arranged in a row. It is required to light up at least 3 of the bulbs, and adjacent bulbs cannot be lit at the same time. Determine the total number of different ways to light up the bulbs.
|
11
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
What is the sum of $x + y$ if the sequence $3, ~8, ~13, \ldots, ~x, ~y, ~33$ forms an arithmetic sequence?
|
51
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
The area of the base of a hemisphere is $144\pi$. A cylinder of the same radius as the hemisphere and height equal to the radius of the hemisphere is attached to its base. What is the total surface area of the combined solid (hemisphere + cylinder)?
|
576\pi
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Monica tosses a fair 6-sided die. If the roll is a prime number, then she wins that amount of dollars (so that, for example, if she rolls 3, then she wins 3 dollars). If the roll is composite, she wins nothing. Otherwise, she loses 3 dollars. What is the expected value of her winnings on one die toss? Express your answer as a dollar value to the nearest cent.
|
\$1.17
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given the real numbers \( x \) and \( y \) satisfy the equations:
\[ 2^x + 4x + 12 = \log_2{(y-1)^3} + 3y + 12 = 0 \]
find the value of \( x + y \).
|
-2
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
The function \(f(x) = 5x^2 - 15x - 2\) has a minimum value when x is negative.
|
-13.25
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Let side $AD$ of convex quadrilateral $ABCD$ be extended through $D$, and let side $BC$ be extended through $C$, to meet in point $E.$ Let $S$ be the degree-sum of angles $CDE$ and $DCE$, and let $S'$ represent the degree-sum of angles $BAD$ and $ABC.$ If $r=S/S'$, then:
|
1
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
As shown in the diagram, \(FGHI\) is a trapezium with side \(GF\) parallel to \(HI\). The lengths of \(FG\) and \(HI\) are 50 and 20 respectively. The point \(J\) is on the side \(FG\) such that the segment \(IJ\) divides the trapezium into two parts of equal area. What is the length of \(FJ\)?
|
35
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given the chord length intercepted by the circle $x^{2}+y^{2}+2x-4y+1=0$ on the line $ax-by+2=0$ $(a > 0, b > 0)$ is 4, find the minimum value of $\frac{1}{a} + \frac{1}{b}$.
|
\frac{3}{2} + \sqrt{2}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Let
\[f(x) = \left\{
\begin{array}{cl}
x^2 + 3 & \text{if $x < 15$}, \\
3x - 2 & \text{if $x \ge 15$}.
\end{array}
\right.\]
Find $f^{-1}(10) + f^{-1}(49).$
|
\sqrt{7} + 17
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Find the number of positive divisors $d$ of $15!=15 \cdot 14 \cdots 2 \cdot 1$ such that $\operatorname{gcd}(d, 60)=5$.
|
36
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A square with side length 8 is cut in half, creating two congruent rectangles. What are the dimensions of one of these rectangles?
|
4 \times 8
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
One day, School A bought 56 kilograms of fruit candy at 8.06 yuan per kilogram. A few days later, School B also needed to buy the same 56 kilograms of fruit candy, but it happened that there was a promotional event, and the price of fruit candy was reduced by 0.56 yuan per kilogram. Additionally, they received 5% extra fruit candy for free. How much less did School B spend compared to School A?
|
51.36
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
How many 6-digit numbers have at least two zeros?
|
73,314
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Find the largest integer $n$ such that $3^{512}-1$ is divisible by $2^{n}$.
|
11
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given the line $l: x-y+4=0$ and the circle $C: \begin{cases}x=1+2\cos \theta \\ y=1+2\sin \theta\end{cases} (\theta$ is a parameter), find the distance from each point on $C$ to $l$.
|
2 \sqrt{2}-2
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Consider a new infinite geometric series: $$\frac{7}{4} + \frac{28}{9} + \frac{112}{27} + \dots$$
Determine the common ratio of this series.
|
\frac{16}{9}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
\frac{3}{2} + \frac{5}{4} + \frac{9}{8} + \frac{17}{16} + \frac{33}{32} + \frac{65}{64} - 7 =
|
-\frac{1}{64}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A certain function $f$ has the properties that $f(3x) = 3f(x)$ for all positive real values of $x$, and that $f(x) = 1 - |x - 2|$ for $1\leq x \leq 3$. Find the smallest $x$ for which $f(x) = f(2001)$.
|
429
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
$44 \times 22$ is equal to
|
$88 \times 11$
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
In a three-dimensional Cartesian coordinate system, there is a sphere with its center at the origin and a radius of 3 units. How many lattice points lie on the surface of the sphere?
|
30
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given the function $f\left(x\right)=x^{2}-2$, find $\lim_{{Δx→0}}\frac{{f(3)-f({3-2Δx})}}{{Δx}}$.
|
12
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Find the smallest positive angle $x$ that satisfies $\sin 2x \sin 3x = \cos 2x \cos 3x,$ in degrees.
|
18^\circ
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Let $p$, $q$, and $r$ be the roots of $x^3 - 2x^2 - x + 3 = 0$. Find $\frac{1}{p-2} + \frac{1}{q-2} + \frac{1}{r-2}$.
|
-3
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
$ABCD$ is a parallelogram with $\angle D$ obtuse. $M$ and $N$ are the feet of the perpendiculars from $D$ to $AB$ and $BC$ respectively. If $DB = DC = 50$ and $DA = 60$, find $DM + DN$.
|
88
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
In the obtuse triangle $ABC$ with $\angle C>90^\circ$, $AM=MB$, $MD\perp BC$, and $EC\perp BC$ ($D$ is on $BC$, $E$ is on $AB$, and $M$ is on $EB$). If the area of $\triangle ABC$ is $24$, then the area of $\triangle BED$ is
|
12
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
For how many integers $N$ between $1$ and $1990$ is the improper fraction $\frac{N^2+7}{N+4}$ not in lowest terms?
|
86
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
For each value of $x$, $g(x)$ is defined to be the minimum value of the three numbers $3x + 3$, $\frac{1}{3}x + 1$, and $-\frac{2}{3}x + 8$. Find the maximum value of $g(x)$.
|
\frac{10}{3}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A function $f(x, y)$ is linear in $x$ and in $y . f(x, y)=\frac{1}{x y}$ for $x, y \in\{3,4\}$. What is $f(5,5)$?
|
\frac{1}{36}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Find a 4-digit perfect square, knowing that the number formed by the first two digits is one more than the number formed by the last two digits.
|
8281
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
In $\triangle ABC$, the sides opposite to angles $A$, $B$, and $C$ are $a$, $b$, and $c$ respectively, which form a geometric progression. Also, $(2a-c)\cos B = b\cos C$.
(Ⅰ) Find the magnitude of angle $B$;
(Ⅱ) Calculate $\frac{1}{\tan A} + \frac{1}{\tan C}$.
|
\frac{2 \sqrt{3}}{3}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given the number $S_{20}$, which denotes an integer whose base-ten representation consists of 20 repetitions of the digit "2", and $S_{2}$, which denotes an integer whose base-ten representation consists of 2 repetitions of the digit "2", determine the number of zeros in the base-ten representation of the quotient $T = S_{20}/S_{2}$.
|
18
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Kelvin the Frog was bored in math class one day, so he wrote all ordered triples $(a, b, c)$ of positive integers such that $a b c=2310$ on a sheet of paper. Find the sum of all the integers he wrote down. In other words, compute $$\sum_{\substack{a b c=2310 \\ a, b, c \in \mathbb{N}}}(a+b+c)$$ where $\mathbb{N}$ denotes the positive integers.
|
49140
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
4.3535… is a decimal, which can be abbreviated as , and the repeating cycle is .
|
35
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Suppose $x, y$, and $z$ are real numbers greater than 1 such that $$\begin{aligned} x^{\log _{y} z} & =2, \\ y^{\log _{z} x} & =4, \text { and } \\ z^{\log _{x} y} & =8 \end{aligned}$$ Compute $\log _{x} y$.
|
\sqrt{3}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Several cuboids with edge lengths of $2, 7, 13$ are arranged in the same direction to form a cube with an edge length of 2002. How many small cuboids does a diagonal of the cube pass through?
|
1210
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Brenda is going from $(-4,5)$ to $(5,-4)$, but she needs to stop by the origin on the way. How far does she have to travel?
|
2\sqrt{41}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Melinda has three empty boxes and $12$ textbooks, three of which are mathematics textbooks. One box will hold any three of her textbooks, one will hold any four of her textbooks, and one will hold any five of her textbooks. If Melinda packs her textbooks into these boxes in random order, the probability that all three mathematics textbooks end up in the same box can be written as $\frac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
|
47
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
On the AMC 8 contest Billy answers 13 questions correctly, answers 7 questions incorrectly and doesn't answer the last 5. What is his score?
|
13
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Natural numbers \( x, y, z \) are such that \( \operatorname{GCD}(\operatorname{LCM}(x, y), z) \cdot \operatorname{LCM}(\operatorname{GCD}(x, y), z) = 1400 \).
What is the maximum value that \( \operatorname{GCD}(\operatorname{LCM}(x, y), z) \) can take?
|
10
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Consider a square pyramid $S-ABCD$ with a height of $h$. The base $ABCD$ is a square with side length 1. Points $S$, $A$, $B$, $C$, and $D$ all lie on the surface of a sphere with radius 1. The task is to find the distance between the center of the base $ABCD$ and the vertex $S$.
|
\frac{\sqrt{2}}{2}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
2005^{2} + 2 \times 2005 \times 1995 + 1995^{2} divided by 800.
|
20000
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Annie and Bonnie are running laps around a $400$-meter oval track. They started together, but Annie has pulled ahead, because she runs $25\%$ faster than Bonnie. How many laps will Annie have run when she first passes Bonnie?
|
5
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
When drawing 20 numbers from 2005 numbers using systematic sampling, calculate the interval of sampling.
|
100
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
What is the largest $2$-digit prime factor of the integer $n = {300\choose 150}$?
|
97
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given the hyperbola $\dfrac {x^{2}}{9}- \dfrac {y^{2}}{27}=1$ with its left and right foci denoted as $F_{1}$ and $F_{2}$ respectively, and $F_{2}$ being the focus of the parabola $y^{2}=2px$, find the area of $\triangle PF_{1}F_{2}$.
|
36 \sqrt {6}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Sets $A$, $B$, and $C$, depicted in the Venn diagram, are such that the total number of elements in set $A$ is three times the total number of elements in set $B$. Their intersection has 1200 elements, and altogether, there are 4200 elements in the union of $A$, $B$, and $C$. If set $C$ intersects only with set $A$ adding 300 more elements to the union, how many elements are in set $A$?
[asy]
label("$A$", (2,67));
label("$B$", (80,67));
label("$C$", (41,10));
draw(Circle((30,45), 22));
draw(Circle((58, 45), 22));
draw(Circle((44, 27), 22));
label("1200", (44, 45));
label("300", (44, 27));
[/asy]
|
3825
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
How many digits does the smallest repeating block in the decimal expansion of $\frac{5}{7}$ contain?
|
6
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given a triangle $ABC$ with sides opposite to angles $A$, $B$, and $C$ being $a$, $b$, and $c$, respectively, and it is given that $(3b-c)\cos A = a\cos C$.
(1) Find the value of $\cos A$;
(2) If the area of $\triangle ABC$ is $S=2\sqrt{2}$, find the minimum value of the perimeter of $\triangle ABC$.
|
2\sqrt{6}+2\sqrt{2}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Let \( a, b, c \) be prime numbers such that \( a^5 \) divides \( b^2 - c \), and \( b + c \) is a perfect square. Find the minimum value of \( abc \).
|
1958
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Simplify $\dfrac{18}{17}\cdot\dfrac{13}{24}\cdot\dfrac{68}{39}$.
|
1
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
What is the greatest common divisor (GCD) and the sum of the numbers 1729 and 867?
|
2596
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A square with side length $8$ is colored white except for $4$ black isosceles right triangular regions with legs of length $2$ in each corner of the square and a black diamond with side length $2\sqrt{2}$ in the center of the square, as shown in the diagram. A circular coin with diameter $1$ is dropped onto the square and lands in a random location where the coin is completely contained within the square. The probability that the coin will cover part of the black region of the square can be written as $\frac{1}{196}\left(a+b\sqrt{2}+\pi\right)$, where $a$ and $b$ are positive integers. What is $a+b$?
|
68
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
In the octagon below all sides have the length $1$ and all angles are equal.
Determine the distance between the corners $A$ and $B$ .
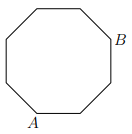
|
1 + \sqrt{2}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Define a function $g :\mathbb{N} \rightarrow \mathbb{R}$ Such that $g(x)=\sqrt{4^x+\sqrt {4^{x+1}+\sqrt{4^{x+2}+...}}}$ .
Find the last 2 digits in the decimal representation of $g(2021)$ .
|
53
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A triangle with angles \( A, B, C \) satisfies the following conditions:
\[
\frac{\sin A + \sin B + \sin C}{\cos A + \cos B + \cos C} = \frac{12}{7},
\]
and
\[
\sin A \sin B \sin C = \frac{12}{25}.
\]
Given that \( \sin C \) takes on three possible values \( s_1, s_2 \), and \( s_3 \), find the value of \( 100 s_1 s_2 s_3 \).
|
48
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Billy's age is three times Brenda's age and twice Joe's age. The sum of their ages is 72. How old is Billy?
|
\frac{432}{11}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
What is the smallest positive integer $n$ such that $\frac{1}{n}$ is a terminating decimal and $n$ contains the digit '3'?
|
3125
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
In the "Nine Chapters on the Mathematical Art," a tetrahedron with all four faces being right-angled triangles is referred to as a "turtle's knee." Given that in the turtle's knee $M-ABC$, $MA \perp$ plane $ABC$, and $MA=AB=BC=2$, the sum of the surface areas of the circumscribed sphere and the inscribed sphere of the turtle's knee is ______.
|
24\pi-8\sqrt{2}\pi
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Each outcome on the spinner below has equal probability. If you spin the spinner three times and form a three-digit number from the three outcomes, such that the first outcome is the hundreds digit, the second outcome is the tens digit and the third outcome is the units digit, what is the probability that you will end up with a three-digit number that is divisible by 4? Express your answer as a common fraction.
[asy]
draw(Circle((0,0),10));
draw((0,0)--(8.7,-5));
draw((0,0)--(-8.7,-5));
draw((0,0)--(0,10));
label("1",(7,7),SW);
label("3",(-7,7),SE);
label("2",(0,-2),S);
draw((0,0)--(3,5),Arrow);
[/asy]
|
\frac{2}{9}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Let $f(x)=x+2$ and $g(x)=x/3.$ Also denote the inverses to these functions as $f^{-1}$ and $g^{-1}.$ Compute \[f(g^{-1}(f^{-1}(f^{-1}(g(f(19)))))).\]
|
11
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
For an arithmetic sequence $a_1, a_2, a_3, \dots,$ let
\[ S_n = a_1 + a_2 + a_3 + \dots + a_n, \]
and let
\[ T_n = S_1 + S_2 + S_3 + \dots + S_n. \]
Given the value of $S_{2023}$, determine the smallest integer $n$ for which you can uniquely determine the value of $T_n$.
|
3034
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A certain product in a shopping mall sells an average of 70 items per day, with a profit of $50 per item. In order to reduce inventory quickly, the mall decides to take appropriate price reduction measures. After investigation, it was found that for each item, for every $1 decrease in price, the mall can sell an additional 2 items per day. Let $x$ represent the price reduction per item. Based on this rule, please answer:<br/>$(1)$ The daily sales volume of the mall increases by ______ items, and the profit per item is ______ dollars. (Express using algebraic expressions involving $x$)<br/>$(2)$ With the above conditions unchanged, how much should the price of each item be reduced so that the mall's daily profit reaches $3572$ dollars.
|
12
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Define a positive integer $n$ to be a factorial tail if there is some positive integer $m$ such that the decimal representation of $m!$ ends with exactly $n$ zeroes. How many positive integers less than $2500$ are not factorial tails?
|
500
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Maria buys computer disks at a price of $4$ for $\$5$ and sells them at a price of $3$ for $\$5$. How many computer disks must she sell in order to make a profit of $\$100$?
|
240
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Four fair eight-sided dice (with faces showing 1 to 8) are rolled. What is the probability that the sum of the numbers on the top faces equals 32?
|
\frac{1}{4096}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Let $x$ and $y$ be positive integers such that $7x^5 = 11y^{13}.$ The minimum possible value of $x$ has a prime factorization $a^cb^d.$ What is $a + b + c + d?$
|
31
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Circle $O$ has chord $A B$. A circle is tangent to $O$ at $T$ and tangent to $A B$ at $X$ such that $A X=2 X B$. What is \frac{A T}{B T}?
|
2
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
In writing the integers from 10 through 99 inclusive, how many times is the digit 7 written?
|
19
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Inside the cube \( ABCD A_1 B_1 C_1 D_1 \) is located the center \( O \) of a sphere with a radius of 10. The sphere intersects the face \( A A_1 D_1 D \) in a circle with a radius of 1, the face \( A_1 B_1 C_1 D_1 \) in a circle with a radius of 1, and the face \( C D D_1 C_1 \) in a circle with a radius of 3. Find the length of the segment \( O D_1 \).
|
17
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
On an $8 \times 8$ chessboard, 6 black rooks and $k$ white rooks are placed on different cells so that each rook only attacks rooks of the opposite color. Compute the maximum possible value of $k$.
|
14
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Farmer Bill's 1000 animals - ducks, cows, and rabbits - are standing in a circle. In order to feel safe, every duck must either be standing next to at least one cow or between two rabbits. If there are 600 ducks, what is the least number of cows there can be for this to be possible?
|
201
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A sphere is inscribed in a cone, and the surface area of the sphere is equal to the area of the base of the cone. Find the cosine of the angle at the vertex in the axial section of the cone.
|
\frac{7}{25}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Five numbers, $a_1$, $a_2$, $a_3$, $a_4$, are drawn randomly and without replacement from the set $\{1, 2, 3, \dots, 50\}$. Four other numbers, $b_1$, $b_2$, $b_3$, $b_4$, are then drawn randomly and without replacement from the remaining set of 46 numbers. Let $p$ be the probability that, after a suitable rotation, a brick of dimensions $a_1 \times a_2 \times a_3 \times a_4$ can be enclosed in a box of dimensions $b_1 \times b_2 \times b_3 \times b_4$, with the sides of the brick parallel to the sides of the box. Compute $p$ in lowest terms and determine the sum of the numerator and denominator.
|
71
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Solve
\[\sqrt{1 + \sqrt{2 + \sqrt{x}}} = \sqrt[3]{1 + \sqrt{x}}.\]
|
49
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
A point $(x,y)$ in the plane is called a lattice point if both $x$ and $y$ are integers. The area of the largest square that contains exactly three lattice points in its interior is closest to
|
5.0
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given the random variable $ξ∼B\left(5,0.5\right)$, and $η=5ξ$, find the respective values of $Eη$ and $Dη$.
|
\frac{125}{4}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
In triangle $PQR,$ $PQ = 24,$ $QR = 25,$ $PR = 7,$ and point $H$ is the intersection of the altitudes (the orthocenter). Points $P',$ $Q',$ and $R',$ are the images of $P,$ $Q,$ and $R,$ respectively, after a $180^\circ$ rotation about $H.$ What is the area of the union of the two regions enclosed by the triangles $PQR$ and $P'Q'R'$?
|
84
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Determine the real values of $x$ such that the triangle with sides $5$, $8$, and $x$ is obtuse.
|
(3, \sqrt{39}) \cup (\sqrt{89}, 13)
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Triangle $ABC$ has positive integer side lengths with $AB=AC$. Let $I$ be the intersection of the bisectors of $\angle B$ and $\angle C$. Suppose $BI=8$. Find the smallest possible perimeter of $\triangle ABC$.
|
108
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Given that in triangle $\triangle ABC$, the sides opposite to angles $A$, $B$, and $C$ are denoted as $a$, $b$, and $c$ respectively, and $\left(a+b\right)\left(\sin A-\sin B\right)=\left(c-b\right)\sin C$ with $a=2$, find the maximum area of triangle $\triangle ABC$.
|
\sqrt{3}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
What is the difference between the largest and smallest numbers in the list $0.023,0.302,0.203,0.320,0.032$?
|
0.297
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
In $\triangle ABC$, points $E$ and $F$ are on $AB$ and $BC$, respectively, such that $AE = BF$ and $BE = CF$. If $\angle BAC = 70^{\circ}$, what is the measure of $\angle ABC$?
|
40^{\circ}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Compute the smallest positive integer $n$ for which $$0<\sqrt[4]{n}-\lfloor\sqrt[4]{n}\rfloor<\frac{1}{2015}$$
|
4097
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Max and Minnie each add up sets of three-digit positive integers. Each of them adds three different three-digit integers whose nine digits are all different. Max creates the largest possible sum. Minnie creates the smallest possible sum. What is the difference between Max's sum and Minnie's sum?
|
1845
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
The graph below shows a portion of the curve defined by the quartic polynomial $P(x)=x^4+ax^3+bx^2+cx+d$.
[asy]
unitsize(0.8 cm);
int i;
real func (real x) {
return(0.5*(x^4/4 - 2*x^3/3 - 3/2*x^2) + 2.7);
}
draw(graph(func,-4.5,4.5));
draw((-4.5,0)--(4.5,0));
draw((0,-5.5)--(0,5.5));
for (i = -4; i <= 4; ++i) {
draw((i,-0.1)--(i,0.1));
}
for (i = -5; i <= 5; ++i) {
draw((-0.1,i)--(0.1,i));
}
label("$-3$", (-3,-0.1), S);
label("$3$", (3,-0.1), S);
label("$10$", (-0.1,5), W);
label("$-10$", (-0.1,-5), W);
limits((-4.5,-5.5),(4.5,5.5),Crop);
[/asy]
Which of the following is the smallest?
A. $P(-1)$
B. The product of the zeros of $P$
C. The product of the non-real zeros of $P$
D. The sum of the coefficients of $P$
E. The sum of the real zeros of $P$
|
\text{C}
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
If $f(x)=\frac{x^5-1}3$, find $f^{-1}(-31/96)$.
|
\frac12
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
For a permutation $p = (a_1,a_2,\ldots,a_9)$ of the digits $1,2,\ldots,9$, let $s(p)$ denote the sum of the three $3$-digit numbers $a_1a_2a_3$, $a_4a_5a_6$, and $a_7a_8a_9$. Let $m$ be the minimum value of $s(p)$ subject to the condition that the units digit of $s(p)$ is $0$. Let $n$ denote the number of permutations $p$ with $s(p) = m$. Find $|m - n|$.
|
162
|
|
agentica-org/DeepScaleR-Preview-Dataset
|
Two spheres are inscribed in a dihedral angle in such a way that they touch each other. The radius of one sphere is 1.5 times the radius of the other, and the line connecting the centers of the spheres forms an angle of $30^{\circ}$ with the edge of the dihedral angle. Find the measure of the dihedral angle. In the answer, write down the cosine of this angle, rounding it to two decimal places if necessary.
|
0.5
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.