title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Solution | is-graph-bipartite | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool check(vector<vector<int>>& graph, int src, vector<int>& color)\n {\n color[src] = 0;\n queue<int>q;\n q.push(src);\n while(!q.empty())\n {\n int u = q.front();\n q.pop();\n for(int i=0;i<graph[u].size();i++)\n {\n if(color[graph[u][i]]==-1)\n {\n color[graph[u][i]] = !color[u];\n q.push(graph[u][i]);\n }\n else if(color[graph[u][i]]==color[u])\n {\n return false;\n }\n }\n }\n return true; \n }\n bool isBipartite(vector<vector<int>>& graph) {\n ios_base::sync_with_stdio(0), cin.tie(0);\n int n = graph.size();\n vector<int>color(n, -1);\n for(int j=0;j<n;j++)\n {\n if((color[j] == -1) && (check(graph, j, color) == false))\n {\n return false;\n }\n }\n return true; \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n color = {}\n def bfs(x):\n q = deque([x])\n color[x] = 1\n while q:\n cur = q.popleft()\n for n in graph[cur]:\n if n not in color:\n color[n] = -color[cur]\n q += n,\n elif color[n] == color[cur]:\n return False\n return True\n \n return all(i in color or bfs(i) for i in range(len(graph)))\n```\n\n```Java []\nclass Solution {\n public boolean isBipartite(int[][] graph) {\n int[] coloured = new int[graph.length];\n Arrays.fill(coloured,-1);\n\n for(int i=0;i<graph.length;i++){\n if(coloured[i]==-1){\n if(!dfs(graph,coloured,i,0)){\n return false;\n }\n }\n }\n return true;\n }\n public boolean dfs(int[][] graph,int[] coloured,int node,int color){\n coloured[node] = color;\n int[] neighbours = graph[node];\n for(int neighbour:neighbours){\n if(coloured[neighbour]==-1){\n if(!dfs(graph,coloured,neighbour,1-color)){\n return false;\n }\n }else if(coloured[neighbour]==color){\n return false;\n }\n }\n return true;\n }\n}\n```\n | 1 | There is an **undirected** graph with `n` nodes, where each node is numbered between `0` and `n - 1`. You are given a 2D array `graph`, where `graph[u]` is an array of nodes that node `u` is adjacent to. More formally, for each `v` in `graph[u]`, there is an undirected edge between node `u` and node `v`. The graph has the following properties:
* There are no self-edges (`graph[u]` does not contain `u`).
* There are no parallel edges (`graph[u]` does not contain duplicate values).
* If `v` is in `graph[u]`, then `u` is in `graph[v]` (the graph is undirected).
* The graph may not be connected, meaning there may be two nodes `u` and `v` such that there is no path between them.
A graph is **bipartite** if the nodes can be partitioned into two independent sets `A` and `B` such that **every** edge in the graph connects a node in set `A` and a node in set `B`.
Return `true` _if and only if it is **bipartite**_.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0,2\],\[0,1,3\],\[0,2\]\]
**Output:** false
**Explanation:** There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
**Example 2:**
**Input:** graph = \[\[1,3\],\[0,2\],\[1,3\],\[0,2\]\]
**Output:** true
**Explanation:** We can partition the nodes into two sets: {0, 2} and {1, 3}.
**Constraints:**
* `graph.length == n`
* `1 <= n <= 100`
* `0 <= graph[u].length < n`
* `0 <= graph[u][i] <= n - 1`
* `graph[u]` does not contain `u`.
* All the values of `graph[u]` are **unique**.
* If `graph[u]` contains `v`, then `graph[v]` contains `u`. | null |
Solution | is-graph-bipartite | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool check(vector<vector<int>>& graph, int src, vector<int>& color)\n {\n color[src] = 0;\n queue<int>q;\n q.push(src);\n while(!q.empty())\n {\n int u = q.front();\n q.pop();\n for(int i=0;i<graph[u].size();i++)\n {\n if(color[graph[u][i]]==-1)\n {\n color[graph[u][i]] = !color[u];\n q.push(graph[u][i]);\n }\n else if(color[graph[u][i]]==color[u])\n {\n return false;\n }\n }\n }\n return true; \n }\n bool isBipartite(vector<vector<int>>& graph) {\n ios_base::sync_with_stdio(0), cin.tie(0);\n int n = graph.size();\n vector<int>color(n, -1);\n for(int j=0;j<n;j++)\n {\n if((color[j] == -1) && (check(graph, j, color) == false))\n {\n return false;\n }\n }\n return true; \n }\n};\n```\n\n```Python3 []\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n color = {}\n def bfs(x):\n q = deque([x])\n color[x] = 1\n while q:\n cur = q.popleft()\n for n in graph[cur]:\n if n not in color:\n color[n] = -color[cur]\n q += n,\n elif color[n] == color[cur]:\n return False\n return True\n \n return all(i in color or bfs(i) for i in range(len(graph)))\n```\n\n```Java []\nclass Solution {\n public boolean isBipartite(int[][] graph) {\n int[] coloured = new int[graph.length];\n Arrays.fill(coloured,-1);\n\n for(int i=0;i<graph.length;i++){\n if(coloured[i]==-1){\n if(!dfs(graph,coloured,i,0)){\n return false;\n }\n }\n }\n return true;\n }\n public boolean dfs(int[][] graph,int[] coloured,int node,int color){\n coloured[node] = color;\n int[] neighbours = graph[node];\n for(int neighbour:neighbours){\n if(coloured[neighbour]==-1){\n if(!dfs(graph,coloured,neighbour,1-color)){\n return false;\n }\n }else if(coloured[neighbour]==color){\n return false;\n }\n }\n return true;\n }\n}\n```\n | 1 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
[Python] Checking for odd length cycles | is-graph-bipartite | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nOne characterization of bipartite graphs is graphs that do not have odd length cycles. So we can check for this by doing a BFS and if we see a node we\'ve already visited, we see how long ago it was. We do this component-wise. It\'s not any better than the two-coloring method, but it\'s just a different perspective on it. \n\n\n# Code\n```\nfrom collections import deque\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n n = len(graph)\n visited = [-1]*len(graph)\n d = {x:graph[x] for x in range(n)}\n for i in range(n):\n if visited[i] < 0:\n q = deque([[i,0]])\n visited[i] = 0\n while q:\n curr, time = q.popleft()\n for vtx in d[curr]:\n if visited[vtx] == -1:\n q.append([vtx, time+1])\n visited[vtx] = time+1\n elif (time+1-visited[vtx])%2 == 1:\n return False\n return True\n\n``` | 1 | There is an **undirected** graph with `n` nodes, where each node is numbered between `0` and `n - 1`. You are given a 2D array `graph`, where `graph[u]` is an array of nodes that node `u` is adjacent to. More formally, for each `v` in `graph[u]`, there is an undirected edge between node `u` and node `v`. The graph has the following properties:
* There are no self-edges (`graph[u]` does not contain `u`).
* There are no parallel edges (`graph[u]` does not contain duplicate values).
* If `v` is in `graph[u]`, then `u` is in `graph[v]` (the graph is undirected).
* The graph may not be connected, meaning there may be two nodes `u` and `v` such that there is no path between them.
A graph is **bipartite** if the nodes can be partitioned into two independent sets `A` and `B` such that **every** edge in the graph connects a node in set `A` and a node in set `B`.
Return `true` _if and only if it is **bipartite**_.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0,2\],\[0,1,3\],\[0,2\]\]
**Output:** false
**Explanation:** There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
**Example 2:**
**Input:** graph = \[\[1,3\],\[0,2\],\[1,3\],\[0,2\]\]
**Output:** true
**Explanation:** We can partition the nodes into two sets: {0, 2} and {1, 3}.
**Constraints:**
* `graph.length == n`
* `1 <= n <= 100`
* `0 <= graph[u].length < n`
* `0 <= graph[u][i] <= n - 1`
* `graph[u]` does not contain `u`.
* All the values of `graph[u]` are **unique**.
* If `graph[u]` contains `v`, then `graph[v]` contains `u`. | null |
[Python] Checking for odd length cycles | is-graph-bipartite | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nOne characterization of bipartite graphs is graphs that do not have odd length cycles. So we can check for this by doing a BFS and if we see a node we\'ve already visited, we see how long ago it was. We do this component-wise. It\'s not any better than the two-coloring method, but it\'s just a different perspective on it. \n\n\n# Code\n```\nfrom collections import deque\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n n = len(graph)\n visited = [-1]*len(graph)\n d = {x:graph[x] for x in range(n)}\n for i in range(n):\n if visited[i] < 0:\n q = deque([[i,0]])\n visited[i] = 0\n while q:\n curr, time = q.popleft()\n for vtx in d[curr]:\n if visited[vtx] == -1:\n q.append([vtx, time+1])\n visited[vtx] = time+1\n elif (time+1-visited[vtx])%2 == 1:\n return False\n return True\n\n``` | 1 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
Image Explanation🏆- [Both BFS & DFS ways] - C++/Java/Python | is-graph-bipartite | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Is Graph Bipartite?` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n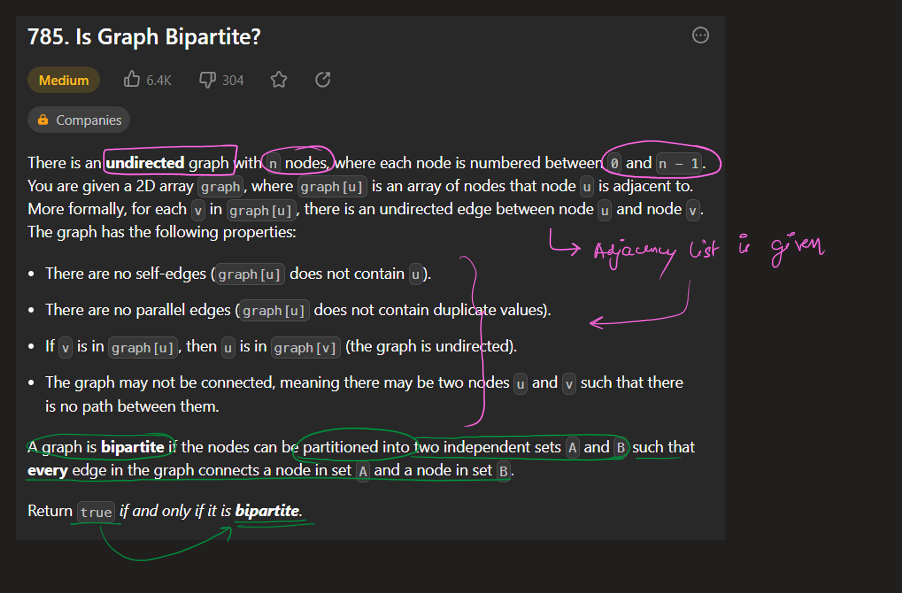\n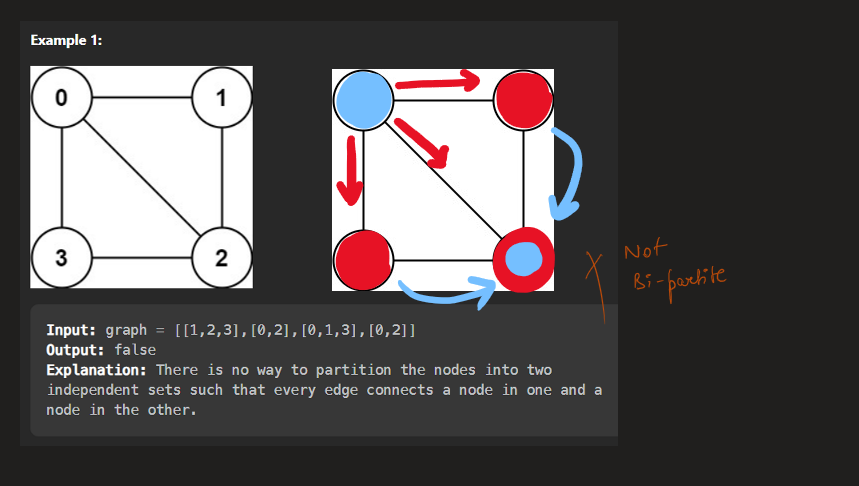\n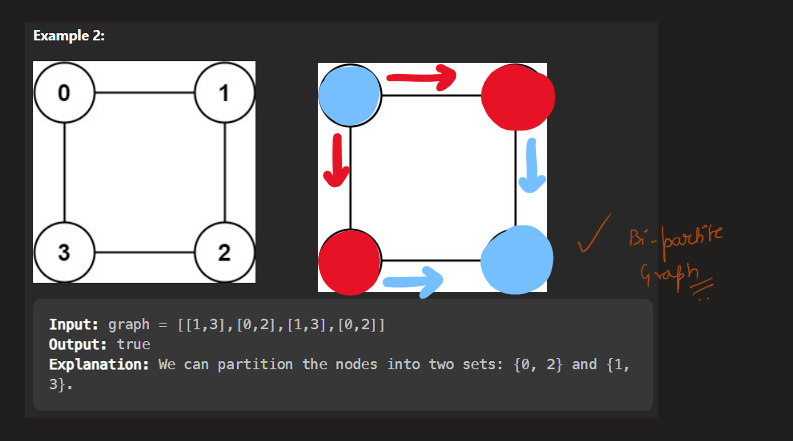\n\n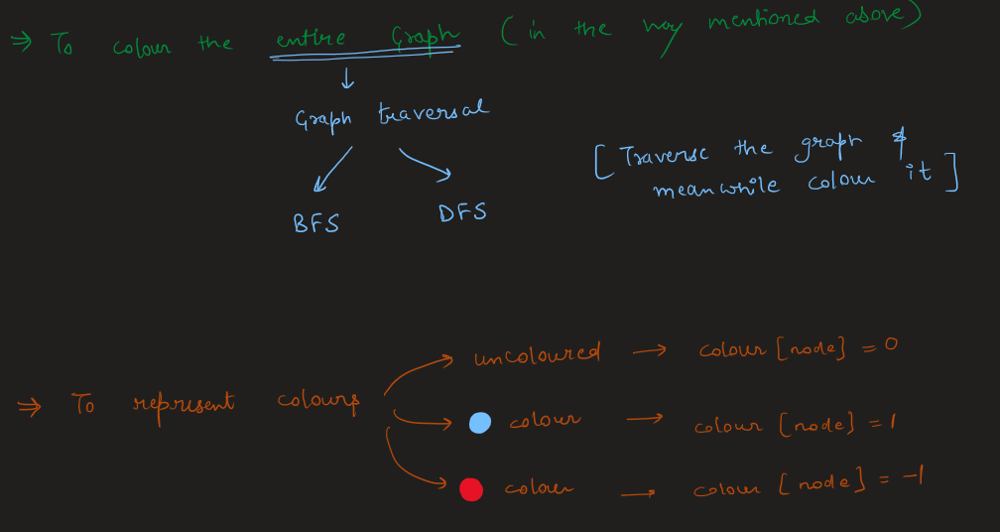\n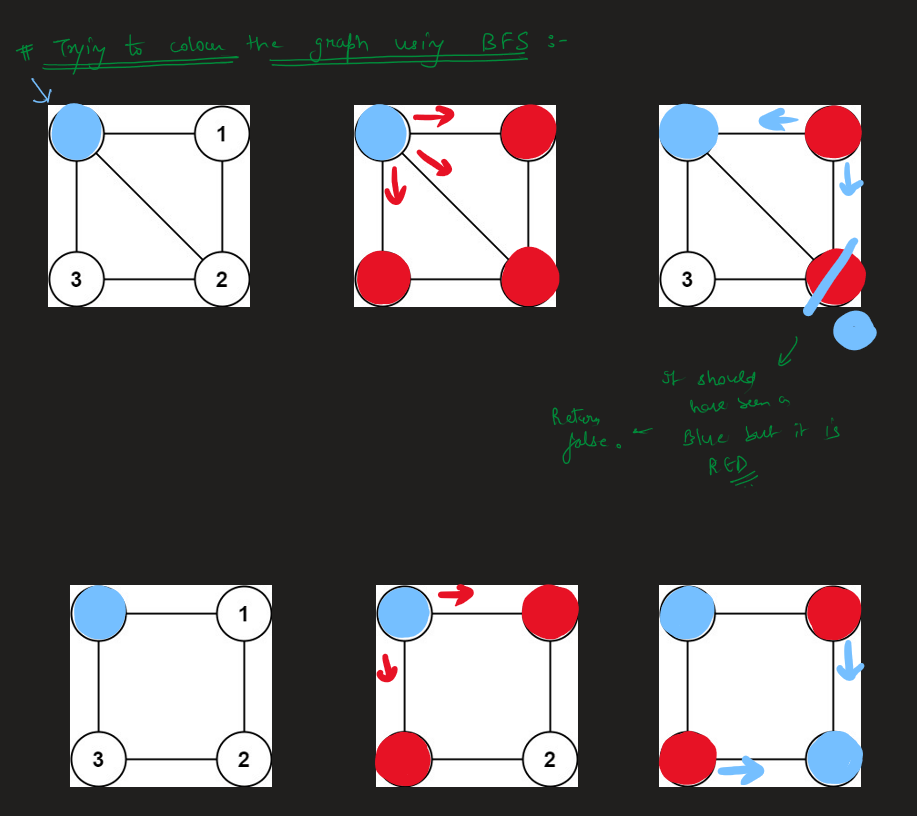\n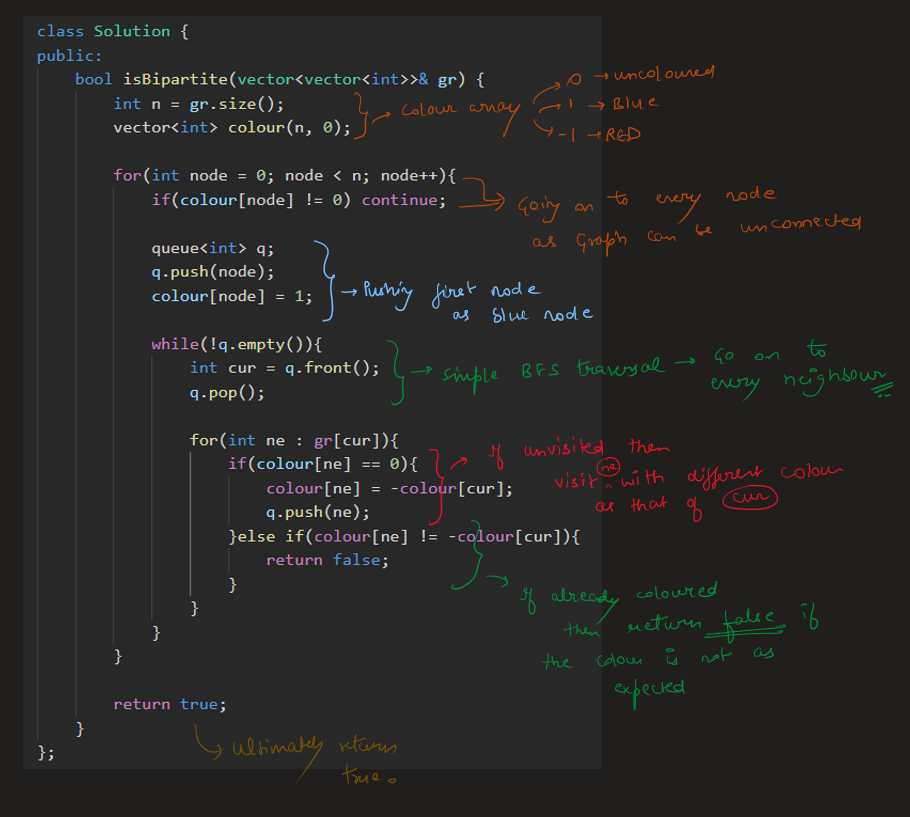\n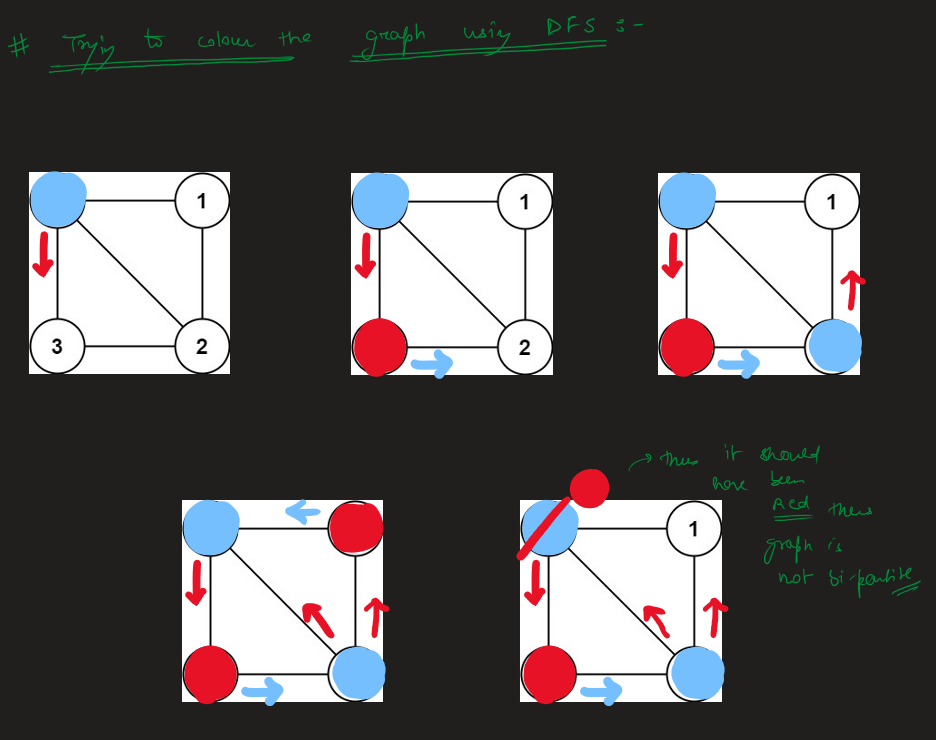\n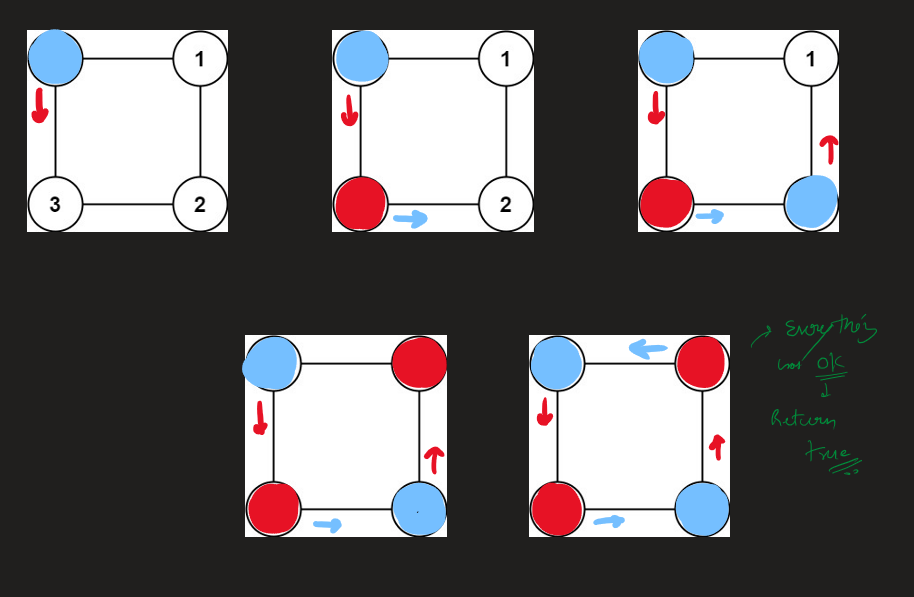\n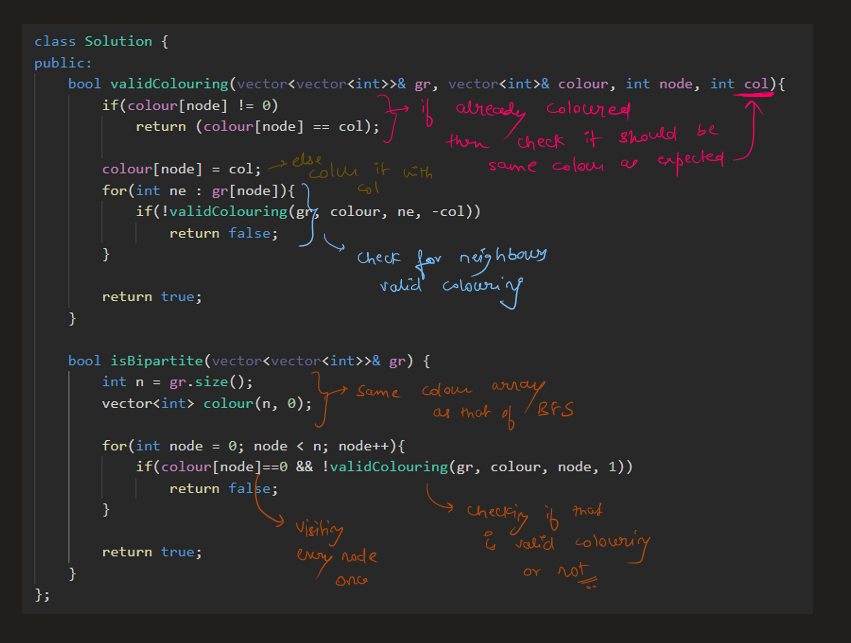\n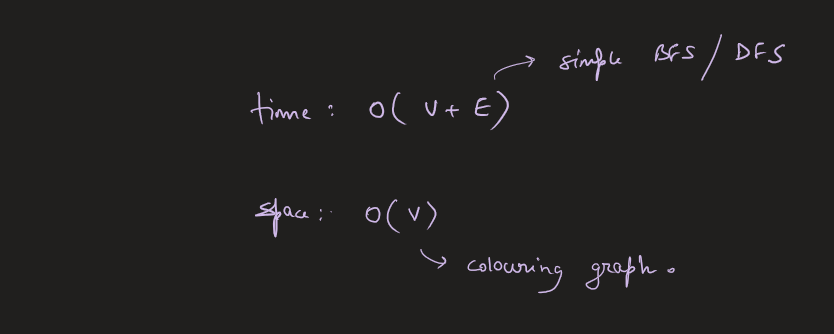\n\n\n\n# BFS Code\n```C++ []\nclass Solution {\npublic:\n bool isBipartite(vector<vector<int>>& gr) {\n int n = gr.size();\n vector<int> colour(n, 0);\n\n for(int node = 0; node < n; node++){\n if(colour[node] != 0) continue;\n\n queue<int> q;\n q.push(node);\n colour[node] = 1;\n\n while(!q.empty()){\n int cur = q.front();\n q.pop();\n\n for(int ne : gr[cur]){\n if(colour[ne] == 0){\n colour[ne] = -colour[cur];\n q.push(ne);\n }else if(colour[ne] != -colour[cur]){\n return false;\n }\n }\n }\n }\n\n return true;\n }\n};\n```\n```Java []\nimport java.util.ArrayDeque;\nimport java.util.Queue;\n\nclass Solution {\n public boolean isBipartite(int[][] gr) {\n int n = gr.length;\n int[] colour = new int[n];\n\n for (int node = 0; node < n; node++) {\n if (colour[node] != 0) {\n continue;\n }\n\n Queue<Integer> q = new ArrayDeque<>();\n q.add(node);\n colour[node] = 1;\n\n while (!q.isEmpty()) {\n int cur = q.poll();\n\n for (int ne : gr[cur]) {\n if (colour[ne] == 0) {\n colour[ne] = -colour[cur];\n q.add(ne);\n } else if (colour[ne] != -colour[cur]) {\n return false;\n }\n }\n }\n }\n\n return true;\n }\n}\n```\n```Python []\nfrom typing import List\nfrom collections import deque\n\nclass Solution:\n def isBipartite(self, gr: List[List[int]]) -> bool:\n n = len(gr)\n colour = [0] * n\n\n for node in range(n):\n if colour[node] != 0:\n continue\n\n q = deque()\n q.append(node)\n colour[node] = 1\n\n while q:\n cur = q.popleft()\n\n for ne in gr[cur]:\n if colour[ne] == 0:\n colour[ne] = -colour[cur]\n q.append(ne)\n elif colour[ne] != -colour[cur]:\n return False\n\n return True\n```\n\n# DFS Code\n```C++ []\nclass Solution {\npublic:\n bool validColouring(vector<vector<int>>& gr, vector<int>& colour, int node, int col){\n if(colour[node] != 0)\n return (colour[node] == col);\n\n colour[node] = col;\n for(int ne : gr[node]){\n if(!validColouring(gr, colour, ne, -col))\n return false;\n }\n\n return true;\n }\n\n bool isBipartite(vector<vector<int>>& gr) {\n int n = gr.size();\n vector<int> colour(n, 0);\n\n for(int node = 0; node < n; node++){\n if(colour[node]==0 && !validColouring(gr, colour, node, 1))\n return false;\n }\n\n return true;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean validColouring(int[][] gr, int[] colour, int node, int col) {\n if (colour[node] != 0)\n return colour[node] == col;\n\n colour[node] = col;\n for (int ne : gr[node]) {\n if (!validColouring(gr, colour, ne, -col))\n return false;\n }\n\n return true;\n }\n\n public boolean isBipartite(int[][] gr) {\n int n = gr.length;\n int[] colour = new int[n];\n\n for (int node = 0; node < n; node++) {\n if (colour[node] == 0 && !validColouring(gr, colour, node, 1))\n return false;\n }\n\n return true;\n }\n}\n```\n```Python []\nclass Solution:\n def validColouring(self, gr, colour, node, col):\n if colour[node] != 0:\n return colour[node] == col\n\n colour[node] = col\n for ne in gr[node]:\n if not self.validColouring(gr, colour, ne, -col):\n return False\n\n return True\n\n def isBipartite(self, gr):\n n = len(gr)\n colour = [0] * n\n\n for node in range(n):\n if colour[node] == 0 and not self.validColouring(gr, colour, node, 1):\n return False\n\n return True\n``` | 48 | There is an **undirected** graph with `n` nodes, where each node is numbered between `0` and `n - 1`. You are given a 2D array `graph`, where `graph[u]` is an array of nodes that node `u` is adjacent to. More formally, for each `v` in `graph[u]`, there is an undirected edge between node `u` and node `v`. The graph has the following properties:
* There are no self-edges (`graph[u]` does not contain `u`).
* There are no parallel edges (`graph[u]` does not contain duplicate values).
* If `v` is in `graph[u]`, then `u` is in `graph[v]` (the graph is undirected).
* The graph may not be connected, meaning there may be two nodes `u` and `v` such that there is no path between them.
A graph is **bipartite** if the nodes can be partitioned into two independent sets `A` and `B` such that **every** edge in the graph connects a node in set `A` and a node in set `B`.
Return `true` _if and only if it is **bipartite**_.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0,2\],\[0,1,3\],\[0,2\]\]
**Output:** false
**Explanation:** There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
**Example 2:**
**Input:** graph = \[\[1,3\],\[0,2\],\[1,3\],\[0,2\]\]
**Output:** true
**Explanation:** We can partition the nodes into two sets: {0, 2} and {1, 3}.
**Constraints:**
* `graph.length == n`
* `1 <= n <= 100`
* `0 <= graph[u].length < n`
* `0 <= graph[u][i] <= n - 1`
* `graph[u]` does not contain `u`.
* All the values of `graph[u]` are **unique**.
* If `graph[u]` contains `v`, then `graph[v]` contains `u`. | null |
Image Explanation🏆- [Both BFS & DFS ways] - C++/Java/Python | is-graph-bipartite | 1 | 1 | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Is Graph Bipartite?` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n\n\n\n\n\n\n\n\n\n\n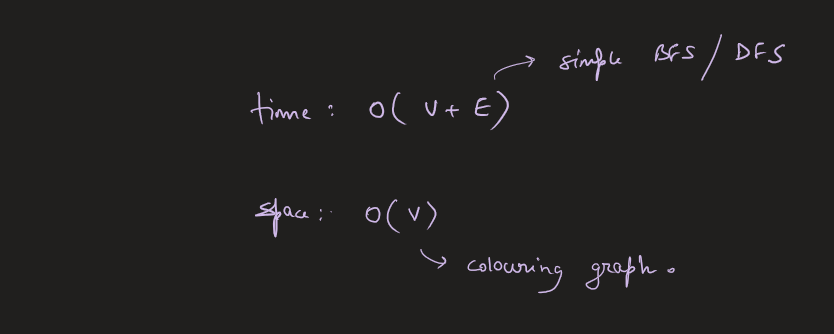\n\n\n\n# BFS Code\n```C++ []\nclass Solution {\npublic:\n bool isBipartite(vector<vector<int>>& gr) {\n int n = gr.size();\n vector<int> colour(n, 0);\n\n for(int node = 0; node < n; node++){\n if(colour[node] != 0) continue;\n\n queue<int> q;\n q.push(node);\n colour[node] = 1;\n\n while(!q.empty()){\n int cur = q.front();\n q.pop();\n\n for(int ne : gr[cur]){\n if(colour[ne] == 0){\n colour[ne] = -colour[cur];\n q.push(ne);\n }else if(colour[ne] != -colour[cur]){\n return false;\n }\n }\n }\n }\n\n return true;\n }\n};\n```\n```Java []\nimport java.util.ArrayDeque;\nimport java.util.Queue;\n\nclass Solution {\n public boolean isBipartite(int[][] gr) {\n int n = gr.length;\n int[] colour = new int[n];\n\n for (int node = 0; node < n; node++) {\n if (colour[node] != 0) {\n continue;\n }\n\n Queue<Integer> q = new ArrayDeque<>();\n q.add(node);\n colour[node] = 1;\n\n while (!q.isEmpty()) {\n int cur = q.poll();\n\n for (int ne : gr[cur]) {\n if (colour[ne] == 0) {\n colour[ne] = -colour[cur];\n q.add(ne);\n } else if (colour[ne] != -colour[cur]) {\n return false;\n }\n }\n }\n }\n\n return true;\n }\n}\n```\n```Python []\nfrom typing import List\nfrom collections import deque\n\nclass Solution:\n def isBipartite(self, gr: List[List[int]]) -> bool:\n n = len(gr)\n colour = [0] * n\n\n for node in range(n):\n if colour[node] != 0:\n continue\n\n q = deque()\n q.append(node)\n colour[node] = 1\n\n while q:\n cur = q.popleft()\n\n for ne in gr[cur]:\n if colour[ne] == 0:\n colour[ne] = -colour[cur]\n q.append(ne)\n elif colour[ne] != -colour[cur]:\n return False\n\n return True\n```\n\n# DFS Code\n```C++ []\nclass Solution {\npublic:\n bool validColouring(vector<vector<int>>& gr, vector<int>& colour, int node, int col){\n if(colour[node] != 0)\n return (colour[node] == col);\n\n colour[node] = col;\n for(int ne : gr[node]){\n if(!validColouring(gr, colour, ne, -col))\n return false;\n }\n\n return true;\n }\n\n bool isBipartite(vector<vector<int>>& gr) {\n int n = gr.size();\n vector<int> colour(n, 0);\n\n for(int node = 0; node < n; node++){\n if(colour[node]==0 && !validColouring(gr, colour, node, 1))\n return false;\n }\n\n return true;\n }\n};\n```\n```Java []\nclass Solution {\n public boolean validColouring(int[][] gr, int[] colour, int node, int col) {\n if (colour[node] != 0)\n return colour[node] == col;\n\n colour[node] = col;\n for (int ne : gr[node]) {\n if (!validColouring(gr, colour, ne, -col))\n return false;\n }\n\n return true;\n }\n\n public boolean isBipartite(int[][] gr) {\n int n = gr.length;\n int[] colour = new int[n];\n\n for (int node = 0; node < n; node++) {\n if (colour[node] == 0 && !validColouring(gr, colour, node, 1))\n return false;\n }\n\n return true;\n }\n}\n```\n```Python []\nclass Solution:\n def validColouring(self, gr, colour, node, col):\n if colour[node] != 0:\n return colour[node] == col\n\n colour[node] = col\n for ne in gr[node]:\n if not self.validColouring(gr, colour, ne, -col):\n return False\n\n return True\n\n def isBipartite(self, gr):\n n = len(gr)\n colour = [0] * n\n\n for node in range(n):\n if colour[node] == 0 and not self.validColouring(gr, colour, node, 1):\n return False\n\n return True\n``` | 48 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
Easiest Python Solution | is-graph-bipartite | 0 | 1 | \n# Code\n```\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n color = [-1] * len(graph)\n for v in range(len(graph)):\n if color[v] == -1:\n stack = [v]\n color[v] = 0\n while stack:\n node = stack.pop()\n for nei in graph[node]:\n if color[nei] == color[node]:\n return False\n if color[nei] == -1:\n color[nei] = color[node] ^ 1\n stack.append(nei)\n return True\n``` | 1 | There is an **undirected** graph with `n` nodes, where each node is numbered between `0` and `n - 1`. You are given a 2D array `graph`, where `graph[u]` is an array of nodes that node `u` is adjacent to. More formally, for each `v` in `graph[u]`, there is an undirected edge between node `u` and node `v`. The graph has the following properties:
* There are no self-edges (`graph[u]` does not contain `u`).
* There are no parallel edges (`graph[u]` does not contain duplicate values).
* If `v` is in `graph[u]`, then `u` is in `graph[v]` (the graph is undirected).
* The graph may not be connected, meaning there may be two nodes `u` and `v` such that there is no path between them.
A graph is **bipartite** if the nodes can be partitioned into two independent sets `A` and `B` such that **every** edge in the graph connects a node in set `A` and a node in set `B`.
Return `true` _if and only if it is **bipartite**_.
**Example 1:**
**Input:** graph = \[\[1,2,3\],\[0,2\],\[0,1,3\],\[0,2\]\]
**Output:** false
**Explanation:** There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
**Example 2:**
**Input:** graph = \[\[1,3\],\[0,2\],\[1,3\],\[0,2\]\]
**Output:** true
**Explanation:** We can partition the nodes into two sets: {0, 2} and {1, 3}.
**Constraints:**
* `graph.length == n`
* `1 <= n <= 100`
* `0 <= graph[u].length < n`
* `0 <= graph[u][i] <= n - 1`
* `graph[u]` does not contain `u`.
* All the values of `graph[u]` are **unique**.
* If `graph[u]` contains `v`, then `graph[v]` contains `u`. | null |
Easiest Python Solution | is-graph-bipartite | 0 | 1 | \n# Code\n```\nclass Solution:\n def isBipartite(self, graph: List[List[int]]) -> bool:\n color = [-1] * len(graph)\n for v in range(len(graph)):\n if color[v] == -1:\n stack = [v]\n color[v] = 0\n while stack:\n node = stack.pop()\n for nei in graph[node]:\n if color[nei] == color[node]:\n return False\n if color[nei] == -1:\n color[nei] = color[node] ^ 1\n stack.append(nei)\n return True\n``` | 1 | You are given two integer arrays of the same length `nums1` and `nums2`. In one operation, you are allowed to swap `nums1[i]` with `nums2[i]`.
* For example, if `nums1 = [1,2,3,8]`, and `nums2 = [5,6,7,4]`, you can swap the element at `i = 3` to obtain `nums1 = [1,2,3,4]` and `nums2 = [5,6,7,8]`.
Return _the minimum number of needed operations to make_ `nums1` _and_ `nums2` _**strictly increasing**_. The test cases are generated so that the given input always makes it possible.
An array `arr` is **strictly increasing** if and only if `arr[0] < arr[1] < arr[2] < ... < arr[arr.length - 1]`.
**Example 1:**
**Input:** nums1 = \[1,3,5,4\], nums2 = \[1,2,3,7\]
**Output:** 1
**Explanation:**
Swap nums1\[3\] and nums2\[3\]. Then the sequences are:
nums1 = \[1, 3, 5, 7\] and nums2 = \[1, 2, 3, 4\]
which are both strictly increasing.
**Example 2:**
**Input:** nums1 = \[0,3,5,8,9\], nums2 = \[2,1,4,6,9\]
**Output:** 1
**Constraints:**
* `2 <= nums1.length <= 105`
* `nums2.length == nums1.length`
* `0 <= nums1[i], nums2[i] <= 2 * 105` | null |
Solution | k-th-smallest-prime-fraction | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double cur_large;\n double ans=99999;\n int ans_row,ans_col;\n int cur_row,cur_col;\n int smaller_count(double mid,vector<int>& arr)\n {\n int row=0, col=0;\n int counter=0;\n cur_large=0;\n for(int i=0;i<arr.size();i++)\n {\n while(col<arr.size() && mid<((double)arr[row])/((double)arr[col]))\n {\n col++;\n }\n if(col<arr.size() && cur_large<((double)arr[row])/((double)arr[col]))\n {\n cur_large=((double)arr[row])/((double)arr[col]);\n cur_row=row;\n cur_col=col;\n }\n counter+=arr.size()-col;\n row++;\n }\n return counter;\n }\n vector<int> kthSmallestPrimeFraction(vector<int>& arr, int k) {\n int n=arr.size();\n double start=0.0;\n double end=1.0;\n int counting;\n while(start<end)\n {\n double mid=(start+end)/2;\n counting=smaller_count(mid,arr);\n if(counting>=k)\n {\n if(ans>cur_large)\n {\n ans=cur_large;\n ans_row=cur_row;\n ans_col=cur_col;\n }\n end=mid;\n if(counting==k)\n break;\n }\n else\n {\n start=mid;\n }\n }\n vector<int> out;\n if(ans==99999)\n {\n return out;\n }\n else\n {\n out.push_back(arr[ans_row]);\n out.push_back(arr[ans_col]);\n return out;\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n def con(value):\n nb_smallest_fraction = 0\n numer = arr[0]\n denom = arr[-1]\n\n slow = 0\n for fast in range(1, len(arr)):\n while slow < fast and arr[slow] / arr[fast] < value:\n if arr[slow] / arr[fast] > numer / denom:\n numer, denom = arr[slow], arr[fast]\n\n slow += 1\n\n nb_smallest_fraction += slow\n\n return nb_smallest_fraction, numer, denom\n\n l = arr[0] / arr[-1]\n r = 1\n\n while l < r:\n m = (l+r) / 2\n\n count, numer, denom = con(m)\n\n if count == k:\n return [numer, denom]\n\n if count > k:\n r = m\n else:\n l = m\n```\n\n```Java []\nclass Solution {\n public int[] kthSmallestPrimeFraction(int[] arr, int k) {\n int n = arr.length;\n \n double low = 0;\n double high = 1.0;\n while(low<high){\n double mid = (low+high)/2;\n int res[] = getFractionsLessThanMid(arr, n, mid);\n \n if(res[0]==k) return new int[]{arr[res[1]],arr[res[2]]};\n else if(res[0]>k) high = mid;\n else low = mid;\n } \n return new int[]{};\n }\n private int[] getFractionsLessThanMid(int arr[], int n, double mid){\n double maxLessThanMid = 0.0;\n int x = 0;\n int y = 0;\n int total = 0;\n int j = 1;\n for(int i = 0 ; i < n-1 ; i++){ \n \n while(j < n && arr[i] > (arr[j] * mid)){\n j++;\n }\n if(j==n) break;\n total += (n-j);\n\n double fraction = (double)arr[i]/arr[j];\n if(fraction > maxLessThanMid){\n maxLessThanMid = fraction;\n x = i;\n y = j;\n }\n }\n return new int[]{total,x,y};\n }\n}\n```\n | 2 | You are given a sorted integer array `arr` containing `1` and **prime** numbers, where all the integers of `arr` are unique. You are also given an integer `k`.
For every `i` and `j` where `0 <= i < j < arr.length`, we consider the fraction `arr[i] / arr[j]`.
Return _the_ `kth` _smallest fraction considered_. Return your answer as an array of integers of size `2`, where `answer[0] == arr[i]` and `answer[1] == arr[j]`.
**Example 1:**
**Input:** arr = \[1,2,3,5\], k = 3
**Output:** \[2,5\]
**Explanation:** The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, and 2/3.
The third fraction is 2/5.
**Example 2:**
**Input:** arr = \[1,7\], k = 1
**Output:** \[1,7\]
**Constraints:**
* `2 <= arr.length <= 1000`
* `1 <= arr[i] <= 3 * 104`
* `arr[0] == 1`
* `arr[i]` is a **prime** number for `i > 0`.
* All the numbers of `arr` are **unique** and sorted in **strictly increasing** order.
* `1 <= k <= arr.length * (arr.length - 1) / 2`
**Follow up:** Can you solve the problem with better than `O(n2)` complexity? | null |
Solution | k-th-smallest-prime-fraction | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double cur_large;\n double ans=99999;\n int ans_row,ans_col;\n int cur_row,cur_col;\n int smaller_count(double mid,vector<int>& arr)\n {\n int row=0, col=0;\n int counter=0;\n cur_large=0;\n for(int i=0;i<arr.size();i++)\n {\n while(col<arr.size() && mid<((double)arr[row])/((double)arr[col]))\n {\n col++;\n }\n if(col<arr.size() && cur_large<((double)arr[row])/((double)arr[col]))\n {\n cur_large=((double)arr[row])/((double)arr[col]);\n cur_row=row;\n cur_col=col;\n }\n counter+=arr.size()-col;\n row++;\n }\n return counter;\n }\n vector<int> kthSmallestPrimeFraction(vector<int>& arr, int k) {\n int n=arr.size();\n double start=0.0;\n double end=1.0;\n int counting;\n while(start<end)\n {\n double mid=(start+end)/2;\n counting=smaller_count(mid,arr);\n if(counting>=k)\n {\n if(ans>cur_large)\n {\n ans=cur_large;\n ans_row=cur_row;\n ans_col=cur_col;\n }\n end=mid;\n if(counting==k)\n break;\n }\n else\n {\n start=mid;\n }\n }\n vector<int> out;\n if(ans==99999)\n {\n return out;\n }\n else\n {\n out.push_back(arr[ans_row]);\n out.push_back(arr[ans_col]);\n return out;\n }\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n def con(value):\n nb_smallest_fraction = 0\n numer = arr[0]\n denom = arr[-1]\n\n slow = 0\n for fast in range(1, len(arr)):\n while slow < fast and arr[slow] / arr[fast] < value:\n if arr[slow] / arr[fast] > numer / denom:\n numer, denom = arr[slow], arr[fast]\n\n slow += 1\n\n nb_smallest_fraction += slow\n\n return nb_smallest_fraction, numer, denom\n\n l = arr[0] / arr[-1]\n r = 1\n\n while l < r:\n m = (l+r) / 2\n\n count, numer, denom = con(m)\n\n if count == k:\n return [numer, denom]\n\n if count > k:\n r = m\n else:\n l = m\n```\n\n```Java []\nclass Solution {\n public int[] kthSmallestPrimeFraction(int[] arr, int k) {\n int n = arr.length;\n \n double low = 0;\n double high = 1.0;\n while(low<high){\n double mid = (low+high)/2;\n int res[] = getFractionsLessThanMid(arr, n, mid);\n \n if(res[0]==k) return new int[]{arr[res[1]],arr[res[2]]};\n else if(res[0]>k) high = mid;\n else low = mid;\n } \n return new int[]{};\n }\n private int[] getFractionsLessThanMid(int arr[], int n, double mid){\n double maxLessThanMid = 0.0;\n int x = 0;\n int y = 0;\n int total = 0;\n int j = 1;\n for(int i = 0 ; i < n-1 ; i++){ \n \n while(j < n && arr[i] > (arr[j] * mid)){\n j++;\n }\n if(j==n) break;\n total += (n-j);\n\n double fraction = (double)arr[i]/arr[j];\n if(fraction > maxLessThanMid){\n maxLessThanMid = fraction;\n x = i;\n y = j;\n }\n }\n return new int[]{total,x,y};\n }\n}\n```\n | 2 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
easy.......python solution | k-th-smallest-prime-fraction | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom fractions import Fraction\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n sol_arr = []\n for i in range(len(arr)-1):\n for j in range(i+1,len(arr)):\n sol_arr.append(arr[i]/arr[j])\n sol_arr = sorted(sol_arr)\n smallest = sol_arr[k-1]\n sol = str(Fraction(str(smallest)).limit_denominator())\n numerator, denominator = sol.split("/")\n return [int(numerator), int(denominator)]\n``` | 1 | You are given a sorted integer array `arr` containing `1` and **prime** numbers, where all the integers of `arr` are unique. You are also given an integer `k`.
For every `i` and `j` where `0 <= i < j < arr.length`, we consider the fraction `arr[i] / arr[j]`.
Return _the_ `kth` _smallest fraction considered_. Return your answer as an array of integers of size `2`, where `answer[0] == arr[i]` and `answer[1] == arr[j]`.
**Example 1:**
**Input:** arr = \[1,2,3,5\], k = 3
**Output:** \[2,5\]
**Explanation:** The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, and 2/3.
The third fraction is 2/5.
**Example 2:**
**Input:** arr = \[1,7\], k = 1
**Output:** \[1,7\]
**Constraints:**
* `2 <= arr.length <= 1000`
* `1 <= arr[i] <= 3 * 104`
* `arr[0] == 1`
* `arr[i]` is a **prime** number for `i > 0`.
* All the numbers of `arr` are **unique** and sorted in **strictly increasing** order.
* `1 <= k <= arr.length * (arr.length - 1) / 2`
**Follow up:** Can you solve the problem with better than `O(n2)` complexity? | null |
easy.......python solution | k-th-smallest-prime-fraction | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom fractions import Fraction\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n sol_arr = []\n for i in range(len(arr)-1):\n for j in range(i+1,len(arr)):\n sol_arr.append(arr[i]/arr[j])\n sol_arr = sorted(sol_arr)\n smallest = sol_arr[k-1]\n sol = str(Fraction(str(smallest)).limit_denominator())\n numerator, denominator = sol.split("/")\n return [int(numerator), int(denominator)]\n``` | 1 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
[Explained] Easiest Python Solution | k-th-smallest-prime-fraction | 0 | 1 | # [Explained] Easiest Python Solution\n\nNote: It is not the most optimal solution, but it is easy and beginner friendly approach.\n```\nclass Solution:\n\n\tdef kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n\t\tif len(arr) > 2:\n\t\t\tres = [] # list for storing the list: [prime fraction of arr[i]/arr[j], arr[i], arr[j]]\n\n\t\t\tfor i in range(len(arr)):\n\t\t\t\tfor j in range(i + 1, len(arr)):\n\t\t\t\t\t# creating and adding the sublist to res\n\t\t\t\t\ttmp = [arr[i] / arr[j], arr[i], arr[j]]\n\t\t\t\t\tres.append(tmp)\n\n\t\t\t# sorting res on the basis of value of arr[i] \n\t\t\tres.sort(key=lambda x: x[0])\n\n\t\t\t# creating and returning the required list\n\t\t\treturn [res[k - 1][1], res[k - 1][2]]\n\t\telse:\n\t\t\treturn arr\n``` | 2 | You are given a sorted integer array `arr` containing `1` and **prime** numbers, where all the integers of `arr` are unique. You are also given an integer `k`.
For every `i` and `j` where `0 <= i < j < arr.length`, we consider the fraction `arr[i] / arr[j]`.
Return _the_ `kth` _smallest fraction considered_. Return your answer as an array of integers of size `2`, where `answer[0] == arr[i]` and `answer[1] == arr[j]`.
**Example 1:**
**Input:** arr = \[1,2,3,5\], k = 3
**Output:** \[2,5\]
**Explanation:** The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, and 2/3.
The third fraction is 2/5.
**Example 2:**
**Input:** arr = \[1,7\], k = 1
**Output:** \[1,7\]
**Constraints:**
* `2 <= arr.length <= 1000`
* `1 <= arr[i] <= 3 * 104`
* `arr[0] == 1`
* `arr[i]` is a **prime** number for `i > 0`.
* All the numbers of `arr` are **unique** and sorted in **strictly increasing** order.
* `1 <= k <= arr.length * (arr.length - 1) / 2`
**Follow up:** Can you solve the problem with better than `O(n2)` complexity? | null |
[Explained] Easiest Python Solution | k-th-smallest-prime-fraction | 0 | 1 | # [Explained] Easiest Python Solution\n\nNote: It is not the most optimal solution, but it is easy and beginner friendly approach.\n```\nclass Solution:\n\n\tdef kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n\t\tif len(arr) > 2:\n\t\t\tres = [] # list for storing the list: [prime fraction of arr[i]/arr[j], arr[i], arr[j]]\n\n\t\t\tfor i in range(len(arr)):\n\t\t\t\tfor j in range(i + 1, len(arr)):\n\t\t\t\t\t# creating and adding the sublist to res\n\t\t\t\t\ttmp = [arr[i] / arr[j], arr[i], arr[j]]\n\t\t\t\t\tres.append(tmp)\n\n\t\t\t# sorting res on the basis of value of arr[i] \n\t\t\tres.sort(key=lambda x: x[0])\n\n\t\t\t# creating and returning the required list\n\t\t\treturn [res[k - 1][1], res[k - 1][2]]\n\t\telse:\n\t\t\treturn arr\n``` | 2 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
[Python 3] MaxHeap | k-th-smallest-prime-fraction | 0 | 1 | ```\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n res = []\n \n for i in range(len(arr)):\n for j in range(i + 1, len(arr)):\n heappush(res, (-(arr[i] / arr[j]), arr[i], arr[j]))\n \n if len(res) > k:\n heappop(res)\n \n return [res[0][1], res[0][2]]\n``` | 5 | You are given a sorted integer array `arr` containing `1` and **prime** numbers, where all the integers of `arr` are unique. You are also given an integer `k`.
For every `i` and `j` where `0 <= i < j < arr.length`, we consider the fraction `arr[i] / arr[j]`.
Return _the_ `kth` _smallest fraction considered_. Return your answer as an array of integers of size `2`, where `answer[0] == arr[i]` and `answer[1] == arr[j]`.
**Example 1:**
**Input:** arr = \[1,2,3,5\], k = 3
**Output:** \[2,5\]
**Explanation:** The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, and 2/3.
The third fraction is 2/5.
**Example 2:**
**Input:** arr = \[1,7\], k = 1
**Output:** \[1,7\]
**Constraints:**
* `2 <= arr.length <= 1000`
* `1 <= arr[i] <= 3 * 104`
* `arr[0] == 1`
* `arr[i]` is a **prime** number for `i > 0`.
* All the numbers of `arr` are **unique** and sorted in **strictly increasing** order.
* `1 <= k <= arr.length * (arr.length - 1) / 2`
**Follow up:** Can you solve the problem with better than `O(n2)` complexity? | null |
[Python 3] MaxHeap | k-th-smallest-prime-fraction | 0 | 1 | ```\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n res = []\n \n for i in range(len(arr)):\n for j in range(i + 1, len(arr)):\n heappush(res, (-(arr[i] / arr[j]), arr[i], arr[j]))\n \n if len(res) > k:\n heappop(res)\n \n return [res[0][1], res[0][2]]\n``` | 5 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Binary Search + Sliding Window (Beats 91.21%) | k-th-smallest-prime-fraction | 0 | 1 | # Intuition\n\nBinary search the possible range of fraction `[0, 1]`. For each possible value `v`, we use sliding window (two pointers) to count the number (`cnt`) of fractions < v, as well as record the largest fraction `l/r` that is < v.\n\nDuring binary search, when `cnt == k` we can return the result `[l, r]`.\n\n# Complexity\n- Time complexity: O(NlogW), where N is array size, and W is the range size between the smallest and the largest fraction, in float number space.\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n N = len(arr)\n def count_less(v):\n """1. the number of fractions < v\n 2. the largest fraction l/r that is < v"""\n li = 0\n cnt, l, r = 0, arr[0], arr[-1]\n for ri in range(1, N):\n while li < ri and arr[li]/arr[ri] < v:\n if arr[li]/arr[ri] > l/r:\n l, r = arr[li], arr[ri]\n li += 1\n cnt += li\n return cnt, l, r\n\n lo, hi = arr[0]/arr[-1], 1\n while lo <= hi:\n v = (lo+hi)/2\n cnt, l, r = count_less(v)\n if cnt == k:\n return [l, r]\n if cnt < k:\n lo = v\n else:\n hi = v\n``` | 4 | You are given a sorted integer array `arr` containing `1` and **prime** numbers, where all the integers of `arr` are unique. You are also given an integer `k`.
For every `i` and `j` where `0 <= i < j < arr.length`, we consider the fraction `arr[i] / arr[j]`.
Return _the_ `kth` _smallest fraction considered_. Return your answer as an array of integers of size `2`, where `answer[0] == arr[i]` and `answer[1] == arr[j]`.
**Example 1:**
**Input:** arr = \[1,2,3,5\], k = 3
**Output:** \[2,5\]
**Explanation:** The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, and 2/3.
The third fraction is 2/5.
**Example 2:**
**Input:** arr = \[1,7\], k = 1
**Output:** \[1,7\]
**Constraints:**
* `2 <= arr.length <= 1000`
* `1 <= arr[i] <= 3 * 104`
* `arr[0] == 1`
* `arr[i]` is a **prime** number for `i > 0`.
* All the numbers of `arr` are **unique** and sorted in **strictly increasing** order.
* `1 <= k <= arr.length * (arr.length - 1) / 2`
**Follow up:** Can you solve the problem with better than `O(n2)` complexity? | null |
Binary Search + Sliding Window (Beats 91.21%) | k-th-smallest-prime-fraction | 0 | 1 | # Intuition\n\nBinary search the possible range of fraction `[0, 1]`. For each possible value `v`, we use sliding window (two pointers) to count the number (`cnt`) of fractions < v, as well as record the largest fraction `l/r` that is < v.\n\nDuring binary search, when `cnt == k` we can return the result `[l, r]`.\n\n# Complexity\n- Time complexity: O(NlogW), where N is array size, and W is the range size between the smallest and the largest fraction, in float number space.\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n N = len(arr)\n def count_less(v):\n """1. the number of fractions < v\n 2. the largest fraction l/r that is < v"""\n li = 0\n cnt, l, r = 0, arr[0], arr[-1]\n for ri in range(1, N):\n while li < ri and arr[li]/arr[ri] < v:\n if arr[li]/arr[ri] > l/r:\n l, r = arr[li], arr[ri]\n li += 1\n cnt += li\n return cnt, l, r\n\n lo, hi = arr[0]/arr[-1], 1\n while lo <= hi:\n v = (lo+hi)/2\n cnt, l, r = count_less(v)\n if cnt == k:\n return [l, r]\n if cnt < k:\n lo = v\n else:\n hi = v\n``` | 4 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Python3 | Solved Using Sorting and Trying Every Possible Pairings | k-th-smallest-prime-fraction | 0 | 1 | ```\nclass Solution:\n #Time-Complexity: O(n^2 + n^2log(n^2)) -> O(n^2*log(n^2)) ->O(n^2*log(n))\n #Space-Complexity: O(n^2)\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n array = []\n for i in range(0, len(arr)-1):\n numerator = arr[i]\n for j in range(i+1, len(arr)):\n denominator = arr[j]\n division = numerator / denominator\n array.append([numerator, denominator, division])\n array.sort(key = lambda x : x[2])\n ans = []\n ans.append(array[k-1][0])\n ans.append(array[k-1][1])\n return ans | 0 | You are given a sorted integer array `arr` containing `1` and **prime** numbers, where all the integers of `arr` are unique. You are also given an integer `k`.
For every `i` and `j` where `0 <= i < j < arr.length`, we consider the fraction `arr[i] / arr[j]`.
Return _the_ `kth` _smallest fraction considered_. Return your answer as an array of integers of size `2`, where `answer[0] == arr[i]` and `answer[1] == arr[j]`.
**Example 1:**
**Input:** arr = \[1,2,3,5\], k = 3
**Output:** \[2,5\]
**Explanation:** The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, and 2/3.
The third fraction is 2/5.
**Example 2:**
**Input:** arr = \[1,7\], k = 1
**Output:** \[1,7\]
**Constraints:**
* `2 <= arr.length <= 1000`
* `1 <= arr[i] <= 3 * 104`
* `arr[0] == 1`
* `arr[i]` is a **prime** number for `i > 0`.
* All the numbers of `arr` are **unique** and sorted in **strictly increasing** order.
* `1 <= k <= arr.length * (arr.length - 1) / 2`
**Follow up:** Can you solve the problem with better than `O(n2)` complexity? | null |
Python3 | Solved Using Sorting and Trying Every Possible Pairings | k-th-smallest-prime-fraction | 0 | 1 | ```\nclass Solution:\n #Time-Complexity: O(n^2 + n^2log(n^2)) -> O(n^2*log(n^2)) ->O(n^2*log(n))\n #Space-Complexity: O(n^2)\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n array = []\n for i in range(0, len(arr)-1):\n numerator = arr[i]\n for j in range(i+1, len(arr)):\n denominator = arr[j]\n division = numerator / denominator\n array.append([numerator, denominator, division])\n array.sort(key = lambda x : x[2])\n ans = []\n ans.append(array[k-1][0])\n ans.append(array[k-1][1])\n return ans | 0 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Python3 easy solution (beats 78.8%) | k-th-smallest-prime-fraction | 0 | 1 | # Code\n```\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n consider = []\n n = len(arr)\n\n for i in range(n):\n for j in range(max(n-k,i+1),n):\n consider.append((arr[i],arr[j]))\n\n consider.sort(key=lambda x: x[0]/x[1])\n return consider[k-1]\n``` | 1 | You are given a sorted integer array `arr` containing `1` and **prime** numbers, where all the integers of `arr` are unique. You are also given an integer `k`.
For every `i` and `j` where `0 <= i < j < arr.length`, we consider the fraction `arr[i] / arr[j]`.
Return _the_ `kth` _smallest fraction considered_. Return your answer as an array of integers of size `2`, where `answer[0] == arr[i]` and `answer[1] == arr[j]`.
**Example 1:**
**Input:** arr = \[1,2,3,5\], k = 3
**Output:** \[2,5\]
**Explanation:** The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, and 2/3.
The third fraction is 2/5.
**Example 2:**
**Input:** arr = \[1,7\], k = 1
**Output:** \[1,7\]
**Constraints:**
* `2 <= arr.length <= 1000`
* `1 <= arr[i] <= 3 * 104`
* `arr[0] == 1`
* `arr[i]` is a **prime** number for `i > 0`.
* All the numbers of `arr` are **unique** and sorted in **strictly increasing** order.
* `1 <= k <= arr.length * (arr.length - 1) / 2`
**Follow up:** Can you solve the problem with better than `O(n2)` complexity? | null |
Python3 easy solution (beats 78.8%) | k-th-smallest-prime-fraction | 0 | 1 | # Code\n```\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n consider = []\n n = len(arr)\n\n for i in range(n):\n for j in range(max(n-k,i+1),n):\n consider.append((arr[i],arr[j]))\n\n consider.sort(key=lambda x: x[0]/x[1])\n return consider[k-1]\n``` | 1 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Python with heap. Don't need to put all N^2 pairs into heap | k-th-smallest-prime-fraction | 0 | 1 | # Intuition\nPut at most len(arr)-1 pairs into heap. Put a new pair in for every pair popped.\n\nE.g \n[1,3,4,5,7,11,13,17] (8 numbers)\nk = 2\n\nDo you really need to put all 64 pairs in????? NOO\nk = 2 so its either [1, 17], [3, 17] or [1, 13]\nSo you put [1,17], [3, 17] into heap.\n\nTake [1,17] from heap, put [1, 13] into heap \nThen take [1,13] from heap and THERE YOU GOOOOOOOO \n\n# Code\n```\nfrom heapq import heappush, heappop\n\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n heap = []\n\n for i in range(min(len(arr)-1, k)):\n heappush(heap, (arr[i]/arr[-1], i, len(arr)-1))\n\n for i in range(k-1):\n # x, y: index of elements in pair\n frac, x, y = heappop(heap)\n if y-1 > x:\n heappush(heap, (arr[x]/arr[y-1], x, y-1))\n\n _, n, d = heappop(heap)\n return [arr[n], arr[d]]\n``` | 0 | You are given a sorted integer array `arr` containing `1` and **prime** numbers, where all the integers of `arr` are unique. You are also given an integer `k`.
For every `i` and `j` where `0 <= i < j < arr.length`, we consider the fraction `arr[i] / arr[j]`.
Return _the_ `kth` _smallest fraction considered_. Return your answer as an array of integers of size `2`, where `answer[0] == arr[i]` and `answer[1] == arr[j]`.
**Example 1:**
**Input:** arr = \[1,2,3,5\], k = 3
**Output:** \[2,5\]
**Explanation:** The fractions to be considered in sorted order are:
1/5, 1/3, 2/5, 1/2, 3/5, and 2/3.
The third fraction is 2/5.
**Example 2:**
**Input:** arr = \[1,7\], k = 1
**Output:** \[1,7\]
**Constraints:**
* `2 <= arr.length <= 1000`
* `1 <= arr[i] <= 3 * 104`
* `arr[0] == 1`
* `arr[i]` is a **prime** number for `i > 0`.
* All the numbers of `arr` are **unique** and sorted in **strictly increasing** order.
* `1 <= k <= arr.length * (arr.length - 1) / 2`
**Follow up:** Can you solve the problem with better than `O(n2)` complexity? | null |
Python with heap. Don't need to put all N^2 pairs into heap | k-th-smallest-prime-fraction | 0 | 1 | # Intuition\nPut at most len(arr)-1 pairs into heap. Put a new pair in for every pair popped.\n\nE.g \n[1,3,4,5,7,11,13,17] (8 numbers)\nk = 2\n\nDo you really need to put all 64 pairs in????? NOO\nk = 2 so its either [1, 17], [3, 17] or [1, 13]\nSo you put [1,17], [3, 17] into heap.\n\nTake [1,17] from heap, put [1, 13] into heap \nThen take [1,13] from heap and THERE YOU GOOOOOOOO \n\n# Code\n```\nfrom heapq import heappush, heappop\n\nclass Solution:\n def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:\n heap = []\n\n for i in range(min(len(arr)-1, k)):\n heappush(heap, (arr[i]/arr[-1], i, len(arr)-1))\n\n for i in range(k-1):\n # x, y: index of elements in pair\n frac, x, y = heappop(heap)\n if y-1 > x:\n heappush(heap, (arr[x]/arr[y-1], x, y-1))\n\n _, n, d = heappop(heap)\n return [arr[n], arr[d]]\n``` | 0 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Solution | cheapest-flights-within-k-stops | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {\n vector<pair<int,int>>adj[n];\n int edges = flights.size();\n for(int i=0; i<edges; i++) {\n int u = flights[i][0];\n int v = flights[i][1];\n int w = flights[i][2];\n adj[u].push_back({v,w});\n }\n vector<int> dist(n, numeric_limits<int>::max());\n queue<pair<int, int>> q;\n q.push({src, 0});\n int stops = 0;\n\n while (stops <= k && !q.empty()) {\n int sz = q.size();\n while (sz--) {\n auto [node, distance] = q.front();\n q.pop();\n for (auto& [neighbour, price] : adj[node]) {\n if (price + distance < dist[neighbour]) {\n dist[neighbour] = price + distance;\n q.push({neighbour, dist[neighbour]});\n }\n }\n }\n stops++;\n }\n return dist[dst] == numeric_limits<int>::max() ? -1 : dist[dst];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:\n adjList = defaultdict(list)\n for flight in flights:\n adjList[flight[0]].append(flight[1:])\n\n cost = [inf] * n\n cost[src] = 0\n q = deque([(src, cost[src])])\n steps = -1\n while steps < k and len(q):\n size = len(q)\n print(q)\n while size:\n curr, curr_cost = q.popleft()\n for nei, path_cost in adjList[curr]:\n if curr_cost + path_cost < cost[nei]:\n q.append((nei, curr_cost + path_cost))\n cost[nei] = curr_cost + path_cost\n size -= 1\n steps += 1\n \n if cost[dst] != inf:\n return cost[dst]\n return -1\n```\n\n```Java []\nclass Solution {\n public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {\n int[] distance = new int[n];\n Arrays.fill(distance, Integer.MAX_VALUE);\n distance[src] = 0;\n for (int i = 0; i <= k; i++) {\n if (isRoutePossible(distance, flights)) {\n break;\n }\n }\n return distance[dst] == Integer.MAX_VALUE ? -1 : distance[dst];\n }\n private boolean isRoutePossible(int[] dist, int[][] flights) {\n int[] copy = Arrays.copyOf(dist, dist.length);\n boolean result = true;\n\n for (int[] flight : flights) {\n int src = flight[0];\n int dst = flight[1];\n int cost = flight[2];\n\n if (copy[src] < Integer.MAX_VALUE && dist[dst] > dist[src] + cost) {\n dist[dst] = cost + copy[src];\n result = false;\n }\n }\n return result;\n }\n}\n```\n | 1 | There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i] = [fromi, toi, pricei]` indicates that there is a flight from city `fromi` to city `toi` with cost `pricei`.
You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
**Example 1:**
**Input:** n = 4, flights = \[\[0,1,100\],\[1,2,100\],\[2,0,100\],\[1,3,600\],\[2,3,200\]\], src = 0, dst = 3, k = 1
**Output:** 700
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities \[0,1,2,3\] is cheaper but is invalid because it uses 2 stops.
**Example 2:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 1
**Output:** 200
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
**Example 3:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 0
**Output:** 500
**Explanation:**
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
**Constraints:**
* `1 <= n <= 100`
* `0 <= flights.length <= (n * (n - 1) / 2)`
* `flights[i].length == 3`
* `0 <= fromi, toi < n`
* `fromi != toi`
* `1 <= pricei <= 104`
* There will not be any multiple flights between two cities.
* `0 <= src, dst, k < n`
* `src != dst` | Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move. |
Solution | cheapest-flights-within-k-stops | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {\n vector<pair<int,int>>adj[n];\n int edges = flights.size();\n for(int i=0; i<edges; i++) {\n int u = flights[i][0];\n int v = flights[i][1];\n int w = flights[i][2];\n adj[u].push_back({v,w});\n }\n vector<int> dist(n, numeric_limits<int>::max());\n queue<pair<int, int>> q;\n q.push({src, 0});\n int stops = 0;\n\n while (stops <= k && !q.empty()) {\n int sz = q.size();\n while (sz--) {\n auto [node, distance] = q.front();\n q.pop();\n for (auto& [neighbour, price] : adj[node]) {\n if (price + distance < dist[neighbour]) {\n dist[neighbour] = price + distance;\n q.push({neighbour, dist[neighbour]});\n }\n }\n }\n stops++;\n }\n return dist[dst] == numeric_limits<int>::max() ? -1 : dist[dst];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:\n adjList = defaultdict(list)\n for flight in flights:\n adjList[flight[0]].append(flight[1:])\n\n cost = [inf] * n\n cost[src] = 0\n q = deque([(src, cost[src])])\n steps = -1\n while steps < k and len(q):\n size = len(q)\n print(q)\n while size:\n curr, curr_cost = q.popleft()\n for nei, path_cost in adjList[curr]:\n if curr_cost + path_cost < cost[nei]:\n q.append((nei, curr_cost + path_cost))\n cost[nei] = curr_cost + path_cost\n size -= 1\n steps += 1\n \n if cost[dst] != inf:\n return cost[dst]\n return -1\n```\n\n```Java []\nclass Solution {\n public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {\n int[] distance = new int[n];\n Arrays.fill(distance, Integer.MAX_VALUE);\n distance[src] = 0;\n for (int i = 0; i <= k; i++) {\n if (isRoutePossible(distance, flights)) {\n break;\n }\n }\n return distance[dst] == Integer.MAX_VALUE ? -1 : distance[dst];\n }\n private boolean isRoutePossible(int[] dist, int[][] flights) {\n int[] copy = Arrays.copyOf(dist, dist.length);\n boolean result = true;\n\n for (int[] flight : flights) {\n int src = flight[0];\n int dst = flight[1];\n int cost = flight[2];\n\n if (copy[src] < Integer.MAX_VALUE && dist[dst] > dist[src] + cost) {\n dist[dst] = cost + copy[src];\n result = false;\n }\n }\n return result;\n }\n}\n```\n | 1 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
SIMPLE PYTHON SOLUTION USING HEAP SORT | cheapest-flights-within-k-stops | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(KLOGN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:\n grid=[[] for i in range(n)]\n for frm,to,cst in flights:\n grid[frm].append((cst,to))\n \n st=[(0,0,src)]\n heapq.heapify(st)\n css=[(float("infinity"),float("infinity"))]*n\n css[src]=(0,0)\n while st:\n cst,stop,x=heapq.heappop(st)\n if x==dst:\n return cst\n if stop<=k:\n for ct,to in grid[x]:\n if css[to][0]>ct+cst or css[to][1]>stop+1:\n css[to]=(ct+cst,stop+1)\n heapq.heappush(st,(cst+ct,stop+1,to))\n\n return -1\n\n\n \n``` | 1 | There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i] = [fromi, toi, pricei]` indicates that there is a flight from city `fromi` to city `toi` with cost `pricei`.
You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
**Example 1:**
**Input:** n = 4, flights = \[\[0,1,100\],\[1,2,100\],\[2,0,100\],\[1,3,600\],\[2,3,200\]\], src = 0, dst = 3, k = 1
**Output:** 700
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities \[0,1,2,3\] is cheaper but is invalid because it uses 2 stops.
**Example 2:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 1
**Output:** 200
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
**Example 3:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 0
**Output:** 500
**Explanation:**
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
**Constraints:**
* `1 <= n <= 100`
* `0 <= flights.length <= (n * (n - 1) / 2)`
* `flights[i].length == 3`
* `0 <= fromi, toi < n`
* `fromi != toi`
* `1 <= pricei <= 104`
* There will not be any multiple flights between two cities.
* `0 <= src, dst, k < n`
* `src != dst` | Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move. |
SIMPLE PYTHON SOLUTION USING HEAP SORT | cheapest-flights-within-k-stops | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(KLOGN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\n\nclass Solution:\n def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:\n grid=[[] for i in range(n)]\n for frm,to,cst in flights:\n grid[frm].append((cst,to))\n \n st=[(0,0,src)]\n heapq.heapify(st)\n css=[(float("infinity"),float("infinity"))]*n\n css[src]=(0,0)\n while st:\n cst,stop,x=heapq.heappop(st)\n if x==dst:\n return cst\n if stop<=k:\n for ct,to in grid[x]:\n if css[to][0]>ct+cst or css[to][1]>stop+1:\n css[to]=(ct+cst,stop+1)\n heapq.heappush(st,(cst+ct,stop+1,to))\n\n return -1\n\n\n \n``` | 1 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
Python BFS solution | cheapest-flights-within-k-stops | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nK stops means we can do K+1 times bfs.\nKeep track the shortest price to each node, if there are cheaper ways to reach the node, update the cost.\n\n# Code\n```\nclass Solution:\n def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:\n graph = defaultdict(dict)\n for s,e,p in flights:\n graph[s][e] = p\n cost = [math.inf for _ in range(n)]\n q = deque([[src, 0]])\n for _ in range(k+1):\n size = len(q)\n for _ in range(size):\n [ele, curCost] = q.popleft()\n for nextNode in graph[ele]:\n nextNodePrice = curCost+graph[ele][nextNode]\n if nextNodePrice<cost[nextNode]:\n cost[nextNode] = nextNodePrice\n q.append([nextNode, nextNodePrice])\n if cost[dst]==math.inf:\n return -1\n return cost[dst]\n\n``` | 1 | There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i] = [fromi, toi, pricei]` indicates that there is a flight from city `fromi` to city `toi` with cost `pricei`.
You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
**Example 1:**
**Input:** n = 4, flights = \[\[0,1,100\],\[1,2,100\],\[2,0,100\],\[1,3,600\],\[2,3,200\]\], src = 0, dst = 3, k = 1
**Output:** 700
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities \[0,1,2,3\] is cheaper but is invalid because it uses 2 stops.
**Example 2:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 1
**Output:** 200
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
**Example 3:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 0
**Output:** 500
**Explanation:**
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
**Constraints:**
* `1 <= n <= 100`
* `0 <= flights.length <= (n * (n - 1) / 2)`
* `flights[i].length == 3`
* `0 <= fromi, toi < n`
* `fromi != toi`
* `1 <= pricei <= 104`
* There will not be any multiple flights between two cities.
* `0 <= src, dst, k < n`
* `src != dst` | Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move. |
Python BFS solution | cheapest-flights-within-k-stops | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nK stops means we can do K+1 times bfs.\nKeep track the shortest price to each node, if there are cheaper ways to reach the node, update the cost.\n\n# Code\n```\nclass Solution:\n def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:\n graph = defaultdict(dict)\n for s,e,p in flights:\n graph[s][e] = p\n cost = [math.inf for _ in range(n)]\n q = deque([[src, 0]])\n for _ in range(k+1):\n size = len(q)\n for _ in range(size):\n [ele, curCost] = q.popleft()\n for nextNode in graph[ele]:\n nextNodePrice = curCost+graph[ele][nextNode]\n if nextNodePrice<cost[nextNode]:\n cost[nextNode] = nextNodePrice\n q.append([nextNode, nextNodePrice])\n if cost[dst]==math.inf:\n return -1\n return cost[dst]\n\n``` | 1 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
Intuitive Heap Approach | cheapest-flights-within-k-stops | 0 | 1 | Maintain a heap to store all the upcoming nodes to visit (currentPrice, currentNode, currentSteps). Steps is to determine the number of stops so far and this number cannot exceed k. When you visit a node, mark it as visited and push all of its neighbors into our current heap. If you meet the destination, update the result variable and continue searching (the minimum result may appear later while travering the graph). After you visit a node and its step is k, remove it out of the visited set as it can be included in another path that contain your minimum cost.\n\n# Code\n```\nclass Solution:\n def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:\n graph = [[] for _ in range(n)]\n for s, d, p in flights:\n graph[s].append((d, p))\n \n heap = [(0, src, 0)]\n visited = set()\n res = float(\'inf\')\n while len(heap):\n currentPrice, current, steps = heappop(heap)\n # mark the current node as visited\n visited.add(current)\n for neighbor, price in graph[current]:\n if neighbor not in visited:\n if neighbor == dst and steps <= k: \n # meet the destination, update result and continue searching\n res = min(res, currentPrice + price)\n continue\n # not worth pushing neighbor that exceeds k stops\n if steps < k: heappush(heap, (currentPrice+price, neighbor, steps+1))\n # if after visiting a node and current steps is k, remove it out of the visited set so that other nodes can revisit the this node again\n if steps == k: visited.remove(current)\n return res if res != float(\'inf\') else -1\n``` | 1 | There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i] = [fromi, toi, pricei]` indicates that there is a flight from city `fromi` to city `toi` with cost `pricei`.
You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
**Example 1:**
**Input:** n = 4, flights = \[\[0,1,100\],\[1,2,100\],\[2,0,100\],\[1,3,600\],\[2,3,200\]\], src = 0, dst = 3, k = 1
**Output:** 700
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities \[0,1,2,3\] is cheaper but is invalid because it uses 2 stops.
**Example 2:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 1
**Output:** 200
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
**Example 3:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 0
**Output:** 500
**Explanation:**
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
**Constraints:**
* `1 <= n <= 100`
* `0 <= flights.length <= (n * (n - 1) / 2)`
* `flights[i].length == 3`
* `0 <= fromi, toi < n`
* `fromi != toi`
* `1 <= pricei <= 104`
* There will not be any multiple flights between two cities.
* `0 <= src, dst, k < n`
* `src != dst` | Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move. |
Intuitive Heap Approach | cheapest-flights-within-k-stops | 0 | 1 | Maintain a heap to store all the upcoming nodes to visit (currentPrice, currentNode, currentSteps). Steps is to determine the number of stops so far and this number cannot exceed k. When you visit a node, mark it as visited and push all of its neighbors into our current heap. If you meet the destination, update the result variable and continue searching (the minimum result may appear later while travering the graph). After you visit a node and its step is k, remove it out of the visited set as it can be included in another path that contain your minimum cost.\n\n# Code\n```\nclass Solution:\n def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:\n graph = [[] for _ in range(n)]\n for s, d, p in flights:\n graph[s].append((d, p))\n \n heap = [(0, src, 0)]\n visited = set()\n res = float(\'inf\')\n while len(heap):\n currentPrice, current, steps = heappop(heap)\n # mark the current node as visited\n visited.add(current)\n for neighbor, price in graph[current]:\n if neighbor not in visited:\n if neighbor == dst and steps <= k: \n # meet the destination, update result and continue searching\n res = min(res, currentPrice + price)\n continue\n # not worth pushing neighbor that exceeds k stops\n if steps < k: heappush(heap, (currentPrice+price, neighbor, steps+1))\n # if after visiting a node and current steps is k, remove it out of the visited set so that other nodes can revisit the this node again\n if steps == k: visited.remove(current)\n return res if res != float(\'inf\') else -1\n``` | 1 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
My simply python BFS solution. | cheapest-flights-within-k-stops | 0 | 1 | \n# Complexity\n- Time complexity: $$O(n*k)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findCheapestPrice(self, n, flights, src, dst, k):\n adj = [[] for _ in range(n)]\n dis = [float("inf")]*n; dis[src] = 0\n\n for a,b,c in flights:\n adj[a].append((b,c))\n\n q = deque([(src,0)])\n for _ in range(k+1):\n for _ in range(len(q)):\n cur,cur_dis = q.popleft()\n for neigh,neigh_dis in adj[cur]:\n if cur_dis+neigh_dis < dis[neigh]:\n dis[neigh] = cur_dis+neigh_dis\n q.append((neigh,dis[neigh]))\n\n return -1 if dis[dst] == float("inf") else dis[dst]\n\n``` | 1 | There are `n` cities connected by some number of flights. You are given an array `flights` where `flights[i] = [fromi, toi, pricei]` indicates that there is a flight from city `fromi` to city `toi` with cost `pricei`.
You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.
**Example 1:**
**Input:** n = 4, flights = \[\[0,1,100\],\[1,2,100\],\[2,0,100\],\[1,3,600\],\[2,3,200\]\], src = 0, dst = 3, k = 1
**Output:** 700
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities \[0,1,2,3\] is cheaper but is invalid because it uses 2 stops.
**Example 2:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 1
**Output:** 200
**Explanation:**
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
**Example 3:**
**Input:** n = 3, flights = \[\[0,1,100\],\[1,2,100\],\[0,2,500\]\], src = 0, dst = 2, k = 0
**Output:** 500
**Explanation:**
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
**Constraints:**
* `1 <= n <= 100`
* `0 <= flights.length <= (n * (n - 1) / 2)`
* `flights[i].length == 3`
* `0 <= fromi, toi < n`
* `fromi != toi`
* `1 <= pricei <= 104`
* There will not be any multiple flights between two cities.
* `0 <= src, dst, k < n`
* `src != dst` | Perform a breadth-first-search, where the nodes are the puzzle boards and edges are if two puzzle boards can be transformed into one another with one move. |
My simply python BFS solution. | cheapest-flights-within-k-stops | 0 | 1 | \n# Complexity\n- Time complexity: $$O(n*k)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findCheapestPrice(self, n, flights, src, dst, k):\n adj = [[] for _ in range(n)]\n dis = [float("inf")]*n; dis[src] = 0\n\n for a,b,c in flights:\n adj[a].append((b,c))\n\n q = deque([(src,0)])\n for _ in range(k+1):\n for _ in range(len(q)):\n cur,cur_dis = q.popleft()\n for neigh,neigh_dis in adj[cur]:\n if cur_dis+neigh_dis < dis[neigh]:\n dis[neigh] = cur_dis+neigh_dis\n q.append((neigh,dis[neigh]))\n\n return -1 if dis[dst] == float("inf") else dis[dst]\n\n``` | 1 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
Easy Understandable Python Code | rotated-digits | 0 | 1 | \n\n# Approach\n- Valid if N contains ATLEAST ```ONE 2, 5, 6, 9```\n AND ``` NO 3, 4 or 7```\n\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n invalid = [3,4,7]\n good = 0\n check = False\n\n for i in range(1,n+1):\n j = i\n \n while j != 0:\n d = j % 10\n \n if d == 2 or d == 5 or d == 6 or d == 9:\n check = True\n \n elif d in invalid:\n check = False\n break\n \n j = j // 10\n\n if check:\n good += 1\n\n check = False \n \n return good\n``` | 4 | An integer `x` is a **good** if after rotating each digit individually by 180 degrees, we get a valid number that is different from `x`. Each digit must be rotated - we cannot choose to leave it alone.
A number is valid if each digit remains a digit after rotation. For example:
* `0`, `1`, and `8` rotate to themselves,
* `2` and `5` rotate to each other (in this case they are rotated in a different direction, in other words, `2` or `5` gets mirrored),
* `6` and `9` rotate to each other, and
* the rest of the numbers do not rotate to any other number and become invalid.
Given an integer `n`, return _the number of **good** integers in the range_ `[1, n]`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are four good numbers in the range \[1, 10\] : 2, 5, 6, 9.
Note that 1 and 10 are not good numbers, since they remain unchanged after rotating.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Example 3:**
**Input:** n = 2
**Output:** 1
**Constraints:**
* `1 <= n <= 104` | Use a binary search. We'll binary search the monotone function "possible(D) = can we use K or less gas stations to ensure each adjacent distance between gas stations is at most D?" |
Easy Understandable Python Code | rotated-digits | 0 | 1 | \n\n# Approach\n- Valid if N contains ATLEAST ```ONE 2, 5, 6, 9```\n AND ``` NO 3, 4 or 7```\n\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n invalid = [3,4,7]\n good = 0\n check = False\n\n for i in range(1,n+1):\n j = i\n \n while j != 0:\n d = j % 10\n \n if d == 2 or d == 5 or d == 6 or d == 9:\n check = True\n \n elif d in invalid:\n check = False\n break\n \n j = j // 10\n\n if check:\n good += 1\n\n check = False \n \n return good\n``` | 4 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
O(nLogbase10n):Time|O(1):Space|Dict | rotated-digits | 0 | 1 | # Intuition\n## PLEASE UPVOTE \nThe goal of the "rotatedDigits" function is to count how many numbers in the range from 1 to n are considered "good" after a specific type of digit rotation. A number is considered "good" if, after rotating its digits, it becomes a different number. Rotating a number means replacing its digits with other digits in a way that results in a valid and different number. For example, 2 becomes 5, and 6 becomes 9, while 1, 8, and 0 remain unchanged. Additionally, a "good" number should not contain any of the "invalid" digits: 3, 4, or 7.\n\n# Approach\nCreate a dictionary dict that maps each digit to its rotated counterpart. For example, 2 maps to 5, 5 maps to 2, 6 maps to 9, 8 maps to 8, and 9 maps to 6. Digits not in this dictionary (0, 1) are self-rotating, meaning they remain unchanged.\n\nCreate a list invalid containing the digits 3, 4, and 7, which are considered "invalid."\n\nDefine a helper function isValid(num) to check if a given number is "good" according to the rules described. It iterates through the digits of the number, checking if any of them are in the list of invalid digits or if any digit changes after rotation. If any of these conditions are met, the number is considered "good."\n\nInitialize a variable ans to 0. This variable will be used to count the "good" numbers in the range from 1 to n.\n\nLoop through numbers from 1 to n, and for each number, call the isValid function to determine if it\'s "good." If it is, increment the ans counter.\n\nReturn the final count ans, which represents the number of "good" numbers in the range from 1 to n.\n\nLet\'s break down the code step by step and explain each part in detail.\n\n```python\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n```\nThis code defines a class named `Solution` and a method called `rotatedDigits`. The `rotatedDigits` method takes an integer `n` as an argument and returns an integer.\n\n```python\n dict = {0:0,1:1,2:5,5:2,6:9,8:8,9:6}\n```\nHere, a dictionary named `dict` is defined. This dictionary is used to map each digit to its corresponding digit after rotation. For example, `0` remains `0`, `1` remains `1`, `2` becomes `5`, `5` becomes `2`, `6` becomes `9`, `8` remains `8`, and `9` becomes `6`. This mapping is used to determine if a digit is valid or not.\n\n```python\n invalid = [3,4,7]\n```\nAn array named `invalid` is defined, containing the digits `3`, `4`, and `7`. These digits are considered invalid because they do not change when rotated, so they are not considered valid numbers.\n\n```python\n def isValid(num):\n flag = 0\n```\nA function named `isValid` is defined, which takes an integer `num` as an argument. The function initializes a variable `flag` to `0`.\n\n```python\n while num:\n```\nThe function enters a `while` loop, which continues until `num` becomes zero.\n\n```python\n val = num % 10\n```\nInside the loop, `val` is assigned the last digit of `num` by taking the remainder of `num` divided by `10`.\n\n```python\n if val in invalid:\n flag = 0\n break\n```\nThe code checks if the value of `val` is in the `invalid` list. If it is, the `flag` is set to `0`, and the loop is exited. This indicates that the number is not valid.\n\n```python\n else:\n if val != dict[val]:\n flag = 1\n```\nIf the `val` is not in the `invalid` list, it checks if the rotated value of `val` (as defined in the `dict`) is different from the original value of `val`. If they are different, it sets the `flag` to `1`, indicating that this digit is part of a valid number.\n\n```python\n num = num // 10\n```\nAfter processing the last digit, the code removes the last digit by performing integer division by `10`. This effectively moves to the next digit in the number.\n\n```python\n return flag\n```\nAfter the loop finishes, the function returns the `flag`, indicating whether the entire number is valid or not.\n\n```python\n ans = 0\n```\nThe variable `ans` is initialized to `0`. This variable will be used to keep track of the count of valid numbers.\n\n```python\n for i in range(1, n + 1):\n```\nA `for` loop is used to iterate through numbers from 1 to `n`, inclusive.\n\n```python\n ans = ans + isValid(i)\n```\nFor each number `i` in the range, the `isValid` function is called to check if `i` is a valid number. If it\'s valid (the `isValid` function returns `1`), the `ans` variable is incremented by `1`.\n\n```python\n return ans\n```\nAfter processing all numbers in the range, the function returns the value of `ans`, which represents the count of valid numbers in the range from 1 to `n`.\n\n# Complexity\n- Time Complexity:\nThe time complexity of this solution is O(n * d), where n is the input number n, and d is the number of digits in the largest number in the range (log10(n)). The loop iterates through all numbers from 1 to n, and for each number, the isValid function checks each of its digits, which takes O(d) time.\n\n- Space Complexity:\nThe space complexity is O(1) because the size of the dictionary and the list of invalid digits is constant and independent of the input n.\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n # Define a dictionary to map digits to their rotated counterparts\n # For example, 0 maps to 0, 1 maps to 1, 2 maps to 5, and so on.\n # This dictionary will be used to determine if a number is valid or not.\n dict = {0: 0, 1: 1, 2: 5, 5: 2, 6: 9, 8: 8, 9: 6}\n\n # Define a list of invalid digits, which are 3, 4, and 7.\n invalid = [3, 4, 7]\n\n # Define a function to check if a number is valid\n def isValid(num):\n flag = 0 # Initialize a flag to 0\n while num:\n val = num % 10 # Get the last digit of the number\n if val in invalid:\n flag = 0 # If the digit is in the invalid list, the number is invalid\n break\n else:\n if val != dict[val]:\n flag = 1 # If the digit has a rotated counterpart, set the flag to 1\n num = num // 10 # Move to the next digit\n return flag # Return the flag (0 for invalid, 1 for valid)\n\n ans = 0 # Initialize a variable to count the number of valid numbers\n for i in range(1, n + 1): # Iterate through numbers from 1 to n (inclusive)\n ans = ans + isValid(i) # Check if the number is valid and increment the count\n return ans # Return the count of valid numbers \n``` | 1 | An integer `x` is a **good** if after rotating each digit individually by 180 degrees, we get a valid number that is different from `x`. Each digit must be rotated - we cannot choose to leave it alone.
A number is valid if each digit remains a digit after rotation. For example:
* `0`, `1`, and `8` rotate to themselves,
* `2` and `5` rotate to each other (in this case they are rotated in a different direction, in other words, `2` or `5` gets mirrored),
* `6` and `9` rotate to each other, and
* the rest of the numbers do not rotate to any other number and become invalid.
Given an integer `n`, return _the number of **good** integers in the range_ `[1, n]`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are four good numbers in the range \[1, 10\] : 2, 5, 6, 9.
Note that 1 and 10 are not good numbers, since they remain unchanged after rotating.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Example 3:**
**Input:** n = 2
**Output:** 1
**Constraints:**
* `1 <= n <= 104` | Use a binary search. We'll binary search the monotone function "possible(D) = can we use K or less gas stations to ensure each adjacent distance between gas stations is at most D?" |
O(nLogbase10n):Time|O(1):Space|Dict | rotated-digits | 0 | 1 | # Intuition\n## PLEASE UPVOTE \nThe goal of the "rotatedDigits" function is to count how many numbers in the range from 1 to n are considered "good" after a specific type of digit rotation. A number is considered "good" if, after rotating its digits, it becomes a different number. Rotating a number means replacing its digits with other digits in a way that results in a valid and different number. For example, 2 becomes 5, and 6 becomes 9, while 1, 8, and 0 remain unchanged. Additionally, a "good" number should not contain any of the "invalid" digits: 3, 4, or 7.\n\n# Approach\nCreate a dictionary dict that maps each digit to its rotated counterpart. For example, 2 maps to 5, 5 maps to 2, 6 maps to 9, 8 maps to 8, and 9 maps to 6. Digits not in this dictionary (0, 1) are self-rotating, meaning they remain unchanged.\n\nCreate a list invalid containing the digits 3, 4, and 7, which are considered "invalid."\n\nDefine a helper function isValid(num) to check if a given number is "good" according to the rules described. It iterates through the digits of the number, checking if any of them are in the list of invalid digits or if any digit changes after rotation. If any of these conditions are met, the number is considered "good."\n\nInitialize a variable ans to 0. This variable will be used to count the "good" numbers in the range from 1 to n.\n\nLoop through numbers from 1 to n, and for each number, call the isValid function to determine if it\'s "good." If it is, increment the ans counter.\n\nReturn the final count ans, which represents the number of "good" numbers in the range from 1 to n.\n\nLet\'s break down the code step by step and explain each part in detail.\n\n```python\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n```\nThis code defines a class named `Solution` and a method called `rotatedDigits`. The `rotatedDigits` method takes an integer `n` as an argument and returns an integer.\n\n```python\n dict = {0:0,1:1,2:5,5:2,6:9,8:8,9:6}\n```\nHere, a dictionary named `dict` is defined. This dictionary is used to map each digit to its corresponding digit after rotation. For example, `0` remains `0`, `1` remains `1`, `2` becomes `5`, `5` becomes `2`, `6` becomes `9`, `8` remains `8`, and `9` becomes `6`. This mapping is used to determine if a digit is valid or not.\n\n```python\n invalid = [3,4,7]\n```\nAn array named `invalid` is defined, containing the digits `3`, `4`, and `7`. These digits are considered invalid because they do not change when rotated, so they are not considered valid numbers.\n\n```python\n def isValid(num):\n flag = 0\n```\nA function named `isValid` is defined, which takes an integer `num` as an argument. The function initializes a variable `flag` to `0`.\n\n```python\n while num:\n```\nThe function enters a `while` loop, which continues until `num` becomes zero.\n\n```python\n val = num % 10\n```\nInside the loop, `val` is assigned the last digit of `num` by taking the remainder of `num` divided by `10`.\n\n```python\n if val in invalid:\n flag = 0\n break\n```\nThe code checks if the value of `val` is in the `invalid` list. If it is, the `flag` is set to `0`, and the loop is exited. This indicates that the number is not valid.\n\n```python\n else:\n if val != dict[val]:\n flag = 1\n```\nIf the `val` is not in the `invalid` list, it checks if the rotated value of `val` (as defined in the `dict`) is different from the original value of `val`. If they are different, it sets the `flag` to `1`, indicating that this digit is part of a valid number.\n\n```python\n num = num // 10\n```\nAfter processing the last digit, the code removes the last digit by performing integer division by `10`. This effectively moves to the next digit in the number.\n\n```python\n return flag\n```\nAfter the loop finishes, the function returns the `flag`, indicating whether the entire number is valid or not.\n\n```python\n ans = 0\n```\nThe variable `ans` is initialized to `0`. This variable will be used to keep track of the count of valid numbers.\n\n```python\n for i in range(1, n + 1):\n```\nA `for` loop is used to iterate through numbers from 1 to `n`, inclusive.\n\n```python\n ans = ans + isValid(i)\n```\nFor each number `i` in the range, the `isValid` function is called to check if `i` is a valid number. If it\'s valid (the `isValid` function returns `1`), the `ans` variable is incremented by `1`.\n\n```python\n return ans\n```\nAfter processing all numbers in the range, the function returns the value of `ans`, which represents the count of valid numbers in the range from 1 to `n`.\n\n# Complexity\n- Time Complexity:\nThe time complexity of this solution is O(n * d), where n is the input number n, and d is the number of digits in the largest number in the range (log10(n)). The loop iterates through all numbers from 1 to n, and for each number, the isValid function checks each of its digits, which takes O(d) time.\n\n- Space Complexity:\nThe space complexity is O(1) because the size of the dictionary and the list of invalid digits is constant and independent of the input n.\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n # Define a dictionary to map digits to their rotated counterparts\n # For example, 0 maps to 0, 1 maps to 1, 2 maps to 5, and so on.\n # This dictionary will be used to determine if a number is valid or not.\n dict = {0: 0, 1: 1, 2: 5, 5: 2, 6: 9, 8: 8, 9: 6}\n\n # Define a list of invalid digits, which are 3, 4, and 7.\n invalid = [3, 4, 7]\n\n # Define a function to check if a number is valid\n def isValid(num):\n flag = 0 # Initialize a flag to 0\n while num:\n val = num % 10 # Get the last digit of the number\n if val in invalid:\n flag = 0 # If the digit is in the invalid list, the number is invalid\n break\n else:\n if val != dict[val]:\n flag = 1 # If the digit has a rotated counterpart, set the flag to 1\n num = num // 10 # Move to the next digit\n return flag # Return the flag (0 for invalid, 1 for valid)\n\n ans = 0 # Initialize a variable to count the number of valid numbers\n for i in range(1, n + 1): # Iterate through numbers from 1 to n (inclusive)\n ans = ans + isValid(i) # Check if the number is valid and increment the count\n return ans # Return the count of valid numbers \n``` | 1 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Solution | rotated-digits | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool good(int x)\n {\n bool ans=false;\n int y;\n while(x>0)\n {\n y=x%10;\n switch(y)\n {\n case 0:\n case 1:\n case 8:\n break;\n case 2:\n case 5:\n case 6:\n case 9:\n ans=true;\n break;\n default:\n return false;\n }\n x/=10;\n }\n return ans;\n }\n int rotatedDigits(int n) {\n int c=0;\n for(int i=1;i<=n;i++)\n {\n if(good(i))\n {\n c++;\n }\n }\n return c;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def restrictedNumbersUsingDigits(self, n: int, digits: list) -> int:\n s = str(n)\n num_smaller_first_digits = len([d for d in digits if d <= int(s[0])])\n num_strictly_smaller_first_digits = len([d for d in digits if d < int(s[0])])\n num_digits = len(digits)\n if len(s) == 1:\n return num_smaller_first_digits\n if int(s[0]) in digits:\n same_first_digit_number = self.restrictedNumbersUsingDigits(int(s[1:]), digits)\n else:\n same_first_digit_number = 0\n different_first_digit_number = num_strictly_smaller_first_digits * num_digits ** (len(s) - 1)\n return same_first_digit_number + different_first_digit_number\n \n def rotatedDigits(self, n: int) -> int:\n all_digits = [0, 1, 2, 5, 6, 8, 9]\n mediocre_digits = [0, 1, 8]\n total_numbers = self.restrictedNumbersUsingDigits(n, all_digits)\n mediocre_numbers = self.restrictedNumbersUsingDigits(n, mediocre_digits)\n return total_numbers - mediocre_numbers\n```\n\n```Java []\nclass Solution {\n int[] available = new int[]{0,1,2,5,6,8,9};\n int[] swaps = new int[]{2,5,6,9};\n public int rotatedDigits(int n) {\n List<Integer> arr = new ArrayList();\n int a = n;\n while(a > 0){\n arr.add(a % 10);\n a/=10;\n }\n int[] nums = new int[arr.size()];\n for(int i = 0; i < arr.size(); i++){\n nums[i] = arr.get(arr.size() - 1 - i);\n }\n return g(nums,0, false);\n }\n int g(int[] A, int index, boolean allowed){\n int ans = 0;\n if(index == A.length - 1){\n for(int i = 0; i < available.length && available[i] <= A[index]; i++){\n if(swapsToDifferent(available[i]) || allowed) {\n ans++;\n }\n }\n }else{\n for(int i = 0; i < available.length && available[i] <= A[index]; i++){\n if(available[i] == A[index]){\n int res = g(A, index + 1, allowed || swapsToDifferent(A[index]));\n ans += res;\n }else{\n int res = f(A.length - index - 1, allowed || swapsToDifferent(available[i]));\n ans += res;\n }\n }\n }\n return ans;\n }\n boolean swapsToDifferent(int number){\n for(int i : swaps){\n if(number == i) return true;\n }\n return false;\n }\n int f(int digits, boolean swapsToDifferent){\n if(digits == 0) return 0;\n if(digits == 1 && !swapsToDifferent) return 4;\n if(digits == 1 && swapsToDifferent) return 7;\n if(digits == 2 && !swapsToDifferent) return 40;\n if(digits == 2 && swapsToDifferent) return 49;\n if(digits == 3 && !swapsToDifferent) return 316;\n if(digits == 3 && swapsToDifferent) return 343;\n return -1;\n }\n}\n```\n | 2 | An integer `x` is a **good** if after rotating each digit individually by 180 degrees, we get a valid number that is different from `x`. Each digit must be rotated - we cannot choose to leave it alone.
A number is valid if each digit remains a digit after rotation. For example:
* `0`, `1`, and `8` rotate to themselves,
* `2` and `5` rotate to each other (in this case they are rotated in a different direction, in other words, `2` or `5` gets mirrored),
* `6` and `9` rotate to each other, and
* the rest of the numbers do not rotate to any other number and become invalid.
Given an integer `n`, return _the number of **good** integers in the range_ `[1, n]`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are four good numbers in the range \[1, 10\] : 2, 5, 6, 9.
Note that 1 and 10 are not good numbers, since they remain unchanged after rotating.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Example 3:**
**Input:** n = 2
**Output:** 1
**Constraints:**
* `1 <= n <= 104` | Use a binary search. We'll binary search the monotone function "possible(D) = can we use K or less gas stations to ensure each adjacent distance between gas stations is at most D?" |
Solution | rotated-digits | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool good(int x)\n {\n bool ans=false;\n int y;\n while(x>0)\n {\n y=x%10;\n switch(y)\n {\n case 0:\n case 1:\n case 8:\n break;\n case 2:\n case 5:\n case 6:\n case 9:\n ans=true;\n break;\n default:\n return false;\n }\n x/=10;\n }\n return ans;\n }\n int rotatedDigits(int n) {\n int c=0;\n for(int i=1;i<=n;i++)\n {\n if(good(i))\n {\n c++;\n }\n }\n return c;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def restrictedNumbersUsingDigits(self, n: int, digits: list) -> int:\n s = str(n)\n num_smaller_first_digits = len([d for d in digits if d <= int(s[0])])\n num_strictly_smaller_first_digits = len([d for d in digits if d < int(s[0])])\n num_digits = len(digits)\n if len(s) == 1:\n return num_smaller_first_digits\n if int(s[0]) in digits:\n same_first_digit_number = self.restrictedNumbersUsingDigits(int(s[1:]), digits)\n else:\n same_first_digit_number = 0\n different_first_digit_number = num_strictly_smaller_first_digits * num_digits ** (len(s) - 1)\n return same_first_digit_number + different_first_digit_number\n \n def rotatedDigits(self, n: int) -> int:\n all_digits = [0, 1, 2, 5, 6, 8, 9]\n mediocre_digits = [0, 1, 8]\n total_numbers = self.restrictedNumbersUsingDigits(n, all_digits)\n mediocre_numbers = self.restrictedNumbersUsingDigits(n, mediocre_digits)\n return total_numbers - mediocre_numbers\n```\n\n```Java []\nclass Solution {\n int[] available = new int[]{0,1,2,5,6,8,9};\n int[] swaps = new int[]{2,5,6,9};\n public int rotatedDigits(int n) {\n List<Integer> arr = new ArrayList();\n int a = n;\n while(a > 0){\n arr.add(a % 10);\n a/=10;\n }\n int[] nums = new int[arr.size()];\n for(int i = 0; i < arr.size(); i++){\n nums[i] = arr.get(arr.size() - 1 - i);\n }\n return g(nums,0, false);\n }\n int g(int[] A, int index, boolean allowed){\n int ans = 0;\n if(index == A.length - 1){\n for(int i = 0; i < available.length && available[i] <= A[index]; i++){\n if(swapsToDifferent(available[i]) || allowed) {\n ans++;\n }\n }\n }else{\n for(int i = 0; i < available.length && available[i] <= A[index]; i++){\n if(available[i] == A[index]){\n int res = g(A, index + 1, allowed || swapsToDifferent(A[index]));\n ans += res;\n }else{\n int res = f(A.length - index - 1, allowed || swapsToDifferent(available[i]));\n ans += res;\n }\n }\n }\n return ans;\n }\n boolean swapsToDifferent(int number){\n for(int i : swaps){\n if(number == i) return true;\n }\n return false;\n }\n int f(int digits, boolean swapsToDifferent){\n if(digits == 0) return 0;\n if(digits == 1 && !swapsToDifferent) return 4;\n if(digits == 1 && swapsToDifferent) return 7;\n if(digits == 2 && !swapsToDifferent) return 40;\n if(digits == 2 && swapsToDifferent) return 49;\n if(digits == 3 && !swapsToDifferent) return 316;\n if(digits == 3 && swapsToDifferent) return 343;\n return -1;\n }\n}\n```\n | 2 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Easy understand solution python O(1) space | rotated-digits | 0 | 1 | ```\ndef rotatedDigits(self, N: int) -> int:\n count = 0\n for d in range(1, N+1):\n d = str(d)\n if \'3\' in d or \'4\' in d or \'7\' in d:\n continue\n if \'2\' in d or \'5\' in d or \'6\' in d or \'9\' in d:\n count+=1\n return count\n``` | 28 | An integer `x` is a **good** if after rotating each digit individually by 180 degrees, we get a valid number that is different from `x`. Each digit must be rotated - we cannot choose to leave it alone.
A number is valid if each digit remains a digit after rotation. For example:
* `0`, `1`, and `8` rotate to themselves,
* `2` and `5` rotate to each other (in this case they are rotated in a different direction, in other words, `2` or `5` gets mirrored),
* `6` and `9` rotate to each other, and
* the rest of the numbers do not rotate to any other number and become invalid.
Given an integer `n`, return _the number of **good** integers in the range_ `[1, n]`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are four good numbers in the range \[1, 10\] : 2, 5, 6, 9.
Note that 1 and 10 are not good numbers, since they remain unchanged after rotating.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Example 3:**
**Input:** n = 2
**Output:** 1
**Constraints:**
* `1 <= n <= 104` | Use a binary search. We'll binary search the monotone function "possible(D) = can we use K or less gas stations to ensure each adjacent distance between gas stations is at most D?" |
Easy understand solution python O(1) space | rotated-digits | 0 | 1 | ```\ndef rotatedDigits(self, N: int) -> int:\n count = 0\n for d in range(1, N+1):\n d = str(d)\n if \'3\' in d or \'4\' in d or \'7\' in d:\n continue\n if \'2\' in d or \'5\' in d or \'6\' in d or \'9\' in d:\n count+=1\n return count\n``` | 28 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Typical DIGIT DP | rotated-digits | 0 | 1 | If you know digit dp then this is trivial\n\nIf you contain a 3 or 4 or 7 then this number cannot be good\n\nIf you contain 2 or 5 or 6 or 9 then this number is automatically good provided that it doesnt contain any 3 or 4 or 7\n\n0,1,8 do nothing. \n\nStore pareamter good, good = True means that the number is going to be good\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n \n n = str(n)\n def helper(strict, pointer, good):\n if pointer == len(n) and good:\n return 1\n if pointer == len(n) and not good: return 0\n currentBound = int(n[pointer])\n s = 0\n if strict:\n for i in [0,1,8]:\n if i < currentBound: s+= helper(False, pointer + 1, good)\n elif i == currentBound: s += helper(True, pointer + 1, good)\n else: pass\n for i in [2,5,6,9]:\n if i < currentBound: s+= helper(False, pointer + 1, True)\n elif i == currentBound: s += helper(True, pointer + 1, True)\n else: pass\n else:\n for i in [0,1,8]:\n s += helper(False, pointer + 1, good)\n for i in [2,5,6,9]:\n s += helper(False, pointer + 1, True) \n return s\n\n return helper(True, 0, False)\n``` | 1 | An integer `x` is a **good** if after rotating each digit individually by 180 degrees, we get a valid number that is different from `x`. Each digit must be rotated - we cannot choose to leave it alone.
A number is valid if each digit remains a digit after rotation. For example:
* `0`, `1`, and `8` rotate to themselves,
* `2` and `5` rotate to each other (in this case they are rotated in a different direction, in other words, `2` or `5` gets mirrored),
* `6` and `9` rotate to each other, and
* the rest of the numbers do not rotate to any other number and become invalid.
Given an integer `n`, return _the number of **good** integers in the range_ `[1, n]`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are four good numbers in the range \[1, 10\] : 2, 5, 6, 9.
Note that 1 and 10 are not good numbers, since they remain unchanged after rotating.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Example 3:**
**Input:** n = 2
**Output:** 1
**Constraints:**
* `1 <= n <= 104` | Use a binary search. We'll binary search the monotone function "possible(D) = can we use K or less gas stations to ensure each adjacent distance between gas stations is at most D?" |
Typical DIGIT DP | rotated-digits | 0 | 1 | If you know digit dp then this is trivial\n\nIf you contain a 3 or 4 or 7 then this number cannot be good\n\nIf you contain 2 or 5 or 6 or 9 then this number is automatically good provided that it doesnt contain any 3 or 4 or 7\n\n0,1,8 do nothing. \n\nStore pareamter good, good = True means that the number is going to be good\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n \n n = str(n)\n def helper(strict, pointer, good):\n if pointer == len(n) and good:\n return 1\n if pointer == len(n) and not good: return 0\n currentBound = int(n[pointer])\n s = 0\n if strict:\n for i in [0,1,8]:\n if i < currentBound: s+= helper(False, pointer + 1, good)\n elif i == currentBound: s += helper(True, pointer + 1, good)\n else: pass\n for i in [2,5,6,9]:\n if i < currentBound: s+= helper(False, pointer + 1, True)\n elif i == currentBound: s += helper(True, pointer + 1, True)\n else: pass\n else:\n for i in [0,1,8]:\n s += helper(False, pointer + 1, good)\n for i in [2,5,6,9]:\n s += helper(False, pointer + 1, True) \n return s\n\n return helper(True, 0, False)\n``` | 1 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Intuitive exhaustive case solution | rotated-digits | 0 | 1 | # Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n invalid = [3,4,7]\n good = 0\n check = False\n\n for i in range(1,n+1):\n j = i\n \n while j != 0:\n d = j % 10\n \n if d == 2 or d == 5 or d == 6 or d == 9:\n check = True\n \n elif d in invalid:\n check = False\n break\n \n j = j // 10\n\n if check:\n good += 1\n\n check = False \n \n return good\n```\n\n# Please Upvote \uD83D\uDE4F | 0 | An integer `x` is a **good** if after rotating each digit individually by 180 degrees, we get a valid number that is different from `x`. Each digit must be rotated - we cannot choose to leave it alone.
A number is valid if each digit remains a digit after rotation. For example:
* `0`, `1`, and `8` rotate to themselves,
* `2` and `5` rotate to each other (in this case they are rotated in a different direction, in other words, `2` or `5` gets mirrored),
* `6` and `9` rotate to each other, and
* the rest of the numbers do not rotate to any other number and become invalid.
Given an integer `n`, return _the number of **good** integers in the range_ `[1, n]`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are four good numbers in the range \[1, 10\] : 2, 5, 6, 9.
Note that 1 and 10 are not good numbers, since they remain unchanged after rotating.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Example 3:**
**Input:** n = 2
**Output:** 1
**Constraints:**
* `1 <= n <= 104` | Use a binary search. We'll binary search the monotone function "possible(D) = can we use K or less gas stations to ensure each adjacent distance between gas stations is at most D?" |
Intuitive exhaustive case solution | rotated-digits | 0 | 1 | # Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n invalid = [3,4,7]\n good = 0\n check = False\n\n for i in range(1,n+1):\n j = i\n \n while j != 0:\n d = j % 10\n \n if d == 2 or d == 5 or d == 6 or d == 9:\n check = True\n \n elif d in invalid:\n check = False\n break\n \n j = j // 10\n\n if check:\n good += 1\n\n check = False \n \n return good\n```\n\n# Please Upvote \uD83D\uDE4F | 0 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Easy understandable solution ||python3 | rotated-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n count=0\n # if n<=1:\n # return 0\n # elif n==2:\n # return 1\n for i in range(1,n+1):\n if \'3\' in str(i) or \'4\' in str(i) or \'7\' in str(i):\n continue\n if \'2\' in str(i) or \'5\' in str(i) or \'6\' in str(i) or \'9\' in str(i):\n count+=1\n \n return count\n\n return count\n \n \n``` | 0 | An integer `x` is a **good** if after rotating each digit individually by 180 degrees, we get a valid number that is different from `x`. Each digit must be rotated - we cannot choose to leave it alone.
A number is valid if each digit remains a digit after rotation. For example:
* `0`, `1`, and `8` rotate to themselves,
* `2` and `5` rotate to each other (in this case they are rotated in a different direction, in other words, `2` or `5` gets mirrored),
* `6` and `9` rotate to each other, and
* the rest of the numbers do not rotate to any other number and become invalid.
Given an integer `n`, return _the number of **good** integers in the range_ `[1, n]`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are four good numbers in the range \[1, 10\] : 2, 5, 6, 9.
Note that 1 and 10 are not good numbers, since they remain unchanged after rotating.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Example 3:**
**Input:** n = 2
**Output:** 1
**Constraints:**
* `1 <= n <= 104` | Use a binary search. We'll binary search the monotone function "possible(D) = can we use K or less gas stations to ensure each adjacent distance between gas stations is at most D?" |
Easy understandable solution ||python3 | rotated-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, n: int) -> int:\n count=0\n # if n<=1:\n # return 0\n # elif n==2:\n # return 1\n for i in range(1,n+1):\n if \'3\' in str(i) or \'4\' in str(i) or \'7\' in str(i):\n continue\n if \'2\' in str(i) or \'5\' in str(i) or \'6\' in str(i) or \'9\' in str(i):\n count+=1\n \n return count\n\n return count\n \n \n``` | 0 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
788: Solution with step by step explanation | rotated-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\n def isGoodNumber(num: int) -> bool:\n```\n\nInside rotatedDigits, we define a helper function isGoodNumber that takes an integer num and returns a boolean. This function will be used to determine if a number is "good" based on its rotated digits.\n\n```\n valid_rotation = False \n```\n\nWe initialize a flag valid_rotation as False. This flag will track whether the current number has any digits that make it valid when rotated.\n\n```\n while num:\n```\n\nWe start a while loop that will continue as long as num is not zero. This loop is used to iterate through each digit of the number.\n\n```\n digit = num % 10\n```\n\nHere, we extract the last digit of num using the modulo operator.\n\n```\n if digit in {3, 4, 7}:\n return False\n```\nIf the current digit is one of 3, 4, or 7, the entire number is deemed invalid when rotated (because these digits don\'t have valid rotations). Therefore, we immediately return False.\n\n```\n if digit in {2, 5, 6, 9}:\n valid_rotation = True\n```\n\nHowever, if the digit is one of 2, 5, 6, or 9, then this digit becomes a different digit upon rotation. We mark this by setting valid_rotation to True.\n\n```\n num //= 10\n```\nWe remove the last digit from num by using integer (floor) division by 10.\n\n```\n return valid_rotation\n```\n\nAfter processing all the digits, we return the value of valid_rotation. If it\'s True, this means the number is "good". If it\'s False, then the number remains unchanged upon rotation.\n\n```\n return sum(isGoodNumber(i) for i in range(1, N + 1))\n```\n\nFinally, we use a generator expression to iterate over all numbers from 1 to N. For each number, we check if it\'s "good" using the isGoodNumber function. The sum() function counts all the numbers that are deemed "good", and we return this count.\n\n# Complexity\n- Time complexity:\nO(n log n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, N: int) -> int:\n def isGoodNumber(num: int) -> bool:\n valid_rotation = False \n \n while num:\n digit = num % 10\n if digit in {3, 4, 7}:\n\n return False\n if digit in {2, 5, 6, 9}:\n valid_rotation = True\n num //= 10\n return valid_rotation\n\n return sum(isGoodNumber(i) for i in range(1, N + 1))\n\n``` | 0 | An integer `x` is a **good** if after rotating each digit individually by 180 degrees, we get a valid number that is different from `x`. Each digit must be rotated - we cannot choose to leave it alone.
A number is valid if each digit remains a digit after rotation. For example:
* `0`, `1`, and `8` rotate to themselves,
* `2` and `5` rotate to each other (in this case they are rotated in a different direction, in other words, `2` or `5` gets mirrored),
* `6` and `9` rotate to each other, and
* the rest of the numbers do not rotate to any other number and become invalid.
Given an integer `n`, return _the number of **good** integers in the range_ `[1, n]`.
**Example 1:**
**Input:** n = 10
**Output:** 4
**Explanation:** There are four good numbers in the range \[1, 10\] : 2, 5, 6, 9.
Note that 1 and 10 are not good numbers, since they remain unchanged after rotating.
**Example 2:**
**Input:** n = 1
**Output:** 0
**Example 3:**
**Input:** n = 2
**Output:** 1
**Constraints:**
* `1 <= n <= 104` | Use a binary search. We'll binary search the monotone function "possible(D) = can we use K or less gas stations to ensure each adjacent distance between gas stations is at most D?" |
788: Solution with step by step explanation | rotated-digits | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\n def isGoodNumber(num: int) -> bool:\n```\n\nInside rotatedDigits, we define a helper function isGoodNumber that takes an integer num and returns a boolean. This function will be used to determine if a number is "good" based on its rotated digits.\n\n```\n valid_rotation = False \n```\n\nWe initialize a flag valid_rotation as False. This flag will track whether the current number has any digits that make it valid when rotated.\n\n```\n while num:\n```\n\nWe start a while loop that will continue as long as num is not zero. This loop is used to iterate through each digit of the number.\n\n```\n digit = num % 10\n```\n\nHere, we extract the last digit of num using the modulo operator.\n\n```\n if digit in {3, 4, 7}:\n return False\n```\nIf the current digit is one of 3, 4, or 7, the entire number is deemed invalid when rotated (because these digits don\'t have valid rotations). Therefore, we immediately return False.\n\n```\n if digit in {2, 5, 6, 9}:\n valid_rotation = True\n```\n\nHowever, if the digit is one of 2, 5, 6, or 9, then this digit becomes a different digit upon rotation. We mark this by setting valid_rotation to True.\n\n```\n num //= 10\n```\nWe remove the last digit from num by using integer (floor) division by 10.\n\n```\n return valid_rotation\n```\n\nAfter processing all the digits, we return the value of valid_rotation. If it\'s True, this means the number is "good". If it\'s False, then the number remains unchanged upon rotation.\n\n```\n return sum(isGoodNumber(i) for i in range(1, N + 1))\n```\n\nFinally, we use a generator expression to iterate over all numbers from 1 to N. For each number, we check if it\'s "good" using the isGoodNumber function. The sum() function counts all the numbers that are deemed "good", and we return this count.\n\n# Complexity\n- Time complexity:\nO(n log n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def rotatedDigits(self, N: int) -> int:\n def isGoodNumber(num: int) -> bool:\n valid_rotation = False \n \n while num:\n digit = num % 10\n if digit in {3, 4, 7}:\n\n return False\n if digit in {2, 5, 6, 9}:\n valid_rotation = True\n num //= 10\n return valid_rotation\n\n return sum(isGoodNumber(i) for i in range(1, N + 1))\n\n``` | 0 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Solution | escape-the-ghosts | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool escapeGhosts(vector<vector<int>>& ghosts, vector<int>& target) {\n int my_distance_from_target = abs(target[0]) + abs(target[1]);\n for( auto &g : ghosts )\n {\n if( my_distance_from_target >= ( abs(g[0] - target[0]) + abs(g[1] - target[1])) )return false;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n ee = abs(target[0]) + abs(target[1])\n for ghost in ghosts:\n if abs(target[0] - ghost[0]) + abs(target[1] - ghost[1]) <= ee:\n return False\n return True\n```\n\n```Java []\nclass Solution {\n public boolean escapeGhosts(int[][] ghosts, int[] target) {\n int len = Math.abs(target[0])+Math.abs(target[1]);\n for(int[] arr:ghosts) if(len >= Math.abs(target[0]-arr[0]) + Math.abs(target[1]-arr[1])) return false;\n return true;\n }\n}\n```\n | 1 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
Solution | escape-the-ghosts | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool escapeGhosts(vector<vector<int>>& ghosts, vector<int>& target) {\n int my_distance_from_target = abs(target[0]) + abs(target[1]);\n for( auto &g : ghosts )\n {\n if( my_distance_from_target >= ( abs(g[0] - target[0]) + abs(g[1] - target[1])) )return false;\n }\n return true;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n ee = abs(target[0]) + abs(target[1])\n for ghost in ghosts:\n if abs(target[0] - ghost[0]) + abs(target[1] - ghost[1]) <= ee:\n return False\n return True\n```\n\n```Java []\nclass Solution {\n public boolean escapeGhosts(int[][] ghosts, int[] target) {\n int len = Math.abs(target[0])+Math.abs(target[1]);\n for(int[] arr:ghosts) if(len >= Math.abs(target[0]-arr[0]) + Math.abs(target[1]-arr[1])) return false;\n return true;\n }\n}\n```\n | 1 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Python Solution for reference | escape-the-ghosts | 0 | 1 | \n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n\n # If any of the ghosts reaches the targert before \n # you, then you lose\n def time(x,y):\n a,b = target\n return max(x,a)-min(x,a) + max(y,b)-min(y,b)\n \n t_p = time(0,0)\n for a,b in ghosts:\n if time(a,b)<= t_p :\n return False \n return True \n``` | 1 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
Python Solution for reference | escape-the-ghosts | 0 | 1 | \n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n\n # If any of the ghosts reaches the targert before \n # you, then you lose\n def time(x,y):\n a,b = target\n return max(x,a)-min(x,a) + max(y,b)-min(y,b)\n \n t_p = time(0,0)\n for a,b in ghosts:\n if time(a,b)<= t_p :\n return False \n return True \n``` | 1 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Python3 | escape-the-ghosts | 0 | 1 | \n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n a=abs(target[0])+abs(target[1])\n for i ,j in ghosts:\n b=abs(target[0]-i)+abs(target[1]-j)\n if b<=a:\n return False\n return True\n``` | 1 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
Python3 | escape-the-ghosts | 0 | 1 | \n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n a=abs(target[0])+abs(target[1])\n for i ,j in ghosts:\n b=abs(target[0]-i)+abs(target[1]-j)\n if b<=a:\n return False\n return True\n``` | 1 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Python 3 || 2 lines, w/ a brief explanation || T/M: 86% / 72% | escape-the-ghosts | 0 | 1 | The problem reduces to whether any ghost`g`has a *manhattan-distance* to`target`that is less than the *manhattan-distance* to`target`from`(0,0)`.\n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n \n dist = lambda x : abs(x[0] - target[0]) + abs(x[1] - target[1])\n\n return dist((0,0)) < min(dist(g) for g in ghosts)\n```\n[https://leetcode.com/problems/escape-the-ghosts/submissions/872215914/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 4 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
Python 3 || 2 lines, w/ a brief explanation || T/M: 86% / 72% | escape-the-ghosts | 0 | 1 | The problem reduces to whether any ghost`g`has a *manhattan-distance* to`target`that is less than the *manhattan-distance* to`target`from`(0,0)`.\n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n \n dist = lambda x : abs(x[0] - target[0]) + abs(x[1] - target[1])\n\n return dist((0,0)) < min(dist(g) for g in ghosts)\n```\n[https://leetcode.com/problems/escape-the-ghosts/submissions/872215914/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*).\n | 4 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
✅ Mathematics is the ultimate savior. | escape-the-ghosts | 0 | 1 | Calculate the `Manhattan distance` between `you` and `all the ghosts` to the `target`. If any of the ghosts are `closer` to the `target` than you are, `you lose`. Otherwise, `you win`.\n\n\nI came across about 3 to 4 problems on LeetCode that involved the concept of "Manhattan distance" in various scenarios. It\'s good to learn, if you\'re not familiar with it.\nsource: https://tinyurl.com/Manhattan-dis\n\n\n# Code\n```\nclass Solution:\n\n def f(self,g,t):\n myDis = abs(t[0])+abs(t[1])\n ghostDis = 1e6\n\n for ghost in g:\n ghostDis = min(ghostDis, abs(ghost[0] - t[0])+abs(ghost[1]- t[1]))\n if ghostDis <= myDis: return False\n \n return True\n\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n return self.f(ghosts,target)\n``` | 0 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
✅ Mathematics is the ultimate savior. | escape-the-ghosts | 0 | 1 | Calculate the `Manhattan distance` between `you` and `all the ghosts` to the `target`. If any of the ghosts are `closer` to the `target` than you are, `you lose`. Otherwise, `you win`.\n\n\nI came across about 3 to 4 problems on LeetCode that involved the concept of "Manhattan distance" in various scenarios. It\'s good to learn, if you\'re not familiar with it.\nsource: https://tinyurl.com/Manhattan-dis\n\n\n# Code\n```\nclass Solution:\n\n def f(self,g,t):\n myDis = abs(t[0])+abs(t[1])\n ghostDis = 1e6\n\n for ghost in g:\n ghostDis = min(ghostDis, abs(ghost[0] - t[0])+abs(ghost[1]- t[1]))\n if ghostDis <= myDis: return False\n \n return True\n\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n return self.f(ghosts,target)\n``` | 0 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
789: Beats 100.00%, Solution with step by step explanation | escape-the-ghosts | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nplayer_distance = abs(target[0]) + abs(target[1])\n```\nWe begin by calculating the distance the player needs to cover to reach the target.\nWe use the Manhattan distance, which is a way to compute the distance between two points in a grid-based path. It\'s the total number of horizontal and vertical steps to go from one point to another.\nabs is a built-in Python function that returns the absolute value of the number.\nSince the player always starts at position [0,0], the Manhattan distance is simply the sum of the absolute values of the target\'s x and y coordinates.\n\n```\nfor ghost in ghosts:\n```\n\nWe then loop through each ghost in the ghosts list to calculate their distances to the target and compare it with the player\'s distance.\n\n```\nghost_distance = abs(ghost[0] - target[0]) + abs(ghost[1] - target[1])\n```\n\nFor each ghost, we compute its Manhattan distance to the target.\nWe subtract the ghost\'s x coordinate from the target\'s x coordinate (and similarly for the y coordinate) to get the horizontal and vertical distances, respectively. Then, we sum up the absolute values of these distances.\n\n```\nif ghost_distance <= player_distance:\n return False\n```\n\nIf the distance of a ghost to the target is less than or equal to the player\'s distance, it means the ghost can intercept or reach the target before the player does. In this case, we immediately return False, indicating the player cannot escape.\n\n```\nreturn True\n```\n\nIf we\'ve gone through all the ghosts and none of them can reach the target before the player, then the function will return True, indicating that the player can escape.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n player_distance = abs(target[0]) + abs(target[1])\n\n for ghost in ghosts:\n ghost_distance = abs(ghost[0] - target[0]) + abs(ghost[1] - target[1])\n\n if ghost_distance <= player_distance:\n return False\n\n return True\n\n``` | 0 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
789: Beats 100.00%, Solution with step by step explanation | escape-the-ghosts | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nplayer_distance = abs(target[0]) + abs(target[1])\n```\nWe begin by calculating the distance the player needs to cover to reach the target.\nWe use the Manhattan distance, which is a way to compute the distance between two points in a grid-based path. It\'s the total number of horizontal and vertical steps to go from one point to another.\nabs is a built-in Python function that returns the absolute value of the number.\nSince the player always starts at position [0,0], the Manhattan distance is simply the sum of the absolute values of the target\'s x and y coordinates.\n\n```\nfor ghost in ghosts:\n```\n\nWe then loop through each ghost in the ghosts list to calculate their distances to the target and compare it with the player\'s distance.\n\n```\nghost_distance = abs(ghost[0] - target[0]) + abs(ghost[1] - target[1])\n```\n\nFor each ghost, we compute its Manhattan distance to the target.\nWe subtract the ghost\'s x coordinate from the target\'s x coordinate (and similarly for the y coordinate) to get the horizontal and vertical distances, respectively. Then, we sum up the absolute values of these distances.\n\n```\nif ghost_distance <= player_distance:\n return False\n```\n\nIf the distance of a ghost to the target is less than or equal to the player\'s distance, it means the ghost can intercept or reach the target before the player does. In this case, we immediately return False, indicating the player cannot escape.\n\n```\nreturn True\n```\n\nIf we\'ve gone through all the ghosts and none of them can reach the target before the player, then the function will return True, indicating that the player can escape.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n player_distance = abs(target[0]) + abs(target[1])\n\n for ghost in ghosts:\n ghost_distance = abs(ghost[0] - target[0]) + abs(ghost[1] - target[1])\n\n if ghost_distance <= player_distance:\n return False\n\n return True\n\n``` | 0 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Python Beats 100% | escape-the-ghosts | 0 | 1 | \n def calculate_distance(self, pointa, pointb):\n return abs(pointa[0] - pointb[0]) + abs(pointa[1] - pointb[1]) \n\n\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n my_distance = self.calculate_distance(target, [0,0])\n ghost_distances = [self.calculate_distance(target, ghost) for ghost in ghosts]\n\n for d in ghost_distances:\n if d <= my_distance:\n return False\n\n return True | 0 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
Python Beats 100% | escape-the-ghosts | 0 | 1 | \n def calculate_distance(self, pointa, pointb):\n return abs(pointa[0] - pointb[0]) + abs(pointa[1] - pointb[1]) \n\n\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n my_distance = self.calculate_distance(target, [0,0])\n ghost_distances = [self.calculate_distance(target, ghost) for ghost in ghosts]\n\n for d in ghost_distances:\n if d <= my_distance:\n return False\n\n return True | 0 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Ye old one liner | escape-the-ghosts | 0 | 1 | # Intuition\nOptimal strategy for ghosts is to always go straight for the target\n\n# Code\n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n return sum(abs(i) for i in target) < min(sum(abs(x-y) for x,y in zip(target, i)) for i in ghosts)\n``` | 0 | You are playing a simplified PAC-MAN game on an infinite 2-D grid. You start at the point `[0, 0]`, and you are given a destination point `target = [xtarget, ytarget]` that you are trying to get to. There are several ghosts on the map with their starting positions given as a 2D array `ghosts`, where `ghosts[i] = [xi, yi]` represents the starting position of the `ith` ghost. All inputs are **integral coordinates**.
Each turn, you and all the ghosts may independently choose to either **move 1 unit** in any of the four cardinal directions: north, east, south, or west, or **stay still**. All actions happen **simultaneously**.
You escape if and only if you can reach the target **before** any ghost reaches you. If you reach any square (including the target) at the **same time** as a ghost, it **does not** count as an escape.
Return `true` _if it is possible to escape regardless of how the ghosts move, otherwise return_ `false`_._
**Example 1:**
**Input:** ghosts = \[\[1,0\],\[0,3\]\], target = \[0,1\]
**Output:** true
**Explanation:** You can reach the destination (0, 1) after 1 turn, while the ghosts located at (1, 0) and (0, 3) cannot catch up with you.
**Example 2:**
**Input:** ghosts = \[\[1,0\]\], target = \[2,0\]
**Output:** false
**Explanation:** You need to reach the destination (2, 0), but the ghost at (1, 0) lies between you and the destination.
**Example 3:**
**Input:** ghosts = \[\[2,0\]\], target = \[1,0\]
**Output:** false
**Explanation:** The ghost can reach the target at the same time as you.
**Constraints:**
* `1 <= ghosts.length <= 100`
* `ghosts[i].length == 2`
* `-104 <= xi, yi <= 104`
* There can be **multiple ghosts** in the same location.
* `target.length == 2`
* `-104 <= xtarget, ytarget <= 104` | null |
Ye old one liner | escape-the-ghosts | 0 | 1 | # Intuition\nOptimal strategy for ghosts is to always go straight for the target\n\n# Code\n```\nclass Solution:\n def escapeGhosts(self, ghosts: List[List[int]], target: List[int]) -> bool:\n return sum(abs(i) for i in target) < min(sum(abs(x-y) for x,y in zip(target, i)) for i in ghosts)\n``` | 0 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Python3 | Recursion + Memoization | domino-and-tromino-tiling | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nMOD = (10**9) + 7\nclass Solution:\n def numTilings(self, n: int) -> int:\n memo = {}\n\n def state(t1, t2):\n if t1 and t2: return 3\n if t1 and not t2: return 1\n if not t1 and t2: return 2\n\n def recur(i, t1, t2):\n if i == n:\n return 1\n if (i, state(t1, t2)) in memo:\n return memo[(i, state(t1, t2))]\n t3, t4 = i+1 < n, i+1 < n\n count = 0\n\n if t1 and t2: count += recur(i+1, True, True)\n if t1 and t2 and t3:\n count += recur(i+1, True, False)\n count += recur(i+1, False, True)\n if t1 and not t2 and t3:\n count += recur(i+1, False, True)\n if not t1 and t2 and t4:\n count += recur(i+1, True, False)\n if not t1 and not t2:\n count += recur(i+1, True, True)\n if t1 and t2 and t3 and t4:\n count += recur(i+1, False, False)\n if t1 and not t2 and t3:\n count += recur(i+1, False, False)\n if not t1 and t2 and t3:\n count += recur(i+1, False, False)\n\n memo[(i, state(t1, t2))] = count\n return count\n\n return recur(0, True, True) % MOD\n``` | 1 | You have two types of tiles: a `2 x 1` domino shape and a tromino shape. You may rotate these shapes.
Given an integer n, return _the number of ways to tile an_ `2 x n` _board_. Since the answer may be very large, return it **modulo** `109 + 7`.
In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Explanation:** The five different ways are show above.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 1000` | Where can the 0 be placed in an ideal permutation? What about the 1? |
Python3 | Recursion + Memoization | domino-and-tromino-tiling | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nMOD = (10**9) + 7\nclass Solution:\n def numTilings(self, n: int) -> int:\n memo = {}\n\n def state(t1, t2):\n if t1 and t2: return 3\n if t1 and not t2: return 1\n if not t1 and t2: return 2\n\n def recur(i, t1, t2):\n if i == n:\n return 1\n if (i, state(t1, t2)) in memo:\n return memo[(i, state(t1, t2))]\n t3, t4 = i+1 < n, i+1 < n\n count = 0\n\n if t1 and t2: count += recur(i+1, True, True)\n if t1 and t2 and t3:\n count += recur(i+1, True, False)\n count += recur(i+1, False, True)\n if t1 and not t2 and t3:\n count += recur(i+1, False, True)\n if not t1 and t2 and t4:\n count += recur(i+1, True, False)\n if not t1 and not t2:\n count += recur(i+1, True, True)\n if t1 and t2 and t3 and t4:\n count += recur(i+1, False, False)\n if t1 and not t2 and t3:\n count += recur(i+1, False, False)\n if not t1 and t2 and t3:\n count += recur(i+1, False, False)\n\n memo[(i, state(t1, t2))] = count\n return count\n\n return recur(0, True, True) % MOD\n``` | 1 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
✅ [Python/JAVA/C/C++] DP || Image Visualized Explanation || 100% Faster || O(N) | domino-and-tromino-tiling | 1 | 1 | * dp[i] denotes the number of ways to tile an 2 * (i + 1) board, note that dp is 0-indexed.\n\t* Intuitively, dp[0] = 1 and dp[1] = 2\n* dpa[i] denotes the number of ways to tile an 2 * i board and 1 more square left below(or above symmetrically).\n\t* Intuitively, dpa[0] = 0 and dpa[1] = 1\n\t* I just explained the case where in i-th column, 2nd row is filled. But it should be noted that the two cases(the other is in i-th column, 1st row is filled) are symmetric and the numbers are both dpa[i], you may imagine dpb[i] = dpa[i] for the second case where i-th column 1st row is filled.\n\n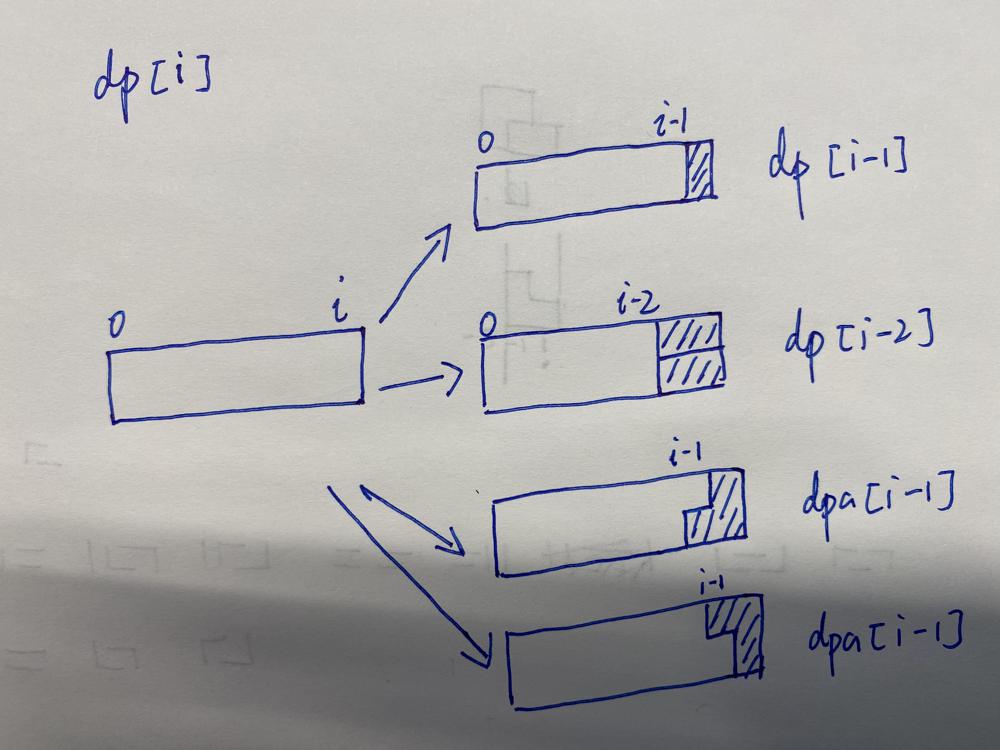\n\nFurther More!\n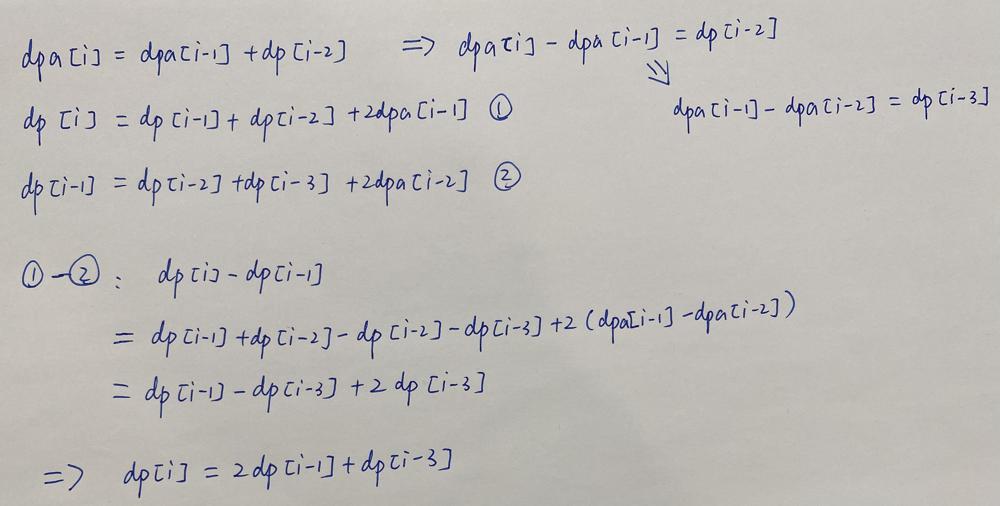\n\n\n\n**If you hava any question, feel free to ask. If you like the solution or the explaination, Please UPVOTE!**\n\n**Python/Python3**\n```\nclass Solution(object):\n def numTilings(self, n):\n dp = [1, 2, 5] + [0] * n\n for i in range(3, n):\n dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % 1000000007\n return dp[n - 1]\n```\n```\nclass Solution(object):\n def numTilings(self, n):\n dp, dpa = [1, 2] + [0] * n, [1] * n\n for i in range(2, n):\n dp[i] = (dp[i - 1] + dp[i - 2] + dpa[i - 1] * 2) % 1000000007\n dpa[i] = (dp[i - 2] + dpa[i - 1]) % 1000000007\n return dp[n - 1]\n```\n**Java**\n```\nclass Solution {\n public int numTilings(int n) {\n long[] dp = new long[n + 3]; dp[0] = 1; dp[1] = 2; dp[2] = 5;\n for (int i = 3; i < n; i ++) {\n dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % 1000000007;\n }\n return (int)dp[n - 1];\n }\n}\n```\n```\nclass Solution {\n public int numTilings(int n) {\n long[] dp = new long[n + 2]; dp[0] = 1; dp[1] = 2;\n long[] dpa = new long[n + 2]; dpa[1] = 1;\n for (int i = 2; i < n; i ++) {\n dp[i] = (dp[i - 1] + dp[i - 2] + dpa[i - 1] * 2) % 1000000007;\n dpa[i] = (dp[i - 2] + dpa[i - 1]) % 1000000007;\n }\n return (int)dp[n - 1];\n }\n}\n```\n**C/C++**\n```\nint numTilings(int n) {\n unsigned int dp[n + 3]; dp[0] = 1; dp[1] = 2; dp[2] = 5;\n for (int i = 3; i < n; i ++) {\n dp[i] = (2 * dp[i - 1] + dp[i - 3]) % 1000000007;\n }\n return dp[n - 1];\n}\n```\n```\nint numTilings(int n){\n if (n == 1) return 1;\n unsigned int dp[n]; dp[0] = 1; dp[1] = 2;\n unsigned int dpa[n]; dpa[1] = 1;\n for (int i = 2; i < n; i ++) {\n dp[i] = (dp[i - 1] + dp[i - 2] + dpa[i - 1] * 2) % 1000000007;\n dpa[i] = (dp[i - 2] + dpa[i - 1]) % 1000000007;\n }\n return dp[n - 1];\n}\n```\n\n**Please UPVOTE!** | 161 | You have two types of tiles: a `2 x 1` domino shape and a tromino shape. You may rotate these shapes.
Given an integer n, return _the number of ways to tile an_ `2 x n` _board_. Since the answer may be very large, return it **modulo** `109 + 7`.
In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Explanation:** The five different ways are show above.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 1000` | Where can the 0 be placed in an ideal permutation? What about the 1? |
✅ [Python/JAVA/C/C++] DP || Image Visualized Explanation || 100% Faster || O(N) | domino-and-tromino-tiling | 1 | 1 | * dp[i] denotes the number of ways to tile an 2 * (i + 1) board, note that dp is 0-indexed.\n\t* Intuitively, dp[0] = 1 and dp[1] = 2\n* dpa[i] denotes the number of ways to tile an 2 * i board and 1 more square left below(or above symmetrically).\n\t* Intuitively, dpa[0] = 0 and dpa[1] = 1\n\t* I just explained the case where in i-th column, 2nd row is filled. But it should be noted that the two cases(the other is in i-th column, 1st row is filled) are symmetric and the numbers are both dpa[i], you may imagine dpb[i] = dpa[i] for the second case where i-th column 1st row is filled.\n\n\n\nFurther More!\n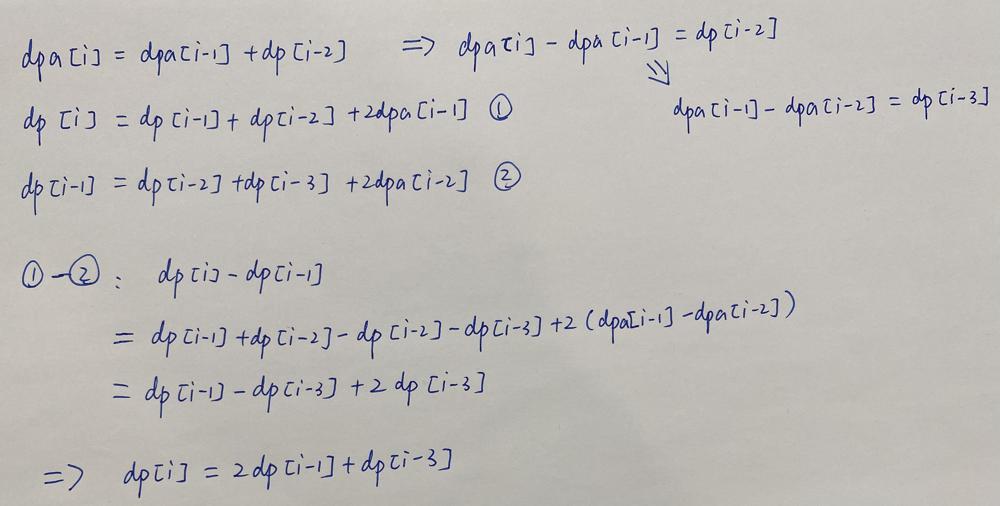\n\n\n\n**If you hava any question, feel free to ask. If you like the solution or the explaination, Please UPVOTE!**\n\n**Python/Python3**\n```\nclass Solution(object):\n def numTilings(self, n):\n dp = [1, 2, 5] + [0] * n\n for i in range(3, n):\n dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % 1000000007\n return dp[n - 1]\n```\n```\nclass Solution(object):\n def numTilings(self, n):\n dp, dpa = [1, 2] + [0] * n, [1] * n\n for i in range(2, n):\n dp[i] = (dp[i - 1] + dp[i - 2] + dpa[i - 1] * 2) % 1000000007\n dpa[i] = (dp[i - 2] + dpa[i - 1]) % 1000000007\n return dp[n - 1]\n```\n**Java**\n```\nclass Solution {\n public int numTilings(int n) {\n long[] dp = new long[n + 3]; dp[0] = 1; dp[1] = 2; dp[2] = 5;\n for (int i = 3; i < n; i ++) {\n dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % 1000000007;\n }\n return (int)dp[n - 1];\n }\n}\n```\n```\nclass Solution {\n public int numTilings(int n) {\n long[] dp = new long[n + 2]; dp[0] = 1; dp[1] = 2;\n long[] dpa = new long[n + 2]; dpa[1] = 1;\n for (int i = 2; i < n; i ++) {\n dp[i] = (dp[i - 1] + dp[i - 2] + dpa[i - 1] * 2) % 1000000007;\n dpa[i] = (dp[i - 2] + dpa[i - 1]) % 1000000007;\n }\n return (int)dp[n - 1];\n }\n}\n```\n**C/C++**\n```\nint numTilings(int n) {\n unsigned int dp[n + 3]; dp[0] = 1; dp[1] = 2; dp[2] = 5;\n for (int i = 3; i < n; i ++) {\n dp[i] = (2 * dp[i - 1] + dp[i - 3]) % 1000000007;\n }\n return dp[n - 1];\n}\n```\n```\nint numTilings(int n){\n if (n == 1) return 1;\n unsigned int dp[n]; dp[0] = 1; dp[1] = 2;\n unsigned int dpa[n]; dpa[1] = 1;\n for (int i = 2; i < n; i ++) {\n dp[i] = (dp[i - 1] + dp[i - 2] + dpa[i - 1] * 2) % 1000000007;\n dpa[i] = (dp[i - 2] + dpa[i - 1]) % 1000000007;\n }\n return dp[n - 1];\n}\n```\n\n**Please UPVOTE!** | 161 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
Python recursive-recursion easy to understand with explanation. | domino-and-tromino-tiling | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRecursion\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nYou start from left to right.\nThe helper function takes 2 arguments , i for the tile number and half to say whether i is just half space(half =true) or i is full space(half = false).\nWe need the following base cases:\n1] when i is n-1(last space full empty half = false)\n2] when i is n-2(second last full empty half = false) . We need this case since if we don\'t have this base case we try to solve this recursively you will not get answer 2 for this case.\n3] when i is n-2(second last half empty half= true). We need this case since if we don\'t have this base and let it solve recursively you won\'t get 1 for this case.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self):\n self.MOD = 1000000007\n \n def numTilings(self, n: int) -> int:\n \n @cache\n def helper(i , half):\n #case where only 1 spaces remaining\n if i== n-1 and not half:\n return 1\n #case where only 2 spaces remaining\n if i== n-2 and not half:\n return 2\n\n #case where only 1.5 spaces remaining\n if i== n-2 and half:\n return 1\n\n #nothing remaining to fill\n if i>n-1:\n return 0\n\n # if i is integer\n if not half:\n return ( helper(i+1, False)\n + helper(i+2, False)\n + 2 * helper(i+1, True) ) % self.MOD\n else:\n return ( helper(i+2, False)\n + helper(i+1, True) % self.MOD\n\n )\n return helper(0, False)\n \n``` | 1 | You have two types of tiles: a `2 x 1` domino shape and a tromino shape. You may rotate these shapes.
Given an integer n, return _the number of ways to tile an_ `2 x n` _board_. Since the answer may be very large, return it **modulo** `109 + 7`.
In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Explanation:** The five different ways are show above.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 1000` | Where can the 0 be placed in an ideal permutation? What about the 1? |
Python recursive-recursion easy to understand with explanation. | domino-and-tromino-tiling | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRecursion\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nYou start from left to right.\nThe helper function takes 2 arguments , i for the tile number and half to say whether i is just half space(half =true) or i is full space(half = false).\nWe need the following base cases:\n1] when i is n-1(last space full empty half = false)\n2] when i is n-2(second last full empty half = false) . We need this case since if we don\'t have this base case we try to solve this recursively you will not get answer 2 for this case.\n3] when i is n-2(second last half empty half= true). We need this case since if we don\'t have this base and let it solve recursively you won\'t get 1 for this case.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self):\n self.MOD = 1000000007\n \n def numTilings(self, n: int) -> int:\n \n @cache\n def helper(i , half):\n #case where only 1 spaces remaining\n if i== n-1 and not half:\n return 1\n #case where only 2 spaces remaining\n if i== n-2 and not half:\n return 2\n\n #case where only 1.5 spaces remaining\n if i== n-2 and half:\n return 1\n\n #nothing remaining to fill\n if i>n-1:\n return 0\n\n # if i is integer\n if not half:\n return ( helper(i+1, False)\n + helper(i+2, False)\n + 2 * helper(i+1, True) ) % self.MOD\n else:\n return ( helper(i+2, False)\n + helper(i+1, True) % self.MOD\n\n )\n return helper(0, False)\n \n``` | 1 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
27ms 98.89% 13.8mb 99.21% Python explained! | domino-and-tromino-tiling | 0 | 1 | # Intuition\nFirst look at the numbers really good and long.\nSearch patterns and the according offsets to reach our values...\nLike sum, fibonacci etc.\n|i | n | sum|off| \n|--|--:|--:|-:|\n1|1|1|+1\n2|2|3|+2\n3|5|8|+3\n4|11|19|+5\n5|24|43|+10\n6|53|96|+21\n7|117|213|+45\n8|258|471|+98\n9|569|1040|+215\n10|1255|\n\nFirst this rather looks like powers of 2.\nBut there are offsets growing irrationally like sums.\n|n | 2^(i-1) | off|\n|--|-:|-:|\n1|1|+0\n2|2|+0\n5|4|+1\n11|8|+3\n24|16|+8\n53|32|+21\n117|64|+53\n258|128|+130\n\nThen it looks like nextN=2*lastN.\n|n | 2*(n-1) | off|\n|--|-:|-:|\n1 |2*0 |(+1)\n2 |2*1 |(+0)\n5 |2*2 |(+1)\n11 |2*5 |(+1)\n24 |2*11 |(+2)\n53 |2*24 |+5\n117 |2*53 |+11\n258 |2*117 |+24\n569 |2*258 |+53\n1255|2*569|+117\n\nThis offsets looks really similar!\n# Approach\ndefaultcases for 1,2,3,4,5.\nthen use this vars: a=5 b=11 c=24\nand for each i up to n:\n(a,b,c)->(b,c,a+c+c)\na\'=b \nb\'=c \nc\'=a+2c\n\nE.g. first defaults:\n1\n2\n5\n11\n24\nThen these jumps from 5,11,24:\n|a|b|c|\n|-|-|-|\n11|24|**53**\n24|53|**117**\n53|117|**258**\n117|258|**569**\n258|569|**1255**\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def numTilings(self, n: int) -> int:\n if n == 1: return 1\n if n == 2: return 2\n if n == 3: return 5\n if n == 4: return 11\n if n == 5: return 24\n a,b,c = 5,11,24 #[a,b,c] => [b,c,a+c+c] => [b,c]+[2*c+a]\n for i in range(6,n+1):\n a,b,c = b,c,2*c+a\n return c % (10**9+7)\n``` | 32 | You have two types of tiles: a `2 x 1` domino shape and a tromino shape. You may rotate these shapes.
Given an integer n, return _the number of ways to tile an_ `2 x n` _board_. Since the answer may be very large, return it **modulo** `109 + 7`.
In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.
**Example 1:**
**Input:** n = 3
**Output:** 5
**Explanation:** The five different ways are show above.
**Example 2:**
**Input:** n = 1
**Output:** 1
**Constraints:**
* `1 <= n <= 1000` | Where can the 0 be placed in an ideal permutation? What about the 1? |
27ms 98.89% 13.8mb 99.21% Python explained! | domino-and-tromino-tiling | 0 | 1 | # Intuition\nFirst look at the numbers really good and long.\nSearch patterns and the according offsets to reach our values...\nLike sum, fibonacci etc.\n|i | n | sum|off| \n|--|--:|--:|-:|\n1|1|1|+1\n2|2|3|+2\n3|5|8|+3\n4|11|19|+5\n5|24|43|+10\n6|53|96|+21\n7|117|213|+45\n8|258|471|+98\n9|569|1040|+215\n10|1255|\n\nFirst this rather looks like powers of 2.\nBut there are offsets growing irrationally like sums.\n|n | 2^(i-1) | off|\n|--|-:|-:|\n1|1|+0\n2|2|+0\n5|4|+1\n11|8|+3\n24|16|+8\n53|32|+21\n117|64|+53\n258|128|+130\n\nThen it looks like nextN=2*lastN.\n|n | 2*(n-1) | off|\n|--|-:|-:|\n1 |2*0 |(+1)\n2 |2*1 |(+0)\n5 |2*2 |(+1)\n11 |2*5 |(+1)\n24 |2*11 |(+2)\n53 |2*24 |+5\n117 |2*53 |+11\n258 |2*117 |+24\n569 |2*258 |+53\n1255|2*569|+117\n\nThis offsets looks really similar!\n# Approach\ndefaultcases for 1,2,3,4,5.\nthen use this vars: a=5 b=11 c=24\nand for each i up to n:\n(a,b,c)->(b,c,a+c+c)\na\'=b \nb\'=c \nc\'=a+2c\n\nE.g. first defaults:\n1\n2\n5\n11\n24\nThen these jumps from 5,11,24:\n|a|b|c|\n|-|-|-|\n11|24|**53**\n24|53|**117**\n53|117|**258**\n117|258|**569**\n258|569|**1255**\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n def numTilings(self, n: int) -> int:\n if n == 1: return 1\n if n == 2: return 2\n if n == 3: return 5\n if n == 4: return 11\n if n == 5: return 24\n a,b,c = 5,11,24 #[a,b,c] => [b,c,a+c+c] => [b,c]+[2*c+a]\n for i in range(6,n+1):\n a,b,c = b,c,2*c+a\n return c % (10**9+7)\n``` | 32 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
Solution | custom-sort-string | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string customSortString(string order, string s) {\n unordered_map<char,int>um;\n for(auto j:s)\n um[j]++;\n string ans;\n for(auto it:order)\n {\n for(int i=0;i<um[it];i++)\n ans+=it;\n um[it]=0;\n }\n for(auto it:um)\n {\n for(int i=0;i<it.second;i++)\n ans+=it.first;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n answer = ""\n mapping = {}\n for sym in s:\n mapping[sym] = mapping.get(sym, 0) + 1\n for sym in order:\n if sym in mapping:\n answer += sym * mapping[sym]\n mapping.pop(sym)\n for sym in mapping.keys():\n answer += sym * mapping.get(sym, 0)\n print(mapping)\n return answer\n```\n\n```Java []\nclass Solution {\n public String customSortString(String order, String s) {\n int[] count = new int[26];\n for (char c : s.toCharArray()) {\n count[c - \'a\']++;\n }\n StringBuilder answer = new StringBuilder();\n for (char c : order.toCharArray()) {\n for (int i = 0; i < count[c - \'a\']; i++) {\n answer.append(c);\n }\n count[c - \'a\'] = 0;\n }\n for (char c = \'a\'; c <= \'z\'; c++) {\n for (int i = 0; i < count[c - \'a\']; i++) {\n answer.append(c);\n }\n }\n return answer.toString();\n }\n}\n```\n | 1 | You are given two strings order and s. All the characters of `order` are **unique** and were sorted in some custom order previously.
Permute the characters of `s` so that they match the order that `order` was sorted. More specifically, if a character `x` occurs before a character `y` in `order`, then `x` should occur before `y` in the permuted string.
Return _any permutation of_ `s` _that satisfies this property_.
**Example 1:**
**Input:** order = "cba ", s = "abcd "
**Output:** "cbad "
**Explanation:**
"a ", "b ", "c " appear in order, so the order of "a ", "b ", "c " should be "c ", "b ", and "a ".
Since "d " does not appear in order, it can be at any position in the returned string. "dcba ", "cdba ", "cbda " are also valid outputs.
**Example 2:**
**Input:** order = "cbafg ", s = "abcd "
**Output:** "cbad "
**Constraints:**
* `1 <= order.length <= 26`
* `1 <= s.length <= 200`
* `order` and `s` consist of lowercase English letters.
* All the characters of `order` are **unique**. | Use recursion. If root.val <= V, you split root.right into two halves, then join it's left half back on root.right. |
Solution | custom-sort-string | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n string customSortString(string order, string s) {\n unordered_map<char,int>um;\n for(auto j:s)\n um[j]++;\n string ans;\n for(auto it:order)\n {\n for(int i=0;i<um[it];i++)\n ans+=it;\n um[it]=0;\n }\n for(auto it:um)\n {\n for(int i=0;i<it.second;i++)\n ans+=it.first;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n answer = ""\n mapping = {}\n for sym in s:\n mapping[sym] = mapping.get(sym, 0) + 1\n for sym in order:\n if sym in mapping:\n answer += sym * mapping[sym]\n mapping.pop(sym)\n for sym in mapping.keys():\n answer += sym * mapping.get(sym, 0)\n print(mapping)\n return answer\n```\n\n```Java []\nclass Solution {\n public String customSortString(String order, String s) {\n int[] count = new int[26];\n for (char c : s.toCharArray()) {\n count[c - \'a\']++;\n }\n StringBuilder answer = new StringBuilder();\n for (char c : order.toCharArray()) {\n for (int i = 0; i < count[c - \'a\']; i++) {\n answer.append(c);\n }\n count[c - \'a\'] = 0;\n }\n for (char c = \'a\'; c <= \'z\'; c++) {\n for (int i = 0; i < count[c - \'a\']; i++) {\n answer.append(c);\n }\n }\n return answer.toString();\n }\n}\n```\n | 1 | There is a city composed of `n x n` blocks, where each block contains a single building shaped like a vertical square prism. You are given a **0-indexed** `n x n` integer matrix `grid` where `grid[r][c]` represents the **height** of the building located in the block at row `r` and column `c`.
A city's **skyline** is the outer contour formed by all the building when viewing the side of the city from a distance. The **skyline** from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of **any number of buildings by any amount** (the amount can be different per building). The height of a `0`\-height building can also be increased. However, increasing the height of a building should **not** affect the city's **skyline** from any cardinal direction.
Return _the **maximum total sum** that the height of the buildings can be increased by **without** changing the city's **skyline** from any cardinal direction_.
**Example 1:**
**Input:** grid = \[\[3,0,8,4\],\[2,4,5,7\],\[9,2,6,3\],\[0,3,1,0\]\]
**Output:** 35
**Explanation:** The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = \[ \[8, 4, 8, 7\],
\[7, 4, 7, 7\],
\[9, 4, 8, 7\],
\[3, 3, 3, 3\] \]
**Example 2:**
**Input:** grid = \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Output:** 0
**Explanation:** Increasing the height of any building will result in the skyline changing.
**Constraints:**
* `n == grid.length`
* `n == grid[r].length`
* `2 <= n <= 50`
* `0 <= grid[r][c] <= 100` | null |
User Friendly soln | custom-sort-string | 0 | 1 | # Intuition\n\nBeats 99% time and space \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing Hashmap\n\n# Complexity\n- Time complexity:\n- O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(26+26) in worst Case\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n s1=Counter(s)\n o1=Counter(order)\n res=""\n for i in order:\n if i in s1:\n res+=i*s1[i]\n for i in s:\n if i not in o1:\n res+=i\n return res\n \n``` | 1 | You are given two strings order and s. All the characters of `order` are **unique** and were sorted in some custom order previously.
Permute the characters of `s` so that they match the order that `order` was sorted. More specifically, if a character `x` occurs before a character `y` in `order`, then `x` should occur before `y` in the permuted string.
Return _any permutation of_ `s` _that satisfies this property_.
**Example 1:**
**Input:** order = "cba ", s = "abcd "
**Output:** "cbad "
**Explanation:**
"a ", "b ", "c " appear in order, so the order of "a ", "b ", "c " should be "c ", "b ", and "a ".
Since "d " does not appear in order, it can be at any position in the returned string. "dcba ", "cdba ", "cbda " are also valid outputs.
**Example 2:**
**Input:** order = "cbafg ", s = "abcd "
**Output:** "cbad "
**Constraints:**
* `1 <= order.length <= 26`
* `1 <= s.length <= 200`
* `order` and `s` consist of lowercase English letters.
* All the characters of `order` are **unique**. | Use recursion. If root.val <= V, you split root.right into two halves, then join it's left half back on root.right. |
User Friendly soln | custom-sort-string | 0 | 1 | # Intuition\n\nBeats 99% time and space \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing Hashmap\n\n# Complexity\n- Time complexity:\n- O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(26+26) in worst Case\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n s1=Counter(s)\n o1=Counter(order)\n res=""\n for i in order:\n if i in s1:\n res+=i*s1[i]\n for i in s:\n if i not in o1:\n res+=i\n return res\n \n``` | 1 | There is a city composed of `n x n` blocks, where each block contains a single building shaped like a vertical square prism. You are given a **0-indexed** `n x n` integer matrix `grid` where `grid[r][c]` represents the **height** of the building located in the block at row `r` and column `c`.
A city's **skyline** is the outer contour formed by all the building when viewing the side of the city from a distance. The **skyline** from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of **any number of buildings by any amount** (the amount can be different per building). The height of a `0`\-height building can also be increased. However, increasing the height of a building should **not** affect the city's **skyline** from any cardinal direction.
Return _the **maximum total sum** that the height of the buildings can be increased by **without** changing the city's **skyline** from any cardinal direction_.
**Example 1:**
**Input:** grid = \[\[3,0,8,4\],\[2,4,5,7\],\[9,2,6,3\],\[0,3,1,0\]\]
**Output:** 35
**Explanation:** The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = \[ \[8, 4, 8, 7\],
\[7, 4, 7, 7\],
\[9, 4, 8, 7\],
\[3, 3, 3, 3\] \]
**Example 2:**
**Input:** grid = \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Output:** 0
**Explanation:** Increasing the height of any building will result in the skyline changing.
**Constraints:**
* `n == grid.length`
* `n == grid[r].length`
* `2 <= n <= 50`
* `0 <= grid[r][c] <= 100` | null |
Python 1 liner | custom-sort-string | 0 | 1 | # Code\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n return "".join(sorted(s, key= lambda x: order.find(x)))\n``` | 1 | You are given two strings order and s. All the characters of `order` are **unique** and were sorted in some custom order previously.
Permute the characters of `s` so that they match the order that `order` was sorted. More specifically, if a character `x` occurs before a character `y` in `order`, then `x` should occur before `y` in the permuted string.
Return _any permutation of_ `s` _that satisfies this property_.
**Example 1:**
**Input:** order = "cba ", s = "abcd "
**Output:** "cbad "
**Explanation:**
"a ", "b ", "c " appear in order, so the order of "a ", "b ", "c " should be "c ", "b ", and "a ".
Since "d " does not appear in order, it can be at any position in the returned string. "dcba ", "cdba ", "cbda " are also valid outputs.
**Example 2:**
**Input:** order = "cbafg ", s = "abcd "
**Output:** "cbad "
**Constraints:**
* `1 <= order.length <= 26`
* `1 <= s.length <= 200`
* `order` and `s` consist of lowercase English letters.
* All the characters of `order` are **unique**. | Use recursion. If root.val <= V, you split root.right into two halves, then join it's left half back on root.right. |
Python 1 liner | custom-sort-string | 0 | 1 | # Code\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n return "".join(sorted(s, key= lambda x: order.find(x)))\n``` | 1 | There is a city composed of `n x n` blocks, where each block contains a single building shaped like a vertical square prism. You are given a **0-indexed** `n x n` integer matrix `grid` where `grid[r][c]` represents the **height** of the building located in the block at row `r` and column `c`.
A city's **skyline** is the outer contour formed by all the building when viewing the side of the city from a distance. The **skyline** from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of **any number of buildings by any amount** (the amount can be different per building). The height of a `0`\-height building can also be increased. However, increasing the height of a building should **not** affect the city's **skyline** from any cardinal direction.
Return _the **maximum total sum** that the height of the buildings can be increased by **without** changing the city's **skyline** from any cardinal direction_.
**Example 1:**
**Input:** grid = \[\[3,0,8,4\],\[2,4,5,7\],\[9,2,6,3\],\[0,3,1,0\]\]
**Output:** 35
**Explanation:** The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = \[ \[8, 4, 8, 7\],
\[7, 4, 7, 7\],
\[9, 4, 8, 7\],
\[3, 3, 3, 3\] \]
**Example 2:**
**Input:** grid = \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Output:** 0
**Explanation:** Increasing the height of any building will result in the skyline changing.
**Constraints:**
* `n == grid.length`
* `n == grid[r].length`
* `2 <= n <= 50`
* `0 <= grid[r][c] <= 100` | null |
791: Beats 95.81%, Solution with step by step explanation | custom-sort-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe use Python\'s Counter from the collections module to achieve this. It creates a dictionary where keys are characters of s and values are their corresponding frequencies.\n\n```\ns_count = Counter(s)\n```\nWe utilize a list comprehension to iterate over each character in order.\nFor each character char in order, we repeat it s_count[char] times.\n\'\'.join([...]) is used to concatenate all the individual pieces into a single string.\n\n```\nresult = \'\'.join([char * s_count[char] for char in order])\n```\n\nWe iterate over each key-value pair in s_count (i.e., char and freq).\nIf char is not present in order, it means it has not been added to our result string yet. Therefore, we append this character to result repeated freq times.\n\n```\nfor char, freq in s_count.items():\n if char not in order:\n result += char * freq\n```\n\nSimply return the constructed result.\n\n```\nreturn result\n```\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n s_count = Counter(s)\n \n result = \'\'.join([char * s_count[char] for char in order])\n \n for char, freq in s_count.items():\n if char not in order:\n result += char * freq\n \n return result\n\n``` | 0 | You are given two strings order and s. All the characters of `order` are **unique** and were sorted in some custom order previously.
Permute the characters of `s` so that they match the order that `order` was sorted. More specifically, if a character `x` occurs before a character `y` in `order`, then `x` should occur before `y` in the permuted string.
Return _any permutation of_ `s` _that satisfies this property_.
**Example 1:**
**Input:** order = "cba ", s = "abcd "
**Output:** "cbad "
**Explanation:**
"a ", "b ", "c " appear in order, so the order of "a ", "b ", "c " should be "c ", "b ", and "a ".
Since "d " does not appear in order, it can be at any position in the returned string. "dcba ", "cdba ", "cbda " are also valid outputs.
**Example 2:**
**Input:** order = "cbafg ", s = "abcd "
**Output:** "cbad "
**Constraints:**
* `1 <= order.length <= 26`
* `1 <= s.length <= 200`
* `order` and `s` consist of lowercase English letters.
* All the characters of `order` are **unique**. | Use recursion. If root.val <= V, you split root.right into two halves, then join it's left half back on root.right. |
791: Beats 95.81%, Solution with step by step explanation | custom-sort-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe use Python\'s Counter from the collections module to achieve this. It creates a dictionary where keys are characters of s and values are their corresponding frequencies.\n\n```\ns_count = Counter(s)\n```\nWe utilize a list comprehension to iterate over each character in order.\nFor each character char in order, we repeat it s_count[char] times.\n\'\'.join([...]) is used to concatenate all the individual pieces into a single string.\n\n```\nresult = \'\'.join([char * s_count[char] for char in order])\n```\n\nWe iterate over each key-value pair in s_count (i.e., char and freq).\nIf char is not present in order, it means it has not been added to our result string yet. Therefore, we append this character to result repeated freq times.\n\n```\nfor char, freq in s_count.items():\n if char not in order:\n result += char * freq\n```\n\nSimply return the constructed result.\n\n```\nreturn result\n```\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n s_count = Counter(s)\n \n result = \'\'.join([char * s_count[char] for char in order])\n \n for char, freq in s_count.items():\n if char not in order:\n result += char * freq\n \n return result\n\n``` | 0 | There is a city composed of `n x n` blocks, where each block contains a single building shaped like a vertical square prism. You are given a **0-indexed** `n x n` integer matrix `grid` where `grid[r][c]` represents the **height** of the building located in the block at row `r` and column `c`.
A city's **skyline** is the outer contour formed by all the building when viewing the side of the city from a distance. The **skyline** from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of **any number of buildings by any amount** (the amount can be different per building). The height of a `0`\-height building can also be increased. However, increasing the height of a building should **not** affect the city's **skyline** from any cardinal direction.
Return _the **maximum total sum** that the height of the buildings can be increased by **without** changing the city's **skyline** from any cardinal direction_.
**Example 1:**
**Input:** grid = \[\[3,0,8,4\],\[2,4,5,7\],\[9,2,6,3\],\[0,3,1,0\]\]
**Output:** 35
**Explanation:** The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = \[ \[8, 4, 8, 7\],
\[7, 4, 7, 7\],
\[9, 4, 8, 7\],
\[3, 3, 3, 3\] \]
**Example 2:**
**Input:** grid = \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Output:** 0
**Explanation:** Increasing the height of any building will result in the skyline changing.
**Constraints:**
* `n == grid.length`
* `n == grid[r].length`
* `2 <= n <= 50`
* `0 <= grid[r][c] <= 100` | null |
Python Easy Solution || Sorting || Hashmap | custom-sort-string | 0 | 1 | # Code\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n dic={}\n dic1={}\n rem=""\n lis=[]\n for i in range(len(order)):\n dic[order[i]]=i\n for i in dic:\n dic1[dic[i]]=i\n for i in s:\n if i in dic:\n lis.append(dic[i])\n else:\n rem+=i\n lis.sort()\n for i in lis:\n rem+=dic1[i]\n return rem\n``` | 2 | You are given two strings order and s. All the characters of `order` are **unique** and were sorted in some custom order previously.
Permute the characters of `s` so that they match the order that `order` was sorted. More specifically, if a character `x` occurs before a character `y` in `order`, then `x` should occur before `y` in the permuted string.
Return _any permutation of_ `s` _that satisfies this property_.
**Example 1:**
**Input:** order = "cba ", s = "abcd "
**Output:** "cbad "
**Explanation:**
"a ", "b ", "c " appear in order, so the order of "a ", "b ", "c " should be "c ", "b ", and "a ".
Since "d " does not appear in order, it can be at any position in the returned string. "dcba ", "cdba ", "cbda " are also valid outputs.
**Example 2:**
**Input:** order = "cbafg ", s = "abcd "
**Output:** "cbad "
**Constraints:**
* `1 <= order.length <= 26`
* `1 <= s.length <= 200`
* `order` and `s` consist of lowercase English letters.
* All the characters of `order` are **unique**. | Use recursion. If root.val <= V, you split root.right into two halves, then join it's left half back on root.right. |
Python Easy Solution || Sorting || Hashmap | custom-sort-string | 0 | 1 | # Code\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n dic={}\n dic1={}\n rem=""\n lis=[]\n for i in range(len(order)):\n dic[order[i]]=i\n for i in dic:\n dic1[dic[i]]=i\n for i in s:\n if i in dic:\n lis.append(dic[i])\n else:\n rem+=i\n lis.sort()\n for i in lis:\n rem+=dic1[i]\n return rem\n``` | 2 | There is a city composed of `n x n` blocks, where each block contains a single building shaped like a vertical square prism. You are given a **0-indexed** `n x n` integer matrix `grid` where `grid[r][c]` represents the **height** of the building located in the block at row `r` and column `c`.
A city's **skyline** is the outer contour formed by all the building when viewing the side of the city from a distance. The **skyline** from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of **any number of buildings by any amount** (the amount can be different per building). The height of a `0`\-height building can also be increased. However, increasing the height of a building should **not** affect the city's **skyline** from any cardinal direction.
Return _the **maximum total sum** that the height of the buildings can be increased by **without** changing the city's **skyline** from any cardinal direction_.
**Example 1:**
**Input:** grid = \[\[3,0,8,4\],\[2,4,5,7\],\[9,2,6,3\],\[0,3,1,0\]\]
**Output:** 35
**Explanation:** The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = \[ \[8, 4, 8, 7\],
\[7, 4, 7, 7\],
\[9, 4, 8, 7\],
\[3, 3, 3, 3\] \]
**Example 2:**
**Input:** grid = \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Output:** 0
**Explanation:** Increasing the height of any building will result in the skyline changing.
**Constraints:**
* `n == grid.length`
* `n == grid[r].length`
* `2 <= n <= 50`
* `0 <= grid[r][c] <= 100` | null |
✅ Simple yet interview friendly | Faster than 99.97% | Custom Sorting in Python | custom-sort-string | 0 | 1 | **Logic for Ranking**\n* There can only be 26 characters in the alphabet so if we can create a rank array of size 26 initially all values as 26\n ```rank = [26, 26, . . . . , 26] ```\n \n* We can rank all characters by giving them 0-25 Order and all characters that are not in Order string will have their value as 26 so they will be concatenated in the end of sorted string\n\n**Method 1:**\nWith use of lambda:\n\n***Faster than 99.97%***\n\n\n\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n\n rank = [26]*26\n \n for i in range(len(order)):\n rank[ord(order[i]) - ord(\'a\')] = i\n\n return "".join(sorted(list(s), key= lambda x: rank[ord(x) - ord(\'a\')]))\n \n```\n**Method 2:**\nWithout lambda:\n\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n \n def serialOrder(x):\n return rank[ord(x) - ord(\'a\')]\n \n rank = [26]*26\n \n for i in range(len(order)):\n rank[ord(order[i]) - ord(\'a\')] = i\n \n \n print(rank)\n arr = [i for i in s]\n \n arr.sort(key= serialOrder)\n \n s = "".join(arr)\n \n return s\n```\n\n**Time Complexity: O(M) + O(NlogN) ~~ O(NlogN)**\n**Space Complexity: O(26) ~~ O(1)**\n\n***I hope this explanation was helpful, please make sure to UPVOTE so that it can rank higher in discussion*** | 8 | You are given two strings order and s. All the characters of `order` are **unique** and were sorted in some custom order previously.
Permute the characters of `s` so that they match the order that `order` was sorted. More specifically, if a character `x` occurs before a character `y` in `order`, then `x` should occur before `y` in the permuted string.
Return _any permutation of_ `s` _that satisfies this property_.
**Example 1:**
**Input:** order = "cba ", s = "abcd "
**Output:** "cbad "
**Explanation:**
"a ", "b ", "c " appear in order, so the order of "a ", "b ", "c " should be "c ", "b ", and "a ".
Since "d " does not appear in order, it can be at any position in the returned string. "dcba ", "cdba ", "cbda " are also valid outputs.
**Example 2:**
**Input:** order = "cbafg ", s = "abcd "
**Output:** "cbad "
**Constraints:**
* `1 <= order.length <= 26`
* `1 <= s.length <= 200`
* `order` and `s` consist of lowercase English letters.
* All the characters of `order` are **unique**. | Use recursion. If root.val <= V, you split root.right into two halves, then join it's left half back on root.right. |
✅ Simple yet interview friendly | Faster than 99.97% | Custom Sorting in Python | custom-sort-string | 0 | 1 | **Logic for Ranking**\n* There can only be 26 characters in the alphabet so if we can create a rank array of size 26 initially all values as 26\n ```rank = [26, 26, . . . . , 26] ```\n \n* We can rank all characters by giving them 0-25 Order and all characters that are not in Order string will have their value as 26 so they will be concatenated in the end of sorted string\n\n**Method 1:**\nWith use of lambda:\n\n***Faster than 99.97%***\n\n\n\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n\n rank = [26]*26\n \n for i in range(len(order)):\n rank[ord(order[i]) - ord(\'a\')] = i\n\n return "".join(sorted(list(s), key= lambda x: rank[ord(x) - ord(\'a\')]))\n \n```\n**Method 2:**\nWithout lambda:\n\n```\nclass Solution:\n def customSortString(self, order: str, s: str) -> str:\n \n def serialOrder(x):\n return rank[ord(x) - ord(\'a\')]\n \n rank = [26]*26\n \n for i in range(len(order)):\n rank[ord(order[i]) - ord(\'a\')] = i\n \n \n print(rank)\n arr = [i for i in s]\n \n arr.sort(key= serialOrder)\n \n s = "".join(arr)\n \n return s\n```\n\n**Time Complexity: O(M) + O(NlogN) ~~ O(NlogN)**\n**Space Complexity: O(26) ~~ O(1)**\n\n***I hope this explanation was helpful, please make sure to UPVOTE so that it can rank higher in discussion*** | 8 | There is a city composed of `n x n` blocks, where each block contains a single building shaped like a vertical square prism. You are given a **0-indexed** `n x n` integer matrix `grid` where `grid[r][c]` represents the **height** of the building located in the block at row `r` and column `c`.
A city's **skyline** is the outer contour formed by all the building when viewing the side of the city from a distance. The **skyline** from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of **any number of buildings by any amount** (the amount can be different per building). The height of a `0`\-height building can also be increased. However, increasing the height of a building should **not** affect the city's **skyline** from any cardinal direction.
Return _the **maximum total sum** that the height of the buildings can be increased by **without** changing the city's **skyline** from any cardinal direction_.
**Example 1:**
**Input:** grid = \[\[3,0,8,4\],\[2,4,5,7\],\[9,2,6,3\],\[0,3,1,0\]\]
**Output:** 35
**Explanation:** The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = \[ \[8, 4, 8, 7\],
\[7, 4, 7, 7\],
\[9, 4, 8, 7\],
\[3, 3, 3, 3\] \]
**Example 2:**
**Input:** grid = \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Output:** 0
**Explanation:** Increasing the height of any building will result in the skyline changing.
**Constraints:**
* `n == grid.length`
* `n == grid[r].length`
* `2 <= n <= 50`
* `0 <= grid[r][c] <= 100` | null |
PYTHON|| FASTER THAN 99.8%|| SC 99%|| EASY | number-of-matching-subsequences | 0 | 1 | ```\n def sub(st):\n pos = -1\n for char in st:\n pos = s.find(char, pos+1)\n if pos == -1: return False\n return True\n return sum(map(sub, words))\n\t```\nIF THIS HELP U KINDLY UPVOTE THIS TO HELP OTHERS TO GET THIS SOLUTION\nIF U DONT GET IT KINDLY COMMENT AND FEEL FREE TO ASK\nAND CORRECT MEIF I AM WRONG | 15 | Given a string `s` and an array of strings `words`, return _the number of_ `words[i]` _that is a subsequence of_ `s`.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "abcde ", words = \[ "a ", "bb ", "acd ", "ace "\]
**Output:** 3
**Explanation:** There are three strings in words that are a subsequence of s: "a ", "acd ", "ace ".
**Example 2:**
**Input:** s = "dsahjpjauf ", words = \[ "ahjpjau ", "ja ", "ahbwzgqnuk ", "tnmlanowax "\]
**Output:** 2
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 50`
* `s` and `words[i]` consist of only lowercase English letters. | null |
PYTHON|| FASTER THAN 99.8%|| SC 99%|| EASY | number-of-matching-subsequences | 0 | 1 | ```\n def sub(st):\n pos = -1\n for char in st:\n pos = s.find(char, pos+1)\n if pos == -1: return False\n return True\n return sum(map(sub, words))\n\t```\nIF THIS HELP U KINDLY UPVOTE THIS TO HELP OTHERS TO GET THIS SOLUTION\nIF U DONT GET IT KINDLY COMMENT AND FEEL FREE TO ASK\nAND CORRECT MEIF I AM WRONG | 15 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
📌 Easy-Approach || Well-explained || 95% faster 🐍 | number-of-matching-subsequences | 0 | 1 | ## IDEA:\n\n\uD83D\uDC49 finding the index of each character in "s" then virtually cutting "s" => from index+1 to last.\n\uD83D\uDC49 repeating above point for all the characters in word, if any ch not found in s then it will return -1.\n\ne.g.-\n\ts="abgheaf"\n\tw=["gef", "gefk"]\n\tindex = -1\n* \tfirst found index of "g" in s[index+1 : ] => "abgheaf", which is 2 (i.e. index=2).\n* \tNow, we find the index of "e" in s[index+1:] => s[2+1:] => s[3:] => "heaf" which results index=4.\n* \tAgain find the index of "f" in s[index+1: ] => s[4+1:] => s[5:] => "af" which gives index=6.\n**Another word:**\n* \tif we are having word as "gefk" then after repeating previous 3 points we will have index=6.\n* \tNow find the index of "k" in s[index+1:] => s[6+1:] => s[7:] =>"" which will give index=-1. i.e. not found.\n\t\n\'\'\'\n\n\tclass Solution:\n def numMatchingSubseq(self, s: str, words: List[str]) -> int:\n \n def is_sub(word):\n index=-1\n for ch in word:\n index=s.find(ch,index+1)\n if index==-1:\n return False\n return True\n \n c=0\n for word in words:\n if is_sub(word):\n c+=1\n \n return c\n\t\t\nfeel free to ask if any doubt. \uD83C\uDFCD\nif you got helpful then please **upvote!!** \uD83E\uDD17 | 29 | Given a string `s` and an array of strings `words`, return _the number of_ `words[i]` _that is a subsequence of_ `s`.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "abcde ", words = \[ "a ", "bb ", "acd ", "ace "\]
**Output:** 3
**Explanation:** There are three strings in words that are a subsequence of s: "a ", "acd ", "ace ".
**Example 2:**
**Input:** s = "dsahjpjauf ", words = \[ "ahjpjau ", "ja ", "ahbwzgqnuk ", "tnmlanowax "\]
**Output:** 2
**Constraints:**
* `1 <= s.length <= 5 * 104`
* `1 <= words.length <= 5000`
* `1 <= words[i].length <= 50`
* `s` and `words[i]` consist of only lowercase English letters. | null |
📌 Easy-Approach || Well-explained || 95% faster 🐍 | number-of-matching-subsequences | 0 | 1 | ## IDEA:\n\n\uD83D\uDC49 finding the index of each character in "s" then virtually cutting "s" => from index+1 to last.\n\uD83D\uDC49 repeating above point for all the characters in word, if any ch not found in s then it will return -1.\n\ne.g.-\n\ts="abgheaf"\n\tw=["gef", "gefk"]\n\tindex = -1\n* \tfirst found index of "g" in s[index+1 : ] => "abgheaf", which is 2 (i.e. index=2).\n* \tNow, we find the index of "e" in s[index+1:] => s[2+1:] => s[3:] => "heaf" which results index=4.\n* \tAgain find the index of "f" in s[index+1: ] => s[4+1:] => s[5:] => "af" which gives index=6.\n**Another word:**\n* \tif we are having word as "gefk" then after repeating previous 3 points we will have index=6.\n* \tNow find the index of "k" in s[index+1:] => s[6+1:] => s[7:] =>"" which will give index=-1. i.e. not found.\n\t\n\'\'\'\n\n\tclass Solution:\n def numMatchingSubseq(self, s: str, words: List[str]) -> int:\n \n def is_sub(word):\n index=-1\n for ch in word:\n index=s.find(ch,index+1)\n if index==-1:\n return False\n return True\n \n c=0\n for word in words:\n if is_sub(word):\n c+=1\n \n return c\n\t\t\nfeel free to ask if any doubt. \uD83C\uDFCD\nif you got helpful then please **upvote!!** \uD83E\uDD17 | 29 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Solution | preimage-size-of-factorial-zeroes-function | 1 | 1 | ```C++ []\nclass Solution {\n#include <random>\npublic:\n int preimageSizeFZF(int k) {\n vector<long long> magicNum;\n long long Num = 0;\n long long power_5 = 5;\n while(Num < 1000000000){\n power_5 = power_5 * 5;\n Num = (power_5 - 1) / 4;\n magicNum.push_back(Num);\n }\n long long nextMagic = 0;\n int current_zero_num;\n for(int i = 0 ; i < magicNum.size() ; i++){\n if(magicNum[i] > k){\n nextMagic = magicNum[i];\n current_zero_num = i;\n break;\n }else if(magicNum[i] == k){\n return 5;\n }\n }\n long long temp_k = k;\n for(int i = current_zero_num ; i >= 0 ; i--){\n if(temp_k>=magicNum[i]-i-1){\n return 0;\n }else{\n if(i == 0){\n return 5;\n }\n while(temp_k - magicNum[i-1] >= 0){\n temp_k = temp_k - magicNum[i-1];\n }\n }\n }\n return 5;\n }\n};\n```\n\n```Python3 []\nfrom math import floor, log\n\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n m = floor(log(4 * k + 1, 5))\n while m:\n unit = (5 ** m - 1) // 4\n if k // unit > 4:\n return 0\n k %= unit\n m -= 1\n\n return 5\n```\n\n```Java []\nclass Solution {\n public int preimageSizeFZF(int k) {\n \n long low = 0;\n long high = (long)Math.pow(10,10);\n \n while(low<=high){\n long mid = low + (high-low)/2;\n long val = mid;\n long ans = 0;\n while(val!=0){\n val/=5;\n ans+=val;\n }\n if(ans==k){\n return 5;\n }else if(ans>k){\n high = mid-1;\n }else{\n low = mid+1;\n }\n }\n return 0;\n }\n}\n```\n | 1 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
Solution | preimage-size-of-factorial-zeroes-function | 1 | 1 | ```C++ []\nclass Solution {\n#include <random>\npublic:\n int preimageSizeFZF(int k) {\n vector<long long> magicNum;\n long long Num = 0;\n long long power_5 = 5;\n while(Num < 1000000000){\n power_5 = power_5 * 5;\n Num = (power_5 - 1) / 4;\n magicNum.push_back(Num);\n }\n long long nextMagic = 0;\n int current_zero_num;\n for(int i = 0 ; i < magicNum.size() ; i++){\n if(magicNum[i] > k){\n nextMagic = magicNum[i];\n current_zero_num = i;\n break;\n }else if(magicNum[i] == k){\n return 5;\n }\n }\n long long temp_k = k;\n for(int i = current_zero_num ; i >= 0 ; i--){\n if(temp_k>=magicNum[i]-i-1){\n return 0;\n }else{\n if(i == 0){\n return 5;\n }\n while(temp_k - magicNum[i-1] >= 0){\n temp_k = temp_k - magicNum[i-1];\n }\n }\n }\n return 5;\n }\n};\n```\n\n```Python3 []\nfrom math import floor, log\n\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n m = floor(log(4 * k + 1, 5))\n while m:\n unit = (5 ** m - 1) // 4\n if k // unit > 4:\n return 0\n k %= unit\n m -= 1\n\n return 5\n```\n\n```Java []\nclass Solution {\n public int preimageSizeFZF(int k) {\n \n long low = 0;\n long high = (long)Math.pow(10,10);\n \n while(low<=high){\n long mid = low + (high-low)/2;\n long val = mid;\n long ans = 0;\n while(val!=0){\n val/=5;\n ans+=val;\n }\n if(ans==k){\n return 5;\n }else if(ans>k){\n high = mid-1;\n }else{\n low = mid+1;\n }\n }\n return 0;\n }\n}\n```\n | 1 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
✔ Python3 Solution | Binary Search | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Binary Search\n```\nclass Solution:\n def preimageSizeFZF(self, k):\n l, r = -1, k\n while l != r:\n n = c = m = (l + r + 1) >> 1\n while n and c <= k: c += (n := n // 5)\n if c < k: l = m\n elif c > k: r = m - 1\n else: return 5\n return 0\n``` | 1 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
✔ Python3 Solution | Binary Search | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Binary Search\n```\nclass Solution:\n def preimageSizeFZF(self, k):\n l, r = -1, k\n while l != r:\n n = c = m = (l + r + 1) >> 1\n while n and c <= k: c += (n := n // 5)\n if c < k: l = m\n elif c > k: r = m - 1\n else: return 5\n return 0\n``` | 1 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Python 3 || 12 lines, bin search, w/explanation || T/M: 88% / 98% | preimage-size-of-factorial-zeroes-function | 0 | 1 | The number of zeros in the decimal representation of an integer is equal to the count of factors of`10` in the integer. The number of `10`-factors in an integer, in turn, is equal to the lesser of the counts of `5`-factors and of `2`-factors in that integer. For an integer n!, it is the count `5`-factors because the count of`2`-factors is at least thrice the count of `5`-factors.\n\nThe plan here is to determine the integers `atMost_k(k)` and `atMost_k(k-1)`, the greatest integers have at most`5`-factors counts of`k` and `k-1` respectively. The solution to the problem is the difference of these quantities. We use a binary search in `atMost_k`.\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int: \n\n def atMost_k(k: int)-> int:\n\n left, right = 0, 5*k + 4\n\n while left <= right:\n mid = (left+right)//2\n count, n = 0, mid\n\n while n:\n n//= 5\n count+= n\n\n if count <= k: left = mid + 1\n else: right = mid - 1\n\n return right\n\n \n return atMost_k(k) - atMost_k(k-1)\n```\n[https://leetcode.com/problems/preimage-size-of-factorial-zeroes-function/submissions/885195088/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1). | 4 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
Python 3 || 12 lines, bin search, w/explanation || T/M: 88% / 98% | preimage-size-of-factorial-zeroes-function | 0 | 1 | The number of zeros in the decimal representation of an integer is equal to the count of factors of`10` in the integer. The number of `10`-factors in an integer, in turn, is equal to the lesser of the counts of `5`-factors and of `2`-factors in that integer. For an integer n!, it is the count `5`-factors because the count of`2`-factors is at least thrice the count of `5`-factors.\n\nThe plan here is to determine the integers `atMost_k(k)` and `atMost_k(k-1)`, the greatest integers have at most`5`-factors counts of`k` and `k-1` respectively. The solution to the problem is the difference of these quantities. We use a binary search in `atMost_k`.\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int: \n\n def atMost_k(k: int)-> int:\n\n left, right = 0, 5*k + 4\n\n while left <= right:\n mid = (left+right)//2\n count, n = 0, mid\n\n while n:\n n//= 5\n count+= n\n\n if count <= k: left = mid + 1\n else: right = mid - 1\n\n return right\n\n \n return atMost_k(k) - atMost_k(k-1)\n```\n[https://leetcode.com/problems/preimage-size-of-factorial-zeroes-function/submissions/885195088/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1). | 4 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
PYTHON SIMPLE BINARY SEARCH BEATS 94%! | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe notice that every occurence of 5 we are added 1 \'0\'\nour approach will be to Binary Search the number of 5\'s needed to get k (if even possible)\n* we have to look for exponents of 5 like 25 225 and so on.\nbecause those add us 2 , 3 and so on \'0\'s.\n\nso the code is simple, count how much zero\'s we get for every value we go threw when we Binary Search, if we didnt find solution it means such k is immposible.\n\n* self exercise: explain why if there is suck k, there are only 5 numbers that satisfy it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nBST : O(log(k))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nsaving the numbers while running: O(log(k))\n\n# Code\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n #init: k = 0\n #every 5 : k += 1\n #sol is either 0 or 5 (!) :)\n r = k\n l = 0\n while l <= r:\n mid = l + (r - l) // 2\n val = 0\n x = mid\n while x > 0:\n x //= 5\n val += x \n val += mid\n if val == k:\n return 5\n elif val < k:\n l = mid + 1\n else:\n r = mid - 1\n return 0\n\n \n``` | 0 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
PYTHON SIMPLE BINARY SEARCH BEATS 94%! | preimage-size-of-factorial-zeroes-function | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe notice that every occurence of 5 we are added 1 \'0\'\nour approach will be to Binary Search the number of 5\'s needed to get k (if even possible)\n* we have to look for exponents of 5 like 25 225 and so on.\nbecause those add us 2 , 3 and so on \'0\'s.\n\nso the code is simple, count how much zero\'s we get for every value we go threw when we Binary Search, if we didnt find solution it means such k is immposible.\n\n* self exercise: explain why if there is suck k, there are only 5 numbers that satisfy it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nBST : O(log(k))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nsaving the numbers while running: O(log(k))\n\n# Code\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n #init: k = 0\n #every 5 : k += 1\n #sol is either 0 or 5 (!) :)\n r = k\n l = 0\n while l <= r:\n mid = l + (r - l) // 2\n val = 0\n x = mid\n while x > 0:\n x //= 5\n val += x \n val += mid\n if val == k:\n return 5\n elif val < k:\n l = mid + 1\n else:\n r = mid - 1\n return 0\n\n \n``` | 0 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
binary search w/ counting trailing zeros | runtime beats 71.08% | preimage-size-of-factorial-zeroes-function | 1 | 1 | # Intuition\nThe problem involves counting the number of non-negative integers x such that the number of trailing zeroes in x! (factorial of x) is equal to a given value k.\n\n# Approach\nHere, `atMost_k` function calculates the number of integers less than or equal to a given value with k trailing zeros by performing a binary search on the possible range of values. The key optimization lies in the efficient calculation of trailing zeros using the count_trailing_zeros function.\n\n# Complexity\n- Time complexity: $$O(logN)$$, where N is the range of possible values.\n- Space complexity: $$O(1)$$ as there is no significant additional space usage.\n\n\n# Code\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n def count_trailing_zeros(n: int) -> int:\n count = 0\n while n > 0:\n n //= 5\n count += n\n return count\n\n def atMost_k(k: int) -> int:\n left, right = 0, 5 * k + 4\n\n while left <= right:\n mid = (left + right) // 2\n count = count_trailing_zeros(mid)\n\n if count <= k:\n left = mid + 1\n else:\n right = mid - 1\n\n return right\n\n return atMost_k(k) - atMost_k(k - 1) \n``` | 0 | Let `f(x)` be the number of zeroes at the end of `x!`. Recall that `x! = 1 * 2 * 3 * ... * x` and by convention, `0! = 1`.
* For example, `f(3) = 0` because `3! = 6` has no zeroes at the end, while `f(11) = 2` because `11! = 39916800` has two zeroes at the end.
Given an integer `k`, return the number of non-negative integers `x` have the property that `f(x) = k`.
**Example 1:**
**Input:** k = 0
**Output:** 5
**Explanation:** 0!, 1!, 2!, 3!, and 4! end with k = 0 zeroes.
**Example 2:**
**Input:** k = 5
**Output:** 0
**Explanation:** There is no x such that x! ends in k = 5 zeroes.
**Example 3:**
**Input:** k = 3
**Output:** 5
**Constraints:**
* `0 <= k <= 109` | Think of the L and R's as people on a horizontal line, where X is a space. The people can't cross each other, and also you can't go from XRX to RXX. |
binary search w/ counting trailing zeros | runtime beats 71.08% | preimage-size-of-factorial-zeroes-function | 1 | 1 | # Intuition\nThe problem involves counting the number of non-negative integers x such that the number of trailing zeroes in x! (factorial of x) is equal to a given value k.\n\n# Approach\nHere, `atMost_k` function calculates the number of integers less than or equal to a given value with k trailing zeros by performing a binary search on the possible range of values. The key optimization lies in the efficient calculation of trailing zeros using the count_trailing_zeros function.\n\n# Complexity\n- Time complexity: $$O(logN)$$, where N is the range of possible values.\n- Space complexity: $$O(1)$$ as there is no significant additional space usage.\n\n\n# Code\n```\nclass Solution:\n def preimageSizeFZF(self, k: int) -> int:\n def count_trailing_zeros(n: int) -> int:\n count = 0\n while n > 0:\n n //= 5\n count += n\n return count\n\n def atMost_k(k: int) -> int:\n left, right = 0, 5 * k + 4\n\n while left <= right:\n mid = (left + right) // 2\n count = count_trailing_zeros(mid)\n\n if count <= k:\n left = mid + 1\n else:\n right = mid - 1\n\n return right\n\n return atMost_k(k) - atMost_k(k - 1) \n``` | 0 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.