title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python Easy Solution | find-eventual-safe-states | 0 | 1 | \n\n# Code\n```\nclass Solution(object):\n def eventualSafeNodes(self, graph):\n """\n :type graph: List[List[int]]\n :rtype: List[int]\n """\n n=len(graph)\n safe={}\n ans=[]\n def dfs(i):\n if i in safe:\n return safe[i]\n safe[i]=False\n for nei in graph[i]:\n if not dfs(nei):\n return safe[i]\n safe[i]=True\n return safe[i]\n\n for i in range(n):\n if dfs(i):\n ans.append(i)\n return ans \n``` | 1 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Python Easy Solution | find-eventual-safe-states | 0 | 1 | \n\n# Code\n```\nclass Solution(object):\n def eventualSafeNodes(self, graph):\n """\n :type graph: List[List[int]]\n :rtype: List[int]\n """\n n=len(graph)\n safe={}\n ans=[]\n def dfs(i):\n if i in safe:\n return safe[i]\n safe[i]=False\n for nei in graph[i]:\n if not dfs(nei):\n return safe[i]\n safe[i]=True\n return safe[i]\n\n for i in range(n):\n if dfs(i):\n ans.append(i)\n return ans \n``` | 1 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Solution | find-eventual-safe-states | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool dfs(vector<int>&vis,vector<int>&path,int start,vector<vector<int>>&graph,vector<int>&ans)\n {\n vis[start]=1;\n path[start]=1;\n for(auto it:graph[start])\n {\n if(vis[it]==0)\n {\n if(dfs(vis,path,it,graph,ans))\n return true;\n }\n else if(path[it]==1)\n return true ;\n }\n path[start]=0;\n ans.push_back(start);\n return false;\n }\n vector<int> eventualSafeNodes(vector<vector<int>>& graph) {\n int n=graph.size();\n vector<int>vis(n,0);\n vector<int>path(n,0);\n vector<int>ans;\n for(int i=0;i<n;i++)\n {\n if(!vis[i])\n dfs(vis,path,i,graph,ans);\n }\n sort(ans.begin(),ans.end());\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n n = len(graph)\n visited, res = [-1] * n, []\n def explore(u):\n visited[u] = 0\n for v in graph[u]:\n if visited[v] == 0 or (visited[v] == -1 and explore(v)): return True\n \n visited[u] = 1\n res.append(u)\n return False\n\n for u in range(n):\n if visited[u] == -1: explore(u)\n\n return sorted(res)\n```\n\n```Java []\nclass Solution {\n public List<Integer> eventualSafeNodes(int[][] graph) {\n ArrayList<Integer> safeStates = new ArrayList<>();\n int vis[] = new int[graph.length];\n\n for(int i=0; i<graph.length; i++) {\n if(isSafe(i, graph , vis)) {\n safeStates.add(i);\n }\n }\n return safeStates;\n }\n public static boolean isSafe(int index, int[][] graph, int vis[]) {\n if(vis[index] == 2) {\n return true;\n }\n if(vis[index] == 1) {\n return false;\n }\n vis[index] = 1;\n int neighbor[] = graph[index];\n\n for(int i=0; i< neighbor.length; i++) {\n if(!isSafe(neighbor[i], graph, vis)) {\n return false;\n }\n }\n vis[index] = 2;\n return true;\n }\n}\n```\n | 2 | There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`.
A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node).
Return _an array containing all the **safe nodes** of the graph_. The answer should be sorted in **ascending** order.
**Example 1:**
**Input:** graph = \[\[1,2\],\[2,3\],\[5\],\[0\],\[5\],\[\],\[\]\]
**Output:** \[2,4,5,6\]
**Explanation:** The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.
**Example 2:**
**Input:** graph = \[\[1,2,3,4\],\[1,2\],\[3,4\],\[0,4\],\[\]\]
**Output:** \[4\]
**Explanation:**
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.
**Constraints:**
* `n == graph.length`
* `1 <= n <= 104`
* `0 <= graph[i].length <= n`
* `0 <= graph[i][j] <= n - 1`
* `graph[i]` is sorted in a strictly increasing order.
* The graph may contain self-loops.
* The number of edges in the graph will be in the range `[1, 4 * 104]`. | null |
Solution | find-eventual-safe-states | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool dfs(vector<int>&vis,vector<int>&path,int start,vector<vector<int>>&graph,vector<int>&ans)\n {\n vis[start]=1;\n path[start]=1;\n for(auto it:graph[start])\n {\n if(vis[it]==0)\n {\n if(dfs(vis,path,it,graph,ans))\n return true;\n }\n else if(path[it]==1)\n return true ;\n }\n path[start]=0;\n ans.push_back(start);\n return false;\n }\n vector<int> eventualSafeNodes(vector<vector<int>>& graph) {\n int n=graph.size();\n vector<int>vis(n,0);\n vector<int>path(n,0);\n vector<int>ans;\n for(int i=0;i<n;i++)\n {\n if(!vis[i])\n dfs(vis,path,i,graph,ans);\n }\n sort(ans.begin(),ans.end());\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:\n n = len(graph)\n visited, res = [-1] * n, []\n def explore(u):\n visited[u] = 0\n for v in graph[u]:\n if visited[v] == 0 or (visited[v] == -1 and explore(v)): return True\n \n visited[u] = 1\n res.append(u)\n return False\n\n for u in range(n):\n if visited[u] == -1: explore(u)\n\n return sorted(res)\n```\n\n```Java []\nclass Solution {\n public List<Integer> eventualSafeNodes(int[][] graph) {\n ArrayList<Integer> safeStates = new ArrayList<>();\n int vis[] = new int[graph.length];\n\n for(int i=0; i<graph.length; i++) {\n if(isSafe(i, graph , vis)) {\n safeStates.add(i);\n }\n }\n return safeStates;\n }\n public static boolean isSafe(int index, int[][] graph, int vis[]) {\n if(vis[index] == 2) {\n return true;\n }\n if(vis[index] == 1) {\n return false;\n }\n vis[index] = 1;\n int neighbor[] = graph[index];\n\n for(int i=0; i< neighbor.length; i++) {\n if(!isSafe(neighbor[i], graph, vis)) {\n return false;\n }\n }\n vis[index] = 2;\n return true;\n }\n}\n```\n | 2 | A **valid encoding** of an array of `words` is any reference string `s` and array of indices `indices` such that:
* `words.length == indices.length`
* The reference string `s` ends with the `'#'` character.
* For each index `indices[i]`, the **substring** of `s` starting from `indices[i]` and up to (but not including) the next `'#'` character is equal to `words[i]`.
Given an array of `words`, return _the **length of the shortest reference string**_ `s` _possible of any **valid encoding** of_ `words`_._
**Example 1:**
**Input:** words = \[ "time ", "me ", "bell "\]
**Output:** 10
**Explanation:** A valid encoding would be s = ` "time#bell# " and indices = [0, 2, 5`\].
words\[0\] = "time ", the substring of s starting from indices\[0\] = 0 to the next '#' is underlined in "time#bell# "
words\[1\] = "me ", the substring of s starting from indices\[1\] = 2 to the next '#' is underlined in "time#bell# "
words\[2\] = "bell ", the substring of s starting from indices\[2\] = 5 to the next '#' is underlined in "time#bell\# "
**Example 2:**
**Input:** words = \[ "t "\]
**Output:** 2
**Explanation:** A valid encoding would be s = "t# " and indices = \[0\].
**Constraints:**
* `1 <= words.length <= 2000`
* `1 <= words[i].length <= 7`
* `words[i]` consists of only lowercase letters. | null |
Solution | bricks-falling-when-hit | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isConnected(vector<vector<bool>>& vis, int& i, int& j){\n if(i==0)\n return true;\n \n if(i>0 && vis[i-1][j])\n return true;\n if(j>0 && vis[i][j-1])\n return true;\n if(i<vis.size()-1 && vis[i+1][j])\n return true;\n if(j<vis[0].size()-1 && vis[i][j+1])\n return true;\n return false;\n }\n vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) {\n vector<int> ans(hits.size(), 0);\n vector<vector<int>> mat = grid;\n for(int i=0; i<hits.size(); i++)\n mat[hits[i][0]][hits[i][1]] = 0;\n vector<vector<bool>> vis(grid.size(), vector<bool> (grid[0].size(), false));\n queue<pair<int, int>> q;\n for(int i=0; i<grid[0].size(); i++){\n if(mat[0][i]==1){\n vis[0][i] = true;\n q.push({0, i});\n }\n }\n while(!q.empty()){\n int idx = q.front().first, jdx = q.front().second;\n q.pop();\n \n if(idx>0 && mat[idx-1][jdx]==1){\n if(!vis[idx-1][jdx])\n q.push({idx-1, jdx});\n vis[idx-1][jdx]=true;\n }\n if(jdx>0 && mat[idx][jdx-1]==1){\n if(!vis[idx][jdx-1])\n q.push({idx, jdx-1});\n vis[idx][jdx-1]=true;\n }\n if(idx<grid.size()-1 && mat[idx+1][jdx]==1){\n if(!vis[idx+1][jdx])\n q.push({idx+1, jdx});\n vis[idx+1][jdx]=true;\n }\n if(jdx<grid[0].size()-1 && mat[idx][jdx+1]==1){\n if(!vis[idx][jdx+1])\n q.push({idx, jdx+1});\n vis[idx][jdx+1]=true;\n }\n }\n for(int i=hits.size()-1; i>=0; i--){\n if(grid[hits[i][0]][hits[i][1]]==0)\n continue;\n mat[hits[i][0]][hits[i][1]] = 1;\n if(!isConnected(vis, hits[i][0], hits[i][1]))\n continue;\n q.push({hits[i][0], hits[i][1]});\n vis[hits[i][0]][hits[i][1]] = true;\n int cnt=0;\n while(!q.empty()){\n int idx = q.front().first, jdx = q.front().second;\n q.pop();\n cnt++;\n if(idx>0 && mat[idx-1][jdx]==1 && !vis[idx-1][jdx]){\n q.push({idx-1, jdx});\n vis[idx-1][jdx]=true;\n }\n if(jdx>0 && mat[idx][jdx-1]==1 && !vis[idx][jdx-1]){\n q.push({idx, jdx-1});\n vis[idx][jdx-1]=true;\n }\n if(idx<grid.size()-1 && mat[idx+1][jdx]==1 && !vis[idx+1][jdx]){\n q.push({idx+1, jdx});\n vis[idx+1][jdx]=true;\n }\n if(jdx<grid[0].size()-1 && mat[idx][jdx+1]==1 && !vis[idx][jdx+1]){\n q.push({idx, jdx+1});\n vis[idx][jdx+1]=true;\n }\n }\n ans[i] = cnt-1;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def hitBricks(\n self, grid: List[List[int]], hits: List[List[int]],\n exhaust=deque(maxlen=0).extend \n ) -> List[int]:\n cells = bytearray(\n (cell_cnt := (len(grid) + 2) \n * (col_cnt := (width := len(grid[0])) + 2))\n ) \n occupied = partial(filter, cells.__getitem__)\n for base, row in zip(\n count((offset := col_cnt + 1) + col_cnt, col_cnt), \n islice(grid, 1, None)\n ):\n cells[base:base + width] = row\n exhaust(map(\n (removed := [-40805] * cell_cnt).__setitem__, \n (((row * col_cnt) + col + offset) for row, col in hits), \n count(-1, -1)\n ))\n base_removals = tuple(map(\n removed.__getitem__, \n (bases := tuple(\n map(offset.__add__, \n filter(grid[0].__getitem__, range(width)))\n ))\n ))\n dists = 1, col_cnt, -1, -col_cnt\n solutions = [0] * len(hits) \n heapify((pending := list(zip(base_removals, bases))))\n while pending:\n hit, at = heappop(pending)\n for to in occupied(map(at.__add__, dists)):\n cells[to] = False\n if (candidate := removed[to]) < hit:\n solutions[(candidate := hit)] += 1\n heappush(pending, (candidate, to))\n return reversed(solutions)\n```\n\n```Java []\nclass Solution {\n public int[] hitBricks(int[][] grid, int[][] hits) {\n int n = grid.length;\n int m = grid[0].length;\n int[] ans = new int[hits.length];\n \n for(int[] hit : hits) {\n grid[hit[0]][hit[1]] *= -1;\n }\n for(int i = 0; i < m; i++) {\n dfs(grid, 0, i);\n }\n for(int i = hits.length-1; i >= 0; i--) {\n int x = hits[i][0];\n int y = hits[i][1];\n if(grid[x][y] == 0) {\n continue;\n } \n grid[x][y] = 1;\n if(connected(grid, x, y, n, m)) {\n ans[i] = dfs(grid, x, y)-1;\n }\n }\n return ans;\n }\n public int dfs(int[][] grid, int x, int y) {\n if(x < 0 || y < 0 || x >= grid.length || y >= grid[0].length || grid[x][y] != 1) {\n return 0;\n }\n grid[x][y] = 2;\n return 1 + dfs(grid, x+1, y) + dfs(grid, x, y+1) + dfs(grid, x-1, y) + dfs(grid, x, y-1);\n }\n public boolean connected(int[][] grid, int x, int y, int n, int m) {\n if(x == 0) {\n return true;\n }\n if(x+1 < n) {\n if(grid[x+1][y] == 2) {\n return true;\n }\n }\n if(x-1 >= 0) {\n if(grid[x-1][y] == 2) {\n return true;\n }\n }\n if(y+1 < m) {\n if(grid[x][y+1] == 2) {\n return true;\n }\n }\n if(y-1 >= 0) {\n if(grid[x][y-1] == 2) {\n return true;\n }\n }\n return false;\n }\n}\n```\n | 1 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
Solution | bricks-falling-when-hit | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool isConnected(vector<vector<bool>>& vis, int& i, int& j){\n if(i==0)\n return true;\n \n if(i>0 && vis[i-1][j])\n return true;\n if(j>0 && vis[i][j-1])\n return true;\n if(i<vis.size()-1 && vis[i+1][j])\n return true;\n if(j<vis[0].size()-1 && vis[i][j+1])\n return true;\n return false;\n }\n vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) {\n vector<int> ans(hits.size(), 0);\n vector<vector<int>> mat = grid;\n for(int i=0; i<hits.size(); i++)\n mat[hits[i][0]][hits[i][1]] = 0;\n vector<vector<bool>> vis(grid.size(), vector<bool> (grid[0].size(), false));\n queue<pair<int, int>> q;\n for(int i=0; i<grid[0].size(); i++){\n if(mat[0][i]==1){\n vis[0][i] = true;\n q.push({0, i});\n }\n }\n while(!q.empty()){\n int idx = q.front().first, jdx = q.front().second;\n q.pop();\n \n if(idx>0 && mat[idx-1][jdx]==1){\n if(!vis[idx-1][jdx])\n q.push({idx-1, jdx});\n vis[idx-1][jdx]=true;\n }\n if(jdx>0 && mat[idx][jdx-1]==1){\n if(!vis[idx][jdx-1])\n q.push({idx, jdx-1});\n vis[idx][jdx-1]=true;\n }\n if(idx<grid.size()-1 && mat[idx+1][jdx]==1){\n if(!vis[idx+1][jdx])\n q.push({idx+1, jdx});\n vis[idx+1][jdx]=true;\n }\n if(jdx<grid[0].size()-1 && mat[idx][jdx+1]==1){\n if(!vis[idx][jdx+1])\n q.push({idx, jdx+1});\n vis[idx][jdx+1]=true;\n }\n }\n for(int i=hits.size()-1; i>=0; i--){\n if(grid[hits[i][0]][hits[i][1]]==0)\n continue;\n mat[hits[i][0]][hits[i][1]] = 1;\n if(!isConnected(vis, hits[i][0], hits[i][1]))\n continue;\n q.push({hits[i][0], hits[i][1]});\n vis[hits[i][0]][hits[i][1]] = true;\n int cnt=0;\n while(!q.empty()){\n int idx = q.front().first, jdx = q.front().second;\n q.pop();\n cnt++;\n if(idx>0 && mat[idx-1][jdx]==1 && !vis[idx-1][jdx]){\n q.push({idx-1, jdx});\n vis[idx-1][jdx]=true;\n }\n if(jdx>0 && mat[idx][jdx-1]==1 && !vis[idx][jdx-1]){\n q.push({idx, jdx-1});\n vis[idx][jdx-1]=true;\n }\n if(idx<grid.size()-1 && mat[idx+1][jdx]==1 && !vis[idx+1][jdx]){\n q.push({idx+1, jdx});\n vis[idx+1][jdx]=true;\n }\n if(jdx<grid[0].size()-1 && mat[idx][jdx+1]==1 && !vis[idx][jdx+1]){\n q.push({idx, jdx+1});\n vis[idx][jdx+1]=true;\n }\n }\n ans[i] = cnt-1;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def hitBricks(\n self, grid: List[List[int]], hits: List[List[int]],\n exhaust=deque(maxlen=0).extend \n ) -> List[int]:\n cells = bytearray(\n (cell_cnt := (len(grid) + 2) \n * (col_cnt := (width := len(grid[0])) + 2))\n ) \n occupied = partial(filter, cells.__getitem__)\n for base, row in zip(\n count((offset := col_cnt + 1) + col_cnt, col_cnt), \n islice(grid, 1, None)\n ):\n cells[base:base + width] = row\n exhaust(map(\n (removed := [-40805] * cell_cnt).__setitem__, \n (((row * col_cnt) + col + offset) for row, col in hits), \n count(-1, -1)\n ))\n base_removals = tuple(map(\n removed.__getitem__, \n (bases := tuple(\n map(offset.__add__, \n filter(grid[0].__getitem__, range(width)))\n ))\n ))\n dists = 1, col_cnt, -1, -col_cnt\n solutions = [0] * len(hits) \n heapify((pending := list(zip(base_removals, bases))))\n while pending:\n hit, at = heappop(pending)\n for to in occupied(map(at.__add__, dists)):\n cells[to] = False\n if (candidate := removed[to]) < hit:\n solutions[(candidate := hit)] += 1\n heappush(pending, (candidate, to))\n return reversed(solutions)\n```\n\n```Java []\nclass Solution {\n public int[] hitBricks(int[][] grid, int[][] hits) {\n int n = grid.length;\n int m = grid[0].length;\n int[] ans = new int[hits.length];\n \n for(int[] hit : hits) {\n grid[hit[0]][hit[1]] *= -1;\n }\n for(int i = 0; i < m; i++) {\n dfs(grid, 0, i);\n }\n for(int i = hits.length-1; i >= 0; i--) {\n int x = hits[i][0];\n int y = hits[i][1];\n if(grid[x][y] == 0) {\n continue;\n } \n grid[x][y] = 1;\n if(connected(grid, x, y, n, m)) {\n ans[i] = dfs(grid, x, y)-1;\n }\n }\n return ans;\n }\n public int dfs(int[][] grid, int x, int y) {\n if(x < 0 || y < 0 || x >= grid.length || y >= grid[0].length || grid[x][y] != 1) {\n return 0;\n }\n grid[x][y] = 2;\n return 1 + dfs(grid, x+1, y) + dfs(grid, x, y+1) + dfs(grid, x-1, y) + dfs(grid, x, y-1);\n }\n public boolean connected(int[][] grid, int x, int y, int n, int m) {\n if(x == 0) {\n return true;\n }\n if(x+1 < n) {\n if(grid[x+1][y] == 2) {\n return true;\n }\n }\n if(x-1 >= 0) {\n if(grid[x-1][y] == 2) {\n return true;\n }\n }\n if(y+1 < m) {\n if(grid[x][y+1] == 2) {\n return true;\n }\n }\n if(y-1 >= 0) {\n if(grid[x][y-1] == 2) {\n return true;\n }\n }\n return false;\n }\n}\n```\n | 1 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
803: Solution with step by step explanation | bricks-falling-when-hit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nclass Solution:\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n # Depth-First Search function to mark connected bricks\n def dfs(x, y):\n # Check for valid brick and bounds\n if not (0 <= x < m and 0 <= y < n) or grid[x][y] != 1:\n return 0\n # Mark the brick as visited to prevent cycles\n grid[x][y] = 2 \n # Count this brick and all connected bricks\n return 1 + sum(dfs(x + dx, y + dy) for dx, dy in dirs if 0 <= x + dx < m and 0 <= y + dy < n)\n \n # Function to check if a brick is stable\n def is_stable(x, y):\n # A brick is stable if it\'s in the top row or connected to a stable brick\n return x == 0 or any((0 <= nx < m and 0 <= ny < n) and grid[nx][ny] == 2 for nx, ny in [(x + dx, y + dy) for dx, dy in dirs])\n \n # Dimensions of the grid and possible move directions\n m, n, dirs = len(grid), len(grid[0]), [(0, 1), (1, 0), (0, -1), (-1, 0)]\n \n # Step 1: Simulate the hits and remove bricks\n for x, y in hits:\n if 0 <= x < m and 0 <= y < n: \n grid[x][y] -= 1\n \n # Step 2: Perform DFS from the top row to find all stable bricks\n for y in range(n):\n dfs(0, y)\n \n # Step 3: Reverse the hits and for each hit, try to make the brick fall if it\'s unstable\n res = []\n for x, y in reversed(hits):\n if 0 <= x < m and 0 <= y < n: \n grid[x][y] += 1\n # Only perform DFS if the current brick is stable\n res.append(dfs(x, y) - 1 if grid[x][y] == 1 and is_stable(x, y) else 0)\n \n # Return the result in the original hit order\n return res[::-1]\n```\n\n# Complexity\n- Time complexity:\nO(m * n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n def dfs(x, y):\n if not (0 <= x < m and 0 <= y < n) or grid[x][y] != 1:\n return 0\n grid[x][y] = 2 \n return 1 + sum(dfs(x + dx, y + dy) for dx, dy in dirs if 0 <= x + dx < m and 0 <= y + dy < n)\n \n def is_stable(x, y):\n return x == 0 or any((0 <= nx < m and 0 <= ny < n) and grid[nx][ny] == 2 for nx, ny in [(x + dx, y + dy) for dx, dy in dirs])\n \n m, n, dirs = len(grid), len(grid[0]), [(0, 1), (1, 0), (0, -1), (-1, 0)]\n \n for x, y in hits:\n if 0 <= x < m and 0 <= y < n: \n grid[x][y] -= 1\n \n for y in range(n):\n dfs(0, y)\n \n res = []\n for x, y in reversed(hits):\n if 0 <= x < m and 0 <= y < n: \n grid[x][y] += 1\n res.append(dfs(x, y) - 1 if grid[x][y] == 1 and is_stable(x, y) else 0)\n \n return res[::-1] \n``` | 0 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
803: Solution with step by step explanation | bricks-falling-when-hit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nclass Solution:\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n # Depth-First Search function to mark connected bricks\n def dfs(x, y):\n # Check for valid brick and bounds\n if not (0 <= x < m and 0 <= y < n) or grid[x][y] != 1:\n return 0\n # Mark the brick as visited to prevent cycles\n grid[x][y] = 2 \n # Count this brick and all connected bricks\n return 1 + sum(dfs(x + dx, y + dy) for dx, dy in dirs if 0 <= x + dx < m and 0 <= y + dy < n)\n \n # Function to check if a brick is stable\n def is_stable(x, y):\n # A brick is stable if it\'s in the top row or connected to a stable brick\n return x == 0 or any((0 <= nx < m and 0 <= ny < n) and grid[nx][ny] == 2 for nx, ny in [(x + dx, y + dy) for dx, dy in dirs])\n \n # Dimensions of the grid and possible move directions\n m, n, dirs = len(grid), len(grid[0]), [(0, 1), (1, 0), (0, -1), (-1, 0)]\n \n # Step 1: Simulate the hits and remove bricks\n for x, y in hits:\n if 0 <= x < m and 0 <= y < n: \n grid[x][y] -= 1\n \n # Step 2: Perform DFS from the top row to find all stable bricks\n for y in range(n):\n dfs(0, y)\n \n # Step 3: Reverse the hits and for each hit, try to make the brick fall if it\'s unstable\n res = []\n for x, y in reversed(hits):\n if 0 <= x < m and 0 <= y < n: \n grid[x][y] += 1\n # Only perform DFS if the current brick is stable\n res.append(dfs(x, y) - 1 if grid[x][y] == 1 and is_stable(x, y) else 0)\n \n # Return the result in the original hit order\n return res[::-1]\n```\n\n# Complexity\n- Time complexity:\nO(m * n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n def dfs(x, y):\n if not (0 <= x < m and 0 <= y < n) or grid[x][y] != 1:\n return 0\n grid[x][y] = 2 \n return 1 + sum(dfs(x + dx, y + dy) for dx, dy in dirs if 0 <= x + dx < m and 0 <= y + dy < n)\n \n def is_stable(x, y):\n return x == 0 or any((0 <= nx < m and 0 <= ny < n) and grid[nx][ny] == 2 for nx, ny in [(x + dx, y + dy) for dx, dy in dirs])\n \n m, n, dirs = len(grid), len(grid[0]), [(0, 1), (1, 0), (0, -1), (-1, 0)]\n \n for x, y in hits:\n if 0 <= x < m and 0 <= y < n: \n grid[x][y] -= 1\n \n for y in range(n):\n dfs(0, y)\n \n res = []\n for x, y in reversed(hits):\n if 0 <= x < m and 0 <= y < n: \n grid[x][y] += 1\n res.append(dfs(x, y) - 1 if grid[x][y] == 1 and is_stable(x, y) else 0)\n \n return res[::-1] \n``` | 0 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Union Find Solution | bricks-falling-when-hit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self):\n\n self.father = {}\n self.block_count = 0\n self.size_of_set = {}\n \n def add(self, x):\n if x in self.father:\n return\n self.father[x] = None\n self.block_count += 1\n self.size_of_set[x] = 1\n \n def find(self, x):\n root = x\n while self.father[root]:\n root = self.father[root]\n \n while x != root:\n old_father = self.father[x]\n self.father[x] = root\n x = old_father\n return root\n \n def merge(self, a, b):\n fa = self.find(a)\n fb = self.find(b)\n if fa != fb:\n self.father[fa] = fb\n self.block_count -= 1\n self.size_of_set[fb] += self.size_of_set[fa]\n \n def is_connected(self, a, b):\n return self.find(a) == self.find(b)\n\n def num_block(self):\n return self.block_count\n \n def get_size_of_set(self, x) -> int:\n root = self.find(x)\n size = self.size_of_set[root]\n return size\n\nclass Solution:\n\n def isValid(self, x, y, grid):\n rows = len(grid)\n cols = len(grid[0])\n if 0 <= x < rows and 0 <= y < cols:\n return True\n return False\n \n def mergeNeighbors(self, i, j, grid, uf):\n DIRECTIONS = [(1, 0), (0, 1), (-1, 0), (0, -1)]\n for dx, dy in DIRECTIONS:\n x, y = i+dx, j+dy\n if self.isValid(x, y, grid) and grid[x][y] == 1:\n uf.merge((i, j),(x, y))\n if i == 0:\n uf.merge((i, j), -100)\n\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n rows = len(grid)\n cols = len(grid[0])\n\n # iterate through hits\n for x, y in hits:\n grid[x][y] -= 1\n \n uf = UnionFind()\n WALL = -100\n uf.add(WALL)\n # connect the 1 on first row to "WALL"\n for j in range(cols):\n if grid[0][j] == 1:\n uf.add((0, j))\n uf.merge(WALL, (0, j))\n \n # add all 1\'s into uf\n for i in range(rows):\n for j in range(cols):\n if grid[i][j] == 1:\n uf.add((i, j))\n \n # connect all connected 1\'s\n for i in range(rows):\n for j in range(cols):\n if grid[i][j] == 1:\n self.mergeNeighbors(i, j, grid, uf)\n \n ans = [0 for _ in range(len(hits))]\n # print(uf.father)\n # print(uf.get_size_of_set(WALL))\n for index in range(len(hits)-1, -1, -1):\n i, j = hits[index]\n grid[i][j] += 1\n after = uf.get_size_of_set(WALL)\n\n if grid[i][j] != 1:\n # indication that nothing falls off\n ans[index] = 0\n continue\n # put i, j back in\n uf.add((i, j))\n self.mergeNeighbors(i, j, grid, uf)\n before = uf.get_size_of_set(WALL)\n # since the one erased does not count\n ans[index] = before - after\n if ans[index] != 0:\n ans[index] -= 1\n # print(uf.father)\n # print(uf.get_size_of_set(WALL))\n \n return ans\n \n \n\n \n``` | 0 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
Union Find Solution | bricks-falling-when-hit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self):\n\n self.father = {}\n self.block_count = 0\n self.size_of_set = {}\n \n def add(self, x):\n if x in self.father:\n return\n self.father[x] = None\n self.block_count += 1\n self.size_of_set[x] = 1\n \n def find(self, x):\n root = x\n while self.father[root]:\n root = self.father[root]\n \n while x != root:\n old_father = self.father[x]\n self.father[x] = root\n x = old_father\n return root\n \n def merge(self, a, b):\n fa = self.find(a)\n fb = self.find(b)\n if fa != fb:\n self.father[fa] = fb\n self.block_count -= 1\n self.size_of_set[fb] += self.size_of_set[fa]\n \n def is_connected(self, a, b):\n return self.find(a) == self.find(b)\n\n def num_block(self):\n return self.block_count\n \n def get_size_of_set(self, x) -> int:\n root = self.find(x)\n size = self.size_of_set[root]\n return size\n\nclass Solution:\n\n def isValid(self, x, y, grid):\n rows = len(grid)\n cols = len(grid[0])\n if 0 <= x < rows and 0 <= y < cols:\n return True\n return False\n \n def mergeNeighbors(self, i, j, grid, uf):\n DIRECTIONS = [(1, 0), (0, 1), (-1, 0), (0, -1)]\n for dx, dy in DIRECTIONS:\n x, y = i+dx, j+dy\n if self.isValid(x, y, grid) and grid[x][y] == 1:\n uf.merge((i, j),(x, y))\n if i == 0:\n uf.merge((i, j), -100)\n\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n rows = len(grid)\n cols = len(grid[0])\n\n # iterate through hits\n for x, y in hits:\n grid[x][y] -= 1\n \n uf = UnionFind()\n WALL = -100\n uf.add(WALL)\n # connect the 1 on first row to "WALL"\n for j in range(cols):\n if grid[0][j] == 1:\n uf.add((0, j))\n uf.merge(WALL, (0, j))\n \n # add all 1\'s into uf\n for i in range(rows):\n for j in range(cols):\n if grid[i][j] == 1:\n uf.add((i, j))\n \n # connect all connected 1\'s\n for i in range(rows):\n for j in range(cols):\n if grid[i][j] == 1:\n self.mergeNeighbors(i, j, grid, uf)\n \n ans = [0 for _ in range(len(hits))]\n # print(uf.father)\n # print(uf.get_size_of_set(WALL))\n for index in range(len(hits)-1, -1, -1):\n i, j = hits[index]\n grid[i][j] += 1\n after = uf.get_size_of_set(WALL)\n\n if grid[i][j] != 1:\n # indication that nothing falls off\n ans[index] = 0\n continue\n # put i, j back in\n uf.add((i, j))\n self.mergeNeighbors(i, j, grid, uf)\n before = uf.get_size_of_set(WALL)\n # since the one erased does not count\n ans[index] = before - after\n if ans[index] != 0:\n ans[index] -= 1\n # print(uf.father)\n # print(uf.get_size_of_set(WALL))\n \n return ans\n \n \n\n \n``` | 0 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
🌟 || Reverse Logic Intuition || 🌟 | bricks-falling-when-hit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\nIntuition:\nHere we go in the reverse order: We add bricks instead of erasing\n\n1-> Remove the bricks which are to be erased from the grid.\n2-> One by one add the bricks which are to be erased and then check if it is connected to \n the top or a component which is connected to the top.\n 2a-> If yes then run a dfs from this point and whichever nodes are connected to this add them as\n potential ans.\n 2b-> If no then it would not contribute any anything to the ans\n\nAt removal time of bricks at the start:\nIf there is a brick at the given position: then make it 0 otherwise make it -1\n"""\n\nclass Solution:\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n m, n = len(grid), len(grid[0])\n\n # DFS to mark all connected nodes to top(Not Falling Bricks) at the beginning of the program\n # To count the number of bricks connected to a brick which is present in the hits\n def dfs(i, j):\n # Base Case -> Out Of Bounds or No Brick Exists \n if not (i >= 0 and i < m and j >= 0 and j < n) or grid[i][j] != 1:\n return 0\n \n ret = 1\n grid[i][j] = 2 # 2 means that this is connected to the top part\n\n # Calling dfs in the four directions\n ret += sum(dfs(x,y) for x,y in [(i-1, j), (i+1, j), (i, j-1), (i, j+1)])\n return ret\n\n # To check if a brick present in hits is connected to the top not falling bricks\n def isConnected(i, j):\n # To be connected to the top the adjacent grid values four diretionally must have atleast a 2 \n # Top connected bricks are marked 2\n return i == 0 or any([0<=x<m and 0<=y<n and grid[x][y]==2 for x, y in [(i-1, j), (i+1, j), (i, j-1), (i, j+1)]])\n\n\n # At each hit mark if there is a brick present there or not\n for i, j in hits:\n grid[i][j] -= 1\n\n # Now we run a dfs from every cell of the first row and mark cells which are connected to top\n for i in range(n):\n dfs(0, i)\n\n # Add the hits in reverse order and store ans for every hit\n res = [0]*len(hits)\n for k in range(len(hits)-1, -1, -1):\n i, j = hits[k]\n\n # Add this brick now -> Make it +1 -> If already this hit place stored -1 then we would\n # Not process it as it does not have any brick at any point in time but if it had a brick\n # then we would have store 0 at that place which now would have become 1 so process it\n # By process I mean -> If this cell is connected to the Top -> (Not Falling Bricks)\n # find no. of cells connected to it by running a dfs around it\n\n grid[i][j] += 1\n\n if grid[i][j] == 1 and isConnected(i, j):\n res[k] = dfs(i, j) - 1\n \n return res\n\n\n\n``` | 0 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
🌟 || Reverse Logic Intuition || 🌟 | bricks-falling-when-hit | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\nIntuition:\nHere we go in the reverse order: We add bricks instead of erasing\n\n1-> Remove the bricks which are to be erased from the grid.\n2-> One by one add the bricks which are to be erased and then check if it is connected to \n the top or a component which is connected to the top.\n 2a-> If yes then run a dfs from this point and whichever nodes are connected to this add them as\n potential ans.\n 2b-> If no then it would not contribute any anything to the ans\n\nAt removal time of bricks at the start:\nIf there is a brick at the given position: then make it 0 otherwise make it -1\n"""\n\nclass Solution:\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n m, n = len(grid), len(grid[0])\n\n # DFS to mark all connected nodes to top(Not Falling Bricks) at the beginning of the program\n # To count the number of bricks connected to a brick which is present in the hits\n def dfs(i, j):\n # Base Case -> Out Of Bounds or No Brick Exists \n if not (i >= 0 and i < m and j >= 0 and j < n) or grid[i][j] != 1:\n return 0\n \n ret = 1\n grid[i][j] = 2 # 2 means that this is connected to the top part\n\n # Calling dfs in the four directions\n ret += sum(dfs(x,y) for x,y in [(i-1, j), (i+1, j), (i, j-1), (i, j+1)])\n return ret\n\n # To check if a brick present in hits is connected to the top not falling bricks\n def isConnected(i, j):\n # To be connected to the top the adjacent grid values four diretionally must have atleast a 2 \n # Top connected bricks are marked 2\n return i == 0 or any([0<=x<m and 0<=y<n and grid[x][y]==2 for x, y in [(i-1, j), (i+1, j), (i, j-1), (i, j+1)]])\n\n\n # At each hit mark if there is a brick present there or not\n for i, j in hits:\n grid[i][j] -= 1\n\n # Now we run a dfs from every cell of the first row and mark cells which are connected to top\n for i in range(n):\n dfs(0, i)\n\n # Add the hits in reverse order and store ans for every hit\n res = [0]*len(hits)\n for k in range(len(hits)-1, -1, -1):\n i, j = hits[k]\n\n # Add this brick now -> Make it +1 -> If already this hit place stored -1 then we would\n # Not process it as it does not have any brick at any point in time but if it had a brick\n # then we would have store 0 at that place which now would have become 1 so process it\n # By process I mean -> If this cell is connected to the Top -> (Not Falling Bricks)\n # find no. of cells connected to it by running a dfs around it\n\n grid[i][j] += 1\n\n if grid[i][j] == 1 and isConnected(i, j):\n res[k] = dfs(i, j) - 1\n \n return res\n\n\n\n``` | 0 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Python 3 | DFS | Explanation | bricks-falling-when-hit | 0 | 1 | - We can do it on regular order, which will take `O(KMN)`, where `K = len(hits), M = len(grid), N = len(grid[0])`\n- If we do it reversely of `hits`, it will take `O(MN) + O(K)` since we can utilize the known information (we know how many nodes is already connected), all points will be at most be visited twice (mark as unstable + mark as stable)\n### Without comments\n<iframe src="https://leetcode.com/playground/6bd6DPwf/shared" frameBorder="0" width="950" height="400"></iframe> \n\n### With comments\n<iframe src="https://leetcode.com/playground/5kRDSxNZ/shared" frameBorder="0" width="950" height="500"></iframe> | 6 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
Python 3 | DFS | Explanation | bricks-falling-when-hit | 0 | 1 | - We can do it on regular order, which will take `O(KMN)`, where `K = len(hits), M = len(grid), N = len(grid[0])`\n- If we do it reversely of `hits`, it will take `O(MN) + O(K)` since we can utilize the known information (we know how many nodes is already connected), all points will be at most be visited twice (mark as unstable + mark as stable)\n### Without comments\n<iframe src="https://leetcode.com/playground/6bd6DPwf/shared" frameBorder="0" width="950" height="400"></iframe> \n\n### With comments\n<iframe src="https://leetcode.com/playground/5kRDSxNZ/shared" frameBorder="0" width="950" height="500"></iframe> | 6 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
[Python3] union-find | bricks-falling-when-hit | 0 | 1 | \n```\nclass UnionFind: \n \n def __init__(self, n): \n self.parent = list(range(n))\n self.rank = [1] * n\n \n def find(self, p): \n if p != self.parent[p]: \n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n \n def union(self, p, q):\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: prt, qrt = qrt, prt\n self.parent[prt] = qrt\n self.rank[qrt] += self.rank[prt]\n return True \n\n\nclass Solution:\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n m, n = len(grid), len(grid[0]) # dimensions \n \n seen = set()\n for i, j in hits: \n if grid[i][j]: \n seen.add((i, j))\n grid[i][j] = 0\n \n uf = UnionFind(m*n+1)\n for i in range(m): \n for j in range(n): \n if i == 0 and grid[i][j]: uf.union(j, m*n)\n if grid[i][j]: \n for ii, jj in (i-1, j), (i, j-1): \n if 0 <= ii < m and 0 <= jj < n and grid[ii][jj]: uf.union(i*n+j, ii*n+jj)\n \n ans = []\n prev = uf.rank[uf.find(m*n)]\n for i, j in reversed(hits): \n if (i, j) in seen: \n grid[i][j] = 1\n if i == 0: uf.union(j, m*n)\n for ii, jj in (i-1, j), (i, j-1), (i, j+1), (i+1, j): \n if 0 <= ii < m and 0 <= jj < n and grid[ii][jj]: uf.union(i*n+j, ii*n+jj)\n rank = uf.rank[uf.find(m*n)]\n ans.append(max(0, rank - prev - 1))\n prev = rank\n else: ans.append(0)\n return ans[::-1]\n``` | 2 | You are given an `m x n` binary `grid`, where each `1` represents a brick and `0` represents an empty space. A brick is **stable** if:
* It is directly connected to the top of the grid, or
* At least one other brick in its four adjacent cells is **stable**.
You are also given an array `hits`, which is a sequence of erasures we want to apply. Each time we want to erase the brick at the location `hits[i] = (rowi, coli)`. The brick on that location (if it exists) will disappear. Some other bricks may no longer be stable because of that erasure and will **fall**. Once a brick falls, it is **immediately** erased from the `grid` (i.e., it does not land on other stable bricks).
Return _an array_ `result`_, where each_ `result[i]` _is the number of bricks that will **fall** after the_ `ith` _erasure is applied._
**Note** that an erasure may refer to a location with no brick, and if it does, no bricks drop.
**Example 1:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,1,0\]\], hits = \[\[1,0\]\]
**Output:** \[2\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,1,0\]\]
We erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,1,1,0\]\]
The two underlined bricks are no longer stable as they are no longer connected to the top nor adjacent to another stable brick, so they will fall. The resulting grid is:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Hence the result is \[2\].
**Example 2:**
**Input:** grid = \[\[1,0,0,0\],\[1,1,0,0\]\], hits = \[\[1,1\],\[1,0\]\]
**Output:** \[0,0\]
**Explanation:** Starting with the grid:
\[\[1,0,0,0\],
\[1,1,0,0\]\]
We erase the underlined brick at (1,1), resulting in the grid:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
All remaining bricks are still stable, so no bricks fall. The grid remains the same:
\[\[1,0,0,0\],
\[1,0,0,0\]\]
Next, we erase the underlined brick at (1,0), resulting in the grid:
\[\[1,0,0,0\],
\[0,0,0,0\]\]
Once again, all remaining bricks are still stable, so no bricks fall.
Hence the result is \[0,0\].
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 200`
* `grid[i][j]` is `0` or `1`.
* `1 <= hits.length <= 4 * 104`
* `hits[i].length == 2`
* `0 <= xi <= m - 1`
* `0 <= yi <= n - 1`
* All `(xi, yi)` are unique. | null |
[Python3] union-find | bricks-falling-when-hit | 0 | 1 | \n```\nclass UnionFind: \n \n def __init__(self, n): \n self.parent = list(range(n))\n self.rank = [1] * n\n \n def find(self, p): \n if p != self.parent[p]: \n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n \n def union(self, p, q):\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: prt, qrt = qrt, prt\n self.parent[prt] = qrt\n self.rank[qrt] += self.rank[prt]\n return True \n\n\nclass Solution:\n def hitBricks(self, grid: List[List[int]], hits: List[List[int]]) -> List[int]:\n m, n = len(grid), len(grid[0]) # dimensions \n \n seen = set()\n for i, j in hits: \n if grid[i][j]: \n seen.add((i, j))\n grid[i][j] = 0\n \n uf = UnionFind(m*n+1)\n for i in range(m): \n for j in range(n): \n if i == 0 and grid[i][j]: uf.union(j, m*n)\n if grid[i][j]: \n for ii, jj in (i-1, j), (i, j-1): \n if 0 <= ii < m and 0 <= jj < n and grid[ii][jj]: uf.union(i*n+j, ii*n+jj)\n \n ans = []\n prev = uf.rank[uf.find(m*n)]\n for i, j in reversed(hits): \n if (i, j) in seen: \n grid[i][j] = 1\n if i == 0: uf.union(j, m*n)\n for ii, jj in (i-1, j), (i, j-1), (i, j+1), (i+1, j): \n if 0 <= ii < m and 0 <= jj < n and grid[ii][jj]: uf.union(i*n+j, ii*n+jj)\n rank = uf.rank[uf.find(m*n)]\n ans.append(max(0, rank - prev - 1))\n prev = rank\n else: ans.append(0)\n return ans[::-1]\n``` | 2 | Given a string `s` and a character `c` that occurs in `s`, return _an array of integers_ `answer` _where_ `answer.length == s.length` _and_ `answer[i]` _is the **distance** from index_ `i` _to the **closest** occurrence of character_ `c` _in_ `s`.
The **distance** between two indices `i` and `j` is `abs(i - j)`, where `abs` is the absolute value function.
**Example 1:**
**Input:** s = "loveleetcode ", c = "e "
**Output:** \[3,2,1,0,1,0,0,1,2,2,1,0\]
**Explanation:** The character 'e' appears at indices 3, 5, 6, and 11 (0-indexed).
The closest occurrence of 'e' for index 0 is at index 3, so the distance is abs(0 - 3) = 3.
The closest occurrence of 'e' for index 1 is at index 3, so the distance is abs(1 - 3) = 2.
For index 4, there is a tie between the 'e' at index 3 and the 'e' at index 5, but the distance is still the same: abs(4 - 3) == abs(4 - 5) = 1.
The closest occurrence of 'e' for index 8 is at index 6, so the distance is abs(8 - 6) = 2.
**Example 2:**
**Input:** s = "aaab ", c = "b "
**Output:** \[3,2,1,0\]
**Constraints:**
* `1 <= s.length <= 104`
* `s[i]` and `c` are lowercase English letters.
* It is guaranteed that `c` occurs at least once in `s`. | null |
Python | Set w/ DP | Beats 95% | unique-morse-code-words | 0 | 1 | # Complexity\n- Time complexity: O(S)\n- Space complexity: O(S) \n\n# Code\n```\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n # potential questions\n # can we expect all lower case\n # can we expect empty words dict\n # will the input be valid? non-numeric?\n converter = [\n ".-","-...","-.-.","-..",".","..-.","--.",\n "....","..",".---","-.-",".-..","--","-.",\n "---",".--.","--.-",".-.","...","-","..-",\n "...-",".--","-..-","-.--","--.."\n ]\n distinct = set()\n\n memo = {}\n def gen_code(word):\n if word in memo:\n return memo[word]\n if not word: return ""\n\n return converter[ord(word[0])-ord(\'a\')] + gen_code(word[1:])\n\n for word in words:\n distinct.add(gen_code(word))\n return len(distinct)\n``` | 1 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Python | Set w/ DP | Beats 95% | unique-morse-code-words | 0 | 1 | # Complexity\n- Time complexity: O(S)\n- Space complexity: O(S) \n\n# Code\n```\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n # potential questions\n # can we expect all lower case\n # can we expect empty words dict\n # will the input be valid? non-numeric?\n converter = [\n ".-","-...","-.-.","-..",".","..-.","--.",\n "....","..",".---","-.-",".-..","--","-.",\n "---",".--.","--.-",".-.","...","-","..-",\n "...-",".--","-..-","-.--","--.."\n ]\n distinct = set()\n\n memo = {}\n def gen_code(word):\n if word in memo:\n return memo[word]\n if not word: return ""\n\n return converter[ord(word[0])-ord(\'a\')] + gen_code(word[1:])\n\n for word in words:\n distinct.add(gen_code(word))\n return len(distinct)\n``` | 1 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Easy solution || Line By Line Explanation || Python || Java || C++ || Ruby | unique-morse-code-words | 1 | 1 | # Beats\n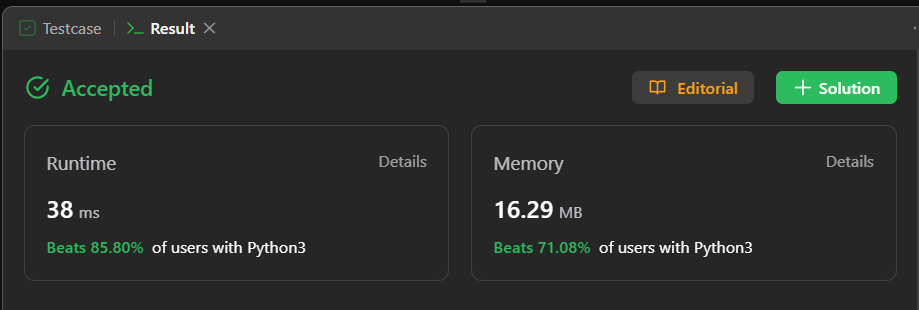\n\n# Intuition\nThe problem asks for the number of different transformations among a list of words, where each word can be represented as a concatenation of Morse code representations for its letters. To solve this, we need to convert each letter in a word to its Morse code equivalent and count the unique representations.\n\n# Approach\n1. Define the English alphabet and Morse code representations:\n - `letters` stores the lowercase English alphabet from \'a\' to \'z\'.\n - `morse_code` stores the corresponding Morse code representations for each letter.\n\n2. Create a dictionary mapping letters to Morse code:\n - `morse_dict` is a dictionary created by zipping `letters` and `morse_code` together. It maps each letter to its Morse code representation.\n\n3. Initialize a list to store words converted to Morse code:\n - `words2` is an empty list that will be used to store the Morse code representations of the input words.\n\n4. Iterate through each word in the input list:\n - For each word in `words`, the code initializes an empty string `k` to store the Morse code for the current word.\n\n5. Iterate through each character in the current word:\n - For each character `i` in the current word, the code appends the Morse code representation of that character (retrieved from `morse_dict`) to the string `k`.\n\n6. Append the Morse code for the current word to the list:\n - After converting the entire word to Morse code and building the string `k`, the code appends `k` to the `words2` list.\n\n7. Return the count of unique Morse code representations:\n - The code returns the length of the set of `words2`. This effectively counts the number of unique Morse code representations in the list and returns that count as the result.\n\n# Complexity\n- Time complexity: The code iterates through each character in each word, so the time complexity is O(n), where n is the total number of characters in all words.\n- Space complexity: The space complexity is O(n) as well because the `words2` list stores Morse code representations for each word.\n\n# Code\n\n```\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n # Define the English alphabet\n letters = "abcdefghijklmnopqrstuvwxyz"\n \n # Define the corresponding Morse code representations\n morse_code = [".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---", "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-", "..-", "...-", ".--", "-..-", "-.--", "--.."]\n\n # Create a dictionary that maps letters to Morse code\n morse_dict = dict(zip(letters, morse_code))\n\n # Initialize a list to store words converted to Morse code\n words2 = []\n\n # Iterate through each word in the input list\n for word in words:\n # Initialize an empty string to store the Morse code for the current word\n k = ""\n \n # Iterate through each character in the current word\n for i in word:\n # Append the Morse code representation of the character to the string\n k += morse_dict[i]\n\n # Append the Morse code for the current word to the list\n words2.append(k) \n\n # Return the count of unique Morse code representations\n return len(set(words2))\n\n```\n\n# Java\n```\nimport java.util.HashSet;\nimport java.util.Set;\n\nclass Solution {\n public int uniqueMorseRepresentations(String[] words) {\n String[] morseCode = {\n ".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---",\n "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-",\n "..-", "...-", ".--", "-..-", "-.--", "--.."\n };\n\n Set<String> uniqueMorse = new HashSet<>();\n\n for (String word : words) {\n StringBuilder morseRepresentation = new StringBuilder();\n for (char c : word.toCharArray()) {\n morseRepresentation.append(morseCode[c - \'a\']);\n }\n uniqueMorse.add(morseRepresentation.toString());\n }\n\n return uniqueMorse.size();\n }\n}\n\n```\n# C++\n```\nclass Solution {\npublic:\n int uniqueMorseRepresentations(vector<string>& words) {\n vector<string> morseCode = {\n ".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---",\n "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-",\n "..-", "...-", ".--", "-..-", "-.--", "--.."\n };\n\n unordered_set<string> uniqueMorse;\n\n for (const string& word : words) {\n string morseRepresentation = "";\n for (char c : word) {\n morseRepresentation += morseCode[c - \'a\'];\n }\n uniqueMorse.insert(morseRepresentation);\n }\n\n return uniqueMorse.size();\n }\n};\n\n```\n# Ruby\n```\nclass Solution\n MORSE_CODE = [\n ".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---",\n "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-",\n "..-", "...-", ".--", "-..-", "-.--", "--.."\n ]\n\n def unique_morse_representations(words)\n unique_morse = Set.new\n\n words.each do |word|\n morse_representation = ""\n word.each_char do |char|\n morse_representation += MORSE_CODE[char.ord - \'a\'.ord]\n end\n unique_morse.add(morse_representation)\n end\n\n unique_morse.size\n end\nend\n\n```\n# javascript\n```\n/**\n * @param {string[]} words\n * @return {number}\n */\nvar uniqueMorseRepresentations = function (words) {\n const morseCode = [\n ".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---",\n "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-", "..-",\n "...-", ".--", "-..-", "-.--", "--.."\n ];\n\n const uniqueMorse = new Set();\n\n for (const word of words) {\n let morseRepresentation = "";\n for (const char of word) {\n morseRepresentation += morseCode[char.charCodeAt(0) - \'a\'.charCodeAt(0)];\n }\n uniqueMorse.add(morseRepresentation);\n }\n\n return uniqueMorse.size;\n};\n\n``` | 15 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Easy solution || Line By Line Explanation || Python || Java || C++ || Ruby | unique-morse-code-words | 1 | 1 | # Beats\n\n\n# Intuition\nThe problem asks for the number of different transformations among a list of words, where each word can be represented as a concatenation of Morse code representations for its letters. To solve this, we need to convert each letter in a word to its Morse code equivalent and count the unique representations.\n\n# Approach\n1. Define the English alphabet and Morse code representations:\n - `letters` stores the lowercase English alphabet from \'a\' to \'z\'.\n - `morse_code` stores the corresponding Morse code representations for each letter.\n\n2. Create a dictionary mapping letters to Morse code:\n - `morse_dict` is a dictionary created by zipping `letters` and `morse_code` together. It maps each letter to its Morse code representation.\n\n3. Initialize a list to store words converted to Morse code:\n - `words2` is an empty list that will be used to store the Morse code representations of the input words.\n\n4. Iterate through each word in the input list:\n - For each word in `words`, the code initializes an empty string `k` to store the Morse code for the current word.\n\n5. Iterate through each character in the current word:\n - For each character `i` in the current word, the code appends the Morse code representation of that character (retrieved from `morse_dict`) to the string `k`.\n\n6. Append the Morse code for the current word to the list:\n - After converting the entire word to Morse code and building the string `k`, the code appends `k` to the `words2` list.\n\n7. Return the count of unique Morse code representations:\n - The code returns the length of the set of `words2`. This effectively counts the number of unique Morse code representations in the list and returns that count as the result.\n\n# Complexity\n- Time complexity: The code iterates through each character in each word, so the time complexity is O(n), where n is the total number of characters in all words.\n- Space complexity: The space complexity is O(n) as well because the `words2` list stores Morse code representations for each word.\n\n# Code\n\n```\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n # Define the English alphabet\n letters = "abcdefghijklmnopqrstuvwxyz"\n \n # Define the corresponding Morse code representations\n morse_code = [".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---", "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-", "..-", "...-", ".--", "-..-", "-.--", "--.."]\n\n # Create a dictionary that maps letters to Morse code\n morse_dict = dict(zip(letters, morse_code))\n\n # Initialize a list to store words converted to Morse code\n words2 = []\n\n # Iterate through each word in the input list\n for word in words:\n # Initialize an empty string to store the Morse code for the current word\n k = ""\n \n # Iterate through each character in the current word\n for i in word:\n # Append the Morse code representation of the character to the string\n k += morse_dict[i]\n\n # Append the Morse code for the current word to the list\n words2.append(k) \n\n # Return the count of unique Morse code representations\n return len(set(words2))\n\n```\n\n# Java\n```\nimport java.util.HashSet;\nimport java.util.Set;\n\nclass Solution {\n public int uniqueMorseRepresentations(String[] words) {\n String[] morseCode = {\n ".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---",\n "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-",\n "..-", "...-", ".--", "-..-", "-.--", "--.."\n };\n\n Set<String> uniqueMorse = new HashSet<>();\n\n for (String word : words) {\n StringBuilder morseRepresentation = new StringBuilder();\n for (char c : word.toCharArray()) {\n morseRepresentation.append(morseCode[c - \'a\']);\n }\n uniqueMorse.add(morseRepresentation.toString());\n }\n\n return uniqueMorse.size();\n }\n}\n\n```\n# C++\n```\nclass Solution {\npublic:\n int uniqueMorseRepresentations(vector<string>& words) {\n vector<string> morseCode = {\n ".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---",\n "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-",\n "..-", "...-", ".--", "-..-", "-.--", "--.."\n };\n\n unordered_set<string> uniqueMorse;\n\n for (const string& word : words) {\n string morseRepresentation = "";\n for (char c : word) {\n morseRepresentation += morseCode[c - \'a\'];\n }\n uniqueMorse.insert(morseRepresentation);\n }\n\n return uniqueMorse.size();\n }\n};\n\n```\n# Ruby\n```\nclass Solution\n MORSE_CODE = [\n ".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---",\n "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-",\n "..-", "...-", ".--", "-..-", "-.--", "--.."\n ]\n\n def unique_morse_representations(words)\n unique_morse = Set.new\n\n words.each do |word|\n morse_representation = ""\n word.each_char do |char|\n morse_representation += MORSE_CODE[char.ord - \'a\'.ord]\n end\n unique_morse.add(morse_representation)\n end\n\n unique_morse.size\n end\nend\n\n```\n# javascript\n```\n/**\n * @param {string[]} words\n * @return {number}\n */\nvar uniqueMorseRepresentations = function (words) {\n const morseCode = [\n ".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---",\n "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-", "..-",\n "...-", ".--", "-..-", "-.--", "--.."\n ];\n\n const uniqueMorse = new Set();\n\n for (const word of words) {\n let morseRepresentation = "";\n for (const char of word) {\n morseRepresentation += morseCode[char.charCodeAt(0) - \'a\'.charCodeAt(0)];\n }\n uniqueMorse.add(morseRepresentation);\n }\n\n return uniqueMorse.size;\n};\n\n``` | 15 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
🔥Clean, Simple 95% using ASCII🔥 | unique-morse-code-words | 0 | 1 | # Approach\n1. Create a list morse that contains Morse code representations for lowercase letters.\n2. For each word in the words list:\n- Use a list comprehension to convert each character to its corresponding Morse code.\n- Determine the index by subtracting the ASCII value of \'a\' (97) from the ASCII value of the character.\n3. Collect and join the Morse code representations for each word.\n4. Count the number of unique Morse code representations using a set.\n# Code\n```\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n morse = [".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]\n res = []\n for x in words:\n res.append(\'\'.join([morse[ord(c)-97] for c in x]))\n return len(set(res))\n```\nplease upvote :D | 1 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
🔥Clean, Simple 95% using ASCII🔥 | unique-morse-code-words | 0 | 1 | # Approach\n1. Create a list morse that contains Morse code representations for lowercase letters.\n2. For each word in the words list:\n- Use a list comprehension to convert each character to its corresponding Morse code.\n- Determine the index by subtracting the ASCII value of \'a\' (97) from the ASCII value of the character.\n3. Collect and join the Morse code representations for each word.\n4. Count the number of unique Morse code representations using a set.\n# Code\n```\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n morse = [".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]\n res = []\n for x in words:\n res.append(\'\'.join([morse[ord(c)-97] for c in x]))\n return len(set(res))\n```\nplease upvote :D | 1 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Simple Easy Solution | Beats 99% | 30 ms | Accepted 🔥🚀🚀 | unique-morse-code-words | 0 | 1 | # Code\n```\nclass Solution:\n def uniqueMorseRepresentations(self, x: List[str]) -> int:\n a=[".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]\n return len(set(["".join([a[ord(i)-97] for i in j]) for j in x]))\n``` | 3 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Simple Easy Solution | Beats 99% | 30 ms | Accepted 🔥🚀🚀 | unique-morse-code-words | 0 | 1 | # Code\n```\nclass Solution:\n def uniqueMorseRepresentations(self, x: List[str]) -> int:\n a=[".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]\n return len(set(["".join([a[ord(i)-97] for i in j]) for j in x]))\n``` | 3 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Python Elegant & Short | Two lines | No loops | unique-morse-code-words | 0 | 1 | \n\tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(n)\n\t\t"""\n\n\t\tMORSE = {\n\t\t\t\'a\': \'.-\', \'b\': \'-...\', \'c\': \'-.-.\', \'d\': \'-..\', \'e\': \'.\', \'f\': \'..-.\', \'g\': \'--.\',\n\t\t\t\'h\': \'....\', \'i\': \'..\', \'j\': \'.---\', \'k\': \'-.-\', \'l\': \'.-..\', \'m\': \'--\', \'n\': \'-.\',\n\t\t\t\'o\': \'---\', \'p\': \'.--.\', \'q\': \'--.-\', \'r\': \'.-.\', \'s\': \'...\', \'t\': \'-\', \'u\': \'..-\',\n\t\t\t\'v\': \'...-\', \'w\': \'.--\', \'x\': \'-..-\', \'y\': \'-.--\', \'z\': \'--..\',\n\t\t}\n\n\t\tdef uniqueMorseRepresentations(self, words: List[str]) -> int:\n\t\t\treturn len(set(map(self.encode, words)))\n\n\t\t@classmethod\n\t\tdef encode(cls, word: str) -> str:\n\t\t\treturn \'\'.join(map(cls.MORSE.get, word))\n | 5 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Python Elegant & Short | Two lines | No loops | unique-morse-code-words | 0 | 1 | \n\tclass Solution:\n\t\t"""\n\t\tTime: O(n)\n\t\tMemory: O(n)\n\t\t"""\n\n\t\tMORSE = {\n\t\t\t\'a\': \'.-\', \'b\': \'-...\', \'c\': \'-.-.\', \'d\': \'-..\', \'e\': \'.\', \'f\': \'..-.\', \'g\': \'--.\',\n\t\t\t\'h\': \'....\', \'i\': \'..\', \'j\': \'.---\', \'k\': \'-.-\', \'l\': \'.-..\', \'m\': \'--\', \'n\': \'-.\',\n\t\t\t\'o\': \'---\', \'p\': \'.--.\', \'q\': \'--.-\', \'r\': \'.-.\', \'s\': \'...\', \'t\': \'-\', \'u\': \'..-\',\n\t\t\t\'v\': \'...-\', \'w\': \'.--\', \'x\': \'-..-\', \'y\': \'-.--\', \'z\': \'--..\',\n\t\t}\n\n\t\tdef uniqueMorseRepresentations(self, words: List[str]) -> int:\n\t\t\treturn len(set(map(self.encode, words)))\n\n\t\t@classmethod\n\t\tdef encode(cls, word: str) -> str:\n\t\t\treturn \'\'.join(map(cls.MORSE.get, word))\n | 5 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
My simple Python3 Solution | unique-morse-code-words | 0 | 1 | \n# Code\n```\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n m = [".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]\n a = "abcdefghijklmnopqrstuvwxyz"\n p = []\n ans = []\n for q in words:\n b = ""\n for i in q:\n b += m[a.index(i)]\n p.append(b)\n for q in p:\n if q not in ans:\n ans.append(q)\n return len(ans)\n``` | 2 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
My simple Python3 Solution | unique-morse-code-words | 0 | 1 | \n# Code\n```\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n m = [".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]\n a = "abcdefghijklmnopqrstuvwxyz"\n p = []\n ans = []\n for q in words:\n b = ""\n for i in q:\n b += m[a.index(i)]\n p.append(b)\n for q in p:\n if q not in ans:\n ans.append(q)\n return len(ans)\n``` | 2 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Solution | unique-morse-code-words | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int uniqueMorseRepresentations(vector<string>& words) {\n vector<string> d = {".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---", "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-", "..-", "...-", ".--", "-..-", "-.--", "--.."};\n unordered_set<string> s;\n for (auto w : words) {\n string code;\n for (auto c : w) code += d[c - \'a\'];\n s.insert(code);\n }\n return s.size();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n\n morse = [".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]\n\n table = {}\n i = \'a\'\n for m in morse:\n table[i] = m\n i = chr(ord(i) + 1)\n pairs = set()\n for word in words:\n string = ""\n for w in word:\n string += table[w]\n pairs.add(string)\n return len(pairs)\n```\n\n```Java []\nclass Solution {\n public int uniqueMorseRepresentations(String[] words) {\n String[] morseCode = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};\n\n Set<String> set = new HashSet<>();\n for(String word : words){\n StringBuilder sb = new StringBuilder();\n for(char c : word.toCharArray()){\n sb.append(morseCode[c - \'a\']);\n }\n set.add(sb.toString());\n } \n return set.size();\n }\n}\n```\n | 4 | International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows:
* `'a'` maps to `".- "`,
* `'b'` maps to `"-... "`,
* `'c'` maps to `"-.-. "`, and so on.
For convenience, the full table for the `26` letters of the English alphabet is given below:
\[ ".- ", "-... ", "-.-. ", "-.. ", ". ", "..-. ", "--. ", ".... ", ".. ", ".--- ", "-.- ", ".-.. ", "-- ", "-. ", "--- ", ".--. ", "--.- ", ".-. ", "... ", "- ", "..- ", "...- ", ".-- ", "-..- ", "-.-- ", "--.. "\]
Given an array of strings `words` where each word can be written as a concatenation of the Morse code of each letter.
* For example, `"cab "` can be written as `"-.-..--... "`, which is the concatenation of `"-.-. "`, `".- "`, and `"-... "`. We will call such a concatenation the **transformation** of a word.
Return _the number of different **transformations** among all words we have_.
**Example 1:**
**Input:** words = \[ "gin ", "zen ", "gig ", "msg "\]
**Output:** 2
**Explanation:** The transformation of each word is:
"gin " -> "--...-. "
"zen " -> "--...-. "
"gig " -> "--...--. "
"msg " -> "--...--. "
There are 2 different transformations: "--...-. " and "--...--. ".
**Example 2:**
**Input:** words = \[ "a "\]
**Output:** 1
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 12`
* `words[i]` consists of lowercase English letters. | null |
Solution | unique-morse-code-words | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int uniqueMorseRepresentations(vector<string>& words) {\n vector<string> d = {".-", "-...", "-.-.", "-..", ".", "..-.", "--.", "....", "..", ".---", "-.-", ".-..", "--", "-.", "---", ".--.", "--.-", ".-.", "...", "-", "..-", "...-", ".--", "-..-", "-.--", "--.."};\n unordered_set<string> s;\n for (auto w : words) {\n string code;\n for (auto c : w) code += d[c - \'a\'];\n s.insert(code);\n }\n return s.size();\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def uniqueMorseRepresentations(self, words: List[str]) -> int:\n\n morse = [".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]\n\n table = {}\n i = \'a\'\n for m in morse:\n table[i] = m\n i = chr(ord(i) + 1)\n pairs = set()\n for word in words:\n string = ""\n for w in word:\n string += table[w]\n pairs.add(string)\n return len(pairs)\n```\n\n```Java []\nclass Solution {\n public int uniqueMorseRepresentations(String[] words) {\n String[] morseCode = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};\n\n Set<String> set = new HashSet<>();\n for(String word : words){\n StringBuilder sb = new StringBuilder();\n for(char c : word.toCharArray()){\n sb.append(morseCode[c - \'a\']);\n }\n set.add(sb.toString());\n } \n return set.size();\n }\n}\n```\n | 4 | You are given two **0-indexed** integer arrays `fronts` and `backs` of length `n`, where the `ith` card has the positive integer `fronts[i]` printed on the front and `backs[i]` printed on the back. Initially, each card is placed on a table such that the front number is facing up and the other is facing down. You may flip over any number of cards (possibly zero).
After flipping the cards, an integer is considered **good** if it is facing down on some card and **not** facing up on any card.
Return _the minimum possible good integer after flipping the cards_. If there are no good integers, return `0`.
**Example 1:**
**Input:** fronts = \[1,2,4,4,7\], backs = \[1,3,4,1,3\]
**Output:** 2
**Explanation:**
If we flip the second card, the face up numbers are \[1,3,4,4,7\] and the face down are \[1,2,4,1,3\].
2 is the minimum good integer as it appears facing down but not facing up.
It can be shown that 2 is the minimum possible good integer obtainable after flipping some cards.
**Example 2:**
**Input:** fronts = \[1\], backs = \[1\]
**Output:** 0
**Explanation:**
There are no good integers no matter how we flip the cards, so we return 0.
**Constraints:**
* `n == fronts.length == backs.length`
* `1 <= n <= 1000`
* `1 <= fronts[i], backs[i] <= 2000` | null |
Solution | split-array-with-same-average | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool splitArraySameAverage(vector<int>& a) {\n int n = a.size(), tot = accumulate(a.begin(), a.end(), 0);\n int M = tot / 2 + 1, N = n / 2 + 1;\n vector <bool> vis(M * N, 0);\n vector <int> q; q.reserve(N/2 * M);\n int cnt = 0;\n for (int i = 1; i <= n / 2; i++) { // n / 2\n if ((tot * i) % n) \n continue ;\n if (int next = i * M + tot * i / n; \n vis[next] == 0) {\n vis[next] = 1;\n q.push_back(next); \n cnt++;\n if (cnt > 5)\n break;\n }\n }\n for (int i = 0; i < n; i++) {\n int nn = q.size();\n for (int j = 0; j < nn; j++) { // 10^4 * 30 / 2\n int next = q[j] - a[i] - M;\n if (next == 0) \n return true;\n if (next > 0 && vis[next] == 0) {\n vis[next] = 1;\n q.push_back(next); \n }\n }\n }\n return false;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def splitArraySameAverage_NEW(self, nums: List[int]) -> bool:\n if len(nums) < 2: return False\n arr = [n*len(nums) for n in nums]\n ave = sum(nums)\n N, P = [], []\n for a in arr:\n if a == ave: return True\n if a > ave: P.append(a-ave)\n else: N.append(ave-a)\n dp_n, dp_p, i, j = 1, 1, 0, 0\n while i < len(N)-1 or j < len(P)-1:\n if i < len(N)-1:\n dp_n |= (dp_n << N[i]); i += 1\n if j < len(P)-1:\n dp_p |= (dp_p << P[j]); j += 1\n if dp_n & dp_p and (dp_n & dp_p != 1):\n return True\n full_dp_n, full_dp_p = (dp_n << N[-1]), (dp_p << P[-1])\n if (full_dp_n & dp_p and (full_dp_n & dp_p != 1)) or (dp_n & full_dp_p and (dp_n & full_dp_p != 1)):\n return True\n return False\n\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n if len(nums) <= 2:\n return False if len(nums) < 2 or nums[0] != nums[1] else True\n s = sum(nums)\n pos, neg = [], []\n for d in [n*len(nums) - s for n in nums]:\n if d == 0: return True\n if d > 0: pos.append(d)\n else: neg.append(-d)\n dp_pos = 0\n for n in pos:\n dp_pos |= (dp_pos << n) + (1 << n)\n dp_pos ^= (1 << sum(pos)) # remove full set\n dp_neg = 0\n for n in neg:\n dp_neg |= (dp_neg << n) + (1 << n)\n if dp_pos & dp_neg:\n return True\n return False\n```\n\n```Java []\nimport java.util.Arrays;\n\npublic class Solution {\n private int[] nums;\n private int[] sums;\n\n public boolean splitArraySameAverage(int[] nums) {\n int len = nums.length;\n if (len == 1) {\n return false;\n }\n Arrays.sort(nums);\n sums = new int[len + 1];\n for (int i = 0; i < len; i++) {\n sums[i + 1] = sums[i] + nums[i];\n }\n int sum = sums[len];\n this.nums = nums;\n for (int i = 1, stop = len / 2; i <= stop; i++) {\n if ((sum * i) % len == 0 && findSum(i, len, (sum * i) / len)) {\n return true;\n }\n }\n return false;\n }\n private boolean findSum(int k, int pos, int target) {\n if (k == 1) {\n while (true) {\n if (nums[--pos] <= target) {\n break;\n }\n }\n return nums[pos] == target;\n }\n for (int i = pos; sums[i] - sums[i-- - k] >= target; ) {\n if (sums[k - 1] <= target - nums[i] && findSum(k - 1, i, target - nums[i])) {\n return true;\n }\n }\n return false;\n }\n}\n```\n | 1 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Solution | split-array-with-same-average | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool splitArraySameAverage(vector<int>& a) {\n int n = a.size(), tot = accumulate(a.begin(), a.end(), 0);\n int M = tot / 2 + 1, N = n / 2 + 1;\n vector <bool> vis(M * N, 0);\n vector <int> q; q.reserve(N/2 * M);\n int cnt = 0;\n for (int i = 1; i <= n / 2; i++) { // n / 2\n if ((tot * i) % n) \n continue ;\n if (int next = i * M + tot * i / n; \n vis[next] == 0) {\n vis[next] = 1;\n q.push_back(next); \n cnt++;\n if (cnt > 5)\n break;\n }\n }\n for (int i = 0; i < n; i++) {\n int nn = q.size();\n for (int j = 0; j < nn; j++) { // 10^4 * 30 / 2\n int next = q[j] - a[i] - M;\n if (next == 0) \n return true;\n if (next > 0 && vis[next] == 0) {\n vis[next] = 1;\n q.push_back(next); \n }\n }\n }\n return false;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def splitArraySameAverage_NEW(self, nums: List[int]) -> bool:\n if len(nums) < 2: return False\n arr = [n*len(nums) for n in nums]\n ave = sum(nums)\n N, P = [], []\n for a in arr:\n if a == ave: return True\n if a > ave: P.append(a-ave)\n else: N.append(ave-a)\n dp_n, dp_p, i, j = 1, 1, 0, 0\n while i < len(N)-1 or j < len(P)-1:\n if i < len(N)-1:\n dp_n |= (dp_n << N[i]); i += 1\n if j < len(P)-1:\n dp_p |= (dp_p << P[j]); j += 1\n if dp_n & dp_p and (dp_n & dp_p != 1):\n return True\n full_dp_n, full_dp_p = (dp_n << N[-1]), (dp_p << P[-1])\n if (full_dp_n & dp_p and (full_dp_n & dp_p != 1)) or (dp_n & full_dp_p and (dp_n & full_dp_p != 1)):\n return True\n return False\n\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n if len(nums) <= 2:\n return False if len(nums) < 2 or nums[0] != nums[1] else True\n s = sum(nums)\n pos, neg = [], []\n for d in [n*len(nums) - s for n in nums]:\n if d == 0: return True\n if d > 0: pos.append(d)\n else: neg.append(-d)\n dp_pos = 0\n for n in pos:\n dp_pos |= (dp_pos << n) + (1 << n)\n dp_pos ^= (1 << sum(pos)) # remove full set\n dp_neg = 0\n for n in neg:\n dp_neg |= (dp_neg << n) + (1 << n)\n if dp_pos & dp_neg:\n return True\n return False\n```\n\n```Java []\nimport java.util.Arrays;\n\npublic class Solution {\n private int[] nums;\n private int[] sums;\n\n public boolean splitArraySameAverage(int[] nums) {\n int len = nums.length;\n if (len == 1) {\n return false;\n }\n Arrays.sort(nums);\n sums = new int[len + 1];\n for (int i = 0; i < len; i++) {\n sums[i + 1] = sums[i] + nums[i];\n }\n int sum = sums[len];\n this.nums = nums;\n for (int i = 1, stop = len / 2; i <= stop; i++) {\n if ((sum * i) % len == 0 && findSum(i, len, (sum * i) / len)) {\n return true;\n }\n }\n return false;\n }\n private boolean findSum(int k, int pos, int target) {\n if (k == 1) {\n while (true) {\n if (nums[--pos] <= target) {\n break;\n }\n }\n return nums[pos] == target;\n }\n for (int i = pos; sums[i] - sums[i-- - k] >= target; ) {\n if (sums[k - 1] <= target - nums[i] && findSum(k - 1, i, target - nums[i])) {\n return true;\n }\n }\n return false;\n }\n}\n```\n | 1 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
Time: O(2n/2)O(2n/2) Space: O(2n/2)O(2n/2) | split-array-with-same-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n n = len(nums)\n summ = sum(nums)\n if not any(i * summ % n == 0 for i in range(1, n // 2 + 1)):\n return False\n\n sums = [set() for _ in range(n // 2 + 1)]\n sums[0].add(0)\n\n for num in nums:\n for i in range(n // 2, 0, -1):\n for val in sums[i - 1]:\n sums[i].add(num + val)\n\n for i in range(1, n // 2 + 1):\n if i * summ % n == 0 and i * summ // n in sums[i]:\n return True\n\n return False\n\n``` | 1 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Time: O(2n/2)O(2n/2) Space: O(2n/2)O(2n/2) | split-array-with-same-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n n = len(nums)\n summ = sum(nums)\n if not any(i * summ % n == 0 for i in range(1, n // 2 + 1)):\n return False\n\n sums = [set() for _ in range(n // 2 + 1)]\n sums[0].add(0)\n\n for num in nums:\n for i in range(n // 2, 0, -1):\n for val in sums[i - 1]:\n sums[i].add(num + val)\n\n for i in range(1, n // 2 + 1):\n if i * summ % n == 0 and i * summ // n in sums[i]:\n return True\n\n return False\n\n``` | 1 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
Simple Math Explanation | split-array-with-same-average | 0 | 1 | ```\nWe need to split array in 2 parts such that the avg is equal\n\n```\n`We know,`\n`SubArrayB + SubArrayA = Sum`---------`eq(1)`\n`X + Y = N `-------------------------------`eq(2)`\n `Where X = len(SubArrayA), Y = len(SubArrayB) , N = len(array)`\n\n`To Prove :` $\\frac{SubArrayA}{X}$ = $\\frac{SubArrayB}{Y}$\n`From eq(1) and eq(2)`\n`--------->` $\\frac{SubArrayA}{X}$ = $\\frac{Sum-SubArrayA}{N-X}$\n`--------->` $SubArrayA\\times (N-X) = (Sum-SubArrayA)\\times X$\n`--------->` $N\\cdot SubArrayA - X\\cdot SubArrayA = X\\cdot Sum - X\\cdot SubArrayA$\n`--------->` $N\\cdot SubArrayA = X\\cdot Sum$\n`--------->` $SubArrayA = \\frac{X\\cdot Sum}{N}$\n\n`So, basically we need to check if ` $\\frac{X\\cdot Sum}{N}$ `exists or not`\n\n# Code\n```\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n \n \n n = len(nums)\n total = sum(nums)\n\n // Creating all possible sums of lens 1 to n\n dic = {}\n dic[0] = {0}\n for i in range(1,n+1):\n dic[i] = set()\n for j in range(i,0,-1):\n for each in dic[j-1]:\n dic[j].add(each+nums[i-1])\n // ------------------------------------------\n for i in range(1,n//2+1):\n // why n/2 , because between the 2 subArray we will \n // always encounter the subarray with smaller length first\n // and we need to check for anyone of the subarray\n if (i*total) % n == 0: \n // if (x * Sum) % n == 0 , then only its possible divide in 2 equal avg\n if (i*total)//n in dic[i]: \n // now as its possible to divide of X len we need to check if the SubArray of len X exist or not\n return True\n return False\n\n\n``` | 2 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Simple Math Explanation | split-array-with-same-average | 0 | 1 | ```\nWe need to split array in 2 parts such that the avg is equal\n\n```\n`We know,`\n`SubArrayB + SubArrayA = Sum`---------`eq(1)`\n`X + Y = N `-------------------------------`eq(2)`\n `Where X = len(SubArrayA), Y = len(SubArrayB) , N = len(array)`\n\n`To Prove :` $\\frac{SubArrayA}{X}$ = $\\frac{SubArrayB}{Y}$\n`From eq(1) and eq(2)`\n`--------->` $\\frac{SubArrayA}{X}$ = $\\frac{Sum-SubArrayA}{N-X}$\n`--------->` $SubArrayA\\times (N-X) = (Sum-SubArrayA)\\times X$\n`--------->` $N\\cdot SubArrayA - X\\cdot SubArrayA = X\\cdot Sum - X\\cdot SubArrayA$\n`--------->` $N\\cdot SubArrayA = X\\cdot Sum$\n`--------->` $SubArrayA = \\frac{X\\cdot Sum}{N}$\n\n`So, basically we need to check if ` $\\frac{X\\cdot Sum}{N}$ `exists or not`\n\n# Code\n```\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n \n \n n = len(nums)\n total = sum(nums)\n\n // Creating all possible sums of lens 1 to n\n dic = {}\n dic[0] = {0}\n for i in range(1,n+1):\n dic[i] = set()\n for j in range(i,0,-1):\n for each in dic[j-1]:\n dic[j].add(each+nums[i-1])\n // ------------------------------------------\n for i in range(1,n//2+1):\n // why n/2 , because between the 2 subArray we will \n // always encounter the subarray with smaller length first\n // and we need to check for anyone of the subarray\n if (i*total) % n == 0: \n // if (x * Sum) % n == 0 , then only its possible divide in 2 equal avg\n if (i*total)//n in dic[i]: \n // now as its possible to divide of X len we need to check if the SubArray of len X exist or not\n return True\n return False\n\n\n``` | 2 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
short python | split-array-with-same-average | 0 | 1 | ```\nclass Solution:\n def splitArraySameAverage(self, A: List[int]) -> bool:\n total = sum(A)\n # The ans does not change if we scale or shift the array\n for i in range(len(A)): A[i] = len(A) * A[i] - total\n # The above ensures that sum(A)=Avg(A)=avg(B)=avg(C)=sum(B)=sum(C)=0\n # So we are looking for a non-empty strict subset of A that sum to 0\n \n A.sort() #help prune the search a bit\n X = set()\n for a in A[:-1]: #excluding last element so it looks for STRICT subset\n X |= { a } | { a + x for x in X if x < 0}\n if 0 in X: return True\n return False\n``` | 7 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
short python | split-array-with-same-average | 0 | 1 | ```\nclass Solution:\n def splitArraySameAverage(self, A: List[int]) -> bool:\n total = sum(A)\n # The ans does not change if we scale or shift the array\n for i in range(len(A)): A[i] = len(A) * A[i] - total\n # The above ensures that sum(A)=Avg(A)=avg(B)=avg(C)=sum(B)=sum(C)=0\n # So we are looking for a non-empty strict subset of A that sum to 0\n \n A.sort() #help prune the search a bit\n X = set()\n for a in A[:-1]: #excluding last element so it looks for STRICT subset\n X |= { a } | { a + x for x in X if x < 0}\n if 0 in X: return True\n return False\n``` | 7 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
Share | split-array-with-same-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n s,n = sum(nums),len(nums)\n l = nums\n @cache\n def f(i, g, j):\n #print(g, i, j)\n nonlocal l\n if g == 0 and i==0:\n return True\n if g<0:\n return False\n if j == len(l):\n return False\n if f(i-1, g-l[j], j+1) or f(i, g, j+1):\n return True\n return False\n for i in range(1, n//2+1):\n if (s*i)%n == 0:\n #print(i)\n g = (s*i) // n\n if f(i, g, 0):\n return True\n return False\n\n``` | 0 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Share | split-array-with-same-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n s,n = sum(nums),len(nums)\n l = nums\n @cache\n def f(i, g, j):\n #print(g, i, j)\n nonlocal l\n if g == 0 and i==0:\n return True\n if g<0:\n return False\n if j == len(l):\n return False\n if f(i-1, g-l[j], j+1) or f(i, g, j+1):\n return True\n return False\n for i in range(1, n//2+1):\n if (s*i)%n == 0:\n #print(i)\n g = (s*i) // n\n if f(i, g, 0):\n return True\n return False\n\n``` | 0 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
805: Solution with step by step explanation | split-array-with-same-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\ntotal_sum = sum(nums)\nn = len(nums)\nif all(total_sum * i % n != 0 for i in range(1, n // 2 + 1)):\n return False\n```\n\nThe sum of all numbers in the array is calculated and stored in total_sum. n is the number of elements in nums. The method then checks if it is mathematically possible to split the array into two with the same average by checking if the total_sum * i is not divisible by n for all i in the range 1 to n//2. If it\'s not divisible for all, it returns False because the split is impossible.\n\n```\npossible_sums = {i: set() for i in range(1, n // 2 + 1)}\npossible_sums[0] = {0}\n```\n\nHere we initialize a dictionary possible_sums where the key is the size of the subset and the value is a set of possible sums that can be formed with subsets of that size. We initialize the size 0 with a set containing just 0 to represent the empty subset.\n\n```\nfor num in nums:\n for i in range(n // 2, 0, -1):\n for prev_sum in possible_sums[i-1]:\n possible_sums[i].add(prev_sum + num)\n```\n\nFor each number in the input array, the code iterates over the possible subset sizes in reverse. It updates the possible sums for each subset size by adding the current number to each of the previously seen sums for subsets of size one smaller.\n\n\n```\nfor i in range(1, n // 2 + 1):\n if total_sum * i % n == 0 and total_sum * i // n in possible_sums[i]:\n return True\nreturn False\n```\n\nThe method then iterates through the possible subset sizes and checks if there is a subset of size i whose sum is the same as i times the average of the whole array. If such a subset exists, it returns True. If the loop completes without finding any such subset, it returns False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n total_sum = sum(nums)\n n = len(nums)\n \n if all(total_sum * i % n != 0 for i in range(1, n // 2 + 1)):\n return False\n\n possible_sums = {i: set() for i in range(1, n // 2 + 1)}\n possible_sums[0] = {0}\n\n for num in nums:\n for i in range(n // 2, 0, -1):\n for prev_sum in possible_sums[i-1]:\n possible_sums[i].add(prev_sum + num)\n\n for i in range(1, n // 2 + 1):\n if total_sum * i % n == 0 and total_sum * i // n in possible_sums[i]:\n return True\n\n return False\n\n``` | 0 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
805: Solution with step by step explanation | split-array-with-same-average | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\ntotal_sum = sum(nums)\nn = len(nums)\nif all(total_sum * i % n != 0 for i in range(1, n // 2 + 1)):\n return False\n```\n\nThe sum of all numbers in the array is calculated and stored in total_sum. n is the number of elements in nums. The method then checks if it is mathematically possible to split the array into two with the same average by checking if the total_sum * i is not divisible by n for all i in the range 1 to n//2. If it\'s not divisible for all, it returns False because the split is impossible.\n\n```\npossible_sums = {i: set() for i in range(1, n // 2 + 1)}\npossible_sums[0] = {0}\n```\n\nHere we initialize a dictionary possible_sums where the key is the size of the subset and the value is a set of possible sums that can be formed with subsets of that size. We initialize the size 0 with a set containing just 0 to represent the empty subset.\n\n```\nfor num in nums:\n for i in range(n // 2, 0, -1):\n for prev_sum in possible_sums[i-1]:\n possible_sums[i].add(prev_sum + num)\n```\n\nFor each number in the input array, the code iterates over the possible subset sizes in reverse. It updates the possible sums for each subset size by adding the current number to each of the previously seen sums for subsets of size one smaller.\n\n\n```\nfor i in range(1, n // 2 + 1):\n if total_sum * i % n == 0 and total_sum * i // n in possible_sums[i]:\n return True\nreturn False\n```\n\nThe method then iterates through the possible subset sizes and checks if there is a subset of size i whose sum is the same as i times the average of the whole array. If such a subset exists, it returns True. If the loop completes without finding any such subset, it returns False.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool:\n total_sum = sum(nums)\n n = len(nums)\n \n if all(total_sum * i % n != 0 for i in range(1, n // 2 + 1)):\n return False\n\n possible_sums = {i: set() for i in range(1, n // 2 + 1)}\n possible_sums[0] = {0}\n\n for num in nums:\n for i in range(n // 2, 0, -1):\n for prev_sum in possible_sums[i-1]:\n possible_sums[i].add(prev_sum + num)\n\n for i in range(1, n // 2 + 1):\n if total_sum * i % n == 0 and total_sum * i // n in possible_sums[i]:\n return True\n\n return False\n\n``` | 0 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
Bitshifted Subset Calculations | Commented and Explained | split-array-with-same-average | 0 | 1 | # Intuition and Approach \n<!-- Describe your first thoughts on how to solve this problem. -->\nFrom the problem, we can notice a few key factors for this implementation. \nThe first is that the number of values can go from 1 to 30. This gives us at most 30 bits we can work within for a bitmask, giving us a chance to use bitmasking for the problem in the space required. Secondly, if we have only 1 value, there is no way to split it (parable of the judgement of Solomon, weirdly enough!). Third, if we have only two values, we can return a comparison of their equality. In all other cases, we now have some work to do. \n\nTo reduce the other cases, notice that for the average to be true across all three \n\nsum(nums) / len(nums) == sum(numsA)/len(numsA) == sum(numsB)/len(numsB) \n\nThis tells us that we can actually look for those sum situations where the arrays of each subtract to 0, or instead could bitshift and to 1. However, we must exclude certain cases when we do so in that manner. First, when we work with subsets that do not yet include all values, the bitshift & of their values must not be 1, otherwise we may have an empty set for the union. In that case, we know one consideration to keep in mind. Similarly, we know that the complete sets with an incomplete of the other should not combine to 1, otherwise we will also have used the full set of one and not the other, and that would also be incorrect. \n\nBased on this we can come to a more complete agreement where we have the balance of the differences in arrays to be useful. But how do we set up these sets of values? \n\nTo answer this, we can shift from working in the array as it is to its scaled form. What value should we scale by? The size of the array originally! \n\nSo then, our process is as follows \nScale all values in our original array of nums by the length of nums \nGet the sum total of the original array of nums, which must also be the average of our scaled array { as sum(nums * len(nums)) / len(nums) = sum(nums)}. \nLoop over our scaled array, and if we find a value that is the average, we can split most assuredly and can return true. Otherwise, if the value is greater than our average, it goes to our positive differences and if less than, our negatives. We send the difference of the value - sum of nums original. This is ensured to be positive with correct ordering, allowing us to utilize bit shifts correctly. \n\nIf we do not arrive at a valid result by the end of this, we now must process our two arrays. We can process them simultaneously if we do so up until the final value in each. To achieve this, we will use a dp_positive and negative value starting at 1, and get the length of each our positive and negative differences. We will also use indices markers for each, and will let them grow up to the total length - 1 for each of the respective indices arrays. \n\nThen, while one or the other of the indices can still grow, \n- if that indice can grow, union in place the respective dp with itself bitshifted by the ith respective difference and increment the appropriate indice \n- if the union of the two dps is strictly gt 1 -> return True, we found a balance \n\nAfterwards, if we have not yet found a balance, there is one last trick. \n\nWe can create the complete dp positive and negative by assigning them to the bitshift of each respective dp with their final difference element. \n\nIf the complete dp positive & dp negative is > 1 -> we also have a true balance. Similarly for the complete dp negative with positive. \n\nIf none of this works, it will never work, return False. \n\n# Complexity\n- Time complexity : Theta(N)\n - We spend O(N) looping over nums to get sum, to get the scaled sum array, to build our differences and to check our unions. This in total takes O(N). We have several early stopping points so we can also say that it is at most N and no less than 1, so we have a tighter upper bound. This lets us say Theta(N) \n\n- Space complexity: O(N) \n - We store the scaled sum and otherwise use integers, so O(N) \n\n# Code\n```\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool :\n # cannot do so for less than 2 nums \n if len(nums) < 2 : \n return False \n elif len(nums) == 2 : \n # can only do so for 2 if we have equality \n return nums[0] == nums[1]\n else : \n # for all others, we must check. \n # start by getting length and sum of nums \n numsL = len(nums)\n sum_nums = sum(nums)\n # get size scaled nums version of nums \n size_scaled_nums = [num * numsL for num in nums]\n # build lists for positive and negative differences \n positive_differences = []\n negative_differences = []\n # loop over size scaled nums \n for ss_num in size_scaled_nums : \n # if we match summation, we can split evenly \n # this is because size scaled nums == sum of nums means \n # size scaled num = average(nums) -> set match that is viable \n if ss_num == sum_nums : \n return True\n elif ss_num > sum_nums : \n # otherwise, append appropriately based on comparisons \n positive_differences.append(ss_num - sum_nums)\n else : \n # note shift to other difference form for positive bit shift later on \n negative_differences.append(sum_nums - ss_num)\n\n # set up for processing our lists of differences \n dp_positive = 1 \n dp_negative = 1 \n # get size of each \n pdL = len(positive_differences)\n ndL = len(negative_differences)\n # positive difference index and negative difference index \n pd_i = 0\n nd_i = 0 \n # excluding maximal indices \n pd_imax = pdL - 1 \n nd_imax = ndL - 1 \n\n # exclude full set calculations -> ignore the final bit shift possibility \n while pd_i < pd_imax or nd_i < nd_imax : \n # if we can update for either, do so \n if pd_i < pd_imax : \n # by union in place with the ith associated difference bit shift on current value \n dp_positive |= (dp_positive << positive_differences[pd_i])\n pd_i += 1 \n if nd_i < nd_imax : \n # similarly for the negative valuations \n dp_negative |= (dp_negative << negative_differences[nd_i])\n nd_i += 1 \n # after updates if we have non-empty set union, return True \n # this is because our positive and negative differences have canceled giving a subset \n # that has a sum of zero for this array of nums \n if dp_positive & dp_negative > 1 : \n return True \n \n # complete positive subset and check for match with negatives excluding full set \n complete_dp_positive = (dp_positive << positive_differences[-1])\n # this lets us have a one off difference matching that balances out \n if (complete_dp_positive & dp_negative) > 1 : \n return True \n\n # complete negative subset and check for match with positives excluding full set \n complete_dp_negative = (dp_negative << negative_differences[-1])\n # similar in the other direction. Do one then the other as bitshift at this size may be costly\n if (complete_dp_negative & dp_positive) > 1 : \n return True \n\n # if we have no differences that cancel, and have no value to split on, and exhaust all else\n # it is not possible, return False \n return False \n``` | 0 | You are given an integer array `nums`.
You should move each element of `nums` into one of the two arrays `A` and `B` such that `A` and `B` are non-empty, and `average(A) == average(B)`.
Return `true` if it is possible to achieve that and `false` otherwise.
**Note** that for an array `arr`, `average(arr)` is the sum of all the elements of `arr` over the length of `arr`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5,6,7,8\]
**Output:** true
**Explanation:** We can split the array into \[1,4,5,8\] and \[2,3,6,7\], and both of them have an average of 4.5.
**Example 2:**
**Input:** nums = \[3,1\]
**Output:** false
**Constraints:**
* `1 <= nums.length <= 30`
* `0 <= nums[i] <= 104` | null |
Bitshifted Subset Calculations | Commented and Explained | split-array-with-same-average | 0 | 1 | # Intuition and Approach \n<!-- Describe your first thoughts on how to solve this problem. -->\nFrom the problem, we can notice a few key factors for this implementation. \nThe first is that the number of values can go from 1 to 30. This gives us at most 30 bits we can work within for a bitmask, giving us a chance to use bitmasking for the problem in the space required. Secondly, if we have only 1 value, there is no way to split it (parable of the judgement of Solomon, weirdly enough!). Third, if we have only two values, we can return a comparison of their equality. In all other cases, we now have some work to do. \n\nTo reduce the other cases, notice that for the average to be true across all three \n\nsum(nums) / len(nums) == sum(numsA)/len(numsA) == sum(numsB)/len(numsB) \n\nThis tells us that we can actually look for those sum situations where the arrays of each subtract to 0, or instead could bitshift and to 1. However, we must exclude certain cases when we do so in that manner. First, when we work with subsets that do not yet include all values, the bitshift & of their values must not be 1, otherwise we may have an empty set for the union. In that case, we know one consideration to keep in mind. Similarly, we know that the complete sets with an incomplete of the other should not combine to 1, otherwise we will also have used the full set of one and not the other, and that would also be incorrect. \n\nBased on this we can come to a more complete agreement where we have the balance of the differences in arrays to be useful. But how do we set up these sets of values? \n\nTo answer this, we can shift from working in the array as it is to its scaled form. What value should we scale by? The size of the array originally! \n\nSo then, our process is as follows \nScale all values in our original array of nums by the length of nums \nGet the sum total of the original array of nums, which must also be the average of our scaled array { as sum(nums * len(nums)) / len(nums) = sum(nums)}. \nLoop over our scaled array, and if we find a value that is the average, we can split most assuredly and can return true. Otherwise, if the value is greater than our average, it goes to our positive differences and if less than, our negatives. We send the difference of the value - sum of nums original. This is ensured to be positive with correct ordering, allowing us to utilize bit shifts correctly. \n\nIf we do not arrive at a valid result by the end of this, we now must process our two arrays. We can process them simultaneously if we do so up until the final value in each. To achieve this, we will use a dp_positive and negative value starting at 1, and get the length of each our positive and negative differences. We will also use indices markers for each, and will let them grow up to the total length - 1 for each of the respective indices arrays. \n\nThen, while one or the other of the indices can still grow, \n- if that indice can grow, union in place the respective dp with itself bitshifted by the ith respective difference and increment the appropriate indice \n- if the union of the two dps is strictly gt 1 -> return True, we found a balance \n\nAfterwards, if we have not yet found a balance, there is one last trick. \n\nWe can create the complete dp positive and negative by assigning them to the bitshift of each respective dp with their final difference element. \n\nIf the complete dp positive & dp negative is > 1 -> we also have a true balance. Similarly for the complete dp negative with positive. \n\nIf none of this works, it will never work, return False. \n\n# Complexity\n- Time complexity : Theta(N)\n - We spend O(N) looping over nums to get sum, to get the scaled sum array, to build our differences and to check our unions. This in total takes O(N). We have several early stopping points so we can also say that it is at most N and no less than 1, so we have a tighter upper bound. This lets us say Theta(N) \n\n- Space complexity: O(N) \n - We store the scaled sum and otherwise use integers, so O(N) \n\n# Code\n```\nclass Solution:\n def splitArraySameAverage(self, nums: List[int]) -> bool :\n # cannot do so for less than 2 nums \n if len(nums) < 2 : \n return False \n elif len(nums) == 2 : \n # can only do so for 2 if we have equality \n return nums[0] == nums[1]\n else : \n # for all others, we must check. \n # start by getting length and sum of nums \n numsL = len(nums)\n sum_nums = sum(nums)\n # get size scaled nums version of nums \n size_scaled_nums = [num * numsL for num in nums]\n # build lists for positive and negative differences \n positive_differences = []\n negative_differences = []\n # loop over size scaled nums \n for ss_num in size_scaled_nums : \n # if we match summation, we can split evenly \n # this is because size scaled nums == sum of nums means \n # size scaled num = average(nums) -> set match that is viable \n if ss_num == sum_nums : \n return True\n elif ss_num > sum_nums : \n # otherwise, append appropriately based on comparisons \n positive_differences.append(ss_num - sum_nums)\n else : \n # note shift to other difference form for positive bit shift later on \n negative_differences.append(sum_nums - ss_num)\n\n # set up for processing our lists of differences \n dp_positive = 1 \n dp_negative = 1 \n # get size of each \n pdL = len(positive_differences)\n ndL = len(negative_differences)\n # positive difference index and negative difference index \n pd_i = 0\n nd_i = 0 \n # excluding maximal indices \n pd_imax = pdL - 1 \n nd_imax = ndL - 1 \n\n # exclude full set calculations -> ignore the final bit shift possibility \n while pd_i < pd_imax or nd_i < nd_imax : \n # if we can update for either, do so \n if pd_i < pd_imax : \n # by union in place with the ith associated difference bit shift on current value \n dp_positive |= (dp_positive << positive_differences[pd_i])\n pd_i += 1 \n if nd_i < nd_imax : \n # similarly for the negative valuations \n dp_negative |= (dp_negative << negative_differences[nd_i])\n nd_i += 1 \n # after updates if we have non-empty set union, return True \n # this is because our positive and negative differences have canceled giving a subset \n # that has a sum of zero for this array of nums \n if dp_positive & dp_negative > 1 : \n return True \n \n # complete positive subset and check for match with negatives excluding full set \n complete_dp_positive = (dp_positive << positive_differences[-1])\n # this lets us have a one off difference matching that balances out \n if (complete_dp_positive & dp_negative) > 1 : \n return True \n\n # complete negative subset and check for match with positives excluding full set \n complete_dp_negative = (dp_negative << negative_differences[-1])\n # similar in the other direction. Do one then the other as bitshift at this size may be costly\n if (complete_dp_negative & dp_positive) > 1 : \n return True \n\n # if we have no differences that cancel, and have no value to split on, and exhaust all else\n # it is not possible, return False \n return False \n``` | 0 | Given an array of unique integers, `arr`, where each integer `arr[i]` is strictly greater than `1`.
We make a binary tree using these integers, and each number may be used for any number of times. Each non-leaf node's value should be equal to the product of the values of its children.
Return _the number of binary trees we can make_. The answer may be too large so return the answer **modulo** `109 + 7`.
**Example 1:**
**Input:** arr = \[2,4\]
**Output:** 3
**Explanation:** We can make these trees: `[2], [4], [4, 2, 2]`
**Example 2:**
**Input:** arr = \[2,4,5,10\]
**Output:** 7
**Explanation:** We can make these trees: `[2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]`.
**Constraints:**
* `1 <= arr.length <= 1000`
* `2 <= arr[i] <= 109`
* All the values of `arr` are **unique**. | null |
Python3 Runtime: 42ms 67.78% Memory: 13.9mb 19.81% | number-of-lines-to-write-string | 0 | 1 | ```\nclass Solution:\n# Runtime: 42ms 67.78% Memory: 13.9mb 19.81%\n# O(n) || O(1)\n def numberOfLines(self, widths, s):\n newLine = 1\n \n width = 0\n \n for char in s:\n charWidth = widths[ord(char) - ord(\'a\')]\n \n if charWidth + width > 100:\n newLine += 1\n width = 0\n \n width += charWidth\n \n return [newLine, width] \n``` | 1 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
Python3 Runtime: 42ms 67.78% Memory: 13.9mb 19.81% | number-of-lines-to-write-string | 0 | 1 | ```\nclass Solution:\n# Runtime: 42ms 67.78% Memory: 13.9mb 19.81%\n# O(n) || O(1)\n def numberOfLines(self, widths, s):\n newLine = 1\n \n width = 0\n \n for char in s:\n charWidth = widths[ord(char) - ord(\'a\')]\n \n if charWidth + width > 100:\n newLine += 1\n width = 0\n \n width += charWidth\n \n return [newLine, width] \n``` | 1 | You are given a string `sentence` that consist of words separated by spaces. Each word consists of lowercase and uppercase letters only.
We would like to convert the sentence to "Goat Latin " (a made-up language similar to Pig Latin.) The rules of Goat Latin are as follows:
* If a word begins with a vowel (`'a'`, `'e'`, `'i'`, `'o'`, or `'u'`), append `"ma "` to the end of the word.
* For example, the word `"apple "` becomes `"applema "`.
* If a word begins with a consonant (i.e., not a vowel), remove the first letter and append it to the end, then add `"ma "`.
* For example, the word `"goat "` becomes `"oatgma "`.
* Add one letter `'a'` to the end of each word per its word index in the sentence, starting with `1`.
* For example, the first word gets `"a "` added to the end, the second word gets `"aa "` added to the end, and so on.
Return _the final sentence representing the conversion from sentence to Goat Latin_.
**Example 1:**
**Input:** sentence = "I speak Goat Latin"
**Output:** "Imaa peaksmaaa oatGmaaaa atinLmaaaaa"
**Example 2:**
**Input:** sentence = "The quick brown fox jumped over the lazy dog"
**Output:** "heTmaa uickqmaaa rownbmaaaa oxfmaaaaa umpedjmaaaaaa overmaaaaaaa hetmaaaaaaaa azylmaaaaaaaaa ogdmaaaaaaaaaa"
**Constraints:**
* `1 <= sentence.length <= 150`
* `sentence` consists of English letters and spaces.
* `sentence` has no leading or trailing spaces.
* All the words in `sentence` are separated by a single space. | null |
✅ Beats 99.76% solutions, ✅ Easy to understand O(n) tc Python code by ✅ BOLT CODING ✅ | number-of-lines-to-write-string | 0 | 1 | # Explanation\nAt first we are initializing pix to 0, min no of lines which will be there is always 1, i for keeping count of index, and a which is ascii of \'a\'.\nWe are then iterating through the s - list of words. In case pix size is <= 100 we increment the pix, incase pix > 100 we increment the line number and initialize the pix back to 0. So now when the while loop ends but pix <= 100 it will print the pix of last line. This way we can print line number and pix in last line.\n\n# Complexity\n- Time complexity: O(n) as we are using a single while loop to iterate over the list\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) as we are using variables to keep track on number of lines and pixel size\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfLines(self, width: List[int], s: str) -> List[int]:\n pix = 0\n line = 1\n i = 0\n a = 97\n while i<len(s):\n if pix<=100:\n pix+=width[ord(s[i])-a]\n i+=1\n if pix>100:\n line+=1\n pix=0\n i-=1\n return [line, pix]\n\n\n\n```\n# Learning\nTo understand problems in simpler ways, need help with projects, want to learn coding from scratch, work on resume level projects, learn data science ...................\n\nSubscribe to Bolt Coding Channel - https://www.youtube.com/@boltcoding | 1 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
✅ Beats 99.76% solutions, ✅ Easy to understand O(n) tc Python code by ✅ BOLT CODING ✅ | number-of-lines-to-write-string | 0 | 1 | # Explanation\nAt first we are initializing pix to 0, min no of lines which will be there is always 1, i for keeping count of index, and a which is ascii of \'a\'.\nWe are then iterating through the s - list of words. In case pix size is <= 100 we increment the pix, incase pix > 100 we increment the line number and initialize the pix back to 0. So now when the while loop ends but pix <= 100 it will print the pix of last line. This way we can print line number and pix in last line.\n\n# Complexity\n- Time complexity: O(n) as we are using a single while loop to iterate over the list\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) as we are using variables to keep track on number of lines and pixel size\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfLines(self, width: List[int], s: str) -> List[int]:\n pix = 0\n line = 1\n i = 0\n a = 97\n while i<len(s):\n if pix<=100:\n pix+=width[ord(s[i])-a]\n i+=1\n if pix>100:\n line+=1\n pix=0\n i-=1\n return [line, pix]\n\n\n\n```\n# Learning\nTo understand problems in simpler ways, need help with projects, want to learn coding from scratch, work on resume level projects, learn data science ...................\n\nSubscribe to Bolt Coding Channel - https://www.youtube.com/@boltcoding | 1 | You are given a string `sentence` that consist of words separated by spaces. Each word consists of lowercase and uppercase letters only.
We would like to convert the sentence to "Goat Latin " (a made-up language similar to Pig Latin.) The rules of Goat Latin are as follows:
* If a word begins with a vowel (`'a'`, `'e'`, `'i'`, `'o'`, or `'u'`), append `"ma "` to the end of the word.
* For example, the word `"apple "` becomes `"applema "`.
* If a word begins with a consonant (i.e., not a vowel), remove the first letter and append it to the end, then add `"ma "`.
* For example, the word `"goat "` becomes `"oatgma "`.
* Add one letter `'a'` to the end of each word per its word index in the sentence, starting with `1`.
* For example, the first word gets `"a "` added to the end, the second word gets `"aa "` added to the end, and so on.
Return _the final sentence representing the conversion from sentence to Goat Latin_.
**Example 1:**
**Input:** sentence = "I speak Goat Latin"
**Output:** "Imaa peaksmaaa oatGmaaaa atinLmaaaaa"
**Example 2:**
**Input:** sentence = "The quick brown fox jumped over the lazy dog"
**Output:** "heTmaa uickqmaaa rownbmaaaa oxfmaaaaa umpedjmaaaaaa overmaaaaaaa hetmaaaaaaaa azylmaaaaaaaaa ogdmaaaaaaaaaa"
**Constraints:**
* `1 <= sentence.length <= 150`
* `sentence` consists of English letters and spaces.
* `sentence` has no leading or trailing spaces.
* All the words in `sentence` are separated by a single space. | null |
Beats 89.81% of users with Python3 | number-of-lines-to-write-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfLines(self, widths: List[int], s: str) -> List[int]:\n out = {}\n l = len(s)\n dd = {chr(i+97):i for i in range(0,26)}\n mx = 100\n temp = 0\n line = 1\n ss = \'\'\n for i in range(l):\n if temp < 100:\n temp += widths[dd[s[i]]]\n if temp <100:\n ss+=s[i]\n\n else:\n if temp ==100:\n out[line] = temp\n line += 1\n temp = 0\n ss = \'\' \n\n if temp >100:\n out[line] = temp - widths[dd[s[i]]]\n line += 1\n temp = widths[dd[s[i]]]\n ss = s[i] \n\n if ss:\n out[line] = temp \n \n \n \n return [len(out),out[len(out)]] \n\n\n\n \n``` | 0 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
Beats 89.81% of users with Python3 | number-of-lines-to-write-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfLines(self, widths: List[int], s: str) -> List[int]:\n out = {}\n l = len(s)\n dd = {chr(i+97):i for i in range(0,26)}\n mx = 100\n temp = 0\n line = 1\n ss = \'\'\n for i in range(l):\n if temp < 100:\n temp += widths[dd[s[i]]]\n if temp <100:\n ss+=s[i]\n\n else:\n if temp ==100:\n out[line] = temp\n line += 1\n temp = 0\n ss = \'\' \n\n if temp >100:\n out[line] = temp - widths[dd[s[i]]]\n line += 1\n temp = widths[dd[s[i]]]\n ss = s[i] \n\n if ss:\n out[line] = temp \n \n \n \n return [len(out),out[len(out)]] \n\n\n\n \n``` | 0 | You are given a string `sentence` that consist of words separated by spaces. Each word consists of lowercase and uppercase letters only.
We would like to convert the sentence to "Goat Latin " (a made-up language similar to Pig Latin.) The rules of Goat Latin are as follows:
* If a word begins with a vowel (`'a'`, `'e'`, `'i'`, `'o'`, or `'u'`), append `"ma "` to the end of the word.
* For example, the word `"apple "` becomes `"applema "`.
* If a word begins with a consonant (i.e., not a vowel), remove the first letter and append it to the end, then add `"ma "`.
* For example, the word `"goat "` becomes `"oatgma "`.
* Add one letter `'a'` to the end of each word per its word index in the sentence, starting with `1`.
* For example, the first word gets `"a "` added to the end, the second word gets `"aa "` added to the end, and so on.
Return _the final sentence representing the conversion from sentence to Goat Latin_.
**Example 1:**
**Input:** sentence = "I speak Goat Latin"
**Output:** "Imaa peaksmaaa oatGmaaaa atinLmaaaaa"
**Example 2:**
**Input:** sentence = "The quick brown fox jumped over the lazy dog"
**Output:** "heTmaa uickqmaaa rownbmaaaa oxfmaaaaa umpedjmaaaaaa overmaaaaaaa hetmaaaaaaaa azylmaaaaaaaaa ogdmaaaaaaaaaa"
**Constraints:**
* `1 <= sentence.length <= 150`
* `sentence` consists of English letters and spaces.
* `sentence` has no leading or trailing spaces.
* All the words in `sentence` are separated by a single space. | null |
Python Simple Solution!! | number-of-lines-to-write-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def numberOfLines(self, widths: List[int], s: str) -> List[int]:\n\n lines, counter = [], 0\n for letter in s:\n index: int = ord(letter) - 97\n if counter + widths[index] > 100:\n lines.append(counter)\n counter = 0\n counter += widths[index]\n \n return [len(lines) + 1, counter]\n \n``` | 0 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
Python Simple Solution!! | number-of-lines-to-write-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def numberOfLines(self, widths: List[int], s: str) -> List[int]:\n\n lines, counter = [], 0\n for letter in s:\n index: int = ord(letter) - 97\n if counter + widths[index] > 100:\n lines.append(counter)\n counter = 0\n counter += widths[index]\n \n return [len(lines) + 1, counter]\n \n``` | 0 | You are given a string `sentence` that consist of words separated by spaces. Each word consists of lowercase and uppercase letters only.
We would like to convert the sentence to "Goat Latin " (a made-up language similar to Pig Latin.) The rules of Goat Latin are as follows:
* If a word begins with a vowel (`'a'`, `'e'`, `'i'`, `'o'`, or `'u'`), append `"ma "` to the end of the word.
* For example, the word `"apple "` becomes `"applema "`.
* If a word begins with a consonant (i.e., not a vowel), remove the first letter and append it to the end, then add `"ma "`.
* For example, the word `"goat "` becomes `"oatgma "`.
* Add one letter `'a'` to the end of each word per its word index in the sentence, starting with `1`.
* For example, the first word gets `"a "` added to the end, the second word gets `"aa "` added to the end, and so on.
Return _the final sentence representing the conversion from sentence to Goat Latin_.
**Example 1:**
**Input:** sentence = "I speak Goat Latin"
**Output:** "Imaa peaksmaaa oatGmaaaa atinLmaaaaa"
**Example 2:**
**Input:** sentence = "The quick brown fox jumped over the lazy dog"
**Output:** "heTmaa uickqmaaa rownbmaaaa oxfmaaaaa umpedjmaaaaaa overmaaaaaaa hetmaaaaaaaa azylmaaaaaaaaa ogdmaaaaaaaaaa"
**Constraints:**
* `1 <= sentence.length <= 150`
* `sentence` consists of English letters and spaces.
* `sentence` has no leading or trailing spaces.
* All the words in `sentence` are separated by a single space. | null |
Python solution | number-of-lines-to-write-string | 0 | 1 | ```\nclass Solution:\n def numberOfLines(self, widths: List[int], s: str) -> List[int]:\n alphabet: str = "abcdefghijklmnopqrstuvwxyz"\n line, total = 0, 0\n\n for letter in s:\n pixel = widths[alphabet.index(letter)]\n if line + pixel > 100:\n total += 1\n line = 0\n line += pixel\n\n return [total + 1, line]\n``` | 0 | You are given a string `s` of lowercase English letters and an array `widths` denoting **how many pixels wide** each lowercase English letter is. Specifically, `widths[0]` is the width of `'a'`, `widths[1]` is the width of `'b'`, and so on.
You are trying to write `s` across several lines, where **each line is no longer than** `100` **pixels**. Starting at the beginning of `s`, write as many letters on the first line such that the total width does not exceed `100` pixels. Then, from where you stopped in `s`, continue writing as many letters as you can on the second line. Continue this process until you have written all of `s`.
Return _an array_ `result` _of length 2 where:_
* `result[0]` _is the total number of lines._
* `result[1]` _is the width of the last line in pixels._
**Example 1:**
**Input:** widths = \[10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "abcdefghijklmnopqrstuvwxyz "
**Output:** \[3,60\]
**Explanation:** You can write s as follows:
abcdefghij // 100 pixels wide
klmnopqrst // 100 pixels wide
uvwxyz // 60 pixels wide
There are a total of 3 lines, and the last line is 60 pixels wide.
**Example 2:**
**Input:** widths = \[4,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10\], s = "bbbcccdddaaa "
**Output:** \[2,4\]
**Explanation:** You can write s as follows:
bbbcccdddaa // 98 pixels wide
a // 4 pixels wide
There are a total of 2 lines, and the last line is 4 pixels wide.
**Constraints:**
* `widths.length == 26`
* `2 <= widths[i] <= 10`
* `1 <= s.length <= 1000`
* `s` contains only lowercase English letters. | null |
Python solution | number-of-lines-to-write-string | 0 | 1 | ```\nclass Solution:\n def numberOfLines(self, widths: List[int], s: str) -> List[int]:\n alphabet: str = "abcdefghijklmnopqrstuvwxyz"\n line, total = 0, 0\n\n for letter in s:\n pixel = widths[alphabet.index(letter)]\n if line + pixel > 100:\n total += 1\n line = 0\n line += pixel\n\n return [total + 1, line]\n``` | 0 | You are given a string `sentence` that consist of words separated by spaces. Each word consists of lowercase and uppercase letters only.
We would like to convert the sentence to "Goat Latin " (a made-up language similar to Pig Latin.) The rules of Goat Latin are as follows:
* If a word begins with a vowel (`'a'`, `'e'`, `'i'`, `'o'`, or `'u'`), append `"ma "` to the end of the word.
* For example, the word `"apple "` becomes `"applema "`.
* If a word begins with a consonant (i.e., not a vowel), remove the first letter and append it to the end, then add `"ma "`.
* For example, the word `"goat "` becomes `"oatgma "`.
* Add one letter `'a'` to the end of each word per its word index in the sentence, starting with `1`.
* For example, the first word gets `"a "` added to the end, the second word gets `"aa "` added to the end, and so on.
Return _the final sentence representing the conversion from sentence to Goat Latin_.
**Example 1:**
**Input:** sentence = "I speak Goat Latin"
**Output:** "Imaa peaksmaaa oatGmaaaa atinLmaaaaa"
**Example 2:**
**Input:** sentence = "The quick brown fox jumped over the lazy dog"
**Output:** "heTmaa uickqmaaa rownbmaaaa oxfmaaaaa umpedjmaaaaaa overmaaaaaaa hetmaaaaaaaa azylmaaaaaaaaa ogdmaaaaaaaaaa"
**Constraints:**
* `1 <= sentence.length <= 150`
* `sentence` consists of English letters and spaces.
* `sentence` has no leading or trailing spaces.
* All the words in `sentence` are separated by a single space. | null |
python3 solution using 2 arrays beats 98% O(N) space | max-increase-to-keep-city-skyline | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nhere a contains maximum in each row\nhere b cointains maximum in each column\nc has max in each column which will be appendded to b\nafter having these we just just need to compare a[i] and b[j] whichever is lower to maintain skyline and then we can just subtract element from the minimum value \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**0(N^2)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(N)**\n# Code\n```\nclass Solution:\n def maxIncreaseKeepingSkyline(self, grid: List[List[int]]) -> int:\n a=[max(i) for i in grid]\n b=[]\n l=len(grid)\n for i in range(l):\n "list comprehension for column"\n c=max([j[i] for j in grid])\n b.append(c)\n ans=0\n for i in range(l):\n for j in range(l):\n "can also have varible m storing min a[i] and b[j]"\n ans+=min(a[i],b[j])-grid[i][j]\n return ans\n``` | 1 | There is a city composed of `n x n` blocks, where each block contains a single building shaped like a vertical square prism. You are given a **0-indexed** `n x n` integer matrix `grid` where `grid[r][c]` represents the **height** of the building located in the block at row `r` and column `c`.
A city's **skyline** is the outer contour formed by all the building when viewing the side of the city from a distance. The **skyline** from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of **any number of buildings by any amount** (the amount can be different per building). The height of a `0`\-height building can also be increased. However, increasing the height of a building should **not** affect the city's **skyline** from any cardinal direction.
Return _the **maximum total sum** that the height of the buildings can be increased by **without** changing the city's **skyline** from any cardinal direction_.
**Example 1:**
**Input:** grid = \[\[3,0,8,4\],\[2,4,5,7\],\[9,2,6,3\],\[0,3,1,0\]\]
**Output:** 35
**Explanation:** The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = \[ \[8, 4, 8, 7\],
\[7, 4, 7, 7\],
\[9, 4, 8, 7\],
\[3, 3, 3, 3\] \]
**Example 2:**
**Input:** grid = \[\[0,0,0\],\[0,0,0\],\[0,0,0\]\]
**Output:** 0
**Explanation:** Increasing the height of any building will result in the skyline changing.
**Constraints:**
* `n == grid.length`
* `n == grid[r].length`
* `2 <= n <= 50`
* `0 <= grid[r][c] <= 100` | null |
python3 solution using 2 arrays beats 98% O(N) space | max-increase-to-keep-city-skyline | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nhere a contains maximum in each row\nhere b cointains maximum in each column\nc has max in each column which will be appendded to b\nafter having these we just just need to compare a[i] and b[j] whichever is lower to maintain skyline and then we can just subtract element from the minimum value \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**0(N^2)**\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(N)**\n# Code\n```\nclass Solution:\n def maxIncreaseKeepingSkyline(self, grid: List[List[int]]) -> int:\n a=[max(i) for i in grid]\n b=[]\n l=len(grid)\n for i in range(l):\n "list comprehension for column"\n c=max([j[i] for j in grid])\n b.append(c)\n ans=0\n for i in range(l):\n for j in range(l):\n "can also have varible m storing min a[i] and b[j]"\n ans+=min(a[i],b[j])-grid[i][j]\n return ans\n``` | 1 | There are `n` persons on a social media website. You are given an integer array `ages` where `ages[i]` is the age of the `ith` person.
A Person `x` will not send a friend request to a person `y` (`x != y`) if any of the following conditions is true:
* `age[y] <= 0.5 * age[x] + 7`
* `age[y] > age[x]`
* `age[y] > 100 && age[x] < 100`
Otherwise, `x` will send a friend request to `y`.
Note that if `x` sends a request to `y`, `y` will not necessarily send a request to `x`. Also, a person will not send a friend request to themself.
Return _the total number of friend requests made_.
**Example 1:**
**Input:** ages = \[16,16\]
**Output:** 2
**Explanation:** 2 people friend request each other.
**Example 2:**
**Input:** ages = \[16,17,18\]
**Output:** 2
**Explanation:** Friend requests are made 17 -> 16, 18 -> 17.
**Example 3:**
**Input:** ages = \[20,30,100,110,120\]
**Output:** 3
**Explanation:** Friend requests are made 110 -> 100, 120 -> 110, 120 -> 100.
**Constraints:**
* `n == ages.length`
* `1 <= n <= 2 * 104`
* `1 <= ages[i] <= 120` | null |
Python3 | 100% time (32ms), 97% memory | Fast int math | soup-servings | 0 | 1 | \n\n\n# Intuition\nMost of this follows similar concepts as the editorial, but instead of adding complexity with dividing by 25 and messing about with adding fractions of fractions, I chose to keep everything integer and keep track of the success count and total count as numerator and denominator. Because of the curveball of tie counting for half, the numerator is doubled in the loop, and at the very end I double the denominator to compensate. \n\nOnly integer subtraction is needed for soup quantities, the chance count is addition. \nMultiplication of the denominator is required when forking to different possibilities, and when updating the answer to common denominator, but in those cases it\'s both multiplying by 4. That is equivalent to bitshift by 2, which i\'ve chosen to replace it with.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n > 4500:\n return 1\n SERVING_OPTIONS = [(100, 0), (75, 25), (50, 50), (25, 75)]\n # (ml_soup_a, ml_soup_b) = [numerator, denominator]\n quantities_chance = {(n, n): [1, 1]}\n q = deque()\n q.appendleft((n, n))\n answer_numerator = 0\n answer_denominator = 1\n while q:\n ml_soup_a, ml_soup_b = q.pop()\n chance_numerator, chance_denominator = quantities_chance.pop((ml_soup_a, ml_soup_b))\n if min(ml_soup_a, ml_soup_b) <= 0:\n while answer_denominator < chance_denominator:\n answer_numerator <<= 2\n answer_denominator <<= 2\n if ml_soup_a <= 0:\n answer_numerator += chance_numerator\n if ml_soup_b > 0:\n answer_numerator += chance_numerator\n continue\n for serving_a, serving_b in SERVING_OPTIONS:\n remaining_soups = (ml_soup_a - serving_a, ml_soup_b - serving_b)\n if remaining_soups not in quantities_chance:\n q.appendleft(remaining_soups)\n quantities_chance[remaining_soups] = [0, chance_denominator << 2]\n quantities_chance[remaining_soups][0] += chance_numerator\n return answer_numerator / (answer_denominator << 1)\n\n\n``` | 3 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Python3 | 100% time (32ms), 97% memory | Fast int math | soup-servings | 0 | 1 | \n\n\n# Intuition\nMost of this follows similar concepts as the editorial, but instead of adding complexity with dividing by 25 and messing about with adding fractions of fractions, I chose to keep everything integer and keep track of the success count and total count as numerator and denominator. Because of the curveball of tie counting for half, the numerator is doubled in the loop, and at the very end I double the denominator to compensate. \n\nOnly integer subtraction is needed for soup quantities, the chance count is addition. \nMultiplication of the denominator is required when forking to different possibilities, and when updating the answer to common denominator, but in those cases it\'s both multiplying by 4. That is equivalent to bitshift by 2, which i\'ve chosen to replace it with.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n > 4500:\n return 1\n SERVING_OPTIONS = [(100, 0), (75, 25), (50, 50), (25, 75)]\n # (ml_soup_a, ml_soup_b) = [numerator, denominator]\n quantities_chance = {(n, n): [1, 1]}\n q = deque()\n q.appendleft((n, n))\n answer_numerator = 0\n answer_denominator = 1\n while q:\n ml_soup_a, ml_soup_b = q.pop()\n chance_numerator, chance_denominator = quantities_chance.pop((ml_soup_a, ml_soup_b))\n if min(ml_soup_a, ml_soup_b) <= 0:\n while answer_denominator < chance_denominator:\n answer_numerator <<= 2\n answer_denominator <<= 2\n if ml_soup_a <= 0:\n answer_numerator += chance_numerator\n if ml_soup_b > 0:\n answer_numerator += chance_numerator\n continue\n for serving_a, serving_b in SERVING_OPTIONS:\n remaining_soups = (ml_soup_a - serving_a, ml_soup_b - serving_b)\n if remaining_soups not in quantities_chance:\n q.appendleft(remaining_soups)\n quantities_chance[remaining_soups] = [0, chance_denominator << 2]\n quantities_chance[remaining_soups][0] += chance_numerator\n return answer_numerator / (answer_denominator << 1)\n\n\n``` | 3 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
Easy Explanation with comment + Video Explanation in Depth || C++ || java || python | soup-servings | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nExplore all the options we have and calculate the probability smartly by reducing n.\n\nFor detailed explanation you can refer to my youtube channel (hindi Language)\nhttps://youtu.be/z7L9f8Lt_lc\n or link in my profile.Here,you can find any solution in playlists monthwise from June 2023 with detailed explanation.i upload daily leetcode solution video with short and precise explanation (5-10) minutes.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. Two vectors `optionA` and `optionB` are defined to represent the servings from bowls A and B, respectively.\n\n2. The `solve` function recursively calculates the probability of bowl A being emptied first given the current quantities of soup in bowls A and B.\n\n3. Base cases in the `solve` function return probabilities for empty or full bowls A and B.\n\n4. The function iterates over the options in `optionA` and `optionB`, updating the remaining soup quantities and probability.\n\n5. The `soupServings` function serves as the entry point, checking if `n` is sufficiently large to return a probability of 1 directly. It initializes a memoization table `dp`.\n\n6. The `solve` function is called with initial quantities `n` in both bowls, and the result is returned.\n\n\n# Complexity\n- Time complexity:$$O(n*n)$$ less than this\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n vector<int>optionA={100,75,50,25};\n vector<int>optionB={0,25,50,75};\n\n double solve(int a, int b, vector<vector<double>> &dp){\n if(a==0&&b==0)\n return 0.5;//half the probability that A and B become empty at the same time\n if(a==0)\n return 1;\n if(b==0) return 0; \n \n if(dp[a][b] != -1) return dp[a][b];\n \n double ans=0;\n for(int k=0;k<4;k++){\n int rema=a-optionA[k];\n int remb=b-optionB[k];\n ans =ans+ 0.25*solve(max(0,rema), max(0,remb), dp);\n }\n \n return dp[a][b]=ans;\n }\n \n double soupServings(int n) {\n if(n>=4800) return 1;//since we want to calculate the probability of a .so we can see that the a will become 0 at fast rate as we increase n because a is decresing at more faster rate and at sume point probaility reaches 1 for soup A will be empty first .\n vector<vector<double>> dp(n+1,vector<double>(n+1,-1));\n return solve(n,n,dp);\n }\n};\n```\n```Java []\n\nclass Solution {\n private int[] optionA = {100, 75, 50, 25};\n private int[] optionB = {0, 25, 50, 75};\n\n private double solve(int a, int b, double[][] dp) {\n if (a == 0 && b == 0)\n return 0.5; // half the probability that A and B become empty at the same time\n if (a == 0)\n return 1;\n if (b == 0)\n return 0;\n\n if (dp[a][b] != -1)\n return dp[a][b];\n\n double ans = 0;\n for (int k = 0; k < 4; k++) {\n int rema = a - optionA[k];\n int remb = b - optionB[k];\n ans += 0.25 * solve(Math.max(0, rema), Math.max(0, remb), dp);\n }\n\n return dp[a][b] = ans;\n }\n\n public double soupServings(int n) {\n if (n >= 4800)\n return 1;\n double[][] dp = new double[n + 1][n + 1];\n for (double[] row : dp) {\n Arrays.fill(row, -1);\n }\n return solve(n, n, dp);\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def __init__(self):\n self.optionA = [100, 75, 50, 25]\n self.optionB = [0, 25, 50, 75]\n\n def solve(self, a, b, dp):\n if a == 0 and b == 0:\n return 0.5 # half the probability that A and B become empty at the same time\n if a == 0:\n return 1\n if b == 0:\n return 0\n\n if dp[a][b] != -1:\n return dp[a][b]\n\n ans = 0\n for k in range(4):\n rema = a - self.optionA[k]\n remb = b - self.optionB[k]\n ans += 0.25 * self.solve(max(0, rema), max(0, remb), dp)\n\n dp[a][b] = ans\n return ans\n\n def soupServings(self, n: int) -> float:\n if n >= 4800:\n return 1\n dp = [[-1] * (n + 1) for _ in range(n + 1)]\n return self.solve(n, n, dp)\n\n```\n\n | 28 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Easy Explanation with comment + Video Explanation in Depth || C++ || java || python | soup-servings | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nExplore all the options we have and calculate the probability smartly by reducing n.\n\nFor detailed explanation you can refer to my youtube channel (hindi Language)\nhttps://youtu.be/z7L9f8Lt_lc\n or link in my profile.Here,you can find any solution in playlists monthwise from June 2023 with detailed explanation.i upload daily leetcode solution video with short and precise explanation (5-10) minutes.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. Two vectors `optionA` and `optionB` are defined to represent the servings from bowls A and B, respectively.\n\n2. The `solve` function recursively calculates the probability of bowl A being emptied first given the current quantities of soup in bowls A and B.\n\n3. Base cases in the `solve` function return probabilities for empty or full bowls A and B.\n\n4. The function iterates over the options in `optionA` and `optionB`, updating the remaining soup quantities and probability.\n\n5. The `soupServings` function serves as the entry point, checking if `n` is sufficiently large to return a probability of 1 directly. It initializes a memoization table `dp`.\n\n6. The `solve` function is called with initial quantities `n` in both bowls, and the result is returned.\n\n\n# Complexity\n- Time complexity:$$O(n*n)$$ less than this\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n*n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` C++ []\nclass Solution {\npublic:\n vector<int>optionA={100,75,50,25};\n vector<int>optionB={0,25,50,75};\n\n double solve(int a, int b, vector<vector<double>> &dp){\n if(a==0&&b==0)\n return 0.5;//half the probability that A and B become empty at the same time\n if(a==0)\n return 1;\n if(b==0) return 0; \n \n if(dp[a][b] != -1) return dp[a][b];\n \n double ans=0;\n for(int k=0;k<4;k++){\n int rema=a-optionA[k];\n int remb=b-optionB[k];\n ans =ans+ 0.25*solve(max(0,rema), max(0,remb), dp);\n }\n \n return dp[a][b]=ans;\n }\n \n double soupServings(int n) {\n if(n>=4800) return 1;//since we want to calculate the probability of a .so we can see that the a will become 0 at fast rate as we increase n because a is decresing at more faster rate and at sume point probaility reaches 1 for soup A will be empty first .\n vector<vector<double>> dp(n+1,vector<double>(n+1,-1));\n return solve(n,n,dp);\n }\n};\n```\n```Java []\n\nclass Solution {\n private int[] optionA = {100, 75, 50, 25};\n private int[] optionB = {0, 25, 50, 75};\n\n private double solve(int a, int b, double[][] dp) {\n if (a == 0 && b == 0)\n return 0.5; // half the probability that A and B become empty at the same time\n if (a == 0)\n return 1;\n if (b == 0)\n return 0;\n\n if (dp[a][b] != -1)\n return dp[a][b];\n\n double ans = 0;\n for (int k = 0; k < 4; k++) {\n int rema = a - optionA[k];\n int remb = b - optionB[k];\n ans += 0.25 * solve(Math.max(0, rema), Math.max(0, remb), dp);\n }\n\n return dp[a][b] = ans;\n }\n\n public double soupServings(int n) {\n if (n >= 4800)\n return 1;\n double[][] dp = new double[n + 1][n + 1];\n for (double[] row : dp) {\n Arrays.fill(row, -1);\n }\n return solve(n, n, dp);\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def __init__(self):\n self.optionA = [100, 75, 50, 25]\n self.optionB = [0, 25, 50, 75]\n\n def solve(self, a, b, dp):\n if a == 0 and b == 0:\n return 0.5 # half the probability that A and B become empty at the same time\n if a == 0:\n return 1\n if b == 0:\n return 0\n\n if dp[a][b] != -1:\n return dp[a][b]\n\n ans = 0\n for k in range(4):\n rema = a - self.optionA[k]\n remb = b - self.optionB[k]\n ans += 0.25 * self.solve(max(0, rema), max(0, remb), dp)\n\n dp[a][b] = ans\n return ans\n\n def soupServings(self, n: int) -> float:\n if n >= 4800:\n return 1\n dp = [[-1] * (n + 1) for _ in range(n + 1)]\n return self.solve(n, n, dp)\n\n```\n\n | 28 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
Python3 👍||⚡100% faster beats 🔥|| clean solution with critical point tips! || simple explain || | soup-servings | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nAs the value of N increases, the winning rate of A approaches 1,therefore, you need to find the critical point, which can significantly increase the execution speed.\n\n\n# Complexity\n- Time complexity: O(n<sup>2</sup>)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n<sup>2</sup>)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def soupServings(self, n: int) -> float:\n @cache\n def dfs(a,b):\n if a<=0 and b <=0:\n return 0.5\n elif a<=0:\n return 1\n elif b<=0:\n return 0\n else:\n return 0.25 * (dfs(a-100,b)+dfs(a-75,b-25)+dfs(a-50,b-50)+dfs(a-25,b-75))\n return 1 if n > 4450 else dfs(n,n) # How to know 4450 ? \u21E3\u21E3\u21E3\n\n # print(dfs(1000,1000)) # 0.9765650521094358\n # print(dfs(10000,10000)) # 0.9999999999159161\n # for i in range(1000,10000):\n # if 1-dfs(i,i) <= 10**(-5):\n # print(i) # 4451\n # break \n``` | 9 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Python3 👍||⚡100% faster beats 🔥|| clean solution with critical point tips! || simple explain || | soup-servings | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nAs the value of N increases, the winning rate of A approaches 1,therefore, you need to find the critical point, which can significantly increase the execution speed.\n\n\n# Complexity\n- Time complexity: O(n<sup>2</sup>)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n<sup>2</sup>)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def soupServings(self, n: int) -> float:\n @cache\n def dfs(a,b):\n if a<=0 and b <=0:\n return 0.5\n elif a<=0:\n return 1\n elif b<=0:\n return 0\n else:\n return 0.25 * (dfs(a-100,b)+dfs(a-75,b-25)+dfs(a-50,b-50)+dfs(a-25,b-75))\n return 1 if n > 4450 else dfs(n,n) # How to know 4450 ? \u21E3\u21E3\u21E3\n\n # print(dfs(1000,1000)) # 0.9765650521094358\n # print(dfs(10000,10000)) # 0.9999999999159161\n # for i in range(1000,10000):\n # if 1-dfs(i,i) <= 10**(-5):\n # print(i) # 4451\n # break \n``` | 9 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
Python short and clean. Functional programming. | soup-servings | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution. Approach 2](https://leetcode.com/problems/soup-servings/editorial/) but shorter and functional.\n\n<!-- # Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$ -->\n\n# Code\nHardcoded saturation point (i.e, `m = 200`)\n```python\nclass Solution:\n def soupServings(self, n: int) -> float:\n m = ceil(n / 25)\n return self.empty_prob(m, m) if m < 200 else 1.0\n \n @cache\n def empty_prob(self, a: int, b: int) -> float:\n match a <= 0, b <= 0:\n case True , True : return 0.5\n case True , False: return 1.0\n case False, True : return 0.0\n case False, False: return sum(\n self.empty_prob(a - da, b - db)\n for da, db in ((4, 0), (3, 1), (2, 2), (1, 3)) \n ) / 4\n\n\n```\n\nDynamic saturation point with incremental memoization:\n```python\nclass Solution:\n probs = []\n\n def soupServings(self, n: int) -> float:\n m, k = ceil(n / 25), len(self.probs)\n self.probs.extend(takewhile(\n lambda x: x <= 1 - 1e-5,\n (self.empty_prob(i, i) for i in range(k, m + 1))\n ))\n return self.probs[m if m < k else -1]\n \n @cache\n def empty_prob(self, a: int, b: int) -> float:\n match a <= 0, b <= 0:\n case True , True : return 0.5\n case True , False: return 1.0\n case False, True : return 0.0\n case False, False: return sum(\n self.empty_prob(a - da, b - db)\n for da, db in ((4, 0), (3, 1), (2, 2), (1, 3)) \n ) / 4\n\n\n``` | 1 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Python short and clean. Functional programming. | soup-servings | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial solution. Approach 2](https://leetcode.com/problems/soup-servings/editorial/) but shorter and functional.\n\n<!-- # Complexity\n- Time complexity: $$O(1)$$\n\n- Space complexity: $$O(1)$$ -->\n\n# Code\nHardcoded saturation point (i.e, `m = 200`)\n```python\nclass Solution:\n def soupServings(self, n: int) -> float:\n m = ceil(n / 25)\n return self.empty_prob(m, m) if m < 200 else 1.0\n \n @cache\n def empty_prob(self, a: int, b: int) -> float:\n match a <= 0, b <= 0:\n case True , True : return 0.5\n case True , False: return 1.0\n case False, True : return 0.0\n case False, False: return sum(\n self.empty_prob(a - da, b - db)\n for da, db in ((4, 0), (3, 1), (2, 2), (1, 3)) \n ) / 4\n\n\n```\n\nDynamic saturation point with incremental memoization:\n```python\nclass Solution:\n probs = []\n\n def soupServings(self, n: int) -> float:\n m, k = ceil(n / 25), len(self.probs)\n self.probs.extend(takewhile(\n lambda x: x <= 1 - 1e-5,\n (self.empty_prob(i, i) for i in range(k, m + 1))\n ))\n return self.probs[m if m < k else -1]\n \n @cache\n def empty_prob(self, a: int, b: int) -> float:\n match a <= 0, b <= 0:\n case True , True : return 0.5\n case True , False: return 1.0\n case False, True : return 0.0\n case False, False: return sum(\n self.empty_prob(a - da, b - db)\n for da, db in ((4, 0), (3, 1), (2, 2), (1, 3)) \n ) / 4\n\n\n``` | 1 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
Python3 97% faster concise code based on cache | soup-servings | 0 | 1 | ```\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n > 4800:\n return 1\n @cache\n def serve(quantityA: int, quantityB: int) -> float:\n if quantityA <= 0 and quantityB <= 0:\n return 0.5\n if quantityA <= 0:\n return 1.0\n if quantityB <= 0:\n return 0.0\n op1 = 0.25 * serve(quantityA - 100, quantityB)\n op2 = 0.25 * serve(quantityA - 75, quantityB - 25)\n op3 = 0.25 * serve(quantityA - 50, quantityB - 50)\n op4 = 0.25 * serve(quantityA - 25, quantityB - 75)\n return op1 + op2 + op3 + op4\n return serve(n, n)\n\n``` | 1 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Python3 97% faster concise code based on cache | soup-servings | 0 | 1 | ```\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n > 4800:\n return 1\n @cache\n def serve(quantityA: int, quantityB: int) -> float:\n if quantityA <= 0 and quantityB <= 0:\n return 0.5\n if quantityA <= 0:\n return 1.0\n if quantityB <= 0:\n return 0.0\n op1 = 0.25 * serve(quantityA - 100, quantityB)\n op2 = 0.25 * serve(quantityA - 75, quantityB - 25)\n op3 = 0.25 * serve(quantityA - 50, quantityB - 50)\n op4 = 0.25 * serve(quantityA - 25, quantityB - 75)\n return op1 + op2 + op3 + op4\n return serve(n, n)\n\n``` | 1 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
BFS with explanation | soup-servings | 0 | 1 | # Intuition\nFirst it is obvious that above some specific value n the result will be 1. So once you have more or less working solution you can find this value and hardcode it. I saw that 5000 is good enough you can definitely tweek this value with binary search to find the first one.\n\nThen you maintain the frontier which consits of dictionary which maps `(soup_a, soup_b) -> cnt` (it stats with `{(N, N): 1}`) and then you iterate until you have something in frontier maitaining the counts.\n\n# Code\n```\nfrom collections import defaultdict\n\nclass Solution:\n def soupServings(self, N: int) -> float:\n if N >= 5000:\n return 1\n \n frontier, mult = {(N, N): 1}, 1\n p1, p2 = 0, 0\n \n while frontier:\n new_frontier, mult = defaultdict(int), mult * 0.25\n for (v1, v2), n in frontier.items():\n for d1, d2 in [(100, 0), (75, 25), (50, 50), (25, 75)]:\n v1_, v2_ = max(0, v1 - d1), max(0, v2 - d2)\n \n if v1_ == 0 and v2_ == 0:\n p2 += n * mult\n elif v1_ == 0:\n p1 += n * mult\n elif v1_ > 0 and v2_ > 0:\n new_frontier[(v1_, v2_)] += n\n \n frontier = new_frontier\n \n return p1 + p2 * 0.5\n \n``` | 1 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
BFS with explanation | soup-servings | 0 | 1 | # Intuition\nFirst it is obvious that above some specific value n the result will be 1. So once you have more or less working solution you can find this value and hardcode it. I saw that 5000 is good enough you can definitely tweek this value with binary search to find the first one.\n\nThen you maintain the frontier which consits of dictionary which maps `(soup_a, soup_b) -> cnt` (it stats with `{(N, N): 1}`) and then you iterate until you have something in frontier maitaining the counts.\n\n# Code\n```\nfrom collections import defaultdict\n\nclass Solution:\n def soupServings(self, N: int) -> float:\n if N >= 5000:\n return 1\n \n frontier, mult = {(N, N): 1}, 1\n p1, p2 = 0, 0\n \n while frontier:\n new_frontier, mult = defaultdict(int), mult * 0.25\n for (v1, v2), n in frontier.items():\n for d1, d2 in [(100, 0), (75, 25), (50, 50), (25, 75)]:\n v1_, v2_ = max(0, v1 - d1), max(0, v2 - d2)\n \n if v1_ == 0 and v2_ == 0:\n p2 += n * mult\n elif v1_ == 0:\n p1 += n * mult\n elif v1_ > 0 and v2_ > 0:\n new_frontier[(v1_, v2_)] += n\n \n frontier = new_frontier\n \n return p1 + p2 * 0.5\n \n``` | 1 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
Solution | soup-servings | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double memo[200][200];\n double soupServings(int N) {\n return N > 4800 ? 1.0 : f((N + 24) / 25, (N + 24) / 25);\n }\n double f(int a, int b) {\n if (a <= 0 && b <= 0) return 0.5;\n if (a <= 0) return 1;\n if (b <= 0) return 0;\n if (memo[a][b] > 0) return memo[a][b];\n memo[a][b] = 0.25 * (f(a-4,b)+f(a-3,b-1)+f(a-2,b-2)+f(a-1,b-3));\n return memo[a][b];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def soupServings(self, n: int) -> float:\n @cache\n def dp(a, b):\n if a <= 0 and b <= 0:\n return 0.5\n if a <= 0:\n return 1\n if b <= 0:\n return 0\n\n return 0.25 * (dp(a - 4, b) + dp(a - 3, b - 1) + dp(a - 2, b - 2) + dp(a - 1, b - 3))\n\n if n > 4800:\n return 1\n\n n = ceil(n / 25)\n return dp(n, n)\n```\n\n```Java []\nclass Solution {\n public double soupServings(int n) {\n \n if (n >= 4800) {\n return 1.0;\n }\n int N = (n + 24) / 25;\n double[][] dp = new double[N + 1][N + 1];\n return helper(dp, N, N);\n }\n private double helper(double[][] dp, int A, int B) {\n if (A <= 0 && B <= 0) {\n return 0.5;\n }\n if (A <= 0) {\n return 1.0;\n }\n if (B <= 0) {\n return 0.0;\n }\n if (dp[A][B] > 0) {\n return dp[A][B];\n }\n dp[A][B] = 0.25 * (helper(dp, A - 4, B) + helper(dp, A - 3, B - 1) + helper(dp, A - 2, B - 2) + helper(dp, A - 1, B - 3));\n return dp[A][B];\n }\n}\n```\n | 1 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Solution | soup-servings | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n double memo[200][200];\n double soupServings(int N) {\n return N > 4800 ? 1.0 : f((N + 24) / 25, (N + 24) / 25);\n }\n double f(int a, int b) {\n if (a <= 0 && b <= 0) return 0.5;\n if (a <= 0) return 1;\n if (b <= 0) return 0;\n if (memo[a][b] > 0) return memo[a][b];\n memo[a][b] = 0.25 * (f(a-4,b)+f(a-3,b-1)+f(a-2,b-2)+f(a-1,b-3));\n return memo[a][b];\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def soupServings(self, n: int) -> float:\n @cache\n def dp(a, b):\n if a <= 0 and b <= 0:\n return 0.5\n if a <= 0:\n return 1\n if b <= 0:\n return 0\n\n return 0.25 * (dp(a - 4, b) + dp(a - 3, b - 1) + dp(a - 2, b - 2) + dp(a - 1, b - 3))\n\n if n > 4800:\n return 1\n\n n = ceil(n / 25)\n return dp(n, n)\n```\n\n```Java []\nclass Solution {\n public double soupServings(int n) {\n \n if (n >= 4800) {\n return 1.0;\n }\n int N = (n + 24) / 25;\n double[][] dp = new double[N + 1][N + 1];\n return helper(dp, N, N);\n }\n private double helper(double[][] dp, int A, int B) {\n if (A <= 0 && B <= 0) {\n return 0.5;\n }\n if (A <= 0) {\n return 1.0;\n }\n if (B <= 0) {\n return 0.0;\n }\n if (dp[A][B] > 0) {\n return dp[A][B];\n }\n dp[A][B] = 0.25 * (helper(dp, A - 4, B) + helper(dp, A - 3, B - 1) + helper(dp, A - 2, B - 2) + helper(dp, A - 1, B - 3));\n return dp[A][B];\n }\n}\n```\n | 1 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
Python3 Solution | soup-servings | 0 | 1 | \n```\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n>4275:\n return 1\n n/=25 \n @cache\n def dfs(a,b):\n if a<=0 and b>0:\n return 1\n\n elif a<=0 and b<=0:\n return 0.5\n\n elif a>0 and b<=0:\n return 0\n\n return (dfs(a-4,b)+dfs(a-3,b-1)+dfs(a-2,b-2)+dfs(a-1,b-3))*0.25\n\n \n return dfs(n,n) \n``` | 2 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Python3 Solution | soup-servings | 0 | 1 | \n```\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n>4275:\n return 1\n n/=25 \n @cache\n def dfs(a,b):\n if a<=0 and b>0:\n return 1\n\n elif a<=0 and b<=0:\n return 0.5\n\n elif a>0 and b<=0:\n return 0\n\n return (dfs(a-4,b)+dfs(a-3,b-1)+dfs(a-2,b-2)+dfs(a-1,b-3))*0.25\n\n \n return dfs(n,n) \n``` | 2 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
🍲 [VIDEO] 100% Soup Servings: A Dive into Dynamic Programming and Probability 🎲 | soup-servings | 1 | 1 | # Intuition\nAt first glance, this problem is about making random choices and observing the outcome. This brings to mind the field of probability. However, since we\'re also dealing with several states (the amounts of soup A and B), it becomes clear that we need to use dynamic programming.\n\nhttps://youtu.be/S-9NmIj2fdQ\n\n# Approach\nOur approach to solving the \'Soup Servings\' problem revolves around a top-down dynamic programming technique, commonly known as memoization. The goal is to calculate the probability of soup A running out first, considering each possible state of soups A and B. Here\'s a detailed breakdown of our approach:\n\n1. **Initial Consideration:** We begin by addressing a particular property of the problem. When \'n\' (the initial quantity of soup in milliliters) is greater than 4451, the probability that soup A will be emptied first approaches 1. To optimize our solution, if \'n\' is greater than 4451, we return 1.0 immediately and avoid further computation. This value is derived empirically, as demonstrated in the code `binary_search_limit` below.\n\n2. **Scaling down \'n\':** The serving sizes in the problem are in multiples of 25 ml. To reduce the scale of the problem and make our computations more efficient, we divide \'n\' by 25 and round up to the nearest integer. This is done using the line `n = (n + 24) // 25`. Now \'n\' represents the number of servings of each soup (each serving being 25 ml), rather than the quantity in milliliters.\n\n3. **State Representation:** We then define the state of the system as a pair (i, j), where \'i\' denotes the remaining amount of soup A and \'j\' indicates the remaining amount of soup B. Each state (i, j) corresponds to a unique scenario with specific remaining quantities of soups A and B.\n\n4. **Memoization Strategy:** To prevent redundant computations, we adopt a memoization strategy. This involves storing the result of each state in a dictionary, named `memo`, after it\'s computed for the first time. Hence, if we encounter a state that\'s already been calculated, we can simply retrieve the result from the `memo` dictionary instead of re-computing it.\n\n5. **Recursive Function:** We formulate a recursive function, `dp(i, j)`, to compute the desired probability. This function takes two parameters, \'i\' and \'j\', representing the remaining quantities of soups A and B, respectively.\n\n - The function initially checks if the current state (i, j) is present in the `memo` dictionary. If it is, the function returns the stored result, thereby avoiding redundant computation.\n\n - If the current state is not in `memo`, the function proceeds to calculate the result based on several scenarios:\n - If both soups A and B are empty (i.e., i <= 0 and j <= 0), the function returns 0.5. This is because, according to the problem statement, we count the event of both soups becoming empty simultaneously as half a success.\n - If only soup A is empty (i.e., i <= 0), the function returns 1.0. This aligns with our goal, which is to calculate the probability of soup A emptying first.\n - If only soup B is empty (i.e., j <= 0), the function returns 0.0, since this scenario does not contribute to the probability of soup A becoming empty first.\n\n - If there are remaining quantities of both soups, the function calculates the probability using the given formula. This formula is derived from the four possible operations for serving the soup, which are equally likely. Each operation serves a different amount of soups A and B, thereby leading to different new states. For instance, the operation "Serve 100 ml of soup A and 0 ml of soup B" leads to the new state (i - 4, j), and so on for the other operations. The function calls itself recursively with these new states, averages the returned probabilities, stores this average in `memo`, and then returns it.\n\nThrough this approach, we can efficiently compute the desired probability by utilizing memoization to evade redundant calculations and recursion to explore all plausible states and transitions.\n\n# Complexity\n- Time complexity: The time complexity is \\(O(n^2)\\) because we need to compute the result for each possible state of soups A and B once, where \'n\' is the initial amount of each soup.\n- Space complexity: The space complexity is also \\(O(n^2)\\) because we need to store the result for each possible state in `memo`.\n\nThis Python code implements the top-down dynamic programming approach we described. It first handles the case where \'n\' is greater than 4451, scales down \'n\' by a factor of 25, and initializes the `memo` dictionary. It then defines the recursive function and calls it to calculate and return the desired probability.\n\n# Code\n```Python []\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n > 4451: \n return 1.0\n n = (n + 24) // 25\n memo = dict()\n \n def dp(i, j):\n if (i, j) in memo:\n return memo[(i, j)]\n if i <= 0 and j <= 0: \n return 0.5\n if i <= 0: \n return 1.0\n if j <= 0: \n return 0.0\n memo[(i, j)] = 0.25 * (dp(i - 4, j) + dp(i - 3, j - 1) + dp(i - 2, j - 2) + dp(i - 1, j - 3))\n return memo[(i, j)]\n \n return dp(n, n)\n```\n``` C++ []\nclass Solution {\npublic:\n double soupServings(int N) {\n if (N > 4451) {\n return 1.0;\n }\n N = (N + 24) / 25;\n std::unordered_map<int, double> memo;\n\n return dp(N, N, memo);\n }\n\nprivate:\n double dp(int a, int b, std::unordered_map<int, double>& memo) {\n if (a <= 0 && b <= 0) {\n return 0.5;\n }\n if (a <= 0) {\n return 1.0;\n }\n if (b <= 0) {\n return 0.0;\n }\n int key = a * 5000 + b;\n if (memo.count(key)) {\n return memo[key];\n }\n memo[key] = 0.25 * (dp(a-4, b, memo) + dp(a-3, b-1, memo) + dp(a-2, b-2, memo) + dp(a-1, b-3, memo));\n return memo[key];\n }\n};\n```\n``` C# []\npublic class Solution {\n Dictionary<Tuple<int, int>, double> memo = new Dictionary<Tuple<int, int>, double>();\n\n public double SoupServings(int N) {\n if (N > 4451) {\n return 1.0;\n }\n N = (N + 24) / 25;\n\n return dp(N, N);\n }\n\n private double dp(int a, int b) {\n if (a <= 0 && b <= 0) {\n return 0.5;\n }\n if (a <= 0) {\n return 1.0;\n }\n if (b <= 0) {\n return 0.0;\n }\n var key = Tuple.Create(a, b);\n if (memo.ContainsKey(key)) {\n return memo[key];\n }\n memo[key] = 0.25 * (dp(a-4, b) + dp(a-3, b-1) + dp(a-2, b-2) + dp(a-1, b-3));\n return memo[key];\n }\n}\n```\n``` Java []\nclass Solution {\n private HashMap<Pair<Integer, Integer>, Double> memo = new HashMap<>();\n\n public double soupServings(int N) {\n if (N > 4451) {\n return 1.0;\n }\n N = (N + 24) / 25;\n\n return dp(N, N);\n }\n\n private double dp(int a, int b) {\n if (a <= 0 && b <= 0) {\n return 0.5;\n }\n if (a <= 0) {\n return 1.0;\n }\n if (b <= 0) {\n return 0.0;\n }\n Pair<Integer, Integer> key = new Pair<>(a, b);\n if (memo.containsKey(key)) {\n return memo.get(key);\n }\n memo.put(key, 0.25 * (dp(a-4, b) + dp(a-3, b-1) + dp(a-2, b-2) + dp(a-1, b-3)));\n return memo.get(key);\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar soupServings = function(N) {\n if (N > 4451) {\n return 1.0;\n }\n N = Math.floor((N + 24) / 25);\n let memo = {};\n\n return dp(N, N);\n\n function dp(a, b) {\n if (a <= 0 && b <= 0) {\n return 0.5;\n }\n if (a <= 0) {\n return 1.0;\n }\n if (b <= 0) {\n return 0.0;\n }\n let key = a * 5000 + b;\n if (key in memo) {\n return memo[key];\n }\n memo[key] = 0.25 * (dp(a-4, b) + dp(a-3, b-1) + dp(a-2, b-2) + dp(a-1, b-3));\n return memo[key];\n }\n};\n```\n\n# How to find 4451 ?\n\nUsing the binary search limit method, we find that the minimum value of \\( n \\) for which the function `soupServings(n)` returns a value that is very close to 1 (within \\( 10^{-5} \\)) is \\( n = 4451 \\).\n\nThis means that for \\( n \\geq 4451 \\), the probability that soup A will be empty first, plus half the probability that A and B become empty at the same time, is effectively 1 (or very close to 1). \n\n``` Python []\n# Let\'s implement a binary search to find the limit\ndef binary_search_limit(low, high, epsilon):\n while high - low > 1:\n mid = low + (high - low) // 2\n result = soupServings(mid)\n if abs(result - 1.0) <= epsilon:\n high = mid\n else:\n low = mid\n return high\n\nepsilon = 10**(-5)\nbinary_search_limit(1000, 5000, epsilon)\n```\n\nIn the context of the problem, this suggests that for initial volumes of soup of 4451 ml or more, it\'s almost certain that soup A will be consumed first. \n\nThe binary search limit method provides an efficient way to find the limit in a continuous domain by progressively narrowing the search interval.\n\n# Video for C++ & JavaScript\nhttps://youtu.be/EDH1zBhebXg\nhttps://youtu.be/LhNJ1biTTR0 | 45 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
🍲 [VIDEO] 100% Soup Servings: A Dive into Dynamic Programming and Probability 🎲 | soup-servings | 1 | 1 | # Intuition\nAt first glance, this problem is about making random choices and observing the outcome. This brings to mind the field of probability. However, since we\'re also dealing with several states (the amounts of soup A and B), it becomes clear that we need to use dynamic programming.\n\nhttps://youtu.be/S-9NmIj2fdQ\n\n# Approach\nOur approach to solving the \'Soup Servings\' problem revolves around a top-down dynamic programming technique, commonly known as memoization. The goal is to calculate the probability of soup A running out first, considering each possible state of soups A and B. Here\'s a detailed breakdown of our approach:\n\n1. **Initial Consideration:** We begin by addressing a particular property of the problem. When \'n\' (the initial quantity of soup in milliliters) is greater than 4451, the probability that soup A will be emptied first approaches 1. To optimize our solution, if \'n\' is greater than 4451, we return 1.0 immediately and avoid further computation. This value is derived empirically, as demonstrated in the code `binary_search_limit` below.\n\n2. **Scaling down \'n\':** The serving sizes in the problem are in multiples of 25 ml. To reduce the scale of the problem and make our computations more efficient, we divide \'n\' by 25 and round up to the nearest integer. This is done using the line `n = (n + 24) // 25`. Now \'n\' represents the number of servings of each soup (each serving being 25 ml), rather than the quantity in milliliters.\n\n3. **State Representation:** We then define the state of the system as a pair (i, j), where \'i\' denotes the remaining amount of soup A and \'j\' indicates the remaining amount of soup B. Each state (i, j) corresponds to a unique scenario with specific remaining quantities of soups A and B.\n\n4. **Memoization Strategy:** To prevent redundant computations, we adopt a memoization strategy. This involves storing the result of each state in a dictionary, named `memo`, after it\'s computed for the first time. Hence, if we encounter a state that\'s already been calculated, we can simply retrieve the result from the `memo` dictionary instead of re-computing it.\n\n5. **Recursive Function:** We formulate a recursive function, `dp(i, j)`, to compute the desired probability. This function takes two parameters, \'i\' and \'j\', representing the remaining quantities of soups A and B, respectively.\n\n - The function initially checks if the current state (i, j) is present in the `memo` dictionary. If it is, the function returns the stored result, thereby avoiding redundant computation.\n\n - If the current state is not in `memo`, the function proceeds to calculate the result based on several scenarios:\n - If both soups A and B are empty (i.e., i <= 0 and j <= 0), the function returns 0.5. This is because, according to the problem statement, we count the event of both soups becoming empty simultaneously as half a success.\n - If only soup A is empty (i.e., i <= 0), the function returns 1.0. This aligns with our goal, which is to calculate the probability of soup A emptying first.\n - If only soup B is empty (i.e., j <= 0), the function returns 0.0, since this scenario does not contribute to the probability of soup A becoming empty first.\n\n - If there are remaining quantities of both soups, the function calculates the probability using the given formula. This formula is derived from the four possible operations for serving the soup, which are equally likely. Each operation serves a different amount of soups A and B, thereby leading to different new states. For instance, the operation "Serve 100 ml of soup A and 0 ml of soup B" leads to the new state (i - 4, j), and so on for the other operations. The function calls itself recursively with these new states, averages the returned probabilities, stores this average in `memo`, and then returns it.\n\nThrough this approach, we can efficiently compute the desired probability by utilizing memoization to evade redundant calculations and recursion to explore all plausible states and transitions.\n\n# Complexity\n- Time complexity: The time complexity is \\(O(n^2)\\) because we need to compute the result for each possible state of soups A and B once, where \'n\' is the initial amount of each soup.\n- Space complexity: The space complexity is also \\(O(n^2)\\) because we need to store the result for each possible state in `memo`.\n\nThis Python code implements the top-down dynamic programming approach we described. It first handles the case where \'n\' is greater than 4451, scales down \'n\' by a factor of 25, and initializes the `memo` dictionary. It then defines the recursive function and calls it to calculate and return the desired probability.\n\n# Code\n```Python []\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n > 4451: \n return 1.0\n n = (n + 24) // 25\n memo = dict()\n \n def dp(i, j):\n if (i, j) in memo:\n return memo[(i, j)]\n if i <= 0 and j <= 0: \n return 0.5\n if i <= 0: \n return 1.0\n if j <= 0: \n return 0.0\n memo[(i, j)] = 0.25 * (dp(i - 4, j) + dp(i - 3, j - 1) + dp(i - 2, j - 2) + dp(i - 1, j - 3))\n return memo[(i, j)]\n \n return dp(n, n)\n```\n``` C++ []\nclass Solution {\npublic:\n double soupServings(int N) {\n if (N > 4451) {\n return 1.0;\n }\n N = (N + 24) / 25;\n std::unordered_map<int, double> memo;\n\n return dp(N, N, memo);\n }\n\nprivate:\n double dp(int a, int b, std::unordered_map<int, double>& memo) {\n if (a <= 0 && b <= 0) {\n return 0.5;\n }\n if (a <= 0) {\n return 1.0;\n }\n if (b <= 0) {\n return 0.0;\n }\n int key = a * 5000 + b;\n if (memo.count(key)) {\n return memo[key];\n }\n memo[key] = 0.25 * (dp(a-4, b, memo) + dp(a-3, b-1, memo) + dp(a-2, b-2, memo) + dp(a-1, b-3, memo));\n return memo[key];\n }\n};\n```\n``` C# []\npublic class Solution {\n Dictionary<Tuple<int, int>, double> memo = new Dictionary<Tuple<int, int>, double>();\n\n public double SoupServings(int N) {\n if (N > 4451) {\n return 1.0;\n }\n N = (N + 24) / 25;\n\n return dp(N, N);\n }\n\n private double dp(int a, int b) {\n if (a <= 0 && b <= 0) {\n return 0.5;\n }\n if (a <= 0) {\n return 1.0;\n }\n if (b <= 0) {\n return 0.0;\n }\n var key = Tuple.Create(a, b);\n if (memo.ContainsKey(key)) {\n return memo[key];\n }\n memo[key] = 0.25 * (dp(a-4, b) + dp(a-3, b-1) + dp(a-2, b-2) + dp(a-1, b-3));\n return memo[key];\n }\n}\n```\n``` Java []\nclass Solution {\n private HashMap<Pair<Integer, Integer>, Double> memo = new HashMap<>();\n\n public double soupServings(int N) {\n if (N > 4451) {\n return 1.0;\n }\n N = (N + 24) / 25;\n\n return dp(N, N);\n }\n\n private double dp(int a, int b) {\n if (a <= 0 && b <= 0) {\n return 0.5;\n }\n if (a <= 0) {\n return 1.0;\n }\n if (b <= 0) {\n return 0.0;\n }\n Pair<Integer, Integer> key = new Pair<>(a, b);\n if (memo.containsKey(key)) {\n return memo.get(key);\n }\n memo.put(key, 0.25 * (dp(a-4, b) + dp(a-3, b-1) + dp(a-2, b-2) + dp(a-1, b-3)));\n return memo.get(key);\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar soupServings = function(N) {\n if (N > 4451) {\n return 1.0;\n }\n N = Math.floor((N + 24) / 25);\n let memo = {};\n\n return dp(N, N);\n\n function dp(a, b) {\n if (a <= 0 && b <= 0) {\n return 0.5;\n }\n if (a <= 0) {\n return 1.0;\n }\n if (b <= 0) {\n return 0.0;\n }\n let key = a * 5000 + b;\n if (key in memo) {\n return memo[key];\n }\n memo[key] = 0.25 * (dp(a-4, b) + dp(a-3, b-1) + dp(a-2, b-2) + dp(a-1, b-3));\n return memo[key];\n }\n};\n```\n\n# How to find 4451 ?\n\nUsing the binary search limit method, we find that the minimum value of \\( n \\) for which the function `soupServings(n)` returns a value that is very close to 1 (within \\( 10^{-5} \\)) is \\( n = 4451 \\).\n\nThis means that for \\( n \\geq 4451 \\), the probability that soup A will be empty first, plus half the probability that A and B become empty at the same time, is effectively 1 (or very close to 1). \n\n``` Python []\n# Let\'s implement a binary search to find the limit\ndef binary_search_limit(low, high, epsilon):\n while high - low > 1:\n mid = low + (high - low) // 2\n result = soupServings(mid)\n if abs(result - 1.0) <= epsilon:\n high = mid\n else:\n low = mid\n return high\n\nepsilon = 10**(-5)\nbinary_search_limit(1000, 5000, epsilon)\n```\n\nIn the context of the problem, this suggests that for initial volumes of soup of 4451 ml or more, it\'s almost certain that soup A will be consumed first. \n\nThe binary search limit method provides an efficient way to find the limit in a continuous domain by progressively narrowing the search interval.\n\n# Video for C++ & JavaScript\nhttps://youtu.be/EDH1zBhebXg\nhttps://youtu.be/LhNJ1biTTR0 | 45 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | soup-servings | 1 | 1 | Python solution beats 100%.\n\n\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/6Wcl2nhDVyo\n\n# Subscribe to my channel from here. I have 234 videos as of July 29th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python solution. Other languages might be differnt a bit.\n\n1. The function `soupServings` takes an integer `n` as input.\n\n2. If `n` is greater than or equal to 4300, the function directly returns 1.0, as the probability of A becoming empty first is highly likely in this case.\n\n3. Otherwise, the function initializes an empty dictionary `memo` to store computed probabilities for different states of the soup.\n\n4. It defines the recursive function `serve(A, B)`, which calculates the probability that A will be empty first given the remaining volumes of soup `A` and `B`.\n\n5. In the `serve` function, it first checks if the current state `(A, B)` has been memoized (i.e., its probability has been calculated before). If so, it returns the memoized probability to avoid redundant calculations.\n\n6. If both `A` and `B` are less than or equal to 0, it means both types of soup are already empty, and it returns 0.5, representing the probability of A and B becoming empty at the same time.\n\n7. If `A` is less than or equal to 0, it means soup A is already empty, and it returns 1.0, representing the probability of A becoming empty first.\n\n8. If `B` is less than or equal to 0, it means soup B is already empty, and it returns 0.0, representing the probability of B becoming empty first (which is 0 as per the problem\'s description).\n\n9. If none of the base cases is met, the function proceeds to calculate the probability of A becoming empty first (represented by the variable `prob`). It does this by considering the four types of operations to serve the soup, each with a 25% probability.\n\n10. The `prob` is calculated by taking 0.25 times the sum of four recursive calls to `serve` with the updated remaining volumes of soup according to the four operations.\n\n11. After computing the probability `prob`, the result is stored in the `memo` dictionary with the current state `(A, B)` as the key.\n\n12. Finally, the function returns the result of the `serve(n, n)` call, which represents the probability that A will be empty first when the initial volumes of soup are both `n`.\n\n```python []\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n >= 4300:\n return 1.0\n \n memo = {}\n\n def serve(A, B):\n if (A, B) in memo:\n return memo[(A, B)]\n \n # probability of A that is empty first\n if A <= 0 and B <= 0:\n return 0.5\n if A <= 0:\n return 1.0\n if B <= 0:\n return 0.0\n \n prob = 0.25 * (serve(A - 100, B) + serve(A - 75, B - 25) + serve(A - 50, B - 50) + serve(A - 25, B - 75))\n memo[(A, B)] = prob\n return prob\n\n return serve(n, n)\n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar soupServings = function(n) {\n if (n >= 4300) {\n return 1.0;\n }\n\n const memo = new Map();\n\n function serve(A, B) {\n if (memo.has(`${A}-${B}`)) {\n return memo.get(`${A}-${B}`);\n }\n\n if (A <= 0 && B <= 0) {\n return 0.5;\n }\n if (A <= 0) {\n return 1.0;\n }\n if (B <= 0) {\n return 0.0;\n }\n\n const prob = 0.25 * (serve(A - 100, B) + serve(A - 75, B - 25) + serve(A - 50, B - 50) + serve(A - 25, B - 75));\n memo.set(`${A}-${B}`, prob);\n return prob;\n }\n\n return serve(n, n); \n};\n```\n```java []\nclass Solution {\n public double soupServings(int n) {\n if (n >= 4300) {\n return 1.0;\n }\n\n Map<String, Double> memo = new HashMap<>();\n\n return serve(n, n, memo); \n }\n\n private double serve(int A, int B, Map<String, Double> memo) {\n String key = A + "-" + B;\n if (memo.containsKey(key)) {\n return memo.get(key);\n }\n\n if (A <= 0 && B <= 0) {\n return 0.5;\n }\n if (A <= 0) {\n return 1.0;\n }\n if (B <= 0) {\n return 0.0;\n }\n\n double prob = 0.25 * (serve(A - 100, B, memo) + serve(A - 75, B - 25, memo) + serve(A - 50, B - 50, memo) + serve(A - 25, B - 75, memo));\n memo.put(key, prob);\n return prob;\n }\n\n}\n```\n```C++ []\nclass Solution {\npublic:\n double soupServings(int n) {\n if (n >= 4300) {\n return 1.0;\n }\n\n std::unordered_map<std::string, double> memo;\n return serve(n, n, memo); \n }\n\nprivate:\n double serve(int A, int B, std::unordered_map<std::string, double>& memo) {\n std::string key = std::to_string(A) + "-" + std::to_string(B);\n if (memo.find(key) != memo.end()) {\n return memo[key];\n }\n\n if (A <= 0 && B <= 0) {\n return 0.5;\n }\n if (A <= 0) {\n return 1.0;\n }\n if (B <= 0) {\n return 0.0;\n }\n\n double prob = 0.25 * (serve(A - 100, B, memo) + serve(A - 75, B - 25, memo) + serve(A - 50, B - 50, memo) + serve(A - 25, B - 75, memo));\n memo[key] = prob;\n return prob;\n } \n};\n```\n | 14 | There are two types of soup: **type A** and **type B**. Initially, we have `n` ml of each type of soup. There are four kinds of operations:
1. Serve `100` ml of **soup A** and `0` ml of **soup B**,
2. Serve `75` ml of **soup A** and `25` ml of **soup B**,
3. Serve `50` ml of **soup A** and `50` ml of **soup B**, and
4. Serve `25` ml of **soup A** and `75` ml of **soup B**.
When we serve some soup, we give it to someone, and we no longer have it. Each turn, we will choose from the four operations with an equal probability `0.25`. If the remaining volume of soup is not enough to complete the operation, we will serve as much as possible. We stop once we no longer have some quantity of both types of soup.
**Note** that we do not have an operation where all `100` ml's of **soup B** are used first.
Return _the probability that **soup A** will be empty first, plus half the probability that **A** and **B** become empty at the same time_. Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** n = 50
**Output:** 0.62500
**Explanation:** If we choose the first two operations, A will become empty first.
For the third operation, A and B will become empty at the same time.
For the fourth operation, B will become empty first.
So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 \* (1 + 1 + 0.5 + 0) = 0.625.
**Example 2:**
**Input:** n = 100
**Output:** 0.71875
**Constraints:**
* `0 <= n <= 109` | null |
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++ | soup-servings | 1 | 1 | Python solution beats 100%.\n\n\n\n# Solution Video\n## *** Please upvote for this article. *** \n\nhttps://youtu.be/6Wcl2nhDVyo\n\n# Subscribe to my channel from here. I have 234 videos as of July 29th\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n---\n\n# Approach\nThis is based on Python solution. Other languages might be differnt a bit.\n\n1. The function `soupServings` takes an integer `n` as input.\n\n2. If `n` is greater than or equal to 4300, the function directly returns 1.0, as the probability of A becoming empty first is highly likely in this case.\n\n3. Otherwise, the function initializes an empty dictionary `memo` to store computed probabilities for different states of the soup.\n\n4. It defines the recursive function `serve(A, B)`, which calculates the probability that A will be empty first given the remaining volumes of soup `A` and `B`.\n\n5. In the `serve` function, it first checks if the current state `(A, B)` has been memoized (i.e., its probability has been calculated before). If so, it returns the memoized probability to avoid redundant calculations.\n\n6. If both `A` and `B` are less than or equal to 0, it means both types of soup are already empty, and it returns 0.5, representing the probability of A and B becoming empty at the same time.\n\n7. If `A` is less than or equal to 0, it means soup A is already empty, and it returns 1.0, representing the probability of A becoming empty first.\n\n8. If `B` is less than or equal to 0, it means soup B is already empty, and it returns 0.0, representing the probability of B becoming empty first (which is 0 as per the problem\'s description).\n\n9. If none of the base cases is met, the function proceeds to calculate the probability of A becoming empty first (represented by the variable `prob`). It does this by considering the four types of operations to serve the soup, each with a 25% probability.\n\n10. The `prob` is calculated by taking 0.25 times the sum of four recursive calls to `serve` with the updated remaining volumes of soup according to the four operations.\n\n11. After computing the probability `prob`, the result is stored in the `memo` dictionary with the current state `(A, B)` as the key.\n\n12. Finally, the function returns the result of the `serve(n, n)` call, which represents the probability that A will be empty first when the initial volumes of soup are both `n`.\n\n```python []\nclass Solution:\n def soupServings(self, n: int) -> float:\n if n >= 4300:\n return 1.0\n \n memo = {}\n\n def serve(A, B):\n if (A, B) in memo:\n return memo[(A, B)]\n \n # probability of A that is empty first\n if A <= 0 and B <= 0:\n return 0.5\n if A <= 0:\n return 1.0\n if B <= 0:\n return 0.0\n \n prob = 0.25 * (serve(A - 100, B) + serve(A - 75, B - 25) + serve(A - 50, B - 50) + serve(A - 25, B - 75))\n memo[(A, B)] = prob\n return prob\n\n return serve(n, n)\n```\n```javascript []\n/**\n * @param {number} n\n * @return {number}\n */\nvar soupServings = function(n) {\n if (n >= 4300) {\n return 1.0;\n }\n\n const memo = new Map();\n\n function serve(A, B) {\n if (memo.has(`${A}-${B}`)) {\n return memo.get(`${A}-${B}`);\n }\n\n if (A <= 0 && B <= 0) {\n return 0.5;\n }\n if (A <= 0) {\n return 1.0;\n }\n if (B <= 0) {\n return 0.0;\n }\n\n const prob = 0.25 * (serve(A - 100, B) + serve(A - 75, B - 25) + serve(A - 50, B - 50) + serve(A - 25, B - 75));\n memo.set(`${A}-${B}`, prob);\n return prob;\n }\n\n return serve(n, n); \n};\n```\n```java []\nclass Solution {\n public double soupServings(int n) {\n if (n >= 4300) {\n return 1.0;\n }\n\n Map<String, Double> memo = new HashMap<>();\n\n return serve(n, n, memo); \n }\n\n private double serve(int A, int B, Map<String, Double> memo) {\n String key = A + "-" + B;\n if (memo.containsKey(key)) {\n return memo.get(key);\n }\n\n if (A <= 0 && B <= 0) {\n return 0.5;\n }\n if (A <= 0) {\n return 1.0;\n }\n if (B <= 0) {\n return 0.0;\n }\n\n double prob = 0.25 * (serve(A - 100, B, memo) + serve(A - 75, B - 25, memo) + serve(A - 50, B - 50, memo) + serve(A - 25, B - 75, memo));\n memo.put(key, prob);\n return prob;\n }\n\n}\n```\n```C++ []\nclass Solution {\npublic:\n double soupServings(int n) {\n if (n >= 4300) {\n return 1.0;\n }\n\n std::unordered_map<std::string, double> memo;\n return serve(n, n, memo); \n }\n\nprivate:\n double serve(int A, int B, std::unordered_map<std::string, double>& memo) {\n std::string key = std::to_string(A) + "-" + std::to_string(B);\n if (memo.find(key) != memo.end()) {\n return memo[key];\n }\n\n if (A <= 0 && B <= 0) {\n return 0.5;\n }\n if (A <= 0) {\n return 1.0;\n }\n if (B <= 0) {\n return 0.0;\n }\n\n double prob = 0.25 * (serve(A - 100, B, memo) + serve(A - 75, B - 25, memo) + serve(A - 50, B - 50, memo) + serve(A - 25, B - 75, memo));\n memo[key] = prob;\n return prob;\n } \n};\n```\n | 14 | You have `n` jobs and `m` workers. You are given three arrays: `difficulty`, `profit`, and `worker` where:
* `difficulty[i]` and `profit[i]` are the difficulty and the profit of the `ith` job, and
* `worker[j]` is the ability of `jth` worker (i.e., the `jth` worker can only complete a job with difficulty at most `worker[j]`).
Every worker can be assigned **at most one job**, but one job can be **completed multiple times**.
* For example, if three workers attempt the same job that pays `$1`, then the total profit will be `$3`. If a worker cannot complete any job, their profit is `$0`.
Return the maximum profit we can achieve after assigning the workers to the jobs.
**Example 1:**
**Input:** difficulty = \[2,4,6,8,10\], profit = \[10,20,30,40,50\], worker = \[4,5,6,7\]
**Output:** 100
**Explanation:** Workers are assigned jobs of difficulty \[4,4,6,6\] and they get a profit of \[20,20,30,30\] separately.
**Example 2:**
**Input:** difficulty = \[85,47,57\], profit = \[24,66,99\], worker = \[40,25,25\]
**Output:** 0
**Constraints:**
* `n == difficulty.length`
* `n == profit.length`
* `m == worker.length`
* `1 <= n, m <= 104`
* `1 <= difficulty[i], profit[i], worker[i] <= 105` | null |
Solution | expressive-words | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool check(string s, string w) {\n int m = s.size(), n = w.size();\n int i = 0, j = 0;\n for (int i2 = 0, j2 = 0; i < m && j < n; i = i2, j = j2) {\n if (s[i] != w[j]) return false;\n while(i2 < m && s[i2] == s[i]) i2++;\n while(j2 < n && w[j2] == w[j]) j2++;\n if ((i2 - i) != (j2 - j) && (i2 - i) < max(3, j2 - j)) return false; \n }\n return i == m && j == n;\n }\n int expressiveWords(string s, vector<string>& words) {\n int ans = 0;\n for (auto& word:words) {\n if (check(s, word)) ans++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n s_streaks = get_streaks(s)\n \n def check(word: str):\n word_streaks = get_streaks(word)\n if len(s_streaks) != len(word_streaks):\n return False\n for (s_letter, s_streak_len), (word_letter, word_streak_len) in zip(s_streaks, word_streaks):\n if s_letter != word_letter:\n return False\n if word_streak_len > s_streak_len:\n return False\n if word_streak_len == s_streak_len:\n continue\n if s_streak_len < 3:\n return False\n return True\n return sum(check(word) for word in words)\n\ndef get_streaks(word: str):\n streak_letter = word[0]\n streak_len = 0\n res = []\n for letter in word:\n if letter == streak_letter:\n streak_len += 1\n else:\n res.append((streak_letter, streak_len))\n streak_letter = letter\n streak_len = 1\n \n res.append((streak_letter, streak_len))\n return res\n```\n\n```Java []\nclass Solution {\n public int expressiveWords(String s, String[] words) {\n int count = 0;\n for (String word : words) {\n if (isStretchy(s, word))\n count += 1;\n }\n return count;\n }\n private boolean isStretchy(String s, String word) {\n int sIndex = 0;\n int wordIndex = 0;\n while (sIndex < s.length() && wordIndex < word.length()) {\n int sLetters = 1;\n char sChar = s.charAt(sIndex);\n while (sIndex + sLetters < s.length() && s.charAt(sIndex + sLetters) == sChar) {\n sLetters++;\n }\n int wordLetters = 1;\n char wordChar = word.charAt(wordIndex);\n while (wordIndex + wordLetters < word.length() && word.charAt(wordIndex + wordLetters) == wordChar) {\n wordLetters++;\n }\n if (sChar != wordChar)\n return false;\n if (sLetters == 2 && wordLetters == 1)\n return false;\n if (sLetters < wordLetters)\n return false;\n sIndex += sLetters;\n wordIndex += wordLetters;\n }\n return sIndex == s.length() && wordIndex == word.length();\n }\n}\n```\n | 1 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Solution | expressive-words | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool check(string s, string w) {\n int m = s.size(), n = w.size();\n int i = 0, j = 0;\n for (int i2 = 0, j2 = 0; i < m && j < n; i = i2, j = j2) {\n if (s[i] != w[j]) return false;\n while(i2 < m && s[i2] == s[i]) i2++;\n while(j2 < n && w[j2] == w[j]) j2++;\n if ((i2 - i) != (j2 - j) && (i2 - i) < max(3, j2 - j)) return false; \n }\n return i == m && j == n;\n }\n int expressiveWords(string s, vector<string>& words) {\n int ans = 0;\n for (auto& word:words) {\n if (check(s, word)) ans++;\n }\n return ans;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n s_streaks = get_streaks(s)\n \n def check(word: str):\n word_streaks = get_streaks(word)\n if len(s_streaks) != len(word_streaks):\n return False\n for (s_letter, s_streak_len), (word_letter, word_streak_len) in zip(s_streaks, word_streaks):\n if s_letter != word_letter:\n return False\n if word_streak_len > s_streak_len:\n return False\n if word_streak_len == s_streak_len:\n continue\n if s_streak_len < 3:\n return False\n return True\n return sum(check(word) for word in words)\n\ndef get_streaks(word: str):\n streak_letter = word[0]\n streak_len = 0\n res = []\n for letter in word:\n if letter == streak_letter:\n streak_len += 1\n else:\n res.append((streak_letter, streak_len))\n streak_letter = letter\n streak_len = 1\n \n res.append((streak_letter, streak_len))\n return res\n```\n\n```Java []\nclass Solution {\n public int expressiveWords(String s, String[] words) {\n int count = 0;\n for (String word : words) {\n if (isStretchy(s, word))\n count += 1;\n }\n return count;\n }\n private boolean isStretchy(String s, String word) {\n int sIndex = 0;\n int wordIndex = 0;\n while (sIndex < s.length() && wordIndex < word.length()) {\n int sLetters = 1;\n char sChar = s.charAt(sIndex);\n while (sIndex + sLetters < s.length() && s.charAt(sIndex + sLetters) == sChar) {\n sLetters++;\n }\n int wordLetters = 1;\n char wordChar = word.charAt(wordIndex);\n while (wordIndex + wordLetters < word.length() && word.charAt(wordIndex + wordLetters) == wordChar) {\n wordLetters++;\n }\n if (sChar != wordChar)\n return false;\n if (sLetters == 2 && wordLetters == 1)\n return false;\n if (sLetters < wordLetters)\n return false;\n sIndex += sLetters;\n wordIndex += wordLetters;\n }\n return sIndex == s.length() && wordIndex == word.length();\n }\n}\n```\n | 1 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
python: easy to understand with helper function | expressive-words | 0 | 1 | # Code\n```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n # edge cases\n if len(s) == 0 and len(words) != 0:\n return False\n if len(words) == 0 and len(s) != 0:\n return False\n if len(s) == 0 and len(words) == 0:\n return True\n \n # helper function, compressing string and extract counts\n def compressor(s_word):\n init_string =[s_word[0]]\n array = []\n start = 0\n for i,c in enumerate(s_word):\n if c == init_string[-1]:\n continue\n array.append(i-start)\n start = i\n init_string += c \n array.append(i-start+1) \n return init_string,array\n\n res = len(words)\n s_split, s_array = compressor(s)\n for word in words:\n word_split = [\'\']\n word_array = []\n word_split,word_array = compressor(word)\n if s_split == word_split:\n for num_s,num_word in zip(s_array,word_array):\n if num_s != num_word and num_s < 3 or num_word > num_s:\n res -= 1\n break\n else:\n res -= 1\n return res\n``` | 1 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
python: easy to understand with helper function | expressive-words | 0 | 1 | # Code\n```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n # edge cases\n if len(s) == 0 and len(words) != 0:\n return False\n if len(words) == 0 and len(s) != 0:\n return False\n if len(s) == 0 and len(words) == 0:\n return True\n \n # helper function, compressing string and extract counts\n def compressor(s_word):\n init_string =[s_word[0]]\n array = []\n start = 0\n for i,c in enumerate(s_word):\n if c == init_string[-1]:\n continue\n array.append(i-start)\n start = i\n init_string += c \n array.append(i-start+1) \n return init_string,array\n\n res = len(words)\n s_split, s_array = compressor(s)\n for word in words:\n word_split = [\'\']\n word_array = []\n word_split,word_array = compressor(word)\n if s_split == word_split:\n for num_s,num_word in zip(s_array,word_array):\n if num_s != num_word and num_s < 3 or num_word > num_s:\n res -= 1\n break\n else:\n res -= 1\n return res\n``` | 1 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
Python 3 || 9 lines, groupby, w/ explanation || T/M: 97% / 17% | expressive-words | 0 | 1 | Here\'s the plan:\n\nFor the string `s` and for each string `word` in `words`, we use `groupby` to construct two tuples per string. The first lists the distinct characters in the string, and second lists the multiplicty of each character in the string.\n\nI think, knowing that, one can figure out the code below. \'The secret of being a bore is to tell everything.\' --Voltaire\n\n```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n\n f = lambda x: (tuple(zip(*[(k, len(tuple(g)))\n for k,g in groupby(x)])))\n \n (sCh, sCt), ans = f(s), 0\n\n for word in words:\n wCh, wCt = f(word)\n\n if sCh == wCh:\n for sc, wc in zip(sCt, wCt):\n \n if sc < wc or (sc < 3 and sc != wc): break\n\n else: ans+= 1 \n\n return ans\n\n```\n[https://leetcode.com/problems/expressive-words/submissions/863514015/](http://)\n\n\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(*N*). | 4 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Python 3 || 9 lines, groupby, w/ explanation || T/M: 97% / 17% | expressive-words | 0 | 1 | Here\'s the plan:\n\nFor the string `s` and for each string `word` in `words`, we use `groupby` to construct two tuples per string. The first lists the distinct characters in the string, and second lists the multiplicty of each character in the string.\n\nI think, knowing that, one can figure out the code below. \'The secret of being a bore is to tell everything.\' --Voltaire\n\n```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n\n f = lambda x: (tuple(zip(*[(k, len(tuple(g)))\n for k,g in groupby(x)])))\n \n (sCh, sCt), ans = f(s), 0\n\n for word in words:\n wCh, wCt = f(word)\n\n if sCh == wCh:\n for sc, wc in zip(sCt, wCt):\n \n if sc < wc or (sc < 3 and sc != wc): break\n\n else: ans+= 1 \n\n return ans\n\n```\n[https://leetcode.com/problems/expressive-words/submissions/863514015/](http://)\n\n\n\nI could be wrong, but I think that time is *O*(*N*) and space is *O*(*N*). | 4 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
Python Solution Without Using Any Special Library With Detailed Explanation | expressive-words | 0 | 1 | In this solution first, I use the process function to get the characters that appear without repeating in the string and also their frequencies. For example for the string "helloo", chars=[\'h\',\'e\',\'l\',\'o\'] and counts=[1,1,2,2]. \nIf any of the strings in the words list has the same characters as S, then it worth further investigation. For further investigation, since the characters are the same, we need to figure out if the word can be extended to S based on the expansion rules or not. \nIf the frequency of the characters are the same or if we need to expand the character in word to be equal in the frequency with the same character in S, the final frequency value of the character will be 3 or more, then it is expandable. If all of the characters in the word are expandable according to this rule, we have a word that can be changed to S, so we only need to return the number of these words. \n```\nclass Solution:\n def expressiveWords(self, S: str, words: List[str]) -> int:\n def process(st):\n if not st:\n return [], []\n chars, counts = [st[0]], [1]\n \n for i in range(1, len(st)):\n if st[i] == chars[-1]:\n counts[-1] += 1\n else:\n chars.append(st[i])\n counts.append(1)\n return chars, counts\n \n\n ans = 0\n s_chars, s_counts = process(S)\n for word in words:\n w_chars, w_counts = process(word)\n \n if s_chars == w_chars:\n counter = 0\n for k in range(len(w_chars)):\n if w_counts[k]==s_counts[k] or (w_counts[k]<s_counts[k] and s_counts[k]>=3):\n counter += 1\n \n if counter ==len(w_chars):\n ans += 1\n\n return ans | 19 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Python Solution Without Using Any Special Library With Detailed Explanation | expressive-words | 0 | 1 | In this solution first, I use the process function to get the characters that appear without repeating in the string and also their frequencies. For example for the string "helloo", chars=[\'h\',\'e\',\'l\',\'o\'] and counts=[1,1,2,2]. \nIf any of the strings in the words list has the same characters as S, then it worth further investigation. For further investigation, since the characters are the same, we need to figure out if the word can be extended to S based on the expansion rules or not. \nIf the frequency of the characters are the same or if we need to expand the character in word to be equal in the frequency with the same character in S, the final frequency value of the character will be 3 or more, then it is expandable. If all of the characters in the word are expandable according to this rule, we have a word that can be changed to S, so we only need to return the number of these words. \n```\nclass Solution:\n def expressiveWords(self, S: str, words: List[str]) -> int:\n def process(st):\n if not st:\n return [], []\n chars, counts = [st[0]], [1]\n \n for i in range(1, len(st)):\n if st[i] == chars[-1]:\n counts[-1] += 1\n else:\n chars.append(st[i])\n counts.append(1)\n return chars, counts\n \n\n ans = 0\n s_chars, s_counts = process(S)\n for word in words:\n w_chars, w_counts = process(word)\n \n if s_chars == w_chars:\n counter = 0\n for k in range(len(w_chars)):\n if w_counts[k]==s_counts[k] or (w_counts[k]<s_counts[k] and s_counts[k]>=3):\n counter += 1\n \n if counter ==len(w_chars):\n ans += 1\n\n return ans | 19 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
Python3 48ms with itertools | expressive-words | 0 | 1 | ```\nfrom typing import List\nfrom itertools import groupby\n\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n """\n split original string into groups\n eg. hello -> ["h", "e", "ll", "o"]\n\n Apply this same grouping to every query string, and then compare each group\n """\n\n def group_comp(src_group: List[str], target_group: List[str]):\n """Check if there are chars from og string missing"""\n if len(src_group) != len(target_group):\n return False\n \n for index, group in enumerate(src_group):\n if group != target_group[index]:\n #if the og group len < 2, meaning we cannot expanding the query group to that\n if len(target_group[index]) <= 2:\n return False\n #different chars\n elif group[0] != target_group[index][0]:\n return False\n #the length of query str group shouldn\'t be longer than the og one\n elif len(group) > len(target_group[index]):\n return False\n \n return True\n \n count = 0\n og_groups = ["".join(group) for _, group in groupby(s)]\n for word in words:\n group = ["".join(group) for _, group in groupby(word)]\n if group_comp(group, og_groups):\n count += 1\n \n return count\n``` | 2 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Python3 48ms with itertools | expressive-words | 0 | 1 | ```\nfrom typing import List\nfrom itertools import groupby\n\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n """\n split original string into groups\n eg. hello -> ["h", "e", "ll", "o"]\n\n Apply this same grouping to every query string, and then compare each group\n """\n\n def group_comp(src_group: List[str], target_group: List[str]):\n """Check if there are chars from og string missing"""\n if len(src_group) != len(target_group):\n return False\n \n for index, group in enumerate(src_group):\n if group != target_group[index]:\n #if the og group len < 2, meaning we cannot expanding the query group to that\n if len(target_group[index]) <= 2:\n return False\n #different chars\n elif group[0] != target_group[index][0]:\n return False\n #the length of query str group shouldn\'t be longer than the og one\n elif len(group) > len(target_group[index]):\n return False\n \n return True\n \n count = 0\n og_groups = ["".join(group) for _, group in groupby(s)]\n for word in words:\n group = ["".join(group) for _, group in groupby(word)]\n if group_comp(group, og_groups):\n count += 1\n \n return count\n``` | 2 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
python 3 || simple solution || O(n)/O(1) | expressive-words | 0 | 1 | ```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n def groupWord(word):\n size = 1\n for i in range(1, len(word)):\n if word[i] == word[i - 1]:\n size += 1\n else:\n yield word[i - 1], size\n size = 1\n \n yield word[-1], size\n yield \' \', 0\n \n res = len(words)\n \n for word in words:\n for (sChar, sSize), (wordChar, wordSize) in zip(groupWord(s), groupWord(word)):\n if sChar != wordChar or sSize < wordSize or wordSize < sSize < 3:\n res -= 1\n break\n \n return res | 1 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
python 3 || simple solution || O(n)/O(1) | expressive-words | 0 | 1 | ```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n def groupWord(word):\n size = 1\n for i in range(1, len(word)):\n if word[i] == word[i - 1]:\n size += 1\n else:\n yield word[i - 1], size\n size = 1\n \n yield word[-1], size\n yield \' \', 0\n \n res = len(words)\n \n for word in words:\n for (sChar, sSize), (wordChar, wordSize) in zip(groupWord(s), groupWord(word)):\n if sChar != wordChar or sSize < wordSize or wordSize < sSize < 3:\n res -= 1\n break\n \n return res | 1 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
Problem description is horrible... but here's simple python solution | expressive-words | 0 | 1 | hope this helps for someone who is also struggling with the description\n```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n \n def summarize(word):\n res = []\n \n n = len(word)\n i, j = 0, 0\n while i<=j and j <= n-1:\n while j <= n-1 and word[j] == word[i]:\n j += 1\n res.append(word[i])\n res.append(j-i)\n i = j\n return res\n \n t = 0 \n start = summarize(s)\n n = len(start)//2\n def compare(w):\n r = summarize(w)\n \n if len(r) != len(start):\n return False \n for i in range(0, 2*n, 2):\n if start[i] != r[i]:\n return False\n elif start[i] == r[i]:\n if start[i+1] < r[i+1]:\n return False\n elif start[i+1] == r[i+1]:\n pass \n elif start[i+1] < 3:\n return False\n return True\n\n for w in words:\n if compare(w):\n t += 1\n return t \n``` | 3 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
Problem description is horrible... but here's simple python solution | expressive-words | 0 | 1 | hope this helps for someone who is also struggling with the description\n```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n \n def summarize(word):\n res = []\n \n n = len(word)\n i, j = 0, 0\n while i<=j and j <= n-1:\n while j <= n-1 and word[j] == word[i]:\n j += 1\n res.append(word[i])\n res.append(j-i)\n i = j\n return res\n \n t = 0 \n start = summarize(s)\n n = len(start)//2\n def compare(w):\n r = summarize(w)\n \n if len(r) != len(start):\n return False \n for i in range(0, 2*n, 2):\n if start[i] != r[i]:\n return False\n elif start[i] == r[i]:\n if start[i+1] < r[i+1]:\n return False\n elif start[i+1] == r[i+1]:\n pass \n elif start[i+1] < 3:\n return False\n return True\n\n for w in words:\n if compare(w):\n t += 1\n return t \n``` | 3 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
python most basic | expressive-words | 0 | 1 | ```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n def check(x):\n i = j = 0\n while i < len(s) and j < len(x):\n counts = 1\n while i<len(s)-1 and s[i]==s[i+1]:\n i+=1\n counts+=1\n countx = 1\n while j<len(x)-1 and x[j]==x[j+1]:\n j+=1\n countx+=1\n if s[i]!=x[j]: return 0\n i+=1\n j+=1\n if counts<countx: return 0\n if countx==counts: continue\n if counts<=2: return 0\n return 1 if i>=len(s) and j>=len(x) else 0\n return sum(check(x) for x in words)\n``` | 4 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
python most basic | expressive-words | 0 | 1 | ```\nclass Solution:\n def expressiveWords(self, s: str, words: List[str]) -> int:\n def check(x):\n i = j = 0\n while i < len(s) and j < len(x):\n counts = 1\n while i<len(s)-1 and s[i]==s[i+1]:\n i+=1\n counts+=1\n countx = 1\n while j<len(x)-1 and x[j]==x[j+1]:\n j+=1\n countx+=1\n if s[i]!=x[j]: return 0\n i+=1\n j+=1\n if counts<countx: return 0\n if countx==counts: continue\n if counts<=2: return 0\n return 1 if i>=len(s) and j>=len(x) else 0\n return sum(check(x) for x in words)\n``` | 4 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
809: Beats 97.96%, Solution with step by step explanation | expressive-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\ndef check(stretchy: str, word: str) -> bool:\n```\n\nInside the main function, a helper function named check is defined. It takes two strings, stretchy and word, and returns a boolean indicating if word can be stretched to match stretchy.\n\n```\ni, j = 0, 0\n```\n\nTwo indices i and j are initialized to zero. They will be used to iterate over the characters in stretchy and word, respectively.\n\n```\nwhile i < len(stretchy) and j < len(word):\n if stretchy[i] != word[j]:\n return False\n```\n\nThis while loop continues until one of the indices reaches the end of its respective string. If the current characters do not match, the function returns False because word cannot be stretched to match stretchy.\n\n```\nlen_s = 1\nwhile i + 1 < len(stretchy) and stretchy[i] == stretchy[i + 1]:\n i += 1\n len_s += 1\n```\n\nHere, the code counts how many identical consecutive characters there are in stretchy, starting from the current index i.\n\n```\nlen_w = 1\nwhile j + 1 < len(word) and word[j] == word[j + 1]:\n j += 1\n len_w += 1\n```\n\nSimilarly, this counts consecutive identical characters in word, starting from the current index j.\n\n```\nif (len_s != len_w and len_s < 3) or len_s < len_w:\n return False\n```\n\nHere, it checks if word can be stretched to match stretchy. If stretchy has less than 3 consecutive characters (and isn\'t identical to word in that part) or word has more consecutive characters than stretchy, it returns False.\n\n```\ni += 1\nj += 1\n```\n\nAfter checking a group of identical characters, both indices are advanced.\n\n```\nreturn i == len(stretchy) and j == len(word)\n```\n\nAfter exiting the loop, the function checks if both indices have reached the end of their respective strings, meaning a potential stretchy match.\n\n```\nreturn sum(check(s, word) for word in words)\n```\n\nFinally, the main function returns the count of words that can be stretched to match s, using a generator expression to apply check to each word.\n\n# Complexity\n- Time complexity:\nO(m * n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def expressiveWords(self, s: str, words: list[str]) -> int:\n def check(stretchy: str, word: str) -> bool:\n i, j = 0, 0\n while i < len(stretchy) and j < len(word):\n if stretchy[i] != word[j]:\n return False\n\n len_s = 1\n while i + 1 < len(stretchy) and stretchy[i] == stretchy[i + 1]:\n i += 1\n len_s += 1\n\n len_w = 1\n while j + 1 < len(word) and word[j] == word[j + 1]:\n j += 1\n len_w += 1\n \n if (len_s != len_w and len_s < 3) or len_s < len_w:\n return False\n\n i += 1\n j += 1\n \n return i == len(stretchy) and j == len(word)\n\n return sum(check(s, word) for word in words)\n\n\n``` | 0 | Sometimes people repeat letters to represent extra feeling. For example:
* `"hello " -> "heeellooo "`
* `"hi " -> "hiiii "`
In these strings like `"heeellooo "`, we have groups of adjacent letters that are all the same: `"h "`, `"eee "`, `"ll "`, `"ooo "`.
You are given a string `s` and an array of query strings `words`. A query word is **stretchy** if it can be made to be equal to `s` by any number of applications of the following extension operation: choose a group consisting of characters `c`, and add some number of characters `c` to the group so that the size of the group is **three or more**.
* For example, starting with `"hello "`, we could do an extension on the group `"o "` to get `"hellooo "`, but we cannot get `"helloo "` since the group `"oo "` has a size less than three. Also, we could do another extension like `"ll " -> "lllll "` to get `"helllllooo "`. If `s = "helllllooo "`, then the query word `"hello "` would be **stretchy** because of these two extension operations: `query = "hello " -> "hellooo " -> "helllllooo " = s`.
Return _the number of query strings that are **stretchy**_.
**Example 1:**
**Input:** s = "heeellooo ", words = \[ "hello ", "hi ", "helo "\]
**Output:** 1
**Explanation:**
We can extend "e " and "o " in the word "hello " to get "heeellooo ".
We can't extend "helo " to get "heeellooo " because the group "ll " is not size 3 or more.
**Example 2:**
**Input:** s = "zzzzzyyyyy ", words = \[ "zzyy ", "zy ", "zyy "\]
**Output:** 3
**Constraints:**
* `1 <= s.length, words.length <= 100`
* `1 <= words[i].length <= 100`
* `s` and `words[i]` consist of lowercase letters. | null |
809: Beats 97.96%, Solution with step by step explanation | expressive-words | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\ndef check(stretchy: str, word: str) -> bool:\n```\n\nInside the main function, a helper function named check is defined. It takes two strings, stretchy and word, and returns a boolean indicating if word can be stretched to match stretchy.\n\n```\ni, j = 0, 0\n```\n\nTwo indices i and j are initialized to zero. They will be used to iterate over the characters in stretchy and word, respectively.\n\n```\nwhile i < len(stretchy) and j < len(word):\n if stretchy[i] != word[j]:\n return False\n```\n\nThis while loop continues until one of the indices reaches the end of its respective string. If the current characters do not match, the function returns False because word cannot be stretched to match stretchy.\n\n```\nlen_s = 1\nwhile i + 1 < len(stretchy) and stretchy[i] == stretchy[i + 1]:\n i += 1\n len_s += 1\n```\n\nHere, the code counts how many identical consecutive characters there are in stretchy, starting from the current index i.\n\n```\nlen_w = 1\nwhile j + 1 < len(word) and word[j] == word[j + 1]:\n j += 1\n len_w += 1\n```\n\nSimilarly, this counts consecutive identical characters in word, starting from the current index j.\n\n```\nif (len_s != len_w and len_s < 3) or len_s < len_w:\n return False\n```\n\nHere, it checks if word can be stretched to match stretchy. If stretchy has less than 3 consecutive characters (and isn\'t identical to word in that part) or word has more consecutive characters than stretchy, it returns False.\n\n```\ni += 1\nj += 1\n```\n\nAfter checking a group of identical characters, both indices are advanced.\n\n```\nreturn i == len(stretchy) and j == len(word)\n```\n\nAfter exiting the loop, the function checks if both indices have reached the end of their respective strings, meaning a potential stretchy match.\n\n```\nreturn sum(check(s, word) for word in words)\n```\n\nFinally, the main function returns the count of words that can be stretched to match s, using a generator expression to apply check to each word.\n\n# Complexity\n- Time complexity:\nO(m * n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def expressiveWords(self, s: str, words: list[str]) -> int:\n def check(stretchy: str, word: str) -> bool:\n i, j = 0, 0\n while i < len(stretchy) and j < len(word):\n if stretchy[i] != word[j]:\n return False\n\n len_s = 1\n while i + 1 < len(stretchy) and stretchy[i] == stretchy[i + 1]:\n i += 1\n len_s += 1\n\n len_w = 1\n while j + 1 < len(word) and word[j] == word[j + 1]:\n j += 1\n len_w += 1\n \n if (len_s != len_w and len_s < 3) or len_s < len_w:\n return False\n\n i += 1\n j += 1\n \n return i == len(stretchy) and j == len(word)\n\n return sum(check(s, word) for word in words)\n\n\n``` | 0 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
Solution | chalkboard-xor-game | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool xorGame(vector<int>& nums) {\n int xo = 0;\n for (int i: nums) xo ^= i;\n return xo == 0 || nums.size() % 2 == 0;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def xorGame(self, nums: List[int]) -> bool:\n xor = 0\n for i in nums:\n xor ^= i\n return len( nums ) % 2 == 0 or xor == 0\n```\n\n```Java []\nclass Solution {\n public boolean xorGame(int[] nums) {\n int x = 0;\n for(int i=0;i<nums.length;i++){\n x^=nums[i];\n }\n return (x==0 || nums.length%2==0);\n }\n}\n```\n | 1 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
Solution | chalkboard-xor-game | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n bool xorGame(vector<int>& nums) {\n int xo = 0;\n for (int i: nums) xo ^= i;\n return xo == 0 || nums.size() % 2 == 0;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def xorGame(self, nums: List[int]) -> bool:\n xor = 0\n for i in nums:\n xor ^= i\n return len( nums ) % 2 == 0 or xor == 0\n```\n\n```Java []\nclass Solution {\n public boolean xorGame(int[] nums) {\n int x = 0;\n for(int i=0;i<nums.length;i++){\n x^=nums[i];\n }\n return (x==0 || nums.length%2==0);\n }\n}\n```\n | 1 | Let's define a function `countUniqueChars(s)` that returns the number of unique characters on `s`.
* For example, calling `countUniqueChars(s)` if `s = "LEETCODE "` then `"L "`, `"T "`, `"C "`, `"O "`, `"D "` are the unique characters since they appear only once in `s`, therefore `countUniqueChars(s) = 5`.
Given a string `s`, return the sum of `countUniqueChars(t)` where `t` is a substring of `s`. The test cases are generated such that the answer fits in a 32-bit integer.
Notice that some substrings can be repeated so in this case you have to count the repeated ones too.
**Example 1:**
**Input:** s = "ABC "
**Output:** 10
**Explanation:** All possible substrings are: "A ", "B ", "C ", "AB ", "BC " and "ABC ".
Every substring is composed with only unique letters.
Sum of lengths of all substring is 1 + 1 + 1 + 2 + 2 + 3 = 10
**Example 2:**
**Input:** s = "ABA "
**Output:** 8
**Explanation:** The same as example 1, except `countUniqueChars`( "ABA ") = 1.
**Example 3:**
**Input:** s = "LEETCODE "
**Output:** 92
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of uppercase English letters only. | null |
The Clever Math Solution Explained - Allows an O(1) Solution if N%2==0 | chalkboard-xor-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nI have no intuition for deriving this :(\n\n# Approach\n\nThere are three cases:\n1. the xor of all the numbers is 0 => Alice wins because the problem says so\n2. the xor is nonzero, and `len(nums)` is even\n3. the xor is nonzero, and `len(nums)` is odd\n\nWhy would we look at even-vs-odd lengths in the first place? No idea. But once you do, the solution can be derived.\n\nLet\'s look at case 2. Here are the order of plays:\n1. since the xor is nonzero, not all the numbers can be the same, otherwise the xor would be 0. Therefore there are at least two unique values. That means at least one is NOT the xor value. Therefore Alice can pick one of the numbers not equal to the xor. The result is an odd number of remaining numbers, and a nonzero xor. Thereofore Alice always has a valid play the length is even.\n2. then Bob plays. Bob is faced with two possibilities\n i. Bob has no good plays: the remaining number(s) all equal the xor. He loses, so Alice wins\n ii. Bob has a good play: he can erase a number and leave the xor nonzero. So he does that and gives it back to Alice: xor nonzero, and an even length array.\n3. Now Alice is back to (1). So she makes a valid play and hands it back to Bob.\n4. Alice always has a valid play. So as the remaining numbers dwindle, Bob is eventually forced to to do (2)(ii).\n\nThe game can\'t go on forever because there are a finite number of numbers. The game can\'t end on Alice\'s turn because she always has a valid play. So the game must end on Bob\'s turn.\n\n\nNow let\'s look at case 3:\n1. Alice has a nonzero xor and an odd number of numbers. This is the same as case 2 play (2) - she\'s in the same situation as Bob!\n2. Then Bob gets back a nonzero xor with an even length array. We showed in case 1\'s step (1) that he will will always have a valid play. He\'s playing as Alice!\n\nSo this is the same as case 2, but with Alice and Bob flipped. So Bob wins.\n\n\nTherefore the code is just\n* check for xor == 0\n* then return True if the array\'s length is even, else return False\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def xorGame(self, nums: List[int]) -> bool:\n # Idea is something like this for the nontrivial xor != 0 case:\n # if length is even: not all the numbers are the same, otherwise xor would be zero.\n # in addition: two+ unique numbers, so one+ is != xor. So Alice can delete that number without setting xor to zero\n # Therefore Alice has a guaranteed play if N % 2 == 0 and xor != 0\n # Then Bob faces a couple of cases:\n # 1. if each unique number he picks results in xor == 0, he loses\n # 2. if Bob picks a safe number, then he passes it back to Alice with xor != 0 and an even number\n # we know that Alice always has a safe play from here. She does that safe play: goto (1)\n\n xor = 0\n for n in nums:\n xor ^= n\n\n return xor == 0 or len(nums) % 2 == 0\n``` | 1 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
The Clever Math Solution Explained - Allows an O(1) Solution if N%2==0 | chalkboard-xor-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nI have no intuition for deriving this :(\n\n# Approach\n\nThere are three cases:\n1. the xor of all the numbers is 0 => Alice wins because the problem says so\n2. the xor is nonzero, and `len(nums)` is even\n3. the xor is nonzero, and `len(nums)` is odd\n\nWhy would we look at even-vs-odd lengths in the first place? No idea. But once you do, the solution can be derived.\n\nLet\'s look at case 2. Here are the order of plays:\n1. since the xor is nonzero, not all the numbers can be the same, otherwise the xor would be 0. Therefore there are at least two unique values. That means at least one is NOT the xor value. Therefore Alice can pick one of the numbers not equal to the xor. The result is an odd number of remaining numbers, and a nonzero xor. Thereofore Alice always has a valid play the length is even.\n2. then Bob plays. Bob is faced with two possibilities\n i. Bob has no good plays: the remaining number(s) all equal the xor. He loses, so Alice wins\n ii. Bob has a good play: he can erase a number and leave the xor nonzero. So he does that and gives it back to Alice: xor nonzero, and an even length array.\n3. Now Alice is back to (1). So she makes a valid play and hands it back to Bob.\n4. Alice always has a valid play. So as the remaining numbers dwindle, Bob is eventually forced to to do (2)(ii).\n\nThe game can\'t go on forever because there are a finite number of numbers. The game can\'t end on Alice\'s turn because she always has a valid play. So the game must end on Bob\'s turn.\n\n\nNow let\'s look at case 3:\n1. Alice has a nonzero xor and an odd number of numbers. This is the same as case 2 play (2) - she\'s in the same situation as Bob!\n2. Then Bob gets back a nonzero xor with an even length array. We showed in case 1\'s step (1) that he will will always have a valid play. He\'s playing as Alice!\n\nSo this is the same as case 2, but with Alice and Bob flipped. So Bob wins.\n\n\nTherefore the code is just\n* check for xor == 0\n* then return True if the array\'s length is even, else return False\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def xorGame(self, nums: List[int]) -> bool:\n # Idea is something like this for the nontrivial xor != 0 case:\n # if length is even: not all the numbers are the same, otherwise xor would be zero.\n # in addition: two+ unique numbers, so one+ is != xor. So Alice can delete that number without setting xor to zero\n # Therefore Alice has a guaranteed play if N % 2 == 0 and xor != 0\n # Then Bob faces a couple of cases:\n # 1. if each unique number he picks results in xor == 0, he loses\n # 2. if Bob picks a safe number, then he passes it back to Alice with xor != 0 and an even number\n # we know that Alice always has a safe play from here. She does that safe play: goto (1)\n\n xor = 0\n for n in nums:\n xor ^= n\n\n return xor == 0 or len(nums) % 2 == 0\n``` | 1 | Let's define a function `countUniqueChars(s)` that returns the number of unique characters on `s`.
* For example, calling `countUniqueChars(s)` if `s = "LEETCODE "` then `"L "`, `"T "`, `"C "`, `"O "`, `"D "` are the unique characters since they appear only once in `s`, therefore `countUniqueChars(s) = 5`.
Given a string `s`, return the sum of `countUniqueChars(t)` where `t` is a substring of `s`. The test cases are generated such that the answer fits in a 32-bit integer.
Notice that some substrings can be repeated so in this case you have to count the repeated ones too.
**Example 1:**
**Input:** s = "ABC "
**Output:** 10
**Explanation:** All possible substrings are: "A ", "B ", "C ", "AB ", "BC " and "ABC ".
Every substring is composed with only unique letters.
Sum of lengths of all substring is 1 + 1 + 1 + 2 + 2 + 3 = 10
**Example 2:**
**Input:** s = "ABA "
**Output:** 8
**Explanation:** The same as example 1, except `countUniqueChars`( "ABA ") = 1.
**Example 3:**
**Input:** s = "LEETCODE "
**Output:** 92
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of uppercase English letters only. | null |
810: Beats 93.00%, Solution with step by step explanation | chalkboard-xor-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nxor_sum = 0\n```\n\nHere, we initialize a variable xor_sum that will hold the XOR of all the numbers in the list. The XOR operation is a bitwise operation where bits that are the same result in 0, and bits that are different result in 1.\n\n```\nfor num in nums:\n xor_sum ^= num\n```\n\nWe loop through each number in the nums list and apply the XOR operation. xor_sum ^= num is shorthand for xor_sum = xor_sum ^ num, which means we continuously XOR the current xor_sum with the next number in the list.\n\n```\nif xor_sum == 0:\n return True\n```\n\nAfter the loop, if the XOR sum of all numbers is 0, Alice wins by default because there are no moves left for Bob to make without losing.\n\n```\nreturn len(nums) % 2 == 0\n```\n\nIf the XOR is not 0, the game outcome is decided by the number of elements in the list. If there\'s an even number of elements, Alice can always mirror Bob\'s moves to maintain an advantage. For instance, if Bob takes a number that doesn\'t make the XOR 0, Alice can take a different number to ensure the XOR doesn\'t become 0 on her turn, leading to a win for her when Bob has no more moves to make. Therefore, if the number of elements is even, Alice wins.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def xorGame(self, nums: List[int]) -> bool:\n xor_sum = 0\n for num in nums:\n xor_sum ^= num\n\n if xor_sum == 0:\n return True\n\n return len(nums) % 2 == 0\n\n``` | 0 | You are given an array of integers `nums` represents the numbers written on a chalkboard.
Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become `0`, then that player loses. The bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is `0`.
Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to `0`, then that player wins.
Return `true` _if and only if Alice wins the game, assuming both players play optimally_.
**Example 1:**
**Input:** nums = \[1,1,2\]
**Output:** false
**Explanation:**
Alice has two choices: erase 1 or erase 2.
If she erases 1, the nums array becomes \[1, 2\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose.
If Alice erases 2 first, now nums become \[1, 1\]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.
**Example 2:**
**Input:** nums = \[0,1\]
**Output:** true
**Example 3:**
**Input:** nums = \[1,2,3\]
**Output:** true
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] < 216` | null |
810: Beats 93.00%, Solution with step by step explanation | chalkboard-xor-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n```\nxor_sum = 0\n```\n\nHere, we initialize a variable xor_sum that will hold the XOR of all the numbers in the list. The XOR operation is a bitwise operation where bits that are the same result in 0, and bits that are different result in 1.\n\n```\nfor num in nums:\n xor_sum ^= num\n```\n\nWe loop through each number in the nums list and apply the XOR operation. xor_sum ^= num is shorthand for xor_sum = xor_sum ^ num, which means we continuously XOR the current xor_sum with the next number in the list.\n\n```\nif xor_sum == 0:\n return True\n```\n\nAfter the loop, if the XOR sum of all numbers is 0, Alice wins by default because there are no moves left for Bob to make without losing.\n\n```\nreturn len(nums) % 2 == 0\n```\n\nIf the XOR is not 0, the game outcome is decided by the number of elements in the list. If there\'s an even number of elements, Alice can always mirror Bob\'s moves to maintain an advantage. For instance, if Bob takes a number that doesn\'t make the XOR 0, Alice can take a different number to ensure the XOR doesn\'t become 0 on her turn, leading to a win for her when Bob has no more moves to make. Therefore, if the number of elements is even, Alice wins.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def xorGame(self, nums: List[int]) -> bool:\n xor_sum = 0\n for num in nums:\n xor_sum ^= num\n\n if xor_sum == 0:\n return True\n\n return len(nums) % 2 == 0\n\n``` | 0 | Let's define a function `countUniqueChars(s)` that returns the number of unique characters on `s`.
* For example, calling `countUniqueChars(s)` if `s = "LEETCODE "` then `"L "`, `"T "`, `"C "`, `"O "`, `"D "` are the unique characters since they appear only once in `s`, therefore `countUniqueChars(s) = 5`.
Given a string `s`, return the sum of `countUniqueChars(t)` where `t` is a substring of `s`. The test cases are generated such that the answer fits in a 32-bit integer.
Notice that some substrings can be repeated so in this case you have to count the repeated ones too.
**Example 1:**
**Input:** s = "ABC "
**Output:** 10
**Explanation:** All possible substrings are: "A ", "B ", "C ", "AB ", "BC " and "ABC ".
Every substring is composed with only unique letters.
Sum of lengths of all substring is 1 + 1 + 1 + 2 + 2 + 3 = 10
**Example 2:**
**Input:** s = "ABA "
**Output:** 8
**Explanation:** The same as example 1, except `countUniqueChars`( "ABA ") = 1.
**Example 3:**
**Input:** s = "LEETCODE "
**Output:** 92
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of uppercase English letters only. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.