markdown
stringlengths 0
1.02M
| code
stringlengths 0
832k
| output
stringlengths 0
1.02M
| license
stringlengths 3
36
| path
stringlengths 6
265
| repo_name
stringlengths 6
127
|
|---|---|---|---|---|---|
Setup If you are running this generator locally(i.e. in a jupyter notebook in conda, just make sure you installed:- RDKit- DeepChem 2.5.0 & above- Tensorflow 2.4.0 & aboveThen, please skip the following part and continue from `Data Preparations`. To increase efficiency, we recommend running this molecule generator in Colab.Then, we'll first need to run the following lines of code, these will download conda with the deepchem environment in colab.
|
#!curl -Lo conda_installer.py https://raw.githubusercontent.com/deepchem/deepchem/master/scripts/colab_install.py
#import conda_installer
#conda_installer.install()
#!/root/miniconda/bin/conda info -e
#!pip install --pre deepchem
#import deepchem
#deepchem.__version__
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Data PreparationsNow we are ready to import some useful functions/packages, along with our model. Import Data
|
import model##our model
from rdkit import Chem
from rdkit.Chem import AllChem
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import deepchem as dc
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Then, we are ready to import our dataset for training. Here, for demonstration, we'll be using this dataset of in-vitro assay that detects inhibition of SARS-CoV 3CL protease via fluorescence.The dataset is originally from [PubChem AID1706](https://pubchem.ncbi.nlm.nih.gov/bioassay/1706), previously handled by [JClinic AIcure](https://www.aicures.mit.edu/) team at MIT into this [binarized label form](https://github.com/yangkevin2/coronavirus_data/blob/master/data/AID1706_binarized_sars.csv).
|
df = pd.read_csv('AID1706_binarized_sars.csv')
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Observe the data above, it contains a 'smiles' column, which stands for the smiles representation of the molecules. There is also an 'activity' column, in which it is the label specifying whether that molecule is considered as hit for the protein.Here, we only need those 405 molecules considered as hits, and we'll be extracting features from them to generate new molecules that may as well be hits.
|
true = df[df['activity']==1]
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Set Minimum Length for molecules Since we'll be using graphic neural network, it might be more helpful and efficient if our graph data are of the same size, thus, we'll eliminate the molecules from the training set that are shorter(i.e. lacking enough atoms) than our desired minimum size.
|
num_atoms = 6 #here the minimum length of molecules is 6
input_df = true['smiles']
df_length = []
for _ in input_df:
df_length.append(Chem.MolFromSmiles(_).GetNumAtoms() )
true['length'] = df_length #create a new column containing each molecule's length
true = true[true['length']>num_atoms] #Here we leave only the ones longer than 6
input_df = true['smiles']
input_df_smiles = input_df.apply(Chem.MolFromSmiles) #convert the smiles representations into rdkit molecules
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Now, we are ready to apply the `featurizer` function to our molecules to convert them into graphs with nodes and edges for training.
|
#input_df = input_df.apply(Chem.MolFromSmiles)
train_set = input_df_smiles.apply( lambda x: model.featurizer(x,max_length = num_atoms))
train_set
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
We'll take one more step to make the train_set into separate nodes and edges, which fits the format later to supply to the model for training
|
nodes_train, edges_train = list(zip(*train_set) )
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Training Now, we're finally ready for generating new molecules. We'll first import some necessay functions from tensorflow.
|
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
The network here we'll be using is Generative Adversarial Network, as mentioned in the project introduction. Here's a great [introduction](https://machinelearningmastery.com/what-are-generative-adversarial-networks-gans/). 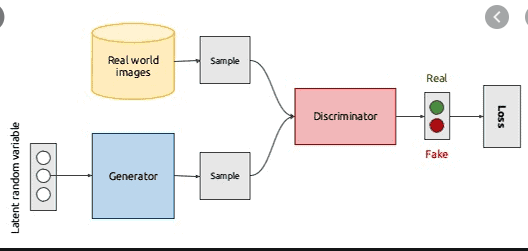 Here we'll first initiate a discriminator and a generator model with the corresponding functions in the package.
|
disc = model.make_discriminator(num_atoms)
gene = model.make_generator(num_atoms, noise_input_shape = 100)
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Then, with the `train_batch` function, we'll supply the necessary inputs and train our network. Upon some experimentations, an epoch of around 160 would be nice for this dataset.
|
generator_trained = model.train_batch(
disc, gene,
np.array(nodes_train), np.array(edges_train),
noise_input_shape = 100, EPOCH = 160, BATCHSIZE = 2,
plot_hist = True, temp_result = False
)
|
>0, d1=0.221, d2=0.833 g=0.681, a1=100, a2=0
>1, d1=0.054, d2=0.714 g=0.569, a1=100, a2=0
>2, d1=0.026, d2=0.725 g=0.631, a1=100, a2=0
>3, d1=0.016, d2=0.894 g=0.636, a1=100, a2=0
>4, d1=0.016, d2=0.920 g=0.612, a1=100, a2=0
>5, d1=0.012, d2=0.789 g=0.684, a1=100, a2=0
>6, d1=0.014, d2=0.733 g=0.622, a1=100, a2=0
>7, d1=0.056, d2=0.671 g=0.798, a1=100, a2=100
>8, d1=0.029, d2=0.587 g=0.653, a1=100, a2=100
>9, d1=0.133, d2=0.537 g=0.753, a1=100, a2=100
>10, d1=0.049, d2=0.640 g=0.839, a1=100, a2=100
>11, d1=0.056, d2=0.789 g=0.836, a1=100, a2=0
>12, d1=0.086, d2=0.564 g=0.916, a1=100, a2=100
>13, d1=0.067, d2=0.550 g=0.963, a1=100, a2=100
>14, d1=0.062, d2=0.575 g=0.940, a1=100, a2=100
>15, d1=0.053, d2=0.534 g=1.019, a1=100, a2=100
>16, d1=0.179, d2=0.594 g=1.087, a1=100, a2=100
>17, d1=0.084, d2=0.471 g=0.987, a1=100, a2=100
>18, d1=0.052, d2=0.366 g=1.226, a1=100, a2=100
>19, d1=0.065, d2=0.404 g=1.220, a1=100, a2=100
>20, d1=0.044, d2=0.311 g=1.274, a1=100, a2=100
>21, d1=0.015, d2=0.231 g=1.567, a1=100, a2=100
>22, d1=0.010, d2=0.222 g=1.838, a1=100, a2=100
>23, d1=0.007, d2=0.177 g=1.903, a1=100, a2=100
>24, d1=0.004, d2=0.139 g=2.155, a1=100, a2=100
>25, d1=0.132, d2=0.111 g=2.316, a1=100, a2=100
>26, d1=0.004, d2=0.139 g=2.556, a1=100, a2=100
>27, d1=0.266, d2=0.133 g=2.131, a1=100, a2=100
>28, d1=0.001, d2=0.199 g=2.211, a1=100, a2=100
>29, d1=0.000, d2=0.252 g=2.585, a1=100, a2=100
>30, d1=0.000, d2=0.187 g=2.543, a1=100, a2=100
>31, d1=0.002, d2=0.081 g=2.454, a1=100, a2=100
>32, d1=0.171, d2=0.061 g=2.837, a1=100, a2=100
>33, d1=0.028, d2=0.045 g=2.858, a1=100, a2=100
>34, d1=0.011, d2=0.072 g=2.627, a1=100, a2=100
>35, d1=2.599, d2=0.115 g=1.308, a1=0, a2=100
>36, d1=0.000, d2=0.505 g=0.549, a1=100, a2=100
>37, d1=0.000, d2=1.463 g=0.292, a1=100, a2=0
>38, d1=0.002, d2=1.086 g=0.689, a1=100, a2=0
>39, d1=0.153, d2=0.643 g=0.861, a1=100, a2=100
>40, d1=0.000, d2=0.353 g=1.862, a1=100, a2=100
>41, d1=0.034, d2=0.143 g=2.683, a1=100, a2=100
>42, d1=0.003, d2=0.110 g=2.784, a1=100, a2=100
>43, d1=0.093, d2=0.058 g=2.977, a1=100, a2=100
>44, d1=0.046, d2=0.051 g=3.051, a1=100, a2=100
>45, d1=0.185, d2=0.062 g=2.922, a1=100, a2=100
>46, d1=0.097, d2=0.070 g=2.670, a1=100, a2=100
>47, d1=0.060, d2=0.073 g=2.444, a1=100, a2=100
>48, d1=0.093, d2=0.156 g=2.385, a1=100, a2=100
>49, d1=0.785, d2=0.346 g=1.026, a1=0, a2=100
>50, d1=0.057, d2=0.869 g=0.667, a1=100, a2=0
>51, d1=0.002, d2=1.001 g=0.564, a1=100, a2=0
>52, d1=0.000, d2=0.764 g=1.047, a1=100, a2=0
>53, d1=0.010, d2=0.362 g=1.586, a1=100, a2=100
>54, d1=0.033, d2=0.230 g=2.469, a1=100, a2=100
>55, d1=0.179, d2=0.134 g=2.554, a1=100, a2=100
>56, d1=0.459, d2=0.103 g=2.356, a1=100, a2=100
>57, d1=0.245, d2=0.185 g=1.769, a1=100, a2=100
>58, d1=0.014, d2=0.227 g=1.229, a1=100, a2=100
>59, d1=0.016, d2=0.699 g=0.882, a1=100, a2=0
>60, d1=0.002, d2=0.534 g=1.192, a1=100, a2=100
>61, d1=0.010, d2=0.335 g=1.630, a1=100, a2=100
>62, d1=0.019, d2=0.283 g=2.246, a1=100, a2=100
>63, d1=0.240, d2=0.132 g=2.547, a1=100, a2=100
>64, d1=0.965, d2=0.219 g=1.534, a1=0, a2=100
>65, d1=0.040, d2=0.529 g=0.950, a1=100, a2=100
>66, d1=0.012, d2=0.611 g=0.978, a1=100, a2=100
>67, d1=0.015, d2=0.576 g=1.311, a1=100, a2=100
>68, d1=0.102, d2=0.214 g=1.840, a1=100, a2=100
>69, d1=0.020, d2=0.140 g=2.544, a1=100, a2=100
>70, d1=5.089, d2=0.314 g=1.231, a1=0, a2=100
>71, d1=0.026, d2=0.700 g=0.556, a1=100, a2=0
>72, d1=0.005, d2=1.299 g=0.460, a1=100, a2=0
>73, d1=0.009, d2=1.033 g=0.791, a1=100, a2=0
>74, d1=0.013, d2=0.343 g=1.408, a1=100, a2=100
>75, d1=0.247, d2=0.267 g=1.740, a1=100, a2=100
>76, d1=0.184, d2=0.172 g=2.105, a1=100, a2=100
>77, d1=0.150, d2=0.133 g=2.297, a1=100, a2=100
>78, d1=0.589, d2=0.112 g=2.557, a1=100, a2=100
>79, d1=0.477, d2=0.232 g=1.474, a1=100, a2=100
>80, d1=0.173, d2=0.360 g=1.034, a1=100, a2=100
>81, d1=0.052, d2=0.790 g=0.936, a1=100, a2=0
>82, d1=0.042, d2=0.537 g=1.135, a1=100, a2=100
>83, d1=0.296, d2=0.363 g=1.152, a1=100, a2=100
>84, d1=0.157, d2=0.377 g=1.283, a1=100, a2=100
>85, d1=0.139, d2=0.436 g=1.445, a1=100, a2=100
>86, d1=0.163, d2=0.343 g=1.370, a1=100, a2=100
>87, d1=0.189, d2=0.290 g=1.576, a1=100, a2=100
>88, d1=1.223, d2=0.548 g=0.822, a1=0, a2=100
>89, d1=0.016, d2=1.042 g=0.499, a1=100, a2=0
>90, d1=0.013, d2=1.033 g=0.829, a1=100, a2=0
>91, d1=0.006, d2=0.589 g=1.421, a1=100, a2=100
>92, d1=0.054, d2=0.160 g=2.414, a1=100, a2=100
>93, d1=0.214, d2=0.070 g=3.094, a1=100, a2=100
>94, d1=0.445, d2=0.089 g=2.564, a1=100, a2=100
>95, d1=2.902, d2=0.180 g=1.358, a1=0, a2=100
>96, d1=0.485, d2=0.684 g=0.625, a1=100, a2=100
>97, d1=0.287, d2=1.296 g=0.405, a1=100, a2=0
>98, d1=0.159, d2=1.149 g=0.689, a1=100, a2=0
>99, d1=0.021, d2=0.557 g=1.405, a1=100, a2=100
>100, d1=0.319, d2=0.243 g=1.905, a1=100, a2=100
>101, d1=0.811, d2=0.241 g=1.523, a1=0, a2=100
>102, d1=0.469, d2=0.439 g=0.987, a1=100, a2=100
>103, d1=0.073, d2=0.760 g=0.698, a1=100, a2=0
>104, d1=0.040, d2=0.762 g=0.869, a1=100, a2=0
>105, d1=0.073, d2=0.444 g=1.453, a1=100, a2=100
>106, d1=0.455, d2=0.272 g=1.632, a1=100, a2=100
>107, d1=0.320, d2=0.365 g=1.416, a1=100, a2=100
>108, d1=0.245, d2=0.409 g=1.245, a1=100, a2=100
>109, d1=0.258, d2=0.572 g=1.146, a1=100, a2=100
>110, d1=0.120, d2=0.447 g=1.538, a1=100, a2=100
>111, d1=2.707, d2=0.376 g=1.343, a1=0, a2=100
>112, d1=3.112, d2=0.604 g=0.873, a1=0, a2=100
>113, d1=0.107, d2=0.750 g=0.873, a1=100, a2=0
>114, d1=0.284, d2=0.682 g=0.905, a1=100, a2=100
>115, d1=1.768, d2=0.717 g=0.824, a1=0, a2=0
>116, d1=0.530, d2=0.822 g=0.560, a1=100, a2=0
>117, d1=0.424, d2=0.984 g=0.613, a1=100, a2=0
>118, d1=1.608, d2=1.398 g=0.244, a1=0, a2=0
>119, d1=4.422, d2=2.402 g=0.135, a1=0, a2=0
>120, d1=0.011, d2=1.998 g=0.321, a1=100, a2=0
>121, d1=0.085, d2=1.066 g=0.815, a1=100, a2=0
>122, d1=0.895, d2=0.444 g=1.495, a1=0, a2=100
>123, d1=2.659, d2=0.288 g=1.417, a1=0, a2=100
>124, d1=1.780, d2=0.450 g=0.869, a1=0, a2=100
>125, d1=2.271, d2=1.046 g=0.324, a1=0, a2=0
>126, d1=0.836, d2=1.970 g=0.123, a1=0, a2=0
>127, d1=0.108, d2=2.396 g=0.103, a1=100, a2=0
>128, d1=0.146, d2=2.371 g=0.174, a1=100, a2=0
>129, d1=0.189, d2=1.623 g=0.424, a1=100, a2=0
>130, d1=0.508, d2=0.877 g=0.876, a1=100, a2=0
>131, d1=0.723, d2=0.423 g=1.367, a1=0, a2=100
>132, d1=1.306, d2=0.292 g=1.445, a1=0, a2=100
>133, d1=0.920, d2=0.318 g=1.378, a1=0, a2=100
>134, d1=1.120, d2=0.481 g=0.827, a1=0, a2=100
>135, d1=0.278, d2=0.763 g=0.562, a1=100, a2=0
>136, d1=0.134, d2=0.901 g=0.555, a1=100, a2=0
>137, d1=0.061, d2=0.816 g=0.864, a1=100, a2=0
>138, d1=0.057, d2=0.451 g=1.533, a1=100, a2=100
>139, d1=0.111, d2=0.214 g=2.145, a1=100, a2=100
>140, d1=0.260, d2=0.107 g=2.451, a1=100, a2=100
>141, d1=4.498, d2=0.209 g=1.266, a1=0, a2=100
>142, d1=0.016, d2=0.681 g=0.672, a1=100, a2=100
>143, d1=0.007, d2=0.952 g=0.702, a1=100, a2=0
>144, d1=0.008, d2=0.624 g=1.337, a1=100, a2=100
>145, d1=0.010, d2=0.241 g=2.114, a1=100, a2=100
>146, d1=2.108, d2=0.121 g=2.536, a1=0, a2=100
>147, d1=4.086, d2=0.111 g=2.315, a1=0, a2=100
>148, d1=1.247, d2=0.177 g=1.781, a1=0, a2=100
>149, d1=2.684, d2=0.377 g=1.026, a1=0, a2=100
>150, d1=0.572, d2=0.701 g=0.710, a1=100, a2=0
>151, d1=0.608, d2=0.899 g=0.571, a1=100, a2=0
>152, d1=0.118, d2=0.904 g=0.592, a1=100, a2=0
>153, d1=0.228, d2=0.837 g=0.735, a1=100, a2=0
>154, d1=0.353, d2=0.671 g=0.912, a1=100, a2=100
>155, d1=0.959, d2=0.563 g=0.985, a1=0, a2=100
>156, d1=0.427, d2=0.478 g=1.184, a1=100, a2=100
>157, d1=0.307, d2=0.348 g=1.438, a1=100, a2=100
>158, d1=0.488, d2=0.286 g=1.383, a1=100, a2=100
>159, d1=0.264, d2=0.333 g=1.312, a1=100, a2=100
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
There are two possible kind of failures regarding a GAN model: model collapse and failure of convergence. Model collapse would often mean that the generative part of the model wouldn't be able to generate diverse outcomes. Failure of convergence between the generative and the discriminative model could likely way be identified as that the loss for the discriminator has gone to zero or close to zero. Observe the above generated plot, in the upper plot, the loss of discriminator has not gone to zero/close to zero, indicating that the model has possibily find a balance between the generator and the discriminator. In the lower plot, the accuracy is fluctuating between 1 and 0, indicating possible variability within the data generated. Therefore, it is reasonable to conclude that within the possible range of epoch and other parameters, the model has successfully avoided the two common types of failures associated with GAN. Rewarding Phase The above `train_batch` function is set to return a trained generator. Thus, we could use that function directly and observe the possible molecules we could get from that function.
|
no, ed = generator_trained(np.random.randint(0,20
, size =(1,100)))#generated nodes and edges
abs(no.numpy()).astype(int).reshape(num_atoms), abs(ed.numpy()).astype(int).reshape(num_atoms,num_atoms)
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
With the `de_featurizer`, we could convert the generated matrix into a smiles molecule and plot it out=)
|
cat, dog = model.de_featurizer(abs(no.numpy()).astype(int).reshape(num_atoms), abs(ed.numpy()).astype(int).reshape(num_atoms,num_atoms))
Chem.MolToSmiles(cat)
Chem.MolFromSmiles(Chem.MolToSmiles(cat))
|
RDKit ERROR: [14:09:13] Explicit valence for atom # 1 O, 5, is greater than permitted
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Brief Result Analysis
|
from rdkit import DataStructs
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
With the rdkit function of comparing similarities, here we'll demonstrate a preliminary analysis of the molecule we've generated. With "CCO" molecule as a control, we could observe that the new molecule we've generated is more similar to a random selected molecule(the fourth molecule) from the initial training set.This may indicate that our model has indeed extracted some features from our original dataset and generated a new molecule that is relevant.
|
DataStructs.FingerprintSimilarity(Chem.RDKFingerprint(Chem.MolFromSmiles("[Li]NBBC=N")), Chem.RDKFingerprint(Chem.MolFromSmiles("CCO")))# compare with the control
#compare with one from the original data
DataStructs.FingerprintSimilarity(Chem.RDKFingerprint(Chem.MolFromSmiles("[Li]NBBC=N")), Chem.RDKFingerprint(Chem.MolFromSmiles("CCN1C2=NC(=O)N(C(=O)C2=NC(=N1)C3=CC=CC=C3)C")))
|
_____no_output_____
|
MIT
|
example.ipynb
|
susanzhang233/mollykill
|
Large DataFrame Tests - NYC CAB
|
BASE_DIR = '/mnt/roscoe/data/fuzzydata/fuzzydatatest/nyc-cab/'
frameworks = ['pandas', 'sqlite', 'modin_dask', 'modin_ray']
all_perfs = []
for f in frameworks:
result_file = glob.glob(f"{BASE_DIR}/{f}/*_perf.csv")[0]
perf_df = pd.read_csv(result_file, index_col=0)
perf_df['end_time_seconds'] = np.cumsum(perf_df.elapsed_time)
perf_df['start_time_seconds'] = perf_df['end_time_seconds'].shift().fillna(0)
perf_df['framework'] = f
all_perfs.append(perf_df)
#plot_gantt(perf_df, title=f'Example Workflow 1.18 GB CSV load/groupby on {f}', x_range=[0.0, 320])
nyc_cab_perfs = pd.concat(all_perfs, ignore_index=True)
new_op_labels = ['load', 'groupby_1', 'groupby_2', 'groupby_3']
nyc_cab_perfs['op'] = np.tile(new_op_labels,4)
pivoted = nyc_cab_perfs.pivot(index='framework', columns='op', values='elapsed_time')
pivoted = pivoted.reindex(['pandas', 'modin_dask', 'modin_ray', 'sqlite'])[new_op_labels]
ax = pivoted.plot.bar(stacked=True)
plt.xticks(rotation=0)
plt.legend()
plt.xlabel('Client')
plt.ylabel('Runtime (Seconds)')
plt.savefig('real_example.pdf', bbox_inches='tight')
|
_____no_output_____
|
MIT
|
examples/Result_Analysis.ipynb
|
suhailrehman/fuzzydata
|
Combined Performance / Scaling Graph
|
BASE_DIR = '/mnt/roscoe/data/fuzzydata/fuzzydata_scaling_test_3/'
frameworks = ['pandas', 'sqlite', 'modin_dask', 'modin_ray']
sizes = ['1000', '10000', '100000', '1000000', '5000000']
all_perfs = []
for framework in frameworks:
for size in sizes:
input_dir = f"{BASE_DIR}/{framework}_{size}/"
try:
#print(f"{input_dir}/*_perf.csv")
perf_file = glob.glob(f"{input_dir}/*_perf.csv")[0]
perf_df = pd.read_csv(perf_file, index_col=0)
perf_df['end_time_seconds'] = np.cumsum(perf_df.elapsed_time)
perf_df['start_time_seconds'] = perf_df['end_time_seconds'].shift().fillna(0)
perf_df['framework'] = framework
perf_df['size'] = size
all_perfs.append(perf_df)
except (IndexError, FileNotFoundError) as e:
#raise(e)
pass
all_perfs_df = pd.concat(all_perfs, ignore_index=True)
total_wf_times = all_perfs_df.loc[all_perfs_df.dst == 'artifact_14'][['framework','size','end_time_seconds']].reset_index(drop=True).pivot(index='size', columns='framework', values='end_time_seconds')
total_wf_times = total_wf_times.rename_axis('Client')
total_wf_times = total_wf_times[['pandas', 'modin_dask', 'modin_ray', 'sqlite']]
total_wf_times
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
font = {'family' : 'serif',
'weight' : 'normal',
'size' : 12}
matplotlib.rc('font', **font)
x_axis_replacements = ['1K', '10K', '100K', '1M', '5M']
plt.figure(figsize=(6,4))
ax = sns.lineplot(data=total_wf_times, markers=True, linewidth=2.5, markersize=10)
plt.xticks(total_wf_times.index, x_axis_replacements)
plt.grid()
plt.xlabel('Base Artifact Number of Rows (r)')
plt.ylabel('Runtime (Seconds)')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=labels)
plt.savefig("scaling.pdf", bbox_inches='tight')
breakdown = all_perfs_df[['framework', 'size', 'op', 'elapsed_time']].groupby(['framework', 'size', 'op']).sum().reset_index()
pivoted_breakdown = breakdown.pivot(index=['size', 'framework'], columns=['op'], values='elapsed_time')
pivoted_breakdown
pivoted_breakdown.plot.bar(stacked=True)
plt.savefig("breakdown.pdf", bbox_inches='tight')
breakdown
# Sources: https://stackoverflow.com/questions/22787209/how-to-have-clusters-of-stacked-bars-with-python-pandas
import pandas as pd
import matplotlib.cm as cm
import numpy as np
import matplotlib.pyplot as plt
def plot_clustered_stacked(dfall, labels=None, title="multiple stacked bar plot", H="/",
x_axis_replacements=None, **kwargs):
"""Given a list of dataframes, with identical columns and index, create a clustered stacked bar plot.
labels is a list of the names of the dataframe, used for the legend
title is a string for the title of the plot
H is the hatch used for identification of the different dataframe"""
n_df = len(dfall)
n_col = len(dfall[0].columns)
n_ind = len(dfall[0].index)
fig = plt.figure(figsize=(6,4))
axe = fig.add_subplot(111)
for df in dfall : # for each data frame
axe = df.plot(kind="bar",
linewidth=0,
stacked=True,
ax=axe,
legend=False,
grid=False,
**kwargs) # make bar plots
hatches = ['', 'oo', '///', '++']
h,l = axe.get_legend_handles_labels() # get the handles we want to modify
for i in range(0, n_df * n_col, n_col): # len(h) = n_col * n_df
for j, pa in enumerate(h[i:i+n_col]):
for rect in pa.patches: # for each index
rect.set_x(rect.get_x() + 1 / float(n_df + 1) * i / float(n_col) -0.1)
rect.set_hatch(hatches[int(i / n_col)]) #edited part
rect.set_width(1 / float(n_df + 1))
axe.set_xticks((np.arange(0, 2 * n_ind, 2) + 1 / float(n_df + 1)) / 2.)
if x_axis_replacements == None:
x_axis_replacements = df.index
axe.set_xticklabels(x_axis_replacements, rotation = 0)
#axe.set_title(title)
# Add invisible data to add another legend
n=[]
for i in range(n_df):
n.append(axe.bar(0, 0, color="gray", hatch=hatches[i]))
l1 = axe.legend(h[:n_col], l[:n_col], loc=[0.38, 0.545])
if labels is not None:
l2 = plt.legend(n, labels)# , loc=[1.01, 0.1])
axe.add_artist(l1)
return axe
cols = ['groupby','load','merge','project','sample']
pbr = pivoted_breakdown.reset_index()
pbr = pbr.set_index('size')
df_splits = [pbr.loc[pbr.framework == f][cols] for f in ['pandas', 'modin_dask', 'modin_ray', 'sqlite']]
# Then, just call :
plot_clustered_stacked(df_splits,['pandas', 'modin_dask', 'modin_ray', 'sqlite'],
x_axis_replacements=x_axis_replacements,
title='Timing Breakdown Per Operation Type')
plt.xlabel('Base Artifact Number of Rows (r)')
plt.ylabel('Runtime (Seconds)')
plt.savefig("breakdown.eps")
pivoted_breakdown.reset_index().set_index('size')
|
_____no_output_____
|
MIT
|
examples/Result_Analysis.ipynb
|
suhailrehman/fuzzydata
|
DataMining TwitterAPIRequirements:- TwitterAccount- TwitterApp credentials ImportsThe following imports are requiered to mine data from Twitter
|
# http://tweepy.readthedocs.io/en/v3.5.0/index.html
import tweepy
# https://api.mongodb.com/python/current/
import pymongo
import json
import sys
|
_____no_output_____
|
MIT
|
jupyter-notebooks/02_DataMining_TwitterAPI.ipynb
|
amarbajric/INDBA-ML
|
Access and Test the TwitterAPIInsert your `CONSUMER_KEY`, `CONSUMER_SECRET`, `ACCESS_TOKEN` and `ACCESS_TOKEN_SECRET` and run the code snippet to test if access is granted. If everything works well 'tweepy...' will be posted to your timeline.
|
# Set the received credentials for your recently created TwitterAPI
CONSUMER_KEY = 'MmiELrtF7fSp3vptCID8jKril'
CONSUMER_SECRET = 'HqtMRk4jpt30uwDOLz30jHqZm6TPN6rj3oHFaL6xFxw2k0GkDC'
ACCESS_TOKEN = '116725830-rkT63AILxR4fpf4kUXd8xJoOcHTsGkKUOKSMpMJQ'
ACCESS_TOKEN_SECRET = 'eKzxfku4GdYu1wWcMr5iusTmhFT35cDWezMU2Olr5UD4i'
# auth with your provided
auth = tweepy.OAuthHandler(CONSUMER_KEY, CONSUMER_SECRET)
auth.set_access_token(ACCESS_TOKEN, ACCESS_TOKEN_SECRET)
# Create an instance for the TwitterApi
twitter = tweepy.API(auth)
status = twitter.update_status('tweepy ...')
print(json.dumps(status._json, indent=1))
|
_____no_output_____
|
MIT
|
jupyter-notebooks/02_DataMining_TwitterAPI.ipynb
|
amarbajric/INDBA-ML
|
mongoDBTo gain access to the mongoDB the library `pymongo` is used.In the first step the mongoDB URL is defined.
|
MONGO_URL = 'mongodb://twitter-mongodb:27017/'
|
_____no_output_____
|
MIT
|
jupyter-notebooks/02_DataMining_TwitterAPI.ipynb
|
amarbajric/INDBA-ML
|
Next, two functions are defined to save and load data from mongoDB.
|
def save_to_mongo(data, mongo_db, mongo_db_coll):
# Connects to the MongoDB server running on
client = pymongo.MongoClient(MONGO_URL)
# Get a reference to a particular database
db = client[mongo_db]
# Reference a particular collection in the database
coll = db[mongo_db_coll]
# Perform a bulk insert and return the IDs
return coll.insert_one(data)
def load_from_mongo(mongo_db, mongo_db_coll, return_cursor=False, criteria=None, projection=None):
# Optionally, use criteria and projection to limit the data that is
# returned - http://docs.mongodb.org/manual/reference/method/db.collection.find/
# Connects to the MongoDB server running on
client = pymongo.MongoClient(MONGO_URL)
# Reference a particular collection in the database
db = client[mongo_db]
# Perform a bulk insert and return the IDs
coll = db[mongo_db_coll]
if criteria is None:
criteria = {}
if projection is None:
cursor = coll.find(criteria)
else:
cursor = coll.find(criteria, projection)
# Returning a cursor is recommended for large amounts of data
if return_cursor:
return cursor
else:
return [ item for item in cursor ]
|
_____no_output_____
|
MIT
|
jupyter-notebooks/02_DataMining_TwitterAPI.ipynb
|
amarbajric/INDBA-ML
|
Stream tweets to mongoDBNow we want to stream tweets to a current trend to the mongoDB.Therefore we ask the TwitterAPI for current Trends within different places. Places are defined with WOEID https://www.flickr.com/places/info/1
|
# WORLD
print('trends WORLD')
trends = twitter.trends_place(1)[0]['trends']
for t in trends[:5]:
print(json.dumps(t['name'],indent=1))
# US
print('\ntrends US')
trends = twitter.trends_place(23424977)[0]['trends']
for t in trends[:5]:
print(json.dumps(t['name'],indent=1))
# AT
print('\ntrends AUSTRIA')
trends = twitter.trends_place(23424750)[0]['trends']
for t in trends[:5]:
print(json.dumps(t['name'],indent=1))
|
_____no_output_____
|
MIT
|
jupyter-notebooks/02_DataMining_TwitterAPI.ipynb
|
amarbajric/INDBA-ML
|
StreamListenertweepy provides a StreamListener that allows to stream live tweets. All streamed tweets are stored to the mongoDB.
|
MONGO_DB = 'trends'
MONGO_COLL = 'tweets'
TREND = '#BestBoyBand'
class CustomStreamListener(tweepy.StreamListener):
def __init__(self, twitter):
self.twitter = twitter
super(tweepy.StreamListener, self).__init__()
self.db = pymongo.MongoClient(MONGO_URL)[MONGO_DB]
self.number = 1
print('Streaming tweets to mongo ...')
def on_data(self, tweet):
self.number += 1
self.db[MONGO_COLL].insert_one(json.loads(tweet))
if self.number % 100 == 0 : print('{} tweets added'.format(self.number))
def on_error(self, status_code):
return True # Don't kill the stream
def on_timeout(self):
return True # Don't kill the stream
sapi = tweepy.streaming.Stream(auth, CustomStreamListener(twitter))
sapi.filter(track=[TREND])
|
_____no_output_____
|
MIT
|
jupyter-notebooks/02_DataMining_TwitterAPI.ipynb
|
amarbajric/INDBA-ML
|
Collect tweets from a specific userIn this use-case we mine data from a specific user.
|
MONGO_DB = 'trump'
MONGO_COLL = 'tweets'
TWITTER_USER = '@realDonaldTrump'
def get_all_tweets(screen_name):
#initialize a list to hold all the tweepy Tweets
alltweets = []
#make initial request for most recent tweets (200 is the maximum allowed count)
new_tweets = twitter.user_timeline(screen_name = screen_name,count=200)
#save most recent tweets
alltweets.extend(new_tweets)
#save the id of the oldest tweet less one
oldest = alltweets[-1].id - 1
#keep grabbing tweets until there are no tweets left to grab
while len(new_tweets) > 0:
#all subsiquent requests use the max_id param to prevent duplicates
new_tweets = twitter.user_timeline(screen_name = screen_name,count=200,max_id=oldest)
#save most recent tweets
alltweets.extend(new_tweets)
#update the id of the oldest tweet less one
oldest = alltweets[-1].id - 1
print("...{} tweets downloaded so far".format(len(alltweets)))
#write tweet objects to JSON
print("Writing tweet objects to MongoDB please wait...")
number = 1
for status in alltweets:
print(save_to_mongo(status._json, MONGO_DB, MONGO_COLL))
number += 1
print("Done - {} tweets saved!".format(number))
#pass in the username of the account you want to download
get_all_tweets(TWITTER_USER)
|
_____no_output_____
|
MIT
|
jupyter-notebooks/02_DataMining_TwitterAPI.ipynb
|
amarbajric/INDBA-ML
|
Load tweets from mongo
|
data = load_from_mongo('trends', 'tweets')
for d in data[:5]:
print(d['text'])
|
_____no_output_____
|
MIT
|
jupyter-notebooks/02_DataMining_TwitterAPI.ipynb
|
amarbajric/INDBA-ML
|
Graphs from the presentation
|
import matplotlib.pyplot as plt
%matplotlib notebook
# create a new figure
plt.figure()
# create x and y coordinates via lists
x = [99, 19, 88, 12, 95, 47, 81, 64, 83, 76]
y = [43, 18, 11, 4, 78, 47, 77, 70, 21, 24]
# scatter the points onto the figure
plt.scatter(x, y)
# create a new figure
plt.figure()
# create x and y values via lists
x = [1, 2, 3, 4, 5, 6, 7, 8]
y = [1, 4, 9, 16, 25, 36, 49, 64]
# plot the line
plt.plot(x, y)
# create a new figure
plt.figure()
# create a list of observations
observations = [5.24, 3.82, 3.73, 5.3 , 3.93, 5.32, 6.43, 4.4 , 5.79, 4.05, 5.34, 5.62, 6.02, 6.08, 6.39, 5.03, 5.34, 4.98, 3.84, 4.91, 6.62, 4.66, 5.06, 2.37, 5. , 3.7 , 5.22, 5.86, 3.88, 4.68, 4.88, 5.01, 3.09, 5.38, 4.78, 6.26, 6.29, 5.77, 4.33, 5.96, 4.74, 4.54, 7.99, 5. , 4.85, 5.68, 3.73, 4.42, 4.99, 4.47, 6.06, 5.88, 4.56, 5.37, 6.39, 4.15]
# create a histogram with 15 intervals
plt.hist(observations, bins=15)
# create a new figure
plt.figure()
# plot a red line with a transparancy of 40%. Label this 'line 1'
plt.plot(x, y, color='red', alpha=0.4, label='line 1')
# make a key appear on the plot
plt.legend()
# import pandas
import pandas as pd
# read in data from a csv
data = pd.read_csv('data/weather.csv', parse_dates=['Date'])
# create a new matplotlib figure
plt.figure()
# plot the temperature over time
plt.plot(data['Date'], data['Temp (C)'])
# add a ylabel
plt.ylabel('Temperature (C)')
plt.figure()
# create inputs
x = ['UK', 'France', 'Germany', 'Spain', 'Italy']
y = [67.5, 65.1, 83.5, 46.7, 60.6]
# plot the chart
plt.bar(x, y)
plt.ylabel('Population (M)')
plt.figure()
# create inputs
x = ['UK', 'France', 'Germany', 'Spain', 'Italy']
y = [67.5, 65.1, 83.5, 46.7, 60.6]
# create a list of colours
colour = ['red', 'green', 'blue', 'orange', 'purple']
# plot the chart with the colors and transparancy
plt.bar(x, y, color=colour, alpha=0.5)
plt.ylabel('Population (M)')
plt.figure()
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
y1 = [2, 4, 6, 8, 10, 12, 14, 16, 18]
y2 = [4, 8, 12, 16, 20, 24, 28, 32, 36]
plt.scatter(x, y1, color='cyan', s=5)
plt.scatter(x, y2, color='violet', s=15)
plt.figure()
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
y1 = [2, 4, 6, 8, 10, 12, 14, 16, 18]
y2 = [4, 8, 12, 16, 20, 24, 28, 32, 36]
size1 = [10, 20, 30, 40, 50, 60, 70, 80, 90]
size2 = [90, 80, 70, 60, 50, 40, 30, 20, 10]
plt.scatter(x, y1, color='cyan', s=size1)
plt.scatter(x, y2, color='violet', s=size2)
co2_file = '../5. Examples of Visual Analytics in Python/data/national/co2_emissions_tonnes_per_person.csv'
gdp_file = '../5. Examples of Visual Analytics in Python/data/national/gdppercapita_us_inflation_adjusted.csv'
pop_file = '../5. Examples of Visual Analytics in Python/data/national/population.csv'
co2_per_cap = pd.read_csv(co2_file, index_col=0, parse_dates=True)
gdp_per_cap = pd.read_csv(gdp_file, index_col=0, parse_dates=True)
population = pd.read_csv(pop_file, index_col=0, parse_dates=True)
plt.figure()
x = gdp_per_cap.loc['2017'] # gdp in 2017
y = co2_per_cap.loc['2017'] # co2 emmissions in 2017
# population in 2017 will give size of points (divide pop by 1M)
size = population.loc['2017'] / 1e6
# scatter points with vector size and some transparancy
plt.scatter(x, y, s=size, alpha=0.5)
# set a log-scale
plt.xscale('log')
plt.yscale('log')
plt.xlabel('GDP per capita, $US')
plt.ylabel('CO2 emissions per person per year, tonnes')
plt.figure()
# create grid of numbers
grid = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
# plot the grid with 'autumn' color map
plt.imshow(grid, cmap='autumn')
# add a colour key
plt.colorbar()
import pandas as pd
data = pd.read_csv("../5. Examples of Visual Analytics in Python/data/stocks/FTSE_stock_prices.csv", index_col=0)
correlation_matrix = data.pct_change().corr()
# create a new figure
plt.figure()
# imshow the grid of correlation
plt.imshow(correlation_matrix, cmap='terrain')
# add a color bar
plt.colorbar()
# remove cluttering x and y ticks
plt.xticks([])
plt.yticks([])
elevation = pd.read_csv('data/UK_elevation.csv', index_col=0)
# create figure
plt.figure()
# imshow data
plt.imshow(elevation, # grid data
vmin=-50, # minimum for colour bar
vmax=500, # maximum for colour bar
cmap='terrain', # terrain style colour map
extent=[-11, 3, 50, 60]) # [x1, x2, y1, y2] plot boundaries
# add axis labels and a title
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.title('UK Elevation Profile')
# add a colourbar
plt.colorbar()
|
_____no_output_____
|
MIT
|
6. Advanced Visualisation Tools/Graphs from the presentation.ipynb
|
nickelnine37/VisualAnalyticsWithPython
|
SOLUCION 1
|
h1 = 0
h2 = 0
m1 = 0
m2 = 0 # 1440 + 24 *6
contador = 0 # 5 + (1440 + ?) * 2 + 144 + 24 + 2= 3057
while [h1, h2, m1, m2] != [2,3,5,9]:
if [h1, h2] == [m2, m1]:
print(h1, h2,":", m1, m2)
m2 = m2 + 1
if m2 == 10:
m2 = 0
m1 = m1 + 1
if m1 == 6:
h2 = h2 + 1
m2 = 0
contador = contador + 1
m2 = m2 + 1
if m2 == 10:
m2 = 0
m1 = m1 + 1
if m1 == 6:
m1 = 0
h2 = h2 +1
if h2 == 10:
h2 = 0
h1 = h1 +1
print("Numero de palindromos: ",contador)
|
_____no_output_____
|
MIT
|
28Octubre.ipynb
|
VxctxrTL/daa_2021_1
|
Solucion 2
|
horario="0000"
contador=0
while horario!="2359":
inv=horario[::-1]
if horario==inv:
contador+=1
print(horario[0:2],":",horario[2:4])
new=int(horario)
new+=1
horario=str(new).zfill(4)
print("son ",contador,"palindromos")
# 2 + (2360 * 4 ) + 24
|
_____no_output_____
|
MIT
|
28Octubre.ipynb
|
VxctxrTL/daa_2021_1
|
Solucion 3
|
lista=[]
for i in range(0,24,1): # 24
for j in range(0,60,1): # 60 1440
if i<10:
if j<10:
lista.append("0"+str(i)+":"+"0"+str(j))
elif j>=10:
lista.append("0"+str(i)+":"+str(j))
else:
if i>=10:
if j<10:
lista.append(str(i)+":"+"0"+str(j))
elif j>=10:
lista.append(str(i)+":"+str(j))
# 1440 + 2 + 1440 + 16 * 2 = 2900
lista2=[]
contador=0
for i in range(len(lista)): # 1440
x=lista[i][::-1]
if x==lista[i]:
lista2.append(x)
contador=contador+1
print(contador)
for j in (lista2):
print(j)
for x in range (0,24,1):
for y in range(0,60,1): #1440 * 3 +13 = 4333
hora=str(x)+":"+str(y)
if x<10:
hora="0"+str(x)+":"+str(y)
if y<10:
hora=str(x)+"0"+":"+str(y)
p=hora[::-1]
if p==hora:
print(f"{hora} es palindromo")
total = int(0) #Contador de numero de palindromos
for hor in range(0,24): #Bucles anidados for para dar aumentar las horas y los minutos al mismo tiempo
for min in range(0,60):
hor_n = str(hor) #Variables
min_n = str(min)
if (hor<10): #USamos condiciones para que las horas y los minutos no rebasen el horario
hor_n = ("0"+hor_n)
if (min<10):
min_n = ("0"+ min_n)
if (hor_n[::-1] == min_n): #Mediante un slicing le damos el formato a las horas para que este empiece desde la derecha
print("{}:{}".format(hor_n,min_n))
total += 1
#1 + 1440 * 5 =7201
|
_____no_output_____
|
MIT
|
28Octubre.ipynb
|
VxctxrTL/daa_2021_1
|
Getting ready
|
import tensorflow as tf
import tensorflow.keras as keras
import pandas as pd
import numpy as np
census_dir = 'https://archive.ics.uci.edu/ml/machine-learning-databases/adult/'
train_path = tf.keras.utils.get_file('adult.data', census_dir + 'adult.data')
test_path = tf.keras.utils.get_file('adult.test', census_dir + 'adult.test')
columns = ['age', 'workclass', 'fnlwgt', 'education', 'education_num', 'marital_status', 'occupation',
'relationship', 'race', 'gender', 'capital_gain', 'capital_loss', 'hours_per_week', 'native_country',
'income_bracket']
train_data = pd.read_csv(train_path, header=None, names=columns)
test_data = pd.read_csv(test_path, header=None, names=columns, skiprows=1)
|
_____no_output_____
|
MIT
|
Chapter 4 - Linear Regression/Using Wide & Deep models.ipynb
|
Young-Picasso/TensorFlow2.x_Cookbook
|
How to do it
|
predictors = ['age', 'workclass', 'education', 'education_num', 'marital_status', 'occupation', 'relationship',
'gender']
y_train = (train_data.income_bracket==' >50K').astype(int)
y_test = (test_data.income_bracket==' >50K').astype(int)
train_data = train_data[predictors]
test_data = test_data[predictors]
train_data[['age', 'education_num']] = train_data[['age', 'education_num']].fillna(train_data[['age', 'education_num']]).mean()
test_data[['age', 'education_num']] = test_data[['age', 'education_num']].fillna(test_data[['age', 'education_num']]).mean()
def define_feature_columns(data_df, numeric_cols, categorical_cols, categorical_embeds, dimension=30):
numeric_columns = []
categorical_columns = []
embeddings = []
for feature_name in numeric_cols:
numeric_columns.append(tf.feature_column.numeric_column(feature_name, dtype=tf.float32))
for feature_name in categorical_cols:
vocabulary = data_df[feature_name].unique()
categorical_columns.append(tf.feature_column.categorical_column_with_vocabulary_list(feature_name, vocabulary))
for feature_name in categorical_embeds:
vocabulary = data_df[feature_name].unique()
to_categorical = tf.feature_column.categorical_column_with_vocabulary_list(feature_name, vocabulary)
embeddings.append(tf.feature_column.embedding_column(to_categorical, dimension=dimension))
return numeric_columns, categorical_columns, embeddings
def create_interactions(interactions_list, buckets=10):
feature_columns = []
for (a, b) in interactions_list:
crossed_feature = tf.feature_column.crossed_column([a, b], hash_bucket_size=buckets)
crossed_feature_one_hot = tf.feature_column.indicator_column(crossed_feature)
feature_columns.append(crossed_feature_one_hot)
return feature_columns
numeric_columns, categorical_columns, embeddings = define_feature_columns(train_data,
numeric_cols=['age', 'education_num'],
categorical_cols=['gender'],
categorical_embeds=['workclass', 'education',
'marital_status', 'occupation',
'relationship'],
dimension=32
)
interactions = create_interactions([['education', 'occupation']], buckets=10)
estimator = tf.estimator.DNNLinearCombinedClassifier(
# wide settings
linear_feature_columns=numeric_columns+categorical_columns+interactions,
linear_optimizer=keras.optimizers.Ftrl(learning_rate=0.0002),
# deep settings
dnn_feature_columns=embeddings,
dnn_hidden_units=[1024, 256, 128, 64],
dnn_optimizer=keras.optimizers.Adam(learning_rate=0.0001))
def make_input_fn(data_df, label_df, num_epochs=10, shuffle=True, batch_size=256):
def input_function():
ds = tf.data.Dataset.from_tensor_slices((dict(data_df), label_df))
if shuffle:
ds = ds.shuffle(1000)
ds = ds.batch(batch_size).repeat(num_epochs)
return ds
return input_function
train_input_fn = make_input_fn(train_data, y_train, num_epochs=100, batch_size=256)
test_input_fn = make_input_fn(test_data, y_test, num_epochs=1, shuffle=False)
estimator.train(input_fn=train_input_fn, steps=1500)
results = estimator.evaluate(input_fn=test_input_fn)
print(results)
def predict_proba(predictor):
preds = list()
for pred in predictor:
preds.append(pred['probabilities'])
return np.array(preds)
predictions = predict_proba(estimator.predict(input_fn=test_input_fn))
print(predictions)
|
INFO:tensorflow:Calling model_fn.
INFO:tensorflow:Done calling model_fn.
INFO:tensorflow:Graph was finalized.
INFO:tensorflow:Restoring parameters from /tmp/tmpxnk3fqlo/model.ckpt-1500
INFO:tensorflow:Running local_init_op.
INFO:tensorflow:Done running local_init_op.
|
MIT
|
Chapter 4 - Linear Regression/Using Wide & Deep models.ipynb
|
Young-Picasso/TensorFlow2.x_Cookbook
|
Automated Machine Learning Forecasting away from training data Contents1. [Introduction](Introduction)2. [Setup](Setup)3. [Data](Data)4. [Prepare remote compute and data.](prepare_remote)4. [Create the configuration and train a forecaster](train)5. [Forecasting from the trained model](forecasting)6. [Forecasting away from training data](forecasting_away) IntroductionThis notebook demonstrates the full interface to the `forecast()` function. The best known and most frequent usage of `forecast` enables forecasting on test sets that immediately follows training data. However, in many use cases it is necessary to continue using the model for some time before retraining it. This happens especially in **high frequency forecasting** when forecasts need to be made more frequently than the model can be retrained. Examples are in Internet of Things and predictive cloud resource scaling.Here we show how to use the `forecast()` function when a time gap exists between training data and prediction period.Terminology:* forecast origin: the last period when the target value is known* forecast periods(s): the period(s) for which the value of the target is desired.* lookback: how many past periods (before forecast origin) the model function depends on. The larger of number of lags and length of rolling window.* prediction context: `lookback` periods immediately preceding the forecast origin Setup Please make sure you have followed the `configuration.ipynb` notebook so that your ML workspace information is saved in the config file.
|
import os
import pandas as pd
import numpy as np
import logging
import warnings
import azureml.core
from azureml.core.dataset import Dataset
from pandas.tseries.frequencies import to_offset
from azureml.core.compute import AmlCompute
from azureml.core.compute import ComputeTarget
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
# Squash warning messages for cleaner output in the notebook
warnings.showwarning = lambda *args, **kwargs: None
np.set_printoptions(precision=4, suppress=True, linewidth=120)
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
|
print("This notebook was created using version 1.8.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
from azureml.core.workspace import Workspace
from azureml.core.experiment import Experiment
from azureml.train.automl import AutoMLConfig
ws = Workspace.from_config()
# choose a name for the run history container in the workspace
experiment_name = 'automl-forecast-function-demo'
experiment = Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['SKU'] = ws.sku
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Run History Name'] = experiment_name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
DataFor the demonstration purposes we will generate the data artificially and use them for the forecasting.
|
TIME_COLUMN_NAME = 'date'
GRAIN_COLUMN_NAME = 'grain'
TARGET_COLUMN_NAME = 'y'
def get_timeseries(train_len: int,
test_len: int,
time_column_name: str,
target_column_name: str,
grain_column_name: str,
grains: int = 1,
freq: str = 'H'):
"""
Return the time series of designed length.
:param train_len: The length of training data (one series).
:type train_len: int
:param test_len: The length of testing data (one series).
:type test_len: int
:param time_column_name: The desired name of a time column.
:type time_column_name: str
:param
:param grains: The number of grains.
:type grains: int
:param freq: The frequency string representing pandas offset.
see https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html
:type freq: str
:returns: the tuple of train and test data sets.
:rtype: tuple
"""
data_train = [] # type: List[pd.DataFrame]
data_test = [] # type: List[pd.DataFrame]
data_length = train_len + test_len
for i in range(grains):
X = pd.DataFrame({
time_column_name: pd.date_range(start='2000-01-01',
periods=data_length,
freq=freq),
target_column_name: np.arange(data_length).astype(float) + np.random.rand(data_length) + i*5,
'ext_predictor': np.asarray(range(42, 42 + data_length)),
grain_column_name: np.repeat('g{}'.format(i), data_length)
})
data_train.append(X[:train_len])
data_test.append(X[train_len:])
X_train = pd.concat(data_train)
y_train = X_train.pop(target_column_name).values
X_test = pd.concat(data_test)
y_test = X_test.pop(target_column_name).values
return X_train, y_train, X_test, y_test
n_test_periods = 6
n_train_periods = 30
X_train, y_train, X_test, y_test = get_timeseries(train_len=n_train_periods,
test_len=n_test_periods,
time_column_name=TIME_COLUMN_NAME,
target_column_name=TARGET_COLUMN_NAME,
grain_column_name=GRAIN_COLUMN_NAME,
grains=2)
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Let's see what the training data looks like.
|
X_train.tail()
# plot the example time series
import matplotlib.pyplot as plt
whole_data = X_train.copy()
target_label = 'y'
whole_data[target_label] = y_train
for g in whole_data.groupby('grain'):
plt.plot(g[1]['date'].values, g[1]['y'].values, label=g[0])
plt.legend()
plt.show()
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Prepare remote compute and data. The [Machine Learning service workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-workspace), is paired with the storage account, which contains the default data store. We will use it to upload the artificial data and create [tabular dataset](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabulardataset?view=azure-ml-py) for training. A tabular dataset defines a series of lazily-evaluated, immutable operations to load data from the data source into tabular representation.
|
# We need to save thw artificial data and then upload them to default workspace datastore.
DATA_PATH = "fc_fn_data"
DATA_PATH_X = "{}/data_train.csv".format(DATA_PATH)
if not os.path.isdir('data'):
os.mkdir('data')
pd.DataFrame(whole_data).to_csv("data/data_train.csv", index=False)
# Upload saved data to the default data store.
ds = ws.get_default_datastore()
ds.upload(src_dir='./data', target_path=DATA_PATH, overwrite=True, show_progress=True)
train_data = Dataset.Tabular.from_delimited_files(path=ds.path(DATA_PATH_X))
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
You will need to create a [compute target](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targetsamlcompute) for your AutoML run. In this tutorial, you create AmlCompute as your training compute resource.
|
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
amlcompute_cluster_name = "fcfn-cluster"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=6)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Create the configuration and train a forecaster First generate the configuration, in which we:* Set metadata columns: target, time column and grain column names.* Validate our data using cross validation with rolling window method.* Set normalized root mean squared error as a metric to select the best model.* Set early termination to True, so the iterations through the models will stop when no improvements in accuracy score will be made.* Set limitations on the length of experiment run to 15 minutes.* Finally, we set the task to be forecasting.* We apply the lag lead operator to the target value i.e. we use the previous values as a predictor for the future ones.
|
lags = [1,2,3]
max_horizon = n_test_periods
time_series_settings = {
'time_column_name': TIME_COLUMN_NAME,
'grain_column_names': [ GRAIN_COLUMN_NAME ],
'max_horizon': max_horizon,
'target_lags': lags
}
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Run the model selection and training process.
|
from azureml.core.workspace import Workspace
from azureml.core.experiment import Experiment
from azureml.train.automl import AutoMLConfig
automl_config = AutoMLConfig(task='forecasting',
debug_log='automl_forecasting_function.log',
primary_metric='normalized_root_mean_squared_error',
experiment_timeout_hours=0.25,
enable_early_stopping=True,
training_data=train_data,
compute_target=compute_target,
n_cross_validations=3,
verbosity = logging.INFO,
max_concurrent_iterations=4,
max_cores_per_iteration=-1,
label_column_name=target_label,
**time_series_settings)
remote_run = experiment.submit(automl_config, show_output=False)
remote_run.wait_for_completion()
# Retrieve the best model to use it further.
_, fitted_model = remote_run.get_output()
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Forecasting from the trained model In this section we will review the `forecast` interface for two main scenarios: forecasting right after the training data, and the more complex interface for forecasting when there is a gap (in the time sense) between training and testing data. X_train is directly followed by the X_testLet's first consider the case when the prediction period immediately follows the training data. This is typical in scenarios where we have the time to retrain the model every time we wish to forecast. Forecasts that are made on daily and slower cadence typically fall into this category. Retraining the model every time benefits the accuracy because the most recent data is often the most informative.We use `X_test` as a **forecast request** to generate the predictions. Typical path: X_test is known, forecast all upcoming periods
|
# The data set contains hourly data, the training set ends at 01/02/2000 at 05:00
# These are predictions we are asking the model to make (does not contain thet target column y),
# for 6 periods beginning with 2000-01-02 06:00, which immediately follows the training data
X_test
y_pred_no_gap, xy_nogap = fitted_model.forecast(X_test)
# xy_nogap contains the predictions in the _automl_target_col column.
# Those same numbers are output in y_pred_no_gap
xy_nogap
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Confidence intervals Forecasting model may be used for the prediction of forecasting intervals by running ```forecast_quantiles()```. This method accepts the same parameters as forecast().
|
quantiles = fitted_model.forecast_quantiles(X_test)
quantiles
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Distribution forecastsOften the figure of interest is not just the point prediction, but the prediction at some quantile of the distribution. This arises when the forecast is used to control some kind of inventory, for example of grocery items or virtual machines for a cloud service. In such case, the control point is usually something like "we want the item to be in stock and not run out 99% of the time". This is called a "service level". Here is how you get quantile forecasts.
|
# specify which quantiles you would like
fitted_model.quantiles = [0.01, 0.5, 0.95]
# use forecast_quantiles function, not the forecast() one
y_pred_quantiles = fitted_model.forecast_quantiles(X_test)
# quantile forecasts returned in a Dataframe along with the time and grain columns
y_pred_quantiles
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Destination-date forecast: "just do something"In some scenarios, the X_test is not known. The forecast is likely to be weak, because it is missing contemporaneous predictors, which we will need to impute. If you still wish to predict forward under the assumption that the last known values will be carried forward, you can forecast out to "destination date". The destination date still needs to fit within the maximum horizon from training.
|
# We will take the destination date as a last date in the test set.
dest = max(X_test[TIME_COLUMN_NAME])
y_pred_dest, xy_dest = fitted_model.forecast(forecast_destination=dest)
# This form also shows how we imputed the predictors which were not given. (Not so well! Use with caution!)
xy_dest
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Forecasting away from training data Suppose we trained a model, some time passed, and now we want to apply the model without re-training. If the model "looks back" -- uses previous values of the target -- then we somehow need to provide those values to the model.The notion of forecast origin comes into play: the forecast origin is **the last period for which we have seen the target value**. This applies per grain, so each grain can have a different forecast origin. The part of data before the forecast origin is the **prediction context**. To provide the context values the model needs when it looks back, we pass definite values in `y_test` (aligned with corresponding times in `X_test`).
|
# generate the same kind of test data we trained on,
# but now make the train set much longer, so that the test set will be in the future
X_context, y_context, X_away, y_away = get_timeseries(train_len=42, # train data was 30 steps long
test_len=4,
time_column_name=TIME_COLUMN_NAME,
target_column_name=TARGET_COLUMN_NAME,
grain_column_name=GRAIN_COLUMN_NAME,
grains=2)
# end of the data we trained on
print(X_train.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].max())
# start of the data we want to predict on
print(X_away.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].min())
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
There is a gap of 12 hours between end of training and beginning of `X_away`. (It looks like 13 because all timestamps point to the start of the one hour periods.) Using only `X_away` will fail without adding context data for the model to consume.
|
try:
y_pred_away, xy_away = fitted_model.forecast(X_away)
xy_away
except Exception as e:
print(e)
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
How should we read that eror message? The forecast origin is at the last time the model saw an actual value of `y` (the target). That was at the end of the training data! The model is attempting to forecast from the end of training data. But the requested forecast periods are past the maximum horizon. We need to provide a define `y` value to establish the forecast origin.We will use this helper function to take the required amount of context from the data preceding the testing data. It's definition is intentionally simplified to keep the idea in the clear.
|
def make_forecasting_query(fulldata, time_column_name, target_column_name, forecast_origin, horizon, lookback):
"""
This function will take the full dataset, and create the query
to predict all values of the grain from the `forecast_origin`
forward for the next `horizon` horizons. Context from previous
`lookback` periods will be included.
fulldata: pandas.DataFrame a time series dataset. Needs to contain X and y.
time_column_name: string which column (must be in fulldata) is the time axis
target_column_name: string which column (must be in fulldata) is to be forecast
forecast_origin: datetime type the last time we (pretend to) have target values
horizon: timedelta how far forward, in time units (not periods)
lookback: timedelta how far back does the model look?
Example:
```
forecast_origin = pd.to_datetime('2012-09-01') + pd.DateOffset(days=5) # forecast 5 days after end of training
print(forecast_origin)
X_query, y_query = make_forecasting_query(data,
forecast_origin = forecast_origin,
horizon = pd.DateOffset(days=7), # 7 days into the future
lookback = pd.DateOffset(days=1), # model has lag 1 period (day)
)
```
"""
X_past = fulldata[ (fulldata[ time_column_name ] > forecast_origin - lookback) &
(fulldata[ time_column_name ] <= forecast_origin)
]
X_future = fulldata[ (fulldata[ time_column_name ] > forecast_origin) &
(fulldata[ time_column_name ] <= forecast_origin + horizon)
]
y_past = X_past.pop(target_column_name).values.astype(np.float)
y_future = X_future.pop(target_column_name).values.astype(np.float)
# Now take y_future and turn it into question marks
y_query = y_future.copy().astype(np.float) # because sometimes life hands you an int
y_query.fill(np.NaN)
print("X_past is " + str(X_past.shape) + " - shaped")
print("X_future is " + str(X_future.shape) + " - shaped")
print("y_past is " + str(y_past.shape) + " - shaped")
print("y_query is " + str(y_query.shape) + " - shaped")
X_pred = pd.concat([X_past, X_future])
y_pred = np.concatenate([y_past, y_query])
return X_pred, y_pred
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Let's see where the context data ends - it ends, by construction, just before the testing data starts.
|
print(X_context.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].agg(['min','max','count']))
print(X_away.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].agg(['min','max','count']))
X_context.tail(5)
# Since the length of the lookback is 3,
# we need to add 3 periods from the context to the request
# so that the model has the data it needs
# Put the X and y back together for a while.
# They like each other and it makes them happy.
X_context[TARGET_COLUMN_NAME] = y_context
X_away[TARGET_COLUMN_NAME] = y_away
fulldata = pd.concat([X_context, X_away])
# forecast origin is the last point of data, which is one 1-hr period before test
forecast_origin = X_away[TIME_COLUMN_NAME].min() - pd.DateOffset(hours=1)
# it is indeed the last point of the context
assert forecast_origin == X_context[TIME_COLUMN_NAME].max()
print("Forecast origin: " + str(forecast_origin))
# the model uses lags and rolling windows to look back in time
n_lookback_periods = max(lags)
lookback = pd.DateOffset(hours=n_lookback_periods)
horizon = pd.DateOffset(hours=max_horizon)
# now make the forecast query from context (refer to figure)
X_pred, y_pred = make_forecasting_query(fulldata, TIME_COLUMN_NAME, TARGET_COLUMN_NAME,
forecast_origin, horizon, lookback)
# show the forecast request aligned
X_show = X_pred.copy()
X_show[TARGET_COLUMN_NAME] = y_pred
X_show
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Note that the forecast origin is at 17:00 for both grains, and periods from 18:00 are to be forecast.
|
# Now everything works
y_pred_away, xy_away = fitted_model.forecast(X_pred, y_pred)
# show the forecast aligned
X_show = xy_away.reset_index()
# without the generated features
X_show[['date', 'grain', 'ext_predictor', '_automl_target_col']]
# prediction is in _automl_target_col
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Forecasting farther than the maximum horizon When the forecast destination, or the latest date in the prediction data frame, is farther into the future than the specified maximum horizon, the `forecast()` function will still make point predictions out to the later date using a recursive operation mode. Internally, the method recursively applies the regular forecaster to generate context so that we can forecast further into the future. To illustrate the use-case and operation of recursive forecasting, we'll consider an example with a single time-series where the forecasting period directly follows the training period and is twice as long as the maximum horizon given at training time.Internally, we apply the forecaster in an iterative manner and finish the forecast task in two interations. In the first iteration, we apply the forecaster and get the prediction for the first max-horizon periods (y_pred1). In the second iteraction, y_pred1 is used as the context to produce the prediction for the next max-horizon periods (y_pred2). The combination of (y_pred1 and y_pred2) gives the results for the total forecast periods. A caveat: forecast accuracy will likely be worse the farther we predict into the future since errors are compounded with recursive application of the forecaster.
|
# generate the same kind of test data we trained on, but with a single grain/time-series and test period twice as long as the max_horizon
_, _, X_test_long, y_test_long = get_timeseries(train_len=n_train_periods,
test_len=max_horizon*2,
time_column_name=TIME_COLUMN_NAME,
target_column_name=TARGET_COLUMN_NAME,
grain_column_name=GRAIN_COLUMN_NAME,
grains=1)
print(X_test_long.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].min())
print(X_test_long.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].max())
# forecast() function will invoke the recursive forecast method internally.
y_pred_long, X_trans_long = fitted_model.forecast(X_test_long)
y_pred_long
# What forecast() function does in this case is equivalent to iterating it twice over the test set as the following.
y_pred1, _ = fitted_model.forecast(X_test_long[:max_horizon])
y_pred_all, _ = fitted_model.forecast(X_test_long, np.concatenate((y_pred1, np.full(max_horizon, np.nan))))
np.array_equal(y_pred_all, y_pred_long)
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
Confidence interval and distributional forecastsAutoML cannot currently estimate forecast errors beyond the maximum horizon set during training, so the `forecast_quantiles()` function will return missing values for quantiles not equal to 0.5 beyond the maximum horizon.
|
fitted_model.forecast_quantiles(X_test_long)
|
_____no_output_____
|
MIT
|
how-to-use-azureml/automated-machine-learning/forecasting-forecast-function/auto-ml-forecasting-function.ipynb
|
hyoshioka0128/MachineLearningNotebooks
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
path =("https://raw.githubusercontent.com/18cse005/DMDW/main/USA_cars_datasets.csv")
data=pd.read_csv(path)
type(data)
data.info
data.shape
data.index
data.columns
data.head()
data.tail()
data.head(10)
data.isnull().sum()
data.dropna(inplace=True) # removed the null values 1st method remove roes when large data we are having
data.isnull().sum()
data.shape
data.head(10)
# 2nd method handling missing value
data['price'].mean()
data['price'].head()
data['price'].replace(np.NaN,data['price'].mean()).head()
|
_____no_output_____
|
Apache-2.0
|
Data_preprocessing.ipynb
|
18cse081/dmdw
|
|
Introduction and Foundations: Titanic Survival Exploration> Udacity Machine Learning Engineer Nanodegree: _Project 0_>> Author: _Ke Zhang_>> Submission Date: _2017-04-27_ (Revision 2) AbstractIn 1912, the ship RMS Titanic struck an iceberg on its maiden voyage and sank, resulting in the deaths of most of its passengers and crew. In this introductory project, we will explore a subset of the RMS Titanic passenger manifest to determine which features best predict whether someone survived or did not survive. To complete this project, you will need to implement several conditional predictions and answer the questions below. Your project submission will be evaluated based on the completion of the code and your responses to the questions. Content- [Getting Started](Getting-Started)- [Making Predictions](Making-Predictions)- [Conclusion](Conclusion)- [References](References)- [Reproduction Environment](Reproduction-Environment) Getting StartedTo begin working with the RMS Titanic passenger data, we'll first need to `import` the functionality we need, and load our data into a `pandas` DataFrame.
|
# Import libraries necessary for this project
import numpy as np
import pandas as pd
from IPython.display import display # Allows the use of display() for DataFrames
# Import supplementary visualizations code visuals.py
import visuals as vs
# Pretty display for notebooks
%matplotlib inline
# Load the dataset
in_file = 'titanic_data.csv'
full_data = pd.read_csv(in_file)
# Print the first few entries of the RMS Titanic data
display(full_data.head())
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
From a sample of the RMS Titanic data, we can see the various features present for each passenger on the ship:- **Survived**: Outcome of survival (0 = No; 1 = Yes)- **Pclass**: Socio-economic class (1 = Upper class; 2 = Middle class; 3 = Lower class)- **Name**: Name of passenger- **Sex**: Sex of the passenger- **Age**: Age of the passenger (Some entries contain `NaN`)- **SibSp**: Number of siblings and spouses of the passenger aboard- **Parch**: Number of parents and children of the passenger aboard- **Ticket**: Ticket number of the passenger- **Fare**: Fare paid by the passenger- **Cabin** Cabin number of the passenger (Some entries contain `NaN`)- **Embarked**: Port of embarkation of the passenger (C = Cherbourg; Q = Queenstown; S = Southampton)Since we're interested in the outcome of survival for each passenger or crew member, we can remove the **Survived** feature from this dataset and store it as its own separate variable `outcomes`. We will use these outcomes as our prediction targets. Run the code cell below to remove **Survived** as a feature of the dataset and store it in `outcomes`.
|
# Store the 'Survived' feature in a new variable and remove it from the dataset
outcomes = full_data['Survived']
data = full_data.drop('Survived', axis = 1)
# Show the new dataset with 'Survived' removed
display(data.head())
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
The very same sample of the RMS Titanic data now shows the **Survived** feature removed from the DataFrame. Note that `data` (the passenger data) and `outcomes` (the outcomes of survival) are now *paired*. That means for any passenger `data.loc[i]`, they have the survival outcome `outcomes[i]`.To measure the performance of our predictions, we need a metric to score our predictions against the true outcomes of survival. Since we are interested in how *accurate* our predictions are, we will calculate the proportion of passengers where our prediction of their survival is correct. Run the code cell below to create our `accuracy_score` function and test a prediction on the first five passengers. **Think:** *Out of the first five passengers, if we predict that all of them survived, what would you expect the accuracy of our predictions to be?*
|
def accuracy_score(truth, pred):
""" Returns accuracy score for input truth and predictions. """
# Ensure that the number of predictions matches number of outcomes
if len(truth) == len(pred):
# Calculate and return the accuracy as a percent
return "Predictions have an accuracy of {:.2f}%.".format((truth == pred).mean()*100)
else:
return "Number of predictions does not match number of outcomes!"
# Test the 'accuracy_score' function
predictions = pd.Series(np.ones(5, dtype = int))
print accuracy_score(outcomes[:5], predictions)
|
Predictions have an accuracy of 60.00%.
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
> **Tip:** If you save an iPython Notebook, the output from running code blocks will also be saved. However, the state of your workspace will be reset once a new session is started. Make sure that you run all of the code blocks from your previous session to reestablish variables and functions before picking up where you last left off. Making PredictionsIf we were asked to make a prediction about any passenger aboard the RMS Titanic whom we knew nothing about, then the best prediction we could make would be that they did not survive. This is because we can assume that a majority of the passengers (more than 50%) did not survive the ship sinking. The `predictions_0` function below will always predict that a passenger did not survive.
|
def predictions_0(data):
""" Model with no features. Always predicts a passenger did not survive. """
predictions = []
for _, passenger in data.iterrows():
# Predict the survival of 'passenger'
predictions.append(0)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_0(data)
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
Question 1*Using the RMS Titanic data, how accurate would a prediction be that none of the passengers survived?* **Hint:** Run the code cell below to see the accuracy of this prediction.
|
print accuracy_score(outcomes, predictions)
|
Predictions have an accuracy of 61.62%.
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
**Answer:** The prediction accuracy is **61.62%** ***Let's take a look at whether the feature **Sex** has any indication of survival rates among passengers using the `survival_stats` function. This function is defined in the `titanic_visualizations.py` Python script included with this project. The first two parameters passed to the function are the RMS Titanic data and passenger survival outcomes, respectively. The third parameter indicates which feature we want to plot survival statistics across. Run the code cell below to plot the survival outcomes of passengers based on their sex.
|
vs.survival_stats(data, outcomes, 'Sex')
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
Examining the survival statistics, a large majority of males did not survive the ship sinking. However, a majority of females *did* survive the ship sinking. Let's build on our previous prediction: If a passenger was female, then we will predict that they survived. Otherwise, we will predict the passenger did not survive. Fill in the missing code below so that the function will make this prediction. **Hint:** You can access the values of each feature for a passenger like a dictionary. For example, `passenger['Sex']` is the sex of the passenger.
|
def predictions_1(data):
""" Model with one feature:
- Predict a passenger survived if they are female. """
predictions = []
for _, passenger in data.iterrows():
predictions.append(True if passenger['Sex'] == 'female'
else False)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_1(data)
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
Question 2*How accurate would a prediction be that all female passengers survived and the remaining passengers did not survive?* **Hint:** Run the code cell below to see the accuracy of this prediction.
|
print accuracy_score(outcomes, predictions)
|
Predictions have an accuracy of 78.68%.
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
**Answer**: **78.68**% ***Using just the **Sex** feature for each passenger, we are able to increase the accuracy of our predictions by a significant margin. Now, let's consider using an additional feature to see if we can further improve our predictions. For example, consider all of the male passengers aboard the RMS Titanic: Can we find a subset of those passengers that had a higher rate of survival? Let's start by looking at the **Age** of each male, by again using the `survival_stats` function. This time, we'll use a fourth parameter to filter out the data so that only passengers with the **Sex** 'male' will be included. Run the code cell below to plot the survival outcomes of male passengers based on their age.
|
vs.survival_stats(data, outcomes, 'Age', ["Sex == 'male'"])
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
Examining the survival statistics, the majority of males younger than 10 survived the ship sinking, whereas most males age 10 or older *did not survive* the ship sinking. Let's continue to build on our previous prediction: If a passenger was female, then we will predict they survive. If a passenger was male and younger than 10, then we will also predict they survive. Otherwise, we will predict they do not survive. Fill in the missing code below so that the function will make this prediction. **Hint:** You can start your implementation of this function using the prediction code you wrote earlier from `predictions_1`.
|
def predictions_2(data):
""" Model with two features:
- Predict a passenger survived if they are female.
- Predict a passenger survived if they are male and younger than 10. """
predictions = []
for _, passenger in data.iterrows():
predictions.append(True if passenger['Sex'] == 'female' or
passenger['Age'] < 10 else False)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_2(data)
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
Question 3*How accurate would a prediction be that all female passengers and all male passengers younger than 10 survived?* **Hint:** Run the code cell below to see the accuracy of this prediction.
|
print accuracy_score(outcomes, predictions)
|
Predictions have an accuracy of 79.35%.
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
**Answer**: **79.35** ***Adding the feature **Age** as a condition in conjunction with **Sex** improves the accuracy by a small margin more than with simply using the feature **Sex** alone. Now it's your turn: Find a series of features and conditions to split the data on to obtain an outcome prediction accuracy of at least 80%. This may require multiple features and multiple levels of conditional statements to succeed. You can use the same feature multiple times with different conditions. **Pclass**, **Sex**, **Age**, **SibSp**, and **Parch** are some suggested features to try.Use the `survival_stats` function below to to examine various survival statistics. **Hint:** To use mulitple filter conditions, put each condition in the list passed as the last argument. Example: `["Sex == 'male'", "Age < 18"]`
|
# survival by Embarked
vs.survival_stats(data, outcomes, 'Embarked')
# survival by Embarked
vs.survival_stats(data, outcomes, 'SibSp')
vs.survival_stats(data, outcomes, 'Age', ["Sex == 'male'", "Age < 18"])
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
We found out earlier that female and children had better chance to survive. In the next step we'll add another criteria 'Pclass' to further distinguish the survival rates among the different groups.
|
# female passengers in the higher pclass had great chance to survive
vs.survival_stats(data, outcomes, 'Pclass', [
"Sex == 'female'"
])
# male passengers in the higher pclass had great chance to survive
vs.survival_stats(data, outcomes, 'Pclass', [
"Sex == 'male'"
])
# more female passengers survived in all age groups
vs.survival_stats(data, outcomes, 'Age', [
"Sex == 'female'",
])
# more male passengers survived only when age < 10
vs.survival_stats(data, outcomes, 'Age', [
"Sex == 'male'",
])
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
It looks like that all female passengers under 20 survived from the accident. Let's check passengers in the lower class to complete our guess.
|
# ... but not in the lower class when they're older than 20
vs.survival_stats(data, outcomes, 'Age', [
"Sex == 'female'",
"Pclass == 3"
])
# ... actually only females under 20 had more survivers in the lower class
vs.survival_stats(data, outcomes, 'Age', [
"Sex == 'male'",
"Pclass == 3"
])
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
> We conclude that in the lower class only female under 20 had better chance to survive. In the other classes all children under 10 and female passengers had more likey survived. Let's check if we have reached our 80% target. After exploring the survival statistics visualization, fill in the missing code below so that the function will make your prediction. Make sure to keep track of the various features and conditions you tried before arriving at your final prediction model. **Hint:** You can start your implementation of this function using the prediction code you wrote earlier from `predictions_2`.
|
def predictions_3(data):
"""
Model with multiple features: Sex, Age and Pclass
Makes a prediction with an accuracy of at least 80%.
"""
predictions = []
for _, passenger in data.iterrows():
if passenger['Age'] < 10:
survived = True
elif passenger['Sex'] == 'female' and not (
passenger['Pclass'] == 3 and passenger['Age'] > 20
):
survived = True
else:
survived = False
predictions.append(survived)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_3(data)
|
_____no_output_____
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
Question 4*Describe the steps you took to implement the final prediction model so that it got an accuracy of at least 80%. What features did you look at? Were certain features more informative than others? Which conditions did you use to split the survival outcomes in the data? How accurate are your predictions?* **Hint:** Run the code cell below to see the accuracy of your predictions.
|
print accuracy_score(outcomes, predictions)
|
Predictions have an accuracy of 80.36%.
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
**Answer**: Using the features *Sex*, *Pclass* and *Age* we increased the accuracy score to **80.36%**.We tried to plot the survival statistics with different features and chose the ones under which conditions the differences were the largest.* some features are just not relevant like *PassengerId* or *Name** some features have to be decoded to be helpful like *Cabin* which could be helpful if we have more information on the location of each cabin* some features are less informative than the others: e.g. we could use *Embarked*, *SibSp* or *Parch* to group the passengers but the resulting model would be more complicated.* Eventually we chose *Sex*, *Pclass* and *Age* as our final features.We derived the conditions to split the survival outcomes from the survival plots. The split conditions are:1. All children under 10 => **survived**2. Female passengers in the upper and middle class, or less than 20 => **survived**3. Others => **died**The final accuracy score was **80.36%**. ConclusionAfter several iterations of exploring and conditioning on the data, you have built a useful algorithm for predicting the survival of each passenger aboard the RMS Titanic. The technique applied in this project is a manual implementation of a simple machine learning model, the *decision tree*. A decision tree splits a set of data into smaller and smaller groups (called *nodes*), by one feature at a time. Each time a subset of the data is split, our predictions become more accurate if each of the resulting subgroups are more homogeneous (contain similar labels) than before. The advantage of having a computer do things for us is that it will be more exhaustive and more precise than our manual exploration above. [This link](http://www.r2d3.us/visual-intro-to-machine-learning-part-1/) provides another introduction into machine learning using a decision tree.A decision tree is just one of many models that come from *supervised learning*. In supervised learning, we attempt to use features of the data to predict or model things with objective outcome labels. That is to say, each of our data points has a known outcome value, such as a categorical, discrete label like `'Survived'`, or a numerical, continuous value like predicting the price of a house. Question 5*Think of a real-world scenario where supervised learning could be applied. What would be the outcome variable that you are trying to predict? Name two features about the data used in this scenario that might be helpful for making the predictions.* **Answer**: A real-world scenario would be that we have a buch of animal photos labeled with the animal type on them and try to recognize new photos with supervised learning model predictions.Useful featrues could be:* number of legs* size of the animal* color of the skin or fur* surrounding environment (tropical, water, air, iceberg etc.)Outcome variable is the animal type. References- [Udacity Website](http://www.udacity.com)- [Pandas Documentation](http://pandas.pydata.org/pandas-docs/stable/) Reproduction Environment
|
import IPython
print IPython.sys_info()
!pip freeze
|
alabaster==0.7.9
anaconda-client==1.6.0
anaconda-navigator==1.4.3
argcomplete==1.0.0
astroid==1.4.9
astropy==1.3
Babel==2.3.4
backports-abc==0.5
backports.shutil-get-terminal-size==1.0.0
backports.ssl-match-hostname==3.4.0.2
beautifulsoup4==4.5.3
bitarray==0.8.1
blaze==0.10.1
bokeh==0.12.4
boto==2.45.0
Bottleneck==1.2.0
cdecimal==2.3
cffi==1.9.1
chardet==2.3.0
chest==0.2.3
click==6.7
cloudpickle==0.2.2
clyent==1.2.2
colorama==0.3.7
comtypes==1.1.2
conda==4.3.15
configobj==5.0.6
configparser==3.5.0
contextlib2==0.5.4
cryptography==1.7.1
cycler==0.10.0
Cython==0.25.2
cytoolz==0.8.2
dask==0.13.0
datashape==0.5.4
decorator==4.0.11
dill==0.2.5
docutils==0.13.1
enum34==1.1.6
et-xmlfile==1.0.1
fastcache==1.0.2
Flask==0.12
Flask-Cors==3.0.2
funcsigs==1.0.2
functools32==3.2.3.post2
futures==3.0.5
gevent==1.2.1
glueviz==0.9.1
greenlet==0.4.11
grin==1.2.1
h5py==2.6.0
HeapDict==1.0.0
idna==2.2
imagesize==0.7.1
ipaddress==1.0.18
ipykernel==4.5.2
ipython==5.1.0
ipython-genutils==0.1.0
ipywidgets==5.2.2
isort==4.2.5
itsdangerous==0.24
jdcal==1.3
jedi==0.9.0
Jinja2==2.9.4
jsonschema==2.5.1
jupyter==1.0.0
jupyter-client==4.4.0
jupyter-console==5.0.0
jupyter-core==4.2.1
lazy-object-proxy==1.2.2
llvmlite==0.15.0
locket==0.2.0
lxml==3.7.2
MarkupSafe==0.23
matplotlib==2.0.0
menuinst==1.4.4
mistune==0.7.3
mpmath==0.19
multipledispatch==0.4.9
nbconvert==4.2.0
nbformat==4.2.0
networkx==1.11
nltk==3.2.2
nose==1.3.7
notebook==4.4.1
numba==0.30.1+0.g8c1033f.dirty
numexpr==2.6.1
numpy==1.11.3
numpydoc==0.6.0
odo==0.5.0
openpyxl==2.4.1
pandas==0.19.2
partd==0.3.7
path.py==0.0.0
pathlib2==2.2.0
patsy==0.4.1
pep8==1.7.0
pickleshare==0.7.4
Pillow==4.0.0
ply==3.9
prompt-toolkit==1.0.9
psutil==5.0.1
py==1.4.32
pyasn1==0.1.9
pycosat==0.6.1
pycparser==2.17
pycrypto==2.6.1
pycurl==7.43.0
pyflakes==1.5.0
pygame==1.9.3
Pygments==2.1.3
pylint==1.6.4
pymongo==3.3.0
pyOpenSSL==16.2.0
pyparsing==2.1.4
pytest==3.0.5
python-dateutil==2.6.0
pytz==2016.10
pywin32==220
PyYAML==3.12
pyzmq==16.0.2
QtAwesome==0.4.3
qtconsole==4.2.1
QtPy==1.2.1
requests==2.12.4
rope==0.9.4
scandir==1.4
scikit-image==0.12.3
scikit-learn==0.18.1
scipy==0.18.1
seaborn==0.7.1
simplegeneric==0.8.1
singledispatch==3.4.0.3
six==1.10.0
snowballstemmer==1.2.1
sockjs-tornado==1.0.3
sphinx==1.5.1
spyder==3.1.2
SQLAlchemy==1.1.5
statsmodels==0.6.1
subprocess32==3.2.7
sympy==1.0
tables==3.2.2
toolz==0.8.2
tornado==4.4.2
traitlets==4.3.1
unicodecsv==0.14.1
wcwidth==0.1.7
Werkzeug==0.11.15
widgetsnbextension==1.2.6
win-unicode-console==0.5
wrapt==1.10.8
xlrd==1.0.0
XlsxWriter==0.9.6
xlwings==0.10.2
xlwt==1.2.0
|
Apache-2.0
|
p0_ss_titanic_survival_exploration/p0_ss_titanic_survival_exploration.ipynb
|
superkley/udacity-mlnd
|
Preclustering and Cluster Enriched Features PurposeThe purpose of this step is to perform a simple pre-clustering using the highly variable features to get a pre-clusters labeling. We then select top enriched features for each cluster (CEF) for further analysis. Input- HVF adata file. Output- HVF adata file with pre-clusters and CEF annotated. Import
|
import seaborn as sns
import anndata
import scanpy as sc
from ALLCools.clustering import cluster_enriched_features, significant_pc_test, log_scale
sns.set_context(context='notebook', font_scale=1.3)
|
_____no_output_____
|
MIT
|
docs/allcools/cell_level/step_by_step/100kb/04a-PreclusteringAndClusterEnrichedFeatures-mCH.ipynb
|
mukamel-lab/ALLCools
|
Parameters
|
adata_path = 'mCH.HVF.h5ad'
# Cluster Enriched Features analysis
top_n=200
alpha=0.05
stat_plot=True
# you may provide a pre calculated cluster version.
# If None, will perform basic clustering using parameters below.
cluster_col = None
# These parameters only used when cluster_col is None
k=25
resolution=1
cluster_plot=True
|
_____no_output_____
|
MIT
|
docs/allcools/cell_level/step_by_step/100kb/04a-PreclusteringAndClusterEnrichedFeatures-mCH.ipynb
|
mukamel-lab/ALLCools
|
Load Data
|
adata = anndata.read_h5ad(adata_path)
|
_____no_output_____
|
MIT
|
docs/allcools/cell_level/step_by_step/100kb/04a-PreclusteringAndClusterEnrichedFeatures-mCH.ipynb
|
mukamel-lab/ALLCools
|
Pre-ClusteringIf cluster label is not provided, will perform basic clustering here
|
if cluster_col is None:
# IMPORTANT
# put the unscaled matrix in adata.raw
adata.raw = adata
log_scale(adata)
sc.tl.pca(adata, n_comps=100)
significant_pc_test(adata, p_cutoff=0.1, update=True)
sc.pp.neighbors(adata, n_neighbors=k)
sc.tl.leiden(adata, resolution=resolution)
if cluster_plot:
sc.tl.umap(adata)
sc.pl.umap(adata, color='leiden')
# return to unscaled X, CEF need to use the unscaled matrix
adata = adata.raw.to_adata()
cluster_col = 'leiden'
|
32 components passed P cutoff of 0.1.
Changing adata.obsm['X_pca'] from shape (16985, 100) to (16985, 32)
|
MIT
|
docs/allcools/cell_level/step_by_step/100kb/04a-PreclusteringAndClusterEnrichedFeatures-mCH.ipynb
|
mukamel-lab/ALLCools
|
Cluster Enriched Features (CEF)
|
cluster_enriched_features(adata,
cluster_col=cluster_col,
top_n=top_n,
alpha=alpha,
stat_plot=True)
|
Found 31 clusters to compute feature enrichment score
Computing enrichment score
Computing enrichment score FDR-corrected P values
Selected 3102 unique features
|
MIT
|
docs/allcools/cell_level/step_by_step/100kb/04a-PreclusteringAndClusterEnrichedFeatures-mCH.ipynb
|
mukamel-lab/ALLCools
|
Save AnnData
|
# save adata
adata.write_h5ad(adata_path)
adata
|
_____no_output_____
|
MIT
|
docs/allcools/cell_level/step_by_step/100kb/04a-PreclusteringAndClusterEnrichedFeatures-mCH.ipynb
|
mukamel-lab/ALLCools
|
Ploting Different Polling Methods
|
pollster_rating = pd.read_csv("pollster-ratings.csv")
Methodologies_frequencies = pollster_rating.Methodology.value_counts()
plt.bar(Methodologies_frequencies.index, Methodologies_frequencies)
plt.xticks(rotation = "vertical")
plt.title("Methodolgies of Diffrent Pollsters")
plt.ylabel("Number of Pollsters")
plt.xlabel("Methodolgy")
|
_____no_output_____
|
CC-BY-4.0
|
pollster-ratings/Visualization.ipynb
|
machinglearnin/data
|
Plotting Poll Size Distribution
|
plt.figure(figsize = (10,6))
plt.hist(pollster_rating['# of Polls'])
plt.title("Distrubution of Polling Sizes Among Diffrent Pollsters")
plt.xlabel("# of Polls Conducted")
plt.show()
|
_____no_output_____
|
CC-BY-4.0
|
pollster-ratings/Visualization.ipynb
|
machinglearnin/data
|
Accuracy of Pollsters
|
#selects only Pollsters with 100+ Polls
frequent_pollsters = pollster_rating[pollster_rating['# of Polls'] > 100]
frequent_pollsters = frequent_pollsters.set_index('Pollster')
#Reformats Races Called Correclty Data so it ban be sorted
Races_called_correctly = frequent_pollsters['Races Called Correctly'].str.rstrip('%').astype(int)
Races_called_correctly = Races_called_correctly.sort_values()
#makes Bar graph
plt.figure(figsize = (6,4))
plt.barh(Races_called_correctly.index, Races_called_correctly)
plt.title("Accuracy of Different Pollsters")
plt.xlabel("Percentage of Races Called Correctly")
plt.show()
|
_____no_output_____
|
CC-BY-4.0
|
pollster-ratings/Visualization.ipynb
|
machinglearnin/data
|
Are More Frequent Pollsters More Accurate?
|
pollster_above_10 = pollster_rating[pollster_rating['# of Polls'] > 100]
plt.figure(figsize = (8,6))
x_list = pollster_above_10['# of Polls']
y_list = pollster_above_10['Races Called Correctly'].str.rstrip('%').astype(int)
plt.scatter(x_list, y_list)
plt.yticks(np.arange(0, 110, 10))
plt.title("Comparison of Pollsters Accuarcy and Frequency of Polling")
plt.xlabel("Number of Polls Conducted")
plt.ylabel("Percentage of Races Called Correctly")
plt.show()
from scipy import stats
slope, intercept, r_value, p_value, std_err = stats.linregress(x_list, y_list)
predictions = slope * x_list + intercept
plt.yticks(np.arange(0, 110, 10))
plt.title("Correlation of Number of Polls and Accuracy")
plt.xlabel("Number of Polls Conducted")
plt.ylabel("Percentage of Races Called Correctly")
plt.scatter(x_list, y_list)
plt.plot(x_list, predictions, color = 'r')
plt.show()
print "R squared:", r_value ** 2
|
_____no_output_____
|
CC-BY-4.0
|
pollster-ratings/Visualization.ipynb
|
machinglearnin/data
|
Before you begin1. Use the [Cloud Resource Manager](https://console.cloud.google.com/cloud-resource-manager) to Create a Cloud Platform project if you do not already have one.2. [Enable billing](https://support.google.com/cloud/answer/6293499enable-billing) for the project.3. [Enable BigQuery](https://console.cloud.google.com/flows/enableapi?apiid=bigquery) APIs for the project. Provide your credentials to the runtime
|
from google.colab import auth
auth.authenticate_user()
print('Authenticated')
|
_____no_output_____
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
Optional: Enable data table displayColab includes the ``google.colab.data_table`` package that can be used to display large pandas dataframes as an interactive data table.It can be enabled with:
|
%load_ext google.colab.data_table
|
_____no_output_____
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
If you would prefer to return to the classic Pandas dataframe display, you can disable this by running:```python%unload_ext google.colab.data_table``` Use BigQuery via magicsThe `google.cloud.bigquery` library also includes a magic command which runs a query and either displays the result or saves it to a variable as a `DataFrame`.
|
# Display query output immediately
%%bigquery --project yourprojectid
SELECT
COUNT(*) as total_rows
FROM `bigquery-public-data.samples.gsod`
# Save output in a variable `df`
%%bigquery --project yourprojectid df
SELECT
COUNT(*) as total_rows
FROM `bigquery-public-data.samples.gsod`
df
|
_____no_output_____
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
Use BigQuery through google-cloud-bigquerySee [BigQuery documentation](https://cloud.google.com/bigquery/docs) and [library reference documentation](https://googlecloudplatform.github.io/google-cloud-python/latest/bigquery/usage.html).The [GSOD sample table](https://bigquery.cloud.google.com/table/bigquery-public-data:samples.gsod) contains weather information collected by NOAA, such as precipitation amounts and wind speeds from late 1929 to early 2010. Declare the Cloud project ID which will be used throughout this notebook
|
project_id = '[your project ID]'
|
_____no_output_____
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
Sample approximately 2000 random rows
|
from google.cloud import bigquery
client = bigquery.Client(project=project_id)
sample_count = 2000
row_count = client.query('''
SELECT
COUNT(*) as total
FROM `bigquery-public-data.samples.gsod`''').to_dataframe().total[0]
df = client.query('''
SELECT
*
FROM
`bigquery-public-data.samples.gsod`
WHERE RAND() < %d/%d
''' % (sample_count, row_count)).to_dataframe()
print('Full dataset has %d rows' % row_count)
|
Full dataset has 114420316 rows
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
Describe the sampled data
|
df.describe()
|
_____no_output_____
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
View the first 10 rows
|
df.head(10)
# 10 highest total_precipitation samples
df.sort_values('total_precipitation', ascending=False).head(10)[['station_number', 'year', 'month', 'day', 'total_precipitation']]
|
_____no_output_____
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
Use BigQuery through pandas-gbqThe `pandas-gbq` library is a community led project by the pandas community. It covers basic functionality, such as writing a DataFrame to BigQuery and running a query, but as a third-party library it may not handle all BigQuery features or use cases.[Pandas GBQ Documentation](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_gbq.html)
|
import pandas as pd
sample_count = 2000
df = pd.io.gbq.read_gbq('''
SELECT name, SUM(number) as count
FROM `bigquery-public-data.usa_names.usa_1910_2013`
WHERE state = 'TX'
GROUP BY name
ORDER BY count DESC
LIMIT 100
''', project_id=project_id, dialect='standard')
df.head()
|
_____no_output_____
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
Syntax highlighting`google.colab.syntax` can be used to add syntax highlighting to any Python string literals which are used in a query later.
|
from google.colab import syntax
query = syntax.sql('''
SELECT
COUNT(*) as total_rows
FROM
`bigquery-public-data.samples.gsod`
''')
pd.io.gbq.read_gbq(query, project_id=project_id, dialect='standard')
|
_____no_output_____
|
MIT
|
Getting_started_with_BigQuery.ipynb
|
darshanbk/100-Days-Of-ML-Code
|
Solving Multi-armed Bandit Problems We will focus on how to solve the multi-armed bandit problem using four strategies, including epsilon-greedy, softmax exploration, upper confidence bound, and Thompson sampling. We will see how they deal with the exploration-exploitation dilemma in their own unique ways. We will also work on a billion-dollar problem, online advertising, and demonstrate how to solve it using a multi-armed bandit algorithm. Finally, we will solve the contextual advertising problem using contextual bandits to make more informed decisions in ad optimization. Creating a multi-armed bandit environment The multi-armed bandit problem is one of the simplest reinforcement learning problems. It is best described as a slot machine with multiple levers (arms), and each lever has a different payout and payout probability. Our goal is to discover the best lever with the maximum return so that we can keep choosing it afterward. Let’s start with a simple multi-armed bandit problem in which the payout and payout probability is fixed for each arm. After creating the environment, we will solve it using the random policy algorithm.
|
import torch
class BanditEnv():
"""
Multi-armed bandit environment
payout_list:
A list of probabilities of the likelihood that a particular bandit will pay out
reward_list:
A list of rewards of the payout that bandit has
"""
def __init__(self, payout_list, reward_list):
self.payout_list = payout_list
self.reward_list = reward_list
def step(self, action):
if torch.rand(1).item() < self.payout_list[action]:
return self.reward_list[action]
return 0
if __name__ == "__main__":
bandit_payout = [0.1, 0.15, 0.3]
bandit_reward = [4, 3, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = [0 for _ in range(n_action)]
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def random_policy():
action = torch.multinomial(torch.ones(n_action), 1).item()
return action
for episode in range(n_episode):
action = random_policy()
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
|
_____no_output_____
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
In the example we just worked on, there are three slot machines. Each machine has a different payout (reward) and payout probability. In each episode, we randomly chose one arm of the machine to pull (one action to execute) and get a payout at a certain probability. Arm 1 is the best arm with the largest average reward. Also, the average rewards start to saturate round 10,000 episodes.This solution seems very naive as we only perform an exploration of all arms. We will come up with more intelligent strategies in the upcoming sections. Solving multi-armed bandit problems with the epsilon-greedy policyInstead of exploring solely with random policy, we can do better with a combination of exploration and exploitation. Here comes the well-known epsilon-greedy policy.Epsilon-greedy for multi-armed bandits exploits the best action the majority of the time and also keeps exploring different actions from time to time. Given a parameter, ε, with a value from 0 to 1, the probabilities of performing exploration and exploitation are ε and 1 - ε, respectively. Similar to other MDP problems, the epsilon-greedy policy selects the best arm with a probability of 1 - ε and performs random exploration with a probability of ε. Epsilon manages the trade-off between exploration and exploitation.
|
import torch
bandit_payout = [0.1, 0.15, 0.3]
bandit_reward = [4, 3, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = [0 for _ in range(n_action)]
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def gen_epsilon_greedy_policy(n_action, epsilon):
def policy_function(Q):
probs = torch.ones(n_action) * epsilon / n_action
best_action = torch.argmax(Q).item()
probs[best_action] += 1.0 - epsilon
action = torch.multinomial(probs, 1).item()
return action
return policy_function
epsilon = 0.2
epsilon_greedy_policy = gen_epsilon_greedy_policy(n_action, epsilon)
Q = torch.zeros(n_action)
for episode in range(n_episode):
action = epsilon_greedy_policy(Q)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
Q[action] = action_total_reward[action] / action_count[action]
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
|
_____no_output_____
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
Arm 1 is the best arm, with the largest average reward at the end. Also, its average reward starts to saturate after around 1,000 episodes. You may wonder whether the epsilon-greedy policy actually outperforms the random policy. Besides the fact that the value for the optimal arm converges earlier with the epsilon-greedy policy, we can also prove that, on average, the reward we get during the course of training is higher with the epsilon-greedy policy than the random policy.We can simply average the reward over all episodes:
|
print(sum(action_total_reward) / n_episode)
|
0.43616
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
Over 100,000 episodes, the average payout is 0.43718 with the epsilon-greedy policy. Repeating the same computation for the random policy solution, we get 0.37902 as the average payout. Solving multi-armed bandit problems with the softmax explorationAs we've seen with epsilon-greedy, when performing exploration we randomly select one of the non-best arms with a probability of ε/|A|. Each non-best arm is treated equivalently regardless of its value in the Q function. Also, the best arm is chosen with a fixed probability regardless of its value. In softmax exploration, an arm is chosen based on a probability from the softmax distribution of the Q function values. With the softmax exploration strategy, the dilemma of exploitation and exploration is solved with a softmax function based on the Q values. Instead of using a fixed pair of probabilities for the best arm and non-best arms, it adjusts the probabilities according to the softmax distribution with the τ parameter as a temperature factor. The higher the value of τ, the more focus will be shifted to exploration.
|
import torch
bandit_payout = [0.1, 0.15, 0.3]
bandit_reward = [4, 3, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = [0 for _ in range(n_action)]
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def gen_softmax_exploration_policy(tau):
def policy_function(Q):
probs = torch.exp(Q / tau)
probs = probs / torch.sum(probs)
action = torch.multinomial(probs, 1).item()
return action
return policy_function
tau = 0.1
softmax_exploration_policy = gen_softmax_exploration_policy(tau)
Q = torch.zeros(n_action)
for episode in range(n_episode):
action = softmax_exploration_policy(Q)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
Q[action] = action_total_reward[action] / action_count[action]
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
|
_____no_output_____
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
Arm 1 is the best arm, with the largest average reward at the end. Also, its average reward starts to saturate after around 800 episodes in this example. Solving multi-armed bandit problems with the upper confidence bound algorithmIn the previous two recipes, we explored random actions in the multi-armed bandit problem with probabilities that are either assigned as fixed values in the epsilon-greedy policy or computed based on the Q-function values in the softmax exploration algorithm. In either algorithm, the probabilities of taking random actions are not adjusted over time. Ideally, we want less exploration as learning progresses. In this recipe, we will use a new algorithm called upper confidence bound to achieve this goal.The upper confidence bound (UCB) algorithm stems from the idea of the confidence interval. In general, the confidence interval is a range of values where the true value lies. In the UCB algorithm, the confidence interval for an arm is a range where the mean reward obtained with this arm lies. The interval is in the form of [lower confidence bound, upper confidence bound] and we only use the upper bound, which is the UCB, to estimate the potential of the arm. The UCB is computed as follows:$$UCB(a) = Q(a) + \sqrt{2log(t)/N(a)}$$Here, t is the number of episodes, and N(a) is the number of times arm a is chosen among t episodes. As learning progresses, the confidence interval shrinks and becomes more and more accurate. The arm to pull is the one with the highest UCB. In this recipe, we solved the multi-armed bandit with the UCB algorithm. It adjusts the exploitation-exploration dilemma according to the number of episodes. For an action with a few data points, its confidence interval is relatively wide, hence, choosing this action is of relatively high uncertainty. With more episodes of the action being selected, the confidence interval becomes narrow and shrinks to its actual value. In this case, it is of high certainty to choose (or not) this action. Finally, the UCB algorithm pulls the arm with the highest UCB in each episode and gains more and more confidence over time.
|
import torch
bandit_payout = [0.1, 0.15, 0.3]
bandit_reward = [4, 3, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = torch.tensor([0. for _ in range(n_action)])
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def upper_confidence_bound(Q, action_count, t):
ucb = torch.sqrt((2 * torch.log(torch.tensor(float(t)))) / action_count) + Q
return torch.argmax(ucb)
Q = torch.empty(n_action)
for episode in range(n_episode):
action = upper_confidence_bound(Q, action_count, episode)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
Q[action] = action_total_reward[action] / action_count[action]
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
|
_____no_output_____
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
Arm 1 is the best arm, with the largest average reward in the end. You may wonder whether UCB actually outperforms the epsilon-greedy policy. We can compute the average reward over the entire training process, and the policy with the highest average reward learns faster.We can simply average the reward over all episodes:
|
print(sum(action_total_reward) / n_episode)
|
0.4433
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
Over 100,000 episodes, the average payout is 0.44605 with UCB, which is higher than 0.43718 with the epsilon-greedy policy. Solving internet advertising problems with a multi-armed banditImagine you are an advertiser working on ad optimization on a website:- There are three different colors of ad background – red, green, and blue. Which one will achieve the best click-through rate (CTR)?- There are three types of wordings of the ad – learn …, free ..., and try .... Which one will achieve the best CTR?For each visitor, we need to choose an ad in order to maximize the CTR over time. How can we solve this?Perhaps you are thinking about A/B testing, where you randomly split the traffic into groups and assign each ad to a different group, and then choose the ad from the group with the highest CTR after a period of observation. However, this is basically a complete exploration, and we are usually unsure of how long the observation period should be and will end up losing a large portion of potential clicks. Besides, in A/B testing, the unknown CTR for an ad is assumed to not change over time. Otherwise, such A/B testing should be re-run periodically.A multi-armed bandit can certainly do better than A/B testing. Each arm is an ad, and the reward for an arm is either 1 (click) or 0 (no click).Let's try to solve it with the UCB algorithm. In this recipe, we solved the ad optimization problem in a multi-armed bandit manner. It overcomes the challenges confronting the A/B testing approach. We used the UCB algorithm to solve the multi-armed (multi-ad) bandit problem; the reward for each arm is either 1 or 0. Instead of pure exploration and no interaction between action and reward, UCB (or other algorithms such as epsilon-greedy and softmax exploration) dynamically switches between exploitation and exploration where necessarly. For an ad with a few data points, the confidence interval is relatively wide, hence, choosing this action is of relatively high uncertainty. With more episodes of the ad being selected, the confidence interval becomes narrow and shrinks to its actual value.
|
import torch
bandit_payout = [0.01, 0.015, 0.03]
bandit_reward = [1, 1, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = torch.tensor([0. for _ in range(n_action)])
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def upper_confidence_bound(Q, action_count, t):
ucb = torch.sqrt((2 * torch.log(torch.tensor(float(t)))) / action_count) + Q
return torch.argmax(ucb)
Q = torch.empty(n_action)
for episode in range(n_episode):
action = upper_confidence_bound(Q, action_count, episode)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
Q[action] = action_total_reward[action] / action_count[action]
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
|
_____no_output_____
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
Ad 2 is the best ad with the highest predicted CTR (average reward) after the model converges.Eventually, we found that ad 2 is the optimal one to choose, which is true. Also, the sooner we figure this out the better, because we will lose fewer potential clicks. In this example, ad 2 outperformed the others after around 1000 episodes. Solving multi-armed bandit problems with the Thompson sampling algorithmIn this recipe, we will tackle the exploitation and exploration dilemma in the advertising bandits problem using another algorithm, Thompson sampling. We will see how it differs greatly from the previous three algorithms.Thompson sampling (TS) is also called Bayesian bandits as it applies the Bayesian way of thinking from the following perspectives:- It is a probabilistic algorithm.- It computes the prior distribution for each arm and samples a value from each distribution.- It then selects the arm with the highest value and observes the reward.- Finally, it updates the prior distribution based on the observed reward. This process is called Bayesian updating.As we have seen that in our ad optimization case, the reward for each arm is either 1 or 0. We can use beta distribution for our prior distribution because the value of the beta distribution is from 0 to 1. The beta distribution is parameterized by two parameters, α and β. α represents the number of times we receive the reward of 1 and β, indicates the number of times we receive the reward of 0.To help you understand the beta distribution better, we will start by looking at several beta distributions before we implement the TS algorithm.
|
import torch
import matplotlib.pyplot as plt
beta1 = torch.distributions.beta.Beta(1, 1)
samples1 = [beta1.sample() for _ in range(100000)]
plt.hist(samples1, range=[0, 1], bins=10)
plt.title('beta(1, 1)')
plt.show()
beta2 = torch.distributions.beta.Beta(5, 1)
samples2 = [beta2.sample() for _ in range(100000)]
plt.hist(samples2, range=[0, 1], bins=10)
plt.title('beta(5, 1)')
plt.show()
beta3 = torch.distributions.beta.Beta(1, 5)
samples3= [beta3.sample() for _ in range(100000)]
plt.hist(samples3, range=[0, 1], bins=10)
plt.title('beta(1, 5)')
plt.show()
beta4 = torch.distributions.beta.Beta(5, 5)
samples4= [beta4.sample() for _ in range(100000)]
plt.hist(samples4, range=[0, 1], bins=10)
plt.title('beta(5, 5)')
plt.show()
bandit_payout = [0.01, 0.015, 0.03]
bandit_reward = [1, 1, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = torch.tensor([0. for _ in range(n_action)])
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
|
_____no_output_____
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
In this recipe, we solved the ad bandits problem with the TS algorithm. The biggest difference between TS and the three other approaches is the adoption of Bayesian optimization. It first computes the prior distribution for each possible arm, and then randomly draws a value from each distribution. It then picks the arm with the highest value and uses the observed outcome to update the prior distribution. The TS policy is both stochastic and greedy. If an ad is more likely to receive clicks, its beta distribution shifts toward 1 and, hence, the value of a random sample tends to be closer to 1.
|
def thompson_sampling(alpha, beta):
prior_values = torch.distributions.beta.Beta(alpha, beta).sample()
return torch.argmax(prior_values)
alpha = torch.ones(n_action)
beta = torch.ones(n_action)
for episode in range(n_episode):
action = thompson_sampling(alpha, beta)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
if reward > 0:
alpha[action] += 1
else:
beta[action] += 1
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
|
_____no_output_____
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
Ad 2 is the best ad, with the highest predicted CTR (average reward). Solving internet advertising problems with contextual banditsYou may notice that in the ad optimization problem, we only care about the ad and ignore other information, such as user information and web page information, that might affect the ad being clicked on or not. In this recipe, we will talk about how we take more information into account beyond the ad itself and solve the problem with contextual bandits.The multi-armed bandit problems we have worked with so far do not involve the concept of state, which is very different from MDPs. We only have several actions, and a reward will be generated that is associated with the action selected. Contextual bandits extend multi-armed bandits by introducing the concept of state. State provides a description of the environment, which helps the agent take more informed actions. In the advertising example, the state could be the user's gender (two states, male and female), the user’s age group (four states, for example), or page category (such as sports, finance, or news). Intuitively, users of certain demographics are more likely to click on an ad on certain pages.It is not difficult to understand contextual bandits. A multi-armed bandit is a single machine with multiple arms, while contextual bandits are a set of such machines (bandits). Each machine in contextual bandits is a state that has multiple arms. The learning goal is to find the best arm (action) for each machine (state).We will work with an advertising example with two states for simplicity. In this recipe, we solved the contextual advertising problem with contextual bandits using the UCB algorithm.
|
import torch
bandit_payout_machines = [
[0.01, 0.015, 0.03],
[0.025, 0.01, 0.015]
]
bandit_reward_machines = [
[1, 1, 1],
[1, 1, 1]
]
n_machine = len(bandit_payout_machines)
bandit_env_machines = [BanditEnv(bandit_payout, bandit_reward)
for bandit_payout, bandit_reward in
zip(bandit_payout_machines, bandit_reward_machines)]
n_episode = 100000
n_action = len(bandit_payout_machines[0])
action_count = torch.zeros(n_machine, n_action)
action_total_reward = torch.zeros(n_machine, n_action)
action_avg_reward = [[[] for action in range(n_action)] for _ in range(n_machine)]
def upper_confidence_bound(Q, action_count, t):
ucb = torch.sqrt((2 * torch.log(torch.tensor(float(t)))) / action_count) + Q
return torch.argmax(ucb)
Q_machines = torch.empty(n_machine, n_action)
for episode in range(n_episode):
state = torch.randint(0, n_machine, (1,)).item()
action = upper_confidence_bound(Q_machines[state], action_count[state], episode)
reward = bandit_env_machines[state].step(action)
action_count[state][action] += 1
action_total_reward[state][action] += reward
Q_machines[state][action] = action_total_reward[state][action] / action_count[state][action]
for a in range(n_action):
if action_count[state][a]:
action_avg_reward[state][a].append(action_total_reward[state][a] / action_count[state][a])
else:
action_avg_reward[state][a].append(0)
import matplotlib.pyplot as plt
for state in range(n_machine):
for action in range(n_action):
plt.plot(action_avg_reward[state][action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time for state {}'.format(state))
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
|
_____no_output_____
|
Apache-2.0
|
_notebooks/2022-01-20-mab.ipynb
|
recohut/notebook
|
Copyright 2018 The TensorFlow Authors.
|
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
|
_____no_output_____
|
Apache-2.0
|
site/zh-cn/guide/ragged_tensor.ipynb
|
RedContritio/docs-l10n
|
不规则张量 在 TensorFlow.org 上查看 在 Google Colab 中运行 在 Github 上查看源代码 {img}下载笔记本 **API 文档:** [`tf.RaggedTensor`](https://tensorflow.google.cn/api_docs/python/tf/RaggedTensor) [`tf.ragged`](https://tensorflow.google.cn/api_docs/python/tf/ragged) 设置
|
!pip install -q tf_nightly
import math
import tensorflow as tf
|
_____no_output_____
|
Apache-2.0
|
site/zh-cn/guide/ragged_tensor.ipynb
|
RedContritio/docs-l10n
|
概述数据有多种形状;张量也应当有多种形状。*不规则张量*是嵌套的可变长度列表的 TensorFlow 等效项。它们使存储和处理包含非均匀形状的数据变得容易,包括:- 可变长度特征,例如电影的演员名单。- 成批的可变长度顺序输入,例如句子或视频剪辑。- 分层输入,例如细分为节、段落、句子和单词的文本文档。- 结构化输入中的各个字段,例如协议缓冲区。 不规则张量的功能有一百多种 TensorFlow 运算支持不规则张量,包括数学运算(如 `tf.add` 和 `tf.reduce_mean`)、数组运算(如 `tf.concat` 和 `tf.tile`)、字符串操作运算(如 `tf.substr`)、控制流运算(如 `tf.while_loop` 和 `tf.map_fn`)等:
|
digits = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
words = tf.ragged.constant([["So", "long"], ["thanks", "for", "all", "the", "fish"]])
print(tf.add(digits, 3))
print(tf.reduce_mean(digits, axis=1))
print(tf.concat([digits, [[5, 3]]], axis=0))
print(tf.tile(digits, [1, 2]))
print(tf.strings.substr(words, 0, 2))
print(tf.map_fn(tf.math.square, digits))
|
_____no_output_____
|
Apache-2.0
|
site/zh-cn/guide/ragged_tensor.ipynb
|
RedContritio/docs-l10n
|
还有专门针对不规则张量的方法和运算,包括工厂方法、转换方法和值映射运算。有关支持的运算列表,请参阅 **`tf.ragged` 包文档**。 许多 TensorFlow API 都支持不规则张量,包括 [Keras](https://tensorflow.google.cn/guide/keras)、[Dataset](https://tensorflow.google.cn/guide/data)、[tf.function](https://tensorflow.google.cn/guide/function)、[SavedModel](https://tensorflow.google.cn/guide/saved_model) 和 [tf.Example](https://tensorflow.google.cn/tutorials/load_data/tfrecord)。有关更多信息,请参阅下面的 **TensorFlow API** 一节。 与普通张量一样,您可以使用 Python 风格的索引来访问不规则张量的特定切片。有关更多信息,请参阅下面的**索引**一节。
|
print(digits[0]) # First row
print(digits[:, :2]) # First two values in each row.
print(digits[:, -2:]) # Last two values in each row.
|
_____no_output_____
|
Apache-2.0
|
site/zh-cn/guide/ragged_tensor.ipynb
|
RedContritio/docs-l10n
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.