question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
4sum
|
A Java Solution with Two Pointers
|
a-java-solution-with-two-pointers-by-hun-74um
|
public List<List<Integer>> fourSum(int[] nums, int target) {\n \tList<List<Integer>> result = new ArrayList<List<Integer>>();\n \tif (nums == nul
|
huntnahan
|
NORMAL
|
2015-05-11T01:01:28+00:00
|
2018-10-12T01:33:28.817316+00:00
| 2,232 | false |
public List<List<Integer>> fourSum(int[] nums, int target) {\n \tList<List<Integer>> result = new ArrayList<List<Integer>>();\n \tif (nums == null || nums.length < 4) {\n \t\treturn result;\n \t}\n \tArrays.sort(nums);\n \tfor (int i = 0; i < nums.length - 3; i ++) {\n \t\tfor (int j = i + 1; j < nums.length - 2; j ++) {\n \t\t\tint head = j + 1;\n \t\t\tint tail = nums.length - 1;\n \t\t\twhile (head < tail) {\n \t\t\t\tint tempSum = nums[i] + nums[j] + nums[head] + nums[tail];\n \t\t\t\tif (tempSum == target) {\n \t\t\t\t\tList<Integer> item = new ArrayList<Integer>();\n \t\t\t\t\titem.add(nums[i]);\n \t\t\t\t\titem.add(nums[j]);\n \t\t\t\t\titem.add(nums[head]);\n \t\t\t\t\titem.add(nums[tail]);\n \t\t\t\t\tif (result.contains(item) == false) {\n \t\t\t\t\t\tresult.add(item);\n \t\t\t\t\t} \n \t\t\t\t\thead ++;\n \t\t\t\t\ttail --;\n \t\t\t\t} else if (tempSum < target) {\n \t\t\t\t\thead ++;\n \t\t\t\t} else {\n \t\t\t\t\ttail --;\n \t\t\t\t}\n \t\t\t}\n \t\t}\n \t}\n \treturn result;\n }
| 8 | 1 |
[]
| 5 |
4sum
|
two pointer approach || easy c++ solution || beats 100%
|
two-pointer-approach-easy-c-solution-bea-jy5w
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Rhythm_1383
|
NORMAL
|
2023-08-16T10:37:15.319109+00:00
|
2023-08-16T10:37:15.319155+00:00
| 1,216 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n vector<vector<int>>v;\n sort(nums.begin(),nums.end());\n int n=nums.size();\n for(int i=0;i<n;i++)\n {\n if(i>0&& nums[i]==nums[i-1])continue;\n for(int j=i+1;j<n;j++)\n {\n if(j!=(i+1) && nums[j]==nums[j-1])continue;\n int k=j+1;\n int l=n-1;\n while(k<l)\n {\n long long sum=nums[i];\n sum+=nums[j];\n sum+=nums[k];\n sum+=nums[l];\n if(sum==target)\n {\n vector<int> temp={nums[i],nums[j],nums[k],nums[l]};\n v.push_back(temp);\n k=k+1;\n l=l-1;\n while(k<l && nums[k]==nums[k-1])k=k+1;\n while(k<l && nums[l]==nums[l+1])l=l-1;\n }\n else if(sum<target)\n {\n k++;\n }\n else{l--;}\n }\n }\n } \n return v;\n }\n};\n```
| 7 | 0 |
['C++']
| 0 |
4sum
|
Python simple two pointer approach
|
python-simple-two-pointer-approach-by-ka-41tn
|
\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n res, n = [], len(nums)\n nums.sort()\n for a i
|
kaii-23
|
NORMAL
|
2022-07-28T07:51:09.622272+00:00
|
2022-07-28T07:51:09.622344+00:00
| 1,185 | false |
```\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n res, n = [], len(nums)\n nums.sort()\n for a in range(n):\n for b in range(a+1, n):\n c = b+1; d = n-1\n while c<d:\n sums = nums[a]+nums[b]+nums[c]+nums[d]\n if sums < target:\n c += 1\n elif sums > target:\n d -= 1\n else:\n toappend = [nums[a],nums[b],nums[c],nums[d]]\n if toappend not in res:\n res.append(toappend)\n c +=1\n d-=1\n return res\n```
| 7 | 0 |
['Two Pointers', 'Python']
| 1 |
4sum
|
DP, TwoSum Style Python Solution
|
dp-twosum-style-python-solution-by-matth-lbpx
|
The idea is that fourSum is just two twoSums\n1. We can treat the input like an N x N matrix of summed values \nwhere eg. nums[0][1] is nums[0] + nums[1]\nTo av
|
matthewaarongo
|
NORMAL
|
2020-05-10T15:49:20.026746+00:00
|
2020-05-10T15:51:22.016907+00:00
| 969 | false |
The idea is that fourSum is just two twoSums\n1. We can treat the input like an N x N matrix of summed values \nwhere eg. nums[0][1] is nums[0] + nums[1]\nTo avoid duplicate calculations we only traverse half the matrix\nstopping right before nums[i][i] because that would be a number plus itself\n\n2. Similar to twoSum, we keep track of sums we\'ve seen so far\nand find the other half we need to add up to the target\nhave = nums[r] - nums[c] basically a new two sum\nneed = target - have\nHere we\'re keeping track of the indexes in an array, with a key of their sum\n\n3. If we find it, make sure that all indexes are unique by counting a unique set\nand making sure they add to up four. Then storying in a set\n\n112 ms\nO(N^2)\n\t\t\n```\nfrom collections import defaultdict\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n # Store a dp style table of [row][col] for each two sum\n dp = {}\n res = set()\n seen = defaultdict(list)\n # 1\n for r in range(len(nums)):\n for c in range(r):\n have = nums[r] + nums[c]\n need = target - have\n # 2\n if need in seen:\n # 3\n for r1,c1 in seen[need]:\n if len({r1,c1,r,c}) == 4:\n res.add( tuple(sorted([nums[r1],nums[c1],nums[r],nums[c]])) ) \n seen[have].append((r, c))\n return res\n```
| 7 | 0 |
['Dynamic Programming', 'Python']
| 5 |
4sum
|
C++ generalized to kSum
|
c-generalized-to-ksum-by-sunhaozhe-9lkw
|
Generalization to k-sum problems\n\nFor k >= 3, the following solution achieves the best time complexity possible which is O( n^{k-1} ).\nc++\n\tvoid kSum(vecto
|
sunhaozhe
|
NORMAL
|
2020-02-22T18:36:27.167272+00:00
|
2020-02-22T18:43:38.166715+00:00
| 1,291 | false |
# Generalization to k-sum problems\n\nFor `k >= 3`, the following solution achieves the best time complexity possible which is `O( n^{k-1} )`.\n```c++\n\tvoid kSum(vector<int>& nums, int target, int k, int start, vector<vector<int>>& res, vector<int>& curr, int sm){\n if(k == 2){\n int i = start, j = nums.size() - 1;\n target -= sm;\n while(i < j){\n if(nums[i] + nums[j] < target) i++;\n else if(nums[i] + nums[j] > target) j--;\n else{\n curr[curr.size() - 2] = nums[i];\n curr[curr.size() - 1] = nums[j];\n res.push_back(curr);\n while(i + 1 < j && nums[i] == nums[i + 1]) i++;\n i++;\n while(i < j - 1 && nums[j] == nums[j - 1]) j--;\n j--;\n }\n }\n return;\n }\n for(int i = start; i + k - 1 < nums.size(); i++){\n curr[curr.size() - k] = nums[i];\n kSum(nums, target, k - 1, i + 1, res, curr, sm + nums[i]);\n while(i + 1 < nums.size() && nums[i] == nums[i + 1]) i++;\n }\n }\n \n inline vector<vector<int>> kSumWrapper(vector<int>& nums, int target, int k){\n vector<vector<int>> res;\n sort(nums.begin(), nums.end());\n vector<int> curr(k, 0);\n kSum(nums, target, k, 0, res, curr, 0);\n return res;\n }\n \n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n return kSumWrapper(nums, target, 4);\n }\n```\n\n************************************************************************************************\n\nFor `k == 2`, the above solution does not achieve the best time complexity possible. One should instead use hash-table approach to achieve `O(n)` time complexity.
| 7 | 0 |
['C++']
| 0 |
4sum
|
kSum Java Solution, intuitive and clean.
|
ksum-java-solution-intuitive-and-clean-b-o079
|
The idea is to decompose the K sum problem into classic 2 sum problem. \nIn Two sum problem, we use head and tail pointer to find the solution.\njava\n publi
|
kaishenou
|
NORMAL
|
2019-02-17T06:39:02.591838+00:00
|
2019-02-17T06:39:02.591900+00:00
| 2,906 | false |
The idea is to decompose the K sum problem into classic 2 sum problem. \nIn Two sum problem, we use head and tail pointer to find the solution.\n```java\n public List<List<Integer>> fourSum(int[] nums, int target) {\n List<List<Integer>> res = new LinkedList<>();\n if(nums == null || nums.length == 0){\n return res;\n }\n Arrays.sort(nums);\n return kSum(4, nums,0,target);\n }\n\n public List<List<Integer>> kSum(int k, int[] nums, int startIndex, int target){\n List<List<Integer>> res = new LinkedList<>();\n if(k > nums.length - startIndex){\n return res;\n }\n if(k == 2){\n int i = startIndex, j = nums.length-1;\n while(i < j){\n if(nums[i] + nums[j] == target){\n List<Integer> temp = new LinkedList<>();\n temp.add(nums[i]);\n temp.add(nums[j]);\n res.add(temp);\n while(i < j && nums[i] == nums[++i]);\n while(i < j && nums[j] == nums[--j]);\n }\n else if(nums[i] + nums[j] < target){\n i++;\n }\n else{\n j--;\n }\n }\n return res;\n }\n else{\n for(int i = startIndex; i < nums.length; i++){\n if(i > startIndex && nums[i] == nums[i-1]){\n continue;\n }\n List<List<Integer>> tempLists = kSum(k - 1, nums, i + 1, target - nums[i]);\n for(List<Integer> temp : tempLists){\n temp.add(0,nums[i]);\n res.add(temp);\n }\n }\n return res;\n }\n }\n```
| 7 | 0 |
[]
| 2 |
4sum
|
O(n^2) method with cpp
|
on2-method-with-cpp-by-weiyang95-vpqp
|
It is very tricky that for cpp user, it would not be that much easier to implement the O(n^2) method since the deduplicate process is a bit disgusting. Here, I
|
weiyang95
|
NORMAL
|
2019-01-14T13:12:15.111771+00:00
|
2019-01-14T13:12:15.111814+00:00
| 1,469 | false |
It is very tricky that for cpp user, it would not be that much easier to implement the O(n^2) method since the deduplicate process is a bit disgusting. Here, I would share my code that solve such problem with built-in unique() function so as to implement the O(n^2) method. If you have any better method, please tell me. \n```\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n vector<vector<int>> result;\n if (nums.size() == 0)\n return result;\n \n unordered_map<int, vector<pair<int, int>>> map;\n for (int i = 0; i < nums.size(); ++i) {\n for (int j = i + 1; j < nums.size(); ++j) {\n map[target - nums[i] - nums[j]].push_back({i, j});\n }\n }\n \n for (int i = 0; i < nums.size(); ++i) {\n for (int j = i + 1; j < nums.size(); ++j) {\n int temp = nums[i] + nums[j];\n if (map.find(temp) != map.end()) {\n for (auto p : map[temp]) {\n if (p.first == i || p.first == j ||\n p.second == i || p.second == j)\n continue; \n result.push_back({nums[p.first], nums[p.second], nums[i], nums[j]});\n \n }\n }\n }\n }\n \n for (int i = 0; i < result.size(); ++i) {\n sort(result[i].begin(), result[i].end());\n }\n sort(result.begin(), result.end());\n result.erase(unique(result.begin(), result.end()), result.end());\n \n return result;\n }\n};\n```
| 7 | 0 |
[]
| 4 |
4sum
|
Simple Solution in Javascript
|
simple-solution-in-javascript-by-yinshen-f3h7
|
var fourSum = function(nums, target) {\n var ret = [];\n \n if(nums.length == 0)\n return ret;\n \n nums.sort(
|
yinsheng
|
NORMAL
|
2015-09-30T06:15:34+00:00
|
2015-09-30T06:15:34+00:00
| 2,460 | false |
var fourSum = function(nums, target) {\n var ret = [];\n \n if(nums.length == 0)\n return ret;\n \n nums.sort(function(a,b){\n return a - b; \n });\n \n for(var i = 0; i < nums.length; i++){\n var target2 = target - nums[i];\n \n for(var j = i + 1; j < nums.length; j++){\n var target3 = target2 - nums[j];\n \n var front = j + 1;\n var back = nums.length - 1;\n \n while(front < back){\n var sum = nums[front] + nums[back];\n \n if(sum < target3)\n front++;\n \n else if(sum > target3)\n back--;\n \n else{\n var temp = new Array(4);\n temp[0] = nums[i];\n temp[1] = nums[j];\n temp[2] = nums[front];\n temp[3] = nums[back];\n ret.push(temp);\n \n while(front < back && nums[front] === temp[2])\n front++;\n \n while(front < back && nums[back] === temp[3])\n back--;\n }\n }\n \n while(j + 1 < nums.length && nums[j + 1] === nums[j]) ++j;\n }\n \n while(i + 1 < nums.length && nums[i + 1] === nums[i]) ++i;\n }\n \n return ret;\n };
| 7 | 1 |
['JavaScript']
| 0 |
4sum
|
Python solution with detailed explanation
|
python-solution-with-detailed-explanatio-6ah2
|
Solution\n\n4Sum https://leetcode.com/problems/4sum/\n\n Brute force solution will be O(N^4).\n Optimized solution will be O(N^3). We will first sort the input.
|
gabbu
|
NORMAL
|
2017-01-19T03:45:47.012000+00:00
|
2017-01-19T03:45:47.012000+00:00
| 1,448 | false |
**Solution**\n\n**4Sum** https://leetcode.com/problems/4sum/\n\n* Brute force solution will be O(N^4).\n* Optimized solution will be O(N^3). We will first sort the input. Then we will use the two pointer technique.\n* We will use the same optimizations which we used in 3SUM problem to avoid duplicates. \n* Reference: https://discuss.leetcode.com/topic/75883/python-solution-with-detailed-explanation\n```\nclass Solution(object):\n def fourSum(self, nums, target):\n """\n :type nums: List[int]\n :type target: int\n :rtype: List[List[int]]\n """\n nums.sort()\n N, result = len(nums), []\n for i in range(N):\n if i > 0 and nums[i] == nums[i-1]:\n continue\n for j in range(i+1, N):\n if j > i+1 and nums[j] == nums[j-1]:\n continue\n x = target - nums[i] - nums[j]\n s,e = j+1, N-1\n while s < e:\n if nums[s]+nums[e] == x:\n result.append([nums[i], nums[j], nums[s], nums[e]])\n s = s+1\n while s < e and nums[s] == nums[s-1]:\n s = s+1\n elif nums[s]+nums[e] < x:\n s = s+1\n else:\n e = e-1\n return result\n```
| 7 | 0 |
[]
| 0 |
4sum
|
Golang concise 26ms solution
|
golang-concise-26ms-solution-by-redtree1-diqw
|
Just pick the first element and then for the remaining array, apply 3 sum.\nO(n^3) .\n\n\nfunc fourSum(nums []int, target int) [][]int {\n\tsort.Ints(nums)\n\tv
|
redtree1112
|
NORMAL
|
2017-02-10T09:00:38.871000+00:00
|
2017-02-10T09:00:38.871000+00:00
| 836 | false |
Just pick the first element and then for the remaining array, apply 3 sum.\n`O(n^3)` .\n\n```\nfunc fourSum(nums []int, target int) [][]int {\n\tsort.Ints(nums)\n\tvar res [][]int\n\tfor i := 0; i < len(nums)-3; i++ {\n\t\tif i != 0 && nums[i] == nums[i-1] {\n\t\t\tcontinue\n\t\t}\n\t\tthreeSum(&res, nums[i], nums[i+1:], target-nums[i])\n\t}\n\treturn res\n}\n\nfunc threeSum(res *[][]int, first int, nums []int, target int) {\n\tnlen := len(nums)\n\tfor i := 0; i < nlen-2; i++ {\n\t\tif i != 0 && nums[i] == nums[i-1] {\n\t\t\tcontinue\n\t\t}\n\n\t\tleft, right := i+1, nlen-1\n\t\tfor left < right {\n\t\t\tsum := nums[i] + nums[left] + nums[right]\n\t\t\tif sum == target {\n\t\t\t\t*res = append(*res, []int{first, nums[i], nums[left], nums[right]})\n\t\t\t\tfor left < right && nums[left] == nums[left+1] {\n\t\t\t\t\tleft++\n\t\t\t\t}\n\t\t\t\tfor left < right && nums[right] == nums[right-1] {\n\t\t\t\t\tright--\n\t\t\t\t}\n\t\t\t\tleft++\n\t\t\t\tright--\n\t\t\t} else if sum < target {\n\t\t\t\tfor left < right && nums[left] == nums[left+1] {\n\t\t\t\t\tleft++\n\t\t\t\t}\n\t\t\t\tleft++\n\t\t\t} else {\n\t\t\t\tfor left < right && nums[right] == nums[right-1] {\n\t\t\t\t\tright--\n\t\t\t\t}\n\t\t\t\tright--\n\t\t\t}\n\t\t}\n\t}\n}\n```
| 7 | 0 |
['Go']
| 0 |
4sum
|
Best Solution for Arrays 🚀 in C++, Python and Java || 100% working
|
best-solution-for-arrays-in-c-python-and-yinp
|
Intuition✨ The problem requires finding all unique quadruplets in the array that sum up to the target.
✨ Sorting the array and using pointers help reduce the pr
|
BladeRunner150
|
NORMAL
|
2025-01-21T16:54:44.946793+00:00
|
2025-01-21T16:54:44.946793+00:00
| 2,430 | false |
# Intuition
✨ The problem requires finding all unique quadruplets in the array that sum up to the target.
✨ Sorting the array and using pointers help reduce the problem's complexity.
# Approach
1️⃣ Sort the array to efficiently skip duplicates.
2️⃣ Use two nested loops to fix the first two numbers.
3️⃣ Use two pointers to find the remaining two numbers that complete the target sum.
4️⃣ Skip duplicates to ensure unique quadruplets.
# Complexity
- Time complexity: $$O(n^3)$$
- Space complexity: $$O(1)$$
# Code
```cpp []
#define ll long long
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
int n = nums.size();
sort(nums.begin(), nums.end());
vector<vector<int>> ans;
for (int i = 0; i < n; i++) {
if (i > 0 && nums[i] == nums[i - 1]) continue;
for (int j = i + 1; j < n; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
ll comp = (ll)target - (nums[i] + nums[j]);
int k = j + 1, l = n - 1;
while (k < l) {
if (nums[k] + nums[l] == comp) {
ans.push_back({nums[i], nums[j], nums[k], nums[l]});
while (k < l && nums[k] == nums[k + 1]) k++;
while (k < l && nums[l] == nums[l - 1]) l--;
k++;
l--;
} else if (nums[k] + nums[l] > comp) l--;
else k++;
}
}
}
return ans;
}
};
```
```python []
Code
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
nums.sort()
n = len(nums)
ans = []
for i in range(n):
if i > 0 and nums[i] == nums[i - 1]:
continue
for j in range(i + 1, n):
if j > i + 1 and nums[j] == nums[j - 1]:
continue
comp = target - (nums[i] + nums[j])
k, l = j + 1, n - 1
while k < l:
if nums[k] + nums[l] == comp:
ans.append([nums[i], nums[j], nums[k], nums[l]])
while k < l and nums[k] == nums[k + 1]:
k += 1
while k < l and nums[l] == nums[l - 1]:
l -= 1
k += 1
l -= 1
elif nums[k] + nums[l] > comp:
l -= 1
else:
k += 1
return ans
```
```java []
Code
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
Arrays.sort(nums);
int n = nums.length;
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (i > 0 && nums[i] == nums[i - 1]) continue;
for (int j = i + 1; j < n; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
long comp = (long)target - (nums[i] + nums[j]);
int k = j + 1, l = n - 1;
while (k < l) {
if (nums[k] + nums[l] == comp) {
ans.add(Arrays.asList(nums[i], nums[j], nums[k], nums[l]));
while (k < l && nums[k] == nums[k + 1]) k++;
while (k < l && nums[l] == nums[l - 1]) l--;
k++;
l--;
} else if (nums[k] + nums[l] > comp) {
l--;
} else {
k++;
}
}
}
}
return ans;
}
}
```
<img src="https://assets.leetcode.com/users/images/7b864aef-f8a2-4d0b-a376-37cdcc64e38c_1735298989.3319144.jpeg" alt="upvote" width="150px">
# Connect with me on LinkedIn for more insights! 🌟 Link in bio
| 6 | 0 |
['Array', 'Two Pointers', 'Sorting', 'Python', 'C++', 'Java', 'Python3']
| 0 |
4sum
|
Two Pointer || JAVA
|
two-pointer-java-by-anki99-hywc
|
IntuitionThe goal is to find all unique quadruplets in the array that sum up to the target. Since a brute force approach would involve iterating through all com
|
anki99
|
NORMAL
|
2025-01-06T17:02:18.596909+00:00
|
2025-04-02T16:54:35.532653+00:00
| 1,505 | false |
# Intuition
The goal is to find all unique quadruplets in the array that sum up to the target. Since a brute force approach would involve iterating through all combinations, which is inefficient, we can use a combination of sorting and the two-pointer technique to reduce the time complexity. Sorting the array helps identify and skip duplicates efficiently while maintaining order for the two-pointer traversal.
# Approach
1. **Sort the Array:** Begin by sorting the input array to simplify the process of handling duplicates and allow the use of two-pointer techniques.
2. **Iterate through the Array:**
- Use two nested loops (`i` and `j`) for the first two numbers of the quadruplet.
- Skip duplicate values for both `i` and `j` to avoid repeating the same quadruplets.
3. **Two-Pointer Technique:**
- For each pair of numbers chosen by `i` and `j`, use two pointers (`left` and `right`) to find the remaining two numbers.
- Adjust the pointers based on the sum:
- If the sum equals the target, add the quadruplet to the result and move both pointers inward while skipping duplicates.
- If the sum is less than the target, move the `left` pointer to increase the sum.
- If the sum is greater than the target, move the `right` pointer to decrease the sum.
4. **Avoid Overflow:** Use `long` for the sum to handle cases where the numbers are near `Integer.MAX_VALUE` or `Integer.MIN_VALUE`.
5. **Return Results:** Convert the results into a list of lists and return them.
# Complexity
- **Time complexity:** `O(n^3)`
- Sorting takes `O(nlog n)`.
- The nested loops (`i`, `j`) and two-pointer traversal take \(O(n^3)\) in total.
- **Space complexity:** \(O(1)\)
- Apart from the result list, no significant additional space is used.
# Code
```java
import java.util.*;
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> result = new ArrayList<>();
if (nums == null || nums.length < 4) {
return result; // Return empty list if not enough elements
}
Arrays.sort(nums); // Sort the array for easier duplicate handling
int n = nums.length;
for (int i = 0; i < n - 3; i++) {
// Skip duplicate values for the first number
if (i > 0 && nums[i] == nums[i - 1]) continue;
for (int j = i + 1; j < n - 2; j++) {
// Skip duplicate values for the second number
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
int left = j + 1;
int right = n - 1;
while (left < right) {
long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
if (sum == target) {
result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
left++;
right--;
// Skip duplicate values for the third and fourth numbers
while (left < right && nums[left] == nums[left - 1]) left++;
while (left < right && nums[right] == nums[right + 1]) right--;
} else if (sum < target) {
left++;
} else {
right--;
}
}
}
}
return result;
}
}
| 6 | 0 |
['Array', 'Two Pointers', 'Sorting', 'Java']
| 2 |
4sum
|
Beats 💯 percent Java, Python,C++ with full explanation of code
|
beats-percent-java-pythonc-with-full-exp-e9nm
|
Intuition\nThis code solves the 4-sum problem, where the goal is to find all unique quadruplets in a list of numbers that add up to a given target. Here\u2019s
|
raghavkwatraa
|
NORMAL
|
2024-10-27T06:09:53.498924+00:00
|
2024-10-27T06:10:41.902685+00:00
| 1,315 | false |
# Intuition\nThis code solves the 4-sum problem, where the goal is to find all unique quadruplets in a list of numbers that add up to a given target. Here\u2019s the step-by-step intuition behind the approach:\n\n# **1. Sort the Array**\n\nSorting the array simplifies the process of finding and skipping duplicates, as well as enables efficient two-pointer traversal to explore possible sums. After sorting, similar numbers are grouped together, making it easier to skip duplicates by comparing adjacent elements.\n\n# **2. Fix Two Elements with Nested Loops (Outer Two Loops)**\n\nThe idea is to break down the problem into smaller parts. By fixing the first two elements in a quadruplet (nums[i] and nums[j]), we transform the 4-sum problem into a simpler 2-sum problem for the remaining two elements (nums[li] and nums[ri]).\n\nLoop over i: The first loop iterates over the array to fix the first element of the quadruplet (nums[i]). If nums[i] is the same as nums[i - 1], it skips this index to avoid duplicate quadruplets.\n\n\nLoop over j: The second loop, starting after i, fixes the second element of the quadruplet (nums[j]). Similarly, it skips duplicates to avoid repeating quadruplets with the same first two elements.\n\n# **3. Use a Two-Pointer Technique for the Remaining Two Elements**\n\nOnce nums[i] and nums[j] are fixed, we use two pointers (li and ri) to find pairs of elements (nums[li] and nums[ri]) that complete the quadruplet to reach the target sum.\n\n\t\u2022\tCalculate the Sum: sum = nums[i] + nums[j] + nums[li] + nums[ri].\n\t\u2022\tCompare with the Target:\n\t\u2022\tIf sum == target: The quadruplet [nums[i], nums[j], nums[li], nums[ri]] is a valid solution, so it\u2019s added to the result list.\n\t\u2022\tIf sum < target: To increase the sum, move the left pointer li one step right.\n\t\u2022\tIf sum > target: To decrease the sum, move the right pointer ri one step left.\n\n# **4. Skip Duplicates with Two Pointers**\n\nAfter finding a valid quadruplet, the code increments li and decrements ri while skipping any duplicates (i.e., if the next element at li or ri is the same as the previous one). This avoids repeating quadruplets with the same third and fourth elements.\n\n# **5. Return the Result**\n\nAfter all loops and pointer movements, the list ans contains all unique quadruplets that sum up to the target.\n\nWhy This Approach Works Efficiently\n\n\t\u2022\tReduced Complexity: By reducing the 4-sum problem to a 2-sum problem using nested loops and two pointers, we keep the solution efficient. Sorting and using two-pointer traversal within a sorted array allows skipping duplicate quadruplets in an orderly way.\n\t\u2022\tAvoids Duplicates: Skipping duplicate elements ensures each quadruplet is unique, reducing unnecessary computations and maintaining optimal performance.\n\n\n# Complexity\n- Time complexity:\n\t1.\tSorting the Array: Sorting nums takes O(n \\log n), where n is the length of the array.\n\t2.\tNested Loops for Fixing the First Two Elements:\n\t\u2022\tThe outer two loops iterate over the array with indices i and j.\n\t\u2022\tFor each fixed pair (i, j), a two-pointer search is performed for the remaining two elements (li and ri).\n\t3.\tTwo-Pointer Search:\n\t\u2022\tFor each pair (i, j), the two-pointer search from li to ri has a time complexity of O(n).\n\t\u2022\tSo, for each pair (i, j), finding pairs with two pointers takes O(n).\n\nPutting it all together:\n\n\t\u2022\tThe two outer loops with indices i and j contribute O(n^2).\n\t\u2022\tThe two-pointer search for each (i, j) combination is O(n).\n\nThus, the total time complexity is:\n\n*# O(n^2 . n) = **O(n^3)***\n\n\n- Space complexity:\n O(n^2)\n\n# Code\n```java []\nclass Solution {\n public List<List<Integer>> fourSum(int[] nums, int target) {\n List<List<Integer>> ans= new ArrayList<>();\n int n = nums.length;\n\n Arrays.sort(nums);\n\n for(int i=0;i<n-3;i++){\n\n if(i > 0 && nums[i-1] == nums[i])\n continue;\n\n for(int j =i+1;j<n-2;j++){\n\n if(j > i+1 && nums[j-1] == nums[j])\n continue;\n int li = j+1;\n int ri = n-1;\n\n while(li<ri){\n long sum = nums[i]+nums[j];\n sum += nums[li]+nums[ri];\n\n if(sum == target){\n ans.add(Arrays.asList(nums[i],nums[j],nums[li],nums[ri]));\n\n li++;\n ri--;\n\n while(li < ri && nums[li-1] == nums[li])li++;\n\n while(li<ri && nums[ri+1] == nums[ri]) ri--;\n } else if(sum < target){\n li++;\n }else{\n ri--;\n }\n }\n }\n }\n return ans;\n }\n}\n```\n```python []\nclass Solution(object):\n def fourSum(self, nums, target):\n ans = []\n n = len(nums)\n\n nums.sort()\n\n for i in range(n - 3):\n if i > 0 and nums[i] == nums[i - 1]:\n continue\n\n for j in range(i + 1, n - 2):\n if j > i + 1 and nums[j] == nums[j - 1]:\n continue\n\n li, ri = j + 1, n - 1\n\n while li < ri:\n total = nums[i] + nums[j] + nums[li] + nums[ri]\n\n if total == target:\n ans.append([nums[i], nums[j], nums[li], nums[ri]])\n\n li += 1\n ri -= 1\n\n while li < ri and nums[li] == nums[li - 1]:\n li += 1\n while li < ri and nums[ri] == nums[ri + 1]:\n ri -= 1\n elif total < target:\n li += 1\n else:\n ri -= 1\n\n return ans\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n std::vector<std::vector<int>> ans;\n int n = nums.size();\n\n std::sort(nums.begin(), nums.end());\n\n for (int i = 0; i < n - 3; i++) {\n if (i > 0 && nums[i] == nums[i - 1]) continue;\n\n for (int j = i + 1; j < n - 2; j++) {\n if (j > i + 1 && nums[j] == nums[j - 1]) continue;\n\n int li = j + 1;\n int ri = n - 1;\n\n while (li < ri) {\n long long sum = static_cast<long long>(nums[i]) + nums[j] + nums[li] + nums[ri];\n\n if (sum == target) {\n ans.push_back({nums[i], nums[j], nums[li], nums[ri]});\n li++;\n ri--;\n\n while (li < ri && nums[li] == nums[li - 1]) li++;\n while (li < ri && nums[ri] == nums[ri + 1]) ri--;\n } else if (sum < target) {\n li++;\n } else {\n ri--;\n }\n }\n }\n }\n\n return ans;\n }\n};\n```\n\n
| 6 | 0 |
['Python', 'C++', 'Java']
| 1 |
4sum
|
⚕️[EASY] INTUITION & EXPLANATION
|
easy-intuition-explanation-by-ramitgangw-rrdl
|
\n\n# \uD83D\uDC93**_PLEASE CONSIDER UPVOTING_**\uD83D\uDC93\n\n \n\n\n# \u2B50 Intuition\nThe problem asks for finding all unique quadruplets (four numbers) in
|
ramitgangwar
|
NORMAL
|
2024-10-10T16:23:57.924285+00:00
|
2024-10-10T16:23:57.924322+00:00
| 1,280 | false |
<div align="center">\n\n# \uD83D\uDC93**_PLEASE CONSIDER UPVOTING_**\uD83D\uDC93\n\n</div>\n\n***\n# \u2B50 Intuition\nThe problem asks for finding all unique quadruplets (four numbers) in an array that add up to a given target. A brute force approach would involve checking every combination of four numbers, but this would be inefficient. Instead, we can leverage sorting and the two-pointer technique, which is often used for the 3-sum problem, to optimize the search for quadruplets.\n\n# \u2B50 Approach\n1. **Sort the array**: Sorting helps in efficiently applying the two-pointer technique and also allows us to skip duplicate elements.\n2. **Two loops for the first two numbers**:\n - Use two nested loops: the outer loop iterates over the first element of the quadruplet (`i`), and the inner loop iterates over the second element (`j`).\n - Skip duplicate elements in both loops to avoid generating duplicate quadruplets.\n3. **Two-pointer technique for the remaining two numbers**:\n - For the remaining two numbers, use a two-pointer approach:\n - Start one pointer `k` from just after `j` and another pointer `l` from the end of the array.\n - Calculate the sum of the four elements: `arr[i] + arr[j] + arr[k] + arr[l]`.\n - If the sum equals the target, add the quadruplet to the result and move both pointers inward while skipping duplicates.\n - If the sum is less than the target, move the left pointer (`k`) to increase the sum.\n - If the sum is greater than the target, move the right pointer (`l`) to decrease the sum.\n4. **Return the result**: The result list contains all unique quadruplets whose sum equals the target.\n\n# \u2B50 Complexity\n- **Time complexity:** \n Sorting the array takes $$O(n \\log n)$$, and we use two nested loops and a two-pointer technique, which results in a total time complexity of $$O(n^3)$$, where $$n$$ is the length of the array.\n\n- **Space complexity:** \n The space complexity is $$O(1)$$ for extra space since we only use a few variables for the two-pointer technique. However, the space complexity for the result list will depend on the number of quadruplets found.\n\n# \u2B50 Code\n```java\nclass Solution {\n public List<List<Integer>> fourSum(int[] arr, int target) {\n List<List<Integer>> ans = new ArrayList<>();\n int len = arr.length;\n\n Arrays.sort(arr);\n\n for (int i = 0; i < len - 3; i++) {\n if (i > 0 && arr[i - 1] == arr[i]) continue;\n\n for (int j = i + 1; j < len - 2; j++) {\n if (j > i + 1 && arr[j - 1] == arr[j]) continue;\n\n int k = j + 1;\n int l = len - 1;\n\n while (k < l) {\n long sum = arr[i] + arr[j];\n sum += arr[k] + arr[l];\n\n if (sum == target) {\n ans.add(Arrays.asList(arr[i], arr[j], arr[k], arr[l]));\n k++;\n l--;\n while (k < l && arr[k - 1] == arr[k]) k++;\n while (k < l && arr[l + 1] == arr[l]) l--;\n } else if (sum < target) {\n k++;\n } else {\n l--;\n }\n }\n }\n }\n\n return ans;\n }\n}\n```
| 6 | 0 |
['Array', 'Two Pointers', 'Sorting', 'Java']
| 0 |
4sum
|
18. 4Sum
|
18-4sum-by-layan_am-i7zu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
layan_am
|
NORMAL
|
2024-06-07T19:56:01.211370+00:00
|
2024-06-07T19:56:01.211390+00:00
| 4,380 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.util.*;\n\nclass Solution {\n public List<List<Integer>> fourSum(int[] nums, int target) {\n List<List<Integer>> result = new ArrayList<>();\n Set<List<Integer>> resultSet = new HashSet<>(); \n \n Arrays.sort(nums); \n \n for (int i = 0; i < nums.length - 3; i++) {\n for (int j = i + 1; j < nums.length - 2; j++) {\n int left = j + 1;\n int right = nums.length - 1;\n \n while (left < right) {\n long sum = (long)nums[i] + nums[j] + nums[left] + nums[right];\n if (sum == target) {\n List<Integer> arr = new ArrayList<>();\n arr.add(nums[i]);\n arr.add(nums[j]);\n arr.add(nums[left]);\n arr.add(nums[right]);\n \n if (!resultSet.contains(arr)) {\n resultSet.add(arr); \n }\n \n left++;\n right--;\n } else if (sum <= target) {\n left++;\n } else if(sum > target){\n right--;\n }\n }\n }\n }\n \n result.addAll(resultSet); \n \n return result;\n }\n}\n```
| 6 | 0 |
['Java']
| 1 |
4sum
|
Most optimal solution 🍃| Detailed explanation ☑️☑️
|
most-optimal-solution-detailed-explanati-h7n3
|
Approach\n1. First, we will sort the entire array.\n2. We will use a loop(say i) that will run from 0 to n-1. This i will represent one of the fixed pointers. I
|
Prabhakar_s_kulkarni
|
NORMAL
|
2024-03-02T17:47:54.707678+00:00
|
2024-03-02T17:47:54.707701+00:00
| 1,275 | false |
# Approach\n1. First, we will sort the entire array.\n2. We will use a loop(say i) that will run from 0 to n-1. This i will represent one of the fixed pointers. In each iteration, this value will be fixed for all different values of the rest of the 3 pointers. Inside the loop, we will first check if the current and the previous element is the same and if it is we will do nothing and continue to the next value of i.\n3. After checking inside the loop, we will introduce another fixed pointer j(runs from i+1 to n-1) using another loop. Inside this second loop, we will again check for duplicate elements and only perform any further operation if the elements are different.\n4. Inside the second loop, there will be 2 moving pointers i.e. k(starts from j+1) and l(starts from the last index). The pointer k will move forward and the pointer l will move backward until they cross each other while the value of i and j will be fixed.\n5. Now we will check the sum i.e. nums[i]+nums[j]+nums[k]+nums[l].\n- If the sum is greater, then we need lesser elements and so we will decrease the value of l.\n- If the sum is lesser than the target, we need a bigger value and so we will increase the value of k. \n- If the sum is equal to the target, we will simply insert the quad i.e. nums[i], nums[j], nums[k], and nums[l] into our answer and move the pointers k and l skipping the duplicate elements(i.e. by checking the adjacent elements while moving the pointers).\n6. Finally, we will have a list of unique quadruplets.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# PS\n- If there\'s any optimal code then do lmk, thank you :)\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n // Get the size of the input vector\n int n = nums.size();\n \n // Sort the input vector to simplify the search process\n sort(nums.begin(), nums.end());\n \n // Vector to store the resulting quadruplets\n vector<vector<int>> temp;\n \n // Loop through each element in the sorted vector\n for (int i = 0; i < n; i++) {\n // Skip duplicates of the first element to avoid duplicate quadruplets\n if (i > 0 && nums[i] == nums[i - 1])\n continue;\n \n // Loop through each element after the first element\n for (int j = i + 1; j < n; j++) {\n // Skip duplicates of the second element to avoid duplicate quadruplets\n if (j > i + 1 && nums[j] == nums[j - 1])\n continue;\n \n // Pointers for the third and fourth elements of the quadruplet\n int k = j + 1;\n int l = n - 1;\n \n // While the third pointer is less than the fourth pointer\n while (k < l) {\n // Calculate the sum of the current quadruplet\n //long long sum = nums[i] + nums[j] + nums[k] + nums[l];\n long long sum = static_cast<long long>(nums[i]) + nums[j] + nums[k] + nums[l];\n\n \n // If the sum equals the target, add the quadruplet to the result vector\n if (sum == target) {\n vector<int> ans = {nums[i], nums[j], nums[k], nums[l]};\n temp.push_back(ans);\n \n // Move the third pointer to the right and the fourth pointer to the left\n k++;\n l--;\n \n // Skip duplicates of the third and fourth elements\n while (k < l && nums[k] == nums[k - 1])\n k++;\n while (k < l && nums[l] == nums[l + 1])\n l--;\n } \n // If the sum is less than the target, move the third pointer to the right\n else if (sum < target) {\n k++;\n } \n // If the sum is greater than the target, move the fourth pointer to the left\n else {\n l--;\n }\n }\n }\n }\n // Return the resulting vector of quadruplets\n return temp;\n }\n};\n\n```\n\n
| 6 | 0 |
['Array', 'Two Pointers', 'Sorting', 'C++']
| 1 |
4sum
|
✅☑[C++/C/Java/Python/Javascript ] || 3 Best Approaches || Hash table || 2 pointers || Sorting 🔥
|
ccjavapythonjavascript-3-best-approaches-sbqy
|
PLEASE UPVOTE IF IT HELPED\n\n---\n\n# Approach\n(also explained in the code)\n\n1. Approach 1: (Using Two Pointers and Sorting with Hash Tables)\n\n2. Approach
|
MarkSPhilip31
|
NORMAL
|
2023-09-04T19:11:59.615262+00:00
|
2023-10-05T04:15:52.792765+00:00
| 897 | false |
# ***PLEASE UPVOTE IF IT HELPED***\n\n---\n\n# Approach\n***(also explained in the code)***\n\n1. **Approach 1:** **(Using Two Pointers and Sorting with Hash Tables)**\n\n2. **Approach 2:** **(Using a Hash Set for Efficiency )**\n\n\n3. **Approach 3:** **(Using Two Pointers and Sorting) (*Simplified*)** ***(Optimized)***\n \n\n# Complexity\n- **Time complexity:**\n1. $$O(n^3)$$\n2. $$O(n^3)$$\n3. $$O(n^3)$$ \n \n- **Space complexity:**\n1. $$O(n)$$\n2. $$O(n)$$\n3. $$O(1)$$\n\n\n# Code\n\n```C++ []\n\n\n -----------Approach 1------------\n\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end()); // Sort the input array.\n vector<vector<int>> ans; // Create a vector to store the result.\n set<vector<int>> pair; // Use a set to store unique quadruplets.\n\n int n = nums.size();\n for (int i = 0; i < n - 3; i++) {\n for (int j = i + 1; j < n - 2; j++) {\n long long newtarget = (long long)target - ((long long)nums[i] + (long long)nums[j]);\n int low = j + 1, high = n - 1;\n\n while (low < high) {\n if (nums[low] + nums[high] < newtarget) {\n low++;\n } else if (nums[low] + nums[high] > newtarget) {\n high--;\n } else {\n pair.insert({nums[i], nums[j], nums[low], nums[high]});\n low++;\n high--;\n }\n }\n }\n }\n\n for (auto a : pair) {\n ans.push_back(a); // Convert the set to a vector for the final result.\n }\n\n return ans;\n }\n};\n\n\n -----------Approach 2------------\n\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n set<vector<int>> st; // Use a set to store unique quadruplets.\n int n = nums.size();\n\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n set<long long> hash; // Use a set to store unique sums.\n\n for (int k = j + 1; k < n; k++) {\n long long sum = nums[i] + nums[j] + nums[k];\n long long forth = target - sum;\n\n if (hash.find(forth) != hash.end()) {\n vector<int> temp = {nums[i], nums[j], nums[k], (int)forth};\n sort(temp.begin(), temp.end());\n st.insert(temp);\n }\n hash.insert(nums[k]);\n }\n }\n }\n\n vector<vector<int>> ans(st.begin(), st.end()); // Convert the set to a vector for the final result.\n return ans;\n }\n};\n\n\n -----------Approach 3------------\n\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n sort(nums.begin(), nums.end()); // Sort the input array.\n vector<vector<int>> ans; // Create a vector to store the result.\n\n int n = nums.size();\n for (int i = 0; i < n - 3; i++) {\n for (int j = i + 1; j < n - 2; j++) {\n long long newtarget = (long long)target - ((long long)nums[i] + (long long)nums[j]);\n int low = j + 1, high = n - 1;\n\n while (low < high) {\n if (nums[low] + nums[high] < newtarget) {\n low++;\n } else if (nums[low] + nums[high] > newtarget) {\n high--;\n } else {\n ans.push_back({nums[i], nums[j], nums[low], nums[high]});\n int index1 = low, index2 = high;\n while (low < high && nums[low] == nums[index1]) low++;\n while (low < high && nums[high] == nums[index2]) high--;\n }\n }\n while (j + 1 < n && nums[j] == nums[j + 1]) j++;\n }\n while (i + 1 < n && nums[i] == nums[i + 1]) i++;\n }\n\n return ans;\n }\n};\n\n\n\n\n\n```\n```Java []\n\n -----------Approach 1------------\n\nclass Solution {\n public List<List<Integer>> fourSum(int[] nums, int target) {\n Arrays.sort(nums); // Sort the input array.\n List<List<Integer>> ans = new ArrayList<>(); // Create a list to store the result.\n Set<List<Integer>> pair = new HashSet<>(); // Use a set to store unique quadruplets.\n\n int n = nums.length;\n for (int i = 0; i < n - 3; i++) {\n for (int j = i + 1; j < n - 2; j++) {\n long newTarget = (long) target - ((long) nums[i] + (long) nums[j]);\n int low = j + 1, high = n - 1;\n\n while (low < high) {\n if (nums[low] + nums[high] < newTarget) {\n low++;\n } else if (nums[low] + nums[high] > newTarget) {\n high--;\n } else {\n pair.add(Arrays.asList(nums[i], nums[j], nums[low], nums[high]));\n low++;\n high--;\n }\n }\n }\n }\n\n ans.addAll(pair);\n return ans;\n }\n}\n\n\n -----------Approach 2------------\n\nclass Solution {\n public List<List<Integer>> fourSum(int[] nums, int target) {\n Set<List<Integer>> set = new HashSet<>(); // Use a set to store unique quadruplets.\n int n = nums.length;\n\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n Set<Long> hash = new HashSet<>(); // Use a set to store unique sums.\n\n for (int k = j + 1; k < n; k++) {\n long sum = (long) nums[i] + nums[j] + nums[k];\n long forth = (long) target - sum;\n\n if (hash.contains(forth)) {\n List<Integer> temp = Arrays.asList(nums[i], nums[j], nums[k], (int) forth);\n Collections.sort(temp);\n set.add(temp);\n }\n hash.add((long) nums[k]);\n }\n }\n }\n\n return new ArrayList<>(set);\n }\n}\n\n\n -----------Approach 3------------\n\nclass Solution {\n public List<List<Integer>> fourSum(int[] nums, int target) {\n Arrays.sort(nums); // Sort the input array.\n List<List<Integer>> ans = new ArrayList<>(); // Create a list to store the result.\n\n int n = nums.length;\n for (int i = 0; i < n - 3; i++) {\n for (int j = i + 1; j < n - 2; j++) {\n long newTarget = (long) target - ((long) nums[i] + (long) nums[j]);\n int low = j + 1, high = n - 1;\n\n while (low < high) {\n if (nums[low] + nums[high] < newTarget) {\n low++;\n } else if (nums[low] + nums[high] > newTarget) {\n high--;\n } else {\n ans.add(Arrays.asList(nums[i], nums[j], nums[low], nums[high]));\n int index1 = low, index2 = high;\n while (low < high && nums[low] == nums[index1]) low++;\n while (low < high && nums[high] == nums[index2]) high--;\n }\n }\n while (j + 1 < n && nums[j] == nums[j + 1]) j++;\n }\n while (i + 1 < n && nums[i] == nums[i + 1]) i++;\n }\n\n return ans;\n }\n}\n\n\n\n```\n\n```C []\n\n\n -----------Approach 1------------\n\n#include <stdio.h>\n#include <stdlib.h>\n#include <string.h>\n\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n\nint** fourSum(int* nums, int numsSize, int target, int* returnSize, int** returnColumnSizes) {\n qsort(nums, numsSize, sizeof(int), compare);\n int** ans = NULL;\n *returnSize = 0;\n\n for (int i = 0; i < numsSize - 3; i++) {\n if (i > 0 && nums[i] == nums[i - 1]) continue;\n for (int j = i + 1; j < numsSize - 2; j++) {\n if (j > i + 1 && nums[j] == nums[j - 1]) continue;\n long long newTarget = (long long)target - nums[i] - nums[j];\n int low = j + 1, high = numsSize - 1;\n\n while (low < high) {\n long long sum = nums[low] + nums[high];\n if (sum < newTarget) {\n low++;\n } else if (sum > newTarget) {\n high--;\n } else {\n (*returnSize)++;\n ans = (int**)realloc(ans, (*returnSize) * sizeof(int*));\n ans[*returnSize - 1] = (int*)malloc(4 * sizeof(int));\n ans[*returnSize - 1][0] = nums[i];\n ans[*returnSize - 1][1] = nums[j];\n ans[*returnSize - 1][2] = nums[low];\n ans[*returnSize - 1][3] = nums[high];\n while (low < high && nums[low] == nums[low + 1]) low++;\n while (low < high && nums[high] == nums[high - 1]) high--;\n low++;\n high--;\n }\n }\n }\n }\n\n *returnColumnSizes = (int*)malloc(*returnSize * sizeof(int));\n for (int i = 0; i < *returnSize; i++) {\n (*returnColumnSizes)[i] = 4;\n }\n\n return ans;\n}\n\n\n -----------Approach 2------------\n\n#include <stdio.h>\n#include <stdlib.h>\n#include <string.h>\n\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n\nint** fourSum(int* nums, int numsSize, int target, int* returnSize, int** returnColumnSizes) {\n int** ans = NULL;\n *returnSize = 0;\n\n qsort(nums, numsSize, sizeof(int), compare);\n\n for (int i = 0; i < numsSize; i++) {\n if (i > 0 && nums[i] == nums[i - 1]) continue;\n for (int j = i + 1; j < numsSize; j++) {\n if (j > i + 1 && nums[j] == nums[j - 1]) continue;\n long long newTarget = (long long)target - nums[i] - nums[j];\n int low = j + 1, high = numsSize - 1;\n\n while (low < high) {\n long long sum = (long long)nums[low] + nums[high];\n if (sum < newTarget) {\n low++;\n } else if (sum > newTarget) {\n high--;\n } else {\n (*returnSize)++;\n ans = (int**)realloc(ans, (*returnSize) * sizeof(int*));\n ans[*returnSize - 1] = (int*)malloc(4 * sizeof(int));\n ans[*returnSize - 1][0] = nums[i];\n ans[*returnSize - 1][1] = nums[j];\n ans[*returnSize - 1][2] = nums[low];\n ans[*returnSize - 1][3] = nums[high];\n while (low < high && nums[low] == nums[low + 1]) low++;\n while (low < high && nums[high] == nums[high - 1]) high--;\n low++;\n high--;\n }\n }\n }\n }\n\n *returnColumnSizes = (int*)malloc(*returnSize * sizeof(int));\n for (int i = 0; i < *returnSize; i++) {\n (*returnColumnSizes)[i] = 4;\n }\n\n return ans;\n}\n\n\n -----------Approach 3------------\n\n\n#include <stdio.h>\n#include <stdlib.h>\n#include <string.h>\n\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n\nint** fourSum(int* nums, int numsSize, int target, int* returnSize, int** returnColumnSizes) {\n int** ans = NULL;\n *returnSize = 0;\n\n qsort(nums, numsSize, sizeof(int), compare);\n\n for (int i = 0; i < numsSize - 3; i++) {\n if (i > 0 && nums[i] == nums[i - 1]) continue;\n for (int j = i + 1; j < numsSize - 2; j++) {\n if (j > i + 1 && nums[j] == nums[j - 1]) continue;\n long long newTarget = (long long)target - nums[i] - nums[j];\n int low = j + 1, high = numsSize - 1;\n\n while (low < high) {\n long long sum = (long long)nums[low] + nums[high];\n if (sum < newTarget) {\n low++;\n } else if (sum > newTarget) {\n high--;\n } else {\n (*returnSize)++;\n ans = (int**)realloc(ans, (*returnSize) * sizeof(int*));\n ans[*returnSize - 1] = (int*)malloc(4 * sizeof(int));\n ans[*returnSize - 1][0] = nums[i];\n ans[*returnSize - 1][1] = nums[j];\n ans[*returnSize - 1][2] = nums[low];\n ans[*returnSize - 1][3] = nums[high];\n while (low < high && nums[low] == nums[low + 1]) low++;\n while (low < high && nums[high] == nums[high - 1]) high--;\n low++;\n high--;\n }\n }\n }\n }\n\n *returnColumnSizes = (int*)malloc(*returnSize * sizeof(int));\n for (int i = 0; i < *returnSize; i++) {\n (*returnColumnSizes)[i] = 4;\n }\n\n return ans;\n}\n\n\n\n\n```\n\n```python []\n\n\n -----------Approach 1------------\n\ndef fourSum(nums, target):\n nums.sort()\n ans = set()\n n = len(nums)\n \n for i in range(n - 3):\n for j in range(i + 1, n - 2):\n new_target = target - nums[i] - nums[j]\n low, high = j + 1, n - 1\n\n while low < high:\n if nums[low] + nums[high] < new_target:\n low += 1\n elif nums[low] + nums[high] > new_target:\n high -= 1\n else:\n ans.add((nums[i], nums[j], nums[low], nums[high]))\n low += 1\n high -= 1\n \n return list(ans)\n\n\n -----------Approach 2------------\n\ndef fourSum(nums, target):\n ans = set()\n n = len(nums)\n\n for i in range(n):\n for j in range(i + 1, n):\n hash_set = set()\n\n for k in range(j + 1, n):\n current_sum = nums[i] + nums[j] + nums[k]\n fourth = target - current_sum\n\n if fourth in hash_set:\n ans.add(tuple(sorted([nums[i], nums[j], nums[k], fourth])))\n hash_set.add(nums[k])\n \n return list(ans)\n\n\n -----------Approach 3------------\n\n\ndef fourSum(nums, target):\n nums.sort()\n ans = []\n n = len(nums)\n \n for i in range(n - 3):\n if i > 0 and nums[i] == nums[i - 1]:\n continue\n for j in range(i + 1, n - 2):\n if j > i + 1 and nums[j] == nums[j - 1]:\n continue\n new_target = target - nums[i] - nums[j]\n low, high = j + 1, n - 1\n\n while low < high:\n current_sum = nums[low] + nums[high]\n if current_sum < new_target:\n low += 1\n elif current_sum > new_target:\n high -= 1\n else:\n ans.append([nums[i], nums[j], nums[low], nums[high]])\n while low < high and nums[low] == nums[low + 1]:\n low += 1\n while low < high and nums[high] == nums[high - 1]:\n high -= 1\n low += 1\n high -= 1\n return ans\n\n\n\n\n```\n\n```javascript []\n\n\n -----------Approach 1------------\n\nvar fourSum = function(nums, target) {\n nums.sort((a, b) => a - b);\n const ans = new Set();\n const n = nums.length;\n\n for (let i = 0; i < n - 3; i++) {\n for (let j = i + 1; j < n - 2; j++) {\n const newTarget = target - nums[i] - nums[j];\n let low = j + 1, high = n - 1;\n\n while (low < high) {\n if (nums[low] + nums[high] < newTarget) {\n low++;\n } else if (nums[low] + nums[high] > newTarget) {\n high--;\n } else {\n ans.add([nums[i], nums[j], nums[low], nums[high]].toString());\n low++;\n high--;\n }\n }\n }\n }\n\n return Array.from(ans).map(item => item.split(\',\').map(Number));\n};\n\n\n -----------Approach 2------------\n\nvar fourSum = function(nums, target) {\n const ans = new Set();\n const n = nums.length;\n\n for (let i = 0; i < n; i++) {\n for (let j = i + 1; j < n; j++) {\n const hash = new Set();\n\n for (let k = j + 1; k < n; k++) {\n const currentSum = nums[i] + nums[j] + nums[k];\n const fourth = target - currentSum;\n\n if (hash.has(fourth)) {\n ans.add([nums[i], nums[j], nums[k], fourth].sort((a, b) => a - b).toString());\n }\n hash.add(nums[k]);\n }\n }\n }\n\n return Array.from(ans).map(item => item.split(\',\').map(Number));\n};\n\n\n -----------Approach 3------------\n\n\nvar fourSum = function(nums, target) {\n nums.sort((a, b) => a - b);\n const ans = [];\n const n = nums.length;\n\n for (let i = 0; i < n - 3; i++) {\n if (i > 0 && nums[i] === nums[i - 1]) continue;\n for (let j = i + 1; j < n - 2; j++) {\n if (j > i + 1 && nums[j] === nums[j - 1]) continue;\n const newTarget = target - nums[i] - nums[j];\n let low = j + 1, high = n - 1;\n\n while (low < high) {\n const currentSum = nums[low] + nums[high];\n if (currentSum < newTarget) {\n low++;\n } else if (currentSum > newTarget) {\n high--;\n } else {\n ans.push([nums[i], nums[j], nums[low], nums[high]]);\n while (low < high && nums[low] === nums[low + 1]) low++;\n while (low < high && nums[high] === nums[high - 1]) high--;\n low++;\n high--;\n }\n }\n }\n }\n\n return ans;\n};\n\n\n\n\n```\n\n\n\n\n\n# ***PLEASE UPVOTE IF IT HELPED***\n\n---\n\n\n---\n\n\n
| 6 | 0 |
['Array', 'Hash Table', 'Two Pointers', 'Binary Search', 'C', 'Sorting', 'Python', 'C++', 'Java', 'JavaScript']
| 1 |
4sum
|
Brute Force ,Optimised, Hashset Approach
|
brute-force-optimised-hashset-approach-b-3540
|
Brute Force--->O(N^4)--->[TLE]\n\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n ans=[]\n n=len(nums)\
|
GANJINAVEEN
|
NORMAL
|
2023-08-22T07:43:30.345530+00:00
|
2023-08-22T07:48:11.161359+00:00
| 1,145 | false |
# Brute Force--->O(N^4)--->[TLE]\n```\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n ans=[]\n n=len(nums)\n for i in range(n-3):\n for j in range(i+1,n-2):\n for k in range(j+1,n-1):\n for l in range(k+1,n):\n temp=nums[i]+nums[j]+nums[k]+nums[l]\n sorted_num=sorted([nums[i],nums[j],nums[k],nums[l]])\n if temp==target and sorted_num not in ans:\n ans.append(sorted_num)\n return ans\n```\n# Optimised Approach-->Two Pointers Appraoch ----> O(N^3)---->[Accepted]\n```\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n ans=[]\n n=len(nums)\n nums.sort()\n for i in range(n-3):\n for j in range(i+1,n-2):\n k=j+1\n l=n-1\n while k<l:\n temp=nums[i]+nums[j]+nums[k]+nums[l]\n sorted_num=sorted([nums[i],nums[j],nums[k],nums[l]])\n if temp==target and sorted_num not in ans:\n ans.append(sorted_num)\n elif temp>target:\n l-=1\n else:\n k+=1\n return ans\n ```\n # Using Hashset----->O(N^3)---->[Accepted]\n ```\n class Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n ans=set()\n n=len(nums)\n nums.sort()\n for i in range(n-3):\n for j in range(i+1,n-2):\n k=j+1\n l=n-1\n while k<l:\n temp=nums[i]+nums[j]+nums[k]+nums[l]\n if temp==target:\n ans.add((nums[i],nums[j],nums[k],nums[l]))\n k+=1\n elif temp>target:\n l-=1\n else:\n k+=1\n return list(ans)\n ```\n # please upvote me it would encourage me alot\n\n
| 6 | 0 |
[]
| 1 |
4sum
|
Best O(N^3) Solution
|
best-on3-solution-by-kumar21ayush03-kv2c
|
Approach\nUsing Two Pointer\n\n# Complexity\n- Time complexity:\nO(n^3)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n vector<vector<i
|
kumar21ayush03
|
NORMAL
|
2023-06-07T13:49:30.610381+00:00
|
2023-06-07T13:49:30.610428+00:00
| 1,648 | false |
# Approach\nUsing Two Pointer\n\n# Complexity\n- Time complexity:\n$$O(n^3)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n int n = nums.size();\n sort(nums.begin(), nums.end());\n vector<vector<int>> quadruplets;\n for (int i = 0; i < n; i++) {\n if (i != 0 && nums[i] == nums[i-1])\n continue;\n for (int j = i+1; j < n; j++) {\n if (j != i+1 && nums[j] == nums[j-1])\n continue;\n int k = j+1, l = n-1; \n while (k < l) {\n long long sum = nums[i] + nums[j];\n sum += nums[k];\n sum += nums[l];\n if (sum == target) {\n vector<int> temp = {nums[i], nums[j], nums[k], nums[l]};\n quadruplets.push_back(temp);\n k++;\n l--;\n while (k < l && nums[k] == nums[k-1]) k++;\n while (k < l && nums[l] == nums[l+1]) l--;\n } else if (sum > target) {\n l--;\n } else {\n k++;\n }\n } \n }\n }\n return quadruplets;\n }\n};\n```
| 6 | 0 |
['C++']
| 0 |
4sum
|
C++ | ⌛| USING 3 SUM | EASY EXPLANATION | BEGINNER FRIENDLY
|
c-using-3-sum-easy-explanation-beginner-bq0gx
|
UPVOTE AGAR SAWAL ASAAN KIYA AAPKE LIYE \uD83D\uDE42.\n# Advice\nDONT GO DIRECTLY TO SOLUTION.UNDERSTAND THE FLOW/APPROACH.\nYOU MUST BE KNOWING HOW TO SOLVE TW
|
codman_1
|
NORMAL
|
2023-04-21T06:50:29.211355+00:00
|
2023-04-21T06:50:29.211381+00:00
| 932 | false |
UPVOTE AGAR SAWAL ASAAN KIYA AAPKE LIYE \uD83D\uDE42.\n# Advice\nDONT GO DIRECTLY TO SOLUTION.UNDERSTAND THE FLOW/APPROACH.\nYOU MUST BE KNOWING HOW TO SOLVE TWO SUM PROBLEM .\n\n# Intuition\nI HAVE SOLVED 3SUM USING 2 SUM .THAT\'S WHY I GOT INTUTION TO SOLVE FOUR SOME(\uD83D\uDE01) USING 3 SUM .\n\n# Approach\n1. IN AN ARRAY AT INDEX I, I TAKE THE ARRAY ELEMENT IN FOUR SUM CONSIDERATION IF NOT PREVIOUSLY TAKEN AND STORE IT IN A VARIABLE A=NUMS[I] .THEN ASK THREE SUM TO FIND TARGET-NUMS[I] IN REMAINING ARRAY.\n\n2. AGAIN IN ARRAY AT INDEX I, TAKE THE ARRAY ELEMENT IN FOUR SUM CONSIDERATION IF NOT PREVIOUSLY TAKEN AND STORE IT IN A VARIABLE B=NUMS[I].THEN ASK FOR TWO SUM TO FIND TARGET-NUMS[I] IN REMAINING ARRAY.\n\n3. SIMPLE TWO SUM PROBLEM\uD83D\uDE0E.\n\n```\nwhile(i<j){\n if(target==nums[i]+nums[j]){\n //STORE IN ANS \n ans.push_back({a,b,nums[i],nums[j]});\n // DISTINCT SUBARRAY SHOULD BE INSIDE VECTOR<VECTOR<INT>>ANS.\n i++,j--;\n while(j>i && nums[j]==nums[j+1])j--;\n while(i<j&&nums[i]==nums[i-1])i++;\n }\n else if(nums[i]+nums[j]>target)j--;\n else{\n ++i;\n }\n }\n\n```\nEXAMPLE : LET ARRAY[-2,-2,-1,0,1,1,2,2].TARGET=0.\n\n\n# Code\n```\nclass Solution {\npublic:\n void twosum(vector<int>&nums,int i,long long target,vector<vector<int>>&ans,int a ,int b){\n int n =nums.size();\n int j=n-1;\n\n while(i<j){\n if(target==nums[i]+nums[j]){\n ans.push_back({a,b,nums[i],nums[j]});\n i++,j--;\n while(j>i && nums[j]==nums[j+1])j--;\n while(i<j&&nums[i]==nums[i-1])i++;\n }\n else if(nums[i]+nums[j]>target)j--;\n else{\n ++i;\n }\n }\n return;\n }\n void threesum(vector<vector<int>>&ans,vector<int>& nums,int j,long long target,int a ) {\n int n =nums.size();\n twosum(nums,j+1,target-nums[j],ans,a,nums[j]);\n\n for(int i =j+1;i<n-2;i++){\n if(nums[i]==nums[i-1])continue;\n int b=nums[i];\n twosum(nums,i+1,target-nums[i],ans,a,b);\n }\n return ;\n }\n vector<vector<int>> fourSum(vector<int>& nums, int t) {\n long long target=t;\n vector<vector<int>>ans;\n sort(nums.begin(),nums.end());\n int n =nums.size();\n\n if(n>=4)threesum(ans,nums,1,target-nums[0],nums[0]);\n if(nums[0]>0 && nums[0]>target)return ans;\n\n for(int i=1;i<n-3;i++){\n if(nums[i]==nums[i-1])continue;\n int a=nums[i];\n threesum(ans,nums,i+1,target-nums[i],a);\n }\n return ans ;\n }\n};\n```\nTHANK YOU \nCODE BY:) AMAN MAURYA
| 6 | 0 |
['C++']
| 0 |
4sum
|
94% javascript fast very easy to understand solution with video explanation!
|
94-javascript-fast-very-easy-to-understa-8tug
|
Here is video for explain if it is helpful please subscribe! :\n\nhttps://youtu.be/U4cX-QMlmgA\n\n# Code\n\n/**\n * @param {number[]} nums\n * @param {number} t
|
rlawnsqja850
|
NORMAL
|
2023-01-15T18:07:28.620814+00:00
|
2023-01-15T18:14:33.070053+00:00
| 2,559 | false |
Here is video for explain if it is helpful please subscribe! :\n\nhttps://youtu.be/U4cX-QMlmgA\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @param {number} target\n * @return {number[][]}\n */\nvar fourSum = function(nums, target) {\n let res = []\n nums.sort((a,b)=>a-b)\n\n for(let i =0; i< nums.length-3;i++){\n for(let j =i+1; j<nums.length-2;j++){\n let f = nums[i];\n let s = nums[j];\n let left = j+1;\n let right = nums.length-1;\n while(left<right){\n let sum = f + s + nums[left] + nums[right];\n if(sum < target) left++\n else if(sum > target) right--\n else {\n res.push([f,s,nums[left],nums[right]]);\n while(nums[left] == nums[left+1])left++\n while(nums[right] == nums[right-1]) right--\n left++\n right--\n }\n }\n while(nums[j] == nums[j+1]) j++\n }\n while(nums[i] == nums[i+1]) i++\n }\n return res\n};\n```
| 6 | 0 |
['JavaScript']
| 0 |
4sum
|
C++ Solution
|
c-solution-by-pranto1209-9t8c
|
Code\n\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n vector<vector<int>> ans;\n sort(nums.begin()
|
pranto1209
|
NORMAL
|
2022-11-15T15:12:03.982401+00:00
|
2023-03-14T08:14:42.962126+00:00
| 1,399 | false |
# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int>& nums, int target) {\n vector<vector<int>> ans;\n sort(nums.begin(), nums.end());\n map<vector<int>, int> mp;\n for(int i=0; i<nums.size()-1; i++) {\n for(int j=i+1; j<nums.size(); j++) {\n int l = j + 1, r = nums.size() - 1; \n while(l < r) {\n long long sum = (long long) nums[i] + nums[j] + nums[l] + nums[r];\n if(sum == target) {\n mp[{nums[i], nums[j], nums[l], nums[r]}]++;\n if(mp[{nums[i], nums[j], nums[l], nums[r]}] == 1) ans.push_back({nums[i], nums[j], nums[l], nums[r]});\n l++;\n r--;\n }\n else if(sum < target) l++;\n else if(sum > target) r--;\n }\n }\n }\n return ans;\n }\n};\n```
| 6 | 0 |
['C++']
| 0 |
4sum
|
✅ JS || Multiple Approaches || Easy to understand
|
js-multiple-approaches-easy-to-understan-e426
|
I just found this Blog and Github repository with solutions to Leetcode problems.\nhttps://leet-codes.blogspot.com/2022/10/4-sum.html\nIt has solutions to almos
|
pmistry_
|
NORMAL
|
2022-11-07T03:06:49.014041+00:00
|
2022-11-07T03:06:49.014074+00:00
| 1,117 | false |
I just found this Blog and Github repository with solutions to Leetcode problems.\nhttps://leet-codes.blogspot.com/2022/10/4-sum.html\nIt has solutions to almost every problem on Leetcode, and I recommend checking it out.\nNote: You can bookmark it as a resource, and approach. Other approaches are in above blog\n<br>\n\n```\nvar fourSum = function (nums, target) {\n let solutionArrays = [];\n\n // Sort the array\n sortedNums = nums.sort((a, b) => a - b);\n\n // Loop through the array (excluding the last 3 entries)\n for (let i = 0; i < sortedNums.length - 3; i++) {\n // Check if this is the same number as the last one\n if (i > 0 && sortedNums[i] == sortedNums[i - 1]) {\n continue;\n }\n\n // Loop through the remaining numbers\n for (let j = i + 1; j < sortedNums.length - 2; j++) {\n // Check if this is the same number as the last one\n if (j > i + 1 && sortedNums[j] == sortedNums[j - 1]) {\n continue;\n }\n\n // Establish a window from the next number to the end of the array\n let left = j + 1;\n let right = sortedNums.length - 1;\n\n // Run until the window is closed\n while (left < right) {\n // Add together the current numbers, and each side of the window\n const total =\n sortedNums[i] +\n sortedNums[j] +\n sortedNums[left] +\n sortedNums[right];\n\n // If we\'ve reached an answer, add it to the array of answers\n if (total == target) {\n solutionArrays.push([\n sortedNums[i],\n sortedNums[j],\n sortedNums[left],\n sortedNums[right],\n ]);\n\n // Move the left-hand edge of the window to the right until it reaches a different number\n do {\n left++;\n } while (sortedNums[left] == sortedNums[left - 1]);\n\n // Move the right-hand edge of the window to the left until it reaches a different number\n do {\n right--;\n } while (sortedNums[right] == sortedNums[right + 1]);\n }\n // If we\'re too low\n else if (total < target) {\n left++;\n }\n // If we\'re too high\n else {\n right--;\n }\n }\n }\n }\n\n return solutionArrays;\n};\n```
| 6 | 0 |
['JavaScript']
| 2 |
4sum
|
JAVA | 2 approaches | Brute and Optimal
|
java-2-approaches-brute-and-optimal-by-s-lgzj
|
Please Upvote :D\n##### 1. Brute force approach (TLE - 288/291 passed):\n\nclass Solution {\n public List<List<Integer>> fourSum(int[] nums, int target) {\n
|
sourin_bruh
|
NORMAL
|
2022-10-09T19:05:21.480169+00:00
|
2022-10-18T10:01:40.156777+00:00
| 4,062 | false |
### **Please Upvote** :D\n##### 1. Brute force approach (TLE - 288/291 passed):\n```\nclass Solution {\n public List<List<Integer>> fourSum(int[] nums, int target) {\n int n = nums.length;\n if (n < 4) return new ArrayList<>(); // it\'d still be handled even if we don\'t write this condition\n Arrays.sort(nums);\n\n Set<List<Integer>> ans = new HashSet<>();\n\n for (int i = 0; i < n; i++) \n for (int j = i + 1; j < n; j++) \n for (int k = j + 1; k < n; k++) \n for (int l = k + 1; l < n; l++) \n if (nums[i] + nums[j] + nums[k] + nums[l] == target) \n ans.add(Arrays.asList(nums[i], nums[j], nums[k], nums[l]));\n\n return new ArrayList(ans);\n }\n}\n\n// TC: O(n * logn) + O(n ^ 4) => O(n ^ 4)\n// SC: O(1) - Ignoring output array\n```\n##### 2. Optimal solution (Two pointers):\nWe iterate using the first for loop and find the remaining 3 elements by the same **[3Sum](https://leetcode.com/problems/3sum/discuss/2397624/JAVA-or-3-approaches)** approach.\n\nOr we can say, we find the first two elements using nested for loops and find the remaining 2 elements by the **[TwoSum](https://leetcode.com/problems/two-sum/discuss/2345909/Java-solution-(brute-force-and-optimized))** approach.\n```\nclass Solution {\n public List<List<Integer>> fourSum(int[] nums, int target) {\n List<List<Integer>> ans = new ArrayList<>();\n int n = nums.length;\n\n Arrays.sort(nums);\n\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n\n long target2 = (long) target - (long) nums[i] - (long) nums[j];\n int lo = j + 1, hi = n - 1;\n\n while (lo < hi) {\n int twoSum = nums[lo] + nums[hi];\n\n if (twoSum < target2) lo++;\n else if (twoSum > target2) hi--;\n else {\n List<Integer> quad = Arrays.asList(nums[i], nums[j], nums[lo], nums[hi]);\n ans.add(quad);\n\n while (lo < hi && nums[lo] == quad.get(2)) lo++;\n while (lo < hi && nums[hi] == quad.get(3)) hi--;\n }\n }\n\n while (j + 1 < n && nums[j] == nums[j + 1]) j++;\n }\n\n while (i + 1 < n && nums[i] == nums[i + 1]) i++;\n }\n\n return ans;\n }\n}\n\n// TC: O(n * logn) + O(n ^ 3) => O(n ^ 3)\n// SC: O(1) - ignoring the output array\n```
| 6 | 0 |
['Two Pointers', 'Java']
| 4 |
4sum
|
BruteForce to Better to Optimal | C++ Multiple Solutions
|
bruteforce-to-better-to-optimal-c-multip-qrji
|
cpp\ntypedef long long ll;\n\n\n// Bruteforce | O(n^4) time | O(n) space\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int> &nums, int targ
|
travanj05
|
NORMAL
|
2022-09-04T20:05:24.659366+00:00
|
2022-10-04T04:39:46.079625+00:00
| 423 | false |
```cpp\ntypedef long long ll;\n\n\n// Bruteforce | O(n^4) time | O(n) space\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int> &nums, int target) {\n int n = nums.size();\n set<vector<int>> st;\n sort(nums.begin(), nums.end());\n for (int i =0; i < n - 3; i++) {\n for (int j = i + 1; j < n - 2; j++) {\n for (int k = j + 1; k < n - 1; k++) {\n for (int t = k + 1; t < n; t++) {\n if ((ll)nums[i] + nums[j] + nums[k] + nums[t] == (ll)target) {\n vector<int> quad = {nums[i], nums[j], nums[k], nums[t]};\n st.insert(quad);\n }\n }\n }\n }\n }\n vector<vector<int>> res(st.begin(), st.end());\n return res;\n }\n};\n\n\n// Bruteforce | O(n^4) time | O(1) space\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int> &nums, int target) {\n int n = nums.size();\n vector<vector<int>> res;\n sort(nums.begin(), nums.end());\n for (int i =0; i < n - 3; i++) {\n for (int j = i + 1; j < n - 2; j++) {\n for (int k = j + 1; k < n - 1; k++) {\n for (int t = k + 1; t < n; t++) {\n if ((ll)nums[i] + nums[j] + nums[k] + nums[t] == (ll)target) {\n vector<int> quad = {nums[i], nums[j], nums[k], nums[t]};\n res.push_back(quad);\n }\n while (t < n - 1 && nums[t] == nums[t + 1]) t++;\n }\n while (k < n - 1 && nums[k] == nums[k + 1]) k++;\n }\n while (j < n - 1 && nums[j] == nums[j + 1]) j++;\n }\n while (i < n - 1 && nums[i] == nums[i + 1]) i++;\n }\n return res;\n }\n};\n\n\n\n// Optimal | O(n^3 * log(n)) time | O(1) space\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int> &nums, int target) {\n int n = nums.size();\n vector<vector<int>> res;\n sort(nums.begin(), nums.end());\n for (int i = 0; i < n - 3; i++) {\n for (int j = i + 1; j < n - 2; j++) {\n for (int k = j + 1; k < n - 1; k++) {\n ll sumOfThree = (ll)nums[i] + (ll)nums[j] + (ll)nums[k];\n int fourthNum = target - sumOfThree;\n if (binary_search(nums.begin() + k + 1, nums.end(), fourthNum)) {\n vector<int> quad = {nums[i], nums[j], nums[k], fourthNum};\n res.push_back(quad);\n }\n while (k < n - 1 && nums[k] == nums[k + 1]) k++;\n }\n while (j < n - 1 && nums[j] == nums[j + 1]) j++;\n }\n while (i < n - 1 && nums[i] == nums[i + 1]) i++;\n }\n return res;\n }\n};\n\n\n\n// Most Optimal | O(n^3) time | O(1) space\nclass Solution {\npublic:\n vector<vector<int>> fourSum(vector<int> &nums, int target) {\n int n = nums.size();\n vector<vector<int>> res;\n sort(nums.begin(), nums.end());\n for (int i = 0; i < n - 3; i++) {\n for (int j = i + 1; j < n - 2; j++) {\n int l = j + 1, r = n - 1;\n ll remSum = (ll)target - (ll)nums[i] - (ll)nums[j];\n while (l < r) {\n ll sumOfLastTwo = nums[l] + nums[r];\n if (sumOfLastTwo < remSum) l++;\n else if (sumOfLastTwo > remSum) r--;\n else {\n vector<int> quad = {nums[i], nums[j], nums[l], nums[r]};\n res.push_back(quad);\n while (l < r && nums[l] == quad[2]) l++;\n while (l < r && nums[r] == quad[3]) r--;\n }\n }\n while (j < n - 1 && nums[j] == nums[j + 1]) j++;\n }\n while (i < n - 1 && nums[i] == nums[i + 1]) i++;\n }\n return res;\n }\n};\n```
| 6 | 0 |
['C', 'C++']
| 1 |
4sum
|
Extension of 2 Sum Solution, works in O(N^3)
|
extension-of-2-sum-solution-works-in-on3-u1sk
|
\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n nums.sort()\n ans = set()\n n = len(nums)\n
|
deleted_user
|
NORMAL
|
2022-04-01T08:18:51.835615+00:00
|
2022-04-01T08:18:51.835647+00:00
| 543 | false |
```\nclass Solution:\n def fourSum(self, nums: List[int], target: int) -> List[List[int]]:\n nums.sort()\n ans = set()\n n = len(nums)\n for i in range(n):\n for j in range(i+1, n):\n # two sum problem solution\n new_target = target - (nums[i] + nums[j])\n start = j+1\n end = n-1\n while end > start:\n if(nums[start] + nums[end] == new_target):\n ans.add((nums[i], nums[j], nums[start], nums[end]))\n end -= 1\n start += 1\n elif nums[start] + nums[end] > new_target:\n end -= 1\n else:\n start += 1\n return ans\n```
| 6 | 0 |
['Two Pointers', 'Python']
| 0 |
4sum
|
C++ Easy Approach faster than 91% , O(n^3) . Two Pointer Approach
|
c-easy-approach-faster-than-91-on3-two-p-n46x
|
\nvector> fourSum(vector& nums, int target) {\n \n vector> ans;\n int n= nums.size();\n \n // If length of array is smaller t
|
Sanskar_Garg
|
NORMAL
|
2022-01-19T08:50:54.311417+00:00
|
2022-01-22T10:22:46.003163+00:00
| 905 | false |
\nvector<vector<int>> fourSum(vector<int>& nums, int target) {\n \n vector<vector<int>> ans;\n int n= nums.size();\n \n // If length of array is smaller than 4 then no quadruplet can be formed.\n if(n<4) return ans;\n \n sort(nums.begin(),nums.end()); // to apply two pointer approach\n \n for(int i=0 ; i<n ; i++){\n \n long long int a = nums[i];\n \n for(int j=i+1 ; j<n ; j++){\n \n long long int b= nums[j];\n \n // two element are now fixed one at i and other at j\n \n // applying two pointer approach over the remaining two\n \n int s = j+1;\n int e = n-1;\n \n \n while(s<e){\n \n long long int x = nums[s];\n long long int y = nums[e];\n \n long long int sum = x+y+a+b;\n \n if(sum == target){\n // Need to make all a,b,c,d back to int as ans is a vector of vector of int\n ans.push_back({int(a),int(b),int(x),int(y)});\n \n // skipping same value of x and y\n \n while(s<e and nums[s] == x){\n s++;\n }\n \n while(s<e and nums[e] == y){\n e--;\n }\n \n }\n \n else if(sum > target){\n e--;\n }\n \n else{\n s++;\n }\n \n }\n \n // skipping same value at jth point\n \n while(j+1<n and nums[j+1] == nums[j]){\n j++;\n } \n \n }\n // skipping same value at ith point\n while(i+1<n and nums[i+1] == nums[i]){\n i++;\n } \n \n }\n \n \n return ans;\n \n \n }
| 6 | 1 |
['Two Pointers', 'C', 'Binary Tree']
| 2 |
4sum
|
4Sum || Two pointer || commented
|
4sum-two-pointer-commented-by-shahid_92-2000
|
\n vector<vector<int>> fourSum(vector<int> nums, int target) {\n int n = nums.size();\n vector<vector<int>> ans;\n //store in set as we nee
|
shahid_92
|
NORMAL
|
2021-07-16T12:28:29.436222+00:00
|
2021-07-16T12:28:29.436254+00:00
| 507 | false |
```\n vector<vector<int>> fourSum(vector<int> nums, int target) {\n int n = nums.size();\n vector<vector<int>> ans;\n //store in set as we need unique quadruplets only\n set<vector<int>> res;\n \n //less than 4 no ans\n if(n < 4) return ans;\n \n sort(begin(nums),end(nums));\n \n for(int i=0;i<n;i++){\n for(int j=i+1;j<n;j++){\n //choose two pointer \n int l = j+1 , r = n-1;\n //calc rest req sum\n int req = target-nums[i]-nums[j];\n while(l < r){\n //if it is our sum take it and inc or dec pointer if we nums[l]==nums[l+1], or otherwise.\n if((nums[l]+nums[r]) == req){\n //take it\n res.insert({nums[i],nums[j],nums[l],nums[r]});\n if(nums[l] == nums[l+1]) l++;\n else r--;\n }\n //if the sum is greater than require dec last pointer to dec sum\n else if((nums[l]+nums[r]) > req){\n r--;\n }\n //otherwise inc\n else{\n l++;\n }\n }\n }\n }\n \n for(auto it : res){\n ans.push_back(it);\n }\n \n return ans;\n }\n```
| 6 | 0 |
['C']
| 1 |
number-of-submatrices-that-sum-to-target
|
[Java/C++/Python] Find the Subarray with Target Sum
|
javacpython-find-the-subarray-with-targe-gcyx
|
Intuition\nPreaquis: 560. Subarray Sum Equals K\nFind the Subarray with Target Sum in linear time.\n\n\n# Explanation\nFor each row, calculate the prefix sum.\n
|
lee215
|
NORMAL
|
2019-06-02T04:03:28.589422+00:00
|
2021-04-18T07:20:49.283225+00:00
| 58,014 | false |
# Intuition\nPreaquis: [560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/description/)\nFind the Subarray with Target Sum in linear time.\n<br>\n\n# Explanation\nFor each row, calculate the prefix sum.\nFor each pair of columns,\ncalculate the accumulated sum of rows.\nNow this problem is same to, "Find the Subarray with Target Sum".\n<br>\n\n# Complexity\nTime `O(mnn)`\nSpace `O(m)`\n<br>\n\n**Java**\n```java\n public int numSubmatrixSumTarget(int[][] A, int target) {\n int res = 0, m = A.length, n = A[0].length;\n for (int i = 0; i < m; i++)\n for (int j = 1; j < n; j++)\n A[i][j] += A[i][j - 1];\n Map<Integer, Integer> counter = new HashMap<>();\n for (int i = 0; i < n; i++) {\n for (int j = i; j < n; j++) {\n counter.clear();\n counter.put(0, 1);\n int cur = 0;\n for (int k = 0; k < m; k++) {\n cur += A[k][j] - (i > 0 ? A[k][i - 1] : 0);\n res += counter.getOrDefault(cur - target, 0);\n counter.put(cur, counter.getOrDefault(cur, 0) + 1);\n }\n }\n }\n return res;\n }\n```\n\n**C++**\n```cpp\n int numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n int res = 0, m = A.size(), n = A[0].size();\n for (int i = 0; i < m; i++)\n for (int j = 1; j < n; j++)\n A[i][j] += A[i][j - 1];\n\n unordered_map<int, int> counter;\n for (int i = 0; i < n; i++) {\n for (int j = i; j < n; j++) {\n counter = {{0,1}};\n int cur = 0;\n for (int k = 0; k < m; k++) {\n cur += A[k][j] - (i > 0 ? A[k][i - 1] : 0);\n res += counter.find(cur - target) != counter.end() ? counter[cur - target] : 0;\n counter[cur]++;\n }\n }\n }\n return res;\n }\n```\n\n**Python:**\n```py\n def numSubmatrixSumTarget(self, A, target):\n m, n = len(A), len(A[0])\n for row in A:\n for i in xrange(n - 1):\n row[i + 1] += row[i]\n res = 0\n for i in xrange(n):\n for j in xrange(i, n):\n c = collections.defaultdict(int)\n cur, c[0] = 0, 1\n for k in xrange(m):\n cur += A[k][j] - (A[k][i - 1] if i > 0 else 0)\n res += c[cur - target]\n c[cur] += 1\n return res\n```\n
| 570 | 16 |
[]
| 64 |
number-of-submatrices-that-sum-to-target
|
Java Solution with Detailed Explanation
|
java-solution-with-detailed-explanation-t681y
|
Before this problem\n>https://leetcode.com/problems/subarray-sum-equals-k/\n>https://leetcode.com/problems/subarray-sum-equals-k/discuss/803317/Java-Solution-wi
|
conor-jiahaochen
|
NORMAL
|
2020-08-21T05:34:56.508445+00:00
|
2021-04-19T11:05:48.114188+00:00
| 8,158 | false |
## Before this problem\n>https://leetcode.com/problems/subarray-sum-equals-k/\n>https://leetcode.com/problems/subarray-sum-equals-k/discuss/803317/Java-Solution-with-Detailed-Explanation\n## Thinkings\n\n1. For a matrix, what is the prefix sum ?\n\n\t sum[x] [y] is the sum of submatrix \n\n\t (The upper left corner is matrix[0] [0], the lower right corner is matrix[x] [y])\n\n\t 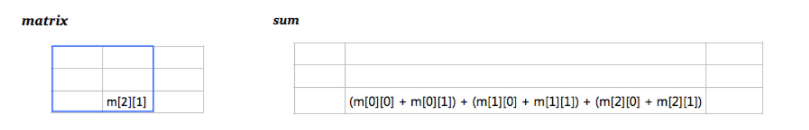\n\n\n2. How to calculate the sum of all submatrices ***whose upper left corners are matrix[0] [0]*** \uFF1F\n\n Step 1. Calculate the prefix sum of each line.\n\n\t \n\n\n ```java\n // Like the one-dimensional prefix sum, \n // in order to prevent index out of range and facilitate calculations,\n // we add an extra column with all 0s at the forefront.\n int line = matrix.length;\n int column = matrix[0].length + 1;\n int[][] sum = new int[line][column]; // Initialization default is all 0\n \n for (int l = 0; l < sum.length; l++){\n // start from the second column\n for (int c = 1; c < sum[0].length; c++){\n sum[l][c] = sum[l][c - 1] + matrix[l][c - 1]; // "c - 1",because of an extra column.\n }\n }\n ```\n\n\t \n\n\n Step 2. Using the prefix sum of each line to calculate the sum of submatrix.\n\n 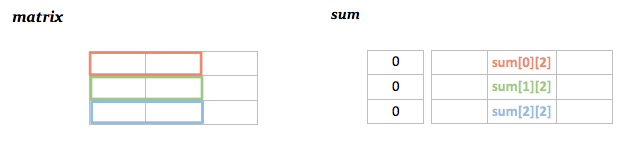\n\n\n ```java\xA0\n sum[1][2] = sum[1][2] + sum[0][2]; // green + orange\n ```\n\n ```java\n sum[2][2] = sum[2][2] + sum[1][2] + sum[0][2]; // blue + green + orange\n ```\n\n So, to caculate any sum of submatrices ***whose upper left corner are matrix[0] [0].***\n\n ```java\n int sumOfSubMatrix = 0;\n \n for(int l = 0; l < line; l++){\n \tsumOfSubMatrix += sum[l][column]; // one of submatrices\n }\n ```\n\n\n\n3. How to find all submatrices ?\n\n 1. Any submatrix needs any two rows and any two columns to form, that is to say, four variables and four nested loops are required.\n\n ```java\n // Use double nested "for" loop to select any two columns\n for (int start = 0; start < column; start++){\n for (int end = start + 1; end < column; end++ ){\n \t// ...\n \t// Then Use double nested "for" loop to select any two lines\n \t}\n }\n ```\n\n 2. Convert 2D to 1D\n\n Step 1 : Use the ***prefix sum of each row*** to calculate the matrix sum between the "start" column and "end" column.\n\n 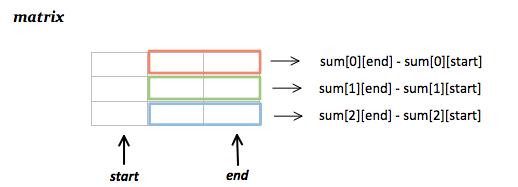\n\n\n Step 2 : Rotate it 90 degrees to the left, ***it can be regarded as a one-dimensional array.***\n\n\t\t \n\n\n Then the problem is transformed into how many sub-arrays whose sum == target ?\n\n ***It\'s the same with >https://leetcode.com/problems/subarray-sum-equals-k/***\n\n Step 3 : In the same way, we can use hashmap to optimize the double nested loop for any two lines, and only need one loop\n\n ```java\n int sumOfSubMatrix = 0;\n Map<Integer, Integer> map = new HashMap<Integer, Integer>();\n map.put(0, 1);\n \n for(int l = 0; l < line; l++){\n // prefix sum\n \tsumOfSubMatrix += sum[l][end] - sum[l][start];\n \n \tif (map.containsKey(sumOfSubMatrix - target))\n \t\tcount += map.get(sumOfSubMatrix - target);\n \n \tmap.put(sumOfSubMatrix, map.getOrDefault(sumOfSubMatrix, 0) + 1);\n ```\n\n \n\n \n\n## Code\n\n```java\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int count = 0;\n int line = matrix.length;\n int column = matrix[0].length + 1;\n int[][] sum = new int[line][column];\n \n for (int i = 0; i < sum.length; i++){\n for (int j = 1; j < sum[0].length; j++){\n sum[i][j] = sum[i][j - 1] + matrix[i][j - 1];\n }\n }\n \n \n for (int start = 0; start < column; start++){\n for (int end = start + 1; end < column; end++ ){\n \n int sumOfSubMatrix = 0;\n Map<Integer, Integer> map = new HashMap<Integer, Integer>();\n map.put(0, 1);\n for(int l = 0; l < line; l++){\n sumOfSubMatrix += sum[l][end] - sum[l][start];\n if (map.containsKey(sumOfSubMatrix - target))\n count += map.get(sumOfSubMatrix - target);\n map.put(sumOfSubMatrix, map.getOrDefault(sumOfSubMatrix, 0) + 1);\n \n }\n }\n }\n \n return count;\n \n }\n}\n```\n\n\n\n## Update\nFor the commet from jun.\n1. What\'s the meaning of this sentence ?\n+ "Any submatrix needs any two rows and any two columns to form, that is to say, four variables and four nested loops are required." \n\n\teg. |0| is the submatrix I want to find, whose index is [0][0]\n\tIn the "sum", the column 1 corresponds to column 0 in "matrix". SO we bound the area like this\n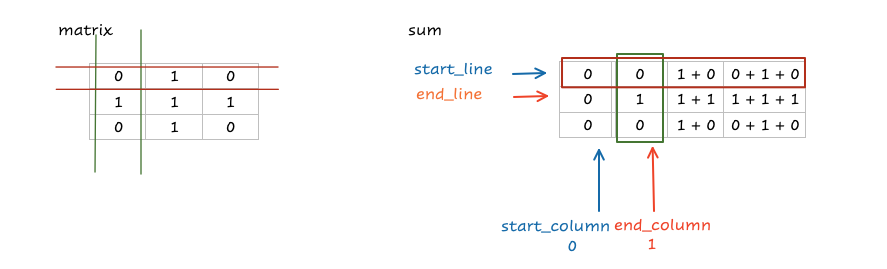\n\nSince we have done prefix sum for every line, we need to do sum[line][end_column] - sum[line][start_column], and in this case elements in start_column is all 0, when we subtract sum[line][0], It actually did nothing.\n\nAlso, since "end_cloumn" starts from "end_cloumn = start_column + 1", it is impossible to treat the first column of "sum" as part of our result.\n\n\n\n\n\n
| 178 | 4 |
['Prefix Sum', 'Java']
| 14 |
number-of-submatrices-that-sum-to-target
|
[C++] O(n^3) Simple 1D Subarray target sum applied to 2D array
|
c-on3-simple-1d-subarray-target-sum-appl-6k25
|
Explaination:\nCheck out how to solve for 1D array 560. Subarray Sum Equals K in O(n) time.\n\nThe solution for 1D array uses running prefix sum.\n We know that
|
phoenixdd
|
NORMAL
|
2019-06-02T04:10:20.723328+00:00
|
2020-03-28T05:35:12.827033+00:00
| 18,378 | false |
**Explaination:**\nCheck out how to solve for 1D array `560. Subarray Sum Equals K` in O(n) time.\n\nThe solution for 1D array uses running prefix sum.\n* We know that to get sum of a subarray `[j,i]` we can calculate using `SUM[0,i] - SUM [0,j-1]`.\n* If this calculation = target then we have a subarray who\'s sum equals target and ends at `i`.\n* Hence at any point `i` we need to find number of occurence of `runningSum - target` since `x + target = runningSum`.\n* We start moving from 1st element to the last and keep adding the value to running sum.\n* We also keep a hash map maintaining number of such sums occured.\n* Thus at any point `i` we have sums from [0,i) stored in hashmap where `i` ranges from `0` to `i` excluding `i`. eg: at `i=3`, we have `SUM[0,0`] , `SUM[0,1]` and `SUM[0,2]`.\n* At each index `i` we can then query the hashmap to find out number of occurences of `runningSum-target` to get number of subarrays ending at `i`.\n\nNow since we know how to find number of subarrays who\'s sum equals target for 1D array.\nWe can convert a 2D matrix of values to 1D matrix whose values equal to that of 2D. Such that they have combination of all rows and apply the same technique.\neg: [[1,2,3,4,5],[2,6,7,8,9]]\n\nWe can break this down to 1 2x5 matrix and 2 1x5 matrix\nThus the 1D value matrices are:\n* We start row wise\n* 1st 1x5 matrix is matrix[0] itself [1,2,3,4,5].\n* We then add second row to previous 1D matrix and get [3,8,10,12,14].\n* We then move on to make matrices with 2nd row of the original matrix as their first row.\n* Since 2nd row is the last we end up with last 1D matrix of [2,6,7,8,9].\n\nWe use the same technique for each 1D matrix created in above steps and keep adding the result for these individual 1D arrays and return that as the result in the end.\n\nIf you notice in the case of 1D array you get results for subarrays of all lengths starting from any point.\nso you are checking rectangles of 1x1, 1x2, 1x3 ..... upto length.\nWhen you apply this to a 2D->1D array at each `i` you are checking rectangles of all sizes starting from `i`.\nwhich looks like ( (1x1, 1x2 ...upto length of row then 2x1, 2x2 ...upto length of a row) .... upto length of columns) for each row in original matrix as their 1st row, hence the result includes all combinations of submatrices.\n\n**Note:** You can make this a little bit faster by sacrificing space and precalculating all prefix sums in the 2D matrix and storing them as in `304. Range Sum Query 2D - Immutable` so that we have a constant lookup for calculating sums, this way we avoid recalculating sums of overlapping rows.\n\n**Solution:**\n```c++\nclass Solution {\npublic:\n int result=0,target;\n unordered_map<int,int> map;\n void get_result(vector<int>& nums) //Get number of subarrays that sum to target.\n {\n int sum=0;\n map.clear();\n map[0]++;\n for(int &i:nums)\n {\n sum+=i;\n result+=map[sum-target]; //get number of subarrays who\'s sum equals target and end at i and add result to global result.\n map[sum]++; //Add the occurence of running sum to map.\n }\n }\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) \n {\n this->target=target;\n vector<int> row(matrix[0].size());\n for(int i=0;i<matrix.size();i++) //Convert 2D array to 1D by row.\n {\n fill(row.begin(),row.end(),0); //Clear vector to start the row with i as starting row.\n for(int j=i;j<matrix.size();j++)\n {\n for(int x=0;x<matrix[0].size();x++) //Add next row\n row[x]+=matrix[j][x];\n get_result(row);\n }\n }\n return result;\n }\n};\n```
| 144 | 1 |
[]
| 13 |
number-of-submatrices-that-sum-to-target
|
✅ Optimization from Brute-Force to Optimized Solution w/ Easy Explanation
|
optimization-from-brute-force-to-optimiz-tgzi
|
There are a few solution mentioned by others but most have directly given the most optimal solution. Here, I will try to start from the brute-force approach and
|
archit91
|
NORMAL
|
2021-04-17T14:26:09.266684+00:00
|
2021-04-17T14:26:09.266711+00:00
| 5,472 | false |
There are a few solution mentioned by others but most have directly given the most optimal solution. Here, I will try to start from the brute-force approach and try to explain the various optimizations that can be done to finally arrive at the optimal solution.\n\n---\n\n\u274C ***Solution - I (Brute-Force Approach) [Rejected]***\n\nLet\'s start with the most basic approach to this problem. Take all the submatrices possible for the given matrix and check if their sum is equal to `target`.\n\n```\nint numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n\tint res = 0, m = size(A), n = size(A[0]);\n\t// calculate sum of each submatrix and check if it is equal to target\n\tfor(int rowStart = 0; rowStart < m; rowStart++)\n\t\tfor(int rowSize = 1; rowStart + rowSize <= m; rowSize++)\n\t\t\tfor(int colStart = 0; colStart < n; colStart++)\n\t\t\t\tfor(int colSize = 1; colStart + colSize <= n; colSize++)\n\t\t\t\t\tif(SUM(A, rowStart, rowSize, colStart, colSize) == target)\n\t\t\t\t\t\tres++;\n\treturn res; \n}\n// Calculates the sum of a submatrix with given bounds\nint SUM(vector<vector<int> > &A, int rStart, int rSize, int cStart, int cSize){\n\tint subMatrixSum = 0;\n\tfor(int i = rStart; i < rStart + rSize; i++)\n\t\tfor(int j = cStart; j < cStart + cSize; j++)\n\t\t\tsubMatrixSum += A[i][j];\n\treturn subMatrixSum;\n}\n```\n\n***Time Complexity :*** **`O((M*N)^3)`**, where `M` is the number of rows and `N` is the number of columns in the given matrix.\n***Space Complexity :*** **`O(1)`**\n\n---\n\n\u2714\uFE0F ***Solution - II (Compute prefix sum for each Row or Column)***\n\nWe can optimize the above approach by reducing the time complexity of the `SUM` function in the above solution. We know that in a given array, the sum of range [i,j] can be calculated by `prefixSum[j] - prefixSum[i - 1]`. We can use this to optimize the solution.\n\nAfter computing prefix sum for each row of matrix (*you can do it for column as well*), we can get the sum of a given range in O(1) time. Thus, for any submatrix of the main matrix, we just need to iterate over all its rows and we can get sum of given range (`[colStart, colEnd]`) in O(1) time.\n\n1. We just start from row 0, calculate the sum for that row for the range `[colStart, colEnd]`.\n2. Extend the sum by perform step-1 for row 1, row 2, ... and so on till last row.\n3. Repeat this process for every `[colStart, colEnd]` combination.\n\n\n```\nint numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n\tint res = 0, m = size(A), n = size(A[0]);\n\t// calculating prefix sum for each row of matrix\n\tfor (int row = 0; row < m; row++)\n\t\tfor (int col = 1; col < n; col++)\n\t\t\tA[row][col] += A[row][col - 1];\n\t// calculate sum of each submatrix and check if it is equal to target\n\tfor (int colStart = 0; colStart < n; colStart++) {\n\t\tfor (int colEnd = colStart; colEnd < n; colEnd++) {\n\t\t\tfor(int rowStart = 0; rowStart < m; rowStart++){\n\t\t\t\tint sum = 0;\n\t\t\t\tfor(int rowEnd = rowStart; rowEnd < m; rowEnd++){\n\t\t\t\t\tsum += A[rowEnd][colEnd] - (colStart ? A[rowEnd][colStart - 1] : 0);\n\t\t\t\t\tif(sum == target) res++;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\treturn res; \n}\n```\n***Time Complexity :*** **`O((M*N)^2)`**, where `M` is the number of rows and `N` is the number of columns in the given matrix.\n***Space Complexity :*** **`O(1)`**, since we are modifying the given matrix itself. If we use a new prefix sum matrix, the space complexity would be `O(M*N)`.\n\n---\n\n\u2714\uFE0F ***Solution - III (Further Optimization in Solution - II)***\n\nWe can further optimize the solution by using hashmap. The optimization done here is similar to the one in solution of [560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/solution/).\n\nBasically, we will be maintaining a running submatrix sum starting from row 0 till m, for a given `[colStart, colEnd]` range. Each sum value and number of its occurence will be stored in hashmap. If there\'s a submatrix which was found such that `cursum` at that time was equal to present sum (`cursum`) - target, then we are sure that there were occurences of submatrices which had sum equal to `target` and the count is given by `mp[cursum - target]`.\n\nIf the explanation didn\'t make the approach clear, I really suggest you to try the *560. Subarray Sum Equals K* problem and read the hashmap solution. It took me some time reading that before I was able to clearly understand this solution.\n\n```\nint numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n\tint res = 0, m = size(A), n = size(A[0]);\n\tfor (int row = 0; row < m; row++)\n\t\tfor (int col = 1; col < n; col++)\n\t\t\tA[row][col] += A[row][col - 1];\n\t// cursum, occurences\n\tunordered_map<int, int> mp;\n\tfor (int colStart = 0; colStart < n; colStart++) {\n\t\tfor (int colEnd = colStart; colEnd < n; colEnd++) {\n\t\t\tint cursum = 0;\n\t\t\tmp = {{0, 1}};\n\t\t\tfor(int row = 0; row < m; row++){\n\t\t\t\tcursum += A[row][colEnd] - (colStart ? A[row][colStart - 1] : 0); \n\t\t\t\t// mp[sum-target] will give number of submatrices found having sum as \'sum - target\'\n\t\t\t\tres += mp[cursum - target];\n\t\t\t\tmp[cursum]++;\n\t\t\t}\n\t\t}\n\t}\n\treturn res; \n}\n```\n***Time Complexity :*** **`O(N*N*M)`**, where `M` is the number of rows and `N` is the number of columns in the given matrix.\n***Space Complexity :*** **`O(N)`**\n\n\n\n---\n---\n\n\uD83D\uDCBB\uD83D\uDC31\u200D\uD83D\uDCBBIf there are any questions or mistakes in my post, please do comment below \uD83D\uDC47 \n\n---\n---
| 136 | 7 |
[]
| 10 |
number-of-submatrices-that-sum-to-target
|
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || EXPLAINED🔥
|
cjavapythonjavascript-2-approaches-expla-g6af
|
PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n\n#### Approach 1(With Maps)\n\n1. Find the prefix sum for each row.\n1. Fo
|
MarkSPhilip31
|
NORMAL
|
2024-01-28T00:21:15.132335+00:00
|
2024-01-28T00:28:54.307035+00:00
| 25,134 | false |
# PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n\n#### ***Approach 1(With Maps)***\n\n1. Find the prefix sum for each row.\n1. For each pair of column find the subarrays sum eqaul to target.\n\n\n\n# Complexity\n- Time complexity:\n $$O(m^2 * n)$$\n*(where m is the number of rows and n is the number of columns in the matrix.)*\n \n\n- Space complexity:\n $$O(m)$$\n \n\n\n# Code\n```C++ []\n\n\n\nclass Solution {\npublic:\n int numSubmatrixSumTarget(std::vector<std::vector<int>>& matrix, int target) {\n int m = matrix.size();\n int n = matrix[0].size();\n\n for (int row = 0; row < m; row++) {\n for (int col = 1; col < n; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n int count = 0;\n\n for (int c1 = 0; c1 < n; c1++) {\n for (int c2 = c1; c2 < n; c2++) {\n std::unordered_map<int, int> map;\n map[0] = 1;\n int sum = 0;\n\n for (int row = 0; row < m; row++) {\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n count += map[sum - target];\n map[sum]++;\n }\n }\n }\n\n return count;\n }\n};\n\n\n\n\n\n```\n```Java []\n\n\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length;\n int n = matrix[0].length;\n\n for (int row = 0; row < m; row++) {\n for (int col = 1; col < n; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n int count = 0;\n\n for (int c1 = 0; c1 < n; c1++) {\n for (int c2 = c1; c2 < n; c2++) {\n Map<Integer, Integer> map = new HashMap<>();\n map.put(0, 1);\n int sum = 0;\n\n for (int row = 0; row < m; row++) {\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n count += map.getOrDefault(sum - target, 0);\n map.put(sum, map.getOrDefault(sum, 0) + 1);\n }\n }\n }\n\n return count;\n }\n}\n\n\n\n```\n```python []\nclass Solution:\n def numSubmatrixSumTarget(self, matrix, target):\n m, n = len(matrix), len(matrix[0])\n\n for row in range(m):\n for col in range(1, n):\n matrix[row][col] += matrix[row][col - 1]\n\n count = 0\n\n for c1 in range(n):\n for c2 in range(c1, n):\n prefix_sum_count = {0: 1}\n sum_val = 0\n\n for row in range(m):\n sum_val += matrix[row][c2] - (matrix[row][c1 - 1] if c1 > 0 else 0)\n count += prefix_sum_count.get(sum_val - target, 0)\n prefix_sum_count[sum_val] = prefix_sum_count.get(sum_val, 0) + 1\n\n return count\n\n\n```\n```javascript []\nvar numSubmatrixSumTarget = function(matrix, target) {\n const m = matrix.length;\n const n = matrix[0].length;\n\n for (let row = 0; row < m; row++) {\n for (let col = 1; col < n; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n let count = 0;\n\n for (let c1 = 0; c1 < n; c1++) {\n for (let c2 = c1; c2 < n; c2++) {\n const map = new Map();\n map.set(0, 1);\n let sum = 0;\n\n for (let row = 0; row < m; row++) {\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n count += map.get(sum - target) || 0;\n map.set(sum, (map.get(sum) || 0) + 1);\n }\n }\n }\n\n return count;\n};\n\n\n\n```\n---\n\n#### ***Approach 2(With Arrays)***\n\n1. Find the prefix sum for each row.\n1. For each pair of column find the subarrays sum eqaul to target.\n\n\n\n# Complexity\n- Time complexity:\n $$O(m^2 * n)$$\n*(where m is the number of rows and n is the number of columns in the matrix.)*\n \n\n- Space complexity:\n $$O(m)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n int subarraySum(vector<int>& nums, int k) {\n int count=0,sum=0;\n map<int,int>mp;\n for(int i=0;i<nums.size();i++)\n {\n sum+=nums[i];\n if(sum==k)\n {\n count++;\n }\n if(mp.find(sum-k)!=mp.end())\n {\n count+=mp[sum-k]; \n }\n mp[sum]++;\n }\n return count;\n }\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int count=0;\n for(int i=0; i<matrix.size(); i++){\n\t\t\t\n vector<int> sum(matrix[0].size(), 0);\n for(int j=i; j<matrix.size(); j++){\n for(int k=0; k<matrix[0].size(); k++){\n sum[k] += matrix[j][k];\n }\n count += subarraySum(sum, target);\n }\n }\n \n return count;\n }\n}; \n\n\n\n\n\n\n```\n```Java []\nimport java.util.HashMap;\nimport java.util.Map;\n\nclass Solution {\n public int subarraySum(int[] nums, int k) {\n int count = 0;\n int sum = 0;\n Map<Integer, Integer> mp = new HashMap<>();\n\n for (int i = 0; i < nums.length; i++) {\n sum += nums[i];\n\n if (sum == k) {\n count++;\n }\n\n if (mp.containsKey(sum - k)) {\n count += mp.get(sum - k);\n }\n\n mp.put(sum, mp.getOrDefault(sum, 0) + 1);\n }\n\n return count;\n }\n\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int count = 0;\n\n for (int i = 0; i < matrix.length; i++) {\n int[] sum = new int[matrix[0].length];\n\n for (int j = i; j < matrix.length; j++) {\n for (int k = 0; k < matrix[0].length; k++) {\n sum[k] += matrix[j][k];\n }\n\n count += subarraySum(sum, target);\n }\n }\n\n return count;\n }\n}\n\n\n\n\n```\n```python []\nfrom typing import List\nfrom collections import defaultdict\n\nclass Solution:\n def subarraySum(self, nums: List[int], k: int) -> int:\n count = 0\n sum_val = 0\n mp = defaultdict(int)\n\n for num in nums:\n sum_val += num\n\n if sum_val == k:\n count += 1\n\n if sum_val - k in mp:\n count += mp[sum_val - k]\n\n mp[sum_val] += 1\n\n return count\n\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n count = 0\n\n for i in range(len(matrix)):\n sum_val = [0] * len(matrix[0])\n\n for j in range(i, len(matrix)):\n for k in range(len(matrix[0])):\n sum_val[k] += matrix[j][k]\n\n count += self.subarraySum(sum_val, target)\n\n return count\n\n\n```\n```javascript []\nclass Solution {\n subarraySum(nums, k) {\n let count = 0;\n let sum = 0;\n const mp = new Map();\n\n for (const num of nums) {\n sum += num;\n\n if (sum === k) {\n count++;\n }\n\n if (mp.has(sum - k)) {\n count += mp.get(sum - k);\n }\n\n mp.set(sum, (mp.get(sum) || 0) + 1);\n }\n\n return count;\n }\n\n numSubmatrixSumTarget(matrix, target) {\n let count = 0;\n\n for (let i = 0; i < matrix.length; i++) {\n const sum = Array(matrix[0].length).fill(0);\n\n for (let j = i; j < matrix.length; j++) {\n for (let k = 0; k < matrix[0].length; k++) {\n sum[k] += matrix[j][k];\n }\n\n count += this.subarraySum(sum, target);\n }\n }\n\n return count;\n }\n}\n\n\n\n\n```\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n---
| 118 | 5 |
['Array', 'Hash Table', 'Matrix', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 16 |
number-of-submatrices-that-sum-to-target
|
Fully explained intuition - 4 solutions | MUST READ | With Image
|
fully-explained-intuition-4-solutions-mu-r5cv
|
Note: that\'s a long read, but I explained the whole thinking process. It\'s going to be worth it if you want to learn and not to memorize solutions :)\n\nIf yo
|
nadaralp
|
NORMAL
|
2022-07-18T08:22:55.448971+00:00
|
2022-07-18T08:45:38.452865+00:00
| 7,169 | false |
Note: that\'s a long read, but I explained the whole thinking process. It\'s going to be worth it if you want to learn and not to memorize solutions :)\n\nIf you found it helpful, please upvote <3\n\n<hr />\n\n\nLet\'s start with the basics\n\nFirst, how do we generate the coordinates for all the submatrices? we need all distinct (x1,y1), (x2,y2) pairs\n\nSo it will be something like this:\n\n```\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m, n = len(matrix), len(matrix[0])\n # Generate all submatrices\n for y1 in range(m):\n for x1 in range(n):\n for y2 in range(y1, m):\n for x2 in range(x1, n):\n print(f"({x1}, {y1}), ({x2, y2})")\n```\n\n\nAnd a brute force would be to count the sum between all pairs of coordinates\n\n```\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m, n = len(matrix), len(matrix[0])\n ans = 0\n \n # Generate all submatrices\n for y1 in range(m):\n for x1 in range(n):\n for y2 in range(y1, m):\n for x2 in range(x1, n):\n # We could sum the distance between the coordinates\n total = 0\n for r in range(y1, y2+1):\n for c in range(x1, x2+1):\n total += matrix[r][c]\n \n if total == target:\n ans += 1\n return ans\n```\n\n\nObviously that\'s too bad of a solution with `n^3*m^3`\n\n# Improvement\n\nIn the last example, we had to iterate from (x1,y1) to (x2,y2) to find the sum.\n\nWe can reduce the time complexity for finding the sum to `O(1)` instead of `O(m*n)`, but how?\n\nBy using `prefix sums` (or prefix matrices one may say), extending the idea of a prefix sum array\n\nLet\'s look at the image below:\n\n\n**UPDATE**: **the value 8 is calculated as `7+6+(-3)-2`. The image has a mistake in it.. Sorry \nAll other calculations are fine**\n**Also the usage of DP in the image is for convenience, it\'s not a dynamic programming question.**\n\n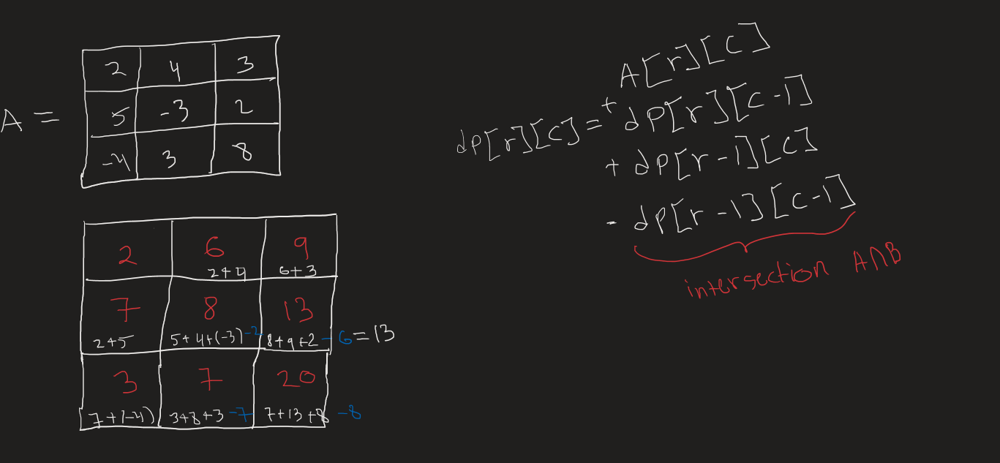\n\nEvery coordinate (x,y) is the matrix sum between origin `(0,0) and (x,y)`\n\nWe can calculate the sum by taking the sum of the matrix above `matrix_sum[row-1][col]`, adding the sum of the matrix behind `matrix_sum[row][col-1]` and removing the intersection, because there is a part that is added twice `matrix_sum[row-1][col-1]`\n\nThen to calculate the sum of some `submatrix (x1,y1), (x2,y2)` we need to add the sum of the matrix that ends at the bottom coordinates, and remove the parts which are unused (again there is an intersection, hence we need to add the intersection because it\'s removed twice)\n\n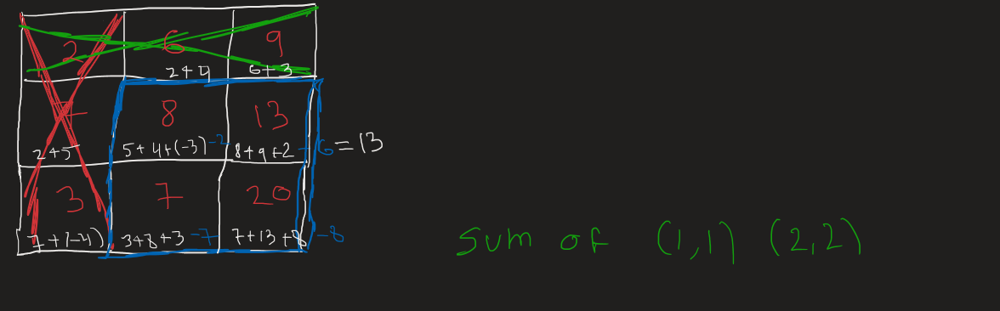\n\n\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m, n = len(matrix), len(matrix[0])\n matrix_sums = [[0 for _ in range(n)] for _ in range(m)]\n \n # Calculate all the submatrices sum with the transition formula we found\n for row in range(m):\n for col in range(n):\n # first cell\n if row == 0 and col == 0:\n matrix_sums[row][col] = matrix[row][col]\n # Rows and columns are like prefix sums, without intersection\n elif row == 0:\n matrix_sums[row][col] = matrix[row][col] + matrix_sums[row][col-1]\n elif col == 0:\n matrix_sums[row][col] = matrix[row][col] + matrix_sums[row-1][col]\n \n # current sum is the sum of the matrix above, to the left and subtract the intersection\n else:\n matrix_sums[row][col] = matrix[row][col] \\\n + (matrix_sums[row][col-1]) \\\n + (matrix_sums[row-1][col]) \\\n - (matrix_sums[row-1][col-1])\n\n \n ans = 0\n # Generate all submatrices\n for y1 in range(m):\n for x1 in range(n):\n for y2 in range(y1, m):\n for x2 in range(x1, n):\n # calculate sum in O(1)\n submatrix_total = matrix_sums[y2][x2] \\\n - (matrix_sums[y2][x1-1] if x1-1 >= 0 else 0) \\\n - (matrix_sums[y1-1][x2] if y1-1 >= 0 else 0) \\\n + (matrix_sums[y1-1][x1-1] if y1-1 >= 0 and x1-1 >= 0 else 0)\n \n if submatrix_total == target:\n ans += 1\n return ans\n```\n\n# Do we really need 2 separate iterations?\nWe can inverse the order of iterations, to build the prefix matrix and calculate in one go\n\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m, n = len(matrix), len(matrix[0])\n matrix_sums = [[0 for _ in range(n)] for _ in range(m)]\n \n ans = 0\n # Generate all submatrices\n for y1 in range(m):\n for x1 in range(n):\n # Calculate matrix_sums\n # first cell\n if y1 == 0 and x1 == 0:\n matrix_sums[y1][x1] = matrix[y1][x1]\n # Rows and columns are like prefix sums, without intersection\n elif y1 == 0:\n matrix_sums[y1][x1] = matrix[y1][x1] + matrix_sums[y1][x1-1]\n elif x1 == 0:\n matrix_sums[y1][x1] = matrix[y1][x1] + matrix_sums[y1-1][x1]\n \n # current sum is the sum of the matrix above, to the left and subtract the intersection\n else:\n matrix_sums[y1][x1] = matrix[y1][x1] \\\n + (matrix_sums[y1][x1-1]) \\\n + (matrix_sums[y1-1][x1]) \\\n - (matrix_sums[y1-1][x1-1])\n \n for y2 in range(y1 + 1):\n for x2 in range(x1 + 1):\n submatrix_total = matrix_sums[y1][x1] \\\n - (matrix_sums[y1][x2-1] if x2-1 >= 0 else 0) \\\n - (matrix_sums[y2-1][x1] if y2-1 >= 0 else 0) \\\n + (matrix_sums[y2-1][x2-1] if y2-1 >= 0 and x2-1 >= 0 else 0)\n \n if submatrix_total == target:\n ans += 1\n return ans\n```\n\n\n# But wait...\nWe can optimize even more!\n\nWe have time complexity of `m^2*n^2` but do we really need the `n^2` ?\n\nInstead, it\'s enough to simply "fix" the vertical coordinates y1, y2 and let x iterate\n\nThis way, we can reduce the problem into **subarray sum equal to target** (1D problem)\n\nFinal complexity: `O(m^2*n)`\n\n# Code\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m, n = len(matrix), len(matrix[0])\n matrix_sums = [[0 for _ in range(n)] for _ in range(m)]\n \n # Calculate all the submatrices sum with the transition formula we found\n for row in range(m):\n for col in range(n):\n # first cell\n if row == 0 and col == 0:\n matrix_sums[row][col] = matrix[row][col]\n # Rows and columns are like prefix sums, without intersection\n elif row == 0:\n matrix_sums[row][col] = matrix[row][col] + matrix_sums[row][col-1]\n elif col == 0:\n matrix_sums[row][col] = matrix[row][col] + matrix_sums[row-1][col]\n \n # current sum is the sum of the matrix above, to the left and subtract the intersection\n else:\n matrix_sums[row][col] = matrix[row][col] \\\n + (matrix_sums[row][col-1]) \\\n + (matrix_sums[row-1][col]) \\\n - (matrix_sums[row-1][col-1])\n\n \n ans = 0\n for y1 in range(m):\n for y2 in range(y1, m):\n # Reduce the problem to subarray sum of target\n subarray_sums = defaultdict(int)\n subarray_sums[0] = 1\n \n for x in range(n):\n matrix_sum = matrix_sums[y2][x]\n \n # Remove to matrix sum above y1\n if y1 > 0:\n matrix_sum -= matrix_sums[y1-1][x]\n \n if matrix_sum - target in subarray_sums:\n ans += subarray_sums[matrix_sum - target]\n \n subarray_sums[matrix_sum] += 1\n return ans\n```
| 102 | 0 |
['Python']
| 4 |
number-of-submatrices-that-sum-to-target
|
Simple Python DP solution
|
simple-python-dp-solution-by-otoc-9xz8
|
Please see and vote for my solution for these similar problems.\n560. Subarray Sum Equals K\n974. Subarray Sums Divisible by K\n325. Maximum Size Subarray Sum E
|
otoc
|
NORMAL
|
2019-07-27T03:47:14.148350+00:00
|
2019-12-06T23:44:49.233046+00:00
| 6,755 | false |
Please see and vote for my solution for these similar problems.\n[560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/discuss/344431/Simple-Python-DP-solution)\n[974. Subarray Sums Divisible by K](https://leetcode.com/problems/subarray-sums-divisible-by-k/discuss/344436/Simple-Python-DP-solution)\n[325. Maximum Size Subarray Sum Equals k](https://leetcode.com/problems/maximum-size-subarray-sum-equals-k/discuss/344432/Simple-Python-DP-solution)\n[1074. Number of Submatrices That Sum to Target](https://leetcode.com/problems/number-of-submatrices-that-sum-to-target/discuss/344440/Simple-Python-DP-solution)\n[363. Max Sum of Rectangle No Larger Than K](https://leetcode.com/problems/max-sum-of-rectangle-no-larger-than-k/discuss/445540/Python-bisect-solution-(960ms-beat-71.25))\n\nFor each row, calculate the prefix sum. For each pair of columns, calculate the sum of rows. \nNow this problem is changed to problem 560 Subarray Sum Equals K.\n```\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m, n = len(matrix), len(matrix[0])\n for x in range(m):\n for y in range(n - 1):\n matrix[x][y+1] += matrix[x][y]\n res = 0\n for y1 in range(n):\n for y2 in range(y1, n):\n preSums = {0: 1}\n s = 0\n for x in range(m):\n s += matrix[x][y2] - (matrix[x][y1-1] if y1 > 0 else 0)\n res += preSums.get(s - target, 0)\n preSums[s] = preSums.get(s, 0) + 1\n return res\n```
| 72 | 3 |
[]
| 4 |
number-of-submatrices-that-sum-to-target
|
[C++] Easy Solution with Explanation
|
c-easy-solution-with-explanation-by-yadv-aw1z
|
Intution :\n We need to apply same logic which we used in : Subarray Sum Equals K. If you have not done this pls check it out first .\n Calculate prefix sum for
|
yadvendrak01
|
NORMAL
|
2021-04-17T11:30:28.840934+00:00
|
2021-04-18T11:28:24.567825+00:00
| 5,138 | false |
**Intution :**\n* We need to apply same logic which we used in : **[Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/)**. If you have not done this pls check it out first .\n* Calculate prefix sum for each row.\n* Calculate sum for each column and check if **sum - target** is there in the DS or not .If it is there then add the count. (DS is data structure , in this question we will use **`unordered_map<int,int> counter`**)\n\t\t** Why sum - target ? Because if sum - target is there in the DS it means that there is a subset whose sum == target.\n\t\tExample : target = 4 \n\t\t***1*** *1 1* 1 \n\t\t***1*** *1 1* 1 \n\t\tsum of bold = 2 , sum of bold + Italic = 6 ,,, 6 - 4 = **2** , it means the italic sub matrix sum = target.\n\n\n**Example** : 4 * 4 matrix , target = 4,\n```\n1 1 1 1\n1 1 1 1\n1 1 1 1\n1 1 1 1\n```\n**1. Calculate prefix sum for each row ;**\n\n```\n1 2 3 4\n1 2 3 4\n1 2 3 4\n1 2 3 4\n```\n\n**2. For every possible range between two columns, accumulate the prefix sum of submartrixes that can be formed between these two columns by adding up the sum of values between these two columns for every row.**\n\nFor first column :\n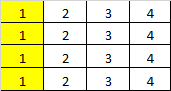\n\n\n```\nSum = 1 + 1 + 1 + 1 =4\nsum - target = 0 , which is there in map so count will be increased by 1.\n```\n\nFor second column :\n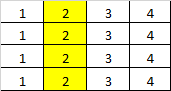\n\n\nHere when row = 1 , 2 - target is not there in the DS so we will add 2 into DS with count 1, **sum = 2** `DS : {{0 , 1 } , {2 , 1}`\nwhen row = 2 , **sum = 4** 4 - target is there so increase count. `DS : {{0 , 1 } , {2 , 1} , { 4 ,1}`\nwhen row = 3 , **sum = 6** 6 - target = 2, which is there in DS so increase count.`DS : {{0 , 1 } , {2 , 1} , { 4 ,1} ,{6,1}`\nwhen row = 4 , **sum = 8** 8 - target = 4 , which is there in DS so increase count. `DS : {{0 , 1 } , {2 , 1} , { 4 ,1} ,{6,1}, {8,1}`\n\n**In this way for each column we will get number of sub matrixes whose sum is equals to target. Like wise we will do this for all the columns . Now the problem is in this way we are missing some sub matrixes**\n\n\nAs you can see in the image for column 2 we have considered 3 sub matrixes :\n1. Yellow 1\'s\n2. boxes with color inside it.\n3. Red border color boxes. so **what we missed ?????**\n\n**We missed the 1\'s in green box. So to count those sub matrixes we need to subtract previous column sum. For this third loop is there which checks if column start is greater than 0 then subtract the sum of previous column and sum.**\n\n```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int rows = matrix.size() , cols = matrix[0].size();\n \n if(rows < 1){\n return 0;\n }\n \n // calculate prefix sum for rows\n for(int row = 0 ; row < rows ; row++){\n for(int col = 1 ; col < cols ;col++){\n matrix[row][col] = matrix[row][col] + matrix[row][col -1];\n }\n }\n \n int count = 0 , sum ;\n unordered_map<int , int> counter;\n for(int colstart = 0 ; colstart < cols ;colstart++){\n for(int col = colstart ; col < cols; col++){\n counter.clear();\n counter[0] = 1;\n sum =0;\n for(int row = 0 ; row < rows ;row++){\n sum += matrix[row][col] - (colstart > 0 ? matrix[row][colstart - 1] : 0 );\n count += (counter.find(sum- target) != counter.end() ? counter[sum-target] : 0);\n counter[sum]++;\n }\n }\n }\n return count;\n }\n};\n```\n\n***Time Complexity : O(row * column^2)\nSpace Complexity :O(N)***\n\n**Update 18/04/2021 :**\n\nIncase anyone else is having same doubt : \n\n\n**Hello,\n\tFeel free to comment for doubts . I will love to clear them . If something is wrong please let me know in comment section.\nThanks !! Happy Coding.**
| 60 | 3 |
['C', 'C++']
| 8 |
number-of-submatrices-that-sum-to-target
|
Java, reduce to 1D array
|
java-reduce-to-1d-array-by-_topspeed-bzwv
|
Similar to "Max Sum of Rectangle No Larger Than K", reduce 2D array to 1D, and find the sub-array sum targeting k.\n\n\npublic int numSubmatrixSumTarget(int[][]
|
_topspeed_
|
NORMAL
|
2019-06-02T04:08:12.949222+00:00
|
2019-06-02T04:09:34.743397+00:00
| 3,596 | false |
Similar to ["Max Sum of Rectangle No Larger Than K"](https://leetcode.com/problems/max-sum-of-rectangle-no-larger-than-k/), reduce 2D array to 1D, and find the sub-array sum targeting k.\n\n```\npublic int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length;\n int n = matrix[0].length;\n int[] array = new int[m];\n int result = 0;\n for(int i = 0; i < n; i++) { //i is the starting column\n Arrays.fill(array, 0);\n for(int j = i; j < n; j++) { //j is the ending column\n for(int k = 0; k < m; k++) {\n array[k] += matrix[k][j];\n }\n result += subarraySum(array, target);\n }\n }\n return result;\n }\n \n public int subarraySum(int[] nums, int k) {\n int sum = 0, result = 0;\n Map<Integer, Integer> preSum = new HashMap<>();\n preSum.put(0, 1);\n \n for (int i = 0; i < nums.length; i++) {\n sum += nums[i];\n if (preSum.containsKey(sum - k)) {\n result += preSum.get(sum - k);\n }\n preSum.put(sum, preSum.getOrDefault(sum, 0) + 1);\n }\n \n return result;\n }\n```
| 60 | 1 |
[]
| 9 |
number-of-submatrices-that-sum-to-target
|
JS, Python, Java, C++ | Short Prefix Sum Solution w/ Explanation
|
js-python-java-c-short-prefix-sum-soluti-iynm
|
(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n
|
sgallivan
|
NORMAL
|
2021-04-17T11:47:51.126025+00:00
|
2021-04-17T21:14:58.886112+00:00
| 4,436 | false |
*(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nThis problem is essentially a **2-dimensional** version of [**#560. Subarray Sum Equals K (S.S.E.K)**](https://leetcode.com/problems/subarray-sum-equals-k/description/). By using a **prefix sum** on each row or each column, we can compress this problem down to either **N^2** iterations of the **O(M)** SSEK, or **M^2** iterations of the **O(N)** SSEK.\n\nIn the SSEK solution, we can find the number of subarrays with the target sum by utilizing a **result map** (**res**) to store the different values found as we iterate through the array while keeping a running sum (**csum**). Just as in the case with a prefix sum array, the sum of a subarray between **i** and **j** is equal to the sum of the subarray from **0** to **j** minus the sum of the subarray from **0** to **i-1**.\n\nRather than iteratively checking if **sum[0,j] - sum[0,i-1] = T** for every pair of **i, j** values, we can flip it around to **sum[0,j] - T = sum[0,i-1]** and since every earlier sum value has been stored in **res**, we can simply perform a lookup on **sum[0,j] - T** to see if there are any matches.\n\nWhen extrapolating this solution to our **2-dimensional** matrix (**M**), we will need to first prefix sum the rows or columns, (which we can do **in-place** to avoid extra space, as we will not need the original values again). Then we should iterate through **M** again in the opposite order of rows/columns where the prefix sums will allow us to treat a group of columns or rows as if it were a **1-dimensional** array and apply the SSEK algorithm.\n\n---\n\n#### ***Implementation:***\n\nPython, oddly, has _much_ better performance with the use of a simple **dict** instead of a **defaultdict** for **res** (Thanks, [@slcheungcasado](https://leetcode.com/slcheungcasado)!)\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **232ms / 44.8MB** (beats 100% / 81%).\n```javascript\nvar numSubmatrixSumTarget = function(M, T) {\n let xlen = M[0].length, ylen = M.length,\n ans = 0, res = new Map(), csum\n for (let i = 0, r = M[0]; i < ylen; r = M[++i]) \n for (let j = 1; j < xlen; j++)\n r[j] += r[j-1]\n for (let j = 0; j < xlen; j++)\n for (let k = j; k < xlen; k++) {\n res.clear(), res.set(0,1), csum = 0\n for (let i = 0; i < ylen; i++) {\n csum += M[i][k] - (j ? M[i][j-1] : 0)\n ans += (res.get(csum - T) || 0)\n res.set(csum, (res.get(csum) || 0) + 1)\n }\n }\n return ans\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **552ms / 15.0MB** (beats 100% / 85%).\n```python\nclass Solution:\n def numSubmatrixSumTarget(self, M: List[List[int]], T: int) -> int:\n xlen, ylen, ans = len(M[0]), len(M), 0\n for r in M:\n for j in range(1, xlen):\n r[j] += r[j-1]\n for j in range(xlen):\n for k in range(j, xlen):\n res, csum = {0: 1}, 0\n for r in M:\n csum += r[k] - (r[j-1] if j else 0)\n if csum - T in res: ans += res[csum-T]\n res[csum] = res[csum] + 1 if csum in res else 1 \n return ans\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **81ms / 39.3MB** (beats 96% / 95%).\n```java\nclass Solution {\n public int numSubmatrixSumTarget(int[][] M, int T) {\n int xlen = M[0].length, ylen = M.length, ans = 0;\n Map<Integer, Integer> res = new HashMap<>();\n for (int[] r : M)\n for (int j = 1; j < xlen; j++)\n r[j] += r[j-1];\n for (int j = 0; j < xlen; j++)\n for (int k = j; k < xlen; k++) {\n res.clear();\n res.put(0,1);\n int csum = 0;\n for (int i = 0; i < ylen; i++) {\n csum += M[i][k] - (j > 0 ? M[i][j-1] : 0);\n ans += res.getOrDefault(csum - T, 0);\n res.put(csum, res.getOrDefault(csum, 0) + 1);\n }\n }\n return ans;\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **484ms / 95.3MB** (beats 96% / 76%).\n```c++\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& M, int T) {\n int xlen = M[0].size(), ylen = M.size(), ans = 0;\n unordered_map<int, int> res;\n for (int i = 0; i < ylen; i++)\n for (int j = 1; j < xlen; j++)\n M[i][j] += M[i][j-1];\n for (int j = 0; j < xlen; j++)\n for (int k = j; k < xlen; k++) {\n res.clear();\n res[0] = 1;\n int csum = 0;\n for (int i = 0; i < ylen; i++) {\n csum += M[i][k] - (j ? M[i][j-1] : 0);\n ans += res.find(csum - T) != res.end() ? res[csum - T] : 0;\n res[csum]++;\n }\n }\n return ans;\n }\n};\n```
| 58 | 8 |
['C', 'Python', 'Java', 'JavaScript']
| 2 |
number-of-submatrices-that-sum-to-target
|
[Python] cumulative sum + dp, explained
|
python-cumulative-sum-dp-explained-by-db-lzbr
|
Let us define by dp[i, j, k] sum of numbers in the rectangle i <= x < j and 0 <= y < m. Why it is enough to evaluate only values on these matrices? Because then
|
dbabichev
|
NORMAL
|
2021-04-17T09:20:26.570451+00:00
|
2021-04-17T09:59:56.407035+00:00
| 2,449 | false |
Let us define by `dp[i, j, k]` sum of numbers in the rectangle `i <= x < j` and `0 <= y < m`. Why it is enough to evaluate only values on these matrices? Because then we can use **2Sum** problem: any sum of elements in submatrix with coordinates `a <= x < b` and `c <= y < d` can be evaluated as difference between sum of `a <= x < b, 0 <= y < d` and sum of `a <= x < b, 0 <= y < c`. So, let us fix `a` and `b`, and say we have sums `S1, S2, ... Sm`. Then we want to find how many differences between these values give us our `target`. The idea is to calculate cumulative sums and keep counter of values, and then check how many we have (we can not use sliding window, because we can have negative values), see problem **560**. Subarray Sum Equals K for more details.\n\nSo, we have in total two stages of our algorithm:\n1. Precompute all sums in rectangles of the type `i <= x < j` and `0 <= y < m`.\n2. For each `n*(n-1)/2` problems with fixed `i` and `j`, solve sumproblem in `O(m)` time.\n\n#### Complexity\nTime complexity is `O(n^2m)`, we need it for both stages. Space complexity is the same.\n\n#### Code\n\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix, target):\n m, n = len(matrix), len(matrix[0])\n dp, ans = {}, 0\n for k in range(m):\n t = [0] + list(accumulate(matrix[k]))\n for i, j in combinations(range(n+1), 2):\n dp[i, j, k] = dp.get((i,j,k-1), 0) + t[j] - t[i]\n \n for i, j in combinations(range(n+1), 2):\n T = Counter([0])\n for k in range(m):\n ans += T[dp[i, j, k] - target]\n T[dp[i, j, k]] += 1\n \n return ans\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**
| 33 | 2 |
['Dynamic Programming']
| 2 |
number-of-submatrices-that-sum-to-target
|
🔥✅✅Beats 99.71% with Proof | Very Easy to Understand | Prefix Sum Approach✅✅🔥
|
beats-9971-with-proof-very-easy-to-under-c9dm
|
Proof - Upvote if you\'re watching the proof\n\n\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe key intuition here is to use
|
areetrahalder
|
NORMAL
|
2024-01-28T04:36:36.120670+00:00
|
2024-01-28T04:36:36.120701+00:00
| 5,503 | false |
# Proof - Upvote if you\'re watching the proof\n\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key intuition here is to use the prefix sum technique to efficiently compute the sum of submatrices. The idea is to preprocess the matrix by calculating the cumulative sum of each row. Then, for any submatrix defined by two column indices `c1` and `c2`, and two row indices `row1` and `row2`, the sum of elements in this submatrix can be computed in constant time using the prefix sum array.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Preprocess the matrix to calculate the cumulative sum for each row. This is done by iterating through each row and updating each element to be the sum of itself and the previous element in the row.\n2. Iterate over all possible pairs of column indices `c1` and `c2`.\n3. For each pair of column indices, iterate over all possible pairs of row indices `row1` and `row2`.\n4. Calculate the sum of the submatrix defined by `c1`, `c2`, `row1`, and `row2` using the preprocessed cumulative sum array.\n5. Use a HashMap to keep track of the frequency of each sum encountered so far.\n6. Check if the current sum minus the target value exists in the HashMap. If it does, increment the count by the frequency of that sum.\n7. Update the HashMap with the current sum.\n8. Return the final count as the result.\n\n# Complexity\n- Time complexity: $$O(m * n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n> where m is the number of rows and n is the number of columns. The nested loops iterate over all possible submatrices, and the inner loop involves constant time operations.\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n> where n is the number of columns. The space is used for the HashMap to store the frequency of sums encountered.\n# Code\n```Java []\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length;\n int n = matrix[0].length;\n\n for (int row = 0; row < m; row++) {\n for (int col = 1; col < n; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n int count = 0;\n\n for (int c1 = 0; c1 < n; c1++) {\n for (int c2 = c1; c2 < n; c2++) {\n Map<Integer, Integer> map = new HashMap<>();\n map.put(0, 1);\n int sum = 0;\n\n for (int row = 0; row < m; row++) {\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n count += map.getOrDefault(sum - target, 0);\n map.put(sum, map.getOrDefault(sum, 0) + 1);\n }\n }\n }\n\n return count;\n }\n}\n```\n```C []\nint numSubmatrixSumTarget(int** matrix, int matrixSize, int* matrixColSize, int target) {\n int m = matrixSize;\n int n = *matrixColSize;\n\n // Preprocess the matrix to calculate cumulative sum for each row\n for (int row = 0; row < m; row++) {\n for (int col = 1; col < n; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n int count = 0;\n\n // Iterate over all possible pairs of column indices c1 and c2\n for (int c1 = 0; c1 < n; c1++) {\n for (int c2 = c1; c2 < n; c2++) {\n int sum = 0;\n int prefixSum[100]; // Assuming a maximum size for the prefix sum array\n\n // Initialize prefix sum array\n for (int i = 0; i < m; i++) {\n prefixSum[i] = 0;\n }\n\n // Iterate over all possible pairs of row indices row1 and row2\n for (int row = 0; row < m; row++) {\n // Calculate the sum of the submatrix using cumulative sum\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n\n // Check if the current sum minus the target exists in the prefix sum array\n if (sum == target) {\n count++;\n }\n\n // Update the prefix sum array\n prefixSum[row] = sum;\n\n // Check if the (sum - target) exists in the prefix sum array\n for (int k = 0; k < row; k++) {\n if (prefixSum[row] - prefixSum[k] == target) {\n count++;\n }\n }\n }\n }\n }\n\n return count;\n}\n```\n```C++ []\nclass Solution\n{\n public:\n Solution()\n {\n cin.tie(NULL);\n cout.tie(NULL);\n ios_base :: sync_with_stdio(false);\n }\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target)\n {\n int ans = 0;\n int n = matrix.size(), m = matrix[0].size();\n for(int left = 0 ; left < m ; left++)\n {\n vector<int>pre(n, 0);\n for(int right = left ; right < m ; right++)\n {\n for(int i = 0 ; i<n; i++)\n {\n pre[i] += matrix[i][right];\n }\n\n for(int i = 0 ; i<n;i++)\n {\n int sum = 0;\n for(int j = i ; j<n; j++)\n {\n sum += pre[j];\n if(sum == target)\n {\n ans += 1;\n }\n }\n }\n }\n }\n return ans;\n }\n};\n```\n```C# []\npublic class Solution {\n public int NumSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.Length;\n int n = matrix[0].Length;\n\n // Preprocess the matrix to calculate the cumulative sum for each row\n for (int row = 0; row < m; row++) {\n for (int col = 1; col < n; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n int count = 0;\n\n // Iterate over all possible pairs of column indices c1 and c2\n for (int c1 = 0; c1 < n; c1++) {\n for (int c2 = c1; c2 < n; c2++) {\n Dictionary<int, int> map = new Dictionary<int, int>();\n map[0] = 1;\n int sum = 0;\n\n // Iterate over all possible pairs of row indices row1 and row2\n for (int row = 0; row < m; row++) {\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n count += map.GetValueOrDefault(sum - target, 0);\n map[sum] = map.GetValueOrDefault(sum, 0) + 1;\n }\n }\n }\n\n return count;\n }\n}\n```\n```Javascript []\n/**\n * @param {number[][]} matrix\n * @param {number} target\n * @return {number}\n */\nvar numSubmatrixSumTarget = function(matrix, target) {\n const m = matrix.length;\n const n = matrix[0].length;\n\n // Preprocess the matrix to calculate cumulative sum for each row\n for (let row = 0; row < m; row++) {\n for (let col = 1; col < n; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n let count = 0;\n\n for (let c1 = 0; c1 < n; c1++) {\n for (let c2 = c1; c2 < n; c2++) {\n const map = new Map();\n map.set(0, 1);\n let sum = 0;\n\n for (let row = 0; row < m; row++) {\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n count += map.get(sum - target) || 0;\n map.set(sum, (map.get(sum) || 0) + 1);\n }\n }\n }\n\n return count;\n};\n```\n```Typescript []\nfunction numSubmatrixSumTarget(matrix: number[][], target: number): number {\n const m = matrix.length;\n const n = matrix[0].length;\n\n for (let row = 0; row < m; row++) {\n for (let col = 1; col < n; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n let count = 0;\n\n for (let c1 = 0; c1 < n; c1++) {\n for (let c2 = c1; c2 < n; c2++) {\n const map = new Map<number, number>();\n map.set(0, 1);\n let sum = 0;\n\n for (let row = 0; row < m; row++) {\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n count += map.get(sum - target) || 0;\n map.set(sum, (map.get(sum) || 0) + 1);\n }\n }\n }\n\n return count;\n}\n```\n```Python []\nclass Solution(object):\n def numSubmatrixSumTarget(self, matrix, target):\n rows, cols = len(matrix), len(matrix[0])\n prefix_sum = [[0] * (cols + 1) for _ in range(rows + 1)]\n\n # Compute the 2D prefix sum\n for i in range(1, rows + 1):\n for j in range(1, cols + 1):\n prefix_sum[i][j] = matrix[i - 1][j - 1] + prefix_sum[i - 1][j] + prefix_sum[i][j - 1] - prefix_sum[i - 1][j - 1]\n\n count = 0\n\n # Iterate through all possible pairs of columns\n for col1 in range(1, cols + 1):\n for col2 in range(col1, cols + 1):\n # Use a hashmap to count the number of subarrays with a given sum\n prefix_sum_map = {0: 1}\n current_sum = 0\n for row in range(1, rows + 1):\n current_sum = prefix_sum[row][col2] - prefix_sum[row][col1 - 1]\n if current_sum - target in prefix_sum_map:\n count += prefix_sum_map[current_sum - target]\n if current_sum in prefix_sum_map:\n prefix_sum_map[current_sum] += 1\n else:\n prefix_sum_map[current_sum] = 1\n\n return count\n```\n```Python3 []\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m, n = len(matrix), len(matrix[0])\n\n # Step 1: Preprocess the matrix to calculate cumulative sum for each row\n for row in range(m):\n for col in range(1, n):\n matrix[row][col] += matrix[row][col - 1]\n\n count = 0\n\n # Step 2: Iterate over all pairs of column indices c1 and c2\n for c1 in range(n):\n for c2 in range(c1, n):\n # Step 3: Iterate over all pairs of row indices row1 and row2\n prefix_sum_map = {0: 1}\n sum_val = 0\n\n # Step 4: Calculate the sum of submatrix using cumulative sum\n for row in range(m):\n sum_val += matrix[row][c2] - (matrix[row][c1 - 1] if c1 > 0 else 0)\n\n # Step 5 and 6: Update count and prefix_sum_map\n count += prefix_sum_map.get(sum_val - target, 0)\n prefix_sum_map[sum_val] = prefix_sum_map.get(sum_val, 0) + 1\n\n # Step 8: Return the final count\n return count\n```\n# Upvote - Please\n\n
| 32 | 1 |
['Array', 'C', 'Prefix Sum', 'Python', 'C++', 'Java', 'TypeScript', 'Python3', 'JavaScript', 'C#']
| 6 |
number-of-submatrices-that-sum-to-target
|
[JAVA] Easy to Understand | Heavily Commented | Detailed Explanation with Pictures
|
java-easy-to-understand-heavily-commente-mgf6
|
Region(Answer)\n\nSo we first need the sum from each of the following regions:\n1. Region(A)\n\t\n2. Region(B)\n\t\n3. Region(C)\n \n4. Region(D)\n \nRegion
|
angzhanh
|
NORMAL
|
2022-07-18T03:14:04.691397+00:00
|
2022-07-18T03:16:38.069588+00:00
| 2,743 | false |
Region(Answer)\n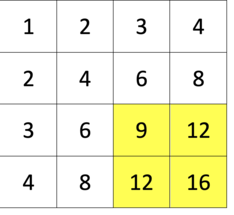\nSo we first need the sum from each of the following regions:\n1. Region(A)\n\t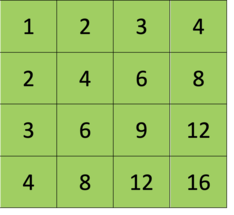\n2. Region(B)\n\t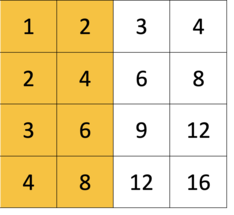\n3. Region(C)\n 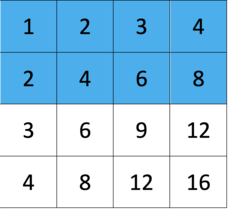\n4. Region(D)\n 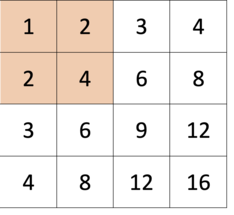\nRegion(Answer) = Region(A) - Region(B) - Region(C) + Region(D)\n```\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length;\n int n = matrix[0].length;\n \n\t\t// aux[i][j] is the sum of sub-matrix which start at [0][0] and end in [i][j]\n int[][] aux = new int[m + 1][n + 1]; // padding on top and left\n for (int i = 1; i < m + 1; i++) {\n for (int j = 1; j < n + 1; j++) {\n\t\t\t\t// draw a picture, you will understand it easily~\n aux[i][j] = matrix[i - 1][j - 1] + aux[i - 1][j] + aux[i][j - 1] - aux[i - 1][j - 1]; \n }\n }\n \n int res = 0;\n\t\t// try each sub-matrix\n for (int x1 = 1; x1 < m + 1; x1++) {\n for (int y1 = 1; y1 < n + 1; y1++) {\n for (int x2 = x1; x2 < m + 1; x2++) {\n for (int y2 = y1; y2 < n + 1; y2++) {\n if (target == aux[x2][y2] - aux[x2][y1 - 1] - aux[x1 - 1][y2] + aux[x1 - 1][y1 - 1])\n res++;\n }\n }\n }\n }\n \n return res;\n }\n}\n```\nPlease vote if it helps\uD83D\uDE06~
| 30 | 1 |
[]
| 2 |
number-of-submatrices-that-sum-to-target
|
[Java] N^4 and N^3 Solutions
|
java-n4-and-n3-solutions-by-hiepit-s87d
|
Solution 1: N^4 ~ 4500ms\njava\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length, n = matrix[
|
hiepit
|
NORMAL
|
2020-02-26T16:47:53.045853+00:00
|
2020-02-29T12:12:58.886167+00:00
| 1,645 | false |
**Solution 1: N^4 ~ 4500ms**\n```java\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length, n = matrix[0].length;\n int[][] sum = new int[m + 1][n + 1];\n for (int i = 1; i <= m; i++) {\n for (int j = 1; j <= n; j++) {\n sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];\n }\n }\n int ans = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n for (int u = i + 1; u <= m; u++) {\n for (int v = j + 1; v <= n; v++) {\n int _sum = sum[u][v] - sum[i][v] - sum[u][j] + sum[i][j];\n if (_sum == target) {\n ans++;\n }\n }\n }\n }\n }\n return ans;\n }\n}\n```\nComplexity:\n- Time: `O((m*n)^2)`\n- Space: `O(m*n)`\n\n**Solution 2 - N^3 ~ 1000ms**\n```java\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length, n = matrix[0].length;\n for (int i = 0; i < m; i++) {\n for (int j = 1; j < n; j++) {\n matrix[i][j] += matrix[i][j - 1];\n }\n }\n int ans = 0;\n for (int i = 0; i < n; i++) {\n for (int j = i; j < n; j++) {\n HashMap<Integer, Integer> map = new HashMap<>();\n map.put(0, 1);\n int right = 0;\n for (int k = 0; k < m; k++) {\n right += matrix[k][j] - (i == 0 ? 0 : matrix[k][i - 1]);\n int left = right - target;\n ans += map.getOrDefault(left, 0);\n map.put(right, map.getOrDefault(right, 0) + 1);\n }\n }\n }\n return ans;\n }\n}\n```\nComplexity:\n- Time: `O(n*n*m)`\n- Space: `O(m)` for map
| 30 | 1 |
[]
| 2 |
number-of-submatrices-that-sum-to-target
|
Number of Submatrices That Sum to Target | JS, Python, Java, C++ | Short Solution w/ Explanation
|
number-of-submatrices-that-sum-to-target-5gam
|
(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n
|
sgallivan
|
NORMAL
|
2021-04-17T11:48:41.706397+00:00
|
2021-04-17T21:15:09.745572+00:00
| 1,126 | false |
*(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nThis problem is essentially a **2-dimensional** version of [**#560. Subarray Sum Equals K (S.S.E.K)**](https://leetcode.com/problems/subarray-sum-equals-k/description/). By using a **prefix sum** on each row or each column, we can compress this problem down to either **N^2** iterations of the **O(M)** SSEK, or **M^2** iterations of the **O(N)** SSEK.\n\nIn the SSEK solution, we can find the number of subarrays with the target sum by utilizing a **result map** (**res**) to store the different values found as we iterate through the array while keeping a running sum (**csum**). Just as in the case with a prefix sum array, the sum of a subarray between **i** and **j** is equal to the sum of the subarray from **0** to **j** minus the sum of the subarray from **0** to **i-1**.\n\nRather than iteratively checking if **sum[0,j] - sum[0,i-1] = T** for every pair of **i, j** values, we can flip it around to **sum[0,j] - T = sum[0,i-1]** and since every earlier sum value has been stored in **res**, we can simply perform a lookup on **sum[0,j] - T** to see if there are any matches.\n\nWhen extrapolating this solution to our **2-dimensional** matrix (**M**), we will need to first prefix sum the rows or columns, (which we can do **in-place** to avoid extra space, as we will not need the original values again). Then we should iterate through **M** again in the opposite order of rows/columns where the prefix sums will allow us to treat a group of columns or rows as if it were a **1-dimensional** array and apply the SSEK algorithm.\n\n---\n\n#### ***Implementation:***\n\nPython, oddly, has _much_ better performance with the use of a simple **dict** instead of a **defaultdict** for **res** (Thanks, [@slcheungcasado](https://leetcode.com/slcheungcasado)!)\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **232ms / 44.8MB** (beats 100% / 81%).\n```javascript\nvar numSubmatrixSumTarget = function(M, T) {\n let xlen = M[0].length, ylen = M.length,\n ans = 0, res = new Map(), csum\n for (let i = 0, r = M[0]; i < ylen; r = M[++i]) \n for (let j = 1; j < xlen; j++)\n r[j] += r[j-1]\n for (let j = 0; j < xlen; j++)\n for (let k = j; k < xlen; k++) {\n res.clear(), res.set(0,1), csum = 0\n for (let i = 0; i < ylen; i++) {\n csum += M[i][k] - (j ? M[i][j-1] : 0)\n ans += (res.get(csum - T) || 0)\n res.set(csum, (res.get(csum) || 0) + 1)\n }\n }\n return ans\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **552ms / 15.0MB** (beats 100% / 85%).\n```python\nclass Solution:\n def numSubmatrixSumTarget(self, M: List[List[int]], T: int) -> int:\n xlen, ylen, ans = len(M[0]), len(M), 0\n for r in M:\n for j in range(1, xlen):\n r[j] += r[j-1]\n for j in range(xlen):\n for k in range(j, xlen):\n res, csum = {0: 1}, 0\n for r in M:\n csum += r[k] - (r[j-1] if j else 0)\n if csum - T in res: ans += res[csum-T]\n res[csum] = res[csum] + 1 if csum in res else 1 \n return ans\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **81ms / 39.3MB** (beats 96% / 95%).\n```java\nclass Solution {\n public int numSubmatrixSumTarget(int[][] M, int T) {\n int xlen = M[0].length, ylen = M.length, ans = 0;\n Map<Integer, Integer> res = new HashMap<>();\n for (int[] r : M)\n for (int j = 1; j < xlen; j++)\n r[j] += r[j-1];\n for (int j = 0; j < xlen; j++)\n for (int k = j; k < xlen; k++) {\n res.clear();\n res.put(0,1);\n int csum = 0;\n for (int i = 0; i < ylen; i++) {\n csum += M[i][k] - (j > 0 ? M[i][j-1] : 0);\n ans += res.getOrDefault(csum - T, 0);\n res.put(csum, res.getOrDefault(csum, 0) + 1);\n }\n }\n return ans;\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **484ms / 95.3MB** (beats 96% / 76%).\n```c++\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& M, int T) {\n int xlen = M[0].size(), ylen = M.size(), ans = 0;\n unordered_map<int, int> res;\n for (int i = 0; i < ylen; i++)\n for (int j = 1; j < xlen; j++)\n M[i][j] += M[i][j-1];\n for (int j = 0; j < xlen; j++)\n for (int k = j; k < xlen; k++) {\n res.clear();\n res[0] = 1;\n int csum = 0;\n for (int i = 0; i < ylen; i++) {\n csum += M[i][k] - (j ? M[i][j-1] : 0);\n ans += res.find(csum - T) != res.end() ? res[csum - T] : 0;\n res[csum]++;\n }\n }\n return ans;\n }\n};\n```
| 27 | 5 |
[]
| 2 |
number-of-submatrices-that-sum-to-target
|
JAVA|| Easy Solution With Explanation || HashMap
|
java-easy-solution-with-explanation-hash-u673
|
Explanation\n\n For each row, calculate the prefix sum.\n For each pair of columns,\n calculate the accumulated sum of rows.\n Now this problem is same to, "Fin
|
shivrastogi
|
NORMAL
|
2022-07-18T02:39:19.254840+00:00
|
2022-07-18T02:39:19.254875+00:00
| 2,534 | false |
Explanation\n\n* For each row, calculate the prefix sum.\n* For each pair of columns,\n* calculate the accumulated sum of rows.\n* Now this problem is same to, "Find the Subarray with Target Sum".\n```\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int row = matrix.length;\n int col = matrix[0].length;\n int res = 0;\n //int[][] sum = new int[row][col];\n \n for(int i = 0; i < row; i++){\n for(int j = 1; j < col; j++){\n //sum[i][j] =sum[i][j-1] + matrix[i][j-1];\n matrix[i][j] += matrix[i][j-1];\n }\n }\n \n for(int start = 0; start < col; start++){\n for(int end = start; end < col; end++){\n int subMatrixSum = 0;\n \n Map<Integer, Integer> countElm = new HashMap<Integer, Integer>();\n countElm.put(0,1);\n \n for(int k = 0; k < row; k++){\n //subMatrixSum += sum[k][end] - sum[k][start];\n int prefixSum = start == 0 ? 0:matrix[k][start-1];\n subMatrixSum += matrix[k][end] - prefixSum;\n \n if(countElm.containsKey(subMatrixSum - target))\n res += countElm.get(subMatrixSum - target);\n \n int r = countElm.getOrDefault(subMatrixSum, 0);\n countElm.put(subMatrixSum, r+1);\n }\n }\n }\n \n return res;\n }\n}\n```
| 19 | 0 |
['Java']
| 1 |
number-of-submatrices-that-sum-to-target
|
✅ Number of Submatrices That Sum to Target | Optimization from Brute-Force Explained!
|
number-of-submatrices-that-sum-to-target-j4jo
|
There are a few solution mentioned by others but most have directly given the most optimal solution. Here, I will try to start from the brute-force approach and
|
archit91
|
NORMAL
|
2021-04-17T14:24:28.391323+00:00
|
2021-04-17T14:26:17.175167+00:00
| 866 | false |
There are a few solution mentioned by others but most have directly given the most optimal solution. Here, I will try to start from the brute-force approach and try to explain the various optimizations that can be done to finally arrive at the optimal solution.\n\n---\n\n\u274C ***Solution - I (Brute-Force Approach) [Rejected]***\n\nLet\'s start with the most basic approach to this problem. Take all the submatrices possible for the given matrix and check if their sum is equal to `target`.\n\n```\nint numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n\tint res = 0, m = size(A), n = size(A[0]);\n\t// calculate sum of each submatrix and check if it is equal to target\n\tfor(int rowStart = 0; rowStart < m; rowStart++)\n\t\tfor(int rowSize = 1; rowStart + rowSize <= m; rowSize++)\n\t\t\tfor(int colStart = 0; colStart < n; colStart++)\n\t\t\t\tfor(int colSize = 1; colStart + colSize <= n; colSize++)\n\t\t\t\t\tif(SUM(A, rowStart, rowSize, colStart, colSize) == target)\n\t\t\t\t\t\tres++;\n\treturn res; \n}\n// Calculates the sum of a submatrix with given bounds\nint SUM(vector<vector<int> > &A, int rStart, int rSize, int cStart, int cSize){\n\tint subMatrixSum = 0;\n\tfor(int i = rStart; i < rStart + rSize; i++)\n\t\tfor(int j = cStart; j < cStart + cSize; j++)\n\t\t\tsubMatrixSum += A[i][j];\n\treturn subMatrixSum;\n}\n```\n\n***Time Complexity :*** **`O((M*N)^3)`**, where `M` is the number of rows and `N` is the number of columns in the given matrix.\n***Space Complexity :*** **`O(1)`**\n\n---\n\n\u2714\uFE0F ***Solution - II (Compute prefix sum for each Row or Column)***\n\nWe can optimize the above approach by reducing the time complexity of the `SUM` function in the above solution. We know that in a given array, the sum of range [i,j] can be calculated by `prefixSum[j] - prefixSum[i - 1]`. We can use this to optimize the solution.\n\nAfter computing prefix sum for each row of matrix (*you can do it for column as well*), we can get the sum of a given range in O(1) time. Thus, for any submatrix of the main matrix, we just need to iterate over all its rows and we can get sum of given range (`[colStart, colEnd]`) in O(1) time.\n\n1. We just start from row 0, calculate the sum for that row for the range `[colStart, colEnd]`.\n2. Extend the sum by perform step-1 for row 1, row 2, ... and so on till last row.\n3. Repeat this process for every `[colStart, colEnd]` combination.\n\n\n```\nint numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n\tint res = 0, m = size(A), n = size(A[0]);\n\t// calculating prefix sum for each row of matrix\n\tfor (int row = 0; row < m; row++)\n\t\tfor (int col = 1; col < n; col++)\n\t\t\tA[row][col] += A[row][col - 1];\n\t// calculate sum of each submatrix and check if it is equal to target\n\tfor (int colStart = 0; colStart < n; colStart++) {\n\t\tfor (int colEnd = colStart; colEnd < n; colEnd++) {\n\t\t\tfor(int rowStart = 0; rowStart < m; rowStart++){\n\t\t\t\tint sum = 0;\n\t\t\t\tfor(int rowEnd = rowStart; rowEnd < m; rowEnd++){\n\t\t\t\t\tsum += A[rowEnd][colEnd] - (colStart ? A[rowEnd][colStart - 1] : 0);\n\t\t\t\t\tif(sum == target) res++;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\treturn res; \n}\n```\n***Time Complexity :*** **`O((M*N)^2)`**, where `M` is the number of rows and `N` is the number of columns in the given matrix.\n***Space Complexity :*** **`O(1)`**, since we are modifying the given matrix itself. If we use a new prefix sum matrix, the space complexity would be `O(M*N)`.\n\n---\n\n\u2714\uFE0F ***Solution - III (Further Optimization in Solution - II)***\n\nWe can further optimize the solution by using hashmap. The optimization done here is similar to the one in solution of [560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/solution/).\n\nBasically, we will be maintaining a running submatrix sum starting from row 0 till m, for a given `[colStart, colEnd]` range. Each sum value and number of its occurence will be stored in hashmap. If there\'s a submatrix which was found such that `cursum` at that time was equal to present sum (`cursum`) - target, then we are sure that there were occurences of submatrices which had sum equal to `target` and the count is given by `mp[cursum - target]`.\n\nIf the explanation didn\'t make the approach clear, I really suggest you to try the *560. Subarray Sum Equals K* problem and read the hashmap solution. It took me some time reading that before I was able to clearly understand this solution.\n\n```\nint numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n\tint res = 0, m = size(A), n = size(A[0]);\n\tfor (int row = 0; row < m; row++)\n\t\tfor (int col = 1; col < n; col++)\n\t\t\tA[row][col] += A[row][col - 1];\n\t// cursum, occurences\n\tunordered_map<int, int> mp;\n\tfor (int colStart = 0; colStart < n; colStart++) {\n\t\tfor (int colEnd = colStart; colEnd < n; colEnd++) {\n\t\t\tint cursum = 0;\n\t\t\tmp = {{0, 1}};\n\t\t\tfor(int row = 0; row < m; row++){\n\t\t\t\tcursum += A[row][colEnd] - (colStart ? A[row][colStart - 1] : 0); \n\t\t\t\t// mp[sum-target] will give number of submatrices found having sum as \'sum - target\'\n\t\t\t\tres += mp[cursum - target];\n\t\t\t\tmp[cursum]++;\n\t\t\t}\n\t\t}\n\t}\n\treturn res; \n}\n```\n***Time Complexity :*** **`O(N*N*M)`**, where `M` is the number of rows and `N` is the number of columns in the given matrix.\n***Space Complexity :*** **`O(N)`**\n\n\n\n---\n---\n\n\uD83D\uDCBB\uD83D\uDC31\u200D\uD83D\uDCBBIf there are any questions or mistakes in my post, please do comment below \uD83D\uDC47 \n\n---\n---
| 17 | 0 |
['C']
| 2 |
number-of-submatrices-that-sum-to-target
|
C++||Explained Detailed||DP-prefix sum
|
cexplained-detaileddp-prefix-sum-by-rang-ktgd
|
!!!Please upvote if you like it..\nThe given question ask to count the number of sub-matrix whose sum of all element is equal to target value.\n\uD83D\uDE2E\u20
|
rango__
|
NORMAL
|
2022-01-18T15:26:21.361899+00:00
|
2022-01-18T15:26:21.361928+00:00
| 980 | false |
**!!!Please upvote if you like it..**\nThe given question ask to `count the number of sub-matrix whose sum of all element is equal to target value.`\n\uD83D\uDE2E\u200D\uD83D\uDCA8\uD83D\uDE2E\u200D\uD83D\uDCA8\uD83D\uDE2E\u200D\uD83D\uDCA8\uD83D\uDE2E\u200D\uD83D\uDCA8\n**How to find all sub-matrix??**\n->Let\'s think about 1-d array when we ask to f`ind all possible sub array we use prefix sum and do it `easily....\n**Here is a case of 2-D matrix..**\nIDEA:\uD83D\uDCAF\n1.To use 2D-prefix sum to store sum of all sub-matrix .\n2.Generate all possible sub matrix-cordinate and find sum and count possible value.\n3.Checking will be of O(1) time.\n\n`1.How to create 2-d prefix sum??`\n[\n` 2.Genrating all possible submatrix co-rdinate:`\nThis can be done using 4-loops that help to all sub-matrix.\n```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n \n int n=matrix.size();\n int m=matrix[0].size();\n int dp[n+1][m+1];//2-ddp for prefix sum\n \n \n for(int i=0;i<=n;i++)\n {\n for(int j=0;j<=m;j++)\n {\n if(i==0||j==0)\n {\n dp[i][j]=0;\n }\n else{\n \n dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+matrix[i-1][j-1];//using prefix dp formulae\n \n }\n }\n }\n int count=0;\n\t\t//generate all possible sub matrix.\n for(int i=1;i<=n;i++)\n {\n for(int j=1;j<=m;j++)\n {\n for(int k=i;k<=n;k++)\n {\n for(int l=j;l<=m;l++)\n {\n int ans=dp[i-1][j-1]+dp[k][l]-dp[i-1][l]-dp[k][j-1];\n if(ans==target)\n {\n count++;\n }\n }\n \n }\n \n }\n }\n return count;\n \n \n \n }\n};\n```\n\n\n\n\n
| 16 | 0 |
['Dynamic Programming', 'C']
| 1 |
number-of-submatrices-that-sum-to-target
|
C++ prefix sum, explanation with pictures (424ms / 9Mb)
|
c-prefix-sum-explanation-with-pictures-4-wsxo
|
The problem is split in two parts. \nFirst, compute 2D prefix sum matrix ps, so that element p[i][j] is equal to the sum of elements in submatrix matrix[x][y] w
|
dalexandr
|
NORMAL
|
2021-04-17T13:25:47.695670+00:00
|
2021-04-17T13:27:15.035618+00:00
| 950 | false |
The problem is split in two parts. \nFirst, compute 2D prefix sum matrix ```ps```, so that element ```p[i][j]``` is equal to the sum of elements in submatrix ```matrix[x][y]``` with ```0 <= x <= i, 0 <= y <= j```. For this purpose we compute 1D prefix sums for the first row and first column and then use the formula:\n```ps[i][j] = matrix[i][j] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1]```\n\n\nHere is illustration:\n<img src="https://assets.leetcode.com/users/images/fad46894-4b59-48a9-a0f8-a6e969cc7b29_1618664366.132954.png" alt="drawing" height="200"/>\n\nThe sum of elements from ```(0,0)``` to ```(i,j)``` consists of element ```matrix[i][j]``` and sums of elemnts in submatrices ```A,B,C```. \n\nSum of elements in ```A``` is simply ```ps[i-1][j-1]```.\nElements in ```B```: ```ps[i][j-1] - ps[i-1][j-1]```.\nElements in ```C```: ```ps[i-1][j] - ps[i-1][j-1]```.\nSumming of all this \n\nSecond part of the solution: use the prefix sum matrix to quickly compute sums of all the possible submatrices:\n<img src="https://assets.leetcode.com/users/images/1d8e4609-5d06-4ad8-b97e-9f4af78e9906_1618665165.0758274.png" alt="drawing" height="250"/>\nSum of elements in submatrix ```matrix[x][y]``` with ```i0 <= x <= i1, j0 <= y <= j1``` is a difference between elements in ```D``` and elements in ```A```,```B``` and ```C```. \n\nSum in ```D``` and ```A``` are prefix sums ```ps[i1][j1]``` and ```ps[i0-1][j0-1]```. For the remaining two submatrices we get:\n```B=ps[i1][j0-1] - ps[i0-1][j0-1]```\n```C=ps[i0-1][j1] - ps[i0-1][j0-1]```\n\nHence, the final formula is:\n```sum = ps[i1][j1]-ps[i1][j0-1]-ps[i0-1][j1]+ps[i0-1][j0-1]```\n\nThe corner cases are when ```j0=0``` or ```i0=0```.\n\n```\nclass Solution {\n int ps[101][101];\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& M, int target) {\n ios_base::sync_with_stdio(false);\n size_t n{ M.size() }, m{ M[0].size() };\n \n\t\t// compute prefix sum\n ps[0][0] = M[0][0];\n for (int i = 1; i < n; i++) ps[i][0] = M[i][0] + ps[i-1][0];\n for (int j = 1; j < m; j++) ps[0][j] = M[0][j] + ps[0][j-1];\n \n for (int i = 1; i < n; i++)\n for (int j = 1; j < m; j++)\n ps[i][j] = M[i][j] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1];\n\n \n int count{};\n // test all submatrices\n for (int i0 = 0; i0 < n; i0++)\n for (int j0 = 0; j0 < m; j0++)\n for (int i1 = i0; i1 < n; i1++)\n for (int j1 = j0; j1 < m; j1++) {\n int sum{ ps[i1][j1] };\n\n if (i0 > 0) sum -= ps[i0 - 1][j1];\n if (j0 > 0) sum -= ps[i1][j0-1];\n if (i0 > 0 && j0 > 0) sum += ps[i0 - 1][j0 - 1];\n\n if (sum == target) count++;\n }\n\n return count;\n }\n};\n```
| 15 | 0 |
[]
| 4 |
number-of-submatrices-that-sum-to-target
|
🔥 BEATS 100% | ✅ [ Py /Java / C++ / C / C# / JS / GO / Rust ]
|
beats-100-py-java-c-c-c-js-go-rust-by-ne-vmv0
|
\nC++ []\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int m = matrix.size(), n = matrix[0].size
|
Neoni_77
|
NORMAL
|
2024-01-28T04:06:38.968071+00:00
|
2024-08-08T17:49:12.541885+00:00
| 5,487 | false |
\n```C++ []\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int m = matrix.size(), n = matrix[0].size(), res = 0;\n\n for (int l = 0; l < n; ++l) {\n int sums[105] = {0};\n for (int r = l; r < n; ++r) {\n for (int i = 0; i < m; ++i) {\n sums[i] += matrix[i][r];\n }\n for (int i = 0; i < m; ++i) {\n int sum = 0;\n for (int j = i; j < m; ++j) {\n sum += sums[j];\n if (sum == target) {\n ++res;\n }\n }\n }\n }\n }\n\n return res;\n }\n};\n\n```\n```Java []\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length, n = matrix[0].length, res = 0;\n\n for (int l = 0; l < n; ++l) {\n int[] sums = new int[105];\n for (int r = l; r < n; ++r) {\n for (int i = 0; i < m; ++i) {\n sums[i] += matrix[i][r];\n }\n for (int i = 0; i < m; ++i) {\n int sum = 0;\n for (int j = i; j < m; ++j) {\n sum += sums[j];\n if (sum == target) {\n ++res;\n }\n }\n }\n }\n }\n\n return res;\n }\n}\n\n```\n```Python []\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n for row in matrix:\n for i in range(len(row)-1):\n row[i+1] += row[i]\n\n count = 0\n for t in range(len(matrix)):\n for b in range(t, -1, -1):\n if t == b:\n cur = matrix[t][:]\n else:\n cur = [cur[i]+matrix[b][i] for i in range(len(matrix[0]))]\n seen = {0: 1}\n for v in cur:\n if v - target in seen:\n count += seen[v - target]\n seen[v] = seen.get(v, 0) + 1\n \n return count\n# not same logic as other codes\n# for python it may not beat 100% .. \n\n```\n```C []\nint numSubmatrixSumTarget(int** matrix, int matrixSize, int* matrixColSize, int target) {\n int m = matrixSize, n = *matrixColSize, res = 0;\n\n for (int l = 0; l < n; ++l) {\n int sums[105] = {0};\n for (int r = l; r < n; ++r) {\n for (int i = 0; i < m; ++i) {\n sums[i] += matrix[i][r];\n }\n for (int i = 0; i < m; ++i) {\n int sum = 0;\n for (int j = i; j < m; ++j) {\n sum += sums[j];\n if (sum == target) {\n ++res;\n }\n }\n }\n }\n }\n\n return res;\n}\n\n```\n```C# []\npublic class Solution {\n public int NumSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.Length, n = matrix[0].Length, res = 0;\n\n for (int l = 0; l < n; ++l) {\n int[] sums = new int[105];\n for (int r = l; r < n; ++r) {\n for (int i = 0; i < m; ++i) {\n sums[i] += matrix[i][r];\n }\n for (int i = 0; i < m; ++i) {\n int sum = 0;\n for (int j = i; j < m; ++j) {\n sum += sums[j];\n if (sum == target) {\n ++res;\n }\n }\n }\n }\n }\n\n return res;\n }\n}\n\n```\n```Javascript []\nvar numSubmatrixSumTarget = function(matrix, target) {\n let m = matrix.length, n = matrix[0].length;\n let res = 0;\n\n for (let l = 0; l < n; ++l) {\n let sums = new Array(105).fill(0);\n for (let r = l; r < n; ++r) {\n for (let i = 0; i < m; ++i) {\n sums[i] += matrix[i][r];\n }\n for (let i = 0; i < m; ++i) {\n let sum = 0;\n for (let j = i; j < m; ++j) {\n sum += sums[j];\n if (sum === target) {\n ++res;\n }\n }\n }\n }\n }\n\n return res;\n};\n\n```\n```GO []\nfunc numSubmatrixSumTarget(matrix [][]int, target int) int {\n m, n := len(matrix), len(matrix[0])\n res := 0\n\n for l := 0; l < n; l++ {\n sums := make([]int, 105)\n for r := l; r < n; r++ {\n for i := 0; i < m; i++ {\n sums[i] += matrix[i][r]\n }\n for i := 0; i < m; i++ {\n sum := 0\n for j := i; j < m; j++ {\n sum += sums[j]\n if sum == target {\n res++\n }\n }\n }\n }\n }\n\n return res\n}\n\n```\n```Rust []\nimpl Solution {\n pub fn num_submatrix_sum_target(matrix: Vec<Vec<i32>>, target: i32) -> i32 {\n let (m, n) = (matrix.len(), matrix[0].len());\n let mut res = 0;\n\n for l in 0..n {\n let mut sums = vec![0; 105];\n for r in l..n {\n for i in 0..m {\n sums[i] += matrix[i][r];\n }\n for i in 0..m {\n let mut sum = 0;\n for j in i..m {\n sum += sums[j];\n if sum == target {\n res += 1;\n }\n }\n }\n }\n }\n\n res\n }\n}\n\n```\n**\u041F\u043E \u0440\u0435\u0448\u0435\u043D\u0438\u044E \u043D\u0430 \u0421++ \u0434\u043E\u0441\u0442\u0438\u0433\u0430\u0435\u0442 100%, \u043F\u043E \u043E\u0441\u0442\u0430\u043B\u044C\u043D\u044B\u043C \u043A\u043E\u0434\u0430\u043C \u043D\u0435 \u0437\u043D\u0430\u044E..\n\u043F\u0440\u043E\u0433\u043E\u043B\u043E\u0441\u0443\u0439\u0442\u0435 \u043F\u043E\u0436\u0430\u043B\u0443\u0439\u0441\u0442\u0430!! \uD83D\uDE0A**\n
| 14 | 0 |
['C', 'Python', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'JavaScript', 'C#']
| 2 |
number-of-submatrices-that-sum-to-target
|
C++ || Easy solution || Detailed explanation
|
c-easy-solution-detailed-explanation-by-j75o2
|
Prerequisite: https://leetcode.com/problems/subarray-sum-equals-k/ (if you don\'t know this question, please first solve it. Otherwise, understanding current pr
|
_Potter_
|
NORMAL
|
2022-07-18T10:11:08.417592+00:00
|
2022-07-18T10:20:20.245942+00:00
| 1,273 | false |
**Prerequisite:** https://leetcode.com/problems/subarray-sum-equals-k/ (if you don\'t know this question, please first solve it. Otherwise, understanding current problem is difficult)\n```\nint subarraySum(vector<int>& nums, int k) {\n\tunordered_map<int,int> um;\n\tum[0] = 1;\n\tint curr = 0;\n\tint ans = 0;\n\tfor(auto it: nums){\n\t\tcurr += it;\n\t\tint rem = curr-k;\n\t\tif(um.find(rem) != um.end()){\n\t\t\tans += um[rem];\n\t\t}\n\t\tum[curr] += 1;\n\t}\n\treturn ans;\n}\n```\n\nBack to this problem:\n```\nclass Solution {\npublic:\n int subarraySum(vector<int> &nums, int k){\n unordered_map<int,int> um;\n um[0] = 1;\n int curr = 0;\n int ans = 0;\n for(auto it: nums){ \n curr += it;\n int rem = curr-k;\n if(um.find(rem) != um.end()){\n ans += um[rem];\n }\n um[curr] += 1;\n }\n return ans;\n }\n \n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int ans = 0;\n\t\t// Each iteration calculates the count for submatrix from row i to matrix.size()\n for(int i=0; i<matrix.size(); i++){\n\t\t\t// Sum stores the sum of the elements from row i to j \n vector<int> sum(matrix[0].size(), 0);\n for(int j=i; j<matrix.size(); j++){\n for(int k=0; k<matrix[0].size(); k++){\n sum[k] += matrix[j][k];\n }\n\t\t\t\t// Now calculate the count for the submatrix from row i to j\n ans += subarraySum(sum, target);\n }\n }\n \n return ans;\n }\n};\n```\n```\ncout << "Upvote the solution if you like it !!" << endl;\n```
| 14 | 0 |
['C', 'C++']
| 0 |
number-of-submatrices-that-sum-to-target
|
C++ Java Python || Subarray Sum || Explained
|
c-java-python-subarray-sum-explained-by-y9ab7
|
Plz Upvote if found helpful\n\nExplaination:\nThis problem is essentially a 2-dimensional version of #560. Subarray Sum Equals K (S.S.E.K). By using a prefix su
|
ankit6378yadav
|
NORMAL
|
2022-07-18T07:56:21.915956+00:00
|
2022-07-18T07:57:23.461125+00:00
| 1,952 | false |
**Plz Upvote if found helpful**\n\n**Explaination:**\nThis problem is essentially a 2-dimensional version of #560. Subarray Sum Equals K (S.S.E.K). By using a prefix sum on each row or each column, we can compress this problem down to either N^2 iterations of the **O(M)** SSEK, or M^2 iterations of the **O(N)** SSEK.\n\nIn the SSEK solution, we can find the number of subarrays with the target sum by utilizing a result map (res) to store the different values found as we iterate through the array while keeping a running sum (csum). Just as in the case with a prefix sum array, the sum of a subarray between i and j is equal to the sum of the subarray from 0 to j minus the sum of the subarray from 0 to i-1.\n\nRather than iteratively checking if sum[0,j] - sum[0,i-1] = T for every pair of i, j values, we can flip it around to sum[0,j] - T = sum[0,i-1] and since every earlier sum value has been stored in res, we can simply perform a lookup on sum[0,j] - T to see if there are any matches.\n\nWhen extrapolating this solution to our 2-dimensional matrix (M), we will need to first prefix sum the rows or columns, (which we can do in-place to avoid extra space, as we will not need the original values again). Then we should iterate through M again in the opposite order of rows/columns where the prefix sums will allow us to treat a group of columns or rows as if it were a 1-dimensional array and apply the SSEK algorithm.\n\n----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------\n**C++ Code**\n```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int rows = matrix.size() , cols = matrix[0].size();\n \n if(rows < 1){\n return 0;\n }\n \n // calculate prefix sum for rows\n for(int row = 0 ; row < rows ; row++){\n for(int col = 1 ; col < cols ;col++){\n matrix[row][col] = matrix[row][col] + matrix[row][col -1];\n }\n }\n \n int count = 0 , sum ;\n unordered_map<int , int> counter;\n for(int colstart = 0 ; colstart < cols ;colstart++){\n for(int col = colstart ; col < cols; col++){\n counter.clear();\n counter[0] = 1;\n sum =0;\n for(int row = 0 ; row < rows ;row++){\n sum += matrix[row][col] - (colstart > 0 ? matrix[row][colstart - 1] : 0 );\n count += (counter.find(sum- target) != counter.end() ? counter[sum-target] : 0);\n counter[sum]++;\n }\n }\n }\n return count;\n }\n};\n```\n\n**Java Code:**\n```\nclass Solution {\n public int numSubmatrixSumTarget(int[][] M, int T) {\n int xlen = M[0].length, ylen = M.length, ans = 0;\n Map<Integer, Integer> res = new HashMap<>();\n for (int[] r : M)\n for (int j = 1; j < xlen; j++)\n r[j] += r[j-1];\n for (int j = 0; j < xlen; j++)\n for (int k = j; k < xlen; k++) {\n res.clear();\n res.put(0,1);\n int csum = 0;\n for (int i = 0; i < ylen; i++) {\n csum += M[i][k] - (j > 0 ? M[i][j-1] : 0);\n ans += res.getOrDefault(csum - T, 0);\n res.put(csum, res.getOrDefault(csum, 0) + 1);\n }\n }\n return ans;\n }\n}\n```\n\n**Python Code**\n```\nclass Solution:\n def numSubmatrixSumTarget(self, M: List[List[int]], T: int) -> int:\n xlen, ylen, ans = len(M[0]), len(M), 0\n for r in M:\n for j in range(1, xlen):\n r[j] += r[j-1]\n for j in range(xlen):\n for k in range(j, xlen):\n res, csum = {0: 1}, 0\n for r in M:\n csum += r[k] - (r[j-1] if j else 0)\n if csum - T in res: ans += res[csum-T]\n res[csum] = res[csum] + 1 if csum in res else 1 \n return ans\n```\n\n**Please Upvote if found Helpful**
| 13 | 0 |
['C', 'Python', 'Java']
| 1 |
number-of-submatrices-that-sum-to-target
|
C++ compact prefix sum explained 65% Speed, 100% Memory
|
c-compact-prefix-sum-explained-65-speed-qw63k
|
For all possible row ranges, calculate cumulative matrix sums column by column identifying when sum equals target or when sum equals a previous sum (in the same
|
adrianlee0118
|
NORMAL
|
2020-04-04T02:17:19.560849+00:00
|
2020-04-12T01:41:50.618428+00:00
| 1,599 | false |
For all possible row ranges, calculate cumulative matrix sums column by column identifying when sum equals target or when sum equals a previous sum (in the same row range) minus the target. In the y direction, the cumulative sum is added to each column incrementally using a vector representing the column sum of interest in the row.\n\n```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int m = matrix.size();\n int n = matrix[0].size();\n int count = 0;\n \n for (int i = 0; i < m; i++){ //Iterating over all possible row ranges between row i and row j\n vector<int> CumulativeColumns = matrix[i]; //Instead of setting up a prefix sum matrix, add to columns as we go row by row\n \n for (int j = i; j < m; j++){\n unordered_map<int,int> sumCount; //track occurrences of corner matrix sums for the current row range\n int totalSum = 0;\n \n for (int k = 0; k < n; k++){\n totalSum += CumulativeColumns[k]; //within the current row range, at every row cumulatively build matrix sums using cumulative column sums column by column\n if (totalSum == target) count++; //if the target is found or if a sum is found that has a difference with a previous sum in the same top/bottom bounds exactly equal to target, add submatrices found\n if (sumCount.count(totalSum-target)) count += sumCount[totalSum-target];\n sumCount[totalSum]++; //Store the current cumulative sum to be used later in the row to calculate target matrix counts \n if (j < m - 1) CumulativeColumns[k] += matrix[j+1][k]; //Increment the cumulative column sum for the next row iteration in the current row range if necessary\n }\n }\n }\n return count;\n }\n};\n```
| 13 | 0 |
[]
| 1 |
number-of-submatrices-that-sum-to-target
|
💥C# | Runtime 111 ms Beats 100.00%, Memory 53.15 MB Beats 76.19% [EXPLAINED]
|
c-runtime-111-ms-beats-10000-memory-5315-crng
|
Intuition\nI want to find all submatrices in a grid that sum up to a given target. To do this efficiently, I first need to understand how to quickly compute the
|
r9n
|
NORMAL
|
2024-09-13T23:11:01.216643+00:00
|
2024-09-13T23:11:01.216661+00:00
| 49 | false |
# Intuition\nI want to find all submatrices in a grid that sum up to a given target. To do this efficiently, I first need to understand how to quickly compute the sum of any submatrix.\n\n# Approach\nPrefix Sums: Calculate vertical prefix sums for quick submatrix sum calculations.\n\nRow Pairs: Iterate through pairs of rows to find submatrices.\n\nHash Map: Use a hash map to track prefix sums and count submatrices that match the target\n\n# Complexity\n- Time complexity:\nO(r^2 * c).\n\n- Space complexity:\nO(c).\n\n# Code\n```csharp []\npublic class Solution {\n // Time O(r^2 * c) | Space O(c), where r = number of rows, c = number of columns\n public int NumSubmatrixSumTarget(int[][] matrix, int target) {\n int rows = matrix.Length, cols = matrix[0].Length, result = 0;\n\n // Compute prefix sums vertically for each column\n for (int r = 1; r < rows; r++) {\n for (int c = 0; c < cols; c++) {\n matrix[r][c] += matrix[r - 1][c];\n }\n }\n\n var sumFreq = new Dictionary<int, int>();\n\n // Iterate over all pairs of rows\n for (int r1 = 0; r1 < rows; r1++) {\n for (int r2 = r1; r2 < rows; r2++) {\n // Calculate the prefix sums for columns in the current row range\n int[] combinedSum = new int[cols];\n for (int c = 0; c < cols; c++) {\n int rowSum = matrix[r2][c] - (r1 > 0 ? matrix[r1 - 1][c] : 0);\n combinedSum[c] = rowSum + (c > 0 ? combinedSum[c - 1] : 0);\n }\n\n // Count submatrices with the target sum\n sumFreq.Clear();\n sumFreq[0] = 1; // Base case\n for (int c = 0; c < cols; c++) {\n int runningSum = combinedSum[c];\n int targetSum = runningSum - target;\n if (sumFreq.TryGetValue(targetSum, out int freq)) {\n result += freq;\n }\n sumFreq[runningSum] = sumFreq.GetValueOrDefault(runningSum, 0) + 1;\n }\n }\n }\n return result;\n }\n}\n\n```
| 11 | 0 |
['C#']
| 0 |
number-of-submatrices-that-sum-to-target
|
Simple And Easy To Understand || 2D converted to 1D || Subarrray sum equal to K
|
simple-and-easy-to-understand-2d-convert-a66y
|
Intuition \nTraverse and calcuate prefix sum\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the
|
viraj2003
|
NORMAL
|
2024-01-28T08:53:56.114266+00:00
|
2024-01-28T08:58:45.798580+00:00
| 887 | false |
# Intuition \nTraverse and calcuate prefix sum\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nJust stored the 2D vector sum into 1D vector and applied subarray sum \n\nFor example let\'s try for \n\nmatrix=[[0 , 1, 0],[1, 1, 1], [0, 1, 0]] Target=3\n\nfor i=0\nIn 1st loop our vector will be (0,1,0) check for sum 3 no subarray \nnow next loop vector will become (1,2,1) check for 3 we will get **two** subarray (1,2) and (2,1) \nnow next loop vector will become (1,3,1) check for 3 we will get **one** subarray (3)\n\nfor i=1\nIn 1st loop our vector will be (1,1,1) check for sum 3 **one** subarray (1,1,1)\nnow next loop vector will become (1,2,1) check for 3 we will **two** subarray (1,2) and (2,1)\n\nfor i=2\nIn 1st loop our vector will be (0,1,0) check for sum 3 no subarray\n\n\nFinally the answer is **6** \n\nIn these way we can convert 2D array in 1D an apply subarray sum equals K method\n\n\n\n# Complexity\n- Time complexity:O(n * n * n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int subarraysum(vector<int>& nums, int k)\n {\n unordered_map<int,int> m;\n m[0]=1;\n int curr=0,ans=0;\n\n for(auto &val:nums)\n {\n curr+=val;\n if(m.find(curr-k)!=m.end())\n {\n ans+=m[curr-k];\n }\n m[curr]++;\n }\n\n return ans;\n }\n int numSubmatrixSumTarget(vector<vector<int>>& mat, int target) {\n int ans=0;\n\n for(int i=0;i<mat.size();i++)\n {\n vector<int> sum(mat[0].size(),0);\n for(int j=i;j<mat.size();j++)\n {\n for(int k=0;k<mat[0].size();k++)\n {\n sum[k]+=mat[j][k];\n }\n \n ans+=subarraysum(sum,target);\n }\n }\n\n return ans;\n }\n};\n```
| 11 | 0 |
['Prefix Sum', 'C++']
| 1 |
number-of-submatrices-that-sum-to-target
|
Simple to Understand Java Code
|
simple-to-understand-java-code-by-saurab-lwqe
|
Complexity\n- Time complexity:\nO(m^2\u2217n)\n- Space complexity:\nO(n)\n# Code\n\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int t
|
Saurabh_Mishra06
|
NORMAL
|
2024-01-28T03:08:55.943188+00:00
|
2024-01-28T03:08:55.943210+00:00
| 1,436 | false |
# Complexity\n- Time complexity:\nO(m^2\u2217n)\n- Space complexity:\nO(n)\n# Code\n```\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int row = matrix.length;\n int col = matrix[0].length;\n int res = 0;\n //int[][] sum = new int[row][col];\n \n for(int i = 0; i < row; i++){\n for(int j = 1; j < col; j++){\n //sum[i][j] =sum[i][j-1] + matrix[i][j-1];\n matrix[i][j] += matrix[i][j-1];\n }\n }\n \n for(int start = 0; start < col; start++){\n for(int end = start; end < col; end++){\n int subMatrixSum = 0;\n \n Map<Integer, Integer> countElm = new HashMap<Integer, Integer>();\n countElm.put(0,1);\n \n for(int k = 0; k < row; k++){\n //subMatrixSum += sum[k][end] - sum[k][start];\n int prefixSum = start == 0 ? 0:matrix[k][start-1];\n subMatrixSum += matrix[k][end] - prefixSum;\n \n if(countElm.containsKey(subMatrixSum - target))\n res += countElm.get(subMatrixSum - target);\n \n int r = countElm.getOrDefault(subMatrixSum, 0);\n countElm.put(subMatrixSum, r+1);\n }\n }\n }\n \n return res;\n }\n}\n```\n\n\n
| 11 | 0 |
['Array', 'Matrix', 'Java']
| 0 |
number-of-submatrices-that-sum-to-target
|
C++ Easy Solution Without Hashmap || Prefix Sum || Easy Understanding
|
c-easy-solution-without-hashmap-prefix-s-zl14
|
C++ Easy Solution Without Hashmap || Prefix Sum || Easy Understanding\n\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, i
|
Conquistador17
|
NORMAL
|
2022-07-18T02:58:18.504803+00:00
|
2022-07-18T02:58:18.504834+00:00
| 4,078 | false |
# **C++ Easy Solution Without Hashmap || Prefix Sum || Easy Understanding**\n```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int n=matrix.size(),m=matrix[0].size(),count=0;\n vector<vector<int>>temp(n+1,vector<int>(m));\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n temp[i+1][j]=temp[i][j]+matrix[i][j];\n }\n }\n for(int i=0;i<n;i++){\n for(int j=i+1;j<=n;j++){\n for(int k=0;k<m;k++){\n int sum=0;\n for(int l=k;l<m;l++){\n sum+=temp[j][l]-temp[i][l];\n if(sum==target){\n // cout<<j<<" "<<i<<" "<<k<<endl;\n count++;\n }\n }\n }\n }\n }\n return count;\n }\n};\n```\n# **Please Share and Upvote**
| 11 | 0 |
['C', 'Prefix Sum', 'C++']
| 6 |
number-of-submatrices-that-sum-to-target
|
C++ Prefix sums time complexity O(row*col*min(row, col))||399 ms Beats 95.82%
|
c-prefix-sums-time-complexity-orowcolmin-s5br
|
Intuition\n Describe your first thoughts on how to solve this problem. \nCompute prefix sums for rows or prefix sums for columns in either way.\nThen use hash m
|
anwendeng
|
NORMAL
|
2024-01-28T08:53:35.045577+00:00
|
2024-01-28T12:16:29.757159+00:00
| 1,154 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCompute prefix sums for rows or prefix sums for columns in either way.\nThen use hash map.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIdea like in [Leetcode 560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/description/)\n\nif col>row, compute it in an alternative way which has TC $O(row^2\\times col)$\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(row\\times col\\times \\min(row, col))$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(row\\times col)$\n# Code ||399 ms Beats 95.82%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int alternative(vector<vector<int>>& matrix, int target, int n, int m){\n // Calculate prefix sums for every column\n for (int j = 0; j < m; j++) {\n for (int i = 1; i < n; i++) {\n matrix[i][j] += matrix[i-1][j];\n }\n }\n int ans= 0; \n for(int r0 = 0 ; r0 < n ; r0++){\n for(int r = r0 ; r < n; r++){\n unordered_map<int , int> f;\n f[0] = 1;\n int sum =0;\n for(int c = 0 ; c < m ; c++){\n int prev=(r0==0) ? 0 : matrix[r0-1][c];\n sum += matrix[r][c]-prev;\n int x=sum-target;\n ans += f.count(x) ? f[x] : 0;\n f[sum]++;\n }\n }\n }\n return ans;\n }\n\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int n = matrix.size(), m = matrix[0].size();\n if ( m>n ) return alternative(matrix, target, n, m);\n\n // Calculate prefix sums for every row\n for (int i = 0; i < n; i++) {\n for (int j = 1; j < m; j++) {\n matrix[i][j] += matrix[i][j-1];\n }\n }\n int ans= 0; \n for(int c0 = 0 ; c0 < m ; c0++){\n for(int c = c0 ; c < m; c++){\n unordered_map<int , int> f;\n f[0] = 1;\n int sum =0;\n for(int r = 0 ; r < n ; r++){\n int prev=(c0==0) ? 0 : matrix[r][c0-1];\n sum += matrix[r][c]-prev;\n int x= sum-target;\n ans += f.count(x) ? f[x] : 0;\n f[sum]++;\n }\n }\n }\n return ans;\n }\n};\n\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```
| 10 | 0 |
['Hash Table', 'Prefix Sum', 'C++']
| 2 |
number-of-submatrices-that-sum-to-target
|
Python/Go O(w^2 * h) by prefix sum [w/ Hint]
|
pythongo-ow2-h-by-prefix-sum-w-hint-by-b-6fxt
|
Python O(w^2 * h) by prefix sum\n\n---\n\nHint:\n\nThis is 2D extented version of Leetcode 560 Subarray Sum Equals K\n\nThe concept of prefix sum and dictionar
|
brianchiang_tw
|
NORMAL
|
2021-04-17T11:09:27.932158+00:00
|
2021-04-23T13:26:26.628974+00:00
| 1,095 | false |
Python O(w^2 * h) by prefix sum\n\n---\n\n**Hint**:\n\nThis is **2D extented version** of [Leetcode 560 Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/)\n\nThe concept of **prefix sum** and **dictionary** technique can be used again to help us.\n\n---\n\n**Implementation** by dictionary in Python\n\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n \n # height and width of matrix\n h, w = len(matrix), len(matrix[0])\n \n\t\t\n # update prefix sum on each row\n for y in range(h):\n for x in range(1,w):\n matrix[y][x] = matrix[y][x] + matrix[y][x-1]\n \n \n # number of submatrices that sum to target\n counter = 0\n \n # sliding windows on x-axis, in range [left, right]\n for left in range(w):\n for right in range(left, w):\n \n # accumulation of area so far\n accumulation = {0: 1}\n \n # area of current submatrices, bounded by [left, right] with height y\n area = 0\n \n # scan each possible height on y-axis\n for y in range(h):\n \n if left > 0:\n area += matrix[y][right] - matrix[y][left-1]\n \n else:\n area += matrix[y][right]\n \n # if ( area - target ) exist, then target must exist in submatrices\n counter += accumulation.get( area - target, 0)\n \n # update dictionary with current accumulation area\n accumulation[area] = accumulation.get(area, 0) + 1\n \n return counter\n```\n\n---\n\n**Implementatin** by map in Go\n\n```\nfunc numSubmatrixSumTarget(matrix [][]int, target int) int {\n \n // height and width of matrix\n h, w := len(matrix), len(matrix[0])\n \n // update prefix sum on each row\n for y := 0 ; y < h ; y++{\n for x:= 1 ; x < w; x++{\n matrix[y][x] = matrix[y][x] + matrix[y][x-1]\n }\n }\n \n // number of submatrices that sum to target\n counter := 0\n \n // sliding windows on x-axis, in range[left, right]\n for left := 0 ; left < w ; left ++{\n for right := left ; right < w ; right++{\n \n // accumulation for area so far\n accumulation := map[int]int{ 0 : 1}\n \n // area of current submatrices, bounded by [left, right] with height y\n area := 0\n \n // scan each possible height on y-axis\n for y := 0 ; y < h ; y++{\n \n if left > 0 {\n area += matrix[y][right] - matrix[y][left-1]\n }else{\n area += matrix[y][right]\n }\n \n // if ( area - target ) exists, then target must exist in submatrices\n counter += accumulation[ (area - target) ]\n \n // update dictionary with current accumulation area\n accumulation[area] += 1\n \n }\n \n }//end of right loop\n \n }//end of left loop\n \n return counter\n \n}\n```\n\n---\n\nRelated leetcode challenge:\n\n[1] [Leetcode 560 Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/)\n\n---\n\nReference:\n\n[1] [Python official docs about dictioanry](https://docs.python.org/3/tutorial/datastructures.html#dictionaries)\n\n[2] [Golang official docs about map[]](https://blog.golang.org/maps)\n\n[3] [Wiki: prefix sum](https://en.wikipedia.org/wiki/Prefix_sum)
| 10 | 0 |
['Sliding Window', 'Prefix Sum', 'Python', 'Go', 'Python3']
| 2 |
number-of-submatrices-that-sum-to-target
|
[C++] Short & Easy Solution
|
c-short-easy-solution-by-hunarbatra-0zm9
|
\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int rows = matrix.size(), cols = matrix[0].size();\n int count = 0;\n
|
hunarbatra
|
NORMAL
|
2020-01-21T12:53:46.767292+00:00
|
2020-01-21T12:53:46.767340+00:00
| 1,913 | false |
```\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int rows = matrix.size(), cols = matrix[0].size();\n int count = 0;\n for(int L=0; L<cols; L++) {\n vector<int> running_rows(rows,0); //intialize the running row\n for(int R=L; R<cols; R++) { //calculate running rows sum\n for(int i=0; i<rows; i++) running_rows[i] += matrix[i][R]; \n int sum = 0;\n unordered_map<int, int> visited;\n for(int i=0; i<rows; i++) { //check for subarrays in every running row\n visited[sum]++;\n sum = sum + running_rows[i];\n if(visited[sum - target]) \n count += visited[sum - target];\n }\n }\n }\n return count;\n }\n```\n\nRuntime - O(cols^2 rows) i.e cubic runtime\nSpace - O(rows)\n\nTo understand what are running rows, watch : https://www.youtube.com/watch?v=-FgseNO-6Gk\nTo understand how I\'m checking for subarrays in every single running row, try : https://leetcode.com/problems/subarray-sum-equals-k/ or check out this video on youtube to understand the solution https://www.youtube.com/watch?v=AmlVSNBHzJg
| 9 | 1 |
['Array', 'C', 'C++']
| 4 |
number-of-submatrices-that-sum-to-target
|
(Java) Simple solution with explanation.
|
java-simple-solution-with-explanation-by-9v1r
|
Counting all sub-arrays with a given sum k for 1-Dimensional array can be used to reduce the time complexity.\n We fix the left and right columns one by one and
|
poorvank
|
NORMAL
|
2019-06-02T04:06:39.485752+00:00
|
2019-06-02T04:08:00.386105+00:00
| 2,736 | false |
* Counting all sub-arrays with a given sum k for 1-Dimensional array can be used to reduce the time complexity.\n* We fix the left and right columns one by one and count sub-arrays for every left and right column pair.\n* The sum of elements in every row from left to right and store these sums in a temporary array say temp[].\n* So temp[i] indicates sum of elements from left to right in row i.\n* Count sub-arrays in temp[] having sum k.\n* Sum up all the counts for each temp[] with different left and right column pairs.\n```\npublic int numSubmatrixSumTarget(int[][] matrix, int target) {\n\n int m = matrix.length;\n int n = matrix[0].length;\n\n int[] temp = new int[m];\n int ans=0;\n for (int left = 0;left<n;left++) {\n Arrays.fill(temp,0);\n for (int right=left;right<n;right++) {\n for (int i=0;i<m;i++) {\n temp[i]+=matrix[i][right];\n }\n ans+= subCount(temp,target);\n }\n }\n return ans;\n }\n\n private int subCount(int[] temp,int target) {\n HashMap<Integer, Integer> prevSum = new HashMap<>();\n\n int res = 0;\n int currentSum = 0;\n\n for (int t : temp) {\n\n currentSum += t;\n if (currentSum == target) {\n res++;\n }\n if (prevSum.containsKey(currentSum - target)) {\n res += prevSum.get(currentSum - target);\n }\n prevSum.merge(currentSum, 1, (a, b) -> a + b);\n }\n\n return res;\n }\n```
| 9 | 1 |
[]
| 1 |
number-of-submatrices-that-sum-to-target
|
[Java] O(n^3) : With Detailed Explanation (step by step)
|
java-on3-with-detailed-explanation-step-jkd7x
|
The idea is to fix the left and right columns one by one and count sub-arrays for every left and right column pair. Calculate sum of elements in every row from
|
kroos9
|
NORMAL
|
2019-07-16T08:24:06.100349+00:00
|
2019-09-25T00:47:55.683487+00:00
| 1,119 | false |
* The idea is to fix the left and right columns one by one and count sub-arrays for every left and right column pair. Calculate sum of elements in every row from left to right and store these sums in an array say temp[]. So temp[i] indicates sum of elements from left to right in row i.\n\n* Count sub-arrays in temp[] having sum equal to target. This count is the number of sub-matrices having sum equal to target with left and right as boundary columns. Sum up all the counts for each temp[] with different left and right column pairs.\n\n```\nclass Solution {\n \n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n // Number of columns\n int n=matrix[0].length;\n // Number of rows\n int m=matrix.length;\n // store the total count of such sub matrices in result variable\n int result=0;\n \n // Fix the left boundary\n for(int left=0;left<n;left++){\n // Fix the right boundary\n int[] temp=new int[m];\n for(int right=left;right<n;right++){\n // Compute sum of row elements between the left and right boundary\n for(int k=0;k<m;k++){\n temp[k]+=matrix[k][right];\n }\n // Check for target sum\n result+=subArraySumToTarget(temp,target);\n }\n }\n return result;\n }\n \n // Works in O(n)\n int subArraySumToTarget(int[] temp,int target){\n // Use a hashmap of running sum and frequency of that sum\n HashMap<Integer,Integer> map=new HashMap<>();\n int runningSum=0;\n int count=0;\n map.put(0,1);\n for(int i=0;i<temp.length;i++){\n runningSum+=temp[i];\n if(map.containsKey(runningSum-target)){\n count+=map.get(runningSum-target);\n }\n map.put(runningSum,map.getOrDefault(runningSum,0)+1);\n }\n return count;\n }\n \n}\n```
| 8 | 0 |
[]
| 0 |
number-of-submatrices-that-sum-to-target
|
✅☑Beats 99.59% Users || Easy Understood Solution with optimized space || 2 Approaches🔥
|
beats-9959-users-easy-understood-solutio-gdqz
|
\n\n# Explanation :- \n\n1. Prefix Sum Calculation:\n - Calculate the prefix sum for each row in the matrix. This is done to efficiently compute the sum of an
|
MindOfshridhar
|
NORMAL
|
2024-01-28T22:16:33.313433+00:00
|
2024-01-28T23:16:57.309435+00:00
| 167 | false |
\n\n# Explanation :- \n\n1. Prefix Sum Calculation:\n - Calculate the prefix sum for each row in the matrix. This is done to efficiently compute the sum of any subarray in constant time.\n2. Iterating Over Column Pairs:\n - Iterate over all possible pairs of columns (start_col and end_col).\n3. Cumulative Sum Calculation:\n - For each pair of columns, iterate over each row and calculate the cumulative sum of elements between start_col and end_col.\n4. Using Dictionary for Prefix Sums:\n - Use a dictionary (prefix_sum_count) to store the count of prefix sums encountered so far.\n5. Counting Submatrices:\n - Check if the complement of the current sum (current_sum - target) exists in the dictionary. If yes, add its count to the result.\n6. Updating Dictionary:\n - Update the dictionary with the current cumulative sum.\n7. Final Result:\n - Return the total count of submatrices with a sum equal to the target value.\n# brute-force approach \n - Time Complexity: O(rows^2 * cols^2).\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n rows, cols = len(matrix), len(matrix[0])\n result = 0\n\n # Iterate over all possible submatrices\n for top_row in range(rows):\n for bottom_row in range(top_row, rows):\n for left_col in range(cols):\n for right_col in range(left_col, cols):\n # Calculate the sum of the current submatrix\n current_sum = 0\n for i in range(top_row, bottom_row + 1):\n for j in range(left_col, right_col + 1):\n current_sum += matrix[i][j]\n\n # Check if the sum is equal to the target\n if current_sum == target:\n result += 1\n\n return result\n\n```\n# Complexity\n- Time complexity: O(cols^2 * rows)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(rows)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# code 1 \n - (T.c & S.c: O(col^2 * row))\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n row, col = len(matrix), len(matrix[0])\n res = 0\n\n # Update cumulative sums for each column in the matrix\n for i in range(row):\n for j in range(1, col):\n matrix[i][j] += matrix[i][j-1]\n\n # Iterate through all possible combinations of start and end columns\n for s_col in range(col):\n for l_col in range(s_col, col):\n # Dictionary to store cumulative sums and their frequencies\n h = {0: 1}\n cums = 0\n for i in range(row):\n # Calculate the cumulative sum for the current submatrix\n cums += matrix[i][l_col] - (matrix[i][s_col-1] if s_col > 0 else 0)\n \n # If the difference between current cumulative sum and target exists in dictionary,\n # increment the result count by the frequency of that difference\n if cums - target in h:\n res += h[cums - target]\n \n # Update the dictionary with the current cumulative sum\n h[cums] = h.get(cums, 0) + 1\n\n return res\n\n```\n# Code 2\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n rows, cols = len(matrix), len(matrix[0])\n\n # Calculate the prefix sum for each row\n for row in matrix:\n for j in range(1, cols):\n row[j] += row[j - 1]\n\n result = 0\n\n # Iterate over all possible pairs of columns\n for start_col in range(cols):\n for end_col in range(start_col, cols):\n # Use a dictionary to store the prefix sum of subarrays in each row\n prefix_sum_count = {0: 1}\n current_sum = 0\n\n # Iterate over each row and calculate the cumulative sum\n for row in matrix:\n current_sum += row[end_col] - (row[start_col - 1] if start_col > 0 else 0)\n\n # Check if the complement (current_sum - target) exists in prefix_sum_count\n complement = current_sum - target\n result += prefix_sum_count.get(complement, 0)\n\n # Update the prefix_sum_count dictionary\n prefix_sum_count[current_sum] = prefix_sum_count.get(current_sum, 0) + 1\n\n return result\n \n```\n\n
| 7 | 0 |
['Array', 'Hash Table', 'Ordered Map', 'Rolling Hash', 'Matrix', 'Counting', 'Hash Function', 'Prefix Sum', 'Python', 'Python3']
| 0 |
number-of-submatrices-that-sum-to-target
|
Simple beginner-level C solution || Prefix sum + Brute force || With clear comments || 中文註解
|
simple-beginner-level-c-solution-prefix-06458
|
\n# Complexity\n- Time complexity: $O(m^2n^2)$\n- Space complexity: $O(mn)$\n Add your space complexity here, e.g. O(n) \n\n# Code\ncpp\n// 1074. Number of Sub
|
paulchen2713
|
NORMAL
|
2024-01-28T00:36:20.394161+00:00
|
2024-01-28T00:36:20.394189+00:00
| 1,108 | false |
\n# Complexity\n- Time complexity: $O(m^2n^2)$\n- Space complexity: $O(mn)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp\n// 1074. Number of Submatrices That Sum to Target\nint** init_2D_array(const int arrSize, const int arrColSize) {\n int** arr = (int**)calloc(arrSize, sizeof(int*));\n for (int i = 0; i < arrSize; i++) {\n arr[i] = (int*)calloc(arrColSize, sizeof(int));\n }\n return arr;\n}\nvoid free_2D_array(int*** arr, const int arrSize, const int arrColSize) {\n for (int i = 0; i < arrSize; i++) {\n free((*arr)[i]);\n }\n free((*arr));\n}\nint numSubmatrixSumTarget(int** matrix, int matrixSize, int* matrixColSize, int target) {\n // Prefix sum + Brute force\n\n // Time complexity: O(m^2*n^2)\n // Space complexity: O(m*n)\n\n // Given a 2D matrix of size m x n and an integer target \n // Find the number of non-empty submatrices whose sum equals target\n\n const int m = matrixSize, n = matrixColSize[0];\n int result = 0; // Record the occurrence count\n \n // Use prefix sum matrix to quickly compute the sum of any submatrix\n int** sums = init_2D_array(m + 1, n + 1);\n\n // Traverse matrix starting from 1 to build the prefix sum matrix \'sums\'\n for (int i = 1; i <= m; i++) {\n for (int j = 1; j <= n; j++) {\n // The sum at current position equals the sum above plus the sum on the left minus \n // the sum on the upper left plus the value of current position in the original matrix\n sums[i][j] = sums[i][j - 1] + sums[i - 1][j] - sums[i - 1][j - 1] + matrix[i - 1][j - 1];\n }\n }\n\n // Then traverse all possible submatrix cases. \n\n // Since a matrix has 4 vertices, the time complexity of traversal is O(n^4). By accessing the \n // results of the prefix sum matrix \'sums\' with coordinates of the 4 vertices, we can obtain the \n // sum of the submatrix in O(1) time.\n\n int temp = 0; // If the calculated value \'temp\' equals target, then increment \'result\'.\n for (int i = 1; i <= m; i++) {\n for (int j = 1; j <= n; j++) {\n for (int p = 1; p <= i; p++) {\n for (int q = 1; q <= j; q++) {\n temp = sums[i][j] - sums[i][q - 1] - sums[p - 1][j] + sums[p - 1][q - 1];\n if (temp == target) result++;\n }\n }\n }\n }\n free_2D_array(&sums, m + 1, n + 1);\n return result;\n}\n```\n```cpp\n// 1074. Number of Submatrices That Sum to Target\nint numSubmatrixSumTarget(int** matrix, int matrixSize, int* matrixColSize, int target) {\n // Prefix sum + Brute force\n\n // Time complexity: O(m^2*n^2)\n // Space compelxity: O(m*n)\n\n // \u7D66\u5B9A\u4E00\u500B\u5927\u5C0F\u70BA m x n \u7684\u4E8C\u7DAD\u77E9\u9663 matrix \u548C\u4E00\u500B\u6574\u6578 target \n // \u8A66\u554F\u6709\u5E7E\u7A2E \u975E\u7A7A\u5B50\u77E9\u9663\u548C\u7B49\u65BC target \u7684\u60C5\u6CC1\n\n const int m = matrixSize, n = matrixColSize[0];\n int result = 0; // \u8A18\u9304\u60C5\u6CC1\u51FA\u73FE\u7684\u6B21\u6578\n \n // \u901A\u904E\u5EFA\u7ACB\u7D2F\u52A0\u548C\u77E9\u9663 \u4F86\u5FEB\u901F\u6C42\u51FA\u4EFB\u610F\u5B50\u77E9\u9663\u7684\u548C\n int** sums = init_2D_array(m + 1, n + 1);\n\n // \u5F9E 1 \u958B\u59CB\u904D\u6B77 matrix \u5EFA\u7ACB\u7D2F\u52A0\u548C\u77E9\u9663\u65BC sums\n for (int i = 1; i <= m; i++) {\n for (int j = 1; j <= n; j++) {\n // \u7576\u524D\u4F4D\u7F6E\u7D2F\u52A0\u548C \u7B49\u65BC \u4E0A\u9762\u7684\u503C \u52A0\u4E0A\u5DE6\u908A\u7684\u503C \u6E1B\u53BB\u5DE6\u4E0A\u7684\u503C \u6700\u5F8C\u52A0\u4E0A\u539F\u77E9\u9663\u4E2D\u7576\u524D\u4F4D\u7F6E\u7684\u503C\n sums[i][j] = sums[i][j - 1] + sums[i - 1][j] - sums[i - 1][j - 1] + matrix[i - 1][j - 1];\n }\n }\n\n // \u63A5\u8457\u904D\u6B77\u6240\u6709\u5B50\u77E9\u9663\u53EF\u80FD\u60C5\u6CC1 \u77E9\u9663\u6709 4 \u500B\u9802\u9EDE \u6240\u4EE5\u904D\u6B77\u6642\u9593\u8907\u96DC\u5EA6\u662F O(n^4) \n // \u7531 4 \u500B\u9802\u9EDE\u5EA7\u6A19\u53BB\u5B58\u53D6\u7D2F\u52A0\u548C\u77E9\u9663 sums \u7684\u7D50\u679C \u61C9\u8A72\u53EF\u4EE5\u5728 O(1) \u5167\u6C42\u5F97\u5B50\u77E9\u9663\u7684\u548C \n \n int temp = 0; // \u5982\u679C\u8A08\u7B97\u503C temp \u7B49\u65BC target \u5247 result++\n for (int i = 1; i <= m; i++) {\n for (int j = 1; j <= n; j++) {\n for (int p = 1; p <= i; p++) {\n for (int q = 1; q <= j; q++) {\n temp = sums[i][j] - sums[i][q - 1] - sums[p - 1][j] + sums[p - 1][q - 1];\n if (temp == target) result++;\n }\n }\n }\n }\n free_2D_array(&sums, m + 1, n + 1);\n return result;\n}\n```
| 7 | 0 |
['Array', 'C', 'Matrix', 'Prefix Sum']
| 1 |
number-of-submatrices-that-sum-to-target
|
Easy prefix Sum approach
|
easy-prefix-sum-approach-by-akshatsaxena-rbpl
|
\nclass Solution {\npublic:\n int dp[101][101];\n int n,m;\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n n=matrix.siz
|
akshatsaxena2017
|
NORMAL
|
2022-07-18T04:54:37.102883+00:00
|
2022-07-18T04:54:37.102917+00:00
| 686 | false |
```\nclass Solution {\npublic:\n int dp[101][101];\n int n,m;\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n n=matrix.size(),m=matrix[0].size();\n fun(matrix);\n int ans=0;\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n int si=i,sj=j;\n \n for(int p=si;p<n;p++){\n for(int q=sj;q<m;q++){\n \n if(p==si && q==sj){\n \n ans+=(target==matrix[p][q])?1:0;\n }else{\n \n ans+=(target==getans(si,sj,p,q))?1:0;\n }\n }\n }\n \n }\n }\n return ans;\n }\n void fun(vector<vector<int>>& matrix){\n dp[0][0]=matrix[0][0]; // Getting the sum of matrix from index(0,0) for every (i,j);\n for(int i=1;i<m;i++){\n dp[0][i]=(dp[0][i-1]+matrix[0][i]);\n }\n for(int i=1;i<n;i++){\n dp[i][0]=(dp[i-1][0]+matrix[i][0]);\n }\n for(int i=1;i<n;i++){\n for(int j=1;j<m;j++){\n dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+matrix[i][j];\n }\n }\n \n }\n \n int getans(int si,int sj,int ei,int ej){\n if(si==0 && sj==0){\n return dp[ei][ej];\n }else if(si==0 && sj!=0){\n return dp[ei][ej]-dp[ei][sj-1];\n }else if(si!=0 && sj==0){\n return dp[ei][ej]-dp[si-1][ej];\n }else{\n return dp[ei][ej]-dp[ei][sj-1]-dp[si-1][ej]+dp[si-1][sj-1];\n }\n \n }\n};\n```
| 7 | 0 |
['Matrix', 'Prefix Sum']
| 2 |
number-of-submatrices-that-sum-to-target
|
✔✔C++ ||91% faster ||easy to understand || Have a look ||explained
|
c-91-faster-easy-to-understand-have-a-lo-q6rf
|
\nclass Solution {\npublic:\n\n // this part you have already solve on leetcode here we are just solving famous leetcode problem number of subarrays with sum
|
priyanshu2001
|
NORMAL
|
2022-07-18T03:49:12.822225+00:00
|
2022-07-18T04:53:20.136383+00:00
| 1,657 | false |
\nclass Solution {\npublic:\n\n // this part you have already solve on leetcode here we are just solving famous leetcode problem number of subarrays with sum k\n\t// we are just converting this bigger problem into one of the most renowed problem\n\t\t\n\t\tint solve(vector<int>&nums,int k)\n {unordered_map<int,int>mp;\n int cs=0;\n int ans=0;\n for(int i=0;i<nums.size();++i)\n {\n cs+=nums[i];\n if(cs==k)\n {\n ans++; \n }\n if(mp.find(cs-k)!=mp.end())\n {\n ans+=mp[cs-k];\n \n }\n mp[cs]++;\n }\n return ans;\n \n }\n int numSubmatrixSumTarget(vector<vector<int>>& a, int t) {\n int ans=0;\n //we will actually work row wise because we already know the problem to find number of subarray in a row with a given sum\n for(int srow=0;srow<a.size();++srow)\n {vector<int>v(a[0].size(),0);\n for(int crow =srow;crow<a.size();++crow)//crow-->currrow\n {\n // now storing sum in a particular array\n for(int j=0;j<a[0].size();++j)\n {\n v[j]+=a[crow][j];\n }\n ans+=solve(v,t);\n }\n }\n \n return ans;\n }\n};\n/*\n**Taking an example**\n**step 1--\nsolving like this\n1 1 1 1->srow v=> 1 1 1 1\n1 1 1 1 v=> 2 2 2 2\n1 1 1 1 v=> 3 3 3 3\n1 1 1 1 v=> 4 4 4 4\nstep 2--\n1 1 1 1 \n1 1 1 1=>srow v=> 1 1 1 1\n1 1 1 1 v=> 2 2 2 2\n1 1 1 1 v=> 3 3 3 3\nstep 3--\n1 1 1 1 \n1 1 1 1\n1 1 1 1 =>srow v=> 1 1 1 1 \n1 1 1 1 v=> 2 2 2 2\nstep 4--\n1 1 1 1 \n1 1 1 1\n1 1 1 1 \n1 1 1 1 =>srow v=> 1 1 1 1 \nevery time we are calculating the cumulative sum starting from the srow index\nand you will get your ans**\n*/\n**Upvote if it helped**
| 7 | 0 |
['C']
| 1 |
number-of-submatrices-that-sum-to-target
|
Full and Explained in Depth || Most Intuitive || [Java/JavaScript/C++/Python]
|
full-and-explained-in-depth-most-intuiti-r5tp
|
Intuition\nLeetcode 560 This is prerequisite to understand this solution, The prerequisite is must.\n\n# Approach\n1. Iterate over all possible starting rows of
|
Shivansu_7
|
NORMAL
|
2024-01-28T15:10:37.658354+00:00
|
2024-01-28T15:10:37.658388+00:00
| 769 | false |
# Intuition\n[Leetcode 560](https://leetcode.com/problems/subarray-sum-equals-k/solutions/4638332/beats-100-in-depth-explained-java-c-python-javascript/) *This is prerequisite to understand this solution, The prerequisite is must.*\n\n# Approach\n1. **Iterate over all possible starting rows of the submatrix:**\n - Begin by selecting a starting row (i) from the matrix. This row will be the top row of the submatrix.\n2. **For each starting row, iterate over all possible ending rows:**\n - Iterate over all rows below the starting row to determine the bottom row (j) of the submatrix.\n3. **Compute the sum of elements column-wise between the starting and ending rows:**\n - Compute the sum of elements within the current submatrix by summing the elements in each column between the selected starting and ending rows.\n4. **For each sumRow, find subarrays with the target sum using a HashMap:**\n - Use a HashMap to store the frequency of prefix sums encountered while iterating through the columns.\n - For each sumRow (running sum of columns), check if there exists a prefix sum that, when subtracted from the current sum, equals the target.\n - If a prefix sum exists indicating a subarray with the target sum, increment the count.\nIncrement count by the number of subarrays found in step 4:\n5. **Accumulate the count of subarrays found with the target sum across all sumRows within the current submatrix.**\n - Repeat steps 1-5 for all combinations of starting and ending rows:\n - Iterate over all possible combinations of starting and ending rows to consider all potential submatrices within the matrix.\n6. **Return the final count:**\n - Iterate through all submatrices, count those with the target sum, and return the total count.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(m * n * n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.length;\n int n = matrix[0].length;\n\n int[] sumRow = new int[n];\n int count = 0;\n\n for(int i=0; i<m; i++) {\n Arrays.fill(sumRow, 0);\n\n for(int j=i; j<m; j++) {\n for(int k=0; k<n; k++) {\n sumRow[k] += matrix[j][k];\n }\n count += subArraySum(sumRow, target);\n }\n }\n return count;\n }\n\n private int subArraySum(int[] arr, int k) {\n int sum = 0;\n int count = 0;\n HashMap<Integer, Integer> map = new HashMap<>();\n map.put(0, 1);\n\n for(int i=0; i<arr.length; i++) {\n sum += arr[i];\n int rem = sum - k;\n \n if(map.containsKey(rem)) {\n count += map.get(rem);\n }\n map.put(sum, map.getOrDefault(sum, 0)+1);\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int m = matrix.size();\n int n = matrix[0].size();\n int count = 0;\n\n for(int i = 0; i < m; i++) {\n vector<int> sumRow(n, 0);\n\n for(int j = i; j < m; j++) {\n for(int k = 0; k < n; k++) {\n sumRow[k] += matrix[j][k];\n }\n count += subArraySum(sumRow, target);\n }\n }\n return count;\n }\n\nprivate:\n int subArraySum(vector<int>& arr, int k) {\n int sum = 0;\n int count = 0;\n unordered_map<int, int> map;\n map[0] = 1;\n\n for(int i = 0; i < arr.size(); i++) {\n sum += arr[i];\n int rem = sum - k;\n \n if(map.find(rem) != map.end()) {\n count += map[rem];\n }\n map[sum] = map.find(sum) != map.end() ? map[sum] + 1 : 1;\n }\n return count;\n }\n};\n```\n```Python []\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m = len(matrix)\n n = len(matrix[0])\n count = 0\n\n for i in range(m):\n sumRow = [0] * n\n\n for j in range(i, m):\n for k in range(n):\n sumRow[k] += matrix[j][k]\n count += self.subArraySum(sumRow, target)\n \n return count\n\n def subArraySum(self, arr: List[int], k: int) -> int:\n sum_map = defaultdict(int)\n sum_map[0] = 1\n total_sum = 0\n count = 0\n\n for num in arr:\n total_sum += num\n rem = total_sum - k\n \n if rem in sum_map:\n count += sum_map[rem]\n sum_map[total_sum] += 1\n\n return count\n```\n```JavaScript []\n/**\n * @param {number[][]} matrix\n * @param {number} target\n * @return {number}\n */\nvar numSubmatrixSumTarget = function(matrix, target) {\n const m = matrix.length;\n const n = matrix[0].length;\n\n const subArraySum = function(arr, k) {\n let sum = 0;\n let count = 0;\n const map = new Map();\n map.set(0, 1);\n\n for (let i = 0; i < arr.length; i++) {\n sum += arr[i];\n const rem = sum - k;\n\n if (map.has(rem)) {\n count += map.get(rem);\n }\n map.set(sum, (map.get(sum) || 0) + 1);\n }\n return count;\n };\n\n let count = 0;\n const sumRow = new Array(n).fill(0);\n\n for (let i = 0; i < m; i++) {\n sumRow.fill(0);\n\n for (let j = i; j < m; j++) {\n for (let k = 0; k < n; k++) {\n sumRow[k] += matrix[j][k];\n }\n count += subArraySum(sumRow, target);\n }\n }\n return count;\n};\n```\n\n---\n\n\n---\n\n\n
| 6 | 0 |
['Matrix', 'C++', 'Java', 'JavaScript']
| 6 |
number-of-submatrices-that-sum-to-target
|
Python3 Solution
|
python3-solution-by-motaharozzaman1996-4w23
|
\n\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n n=len(matrix)\n m=len(matrix[0])\n
|
Motaharozzaman1996
|
NORMAL
|
2024-01-28T01:54:44.090750+00:00
|
2024-01-28T01:54:44.090767+00:00
| 1,473 | false |
\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n n=len(matrix)\n m=len(matrix[0])\n ans=0\n for r in matrix:\n for i in range(1,len(r)):\n r[i]+=r[i-1]\n for start in range(m):\n for end in range(start,m):\n lookup=defaultdict(int)\n cumsum=0\n lookup[0]=1\n for k in range(n):\n cumsum+=matrix[k][end] - (matrix[k][start-1] if start !=0 else 0)\n if cumsum -target in lookup:\n ans+=lookup[cumsum-target]\n lookup[cumsum]+=1\n return ans \n```
| 6 | 0 |
['Python', 'Python3']
| 0 |
number-of-submatrices-that-sum-to-target
|
High-Speed Solution: Outpacing 95% of Submissions with Efficient Algorithm Design
|
high-speed-solution-outpacing-95-of-subm-wbwp
|
Intuition\nWhen faced with a problem involving the sum of submatrices, a common strategy is to utilize cumulative sums, which allow for the efficient computatio
|
kancheti
|
NORMAL
|
2024-01-28T01:21:27.155362+00:00
|
2024-01-28T01:21:27.155380+00:00
| 743 | false |
# Intuition\nWhen faced with a problem involving the sum of submatrices, a common strategy is to utilize cumulative sums, which allow for the efficient computation of the sum of any submatrix. However, a brute-force approach that considers all possible submatrices can be inefficient for large matrices. To optimize, we can combine the cumulative sum technique with a hashmap to efficiently count the occurrences of sums, thus allowing us to quickly determine if a particular submatrix sum equals the target.\n\n# Approach\nPrecompute Cumulative Sums: Calculate the cumulative sum for each cell in the matrix. Each cell\'s cumulative sum represents the total sum of the submatrix starting from the top-left corner (0,0) to the current cell.\n\nIterate Over Row Pairs: Fix two rows at a time (r1 and r2). This allows us to consider submatrices between these two rows.\n\nCalculate Column Sums and Use HashMap: For each pair of fixed rows, iterate through the columns and calculate the cumulative sum for columns within these rows. Use a hashmap to store the frequency of each cumulative sum. If the current cumulative sum minus the target is found in the hashmap, it indicates the existence of a submatrix summing to the target.\n\nCounting Submatrices: For every occurrence of a sum that, when subtracted from the current cumulative sum equals the target, increment the count. This count ultimately represents the total number of submatrices summing to the target.\n\n# Complexity\nTime complexity: The time complexity is O(n*n*n), where n is the number of rows (or columns) in the square matrix. For non-square matrices with dimensions m x n, the complexity is O(m*m*n). This complexity arises from iterating over every pair of rows and computing cumulative sums for each column in each pair.\n\nSpace complexity: The space complexity is O(m*n) for storing the cumulative sums. The space used by the hashmap can be considered as O(n) in the worst case, but this does not significantly affect the overall space complexity.\n\n\n\n# Code\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix, target):\n rows, cols = len(matrix), len(matrix[0])\n count = 0\n\n # Precompute the cumulative sum for the matrix\n cum_sum = [[0] * (cols + 1) for _ in range(rows + 1)]\n for r in range(rows):\n for c in range(cols):\n cum_sum[r+1][c+1] = cum_sum[r+1][c] + cum_sum[r][c+1] - cum_sum[r][c] + matrix[r][c]\n\n # Use hash map to find the target sum for submatrices\n for r1 in range(1, rows + 1):\n for r2 in range(r1, rows + 1):\n sum_count = {0: 1}\n cur_sum = 0\n for c in range(1, cols + 1):\n cur_sum = cum_sum[r2][c] - cum_sum[r1-1][c]\n count += sum_count.get(cur_sum - target, 0)\n sum_count[cur_sum] = sum_count.get(cur_sum, 0) + 1\n\n return count\n\n```
| 6 | 0 |
['Array', 'Hash Table', 'Matrix', 'Prefix Sum', 'Python3']
| 0 |
number-of-submatrices-that-sum-to-target
|
C++ || Easy to Understand || EXPLAINED || PREFIX + MAP
|
c-easy-to-understand-explained-prefix-ma-gvyn
|
HOPE IT HELPS...\n\nCODE : \n\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& mat, int target) {\n int r,c;\n r = m
|
The_Insyder
|
NORMAL
|
2022-07-18T07:13:34.582398+00:00
|
2022-07-18T07:14:24.605104+00:00
| 648 | false |
HOPE IT HELPS...\n\nCODE : \n```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& mat, int target) {\n int r,c;\n r = mat.size();\n c = mat[0].size();\n int prefix[r+1][c];\n prefix[r-1][c-1] = mat[r-1][c-1];\n prefix[r][c-1] = 0;\n for(int i = c-2 ; i >= 0 ; i--)\n {\n prefix[r-1][i] = prefix[r-1][i+1] + mat[r-1][i];\n prefix[r][i] = 0;\n }\n for(int j = r-2 ; j >= 0 ; j--)\n prefix[j][c-1] = prefix[j+1][c-1] + mat[j][c-1];\n for(int i = r-2 ; i >= 0 ; i--)\n for(int j = c-2 ; j >= 0 ;j--)\n prefix[i][j] = prefix[i+1][j] + prefix[i][j+1] - prefix[i+1][j+1] + mat[i][j];\n \n int cnt = 0;\n for(int i = 0 ; i < r ; i++)\n {\n for(int j = i+1; j <= r ; j++)\n {\n map<int , int> mp;\n mp[0] = 1;\n for(int k = c-1 ; k >= 0 ; k--)\n {\n int sum = prefix[i][k] - prefix[j][k];\n int reqSum = sum - target;\n cnt += mp[reqSum];\n mp[sum]++;\n }\n }\n }\n return cnt;\n }\n};\n```\n\nEXPLANATION (By pictures) : \n\n\n\n\n\n\nCOMPLEXITY : \n\n\n\n\n\n
| 6 | 0 |
['Prefix Sum']
| 2 |
number-of-submatrices-that-sum-to-target
|
C++||Hashmap||Easy & Understandable
|
chashmapeasy-understandable-by-prince_72-fes0
|
\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n int res = 0, m = A.size(), n = A[0].size();\n\t\tfor (
|
prince_725
|
NORMAL
|
2022-07-18T06:07:31.267655+00:00
|
2022-07-18T06:07:31.267694+00:00
| 1,286 | false |
```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& A, int target) {\n int res = 0, m = A.size(), n = A[0].size();\n\t\tfor (int i = 0; i < m; i++)\n\t\t\tfor (int j = 1; j < n; j++)\n\t\t\t\tA[i][j] += A[i][j - 1];\n\n\t\tunordered_map<int, int> counter;\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tfor (int j = i; j < n; j++) {\n\t\t\t\tcounter = {{0,1}};\n\t\t\t\tint cur = 0;\n\t\t\t\tfor (int k = 0; k < m; k++) {\n\t\t\t\t cur += A[k][j] - (i > 0 ? A[k][i - 1] : 0);\n\t\t\t\t res += counter.find(cur - target) != counter.end() ? counter[cur - target] : 0;\n\t\t\t\t counter[cur]++;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn res;\n }\n};\n```
| 6 | 1 |
['C']
| 0 |
number-of-submatrices-that-sum-to-target
|
CPP BRUTE FORCE O(n^6) time complexity, just for fun, TIME LIMIT EXCEEDS
|
cpp-brute-force-on6-time-complexity-just-opek
|
\nclass Solution {\npublic:\n \n int sum(vector<vector<int>>& matrix, int i,int j,int k,int l){\n int s=0;\n for(int p=i;p<=k;p++){\n
|
chase_master_kohli
|
NORMAL
|
2020-05-08T09:23:27.737834+00:00
|
2020-05-08T09:23:38.886218+00:00
| 264 | false |
```\nclass Solution {\npublic:\n \n int sum(vector<vector<int>>& matrix, int i,int j,int k,int l){\n int s=0;\n for(int p=i;p<=k;p++){\n for(int q=j;q<=l;q++){\n s+=matrix[p][q];\n }\n }\n return s;\n }\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int c=0;\n for(int i=0;i<matrix.size();i++){\n for(int j=0;j<matrix[i].size();j++){\n for(int k=i;k<matrix.size();k++){\n for(int l=j;l<matrix[k].size();l++){\n if(sum(matrix,i,j,k,l)==target)\n c++;\n }\n }\n }\n }\n return c;\n }\n};\n```
| 6 | 1 |
[]
| 1 |
number-of-submatrices-that-sum-to-target
|
[Java] O(R*R*C) or O(C*C*R) Solution
|
java-orrc-or-occr-solution-by-frenkiedej-0ijp
|
Convert it to 1-D array, then the problem turns into "search for subarray sums that equal to the target", which uses hashmap to track prefix sum count during it
|
frenkiedejong
|
NORMAL
|
2020-01-28T05:52:10.678557+00:00
|
2020-01-28T05:52:26.648525+00:00
| 462 | false |
* Convert it to 1-D array, then the problem turns into "search for subarray sums that equal to the target", which uses hashmap to track prefix sum count during iteration.\n```\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int res = 0, r = matrix.length, c = matrix[0].length;\n \n for (int i = 0; i < c; i++) {\n int[] rowSums = new int[r];\n for (int j = i; j < c; j++) {\n Map<Integer, Integer> count = new HashMap<>();\n count.put(0, 1);\n int prefixSum = 0;\n for (int k = 0; k < r; k++) {\n rowSums[k] += matrix[k][j];\n prefixSum += rowSums[k];\n res += count.getOrDefault(prefixSum - target, 0);\n count.put(prefixSum, count.getOrDefault(prefixSum, 0) + 1);\n }\n }\n }\n \n return res;\n }\n}\n```
| 6 | 0 |
[]
| 0 |
number-of-submatrices-that-sum-to-target
|
C++ | O(n^4) TIme | O(n) Space
|
c-on4-time-on-space-by-sohelshk7-w1a9
|
\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n \n int n = matrix.size(), m = matrix[0].si
|
sohelshk7
|
NORMAL
|
2022-07-18T17:50:55.325480+00:00
|
2022-07-18T17:50:55.325521+00:00
| 671 | false |
```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n \n int n = matrix.size(), m = matrix[0].size(), ans = 0;\n \n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n \n vector<int>tmp(m, 0);\n for(int k=i; k<n; k++){\n int s = 0;\n for(int l=j; l<m; l++){\n s += matrix[k][l];\n tmp[l] += s;\n if(tmp[l]==target)\n ans++;\n }\n }\n \n }\n }\n \n return ans;\n }\n};\n```\n\nComplextiy:\n\u2981\tTime: O((m*n)^2)\n\u2981\tSpace: O(n)\n
| 5 | 0 |
['C', 'Matrix', 'Prefix Sum', 'C++']
| 0 |
number-of-submatrices-that-sum-to-target
|
O(N^3) Solution | C++ | Approach Fully Explained | Must Watch
|
on3-solution-c-approach-fully-explained-36x7k
|
\nclass Solution {\npublic:\n /*\n \n APPROACH :\n \n GIVEN ARRAY\n \n 0 1 0\n 1 1 1\n 0 1 0\n \n no of rows(m) = 3;\n no of
|
dibyajyotidhar
|
NORMAL
|
2020-08-28T08:13:04.695108+00:00
|
2020-08-28T08:13:04.695150+00:00
| 384 | false |
```\nclass Solution {\npublic:\n /*\n \n APPROACH :\n \n GIVEN ARRAY\n \n 0 1 0\n 1 1 1\n 0 1 0\n \n no of rows(m) = 3;\n no of cols(n) = 4;\n \n First construct a prefix sum array of size {m+1 , n}\n \n And calculate prefix sum for every column\n \n Prefix Sum array\n 0 0 0\n 0 1 0\n 1 2 1\n 1 3 1\n \n Now for each row\n \n We search for all the downward sub matrics end {i,j}\n here i>=row and i<m\n and j>=0 and j<n\n \n we sum prefixSum[i+1][0] to prefixSum[i+1][j] to calulate sum of all the elements from (0,0) to (i,j) (Let Say sum)\n we sum prefixSum[row][0] to prefixSum[row][j] to calulate sum of all the elements from (0,0) to (row-1,j) (Let Say Subsum)\n \n for each j\n if we subtract sum = (sum- Subsum), we get sum of all the elements from (row,0) to (i,j)\n \n if(sum=target) in increase the counter\n \n for for this sum we check if (sum-target) exists in the map or not;\n if exsits we can confirm that how many times we have encountered an l (0<l<j) \n Such that\n sum of all the elements from (row,0) to (i,l) is (sum-target)\n Which indirectly confirms sum of all the elements from (row,l+1) to (i,j) is target\n \n Increase mp[sum] by 1\n \n \n */\n \n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n \n \n int m = matrix.size();\n int n = matrix[0].size();\n \n int pre[m+1][n];\n for(int i=0;i<=m;i++){\n for(int j=0;j<n;j++){\n pre[i][j]=0;\n }\n }\n \n for(int j=0;j<n;j++){\n for(int i=0;i<m;i++){\n \n pre[i+1][j]=pre[i][j]+matrix[i][j];\n }\n }\n \n unordered_map<int,int> mp;\n int cnt=0;\n /* \n 0 0 0\n 0 1 0\n 1 2 1\n 0 3 0\n */\n \n for(int row =0 ; row<m; row++){\n \n for(int i=row; i<m;i++){\n mp.clear();\n int sum=0;\n for(int j=0; j<n;j++){\n sum+= pre[i+1][j]-pre[row][j];\n if(sum==target)\n cnt++;\n if(mp.find(sum-target)!=mp.end()){\n cnt+=mp[sum-target];\n }\n mp[sum]++;\n }\n }\n }\n \n return cnt;\n }\n};\n```
| 5 | 1 |
[]
| 0 |
number-of-submatrices-that-sum-to-target
|
JavaScript 2D Prefix Sums - Clean and Simple
|
javascript-2d-prefix-sums-clean-and-simp-e67d
|
js\nvar numSubmatrixSumTarget = function(matrix, target) {\n const prefixSums = new Array(matrix.length + 1)\n .fill()\n .map(() => new Array(m
|
l33t1234
|
NORMAL
|
2020-08-19T19:16:31.274771+00:00
|
2020-08-19T19:16:54.741486+00:00
| 413 | false |
```js\nvar numSubmatrixSumTarget = function(matrix, target) {\n const prefixSums = new Array(matrix.length + 1)\n .fill()\n .map(() => new Array(matrix[0].length + 1).fill(0));\n \n for (let i = 1; i <= matrix.length; i++) {\n for (let j = 1; j <= matrix[0].length; j++) {\n prefixSums[i][j] = matrix[i-1][j-1] + prefixSums[i-1][j] + prefixSums[i][j-1] - prefixSums[i-1][j-1];\n }\n }\n \n let count = 0;\n for (let r1 = 1; r1 <= matrix.length; r1++) {\n for (let r2 = r1; r2 <= matrix.length; r2++) {\n const counts = {};\n counts[0] = 1;\n for (let c = 1; c <= matrix[0].length; c++) {\n const sum = prefixSums[r2][c] - prefixSums[r1 - 1][c];\n count += counts[sum - target] || 0;\n counts[sum] = (counts[sum] || 0) + 1;\n }\n }\n }\n \n return count;\n};\n```
| 5 | 0 |
['JavaScript']
| 0 |
number-of-submatrices-that-sum-to-target
|
C++ | Prefix Sum | Subarray Sum based Explanation
|
c-prefix-sum-subarray-sum-based-explanat-us6x
|
The problem can be reduced to finding subarray sum in a 1D array with target value. We can find the 1D subarray sum for each combination of rows and then each s
|
jainkartik203
|
NORMAL
|
2020-07-21T15:05:52.184546+00:00
|
2020-07-21T17:27:27.616451+00:00
| 736 | false |
The problem can be reduced to finding subarray sum in a 1D array with target value. We can find the 1D subarray sum for each combination of rows and then each subarray sum takes O(n) which makes the total time complexity O(n^3) since there will be n^2 combinations of rows.\n\nFirst we calculate the row prefix sum for the matrix so that each time we need to find the elements of rows r1 to r2 we can get it in O(n) since we won\'t need to sum all the elements in the row range again. And the sum of that row range can be calculated as sum[r2] - sum[r1-1]. \nFor Example1 the row prefix sum matrix would be: \n```\n0 1 0 0 1 0\n1 1 1 => 1 2 1\n0 1 0 1 3 1\n\nRange [1,2] would sum to: [1 3 1]-[0 1 0] = [1 2 1] in the original matrix.\n```\nAnd then we can find the subarray sum equal to target in the above formed 1D array in linear time. For this refer [@560](https://leetcode.com/problems/subarray-sum-equals-k). And in the above 1D array any subarray sum from index l,r would correspond to sum of submatrix having upper left as [r1,l] and lower right as [r2,r]. Thus we can just find the subarray sum for a 1D array for each combination of rows and we would be covering all the possible submatrices.\n\n**Implementation:**\n\n```\nclass Solution {\npublic:\n int checksub(vector<vector<int>>& matrix,int r1,int r2,int target){\n unordered_map<int,int> m;\n int curr=0,ans=0;\n m[0]=1;\n\t\t// ith element of 1D array = matrix[r2][i]-matrix[r1-1][i]\n for(int i=0;i<matrix[0].size();i++){ \n if(r1>0) \n curr+=matrix[r2][i]-matrix[r1-1][i];\n else\n curr+=matrix[r2][i];\n \n if(m.find(curr-target)!=m.end())\n ans+=m[curr-target];\n m[curr]++;\n }\n \n return ans;\n }\n \n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n \n int m=matrix.size(),n=matrix[0].size();\n if(m==0 || n==0)\n return 0;\n vector<vector<int>> dp(m,vector<int>(n,0));\n for(int i=0;i<m;i++) // Creating row prefix sum matrix\n for(int j=0;j<n;j++){\n if(i>0)\n matrix[i][j]+=matrix[i-1][j];\n }\n int ans=0;\n for(int i=0;i<m;i++) // For each row pair find 1D subarray sum with target\n for(int j=i;j<m;j++) \n ans+=checksub(matrix,i,j,target);\n return ans;\n }\n};\n```
| 5 | 0 |
[]
| 2 |
number-of-submatrices-that-sum-to-target
|
Vertical And Horizontal Prefix Sum | Java | C++
|
vertical-and-horizontal-prefix-sum-java-01nm6
|
Intuition, approach, and complexity discussed in video solution in detail.\nhttps://youtu.be/otmammzWYgI\n\n# Code\nJava\n\nclass Solution {\n public int num
|
Fly_ing__Rhi_no
|
NORMAL
|
2024-01-28T12:30:19.030777+00:00
|
2024-01-28T12:31:46.260078+00:00
| 1,290 | false |
# Intuition, approach, and complexity discussed in video solution in detail.\nhttps://youtu.be/otmammzWYgI\n\n# Code\nJava\n```\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n int rows = matrix.length, cols = matrix[0].length;\n \n for(int[] row : matrix){\n for(int col = 1; col < cols; col++){\n row[col] += row[col-1];\n }\n }\n \n int sumCnt = 0;\n \n for(int left = 0; left < cols; left++){\n for(int right = left; right < cols; right++){\n int currPrefSum = 0;\n Map<Integer, Integer> sumFreq = new HashMap<>();\n sumFreq.put(0, 1);\n \n for(int r = 0; r < rows; r++){\n int prefSumCurrRow = matrix[r][right] - ((left - 1 > -1) ? matrix[r][left - 1] : 0);\n currPrefSum += prefSumCurrRow;\n if(sumFreq.containsKey(currPrefSum - target)){\n sumCnt += sumFreq.get(currPrefSum - target);\n }\n sumFreq.put(currPrefSum, sumFreq.getOrDefault(currPrefSum, 0) + 1);\n }\n }\n }\n return sumCnt;\n }\n}\n\n\n```\nC++\n```\nclass Solution {\nprivate:\n void printMat(vector<vector<int>> mat){\n for(auto &row : mat){\n for(auto val : row){\n cout<<val<<" ";\n }\n cout<<endl;\n }\n cout<<endl;\n } \npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int rows = matrix.size(), cols = matrix[0].size();\n for(auto &row : matrix){\n for(int col = 1; col < cols; col++){\n row[col] += row[col-1];\n }\n }\n int sumCnt = 0;\n for(int left = 0; left < cols; left++){\n for(int right = left; right < cols; right++){\n int currPrefSum = 0;\n unordered_map<int, int> sumFreq;\n sumFreq[0]++;\n for(int r = 0; r < rows; r++){\n int prefSumCurrRow = matrix[r][right] - ((left - 1 > -1) ? matrix[r][left - 1] : 0);\n currPrefSum += prefSumCurrRow;\n if(sumFreq.count(currPrefSum-target)){\n sumCnt += sumFreq[currPrefSum-target];\n }\n sumFreq[currPrefSum]++;\n }\n }\n }\n return sumCnt;\n }\n};\n```
| 4 | 0 |
['Prefix Sum', 'C++', 'Java']
| 1 |
number-of-submatrices-that-sum-to-target
|
Easy Approach Using Map and prefix sum 🔥
|
easy-approach-using-map-and-prefix-sum-b-bult
|
\n# Complexity\n- Time complexity:\n O(mmn)\n- Space complexity:\n O(N)\n\n# Code\n\nclass Solution {\npublic:\n int getCount(vector<int> &prefix, int
|
omkarmundlik11
|
NORMAL
|
2024-01-28T10:41:51.429297+00:00
|
2024-01-28T10:41:51.429318+00:00
| 535 | false |
\n# Complexity\n- Time complexity:\n O(m*m*n)\n- Space complexity:\n O(N)\n\n# Code\n```\nclass Solution {\npublic:\n int getCount(vector<int> &prefix, int target){\n unordered_map<int,int> m;\n int sum = 0;\n int ans = 0;\n m[0]=1;\n for(auto i : prefix){\n sum += i;\n if(m[sum-target] > 0){\n ans += m[sum-target];\n }\n m[sum]++;\n }\n return ans;\n }\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int m = matrix.size();\n int n = matrix[0].size();\n int ans = 0;\n for(int i=0;i<m; i++){\n vector<int> prefix(n, 0);\n for(int j=i; j<m; j++){\n for(int k=0;k<n;k++){\n prefix[k] += matrix[j][k];\n }\n ans += getCount(prefix, target);\n }\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
number-of-submatrices-that-sum-to-target
|
JAVA Solution Explained in HINDI
|
java-solution-explained-in-hindi-by-the_-0cbi
|
https://youtu.be/rCTugCzGFV4\n\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvot
|
The_elite
|
NORMAL
|
2024-01-28T10:13:36.021832+00:00
|
2024-01-28T10:13:36.021867+00:00
| 328 | false |
https://youtu.be/rCTugCzGFV4\n\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\nSubscribe link:- https://youtube.com/@quantumCode7?si=NzjWYmiCbqfFBUJE\n\nSubscribe Goal:- 100\nCurrent Subscriber:- 82\n\n# Code\n```\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target) {\n \n int m = matrix.length;\n int n = matrix[0].length;\n\n int sumRow[] = new int[n];\n int ans = 0;\n\n for(int i = 0; i < m; i++) { // i is the starting row\n Arrays.fill(sumRow, 0);\n for(int j = i; j < m; j++) { // j is the ending row\n for(int k = 0; k < n; k++) { // k is the column\n sumRow[k] += matrix[j][k];\n }\n ans += subarraySum(sumRow, target);\n }\n }\n return ans;\n }\n\n public int subarraySum(int[] nums, int k) {\n \n int sum = 0;\n int ans = 0;\n\n Map<Integer, Integer> prefixSum = new HashMap<>();\n prefixSum.put(0, 1);\n\n for(int i = 0; i < nums.length; i++) {\n sum += nums[i];\n if(prefixSum.containsKey(sum - k)) {\n ans += prefixSum.get(sum - k);\n }\n prefixSum.put(sum, prefixSum.getOrDefault(sum, 0) + 1);\n }\n return ans;\n }\n}\n```
| 4 | 0 |
['Java']
| 0 |
number-of-submatrices-that-sum-to-target
|
🌟 JavaScript || Professional Approach and In-Depth Explanation
|
javascript-professional-approach-and-in-eev2q
|
Intuition\nThe problem involves finding the number of submatrices in a given matrix such that the sum of elements in the submatrix is equal to a target value. T
|
withaarzoo
|
NORMAL
|
2024-01-28T06:07:23.287227+00:00
|
2024-01-28T06:07:23.287270+00:00
| 1,035 | false |
## Intuition\nThe problem involves finding the number of submatrices in a given matrix such that the sum of elements in the submatrix is equal to a target value. The intuition here is to use the cumulative sum to efficiently calculate the sum of elements in any submatrix. By considering all possible pairs of columns and using a hashmap to keep track of cumulative sums, we can efficiently count the submatrices meeting the target sum condition.\n\n## Approach\n1. **Cumulative Sum Precomputation:** Iterate through each row and precompute the cumulative sum for each element in that row. This step is essential for efficient computation of submatrix sums.\n \n2. **Pair of Columns Iteration:** Use two nested loops to iterate through all possible pairs of columns (`c1` and `c2`). This defines the left and right boundaries of the submatrix.\n\n3. **HashMap for Cumulative Sums:** For each pair of columns, iterate through all rows and calculate the sum of elements in the submatrix formed by those columns. Keep track of the cumulative sum using a hashmap (`map`). \n\n4. **Counting Submatrices:** Update a counter (`count`) based on the occurrences of specific cumulative sums in the hashmap. If the difference between the current cumulative sum and the target sum exists in the hashmap, increment the counter by the corresponding frequency.\n\n5. **Update Hashmap:** Update the hashmap with the current cumulative sum\'s frequency.\n\n## Complexity\n- **Time complexity:** The cumulative sum precomputation takes $$O(rows \\times cols)$$ time. The subsequent pair of columns iteration involves iterating through each element in the matrix, resulting in $$O(rows \\times cols \\times cols)$$ time complexity. Overall, the time complexity is $$O(rows \\times cols \\times cols)$$.\n\n- **Space complexity:** The space complexity is $$O(rows \\times cols)$$ for storing the cumulative sum matrix. Additionally, the hashmap (`map`) has a space complexity of $$O(rows)$$, where each entry corresponds to a unique cumulative sum. Hence, the overall space complexity is $$O(rows \\times cols)$$.\n\n# Code\n```\nvar numSubmatrixSumTarget = function(matrix, target) {\n const rows = matrix.length;\n const cols = matrix[0].length;\n\n // Precompute the cumulative sum for each row\n for (let row = 0; row < rows; row++) {\n for (let col = 1; col < cols; col++) {\n matrix[row][col] += matrix[row][col - 1];\n }\n }\n\n let count = 0;\n\n // Iterate through all possible pairs of columns\n for (let c1 = 0; c1 < cols; c1++) {\n for (let c2 = c1; c2 < cols; c2++) {\n const map = new Map();\n map.set(0, 1);\n let sum = 0;\n\n // Iterate through all rows and calculate the sum\n for (let row = 0; row < rows; row++) {\n sum += matrix[row][c2] - (c1 > 0 ? matrix[row][c1 - 1] : 0);\n\n // Check if there is a subarray with sum equal to target\n count += map.get(sum - target) || 0;\n\n // Update the frequency of the current sum\n map.set(sum, (map.get(sum) || 0) + 1);\n }\n }\n }\n\n return count;\n};\n\n```
| 4 | 0 |
['JavaScript']
| 6 |
number-of-submatrices-that-sum-to-target
|
Submatrices Sum To Target: Efficient Matrix + Map Algo
|
submatrices-sum-to-target-efficient-matr-yba1
|
Intuition\nThe intuition is to reduce the problem from 2D to 1D by using prefix sums and then apply a technique similar to "Two Sum" on the 1D array.\n Describe
|
madhusudanrathi99
|
NORMAL
|
2024-01-28T01:44:04.152220+00:00
|
2024-03-04T02:36:16.512827+00:00
| 439 | false |
# Intuition\nThe intuition is to reduce the problem from 2D to 1D by using prefix sums and then apply a technique similar to "Two Sum" on the 1D array.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. **Calculate Prefix Sums**: \nFirst, we calculate the prefix sum for each row in the `matrix`. This will help us to quickly calculate the sum of elements in any column between two rows.\n2. **Iterate Over Columns**: \nThen, we iterate over all pairs of columns and calculate the sum of elements between these two columns for every row. This effectively gives us a 1D array.\n3. **Use a Dictionary**: \nWe use a dictionary (HashMap) to keep track of the sum and its frequency. The key is the sum and the value is the frequency of this sum. We initialize the map with (0,1) because we have one submatrix (an empty one) that sums up to 0.\n4. **Check for Target Sum**: \nFor each sum, we check if `sum - target` is in the map. If it is, we add the frequency of `sum - target` to the count. This is because for each pair (i,j) where `sum[i] - sum[j] = target`, there is one more submatrix that sums up to the target.\n5. **Return Count**: \nFinally, we return the count.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N^2 * M)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(M)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int NumSubmatrixSumTarget(int[][] matrix, int target) {\n int m = matrix.Length;\n int n = matrix[0].Length;\n for(int i = 0; i < m; i++) {\n for(int j = 1; j < n; j++) {\n matrix[i][j] += matrix[i][j - 1];\n }\n }\n\n int count = 0;\n for(int i = 0; i < n; i++) {\n for(int j = i; j < n; j++) {\n Dictionary<int, int> map = new();\n map[0] = 1;\n int sum = 0;\n for(int k = 0; k < m; k++) {\n sum += matrix[k][j];\n if(i > 0)\n sum -= matrix[k][i - 1];\n if(map.ContainsKey(sum - target))\n count += map[sum - target];\n if(!map.ContainsKey(sum))\n map[sum] = 0;\n map[sum]++;\n }\n }\n }\n\n return count;\n }\n}\n```
| 4 | 0 |
['Array', 'Hash Table', 'Matrix', 'Prefix Sum', 'C#']
| 0 |
number-of-submatrices-that-sum-to-target
|
Java Using HashMap
|
java-using-hashmap-by-aditya_jain_258455-34x9
|
\nclass Solution {\n\tpublic int numSubmatrixSumTarget(int[][] arr, int target) {\n\t\tint n = arr.length;\n\t\tint m = arr[0].length;\n\t\tint count = 0;\n\t\t
|
Aditya_jain_2584550188
|
NORMAL
|
2022-09-05T05:58:05.490402+00:00
|
2022-09-05T05:58:05.490456+00:00
| 442 | false |
```\nclass Solution {\n\tpublic int numSubmatrixSumTarget(int[][] arr, int target) {\n\t\tint n = arr.length;\n\t\tint m = arr[0].length;\n\t\tint count = 0;\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tint[] temp = new int[m];\n\t\t\tfor (int row = i; row < n; row++) {\n\t\t\t\tfor (int col = 0; col < m; col++) {\n\t\t\t\t\ttemp[col] += arr[row][col];\n\t\t\t\t}\n\t\t\t\tcount += helper(temp, target);\n\t\t\t}\n\t\t}\n\t\treturn count;\n\t}\n\n\tpublic int helper(int[] arr, int target) {\n\t\tHashMap<Integer, Integer> map = new HashMap<>();\n\t\tmap.put(0, 1);\n\t\tint count = 0, sum = 0;\n\t\tfor (int i = 0; i < arr.length; i++) {\n\t\t\tsum += arr[i];\n\t\t\tcount += map.getOrDefault(sum - target, 0);\n\t\t\tmap.put(sum, map.getOrDefault(sum, 0) + 1);\n\t\t}\n\t\treturn count;\n\t}\n}\n```
| 4 | 0 |
['Java']
| 0 |
number-of-submatrices-that-sum-to-target
|
Very Easy Explanation & Solution || Subarray sum equal to K
|
very-easy-explanation-solution-subarray-sc1u6
|
Before you go with this problem I will suggest you to first solve Subarray Sum Equal to K. This problem is quite modified version of that problem. Upvote if you
|
umeshbagade
|
NORMAL
|
2022-07-18T18:30:10.387094+00:00
|
2022-07-18T18:33:27.203074+00:00
| 465 | false |
Before you go with this problem I will suggest you to first solve [Subarray Sum Equal to K](https://leetcode.com/problems/subarray-sum-equals-k/). This problem is quite modified version of that problem. Upvote if you like it.\n\n\n**Approach**\nFirst we will find the subarrays that contribute to sum equal to target, considering each row.\n\n| a | b | c | ------------------row1 \n| d | e | f | ------------------row2\n| g | h | i |-------------------row3\n\n\n\nCombine consecutive rows and find answer again, as submatrix can also combination of two or more rows.\n\n| a | b | c | ------find for this\n| d+a | e+b | f+c | -----find for this row\n| g+d+a | h+e+b | i+f+c | ------find for this row\n\nsimilarly,\n\n| d | e | f | -----for this row\n| g+d | h+e | i+f | -----for this row\n\nand,\n| g | h | i | -----for this row\n\n\nadd the answers of all these rows, and have the final answer,\n\n\n**My Solution**\n```\nclass Solution {\npublic:\n int sumEqualToK(vector<int>& nums, int k)\n {\n unordered_map<int,int> mp;\n mp[0] =1;\n int sum = 0,ans=0;\n for(int i=0;i<nums.size();i++)\n {\n sum += nums[i];\n ans += mp[sum-k]; \n mp[sum]++;\n }\n return ans;\n }\n \n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n \n int count=0;\n for(int i=0;i<matrix.size();i++)\n {\n vector<int> prefSum(matrix[i].size(),0);\n for(int j=i;j<matrix.size();j++)\n {\n for(int k=0;k<matrix[j].size();k++)\n {\n prefSum[k] += matrix[j][k];\n }\n count += sumEqualToK(prefSum, target);\n\n } \n }\n return count;\n \n }\n};\n```\n\n\n
| 4 | 0 |
['Dynamic Programming', 'C', 'C++']
| 1 |
number-of-submatrices-that-sum-to-target
|
Brute force and Optimised (Number of Submatrices That Sum to Target)
|
brute-force-and-optimised-number-of-subm-kbmb
|
From Bruteforce to optimised code.\nBrute force code(TLE)\nSimply check sum of all possible (x1, y1), (x2, y2) pairs in matrix.\nWe can easily optmise this usin
|
anubhav100rao
|
NORMAL
|
2022-07-18T05:11:54.229376+00:00
|
2022-07-18T05:11:54.229407+00:00
| 232 | false |
From Bruteforce to optimised code.\n**Brute force code(TLE)**\nSimply check sum of all possible (x1, y1), (x2, y2) pairs in matrix.\nWe can easily optmise this using prefix 2 D array\n```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int n = matrix.size(), m = matrix[0].size();\n\n vector<vector<int>>pre(n + 1, vector<int>(m + 1, 0));\n\n for(int i = 1; i<=n; i++)\n for(int j = 1; j<=m; j++)\n pre[i][j] += pre[i-1][j] + pre[i][j-1] - pre[i-1][j-1] + matrix[i-1][j-1];\n\n int cnt = 0;\n\n for(int i = 1; i<=n; i++) {\n for(int j = 1; j<=m; j++) {\n for(int k = i; k <= n; k++) {\n for(int l = j; l <=m; l++) {\n if(pre[k][l] - pre[k][j-1] - pre[i - 1][l] + pre[i - 1][j - 1] == target) {\n cout << k << " " << l << " " << i << " " << j << "\\n";\n cnt++;\n }\n }\n }\n }\n } \n\n return cnt;\n }\n};\n```\nBut this code leads to TLE since it is O(N^4)\n\n**Optimised approach**\nWe can iterate over all column pairs and store the prefix sum of rows between two columns.\n```\nclass Solution {\npublic:\n int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {\n int n = matrix.size(), m = matrix[0].size();\n\n vector<vector<int>>pre(n + 1, vector<int>(m + 1, 0));\n\n for(int i = 1; i<=n; i++)\n for(int j = 1; j<=m; j++)\n pre[i][j] = matrix[i-1][j-1] + pre[i][j-1];\n\n\n unordered_map<int, int>hsh;\n int res = 0;\n\n for(int col1 = 1; col1 <= m; col1++) {\n for(int col2 = col1; col2 <= m; col2++) {\n hsh = {{0, 1}};\n int curr = 0;\n for(int row = 1; row <= n; row++) {\n curr += pre[row][col2] - pre[row][col1 - 1];\n if(hsh.count(curr - target))\n res += hsh[curr - target];\n hsh[curr]++;\n }\n }\n }\n return res;\n }\n};\n```\nTime Complexity: O(N^3)\n\nThank You \u2764\uFE0F
| 4 | 0 |
[]
| 0 |
number-of-submatrices-that-sum-to-target
|
✔️ C++ || Easy || Prefix-Sum || Sliding Window
|
c-easy-prefix-sum-sliding-window-by-sura-ua7h
|
\nclass Solution\n{\n public:\n int numSubmatrixSumTarget(vector<vector < int>> &matrix, int target)\n {\n int m = matrix.size();\n
|
suraj_08
|
NORMAL
|
2022-07-18T03:08:08.242468+00:00
|
2022-07-18T03:08:08.242508+00:00
| 762 | false |
````\nclass Solution\n{\n public:\n int numSubmatrixSumTarget(vector<vector < int>> &matrix, int target)\n {\n int m = matrix.size();\n int n = matrix[0].size();\n \n for (int i = 0; i < m; i++)\n {\n for (int j = 1; j < n; j++)\n {\n matrix[i][j] += matrix[i][j - 1];\n }\n }\n \n int count = 0;\n \n for (int i = 0; i < n; i++)\n {\n for (int j = i; j < n; j++)\n {\n map<int, int> mp;\n mp[0] = 1;\n int sum = 0;\n for (int k = 0; k < m; k++)\n {\n sum += matrix[k][j] - (i > 0 ? matrix[k][i - 1] : 0);\n count += mp[sum - target];\n mp[sum]++;\n }\n }\n }\n \n return count;\n }\n};\n````
| 4 | 0 |
['C', 'Sliding Window', 'Prefix Sum']
| 1 |
number-of-submatrices-that-sum-to-target
|
python beat 97.25% easy understanding
|
python-beat-9725-easy-understanding-by-j-j4h4
|
\nclass Solution(object):\n def numSubmatrixSumTarget(self, matrix, target):\n m = len(matrix[0])\n n = len(matrix)\n res = 0\n \
|
jason0323
|
NORMAL
|
2020-06-18T04:14:09.684434+00:00
|
2020-06-18T04:14:09.684475+00:00
| 280 | false |
```\nclass Solution(object):\n def numSubmatrixSumTarget(self, matrix, target):\n m = len(matrix[0])\n n = len(matrix)\n res = 0\n \n prefix = [[0] * m for _ in range(n)]\n \n \n for i in range(n):\n for j in range(m):\n if i == 0:\n prefix[i][j] = matrix[i][j]\n else:\n prefix[i][j] = matrix[i][j] + prefix[i-1][j]\n \n for i in range(n):\n for j in range(i, n):\n d = {0:1}\n cur = 0\n for k in range(m):\n if i == 0:\n cur += prefix[j][k]\n else:\n cur += prefix[j][k] - prefix[i-1][k]\n \n if cur - target in d:\n res += d[cur-target]\n\n if cur in d:\n d[cur] += 1\n else:\n d[cur] = 1\n return res\n```
| 4 | 0 |
[]
| 0 |
number-of-submatrices-that-sum-to-target
|
Python Solution O(n^3) beats 98%
|
python-solution-on3-beats-98-by-user8307-xgff
|
This question is related to https://leetcode.com/problems/subarray-sum-equals-k/. We can use the same idea to find out the number of subarray with target sum fo
|
user8307e
|
NORMAL
|
2020-01-04T21:51:43.850834+00:00
|
2020-01-04T21:51:43.850868+00:00
| 965 | false |
This question is related to https://leetcode.com/problems/subarray-sum-equals-k/. We can use the same idea to find out the number of subarray with target sum for one row in linear time. Basically, we generate O(m^2) combinations of rows and apply O(n) algorithm to find the target sum for each combination. \n\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n if not matrix:\n return 0\n \n def num_for_one_row(nums):\n prev = {}\n prev[0] = 1\n cur_sum = 0\n ans = 0\n for num in nums:\n cur_sum += num\n if cur_sum - target in prev:\n ans += prev[cur_sum - target]\n if cur_sum not in prev:\n prev[cur_sum] = 1\n else:\n prev[cur_sum] += 1\n return ans \n \n res = 0\n m = len(matrix)\n n = len(matrix[0])\n \n for i in range(m):\n nums = [0]*n\n for j in range(i,m):\n for k in range(n):\n nums[k]+=matrix[j][k]\n res += num_for_one_row(nums)\n \n return res\n```\n\nIn this solution, the time complexity is O(m^2*n) where m is the number of rows and n is the number of columns. The space complexity is O(n).
| 4 | 0 |
['Python', 'Python3']
| 2 |
number-of-submatrices-that-sum-to-target
|
Python Simple Intuitive Solution
|
python-simple-intuitive-solution-by-zou_-agwg
|
\nfrom collections import defaultdict\nclass Solution(object):\n def numSubmatrixSumTarget(self, matrix, target):\n """\n :type matrix: List[Li
|
zou_zheng
|
NORMAL
|
2019-09-28T15:10:06.015949+00:00
|
2019-09-28T15:10:06.016001+00:00
| 670 | false |
```\nfrom collections import defaultdict\nclass Solution(object):\n def numSubmatrixSumTarget(self, matrix, target):\n """\n :type matrix: List[List[int]]\n :type target: int\n :rtype: int\n """\n res = 0\n row,col = len(matrix),len(matrix[0])\n for k in xrange(row):\n nums = [0 for _ in xrange(col)]\n for i in xrange(k,row):\n for j in xrange(col):\n nums[j] += matrix[i][j]\n res += self.check(nums,target)\n return res\n \n def check(self,nums,target):\n counter,res = defaultdict(int),0\n counter[0],cum_sum = 1,0\n for i,num in enumerate(nums):\n cum_sum += num\n res += counter[cum_sum - target]\n counter[cum_sum] += 1\n return res\n```
| 4 | 1 |
[]
| 0 |
number-of-submatrices-that-sum-to-target
|
Easy solution biginner friendly | Very easy to understand
|
easy-solution-biginner-friendly-very-eas-t57k
|
Approach\n# \n1. Cumulative Sum for Each Row:\n\n The algorithm starts by computing the cumulative sum for each row in the matrix A. This is done to efficiently
|
Rockposedon
|
NORMAL
|
2024-01-28T08:43:05.397431+00:00
|
2024-01-28T08:43:05.397449+00:00
| 181 | false |
## Approach\n# \n1. Cumulative Sum for Each Row:\n\n* The algorithm starts by computing the cumulative sum for each row in the matrix A. This is done to efficiently calculate the sum of elements in any submatrix.\n# \n2. Iterate Over All Possible Column Pairs:\n\n* The algorithm uses two nested loops to iterate over all possible pairs of columns, denoted by (i, j).\n* For each pair of columns, it calculates the cumulative sum of elements in the submatrix between those columns for each row.\n# \n3. Count Submatrices with Target Sum:\n\n* For each submatrix, the algorithm maintains a defaultdict (c) to count the occurrences of cumulative sums.\n* It uses the variable cur to represent the current sum of elements in the submatrix.\n* The algorithm checks if cur - target has been encountered before. If so, it increments the result (res) by the count of occurrences stored in c[cur - target].\n* The counter c is then updated to reflect the occurrence of the current cumulative sum.\n\n# \n4. Return Result:\n* The final result (res) represents the count of submatrices whose sum meets the target criteria.\n\n## Solution\n```\nclass Solution:\n def numSubmatrixSumTarget(self, A: List[List[int]], target: int) -> int:\n # Get the dimensions of the matrix\n m, n = len(A), len(A[0])\n\n # Compute the cumulative sum for each row\n for row in A:\n for i in range(n - 1):\n row[i + 1] += row[i]\n\n res = 0 # Initialize the result variable to count submatrices\n\n # Iterate over all possible pairs of columns\n for i in range(n):\n for j in range(i, n):\n c = collections.defaultdict(int)\n cur, c[0] = 0, 1 # Initialize the current sum and a counter for cumulative sums\n\n # Iterate over each row to calculate the submatrix sum\n for k in range(m):\n # Update the current sum based on the cumulative row sums\n cur += A[k][j] - (A[k][i - 1] if i > 0 else 0)\n\n # Count submatrices with the target sum using cumulative sums\n res += c[cur - target]\n\n # Update the counter for the current cumulative sum\n c[cur] += 1\n\n return res\n```
| 3 | 0 |
['Python', 'Python3']
| 0 |
number-of-submatrices-that-sum-to-target
|
Beats 91% fully explained
|
beats-91-fully-explained-by-deepeshoverc-0lc0
|
Intuition\nThe numSubmatrixSumTarget function calculates the number of submatrices within the given matrix that sum up to the target value.\n\n# Approach\nItera
|
deepeshovercoder
|
NORMAL
|
2024-01-28T04:03:24.942146+00:00
|
2024-01-28T04:03:24.942167+00:00
| 104 | false |
# Intuition\nThe numSubmatrixSumTarget function calculates the number of submatrices within the given matrix that sum up to the target value.\n\n# Approach\nIterate through each row of the matrix (i):\nFor each row, initialize a prefix sum array (prefixSums) to store the cumulative sums of elements in that row.\nIterate through each subsequent row (j) starting from i:\nUpdate the prefixSums array to include the cumulative sums of elements in the current row (j).\nUse a hashmap (seen) to keep track of the cumulative sums encountered so far and their frequencies.\nInitialize currentSum to 0 to keep track of the cumulative sum of subarrays.\nIterate through each column (k) to calculate the cumulative sum (currentSum) of subarrays ending at column k.\nCheck if there exists a previous subarray with the required complement (currentSum - target). If so, increment the count by the frequency of that complement in seen.\nUpdate the hashmap seen with the current cumulative sum (currentSum).\nAfter processing all submatrices, return the count, which represents the number of submatrices with the target sum.\n\n\n# Complexity\n- Time complexity:\nO(m^2 * n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nfunction numSubmatrixSumTarget(matrix, target) {\n const m = matrix.length;\n const n = matrix[0].length;\n let count = 0;\n\n for (let i = 0; i < m; i++) {\n const prefixSums = new Array(n).fill(0);\n for (let j = i; j < m; j++) {\n for (let k = 0; k < n; k++) {\n prefixSums[k] += matrix[j][k];\n }\n const seen = new Map();\n seen.set(0, 1); \n let currentSum = 0;\n for (let k = 0; k < n; k++) {\n currentSum += prefixSums[k];\n count += seen.get(currentSum - target) || 0; \n seen.set(currentSum, (seen.get(currentSum) || 0) + 1);\n }\n }\n }\n\n return count;\n}\n\n```
| 3 | 0 |
['JavaScript']
| 0 |
number-of-submatrices-that-sum-to-target
|
Simple code with explanation
|
simple-code-with-explanation-by-mullachv-msaj
|
Intuition\nThis solution was inspired by the Editorial and is a structure worth memorizing. Prefix sums for 2D matrix can be constructed using the following. We
|
mullachv
|
NORMAL
|
2024-01-28T04:00:24.183291+00:00
|
2024-01-28T04:00:24.183329+00:00
| 143 | false |
# Intuition\nThis solution was inspired by the Editorial and is a structure worth memorizing. Prefix sums for 2D matrix can be constructed using the following. We recollect that prefix sums for a 2D case involves capturing the sum of all the values from cell (0,0) to cell (row, col) inclusive:\n```\nm, n = len(matrix), len(matrix[0])\n\n# add an extra row and column to avoid index checks such as i >= 1 etc.\nps = [[0]*(n+1) for _ in range(m+1)]\n\n#\n# remember that adding the extra row and column now makes \n# the reference to the original matrix 1-based indexing, matrix[i-1][j-1]\n#\nfor i in range(1, m+1):\n for j in range(1, n+1):\n ps[i][j] = ps[i][j-1] + ps[i-1][j] - ps[i-1][j-1] + matrix[i-1][j-1]\n\n```\n\n# Approach\nNow we can compute the sums for any rectangular portion of the grid by using nested loops over rows and then over columns. This is what the editorial calls reducing it to a 1D problem. However to do that we\'ll use a dictionary before scanning the cols for the row, and initialize it with a count `1` for a sum of `0`:\n\n```\nfor r1 in range(1, m+1):\n for r2 in range(r1, m+1):\n dt = defaultdict(int)\n dt[0] = 1\n for col in range(1, n+1):\n # compute sum for (r1,1) to (r2,col) \n curr_sum = ps[r2][col] - ps[r1 - 1][col]\n\n # check whether there exists a previous sum A s.t. curr_sum - A == target\n count += dt[curr_sum - target]\n\n # increment counter for curr_sum\n dt[curr_sum] += 1\n\nreturn count\n```\n\n# Complexity\n- Time complexity:\n$O(m^2n)$ where $m$ is the number of rows and $n$ is the number of columns in matrix\n\n- Space complexity:\n$O(mn)$\n\n# Code\n```\nclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m, n = len(matrix), len(matrix[0])\n\n # 2D prefix sum\n ps = [[0]*(n+1) for _ in range(m+1)]\n\n for i in range(1, m+1):\n for j in range(1, n+1):\n ps[i][j] = ps[i][j-1] + ps[i-1][j] - ps[i-1][j-1] + matrix[i-1][j-1]\n \n count = 0\n for r1 in range(1, m+1):\n for r2 in range(r1, m+1):\n dt = defaultdict(int)\n dt[0] = 1\n\n for col in range(1, n+1):\n curr_sum = ps[r2][col] - ps[r1 - 1][col]\n count += dt[curr_sum - target]\n dt[curr_sum] += 1\n\n return count\n \n```
| 3 | 0 |
['Python3']
| 1 |
number-of-submatrices-that-sum-to-target
|
Swift💯1liner
|
swift1liner-by-upvotethispls-k7xa
|
One-Liner, terse \uD83D\uDE44 (accepted answer)\n\nclass Solution {\n func numSubmatrixSumTarget(_ m: [[Int]], _ t: Int) -> Int {\n m[0].indices.reduc
|
UpvoteThisPls
|
NORMAL
|
2024-01-28T01:31:45.475837+00:00
|
2024-09-11T22:33:28.680810+00:00
| 196 | false |
**One-Liner, terse \uD83D\uDE44 (accepted answer)**\n```\nclass Solution {\n func numSubmatrixSumTarget(_ m: [[Int]], _ t: Int) -> Int {\n m[0].indices.reduce((0,m.map{$0.reduce(into:[0]){$0+=[$0.last!+$1]}})){d,i in ((i..<d.1[0].count-1).reduce(d.0){r,j in d.1.reduce(into:(r,[0:1],0)){a,b in a.2+=b[j+1]-b[i];a.0+=a.1[a.2-t] ?? 0;a.1[a.2,default:0]+=1}.0},d.1)}.0\n }\n}\n```\n\n---\n\n**One-Liner, expanded and annotated (accepted answer)**\n```\nimport Algorithms\n\nclass Solution {\n func numSubmatrixSumTarget(_ matrix: [[Int]], _ target: Int) -> Int {\n matrix[0].indices.reduce(0) { result, i in\n (i..<matrix[0].count).reduce(result) {result, j in\n matrix.reduce(into: (\n result: result,\n counts: [0:1],\n cur: 0\n )) { data, row in\n let prefixSums = row.reductions(0, +)\n data.cur += prefixSums[j+1] - prefixSums[i]\n data.result += data.counts[data.cur - target, default:0]\n data.counts[data.cur, default:0] += 1\n }\n .result\n }\n }\n }\n}\n```
| 3 | 0 |
['Swift']
| 2 |
number-of-submatrices-that-sum-to-target
|
Java
|
java-by-gadmo-uv2l
|
Presum rects from top-left corner (0, 0) to each btm-right corner and checking all options at O(n^2 * M^2)Code
|
gadmo
|
NORMAL
|
2024-01-28T00:35:37.475282+00:00
|
2025-01-09T00:39:27.288571+00:00
| 213 | false |
Presum rects from top-left corner (0, 0) to each btm-right corner and checking all options at O(n^2 * M^2)
# Code
```
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int m = matrix.length, n = matrix[0].length, ans = 0;
int presum[][] = new int [m][n]; // rects sums of (0, 0, i , j) coordinates
for (int i = 0; i < m; i++){
for (int j = 0; j < n; j++){
presum[i][j] = matrix[i][j];
if (i > 0) presum[i][j] += presum[i - 1][j];
if (j > 0) presum[i][j] += presum[i][j - 1];
if (i > 0 && j > 0) presum[i][j] -= presum[i - 1][j - 1]; // since it been added twice
}
}
for (int i = 0; i < m; i++){
for (int j = 0; j < n; j++){
for (int h = -1; h < i; h++){ // upper corner
for (int w = -1; w < j; w++){ // left corner
int sum = presum[i][j];
if (h >= 0) sum -= presum[h][j];
if (w >= 0) sum -= presum[i][w];
if (h >= 0 && w >= 0) sum += presum[h][w];
if (sum == target) ans++;
}
}
}
}
return ans;
}
}
```
| 3 | 1 |
['Java']
| 0 |
number-of-submatrices-that-sum-to-target
|
C# | Detailed Explained solution | with workflow
|
c-detailed-explained-solution-with-workf-c9qt
|
Steps involved here:\n1. We will create a prefixSum Array - (Loops1 in diagram)\n2. We use LoopA to leave behind the checked columns. Each iteration the matrix
|
rahulvc
|
NORMAL
|
2022-07-18T16:55:47.046827+00:00
|
2022-07-18T17:04:49.624939+00:00
| 130 | false |
Steps involved here:\n1. We will create a prefixSum Array - (Loops1 in diagram)\n2. We use LoopA to leave behind the checked columns. Each iteration the matrix which we will check will decrease by 1 column.\nthis line will take care of that - \n\n\n\n3. LoopB to check all the posisble sums in the active sub matrix\n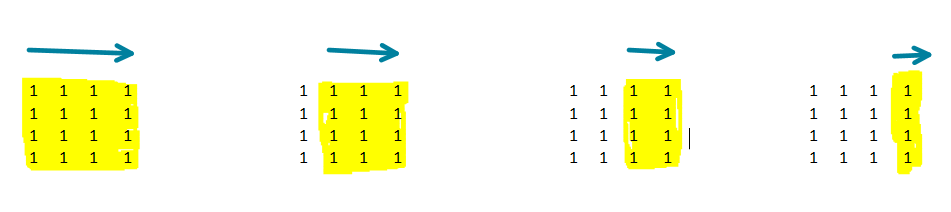\n\n\n4. Loop C to iterate over each row and find the number of sums we can get.\n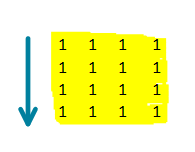\n\n\n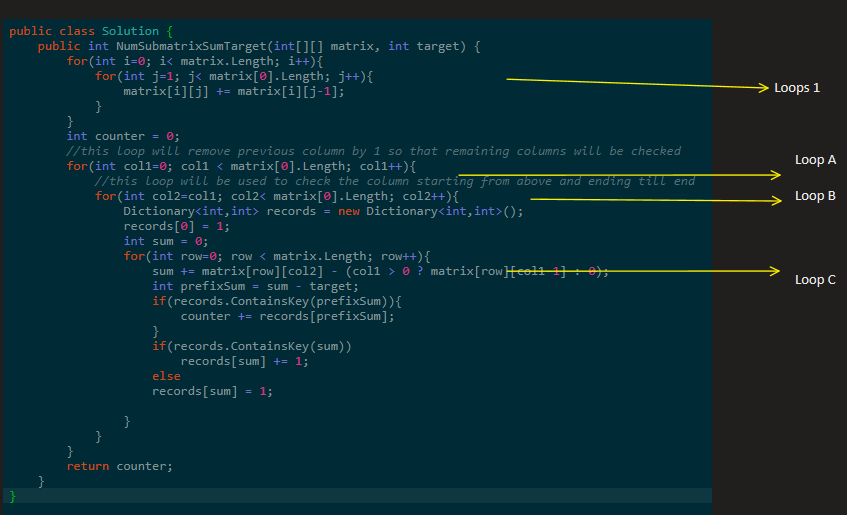\n\n```\npublic class Solution {\n public int NumSubmatrixSumTarget(int[][] matrix, int target) {\n for(int i=0; i< matrix.Length; i++){\n for(int j=1; j< matrix[0].Length; j++){\n matrix[i][j] += matrix[i][j-1]; \n }\n }\n int counter = 0;\n //this loop will remove previous column by 1 so that remaining columns will be checked\n for(int col1=0; col1 < matrix[0].Length; col1++){\n //this loop will be used to check the column starting from above and ending till end\n for(int col2=col1; col2< matrix[0].Length; col2++){\n Dictionary<int,int> records = new Dictionary<int,int>();\n records[0] = 1;\n int sum = 0;\n for(int row=0; row < matrix.Length; row++){\n sum += matrix[row][col2] - (col1 > 0 ? matrix[row][col1-1] : 0);\n int prefixSum = sum - target;\n if(records.ContainsKey(prefixSum)){\n counter += records[prefixSum];\n }\n if(records.ContainsKey(sum))\n records[sum] += 1;\n else\n records[sum] = 1;\n \n }\n }\n }\n return counter;\n }\n}\n```
| 3 | 0 |
['C#']
| 0 |
number-of-submatrices-that-sum-to-target
|
Python | 99.94% Fastest
|
python-9994-fastest-by-sahil329-uzpl
|
\ndef numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int: \n n,m = len(matrix),len(matrix[0])\n dp = [[0]*m for _ in rang
|
sahil329
|
NORMAL
|
2022-07-18T08:15:18.422431+00:00
|
2022-07-18T08:15:18.422480+00:00
| 517 | false |
```\ndef numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int: \n n,m = len(matrix),len(matrix[0])\n dp = [[0]*m for _ in range(n)]\n \n # make prefix sum for every row\n for i in range(n):\n for j in range(m):\n dp[i][j] = matrix[i][j] + (dp[i][j-1] if j-1>=0 else 0)\n # print(*dp,sep="\\n") \n ans = 0\n # for every column see row sum\n for i in range(m):\n for j in range(i,m):\n d = {0:1}\n s = 0\n for r in range(n):\n s += dp[r][j] - (dp[r][i-1] if i-1>=0 else 0)\n if s-target in d:\n ans += d[s-target] \n \n if s in d:\n d[s] += 1\n else:\n d[s] = 1\n \n return ans\n```
| 3 | 0 |
['Dynamic Programming', 'Prefix Sum']
| 0 |
number-of-submatrices-that-sum-to-target
|
Python | prefix sum + hashmap, with explanation
|
python-prefix-sum-hashmap-with-explanati-mfke
|
To solve this probelm, let us solve 560. Subarray Sum Equals K at first.\n\n### 560. Subarray Sum Equals K\nThe basic idea it to handle this problem with hashma
|
YuOfferPlusPlus
|
NORMAL
|
2022-07-18T08:00:48.371284+00:00
|
2022-07-18T08:00:48.371325+00:00
| 368 | false |
To solve this probelm, let us solve [560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/) at first.\n\n### 560. Subarray Sum Equals K\nThe basic idea it to handle this problem with `hashmap`. The hashmap will store with the key being any particular `sum`, and the value being the number of time it has happened yet. Suppose we iterate the arrary from left to right and keep track of cumulative sum up to `i` in each position.\n\nIf there is an increase of `k` in `preSum[i]`, we can find `preSum[j] = preSum[i] + k`. (j > i)\n\nThe origin problem `find a subarry whose sum equals to k (preSum[j] - preSum[i])` can be changed to `find a subarray whose sum equals to preSum[i] (preSum[j] - k)`\n\nSo, the solution is here:\n```python\n```python\nclass Solution:\n def subarraySum(self, nums: List[int], k: int) -> int:\n ans = 0\n pre_sum = 0\n res = defaultdict(int)\n res[0] = 1 # it means that we\'ve already seen sum of 0 once before iterating the list.\n \n for num in nums:\n pre_sum += num\n ans += res[pre_sum - k]\n res[pre_sum] += 1\n return ans\n```\n\n### 1074. Number of Submatrices That Sum to Target\nActually, this problem is a variation of `560`. We enumerate the submatrixs by setting different `upper` and `lower` boundaries. Then we calculate the `sum` of each column. So the origin problem can be changed to:\n- Given an array of integers nums and an integer k, return the total number of subarrays whose sum equals to k.\n\nFor the calculation of sum of each column, every time we extend lower boundary `j` downwards, the elements in the `jth` row of the matrix are added to the `sum`.\n\n```python\nclass Solution:\n def numSubmatrixSumTarget(self, M: List[List[int]], T: int) -> int:\n def subarrSum(nums, target):\n res = defaultdict(int)\n res[0] = 1\n ans, pre_sum = 0, 0\n \n for num in nums:\n pre_sum += num\n ans += res[pre_sum - target]\n res[pre_sum] += 1\n return ans\n \n \n rows, cols = len(M), len(M[0])\n ans = 0\n for i1 in range(rows):\n total = [0]*cols\n for i2 in range(i1, rows):\n for j in range(cols):\n total[j] += M[i2][j]\n ans += subarrSum(total, T)\n return ans\n```
| 3 | 0 |
['Prefix Sum', 'Python']
| 1 |
number-of-submatrices-that-sum-to-target
|
91% Faster and Memory efficient solution
|
91-faster-and-memory-efficient-solution-md1nx
|
\t\n\tclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m = len(matrix)\n n = len(matrix[0])\n
|
anuvabtest
|
NORMAL
|
2022-07-18T03:58:58.735022+00:00
|
2022-07-18T03:58:58.735051+00:00
| 592 | false |
\t\n\tclass Solution:\n def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:\n m = len(matrix)\n n = len(matrix[0])\n \n ans = 0\n \n for i in range(m): # enum upper bound\n total = [0] * n\n \n for j in range(i, m): # enum lower bound\n for c in range(n):\n # update each row\'s sum\n total[c] += matrix[j][c]\n \n ans += self.subarrSum(total, target)\n \n \n return ans\n \n \n \n def subarrSum(self, nums, k):\n hashmap = defaultdict(int)\n hashmap[0] = 1\n\n cnt = presum = 0\n for x in nums:\n presum += x \n\n if presum - k in hashmap:\n cnt += hashmap[presum-k]\n\n hashmap[presum] += 1\n\n return cnt
| 3 | 0 |
['Python']
| 0 |
number-of-submatrices-that-sum-to-target
|
Rust: Prefix Sum DP + HashMap for O(m * n * n)
|
rust-prefix-sum-dp-hashmap-for-om-n-n-by-28qz
|
Firstly make a basic prefix sum DP solution for O(m * m * n * n) time.\nrust\npub fn num_submatrix_sum_target_old(matrix: Vec<Vec<i32>>, target: i32) -> i32 {\n
|
Minamikaze392
|
NORMAL
|
2022-07-18T03:24:48.670677+00:00
|
2022-07-18T03:29:17.089898+00:00
| 96 | false |
Firstly make a basic prefix sum DP solution for O(m * m * n * n) time.\n```rust\npub fn num_submatrix_sum_target_old(matrix: Vec<Vec<i32>>, target: i32) -> i32 {\n let mut dp = vec![vec![0; matrix[0].len() + 1]; matrix.len() + 1];\n let mut ans = 0; \n for i in 0..matrix.len() {\n for j in 0..matrix[0].len() {\n dp[i + 1][j + 1] = dp[i + 1][j] + dp[i][j + 1] - dp[i][j] + matrix[i][j];\n for x in 0..i + 1 {\n for y in 0..j + 1 {\n if dp[i + 1][j + 1] - dp[i + 1][y] - (dp[x][j + 1] - dp[x][y]) == target {\n ans += 1;\n }\n }\n }\n }\n }\n ans\n}\n```\nThen we can find that the count of previous results of `dp[x][j + 1] - dp[x][y]` can be grouped up with a HashMap. Simple modification but having a O(m * n * n) space HashMap.\n```rust\npub fn num_submatrix_sum_target_hash(matrix: Vec<Vec<i32>>, target: i32) -> i32 {\n let mut dp = vec![vec![0; matrix[0].len() + 1]; matrix.len() + 1];\n let mut ans = 0; \n let mut hash: HashMap<(usize, usize, i32), i32> = HashMap::new();\n for j in 0..matrix[0].len() {\n for y in 0..j + 1 {\n hash.insert((y, j + 1, 0), 1);\n }\n }\n for i in 0..matrix.len() {\n for j in 0..matrix[0].len() {\n dp[i + 1][j + 1] = dp[i + 1][j] + dp[i][j + 1] - dp[i][j] + matrix[i][j];\n for y in 0..j + 1 {\n let diff = dp[i + 1][j + 1] - dp[i + 1][y];\n if let Some(c) = hash.get(&(y, j + 1, diff - target)) {\n ans += c;\n }\n *hash.entry((y, j + 1, diff)).or_insert(0) += 1;\n }\n }\n }\n ans\n}\n```\nThen optimize the HashMap space usage by eliminating the `(y, j + 1)` part, making it O(n) space.\n```rust\npub fn num_submatrix_sum_target(matrix: Vec<Vec<i32>>, target: i32) -> i32 {\n let mut dp = vec![vec![0; matrix[0].len() + 1]; matrix.len() + 1];\n let mut ans = 0;\n for i in 0..matrix.len() {\n for j in 0..matrix[0].len() {\n dp[i + 1][j + 1] = dp[i + 1][j] + dp[i][j + 1] - dp[i][j] + matrix[i][j];\n }\n }\n for j in 0..matrix[0].len() {\n for y in 0..j + 1 {\n let mut hash: HashMap<i32, i32> = HashMap::new();\n hash.insert(0, 1);\n for i in 0..matrix.len() {\n let diff = dp[i + 1][j + 1] - dp[i + 1][y];\n if let Some(c) = hash.get(&(diff - target)) {\n ans += c;\n }\n *hash.entry(diff).or_insert(0) += 1;\n }\n }\n }\n ans\n}\n```
| 3 | 0 |
['Prefix Sum', 'Rust']
| 0 |
number-of-submatrices-that-sum-to-target
|
🗓️ Daily LeetCoding Challenge July, Day 18
|
daily-leetcoding-challenge-july-day-18-b-n0sy
|
This problem is the Daily LeetCoding Challenge for July, Day 18. Feel free to share anything related to this problem here! You can ask questions, discuss what y
|
leetcode
|
OFFICIAL
|
2022-07-18T00:00:11.441475+00:00
|
2022-07-18T00:00:11.441511+00:00
| 2,106 | false |
This problem is the Daily LeetCoding Challenge for July, Day 18.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/number-of-submatrices-that-sum-to-target/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain these 2 approaches in the official solution</summary>
**Approach 1:** Number of Subarrays that Sum to Target: Horizontal 1D Prefix Sum
**Approach 2:** Number of Subarrays that Sum to Target: Vertical 1D Prefix Sum
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 3 | 0 |
[]
| 14 |
number-of-submatrices-that-sum-to-target
|
JAVA||EASY||EXPLAINED||VERY SIMPLE O(M*N*M)`
|
javaeasyexplainedvery-simple-omnm-by-asp-4kty
|
\nsee u can first find the row prefix sum\nthen take two pointer one on 0 and other on say x then traverse row and as u did in to find the subarray sum equal t
|
asppanda
|
NORMAL
|
2022-06-09T00:20:47.704056+00:00
|
2022-06-09T00:20:47.704093+00:00
| 448 | false |
```\nsee u can first find the row prefix sum\nthen take two pointer one on 0 and other on say x then traverse row and as u did in to find the subarray sum equal to k just do that that is sum-target+target=sum if u can store sum at some point u will realise that u are finding target because sum-(sum-target)=target if u have the count of sum-target u hv to just add it up\n```\n\n\n```\nclass Solution {\n public int numSubmatrixSumTarget(int[][] matrix, int target)\n {\n int n=matrix.length;\n int m=matrix[0].length;\n long dp[][]=new long[n][m];\n for(int i=0;i<n;i++)\n {\n dp[i][0]=matrix[i][0];\n }\n for(int i=0;i<n;i++)\n {\n for(int j=1;j<m;j++)\n {\n dp[i][j]=dp[i][j-1]+matrix[i][j];\n }\n }\n int count=0;\n for(int start=0;start<m;start++)\n {\n for(int end=start;end<m;end++)\n {\n HashMap<Long,Integer> map=new HashMap<Long,Integer>();\n long sum=0;\n for(int i=0;i<n;i++)\n {\n map.put(sum,map.getOrDefault(sum,0)+1);\n long pre=start!=0?dp[i][start-1]:0;\n sum+=dp[i][end]-pre;\n if(map.containsKey(sum-target))\n {\n count+=map.get(sum-target);\n }\n }\n }\n }\n return count;\n \n }\n}\n```\n\n# ***PLS UPVOTE IF U LIKE THE SOLUTION* **
| 3 | 0 |
['Dynamic Programming', 'Prefix Sum', 'Java']
| 0 |
number-of-submatrices-that-sum-to-target
|
C++ || Easy to Understand
|
c-easy-to-understand-by-singhaaaa-pt4b
|
\n\nclass Solution {\npublic:\n\n int numSubmatrixSumTarget(vector>& A, int k) {\n // same logic as count subarray with sum k HASHING\n \n
|
singhaaaa
|
NORMAL
|
2021-06-14T11:28:00.449399+00:00
|
2021-06-14T11:28:00.449429+00:00
| 559 | false |
\n\nclass Solution {\npublic:\n\n int numSubmatrixSumTarget(vector<vector<int>>& A, int k) {\n // same logic as count subarray with sum k HASHING\n \n int row = A.size();\n int col = A[0].size();\n \n\t\t//Calculating Prefix Sum of Columns\n for(int i=0;i<row;i++)\n {\n for(int j=1;j<col;j++)\n A[i][j]+=A[i][j-1]; \n }\n \n int count = 0;\n \n for(int c1=0;c1<col;c1++)\n {\n for(int c2=c1;c2<col;c2++)\n {\n unordered_map<int,int>mp;\n int sum=0;\n mp[sum]=1;\n \n for(int r=0;r<row;r++)\n {\n sum +=A[r][c2] - (c1>0 ? A[r][c1-1] : 0);\n \n if(mp.find(sum-k)!=mp.end())\n count+=mp[sum-k];\n \n mp[sum]+=1;\n }\n }\n }\n return count;\n }\n};
| 3 | 1 |
['C', 'C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.