question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-average-difference
|
With Explanation Comments: Time: 214 ms (42.49%), Space: 78.3 MB (94.22%)
|
with-explanation-comments-time-214-ms-42-phmu
|
Like it? ->Upvote please! \u30C4\n\nTC: O(n) //iterate the array\nSC: O(1)\n\n\n\'\'\'\nclass Solution {\npublic:\n \n int minimumAverageDifference(vect
|
deleted_user
|
NORMAL
|
2022-09-19T12:16:48.952822+00:00
|
2022-09-19T12:16:48.952861+00:00
| 61 | false |
**Like it? ->Upvote please!** \u30C4\n\nTC: O(n) //iterate the array\nSC: O(1)\n\n\n\'\'\'\nclass Solution {\npublic:\n \n int minimumAverageDifference(vector<int>& nums) {\n \n //initialize two sum variables-> one from the left or start & one from the right or end\n long long sumLeft=0, sumRight=0, minAvg=INT_MAX, index=0;\n \n //loop to get the sumRight value\n for(int num:nums)\n sumRight+=num;\n //btw, you can use {sumRight=accumulate(nums.begin(), nums.end(), 0LL)} instead\n \n //loop over the whole array elements\n for(int i=0;i<nums.size();i++){\n \n //add the current value to the left sum-> (i+1) elements\n sumLeft+=nums[i];\n //subtract the current value from the right sum-> (n-i-1) elements\n sumRight-=nums[i];\n \n //average for the left sum-> sum value / the number of left elements\n int avgLeft=sumLeft/(i+1);\n //average for the right sum-> sum value / the number of right elements & if you\'re in the last position-> avg will be 0\n int avgRight= (i==nums.size()-1) ? 0 : sumRight/(nums.size()-i-1);\n \n \n //check if the absolute difference between the two averages is smaller than the lowest possible avg\n if(abs(avgLeft-avgRight) < minAvg){\n //replace the avg value with the lower one\n minAvg=abs(avgLeft-avgRight);\n //also, save the current index of the lower one\n index=i;\n }\n \n }\n \n //return the lowest index value\n return index;\n }\n};\n\'\'\'\n\n**Like it? ->Upvote please!** \u30C4\n**If still not understood, feel free to comment. I will help you out**\n**Happy Coding :)**
| 2 | 0 |
['Array', 'C', 'Prefix Sum', 'C++']
| 0 |
minimum-average-difference
|
Using Prefix,Suffix Sum
|
using-prefixsuffix-sum-by-gurnam44-0dtk
|
\n\n\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n vector<long long> left(nums.size());\n vector<long long>
|
gurnam44
|
NORMAL
|
2022-05-12T17:47:51.058874+00:00
|
2022-05-12T17:47:51.058916+00:00
| 108 | false |
\n\n```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n vector<long long> left(nums.size());\n vector<long long> right(nums.size());\n right[nums.size()-1]=0;\n left[0]=nums[0];\n for(int i=1;i<nums.size();i++)\n {\n left[i]=left[i-1]+nums[i];\n \n }\n for(int i=nums.size()-2;i>=0;i--)\n {\n right[i]=right[i+1]+nums[i+1];\n \n }\n \n int d=1e7;\n int ans;\n int n=nums.size()-1;\n for(int i=0;i<nums.size();i++)\n {\n //cout<<n-i;\n if(i==nums.size()-1)\n {\n if(left[i]/(i+1)<d)\n {\n ans=i;\n }\n }\n else{\n int a=abs(left[i]/(i+1)-right[i]/(n-i));\n if(a<d)\n {\n \n d=a;\n ans=i;\n }\n }\n }\n return ans;\n }\n};\n```\n\n\n\n\n \n
| 2 | 0 |
['C', 'Prefix Sum', 'C++']
| 0 |
minimum-average-difference
|
Golang prefix sum solution
|
golang-prefix-sum-solution-by-tjucoder-sdsq
|
go\nfunc minimumAverageDifference(nums []int) int {\n\tsummation := make([]int, len(nums))\n\tsummation[0] = nums[0]\n\tfor i := 1; i < len(summation); i++ {\n\
|
tjucoder
|
NORMAL
|
2022-05-03T07:01:18.537633+00:00
|
2022-05-03T07:01:18.537670+00:00
| 81 | false |
```go\nfunc minimumAverageDifference(nums []int) int {\n\tsummation := make([]int, len(nums))\n\tsummation[0] = nums[0]\n\tfor i := 1; i < len(summation); i++ {\n\t\tsummation[i] = summation[i-1] + nums[i]\n\t}\n\tindex := len(nums) - 1\n\tminDiff := abs(summation[len(nums)-1] / len(nums))\n\tfor i := 0; i < len(summation)-1; i++ {\n\t\tcurDiff := abs(summation[i]/(i+1) - (summation[len(nums)-1]-summation[i])/(len(nums)-i-1))\n\t\t// index might be len(nums) - 1, so we must check index with i while curDiff equal to minDiff\n\t\tif curDiff < minDiff || (curDiff == minDiff && i < index) {\n\t\t\tminDiff, index = curDiff, i\n\t\t}\n\t}\n\treturn index\n}\n\nfunc abs(v int) int {\n\tif v > 0 {\n\t\treturn v\n\t}\n\treturn v * -1\n}\n```
| 2 | 0 |
['Go']
| 0 |
minimum-average-difference
|
Prefix sum solution
|
prefix-sum-solution-by-richbit-sqh5
|
Find the prefix sum from the start of the array to the end of the array. The loop through the array, keeping track of the minimum average difference at each ind
|
Richbytes
|
NORMAL
|
2022-04-30T17:31:59.894628+00:00
|
2022-04-30T17:32:26.811668+00:00
| 228 | false |
Find the prefix sum from the start of the array to the end of the array. The loop through the array, keeping track of the minimum average difference at each index\n```\ndef minimumAverageDifference(self, nums: List[int]) -> int:\n \n pre_sum=[]\n pre=0\n for i in range(len(nums)):\n pre+=nums[i]\n pre_sum.append(pre)\n max_sum=pre_sum[-1]\n \n min_dif=float(\'+inf\')\n idx=0\n n=len(nums)\n for i in range(len(nums)):\n if i!=n-1:\n present=(pre_sum[i]//(i+1)) -((max_sum-pre_sum[i])//(n-i-1))\n else:\n present=pre_sum[i]//(i+1)\n \n present=abs(present)\n if present<min_dif:\n idx=i\n min_dif=present\n \n return idx\n```
| 2 | 0 |
['Prefix Sum', 'Python']
| 1 |
minimum-average-difference
|
SIMPLE SOLUTION || c++ || O(1) space
|
simple-solution-c-o1-space-by-deepanshu_-zxqe
|
\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n int ans=INT_MAX;\n long long total=0; \n int n=nums.s
|
Deepanshu_Dhakate
|
NORMAL
|
2022-04-30T16:11:55.203926+00:00
|
2022-04-30T16:11:55.203953+00:00
| 93 | false |
```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n int ans=INT_MAX;\n long long total=0; \n int n=nums.size(); //size of vector\n \n for(int i=0;i<n;i++){\n total+=nums[i]; //total sum of all elements\n }\n \n long long curr=0;\n int ind=-1;\n for(int i=0;i<n-1;i++){\n curr+=nums[i]; //sum of elements upto current index i\n long long last=total-curr; //sum of remaining elements\n long long p=abs((curr/(i+1))-(last/(n-i-1))); //average \n if(p<ans){ // taking min average difference and updating index\n ans=p;\n ind=i;\n }\n }\n long long p=(total/n);\n if(p<ans){ // taking min average difference and updating index for last index (n-1)\n ans=p;\n ind=n-1;\n }\n \n return ind; //return index of min average difference\n }\n};\n\n\n\n```
| 2 | 0 |
['Prefix Sum']
| 0 |
minimum-average-difference
|
C++ super easy solution using prefix sum method
|
c-super-easy-solution-using-prefix-sum-m-1rd6
|
\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n long long sum = 0;\n for (int i:nums){\n sum+=i;\n
|
harsh3958
|
NORMAL
|
2022-04-30T16:01:55.779596+00:00
|
2022-04-30T16:01:55.779633+00:00
| 298 | false |
```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n long long sum = 0;\n for (int i:nums){\n sum+=i;\n }\n long long temp = 0;\n int mad = INT_MAX;\n int ans = 0;\n int n = nums.size();\n for (int i=0;i<n;i++){\n temp+=nums[i];\n int a1 = temp/(i+1);\n int a2 = (n-i-1)!=0 ? (sum-temp)/(n-i-1) : 0;\n int curr = abs(a1-a2);\n if (curr<mad){\n ans = i;\n mad = curr;\n }\n }\n return ans;\n }\n};\n```\n\n**Please upvote if you like it. Thanks :)**
| 2 | 0 |
['C', 'Prefix Sum']
| 0 |
minimum-average-difference
|
C++ || EASY TO UNDERSTAND || Simple Solution
|
c-easy-to-understand-simple-solution-by-7vksf
|
\n#define ll long long int\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n ll n=nums.size();\n vector<ll> pref
|
aarindey
|
NORMAL
|
2022-04-30T16:01:34.225409+00:00
|
2022-04-30T16:01:34.225438+00:00
| 518 | false |
```\n#define ll long long int\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n ll n=nums.size();\n vector<ll> prefix(n);\n prefix[0]=nums[0];\n for(ll i=1;i<n;i++)\n {\n prefix[i]=nums[i]+prefix[i-1];\n }\n ll mini=INT_MAX; \n ll left,right;\n ll ans=0;\n for(ll i=0;i<n;i++)\n {\n left=prefix[i];\n ll l,r;\n l=i+1;\n r=n-i-1;\n ll v1,v2;\n if(i==n-1)\n {\n right=0;\n v1=left/l;\n v2=0;\n }\n else \n {\n right=prefix[n-1]-prefix[i];\n v1=left/l;\n v2=right/r;\n }\n \n ll x=abs(v1-v2);\n if(x<mini)\n {\n mini=x;\n ans=i;\n \n } \n }\n return ans;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
minimum-average-difference
|
IIT | Simple appraoch | C++ | O(N)& O(1) |
|
iit-simple-appraoch-c-on-o1-by-iitian_01-s7dd
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
iitian_010u
|
NORMAL
|
2025-02-13T07:50:23.447443+00:00
|
2025-02-13T07:50:23.447443+00:00
| 25 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minimumAverageDifference(vector<int>& nums) {
int n = nums.size();
if (n == 1) return 0;
long long left = 0, sum = accumulate(nums.begin(), nums.end(), 0LL);
int ans = -1, diff = INT_MAX;
for (int i = 0; i < n; ++i) {
left += nums[i];
long long l = left / (i + 1);
long long r = (i == n - 1) ? 0 : (sum - left) / (n - i - 1); // Avoid division by zero
int new_diff = abs(l - r);
if (new_diff < diff) {
ans = i;
diff = new_diff;
}
}
return ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
minimum-average-difference
|
Python | Simple | Beats 100% | O(n) Time & Space | 😊
|
python-simple-beats-100-on-time-space-by-5n9i
|
Complexity
Time complexity: O(n)
Space complexity: O(n)
Code
|
ashishgupta291
|
NORMAL
|
2025-02-06T10:47:10.280487+00:00
|
2025-02-06T10:47:10.280487+00:00
| 17 | false |
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
class Solution(object):
def minimumAverageDifference(self, nums):
tot = sum(nums)
n = len(nums)
min_i = None
min_abs_diff= float('inf')
curr_sum=0
for i in range(n):
curr_sum+=nums[i]
t = abs((curr_sum//(i+1))-((tot-curr_sum)//(n-i-1) if tot-curr_sum else 0 ))
if t <min_abs_diff:
min_i = i
min_abs_diff = t
return min_i
```
| 1 | 0 |
['Python']
| 0 |
minimum-average-difference
|
Minimum Average Difference
|
minimum-average-difference-by-kartixriva-x26v
|
IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(1)Code
|
kartixrivastava
|
NORMAL
|
2025-02-04T13:58:59.188821+00:00
|
2025-02-04T13:58:59.188821+00:00
| 23 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```cpp []
class Solution {
public:
int minimumAverageDifference(vector<int>& nums) {
int n = nums.size();
if (n == 1)
return 0; // handle the edge case
long long totalSum = 0, currentSum = 0;
for (int i : nums) {
totalSum += i; // stored total sum in a variable
}
int difference = INT_MAX;
int ans = -1; // initially give any random value to the answer
for (int i = 0; i < n; i++) {
currentSum += nums[i];
long long left = currentSum / (i + 1); // left average for every current sum (Or, you can say, for every i)
long long right =
(i == n - 1) ? 0 : (totalSum - currentSum) / (n - i - 1); // used ternary operator
int currentDifference = abs(left - right);
if (currentDifference < difference) {
difference = currentDifference; // if the current difference is less than the previous one, change the value of previous to the current difference
ans = i; //store the index to the answer as well
}
}
return ans;
}
};
```
| 1 | 0 |
['Array', 'Prefix Sum', 'C++']
| 0 |
minimum-average-difference
|
O(n) very Easy And Intutive Solution || JAVA
|
on-very-easy-and-intutive-solution-java-gjkps
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ayush0704
|
NORMAL
|
2024-06-05T17:32:06.251224+00:00
|
2024-06-05T17:32:06.251247+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minimumAverageDifference(int[] nums) {\n int diff = Integer.MAX_VALUE;\n int i = 0;\n int n = nums.length;\n int ans = -1;\n long totalsum = 0;\n for(int T:nums){\n totalsum+= T;\n }\n long leftsum = 0;\n while(i<nums.length){\n leftsum += nums[i];\n long rightsum = totalsum - leftsum;\n int lsavg = (int)(leftsum/(i+1));\n int rsavg = (i == n - 1) ? 0 : (int)(rightsum / (n - i - 1));\n int currdiff = Math.abs(lsavg-rsavg);\n if(currdiff<diff){\n diff = currdiff;\n ans = i;\n }\n i++;\n }\n return ans;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
minimum-average-difference
|
JAVA one loop Solution
|
java-one-loop-solution-by-ansh29-q19z
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
AnsH29
|
NORMAL
|
2024-03-14T07:57:57.041773+00:00
|
2024-03-14T07:57:57.041801+00:00
| 16 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minimumAverageDifference(int[] nums) {\n\n double[] prefix = new double[nums.length + 1]; \n for (int i=0;i<nums.length;i++){\n prefix[i + 1] = prefix[i] + nums[i];\n }\n int bestIndex = 0;\n int best = Integer.MAX_VALUE;\n for (int i=0;i<nums.length;i++){\n int prefixAverage = (int) Math.floor(prefix[i + 1] / (i + 1));\n int suffixAverage = (int) Math.floor((prefix[nums.length]-prefix[i + 1])/(nums.length-i-1));\n int averageDifference = Math.abs(prefixAverage - suffixAverage);\n if (averageDifference < best) {\n best = averageDifference;\n bestIndex = i;\n }\n }\n return bestIndex;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
minimum-average-difference
|
2256. Simple C++ solution
|
2256-simple-c-solution-by-shreyash_153-1z3n
|
Code\n\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n vector<long long int>v,u;\n long long int ans=0;\n
|
shreyash_153
|
NORMAL
|
2023-08-20T18:11:15.272176+00:00
|
2023-09-06T08:40:17.404841+00:00
| 4 | false |
# Code\n```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n vector<long long int>v,u;\n long long int ans=0;\n for(int i=0;i<nums.size();i++)\n {\n ans+=nums[i];\n v.push_back(ans/(i+1));\n }\n ans=0;\n u.push_back(ans);\n for(int j=nums.size()-1;j>=1;j--)\n {\n ans+=nums[j];\n u.push_back(ans/(nums.size()-j));\n }\n reverse(u.begin(),u.end());\n int k=0;\n int a=abs(u[0]-v[0]);\n for(int i=1;i<u.size();i++)\n {\n if(abs(u[i]-v[i])<a)\n {\n a=abs(u[i]-v[i]);\n k=i;\n }\n }\n return k;\n }\n};\n```
| 1 | 0 |
['Array', 'Prefix Sum', 'C++']
| 0 |
minimum-average-difference
|
Easy C++ solution || Very simple approach || Beats 95% in both !!
|
easy-c-solution-very-simple-approach-bea-03x8
|
Code\n\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n int n = nums.size(), ans = 0, min_avg_diff = INT_MAX;\n
|
prathams29
|
NORMAL
|
2023-07-03T15:06:30.666637+00:00
|
2023-07-03T15:06:30.666662+00:00
| 38 | false |
# Code\n```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n int n = nums.size(), ans = 0, min_avg_diff = INT_MAX;\n long long int sumRight = 0, sumLeft = 0, avgLeft = 0, avgRight = 0; \n for(int i=0; i<n; i++)\n sumRight += nums[i];\n for(int i=0; i<n; i++)\n {\n sumLeft += nums[i];\n sumRight -= nums[i];\n avgLeft = sumLeft/(i+1);\n avgRight = i==(n-1) ? 0 : sumRight/(n-i-1);\n int val = abs(avgLeft - avgRight);\n if(val < min_avg_diff){\n min_avg_diff = val;\n ans = i;\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
minimum-average-difference
|
Easy Java Solution 91% | Easy Approach |
|
easy-java-solution-91-easy-approach-by-s-lwle
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
SaikatDass
|
NORMAL
|
2023-03-07T07:22:50.902623+00:00
|
2023-03-07T07:22:50.902667+00:00
| 29 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minimumAverageDifference(int[] nums) {\n int n = nums.length, pos = 0;\n long min = Integer.MAX_VALUE;\n long right = 0, left = 0, sum = 0;\n for(int i = 0; i < n; i++){\n sum += nums[i];\n }\n long val = 0;\n for(int i = 0; i < n; i++){\n left += nums[i];\n right = sum - left;\n if(i == n - 1)\n val = Math.abs(left / n);\n else if(i < n - 1)\n val = Math.abs((left / (i + 1)) - (right / (n - i - 1)));\n if(val < min){\n min = val;\n pos = i;\n }\n }\n return pos;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
minimum-average-difference
|
C++ | Easy and Simple | 90% fast
|
c-easy-and-simple-90-fast-by-vaibhav_sho-qdgx
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
VAIBHAV_SHORAN
|
NORMAL
|
2023-01-12T15:23:34.159686+00:00
|
2023-01-12T15:23:34.159742+00:00
| 31 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n if(nums.size() == 1) return 0;\n long long int sum1 = 0, sum2 = 0;\n\n for(int i=0; i<nums.size(); i++) sum2 += nums[i];\n\n int ans = -1;\n int cnt = INT_MAX;\n\n int n = nums.size();\n for(int i=0; i<n-1; i++){\n sum1 += nums[i];\n sum2 -= nums[i];\n\n long long int a = sum1/(i+1);\n long long int b = sum2/(n-i-1);\n\n if(cnt > abs(a-b)){\n cnt = abs(a-b);\n ans = i;\n }\n }\n\n sum1 += nums[n-1];\n if(sum1/n < cnt){\n ans = n-1;\n }\n\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
minimum-average-difference
|
JAVA - EASY
|
java-easy-by-adityasharma15-g4l7
|
\nclass Solution {\n public int minimumAverageDifference(int[] nums) {\n long totalSum = 0;\n for(int num: nums) {\n totalSum += num
|
adityasharma15
|
NORMAL
|
2022-12-10T13:38:28.108176+00:00
|
2022-12-10T13:38:28.108233+00:00
| 46 | false |
```\nclass Solution {\n public int minimumAverageDifference(int[] nums) {\n long totalSum = 0;\n for(int num: nums) {\n totalSum += num;\n }\n\n long currSum = 0, minAvgDiff = Integer.MAX_VALUE;\n int minAvgIdx = 0;\n for(int idx = 0; idx<nums.length; idx++) {\n currSum += nums[idx];\n long leftAvg = currSum/(idx+1);\n long rightSum = totalSum - currSum;\n boolean isLastElement = idx == nums.length-1;\n long rightAvg = isLastElement ? 0 : rightSum/(nums.length-idx-1); \n long diffAvg = Math.abs(leftAvg-rightAvg);\n \n if(diffAvg<minAvgDiff) {\n minAvgDiff = diffAvg;\n minAvgIdx = idx;\n }\n }\n \n return minAvgIdx;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
minimum-average-difference
|
✅ C++ using prefix sum, detailed explanation, one pass, O(nlongn)
|
c-using-prefix-sum-detailed-explanation-yoa6s
|
\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n vector<long> prefixSum(nums.size(), 0);\n \n long sum
|
user3619T
|
NORMAL
|
2022-12-04T19:33:02.698030+00:00
|
2022-12-04T19:34:18.312888+00:00
| 17 | false |
```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n vector<long> prefixSum(nums.size(), 0);\n \n long sum = 0;\n \n // store the accumulated sum at the index \n for (int i = 0; i < nums.size(); i ++) {\n sum += nums[i];\n prefixSum[i] = sum;\n }\n \n vector<pair<long,int>> vec; // set up a vec to store pairs with the first one as the res and the second one as the index\n \n for (int i = 0; i < nums.size(); i++) {\n long firstPartSum = prefixSum[i];\n long secondPartSum = prefixSum[nums.size()-1] - firstPartSum; \n // the second part sum is just the last item from the vec subtract the firstPart sum\n long firstPartSumAverage = firstPartSum/ (i+1);\n long secondPartSumAverage = 0;\n if (secondPartSum != 0) {\n secondPartSumAverage = secondPartSum/(nums.size() - (i+1));\n }\n long res = abs(firstPartSumAverage - secondPartSumAverage);\n vec.push_back({res, i});\n // once we have the result store the result as a pair of {res, index} to vec\n }\n \n sort(vec.begin(), vec.end()); // sort the vec from smallest to biggest\n \n return vec[0].second; // just return the first item\'s index from the vec\n }\n};\n```
| 1 | 0 |
['C']
| 0 |
minimum-average-difference
|
O(1) Space | O(N) Time | Java
|
o1-space-on-time-java-by-heraaijaz-x0xn
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe calculate the sum of all elements beforehand, which is of O(N) complexity\nWe store
|
heraAijaz
|
NORMAL
|
2022-12-04T19:22:07.107770+00:00
|
2022-12-04T19:22:07.107799+00:00
| 11 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe calculate the sum of all elements beforehand, which is of O(N) complexity\nWe store the prefix sum in a variable as we traverse through the array, this is the sum of the left part of the partition. \nTo calculate the right sum, there are two conditions\n1. if the no. of elements is zero, then we simply subtract 0 from the left average\n2. if the no. of elements is greater than zero, then we find the right sum by subtracting current left sum from the total sum\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Note\nHere, we use \'long\' datatype instead of int for all the variables storing elements as \'int\' range is not enough for all the testcases, for indices we use \'int\'. \n\n# Code\n```\nclass Solution {\n public int minimumAverageDifference(int[] nums) {\n int n = nums.length;\n if (n == 1) return 0;\n\n long tot = 0;\n for(int i : nums) \n tot += i;\n\n long left = 0;\n long minDiff = Integer.MAX_VALUE;\n int ans = -1;\n for (int i = 0; i < n; ++i) {\n left += nums[i];\n long right = tot - left; \n long diff = Math.abs((left / (i + 1)) - \n ((n - i == 1) ? 0: right / (n - i - 1)));\n \n if (diff < minDiff) {\n minDiff = diff;\n ans = i;\n }\n }\n return ans;\n }\n}\n```
| 1 | 0 |
['Prefix Sum', 'Java']
| 0 |
minimum-average-difference
|
using java
|
using-java-by-lavkush_173-jttu
|
class Solution {\n public int minimumAverageDifference(int[] nums) {\n\tint len = nums.length, res = 0;\n\tlong min = Integer.MAX_VALUE, sum = 0, leftSum = 0
|
Lavkush_173
|
NORMAL
|
2022-12-04T18:49:55.611721+00:00
|
2022-12-04T18:49:55.611766+00:00
| 10 | false |
class Solution {\n public int minimumAverageDifference(int[] nums) {\n\tint len = nums.length, res = 0;\n\tlong min = Integer.MAX_VALUE, sum = 0, leftSum = 0, rightSum = 0;\n\tfor (int num : nums)\n\t\tsum += num;\n\tfor (int i = 0; i < len; i++) {\n\t\tleftSum += nums[i];\n\t\trightSum = sum - leftSum;\n\t\tlong diff = Math.abs(leftSum / (i + 1) - (len - i == 1 ? 0 : rightSum / (len -i - 1)));\n\t\tif (diff < min) {\n\t\t\tmin = diff;\n\t\t\tres = i;\n\t\t}\n\t}\n\treturn res;\n}\n}
| 1 | 0 |
[]
| 0 |
minimum-average-difference
|
C++|| My Solution || Easy to understand
|
c-my-solution-easy-to-understand-by-r4j4-o9pw
|
Calculating the prefix sum will make the problem easy.\n\n\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n \n
|
r4j4t
|
NORMAL
|
2022-12-04T18:36:38.861876+00:00
|
2022-12-04T18:36:38.861964+00:00
| 49 | false |
Calculating the prefix sum will make the problem easy.\n\n```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n \n vector<long long> prefix;\n prefix.push_back(nums[0]);\n \n \n for(int i=1;i<nums.size();i++){\n prefix.push_back(nums[i]+prefix[i-1]);\n }\n \n int min = INT_MAX;\n int min_index = 0;\n for(int i=0;i<nums.size();i++){\n int diff;\n if(nums.size() - i - 1==0)\n diff = (prefix[i]/(i+1));\n else\n diff = (prefix[i]/(i+1)) - (prefix[nums.size()-1]-prefix[i])/(nums.size() - i - 1);\n \n diff = abs(diff);\n if(diff<min){\n min = diff;\n min_index = i;\n }\n }\n \n return min_index;\n }\n};\n```
| 1 | 0 |
['C', 'C++']
| 0 |
minimum-average-difference
|
Solution in java with time complexity : O(N) and Space O(1)
|
solution-in-java-with-time-complexity-on-v2iv
|
Intuition\n \n\n# Approach\n Runing sum \n\n# Complexity\n- Time complexity:\n O(N) \n\n- Space complexity:\n O(1) \n\n# Code\n\nclass Solution {\n public i
|
LC-Guddu1cse
|
NORMAL
|
2022-12-04T17:58:37.552032+00:00
|
2022-12-04T17:58:37.552074+00:00
| 11 | false |
# Intuition\n<!-- -->\n\n# Approach\n<!-- Runing sum -->\n\n# Complexity\n- Time complexity:\n<!-- O(N) -->\n\n- Space complexity:\n<!-- O(1) -->\n\n# Code\n```\nclass Solution {\n public int minimumAverageDifference(int[] nums) {\n\n long min=Long.MAX_VALUE;\n\n long sum = 0L;\n\n for(int y : nums) sum+=y;\n\n int x=0;\n long currSum=0;\n int ans=0;\n int y=0;\n if(sum==0) return 0;\n\n\n for(; y<nums.length-1 ; y++){\n x++;\n currSum+=nums[y];\n sum-=nums[y];\n long avg=Math.abs(((long)currSum/x) - ((long)sum/(nums.length-x)));\n if(min > avg ){\n min=avg;\n ans=y;\n }\n }\n currSum+=sum;\n sum=0;\n\n if(min>currSum/nums.length) ans=y;\n\n\n\n return ans;\n \n }\n}\n```
| 1 | 0 |
['Prefix Sum', 'Java']
| 0 |
minimum-average-difference
|
c++ easy solution (o(n))
|
c-easy-solution-on-by-abhinav_pathak4-n6jt
|
\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(1)\n\n# Code\n\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nu
|
Abhinav_pathak4
|
NORMAL
|
2022-12-04T16:23:27.292851+00:00
|
2022-12-04T16:24:24.124647+00:00
| 21 | false |
\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n int ans;\n int c_min = INT_MAX;\n long long int avg = 0;\n if(nums.size() == 1) return 0;\n long long int total = 0;\n for(int i = 0; i<nums.size(); i++){\n total += nums[i];\n }\n for(int i = 0; i<nums.size(); i++){\n avg += nums[i];\n long long int c_avg = 0;\n c_avg = total - avg;\n if(nums.size()-1-i != 0)\n c_avg = c_avg/(nums.size()-1-i);\n else c_avg = 0;\n int aavg = avg/(i+1);\n if(abs(c_avg - aavg) < c_min){\n c_min = abs(c_avg-aavg);\n ans = i;\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
minimum-average-difference
|
Simple prefix sum || C++
|
simple-prefix-sum-c-by-daring_jackson-x7jr
|
\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n int n = nums.size();\n vector<long long> pref(n+1,0);\n
|
daring_jackson
|
NORMAL
|
2022-12-04T15:29:46.818837+00:00
|
2022-12-04T15:29:46.818876+00:00
| 20 | false |
```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n int n = nums.size();\n vector<long long> pref(n+1,0);\n for(int i=1;i<=n;i++){\n pref[i] = pref[i-1] + nums[i-1];\n }\n int ans = INT_MAX;\n int index = 0;\n for(int i = 1;i<=n;i++){\n long long temp =(long long) abs(((pref[i]-pref[0])/(i)) - ((pref[n]-pref[i])/(n-i==0?1:n-i)));\n cout<<temp<<endl;\n if(temp<ans){\n ans = temp;\n index=i-1;\n }\n }\n return index;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
minimum-average-difference
|
Minimum Average Difference ( 96.81% of C++ ) - with comments
|
minimum-average-difference-9681-of-c-wit-k37q
|
Intuition: We just have to take average difference and return the index giving minimum average difference.\n\nApproach:\n1) Take outtotalwhich will be sum of al
|
Neha22_04
|
NORMAL
|
2022-12-04T15:28:45.788948+00:00
|
2022-12-04T15:29:46.089109+00:00
| 37 | false |
**Intuition:** We just have to take average difference and return the index giving minimum average difference.\n\n**Approach:**\n1) Take out` total `which will be sum of all n elements and `sum` which will be the sum till ith index.\n2) Calculate the the average till ith index and average till (n-1-i) th index.\n3) Now take absolute diff btw the average till ith index and average till (n-1-i) th index and keep tracking the index giving minimum diff.\n4) Return the index giving minimum diff.\n\n```\nclass Solution {\npublic:\n int minimumAverageDifference(vector<int>& nums) {\n \n\t //total will store the sum of all the elements of nums\n long long total=0; \n\t\t//sum will store the sum upto ith index\n long long sum=0; \n\t // mini stores the minimum average difference\n long long mini=INT_MAX; \n\t\t//ans will store the index of minimum average difference\n int ans=0; \n \n //finding the sum of all the elements of nums\n for(int i=0;i<nums.size();i++){\n total+=nums[i];\n }\n \n for(int i=0;i<nums.size();i++){ \n sum+=nums[i];\n long long t=total-sum;\n long long temp=nums.size()-i-1; //number of elements in the\n\t\t\t// last n - i - 1 elements\n int avg=0;\n if(temp==0){\n avg=sum/(i+1); // average of the first i + 1 elements of nums\n }\n else{\n //avg will store the absolute difference between the average of\n\t\t\t//the first i + 1 elements of nums and the average of the\n\t\t\t//last n - i - 1 elements\n avg=(abs(sum/(i+1) - (t/temp)));\n }\n \n //if mini is greater than the avg then insert avg in mini and \n\t\t\t//store the index in ans\n if(mini>avg){\n mini=avg;\n ans=i;\n }\n }\n \n //returns the index of minimum average difference\n return ans;\n }\n};\n\n```\n\n**Time Complexity = O(n)\nSpace Complexity = O(1)**\n\n\n
| 1 | 0 |
['Array', 'C++']
| 0 |
minimum-average-difference
|
almost 1 hr utilised java solution
|
almost-1-hr-utilised-java-solution-by-ca-mp8n
|
class Solution {\n public int minimumAverageDifference(int[] nums) {\n long sum=0;\n for(int i=0;i<nums.length;i++)\n {\n sum
|
callmecomder
|
NORMAL
|
2022-12-04T14:53:51.710412+00:00
|
2022-12-04T14:53:51.710438+00:00
| 8 | false |
# class Solution {\n public int minimumAverageDifference(int[] nums) {\n long sum=0;\n for(int i=0;i<nums.length;i++)\n {\n sum+=nums[i];\n }\n long avg=0,rsum=0,lsum=0,min=Integer.MAX_VALUE;\n int indx=0;\n int c=1;\n for(int i=0;i<nums.length-1;i++)\n {\n lsum+=nums[i];\n rsum=(sum-lsum)/((nums.length)-(i+1));\n avg=Math.abs((lsum/c)-rsum);\n if(avg<min)\n {\n min=avg;\n indx=i;\n }\n c++;\n }\n avg=Math.abs(sum/nums.length);\n if(avg<min)\n {\n indx=nums.length-1;\n }\n return indx;\n }\n}
| 1 | 0 |
['Prefix Sum', 'Java']
| 0 |
largest-1-bordered-square
|
c++, beats 100% (both time and memory) concise, with algorithm and image
|
c-beats-100-both-time-and-memory-concise-7xb2
|
Create auxillary horizontal and vertical arrays first\nFor example : \n\n\nThen starting from bottom right,for every i,j ; we find small=min (ver[i][j], hor[i][
|
goelrishabh5
|
NORMAL
|
2019-07-28T04:09:42.193057+00:00
|
2019-07-28T07:11:16.807629+00:00
| 12,891 | false |
Create auxillary horizontal and vertical arrays first\nFor example : \n\n\nThen starting from bottom right,for every i,j ; we find small=min (ver[i][j], hor[i][j]) (marked in orange) , then look at all distances in [1,small] vertically in hor array and horizontally in ver array. If values(shown in blue) are greater than small and if small is greater than curr result, then we update result\n\n\n\n```\n int findLargestSquare(vector<vector<int>>& mat) \n { \n int max = 0; int m = mat.size() , n = mat[0].size();\n vector<vector<int>> hor(m,vector<int> (n,0)) , ver(m,vector<int> (n,0));\n \n for (int i=0; i<m; i++) { \n for (int j=0; j<n; j++) { \n if (mat[i][j] == 1) \n { \n hor[i][j] = (j==0)? 1: hor[i][j-1] + 1; // auxillary horizontal array\n ver[i][j] = (i==0)? 1: ver[i-1][j] + 1; // auxillary vertical array\n } \n } \n } \n \n for (int i = m-1; i>=0; i--) { \n for (int j = n-1; j>=0; j--) { \n int small = min(hor[i][j], ver[i][j]); // choose smallest of horizontal and vertical value\n while (small > max) { \n if (ver[i][j-small+1] >= small && hor[i-small+1][j] >= small) // check if square exists with \'small\' length\n max = small; \n small--; \n } \n } \n } \n return max*max; \n} \n \n int largest1BorderedSquare(vector<vector<int>>& grid) {\n return findLargestSquare(grid); \n }\n```
| 271 | 4 |
['C', 'Matrix']
| 32 |
largest-1-bordered-square
|
[Java/C++/Python] Straight Forward
|
javacpython-straight-forward-by-lee215-sn1v
|
Explanation\n1. Count the number of consecutive 1s on the top and on the left.\n2. From length of edge l = min(m,n) to l = 1, check if the 1-bordered square exi
|
lee215
|
NORMAL
|
2019-07-28T04:03:20.568902+00:00
|
2019-07-28T04:03:20.568944+00:00
| 13,071 | false |
## **Explanation**\n1. Count the number of consecutive 1s on the top and on the left.\n2. From length of edge `l = min(m,n)` to `l = 1`, check if the 1-bordered square exist.\n<br>\n\n## **Complexity**\nTime `O(N^3)`\nSpace `O(N^2)`\n<br>\n\n**Java:**\n```java\nclass Solution {\n public int largest1BorderedSquare(int[][] A) {\n int m = A.length, n = A[0].length;\n int[][] left = new int[m][n], top = new int[m][n];\n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n if (A[i][j] > 0) {\n left[i][j] = j > 0 ? left[i][j - 1] + 1 : 1;\n top[i][j] = i > 0 ? top[i - 1][j] + 1 : 1;\n }\n }\n }\n for (int l = Math.min(m, n); l > 0; --l)\n for (int i = 0; i < m - l + 1; ++i)\n for (int j = 0; j < n - l + 1; ++j)\n if (top[i + l - 1][j] >= l &&\n top[i + l - 1][j + l - 1] >= l &&\n left[i][j + l - 1] >= l &&\n left[i + l - 1][j + l - 1] >= l)\n return l * l;\n return 0;\n }\n}\n```\n\n**C++:**\n```cpp\n int largest1BorderedSquare(vector<vector<int>>& A) {\n int m = A.size(), n = A[0].size();\n vector<vector<int>> left(m, vector<int>(n)), top(m, vector<int>(n));\n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n left[i][j] = A[i][j] + (j && A[i][j] ? left[i][j - 1] : 0);\n top[i][j] = A[i][j] + (i && A[i][j] ? top[i - 1][j] : 0);\n }\n }\n for (int l = min(m, n); l > 0; --l)\n for (int i = 0; i < m - l + 1; ++i)\n for (int j = 0; j < n - l + 1; ++j)\n if (min({top[i + l - 1][j], top[i + l - 1][j + l - 1], left[i][j + l - 1], left[i + l - 1][j + l - 1]}) >= l)\n return l * l;\n return 0;\n }\n```\n\n**Python:**\n```python\n def largest1BorderedSquare(self, A):\n m, n = len(A), len(A[0])\n res = 0\n top, left = [a[:] for a in A], [a[:] for a in A]\n for i in xrange(m):\n for j in xrange(n):\n if A[i][j]:\n if i: top[i][j] = top[i - 1][j] + 1\n if j: left[i][j] = left[i][j - 1] + 1\n for r in xrange(min(m, n), 0, -1):\n for i in xrange(m - r + 1):\n for j in xrange(n - r + 1):\n if min(top[i + r - 1][j], top[i + r - 1][j + r - 1], left[i]\n [j + r - 1], left[i + r - 1][j + r - 1]) >= r:\n return r * r\n return 0\n```\n
| 107 | 6 |
[]
| 16 |
largest-1-bordered-square
|
Python O(N^3) time complexity with graphic illustration
|
python-on3-time-complexity-with-graphic-mnekw
|
At each point that is not 0, we try to construct the largest square that uses the point as the lower right corner that satisties the condition.\n\nConsider the
|
basi4869
|
NORMAL
|
2019-07-28T04:56:51.004783+00:00
|
2019-07-28T05:26:39.394245+00:00
| 2,308 | false |
At each point that is not `0`, we try to construct the largest square that uses the point as the lower right corner that satisties the condition.\n\nConsider the point at `(3, 3)`, highlighted in red below. We first find how many `1` are above it (including itself, and how many `1` are on its left, including itself. In this case, we have 4 above and 4 on the left. The largest possible square we can construct here is capped by the minimum of the two numbers, `min(4, 4) = 4`.\n\n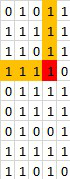\n\nNext, we go try out these 4 possibilities, starting from the largest. So we try the following 4 green corners, starting from the furthest one from our red point. When we try these green points, we are interested in whether there are enough `1` on the right and below the green point to complete a square with the beams extended from the red point. This condition is that **the minimum between the numbers of 1\'s on the right and below the green point is greater than or equal to the distance between the green and the red points**.\n\n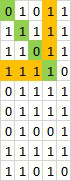\n\nTry the first one, its distance from the red point is 4, there is 0 on its right and 0 below it. `min(0, 0) < 4`, so not valid.\n\n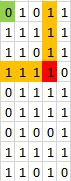\n\nTry the second one, its distance from the red point is 3, there is 4 on its right and 8 below it. `min(4, 8) >= 3`. So we have found a square of size `3*3`.\n\n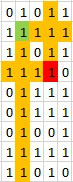\n\n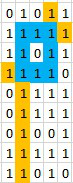\n\nTo facilitate this process, I first find how many 1s are above, below, on the left, and on the right of each point, including the point itself.\n\n```python\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n R, C = len(grid), len(grid[0])\n up = [[0 for _ in range(C)] for _ in range(R)]\n down = [[0 for _ in range(C)] for _ in range(R)]\n left = [[0 for _ in range(C)] for _ in range(R)]\n right = [[0 for _ in range(C)] for _ in range(R)]\n \n for r in range(R):\n for c in range(C):\n if r == 0:\n up[r][c] = grid[r][c]\n else:\n up[r][c] = grid[r][c] + up[r-1][c] if grid[r][c] == 1 else 0\n \n for r in range(R-1, -1, -1):\n for c in range(C):\n if r == R-1:\n down[r][c] = grid[r][c]\n else:\n down[r][c] = grid[r][c] + down[r+1][c] if grid[r][c] == 1 else 0\n \n for c in range(C):\n for r in range(R):\n if c == 0:\n left[r][c] = grid[r][c]\n else:\n left[r][c] = grid[r][c] + left[r][c-1] if grid[r][c] == 1 else 0\n \n for c in range(C-1, -1, -1):\n for r in range(R):\n if c == C-1:\n right[r][c] = grid[r][c]\n else:\n right[r][c] = grid[r][c] + right[r][c+1] if grid[r][c] == 1 else 0\n \n res = 0\n \n for r in range(R):\n for c in range(C):\n if grid[r][c] == 0:\n continue\n side = min(up[r][c], left[r][c])\n for i in range(side-1, -1, -1):\n if i < res:\n break\n if min(down[r-i][c-i], right[r-i][c-i]) >= i + 1:\n res = max(res, i + 1)\n break\n return res * res\n```\n\n \n \n \n \n \n \n \n \n \n \n \n \n \n \n \n \n \n \n
| 35 | 0 |
[]
| 2 |
largest-1-bordered-square
|
clean JAVA DP over 100% ! just to store the maximum possibility
|
clean-java-dp-over-100-just-to-store-the-n5cp
|
The main trick here is to use two dp 2d array to respectively store the maximum left-side outreach point and top-side outreach point. \n\nBy using these two dp,
|
sumonon
|
NORMAL
|
2019-07-28T04:44:10.805486+00:00
|
2019-07-28T05:00:22.235672+00:00
| 3,639 | false |
The main trick here is to use two dp 2d array to respectively store the maximum left-side outreach point and top-side outreach point. \n\nBy using these two dp, we can directly be inferred whether currenly possible length is valid or not. \n\nSo in the third for loop, we just need to test the current possible length step by step, from the maximum point to the closest. (Early stop when found the valid length helps to reduce time).\n\ngoelrishabh5\'s image might help you to understand the meaning of outreach point\nhttps://leetcode.com/problems/largest-1-bordered-square/discuss/345265/c%2B%2B-beats-100-(both-time-and-memory)-concise-with-algorithm-and-image\n\nPlease be free to leave any question~ GOOD LUCK\n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n if (grid.length==0) return 0;\n int[][] dpr = new int[grid.length+1][grid[0].length+1];\n int[][] dpc = new int[grid.length+1][grid[0].length+1];\n int dist, max=0;\n for (int r=1;r<=grid.length;r++){\n for (int c=1;c<=grid[0].length;c++){\n if (grid[r-1][c-1]==0) continue;\n dpr[r][c] = dpr[r-1][c]+1;\n dpc[r][c] = dpc[r][c-1]+1;\n dist = Math.min(dpr[r][c],dpc[r][c]);\n for (int i=dist;i>=1;i--){\n if (dpr[r][c-i+1]>=i \n && dpc[r-i+1][c]>=i){\n max = Math.max(max, i*i);\n break;\n }\n }\n }\n }\n return max;\n }\n}\n```
| 33 | 1 |
[]
| 2 |
largest-1-bordered-square
|
Java DP Solution with Videos Explained
|
java-dp-solution-with-videos-explained-b-qynn
|
English\n\n\n# Chinese\n\n\n# Code\njava\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n if (grid == null || grid.length == 0)
|
strong_painkiller
|
NORMAL
|
2019-07-28T11:39:11.652308+00:00
|
2019-11-06T12:50:17.280584+00:00
| 2,421 | false |
# English\n<iframe width="560" height="315" src="https://www.youtube.com/embed/MC41ZqLqhWU" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>\n\n# Chinese\n<iframe width="560" height="315" src="https://www.youtube.com/embed/7IkOZOwc-Mc" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>\n\n# Code\n```java\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n if (grid == null || grid.length == 0) return 0;\n int m = grid.length, n = grid[0].length;\n int[][][] dp = new int[m + 1][n + 1][2];\n int max = 0;\n\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == 1) {\n dp[i + 1][j + 1][0] = dp[i][j + 1][0] + 1;\n dp[i + 1][j + 1][1] = dp[i + 1][j][1] + 1;\n\n int len = Math.min(dp[i + 1][j + 1][0], dp[i + 1][j + 1][1]);\n for (int k = len; k > max; k--) {\n int len1 = Math.min(dp[i + 1 - k + 1][j + 1][1], dp[i + 1][j + 1 - k + 1][0]);\n if (len1 >= k) {\n max = Math.max(max, k);\n }\n }\n } else {\n dp[i + 1][j + 1][0] = 0;\n dp[i + 1][j + 1][1] = 0;\n }\n }\n }\n\n return max * max;\n }\n}\n```
| 20 | 1 |
['Dynamic Programming', 'Java']
| 4 |
largest-1-bordered-square
|
[Java] One pass 12 liner DP code w/ explanation and analysis.
|
java-one-pass-12-liner-dp-code-w-explana-dz90
|
Use two 2-D arrays to record the count of consecutive 1\'s horizontally and vertically, respectively;\n2. a) horizontal[i + 1][j + 1] and horizontal[i + 2 - len
|
rock
|
NORMAL
|
2019-07-28T10:18:30.031329+00:00
|
2019-07-29T12:22:37.628058+00:00
| 950 | false |
1. Use two 2-D arrays to record the count of consecutive `1\'s` horizontally and vertically, respectively;\n2. a) `horizontal[i + 1][j + 1]` and `horizontal[i + 2 - len][j + 1]` indicate the count of consecutive `1\'s` ending at `j` on row `i` and `i + 1 - len`, respectively; \nb) `vertical[i + 1][j + 1]` and `vertical[i + 1][j + 2 - len]` indicate the count of consecutive `1\'s` ending at `i` on column `j` and `j + 1 - len`, respectively; \n3. The minimum of the above 4 values in the arrays is greater or equal to `len`, then `len` is the length of the required square.\n4. Loop through `grid` to update the max area of the square met the requirement. \n\n```\n public int largest1BorderedSquare(int[][] grid) {\n int area = 0, m = grid.length, n = m == 0 ? 0 : grid[0].length;\n int[][] horizontal = new int[m + 1][n + 1], vertical = new int[m + 1][n + 1];\n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n horizontal[i + 1][j + 1] = grid[i][j] == 0 ? 0 : 1 + horizontal[i + 1][j]; \n vertical[i + 1][j + 1] = grid[i][j] == 0 ? 0 : 1 + vertical[i][j + 1]; \n for (int len = Math.min(horizontal[i + 1][j + 1], vertical[i + 1][j + 1]); area < len * len; --len)\n if (Math.min(horizontal[i + 2 - len][j + 1], vertical[i + 1][j + 2 - len]) >= len)\n area = len * len;\n }\n }\n return area;\n }\n```\n\n**Analysis:**\n\n Time: O(m * n * min(m, n)), space: O(m * n), where m = grid.length, n = grid[0].length.
| 8 | 3 |
[]
| 0 |
largest-1-bordered-square
|
Java DP Solution, beats 100%(both time and memory)
|
java-dp-solution-beats-100both-time-and-j7bgv
|
\u8BB0\u5F55\u6BCF\u4E2A\u70B9\uFF08\u7B97\u8FD9\u4E2A\u70B9\u672C\u8EAB\uFF09\u5DE6\u8FB9\u8FDE\u7EED\u76841\u7684\u4E2A\u6570\uFF0C\u4E0A\u8FB9\u8FDE\u7EED\u7
|
dinary
|
NORMAL
|
2019-07-28T08:00:06.093422+00:00
|
2019-07-28T08:01:39.526853+00:00
| 873 | false |
\u8BB0\u5F55\u6BCF\u4E2A\u70B9\uFF08\u7B97\u8FD9\u4E2A\u70B9\u672C\u8EAB\uFF09\u5DE6\u8FB9\u8FDE\u7EED\u76841\u7684\u4E2A\u6570\uFF0C\u4E0A\u8FB9\u8FDE\u7EED\u76841\u7684\u4E2A\u6570\u3002\u7136\u540E\u9009\u4E24\u8005\u4E2D\u8F83\u5C0F\u7684\u90A3\u4E2Ax\uFF0C\u5206\u522B\u4ECEx\u52301\u4F5C\u4E3A\u8FB9\u957F\uFF0C\u770B\u662F\u5426\u5B58\u5728\u5408\u6CD5\u7684\u6B63\u65B9\u5F62\u3002\nmemorize the number of consecutive 1s on the top and on the left for every cell (include the cell itself)\uFF0Cpick the minimum one as side length of potential quare. (sorry for my awful English)\n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[][] left = new int[m][n], top = new int[m][n];\n int res = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (i == 0) {\n top[i][j] = grid[i][j];\n } else {\n top[i][j] = grid[i][j] == 0? 0 : top[i-1][j] + 1;\n }\n if (j == 0) {\n left[i][j] = grid[i][j];\n } else {\n left[i][j] = grid[i][j] == 0? 0 : left[i][j-1] + 1;\n }\n for (int l = Math.min(top[i][j], left[i][j]); l >= 1; l--) {\n\t\t\t\t// \u5DF2\u77E5\u4E0B\u9762\u7684\u8FB9\u548C\u53F3\u4FA7\u8FB9\u5408\u6CD5\uFF0C\u770B\u4E0A\u8FB9\u548C\u5DE6\u4FA7\u8FB9\u662F\u5426\u5408\u6CD5\n if (left[i-l+1][j] >= l && top[i][j-l+1] >= l) {\n res = Math.max(res, l * l);\n break;\n }\n }\n }\n }\n return res;\n }\n}\n```\n
| 8 | 0 |
['Dynamic Programming', 'Java']
| 1 |
largest-1-bordered-square
|
Python DP with explanation, faster than 90% runtime and less than 100% space.
|
python-dp-with-explanation-faster-than-9-kb6r
|
construct dp matrix, each element dp[i][j] is a tuple that stores the length of consecutive 1s ending with grid[i][j] in horizontal and vertical directions. \n2
|
specialforceatp
|
NORMAL
|
2019-12-15T01:55:36.098336+00:00
|
2019-12-15T01:55:36.098390+00:00
| 791 | false |
1. construct dp matrix, each element dp[i][j] is a tuple that stores the length of consecutive 1s ending with grid[i][j] in horizontal and vertical directions. \n2. res stores the length of the longest subgrids with all 1 edges.\n3. at dp[i][j], if dp[i][j]>res, we check the subgrids with edge length ranging from res+1 to min(dp[i][j]). for edge length of L, we just need to check information stored in dp[i][j-L+1] and dp[i-L+1][j]. update res if we find a larger subgrids.\n4. return res squared.\n\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n r,c = len(grid),len(grid[0])\n \n dp = [[(0,0) for j in range(c)] for i in range(r)]\n \n if grid[0][0]==1:\n dp[0][0]=(1,1)\n \n \n res = 0\n \n for i in range(r):\n for j in range(c):\n if grid[i][j]==1:\n dp[i][j] = (dp[i][max(j-1,0)][0]+1,dp[max(i-1,0)][j][1]+1)\n else:\n dp[i][j] = (0,0)\n \n if dp[i][j][0]>res and dp[i][j][1]>res:\n l = res + 1\n if l!=1:\n while(l<=dp[i][j][0] and l<=dp[i][j][1]):\n if dp[i][j-l+1][1]>=l and dp[i-l+1][j][0]>=l:\n \n res = l\n\n l+=1\n else:\n res = 1\n \n return res**2\n \n \n \n```
| 6 | 0 |
[]
| 0 |
largest-1-bordered-square
|
C++ O(n ^ 3)
|
c-on-3-by-votrubac-mgbx
|
Accumulate the number of consecutive horizontal and vertical 1s in two helper grids.\n\nThen, starting from the maximum possible square size sz_s, check the len
|
votrubac
|
NORMAL
|
2019-07-28T04:27:24.148522+00:00
|
2019-07-28T04:50:44.952378+00:00
| 1,363 | false |
Accumulate the number of consecutive horizontal and vertical ```1```s in two helper grids.\n\nThen, starting from the maximum possible square size ```sz_s```, check the length of 4 sides using the helper grids.\n```\nint largest1BorderedSquare(vector<vector<int>>& grid) {\n auto sz_x = grid.size(), sz_y = grid[0].size();\n vector<vector<int>> sx(sz_x, vector<int>(sz_y)), sy(sz_x, vector<int>(sz_y));\n for (auto x = 0; x < sz_x; ++x)\n for (auto y = 0; y < sz_y; ++y)\n if (grid[x][y] == 0) sx[x][y] = sy[x][y] = 0;\n else {\n sx[x][y] = 1 + (y == 0 ? 0 : sx[x][y - 1]);\n sy[x][y] = 1 + (x == 0 ? 0 : sy[x - 1][y]);\n }\n for (int sz_s = min(sz_y, sz_x) - 1; sz_s >= 0; --sz_s)\n for (auto x = 0; x + sz_s < sz_x; ++x)\n for (auto y = 0; y + sz_s < sz_y; ++y) {\n if (sx[x][y + sz_s] > sz_s && sx[x + sz_s][y + sz_s] > sz_s &&\n sy[x + sz_s][y] > sz_s && sy[x + sz_s][y + sz_s] > sz_s) return (sz_s + 1) * (sz_s + 1);\n }\n return 0;\n}\n```
| 6 | 1 |
[]
| 4 |
largest-1-bordered-square
|
✅✔️Easy and clean Implementation || C++ Solution ✈️✈️✈️✈️✈️
|
easy-and-clean-implementation-c-solution-90ty
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ajay_1134
|
NORMAL
|
2023-08-04T12:32:44.668346+00:00
|
2023-08-04T12:32:44.668376+00:00
| 452 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n void fillrd(int r, int c, vector<vector<int>>&rd, int n, int m, vector<vector<int>>& grid){\n int rcnt = 0, ccnt = 0;\n for(int j=c; j<m; j++){\n if(grid[r][j] == 0) break;\n rcnt++;\n }\n for(int i=r; i<n; i++){\n if(grid[i][c] == 0) break;\n ccnt++;\n }\n rd[r][c] = min(rcnt,ccnt);\n }\n\n void filllu(int r, int c, vector<vector<int>>&lu, int n, int m, vector<vector<int>>& grid){\n int rcnt = 0, ccnt = 0;\n for(int j=c; j>=0; j--){\n if(grid[r][j] == 0) break;\n rcnt++;\n }\n for(int i=r; i>=0; i--){\n if(grid[i][c] == 0) break;\n ccnt++;\n }\n lu[r][c] = min(rcnt,ccnt);\n }\n\n int solve(int r, int c, vector<vector<int>>&rd,vector<vector<int>>&lu){\n for(int sz=rd[r][c]; sz>0; sz--){\n if(lu[r+sz-1][c+sz-1] >= sz) return sz;\n }\n return 1;\n }\n\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n vector<vector<int>>rd(n,vector<int>(m));\n vector<vector<int>>lu(n,vector<int>(m));\n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n fillrd(i,j,rd,n,m,grid);\n filllu(i,j,lu,n,m,grid);\n }\n }\n int ans = 0;\n for(int i=0; i<n; i++){\n for(int j=0; j<m; j++){\n if(grid[i][j] == 1) ans = max(ans, solve(i,j,rd,lu));\n }\n }\n return ans*ans;\n }\n};\n```
| 4 | 0 |
['Array', 'Matrix', 'Prefix Sum', 'C++']
| 0 |
largest-1-bordered-square
|
C++ DP Solution
|
c-dp-solution-by-gaurav2k20-vzro
|
\nstruct Co{\n int x;\n int y; \n}; \nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m=grid.size();
|
gaurav2k20
|
NORMAL
|
2022-03-04T08:11:27.535891+00:00
|
2022-03-04T08:12:25.102154+00:00
| 867 | false |
```\nstruct Co{\n int x;\n int y; \n}; \nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m=grid.size(); \n int n=grid[0].size(); \n \n vector<vector<Co>>dp(m,vector<Co>(n,{0,0}));\n if(grid[0][0]){\n dp[0][0]={1,1}; \n }\n for(int i=1;i<m;i++){\n if(grid[i][0]!=0){\n dp[i][0]={1+dp[i-1][0].x,1}; \n }\n }\n \n for(int j=1;j<n;j++){\n if(grid[0][j]!=0){\n dp[0][j]={1,dp[0][j-1].y+1}; \n }\n }\n \n for(int i=1;i<m;i++){\n for(int j=1;j<n;j++){\n if(grid[i][j]!=0) dp[i][j]={dp[i-1][j].x+1,dp[i][j-1].y+1}; \n }\n }\n int ans=0; \n for(int i=m-1;i>=0;i--){\n for(int j=n-1;j>=0;j--){\n int mini; \n if(dp[i][j].x) mini= min(dp[i][j].x,dp[i][j].y); \n else continue; \n mini--; \n while(mini>=0){\n if( dp[i-mini][j].y>=mini and dp[i][j-mini].x>=mini and grid[i-mini][j-mini]==1){\n ans=max(ans,mini+1); \n break; \n }\n mini--; \n \n }\n \n }\n }\n ans=ans*ans; \n return ans; \n }\n};\n```
| 4 | 0 |
['Dynamic Programming']
| 0 |
largest-1-bordered-square
|
Python 3 | Prefix-sum, DP, O(N^3) | Explanation
|
python-3-prefix-sum-dp-on3-explanation-b-v0gs
|
Implementation as hint section suggested\n- See below comments for more detail\n\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -
|
idontknoooo
|
NORMAL
|
2021-08-30T15:32:01.595210+00:00
|
2021-08-30T15:32:01.595255+00:00
| 741 | false |
- Implementation as __*hint*__ section suggested\n- See below comments for more detail\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n dp = [[(0, 0)] * (n) for _ in range((m))] \n for i in range(m): # calculate prefix-sum as `hint` section suggested\n for j in range(n):\n if not grid[i][j]:\n continue\n dp[i][j] = (dp[i][j][0] + dp[i-1][j][0] + 1, dp[i][j][1] + dp[i][j-1][1] + 1)\n for win in range(min(m, n)-1, -1, -1): # for each window size\n for i in range(m-win): # for each x-axis\n for j in range(n-win): # for each y-axis\n if not grid[i][j]: continue # determine whether square of (i, j), (i+win, j+win) is 1-boarded\n x1, y1 = dp[i+win][j+win] # bottom-right corner\n x2, y2 = dp[i][j+win] # upper-right corner\n x3, y3 = dp[i+win][j] # bottom-left corner\n x4, y4 = dp[i][j] # upper-left corner\n if y1 - y3 == x1 - x2 == y2 - y4 == x3 - x4 == win:\n return (win+1) * (win+1)\n return 0\n```
| 4 | 0 |
['Dynamic Programming', 'Matrix', 'Python', 'Python3']
| 0 |
largest-1-bordered-square
|
java, 3ms, easy to understand
|
java-3ms-easy-to-understand-by-yuzhouwu-8uzs
|
class Solution {\n public int largest1BorderedSquare(int[][] grid) {\n if(grid.length == 0) return 0;\n int m = grid.length, n = grid[0].length
|
yuzhouwu
|
NORMAL
|
2019-07-28T04:04:04.141243+00:00
|
2019-07-28T04:04:04.141300+00:00
| 663 | false |
class Solution {\n public int largest1BorderedSquare(int[][] grid) {\n if(grid.length == 0) return 0;\n int m = grid.length, n = grid[0].length;\n int hor[][] = new int[m][n]; \n int ver[][] = new int[m][n];\n for (int i = 0; i < m; i++){\n for(int j = 0; j < n; j++){\n if(grid[i][j] == 1){\n hor[i][j] = j == 0? 1 : hor[i][j-1] + 1;\n ver[i][j] = i == 0? 1 : ver[i-1][j] + 1;\n }\n }\n }\n int max = 0;\n for(int i = m-1; i >= 0; i--){\n for(int j = n-1; j >= 0; j--){\n int edge = Math.min(hor[i][j], ver[i][j]);\n while(edge > max){\n if(ver[i][j-edge+1] >= edge && hor[i-edge+1][j] >= edge) max = edge;\n edge--;\n }\n }\n }\n return max * max;\n }\n}
| 4 | 2 |
[]
| 3 |
largest-1-bordered-square
|
C++ straightforward matrix
|
c-straightforward-matrix-by-wzypangpang-9euo
|
\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n vector<vecto
|
wzypangpang
|
NORMAL
|
2021-09-16T19:56:28.761198+00:00
|
2021-09-16T19:56:28.761246+00:00
| 426 | false |
```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n vector<vector<int>> mr(m, vector<int>(n, 0));\n vector<vector<int>> mc(m, vector<int>(n, 0));\n \n for(int i=0; i<m; ++i){\n for(int j=0; j<n; ++j){\n if(j == 0) {\n mr[i][j] = grid[i][j];\n } else {\n mr[i][j] = grid[i][j] == 0 ? 0 : mr[i][j-1] + 1;\n }\n }\n }\n \n for(int j=0; j<n; ++j){\n for(int i=0; i<m; ++i){\n if(i == 0) {\n mc[i][j] = grid[i][j];\n } else {\n mc[i][j] = grid[i][j] == 0 ? 0 : mc[i-1][j] + 1;\n }\n }\n }\n \n int ans = 0;\n for(int i=0; i<m; ++i) {\n for(int j=0; j<n; ++j) {\n for(int len=0; i+len < m && j+len < n; ++len) {\n if(mr[i][j+len] > len && mc[i+len][j] > len && mr[i+len][j+len] > len && mc[i+len][j+len] > len) {\n ans = max(ans, len+1);\n }\n }\n }\n }\n \n return ans * ans;\n }\n};\n```
| 3 | 0 |
[]
| 0 |
largest-1-bordered-square
|
O(n^2) space and runtime. Sophisticated. With explanation. How to improve explanation/code?
|
on2-space-and-runtime-sophisticated-with-k1i4
|
Please comment for any suggestions how to explain better, code cleaner and any point, which should be clarified.\n\nI assume for simplicity that n is the maximu
|
Iwadev
|
NORMAL
|
2021-05-21T13:53:20.293266+00:00
|
2021-05-21T14:01:01.198498+00:00
| 435 | false |
Please **comment** for any suggestions how to *explain better*, *code cleaner* and any point, which should be clarified.\n\nI assume for simplicity that n is the maximum side length of the grid and show runtime O(n^2). The analysis can be adapted to non-rectangular grids to show that the runtime is, in fact, linear in n* m, the number of entries of the grid. This is asymtotically optimal. \n\nBefore we try ourselves finding full squares, we ask ourselves the following question:\nGiven a position (x,y) what is the longest possible sqare at this corner if we are allowed to set all values outside of row x and column y to 1. In other word, we are looking vor the maximum size of such a shape (where * denotes any value) where the upper right corner is (x,y).\n1 1 1 1 \n1 * * * \n1 * * *\n1 * * *\nThis value is UpperLeft[y][x];\nIn order to compute it efficiently (i.e. in time O(n^2)) we make yet another observation: If h is maximal such that \ngrid[y][x]=UpperLeft[y+1][x]=... UpperLeft[y+h-1][x]=1 and w is maximal such that grid[y][x]=UpperLeft[y][x+1]=... UpperLeft[y][x+w-1]=1 then UpperLeft[y][x]=min(w,h).\n\nAnaloguously we define LowerRight[y][x] to be the maximum size of a square whose lower right corner is (x,y) if we are allowed to set all values outside of column y and row x to 1. It corresponds to the following shape:\n, * * * 1 \n, * * * 1\n, * * * 1\n, 1 1 1 1\n(Commas are only added for formatting reasons.) It is computed analoguously to UpperLeft.\n\nNow we have the following observation: There exists a 1-Bordered Square with side length s and upper right corner (x,y) --- the lower left corner is thus (x+s-1,y+s-1) --- if and only if UpperLeft[y][x]>=s and LowerRight[y+s-1,y+s-1]>=s.\nWe now implement the following **subroutine** in linear time: Given a value best and a value d, we consider the diagonal defined by x-y=d; we then find out, whether there exists a 1-Bordered Square whose upper right and lower left corner lie in the diagonal and whose side-length is at least left. \n\nThe idea is the following. We start on the upper left of the diagonal x+d=y and proceed downwards (rightwards). The point (leftX,leftY) starts by (0,0) while (rightX,rightY)=(leftX+best,leftX+best). Whenever (leftX,leftY) could be a corner of a Square of sidelength at least best+1, i.e. if UpperLeft[leftY][leftX]>best, we add this corner to a stack. If (rightX,rightY) is a suitable lower right corner, i.e. rval=LowerRight[rightY][rightX]>best we check the values in the upper left corners if they form a Square. If the top element of the stack has distance *dist* more than rval from (rightX,right Y) there is no suitable square at that point. The situation might look like the following:\n1 1 1 1 1 1\n1 * * * * 0\n1 * * * * 1\n1 * * * * 1\n1 * * * * 1\n1 1 1 1 1 1 The two sides starting at the lower right corner do not reach the two sides starting at the upper left.\n\nOn the other hand, let lval be the value of UpperLeft of the top element of the stack. if(lval< dist). The top element is not a suitable left corner anymore. Furthermore, it will not be a suitable corner to any right corner we encounter later in the stack. We can pop/remove it. The situation could be the following:\n1 1 1 1 0 1\n1 * * * * 1\n1 * * * * 1\n1 * * * * 1\n1 * * * * 1\n1 1 1 1 1 1 The two sides at the upper left are not long enough.\nWe repeat the process till either the stack is empty or the right corner has rval smaller then the distance to the top element of the stack **or** till both the top element of the stack and the lower right corner have UpperLeft resp. LowerRight at least their distance *dist*. In this case they form a square of side length *dist*. Since we only put elements in the stack, which ahve distance at lest best+1 from the lower right corner, this square has side length at least *best*. One can also note that if such a square exists, the subroutine will find such a square (though not necessarily the best one). Finally, for the runtime, one should observe that the soubroutine whenever it checks a lower right corner either pops an element from the stack or finds out whether the right corner can be the right corner of a square of side length at least best+1. Since there are only n (number of element s on a diagonal) right corners and also at most n elements (corresponding to upper left corners) get added to the stack, this subroutine has runtime O(n).\n\nOur algorithm now does the following. Set best=0. For each diagonal check using our **subroutine** if it contains a square of size at least best+1. If so, set best to the size of the largest square found and repeat. Else, consider the next diagonal. \nIn each iteration we either increase best or consider a new diagonal. Since there are only 2n-1 diagonals and best cannot exceed n this means we use our subroutine at most 3n times. We get quadratic running time.\n\nPlease **comment** for any suggestions how to *explain better*, *code cleaner* and any point, which should be clarified.\n\nAs a new **challenge**, bring down the space requirements to O(n). You are not allowed to change the entries of *grid*, that is cheating. I am certain it is possible.\n\n\n```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n \n vector<vector<int>> upperLeft(grid.size(),vector<int>(grid[0].size()));\n vector<vector<int>> lowerRight(grid.size(),vector<int>(grid[0].size()));\n \n for(int i=0;i<grid.size();++i){\n computeHorizontalSums(upperLeft[i].rbegin(),upperLeft[i].rend(),grid[i].rbegin());\n computeHorizontalSums(lowerRight[i].begin(),lowerRight[i].end(),grid[i].begin());\n }\n updateVerticalSums(upperLeft.rbegin(),upperLeft.rend(),grid.rbegin());\n updateVerticalSums(lowerRight.begin(),lowerRight.end(),grid.begin());\n \n int best=0;\n \n for(int diagonal=1-grid.size(); diagonal<(int)grid[0].size(); ++diagonal){\n bool couldImproveBest;\n do{\n couldImproveBest=false;\n int rightX,leftX,rightY,leftY;\n rightX=leftX=max(0,diagonal);\n rightY=leftY=max(-diagonal,0);\n int count=0;\n \n\n //(rightX,rightY) becomes the first point on the diagonal with distance best+1\n while(rightY<grid.size() && rightX<grid[0].size() &&count<best){\n count++;\n rightX++;\n rightY++;\n }\n if(rightY<grid.size() && rightX<grid[0].size()){\n stack<pair<int,int>> possibleUpperLeftCorner;\n while(rightY<grid.size() && rightX<grid[0].size()){\n if(upperLeft[leftY][leftX]>best){\n possibleUpperLeftCorner.push(make_pair(leftX,leftY));\n }\n int rval=lowerRight[rightY][rightX];\n if(rval>best){\n int dist=INT_MAX;\n if(!possibleUpperLeftCorner.empty())\n dist=rightX-possibleUpperLeftCorner.top().first+1;\n while(rval>=dist){\n pair<int,int> current=possibleUpperLeftCorner.top();\n int lval=upperLeft[current.second][current.first];\n if(lval>=dist){\n best=dist;\n couldImproveBest=true;\n }\n \n possibleUpperLeftCorner.pop();\n if(possibleUpperLeftCorner.empty())\n dist=INT_MAX;\n else\n dist=rightX-possibleUpperLeftCorner.top().first+1;\n }\n }\n rightX++;\n rightY++;\n leftX++;\n leftY++;\n }\n }\n }while(couldImproveBest);\n }\n \n return best*best;\n }\nprivate:\n template <class RandomAccessIterator> void computeHorizontalSums(RandomAccessIterator begin, RandomAccessIterator end, RandomAccessIterator gridposition){\n if(*gridposition)\n *begin=1;\n else\n *begin=0;\n begin++;\n while(begin!=end){\n gridposition++;\n if(*gridposition)\n *begin=*(begin-1)+1;\n else\n *begin=0;\n begin++;\n }\n }\n template <class RandomAccessIterator> void updateVerticalSums(RandomAccessIterator begin, RandomAccessIterator end, RandomAccessIterator gridposition){\n int n=begin->size();\n \n for(int i=0;i<n;++i){\n RandomAccessIterator pos=gridposition;\n int sum=0;\n for(RandomAccessIterator it=begin;it!=end;++it){\n if((*pos)[i])\n sum++;\n else\n sum=0;\n pos++;\n (*it)[i]=min((*it)[i],sum);\n }\n }\n }\n};\n```
| 3 | 1 |
[]
| 0 |
largest-1-bordered-square
|
python, dp, faster than 98+%
|
python-dp-faster-than-98-by-dustlihy-512g
|
If anyone doesn\'t understand my solution, comment.\n\n\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n
|
dustlihy
|
NORMAL
|
2021-05-02T10:10:06.200634+00:00
|
2021-06-09T10:45:25.869083+00:00
| 674 | false |
If anyone doesn\'t understand my solution, comment.\n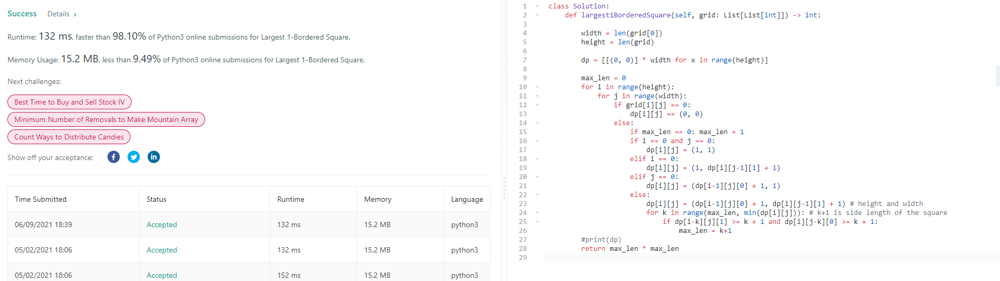\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n width = len(grid[0])\n height = len(grid)\n \n dp = [[(0, 0)] * width for x in range(height)]\n \n max_len = 0\n for i in range(height):\n for j in range(width):\n if grid[i][j] == 0:\n dp[i][j] == (0, 0)\n else:\n if max_len == 0: max_len = 1\n if i == 0 and j == 0: \n dp[i][j] = (1, 1)\n elif i == 0:\n dp[i][j] = (1, dp[i][j-1][1] + 1)\n elif j == 0:\n dp[i][j] = (dp[i-1][j][0] + 1, 1)\n else:\n dp[i][j] = (dp[i-1][j][0] + 1, dp[i][j-1][1] + 1) # height and width\n for k in range(max_len, min(dp[i][j])): # k+1 is side length of the square\n if dp[i-k][j][1] >= k + 1 and dp[i][j-k][0] >= k + 1:\n max_len = k+1\n #print(dp)\n return max_len * max_len\n```\nThe image below maybe help you understand the magic.\n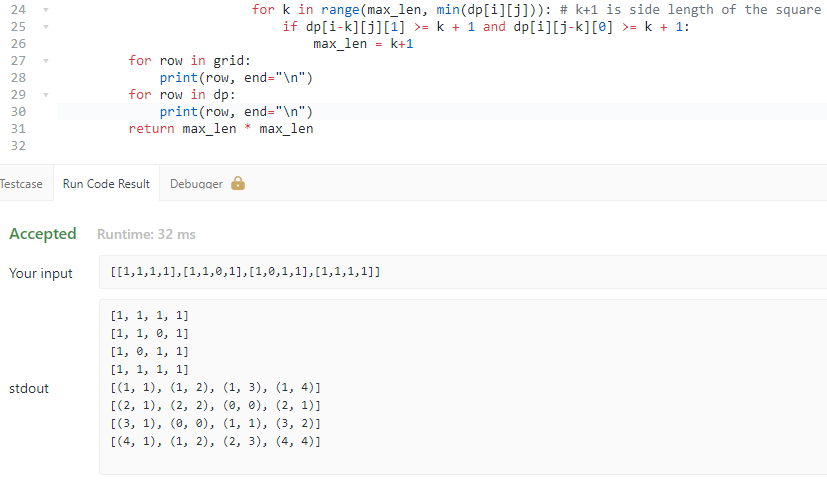\n
| 3 | 0 |
['Dynamic Programming', 'Python', 'Python3']
| 2 |
largest-1-bordered-square
|
Java simple prefix dp
|
java-simple-prefix-dp-by-hobiter-60s8
|
\n public int largest1BorderedSquare(int[][] g) {\n int res = 0, m = g.length, n = g[0].length, dp[][][] = new int[m + 1][n + 1][2];\n for (int
|
hobiter
|
NORMAL
|
2020-06-09T06:09:31.980279+00:00
|
2020-06-09T06:09:31.980328+00:00
| 499 | false |
```\n public int largest1BorderedSquare(int[][] g) {\n int res = 0, m = g.length, n = g[0].length, dp[][][] = new int[m + 1][n + 1][2];\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (g[i][j] == 0) continue;\n dp[i+1][j+1][0] += dp[i][j+1][0] + 1;\n dp[i+1][j+1][1] += dp[i+1][j][1] + 1;\n int pre = Math.min(dp[i+1][j+1][0], dp[i+1][j+1][1]);\n if (pre <= res) continue;\n for (int k = pre; k > res; k--) {\n if (dp[i + 1 - k + 1][j + 1][1] >= k && dp[i + 1][j + 1 - k + 1][0] >= k) {\n res = k;\n break;\n }\n }\n }\n }\n return res * res;\n }\n```
| 3 | 0 |
[]
| 0 |
largest-1-bordered-square
|
C++ O(n²)time and O(n²)space
|
c-on2time-and-on2space-by-dw_rudolph-sk61
|
use left and up to record the numbers of one along two lines\u2014\u2014row and column\nthen use the requirement that the area should be square to select suitab
|
dw_rudolph
|
NORMAL
|
2020-04-15T15:26:34.402946+00:00
|
2020-04-15T15:26:34.402985+00:00
| 343 | false |
use left and up to record the numbers of one along two lines\u2014\u2014row and column\nthen use the requirement that the area should be square to select suitable situation\nFinally,it should be paid attention that we should try every situation until the number is equal to current max number\n\n```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m=grid.size(),n=grid[0].size();\n int res=0;\n vector<vector<int>> left(m,vector<int>(n,0)),up(m,vector<int>(n,0));\n for(int i=0;i<m;++i){\n for(int j=0;j<n;++j){\n left[i][j]= grid[i][j]==0?0:j>=1?left[i][j-1]+1:grid[i][0];\n up[i][j]= grid[i][j]==0?0:i>=1?up[i-1][j]+1:grid[0][j];\n int t=min(left[i][j],up[i][j]);\n while(t>res){\n int U=i-t+1,L=j-t+1;\n if(up[i][L]>=t && left[U][j]>=t) res=max(res,t);\n --t;\n }\n }\n }\n return res*res;\n }\n};\n```
| 3 | 4 |
[]
| 2 |
largest-1-bordered-square
|
Python3: FT 100%: TC O(M^2 N), SC O(M N): Mostly DP with a Few Optimizations
|
python3-ft-100-tc-om2-n-sc-om-n-mostly-d-bgt1
|
Intuition\n\nFor most problems involving squares or sides in grids, we usually need to know the number of consecutive ones. We can do this with O(M N) DP.\n\nIn
|
biggestchungus
|
NORMAL
|
2023-12-04T22:49:20.295755+00:00
|
2023-12-04T22:49:20.295781+00:00
| 241 | false |
# Intuition\n\nFor most problems involving squares or sides in grids, we usually need to know the number of consecutive ones. We can do this with O(M N) DP.\n\nIn this case, 1-bordered squares mean we need to find cells with a specific number of consecutive 1s down and to the right. So we\'re probably on the right track.\n\nIn more detail: to form a 1-bordered region of size `k x k` with the upper-left corner at `r, c` we need\n* at `r, c`: `k` consecutive 1\'s going down\n* at `r, c`: `k` consecutive 1\'s going right\n* at `r+k-1, c`: `k` consecutive 1\'s going right\n* at `r, c+k-1`: `k` consecutive 1\'s going down\n\nHere\'s some ASCII art:\n```a\n (r,c) k ones\n \\ --------->\n k | 1 1 1 1 |\nones | 1 1 | k ones\n | 1 1 |\n | 1 1 1 1 V\n ------------>\n k ones\n```\n\nAt `r,c`:\n* suppose we have `D` 1s going down\n* and we have `R` 1s going right\n* then the largest *square* we can form has side length `min(D,R)`\n* so we know the largest side length to check\n\nWe can use DP to get the consecutive ones in both directions. Then we can iterate over the grid and find the largest square with each upper-left coordinate. The best answer is the max square size over all (r,c) starting locations (i.e. all O(M N) choices for the upper-left).\n\n# Approach\n\n## Consecutive Ones Down and Left\n\nA (somewhat) common DP operation for grids is getting the number of consecutive ones in some direction. This shows up in a lot of "skyline" problems too, or places where you need to quickly get information about consecutive elements meeting some criterion.\n\nFor consecutive ones going right:\n* if the right-most element is 0, the count is zero\n* if the right-most element is 1, the count is one\n* for each r < R-1\n * if the current element is 1, the count is 1 plus the number of consecutive ones starting one element to the right: we take the `k` 1\'s off to the right, and add 1 for the current element\n * if the current element is 0, the count is 0\n\nSome more ASCII art to explain what we\'re doing:\n```\nrow: 0 1 1 1 0 0 1 1 0 1 1 1 1 0\nconsecutive ones to right: 0 3 2 1 0 0 2 1 0 4 3 2 1 0\n```\n\nThe same logic applies to consecutive ones downward, but with rows/columns flipped. Same idea, just be careful about R vs. C.\n\n## Main Loop\n\nFor all `r,c` coordinates, we can find the max edge length using `min(down[r][c], right[r][c])`. Any edge longer than that will have a zero along at least one edge, or go out of bounds.\n\nThen for each possible side length `l`, we check\n* if we go the bottom-left corner, are there `l` ones to the right?\n* if we go to the top-right corner, are there `l` ones going down?\n\nIf the answer to both is yes, then we have a square of side length `l`.\n\n## Optimizations\n\nWe want the cumulative max over all starting locations. Therefore we only care about improving the current max.\n\n### Early Break in R/C Loops\n\nIf we\'re at (r,c) and the current best side length is `best`, then a new best square would end at least at `r+best+1-1, c+best+1-1 == r+best, c+best`.\n\nIf those coordinates are out of bounds, we can\'t possibly improve on the best. So I added an early `break` statement to the outermost loop (rows), and adjusted the upper bound of the inner loop (cols).\n\n### Try Longest First\n\nSince we want the maximum, we don\'t care about *all* the edge lengths we can form at `r,c` - we just want the max. So I iterate from the longest length downward, and break if/when we get a length. This way we look at the fewest squares possible.\n\n### Only Try Larger Squares\n\nSimilar to "Try Longest First," we know that the only squares that can improve the current `best` have side length `best+1` or longer.\n\nSo I only check lengths from `longest` to `best+1` in descending order. If we find a square, we know this is a new best (because we *only* consider lengths that will be a new best) so we set `best = l` directly.\n\n# Complexity\n- Time complexity: O(M^2 N)\n - M is the shorter axis\n - N is the longer axis\n - analysis: we do O(M N) iterations, over most upper-left coordintes `r, c`. In each iteration, we look at longest possible edge length, which is O(M). So we do O(M M N) work total.\n - the `down` and `left` DP grids only take O(M N)\n\n- Space complexity: O(M N) because we form `down` and `right` DP grids\n\nIn practice I think the complexity is typically lot lower because we only iterate over lengths from `min(down[r][c], right[r][c])` down to `best+1`\n* for early r,c coordinates, usually one axis will have many fewer consecutive ones than the other. The worst case would be a lot of downward and rightward lines of 1s\n* for later r,c coordinates, the current best increases so the number of side lengths we check decreases\n* for very late r,c coordintes, given the current best, we skip checking late r and c values entirely\n\nSo the effective size of the grid decreases over time, and the range of the loop decreases over time. If there\'s a large rectangle early then the "Only Try Larger Rectangles" optimization means we don\'t actually iterate over any candidate squares at all.\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n R = len(grid)\n C = len(grid[0])\n\n # want largest square subgrid: min(R,C) side length\n # max(R,C)-min(R,C)+1 different offsets in other direction\n\n # Reread problem, a lot easier than I thought (we\'re not counting\n # number of 1-bordered squares in the largest square) - we want\n # the size of the largest 1-bordered square\n\n # the grid already gives us the size of 1x1 squares\n # DP?\n # for x 1 1 1 1 1\n # 1 1\n # 1 1\n # 1 1 1 1 4x4\n\n # if we knew\n # x has 6 left and 4 down ones, including x\n # So max grid size at x is 4x4\n # We can look at right[x + (3,0)] -> get 4\n # and look at down[x + (0,3)] -> get 4\n # so we have a 4x4\n\n # For a MxN grid, the max number of 1s at any cell would be O(M) down and O(N) right\n # for each one we\'d do O(min(M,N)) ops\n # so if shorter axis is M and longer is N, then we\'d do O(MN) iterations, and O(M) ops per iteration\n \n # Can we go faster? I don\'t think so, but I have no proof.\n\n # foo[r][c] is number of consec. 1s, including (r,c), right/down starting at (r,c)\n right = [[0]*C for _ in range(R)]\n down = [[0]*C for _ in range(R)]\n\n for r in range(R):\n right[r][C-1] = grid[r][C-1]\n for c in range(C-2, -1, -1):\n if grid[r][c]:\n right[r][c] = right[r][c+1] + 1\n # else: leave it zero\n\n for c in range(C):\n down[R-1][c] = grid[R-1][c]\n for r in range(R-2, -1, -1):\n if grid[r][c]:\n down[r][c] = down[r+1][c] + 1\n\n L = min(R,C)\n best = 0\n for r in range(R):\n # break early if we can\'t improve on the best; new best would need row index >= r+(best+1)-1\n if r+best >= R: break\n for c in range(C-best):\n longest = min(down[r][c], right[r][c])\n # only candidates > best can change the answer\n for l in range(longest, best, -1):\n if right[r+l-1][c] >= l and down[r][c+l-1] >= l:\n best = l\n break\n \n return best**2 # FIX: area, not side length\n```
| 2 | 0 |
['Python3']
| 0 |
largest-1-bordered-square
|
✔ Python3 Solution | O(n * m * min(n, m))
|
python3-solution-on-m-minn-m-by-satyam20-8mx1
|
Complexity\n- Time complexity: O(n * m * min(n, m))\n- Space complexity: O(n * m)\n\n# Code\n\nclass Solution:\n def largest1BorderedSquare(self, A):\n
|
satyam2001
|
NORMAL
|
2023-01-04T13:36:08.054318+00:00
|
2023-01-04T13:44:47.187960+00:00
| 778 | false |
# Complexity\n- Time complexity: $$O(n * m * min(n, m))$$\n- Space complexity: $$O(n * m)$$\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, A):\n n, m, ans = len(A), len(A[0]), 0\n H, V = [row[:] for row in A], [row[:] for row in A]\n for i in range(n):\n for j in range(m):\n if i and H[i][j]: H[i][j] += H[i - 1][j]\n if j and V[i][j]: V[i][j] += V[i][j - 1]\n for i in range(n):\n for j in range(m):\n for k in range(min(H[i][j], V[i][j]), ans, -1):\n if V[i - k + 1][j] >= k and H[i][j - k + 1] >= k:\n ans = k\n break\n return ans * ans\n```
| 2 | 0 |
['Matrix', 'Python3']
| 0 |
largest-1-bordered-square
|
[C++] Compact solution, 12 lines
|
c-compact-solution-12-lines-by-qyryq-qk75
|
\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n vector<vector<int>> U(grid), L(grid); // up, left\n si
|
qyryq
|
NORMAL
|
2022-05-20T19:29:45.831692+00:00
|
2023-10-31T21:18:48.721713+00:00
| 470 | false |
```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n vector<vector<int>> U(grid), L(grid); // up, left\n size_t largest = 0;\n for (size_t i = 0; i < grid.size(); i++)\n for (size_t j = 0; j < grid[0].size(); j++)\n if (grid[i][j]) {\n L[i][j] += j > 0 ? L[i][j-1] : 0;\n U[i][j] += i > 0 ? U[i-1][j] : 0;\n for (size_t lim = min(L[i][j], U[i][j]), k = largest; k < lim; k++)\n if (L[i-k][j] > k && U[i][j-k] > k)\n largest = k+1;\n }\n return largest*largest;\n }\n};\n```
| 2 | 0 |
['Dynamic Programming', 'C++']
| 0 |
largest-1-bordered-square
|
C++ | 91% faster | horizonatal and vertical precalculation
|
c-91-faster-horizonatal-and-vertical-pre-o80j
|
\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n vector<vector<int>> hb(grid.size(),vector<int>(grid[0].size(),
|
armangupta48
|
NORMAL
|
2021-04-30T19:12:42.117122+00:00
|
2021-04-30T19:12:42.117152+00:00
| 415 | false |
```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n vector<vector<int>> hb(grid.size(),vector<int>(grid[0].size(),0));\n vector<vector<int>> vb(grid.size(),vector<int>(grid[0].size(),0));\n for(int i = 0;i<grid.size();i++)\n {\n for(int j = 0;j<grid[0].size();j++)\n {\n if(grid[i][j]==1)\n {\n if(j>0)\n {\n hb[i][j] = hb[i][j-1]; \n }\n if(i>0) vb[i][j] = vb[i-1][j];\n \n hb[i][j]+=1;\n vb[i][j]+=1;\n }\n }\n }\n int ans = 0;\n for(int i = 0;i<grid.size();i++)\n {\n for(int j = 0;j<grid[0].size();j++)\n {\n int size = min(hb[i][j],vb[i][j]);\n if(size==0) continue;\n for(int k = size;k>0;k--)\n {\n if(hb[i-k+1][j]>=k && vb[i][j-k+1]>=k)\n {\n ans = max(ans,k);\n }\n }\n }\n }\n return ans*ans;\n }\n};\n```
| 2 | 0 |
['Dynamic Programming', 'C']
| 0 |
largest-1-bordered-square
|
C#, O(mn * min(m,n)) DP solution, beats 100%
|
c-omn-minmn-dp-solution-beats-100-by-ede-y2mn
|
\npublic class Solution {\n public int Largest1BorderedSquare(int[][] grid) {\n int height = grid.Length;\n int width = grid[0].Length;\n
|
edevyatkin
|
NORMAL
|
2021-03-08T08:44:38.236011+00:00
|
2021-03-08T08:44:38.236047+00:00
| 217 | false |
```\npublic class Solution {\n public int Largest1BorderedSquare(int[][] grid) {\n int height = grid.Length;\n int width = grid[0].Length;\n int border = 0;\n var dp = new (int Left, int Top)[height+1][];\n for (int row = 0; row <= height; row++)\n dp[row] = new (int Left, int Top)[width+1];\n for (int i = 1; i <= height; i++) {\n for (int j = 1; j <= width; j++) {\n if (grid[i-1][j-1] == 0)\n continue;\n border = Math.Max(border, 1);\n int left = dp[i][j-1].Left;\n int top = dp[i-1][j].Top;\n int corner = Math.Min(left, top);\n while (corner > 0) {\n if (Math.Min(dp[i-corner][j].Left, dp[i][j-corner].Top) >= corner+1) {\n border = Math.Max(border, corner+1);\n break;\n }\n corner--;\n }\n dp[i][j].Left = left + 1;\n dp[i][j].Top = top + 1;\n }\n }\n \n return border*border;\n }\n}\n```
| 2 | 0 |
['Dynamic Programming', 'C#']
| 0 |
largest-1-bordered-square
|
[Java] Two solutions explained. O(n³) time and O(1) space
|
java-two-solutions-explained-on3-time-an-5aql
|
Simple O(n\u2074) solution passes in 450 ms. Idea is following:\nIterate over possible length O(n)\nIterate over possible starting position O(n\xB2)\nCheck if p
|
roka
|
NORMAL
|
2020-06-21T12:09:33.497220+00:00
|
2020-06-21T12:09:33.497251+00:00
| 204 | false |
Simple `O(n\u2074)` solution passes in 450 ms. Idea is following:\nIterate over possible length `O(n)`\nIterate over possible starting position `O(n\xB2)`\nCheck if possition is valid for given length `O(n)`\nOverall `O(n\u2074)` and `O(1)` space\n\n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int n = grid.length;\n int m = grid[0].length;\n for (int length = Math.min(n, m); length > 0; length--) {\n for (int i = 0; i + length <= n; i++) {\n for (int j = 0; j + length <= m; j++) {\n boolean flag = true;\n \n for (int g = 0; g < length; g++) {\n flag &= grid[i + g][j] == 1;\n flag &= grid[i + g][j + length - 1] == 1;\n \n flag &= grid[i][j + g] == 1;\n flag &= grid[i + length - 1][j + g] == 1;\n }\n \n if (flag) {\n return length * length;\n }\n }\n }\n }\n \n return 0;\n }\n}\n```\n\nWe can improve our solution with following idea:\nFor each cell `grid[i][j]` we should maintain number of `1` above and number of `1` to the left. With this information we can check if subgrid is valid in `O(n\xB3)` time.\nWe can even simplify our solution to use `O(1)` space by using input array for precomputing.\nThis solution runs in 3 ms\n\n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int n = grid.length;\n int m = grid[0].length;\n \n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (grid[i][j] == 0)\n continue;\n \n int left = 1;\n if (j > 0) {\n left = grid[i][j - 1] % 1000 + 1;\n }\n \n int top = 1;\n if (i > 0) {\n top = grid[i - 1][j] / 1000 + 1;\n }\n \n grid[i][j] = left + top * 1000;\n }\n }\n \n int answer = 0;\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n int length = Math.min(grid[i][j] % 1000, grid[i][j] / 1000);\n \n for (int g = answer; g < length; g++) {\n if (grid[i][j - g] / 1000 > g && grid[i - g][j] % 1000 > g) {\n answer = Math.max(answer, g + 1);\n }\n }\n }\n }\n \n return answer * answer;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
largest-1-bordered-square
|
Javascript and C++ solutions
|
javascript-and-c-solutions-by-claytonjwo-b8th
|
Synopsis:\n\nUse a naive DP algorithm to pre-calculate the prefix sequential sums per row and column of the input matrix A. Then use these pre-calculations for
|
claytonjwong
|
NORMAL
|
2020-06-11T12:50:34.654889+00:00
|
2020-06-11T13:09:04.404309+00:00
| 257 | false |
**Synopsis:**\n\nUse a naive DP algorithm to pre-calculate the prefix *sequential* sums per row and column of the input matrix `A`. Then use these pre-calculations for O(1) lookups to determine if a sequential line of 1s exists for each of the 4 edges which can form a bordered sqaure. Iterate through each cell of `i`,`j` of `A` and consider `i`,`j` as the top-left corner of a candidate bordered square of length `k`. The corners of each candidate square are as follows for a square of length `k`:\n\n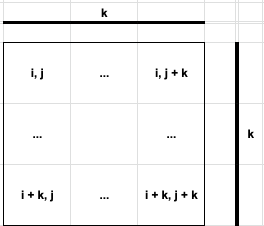\n\nThus, when checking for a square border, we need to check if the top/bottom rows of the border are all 1s and we need to check if the left/right columns of the border are all 1s. The pre-calculated prefix sequential sums can be used to perform these 4 checks along the candidate square border by comparing the absolute difference between each corner cell\'s pre-calculated values and `k`. If the difference is equal to `k`, then we know sequential 1s exist for the edge under consideration.\n\n**Example 1:**\n\n**Input:** A = [[1,1,1],[1,0,1],[1,1,1]]\n**Output:** 9\n\n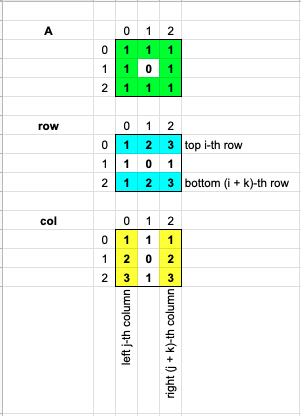\n\nIn the diagram above, the answer is highlighted in green, (ie. a 3x3 square) starting at top-left cell `i = 0`, `j = 0`. `k` is 0-base indexed, thus the border length `k = 2`, when we check each of the 4 sides:\n\n* Check the top/bottom rows highlighted in blue and observe `3 - 1 == 2` \u2705 \n\t* `row[i][j + k] - row[i][j] == k`\n\t* `row[i + k][j + k] - row[i + k][j] == k`\n* Check the left/right columns highlighted in yellow and observe `3 - 1 == 2` \u2705\n\t* `col[i + k][j] - col[i][j] == k`\n\t* `col[i + k][j + k] - col[i][j + k] == k`\n\nThis candidate square is `ok` since all 4 edges contain sequential 1s and the maximum side length `max` is then `k + 1` for edge end-points inclusive.\n\n---\n\n*Javascript*\n```\nlet largest1BorderedSquare = (A, max = 0) => {\n let M = A.length,\n N = A[0].length;\n let row = [...Array(M)].map(_ => Array(N).fill(0)),\n col = [...Array(M)].map(_ => Array(N).fill(0));\n let ok = (i, j, k) => A[i][j]\n && row[i][j + k] - row[i][j] == k // top i-th row\n && col[i + k][j] - col[i][j] == k // left j-th col\n && row[i + k][j + k] - row[i + k][j] == k // bottom (i + k)-th row\n && col[i + k][j + k] - col[i][j + k] == k; // right (j + k)-th col\n row[0][0] = A[0][0];\n col[0][0] = A[0][0];\n for (let i = 0; i < M; ++i)\n for (let j = 0; j < N; ++j)\n row[i][j] = !A[i][j] ? 0 : 1 + (0 <= j - 1 ? row[i][j - 1] : 0), // prefix sequential sums per row\n col[i][j] = !A[i][j] ? 0 : 1 + (0 <= i - 1 ? col[i - 1][j] : 0); // prefix sequential sums per col\n for (let i = 0; i < M; ++i)\n for (let j = 0; j < N; ++j)\n for (let k = 0; i + k < M && j + k < N; ++k)\n max = Math.max(max, ok(i, j, k) ? k + 1 : 0); // k + 1 for edge end-points inclusive\n return max * max; // max length squared == max 2D square area \uD83C\uDFAF\n};\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n int largest1BorderedSquare(VVI& A, int max = 0) {\n int M = A.size(),\n N = A[0].size();\n VVI row(M, VI(N)),\n col(M, VI(N));\n auto ok = [&](auto i, auto j, auto k) {\n return A[i][j]\n && row[i][j + k] - row[i][j] == k // top i-th row\n && col[i + k][j] - col[i][j] == k // left j-th col\n && row[i + k][j + k] - row[i + k][j] == k // bottom (i + k)-th row\n && col[i + k][j + k] - col[i][j + k] == k; // right (j + k)-th col\n };\n row[0][0] = A[0][0];\n col[0][0] = A[0][0];\n for (auto i{ 0 }; i < M; ++i)\n for (auto j{ 0 }; j < N; ++j)\n row[i][j] = !A[i][j] ? 0 : 1 + (0 <= j - 1 ? row[i][j - 1] : 0),\n col[i][j] = !A[i][j] ? 0 : 1 + (0 <= i - 1 ? col[i - 1][j] : 0);\n for (auto i{ 0 }; i < M; ++i)\n for (auto j{ 0 }; j < N; ++j)\n for (auto k{ 0 }; i + k < M && j + k < N; ++k)\n if (ok(i, j, k))\n max = std::max(max, k + 1); // k + 1 for edge end-points inclusive \n return max * max; // max length squared == max 2D square area \uD83C\uDFAF\n }\n};\n```
| 2 | 0 |
[]
| 0 |
largest-1-bordered-square
|
Java DP Solution
|
java-dp-solution-by-sycmtic-2ifz
|
\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[][][] dp = new int[m +
|
sycmtic
|
NORMAL
|
2019-07-30T12:28:47.769921+00:00
|
2019-07-30T12:28:47.769966+00:00
| 400 | false |
```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[][][] dp = new int[m + 1][n + 1][2];\n int max = 0;\n for (int i = 1; i <= m; i++) {\n for (int j = 1; j <= n; j++) {\n if (grid[i - 1][j - 1] == 1) {\n dp[i][j][0] = dp[i][j - 1][0] + 1;\n dp[i][j][1] = dp[i - 1][j][1] + 1;\n int side = Math.min(dp[i][j][0], dp[i][j][1]);\n \n for (int k = side; k > 0; k--) {\n if (dp[i - k + 1][j][0] >= k && dp[i][j - k + 1][1] >= k) {\n max = Math.max(max, k);\n }\n }\n }\n }\n }\n return max * max;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
largest-1-bordered-square
|
Simple Python O(N**3)
|
simple-python-on3-by-davyjing-e8kv
|
\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n memo_h = {}\n memo_v = {}\n for i in range(len(gri
|
davyjing
|
NORMAL
|
2019-07-28T04:06:37.780396+00:00
|
2019-07-28T04:06:37.780431+00:00
| 302 | false |
```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n memo_h = {}\n memo_v = {}\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n memo_v[(i,j)] = 0\n for k in range(i,len(grid)):\n if grid[k][j]:\n memo_v[(i,j)] = k-i+1\n else:\n break\n memo_h[(i,j)] = 0\n for k in range(j,len(grid[0])):\n if grid[i][k]:\n memo_h[(i,j)] = k - j+1\n else:\n break\n res = 0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n k = 1\n while i+k <= len(grid) and j + k <= len(grid[0]):\n if memo_v[(i,j)] >= k and memo_h[(i,j)] >= k and memo_v[(i,j+k-1)] >= k and memo_h[(i+k-1,j)] >= k:\n res = max(res,k*k)\n k += 1\n return res\n```
| 2 | 1 |
[]
| 0 |
largest-1-bordered-square
|
Java, brute force, 6ms
|
java-brute-force-6ms-by-ivan666-s6yu
|
I think the code is quite straight forward, I use two helper functions to find the largest sqaure we can find at each point with some early stop conditions. I t
|
ivan666
|
NORMAL
|
2019-07-28T04:03:02.365931+00:00
|
2019-07-28T04:14:18.505323+00:00
| 321 | false |
I think the code is quite straight forward, I use two helper functions to find the largest sqaure we can find at each point with some early stop conditions. I think there is a lot space to improve, but still this is a very naive and straight forward way to get in an interview or this contest\n```\nclass Solution {\n int max = 0;\n public int largest1BorderedSquare(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n for(int i = 0; i < m; i++){\n if(m - i < max) break;\n for(int j = 0; j < n ; j++){\n if(n - j < max) break;\n if(grid[i][j] == 1){\n int l = getL(grid, i, j);\n max = Math.max(l, max);\n }\n }\n }\n return max*max; \n }\n\t\n\t//check left and top\n \n private int getL(int[][] grid, int x, int y){\n int res = 0, cur = 0;\n for(int i = 0; x+i < grid.length && y + i < grid[0].length; i++){\n if(grid[x+i][y] == 1 && grid[x][y+i] ==1) {\n cur++;\n if(isBS(grid, x, y, cur)) res = cur;\n }\n else break;\n }\n return res;\n }\n\t\n\t//check right and bottom\n \n private boolean isBS(int[][] grid, int x, int y, int l){\n for(int i = 0; i < l; i++){\n if(grid[x+l-1][y+i] ==0 || grid[x+i][y+l-1] ==0) return false;\n }\n return true;\n }\n}
| 2 | 1 |
[]
| 0 |
largest-1-bordered-square
|
Easy & Efficient code Largest 1-Bordered Square
|
easy-efficient-code-largest-1-bordered-s-l7bg
|
IntuitionThe problem requires finding the largest square with all 1s on its border in a binary grid. To efficiently check for valid squares, we need to precompu
|
Ansari_07
|
NORMAL
|
2025-02-26T08:19:59.235063+00:00
|
2025-02-26T08:19:59.235063+00:00
| 67 | false |
# Intuition
The problem requires finding the largest square with all `1`s on its border in a binary grid. To efficiently check for valid squares, we need to precompute how many `1`s extend **rightward** and **downward** from each cell.
Instead of checking every possible square from scratch (which would be inefficient), we leverage **precomputed prefix values** to verify the existence of valid bordered squares in **constant time**.
---
# Approach
1. **Precompute Right and Down Matrices**
- `right[i][j]`: Number of consecutive `1`s to the right of `grid[i][j]`.
- `down[i][j]`: Number of consecutive `1`s downward from `grid[i][j]`.
2. **Iterate Through Each Cell**
- Determine the maximum possible side length (`maxside`) for a square starting at `(i, j)`.
- Try to form a square of side `maxside` by checking:
- If the **bottom row** has at least `side` consecutive `1`s (`right[i + side - 1][j]`).
- If the **rightmost column** has at least `side` consecutive `1`s (`down[i][j + side - 1]`).
- **Update `maxsize`** accordingly.
3. **Return `maxsize * maxsize`** as the area of the largest valid square.
---
# Complexity
- **Precomputing `right` and `down` arrays:**
- Each cell is processed once: $$O(m imes n)$$
- **Checking for the largest square:**
- In the worst case, we check each cell and iterate over possible side lengths: $$O(m imes n)$$
- **Overall Complexity:** $$O(m imes n)$$
- Efficient for large grids.
- **Space Complexity:** $$O(m imes n)$$
- We store two additional matrices (`right` and `down`), making it $$O(m imes n)$$ extra space.
---
# Code
```cpp
class Solution {
public:
int largest1BorderedSquare(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
vector<vector<int>> right(n, vector<int>(m, 0));
vector<vector<int>> down(n, vector<int>(m, 0));
// Precompute right and down arrays
for (int i = n - 1; i >= 0; i--) {
for (int j = m - 1; j >= 0; j--) {
if (grid[i][j] == 1) {
right[i][j] = (j == m - 1) ? 1 : 1 + right[i][j + 1];
down[i][j] = (i == n - 1) ? 1 : 1 + down[i + 1][j];
}
}
}
int maxsize = 0;
// Iterate to find the largest square
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int maxside = min(right[i][j], down[i][j]);
for (int side = maxside; side > maxsize; side--) { // Early stopping
if (right[i + side - 1][j] >= side && down[i][j + side - 1] >= side) {
maxsize = side;
break; // No need to check smaller sizes
}
}
}
}
return maxsize * maxsize;
}
};
```
---
# Key Optimizations
✅ **Handles Rectangular Grids** (supports `m × n`, not just `n × n`)
✅ **Early Stopping** (Avoids unnecessary iterations by breaking early when a valid square is found)
✅ **Optimized Side-Length Search** (Only checks sizes greater than the current `maxsize`)
This solution efficiently finds the largest 1-bordered square in any binary grid. 🚀
| 1 | 0 |
['C++']
| 0 |
largest-1-bordered-square
|
Explained
|
explained-by-rickienol-ke9e
|
IntuitionTo avoid repeated work, process the grid first;ApproachStore in all potential upper left corners the largest possible side length of the square, based
|
rickienol
|
NORMAL
|
2025-02-22T14:06:09.407623+00:00
|
2025-02-22T14:06:09.407623+00:00
| 30 | false |
# Intuition
To avoid repeated work, process the grid first;
# Approach
Store in all potential upper left corners the largest possible side length of the square, based on the number of consecutive 1's horizontally and vertically.
Also store in all potential bottom right corners likewise.
Then find the largest pair of upper-left and bottom-right corner.
# Complexity
- Time complexity:
$$O(n^2)$$
# Code
```cpp []
class Solution {
public:
int largest1BorderedSquare(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
// Check if there is a 1, if not, return 0;
bool hasOne = false;
for (int i=0;i<m;i++) {
for (int j=0;j<n;j++) {
if (grid[i][j]==1) {hasOne = true; break;}
}
if (hasOne) break;
}
if (!hasOne) return 0;
// create 4 matrices, each entry stores:
// in A: the longest horizontal side length with entry position being the right end;
// in B: the longest vertical side length with entry position being the bottom end;
// in C: the longest horizontal side length with entry position being the left end;
// in D: the longest vertical side length with entry position being the top end;
vector<vector<int>> A = grid, B = grid, C = grid, D = grid;
for (int i=0;i<m;i++) {
for (int j=0;j<n;j++) {
if (j>0&&A[i][j-1]!=0&&A[i][j]!=0) A[i][j]+=A[i][j-1];
if (j>0&&C[i][n-j]!=0&&C[i][n-j-1]!=0) C[i][n-j-1]+=C[i][n-j];
if (i>0&&B[i-1][j]!=0&&B[i][j]!=0) B[i][j]+=B[i-1][j];
if (i>0&&D[m-i][j]!=0&&D[m-i-1][j]!=0) D[m-i-1][j]+=D[m-i][j];
}
}
// Update A and C such that each entry stores the longest segment length that can be both vertical and horizontal, with the position of each entry being:
// in A: the bottom right corner;
// in C: the upper left corner;
for (int i=0;i<m;i++) {
for (int j=0;j<n;j++) {
A[i][j] = min(A[i][j],B[i][j]);
C[i][j] = min(C[i][j],D[i][j]);
}
}
int res = 1;
// loop through C, the upper left corner, and check if the bottom right corner is in A;
for (int i=0;i<m;i++) {
for (int j=0;j<n;j++) {
for (int a=C[i][j]; a>res; a--) {
if (A[i+a-1][j+a-1]>=a) {
res = a;
break;
}
}
}
}
return res*res;
}
};
```
| 1 | 0 |
['C++']
| 0 |
largest-1-bordered-square
|
Java code (Recursion/Backtracking)
|
java-code-recursionbacktracking-by-anike-oyay
|
Intuition
What we want: We need to find the biggest square in the grid where every cell along its border is a 1.
Key idea: Even if a smaller square doesn’t w
|
Aniket-Yadav
|
NORMAL
|
2025-02-20T08:58:27.350772+00:00
|
2025-02-20T08:58:27.350772+00:00
| 18 | false |
# Intuition
- **What we want**: We need to find the biggest square in the grid where every cell along its border is a 1.
- **Key idea**: Even if a smaller square doesn’t work because one of its border cells is 0, a bigger square might work because that 0 could end up inside the square (and we only care about the border).
# Approach
1. **Start at Every 1:**
Look at every cell in the grid. If it’s a 1, consider it as the top-left corner of a square.
2. **Try Different Sizes:**
From that starting cell, try making squares of different sizes (like 1x1, 2x2, 3x3, etc.) as long as the square fits in the grid.
3. **Check the Border:**
For each square, check if all the cells along its edges (top, bottom, left, right) are 1.
4. **Keep the Largest:**
If the square’s border is all 1s, update your record of the largest square you’ve found.
5. **Final Answer:**
After checking all possible squares, return the area (side length squared) of the largest valid square.
# Complexity
- Time complexity:
For every cell, we try many square sizes and check each square’s border. This makes the algorithm slower on large grids. In the worst-case, it can be thought of as checking about m × n × (size^2) cells, where m and n are the grid’s dimensions.
- Space complexity:
The primary extra space used is due to recursion. The maximum depth of recursion is K (the largest square side length). Hence, the space complexity is O(min(m, n)) (excluding the input grid).
# Code
```java []
class Solution {
int rows, cols, maxSquare;
int[][] grid;
public int largest1BorderedSquare(int[][] g) {
if (g == null || g.length == 0 || g[0].length == 0) return 0;
grid = g;
rows = grid.length;
cols = grid[0].length;
maxSquare = 0;
// Try every cell as the top-left corner.
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (grid[i][j] == 1) { // Only consider if the top-left is 1.
backtrack(i, j, 1);
}
}
}
return maxSquare * maxSquare;
}
// Recursively check all possible square sizes from (i, j)
private void backtrack(int i, int j, int size) {
// If the square goes out of bounds, stop recursion.
if (i + size > rows || j + size > cols) return;
// Check if the current square's border is all 1s.
if (isValidBorder(i, j, size)) {
if (size > maxSquare) {
maxSquare = size;
}
}
// Regardless of current validity, try a larger square.
backtrack(i, j, size + 1);
}
// Check if the square with top-left at (i, j) and side length 'size'
// has all 1s on its border.
private boolean isValidBorder(int i, int j, int size) {
// Check top and bottom rows.
for (int col = j; col < j + size; col++) {
if (grid[i][col] == 0) return false; // Top border
if (grid[i + size - 1][col] == 0) return false; // Bottom border
}
// Check left and right columns (excluding corners already checked).
for (int row = i + 1; row < i + size - 1; row++) {
if (grid[row][j] == 0) return false; // Left border
if (grid[row][j + size - 1] == 0) return false; // Right border
}
return true;
}
}
```
| 1 | 0 |
['Backtracking', 'Recursion', 'Java']
| 0 |
largest-1-bordered-square
|
[Java] ✅ PREFIX SUM ✅ CLEAN CODE ✅ CLEAN EXPLANATIONS
|
java-prefix-sum-clean-code-clean-explana-0ofm
|
Approach\n1. Compute the row and column prefixes of count of 1 and store them in an 2 x int[][] \n - EG: [[1,1,0,0,1],[0,1,0,1,0] \n - rowPrefix [[1,2,2,2
|
StefanelStan
|
NORMAL
|
2024-04-27T17:47:39.150639+00:00
|
2024-04-27T17:47:39.150669+00:00
| 91 | false |
# Approach\n1. Compute the row and column prefixes of count of 1 and store them in an 2 x int[][] \n - EG: [[1,1,0,0,1],[0,1,0,1,0] \n - rowPrefix [[1,2,2,2,3],[0,1,1,2,2]] -> count of 1s on each row\n - colPrefix [[1,1,0,0,1],[1,2,0,1,1]] -> count of 1s on each column by row.\n2. Knowing this, we can apply interval count:\n - number of 1s at on row 0 between index 3 and 7 is rowPrefix[0][7] - rowPrefix[0][2].\n - number of 1s on column 3 between rows 2 and 8 is colPrefix[8][3] - colPrefix[1][3]\n3. In 2 fors (i - rows, j columns, stopping when i,j < length - range)\n - Find the further diagonal point from i & j that sits at the edge of a square.\n - the furthest point if Math.min(n - i, m - j)\n - From the furthest, try to determine if the 4 borders (aka interval counts) equal range.\n - Stop when you find a range or when current range goes below the largest range found so far.\n\n# Complexity\n- Time complexity:$$O(n * m * min(m, n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n * m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int[][] rowPrefix = new int[grid.length][grid[0].length];\n int[][] colPrefix = new int[grid.length][grid[0].length];\n getPrefixes(grid, rowPrefix, colPrefix);\n return findLargestBorder(grid, rowPrefix, colPrefix);\n }\n\n private void getPrefixes(int[][] grid, int[][] rowPrefix, int[][] colPrefix) {\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n rowPrefix[i][j] = grid[i][j] + (j == 0 ? 0 : rowPrefix[i][j - 1]);\n colPrefix[i][j] = grid[i][j] + (i == 0 ? 0 : colPrefix[i - 1][j]);\n }\n }\n }\n\n private int findLargestBorder(int[][] grid, int[][] rowPrefix, int[][] colPrefix) {\n int largest = 0;\n boolean found = false;\n for (int i = 0; i < grid.length - largest; i++) {\n for (int j = 0; j < grid[i].length - largest; j++) {\n if (grid[i][j] == 1) {\n found = true;\n largest = Math.max(largest, shrinkBorder(grid, i, j, rowPrefix, colPrefix, largest));\n }\n }\n }\n return !found ? 0 : (int)Math.pow(1 + largest, 2);\n }\n\n private int shrinkBorder(int[][] grid, int x, int y, int[][] rowPrefix, int[][] colPrefix, int largest) {\n int range = Math.min(grid.length - x, grid[0].length - y) - 1;\n while (range > largest) {\n if (isValidBorder(grid, x, y, range, rowPrefix, colPrefix)) {\n break;\n }\n range--;\n }\n return range; \n }\n\n private boolean isValidBorder(int[][] grid, int x, int y, int range, int[][] rowPrefix, int[][] colPrefix) {\n return 1 + range == rowPrefix[x][y + range] - (y == 0 ? 0 : rowPrefix[x][y-1])\n && 1 + range == rowPrefix[x + range][y + range] - (y == 0 ? 0 : rowPrefix[x + range][y-1])\n && 1 + range == colPrefix[x + range][y] - (x == 0 ? 0 : colPrefix[x-1][y])\n && 1 + range == colPrefix[x + range][y + range] - (x == 0 ? 0 : colPrefix[x-1][y + range]);\n }\n}\n```
| 1 | 0 |
['Prefix Sum', 'Java']
| 0 |
largest-1-bordered-square
|
O(n^2*Log(n)) fastest in theory
|
on2logn-fastest-in-theory-by-nsknojj-tzse
|
Approach\n1. \u9884\u5904\u7406\u6C42\u51FA\u6BCF\u4E2A\u683C\u5B50\u6CBF\u77401\u8D70\u5411\u5DE6\u3001\u4E0A\u3001\u53F3\u3001\u4E0B\uFF0C\u80FD\u5EF6\u4F38\u
|
nsknojj
|
NORMAL
|
2023-11-22T05:41:56.797968+00:00
|
2023-11-22T06:17:28.674136+00:00
| 80 | false |
# Approach\n1. \u9884\u5904\u7406\u6C42\u51FA\u6BCF\u4E2A\u683C\u5B50\u6CBF\u77401\u8D70\u5411\u5DE6\u3001\u4E0A\u3001\u53F3\u3001\u4E0B\uFF0C\u80FD\u5EF6\u4F38\u7684\u6700\u957F\u957F\u5EA6\n2. \u5BF9\u6BCF\u4E2A\u683C\u5B50grid[i][j]\uFF0C\u53F3\u548C\u4E0B\u4E2D\u80FD\u5EF6\u4F38\u7684\u8F83\u5C0F\u503C\u5B58\u653E\u4E3Aa[i][j]\uFF0C\u5DE6\u548C\u4E0A\u4E2D\u80FD\u5EF6\u4F38\u7684\u8F83\u5C0F\u503C\u5B58\u653E\u4E3Ab[i][j]\u3002\n3. \u663E\u7136\uFF0C\u5BF9\u4E8E\u4E00\u4E2A\u5DE6\u4E0A\u89D2\u4E3A(x1, y1)\uFF0C\u53F3\u4E0B\u89D2\u4E3A(x2, y2)\u7684\u6B63\u65B9\u5F62\uFF0C\u6EE1\u8DB3a[x1][y1] >= x2 - x1 + 1 \u4E14 b[x2][y2] >= x2 - x1 + 1\u3002\uFF08\u89D2\u7684\u5EF6\u4F38\u957F\u5EA6\u5927\u4E8E\u7B49\u4E8E\u8FB9\u957F\uFF09\n4. \u6240\u6709\u6B63\u65B9\u5F62\u7684\u5DE6\u4E0A\u548C\u53F3\u4E0B\u4E24\u4E2A\u683C\u5B50\u5FC5\u5B9A\u5728\u540C\u4E00\u5BF9\u89D2\u7EBF\u4E0A\u3002\u5728\u4E00\u4E2A M * N \u7684\u7F51\u683C\u4E2D\u5BF9\u89D2\u7EBF\u7684\u4E2A\u6570\u662F M + N - 1\u4E2A\uFF0C\u6211\u4EEC\u5C1D\u8BD5\u679A\u4E3E\u6CBF\u7740\u6BCF\u4E00\u4E2A\u5BF9\u89D2\u7EBF\u4ECE\u5DE6\u4E0A\u5230\u53F3\u4E0B\u679A\u4E3E\u3002\n5. \u5F53\u679A\u4E3E\u5230(x2, y2)\u4F5C\u4E3A\u53F3\u4E0B\u89D2\u65F6\uFF0C\u6211\u4EEC\u9700\u8981\u627E\u5230\u4E00\u4E2A\u6700\u9760\u5DE6\u4E0A\u7684(x1, y1)\uFF0C\u4F7F\u5F97\u6B65\u9AA43\u4E2D\u7684\u4E0D\u7B49\u5F0F\u6EE1\u8DB3\u3002\u5BF9\u5B83\u8FDB\u884C\u53D8\u6362\u5F97\u5230\na[x1][y1] + x1 >= x2 + 1\nx1 >= x2 - b[x2][y2] + 1\n\u7B49\u5F0F\u7684\u53F3\u8FB9\u5728\u679A\u4E3E\u5230(x2,y2)\u65F6\u662F\u56FA\u5B9A\u7684\u503C\uFF0C\u6211\u4EEC\u8981\u6C42\u7684\u662F\u6EE1\u8DB3\u8FD9\u4E2A\u4E0D\u7B49\u5F0F\u7684\u6700\u5C0F\u7684x1\u3002y1\u5176\u5B9E\u5E76\u4E0D\u91CD\u8981\uFF0C\u56E0\u4E3A\u5728\u4E00\u4E2A\u5BF9\u89D2\u7EBF\u91CC\u4ECEx1\u80FD\u8BA1\u7B97\u51FAy1\u3002\n6. \u770B\u7B2C\u4E00\u4E2A\u4E0D\u7B49\u5F0F\uFF0Cx2 + 1 \u5728\u679A\u4E3E\u8FC7\u7A0B\u4E2D\u4F1A\u9010\u6E10\u589E\u5927\uFF0C\u6240\u4EE5\u6EE1\u8DB3a[x1][y1] + x1 >= x2 + 1\u7684x1\u4F1A\u8D8A\u6765\u8D8A\u5C11\u3002 \u770B\u7B2C\u4E8C\u4E2A\u4E0D\u7B49\u5F0F\uFF0C\u53EA\u662F\u8981\u6C42\u4E00\u4E2A\u6BD4x2 - b[x2][y2] + 1\u5927\u6216\u76F8\u7B49\u7684x1\u3002\n7. \u6240\u4EE5\uFF0C\u5728\u679A\u4E3E\u8FC7\u7A0B\u4E2D\uFF0C\u6211\u4EEC\u628A\u51FA\u73B0\u7684a[x1][y1] + x1\u5B58\u50A8\u4E0B\u6765\uFF0C\u7528TreeSet\u7EF4\u62A4\uFF0C\u5F53\u67D0\u4E9Ba[x1][y1] + x1\u4E0D\u6EE1\u8DB3\u7B2C\u4E00\u4E2A\u4E0D\u7B49\u5F0F\u65F6\uFF0C\u5C06\u5B83\u4EEC\u8E22\u51FA\u3002\u5BF9\u4E8E\u6BCF\u4E00\u6B21\u679A\u4E3E\uFF0C\u6211\u4EEC\u9700\u8981\u6C42\u8FD8\u6EE1\u8DB3\u7B2C\u4E00\u4E2A\u4E0D\u7B49\u5F0F\u7684x1\u4E2D\uFF0C\u6700\u5C0F\u7684\u5927\u4E8E\u7B49\u4E8Ex2 - b[x2][y2] + 1\u7684\u90A3\u4E2A\u3002\n\n# Complexity\n- Time complexity: $$O(n^2log(n))$$\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n class Summation implements Comparable<Summation> {\n int sum;\n int i;\n public Summation(int sum, int i) {\n this.sum = sum;\n this.i = i;\n // System.out.println("Summation " + sum + "," + i);\n }\n @Override\n public int compareTo(Summation otherSum) {\n if (this.sum == otherSum.sum) return this.i - otherSum.i;\n return this.sum - otherSum.sum;\n }\n }\n\n public int largest1BorderedSquare(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[][] leftToRight = new int[m+1][n+1];\n int[][] topToDown = new int[m+1][n+1];\n\n int[][] rightToLeft = new int[m+2][n+2];\n int[][] downToTop = new int[m+2][n+2];\n int[][] a = new int[m+1][n+1];\n int[][] b = new int[m+1][n+1];\n\n for (int i = 1; i <= m; i ++) {\n for (int j = 1; j <= n; j ++) {\n if (grid[i-1][j-1] == 0) continue;\n leftToRight[i][j] = leftToRight[i][j-1] + 1;\n topToDown[i][j] = topToDown[i-1][j] + 1;\n b[i][j] = Math.min(leftToRight[i][j], topToDown[i][j]);\n }\n }\n\n for (int i = m; i >= 1; i --) {\n for (int j = n; j >= 1; j --) {\n if (grid[i-1][j-1] == 0) continue;\n rightToLeft[i][j] = rightToLeft[i][j+1] + 1;\n downToTop[i][j] = downToTop[i+1][j] + 1;\n a[i][j] = Math.min(rightToLeft[i][j], downToTop[i][j]);\n }\n }\n\n TreeSet<Summation> summation = new TreeSet<>();\n TreeSet<Integer> indexSet = new TreeSet<>();\n\n int ans = 0;\n\n for (int r = 1; r <= n + m - 1; r ++) {\n int i, j;\n if (r > m) {\n i = 1; j = r - m + 1;\n } else {\n i = r; j = 1;\n }\n summation.clear();\n indexSet.clear();\n for (; i <= m && j <= n; i++, j++) {\n if (a[i][j] >= 1) {\n summation.add(new Summation(a[i][j] + i, i));\n indexSet.add(i);\n }\n while (!summation.isEmpty() && summation.first().sum < i + 1) {\n indexSet.remove(summation.first().i);\n summation.pollFirst();\n }\n if (b[i][j] <= ans) continue;\n Integer ceil = indexSet.ceiling(i - b[i][j] + 1);\n if (ceil != null) {\n ans = Math.max(ans, i - ceil + 1);\n }\n }\n\n }\n return ans * ans;\n }\n}\n```
| 1 | 1 |
['Java']
| 0 |
largest-1-bordered-square
|
RAM RAM SARAEYA NU
|
ram-ram-saraeya-nu-by-josephstarkrgb-of43
|
class Solution {\n public:\n int largest1BorderedSquare(vector>& grid) \n {\n int n=grid.size();\n int m=grid[0].size();\
|
josephstarkrgb
|
NORMAL
|
2023-08-25T12:46:35.004592+00:00
|
2023-08-25T12:46:35.004616+00:00
| 148 | false |
class Solution {\n public:\n int largest1BorderedSquare(vector<vector<int>>& grid) \n {\n int n=grid.size();\n int m=grid[0].size();\n vector<vector<pair<int,int>>> dp(n+1,vector<pair<int,int>> (m+1));\n\n for(int i=n-1;i>=0;i--)\n {\n for(int j=m-1;j>=0;j--)\n {\n if(grid[i][j]==0)\n continue;\n dp[i][j].first=dp[i][j+1].first+1;\n dp[i][j].second=dp[i+1][j].second+1;\n }\n } \n\n int ans=0;\n\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n int e=min(dp[i][j].first,dp[i][j].second);\n int k=e;\n for(k=e;k>0;k--)\n {\n if(dp[i][j+k-1].second>=k && dp[i+k-1][j].first>=k)\n break;\n }\n ans=max(ans,k);\n }\n }\n\n return ans*ans;\n }\n };\n
| 1 | 0 |
['C++']
| 0 |
largest-1-bordered-square
|
Explained and Commented Solution
|
explained-and-commented-solution-by-dari-hfq9
|
\n\nclass Solution {\npublic:\n int findLargestSquare(vector<vector<int>>& mat) \n { \n int max = 0; int m = mat.size() , n = mat[0].size();\n vect
|
darian-catalin-cucer
|
NORMAL
|
2023-01-28T22:07:03.948987+00:00
|
2023-01-28T22:07:03.949013+00:00
| 144 | false |
\n```\nclass Solution {\npublic:\n int findLargestSquare(vector<vector<int>>& mat) \n { \n int max = 0; int m = mat.size() , n = mat[0].size();\n vector<vector<int>> hor(m,vector<int> (n,0)) , ver(m,vector<int> (n,0));\n \n for (int i=0; i<m; i++) { \n for (int j=0; j<n; j++) { \n if (mat[i][j] == 1) \n { \n hor[i][j] = (j==0)? 1: hor[i][j-1] + 1; // auxillary horizontal array\n ver[i][j] = (i==0)? 1: ver[i-1][j] + 1; // auxillary vertical array\n } \n } \n } \n \n for (int i = m-1; i>=0; i--) { \n for (int j = n-1; j>=0; j--) { \n int small = min(hor[i][j], ver[i][j]); // choose smallest of horizontal and vertical value\n while (small > max) { \n if (ver[i][j-small+1] >= small && hor[i-small+1][j] >= small) // check if square exists with \'small\' length\n max = small; \n small--; \n } \n } \n } \n return max*max; \n} \n \n int largest1BorderedSquare(vector<vector<int>>& grid) {\n return findLargestSquare(grid); \n }\n};\n```
| 1 | 0 |
['C++']
| 1 |
largest-1-bordered-square
|
Kotlin prefix sum
|
kotlin-prefix-sum-by-c4tdog-eiak
|
Code\n\nclass Solution {\n fun largest1BorderedSquare(g: Array<IntArray>): Int {\n var a = Array<Array<IntArray>>(g.size, { Array(g[0].size, { IntArra
|
c4tdog
|
NORMAL
|
2023-01-17T01:35:57.524298+00:00
|
2023-01-17T01:35:57.524335+00:00
| 127 | false |
# Code\n```\nclass Solution {\n fun largest1BorderedSquare(g: Array<IntArray>): Int {\n var a = Array<Array<IntArray>>(g.size, { Array(g[0].size, { IntArray(4, { 0 }) }) })\n\n for (r in 0..g.size - 1) {\n var t = a[r]\n\n var z = 0\n for (c in 0..g[0].size - 1) {\n if (g[r][c] == 1) {\n z++\n t[c][0] = z\n } else z = 0\n }\n z = 0\n for (c in g[0].size - 1 downTo 0) {\n if (g[r][c] == 1) {\n z++\n t[c][1] = z\n } else z = 0\n }\n }\n\n for (c in 0..g[0].size - 1) {\n var z = 0\n for (r in 0..g.size - 1) {\n if (g[r][c] == 1) {\n z++\n a[r][c][2] = z\n } else z = 0\n }\n\n z = 0\n for (r in g.size - 1 downTo 0) {\n if (g[r][c] == 1) {\n z++\n a[r][c][3] = z\n } else z = 0\n }\n }\n\n var res = 0\n\n for (r in 0..g.size - 1) {\n for (c in 0..g[0].size - 1) {\n if (g[r][c] == 1) {\n var m = Math.min(a[r][c][1], a[r][c][3])\n if (m <= res) continue\n \n var diff = m - (res + 1)\n\n // check all from m downTo current res + 1\n for (k in 0..diff) {\n var row = r + (m - 1 - k)\n var col = c + (m - 1 - k)\n if (a[row][col][0] >= m - k && a[row][col][2] >= m - k) {\n res = m - k\n break\n }\n }\n }\n }\n }\n\n return res * res\n }\n}\n```
| 1 | 0 |
['Prefix Sum', 'Kotlin']
| 0 |
largest-1-bordered-square
|
Python (Simple DP)
|
python-simple-dp-by-rnotappl-4hwo
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rnotappl
|
NORMAL
|
2022-11-29T11:19:54.755379+00:00
|
2022-11-29T11:19:54.755435+00:00
| 150 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largest1BorderedSquare(self, grid):\n n, m = len(grid), len(grid[0])\n\n top, left = [i[:] for i in grid], [i[:] for i in grid]\n\n for i in range(n):\n for j in range(m):\n if grid[i][j] == 1:\n if i: top[i][j] = top[i-1][j] + 1\n if j: left[i][j] = left[i][j-1] + 1\n\n\n for r in range(min(m,n),0,-1):\n for i in range(n-r+1):\n for j in range(m-r+1):\n if min(top[i+r-1][j],top[i+r-1][j+r-1],left[i][j+r-1],left[i+r-1][j+r-1]) >= r:\n return r*r\n\n return 0\n\n\n \n\n\n\n\n \n\n\n\n\n\n\n \n\n\n\n\n\n \n\n \n\n\n\n\n\n\n\n \n\n\n\n```
| 1 | 0 |
['Python3']
| 0 |
largest-1-bordered-square
|
largest 1 bordered square java solution
|
largest-1-bordered-square-java-solution-3rke4
|
**\n\n\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n\t\tint maxLengthSquare=0;\n\t\tfor(int row=0; row<grid.length; row++){\n\t\t\t
|
siddhantdhandore9
|
NORMAL
|
2022-07-01T11:28:58.829521+00:00
|
2022-07-01T11:28:58.829550+00:00
| 195 | false |
**\n\n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n\t\tint maxLengthSquare=0;\n\t\tfor(int row=0; row<grid.length; row++){\n\t\t\tfor(int col=0; col<grid[0].length; col++){\n\t\t\t\tif(grid[row][col]==1){\n\t\t\t\t\tint nextRowCol=0;\n\t\t\t\t\twhile(row+nextRowCol<grid.length && col+nextRowCol<grid[0].length && grid[row+nextRowCol][col]==1 && grid[row][col+nextRowCol]==1){\n\t\t\t\t\t\tint newRow = row+nextRowCol;\n\t\t\t\t\t\tint newCol = col+nextRowCol;\n\t\t\t\t\t\tint counter=0;\n\t\t\t\t\t\twhile(newCol>=col && newRow >= row && grid[row+nextRowCol][newCol]==1 && grid[newRow][col+nextRowCol]==1){\n\t\t\t\t\t\t\tcounter+=1;\n\t\t\t\t\t\t\tnewCol-=1;\n\t\t\t\t\t\t\tnewRow-=1;\n\t\t\t\t\t\t}\n\t\t\t\t\t\tif(counter==nextRowCol+1 && counter>=maxLengthSquare){\n\t\t\t\t\t\t\tmaxLengthSquare=counter;\n\t\t\t\t\t\t} \n\t\t\t\t\t\tnextRowCol+=1;\n\t\t\t\t\t}\n\t\t\t\t\t\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn maxLengthSquare*maxLengthSquare;\n\t\n }\n}\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
Easy-understanding solution
|
easy-understanding-solution-by-shubham_k-3xxa
|
\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m = grid.size();\n int n= grid[0].size();\n
|
shubham_kushwaha
|
NORMAL
|
2022-07-01T06:43:23.392533+00:00
|
2022-07-01T06:43:23.392605+00:00
| 443 | false |
```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m = grid.size();\n int n= grid[0].size();\n vector<vector<int>>left(m,vector<int>(n,0));\n vector<vector<int>>down(m,vector<int>(n,0));\n for(int i = 0;i<m;i++){\n left[i][n-1] = grid[i][n-1];\n }\n for(int i = 0;i<m;i++){\n for(int j = n-2;j>=0;j--){\n //now make the left grid\n if(grid[i][j] == 0){\n left[i][j] = 0;\n }\n else{\n left[i][j] += left[i][j+1]+1;\n }\n }\n }\n for(int i = 0;i<n;i++){\n down[m-1][i] = grid[m-1][i];\n }\n for(int i = m-2;i>=0 ;i--){\n for(int j= 0;j<n;j++){\n if(grid[i][j] == 0){\n down[i][j] = 0;\n }\n else{\n down[i][j]+= down[i+1][j]+1;\n }\n }\n }\n for(int i = 0;i<m;i++){\n for(int j = 0;j<n;j++){\n cout<<left[i][j] <<\' \';\n }\n cout<<endl;\n }\n cout<<endl;\n for(int i = 0;i<m;i++){\n for(int j = 0;j<n;j++){\n cout<<down[i][j] <<\' \';\n }\n cout<<endl;\n }\n // now take the minimum of the values of the required\n int ans = 0;\n for(int i = 0;i<m;i++){\n for(int j = 0;j<n;j++){\n // take the minimum of the values of the \n if(grid[i][j] == 1){\n int ci = i;\n int cj = j;\n int w = min(left[i][j],down[i][j]);\n // now serach in the left and down when no of the 1\'s become equal\n for(int k = 0;k<w;k++){\n // size of the square of the submatrix\n if(k == 0){\n ans = max(ans,1);\n }\n else{\n // now make it maximum value of the \n if(down[ci][cj+k] >= k+1 && left[ci+k][cj] >=k+1){\n ans = max(ans,(k+1)*(k+1));\n }\n }\n\n }\n }\n \n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C']
| 1 |
largest-1-bordered-square
|
JAVA | kind of dp
|
java-kind-of-dp-by-crackitsean-yihh
|
\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int m=grid.length;\n int n=grid[0].length;\n\t\t// rows[r][c] is the l
|
CrackItSean
|
NORMAL
|
2022-04-04T02:32:38.396002+00:00
|
2022-04-04T02:32:38.396063+00:00
| 170 | false |
```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int m=grid.length;\n int n=grid[0].length;\n\t\t// rows[r][c] is the length of the line ended at [r,c] on row r\n int[][] rows=new int[m][n]; \n\t\t// the length of the line ended at [r,c] on colume c\n int[][] cols=new int[m][n];\n int res=0;\n for(int r=0;r<m;r++){\n for(int c=0;c<n;c++){\n if(grid[r][c]==0){\n rows[r][c]=0;\n cols[r][c]=0;\n }else{\n rows[r][c]=c==0?1:rows[r][c-1]+1;\n cols[r][c]=r==0?1:cols[r-1][c]+1;\n if(res>=rows[r][c]||res>=cols[r][c]){\n continue;\n }\n res=Math.max(res,getD(rows,cols,r,c));\n }\n }\n }\n return res*res;\n }\n \n\t// get the dimension of the largest square which bottom-right point is [row,col]\n private int getD(int[][] rows,int[][] cols,int row,int col){\n int len=Math.min(rows[row][col],cols[row][col]);\n for(int i=len-1;i>=0;i--){\n if(rows[row-i][col]>i && cols[row][col-i]>i){\n return i+1;\n }\n }\n return 1;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
largest-1-bordered-square
|
[Java] Built with vertical and horizontal grids
|
java-built-with-vertical-and-horizontal-x89mt
|
\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n \n int m = grid.length;\n int n = grid[0].length;\n \n
|
thinkman
|
NORMAL
|
2021-12-29T16:58:47.953136+00:00
|
2021-12-29T17:00:10.800719+00:00
| 146 | false |
```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n \n int m = grid.length;\n int n = grid[0].length;\n \n int[][] ver = new int[m][n];\n int[][] hor = new int[m][n];\n \n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (grid[j][i] == 1) {\n ver[j][i] = j == 0 ? ver[j][i] = 1 : ver[j-1][i] + 1; \n } else {\n ver[j][i] = 0;\n }\n }\n }\n \n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == 1) {\n hor[i][j] = j == 0 ? hor[i][j] = 1 : hor[i][j-1] + 1;\n } else {\n hor[i][j] = 0;\n }\n }\n }\n \n int max = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n \n boolean found = false;\n for (int len = Math.min(ver[i][j], hor[i][j]); len > max && !found; len--) {\n \n if (ver[i][j+1-len] >= len && hor[i+1-len][j] >= len) {\n max = len;\n found = true;\n }\n }\n }\n }\n \n return max * max;\n }\n}\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
C++, faster than 100%
|
c-faster-than-100-by-prakhar009-um9l
|
\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& a){\n int n=a.size(),m=a[0].size(),left[n+1][m+1],top[n+1][m+1],i,j,ans=
|
prakhar009
|
NORMAL
|
2021-07-27T08:19:25.444480+00:00
|
2021-07-27T08:20:29.079649+00:00
| 255 | false |
```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& a){\n int n=a.size(),m=a[0].size(),left[n+1][m+1],top[n+1][m+1],i,j,ans=0;\n memset(left,0,sizeof(left));\n memset(top,0,sizeof(top));\n for(i=1;i<=n;i++){\n for(j=1;j<=m;j++){\n if(a[i-1][j-1]==1){\n left[i][j]=1+left[i][j-1];\n top[i][j]=1+top[i-1][j];\n int mn=min(top[i][j],left[i][j]),flag=0;\n while(mn>0){\n if(top[i][j-mn+1]>=mn&&left[i-mn+1][j]>=mn){\n ans=max(ans,mn);flag=1;\n }\n mn--;if(flag)break;\n }\n }\n }\n }\n return ans*ans;\n \n }\n};\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
C++ Concise solution with comments: time-N^3; Memory: N^2
|
c-concise-solution-with-comments-time-n3-smzz
|
1) Intruducing and calculating two grids for storing prefix sum on columns & rows rescpectively. \n2) Checking all sub-grids from bigger size down, verifying a
|
xiaoping3418
|
NORMAL
|
2021-06-20T02:15:12.213479+00:00
|
2021-06-20T12:14:57.631471+00:00
| 218 | false |
1) Intruducing and calculating two grids for storing prefix sum on columns & rows rescpectively. \n2) Checking all sub-grids from bigger size down, verifying all four edges to see all of them are with 1\'s \n~~~\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n // prefix sum on columns\n vector<vector<int>> sumC(m, vector<int>(n + 1, 0));\n // prefix sum on rows\n vector<vector<int>> sumR(m + 1, vector<int>(n, 0));\n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n sumC[i][j + 1] = sumC[i][j] + grid[i][j];\n }\n }\n for (int j = 0; j < n; ++j) {\n for (int i = 0; i < m; ++i) {\n sumR[i + 1][j] = sumR[i][j] + grid[i][j];\n }\n }\n \n // check all sub-grids from bigger size down\n // by verifying if all four edges are all with 1\'s\n for (int s = min(m, n); s > 0; --s) {\n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n if (s + i > m || s + j > n) continue;\n bool flag = true;\n if (sumR[s+i][j] - sumR[i][j] < s) flag = false;\n if (sumR[s+i][j+s-1] - sumR[i][j+s-1] < s) flag = false;\n if (sumC[i][j+s] - sumC[i][j] < s) flag = false;\n if (sumC[s+i-1][j+s] - sumC[s+i-1][j] < s) flag = false;\n if (flag == true) return s * s;\n }\n }\n }\n return 0;\n }\n};\n~~~\n
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
3ms 95% Faster Solution
|
3ms-95-faster-solution-by-shivam_gupta-3zps
|
java code is:\n# \n\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int n=grid.length,m=grid[0].length;\n int left[][]=
|
shivam_gupta_
|
NORMAL
|
2021-05-08T10:30:30.447992+00:00
|
2021-05-08T10:30:30.448031+00:00
| 99 | false |
java code is:\n# \n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int n=grid.length,m=grid[0].length;\n int left[][]=new int[n][m];\n int down[][]=new int[n][m];\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n left[i][j]=grid[i][j]==0 ? 0 : 1+(j-1>=0 ? left[i][j-1] : 0);\n down[i][j]=grid[i][j]==0 ? 0 : 1+(i-1>=0 ? down[i-1][j] : 0);\n }\n }\n int res=0;\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n int min=Math.min(down[i][j],left[i][j]);\n while(min>res){\n if(left[i-min+1][j]>=min && down[i][j-min+1]>=min){\n res=min;\n break;\n }\n min--;\n } \n }\n }\n return res*res;\n }\n}\n```\n***Please,Upvote if this is helpful***
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
Simple JAVA Solution, 4ms faster than 73%
|
simple-java-solution-4ms-faster-than-73-s8g64
|
\tclass Solution {\n\t\tpublic int largest1BorderedSquare(int[][] grid) {\n\t\t\tint n = grid.length, m = grid[0].length;\n\t\t\tint ans = 0;\n\t\t\tint[][] h =
|
user_07
|
NORMAL
|
2021-04-21T17:54:39.268752+00:00
|
2021-04-21T17:54:39.268797+00:00
| 318 | false |
\tclass Solution {\n\t\tpublic int largest1BorderedSquare(int[][] grid) {\n\t\t\tint n = grid.length, m = grid[0].length;\n\t\t\tint ans = 0;\n\t\t\tint[][] h = new int[n+1][m+1];\n\t\t\tint[][] v = new int[n+1][m+1];\n\t\t\tfor(int i=1;i<=n;i++){\n\t\t\t\tfor(int j=1;j<=m;j++){\n\t\t\t\t\tif(grid[i-1][j-1]==1){\n\t\t\t\t\t\tv[i][j] = 1+v[i-1][j];\n\t\t\t\t\t\th[i][j] = 1+h[i][j-1];\n\t\t\t\t\t\tint t = Math.min(v[i-1][j],h[i][j-1]);\n\t\t\t\t\t\tfor(int k=t;k>=0;k--){\n\t\t\t\t\t\t\tif(v[i][j-k]>=k+1&&h[i-k][j]>=k){\n\t\t\t\t\t\t\t\tans = Math.max(ans,k+1);\n\t\t\t\t\t\t\t\tbreak;\n\t\t\t\t\t\t\t}\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn ans*ans;\n\t\t}\n\t}
| 1 | 0 |
['Java']
| 0 |
largest-1-bordered-square
|
[python3] illustrated explanation
|
python3-illustrated-explanation-by-wilme-vgx6
|
\n\n\n\n\ndef largest1BorderedSquare(self, grid: List[List[int]]) -> int: # pylint: disable=invalid-name\n """ O(N^3)T O(N^2)S """\n size_y, siz
|
wilmerkrisp
|
NORMAL
|
2020-07-25T08:56:17.531653+00:00
|
2020-07-25T08:56:17.531703+00:00
| 212 | false |
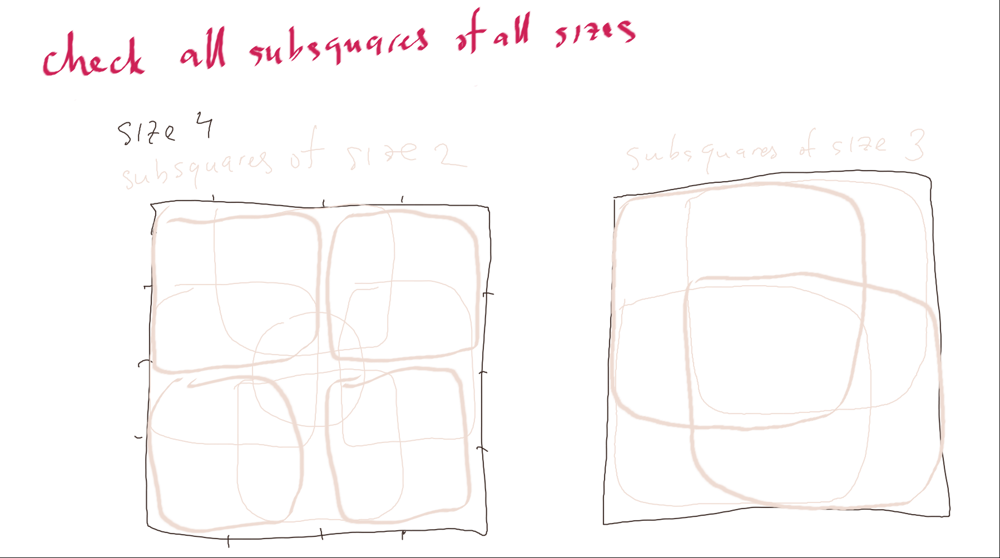\n\n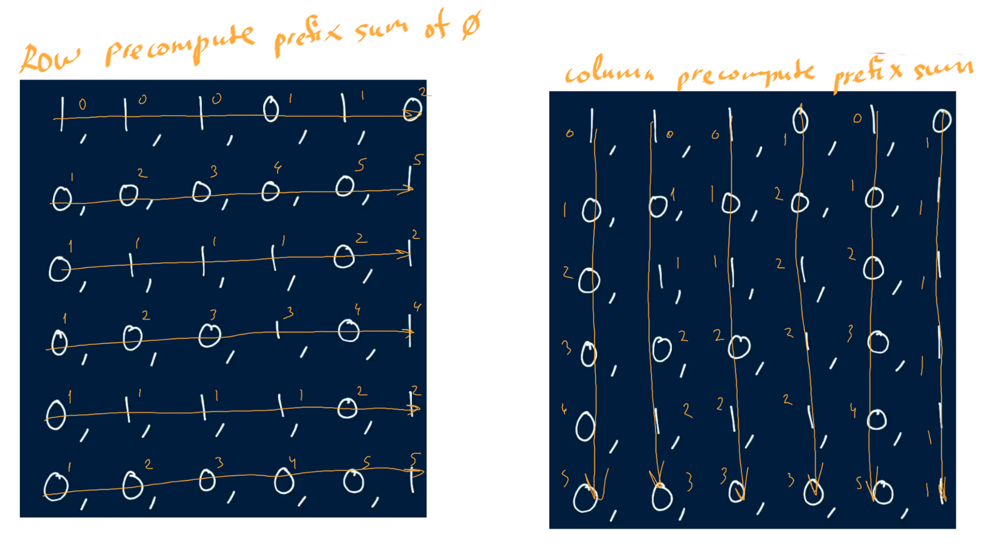\n\n```\ndef largest1BorderedSquare(self, grid: List[List[int]]) -> int: # pylint: disable=invalid-name\n """ O(N^3)T O(N^2)S """\n size_y, size_x, size_max, largest = len(grid), len(grid[0]), max(len(grid), len(grid[0])), 1 if sum(itertools.chain.from_iterable(grid)) > 0 else 0 #for 1-size square\n prefixes = [[(0, 0)] * (size_x + 1) for _ in range(size_y + 1)]\n\n # precompute row,column prefix summs\n for y, row in enumerate(grid, start=1):\n for x, num in enumerate(row, start=1):\n (prev_y, _), (_, prev_x) = prefixes[y - 1][x], prefixes[y][x - 1]\n prefixes[y][x] = (1 + prev_y, 1 + prev_x) if grid[y - 1][x - 1] else (prev_y, prev_x)\n\n def check_square(x1, y1, x2, y2): # [x1:x2] [y1:y2]\n nonlocal largest\n if not (0 <= x1 < size_x) or not (0 <= x2 < size_x) or not (0 <= y1 < size_y) or not (0 <= y2 < size_y): # because grid may be not squared\n return False\n\n size, x1, y1, x2, y2 = x2 - x1 + 1, x1 + 1, y1 + 1, x2 + 1, y2 + 1\n left_vertical = prefixes[y2][x1][0] - prefixes[y1 - 1][x1][0]\n right_vertical = prefixes[y2][x2][0] - prefixes[y1 - 1][x2][0]\n upper_gorizontal = prefixes[y1][x2][1] - prefixes[y1][x1 - 1][1]\n lower_gorizontal = prefixes[y2][x2][1] - prefixes[y2][x1 - 1][1]\n\n if left_vertical == right_vertical == upper_gorizontal == lower_gorizontal == size:\n largest = max(largest, size) # find max square\n \n\n # check all squares\n for size in range(2, size_max + 1):\n for y, row in enumerate(grid):\n for x, num in enumerate(row):\n check_square(x, y, x + size - 1, y + size - 1)\n\n return largest * largest\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
C++ dp with Explanation
|
c-dp-with-explanation-by-f20180119-rmu4
|
After hardcoding for edge cases which include - presence of only zeros, rows = 1 or columns = 1 we move to the dp part.\nHere I have used 2 dimensional vector
|
f20180119
|
NORMAL
|
2020-07-16T13:10:51.162769+00:00
|
2020-07-16T13:13:13.093059+00:00
| 220 | false |
After hardcoding for edge cases which include - presence of only zeros, rows = 1 or columns = 1 we move to the dp part.\nHere I have used 2 dimensional vector of pairs. Each element of the vector for example say the pair at the ith row and the jth column is of the form (top, left). Top stores the count of continuous ones above this position in the input array and left stores the count of continuous ones to the left of this position in the input array. Also note that if grid[i][j] = 0 then dp[i][j] = {0,0}\nNow for example an input vector\n1 0 1 1 \n1 1 1 1\n1 1 0 1\n1 1 1 1\nThe dp shall be of the form\n(0,0) (0,0) (0,0) (0,1) \n(1,0) (0,1) (1,2) (1,3) \n(2,0) (1,1) (0,0) (2,0) \n(3,0) (2,1) (0,2) (3,3)\n\nFrom simple observation it is clear that the ans is 9. But how do we reach at this conclusion from this dp array?\nWhat we need to do now is for each dp pair such that both elements are greater than 0 we will take the minimum of the two and if this minimum is say x, then we have to go x boxes up and x boxes left. The pair which is x boxes up must have atleast x number of ones on it\u2019s left and the pair which is x boxes left must have atleast x number of ones on top of it. If it is then calculate it\u2019s area and keep track of the maximum. \nThe trick here is for the input array I wrote above the ans is 9 consisting of the location (3,3)\u2014{zero based indexing} as the bottom right of the square but the minimum of 3 and 3 is 3. So, x = 3, but this doesn\u2019t satisfy our conditions so we need to run a while loop such that it will run from 3 to 1. So, when x becomes 2 we get the ans. \nThe code is:-\n \n \n```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n if(grid.size()==0)\n return 0;\n int n = grid.size();\n int m = grid[0].size();\n bool flag = false;\n vector<vector<pair<int,int>>>dp(n, vector<pair<int,int>>(m, {0,0}));\n for(int i = 0; i<n; i++){\n for(int j = 0; j<m; j++){\n if(grid[i][j]==0)\n dp[i][j] ={0,0};\n else{\n flag = true;\n int left = 0, top = 0;\n if(i!=0){\n if(grid[i-1][j]==0)\n top = 0;\n else\n top = dp[i-1][j].first+1;\n }\n if(j!=0){\n if(grid[i][j-1]==0)\n left = 0;\n else\n left = dp[i][j-1].second+1;\n }\n dp[i][j] = {top,left};\n }\n }\n }\n if(!flag)\n return 0;\n if(n==1 || m==1)\n return 1;\n int ans = 1;\n for(int i = 0; i<n; i++){\n for(int j = 0; j<m; j++){\n if(dp[i][j].first >0 && dp[i][j].second>0){\n int x = min(dp[i][j].first, dp[i][j].second);\n while(x){\n int top = dp[i-x][j].second;\n int left = dp[i][j-x].first;\n int mini = min({top, left, x});\n if(top>=x && left>=x)\n ans = max(ans, (mini+1)*(mini+1));\n x--;\n }\n }\n }\n }\n return ans;\n //return ans;\n }\n};\n```
| 1 | 0 |
[]
| 1 |
largest-1-bordered-square
|
C++, beats 100% (both time and memory)
|
c-beats-100-both-time-and-memory-by-ruih-w3fm
|
\nclass Solution {\npublic:\n Solution() {ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr);}\n \n int largest1BorderedSquare(
|
ruihou
|
NORMAL
|
2020-04-16T07:10:38.601243+00:00
|
2020-04-16T07:10:38.601277+00:00
| 245 | false |
```\nclass Solution {\npublic:\n Solution() {ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr);}\n \n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n int top[m][n], left[m][n]; //grid[i][j]\u4E3A\u4E2D\u5FC3\uFF0C\u5411\u4E0A\u5411\u5DE6\u5947\u65701\u7684\u4E2A\u6570\n for(int i=0; i<m; ++i)for(int j=0; j<n; ++j){\n top[i][j] = grid[i][j] ? (i>0 ? top[i-1][j]+1 : 1) : 0;\n left[i][j] = grid[i][j] ? (j>0 ? left[i][j-1]+1 : 1) : 0;\n }\n vector<vector<int>> dp(grid);\n for(int i=1; i<m; ++i) for(int j=1; j<n; ++j){\n if(dp[i][j] == 0) continue;\n int step = min(top[i][j], left[i][j])-1; //\u6B63\u65B9\u5F62\u7684\u5E95\u8FB9\u3001\u53F3\u8FB9\u7684\u6700\u5C0F\u503C\n for(; step > 0; --step){\n if(j < step || i < step) continue;\n if(step <= min(top[i][j-step], left[i-step][j])) break; //\u6B63\u65B9\u5F62\u7684\u5DE6\u8FB9\u3001\u9876\u8FB9\u7684\u6700\u5C0F\u503C\n }\n dp[i][j] = dp[i-step][j-step]==0 ? 1 : (step+1) * (step+1); //\u5DE6\u4E0A\u70B9\u4E0D\u80FD\u4E3A0\n }\n int res = 0;\n for(int i=0; i<m; ++i) for(int j=0; j<n; ++j) res = max(res, dp[i][j]);\n return res;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
[Python] Time O(n*m*min(n, m)), Space O(n*m), DP Super Concise but Easy to Understand
|
python-time-onmminn-m-space-onm-dp-super-bxw9
|
\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n left = [[0 for _ in range(len(grid[0]))] for _ in range(len(grid
|
ztonege
|
NORMAL
|
2020-03-29T05:41:30.097131+00:00
|
2020-03-29T05:41:30.097186+00:00
| 196 | false |
```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n left = [[0 for _ in range(len(grid[0]))] for _ in range(len(grid))]\n top = [[0 for _ in range(len(grid[0]))] for _ in range(len(grid))]\n \n max_side = 0\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n top[i][j] = top[i-1][j]+1 if i>0 and grid[i][j] else grid[i][j]\n left[i][j] = left[i][j-1]+1 if j>0 and grid[i][j] else grid[i][j]\n for side in range(min(top[i][j], left[i][j]), max_side, -1):\n if left[i-side+1][j] >= side and top[i][j-side+1] >= side:\n max_side = side\n return max_side**2\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
C++ DP Solution !!!
|
c-dp-solution-by-kylewzk-3sx1
|
\n int largest1BorderedSquare(vector<vector<int>>& g) {\n int res = 0, cur = 0, m = g.size(), n = g[0].size();\n vector<vector<int>> ver(m, vec
|
kylewzk
|
NORMAL
|
2020-02-06T07:39:25.586513+00:00
|
2020-02-06T07:39:25.586808+00:00
| 249 | false |
```\n int largest1BorderedSquare(vector<vector<int>>& g) {\n int res = 0, cur = 0, m = g.size(), n = g[0].size();\n vector<vector<int>> ver(m, vector<int>(n, 0)), hor(m, vector<int>(n, 0));\n \n for(int i = 0; i < m; i++) {\n for(int j = 0; j < n; j++) {\n if(g[i][j]) {\n ver[i][j] = 1 + (i == 0 ? 0 : ver[i-1][j]);\n hor[i][j] = 1 + (j == 0 ? 0 : hor[i][j-1]);\n }\n }\n }\n \n for(int i = m-1; i >= 0; i--) {\n for(int j = n-1; j >= 0; j--) {\n int len = min(ver[i][j], hor[i][j]);\n while(len > res) {\n if(ver[i][j-len+1] >= len && hor[i-len+1][j] >= len) {\n res = len;\n break;\n } else {\n len--;\n }\n }\n }\n }\n return res*res;\n }\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
easy understand python DP 160ms
|
easy-understand-python-dp-160ms-by-15600-vaqc
|
\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n M,N,count=len(grid),len(grid[0]),0\n dp=[[[0,0]for _ in r
|
15600158088
|
NORMAL
|
2020-01-06T14:06:20.815718+00:00
|
2020-01-06T14:06:20.815751+00:00
| 381 | false |
```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n M,N,count=len(grid),len(grid[0]),0\n dp=[[[0,0]for _ in range(N+1)]for _ in range(M+1)]\n for i in range(1,M+1):\n for j in range(1,N+1):\n if grid[i-1][j-1]==1:\n dp[i][j][0],dp[i][j][1]=dp[i-1][j][0]+1,dp[i][j-1][1]+1\n for k in range(min(dp[i][j][0],dp[i][j][1]),count,-1):\n if min(dp[i-k+1][j][1],dp[i][j-k+1][0])>=k:\n count=max(count,k)\n break\n return count**2\n```
| 1 | 0 |
['Dynamic Programming', 'Python']
| 1 |
largest-1-bordered-square
|
Java DP Solution
|
java-dp-solution-by-rebecca-a397
|
\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n //Sanity check\n if (grid == null || grid.length < 1 || grid[0].length
|
rebecca_
|
NORMAL
|
2019-09-05T19:33:52.147670+00:00
|
2019-09-05T19:33:52.147709+00:00
| 254 | false |
```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n //Sanity check\n if (grid == null || grid.length < 1 || grid[0].length < 1) {\n return 0;\n }\n int rows = grid.length;\n int cols = grid[0].length;\n int[][] rightToLeft = new int[rows][cols];\n int[][] bottomToTop = new int[rows][cols];\n int max = 0;\n //Pre-processing\n for (int i = 0; i < rows; i++) {\n rightToLeft[i][cols - 1] = grid[i][cols - 1];\n }\n for (int i = 0; i < rows; i++) {\n for (int j = cols - 2; j >= 0; j--) {\n if (grid[i][j] == 0) {\n rightToLeft[i][j] = 0;\n } else{\n rightToLeft[i][j] = rightToLeft[i][j + 1] + 1;\n }\n }\n }\n for (int j = 0; j < cols; j++) {\n bottomToTop[rows - 1][j] = grid[rows - 1][j];\n }\n for (int i = rows - 2; i >= 0; i--) {\n for (int j = 0; j < cols; j++) {\n if (grid[i][j] == 0) {\n bottomToTop[i][j] = 0;\n } else {\n bottomToTop[i][j] = bottomToTop[i + 1][j] + 1;\n }\n }\n }\n //Iterate each possible solution\n for (int i = 0; i < rows; i++) {\n for (int j = 0; j < cols; j++) {\n int n = Math.min(rightToLeft[i][j], bottomToTop[i][j]);\n for(int k = n; k > 0; k--) {\n if (rightToLeft[i + k - 1][j] >= k && bottomToTop[i][j + k - 1] >= k){\n max = Math.max(max, k);\n break;\n }\n }\n }\n }\n return max * max;\n }\n}\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
[C++] Nice, concise solution (runtime: 0 ms)
|
c-nice-concise-solution-runtime-0-ms-by-q6w3t
|
Others have come up with fundamentally the same solution, time complexity O(R * C * min(R, C)).\n\nBut I thought I\'d share my version anyway. It\'s concise, an
|
mhelvens
|
NORMAL
|
2019-08-03T16:52:00.257700+00:00
|
2019-08-03T16:52:00.257731+00:00
| 413 | false |
Others have come up with fundamentally the same solution, time complexity _O(R * C * min(R, C))_.\n\nBut I thought I\'d share my version anyway. It\'s concise, and it has some nice optimizations in the final code-block. For example, we never test a square unless it can beat our current best length.\n\n```C++\nint largest1BorderedSquare(vector<vector<int>>& grid) {\n // grid size\n const int R = grid.size();\n const int C = grid[0].size();\n\n // record the reach of 1\'s from every cell\n auto right = grid;\n auto down = move(grid);\n for (int r = 0; r < R; ++r)\n for (int c = C-2; c >= 0; --c)\n right[r][c] *= right[r][c+1] + 1;\n for (int c = 0; c < C; ++c)\n for (int r = R-2; r >= 0; --r)\n down[r][c] *= down[r+1][c] + 1;\n\n // find the largest 1-bordered square\n int length = 0;\n for (int r = 0; r < R - length; ++r)\n for (int c = 0; c < C - length; ++c)\n for (int dist = min(right[r][c], down[r][c]); dist > length; --dist)\n if (dist <= min(right[r+dist-1][c], down[r][c+dist-1]))\n length = dist;\n\n return length * length;\n}\n```
| 1 | 0 |
['C']
| 0 |
largest-1-bordered-square
|
O(N^2logN) solution
|
on2logn-solution-by-htfy96-y0rm
|
The basic idea is to preprocess the length of two types of gadget at each position:\n\n[X is current position]\nType A:\ntext\n 1\n 1\n1 1 X\n\nwhich has
|
htfy96
|
NORMAL
|
2019-07-29T03:57:42.011929+00:00
|
2019-07-29T04:01:15.464821+00:00
| 215 | false |
The basic idea is to preprocess the length of two types of gadget at each position:\n\n[X is current position]\nType A:\n```text\n 1\n 1\n1 1 X\n```\nwhich has length min(left[i, j], top[i, j]). Here it\'s 3.\n\nType B:\n```\nX 1 1\n1\n1\n```\n\nwhich has length min(right[i, j], bottom[i, j]), which is 3 in this example.\n\nThen, for each top-left -> bottom right diagnal line, we try to match these two types of gadget. Assume we are currently at row `i` with gadget A of length `dself`, we want to find matching gadget Bs at row `i\' <= i` with gadget length `d_i\'` (i.e., min(r[i\', j\'], b[i\', j\'])) and choose the one that forms a max border square, i.e.,\n1) `i - dself + 1` <= `i\'` <= `i`\n2) `i\' + d_i\'` >= `i`\n\nAnd the one that forms the largest square is the minimal `i\'` that satisfies the above conditions.\n\nWe can maintain two balance trees for each of the condition. For each `i`, we first add `i + d_i` to `max_reach` tree and `i` to `s` tree. Then, note that `i` is increasing, so we can pop all `i\'` along with their entries in `s` that have `i\' + d_i\' < i`. After this operation, all entries in `s` and `max_reach` satisfies condition 2). Therefore, we can use a binary search in `s` tree to find the minimum `i\'` s.t., `i - dself + 1 <= i\'`.\n\n```cpp\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n const int m = grid.size(), n = grid[0].size();\n // consecutive 1s to left/right/top/bottom\n vector<int> l(m * n), r(m * n), t(m * n), b (m * n);\n auto idx = [m, n](int i, int j) {\n return i * n + j;\n };\n for (int i=0; i<m; ++i) {\n l[idx(i, 0)] = grid[i][0];\n for (int j= 1; j<n; ++j)\n l[idx(i, j)] = grid[i][j] ? l[idx(i, j-1)] + 1 : 0;\n r[idx(i, n-1)] = grid[i][n-1];\n for (int j =n-2; j>=0; --j)\n r[idx(i, j)] = grid[i][j] ? r[idx(i, j+1)] + 1 : 0;\n }\n for (int j=0; j<n; ++j) {\n t[idx(0, j)] = grid[0][j];\n for (int i=1; i<m; ++i)\n t[idx(i, j)] = grid[i][j] ? t[idx(i-1, j)] + 1 : 0;\n b[idx(m-1, j)] = grid[m-1][j];\n for (int i=m-2; i>=0; --i)\n b[idx(i, j)] = grid[i][j] ? b[idx(i+1, j)] + 1 : 0;\n }\n int ans = 0;\n // for each topleft -> bottomright diagnal line with i - j = d\n for (int d = -max(m, n); d <= max(m, n); ++d)\n {\n set<pair<int, int>> max_reach; // <i\' + min(r, b), i\'>\n set<int> s; // all i\' in max_reach\n for (int i = 0; i < m; ++i)\n {\n int j = i - d;\n if (j >= n) break;\n if (j < 0) continue;\n int dself = min(t[idx(i, j)], l[idx(i, j)]);\n // find minimum i\' from i - dself + 1, s.t. \n // i\' + min(r[i\', j\'], b[i\', j\']) >= i\n s.insert(i);\n max_reach.insert(make_pair(i + min(r[idx(i, j)], b[idx(i, j)]), i));\n while (!max_reach.empty() && max_reach.begin()->first < i)\n {\n s.erase(max_reach.begin()->second);\n max_reach.erase(max_reach.begin());\n }\n auto it = s.lower_bound(i - dself + 1);\n if (it != s.end())\n ans = max(ans, (i - *it + 1) * (i - *it + 1));\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Binary Search Tree']
| 1 |
largest-1-bordered-square
|
Share my clear python solution
|
share-my-clear-python-solution-by-jie69-0ecp
|
\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n if not grid:\n return 0\n \n
|
jie69
|
NORMAL
|
2019-07-28T17:48:49.746987+00:00
|
2019-07-28T17:48:49.747018+00:00
| 135 | false |
```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n if not grid:\n return 0\n \n res = 0\n \n m = len(grid)\n n = len(grid[0])\n \n \n height = [[0] * n for _ in range(m)]\n left = [[0] * n for _ in range(m)]\n \n for i in range(m):\n \n for j in range(n):\n \n if grid[i][j] != 0:\n \n if j > 0 and grid[i][j-1] !=0:\n left[i][j] = grid[i][j] + left[i][j-1]\n else:\n left[i][j] = grid[i][j]\n \n if i > 0 and grid[i-1][j]!=0:\n height[i][j] = grid[i][j] + height[i-1][j]\n else:\n height[i][j] = grid[i][j]\n \n \n for i in range(m):\n \n for j in range(n):\n \n if grid[i][j] !=0:\n \n for k in range(min(left[i][j],height[i][j])):\n \n if i-k>= 0 and left[i-k][j] >= k+1 and j-k >=0 and height[i][j-k] >= k+1:\n res = max(res,(k+1)**2)\n \n return res\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
Python solution
|
python-solution-by-cslzy-hh14
|
python\nclass Solution(object):\n def largest1BorderedSquare(self, grid):\n """\n :type grid: List[List[int]]\n :rtype: int\n """
|
cslzy
|
NORMAL
|
2019-07-28T08:42:49.485361+00:00
|
2019-07-28T08:42:49.485393+00:00
| 144 | false |
```python\nclass Solution(object):\n def largest1BorderedSquare(self, grid):\n """\n :type grid: List[List[int]]\n :rtype: int\n """\n if not grid:\n return 0\n \n h = len(grid)\n w = len(grid[0])\n \n ver = [[0 for i in range(w)] for i in range(h)]\n hon = [[0 for i in range(w)] for i in range(h)]\n \n for i in range(w):\n ver[0][i] = grid[0][i]\n \n for i in range(1, h):\n for j in range(w):\n if grid[i][j] == 1:\n ver[i][j] = 1 + ver[i - 1][j]\n \n \n for i in range(h):\n hon[i][0] = grid[i][0]\n \n for i in range(h):\n for j in range(1, w):\n if grid[i][j] == 1:\n hon[i][j] = 1 + hon[i][j - 1]\n \n\n res = 0\n for i in range(h):\n for j in range(w):\n hv = hon[i][j]\n vv = ver[i][j]\n m = min(hv, vv)\n k = 0\n imax = 0\n while m - k > 0:\n hk = hon[i - k][j]\n vk = ver[i][j - k]\n if hk > k and vk > k:\n imax = max(imax, (k + 1) ** 2)\n k += 1\n \n res = max(res, imax)\n \n \n return res\n \n \n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
Java Solution With Explanation
|
java-solution-with-explanation-by-naveen-stg5
|
Idea\nleft[i][j] indicates how far left can we go from [i][j] cell.\nup[i][j] indicates how far up can we go from [i][j] cell.\n\nNow, at every [i][j], we will
|
naveen_kothamasu
|
NORMAL
|
2019-07-28T08:07:56.874185+00:00
|
2019-07-28T08:09:48.424451+00:00
| 157 | false |
**Idea**\n`left[i][j]` indicates how far left can we go from `[i][j]` cell.\n`up[i][j]` indicates how far up can we go from `[i][j]` cell.\n\nNow, at every `[i][j]`, we will start with verifying max square has `1-border`. The max square has length `d` which is the min of `left[i][j]` and `up[i][j]` (i.e. since it is a square, how far up and left we can go will be determined by the min of those two, right?).\nNow, we may not have max square with `d`, how do we check? we move up `d` steps and check the `left` there to see if that cell has the value at least `d`, why? then we can go left from there by `d` steps to form the square. Similar check - we move left `d` steps and check the `up` there.\nand then we will keep trying smaller square at `d-1`, if the above checks fail.\n\n```\npublic int largest1BorderedSquare(int[][] g) {\n int m = g.length, n = g[0].length;\n int[][] left = new int[m][n], up = new int[m][n];\n for(int i=0; i < m; i++){\n left[i][0] = g[i][0];\n for(int j=1; j < n; j++)\n if(g[i][j] == 1)\n left[i][j] = 1+left[i][j-1];\n }\n for(int j=0; j < n; j++){\n up[0][j] = g[0][j];\n for(int i=1; i < m; i++)\n if(g[i][j] == 1)\n up[i][j] = 1+up[i-1][j];\n }\n int max = 0;\n for(int i=0; i < m; i++){\n for(int j=0; j < n; j++){\n int d = Math.min(left[i][j], up[i][j]);\n while(d > 1){\n if(left[i-(d-1)][j] >= d && up[i][j-(d-1)] >= d)\n break;\n --d;\n }\n max = Math.max(max, d*d);\n }\n }\n return max;\n }\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
[JAVA] Brute Force Solution
|
java-brute-force-solution-by-umn-hkc-x8bn
|
\n public int largest1BorderedSquare(int[][] grid) {\n if (grid == null || grid.length == 0 || grid[0].length == 0) return 0;\n int max = 0;\n
|
umn-hkc
|
NORMAL
|
2019-07-28T04:34:05.497609+00:00
|
2019-07-28T13:34:36.325065+00:00
| 195 | false |
```\n public int largest1BorderedSquare(int[][] grid) {\n if (grid == null || grid.length == 0 || grid[0].length == 0) return 0;\n int max = 0;\n int m = grid.length;\n int n = grid[0].length;\n for (int side = 1; side <= Math.min(m, n); side++) {\n for (int i = 0; i <= m - side; i++) {\n for (int j = 0; j <= n - side; j++) {\n if (max < side) {\n if (isValid(grid, i, j, side)) {\n max = side;\n }\n }\n }\n }\n }\n return max * max;\n }\n public boolean isValid(int[][] grid, int x, int y, int side) {\n for (int i = x; i < x + side; i++) {\n if (grid[i][y] != 1) return false;\n if (grid[i][y + side - 1] != 1) return false;\n }\n for (int i = y; i < y + side; i++) {\n if (grid[x][i] != 1) return false;\n if (grid[x + side - 1][i] != 1) return false;\n }\n return true;\n }\n```
| 1 | 0 |
[]
| 0 |
largest-1-bordered-square
|
Python Bruteforce O(N^4) Passed
|
python-bruteforce-on4-passed-by-doudouzi-58kg
|
Did not think it will pass, 1400 ms\n\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n def checkOnes(r1,
|
doudouzi
|
NORMAL
|
2019-07-28T04:22:32.367589+00:00
|
2019-07-28T04:22:32.367629+00:00
| 256 | false |
Did not think it will pass, 1400 ms\n```\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n \n def checkOnes(r1, c1, r2, c2):\n for i in range(c1, c2+1):\n if grid[r1][i] == 0: return False\n for i in range(c1, c2+1):\n if grid[r2][i] == 0: return False\n for j in range(r1, r2+1):\n if grid[j][c1] == 0: return False\n for j in range(r1, r2+1):\n if grid[j][c2] == 0: return False \n return True\n \n count = 0\n rowN, colN = len(grid), len(grid[0])\n for r2 in range(rowN-1, -1, -1):\n for c2 in range(colN-1, -1, -1):\n shift = min(r2, c2)\n for r1 in range(r2 - shift, r2+1):\n if count >= (r2 - r1 + 1)**2: break\n c1 = c2 - (r2 - r1) \n if checkOnes(r1, c1, r2, c2):\n # print(r1, c1, r2, c2)\n count = max(count, (r2 - r1 + 1)**2)\n break\n \n return count\n```
| 1 | 0 |
[]
| 3 |
largest-1-bordered-square
|
Python O(n*3) solution
|
python-on3-solution-by-cubicon-03aq
|
\ndef largest1BorderedSquare(self, g: List[List[int]]) -> int:\n rows,cols = len(g), len(g[0])\n a = [[0] * cols for _ in range(rows)]\n a[
|
Cubicon
|
NORMAL
|
2019-07-28T04:05:31.233819+00:00
|
2019-07-28T04:10:13.719191+00:00
| 149 | false |
```\ndef largest1BorderedSquare(self, g: List[List[int]]) -> int:\n rows,cols = len(g), len(g[0])\n a = [[0] * cols for _ in range(rows)]\n a[0][0] = [g[0][0] , g[0][0]]\n for i in range(1, rows):\n a[i][0] = [g[i][0], 0 if g[i][0] == 0 else a[i-1][0][1] + 1]\n for j in range(1, cols):\n a[0][j] = [0 if g[0][j] == 0 else a[0][j-1][0] + 1, g[0][j]]\n \n res = max(0, sum(sum(g,[])) > 0)\n for i in range(1, rows):\n for j in range(1, cols):\n a[i][j] = [0, 0]\n if not g[i][j]: continue\n \n a[i][j][0] = 0 if not g[i][j] else a[i][j-1][0] + 1\n a[i][j][1] = 0 if not g[i][j] else a[i-1][j][1] + 1\n \n res = max(1, res)\n for x in range(min(a[i][j][0], a[i][j][1])-1, 0, -1):\n if a[i][j-x][1] >= x+1 and a[i-x][j][0] >= x+1:\n res = max(res, x+1)\n break\n return res * res\n```
| 1 | 1 |
[]
| 0 |
largest-1-bordered-square
|
Easy to understand C++ Solution with Explanation
|
easy-to-understand-c-solution-with-expla-my5c
|
\'hor\' count horizontal consecutive 1s & \'ver\' count vertical consecutive 1s for each position.\n* Then from bottom to top we check what is the maximum size
|
roy-sourov
|
NORMAL
|
2019-07-28T04:04:51.308475+00:00
|
2019-07-28T04:18:32.299070+00:00
| 177 | false |
* \'hor\' count horizontal consecutive 1s & \'ver\' count vertical consecutive 1s for each position.\n* Then from bottom to top we check what is the maximum size square we can achieve from the current location.\n\n```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int result=0;\n int m=grid.size(),n=grid[0].size();\n vector<vector<int>> hor(m,vector<int>(n,0)); \n vector<vector<int>> ver(m,vector<int>(n,0));\n \n \n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(j==0 && grid[i][j]==1) ver[i][j]=1;\n else if(j!=0 && grid[i][j]==1) ver[i][j]=ver[i][j-1]+1;\n \n if(i==0 && grid[i][j]==1) hor[i][j]=1;\n else if(i!=0 && grid[i][j]==1) hor[i][j]=hor[i-1][j]+1;\n }\n }\n \n \n for(int i=m-1;i>=0;i--){\n for(int j=n-1;j>=0;j--){\n int sqr=min(ver[i][j],hor[i][j]);\n \n while(sqr>result){\n if(ver[i-sqr+1][j]>=sqr && hor[i][j-sqr+1]>=sqr) result=sqr;\n sqr--;\n }\n }\n }\n \n return result*result; \n \n }\n};\n```
| 1 | 0 |
[]
| 1 |
largest-1-bordered-square
|
1139. Largest 1-Bordered Square
|
1139-largest-1-bordered-square-by-g8xd0q-vrgh
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-11T18:00:00.595445+00:00
|
2025-01-11T18:00:00.595445+00:00
| 8 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int largest1BorderedSquare(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] left = new int[m][n], up = new int[m][n];
int maxSize = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
left[i][j] = (j > 0) ? left[i][j - 1] + 1 : 1;
up[i][j] = (i > 0) ? up[i - 1][j] + 1 : 1;
int side = Math.min(left[i][j], up[i][j]);
while (side > maxSize) {
if (up[i][j - side + 1] >= side && left[i - side + 1][j] >= side) {
maxSize = side;
}
side--;
}
}
}
}
return maxSize * maxSize;
}
}
```
| 0 | 0 |
['Java']
| 0 |
largest-1-bordered-square
|
Daily Challenge | Day 20
|
daily-challenge-day-20-by-famous_chef-pbud
|
\n\n# Code\ncpp []\nclass Solution {\npublic:\n int rows, cols;\n int largestSquare(int x, int y, vector<vector<int>>& grid, vector<vector<int>>& hor, vec
|
suvro_datta
|
NORMAL
|
2024-10-04T10:11:49.677154+00:00
|
2024-10-04T10:11:49.677177+00:00
| 15 | false |
\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int rows, cols;\n int largestSquare(int x, int y, vector<vector<int>>& grid, vector<vector<int>>& hor, vector<vector<int>>& ver) {\n int len = min(hor[x][y], ver[x][y]) - 1;// min dist b/w horiz & vert. line containing ones \n for(int i = len; i >= 0; i--) { // shrink if unable to make\n if(i+x < rows && i+y < cols && ver[x][y+i] > i && hor[i+x][y] > i)\n return (i+1) * (i+1);\n }\n\n return 0; \n }\n\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n rows = grid.size(), cols = grid[0].size();\n\n vector<vector<int>> hor( rows , vector<int> (cols)); \n vector<vector<int>> ver( rows , vector<int> (cols)); \n\n // count no. of 1\'s from right to i,j (<----- this dir. in grid)\n for(int i = 0; i < rows; i++) {\n int cnt = 0;\n for(int j = cols - 1; j >= 0; j--) {\n if(grid[i][j]) ++cnt;\n else cnt = 0;\n hor[i][j] = cnt;\n }\n }\n\n for(int i = 0; i < cols; i++) {\n int cnt = 0;\n for(int j = rows-1; j >= 0; j--) {\n if(grid[j][i]) ++cnt;\n else cnt = 0;\n ver[j][i] = cnt;\n }\n }\n\n int mx = 0;\n for(int i = 0; i < rows; i++) {\n for(int j = 0; j < cols; j++) {\n int size = largestSquare(i, j, grid, hor, ver);\n mx = max(mx, size);\n }\n }\n\n return mx;\n }\n};\n\n/*\n[ 1,1,1 ],\n[ 1,0,1 ],\n[ 1,1,1 ],\n*/\n```
| 0 | 0 |
['C++']
| 0 |
largest-1-bordered-square
|
DP Prefix sum Row and Col - Java O(N^3)|O(N^2)
|
dp-prefix-sum-row-and-col-java-on3on2-by-tzgf
|
Intuition\n Describe your first thoughts on how to solve this problem. \nCalcuate 2 DP tables, one (dpRow) for consecutive cell 1 in row and another (dpCol) for
|
wangcai20
|
NORMAL
|
2024-09-22T17:56:48.019458+00:00
|
2024-09-22T17:56:48.019497+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCalcuate 2 DP tables, one (dpRow) for consecutive cell `1` in row and another (dpCol) for consecurity cell `1` in column. The min of each cell across the two DP tables is the longest possible length of right vertical side and bottom horizontal side of the square. \n\nThen for each cell, check the possible top horizontal side and left vertical side to see if they exist, capture the max along the way.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int n = grid.length + 1, m = grid[0].length + 1, res = 0;\n int[][] dpRow = new int[n][m], dpCol = new int[n][m];\n for (int i = 1; i < n; i++)\n for (int j = 1; j < m; j++)\n if (grid[i - 1][j - 1] != 0) {\n // prefix sum row and col\n dpRow[i][j] = dpRow[i][j - 1] + 1;\n dpCol[i][j] = dpCol[i - 1][j] + 1;\n // check square\n int side = Math.min(dpRow[i][j], dpCol[i][j]);\n for (int k = side; k > res; k--)\n if (i >= k && j >= k\n && dpRow[i - k + 1][j] >= k && dpCol[i][j - k + 1] >= k) {\n res = k;\n // System.out.printf("i:%d,j:%d,k:%d\\n", i, j, k);\n break;\n }\n }\n return res * res;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
largest-1-bordered-square
|
Simple Java Sol. | Beats 98% | Explanation
|
simple-java-sol-beats-98-explanation-by-0xsay
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Simple brute force\n\n# Complexity\n- Time complexity:\n O(n^3)\n\n- Spa
|
harshjaiswal9450
|
NORMAL
|
2024-08-01T08:49:01.414504+00:00
|
2024-08-01T08:50:20.747331+00:00
| 40 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n Simple brute force\n\n# Complexity\n- Time complexity:\n O(n^3)\n\n- Space complexity:\n O(n^2)\n\n# Code\n```\nclass Solution {\n\n public int largest1BorderedSquare(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[][] hor = new int[m][n];\n int[][] ver = new int[m][n];\n \n for(int i=0; i<grid.length; i++){ // count no. of 1\'s from right to i,j (<----- this dir. in grid)\n int cnt = 0;\n for(int j =n-1; j >= 0; j--){\n if(grid[i][j] == 1)\n cnt++;\n else cnt = 0;\n hor[i][j] = cnt;\n }\n }\n \n\n for(int i=0; i<grid[0].length; i++){ // count no. of 1\'s from bottom to j,i\n // ^\n // |\n // | this dir. in grid\n int cnt = 0;\n for(int j =m-1; j >= 0; j--){\n if(grid[j][i] == 1)\n cnt++;\n else cnt = 0;\n ver[j][i] = cnt;\n }\n }\n \n int max = 0;\n for(int i =0; i<m; i++){\n for(int j =0; j<n; j++){\n int size = largestSquare(grid,i,j,hor,ver); // start from every possible idx\n max= Math.max(max, size);\n }\n }\n return max;\n }\n\n private int largestSquare(int[][] grid, int x, int y, int[][] hor, int[][] ver) {\n if (x<0 || y<0 || x >= grid.length || y >= grid[0].length || grid[x][y] == 0) return 0;\n\n int len = Math.min(hor[x][y],ver[x][y]) -1;// min dist b/w horiz & vert. line containing ones \n\n for(int i =len; i>=0; i--){ // shrink if unable to make\n if(i+x < grid.length && i+y <grid[0].length && ver[x][y+i]> i && hor[i+x][y] > i)\n return (i+1)*(i+1);\n }\n\n return 0; \n }\n}\n\n```
| 0 | 0 |
['Array', 'Dynamic Programming', 'Recursion', 'Matrix', 'Java']
| 0 |
largest-1-bordered-square
|
scala twoliner with prefix sum
|
scala-twoliner-with-prefix-sum-by-vitito-7fde
|
scala\nobject Solution {\n def largest1BorderedSquare(grid: Array[Array[Int]]): Int = {\n lazy val (px,py) = (grid.transpose.map(_.scanLeft(0)(_ + _)).trans
|
vititov
|
NORMAL
|
2024-07-22T20:40:08.531024+00:00
|
2024-07-22T20:40:08.531055+00:00
| 1 | false |
```scala\nobject Solution {\n def largest1BorderedSquare(grid: Array[Array[Int]]): Int = {\n lazy val (px,py) = (grid.transpose.map(_.scanLeft(0)(_ + _)).transpose, grid.map(_.scanLeft(0)(_ + _)))\n (for{\n sz <- (grid.size min grid.head.size) to 1 by -1\n i <- (0 to grid.size-sz)\n j <- (0 to grid.head.size-sz)\n } yield {Option.when(Seq(\n px(i+sz)(j)-px(i)(j), px(i+sz)(j+sz-1)-px(i)(j+sz-1),\n py(i)(j+sz)-py(i)(j), py(i+sz-1)(j+sz)-py(i+sz-1)(j)\n ).sum == 4*sz)(sz*sz)\n }).flatten.headOption.getOrElse(0)\n }\n}\n```
| 0 | 0 |
['Matrix', 'Prefix Sum', 'Scala']
| 0 |
largest-1-bordered-square
|
C++ || Pre-Count || Time 8ms >83% || Space 14MB >60%
|
c-pre-count-time-8ms-83-space-14mb-60-by-71hi
|
Approach\nWe want to start form the largest square, check if it is 1-bordered, and if not move on to the next largest square. This is done with plain iteration.
|
BillyLjm
|
NORMAL
|
2024-06-27T16:50:05.700653+00:00
|
2024-06-27T16:50:05.700684+00:00
| 24 | false |
# Approach\nWe want to start form the largest square, check if it is 1-bordered, and if not move on to the next largest square. This is done with plain iteration. To efficiently check if a square is 1-bordered, we can pre-count the number of consecutive 1\'s across the rows and the columns. Then we can immediately check if a square if 1-bordered by accessing the pre-counted values for the 4 corners.\n\n# Complexity\n- Time complexity:\nO(n*m^2) *, where n and m are the large and smaller dimensions of the grid respectively*\n\n- Space complexity:\nO(n*m) *, where n and m are the large and smaller dimensions of the grid respectively*\n\n# Code\n```\nclass Solution {\npublic:\n\tint largest1BorderedSquare(vector<vector<int>>& grid) {\n\t\tvector<vector<int>> cntrows(grid.size(), vector<int>(grid[0].size()));\n\t\tvector<vector<int>> cntcols(grid.size(), vector<int>(grid[0].size()));\n\n\t\t// pre-count consecutive 1\'s across rows\n\t\tfor (int j = 0; j < grid[0].size(); j++) {\n\t\t\tcntrows[0][j] = grid[0][j];\n\t\t}\n\t\tfor (int i = 1; i < grid.size(); i++) {\n\t\t\tfor (int j = 0; j < grid[0].size(); j++) {\n\t\t\t\tcntrows[i][j] = grid[i][j] * (cntrows[i - 1][j] + 1);\n\t\t\t}\n\t\t}\n\n\t\t// pre-count consecutive 1\'s across cols\n\t\tfor (int j = 0; j < grid.size(); j++) {\n\t\t\tcntcols[j][0] = grid[j][0];\n\t\t}\n\t\tfor (int i = 1; i < grid[0].size(); i++) {\n\t\t\tfor (int j = 0; j < grid.size(); j++) {\n\t\t\t\tcntcols[j][i] = grid[j][i] * (cntcols[j][i - 1] + 1);\n\t\t\t}\n\t\t}\n\n\t\t// check progressively smaller square\n\t\tfor (int dimm = min(grid.size(), grid[0].size()); dimm >= 0; dimm--) {\n\t\t\tfor (int i = 0; i < grid.size() - dimm; i++) {\n\t\t\t\tfor (int j = 0; j < grid[0].size() - dimm; j++) {\n\t\t\t\t\tif (cntrows[i + dimm][j] > dimm &&\n\t\t\t\t\t\tcntrows[i + dimm][j + dimm] > dimm &&\n\t\t\t\t\t\tcntcols[i][j + dimm] > dimm &&\n\t\t\t\t\t\tcntcols[i + dimm][j + dimm] > dimm) {\n\t\t\t\t\t\treturn (dimm + 1) * (dimm + 1);\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\n\t\t// no 1-bordered square found\n\t\treturn 0;\n\t}\n};\n```
| 0 | 0 |
['C++']
| 0 |
largest-1-bordered-square
|
Dynamic Programming
|
dynamic-programming-by-priyankshah25-gabf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
priyankshah25
|
NORMAL
|
2024-06-01T21:17:23.182990+00:00
|
2024-06-01T21:17:23.183017+00:00
| 20 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n\n int[][]hbox = new int [grid.length][grid[0].length];\n int [][]vbox = new int [grid.length][grid[0].length];\n for(int i = 0; i< grid.length; i++)\n {\n for(int j =0;j< grid[0].length;j++)\n {\n if(grid[i][j] == 1)\n {\n if(j>0){\n hbox[i][j]= hbox[i][j-1];\n }\n if(i> 0)\n {\n vbox[i][j] = vbox[i-1][j];\n \n }\n hbox[i][j] += 1;\n vbox[i][j] += 1;\n }\n }\n }\n for(int[] a: hbox){\n System.out.println(Arrays.toString(a));\n }\n System.out.println();\n for(int[]a : vbox)\n {\n System.out.println(Arrays.toString(a));\n }\n int output =0;\n for(int i = 0; i<grid.length; i++)\n {\n for(int j = 0; j< grid[0].length;j++) \n {\n int size = Math.min(vbox[i][j],hbox[i][j]);\n if(size == 0)continue;\n for(int k = size; k > output; k--){\n\n if(hbox[i-k+1][j]>= k && vbox[i][j-k+1]>= k)\n {\n output = Math.max(output,k);\n }\n }\n }\n }\nreturn output * output;\n }\n\n}\n```
| 0 | 0 |
['Java']
| 0 |
largest-1-bordered-square
|
[Go] Compare halves of squares
|
go-compare-halves-of-squares-by-ivan-272-laef
|
\nfunc min(x, y int) int {\n if x < y {\n return x\n }\n return y\n}\n\nfunc max(x, y int) int {\n if x > y {\n return x\n }\n r
|
ivan-2727
|
NORMAL
|
2024-05-13T22:35:32.612593+00:00
|
2024-05-13T22:35:32.612615+00:00
| 5 | false |
```\nfunc min(x, y int) int {\n if x < y {\n return x\n }\n return y\n}\n\nfunc max(x, y int) int {\n if x > y {\n return x\n }\n return y\n}\n\nfunc largest1BorderedSquare(grid [][]int) int {\n ans := 0\n m := len(grid)\n n := len(grid[0])\n side := make([][]int, m)\n for i := 0; i < m; i++ {\n side[i] = make([]int, n)\n for j := 0; j < n; j++ {\n if grid[i][j] != 1 {\n continue\n }\n down := 0\n for k := i; k < m; k++ {\n if grid[k][j] == 1 {\n down += 1\n } else {\n break\n }\n }\n right := 0\n for k := j; k < n; k++ {\n if grid[i][k] == 1 {\n right += 1\n } else {\n break\n }\n }\n side[i][j] = min(down, right)\n for k := 0; k <= min(i, j); k++ {\n if grid[i-k][j] == 1 && grid[i][j-k] == 1 {\n if side[i-k][j-k] >= k {\n ans = max(ans, (k+1)*(k+1))\n }\n } else {\n break\n }\n }\n }\n }\n return ans\n}\n```
| 0 | 0 |
['Dynamic Programming', 'Go']
| 0 |
largest-1-bordered-square
|
1139. Largest 1-Bordered Square.cpp
|
1139-largest-1-bordered-squarecpp-by-202-bfsc
|
Code\n\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) { \n int r = grid.size();\n int c = grid[0].si
|
202021ganesh
|
NORMAL
|
2024-05-04T16:52:31.921947+00:00
|
2024-05-04T16:52:31.921971+00:00
| 3 | false |
**Code**\n```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) { \n int r = grid.size();\n int c = grid[0].size();\n int hdp[r][c];\n int vdp[r][c]; \n int maxSquareL = 0;\n int squareL = 0;\n for(int i=0;i<r;i++)\n {\n for(int j=0;j<c;j++)\n {\n if(grid[i][j]==1)\n {\n hdp[i][j] = j>0?(1+hdp[i][j-1]):1;\n vdp[i][j] = i>0?(1+vdp[i-1][j]):1; \n }\n else\n {\n hdp[i][j] = 0;\n vdp[i][j] = 0; \n }\n int minL = min(hdp[i][j],vdp[i][j]);\n if(minL>maxSquareL)\n {\n while(minL>maxSquareL)\n {\n if(hdp[i+1-minL][j]>=minL && vdp[i][j+1-minL]>=minL)\n {\n squareL = minL;\n break;\n }\n minL--;\n } \n }\n else\n squareL = grid[i][j];\n \n if(maxSquareL<squareL)maxSquareL=squareL;\n } \n } \n return maxSquareL * maxSquareL;\n }\n};\n```
| 0 | 0 |
['C']
| 0 |
largest-1-bordered-square
|
1139. Largest 1-Bordered Square
|
1139-largest-1-bordered-square-by-zhihui-ym45
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\u9898\u76EE\u7ED9\u5B9A\u7684\u6570\u636E\u89C4\u6A21\u662F100 \u6839\u636E\u6700\u592
|
zhihuijie1
|
NORMAL
|
2024-04-22T03:11:39.665865+00:00
|
2024-04-22T03:11:39.665885+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\u9898\u76EE\u7ED9\u5B9A\u7684\u6570\u636E\u89C4\u6A21\u662F100 \u6839\u636E\u6700\u5927\u6570\u636E\u89C4\u6A21\u662F10^8\u53EF\u4EE5\u5927\u81F4\u7684\u731C\u5230\uFF0C\u590D\u6742\u5EA6\u662FN^3\u662F\u53EF\u4EE5\u7684\u3002\u5728\u4E00\u4E2A\u77E9\u9635\u4E2D\u67E5\u627E\u6240\u6709\u957F\u65B9\u5F62\u7684\u65F6\u95F4\u590D\u6742\u5EA6\u662FN^4 - \u9996\u5148\u968F\u673A\u627E\u4E00\u4E2A\u70B9(\u5DE6\u4E0A)\u7684\u65F6\u95F4\u590D\u6742\u5EA6\u662FN^2 \u7136\u540E\u518D\u968F\u673A\u627E\u4E00\u4E2A\u70B9(\u53F3\u4E0B)\u7684\u65F6\u95F4\u590D\u6742\u5EA6\u4E5F\u662FN^2,\u5728\u4E00\u4E2A\u77E9\u9635\u4E2D\u67E5\u627E\u6240\u6709\u6B63\u65B9\u5F62\u7684\u65F6\u95F4\u590D\u6742\u5EA6\u662FN^3 - \u9996\u5148\u968F\u673A\u627E\u4E00\u4E2A\u70B9(\u5DE6\u4E0A)\u7684\u65F6\u95F4\u590D\u6742\u5EA6\u662FN^2 \u7136\u540E\u518D\u968F\u673A\u627E\u4E00\u4E2A\u70B9(\u53F3\u4E0B)\u7684\u65F6\u95F4\u590D\u6742\u5EA6\u662FN,\u73B0\u5728\u5728\u77E9\u9635\u4E2D\u968F\u673A\u627E\u5230\u4E00\u4E2A\u6B63\u65B9\u5F62\u7684\u65F6\u95F4\u590D\u6742\u5EA6\u5DF2\u7ECF\u8FBE\u5230N^3\u4E86\uFF0C\u90A3\u4E48\u5224\u65AD\u8FB9\u754C\u6784\u6210\u7684\u5B50\u7F51\u9762\u79EF\u7684\u590D\u6742\u5EA6\u5FC5\u987B\u662FO(1),\u6240\u4EE5\u8981\u5BF9\u6570\u7EC4\u8FDB\u884C\u9884\u5904\u7406\uFF0C\u60F3\u8981\u7684\u6548\u679C\u662F\u968F\u673A\u4E00\u4E2A\u70B9(i,j)\u5C31\u53EF\u4EE5\u5F97\u5230\u5176\u53F3\u8FB9\u6700\u957F\u7684\u8FDE\u7EED1\u6709\u51E0\u4E2A\uFF0C\u5176\u4E0B\u8FB9\u6700\u957F\u8FDE\u7EED\u76841\u6709\u51E0\u4E2A\u3002\u7ECF\u9884\u5904\u7406\u4E4B\u540E\uFF0C\u6211\u53EF\u4EE5\u5FEB\u901F\u7684\u5224\u65AD\u51FA\u5F53\u524D\u7684\u6B63\u65B9\u884C\u662F\u5426\u662F\u8FB9\u957F\u4E3A1\u73AF\u6210\u7684\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nN^3\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n public static int largest1BorderedSquare(int[][] m) {\n if (m == null || m.length == 0 || m[0].length == 0) {\n return 0;\n }\n int N = m.length;\n int M = m[0].length;\n int ans = 0;\n //\u5BF9\u6570\u7EC4\u8FDB\u884C\u9884\u5904\u7406 \u65F6\u95F4\u590D\u6742\u5EA6\u662FN^2\n int[][] right = rightPreprocessing(m);\n int[][] down = downPreprocessing(m);\n\n for (int i = 0; i < N; i++) {\n for (int j = 0; j < M; j++) {\n\n //[i,j]\u662F\u5DE6\u4E0A\u70B9\n for (int k = 1; k <= Math.min(N - i, M - j); k++) {\n if (right[i][j] >= k && down[i][j] >= k && down[i][j + k - 1] >= k && right[i + k - 1][j] >= k) {\n ans = Math.max(ans, k * k);\n }\n }\n }\n }\n return ans;\n }\n\n //\u5411\u53F3\u8FDB\u884C\u9884\u5904\u7406\n private static int[][] rightPreprocessing(int[][] m) {\n int N = m.length;\n int M = m[0].length;\n int[][] right = new int[N][M];\n\n //\u4ECE\u53F3\u5F80\u5DE6\u8FDB\u884C\u9884\u5904\u7406\n for (int i = 0; i < N; i++) {\n for (int j = M - 1; j >= 0; j--) {\n if (m[i][j] == 0) {\n right[i][j] = 0;\n } else {\n right[i][j] = j + 1 < M && right[i][j + 1] != 0 ? 1 + right[i][j + 1] : 1;\n }\n }\n }\n return right;\n }\n\n //\u5411\u4E0B\u8FDB\u884C\u9884\u5904\u7406\n private static int[][] downPreprocessing(int[][] m) {\n int N = m.length;\n int M = m[0].length;\n int[][] down = new int[N][M];\n\n //\u4ECE\u4E0B\u5F80\u4E0A\u8FDB\u884C\u9884\u5904\u7406\n for (int i = N - 1; i >= 0; i--) {\n for (int j = 0; j < M; j++) {\n if (m[i][j] == 0) {\n down[i][j] = 0;\n } else {\n down[i][j] = i + 1 < N && down[i + 1][j] != 0 ? 1 + down[i + 1][j] : 1;\n }\n }\n }\n return down;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
largest-1-bordered-square
|
Simple python3 solution | Dynamic Programming
|
simple-python3-solution-dynamic-programm-yb0y
|
Complexity\n- Time complexity: O(m \cdot n \cdot \min(n, m))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(m \cdot n)\n Add your space co
|
tigprog
|
NORMAL
|
2024-03-26T22:47:08.910056+00:00
|
2024-03-26T22:47:08.910081+00:00
| 69 | false |
# Complexity\n- Time complexity: $$O(m \\cdot n \\cdot \\min(n, m))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m \\cdot n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n``` python3 []\nclass Solution:\n def largest1BorderedSquare(self, grid: List[List[int]]) -> int:\n def get_dp(iter_lines):\n result = {}\n for i, line in enumerate(iter_lines):\n j = 0\n for elem, it in groupby(line):\n length = sum(1 for _ in it)\n if elem == 0: # skip zeros\n j += length\n continue\n for minus in range(length):\n result[(i, j)] = length - minus\n j += 1\n return result\n\n dp_lines = get_dp(grid)\n if len(dp_lines) == 0:\n return 0\n\n n = len(grid)\n m = len(grid[0])\n dp_rows = get_dp(\n (grid[i][j] for i in range(n))\n for j in range(m)\n )\n\n def get_square_side(i, j):\n max_length = min(\n dp_lines[(i, j)],\n dp_rows[(j, i)],\n )\n for size in range(max_length, 1, -1):\n if (\n dp_lines[(i + size - 1, j)] >= size\n and dp_rows[(j + size - 1, i)] >= size\n ):\n return size\n return 1\n \n result = max(\n get_square_side(i, j)\n for i, line in enumerate(grid)\n for j, elem in enumerate(line)\n if elem != 0\n )\n return result ** 2\n```
| 0 | 0 |
['Dynamic Programming', 'Matrix', 'Iterator', 'Prefix Sum', 'Python3']
| 0 |
largest-1-bordered-square
|
C++ | DP
|
c-dp-by-rohilla_himanshu-zf92
|
Intuition & Approach\n Describe your first thoughts on how to solve this problem. \nPrefix sum is hinted by forming a square, at a point we can get to know if i
|
rohilla_himanshu
|
NORMAL
|
2024-03-24T16:44:58.900715+00:00
|
2024-03-24T16:44:58.900750+00:00
| 54 | false |
# Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nPrefix sum is hinted by forming a square, at a point we can get to know if its a square if number of 1\'s form a square.\nSo, compute prefixSum for both rows and cols, and process the complete array again.\n\n# Complexity\n- Time complexity: O(rows*cols*min(rows, cols))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(rows*cols)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int largest1BorderedSquare(vector<vector<int>>& grid) {\n int rows = grid.size(), cols = grid[0].size();\n int res = 0;\n bool ones = false;\n int rowSum[rows][cols], colSum[rows][cols];\n // vector<vector<int>> rowSum(rows, vector<int>(cols, 0)), colSum(rows, vector<int>(cols, 0));\n \n // calculate the prefix sum\n for(int i = 0; i < rows; i++)\n {\n for(int j = 0; j < cols; j++)\n {\n if(grid[i][j] == 0)\n rowSum[i][j] = colSum[i][j] = 0;\n else\n {\n ones = true;\n rowSum[i][j] = j > 0 ? rowSum[i][j-1] + 1 : 1;\n colSum[i][j] = i > 0 ? colSum[i-1][j] + 1 : 1;\n }\n }\n }\n\n // now compute the actual result by taking each point and then \\\n calculate the maximum square area possible.\n for(int i = 1; i < rows; i++)\n {\n for(int j = 1; j < cols; j++)\n {\n // i, j\n // traverse the complete length.\n\n int maxLen = min(i, j); // how many steps we can move up to check.\n int bottomRow = rowSum[i][j], bottomCol = colSum[i][j];\n for(int k = maxLen; k >= 1; k--)\n {\n int newRow = rowSum[i-k][j], newCol = colSum[i][j-k];\n int len = k+1;\n int minNum = min(bottomRow, min(bottomCol, min(newRow, newCol)));\n\n if(minNum >= len)\n {\n res = max(res, len*len);\n break;\n }\n }\n }\n }\n return res == 0 ? ones : res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
largest-1-bordered-square
|
Easy to under simple java solution
|
easy-to-under-simple-java-solution-by-vs-vua1
|
Intuition\nReferred other solutions, and made changes easier for me to understand. \n\n# Approach\nStore left to right sum array and top to bottom sum array. Ev
|
vsriram
|
NORMAL
|
2024-03-22T05:53:14.830278+00:00
|
2024-03-22T05:53:14.830297+00:00
| 15 | false |
# Intuition\nReferred other solutions, and made changes easier for me to understand. \n\n# Approach\nStore left to right sum array and top to bottom sum array. Every point in this array is considered bottom right point of a square and check if top right and bottom left corners of square satisfy the required condition of minimum number of 1s.\n\n# Complexity\n- Time complexity: Worst case O(N^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int largest1BorderedSquare(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[][] left = new int[m][n];\n int[][] top = new int[m][n];\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == 1) {\n left[i][j] = j > 0 ? left[i][j-1] + 1 : 1;\n top[i][j] = i > 0 ? top[i-1][j] + 1 : 1;\n }\n }\n }\n int res = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int limit = Math.min(left[i][j], top[i][j]); // Maximum possible square from this bottom right point\n for (int k = limit; k > 0; k--) {\n if (left[i-k+1][j] >= k && top[i][j-k+1] >= k) { // Check if corresponding bottom left and top right points satisfy required number of 1s\n res = Math.max(res, k * k);\n break;\n }\n }\n }\n }\n return res;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.