question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
rle-iterator
|
Easy Java Solution TC: O(N), SC: O(1)
|
easy-java-solution-tc-on-sc-o1-by-amaaty-bqf7
|
Intuition\n Describe your first thoughts on how to solve this problem. \nEven indexes show the frequency of the corresponding next number.\nWe can decrement thi
|
amaatya
|
NORMAL
|
2023-10-05T11:32:26.280471+00:00
|
2023-10-05T11:32:26.280492+00:00
| 369 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEven indexes show the frequency of the corresponding next number.\nWe can decrement this number to see if there is anything left to add with the next number.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nKeep a reference to the even indexes. In a loop till ```n``` is more than zero, decrement the frequency if it is more than n. Otherwise, decrement ```n``` by the difference. Don\'t forget to check the reference pointer going out of bound.\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass RLEIterator {\n int pointer;\n int[] encoded;\n\n public RLEIterator(int[] encoding) {\n pointer = 0;\n encoded = Arrays.copyOf(encoding, encoding.length);\n }\n \n public int next(int n) {\n while(n > 0) {\n // check out of bound condition\n if (pointer >= encoded.length) return -1;\n\n // Only two cases possible\n // 1. Frequency is more than n -> Decrease the frequency by n\n // 2. Frequency is less than n -> Decrease n by the difference\n if (encoded[pointer] >= n) {\n encoded[pointer] -= n;\n return encoded[pointer + 1];\n } else {\n n = n - encoded[pointer];\n // move the reference to the next frequency location\n pointer += 2;\n }\n }\n\n return encoded[pointer + 1];\n }\n}\n\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(encoding);\n * int param_1 = obj.next(n);\n */\n```
| 3 | 0 |
['Java']
| 0 |
rle-iterator
|
Short and Easy c++ solution
|
short-and-easy-c-solution-by-sanchi285-rzkr
|
\n\n\nclass RLEIterator {\npublic:\n \n int mp;\n vector<int> arr;\n RLEIterator(vector<int>& encoding) {\n mp=0;\n arr.clear();\n
|
sanchi285
|
NORMAL
|
2022-01-24T09:26:19.826090+00:00
|
2022-01-24T09:26:19.826121+00:00
| 91 | false |
\n\n```\nclass RLEIterator {\npublic:\n \n int mp;\n vector<int> arr;\n RLEIterator(vector<int>& encoding) {\n mp=0;\n arr.clear();\n for(int i=0;i<encoding.size();i++){\n arr.emplace_back(encoding[i]);\n }\n }\n \n int next(int n) {\n \n while(mp<arr.size()){\n if(arr[mp]-n>=0){\n arr[mp]-=n;\n return arr[mp+1];\n }\n else{\n n= n-arr[mp];\n mp+=2;\n }\n }\n \n return -1;\n }\n};\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator* obj = new RLEIterator(encoding);\n * int param_1 = obj->next(n);\n */\n```\n
| 3 | 0 |
[]
| 0 |
rle-iterator
|
Java : Simple Stack Solution
|
java-simple-stack-solution-by-saiharini-i45r
|
\nclass RLEIterator {\n protected Stack<int[]> s;\n public RLEIterator(int[] encoding) {\n s = new Stack<>();\n int lgt = encoding.length;\n
|
saiharini
|
NORMAL
|
2021-12-29T07:56:52.820084+00:00
|
2021-12-29T07:56:52.820120+00:00
| 165 | false |
```\nclass RLEIterator {\n protected Stack<int[]> s;\n public RLEIterator(int[] encoding) {\n s = new Stack<>();\n int lgt = encoding.length;\n for(int i=lgt-1;i>=0;){\n int val = encoding[i];\n int count = encoding[i-1];\n i=i-2;\n if(count == 0){\n continue;\n }\n if(!s.isEmpty() && s.peek()[0] == val){\n int[] top = s.pop();\n count+=top[1];\n }\n s.push(new int[]{val, count});\n }\n \n }\n \n public int next(int n) {\n int ctr = n;\n int res = -1;\n while(ctr>0 && !s.isEmpty()){\n int[] top = s.pop();\n if(top[1] < ctr){\n ctr-=top[1];\n }else{\n res = top[0];\n if(top[1]-ctr != 0){\n s.push(new int[]{top[0], top[1]-ctr});\n }\n break;\n }\n }\n return res;\n }\n}\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(encoding);\n * int param_1 = obj.next(n);\n */\n ```
| 3 | 0 |
['Stack', 'Java']
| 0 |
rle-iterator
|
Recursive approach | no extra space | beats 100% users
|
recursive-approach-no-extra-space-beats-1wezv
|
Approach\n- Keep a pointer to the index which represents total occurence of front element\n- for next operation check if cuurent element can satisfy it if yes t
|
anupsingh556
|
NORMAL
|
2024-03-23T07:28:21.459502+00:00
|
2024-03-23T07:28:21.459539+00:00
| 79 | false |
# Approach\n- Keep a pointer to the index which represents total occurence of front element\n- for next operation check if cuurent element can satisfy it if yes then reduce its occurence to total element you are removing If not reduce n to amount it can be fullfilled from front number and recursively call again\n\n# Code\n```\nclass RLEIterator {\npublic:\n vector<int> enc;int pointer;\n RLEIterator(vector<int>& e) {\n enc = e;\n pointer=0;\n }\n \n int next(int n) {\n if(pointer>=enc.size())return -1;\n if(n<=enc[pointer]) {\n enc[pointer] = enc[pointer]-n;\n return enc[pointer+1];\n }\n n = n - enc[pointer];\n enc[pointer]=0;pointer+=2;\n return next(n);\n }\n};\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator* obj = new RLEIterator(encoding);\n * int param_1 = obj->next(n);\n */\n```
| 2 | 0 |
['C++']
| 0 |
rle-iterator
|
Solution
|
solution-by-deleted_user-1yzc
|
C++ []\nclass RLEIterator {\npublic:\n RLEIterator(const std::vector<int>& encoding)\n {\n m_encodings.reserve(encoding.size() / 2);\n for (
|
deleted_user
|
NORMAL
|
2023-05-11T22:05:15.498563+00:00
|
2023-05-11T22:12:50.101882+00:00
| 630 | false |
```C++ []\nclass RLEIterator {\npublic:\n RLEIterator(const std::vector<int>& encoding)\n {\n m_encodings.reserve(encoding.size() / 2);\n for (int i = 0; i < encoding.size(); i += 2) {\n const int count = encoding[i];\n const int number = encoding[i + 1];\n m_encodings.emplace_back(count, number);\n }\n }\n int next(int n)\n {\n while (m_current_idx < m_encodings.size() && m_encodings[m_current_idx].first < n) {\n n -= m_encodings[m_current_idx].first;\n m_encodings[m_current_idx].first = 0;\n ++m_current_idx;\n }\n if (m_current_idx >= m_encodings.size())\n return -1;\n m_encodings[m_current_idx].first -= n;\n return m_encodings[m_current_idx].second;\n }\nprivate:\n int m_current_idx = 0;\n std::vector<std::pair<int, int>> m_encodings;\n};\n```\n\n```Python3 []\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n while self.lst and n>0:\n if n<=self.lst[0]:\n self.lst[0]-=n \n n=0\n num=self.lst[1]\n else:\n n-=self.lst[0]\n self.lst[0]=0\n if self.lst[0]==0:\n self.lst.pop(0)\n self.lst.pop(0)\n if n>0:\n return -1\n return num\n```\n\n```Java []\nclass RLEIterator {\n public int[] encoding;\n public int index;\n public RLEIterator(int[] encoding) {\n this.encoding = encoding;\n this.index = 0;\n }\n public int next(int n) { \n while (n > 0 && index < encoding.length) {\n if (encoding[index] < n) {\n n -= encoding[index];\n encoding[index] = 0;\n index += 2;\n } else {\n encoding[index] -= n;\n n = 0;\n }\n }\n if (index >= encoding.length) return -1;\n return encoding[index + 1];\n }\n}\n```\n
| 2 | 0 |
['C++', 'Java', 'Python3']
| 0 |
rle-iterator
|
C++ | Binary Search | Faster than100%
|
c-binary-search-faster-than100-by-iamron-o32d
|
\n#define ll long long int\nclass RLEIterator {\npublic:\n vector<ll> prefix,val;\n ll idx;\n RLEIterator(vector<int>& en) {\n ll sum = 0;\n
|
iamronnie847
|
NORMAL
|
2023-02-08T17:46:00.946271+00:00
|
2023-02-08T17:46:00.946315+00:00
| 284 | false |
```\n#define ll long long int\nclass RLEIterator {\npublic:\n vector<ll> prefix,val;\n ll idx;\n RLEIterator(vector<int>& en) {\n ll sum = 0;\n for(int i=0;i<en.size()-1;i+=2){\n sum += en[i];\n prefix.push_back(sum);\n val.push_back(en[i+1]);\n }\n idx = 0;\n }\n \n int next(int n) {\n idx += n;\n auto it = lower_bound(prefix.begin(),prefix.end(),idx);\n if(it == prefix.end())\n return -1;\n return val[it-prefix.begin()];\n }\n};\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator* obj = new RLEIterator(encoding);\n * int param_1 = obj->next(n);\n */\n```
| 2 | 0 |
['C', 'Binary Tree']
| 0 |
rle-iterator
|
C++ || Simple || Short || Easy to understand
|
c-simple-short-easy-to-understand-by-van-5bsw
|
\n\n# Code\n\nclass RLEIterator {\npublic:\n vector<int> arr;\n int l = 0;\n int size;\n RLEIterator(vector<int>& encoding) {\n arr = encodin
|
agg_vansh
|
NORMAL
|
2022-11-17T09:03:42.232915+00:00
|
2022-11-17T09:04:13.890213+00:00
| 289 | false |
\n\n# Code\n```\nclass RLEIterator {\npublic:\n vector<int> arr;\n int l = 0;\n int size;\n RLEIterator(vector<int>& encoding) {\n arr = encoding;\n size = arr.size();\n }\n \n int next(int n) { \n while(l < size && arr[l] < n){\n n -= arr[l];\n l += 2;\n }\n if(l < size && arr[l] >= n){\n arr[l] -= n;\n return arr[l+1];\n }\n return -1;\n }\n};\n\n// just dry run the code \n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator* obj = new RLEIterator(encoding);\n * int param_1 = obj->next(n);\n */\n```
| 2 | 0 |
['C++']
| 0 |
rle-iterator
|
Explanation of O(NLogN) solution
|
explanation-of-onlogn-solution-by-sunder-z8vi
|
Very nice Java solution was provided here: https://leetcode.com/problems/rle-iterator/discuss/204726/Three-solutions-you-would-want-to-discuss-in-an-interview-(
|
sunder_thinkit
|
NORMAL
|
2022-11-12T15:41:00.195933+00:00
|
2022-11-12T15:41:00.195964+00:00
| 120 | false |
Very nice Java solution was provided here: https://leetcode.com/problems/rle-iterator/discuss/204726/Three-solutions-you-would-want-to-discuss-in-an-interview-(O(n)-O(logn)-and-O(1)-lookup) in using BinarySearch (O(log N)) by storing cumulative count !!\nJust to unravel the solution:\n\nInput-> [3 8 0 9 2 5]\n\n1. Create two Arrays: One that stores the count and other that stores the number with that count\nCount Array : [3 0 2]\nNumber Array: [8 9 5]\n\n2. Now transform the "Count Array" by storing the cumulative count; this way we will be able to get the actual position or interval of the number\nCumulative Count Array: [3, 3+0, 3+0+2] -> [3 3 5]; Note: if the count is 0 in Count array, don\'t even store it to keep it cleaner -> [3 5]\nCumulative Count Array: [3 5]\nNumber Array : [8 5]\n\n3. With this cumulative count, we have actually been able to capture the positions or intervals of the numbers. Space complexity is still O(N/2) -> 0(N)\n[3 5] -> means positions 1 to 3 is the first number 8 and positions 4 to 5 is the second number 5\n\n4. Now, if they are asking us to find the number at position n ( this is a rolling position every time next() is called), we Binary Search the position in the Cumulative County Array\nand return the number in Number Array in that position or in that interval.\n\n5. First Time: n = (2); Binary Search 2 in Cumulative Count Array (CCA)\nLogic: Find n such that its less than or equal to a number in the CCA and greater than the previous number in CCA. Its position 1 -> So, return Number in\nposition 1.\n\n\tSecond Time: n = n + (1) = 3; Binary Search 3 in CCA -> Still its position 1.\n\n\tThird Time : n = n + (2) = 5; Binary Search 5 in CCA ->its position 2- > So, return Number in position 2.\n\n\tFourth Time : n = n + (1) = 6; Binary Search 6 in CCA -> Not available and so return -1.\n\nAs its a Binary Search, time complexity is O(log N).
| 2 | 0 |
[]
| 0 |
rle-iterator
|
Easy python solution
|
easy-python-solution-by-shubham_1307-e0e0
|
\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n w
|
shubham_1307
|
NORMAL
|
2022-11-10T04:35:06.575708+00:00
|
2022-11-10T04:35:06.575752+00:00
| 895 | false |
```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.lst=encoding\n\n def next(self, n: int) -> int:\n num=-1\n while self.lst and n>0:\n if n<=self.lst[0]:\n self.lst[0]-=n \n n=0\n num=self.lst[1]\n else:\n n-=self.lst[0]\n self.lst[0]=0\n if self.lst[0]==0:\n self.lst.pop(0)\n self.lst.pop(0)\n if n>0:\n return -1\n return num\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
rle-iterator
|
Python simple deque solution
|
python-simple-deque-solution-by-vincent_-mfz9
|
\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.dq = deque(encoding)\n\n def next(self, n: int) -> int:\n ans = -1\
|
vincent_great
|
NORMAL
|
2022-07-23T03:00:12.994938+00:00
|
2022-07-23T03:00:12.994982+00:00
| 256 | false |
```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.dq = deque(encoding)\n\n def next(self, n: int) -> int:\n ans = -1\n while(n>0):\n if not self.dq:\n return -1\n if self.dq[0]>n:\n self.dq[0] -= n\n n = 0\n ans = self.dq[1]\n else:\n n -= self.dq.popleft()\n ans = self.dq.popleft()\n \n return ans\n```
| 2 | 0 |
[]
| 1 |
rle-iterator
|
std::map, O(log(N)
|
stdmap-ologn-by-the_2nd_derivative-9cjg
|
The idea is simple,\nFor every number n, we store the last index of occuring i in a map such that map[i] = n then for every query we just find the lower_bound f
|
The_2nd_Derivative
|
NORMAL
|
2022-03-27T12:37:53.142095+00:00
|
2022-03-27T12:39:26.241322+00:00
| 214 | false |
The idea is simple,\nFor every number `n`, we store the last index of occuring `i` in a map such that `map[i] = n` then for every query we just find the `lower_bound` for the index :)\nfor example, let\'s take sample test case :\n`encoding = [3, 8, 0, 9, 2, 5];`\narray = `8 8 8 5 5`\nindex =` 0 1 2 3 4`\nhence, map becomes `mp = {{2 : 8}, {4 : 5}}`\n**code : **\n```\nclass RLEIterator {\nprivate:\n long long idx = -1, sz = 0;\n map<long long, long long> mp;\npublic:\n RLEIterator(vector<int>& encoding) {\n long long cur = -1;\n for (int i=0; i<encoding.size()-1;i+=2) {\n if (encoding[i] > 0) {\n cur += encoding[i];\n mp[cur] = encoding[i+1];\n sz = cur+1;\n }\n }\n }\n \n int next(int n) {\n idx += n;\n if (idx < sz) {\n auto it = mp.lower_bound(idx);\n return it->second;\n } else return -1;\n }\n};\n```
| 2 | 0 |
[]
| 1 |
rle-iterator
|
c++ prefix sum -> binary search O(lgn) per query
|
c-prefix-sum-binary-search-olgn-per-quer-6pwi
|
\nclass RLEIterator {\npublic:\n RLEIterator(vector<int>& encoding) {\n long psum = 0;\n for (int i = 0; i < encoding.size(); i += 2) {\n
|
colinyoyo26
|
NORMAL
|
2021-12-14T02:42:01.725592+00:00
|
2021-12-14T02:43:13.597581+00:00
| 147 | false |
```\nclass RLEIterator {\npublic:\n RLEIterator(vector<int>& encoding) {\n long psum = 0;\n for (int i = 0; i < encoding.size(); i += 2) {\n val.push_back(encoding[i + 1]);\n psum += encoding[i];\n cnt.push_back(psum);\n }\n val.push_back(-1);\n }\n \n int next(int n) {\n n_ += n;\n auto i = lower_bound(cnt.begin(), cnt.end(), n_) - cnt.begin();\n return val[i];\n }\n vector<long> val, cnt;\n long n_ = 0;\n};\n```
| 2 | 0 |
[]
| 1 |
rle-iterator
|
Python 3 & Java | Deque | Explanation
|
python-3-java-deque-explanation-by-idont-oqyq
|
Explanation\n- Intuition is pretty much just a simulation of the process, you can totally use array operation instead of Deque. Deque seems more straight forwar
|
idontknoooo
|
NORMAL
|
2021-07-02T18:37:21.421405+00:00
|
2021-07-02T18:37:21.421445+00:00
| 350 | false |
### Explanation\n- Intuition is pretty much just a simulation of the process, you can totally use array operation instead of Deque. Deque seems more straight forward to simulate the process.\n- While `n` is greater than total count of current available number (`self.q[0]`), meaning current number is not enough to exhaust `n`, thus:\n\t- `n = n - self.q[0]`, then\n\t- popleft twice to clear count & value\n- If `n` is less than or equal to total count of current available number (`self.q[0]`), meaning current number has enough count to exhaust `n`, thus:\n\t- `self.q[0] -= n`, then\n\t- No need to pop since there might be some leftover for current number\n- If `n` is exhausted, return current number (`self.q[1]`)\n- Otherwise, return `-1` (meaning we failed to exhaust `n` using `self.q`)\n### Implementation\n<iframe src="https://leetcode.com/playground/KomHCN9z/shared" frameBorder="0" width="600" height="500"></iframe>
| 2 | 0 |
['Queue', 'Simulation', 'Python', 'Python3']
| 2 |
rle-iterator
|
C++ solution with iterators, no need to store array
|
c-solution-with-iterators-no-need-to-sto-itcy
|
The following solution makes use of iterators , instead of having to save full array.\n\n\nclass RLEIterator {\npublic:\n vector<int>::iterator curIndex, end
|
srishti31
|
NORMAL
|
2021-04-26T19:58:52.278683+00:00
|
2021-04-26T19:58:52.278727+00:00
| 222 | false |
The following solution makes use of iterators , instead of having to save full array.\n\n```\nclass RLEIterator {\npublic:\n vector<int>::iterator curIndex, end;\n RLEIterator(vector<int>& A) {\n curIndex = A.begin();\n end = A.end();\n }\n \n int next(int n) {\n while (curIndex != end && *curIndex < n) {\n n -= *curIndex;\n curIndex += 2;\n }\n if (curIndex != end && *curIndex >= n) {\n (*curIndex) -= n;\n return *(curIndex+1);\n }\n return -1;\n }\n};\n```
| 2 | 0 |
[]
| 1 |
rle-iterator
|
Python3 commented just keep a current position pointer
|
python3-commented-just-keep-a-current-po-9q6k
|
Runtime: 36 ms, faster than 75.00% of Python3 online submissions for RLE Iterator.\nMemory Usage: 14.6 MB, less than 45.57% of Python3 online submissions for RL
|
zetinator
|
NORMAL
|
2020-11-15T19:21:32.911902+00:00
|
2020-11-15T19:21:32.911935+00:00
| 342 | false |
*Runtime: 36 ms, faster than 75.00% of Python3 online submissions for RLE Iterator.\nMemory Usage: 14.6 MB, less than 45.57% of Python3 online submissions for RLE Iterator.*\n\n```python\nclass RLEIterator:\n def __init__(self, A: List[int]):\n self.pointer = 0\n self.nums = []\n self.repetitions = []\n for i in range(0, len(A) - 1, 2):\n repetition, num = A[i], A[i + 1]\n # avoid empty nums\n if repetition:\n self.nums.append(num)\n self.repetitions.append(repetition)\n\n def next(self, n: int) -> int:\n # chekc if we supass\n while n:\n # check index out of range\n if self.pointer == len(self.repetitions):\n return -1\n # move pointer\n if n > self.repetitions[self.pointer]:\n # reduce n\n n -= self.repetitions[self.pointer]\n # move pointer to next num\n self.pointer += 1\n else:\n # reduce repetitions left\n self.repetitions[self.pointer] -= n\n n = 0\n return self.nums[self.pointer]\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
rle-iterator
|
Python 36 ms, 100%
|
python-36-ms-100-by-yashb_dev-vrjx
|
\nclass RLEIterator:\n\n def __init__(self, A):\n """\n :type A: List[int]\n """\n global a\n a = []\n for x in ran
|
yashb_dev
|
NORMAL
|
2019-01-24T18:51:40.227198+00:00
|
2019-01-24T18:51:40.227265+00:00
| 603 | false |
```\nclass RLEIterator:\n\n def __init__(self, A):\n """\n :type A: List[int]\n """\n global a\n a = []\n for x in range(int(len(A)/2)):\n if A[2*x] != 0:\n a.insert(0, [A[2*x],A[2*x+1]])\n\n def next(self, n):\n """\n :type n: int\n :rtype: int\n """\n global a\n while n > 0:\n if a:\n i = a.pop()\n if i[0] >= n:\n i[0] -= n\n if i[0] != 0:\n a.append(i)\n return i[1]\n else:\n n-= i[0] \n else:\n return -1\n```\n\nCould probably make it much cleaner, but I don\'t really know what I did. Let me know if you guys figure it out.
| 2 | 1 |
[]
| 1 |
rle-iterator
|
O(1) Space O(input_arr.length) Time
|
o1-space-oinput_arrlength-time-by-google-fof5
|
\nclass RLEIterator {\n int[] arr;\n int idx;\n public RLEIterator(int[] A) {\n this.arr = A;\n this.idx = 0;\n }\n \n public in
|
google8
|
NORMAL
|
2019-01-08T02:44:51.368072+00:00
|
2019-01-08T02:44:51.368114+00:00
| 345 | false |
```\nclass RLEIterator {\n int[] arr;\n int idx;\n public RLEIterator(int[] A) {\n this.arr = A;\n this.idx = 0;\n }\n \n public int next(int n) {\n while (idx < arr.length) {\n if (n > arr[idx]) {\n n -= arr[idx];\n idx += 2;\n } else {\n arr[idx] -= n;\n return arr[idx + 1];\n }\n }\n return -1;\n }\n}\n```
| 2 | 0 |
[]
| 1 |
rle-iterator
|
Readable Javascript Solution
|
readable-javascript-solution-by-codingba-1qaa
|
Javascript solution of https://leetcode.com/problems/rle-iterator/discuss/168294/Java-Straightforward-Solution-O(n)-time-O(1)-space\n\nTo me, this seems like a
|
codingbarista
|
NORMAL
|
2018-11-12T06:22:54.035930+00:00
|
2018-11-12T06:22:54.035979+00:00
| 202 | false |
Javascript solution of https://leetcode.com/problems/rle-iterator/discuss/168294/Java-Straightforward-Solution-O(n)-time-O(1)-space\n\nTo me, this seems like a greedy problem\nGreedy choice: retire many number as possible.\n\n```\nvar RLEIterator = function(A) {\n this.A = A;\n this.index = 0;\n};\n\nRLEIterator.prototype.next = function(n) {\n while (this.index < this.A.length && n > this.A[this.index]) {\n n -= this.A[this.index];\n this.index += 2;\n }\n \n if (this.index < this.A.length) {\n this.A[this.index] -= n;\n return this.A[this.index + 1];\n }\n \n return -1;\n};\n```
| 2 | 0 |
[]
| 0 |
rle-iterator
|
TreeMap, Java O(log(n)) time next function
|
treemap-java-ologn-time-next-function-by-4m6n
|
\nclass RLEIterator {\n TreeMap<Long, Integer> map = new TreeMap<>();\n long cur = 0;\n public RLEIterator(int[] A) {\n long count = 0;\n
|
chanchopee
|
NORMAL
|
2018-10-13T03:55:31.208615+00:00
|
2018-10-13T03:55:31.208653+00:00
| 119 | false |
```\nclass RLEIterator {\n TreeMap<Long, Integer> map = new TreeMap<>();\n long cur = 0;\n public RLEIterator(int[] A) {\n long count = 0;\n for (int i = 0; i < A.length - 1; i += 2) {\n if (A[i] == 0) continue;\n count += A[i];\n map.put(count, A[i + 1]);\n }\n }\n \n public int next(int n) {\n cur += n;\n Long val = map.ceilingKey(cur);\n if (val == null) return -1;\n return map.get(val);\n }\n}\n```
| 2 | 0 |
[]
| 0 |
rle-iterator
|
python3 coroutine beat 100%
|
python3-coroutine-beat-100-by-freestylez-6ffk
|
The problem is to implement an iterator, my first thought is to use a generator. However, the iterator accepts an input. That will be a python coroutine. \n\n\n
|
freestylezhy
|
NORMAL
|
2018-09-14T17:31:01.636226+00:00
|
2018-09-14T17:31:01.636272+00:00
| 199 | false |
The problem is to implement an iterator, my first thought is to use a generator. However, the iterator accepts an input. That will be a python coroutine. \n\n```\n def __init__(self, A):\n """\n :type A: List[int]\n """ \n def my_gen(data):\n i = 0\n n = yield\n while True:\n try:\n count = data[i]\n value = data[i + 1]\n i += 2\n except:\n yield -1\n\n while count > 0:\n if n <= count:\n count -= n\n n = yield value\n else:\n n -= count\n count = 0\n \n self.gen = my_gen(A)\n next(self.gen)\n \n \n def next(self, n):\n """\n :type n: int\n :rtype: int\n """\n return self.gen.send(n)\n```
| 2 | 0 |
[]
| 1 |
rle-iterator
|
Short Java Solution
|
short-java-solution-by-climberig-a02g
|
```\nclass RLEIterator {\n int a[], i;\n\n public RLEIterator(int[] a) { this.a = a;}\n\n public int next(int n) {\n for (; i <
|
climberig
|
NORMAL
|
2018-09-09T19:25:36.909920+00:00
|
2018-09-30T17:35:50.198260+00:00
| 151 | false |
```\nclass RLEIterator {\n int a[], i;\n\n public RLEIterator(int[] a) { this.a = a;}\n\n public int next(int n) {\n for (; i < a.length; i += 2)\n if (n > a[i])\n n -= a[i];\n else {\n a[i] -= n;\n return a[i + 1];\n }\n return -1;\n }\n }
| 2 | 2 |
[]
| 0 |
rle-iterator
|
JAVA 3-liner next()
|
java-3-liner-next-by-shreyansh94-376a
|
\nclass RLEIterator {\n int index = 0, i; \n int[] a; \n \n public RLEIterator(int[] A) {\n a = A;\n }\n \n public int next(int n) {
|
shreyansh94
|
NORMAL
|
2018-09-09T03:52:03.806867+00:00
|
2018-09-09T16:30:28.023733+00:00
| 190 | false |
```\nclass RLEIterator {\n int index = 0, i; \n int[] a; \n \n public RLEIterator(int[] A) {\n a = A;\n }\n \n public int next(int n) {\n for(i = index; i < a.length && n>a[i]; n -= a[i], i+=2, index=i);\n if(i < a.length ) a[i]-=n; \n return i < a.length ? a[i+1] : -1; \n }\n}\n```
| 2 | 2 |
[]
| 0 |
rle-iterator
|
C++ 100% faster deque based solution
|
c-100-faster-deque-based-solution-by-sj4-xvvc
|
IntuitionMaintain a deque and do ops from top of it.Complexity
Time complexity: O(n2)
Space complexity: O(n)
Code
|
SJ4u
|
NORMAL
|
2025-03-31T12:26:38.383423+00:00
|
2025-03-31T12:26:38.383423+00:00
| 11 | false |
# Intuition
Maintain a deque and do ops from top of it.
# Complexity
- Time complexity: $$O(n^2)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class RLEIterator {
public:
deque<pair<int,int>>q;
RLEIterator(vector<int>& encoding) {
// populate freq, num to queue
for(int i=0;i<encoding.size();i+=2){
if(encoding[i] == 0)
continue;
q.push_back({encoding[i],encoding[i+1]});
}
}
int next(int n) {
while(q.size()){
int freq = q.front().first, num = q.front().second;
q.pop_front();
if(n-freq>0){
n-=freq; // more exhaustion needed
} else if(n-freq ==0){
return num; // all consumed
} else{
q.push_front({freq-n,num}); // give remaining back to deque of current.
return num;
}
}
return -1;
}
};
/**
* Your RLEIterator object will be instantiated and called as such:
* RLEIterator* obj = new RLEIterator(encoding);
* int param_1 = obj->next(n);
*/
```
| 1 | 0 |
['C++']
| 1 |
rle-iterator
|
Python3 deque solution
|
python3-deque-solution-by-pp811-kpdw
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUse a deque in python to add from right in init function and consume from left in next
|
pp811
|
NORMAL
|
2024-02-19T02:01:03.386688+00:00
|
2024-02-19T02:01:03.386719+00:00
| 139 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse a deque in python to add from right in init function and consume from left in next function. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N) for init and O(1) for next\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.qrle = deque()\n n = len(encoding)\n for i in range(0, n, 2):\n count, elem = encoding[i], encoding[i+1]\n if count:\n self.qrle.append((count, elem)) \n\n def next(self, n: int) -> int:\n last_elem = 0\n while n:\n if not self.qrle:\n last_elem = -1\n break\n \n count, elem = self.qrle.popleft()\n if count >= n:\n last_elem = elem\n if count > n: self.qrle.appendleft((count-n, elem))\n break\n else:\n n -= count\n \n return last_elem\n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n```
| 1 | 0 |
['Python3']
| 1 |
rle-iterator
|
Java | 5ms | Simple Solution
|
java-5ms-simple-solution-by-ayush172-hrjw
|
Code\n\nclass RLEIterator {\n int i, len, val = -1;\n int[] list;\n public RLEIterator(int[] encoding) {\n i=0;\n len = encoding.length;\
|
ayush172
|
NORMAL
|
2023-11-09T07:28:06.732225+00:00
|
2023-11-09T07:30:42.761380+00:00
| 8 | false |
# Code\n```\nclass RLEIterator {\n int i, len, val = -1;\n int[] list;\n public RLEIterator(int[] encoding) {\n i=0;\n len = encoding.length;\n list = encoding;\n }\n \n public int next(int n) {\n if(i >= len-1) return -1;\n\n int ans = -1;\n // Reduce the count and return the number\n if(list[i] - n > 0){\n list[i] -= n;\n ans = list[i+1];\n }\n // Return the number and Move iterator to next group\n else if(list[i] - n == 0){\n ans = list[i+1];\n i += 2; \n }\n // Move iterator to next group and recursively call next with n-list[i]\n else{\n int newN = n - list[i];\n i += 2;\n ans = next(newN);\n }\n return ans;\n }\n}\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(encoding);\n * int param_1 = obj.next(n);\n */\n```
| 1 | 0 |
['Java']
| 0 |
rle-iterator
|
Simple Java Solution with LinkedHashMap
|
simple-java-solution-with-linkedhashmap-qvu0k
|
\npublic class RLEIterator {\n\n long p = 0;\n Map<Long, Integer> hm = new LinkedHashMap<>();\n\n public RLEIterator(int[] encoding) {\n long k
|
jsnmrrssy
|
NORMAL
|
2023-06-20T13:07:01.726525+00:00
|
2023-06-20T13:07:01.726544+00:00
| 14 | false |
```\npublic class RLEIterator {\n\n long p = 0;\n Map<Long, Integer> hm = new LinkedHashMap<>();\n\n public RLEIterator(int[] encoding) {\n long k = 0;\n for (int i = 0; i < encoding.length; i += 2) {\n k += encoding[i];\n if (encoding[i] > 0) {\n hm.put(k, encoding[i + 1]);\n }\n }\n }\n\n public int next(int n) {\n p += n;\n for (Long key : hm.keySet()) {\n if (key >= p) {\n return hm.get(key);\n }\n }\n return -1;\n }\n}\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(encoding);\n * int param_1 = obj.next(n);\n */\n```
| 1 | 0 |
['Java']
| 1 |
rle-iterator
|
very easy to understand || must see
|
very-easy-to-understand-must-see-by-aksh-n1yj
|
Code\n\nstatic int fast_io = []() \n{ \n std::ios::sync_with_stdio(false); \n cin.tie(nullptr); \n cout.tie(nullptr); \n return 0; \n}();\n\n#ifdef
|
akshat0610
|
NORMAL
|
2023-03-14T17:15:25.681333+00:00
|
2023-03-14T17:15:25.681382+00:00
| 701 | false |
# Code\n```\nstatic int fast_io = []() \n{ \n std::ios::sync_with_stdio(false); \n cin.tie(nullptr); \n cout.tie(nullptr); \n return 0; \n}();\n\n#ifdef LOCAL\n freopen("input.txt", "r" , stdin);\n freopen("output.txt", "w", stdout);\n#endif\n\nclass RLEIterator {\npublic:\n int idx;\n vector<int>v;\n RLEIterator(vector<int>& encoding) \n {\n idx = 0;\n v = encoding;\n }\n \n int next(int n) \n {\n while(idx < v.size()-1 and (v[idx] == 0 or v[idx] < n))\n {\n n = n - v[idx];\n idx = idx + 2;\n } \n\n if(idx >= v.size()-1)\n return -1;\n\n if(idx < v.size()-1 and v[idx] > n)\n {\n v[idx] = v[idx] - n;\n return v[idx+1];\n }\n else if(idx < v.size()-1 and v[idx] == n)\n {\n int ele = v[idx+1];\n v[idx] = v[idx] - n;\n idx = idx + 2;\n return ele;\n }\n return -1;\n }\n};\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator* obj = new RLEIterator(encoding);\n * int param_1 = obj->next(n);\n */\n```
| 1 | 0 |
['Array', 'Design', 'Counting', 'Iterator', 'C++']
| 0 |
rle-iterator
|
[C++][Short][Simple] Just a Stack
|
cshortsimple-just-a-stack-by-unstoppable-bv66
|
```\nclass RLEIterator {\npublic:\n stack> st;\n \n RLEIterator(vector& encoding) {\n for (int i = encoding.size() - 1; i >= 0; i -= 2) {\n
|
Unstoppable_Train
|
NORMAL
|
2023-01-04T10:46:31.479661+00:00
|
2023-01-04T10:47:19.989881+00:00
| 113 | false |
```\nclass RLEIterator {\npublic:\n stack<pair<int, int>> st;\n \n RLEIterator(vector<int>& encoding) {\n for (int i = encoding.size() - 1; i >= 0; i -= 2) {\n if (encoding[i - 1] <= 0) continue;\n \n // Will hold each value and its frequency\n st.push({ encoding[i], encoding[i - 1] });\n }\n }\n \n int next(int n) {\n int originalN = n;\n \n while(!st.empty()) {\n auto [ value, freq ] = st.top(); st.pop();\n \n originalN = n;\n n -= freq;\n freq -= originalN;\n \n // IF we didn\'t consume all the frequency of the element, then push it back again\n if (freq > 0) {\n st.push({ value, freq }); \n }\n \n // If we moved forward n steps, then we return the value\n if (n <= 0) {\n return value;\n }\n }\n \n return -1;\n }\n};\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator* obj = new RLEIterator(encoding);\n * int param_1 = obj->next(n);\n */
| 1 | 0 |
['Stack', 'C', 'C++']
| 0 |
rle-iterator
|
Python prefix sum and bisect
|
python-prefix-sum-and-bisect-by-bac2qh-5732
|
Thoughts: \n\n- For an even index i, encoding[i] is the number of appreances of the encoding[i+1] in the list \n- Create two array, one for number of appearance
|
bac2qh
|
NORMAL
|
2022-08-24T19:54:52.341190+00:00
|
2022-08-24T19:58:51.369490+00:00
| 31 | false |
#### Thoughts: \n\n- For an even index i, `encoding[i]` is the number of appreances of the `encoding[i+1]` in the list \n- Create two array, one for number of appearance `self.counts` the other for the corresponding value `self.vals` . \n- Transform `self.counts` to prefix sum\n- Now you can binary search the insertion index while maintaining the sorted order of the `self.counts`. You can do this easily in Python with `bisect` library. \n\n#### Example \n\n[3, 8, 0, 9, 2, 5] is an encoding of [8, 8, 8, 5, 5] \nself.counts = [3, 2]\nself.vals = [8, 5] \nwhat you want to do now is to return 8 for query at index 0, 1, 2 and 5 for query at index 3, 4, and -1 for anything beyond \n\n#### Solution \n\n```Python \nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.counts = [-1] # -1 to avoid indexing error \n self.vals = []\n for i in range(len(encoding) // 2): \n count, val = encoding[i*2], encoding[i*2+1] \n if count > 0: \n self.counts.append(count)\n if len(self.counts) > 1: \n self.counts[-1] += self.counts[-2] # build the prefix sum \n self.vals.append(val)\n self.idx = -1 # an internal counter for handelling next calls \n\n\t# I created my own bisect module here but in python it\'s built-in \n def bi(self, idx): \n if idx > self.counts[-1]: \n return -1 \n l, r = 0, len(self.counts) - 1\n while l <= r: \n mid = l + (r - l) // 2\n if self.counts[mid] < idx <= self.counts[mid+1]:\n return mid \n if idx > self.counts[mid+1]: \n l = mid + 1\n else: \n r = mid - 1\n \n def next(self, n: int) -> int:\n self.idx += n \n # i = self.bi(self.idx)\n i = bisect.bisect_left(self.counts, self.idx) - 1\n return self.vals[i] if i < len(self.vals) else -1\n```
| 1 | 0 |
['Prefix Sum', 'Python']
| 0 |
rle-iterator
|
[Java] Simple Iteration O(1) space
|
java-simple-iteration-o1-space-by-java-l-10fz
|
```\nclass RLEIterator {\n \n private final int[] encoding;\n private final int size;\n \n int encodeIndex = 0;\n\n public RLEIterator(int
|
java-lang-goutam
|
NORMAL
|
2022-08-13T13:08:31.332204+00:00
|
2022-08-13T13:10:55.166783+00:00
| 158 | false |
```\nclass RLEIterator {\n \n private final int[] encoding;\n private final int size;\n \n int encodeIndex = 0;\n\n public RLEIterator(int[] encoding) {\n this.encoding = encoding;\n this.size = encoding.length;\n }\n \n public int next(int n) {\n \n while (encodeIndex < size) {\n if (encoding[encodeIndex] <= n) {\n if (encoding[encodeIndex] != 0) n -= encoding[encodeIndex];\n encodeIndex+=2;\n if (n == 0) return encoding[encodeIndex - 1];\n } else {\n encoding[encodeIndex] -= n;\n return encoding[encodeIndex + 1];\n }\n }\n \n return -1;\n }\n}\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(encoding);\n * int param_1 = obj.next(n);\n */
| 1 | 0 |
[]
| 0 |
rle-iterator
|
Clean/Readable C++ optimal solution. :)
|
cleanreadable-c-optimal-solution-by-dave-sv4e
|
\nclass RLEIterator \n{\n public:\n RLEIterator(vector<int> &encoding) : m_encoding{encoding}\n {\n }\n\n int next(int n) \n
|
dave4444
|
NORMAL
|
2022-07-23T17:41:45.916201+00:00
|
2022-07-23T17:41:45.916245+00:00
| 201 | false |
```\nclass RLEIterator \n{\n public:\n RLEIterator(vector<int> &encoding) : m_encoding{encoding}\n {\n }\n\n int next(int n) \n {\n while (m_iterator < m_encoding.size())\n {\n if (m_encoding[m_iterator] >= n)\n {\n m_encoding[m_iterator] -= n;\n return m_encoding[m_iterator + 1];\n }\n else\n {\n n -= m_encoding[m_iterator];\n m_iterator += 2;\n }\n }\n \n return -1;\n }\n \n private:\n std::vector<int> &m_encoding;\n int m_iterator{0};\n \n};\n```
| 1 | 0 |
['C']
| 0 |
rle-iterator
|
Python (Simple Maths)
|
python-simple-maths-by-rnotappl-st66
|
\n def init(self, encoding):\n self.encoding = encoding\n self.idx = 0\n\n def next(self, n):\n while self.idx < len(self.encoding):\
|
rnotappl
|
NORMAL
|
2022-05-07T19:08:52.205204+00:00
|
2022-05-07T19:08:52.205273+00:00
| 58 | false |
\n def __init__(self, encoding):\n self.encoding = encoding\n self.idx = 0\n\n def next(self, n):\n while self.idx < len(self.encoding):\n if self.encoding[self.idx] >= n:\n self.encoding[self.idx] -= n\n return self.encoding[self.idx+1]\n else:\n n -= self.encoding[self.idx]\n self.idx += 2\n \n return -1
| 1 | 0 |
[]
| 0 |
rle-iterator
|
Simple recursive Python3
|
simple-recursive-python3-by-brynna-yyoe
|
Simple solution beats 34% on runtime and 75% on memory.\n\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.encoding = encoding\
|
brynna
|
NORMAL
|
2022-05-07T06:24:06.929770+00:00
|
2022-05-07T06:24:06.929822+00:00
| 210 | false |
Simple solution beats 34% on runtime and 75% on memory.\n```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.encoding = encoding\n\n def next(self, n: int) -> int:\n \n if self.encoding:\n \n count = self.encoding[0]\n \n if count >= n:\n\t\t\t\t# Partially exhaust and return the current value.\n self.encoding[0] -= n\n return self.encoding[1]\n \n # Exhaust all of current value and continue.\n self.encoding = self.encoding[2:]\n return self.next(n - count)\n \n return -1\n```
| 1 | 0 |
['Recursion', 'Python']
| 1 |
rle-iterator
|
[Java] O(n) | Straight Forward
|
java-on-straight-forward-by-ninad07-ynrd
|
\nclass RLEIterator {\n int[] arr;\n int index;\n public RLEIterator(int[] encoding) {\n arr = encoding;\n index = 0;\n }\n \n p
|
Ninad07
|
NORMAL
|
2022-04-18T12:58:32.582696+00:00
|
2022-04-18T12:58:32.582744+00:00
| 165 | false |
```\nclass RLEIterator {\n int[] arr;\n int index;\n public RLEIterator(int[] encoding) {\n arr = encoding;\n index = 0;\n }\n \n public int next(int n) {\n int curr = 0;\n\t\t\n\t\t// Exhausting the next n elements\n while(index < arr.length && arr[index] < n) {\n n -= arr[index];\n arr[index] = 0;\n index += 2;\n }\n \n\t\t// No elements left\n if(index + 1 >= arr.length) return -1;\n\t\t\n\t\t// Update the current value\n arr[index] -= n;\n \n return arr[index + 1];\n }\n}\n\n```
| 1 | 0 |
['Java']
| 0 |
rle-iterator
|
Javascript Solution beating 100% in O(1) space and O(n) time
|
javascript-solution-beating-100-in-o1-sp-yqgu
|
Looking at the solution, seems like a simple producer consumer problem.\n\nnext(n) \nshould first produce i.e. iterate n places\nthen check while n is less than
|
_rajparekh
|
NORMAL
|
2022-02-16T17:45:47.068110+00:00
|
2022-02-16T17:46:39.860347+00:00
| 119 | false |
Looking at the solution, seems like a simple producer consumer problem.\n\nnext(n) \nshould first produce i.e. iterate n places\nthen check while n is less than allowed limit\nkeep consuming\n\nif you are out of bound return -1\n\nor else return next position\n\n```\n/**\n * @param {number[]} encoding\n */\nvar RLEIterator = function(encoding) {\n this.arr = encoding\n \n this.itrSum = 0\n this.itrPtr = 0\n};\n\n/** \n * @param {number} n\n * @return {number}\n */\nRLEIterator.prototype.next = function(n) {\n\t// PRODUCE\n this.itrSum += n\n \n\t// IF ABOVE LIMIT CONSUME\n while (this.arr[this.itrPtr] < this.itrSum) {\n this.itrSum -= this.arr[this.itrPtr]\n this.itrPtr += 2\n }\n \n\t// OUT OF BOUNDS\n if (this.itrPtr >= this.arr.length) {\n return -1\n }\n \n\t// RETURN NEXT\n return this.arr[this.itrPtr+1]\n};\n\n/** \n * Your RLEIterator object will be instantiated and called as such:\n * var obj = new RLEIterator(encoding)\n * var param_1 = obj.next(n)\n */\n```\n\nP.S. This is my first try at LC\'s discuss so please any feedback helps me! Thanks!
| 1 | 0 |
['JavaScript']
| 0 |
rle-iterator
|
[C++] O(n) simple solution with comments
|
c-on-simple-solution-with-comments-by-fg-l8b9
|
\nclass RLEIterator {\npublic:\n \n vector<int> enc; // the encoding vector\n int curr_val = -1; // the current value in the encoding vector that we po
|
fgodinho123
|
NORMAL
|
2022-02-02T20:55:54.457103+00:00
|
2022-02-02T20:57:04.739548+00:00
| 225 | false |
```\nclass RLEIterator {\npublic:\n \n vector<int> enc; // the encoding vector\n int curr_val = -1; // the current value in the encoding vector that we point to\n int curr_count = 0; // the current count of curr_val\n int enc_pointer = 0; // the position in encoding vector that we currently point to\n \n RLEIterator(vector<int>& encoding) {\n enc = encoding; \n }\n \n int next(int n) {\n \n for(int i = 0; i < n; ){\n\t\t\t\n\t\t\t// if curr_count is 0, get the next element in the encoding vector\n if(curr_count == 0){\n if(enc_pointer >= enc.size()) return -1;\n curr_count = enc[enc_pointer++];\n curr_val = enc[enc_pointer++];\n }\n\t\t\t\n\t\t\t// if curr_count is greater than the amount that remains to be exhausted,\n\t\t\t// we can decrement curr_count and then return the current value\n if(n - i <= curr_count){\n curr_count -= n - i;\n return curr_val;\n }\n \n\t\t\t// otherwise, we increment i be the amount that is possible to be exhausted and set curr_count to 0 \n i += curr_count;\n curr_count = 0; // we set curr_count to 0 because we have exhausted all remaining elements of value curr_val\n }\n return -1;\n \n }\n};\n```
| 1 | 0 |
['C', 'C++']
| 0 |
rle-iterator
|
Java 3ms beats 100%, very clear code
|
java-3ms-beats-100-very-clear-code-by-te-f5kk
|
\n/*\nRuntime: 3 ms, faster than 100.00% of Java online submissions for RLE Iterator.\nMemory Usage: 42 MB, less than 5.01% of Java online submissions for RLE I
|
texastim
|
NORMAL
|
2022-01-28T16:00:52.100081+00:00
|
2022-01-28T16:05:31.542646+00:00
| 108 | false |
```\n/*\nRuntime: 3 ms, faster than 100.00% of Java online submissions for RLE Iterator.\nMemory Usage: 42 MB, less than 5.01% of Java online submissions for RLE Iterator.\n*/\n\nclass RLEIterator {\n \n int[] arr;\n int indexIntoArr;\n\n public RLEIterator(int[] encoding) {\n // even indices are: number of times\n // odd indices are: what integer value\n \n this.arr = encoding;\n this.indexIntoArr = 0;\n }\n \n public int next(int n) {\n \n // guard clause\n\t\tif (this.indexIntoArr >= this.arr.length) {\n return -1;\n }\n \n if (n < this.arr[this.indexIntoArr]) {\n this.arr[this.indexIntoArr] -= n;\n return this.arr[this.indexIntoArr + 1];\n \n } else if (n == this.arr[this.indexIntoArr]) {\n int toReturn = this.arr[this.indexIntoArr + 1];\n this.indexIntoArr += 2;\n return toReturn;\n \n } else { // n > this.arr[this.indexIntoArr]\n n -= this.arr[this.indexIntoArr];\n this.indexIntoArr += 2;\n return this.next(n);\n }\n }\n}\n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
easy java treemap solution
|
easy-java-treemap-solution-by-silver__bu-3pcl
|
\nclass RLEIterator {\n long pos;\n long currPos =0;\n int flag =0;\n TreeMap<Long,Integer> map;\n public RLEIterator(int[] e) {\n pos =0
|
silver__bullet
|
NORMAL
|
2021-12-04T22:25:35.733857+00:00
|
2021-12-04T22:26:22.562906+00:00
| 81 | false |
```\nclass RLEIterator {\n long pos;\n long currPos =0;\n int flag =0;\n TreeMap<Long,Integer> map;\n public RLEIterator(int[] e) {\n pos =0;\n map = new TreeMap<>();\n // TreeMap to store the range of encoded values example [0-3]: 8, [3-5]:8 \n for(int i=0;i<e.length-1;i+=2){\n if(e[i]==0) continue;\n pos += e[i];\n map.put(pos,e[i+1]);\n }\n \n }\n \n public int next(int n) {\n if(flag==1) return -1;\n if(currPos+n>pos) {\n flag=1;\n return -1;\n }\n currPos+=n;\n return map.get(map.ceilingKey(currPos));\n \n }\n}\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(encoding);\n * int param_1 = obj.next(n);\n */\n```
| 1 | 0 |
['Tree', 'Java']
| 1 |
rle-iterator
|
84% Faster || Easy Solution || C++ || O(n) Time
|
84-faster-easy-solution-c-on-time-by-_mu-0e89
|
\nclass RLEIterator {\npublic:\n \n vector<int> e;\n int id = 0;\n RLEIterator(vector<int>& encoding) {\n e = encoding;\n }\n \n int
|
_muhammad
|
NORMAL
|
2021-12-03T12:00:06.835228+00:00
|
2021-12-03T12:00:21.555199+00:00
| 125 | false |
```\nclass RLEIterator {\npublic:\n \n vector<int> e;\n int id = 0;\n RLEIterator(vector<int>& encoding) {\n e = encoding;\n }\n \n int next(int n) {\n while ( id < e.size() && n > 0 ) {\n if ( n <= e[id] ) {\n e[id] -= n;\n return e[id+1];\n }\n else {\n n -= e[id];\n id += 2;\n }\n }\n \n return -1;\n }\n};\n```
| 1 | 0 |
['C']
| 0 |
rle-iterator
|
Java || Explained question || Explained steps to solve || O(N)
|
java-explained-question-explained-steps-ntn6y
|
// The encoding[] array is the encoded version of some array. Every even pos \'i\' (0, 2, 4, 6,...) in this encoded array tells how many elements at encoding[i
|
ICodeToSurvive
|
NORMAL
|
2021-11-29T16:15:43.409833+00:00
|
2021-11-29T16:15:43.409878+00:00
| 71 | false |
// The encoding[] array is the encoded version of some array. Every even pos \'i\' (0, 2, 4, 6,...) in this encoded array tells how many elements at encoding[i + 1] are there(consecutively) in original array\n// Ex : [8,8,8,5,5] -> [3,8,2,5] -> this means that there are 3 ->8s and 2 -> 5s in original array which we can clearly see\n// Also [8,8,8,5,5] ->[3,8,0,9,2,5] -> 3 -> 8s, 0 -> 9s, 2 -> 5s. There are 0 9s which is also true so this encoded array is also valid\n\n// Do following steps to give next\n// 1. Maintain index (this tells at which index of encoded array are we pointing, even after some exhauting has happened)\n// 2. check if \'n\' <= A[index] -> we are trying to see if the number at position \'n\' int he original array is still there (since we exhaust numbers -> meaning we remove them)\n// For ex -> n = 2, index 0, A[index] = 3\n// This means that we wants to fetch 2nd number from the original element and A[index] = 3 means that there are 3 same elements so we return A[index + 1] (which contains the actual value) and reduce the value of A[index] ny n. So now A[index] = 3 - 2 = 1 (this means that we have exhausted 2 8s, and now only 1 8 is left) -> [8 ,5 , 5]\n// 3. If the n > A[index], this means that we wanted to fetch a number from original array at pos \'n\' but the current index at A, A[index] does not point to that nth position number, so we need to update our index and exhaust all the lements befre that nth element\n\n// TC : O(N)\n// SC : O(1)\n\n```\nclass RLEIterator {\n\n int[] A;\n int index;\n public RLEIterator(int[] encoding) {\n this.A = encoding;\n this.index = 0;\n }\n \n public int next(int n) {\n while(index < A.length) {\n if(n <= A[index]) { // step 2\n A[index] -= n;\n return A[index + 1];\n } // step 3\n n = n - A[index];\n index = index + 2;\n }\n return -1;\n }\n}\n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
C++ || SIMPLE SOLUTION || O(n) || Easy To Understand
|
c-simple-solution-on-easy-to-understand-cpttl
|
first copy all elements in another vector then \nStart understanding from the nested if else \n\n\n\nclass RLEIterator {\n private: vector<int>v;\npublic:\n
|
Shikhar_dhyani
|
NORMAL
|
2021-10-25T18:27:09.873880+00:00
|
2021-10-25T18:27:09.873923+00:00
| 64 | false |
first copy all elements in another vector then \nStart understanding from the nested if else \n\n```\n\nclass RLEIterator {\n private: vector<int>v;\npublic:\n long long int size(vector<int>&v)\n {\n long long int n=0;\n for(int i=0;i<v.size();i=i+2)\n n+=v[i];\n return n;\n }\n RLEIterator(vector<int>& encoding) {\n for(int i=0;i<encoding.size();i++)\n v.push_back(encoding[i]);\n }\n \n int next(int n) {\n if(v.size()==0||n>size(v))\n { v.clear(); \n return -1;}\n if(n<v[0]) //from here\n {\n v[0]=v[0]-n;\n return v[1];\n }\n else if(n==v[0])\n {\n int temp=v[1];\n auto it=v.begin();\n auto jt=v.begin()+2;\n v.erase(it,jt);\n return temp;\n }\n else {\n if(n>size(v))\n { v.clear(); \n return -1;}\n auto it=v.begin();\n auto jt=v.begin()+2;\n n=n-v[0];\n v.erase(it,jt);\n return next(n);\n }\n }\n};\n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
Easy understanding solution
|
easy-understanding-solution-by-pvs_prane-6uly
|
Easy understanding Java solution using pointer with detailed description.\nTime Complexity: O(n)\nSpace Complexity: O(1)\n\n\nclass RLEIterator {\n \n //
|
pvs_praneeth
|
NORMAL
|
2021-10-10T22:17:13.462055+00:00
|
2022-03-14T17:11:31.186425+00:00
| 166 | false |
Easy understanding Java solution using pointer with detailed description.\nTime Complexity: O(n)\nSpace Complexity: O(1)\n\n```\nclass RLEIterator {\n \n // Index ptr keeps track of the element that needs to be returned.\n int diff;\n int index;\n int[] enc;\n\n // Initializing the diff varaible to the first element of the encoding.\n // Initializing the index ptr to the 1st return element.\n public RLEIterator(int[] encoding) {\n enc = encoding;\n index = 1;\n diff = encoding[0];\n }\n \n public int next(int n) {\n \n // Verify if the index ptr is out of the encoding array.\n if(index >= enc.length){\n return -1;\n }\n \n // Subtract the given number from the current diff.\n // By doing aobve we are exhausting n elements from the array.\n diff -= n;\n \n // If the difference value is >= 0, then the index ptr remains at the same location.\n // If the difference value is < 0, then we have exhausted all the curr elements.\n while(diff < 0){\n // We move the ptr to the next available ele.\n index += 2;\n // If the index is out of bounds then we have exhausted all ele from the array.\n if(index >= enc.length){\n return -1;\n }\n // If the index is in the limits, then update the global diff.\n diff += enc[index-1];\n }\n // Set the new remaining ele count in the array.\n enc[index-1] = diff;\n return enc[index];\n }\n}\n```\n\nPlease upvote if this looks simple & easy to understand/implement. Thanks :)
| 1 | 0 |
['Iterator', 'Java']
| 0 |
rle-iterator
|
Java O(n) Solution O(1) space
|
java-on-solution-o1-space-by-mahi_10-0176
|
\n//Pointer will move by 2\nclass RLEIterator {\n\n int[] enc;\n int pointer;\n public RLEIterator(int[] encoding) {\n this.enc = encoding;\n
|
mahi_10
|
NORMAL
|
2021-10-10T03:21:43.673028+00:00
|
2021-10-10T03:21:43.673057+00:00
| 109 | false |
```\n//Pointer will move by 2\nclass RLEIterator {\n\n int[] enc;\n int pointer;\n public RLEIterator(int[] encoding) {\n this.enc = encoding;\n this.pointer = 0;\n }\n \n public int next(int n) {\n int lastIndex = -1;\n while (n > 0 && pointer < enc.length) {\n \n if (n <= enc[pointer]){ \n enc[pointer] = enc[pointer] - n; \n n = 0;\n lastIndex = enc[pointer+1]; \n }\n else {\n n = n - enc[pointer]; \n enc[pointer] = 0;\n pointer = pointer +2; \n }\n }\n return lastIndex; \n }\n}\n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
Java Prefix Sum + Binary Search, O(logn) next
|
java-prefix-sum-binary-search-ologn-next-aetw
|
First we do prefix sum of all available items in the new array A.\nIn each call, we find the smallest index, where the number of elements is enough to cover our
|
migfulcrum
|
NORMAL
|
2021-09-30T12:31:52.590646+00:00
|
2021-09-30T12:35:56.609140+00:00
| 150 | false |
First we do prefix sum of all available items in the new array `A`.\nIn each call, we find the smallest index, where the number of elements is enough to cover our query. \nLeft boundry of binary search keeps getting closer to the end at each call. \n\nClassic binary search diffs:\n`& ~1` drops the last bit for each number, this way we always look at the number of items, not the item.\n`l = m + 2` to go to next next item count\n\nTime:\n`Init - O(N)`\n`next - O(logN)`\n\nSpace:\n`O(N)`\n```\nclass RLEIterator {\n \n long [] A;\n long taken = 0;\n int l = 0;\n\n public RLEIterator(int[] encoding) {\n this.A = new long[encoding.length];\n for(int i = 0; i < encoding.length ; i += 2) {\n this.A[i] = encoding[i] + (i > 0 ? A[i - 2] : 0);\n this.A[i + 1] = encoding[i + 1];\n }\n }\n\n public int next(int n) {\n taken += n;\n if(l >= A.length || taken > A[A.length - 2]) {\n return -1;\n }\n int r = A.length - 2;\n while(l < r) {\n int m = ((r - l) / 2 + l) & ~1;\n if(A[m] >= taken) {\n r = m;\n } else {\n l = m + 2;\n }\n }\n return l >= A.length ? -1: (int) A[l + 1];\n } \n}\n```
| 1 | 0 |
[]
| 1 |
rle-iterator
|
Python3 solution
|
python3-solution-by-eklavyajoshi-5y5q
|
\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.encoding = encoding\n self.x = 0\n def next(self, n: int) -> int:\n
|
EklavyaJoshi
|
NORMAL
|
2021-09-24T07:31:07.897902+00:00
|
2021-09-24T07:32:38.927911+00:00
| 106 | false |
```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n self.encoding = encoding\n self.x = 0\n def next(self, n: int) -> int:\n for i in range(self.x,len(self.encoding)):\n if i%2 == 0:\n if self.encoding[i] > 0:\n if self.encoding[i] >= n:\n self.encoding[i] -= n\n return self.encoding[i+1]\n else:\n n -= self.encoding[i]\n self.x = i+2\n if n > 0:\n return -1\n```\n**If you like this solution, please upvote for this**
| 1 | 1 |
['Python3']
| 0 |
rle-iterator
|
Python 16ms (beats 100%)
|
python-16ms-beats-100-by-user9112qd-7qlm
|
\nclass RLEIterator(object):\n def __init__(self, encoding):\n """\n :type encoding: List[int]\n """\n \n self.arr = []\n
|
user9112QD
|
NORMAL
|
2021-09-21T18:33:03.709898+00:00
|
2021-09-21T18:33:03.709945+00:00
| 54 | false |
```\nclass RLEIterator(object):\n def __init__(self, encoding):\n """\n :type encoding: List[int]\n """\n \n self.arr = []\n for i in range(0, len(encoding), 2):\n cnt = encoding[i]\n x = encoding[i + 1]\n if cnt > 0:\n self.arr.append((x, cnt))\n \n def next(self, n):\n """\n :type n: int\n :rtype: int\n """\n last = None\n while len(self.arr) > 0:\n x, cnt = self.arr[0]\n last = x\n diff = cnt - n\n if diff <= 0:\n n -= cnt\n self.arr = self.arr[1:]\n if diff == 0:\n break\n else:\n self.arr[0] = (x, cnt - n)\n n = 0\n break\n \n if n > 0:\n return -1\n return last\n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
C++ Solution that Google interviewers will fail you
|
c-solution-that-google-interviewers-will-jrlm
|
\nclass RLEIterator\n{\npublic:\n RLEIterator(vector<int>& encoding) : m_cur_pos(0)\n {\n const int SIZE = encoding.size();\n \n int
|
zhenzhongluo
|
NORMAL
|
2021-08-30T04:41:48.151164+00:00
|
2021-08-30T04:41:48.151199+00:00
| 95 | false |
```\nclass RLEIterator\n{\npublic:\n RLEIterator(vector<int>& encoding) : m_cur_pos(0)\n {\n const int SIZE = encoding.size();\n \n int target_value = encoding[1];\n \n for(int index = 0; \n index < (SIZE -1);\n index += 2)\n {\n const int cur_frequency = encoding[index];\n \n if(cur_frequency == 0)\n {\n continue;\n }\n \n const int cur_value = encoding[index +1];\n \n if(cur_value != target_value)\n {\n target_value = cur_value;\n \n ++m_cur_pos;\n }\n \n m_position_KEY_value_frequency_VALUE_map[m_cur_pos].first = cur_value;\n m_position_KEY_value_frequency_VALUE_map[m_cur_pos].second += cur_frequency;\n }\n \n // RESET\n m_cur_pos = 0;\n }\n \n int next(int num_values_to_be_removed) \n {\n int target_value = m_position_KEY_value_frequency_VALUE_map[m_cur_pos].first;\n \n m_position_KEY_value_frequency_VALUE_map[m_cur_pos].second -= num_values_to_be_removed;\n \n int remainder_frequency = 0;\n \n while(m_cur_pos < m_position_KEY_value_frequency_VALUE_map.size() &&\n m_position_KEY_value_frequency_VALUE_map[m_cur_pos].second < 0)\n {\n remainder_frequency = m_position_KEY_value_frequency_VALUE_map[m_cur_pos].second;\n \n ++m_cur_pos;\n \n if(m_position_KEY_value_frequency_VALUE_map.count(m_cur_pos))\n {\n target_value = m_position_KEY_value_frequency_VALUE_map[m_cur_pos].first;\n \n m_position_KEY_value_frequency_VALUE_map[m_cur_pos].second += remainder_frequency; \n }\n \n else\n {\n return -1;\n }\n }\n \n return target_value;\n }\n \nprivate:\n \n int m_cur_pos;\n \n // Key = position\n // Value = pair<cur_value, cur_frequency>\n unordered_map<int, pair<int, int>> m_position_KEY_value_frequency_VALUE_map;\n};\n\n\n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
[Python3/Python] Simple brute force method. Readable solution with comments.
|
python3python-simple-brute-force-method-0k0oi
|
\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n \n # Init\n self.__x = [] # Elements\n self.__nums_x = [] # N
|
ssshukla26
|
NORMAL
|
2021-08-28T16:13:01.355865+00:00
|
2021-08-28T16:17:26.454508+00:00
| 89 | false |
```\nclass RLEIterator:\n\n def __init__(self, encoding: List[int]):\n \n # Init\n self.__x = [] # Elements\n self.__nums_x = [] # Number of occurence of respective Elements\n self.__i = 0 # Current index from where one should start consuming\n \n for i in range(0,len(encoding),2):\n if encoding[i] > 0: # Discard any element with zero or less encoding\n self.__nums_x.append(encoding[i])\n self.__x.append(encoding[i+1])\n \n self.__m = len(self.__x) # No. of elements\n return\n \n\n def next(self, n: int) -> int:\n \n res = -1\n \n while n:\n \n # If index is greater or equal to no. of element\n # the array is exhausted, break and return -1\n if self.__i >= self.__m:\n res = -1\n break\n else:\n \n # Get the current index\n k = self.__i\n \n # Get the current element\n res = self.__x[k]\n \n # If no. of occurrence of an element is\n # greater than the number of element to be\n # consumed, then update the no. of occurrence\n # of an element to be n less than the current value.\n # Make n "0" as all slots are consumed.\n if self.__nums_x[k] > n:\n self.__nums_x[k] -= n\n n = 0\n else:\n \n # If no. of occurrence of an element is\n # less or equal than the number of element to be\n # consumed, then update the n to be \n\t\t\t\t\t# less than no. of occurrence of the current element.\n # Make no. of occurence of current element "0".\n # Update the index, to indicate consumption of next element.\n n -= self.__nums_x[k]\n self.__nums_x[k] = 0\n self.__i = self.__i + 1\n \n return res\n \n\n\n# Your RLEIterator object will be instantiated and called as such:\n# obj = RLEIterator(encoding)\n# param_1 = obj.next(n)\n```
| 1 | 1 |
['Python', 'Python3']
| 0 |
rle-iterator
|
Java Easy Understanding Deque solution
|
java-easy-understanding-deque-solution-b-1ypi
|
\nclass RLEIterator {\n Deque<Pair<Integer,Integer>> deque = new ArrayDeque(); //key: num frequency, value: num value\n \n public RLEIterator(int[] enc
|
darkrwe
|
NORMAL
|
2021-08-06T16:22:07.284051+00:00
|
2021-08-06T16:34:01.135163+00:00
| 145 | false |
```\nclass RLEIterator {\n Deque<Pair<Integer,Integer>> deque = new ArrayDeque(); //key: num frequency, value: num value\n \n public RLEIterator(int[] encoding) {\n for(int i = 0 ; i + 1 < encoding.length; i= i+2){\n if(encoding[i] != 0)\n deque.add(new Pair(encoding[i], encoding[i+1]));\n }\n }\n \n public int next(int n) {\n Pair<Integer,Integer> item = deque.peek();\n if(item == null)\n return -1;\n if(item.getKey() > n) //decrement the num frequency\n decrementFrequency(item, n);\n else if (item.getKey() == n) //just remove the item from queue\n deque.poll();\n else { // need to go and find another candidate to pass it also\n while( item != null && n > item.getKey()){\n n = n - item.getKey();\n deque.poll();\n item = deque.peek();\n }\n if(item == null)\n return -1;\n else\n decrementFrequency(item, n);\n }\n return item.getValue();\n }\n \n private void decrementFrequency(Pair<Integer,Integer> item,int n){\n int key = item.getKey() - n;\n deque.poll();\n deque.addFirst(new Pair(key, item.getValue()));\n }\n}\n\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(encoding);\n * int param_1 = obj.next(n);\n */\n```
| 1 | 0 |
['Queue', 'Java']
| 0 |
rle-iterator
|
Java TreeMap Solution
|
java-treemap-solution-by-ayyild1z-qg20
|
Java\nclass RLEIterator {\n \n long pos = -1;\n TreeMap<Long, Integer> map = new TreeMap<>();\n\n public RLEIterator(int[] encoding) {\n long
|
ayyild1z
|
NORMAL
|
2021-07-05T21:32:30.109276+00:00
|
2021-07-05T21:32:30.109325+00:00
| 131 | false |
```Java\nclass RLEIterator {\n \n long pos = -1;\n TreeMap<Long, Integer> map = new TreeMap<>();\n\n public RLEIterator(int[] encoding) {\n long curr = 0;\n for(int i=0; i < encoding.length; i+=2){\n int cnt = encoding[i];\n int num = encoding[i+1];\n \n if(cnt <= 0) continue;\n \n curr += cnt;\n map.put(curr, num);\n }\n }\n \n public int next(int n) {\n pos += n;\n Long key = map.higherKey(pos);\n return key == null ? -1 : map.get(key);\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
rle-iterator
|
Java | Easy | Using Double Ended Queue
|
java-easy-using-double-ended-queue-by-us-n2f4
|
\nclass RLEIterator {\n ArrayDeque<Integer> q;\n public RLEIterator(int[] encoding) {\n q = new ArrayDeque<>();\n for(int val : encoding){\
|
user8540kj
|
NORMAL
|
2021-06-28T12:23:53.069825+00:00
|
2021-06-28T12:23:53.069856+00:00
| 88 | false |
```\nclass RLEIterator {\n ArrayDeque<Integer> q;\n public RLEIterator(int[] encoding) {\n q = new ArrayDeque<>();\n for(int val : encoding){\n q.addLast(val);\n }\n }\n \n public int next(int n) {\n int le = -1;\n while(n > 0 && q.size() >= 2){\n int freq = q.removeFirst();\n int num = q.removeFirst();\n if(freq >= n){\n freq = freq - n;\n \n if(freq !=0 ){ \n q.addFirst(num);\n q.addFirst(freq);\n }\n return num;\n }\n else{\n n = n - freq;\n }\n le = num;\n }\n if(n != 0) return -1;\n \n return le;\n }\n}\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(encoding);\n * int param_1 = obj.next(n);\n */\n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
C++ solution- trick is NOT to create the actual array from the encoding
|
c-solution-trick-is-not-to-create-the-ac-n12c
|
As described in the title, I was creating a vector of original items from encoding and then applying the operation of next on it. It gave me TLE. So just keep t
|
maitreya47
|
NORMAL
|
2021-06-21T05:58:57.884581+00:00
|
2021-06-21T05:59:19.323652+00:00
| 111 | false |
As described in the title, I was creating a vector of original items from encoding and then applying the operation of next on it. It gave me TLE. So just keep the encoding as it is and do the math on current index.\n```\nclass RLEIterator {\npublic:\n int index;\n vector<int> e;\n RLEIterator(vector<int>& encoding) {\n index=0;\n e = encoding;\n }\n \n int next(int n) {\n while(index<e.size())\n {\n if(e[index]>=n)\n {\n e[index]-=n;\n return e[index+1];\n }\n else\n {\n n-=e[index];\n index+=2;\n }\n }\n return -1;\n }\n};\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator* obj = new RLEIterator(encoding);\n * int param_1 = obj->next(n);\n */\n ```
| 1 | 0 |
['C']
| 0 |
rle-iterator
|
Clean java code beats 94% O(N) with intuition
|
clean-java-code-beats-94-on-with-intuiti-0id5
|
\n/**\n\tIntuition: Take a current pointer with starting index. For each of the next call, search for an index which has \n\tpositive run length and return the
|
ngeek
|
NORMAL
|
2021-06-17T01:47:12.513049+00:00
|
2021-06-17T01:47:55.239333+00:00
| 90 | false |
```\n/**\n\tIntuition: Take a current pointer with starting index. For each of the next call, search for an index which has \n\tpositive run length and return the element. Else keep moving forward until a value > n is found. \n\tTime Complexity: O(N) \n\tSpace Complexity: O(constant). \n**/\nclass RLEIterator {\n\n int[] e;\n int cur;\n \n public RLEIterator(int[] encoding) {\n e = encoding; \n cur = 0;\n }\n \n public int next(int n) {\n // System.out.println(Arrays.toString(e));\n while(cur < e.length - 1) {\n if(n > e[cur]) {\n n = n - e[cur];\n e[cur] = 0;\n cur += 2;\n } else {\n e[cur] -= n;\n return e[cur + 1];\n }\n }\n return -1;\n }\n}\n```\n
| 1 | 0 |
[]
| 0 |
rle-iterator
|
C++ Clean Solution! ✓
|
c-clean-solution-by-satj-3jh1
|
\nclass RLEIterator {\npublic:\n vector <int> b;\n int i;\n RLEIterator(vector<int>& a) {\n b = a;\n i = 0;\n }\n int next(int n) {
|
satj
|
NORMAL
|
2021-06-15T08:27:20.945923+00:00
|
2021-06-15T08:31:30.826568+00:00
| 133 | false |
```\nclass RLEIterator {\npublic:\n vector <int> b;\n int i;\n RLEIterator(vector<int>& a) {\n b = a;\n i = 0;\n }\n int next(int n) {\n if (i == b.size()) return -1;\n if (n <= b[i]) {\n b[i] -= n;\n return b[i + 1];\n }\n n -= b[i];\n i += 2;\n return next(n);\n }\n};\n```
| 1 | 0 |
['Recursion', 'C', 'C++']
| 0 |
rle-iterator
|
[Python3] loop through array
|
python3-loop-through-array-by-ye15-rk1h
|
\n\nclass RLEIterator:\n\n def __init__(self, A: List[int]):\n self.rle = A\n self.k = 0 \n\n def next(self, n: int) -> int:\n while
|
ye15
|
NORMAL
|
2021-06-08T02:15:58.209502+00:00
|
2021-06-08T02:15:58.209541+00:00
| 74 | false |
\n```\nclass RLEIterator:\n\n def __init__(self, A: List[int]):\n self.rle = A\n self.k = 0 \n\n def next(self, n: int) -> int:\n while self.k < len(self.rle) and n > self.rle[self.k]: \n n -= self.rle[self.k]\n self.k += 2 \n if self.k < len(self.rle): \n self.rle[self.k] -= n\n return self.rle[self.k+1]\n return -1 \n```
| 1 | 1 |
['Python3']
| 1 |
rle-iterator
|
Java modular solution (5 ms, faster than 92%)
|
java-modular-solution-5-ms-faster-than-9-7pm1
|
Lengthy, but easy to understand solution\n\nclass RLEIterator {\n\n\tint[] encoding;\n\tint index;\n\n public RLEIterator(int[] encoding) {\n this.enc
|
texens
|
NORMAL
|
2021-06-05T18:23:28.802982+00:00
|
2021-06-05T18:23:28.803022+00:00
| 117 | false |
Lengthy, but easy to understand solution\n```\nclass RLEIterator {\n\n\tint[] encoding;\n\tint index;\n\n public RLEIterator(int[] encoding) {\n this.encoding = encoding;\n this.index = 0;\n }\n\n public int next(int n) {\n\t\t// remove the first n-1 elements\n this.remove(n - 1);\n\t\t\n\t\t// remove any prefix zeroes\n this.removePrefixZeroes();\n\t\t\n\t\t// peek the latest value\n int res = this.peek();\n\t\t\n\t\t// now remove the last value i.e. nth value\n this.remove(1);\n\n return res;\n }\n\n\t// removes n values\n private void remove(int n) {\n for (int i = n; i > 0; ) {\n this.removePrefixZeroes();\n if (this.index >= this.encoding.length) return;\n if (this.encoding[this.index] <= i) {\n i -= this.encoding[this.index];\n this.index += 2;\n } else {\n this.encoding[this.index] = this.encoding[this.index] - i;\n i = 0;\n }\n }\n }\n\n\t// removes any prefix 0s, such as 0,9\n private void removePrefixZeroes() {\n if (this.index >= this.encoding.length) return;\n if (this.encoding[this.index] == 0) {\n this.index += 2;\n this.removePrefixZeroes();\n }\n }\n\n\t// just take a peek at the value, don\'t remove it\n private int peek() {\n if (this.index >= this.encoding.length) return -1;\n return this.encoding[this.index + 1];\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
rle-iterator
|
Straightforward Java Solution
|
straightforward-java-solution-by-mycafeb-fx9m
|
\nclass RLEIterator {\n \n int pos = 1;\n int num = 0;\n int val = 0;\n int[] A;\n\n public RLEIterator(int[] A) {\n this.A = A;\n }
|
mycafebabe
|
NORMAL
|
2021-05-31T23:27:29.859960+00:00
|
2021-05-31T23:27:29.860001+00:00
| 93 | false |
```\nclass RLEIterator {\n \n int pos = 1;\n int num = 0;\n int val = 0;\n int[] A;\n\n public RLEIterator(int[] A) {\n this.A = A;\n }\n \n public int next(int n) {\n while (pos < A.length && num < n) {\n num += A[pos - 1];\n val = A[pos];\n pos += 2;\n }\n num -= n; // substract the n before return anything\n if (pos > A.length && num < 0) {\n return -1;\n }\n return val;\n }\n}\n\n```
| 1 | 0 |
[]
| 1 |
rle-iterator
|
Simple O(LogN) C++ solution using map
|
simple-ologn-c-solution-using-map-by-nik-sjro
|
\nmap<long, long> cache;\n //storing end index\n long currIdx;\n\n RLEIterator(vector<int>& A) \n {\n long end = 0;\n for(int i=0; i<A
|
nikhilm23
|
NORMAL
|
2020-10-20T23:00:45.353530+00:00
|
2020-10-20T23:00:45.353569+00:00
| 141 | false |
```\nmap<long, long> cache;\n //storing end index\n long currIdx;\n\n RLEIterator(vector<int>& A) \n {\n long end = 0;\n for(int i=0; i<A.size(); i=i+2)\n {\n if(A[i]==0)\n continue;\n end += A[i];\n cache[end] = A[i+1];\n }\n currIdx = 0;\n }\n \n int next(int n) \n {\n currIdx += n;\n auto itr = cache.lower_bound(currIdx);\n if(itr->first < currIdx)\n return -1;\n return itr->second;\n }\n```
| 1 | 0 |
['C', 'C++']
| 0 |
rle-iterator
|
Clean Python solution with explanation using Bisect Left / Binary Search
|
clean-python-solution-with-explanation-u-nws5
|
Idea is simple:\nA = [3,8,0,9,2,5]\ncounts[i] keeps count of numbers that need to be removed before A[2i + 1] can be removed\ncounts = [3, 3, 5]\nIf we are aske
|
random_leetcoder
|
NORMAL
|
2020-10-03T17:57:27.582426+00:00
|
2020-10-03T20:15:02.702351+00:00
| 89 | false |
Idea is simple:\nA = [3,8,0,9,2,5]\ncounts[i] keeps count of numbers that need to be removed before A[2i + 1] can be removed\ncounts = [3, 3, 5]\nIf we are asked to remove 4 numbers, All we need to do is bisect left counts array for 4. Bisect left gives us i = 2 which corresponds to 2i + 1 in A, which is 5. So, 5 is our answer.\n```\nfrom bisect import bisect_left as bl\nclass RLEIterator:\n\n def __init__(self, A: List[int]):\n self.A = A\n self.removed = 0\n self.counts = A[::2]\n for i in range(1, len(self.counts)):\n self.counts[i] += self.counts[i-1]\n self.total = self.counts[-1] if self.counts else 0\n\n def next(self, n: int) -> int:\n if self.removed >= self.total:\n return -1\n self.removed += n\n i = bl(self.counts, self.removed)\n if i >= len(self.counts):\n return -1\n return self.A[2*i+1]\n\t\t```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
Ruby with Recursion
|
ruby-with-recursion-by-woahlag-tesv
|
\nclass RLEIterator\n def initialize(a)\n @array = a \n end\n\n def next(n)\n return -1 if @array.empty?\n \n if @arra
|
woahlag
|
NORMAL
|
2020-05-18T01:57:22.533859+00:00
|
2020-05-18T01:57:22.533913+00:00
| 65 | false |
```\nclass RLEIterator\n def initialize(a)\n @array = a \n end\n\n def next(n)\n return -1 if @array.empty?\n \n if @array[0] == n\n value = @array[1]\n @array = @array[2..-1]\n value\n elsif @array[0] > n\n value = @array[1]\n @array[0] -= n\n value\n else\n removed = @array[0]\n @array = @array[2..-1]\n self.next(n-removed)\n end\n end\nend\n```
| 1 | 0 |
['Ruby']
| 1 |
rle-iterator
|
JAVA solution, using only a List. 4ms beats 100% of current Java submissions.
|
java-solution-using-only-a-list-4ms-beat-46ew
|
/ This stores the the pair of frequency, value. Which we will use to derive the encoded sequence. */\n List encodedPairs = new ArrayList<>();\n\n / This s
|
ridgetastic
|
NORMAL
|
2019-11-15T08:38:29.666538+00:00
|
2019-11-15T08:38:54.641698+00:00
| 282 | false |
/** This stores the the pair of frequency, value. Which we will use to derive the encoded sequence. */\n List<int[]> encodedPairs = new ArrayList<>();\n\n /** This stores the pointer to the next encoded string value that we are on. */\n int currentIndex = 0;\n\n /** The constructor will store the pairs into the list. */\n public RLEIterator(int[] A) {\n int i=0;\n while (i < A.length) {\n int freq = A[i];\n int val = A[i+1];\n encodedPairs.add(new int[]{freq,val});\n i+=2;\n }\n }\n\n public int next(int n) {\n while (n > 0) {\n if (currentIndex < encodedPairs.size()) {\n int[] pair = encodedPairs.get(currentIndex);\n /** Subtract from n the frequencies in the current pair until we land on the pair where the frequency count is > what is left of n */\n if (n - pair[0] > 0) {\n n -= pair[0];\n currentIndex++;\n continue;\n } else {\n /** We need to update the list value here for the next call to this method. */\n encodedPairs.set(currentIndex, new int[]{pair[0]-n,pair[1]});\n }\n return pair[1];\n } else {\n return -1;\n }\n }\n return -1;\n }\n
| 1 | 0 |
[]
| 0 |
rle-iterator
|
C# Solution
|
c-solution-by-leonhard_euler-mgot
|
\npublic class RLEIterator \n{\n int index;\n int [] array;\n\n public RLEIterator(int[] A) \n {\n array = A;\n index = 0;\n }\n
|
Leonhard_Euler
|
NORMAL
|
2019-10-28T06:17:19.770166+00:00
|
2019-10-28T06:17:19.770203+00:00
| 106 | false |
```\npublic class RLEIterator \n{\n int index;\n int [] array;\n\n public RLEIterator(int[] A) \n {\n array = A;\n index = 0;\n }\n \n public int Next(int n) \n {\n while(index < array.Length && n > array[index])\n {\n n = n - array[index];\n index += 2;\n }\n \n if(index >= array.Length)\n return -1;\n \n array[index] = array[index] - n;\n return array[index + 1];\n }\n}\n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
O(logN) search time, O(n) space solution with Cumulative Sum and Binary Search
|
ologn-search-time-on-space-solution-with-unez
|
Overall Time Complexity O(N),\n\t\n\tConstructor method: \n\tinitialize a cumulative sum variable. loop through the array, increment the cumulative sum value if
|
julan
|
NORMAL
|
2019-09-20T18:57:28.150244+00:00
|
2019-09-20T18:57:28.150316+00:00
| 104 | false |
Overall Time Complexity O(N),\n\t\n\t**Constructor method:** \n\tinitialize a cumulative sum variable. loop through the array, increment the cumulative sum value if frequency is not zero, insert the sum variable and array value into index list and value list respectively\n\t\n\t**Next method:**\n\tUpdate the global cumulative sum variable, do a binary search from the index list, find the smallest index value which is just greater than or equal to updated global variable. return the value from corresponding value list. \n\t\n\tFollowing is the code:\n\t\n\t\tpublic long cumulative_ind = 0;\n\t\tpublic List<long> index_list = new List<long>();\n\t\tpublic List<int> value_list = new List<int>();\n\n\t\tpublic RLEIterator(int[] A) {\n\t\t\tint len = A.Length;\n\t\t\tlong current_cummutive = 0;\n\t\t\tfor (int i = 0; i < len; i+= 2) {\n\t\t\t\tif (A[i] != 0) {\n\t\t\t\t\tcurrent_cummutive += A[i];\n\t\t\t\t\tindex_list.Add(current_cummutive);\n\t\t\t\t\tvalue_list.Add(A[i+1]);\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\n\t\tpublic int Next(int n) {\n\t\t\tcumulative_ind += n; \n\t\t\t\n\t\t\tif (index_list[0] >= cumulative_ind) return value_list[0];\n\t\t\t// if cumulative sum is greater than the decoded array length, simply return -1;\n\t\t\tif (index_list[index_list.Count() - 1] < cumulative_ind) return -1;\n\t\t\t\n\t\t\tint st = 0; int end = index_list.Count() - 1;\n\t\t\twhile (st <= end) {\n\t\t\t\tint mid = (st + end)/2;\n\t\t\t\tif (index_list[mid] == cumulative_ind) return value_list[mid];\n\t\t\t\telse if (index_list[mid] <= cumulative_ind) {\n\t\t\t\t\tst += 1;\n\t\t\t\t} else {\n\t\t\t\t\tend -= 1;\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn value_list[st];\n\t\t}
| 1 | 0 |
[]
| 0 |
rle-iterator
|
C++ 8ms 99% easy to follow O(1) space
|
c-8ms-99-easy-to-follow-o1-space-by-pigh-ptfu
|
\nclass RLEIterator {\n int idx_ = 0; \n int used_ = 0;\n vector<int>& theA_;\npublic:\n RLEIterator(vector<int>& A): theA_(A) { }\n\n int next(int n) {\n
|
pighaslc
|
NORMAL
|
2019-05-13T00:06:37.893060+00:00
|
2019-05-13T00:06:52.374796+00:00
| 433 | false |
```\nclass RLEIterator {\n int idx_ = 0; \n int used_ = 0;\n vector<int>& theA_;\npublic:\n RLEIterator(vector<int>& A): theA_(A) { }\n\n int next(int n) {\n for(; idx_<theA_.size(); idx_ += 2) {\n if(theA_[idx_] - used_ > n) {\n used_ += n;\n return theA_[idx_+1];\n }\n else if (theA_[idx_] - used_ == n) {\n used_ = 0;\n idx_ += 2;\n return theA_[idx_-1];\n }\n else {\n n -= theA_[idx_] - used_;\n used_ = 0;\n }\n }\n \n return -1;\n }\n};\n```
| 1 | 1 |
[]
| 0 |
rle-iterator
|
One loop solution (javascript) - 56ms
|
one-loop-solution-javascript-56ms-by-efo-2hx5
|
\nvar RLEIterator = function(A) {\n this.nums = A;\n this.currentIndex = 0;\n};\n\n/** \n * @param {number} n\n * @return {number}\n */\nRLEIterator.proto
|
eforce
|
NORMAL
|
2018-12-25T08:19:37.449790+00:00
|
2018-12-25T08:19:37.449833+00:00
| 193 | false |
```\nvar RLEIterator = function(A) {\n this.nums = A;\n this.currentIndex = 0;\n};\n\n/** \n * @param {number} n\n * @return {number}\n */\nRLEIterator.prototype.next = function(n) {\n for (var i = this.currentIndex; i < this.nums.length; i += 2) {\n if (this.nums[i] >= n) {\n this.nums[i] -= n;\n return this.nums[i + 1];\n } else {\n n -= this.nums[i];\n this.currentIndex += 2;\n }\n }\n \n return -1;\n};\n```
| 1 | 0 |
[]
| 1 |
rle-iterator
|
Python simple solution beats 95% python codes - O(n)
|
python-simple-solution-beats-95-python-c-iq7w
|
class RLEIterator(object): def __init__(self, A): """ :type A: List[int] """ self.inputList = A def next(self, n): """ :type n: int
|
leetcoderkp
|
NORMAL
|
2018-11-09T23:40:29.437511+00:00
|
2018-11-09T23:40:29.437565+00:00
| 470 | false |
class RLEIterator(object):
def __init__(self, A):
"""
:type A: List[int]
"""
self.inputList = A
def next(self, n):
"""
:type n: int
:rtype: int
"""
index = 0
while index < len(self.inputList):
if self.inputList[index] == 0:
self.inputList = self.inputList[index+2:]
elif n <= self.inputList[index]:
output = self.inputList[index+1]
self.inputList[index] -= n
return output
else:
n -= self.inputList[index]
self.inputList = self.inputList[index+2:]
if n > 0:
return -1
| 1 | 0 |
[]
| 1 |
rle-iterator
|
Java super easy O(n) time O(1) space solution! Clean code!
|
java-super-easy-on-time-o1-space-solutio-14y6
|
```\nclass RLEIterator {\n int index=0;\n long sum=0, cur=0;\n int[] nums;\n public RLEIterator(int[] A) {\n nums=A;\n sum=A[0];\n
|
michaelz
|
NORMAL
|
2018-10-28T21:46:19.729696+00:00
|
2018-10-28T21:46:19.729735+00:00
| 302 | false |
```\nclass RLEIterator {\n int index=0;\n long sum=0, cur=0;\n int[] nums;\n public RLEIterator(int[] A) {\n nums=A;\n sum=A[0];\n }\n \n public int next(int n) {\n if(index>=nums.length) return -1;\n cur+=n;\n while(cur>sum&&index<nums.length) {\n index+=2;\n if(index<nums.length) sum+=nums[index];\n } \n if(index<nums.length) return nums[index+1];\n else return -1;\n }\n}
| 1 | 0 |
[]
| 0 |
rle-iterator
|
Java easy to understand solution
|
java-easy-to-understand-solution-by-daij-vq91
|
\nclass RLEIterator {\n int A[];\n int index = 0;//indicate the current start of the array(number of times)\n public RLEIterator(int[] A) {\n th
|
daijidj
|
NORMAL
|
2018-10-28T05:07:39.215644+00:00
|
2018-10-28T05:07:39.215683+00:00
| 91 | false |
```\nclass RLEIterator {\n int A[];\n int index = 0;//indicate the current start of the array(number of times)\n public RLEIterator(int[] A) {\n this.A = A;\n }\n \n public int next(int n) {\n while(index + 1 < A.length){//valid\n if(n > A[index]){\n n -= A[index];\n index += 2;\n }else {//smaller or equal\n A[index] -= n;\n return A[index + 1];\n }\n }\n return -1;\n }\n}\n```
| 1 | 1 |
[]
| 0 |
rle-iterator
|
Easy Python with Binary Search
|
easy-python-with-binary-search-by-localh-2q3i
|
\nclass RLEIterator:\n\n def __init__(self, A):\n """\n :type A: List[int]\n """\n self.rle = []\n self.times = [A[0]] \n
|
localhostghost
|
NORMAL
|
2018-10-24T04:04:11.232901+00:00
|
2018-10-24T04:04:11.232961+00:00
| 141 | false |
```\nclass RLEIterator:\n\n def __init__(self, A):\n """\n :type A: List[int]\n """\n self.rle = []\n self.times = [A[0]] \n self.ptr = 0\n for i in range(1,len(A),2):\n if A[i-1]:\n self.rle.append(A[i])\n for i in range(2, len(A), 2):\n if A[i]:\n self.times.append(self.times[-1] + A[i])\n\n def next(self, n):\n """\n :type n: int\n :rtype: int\n """\n self.ptr += n\n if self.ptr > self.times[-1]:\n return -1\n idx = bisect.bisect_left(self.times, self.ptr)\n return self.rle[idx]\n \n\n```\n\nCondensed Version\n\n```\nclass RLEIterator:\n\n def __init__(self, A):\n """\n :type A: List[int]\n """\n self.rle = []\n self.ptr = cnt = 0\n for i, j in zip(A[::2], A[1::2]):\n if i != 0:\n cnt += i \n self.rle.append((cnt, j)) \n def next(self, n):\n """\n :type n: int\n :rtype: int\n """\n self.ptr += n\n if self.ptr > self.rle[-1][0]:\n return -1\n target = bisect.bisect_left(self.rle, (self.ptr,))\n return self.rle[target][1] \n```
| 1 | 0 |
[]
| 0 |
rle-iterator
|
Python Binary Search Solution, beats 100%
|
python-binary-search-solution-beats-100-qn22y
|
``` class RLEIterator: def __init__(self, A): """ :type A: List[int] """ cnt = 0 self.index, self.value = list(), list() for num, i in z
|
andysim3d
|
NORMAL
|
2018-09-29T18:05:01.358706+00:00
|
2018-09-29T18:05:01.358755+00:00
| 112 | false |
```
class RLEIterator:
def __init__(self, A):
"""
:type A: List[int]
"""
cnt = 0
self.index, self.value = list(), list()
for num, i in zip(A[::2], A[1::2]):
if num == 0:
continue
cnt += num
self.index.append(cnt)
self.value.append(i)
self.indicator = 0
self.size = cnt
def next(self, n):
"""
:type n: int
:rtype: int
"""
self.indicator += n
if self.indicator >= self.size:
return -1
ind = bisect.bisect_left(self.index, self.indicator)
return self.value[ind]
```
| 1 | 0 |
[]
| 1 |
rle-iterator
|
Java Solution
|
java-solution-by-vidhushini1993-cppk
|
\nclass RLEIterator {\n int[] A;\n int idx;\n public RLEIterator(int[] A) {\n this.A=A;\n idx=0;\n }\n \n public int next(int n) {\n
|
vidhushini1993
|
NORMAL
|
2018-09-12T12:26:41.835912+00:00
|
2018-10-04T20:25:11.447841+00:00
| 102 | false |
```\nclass RLEIterator {\n int[] A;\n int idx;\n public RLEIterator(int[] A) {\n this.A=A;\n idx=0;\n }\n \n public int next(int n) {\n \n while(idx<A.length && n>A[idx]) {\n n=n-A[idx];\n idx+=2;\n }\n if(idx>=A.length){\n return -1;\n }\n A[idx]=A[idx]-n;\n return A[idx+1];\n }\n}\n\n/**\n * Your RLEIterator object will be instantiated and called as such:\n * RLEIterator obj = new RLEIterator(A);\n * int param_1 = obj.next(n);\n */\n ```
| 1 | 1 |
[]
| 0 |
rle-iterator
|
Python solution with comments [24ms]
|
python-solution-with-comments-24ms-by-ga-mzxg
|
The idea is to keep track of the current counter/value. I have a temp value that stores how much of the current value has been "next" but not completely done ye
|
gavinlinasd
|
NORMAL
|
2018-09-12T10:06:02.060773+00:00
|
2018-09-14T18:35:05.320802+00:00
| 175 | false |
The idea is to keep track of the current counter/value. I have a temp value that stores how much of the current value has been "next" but not completely done yet. This makes it easier when I need to move the counter.\n```\nclass RLEIterator(object):\n\n def __init__(self, A):\n """\n :type A: List[int]\n """\n self._counts = A[0::2]\n self._vals = A[1::2]\n self._index = 0 # the current index of the iteration\n self._next = 0 # how many next has been called on the current value\n self._len = len(self._vals)\n \n\n def next(self, n):\n """\n :type n: int\n :rtype: int\n """\n\n remains = self._next + n\n # Moving the counter based on how many next elements we have to skip.\n while self._index < self._len and remains > self._counts[self._index] :\n remains -= self._counts[self._index]\n self._index += 1\n \n # already run out\n if self._index >= self._len:\n return -1\n else:\n self._next = temp\n return self._vals[self._index]\n```
| 1 | 1 |
[]
| 0 |
rle-iterator
|
python beats 100%
|
python-beats-100-by-jingmlc-w2v0
|
python\nclass RLEIterator(object):\n\n def __init__(self, A):\n """\n :type A: List[int]\n """\n self.index = []\n self.da
|
jingmlc
|
NORMAL
|
2018-09-11T16:21:25.100161+00:00
|
2018-09-12T13:44:30.315879+00:00
| 86 | false |
```python\nclass RLEIterator(object):\n\n def __init__(self, A):\n """\n :type A: List[int]\n """\n self.index = []\n self.data = []\n for i,r in enumerate(A):\n if i % 2 == 0 and r > 0 :\n self.index.append(r)\n self.data.append(A[i+1])\n self.dlen = sum(self.index)\n \n\n def next(self, n):\n """\n :type n: int\n :rtype: int\n """\n if n > self.dlen:\n self.data = []\n self.index = []\n self.dlen = 0\n return -1\n else:\n for i,no in enumerate(self.index):\n if no < n:\n self.dlen -= no\n n -= no\n else:\n self.dlen -= n\n self.index[i] -= n\n break\n \n self.data = self.data[i:]\n self.index = self.index[i:]\n return self.data[0]\n```
| 1 | 1 |
[]
| 0 |
rle-iterator
|
Java Solution: With detailed explanation
|
java-solution-with-detailed-explanation-hd7k6
|
Approach\nIf we expand the sequence and store them in a temporary datastructure like LinkedList. Then we can return the elements as and when the next() gets ca
|
rkg
|
NORMAL
|
2018-09-09T05:35:55.484893+00:00
|
2018-09-09T05:35:55.484936+00:00
| 182 | false |
# Approach\nIf we expand the sequence and store them in a temporary datastructure like LinkedList. Then we can return the elements as and when the next() gets called. For example: [3,8,0,9,2,5] gets expanded and stored as 3 times 8, 0 times 9 and 2 times 5 i.e., [8,8,8,5,5]. When next() gets called with n = 2, remove first 2 elements from the array from front and return the last element. \n# Optimization\nThe above approach works well, but the problem is when the run length of a sequence is high as mentioned in the problem statement(10^9), then the space usage will also be high. If we check the above approach carefully we actually don\'t need this new linkedList(or stack or any other) data structure. We only need to maintain the currentElement and the remaining run length of that element. Hence, the new approach with optimization is given below.\n# Algorithm\n1. Store the incoming sequence as it is. Maintain the state of the current run length and element as mentioned below.\n\t\t\ti. int A[] // input sequence.\n\t\t\tii. currentNum = -1 // Current element to return as part of next()\n\t\t\tiii. runLen = 0 // run length of currentNum\n\t\t\tiv. nextIdx = 0 // next index of the currentNum.\n2. When next() gets called with n.\n 1. Case1: Can we accomodate n with existing runLenght? Check if n <= remainingRunLength. If yes then update remainingRunLength by subtracting n from it.\n 2. Case2: If we are at the end of the sequence ? Check if nextIdx >= A.length. If yes then its not possible to continue further. So, at this point our output can be only 2 values either -1 or the currentNum. If runLength != 0 then the last exhaust Number will be -1 otherwise it\'ll be curretNum(which was set in previous call to next(), and it can be either -1 or some valid number). So, return that.\n 3. Case3: Iterate over the Seq using nextIdx. Remember nextIdx should be incremented by 2 as A[i] is the runLength and A[i+1] is the actual number. It\'s guaranteed that length of sequence A is always even. So, it\'s ok to increment twice in the loop and update the current runLength and currentNumber. Also, keep updating the n by subtracting runLength from n. This helps solve when n spans across multiple sequence. \n 4. Case3 continued: After we exit while loop check if n is still greater than zero. This is because during last runLength updated, runLength grew beyond n, hence we came out of while loop. So, check if n > 0 then update the runLength accordingly and return the output. Code is given below.\n3. Run Time Complexity O(N) --> N sequence length. Space complexity is constant. We can probably optimize space complexity by removing one or two variables but it takes away the readability and doesn\'t give any major improvements. \n4. Please feel free to comment. Thank you \n# Code\n```\nclass RLEIterator {\n int runLen ;\n int currentNum ;\n int[] A ;\n int nextIdx ;\n \n public RLEIterator(int[] A) {\n this.A = A; // Store the sequence as it is\n this.nextIdx = 0 ; // nextIdx in the above sequence\n this.runLen = 0 ; // remaining runLength\n this.currentNum = -1 ; // current Sequence or Number to return as part of next\n }\n \n public int next(int n) {\n if (n <= runLen){ //case1\n runLen -= n ;\n return currentNum ;\n }\n if (nextIdx >= A.length) { // case2\n if (runLen != 0 && n > runLen) {\n runLen -= n ;\n currentNum = -1 ;\n }\n\n return currentNum ;\n }\n while ( n >= runLen && nextIdx < A.length) { // case 3\n n -= runLen ;\n runLen = A[nextIdx++] ;\n currentNum = A[nextIdx++] ;\n }\n\n int ret = -1 ;\n if ( n > 0 ) { //case3 continued\n runLen -= n ;\n ret = currentNum ;\n }\n\n return ret ;\n }\n}\n```\n\n\n\t\t\t\n\t\t\t
| 1 | 0 |
[]
| 0 |
rle-iterator
|
Simple C++ solution O(n) time
|
simple-c-solution-on-time-by-limitless-vkzv
|
Instead of expanding the array, keep the index in the vector which will point to the current element from which we have to start exhausting the elements.\n\n\n
|
limitless_
|
NORMAL
|
2018-09-09T05:10:03.127002+00:00
|
2018-09-09T21:00:06.406151+00:00
| 164 | false |
Instead of expanding the array, keep the index in the vector which will point to the current element from which we have to start exhausting the elements.\n\n```\nclass RLEIterator {\n vector<int> values;\n int index = 0, size;\npublic:\n RLEIterator(vector<int> A) {\n values = A;\n size = values.size();\n }\n \n int next(int n) {\n if (n > 0) {\n while (index < size) {\n if (values[index] == 0) { //If count = 0, then no need to check that element\n index += 2;\n } else if (values[index] < n) {\n n = n - values[index];\n index += 2;\n } else if (values[index] >= n) {\n values[index] = values[index] - n;\n return values[index + 1];\n }\n }\n }\n return -1;\n }\n};\n```
| 1 | 1 |
[]
| 0 |
rle-iterator
|
Super Simple Java Using Stack with Explanation
|
super-simple-java-using-stack-with-expla-or0v
|
\nclass RLEIterator {\n Stack<int[]> stack;\n public RLEIterator(int[] A) {\n stack=new Stack<>();\n int len=A.length; \n for(int i=l
|
bmask
|
NORMAL
|
2018-09-09T03:19:37.520782+00:00
|
2018-09-09T03:25:21.211899+00:00
| 260 | false |
```\nclass RLEIterator {\n Stack<int[]> stack;\n public RLEIterator(int[] A) {\n stack=new Stack<>();\n int len=A.length; \n for(int i=len-1; i>0; i-=2) { // we read from right to left as we use stack and we want index 0 at the top\n if(A[i-1]>0) stack.push(new int[]{A[i],A[i-1]}); //Records the count of each integer which is i-1 in a stack (except zeros) \n }\n }\n \n public int next(int n) {\n if(stack.isEmpty()) return -1; // if stack is empty means there is nothing left\n int count=0; int prev=-1;\n while(!stack.isEmpty() && count<n) { // pop the data from stack till count>=n\n count+=stack.peek()[1];\n prev=stack.peek()[0];\n stack.pop();\n }\n if(count<n) return -1; // if count is still smaller, then there is nothing to return\n if(count==n) return prev; // if count is equals N then there is no reminder to push to the stack\n count-=n; \n stack.push(new int[]{prev,count}); // push the remindar count into the stack again\n return prev;\n }\n}\n```
| 1 | 1 |
[]
| 0 |
rle-iterator
|
Verbose Solution - Java - O(n) time over all calls - O(1) space
|
verbose-solution-java-on-time-over-all-c-tnz5
|
Hop over the count of the numbers on even positions until n > 0 \nwhen n <= 0 return the odd position number next to the current location. \n\n\nclass RLEIterat
|
shreyansh94
|
NORMAL
|
2018-09-09T03:19:21.615595+00:00
|
2018-09-11T01:23:17.929117+00:00
| 261 | false |
Hop over the count of the numbers on even positions until `n > 0` \nwhen `n <= 0` return the odd position number next to the current location. \n\n```\nclass RLEIterator {\n int index; \n int[] a; \n \n public RLEIterator(int[] A) {\n a = A; \n index = 0; \n }\n \n public int next(int n) {\n for(int i = index; i < a.length; i+=2, index=i){\n if(n <= a[i]){\n a[i] -= n;\n return a[i+1]; \n }else{\n n -= a[i]; \n }\n }\n return -1; \n }\n}\n```
| 1 | 1 |
[]
| 1 |
rle-iterator
|
Using state variables for the object
|
using-state-variables-for-the-object-by-r7p66
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
skj96
|
NORMAL
|
2025-04-07T20:12:56.063526+00:00
|
2025-04-07T20:12:56.063526+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class RLEIterator {
int currentIdx;
int[] encoding;
public RLEIterator(int[] encoding) {
currentIdx=0;
this.encoding = encoding;
}
public int next(int n) {
while(currentIdx< encoding.length) {
if(n<=encoding[currentIdx]){
encoding[currentIdx]-=n;
return encoding[currentIdx+1];
}else{
n-=encoding[currentIdx];
currentIdx+=2;
}
}
return -1;
}
}
/**
* Your RLEIterator object will be instantiated and called as such:
* RLEIterator obj = new RLEIterator(encoding);
* int param_1 = obj.next(n);
*/
```
| 0 | 0 |
['Java']
| 0 |
rle-iterator
|
Java O(n) Time and O(1) Space Approach without Modifying the Input Array
|
java-on-time-and-o1-space-approach-witho-03ou
|
IntuitionImplement an iterator that uses constant space, and does not modify the original array.Algorithm
Maintain an extra variable repetitionsRemaining to kee
|
kcstar
|
NORMAL
|
2025-03-26T23:25:19.463976+00:00
|
2025-03-26T23:25:19.463976+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Implement an iterator that uses constant space, and does not modify the original array.
# Algorithm
<!-- Describe your approach to solving the problem. -->
1. Maintain an extra variable *repetitionsRemaining* to keep track of how many of each current number are available to exhaust. That way, updates on the number counts can be performed on that variable instead of the original array.
2. Exhaust numbers until we reach an element that has enough numbers to exhaust for the remaining n. That will be the element that is to be returned in the next step. If we reach the end of the array before this is fulfilled, then there are not enough numbers, in which case return -1.
3. Exhaust any remaining n numbers from that element from the previous step, then return that element.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$ In the worst-case scenario, the entire array will need to be traversed to exhaust n elements.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(1)$$ Regardless of input array length or n, this implementation will always use three variables.
# Code
```java []
class RLEIterator {
private int[] encoding;
private int index;
private int repetitionsRemaining;
public RLEIterator(int[] encoding) {
this.encoding = encoding;
index = 0;
repetitionsRemaining = (encoding.length >= 2) ? encoding[0] : 0;
}
// This implementation does not produce any side effects
public int next(int n) {
if (n <= 0 || index + 1 >= encoding.length) {
return -1;
}
while (repetitionsRemaining < n) {
n -= repetitionsRemaining;
index += 2;
// End of array check
if (index + 1 >= encoding.length) {
return -1;
}
repetitionsRemaining = encoding[index];
}
repetitionsRemaining -= n;
return encoding[index + 1];
}
}
/**
* Your RLEIterator object will be instantiated and called as such:
* RLEIterator obj = new RLEIterator(encoding);
* int param_1 = obj.next(n);
*/
```
| 0 | 0 |
['Array', 'Design', 'Counting', 'Iterator', 'Java']
| 0 |
rle-iterator
|
JS solution
|
js-solution-by-sunnat_dev_2011-6b99
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
sunnat_dev_2011
|
NORMAL
|
2025-03-20T18:15:54.957590+00:00
|
2025-03-20T18:15:54.957590+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {number[]} encoding
*/
var RLEIterator = function(encoding) {
this.arr = encoding
this.itrSum = 0
this.itrPtr = 0
};
/**
* @param {number} n
* @return {number}
*/
RLEIterator.prototype.next = function(n) {
// PRODUCE
this.itrSum += n
// IF ABOVE LIMIT CONSUME
while (this.arr[this.itrPtr] < this.itrSum) {
this.itrSum -= this.arr[this.itrPtr]
this.itrPtr += 2
}
// OUT OF BOUNDS
if (this.itrPtr >= this.arr.length) {
return -1
}
// RETURN NEXT
return this.arr[this.itrPtr+1]
};
/**
* Your RLEIterator object will be instantiated and called as such:
* var obj = new RLEIterator(encoding)
* var param_1 = obj.next(n)
*/
```
| 0 | 0 |
['JavaScript']
| 0 |
rle-iterator
|
JS solution
|
js-solution-by-sunnat_dev_2011-89y9
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
sunnat_dev_2011
|
NORMAL
|
2025-03-20T18:15:52.574730+00:00
|
2025-03-20T18:15:52.574730+00:00
| 0 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {number[]} encoding
*/
var RLEIterator = function(encoding) {
this.arr = encoding
this.itrSum = 0
this.itrPtr = 0
};
/**
* @param {number} n
* @return {number}
*/
RLEIterator.prototype.next = function(n) {
// PRODUCE
this.itrSum += n
// IF ABOVE LIMIT CONSUME
while (this.arr[this.itrPtr] < this.itrSum) {
this.itrSum -= this.arr[this.itrPtr]
this.itrPtr += 2
}
// OUT OF BOUNDS
if (this.itrPtr >= this.arr.length) {
return -1
}
// RETURN NEXT
return this.arr[this.itrPtr+1]
};
/**
* Your RLEIterator object will be instantiated and called as such:
* var obj = new RLEIterator(encoding)
* var param_1 = obj.next(n)
*/
```
| 0 | 0 |
['JavaScript']
| 0 |
count-substrings-that-differ-by-one-character
|
C++/Java/Python3 O(n ^ 3) => O(n ^ 2)
|
cjavapython3-on-3-on-2-by-votrubac-bmr3
|
I misread the description and got wrong answer first time. Then I got TLE as I tried to use a map or a trie. I thought about using a rolling hash, but it sounde
|
votrubac
|
NORMAL
|
2020-10-31T16:01:44.064906+00:00
|
2020-10-31T19:26:11.495766+00:00
| 16,285 | false |
I misread the description and got wrong answer first time. Then I got TLE as I tried to use a map or a trie. I thought about using a rolling hash, but it sounded too complicated.\n\nFinally, I looked at the constraint and thought a simple cubic solution should do. We analyze all pairs of starting points in our strings (which is O(n ^2)), and the trick is to count substrings in a linear time.\n\n> Update: we can also count substrings in O(1) time if we precompute. Check approach 3 below.\n\n#### Approach 1: Compare and Expand\nWe compare strings starting from `s[i]` and `t[j]`, and track the number of mismatched characters `miss`:\n- 0: continue our comparison\n- 1: we found a substring - increment res and continue our comparison\n- 2: break from the loop.\n\n**C++**\n```cpp\nint countSubstrings(string &s, string &t) {\n int res = 0;\n for (int i = 0; i < s.size(); ++i) {\n for (int j = 0; j < t.size(); ++j) {\n int miss = 0;\n for (int pos = 0; i + pos < s.size() && j + pos < t.size(); ++pos) {\n if (s[i + pos] != t[j + pos] && ++miss > 1)\n break;\n res += miss;\n }\n }\n }\n return res;\n}\n```\n**Java**\n```java\npublic int countSubstrings(String s, String t) {\n int res = 0;\n for (int i = 0; i < s.length(); ++i) {\n for (int j = 0; j < t.length(); ++j) {\n int miss = 0;\n for (int pos = 0; i + pos < s.length() && j + pos < t.length(); ++pos) {\n if (s.charAt(i + pos) != t.charAt(j + pos) && ++miss > 1)\n break;\n res += miss;\n }\n }\n }\n return res; \n}\n```\n\n**Python 3**\n```python\nclass Solution:\n def countSubstrings(self, s: str, t: str) -> int:\n res = 0\n for i in range(len(s)):\n for j in range(len(t)):\n miss, pos = 0, 0\n while i + pos < len(s) and j + pos < len(t) and miss < 2:\n miss += s[i + pos] != t[j + pos]\n res += miss == 1\n pos += 1\n return res\n```\n**Complexity Analysis**\n- Time: O(n ^ 3), as we have three nested loops.\n- Memory: O(1).\n#### Approach 2: Process Missmatches\nAlternativelly, we can process all pair of missmatched characters `s[i]` and `t[j]`. Starting from the missmatch, we count matching characters to the left `l` and to the right `r`. The total number of substrings will be `l * r`.\n**C++**\n```cpp\nint countSubstrings(string &s, string &t) {\n int res = 0;\n for (int i = 0; i < s.size(); ++i)\n for (int j = 0; j < t.size(); ++j) {\n if (s[i] != t[j]) {\n int l = 1, r = 1;\n while (min(i - l, j - l) >= 0 && s[i - l] == t[j - l])\n ++l;\n while (i + r < s.size() && j + r < t.size() && s[i + r] == t[j + r])\n ++r;\n res += l * r;\n }\n }\n return res;\n}\n```\n**Complexity Analysis**\n- Same as for approach above.\n#### Approach 3: Process Missmatches + DP\nThis is the same as approach 2 above, but we use DP to precompute sizes of a matching substring ending at position `[i][j]` (`dpl`), and starting from position `[i][j]` (`dpr`).\n**C++**\n```cpp\nint countSubstrings(string &s, string &t) {\n int res = 0;\n int dpl[101][101] = {}, dpr[101][101] = {};\n for (int i = 1; i <= s.size(); ++i)\n for (int j = 1; j <= t.size(); ++j)\n if (s[i - 1] == t[j - 1])\n dpl[i][j] = 1 + dpl[i - 1][j - 1];\n for (int i = s.size(); i > 0; --i)\n for (int j = t.size(); j > 0; --j)\n if (s[i - 1] == t[j - 1])\n dpr[i - 1][j - 1] = 1 + dpr[i][j];\n for (int i = 0; i < s.size(); ++i)\n for (int j = 0; j < t.size(); ++j)\n if (s[i] != t[j])\n res += (dpl[i][j] + 1) * (dpr[i + 1][j + 1] + 1);\n return res;\n}\n```\n**Complexity Analysis**\n- Time: O(n ^ 2), we have two nested loops to precompute sizes, and count substrings.\n- Memory: O(n ^ 2) for the memoisation.
| 252 | 11 |
[]
| 31 |
count-substrings-that-differ-by-one-character
|
[Java/C++/Python] Time O(nm), Space O(1)
|
javacpython-time-onm-space-o1-by-lee215-gtdh
|
Intuition\nChoose a start point for s and a start point for t, and then compare characters one by one.\n\n\n# Explanation\nTry to match from s[i] and t[j],\nwhe
|
lee215
|
NORMAL
|
2020-10-31T18:35:17.986688+00:00
|
2020-12-01T07:01:40.019073+00:00
| 13,127 | false |
# **Intuition**\nChoose a start point for `s` and a start point for `t`, and then compare characters one by one.\n<br>\n\n# **Explanation**\nTry to match from s[i] and t[j],\nwhere i = 0 or j = 0.\n\n`cur` is the current number of consecutive same characters.\n`pre` is the previous number of consecutive same characters.\n<br>\n\n# **Complexity**\nTime `O(mn)`\nSpace `O(1)`\n<br>\n\n**Java**\n```java\n public int countSubstrings(String s, String t) {\n int res = 0 ;\n for (int i = 0; i < s.length(); ++i)\n res += helper(s, t, i, 0);\n for (int j = 1; j < t.length(); ++j)\n res += helper(s, t, 0, j);\n return res;\n }\n\n\n public int helper(String s, String t, int i, int j) {\n int res = 0, pre = 0, cur = 0;\n for (int n = s.length(), m = t.length(); i < n && j < m; ++i, ++j) {\n cur++;\n if (s.charAt(i) != t.charAt(j)) {\n pre = cur;\n cur = 0;\n }\n res += pre;\n }\n return res;\n }\n```\n**C++**\n```cpp\n int countSubstrings(string s, string t) {\n int res = 0 ;\n for (int i = 0; i < s.length(); ++i)\n res += helper(s, t, i, 0);\n for (int j = 1; j < t.length(); ++j)\n res += helper(s, t, 0, j);\n return res;\n }\n\n int helper(string s, string t, int i, int j) {\n int res = 0, pre = 0, cur = 0;\n for (int n = s.length(), m = t.length(); i < n && j < m; ++i, ++j) {\n cur++;\n if (s[i] != t[j])\n pre = cur, cur = 0;\n res += pre;\n }\n return res;\n }\n```\n\n**Python:**\n```py\n def countSubstrings(self, s, t):\n n, m = len(s), len(t)\n\n def test(i, j):\n res = pre = cur = 0\n for k in xrange(min(n - i, m - j)):\n cur += 1\n if s[i + k] != t[j + k]:\n pre, cur = cur, 0\n res += pre\n return res\n return sum(test(i, 0) for i in xrange(n)) + sum(test(0, j) for j in xrange(1, m))\n```\n
| 166 | 9 |
[]
| 20 |
count-substrings-that-differ-by-one-character
|
C++ DP (Detailed Explanation with Examples)
|
c-dp-detailed-explanation-with-examples-8r7b4
|
dp[i][j] is the number of substrings which are equal and end at s[i-1],t[j-1] respectively.\ndp1[i][j] is the number of substrings which end at s[i-1],t[j-1] an
|
Modern_Seneca
|
NORMAL
|
2021-10-16T03:06:16.463005+00:00
|
2021-10-17T15:40:28.160761+00:00
| 4,926 | false |
dp[i][j] is the number of substrings which are equal and end at s[i-1],t[j-1] respectively.\ndp1[i][j] is the number of substrings which end at s[i-1],t[j-1] and differ by 1 char.\n\n**if s[i-1]==t[j-1]**, we can say that dp[i][j] is 1+dp[i-1][j-1] because all those substrings from dp[i-1][j-1] can be costructed here and the +1 corresponds to the substring which contains only the last character(s[i-1],t[j-1]). Here, dp1[i-1][j-1] will be dp1[i-1][j-1] because all those substrings from dp1[i-1][j-1] can be costructed here by appending the extra character(s[i-1],t[j-1]) which is same in both substrings.\n\n**Example:** \nAssume that dp[i-1][j-1] has substrings {"ab","ab"}. Lets say s[i-1]=t[j-1]=\'c\'. \nNow dp[i][j] will have {"abc","abc"},{"c","c"}.(which is one extra substring than dp[i-1][j-1]).\nAssume dp1[i-1][j-1] has subtrings {"ab","ae"}. Lets say s[i-1]=t[j-1]=\'c\'.\nNow dp1[i][j] will have {"abc","aec"} \n\n\n**if s[i-1]!=t[j-1]**, dp[i][j] will be zero because we can\'t construct equal substrings which end at s[i-1] and t[j-1] respectively. dp1[i][j] becomes 1+dp[i-1][j-1] because we can append this unequal chars(s[i-1],t[j-1]) to all those equal substrings of dp[i-1][j-1]. \n\n**Example:** \nAssume that dp[i-1][j-1] has substrings {"ab","ab"}. Lets say s[i-1]=\'c\' ans t[j-1]=\'d\'. \nNow dp[i][j] will have no equal substrings which end at s[i-1] and t[j-1].\nBut dp1[i][j] will have {"abc","abd"},{"c","d"} \n\n```\nint countSubstrings(string s, string t) {\n int n = s.length();\n int m = t.length();\n vector<vector<int>> dp(n+1,vector<int>(m+1));\n vector<vector<int>> dp1(n+1,vector<int>(m+1));\n int ans = 0;\n \n for(int i=1;i<=n;i++)\n {\n for(int j=1;j<=m;j++)\n {\n if(s[i-1]==t[j-1])\n {\n dp[i][j] = 1+dp[i-1][j-1];\n dp1[i][j] = dp1[i-1][j-1];\n }\n else\n dp1[i][j] = 1+dp[i-1][j-1];\n ans += dp1[i][j];\n }\n }\n return ans;\n }\n```
| 96 | 1 |
[]
| 6 |
count-substrings-that-differ-by-one-character
|
[Java] clean O(MN)-time O(1)-space Dynamic Programming Solution || with comments
|
java-clean-omn-time-o1-space-dynamic-pro-o1ub
|
This article aims to: \n1. give a clear definition of entries of 2-Dimension DP-table\n2. give a clear relationship between big problem and sub-problems\n3. opt
|
xieyun95
|
NORMAL
|
2021-04-29T21:39:26.161933+00:00
|
2021-04-29T22:46:06.136848+00:00
| 4,295 | false |
This article aims to: \n1. give a clear definition of entries of 2-Dimension DP-table\n2. give a clear relationship between big problem and sub-problems\n3. optimize the "naive" DP-Solution into a O(1)-space Solution\n\nFor some people (myself included), directly coming up with an O(1)-Space Solution is neither easy nor straightforward. So I believe it nice to start with the relatively simple solution first. Then optimize the solution by observing its structure. I believe this is a more of less natural process for the interviewer. \n\nOf course for those who just want the "best" solution, feel free to just go to the very bottom of the article and check the **solution (version 4)**; \n\nFirst of all, let\'s start with the "2-Dimensional" DP-table. Here it seems that it\'s 3-Dimensinoal. However, the third dimension consist just two states. What really matter the most are the index pair (i, j); \n\nFor each (i, j), we count the pairs of substrings (sub_s, sub_t) such that\n1. the last digit of sub_s is s[i]\n2. the last digit of sub_t is t[j]\n \nThen define the entries in dp-table as:\n* dp\\[i\\]\\[j\\]\\[0\\] : number of such pairs of (sub_s, sub_t) that differs by 0 char\n* dp\\[i\\]\\[j\\]\\[1\\] : number of such pairs of (sub_s, sub_t) that differs by 1 char \n \nThen relation of bigger problem and sub-problem is very straightforward: \n```\nif (s[i] == t[j])\n\tdp[i][j][0] = dp[i-1][j-1][0] + 1 // plus the substring (s[i], t[j])\n\tdp[i][j][1] = dp[i-1][j-1][1]\nelse \n\tdp[i][j][0] = 0\n\tdp[i][j][1] = dp[i-1][j-1][0] + 1 // plus the substring (s[i], t[j])\n```\n\nThe most basic DP-Solution is as follows: \n\n```\n// version 1 : O(mn) space\nclass Solution {\n public int countSubstrings(String s, String t) {\n int m = s.length(), n = t.length();\n\n int[][][] dp = new int[m][n][2];\n \n int res = 0;\n // first col s[0:i] match t[0:0]\n for (int i = 0; i < m; i++) {\n dp[i][0][0] = (s.charAt(i) == t.charAt(0)) ? 1 : 0;\n dp[i][0][1] = (s.charAt(i) == t.charAt(0)) ? 0 : 1;\n res += dp[i][0][1];\n }\n \n \n // first row s[0:0] match t[0:j]\n for (int j = 1; j < n; j++) {\n dp[0][j][0] = (s.charAt(0) == t.charAt(j)) ? 1 : 0;\n dp[0][j][1] = (s.charAt(0) == t.charAt(j)) ? 0 : 1;\n res += dp[0][j][1];\n }\n \n for (int i = 1; i < m; i++) {\n for (int j = 1; j < n; j++) {\n dp[i][j][0] = (s.charAt(i) == t.charAt(j)) ? dp[i-1][j-1][0] + 1 : 0;\n dp[i][j][1] = (s.charAt(i) == t.charAt(j)) ? dp[i-1][j-1][1] : dp[i-1][j-1][0] + 1;\n res += dp[i][j][1];\n }\n }\n\n return res;\n }\n}\n```\n\nOr we can rewrite the solution in this compact way: \n\n```\n// version 2 : O(MN) space\nclass Solution {\n public int countSubstrings(String s, String t) {\n int m = s.length(), n = t.length(), res = 0;\n int[][][] dp = new int[m+1][n+1][2];\n \n // dp[i][j] : count for s[0:i) & t[0:j)\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n dp[i+1][j+1][0] = (s.charAt(i) == t.charAt(j)) ? dp[i][j][0] + 1 : 0;\n dp[i+1][j+1][1] = (s.charAt(i) == t.charAt(j)) ? dp[i][j][1] : dp[i][j][0] + 1;\n res += dp[i+1][j+1][1];\n }\n }\n \n return res;\n }\n}\n```\n\nNoticing that we only need the left-top entry to calculate current entry. Namely, to calculate dp\\[i+1\\]\\[j+1\\], we only need the values of dp\\[i\\]\\[j\\]. Optimizing the solution into O(min(M,N))-Space is straightforward: \n```\n// version 3: O(min(M, N)) space\nclass Solution {\n public int countSubstrings(String s, String t) {\n int m = s.length(), n = t.length();\n if (m < n) return countSubstrings(t, s);\n \n int res = 0;\n int[][] dp = new int[n+1][2];\n \n for (int i = 0; i < m; i++) {\n int[][] next = new int[n+1][2];\n for (int j = 0; j < n; j++) {\n next[j+1][0] = (s.charAt(i) == t.charAt(j)) ? dp[j][0] + 1 : 0;\n next[j+1][1] = (s.charAt(i) == t.charAt(j)) ? dp[j][1] : dp[j][0] + 1;\n res += next[j+1][1];\n }\n \n dp = next;\n }\n \n return res;\n }\n}\n```\n\nFurther more, we may reduce the Space Complexity to O(1). To traverse the whole table, we only need to start traversing from the top and left boundary. Then for each starting point, we just traverse its right-bottom entry until we hit right/bottom boundary. \n\nThis Solution (version 4) is formulated from version 2: \n\n```\n// version 4: O(1)- space\nclass Solution {\n private String s;\n private String t;\n private int res = 0;\n public int countSubstrings(String s, String t) {\n this.s = s;\n this.t = t;\n \n // starting from left boundary dp[0][0], dp[1][0], ..., dp[m-1][0]\n for (int i = 0; i < s.length(); i++) {\n traverseRightBottom(i, 0);\n }\n \n // starting from top boundary dp[0][1], dp[0][2], ..., dp[0][n-1]\n for (int j = 1; j < t.length(); j++) {\n traverseRightBottom(0, j);\n }\n \n return res;\n }\n \n private void traverseRightBottom(int i, int j) {\n int prev0 = 0; // dp[i][j][0]\n int prev1 = 0; // dp[i][j][1]\n \n while (i < s.length() && j < t.length()) {\n boolean match = (s.charAt(i++) == t.charAt(j++));\n int curr0 = match ? prev0 + 1 : 0; // dp[i+1][j+1][0]\n int curr1 = match ? prev1 : prev0 + 1; // dp[i+1][j+1][1]\n \n res += curr1; \n \n prev0 = curr0;\n prev1 = curr1;\n }\n }\n}\n```
| 75 | 0 |
['Dynamic Programming', 'Java']
| 10 |
count-substrings-that-differ-by-one-character
|
C++ O(N^3) with explanation
|
c-on3-with-explanation-by-lzl124631x-0u2k
|
See my latest update in repo LeetCode\n\n## Solution 1.\n\nIntuition: We can find each pair of s[i] != t[j]. Then try to extend both sides when s[i + t] == t[j
|
lzl124631x
|
NORMAL
|
2020-10-31T16:01:20.744619+00:00
|
2020-11-11T09:26:05.560252+00:00
| 3,435 | false |
See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1.\n\nIntuition: We can find each pair of `s[i] != t[j]`. Then try to extend both sides when `s[i + t] == t[j + t]`. If we have `left` steps extended on the left side and `right` steps on the right side, we have `(left + 1) * (right + 1)` options for this `{ i, j }` case.\n\nExample:\n\n```\ns = xbabc\nt = ybbbc\n```\n\nFor `i = 2` and `j = 2`, we have `s[i] = a` and `t[j] = b` that doesn\'t match. Now look leftwards, we can extend left-side by 1 time due to `b`, and extend right-side by 2 times due to `bc`. So for this specific center `{ i = 2, j = 2 }`, we have `2 * 3 = 6` options.\n\n```cpp\n// OJ: https://leetcode.com/contest/biweekly-contest-38/problems/count-substrings-that-differ-by-one-character/\n// Author: github.com/lzl124631x\n// Time: O(N^3)\n// Space: O(1)\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int M = s.size(), N = t.size(), ans = 0;\n for (int i = 0; i < M; ++i) {\n for (int j = 0; j < N; ++j) {\n if (s[i] == t[j]) continue;\n int left = 1, right = 1;\n while (i - left >= 0 && j - left >= 0 && s[i - left] == t[j - left]) ++left;\n while (i + right < M && j + right < N && s[i + right] == t[j + right]) ++right;\n ans += left * right;\n }\n }\n return ans;\n }\n};\n```
| 68 | 1 |
[]
| 5 |
count-substrings-that-differ-by-one-character
|
Java 3ms | easy to understand code
|
java-3ms-easy-to-understand-code-by-yunj-btx3
|
\n\nSince the substring need to have one and only one different character, we start with finding differenct characters in String s and String t. Then, we work b
|
yunjinglee
|
NORMAL
|
2020-10-31T22:24:39.756320+00:00
|
2020-10-31T23:48:28.438422+00:00
| 2,015 | false |
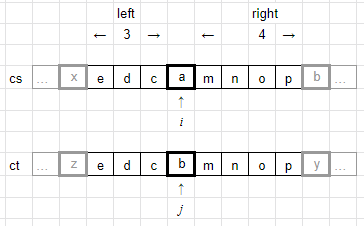\n\nSince the substring need to have one and only one different character, we start with finding differenct characters in String s and String t. Then, we work both backward and forward to find longest matching distance: left and right. In this example, we can choose 0 to 3 characters from left, that has 4 choice. We can also choose 0 to 4 characters from right, that has 5 choice. The total combination with only 1 different character produced by characters in position i and j is (left+1) * (right + 1) = 4 * 5 = 20. Sum all the combination at different i and j would give us result.\n\n```\npublic int countSubstrings(String s, String t) {\n\tchar[] cs = s.toCharArray();\n\tchar[] ct = t.toCharArray();\n\n\tint total = 0;\n\tfor (int i = 0 ; i < cs.length; ++i) {\n\t\tfor (int j = 0 ; j < ct.length ; ++j) {\n\n\t\t\tif (cs[i] == ct[j]) continue;\n\n\t\t\tint left = 0;\n\t\t\tint x = i-1, y = j-1;\n\t\t\twhile(x >= 0 && y >= 0) {\n\t\t\t\tif (cs[x--] == ct[y--])\n\t\t\t\t\t++left;\n\t\t\t\telse\n\t\t\t\t\tbreak;\n\t\t\t}\n\n\t\t\tint right = 0;\n\t\t\tx = i+1;\n\t\t\ty = j+1;\n\t\t\twhile(x < cs.length && y < ct.length) {\n\t\t\t\tif (cs[x++] == ct[y++])\n\t\t\t\t\t++right;\n\t\t\t\telse\n\t\t\t\t\tbreak;\n\t\t\t}\n\n\t\t\ttotal += (left + 1) * (right + 1);\n\t\t}\n\t}\n\treturn total;\n}\n```\n\n\n
| 29 | 1 |
['Java']
| 4 |
count-substrings-that-differ-by-one-character
|
100% FASTER CPP SOLUTION || DP || EXPLAINED
|
100-faster-cpp-solution-dp-explained-by-da0e6
|
\nclass Solution {\npublic:\n \n \n// EXPLANATION:\n \n// Took two Dps.\n\n// 1st dp for storing the number of substrings where the las
|
dd_07
|
NORMAL
|
2022-01-04T17:46:52.419097+00:00
|
2022-01-04T17:46:52.419141+00:00
| 1,974 | false |
```\nclass Solution {\npublic:\n \n \n// EXPLANATION:\n \n// Took two Dps.\n\n// 1st dp for storing the number of substrings where the last character i.e s[i-1]=t[j-1]\n// 2nd dp for storing the number of exactly 1 diff char ending with s[i-1]\n \n// now if s[i-1]==t[j-1], then dp1[i][j]=dp1[i-1][j-1]+1 and dp2[i][j]=dp2[i-1][j-1]\n// else if s[i-1]!=t[j-1], then dp1[i][j]=0 and dp2[i][j]=1+dp1[i-1][j-1]\n// add the ans with dp2[i][j]\n \n// return ans\n \n #define ll long long \n int countSubstrings(string s, string t) {\n ll n=s.length();\n ll m=t.length();\n ll dp1[n+1][m+1],dp2[n+1][m+1];\n for(ll i=0;i<n;i++){\n dp1[i][0]=0; dp2[i][0]=0;\n }\n for(ll i=0;i<m;i++){\n dp1[0][i]=0; dp2[0][i]=0;\n }\n ll ans=0;\n for(ll i=1;i<n+1;i++){\n for(ll j=1;j<m+1;j++){\n if(s[i-1]==t[j-1]){\n dp1[i][j]=1+dp1[i-1][j-1];\n dp2[i][j]=dp2[i-1][j-1];\n ans+=dp2[i][j];\n }\n else{\n dp1[i][j]=0;\n dp2[i][j]=1+dp1[i-1][j-1];\n ans+=dp2[i][j];\n }\n }\n }\n return ans;\n }\n \n // KINDLY DO UPVOTE IF YOU LIKE THE EXPLANATION :)\n};\n```
| 23 | 1 |
['Dynamic Programming']
| 2 |
count-substrings-that-differ-by-one-character
|
[C++] Brute Force, 4ms
|
c-brute-force-4ms-by-rudy-ft5f
|
Time complexity, O(n^3) c++ class Solution { public: int countSubstrings(string s, string t) { int cnt = 0; for (int i = 0; i < s.length(); i++) {
|
rudy__
|
NORMAL
|
2020-10-31T18:38:32.294077+00:00
|
2020-10-31T18:38:32.294120+00:00
| 1,889 | false |
Time complexity, `O(n^3)`
```c++
class Solution {
public:
int countSubstrings(string s, string t) {
int cnt = 0;
for (int i = 0; i < s.length(); i++) {
for (int j = 0; j < t.length(); j++) {
int diff = 0;
for (int k = 0; k < std::min(s.length() - i, t.length() - j); k++) {
if (s[k + i] != t[k + j]) diff++;
if (diff > 1) break;
cnt += diff;
}
}
}
return cnt;
}
};
```
| 19 | 0 |
[]
| 2 |
count-substrings-that-differ-by-one-character
|
C++ O(n^2) solutioin - 4ms beat 100%
|
c-on2-solutioin-4ms-beat-100-by-szzzwno1-dmr9
|
Idea is: for each (i, j) pair, where i in the index in s and j is the index in t, if they are not the same, we then basically need to calculate what is the long
|
szzzwno123
|
NORMAL
|
2020-10-31T16:05:02.554030+00:00
|
2020-10-31T16:08:46.381873+00:00
| 1,749 | false |
Idea is: for each (i, j) pair, where i in the index in s and j is the index in t, if they are not the same, we then basically need to calculate what is the longest substring ends at s[i - 1] and t[j - 1] such that they are the same, and what is the longest substring starts at s[i + 1] and t[j + 1] such that they are the same. Then we can use combinatorics to determine how many valid substring pair that contains s[i] and t[j].\n\nSee code below (can be cleaned up a bit):\n```\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n // dp[i][j] := longest substring ends at s[i] and t[j] such that they are equal\n\t\t// dp2[i][j] := longest substring starts at s[i] and t[j] such that they are equal\n int m = s.length(), n = t.length();\n vector<vector<int>> dp(m + 2, vector<int>(n + 2));\n vector<vector<int>> dp2(m + 2, vector<int>(n + 2));\n \n {\n dp[1][1] = s[0] == t[0];\n\n for (int i = 1; i <= m; i++)\n dp[i][1] = s[i - 1] == t[0];\n\n for (int j = 1; j <= n; j++)\n dp[1][j] = s[0] == t[j - 1];\n\n for (int i = 2; i <= m; i++)\n for (int j = 2; j <= n; j++) {\n if (s[i - 1] == t[j - 1])\n dp[i][j] = 1 + dp[i - 1][j - 1];\n }\n }\n \n {\n dp2[m][n] = s[m - 1] == t[n - 1];\n \n for (int i = 1; i <= m; i++)\n dp2[i][n] = s[i - 1] == t[n - 1];\n\n for (int j = 1; j <= n; j++)\n dp2[m][j] = s[m - 1] == t[j - 1];\n \n for (int i = m - 1; i >= 1; i--)\n for (int j = n - 1; j >= 1; j--) {\n if (s[i - 1] == t[j - 1])\n dp2[i][j] = 1 + dp2[i + 1][j + 1];\n }\n }\n \n int res = 0;\n \n for (int i = 0; i < m; i++)\n for (int j = 0; j < n; j++) {\n if (s[i] != t[j]) {\n res += (dp[i][j] + 1) * (dp2[i + 2][j + 2] + 1);\n }\n }\n\n return res;\n \n }\n};\n```
| 17 | 1 |
[]
| 1 |
count-substrings-that-differ-by-one-character
|
Dynamic programming O(n^2)
|
dynamic-programming-on2-by-prakhar_11-o4np
|
We can do it in O(n^2) complexity by following way:\n\ndp[i][j]]: keep track of number of substring for s and t that ends at position i and j respectively such
|
prakhar_11
|
NORMAL
|
2020-10-31T16:31:14.537837+00:00
|
2020-10-31T16:32:19.174112+00:00
| 2,174 | false |
We can do it in O(n^2) complexity by following way:\n\n**dp[i][j]]**: keep track of number of substring for s and t that ends at position i and j respectively such that they are exactly equal.\n**dp2[i][j]]**: keep track of number of substring for s and t that ends at position i and j respectively such that they differ by one character.\n\nthen transitions are as follows:\nif they character at i and j are equal then:\ndp[i][j]= dp[i-1][j-1] \ndp2[i][jj]= dp2[i-1][j-1]+1\notherwise \ndp[i][j]= dp[i-1][j-1]+1\ndp2[i][j]=0 \n The answer is summation of all value of dp[i][j]\n```\nclass Solution {\npublic:\n #define ll int\n ll dp[101][101]; \n ll dp2[101][101]; \n int countSubstrings(string s, string t) {\n \n \n ll ans=0 ;\n for(ll i=0;i<s.size();i++)\n {\n for(ll j =0;j<s.size();j++)\n {\n dp[i][j]=0;\n dp2[i][j]=0;\n }\n }\n for(ll i=0;i<s.size();i++)\n {\n for(ll j =0;j<t.size();j++)\n {\n \n if(s[i]==t[j])\n {\n ll x=i-1>=0 && j-1>=0 ? dp[i-1][j-1]:0;\n ll y= i-1>=0 && j-1>=0?dp2[i-1][j-1]:0;\n dp[i][j]=x;\n dp2[i][j]=y+1; \n }\n else\n {\n ll x= i-1>=0 && j-1>=0?dp2[i-1][j-1]:0;\n dp[i][j]=x+1;\n dp2[i][j]=0; \n }\n ans+=dp[i][j];\n }\n }\n \n return ans; \n }\n};\n```
| 14 | 0 |
[]
| 5 |
count-substrings-that-differ-by-one-character
|
C++ DP Solution
|
c-dp-solution-by-loktan-au6z
|
\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int ans = 0;\n int m = s.size(), n = t.size();\n\t\t//f: amount of su
|
loktan
|
NORMAL
|
2020-11-06T09:06:48.240012+00:00
|
2020-11-06T09:06:48.240044+00:00
| 1,027 | false |
```\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int ans = 0;\n int m = s.size(), n = t.size();\n\t\t//f: amount of substrings differ by 1 character till s[i]t[j]\n\t\t//i j begin from 1\n vector<vector<int>> f(m + 1, vector<int>(n + 1)); \n\t\t//g: amount of substrings that are the same till s[i]t[j]\n auto g = f;\n \n for (int i = 1; i <= m; i++) {\n for (int j = 1; j <= n; j++) {\n\t\t\t\t//if they are the same\n if (s[i-1] == t[j-1]) {\n g[i][j] = g[i-1][j-1] + 1; //add g[i][j] by 1\n f[i][j] += f[i-1][j-1]; //f[i][j] wont change\n }\n else {\n f[i][j] += g[i-1][j-1] + 1; \n \n }\n ans += f[i][j];\n }\n }\n return ans;\n }\n};\n\n```
| 11 | 0 |
[]
| 1 |
count-substrings-that-differ-by-one-character
|
[c++] || two pointer Approach || 100% faster than any other c++ solution.
|
c-two-pointer-approach-100-faster-than-a-qwdq
|
\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int ans = 0;\n for(int i=0;i<s.size();i++){\n for(int j=0;
|
Prajyotb9
|
NORMAL
|
2021-05-07T10:05:11.089765+00:00
|
2021-05-07T10:05:11.089809+00:00
| 1,000 | false |
```\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int ans = 0;\n for(int i=0;i<s.size();i++){\n for(int j=0;j<t.size();j++){\n int x = i;\n int y = j;\n int temp = 0;\n while( x<s.size() && y<t.size() ){\n if(s[x]!=t[y]){\n temp++;\n }\n if(temp==1){\n ans += 1;\n }\n if(temp>=2){\n break;\n }\n x++;\n y++;\n }\n }\n }\n return ans;\n }\n};\n```
| 10 | 1 |
[]
| 1 |
count-substrings-that-differ-by-one-character
|
Dynamic Programming Detailed Thought process
|
dynamic-programming-detailed-thought-pro-sjfs
|
Think of all the possible scenarios:\nI will consider state as (i,j)\nMy state here is I am going to lookout for all the substrings differing by one character a
|
UnLuckyGuy
|
NORMAL
|
2022-06-07T18:15:43.567170+00:00
|
2022-06-07T18:15:43.567218+00:00
| 1,005 | false |
Think of all the possible scenarios:\nI will consider state as (i,j)\nMy state here is I am going to lookout for all the substrings differing by one character and ending at \'i\' and \'j\'\n\nSo, if (s[i-1] == t[i-1])\n state(i,j) = state(i-1,j-1)\n\t else\n\t state(i,j) = 1 + [all same substrs ending in (i-1) and (j-1)]\n\t\t \nTo get all the equal substrs, we apply another simple dp.\n\nMy answer is summation of all states(i,j)\n\n```\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int len1 = s.length();\n int len2 = t.length();\n vector<vector<int>> sameStr(len1+1,vector<int>(len2+1, 0));\n \n for(int i = 1; i <= len1; i++){\n for(int j = 1; j <= len2; j++){\n if(s[i-1] == t[j-1]){\n sameStr[i][j] = 1 + sameStr[i-1][j-1];\n }\n }\n }\n \n vector<vector<int>>diffStr(len1+1,vector<int>(len2+1,0));\n int cnt = 0;\n for(int i = 1; i <= len1; i++){\n for(int j = 1; j <= len2; j++){\n if(s[i-1] != t[j-1]){\n diffStr[i][j] = 1 + sameStr[i-1][j-1]; \n } else {\n diffStr[i][j] = diffStr[i-1][j-1];\n }\n cnt += diffStr[i][j];\n }\n }\n return cnt;\n }\n};\n```
| 8 | 0 |
['Dynamic Programming']
| 0 |
count-substrings-that-differ-by-one-character
|
C++ Code | Brute Force and DP both approaches
|
c-code-brute-force-and-dp-both-approache-f940
|
\n//BRUTE FORCE\n\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int ans = 0; // for holding answer\n int len1 = s.l
|
103_simran
|
NORMAL
|
2022-04-18T18:41:58.264820+00:00
|
2022-04-18T18:42:40.226058+00:00
| 1,346 | false |
```\n//BRUTE FORCE\n\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int ans = 0; // for holding answer\n int len1 = s.length(), len2 = t.length(); // compute length of both strings "s" and "t"\n for(int i = 1; i <= len1; i++) // length of both substrings of s and t\n {\n for(int j = 0; j+i <= len1; j++) // find subtring of s of length i\n {\n string s1 = s.substr(j, i); // s1 -> subtring of s of length i\n for(int k = 0; k+i <= len2; k++) // subtring of t of length i\n {\n string t1 = t.substr(k, i); // t1 -> subtring of t of length i\n int f = 1;\n for(int p = 0; p < i; p++) // compare the characters of both s1 and t1 substrings \n {\n if(s1[p] != t1[p])\n f--;\n }\n if(f == 0) ans++; // if they differ by only one character, then add the count\n }\n }\n }\n return ans; // return final answer\n }\n};\n\n\n// DP Approach\n\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int ans = 0;\n int len1 = s.length(), len2 = t.length();\n vector<vector<int>> same(len1+1, vector<int>(len2+1, 0)); // if s[i-1] == t[j-1]\n auto differ = same; // if s[i-1] != t[j-1]\n for(int i = 1; i <= len1; i++)\n {\n for(int j = 1; j <= len2; j++)\n {\n if(s[i-1] == t[j-1]) \n {\n same[i][j] = 1 + same[i-1][j-1]; // if it is same then just add 1 more to the count of substrings having equal characters\n differ[i][j] = differ[i-1][j-1]; // number of differing substrings by one character will remain same\n }\n else \n differ[i][j] = same[i-1][j-1] + 1; // add 1 to the substrings having same character upto i-1 of string s and j-1 of string t\n ans += differ[i][j]; // add the differing substrings count to final answer\n }\n }\n return ans; // return final answer\n }\n};\n```
| 8 | 0 |
['String', 'Dynamic Programming', 'C++']
| 1 |
count-substrings-that-differ-by-one-character
|
C++ 100% fast O(m*n)
|
c-100-fast-omn-by-aakashiitd18-t2ju
|
same[i][j] represent the length of maximum substring ending at i in string t and j in string s.\ndiff[i][j] represent the length of maximum substring ending at
|
aakashiitd18
|
NORMAL
|
2022-07-12T07:52:00.368124+00:00
|
2022-07-12T07:52:00.368165+00:00
| 624 | false |
same[i][j] represent the length of maximum substring ending at i in string t and j in string s.\ndiff[i][j] represent the length of maximum substring ending at i in string t and j in string s with only 1 element different.\nThe memory can be reduced by just using only 2 rows as we require only (i-1)th row for calculating ith row.\n\n\t\t\'\'\' \n\t\tint n = s.length(), m = t.length();\n vector<vector<int>> same(n+1,vector<int> (m+1,0));\n vector<vector<int>> diff(n+1,vector<int> (m+1,0));\n int ans = 0;\n for(int i =1;i<=n;i++)\n {\n for(int j = 1;j<=m;j++)\n {\n if(s[i-1]==t[j-1])\n {\n same[i][j] = 1+same[i-1][j-1];\n diff[i][j] = diff[i-1][j-1];\n }\n else\n {\n same[i][j] = 0;\n diff[i][j] = 1+same[i-1][j-1];\n }\n ans+=diff[i][j];\n } \n }\n return ans;\n\t\t\'\'\'
| 7 | 0 |
['Dynamic Programming', 'C']
| 0 |
count-substrings-that-differ-by-one-character
|
C++ || 0 ms || 100% faster || 2 pointer
|
c-0-ms-100-faster-2-pointer-by-aynburnt-01at
|
\n\nstatic auto _____ = [](){\n std::ios::sync_with_stdio(0);\n std::cin.tie(0);\n return 0;\n}();\n\nclass Solution {\npublic:\n int countSubstring
|
aynburnt
|
NORMAL
|
2021-06-04T05:57:06.142730+00:00
|
2021-06-04T05:57:06.142777+00:00
| 588 | false |
```\n\nstatic auto _____ = [](){\n std::ios::sync_with_stdio(0);\n std::cin.tie(0);\n return 0;\n}();\n\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int ans=0;\n for(int i=0; i<s.length(); i++){\n for(int j=0; j<t.length(); j++){\n int x=i, y=j, diff=0;\n while(x<(int)s.length() && y<(int)t.length()){\n if(s[x++] != t[y++]){\n diff++;\n if(diff>1)break;\n }\n if(diff==1)ans++;\n }\n }\n }\n return ans;\n }\n};\n```\n# if you find it helpful, plz upvote
| 7 | 0 |
[]
| 1 |
count-substrings-that-differ-by-one-character
|
100%solution C++ { without hash}
|
100solution-c-without-hash-by-satishsss-gwkt
|
\nIn this question you might think to just generate all the substring of both the arrays and then compare \neach one of them for exactly one different character
|
Satishsss
|
NORMAL
|
2020-12-22T07:18:51.035844+00:00
|
2020-12-22T07:18:51.035888+00:00
| 535 | false |
``` \nIn this question you might think to just generate all the substring of both the arrays and then compare \neach one of them for exactly one different character .. \nthis solution can be easily optimised .. \nyou can think that do we really need to generate all the substring and store them in some hash and then compare\n\nyou can easily apply two pointer\'s like approach and optimise the algo..\n\n\nsuppose string s="aba"\nand string t="baba"\n\n\nkeep i pointer on s and iterate through all j in t and check for exact difference of one \ncontinue the loop until you reach the length or get difference more than one \n\n```\n\n\nclass Solution {\npublic:\n int countSubstrings(string s, string t) {\n int lens=s.length();\n int lent=t.length();\n \n int ans=0;\n \n for(int I=0;I<lens;I++){\n \n for(int J=0;J<lent;J++){\n int i=I;\n int j=J;\n int diff=0;\n while(i<lens and j<lent and diff<=1){\n if(s[i]!=t[j])\n diff++;\n if(diff==1)\n ans++;\n i++;\n j++;\n }\n }\n }\n \n return ans;\n }\n};
| 7 | 1 |
[]
| 2 |
count-substrings-that-differ-by-one-character
|
97% TC and 95% SC easy python solution with explanation
|
97-tc-and-95-sc-easy-python-solution-wit-h0yf
|
Believe me, this ques is like must to have in the mind, as this gonna help you solve many such questions.\n1. We have to calculate all substrings which differ b
|
nitanshritulon
|
NORMAL
|
2022-08-27T14:52:20.252056+00:00
|
2022-08-27T15:04:04.523232+00:00
| 1,263 | false |
Believe me, this ques is like must to have in the mind, as this gonna help you solve many such questions.\n1. We have to calculate all substrings which differ by just a character.\n2. So, maintain 2 states, first one will be for the count of substrings which is present in "t" string as well(all characters equal). The second one will keep the count with 1 different character.\n3. Traverse the 2 strings using 2 pointers using 2 loops. If the char which are being pointed are same, which means we will have our ans from already differed strings, which already have a character different. So just use that.\n4. If they are different, then go for all the strings which have all the characters same, because the current is gonna be a different one.\n5. Now just keep maintaining these 2 states for all the indices.\n6. Didn\'t get it, read it for 3-4 times atleast. And you\'re free to comment down :)\n```\ndef countSubstrings(self, s: str, t: str) -> int:\n\tls, lt = len(s), len(t)\n\tequal_prev, unequal_prev = [0] * (lt+1), [0] * (lt+1)\n\tans = 0\n\tfor i in range(ls):\n\t\tequal_curr, unequal_curr = [0] * (lt+1), [0] * (lt+1)\n\t\tfor j in range(lt):\n\t\t\tif(s[i] == t[j]):\n\t\t\t\tequal_curr[j+1] = 1+equal_prev[j]\n\t\t\tunequal_curr[j+1] = 1+equal_prev[j] if(s[i] != t[j]) else unequal_prev[j]\n\t\t\tans += unequal_curr[j+1]\n\t\tequal_prev, unequal_prev = equal_curr, unequal_curr\n\treturn ans\n```
| 6 | 0 |
['Dynamic Programming', 'Python', 'Python3']
| 0 |
count-substrings-that-differ-by-one-character
|
[Python3] top-down & bottom-up dp
|
python3-top-down-bottom-up-dp-by-ye15-nevt
|
\n\nclass Solution:\n def countSubstrings(self, s: str, t: str) -> int:\n m, n = len(s), len(t) \n \n @cache\n def fn(i, j, k): \
|
ye15
|
NORMAL
|
2021-03-09T17:36:07.075278+00:00
|
2021-03-09T17:36:07.075326+00:00
| 819 | false |
\n```\nclass Solution:\n def countSubstrings(self, s: str, t: str) -> int:\n m, n = len(s), len(t) \n \n @cache\n def fn(i, j, k): \n """Return number of substrings ending at s[i] and t[j] with k=0/1 difference."""\n if i < 0 or j < 0: return 0 \n if s[i] == t[j]: return fn(i-1, j-1, k) + (k==0)\n else: return 0 if k == 0 else 1 + fn(i-1, j-1, 0)\n \n return sum(fn(i, j, 1) for i in range(m) for j in range(n))\n```\n\n```\nclass Solution:\n def countSubstrings(self, s: str, t: str) -> int:\n m, n = len(s), len(t)\n dp0 = [[0]*(n+1) for _ in range(m+1)] # 0-mismatch\n dp1 = [[0]*(n+1) for _ in range(m+1)] # 1-mismatch\n \n ans = 0\n for i in range(m):\n for j in range(n):\n if s[i] == t[j]: \n dp0[i+1][j+1] = 1 + dp0[i][j]\n dp1[i+1][j+1] = dp1[i][j]\n else: \n dp0[i+1][j+1] = 0\n dp1[i+1][j+1] = 1 + dp0[i][j]\n ans += dp1[i+1][j+1]\n return ans \n```
| 6 | 0 |
['Python3']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.