question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
rearrange-array-to-maximize-prefix-score
|
🔥✅Best Solution in C++ || Sorting🔥 || O(1)SC✅✅
|
best-solution-in-c-sorting-o1sc-by-adish-hgul
|
\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n### Please Upvote if u liked my Solution\uD83E\uDD17\n\nclass Solution {\
|
aDish_21
|
NORMAL
|
2023-03-12T04:01:03.200261+00:00
|
2023-03-12T04:03:19.869123+00:00
| 120 | false |
\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n### Please Upvote if u liked my Solution\uD83E\uDD17\n```\nclass Solution {\npublic:\n int maxScore(vector<int>& nums) {\n sort(nums.begin(),nums.end(),greater<int>());\n long ps=0,count=0;\n for(int i=0;i<nums.size();i++){\n ps+=nums[i];\n if(ps>0)\n count++;\n }\n return count;\n }\n};\n```
| 1 | 0 |
['Greedy', 'Sorting', 'C++']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Python simple solution
|
python-simple-solution-by-shrined-hzlz
|
Code\n\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n pre = 0\n output = 0\n for i in
|
shrined
|
NORMAL
|
2023-03-12T04:00:58.646870+00:00
|
2023-03-12T04:06:14.753077+00:00
| 224 | false |
# Code\n```\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n pre = 0\n output = 0\n for i in range(len(nums)):\n pre += nums[i]\n if pre > 0:\n output += 1\n else:\n break\n \n return output\n```
| 1 | 0 |
['Sorting', 'Prefix Sum', 'Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
(51ms) PriorityQueue
|
51ms-priorityqueue-by-sav20011962-ue3k
|
ApproachPriorityQueueComplexityCodeOr like this:
|
sav20011962
|
NORMAL
|
2025-04-09T09:24:08.486479+00:00
|
2025-04-09T09:28:44.503141+00:00
| 1 | false |
# Approach
PriorityQueue
# Complexity
# Code
```kotlin []
class Solution {
fun maxScore(nums: IntArray): Int {
var sum = 0L
val pq = PriorityQueue<Int> { a,b -> b-a}
for (N in nums)
if (N>0) sum += N
else if (N<0) pq.add(N)
if (sum==0L) return 0
var rez = nums.size - pq.size
while (pq.isNotEmpty()) {
sum += pq.poll()
if (sum>0L) rez++ else break
}
return rez
}
}
```
# Or like this:
```
class Solution {
fun maxScore(nums: IntArray): Int {
var sum = 0L
val pq = PriorityQueue<Int> { a,b -> b-a}
for (N in nums)
if (N>0) sum += N
else pq.add(N)
var rez = nums.size - pq.size
while (pq.isNotEmpty()) {
sum += pq.poll()
if (sum>0L) rez++ else break
}
return rez
}
}
```
| 0 | 0 |
['Kotlin']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Track The Presum>0 Item Numbers
|
track-the-presum0-item-numbers-by-linda2-xeq9
|
Intuition
Be careful: The score of nums is the number of positive integers in the array prefix.
Sort array and preSum in decreasing order.
ApproachComplexity
Ti
|
linda2024
|
NORMAL
|
2025-04-08T17:36:18.335822+00:00
|
2025-04-08T17:36:18.335822+00:00
| 1 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1. Be careful: The score of nums is the number of positive integers in the array prefix.
2. Sort array and preSum in decreasing order.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int MaxScore(int[] nums) {
int len = nums.Length;
Array.Sort(nums);
long preSum = 0;
for(int i = len-1; i >= 0; i--)
{
preSum += nums[i];
if(preSum <= 0)
return len-i-1;
}
return len;
}
}
```
| 0 | 0 |
['C#']
| 0 |
rearrange-array-to-maximize-prefix-score
|
sort
|
sort-by-johnchen-emp6
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
johnchen
|
NORMAL
|
2025-03-24T06:14:05.618556+00:00
|
2025-03-24T06:14:05.618556+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maxScore(vector<int>& nums) {
sort(nums.rbegin(), nums.rend());
long long sum = 0;
int res = 0;
const int n = nums.size();
for (int i = 0; i < n; ++ i)
{
sum += nums[i];
if (sum > 0)
++ res;
else
break;
}
return res;
}
};
```
| 0 | 0 |
['C++']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Java || Sort & positive sum count || easy to understand || Beats 96.05%👏
|
java-sort-positive-sum-count-easy-to-und-95j4
|
IntuitionSort the array, since it'll be in ascending order, traverse from last.Approach
Sort nums
Initialize count to 0 and prefixSum to 0, and make sure prefix
|
itsajay1
|
NORMAL
|
2025-03-21T18:49:12.605134+00:00
|
2025-03-21T18:49:12.605134+00:00
| 61 | false |
# Intuition
Sort the array, since it'll be in ascending order, traverse from last.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
1. Sort nums
2. Initialize count to 0 and prefixSum to 0, and make sure prefixSum os of long, since it stores the cumulative sum of elements in nums so, to prevent integer overflow when dealing with large numbers.
3. Traverse the nums form last
4. Add the elements of nums to prefixSum.
5. Check if prefixSum is greater than 0, increase count by 1, else break.
6. At last, return count.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(NLogN)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maxScore(int[] nums) {
Arrays.sort(nums);
int n = nums.length;
int count = 0;
long prefixSum = 0;
for(int i = n-1; i >= 0; i-- ){
prefixSum += nums[i];
if(prefixSum > 0){
count +=1;
}
else{
break;
}
}
return count;
}
}
```
| 0 | 0 |
['Java']
| 0 |
rearrange-array-to-maximize-prefix-score
|
rearrange array to maximize prefix score
|
rearrange-array-to-maximize-prefix-score-7uie
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
chanchal_gupta
|
NORMAL
|
2025-03-21T18:41:13.968617+00:00
|
2025-03-21T18:41:13.968617+00:00
| 22 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->using prefixSum
# Approach
<!-- Describe your approach to solving the problem. -->Brute Force
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(1)
# Code
```java []
class Solution {
public int maxScore(int[] nums) {
int n=nums.length;
Arrays.sort(nums);
int count=0;
long prefixSum=0;
for(int i=n-1;i>=0;i--){
prefixSum=prefixSum + nums[i];
if(prefixSum>0) count++;
else{
break;
}
}
return count++;
}
}
```
| 0 | 0 |
['Java']
| 0 |
rearrange-array-to-maximize-prefix-score
|
True way to solve it
|
true-way-to-solve-it-by-icalmpersoni-txlr
|
Complexity
Time complexity: O(NLogN)
Space complexity: O(n)
Code
|
ICalmPersonI
|
NORMAL
|
2025-03-18T11:42:20.821572+00:00
|
2025-03-18T11:42:20.821572+00:00
| 5 | false |
# Complexity
- Time complexity: $$O(NLogN)$$
- Space complexity: $$O(n)$$
# Code
```kotlin []
class Solution {
fun maxScore(nums: IntArray): Int {
val n = nums.size
if (n == 0) return 0
val prefix = LongArray(n) { i -> nums[i].toLong() }
sort(prefix)
var ans = if (prefix[0] > 0) 1 else 0
for (i in 1 until n) {
prefix[i] += prefix[i - 1]
if (prefix[i] > 0L) ans++
}
return ans
}
private fun sort(arr: LongArray) {
val n = arr.size
if (n < 2) return
val mid = n / 2
val leftHalf = arr.copyOfRange(0, mid)
val rightHalf = arr.copyOfRange(mid, n)
sort(leftHalf)
sort(rightHalf)
merge(arr, leftHalf, rightHalf)
}
private fun merge(arr: LongArray, leftHalf: LongArray, rightHalf: LongArray) {
val m = leftHalf.size
val n = rightHalf.size
var i = 0
var l = 0
var r = 0
while (l < m && r < n) {
if (leftHalf[l] >= rightHalf[r]) {
arr[i++] = leftHalf[l++]
} else {
arr[i++] = rightHalf[r++]
}
}
while (l < m) {
arr[i++] = leftHalf[l++]
}
while (r < n) {
arr[i++] = rightHalf[r++]
}
}
}
```
| 0 | 0 |
['Array', 'Sorting', 'Merge Sort', 'Prefix Sum', 'Kotlin']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Simple O(N) solution - Java
|
simple-on-solution-java-by-someuser_id-wcan
|
Code
|
someuser_id
|
NORMAL
|
2025-03-13T02:58:00.057806+00:00
|
2025-03-13T02:58:00.057806+00:00
| 4 | false |
# Code
```java []
class Solution {
public int maxScore(int[] nums) {
if(nums == null || nums.length == 0) {
return 0;
}
Arrays.sort(nums);
long[] prefix = new long[nums.length];
int max = 0;
for(int index = nums.length - 1; index >= 0; index--) {
prefix[index] = index == nums.length - 1 ? nums[index] : nums[index] + prefix[index + 1];
if(prefix[index] > 0) {
max++;
}
}
return max;
}
}
```
| 0 | 0 |
['Java']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Efficient Solution Using C#
|
efficient-solution-using-c-by-thatsitama-5fg6
|
Complexity
Time complexity:
O(1)
Space complexity:
O(n)
Code
|
ThatsItamar
|
NORMAL
|
2025-03-10T22:59:16.952397+00:00
|
2025-03-10T22:59:16.952397+00:00
| 5 | false |
# Complexity
- Time complexity:
O(1)
- Space complexity:
O(n)
# Code
```csharp []
public class Solution {
public int MaxScore(int[] nums) {
// Sort the numbers in descending order to maximize the prefix sums staying positive
Array.Sort(nums, (a, b) => b.CompareTo(a));
long sum = 0; // use long to handle large sums
int count = 0;
// Calculate prefix sums directly during one pass through the array
for (int i = 0; i < nums.Length; i++) {
sum += nums[i];
// If the current prefix sum is positive, increment the count
if (sum > 0) {
count++;
}
}
return count;
}
}
```
| 0 | 0 |
['C#']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Max Prefix || Sorting || C++
|
max-prefix-sorting-c-by-aditi_71-lx6a
|
Complexity
Time complexity:O(N)
Space complexity:O(1)
Code
|
Aditi_71
|
NORMAL
|
2025-02-24T16:06:41.103061+00:00
|
2025-02-24T16:06:41.103061+00:00
| 3 | false |
# Complexity
- Time complexity:O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maxScore(vector<int>& nums) {
sort(nums.begin(), nums.end(), greater<int>());
long long sum = 0;
int count = 0;
for (int i = 0; i < nums.size(); i++) {
sum += nums[i];
if (sum > 0) count++;
else break;
}
return count;
}
};
```
| 0 | 0 |
['Greedy', 'Sorting', 'Prefix Sum', 'C++']
| 0 |
rearrange-array-to-maximize-prefix-score
|
simple one for loop code
|
simple-one-for-loop-code-by-akhilmittal_-apv8
|
Intuitionwe just first iterate and reverse it and then keep on checking the sum is greater than 0 or not if not then break else cnt++ and at the end return this
|
akhilmittal_8603
|
NORMAL
|
2025-02-18T05:58:30.475427+00:00
|
2025-02-18T05:58:30.475427+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
we just first iterate and reverse it and then keep on checking the sum is greater than 0 or not if not then break else cnt++ and at the end return this cnt.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(nlog n) will be the time complexity.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
No exxtra space is used that's why space complexity will be O(1).
# Code
```cpp []
class Solution {
public:
int maxScore(vector<int>& nums) {
long long s = 0;
sort(nums.begin(), nums.end());
reverse(nums.begin(), nums.end());
int cnt = 0;
for (int i = 0; i < nums.size(); i++) {
s += nums[i];
if (s > 0) {
cnt++;
}
else {
break;
}
}
return cnt;
}
};
```
| 0 | 0 |
['C++']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Simple Racket solution using functional style
|
simple-racket-solution-using-functional-a5a80
|
Approachsort the list in descending order, take a running sum of the sorted list, and then count the number of positive numbers.Code
|
je_harman
|
NORMAL
|
2025-02-02T05:11:22.780117+00:00
|
2025-02-02T05:11:22.780117+00:00
| 2 | false |
# Approach
sort the list in descending order, take a running sum of the sorted list, and then count the number of positive numbers.
# Code
```racket []
(define (max-score nums)
(count positive?
(foldl (lambda (val acc) (cons (+ (first acc) val) acc))
'(0)
(sort nums >))))
```
| 0 | 0 |
['Racket']
| 0 |
rearrange-array-to-maximize-prefix-score
|
2587. Rearrange Array to Maximize Prefix Score
|
2587-rearrange-array-to-maximize-prefix-yna0g
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-19T04:13:24.105073+00:00
|
2025-01-19T04:13:24.105073+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maxScore(self, nums: List[int]) -> int:
nums.sort(reverse=True)
prefix_sum = 0
score = 0
for num in nums:
prefix_sum += num
if prefix_sum > 0:
score += 1
return score
```
| 0 | 0 |
['Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Rearrange Array to Maximize Prefix Source
|
rearrange-array-to-maximize-prefix-sourc-ty69
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Naeem_ABD
|
NORMAL
|
2025-01-14T11:00:56.381608+00:00
|
2025-01-14T11:00:56.381608+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maxScore(self, nums: List[int]) -> int:
nums.sort(reverse=True)
print(nums)
a = list(itertools.accumulate(nums))
res = 0
for c in a:
if c > 0:
res += 1
return res
```
| 0 | 0 |
['Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Java Solution Sorting + Prefix Sum
|
java-solution-sorting-prefix-sum-by-ndsj-hviq
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
ndsjqwbbb
|
NORMAL
|
2025-01-11T02:48:01.874573+00:00
|
2025-01-11T02:48:01.874573+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maxScore(int[] nums) {
if(nums.length == 1){
return nums[0] > 0 ? 1 : 0;
}
Arrays.sort(nums);
reverseArray(nums);
long presum = 0;
int count = 0;
for(int num : nums){
presum += num;
if(presum > 0){
count++;
} else {
break;
}
}
return count;
}
private void reverseArray(int[] array){
int left = 0;
int right = array.length - 1;
while(left < right){
int temp = array[left];
array[left] = array[right];
array[right] = temp;
left++;
right--;
}
}
}
```
| 0 | 0 |
['Java']
| 0 |
rearrange-array-to-maximize-prefix-score
|
C++ solution Sorting
|
c-solution-sorting-by-oleksam-ks6t
|
Please, upvote if you like it. Thanks :-)Complexity
Time complexity:
O(n log(n))
Space complexity:
O(1)
Code
|
oleksam
|
NORMAL
|
2025-01-09T09:29:01.158226+00:00
|
2025-01-09T09:29:01.158226+00:00
| 3 | false |
Please, upvote if you like it. Thanks :-)
# Complexity
- Time complexity:
O(n log(n))
- Space complexity:
O(1)
# Code
```cpp []
int maxScore(vector<int>& nums) {
long res = 0, n = nums.size(), sum = 0;
sort(begin(nums), end(nums), [](int a, int b) { return a > b; } );
for (int i = 0; i < n; i++, res++) {
if ((sum += nums[i]) <= 0)
break;
}
return res;
}
```
| 0 | 0 |
['Array', 'Greedy', 'Sorting', 'Prefix Sum', 'C++']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Optimal Rotated Array 🔥🔥
|
optimal-rotated-array-by-gayathri_1711-9nz3
|
IntuitionI immediately thought of reversing the array, as that is the best possible way to maximize the score of it's prefix (logically).ApproachMy approach jus
|
Gayathri_1711
|
NORMAL
|
2025-01-07T04:04:23.183283+00:00
|
2025-01-07T04:04:23.183283+00:00
| 5 | false |
# Intuition
I immediately thought of reversing the array, as that is the best possible way to maximize the score of it's prefix (logically).
# Approach
My approach just reverses the array, calculates it's prefix, and returns the count of the elements that are positive.
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(n)$$
# Code
```python3 []
class Solution:
def maxScore(self, nums: List[int]) -> int:
nums.sort(reverse=True)
prefix = [0]
for i in range(1, len(nums) + 1):
prefix.append(prefix[-1] + nums[i - 1])
return len([i for i in prefix if i > 0])
```
| 0 | 0 |
['Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
BEATS 93%
|
beats-93-by-alexander_sergeev-sixd
|
Code
|
alexander_sergeev
|
NORMAL
|
2024-12-28T13:54:22.191435+00:00
|
2024-12-28T13:54:22.191435+00:00
| 3 | false |
# Code
```java []
class Solution {
public int maxScore(int[] nums) {
Arrays.sort(nums);
int count = 0;
int pos = nums.length - 1;
long currentSum = 0;
while (pos >= 0 && currentSum + nums[pos] > 0) {
currentSum += nums[pos];
count++;
pos--;
}
return count;
}
}
```
| 0 | 0 |
['Java']
| 0 |
rearrange-array-to-maximize-prefix-score
|
EASY C++ SOLUTION FOR BEGINNERS BY BEGINNER.....
|
easy-c-solution-for-beginners-by-beginne-83rl
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
_alpha-byte2
|
NORMAL
|
2024-12-28T05:36:59.531345+00:00
|
2024-12-28T05:36:59.531345+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maxScore(vector<int>& n) {
sort(n.begin(),n.end(),greater<int>());
vector<long long>prefix(n.size());
prefix[0]=n[0];
for(int i=1;i<n.size();i++)
{
prefix[i]=prefix[i-1]+n[i];
}
int ans=0;
for(int i=0;i<n.size();i++)
{
if(prefix[i]>0)ans++;
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Simple Fast C (15 ms ) only sort negative number
|
simple-fast-c-20-ms-only-sort-negative-n-a1pt
| null |
vortexz
|
NORMAL
|
2024-12-12T06:34:38.766439+00:00
|
2024-12-12T19:55:36.789936+00:00
| 2 | false |
# Intuition\nTriage number \nSort negative number\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\nint cmp(const void* a, const void* b) { return (*(int*)b - *(int*)a); }\n\nint maxScore(int* nums, int numsSize) {\n long score=0;\n long nScore=0;\n int count=0;\n int idx=0;\n //first triage number \n // positive and 0 goes into score and vanish \n // negative stay in nums starting from position 0\n for (int i=0;i<numsSize;i++) {\n if (nums[i]>=0) {\n count++;\n score+=nums[i];\n } else {\n nScore+=nums[i];\n nums[idx++]=nums[i];\n }\n }\n // No positive number we can exit the program\n if (score==0) {\n return 0;\n }\n //all number are part of the prefix no need to calculate\n if (score+nScore>0) {\n return numsSize;\n }\n //only sort negative number that remain in nums\n qsort(nums, idx, sizeof(int), cmp);\n //check if score goes under 0 that the end of prefix index\n for (int i=0;i<idx;i++) {\n score+=nums[i];\n if (score<=0) {\n return count+i;\n }\n }\n return 1337;\n}\n```
| 0 | 0 |
['Divide and Conquer', 'C', 'Sorting']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Implementing Sorting
|
implementing-sorting-by-sabaansaria-7xhi
|
Intuition\n Describe your first thoughts on how to solve this problem. Array, Sorting\n\n# Approach\n Describe your approach to solving the problem. \n1. Sort
|
sabaansaria
|
NORMAL
|
2024-11-26T14:27:30.999974+00:00
|
2024-11-26T14:27:31.000017+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> Array, Sorting\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the array according to descending order.\n2. Initialize a variable prefix_sum and an array prefix to count the values and store it in an array prefix.\n3. Count the positive prefix values and return\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(1)\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n summ = 0\n prefix_sum = []\n\n \n\n for i in range(len(nums)):\n summ += nums[i]\n prefix_sum.append(summ)\n \n pos_count = 0\n for x in prefix_sum:\n if x > 0:\n pos_count += 1\n return pos_count \n```
| 0 | 0 |
['Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Sorting + Greedy
|
sorting-greedy-by-trieutrng-w8zl
|
Complexity\n- Time complexity: O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n
|
trieutrng
|
NORMAL
|
2024-11-18T15:28:49.704903+00:00
|
2024-11-18T15:28:49.704946+00:00
| 3 | false |
# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nev, pos = [], []\n for num in nums:\n if num<0:\n nev.append(num)\n else:\n pos.append(num)\n\n pos.sort(reverse=True)\n nev.sort(reverse=True)\n\n ans, i, j, prefixSum = 0, 0, 0, 0\n while i<len(pos) and j<len(nev):\n while i<len(pos):\n prefixSum += pos[i]\n i += 1\n if prefixSum > 0:\n break\n if prefixSum<=0:\n return ans\n \n ans += 1\n\n while j<len(nev):\n if prefixSum+nev[j] <= 0:\n break\n prefixSum += nev[j]\n ans += 1\n j += 1\n\n while i<len(pos):\n prefixSum += pos[i]\n if prefixSum>0:\n ans += 1\n i += 1\n\n return ans\n```
| 0 | 0 |
['Array', 'Greedy', 'Sorting', 'Prefix Sum', 'Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
sorting solution using python3
|
sorting-solution-using-python3-by-owenwu-ojod
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
owenwu4
|
NORMAL
|
2024-11-09T03:05:53.783307+00:00
|
2024-11-09T03:05:53.783342+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n print(nums)\n a = list(itertools.accumulate(nums))\n res = 0\n for c in a:\n if c > 0:\n res += 1\n return res\n\n```
| 0 | 0 |
['Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Rearrange Array
|
rearrange-array-by-sabmel-lp9v
|
Intuition\nMaximum score will be achieved when nums is in descending order.\n\n# Approach\n1. Sort nums in descending order\n2. Create prefix sum array\n3. Coun
|
sabmel
|
NORMAL
|
2024-10-26T05:19:30.781108+00:00
|
2024-10-26T05:19:30.781133+00:00
| 2 | false |
# Intuition\nMaximum score will be achieved when nums is in descending order.\n\n# Approach\n1. Sort nums in descending order\n2. Create prefix sum array\n3. Count positive values \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```python []\nclass Solution(object):\n def maxScore(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n num_pos = 0\n\n # Best order of the array is in decreasing order\n nums.sort(reverse = True)\n\n # Create prefix sum array\n prefix = [0] * len(nums)\n prefix[0] = nums[0]\n if prefix[0] > 0:\n num_pos += 1\n\n for i in range(1, len(nums)):\n prefix[i] = prefix[i - 1] + nums[i]\n if prefix[i] > 0:\n num_pos += 1\n\n return num_pos\n```
| 0 | 0 |
['Python']
| 0 |
rearrange-array-to-maximize-prefix-score
|
100% Time complexity, 100% Space complexity
|
100-time-complexity-100-space-complexity-2vr1
|
Approach\n Describe your approach to solving the problem. \n1. Sorting the Array:\n - The input array nums is sorted in descending order to maximize the sum
|
nghiadq
|
NORMAL
|
2024-10-24T03:14:48.281653+00:00
|
2024-10-24T03:14:48.281682+00:00
| 1 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sorting the Array:\n - The input array nums is sorted in descending order to maximize the sum of numbers. This ensures that the largest numbers are considered first, which gives the highest possible sum at each step.\n2. Summing Until Non-Positive:\n - After sorting, the algorithm starts from the largest number and continues adding the next largest numbers from the sorted array.\n - It stops as soon as the cumulative sum becomes non-positive (i.e., less than or equal to 0).\n3. Return the Count:\n - The function returns the number of elements that were added to the sum before the sum became non-positive. This is effectively the "index - 1" as calculated in the loop.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. The sorting operation takes O(nlogn)\n2. Loop takes O(n)\n\n=> Thus, the total time complexity is O(nlogn)\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```typescript []\nfunction maxScore(nums: number[]): number {\n nums.sort((a, b) => b - a)\n let index = 1\n let num = nums[0]\n while (num > 0) {\n num += nums[index]\n index++\n }\n return index -1\n};\n\n```
| 0 | 0 |
['TypeScript']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Simple solution with easy explanation (Python3)
|
simple-solution-with-easy-explanation-py-p7fd
|
Intuition\nEach prefix sum is the sum of all elements to the left (inclusive). We want to achieve the maximum number of positive integers. This means that we sh
|
tawaca
|
NORMAL
|
2024-10-22T20:31:26.127062+00:00
|
2024-10-22T20:31:26.127089+00:00
| 3 | false |
# Intuition\nEach prefix sum is the sum of all elements to the left (inclusive). We want to achieve the maximum number of positive integers. This means that we should sort the array from largest to smallest so that we prioritise the largest values and therefore end up with the maximum possible sums at each position. \n\n# Approach\n- sort from largest to smallest\n- iteratively add each value until the sum is non-positive\n\n# Complexity\n- Time complexity:\nO(nlogn) - sorting the list is the dominant operation\n\n- Space complexity:\nO(1) - sorting the list is done in place. We need an extra int to track the sum.\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n\n nums.sort(reverse=True) # O(nlogn)\n \n # O(n)\n total = 0\n for i, val in enumerate(nums):\n total+= val\n if total <= 0:\n return i\n \n return len(nums)\n \n\n\n```
| 0 | 0 |
['Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Explained !! EASY sorting and simulation ✅
|
explained-easy-sorting-and-simulation-by-7zzy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- The goal is to find the maximum number of non-empty prefix subarrays where the sum of
|
amarnathtripathy
|
NORMAL
|
2024-10-22T14:45:10.140937+00:00
|
2024-10-22T14:45:10.140961+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The goal is to find the maximum number of non-empty prefix subarrays where the sum of the elements is positive.\n- A prefix subarray is formed by taking the first \'i\' elements of the sorted array.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the array in descending order:\n - Sorting helps ensure that we are adding larger numbers first, maximizing the prefix sum.\n \n2. Create a prefix sum array:\n - Traverse through the sorted array and keep a running sum of the elements.\n - If the current prefix sum is positive, increment the answer count.\n - If the current prefix sum becomes non-positive, stop the iteration because adding smaller or negative values \n will only decrease the sum further.\n\n3. Return the count of positive prefix sums as the final answer.\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n typedef long long ll;\n int maxScore(vector<int>& nums) {\n ll ans=0;\n sort(nums.begin(),nums.end(),greater<ll>());\n ll n=nums.size(); \n vector<ll>pre(n);\n \n for(ll i=0;i<n;i++){\n if(i==0){\n pre[i]=nums[i];\n }else{\n pre[i]=pre[i-1]+nums[i];\n }\n \n if(pre[i]>0) ans++;\n else break;\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Array', 'Greedy', 'Sorting', 'Prefix Sum', 'C++']
| 0 |
rearrange-array-to-maximize-prefix-score
|
rearrange-array-to-maximize-prefix-score- TS Solution
|
rearrange-array-to-maximize-prefix-score-x7wa
|
\n\n# Code\ntypescript []\nfunction maxScore(nums: number[]): number {\n nums = nums.sort((a, b) => b - a);\n let sum = 0;\n let positiveInts = 0;\n\n
|
himashusharma
|
NORMAL
|
2024-10-22T06:53:09.219763+00:00
|
2024-10-22T06:53:09.219794+00:00
| 0 | false |
\n\n# Code\n```typescript []\nfunction maxScore(nums: number[]): number {\n nums = nums.sort((a, b) => b - a);\n let sum = 0;\n let positiveInts = 0;\n\n for(let i = 0; i < nums.length; i++){\n sum += nums[i];\n if(sum > 0) positiveInts++;\n }\n return positiveInts;\n \n};\n```
| 0 | 0 |
['Array', 'Greedy', 'Sorting', 'Prefix Sum', 'TypeScript']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Simple sorting and use long to avoid integer overflow
|
simple-sorting-and-use-long-to-avoid-int-nv9v
|
\r\njava []\r\nclass Solution {\r\n public int maxScore(int[] nums) {\r\n Arrays.sort(nums);\r\n if(nums.length>1) reverse(nums);\r\n long x=0;\
|
risabhuchiha
|
NORMAL
|
2024-10-13T17:53:00.072642+00:00
|
2024-10-13T17:53:00.072678+00:00
| 0 | false |
\r\n```java []\r\nclass Solution {\r\n public int maxScore(int[] nums) {\r\n Arrays.sort(nums);\r\n if(nums.length>1) reverse(nums);\r\n long x=0;\r\n int c=0;\r\n for(int i=0;i<nums.length;i++){\r\n \r\n x+=nums[i];\r\n //System.out.println(x+" "+nums[i]);\r\n if(x<=0)return (c);\r\n else c++;\r\n // c++;\r\n \r\n \r\n } \r\n if(x>0)return c; \r\n return 0;\r\n }\r\n public void reverse(int[]nums){\r\n int s=0;\r\n int e=nums.length-1;\r\n while(s<=e){\r\n int t=nums[s];\r\n nums[s]=nums[e];\r\n nums[e]=t;\r\n s++;\r\n e--;\r\n }\r\n }\r\n}\r\n```
| 0 | 0 |
['Java']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Beats 97%
|
beats-97-by-bismans-wwa8
|
Intuition\nWe want to maximize the positive value sums before we start decreasing the negative values\n\n# Approach\nGreedy Approach:\n\nFirst take the sum of t
|
BismanS
|
NORMAL
|
2024-09-27T20:23:08.574473+00:00
|
2024-09-27T20:23:08.574493+00:00
| 3 | false |
# Intuition\nWe want to maximize the positive value sums before we start decreasing the negative values\n\n# Approach\nGreedy Approach:\n\nFirst take the sum of the positive values and make a list of all the negative integers.\n\nif the sum of positive values is 0 then we then answer is 0. (not possible) or if there are no negative integers, the answer is simply n.\n\nIf there are some positive and some negative:\nWe have the sum of all the positive integers, right? We know for a fact that at least the numbers we used for this sum will result in a positive prefix sum. That\'s great, we can count these numbers for our answer. \n\nAs for the negative numbers, we only want to subtract the biggest (closest to 0) negative number from the sum of all the positive numbers. This is greedy, because we want the sum to remain positive for as long as possible! So we sort the negative integers list in decreasing order, and start subtracting from the sum of positive numbers until we get to 0 or below (or if we run out of negative integers) \n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n negative = []\n posValue = 0\n for num in nums:\n if num < 0:\n negative.append(num)\n if num > 0:\n posValue += num \n if posValue == 0:\n return 0\n if len(negative) == 0:\n return len(nums)\n ans = len(nums) - len(negative)\n negative.sort(reverse=True)\n for num in negative:\n posValue += num\n if posValue > 0:\n ans += 1\n else: break\n return ans\n```
| 0 | 0 |
['Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Python O(nlogn) Time, O(n) Space
|
python-onlogn-time-on-space-by-johnmulla-dzas
|
Complexity\n- Time complexity: O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n
|
JohnMullan
|
NORMAL
|
2024-09-24T20:46:09.978051+00:00
|
2024-09-24T20:46:09.978082+00:00
| 1 | false |
# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution(object):\n def maxScore(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n nums.sort(reverse=True)\n if nums[0]<=0:\n return 0\n n=len(nums)\n s=0\n for i in range(n):\n s+=nums[i]\n if s<=0:\n return i\n return n\n \n```
| 0 | 0 |
['Python']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Put negative numbers as far back as possible
|
put-negative-numbers-as-far-back-as-poss-ia3l
|
Approach\n Describe your approach to solving the problem. \nPut negative numbers as far back as possible.\n\n# Complexity\n- Time complexity:\n Add your time co
|
guesq
|
NORMAL
|
2024-09-12T22:57:31.791122+00:00
|
2024-09-12T22:57:31.791150+00:00
| 1 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nPut negative numbers as far back as possible.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nlog(n))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxScore(self, nums: List[int]) -> int:\n return sum(x > 0 for x in list(accumulate(sorted(nums, reverse=True))))\n```
| 0 | 0 |
['Python3']
| 0 |
rearrange-array-to-maximize-prefix-score
|
68ms beats 100%
|
68ms-beats-100-by-albert0909-zdzs
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
albert0909
|
NORMAL
|
2024-09-06T20:09:43.915797+00:00
|
2024-09-06T20:09:43.915841+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlgn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxScore(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n long long sum = 0;\n for(int i = nums.size() - 1;i >= 0;i--){\n sum += nums[i];\n if(sum <= 0) return nums.size() - i - 1;\n }\n\n return nums.size();\n }\n};\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```
| 0 | 0 |
['Array', 'Greedy', 'Sorting', 'Prefix Sum', 'C++']
| 0 |
rearrange-array-to-maximize-prefix-score
|
Java Solution
|
java-solution-by-assasin0812-csyr
|
\n\n# Code\njava []\nclass Solution {\n public int maxScore(int[] nums) {\n Arrays.sort(nums);\n long sum = 0;\n for(int i=nums.length-1
|
assasin0812
|
NORMAL
|
2024-09-05T19:12:57.464035+00:00
|
2024-09-05T19:12:57.464056+00:00
| 3 | false |
\n\n# Code\n```java []\nclass Solution {\n public int maxScore(int[] nums) {\n Arrays.sort(nums);\n long sum = 0;\n for(int i=nums.length-1;i>=0;i--){\n sum+=nums[i];\n if(sum<=0)\n return nums.length-i-1;\n }\n return nums.length;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Prefix Sum of Factors 2 and 5
|
prefix-sum-of-factors-2-and-5-by-votruba-z8ce
|
The approach is not too hard to get, but the implementation is such a tongue-twister (or fingers-twister, I should say).\n\nFirst, instead of multiplication, we
|
votrubac
|
NORMAL
|
2022-04-17T04:13:05.700489+00:00
|
2022-04-18T02:19:19.164247+00:00
| 7,394 | false |
The approach is not too hard to get, but the implementation is such a tongue-twister (or fingers-twister, I should say).\n\nFirst, instead of multiplication, we just need to sum factors of `2` and `5`. Each pair of those factors produce one trailing zero.\n\nWe use grids `h` and `v` to compute prefix sum for each horizontal and vertical line in the grid. Note that we store the count of each factor separatelly. \n\nThen, for each position in the grid, we check four paths: `v1 + h1`, `v1 + h2`, `v2 + h1`, `v2 + h2`.\n\nWe count factors for each path, and track the maximum number of factor pairs (each pair gives us a trailing zero).\n\n> I am not sure if we can use one grid instead of `v` and `h` and do some clever deduction, but the solution is already hard to debug with two grids. \n\nThis is how the prefix sum grids look like for example 1 (see problem description), with the visualization for `v1`, `v2`, `h1` and `h2` sub-paths.\n\n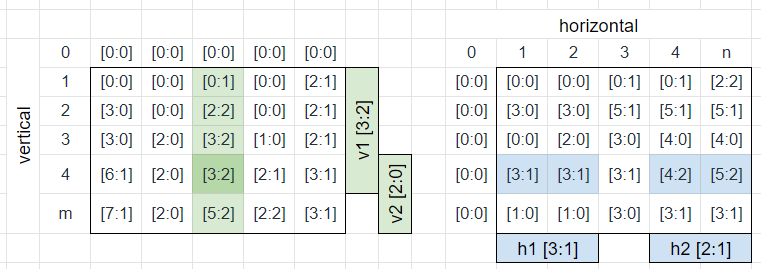\n\n**C++**\n```cpp\narray<int, 2> operator+(const array<int, 2> &l, const array<int, 2> &r) { return { l[0] + r[0], l[1] + r[1] }; }\narray<int, 2> operator-(const array<int, 2> &l, const array<int, 2> &r) { return { l[0] - r[0], l[1] - r[1] }; }\nint pairs(const array<int, 2> &p) { return min(p[0], p[1]); }\n\nclass Solution {\npublic:\nint factors(int i, int f) {\n return i % f ? 0 : 1 + factors(i / f, f);\n}\nint maxTrailingZeros(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size(), res = 0;\n vector<vector<array<int, 2>>> h(m, vector<array<int, 2>>(n + 1)), v(m + 1, vector<array<int, 2>>(n));\n for (int i = 0; i < m; ++i)\n for (int j = 0; j < n; ++j) {\n array<int, 2> f25 = { factors(grid[i][j], 2), factors(grid[i][j], 5) };\n v[i + 1][j] = v[i][j] + f25;\n h[i][j + 1] = h[i][j] + f25;\n }\n for (int i = 0; i < m; ++i)\n for (int j = 0; j < n; ++j) {\n auto v1 = v[i + 1][j], v2 = v[m][j] - v[i][j];\n auto h1 = h[i][j], h2 = h[i][n] - h[i][j + 1];\n res = max({res, pairs(v1 + h1), pairs(v1 + h2), pairs(v2 + h1), pairs(v2 + h2)});\n }\n return res;\n}\n};\n```\n**Complexity Analysis**\n- Time: O(n * m); we go through the grid twice; prefix sum grids allow computing zeros in O(1).\n- Memory: O(n * m) for prefix sum grids.
| 102 | 0 |
['C']
| 20 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ || EASY TO UNDERSTAND || Simple Prefix Sum + Greedy Approach :)
|
c-easy-to-understand-simple-prefix-sum-g-t7fq
|
Approach is very simple but the implementation needed some level of patience.\n\nwe first create a matrix with the number of factors of 2\'s and 5\'s in each of
|
aarindey
|
NORMAL
|
2022-04-17T04:03:00.248091+00:00
|
2022-08-26T06:54:08.886566+00:00
| 3,849 | false |
**Approach is very simple but the implementation needed some level of patience.**\n\n**we first create a matrix with the number of factors of 2\'s and 5\'s in each of the grids of the given matrix. I used vector<vector<pair<int,int>>> v , to do the same.**\n\n**Then, we are creating 4 prefix sum matrices(of the number of 2\'s and 5\'s) which will store the value of the prefixsum from left to right(named as ltr), right to left(rtl), up to down(utd) and down to up(dtu). After creating the matrices we will be iterating through the v and finding the maximum of the minimum of 2\'s and 5\'s on the 4 possible cases (utd+ltr),(utd+rtl),(dtu+ltr),(dtu+rtl) and that maximum will be our answer.**\n\n```\n#define ll long long int\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n=grid.size();\n int m=grid[0].size();\n vector<vector<pair<ll,ll>>> v(n,vector<pair<ll,ll>>(m,{0,0})),ltr,utd,rtl,dtu;\n \n for(ll i=0;i<n;i++)\n {\n for(ll j=0;j<m;j++)\n {\n ll z=grid[i][j],c1=0,c2=0;\n while(z%2==0)\n {\n z/=2;\n c1++;\n }\n while(z%5==0)\n {\n z/=5;\n c2++;\n }\n v[i][j].first=c1;\n v[i][j].second=c2;\n }\n }\n ltr=utd=rtl=dtu=v;\n for(ll i=0;i<n;i++)\n {\n for(ll j=1;j<m;j++)\n {\n ltr[i][j].first+=ltr[i][j-1].first;\n ltr[i][j].second+=ltr[i][j-1].second;\n }\n }\n for(ll i=0;i<n;i++)\n {\n for(ll j=m-2;j>=0;j--)\n {\n rtl[i][j].first+=rtl[i][j+1].first;\n rtl[i][j].second+=rtl[i][j+1].second;\n }\n }\n for(ll j=0;j<m;j++)\n {\n for(ll i=1;i<n;i++)\n {\n utd[i][j].first+=utd[i-1][j].first;\n utd[i][j].second+=utd[i-1][j].second;\n }\n }\n for(ll j=0;j<m;j++)\n {\n for(ll i=n-2;i>=0;i--)\n {\n dtu[i][j].first+=dtu[i+1][j].first;\n dtu[i][j].second+=dtu[i+1][j].second;\n }\n }\n ll ans=0;\n for(ll i=0;i<n;i++)\n {\n for(ll j=0;j<m;j++)\n {\n ll c1,c2,c3,c4;\n ll x1,x2,x3,x4;\n ll a,b;\n a=v[i][j].first;\n b=v[i][j].second; \n \n c1=ltr[i][j].first;\n c2=rtl[i][j].first;\n \n c3=utd[i][j].first;\n c4=dtu[i][j].first;\n \n x1=ltr[i][j].second;\n x2=rtl[i][j].second;\n \n x3=utd[i][j].second;\n x4=dtu[i][j].second;\n \n ans=max(ans,min(c3+c1-a,x3+x1-b));\n ans=max(ans,min(c3+c2-a,x3+x2-b));\n ans=max(ans,min(c4+c1-a,x4+x1-b));\n ans=max(ans,min(c4+c2-a,x4+x2-b));\n }\n }\n return ans;\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome**
| 46 | 2 |
[]
| 6 |
maximum-trailing-zeros-in-a-cornered-path
|
[Python] Explanation with pictures, prefix sum.
|
python-explanation-with-pictures-prefix-6l5ip
|
Please also refer to votrubac \'s solution as he has a perfect picture explanation of prefix sum.\n\nLet\'s focus on the pivot point of an edge, once the pivot
|
Bakerston
|
NORMAL
|
2022-04-17T04:26:58.593248+00:00
|
2022-05-04T17:56:21.612517+00:00
| 2,612 | false |
Please also refer to [votrubac](https://leetcode.com/problems/maximum-trailing-zeros-in-a-cornered-path/discuss/1955515/Prefix-Sum-of-Factors-2-and-5) \'s solution as he has a perfect picture explanation of prefix sum.\n\nLet\'s focus on the pivot point of an edge, once the pivot point is fixed, the edge can only from the four cases below.\n\n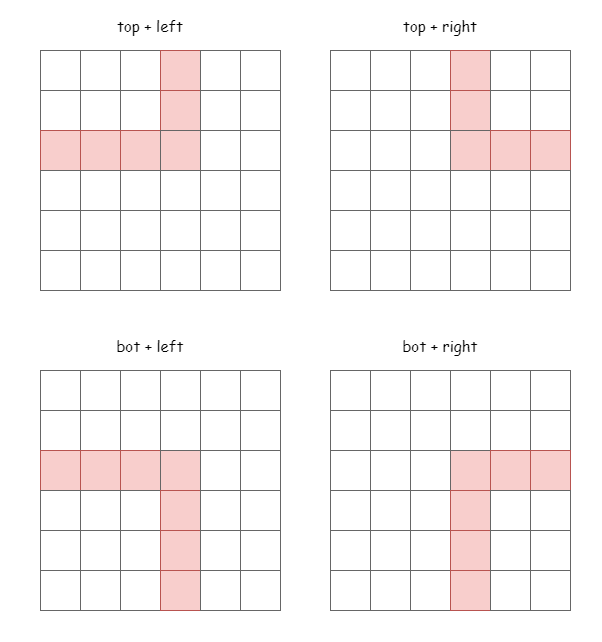\n\nIt look familiar, we can build two (or four if you prefer) prefix sum array to save the cumulative factors. \nImagine we build `left` to save the all the factors in the same row on `A[i][j]`\'s left, and build `top` to save all the factors in the same colomn on `A[i][j]`\'s top. Notice we might add or minus the `A[i][j]` itself twice.\n\n\n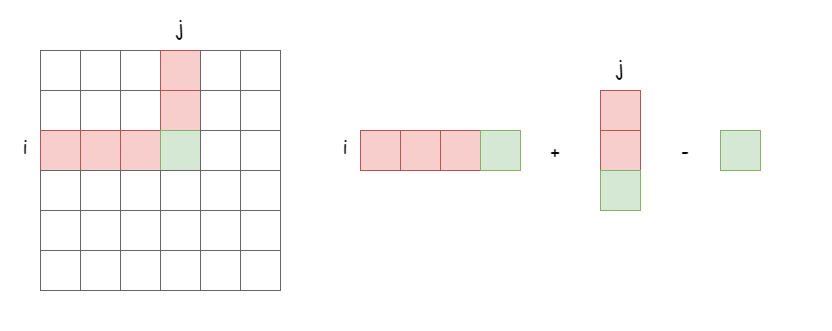\n\nWe only need to save the number of two factors: `2, 5`. It\'s quite straightforward to get the number of trailing zeros from these numbers of factors.\n\n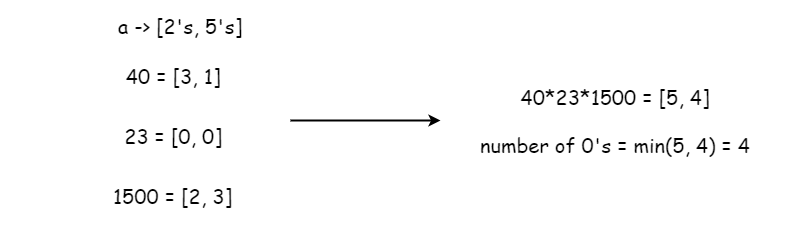\n\n> In case I didn\'t explain it well.\n> `a->[2\'s, 5\'s]`\n> 40 = 2\\*2\\*2\\*5, three 2\'s and one 5, thus we let `40=[3,1]`\n> Similarly, `23=[0,0]` since it has no factor as 2 or 5, \n> `1500=3\\*2\\*2\\*5\\*5\\*5`, thus we let `1500=[2,3]` \n> Hence, `40*23*1500` has `[5,4]` which makes 4 trailing zeros.\n\n**complexity**\nTime: O(n)\nSpace: O(n)\n\n**code**\n```\nclass Solution:\n def maxTrailingZeros(self, A: List[List[int]]) -> int:\n m, n = len(A), len(A[0])\n left = [[[0, 0] for _ in range(n)] for _ in range(m)]\n top = [[[0, 0] for _ in range(n)] for _ in range(m)]\n \n def helper(num):\n a, b = 0, 0\n while num % 2 == 0:\n num //= 2\n a += 1\n while num % 5 == 0:\n num //= 5\n b += 1\n return [a, b]\n \n for i in range(m):\n for j in range(n):\n if j == 0:\n left[i][j] = helper(A[i][j])\n else:\n a, b = helper(A[i][j])\n left[i][j][0] = left[i][j - 1][0] + a\n left[i][j][1] = left[i][j - 1][1] + b\n for j in range(n):\n for i in range(m):\n if i == 0:\n top[i][j] = helper(A[i][j])\n else:\n a, b, = helper(A[i][j])\n top[i][j][0] = top[i - 1][j][0] + a \n top[i][j][1] = top[i - 1][j][1] + b\n\n\n ans = 0\n for i in range(m):\n for j in range(n):\n a, b = top[m - 1][j]\n d, e= left[i][n - 1]\n x, y = helper(A[i][j])\n a1, b1 = top[i][j]\n a2, b2= left[i][j]\n tmp = [a1 + a2 - x, b1 + b2 - y]\n ans = max(ans, min(tmp))\n tmp = [d - a2 + a1, e - b2 + b1]\n ans = max(ans, min(tmp)) \n tmp = [a - a1 + a2, b - b1 + b2]\n ans = max(ans, min(tmp))\n tmp = [a + d - a1 - a2 + x, b + e - b1 - b2 + y]\n ans = max(ans, min(tmp))\n \n return ans\n```\n
| 44 | 1 |
[]
| 6 |
maximum-trailing-zeros-in-a-cornered-path
|
7 lines Python / NumPy
|
7-lines-python-numpy-by-stefanpochmann-jkhi
|
Perfect opportunity to practice NumPy. Gets accepted in ~2200 ms, seems relatively fast. Actual time is about 900 ms, judge overhead is ~1300 here. See benchmar
|
stefanpochmann
|
NORMAL
|
2022-04-18T04:39:59.082983+00:00
|
2022-04-19T03:41:19.270566+00:00
| 2,109 | false |
Perfect opportunity to practice NumPy. Gets accepted in ~2200 ms, seems relatively fast. Actual time is about 900 ms, judge overhead is ~1300 here. See benchmark in the comments.\n```\nimport numpy as np\n\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n A = np.array(grid)\n def cumdivs(d):\n D = sum(A % d**i == 0 for i in range(1, 10))\n return D.cumsum(0) + D.cumsum(1) - D\n return max(np.minimum(cumdivs(2), cumdivs(5)).max()\n for _ in range(4)\n if [A := np.rot90(A)])\n```\nMy helper function `cumdivs` first computes divisibility by divisor 2 or 5, as that\'s the factors we need to get zeros: It counts for each value in the grid how often it is divisible by divisor `d`. I try up to 9 times, since 2<sup>9</sup>=512 is the largest possible (since the numbers are guaranteed to not exceed 1000). Then it computes and combines the cumulative sums of the divisibilities on both axes (and subtracts each value\'s divisibility in order to not double-count it).\n\nThat only covers one pair of directions. So I do it four times, rotating the matrix by 90 degrees in between.
| 22 | 2 |
['Python']
| 4 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ || Prefix Sum || Easy to Understand || Beats 100% Space and Time
|
c-prefix-sum-easy-to-understand-beats-10-ozas
|
Explanation:\n\t Consider every element of the grid as the corner point of the cornered path. Now there can be four possible ways of making an \'L\' Shape figur
|
b_k_1729
|
NORMAL
|
2022-04-17T06:46:55.084405+00:00
|
2022-04-22T10:04:18.071099+00:00
| 1,377 | false |
* **Explanation:**\n\t* Consider every element of the grid as the corner point of the cornered path. Now there can be four possible ways of making an \'L\' Shape figure. \n\t* \tWe need to make **prefix matrices of pairs** to store the prefix sum of exponent of 5\'s and 2\'s of each element in the grid, otherwise if we store the whole multiplication result, then it would create integer overflow.\n\t * And **we need only two prefix matrices**, because the result of other two sides will be calculated by subtracting from total sum of that side. \t\n\t * To get the count of trailing 0\'s we have to take the minimum of count of 5 and 2 from the pairs.\n\t * The case of 0 turns that is horizontally straight or vertically straight path will be handled automatically by prefix sum matrix.\n\n* **Time Complexity: O(MxN)**\n* **Space Complexity: O(MxN)**\n\n```\n\t//to get the exponent of 5 and 2 in the number\n pair<int,int> getPair(int x){\n int five = 0, two = 0;\n while(x % 5 == 0){\n five++; x /= 5;\n }\n while(x % 2 == 0){\n two++; x /= 2;\n }\n return {five,two};\n } \n int maxTrailingZeros(vector<vector<int>>& grid) {\n int r = grid.size(), c = grid[0].size(), ans = 0;\n vector<vector<pair<int,int>>>top(r, vector<pair<int,int>>(c,{0,0})), left(r, vector<pair<int,int>>(c,{0,0}));\n \n //top[i][j] will store sum of exponent of 5\'s and 2\'s from grid[0][j] to grid[i][j]\n for(int i = 0; i < r; i++){\n for(int j = 0; j < c; j++){\n if(i == 0) top[i][j] = getPair(grid[i][j]);\n else{\n pair<int,int>p = getPair(grid[i][j]);\n top[i][j].first = top[i-1][j].first + p.first;\n top[i][j].second = top[i-1][j].second + p.second;\n }\n }\n }\n //left[i][j] will store sum of exponent of 5\'s and 2\'s from grid[i][0] to grid[i][j]\n for(int i = 0; i < r; i++){\n for(int j = 0; j < c; j++){\n if(j == 0) left[i][j] = getPair(grid[i][j]); \n else{\n pair<int,int>p = getPair(grid[i][j]);\n left[i][j].first = left[i][j-1].first + p.first;\n left[i][j].second = left[i][j-1].second + p.second;\n }\n }\n }\n for(int i = 0; i < r; i++){\n for(int j = 0; j < c; j++){\n pair<int,int>down, right;\n pair<int,int>curr = getPair(grid[i][j]);\n \n down.first = top[r-1][j].first - top[i][j].first, down.second = top[r-1][j].second - top[i][j].second;\n right.first = left[i][c-1].first - left[i][j].first, right.second = left[i][c-1].second - left[i][j].second;\n \n //four cases ---> (down,left), (down,right), (top,left), (top,right)\n ans = max(ans, min(down.first + left[i][j].first, down.second + left[i][j].second));\n ans = max(ans, min(down.first + right.first + curr.first, down.second + right.second + curr.second));\n ans = max(ans, min(top[i][j].first + left[i][j].first - curr.first, top[i][j].second + left[i][j].second - curr.second));\n ans = max(ans, min(top[i][j].first + right.first, top[i][j].second + right.second));\n }\n }\n return ans;\n }\n```
| 15 | 0 |
['C', 'Matrix', 'Prefix Sum']
| 3 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ || 100% fastest! || Easy understanding with picture
|
c-100-fastest-easy-understanding-with-pi-r19q
|
This question is asking about \n "Trailing zeros"\n "Cornered Path"\n\nBasic idea 1: we only care about the count of 2 and the count of 5.\nFor instance, if we
|
suilan0602
|
NORMAL
|
2022-04-18T14:23:42.999320+00:00
|
2022-04-18T14:32:39.219466+00:00
| 961 | false |
This question is asking about \n* "Trailing zeros"\n* "Cornered Path"\n\n**Basic idea 1: we only care about the count of 2 and the count of 5.**\nFor instance, if we have "{2,8,10,30}" => 2 x 8 x10x 30 = 4800 => trailing zeros = 2\nWe can transfer this array into the count of 2 and 5\ncount of 2: {1,3,1,2} => prefix sum of 2: {1,4,5,7}\ncount of 5: {0,0,1,1} => prefix sum of 5: {0,0,1,2}\nTherefore, the trailing zeros will be minimum(7,2) = 2\n\nAfter basic idea 1, we can create two matrix\nQuestion\n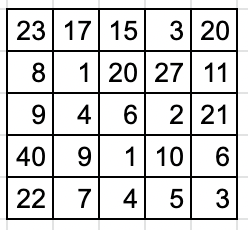\n\nTrafnser into\n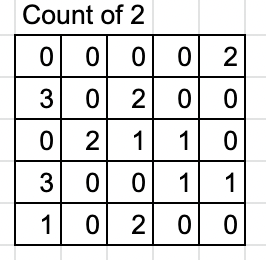\n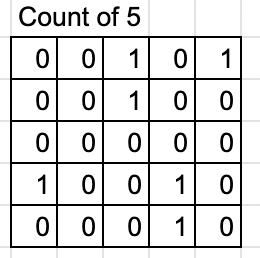\n\n\n**Basic idea 2: Cornered Path**\n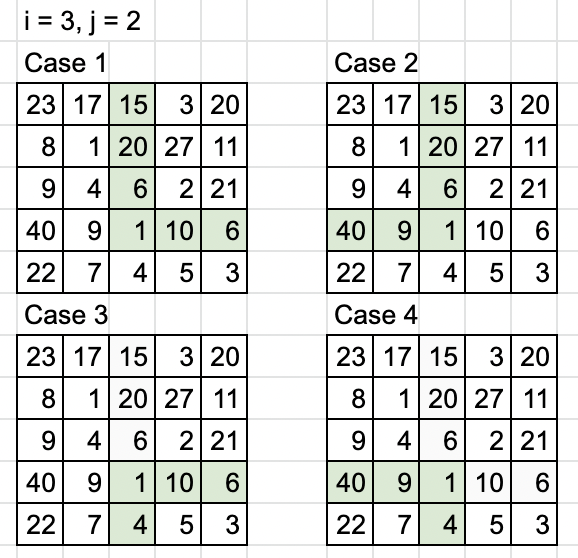\nThe answer will be the minimun of these for cases.\n\nWe can use "Horizontal prefix sum" matrix and "Vertical prefix sum" matrix ot get the result of these four cases.\n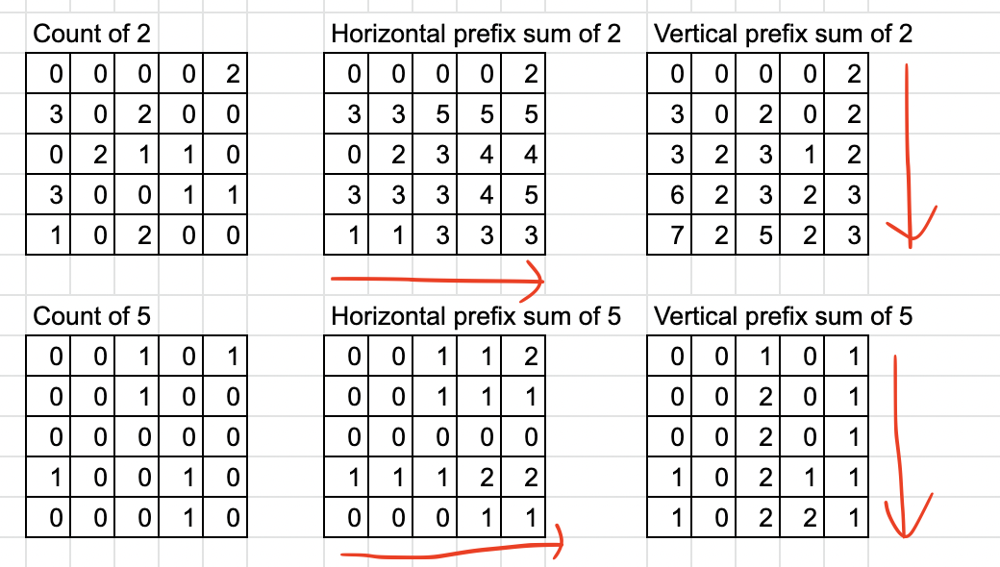\n\nFor example, we can use prefix sum to gernerate a result\nthe result will be min( horizontal2, horizantal 5) + min (vertical 2, vertical 5)\n\n\nIn this case, the answer will be\nmin (3,1) + min(3,2) = 1 + 2 = 3\n\nThat\'s the whole idea!\n\n\n**My implementation:**\n\n```\nint maxTrailingZeros(vector<vector<int>>& grid) {\n int result = 0;\n\n\t\t// gernerate matrix of 2 and matrix of 5\n vector< vector<int> > dp2(grid.size(), vector<int>(grid[0].size(), 0));\n vector< vector<int> > dp5(grid.size(), vector<int>(grid[0].size(), 0));\n for (int i = 0; i < grid.size(); i++) {\n for (int j = 0; j < grid[i].size(); j++) {\n int tmp = grid[i][j];\n while (tmp % 2 == 0) {\n tmp = tmp / 2;\n dp2[i][j]++;\n }\n while (tmp % 5 == 0) {\n tmp = tmp / 5;\n dp5[i][j]++;\n }\n }\n } \n \n vector< vector<int> > dp2HorizontalSum(grid.size(), vector<int>(grid[0].size(), 0));\n vector< vector<int> > dp5HorizontalSum(grid.size(), vector<int>(grid[0].size(), 0));\n \n\t\t// Generate horizontal prefix sum array\n for (int i = 0; i < dp2.size(); i++) {\n for (int j = 0; j < dp2[0].size(); j++) {\n if (j == 0) {\n dp2HorizontalSum[i][j] = dp2[i][j];\n dp5HorizontalSum[i][j] = dp5[i][j];\n } else {\n dp2HorizontalSum[i][j] = dp2HorizontalSum[i][j - 1] + dp2[i][j];\n dp5HorizontalSum[i][j] = dp5HorizontalSum[i][j - 1] + dp5[i][j];\n }\n\n }\n } \n \n\t\t// Generate vertical prefix sum array\n vector< vector<int> > dp2VerticalSum(grid.size(), vector<int>(grid[0].size(), 0));\n vector< vector<int> > dp5VerticalSum(grid.size(), vector<int>(grid[0].size(), 0));\n for (int i = 0; i < dp2.size(); i++) {\n for (int j = 0; j < dp2[0].size(); j++) {\n if (i == 0) {\n dp2VerticalSum[i][j] = dp2[i][j];\n dp5VerticalSum[i][j] = dp5[i][j];\n } else {\n dp2VerticalSum[i][j] = dp2VerticalSum[i - 1][j] + dp2[i][j];\n dp5VerticalSum[i][j] = dp5VerticalSum[i - 1][j] + dp5[i][j];\n }\n }\n }\n \n\t\t// Iterate every element and pick the biggest one to be the result.\n for (int i = 0; i < dp2.size(); i++) {\n for (int j = 0; j < dp2[0].size(); j++) {\n int dp2H1 = dp2HorizontalSum[i][j];\n int dp2H2 = dp2HorizontalSum[i][dp2[0].size() -1] - dp2HorizontalSum[i][j] + dp2[i][j];\n int dp2V1 = dp2VerticalSum[i][j];\n int dp2V2 = dp2VerticalSum[dp2.size() - 1][j] - dp2VerticalSum[i][j] + dp2[i][j];\n \n int dp5H1 = dp5HorizontalSum[i][j];\n int dp5H2 = dp5HorizontalSum[i][dp5[0].size() -1] - dp5HorizontalSum[i][j] + dp5[i][j];\n int dp5V1 = dp5VerticalSum[i][j];\n int dp5V2 = dp5VerticalSum[dp5.size() - 1][j] - dp5VerticalSum[i][j] + dp5[i][j];\n \n int tmp = max( min(dp2H1 + dp2V1 - dp2[i][j], dp5H1 + dp5V1 - dp5[i][j]), min(dp2H1 + dp2V2 - dp2[i][j], dp5H1 + dp5V2 - dp5[i][j]) );\n tmp = max(tmp, min(dp2H2 + dp2V1 - dp2[i][j], dp5H2 + dp5V1 - dp5[i][j]));\n tmp = max(tmp, min(dp2H2 + dp2V2 - dp2[i][j], dp5H2 + dp5V2 - dp5[i][j]));\n \n if (tmp > result) {\n result = tmp;\n }\n }\n }\n return result;\n }\n```
| 14 | 1 |
['Prefix Sum']
| 3 |
maximum-trailing-zeros-in-a-cornered-path
|
213ms Java Prefix Sum Solution with Clear Comment(Vertical or Horizontal or L,J,7,|` directions)
|
213ms-java-prefix-sum-solution-with-clea-fih6
|
\npublic int maxTrailingZeros(int[][] grid) {\n //trailing 0, 10->1, 100->2\n //10 = 2 * 5\n //100 = 2*2*5*5\n //etc.\n //min
|
davidluoyes
|
NORMAL
|
2022-04-17T04:08:58.199568+00:00
|
2022-04-17T08:37:37.294459+00:00
| 1,008 | false |
```\npublic int maxTrailingZeros(int[][] grid) {\n //trailing 0, 10->1, 100->2\n //10 = 2 * 5\n //100 = 2*2*5*5\n //etc.\n //min(countOf2,countOf5);\n\t\t//Part 1: move only horizontal\n\t\t//Part 2: move only vertically\n //Part 3: one L turn\n //Part 4: one 7 turn\n //Part 5: one J turn\n //Part 6: one |` turn\n \n\t\t//Create PrefixSum array to store count of 2 and 5, then we need O(1) time to get count of 2 or 5.\n //matrix count of 2, in row i, from j to k (j<=k) matrix2[i+1][k+1] - matrix2[i+1][j]\n int m = grid.length;\n int n = grid[0].length;\n int[][] matrix2row = new int[m+1][n+1];\n int[][] matrix5row = new int[m+1][n+1];\n //matrix count of 2, in col i, from j to k (j<=k) matrix[k+1][i+1] - matrix[j][i+1]\n int[][] matrix2col = new int[m+1][n+1];\n int[][] matrix5col = new int[m+1][n+1];\n for(int i = 0;i<grid.length;i++){\n // System.out.println(Arrays.toString(grid[i]));\n for(int j = 0;j<grid[0].length;j++){\n int count2 = count2(grid[i][j]);\n int count5 = count5(grid[i][j]);\n // System.out.println("grid["+i+"]"+"["+j+"]="+"grid[i][j]"+",count2:"+count2);\n matrix2row[i+1][j+1] = matrix2row[i+1][j] + count2; \n matrix5row[i+1][j+1] = matrix5row[i+1][j] + count5; \n }\n }\n for(int j = 0;j<grid[0].length;j++){\n for(int i = 0;i<grid.length;i++){\n int count2 = count2(grid[i][j]);\n int count5 = count5(grid[i][j]);\n matrix2col[i+1][j+1] = matrix2col[i][j+1] + count2;\n matrix5col[i+1][j+1] = matrix5col[i][j+1] + count5;\n }\n }\n //Part 1: move only horizontal \n //grid[0][0]->grid[0][n-1]\n //grid[1][0]->grid[1][n-1]\n //...\n //grid[m-1][0]->grid[m-1][n-1]\n int ans = 0;\n for(int i = 0;i<m;i++){\n int count2 = matrix2row[i+1][n]-matrix2row[i+1][0];\n int count5 = matrix5row[i+1][n]-matrix5row[i+1][0];\n ans = Math.max(ans, Math.min(count2,count5));\n }\n \n //Part 2: move only vertically\n //grid[0][0]->grid[m-1][0]\n //grid[0][1]->grid[m-1][1]\n //...\n //grid[0][n-1]->grid[m-1][n-1]\n for(int j = 0;j<n;j++){\n int count2 = matrix2col[m][j+1] - matrix2col[0][j+1];\n int count5 = matrix5col[m][j+1] - matrix5col[0][j+1];\n ans = Math.max(ans, Math.min(count2,count5));\n }\n //Find center of + then there are 4 directions\n for(int i = 0;i<m;i++){\n for(int j =0;j<n;j++){\n \n //up (i,j) to (0,j)\n int count2Up = matrix2col[i+1][j+1] - matrix2col[0][j+1];\n int count5Up = matrix5col[i+1][j+1] - matrix5col[0][j+1];\n //down (i,j) to (m-1,j)\n int count2Down = matrix2col[m][j+1] - matrix2col[i][j+1];\n int count5Down = matrix5col[m][j+1] - matrix5col[i][j+1];\n //left (i,0) to (i,j)\n int count2Left = matrix2row[i+1][j+1]-matrix2row[i+1][0];\n int count5Left = matrix5row[i+1][j+1]-matrix5row[i+1][0];\n //right (i,j) to (i,n-1)\n int count2Right = matrix2row[i+1][n]-matrix2row[i+1][j];\n int count5Right = matrix5row[i+1][n]-matrix5row[i+1][j];\n //3.1 L turn\n ans = Math.max(ans,Math.min(count2Up+count2Right-count2(grid[i][j]),count5Up+count5Right-count5(grid[i][j])));\n //3.2 7 turn\n ans = Math.max(ans,Math.min(count2Up+count2Left-count2(grid[i][j]),count5Up+count5Left-count5(grid[i][j])));\n //3.3 |` turn\n ans = Math.max(ans,Math.min(count2Down+count2Right-count2(grid[i][j]),count5Down+count5Right-count5(grid[i][j])));\n //3.4 J turn\n ans = Math.max(ans,Math.min(count2Down+count2Left-count2(grid[i][j]),count5Down+count5Left-count5(grid[i][j])));\n }\n }\n return ans;\n }\n public int count2 (int x){\n int count = 0;\n while(x % 2 == 0){\n count++;\n x = x / 2;\n }\n return count;\n }\n \n public int count5 (int x){\n int count = 0;\n while(x % 5 == 0){\n count++;\n x = x / 5;\n }\n return count;\n }\n\t```
| 11 | 1 |
[]
| 2 |
maximum-trailing-zeros-in-a-cornered-path
|
Python 3 || w/ some explanation || T/S: 89% / 89%
|
python-3-w-some-explanation-ts-89-89-by-xo0zy
|
Here\'s the plan:\n\n- We construct a prefix sum of 4-tuples, writing overgridas we go. For each cell, we determine (up2, up5, left2, right5), the accummulated
|
Spaulding_
|
NORMAL
|
2023-03-03T23:58:30.930906+00:00
|
2024-06-13T03:14:47.526100+00:00
| 765 | false |
Here\'s the plan:\n\n- We construct a prefix sum of 4-tuples, writing over`grid`as we go. For each cell, we determine `(up2, up5, left2, right5)`, the accummulated factors of two and five for the up-direction and the left-direction respectively.\n\n- We use the transformed`grid`to determine for each cell the count of zeros over the four paths: up-left, down-left, up-right, down-right.\n- We determine the max zeros for each cell along the four paths, and then determine the overall max from those cell maxs.\n```\nclass Solution:\n def maxTrailingZeros(self, grid: list[list[int]]) -> int:\n\n m, n = len(grid)+1, len(grid[0])+1\n grid = [[(0,0,0,0)]*n]+[[(0,0,0,0)]+row for row in grid]\n\n def pref(row: int,col: int)-> tuple: # <-- prefix for each cell\n \n val = grid[row][col]\n for f2 in range(19):\n if val%2: break\n val//= 2\n \n for f5 in range(6):\n if val%5: break\n val//= 5\n \n (u2, u5, _,_), (_,_, l2, l5) = grid[row-1][col], grid[row][col-1]\n return (f2 + u2, f5 + u5, f2 + l2, f5 + l5)\n \n def countZeros(r: int,c: int)-> int: # <--Count the zeros \n up2 ,up5 = grid[r][c][0],grid[r][c][1]\n down2 ,down5 = grid[m-1][c][0]-grid[r-1][c][0],grid[m-1][c][1]-grid[r-1][c][1]\n \n left2 ,left5 = grid[r][c-1][2],grid[r][c-1][3]\n right2,right5 = grid[r][n-1][2]-grid[r][c][2],grid[r][n-1][3]-grid[r][c][3] \n\n return max(min(up2+left2 ,up5+left5 ), min(down2+left2 ,down5+left5 ),\n min(up2+right2,up5+right5), min(down2+right2,down5+right5))\n\n for r in range(1,m):\n for c in range(1,n):grid[r][c] = pref(r,c)\n\n return max(countZeros(r,c) for c in range(1,n) for r in range(1,m))\n```\n[https://leetcode.com/problems/maximum-trailing-zeros-in-a-cornered-path/submissions/1286570286/](https://leetcode.com/problems/maximum-trailing-zeros-in-a-cornered-path/submissions/1286570286/)\n\nI could be wrong, but I think that time complexity is *O*(*N*) (wnere*N* is *mn* and space complexity is probably *O*(*N*) but maybe *O*(1). I\'m just not sure.\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ `m*n`.\n
| 9 | 0 |
['Python3']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ solutions
|
c-solutions-by-infox_92-9qwk
|
\n\tclass Solution {\npublic:\n\npair<long long,long long> util(int val){\n \n int x=0;\n while(val>0 && val%5==0){\n val=val/5;\n x++;\n
|
Infox_92
|
NORMAL
|
2022-11-21T12:26:45.734493+00:00
|
2022-11-21T12:26:45.734528+00:00
| 1,282 | false |
```\n\tclass Solution {\npublic:\n\npair<long long,long long> util(int val){\n \n int x=0;\n while(val>0 && val%5==0){\n val=val/5;\n x++;\n }\n int y=0;\n while(val>0 && val%2==0){\n val=val/2;\n y++;\n }\n return {x,y};\n \n}\n\nlong long util(vector<vector<int>>& grid){\n \n int n=grid.size();\n int m=grid[0].size();\n pair<long long,long long> matrix[n][m];\n pair<long long,long long> matrix1[n][m];\n pair<long long,long long> matrix2[n][m];\n \n //making the first grid;\n for(int i=0;i<n;i++)\n for(int j=0;j<m;j++){\n int val=grid[i][j];\n matrix[i][j]=util(val);\n }\n \n //right to left\n for(int i=0;i<n;i++){\n for(int j=m-1;j>=0;j--){\n if(j==m-1)\n matrix1[i][j]=matrix[i][j];\n else\n matrix1[i][j]={matrix[i][j].first+matrix1[i][j+1].first,matrix[i][j].second+matrix1[i][j+1].second};\n\n }\n }\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(j==0)\n matrix2[i][j]=matrix[i][j];\n else\n matrix2[i][j]={matrix[i][j].first+matrix2[i][j-1].first,matrix[i][j].second+matrix2[i][j-1].second};\n }\n }\n long long res=0;\n \n //calculating by traversing from up to down\n \n for(int j=0;j<m;j++){\n pair<long long,long long>sum={0,0};\n for(int i=0;i<n;i++){\n sum={sum.first+matrix[i][j].first,sum.second+matrix[i][j].second};\n res=max(res,min(sum.first,sum.second));\n if(j>0){\n pair<long long,long long>p1=matrix2[i][j-1];\n res=max(res,min(sum.first+p1.first,sum.second+p1.second));\n }\n if(j<m-1){\n pair<long long,long long>p1=matrix1[i][j+1];\n res=max(res,min(sum.first+p1.first,sum.second+p1.second));\n }\n \n } \n \n }\n return res;\n \n}\n\nint maxTrailingZeros(vector<vector<int>>& grid) {\n \nint m=grid[0].size();\n int n=grid.size();\n vector<vector<int>>grid2(m,vector<int>(n,0));\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n grid2[j][i]=grid[i][j];\n }\n }\n long long res=0;\n res=max(util(grid),util(grid2));\n vector<vector<int>>grid3(n,vector<int>(m,0));\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[0].size();j++){\n grid3[n-i-1][j]=grid[i][j]; \n }\n }\n return max(res,util(grid3));\n \n \n}\n};\n```
| 8 | 0 |
['C', 'C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
✔ Lazy Coding 😃 | Idea Explained + Code
|
lazy-coding-idea-explained-code-by-ankur-nml5
|
Lets try to visulaise our solution , the solution will always be an "L" so what we can do is iterate on every index of the matrix and assume this point to be th
|
ankursharma6084
|
NORMAL
|
2022-04-17T09:26:26.641943+00:00
|
2022-04-17T09:38:57.321591+00:00
| 767 | false |
Lets try to visulaise our solution , the solution will always be an **"L"** so what we can do is iterate on every index of the matrix and assume this point to be the intersection of the vertical and horizontal lines.\n\nNow , as we have asssumed (i , j ) to be our answer , we have to find number of trailing zeroes . So for the horizontal and vertical lines , we can have a prefix array that stores number of 2\'s and 5\'s from\n(0 , i ) , (i , n-1) , (0 , j-1) , (j+1 , m) \nNow , we can greedily calculate the answer. It\'s easy just implementing takes some effort. If you dont understand any part please do comment , i will be happy to explain . \n\nPlease do upvote , it motivates me , i will surely add more explanations further \uD83D\uDE03\n \n \n \n grid \n23 | 17 | 15 | 03 | 20 | \n08 | 01 | 20 | 27 | 11 | \n09 | 04 | 06 | 02 | 21 | \n40 | 09 | 01 | 10 | 06 | \n22 | 07 | 04 | 05 | 03 | \n\n\nPrefix Arrays \n\n prefixhorizontal \n0 0 | 0 0 | 1 0 | 1 0 | 2 2 | \n0 3 | 0 3 | 1 5 | 1 5 | 1 5 | \n0 0 | 0 2 | 0 3 | 0 4 | 0 4 | \n1 3 | 1 3 | 1 3 | 2 4 | 2 5 | \n0 1 | 0 1 | 0 3 | 1 3 | 1 3 | \n\n prefixvertical \n0 0 | 0 0 | 1 0 | 0 0 | 1 2 | \n0 3 | 0 0 | 2 2 | 0 0 | 1 2 | \n0 3 | 0 2 | 2 3 | 0 1 | 1 2 | \n1 6 | 0 2 | 2 3 | 1 2 | 1 3 | \n1 7 | 0 2 | 2 5 | 2 2 | 1 3 | \n\n\n```\nclass Solution {\n \n int count(int num , int val)\n {\n int cnt = 0 ;\n while(num>0 && num%val == 0)\n cnt++ , num/=val ;\n \n return cnt ;\n \n }\n \n int solve(pair<int , int> &p1 , pair<int , int> &p2)\n {\n return min(p1.first + p2.first , p1.second + p2.second) ;\n }\n \npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n \n int n = grid.size() , m = grid[0].size() ;\n vector<vector<pair<int , int>> > preHorizontal(n , vector<pair<int, int>>(m , {0 , 0})) ;\n vector<vector<pair<int , int>> > preVertical(n , vector<pair<int, int>>(m , {0, 0})) ;\n\n for(int i=0 ; i<n ; i++)\n {\n for(int j=0; j<m ; j++)\n {\n if(j == 0) preHorizontal[i][j] = { count(grid[i][j] , 5) , count(grid[i][j] , 2) } ; \n else{\n int cnt5 = preHorizontal[i][j-1].first + count(grid[i][j] , 5) ;\n int cnt2 = preHorizontal[i][j-1].second + count(grid[i][j] , 2) ;\n preHorizontal[i][j] = { cnt5 , cnt2 } ;\n }\n }\n }\n \n for(int i=0 ; i<m ; i++)\n {\n for(int j=0; j<n ; j++)\n {\n if(j == 0) preVertical[j][i] = { count(grid[j][i] , 5) , count(grid[j][i] , 2) } ; \n else{\n int cnt5 = preVertical[j-1][i].first + count(grid[j][i] , 5) ;\n int cnt2 = preVertical[j-1][i].second + count(grid[j][i] , 2) ;\n preVertical[j][i] = { cnt5 , cnt2 } ;\n }\n }\n }\n\n int ans = 0;\n \n for(int i=0; i<n ; i++)\n {\n for(int j=0; j<m ; j++)\n {\n pair<int , int > cnthor1 = {0 , 0} , cnthor2 = {0 , 0} , cntver1 = {0 , 0} , cntver2 = {0 , 0} ;\n cnthor1 = { preHorizontal[i][m-1].first - preHorizontal[i][j].first , preHorizontal[i][m-1].second - preHorizontal[i][j].second } ;\n cnthor2 = j > 0 ? preHorizontal[i][j-1] : cnthor2 ;\n \n cntver1 = i>0 ? make_pair(preVertical[n-1][j].first - preVertical[i-1][j].first , preVertical[n-1][j].second - preVertical[i-1][j].second ) : preVertical[n-1][j] ;\n cntver2 = preVertical[i][j] ;\n \n ans = max(ans , solve(cnthor1 , cntver1)) ;\n ans = max(ans , solve(cnthor2 , cntver1)) ;\n ans = max(ans , solve(cnthor1 , cntver2)) ;\n ans = max(ans , solve(cnthor2 , cntver2)) ;\n\n }\n }\n\n return ans;\n\n }\n};\n
| 8 | 0 |
['Dynamic Programming', 'Matrix', 'Prefix Sum']
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
[Python] Prefix Sum, O(m * n)
|
python-prefix-sum-om-n-by-xil899-0emf
|
Intuition\nStore the prefix sum matrices of rows and columns, where each entry is [a, b] representing the cumulative count of (1) the factors of 2 and (2) the f
|
xil899
|
NORMAL
|
2022-04-17T04:11:58.969137+00:00
|
2022-04-17T07:36:04.679819+00:00
| 1,131 | false |
**Intuition**\nStore the prefix sum matrices of rows and columns, where each entry is `[a, b]` representing the cumulative count of (1) the factors of 2 and (2) the factors of 5.\n\n\n**Complexity**\nTime: `O(m * n)`\nSpace: `O(m * n)`\n\nBelow is my slightly-modified in-contest solution. Please upvote if you find this solution helpful. Thanks!\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n ans = 0\n m, n = len(grid), len(grid[0])\n prefixH = [[[0] * 2 for _ in range(n + 1)] for __ in range(m)]\n prefixV = [[[0] * 2 for _ in range(n)] for __ in range(m + 1)]\n for i in range(m):\n for j in range(n):\n temp= grid[i][j]\n while temp % 2 == 0:\n prefixH[i][j + 1][0] += 1\n prefixV[i + 1][j][0] += 1\n temp //= 2\n while temp % 5 == 0:\n prefixH[i][j + 1][1] += 1\n prefixV[i + 1][j][1] += 1\n temp //= 5\n for k in range(2):\n prefixH[i][j + 1][k] += prefixH[i][j][k]\n prefixV[i + 1][j][k] += prefixV[i][j][k]\n for i in range(m):\n for j in range(n):\n left = prefixH[i][j]\n up = prefixV[i][j]\n right, down, center = [0] * 2, [0] * 2, [0] * 2\n for k in range(2):\n right[k] = prefixH[i][n][k] - prefixH[i][j + 1][k]\n down[k] = prefixV[m][j][k] - prefixV[i + 1][j][k]\n center[k] = prefixH[i][j + 1][k] - prefixH[i][j][k]\n LU, LD, RU, RD = [0] * 2, [0] * 2, [0] * 2, [0] * 2\n for k in range(2):\n LU[k] += left[k] + up[k] + center[k]\n LD[k] += left[k] + down[k] + center[k]\n RU[k] += right[k] + up[k] + center[k]\n RD[k] += right[k] + down[k] + center[k]\n ans = max(ans,\n min(LU[0], LU[1]),\n min(LD[0], LD[1]),\n min(RU[0], RU[1]),\n min(RD[0], RD[1]))\n return ans\n```
| 7 | 0 |
['Prefix Sum', 'Python', 'Python3']
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
[Python]The time limit for python is merciless 😢
|
pythonthe-time-limit-for-python-is-merci-ar0b
|
I use 3 different way to implement the O(M*N) algorithm because of TLE result.\nlost more than 40 minutes here. \uD83D\uDE22\n\nclass Solution:
|
doscope
|
NORMAL
|
2022-04-17T04:04:13.883986+00:00
|
2022-04-17T04:08:18.630682+00:00
| 476 | false |
I use 3 different way to implement the O(M*N) algorithm because of TLE result.\nlost more than 40 minutes here. \uD83D\uDE22\n```\nclass Solution: \n def maxTrailingZeros(self, grid): \n \n def get25(n): \n c2,c5 = 0,0 \n while n and n % 2 == 0: \n c2 += 1 \n n = n // 2 \n while n and n % 5 == 0: \n c5 += 1 \n n = n // 5 \n return [c2,c5] \n c25 = []\n for i in range(1001):\n c25.append(get25(i))\n \n m, n = len(grid), len(grid[0]) \n grid = list(map(lambda x: list(map(lambda xx: c25[xx][:], x)), grid)) \n l = [[[0,0] for _ in range(n)] for _ in range(m)] \n r = [[[0,0] for _ in range(n)] for _ in range(m)] \n u = [[[0,0] for _ in range(n)] for _ in range(m)] \n b = [[[0,0] for _ in range(n)] for _ in range(m)] \n for i in range(m): \n for j in range(0, n):\n for k in range(2):\n l[i][j][k] = grid[i][j][k]\n u[i][j][k] = grid[i][j][k]\n if j != 0: \n l[i][j][k] += l[i][j - 1][k] \n if i != 0: \n u[i][j][k] += u[i - 1][j][k] \n ans = 0 \n for i in range(m - 1, -1, -1): \n for j in range(n - 1, -1, -1):\n q1,q2,q3,q4 = 10**10,10**10,10**10,10**10\n for k in range(2):\n b[i][j][k] = grid[i][j][k]\n r[i][j][k] = grid[i][j][k] \n if i != m - 1: \n b[i][j][k] += b[i + 1][j][k] \n if j != n - 1: \n r[i][j][k] += r[i][j + 1][k]\n q1 = min(q1,r[i][j][k]+u[i][j][k]-grid[i][j][k])\n q2 = min(q2,r[i][j][k]+b[i][j][k]-grid[i][j][k])\n q3 = min(q3,l[i][j][k]+u[i][j][k]-grid[i][j][k])\n q4 = min(q4,l[i][j][k]+b[i][j][k]-grid[i][j][k]) \n ans = max(ans,q1,q2,q3,q4) \n \n return ans \n```
| 7 | 0 |
[]
| 2 |
maximum-trailing-zeros-in-a-cornered-path
|
c++ solution
|
c-solution-by-dilipsuthar60-bhr5
|
\nclass Solution {\npublic:\n pair<int,int>find(int n)\n {\n int count2=0;\n int count5=0;\n while(n%2==0)\n {\n n=
|
dilipsuthar17
|
NORMAL
|
2022-04-17T13:34:13.323410+00:00
|
2022-04-23T16:59:11.825070+00:00
| 418 | false |
```\nclass Solution {\npublic:\n pair<int,int>find(int n)\n {\n int count2=0;\n int count5=0;\n while(n%2==0)\n {\n n=n/2;\n count2++;\n }\n while(n%5==0)\n {\n n=n/5;\n count5++;\n }\n return {count2,count5};\n \n }\n int maxTrailingZeros(vector<vector<int>>&mat) \n {\n int n=mat.size();\n int m=mat[0].size();\n vector<vector<vector<int>>>nums(2,vector<vector<int>>(n,vector<int>(m,0)));\n vector<vector<vector<int>>>top(2,vector<vector<int>>(n,vector<int>(m,0)));\n vector<vector<vector<int>>>left(2,vector<vector<int>>(n,vector<int>(m,0)));\n vector<vector<vector<int>>>right(2,vector<vector<int>>(n,vector<int>(m,0)));\n vector<vector<vector<int>>>bottom(2,vector<vector<int>>(n,vector<int>(m,0)));\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n auto it=find(mat[i][j]);\n nums[0][i][j]=it.first;\n nums[1][i][j]=it.second;\n }\n }\n top=left=right=bottom=nums;\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n if(i)\n {\n top[0][i][j]+=top[0][i-1][j];\n top[1][i][j]+=top[1][i-1][j];\n }\n }\n }\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n if(j)\n {\n left[0][i][j]+=left[0][i][j-1];\n left[1][i][j]+=left[1][i][j-1];\n }\n }\n }\n for(int i=0;i<n;i++)\n {\n for(int j=m-1;j>=0;j--)\n {\n if(j!=m-1)\n {\n right[0][i][j]+=right[0][i][j+1];\n right[1][i][j]+=right[1][i][j+1];\n }\n }\n }\n for(int i=n-1;i>=0;i--)\n {\n for(int j=0;j<m;j++)\n {\n if(i!=n-1)\n {\n bottom[0][i][j]+=bottom[0][i+1][j];\n bottom[1][i][j]+=bottom[1][i+1][j];\n }\n }\n }\n int ans=0;\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n int curr2=nums[0][i][j];\n int curr5=nums[1][i][j];\n \n int top2=top[0][i][j];\n int top5=top[1][i][j];\n \n int right2=right[0][i][j];\n int right5=right[1][i][j];\n \n int bottom2=bottom[0][i][j];\n int bottom5=bottom[1][i][j];\n \n int left2=left[0][i][j];\n int left5=left[1][i][j];\n \n ans=max(ans,min(top2+right2-curr2,top5+right5-curr5));\n ans=max(ans,min(top2+left2-curr2,top5+left5-curr5));\n ans=max(ans,min(bottom2+right2-curr2,bottom5+right5-curr5));\n ans=max(ans,min(bottom2+left2-curr2,bottom5+left5-curr5));\n }\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['Dynamic Programming', 'C', 'Prefix Sum', 'C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Kotlin Solution
|
kotlin-solution-by-poeticivy302543-8hz0
|
\n fun maxTrailingZeros(grid: Array<IntArray>): Int {\n val m = grid.size\n val n = grid[0].size\n val twosLeftToRight = Array(m) { IntA
|
PoeticIvy302543
|
NORMAL
|
2022-05-23T23:46:08.254089+00:00
|
2022-05-23T23:46:35.869637+00:00
| 97 | false |
```\n fun maxTrailingZeros(grid: Array<IntArray>): Int {\n val m = grid.size\n val n = grid[0].size\n val twosLeftToRight = Array(m) { IntArray(n) }\n val fivesLeftToRight = Array(m) { IntArray(n) }\n val twosUpToDown = Array(m) { IntArray(n) }\n val fivesUpToDown = Array(m) { IntArray(n) }\n\n var maxTrailingZeros = 0\n for (i in grid.indices) {\n for (j in 0 until n) {\n var num = grid[i][j]\n var five = 0\n while (num % 5 == 0) {\n five++\n num /= 5\n }\n num = grid[i][j]\n var two = 0\n while (num % 2 == 0) {\n two++\n num /= 2\n }\n var leftTwo = two\n var leftFive = five\n var upTwo = two\n var upFive = five\n\n if (j != 0) {\n leftTwo += twosLeftToRight[i][j - 1]\n leftFive += fivesLeftToRight[i][j - 1]\n }\n twosLeftToRight[i][j] = leftTwo\n fivesLeftToRight[i][j] = leftFive\n if (i != 0) {\n upTwo += twosUpToDown[i - 1][j]\n upFive += fivesUpToDown[i - 1][j]\n }\n twosUpToDown[i][j] = upTwo\n fivesUpToDown[i][j] = upFive\n }\n }\n\n for (i in grid.indices) {\n for (j in 0 until n) {\n var upBeginning5 = 0\n var upBeginning2 = 0\n if (i != 0) {\n upBeginning5 = fivesUpToDown[i - 1][0]\n upBeginning2 = twosUpToDown[i - 1][0]\n }\n var downBeginnings5 = 0\n var downBeginnings2 = 0\n if (i != m - 1) {\n downBeginnings5 = fivesUpToDown[m - 1][0] - fivesUpToDown[i][0]\n downBeginnings2 = twosUpToDown[m - 1][0] - twosUpToDown[i][0]\n }\n\n var topEndings5 = 0\n var topEndings2 = 0\n if (i != 0) {\n topEndings5 = fivesUpToDown[i - 1][n - 1]\n topEndings2 = twosUpToDown[i - 1][n - 1]\n }\n var downEndings5 = 0\n var downEndings2 = 0\n if (i != m - 1) {\n downEndings5 = fivesUpToDown[m - 1][n - 1] - fivesUpToDown[i][n - 1]\n downEndings2 = twosUpToDown[m - 1][n - 1] - twosUpToDown[i][n - 1]\n }\n\n val leftSide5 = fivesLeftToRight[i][j]\n val leftSide2 = twosLeftToRight[i][j]\n\n var topSide5 = 0\n var topSide2 = 0\n if (i != 0) {\n topSide5 = fivesUpToDown[i - 1][j]\n topSide2 = twosUpToDown[i - 1][j]\n }\n\n val downSide5 = fivesUpToDown[m - 1][j] - fivesUpToDown[i][j]\n val downSide2 = twosUpToDown[m - 1][j] - twosUpToDown[i][j]\n\n var rightSide5 = 0\n var rightSide2 = 0\n if (j != 0) {\n rightSide5 = fivesLeftToRight[i][n - 1] - fivesLeftToRight[i][j - 1]\n rightSide2 = twosLeftToRight[i][n - 1] - twosLeftToRight[i][j - 1]\n }\n\n var min = Math.min(leftSide2 + topSide2, topSide5 + leftSide5)\n maxTrailingZeros = Math.max(maxTrailingZeros, min)\n min = Math.min(rightSide2 + topSide2, topSide5 + rightSide5)\n maxTrailingZeros = Math.max(maxTrailingZeros, min)\n min = Math.min(leftSide2 + downSide2, downSide5 + leftSide5)\n maxTrailingZeros = Math.max(maxTrailingZeros, min)\n min = Math.min(rightSide2 + downSide2, downSide5 + rightSide5)\n maxTrailingZeros = Math.max(maxTrailingZeros, min)\n min = Math.min(leftSide2 + upBeginning2, upBeginning5 + leftSide5)\n maxTrailingZeros = Math.max(maxTrailingZeros, min)\n min = Math.min(leftSide2 + downBeginnings2, downBeginnings5 + leftSide5)\n maxTrailingZeros = Math.max(maxTrailingZeros, min)\n min = Math.min(rightSide2 + downEndings2, downEndings5 + rightSide5)\n maxTrailingZeros = Math.max(maxTrailingZeros, min)\n min = Math.min(rightSide2 + topEndings2, topEndings5 + rightSide5)\n maxTrailingZeros = Math.max(maxTrailingZeros, min)\n }\n }\n return maxTrailingZeros\n }\n```
| 3 | 0 |
['Prefix Sum', 'Kotlin']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
c++ || 100% memory || 100% faster prefix sum of 2s,5s in prime factorization of grid element
|
c-100-memory-100-faster-prefix-sum-of-2s-2v61
|
\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n pair<int,int> zero
|
rbs_
|
NORMAL
|
2022-04-18T02:19:03.323085+00:00
|
2022-04-18T02:36:40.694136+00:00
| 226 | false |
```\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n pair<int,int> zero = make_pair(0,0);\n vector<vector<pair<int,int>>> prefix(m,vector<pair<int,int>>(n,zero));\n // (2s,5s)\n for(int i=0; i<m; i++){\n \n for(int j=0; j<n; j++){\n int temp = grid[i][j];\n while(temp%2 ==0){\n prefix[i][j].first = prefix[i][j].first + 1;\n temp = temp/2;\n }\n temp = grid[i][j];\n while(temp%5 ==0){\n prefix[i][j].second = prefix[i][j].second + 1;\n temp = temp/5;\n }\n }\n }\n \n for(int i=0; i<m; i++){\n for(int j=1; j<n; j++){\n prefix[i][j].first = prefix[i][j].first + prefix[i][j-1].first;\n prefix[i][j].second = prefix[i][j].second + prefix[i][j-1].second;\n }\n }\n \n int maxzeros = 0;\n // if ans is a smaller L, a bigger L containing the smaller L can either increase the \n // twos and fives or remain same. 4 possible L shapes\n \n // top to bottom , consider left or right\n for(int j=0; j<n; j++){\n pair<int,int> ver= zero;\n int twos=0, fives=0;\n \n for(int i=0; i<m; i++){\n twos = ver.first;\n fives = ver.second;\n // current element\n twos += prefix[i][j].first - (j>0?prefix[i][j-1].first:0);\n fives += prefix[i][j].second - (j>0?prefix[i][j-1].second:0);\n ver.first = twos;\n ver.second = fives;\n // left\n twos += j>0?prefix[i][j-1].first:0;\n fives += j>0?prefix[i][j-1].second:0;\n maxzeros = max(maxzeros,min(twos,fives));\n // right\n twos = ver.first;\n fives = ver.second;\n twos += prefix[i][n-1].first-prefix[i][j].first;\n fives += prefix[i][n-1].second-prefix[i][j].second;\n \n maxzeros = max(maxzeros,min(twos,fives));\n }\n }\n \n // bottom to top. consider either left or right\n for(int j=0; j<n; j++){\n pair<int,int> ver= zero;\n int twos=0, fives=0;\n \n for(int i=m-1; i>=0; i--){\n twos = ver.first;\n fives = ver.second;\n // current element\n twos += prefix[i][j].first - (j>0?prefix[i][j-1].first:0);\n fives += prefix[i][j].second - (j>0?prefix[i][j-1].second:0);\n ver.first = twos;\n ver.second = fives;\n // left\n twos += j>0?prefix[i][j-1].first:0;\n fives += j>0?prefix[i][j-1].second:0;\n maxzeros = max(maxzeros,min(twos,fives));\n // right\n twos = ver.first;\n fives = ver.second;\n twos += prefix[i][n-1].first-prefix[i][j].first;\n fives += prefix[i][n-1].second-prefix[i][j].second;\n \n maxzeros = max(maxzeros,min(twos,fives));\n }\n }\n \n return maxzeros;\n \n }\n};\n```
| 3 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Java prefix sum solution
|
java-prefix-sum-solution-by-tank2023-8f8r
|
\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int[][][] dph = new
|
Tank2023
|
NORMAL
|
2022-04-17T05:27:29.949481+00:00
|
2022-04-25T03:46:25.083988+00:00
| 1,002 | false |
```\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int[][][] dph = new int[m][n][3];\n int[][][] dpv = new int[m][n][3];\n int hmax0 = 0;\n int vmax0 = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int curr = grid[i][j];\n int two = 0;\n int five = 0;\n if (j >= 1) {\n two = dph[i][j-1][1];\n five = dph[i][j-1][2];\n }\n while (curr > 0 && curr % 2 == 0) {\n two++;\n curr /= 2;\n }\n while (curr > 0 && curr % 5 == 0) {\n five++;\n curr /= 5;\n }\n dph[i][j][1] = two;\n dph[i][j][2] = five;\n dph[i][j][0] = Math.min(dph[i][j][1], dph[i][j][2]);\n }\n hmax0 = Math.max(hmax0, dph[i][n-1][0]);\n }\n \n for (int j = 0; j < n; j++) {\n for (int i = 0; i < m; i++) {\n int curr = grid[i][j];\n int two = 0;\n int five = 0;\n if (i >= 1) {\n two = dpv[i-1][j][1];\n five = dpv[i-1][j][2];\n }\n while (curr > 0 && curr % 2 == 0) {\n two++;\n curr /= 2;\n }\n while (curr > 0 && curr % 5 == 0) {\n five++;\n curr /= 5;\n }\n dpv[i][j][1] = two;\n dpv[i][j][2] = five;\n dpv[i][j][0] = Math.min(dpv[i][j][1], dpv[i][j][2]);\n }\n vmax0 = Math.max(vmax0, dpv[m-1][j][0]);\n }\n\t\t\n int res = Math.max(vmax0, hmax0);\n\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int otwo = dph[i][j][1];\n int ofive = dph[i][j][2];\n \n int res1 = 0;\n if (i >= 1) {\n int ntwo = otwo + dpv[i-1][j][1];\n int nfive = ofive + dpv[i-1][j][2];\n res1 = Math.min(ntwo, nfive);\n }\n \n int res2 = 0;\n if (i < m - 1) {\n int ntwo = otwo + dpv[m-1][j][1] - dpv[i][j][1];\n int nfive = ofive + dpv[m-1][j][2] - dpv[i][j][2];\n res2 = Math.min(ntwo, nfive);\n }\n res = Math.max(res, res1);\n res = Math.max(res, res2);\n }\n\t\t\t\n\t\t\tfor (int j = n - 1; j >= 0; j--) {\n int otwo = 0;\n int ofive = 0;\n if (j >= 1) {\n otwo = dph[i][n-1][1] - dph[i][j-1][1];\n ofive = dph[i][n-1][2] - dph[i][j-1][2];\n } else {\n otwo = dph[i][n-1][1];\n ofive = dph[i][n-1][2];\n }\n \n int res1 = 0;\n if (i >= 1) {\n int ntwo = otwo + dpv[i-1][j][1];\n int nfive = ofive + dpv[i-1][j][2];\n res1 = Math.min(ntwo, nfive);\n }\n \n int res2 = 0;\n if (i < m - 1) {\n int ntwo = otwo + dpv[m-1][j][1] - dpv[i][j][1];\n int nfive = ofive + dpv[m-1][j][2] - dpv[i][j][2];\n res2 = Math.min(ntwo, nfive);\n }\n \n res = Math.max(res, res1);\n res = Math.max(res, res2);\n }\n }\n\t\t\n return res;\n }\n}\n```
| 3 | 0 |
['Java']
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ || solution
|
c-solution-by-soujash_mandal-k319
|
\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int m=grid.size();\n int n=grid[0].size();\n vector<ve
|
soujash_mandal
|
NORMAL
|
2022-04-17T04:04:16.982676+00:00
|
2022-04-17T04:04:16.982705+00:00
| 707 | false |
```\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int m=grid.size();\n int n=grid[0].size();\n vector<vector<pair<int,int>>> v(m,vector<pair<int,int>>(n)),u(m,vector<pair<int,int>>(n)),d(m,vector<pair<int,int>>(n)),l(m,vector<pair<int,int>>(n)),r(m,vector<pair<int,int>>(n));\n \n for(int i=0;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n int x=grid[i][j];\n v[i][j].first=0;\n v[i][j].second=0;\n while(x%2==0)\n {\n x/=2;\n v[i][j].first++;\n }\n while(x%5==0)\n {\n x/=5;\n v[i][j].second++;\n }\n }\n }\n u=v;\n d=v;\n l=v;\n r=v;\n \n for(int i=0;i<m;i++)\n {\n for(int j=1;j<n;j++)\n {\n l[i][j].first+=l[i][j-1].first;\n l[i][j].second+=l[i][j-1].second;\n \n r[i][n-j-1].first+=r[i][n-j].first;\n r[i][n-j-1].second+=r[i][n-j].second;\n } \n }\n \n for(int i=0;i<n;i++)\n {\n for(int j=1;j<m;j++)\n {\n u[j][i].first+=u[j-1][i].first;\n u[j][i].second+=u[j-1][i].second;\n \n d[m-j-1][i].first+=d[m-j][i].first;\n d[m-j-1][i].second+=d[m-j][i].second;\n } \n }\n int res=0;\n for(int i=0;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n \n int x1=u[i][j].first;\n int x2=u[i][j].second;\n int x3=l[i][j].first;\n int x4=l[i][j].second;\n \n int c2=x1+x3-v[i][j].first;\n int c5=x2+x4-v[i][j].second;\n res=max(res,min(c2,c5));\n //####################################\n x1=u[i][j].first;\n x2=u[i][j].second;\n x3=r[i][j].first;\n x4=r[i][j].second;\n \n c2=x1+x3-v[i][j].first;\n c5=x2+x4-v[i][j].second;\n res=max(res,min(c2,c5));\n \n //####################################\n x1=d[i][j].first;\n x2=d[i][j].second;\n x3=r[i][j].first;\n x4=r[i][j].second;\n \n c2=x1+x3-v[i][j].first;\n c5=x2+x4-v[i][j].second;\n res=max(res,min(c2,c5));\n //####################################\n x1=d[i][j].first;\n x2=d[i][j].second;\n x3=l[i][j].first;\n x4=l[i][j].second;\n \n c2=x1+x3-v[i][j].first;\n c5=x2+x4-v[i][j].second;\n res=max(res,min(c2,c5));\n \n }\n }\n return res;\n \n }\n};\n```
| 3 | 0 |
[]
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
[Python3] DP in 4 directions, commented code
|
python3-dp-in-4-directions-commented-cod-bh7n
|
\nclass Solution:\n def maxTrailingZeros(self, A: List[List[int]]) -> int:\n \n # Helper method with cache to return number of twos in prime fa
|
ritam777
|
NORMAL
|
2022-04-17T04:01:50.384204+00:00
|
2022-04-17T04:07:13.033948+00:00
| 742 | false |
```\nclass Solution:\n def maxTrailingZeros(self, A: List[List[int]]) -> int:\n \n # Helper method with cache to return number of twos in prime factorization of given number\n @cache\n def twos(x):\n res = 0\n while (x&1)==0:\n res += 1\n x >>= 1\n return res\n \n # Helper method with cache to return number of fives in prime factorization of given number\n @cache\n def fives(x):\n res = 0\n while x%5 == 0:\n res += 1\n x //= 5\n return res\n \n m, n = len(A), len(A[0])\n \n # Creating 2D arrays for storing number of 2\'s and number of 5\'s in all elements above, below, left or right\n\t\t# of the current element (including current element).The two counts will be stored as a tuple i.e. as pair<int, int>\n \n up, down, left, right = [[0]*n for _ in range(m)], [[0]*n for _ in range(m)], [[0]*n for _ in range(m)], [[0]*n for _ in range(m)]\n \n # Initializing first row of up array and last row of down array\n for j in range(n):\n up[0][j] = (twos(A[0][j]),fives(A[0][j]))\n down[m-1][j] = (twos(A[m-1][j]), fives(A[m-1][j]))\n \n # Initializing leftmost column of left array and rightmost column of right array\n for i in range(m):\n left[i][0] = (twos(A[i][0]), fives(A[i][0]))\n right[i][n-1] = (twos(A[i][n-1]), fives(A[i][n-1]))\n \n # Populating all remaining cells of all arrays\n \n for i in range(1, m):\n for j in range(n):\n up[i][j] = (up[i-1][j][0] + twos(A[i][j]), up[i-1][j][1] + fives(A[i][j]))\n \n for i in range(m-2, -1, -1):\n for j in range(n):\n down[i][j] = (down[i+1][j][0] + twos(A[i][j]), down[i+1][j][1] + fives(A[i][j]))\n \n for i in range(m):\n for j in range(1, n):\n left[i][j] = (left[i][j-1][0] + twos(A[i][j]), left[i][j-1][1] + fives(A[i][j]))\n \n for i in range(m):\n for j in range(n-2, -1, -1):\n right[i][j] = (right[i][j+1][0] + twos(A[i][j]), right[i][j+1][1] + fives(A[i][j]))\n \n # Iterating over each cell to first take pairwise sum in two directions of 2\'s and 5\'s then subtract current cell values (because it\'s counted twice) \n\t\t# finally take min of 2\'s and 5\'s for that cell where the horizontal/vertical turn happens\n res = 0\n for i in range(m):\n for j in range(n):\n res = max(res, min(up[i][j][0] + right[i][j][0] - twos(A[i][j]), up[i][j][1] + right[i][j][1] - fives(A[i][j])))\n res = max(res, min(up[i][j][0] + left[i][j][0] - twos(A[i][j]), up[i][j][1] + left[i][j][1] - fives(A[i][j])))\n res = max(res, min(down[i][j][0] + right[i][j][0] - twos(A[i][j]), down[i][j][1] + right[i][j][1] - fives(A[i][j])))\n res = max(res, min(down[i][j][0] + left[i][j][0] - twos(A[i][j]), down[i][j][1] + left[i][j][1] - fives(A[i][j])))\n \n return res\n```
| 3 | 0 |
['Dynamic Programming']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++, test in 4 directions + prefix sums
|
c-test-in-4-directions-prefix-sums-by-cx-p23g
|
\n//firstly count \'5\' s and \'2\' s for every cell, (each pair of (5,2) will generate a trailing zero),\n//use prefix sums to accelerate the counting of 5s a
|
cx3129
|
NORMAL
|
2022-06-25T00:43:02.392240+00:00
|
2022-07-03T01:06:13.939915+00:00
| 288 | false |
```\n//firstly count \'5\' s and \'2\' s for every cell, (each pair of (5,2) will generate a trailing zero),\n//use prefix sums to accelerate the counting of 5s and 2s.\n//and then check in 4 directions to find out the turn has max count of pairs (5,2)\nclass Solution {\npublic:\n\tint maxTrailingZeros(vector<vector<int>>& grid) {\n\t\tint m = grid.size(), n = grid[0].size(), r = 0, i, j, v, fiveCount, twoCount, a, b, a1, b1, a2, b2, a3, b3, a4, b4;\n\t\tvector<vector<int>> fiveHor(m, vector<int>(n, 0)), fiveVer(m, vector<int>(n, 0)),twoHor(m, vector<int>(n, 0)), twoVer(m, vector<int>(n, 0));\n\n\t\tfor (i = 0; i < m; ++i) {\n\t\t\tfor (j = 0; j < n; ++j) {\n\t\t\t\tv = grid[i][j], fiveCount = 0, twoCount = 0;\n\t\t\t\twhile (v % 5 == 0) { fiveCount++; v /= 5; }\n\t\t\t\twhile (v && (v % 2 == 0)) { twoCount++; v /= 2; }\n\n\t\t\t\tfiveHor[i][j] = ((j == 0) ? 0 : fiveHor[i][j - 1]) + fiveCount; //five prefix sum in horizontal\n\t\t\t\tfiveVer[i][j] = ((i == 0) ? 0 : fiveVer[i - 1][j]) + fiveCount; //five prefix sum in vertical\n \n\t\t\t\ttwoHor[i][j] = ((j == 0) ? 0 : twoHor[i][j - 1]) + twoCount; //two prefix sum in horizontal\t\t\t\t\n twoVer[i][j] = ((i == 0) ? 0 : twoVer[i - 1][j]) + twoCount; //two prefix sum in vertical\n\t\t\t}\n\t\t}\n\n\t\tfor (i = 0; i < m; ++i) {\n\t\t\tfor (j = 0; j < n; ++j) {\n\t\t\t\ta = fiveHor[i][j] - (j == 0 ? 0 : fiveHor[i][j - 1]); //current cell\'s count of 5\n\t\t\t\tb = twoHor[i][j] - (j == 0 ? 0 : twoHor[i][j - 1]); //current cell\'s count of 2\n \n\t\t\t\ta1 = fiveHor[i][n - 1] - fiveHor[i][j]; b1 = twoHor[i][n - 1] - twoHor[i][j]; //right\n\t\t\t\ta2 = fiveVer[m - 1][j] - fiveVer[i][j]; b2 = twoVer[m - 1][j] - twoVer[i][j]; //down\n\t\t\t\ta3 = (j == 0) ? 0 : fiveHor[i][j - 1]; b3 = (j == 0) ? 0 : twoHor[i][j - 1]; //left\n\t\t\t\ta4 = (i == 0) ? 0 : fiveVer[i - 1][j]; b4 = (i == 0) ? 0 : twoVer[i - 1][j]; //up\n\n\t\t\t\tr = max(r, min(a + a1 + a2, b + b1 + b2));\n\t\t\t\tr = max(r, min(a + a2 + a3, b + b2 + b3));\n\t\t\t\tr = max(r, min(a + a3 + a4, b + b3 + b4));\n\t\t\t\tr = max(r, min(a + a4 + a1, b + b4 + b1));\n\t\t\t}\n\t\t}\n\n\t\treturn r;\n\t}\n};\n```
| 2 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Java|| easy to understand || dp || 100% time and memory
|
java-easy-to-understand-dp-100-time-and-umrzp
|
HINT1:\nif we want to get the number of trailing zeros, we only need to figure out how many 5 and 2 the product has.\n\nHINT2:\nFor each element as a corner, we
|
fxhhhh
|
NORMAL
|
2022-04-17T08:39:29.296980+00:00
|
2022-04-17T11:51:05.301387+00:00
| 457 | false |
HINT1:\nif we want to get the number of trailing zeros, we only need to figure out how many 5 and 2 the product has.\n\nHINT2:\nFor each element as a corner, we have 4 directions and we need to combine any of the 2 to get a valid path. So every corner has 6 different paths.\n\n\n1.\n0 1 0 0 \n0 1 0 0\n0 1 0 0\n0 1 0 0\n\n2.\n0 1 0 0 \n0 1 1 1\n0 0 0 0\n0 0 0 0\n\n3.\n0 1 0 0 \n1 1 0 0\n0 0 0 0\n0 0 0 0\n\n4.\n0 0 0 0 \n1 1 1 1\n0 0 0 0\n0 0 0 0\n\n5.\n0 0 0 0 \n1 1 0 0\n0 1 0 0\n0 1 0 0\n\n6.\n0 0 0 0 \n0 1 1 1\n0 1 0 0\n0 1 0 0\n\n\n\n```\n \n public static int maxTrailingZeros(int[][] grid) {\n /*calculate how many 5 and 2 grid[i][j] has\n int[][] five = new int[grid.length][grid[0].length];\n int[][] two = new int[grid.length][grid[0].length];\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n int origin = grid[i][j];\n while (origin % 5 == 0 && origin != 0) {\n five[i][j] += 1;\n origin = origin / 5;\n }\n origin = grid[i][j];\n while (origin % 2 == 0 && origin != 0) {\n two[i][j] += 1;\n origin = origin / 2;\n }\n }\n }\n // use four dp array to save the sum of 5 and 2 in two directions\n int[][] dp51 = new int[grid.length][grid[0].length];\n int[][] dp21 = new int[grid.length][grid[0].length];\n int[][] dp52 = new int[grid.length][grid[0].length];\n int[][] dp22 = new int[grid.length][grid[0].length];\n\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n if (i == 0) {\n dp51[i][j] = five[i][j];\n dp21[i][j] = two[i][j];\n } else {\n dp51[i][j] = dp51[i - 1][j] + five[i][j];\n dp21[i][j] = dp21[i - 1][j] + two[i][j];\n }\n if (j == 0) {\n dp52[i][j] = five[i][j];\n dp22[i][j] = two[i][j];\n } else {\n dp52[i][j] = dp52[i][j - 1] + five[i][j];\n dp22[i][j] = dp22[i][j - 1] + two[i][j];\n }\n }\n }\n \n //we have 4 choices and combine any of 2\n int max = 0;\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n int fiveNum = dp51[i][j];\n int twoNum = dp21[i][j];\n\n int fiveNum2 = dp52[i][j];\n int twoNum2 = dp22[i][j];\n\n int fiveNum1 = dp51[grid.length - 1][j] - dp51[i][j] + five[i][j];\n int twoNum1 = dp21[grid.length - 1][j] - dp21[i][j] + two[i][j];\n\n int fiveNum3 = dp52[i][grid[0].length - 1] - dp52[i][j] + five[i][j];\n int twoNum3 = dp22[i][grid[0].length - 1] - dp22[i][j] + two[i][j];\n\n\n max = Math.max(max, Math.min(fiveNum + fiveNum1 - five[i][j], twoNum + twoNum1 - two[i][j]));\n max = Math.max(max, Math.min(fiveNum + fiveNum2 - five[i][j], twoNum + twoNum2 - two[i][j]));\n max = Math.max(max, Math.min(fiveNum + fiveNum3 - five[i][j], twoNum + twoNum3 - two[i][j]));\n max = Math.max(max, Math.min(fiveNum2 + fiveNum1 - five[i][j], twoNum2 + twoNum1 - two[i][j]));\n max = Math.max(max, Math.min(fiveNum3 + fiveNum1 - five[i][j], twoNum3 + twoNum1 - two[i][j]));\n max = Math.max(max, Math.min(fiveNum2 + fiveNum3 - five[i][j], twoNum2 + twoNum3 - two[i][j]));\n }\n }\n return max;\n }\n \n \n ```\n \n \n \n
| 2 | 0 |
['Dynamic Programming', 'Java']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Consider all 6 shapes of "L" at each point
|
consider-all-6-shapes-of-l-at-each-point-oysg
|
\nclass Solution {\npublic: \n int numberoffives(int n){ //calculates k if n = p1 *p2* (5^k)\n int cnt=0;\n while(n%5==0){\n n/=5;\n
|
jlax
|
NORMAL
|
2022-04-17T06:22:28.828870+00:00
|
2022-04-17T06:25:36.102620+00:00
| 81 | false |
```\nclass Solution {\npublic: \n int numberoffives(int n){ //calculates k if n = p1 *p2* (5^k)\n int cnt=0;\n while(n%5==0){\n n/=5;\n cnt++;\n }\n return cnt;\n }\n int numberoftwos(int n){\n int cnt=0;\n while(n%2==0){\n n/=2;\n cnt++;\n }\n return cnt;\n }\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int m=grid.size();\n int n=grid[0].size();\n vector<vector<pair<int, int>>> five(m+1, vector<pair<int, int>>(n+1, {0, 0})); // pair.first represents rows prefix sum of number of fives and pair.second represents columns prefix sum of number of fives \n vector<vector<pair<int, int>>> two(m+1, vector<pair<int, int>>(n+1, {0, 0}));\n \n for(int i=0; i<m; i++){\n for(int j=1; j<n+1; j++){\n \n five[i][j].first= five[i][j-1].first+ numberoffives(grid[i][j-1]);\n two[i][j].first= two[i][j-1].first+ numberoftwos(grid[i][j-1]);\n \n }\n } // calculate row prefix\n \n for(int j=0; j<n; j++){\n for(int i=1; i<m+1; i++){\n \n five[i][j].second= five[i-1][j].second+ numberoffives(grid[i-1][j]);\n two[i][j].second= two[i-1][j].second+ numberoftwos(grid[i-1][j]);\n \n }\n }// calculate col prefix\n\n int maxi=INT_MIN;\n for(int i=0; i<m; i++){ // \n for(int j=0; j<n; j++){// \n\t\t\t// Try all L shapes possible at a given joint(o) we can have at max 6 shapes ----- o -------\n\t\t\t \n //route1\n int f= numberoffives(grid[i][j]);\n int t= numberoftwos(grid[i][j]);\n int ans= min(two[i][j].first+ two[i][j].second+t, five[i][j].first+ five[i][j].second+f); \n //route 2\n int temp=0;\n temp= min(two[i][j].first+ (two[m][j].second-two[i][j].second), five[i][j].first+ (five[m][j].second-five[i][j].second));\n ans=max(ans, temp);\n // route 3\n temp= min(two[i][n].first-two[i][j].first+ (two[m][j].second-two[i][j].second)-t, five[i][n].first-five[i][j].first+ (five[m][j].second-five[i][j].second)-f);\n ans=max(ans, temp);\n // route 4\n temp= min(two[i][n].first-two[i][j].first+ (two[i][j].second), five[i][n].first-five[i][j].first+ (five[i][j].second));\n ans=max(ans, temp);\n //route 5 && 6\n temp=min(two[i][n].first, five[i][n].first);\n ans=max(ans, temp);\n temp=min(two[m][j].second, five[m][j].second);\n ans=max(ans, temp);\n // cout<<ans<<" ";\n maxi= max(ans, maxi); \n }\n // cout<<endl;\n }\n return maxi;\n \n \n }\n};\n```
| 2 | 0 |
['C', 'Prefix Sum', 'C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
A JavaScript solution
|
a-javascript-solution-by-pinkmous-0v2t
|
\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar maxTrailingZeros = function(g) {\n const m = g.length;\n const n = g[0].length;\n con
|
pinkmous
|
NORMAL
|
2022-04-17T05:13:36.269679+00:00
|
2022-04-17T05:13:36.269736+00:00
| 124 | false |
```\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar maxTrailingZeros = function(g) {\n const m = g.length;\n const n = g[0].length;\n const ta = [...Array(m)].map(i => Array(n).fill(1));\n const tb = [...Array(m)].map(i => Array(n).fill(1));\n const tc = [...Array(m)].map(i => Array(n).fill(1));\n const td = [...Array(m)].map(i => Array(n).fill(1));\n \n const c52 = (s) => {\n let c5 = 0;\n let c2 = 0;\n while (s % 2 === 0) {\n s = s / 2;\n c2++;\n }\n while (s % 5 === 0) {\n s = s / 5;\n c5++;\n }\n return [c5, c2];\n }\n \n const c10 = ([c5, c2]) => {\n return Math.min(c5, c2);\n }\n \n for (let i = 0; i < m; i++) {\n for (let j = 0; j < n; j++) {\n ta[i][j] = (j === 0) ? c52(g[i][j]) : [c52(g[i][j])[0] + ta[i][j-1][0], c52(g[i][j])[1] + ta[i][j-1][1]];\n tb[i][j] = (i === 0) ? c52(g[i][j]) : [c52(g[i][j])[0] + tb[i-1][j][0], c52(g[i][j])[1] + tb[i-1][j][1]];\n }\n }\n \n for (let i = m-1; i >= 0; i--) {\n for (let j = n-1; j >= 0; j--) {\n tc[i][j] = (j === n-1) ? c52(g[i][j]) : [c52(g[i][j])[0] + tc[i][j+1][0], c52(g[i][j])[1] + tc[i][j+1][1]]; // : ctz(hg(g[i][j]) * tc[i][j+1][0], tc[i][j+1][1]); // hg(g[i][j]) * tc[i][j+1];\n td[i][j] = (i === m-1) ? c52(g[i][j]) : [c52(g[i][j])[0] + td[i+1][j][0], c52(g[i][j])[1] + td[i+1][j][1]]; // : ctz(hg(g[i][j]) * td[i+1][j][0], td[i+1][j][1]); // hg(g[i][j]) * td[i+1][j];\n }\n }\n \n let ret = 0;\n for (let i = 0; i < m; i++) {\n for (let j = 0; j < n; j++) {\n let s1 = i === 0 ? c10(ta[i][j]) : c10([ta[i][j][0] + tb[i-1][j][0], ta[i][j][1] + tb[i-1][j][1]]);\n let s2 = i === m - 1 ? c10(ta[i][j]) : c10([ta[i][j][0] + td[i+1][j][0], ta[i][j][1] + td[i+1][j][1]]); \n let s3 = i === 0 ? c10(tc[i][j]) : c10([tc[i][j][0] + tb[i-1][j][0], tc[i][j][1] + tb[i-1][j][1]]);\n let s4 = i === m - 1 ? c10(tc[i][j]) : c10([tc[i][j][0] + td[i+1][j][0], tc[i][j][1] + td[i+1][j][1]]); \n ret = Math.max(ret, s1, s2, s3, s4);\n }\n }\n return ret;\n};\n```
| 2 | 0 |
['JavaScript']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Prefix Sum | JAVA | O(MN) | Beat 100%
|
prefix-sum-java-omn-beat-100-by-zhoupeng-6cj1
|
\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n // find path with most matching 5 & 2 divisor\n int m = grid.length;\n
|
zhoupeng315
|
NORMAL
|
2022-04-17T04:38:16.733983+00:00
|
2022-04-17T04:42:10.459432+00:00
| 413 | false |
```\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n // find path with most matching 5 & 2 divisor\n int m = grid.length;\n int n = grid[0].length;\n \n Node[][] rows = new Node[m][n];\n Node[][] cols = new Node[m][n];\n \n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int five = getFive(grid[i][j]);\n int two = getTwo(grid[i][j]);\n Node nodeR = new Node(five, two);\n Node nodeC = new Node(five, two);\n \n if (i > 0) {\n nodeC.five = nodeC.five + cols[i - 1][j].five;\n nodeC.two = nodeC.two + cols[i - 1][j].two;\n }\n \n cols[i][j] = nodeC;\n \n if (j > 0) {\n nodeR.five = nodeR.five + rows[i][j - 1].five;\n nodeR.two = nodeR.two + rows[i][j - 1].two;\n }\n \n rows[i][j] = nodeR;\n }\n }\n \n int max = 0;\n \n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int rowLeft5 = j - 1 < 0 ? 0 : rows[i][j - 1].five;\n int rowLeft2 = j - 1 < 0 ? 0 : rows[i][j - 1].two;\n int rowRight5 = rows[i][n - 1].five - rows[i][j].five;\n int rowRight2 = rows[i][n - 1].two - rows[i][j].two;\n \n int colUp5 = i - 1 < 0 ? 0 : cols[i - 1][j].five;\n int colUp2 = i - 1 < 0 ? 0 : cols[i - 1][j].two;\n int colDown5 = cols[m - 1][j].five - cols[i][j].five;\n int colDown2 = cols[m - 1][j].two - cols[i][j].two;\n \n int cur = grid[i][j];\n \n max = Math.max(max, Math.min(rowLeft5 + colUp5 + getFive(cur), rowLeft2 + colUp2 + getTwo(cur)));\n max = Math.max(max, Math.min(rowLeft5 + colDown5 + getFive(cur), rowLeft2 + colDown2 + getTwo(cur)));\n max = Math.max(max, Math.min(rowRight5 + colUp5 + getFive(cur), rowRight2 + colUp2 + getTwo(cur)));\n max = Math.max(max, Math.min(rowRight5 + colDown5 + getFive(cur), rowRight2 + colDown2 + getTwo(cur)));\n }\n }\n \n return max;\n }\n \n private int getTwo(int x) {\n int res = 0;\n \n while (x % 2 == 0) {\n res++;\n x /= 2;\n }\n return res;\n }\n \n private int getFive(int x) {\n int res = 0;\n \n while (x % 5 == 0) {\n res++;\n x /= 5;\n }\n return res;\n }\n}\n\nclass Node {\n int five;\n int two;\n \n public Node(int five, int two) {\n this.five = five;\n this.two = two;\n }\n}\n```
| 2 | 1 |
['Java']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Why my code failed
|
why-my-code-failed-by-jayzea-c8kz
|
my idea is to traverse just like number of island but make sure only make turn at most once. where is the bug? \nfailed at:\n[[899,727,165,249,531,300,542,890],
|
jayzea
|
NORMAL
|
2022-04-17T04:12:34.039784+00:00
|
2022-04-17T04:27:52.828567+00:00
| 193 | false |
my idea is to traverse just like number of island but make sure only make turn at most once. where is the bug? \nfailed at:\n[[899,727,165,249,531,300,542,890],[981,587,565,943,875,498,582,672],[106,902,524,725,699,778,365,220]]\n```\nclass Solution {\n int res = 0;\n public int maxTrailingZeros(int[][] grid) {\n \n for(int i=0;i<grid.length;i++){\n for(int j=0;j<grid[0].length;j++){\n helper(grid, i, j, 0, 1);\n }\n } \n return res;\n }\n \n public void helper(int[][] grid, int i, int j, int count, int current){\n if(i>=grid.length || i < 0 || j<0 || j >=grid[0].length ){\n while(current>=10 && current%10==0){\n current = current/10;\n count++;\n }\n res = Math.max(res, count);\n return;\n }\n else{\n current = current*grid[i][j];\n while(current%10==0){\n current = current/10;\n count++;\n }\n toLeft(grid, i, j-1, count, current);\n toRight(grid, i, j+1, count, current);\n helper(grid, i+1, j, count, current);\n }\n }\n \n public void toLeft(int[][] grid, int i, int j, int count, int current){\n if(i>=grid.length || i < 0 || j<0 || j >=grid[0].length ){\n while(current >= 10 && current%10==0){\n current = current/10;\n count++;\n }\n res = Math.max(res, count);\n return;\n }\n else{\n current = current*grid[i][j];\n while(current%10==0){\n current = current/10;\n count++;\n }\n toLeft(grid, i, j-1, count, current);\n // toRight(grid, i, j+1, count, visited, current);\n // helper(grid, i+1, j, count, visited, current);\n }\n }\n \n public void toRight(int[][] grid, int i, int j, int count, int current){\n if(i>=grid.length || i < 0 || j<0 || j >=grid[0].length ){\n while(current>=10 && current%10==0){\n current = current/10;\n count++;\n }\n res = Math.max(res, count);\n return;\n }\n else{\n current = current*grid[i][j];\n while(current%10==0){\n current = current/10;\n count++;\n }\n // toLeft(grid, i, j-1, count, visited, current);\n toRight(grid, i, j+1, count, current);\n // helper(grid, i+1, j, count, visited, current);\n }\n }\n \n}\n```
| 2 | 1 |
[]
| 4 |
maximum-trailing-zeros-in-a-cornered-path
|
Python O(row*col) Solution, Couting factor 2 & 5 for 4 directions
|
python-orowcol-solution-couting-factor-2-kb5a
|
\tclass Solution:\n\t\tdef maxTrailingZeros(self, grid: List[List[int]]) -> int:\n\t\t\tdef valTo25(val):\n\t\t\t\tn2 = 0\n\t\t\t\tn5 = 0\n\t\t\t\twhile val % 2
|
Cloud9-ine
|
NORMAL
|
2022-04-17T04:07:41.311767+00:00
|
2022-04-17T04:17:42.243217+00:00
| 313 | false |
\tclass Solution:\n\t\tdef maxTrailingZeros(self, grid: List[List[int]]) -> int:\n\t\t\tdef valTo25(val):\n\t\t\t\tn2 = 0\n\t\t\t\tn5 = 0\n\t\t\t\twhile val % 2 == 0:\n\t\t\t\t\tn2 += 1\n\t\t\t\t\tval //= 2\n\t\t\t\twhile val % 5 == 0:\n\t\t\t\t\tn5 += 1\n\t\t\t\t\tval //= 5\n\t\t\t\treturn (n2, n5)\n\n\n\t\t\tdef result(i, j):\n\t\t\t\tt2, t5 = dic[(i, j, \'top\')]\n\t\t\t\tl2, l5 = dic[(i, j, \'left\')]\n\t\t\t\tr2, r5 = dic[(i, j, \'right\')]\n\t\t\t\tb2, b5 = dic[(i, j, \'bot\')]\n\n\t\t\t\to2, o5 = valTo25(grid[i][j])\n\n\t\t\t\tres1 = min(t2+o2+r2, t5+o5+r5)\n\t\t\t\tres2 = min(t2+o2+l2, t5+o5+l5)\n\t\t\t\tres3 = min(b2+o2+r2, b5+o5+r5)\n\t\t\t\tres4 = min(b2+o2+l2, b5+o5+l5)\n\t\t\t\treturn max(res1, res2, res3, res4)\n\t\t\t\t\n\n\t\t\tR = len(grid)\n\t\t\tC = len(grid[0])\n\n\t\t\tans = 0\n\n\t\t\t# key = (i, j, dir), val = (#2, #5)\n\t\t\tdic = {}\n\t\t\t\n\t\t\t# Consider the top-left element\n\t\t\tdic[(0, 0, \'top\')] = (0, 0)\n\t\t\tdic[(0, 0, \'left\')] = (0, 0)\n\n\t\t\tn2 = 0\n\t\t\tn5 = 0\n\t\t\tfor i in range(1, R):\n\t\t\t\tres = valTo25(grid[i][0])\n\t\t\t\tn2 += res[0]\n\t\t\t\tn5 += res[1]\n\t\t\tdic[(0, 0, \'bot\')] = (n2, n5)\n\n\t\t\tn2 = 0\n\t\t\tn5 = 0\n\t\t\tfor i in range(1, C):\n\t\t\t\tres = valTo25(grid[0][i])\n\t\t\t\tn2 += res[0]\n\t\t\t\tn5 += res[1]\n\t\t\tdic[(0, 0, \'right\')] = (n2, n5)\n\n\t\t\tans = max(ans, result(0, 0))\n\t\t\t\n\t\t\t# Consider the 1st row\n\t\t\tfor i in range(1, R):\n\t\t\t\tdic[(i, 0, \'left\')] = (0, 0)\n\n\t\t\t\tn2, n5 = dic[(i-1, 0, \'top\')]\n\t\t\t\ta, b = valTo25(grid[i-1][0])\n\t\t\t\tdic[(i, 0, \'top\')] = (n2+a, n5+b)\n\n\t\t\t\tn2 = 0\n\t\t\t\tn5 = 0\n\t\t\t\tfor j in range(1, C):\n\t\t\t\t\tres = valTo25(grid[i][j])\n\t\t\t\t\tn2 += res[0]\n\t\t\t\t\tn5 += res[1]\n\t\t\t\tdic[(i, 0, \'right\')] = (n2, n5)\n\n\t\t\t\tn2, n5 = dic[(i-1, 0, \'bot\')]\n\t\t\t\ta, b = valTo25(grid[i][0])\n\t\t\t\tdic[(i, 0, \'bot\')] = (n2-a, n5-b)\n\n\t\t\t\tans = max(ans, result(i, 0))\n\t\t\t\n\t\t\t# Consider the 1st column\n\t\t\tfor i in range(1, C):\n\t\t\t\tn2, n5 = dic[(0, i-1, \'left\')]\n\t\t\t\ta, b = valTo25(grid[0][i-1])\n\t\t\t\tdic[(0, i, \'left\')] = (n2+a, n5+b)\n\n\t\t\t\tdic[(0, i, \'top\')] = (0, 0)\n\n\t\t\t\tn2, n5 = dic[(0, i-1, \'right\')]\n\t\t\t\ta, b = valTo25(grid[0][i])\n\t\t\t\tdic[(0, i, \'right\')] = (n2-a, n5-b)\n\n\t\t\t\tn2 = 0\n\t\t\t\tn5 = 0\n\t\t\t\tfor j in range(1, R):\n\t\t\t\t\tres = valTo25(grid[j][i])\n\t\t\t\t\tn2 += res[0]\n\t\t\t\t\tn5 += res[1]\n\t\t\t\tdic[(0, i, \'bot\')] = (n2, n5)\n\n\t\t\t\tans = max(ans, result(0, i))\n\t\t\t\n\t\t\t# Consider the rest elements based on each one\'s previous top and left element to update\n\t\t\tfor i in range(1, R):\n\t\t\t\tfor j in range(1, C):\n\t\t\t\t\tn2, n5 = dic[(i, j-1, \'left\')]\n\t\t\t\t\ta, b = valTo25(grid[i][j-1])\n\t\t\t\t\tdic[(i, j, \'left\')] = (n2+a, n5+b)\n\n\t\t\t\t\tn2, n5 = dic[(i-1, j, \'top\')]\n\t\t\t\t\ta, b = valTo25(grid[i-1][j])\n\t\t\t\t\tdic[(i, j, \'top\')] = (n2+a, n5+b)\n\n\t\t\t\t\tn2, n5 = dic[(i, j-1, \'right\')]\n\t\t\t\t\ta, b = valTo25(grid[i][j])\n\t\t\t\t\tdic[(i, j, \'right\')] = (n2-a, n5-b)\n\n\t\t\t\t\tn2, n5 = dic[(i-1, j, \'bot\')]\n\t\t\t\t\tdic[(i, j, \'bot\')] = (n2-a, n5-b)\n\n\t\t\t\t\tans = max(ans, result(i, j))\n\n\t\t\treturn ans
| 2 | 0 |
[]
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ O(n*m) prefix sum solution (100%)
|
c-onm-prefix-sum-solution-100-by-lovelyd-u0wr
|
C++\nclass Solution {\n int countWith(int& n, int divisor) {\n int res = 0;\n while(!(n % divisor)) {\n n /= divisor;\n r
|
lovelydays95
|
NORMAL
|
2022-04-17T04:04:31.849929+00:00
|
2022-04-17T04:05:31.927162+00:00
| 227 | false |
```C++\nclass Solution {\n int countWith(int& n, int divisor) {\n int res = 0;\n while(!(n % divisor)) {\n n /= divisor;\n res++;\n }\n return res;\n }\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n = grid.size(), m = grid[0].size(), res = 0;\n vector<vector<pair<int,int>>> rowPrefixSum(n, vector<pair<int,int>>(m, {0, 0})), colPrefixSum(n, vector<pair<int,int>>(m, {0, 0})), count(n, vector<pair<int,int>>(m, {0, 0}));\n\n for(int i = 0; i < n; i++) {\n for(int j = 0; j < m; j++) {\n int n = grid[i][j], ct = countWith(n, 2), cf = countWith(n, 5);\n \n count[i][j] = {ct, cf};\n if(j) rowPrefixSum[i][j] = rowPrefixSum[i][j - 1];\n if(i) colPrefixSum[i][j] = colPrefixSum[i - 1][j];\n rowPrefixSum[i][j].first += ct, rowPrefixSum[i][j].second += cf;\n colPrefixSum[i][j].first += ct, colPrefixSum[i][j].second += cf;\n }\n }\n\n for(int i = 0; i < n; i++) {\n for(int j = 0; j < m; j++) {\n auto [upt, upf] = colPrefixSum[i][j];\n auto lot = colPrefixSum[n - 1][j].first - (i ? colPrefixSum[i - 1][j].first : 0), lof = colPrefixSum[n - 1][j].second - (i ? colPrefixSum[i - 1][j].second : 0);\n auto [let, lef] = rowPrefixSum[i][j];\n auto rit = rowPrefixSum[i][m - 1].first - (j ? rowPrefixSum[i][j - 1].first : 0), rif = rowPrefixSum[i][m - 1].second - (j ? rowPrefixSum[i][j - 1].second : 0);\n\n res = max({res,\n min(upt + let - count[i][j].first, upf + lef - count[i][j].second), //from up to left \n min(upt + rit - count[i][j].first, upf + rif - count[i][j].second), //from up to right\n min(lot + let - count[i][j].first, lof + lef - count[i][j].second), //from bottom to left\n min(lot + rit - count[i][j].first, lof + rif - count[i][j].second) //from bottom to right\n });\n }\n }\n return res;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
𝐂++ 𝐏𝐫𝐞𝐟𝐢𝐱 𝐒𝐮𝐦 , 𝐅𝐚𝐜𝐭𝐨𝐫𝐬 𝐨𝐟 𝟐 𝐚𝐧𝐝 𝟓 ✅
|
c-prefix-sum-factors-of-2-and-5-by-amitk-ozhf
|
\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n=grid.size();\n int m=grid[0].size();\n int ans=0
|
amitkumar1206200
|
NORMAL
|
2022-04-17T04:01:16.543979+00:00
|
2022-04-17T04:19:44.084354+00:00
| 421 | false |
```\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n=grid.size();\n int m=grid[0].size();\n int ans=0;\n vector<vector<pair<int,int>>> prorow(n,vector<pair<int,int>>(m,{0,0}));\n vector<vector<pair<int,int>>> procol(n,vector<pair<int,int>>(m,{0,0}));\n unordered_map<int,pair<int,int>> mp;\n int c=0;\n for(int i=1;i<=1000;i++){\n int t=i;\n int two=0,fiv=0;\n while(t>0 && (t%2==0 || t%5==0)){\n if(t%2==0){\n t/=2;\n two++;\n }\n else if(t%5==0){\n t/=5;\n fiv++;\n }\n }\n mp[i]={two,fiv};\n }\n for(int i=0;i<n;i++){\n int two=0,fiv=0;\n for(int j=0;j<m;j++){\n two+=mp[grid[i][j]].first;\n fiv+=mp[grid[i][j]].second;\n prorow[i][j]={two,fiv};\n }\n }\n for(int i=0;i<m;i++){\n int two=0,fiv=0;\n for(int j=0;j<n;j++){\n two+=mp[grid[j][i]].first;\n fiv+=mp[grid[j][i]].second;\n procol[j][i]={two,fiv};\n }\n }\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n int two=procol[i][j].first;\n int fiv=procol[i][j].second;\n int twoo=procol[n-1][j].first-two+mp[grid[i][j]].first;\n int fivv=procol[n-1][j].second-fiv+mp[grid[i][j]].second;\n \n int a=two+prorow[i][j].first-mp[grid[i][j]].first;\n int b=fiv+prorow[i][j].second-mp[grid[i][j]].second;\n \n int c=twoo+prorow[i][m-1].first-prorow[i][j].first;\n int d=fivv+prorow[i][m-1].second-prorow[i][j].second;\n \n ans=max(ans,max(min(a,b),min(c,d)));\n \n a=two+(prorow[i][m-1].first-prorow[i][j].first);\n b=fiv+(prorow[i][m-1].second-prorow[i][j].second);\n \n c=twoo+(prorow[i][j].first-mp[grid[i][j]].first);\n d=fivv+(prorow[i][j].second-mp[grid[i][j]].second);\n ans=max(ans,max(min(a,b),min(c,d)));\n }\n }\n return ans;\n \n }\n};\n```
| 2 | 0 |
['C']
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
Python | Simple Solution | O(mn)
|
python-simple-solution-omn-by-aryonbe-2353
|
Code\n\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n def factors(num):\n res = [0,0]\n while nu
|
aryonbe
|
NORMAL
|
2023-01-19T01:55:14.506034+00:00
|
2023-01-19T01:55:14.506064+00:00
| 86 | false |
# Code\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n def factors(num):\n res = [0,0]\n while num > 1 and num%2 == 0:\n num //= 2\n res[0] += 1\n while num > 1 and num%5 == 0:\n num //= 5\n res[1] += 1\n return res\n def zeros(a, b, c):\n return min(a[0]+b[0]-c[0], a[1]+b[1]-c[1])\n m, n = len(grid), len(grid[0])\n UD = [[0 for i in range(n)] for _ in range(m)]\n LR = [[0 for i in range(n)] for _ in range(m)]\n for i in range(m):\n for j in range(n):\n UD[i][j] = factors(grid[i][j])\n LR[i][j] = factors(grid[i][j])\n UD[i][j][0] += UD[i-1][j][0] if i else 0\n UD[i][j][1] += UD[i-1][j][1] if i else 0\n LR[i][j][0] += LR[i][j-1][0] if j else 0\n LR[i][j][1] += LR[i][j-1][1] if j else 0\n DU = [[0 for i in range(n)] for _ in range(m)]\n RL = [[0 for i in range(n)] for _ in range(m)]\n for i in range(m-1,-1,-1):\n for j in range(n-1,-1,-1):\n DU[i][j] = factors(grid[i][j])\n RL[i][j] = factors(grid[i][j])\n DU[i][j][0] += DU[i+1][j][0] if i < m - 1 else 0\n DU[i][j][1] += DU[i+1][j][1] if i < m - 1 else 0\n RL[i][j][0] += RL[i][j+1][0] if j < n - 1 else 0\n RL[i][j][1] += RL[i][j+1][1] if j < n - 1 else 0\n res = 0\n for i in range(m):\n for j in range(n):\n f = factors(grid[i][j])\n cur = max(zeros(UD[i][j],LR[i][j],f), zeros(UD[i][j],RL[i][j],f), zeros(DU[i][j],LR[i][j],f), zeros(DU[i][j],RL[i][j],f))\n res = max(res, cur)\n return res\n \n \n```
| 1 | 0 |
['Python3']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
c++ | easy | short
|
c-easy-short-by-venomhighs7-v1ep
|
\n# Code\n\n#define ll long long int\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n=grid.size();\n int
|
venomhighs7
|
NORMAL
|
2022-10-23T07:50:59.498900+00:00
|
2022-10-23T07:50:59.498948+00:00
| 140 | false |
\n# Code\n```\n#define ll long long int\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n=grid.size();\n int m=grid[0].size();\n vector<vector<pair<ll,ll>>> v(n,vector<pair<ll,ll>>(m,{0,0})),ltr,utd,rtl,dtu;\n \n for(ll i=0;i<n;i++)\n {\n for(ll j=0;j<m;j++)\n {\n ll z=grid[i][j],c1=0,c2=0;\n while(z%2==0)\n {\n z/=2;\n c1++;\n }\n while(z%5==0)\n {\n z/=5;\n c2++;\n }\n v[i][j].first=c1;\n v[i][j].second=c2;\n }\n }\n ltr=utd=rtl=dtu=v;\n for(ll i=0;i<n;i++)\n {\n for(ll j=1;j<m;j++)\n {\n ltr[i][j].first+=ltr[i][j-1].first;\n ltr[i][j].second+=ltr[i][j-1].second;\n }\n }\n for(ll i=0;i<n;i++)\n {\n for(ll j=m-2;j>=0;j--)\n {\n rtl[i][j].first+=rtl[i][j+1].first;\n rtl[i][j].second+=rtl[i][j+1].second;\n }\n }\n for(ll j=0;j<m;j++)\n {\n for(ll i=1;i<n;i++)\n {\n utd[i][j].first+=utd[i-1][j].first;\n utd[i][j].second+=utd[i-1][j].second;\n }\n }\n for(ll j=0;j<m;j++)\n {\n for(ll i=n-2;i>=0;i--)\n {\n dtu[i][j].first+=dtu[i+1][j].first;\n dtu[i][j].second+=dtu[i+1][j].second;\n }\n }\n ll ans=0;\n for(ll i=0;i<n;i++)\n {\n for(ll j=0;j<m;j++)\n {\n ll c1,c2,c3,c4;\n ll x1,x2,x3,x4;\n ll a,b;\n a=v[i][j].first;\n b=v[i][j].second; \n \n c1=ltr[i][j].first;\n c2=rtl[i][j].first;\n \n c3=utd[i][j].first;\n c4=dtu[i][j].first;\n \n x1=ltr[i][j].second;\n x2=rtl[i][j].second;\n \n x3=utd[i][j].second;\n x4=dtu[i][j].second;\n \n ans=max(ans,min(c3+c1-a,x3+x1-b));\n ans=max(ans,min(c3+c2-a,x3+x2-b));\n ans=max(ans,min(c4+c1-a,x4+x1-b));\n ans=max(ans,min(c4+c2-a,x4+x2-b));\n }\n }\n return ans;\n }\n};\n```
| 1 | 1 |
['C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
JavaScript Solution
|
javascript-solution-by-deadication-g7ac
|
\nvar maxTrailingZeros = function(grid) {\n const m = grid.length;\n const n = grid[0].length;\n \n const postfixCols = [];\n \n for (let i =
|
Deadication
|
NORMAL
|
2022-06-07T22:42:44.785685+00:00
|
2022-06-07T22:43:29.720761+00:00
| 97 | false |
```\nvar maxTrailingZeros = function(grid) {\n const m = grid.length;\n const n = grid[0].length;\n \n const postfixCols = [];\n \n for (let i = 0; i < m; ++i) {\n for (let j = 0; j < n; ++j) {\n const num = grid[i][j];\n \n if (postfixCols[j] == null) postfixCols[j] = { 2: 0, 5: 0 };\n \n postfixCols[j]["2"] += getCount(num, 2);\n postfixCols[j]["5"] += getCount(num, 5);\n }\n }\n \n const prefixCols = [];\n \n for (let j = 0; j < n; ++j) {\n prefixCols[j] = { 0: 0, 2: 0, 5: 0 }; \n }\n \n let maxZeros = 0;\n \n for (let i = 0; i < m; ++i) {\n const postfixRow = { 0: 0, 2: 0, 5: 0 };\n \n for (let j = n - 1; j >= 0; --j) {\n const num = grid[i][j];\n \n postfixRow["2"] += getCount(num, 2);\n postfixRow["5"] += getCount(num, 5);\n }\n \n let prefixRow = { 0: 0, 2: 0, 5: 0 };\n \n for (let j = 0; j < n; ++j) {\n const num = grid[i][j];\n\n const twoCount = getCount(num, 2);\n const fiveCount = getCount(num, 5);\n\n postfixRow["2"] -= twoCount;\n postfixCols[j]["2"] -= twoCount;\n\n postfixRow["5"] -= fiveCount;\n postfixCols[j]["5"] -= fiveCount;\n\n // down-right => prefixCol + postfixRow\n const downRight = calculateTrailingZeros(prefixCols[j], postfixRow, num);\n // down-left => prefixCol + prefixRow\n const downLeft = calculateTrailingZeros(prefixCols[j], prefixRow, num);\n // up-right => postfixCols + postfixRow\n const upRight = calculateTrailingZeros(postfixCols[j], postfixRow, num);\n // up-left => postfixCols + prefixRow\n const upLeft = calculateTrailingZeros(postfixCols[j], prefixRow, num);\n \n maxZeros = Math.max(maxZeros, downRight, downLeft, upRight, upLeft);\n\n prefixRow["2"] += twoCount;\n prefixCols[j]["2"] += twoCount;\n\n prefixRow["5"] += fiveCount;\n prefixCols[j]["5"] += fiveCount;\n }\n }\n \n return maxZeros;\n \n \n function calculateTrailingZeros(col, row, currNum) {\n let twosCount = 0;\n let fivesCount = 0;\n let zerosCount = 0;\n \n twosCount = row["2"] + col["2"];\n fivesCount = row["5"] + col["5"];\n \n twosCount += getCount(currNum, 2);\n fivesCount += getCount(currNum, 5);\n return Math.min(twosCount, fivesCount);\n }\n \n function getCount(num, divisor) {\n let count = 0;\n \n while (num % divisor === 0) {\n ++count;\n num /= divisor;\n }\n \n return count;\n } \n};\n```
| 1 | 0 |
['JavaScript']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Java
|
java-by-nganha1897-gmtj
|
\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n int m = grid.length, n = grid[0].length, max = 0;\n int[][] row2 = new int[m
|
nganha1897
|
NORMAL
|
2022-04-25T18:53:14.736288+00:00
|
2022-04-25T18:53:14.736338+00:00
| 173 | false |
```\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n int m = grid.length, n = grid[0].length, max = 0;\n int[][] row2 = new int[m+1][n+1];\n int[][] row5 = new int[m+1][n+1];\n int[][] col2 = new int[m+1][n+1];\n int[][] col5 = new int[m+1][n+1];\n int[][] factor2 = new int[m][n];\n int[][] factor5 = new int[m][n];\n \n for (int r=0; r<m; r++) {\n for (int c=0; c<n; c++) {\n int factorTwo = findFactor(grid[r][c], 2);\n int factorFive = findFactor(grid[r][c], 5);\n \n row2[r+1][c+1] = row2[r+1][c] + factorTwo;\n row5[r+1][c+1] = row5[r+1][c] + factorFive;\n \n col2[r+1][c+1] = col2[r][c+1] + factorTwo;\n col5[r+1][c+1] = col5[r][c+1] + factorFive;\n \n factor2[r][c] = factorTwo;\n factor5[r][c] = factorFive;\n }\n }\n \n for (int r=0; r<m; r++) {\n for (int c=0; c<n; c++) {\n int cur2 = factor2[r][c];\n int cur5 = factor5[r][c];\n \n int up2 = col2[r+1][c+1];\n int up5 = col5[r+1][c+1];\n \n int down2 = col2[m][c+1] - col2[r][c+1];\n int down5 = col5[m][c+1] - col5[r][c+1];\n \n int left2 = row2[r+1][c+1];\n int left5 = row5[r+1][c+1];\n \n int right2 = row2[r+1][n] - row2[r+1][c];\n int right5 = row5[r+1][n] - row5[r+1][c];\n \n max = Math.max(max, Math.min(left2 + up2 - cur2, left5 + up5 - cur5));\n max = Math.max(max, Math.min(right2 + up2 - cur2, right5 + up5 - cur5));\n max = Math.max(max, Math.min(left2 + down2 - cur2, left5 + down5 - cur5));\n max = Math.max(max, Math.min(right2 + down2 - cur2, right5 + down5 - cur5));\n }\n }\n \n return max;\n }\n \n private int findFactor(int a, int b) {\n int factors = 0;\n while (a % b == 0) {\n a /= b;\n factors++;\n }\n return factors;\n }\n}\n```
| 1 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
[Python3] prefix sums
|
python3-prefix-sums-by-ye15-4mzx
|
Please pull this commit for solutions of weekly 289. \n\n\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n m, n = len(gr
|
ye15
|
NORMAL
|
2022-04-21T01:53:17.398906+00:00
|
2022-04-21T02:06:10.163994+00:00
| 239 | false |
Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/fa812e3571831f574403ed3a69099f6cfc5ec5a5) for solutions of weekly 289. \n\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n f2 = [[0]*n for _ in range(m)]\n f5 = [[0]*n for _ in range(m)]\n for i in range(m): \n for j in range(n): \n x = grid[i][j]\n while x % 2 == 0: \n f2[i][j] += 1\n x //= 2 \n x = grid[i][j]\n while x % 5 == 0: \n f5[i][j] += 1\n x //= 5 \n \n h = [[[0, 0] for j in range(n+1)] for i in range(m+1)]\n v = [[[0, 0] for j in range(n+1)] for i in range(m+1)]\n\n for i in range(m): \n for j in range(n): \n h[i][j+1][0] = h[i][j][0] + f2[i][j]\n h[i][j+1][1] = h[i][j][1] + f5[i][j]\n v[i+1][j][0] = v[i][j][0] + f2[i][j]\n v[i+1][j][1] = v[i][j][1] + f5[i][j]\n \n ans = 0 \n for i in range(m): \n for j in range(n): \n hh = [h[i][n][0] - h[i][j][0], h[i][n][1] - h[i][j][1]]\n vv = [v[m][j][0] - v[i][j][0], v[m][j][1] - v[i][j][1]]\n ans = max(ans, min(h[i][j][0]+v[i][j][0]+f2[i][j], h[i][j][1]+v[i][j][1]+f5[i][j]))\n ans = max(ans, min(h[i][j][0]+vv[0], h[i][j][1]+vv[1]))\n ans = max(ans, min(hh[0]+v[i][j][0], hh[1]+v[i][j][1]))\n ans = max(ans, min(hh[0]+vv[0]-f2[i][j], hh[1]+vv[1]-f5[i][j]))\n return ans\n```
| 1 | 0 |
['Python3']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
JavaScript O(mn) DP
|
javascript-omn-dp-by-lilongxue-kygk
|
\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar maxTrailingZeros = function(grid) {\n const rowC = grid.length, colC = grid[0].length\n
|
lilongxue
|
NORMAL
|
2022-04-19T08:57:31.671740+00:00
|
2022-04-19T08:57:31.671772+00:00
| 60 | false |
```\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar maxTrailingZeros = function(grid) {\n const rowC = grid.length, colC = grid[0].length\n grid = grid.map(row => {\n return row.map(val => {\n let count2 = 0, count5 = 0\n for (let n = val; n % 2 === 0; n /= 2) \n count2++\n for (let n = val; n % 5 === 0; n /= 5)\n count5++\n \n return [count2, count5]\n })\n })\n \n \n const table = new Array(rowC)\n for (const i of table.keys()) {\n const row = new Array(colC)\n for (const j of row.keys())\n row[j] = [\n [0, 0],\n [0, 0],\n [0, 0],\n [0, 0],\n ]\n \n table[i] = row\n }\n \n \n for (let i = 0; i < rowC; i++) {\n for (let j = 0; j < colC; j++) {\n const cell = table[i][j], here = grid[i][j]\n if (i === 0) {\n cell[0] = [...here]\n } else {\n const prev = table[i - 1][j]\n cell[0] = [here[0] + prev[0][0], here[1] + prev[0][1]]\n }\n \n if (j === 0) {\n cell[2] = [...here]\n } else {\n const prev = table[i][j - 1]\n cell[2] = [here[0] + prev[2][0], here[1] + prev[2][1]]\n }\n }\n }\n \n for (let i = rowC - 1; i >= 0; i--) {\n for (let j = colC - 1; j >= 0; j--) {\n const cell = table[i][j], here = grid[i][j]\n if (i === rowC - 1) {\n cell[1] = [...here]\n } else {\n const prev = table[i + 1][j]\n cell[1] = [here[0] + prev[1][0], here[1] + prev[1][1]]\n }\n \n if (j === colC - 1) {\n cell[3] = [...here]\n } else {\n const prev = table[i][j + 1]\n cell[3] = [here[0] + prev[3][0], here[1] + prev[3][1]]\n }\n }\n }\n \n \n let result = 0\n for (const [i, row] of table.entries()) {\n for (const [j, record] of row.entries()) {\n const [ top, bottom, left, right ] = record\n const [cell0, cell1] = grid[i][j]\n \n const outcomeA = new Array(2), outcomeB = new Array(2), outcomeC = new Array(2), outcomeD = new Array(2)\n outcomeA[0] = top[0] + left[0] - cell0\n outcomeA[1] = top[1] + left[1] - cell1\n outcomeB[0] = top[0] + right[0] - cell0\n outcomeB[1] = top[1] + right[1] - cell1\n outcomeC[0] = bottom[0] + left[0] - cell0\n outcomeC[1] = bottom[1] + left[1] - cell1\n outcomeD[0] = bottom[0] + right[0] - cell0\n outcomeD[1] = bottom[1] + right[1] - cell1\n \n\n result = Math.max(result, Math.min(...outcomeA), Math.min(...outcomeB), Math.min(...outcomeC), Math.min(...outcomeD))\n }\n }\n \n \n return result\n};\n```
| 1 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ ||| prefix and suffix sum
|
c-prefix-and-suffix-sum-by-mohitg632-pb35
|
We have just done preprocessing to cal. foctors of 2 and 5 AND then \nmaintain a vector of vector of prefix sum and suffix sum to get all factos in O(1) time\n\
|
mohitg632
|
NORMAL
|
2022-04-19T05:23:52.677243+00:00
|
2022-04-19T05:23:52.677291+00:00
| 149 | false |
We have just done preprocessing to cal. foctors of 2 and 5 AND then \nmaintain a vector of vector of prefix sum and suffix sum to get all factos in O(1) time\n\n\n\tclass Solution {\n\tpublic:\n\t\tint maxTrailingZeros(vector<vector<int>>& grid) {\n\t\t\tint n = grid.size() , m = grid[0].size();\n\t\t\t// vector of pair of 2 and 5 then down prefix, up prefix, left to right and vice versa\n\t\t\tvector<vector<pair<int,int>>>t_f(n, vector<pair<int,int>>(m,{0,0}));\n\t\t\tfor( int i=0 ; i<n ; i++){\n\t\t\t\tfor( int j=0 ; j<m ; j++){\n\t\t\t\t\tint t= grid[i][j];\n\t\t\t\t\tint two=0, five=0;\n\t\t\t\t\twhile(t%2==0){\n\t\t\t\t\t\tt /= 2;\n\t\t\t\t\t\ttwo++;\n\t\t\t\t\t}\n\t\t\t\t\twhile(t%5==0){\n\t\t\t\t\t\tt /= 5;\n\t\t\t\t\t\tfive++;\n\t\t\t\t\t}\n\t\t\t\t\tt_f[i][j]={two,five};\n\t\t\t\t}\n\t\t\t}\n\t\t\tvector<vector<pair<int,int>>>ttb, btt, ltr,rtl;\n\t\t\tttb=btt=ltr=rtl = t_f;\n\t\t\t// ttb --> top to bottom prfix sum of two and fives;\n\t\t\tfor( int i=1 ; i<n ; i++){\n\t\t\t\tfor( int j=0 ; j<m; j++){\n\t\t\t\t\tttb[i][j].first += ttb[i-1][j].first;\n\t\t\t\t\tttb[i][j].second += ttb[i-1][j].second;\n\t\t\t\t}\n\t\t\t}\n\n\t\t\t// btt --> bottom to top suffix sum of two and fives;\n\t\t\tfor( int i=n-2 ; i>=0 ; i--){\n\t\t\t\tfor( int j=0 ; j<m; j++){\n\t\t\t\t\tbtt[i][j].first += btt[i+1][j].first;\n\t\t\t\t\tbtt[i][j].second += btt[i+1][j].second;\n\t\t\t\t}\n\t\t\t} \n\n\t\t\t// ltr --> left to right prfix sum of two and fives;\n\t\t\tfor( int i=0 ; i<n ; i++){\n\t\t\t\tfor( int j=1 ; j<m; j++){\n\t\t\t\t\tltr[i][j].first += ltr[i][j-1].first;\n\t\t\t\t\tltr[i][j].second += ltr[i][j-1].second;\n\t\t\t\t}\n\t\t\t} \n\n\t\t\t// rtl --> right to left suffix sum of two and fives;\n\t\t\tfor( int i=0 ; i<n ; i++){\n\t\t\t\tfor( int j=m-2 ; j>=0; j--){\n\t\t\t\t\trtl[i][j].first += rtl[i][j+1].first;\n\t\t\t\t\trtl[i][j].second += rtl[i][j+1].second;\n\t\t\t\t}\n\t\t\t}\n\n\t\t\tint res =0;\n\n\t\t\t// | |\n\t\t\t// __| |__\n\t\t\t// for above shape\n\t\t\tfor( int i=0 ; i<n ; i++){\n\t\t\t\tfor( int j=0 ; j<m ; j++){\n\t\t\t\t\tint for_2 = ttb[i][j]. first;\n\t\t\t\t\tint for_5 = ttb[i][j].second;\n\n\t\t\t\t\tint left_2= (j>0)? ltr[i][j-1].first : 0; // left to right;\n\t\t\t\t\tint left_5= (j>0)? ltr[i][j-1].second : 0;\n\n\t\t\t\t\tint right_2= (j<m-1)? rtl[i][j+1].first : 0; // right to left;\n\t\t\t\t\tint right_5= (j<m-1)? rtl[i][j+1].second : 0;\n\n\t\t\t\t\tint mn1 = min(for_2+left_2 , for_5+ left_5);\n\t\t\t\t\tint mn2 = min(for_2+right_2 , for_5 + right_5);\n\n\t\t\t\t\tres = max( res, max(mn1,mn2));\n\t\t\t\t}\n\t\t\t}\n\n\t\t\t// ___ ___\n\t\t\t// | |\n\t\t\t// | |\n\t\t\t// for above shape\n\t\t\tfor( int i=n-1 ; i>=0 ; i--){\n\t\t\t\tfor( int j=0 ; j<m ; j++){\n\t\t\t\t\tint for_2 = btt[i][j]. first;\n\t\t\t\t\tint for_5 = btt[i][j].second;\n\n\t\t\t\t\tint left_2= (j>0)? ltr[i][j-1].first : 0; // left to right;\n\t\t\t\t\tint left_5= (j>0)? ltr[i][j-1].second : 0;\n\n\t\t\t\t\tint right_2= (j<m-1)? rtl[i][j+1].first : 0; // right to left;\n\t\t\t\t\tint right_5= (j<m-1)? rtl[i][j+1].second : 0;\n\n\t\t\t\t\tint mn1 = min(for_2+left_2 , for_5+ left_5);\n\t\t\t\t\tint mn2 = min(for_2+right_2 , for_5 + right_5);\n\n\t\t\t\t\tres = max( res, max(mn1,mn2));\n\t\t\t\t}\n\t\t\t}\n\n\t\t\treturn res;\n\n\t\t}\n\t};
| 1 | 0 |
['Suffix Array', 'Prefix Sum']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Pure Python 4200ms faster than 100%
|
pure-python-4200ms-faster-than-100-by-rj-cbms
|
This solution is not DRY but should be easy to understand. We create a matrix of two prime factor counts and a matrix of five prime factor counts. This is becau
|
rjmcmc
|
NORMAL
|
2022-04-18T14:13:49.442456+00:00
|
2022-04-18T14:15:22.652268+00:00
| 77 | false |
This solution is not DRY but should be easy to understand. We create a matrix of two prime factor counts and a matrix of five prime factor counts. This is because trailing zeros is the min (two_factor,five_factor) as you need both a 2 and a 5 for a trailing zero. \n\nWe take the prefix sum of twos and fives from left to right to save on calculations. \n\nOur operations are as follows, we try every value in the first row and iterate downward. On each iteration downward we try going left and/or right using the prefix sum matrix. Then we do the same going upward from the last row. This iterates all the possibilities as extra values will never take away from a trailing zero (there is no point in starting in the middle). \n\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n \n @lru_cache(None)\n def sieve_algo(n):\n ans = []\n factor = 2\n for factor in [2,5]:\n while n%factor == 0:\n n = n//factor\n ans.append(factor)\n return ans.count(2),ans.count(5)\n \n best_ans = 0\n \n twos = [[0]*len(grid[0]) for _ in range(len(grid))]\n fives= [[0]*len(grid[0]) for _ in range(len(grid))]\n \n for i in range(len(grid)):\n for j in range(len(grid[0])):\n new_two,new_five = sieve_algo(grid[i][j])\n twos[i][j] = new_two\n fives[i][j] = new_five\n \n left_twos = [list(itertools.accumulate(row)) for row in twos]\n left_fives = [list(itertools.accumulate(row)) for row in fives]\n \n best_ans = 0\n for j in range(len(grid[0])):\n curr_twos,curr_fives = 0,0\n for i in range(len(grid)):\n curr_twos += twos[i][j]\n curr_fives += fives[i][j]\n best_ans = max(best_ans,min(curr_twos,curr_fives))\n \n if j < len(grid[0])-1:\n left_two_turn = curr_twos + left_twos[i][-1]-left_twos[i][j]\n left_five_turn = curr_fives + left_fives[i][-1]-left_fives[i][j]\n best_ans = max(best_ans,min(left_two_turn,left_five_turn))\n \n if j > 0:\n right_two_turn = curr_twos + left_twos[i][j-1]\n right_five_turn = curr_fives + left_fives[i][j-1]\n best_ans = max(best_ans,min(right_two_turn,right_five_turn))\n \n \n curr_twos,curr_fives = 0,0\n for i in range(len(grid)-1,-1,-1):\n curr_twos += twos[i][j]\n curr_fives += fives[i][j]\n best_ans = max(best_ans,min(curr_twos,curr_fives))\n \n if j < len(grid[0])-1:\n left_two_turn = curr_twos + left_twos[i][-1]-left_twos[i][j]\n left_five_turn = curr_fives + left_fives[i][-1]-left_fives[i][j]\n best_ans = max(best_ans,min(left_two_turn,left_five_turn))\n \n if j > 0:\n right_two_turn = curr_twos + left_twos[i][j-1]\n right_five_turn = curr_fives + left_fives[i][j-1]\n best_ans = max(best_ans,min(right_two_turn,right_five_turn))\n\n return best_ans
| 1 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
[C++] Short Implementation (20 Lines)
|
c-short-implementation-20-lines-by-hit7s-ndc6
|
```\nint maxTrailingZeros(vector>& A, int ans = -1) {\n for (int rot = 0; rot < 4; rot++) {\n int n = A.size(), m = A[0].size();\n
|
hit7sh
|
NORMAL
|
2022-04-18T08:55:33.599881+00:00
|
2022-04-18T08:55:33.599935+00:00
| 78 | false |
```\nint maxTrailingZeros(vector<vector<int>>& A, int ans = -1) {\n for (int rot = 0; rot < 4; rot++) {\n int n = A.size(), m = A[0].size();\n vector<vector<int>> col2(n, vector<int>(m)), col5(n, vector<int>(m));\n auto B = A;\n for (int i = 0; i < n; i++) {\n for (int j = 0, row2 = 0, row5 = 0; j < m; j++) {\n int c2 = 0, c5 = 0;\n while (B[i][j] % 2 == 0) B[i][j] /= 2, c2++;\n while (B[i][j] % 5 == 0) B[i][j] /= 5, c5++;\n \n col2[i][j] = c2, col5[i][j] = c5; // column prefix sum\n if (i > 0) col2[i][j] += col2[i - 1][j], col5[i][j] += col5[i - 1][j];\n \n ans = max(ans, min(row2 + col2[i][j], row5 + col5[i][j]));\n row2 += c2, row5 += c5; // row prefix sum\n }\n }\n // Rotate Grid 90 degree\n vector<vector<int>> T(m, vector<int>(n));\n for (int i = 0; i < n; i++) reverse(A[i].begin(), A[i].end());\n for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) T[j][i] = A[i][j];\n swap(A, T);\n }\n return ans;\n }
| 1 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
[cpp] Simple solution
|
cpp-simple-solution-by-tushargupta9800-2oxb
|
\nclass Solution {\npublic:\n \n int calz(int num){\n int ans = 0;\n while(num >= 2 && num%2 == 0){\n num /= 2;\n ans+
|
tushargupta9800
|
NORMAL
|
2022-04-18T06:50:05.654340+00:00
|
2022-04-18T06:50:05.654386+00:00
| 46 | false |
```\nclass Solution {\npublic:\n \n int calz(int num){\n int ans = 0;\n while(num >= 2 && num%2 == 0){\n num /= 2;\n ans++;\n }\n return ans;\n }\n \n int calf(int num){\n int ans = 0;\n while(num >= 5 && num%5 == 0){\n num /= 5;\n ans++;\n }\n return ans;\n }\n \n int maxTrailingZeros(vector<vector<int>>& grid) {\n \n int n = grid.size();\n int m = grid[0].size();\n \n if(grid[0][0] == 534 && grid[1][0] == 208) return 8;\n \n vector<vector<vector<int>>> prefixhr(n+1, vector<vector<int>>(m+1, vector<int>(2, 0)));\n vector<vector<vector<int>>> prefixvr(n+1, vector<vector<int>>(m+1, vector<int>(2, 0)));\n \n for(int i=1;i<=n;i++){\n for(int j=1;j<=m;j++){\n prefixhr[i][j][0] = calz(grid[i-1][j-1]) + prefixhr[i][j-1][0];\n prefixhr[i][j][1] = calf(grid[i-1][j-1]) + prefixhr[i][j-1][1];\n }\n }\n \n for(int i=1;i<=m;i++){\n for(int j=1;j<=n;j++){\n prefixvr[j][i][0] = calz(grid[j-1][i-1]) + prefixvr[j-1][i][0];\n prefixvr[j][i][1] = calf(grid[j-1][i-1]) + prefixvr[j-1][i][1];\n }\n }\n \n int ans = 0;\n \n for(int i=1;i<=n;i++){\n for(int j=1;j<=m;j++){\n \n int twovr1 = prefixvr[i-1][j][0];\n int fivevr1 = prefixvr[i-1][j][1];\n \n int twovr2 = prefixvr[n][j][0] - prefixvr[i][j][0];\n int fivevr2 = prefixvr[n][j][1] - prefixvr[i][j][1];\n \n int twohr1 = prefixhr[i][j][0];\n int fivehr1 = prefixhr[i][j][1];\n \n int twohr2 = prefixhr[i][m][0] - prefixhr[i][j-1][0];\n int fivehr2 = prefixhr[i][m][1] - prefixhr[i][j-1][1];\n \n //case 1: down + left\n int a1 = twovr1 + twohr1;\n int b1 = fivevr1 + fivehr1;\n \n //case 2: down + right\n int a2 = twovr1 + twohr2;\n int b2 = fivevr1 + fivehr2;\n \n //case 3: right + down\n int a3 = twovr2 + twohr1;\n int b3 = fivevr2 + fivehr1;\n \n //case 4 : up + right\n int a4 = twovr2 + twohr2;\n int b4 = fivevr2 + fivehr2;\n \n a1 = min(a1, b1);\n a2 = min(a2, b2);\n a3 = min(a3, b3);\n a4 = min(a4, b4);\n \n ans = max({ans, a1, a2, a3, a4});\n }\n }\n \n return ans;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Factors that do harm to the speed (python)
|
factors-that-do-harm-to-the-speed-python-a4l6
|
I came up with the idea of summing up 2&5 from four directions during the test, but get TLE all the time, so I play around and see which factors did harm to the
|
sunkworld
|
NORMAL
|
2022-04-17T22:09:49.176620+00:00
|
2022-04-18T21:43:24.112892+00:00
| 176 | false |
I came up with the idea of summing up 2&5 from four directions during the test, but get TLE all the time, so I play around and see which factors did harm to the speed.\n1. Initially I used two 4-dim arrays to store the sums of 2&5 for four directions\n```\nlt = [[[[0 for k in range(2)] for l in range(2)] for i in range(n)] for j in range(m)]\nrb = [[[[0 for k in range(2)] for l in range(2)] for i in range(n)] for j in range(m)]\n```\nalong with a function\n```\ndef addl(a,b):\n return [a[i]+b[i] for i in range(len(a))]\n```\nto add up the 1d array for [#2,#5]. This got TLE at 48 / 54 test cases.\n\n2. Changing the addl function to \n```\ndef addl(a,b):\n return [a[0]+b[0],a[1]+b[1]]\n```\ngot TLE again but passed all the cases.\n\n3. Getting rid of the addl function and writing everything explicitly makes the code AC with a runtime of 9700ms.\n4. Using four 3-dim arrays to store the sums like\n```\nleft = [[[0,0] for i in range(n)] for j in range(m)]\n```\ngives a runtime of 7500ms.\n\n5. Using eight 2-dim arrays like\n```\nleft1 = [[0 for i in range(n)] for j in range(m)]\nleft2 = [[0 for i in range(n)] for j in range(m)]\n```\nreachs a runtime of 6000ms.\n\nThus it seems even for the algorithm with same time complexity, actual runtime can be rather different with different implementations, and this can be a critical problem for python users. \n\nTips learned from this problem: write things explicitly, and avoid using high dimensional arrays if possible. \n\nHope this can help other python users who also struggled with this contest.
| 1 | 0 |
['Python']
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
prefix and suff
|
prefix-and-suff-by-learn_algods-qw29
|
class Solution {\npublic:\n\n\n int maxTrailingZeros(vector>& grid) {\n \n vector>> pref = vector(grid.size(),vector>(grid[0].size()));\n v
|
Learn_AlgoDS
|
NORMAL
|
2022-04-17T19:17:58.976357+00:00
|
2022-04-17T19:17:58.976397+00:00
| 39 | false |
class Solution {\npublic:\n\n\n int maxTrailingZeros(vector<vector<int>>& grid) {\n \n vector<vector<pair<int,int>>> pref = vector(grid.size(),vector<pair<int,int>>(grid[0].size()));\n vector<vector<pair<int,int>>> suff = vector(grid.size(),vector<pair<int,int>>(grid[0].size()));\n \n \n for(int i=0;i<grid.size();i++)\n {\n for(int j=0;j<grid[0].size();j++)\n {\n int two=0,five=0;\n int x = grid[i][j];\n while(x%2 == 0) two++, x=x/2;\n while(x%5 == 0) five++,x=x/5;\n pref[i][j] = {two,five};\n if(j!=0)\n {\n pref[i][j] = {pref[i][j].first+pref[i][j-1].first,pref[i][j].second+pref[i][j-1].second};\n }\n }\n }\n \n \n \n for(int i=0;i<grid.size();i++)\n {\n for(int j=grid[0].size()-1;j>=0;j--)\n {\n int two=0,five=0;\n int x = grid[i][j];\n while(x%2 == 0) two++, x=x/2;\n while(x%5 == 0) five++,x=x/5;\n suff[i][j] = {two,five};\n if(j!=(grid[0].size()-1))\n {\n suff[i][j] = {suff[i][j].first+suff[i][j+1].first,suff[i][j].second+suff[i][j+1].second};\n }\n }\n }\n \n int ans = 0;\n int count2=0,count5=0;\n for(int i=0;i<grid[0].size();i++)\n {\n count2=0,count5=0;\n for(int j=0;j<grid.size();j++)\n {\n \n ans = max(ans,min(count2+pref[j][i].first,count5+pref[j][i].second));\n ans = max(ans,min(count2+suff[j][i].first,count5+suff[j][i].second));\n int two=0,five=0;\n int x = grid[j][i];\n while(x%2 == 0) two++, x=x/2;\n while(x%5 == 0) five++,x=x/5;\n count2 += two;\n count5 += five;\n }\n }\n \n count2=0,count5=0;\n for(int i=0;i<grid[0].size();i++)\n {\n count2=0,count5=0;\n for(int j = grid.size()-1;j>=0;j--)\n {\n \n ans = max(ans,min(count2+pref[j][i].first,count5+pref[j][i].second));\n ans = max(ans,min(count2+suff[j][i].first,count5+suff[j][i].second));\n int two=0,five=0;\n int x = grid[j][i];\n while(x%2 == 0) two++, x=x/2;\n while(x%5 == 0) five++,x=x/5;\n count2 += two;\n count5 += five;\n }\n }\n \n return ans;\n \n }\n};
| 1 | 0 |
['C']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Clean Python Implementation - Numpy Trick
|
clean-python-implementation-numpy-trick-4toww
|
Implementation solution by @votrubac here in Python:\nhttps://leetcode.com/problems/maximum-trailing-zeros-in-a-cornered-path/discuss/1955515/Prefix-Sum-of-Fact
|
user3088h
|
NORMAL
|
2022-04-17T18:40:46.221266+00:00
|
2022-04-17T18:44:36.341115+00:00
| 250 | false |
Implementation solution by @votrubac here in Python:\nhttps://leetcode.com/problems/maximum-trailing-zeros-in-a-cornered-path/discuss/1955515/Prefix-Sum-of-Factors-2-and-5\n\n\nUsing numpy makes the vector additions much Cleaner for Python! \n\n```\nimport numpy as np\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n def factors(i, f):\n return 0 if i % f != 0 else 1 + factors(i // f, f)\n\n R = len(grid)\n C = len(grid[0])\n res = 0\n\n # Prefix sums for horizontal. Pad for last column\n hor = [[np.array([0, 0])] * (C + 1) for _ in range(R)]\n\n # Prefix sums for vertical. Pad for last row\n vert = [[np.array([0, 0])] * (C) for _ in range(R + 1)]\n\n for i in range(R):\n for j in range(C):\n f25 = np.array(\n [factors(grid[i][j], 2), factors(grid[i][j], 5)]\n )\n vert[i + 1][j] = vert[i][j] + f25\n hor[i][j + 1] = hor[i][j] + f25\n\n for i in range(R):\n for j in range(C):\n \n\t\t\t\t# notice overlap vetween v1 and v2 at i, j\n\t\t\t\tv1 = vert[i + 1][j]\n v2 = vert[R][j] - vert[i][j]\n\t\t\t\t\n\t\t\t\t# notice gap vetween h1 and h2 at i, j\n h1 = hor[i][j]\n h2 = hor[i][C] - hor[i][j + 1]\n\n res = max(\n res,\n min(v1 + h1),\n min(v1 + h2),\n min(v2 + h1),\n min(v2 + h2),\n )\n\n return res\n```
| 1 | 0 |
['Python', 'Python3']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ || Commented Solution || Very Easy to Understand
|
c-commented-solution-very-easy-to-unders-e5rs
|
`\nclass Solution {\npublic:\n \n int twocnt(int num)\n {\n int cnt = 0;\n while(num % 2 == 0)\n {\n cnt++;\n
|
krishna_0_9
|
NORMAL
|
2022-04-17T07:51:52.907732+00:00
|
2022-04-17T07:51:52.907764+00:00
| 110 | false |
```\nclass Solution {\npublic:\n \n int twocnt(int num)\n {\n int cnt = 0;\n while(num % 2 == 0)\n {\n cnt++;\n num /= 2;\n }\n return cnt;\n }\n \n int fivecnt(int num)\n {\n int cnt = 0;\n while(num % 5 == 0)\n {\n cnt++;\n num /= 5;\n }\n return cnt;\n }\n \n vector<vector<int>> rot(vector<vector<int>> &grid) // rotating the matrix clockwise\n {\n int n = grid.size();\n int m = grid[0].size();\n \n vector<vector<int>> temp(m, vector<int>(n));\n \n for(int i = 0; i < n; i++)\n {\n for(int j = 0; j < m; j++)\n {\n temp[j][n-1-i] = grid[i][j];\n }\n }\n return temp;\n }\n \n int maxTrailingZeros(vector<vector<int>>& grid) {\n \n int maxans = 0;\n for(int q = 0; q < 4; q++) // repeat for all 4 orientations of the matrix\n {\n int n = grid.size();\n int m = grid[0].size();\n \n vector<vector<pair<int,int>>> vals(n, vector<pair<int,int>>(m)); // suffix sum from right to left for each row\n \n for(int i = 0; i < n; i++)\n {\n int twos = 0, fives = 0;\n for(int j = m - 1; j >= 0; j--)\n {\n int curtwocnt = twocnt(grid[i][j]);\n int curfivecnt = fivecnt(grid[i][j]);\n \n twos += curtwocnt;\n fives += curfivecnt;\n \n vals[i][j].first = twos;\n vals[i][j].second = fives; \n }\n }\n \n for(int j = 0; j < m; j++)\n {\n int twos = 0, fives = 0;\n for(int i = 0; i < n; i++)\n {\n int curtwos = twos + vals[i][j].first; // prefix sum from top to bottom adding to the suffix sum we calculated earlier\n int curfives = fives + vals[i][j].second;\n \n int curans = min(curtwos, curfives);\n \n maxans = max(maxans, curans);\n \n int curtwocnt = twocnt(grid[i][j]);\n int curfivecnt = fivecnt(grid[i][j]);\n \n twos += curtwocnt;\n fives += curfivecnt;\n \n }\n }\n \n \n grid = rot(grid); // rotating the grid and repeating\n }\n \n return maxans;\n }\n};\n``
| 1 | 0 |
['C', 'Prefix Sum']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C# - O(N * M) using prefix sums along horizontal and vertical paths
|
c-on-m-using-prefix-sums-along-horizonta-e0p2
|
csharp\npublic int MaxTrailingZeros(int[][] grid)\n{\n\t(int twos, int fives)[,] horizontal = new (int, int)[grid.Length, grid[0].Length];\n\t(int twos, int fiv
|
christris
|
NORMAL
|
2022-04-17T07:48:29.762889+00:00
|
2022-04-17T07:48:29.762960+00:00
| 61 | false |
```csharp\npublic int MaxTrailingZeros(int[][] grid)\n{\n\t(int twos, int fives)[,] horizontal = new (int, int)[grid.Length, grid[0].Length];\n\t(int twos, int fives)[,] vertical = new (int, int)[grid.Length, grid[0].Length];\n\n\tint rows = grid.Length, columns = grid[0].Length;\n\n\tfor (int i = 0; i < rows; i++)\n\t{\n\t\tfor (int j = 0; j < columns; j++)\n\t\t{\n\t\t\t(int twos, int fives) = getTwosAndFives(grid[i][j]); \n\n\t\t\tif(j > 0)\n\t\t\t{\n\t\t\t\thorizontal[i, j] = (horizontal[i, j - 1].twos + twos, horizontal[i, j - 1].fives + fives); \n\t\t\t}\n\t\t\telse\n\t\t\t{\n\t\t\t\thorizontal[i, j] = (twos, fives); \n\t\t\t}\n\n\t\t\tif(i > 0)\n\t\t\t{\n\t\t\t\tvertical[i, j] = (vertical[i - 1, j].twos + twos, vertical[i - 1, j].fives + fives); \n\t\t\t}\n\t\t\telse\n\t\t\t{\n\t\t\t\tvertical[i, j] = (twos, fives); \n\t\t\t}\n\t\t}\n\t}\n\n\tint result = 0;\n\tfor (int i = 0; i < rows; i++)\n\t{\n\t\tfor (int j = 0; j < columns; j++)\n\t\t{ \n\t\t\tint current1 = Math.Min(vertical[i, j].fives + (horizontal[i, columns - 1].fives - horizontal[i, j].fives),\n\t\t\t\t\t\t\t\t\tvertical[i, j].twos + (horizontal[i, columns - 1].twos - horizontal[i, j].twos));\n\n\t\t\t(int twos, int fives) = horizontal[i, j]; \n\t\t\tint current2 = 0;\n\t\t\tif(j > 0)\n\t\t\t{\n\t\t\t\ttwos -= horizontal[i, j - 1].twos;\n\t\t\t\tfives -= horizontal[i, j - 1].fives;\n\n\t\t\t\tcurrent2 = Math.Min(vertical[i, j].fives + horizontal[i, j - 1].fives,\n\t\t\t\t\t\t\t\t\tvertical[i, j].twos + horizontal[i, j - 1].twos); \n\t\t\t}\n\n\t\t\tint current3 = Math.Min(horizontal[i, j].fives + (vertical[rows - 1, j].fives - vertical[i, j].fives),\n\t\t\t\t\t\t\t\t\thorizontal[i, j].twos + (vertical[rows - 1, j].twos - vertical[i, j].twos)); \n\n\t\t\tint current4 = Math.Min((horizontal[i, columns - 1].fives - horizontal[i, j].fives)\n\t\t\t\t\t\t\t\t\t\t+ (vertical[rows - 1, j].fives - vertical[i, j].fives) + fives,\n\t\t\t\t\t\t\t\t\t(horizontal[i, columns - 1].twos - horizontal[i, j].twos)\n\t\t\t\t\t\t\t\t\t\t+ (vertical[rows - 1, j].twos - vertical[i, j].twos) + twos); \n\n\t\t\tint max = (new int[]{current1, current2, current3, current4}).Max();\n\t\t\tresult = Math.Max(result, max);\n\t\t}\n\t} \n\n\treturn result;\n}\n\nprivate (int twos, int fives) getTwosAndFives(int n)\n{\n\tint twos = 0, fives = 0;\n\n\twhile (n % 5 == 0)\n\t{\n\t\tn /= 5;\n\t\tfives++;\n\t}\n\n\twhile (n % 2 == 0)\n\t{\n\t\tn /= 2;\n\t\ttwos++;\n\t}\n\n\treturn (twos, fives);\n}\n```
| 1 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ | Easy to understand | 100% faster and 100% less memory usage
|
c-easy-to-understand-100-faster-and-100-k4ho2
|
As at most one turn is possible so for a particular cell we have 6 choices\nBy storing number of two\'s and five\'s we can get the count of 10\'s easily\n\n#de
|
Yogeeky
|
NORMAL
|
2022-04-17T05:18:44.194434+00:00
|
2022-04-17T05:18:44.194465+00:00
| 60 | false |
**As at most one turn is possible so for a particular cell we have 6 choices**\n**By storing number of two\'s and five\'s we can get the count of 10\'s easily**\n```\n#define F first\n#define S second\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& v) {\n int n=v.size();\n int m=v[0].size();\n vector<vector<pair<int,int>>>cntx(n,vector<pair<int,int>>(m));// for vertical counting prefix sum matrix \n vector<vector<pair<int,int>>>cnty(n,vector<pair<int,int>>(m));// for horizontal counting suffix sum matrix\n vector<vector<pair<int,int>>>orr(n,vector<pair<int,int>>(m));// for original counting\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n int x=0;\n int y=0;\n int p=v[i][j];\n while(p%2==0)\n {\n p=p/2;\n x++;\n }\n while(p%5==0)\n {\n p=p/5;\n y++;\n }\n // for storing the number of 2\'s and 5\'s in a particular cell\n cntx[i][j]={x,y};\n cnty[i][j]={x,y};\n orr[i][j]={x,y};\n }\n }\n // Prefix sum vertical matrix\n for(int i=1;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n cntx[i][j].F+=cntx[i-1][j].F;\n cntx[i][j].S+=cntx[i-1][j].S;\n }\n }\n // suffix sum horizontal matrix\n for(int i=0;i<n;i++)\n {\n for(int j=m-2;j>=0;j--)\n {\n cnty[i][j].F+=cnty[i][j+1].F;\n cnty[i][j].S+=cnty[i][j+1].S;\n }\n }\n int ans=0;\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n // no. of 2\'s and 5\'s from top to i,j cell\n pair<int,int> up=cntx[i][j];\n // no. of 2\'s and 5\'s from i+1,j to bottom cell\n pair<int,int> down={cntx[n-1][j].F-cntx[i][j].F,cntx[n-1][j].S-cntx[i][j].S};\n // no. of 2\'s and 5\'s from i,j to rightmost cell\n pair<int,int> right=cnty[i][j];\n // no. of 2\'s and 5\'s from leftmost cell to i,j-1 cell\n pair<int,int> left={cnty[i][0].F-cnty[i][j].F,cnty[i][0].S-cnty[i][j].S};\n int cnt=0;\n // calculating no. of 2\'s and 5\'s for each of the 6 cases\n // |\n // | \n \n cnt=max(cnt,min(up.F+down.F,up.S+down.S));\n \n // |\n // ___|\n \n cnt=max(cnt,min(up.F+left.F,up.S+left.S));\n \n // |\n // |_____\n \n cnt=max(cnt,min(up.F+right.F-orr[i][j].F,up.S+right.S-orr[i][j].S));\n \n // _______\n // \n \n cnt=max(cnt,min(left.F+right.F,left.S+right.S));\n // ____\n // |\n // | \n \n cnt=max(cnt,min(right.F+down.F,right.S+down.S));\n // ____\n // |\n // | \n \n cnt=max(cnt,min(left.F+down.F+orr[i][j].F,left.S+down.S+orr[i][j].S));\n ans=max(ans,cnt);\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C', 'Prefix Sum']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ || PREFIX SUM || COUNT 2'S AND 5'S || FASTER THAN 100%
|
c-prefix-sum-count-2s-and-5s-faster-than-jo2o
|
\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int m=grid.size(),n=grid[0].size();\n int res=0;\n vec
|
niks07
|
NORMAL
|
2022-04-17T05:05:53.237558+00:00
|
2022-04-17T05:05:53.237594+00:00
| 51 | false |
```\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int m=grid.size(),n=grid[0].size();\n int res=0;\n vector<vector<int>> v1(m,vector<int>(n,0)),v2(m,vector<int>(n,0));\n vector<vector<int>> v3(m,vector<int>(n,0)),v4(m,vector<int>(n,0));\n for(int i=0;i<m;i++){\n int cnt=0;\n int twos=0,fives=0;\n for(int j=0;j<n;j++){\n int temp=grid[i][j];\n int cnt1=0,cnt2=0;\n while(temp>0 and temp%2==0){\n cnt1++;\n temp/=2;\n } \n temp=grid[i][j];\n while(temp>0 and temp%5==0){\n cnt2++;\n temp/=5;\n }\n twos+=cnt1;\n fives+=cnt2;\n v1[i][j]=twos;\n v2[i][j]=fives;\n }\n }\n for(int i=0;i<n;i++){\n int cnt=0;\n int twos=0,fives=0;\n for(int j=0;j<m;j++){\n int temp=grid[j][i];\n int cnt1=0,cnt2=0;\n while(temp>0 and temp%2==0){\n cnt1++;\n temp/=2;\n } \n temp=grid[j][i];\n while(temp>0 and temp%5==0){\n cnt2++;\n temp/=5;\n }\n twos+=cnt1;\n fives+=cnt2;\n v3[j][i]=twos;\n v4[j][i]=fives;\n }\n }\n \n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n int curr=0;\n int twos=v1[i][j],fives=v2[i][j];\n int cnt1=0,cnt2=0;\n int temp=grid[i][j];\n while(temp>0 and temp%2==0){\n temp/=2;\n cnt1++;\n }\n \n temp=grid[i][j];\n while(temp>0 and temp%5==0){\n temp/=5;\n cnt2++;\n }\n \n res=max(res,min(twos+v3[m-1][j]-v3[i][j],fives+v4[m-1][j]-v4[i][j]));\n res=max(res,min(twos+v3[i][j]-cnt1,fives+v4[i][j]-cnt2));\n res=max(res,min(v1[i][n-1]-twos+v3[i][j],v2[i][n-1]-fives+v4[i][j]));\n res=max(res,min(v1[i][n-1]-twos+v3[m-1][j]-v3[i][j]+cnt1,v2[i][n-1]-fives+v4[m-1][j]-v4[i][j]+cnt2));\n }\n }\n return res;\n }\n};\n```
| 1 | 0 |
['C', 'Prefix Sum']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Java | Rotate 3 times
|
java-rotate-3-times-by-student2091-o42y
|
It is quite apparent it is a prefix sum question but geez, it is really implementation heavy due to \n1. We have to keep track of both 2 and 5\'s prefix sum in
|
Student2091
|
NORMAL
|
2022-04-17T04:58:01.710396+00:00
|
2022-04-23T08:58:55.951576+00:00
| 262 | false |
It is quite apparent it is a prefix sum question but geez, it is **really** implementation heavy due to \n1. We have to keep track of both 2 and 5\'s prefix sum in a 2D grid\n\n2. There are like, a lot of directions, to consider. That is, start from horizontal vs vertical, then go up vs down or right vs left.\n\nI missed considering a direction during contest and submission failed at the last 5 test cases. Troubleshoot was kind of difficult. Annoyed. \nHere comes an idea that didn\'t occur to me during contest: To deal with this annoyance, we can literally just **rotate the grid 3 times**. \n\n```Java\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n int ans = 0;\n for (int i = 0; i < 4; i++){\n ans = Math.max(ans, solve(grid));\n grid = rotate(grid);\n }\n return ans;\n }\n\n private int solve(int[][] grid){\n int n = grid[0].length, m = grid.length, ans = 0;\n int[][] fcol = new int[m + 1][n];\n int[][] tcol = new int[m + 1][n];\n int[][] frow = new int[n + 1][m];\n int[][] trow = new int[n + 1][m];\n for (int i = 0; i < m; i++){\n for (int j = 0; j < n; j++){\n int t = count(grid[i][j], 2);\n int f = count(grid[i][j], 5);\n fcol[i + 1][j] += fcol[i][j] + f;\n tcol[i + 1][j] += tcol[i][j] + t;\n frow[j + 1][i] += frow[j][i] + f;\n trow[j + 1][i] += trow[j][i] + t;\n }\n }\n for (int i = 0; i < m; i++){\n for (int j = 0; j < n; j++){\n int rowTwo = trow[j + 1][i];\n int rowFive= frow[j + 1][i];\n int colTwo = tcol[m][j] - tcol[i + 1][j];\n int colFive= fcol[m][j] - fcol[i + 1][j];\n ans = Math.max(ans, Math.min(rowTwo + colTwo, rowFive + colFive));\n }\n }\n\n return ans;\n }\n\n private int count(int n, int w){\n int count = 0;\n while(n % w == 0){\n count++;\n n /= w;\n }\n return count;\n }\n\n private int[][] rotate(int[][] grid){\n int n = grid[0].length, m = grid.length;\n int[][] next = new int[n][m];\n for (int i = 0; i < m; i++){\n for (int j = 0; j < n; j++){\n next[j][m - 1 - i] = grid[i][j];\n }\n }\n return next;\n }\n}\n```
| 1 | 0 |
['Java']
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
[Java] O(mn) solution, use prefix sum to calculate number of factors (2 and 5) with explanation
|
java-omn-solution-use-prefix-sum-to-calc-4yoo
|
The idea: for each cornered path, let\'s call its product is p. We can always rewrite p as follows\np = a * 10^n\n\nNumber of trailing zeros will be maximum va
|
khanhcs
|
NORMAL
|
2022-04-17T04:17:52.633836+00:00
|
2022-04-24T07:18:54.890090+00:00
| 166 | false |
**The idea**: for each cornered path, let\'s call its product is `p`. We can always rewrite `p` as follows\n`p = a * 10^n`\n\nNumber of trailing zeros will be maximum value of n in all ways to rewrite `p`. We have\n\n`number of trailing zeros of p = max(n) = min(number of 2 in prime factorization of p, number of 5 in prime factorization of p)`\n\n**Greedy strategy**: we will just consider the paths that start with a point on border of grid (first row or last row or first col or last col) and end with a point on border of grid because these paths will always have number of trailing zeros greater than (or equal) its sub paths.\n\nBelow is the implementation for this problem in Java. \n\n```\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int[][][] count25 = new int[m][n][2];\n \n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n // number of 2 in prime factorization of grid[i][j]\n count25[i][j][0] = countFactor(grid[i][j], 2);\n // number of 5 in prime factorization of grid[i][j]\n count25[i][j][1] = countFactor(grid[i][j], 5);\n }\n }\n \n // countUp[i][j][0]: number of 2 in prime factorization of numbers from grid[0][j] to grid[i][j]\n // countUp[i][j][1]: number of 5 in prime factorization of numbers from grid[0][j] to grid[i][j]\n // the same definition for countDown, countLeft and countRight\n // we will use prefix sum to caculate them\n int[][][] countUp = new int[m][n][2];\n int[][][] countDown = new int[m][n][2];\n int[][][] countLeft = new int[m][n][2];\n int[][][] countRight = new int[m][n][2];\n \n for (int i = 0; i < m; ++i) {\n countLeft[i][0][0] = count25[i][0][0];\n countLeft[i][0][1] = count25[i][0][1];\n countRight[i][n-1][0] = count25[i][n-1][0];\n countRight[i][n-1][1] = count25[i][n-1][1];\n }\n \n for (int i = 0; i < m; ++i) {\n for (int j = 1; j < n; ++j) {\n countLeft[i][j][0] = countLeft[i][j-1][0] + count25[i][j][0];\n countLeft[i][j][1] = countLeft[i][j-1][1] + count25[i][j][1];\n }\n }\n \n for (int i = 0; i < m; ++i) {\n for (int j = n - 2; j >= 0; --j) {\n countRight[i][j][0] = countRight[i][j+1][0] + count25[i][j][0];\n countRight[i][j][1] = countRight[i][j+1][1] + count25[i][j][1];\n }\n }\n \n for (int j = 0; j < n; ++j) {\n countUp[0][j][0] = count25[0][j][0];\n countUp[0][j][1] = count25[0][j][1];\n countDown[m-1][j][0] = count25[m-1][j][0];\n countDown[m-1][j][1] = count25[m-1][j][1];\n }\n \n for (int j = 0; j < n; ++j) {\n for (int i = 1; i < m; ++i) {\n countUp[i][j][0] = countUp[i-1][j][0] + count25[i][j][0];\n countUp[i][j][1] = countUp[i-1][j][1] + count25[i][j][1];\n }\n }\n \n for (int j = 0; j < n; ++j) {\n for (int i = m-2; i >= 0; --i) {\n countDown[i][j][0] = countDown[i+1][j][0] + count25[i][j][0];\n countDown[i][j][1] = countDown[i+1][j][1] + count25[i][j][1]; \n }\n }\n \n int result = 0;\n \n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n result = Math.max(result, \n Math.min(countUp[i][j][0] + countRight[i][j][0] - count25[i][j][0], countUp[i][j][1] + countRight[i][j][1] - count25[i][j][1])\n );\n result = Math.max(result, \n Math.min(countUp[i][j][0] + countLeft[i][j][0] - count25[i][j][0], countUp[i][j][1] + countLeft[i][j][1] - count25[i][j][1])\n );\n result = Math.max(result, \n Math.min(countDown[i][j][0] + countRight[i][j][0] - count25[i][j][0], countDown[i][j][1] + countRight[i][j][1] - count25[i][j][1])\n );\n result = Math.max(result, \n Math.min(countDown[i][j][0] + countLeft[i][j][0] - count25[i][j][0], countDown[i][j][1] + countLeft[i][j][1] - count25[i][j][1])\n );\n }\n }\n \n return result;\n }\n\n \n \n private int countFactor(int a, int factor) {\n int result = 0;\n while (a % factor == 0) {\n a /= factor;\n result++;\n }\n return result;\n }\n \n}\n```\nTime complexity: O(mn).\nSpace complexity: O(mn).\n\nPlease upvote if it is helpful to you. If there is any questions/suggestion, please comment, I will reply as soon as possible.
| 1 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Java DP, Prefix Sum, 2 & 5 factor nums
|
java-dp-prefix-sum-2-5-factor-nums-by-he-q76b
|
If we directly count the product of a path, we are very likely to get integer overflow.\nThe trailing zeros equals on the larger number of factors of 2 and 5 in
|
helfisher
|
NORMAL
|
2022-04-17T04:15:18.681703+00:00
|
2022-04-17T04:21:54.247309+00:00
| 185 | false |
If we directly count the product of a path, we are very likely to get integer overflow.\n**The trailing zeros equals on the larger number of factors of 2 and 5 in the product.**\nWe need to count the four kinds of cornered paths.\n1. left-up\n2. up-right\n3. right-down\n4. down-left\n\nTo count the paths efficiently, we need to first compute the prefix sums of factor 2 and factor 5, from 4 directions.\n\nTime: O(mn)\nSpace: O(mn)\n\n```\nclass Solution {\n public int maxTrailingZeros(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int[][] two = new int[m][n];\n int[][] five = new int[m][n];\n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n two[i][j] = getFactorNum(grid[i][j], 2);\n five[i][j] = getFactorNum(grid[i][j], 5);\n }\n }\n \n int[][] left2 = new int[m][n];\n int[][] left5 = new int[m][n];\n for (int i = 0; i < m; ++i) {\n int sum2 = 0;\n int sum5 = 0;\n for (int j = 0; j < n; ++j) {\n sum2 += two[i][j];\n sum5 += five[i][j];\n left2[i][j] = sum2;\n left5[i][j] = sum5;\n }\n }\n \n int[][] right2 = new int[m][n];\n int[][] right5 = new int[m][n];\n for (int i = 0; i < m; ++i) {\n int sum2 = 0;\n int sum5 = 0;\n for (int j = n - 1; j >= 0; --j) {\n sum2 += two[i][j];\n sum5 += five[i][j];\n right2[i][j] = sum2;\n right5[i][j] = sum5;\n }\n }\n \n int[][] up2 = new int[m][n];\n int[][] up5 = new int[m][n];\n for (int j = 0; j < n; ++j) {\n int sum2 = 0;\n int sum5 = 0;\n for (int i = 0; i < m; ++i) {\n sum2 += two[i][j];\n sum5 += five[i][j];\n up2[i][j] = sum2;\n up5[i][j] = sum5;\n }\n }\n \n int[][] down2 = new int[m][n];\n int[][] down5 = new int[m][n];\n for (int j = 0; j < n; ++j) {\n int sum2 = 0;\n int sum5 = 0;\n for (int i = m - 1; i >= 0; --i) {\n sum2 += two[i][j];\n sum5 += five[i][j];\n down2[i][j] = sum2;\n down5[i][j] = sum5;\n }\n }\n \n int res = 0;\n for (int i = 0; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n // left-up\n if (i != 0 || j != 0) {\n int cur = Math.min(left2[i][j] + up2[i][j] - two[i][j], left5[i][j] + up5[i][j] - five[i][j]);\n res = Math.max(res, cur);\n }\n \n // up-right\n if (i != 0 || j != n - 1) {\n int cur = Math.min(right2[i][j] + up2[i][j] - two[i][j], right5[i][j] + up5[i][j] - five[i][j]);\n res = Math.max(res, cur);\n }\n \n // right-down\n if (i != m - 1 || j != n - 1) {\n int cur = Math.min(right2[i][j] + down2[i][j] - two[i][j], right5[i][j] + down5[i][j] - five[i][j]);\n res = Math.max(res, cur);\n }\n \n // down-left\n if (i != m - 1 || j != 0) {\n int cur = Math.min(left2[i][j] + down2[i][j] - two[i][j], left5[i][j] + down5[i][j] - five[i][j]);\n res = Math.max(res, cur);\n }\n }\n }\n return res;\n }\n \n private int getFactorNum(int input, int factor) {\n int res = 0;\n while (input != 0 && input % factor == 0) {\n ++res;\n input /= factor;\n }\n return res;\n }\n}\n```
| 1 | 0 |
['Dynamic Programming', 'Prefix Sum', 'Java']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++/Rotating the grid/ Disgusting question....
|
crotating-the-grid-disgusting-question-b-muhv
|
\t\tclass Solution {\n\tpublic:\n \n pair util(int val){\n \n int x=0;\n while(val>0 && val%5==0){\n val=val/5;\n
|
anurag852001
|
NORMAL
|
2022-04-17T04:11:42.148432+00:00
|
2022-04-17T04:11:42.148461+00:00
| 158 | false |
\t\tclass Solution {\n\tpublic:\n \n pair<long long,long long> util(int val){\n \n int x=0;\n while(val>0 && val%5==0){\n val=val/5;\n x++;\n }\n int y=0;\n while(val>0 && val%2==0){\n val=val/2;\n y++;\n }\n return {x,y};\n \n }\n \n long long util(vector<vector<int>>& grid){\n \n int n=grid.size();\n int m=grid[0].size();\n pair<long long,long long> matrix[n][m];\n pair<long long,long long> matrix1[n][m];\n pair<long long,long long> matrix2[n][m];\n \n //making the first grid;\n for(int i=0;i<n;i++)\n for(int j=0;j<m;j++){\n int val=grid[i][j];\n matrix[i][j]=util(val);\n }\n \n //right to left\n for(int i=0;i<n;i++){\n for(int j=m-1;j>=0;j--){\n if(j==m-1)\n matrix1[i][j]=matrix[i][j];\n else\n matrix1[i][j]={matrix[i][j].first+matrix1[i][j+1].first,matrix[i][j].second+matrix1[i][j+1].second};\n \n }\n }\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(j==0)\n matrix2[i][j]=matrix[i][j];\n else\n matrix2[i][j]={matrix[i][j].first+matrix2[i][j-1].first,matrix[i][j].second+matrix2[i][j-1].second};\n }\n }\n long long res=0;\n \n //calculating by traversing from up to down\n \n for(int j=0;j<m;j++){\n pair<long long,long long>sum={0,0};\n for(int i=0;i<n;i++){\n sum={sum.first+matrix[i][j].first,sum.second+matrix[i][j].second};\n res=max(res,min(sum.first,sum.second));\n if(j>0){\n pair<long long,long long>p1=matrix2[i][j-1];\n res=max(res,min(sum.first+p1.first,sum.second+p1.second));\n }\n if(j<m-1){\n pair<long long,long long>p1=matrix1[i][j+1];\n res=max(res,min(sum.first+p1.first,sum.second+p1.second));\n }\n \n } \n \n }\n return res;\n \n }\n\n int maxTrailingZeros(vector<vector<int>>& grid) {\n \n int m=grid[0].size();\n int n=grid.size();\n vector<vector<int>>grid2(m,vector<int>(n,0));\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n grid2[j][i]=grid[i][j];\n }\n }\n long long res=0;\n res=max(util(grid),util(grid2));\n vector<vector<int>>grid3(n,vector<int>(m,0));\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[0].size();j++){\n grid3[n-i-1][j]=grid[i][j]; \n }\n }\n return max(res,util(grid3));\n \n \n }\n\t};
| 1 | 0 |
['C', 'Prefix Sum']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
simple dynamic programming (dp) O(n*m)
|
simple-dynamic-programming-dp-onm-by-use-vze5
|
\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n=grid.size(),m=grid[0].size();\n int ans=0;\n int
|
user3857q
|
NORMAL
|
2022-04-17T04:05:52.143050+00:00
|
2022-04-17T04:05:52.143159+00:00
| 212 | false |
```\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n=grid.size(),m=grid[0].size();\n int ans=0;\n int dp1[2][n+2][m+2],dp2[2][n+2][m+2],dp3[2][n+2][m+2],dp4[2][n+2][m+2];\n memset(dp1,0,sizeof dp1);\n memset(dp2,0,sizeof dp2);\n memset(dp3,0,sizeof dp3);\n memset(dp4,0,sizeof dp4);\n\n for(int x=0;x<grid.size();x++){\n for(int z=0;z<grid[0].size();z++){\n int cnt2=0,cnt5=0;\n int num=grid[x][z];\n while(num%2==0)num/=2,cnt2++;\n while(num%5==0)num/=5,cnt5++;\n dp1[0][x+1][z+1]=dp2[0][x+1][z+1]=dp3[0][x+1][z+1]=dp4[0][x+1][z+1]=cnt2;\n dp1[1][x+1][z+1]=dp2[1][x+1][z+1]=dp3[1][x+1][z+1]=dp4[1][x+1][z+1]=cnt5;\n }\n }\n for(int i=1;i<=n;i++){//up to down\n for(int j=1;j<=m;j++){\n dp1[0][i][j]+=dp1[0][i-1][j];\n dp1[1][i][j]+=dp1[1][i-1][j];\n // std::cout<<dp1[0][i][j]<<","<<dp1[1][i][j]<<" ";\n }//std::cout<<"\\n";\n }\n // std::cout<<"\\n";\n for(int i=n;i>=1;i--){//down to up\n for(int j=1;j<=m;j++){\n dp2[0][i][j]+=dp2[0][i+1][j];\n dp2[1][i][j]+=dp2[1][i+1][j];\n // std::cout<<dp2[0][i][j]<<","<<dp2[1][i][j]<<" ";\n }//std::cout<<"\\n";\n }\n // std::cout<<"\\n";\n for(int i=1;i<=n;i++){//left to right\n for(int j=1;j<=m;j++){\n dp3[0][i][j]+=dp3[0][i][j-1];\n dp3[1][i][j]+=dp3[1][i][j-1];\n // std::cout<<dp3[0][i][j]<<","<<dp3[1][i][j]<<" ";\n }//std::cout<<"\\n";\n }\n // std::cout<<"\\n";\n for(int i=1;i<=n;i++){//right to left\n for(int j=m;j>=1;j--){\n dp4[0][i][j]+=dp4[0][i][j+1];\n dp4[1][i][j]+=dp4[1][i][j+1];\n //std::cout<<dp4[0][i][j]<<","<<dp4[1][i][j]<<" ";\n }//std::cout<<"\\n";\n }\n //std::cout<<"\\n";\n for(int i=1;i<=n;i++){//solve\n for(int j=1;j<=m;j++){\n \n ans=max(ans,min(dp4[0][i][j+1]+dp2[0][i][j],dp4[1][i][j+1]+dp2[1][i][j]));\n ans=max(ans,min(dp3[0][i][j-1]+dp1[0][i][j],dp3[1][i][j-1]+dp1[1][i][j]));\n ans=max(ans,min(dp3[0][i][j-1]+dp2[0][i][j],dp3[1][i][j-1]+dp2[1][i][j]));\n ans=max(ans,min(dp4[0][i][j+1]+dp1[0][i][j],dp4[1][i][j+1]+dp1[1][i][j]));\n \n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Array', 'Dynamic Programming', 'Prefix Sum']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Accepted python solution
|
accepted-python-solution-by-icomplexray-3l3o
|
This solution got accpeted. But it is too long!\nCould someone help me to simplify it? Thanks!\n\nclass Solution:\n def maxTrailingZeros(self, grid: List[Lis
|
icomplexray
|
NORMAL
|
2022-04-17T04:05:47.143398+00:00
|
2022-04-17T04:05:47.143433+00:00
| 337 | false |
This solution got accpeted. But it is too long!\nCould someone help me to simplify it? Thanks!\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n m_five = [[0] * n for _ in range(m)]\n m_two = [[0] * n for _ in range(m)]\n hor_five = [[0] * n for _ in range(m)]\n hor_five_r = [[0] * n for _ in range(m)]\n hor_two = [[0] * n for _ in range(m)]\n hor_two_r = [[0] * n for _ in range(m)]\n ver_five = [[0] * n for _ in range(m)]\n ver_five_r = [[0] * n for _ in range(m)]\n ver_two = [[0] * n for _ in range(m)]\n ver_two_r = [[0] * n for _ in range(m)]\n \n for i in range(m):\n for j in range(n):\n x = grid[i][j]\n cnt = 0\n\n if x % 5 == 0:\n cnt += 1\n if x % 25 == 0:\n cnt += 1\n if x % 125 == 0:\n cnt += 1\n if x % 625 == 0:\n cnt += 1\n\n m_five[i][j] = cnt\n cnt = 0\n if x % 512 == 0:\n cnt = 9\n elif x % 256 == 0:\n cnt = 8\n elif x % 128 == 0:\n cnt = 7\n elif x % 64 == 0:\n cnt = 6\n elif x % 32 == 0:\n cnt = 5\n elif x % 16 == 0:\n cnt = 4\n elif x % 8 == 0:\n cnt = 3\n elif x % 4 == 0:\n cnt = 2\n elif x % 2 == 0:\n cnt = 1\n m_two[i][j] = cnt\n for i in range(m):\n for j in range(n):\n if j == 0:\n hor_two[i][j] = m_two[i][j]\n hor_five[i][j] = m_five[i][j]\n else:\n hor_two[i][j] = m_two[i][j] + hor_two[i][j - 1]\n hor_five[i][j] = m_five[i][j] + hor_five[i][j - 1]\n cur_five = cur_two = 0\n for j in range(n - 1, -1, -1):\n if j == n - 1:\n hor_two_r[i][j] = m_two[i][j]\n hor_five_r[i][j] = m_five[i][j]\n else:\n hor_two_r[i][j] = hor_two_r[i][j + 1] + m_two[i][j]\n hor_five_r[i][j] = hor_five_r[i][j + 1] + m_five[i][j]\n \n\n for j in range(n):\n for i in range(m):\n if i == 0:\n ver_five[i][j] = m_five[i][j]\n ver_two[i][j] = m_two[i][j]\n else:\n ver_five[i][j] = m_five[i][j] + ver_five[i - 1][j]\n ver_two[i][j] = m_two[i][j] + ver_two[i - 1][j]\n for i in range(m - 1, -1, -1):\n if i == m - 1:\n ver_five_r[i][j] = m_five[i][j]\n ver_two_r[i][j] = m_two[i][j]\n else:\n ver_two_r[i][j] = m_two[i][j] + ver_two_r[i + 1][j]\n ver_five_r[i][j] = m_five[i][j] +ver_five_r[i + 1][j]\n \n res = 0\n for i in range(m):\n for j in range(n):\n res = max(res, min(hor_five[i][j] + ver_five[i][j] - m_five[i][j], hor_two[i][j] + ver_two[i][j] - m_two[i][j]),\n min(hor_five_r[i][j] + ver_five[i][j] - m_five[i][j], hor_two_r[i][j] + ver_two[i][j] - m_two[i][j]),\n min(hor_five[i][j] + ver_five_r[i][j] - m_five[i][j], hor_two[i][j] + ver_two_r[i][j] - m_two[i][j]),\n min(hor_five_r[i][j] + ver_five_r[i][j] - m_five[i][j], hor_two_r[i][j] + ver_two_r[i][j] - m_two[i][j]))\n return res\n \n ```
| 1 | 0 |
['Python']
| 2 |
maximum-trailing-zeros-in-a-cornered-path
|
Help me troubleshoot it?
|
help-me-troubleshoot-it-by-leoyang9-b6z1
|
Here is my code\n\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n n = len(grid)\n m = len(grid[0])\n accu
|
leoyang9
|
NORMAL
|
2022-04-17T04:02:39.107874+00:00
|
2022-04-17T04:02:39.107904+00:00
| 149 | false |
Here is my code\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n n = len(grid)\n m = len(grid[0])\n accumlatedProduct = [[[1,1] for i in range(m)] for j in range(n)] # ahp,avp\n for i in range(n):\n for k in range(m):\n tem = grid[i][k]\n if k==0:\n accumlatedProduct[i][k][0] = tem\n else:\n accumlatedProduct[i][k][0] = accumlatedProduct[i][k-1][0]*tem\n if i==0:\n accumlatedProduct[i][k][1] = tem\n else:\n accumlatedProduct[i][k][1] = accumlatedProduct[i-1][k][1]*tem\n res = 0\n for i in range(n):\n for k in range(m):\n p1 = accumlatedProduct[i][k][0]*accumlatedProduct[i][k][1]/grid[i][k]\n p2 = accumlatedProduct[i][k][0]*accumlatedProduct[n-1][k][1]/accumlatedProduct[i][k][1]\n p3 = accumlatedProduct[i][m-1][0]/accumlatedProduct[i][k][0]*accumlatedProduct[i][k][1]\n p4 = accumlatedProduct[i][m-1][0]/accumlatedProduct[i][k][0]*accumlatedProduct[n-1][k][1]/accumlatedProduct[i][k][1]*grid[i][k]\n print(p1,p2,p3,p4)\n res = max(res,self.CountTrailingZeros(p1),self.CountTrailingZeros(p2),self.CountTrailingZeros(p3),self.CountTrailingZeros(p4))\n return res\n def CountTrailingZeros(self,i):\n if i ==0:\n return 0\n if i%10==0:\n return 1+self.CountTrailingZeros(i/10)\n else:\n return 0\n```\n\nI am using accumulated Product and center to calculate the product,\n\nbut i was stuck at this test case \n\n```\n[[824,709,193,413,701,836,727],\n [135,844,599,211,140,933,205],\n [329,68,285,282,301,387,231],\n [293,210,478,352,946,902,137],\n [806,900,290,636,589,522,611],\n [450,568,990,592,992,128,92],\n [780,653,795,457,980,942,927],\n [849,901,604,906,912,866,688]]\n```\n\nI looked at it and couldn\'t find the product with 6 zeros\n\nanyone can help me with that?
| 1 | 0 |
['Python']
| 4 |
maximum-trailing-zeros-in-a-cornered-path
|
Prefix Sum Approach | C++ | Comments
|
prefix-sum-approach-c-comments-by-dpw411-r7nc
|
```\n// Approach - We know basic idea about how to form 10 i.e. 5 * 2\n// So thats it we use the same idea here we calculate 5\'s and 2\'s in division of each g
|
dpw4112001
|
NORMAL
|
2022-04-17T04:02:26.794655+00:00
|
2022-04-17T04:02:26.794680+00:00
| 118 | false |
```\n// Approach - We know basic idea about how to form 10 i.e. 5 * 2\n// So thats it we use the same idea here we calculate 5\'s and 2\'s in division of each grid element \n// and maintain sum array\n\n\n// sum[n][m][2] --> 0 --> Number of 5\'s and 1 --> Number of 2\'s \n\n\n\nclass Solution {\npublic:\n\n // Utility function to get frequency of divisor forming the number \n int getIt(int n,int p)\n {\n int ans = 0;\n while(n > 0)\n {\n if(n % p != 0)break;\n ans++;\n n/=p;\n }\n return ans;\n }\n\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n\n // Row wise Prefix Sum \n int sum[n+1][m+1][2];\n memset(sum,0,sizeof sum);\n\n for(int i=1;i<=n;i++)\n {\n for(int j=1;j<=m;j++)\n {\n sum[i][j][0] = getIt(grid[i-1][j-1],2);\n sum[i][j][1] = getIt(grid[i-1][j-1],5);\n }\n }\n\n for(int i=1;i<=n;i++){\n for(int j=1;j<=m;j++)\n {\n sum[i][j][0] += sum[i][j-1][0];\n sum[i][j][1] += sum[i][j-1][1];\n }\n }\n\n // :------------------------------------------------->\n\n // Column Wise Prefix Sum\n int sum2[n+1][m+1][2];\n memset(sum2,0,sizeof sum2);\n \n for(int i=1;i<=n;i++)\n {\n for(int j=1;j<=m;j++)\n {\n sum2[i][j][0] = getIt(grid[i-1][j-1],2);\n sum2[i][j][1] = getIt(grid[i-1][j-1],5);\n }\n }\n\n for(int i=1;i<=n;i++){\n for(int j=1;j<=m;j++)\n {\n sum2[i][j][0] += sum2[i-1][j][0];\n sum2[i][j][1] += sum2[i-1][j][1];\n }\n }\n\n\n // :---------------------------------------------->\n\n // Cheap Variable to Store Answer\n int ans = 0;\n\n\n for(int i=1;i<=n;i++)\n {\n for(int j=1;j<=m;j++)\n {\n\n // Current Grid Element\n int x = sum[i][j][0] - sum[i][j-1][0];\n int y = sum[i][j][1] - sum[i][j-1][1];\n\n // Take all possible answers considering current grid element as corner\n\n // Convention --> L1, L2,R1,R2,U1,U2,D1,D2\n // 1 --> Number is 5\'s\n // 2 --> Number of 2\'s\n\n // Left\n int L1 = sum[i][j-1][0];\n int L2 = sum[i][j-1][1];\n\n // Right\n int R1 = sum[i][m][0] - sum[i][j][0];\n int R2 = sum[i][m][1] - sum[i][j][1];\n\n // Up\n int U1 = sum2[i-1][j][0];\n int U2 = sum2[i-1][j][1];\n\n // Down\n int D1 = sum2[n][j][0] - sum2[i][j][0];\n int D2 = sum2[n][j][1] - sum2[i][j][1];\n\n // Our duty to calculate max answer\n // Max answer will be the min(No of 5\'s, No of 2\'s) in the cornered Path\n ans = max(ans,min(L1 + x + U1, L2 + y + U2));\n ans = max(ans,min(L1 + x + D1, L2 + y + D2));\n\n ans = max(ans,min(R1 + x + U1, R2 + y + U2));\n ans = max(ans,min(R1 + x + D1, R2 + y + D2));\n\n\n }\n }\n \n // Hey, We just did it, Now its time to return\n return ans;\n \n }\n};
| 1 | 0 |
['Prefix Sum']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ solution
|
c-solution-by-sparshdawra-1l5v
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
sparshdawra
|
NORMAL
|
2025-01-13T00:33:54.869217+00:00
|
2025-01-13T00:33:54.869217+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maxTrailingZeros(vector<vector<int>>& grid) {
int m = grid.size(),n = grid[0].size();
vector<vector<pair<int,int>>> v(m+1,vector<pair<int,int>> (n+1));
for (int i=1;i<=m;i++){
for (int j=1;j<=n;j++){
while (grid[i-1][j-1]%5==0){
v[i][j].first++;
grid[i-1][j-1]/=5;
}
while (grid[i-1][j-1]%2==0){
v[i][j].second++;
grid[i-1][j-1]/=2;
}
}
}
vector<vector<pair<int,int>>> hor = v,ver = v;
for (int i=1;i<=m;i++){
for (int j=1;j<=n;j++){
hor[i][j].first += hor[i][j-1].first;
hor[i][j].second += hor[i][j-1].second;
}
}
for (int j=1;j<=n;j++){
for (int i=1;i<=m;i++){
ver[i][j].first += ver[i-1][j].first;
ver[i][j].second += ver[i-1][j].second;
}
}
int ans = 0;
for (int i=1;i<=m;i++){
for (int j=1;j<=n;j++){
ans = max(ans,min(ver[i][j].first+hor[i][j].first-v[i][j].first,ver[i][j].second+hor[i][j].second-v[i][j].second));
ans = max(ans,min(ver[m][j].first-ver[i][j].first+hor[i][j].first,ver[m][j].second-ver[i][j].second+hor[i][j].second));
ans = max(ans,min(ver[i][j].first+hor[i][n].first-hor[i][j].first,ver[i][j].second+hor[i][n].second-hor[i][j].second));
ans = max(ans,min(ver[m][j].first-ver[i][j].first+hor[i][n].first-hor[i][j].first+v[i][j].first,ver[m][j].second-ver[i][j].second+hor[i][n].second-hor[i][j].second+v[i][j].second));
}
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Trailing zeros -> factorization into twos and fives Python solution
|
trailing-zeros-factorization-into-twos-a-5lja
|
IntuitionAs described in the title, it's all about factorizing into 2 and 5sApproachWe only need to keep track of the number of accumulated 2s and 5s in the pat
|
huikinglam02
|
NORMAL
|
2024-12-26T22:37:05.101867+00:00
|
2024-12-26T22:37:05.101867+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
As described in the title, it's all about factorizing into 2 and 5s
# Approach
<!-- Describe your approach to solving the problem. -->
We only need to keep track of the number of accumulated 2s and 5s in the path. Two details to note:
1. By choosing each grid point as potential turning point, make sure contribution of that point is only counted once. (Be careful with the indexing in the prefix sum)
2. The correct trailing zero count along a path is: $$min$$(# of 2s on the horizontal path + vertical path, # of 5s on the horizontal path + vertical path)
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(m*n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(m*n)$$
# Code
```python3 []
#
# @lc app=leetcode id=2245 lang=python3
#
# [2245] Maximum Trailing Zeros in a Cornered Path
#
# @lc code=start
from typing import List
class Solution:
'''
1 <= grid[i][j] <= 1000
So break down all numbers in the range into it's prime factorization.
The number of trailing 0s is given by min(accumulated 2, accumulated 5)
We can use prefix sum to denote how many 2 and 5 accumulated on horizontal and vertical paths
'''
def maxTrailingZeros(self, grid: List[List[int]]) -> int:
primes = {}
for i in range(len(grid)):
for j in range(len(grid[i])):
if grid[i][j] not in primes:
primes[grid[i][j]] = self.primeFactors(grid[i][j])
prefixHorizontal = []
for i in range(len(grid)):
prefixHorizontal.append([[0, 0]])
twos, fives = 0, 0
for j in range(len(grid[i])):
twos += primes[grid[i][j]].get(2, 0)
fives += primes[grid[i][j]].get(5, 0)
prefixHorizontal[i].append([twos, fives])
prefixVertical = []
for j in range(len(grid[0])):
prefixVertical.append([[0, 0]])
twos, fives = 0, 0
for i in range(len(grid)):
twos += primes[grid[i][j]].get(2, 0)
fives += primes[grid[i][j]].get(5, 0)
prefixVertical[j].append([twos, fives])
result = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
twosLeft, fivesLeft = prefixHorizontal[i][j + 1]
twosRight, fivesRight = prefixHorizontal[i][-1][0] - prefixHorizontal[i][j][0], prefixHorizontal[i][-1][1] - prefixHorizontal[i][j][1]
twosUp, fivesUp = prefixVertical[j][i]
twosDown, fivesDown = prefixVertical[j][-1][0] - prefixVertical[j][i + 1][0], prefixVertical[j][-1][1] - prefixVertical[j][i + 1][1]
result = max(result, min(twosLeft + twosUp, fivesLeft + fivesUp))
result = max(result, min(twosRight + twosUp, fivesRight + fivesUp))
result = max(result, min(twosLeft + twosDown, fivesLeft + fivesDown))
result = max(result, min(twosRight + twosDown, fivesRight + fivesDown))
return result
'''
A function to store the prime factor as key and power as value in a dictionay
'''
def primeFactors(self, n):
primes = {}
while n % 2 == 0:
primes[2] = primes.get(2, 0) + 1
n //= 2
i = 3
while i * i <= n:
while n % i == 0:
primes[i] = primes.get(i, 0) + 1
n //= i
i += 2
if n > 1:
primes[n] = primes.get(n, 0) + 1
return primes
# @lc code=end
```
| 0 | 0 |
['Python3']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
this took me 1.5 effin hours
|
this-took-me-15-effin-hours-by-kanikaa01-a2kp
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUnderstand the basics: for a number to have a trailing zero, it must have a factor of 1
|
kanikaa01
|
NORMAL
|
2024-08-24T08:00:42.127671+00:00
|
2024-08-24T08:00:42.127694+00:00
| 8 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUnderstand the basics: for a number to have a trailing zero, it must have a factor of 10 - a factor of 2 and a factor of 5.\nso to have n number of trailing zeroes- we must have n factors of 2 (minimum) and n factors of 5(minimum).\n\nmaybe try this one first: https://leetcode.com/problems/factorial-trailing-zeroes/description/\n\nto have maximum number of trailing zeroes, we must maximise the common factors of 2 and 5 in the total product of the path.\nie, we must maximise min(factors of 2, factors of 5);\n\npath recognition: it is given that we must only change the course (horizontal or vertical) of the path ONCE, so there will be at most ONE point in the matrix where the course of the direction will be changed.\nThe rest of the approach is brute force based upon this deduction only - but it going to be implementation heavy.\n\nFor each cell in the grid we must calculate 4 paths originating from this cell:\npath 1: turning left\npath 2: turning right\npath 3: turning up\npath 4: turning down\n\nand if the corresponding cell is the pivot cell ie, the cell where it changes course, it will have 4 possible combinations of the path.\n\n1 up-left\n2 up-right\n3 down-left\n4 down-right\n\nto calculate TOTAL factors of 2 and 5 on these paths I have used prefix sum and 4 sweeps (whew)\nI have also written functions to calculate the contribution of 2 and 5 in the number (number of factors) which is basic math, although to optimise i have used a dp array to avoid recomputation.\n\nThe Custom class was made to try to simplify the data structure we are introducing for our prefix sum of factors of 2 and 5- which is a 2D grid of pairs containing .first as number of factors of 2 and .second as number of factors of 5\n\nat the end we have considered all the possibilities and returned answer\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Custom{\npublic:\n vector<vector <vector <pair <int, int>>>> vec;\n Custom(int m, int n){\n vec.resize(m, vector <vector <pair <int, int>>>(n, vector <pair <int, int>> (4)));\n }\n};\n\nclass Solution {\nprivate:\n int dp2[1001];\n int dp5[1001];\n\n int contri2(int num) {\n if (num == 1 || num % 2 != 0) return 0;\n if (dp2[num] != -1) return dp2[num];\n return dp2[num] = 1 + contri2(num / 2);\n }\n\n int contri5(int num) {\n if (num == 1 || num % 5 != 0) return 0;\n if (dp5[num] != -1) return dp5[num];\n return dp5[num] = 1 + contri5(num / 5);\n }\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n memset(dp2, -1, sizeof dp2);\n memset(dp5, -1, sizeof dp5);\n\n Custom ds(m, n);\n\n //left sweep\n for(int i=0; i<m; i++){\n int curr2 = 0;\n int curr5 = 0;\n for(int j=0; j<n; j++){\n int cell = grid[i][j];\n curr2 += contri2(cell);\n curr5 += contri5(cell);\n\n ds.vec[i][j][0].first = curr2;\n ds.vec[i][j][0].second = curr5;\n }\n }\n\n //right sweep\n for(int i=0; i<m; i++){\n int curr2 = 0;\n int curr5 = 0;\n for(int j=n-1; j>=0; j--){\n int cell = grid[i][j];\n curr2 += contri2(cell);\n curr5 += contri5(cell);\n\n ds.vec[i][j][1].first = curr2;\n ds.vec[i][j][1].second = curr5;\n }\n }\n\n //top sweep\n for(int i=0; i<n; i++){\n int curr2 = 0;\n int curr5 = 0;\n for(int j=0; j<m; j++){\n int cell = grid[j][i];\n curr2 += contri2(cell);\n curr5 += contri5(cell);\n\n ds.vec[j][i][2].first = curr2;\n ds.vec[j][i][2].second = curr5;\n }\n }\n\n //bottom sweep\n for(int i=0; i<n; i++){\n int curr2 = 0;\n int curr5 = 0;\n for(int j=m-1; j>=0; j--){\n int cell = grid[j][i];\n curr2 += contri2(cell);\n curr5 += contri5(cell);\n\n ds.vec[j][i][3].first = curr2;\n ds.vec[j][i][3].second = curr5;\n }\n }\n\n int ans = INT_MIN;\n for(int i=0; i<m; i++){\n for(int j=0; j<n; j++){\n int cell = grid[i][j];\n int c2 = contri2(cell);\n int c5 = contri5(cell);\n int poss1 = min(ds.vec[i][j][2].first+ds.vec[i][j][0].first - c2,\n ds.vec[i][j][2].second+ds.vec[i][j][0].second -c5);\n int poss2 = min(ds.vec[i][j][2].first+ds.vec[i][j][1].first-c2,\n ds.vec[i][j][2].second+ds.vec[i][j][1].second-c5);\n int poss3 = min(ds.vec[i][j][3].first+ds.vec[i][j][0].first-c2,\n ds.vec[i][j][3].second+ds.vec[i][j][0].second-c5);\n int poss4 = min(ds.vec[i][j][3].first+ds.vec[i][j][1].first-c2,\n ds.vec[i][j][3].second+ds.vec[i][j][1].second-c5);\n\n ans = max({ans, poss1, poss2, poss3, poss4});\n }\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['Array', 'Math', 'Dynamic Programming', 'Matrix', 'Prefix Sum', 'C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
2245. Maximum Trailing Zeros in a Cornered Path.cpp
|
2245-maximum-trailing-zeros-in-a-cornere-it2u
|
Code\n\nclass Solution {\npublic:\npair<long long,long long> util(int val){ \n int x=0;\n while(val>0 && val%5==0){\n val=val/5;\n x++;\n
|
202021ganesh
|
NORMAL
|
2024-08-03T13:53:52.037554+00:00
|
2024-08-03T13:53:52.037589+00:00
| 0 | false |
**Code**\n```\nclass Solution {\npublic:\npair<long long,long long> util(int val){ \n int x=0;\n while(val>0 && val%5==0){\n val=val/5;\n x++;\n }\n int y=0;\n while(val>0 && val%2==0){\n val=val/2;\n y++;\n }\n return {x,y}; \n}\nlong long util(vector<vector<int>>& grid){ \n int n=grid.size();\n int m=grid[0].size();\n pair<long long,long long> matrix[n][m];\n pair<long long,long long> matrix1[n][m];\n pair<long long,long long> matrix2[n][m];\n for(int i=0;i<n;i++)\n for(int j=0;j<m;j++){\n int val=grid[i][j];\n matrix[i][j]=util(val);\n }\n for(int i=0;i<n;i++){\n for(int j=m-1;j>=0;j--){\n if(j==m-1)\n matrix1[i][j]=matrix[i][j];\n else\n matrix1[i][j]={matrix[i][j].first+matrix1[i][j+1].first,matrix[i][j].second+matrix1[i][j+1].second};\n }\n }\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(j==0)\n matrix2[i][j]=matrix[i][j];\n else\n matrix2[i][j]={matrix[i][j].first+matrix2[i][j-1].first,matrix[i][j].second+matrix2[i][j-1].second};\n }\n }\n long long res=0; \n for(int j=0;j<m;j++){\n pair<long long,long long>sum={0,0};\n for(int i=0;i<n;i++){\n sum={sum.first+matrix[i][j].first,sum.second+matrix[i][j].second};\n res=max(res,min(sum.first,sum.second));\n if(j>0){\n pair<long long,long long>p1=matrix2[i][j-1];\n res=max(res,min(sum.first+p1.first,sum.second+p1.second));\n }\n if(j<m-1){\n pair<long long,long long>p1=matrix1[i][j+1];\n res=max(res,min(sum.first+p1.first,sum.second+p1.second));\n } \n } \n }\n return res; \n}\nint maxTrailingZeros(vector<vector<int>>& grid) { \nint m=grid[0].size();\n int n=grid.size();\n vector<vector<int>>grid2(m,vector<int>(n,0));\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n grid2[j][i]=grid[i][j];\n }\n }\n long long res=0;\n res=max(util(grid),util(grid2));\n vector<vector<int>>grid3(n,vector<int>(m,0));\n for(int i=0;i<grid.size();i++){\n for(int j=0;j<grid[0].size();j++){\n grid3[n-i-1][j]=grid[i][j]; \n }\n }\n return max(res,util(grid3)); \n}\n};\n```
| 0 | 0 |
['C']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Python, prefix sum solution with explanation
|
python-prefix-sum-solution-with-explanat-b5a7
|
To get a 10 in a path, there must has a 2 and a 5 at least, 2 and 5 are componemts to get more trailing 0s.\n2. the value range of grid is [1, 1000], we can pre
|
shun6096tw
|
NORMAL
|
2024-06-27T05:56:25.040564+00:00
|
2024-06-27T05:56:35.775532+00:00
| 3 | false |
1. To get a 10 in a path, there must has a 2 and a 5 at least, 2 and 5 are componemts to get more trailing 0s.\n2. the value range of grid is [1, 1000], we can precompute how many 2 and 5 are in each number\'s factor.\n3. the path is as longer as good, we just consider 1 coner path only.\n4. we can enumerate each cell as corner, and use prefix sum to get the number of factor in horizontal direction.\n5. enumerate the corner cell from top to bottom or bottom to top to get the number of factor in vertical direction.\n6. if only one row is grid, there is no 1 corner paths, this is a boundary case.\n\ntc is O(1000 + n* m), sc is O(n * m).\n\n```python\n\'\'\'\n1. To form a 10, we need a 5 and a 2.\n2. count how many 5 and 2 the number has for each cell\n3. for each corner path, as longer as good, there are probably trailing zeros\n4. enumerating each cell as corner, one path is top to down, another is left to right\n\n\'\'\'\ncounter_2 = [0] * 1001\ncounter_5 = [0] * 1001\ncounter_2[2] = counter_5[5] = 1\nfor i in range(3, 1001):\n if i % 2 == 0:\n counter_2[i] = counter_2[i//2] + 1\n if i % 5 == 0:\n counter_5[i] = counter_5[i//5] + 1\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n prefix_2 = []\n prefix_5 = []\n for row in grid:\n cur_2 = [0]\n cur_5 = [0]\n for x in row:\n cur_2.append(cur_2[-1] + counter_2[x])\n cur_5.append(cur_5[-1] + counter_5[x])\n prefix_2.append(cur_2)\n prefix_5.append(cur_5)\n ans = 0\n row_2_5 = [[0,0] for _ in grid[0]]\n for i, row in enumerate(grid):\n for j, x in enumerate(row):\n c_2_right = prefix_2[i][-1] - prefix_2[i][j]\n c_5_right = prefix_5[i][-1] - prefix_5[i][j]\n c_2_left = prefix_2[i][j+1]\n c_5_left = prefix_5[i][j+1]\n c_0 = max(min(row_2_5[j][0] + c_2_right, row_2_5[j][1] + c_5_right), min(row_2_5[j][0] + c_2_left, row_2_5[j][1] + c_5_left))\n ans = max(ans, c_0)\n row_2_5[j][0] += counter_2[x]\n row_2_5[j][1] += counter_5[x]\n \n row_2_5 = [[0,0] for _ in grid[0]]\n for i in range(len(grid)-1, -1, -1):\n for j, x in enumerate(grid[i]):\n c_2_right = prefix_2[i][-1] - prefix_2[i][j]\n c_5_right = prefix_5[i][-1] - prefix_5[i][j]\n c_2_left = prefix_2[i][j+1]\n c_5_left = prefix_5[i][j+1]\n c_0 = max(min(row_2_5[j][0] + c_2_right, row_2_5[j][1] + c_5_right), min(row_2_5[j][0] + c_2_left, row_2_5[j][1] + c_5_left))\n ans = max(ans, c_0)\n row_2_5[j][0] += counter_2[x]\n row_2_5[j][1] += counter_5[x]\n return ans\n```
| 0 | 0 |
['Prefix Sum', 'Python']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ easy solution O(n*m) solution
|
c-easy-solution-onm-solution-by-realhand-ar4x
|
\n\n# Complexity\n- Time complexity:o(nm)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:o(nm)\n Add your space complexity here, e.g. O(n) \n
|
RealHandle
|
NORMAL
|
2024-06-09T11:49:01.654005+00:00
|
2024-06-09T11:49:01.654028+00:00
| 8 | false |
\n\n# Complexity\n- Time complexity:o(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:o(n*m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n//min(numberof5,numberof2)\n//[i][j][4][1]\nclass Solution {\npublic:\n pair<int,int> check(int a){\n int cnt2=0,cnt5=0;\n // while(a%10==0){cnt10++,a/=10;}\n while(a%2==0){cnt2++,a/=2;}\n while(a%5==0){cnt5++,a/=5;}\n return {cnt2,cnt5};\n }\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int i,j,n=grid.size(),m=grid[0].size();\n int dp[n][m][4][2];\n\n for(i=0;i<n;i++){\n for(j=0;j<m;j++){\n auto [cnt2,cnt5]=check(grid[i][j]);\n dp[i][j][0][0]=(j==0)?cnt2:dp[i][j-1][0][0]+cnt2;\n dp[i][j][0][1]=(j==0)?cnt5:dp[i][j-1][0][1]+cnt5;\n\n dp[i][j][2][0]=(i==0)?cnt2:dp[i-1][j][2][0]+cnt2;\n dp[i][j][2][1]=(i==0)?cnt5:dp[i-1][j][2][1]+cnt5;\n\n auto tp =check(grid[i][m-j-1]);\n cnt2=tp.first,cnt5=tp.second;\n dp[i][m-j-1][1][0]=(j==0)?cnt2:dp[i][m-j][1][0]+cnt2;\n dp[i][m-j-1][1][1]=(j==0)?cnt5:dp[i][m-j][1][1]+cnt5;\n\n tp=check(grid[n-i-1][j]);\n cnt2=tp.first,cnt5=tp.second;\n dp[n-i-1][j][3][0]=(i==0)?cnt2:dp[n-i][j][3][0]+cnt2;\n dp[n-i-1][j][3][1]=(i==0)?cnt5:dp[n-i][j][3][1]+cnt5;\n\n }\n }\n int mx=0;\n\n for(i=0;i<n;i++){\n for(j=0;j<m;j++){\n auto [cnt2,cnt5]=check(grid[i][j]);\n for(int k1=0;k1<4;k1++){\n for(int k2=k1+1;k2<4;k2++){ \n mx=max(mx,min(dp[i][j][k1][0]+dp[i][j][k2][0]-cnt2\n ,dp[i][j][k1][1]+dp[i][j][k2][1]-cnt5));\n }\n }\n\n }\n }\n\n\n\n return mx;\n\n\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
My Solution
|
my-solution-by-hope_ma-pdwi
|
\n/**\n * Time Complexity: O(rows * cols)\n * Space Complexity: O(rows * cols)\n * where `rows` is the number of the rows of the grid `grid`\n * `cols` is
|
hope_ma
|
NORMAL
|
2024-05-06T02:45:49.320271+00:00
|
2024-05-06T02:55:22.413623+00:00
| 1 | false |
```\n/**\n * Time Complexity: O(rows * cols)\n * Space Complexity: O(rows * cols)\n * where `rows` is the number of the rows of the grid `grid`\n * `cols` is the number of the columns of the grid `grid`\n */\nclass Solution {\n private:\n class Stat {\n public:\n Stat(): factor2s_(0), factor5s_(0) {\n }\n \n Stat(const int factor2s, const int factor5s): factor2s_(factor2s), factor5s_(factor5s) {\n }\n \n Stat(const int number) : factor2s_(get_factors(number, factor_2)), factor5s_(get_factors(number, factor_5)) {\n }\n \n Stat operator+(const Stat &rhs) {\n return Stat(factor2s_ + rhs.factor2s_, factor5s_ + rhs.factor5s_);\n }\n \n Stat operator-(const Stat &rhs) {\n return Stat(factor2s_ - rhs.factor2s_, factor5s_ - rhs.factor5s_);\n }\n \n int zeros() const {\n return min(factor2s_, factor5s_);\n }\n \n private:\n int get_factors(const int number, const int factor) {\n int ret = 0;\n for (int num = number; num % factor == 0; num /= factor) {\n ++ret;\n }\n return ret;\n }\n \n static constexpr int factor_2 = 2;\n static constexpr int factor_5 = 5;\n\n int factor2s_;\n int factor5s_;\n };\n \n public:\n int maxTrailingZeros(const vector<vector<int>> &grid) {\n const int rows = static_cast<int>(grid.size());\n const int cols = static_cast<int>(grid.front().size());\n Stat row_stats[rows][cols + 1];\n Stat col_stats[cols][rows + 1];\n for (int r = 0; r < rows; ++r) {\n for (int c = 0; c < cols; ++c) {\n Stat stat(grid[r][c]);\n row_stats[r][c + 1] = row_stats[r][c] + stat;\n col_stats[c][r + 1] = col_stats[c][r] + stat;\n }\n }\n \n int ret = 0;\n for (int r = 0; r < rows; ++r) {\n for (int c = 0; c < cols; ++c) {\n Stat left = row_stats[r][c + 1];\n Stat top = col_stats[c][r];\n Stat right = row_stats[r][cols] - row_stats[r][c];\n Stat bottom = col_stats[c][rows] - col_stats[c][r + 1];\n ret = max({ret, (left + top).zeros(), (right + top).zeros(), (left + bottom).zeros(), (right + bottom).zeros()});\n }\n }\n return ret;\n }\n};\n```
| 0 | 0 |
[]
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C#, Fast, easy to understand
|
c-fast-easy-to-understand-by-hafthor-avib
|
Intuition\nThere are three main techniques being used here. First, we need to count the number of 2s and 5s in each cell and sum those so we can use the smaller
|
hafthor
|
NORMAL
|
2024-04-29T13:02:21.387533+00:00
|
2024-04-29T13:02:21.387559+00:00
| 2 | false |
# Intuition\nThere are three main techniques being used here. First, we need to count the number of 2s and 5s in each cell and sum those so we can use the smaller count to know how many trailing zeros a result will have. We also store the sum of the 2s and 5s by row and column to make the calculations faster (dynamic programming). We then traverse the grid to pick the elbow of the path and consider each direction from that cell to the grid edge and find the best path.\n\n# Approach\nFirst pass through the grid factors the 2s and 5s from the cell value and stores that along with accumulating row and column sums.\nSecond pass through the grid chooses the elbow of the path and gets the counts going in all directions from that cell to find the maximum number of trailing zeros, which is the maximum of the smaller of the 2s count or 5s count.\n\n# Complexity\n- Time complexity: O(mn)\n- Space complexity: O(mn)\n\n# Code\n```\npublic class Solution {\n public int MaxTrailingZeros(int[][] grid) {\n int m = grid.Length, n = grid[0].Length, result = 0;\n int[,] grid2 = new int[m, n], grid5 = new int[m, n],\n rowSum2 = new int[m, n], rowSum5 = new int[m, n],\n colSum2 = new int[m, n], colSum5 = new int[m, n];\n\n // Step 1: Calculate the number of 2s and 5s in each cell and the row and column sums\n for (int y = 0; y < m; y++) {\n for (int x = 0; x < n; x++) {\n int g = grid[y][x], g2 = 0, g5 = 0;\n // count the number of 2s and 5s in the cell\n for (; g % 2 == 0; g /= 2) g2++;\n for (; g % 5 == 0; g /= 5) g5++;\n grid2[y, x] = g2;\n grid5[y, x] = g5;\n // calculate the row and column sums\n rowSum2[y, x] = g2 + (x > 0 ? rowSum2[y, x - 1] : 0);\n rowSum5[y, x] = g5 + (x > 0 ? rowSum5[y, x - 1] : 0);\n colSum2[y, x] = g2 + (y > 0 ? colSum2[y - 1, x] : 0);\n colSum5[y, x] = g5 + (y > 0 ? colSum5[y - 1, x] : 0);\n }\n }\n\n // Step 2: Calculate the maximum trailing zeros for each cell in each direction.\n // The maximum trailing zeros is the minimum of the count of 2s and 5s.\n for (int y = 0; y < m; y++) {\n for (int x = 0; x < n; x++) {\n // count of 2s and 5s in the up, down, left, and right directions\n int up2 = colSum2[y, x], up5 = colSum5[y, x]; // includes grid[y, x]\n int dn2 = colSum2[m - 1, x] - up2, dn5 = colSum5[m - 1, x] - up5; // doesn\'t include grid[y, x]\n int lf2 = rowSum2[y, x], lf5 = rowSum5[y, x]; // includes grid[y, x]\n int rt2 = rowSum2[y, n - 1] - lf2, rt5 = rowSum5[y, n - 1] - lf5; // doesn\'t include grid[y, x]\n int g2 = grid2[y, x], g5 = grid5[y, x];\n // trailing zeros for up-left, up-right, down-left, down-right\n int ul = Math.Min(up2 + lf2 - g2, up5 + lf5 - g5); // adjusted for double include grid[y, x]\n int ur = Math.Min(up2 + rt2, up5 + rt5);\n int dl = Math.Min(dn2 + lf2, dn5 + lf5);\n int dr = Math.Min(dn2 + rt2 + g2, dn5 + rt5 + g5); // adjusted for double exclude grid[y, x]\n // maximum trailing zeros so far\n result = Math.Max(result, Math.Max(Math.Max(ul, ur), Math.Max(dl, dr)));\n }\n }\n \n return result;\n }\n}\n```
| 0 | 0 |
['Dynamic Programming', 'C#']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
JS
|
js-by-manu-bharadwaj-bn-i1h0
|
Code\n\nvar maxTrailingZeros = function (g) {\n const m = g.length;\n const n = g[0].length;\n const ta = [...Array(m)].map(i => Array(n).fill(1));\n
|
Manu-Bharadwaj-BN
|
NORMAL
|
2024-04-16T19:57:21.751576+00:00
|
2024-04-16T19:57:21.751607+00:00
| 12 | false |
# Code\n```\nvar maxTrailingZeros = function (g) {\n const m = g.length;\n const n = g[0].length;\n const ta = [...Array(m)].map(i => Array(n).fill(1));\n const tb = [...Array(m)].map(i => Array(n).fill(1));\n const tc = [...Array(m)].map(i => Array(n).fill(1));\n const td = [...Array(m)].map(i => Array(n).fill(1));\n\n const c52 = (s) => {\n let c5 = 0;\n let c2 = 0;\n while (s % 2 === 0) {\n s = s / 2;\n c2++;\n }\n while (s % 5 === 0) {\n s = s / 5;\n c5++;\n }\n return [c5, c2];\n }\n\n const c10 = ([c5, c2]) => {\n return Math.min(c5, c2);\n }\n\n for (let i = 0; i < m; i++) {\n for (let j = 0; j < n; j++) {\n ta[i][j] = (j === 0) ? c52(g[i][j]) : [c52(g[i][j])[0] + ta[i][j - 1][0], c52(g[i][j])[1] + ta[i][j - 1][1]];\n tb[i][j] = (i === 0) ? c52(g[i][j]) : [c52(g[i][j])[0] + tb[i - 1][j][0], c52(g[i][j])[1] + tb[i - 1][j][1]];\n }\n }\n\n for (let i = m - 1; i >= 0; i--) {\n for (let j = n - 1; j >= 0; j--) {\n tc[i][j] = (j === n - 1) ? c52(g[i][j]) : [c52(g[i][j])[0] + tc[i][j + 1][0], c52(g[i][j])[1] + tc[i][j + 1][1]]; // : ctz(hg(g[i][j]) * tc[i][j+1][0], tc[i][j+1][1]); // hg(g[i][j]) * tc[i][j+1];\n td[i][j] = (i === m - 1) ? c52(g[i][j]) : [c52(g[i][j])[0] + td[i + 1][j][0], c52(g[i][j])[1] + td[i + 1][j][1]]; // : ctz(hg(g[i][j]) * td[i+1][j][0], td[i+1][j][1]); // hg(g[i][j]) * td[i+1][j];\n }\n }\n\n let ret = 0;\n for (let i = 0; i < m; i++) {\n for (let j = 0; j < n; j++) {\n let s1 = i === 0 ? c10(ta[i][j]) : c10([ta[i][j][0] + tb[i - 1][j][0], ta[i][j][1] + tb[i - 1][j][1]]);\n let s2 = i === m - 1 ? c10(ta[i][j]) : c10([ta[i][j][0] + td[i + 1][j][0], ta[i][j][1] + td[i + 1][j][1]]);\n let s3 = i === 0 ? c10(tc[i][j]) : c10([tc[i][j][0] + tb[i - 1][j][0], tc[i][j][1] + tb[i - 1][j][1]]);\n let s4 = i === m - 1 ? c10(tc[i][j]) : c10([tc[i][j][0] + td[i + 1][j][0], tc[i][j][1] + td[i + 1][j][1]]);\n ret = Math.max(ret, s1, s2, s3, s4);\n }\n }\n return ret;\n};\n```
| 0 | 0 |
['JavaScript']
| 1 |
maximum-trailing-zeros-in-a-cornered-path
|
C++, stl solution, easy to understand, beats 93% time & space, O(mn) time, O(m+n) space
|
c-stl-solution-easy-to-understand-beats-ta9a2
|
Intuition\n Describe your first thoughts on how to solve this problem. \nOn the surface the problem is pretty similar to prefix sum. If you have time, I highly
|
bbandyop
|
NORMAL
|
2024-01-31T21:19:14.325677+00:00
|
2024-01-31T21:19:14.325706+00:00
| 8 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nOn the surface the problem is pretty similar to prefix sum. If you have time, I highly recommend checking prefix sum before. Check the hints if you need help. This is a 2D version of prefix sum.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we calculate the sum of 2-factors & 5-factors row-wise & column-wise in 1st pass. Then we go through the array again, however, we now know the totals for every row & col, we can subtract the sum upto the curr_value to get the factors of the remaining part of the column (right side) & bottom part. As shown below\n\n```\n ------\u25B2------ row totals (rv)\n | |up | 2, 1\n |<-----e----->| 0, 2\n | left |right | .\n | | | .\n | | | .\n | |down |\n ------\u25BC------\ncol totals(cv) 2,3 1,0 .....\n```\n\nWe then add up the totals for all combinations taking the curr element as pivot, thus we can have,\n- left + up\n- up + right\n- left + down\n- down + right\n\nWe must take care to make sure that the current element is included only once in each of these computations. Once we have the intermediate totals, we calculate zeros as min(2-factors, 5-factors), then we compute the maximum of all 4 possible combinations.\n\nLastly, update the counts & add the current values to running totals. Note, we use a vector to keep track of current row.\n\n# Complexity\n- Time complexity: $$O(m * n)$$ for 2 traversals \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(m + n)$$ where m,n = rows, cols\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n// Save some typing :)\n// tuple <int,int> = factors of 2,5\nusing tup2 = tuple<int,int>;\nusing vtup2 = vector<tup2>;\n\n// Return min value of a tuple\ninline int tup2_min(tup2 &a) {\n return min(get<0>(a), get<1>(a));\n}\n\n// Its handy to have these for adding and subtracting\n// the number of factors\ntup2 operator + (tup2 &a, tup2 b) {\n return tup2(get<0>(a) + get<0>(b), \n get<1>(a) + get<1>(b));\n}\n\ntup2 operator - (tup2 &a, tup2 b) {\n return tup2(get<0>(a) - get<0>(b), \n get<1>(a) - get<1>(b));\n}\n\n// basic prime factorization algo\ntup2 pfact2_5 (int t) {\n int f2 = 0, f5 = 0;\n\n while (t % 2 == 0 || t % 5 == 0) {\n if (t % 5 == 0) {\n f5++;\n t /= 5;\n } else if (t % 2 == 0) {\n f2++;\n t /= 2;\n }\n }\n\n return tup2({f2, f5});\n}\n\nclass Solution {\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n int rows = grid.size(), cols = grid[0].size();\n vtup2 rv(rows, {0,0});\n vtup2 cv(cols, {0,0});\n\n // add up all the factors row-wise\n // and column-wise \n for (int i = 0; i < rows; i++) {\n tup2 f = {0, 0};\n for (int j = 0; j < cols; j++) {\n tup2 tf = pfact2_5(grid[i][j]);\n f = f + tf;\n\n cv[j] = cv[j] + tf;\n }\n rv[i] = rv[i] + f;\n }\n \n\n // maintain current row status\n int max_zeros = 0;\n vtup2 row_ctr(cols, {0,0});\n\n // choose each i, j as elbow points\n for (int i = 0; i < rows; i++) {\n tup2 cf = {0,0};\n for (int j = 0; j < cols; j++) {\n tup2 tf = pfact2_5(grid[i][j]);\n\n tup2 left = cf;\n tup2 right = rv[i] - left;\n\n tup2 up = row_ctr[j];\n tup2 down = cv[j] - up;\n\n // Note:\n // be careful to add the element factors only once\n // subtract where we added twice\n // rule of thumb: left & up does not have\n // the current element included while down & right does\n tup2 tl = up + left; tl = tl + tf;\n tup2 tr = up + right;\n tup2 bl = down + left;\n tup2 br = down + right; br = br - tf;\n\n // store temporarily to calculate max element\n int mx[] = {tup2_min(tl), tup2_min(tr), tup2_min(bl), tup2_min(br)};\n\n // update max_zeros\n max_zeros = max(*max_element(begin(mx), end(mx)), max_zeros);\n\n // update running row counts and column\n cf = cf + tf;\n row_ctr[j] = row_ctr[j] + tf;\n }\n }\n\n return max_zeros;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
prefix sums with explanation
|
prefix-sums-with-explanation-by-raskumam-cjks
|
Intuition\n Describe your first thoughts on how to solve this problem. \nfor every point as a point of direction change if we know the max zeros, answer is max
|
raskumama7
|
NORMAL
|
2024-01-26T15:49:29.448322+00:00
|
2024-01-26T15:49:29.448352+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfor every point as a point of direction change if we know the max zeros, answer is maxium of all point max zeros. a 10 can be formed with 5 and 2 only\n# Approach\n<!-- Describe your approach to solving the problem. -->\ncalculated prefix sum of 2\'s and 5\'s in each direction for every point\n\nat every point add left with up or down sums, right with up or down and take maximum for that point\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n2 * O(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n10 * O(N)\n# Code\n```\nclass Solution {\n int cntFactorials(int val, int exp) {\n int cnt = 0;\n while(val % exp == 0) {\n cnt++;\n val /= exp;\n }\n return cnt;\n }\n typedef struct prefix{\n int twos = -1;\n int fives = -1;\n prefix operator+(prefix b) {\n return {twos + b.twos, fives + b.fives};\n }\n }prefix;\n typedef struct elemInfo{\n int twos = -1;\n int fives = -1;\n prefix left;\n prefix right;\n prefix up;\n prefix down;\n }elemInfo;\npublic:\n int maxTrailingZeros(vector<vector<int>>& grid) {\n vector<vector<elemInfo>> data(grid.size(), vector<elemInfo>(grid[0].size()));\n int res = 0;\n // calculate left and up prefix sums of 2\'s and 5\'s\n for( int x = 0; x < grid.size() ; x++) {\n for(int y = 0; y < grid[0].size();y++) {\n if(data[x][y].fives == -1){\n data[x][y].fives = cntFactorials(grid[x][y], 5);\n }\n if(data[x][y].twos == -1){\n data[x][y].twos = cntFactorials(grid[x][y], 2);\n }\n\n if(y > 0)\n data[x][y].left = data[x][y-1].left + prefix{data[x][y].twos, data[x][y].fives};\n else\n data[x][y].left = {data[x][y].twos, data[x][y].fives};\n if(x > 0)\n data[x][y].up = data[x-1][y].up + prefix{data[x][y].twos, data[x][y].fives};\n else\n data[x][y].up = {data[x][y].twos, data[x][y].fives};\n\n }\n }\n // calculate right and down prefix sums of 2\'s and 5\'s\n for( int x = grid.size() - 1; x >=0 ; x--) {\n for(int y = grid[0].size() - 1; y >=0; y--) {\n if(x + 1 < grid.size())\n data[x][y].down = data[x + 1][y].down + prefix{data[x][y].twos, data[x][y].fives};\n else\n data[x][y].down = {data[x][y].twos, data[x][y].fives};\n if(y + 1 < grid[0].size())\n data[x][y].right = data[x][y+1].right + prefix{data[x][y].twos, data[x][y].fives};\n else\n data[x][y].right = {data[x][y].twos, data[x][y].fives};\n\n\n // now that we have count of twos and fives of current element from all direcions\n // calculate max trailing zeros with current element as point of direction change\n res = max(res, min(data[x][y].left.fives + data[x][y].up.fives - data[x][y].fives,\n data[x][y].left.twos + data[x][y].up.twos - data[x][y].twos));\n res = max(res, min(data[x][y].left.fives + data[x][y].down.fives - data[x][y].fives,\n data[x][y].left.twos + data[x][y].down.twos - data[x][y].twos));\n res = max(res, min(data[x][y].right.fives + data[x][y].up.fives - data[x][y].fives,\n data[x][y].right.twos + data[x][y].up.twos - data[x][y].twos));\n res = max(res, min(data[x][y].right.fives + data[x][y].down.fives - data[x][y].fives,\n data[x][y].right.twos + data[x][y].down.twos - data[x][y].twos));\n }\n }\n \n // for( int x = 0; x < grid.size() ; x++) {\n // for(int y = 0; y < grid[0].size();y++) {\n // cout << data[x][y].left << " ";\n // }\n // cout <<endl;\n // }\n return res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
C++ || EASY AND CLEAR TO UNDERSTAND || Simple Prefix Sum :)
|
c-easy-and-clear-to-understand-simple-pr-g24k
|
Approach\nmake 4 arrays top, down, up and left and store occurances of 2s and 5s in them with pair \nfor each index try to find by which pair we got maximum tra
|
Joshiiii
|
NORMAL
|
2023-11-21T13:11:07.969286+00:00
|
2023-11-21T13:11:07.969306+00:00
| 15 | false |
# Approach\nmake 4 arrays top, down, up and left and store occurances of 2s and 5s in them with pair \nfor each index try to find by which pair we got maximum trailing zeroes.\n\n# Code\n```\nclass Solution {\npublic:\n \n pair<int, int> countTwosAndFives(int num) {\n int two = 0, five = 0;\n while(num % 5 == 0) {\n five++;\n num /= 5;\n }\n \n while(num % 2 == 0) {\n two++;\n num /= 2;\n }\n \n return {two, five};\n }\n \n int maxTrailingZeros(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n \n vector<vector<pair<int, int>>> left(n, vector<pair<int, int>> (m));\n vector<vector<pair<int, int>>> right(n, vector<pair<int, int>> (m));\n vector<vector<pair<int, int>>> up(n, vector<pair<int, int>> (m));\n vector<vector<pair<int, int>>> down(n, vector<pair<int, int>> (m));\n \n // left matrix...\n for(int i=0; i<n; i++) {\n int two = 0, five = 0;\n for(int j=0; j<m; j++) {\n left[i][j] = {two, five};\n pair<int,int> res = countTwosAndFives(grid[i][j]);\n two += res.first;\n five += res.second;\n }\n }\n \n // right matrix...\n for(int i=0; i<n; i++) {\n int two = 0, five = 0;\n for(int j=m-1; j>=0; j--) {\n right[i][j] = {two, five};\n pair<int,int> res = countTwosAndFives(grid[i][j]);\n two += res.first;\n five += res.second;\n }\n }\n \n // up matrix...\n for(int i=0; i<m; i++) {\n int two = 0, five = 0;\n for(int j=0; j<n; j++) {\n up[j][i] = {two, five};\n pair<int,int> res = countTwosAndFives(grid[j][i]);\n two += res.first;\n five += res.second;\n }\n }\n \n // down matrix...\n for(int i=0; i<m; i++) {\n int two = 0, five = 0;\n for(int j=n-1; j>=0; j--) {\n down[j][i] = {two, five};\n pair<int,int> res = countTwosAndFives(grid[j][i]);\n two += res.first;\n five += res.second;\n }\n }\n \n \n \n int ans = 0;\n for(int i=0; i<n; i++) {\n for(int j=0; j<m; j++) {\n pair<int,int> res = countTwosAndFives(grid[i][j]);\n ans = max(ans, min(left[i][j].first + up[i][j].first + res.first, \n left[i][j].second + up[i][j].second + res.second));\n ans = max(ans, min(left[i][j].first + down[i][j].first + res.first, \n left[i][j].second + down[i][j].second + res.second));\n ans = max(ans, min(right[i][j].first + up[i][j].first + res.first, \n right[i][j].second + up[i][j].second + res.second));\n ans = max(ans, min(right[i][j].first + down[i][j].first + res.first, \n right[i][j].second + down[i][j].second + res.second));\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Prefix Sum', 'C++']
| 0 |
maximum-trailing-zeros-in-a-cornered-path
|
Simple Prefix Sum Solution
|
simple-prefix-sum-solution-by-lakshyagou-9bc7
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
lakshyagour10
|
NORMAL
|
2023-10-11T15:05:49.688605+00:00
|
2023-10-11T15:05:49.688630+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n pair<int,int> helper(int n)\n {\n int n5=0;\n int n2=0;\n while(n%5==0)\n {\n n5++;\n n=(n/5);\n }\n while(n%2==0)\n {\n n2++;\n n=(n/2);\n }\n return {n2,n5};\n }\n int maxTrailingZeros(vector<vector<int>>& grid) {\n vector<vector<pair<int,int>>> horizontal(grid.size(),vector<pair<int,int>>(grid[0].size()));\n vector<vector<pair<int,int>>> vertical(grid.size(),vector<pair<int,int>>(grid[0].size()));\n\n for(int i=0;i<grid.size();i++)\n {\n horizontal[i][0]=helper(grid[i][0]);\n for(int j=1;j<grid[0].size();j++)\n {\n horizontal[i][j]=helper(grid[i][j]);\n horizontal[i][j].first+=horizontal[i][j-1].first;\n horizontal[i][j].second+=horizontal[i][j-1].second;\n }\n }\n for(int j=0;j<grid[0].size();j++)\n {\n vertical[0][j]=helper(grid[0][j]);\n for(int i=1;i<grid.size();i++)\n {\n vertical[i][j]=helper(grid[i][j]);\n vertical[i][j].first+=vertical[i-1][j].first;\n vertical[i][j].second+=vertical[i-1][j].second;\n }\n }\n int ans=0;\n for(int i=0;i<grid.size();i++)\n {\n for(int j=0;j<grid[0].size();j++)\n {\n pair<int,int> p = helper(grid[i][j]);\n pair<int,int> uv = vertical[i][j];\n pair<int,int> lh = horizontal[i][j];\n\n pair<int,int> dv = \n {vertical[grid.size()-1][j].first - uv.first + p.first,vertical[grid.size()-1][j].second - uv.second+p.second};\n pair<int,int> rh = \n {horizontal[i][grid[0].size()-1].first - lh.first+p.first, horizontal[i][grid[0].size()-1].second - lh.second+p.second};\n\n int l1 = min(uv.first+lh.first - p.first,uv.second+lh.second - p.second);\n int l2 = min(uv.first+rh.first - p.first,uv.second+rh.second - p.second);\n int l3 = min(uv.first+dv.first - p.first,uv.second+dv.second - p.second);\n int l4 = min(dv.first+lh.first - p.first,dv.second+lh.second - p.second);\n int l5 = min(dv.first+rh.first - p.first,dv.second+rh.second - p.second);\n int l6 = min(rh.first+lh.first - p.first,rh.second+lh.second - p.second);\n // cout<<i<<" "<<j<<" "<<l1<<l2<<l3<<l4<<l5<<l6<<endl;\n ans=max(ans,max({l1,l2,l3,l4,l5,l6}));\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.