question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-losers-of-the-circular-game
|
Using Math model, Hashmap and Recursion
|
using-math-model-hashmap-and-recursion-b-c8xd
|
Intuition\n Describe your first thoughts on how to solve this problem. \nI will post it later.\n\n# Approach\n Describe your approach to solving the problem. \n
|
Sharath_Payili
|
NORMAL
|
2024-08-30T02:01:47.090271+00:00
|
2024-08-30T02:01:47.090304+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI will post it later.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n Set<Integer> set = new HashSet<>();\n int win = winner(1, n, k, 0, set);\n int len = n - set.size();\n int[] res = new int[len];\n while (len - 1 > -1) {\n if (!set.contains(n)) {\n res[len-1] = n;\n len--;\n }\n n--;\n }\n return res;\n }\n private int winner(int player, int num, int steps, int count, Set<Integer> ballCount) {\n boolean entry = ballCount.add(player);\n if (!entry) {\n return player;\n } else {\n count++;\n int newSteps = count * steps;\n if (player + newSteps <= num) {\n player = player + newSteps;\n return winner(player, num, steps, count, ballCount);\n } else {\n player = (player + newSteps - num) % num;\n if (player == 0) return winner(num, num, steps, count, ballCount);\n else return winner(player, num, steps, count, ballCount);\n }\n }\n }\n}\n```
| 0 | 0 |
['Hash Table', 'Math', 'Recursion', 'Java']
| 0 |
find-the-losers-of-the-circular-game
|
Python 3 | Hash Table | Time O(n) | Space O(n) | Easy code
|
python-3-hash-table-time-on-space-on-eas-qxj8
|
Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\npython3 []\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> Li
|
George_SRE
|
NORMAL
|
2024-08-22T15:02:15.642151+00:00
|
2024-08-22T15:02:15.642187+00:00
| 5 | false |
# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```python3 []\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> List[int]:\n dictSet = set()\n count = 0\n\n for i in range(1, n + 1):\n dictSet.add(i)\n # {1, 2, 3, 4, 5}\n\n for j in range(n): \n\n count = (count + (k * j)) % n\n\n if count + 1 not in dictSet: # 1) {1, 2, 3, 4, 5}\n break # 2) {2, 3, 4, 5}\n else: # 3) {2, 4, 5}\n dictSet.remove(count + 1) # 4) {4, 5}\n # {4, 5}\n return list(dictSet) # [4,5]\n```
| 0 | 0 |
['Array', 'Hash Table', 'Python3']
| 0 |
find-the-losers-of-the-circular-game
|
Bruteforce
|
bruteforce-by-amritbskt-1h0o
|
Code\n\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n int arr[50]={0};\n int i=1;\n int K=k;\n whi
|
amritbskt
|
NORMAL
|
2024-08-16T09:27:28.311309+00:00
|
2024-08-16T09:27:28.311377+00:00
| 0 | false |
# Code\n```\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n int arr[50]={0};\n int i=1;\n int K=k;\n while(1){\n if(arr[i-1]==1)\n break;\n arr[i-1]=1;\n i= (i+K)%n;\n if(i==0) i=n;\n K+=k;\n } \n vector<int> result;\n for(int k=0;k<n;k++){\n if(arr[k]==0) result.push_back(k+1);\n }\n return result;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-losers-of-the-circular-game
|
filter
|
filter-by-user5400vw-xcgh
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
user5400vw
|
NORMAL
|
2024-08-13T04:32:52.533811+00:00
|
2024-08-13T04:32:52.533846+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nimpl Solution {\n pub fn circular_game_losers(n: i32, k: i32) -> Vec<i32> {\n // keep track of who\'s touched the ball\n let mut whostouched: Vec<bool> = vec![false; n as usize];\n let mut step = 1;\n let mut cnt = 0;\n whostouched[0] = true;\n\n loop {\n cnt+=k*step;\n let player = (cnt%n) as usize;\n if whostouched[player] {\n break;\n }\n whostouched[player] = true;\n step+=1;\n }\n (0..n).filter(|&i| !whostouched[i as usize]).map(|v| v+1 ).collect()\n }\n}\n```
| 0 | 0 |
['Rust']
| 0 |
find-the-losers-of-the-circular-game
|
Circular Game Losers Identification Algorithm
|
circular-game-losers-identification-algo-5pz4
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nI approached the problem by first initializing an array with values from
|
traezeeofor
|
NORMAL
|
2024-08-11T05:57:21.949147+00:00
|
2024-08-11T05:57:21.949179+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nI approached the problem by first initializing an array with values from 1 to n, representing the players in the circular game. I then simulated the game by keeping track of the receivers of the pass and the current start position. I used a while loop to continue the game until a player receives the pass for the second time. I stored the receivers in an array and then mapped it to get the actual player numbers. Finally, I filtered the initial array to get the players who did not receive the pass twice, thus identifying the losers.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunction circularGameLosers(n: number, k: number): number[] {\n let valus = Array.from({ length: n }, (v, i) => i + 1);\n let receivers: number[] = [0];\n let start = 0;\n let count = 1;\n\n while (receivers.filter((el) => el === start).length !== 2) {\n start = (start + (count * k)) % n;\n receivers.push(start);\n count++;\n }\n\n let receivers2 = receivers.map((el) => el + 1);\n\n return valus.filter((el) => !receivers2.includes(el));\n};\n```
| 0 | 0 |
['TypeScript']
| 0 |
find-the-losers-of-the-circular-game
|
find-the-losers-of-the-circular-game
|
find-the-losers-of-the-circular-game-by-hrv5g
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
gxImdamNVX
|
NORMAL
|
2024-07-23T06:21:18.635503+00:00
|
2024-07-23T06:21:18.635533+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] circularGameLosers(int n, int k) \n {\n\n int sum=k+1;\n int i=2,j=0;\n int index=sum%n;\n if(index==0)\n {\n index=n;\n }\n \n Set<Integer> set = new HashSet<>();\n set.add(1);\n int[] ans1 ={};\n if(n==1)\n {\n return ans1;\n }\n while(!set.contains(index))\n {\n \n \n // System.out.println(index);\n if(!set.contains(index))\n {\n set.add(index);\n }\n sum=sum+i*k;\n i++;\n index=sum%n;\n if(index==0)\n {\n index=n;\n }\n }\n //System.out.println(set);\n \n int[] ans =new int[n-set.size()];\n for(i=1;i<=n;i++)\n {\n if(!set.contains(i))\n {\n ans[j]=i;\n // System.out.println(ans[j]);\n j++;\n }\n }\n return ans;\n \n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-losers-of-the-circular-game
|
easy solution
|
easy-solution-by-srikanth111-784v
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
srikanth111
|
NORMAL
|
2024-07-06T11:01:58.624433+00:00
|
2024-07-06T11:01:58.624466+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n ios_base::sync_with_stdio(false);\n\n vector<bool> list(n + 1, false);\n vector<int> losers;\n int player = 1, j = 1;\n list[player] = true;\n while (true) {\n player = player+(k * j++);\n (player > n) ? player %= n ,player==0 ? player=n:0: 0;\n \n if (!list[player]) list[player] = true;\n else break;\n }\n for (int i = 1; i < n + 1; ++i) if (!list[i]) losers.push_back(i);\n return losers;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-losers-of-the-circular-game
|
Simple Java Solution
|
simple-java-solution-by-mridsmittal-mhvd
|
\n\n# Code\n\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n boolean visited[] = new boolean[n];\n int x=0;\n int
|
mridsmittal
|
NORMAL
|
2024-07-06T02:34:03.519056+00:00
|
2024-07-06T02:34:03.519083+00:00
| 4 | false |
\n\n# Code\n```\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n boolean visited[] = new boolean[n];\n int x=0;\n int i=1;\n int visCount =0;\n while(!visited[x]){\n visited[x]=true;\n visCount++;\n x=(x+i*k)%n;\n i++;\n }\n int ar[] = new int[n-visCount];\n int pos =0;\n for(int a=0;a<visited.length;a++){\n if(!visited[a]){\n ar[pos]=a+1;\n pos++;\n }\n\n }\n return ar;\n\n \n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-losers-of-the-circular-game
|
Rust beats 100%
|
rust-beats-100-by-grimerssy-5r44
|
Code\n\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn circular_game_losers(n: i32, k: i32) -> Vec<i32> {\n let winners = core::iter::succ
|
grimerssy
|
NORMAL
|
2024-07-04T17:58:39.638377+00:00
|
2024-07-04T17:58:39.638409+00:00
| 2 | false |
# Code\n```\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn circular_game_losers(n: i32, k: i32) -> Vec<i32> {\n let winners = core::iter::successors(Some((0, 0)), |(a, b)| Some((a + k, a + b)))\n .skip(1)\n .map(|(_, steps)| steps % n + 1)\n .try_fold(HashSet::new(), |mut friends, friend| {\n match friends.insert(friend) {\n true => Ok(friends),\n false => Err(friends),\n }\n })\n .unwrap_err();\n (1..=n).filter(|friend| !winners.contains(friend)).collect()\n }\n}\n```
| 0 | 0 |
['Rust']
| 0 |
find-the-losers-of-the-circular-game
|
Easy to understand - Java
|
easy-to-understand-java-by-ungureanu_ovi-pnd9
|
Disclaimer: Like/Upvode if you like the solutions as it help me a lot guys :D\n\n# Intuition\n\nThe problem is about simulating a circular game where players ar
|
Ungureanu_Ovidiu
|
NORMAL
|
2024-07-02T21:37:45.416809+00:00
|
2024-07-02T21:37:45.416836+00:00
| 4 | false |
##### Disclaimer: Like/Upvode if you like the solutions as it help me a lot guys :D\n\n# Intuition\n\nThe problem is about simulating a circular game where players are eliminated in a cyclic manner with an increasing step size. By keeping track of eliminated players using a boolean array, we can determine which players remain at the end.\n\n## Approach\n\n1. **Initialize Players**:\n - Use a boolean array `players` of size `n` to track whether a player is eliminated (`true`) or not (`false`).\n - Initialize `currentK` to `k` and the current index `i` to `0`.\n\n2. **Simulate Elimination**:\n - While loop to simulate the elimination process:\n - If the current player `i` is already eliminated, break the loop.\n - Mark the current player `i` as eliminated.\n - Move to the next player by updating `i` to `(i + currentK) % n`.\n - Increase `currentK` by `k` for the next elimination step.\n\n3. **Determine Losers**:\n - Create an `ArrayList` to store the indices of players who were never eliminated.\n - Iterate through the `players` array, adding the 1-based index of players who are still in the game to the `ArrayList`.\n\n4. **Convert to Array**:\n - Convert the `ArrayList` to an `int[]` array to meet the return type requirement.\n\n5. **Return Result**:\n - Return the array of players who were never eliminated.\n\n## Complexity\n\n- **Time Complexity**: O(n), where n is the number of players. The while loop and subsequent for loop each iterate at most `n` times.\n\n- **Space Complexity**: O(n), where n is the number of players. This space is used by the boolean array and the `ArrayList`.\n\n## Code\n\n```Java\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n boolean[] players = new boolean[n];\n int currentK = k;\n int i = 0;\n\n while (true) {\n if (players[i]) {\n break;\n }\n players[i] = true;\n i = (i + currentK) % n;\n currentK += k;\n }\n\n ArrayList<Integer> losers = new ArrayList<>();\n for (int j = 0; j < n; j++) {\n if (!players[j]) {\n losers.add(j + 1);\n }\n }\n\n int[] result = new int[losers.size()];\n for (int j = 0; j < losers.size(); j++) {\n result[j] = losers.get(j);\n }\n\n return result;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-losers-of-the-circular-game
|
C++ solution simulation
|
c-solution-simulation-by-oleksam-fkgi
|
\n// Please, upvote if you like it. Thanks :-)\nvector<int> circularGameLosers(int n, int k) {\n\tvector<int> game(n, 0);\n\tint nextSteps = 0, curPlayer = 0;\n
|
oleksam
|
NORMAL
|
2024-07-02T09:31:48.592068+00:00
|
2024-07-02T09:31:48.592092+00:00
| 1 | false |
```\n// Please, upvote if you like it. Thanks :-)\nvector<int> circularGameLosers(int n, int k) {\n\tvector<int> game(n, 0);\n\tint nextSteps = 0, curPlayer = 0;\n\twhile (true) {\n\t\tcurPlayer += nextSteps;\n\t\tif (++game[curPlayer % n] > 1)\n\t\t\tbreak;\n\t\tnextSteps += k;\n\t}\n\tvector<int> res;\n\tfor (int i = 0; i < n; i++)\n\t\tif (game[i] == 0)\n\t\t\tres.push_back(i + 1);\n\treturn res;\n}\n```
| 0 | 0 |
['C', 'C++']
| 0 |
find-the-losers-of-the-circular-game
|
2682. Find the Losers of the Circular Game
|
2682-find-the-losers-of-the-circular-gam-iz6y
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
GayatriSowmya
|
NORMAL
|
2024-06-15T17:22:20.692550+00:00
|
2024-06-15T17:22:20.692600+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def circularGameLosers(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: List[int]\n """\n visited = set()\n curr = 0\n s = 1\n visited.add(0)\n while True:\n curr = (curr + s * k) % n\n if curr in visited:\n break\n visited.add(curr)\n s += 1\n \n # Convert from 0-based index to 1-based index\n visited = {x + 1 for x in visited}\n \n # All friends who did not receive the ball\n losers = [i for i in range(1, n + 1) if i not in visited]\n \n return sorted(losers)\n\n \n \n```
| 0 | 0 |
['Python']
| 0 |
find-the-losers-of-the-circular-game
|
C++👨🏻💻 | Easy ✅| Do what Que Says 🫡
|
c-easy-do-what-que-says-by-pavesh_kanung-6lol
|
Intuition\nDo What Question Says. Here, I am visiting every person and marking it visited if it was not visited before. The loop ends when we visit to a person
|
Pavesh_Kanungo
|
NORMAL
|
2024-06-12T04:29:53.951092+00:00
|
2024-06-12T04:29:53.951124+00:00
| 4 | false |
# Intuition\n**Do What Question Says**. Here, I am visiting every person and marking it visited if it was not visited before. The loop ends when we visit to a person who was visited before.\n\n# Approach\nTaken a vector vis (visited, we can say) which will mark according to the number of the person. Here, I have taken the vector of size \'n+1\', here index 0 has no use.\nStarting from pos = 1 to till we go.\nif(pos==0) then I making pos = n, means pos is divisible by n so it must be \'n\' as we are representing the numbers on the range of 1 to n only.\n\n# Complexity\n- Time complexity:\nIn the worst case, we are visiting every node so **TC = O(N)**\n\n- Space complexity:\n**SC = O(N) + O(N) = O(N)**, for visited vector and ans vector\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n vector<int> vis(n+1, 0);\n\n int pos = 1;\n int i=1;\n vis[1] = -1;\n while(true){\n pos = ( i*k + pos ) % n;\n if(pos == 0) pos = n;\n if(vis[pos] == -1){\n break;\n }\n vis[pos] = -1;\n i++;\n }\n\n vector<int> ans;\n for(int i=1; i<=n; i++){\n if(vis[i] == 0) ans.push_back(i);\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['Array', 'C++']
| 0 |
find-the-losers-of-the-circular-game
|
Easy | Simple to Understand
|
easy-simple-to-understand-by-sat_yam_09-4t93
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Sat_yam_09
|
NORMAL
|
2024-06-10T17:41:50.042261+00:00
|
2024-06-10T17:41:50.042290+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n vector<int> vec(n+1,0);\n int i=1;\n int cur=1;\n vec[1]++;\n while(true){\n int p=i*k;\n cur=cur+p;\n if(cur%n!=0)\n cur=cur%n;\n else{\n cur=n;\n }\n \n vec[cur]++;\n if(vec[cur]==2) break;\n i++; \n }\n\n vector<int> ans;\n for(int x=1;x<vec.size();x++){\n if(vec[x]==0){\n ans.push_back(x);\n }\n }\n return ans;\n } \n\n\n \n\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-losers-of-the-circular-game
|
Beats 100.00% of users with Swift
|
beats-10000-of-users-with-swift-by-victo-3ydt
|
\n\nclass Solution {\n func circularGameLosers(_ n: Int, _ k: Int) -> [Int] {\n var set_friends : Set<Int> = []\n var player = 0\n var c
|
Victor-SMK
|
NORMAL
|
2024-06-06T18:27:38.967353+00:00
|
2024-06-06T18:27:38.967406+00:00
| 6 | false |
\n```\nclass Solution {\n func circularGameLosers(_ n: Int, _ k: Int) -> [Int] {\n var set_friends : Set<Int> = []\n var player = 0\n var count = 0\n var ans = [Int]()\n\n while !set_friends.contains(player){\n set_friends.insert(player)\n count += 1\n player = (player + count*k) % n\n }\n\n for i in 0..<n {\n if !set_friends.contains(i){\n ans.append(i + 1)\n }\n }\n\n return ans\n }\n}\n```
| 0 | 0 |
['Swift']
| 0 |
find-the-losers-of-the-circular-game
|
My solution
|
my-solution-by-navjotsaroa-7w1h
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
NavjotSaroa
|
NORMAL
|
2024-06-02T00:35:39.427025+00:00
|
2024-06-02T00:35:39.427047+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def circularGameLosers(self, n, k):\n """\n :type n: int\n :type k: int\n :rtype: List[int]\n """\n members = [i for i in range(n)]\n held = []\n holder = 0\n i = 1\n\n while True:\n held.append(holder)\n holder = (holder + (i * k)) % (n)\n if holder in held:\n break\n\n i += 1\n \n return [j+1 for j in members if j not in held]\n\n```
| 0 | 0 |
['Python']
| 0 |
find-the-losers-of-the-circular-game
|
C# Just Solution with Linq
|
c-just-solution-with-linq-by-ilya-a-f-abtq
|
csharp\npublic class Solution\n{\n public int[] CircularGameLosers(int n, int k)\n {\n var friends = Enumerable.Range(1, n).ToHashSet();\n\n
|
ilya-a-f
|
NORMAL
|
2024-05-11T18:52:47.831590+00:00
|
2024-05-11T19:09:13.085067+00:00
| 9 | false |
```csharp\npublic class Solution\n{\n public int[] CircularGameLosers(int n, int k)\n {\n var friends = Enumerable.Range(1, n).ToHashSet();\n\n Enumerable.Range(0, n)\n .Select(turn => k * turn * (turn + 1) / 2)\n .TakeWhile(i => friends.Remove(i % n + 1))\n .Count();\n\n return friends.Order().ToArray();\n }\n}\n```
| 0 | 0 |
['Hash Table', 'Simulation', 'C#']
| 0 |
find-the-losers-of-the-circular-game
|
Set + stream
|
set-stream-by-ihatealgothrim-hkx9
|
\n# Code\n\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n Set<Integer> set = new HashSet<>();\n int index = 0;\n
|
IHateAlgothrim
|
NORMAL
|
2024-05-11T06:51:00.871064+00:00
|
2024-05-11T06:51:00.871105+00:00
| 0 | false |
\n# Code\n```\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n Set<Integer> set = new HashSet<>();\n int index = 0;\n int i = 1;\n set.add(0);\n\n while (true) {\n int idx = (i++ * k + index) % n;\n if (!set.add(idx)) break;\n index = idx;\n }\n\n return IntStream.range(1, n)\n .filter(idx -> !set.contains(idx))\n .map(idx -> idx + 1)\n .toArray();\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-losers-of-the-circular-game
|
Java Solution || Functional Programming || HashSets<>
|
java-solution-functional-programming-has-epbv
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
hramir
|
NORMAL
|
2024-05-11T04:29:00.032085+00:00
|
2024-05-11T04:29:00.032104+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n int ball = 0;\n int multiplier = 0;\n Set<Integer> visited = new HashSet<Integer>();\n visited.add(0);\n while (true) {\n multiplier++;\n ball = (ball + multiplier * k) % n;\n if (visited.contains(ball)) { break; }\n visited.add(ball);\n }\n Set<Integer> newVisited = visited.stream().map(\n i -> i + 1\n ).collect(Collectors.toSet());\n return IntStream.range(1, n + 1).filter(\n i -> !newVisited.contains(i)\n ).toArray();\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-losers-of-the-circular-game
|
[💾💾💾] 🥷👨💻💀
|
by-jwl-7-cucj
|
Intuition\nPass the ball around and whoever doesn\'t get to touch the cool ball is a loser.\n\n# Approach\nSimulate the game with a loop from 1 to n, keeping tr
|
jwl-7
|
NORMAL
|
2024-05-09T07:19:32.146368+00:00
|
2024-05-09T10:09:08.364450+00:00
| 2 | false |
# Intuition\nPass the ball around and whoever doesn\'t get to touch the cool ball is a loser.\n\n# Approach\nSimulate the game with a loop from `1 to n`, keeping track of the `losers` in a set. Remove players from `losers` that receive the ball `b`.\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> set[int]:\n losers = set(range(1, n + 1))\n b = 1\n\n for i in range(1, n + 1):\n losers.discard(b)\n b = (b + k * i - 1) % n + 1\n\n if b not in losers:\n break\n\n return losers\n```
| 0 | 0 |
['Simulation', 'Python3']
| 0 |
find-the-losers-of-the-circular-game
|
Pass yo partner around, ezzzz....
|
pass-yo-partner-around-ezzzz-by-robert96-7puv
|
Intuition\n1)Keep track of where the ball has been by using a set seen\n2)Move the ball be adding its currentPos + (how many times its been passed) *(k). Then m
|
robert961
|
NORMAL
|
2024-05-08T16:43:53.457275+00:00
|
2024-05-08T16:43:53.457311+00:00
| 5 | false |
# Intuition\n1)Keep track of where the ball has been by using a set seen\n2)Move the ball be adding its currentPos + (how many times its been passed) *(k). Then mod it by n\n3)Do this until you land on a space that is already in seen\n4)Substract all the numbers in the range(n) from seen and increase them by 1\n5)Return 4) in sorted fashion\n# Code\n```\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> List[int]:\n seen = set()\n currPos, passes = 0,1\n while currPos not in seen:\n seen.add(currPos)\n currPos = (currPos + passes*k) % n\n passes+= 1\n \n ans = set([i for i in range(n)]) - seen\n return sorted([i + 1 for i in ans]) \n```
| 0 | 0 |
['Python3']
| 0 |
find-the-losers-of-the-circular-game
|
Very Simple And Easy Solution | JAVA
|
very-simple-and-easy-solution-java-by-su-g2dg
|
\n\n# Code\n\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n if(n==1){\n return new int[]{};\n }\n bool
|
sumo25
|
NORMAL
|
2024-04-29T12:55:43.799748+00:00
|
2024-04-29T12:55:43.799769+00:00
| 0 | false |
\n\n# Code\n```\nclass Solution {\n public int[] circularGameLosers(int n, int k) {\n if(n==1){\n return new int[]{};\n }\n boolean[] check=new boolean[n];\n int c=1;\n check[0]=true;\n int go=1;\n while(true){\n go=(go+k*c)%n;\n if(go==0){\n if(check[n-1]){\n break;\n }\n check[n-1]=true;\n }\n else{\n if(check[go-1]){\n break;\n }\n check[go-1]=true;\n }\n c++;\n \n }\n List<Integer> ls = new ArrayList<>();\n for(int i=0;i<n;i++){\n if(!check[i]){\n ls.add(i+1);\n }\n }\n int[] ans=new int[ls.size()];\n for(int i=0;i<ls.size();i++){\n ans[i]=ls.get(i);\n }\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-losers-of-the-circular-game
|
CPP CODE
|
cpp-code-by-vineethsellamuthu1-59ho
|
Code\n\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n vector<int>ans(n,1);\n vector<int>ans2;\n int i=2;\
|
vineethsellamuthu1
|
NORMAL
|
2024-04-20T12:27:15.890080+00:00
|
2024-04-20T12:27:15.890109+00:00
| 2 | false |
# Code\n```\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n vector<int>ans(n,1);\n vector<int>ans2;\n int i=2;\n ans[0]=0;\n int first=0,temp=k;\n \n while(true)\n {\n \n first=(first+temp)%n;\n if(ans[first]==0) break;\n else\n {\n\n ans[first]=0;\n temp=k*i;\n i++;\n }\n }\n for(int j=0;j<ans.size();j++)\n {\n if(ans[j]==1) {ans2.push_back(j+1);}\n }\n return ans2;\n \n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
find-the-losers-of-the-circular-game
|
Simulate, keep track of visited with set, 79% speed
|
simulate-keep-track-of-visited-with-set-ni6d4
|
image.png\n\n\n# Code\n\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> List[int]:\n pos, i = 0, 1\n visited = {pos}\n
|
evgenysh
|
NORMAL
|
2024-04-16T10:09:00.667689+00:00
|
2024-04-16T10:09:00.667708+00:00
| 2 | false |
image.png\n\n\n# Code\n```\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> List[int]:\n pos, i = 0, 1\n visited = {pos}\n while True:\n new_pos = (pos + i * k) % n\n if new_pos in visited:\n break\n visited.add(new_pos)\n pos = new_pos\n i += 1\n return [j + 1 for j in range(n) if j not in visited]\n```
| 0 | 0 |
['Python3']
| 0 |
find-the-losers-of-the-circular-game
|
Javascript using Sets and Arrays - readable [Beats 93.79% of users with JavaScript]
|
javascript-using-sets-and-arrays-readabl-i9dm
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Kishor1995
|
NORMAL
|
2024-04-04T11:36:16.323049+00:00
|
2024-04-04T11:36:16.323079+00:00
| 15 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number} n\n * @param {number} k\n * @return {number[]}\n */\nvar circularGameLosers = function(n, k) {\n const setLosers = new Set();\n const setWinners = new Set();\n for(let indexI=1; indexI<=n; indexI++){\n setLosers.add(indexI);\n }\n let indexJ=1;\n let indexMultiply = 1;\n while(true){\n if(setWinners.has(indexJ)) break;\n setWinners.add(indexJ);\n setLosers.delete(indexJ);\n indexJ = indexJ+((indexMultiply*k)%n);\n indexMultiply++;\n if(indexJ>n) indexJ=indexJ%n;\n }\n\n return Array.from(setLosers);\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
find-the-losers-of-the-circular-game
|
Simple solution using while loop
|
simple-solution-using-while-loop-by-vinu-5b3u
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vinuaqua4u
|
NORMAL
|
2024-03-29T14:21:16.458180+00:00
|
2024-03-29T14:21:16.458204+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: o(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: o(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> List[int]:\n rec, i, t = [], 0, 1\n while True:\n if i in rec: break\n rec.append(i)\n i = (i + (k * t)) % (n)\n t += 1\n \n op = []\n for i in range(n):\n if i not in rec:\n op.append(i + 1)\n return op\n \n```
| 0 | 0 |
['Python3']
| 0 |
find-the-losers-of-the-circular-game
|
Another simulation.
|
another-simulation-by-scarletpumpernicke-g75d
|
\n\n# Code\n\n/**\n * @param {number} n\n * @param {number} k\n * @return {number[]}\n */\nvar circularGameLosers = function(n, k) {\n const players = new Se
|
ScarletPumpernickel
|
NORMAL
|
2024-03-12T18:37:57.997237+00:00
|
2024-03-12T18:37:57.997261+00:00
| 10 | false |
\n\n# Code\n```\n/**\n * @param {number} n\n * @param {number} k\n * @return {number[]}\n */\nvar circularGameLosers = function(n, k) {\n const players = new Set(Array.from({length: n}, (_, idx) => idx + 1));\n let i = 1;\n let f = 1;\n while(players.has(i)){\n players.delete(i);\n i = (i + (k * f)) % n || n;\n f++;\n }\n return [...players];\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
find-the-losers-of-the-circular-game
|
100% beat. 20 ms.
|
100-beat-20-ms-by-jsleitor-ftm9
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
jsleitor
|
NORMAL
|
2024-03-06T13:56:12.515053+00:00
|
2024-03-06T13:56:12.515079+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def circularGameLosers(self, n, k):\n\n # creating array of elements who in future will loosers \n loosers = set(range(1, n+1))\n\n # initialize the position\n step = 1\n\n # multiplied value on every step\n mult = 1\n\n # Start the game! (loop will continue untill loosers have spep, if not, then that player already taken ball and we should end the game)\n while step in loosers:\n\n # remove current elem from user because we selected it\n loosers.remove(step)\n\n # calculate next step by that formula\n step = (step + mult * k) % n\n\n # fix corner step when step is 0\n step = step or n\n\n # increase multiply\n mult += 1 \n\n # now just return loosers array after loop ends\n return loosers\n```
| 0 | 0 |
['Python']
| 0 |
find-the-losers-of-the-circular-game
|
Solution
|
solution-by-priismo-162w
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
priismo
|
NORMAL
|
2024-02-28T13:30:41.462538+00:00
|
2024-02-28T13:30:41.462571+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 8 ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 15.17 MB\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n std::vector<int> res;\n int l = 1, y = 1;\n std::unordered_map<int, int> play;\n for (int r = 0; r != n; ++r) {\n play[r + 1] = 0;\n }\n for (bool i = true; i; ++y) {\n ++play[l];\n if (play[l] == 2) {\n i = false;\n break;\n }\n l += (y * k);\n for (; l > n; ) {\n l -= n;\n }\n }\n for (const auto& [play, ball] : play) {\n if (ball == 0) {\n res.push_back(play);\n }\n }\n std::sort(res.begin(), res.end());\n return res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-losers-of-the-circular-game
|
Simple Python solution using Set
|
simple-python-solution-using-set-by-aksh-wyc5
|
Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> List[int]:\n
|
akshaychavan7
|
NORMAL
|
2024-02-27T02:42:25.211262+00:00
|
2024-02-27T02:42:25.211287+00:00
| 1 | false |
# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def circularGameLosers(self, n: int, k: int) -> List[int]:\n winners = set()\n pos, i = 0, 1\n winners.add(1)\n while True:\n pos = (pos+(k*i))%(n)\n if pos+1 in winners:\n break\n winners.add(pos+1)\n i+=1\n result = []\n for t in range(1, n+1):\n if t not in winners: result.append(t)\n return result\n\n```
| 0 | 0 |
['Python3']
| 0 |
find-the-losers-of-the-circular-game
|
Elixir, MapSet
|
elixir-mapset-by-lykos_unleashed-omxi
|
Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n\ndefmodule Solution do\n @spec circular_game_losers(n :: integer, k :: integer) :
|
Lykos_unleashed
|
NORMAL
|
2024-02-19T08:07:18.798219+00:00
|
2024-02-19T08:07:18.798242+00:00
| 0 | false |
# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\ndefmodule Solution do\n @spec circular_game_losers(n :: integer, k :: integer) :: [integer]\n def circular_game_losers(n, k) do\n winners = do_game(1, 1, k, n, MapSet.new([1]))\n for x <- n..1, !MapSet.member?(winners, x), reduce: [] do\n acc -> [x | acc]\n end\n end\n\n defp do_game(cur_pos, i, k, n, winners) do\n next_pos = cur_pos + (i * k) |> rem(n) |> then(fn pos -> if pos == 0, do: n, else: pos end)\n if MapSet.member?(winners, next_pos), do: winners,\n else: do_game(next_pos, i + 1, k, n, MapSet.put(winners, next_pos))\n end\nend\n```
| 0 | 0 |
['Elixir']
| 0 |
find-the-losers-of-the-circular-game
|
Eliminate players that got the ball until you try to erase someone that's not there
|
eliminate-players-that-got-the-ball-unti-mz76
|
Intuition\nCreate all possible losers, and start eliminating possibilities.\n\n# Approach\nHelper function- helps find the player that got the ball and erases h
|
mayan3259
|
NORMAL
|
2024-02-17T18:30:20.284154+00:00
|
2024-02-17T18:30:20.284184+00:00
| 3 | false |
# Intuition\nCreate all possible losers, and start eliminating possibilities.\n\n# Approach\nHelper function- helps find the player that got the ball and erases him. If he\'s not in the result vector, it means he already had the ball, so we\'re done playing (returns false).\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$ --> We\'re playing $$n$$ moves at the most.\n`std::find` has $$O(n)$$ running time, and we\'re running it $$O(n)$$ times. \n\n- Space complexity:\n$$O(n)$$ --> Added the `res` vector for the result.\n\n# Code\n```\nclass Solution {\npublic:\n bool findAndErase(vector<int>& vec, int val) {\n auto it = std::find(vec.begin(), vec.end(), val);\n if (it == vec.end())\n return false;\n vec.erase(it);\n return true;\n }\n\n vector<int> circularGameLosers(int n, int k) {\n vector<int> res;\n res.reserve(n - 1); // Player 1 can never lose\n for (auto i = 2; i <= n; i++) {\n res.push_back(i);\n }\n\n int ballPos(1);\n for (auto i = 1; i <= n; i++) {\n ballPos += k * i;\n // mod isn\'t enough here\n while (ballPos > n)\n ballPos -= n;\n if (!findAndErase(res, ballPos))\n break; // Player got the ball twice\n }\n\n return res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-losers-of-the-circular-game
|
A simple solution
|
a-simple-solution-by-jiny680-tz1i
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g
|
jiny680
|
NORMAL
|
2024-02-17T11:28:15.864738+00:00
|
2024-02-17T11:28:15.864757+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\n\nint *circularGameLosers(int n, int k, int *returnSize)\n{\n\tint aux[n], i, pos, add;\n\tint *res, count;\n\n\taux[0] = 1;\n\tfor ( i = 1; i < n; i++ )\n\t\taux[i] = 0;\n\n\tfor ( pos = 0, add = 0, count = 1; ; )\n\t{\n\t\tadd += k;\n\t\tpos += add;\n\n\t\tif ( aux[pos % n] == 1 )\n\t\t\tbreak;\n\n\t\tcount++;\n\t\taux[pos % n] = 1;\n\t}\n\n\tres = malloc( (n - count) * sizeof( int ) );\n\t*returnSize = n - count;\n\n\tfor ( i = 0, pos = 0; i < n; i++ )\n\t\tif ( aux[i] == 0 )\n\t\t\tres[pos++] = i + 1;\n\n\treturn res;\n}\n```
| 0 | 0 |
['C']
| 0 |
find-the-losers-of-the-circular-game
|
beats 100% of users with dart(time & memory)
|
beats-100-of-users-with-darttime-memory-dggni
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
m7medmahgoop
|
NORMAL
|
2024-02-15T23:43:20.035576+00:00
|
2024-02-15T23:43:20.035607+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n List<int> circularGameLosers(int n, int k) {\n Map winPlayers = {};\n int newPlayer = 1;\n int i = 1;\n while (checkEnd(winPlayers, newPlayer)) {\n winPlayers[newPlayer] = 1;\n newPlayer = getNext(newPlayer, k * i, n);\n i++;\n }\n List<int> loserPlayers = getLosers(winPlayers, n);\n return loserPlayers;\n }\n\n List<int> getLosers(Map winPlayers, int maxPlayer) {\n List<int> loserPlayers = [];\n for (int i = 1; i <= maxPlayer; i++) {\n if (!winPlayers.containsKey(i)) {\n loserPlayers.add(i);\n }\n }\n return loserPlayers;\n }\n\n bool checkEnd(Map winPlayers, int newPlayer) {\n if (winPlayers[newPlayer] == 1) {\n return false;\n } else {\n return true;\n }\n }\n\n int getNext(int newPlayer, int steps, int maxPlayer) {\n if (steps > maxPlayer) {\n steps = steps % maxPlayer;\n }\n if (steps + newPlayer > maxPlayer) {\n newPlayer = steps + newPlayer - maxPlayer;\n return newPlayer;\n }\n newPlayer += steps;\n return newPlayer;\n }\n}\n```
| 0 | 0 |
['Dart']
| 0 |
find-the-losers-of-the-circular-game
|
Simple C++ using vector to keep track of how many times the ball has been to each player
|
simple-c-using-vector-to-keep-track-of-h-rq68
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sanket26k
|
NORMAL
|
2024-02-13T10:05:24.164573+00:00
|
2024-02-13T10:05:24.164606+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> circularGameLosers(int n, int k) {\n vector<int> v(n,0);\n vector<int> losers;\n int i=0;\n int j=0;\n while(v[i] < 1)\n {\n v[i]++;\n i += ++j*k;\n i %= n;\n }\n\n for (int p=0; p<v.size(); p++)\n if (v[p]==0)\n losers.push_back(p+1);\n\n return losers;\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
minimum-cost-to-reach-destination-in-time
|
C++ Solution | Dijkstra’s Algorithm
|
c-solution-dijkstras-algorithm-by-invuln-6gu2
|
Solution\n\nThe problem can be solved using standard Dijkstra algorithm with slight modifications.\n\n- In priority queue for each vertex a vector corresponding
|
invulnerable
|
NORMAL
|
2021-07-10T16:01:52.723159+00:00
|
2021-07-11T06:46:57.060342+00:00
| 17,960 | false |
**Solution**\n\nThe problem can be solved using standard Dijkstra algorithm with slight modifications.\n\n- In priority queue for each vertex a vector corresponding to {cost, time, vertex} is stored.\n- The priority queue will be a min-heap, the vectors will be arranged first by cost and then by time.\n- Source vertex (0) will be push into min-heap first.\n- Follow the standard dijkstra by popping vertices and traverse the connected edges.\n- The difference here will be that only those edges will be traversed which will not cause the time to exceed `maxTime`.\n- Also a new entry will be pushed to heap if the cost or time of vertex will reduce.\n- At the end return the cost of destination vertex(`dest`).\n\n**Note**: The reason for including extra condition which is allowing to traverse edges which cause the time to reduce is that it is possible that these edges led us to destination. However if we just traverse those edge causing cost to decrease then we are ignoring the time which can lead us to a non-optimal answer or even a case where time exceed the `maxTime` leading us to return `-1`.\n\n**Code**\n```\nclass Solution {\npublic:\n vector<vector<int>> adj[1001];\n int cost[1001], time[1001];\n \n int dijkstra(int src, int dest, int maxTime) {\n \n for (int i = 1; i <= dest; i++) {\n cost[i] = INT_MAX;\n time[i] = INT_MAX;\n }\n \n priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;\n pq.push({cost[src], time[src], src});\n \n while (pq.empty() == 0) {\n vector<int> z = pq.top(); pq.pop();\n \n int c = z[0]; // cost\n int t = z[1]; // time\n int v = z[2]; // vertex\n \n for (int i=0;i<adj[v].size();i++) {\n \n\t\t\t // if this edge does not cause the time to exceed maxTime\n if (t + adj[v][i][1] <= maxTime) {\n \n\t\t\t\t // if cost will decrease\n if (cost[adj[v][i][0]] > c + adj[v][i][2]) {\n cost[adj[v][i][0]] = c + adj[v][i][2];\n \n time[adj[v][i][0]] = t + adj[v][i][1];\n pq.push({cost[adj[v][i][0]], time[adj[v][i][0]], adj[v][i][0]});\n }\n \n\t\t\t\t\t// if time will decrease\n else if (time[adj[v][i][0]] > t + adj[v][i][1]) {\n time[adj[v][i][0]] = t + adj[v][i][1];\n pq.push({c + adj[v][i][2], time[adj[v][i][0]], adj[v][i][0]});\n }\n }\n }\n }\n \n return cost[dest];\n }\n \n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& fee) {\n int i, x, y, t, e = edges.size(), n = fee.size();\n \n for (i=0;i<e;i++) {\n x = edges[i][0];\n y = edges[i][1];\n t = edges[i][2];\n \n adj[x].push_back({y, t, fee[y]});\n adj[y].push_back({x, t, fee[x]});\n }\n \n cost[0] = fee[0];\n time[0] = 0;\n \n int ans = dijkstra(0, n-1, maxTime);\n \n if(ans == INT_MAX)\n return -1;\n \n return ans;\n }\n};\n```
| 135 | 7 |
[]
| 24 |
minimum-cost-to-reach-destination-in-time
|
Python3 - Modified Djikstra's
|
python3-modified-djikstras-by-ampl3t1m3-97fy
|
The problem is very similar to cheapest flight within K stops.\nhttps://leetcode.com/problems/cheapest-flights-within-k-stops/ \n\n\n\n\nclass Solution:\n de
|
ampl3t1m3
|
NORMAL
|
2021-07-10T16:04:08.628348+00:00
|
2021-07-11T23:35:49.621123+00:00
| 4,728 | false |
The problem is very similar to cheapest flight within K stops.\nhttps://leetcode.com/problems/cheapest-flights-within-k-stops/ \n\n\n\n```\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n n = len(passingFees)\n \n g = [[] for i in range(n)]\n for e in edges:\n g[e[0]].append((e[1], e[2]))\n g[e[1]].append((e[0], e[2]))\n \n times = {}\n \n pq = [(passingFees[0],0,0)]\n \n while pq:\n cost, node, time = heapq.heappop(pq)\n \n if time > maxTime:\n continue\n \n if node == n-1:\n return cost\n \n if node not in times or times[node] > time:\n times[node] = time\n for nbor, trip in g[node]:\n heapq.heappush(pq, (passingFees[nbor]+cost, nbor, time+trip))\n \n \n \n return -1\n```\n\nEdit - A lot of folks have question over why we need to consider costlier routes later for the same node. Hope the below image clarifies those questions.\n\n\n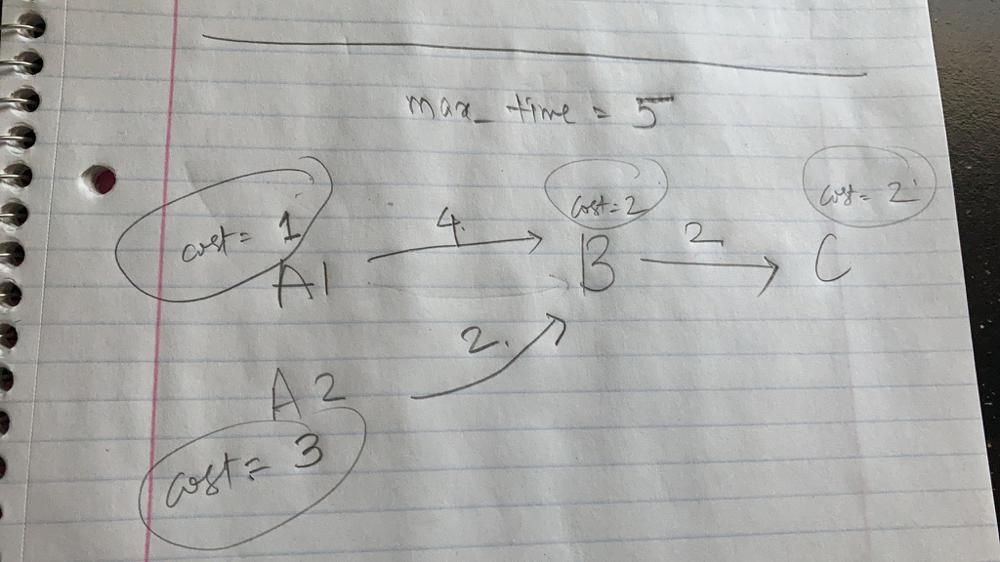\n\n\nIn this image - B is discovered first via the node A1, but the route A1-B-C does not meet the time constraint. \n\nThen B is again discovered via the node A2, this time the cost is more, but the time to reach C via A2-B-C meets the time constraint.\n\n
| 56 | 1 |
[]
| 11 |
minimum-cost-to-reach-destination-in-time
|
Java Solution PriorityQueue
|
java-solution-priorityqueue-by-profchi-bya7
|
Please upvote if you like the solution :)\n\n\nclass Solution {\n List<int []> [] graph;\n \n public int minCost(int maxTime, int[][] edges, int[] pass
|
profchi
|
NORMAL
|
2021-07-10T16:04:44.087504+00:00
|
2021-07-10T16:05:21.715732+00:00
| 3,309 | false |
Please upvote if you like the solution :)\n\n```\nclass Solution {\n List<int []> [] graph;\n \n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = passingFees.length;\n graph = new List [n];\n \n int [] minTime = new int [n];\n \n Arrays.fill(minTime, Integer.MAX_VALUE);\n \n for (int i = 0; i < n; ++i){\n graph[i] = new ArrayList<>();\n }\n \n for (int [] edge : edges){\n graph[edge[0]].add(new int [] {edge[1], edge[2] });\n graph[edge[1]].add(new int [] {edge[0], edge[2] });\n }\n \n PriorityQueue<int []> queue = new PriorityQueue<>((a, b) -> a[1] - b[1]);\n \n queue.add(new int [] {0, passingFees[0], 0});\n \n // node, fee, time spent\n int [] current;\n int size;\n \n int time, score;\n \n while (!queue.isEmpty()){\n current = queue.poll();\n \n if (current[2] >= minTime[current[0]])\n continue;\n \n minTime[current[0]] = current[2];\n \n if (current[0] == n - 1)\n return current[1];\n \n for (int [] next : graph[current[0]]){\n time = current[2] + next[1];\n score = current[1] + passingFees[next[0]];\n \n if (time > maxTime)\n continue;\n else if (time > minTime[next[0]])\n continue;\n \n queue.add(new int [] { next[0], score, time });\n }\n }\n \n return -1;\n }\n}\n```
| 34 | 1 |
[]
| 8 |
minimum-cost-to-reach-destination-in-time
|
C++ Dijkstra
|
c-dijkstra-by-lzl124631x-6s7n
|
See my latest update in repo LeetCode\n\n## Solution 1. Dijkstra\n\nUse a min-heap to have the nodes with the smallest cost at the top.\n\n\n\n\ncpp\n// OJ: htt
|
lzl124631x
|
NORMAL
|
2021-07-10T16:34:12.277774+00:00
|
2021-07-23T17:09:41.912372+00:00
| 2,819 | false |
See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Dijkstra\n\nUse a min-heap to have the nodes with the smallest cost at the top.\n\n\n\n\n```cpp\n// OJ: https://leetcode.com/problems/minimum-cost-to-reach-destination-in-time/\n// Author: github.com/lzl124631x\n// Time: O(ElogE)\n// Space: O(V + E)\nclass Solution {\n typedef array<int, 3> Node; // node, time, cost\npublic:\n int minCost(int maxTime, vector<vector<int>>& E, vector<int>& F) {\n int N = F.size();\n vector<unordered_map<int, int>> G(N);\n vector<int> minTime(N, maxTime + 1);\n for (auto &e : E) {\n int u = e[0], v = e[1], t = e[2];\n if (G[u].count(v)) { // For duplicated edges, we just need to keep track of the edge with smallest time.\n G[u][v] = G[v][u] = min(G[u][v], t);\n } else {\n G[u][v] = G[v][u] = t;\n }\n }\n auto cmp = [](auto &a, auto &b) { return a[2] > b[2]; }; // min-heap: Heap top is the node with the smallest cost to reach\n priority_queue<Node, vector<Node>, decltype(cmp)> pq(cmp);\n pq.push({0, 0, F[0]});\n minTime[0] = 0;\n while (pq.size()) {\n auto [u, time, c] = pq.top();\n pq.pop();\n if (u == N - 1) return c;\n for (auto &[v, t] : G[u]) {\n int nt = time + t, nc = c + F[v];\n if (nt < minTime[v]) {\n minTime[v] = nt;\n pq.push({v, nt, nc});\n }\n }\n }\n return -1;\n }\n};\n```
| 33 | 3 |
[]
| 8 |
minimum-cost-to-reach-destination-in-time
|
Easy top down DP + Memoization
|
easy-top-down-dp-memoization-by-shivaye-008d
|
\nclass Solution {\npublic:\n unordered_map<int,vector<pair<int,int>>> adj;\n int dp[1002][1002];\n int go(int sum,vector<int> &cost,int src=0)\n {\
|
shivaye
|
NORMAL
|
2021-07-10T16:38:18.239965+00:00
|
2021-07-10T16:39:21.564147+00:00
| 3,414 | false |
```\nclass Solution {\npublic:\n unordered_map<int,vector<pair<int,int>>> adj;\n int dp[1002][1002];\n int go(int sum,vector<int> &cost,int src=0)\n {\n if(sum<0)\n return INT_MAX-1000;\n if(src==cost.size()-1)\n return sum>=0?0:INT_MAX-1000;\n if(dp[sum][src]!=-1)\n return dp[sum][src];\n int res=INT_MAX-1000;\n for(auto i:adj[src])\n {\n res=min(res,cost[src]+go(sum-i.second,cost,i.first));\n }\n return dp[sum][src]=res;\n }\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& cost) \n {\n memset(dp,-1,sizeof(dp));\n adj.clear();\n for(auto i:edges)\n {\n adj[i[0]].push_back({i[1],i[2]});\n adj[i[1]].push_back({i[0],i[2]});\n }\n int ans=go(maxTime,cost);\n if(ans==2147482647)\n return -1;\n return cost[size(cost)-1]+ans;\n }\n};\n```
| 32 | 1 |
['Dynamic Programming', 'Memoization']
| 7 |
minimum-cost-to-reach-destination-in-time
|
[Java] 20 Lines Bottom-Up DP | Clear Explanation |
|
java-20-lines-bottom-up-dp-clear-explana-mxmi
|
Explaination:\n Create a 2D matrix dp[maxTime+1][n] and initialise the elements to infinity. \n dp[t][i]stores the minimum cost to reach node i at time = t .
|
000prime
|
NORMAL
|
2021-07-27T16:41:49.280217+00:00
|
2021-07-28T02:33:22.396386+00:00
| 1,859 | false |
# Explaination:\n* Create a 2D matrix `dp[maxTime+1][n]` and initialise the elements to `infinity`. \n* `dp[t][i] `stores the minimum cost to reach node `i` **at `time = t`** . \n* At `t = 0`, you are at `source = 0`, \n* Since you have to pay fees to be even present at a node, so you start the journey with minimum fees of `fee[source]` . So update the dp as `dp[0][0] = fee[source]`. \n* Now start looping from `currTime = 0` to `currTime = maxTime`. For each `currTime`, loop through every `edge {a,b,timeCost}`. \n* If `dp[currTime][i] == infinity`, then it means that node` i` was not reachable **at** `t = currTime`\n* So, while looping through every `edge {a,b,timeCost}`, check if `dp[currTime][a] == infinity` or `dp[currTime][b] == infinity` before making any change to dp state.\n* Let `fromNode = a` and `toNode = b` (we have to again swap these to handle bidirectional movement )\n* If `dp[currTime][fromNode] != infinity`, then it means at` t = currTime` we have managed to reach `fromNode` so we can traverse to `toNode` at `timeCost`, hence we will reach `toNode` at `reachTime = currTime + timeCost`\n* If this `reachTime <= maxTime`, update the cost in `dp`\n* After the dp is populated, loop through from `t = 0` to `t = maxTime` and pick the minCost from `dp[t][n]`\n\n\n-----\n**Request:** Please upvote this post if you found it helpful. This is the only way you can show your gratitude for my work.\n\n------\n\n\n\n# Code:\n<iframe src="https://leetcode.com/playground/2BNqd9sJ/shared" frameBorder="0" width="1000" height="420"></iframe>\n
| 25 | 0 |
['Dynamic Programming', 'Java']
| 5 |
minimum-cost-to-reach-destination-in-time
|
C++ Solution | 100% | Knapsack DP Problem in Graph
|
c-solution-100-knapsack-dp-problem-in-gr-dwha
|
we can assume it as a knapsack DP problem with passtime as cost[n], maxTime as Total Weight,edge time as weight[n]. we have to minimize the total cost with a We
|
lekhrajparihar
|
NORMAL
|
2021-07-10T18:21:09.090315+00:00
|
2021-07-10T18:21:09.090360+00:00
| 1,991 | false |
we can assume it as a knapsack DP problem with passtime as cost[n], maxTime as Total Weight,edge time as weight[n]. we have to minimize the total cost with a Weight Constraints (maxTime).\nHere is the recursive approach with memoization.\n```\nclass Solution {\npublic:\n int dp[1001][1001];\n int solve(int time,vector<pair<int,int>> adj[],int v,vector<int> &pass){\n if(time<0) return INT_MAX;\n int n = pass.size();\n if(v==n-1){\n return pass[v];\n }\n if(dp[v][time]!=-1) return dp[v][time];\n int cost = INT_MAX;\n for(auto &x:adj[v]){\n int u = x.first;\n int temp = x.second;\n if(temp<=time){\n int sol = solve(time-temp,adj,u,pass);\n cost = min(cost,sol);\n }\n }\n if(cost==INT_MAX) return dp[v][time] = INT_MAX;\n return dp[v][time] = cost + pass[v]; \n }\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& pass) {\n memset(dp,-1,sizeof(dp));\n int n = pass.size();\n vector<pair<int,int>> adj[n];\n for(int i = 0;i<edges.size();i++){\n adj[edges[i][0]].push_back(make_pair(edges[i][1],edges[i][2]));\n adj[edges[i][1]].push_back(make_pair(edges[i][0],edges[i][2]));\n \n }\n int ans = solve(maxTime,adj,0,pass);\n if(ans==INT_MAX) return -1;\n return ans;\n }\n};\n```\nPlease leave a comment if needs help.\nIf you like it ...please upvote so that it can reach to other people also.
| 21 | 1 |
['Dynamic Programming', 'C++']
| 5 |
minimum-cost-to-reach-destination-in-time
|
Modified Dijkstra's
|
modified-dijkstras-by-votrubac-n5sh
|
We run Dijkstra, and for each node we track the sorted list of {fee, time}. This allows us to prune costly paths that do not save us time.\n \nI initially did n
|
votrubac
|
NORMAL
|
2021-07-10T16:09:42.412509+00:00
|
2021-07-10T18:34:06.646475+00:00
| 3,047 | false |
We run Dijkstra, and for each node we track the sorted list of `{fee, time}`. This allows us to prune costly paths that do not save us time.\n \nI initially did not use the min heap for the queue, and got TLE. \n\n**C++**\n```cpp\nint minCost(int maxTime, vector<vector<int>>& edges, vector<int>& fees) {\n vector<set<array<int, 2>>> state(fees.size()); // city: {fee, time}\n vector<vector<array<int, 2>>> al(fees.size()); // city i : {city j, time}\n for (auto &e : edges) {\n al[e[0]].push_back({e[1], e[2]});\n al[e[1]].push_back({e[0], e[2]});\n }\n priority_queue<array<int, 3>, vector<array<int, 3>>, greater<array<int, 3>>> q;\n q.push({fees[0], 0, 0}); // {fee, time, city}\n while(!q.empty()) {\n auto [fee, time, city] = q.top(); q.pop();\n if (city == fees.size() - 1)\n return fee;\n for (auto [city1, time1] : al[city]) {\n if (time + time1 <= maxTime) {\n auto it = state[city1].upper_bound({fee + fees[city1], time + time1});\n if (it == begin(state[city1]) || (*prev(it))[1] > time + time1) {\n state[city1].insert({fee + fees[city1], time + time1});\n q.push({fee + fees[city1], time + time1, city1 });\n }\n }\n }\n }\n return -1;\n}\n```
| 19 | 6 |
['C']
| 5 |
minimum-cost-to-reach-destination-in-time
|
🔥 21ms | beats 100% | Dijkstra with optimization
|
21ms-beats-100-dijkstra-with-optimizatio-9gf5
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
byegates
|
NORMAL
|
2023-02-10T00:02:27.915473+00:00
|
2023-02-10T04:32:37.933416+00:00
| 2,335 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Standard Dijkstra, [40ms](https://leetcode.com/problems/minimum-cost-to-reach-destination-in-time/submissions/894999497/)\n```java\nclass Solution {\n record Node(int i, int t) {}\n record Cell(int i, int t, int c) {}\n public int minCost(int maxTime, int[][] edges, int[] fees) {\n int n = fees.length;\n\n // create the adjacency list graph\n List<Node>[] g = new List[n];\n for (int i = 0; i < n; i++) g[i] = new ArrayList<>();\n for (var e : edges) {\n g[e[0]].add(new Node(e[1], e[2]));\n g[e[1]].add(new Node(e[0], e[2]));\n }\n\n // Dijkstra\n Queue<Cell> q = new PriorityQueue<>((a, b) -> a.c == b.c ? a.t - b.t : a.c - b.c);\n int[] T = new int[n]; // 1. visited: de-dup 2. de-dup on worst time\n\n q.offer(new Cell(0, 0, fees[0]));\n Arrays.fill(T, maxTime + 1);\n T[0] = 0;\n\n while (!q.isEmpty()) {\n var cur = q.poll();\n if (cur.i == n-1) return cur.c;\n \n for (var nei : g[cur.i]) {\n int t2 = cur.t + nei.t;\n if (t2 >= T[nei.i]) continue; // if time is worst, no reason to continue\n T[nei.i] = t2;\n q.offer(new Cell(nei.i, t2, cur.c + fees[nei.i]));\n }\n }\n\n return -1;\n }\n}\n```\n\n# Optimize on time, early pruning [21ms](https://leetcode.com/problems/minimum-cost-to-reach-destination-in-time/submissions/895019270/)\n```java\nclass Solution {\n record Node(int i, int t) {}\n record Cell(int i, int t, int c) {}\n public int minCost(int maxTime, int[][] edges, int[] fees) {\n int n = fees.length;\n\n // create the graph\n List<Node>[] g = new List[n];\n for (int i = 0; i < n; i++) g[i] = new ArrayList<>();\n for (var e : edges) {\n g[e[0]].add(new Node(e[1], e[2]));\n g[e[1]].add(new Node(e[0], e[2]));\n }\n\n // min time from end to each node\n int[] time = new int[n];\n Arrays.fill(time, Integer.MAX_VALUE);\n time[n-1] = 0;\n Queue<Integer> q = new PriorityQueue<>((a, b) -> time[a] - time[b]);\n q.offer(n-1);\n while (!q.isEmpty()) {\n int cur = q.poll();\n for (var nei : g[cur]) {\n int t2 = time[cur] + nei.t;\n if (t2 >= time[nei.i]) continue;\n time[nei.i] = t2;\n q.offer(nei.i);\n }\n }\n\n // Dijkstra\n Queue<Cell> q2 = new PriorityQueue<>((a, b) -> a.c - b.c);\n int[] T = new int[n]; // 1. visited: de-dup 2. de-dup on worst time\n\n q2.offer(new Cell(0, 0, fees[0]));\n Arrays.fill(T, maxTime + 1);\n T[0] = 0;\n\n while (!q2.isEmpty()) {\n var cur = q2.poll();\n if (cur.i == n-1) return cur.c;\n \n for (var nei : g[cur.i]) {\n int t2 = cur.t + nei.t;\n if (time[nei.i] + t2 > maxTime) continue; // at this point we know we can skip\n if (t2 >= T[nei.i]) continue; // if time is worst, no reason to continue\n T[nei.i] = t2;\n q2.offer(new Cell(nei.i, t2, cur.c + fees[nei.i]));\n }\n }\n\n return -1;\n }\n}\n```\n
| 16 | 0 |
['Java']
| 4 |
minimum-cost-to-reach-destination-in-time
|
Simple Dijstra algorithm with explanation | CPP
|
simple-dijstra-algorithm-with-explanatio-9zln
|
```\n//Basically the problem is Single source shortest path problem with time constraint.\n\n// DIJSTRA ALGO\n//PLEASE GUYZ UPVOTE IT!!! THANK YOU\n\n\n\n\n\n#d
|
kaushik8511
|
NORMAL
|
2021-07-10T16:03:02.770481+00:00
|
2021-07-10T16:11:13.812635+00:00
| 1,139 | false |
```\n//Basically the problem is Single source shortest path problem with time constraint.\n\n// DIJSTRA ALGO\n//PLEASE GUYZ UPVOTE IT!!! THANK YOU\n\n\n\n\n\n#define pr pair<int, pair<int, int>>\n#define ll long long int\n\nclass Solution {\npublic:\n\n \n int minCost(int maxTime, vector<vector<int>>& ed, vector<int>& pass) {\n int n = pass.size();\n vector<pair<int, int>> adj[n];\n \n //making a graph\n for(vector<int> e: ed) {\n adj[e[0]].push_back({e[1], e[2]});\n adj[e[1]].push_back({e[0], e[2]});\n }\n \n //taking min priority queue as {cost, vertex, time} \n priority_queue<pr, vector<pr>, greater<pr>> pq;\n //Initial vertex\n pq.push({pass[0], {0, 0}});\n \n //map to track of vertex which is visited with minimum time\n //It maps vertex and minimum time to reach that vertex\n unordered_map<int, int> vis;\n \n \n //Simple Dijstra algorithm\n while(!pq.empty()) {\n pr crr = pq.top(); pq.pop();\n int curr = crr.second.first, time = crr.second.second, cost = crr.first;\n \n //Destination\n if(curr == n-1) return cost;\n \n //Visited with current time\n vis[curr] = time;\n \n for(pair<int, int> p: adj[curr]) {\n int ad = p.first, ctime = p.second;\n int ttime = time + ctime;\n \n //if vertex is not visited or vertex is visited prior but with more time, we push it into queue else continue\n if(vis.find(ad) != vis.end() && vis[ad] <= ttime) continue;\n vis[ad] = ttime;\n //check if total time is less or equal to maxTime\n if(ttime <= maxTime) pq.push({cost + pass[ad], {ad, ttime}});\n }\n \n }\n \n //Not possible\n return -1;\n \n //If you understood please upvote!!!\n }\n};\n
| 13 | 3 |
['Graph', 'C', 'Heap (Priority Queue)', 'C++']
| 2 |
minimum-cost-to-reach-destination-in-time
|
[C++] Dijkstra | Track time taken instead of visited nodes | Picture illustration
|
c-dijkstra-track-time-taken-instead-of-v-9vbj
|
This problem is very similar to 787. Cheapest Flights Within K Stops\nIn dijkstra algo, we keep track of minimum distance, and we stop traversing node once it i
|
ujjaldas223
|
NORMAL
|
2021-08-06T17:01:32.304535+00:00
|
2021-08-08T11:53:17.539838+00:00
| 1,201 | false |
This problem is very similar to **787. Cheapest Flights Within K Stops**\nIn dijkstra algo, we keep track of minimum distance, and we stop traversing node once it is visited.\n\nWe do so, because we know that once a node is processed with minimum distance, no matter what other routes we take, it will no more be minimum.\n\nWe can take similar idea here. The condition is that, we are allowed to visit a node as long as we can visit within `maxTime` minutes.\n\nLet\'s take an example below-\n\nFor the simplicity, I have taken time spent for each path as per the below graph, and `maxTime` as 5.\n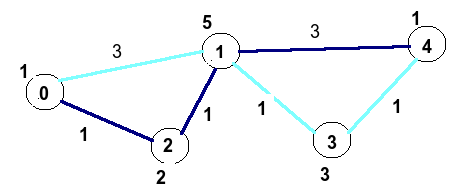\n\nFrom the above, there are two possible paths [sky, blue] to reach destination. \nEach path will take 5 mins, and cost of sky path will be 10, where as cost of blue path will be 9.\n\nNotice that, to reach node-1 from node-0, we can take sky or blue path. \nAt first glance, we can pick sky path, because it will give us minimum cost(1 + 5) as compared to blue path(1 + 2 + 5).\n\nBut later on, sky path will be more costlier to us than blue path. So we should be considering every possible path as long as the total time spent doesn\'t exceed the `maxTime`. \n\nWhenever we notice that the new time spent to reach a particular node exceeds the previous time spent, we will stop considering the node.\n\nRest, it will be as similar as dijkstra algo.\n\n<iframe src="https://leetcode.com/playground/NLiZpaAy/shared" frameBorder="0" width="900" height="700"></iframe>\n\nTime and space complexity will be same as dijkstra algo.
| 11 | 0 |
[]
| 3 |
minimum-cost-to-reach-destination-in-time
|
C++ solution using Dijkstra's algorithm || commented
|
c-solution-using-dijkstras-algorithm-com-yq68
|
\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& e, vector<int>& fees) {\n \n //the number of nodes\n int n=f
|
saiteja_balla0413
|
NORMAL
|
2021-07-10T17:55:16.732502+00:00
|
2021-07-10T17:55:16.732536+00:00
| 1,009 | false |
```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& e, vector<int>& fees) {\n \n //the number of nodes\n int n=fees.size();\n \n using pi=pair<int,pair<int,int>> ;\n //min heap \n //pq contains the format {cost,{time,node}} \n priority_queue<pi,vector<pi>,greater<pi>> pq;\n \n \n //create a adjacency list\n vector<vector<pair<int,int>>> adj(fees.size());\n \n for(int i=0;i<e.size();i++)\n {\n adj[e[i][0]].push_back({e[i][1],e[i][2]});\n adj[e[i][1]].push_back({e[i][0],e[i][2]});\n }\n \n \n vector<int> cost(n,INT_MAX);\n vector<int> time(n,INT_MAX);\n cost[0]=fees[0];\n time[0]=0;\n \n pq.push({cost[0],{time[0],0}});\n while(!pq.empty())\n {\n auto [currCost,v]=pq.top();\n auto [currMin,node]=v;\n pq.pop();\n for(auto [x,t] : adj[node])\n {\n \n //if you can reach the city in <=maxTime\n if(currMin + t <= maxTime)\n {\n //check if the cost can be decreased\n if(cost[x] > currCost+fees[x])\n {\n cost[x]=currCost+fees[x];\n \n time[x] = currMin + t;\n //push it into pq\n pq.push({cost[x],{time[x],x}});\n }\n \n //if the cost of the current node cannot be decreased then check\n //if we can decrease the time of the node\n else if(time[x] > currMin+t)\n {\n //update the time\n time[x]=currMin+t;\n //push it into pq\n pq.push({currCost+fees[x],{time[x],x}});\n \n }\n }\n }\n }\n return cost[n-1]==INT_MAX ? -1 : cost[n-1];\n }\n};\n```\n**Upvote if this helps you :)**
| 11 | 1 |
['C']
| 1 |
minimum-cost-to-reach-destination-in-time
|
C++ | DP (Recursive) | Dijkstra (Two Approach)
|
c-dp-recursive-dijkstra-two-approach-by-o3sjd
|
Code: (Using dp)\n\nclass Solution{\npublic:\n int dp[1002][1002], n;\n int solve(int maxTime, int src, vector<int> &cost, vector<pair<int, int>> g[])\n
|
pkacb
|
NORMAL
|
2023-06-29T13:30:17.363673+00:00
|
2023-06-29T13:30:17.363705+00:00
| 603 | false |
# Code: (Using dp)\n```\nclass Solution{\npublic:\n int dp[1002][1002], n;\n int solve(int maxTime, int src, vector<int> &cost, vector<pair<int, int>> g[])\n {\n if (maxTime < 0)\n return 1e9;\n\n if (src == n - 1)\n return maxTime >= 0 ? cost[n - 1] : 1e9;\n\n if (dp[maxTime][src] != -1)\n return dp[maxTime][src];\n\n int ans = 1e9;\n for (auto [child, time] : g[src])\n ans = min(ans, cost[src] + solve(maxTime - time, child, cost, g));\n\n return dp[maxTime][src] = ans;\n }\n\n int minCost(int maxTime, vector<vector<int>> &edges, vector<int> &cost)\n {\n n = cost.size();\n vector<pair<int, int>> g[n];\n memset(dp, -1, sizeof(dp));\n for (auto edge : edges)\n {\n g[edge[0]].push_back({edge[1], edge[2]});\n g[edge[1]].push_back({edge[0], edge[2]});\n }\n int ans = solve(maxTime, 0, cost, g);\n return ans == 1e9 ? -1 : ans;\n }\n};\n\n```\n\n\n# Code: (Using Dijkstra)\n```\nclass Solution {\npublic:\n struct comp{\n int fees, time, node;\n };\n\n struct graph_comp{\n int child, time, fees;\n };\n\n struct myCmp{\n bool operator()(comp below, comp above)\n {\n if(below.fees == above.fees)\n return below.time > above.time;\n \n return below.fees > above.fees;\n }\n };\n\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int n = passingFees.size();\n vector<graph_comp> g[n];\n for(auto edge : edges)\n {\n g[edge[0]].push_back({edge[1], edge[2], passingFees[edge[1]]});\n g[edge[1]].push_back({edge[0], edge[2], passingFees[edge[0]]});\n }\n\n priority_queue<comp, vector<comp>, myCmp> pq;\n vector<int> cost(n, 1e9);\n vector<int> time(n, 1e9);\n\n cost[0] = passingFees[0];\n time[0] = 0;\n pq.push({cost[0], time[0], 0});\n\n while(!pq.empty())\n {\n auto par = pq.top();\n pq.pop();\n\n for(auto curr : g[par.node])\n {\n if(par.time + curr.time > maxTime)\n continue;\n \n if(cost[curr.child] > par.fees + curr.fees)\n {\n cost[curr.child] = par.fees + curr.fees;\n time[curr.child] = par.time + curr.time;\n pq.push({cost[curr.child], time[curr.child], curr.child});\n }\n else if(time[curr.child] > par.time + curr.time)\n {\n time[curr.child] = par.time + curr.time;\n pq.push({par.fees + curr.fees, time[curr.child], curr.child});\n }\n\n }\n }\n\n return cost[n - 1] == 1e9 ? -1 : cost[n - 1];\n }\n};\n```
| 8 | 0 |
['Dynamic Programming', 'Graph', 'Recursion', 'Shortest Path', 'C++']
| 1 |
minimum-cost-to-reach-destination-in-time
|
C++ | Dijkstra | Simple Solution
|
c-dijkstra-simple-solution-by-sourabcode-aq2c
|
```\nclass Solution {\npublic:\n int minCost(int maxTime, vector>& edges, vector& passingFees) {\n int minfs = INT_MAX;\n \n vector> adj
|
SourabCodes
|
NORMAL
|
2023-01-03T00:07:56.461501+00:00
|
2023-01-03T18:49:08.741131+00:00
| 1,080 | false |
```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int minfs = INT_MAX;\n \n vector<pair<int,int>> adj[passingFees.size()];\n \n // Creating the adjacency list...\n for(auto it : edges){\n adj[it[0]].push_back({it[1],it[2]});\n adj[it[1]].push_back({it[0],it[2]});\n }\n \n // Initialising time and cost array which will be populated as time[i] = minimum time to reach ith node...\n vector<int> time(passingFees.size(),INT_MAX);\n \n // cost[i] = min cost to reach ith node from 0...\n vector<int> cost(passingFees.size(),INT_MAX);\n \n cost[0] = passingFees[0];\n time[0] = 0;\n \n // Creating min-heap which will keep sorted values in priority of { cost, time, node }...\n priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>,greater<pair<int,pair<int,int>>>> pq;\n \n pq.push({cost[0],{0,0}});\n \n // Dijkstra\'s Algo...\n while(!pq.empty()){\n auto tops = pq.top();\n pq.pop();\n \n int node = tops.second.second;\n \n int cst = tops.first;\n int tm = tops.second.first;\n \n if(node == passingFees.size() - 1 && tm <= maxTime){\n \n // If we have reached the n-1th node then return the cost...\n return minfs = min(minfs,cst);\n }\n \n for(auto it : adj[node]){\n int nowdtm = it.second;\n int nowcst = passingFees[it.first];\n \n // push the node if its cheaper and time to reach it is less than maxTime...\n if(tm + nowdtm <= maxTime && cost[it.first] >= cst + nowcst){\n cost[it.first] = cst + nowcst;\n time[it.first] = nowdtm + tm;\n pq.push({cst + nowcst,{nowdtm + tm,it.first}});\n }\n \n // push the node if time to reach it is less than the time it took before..\n else if(nowdtm + tm < time[it.first]){\n time[it.first] = nowdtm + tm;\n pq.push({cst + nowcst,{nowdtm + tm,it.first}});\n }\n }\n \n }\n \n // If the distance from 0 - N-1 node is not updated then its impossible to reach...\n if(minfs == INT_MAX) return -1;\n return minfs;\n \n }\n};
| 8 | 0 |
['Graph', 'C']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Python 3: Modified Dijkstra
|
python-3-modified-dijkstra-by-biggestchu-o1qg
|
Intuition\n\nThis is a tough problem. My original solution was a lot slower, but still decent, based on Fenwick trees for each node.\n\nThe solution here is a L
|
biggestchungus
|
NORMAL
|
2024-07-30T09:57:00.164447+00:00
|
2024-08-11T03:03:48.006881+00:00
| 377 | false |
# Intuition\n\nThis is a tough problem. My original solution was a lot slower, but still decent, based on Fenwick trees for each node.\n\nThe solution here is a LOT faster, I reverse-engineered it from the fastest submission and figured I\'d explain it... if only for my own review.\n\n## Cheapest Path: Dijkstra\n\nIf the time constraint didn\'t exist this would be a medium problem because it would just be Dijkstra\'s algorithm. The cost to visit each node `v` is the cost of the path to `u`, plus the cost to pass through `v`.\n\nThe cost doesn\'t actually depend on the edges at all, it only depends on the nodes which is interesting. But Dijkstra only requires the costs of paths so we\'re still fine.\n\n## Including Distance: Exploring More Expensive Paths\n\nSomething less known about Dijkstra is that we can refactor the algorithm a bit to revisit nodes via paths longer than the shortest one. We just need to modify or remove the usual "if this isn\'t the optimal path, ignore this path" logic (`if c > cost[u]` part of this code).\n\nIn the prior paragraph "longer" really means "more expensive," whatever increases the thing we order the heap/priority queue by in Dijkstra\'s algo.\n\nFor this problem we will need to visit more expensive paths in the interest of reducing the time spent.\n\n## Modifying Dijkstra: Order by Cost, Dual Criteria\n\nWe want the cheapest path so we use Dijkstra\'s algorithm with respect to cost. **We\'ll explore valid paths in order by cost until we find one that reaches `n-1` within the time limit**... or exhaust all relevant options.\n\nThe key to this problem is the *relevant options* part. There are two reasons we\'d want to explore from node `v`:\n* the usual one: we find a new cheapest path to `v`\n* in this problem: we found a new fastest (least time) path to `v`\n\nThe first one is pretty obvious, we need to find the minimum cost path, so when we find a new fastest path, we need to push it to the heap.\n\nThe second one is a LOT less obvious. It requires a lot of insight and understanding of Dijkstra\'s algorithm.\n* when we pop each next path, to some node `u`, from the heap, it\'s ordered by *cost*. So over time we\'re exploring more and more expensive paths\n* **we have a cost-time tradeoff. In general the cheapest path will NOT be the lowest time**, and vice-versa\n * **there\'s an "optimal frontier" or "Pareto front" that describes the best cost for each arrival time and vice-versa**\n * my original algo that I mentioned, based on Fenwick trees, found this optimal frontier literally\n * but we don\'t need the whole frontier, we just need the single cheapest path that satisfies the arrival time criterion\n\nA `(cost, time)` point belongs on the optimal frontier when `time < time\'` for all `cost\' < cost` for all `(cost\', time\')` currently on the frontier. In other words, we only bother adding expensive paths to the frontier if they reduce the minimum time. There\'s no reason to spend more to get to a node later.\n\nNow we need to remember that\n* we\'re doing Dijkstra ordered by cost: we pop nodes `u` in order by cost\n* and **the cost to visit a node only depends on the node**\n\nThat means the cost to visit node `v` from here is\n* the cheapest prior node `u`\n* plus the cost to visit `v` from `u`\n\nWe know the second part is constant with respect to `u`, it\'s just `passingFees[v]`. That means the cheapest path to `v` is the cheapest path to `v`. **Since we\'re doing Dijkstra in cost order, by popping each node `u` in order, we\'re also popping the path to each adjacent node in cost order as well.** There will never be a later path that is cheaper. So we\'ll never have to consider inserting a new `(cost, time)` entry in the frontier with a lower cost: because *this node right now* leads to the lowest cost.\n\nIn fact, this means **we\'re always considering new (cost, time) points on the optimal frontier for `v` where `cost` is at least as high as all prior costs we\'ve seen.** In other words we\'re always considering a new point on the very edge of the frontier, the high-cost region.\n\n**An optimal frontier can be represented as a stack, increasing in `cost` in this case and decreasing by `time`.** That means each candidate `(cost_to_v, time_to_v)` we pop always has a `cost_to_v` that is at least as large. And following the logic above, that means `time_to_v` must be a new lowest value for it to be part of the frontier.\n\n**The optimal frontier therfore simplifies to just storing the lowest arrival time we\'ve see for each node.**\n\n## Final Thoughts\n\nThe giant simplification from "optimal frontier" to "just record min cost" is enabled by the fact that cost only depends on the node, not on the edges. That\'s why exploring paths to `u` in cost order is equivalent to exploring paths to a specific other node `v` in cost order: because any other `u\' -> v` path would have `cost(u\') >= cost(u)` and the path cost doesn\'t depend on `u -> v`.\n\nIf it did, e.g. `passingCost` depended on both the source and destination nodes for each edge, we\'d have a different picture. Then we wouldn\'t have the special property that we\'re popping paths to each adjacent node `v` in order by cost, so we\'d have to worry about popping an expensive path with low time early, and then falsely discarding a later medium cost path with higher time later on just because it\'s not the lowest time we\'ve seen - we don\'t demand the lowest time, just a time <= maxTime.\n\nFor this more complicated situation I think we\'d need to return to the optimal frontier - we\'d want to\n* make sure we explore paths in order by cost as we\'ve done before\n* but also make sure we explore all points on the optimal frontier, exhausting cheap paths before medium cost paths, and medium costs before the most expensive ones\n* and in general we would not encounter points on the optimal frontier in cost order, or in time order. It depends on the mix of cost and time weights\n\nWe can use a segment tree or Fenwick tree to efficiently query an optimal frontier, but that\'s a story for a later time. This is already super long.\n\n# Complexity\n\nI don\'t know.\n\nNormal Dijkstra implemented like this is `O(E log(E))` where we only process each node (looking at its neighbors) when we find the cheapest path. There\'s only one cheapest path so we only iterate over neighbors once per node, and for each neighbor, we push to a big heap. That means `O(E)` pushes, and thus `O(E)` things in the heap, and thus `O(E log(E))` is the time complexity.\n\nBut in this case we might push a node to the heap many times:\n* a first time with the lowest cost, highest time\n* then later with a slightly higher cost, slightly lower time\n* and later with a slightly higher cost, slightly higher time\n* .. and so on\n\nThat suggests that every possible combination of nodes we visit would result in pushing a new node to the path.\n\nBut in practice this algorithm doesn\'t scale with the total possible paths which is exponential.\n\nThat means I probably need fancier complexity analysis tools to figure out what the complexity really is.\n\n# Code\n```\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n\n n = len(passingFees)\n\n # adjacency list # TODO: only use shortest path between each pair\n adj = [[] for _ in range(n)]\n for u, v, dt in edges:\n if dt > maxTime: continue\n adj[u].append((v, dt))\n adj[v].append((u, dt))\n\n # modified Dijkstra\n # > main idea: explore paths in order by cost\n # > ideally the minimum cost path satisifes the maxTime limit\n # > but if not, we\'ll need to consider more expensive paths\n # so we also should visit shorter paths as well\n times = [math.inf]*n\n costs = [math.inf]*n\n times[0] = 0\n costs[0] = passingFees[0]\n pq = [(costs[0], times[0], 0)] # explore by cost asc | time <= maxTime\n while pq:\n c, t, u = heappop(pq)\n\n if u == n-1:\n return c # first encounter of n-1 ord by cost: we found the min cost\n\n if c > costs[u] and t > times[u]: continue # stale entry in heap\n\n # this path to u is either the minimum cost, or the minimum time\n # for costs > u as we explore by costs > u\n for v, dt in adj[u]:\n vt = t+dt\n vc = c+passingFees[v]\n\n if vt > maxTime: continue # illegal path\n \n if vc < costs[v]:\n # new lowest cost, want to explore all legal paths from here to get the min cost\n costs[v] = vc\n heappush(pq, (vc, vt, v))\n elif vt < times[v]:\n # higher cost than current min-cost path, but less time. worth exploring\n times[v] = vt\n heappush(pq, (vc, vt, v))\n # else: neither the best cost nor best time, ignore it\n\n return -1 # never encountered n-1 via a path of suitable distance\n```\n\n# BONUS: The Fenwick Trees Solution\n\nIn this problem, as explained above, we don\'t actually need a Fenwick tree.\n\nBut if, hypothetically, the problem were different and the Fenwick tree / decreasing stack didn\'t just devolve to a 0/1 stack, then we\'ll need a Fenwick tree or other ordered collection.\n\nExample: suppose the times and costs were both edge-specific such that we had `edges = [(u, v, time, cost)..]`. Then for every node there would be a tradeoff between\n* spending a lot to get there asap\n* or cutting costs and getting there late\n\nAnd in this case with arbitrary values per edge, there\'s no guarantee that we\'d see `cost[v]` values in order.\n\n## Interview-Friendly Fenwick Tree\n\nThe code below has a Fenwick tree for every single node in an easy-to-write format you can do duing an interview.\n\nIf you\'re not familiar with Fenwick trees see this [CP Algorithms page](https://cp-algorithms.com/data_structures/fenwick.html) for a primer. It\'s a pretty confusing primer, but oh well.\n\nHere\'s [another explanation](https://leetcode.com/problems/count-number-of-teams/solutions/5555721/python-3-ft-97-tc-on-logmax-sc-omax-fenwick-tree/) that I personally wrote for another LC problem, I think that makes more intuitive sense at least.\n\nThere\'s a related interview-friendly segment tree implementation, but that\'s beyond the scope of this problem.\n\n## Why Use a Fenwick Tree\n\nIn a normal Dijkstra\'s algorithm we want to explore the best paths in order, such that the first time we encounter a node is the best time.\n\nBut in this case we have many possible (time, cost) combinations. As explained above these form an optimal frontier where we can find the cheapest way to arrive at a given node within a certain time limit and vice-versa.\n\nWhen we consider exploring from a node (called "relaxation" in SPFA terms), we only want to do the exploration work if it will give us new best answers.\n\nSo what we do is\n* have a Fenwick tree whose indices are time units, 1..maxTime\n* then if we find that we can reach a node at `time, cost`, then we should only explore from that node if it\'s cheaper than all other known `(time\' <= time, cost\')` combinations known thus far. Otherwise there\'s a way to get to the node at least as soon, AND cheaper.\n* we can find the min cost over `1..time` directly using the Fenwick tree\n\nIf we find a new best (time, cost) combination (i.e. one on the optimal frontier), then we add it to the frontier by storing it in the Fenwick tree.\n\nThe nice thing about Fenwick, and the reason I chose it, is that adding a point to the optimal frontier will automatically make all later queries over that time return the new minimum cost.\n\nIn contrast, if you used a sorted set for the frontier for example, then you\'d have to spend `O(N log(N))` time or more removing later entries that may no longer be on the optimal frontier.\n\nSo Fenwick is a nice way to handle this.\n\n**Note here that the Fenwick trees here store cumulative minimum costs.** Usually they store sums, but you can use Fenwick trees for min *if and only if each element is non-increasing over the whole algorithm.* That\'s because if you reduce an element, the minimum decreases and we can accumulate or "bubble" that change up through the tree. But if it increases, then we need to recompute all parents\' minima and you can\'t do that efficiently with a Fenwick tree.\n\n## The Fenwick Code\n\n```\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n\n # a Fenwick tree per node, O(maxTime*n) memory\n n = len(passingFees)\n costTrees = [[math.inf]*(maxTime+2) for _ in range(n)]\n \n def minCost(u: int, t: int) -> float:\n """Returns the minimum cost over paths reaching u in time <= t"""\n t += 1 # since we want the min cost for time 0 as well\n ans = math.inf\n while t:\n ans = min(ans, costTrees[u][t])\n t &= t-1\n return ans\n\n def reduceCost(u: int, t: int, c: int) -> None:\n tree = costTrees[u]\n t += 1\n while t < maxTime+2:\n tree[t] = min(tree[t], c)\n t += t & -t\n\n # adjacency list, handle parallel edges by recording only the minimum-weight one\n adj = [defaultdict(lambda: math.inf) for _ in range(n)]\n for u, v, t in edges:\n if t > maxTime: continue\n\n adj[u][v] = min(adj[u][v], t)\n adj[v][u] = min(adj[v][u], t)\n\n pq = [(0, passingFees[0], 0)] # time, cost, u\n reduceCost(u=0, t=0, c=passingFees[0])\n while pq:\n t, c, u = heappop(pq)\n\n if c > minCost(u, t):\n continue # stale entry\n\n for v, dt in adj[u].items():\n tv = t+dt\n cv = c + passingFees[v]\n\n if tv > maxTime:\n continue\n if cv >= minCost(v, tv): \n continue # already enqueued a cheaper path at least as fast\n\n # record that we have a new cheapest path to v, costing cv, so we don\'t later\n # push any paths with t\' >= t and c\' >= cv\n reduceCost(v, tv, cv)\n heappush(pq, (tv, cv, v))\n\n # explored all paths from 0 to all other nodes, in time order, ensuring cost\n # drops monotonically with time to its minimum value\n \n min_cost = min(costTrees[n-1])\n return min_cost if min_cost < math.inf else -1\n```
| 6 | 0 |
['Python3']
| 3 |
minimum-cost-to-reach-destination-in-time
|
Simple dijkstra's implementation c++ smooth af !!
|
simple-dijkstras-implementation-c-smooth-dn5t
|
\n#define pb push_back\n#define F first\n#define S second\n#define pii pair<int,int>\n#define vi vector<int>\n#define vii vector<pii>\n#define vvi vector<vector
|
binayKr
|
NORMAL
|
2022-09-11T10:22:56.732536+00:00
|
2022-09-11T10:23:08.167792+00:00
| 614 | false |
```\n#define pb push_back\n#define F first\n#define S second\n#define pii pair<int,int>\n#define vi vector<int>\n#define vii vector<pii>\n#define vvi vector<vector<int>>\n#define vvpii vector<vector<pair<int,int>>>\n#define vc vector\n\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& pass) {\n int n = pass.size();\n vvpii g(n);\n for(auto it : edges)\n {\n g[it[0]].pb({it[1],it[2]});\n g[it[1]].pb({it[0],it[2]});\n }\n \n priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;\n pq.push({pass[0], 0, 0});\n vector<int> time(n,maxTime + 1);\n time[0] = 0;\n \n \n while(!pq.empty())\n {\n int curr_cost = pq.top()[0];\n int curr_node = pq.top()[1];\n int curr_time = pq.top()[2];\n pq.pop();\n \n if(curr_node == n-1) return curr_cost;\n \n for(auto [v,t] : g[curr_node])\n {\n int newTime = curr_time + t, newCost = curr_cost + pass[v];\n if(newTime < time[v])\n {\n time[v] = newTime;\n pq.push({newCost, v, newTime});\n }\n }\n }\n \n return -1;\n }\n};\n```
| 6 | 0 |
['C']
| 1 |
minimum-cost-to-reach-destination-in-time
|
[Java] DFS + DP[Memoisation] | Simple Solution
|
java-dfs-dpmemoisation-simple-solution-b-tjwd
|
\nclass Solution {\n class Edge {\n int src, nbr, wt;\n public Edge(int src, int nbr, int wt) {\n this.src = src;\n this.
|
eshan1809
|
NORMAL
|
2021-07-20T04:38:49.997708+00:00
|
2021-07-20T04:38:49.997738+00:00
| 666 | false |
```\nclass Solution {\n class Edge {\n int src, nbr, wt;\n public Edge(int src, int nbr, int wt) {\n this.src = src;\n this.nbr = nbr;\n this.wt = wt;\n }\n }\n\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = passingFees.length;\n List<Edge>[] graph = new ArrayList[n];\n for(int i = 0; i < n; i++)\n graph[i] = new ArrayList<>();\n for(int[] edge : edges){\n graph[edge[0]].add(new Edge(edge[0], edge[1], edge[2]));\n graph[edge[1]].add(new Edge(edge[1], edge[0], edge[2]));\n }\n return DFS(graph, 0, maxTime, passingFees, new Integer[1001][maxTime + 1]);\n }\n \n private int DFS(List<Edge>[] graph, int src, int remTime, int[] passingFees, Integer[][] dp){\n if(remTime < 0)\n return -1;\n if(dp[src][remTime] != null)\n return dp[src][remTime];\n if(src == passingFees.length - 1)\n return (dp[src][remTime] = passingFees[src]);\n int min = -1;\n for(Edge e : graph[src]){\n int x = DFS(graph, e.nbr, remTime - e.wt, passingFees, dp);\n if(min == -1)\n min = x;\n else if(x != -1)\n min = Math.min(min, x);\n }\n if(min == -1)\n return (dp[src][remTime] = -1);\n return (dp[src][remTime] = min + passingFees[src]);\n }\n}\n```
| 5 | 0 |
[]
| 3 |
minimum-cost-to-reach-destination-in-time
|
JAVA | PriorityQueue | 100% faster
|
java-priorityqueue-100-faster-by-lokeshm-pl03
|
\tclass Solution {\n\t\tpublic int minCost(int maxTime, int[][] edges, int[] Fees) {\n\n\t\t\tint target=Fees.length-1;\n\t\t\tint[] visited=new int[Fees.length
|
lokeshmari2803
|
NORMAL
|
2021-07-10T18:03:45.177637+00:00
|
2021-07-10T18:56:44.544429+00:00
| 903 | false |
\tclass Solution {\n\t\tpublic int minCost(int maxTime, int[][] edges, int[] Fees) {\n\n\t\t\tint target=Fees.length-1;\n\t\t\tint[] visited=new int[Fees.length];\n\t\t\tArrays.fill(visited,-1);\n\t\t\tMap<Integer,List<int[]>> map=new HashMap<>();\n\n\t\t\tfor(int[] x: edges){\n\t\t\t\tint u=x[0];\n\t\t\t\tint v=x[1];\n\t\t\t\tint time=x[2];\n\n\t\t\t\tmap.putIfAbsent(u,new ArrayList<>());\n\t\t\t\tmap.putIfAbsent(v,new ArrayList<>());\n\t\t\t\tmap.get(u).add(new int[]{v,time});\n\t\t\t\tmap.get(v).add(new int[]{u,time});\n\t\t\t}\n\n\t\t\tPriorityQueue<int[]> queue=new PriorityQueue<>((a,b)->a[1]==b[1] ? a[2]-b[2] : a[1]-b[1]);\n\t\t\tqueue.add(new int[]{0,Fees[0],0});\n\t\t\tvisited[0]=0;\n\t\t\twhile(!queue.isEmpty()){\n\t\t\t\tint[] curr=queue.poll();\n\t\t\t\tint u=curr[0];\n\t\t\t\tint cost=curr[1];\n\t\t\t\tint time=curr[2];\n\t\t\t\tif(u==target)\n\t\t\t\t\t return cost;\n\t\t\t\tfor(int next[] : map.get(u)){\n\t\t\t\t\tint v=next[0];\n\t\t\t\t\tif(visited[v]!=-1 && time+next[1]>=visited[v])\n\t\t\t\t\t\tcontinue;\n\t\t\t\t\tvisited[v]=time+next[1];\n\t\t\t\t\tif(time+next[1]<=maxTime){\n\t\t\t\t\t\tqueue.add(new int[]{v,cost+Fees[v],time+next[1]});\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\n\t\t\treturn -1;\n\t\t}\n\t}
| 5 | 0 |
['Heap (Priority Queue)', 'Java']
| 1 |
minimum-cost-to-reach-destination-in-time
|
C++ Simple DFS + Memo (Knapsack) Solution
|
c-simple-dfs-memo-knapsack-solution-by-h-752o
|
\nclass Solution {\npublic:\n int dp[1001][1001],n;\n int dfs(int curr,int k,vector<vector<pair<int,int>>>& g, vector<int>& cost){\n if(curr==n-1)
|
harshseta003
|
NORMAL
|
2022-08-04T06:36:56.784347+00:00
|
2022-08-04T06:36:56.784389+00:00
| 427 | false |
```\nclass Solution {\npublic:\n int dp[1001][1001],n;\n int dfs(int curr,int k,vector<vector<pair<int,int>>>& g, vector<int>& cost){\n if(curr==n-1) // if destination reached, return it\'s cost\n return cost[n-1];\n if(dp[curr][k]!=-1) // if already computed, return it\n return dp[curr][k];\n int mn=INT_MAX;\n for(int i=0;i<g[curr].size();i++){\n if(k<g[curr][i].second) // if time to visit the node, is less than remaining time, continue\n continue;\n int a=dfs(g[curr][i].first,k-g[curr][i].second,g,cost);\n if(a!=INT_MAX)\n mn=min(mn,cost[curr]+a);\n }\n return dp[curr][k]=mn;\n }\n int minCost(int k, vector<vector<int>>& edges, vector<int>& cost) {\n n=cost.size();\n int l=edges.size();\n vector<vector<pair<int,int>>>g(n);\n for(int i=0;i<l;i++){\n g[edges[i][0]].push_back({edges[i][1],edges[i][2]});\n g[edges[i][1]].push_back({edges[i][0],edges[i][2]});\n }\n memset(dp,-1,sizeof(dp));\n dfs(0,k,g,cost); \n return dp[0][k]==INT_MAX?-1:dp[0][k];\n }\n};\n```
| 4 | 0 |
['Dynamic Programming', 'Depth-First Search', 'Memoization', 'C']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Dijkstra's with slight modification
|
dijkstras-with-slight-modification-by-qn-cd8x
|
This concept can be generalised whenever minimization based on two things need to be done and when a parameter has to be just smaller than a threshold. \n1) In
|
qnalkumar
|
NORMAL
|
2021-12-09T07:47:51.632194+00:00
|
2021-12-09T07:47:51.632236+00:00
| 410 | false |
This concept can be generalised whenever minimization based on two things need to be done and when a parameter has to be just smaller than a threshold. \n1) In such a case , we will make a min heap kind of thing with key or thing to minimize being the minimum value which we must return.\n2) The second parameter must be minimized for the cases if the first parameter minimization is not done.\n\nThat is, priority wise minimization have to be considered.\n\nIn this question, we find that we have 2 reasons for putting an element in the multiset.\n1) If cost is decreased, and time required <= threshold time.\n2) Else if cost of the next won\'t be reduced, then we have to see if the time for next node is minimized, so that there is a possibility that some unexplored nodes are found.\n\nSo, performing these 2 cases, we wiil receive the most optimal cost to reach (n-1)th node following the threshold constraint.\n\nC++ code\n```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& fees) {\n \n int n = fees.size();\n \n vector<pair<int,int>> vt[n];\n \n for(int i=0;i<edges.size();i++)\n {\n vt[edges[i][0]].push_back({edges[i][1],edges[i][2]});\n \n vt[edges[i][1]].push_back({edges[i][0],edges[i][2]});\n }\n \n multiset<pair<int,pair<int,int>>> ms;\n \n ms.insert({fees[0],{0,0}});\n \n vector<int> tim(n,INT_MAX);\n tim[0]= 0;\n \n vector<int> cost(n,INT_MAX);\n \n \n while(!ms.empty())\n {\n pair<int,pair<int,int>> hr= *ms.begin();\n \n int cst= hr.first;\n int cur= hr.second.first;\n int tm= hr.second.second;\n \n ms.erase(ms.begin());\n \n \n if(cur==n-1)\n return cost[cur];\n \n for(auto it:vt[cur])\n {\n if(tm+it.second<=maxTime)\n {\n if(cst+fees[it.first] < cost[it.first])\n {\n cost[it.first]= cst+fees[it.first];\n tim[it.first]= tm+it.second; \n ms.insert({cost[it.first],{it.first,tm+ it.second}});\n }\n \n else if( (tim[it.first] > tm + it.second)){\n \n tim[it.first]= tm+it.second;\n ms.insert({cst+fees[it.first],{it.first,tm + it.second}}); \n }\n }\n \n }\n }\n return -1;\n \n }\n};\n```
| 4 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
[Python3] Easy Bellman-Ford solution
|
python3-easy-bellman-ford-solution-by-ni-1s2x
|
dp solution.\n\npython\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n \'\'\'\n Ti
|
nightybear
|
NORMAL
|
2021-08-23T18:34:55.263811+00:00
|
2021-08-23T18:34:55.263861+00:00
| 376 | false |
dp solution.\n\n```python\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n \'\'\'\n Time: O((m+n)* maxtime), where m is length of edges\n Space: O(n*maxtime)\n \'\'\'\n n = len(passingFees)\n dp = [[math.inf]*(n) for _ in range(maxTime+1)]\n dp[0][0] = passingFees[0]\n\n ans = math.inf\n for k in range(1, maxTime+1):\n for x, y, time in edges:\n if k >= time:\n # dual direction\n dp[k][y] = min(dp[k][y], dp[k-time][x] + passingFees[y])\n dp[k][x] = min(dp[k][x], dp[k-time][y] + passingFees[x])\n \n ans = min(ans, dp[k][n-1])\n \n if ans == math.inf:\n return -1\n return ans\n```
| 4 | 0 |
['Dynamic Programming', 'Python']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Minimum Cost to Complete Journey with Time Constraint Using Dijkstra's Algorithm
|
minimum-cost-to-complete-journey-with-ti-b721
|
Intuition
The problem is essentially about finding the shortest path in a weighted graph, where the nodes represent cities, and the edges represent roads conne
|
BharathDurai
|
NORMAL
|
2025-03-20T10:28:33.477456+00:00
|
2025-03-20T10:28:33.477456+00:00
| 156 | false |
### **Intuition**
- The problem is essentially about finding the **shortest path** in a **weighted graph**, where the nodes represent cities, and the edges represent roads connecting these cities with certain travel times. The challenge here is that, in addition to the usual **distance or path cost**, we also have an additional **cost constraint**, i.e., the passing fee for each city you visit. You want to minimize this total cost while respecting the constraint on the total travel time.
- To solve this, we need to explore different paths from the starting city to the destination city, but we must ensure that:
1. The **time** taken to travel doesn't exceed the `maxTime`.
2. The **cost** of passing through the cities is minimized.
- This problem can be approached by using **Dijkstra's algorithm** with a slight modification:
- Instead of just tracking the shortest distance to a node, we also track the **total cost** incurred from passing through the cities.
- We maintain a priority queue to always process the path that has the minimum **cost** (and within the allowed **time**).
---
### **Approach**
1. **Graph Representation**:
We start by building an adjacency list (graph) where each node (city) is connected to its neighbors via roads (edges). Each edge has a travel time.
2. **Priority Queue**:
We use a **min-heap (priority queue)** to always expand the node with the minimum total cost and time to reach it. This allows us to efficiently explore paths with lower costs first.
3. **Tracking Costs and Times**:
- `costs[i]`: Tracks the minimum cost to reach city `i`. We initialize it to infinity for all cities except the starting city (city 0), which has a cost equal to its passing fee.
- `times[i]`: Tracks the minimum time required to reach city `i`. We initialize it to `maxTime + 1` for all cities, except for city 0, which has a time of 0.
4. **Exploring Neighbors**:
For each city, we explore all of its neighbors. For each neighboring city, we compute the new time and cost if we were to travel from the current city. If the new time exceeds `maxTime`, we skip that path. Otherwise, if the new cost is lower than the previously recorded cost for that city, we update the cost and time and add the neighbor to the priority queue for further exploration.
5. **Termination**:
If we reach the destination city (`n - 1`), we return the total cost incurred to reach it. If no valid path exists within the time constraint, return `-1`.
---
### **Complexity**
- **Time complexity**:
The algorithm primarily operates by extracting elements from the priority queue and relaxing edges. The priority queue supports insertions and extractions in **O(log n)** time.
Since we process each edge and each node at most once, the total time complexity is **O(E log V)**, where:
- **E** is the number of edges (roads),
- **V** is the number of vertices (cities).
- **Space complexity**:
We store the graph in an adjacency list, which requires **O(E)** space. Additionally, we store the `costs`, `times`, and the priority queue, which requires **O(V)** space. Thus, the total space complexity is **O(V + E)**.
# Code
```python3 []
import heapq
from collections import defaultdict
from typing import List
class Solution:
def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:
# Number of cities
n = len(passingFees)
# Create a graph to store cities and the time required to travel between them
graph = defaultdict(list)
# Fill the graph with the roads (edges)
for u, v, time in edges:
graph[u].append((v, time))
graph[v].append((u, time))
# Initialize cost array: costs[i] will hold the minimum cost to reach city i
costs = [float("inf")] * n
# Initialize time array: times[i] will hold the minimum time to reach city i
times = [maxTime + 1] * n
# Starting at city 0 with its passing fee
times[0] = 0
costs[0] = passingFees[0]
# Min-heap (priority queue) to always expand the node with the least cost and time
queue = [(passingFees[0], 0, 0)] # (current total cost, current time, current city)
while queue:
# Pop the city with the smallest cost and time from the priority queue
curr_cost, curr_time, curr_city = heapq.heappop(queue)
# If we have reached the destination city (city n - 1), return the cost
if curr_city == n - 1:
return curr_cost
# Explore all the neighboring cities (neighbors and the time to reach them)
for next_city, travel_time in graph[curr_city]:
# If traveling to the next city exceeds the maxTime, skip this path
if curr_time + travel_time > maxTime:
continue
# Calculate the new time and cost after moving to the next city
new_time = curr_time + travel_time
new_cost = curr_cost + passingFees[next_city]
# If we find a cheaper way to reach next_city, update the cost and time
if new_cost < costs[next_city] or new_time < times[next_city]:
costs[next_city] = new_cost
times[next_city] = new_time
# Push the updated city state into the priority queue
heapq.heappush(queue, (new_cost, new_time, next_city))
# If we cannot reach the destination city within the allowed time, return -1
return -1
```
| 3 | 0 |
['Graph', 'Python3']
| 1 |
minimum-cost-to-reach-destination-in-time
|
Simple C++ solution | Dijkstra's Algorithm | Runtime : 214ms
|
simple-c-solution-dijkstras-algorithm-ru-jzbf
|
if you like my approach please hit the upvote button : )\n
|
HustlerNitin
|
NORMAL
|
2022-01-25T10:16:43.079516+00:00
|
2022-01-25T10:18:03.581294+00:00
| 572 | false |
**if you like my approach please hit the upvote button : )**\n<iframe src="https://leetcode.com/playground/8FjPYQu8/shared" frameBorder="0" width="1000" height="600"></iframe>
| 3 | 0 |
['Breadth-First Search', 'C', 'Heap (Priority Queue)', 'C++']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Java || Dijkstra - Clean Code || 35ms Faster than 100%
|
java-dijkstra-clean-code-35ms-faster-tha-lpwg
|
I messed up basic Dijkstra and couldn\'t solve this during the contest. The idea is same as Dijkstra, with the only difference here is that we need to maintain
|
shune
|
NORMAL
|
2021-07-10T17:53:24.653995+00:00
|
2021-07-10T21:33:07.639295+00:00
| 322 | false |
I messed up basic Dijkstra and couldn\'t solve this during the contest. The idea is same as Dijkstra, with the only difference here is that we need to maintain another array to track the amount of `time` taken to reach every vertex. Unlike basic Dijkstra, this helps us to also keep the intermediate solutions with larger cost but lesser time in the priority queue. At every node we encounter in our path, we check if we\'ve reached the node before. If we\'ve reached the node before with a higher fees or with a higher time, we update the fees/time accordingly and add the node to the priority-queue.\n\n```\nclass Solution {\n \n public int minCost(int maxTime, int[][] edges, int[] fees) {\n List<List<int[]>> graph = new ArrayList();\n for (int i=0;i<fees.length;i++) {\n graph.add(new ArrayList());\n }\n for (int[] edge: edges) {\n graph.get(edge[0]).add(new int[]{edge[1], edge[2]});\n graph.get(edge[1]).add(new int[]{edge[0], edge[2]});\n }\n int[] fees2Reach = new int[fees.length];\n int[] time2Reach = new int[fees.length];\n Arrays.fill(time2Reach, Integer.MAX_VALUE);\n Arrays.fill(fees2Reach, Integer.MAX_VALUE);\n time2Reach[0] = 0;\n fees2Reach[0] = fees[0];\n // sort by fees since we need minimum cost\n PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> {\n return a[1] - b[1];\n });\n pq.offer(new int[]{0, fees[0], 0}); // time, fees, city\n while (!pq.isEmpty()) {\n int[] arr = pq.poll();\n if (arr[2]==fees.length-1) return arr[1]; // reached last city\n for (int[] vertTime: graph.get(arr[2])) {\n int vertex = vertTime[0];\n int time = vertTime[1];\n if (arr[0] + time > maxTime) continue;\n if (arr[0] + time < time2Reach[vertex]) {\n time2Reach[vertex] = arr[0] + time;\n fees2Reach[vertex] = arr[1] + fees[vertex];\n pq.offer(new int[]{arr[0] + time, arr[1] + fees[vertex], vertex});\n } else if (arr[1] + fees[vertex] < fees2Reach[vertex]) {\n fees2Reach[vertex] = arr[1] + fees[vertex];\n pq.offer(new int[]{arr[0] + time, arr[1] + fees[vertex], vertex});\n }\n }\n }\n return -1;\n }\n}\n```
| 3 | 0 |
[]
| 1 |
minimum-cost-to-reach-destination-in-time
|
EXPLAINED PYTHON SOLUTION ✅🔥 DP SOLUTION | GRAPH | TABULATION
|
explained-python-solution-dp-solution-gr-qgzq
|
Intuition\nIn the problem we are asked to find a path which has less than the max permitted travel time and has the minimum cost compared to other valid paths i
|
Prathamesh7x
|
NORMAL
|
2024-07-11T13:40:38.220345+00:00
|
2024-07-11T13:40:38.220373+00:00
| 150 | false |
# Intuition\nIn the problem we are asked to find a path which has less than the max permitted travel time and has the minimum cost compared to other valid paths if any. If no such paths are available then return -1.\n\n# Approach\nWe can start by mapping the graph. We will map in a **bidirectional** way. We will initialize a 2D DP array whose **dp[i][j]** will represent the **minimum** cost of reaching *i-th* node in **j** minutes. We will the start from the 0th node and explore it\'s neighbours. We will compute the new distance as the distance to **current node + distance to the next node**. If the distance (time) is less than or equal to max permitted time then we can move to computing the new cost. New cost can be computed as **cost to get to current node + cost to next node**. If the new cost if less than the existing cost to neighbouring node with the newly computed time then we can update it\'s time and append the new node and new time to the queue. At last, If the minimum of the last row of DP array if infinity then it means it is **impossible** to reach the node in given constraints so we return -1 else return the minimum value.\n\n# Complexity\n- Time complexity: $$O(E+N*T)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(E+N*T)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import deque, defaultdict\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n graph = defaultdict(list)\n n = len(passingFees)\n for src, dest, time in edges:\n graph[src].append((dest, time))\n graph[dest].append((src, time))\n\n dp = [[float(\'inf\')] * (maxTime + 1) for _ in range(n)]\n dp[0][0] = passingFees[0]\n queue = deque([(0, 0)])\n while queue:\n current_node, current_time = queue.popleft()\n for nei, nei_time in graph[current_node]:\n new_time = current_time + nei_time\n if new_time <= maxTime:\n new_cost = dp[current_node][current_time] + passingFees[nei]\n if new_cost < dp[nei][new_time]:\n dp[nei][new_time] = new_cost\n queue.append((nei, new_time))\n \n min_cost = min(dp[n-1])\n return min_cost if min_cost != float(\'inf\') else -1\n```
| 2 | 0 |
['Array', 'Dynamic Programming', 'Graph', 'Python', 'Python3']
| 0 |
minimum-cost-to-reach-destination-in-time
|
C++ Dijkstra's
|
c-dijkstras-by-deerishi-r0jn
|
\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO((E+V)log(V))\n\n- Space complexity:\n Add your space complexity here, e.g. O(n
|
deerishi
|
NORMAL
|
2024-04-25T16:00:04.726987+00:00
|
2024-04-25T16:00:04.727027+00:00
| 121 | false |
\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO((E+V)log(V))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(V) where V is the number of vertices.\n\n# Code\n```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int n=passingFees.size();\n vector<vector<array<int,2>>> graph(n+1);\n for(auto e:edges){\n int x=e[0],y=e[1],cost=e[2];\n graph[x].push_back({y,cost});graph[y].push_back({x,cost});\n }\n\n priority_queue<array<int,3>,vector<array<int,3>>> pq;\n\n pq.push({-passingFees[0],0,0});\n\n vector<int> minimumTimeVisited(n+1,INT_MAX);\n while(pq.size()){\n auto [cost,node,time]=pq.top();pq.pop();\n if(minimumTimeVisited[node]<=time) continue;\n minimumTimeVisited[node]=time;\n\n if(node==n-1 and time<=maxTime) return -cost;\n\n for(auto [ne,w]:graph[node]){\n pq.push({-(-cost+passingFees[ne]),ne,time+w});\n }\n }\n\n return -1;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
minimum-cost-to-reach-destination-in-time
|
C++ solution || Dijkstra's Algorithm Approach
|
c-solution-dijkstras-algorithm-approach-kyyxk
|
\n# Complexity\n- Time complexity:\nO(Elog(V))\n- Space complexity:\nO(V)\n# Code\n\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>
|
LetapKartik
|
NORMAL
|
2023-08-11T10:04:30.014039+00:00
|
2023-08-11T10:04:30.014060+00:00
| 159 | false |
\n# Complexity\n- Time complexity:\n$$O(Elog(V))$$\n- Space complexity:\n$$O(V)$$\n# Code\n```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int n = passingFees.size();\n vector<int>costs(n,INT_MAX);\n vector<int>totaltime(n,INT_MAX);\n costs[0] = passingFees[0];\n totaltime[0] = 0;\n vector<vector<pair<int,int>>>graph(n);\n for(auto nxt : edges){\n graph[nxt[0]].push_back({nxt[1],nxt[2]});\n graph[nxt[1]].push_back({nxt[0],nxt[2]});\n }\n priority_queue<pair<int,pair<int,int>>, vector<pair<int,pair<int,int>>>, greater<pair<int,pair<int,int>>>>pq;\n ////////// {cost, node, time}\n pq.push({costs[0],{totaltime[0],0}});\n\n while (!pq.empty())\n {\n int paid = pq.top().first, time = pq.top().second.first, node = pq.top().second.second;\n pq.pop();\n \n for(auto it : graph[node]){\n if(time+it.second <= maxTime){\n if(paid + passingFees[it.first] < costs[it.first]){\n costs[it.first]=paid+passingFees[it.first];\n totaltime[it.first] = time+it.second;\n pq.push({costs[it.first], {totaltime[it.first], it.first}});\n }else if(time + it.second < totaltime[it.first]){\n totaltime[it.first] = time+it.second;\n pq.push({paid+passingFees[it.first], {totaltime[it.first], it.first}});\n }\n \n }\n }\n }\n if(costs[n-1] != INT_MAX){\n return costs[n-1];\n }\n return -1;\n }\n};\n```
| 2 | 0 |
['Breadth-First Search', 'Graph', 'Shortest Path', 'C++']
| 0 |
minimum-cost-to-reach-destination-in-time
|
C++ Modified Dijkstra : Worst case O(ElogV) time O(E + V) space
|
c-modified-dijkstra-worst-case-oelogv-ti-6jm7
|
\tclass Solution {\n\tpublic:\n int\n minCost(int maxTime, vector>& edges, vector& passingFees) {\n // Problem is modeled as an undirected graph wh
|
gopalanhsv
|
NORMAL
|
2022-08-10T17:54:20.480136+00:00
|
2022-08-10T17:54:20.480179+00:00
| 194 | false |
\tclass Solution {\n\tpublic:\n int\n minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n // Problem is modeled as an undirected graph wherein :-\n // Cities are the graph vertices\n // Bidirectional roads between cities are graph edges between vertices\n // representing cities. Travel time between cities is the edge cost.\n // The minimum journey between first city (0) and last city (n - 1)\n // would be the shortest path between the two vertices based on the \n // two parameters; total edge travel time not exceeding the maxTime\n // and total passing time of all path vertices on the path being the\n // minimum => modified Dijkstra with two constraints\n return minCostViaModifiedDijkstra(maxTime, edges, passingFees);\n }\n \n\tprivate:\n \n // Models the edge between 2 graph vertices (i.e. road between cities)\n typedef struct _EdgeInfo {\n // Neighbour vertex\n int nv;\n // Edge cost\n int cost;\n } EdgeInfoT;\n \n int\n minCostViaModifiedDijkstra(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n \n // Construct graph\n buildGraph(edges);\n \n // Modified Dijkstra operating on two constraints to find the shortest path\n // betwen 0 and \'n - 1\' vertices\n // 1. Commence from vertex 0 with path cost being passing fee of vertex\n // 0 at time \'0\'. Add vertex 0 to priority queue (PQ)\n // 2. Select a vertex from the PQ to processed. Vertex which can reached\n // with least edge travel time is prioritised over others stored as\n // this reduces the chance of travel time hitting maxTime leading to\n // journey termination. Tie breaker amongst vertices with same travel\n // time is by preferring the vertex with shortest path cost (sum of all\n // vertex passing times on the path)\n // 3. Skip processing the selected vertex \'v\'; if the vertex was already\n // reached earlier via a journey path earlier with lesser total travel\n // time and lesser path cost\n // 4. Update the total travel time and path cost for the selected vertex\n // with the new values\n // 5. Explore all neighbour vertices of the selected vertex \'v\'\n // 6. Neigbour vertices of \'v\' which can be reached within the max allowable\n // travel time are added to the PQ for processing in the subsequent\n // iterations\n // 7. Go to step 2 as long as there is vertex in the PQ for processing\n \n // Vertex reachability information\n typedef struct _VertexInfo {\n // Vertex\n int v;\n // Total travel time to reach vertex \'v\' (sum of edge times)\n // from start vertex \'0\'\n long time;\n // Total path cost to reach vertex \'v\' (sum of passing times\n // of all vertices on the path) from start vertex \'0\'\n long pathCost;\n } VertexInfoT;\n \n typedef struct _VertexInfoCmpObj {\n bool\n operator()(const VertexInfoT& vi1, const VertexInfoT& vi2) {\n // Prefer vertex with lower journey cost if the travel times\n // are same; else prefer vertex with lesser travel time\n if (vi1.time == vi2.time) {\n return vi1.pathCost > vi2.pathCost;\n }\n return vi1.time > vi2.time;\n }\n } VertexInfoCmpObj;\n // Priority Queue of vertex reachability information\n priority_queue<VertexInfoT, vector<VertexInfoT>, VertexInfoCmpObj> pq;\n \n int nVertices = passingFees.size();\n // Tracks the minimum journey/path cost to each vertex from vertex 0\n vector<long> minCostV(nVertices, numeric_limits<int>::max());\n // Tracks the minimum travel time cost to each vertex from vertex 0\n vector<long> minTimeV(nVertices, numeric_limits<int>::max());\n \n // Step 1. Start from vertex 0. Add to PQ\n minCostV[0] = 0;\n VertexInfoT vi;\n vi.v = 0;\n vi.time = 0;\n vi.pathCost = passingFees[0];\n pq.push(vi);\n \n while (!pq.empty()) {\n // Step 2. Select and dequeue the vertex at front of PQ\n auto reachableVertexInfo = pq.top();\n pq.pop();\n // Selected vertex params\n auto v = reachableVertexInfo.v;\n auto time = reachableVertexInfo.time;\n auto pCost = reachableVertexInfo.pathCost;\n \n // Step 3. Selected vertex was reachable from vertex \'0\' via a \n // path with lesser/same travel time and path cost. So no sense\n // in processing the vertex this time\n if ((time >= minTimeV[v]) &&\n (pCost >= minCostV[v])) {\n continue;\n }\n \n // Step 4. Update total travel time and path cost to reach\n // selected vertex as per new reacahbility info\n minCostV[v] = min(minCostV[v], pCost);\n minTimeV[v] = min(minTimeV[v], time);\n \n // Step 5. Iterate over each neighbor of selected vertex\n auto & nbrInfoV = _adjList[v];\n for (auto & nbrInfo : nbrInfoV) {\n auto edgeCost = nbrInfo.cost;\n auto nv = nbrInfo.nv;\n if (edgeCost + time <= maxTime) {\n // Neighbour reachable from vertex from vertex \'0\' within\n // the max allowable travel time. Enqueue vertex to PQ\n // for further processing\n VertexInfoT nvInfo;\n nvInfo.v = nv;\n // Update the travel time and path cost to neighbpur \'nv\'\n // via last hop as current select vertex\n nvInfo.time = edgeCost + time;\n nvInfo.pathCost = pCost + passingFees[nv];\n pq.push(nvInfo);\n }\n }\n }\n \n \n int minCostToDest = minCostV[nVertices - 1];\n return (minCostToDest == numeric_limits<int>::max()) ? -1 : minCostToDest;\n }\n \n void\n buildGraph(vector<vector<int>>& edges) {\n // Iterate over each edge of the graph\n for (auto & edge : edges) {\n // Edge vertices and cost\n auto u = edge[0];\n auto v = edge[1];\n auto cost = edge[2];\n // Bidirectional edge - add both (u, v) and (v, u) to\n // graph adjacency list\n EdgeInfoT e;\n e.cost = cost;\n e.nv = v;\n _adjList[u].emplace_back(e);\n e.nv = u;\n _adjList[v].emplace_back(e);\n }\n }\n \n // Data members\n \n // Graph Adjacency list representation. Maps each vertex to list of\n // edges incident on the vertex. Edge information consists of neighbour\n // vertex and edge cost tuples\n unordered_map<int, vector<EdgeInfoT> > _adjList;\n\t};
| 2 | 0 |
['Heap (Priority Queue)']
| 2 |
minimum-cost-to-reach-destination-in-time
|
C++ 2 Solutions | DP | Dijkstra's Algorithm
|
c-2-solutions-dp-dijkstras-algorithm-by-eww8b
|
Dynamic Programming\n\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int PASS_MAX = 1
|
alexlee1999
|
NORMAL
|
2022-06-25T17:17:05.514329+00:00
|
2022-06-25T17:17:05.514373+00:00
| 518 | false |
Dynamic Programming\n```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int PASS_MAX = 10000000;\n vector<vector<int>> dp(maxTime + 1, vector<int>(passingFees.size(), PASS_MAX));\n \n dp[0][0] = passingFees[0];\n for (int i=1; i<=maxTime; ++i) {\n for (int j=0; j<edges.size(); ++j) {\n if (edges[j][2] > i) {\n continue;\n }\n int city1 = edges[j][0];\n int city2 = edges[j][1];\n int time = edges[j][2];\n dp[i][city1] = min(dp[i][city1], dp[i - time][city2] + passingFees[city1]);\n dp[i][city2] = min(dp[i][city2], dp[i - time][city1] + passingFees[city2]);\n }\n }\n int ans = PASS_MAX;\n for (int i=0; i<=maxTime; ++i) {\n ans = min(ans, dp[i][passingFees.size()-1]);\n }\n if (ans == PASS_MAX) {\n return -1;\n }\n return ans;\n }\n};\n// Time : O(TE) T = maxtime E = edge\n// Space : O(TN)\n```\nDijkstra\'s Algorithm\n```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int n = passingFees.size();\n priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> myHeap;\n \n vector<vector<pair<int, int>>> edge (n, vector<pair<int, int>>());\n for (int i=0; i<edges.size(); ++i) {\n edge[edges[i][0]].push_back({edges[i][1], edges[i][2]});\n edge[edges[i][1]].push_back({edges[i][0], edges[i][2]});\n }\n vector<int> dist(n, INT_MAX);\n dist[0] = 0;\n myHeap.push({passingFees[0], {0, 0}});\n while (!myHeap.empty()) {\n int node = myHeap.top().second.first;\n int fee = myHeap.top().first;\n int time = myHeap.top().second.second;\n myHeap.pop();\n \n if (node == n - 1) {\n return fee;\n }\n for (int i=0; i<edge[node].size(); ++i) {\n int neighbor = edge[node][i].first;\n int travel_time = edge[node][i].second;\n if (time + travel_time > maxTime) {\n continue;\n }\n if (dist[neighbor] > time + travel_time) {\n dist[neighbor] = time + travel_time;\n myHeap.push({fee + passingFees[neighbor], {neighbor, time + travel_time}});\n }\n }\n }\n return -1;\n }\n};\n// Time : O(Elogn)\n// Space : O(n + E)\n```
| 2 | 0 |
['Dynamic Programming', 'C']
| 1 |
minimum-cost-to-reach-destination-in-time
|
Why simple DFS isn't working?
|
why-simple-dfs-isnt-working-by-deeshantk-yczh
|
I have a simple DFS code. Why isn\'t it working.\n\nIt is saying Wrong Answer.\n\n\nclass Solution {\npublic:\n int ans = INT_MAX, n, t;\n void dfs(vector
|
deeshantk
|
NORMAL
|
2022-02-23T15:58:32.852461+00:00
|
2022-02-23T15:58:32.852492+00:00
| 202 | false |
I have a simple DFS code. Why isn\'t it working.\n\nIt is saying Wrong Answer.\n\n```\nclass Solution {\npublic:\n int ans = INT_MAX, n, t;\n void dfs(vector<vector<pair<int, int>>>& graph, vector<int>& vis, int curr, int time, int total, vector<int>& pass){\n // cout<<curr<<"->"<<total<<" ";\n // total += pass[curr];\n // if(total > 862) return;\n if(time > t) return; \n if(curr == n-1){\n ans = min(ans, total);\n return;\n }\n \n vis[curr] = 1;\n for(pair<int, int> i: graph[curr]){\n if(vis[i.first] == 2 or vis[i.first] == 1) continue;\n dfs(graph, vis, i.first, time+i.second, total+pass[i.first], pass);\n // cout<<ans<<" ";\n }\n vis[curr] = 2;\n \n }\n \n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& pass) {\n ans = INT_MAX;\n n = pass.size();\n vector<int> vis(n);\n //flag = false;\n t = maxTime;\n vector<vector<pair<int, int>>> graph(n, vector<pair<int, int>>());\n for(vector<int> i: edges){\n graph[i[0]].push_back({i[1], i[2]});\n graph[i[1]].push_back({i[0], i[2]});\n }\n \n dfs(graph, vis, 0, 0, pass[0], pass);\n \n return ans == INT_MAX? -1: ans;\n }\n};\n```\nAny help will be appriciated :)
| 2 | 0 |
[]
| 1 |
minimum-cost-to-reach-destination-in-time
|
Python Dijkstra's Algorithm Solution with Explanation
|
python-dijkstras-algorithm-solution-with-rif3
|
We can simply apply Djikstra\'s Algorithm based on the cost as the key to expand paths. However, we need to prune paths that exceed the max time. As well, we mi
|
zlax
|
NORMAL
|
2021-11-25T10:02:35.065661+00:00
|
2021-11-25T10:02:35.065693+00:00
| 431 | false |
We can simply apply Djikstra\'s Algorithm based on the cost as the key to expand paths. However, we need to prune paths that exceed the max time. As well, we might want to revisit nodes that costed less time even though they had a higher cost. This lets us try all valid paths incase the min cost path goes past the max time limit.\n\n```\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n n = len(passingFees)\n heap = [(passingFees[0],0,0)] # (cost, time, curr)\n nodeToTime = {}\n \n \n edgesDict = defaultdict(list)\n for a,b,time in edges:\n edgesDict[a].append((b,time))\n edgesDict[b].append((a, time))\n \n while heap:\n cost, time, curr = heappop(heap)\n \n if time > maxTime:\n continue\n \n if curr == n - 1:\n return cost\n \n # No point in visting this node again if it was visited before with a lower cost AND lower time.\n if curr not in nodeToTime or nodeToTime[curr] > time:\n \n nodeToTime[curr] = time\n\n for nextNode, travelTime in edgesDict[curr]:\n heappush(heap, (cost + passingFees[nextNode], time + travelTime, nextNode))\n \n return -1\n```
| 2 | 0 |
[]
| 2 |
minimum-cost-to-reach-destination-in-time
|
C++ Solution || DP with Dijkstra || Easy to understand
|
c-solution-dp-with-dijkstra-easy-to-unde-8lx6
|
Below solution combines DP with Dijkstra\'s algorithm to achive the min cost possible. Do comment if anything is not clear.\n\n```\ntypedef pair> pii;\n\nclass
|
sumantk778
|
NORMAL
|
2021-08-18T08:58:11.179112+00:00
|
2021-08-18T09:01:59.513981+00:00
| 587 | false |
Below solution combines DP with Dijkstra\'s algorithm to achive the min cost possible. Do comment if anything is not clear.\n\n```\ntypedef pair<int,pair<int,int>> pii;\n\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int n=passingFees.size();\n\n\t//state of dp(i,j) : stores the min cost to reach city \'i\' in \'j\' max time;\n int dp[n][maxTime+1];\n \n\t\t\n\t\t//without using another array for time will result in TLE since it will explore more paths, hence \n\t\t//using another array that stores the min time the city was discovered. This improves the TC to a \n\t\t//huge extent as it prunes some path.\n\t\t\n int ttime[n];\n for(int i=0;i<n;i++){\n ttime[i]=INT_MAX;\n for(int j=0;j<=maxTime;j++){\n dp[i][j]=INT_MAX;\n }\n }\n ttime[0]=0;\n dp[0][0]=passingFees[0];\n \n vector<vector<int>>adj[n];\n for(auto x:edges){\n adj[x[0]].push_back({x[1],x[2]});\n adj[x[1]].push_back({x[0],x[2]});\n }\n \n\t\t// first priority is to minimise the cost associated with the path, {cost, city, time}\n priority_queue<pii,vector<pii>,greater<pii>>minHeap;\n minHeap.push({passingFees[0],{0,0}});\n \n while(!minHeap.empty()){\n auto top=minHeap.top();\n minHeap.pop();\n \n\t\t int u=top.second.first; \n int time=top.second.second;\n int cost=top.first;\n\n\t\t\tif(u==n-1)return cost;\n\n\t\t\tttime[u]=time;\n \n for(auto x:adj[u]){\n\t\t\t// this is the pruning part, where we are only exploring paths that can be reached earlier than \n\t\t\t//the time already required.\n if(time+x[1]<ttime[x[0]]){\n if(time+x[1]<=maxTime){\n\t\t\t\t\t//now we are checking if the cost to reach the neighbor is less than the already minimum \n\t\t\t\t\t//cost, denoted by dp[x[0]][time+x[1]], denoting min cost to reach x[0] in \'time+x[1]\' max \n\t\t\t\t\t//time.\n if(cost+passingFees[x[0]]<dp[x[0]][time+x[1]] ){\n dp[x[0]][time+x[1]]=cost+passingFees[x[0]];\n ttime[x[0]]=time+x[1];\n minHeap.push({dp[x[0]][time+x[1]],{x[0],time+x[1]}});\n }\n }\n }\n }\n }\n return -1;\n }\n};\n
| 2 | 0 |
['Dynamic Programming', 'C', 'Heap (Priority Queue)']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Simple Java Djikstra
|
simple-java-djikstra-by-darkrwe-55hx
|
\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = passingFees.length;\n int destination = n-1;
|
darkrwe
|
NORMAL
|
2021-08-15T11:57:10.203014+00:00
|
2021-08-15T11:57:10.203047+00:00
| 340 | false |
```\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = passingFees.length;\n int destination = n-1;\n int source = 0;\n Integer[] timeHold = new Integer[n];\n Arrays.fill(timeHold, Integer.MAX_VALUE);\n\n Map<Integer,List<int[]>> graph = new HashMap();\n for(int[] edge : edges){\n int src = edge[0];\n int dst = edge[1];\n int time = edge[2];\n graph.putIfAbsent(src,new ArrayList());\n graph.putIfAbsent(dst,new ArrayList());\n graph.get(src).add(new int[]{dst,time});\n graph.get(dst).add(new int[]{src,time});\n }\n \n PriorityQueue<int[]> pq = new PriorityQueue<int[]>( (a, b) -> a[1] - b[1] ); //a[0] = city, a[1] = cost, a[2] = time\n pq.offer(new int[]{source, passingFees[source], 0});\n timeHold[0] = 0;\n while(!pq.isEmpty()){\n int[] node = pq.poll();\n int src = node[0];\n int fee = node[1];\n int time = node[2];\n\n if(src == destination) // check whether destination reached ?\n return fee;\n \n for(int[] nei : graph.get(src)){\n \n int neiNode = nei[0];\n int neiTime = nei[1];\n \n if(time + neiTime > maxTime) // we cannot exceed maxTime, return .. \n continue;\n \n if(time + neiTime < timeHold[neiNode]){\n timeHold[neiNode] = time + neiTime; //we found lesser time update time Array and add this node to pq..\n pq.add(new int[]{neiNode, fee + passingFees[neiNode], timeHold[neiNode]});\n }\n }\n }\n return -1;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
minimum-cost-to-reach-destination-in-time
|
JAVA | 34 ms | Clean Memoization & Dijkstra's Algo
|
java-34-ms-clean-memoization-dijkstras-a-t37t
|
\nDijkstra\'s Algo : 34 ms\n\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] costVtx) {\n int N = costVtx.length;\n Ar
|
siddhantgupta792000
|
NORMAL
|
2021-08-08T15:46:23.354413+00:00
|
2021-08-09T09:08:31.147816+00:00
| 498 | false |
```\nDijkstra\'s Algo : 34 ms\n\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] costVtx) {\n int N = costVtx.length;\n ArrayList<int[]>[] graph = new ArrayList[N];\n for(int i = 0; i < N ; i++) graph[i] = new ArrayList<>();\n \n for(int[] e : edges){\n int u = e[0], v = e[1], w = e[2];\n graph[u].add(new int[]{v, w});\n graph[v].add(new int[]{u, w});\n }\n int[] timeHold = new int[N];\n Arrays.fill(timeHold, (int) 1e9);\n PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> {\n return a[1] - b[1];\n });\n // vtx | cost | time \n pq.add(new int[]{0, costVtx[0], 0});\n timeHold[0] = 0;\n while(!pq.isEmpty()){\n int[] p = pq.remove();\n int vtx = p[0], cost = p[1], time = p[2]; \n if(vtx == costVtx.length - 1) return cost;\n for(int[] e : graph[vtx]){\n int v = e[0], n_time = e[1];\n if(time + n_time > maxTime) continue;\n if(time + n_time < timeHold[v]){\n timeHold[v] = n_time + time;\n pq.add(new int[]{v, cost + costVtx[v], timeHold[v]});\n }\n }\n }\n return -1;\n }\n}\n\nMemoization : 234 ms\n\nclass Solution {\n ArrayList<int[]>[] graph;\n int[][] dp;\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = 1000;\n dp = new int[1001][maxTime + 1];\n for(int[] d : dp) Arrays.fill(d, -1);\n graph = new ArrayList[n];\n for(int i = 0; i < n ; i++){\n graph[i] = new ArrayList<>();\n }\n for(int[] e : edges){\n int u = e[0], v = e[1], w = e[2];\n graph[u].add(new int[]{v,w});\n graph[v].add(new int[]{u,w});\n }\n int ans = costMaker(maxTime, passingFees, 0);\n return ans >= (int) 1e8 ? -1 : ans;\n }\n \n public int costMaker(int time, int[] fees, int src){\n if(time < 0) return (int) 1e8;\n if(src == fees.length - 1) return dp[src][time] = fees[src];\n if(dp[src][time] != -1) return dp[src][time];\n int cost = (int) 1e8;\n for(int[] e : graph[src]){\n int v = e[0], w = e[1];\n cost = Math.min(cost, costMaker(time - w, fees, v));\n }\n return dp[src][time] = cost + fees[src];\n }\n}\n\n\n```\n
| 2 | 0 |
['Dynamic Programming', 'Depth-First Search', 'Memoization', 'Java']
| 2 |
minimum-cost-to-reach-destination-in-time
|
C++ Solution | Modified Dijkstra
|
c-solution-modified-dijkstra-by-oliver_b-ss39
|
\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n \n int n=passingFees.size();\n
|
oliver_bowman
|
NORMAL
|
2021-08-01T11:02:50.442775+00:00
|
2021-08-01T11:02:50.442807+00:00
| 342 | false |
```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n \n int n=passingFees.size();\n vector<vector<pair<int,int>>>mat(n);\n vector<int>cost(n,INT_MAX);\n vector<int>time(n,INT_MAX);\n for(auto x:edges)\n {\n mat[x[0]].push_back({x[1],x[2]});\n mat[x[1]].push_back({x[0],x[2]});\n }\n \n priority_queue<vector<int>,vector<vector<int>>, greater<vector<int>>>pq;\n cost[0]=passingFees[0];\n time[0]=0;\n pq.push({cost[0],time[0],0});\n \n while(!pq.empty())\n {\n auto t =pq.top();\n pq.pop();\n {\n for(auto x:mat[t[2]])\n {\n int t_x =x.second;\n int y=x.first;\n if((cost[y]>t[0]+passingFees[y]) ||(time[y]>t[1]+t_x))\n {\n if(t[1]+t_x<=maxTime)\n {\n if(cost[y]>t[0]+passingFees[y])\n {\n cost[y]=t[0]+passingFees[y];\n time[y]=t[1]+t_x;\n pq.push({cost[y],time[y],y}); \n }\n else if(time[y]>t[1]+t_x)\n {\n time[y]=t[1]+t_x;\n pq.push({t[0]+passingFees[y],time[y],y}); \n }\n \n }\n }\n }\n }\n }\n if(time[n-1]>maxTime||cost[n-1]==INT_MAX)\n return -1;\n else\n return cost[n-1];\n \n }\n};\n```
| 2 | 0 |
['C']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Optimised Dijkstra Algo C++
|
optimised-dijkstra-algo-c-by-kunalsuri-cp29
|
\nclass Solution {\npublic:\n // dry run kia for whole day.... maja aa gya\n vector<vector<int>> graph[1001];\n int time[1001], cost[1001];\n int di
|
kunalsuri
|
NORMAL
|
2021-07-31T18:12:43.835041+00:00
|
2021-07-31T18:12:43.835085+00:00
| 280 | false |
```\nclass Solution {\npublic:\n // dry run kia for whole day.... maja aa gya\n vector<vector<int>> graph[1001];\n int time[1001], cost[1001];\n int dijikstra(int src, int dest, int maxTime) {\n for (int i = 1; i <= dest; ++i) {\n time[i] = INT_MAX;\n cost[i] = INT_MAX;\n }\n priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;\n pq.push({cost[src], time[src], src});\n while (!pq.empty()) {\n vector<int> temp = pq.top(); pq.pop();\n int c = temp[0];\n int t = temp[1];\n int u = temp[2];\n \n for (int i = 0; i < graph[u].size(); ++i) {\n if (t + graph[u][i][1] <= maxTime) {\n if (c + graph[u][i][2] < cost[graph[u][i][0]]) {\n cost[graph[u][i][0]] = c + graph[u][i][2];\n time[graph[u][i][0]] = t + graph[u][i][1];\n pq.push({cost[graph[u][i][0]], time[graph[u][i][0]], graph[u][i][0]});\n } else if (graph[u][i][1] + t < time[graph[u][i][0]]) {\n time[graph[u][i][0]] = graph[u][i][1] + t;\n pq.push({c + graph[u][i][2], time[graph[u][i][0]], graph[u][i][0]});\n }\n }\n }\n }\n return cost[dest];\n }\n int minCost(int maxTime, vector<vector<int>>& arr, vector<int>& fee) {\n int n = arr.size();\n // graph.assign(n, vector<int>());\n // time.assign(n, INT_MAX);\n // cost.assign(n, INT_MAX);\n \n for (int i = 0; i < n; ++i) {\n int u = arr[i][0];\n int v = arr[i][1];\n int t = arr[i][2];\n \n graph[u].push_back({v, t, fee[v]});\n graph[v].push_back({u, t, fee[u]});\n }\n \n cost[0] = fee[0];\n time[0] = 0;\n \n int ans = dijikstra(0, fee.size() - 1, maxTime);\n if (ans == INT_MAX) return -1;\n return ans;\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Java Solution | Dijkstra | Best First Search
|
java-solution-dijkstra-best-first-search-v2jv
|
The base idea is to extend Dijkstra algorithm, or better to be called "Best first search" for easy understanding. Despite being wikipedia, I really recommend a
|
fate3439
|
NORMAL
|
2021-07-14T22:12:32.324824+00:00
|
2021-07-14T22:12:32.324855+00:00
| 242 | false |
The base idea is to extend Dijkstra algorithm, or better to be called "Best first search" for easy understanding. Despite being wikipedia, I really recommend a deep read of it https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm. We maintain a Priority Queue, and the Queue tracks best candidates that could lead to desired outcome: minimum cost to the destination.\n\nBut, how do you model the constraint of time? You can just play blind for now, ignore it being a constraint, check every item in the queue as you would in regular single source best path problem, AND, whenever you find a solution, that is we reached the destination using best candidates from Priority Queue, you check the arrival time! If it exceeds the limit, we just dig into our queue again, until we found one, return the cost, or we give up, return -1.\n\nNow, several traps / important insights of this problem:\n\n- You must also insert a <location, time, cost> tuple into the queue even when the cost is sub-optimal. Why? Bcoz the optimal guy *could* result in time out! Therefore, you must also *compromise* by adding sub optimal tuples. But again, if we behave desperate by adding anything, you will get TLE... So, we only add tuples when there are *potential for improvements*, that is\n\t- reduce in cost OR\n\t- reduce in time cost.\n- Another early stopping opportunity: before you insert tuples into the queue, if its present time cost already > maxTime, we avoid insertion.\n\nNow we have walked through the general ideas + the problem specific tricks, here is the java code. Note that the comparator is kind of niche, you can just compare only on cost, and still acquire the similar performance, hinting the case of same cost different time has low impact on the overall computation.\n\n```\nclass Record {\n int loc;\n int cost;\n int time;\n \n public Record(int loc, int cost, int time) {\n this.loc = loc;\n this.cost = cost;\n this.time = time;\n }\n \n public int compareTo(Record other) {\n // First compare cost, if same, track time.\n if (this.cost > other.cost) {\n return 1;\n } else if (this.cost < other.cost) {\n return -1;\n } else if (this.time > other.time) {\n return 1;\n } else if (this.time < other.time) {\n return -1;\n } else {\n return 0;\n }\n }\n}\n\nclass RecordCompare implements Comparator<Record> {\n @Override\n public int compare (Record a, Record b) {\n return a.compareTo(b);\n }\n}\n\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n // Build adj matrix of time cost.\n int[][] time_adj = new int[passingFees.length][passingFees.length];\n for (int i = 0; i < time_adj.length; i++) {\n for (int j = 0; j < time_adj[0].length; j++) {\n time_adj[i][j] = -1;\n }\n }\n \n for (int[] rd : edges) {\n if (time_adj[rd[0]][rd[1]] == -1 ||\n time_adj[rd[0]][rd[1]] > rd[2]) {\n time_adj[rd[0]][rd[1]] = rd[2];\n time_adj[rd[1]][rd[0]] = rd[2];\n }\n }\n \n // Best first search as if Dijkstra algorithm.\n // PQ which tracks the cost. \n // PriorityQueue<Record> bestQueue = new PriorityQueue<Record>(10, \n // ((o1, o2) -> o1.cost - o2.cost));\n PriorityQueue<Record> bestQueue = new PriorityQueue<Record>(10, new RecordCompare());\n \n bestQueue.offer(new Record(0, passingFees[0], 0));\n // Helper arrays for early stopping. We don\'t need to explore worse \n // candidates vs. those in the bestQueue.\n int[] bestTime = new int[passingFees.length];\n int[] bestCost = new int[passingFees.length];\n bestTime[0] = 0;\n bestCost[0] = passingFees[0];\n for (int i = 1; i < passingFees.length; i++) {\n bestTime[i] = maxTime + 1;\n bestCost[i] = Integer.MAX_VALUE;\n }\n \n while (bestQueue.size() >0) {\n Record curNode = bestQueue.poll();\n \n // Check result.\n if (curNode.loc == passingFees.length - 1 &&\n curNode.time <= maxTime) {\n return curNode.cost;\n }\n \n for (int i = 0; i < passingFees.length; i++) {\n if (i == curNode.loc) {\n continue;\n }\n \n if (time_adj[curNode.loc][i] != -1 &&\n (bestTime[i] > (curNode.time + time_adj[curNode.loc][i]) ||\n bestCost[i] > (curNode.cost + passingFees[i]))\n ) {\n \n // No hope, early stop.\n if (curNode.time + time_adj[curNode.loc][i] > maxTime) {\n continue;\n }\n \n bestTime[i] = (curNode.time + time_adj[curNode.loc][i]);\n bestCost[i] = (curNode.cost + passingFees[i]);\n \n bestQueue.offer(new Record(i, bestCost[i], bestTime[i]));\n }\n }\n \n }\n \n return -1;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
Easiest C++ DP Solution : )
|
easiest-c-dp-solution-by-asmitpapney-5udo
|
\nclass Solution {\npublic:\n \n int t[1001][1001];\n \n int Solve(vector<pair<int,int> > A[] , vector<int>&money , int node , int time , int Target
|
asmitpapney
|
NORMAL
|
2021-07-10T16:27:44.972908+00:00
|
2021-07-10T16:29:18.482002+00:00
| 271 | false |
```\nclass Solution {\npublic:\n \n int t[1001][1001];\n \n int Solve(vector<pair<int,int> > A[] , vector<int>&money , int node , int time , int Target , int maxTime)\n {\n\n if(time>maxTime)\n return 100000000;\n \n if(node==Target)\n {\n return money[Target] ;\n }\n \n if(t[node][time]!=-1) return t[node][time] ; \n \n int Ans = 100000000 ;\n for(auto child:A[node])\n {\n \n if( time+child.second<=maxTime)\n { \n int temp = money[node]+Solve(A,money,child.first,time+child.second,Target,maxTime) ;\n \n Ans = min(Ans,temp) ;\n }\n }\n \n \n \n return t[node][time] =Ans; \n }\n \n \n \n \n \n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& A) {\n int N = edges.size() ;\n vector<pair<int,int>> V[N+1] ;\n int n = -1;\n for(auto x:edges){\n V[x[0]].push_back({x[1],x[2]}) ;\n V[x[1]].push_back({x[0],x[2]}) ;\n n = max({n,x[0],x[1]});\n }\n \n memset(t,-1,sizeof(t)) ;\n \n int Ans = Solve(V,A,0,0,n,maxTime) ;\n \n return (Ans<100000000)?Ans:-1 ;\n}\n};\n```
| 2 | 0 |
['Dynamic Programming']
| 1 |
minimum-cost-to-reach-destination-in-time
|
[C++] explained
|
c-explained-by-dbolohan-g2el
|
First convert the edges vector to adjacency list.\nWe use a priority queue to store the cities we can visit and to extract the one with the lowest cost.\nAs we
|
dbolohan
|
NORMAL
|
2021-07-10T16:01:12.538345+00:00
|
2021-07-10T16:02:06.378013+00:00
| 334 | false |
First convert the edges vector to adjacency list.\nWe use a priority queue to store the cities we can visit and to extract the one with the lowest cost.\nAs we extract a city from the priority queue, we check if it\'s the destination. If it\'s not, we add to the priority queue the adjacent cities.\nTo avoid making back and forward moves between two cities, we use a "seen" vector which stores the best time we have seen for that city.\nWhen we extract a city from the priority queue and we have seen it before with a better time, then we know the cost was also better (as it was extracted earlier), so we should not process it again.\n```\nclass Solution {\nprivate:\n class City{\n public:\n int i;\n int cost;\n int time;\n City(int i, int cost, int time):i(i), cost(cost), time(time){}\n };\n struct cityComparator{\n bool operator()(City const& c1, City const& c2){\n return c1.cost > c2.cost;\n }\n };\npublic: \n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int n = passingFees.size();\n priority_queue<City, vector<City>, cityComparator> cq;\n cq.push(City(0, passingFees[0], 0));\n vector<vector<pair<int, int>>> adj(n);\n for (vector<int> &edge: edges){\n adj[edge[0]].push_back(make_pair(edge[1], edge[2]));\n adj[edge[1]].push_back(make_pair(edge[0], edge[2]));\n }\n vector<int> seen(n, maxTime + 1);\n while (!cq.empty()){\n City c = cq.top();\n cq.pop();\n if (seen[c.i] <= c.time)\n continue;\n seen[c.i] = c.time;\n if (c.i == n - 1 && c.time <= maxTime)\n return c.cost;\n for (int i = 0; i < adj[c.i].size(); i++){\n int ni = adj[c.i][i].first;\n int nt = adj[c.i][i].second;\n if (c.time + nt < seen[ni]){\n cq.push(City(ni, c.cost + passingFees[ni], c.time + nt));\n }\n }\n }\n return -1;\n }\n};\n```\nm = max(n, edges.length)\nComplexity in worst case is O(m * maxTime * log(m * maxTime)). Because every city could be the top of the priority queue at most maxTime times. Processing all the neighbours for all the n cities would be edges.length.\nHowever, in the average case it\'s much better.
| 2 | 2 |
['C', 'Heap (Priority Queue)']
| 1 |
minimum-cost-to-reach-destination-in-time
|
Dijkstra's Algorithm || Java || Easy Solution
|
dijkstras-algorithm-java-easy-solution-b-tlmd
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
vermaanshul975
|
NORMAL
|
2025-04-01T04:06:56.429464+00:00
|
2025-04-01T04:06:56.429464+00:00
| 69 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minCost(int maxTime, int[][] edges, int[] passingFees) {
int n = passingFees.length;
List<int[]>[] adj = new ArrayList[n];
for (int i = 0; i < n; i++) adj[i] = new ArrayList<>();
for (int[] edge : edges) {
int u = edge[0], v = edge[1], time = edge[2];
adj[u].add(new int[]{v, time});
adj[v].add(new int[]{u, time});
}
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
pq.offer(new int[]{passingFees[0], 0, 0});
int[] minTime = new int[n];
Arrays.fill(minTime, Integer.MAX_VALUE);
minTime[0] = 0;
while (!pq.isEmpty()) {
int[] curr = pq.poll();
int cost = curr[0], time = curr[1], city = curr[2];
if (city == n - 1) return cost;
for (int[] neighbor : adj[city]) {
int nextCity = neighbor[0], travelTime = neighbor[1];
int newTime = time + travelTime, newCost = cost + passingFees[nextCity];
if (newTime <= maxTime && newTime < minTime[nextCity]) {
minTime[nextCity] = newTime;
pq.offer(new int[]{newCost, newTime, nextCity});
}
}
}
return -1;
}
}
```
| 1 | 0 |
['Java']
| 0 |
minimum-cost-to-reach-destination-in-time
|
c++ solution | easiest dp solution
|
c-solution-easiest-dp-solution-by-dshiva-4d5z
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
dshivank630
|
NORMAL
|
2025-02-18T07:23:00.528804+00:00
|
2025-02-18T07:23:00.528804+00:00
| 126 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
// lc
#define vi vector<int>
#define vvii vector<vi>
#define vpii vector<pair<int,int>>
#define pii pair<int,int>
#define ll long long int
#define vs vector<string>
#define mii map<int, int>
#define umii unordered_map<int, int>
#define lb lower_bound
#define ub upper_bound
#define all(x) x.begin(), x.end()
#define sall(x) sort(x.begin(), x.end());
#define rall(x) sort(x.rbegin(), x.rend())
#define pb push_back
#define in insert
#define ff first
#define ss second
#define rep(i, a, b) for (int i = a; i < b; i++)
#define all(x) x.begin(), x.end()
#define sall(x) sort(x.begin(), x.end());
#define rall(x) sort(x.rbegin(), x.rend())
#define MAX(x) *max_element(x.begin(), x.end())
#define MIN(x) *min_element(x.begin(), x.end())
#define SUM(X) accumulate(X.begin(), X.end(), 0LL)
#define rev(a) reverse(a.begin(), a.end());
const int mod = 1e9 + 7;
class Solution {
public:
int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
int n = passingFees.size();
vi cost(n,INT_MAX), time(n,INT_MAX);
vector<vpii> adj(n);
for(auto it: edges) {
adj[it[0]].pb({it[1], it[2]});
adj[it[1]].pb({it[0], it[2]});
}
// dp is much easier here
vvii dp(n+1,vi(maxTime+1,-1));
auto rec = [&](int node, int time, auto &&self)->int{
if(node == n-1) return passingFees[node];
if(dp[node][time] != -1) return dp[node][time];
int ans = 1e9;
for(auto it: adj[node]){
int v = it.ff;
int t = it.ss;
if(time + t <= maxTime) {
ans = min(ans, passingFees[node] + self(v, t+time, self));
}
}
return dp[node][time] = ans;
};
int ans = rec(0,0,rec);
return (ans >= 1e9) ? -1 : ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
minimum-cost-to-reach-destination-in-time
|
c++ dijkstra solution
|
easiest-c-solution-recursive-memoization-lfgt
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
dshivank630
|
NORMAL
|
2025-02-18T07:21:47.151294+00:00
|
2025-02-18T07:22:34.729634+00:00
| 118 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
// lc
#define vi vector<int>
#define vvii vector<vi>
#define vpii vector<pair<int,int>>
#define pii pair<int,int>
#define ll long long int
#define vs vector<string>
#define mii map<int, int>
#define umii unordered_map<int, int>
#define lb lower_bound
#define ub upper_bound
#define all(x) x.begin(), x.end()
#define sall(x) sort(x.begin(), x.end());
#define rall(x) sort(x.rbegin(), x.rend())
#define pb push_back
#define in insert
#define ff first
#define ss second
#define rep(i, a, b) for (int i = a; i < b; i++)
#define all(x) x.begin(), x.end()
#define sall(x) sort(x.begin(), x.end());
#define rall(x) sort(x.rbegin(), x.rend())
#define MAX(x) *max_element(x.begin(), x.end())
#define MIN(x) *min_element(x.begin(), x.end())
#define SUM(X) accumulate(X.begin(), X.end(), 0LL)
#define rev(a) reverse(a.begin(), a.end());
const int mod = 1e9 + 7;
class Solution {
public:
int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
int n = passingFees.size();
vi cost(n,INT_MAX), time(n,INT_MAX);
vector<vpii> adj(n);
for(auto it: edges) {
adj[it[0]].pb({it[1], it[2]});
adj[it[1]].pb({it[0], it[2]});
}
// map<pair<int,pii>,int> dp;
// auto rec = [&](int node, int par, int time, auto &&self)->int{
// if(node == n-1) return passingFees[node];
// if(dp.count({node, {par, time}})) return dp[{node, {par, time}}];
// int ans = INT_MAX;
// for(auto it: adj[node]){
// int v = it.ff;
// int t = it.ss;
// if((v != par) and (time + t <= maxTime)) {
// ans = min(ans, passingFees[node] + self(v, node, t+time, self));
// }
// }
// return dp[{node, {par, time}}] = ans;
// };
// int ans = rec(0,-1,0,rec);
// return (ans >= INT_MAX) ? -1 : ans;
priority_queue<pair<int,pii>, vector<pair<int,pii>>, greater<>> pq;
pq.push({0,{0,0}});
cost[0] = 0;
time[0] = 0;
while(pq.size()) {
int c = pq.top().ff;
int t = pq.top().ss.ff;
int node = pq.top().ss.ss;
pq.pop();
for(auto it: adj[node]) {
int v = it.ff;
int tt = it.ss;
if(t + tt <= maxTime) {
if((cost[v] >= c + passingFees[v])) {
cost[v] = c + passingFees[v];
time[v] = t + tt;
pq.push({cost[v], {time[v], v}});
} else if((t + tt < time[v])) {
time[v] = t + tt;
pq.push({c + passingFees[v], {time[v], v}});
}
}
}
}
// rep(i,0,n) cout<<cost[i]<<" ";
// cout<<endl;
int c = cost[n-1];
if(c>=INT_MAX) return -1;
cout<<c<<" "<<passingFees[0]<<endl;
return (c + passingFees[0]);
}
};
```
| 1 | 0 |
['C++']
| 0 |
minimum-cost-to-reach-destination-in-time
|
✅Dijkstra Algo | JAVA | Easy to understand
|
dijkstra-algo-java-easy-to-understand-by-fq0t
|
Code
|
Orangjustice777
|
NORMAL
|
2025-01-09T17:25:29.690136+00:00
|
2025-01-09T17:25:29.690136+00:00
| 20 | false |
# Code
```java []
class Solution {
public int minCost(int maxTime, int[][] edges, int[] fee) {
List<List<int[]>> adjList = new ArrayList<>();
for (int i = 0; i < fee.length; i++) {
adjList.add(new ArrayList<>());
}
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
int t = edge[2];
adjList.get(u).add(new int[]{v, t});
adjList.get(v).add(new int[]{u, t});
}
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> {
if (a[1] == b[1]) {
return a[2] - b[2];
}
return a[1] - b[1];
});
pq.add(new int[]{0, fee[0], 0});
int n = fee.length;
int[] dist = new int[n];
int[] times = new int[n];
Arrays.fill(dist, Integer.MAX_VALUE);
Arrays.fill(times, Integer.MAX_VALUE);
dist[0] = 0;
times[0] = 0;
while (!pq.isEmpty()) {
int[] curr = pq.poll();
int node = curr[0];
int cost = curr[1];
int time = curr[2];
if (time > maxTime) {
continue;
}
if (node == n - 1) return cost;
for (int[] neighbor : adjList.get(node)) {
int neiNode = neighbor[0];
int neiCost = fee[neiNode];
if (cost + neiCost < dist[neiNode]) {
dist[neiNode] = cost + neiCost;
pq.add(new int[]{neiNode, cost + neiCost, time + neighbor[1]});
times[neiNode] = time + neighbor[1];
} else if (time + neighbor[1] < times[neiNode]) {
pq.add(new int[]{neiNode, cost + neiCost, time + neighbor[1]});
times[neiNode] = time + neighbor[1];
}
}
}
return dist[n - 1] == Integer.MAX_VALUE || times[n - 1] > maxTime ? -1 : dist[n - 1];
}
}
```
| 1 | 1 |
['Java']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Java Solution | Using DP
|
java-solution-using-dp-by-dhyan098-aynt
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
dhyan098
|
NORMAL
|
2024-05-09T18:05:43.496552+00:00
|
2024-05-09T18:05:43.496578+00:00
| 32 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(maxTime * edges.length)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(maxTime * passingFees.length)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int dp[][] = new int[maxTime+1][passingFees.length];\n\n for (int i=0; i<=maxTime; i++) {\n for(int j=0; j<passingFees.length; j++) {\n dp[i][j] = Integer.MAX_VALUE;\n }\n }\n\n dp[0][0] = passingFees[0];\n \n int reachTime = 0;\n int city1, city2;\n\n for (int i=0; i<=maxTime; i++) {\n for (int j=0; j<edges.length; j++) {\n reachTime = i+edges[j][2];\n city1 = edges[j][0];\n city2 = edges[j][1];\n\n if (reachTime <= maxTime) {\n if (dp[i][city1] != Integer.MAX_VALUE) dp[reachTime][city2] = Math.min(dp[reachTime][city2], dp[i][city1] + passingFees[city2]);\n if (dp[i][city2] != Integer.MAX_VALUE) dp[reachTime][city1] = Math.min(dp[reachTime][city1], dp[i][city2] + passingFees[city1]);\n }\n }\n }\n\n int res = Integer.MAX_VALUE;\n for (int i=0; i<=maxTime; i++) res = Math.min(res, dp[i][passingFees.length-1]);\n\n return (res != Integer.MAX_VALUE) ? res : -1;\n }\n}\n```
| 1 | 0 |
['Dynamic Programming', 'Graph', 'Java']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Optimized and cleaned Swift conversion of the most popular C++ solution
|
optimized-and-cleaned-swift-conversion-o-dxyj
|
Intuition\n\nI had trouble figuring out how to store the most optimal route while at the same time ensuring we\'re not timing out. Normal Dijkstra applications
|
lucasvandongen
|
NORMAL
|
2024-04-13T22:07:39.136115+00:00
|
2024-04-13T22:07:39.136135+00:00
| 3 | false |
# Intuition\n\nI had trouble figuring out how to store the most optimal route while at the same time ensuring we\'re not timing out. Normal Dijkstra applications have only one score.\n\n# Approach\n\nSince I tanked this one myself I tried to find a Swift solution first, which didn\'t exist, then in different langauges. There were actually a few that didn\'t make it to the end either, so I guess I was not the only one struggling.\n\nI used the following (currently most popular) answer written in C++ and converted it automatically to Swift:\nhttps://leetcode.com/problems/minimum-cost-to-reach-destination-in-time/solutions/1328953/c-solution-dijkstra-s-algorithm/\n\nThis passed the test, and judging by the numbers, also as the first Swift user.\n\nHowever the solution was not super readable and it also seemed to take some unnecessary steps. I cleaned it up and it performed about 10% faster than the original conversion I had before\n\n# Complexity\n\nTime complexity:\nO(V*Vlog V) according to the author\n\n# Code\n```\nstruct PathInfo {\n let cost: Int\n let time: Int\n let city: Int\n}\n\nstruct Edge {\n let destination: Int\n let travelTime: Int\n let fee: Int\n}\n\nclass Solution {\n var adjacencyList = [[Edge]](repeating: [], count: 1001)\n var cost = [Int](repeating: Int.max, count: 1001)\n var time = [Int](repeating: Int.max, count: 1001)\n\n func dijkstra(source: Int, destination: Int, maxTime: Int) -> Int {\n var priorityQueue = [PathInfo]()\n priorityQueue.append(PathInfo(cost: cost[source], time: 0, city: source))\n\n while !priorityQueue.isEmpty {\n let currentPath = priorityQueue.removeFirst()\n\n for edge in adjacencyList[currentPath.city] {\n let newTime = currentPath.time + edge.travelTime\n\n if newTime <= maxTime {\n let totalCost = currentPath.cost + edge.fee\n\n if cost[edge.destination] > totalCost {\n cost[edge.destination] = totalCost\n } else if time[edge.destination] <= newTime {\n continue\n }\n\n time[edge.destination] = newTime\n\n priorityQueue.append(PathInfo(cost: totalCost, time: newTime, city: edge.destination))\n }\n }\n \n priorityQueue.sort { $0.cost < $1.cost }\n }\n\n return cost[destination]\n }\n\n func minCost(_ maxTime: Int, _ edges: [[Int]], _ passingFees: [Int]) -> Int {\n for edge in edges {\n let city1 = edge[0]\n let city2 = edge[1]\n let travelTime = edge[2]\n\n adjacencyList[city1].append(Edge(destination: city2, travelTime: travelTime, fee: passingFees[city2]))\n adjacencyList[city2].append(Edge(destination: city1, travelTime: travelTime, fee: passingFees[city1]))\n }\n\n cost[0] = passingFees[0]\n time[0] = 0\n\n let answer = dijkstra(source: 0, destination: passingFees.count - 1, maxTime: maxTime)\n return answer == Int.max ? -1 : answer\n }\n}\n```
| 1 | 0 |
['Swift']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Simple Dijkstra's algorithm | C++ | Java | Python
|
simple-dijkstras-algorithm-c-java-python-cer5
|
Intuition\nSince source-single destination. Bellman-ford and Dijkstra come to mind? \n\n# Approach\nDijksta\'s algorithm. You can hear more in the linked video:
|
justcoding777
|
NORMAL
|
2023-09-07T23:30:11.471624+00:00
|
2023-09-07T23:31:04.560522+00:00
| 368 | false |
# Intuition\nSince source-single destination. Bellman-ford and Dijkstra come to mind? \n\n# Approach\nDijksta\'s algorithm. You can hear more in the linked video: \n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(N log N)\n\n# Code\n```java []\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = passingFees.length;\n List<Edge>[] adj = new ArrayList[n];\n for (int k = 0; k < n; k++) {\n adj[k] = new ArrayList();\n }\n for (int k = 0; k < edges.length; k++) {\n int[] edge = edges[k];\n int u = edge[0];\n int v = edge[1];\n int t = edge[2];\n adj[u].add(new Edge(v, t, passingFees[v]));\n adj[v].add(new Edge(u, t, passingFees[u]));\n }\n\n int[] minTime = new int[n];\n Arrays.fill(minTime, Integer.MAX_VALUE);\n\n PriorityQueue<Edge> pq = new PriorityQueue<>((a, b)-> (a.cost == b.cost)? a.time - b.time : a.cost - b.cost);// Consider only cost for ordering\n pq.add(new Edge(0, 0, passingFees[0]));\n\n while (!pq.isEmpty()) {\n Edge current = pq.poll();\n int currentNode = current.node;\n int currentTime = current.time;\n int currentCost = current.cost;\n\n if (currentTime > maxTime || currentTime >= minTime[currentNode]){\n continue;\n }\n \n if (currentNode == n - 1) {\n return currentCost; // We have reached the destination\n }\n\n minTime[currentNode] = currentTime; // Update the minTime for this node\n\n for (Edge neighborEdge : adj[currentNode]) {\n int neighbor = neighborEdge.node;\n int newTime = neighborEdge.time + currentTime;\n int newCost = neighborEdge.cost + currentCost;\n\n if (newTime <= maxTime) {\n pq.add(new Edge(neighbor, newTime, newCost));\n }\n }\n }\n\n return -1; // If we can\'t reach the destination within maxTime\n }\n\n public class Edge {\n int node;\n int time;\n int cost;\n\n public Edge(int node, int time, int cost) {\n this.node = node;\n this.time = time;\n this.cost = cost;\n }\n }\n}\n```\n```python []\nfrom heapq import heappush, heappop\n\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n n = len(passingFees)\n adj = [[] for _ in range(n)]\n for edge in edges:\n u, v, t = edge\n adj[u].append((v, t, passingFees[v]))\n adj[v].append((u, t, passingFees[u]))\n\n minTime = [float(\'inf\') for _ in range(n)]\n pq = []\n heappush(pq, (passingFees[0], 0, 0)) # cost, time, node\n\n while pq:\n cost, time, node = heappop(pq)\n\n if time > maxTime or time >= minTime[node]:\n continue\n\n if node == n - 1:\n return cost\n\n minTime[node] = time\n\n for v, t, c in adj[node]:\n if time + t <= maxTime:\n heappush(pq, (cost + c, time + t, v))\n\n return -1\n```\n```c++ []\n#include <vector>\n#include <queue>\n\nusing namespace std;\n\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int n = passingFees.size();\n vector<vector<pair<int, pair<int, int>>>> adj(n); // {node, {time, cost}}\n \n for(auto& edge : edges) {\n int u = edge[0], v = edge[1], t = edge[2];\n adj[u].push_back({v, {t, passingFees[v]}});\n adj[v].push_back({u, {t, passingFees[u]}});\n }\n\n vector<int> minTime(n, INT_MAX);\n priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> pq; // {cost, {time, node}}\n pq.push({passingFees[0], {0, 0}});\n \n while(!pq.empty()) {\n int cost = pq.top().first, time = pq.top().second.first, node = pq.top().second.second;\n pq.pop();\n\n if(time > maxTime || time >= minTime[node]) continue;\n\n if(node == n - 1) return cost;\n\n minTime[node] = time;\n\n for(auto& next : adj[node]) {\n int v = next.first, t = next.second.first, c = next.second.second;\n if(time + t <= maxTime) {\n pq.push({cost + c, {time + t, v}});\n }\n }\n }\n\n return -1;\n }\n};\n\n```
| 1 | 0 |
['Breadth-First Search', 'Heap (Priority Queue)', 'Python', 'C++', 'Java']
| 0 |
minimum-cost-to-reach-destination-in-time
|
c++ | easy | short
|
c-easy-short-by-venomhighs7-aa4u
|
\n\n# Code\n\nclass Solution {\npublic:\n int dp[1001][1001];\n int solve(int time,vector<pair<int,int>> adj[],int v,vector<int> &pass){\n if(time<
|
venomhighs7
|
NORMAL
|
2022-11-09T04:01:13.010568+00:00
|
2022-11-09T04:01:13.010634+00:00
| 1,807 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n int dp[1001][1001];\n int solve(int time,vector<pair<int,int>> adj[],int v,vector<int> &pass){\n if(time<0) return INT_MAX;\n int n = pass.size();\n if(v==n-1){\n return pass[v];\n }\n if(dp[v][time]!=-1) return dp[v][time];\n int cost = INT_MAX;\n for(auto &x:adj[v]){\n int u = x.first;\n int temp = x.second;\n if(temp<=time){\n int sol = solve(time-temp,adj,u,pass);\n cost = min(cost,sol);\n }\n }\n if(cost==INT_MAX) return dp[v][time] = INT_MAX;\n return dp[v][time] = cost + pass[v]; \n }\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& pass) {\n memset(dp,-1,sizeof(dp));\n int n = pass.size();\n vector<pair<int,int>> adj[n];\n for(int i = 0;i<edges.size();i++){\n adj[edges[i][0]].push_back(make_pair(edges[i][1],edges[i][2]));\n adj[edges[i][1]].push_back(make_pair(edges[i][0],edges[i][2]));\n \n }\n int ans = solve(maxTime,adj,0,pass);\n if(ans==INT_MAX) return -1;\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Easy C++ Solution | Memoization
|
easy-c-solution-memoization-by-rac101ran-oi6g
|
\nclass Solution {\npublic:\n long dp[1001][1001];\n vector<pair<int,int>> ed[1001];\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>
|
rac101ran
|
NORMAL
|
2022-10-16T11:58:23.081688+00:00
|
2022-10-16T11:58:23.081713+00:00
| 36 | false |
```\nclass Solution {\npublic:\n long dp[1001][1001];\n vector<pair<int,int>> ed[1001];\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n memset(dp,-1,sizeof(dp));\n int n = passingFees.size();\n for(int i=0; i<edges.size(); i++) {\n ed[edges[i][0]].push_back({edges[i][1],edges[i][2]});\n ed[edges[i][1]].push_back({edges[i][0],edges[i][2]});\n }\n long ans = solve(0,maxTime,passingFees);\n return ans == INT_MAX ? -1 : ans;\n }\n long solve(int src,int time,vector<int> &fees) {\n if(src == fees.size() - 1) return fees[src];\n if(dp[src][time]!=-1) return dp[src][time];\n long cnt = INT_MAX;\n for(auto e : ed[src]) {\n if(time-e.second>=0) {\n cnt = min(cnt,fees[src]+solve(e.first,time-e.second,fees));\n }\n }\n return dp[src][time] = cnt;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C']
| 0 |
minimum-cost-to-reach-destination-in-time
|
3 state Djikstra | C++ | 71%
|
3-state-djikstra-c-71-by-cherryorc987-24ch
|
\n//less cost are covered first hence only time contraint.\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& pas
|
cherryorc987
|
NORMAL
|
2022-07-18T23:57:32.304746+00:00
|
2022-07-18T23:57:32.304786+00:00
| 145 | false |
```\n//less cost are covered first hence only time contraint.\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n int n=passingFees.size();\n vector<vector<pair<int,int>>> adj(n);\n for(auto it: edges){\n adj[it[0]].push_back({it[1],it[2]});\n adj[it[1]].push_back({it[0],it[2]});\n }\n set<vector<int>> s;\n vector<int> vis(n,1005);\n s.insert({passingFees[0],0,0});\n vis[0]=0;\n while(!s.empty()){\n vector<int> x=*s.begin();\n s.erase(s.begin());\n if(x[1]==n-1)\n return x[0];\n for(auto it: adj[x[1]]){\n if(x[2]+it.second<vis[it.first] && x[2]+it.second<=maxTime){\n vis[it.first]=x[2]+it.second;\n s.insert({x[0]+passingFees[it.first],it.first,x[2]+it.second});\n }\n }\n }\n return -1;\n }\n};\n```
| 1 | 0 |
['C']
| 0 |
minimum-cost-to-reach-destination-in-time
|
C++ | Easy Simple TopDown DP | Memomization
|
c-easy-simple-topdown-dp-memomization-by-heph
|
\nclass Solution {\npublic:\n \n int solve(vector<vector<pair<int,int>>>& a, vector<int>& p,vector<vector<int>>& dp,int n,int t,int q){\n if(t<0)\n
|
mysterious_lord
|
NORMAL
|
2022-06-12T12:57:52.820510+00:00
|
2022-06-12T12:57:52.820557+00:00
| 324 | false |
```\nclass Solution {\npublic:\n \n int solve(vector<vector<pair<int,int>>>& a, vector<int>& p,vector<vector<int>>& dp,int n,int t,int q){\n if(t<0)\n return INT_MAX;\n if(q==n-1)\n return p[q];\n if(dp[q][t]!=-1)\n return dp[q][t];\n \n int ans=INT_MAX;\n for(auto& x:a[q]){\n int res=solve(a,p,dp,n,t-x.second,x.first);\n ans=min(ans,(res==INT_MAX?res:res+p[q]));\n }\n return dp[q][t]=ans;\n }\n \n int minCost(int t, vector<vector<int>>& g, vector<int>& p) {\n int n=p.size();\n vector<vector<int>> dp(n,vector<int>(t+1,-1));\n vector<vector<pair<int,int>>> a(n);\n for(auto& x:g){\n a[x[0]].push_back({x[1],x[2]});\n a[x[1]].push_back({x[0],x[2]});\n }\n int ans=solve(a,p,dp,n,t,0);\n return ans==INT_MAX?-1:ans;\n }\n};\n```\n**Don\'t forget to upvote**
| 1 | 0 |
['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Javascript Solution using Djikstra's
|
javascript-solution-using-djikstras-by-m-rssy
|
There\'s two key points to solving this problem. \n\nFirstly you need a way to ensure you only add to the queue when it will either be a benefit to cost or time
|
mygosity
|
NORMAL
|
2022-06-12T10:05:47.898262+00:00
|
2022-10-27T21:16:55.434191+00:00
| 254 | false |
There\'s two key points to solving this problem. \n\nFirstly you need a way to ensure you only add to the queue when it will either be a benefit to cost or time. And the 2nd thing to note is that there could be more than one edge with a different time factor so you should only try to store the best time for each edge.\n\nWith that in mind the solution below is an application of Djikstra\'s algorithm to solve for best cost vs a limit on max time.\n\n```\nvar minCost = function (maxTime, edges, passingFees) {\n const n = passingFees.length;\n const graph = new Array(n);\n\n for (let i = 0; i < edges.length; ++i) {\n const [from, to, time] = edges[i];\n\n graph[from] = graph[from] || [];\n graph[from][to] = Math.min(graph[from][to] ?? Infinity, time);\n\n graph[to] = graph[to] || [];\n graph[to][from] = Math.min(graph[to][from] ?? Infinity, time);\n }\n\n const q = new MinPriorityQueue();\n q.enqueue([0, 0], passingFees[0]);\n\n const bestTimes = new Array(n).fill(Infinity);\n\n while (q.size()) {\n const { element, priority } = q.dequeue();\n const [currNode, currTime] = element;\n \n if (currNode === n - 1) {\n return priority;\n }\n\n for (const node in graph[currNode]) {\n const nextNode = parseInt(node);\n const nextTime = graph[currNode][node] + currTime;\n\n if (nextTime <= maxTime && nextTime < bestTimes[nextNode]) {\n bestTimes[nextNode] = nextTime;\n q.enqueue([nextNode, nextTime], passingFees[nextNode] + priority);\n }\n }\n }\n return -1;\n};\n```\n\nEdited thanks to @da5idf
| 1 | 0 |
['JavaScript']
| 1 |
minimum-cost-to-reach-destination-in-time
|
Java || Dijkstra || faster than 90.46% || less memo than 95.41%
|
java-dijkstra-faster-than-9046-less-memo-5veq
|
\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = passingFees.length;\n List<int[]>[] graph =
|
funingteng
|
NORMAL
|
2022-06-03T02:13:44.434612+00:00
|
2022-06-03T02:13:44.434651+00:00
| 385 | false |
```\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = passingFees.length;\n List<int[]>[] graph = buildGraph(n, edges);\n\t\t// priority queue makes sure we are polling lowest fee every time\n PriorityQueue<Node> q = new PriorityQueue<>((a, b) -> Integer.compare(a.fee, b.fee));\n\t\t// The visited records the minimum time to reach that node\n int[] visited = new int[n];\n Arrays.fill(visited, Integer.MAX_VALUE);\n q.offer(new Node(passingFees[0], 0, 0));\n while (!q.isEmpty()) {\n Node c = q.poll();\n if (c.city == n - 1) return c.fee; \n for (int[] neighbor: graph[c.city]) {\n if (c.time + neighbor[1] > maxTime) continue;\n int newTime = c.time + neighbor[1];\n\t\t\t\t// only if new time to reach the node becomes smaller we have better chance to reach destination\n if (newTime < visited[neighbor[0]]) {\n visited[neighbor[0]] = newTime;\n q.offer(new Node(passingFees[neighbor[0]] + c.fee, c.time + neighbor[1], neighbor[0]));\n } \n }\n }\n return -1;\n }\n private List<int[]>[] buildGraph(int n, int[][] edges) {\n List<int[]>[] graph = new List[n];\n Arrays.setAll(graph, r -> new ArrayList<>());\n for (int[] edge: edges) {\n int from = edge[0];\n int to = edge[1];\n int time = edge[2];\n graph[from].add(new int[] { to, time });\n graph[to].add(new int[] { from, time });\n }\n return graph;\n }\n private static class Node {\n int fee;\n int time;\n int city;\n public Node(int fee, int time, int city) {\n this.fee = fee;\n this.time = time;\n this.city = city;\n }\n }\n}\n```
| 1 | 0 |
['Java']
| 1 |
minimum-cost-to-reach-destination-in-time
|
[C++] Dijkstra's algorithm | Intuitive | Beats 99 %
|
c-dijkstras-algorithm-intuitive-beats-99-rdaa
|
\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& fee) {\n int n = fee.size();\n vector<vector<pa
|
dragoljub-duric
|
NORMAL
|
2022-05-12T12:43:06.256315+00:00
|
2022-05-12T12:43:06.256357+00:00
| 271 | false |
```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& fee) {\n int n = fee.size();\n vector<vector<pair<int, int>>> adj(n, vector<pair<int, int>>());\n \n for(vector<int>& e: edges){\n int u = e[0], v = e[1], t = e[2];\n adj[u].push_back({t, v});\n adj[v].push_back({t, u});\n }\n \n vector<int> times(n, maxTime + 1);\n auto cmp = [](auto& a, auto& b) {return a[0] > b[0];};\n priority_queue<array<int, 3>, vector<array<int, 3>>, decltype(cmp)> q(cmp);\n \n q.push({fee[0], 0, 0});\n \n while(q.size() > 0){\n auto [price, t, u] = q.top();\n q.pop();\n \n if(u == n - 1) return price;\n \n //if we already process \'u\' (than previously it had smaller price)\n //and if then it had time at most \'t\' time we can skip\n //otherwise \'t\' is the smallest time for \'u\' until now\n if(times[u] <= t) continue;\n else times[u] = t;\n \n for(auto& [t1, v]: adj[u]){\n //again same reasoning\n if(times[v] <= t + t1) continue;\n q.push({price + fee[v], t1 + t, v});\n }\n }\n return -1;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
[C++] Simple to understand DP solution.
|
c-simple-to-understand-dp-solution-by-_j-7ssf
|
\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n const int INF = 1e9 + 5;\n int
|
_julian5rk
|
NORMAL
|
2022-03-28T10:37:33.819214+00:00
|
2022-03-28T10:37:33.819258+00:00
| 178 | false |
```\nclass Solution {\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n const int INF = 1e9 + 5;\n int n = passingFees.size();\n vector<vector<pair<int, int>>> adj(n);\n for(auto e: edges) {\n int u = e[0];\n int v = e[1];\n int w = e[2];\n adj[u].push_back({v, w});\n adj[v].push_back({u, w});\n }\n vector<vector<int>> dp(maxTime+1, vector<int>(n, INF));\n //dp[i][j] = min cost to reach city j, int time i\n dp[0][0] = passingFees[0];\n for(int t=0; t<=maxTime; ++t) {\n for(int u=0; u<n; u++) {\n if(dp[t][u] >= INF)continue;\n for(auto [v, time]: adj[u]) {\n int t2 = t + time;\n if(t2 > maxTime)continue;\n dp[t2][v] = min(dp[t2][v], dp[t][u] + passingFees[v]);\n }\n }\n }\n int res = INF;\n for(int t=0; t<=maxTime; ++t) {\n res = min(res, dp[t][n-1]);\n }\n if(res >= INF)return -1;\n return res;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming']
| 0 |
minimum-cost-to-reach-destination-in-time
|
Easy DP✌🙏✌
|
easy-dp-by-rahul7777-1d68
|
\t#define pi pair\n\n\tclass Solution {\n\t\tint dp[1001][1001];\n\t\tint f(vector g[],int u,int currTime,int&maxTime,vector& passingFees){\n\t\t\tif(currTime >
|
rahul7777
|
NORMAL
|
2022-03-23T05:50:08.672003+00:00
|
2022-03-23T05:50:23.745803+00:00
| 138 | false |
\t#define pi pair<int,int>\n\n\tclass Solution {\n\t\tint dp[1001][1001];\n\t\tint f(vector<pi> g[],int u,int currTime,int&maxTime,vector<int>& passingFees){\n\t\t\tif(currTime > maxTime) return (1e8);\n\t\t\tif(u == passingFees.size()-1) return passingFees[u];\n\t\t\tif(dp[u][currTime]!=-1) return dp[u][currTime];\n\n\t\t\tint ans = (1e8);\n\t\t\tfor(auto [cost,v]:g[u]){\n\t\t\t\tans = min(ans,f(g,v,currTime + cost,maxTime,passingFees));\n\t\t\t}\n\t\t\treturn dp[u][currTime] = ans + passingFees[u];\n\t\t}\n\tpublic:\n\t\tint minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n\t\t\tint n = passingFees.size();\n\t\t\tvector<pi> g[n];\n\t\t\tfor(auto it:edges){\n\t\t\t\tg[it[0]].push_back({it[2],it[1]});\n\t\t\t\tg[it[1]].push_back({it[2],it[0]});\n\t\t\t}\n\t\t\tmemset(dp,-1,sizeof dp);\n\t\t\tint ans = f(g,0,0,maxTime,passingFees);\n\t\t\treturn (ans>=(1e8)?-1:ans);\n\t\t}\n\t};
| 1 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
Modified Dijkstra's with intuition
|
modified-dijkstras-with-intuition-by-gup-wzc0
|
Instead of visited array that we normally put we have to make visited for time as there may exists a solution with more cost but with desired time and we have v
|
Gupta-Vandana
|
NORMAL
|
2022-03-03T06:10:13.865333+00:00
|
2022-03-03T06:10:13.865376+00:00
| 362 | false |
Instead of visited array that we normally put we have to make visited for time as there may exists a solution with more cost but with desired time and we have visited array for a node which might be come in the path of optimal solution we will miss the best solution\n\n```\nclass Solution {\n\n\tpublic int minCost(int maxTime, int[][] edges, int[] passingFees) {\n\t\tint dest = passingFees.length - 1;\n\t\tArrayList<Edge>[] graph = new ArrayList[passingFees.length];\n\t\tfor (int i = 0; i < graph.length; i++) {\n\t\t\tgraph[i] = new ArrayList();\n\t\t}\n\t\tfor (int i = 0; i < edges.length; i++) {\n\t\t\tint src = edges[i][0];\n\t\t\tint nbr = edges[i][1];\n\t\t\tint time = edges[i][2];\n\t\t\tgraph[src].add(new Edge(nbr, time, passingFees[src]));\n\t\t\tgraph[nbr].add(new Edge(src, time, passingFees[nbr]));\n\n\t\t}\n\t\tint[] visited = new int[passingFees.length];\n\t\tArrays.fill(visited, -1);\n\t\tPriorityQueue<Edge> q = new PriorityQueue<>();\n\t\tq.add(new Edge(0, 0, passingFees[0]));\n\t\twhile (!q.isEmpty()) {\n\t\t\tEdge r = q.poll();\n\t\t\tif (r.nbr == dest)\n\t\t\t\treturn r.fees;\n\t\t\tfor (Edge nbr : graph[r.nbr]) {\n\t\t\t\tif (visited[nbr.nbr] != -1 && r.time + nbr.time >= visited[nbr.nbr])\n\t\t\t\t\tcontinue;\n\t\t\t\tvisited[nbr.nbr] = r.time + nbr.time;\n\t\t\t\tif (r.time + nbr.time <= maxTime) {\n\t\t\t\t\tq.add(new Edge(nbr.nbr, r.time + nbr.time, r.fees + passingFees[nbr.nbr]));\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn -1;\n\t}\n\n\tpublic static class Edge implements Comparable<Edge> {\n\n\t\tint nbr;\n\t\tint time;\n\t\tint fees;\n\n\t\tpublic Edge(int nbr, int time, int fees) {\n\n\t\t\tthis.nbr = nbr;\n\t\t\tthis.time = time;\n\t\t\tthis.fees = fees;\n\t\t}\n\n\t\tpublic int compareTo(Edge o) {\n\t\t\treturn this.fees - o.fees;\n\t\t}\n\t}\n}
| 1 | 0 |
['Breadth-First Search', 'Heap (Priority Queue)', 'Java']
| 1 |
minimum-cost-to-reach-destination-in-time
|
JAVA SIMPLE SOLUTION runtime:- 56ms
|
java-simple-solution-runtime-56ms-by-rad-4aji
|
\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n ArrayList<ArrayList<road>> country= new ArrayList<ArrayList
|
RadicalRed
|
NORMAL
|
2022-01-28T12:22:58.344291+00:00
|
2022-01-28T12:22:58.344324+00:00
| 180 | false |
```\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n ArrayList<ArrayList<road>> country= new ArrayList<ArrayList<road>>();\n int l=passingFees.length;\n for(int i=0;i<l;i++)\n {\n country.add(new ArrayList<road>());\n }\n for(int i=0;i<edges.length;i++)\n {\n country.get(edges[i][0]).add(new road(edges[i][1],edges[i][2]));\n country.get(edges[i][1]).add(new road(edges[i][0],edges[i][2]));\n }\n return smartdrive(maxTime,0,l-1,passingFees,country);\n }\n public int smartdrive(int maxTime, int s, int e, int []fees, ArrayList<ArrayList<road>> country)\n {\n PriorityQueue<costpriority> order= new PriorityQueue<costpriority>(new prioritycomparator());\n order.offer( new costpriority(fees[s],s,0));\n int []cost= new int[fees.length];\n int []time= new int[fees.length];\n Arrays.fill(cost,Integer.MAX_VALUE);\n Arrays.fill(time,Integer.MAX_VALUE);\n cost[s]=fees[s];\n time[s]=0;\n while(order.size()>0)\n {\n costpriority top=order.poll();\n int c=top.cost;\n int x=top.city;\n int t=top.time;\n if(t>maxTime)\n continue;\n if(x==e)\n return c;\n for(road i:country.get(x))\n {\n if(fees[i.city]+c<cost[i.city])\n {\n cost[i.city]=fees[i.city]+c;\n time[i.city]=i.time+t;\n order.offer(new costpriority(cost[i.city],i.city,time[i.city]));\n }\n if(i.time+t<time[i.city])\n {\n time[i.city]=i.time+t;\n order.offer(new costpriority(fees[i.city]+c,i.city,time[i.city]));\n }\n }\n }\n return -1;\n }\n class road{\n int city;\n int time;\n road(int city,int time)\n {\n this.city=city;\n this.time=time;\n }\n }\n class prioritycomparator implements Comparator<costpriority>{\n public int compare(costpriority a, costpriority b)\n {\n return a.cost-b.cost;\n }\n }\n class costpriority{\n int cost;\n int city;\n int time;\n costpriority(int cost, int city, int time)\n {\n this.cost=cost;\n this.city=city;\n this.time=time;\n }\n \n }\n}\n```
| 1 | 0 |
['Heap (Priority Queue)']
| 1 |
minimum-cost-to-reach-destination-in-time
|
C++ Dijkastra + DP.
|
c-dijkastra-dp-by-jus2havfun-iyxk
|
\nclass Solution {\n typedef pair<int, int> edge;\n struct cmp {\n bool operator()(const array<int, 3> &first,\n const array
|
jus2havfun
|
NORMAL
|
2021-12-28T19:43:07.616137+00:00
|
2021-12-28T19:43:07.616177+00:00
| 194 | false |
```\nclass Solution {\n typedef pair<int, int> edge;\n struct cmp {\n bool operator()(const array<int, 3> &first,\n const array<int, 3> &second) {\n return first[2] > second[2];\n }\n };\npublic:\n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n unordered_map<int, vector<edge>> g;\n for (auto v: edges) {\n g[v[0]].push_back({v[1], v[2]});\n g[v[1]].push_back({v[0], v[2]});\n }\n int n = passingFees.size();\n std::priority_queue<array<int, 3>, vector<array<int, 3>>,\n cmp> q;\n q.push({0, 0, passingFees[0]});\n vector<int> nodeTimes(n, INT_MAX);\n vector<vector<int>> dp(n, vector<int>(maxTime+1, INT_MAX));\n while (q.empty() == false) {\n auto [start, time, cost] = q.top();\n if (start == n-1) break;\n q.pop();\n for (auto [node, ntime]: g[start]) {\n if (time+ntime <= nodeTimes[node]) {\n if (time+ntime <= maxTime) {\n if (passingFees[node]+cost <= dp[node][time+ntime]) {\n nodeTimes[node] = time+ntime;\n dp[node][time+ntime] = passingFees[node]+cost;\n q.push({node, time+ntime, cost+passingFees[node]});\n }\n }\n }\n }\n }\n return (q.empty())?-1: *std::min_element(std::begin(dp[n-1]), std::end(dp[n-1])); \n }\n};\n```
| 1 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
c++ solution
|
c-solution-by-dilipsuthar60-ab3p
|
\nclass Solution\n{\npublic:\n int minCost(int maxtime,vector<vector<int>>&nums,vector<int>&fee) \n {\n int n=fee.size();\n vector<pair<int,
|
dilipsuthar17
|
NORMAL
|
2021-11-14T17:02:51.760139+00:00
|
2021-11-14T17:02:51.760185+00:00
| 283 | false |
```\nclass Solution\n{\npublic:\n int minCost(int maxtime,vector<vector<int>>&nums,vector<int>&fee) \n {\n int n=fee.size();\n vector<pair<int,int>>dp[n+100];\n vector<int>dis(n+1000,INT_MAX);\n for(auto it:nums)\n {\n dp[it[0]].push_back({it[1],it[2]});\n dp[it[1]].push_back({it[0],it[2]});\n }\n priority_queue<vector<int>,vector<vector<int>>,greater<vector<int>>>pq;\n pq.push({fee[0],0,0});\n while(pq.size())\n {\n auto temp=pq.top();\n pq.pop();\n int f=temp[0];\n int time=temp[1];\n int node=temp[2];\n if(node==n-1)\n {\n return f;\n }\n for(auto it:dp[node])\n {\n int new_time=time+it.second;\n if(new_time<=maxtime&&dis[it.first]>time+it.second)\n {\n dis[it.first]=new_time;\n pq.push({f+fee[it.first],new_time,it.first});\n }\n }\n }\n return -1;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'C', 'C++']
| 1 |
minimum-cost-to-reach-destination-in-time
|
[Python] Dijkstra Algorithm
|
python-dijkstra-algorithm-by-ksanjeev555-mz9n
|
Main observation is that we might reach the same node again searching for path that is under our time limit. Hence we apply BFS on that node again (if already a
|
ksanjeev555
|
NORMAL
|
2021-10-16T10:20:50.603795+00:00
|
2021-10-16T10:20:50.603827+00:00
| 237 | false |
Main observation is that we might reach the same node again searching for path that is under our time limit. Hence we apply BFS on that node again (if already applied) instead of dropping.\n```\nfrom collections import defaultdict\nfrom heapq import heappop,heappush\nclass Solution:\n mn = float(\'inf\')\n def minCost(self, mxt: int, edges: List[List[int]], fees: List[int]) -> int:\n n = len(fees)\n adj = defaultdict(list)\n tms = defaultdict(lambda : float(\'inf\')) ### need this dictionary to account the reaching time at ith node. \n for x,y,t in edges:\n adj[x].append([y,t])\n adj[y].append([x,t])\n qu = []\n heappush(qu,(fees[0],0,0))\n while qu:\n fee,tm,nd = heappop(qu)\n if tm > mxt :\n continue\n if nd == n-1 :\n return fee\n if tm < tms[nd]: ### simply if we come again at the same node and in lesser time we allow bfs over that node. \n for dest,time in adj[nd]:\n heappush(qu,(fee+fees[dest],tm+time,dest))\n tms[nd] = min(tms[nd],tm) ## store the min reachable time at the node\n return -1\n\t\t
| 1 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
Bellman Ford + Python3
|
bellman-ford-python3-by-zhangzuxin007-9t2r
|
\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n n = len(passingFees)\n f = [[floa
|
zhangzuxin007
|
NORMAL
|
2021-09-13T14:24:14.875140+00:00
|
2021-09-13T14:24:14.875192+00:00
| 141 | false |
```\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n n = len(passingFees)\n f = [[float("inf")] * n for _ in range(maxTime + 1)]\n f[0][0] = passingFees[0]\n for t in range(1, maxTime + 1):\n for i, j, cost in edges:\n if cost <= t:\n f[t][i] = min(f[t][i], f[t - cost][j] + passingFees[i])\n f[t][j] = min(f[t][j], f[t - cost][i] + passingFees[j])\n ans = min(f[t][n - 1] for t in range(1, maxTime + 1))\n return -1 if ans == float("inf") else ans\n```
| 1 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
[java] | min_heap | dijkstra | easy | priority queue
|
java-min_heap-dijkstra-easy-priority-que-8hvb
|
Please comment incase of any questions\n\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n Map<Integer,Map<Int
|
codehuman
|
NORMAL
|
2021-09-11T08:32:44.456600+00:00
|
2021-09-11T08:32:44.456642+00:00
| 129 | false |
Please comment incase of any questions\n```\nclass Solution {\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n Map<Integer,Map<Integer,Integer>> adjGrp = new HashMap<>();\n adjGrp = getAdjGrp(edges);\n int n = passingFees.length;\n if(noValidPath(adjGrp,n))\n return -1;\n int[] timeTaken = new int[n];\n Arrays.fill(timeTaken,Integer.MAX_VALUE);\n PriorityQueue<int[]> minHeap = new PriorityQueue<>((a,b) -> a[1]-b[1]); \n timeTaken[0] = 0; //0 is the staring point\n minHeap.offer(new int[]{0,passingFees[0],0});\n int dest = n-1;\n while(!minHeap.isEmpty()){\n int[] nodeSrc = minHeap.poll();\n int currTime = nodeSrc[2];\n int currCost = nodeSrc[1];\n int u = nodeSrc[0];\n if(u == dest){\n return currCost;\n }\n for(Map.Entry<Integer,Integer> vertex : adjGrp.get(u).entrySet()){\n int v = vertex.getKey();\n int time = vertex.getValue();\n int fee = passingFees[v]; \n if(currTime+time > maxTime)\n continue; \n if(currTime+time < timeTaken[v]){\n timeTaken[v] = currTime+time;\n minHeap.offer(new int[]{v,fee+currCost,timeTaken[v]}); \n } \n } \n }\n return -1; \n \n \n }\n public boolean noValidPath(Map<Integer,Map<Integer,Integer>> adjGrp , int n ){\n for(int i = 0 ; i < n ;i++){\n if(!adjGrp.containsKey(i))\n return true;\n }\n return false;\n }\n \n //Optimization by taking on fastest road if 2 available \n public Map<Integer,Map<Integer,Integer>> getAdjGrp(int[][] edges){\n Map<Integer,Map<Integer,Integer>> adjGrp = new HashMap<>();\n for(int i=0;i<edges.length;i++){\n int u = edges[i][0];\n int v = edges[i][1];\n int t = edges[i][2];\n adjGrp.putIfAbsent(u,new HashMap<Integer,Integer>());\n adjGrp.putIfAbsent(v,new HashMap<Integer,Integer>()); \n if(!adjGrp.get(u).containsKey(v))\n adjGrp.get(u).put(v,t); \n else{\n if(adjGrp.get(u).get(v) > t) {\n adjGrp.get(u).put(v,t); \n }\n }\n if(!adjGrp.get(v).containsKey(u))\n adjGrp.get(v).put(u,t); \n else{\n if(adjGrp.get(v).get(u) > t )\n adjGrp.get(v).put(u,t);\n }\n \n }\n return adjGrp; \n }\n}\n```
| 1 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
[PYTHON3] BFS + Pruning
|
python3-bfs-pruning-by-irt-70fh
|
Minimum cost problem can be reduced to BFS problem. We need to add the time constraints. So we pick the minimum cost node from the heap and when adding adjacenc
|
irt
|
NORMAL
|
2021-08-29T04:00:37.469509+00:00
|
2021-08-29T04:00:37.469547+00:00
| 148 | false |
Minimum cost problem can be reduced to BFS problem. We need to add the time constraints. So we pick the minimum cost node from the heap and when adding adjacenct nodes of the picked node, we select them only if time can be reduced. We do not need to check cost since earliest visit to a node will have the minimum cost.\n```\nfrom collections import defaultdict\nfrom heapq import heappush, heappop\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n n = len(passingFees)\n adjacency = defaultdict(list)\n min_times = {}\n for src,dst,time in edges:\n adjacency[src].append([dst,time])\n adjacency[dst].append([src,time])\n \n heap = []\n heappush(heap, (passingFees[0],0,0))\n min_times[0] = 0\n while heap:\n cost,time,node = heappop(heap)\n if node==n-1:\n return cost\n for dst,distance in adjacency[node]:\n if time+distance<=maxTime and min_times.get(dst,float(\'inf\'))>time+distance:\n min_times[dst] = time+distance\n heappush(heap, ( cost+passingFees[dst], time+distance,dst))\n return -1\n```
| 1 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
Almost Same problem as 787. Cheapest Flights Within K Stops
|
almost-same-problem-as-787-cheapest-flig-x9t5
|
Using two arrays (minCost and minTime) to do relaxation in Dijkstra search\n\n787. Cheapest Flights Within K Stops\n\n public int findCheapestPrice(int n, in
|
chenzuojing
|
NORMAL
|
2021-08-23T02:25:50.017556+00:00
|
2021-08-23T02:28:23.477993+00:00
| 260 | false |
Using two arrays (minCost and minTime) to do relaxation in Dijkstra search\n\n787. Cheapest Flights Within K Stops\n```\n public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {\n HashMap<Integer, Integer>[] graph = new HashMap[n];\n for (int i = 0; i < n; i++)\n graph[i] = new HashMap<>();\n for (int[] flight : flights)\n graph[flight[0]].put(flight[1], flight[2]);\n\n int[] minCosts = new int[n], minStops = new int[n];\n Arrays.fill(minCosts, Integer.MAX_VALUE);\n Arrays.fill(minStops, Integer.MAX_VALUE);\n minCosts[src] = 0;\n minStops[src] = 0;\n\n // The priority queue would contain (node, cost, stops)\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);\n pq.offer(new int[]{src, 0, 0});\n\n while (!pq.isEmpty()) {\n int[] info = pq.poll();\n int node = info[0], costs = info[1], stops = info[2];\n\n if (node == dst) return costs;\n\n for (int nextNode : graph[node].keySet()) {\n int price = graph[node].get(nextNode);\n if (stops > k) continue;\n if (costs + price < minCosts[nextNode]) {\n pq.offer(new int[]{nextNode, costs + price, stops + 1});\n minCosts[nextNode] = costs + price;\n minStops[nextNode] = stops + 1;\n } else if (stops + 1 < minStops[nextNode]) {\n pq.offer(new int[]{nextNode, costs + price, stops + 1});\n minStops[nextNode] = stops + 1;\n }\n }\n }\n\n return -1;\n }\n```\n\n\n1928. Minimum Cost to Reach Destination in Time\n```\n public int minCost(int maxTime, int[][] edges, int[] passingFees) {\n int n = passingFees.length;\n int[] minTime = new int[n];\n int[] minCosts = new int[n];\n Arrays.fill(minTime, Integer.MAX_VALUE);\n Arrays.fill(minCosts, Integer.MAX_VALUE);\n minTime[0] = 0;\n minCosts[0] = passingFees[0];\n\n HashMap<Integer, Integer>[] graph = new HashMap[n];\n for (int i = 0; i < n; i++)\n graph[i] = new HashMap<>();\n for (int[] e : edges) {\n if (!graph[e[0]].containsKey(e[1]) || graph[e[0]].get(e[1]) > e[2])\n graph[e[0]].put(e[1], e[2]);\n if (!graph[e[1]].containsKey(e[0]) || graph[e[1]].get(e[0]) > e[2])\n graph[e[1]].put(e[0], e[2]);\n }\n\n // The priority queue would contain (node, cost, time)\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);\n pq.offer(new int[]{0, passingFees[0], 0});\n\n while (!pq.isEmpty()) {\n int[] info = pq.poll();\n int node = info[0], costs = info[1], time = info[2];\n if (node == n - 1) return costs;\n\n for (int nextNode : graph[node].keySet()) {\n int passingTime = graph[node].get(nextNode);\n int newFee = passingFees[nextNode];\n if (time + passingTime > maxTime) continue;\n\n if (costs + newFee < minCosts[nextNode]) {\n pq.offer(new int[]{nextNode, costs + newFee, time + passingTime});\n minCosts[nextNode] = costs + newFee;\n minTime[nextNode] = time + passingTime;\n } else if (time + passingTime < minTime[nextNode]) {\n pq.offer(new int[]{nextNode, costs + newFee, time + passingTime});\n minTime[nextNode] = time + passingTime;\n }\n }\n }\n\n return -1;\n }\n```
| 1 | 0 |
[]
| 0 |
minimum-cost-to-reach-destination-in-time
|
[C++] clean DP memoization
|
c-clean-dp-memoization-by-yunqu-iddy
|
For next try to use pairs inside the vector to avoid TLE. next stores the next stop information and the time used on the road.\n\ncpp\nclass Solution {\npublic:
|
yunqu
|
NORMAL
|
2021-08-06T20:48:07.783515+00:00
|
2021-08-06T20:48:32.194408+00:00
| 144 | false |
For `next` try to use pairs inside the vector to avoid TLE. `next` stores the next stop information and the time used on the road.\n\n```cpp\nclass Solution {\npublic:\n int maxi;\n int n;\n vector<vector<int>> memo;\n vector<vector<pair<int, int>>> next;\n \n int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {\n maxi = maxTime;\n n = passingFees.size();\n memo.assign(n, vector<int>(maxi + 1, -1));\n next.assign(n, vector<pair<int, int>>{});\n for (auto e: edges){\n next[e[0]].push_back({e[1], e[2]});\n next[e[1]].push_back({e[0], e[2]});\n }\n int ans = dp(passingFees, 0, 0, 0);\n return (ans == INT_MAX/2) ? -1: ans;\n }\n \n int dp(vector<int>& passingFees, int i, int time, int cost){\n if (time > maxi) return INT_MAX/2;\n if (i == n - 1)\n return passingFees[i];\n if (memo[i][time] < 0){\n memo[i][time] = INT_MAX/2;\n for (auto p: next[i]){\n int j = p.first, t = p.second;\n memo[i][time] = min(memo[i][time],\n passingFees[i] + dp(passingFees, j, time + t, cost));\n }\n }\n return memo[i][time];\n }\n};\n```
| 1 | 1 |
[]
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.