question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-value-of-the-partition
|
Beats 95% in time complexity, simple and understandable
|
beats-95-in-time-complexity-simple-and-u-19dn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
andrew_xv
|
NORMAL
|
2024-09-16T12:41:22.965591+00:00
|
2024-09-16T12:43:58.241748+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n log n)\n# Code\n```csharp []\npublic class Solution {\n public int FindValueOfPartition(int[] nums) {\n Array.Sort(nums);\n int lowest = Math.Abs(nums[0] - nums[1]);\n for (int i = 0; i < nums.Length - 1; i++){\n if(Math.Abs(nums[i] - nums[i + 1]) < lowest){\n lowest = Math.Abs(nums[i] - nums[i + 1]);\n }\n }\n return lowest;\n }\n}\n```
| 0 | 0 |
['C#']
| 0 |
find-the-value-of-the-partition
|
very very very very easy easy
|
very-very-very-very-easy-easy-by-rajan_s-wb6p
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rajan_singh5639
|
NORMAL
|
2024-09-11T04:47:53.260111+00:00
|
2024-09-11T04:47:53.260135+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n int n = nums.size();\n\n sort(nums.begin() , nums.end());\n\nint mx = INT_MAX;\n\n\nfor(int i =0; i<nums.size()-1; i++)\n{\nmx = min(mx,abs(nums[i] - nums[i+1]));\n\n}\n\n\n return mx; \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-value-of-the-partition
|
Intuitive and simple solution
|
intuitive-and-simple-solution-by-kristia-252l
|
Approach\n1. Sort the array\n2. Find the two numbers that are the closest to each other\n3. Split the list at those two numbers \n4. Perform the calculation\n\n
|
Kristian97
|
NORMAL
|
2024-09-02T07:04:01.723850+00:00
|
2024-09-02T07:04:01.723889+00:00
| 0 | false |
# Approach\n1. Sort the array\n2. Find the two numbers that are the closest to each other\n3. Split the list at those two numbers \n4. Perform the calculation\n\n\n# Code\n```csharp []\npublic class Solution {\n public int FindValueOfPartition(int[] nums) {\n Array.Sort(nums);\n int minDiff = 2147483647; // maximum value an int can have\n int place = default;\n for(int i = 1; i < nums.Length; i++){\n if(nums[i] - nums [i -1] < minDiff){\n minDiff = nums[i] - nums [i -1];\n place = i;\n }\n }\n int[] nums1 = nums.Take(place).ToArray();\n int[] nums2 = nums.Skip(place).ToArray();\n return Math.Abs(nums1.Max() - nums2.Min());\n }\n}\n```
| 0 | 0 |
['C#']
| 0 |
find-the-value-of-the-partition
|
Easy solution
|
easy-solution-by-jayprakashyadav2535-zexe
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
jpppyadav1234
|
NORMAL
|
2024-08-28T13:08:42.632006+00:00
|
2024-08-28T13:08:42.632040+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int minie=INT_MAX;\n for(int i=1;i<nums.size();i++)\n {\n minie=min(minie,nums[i]-nums[i-1]);\n }\n return minie;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-value-of-the-partition
|
Very Easy solution Just sort and calculate minimum of arrays element .
|
very-easy-solution-just-sort-and-calcula-4xmk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nSort the array first and then calculate the difference between array cons
|
jpppyadav1234
|
NORMAL
|
2024-08-28T13:07:14.998149+00:00
|
2024-08-28T13:07:14.998184+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSort the array first and then calculate the difference between array consecutive elemnts and return minimum difference.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int minie=INT_MAX;\n for(int i=1;i<nums.size();i++)\n {\n minie=min(minie,nums[i]-nums[i-1]);\n }\n return minie;\n }\n};\n```\n\n\n\n
| 0 | 0 |
['C++', 'Java']
| 0 |
find-the-value-of-the-partition
|
✅ 2 line solution ✅ Beats 100% ✅
|
2-line-solution-beats-100-by-menezes1997-d0ou
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
menezes1997
|
NORMAL
|
2024-08-25T09:14:22.789006+00:00
|
2024-08-25T09:14:22.789030+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int findValueOfPartition(int[] nums) {\n Arrays.sort(nums);\n int minDiff = nums[1] - nums[0];\n for(int i = 2; i < nums.length; i++){\n minDiff = Math.min(nums[i] - nums[i - 1], minDiff);\n }\n return minDiff;\n }\n}\n```
| 0 | 0 |
['Sorting', 'Java']
| 0 |
find-the-value-of-the-partition
|
Solution with Javascript
|
solution-with-javascript-by-manhhungit37-9o0n
|
Code\njavascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findValueOfPartition = function(nums) {\n nums.sort((a, b) => a - b);\n
|
manhhungit37
|
NORMAL
|
2024-08-21T09:20:19.250673+00:00
|
2024-08-21T09:20:19.250706+00:00
| 2 | false |
# Code\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findValueOfPartition = function(nums) {\n nums.sort((a, b) => a - b);\n let min = Number.POSITIVE_INFINITY;\n for (let i = 1; i < nums.length; i++) {\n if (Math.abs(nums[i] - nums[i-1]) < min) min = Math.abs(nums[i] - nums[i-1]);\n }\n return min;\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
find-the-value-of-the-partition
|
Easiest Solution Ever
|
easiest-solution-ever-by-ameyapradippotd-sskd
|
Intuition\nHmm... perhaps sorting would make things much easier\n\n# Approach\nfirst sort the array and calcualte the minimum difference between 2 consecutive i
|
ameyapradippotdar
|
NORMAL
|
2024-08-13T06:17:10.178727+00:00
|
2024-08-13T06:17:10.178755+00:00
| 0 | false |
# Intuition\nHmm... perhaps sorting would make things much easier\n\n# Approach\nfirst sort the array and calcualte the minimum difference between 2 consecutive integers, this works cuz when the array is sorted, the smallest difference between any two elements that are next to each other in the sorted array will naturally give you the smallest value of the partition. This is because the two consecutive elements are the closest in value, and when you split the array between them, you get the smallest possible difference.\n\n\n# Complexity\n- Time complexity:\nO(NLogN)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def findValueOfPartition(self, nums: List[int]) -> int:\n nums.sort()\n _min=10**9\n for i in range(len(nums)-1):\n _min=min(nums[i+1]-nums[i],_min)\n return _min\n```
| 0 | 0 |
['Python3']
| 0 |
find-the-value-of-the-partition
|
TypeScript single line || Solution by Navyendhu Menon
|
typescript-single-line-solution-by-navye-zeyn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
navyendhummenon
|
NORMAL
|
2024-08-01T10:11:20.776605+00:00
|
2024-08-01T10:11:20.776635+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunction findValueOfPartition(nums: number[]): number {\n\n return Math.min(...nums.sort((a, b) => a - b).slice(1).map((num, index) => num - nums[index]))\n\n\n};\n```
| 0 | 0 |
['TypeScript']
| 0 |
find-the-value-of-the-partition
|
Js One Line || Solution by Navyendhu Menon
|
js-one-line-solution-by-navyendhu-menon-dizfd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
navyendhummenon
|
NORMAL
|
2024-08-01T10:09:31.965102+00:00
|
2024-08-01T10:09:31.965142+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findValueOfPartition = function(nums) {\n\n return Math.min(...nums.sort((a, b) => a - b).slice(1).map((num, index) => num - nums[index]))\n\n};\n```
| 0 | 0 |
['JavaScript']
| 0 |
find-the-value-of-the-partition
|
🔥 Go/Python One Line Solution | Beat 97% | With Explanation 🔥
|
gopython-one-line-solution-beat-97-with-kr2w1
|
Approach\n Describe your approach to solving the problem. \nSort nums first and the minimum difference between two neighboured element is the answer.\n\n# Compl
|
ConstantineJin
|
NORMAL
|
2024-07-26T01:27:35.971251+00:00
|
2024-07-26T01:27:35.971279+00:00
| 1 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nSort `nums` first and the minimum difference between two neighboured element is the answer.\n\n# Complexity\n- Time complexity: $$O(n\\text{log}n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Python []\nclass Solution:\n def findValueOfPartition(self, nums: List[int]) -> int:\n return min(y - x for x, y in pairwise(sorted(nums)))\n```\n```Go []\nfunc findValueOfPartition(nums []int) int {\n\tsort.Ints(nums)\n\tans := nums[1] - nums[0]\n\tfor i := 2; i < len(nums); i++ {\n\t\tans = min(ans, nums[i]-nums[i-1])\n\t}\n\treturn ans\n}\n```
| 0 | 0 |
['Sorting', 'Go', 'Python3']
| 0 |
find-the-value-of-the-partition
|
simple and easy O(N) solution💡🚀
|
simple-and-easy-on-solution-by-chyntu-xv1n
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
chyntu
|
NORMAL
|
2024-07-03T11:21:39.607533+00:00
|
2024-07-03T11:21:39.607570+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findValueOfPartition(self, nums: List[int]) -> int:\n \n nums.sort()\n res = float(\'inf\')\n\n for i in range(0, len(nums) - 1):\n res = min(res, nums[i + 1] - nums[i])\n \n return res\n```
| 0 | 0 |
['Array', 'Sorting', 'Python3']
| 0 |
find-the-value-of-the-partition
|
Easiest solution || C++
|
easiest-solution-c-by-saurabhyadav_45-z5s2
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
SaurabhYadav_45
|
NORMAL
|
2024-07-01T14:42:52.094702+00:00
|
2024-07-01T14:42:52.094738+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int minAns = INT_MAX;\n for(int i=1; i<nums.size(); i++){\n minAns = min(nums[i]-nums[i-1], minAns);\n }\n return minAns;\n }\n};\n```
| 0 | 0 |
['Array', 'Sorting', 'C++']
| 0 |
find-the-value-of-the-partition
|
scala sliding oneliner
|
scala-sliding-oneliner-by-vititov-wk8t
|
scala\nobject Solution {\n def findValueOfPartition(nums: Array[Int]): Int = \n nums.sorted.sliding(2,1).map(a => a.last-a.head).min\n}\n
|
vititov
|
NORMAL
|
2024-06-30T21:13:03.098533+00:00
|
2024-06-30T21:13:03.098558+00:00
| 0 | false |
```scala\nobject Solution {\n def findValueOfPartition(nums: Array[Int]): Int = \n nums.sorted.sliding(2,1).map(a => a.last-a.head).min\n}\n```
| 0 | 0 |
['Two Pointers', 'Sliding Window', 'Sorting', 'Scala']
| 0 |
find-the-value-of-the-partition
|
C++ find 2 closest adjacent numbers
|
c-find-2-closest-adjacent-numbers-by-the-27w7
|
We may cut the array into 2 parts so that max of part 1 is adjacent to min of second ( that means we will cut the sorted array by mid of that adjacent numbers)
|
the_ghuly
|
NORMAL
|
2024-06-16T10:23:39.872999+00:00
|
2024-06-16T10:23:39.873029+00:00
| 2 | false |
We may cut the array into 2 parts so that max of part 1 is adjacent to min of second ( that means we will cut the sorted array by mid of that adjacent numbers) \nSo the problem is about findig closest adjacent numbers in sorted array.\n```\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n sort(begin(nums),end(nums));\n int min = INT_MAX;\n for(int i = 1;i<nums.size();++i)\n {\n min= std::min(min,nums[i]-nums[i-1]);\n }\n return min;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-value-of-the-partition
|
C++ Sorting ; Beats 99% of other submissions.
|
c-sorting-beats-99-of-other-submissions-2zmuo
|
Intuition\nSorting the array will provide us with the absolute difference between every adjacent elements, this will in turn make it clear as to where the inter
|
SHUBHAM_KARKI_29
|
NORMAL
|
2024-06-02T18:48:35.537784+00:00
|
2024-06-02T18:48:35.537802+00:00
| 2 | false |
# Intuition\nSorting the array will provide us with the absolute difference between every adjacent elements, this will in turn make it clear as to where the intersection point should.\n\n# Approach\nSorted the array in a non-decreasing order. The result variable keeps track of the minimum absolute difference between every adjacent elements.\n\n# Complexity\n- Time complexity:\nO(N LogN)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n std::ios::sync_with_stdio(false);\n cin.tie(NULL);\n\n sort(nums.begin(), nums.end());\n\n int n = nums.size();\n int result = INT_MAX;\n\n for (int i = 1; i < n; i++) {\n result = min(result, nums[i] - nums[i-1]);\n }\n\n return result;\n }\n};\n```
| 0 | 0 |
['Sorting', 'C++']
| 0 |
find-the-value-of-the-partition
|
Python easy to read and understand | sort
|
python-easy-to-read-and-understand-sort-hfchx
|
```\nclass Solution:\n def findValueOfPartition(self, nums: List[int]) -> int:\n nums.sort()\n res = float("inf")\n for i in range(1, le
|
sanial2001
|
NORMAL
|
2024-05-30T18:57:24.203869+00:00
|
2024-05-30T18:57:24.203886+00:00
| 0 | false |
```\nclass Solution:\n def findValueOfPartition(self, nums: List[int]) -> int:\n nums.sort()\n res = float("inf")\n for i in range(1, len(nums)):\n res = min(res, nums[i]-nums[i-1])\n return res
| 0 | 0 |
['Sorting', 'Python', 'Python3']
| 0 |
find-the-value-of-the-partition
|
Beats 100% One-Line Method
|
beats-100-one-line-method-by-charnavoki-ujkl
|
\n\n\n# Code\n\nvar findValueOfPartition = nums => Math.min(...nums.sort((a, b) => a - b).map((v, i, a) => a[i + 1] - v).slice(0, -1));\n\n\n##### please upvote
|
charnavoki
|
NORMAL
|
2024-05-19T08:55:42.520310+00:00
|
2024-05-19T08:55:42.520340+00:00
| 8 | false |
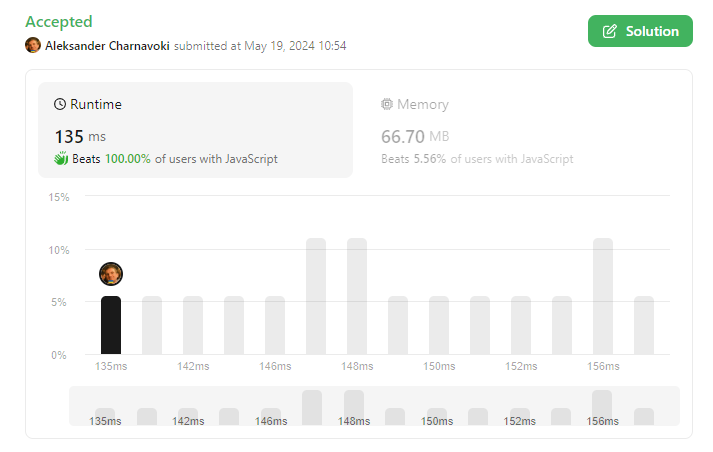\n\n\n# Code\n```\nvar findValueOfPartition = nums => Math.min(...nums.sort((a, b) => a - b).map((v, i, a) => a[i + 1] - v).slice(0, -1));\n```\n\n##### please upvote, you motivate me to solve problems in original ways
| 0 | 0 |
['JavaScript']
| 0 |
find-the-value-of-the-partition
|
cpp
|
cpp-by-pankajkumar101-vcaw
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
PankajKumar101
|
NORMAL
|
2024-05-14T16:22:58.547469+00:00
|
2024-05-14T16:22:58.547491+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int n = nums.size();\n int ans = nums[n-1];\n for(int i = 1; i < n; i++){\n ans = min(ans,nums[i]-nums[i-1]);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-value-of-the-partition
|
Sorting C++
|
sorting-c-by-samarthkadam-tz8x
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
SamarthKadam
|
NORMAL
|
2024-05-12T07:34:01.669772+00:00
|
2024-05-12T07:34:01.669795+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int diff=INT_MAX;\n for(int i=0;i<nums.size()-1;i++)\n {\n if(nums[i+1]-nums[i]<diff)\n diff=nums[i+1]-nums[i];\n }\n return diff;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-value-of-the-partition
|
medium made easier......
|
medium-made-easier-by-kabirrr_03-1rwm
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
kabirrr_03
|
NORMAL
|
2024-05-06T16:32:27.820277+00:00
|
2024-05-06T16:32:27.820305+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findValueOfPartition(int[] nums) {\n Arrays.sort(nums);\n int ans=Integer.MAX_VALUE;\n for(int i=1; i<nums.length; i++){\n ans=Math.min(ans, nums[i]-nums[i-1]);\n }\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-value-of-the-partition
|
CPP CODE :
|
cpp-code-by-vineethsellamuthu1-pkbr
|
Code\n\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n sort(nums.begin() , nums.end());\n int ans = INT_MAX;\n
|
vineethsellamuthu1
|
NORMAL
|
2024-04-30T11:19:13.608891+00:00
|
2024-04-30T11:19:13.608915+00:00
| 0 | false |
# Code\n```\nclass Solution {\npublic:\n int findValueOfPartition(vector<int>& nums) {\n sort(nums.begin() , nums.end());\n int ans = INT_MAX;\n for(int i=1;i<nums.size();i++){\n ans = min(ans,nums[i] - nums[i-1]);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
find-the-value-of-the-partition
|
Beats 98%
|
beats-98-by-obose-d64b
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nThe problem seems to be
|
Obose
|
NORMAL
|
2024-04-27T05:12:45.649675+00:00
|
2024-04-27T05:12:45.649696+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem seems to be asking for the minimum difference between any two adjacent elements in a list of integers. Here\'s my approach to solving it:\n\nSort the list of integers in ascending order. This will allow us to easily compare adjacent elements.\nIterate through the sorted list, and for each pair of adjacent elements, compute their difference.\nKeep track of the minimum difference found so far.\nReturn the minimum difference.\n\n# Complexity\n- Time complexity: O(n log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findValueOfPartition(self, nums: List[int]) -> int:\n nums.sort()\n return min(nums[i] - nums[i-1] for i in range(1, len(nums)))\n\n```
| 0 | 0 |
['Python3']
| 0 |
find-the-value-of-the-partition
|
Sort, take difference!
|
sort-take-difference-by-robert961-r7l9
|
Intuition\nObservation: We need to make 2 arrays, however we can break the array anyway we want!\n\nWe want the largest element in Array1 to be the closest to t
|
robert961
|
NORMAL
|
2024-04-26T16:42:17.111458+00:00
|
2024-04-26T16:42:17.111505+00:00
| 1 | false |
# Intuition\nObservation: We need to make 2 arrays, however we can break the array anyway we want!\n\nWe want the largest element in Array1 to be the closest to the smallest element in Array2!\n\nWhy not sort it and check the difference between elements!\n\nReturn the smallest difference.\n\n# Code\n```\nclass Solution:\n def findValueOfPartition(self, nums: List[int]) -> int:\n min_diff = float(\'inf\')\n for prev, curr in zip(sorted(nums), sorted(nums)[1:]):\n min_diff = min(min_diff, curr - prev)\n return min_diff\n\n \n```
| 0 | 0 |
['Python3']
| 0 |
find-the-value-of-the-partition
|
Sort, take difference!
|
sort-take-difference-by-robert961-h4io
|
Intuition\nObservation: We need to make 2 arrays, however we can break the array anyway we want!\n\nWe want the largest element in Array1 to be the closest to t
|
robert961
|
NORMAL
|
2024-04-26T16:42:13.070263+00:00
|
2024-04-26T16:42:13.070297+00:00
| 0 | false |
# Intuition\nObservation: We need to make 2 arrays, however we can break the array anyway we want!\n\nWe want the largest element in Array1 to be the closest to the smallest element in Array2!\n\nWhy not sort it and check the difference between elements!\n\nReturn the smallest difference.\n\n# Code\n```\nclass Solution:\n def findValueOfPartition(self, nums: List[int]) -> int:\n min_diff = float(\'inf\')\n for prev, curr in zip(sorted(nums), sorted(nums)[1:]):\n min_diff = min(min_diff, curr - prev)\n return min_diff\n\n \n```
| 0 | 0 |
['Python3']
| 0 |
find-the-value-of-the-partition
|
Beats 100% ✅✅ Easy Solution, Sorting Approach.
|
beats-100-easy-solution-sorting-approach-r55u
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Nikhil2910--
|
NORMAL
|
2024-04-23T16:44:28.359425+00:00
|
2024-04-23T16:44:28.359447+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findValueOfPartition(int[] nums) {\n int n = nums.length, ans = Integer.MAX_VALUE;\n Arrays.sort(nums);\n \n for (var i=0; i < n-1; i++)\n ans = Math.min(ans, nums[i+1] - nums[i]);\n \n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-value-of-the-partition
|
Using sorting
|
using-sorting-by-mukhammadazizkhon-f46i
|
Intuition\nSort the array to find two numbers with minimum difference in linear time\n\n# Approach\nFirst of all, we need to sort the array. After sorting, we c
|
mukhammadazizkhon
|
NORMAL
|
2024-04-21T22:13:09.530894+00:00
|
2024-04-21T22:13:09.530918+00:00
| 1 | false |
# Intuition\nSort the array to find two numbers with minimum difference in linear time\n\n# Approach\nFirst of all, we need to sort the array. After sorting, we can find two numbers which have minimum absolute difference in linear time. If we find these two numbers which form absolute minimum difference, then we can conclude these numbers can be put in one of the arrays and we can return their absolute difference as the result.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public int findValueOfPartition(int[] nums) {\n Arrays.sort(nums);\n int result = 1000000000;\n for (int i = 0; i < nums.length - 1; i++) {\n result = Math.min(result, nums[i + 1] - nums[i]);\n }\n return result;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
find-the-value-of-the-partition
|
[Java] ✅ 18ms✅ beats 100% ✅ CLEAN CODE ✅ CLEAR EXPLANATIONS
|
java-18ms-beats-100-clean-code-clear-exp-1jxf
|
Approach\n1. Looking at the requirement of max(nums1) - min(nums2) we realize that we need the max from nums1 to be as close as possible with min from nums2.\n2
|
StefanelStan
|
NORMAL
|
2024-04-20T15:14:27.829011+00:00
|
2024-04-20T15:14:27.829028+00:00
| 8 | false |
# Approach\n1. Looking at the requirement of max(nums1) - min(nums2) we realize that we need the max from nums1 to be as close as possible with min from nums2.\n2. This is only possible if we SORT the numbers and we compare two at a time.\n3. Thus, when comparing numbers [a] and [a+1], it is guaranteed that [a] is max of num1 and [a+1] min of nums2.\n4. Sort them and compare each [i] with [i+1], returning their min difference.\n\n# Complexity\n- Time complexity:$$O(n * log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findValueOfPartition(int[] nums) {\n Arrays.sort(nums);\n int partitionValue = Integer.MAX_VALUE;\n for (int i = 1; i < nums.length && partitionValue != 0; i++) {\n partitionValue = Math.min(partitionValue, nums[i] - nums[i-1]);\n }\n return partitionValue;\n }\n}\n```
| 0 | 0 |
['Sorting', 'Java']
| 0 |
maximum-earnings-from-taxi
|
[C++/Python] DP - O(M+N) - Clean & Concise
|
cpython-dp-omn-clean-concise-by-hiepit-hnny
|
Idea\n- Let dp[i] is the maximum dollars we can get if we start at point i, where 1 <= i <= n.\n- We need to build our dp in reversed order, we iterate i in [n-
|
hiepit
|
NORMAL
|
2021-09-18T16:04:24.110483+00:00
|
2021-09-18T16:56:02.368875+00:00
| 14,518 | false |
**Idea**\n- Let `dp[i]` is the maximum dollars we can get if we start at point `i`, where `1 <= i <= n`.\n- We need to build our dp in reversed order, we iterate `i` in `[n-1..1]` then,\n\t- There are 2 main options:\n\t\t- Picking up rides `{e, d}` start at point `i`, we can get maximum of `dp[i] = dp[e] + d` dollars. (Of course, we need to build rides start at `i`, let say `rideStartAt[i] = [{end, dollar}]` first)\n\t\t- Don\'t pick any ride, `dp[i] = dp[i+1]`.\n\t- Choose the maximum `dp[i]` among above options.\n- Finally, `dp[1]` is our answer.\n\n**Python 3**\n```python\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n rideStartAt = defaultdict(list)\n for s, e, t in rides:\n rideStartAt[s].append([e, e - s + t]) # [end, dollar]\n\n dp = [0] * (n + 1)\n for i in range(n - 1, 0, -1):\n for e, d in rideStartAt[i]:\n dp[i] = max(dp[i], dp[e] + d)\n dp[i] = max(dp[i], dp[i + 1])\n\n return dp[1]\n```\n\n**C++**\n```c++\n#define pii pair<int, int>\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<vector<pii>> rideStartAt(n);\n for (auto& ride : rides) {\n int s = ride[0], e = ride[1], t = ride[2];\n rideStartAt[s].push_back({e, e - s + t}); // [end, dollar]\n }\n vector<long long> dp(n+1);\n for (int i = n-1; i >= 1; --i) {\n for (auto& [e, d] : rideStartAt[i]) {\n dp[i] = max(dp[i], dp[e] + d);\n }\n dp[i] = max(dp[i], dp[i + 1]);\n }\n return dp[1];\n }\n};\n```\n\n**Complexity**\n- Time: `O(M + N)`, where `N <= 10^5` is number points, `M <= 4*10^4` is length of `rides` array.\n- Space: `O(M + N)`\n\nIf you think this **post is useful**, I\'m happy if you **give a vote**. Any **questions or discussions are welcome!** Thank a lot.
| 204 | 7 |
[]
| 22 |
maximum-earnings-from-taxi
|
[Java/C++/Python] DP solution
|
javacpython-dp-solution-by-lee215-qnxc
|
Explanation\nSort A, solve it like Knapsack dp.\n\n\n# Complexity\nTime O(n + klogk), k = A.length\nSpace O(n)\n\n\nJava\njava\n public long maxTaxiEarnings(
|
lee215
|
NORMAL
|
2021-09-18T16:04:58.688243+00:00
|
2021-09-18T16:30:44.475789+00:00
| 13,840 | false |
# **Explanation**\nSort `A`, solve it like Knapsack dp.\n<br>\n\n# **Complexity**\nTime `O(n + klogk), k = A.length`\nSpace `O(n)`\n<br>\n\n**Java**\n```java\n public long maxTaxiEarnings(int n, int[][] A) {\n Arrays.sort(A, (a, b) -> a[0] - b[0]);\n long[] dp = new long[n + 1];\n int j = 0;\n for(int i = 1; i <= n; ++i) {\n dp[i] = Math.max(dp[i], dp[i - 1]);\n while (j < A.length && A[j][0] == i) {\n dp[A[j][1]] = Math.max(dp[A[j][1]], dp[i] + A[j][1] - A[j][0] + A[j][2]);\n ++j;\n }\n }\n return dp[n];\n }\n```\n**C++**\n```cpp\n long long maxTaxiEarnings(int n, vector<vector<int>>& A) {\n sort(A.begin(), A.end());\n vector<long long> dp(n+1);\n int j = 0;\n for(int i = 1; i <= n; ++i) {\n dp[i] = max(dp[i], dp[i - 1]);\n while (j < A.size() && A[j][0] == i)\n dp[A[j++][1]] = max(dp[A[j][1]], dp[i] + A[j][1] - A[j][0] + A[j][2]);\n }\n return dp[n];\n }\n```\n\n**Python**\n```py\n def maxTaxiEarnings(self, n, A):\n dp = [0] * (n + 1)\n A.sort()\n for i in xrange(n - 1, -1, -1):\n dp[i] = dp[i + 1]\n while A and i == A[-1][0]:\n s, e, t = A.pop()\n dp[i] = max(dp[i], dp[e] + e - s + t)\n return dp[0]\n```\n
| 86 | 7 |
[]
| 14 |
maximum-earnings-from-taxi
|
C++ || Brute ( Recursion ) -> Better ( DP ) -> Optimal ( DP + Binary Search ) || Clear and Concise
|
c-brute-recursion-better-dp-optimal-dp-b-seg8
|
1. Brute Force ( Recursion )\n In brute force we use simple recursion technique and opt between two choices:\n1. Opt for an ride and add value to the answer\n2.
|
jk20
|
NORMAL
|
2021-12-05T13:25:59.475807+00:00
|
2021-12-05T13:25:59.475848+00:00
| 4,668 | false |
## 1. Brute Force ( Recursion )\n In brute force we use simple recursion technique and opt between two choices:\n1. Opt for an ride and add value to the answer\n2. Skip the ride and move ahead\n\n```\nclass Solution {\npublic:\n long long recur(vector<vector<int>>&rides,int nn,int idx)\n {\n if(idx>=nn)\n return 0;\n int i;\n for(i=idx+1;i<nn;i++)\n {\n if(rides[i][0]>=rides[idx][1])\n break;\n }\n long long op1=recur(rides,nn,idx+1);\n long long op2=rides[idx][1]-rides[idx][0]+rides[idx][2]+recur(rides,nn,i);\n \n return max(op1,op2);\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n \n sort(rides.begin(),rides.end());\n int nn=rides.size();\n \n return recur(rides,nn,0);\n }\n};\n```\n\n## 2. Better Approach ( Recursion + Memoization )\n\n```\nclass Solution {\npublic:\n long long dp[(int)1e5];\n long long recur(vector<vector<int>>&rides,int nn,int idx)\n {\n if(idx>=nn)\n return 0;\n int i;\n if(dp[idx]!=-1)\n return dp[idx];\n for(i=idx+1;i<nn;i++)\n {\n if(rides[i][0]>=rides[idx][1])\n break;\n }\n long long op1=recur(rides,nn,idx+1);\n long long op2=rides[idx][1]-rides[idx][0]+rides[idx][2]+recur(rides,nn,i);\n \n return dp[idx]=max(op1,op2);\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n \n sort(rides.begin(),rides.end());\n int nn=rides.size();\n memset(dp,-1,sizeof dp);\n return recur(rides,nn,0);\n }\n};\n```\n\n## 3. Optimal Approach ( Recursion + Memoization + Binary Search )\n\n```\nclass Solution {\npublic:\n long long dp[(int)1e5];\n int find(vector<vector<int>>&events,int start,int toFind)\n {\n int low=start;\n int high=events.size()-1;\n int ans=-1;\n while(low<=high)\n {\n int mid=(low+high)/2;\n \n if(events[mid][0]>=toFind)\n {\n ans=mid;\n high=mid-1;\n }\n else\n {\n low=mid+1;\n }\n }\n \n return ans;\n \n }\n long long recur(vector<vector<int>>&rides,int nn,int idx)\n {\n if(idx>=nn)\n return 0;\n if(idx<0)\n return 0;\n if(dp[idx]!=-1)\n return dp[idx];\n \n /* O(n) time in worst case */\n // for(i=idx+1;i<nn;i++)\n // {\n // if(rides[i][0]>=rides[idx][1])\n // break;\n // }\n \n /* O(logn) time in worst case Binary Search */\n int i=find(rides,idx+1,rides[idx][1]);\n long long op1=recur(rides,nn,idx+1);\n long long op2=rides[idx][1]-rides[idx][0]+rides[idx][2]+recur(rides,nn,i);\n \n return dp[idx]=max(op1,op2);\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n \n sort(rides.begin(),rides.end());\n int nn=rides.size();\n memset(dp,-1,sizeof dp);\n return recur(rides,nn,0);\n }\n};\n```\n\n\n**Pls upvote if you found the post to be helpful.**\n\n
| 50 | 0 |
['Dynamic Programming', 'Recursion', 'C', 'Binary Tree', 'C++']
| 5 |
maximum-earnings-from-taxi
|
[Python] dp with binary search, explained
|
python-dp-with-binary-search-explained-b-fuel
|
This problem is very similar to problem 1235. Maximum Profit in Job Scheduling. The only difference is what profit we have given our ride: it is calculated as r
|
dbabichev
|
NORMAL
|
2021-09-18T16:01:39.766335+00:00
|
2021-09-18T16:01:39.766474+00:00
| 4,314 | false |
This problem is very similar to problem **1235.** Maximum Profit in Job Scheduling. The only difference is what profit we have given our ride: it is calculated as `rides[k][2] - rides[k][0] + rides[k][1]`.\n\n#### Complexity\nIt is `O(m log m)`, where `m = len(rides)`.\n\n#### Code\n```python\nimport bisect\n\nclass Solution:\n def maxTaxiEarnings(self, n, rides):\n rides = sorted(rides)\n S = [i[0] for i in rides]\n \n m = len(rides)\n dp = [0]*(m+1)\n for k in range(m-1, -1, -1):\n temp = bisect_left(S, rides[k][1])\n dp[k] = max(dp[k+1], rides[k][2] - rides[k][0] + rides[k][1] + dp[temp])\n \n return dp[0]\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**
| 39 | 4 |
['Binary Search', 'Dynamic Programming']
| 6 |
maximum-earnings-from-taxi
|
[C++] DP with Binary Search solution
|
c-dp-with-binary-search-solution-by-mani-y7ja
|
\nclass Solution {\n long long dp[100005];\n\t// Searching for next passenger who can sit in the car\n int binarySearch(vector<vector<int>>& rides,int va
|
manishbishnoi897
|
NORMAL
|
2021-09-18T16:06:47.735931+00:00
|
2021-09-18T16:41:31.152128+00:00
| 3,439 | false |
```\nclass Solution {\n long long dp[100005];\n\t// Searching for next passenger who can sit in the car\n int binarySearch(vector<vector<int>>& rides,int val){\n int s=0,e=rides.size()-1;\n int ans=rides.size();\n while(s<=e){\n int mid = s + (e-s)/2;\n if(rides[mid][0]>=val){\n ans=mid;\n e=mid-1;\n }\n else{\n s=mid+1;\n }\n }\n return ans;\n }\n \n long long helper(int i,vector<vector<int>>& rides){\n if(i==rides.size()){\n return 0;\n }\n if(dp[i]!=-1) return dp[i];\n long long op1 = helper(i+1,rides); // We didn\'t pick this ith passenger\n int idx = binarySearch(rides,rides[i][1]); \n long long op2 = rides[i][1]-rides[i][0] + rides[i][2] + helper(idx,rides); // We pick this ith passenger\n return dp[i]=max(op1,op2);\n }\n \n \npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n memset(dp,-1,sizeof dp);\n sort(rides.begin(),rides.end());\n return helper(0,rides);\n }\n};\n```\n**Hit Upvote if you like :)**
| 30 | 2 |
['Binary Search', 'Dynamic Programming', 'C']
| 3 |
maximum-earnings-from-taxi
|
DP with Sweep
|
dp-with-sweep-by-votrubac-73on
|
Sort the rides and then process rides in order of their pick-up points. Track the max profit for each point in dp.\n\nSince we are using an array, we need to al
|
votrubac
|
NORMAL
|
2021-09-18T22:41:58.019870+00:00
|
2021-09-19T05:34:54.965466+00:00
| 3,145 | false |
Sort the rides and then process rides in order of their pick-up points. Track the max profit for each point in `dp`.\n\nSince we are using an array, we need to also do the sweep to carry forward the max profit till the next pick-up point.\n\n**C++**\n```cpp\nlong long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n long long dp[100001] = {}, pos = 0;\n sort(begin(rides), end(rides));\n for (const auto &r : rides) {\n for (; pos < r[0]; ++pos)\n dp[pos + 1] = max(dp[pos + 1], dp[pos]);\n dp[r[1]] = max(dp[r[1]], dp[r[0]] + r[1] - r[0] + r[2]);\n }\n return *max_element(begin(dp), begin(dp) + n + 1);\n}\n```\n**Complexity Analysis**\n- Time: O(m log m), where `m` is the number of rides. This is under the assumption that `m log m` would be larger than `n`.\n- Memory: O(n) for tabulation.
| 25 | 2 |
[]
| 3 |
maximum-earnings-from-taxi
|
c++ | memoization + binary search
|
c-memoization-binary-search-by-_seg_faul-5sba
|
Idea\nFor every ar[i], I have 2 options: attend or not attend.\nIn case I don\'t attend, simply proceed forward by doing pos+1.\nIn case we attend a particular
|
_seg_fault
|
NORMAL
|
2021-09-18T16:12:36.371485+00:00
|
2021-09-21T07:26:13.842240+00:00
| 2,364 | false |
<b>Idea</b>\nFor every `ar[i]`, I have 2 options: attend or not attend.\nIn case I don\'t attend, simply proceed forward by doing `pos+1`.\nIn case we attend a particular trip, find the next index from which, we can attend trips without intersecting with the current trip. If we do this search linearly, our time complexity will reach O(`n^2`). So, we sort the array beforehand with respect to the start of the trip and using binary search, find the next index. This brings the time complexity to O(`n*logn`). Finally, we memoize our results to save repeated calculations.\nPlease comment if anything is unclear.\n```\nlong long dp[30001];\nclass Solution {\npublic:\nlong long help(vector<vector<int>> &ar,int pos){\n int n=ar.size();\n if(pos==n) return 0;\n if(dp[pos]!=-1) return dp[pos];\n // either I attend ar[pos] trip or not\n long long ans=help(ar,pos+1);\n // find the first starting time JUST greater than ending time of ar[pos] in log(n) time using binary search\n int lo=pos+1,hi=n-1,nextPos=n;\n while (lo<=hi){\n int mid=lo+(hi-lo)/2;\n if(ar[mid][0]>=ar[pos][1]){\n nextPos=mid;\n hi=mid-1;\n }else lo=mid+1;\n }\n dp[pos]=max(ans,ar[pos][2]+help(ar,nextPos));\n return dp[pos];\n}\n\nlong long maxTaxiEarnings(int n, vector<vector<int>>& ar) {\n memset(dp,-1,sizeof(dp));\n for(auto &it:ar) it[2]+=it[1]-it[0];\n sort(ar.begin(),ar.end());\n return help(ar,0);\n}\n};\n```
| 19 | 0 |
['Memoization', 'Binary Tree']
| 3 |
maximum-earnings-from-taxi
|
✅C++ || Recursion->Memoization->Tabulation || 01-Knapsack
|
c-recursion-memoization-tabulation-01-kn-9ez0
|
Method -1 [Recursion]\n\n\n\nT->O(Expo) && S->O(m) [Recursion stack space]\n\n\tclass Solution {\n\t\tpublic:\n\t\t\tlong long f(int i,vector>& r, vector& st,in
|
abhinav_0107
|
NORMAL
|
2022-10-01T12:25:35.969880+00:00
|
2022-10-01T12:26:05.392433+00:00
| 1,948 | false |
# Method -1 [Recursion]\n\n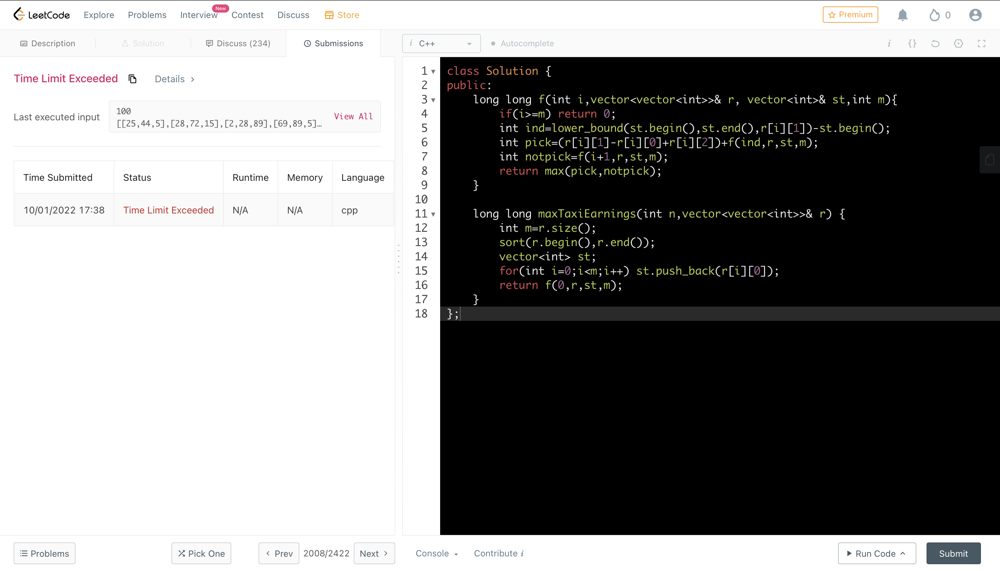\n\n**T->O(Expo) && S->O(m) [Recursion stack space]**\n\n\tclass Solution {\n\t\tpublic:\n\t\t\tlong long f(int i,vector<vector<int>>& r, vector<int>& st,int m){\n\t\t\t\tif(i>=m) return 0;\n\t\t\t\tint ind=lower_bound(st.begin(),st.end(),r[i][1])-st.begin();\n\t\t\t\tint pick=(r[i][1]-r[i][0]+r[i][2])+f(ind,r,st,m);\n\t\t\t\tint notpick=f(i+1,r,st,m);\n\t\t\t\treturn max(pick,notpick);\n\t\t\t}\n\n\t\t\tlong long maxTaxiEarnings(int n,vector<vector<int>>& r) {\n\t\t\t\tint m=r.size();\n\t\t\t\tsort(r.begin(),r.end());\n\t\t\t\tvector<int> st;\n\t\t\t\tfor(int i=0;i<m;i++) st.push_back(r[i][0]);\n\t\t\t\treturn f(0,r,st,m);\n\t\t\t}\n\t\t};\n\t\t\n# Method - 2 [Memoization]\t\n\n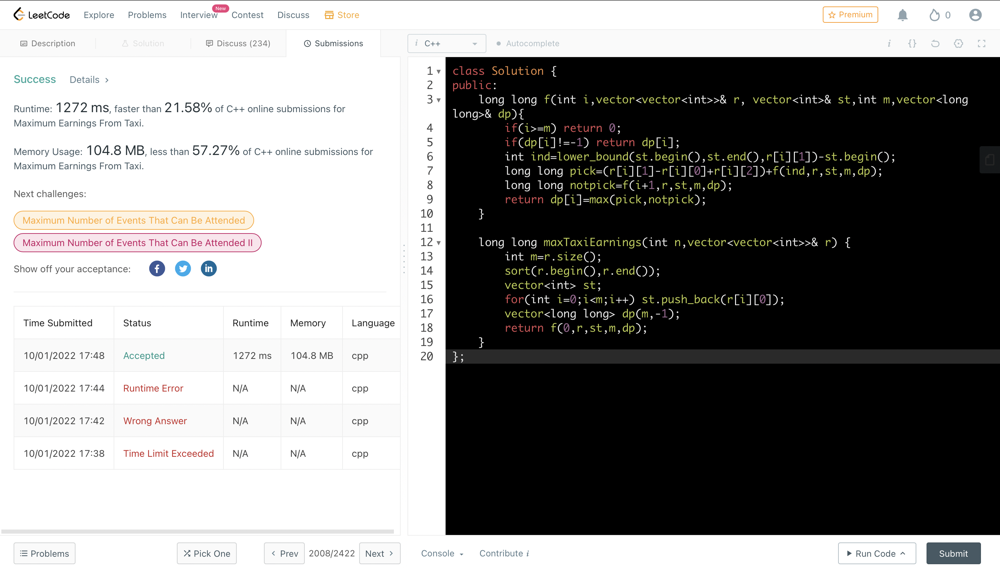\n\n**T->O(m) && S->O(m) + O(m) [Recursion stack space]**\n\n\tclass Solution {\n\tpublic:\n\t\tlong long f(int i,vector<vector<int>>& r, vector<int>& st,int m,vector<long long>& dp){\n\t\t\tif(i>=m) return 0;\n\t\t\tif(dp[i]!=-1) return dp[i];\n\t\t\tint ind=lower_bound(st.begin(),st.end(),r[i][1])-st.begin();\n\t\t\tlong long pick=(r[i][1]-r[i][0]+r[i][2])+f(ind,r,st,m,dp);\n\t\t\tlong long notpick=f(i+1,r,st,m,dp);\n\t\t\treturn dp[i]=max(pick,notpick);\n\t\t}\n\n\t\tlong long maxTaxiEarnings(int n,vector<vector<int>>& r) {\n\t\t\tint m=r.size();\n\t\t\tsort(r.begin(),r.end());\n\t\t\tvector<int> st;\n\t\t\tfor(int i=0;i<m;i++) st.push_back(r[i][0]);\n\t\t\tvector<long long> dp(m,-1);\n\t\t\treturn f(0,r,st,m,dp);\n\t\t}\n\t};\n\t\n# Method -3 [Tabulation]\n\n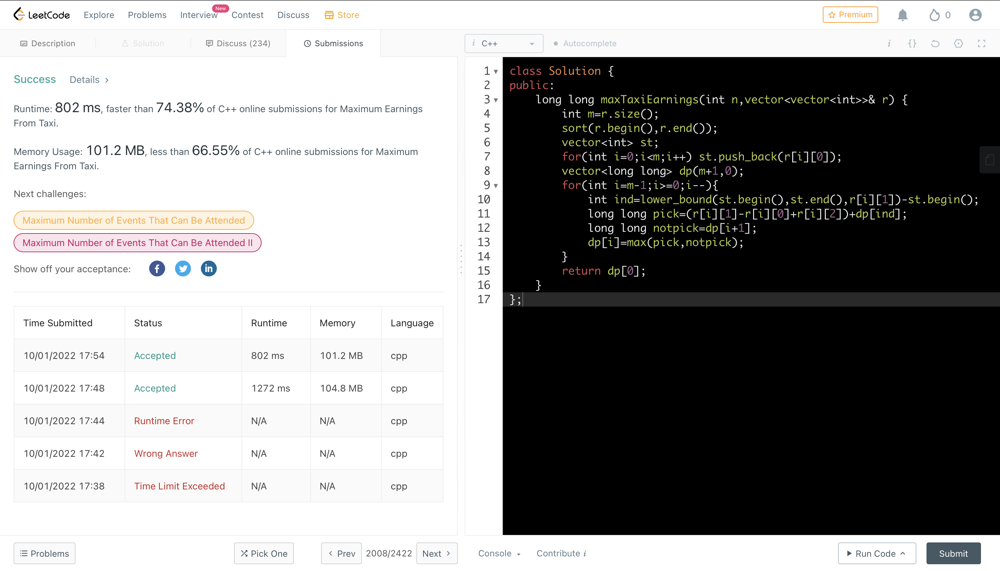\n\n\n**T->O(m) && S->O(m)**\n\n\tclass Solution {\n\tpublic:\n\t\tlong long maxTaxiEarnings(int n,vector<vector<int>>& r) {\n\t\t\tint m=r.size();\n\t\t\tsort(r.begin(),r.end());\n\t\t\tvector<int> st;\n\t\t\tfor(int i=0;i<m;i++) st.push_back(r[i][0]);\n\t\t\tvector<long long> dp(m+1,0);\n\t\t\tfor(int i=m-1;i>=0;i--){\n\t\t\t\tint ind=lower_bound(st.begin(),st.end(),r[i][1])-st.begin();\n\t\t\t\tlong long pick=(r[i][1]-r[i][0]+r[i][2])+dp[ind];\n\t\t\t\tlong long notpick=dp[i+1];\n\t\t\t\tdp[i]=max(pick,notpick);\n\t\t\t}\n\t\t\treturn dp[0];\n\t\t}\n\t};\n
| 17 | 1 |
['Binary Search', 'Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++']
| 2 |
maximum-earnings-from-taxi
|
weighted Job Scheduling , C++
|
weighted-job-scheduling-c-by-itz_pankaj-ef2l
|
\n\nWe have two choice\n\nTake this job with the last non overlapping job\nDon\'t take this job\nSo, for the first option we have to compute which job is not ov
|
itz_pankaj
|
NORMAL
|
2021-09-18T16:02:16.836312+00:00
|
2021-09-18T16:07:00.957931+00:00
| 3,179 | false |
\n\nWe have two choice\n\nTake this job with the last non overlapping job\nDon\'t take this job\nSo, for the first option we have to compute which job is not overlapping to this job. It takes O(N) to compute for each job.\nAnd for the second option we just take its previous profit without including current job.\n```\n#define ll long long \nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& jobs) \n {\n for(auto &x:jobs) x[2] += x[1]-x[0];\n \n map<ll,ll> dp;\n \n sort(jobs.begin(), jobs.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] > b[0];\n });\n ll maxT = 0;\n for (auto job : jobs) {\n auto it = dp.lower_bound(job[1]);\n ll pre = (it == dp.end()) ? 0 : it->second;\n maxT = max(maxT, job[2] + pre);\n dp[job[0]] = maxT;\n }\n \n return maxT;\n \n }\n};\n```
| 17 | 0 |
[]
| 2 |
maximum-earnings-from-taxi
|
C++ | Recursion + DP | Workaround from TLE
|
c-recursion-dp-workaround-from-tle-by-sh-2nf5
|
TLE - 65/82 TC passed\nMy first try was pretty straight forward, include and don\'t include current ride\n\nclass Solution {\npublic:\n long long helper(int
|
shield75_
|
NORMAL
|
2021-09-18T17:56:45.447750+00:00
|
2021-10-06T09:08:14.970615+00:00
| 1,412 | false |
1. TLE - 65/82 TC passed\nMy first try was pretty straight forward, include and don\'t include current ride\n```\nclass Solution {\npublic:\n long long helper(int &n, vector<vector<int>>& rides,int i,int laststop,vector<long long> &dp)\n {\n if(i==rides.size()) return 0;\n if(dp[laststop]!=-1) return dp[laststop];\n long long ans=0;\n int profit=rides[i][1]-rides[i][0]+rides[i][2];\n ans=max(helper(n,rides,i+1,laststop,dp),rides[i][0]>=laststop?profit+helper(n,rides,i+1,rides[i][1],dp):0);\n return dp[laststop]=ans;\n }\n \n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<long long> dp(n+1,-1);\n sort(rides.begin(),rides.end());\n return helper(n,rides,0,1,dp);\n }\n};\n```\n\n2. TLE - 70/82 TC passed\nThen i want to start including the ride only if it\'s start point is greater than current stop.\nand changed my DP to calculate at a given position i rather than laststop.\n```\nclass Solution {\npublic:\n long long helper(int &n, vector<vector<int>>& rides,int i,int laststop,vector<long long> &dp)\n {\n if(i==rides.size()) return 0;\n if(dp[i]!=-1) return dp[i];\n long long ans=0;\n int profit=rides[i][1]-rides[i][0]+rides[i][2];\n int j=i+1;\n while(j<rides.size() && rides[j][0]<rides[i][1]) j++;\n ans=max(helper(n,rides,i+1,laststop,dp),profit+helper(n,rides,j,rides[i][1],dp));\n return dp[i]=ans;\n }\n \n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<long long> dp(rides.size(),-1);\n sort(rides.begin(),rides.end());\n return helper(n,rides,0,1,dp);\n }\n};\n```\n\n3. Passing solution.\nCouldn\'t think to use binary search above because i thought since we already sorted and next valid ride will be close by. Thanks to intelligent people to discuss, i immediately corrected my mistake and it passed.\n```\nclass Solution {\npublic:\n long long helper(int &n, vector<vector<int>>& rides,int i,int laststop,vector<long long> &dp)\n {\n if(i==rides.size()) return 0;\n if(dp[i]!=-1) return dp[i];\n long long ans=0;\n int profit=rides[i][1]-rides[i][0]+rides[i][2];\n int end=rides.size()-1,start=i+1,mid,next=end+1;\n while(start<=end) \n {\n mid=start+(end-start)/2;\n if(rides[mid][0]>=rides[i][1])\n {\n next=mid;\n end=mid-1;\n }\n else start=mid+1;\n }\n ans=max(helper(n,rides,i+1,laststop,dp),profit+helper(n,rides,next,rides[i][1],dp));\n return dp[i]=ans;\n }\n \n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<long long> dp(rides.size(),-1);\n sort(rides.begin(),rides.end());\n return helper(n,rides,0,1,dp);\n }\n};\n```
| 14 | 0 |
['Dynamic Programming', 'Recursion', 'C', 'Binary Tree', 'C++']
| 4 |
maximum-earnings-from-taxi
|
Java | Time : O(n) | Space : O(n) | Dp
|
java-time-on-space-on-dp-by-rickypason-kxrs
|
\n//Example\n//Input : [[1,6,1],[3,10,2],[10,12,3],[11,12,2],[12,15,2],[13,18,1]]\n//Output : 20\n\n//1. Build map {key : end point, value : list of rides ends
|
rickypason
|
NORMAL
|
2022-05-18T06:01:14.638274+00:00
|
2022-05-18T06:01:14.638297+00:00
| 868 | false |
```\n//Example\n//Input : [[1,6,1],[3,10,2],[10,12,3],[11,12,2],[12,15,2],[13,18,1]]\n//Output : 20\n\n//1. Build map {key : end point, value : list of rides ends at key}\n//{\n//(6, [1,6,1]),\n//(10,[3,10,2]),\n//(12,[10,12,3], [11,12,2]),\n//(15, [12,15,2]),\n//(18, [13,18,1])\n//}\n\n//2. Consider sub problems, what is the max earn till i (0<=i<=n) ?\n// we denote its value as dp[i]\n\n//3, eventually, we want to build up solution dp[i] from previous calculated \n// solutions to previous subproblems. => dp transition function\n// how do we know about this ? more examples ....\n\n//dp[0], dp[1], dp[2], dp[3], dp[4], dp[5], -> no possible passenger dropping, no gain\n\n// i = 6\n// dp[6] = Math.max(choice 1, choice 2)\n// choice 1 : we did not pick up passenger 1, dp[6] = dp[5] = 0\n// choice 2 : we picked up passenger 1, dp[6] = end_1 - start_1 + tip_1 = 6\n// dp[6] = Math.max(0, 6) = 6\n\n//dp[7], dp[8], dp[9] = dp[6] -> no possible passenger dropping, no gain, dp value remains\n\n// i = 10\n//dp[10] = Math.max(choice 1, choice 2)\n//choice 1 : we did not pick up passenger 2, dp[10] = dp[9] = 6\n//choice 2 : we picked up passenger 2, since passenger starts at i = 3, we have\n// dp[10] = dp[3] + gain from passenger 2 = 0 + 9 = 9\n// dp[10] = Math.max(6,9) = 9\n\n\n//dp[11] = dp[10] = 9\n\n//i = 12 (tricky one!!)\n//dp[12] = Math.max(choice 1, choice 2, choice 3)\n//choice 1 : we did not pick up any passenger end at i = 12, dp[12] = dp[11] = 9\n//choice 2 : we picked up passenger 3,\n// dp[12] = dp[10] + gain from passenger 3 = 9 + 5 = 14\n//choice 3 : we picked up passenger 4\n// dp[12] = dp[11] + gain from passenger 4 = 9 + 3 = 12\n//dp[12] = Math.max(choice 1, choice 2, choice 3) = 14\n\n// so.... I think you get the gist by far ..\n\n\n\n\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] rides) {\n Map<Integer,List<int[]>> map = new HashMap<>();\n for(int[] ride:rides){\n map.putIfAbsent(ride[1],new ArrayList<int[]>());\n map.get(ride[1]).add(ride);\n }\n long[] dp = new long[n+1];\n for(int i=1;i<=n;i++){\n dp[i] = dp[i-1];\n if(map.containsKey(i)){\n for(int[] r:map.get(i)){\n dp[i] = Math.max(dp[i],r[1]-r[0]+r[2]+dp[r[0]]);\n }\n }\n }\n return dp[n];\n }\n}\n```
| 13 | 0 |
['Dynamic Programming']
| 2 |
maximum-earnings-from-taxi
|
Easy DP - Explained - O(n)
|
easy-dp-explained-on-by-azhw1983-wuep
|
Please upvote if you find the solution helpful :) Thanks!\n\n\n# Approach 1: DP\n# Time: O(n)\n# Space: O(n)\n\n# Intuition: \n# We want to loop from location
|
azhw1983
|
NORMAL
|
2022-01-09T16:12:20.446229+00:00
|
2022-01-09T16:12:20.446271+00:00
| 1,627 | false |
# Please upvote if you find the solution helpful :) Thanks!\n\n```\n# Approach 1: DP\n# Time: O(n)\n# Space: O(n)\n\n# Intuition: \n# We want to loop from location = 1 to n and at each step check if this location is an end point or not .\n# If it is an end point then we check all of its corresponding start points and get the maximum fare we can earn .\n# In order to quickly check if this number is an end point or not maintain a hashmap where keys="end point" and the values="[start_point, tip]""\n\ndef maxTaxiEarnings(n, rides):\n """\n :type n: int\n :type rides: List[List[int]]\n :rtype: int\n """\n import collections\n hashmap = collections.defaultdict(list)\n for start, end, tip in rides:\n hashmap[end].append((start, tip))\n\n dp = [0]*(n+1)\n for location in range(1, n+1):\n # taxi driver has the fare from the previous location, let\'s see if he/she can make more money by dropping someone at the current location\n # we check that by checking if the current location is an end point, among the ones gathered as hashmap keys\n dp[location] = dp[location-1] \n if location in hashmap:\n profitDroppingPassengersHere = 0\n # for each ending trip at the current \'location\'\n for start, tip in hashmap[location]:\n profitDroppingPassengersHere = max(profitDroppingPassengersHere, location - start + tip + dp[start])\n # update the dp\n dp[location] = max(dp[location], profitDroppingPassengersHere)\n\n return dp[n]\n```
| 11 | 0 |
['Dynamic Programming', 'Python']
| 3 |
maximum-earnings-from-taxi
|
"Maximum Earnings From Taxi" [C++ DP]- Easy Solution
|
maximum-earnings-from-taxi-c-dp-easy-sol-cbpc
|
C++ Easy Dynamic Programming Solution :-\nOur task is to choose passengers optimally such that total number of dollars will be Maximum. We are using a hashmap t
|
sagnik_mitra
|
NORMAL
|
2021-09-20T06:16:07.989959+00:00
|
2021-09-20T06:16:07.989999+00:00
| 2,467 | false |
### C++ Easy Dynamic Programming Solution :-\nOur task is to choose passengers optimally such that total number of dollars will be **Maximum**. We are using a hashmap to keep track of all the destination points which have the same boarding point of the passengers. After that we are using Dynamic Programming to choose the optimal starting point and the optimal destination point to get the max profit.\n\n* **Code** :-\n```\nclass Solution {\npublic:\n map<int,vector<pair<int,int>>> mpp; // To store the destination points and total number of dollars\n vector<long long> memo;\n Solution(){\n mpp.clear(); // Initializing the map\n memo.resize(100005,-1); // Initializing the vector with -1\n }\n long long dp(int idx,int n){\n if(idx>n) return 0; // The journey of the taxi ends\n if(memo[idx]!=-1) return memo[idx]; // If this subproblem is already solved, directly getting the answer\n long long ans=0;\n for(auto x:mpp[idx]){\n ans=max(ans,dp(x.first,n)+x.second); // Determining which schedule should we take to get max profit\n }\n\t\t// If there is no schedule at that starting point the ans will be 0 and proceed to the next condition\n ans=max(ans,dp(idx+1,n)); // Checking if we get the max profit by not taking the particular starting point\n // cout<<idx<<" "<<ans<<endl;\n return memo[idx]=ans;\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n for(auto x: rides){\n mpp[x[0]].push_back({x[1],(x[1]-x[0]+x[2])}); // Storing the destination points and total number of dollars of the passenges of same starting point.\n }\n return dp(1,n); // Finally we get our answer :)\n }\n\t// Happy Coding\n};\n```\n\n* Time Complexity :- O(n*logn)\n* Space Complexity :- O(n)\n\nIf you like the blog make sure you hit the Upvote button. Thanks in Advance :)\n
| 11 | 0 |
['Dynamic Programming']
| 2 |
maximum-earnings-from-taxi
|
Java | PriorityQueue | O(NlogN) time | O(N) space | Easy solution same as max profit in job schedule
|
java-priorityqueue-onlogn-time-on-space-nld1m
|
Approach\n Describe your first thoughts on how to solve this problem. \nIntuition behind this is same as maximum profit in job scheduling problem.\n1. Sort ride
|
achinyar
|
NORMAL
|
2022-11-27T03:44:56.885651+00:00
|
2022-12-07T03:09:44.611075+00:00
| 1,773 | false |
# Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition behind this is same as maximum profit in job scheduling problem.\n1. Sort rides based on start time.\n2. Use min heap(priority queue) while comparing end time.\n3. Keep adding to the queue with cumulative profit. \n4. Keep track of max profit.\n\nNote : Used Long array in queue instead of int array, since max value can be long and if int array was used, some of the test cases fail.\n\n# Complexity\n- Time complexity:O(NlogN)\n Sorting ride take O(NlogN). Iterating through each ride would take O(N). Hence total is (N + NlogN) = O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n \n\n- Space complexity: O(N). We store each ride in the queue ammounting to worst case O(N) time.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] rides) {\n //Sort based on start time\n Arrays.sort(rides, (a,b) -> a[0] - b[0]);\n long max = 0;\n\n //Storing Long array instead of Int array, since max value is long.\n //Sort based on end time\n PriorityQueue<long[]> myQueue = new PriorityQueue<long[]>((a,b) -> Long.compare(a[0],b[0]));\n\n for (int i = 0; i < rides.length; i++) {\n int start = rides[i][0];\n int end = rides[i][1];\n long profit = end - start + Long.valueOf(rides[i][2]);\n\n while (!myQueue.isEmpty() && start >= myQueue.peek()[0]) {\n max = Math.max(max, myQueue.peek()[1]);\n myQueue.poll();\n }\n myQueue.offer(new long[] {end, profit + max});\n }\n\n while (!myQueue.isEmpty()) {\n max = Math.max(max, myQueue.poll()[1]);\n }\n\n return max;\n }\n}\n\n```
| 10 | 0 |
['Heap (Priority Queue)', 'Java']
| 1 |
maximum-earnings-from-taxi
|
[JAVA] 2 DP approaches from naive recursive to tabulation
|
java-2-dp-approaches-from-naive-recursiv-z1cg
|
second approach - using n, and find maximum for every i from 1 to n\n\n/**\n * naive recursive using n\n * time = 2 ^ n ?\n */\npublic long maxTaxiEarnings7(int
|
luffyzhou
|
NORMAL
|
2022-02-17T20:34:07.622712+00:00
|
2022-02-17T20:34:41.024686+00:00
| 873 | false |
**second approach - using n, and find maximum for every i from 1 to n**\n```\n/**\n * naive recursive using n\n * time = 2 ^ n ?\n */\npublic long maxTaxiEarnings7(int n, int[][] rides) {\n\treturn helper(rides, n, 0);\n}\n\nprivate long helper(int[][] rides, int n, int curPoint) {\n\tif (curPoint == n)\n\t\treturn 0;\n\tlong include = 0;\n\tfor (int i = 0; i < rides.length; i++) {\n\t\tif (rides[i][0] == curPoint) {\n\t\t\tint[] ride = rides[i];\n\t\t\tinclude = Math.max(include, ride[1] - ride[0] + ride[2] + helper(rides, n, ride[1]));\n\t\t}\n\t}\n\tlong exclude = helper(rides, n, curPoint + 1);\n\treturn Math.max(include, exclude);\n}\n```\n```\n/**\n * bottom up tabulation\n * time = m * n, where m = rides.length\n */\npublic long maxTaxiEarnings8(int n, int[][] rides) {\n\tlong[] dp = new long[n + 1];\n\tfor (int curPoint = n - 1; curPoint >= 0; curPoint--) {\n\t\tlong include = 0;\n\t\tfor (int i = 0; i < rides.length; i++) {\n\t\t\tif (rides[i][0] == curPoint) {\n\t\t\t\tint[] ride = rides[i];\n\t\t\t\tinclude = Math.max(include, ride[1] - ride[0] + ride[2] +\n\t\t\t\t\t\tdp[ride[1]]);\n\t\t\t}\n\t\t}\n\t\tlong exclude = dp[curPoint + 1];\n\t\tdp[curPoint] = Math.max(include, exclude);\n\t}\n\treturn dp[0];\n}\n```\n```\n/**\n * bottom up tabulation with time optimization\n * time = m * log(m) + m + n\n * from maxTaxiEarnings8, we see that we have an inner for-loop\n * for finding all the rides that start at curPoint, however,\n * if we sort rides, then we don\'t have to iterate through all the\n * rides again, we just need to keep a pointer for rides that goes\n * in decreasing order\n */\npublic long maxTaxiEarnings9(int n, int[][] rides) {\n\tArrays.sort(rides, (o1, o2) -> Integer.compare(o1[0], o2[0]));\n\tlong[] dp = new long[n + 1];\n\tint curRide = rides.length - 1;\n\tfor (int curPoint = n - 1; curPoint >= 0; curPoint--) {\n\t\tlong include = 0;\n\t\twhile (curRide >= 0 && rides[curRide][0] == curPoint) {\n\t\t\tint[] ride = rides[curRide];\n\t\t\tinclude = Math.max(include, ride[1] - ride[0] + ride[2] +\n\t\t\t\t\tdp[ride[1]]);\n\t\t\tcurRide--;\n\t\t}\n\t\tlong exclude = dp[curPoint + 1];\n\t\tdp[curPoint] = Math.max(include, exclude);\n\t}\n\treturn dp[0];\n}\n```\n\n\n**first approach - only using an index for rides**\n```\n/**\n * naive recursive\n * time = 2 ^ m * m, where m = rides.length\n * 2 ^ m = include or exclude\n * m = cost of findNextAvailableRide\n */\npublic long maxTaxiEarnings4(int n, int[][] rides) {\n\tArrays.sort(rides, (o1, o2) -> Integer.compare(o1[0], o2[0]));\n\treturn helper(rides, 0);\n}\n\nprivate long helper(int[][] rides, int idx) {\n\tif (idx == rides.length)\n\t\treturn 0;\n\tint[] curRide = rides[idx];\n\tint nextAvailableRide = findNextAvailableRide(rides, idx, curRide[1]);\n\tlong include = curRide[1] - curRide[0] + curRide[2]\n\t\t\t+ helper(rides, nextAvailableRide);\n\tlong exclude = helper(rides, idx + 1);\n\treturn Math.max(include, exclude);\n}\n\nprivate int findNextAvailableRide(int[][] rides, int cur, int preEnd) {\n\tfor (int i = cur + 1; i < rides.length; i++) {\n\t\tif (rides[i][0] >= preEnd)\n\t\t\treturn i;\n\t}\n\treturn rides.length;\n}\n```\n```\n/**\n * dp bottom up\n * time = m * m, where m = rides.length\n * first m = for loop\n * second m = cost of findNextAvailableRide\n * space = m\n */\npublic long maxTaxiEarnings5(int n, int[][] rides) {\n\tArrays.sort(rides, (o1, o2) -> Integer.compare(o1[0], o2[0]));\n\tint m = rides.length;\n\tlong[] dp = new long[m + 1];\n\tfor (int idx = m - 1; idx >= 0; idx--) {\n\t\tint[] curRide = rides[idx];\n\t\tint nextAvailableRide = findNextAvailableRide(rides, idx, curRide[1]);\n\t\tlong include = curRide[1] - curRide[0] + curRide[2] + dp[nextAvailableRide];\n\t\tlong exclude = dp[idx + 1];\n\t\tdp[idx] = Math.max(include, exclude);\n\t}\n\treturn dp[0];\n}\n```\n```\n/**\n * dp bottom up using binary search\n * time = m * log(m)\n * m = for loop\n * log(m) = cost of findNextAvailableRideBS\n */\npublic long maxTaxiEarnings6(int n, int[][] rides) {\n\tArrays.sort(rides, (o1, o2) -> Integer.compare(o1[0], o2[0]));\n\tint m = rides.length;\n\tlong[] dp = new long[m + 1];\n\tfor (int idx = m - 1; idx >= 0; idx--) {\n\t\tint[] curRide = rides[idx];\n\t\tint nextAvailableRide = findNextAvailableRideBS(rides, idx, curRide[1]);\n\t\tlong include = curRide[1] - curRide[0] + curRide[2] + dp[nextAvailableRide];\n\t\tlong exclude = dp[idx + 1];\n\t\tdp[idx] = Math.max(include, exclude);\n\t}\n\treturn dp[0];\n}\n\nprivate int findNextAvailableRideBS(int[][] rides, int lo, int preEnd) {\n\tint hi = rides.length;\n\twhile (lo < hi) {\n\t\tint mid = lo + (hi - lo) / 2;\n\t\tif (rides[mid][0] < preEnd)\n\t\t\tlo = mid + 1;\n\t\telse\n\t\t\thi = mid;\n\t}\n\treturn lo;\n}\n```
| 7 | 0 |
['Dynamic Programming']
| 2 |
maximum-earnings-from-taxi
|
Top Down DP | Binary Search [Python]
|
top-down-dp-binary-search-python-by-vegi-9i8s
|
\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n dp={}\n rides.sort(key=lambda x:x[0]) #sorting based on
|
vegishanmukh7
|
NORMAL
|
2021-09-18T16:04:51.003773+00:00
|
2021-09-18T16:04:51.003804+00:00
| 1,048 | false |
```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n dp={}\n rides.sort(key=lambda x:x[0]) #sorting based on start points\n def recurse(i):\n if(i>=len(rides)):return 0 #no other taxi rides left\n if(i in dp):return dp[i]\n x=recurse(i+1) #not considering i\'th ride\n #binary searching for the value in right of i to find the next ride\n l=i\n r=len(rides)\n while(l<r):\n mid=(l+r)//2\n if(rides[mid][0]>=rides[i][1]):\n r=mid\n else:\n l=mid+1\n x=max(x,rides[i][1]-rides[i][0]+rides[i][2]) #considering i as last element\n x=max(x,recurse(r)+rides[i][1]-rides[i][0]+rides[i][2]) #considering i and next ride\n dp[i]=x\n return x\n return fun(0)\n```\n
| 7 | 0 |
[]
| 0 |
maximum-earnings-from-taxi
|
Recursion->Memoization->Tabulation
|
recursion-memoization-tabulation-by-ved0-55yj
|
Recursion\n\nclass Solution {\npublic:\n int getNextCurr(vector<vector<int>>& rides,int start,int key){\n int end=rides.size()-1;\n int nextCur
|
Ved07
|
NORMAL
|
2023-06-07T18:56:46.123557+00:00
|
2023-06-07T18:56:46.123591+00:00
| 915 | false |
# Recursion\n```\nclass Solution {\npublic:\n int getNextCurr(vector<vector<int>>& rides,int start,int key){\n int end=rides.size()-1;\n int nextCurr=rides.size();\n while(start<=end){\n int mid=(start+end)/2;\n if(rides[mid][0]>=key){\n nextCurr=mid;\n end=mid-1;\n }\n else start=mid+1;\n }\n return nextCurr;\n\n }\n long long maxIncome(int curr,vector<vector<int>>& rides){\n if(curr==rides.size())return 0;\n long long notpick=maxIncome(curr+1,rides);\n int nextCurr=getNextCurr(rides,curr,rides[curr][1]);\n long long pick=(rides[curr][1]-rides[curr][0]+rides[curr][2])+maxIncome(nextCurr,rides);\n return max(pick,notpick);\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n sort(rides.begin(),rides.end());\n return maxIncome(0,rides);\n \n }\n};\n```\n# Memoization\n```\nclass Solution {\npublic:\n int getNextCurr(vector<vector<int>>& rides,int start,int key){\n int end=rides.size()-1;\n int nextCurr=rides.size();\n while(start<=end){\n int mid=(start+end)/2;\n if(rides[mid][0]>=key){\n nextCurr=mid;\n end=mid-1;\n }\n else start=mid+1;\n }\n return nextCurr;\n\n }\n long long maxIncome(int curr,vector<vector<int>>& rides,vector<long long>& dp){\n if(curr==rides.size())return 0;\n if(dp[curr]!=-1) return dp[curr];\n long long notpick=maxIncome(curr+1,rides,dp);\n int nextCurr=getNextCurr(rides,curr,rides[curr][1]);\n long long pick=(rides[curr][1]-rides[curr][0]+rides[curr][2])+maxIncome(nextCurr,rides,dp);\n return dp[curr]=max(pick,notpick);\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n sort(rides.begin(),rides.end());\n vector<long long> dp(rides.size(),-1);\n return maxIncome(0,rides,dp);\n \n }\n};\n```\n\n# Tabulation\n```\nclass Solution {\npublic:\n int getNextCurr(vector<vector<int>>& rides,int start,int key){\n int end=rides.size()-1;\n int nextCurr=rides.size();\n while(start<=end){\n int mid=(start+end)/2;\n if(rides[mid][0]>=key){\n nextCurr=mid;\n end=mid-1;\n }\n else start=mid+1;\n }\n return nextCurr;\n\n }\n\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n sort(rides.begin(),rides.end());\n vector<long long> dp(rides.size()+1,0);\n for(int curr=rides.size()-1;curr>=0;curr--){\n long long notpick=dp[curr+1];\n int nextCurr=getNextCurr(rides,curr,rides[curr][1]);\n long long pick=((long long)rides[curr][1]-(long long)rides[curr][0]+(long long)rides[curr][2])+dp[nextCurr];\n dp[curr]=max(pick,notpick);\n\n }\n return dp[0];\n \n }\n};\n```
| 5 | 0 |
['Binary Search', 'Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 1 |
maximum-earnings-from-taxi
|
Java DP 10 lines of clean code, beat 65%
|
java-dp-10-lines-of-clean-code-beat-65-b-ehl6
|
\npublic long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides, (a, b) -> (a[1] - b[1]));\n TreeMap<Integer, Long> dp = new TreeMap<>()
|
guibin
|
NORMAL
|
2021-11-07T05:56:22.009140+00:00
|
2021-11-07T05:57:13.922654+00:00
| 1,020 | false |
```\npublic long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides, (a, b) -> (a[1] - b[1]));\n TreeMap<Integer, Long> dp = new TreeMap<>();\n dp.put(0, 0L);\n for (int[] ride : rides) {\n long currEarning = ride[1] - ride[0] + ride[2] + dp.floorEntry(ride[0]).getValue();\n if (currEarning > dp.lastEntry().getValue()) {\n dp.put(ride[1], currEarning);\n } \n }\n return dp.lastEntry().getValue();\n }\n```
| 5 | 0 |
['Dynamic Programming', 'Java']
| 1 |
maximum-earnings-from-taxi
|
[Python] Solution - Maximum Earnings from Taxi
|
python-solution-maximum-earnings-from-ta-94md
|
\nProblem : To find the maximum earnings.\n\nIdea : Start to think in this way that we can track the maximum earning at each point .\neg : n = 20, rides = [[1,
|
sasha59
|
NORMAL
|
2021-09-25T14:30:23.129296+00:00
|
2021-09-25T14:30:23.129328+00:00
| 3,621 | false |
\n**Problem** : To find the maximum earnings.\n\n**Idea** : Start to think in this way that we can track the maximum earning at each point .\neg : n = 20, rides = [[1,6,1],[3,10,2],[10,12,3],[11,12,2],[12,15,2],[13,18,1]]\n\nWe want to loop from i = 1 to n and at each step check if this i is an end point or not .\nif it is an end point then we check all of its corresponding start points and get the maximum earning we can make .\n\n i | 0 | 1 | 2 | 3 | 4 | 5\ndp| 0 | 0 | 0 | 0 | 0 | 0\n\nWhen i=6 ,\nwe check if 6 is an end point in the given array of rides \nyes it is \n(Note : -In order to quickly check if this number is an end point or not I am maintaining a dictionary where \nkey=end point and the value is [start_point,tip])\n\nnow I loop through all the corresponding start points whose end point is i\ntemp_profit = i(end_point) - start_point + tip \nbut in order to get the total profit at this end point (i) I also have to consider adding dp[start_point]\n\nWhat this means is **max_profit achieved till the start point (i.e dp[start])+ profit achieved from start_point to this end_point(i)\n(i.e end_point(i)-start_point+tip)**\n\nHence the eqn : \n****\n dp[i] = max(dp[i-1],end_point-start_point+tip+dp[start])\n****\n\nSolution :\n\n```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n \n d = {}\n for start,end,tip in rides:\n if end not in d:\n d[end] =[[start,tip]]\n else:\n d[end].append([start,tip])\n \n \n dp = [0]*(n+1)\n dp[0] = 0\n \n for i in range(1,n+1):\n dp[i] = dp[i-1]\n if i in d:\n temp_profit = 0\n for start,tip in d[i]:\n if (i-start)+tip+dp[start] > temp_profit:\n temp_profit = i-start+tip+dp[start]\n dp[i] = max(dp[i],temp_profit)\n \n \n return dp[-1]\n```\nT.C : O(n)\n
| 5 | 1 |
['Dynamic Programming', 'Python', 'Python3']
| 2 |
maximum-earnings-from-taxi
|
C++ DP + Binary Search
|
c-dp-binary-search-by-lzl124631x-ou99
|
See my latest update in repo LeetCode\n## Solution 1. DP + Binary Search\n\nIntuition: Almost the same as the classic problem 1235. Maximum Profit in Job Schedu
|
lzl124631x
|
NORMAL
|
2021-09-18T16:01:11.605116+00:00
|
2021-09-25T10:20:40.574228+00:00
| 1,034 | false |
See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n## Solution 1. DP + Binary Search\n\n**Intuition**: Almost the same as the classic problem [1235. Maximum Profit in Job Scheduling (Hard)](https://leetcode.com/problems/maximum-profit-in-job-scheduling/).\n\n**Algorithm**:\n* Sort the array in descending order of `start`.\n* Store the maximum profit we can get in range `[start, Infinity)` in a `map<int, long long> m`.\n* For each `A[i]`, `m[start[i]]` is either:\n * The maximum profit we\'ve seen thus far.\n * Or, `profit[i] + (end[i] - start[i]) + P(end[i])`, where `P` is the maximum profit we can get in range `[end[i], Infinity)`. We can get this `P` value by binary searching the map `m` -- `P(end[i]) = m.lower_bound(end[i])->second`.\n\n```cpp\n// OJ: https://leetcode.com/contest/biweekly-contest-61/problems/maximum-earnings-from-taxi/\n// Author: github.com/lzl124631x\n// Time: O(NlogN)\n// Space: O(N)\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& A) {\n sort(begin(A), end(A), [](auto &a, auto &b) { return a[0] > b[0]; }); // Sort the array in descending order of `start`\n map<int, long long> m{{INT_MAX,0}}; // `dp` value. A mapping from a `start` point to the maximum profit we can get in range `[start, Infinity)`\n long long ans = 0;\n for (auto &r : A) {\n int s = r[0], e = r[1], p = r[2];\n m[s] = max(ans, p + e - s + m.lower_bound(e)->second);\n ans = max(ans, m[s]);\n }\n return ans;\n }\n};\n```
| 5 | 2 |
[]
| 2 |
maximum-earnings-from-taxi
|
Python - Longest Path in DAG, Simple Solution
|
python-longest-path-in-dag-simple-soluti-1lcs
|
My approach is slower than others, but intuitive. Our goal is to set the problem as a graph question. The graph will be a DAG, and as a result we can efficientl
|
noahantisseril
|
NORMAL
|
2024-08-01T16:17:15.863728+00:00
|
2025-02-04T00:53:53.892533+00:00
| 314 | false |
My approach is slower than others, but intuitive. Our goal is to set the problem as a graph question. The graph will be a DAG, and as a result we can efficiently calculate the longest weighted path. When visiting a point, we update its neighbors to have the maximum possible earnings upon reaching that point.
The only caveat to the problem is that we can accumulate our earnings even without a direct path. For instance, we can keep our earnings from point 12 to point 13, even if there is no ride marking an edge between the two. We can account for this by keeping track of the largest earnings we have seen before our current point, and adding those earnings to the current point if greater.
# Code
```
class Solution:
def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:
g = defaultdict(list)
for start, end, tip in rides:
g[start].append((end, end - start + tip))
profit = defaultdict(int)
prev_best = 0
for u in range(1, n + 1):
prev_best = max(prev_best, profit[u])
profit[u] = prev_best
for v, w in g[u]:
profit[v] = max(profit[v], profit[u] + w)
return prev_best
```
| 4 | 0 |
['Python3']
| 1 |
maximum-earnings-from-taxi
|
✅C++ || Explained || Recursion->Memoization->Binary Search
|
c-explained-recursion-memoization-binary-z7q3
|
Intuition:\n\nour idea behind solving this problem is simple\n* we will sort all rides according to passenger arriving time\n* now we keep checking all possible
|
yashsachan
|
NORMAL
|
2023-10-06T15:20:59.436992+00:00
|
2023-10-06T15:21:24.805386+00:00
| 387 | false |
Intuition:\n\nour idea behind solving this problem is simple`\n* we will sort all rides according to passenger arriving time\n* now we keep checking all possible earnings by: if the passenger picked up or if he\'s not.\n* we can only pick the passenger if the ride end time of our current passenger is more than or equal to arrival time of next passenger( as two passenger can\'t be given ride together), this is what we check inside our for loop.\n* Case 1: if we pick the passenger then we can only pick next passenger after this ride end so update the index till next possible time\n* Case 2: if we does\'nt pick the passenger we can simply move on to next passenger so increase index by 1.\n\n\n\n**Recursion (TLE):**\n\n```\nclass Solution {\npublic:\n long long solve(int index,int n,vector<vector<int>>& rides)\n {\n if(index>=rides.size())return 0;\n \n int i=0;\n for(i=index+1;i<rides.size();i++)\n {\n if(rides[i][0]>=rides[index][1])break;\n }\n int pick=rides[index][1]-rides[index][0]+rides[index][2]+solve(i,n,rides);\n int notpick=solve(index+1,n,rides);\n return max(pick,notpick);\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n sort(rides.begin(),rides.end());\n return solve(0,n,rides);\n }\n};\n```\n\n**Recursion with Memoization:( TLE again on large test cases)**\n```\nclass Solution {\npublic:\n long long solve(int index,int n,vector<vector<int>>& rides,vector<long long> &dp)\n {\n if(index>=rides.size())return 0;\n if(dp[index]!=-1)return dp[index];\n int i=0;\n for(i=index+1;i<rides.size();i++)\n {\n if(rides[i][0]>=rides[index][1])break;\n }\n long long pick=rides[index][1]-rides[index][0]+rides[index][2]+solve(i,n,rides,dp);\n long long notpick=solve(index+1,n,rides,dp);\n return dp[index]=max(pick,notpick);\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<long long> dp(rides.size()+1,-1);\n sort(rides.begin(),rides.end());\n return solve(0,n,rides,dp);\n }\n};\n```\n\u2705\u2705**Recursion Memoization with Binary search:**\n`in this approach in order to find our next possible passenger we use binary search`\n\n```\nclass Solution {\npublic:\n long long solve(int index,int n,vector<vector<int>>& rides,vector<long long> &dp)\n {\n if(index>=rides.size())return 0;\n if(dp[index]!=-1)return dp[index];\n int i=rides.size();\n int low=index+1,high=rides.size()-1;\n while(low<=high)\n {\n int mid=(low+high)/2;\n if(rides[mid][0]>=rides[index][1])\n {\n i=mid;\n high=mid-1;\n }\n else\n low=mid+1;\n }\n long long pick=rides[index][1]-rides[index][0]+rides[index][2]+solve(i,n,rides,dp);\n long long notpick=solve(index+1,n,rides,dp);\n return dp[index]=max(pick,notpick);\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<long long> dp(rides.size()+1,-1);\n sort(rides.begin(),rides.end());\n return solve(0,n,rides,dp);\n }\n};\n```
| 4 | 0 |
['Binary Search', 'Recursion', 'Memoization']
| 2 |
maximum-earnings-from-taxi
|
Java Solution | DP | TC : O(n * log(n))
|
java-solution-dp-tc-on-logn-by-nitwmanis-93s6
|
\nclass Solution {\n private static class Job {\n\t\tprivate int start;\n\t\tprivate int end;\n\t\tprivate int profit;\n\n\t\tpublic Job(int start, int end,
|
nitwmanish
|
NORMAL
|
2022-11-26T05:35:39.376212+00:00
|
2022-11-26T05:35:39.376235+00:00
| 334 | false |
```\nclass Solution {\n private static class Job {\n\t\tprivate int start;\n\t\tprivate int end;\n\t\tprivate int profit;\n\n\t\tpublic Job(int start, int end, int profit) {\n\t\t\tthis.start = start;\n\t\t\tthis.end = end;\n\t\t\tthis.profit = profit;\n\t\t}\n\t}\n \n private int binarySearch(Job jobs[], int index) {\n\t\tint low = 0;\n\t\tint high = index - 1;\n\t\tint ans = -1;\n\t\twhile (low <= high) {\n\t\t\tint mid = low + (high - low) / 2;\n\t\t\tif (jobs[mid].end <= jobs[index].start) {\n\t\t\t\tans = mid;\n\t\t\t\tlow = mid + 1;\n\t\t\t} else {\n\t\t\t\thigh = mid - 1;\n\t\t\t}\n\t\t}\n\t\treturn ans;\n\t}\n \n public long maxTaxiEarnings(int n, int[][] rides) {\n\t\tJob jobs[] = new Job[rides.length];\n\t\tfor (int i = 0; i < rides.length; i++) {\n\t\t\tjobs[i] = new Job(rides[i][0], rides[i][1], rides[i][1] - rides[i][0] + rides[i][2]);\n\t\t}\n\t\tArrays.sort(jobs, (j1, j2) -> (j1.end - j2.end));\n\t\tlong[] dp = new long[rides.length];\n\t\tdp[0] = jobs[0].profit;\n\t\tfor (int i = 1; i < jobs.length; i++) {\n\t\t\tlong include = jobs[i].profit;\n\t\t\tint index = binarySearch(jobs, i);\n\t\t\tif (index != -1) {\n\t\t\t\tinclude += dp[index];\n\t\t\t}\n\t\t\tdp[i] = Math.max(include, dp[i - 1]);\n\t\t}\n\t\treturn dp[rides.length - 1];\n }\n}\n```
| 4 | 0 |
['Sorting', 'Binary Tree', 'Java']
| 0 |
maximum-earnings-from-taxi
|
[C++]Simple C++ Code
|
csimple-c-code-by-prosenjitkundu760-bi9r
|
\n# If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n i
|
_pros_
|
NORMAL
|
2022-08-11T16:58:07.351970+00:00
|
2022-08-11T16:58:07.352011+00:00
| 609 | false |
\n# **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n int BinarySearch(int &val, int &e, int &s, vector<vector<int>>& rides)\n {\n int end = e-1, start = s+1, ans = e;\n while(start <= end)\n {\n int mid = start + (end - start)/2;\n if(rides[mid][0] >= val)\n {\n ans = mid;\n end = mid-1;\n }\n else\n start = mid+1;\n }\n return ans;\n }\n long long dfs(vector<long long> &dp, vector<vector<int>>& rides, int i, int &n)\n {\n if(i >= n) return 0;\n if(dp[i] != -1) \n return dp[i];\n int val = BinarySearch(rides[i][1], n, i, rides);\n long long price = rides[i][1]-rides[i][0]+rides[i][2];\n return dp[i] = max(dfs(dp, rides, i+1, n),price + dfs(dp, rides, val, n));\n }\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n int m = rides.size();\n sort(rides.begin(), rides.end());\n vector<long long> dp(m, -1);\n return dfs(dp, rides, 0, m);\n }\n};\n```
| 4 | 1 |
['Dynamic Programming', 'Memoization', 'C', 'Binary Tree']
| 0 |
maximum-earnings-from-taxi
|
java commented code.
|
java-commented-code-by-helianthus1588-j0ef
|
```\npublic long maxTaxiEarnings(int n, int[][] rides) {\n int num = rides.length;\n int[][] jobs = new int[num][3];\n for (int i = 0; i <
|
Helianthus1588
|
NORMAL
|
2021-09-24T09:10:47.848304+00:00
|
2021-09-24T09:14:45.922336+00:00
| 425 | false |
```\npublic long maxTaxiEarnings(int n, int[][] rides) {\n int num = rides.length;\n int[][] jobs = new int[num][3];\n for (int i = 0; i < num; i++) {\n jobs[i] = new int[] {rides[i][0], rides[i][1], rides[i][1] - rides[i][0] + rides[i][2]};\n }\n Arrays.sort(jobs, (a, b)->a[1] - b[1]);\n\t\t\n\t\t// create a treemap that contain only max "earning" we get till current "endtime"\n\t\t// TreeMap<endTime, earning>\n TreeMap<Integer, Long> dp = new TreeMap<>();\n dp.put(0, 0L);\n for (int[] job : jobs) {\n\t\t\n\t\t // find what is max earning acheived before startTime of current job and add current earning\n Long cur = dp.floorEntry(job[0]).getValue() + job[2];\n if (cur > dp.lastEntry().getValue())\n\t\t\t\t\n\t\t\t\t//if new cur is max than the top earning in treemap than add new earning \n dp.put(job[1], cur);\n }\n\t\t\n\t\t//finally return the top value which is max earning\n return dp.lastEntry().getValue();\n\n }\n\t\n\t\n\tSimilar Problem:\n\t[1235. Maximum Profit in Job Scheduling](https://leetcode.com/problems/maximum-profit-in-job-scheduling/)
| 4 | 1 |
['Tree', 'Sorting', 'Java']
| 1 |
maximum-earnings-from-taxi
|
[C++ DP]
|
c-dp-by-mk_kr_24-y96q
|
\n\nclass Solution {\npublic:\n static bool fun(vector<int> &a, vector<int> &b){\n return a[1] > b[1];\n }\n long long maxTaxiEarnings(int n, ve
|
mk_kr_24
|
NORMAL
|
2021-09-22T04:51:09.592107+00:00
|
2021-09-22T04:51:09.592149+00:00
| 329 | false |
```\n\nclass Solution {\npublic:\n static bool fun(vector<int> &a, vector<int> &b){\n return a[1] > b[1];\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& r) {\n sort(r.begin(), r.end(), fun);\n vector<long long> dp(n+2, 0);\n long long ans= 0;\n int j= 0;\n for(int i= n;i>= 1; i--)\n {\n ans= max(ans, dp[i]);\n while(j!= r.size()&&r[j][1]==i)\n {\n dp[r[j][0]]= max(r[j][1]-r[j][0]+r[j][2]+ans, dp[r[j][0]]);\n j++;\n }\n }\n return ans;\n }\n};\n```
| 4 | 1 |
[]
| 0 |
maximum-earnings-from-taxi
|
🎨 The ART of Dynamic Programming
|
the-art-of-dynamic-programming-by-clayto-64n5
|
\uD83C\uDFA8 The ART of Dynamic Programming\n\nLet dp[j] denote the optimal earnings ending at index j. There are 2 possibilties to consider for each jth endin
|
claytonjwong
|
NORMAL
|
2021-09-20T16:28:46.853994+00:00
|
2021-09-21T15:33:41.299571+00:00
| 496 | false |
[\uD83C\uDFA8 The ART of Dynamic Programming](https://leetcode.com/discuss/general-discussion/712010/The-ART-of-Dynamic-Programming-An-Intuitive-Approach%3A-from-Apprentice-to-Master)\n\nLet `dp[j]` denote the optimal earnings ending at index `j`. There are 2 possibilties to consider for each `j`<sup>th</sup> ending position\'s intervals:\n\n* **Case 1:** *include* the interval `i..j` with tip `k`\n* **Case 2:** *exclude* the interval `i..j` with tip `k`\n\nWhen we *include* the interval `i..j`, we add the interval\'s earnings onto the previous optimal earnings ending at index `i` inclusive.\nWhen we *exclude* the interval `i..j`, we update the current optimal earnings ending at `j` to the previous optimal earnings ending at `j - 1`.\n\n**Similar Problem:** [1235. Maximum Profit in Job Scheduling](https://leetcode.com/problems/maximum-profit-in-job-scheduling/discuss/1477025/The-ART-of-Dynamic-Programming)\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun maxTaxiEarnings(N: Int, A: Array<IntArray>): Long {\n var dp = LongArray(N + 1) { 0 }\n var m = mutableMapOf<Int, MutableList<Pair<Int, Int>>>()\n for ((i, j, k) in A) {\n if (!m.contains(j))\n m[j] = mutableListOf<Pair<Int, Int>>()\n m[j]!!.add(Pair(i, k))\n }\n for (j in 1..N) {\n if (!m.contains(j)) {\n dp[j] = dp[j - 1]\n continue\n }\n for ((i, k) in m[j]!!) {\n var include = dp[i] + j - i + k\n var exclude = dp[j - 1]\n dp[j] = listOf(dp[j], include, exclude).max()!!\n }\n }\n return dp[N]\n }\n}\n```\n\n*Javascript*\n```\nlet maxTaxiEarnings = (N, A, m = new Map()) => {\n let dp = Array(N + 1).fill(0);\n for (let [i, j, k] of A) {\n if (!m.has(j))\n m.set(j, []);\n m.get(j).push([i, k]);\n }\n for (let j = 1; j <= N; ++j) {\n if (!m.has(j)) {\n dp[j] = dp[j - 1];\n continue;\n }\n for (let [i, k] of m.get(j)) {\n let include = dp[i] + j - i + k,\n exclude = dp[j - 1];\n dp[j] = Math.max(dp[j], include, exclude);\n }\n }\n return dp[N];\n};\n```\n\n*Python3*\n```\nclass Solution:\n def maxTaxiEarnings(self, N: int, A: List[List[int]]) -> int:\n m = {}\n for i, j, k in A:\n if j not in m:\n m[j] = []\n m[j].append([i, k])\n dp = [0] * (N + 1)\n for j in range(1, N + 1):\n if j not in m:\n dp[j] = dp[j - 1]\n continue\n for i, k in m[j]:\n include = dp[i] + j - i + k\n exclude = dp[j - 1]\n dp[j] = max(dp[j], include, exclude)\n return dp[N]\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using LL = long long;\n using VL = vector<LL>;\n using VI = vector<int>;\n using VVI = vector<VI>;\n using Pair = pair<int, int>;\n using Pairs = vector<Pair>;\n using Map = unordered_map<int, Pairs>;\n LL maxTaxiEarnings(int N, VVI& A, Map m = {}) {\n VL dp(N + 1);\n for (auto& ride: A) {\n auto [i, j, k] = tie(ride[0], ride[1], ride[2]);\n m[j].emplace_back(i, k);\n }\n for (auto j{ 1 }; j <= N; ++j) {\n if (m.find(j) == m.end()) {\n dp[j] = dp[j - 1];\n continue;\n }\n for (auto [i, k]: m[j]) {\n LL include = dp[i] + j - i + k,\n exclude = dp[j - 1];\n dp[j] = max({ dp[j], include, exclude });\n }\n }\n return dp[N];\n }\n};\n```
| 4 | 0 |
[]
| 0 |
maximum-earnings-from-taxi
|
Java TreeMap solution
|
java-treemap-solution-by-aravindsys-sm1u
|
\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] rides) {\n TreeMap<Integer,Long> maps = new TreeMap<Integer,Long>();\n Arrays.s
|
aravindsys
|
NORMAL
|
2021-09-18T17:14:27.365991+00:00
|
2021-09-18T17:14:27.366026+00:00
| 964 | false |
```\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] rides) {\n TreeMap<Integer,Long> maps = new TreeMap<Integer,Long>();\n Arrays.sort(rides,(a,b) -> a[1] - b[1]);\n maps.put(0,0L);\n for(int i = 0; i < rides.length; i++){\n Map.Entry<Integer,Long> e = maps.floorEntry(rides[i][0]);\n long p = 0L;\n if(maps.containsKey(rides[i][1]))\n p = maps.get(rides[i][1]);\n long q = e.getValue() + (rides[i][1] - rides[i][0] + rides[i][2]);\n if(q > p && maps.lastEntry().getValue() < q){\n maps.put(rides[i][1],q);\n }\n maps.put(0,0L);\n }\n return maps.lastEntry().getValue();\n }\n}\n```
| 4 | 0 |
['Tree', 'Java']
| 0 |
maximum-earnings-from-taxi
|
C++||DP with Binary Search with detailed comments
|
cdp-with-binary-search-with-detailed-com-2ilf
|
Please do upvote if found helpful\n\nclass Solution {\npublic:\n \n long long dp[100000];\n \n long long solve(vector<vector<int>>& pairs, int curr,
|
notacodinggeek
|
NORMAL
|
2021-09-18T16:05:10.951333+00:00
|
2021-09-22T03:30:39.271276+00:00
| 486 | false |
**Please do upvote if found helpful**\n```\nclass Solution {\npublic:\n \n long long dp[100000];\n \n long long solve(vector<vector<int>>& pairs, int curr, int n){\n if(curr>=n) return 0;\n if(dp[curr]!=-1) return dp[curr];\n long long op1=solve(pairs,curr+1,n); //option 1 is to leave the current passenger\n long long op2=pairs[curr][2]; //option 2 is to take the current passenger\n long long tos=pairs[curr][1]; //if we are deciding to take the passenger then we need find the next passenger that we can pick (tos variable name here means toSearch)\n long long s=curr; //curr index is our starting index\n long long e=n-1; // n-1 is the last index\n long long i=-1;\n \n while(s<=e){\n long long mid=s+(e-s)/2;\n if(pairs[mid][0]<tos){ // if the start time is less than the end time of the passenger we decided to pick then we can\'t pick this passenger\n s=mid+1;\n }else{\n i=mid; //updating i with possible index of the passenger we can pick, we need to get the first possible index\n e=mid-1;\n }\n }\n \n if(i!=-1) op2+=solve(pairs,i,n); // if i!=-1 implies we found a possuble passenger we can take, so we\'ll add the answer that we\'ll get from there\n \n return dp[curr]= max(op1,op2); // returning the maximum of option 1 and option 2\n }\n \n\t\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n memset(dp,-1,sizeof(dp));\n int sz=rides.size();\n vector<vector<int>> pairs; // converting to a new vector with start, end and profit\n for(int i=0;i<sz;i++) pairs.push_back({rides[i][0],rides[i][1],(rides[i][1]-rides[i][0]+rides[i][2])}); \n sort(pairs.begin(),pairs.end()); //sorting on the basis of start time\n return solve(pairs,0,sz);\n \n }\n};\n```
| 4 | 0 |
[]
| 0 |
maximum-earnings-from-taxi
|
C++ | DP | Concise|similar to Job Scheduling
|
c-dp-concisesimilar-to-job-scheduling-by-nng6
|
This question is same as Maximum Profit in Job Scheduling this question\n\n1. Start from the last passenger(having largest start(i)) and move backwards. (used p
|
aman282571
|
NORMAL
|
2021-09-18T16:00:51.118319+00:00
|
2021-09-18T16:03:44.164849+00:00
| 737 | false |
This question is same as [Maximum Profit in Job Scheduling](https://leetcode.com/problems/maximum-profit-in-job-scheduling/) this question\n```\n1. Start from the last passenger(having largest start(i)) and move backwards. (used priority_queue)\n2. As we move backwards for each start(i) store the maximum amount that\n we can get from from that position onwards.\n 3.Maximum amount at any start(i)=amount of current ride +max. amount after current rides completes(lower_bound of end(i) of current ride. \n```\nTime complexity:- O(nlog(n))\nSpace complexity:- O(n)\n```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n priority_queue<vector<int>>pq;\n for(auto & i:rides)\n pq.push(i);\n long long ans=0;\n map<int,long long>mp;\n while(!pq.empty())\n {\n auto vec=pq.top();\n pq.pop();\n long long p=vec[1]-vec[0]+vec[2];\n auto it=mp.lower_bound(vec[1]);\n if(it!=mp.end())\n p+=it->second;\n mp[vec[0]]=max(ans,p);\n ans=max(ans,p);\n }\n return ans;\n }\n};\n```\nDo **UPVOTE** if it helps :)\nIf you have any doubt then please ask in comment section.
| 4 | 0 |
['Dynamic Programming', 'C']
| 1 |
maximum-earnings-from-taxi
|
C++ DP Solution. O(N + klogk)/O(N)
|
c-dp-solution-on-klogkon-by-chejianchao-77qx
|
Idea\nFor each point we have:\ndp[i] = max(dp[i], dp[i - 1])\n\nFor each ride we have:\ndp[end] = max(dp[end], end -start + dp[start] + tip);\n\nclass Solution
|
chejianchao
|
NORMAL
|
2021-09-18T16:00:51.034388+00:00
|
2021-09-18T16:04:00.687902+00:00
| 414 | false |
### Idea\nFor each point we have:\n`dp[i] = max(dp[i], dp[i - 1])`\n\nFor each ride we have:\n`dp[end] = max(dp[end], end -start + dp[start] + tip);`\n```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<long long> dp(n + 1);\n sort(rides.begin(), rides.end());\n int j = 0;\n for(int i = 1; i <= n; i++) {\n dp[i] = max(dp[i], dp[i - 1]);\n while(j < rides.size() && rides[j][0] == i) {\n long long start = rides[j][0];\n long long end = rides[j][1];\n long long tip = rides[j][2];\n dp[end] = max(dp[end], end -start + dp[start] + tip);\n ++j;\n }\n }\n return dp[n];\n }\n};\n```\n
| 4 | 2 |
[]
| 0 |
maximum-earnings-from-taxi
|
Easy commented code using lower bound(learn how to use lb for vec of vec)
|
easy-commented-code-using-lower-boundlea-ii3a
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
amit_geek
|
NORMAL
|
2023-08-22T14:38:33.222167+00:00
|
2023-08-22T14:38:33.222196+00:00
| 788 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n \n long long dp[100000]; // Dynamic programming table to store calculated results\n \n\n // Recursive function to calculate the maximum taxi earnings starting from index \'start\'\n long long giveAns(vector<vector<int>>& rides, int start) {\n // Base case: If the current index is beyond the rides array, return 0\n if (start >= rides.size()) return 0;\n \n // If the result for the current index has already been calculated, return it\n if (dp[start] != -1) return dp[start];\n \n // Find the position to jump to using binary search on the end times of rides\n auto it = lower_bound(rides.begin(), rides.end(), rides[start][1],\n [](auto& vec, int value) { return vec[0] < value; });\n \n // Calculate earnings if the current ride is taken (x) and if it\'s skipped (y)\n long long x = rides[start][2] + rides[start][1] - rides[start][0] +\n giveAns(rides, it - rides.begin()); // Recursive call\n long long y = giveAns(rides, start + 1); // Recursive call\n \n // Store the maximum earnings for the current index in dp table and return it\n return dp[start] = max(x, y);\n }\n \n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n memset(dp, -1, sizeof(dp)); // Initialize the dp table with -1\n sort(rides.begin(), rides.end()); // Sort rides based on start times\n \n // Call the recursive function starting from the first ride\n return giveAns(rides, 0);\n }\n};\n\n```
| 3 | 0 |
['Binary Search', 'Memoization', 'C++']
| 0 |
maximum-earnings-from-taxi
|
Brute Force Recursion -> Memoization -> Memoization + BinarySearch
|
brute-force-recursion-memoization-memoiz-fbmm
|
Brute Force Intuition + Approach\n1. Sort rides array by pickup time, break ties by dropoff time\n2. Start from ride[0] with earliest pickup time, then recursiv
|
irving09
|
NORMAL
|
2023-04-16T08:16:29.107077+00:00
|
2023-04-16T08:16:29.107106+00:00
| 316 | false |
# Brute Force Intuition + Approach\n1. Sort rides array by pickup time, break ties by dropoff time\n2. Start from `ride[0]` with earliest pickup time, then recursively choose to \n- take the current ride\'s profit\n- Or choose to not not take it\n\nThere is one condition wether you can take the ride or not\nand be able to take the profit, and that is \nit must not conflict with any other rides you have picked up so far.\n3. From the current ride, find the next earliest ride that does not have a conflict. Because we sorted the array by pickup time, we just need to find the ride which has a `pickup_time >= current_ride_drop_off_time`\n\n# Complexity\n- Time complexity:\n```\n O(nlogn) + O(n * 2^n) = O(n2^n)\n sorting finding take ride\n nextRide or not take\n i.e. 2 possibilities \n each recursion,\n and depth is n\n\n```\n\n- Space complexity: `O(n) stack space`\n\n# Code\n```\n public long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);\n\n // Start from rides[0] with earliest pickup time\n return recurse(rides, 0);\n }\n\n public long recurse(int[][] rides, int currentRide) {\n int n = rides.length;\n // we have considered all possibilities for each ride,\n // return 0 profit\n if (currentRide >= n)\n return 0;\n\n // From the current ride\'s dropoff,\n // find the next earliest ride who has a pickup with no a conflict\n int nextRide;\n for (nextRide = currentRide + 1; nextRide < n; nextRide++) {\n int nextRidePickup = rides[nextRide][0];\n int currRideDropoff = rides[currentRide][1];\n\n if (nextRidePickup >= currRideDropoff)\n break;\n }\n\n int pickup = rides[currentRide][0];\n int dropoff = rides[currentRide][1];\n int tip = rides[currentRide][2];\n long profit = dropoff - pickup + tip;\n\n // nextRide may be within the rides array range,\n // or there is no valid ride, in which nextRide is assigned value n\n long profitIfTaken = profit + recurse(rides, nextRide);\n long profitIfNotTaken = recurse(rides, currentRide + 1);\n\n return Math.max(\n profitIfTaken,\n profitIfNotTaken\n );\n }\n```\n\n# Brute Force with Caching - Memoization Intuition\nSame idea as brute force, except we add a cache every recursion,\nto avoid making the same recursive calls over and over on\nthe same input parameter (`currentRide`).\n\n# Complexity\n- Time complexity:\n```\nO(nlogn) + O( n x n ) = O(n^2)\n sorting finding the because of caching,\n next ride 2^n is bounded to n now,\n because of caching\n limited to size n\n```\n- Space complexity: `O(n) stack space + cache size`\n\n# Code\n\n```\n private static final long CACHE_MISS = -1L;\n\n public long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);\n long[] cache = new long[rides.length];\n Arrays.fill(cache, CACHE_MISS);\n return recurse(rides, 0, cache);\n }\n\n public long recurse(int[][] rides, int currentRide, long[] cache) {\n int n = rides.length;\n if (currentRide >= n)\n return 0;\n \n if (cache[currentRide] != CACHE_MISS)\n return cache[currentRide];\n\n int pickup = rides[currentRide][0];\n int dropoff = rides[currentRide][1];\n int tip = rides[currentRide][2];\n long profit = dropoff - pickup + tip;\n\n int nextRide;\n for (nextRide = currentRide + 1; nextRide < n; nextRide++) {\n int nextRidePickup = rides[nextRide][0];\n int currRideDropoff = rides[currentRide][1];\n\n if (nextRidePickup >= currRideDropoff)\n break;\n }\n\n long profitIfTaken = profit + recurse(rides, nextRide, cache);\n long profitIfNotTaken = recurse(rides, currentRide + 1, cache);\n\n return cache[currentRide] = Math.max(\n profitIfTaken,\n profitIfNotTaken\n );\n }\n```\n\n# Optimization with binary search and building on top of previous approach\nSame idea as memoization, except we find the next ride using binary search instead of linear, sequential for loop.\n\n# Complexity\n- Time complexity:\n```\nO(nlogn) + O( logn x n ) = O(nlogn)\n sorting finding the because of caching,\n next ride 2^n is bounded to n now,\n because of caching\n limited to size n\n```\n- Space complexity: `O(n) stack space + cache size`\n\n\n# Code\n```\nclass Solution {\n\n private static final long CACHE_MISS = -1L;\n\n public long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);\n long[] cache = new long[rides.length];\n Arrays.fill(cache, CACHE_MISS);\n return recurse(rides, 0, cache);\n }\n\n public long recurse(int[][] rides, int currentRide, long[] cache) {\n int n = rides.length;\n if (currentRide >= n)\n return 0;\n \n if (cache[currentRide] != CACHE_MISS)\n return cache[currentRide];\n\n int pickup = rides[currentRide][0];\n int dropoff = rides[currentRide][1];\n int tip = rides[currentRide][2];\n long profit = dropoff - pickup + tip;\n\n int nextRide = binarySearch(rides, dropoff, currentRide + 1, n - 1);\n for (nextRide = currentRide + 1; nextRide < n; nextRide++) {\n int nextRidePickup = rides[nextRide][0];\n int currRideDropoff = rides[currentRide][1];\n\n if (nextRidePickup >= currRideDropoff)\n break;\n }\n\n long profitIfTaken = nextRide >= 0 ? profit + recurse(rides, nextRide, cache) : profit;\n long profitIfNotTaken = recurse(rides, currentRide + 1, cache);\n\n return cache[currentRide] = Math.max(\n profitIfTaken,\n profitIfNotTaken\n );\n }\n\n public int binarySearch(int[][] rides, int dropoff, int l, int r) {\n int result = -1;\n while (l <= r) {\n int nextRide = l + (r - l) / 2;\n int nextRidePickup = rides[nextRide][0];\n\n if (nextRidePickup >= dropoff) {\n result = nextRide;\n r = nextRide - 1;\n } else {\n l = nextRide + 1;\n }\n }\n\n return result;\n }\n}\n```
| 3 | 0 |
['Java']
| 1 |
maximum-earnings-from-taxi
|
python3 sorting+dynamic programming(with explicit explanation + test case)
|
python3-sortingdynamic-programmingwith-e-f3hc
|
Intuition\nthis question is similar to leetcode 80: maximum number of events that can be attended, the two question uses simiar sorting and usage of stack/heap.
|
SergioDeLaRosa
|
NORMAL
|
2023-01-27T09:38:08.020041+00:00
|
2023-01-27T09:38:08.020090+00:00
| 718 | false |
# Intuition\nthis question is similar to [leetcode 80: maximum number of events that can be attended](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/), the two question uses simiar sorting and usage of stack/heap. In this solution, I used dynamic programming to use an array to keep track of whats the maximum amount of money the driver has made by the time he switched to direction ```i```\n\n# Approach\nfirst we sort the rides based on the end direction, and break ties using the starting direction. In Python3, we can do the sorting using ```rides = sorted(rides, key=lambda x: (x[1], x[0]))```\n\nnext we build a array of size ```n+1``` to keep track of whats the maximum amount of money the drive can make by the time he switched to direction ```i```\n\nthen we began the algorithm\'s iterative part where we iterate over each direction, at each direction we store in our stack the rides that ends in current direction, then the maximum money the driver can make at index ```i``` is ```dp[i] = max(dp[start]+end-start+tip, dp[d])```\n\nthen in the end, compare the current ```dp[i]``` with previous value ```dp[i-1]```, and set ```dp[i] = max(dp[i], dp[i-1])```\n\nfor a detailed example, for test case:\n```sol = Solution()\nn = 10\nrides = [[2,3,6],[8,9,8],[5,9,7],[8,9,1],[2,9,2],[9,10,6],[7,10,10],[6,7,9],[4,9,7],[2,3,1]]\n```\n\nafter sorting, rides becomes:\n```\nrides = [[2, 3, 6], [2, 3, 1], [6, 7, 9], [2, 9, 2], [4, 9, 7], [5, 9, 7], [8, 9, 8], [8, 9, 1], [7, 10, 10], [9, 10, 6]]\n```\n\nthe dp array looks like this:\n```\ndp = [0, 0, 0, 7, 7, 7, 7, 17, 17, 26, 33]\n```\n\nthen we simply ```return max(dp)```\n\n# Complexity\n- Time complexity:\nlet ```k = len(rides)```\n$$O(max(n, k))$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```python\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n # rides based on the end direction, and break ties using the starting direction\n rides = sorted(rides, key=lambda x: (x[1], x[0]))\n l = []\n dp = [0] * (n+1)\n idx = 0\n\n # iterate over each end direction\n for d in range(1, n+1):\n\n stack = []\n # store all rides that ends up in current direction\n while idx < len(rides) and rides[idx][1] == d:\n stack.append(rides[idx])\n idx += 1\n\n # calculate the maximum money that can me made in current direction\n while stack:\n start, end, tip = stack.pop()\n dp[d] = max(dp[d], dp[start]+end-start+tip)\n # compare with last direction and keeping the maximum\n dp[d] = max(dp[d], dp[d-1])\n return max(dp)\n```\n\nif my solution has helped you, please consider upvoting my anwser, thank you :)\n\n
| 3 | 0 |
['Python3']
| 2 |
maximum-earnings-from-taxi
|
[DP+Lower Bound] Easy and Understandable
|
dplower-bound-easy-and-understandable-by-vhw0
|
\nclass Solution {\npublic:\n long long dp[100005];\n \n \n long long fuck(vector<vector<int>>& rides, int i, vector<int> &start){\n if(i >=
|
zoooop
|
NORMAL
|
2022-04-27T18:35:05.807698+00:00
|
2022-04-27T18:35:05.807735+00:00
| 303 | false |
```\nclass Solution {\npublic:\n long long dp[100005];\n \n \n long long fuck(vector<vector<int>>& rides, int i, vector<int> &start){\n if(i >= rides.size())\n return 0;\n \n if(dp[i]!=-1)\n return dp[i];\n long long a = fuck(rides,i+1,start);\n long long add = lower_bound(start.begin(),start.end(),rides[i][1])-start.begin();\n long long b = rides[i][1]-rides[i][0]+rides[i][2] + fuck(rides,add,start);\n return dp[i] = max(a,b);\n }\n \n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n memset(dp,-1,sizeof(dp));\n sort(rides.begin(),rides.end());\n int m = rides.size();\n vector<int> start(m);\n for(int i=0;i<m;i++){\n start[i] = rides[i][0];\n }\n return fuck(rides,0,start);\n }\n};\n```
| 3 | 0 |
['Dynamic Programming', 'C', 'Binary Tree']
| 0 |
maximum-earnings-from-taxi
|
C++ || DP || MEMOIZATION || BINARY SEARCH
|
c-dp-memoization-binary-search-by-easy_c-0c96
|
```\nclass Solution {\npublic:\n long long dp[(int)1e5];\n int nextPosition(vector>& rides, int val, int idx){\n int l = idx ;\n int h = r
|
Easy_coder
|
NORMAL
|
2022-01-21T20:20:27.480163+00:00
|
2022-01-21T20:20:27.480196+00:00
| 641 | false |
```\nclass Solution {\npublic:\n long long dp[(int)1e5];\n int nextPosition(vector<vector<int>>& rides, int val, int idx){\n int l = idx ;\n int h = rides.size() - 1;\n int pos = - 1;\n int mid;\n \n while(l <= h){\n mid = l + (h - l)/2;\n if(rides[mid][0] >= val){\n pos = mid;\n h = mid - 1;\n }\n else l = mid + 1;\n }\n return pos;\n \n }\n \n long long solve(vector<vector<int>>& rides, int idx){\n if(idx >= rides.size()) return 0;\n \n if(dp[idx] != -1) return dp[idx];\n // option 1 is to not consider this passenger\n \n long long op1 = solve(rides, idx + 1);\n \n // option 2 is to consider this passenger\n \n int nextPos = nextPosition(rides, rides[idx][1], idx);\n \n long long op2 = rides[idx][1] - rides[idx][0] + rides[idx][2] + solve(rides,nextPos);\n \n return dp[idx] = max(op1,op2);\n }\n \n \n \n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n sort(rides.begin(),rides.end());\n memset(dp,-1,sizeof(dp));\n return solve(rides,0);\n }\n};
| 3 | 0 |
['Dynamic Programming', 'Memoization', 'C', 'Binary Tree']
| 0 |
maximum-earnings-from-taxi
|
simple python solution | faster than 92.61% | with comments
|
simple-python-solution-faster-than-9261-5gn2z
|
O(n + k * log(k)) where k == len(rides)\n\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n ans = [0 for i in ran
|
solacerxt
|
NORMAL
|
2021-10-29T17:10:55.496718+00:00
|
2021-10-29T17:18:34.331216+00:00
| 473 | false |
O(n + k * log(k)) where k == len(rides)\n```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n ans = [0 for i in range(n + 1)] #storage for answer on each point\n end = 0\n \n for p in sorted(rides, key = lambda x: x[1]): #sort list by ends of rides in ascending order\n for i in range(end + 1, p[1]): ans[i] = ans[i - 1] #set maximum earning for points from last end until the end of current ride\n s = p[1] - p[0] + p[2] + ans[p[0]] #calculate earning, in ans[p[0]] we have maximum earning in the start of current ride\n ans[p[1]] = max(ans[p[1]], ans[p[1] - 1], s) #ans[p[1]] is included for cases when the last end is equal to current\n\t\t\tend = p[1]\n \n return ans[end]\n\n```\n\n
| 3 | 1 |
['Dynamic Programming', 'Sorting', 'Python']
| 0 |
maximum-earnings-from-taxi
|
[Python3] dp
|
python3-dp-by-ye15-ncf6
|
Please check out this commit for the solutions of biweekly 61. \n\ntop-down\n\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) ->
|
ye15
|
NORMAL
|
2021-09-18T21:35:16.438806+00:00
|
2021-09-18T22:25:20.579749+00:00
| 362 | false |
Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/0dcbb71853720dc380becdd8968bf94bdf419b7d) for the solutions of biweekly 61. \n\n**top-down**\n```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n mp = {}\n for start, end, tip in rides: \n mp.setdefault(start, []).append((end, tip))\n \n @cache\n def fn(x): \n """Return max earning at x."""\n if x == n: return 0 \n ans = fn(x+1)\n for xx, tip in mp.get(x, []): \n ans = max(ans, xx - x + tip + fn(xx))\n return ans \n \n return fn(1)\n```\n\n**bottom-up**\n```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n mp = {}\n for start, end, tip in rides: \n mp.setdefault(start, []).append((end, tip))\n \n dp = [0]*(n+1)\n for x in range(n-1, 0, -1): \n dp[x] = dp[x+1]\n for xx, tip in mp.get(x, []): \n dp[x] = max(dp[x], xx - x + tip + dp[xx])\n return dp[1]\n```
| 3 | 0 |
['Python3']
| 1 |
maximum-earnings-from-taxi
|
Java Solution with Recursion Memoization and binary search
|
java-solution-with-recursion-memoization-if81
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is to find which points to take and which points to discard.\nIf first poin
|
priyanshuboss
|
NORMAL
|
2024-06-03T07:36:46.397408+00:00
|
2024-06-03T07:36:46.397425+00:00
| 317 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to find which points to take and which points to discard.\nIf first point is taken the next point can only be selected when the trip of first point got completed i.e the end point of first trip is less than or equal to start point of next trip\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem is similar to knapsack problem where we have to select and discard the points.\nFirst we sort all the trip with starting points so than we can compute \nchronologically\nAfter that we will iterate throgh the points selecting and rejecting based on out criteria. In order to search the next point we can use binary search\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n long dp[];\n\n Solution(){\n dp=new long[100001];\n\n Arrays.fill(dp,-1);\n }\n\n int findNextStartTime(int rides[][], int start,int target){\n int beg = start;\n int end=rides.length-1;\n int res=-1;\n\n while(beg<=end){\n int mid = (beg + end)/2;\n\n if(rides[mid][0] >= target){\n res = mid;\n end=mid-1;\n }else{\n beg=mid+1;\n }\n }\n\n return res;\n }\n\n \n public long maxTaxiEarnings(int n, int[][] rides) {\n int ridesLen = rides.length;\n int idx=0;\n\n Arrays.sort(rides,new Comparator<int[]>(){\n public int compare(int x[], int y[]){\n return Integer.compare(x[0],y[0]);\n }\n });\n\n long ans = solve(rides,ridesLen,idx);\n\n return ans;\n }\n\n long solve(int rides[][], int ridesLen, int idx){\n\n if(idx >= ridesLen){\n return 0;\n }\n\n if(idx < 0){\n return 0;\n }\n\n if(dp[idx] != -1){\n return dp[idx];\n }\n\n //need to select the next point which chan be picked\n int i=0;\n \n // for(i=idx+1;i<ridesLen;i++){\n // //the point can be picked when the first trip ends\n // //i.e if endTime of first trip is less than or equal start time of\n // //next trip\n\n // if(rides[idx][1] <= rides[i][0]){\n // break;\n // }\n \n // }\n\n i=findNextStartTime(rides,idx+1,rides[idx][1]);\n\n long pick = rides[idx][1] - rides[idx][0]+rides[idx][2] + solve(rides,ridesLen,i);\n long notPick =solve(rides,ridesLen,idx+1);\n\n return dp[idx] = Math.max(pick,notPick);\n }\n}\n```
| 2 | 0 |
['Binary Search', 'Recursion', 'Memoization', 'Java']
| 0 |
maximum-earnings-from-taxi
|
100% Python3 || Dynamic Programming + Binary Search || EASY AND SIMPLE EXPLANATION (8 LINES)
|
100-python3-dynamic-programming-binary-s-1qz2
|
Intuition\nI solved the problem Maximum events that can be attended II before attempting this so I already knew the approach. \n# Bottom Up Approach\n Sort the
|
IshaanShettigar
|
NORMAL
|
2023-07-27T13:12:30.727075+00:00
|
2023-07-27T13:12:30.727108+00:00
| 80 | false |
# Intuition\nI solved the problem ***Maximum events that can be attended II*** before attempting this so I already knew the approach. \n# Bottom Up Approach\n* Sort the array `rides`\n* keep a separate array `starts`\n* `n=len(rides)` NOT the same `n` given in the question, its useless\n* dp[index] indicates the max profit we can get when we are at index i in the rides array. (NOT AT THE iTH point in the road)\n* At each step we can either take the ride or skip it. If we take it we need to add the profit, if you dont we dont.\n* Every time we take the ride we need to find the next **VALID** start point for us. Since we have sorted the array, we can use binary search for this. We simple search in the `start` array for the index that immediately follows the current end given by `rides[i][1]`. `nextIndex = bisect.bisect_left(start,rides[i][1])` \n* We then use the above mentioned recurrence relation. `dp[i] = max(profit + dp[nextIndex], dp[i+1)`\n* If we dont take the ride we simply go to `i+1`. \n\n\n# Code\n```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n rides.sort()\n n = len(rides)\n dp = [0]*(n+1)\n start = [s for s,e,t in rides]\n\n for i in range(n-1,-1,-1):\n nextIndex = bisect_left(start,rides[i][1])\n dp[i] = max(dp[i+1], rides[i][1]-rides[i][0]+rides[i][2] + dp[nextIndex])\n\n return dp[0]\n```
| 2 | 0 |
['Python3']
| 0 |
maximum-earnings-from-taxi
|
Easy 2 understand unique short TreeMap solution!
|
easy-2-understand-unique-short-treemap-s-uxu4
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
alphamonster0047
|
NORMAL
|
2023-07-26T01:08:40.434762+00:00
|
2023-07-26T01:08:40.434791+00:00
| 216 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides, (a,b)->(a[1]-b[1]));\n TreeMap<Integer, Long> dp=new TreeMap<>();\n dp.put(0, 0L);\n for(int[] ride:rides){\n Long currProfit = dp.floorEntry(ride[0]).getValue() + (ride[1]-ride[0]+ride[2]);\n if(currProfit>dp.lastEntry().getValue()){\n dp.put(ride[1], currProfit);\n }\n }\n return dp.lastEntry().getValue();\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
maximum-earnings-from-taxi
|
Recursion + Memoization + Binary Search || C++
|
recursion-memoization-binary-search-c-by-8k82
|
Very similar to LeetCode 2054. Two Best Non-Overlapping Events\n# Code\n\nclass Solution \n{\npublic:\n long long dp[100000];\n long long f(int i, vector<
|
lotus18
|
NORMAL
|
2023-03-06T07:25:38.280812+00:00
|
2023-03-06T07:26:44.913366+00:00
| 262 | false |
Very similar to LeetCode 2054. Two Best Non-Overlapping Events\n# Code\n```\nclass Solution \n{\npublic:\n long long dp[100000];\n long long f(int i, vector<vector<int>>& rides)\n {\n if(i==rides.size()) return 0;\n\n if(dp[i]!=-1) return dp[i];\n\n vector<int>ans={rides[i][1]-1,INT_MAX,INT_MAX};\n int nextindex=upper_bound(begin(rides),end(rides),ans)-begin(rides);\n \n return dp[i]=max(rides[i][1]-rides[i][0]+rides[i][2]+f(nextindex,rides),f(i+1,rides));\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) \n {\n memset(dp,-1,sizeof(dp));\n sort(rides.begin(),rides.end());\n return f(0,rides);\n }\n};\n```
| 2 | 0 |
['Binary Search', 'Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 0 |
maximum-earnings-from-taxi
|
C++ | O(N) | Easy to Understand
|
c-on-easy-to-understand-by-user3063c-oz46
|
Runtime: 537 ms, faster than 96.31% of C++ online submissions for Maximum Earnings From Taxi.\nMemory Usage: 122.5 MB, less than 30.66% of C++ online submission
|
user3063c
|
NORMAL
|
2022-06-04T02:37:07.658793+00:00
|
2022-06-04T02:37:07.658839+00:00
| 298 | false |
Runtime: 537 ms, faster than 96.31% of C++ online submissions for Maximum Earnings From Taxi.\nMemory Usage: 122.5 MB, less than 30.66% of C++ online submissions for Maximum Earnings From Taxi.\n\n\n```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<pair<int,int>> roads[n+1];\n for(vector<int> v: rides) {\n roads[v[1]].push_back({v[0], v[1]-v[0]+v[2]});\n }\n long long dp[n+1];\n memset(dp, 0, sizeof(dp));\n for(int i=2; i<=n; i++) {\n dp[i] = dp[i-1];\n for(auto j: roads[i]) {\n dp[i] = max(dp[i], j.second + dp[j.first]);\n }\n }\n return dp[n];\n }\n};\n```
| 2 | 0 |
['Dynamic Programming', 'Graph']
| 0 |
maximum-earnings-from-taxi
|
Python Top-Down DP approach beginner friendly with comments!
|
python-top-down-dp-approach-beginner-fri-9zib
|
\ndef maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n\n # sort rides based on start times.\n rides.sort(key=lambda x: x[0])\n\n @cache\
|
vineeth_moturu
|
NORMAL
|
2022-05-16T20:25:19.467223+00:00
|
2022-05-16T20:28:08.927759+00:00
| 446 | false |
```\ndef maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n\n # sort rides based on start times.\n rides.sort(key=lambda x: x[0])\n\n @cache\n def dp(i):\n if i >= len(rides):\n return 0\n\n # maxProfit if you skip the current ride and take next one.\n maxProfit = dp(i + 1)\n\n ride = rides[i]\n\n # i did [ride[1], x, x] so as to compatible with rides array format. \n\t\t# Note. It only considers the first element in array\n idx = bisect.bisect_left(rides, [ride[1], 0, 0]) \n\n # calculate profit\n profit = ride[1] - ride[0] + ride[2]\n\n # maxProfit will be max between:\n # 1)you skip the current ride and next ride in sequence(above) or \n # 2) you take current ride and then go to next ride after it\'s end\n maxProfit = max(maxProfit, dp(idx) + profit)\n\n return maxProfit\n\n res = dp(0)\n\n return res\n```
| 2 | 0 |
['Python']
| 1 |
maximum-earnings-from-taxi
|
[Python] Fast Clean Python DP Solution (6 lines)
|
python-fast-clean-python-dp-solution-6-l-sa2q
|
First of all, sort by start time so you can reliably use bisect to find next index.\n\n\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List
|
true-detective
|
NORMAL
|
2022-03-11T10:43:35.038937+00:00
|
2022-03-11T10:45:54.496878+00:00
| 278 | false |
First of all, sort by start time so you can reliably use bisect to find next index.\n\n```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n rides.sort(key=lambda x: x[0])\n res = [0] * (len(rides) + 1)\n for i in range(len(rides) - 1, -1, -1):\n idx = bisect.bisect(rides, [rides[i][1]])\n res[i] = max(res[idx] + rides[i][1] - rides[i][0] + rides[i][2], res[i + 1])\n\n return res[0]\n```
| 2 | 0 |
[]
| 1 |
maximum-earnings-from-taxi
|
Easy to understand solution in python
|
easy-to-understand-solution-in-python-by-m8ti
|
```\nfrom collections import *\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n d = defaultdict(list)\n d
|
rohit_vishwas_
|
NORMAL
|
2022-03-06T20:26:55.571838+00:00
|
2022-03-06T20:31:22.185511+00:00
| 434 | false |
```\nfrom collections import *\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n d = defaultdict(list)\n dp = [0] * (n+1)\n for s,e,v in rides:\n d[e].append((s,v))\n for i in range(1,n+1):\n mxm = dp[i-1]\n for s,v in d[i]:\n mxm = max(mxm,i - s + v + dp[s])\n dp[i] = mxm\n return dp[-1]
| 2 | 0 |
['Dynamic Programming', 'Python', 'Python3']
| 0 |
maximum-earnings-from-taxi
|
Maximum Earnings From Taxi | C++ | DP | NLogN
|
maximum-earnings-from-taxi-c-dp-nlogn-by-apzs
|
Same as Maximum Profit in Job Scheduling\n\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& A) {\n sort(begin(A), en
|
renu_apk
|
NORMAL
|
2022-01-15T09:21:28.679961+00:00
|
2022-01-15T09:23:05.529689+00:00
| 315 | false |
Same as [Maximum Profit in Job Scheduling](https://leetcode.com/problems/maximum-profit-in-job-scheduling/)\n```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& A) {\n sort(begin(A), end(A), [&](auto& a, auto& b){\n return a[1] < b[1];\n });\n \n int m = A.size();\n long dp[m];\n dp[0] = A[0][1] - A[0][0] + A[0][2];\n \n auto BS = [&](int i){\n int l = 0, r = i - 1, ans = -1;\n while(l <= r){\n int m = l + (r - l) / 2;\n if(A[m][1] <= A[i][0]){\n ans = m;\n l = m + 1;\n }\n else r = m - 1;\n }\n return ans;\n };\n \n for(int i = 1; i < m; i++){\n long pick = A[i][1] - A[i][0] + A[i][2];\n int idx = BS(i);\n if(idx != -1) pick += dp[idx];\n long discard = dp[i - 1];\n dp[i] = max(pick, discard);\n }\n \n return dp[m - 1];\n }\n};\n```
| 2 | 0 |
['Dynamic Programming']
| 0 |
maximum-earnings-from-taxi
|
C++ DP
|
c-dp-by-electronaota-wr9e
|
\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<long long> dp(n + 1);\n sort(rides.begin(), rides.e
|
Electronaota
|
NORMAL
|
2022-01-05T16:36:23.726412+00:00
|
2022-01-05T16:36:23.726453+00:00
| 407 | false |
```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n vector<long long> dp(n + 1);\n sort(rides.begin(), rides.end(), [](auto &f, auto&s)->bool { return f[1] < s[1]; });\n for (int i = 1, j = 0; i <= n; ++i) {\n dp[i] = dp[i - 1];\n while (j < rides.size() && i == rides[j][1]) {\n int s = rides[j][0], t = rides[j][2];\n dp[i] = max(dp[i], dp[s] + i - s + t);\n ++j;\n }\n }\n return dp[n];\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
maximum-earnings-from-taxi
|
Python3 sort by end, no reverse order
|
python3-sort-by-end-no-reverse-order-by-oas20
|
```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n rides = sorted(rides, key=lambda x: x[1])\n E = [i[1
|
yuyang339
|
NORMAL
|
2021-12-04T12:52:26.937819+00:00
|
2021-12-04T12:52:26.937848+00:00
| 255 | false |
```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n rides = sorted(rides, key=lambda x: x[1])\n E = [i[1] for i in rides]\n \n m = len(rides)\n dp = [0]*(m+1)\n for k in range(1, m+1):\n temp = bisect.bisect_right(E, rides[k-1][0])\n dp[k] = max(dp[k-1], rides[k-1][2] - rides[k-1][0] + rides[k-1][1] + dp[temp])\n \n return dp[-1]
| 2 | 0 |
[]
| 0 |
maximum-earnings-from-taxi
|
One template for max profit from Events/Jobs selection questions
|
one-template-for-max-profit-from-eventsj-xurc
|
\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int: \n rides.sort()\n for job in rides:\n j
|
ShivamBunge
|
NORMAL
|
2021-11-03T07:51:20.734508+00:00
|
2021-11-03T07:55:57.725921+00:00
| 398 | false |
```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int: \n rides.sort()\n for job in rides:\n job[2]+=job[1]-job[0]\n \n heap=[]\n cur=ans=0\n for start,e,p in rides:\n \n while heap and heap[0][0]<=start: \n _,val=heappop(heap)\n cur=max(cur,val)\n heappush(heap,(e,cur+p))\n \n ans=max(ans,cur+p)\n \n return ans\n```\n\n[Maximum Profit in Job Scheduling ](https://leetcode.com/problems/maximum-profit-in-job-scheduling/)\nfor every job we store the max profit before the start of this job + cur job profit (if its not overlapping) in a heap, so that we can use these values again for calculating profit during next job\n```\ndef jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:\n jobs= list(zip(startTime,endTime,profit))\n jobs.sort()\n print(jobs)\n heap=[]\n cur=ans=0\n for start,e,p in jobs: \n while heap and heap[0][0]<=start: #checks for non overlapping\n _,val=heappop(heap)\n cur=max(cur,val)\n \n heappush(heap,(e,cur+p)) \n ans=max(ans,cur+p)\n \n return ans \n \n```\n[2054. Two Best Non-Overlapping Events](https://leetcode.com/problems/two-best-non-overlapping-events/)\n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n \n events.sort()\n res=0\n cur=0\n heap=[]\n for left,r,v in events:\n heappush(heap,(r,v))\n \n while heap and heap[0][0]<left:\n R,val=heappop(heap)\n cur=max(cur,val)\n res=max(res,cur+v)\n \n return res\n```
| 2 | 0 |
['Heap (Priority Queue)', 'Python']
| 0 |
maximum-earnings-from-taxi
|
JAVA HEAP
|
java-heap-by-xxsidxx-5rma
|
\nclass Solution {\n class pair{\n int end;\n long profit;\n pair(int end,long profit){\n this.end=end;\n this.pro
|
xxsidxx
|
NORMAL
|
2021-09-26T06:05:54.372347+00:00
|
2021-09-26T06:05:54.372411+00:00
| 289 | false |
```\nclass Solution {\n class pair{\n int end;\n long profit;\n pair(int end,long profit){\n this.end=end;\n this.profit=profit;\n }\n }\n public long maxTaxiEarnings(int n, int[][] rides) {\n \n Arrays.sort(rides,(a,b)->{\n return a[0]-b[0];\n });\n \n long max=0;\n \n PriorityQueue<pair> pq=new PriorityQueue<>((a,b)->{\n return a.end-b.end;\n });\n \n \n long ans=0;\n for(int i=0;i<rides.length;i++){\n while(pq.size()>0&&pq.peek().end<=rides[i][0]){\n max=Math.max(max,pq.poll().profit);\n }\n pq.add(new pair(rides[i][1],rides[i][1]-rides[i][0]+rides[i][2]+max));\n ans=Math.max(rides[i][1]-rides[i][0]+rides[i][2]+max,ans);\n }\n \n return ans;\n\n \n }\n}\n```
| 2 | 0 |
[]
| 0 |
maximum-earnings-from-taxi
|
[Java][dp][recursion] seems simple
|
javadprecursion-seems-simple-by-anushbej-c218
|
\nclass Solution {\n //dp[i] is maximum earning starting from ith ride\n public static long dp[];\n public long maxTaxiEarnings(int n, int[][] rides) {
|
anushbejgum
|
NORMAL
|
2021-09-23T16:17:43.620613+00:00
|
2021-09-23T16:18:53.731079+00:00
| 195 | false |
```\nclass Solution {\n //dp[i] is maximum earning starting from ith ride\n public static long dp[];\n public long maxTaxiEarnings(int n, int[][] rides) {\n //Sort based on start point\n Arrays.sort(rides, (a,b)->a[0] - b[0]);\n dp = new long[rides.length];\n Arrays.fill(dp, -1);\n return maxTaxiEarningsHelper(n, rides, 0);\n }\n \n public long maxTaxiEarningsHelper(int n, int[][] rides, int start) {\n if(start >= rides.length) {\n return 0;\n }\n if(dp[start] != -1) {\n return dp[start];\n }\n long earn = (rides[start][1] - rides[start][0]) + rides[start][2];\n long pick = earn;\n for (int i=start+1;i<rides.length;i++) {\n if(rides[i][0] >= rides[start][1]) {\n //next eligible ride is ith ride\n pick += maxTaxiEarningsHelper(n, rides, i);\n break;\n }\n }\n //pick the next ride\n long nonpick = maxTaxiEarningsHelper(n, rides, start + 1);\n dp[start] = Math.max(nonpick, pick);\n return dp[start];\n }\n}\n```\n\n
| 2 | 1 |
[]
| 2 |
maximum-earnings-from-taxi
|
Classical "Weighted Job Scheduling" problem | [JS] [DP,Binary Search]
|
classical-weighted-job-scheduling-proble-qovw
|
\n// Same as https://leetcode.com/problems/maximum-profit-in-job-scheduling/\n// Time -> O(nlogn), where n = length of rides array\n// Space -> O(n), where n =
|
c_jain
|
NORMAL
|
2021-09-19T10:50:30.107680+00:00
|
2021-09-19T10:50:30.107715+00:00
| 320 | false |
```\n// Same as https://leetcode.com/problems/maximum-profit-in-job-scheduling/\n// Time -> O(nlogn), where n = length of rides array\n// Space -> O(n), where n = length of rides array\n\n/**\n * @param {number} n\n * @param {number[][]} rides\n * @return {number}\n */\nvar maxTaxiEarnings = function(n, rides) {\n \n const len = rides.length\n \n rides.sort((a,b) => {\n return a[1] - b[1]\n })\n \n // Binary search\n function binarySearch(idx) {\n let low = 0, high = idx\n \n while(low < high) {\n let mid = Math.trunc((low+high)/2)\n \n if(rides[mid][1] <= rides[idx][0]) low = mid+1\n else high = mid\n }\n \n return high === 0 ? -1 : high-1\n }\n \n let dp = new Array(len).fill(0)\n dp[0] = rides[0][2] + (rides[0][1] - rides[0][0])\n \n for(let i=1; i<len; i++) {\n dp[i] = rides[i][2] + (rides[i][1] - rides[i][0])\n let j = binarySearch(i)\n \n if(j !== -1)\n dp[i] += dp[j]\n \n dp[i] = Math.max(dp[i], dp[i-1])\n }\n \n return dp[len-1]\n};\n```
| 2 | 0 |
['JavaScript']
| 0 |
maximum-earnings-from-taxi
|
c++ solution
|
c-solution-by-dilipsuthar60-g7go-2
|
\nclass Solution {\npublic:\n static bool cmp(vector<int>&v1,vector<int>&v2)\n {\n return v1[1]<v2[1];\n }\n long long maxTaxiEarnings(int n,
|
dilipsuthar17
|
NORMAL
|
2021-09-19T05:15:10.885838+00:00
|
2021-09-19T05:15:10.885882+00:00
| 315 | false |
```\nclass Solution {\npublic:\n static bool cmp(vector<int>&v1,vector<int>&v2)\n {\n return v1[1]<v2[1];\n }\n long long maxTaxiEarnings(int n, vector<vector<int>>& nums) \n {\n for(auto &it:nums)\n {\n it[2]+=(it[1]-it[0]);\n }\n using ll=long long;\n n=nums.size();\n vector<ll>dp(n+10,0);\n sort(nums.begin(),nums.end(),cmp);\n dp[0]=nums[0][2];\n for(int i=1;i<n;i++)\n {\n int s=nums[i][0];\n int e=nums[i][1];\n ll cost=nums[i][2];\n int l=0;\n int r=i-1;\n int index=-1;\n while(l<=r)\n {\n int mid=(l+r)/2;\n if(nums[mid][1]<=s)\n {\n index=mid;\n l=mid+1;\n }\n else\n {\n r=mid-1;\n }\n }\n if(index!=-1)\n {\n cost+=dp[index];\n }\n dp[i]=max(dp[i-1],cost);\n }\n return dp[n-1];\n }\n};\n```
| 2 | 0 |
['C', 'Binary Tree', 'C++']
| 0 |
maximum-earnings-from-taxi
|
(C++) 2008. Maximum Earnings From Taxi
|
c-2008-maximum-earnings-from-taxi-by-qee-nuaw
|
\n\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n unordered_map<int, vector<pair<int, int>>> mp; \n
|
qeetcode
|
NORMAL
|
2021-09-18T22:05:02.777627+00:00
|
2021-09-18T22:05:02.777680+00:00
| 446 | false |
\n```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n unordered_map<int, vector<pair<int, int>>> mp; \n for (auto& x : rides) \n mp[x[0]].emplace_back(x[1], x[2]); \n \n vector<long long> dp(n+1); \n for (int x = n-1; x >= 1; --x) {\n dp[x] = dp[x+1]; \n for (auto& [xx, tip] : mp[x]) \n dp[x] = max(dp[x], xx - x + tip + dp[xx]); \n }\n return dp[1]; \n }\n};\n```
| 2 | 0 |
['C']
| 1 |
maximum-earnings-from-taxi
|
DP + Binary search. Simple solution. 6 lines
|
dp-binary-search-simple-solution-6-lines-uyq2
|
\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n earn = [0]\n rides.sort(key = itemgetter(1))\n f
|
xxxxkav
|
NORMAL
|
2024-09-09T20:34:42.041346+00:00
|
2024-09-09T20:35:11.739685+00:00
| 37 | false |
```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n earn = [0]\n rides.sort(key = itemgetter(1))\n for i, (start, end, tip) in enumerate(rides):\n j = bisect_right(rides, start, key = itemgetter(1), hi = i)\n earn.append(max(end - start + tip + earn[j], earn[-1]))\n return earn[-1]\n```
| 1 | 1 |
['Binary Search', 'Dynamic Programming', 'Python3']
| 1 |
maximum-earnings-from-taxi
|
Multiple solutions with detailed thought process (quadratic - TLE, binary search and optimal)
|
multiple-solutions-with-detailed-thought-z4wp
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Tag01
|
NORMAL
|
2023-06-07T00:10:24.035113+00:00
|
2023-06-07T00:10:24.035170+00:00
| 51 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n """\n We can see that this is an optimization problem that is asking us to maximize the money that we can get\n by moving passengers. At a time, there can only be one passenger in our taxi. This hints us to go in the \n brute force, careful brute force (dynamic programming by eliminating overlapping subproblems, providing we\n can prove that an optimal substructure exists in our recurrence relation) or a greedy solution.\n\n Let\'s see how we can approach this in a brute force way:\n If we are looking at a passenger i, there are multiple choices we have, we can either choose this passenger, \n or we can choose any other passenger that\'s overlapping with this one. So, let\'s try all the passengers. \n Let\'s sort the rides by their end points (we\'ll look at it from right to left). Let\'s say i and i-1 have an overlap.\n If we pick ith passenger, then we need to solve the subproblem for i-2 passenger. If we pick the (i-1)st passenger, \n we again need to solve the subproblem for i-2 (i-2 and i-1 don\'t have an overlap). So, there are overlapping \n subproblems, which we can eliminate by dynamic programming.\n\n Let\'s define our recurrence relation as:\n f(i) = the max earning that we can get from rides 1...i\n Mathematically:\n f(i) = max [ f(i-1), f(i-j) + earning(i) ], j = the first ride from end that doesn\'t overlap with the ith ride\n\n The number of total subproblems to solve will be the same as the number of rides. So we can create a 1d table\n of size len(rides) + 1, with table[0] as the base case where there are no rides so 0 money is to be made.\n\n Each subproblem f(i) depends only on the values of i to the left, so there is a top-sort order which allows us\n to solve subproblems incrementally from i=1 to i=len(rides)+1. At the end of this the answer would be in \n table[len(rides)] (or in other words, the max earning from rides 1...len(rides))\n\n\n Now on to implementation:\n 1. If we implementing the recurrence as is i.e. with two for loops (the inner for loop looks for the non overlapping\n ride), we run into Time limit exceeded error. T(n) = O(#rides^2)\n\n 2. We can overcome that with using binary search (since all the rides are sorted by their end times). You can see \n both the implementations below. T(n) = O(#rides * log(#rides))\n\n\n So far in the above implementation, we haven\'t used "n". I was not sure what\'s the purpose of that. Then, I came \n across a solution (https://leetcode.com/problems/maximum-earnings-from-taxi/solutions/1470935/c-python-dp-o-m-n-clean-concise/), that helped me understand how this solution could be improved further. \n \n Instead of looking at the rides, we can look at each point and define the recurrence (in a similar way) as:\n f(i) = the max earning that we can get by finishing at point i.\n Mathematically:\n f(i) = max [ f(i-1), f(i-j) + reward(i) for all the rides that end at i ]\n \n With this recurrence, the max subproblems are n. And we can solve them in a similar way from left to right. But,\n before implementing the recurrence we need to create a map so that we can easily get all the rides that end at \n a particular point.\n This processes all the n points, and only processes each ride only once. So gives a total of O(n + #rides) solution.\n\n Hope this is helpful to someone!\n """\n\n # The optimal solution\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n ridesEndingAt = defaultdict(list)\n for ride in rides:\n start, end, tip = ride\n ridesEndingAt[end].append([start, end-start+tip])\n \n table = [0]*(n+1)\n for i in range(1, n+1):\n # If we don\'t choose the rides ending at point i\n maxEarningWithoutAnyRideEndingAti = table[i-1]\n\n # If we choose the rides ending at point i, then for all the rides that end at this point\n # we look for their starting point, and get the max earning up to that point. And then, among those\n # rides, we choose the ride that gets us the maximum earning\n maxEarningFromRide = 0\n for rideEdningAti in ridesEndingAt[i]:\n startPoint, earningFromTheRide = rideEdningAti\n maxEarningFromRide = max(maxEarningFromRide, earningFromTheRide + table[startPoint])\n \n maxEarning = max(maxEarningWithoutAnyRideEndingAti, maxEarningFromRide)\n table[i] = maxEarning\n return table[-1]\n\n\n # Improving performance with binary search\n def maxTaxiEarningsBinarySearch(self, n: int, rides: List[List[int]]) -> int:\n total_rides = len(rides)\n rides.sort(key=lambda x:x[1])\n table = [0]*(len(rides)+1)\n \n for i in range(1, len(rides) + 1):\n # Fill in table[i]\n currRide = rides[i-1]\n \n # If we don\'t choose the current ride\n maxEarningWithoutCurrentRide = table[i-1]\n \n # If we choose the current ride\n earningUpToPrevRide = 0\n low, high = 0, i-2\n while low <= high:\n mid = low + (high - low) // 2\n # Find the first ride that has end point before the start point of the current ride\n midRide = rides[mid]\n if midRide[1] <= currRide[0]:\n low = mid + 1\n else:\n high = mid - 1\n # high is pointing to the first ride that has end point before the start point of the current ride.\n earningUpToPrevRide = table[high+1]\n currentRideEarning = currRide[1] - currRide[0] + currRide[2]\n \n table[i] = max(maxEarningWithoutCurrentRide, currentRideEarning + earningUpToPrevRide)\n return table[-1]\n\n def maxTaxiEarningsQuadratic(self, n: int, rides: List[List[int]]) -> int:\n total_rides = len(rides)\n rides.sort(key=lambda x:x[1])\n table = [0]*(len(rides)+1)\n\n for i in range(1, total_rides+1):\n # Fill in table[i]\n currRide = rides[i-1]\n\n # If we don\'t choose currRide, max earning is the same as table[i-1]\n maxEarningWithoutCurrentRide = table[i-1]\n\n # If we choose currRide, max earning would be the earning from the current ride plus the \n # earning from the last ride that didn\'t overlap with the current ride\n currRideEarning = currRide[1] - currRide[0] + currRide[2]\n earningUpToLastRide = 0\n for j in range(i-2, -1, -1):\n prevRide = rides[j]\n if prevRide[1] <= currRide[0]:\n # We found the last ride that doesn\'t overlap with current ride\n earningUpToLastRide = table[j+1] # index into table is 1 + the ride index\n break\n \n table[i] = max(maxEarningWithoutCurrentRide, currRideEarning + earningUpToLastRide)\n\n return table[-1]\n\n\n # For this method, we defined the recurrence slightly differently. \n # f(i) = the max earning that we make if we select the ith ride.\n # In the end, the max of the DP table is the max earning.\n def maxTaxiEarnings2(self, n: int, rides: List[List[int]]) -> int:\n rides.sort(key=lambda x:x[1])\n table = [0]*n\n table[0] = rides[0][1] - rides[0][0] + rides[0][2]\n\n for i in range(1, len(rides)):\n reward = rides[i][1] - rides[i][0] + rides[i][2]\n prevReward = 0\n for j in range(0, i):\n if rides[j][1] <= rides[i][0]:\n prevReward = max(prevReward, table[j])\n table[i] = prevReward + reward\n \n return max(table)\n```
| 1 | 0 |
['Binary Search', 'Dynamic Programming', 'Python3']
| 0 |
maximum-earnings-from-taxi
|
simple java solution beats 98% using Map O(n) solution
|
simple-java-solution-beats-98-using-map-t662q
|
please upvote if you like the solution \ntime-O(n)\nspace-O(n)\n\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] a) {\n Map<Integer,Lis
|
sonam_negi
|
NORMAL
|
2023-01-13T17:18:25.595150+00:00
|
2023-01-13T18:05:49.634098+00:00
| 149 | false |
please upvote if you like the solution \ntime-O(n)\nspace-O(n)\n```\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] a) {\n Map<Integer,List<pair>> map = new HashMap<>();\n long dp[]=new long [n+1];\n for(int x[]:a){\n if(!map.containsKey(x[1]))map.put(x[1],new ArrayList<>());\n map.get(x[1]).add(new pair(x[0],x[2]));\n }\n for(int i=1;i<=n;i++){\n if(map.containsKey(i)){\n for(pair x:map.get(i)){\n long cur=i-x.s+x.val;\n dp[i]=Math.max(cur+dp[x.s],dp[i]);\n dp[i]=Math.max(dp[i],dp[i-1]);\n }\n }else dp[i]= dp[i-1];\n }\n \n return dp[n];\n }\n}\nclass pair{\n int s,val;\n pair(int s,int val){\n this.s=s;\n this.val=val;\n }\n}\n```
| 1 | 0 |
['Dynamic Programming', 'Java']
| 0 |
maximum-earnings-from-taxi
|
✅C++ || Recursion->Memoization
|
c-recursion-memoization-by-akshat0610-pb0e
|
\nclass Solution {\npublic:\nunordered_map<long long,vector<pair<long long,long long>>>mp;\nvector<long long>dp;\nlong long maxTaxiEarnings(int n, vector<vector
|
akshat0610
|
NORMAL
|
2022-10-03T09:31:25.838402+00:00
|
2022-10-03T09:31:25.838444+00:00
| 2,378 | false |
```\nclass Solution {\npublic:\nunordered_map<long long,vector<pair<long long,long long>>>mp;\nvector<long long>dp;\nlong long maxTaxiEarnings(int n, vector<vector<int>>& arr) \n{\n\t long long currpos=1;\n\t dp.resize(n+1,-1);\n\t for(int i=0;i<arr.size();i++)\n\t {\n\t \tvector<int>temp=arr[i];\n\t \tlong long int start=temp[0];\n\t \tlong long int end=temp[1];\n\t \tlong long int tip=temp[2];\n\t \t\n\t \tmp[start].push_back(make_pair(end,tip));\n } \n return fun(currpos,n);\n}\nlong long fun(long long currpos,int &n)\n{\n\t//base case\n\tif(currpos==n)\n\t{\n\t\treturn 0;\n\t}\n\tif(dp[currpos]!=-1)\n\t{\n\t\treturn dp[currpos];\n\t}\n\tif(mp[currpos].size()>0) //we have passengers on this point\n\t{\n\t\tlong long choise1=INT_MIN;\n\t\tfor(int i=0;i<mp[currpos].size();i++)\n\t\t{\n\t\t\t//basically we dont have option for the passengers need to carry all of them atleast one time\n\t\t\t//take choise we will consider here\n\t\t auto p = mp[currpos][i];\n\t\t \n\t\t long long start=currpos;\n\t\t long long end=p.first;\n\t\t long long tip=p.second;\n\t\t \n long long temp = (end-start+tip) + fun(end,n) + 0LL;\n \n choise1=max(choise1,temp);\n\t\t}\n\t long long choise2 = 0 + fun(currpos+1,n);\n\t return dp[currpos]= max(choise1,choise2);\n\t}\n\telse if(mp[currpos].size()==0) //we dont have passengers on the currpos \n\t{\n\t \treturn dp[currpos] = 0 + fun(currpos+1,n);\n\t}\n\treturn 0; //this will never get encounterd\n}\n};\n```
| 1 | 0 |
['Dynamic Programming', 'Memoization', 'C', 'C++']
| 0 |
maximum-earnings-from-taxi
|
Scala DP with PriorityQueue
|
scala-dp-with-priorityqueue-by-maxmtmn-pijh
|
\nimport scala.collection.mutable\n\nobject Solution {\n def maxTaxiEarnings(n: Int, rides: Array[Array[Int]]): Long = {\n val ridesByEnd = mutable.Prio
|
maxmtmn
|
NORMAL
|
2022-09-24T20:25:43.114561+00:00
|
2022-10-01T01:39:05.143598+00:00
| 413 | false |
```\nimport scala.collection.mutable\n\nobject Solution {\n def maxTaxiEarnings(n: Int, rides: Array[Array[Int]]): Long = {\n val ridesByEnd = mutable.PriorityQueue.from(rides)(\n Ordering.by((item: Array[Int]) => item(1)).reverse\n )\n val maxAtPoint = Array.fill(n+1)(0L)\n (1 to n).foreach {\n v =>\n while(ridesByEnd.nonEmpty && ridesByEnd.head(1) == v) {\n ridesByEnd.dequeue() match {\n case Array(start, end, tip) =>\n val value = (end - start + tip)\n maxAtPoint(end) =\n // either continue prev ride or start one of new rides\n (value + maxAtPoint(start)) max maxAtPoint(end)\n }\n }\n maxAtPoint(v) = maxAtPoint(v - 1) max maxAtPoint(v)\n }\n maxAtPoint(n)\n }\n }\n ```
| 1 | 0 |
['Scala']
| 1 |
maximum-earnings-from-taxi
|
Priority Queue | Greedy | Easy Explaination | C++
|
priority-queue-greedy-easy-explaination-umseb
|
Intitution\nsort the rides vector according to first day \nfor each day remove the rides that are ending on that day and take the maximum of the earning you are
|
athar_mohammad
|
NORMAL
|
2022-09-02T09:45:13.799821+00:00
|
2022-09-02T09:45:13.799866+00:00
| 243 | false |
**Intitution**\nsort the rides vector according to first day \nfor each day remove the rides that are ending on that day and take the maximum of the earning you are making till that day\nAlso each day see which rides are starting and push them in the min-priority-queue such that ride with smallest end day comes first and add the maximum earnings that can be made till that day so that any ride starting that day will have maximum earning they can have considering all the days before\nreturn the maximum earning\n\n```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n priority_queue<pair<int64_t,int64_t>,vector<pair<int64_t,int64_t>>,greater<pair<int64_t,int64_t>>>pq;\n int64_t ind = 0,mx = 0;\n int64_t N = (int64_t)rides.size();\n sort(rides.begin(),rides.end());\n for(int64_t i = 1; i<= n; i++){\n while(!pq.empty() && pq.top().first <= i){\n mx = max(mx,pq.top().second);\n pq.pop();\n }\n while(ind < N && rides[ind][0] == i){\n pq.push({rides[ind][1],rides[ind][1]-rides[ind][0]+rides[ind][2]+mx});\n ind++;\n }\n }\n return mx;\n }\n};\n```
| 1 | 0 |
['Greedy', 'C', 'Heap (Priority Queue)']
| 0 |
maximum-earnings-from-taxi
|
Maximum Earnings From Taxi (c++)
|
maximum-earnings-from-taxi-c-by-cse19000-wud4
|
\nclass Solution {\npublic:\n bool static mycomp(vector<int>&a, vector<int>&b){\n return a[1]<b[1];\n}\n int find_lowerbound(int n, vector<int>&endtime,
|
cse190001048
|
NORMAL
|
2022-09-01T16:35:30.577091+00:00
|
2022-09-01T16:36:40.816809+00:00
| 175 | false |
```\nclass Solution {\npublic:\n bool static mycomp(vector<int>&a, vector<int>&b){\n return a[1]<b[1];\n}\n int find_lowerbound(int n, vector<int>&endtime, int x){\n int l=0; int r=n-1;\n int ans=-1;\n while(l<=r){\n int mid=l+(r-l)/2;\n if(endtime[mid]<=x){\n ans=mid;\n l=mid+1;\n }\n else{\n r=mid-1;\n }\n }\n return ans;\n }\n long long maxTaxiEarnings(int m, vector<vector<int>>&arr) {\n int n=arr.size();\n sort(arr.begin(), arr.end(), mycomp);\n vector<int>endtime;\n for(int i=0; i<n; i++){\n endtime.push_back(arr[i][1]);\n }\n long long dp[n];\n dp[0]=arr[0][2]+arr[0][1]-arr[0][0];\n for(int i=1; i<n; i++){\n int ind=find_lowerbound(i, endtime, arr[i][0]); \n long long profit=arr[i][2]+arr[i][1]-arr[i][0];\n if(ind>=0){\n profit+=dp[ind];\n }\n dp[i]=max(dp[i-1], profit);\n }\n return dp[n-1];\n }\n};\n```
| 1 | 0 |
['Binary Search', 'Dynamic Programming', 'C']
| 0 |
maximum-earnings-from-taxi
|
C++| DP Memorization + Binary Search | Easy Code
|
c-dp-memorization-binary-search-easy-cod-vc75
|
Please Upvote :)\n\n\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n sort(rides.begin(),rides.end());\n
|
ankit4601
|
NORMAL
|
2022-07-27T11:33:55.898487+00:00
|
2022-07-27T11:33:55.898535+00:00
| 463 | false |
Please Upvote :)\n\n```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n sort(rides.begin(),rides.end());\n vector<long long> dp(rides.size(),-1);\n return fun(rides,dp,0);\n }\n long long fun(vector<vector<int>>& v,vector<long long>& dp, int i)\n {\n if(i>=v.size())\n return 0;\n \n if(dp[i]!=-1)\n return dp[i];\n \n long long t=fun(v,dp,i+1);\n int next=search(v,v[i][1],i);\n long long sum=v[i][2]+v[i][1]-v[i][0];\n t=max(t,sum+fun(v,dp,next));\n \n return dp[i]=t;\n }\n int search(vector<vector<int>>& v,int val,int i)\n {\n int l=i+1;\n int r=v.size()-1;\n int res=v.size();\n \n while(l<=r)\n {\n int mid=(l+r)/2;\n \n if(v[mid][0]>=val)\n {\n res=mid;\n r=mid-1;\n }\n else\n l=mid+1;\n }\n return res;\n }\n};\n```
| 1 | 0 |
['Dynamic Programming', 'Memoization', 'C', 'Binary Tree', 'C++']
| 0 |
maximum-earnings-from-taxi
|
C++ DP
|
c-dp-by-wzypangpang-qbux
|
\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n auto cmp = [](vector<int>& v1, vector<int>& v2) {\n
|
wzypangpang
|
NORMAL
|
2022-07-14T03:31:20.954469+00:00
|
2022-07-14T03:31:20.954512+00:00
| 250 | false |
```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n auto cmp = [](vector<int>& v1, vector<int>& v2) {\n return v1[1] < v2[1];\n };\n sort(rides.begin(), rides.end(), cmp);\n \n vector<long long> dp(n+1, 0);\n \n long long mx = 0;\n long long last = 0;\n for(int i=0; i<rides.size(); ++i) {\n vector<int> r = rides[i];\n while(last < r[1]) {\n dp[last] = mx;\n last++;\n }\n dp[r[1]] = max(mx, dp[r[0]] + r[2] + r[1] - r[0]);\n mx = max(mx, dp[r[1]]);\n }\n return mx;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
maximum-earnings-from-taxi
|
[Java] | priorityQueue 0(nlogn)
|
java-priorityqueue-0nlogn-by-harshit01-5m1c
|
\nclass Solution {\n //easy solution by priorityQueue\n public long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides,(a,b)->a[0]-b[0]);\
|
harshit01
|
NORMAL
|
2022-07-11T12:19:22.402787+00:00
|
2022-07-11T12:19:22.402830+00:00
| 152 | false |
```\nclass Solution {\n //easy solution by priorityQueue\n public long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides,(a,b)->a[0]-b[0]);\n \n PriorityQueue<long[]>pq=new PriorityQueue<>((a,b)->Long.compare(a[0],b[0]));\n long maxf=0;\n \n for(int i=0;i<rides.length;i++){\n while(pq.size() > 0 && pq.peek()[0] <= rides[i][0])\n maxf=Math.max(maxf,pq.remove()[1]);\n \n pq.add(new long[]{rides[i][1],rides[i][1]-rides[i][0]+rides[i][2]+maxf});\n }\n long sum=0;\n \n while(pq.size() > 0)\n sum=Math.max(sum,pq.remove()[1]);\n \n return sum;\n \n }\n}\n```
| 1 | 0 |
[]
| 0 |
maximum-earnings-from-taxi
|
Java DP + Binary Search
|
java-dp-binary-search-by-mi1-t2gv
|
Lets sort the array by start times and then we have 2 options , either pick the passinger or dont. If we pick then since we cant pick any one until we drop we
|
mi1
|
NORMAL
|
2022-07-04T10:04:10.800487+00:00
|
2022-07-04T10:04:10.800521+00:00
| 172 | false |
Lets sort the array by start times and then we have 2 options , either pick the passinger or dont. If we pick then since we cant pick any one until we drop we can can find the next index using binary search.\n\n```\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] rides) {\n long[] dp = new long[rides.length+1];\n Arrays.fill(dp,-1);\n Arrays.sort(rides,(o1,o2)->Integer.compare(o1[0],o2[0]));\n return go(rides,0,dp);\n }\n \n private long go(int [][] rides,int idx,long[]dp){\n if(idx>=rides.length){\n return 0;\n }\n \n //System.out.println(idx);\n if(dp[idx]!=-1){\n return dp[idx];\n }\n \n // pick passinger\n long best = rides[idx][1]-rides[idx][0]+rides[idx][2]+go(rides,getNextIdx(idx,rides[idx][1],rides),dp);\n // dont pick passinger\n best = Math.max(best,go(rides,idx+1,dp));\n \n return dp[idx]=best;\n }\n \n private int getNextIdx(int curr, int endTime,int[][] rides){\n int start = curr,end = rides.length-1,ans = rides.length;\n while(start<=end){\n int mid = start + (end-start)/2;\n if(rides[mid][0]>=endTime){\n ans = mid;\n end = mid-1;\n }else{\n start = mid+1;\n }\n }\n return ans;\n }\n}\n```
| 1 | 0 |
[]
| 1 |
maximum-earnings-from-taxi
|
JAVA || 1-D DP || BINARY SEARCH || EASY TO UNDERSTAND
|
java-1-d-dp-binary-search-easy-to-unders-k4cz
|
\nclass Solution {\n public long maxTaxiEarnings(int max, int[][] rides) \n {\n int n=rides.length;\n Arrays.sort(rides,(a,b)->a[0]!=b[0]?a[
|
29nidhishah
|
NORMAL
|
2022-06-23T06:53:31.614509+00:00
|
2022-06-23T06:53:31.614545+00:00
| 631 | false |
```\nclass Solution {\n public long maxTaxiEarnings(int max, int[][] rides) \n {\n int n=rides.length;\n Arrays.sort(rides,(a,b)->a[0]!=b[0]?a[0]-b[0]:a[1]!=b[1]?a[1]-b[1]:a[2]-b[2]);\n \n \n long dp[]=new long[n+1];\n dp[n-1]=rides[n-1][1]-rides[n-1][0]+rides[n-1][2];\n \n for(int i=n-2;i>=0;i--)\n {\n int location=rides[i][1];\n int pos=binarySearch(rides,location,i+1,n-1);\n \n long money=dp[pos]+rides[i][1]-rides[i][0]+rides[i][2];\n dp[i]=Math.max(money,dp[i+1]);\n }\n \n return dp[0];\n }\n \n public int binarySearch(int rides[][],int target,int start,int end)\n {\n int ans=rides.length;\n while(start<=end)\n {\n int mid=start+(end-start)/2;\n \n if(rides[mid][0]>=target)\n {\n ans=mid;\n end=mid-1;\n }\n else\n {\n start=mid+1;\n }\n }\n \n return ans;\n }\n \n}\n```
| 1 | 0 |
['Dynamic Programming', 'Java']
| 1 |
maximum-earnings-from-taxi
|
✔ Python Solution | DP | 2 Solutions
|
python-solution-dp-2-solutions-by-satyam-rqr0
|
Solution 1\n\nTime : O(n)\nSpace : O(n)\n\n\nclass Solution:\n def maxTaxiEarnings(self, n, A):\n A.sort()\n dp = [0] * (n+1)\n for i in
|
satyam2001
|
NORMAL
|
2022-06-20T08:47:10.944273+00:00
|
2022-06-20T08:47:56.803881+00:00
| 436 | false |
**Solution 1**\n\n```Time``` : ```O(n)```\n```Space``` : ```O(n)```\n\n```\nclass Solution:\n def maxTaxiEarnings(self, n, A):\n A.sort()\n dp = [0] * (n+1)\n for i in range(n-1,-1,-1):\n dp[i] = dp[i+1]\n while A and i == A[-1][0]:\n s,e,t = A.pop()\n dp[i] = max(dp[i],dp[e] + e + t - s)\n return dp[0]\n```\n\n**Solution 2**\n\n```Time``` : ```O(kLog(k))```\n```Space``` : ```O(k)```\n\n```\nclass Solution:\n def maxTaxiEarnings(self, n, A):\n A.sort(key = lambda x:x[1])\n dp = [(0,0)]\n for s,e,t in A:\n i = bisect.bisect(dp,s, key = lambda x:x[0]) - 1\n profit = e + t - s + dp[i][1]\n if profit > dp[-1][1]:\n dp.append((e , profit))\n return dp[-1][1]\n```
| 1 | 0 |
['Dynamic Programming', 'Binary Tree', 'Python']
| 0 |
maximum-earnings-from-taxi
|
C++ Explained in Comments
|
c-explained-in-comments-by-mercer80-obgb
|
\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n \n \n //temp is the heart of the algorithm
|
mercer80
|
NORMAL
|
2022-06-08T16:29:19.593365+00:00
|
2022-06-12T07:47:53.190663+00:00
| 271 | false |
```\nclass Solution {\npublic:\n long long maxTaxiEarnings(int n, vector<vector<int>>& rides) {\n \n \n //temp is the heart of the algorithm here it contains pair\n //{start_time,end-start+tip}\n /*********************************************/\n vector<pair<int,int>> temp[n+1];//Array of vectors\n //this temp contains starting time, end-start+tip as pair for a particular finish time\n \n for(auto x:rides)\n temp[x[1]].push_back({x[0],x[1]-x[0]+x[2]});\n //here we push the pair in the temp[finish time]\n \n \n /*********************************************/\n vector<long long >dp(n+1,0);\n \n // dp0 =0 and dp 1=0 \n // dp[i] means\n for(int i=2;i<=n;i++)\n {\n dp[i]=dp[i-1]; // dont choose \n \n for(auto it : temp[i])\n {\n dp[i]=max(dp[i],it.second+dp[it.first]);\n }\n \n }\n return dp[n];\n \n }\n};\n```
| 1 | 0 |
[]
| 0 |
maximum-earnings-from-taxi
|
Scala
|
scala-by-fairgrieve-hqln
|
\nobject Solution {\n def maxTaxiEarnings(n: Int, rides: Array[Array[Int]]): Long = {\n val startToEndAndTip = rides.groupMap(_(0)) { case Array(_, end, tip
|
fairgrieve
|
NORMAL
|
2022-05-12T07:31:08.026907+00:00
|
2022-05-12T07:31:54.222460+00:00
| 64 | false |
```\nobject Solution {\n def maxTaxiEarnings(n: Int, rides: Array[Array[Int]]): Long = {\n val startToEndAndTip = rides.groupMap(_(0)) { case Array(_, end, tip) => (end, tip) }.withDefaultValue(Array.empty)\n (1 until n)\n .foldRight(IndexedSeq(0L)) {\n case (start, dp) => dp.prepended {\n Iterator(dp(0))\n .concat {\n startToEndAndTip(start).iterator.map {\n case (end, tip) =>\n val distance = end - start\n (distance + tip) + dp(distance - 1)\n }\n }\n .max\n }\n }\n .head\n }\n}\n```
| 1 | 0 |
['Scala']
| 0 |
maximum-earnings-from-taxi
|
Java Recursion, Memoization TLE, Any Idea?
|
java-recursion-memoization-tle-any-idea-x9efa
|
Hi, thinking as top down, looks me more intuitive. I implemented a solution by using recursion and memoization. But I still get TLE. Do you have any idea?\n- S
|
serhattural12
|
NORMAL
|
2022-04-26T06:28:14.909260+00:00
|
2022-04-26T06:28:14.909306+00:00
| 128 | false |
Hi, thinking as top down, looks me more intuitive. I implemented a solution by using recursion and memoization. But I still get TLE. Do you have any idea?\n- Sort the rides by start time\n- Iterate on the rides and you have 2 option: take or not take. (recursion)\n- Keep a variable previous end to check current ride can be take. (if start of current is smaller than prev end you cannot take)\n\n```\n\tpublic long maxTaxiEarnings(int n, int[][] rides) {\n Arrays.sort(rides, (x1,x2) -> Integer.compare(x1[0], x2[0]));\n int result = getMaxRidings(rides, 0, 0, new Integer[n+1]); \n return result;\n }\n \n private int getMaxRidings(int[][] rides, int i, int prevEnd, Integer[] memo) {\n if(i>= rides.length)\n return 0;\n \n int start = rides[i][0];\n int end = rides[i][1];\n int tip = rides[i][2];\n \n if(memo[prevEnd]!=null)\n return memo[prevEnd];\n \n int result1 = Integer.MIN_VALUE;\n if(prevEnd<=start) { \n int profit = end-start+tip;\n result1 = profit + getMaxRidings(rides, i+1, Math.max(prevEnd, end), memo);\n }\n int result2 = getMaxRidings(rides, i+1, prevEnd, memo);\n \n memo[prevEnd] = Math.max(result1, result2);\n return memo[prevEnd];\n }\n```
| 1 | 0 |
[]
| 2 |
maximum-earnings-from-taxi
|
C++ memoized solution using simple binary search
|
c-memoized-solution-using-simple-binary-tciim
|
\n long long dp[1000005];\n int nextpos(vector<vector<int>>& rides , int val , int idx )\n {\n int l=idx;\n int h=rides.size()-1;\n i
|
KR_SK_01_In
|
NORMAL
|
2022-03-25T07:58:42.620745+00:00
|
2022-03-25T07:58:42.620783+00:00
| 178 | false |
```\n long long dp[1000005];\n int nextpos(vector<vector<int>>& rides , int val , int idx )\n {\n int l=idx;\n int h=rides.size()-1;\n int pos=h+1;\n \n while(l<=h)\n {\n int mid=(l+(h-l)/2);\n \n if(rides[mid][0]>=val)\n {\n pos=mid;\n h=mid-1;\n }\n else\n {\n l=mid+1;\n }\n }\n \n return pos;\n }\n long long func( vector<vector<int>>& rides , int i , int n )\n {\n if(i>=n)\n {\n return 0;\n }\n \n if(dp[i]!=-1)\n {\n return dp[i];\n }\n long long val1;\n \n val1=func(rides , i+1 , n);\n \n int idx=nextpos(rides , rides[i][1] , i);\n \n long long val2= (long long)(rides[i][1]-rides[i][0] + rides[i][2] )+ (long long)func(rides , idx , n );\n \n return dp[i]= max(val1 , val2);\n }\n long long maxTaxiEarnings(int m, vector<vector<int>>& rides) {\n \n memset(dp , -1 , sizeof(dp));\n \n \n sort(rides.begin(),rides.end());\n return func(rides , 0 , rides.size());\n \n \n \n \n \n \n }\n```
| 1 | 0 |
['Dynamic Programming', 'Memoization', 'C', 'Binary Tree', 'C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.