question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
reorder-list
|
Best Explanation Ever \(@^0^@)/
|
best-explanation-ever-0-by-hi-ravi-ts2n
|
\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val)
|
hi-ravi
|
NORMAL
|
2022-07-14T06:41:31.429856+00:00
|
2022-07-14T06:41:31.429899+00:00
| 154 | false |
```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public void reorderList(ListNode head) {\n if(head==null||head.next==null)return ;\n \n //Find the middle of the list\n ListNode slow = head;//slow head pe\n ListNode fast = head.next;//fast head.next se\n while(fast!=null&&fast.next!=null){//slow humare middle pe poch jayega\n slow = slow.next;\n fast = fast.next.next;\n }\n \n //Reverse the half after middle 1->2->3->4->5->6 to 1->2->3->6->5->4\n ListNode second =slow.next;//Second is At the starting point of second half\n ListNode prev = null;\n slow.next = null;//last node of first half pointing to null\n while(second!=null){// basic reversing function\n ListNode forw = second.next;\n second.next = prev;\n prev =second;\n second = forw;\n }\n \n //give output as prev as the head of the reverse linked list\n //Start reorder one by one 1->2->3->6->5->4 to 1->6->2->5->3->4\n \n \n ListNode first = head;//first pointer at the head of first list\n second = prev;//second pointet at the head of the second reverse list\n while(second!=null){//merging function\n ListNode temp1=first.next;//temp1 to store the next value of first half\n ListNode temp2 = second.next;//temp 2 to store the next value of second half\n first.next = second;\n second.next =temp1;\n first = temp1;//reseting first\n second = temp2;//resenting second\n }\n }\n} \n```\n<hr>\n<hr>\n\n***TIME COMPLEXITY = 0(N)\nSPACE COMPLEXITY =O(1)*\n\n<hr>\n<hr>\n
| 7 | 0 |
[]
| 0 |
reorder-list
|
3 step C++ iterative solution | Easy to Understand | O(1) space in-place
|
3-step-c-iterative-solution-easy-to-unde-9wak
|
Steps:\n1) Find the middle node of the linked list\n2) Reverse the second half of the linked list\n3) Merge two linked lists\n\n\t\tGiven: 1 --> 2 -->
|
rahulmittall
|
NORMAL
|
2022-05-03T05:38:06.676247+00:00
|
2022-05-03T05:38:06.676292+00:00
| 273 | false |
**Steps:**\n1) Find the middle node of the linked list\n2) Reverse the second half of the linked list\n3) Merge two linked lists\n\n\t\tGiven: 1 --> 2 --> 3 --> 4 --> 5\n\t\t\n\t\tAfter Step 1: 1 --> 2 --> 3 --> 4 --> 5\n\t\t\t\t\t\t\t\t |\n\t\t\t\t\t\t\t\t slow\n\t\t\t\t\t\t\t\t\t\n\t\tAfter Step 2: 1 --> 2 --> 3 5--> 4\n |\n\t\t\t\t\t\t \t\t \t prev\n\t\t\t\t\t\t\t\t\t\t\t\t\n\t\tAfter Step 3: 1 --> 5 --> 2 --> 4 --> 3\n```\nclass Solution {\npublic:\n void reorderList(ListNode* head) {\n if(!head->next) return;\n \n // Finding middle of linked list\n ListNode* slow=head;\n ListNode* fast=head;\n while(fast->next and fast->next->next){\n slow=slow->next;\n fast=fast->next->next;\n }\n \n // Reversing the second half of the linked list\n ListNode* prev=NULL;\n ListNode* curr = slow->next;\n while(curr){\n ListNode* nextt = curr->next;\n curr->next = prev;\n prev = curr;\n curr=nextt;\n }\n slow->next = NULL;\n \n // Merge two lists \n ListNode* head1=head;\n ListNode* head2=prev;\n while(head2){\n ListNode* temp = head1->next;\n head1->next = head2;\n head1=head1->next;\n head2= temp;\n }\n \n }\n};\n\n\n\n
| 7 | 0 |
['Linked List', 'C', 'Iterator']
| 0 |
reorder-list
|
[Rust] Itertaive, in-place re-ordering with O(1) additional space
|
rust-itertaive-in-place-re-ordering-with-w142
|
\nrust\nuse std::hint::unreachable_unchecked;\n\npub fn reorder_list(head: &mut Option<Box<ListNode>>) {\n // Find how many nodes are in the list;\n let m
|
keep_of_kalessin
|
NORMAL
|
2021-09-26T20:39:58.289942+00:00
|
2022-12-31T10:15:55.213113+00:00
| 579 | false |
\n```rust\nuse std::hint::unreachable_unchecked;\n\npub fn reorder_list(head: &mut Option<Box<ListNode>>) {\n // Find how many nodes are in the list;\n let mut count = 0;\n let mut list = &*head;\n\n while let Some(node) = list {\n list = &node.next;\n count += 1;\n }\n\n // If there are less than two nodes, then there is nothing to do\n if count <= 2 {\n return;\n }\n\n // Reach the middle of the list in order to split in to two lists\n let mut half = head.as_mut();\n for _ in 0..count / 2 {\n match half {\n // SAFETY: we have counted the number of nodes, so we know there are more nodes\n None => unsafe { unreachable_unchecked() },\n Some(node) => {\n half = node.next.as_mut();\n }\n }\n }\n\n // Reverse the second half\n let mut half = match half {\n // SAFETY: we have counted the number of nodes, so we know there are more nodes\n None => unsafe { unreachable_unchecked() },\n Some(node) => node.next.take(),\n };\n\n let mut reversed = ListNode::new(0);\n while let Some(mut node) = half.take() {\n half = node.next.take();\n node.next = reversed.next.take();\n reversed.next = Some(node);\n }\n\n // merge the two lists, tail points to the node in the first list\n // that has to be disconnected in order to put a node from the reversed\n // list in its place. Then it\'s reattached as "next" of the new node\n let mut tail = match head.as_mut() {\n // SAFETY: we know there is node at HEAD\n None => unsafe { unreachable_unchecked() },\n Some(node) => &mut node.next,\n };\n\n while tail.is_some() && reversed.next.is_some() {\n // SAFETY: We know there is a reversed.next because we already checked it\n let mut rev = reversed.next.take().unwrap();\n reversed.next = rev.next.take();\n\n rev.next = tail.take();\n *tail = Some(rev);\n tail = &mut tail.as_mut().unwrap().next;\n if let Some(node) = tail {\n tail = &mut node.next;\n }\n }\n}\n```
| 7 | 0 |
['Rust']
| 1 |
reorder-list
|
Python. faster than 95.06%. O(n), Super simple & clear solution.
|
python-faster-than-9506-on-super-simple-fsw70
|
\tclass Solution:\n\t\tdef reorderList(self, head: ListNode) -> None:\n\t\t\tif not head: return head\n\t\t\tslow, fast = head, head\n\t\t\twhile fast.next and
|
m-d-f
|
NORMAL
|
2021-02-10T20:28:28.305763+00:00
|
2021-02-10T20:28:28.305792+00:00
| 1,545 | false |
\tclass Solution:\n\t\tdef reorderList(self, head: ListNode) -> None:\n\t\t\tif not head: return head\n\t\t\tslow, fast = head, head\n\t\t\twhile fast.next and fast.next.next:\n\t\t\t\tslow = slow.next\n\t\t\t\tfast = fast.next.next\n\t\t\t\n\t\t\tprev, cur = None, slow.next\n\t\t\twhile cur:\n\t\t\t\tsave = cur.next\n\t\t\t\tcur.next = prev\n\t\t\t\tprev = cur\n\t\t\t\tcur = save\n\t\t\tslow.next = None\n\t\t\t\n\t\t\thead2 = prev\n\t\t\twhile head2:\n\t\t\t\tsave1 = head.next\n\t\t\t\thead.next = head2\n\t\t\t\thead = head2\n\t\t\t\thead2 = save1
| 7 | 0 |
['Linked List', 'Python', 'Python3']
| 1 |
reorder-list
|
Rust 4ms
|
rust-4ms-by-pedantic-ch9j
|
Very long solution.\n1. Calculate the length\n2. Traverse half way\n3. Reverse the second half\n4. Merge\n\n\nimpl Solution {\n pub fn reorder_list(head: &mu
|
pedantic
|
NORMAL
|
2020-08-21T01:05:51.871833+00:00
|
2020-08-21T01:05:51.871879+00:00
| 282 | false |
Very long solution.\n1. Calculate the length\n2. Traverse half way\n3. Reverse the second half\n4. Merge\n\n```\nimpl Solution {\n pub fn reorder_list(head: &mut Option<Box<ListNode>>) {\n let len = Self::length(&head);\n\n let mut ptr = head.as_mut();\n for _ in 0..(len / 2) {\n if let Some(node) = ptr {\n ptr = node.next.as_mut();\n }\n }\n\n if let Some(node) = ptr {\n let reverse = Self::reverse(node.next.take(), None);\n\n if let Some(node) = head {\n node.next = Self::merge(reverse, node.next.take(), len - 1);\n }\n }\n }\n\n fn length(mut head: &Option<Box<ListNode>>) -> usize {\n let mut count = 0;\n while let Some(node) = head {\n head = &node.next;\n count += 1;\n }\n count\n }\n\n fn reverse(\n head: Option<Box<ListNode>>,\n accumulator: Option<Box<ListNode>>,\n ) -> Option<Box<ListNode>> {\n match head {\n None => accumulator,\n Some(mut node) => {\n let next = node.next;\n node.next = accumulator;\n\n Self::reverse(next, Some(node))\n }\n }\n }\n\n fn merge(\n mut left: Option<Box<ListNode>>,\n right: Option<Box<ListNode>>,\n count: usize,\n ) -> Option<Box<ListNode>> {\n if count == 0 {\n None\n } else {\n match (left.as_mut(), right.as_ref()) {\n (None, None) => None,\n (Some(_), None) => left,\n (None, Some(_)) => right,\n (Some(l), Some(_)) => {\n l.next = Self::merge(right, l.next.take(), count - 1);\n left\n }\n }\n }\n }\n}\n```
| 7 | 0 |
[]
| 1 |
reorder-list
|
JAVA - Easy Solution using ArrayList and 2 Pointers
|
java-easy-solution-using-arraylist-and-2-o0g1
|
\npublic void reorderList(ListNode head) {\n\tList<ListNode> l = new ArrayList<>();\n\tfor(ListNode iter = head; iter!=null; iter = iter.next)\n\t\tl.add(iter);
|
anubhavjindal
|
NORMAL
|
2020-03-07T23:36:33.168094+00:00
|
2020-03-07T23:36:33.168145+00:00
| 259 | false |
```\npublic void reorderList(ListNode head) {\n\tList<ListNode> l = new ArrayList<>();\n\tfor(ListNode iter = head; iter!=null; iter = iter.next)\n\t\tl.add(iter);\n\tint lo = 0, hi = l.size()-1;\n\tListNode dummy = new ListNode(-1);\n\twhile(lo <= hi) {\n\t\tdummy.next = l.get(lo++);\n\t\tdummy = dummy.next;\n\t\tdummy.next = l.get(hi--);\n\t\tdummy = dummy.next;\n\t}\n\tdummy.next = null; // eliminate the cycle\n}\n```
| 7 | 0 |
[]
| 1 |
reorder-list
|
[JavaScript] Easy to understand - 2 solutions - 72ms
|
javascript-easy-to-understand-2-solution-zflu
|
The first solution, it\'s a normal one, and I think it\'s more in line with the requirements "NOT modify the node". Here is the algorithm:\n\n1. Traversal the l
|
poppinlp
|
NORMAL
|
2019-09-23T08:10:06.409782+00:00
|
2019-09-23T08:10:06.409836+00:00
| 1,376 | false |
The first solution, it\'s a normal one, and I think it\'s more in line with the requirements "NOT modify the node". Here is the algorithm:\n\n1. Traversal the linked list to find the middle node\n2. Reverse the latter half\n3. Reorder the whole linked list\n\n```js\nconst reorderList = head => {\n if (!head || !head.next || !head.next.next) return head;\n\n let slow = head;\n let fast = head.next;\n while (fast && fast.next) {\n slow = slow.next;\n fast = fast.next.next;\n }\n\n let prev = slow.next;\n let tail = prev.next;\n while (tail) {\n const next = tail.next;\n tail.next = prev;\n prev = tail;\n tail = next;\n }\n slow.next.next = null;\n slow.next = prev;\n\n let left = head;\n let right = slow.next;\n slow.next = null;\n while (left && right) {\n const ln = left.next;\n const rn = right.next;\n left.next = right;\n right.next = ln;\n left = ln;\n right = rn;\n }\n\n return head;\n};\n```\n\nThe second solution, may be a little cheating, by which I mean I add a pointer for each node link to the previous one. I\'m not pretty sure that it\'s modify the values of node or not. And here\'s the algorithm:\n\n1. Traversal the linked list and convert it to a doubly linked list\n2. Reorder the whole linked list from both 2 side\n\n```js\nconst reorderList = head => {\n if (!head || !head.next) return head;\n let prev = head;\n let tail = head.next;\n while (tail) {\n tail.prev = prev;\n prev = tail;\n tail = tail.next;\n }\n let cur = head;\n while (cur !== prev && cur.prev !== prev) {\n const next = cur.next;\n cur.next = prev;\n prev.next = next;\n prev = prev.prev;\n cur = next;\n }\n cur.next = null;\n return head;\n};\n```
| 7 | 1 |
['JavaScript']
| 1 |
reorder-list
|
[C++] O(n) time, O(1) space solution
|
c-on-time-o1-space-solution-by-arthur960-mrex
|
First Split the list in half.\n2. Reverse the second linked list.\n3. Merge two lists together.\n\n\nclass Solution {\npublic:\n void reorderList(ListNode* h
|
arthur960304
|
NORMAL
|
2019-08-16T09:39:05.227417+00:00
|
2019-08-16T09:39:40.183243+00:00
| 651 | false |
1. First Split the list in half.\n2. Reverse the second linked list.\n3. Merge two lists together.\n\n```\nclass Solution {\npublic:\n void reorderList(ListNode* head) {\n if(!head) return;\n \n // Cut the list in half\n ListNode* head2 = cutInHalf(head);\n \n // Reverse the second part of the list\n head2 = reverse(head2);\n \n // Merge two list\n merge(head, head2);\n }\n \n ListNode* cutInHalf(ListNode* head) {\n ListNode* slow = head;\n ListNode* fast = head;\n \n while(fast->next && fast->next->next) {\n slow = slow->next;\n fast = fast->next->next;\n }\n \n // Cut in half\n ListNode* mid = slow->next;\n slow->next = NULL;\n \n return mid;\n }\n \n ListNode* reverse(ListNode* head) {\n if(!head) return NULL;\n \n ListNode* curr = head;\n ListNode* temp = head;\n ListNode* prev = NULL;\n \n while(curr) {\n temp = curr->next;\n curr->next = prev;\n prev = curr;\n curr = temp;\n }\n return prev;\n }\n \n \n void merge(ListNode* p, ListNode* q) {\n if(!p) return;\n if(!q) return;\n \n while(p && q) {\n ListNode* pTemp = p->next;\n ListNode* qTemp = q->next;\n p->next = q;\n p = pTemp;\n q->next = p;\n q = qTemp;\n }\n }\n};\n```
| 7 | 0 |
['C']
| 2 |
reorder-list
|
Accepted Answer in Java
|
accepted-answer-in-java-by-wei14-0mzu
|
/**\n * Definition for singly-linked list.\n * class ListNode {\n * int val;\n * ListNode next;\n * ListNode(int x) {\n *
|
wei14
|
NORMAL
|
2014-10-15T23:41:06+00:00
|
2014-10-15T23:41:06+00:00
| 2,730 | false |
/**\n * Definition for singly-linked list.\n * class ListNode {\n * int val;\n * ListNode next;\n * ListNode(int x) {\n * val = x;\n * next = null;\n * }\n * }\n */\n public class Solution {\n \n private ListNode start;\n \n public void reorderList(ListNode head) {\n \n // 1. find the middle point\n if(head == null || head.next == null || head.next.next == null)return;\n \n ListNode a1 = head, a2 = head;\n \n while(a2.next!=null){\n // a1 step = 1\n a1 = a1.next;\n // a2 step = 2\n a2 = a2.next;\n if(a2.next==null)break;\n else a2 = a2.next;\n }\n // a1 now points to middle, a2 points to last elem\n \n // 2. reverse the second half of the list\n this.reverseList(a1);\n \n // 3. merge two lists\n ListNode p = head, t1 = head, t2 = head;\n while(a2!=a1){ // start from both side of the list. when a1, a2 meet, the merge finishes.\n t1 = p;\n t2 = a2;\n p = p.next;\n a2 = a2.next;\n \n t2.next = t1.next;\n t1.next = t2;\n }\n }\n \n // use recursion to reverse the right part of the list\n private ListNode reverseList(ListNode n){\n \n if(n.next == null){\n // mark the last node\n // this.start = n;\n return n;\n }\n \n reverseList(n.next).next = n;\n n.next = null;\n return n;\n }\n }
| 7 | 0 |
['Java']
| 1 |
reorder-list
|
143. Reorder List
|
143-reorder-list-by-doaaosamak-0fja
|
Code\n\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\
|
DoaaOsamaK
|
NORMAL
|
2024-03-23T12:45:16.058563+00:00
|
2024-03-23T12:45:16.058598+00:00
| 22 | false |
# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* reverse(ListNode *head){\n if(!head) return NULL;\n ListNode *prev = NULL;\n ListNode *curr = head;\n ListNode *nextNode = NULL;\n while(curr){\n nextNode = curr->next;\n curr->next = prev;\n prev = curr;\n curr = nextNode;\n }\n return prev;\n }\n\n void merge(ListNode *list1, ListNode *list2){\n while(list2) {\n ListNode *nextNode = list1->next;\n list1->next = list2;\n list1 = list2;\n list2 = nextNode;\n\n }\n\n }\n void reorderList(ListNode* head) {\n if(!head || !head->next) return;\n ListNode *slow = head;\n ListNode *fast = head;\n ListNode *prev = head;\n while(fast && fast->next){\n prev = slow;\n fast = fast->next->next;\n slow = slow->next;\n }\n prev->next = NULL;\n ListNode *list1 = head;\n ListNode *list2 = reverse(slow);\n merge(list1,list2);\n }\n};\n```
| 6 | 0 |
['C++']
| 0 |
reorder-list
|
✅Easy✨ ||C++|| Beats 100% || With Explanation||
|
easy-c-beats-100-with-explanation-by-ola-e8c9
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThere are many ways to solve this problem like by stack, recursion, two pointer. Here w
|
olakade33
|
NORMAL
|
2024-03-23T07:37:36.354291+00:00
|
2024-03-23T07:37:36.354322+00:00
| 374 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are many ways to solve this problem like by stack, recursion, two pointer. Here we have used most effective by solving this question in the vector arr and rearranging the nodes as follows.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Save Addresses: Traverse the linked list and save the addresses of all nodes in a vector arr.\n\n2. Set Pointers: After saving all addresses, initialize two pointers i and j to the beginning and end of the vector respectively. Also, initialize a pointer t1 to the first element of the vector.\n\n3. Rearrange Nodes: In a loop, rearrange the pointers to reorder the list. The basic idea is to take the node pointed by j and set it as the next node of the node pointed by i, then move j backward. Next, take the node pointed by i and set it as the next node of the node pointed by j, then move i forward. Repeat this process until i becomes greater than or equal to j.\n\n4. Terminate the List: After the loop, ensure proper termination of the reordered list by setting the next pointer of the last node to nullptr.\n\nThis approach ensures that we are properly rearranging the pointers to reorder the list while traversing it just once.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n void reorderList(ListNode* head) {\n if (!head || !head->next)\n return; // No need to reorder for empty or single node list\n\n vector<ListNode*> arr; // to save address of all list nodes\n ListNode* temp = head;\n\n while (temp != nullptr) {\n arr.push_back(temp);\n temp = temp->next;\n }\n\n int i = 0, j = arr.size() - 1;\n while (i < j) {\n arr[i]->next = arr[j];\n i++;\n\n if (i == j) break; // Break if i and j meet\n\n arr[j]->next = arr[i];\n j--;\n }\n arr[i]->next = nullptr;\n }\n};\n```
| 6 | 0 |
['C++']
| 0 |
reorder-list
|
Easy C++ || beats 99.47% || 3 Easy Steps || TC: O(n) , SC: O(1) || Explanation With Diagram
|
easy-c-beats-9947-3-easy-steps-tc-on-sc-16ivs
|
Intuition\nSee picture I Uploaded below. Its 80% observation and 20% code.\nIf you have done another problem where we reverse a linked list, CONGRATULATIONS, yo
|
kalki299
|
NORMAL
|
2024-03-23T05:11:03.024641+00:00
|
2024-03-23T07:33:03.731559+00:00
| 547 | false |
# Intuition\nSee picture I Uploaded below. Its 80% observation and 20% code.\nIf you have done another problem where we reverse a linked list, CONGRATULATIONS, you are left with 10% of code.\n# Approach\nSTEP 1: Break the list in 2 halves using SLOW and FAST pointer.\nSTEP 2: Reverse the 2nd part.\nSTEP 3: JOIN the corresponding element (eg: 1st and 1st, 2nd and 2nd). See picutre i uploaded.\n**PLS UPVOTE THIS POST, I NEED MY FIRST BADGE**\n\n\n\n\n\n# Complexity\n- Time complexity:\n**O(n)**\n- Space complexity:\n**O(1)**\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\nprivate:\n ListNode* reverseLL(ListNode* head){\n // just a code for reversing a linked list\n if (!head || !head->next) return head;\n ListNode * prev = nullptr;\n ListNode * next = nullptr;\n ListNode * temp = head;\n\n while (temp){\n next = temp->next;\n temp->next = prev;\n prev = temp;\n temp = next;\n }\n return prev;\n }\npublic:\n void reorderList(ListNode* head) {\n // step 1 find the start of second half of ll\n ListNode * slow = head;\n ListNode * fast = head;\n ListNode* head2 = nullptr;\n\n while (fast->next && fast->next->next){\n slow = slow->next;\n fast = fast->next ->next;\n }\n // step2: reverse the second half\n head2 = reverseLL(slow->next);\n\n // disconnect both halves\n slow->next =nullptr;\n \n // 3 finally point the ith element of each part\n ListNode * a = head;\n ListNode * b = head2;\n\n while (a && b){\n ListNode * a2 = a->next;\n ListNode * b2 = b->next;\n b->next = a2;\n a->next = b;\n if (a2 && !b2) {\n b->next = a2;\n return;\n }\n a=a2; b=b2;\n } \n }\n};\n\n```
| 6 | 0 |
['Linked List', 'C++']
| 1 |
reorder-list
|
Simple Java Solution
|
simple-java-solution-by-keerthivarmank-pgrd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
KeerthiVarmanK
|
NORMAL
|
2024-01-02T13:29:35.518859+00:00
|
2024-01-02T13:29:35.518884+00:00
| 820 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public void reorderList(ListNode head) {\n List<ListNode> arr = new ArrayList<>();\n ListNode node = head;\n while(node != null) {\n arr.add(node);\n node = node.next;\n }\n node = head;\n for(int i = 0 ; i < arr.size()/2 ; i++) {\n ListNode ins = arr.get(arr.size()-i-1);\n ListNode insP = arr.get(arr.size()-i-2);\n insP.next = null;\n ListNode rn = node.next;\n node.next = ins;\n ins.next = rn;\n if(rn != null) node = rn;\n }\n }\n}\n```
| 6 | 1 |
['Java']
| 0 |
reorder-list
|
C++ Easy Deque Solution Beats 99.71%
|
c-easy-deque-solution-beats-9971-by-zeri-kite
|
\n# Code\n\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr)
|
zerin_xahan
|
NORMAL
|
2023-01-19T05:43:38.894248+00:00
|
2023-01-19T05:43:38.894295+00:00
| 1,067 | false |
\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n void reorderList(ListNode* head) {\n deque<ListNode*> q;\n ListNode* tmp=head;\n while(tmp!=NULL)\n {\n q.push_back(tmp);\n tmp=tmp->next;\n q.back()->next=NULL;\n }\n q.pop_front();\n bool f=1;\n while(!q.empty())\n {\n if(!f)\n {\n head->next=q.front();\n q.pop_front();\n }\n else\n {\n head->next=q.back();\n q.pop_back();\n }\n head=head->next;\n f=!f;\n }\n }\n};\n```
| 6 | 0 |
['C++']
| 1 |
reorder-list
|
C++ code with Proper explanation & Diagram
|
c-code-with-proper-explanation-diagram-b-vi19
|
\n\n\nHere is full explanation of the code i think you guys like these and plz upvote this !\n\nclass Solution {\npublic:\n ListNode getmid(ListNode &head)\n
|
noobjitu
|
NORMAL
|
2022-10-23T15:12:23.848614+00:00
|
2022-10-23T15:12:23.848667+00:00
| 557 | false |
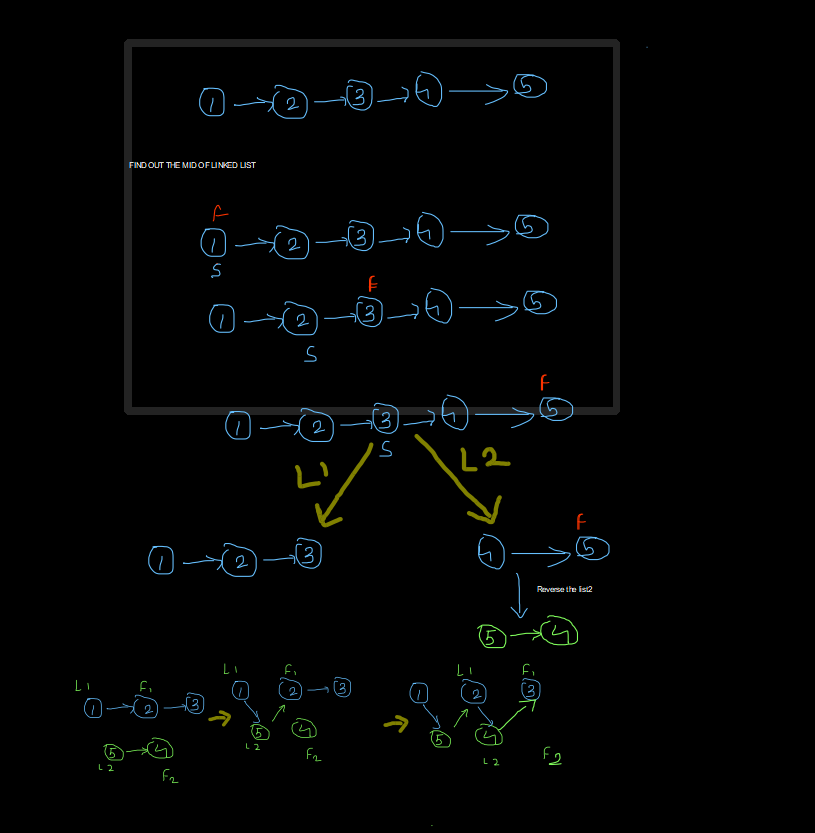\n\n\nHere is full explanation of the code i think you guys like these and plz upvote this !\n\nclass Solution {\npublic:\n ListNode* getmid(ListNode* &head)\n {\n ListNode* slow = head;\n ListNode* fast = head;\n while(fast != NULL && fast -> next != NULL)\n {\n slow = slow -> next;\n fast = fast -> next -> next;\n }\n return slow;\n }\n ListNode* reverse(ListNode* head)\n {\n ListNode* prev = NULL;\n ListNode* curr = head;\n ListNode* forward = NULL;\n while(curr != NULL)\n {\n forward = curr -> next;\n curr -> next = prev;\n prev = curr;\n curr = forward;\n }\n return prev;\n }\n void reorderList(ListNode* head) {\n if(head == NULL || head -> next == NULL)return;\n // find the mid of the linked list\n ListNode* mid = getmid(head); \n ListNode* l1 = head;\n ListNode* l2 = (mid -> next);\n mid -> next = NULL;\n l2 = reverse(l2);\n \n while( l2 != NULL)\n {\n ListNode* f1 =l1 -> next;\n ListNode* f2 = l2 -> next;\n l1 -> next = l2;\n l2 -> next = f1;\n l1 = f1;\n l2 = f2;\n \n }\n }\n};
| 6 | 0 |
['C']
| 0 |
reorder-list
|
C++ || Simple And Easy Approach
|
c-simple-and-easy-approach-by-garvit14-qzmq
|
\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n *
|
garvit14
|
NORMAL
|
2022-08-31T04:41:51.380036+00:00
|
2022-08-31T04:41:51.380078+00:00
| 1,011 | false |
```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n void reorderList(ListNode* head) {\n \n// step 1 : Finding the middle of the list in order to split it in 2 parts\n ListNode *slow=head;\n ListNode *fast=head->next;\n \n while(fast&&fast->next)\n {\n slow=slow->next;\n fast=fast->next->next;\n }\n \n ListNode *head2=slow->next;\n slow->next=NULL;\n \n// step 2 : Reversing the 2nd half of the list\n ListNode *forward=NULL;\n ListNode *prev=NULL;\n ListNode *curr=head2;\n \n while(curr)\n {\n forward=curr->next;\n curr->next=prev;\n prev=curr;\n curr=forward;\n }\n \n// Step 3 : Merge the 2 lists \n head2=prev;\n while(head2)\n {\n ListNode *ptr1=head->next;\n ListNode *ptr2=head2->next;\n \n head->next=head2;\n head2->next=ptr1;\n head=ptr1;\n head2=ptr2;\n \n }\n }\n};\n```\nIf you like my solution plz upvote.
| 6 | 0 |
['Linked List', 'C', 'C++']
| 1 |
reorder-list
|
✅ C++ Solution || Recursive Approch || Short Code || Using stack frame of Recursion
|
c-solution-recursive-approch-short-code-2bgyz
|
In this problem, the basic idea I have used is that we will use the stack frame of each recursive stage.\n\nHere we are doing all thing while returnning from th
|
Sandip_1999
|
NORMAL
|
2022-06-25T11:04:21.254204+00:00
|
2022-06-25T11:06:42.779888+00:00
| 365 | false |
In this problem, the basic idea I have used is that we will use the **stack frame of each recursive stage**.\n\nHere we are doing all thing while returnning from the last node.\n\nHere we will 1st recursivelly traverse to the end of the list then connect first element with last element and last element with 2ndnelement. So, 1st-->last-->2nd this will be our new pattern and we are still on the last stack frame of recursive stack, from here we will return 3rd node which is named as 2nd here(I will use "2nd" name here ) . Now we wiil be on the 2nd last stack frame of recursion, now we will connect 2nd with with 2nd last node now again we repeat above steps untill :-\n1.)curr node(from start)become NULL or\n2.) curr node (from start) and temp (node from current stack frame) are equal or \n3.)current->next == temp.\n\nLets take an :-\n\n\n\t*If you find it helpful then upvote pls..*\n\n```\nListNode *sol(ListNode *head, ListNode *temp)\n {\n if(temp == NULL)return head;\n \n ListNode *curr = sol(head, temp->next);\n \n if(!curr)return NULL;\n if(curr==temp){\n curr->next = NULL;\n return NULL;\n }\n if(curr->next == temp)\n {\n temp->next=NULL;\n return NULL;\n }\n \n temp->next = curr->next;\n curr->next = temp;\n curr = temp->next;\n \n return curr;\n }\n void reorderList(ListNode* head) {\n sol(head, head);\n }\n\t\n
| 6 | 0 |
['Linked List', 'Recursion', 'C']
| 0 |
reorder-list
|
JAVA || O(N) Time || O(1) space
|
java-on-time-o1-space-by-gauravchoudhary-pfar
|
\nclass Solution {\n \n public static ListNode middleOfLL(ListNode head){\n if(head==null){\n return head;\n }\n\n ListNod
|
gauravchoudhary7070
|
NORMAL
|
2022-06-09T21:06:06.733292+00:00
|
2022-06-09T21:07:16.009100+00:00
| 453 | false |
```\nclass Solution {\n \n public static ListNode middleOfLL(ListNode head){\n if(head==null){\n return head;\n }\n\n ListNode slow = head;\n ListNode fast = head;\n\n while(fast.next!=null && fast.next.next!=null){\n slow = slow.next;\n fast = fast.next.next;\n }\n\n return slow;\n\n }\n\n public static ListNode reverseOfLL(ListNode head){\n ListNode prev = null;\n ListNode curr = head;\n\n while(curr!=null){\n //preserve\n ListNode next = curr.next; \n\n //link;\n curr.next = prev;\n \n //move\n prev = curr; \n curr = next;\n }\n\n return prev;\n }\n \n \n public void reorderList(ListNode head) {\n \n ListNode mid = middleOfLL(head);\n ListNode nh = mid.next;\n\n mid.next = null; //break link\n\n nh = reverseOfLL(nh);\n\n ListNode p1 = head;\n ListNode p2 = nh;\n\n while(p2!=null){\n //preserve\n ListNode n1 = p1.next;\n ListNode n2 = p2.next;\n\n //link;\n p1.next = p2;\n p2.next = n1;\n\n //move\n p1 = n1;\n p2 = n2;\n \n } \n\n }\n \n}\n```
| 6 | 0 |
['Linked List', 'Java']
| 0 |
reorder-list
|
[c++] Easy solution + explanation | half + reverse + merge
|
c-easy-solution-explanation-half-reverse-rl0p
|
At first we define some basic function len() , at().\n\n len() will return the length of the linked list:\n\tcpp\n\tint len(ListNode* head) {\n\t\tint c = 0;\n\
|
steinum
|
NORMAL
|
2021-12-22T08:37:38.511094+00:00
|
2022-02-16T02:48:46.105780+00:00
| 164 | false |
At first we define some basic function ```len()``` , ```at()```.\n\n* `len()` will return the length of the linked list:\n\t```cpp\n\tint len(ListNode* head) {\n\t\tint c = 0;\n\t\tfor (; head; head = head->next, c++);\n\t\treturn c;\n\t}\n\t```\n* `at()` will give you the address of `i-th` index of a linked list:\n\t```cpp\n\tListNode* at(ListNode* head, int i) {\n\t\tfor (; i--; head = head->next);\n\t\treturn head;\n\t}\n\t```\n* now make a function `half()` that will split the array into half and retun the head of that two list:\n\t```cpp\n\tpair<ListNode*, ListNode*> half(ListNode* head) {\n\t\tif (!head) return {0, 0};\n\t\tListNode *m = at(head, (len(head) - 1) / 2), *y = m->next;\n\t\tm->next = 0;\n\t\treturn {head, y};\n\t}\n\t```\n* make a function `reverse()` that will reverse a linked-list [here i write an easy recursion, the function will return the head and tail of the reversed linked list]:\n\t```cpp\n\tpair<ListNode*, ListNode*> reverse(ListNode* head) {\n\t\tif (!head)return {0, 0};\n\t\tif (!head -> next) return {head, head};\n\t\tauto [x, y] = reverse(head -> next);\n\t\ty -> next = head;\n\t\thead -> next = 0;\n\t\treturn {x, head};\n\t}\n\t```\n* make a `merge()` function to merge two linked list [i.e: x0 -> x1 -> x2 -> ... + y0 -> y1 -> y2 -> ... = x0 -> y0 -> x1 -> y1 -> ...]:\n\t```cpp\n\tListNode* merge(ListNode *x, ListNode *y) {\n\t\tif (!x || !y) return x ? x : y;\n\t\ty = merge(y, x -> next);\n\t\tx -> next = y;\n\t\treturn x;\n\t}\n\t```\n* Now to **reorderList** you can just `half()` + `reverse()` + `merge()` :\n\t``` cpp\n\tvoid reorderList(ListNode* head) {\n\t\tauto [x, y] = half(head);\n\t\ty = reverse(y).first;\n\t\tmerge(x, y);\n\t}\n\t```\n\t\n\t\n\tFull solution:\n\t```cpp\n\t/**\n\t * Definition for singly-linked list.\n\t * struct ListNode {\n\t * int val;\n\t * ListNode *next;\n\t * ListNode() : val(0), next(nullptr) {}\n\t * ListNode(int x) : val(x), next(nullptr) {}\n\t * ListNode(int x, ListNode *next) : val(x), next(next) {}\n\t * };\n\t */\n\tclass Solution {\n\t\tint len(ListNode* head) {\n\t\t\tint c = 0;\n\t\t\tfor (; head; head = head->next, c++);\n\t\t\treturn c;\n\t\t}\n\t\tListNode* at(ListNode* head, int i) {\n\t\t\tfor (; i--; head = head->next);\n\t\t\treturn head;\n\t\t}\n\t\tpair<ListNode*, ListNode*> half(ListNode* head) {\n\t\t\tif (!head) return {0, 0};\n\t\t\tListNode *m = at(head, (len(head) - 1) / 2), *y = m->next;\n\t\t\tm->next = 0;\n\t\t\treturn {head, y};\n\t\t}\n\t\tpair<ListNode*, ListNode*> reverse(ListNode* head) {\n\t\t\tif (!head)return {0, 0};\n\t\t\tif (!head -> next) return {head, head};\n\t\t\tauto [x, y] = reverse(head -> next);\n\t\t\ty -> next = head;\n\t\t\thead -> next = 0;\n\t\t\treturn {x, head};\n\t\t}\n\t\tListNode* merge(ListNode *x, ListNode *y) {\n\t\t\tif (!x || !y) return x ? x : y;\n\t\t\ty = merge(y, x -> next);\n\t\t\tx -> next = y;\n\t\t\treturn x;\n\t\t}\n\tpublic:\n\t\tvoid reorderList(ListNode* head) {\n\t\t\tauto [x, y] = half(head);\n\t\t\ty = reverse(y).first;\n\t\t\thead = merge(x, y);\n\t\t}\n\t};\n\t```\n\t\n\t\n\tNow its time to upvote my solution ^_^ \n
| 6 | 0 |
['Linked List']
| 1 |
reorder-list
|
C++ O(n) Time & O(1) Space | Iterative approach.
|
c-on-time-o1-space-iterative-approach-by-dbh9
|
The idea here is to update our input list by reversing the second half of the list.\nWe find the middle of the List, and call the reverseList(), which returns b
|
akashchouhan16
|
NORMAL
|
2021-08-10T07:40:55.098314+00:00
|
2021-08-10T07:40:55.098356+00:00
| 208 | false |
The idea here is to update our input list by reversing the second half of the list.\nWe find the middle of the List, and call the ```reverseList()```, which returns back the head from the right side. After this, we will have two pointers, one pointing to the input head node (on the left) and the new head (on the right side) with the second half reversed. [**O(n)** time]\n```c++\n\t 1->2->3->4->null;\n\t //After rearrangements\n\t (head1) 1->2-> null <-3<-4 (head2)\n```\n\nNow we can alternatively pick nodes and update the links to create the required list and finally update our input head. [**O(n)** time.]\n```c++\nListNode *reverseList(ListNode *h){\n ListNode *r = nullptr, *q = nullptr, *p = h;\n do{\n r = q;\n q = p;\n p = p->next;\n q->next = r;\n }while(p);\n return q;\n }\n void reorderList(ListNode* head) {\n if(!head || !head->next) return;\n \n ListNode *ptr1 = head, *ptr2 = head;\n while(ptr2 and ptr2->next){\n ptr1 = ptr1->next;\n ptr2 = ptr2->next->next;\n }\n\n ptr2 = reverseList(ptr1);\n ptr1 = head; \n \n ListNode *header = new ListNode(-1);\n ListNode *p = header;\n\t\t// mutex will strictly iterate between 0 & 1 to pick nodes.\n int mutex = 1; \n while(ptr1 and ptr2){\n if(mutex){\n p->next = ptr1;\n p = ptr1;\n ptr1 = ptr1->next;\n p->next = nullptr;\n }else{\n p->next = ptr2;\n p = ptr2;\n ptr2 = ptr2->next;\n p->next =nullptr;\n }\n mutex = (1 + mutex)%2;\n }\n\t\t//update the input head node and return.\n head = header->next;\n return;\n }\n\n```\n
| 6 | 1 |
[]
| 0 |
reorder-list
|
Python Simple Solution Explained (video + code)
|
python-simple-solution-explained-video-c-t5zc
|
https://www.youtube.com/watch?v=To_uAJRu8NQ\n\n\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n#
|
spec_he123
|
NORMAL
|
2020-08-20T12:07:34.258933+00:00
|
2020-08-20T12:07:34.258980+00:00
| 987 | false |
https://www.youtube.com/watch?v=To_uAJRu8NQ\n[](https://www.youtube.com/watch?v=To_uAJRu8NQ)\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nfrom collections import deque\nclass Solution:\n def reorderList(self, head: ListNode) -> None:\n """\n Do not return anything, modify head in-place instead.\n """\n if not head:\n return\n \n q = deque()\n node = head\n while True:\n node = node.next\n if not node:\n break\n q.append(node)\n \n while q:\n if head:\n temp = q.pop()\n head.next = temp\n head = head.next\n \n if head and q:\n temp = q.popleft()\n head.next = temp\n head = head.next\n \n head.next = None\n```
| 6 | 0 |
['Linked List', 'Python', 'Python3']
| 1 |
reorder-list
|
Simple JavaScript solution [87%, 50%]
|
simple-javascript-solution-87-50-by-i-lo-9khp
|
Runtime: 80 ms, faster than 87.16% of JavaScript online submissions for Reorder List.\nMemory Usage: 41.8 MB, less than 50.00% of JavaScript online submissions
|
i-love-typescript
|
NORMAL
|
2020-05-01T00:50:47.612356+00:00
|
2020-05-01T00:50:47.612453+00:00
| 1,130 | false |
Runtime: 80 ms, faster than 87.16% of JavaScript online submissions for Reorder List.\nMemory Usage: 41.8 MB, less than 50.00% of JavaScript online submissions for Reorder List.\n```\nfunction reorderList(head) {\n const arr = [];\n let index = head;\n \n while (index) {\n arr.push(index);\n index = index.next;\n }\n\n for (let l = 0; l < arr.length; l++) {\n let r = arr.length - 1 - l;\n if (l >= r) { arr[l].next = null; break; }\n arr[l].next = arr[r];\n arr[r].next = arr[l + 1];\n }\n}\n```
| 6 | 0 |
['JavaScript']
| 3 |
reorder-list
|
Concise and Straightforward Python Solution (find mid - reverse - merge)
|
concise-and-straightforward-python-solut-we2j
|
\nclass Solution:\n def reorderList(self, head: ListNode) -> None:\n if not head:\n return head\n \n # find mid point \n
|
haz_o
|
NORMAL
|
2019-10-12T19:55:25.850872+00:00
|
2019-11-05T02:51:41.950438+00:00
| 1,240 | false |
```\nclass Solution:\n def reorderList(self, head: ListNode) -> None:\n if not head:\n return head\n \n # find mid point \n slow = fast = head\n \n while fast and fast.next:\n slow = slow.next\n fast = fast.next.next\n \n # reverse the second half in-place\n # slow.next: the start point of reverse\n \n head2 = None\n\t\tcurr = slow.next\n\t\tslow.next = None\n while slow.next:\n next = curr.next\n curr.next = head2\n head2 = curr\n curr = next\n \n # merge in-place\n first, second = head, head2\n \n while second:\n first.next, first = second, first.next\n second.next, second = first, second.next\n return\n```
| 6 | 0 |
['Python', 'Python3']
| 3 |
reorder-list
|
cpp solution using a stack and a queue
|
cpp-solution-using-a-stack-and-a-queue-b-k3v5
|
c++\nvoid reorderList(ListNode* head) {\n stack<ListNode*> s;\n queue<ListNode*> q;\n int len = 0, count = 0;\n ListNode dummyHead(0);\n ListNode
|
lintongmao
|
NORMAL
|
2019-03-29T07:48:27.277844+00:00
|
2019-03-29T07:48:27.277888+00:00
| 559 | false |
```c++\nvoid reorderList(ListNode* head) {\n stack<ListNode*> s;\n queue<ListNode*> q;\n int len = 0, count = 0;\n ListNode dummyHead(0);\n ListNode *p = head;\n while(p){\n s.push(p);\n q.push(p);\n p = p->next;\n len++;\n }\n p = &dummyHead;\n while(count < len){\n p->next = q.front();\n q.front()->next = s.top();\n p = s.top();\n q.pop();\n s.pop();\n count += 2;\n }\n p->next = NULL;\n}\n```
| 6 | 0 |
['C++']
| 3 |
reorder-list
|
My python solution with some comments. O(1) space (easy to understand)
|
my-python-solution-with-some-comments-o1-d6lf
|
\nclass Solution:\n def reorderList(self, head):\n """\n :type head: ListNode\n :rtype: void Do not return anything, modify head in-plac
|
newstark
|
NORMAL
|
2018-07-01T02:59:12.095880+00:00
|
2018-10-03T06:58:09.642517+00:00
| 435 | false |
```\nclass Solution:\n def reorderList(self, head):\n """\n :type head: ListNode\n :rtype: void Do not return anything, modify head in-place instead.\n """\n if head and head.next and head.next.next: #check if the list has two more nodes\n \n # partition the nodes into two parts\n pre, slow, fast = ListNode(None), head, head\n while fast and fast.next:\n pre, slow, fast = slow, slow.next, fast.next.next\n pre.next = None\n \n # reverse the second half\n temp = None\n while slow:\n nxt = slow.next\n slow.next = temp\n temp = slow\n slow = nxt\n \n # reorder two parts\n dummy = head\n while dummy and temp:\n nxt= dummy.next\n dummy.next,dummy,temp = temp, temp, nxt\n```\nInput: [1,2,3,4,5,6]\nStep 1: partition the input into two parts -- head: [1,2,3], slow: [4,5,6]\nStep 2: reverse slow, temp: [6,5,4]\nStep 3: at the first node of head, temp is inserted. then head.next is inserted, etc.
| 6 | 0 |
[]
| 1 |
reorder-list
|
My java solution with a hashmap
|
my-java-solution-with-a-hashmap-by-scott-fq4k
|
public void reorderList(ListNode head) {\n \t \n \t HashMap <Integer,ListNode> nodeMap = new HashMap<Integer,ListNode> ();\n \t int len =
|
scott
|
NORMAL
|
2014-10-10T12:21:18+00:00
|
2014-10-10T12:21:18+00:00
| 628 | false |
public void reorderList(ListNode head) {\n \t \n \t HashMap <Integer,ListNode> nodeMap = new HashMap<Integer,ListNode> ();\n \t int len = 0 ;\n \t ListNode p = head ; \n \t \n \t while (p != null) {\n \t \tnodeMap.put(len++, p);\n \t \tp = p.next ;\n \t }\n \t \n \t \n \t int i = 0 ; \n \t int j = len - 1 ;\n \t for (; i < j - 1 ; ++i ,--j) {\t \t\n \t \tListNode tmp = nodeMap.get(i).next ;\n \t \tnodeMap.get(i).next = nodeMap.get(j);\n \t \tnodeMap.get(j).next = tmp ;\n \t \tnodeMap.get(j - 1).next = null;\n \t \t\n \t }
| 6 | 0 |
[]
| 1 |
reorder-list
|
Try this strange solution **NOT INPLACE REORDERING** c++
|
try-this-strange-solution-not-inplace-re-5cyj
|
IntuitionThe problem requires us to reorder a linked list such that nodes are arranged in the following pattern:
1st → last → 2nd → second last → 3rd → ... and
|
prashant_71200
|
NORMAL
|
2025-02-10T11:06:41.845058+00:00
|
2025-02-10T11:06:41.845058+00:00
| 253 | false |
# Intuition
The problem requires us to reorder a linked list such that nodes are arranged in the following pattern:
1st → last → 2nd → second last → 3rd → ... and so on.
To achieve this, we need to access the last nodes efficiently. A stack (LIFO structure) helps store the nodes in reverse order, allowing us to pop elements in the required sequence.
# Approach
1) Store Nodes in a Stack:
* Traverse the linked list and push all nodes onto a stack.
* This allows us to access the last node first (LIFO order).
Reorder the List:
2) Start from the head node (t2 = head).
* Iteratively pop elements from the stack and insert them between the current node and its next node.
* Stop when we reach the middle of the list.
3) Handle the Last Node:
* Ensure the last node points to nullptr to avoid cyclic connections.
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(N)
# Code
```cpp []
class Solution {
public:
void reorderList(ListNode* head) {
if (!head || !head->next || !head->next->next) return; // Edge cases
ListNode* t = head;
stack<ListNode*> st;
// Push all nodes onto the stack
while (t) {
st.push(t);
t = t->next;
}
ListNode* t2 = head;
int n = st.size();
// Reordering process
for (int i = 0; i < n / 2; i++) {
ListNode* top = st.top();
st.pop();
top->next = t2->next;
t2->next = top;
t2 = top->next;
}
// Ensure the last node points to NULL to avoid cycles
if (t2) t2->next = nullptr;
}
};
```
| 5 | 0 |
['C++']
| 0 |
find-minimum-in-rotated-sorted-array
|
Beat 100%: Very Simple (Python), Very Detailed Explanation
|
beat-100-very-simple-python-very-detaile-pzak
|
\nclass Solution:\n def findMin(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n # set left and right boun
|
water1111
|
NORMAL
|
2018-08-12T02:21:45.961637+00:00
|
2020-04-10T21:01:01.443347+00:00
| 87,438 | false |
```\nclass Solution:\n def findMin(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n # set left and right bounds\n left, right = 0, len(nums)-1\n \n # left and right both converge to the minimum index;\n # DO NOT use left <= right because that would loop forever\n while left < right:\n # find the middle value between the left and right bounds (their average);\n\t\t\t# can equivalently do: mid = left + (right - left) // 2,\n\t\t\t# if we are concerned left + right would cause overflow (which would occur\n\t\t\t# if we are searching a massive array using a language like Java or C that has\n\t\t\t# fixed size integer types)\n mid = (left + right) // 2\n \n # the main idea for our checks is to converge the left and right bounds on the start\n # of the pivot, and never disqualify the index for a possible minimum value.\n\n # in normal binary search, we have a target to match exactly,\n # and would have a specific branch for if nums[mid] == target.\n # we do not have a specific target here, so we just have simple if/else.\n \n if nums[mid] > nums[right]:\n # we KNOW the pivot must be to the right of the middle:\n # if nums[mid] > nums[right], we KNOW that the\n # pivot/minimum value must have occurred somewhere to the right\n # of mid, which is why the values wrapped around and became smaller.\n\n # example: [3,4,5,6,7,8,9,1,2] \n # in the first iteration, when we start with mid index = 4, right index = 9.\n # if nums[mid] > nums[right], we know that at some point to the right of mid,\n # the pivot must have occurred, which is why the values wrapped around\n # so that nums[right] is less then nums[mid]\n\n # we know that the number at mid is greater than at least\n # one number to the right, so we can use mid + 1 and\n # never consider mid again; we know there is at least\n # one value smaller than it on the right\n left = mid + 1\n\n else:\n # here, nums[mid] <= nums[right]:\n # we KNOW the pivot must be at mid or to the left of mid:\n # if nums[mid] <= nums[right], we KNOW that the pivot was not encountered\n # to the right of middle, because that means the values would wrap around\n # and become smaller (which is caught in the above if statement).\n # this leaves the possible pivot point to be at index <= mid.\n \n # example: [8,9,1,2,3,4,5,6,7]\n # in the first iteration, when we start with mid index = 4, right index = 9.\n # if nums[mid] <= nums[right], we know the numbers continued increasing to\n # the right of mid, so they never reached the pivot and wrapped around.\n # therefore, we know the pivot must be at index <= mid.\n\n # we know that nums[mid] <= nums[right].\n # therefore, we know it is possible for the mid index to store a smaller\n # value than at least one other index in the list (at right), so we do\n # not discard it by doing right = mid - 1. it still might have the minimum value.\n right = mid\n \n # at this point, left and right converge to a single index (for minimum value) since\n # our if/else forces the bounds of left/right to shrink each iteration:\n\n # when left bound increases, it does not disqualify a value\n # that could be smaller than something else (we know nums[mid] > nums[right],\n # so nums[right] wins and we ignore mid and everything to the left of mid).\n\n # when right bound decreases, it also does not disqualify a\n # value that could be smaller than something else (we know nums[mid] <= nums[right],\n # so nums[mid] wins and we keep it for now).\n\n # so we shrink the left/right bounds to one value,\n # without ever disqualifying a possible minimum\n return nums[left]\n```
| 1,386 | 4 |
[]
| 101 |
find-minimum-in-rotated-sorted-array
|
Compact and clean C++ solution
|
compact-and-clean-c-solution-by-changhaz-pqkv
|
Classic binary search problem. \n\nLooking at subarray with index [start,end]. We can find out that if the first member is less than the last member, there's no
|
changhaz
|
NORMAL
|
2014-10-16T04:55:20+00:00
|
2018-10-12T10:07:59.063168+00:00
| 96,068 | false |
Classic binary search problem. \n\nLooking at subarray with index [start,end]. We can find out that if the first member is less than the last member, there's no rotation in the array. So we could directly return the first element in this subarray.\n\nIf the first element is larger than the last one, then we compute the element in the middle, and compare it with the first element. If value of the element in the middle is larger than the first element, we know the rotation is at the second half of this array. Else, it is in the first half in the array.\n \nWelcome to put your comments and suggestions.\n \n\n int findMin(vector<int> &num) {\n int start=0,end=num.size()-1;\n \n while (start<end) {\n if (num[start]<num[end])\n return num[start];\n \n int mid = (start+end)/2;\n \n if (num[mid]>=num[start]) {\n start = mid+1;\n } else {\n end = mid;\n }\n }\n \n return num[start];\n }\n\nSome corner cases will be discussed [here][1]\n\n\n \n\n\n [1]: http://changhaz.wordpress.com/2014/10/15/leetcode-find-minimum-in-rotated-sorted-array/
| 542 | 13 |
[]
| 75 |
find-minimum-in-rotated-sorted-array
|
A concise solution with proof in the comment
|
a-concise-solution-with-proof-in-the-com-mrt0
|
class Solution {\n public:\n int findMin(vector<int> &num) {\n int low = 0, high = num.size() - 1;\n // loop invariant: 1. low <
|
chuchao333
|
NORMAL
|
2014-12-17T05:43:46+00:00
|
2018-10-06T14:11:45.234361+00:00
| 45,822 | false |
class Solution {\n public:\n int findMin(vector<int> &num) {\n int low = 0, high = num.size() - 1;\n // loop invariant: 1. low < high\n // 2. mid != high and thus A[mid] != A[high] (no duplicate exists)\n // 3. minimum is between [low, high]\n // The proof that the loop will exit: after each iteration either the 'high' decreases\n // or the 'low' increases, so the interval [low, high] will always shrink.\n while (low < high) {\n auto mid = low + (high - low) / 2;\n if (num[mid] < num[high])\n // the mininum is in the left part\n high = mid;\n else if (num[mid] > num[high])\n // the mininum is in the right part\n low = mid + 1;\n }\n \n return num[low];\n }\n };
| 278 | 5 |
['Binary Tree']
| 31 |
find-minimum-in-rotated-sorted-array
|
Solution
|
solution-by-deleted_user-42tv
|
C++ []\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int n = nums.size();\n int low=0, high=n-1;\n \n while(low
|
deleted_user
|
NORMAL
|
2023-02-12T13:17:42.356701+00:00
|
2023-03-09T12:27:51.816646+00:00
| 47,746 | false |
```C++ []\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int n = nums.size();\n int low=0, high=n-1;\n \n while(low<high){\n if(nums[low] <= nums[high]) return nums[low];\n int mid = low + (high-low)/2;\n if(nums[low] > nums[mid]){\n high=mid;\n } else if(nums[mid] > nums[high]) {\n low=mid+1;\n } \n }\n if(nums[low] <= nums[high]) return nums[low];\n return -1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n l, r = 0, len(nums) - 1\n\n while l < r:\n m = l + (r - l)\n\n if nums[m] > nums[r]:\n l = m + 1\n \n else:\n r = m \n\n return nums[l] \n```\n\n```Java []\nclass Solution {\n public int findMin(int[] nums) {\n int l = 0;\n int r = nums.length - 1;\n\n while (l < r) {\n final int m = (l + r) / 2;\n if (nums[m] < nums[r])\n r = m;\n else\n l = m + 1;\n }\n\n return nums[l];\n }\n}\n```\n
| 234 | 5 |
['C++', 'Java', 'Python3']
| 16 |
find-minimum-in-rotated-sorted-array
|
Java solution with binary search
|
java-solution-with-binary-search-by-chas-z3tz
|
The minimum element must satisfy one of two conditions: 1) If rotate, A[min] < A[min - 1]; 2) If not, A[0]. Therefore, we can use binary search: check the middl
|
chase1991
|
NORMAL
|
2014-11-16T02:35:52+00:00
|
2018-10-02T17:36:33.723177+00:00
| 66,508 | false |
The minimum element must satisfy one of two conditions: 1) If rotate, A[min] < A[min - 1]; 2) If not, A[0]. Therefore, we can use binary search: check the middle element, if it is less than previous one, then it is minimum. If not, there are 2 conditions as well: If it is greater than both left and right element, then minimum element should be on its right, otherwise on its left.\n\n public class Solution {\n public int findMin(int[] num) {\n if (num == null || num.length == 0) {\n return 0;\n }\n if (num.length == 1) {\n return num[0];\n }\n int start = 0, end = num.length - 1;\n while (start < end) {\n int mid = (start + end) / 2;\n if (mid > 0 && num[mid] < num[mid - 1]) {\n return num[mid];\n }\n if (num[start] <= num[mid] && num[mid] > num[end]) {\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n return num[start];\n }\n }
| 149 | 6 |
['Binary Tree', 'Java']
| 43 |
find-minimum-in-rotated-sorted-array
|
Fastest (100%) || Easiest || Shortest || Binary Search || Multiple Langs
|
fastest-100-easiest-shortest-binary-sear-2ysf
|
\n\n# Approach\nPicture this: You\'re exploring a treasure-filled island, but the path to the treasure is tricky\u2014it\'s like a maze. Now, this approach is l
|
gameboey
|
NORMAL
|
2024-05-12T22:28:42.724325+00:00
|
2024-05-12T22:29:43.130709+00:00
| 30,457 | false |
\n\n# Approach\nPicture this: You\'re exploring a treasure-filled island, but the path to the treasure is tricky\u2014it\'s like a maze. Now, this approach is like having a smart compass that helps you navigate through the maze efficiently.\n\nHere\'s how Franky (from OnePiece) would break it down:\n\n1. **Setting sail**: You start with two markers, one at the beginning of the path (let\'s call it "left") and one at the end (that\'s "right"). These markers help you keep track of where you are.\n\n2. **Sailing through the maze**: You sail through the maze using a special technique called "binary search". It\'s like cutting the maze in half each time to find the quickest route to the treasure.\n\n3. **Calculating the midpoint**: At each intersection, you calculate the midpoint to decide which direction to go next.\n\n4. **Reading the signs**: Now, here\'s the trick\u2014when you reach an intersection, you check the signs. If the sign at the midpoint points toa smaller number than the one at the end of the path, you know the treasure is in the left half. So, you adjust your right marker to the midpoint.\n\n5. **Deciding the route**: But if the sign at the midpoint suggests the number is larger than the one at the end of the path, it means the treasure is likely in the right half. So, you move your left marker to just after the midpoint.\n\n6. **Narrowing down**: You keep repeating this process, narrowing down your search until your markers converge.\n\n7. **Treasure found!**: When your markers meet, it means you\'ve found the smallest number, which is like discovering the treasure in the maze. That\'s the number you return\u2014it\'s the minimum value in the rotated array.\n\nSo, with this clever compass-like approach, you efficiently navigate through the maze of numbers and find your treasure in no time! That\'s the spirit of adventure, just like sailing with the Straw Hat Pirates!\n\n\n# Dry - Run\nLet\'s dry run the provided solution with the example `nums = [4,5,6,7,0,1,2]`:\n\nInitial state:\n- `left = 0`, `right = 6`.\n- `mid = 3`, `nums[mid] = 7`, `nums[right] = 2`.\n\nSince `nums[mid] >= nums[right]`, we update `left = mid + 1 = 4`.\n\nAfter the first iteration:\n- `left = 4`, `right = 6`.\n- `mid = 5`, `nums[mid] = 1`, `nums[right] = 2`.\n\nSince `nums[mid] < nums[right]`, we update `right = mid = 5`.\n\nAfter the second iteration:\n- `left = 4`, `right = 5`.\n- `mid = 4`, `nums[mid] = 0`, `nums[right] = 1`.\n\nSince `nums[mid] < nums[right]`, we update `right = mid = 4`.\n\nAfter the third iteration:\n- `left = 4`, `right = 4`.\n\nThe loop stops as `left` is no longer less than `right`, and the algorithm returns `nums[left]`, which is `0`.\n\nSo, for the input `nums = [4,5,6,7,0,1,2]`, the output of the algorithm is `0`, which is correct. \n\n# Complexity\n- Time complexity: O(logn)\n\n- Space complexity: O(1)\n\n# Code\n```C++ []\n#pragma GCC optimize ("Ofast")\n#pragma GCC target ("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx")\n#pragma GCC optimize ("-ffloat-store")\n\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);\n int left = 0, right = nums.size() - 1;\n\n while(left < right) {\n int mid = left + (right - left) / 2;\n if(nums[mid] < nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left];\n }\n};\n```\n```java []\nclass Solution {\n public int findMin(int[] nums) {\n int left = 0, right = nums.length - 1;\n while(left < right) {\n int mid = left + (right - left) / 2;\n\n if(nums[mid] < nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left];\n }\n}\n```\n```python []\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n left, right = 0, len(nums) - 1\n while left < right:\n mid = left + (right - left) // 2\n if nums[mid] < nums[right]:\n right = mid\n else:\n left = mid + 1\n \n return nums[left]\n```\n```C []\nint findMin(int* nums, int numsSize) {\n int left = 0, right = numsSize - 1;\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (nums[mid] < nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left];\n}\n```\n```C# []\npublic class Solution {\n public int FindMin(int[] nums) {\n int left = 0, right = nums.Length - 1;\n while (left <right) {\n int mid = left + (right - left) / 2;\n if (nums[mid] < nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n \n return nums[left];\n }\n}\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findMin = function(nums) {\n let left = 0, right = nums.length - 1;\n while (left < right) {\n let mid = Math.floor(left + (right - left) / 2);\n \n if (nums[mid] < nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n return nums[left];\n};\n```\n```Kotlin []\nclass Solution {\n fun findMin(nums: IntArray): Int {\n var left = 0\n var right = nums.size - 1\n while (left < right) {\n val mid = left + (right - left) / 2\n if (nums[mid] < nums[right]) {\n right = mid\n } else {\n left = mid + 1\n }\n }\n \n return nums[left]\n }\n}\n```\n\n## **"Ahoy there, navigator! We\'re diving into a sea of numbers, searching for the tiniest treasure in this digital jungle. But fear not, \'cause with this Super-duper binary search trick, we\'re slicing through those digits like a hot knife through butter! Who needs a compass when you\'ve got code? Let\'s navigate these waters and uncover that hidden gem, Super-style!"** \uD83C\uDFF4\u200D\u2620\uFE0F\n\n\n
| 147 | 0 |
['Array', 'Binary Search', 'C', 'C++', 'Java', 'Python3', 'Kotlin', 'JavaScript', 'C#']
| 13 |
find-minimum-in-rotated-sorted-array
|
Using part of input array to compare numbers.
|
using-part-of-input-array-to-compare-num-jiiz
|
IntuitionUse part of input array to compare numbers.Solution Video⭐️⭐️ Don't forget to subscribe to my channel! ⭐️⭐️■ Subscribe URL
http://www.youtube.com/chann
|
niits
|
NORMAL
|
2024-12-16T02:55:42.776102+00:00
|
2024-12-16T02:55:42.776102+00:00
| 12,628 | false |
# Intuition\nUse part of input array to compare numbers.\n\n# Solution Video\n\nhttps://youtu.be/JiNsSV16vLU\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 10,666\nThank you for your support!\n\n---\n\n# Approach\nThe description says "You must write an algorithm that runs in $$O(log n)$$ time.", so we will solve this question with `Binary Search`.\n\n```\nInput: nums = [3,4,5,1,2]\n```\nLet me put left, right and middle pointer.\n\n```\n[3,4,5,1,2]\n L M R\n```\nTypical Binary Search is like this.\n\n---\n\n\nIf a middle number is greater than a target number, we move `right` to `middle - 1`. On the other hand if the middle number is less than the target number, we will move `left` to `middle + 1`.\n\n**Binary search assumes that the input is sorted.**\n\n---\n\nThe target number for this question is a minimum number in the input, but problem here is that input array is rorated a few times.\n\n### How can we decide to move left or right pointer?\n\nIt\'s tough to think about whole array but part of array is still sorted in ascending order, even if the input is rotated.\n\nFor example,\n\n```\n[0,1,2,3,4,5]\n\u2193\n[4,5,0,1,2,3]\n```\nRotated twice. Between `4` and `5`, they are sorted and between `0` and `3`, they are also sorted. We will use those parts of array.\n\nLet\'s go back to main story.\n\nMy strategy is to compare middle number with right number. In this case, `5` and `2`.\n\n```\n[3,4,5,1,2]\n L M R\n```\n`5` is greater than `2`. That means we don\'t know how many numbers we have on the right side of the middle number, but we can say the numbers return to the minimum value and then begin to increase again on the right side of the middle number.\n\nTo prove that, let\'s think about this example quickly.\n\n```\n[1,2,3,4,5]\n L M R\n```\nIn this case, `3` is less than `5`. **That means minimum number is definitely on the left side of the middle number. That\'s because input array is sorted and the last number(= right number) is greater than middle number. We are sure that the numbers increase from middle to right.**\n\nLet\'s go back to main story again.\n\n```\n[3,4,5,1,2]\n L M R\n```\nMiddle number is greater than right number, so we can say at some point, the numbers return to minimum value. That\'s why we should move the left pointer to `middle pointer + 1`.\n\n```\n[3,4,5,1,2]\n M L R\n```\n\nNext, middle pointer should be...\n\n```\n[3,4,5,1,2]\n L R\n M\n```\n\nCompare `1` with `2`. The `middle` number is less than the `right` number, so we are sure that the minimum number is on the left of the middle number.\n\nThere is one point when we move right pointer.\n\n---\n\n\u2B50\uFE0F Points\n\nWhen we move `right` pointer to left side, we will update `right` pointer with `middle pointer`. On the other hand when we move `left` pointer, we will update `left` pointer with `middle pointer + 1`.\n\nWhy? Let\'s think about this case.\n\n```\n[1,2,3,4,5]\n L M R\n```\nCompare `3` with `5`. We will move the `right` pointer to left side. In this case, we only know that the middle number is smaller than the right number, so **the middle number could still be the minimum value.** \n\n```\n[3,4,5,1,2]\n L M R\n```\n\nIn this case, since the middle number is greater than the right number, **it\u2019s impossible for the middle number to be the minimum value.** That\'s why we can update `left` pointer with `middle pointer + 1`.\n\n---\n\nLet\'s go back to main story again.\n\nIn this case, we will update `right` pointer with `middle` pointer.\n\n```\n[3,4,5,1,2]\n L R\n M\n\n\u2193\n\n[3,4,5,1,2]\n L \n M\n R\n```\nNow `L == R`. We stop itertaion.\n\n```\nreturn 1(= left number or right number)\n```\n\n---\n\nhttps://youtu.be/bU_dXCOWHls\n\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n \n left = 0\n right = len(nums) - 1\n\n while left < right:\n mid = (left + right) // 2\n\n if nums[mid] <= nums[right]:\n right = mid\n else:\n left = mid + 1\n \n return nums[left]\n```\n```javascript []\nvar findMin = function(nums) {\n let left = 0;\n let right = nums.length - 1;\n\n while (left < right) {\n const mid = Math.floor((left + right) / 2);\n\n if (nums[mid] <= nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left]; \n};\n```\n```java []\nclass Solution {\n public int findMin(int[] nums) {\n int left = 0;\n int right = nums.length - 1;\n\n while (left < right) {\n int mid = left + (right - left) / 2;\n\n if (nums[mid] <= nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left]; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int left = 0;\n int right = nums.size() - 1;\n\n while (left < right) {\n int mid = left + (right - left) / 2;\n\n if (nums[mid] <= nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left]; \n }\n};\n```\n\n# Step by Step Algorithm\n\n1. **Initialize Pointers**\n\n ```python\n left = 0\n right = len(nums) - 1\n ```\n\n - We define two pointers, `left` and `right`.\n - `left` starts at the beginning of the array (`0`), and `right` starts at the last index (`len(nums) - 1`).\n - The goal is to narrow down the range between `left` and `right` until we find the minimum element.\n\n2. **Binary Search Loop**\n\n ```python\n while left < right:\n ```\n\n - We enter a loop that continues as long as `left` is less than `right`.\n - This loop performs a binary search to locate the minimum value in the rotated sorted array.\n\n3. **Calculate Midpoint**\n\n ```python\n mid = (left + right) // 2\n ```\n\n - We calculate the midpoint `mid` by taking the integer division of `(left + right) / 2`.\n - `mid` represents the middle index of the current subarray defined by `left` and `right`.\n\n4. **Compare Midpoint with Right Element**\n\n ```python\n if nums[mid] <= nums[right]:\n right = mid\n ```\n\n - If the element at `mid` is less than or equal to the element at `right`, this means the minimum element could be at `mid` or to its left (in the left half of the current subarray).\n - We update `right` to `mid`, effectively discarding the right half of the array in the next iteration.\n\n5. **Move Left Pointer**\n\n ```python\n else:\n left = mid + 1\n ```\n\n - If `nums[mid]` is greater than `nums[right]`, this means the minimum element must be in the right half of the current subarray.\n - We update `left` to `mid + 1`, moving it to the right half of the array for the next iteration.\n\n6. **Return Minimum Element**\n\n ```python\n return nums[left]\n ```\n\n - Once the loop exits (when `left == right`), both `left` and `right` will be pointing to the minimum element in the array.\n - We return `nums[left]` as the minimum value.\n\n\n---\n\nThank you for reading my post.\n\n##### \u2B50\uFE0F Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n##### \u2B50\uFE0F Related Video\n#33 Search in Rotated Sorted Array\n\nhttps://youtu.be/dO9OZJP_Hm8
| 118 | 0 |
['Array', 'Binary Search', 'C++', 'Java', 'Python3', 'JavaScript']
| 3 |
find-minimum-in-rotated-sorted-array
|
4ms simple C++ code with explanation
|
4ms-simple-c-code-with-explanation-by-ja-510r
|
In this problem, we have only three cases. \n\nCase 1. The leftmost value is less than the rightmost value in the list: This means that the list is not rotated.
|
jaewoo
|
NORMAL
|
2015-05-25T23:33:48+00:00
|
2018-09-14T08:39:07.568448+00:00
| 23,000 | false |
In this problem, we have only three cases. \n\nCase 1. The leftmost value is less than the rightmost value in the list: This means that the list is not rotated. \ne.g> [1 2 3 4 5 6 7 ]\n\nCase 2. The value in the middle of the list is greater than the leftmost and rightmost values in the list. \ne.g> [ 4 5 6 7 0 1 2 3 ]\n\nCase 3. The value in the middle of the list is less than the leftmost and rightmost values in the list. \ne.g> [ 5 6 7 0 1 2 3 4 ]\n\nAs you see in the examples above, if we have case 1, we just return the leftmost value in the list. If we have case 2, we just move to the right side of the list. If we have case 3 we need to move to the left side of the list. \n\nFollowing is the code that implements the concept described above.\n\n int findMin(vector<int>& nums) {\n int left = 0, right = nums.size() - 1;\n while(left < right) {\n if(nums[left] < nums[right]) \n return nums[left];\n \n int mid = (left + right)/2;\n if(nums[mid] > nums[right])\n left = mid + 1;\n else\n right = mid;\n }\n \n return nums[left];\n }
| 84 | 2 |
[]
| 15 |
find-minimum-in-rotated-sorted-array
|
[Python] Binary Search with Picture - Clean & Concise
|
python-binary-search-with-picture-clean-ooxh2
|
Idea
This is a simple version of this problem 33. Search in Rotated Sorted Array.
Firstly, we check edge cases (when index of the minimum number is 0):
If len(
|
hiepit
|
NORMAL
|
2021-08-31T09:35:43.662607+00:00
|
2025-03-19T15:08:56.023171+00:00
| 6,542 | false |
**Idea**
- This is a simple version of this problem [33. Search in Rotated Sorted Array](https://leetcode.com/problems/search-in-rotated-sorted-array/).
- Firstly, we check edge cases (when index of the minimum number is 0):
- If len(nums) == 1 return nums[0]
- If nums[0] < nums[n-1] return nums[0]
- Binary search, left = 0, right = n-1
- mid = (left + right) / 2
- If nums[mid-1] > nums[mid] then nums[mid] is the minimum
- If nums[mid] > nums[right] then search on the right side, because smaller elements are in the right side
- Else search on the left side.
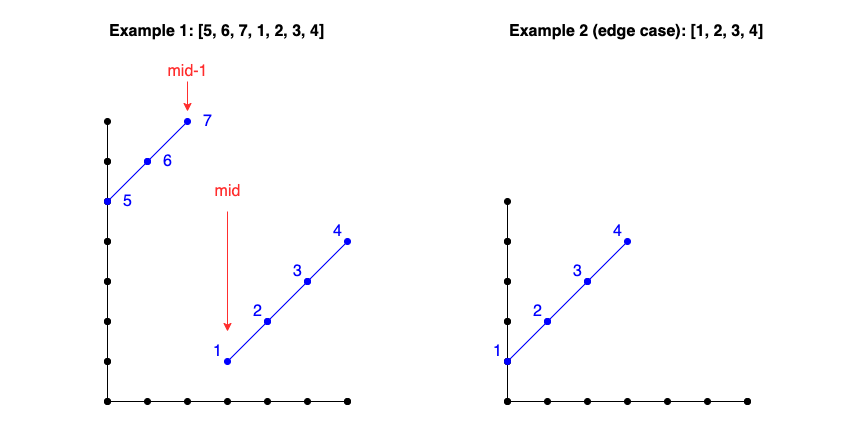
```python
class Solution:
def findMin(self, nums: List[int]) -> int:
if nums[0] <= nums[-1]: # Already sorted
return nums[0]
left = 1
right = len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid-1] > nums[mid]:
return nums[mid]
if nums[mid] > nums[right]:
left = mid + 1
else:
right = mid - 1
```
Complexity:
- Time: `O(logN)`
- Space: `O(1)`
| 82 | 1 |
['Binary Search']
| 12 |
find-minimum-in-rotated-sorted-array
|
9-line python clean code
|
9-line-python-clean-code-by-2wyyw2882-t5e9
|
Just use binary search\n\n class Solution(object):\n def findMin(self, nums):\n """\n :type nums: List[int]\n :rtype:
|
2wyyw2882
|
NORMAL
|
2015-10-11T16:43:01+00:00
|
2018-10-05T20:18:27.441945+00:00
| 13,555 | false |
Just use binary search\n\n class Solution(object):\n def findMin(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n i = 0\n j = len(nums) - 1\n while i < j:\n m = i + (j - i) / 2\n if nums[m] > nums[j]:\n i = m + 1\n else:\n j = m\n return nums[i]
| 61 | 2 |
[]
| 8 |
find-minimum-in-rotated-sorted-array
|
Simplest and fastest C++ solution O(lg N), you can't beat this!
|
simplest-and-fastest-c-solution-olg-n-yo-pgba
|
Binary search: basically eliminate the impossible elements by half each time by exploiting the sorted property.\n\n int findMin(vector &num) {\n
|
1337beef
|
NORMAL
|
2014-11-12T16:24:03+00:00
|
2014-11-12T16:24:03+00:00
| 16,171 | false |
Binary search: basically eliminate the impossible elements by half each time by exploiting the sorted property.\n\n int findMin(vector<int> &num) {\n int lo =0, hi = num.size()-1;\n while(lo<hi){\n int mid=(lo+hi)/2;\n if(num[mid]>num[hi]) lo=mid+1;\n else hi=mid;\n }\n return num[lo];\n }
| 61 | 8 |
[]
| 14 |
find-minimum-in-rotated-sorted-array
|
Clean JavaScript solution
|
clean-javascript-solution-by-hongbo-miao-q7c4
|
\nconst findMin = (nums) => {\n let l = 0;\n let r = nums.length - 1;\n while (l < r) {\n const m = ~~((l + r) / 2);\n if (nums[m] > nums[r]) l = m + 1
|
hongbo-miao
|
NORMAL
|
2019-10-12T20:52:07.048977+00:00
|
2021-12-25T07:43:49.311033+00:00
| 6,934 | false |
```\nconst findMin = (nums) => {\n let l = 0;\n let r = nums.length - 1;\n while (l < r) {\n const m = ~~((l + r) / 2);\n if (nums[m] > nums[r]) l = m + 1;\n else r = m;\n }\n return nums[l];\n};\n```\n
| 57 | 2 |
['Binary Tree', 'JavaScript']
| 9 |
find-minimum-in-rotated-sorted-array
|
1-2 lines Ruby/Python
|
1-2-lines-rubypython-by-stefanpochmann-6w28
|
Use binary search to find the first number that's less than or equal to the last.\n\n---\n\nRuby\n\nDirect translation of the above sentence into Ruby.\n\n d
|
stefanpochmann
|
NORMAL
|
2016-01-21T01:14:21+00:00
|
2018-09-04T23:30:15.327781+00:00
| 10,464 | false |
Use binary search to find the first number that's less than or equal to the last.\n\n---\n\n**Ruby**\n\nDirect translation of the above sentence into Ruby.\n\n def find_min(nums)\n nums.bsearch { |num| num <= nums.last }\n end\n\n---\n\n**Python**\n\nA little hack.\n\n class Solution:\n def findMin(self, nums):\n self.__getitem__ = lambda i: nums[i] <= nums[-1]\n return nums[bisect.bisect(self, False, 0, len(nums))]
| 41 | 7 |
['Python', 'Ruby']
| 14 |
find-minimum-in-rotated-sorted-array
|
Without min comparison | Detailed explanation
|
without-min-comparison-detailed-explanat-im0j
|
Intuition\nGiven that we should use binary search to find the minimum element in the rotated sorted array.\nAs all binary search problems, we have two pointers:
|
younus_baig
|
NORMAL
|
2023-04-15T01:56:43.007690+00:00
|
2023-04-15T04:54:13.743782+00:00
| 4,710 | false |
# Intuition\nGiven that we should **us**e **bi**nary **se**arch to **fi**nd **th**e **mi**nimum **el**ement in the **ro**tated **so**rted **ar**ray.\nAs all binary search problems, we have **tw**o **po**inters: \'low\' and \'high\', and we find \'mid\' using \'low\' and \'high\'.\n\nOur **main objective** here is to find the direction of traversal since we do not have an idea on the number of rotations. \n\n# Approach\n1. Initialize `low = 0 and high = len(nums) - 1`.\n2. Iterate until `low <= high`.\n3. We can find whether the array has been rotated or not using\n `nums[low] <= nums[high]` <br>\nFor example, here the `array is not rotated` and hence nums[low] < nums[high]\n\nHere, we see that nums[low] > nums[high]. Therefore, the `array is rotated`.\n\n\n4. If the **ar**ray is **not rotated**, `return nums[low]`.\n5. If the **ar**ray is **rotated**, we will have to now **fi**nd the **di**rection of **tr**aversal from \'mid\'.\n6. Calculate `mid = (low + high)//2`\n7. Based on the **c**omparison **be**tween **nums[low]** and **nums[mid]**, we can determine whether we have to move left or right from mid.\n\n8. If `nums[low] > nums[mid]: high = mid`\n9. Else ` low = mid + 1`\n\n\n# Complexity\n- Time complexity: O(logN)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n\n # Initialize low and high\n low, high = 0, len(nums) - 1\n\n # Iterate until low <= high\n while low <= high:\n\n # Check if the array is not rotated\n if nums[low] <= nums[high]:\n # Return nums[low] when the array is not rotated\n return nums[low]\n\n # Initialize mid if the array is rotated\n mid = (low + high)//2\n\n # Check the direction of traversal, \n # refer the image for explanation\n if nums[low] > nums[mid]:\n high = mid\n else:\n low = mid + 1\n```
| 40 | 0 |
['Array', 'Binary Search', 'Python3']
| 7 |
find-minimum-in-rotated-sorted-array
|
9-line java code, beats 95.14% run times
|
9-line-java-code-beats-9514-run-times-by-m199
|
if the array is indeed rotated by some pivot, there are only 2 possibilities\n\n> 1. a[mid] > a[left] && a[mid] > a[right], meaning we are on the bigger part, t
|
mach7
|
NORMAL
|
2016-01-20T23:35:40+00:00
|
2016-01-20T23:35:40+00:00
| 13,520 | false |
if the array is indeed rotated by some pivot, there are only 2 possibilities\n\n> 1. a[mid] > a[left] && a[mid] > a[right], meaning we are on the bigger part, the smaller part is on our right, so go right\n\n> 2. a[mid] < a[left] && a[mid] < a[right], meaning we are on the smaller part, to find the smallest element, go left\n\nif the array is not rotated (actually one rotating cycle completed), we just need to go left, in this case a[mid] < a[right] always holds.\n\ncombining the cases above, we conclude that\n> if a[mid] > a[right], go right; if a[mid] < a[right], go left.\n\n public class Solution {\n public int findMin(int[] nums) {\n if (nums==null || nums.length==0) { return Integer.MIN_VALUE; } \n int left = 0, right = nums.length-1;\n while (left < right-1) { // while (left < right-1) is a useful technique\n int mid = left + (right-left)/2;\n if (nums[mid] > nums[right]) { left = mid; }\n else { right = mid; }\n }\n if (nums[left] > nums[right]) { return nums[right]; }\n return nums[left];\n }\n }
| 39 | 1 |
['Java']
| 10 |
find-minimum-in-rotated-sorted-array
|
Javascript Solution using Binary Search in O(logn) time (w/ explanation)
|
javascript-solution-using-binary-search-rnsfg
|
Explanation\nMy solution for this problem utilises Binary Search. The reason I chose binary search was that the question mentioned that the solution has to have
|
AmehPls
|
NORMAL
|
2021-11-27T08:23:54.275654+00:00
|
2021-11-27T08:23:54.275684+00:00
| 3,967 | false |
## Explanation\nMy solution for this problem utilises **Binary Search**. The reason I chose binary search was that the question mentioned that the solution has to have a time complexity of O(logn). The naive method of iterating through the array and updating a variable to keep track of the minimum would be linear, O(n). Since binary search is known to have a time complexity of O(logn) I decided to go down that route.\n\nBut how do we use binary search for this problem? Here are the brief steps to my solution:\n\n1. Left and right are 2 pointers that keep track of the start and end of the subarray that we are currently searching.\n\n2. Within the loop, a mid pointer is calculated to be half the sum of left and right. We then start to compare the value at the mid pointer and the value at the right pointer. From here, there can only be 2 case:\n\n\t(a) nums[mid] > nums[right]\n\tFor an un-rotated sorted array, we can easily understand that there can never be a case where nums[mid] would ever be greater than nums[right]. However, this condition can happen in a rotated array if the mid pointer is residing on the left side of the rotated array. Once we know that the mid pointer is at the left side of the array, we can start to cut down our search to only the right side since we know that the minimum value can never be in the left side. Hence, we update the left pointer to be mid + 1, indicating that we are now searching the right side.\n\t\n\t(b) nums[mid] <= nums[right]\n\tThis condition will tell us that the subarray that we are currently searching is now a properly sorted array which is un-rotated. To get the minimum value of this subarray, we simply have to keep adjusting the right pointer to the left by setting the mid pointer as the right pointer, cutting down our serach to only the left half of this subarray. Eventually, we will reach the left most element of this subarray.\n\t\n\t***Note:*\n\t*For a sorted array of [4,5,6,7,0,1,2], the left side refers to the portion of the array on the left of the minimum value [4,5,6,7] and the right side refers to the portion of the array from the minimum value onwards [0,1,2].***\n\t\n3. Lastly, the while loop only ceases once the search is complete (the right and left pointer passes each other). At this point, the answer that we want will lie in nums[left].\n\t\n## Performance\n\nThe time complexity of this solution is, **O(logn)**, since at every stage of binary search, we are splitting the array into half.\n\nHere are the details of my submission:\nRuntime: 80 ms, faster than 42.33% \nMemory Usage: 39.2 MB, less than 29.36% \n\n## Code\n\n```\nvar findMin = function(nums) {\n var left = 0,\n right = nums.length - 1\n \n while (left < right){\n var mid = Math.floor((left + right)/2)\n if (nums[mid] > nums[right]) left = mid + 1\n else right = mid\n }\n return nums[left]\n};\n```\n\nI hope this helps! Do let me know if there are any lapses in my explanation and/or if my solution can be improved in any way :)
| 36 | 0 |
['Binary Tree', 'JavaScript']
| 6 |
find-minimum-in-rotated-sorted-array
|
My binary-search solution in Python with disscussing
|
my-binary-search-solution-in-python-with-gm3f
|
class Solution:\n # @param num, a list of integer\n # @return an integer\n def findMin(self, num):\n first, last = 0, len(num) -
|
backofhan
|
NORMAL
|
2015-01-15T02:06:21+00:00
|
2018-10-03T01:56:09.256663+00:00
| 7,961 | false |
class Solution:\n # @param num, a list of integer\n # @return an integer\n def findMin(self, num):\n first, last = 0, len(num) - 1\n while first < last:\n midpoint = (first + last) // 2\n if num[midpoint] > num[last]:\n first = midpoint + 1\n else:\n last = midpoint\n return num[first]\n\nThis solution has a time complexity of O(log(n)) and takes about 50 ms to run.\nIn python, things are little bit different from the ones in C++ or Java. I am told that each python statement will be translated into one or several c function invocations. So less statements almost always means higher performance. I tried the one line solution "return min(num)" in this subject. It is really a system cheating and has a complexity of O(n). But it yields the identical running time as the binary-search solution. I am not sure about the test inputs. However I think we should have some large ones to make the difference (O(n) VS O(log(n))) visible. I guess we need some inputs which have 100 k or even more numbers.
| 32 | 0 |
['Binary Tree', 'Python']
| 6 |
find-minimum-in-rotated-sorted-array
|
C / C++ Simple and Clean Solution, O(logn), With Comments
|
c-c-simple-and-clean-solution-ologn-with-xxyo
|
C++:\n\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int r = nums.size()-1, l = 0, mid;\n if (!r) return nums[0]; // only one
|
yehudisk
|
NORMAL
|
2021-08-31T07:12:20.469160+00:00
|
2021-08-31T07:45:26.568622+00:00
| 4,077 | false |
**C++:**\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int r = nums.size()-1, l = 0, mid;\n if (!r) return nums[0]; // only one element\n\n while (l < r)\n {\n mid = l + (r - l) / 2;\n\n // got a part that is not rotated\n if (nums[l] < nums[r]) return nums[l]; \n\n // mid is larger than right - min is in right side\n else if (nums[mid] > nums[r]) l = mid + 1;\n\n // mid is smaller than right - min is in left side (including mid)\n else r = mid;\n }\n return nums[l];\n }\n};\n```\n****\n**C:**\n```\nint findMin(int* nums, int numsSize){\n int r = numsSize-1, l = 0, mid;\n if (!r) return nums[0]; // only one element\n\n while (l < r)\n {\n mid = l + (r - l) / 2;\n\n // got a part that is not rotated\n if (nums[l] < nums[r]) return nums[l]; \n\n // mid is larger than right - min is in right side\n else if (nums[mid] > nums[r]) l = mid + 1;\n\n // mid is smaller than right - min is in left side (including mid)\n else r = mid;\n }\n return nums[l];\n}\n```\n**Like it? please upvote!**
| 29 | 0 |
['C']
| 5 |
find-minimum-in-rotated-sorted-array
|
[Python] Recursive binary search, explained
|
python-recursive-binary-search-explained-3bqv
|
In fact this problem is very similar to problem 0033, but here we need to find not target element, but minimum. We can use exactly the same logic:\n\n1. if nums
|
dbabichev
|
NORMAL
|
2021-08-31T07:20:23.470489+00:00
|
2021-08-31T07:20:23.470584+00:00
| 1,421 | false |
In fact this problem is very similar to problem **0033**, but here we need to find not target element, but minimum. We can use exactly the same logic:\n\n1. `if nums[end] < nums[mid]`, this means that minimum we are looking for is situated in the right half.\n2. `elif nums[end] > nums[mid]` means that minimum we are looking for is situated in the left half.\n3. `if end - start <= 1` means that we have interval of length `1` or `2`, so we can directly check minimum.\n\nAlso here I did it in recursive, not iterative way just for the purpose of exercise.\n\n#### Complexity\nIt is `O(log n)` for time and space.\n\n#### Code\n```python\nclass Solution: \n def findMin(self, nums):\n def dfs(start, end):\n if end - start <= 1:\n return min(nums[start], nums[end])\n\n mid = (start + end)//2\n if nums[end] < nums[mid]:\n return dfs(mid + 1, end)\n elif nums[end] > nums[mid]:\n return dfs(start, mid)\n\n return dfs(0, len(nums) - 1)\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**
| 26 | 1 |
['Binary Search']
| 5 |
find-minimum-in-rotated-sorted-array
|
Updated binary search 😊
|
updated-binary-search-by-kukuxer-4gi8
|
\n\n# Approach\nIf nums[mid] > nums[right], it means the pivot (the point of rotation) is on the right side. The minimum element is on the right side of the arr
|
kukuxer
|
NORMAL
|
2024-02-22T17:23:52.940953+00:00
|
2024-02-22T17:23:52.940985+00:00
| 2,187 | false |
\n\n# Approach\nIf nums[mid] > nums[right], it means the pivot (the point of rotation) is on the right side. The minimum element is on the right side of the array. So, update left = mid + 1.\n\n If nums[mid] <= nums[right], it means the pivot is on the left side, or mid itself might be the minimum element. So, update right = mid.\n\n**Bold**\n# Complexity\n- Time complexity:\nO(log n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public int findMin(int[] nums) {\n int l=0, r = nums.length -1 ; // l - left, r - right\n int m; //mid\n while(l < r){\n m = l+(r-l)/2; //default mid\n if(nums[m] > nums[r]){ \n l = m+1;\n }else{ \n r = m;\n }\n }\n return nums[l];\n }\n}\n\n```\n\n
| 24 | 0 |
['Java']
| 2 |
find-minimum-in-rotated-sorted-array
|
Very Simple Java Binary Search
|
very-simple-java-binary-search-by-zhibzh-26nj
|
public class Solution {\n public int findMin(int[] num) {\n int low = 0;\n int high = num.length - 1;\n while(low < high){\n
|
zhibzhang
|
NORMAL
|
2015-04-20T19:47:55+00:00
|
2018-10-21T15:49:54.030288+00:00
| 7,763 | false |
public class Solution {\n public int findMin(int[] num) {\n int low = 0;\n int high = num.length - 1;\n while(low < high){\n int mid = (low + high) / 2;\n if(num[high] < num[mid]){\n low = mid + 1;\n } else {\n high = mid;\n }\n }\n return num[high];\n }\n}
| 24 | 0 |
['Binary Tree', 'Java']
| 7 |
find-minimum-in-rotated-sorted-array
|
Easiest solution valid for both duplicate and non duplicate
|
easiest-solution-valid-for-both-duplicat-n5th
|
Time complexity: O(log(n))\n\nclass Solution {\npublic:\n int findMin(vector<int>& n) {\n int s=0,l=n.size();\n int e =l-1;\n while(s<e)
|
vatsalkesarwani
|
NORMAL
|
2021-08-03T15:47:12.664858+00:00
|
2021-08-03T15:47:12.664904+00:00
| 3,845 | false |
Time complexity: O(log(n))\n```\nclass Solution {\npublic:\n int findMin(vector<int>& n) {\n int s=0,l=n.size();\n int e =l-1;\n while(s<e){\n int m = s+(e-s)/2;\n if(n[m] > n[e]) s=m+1; // left side has small values (rotated array)\n else if(n[m] < n[e]) e=m; // right side has small value (not rotated)\n else e--; // mid value equal to end move towards small\n }\n return n[s];\n }\n};\n```
| 23 | 0 |
['Binary Search', 'C', 'Binary Tree', 'C++']
| 3 |
find-minimum-in-rotated-sorted-array
|
C++/Java/Python/JavaScript || ✅🚀 Time: O(log n) & Space: O(1) Simple Code || ✔️🔥With Explanation
|
cjavapythonjavascript-time-olog-n-space-ooot1
|
Intuition:\nThe code aims to find the minimum element in a rotated sorted array. It utilizes the binary search algorithm to efficiently narrow down the search s
|
devanshupatel
|
NORMAL
|
2023-05-20T14:32:35.600386+00:00
|
2023-05-22T14:06:38.897884+00:00
| 6,447 | false |
# **Intuition:**\nThe code aims to find the minimum element in a rotated sorted array. It utilizes the binary search algorithm to efficiently narrow down the search space and locate the minimum element.\n\n# **Approach:**\n1. Initialize two pointers, `left` and `right`, representing the start and end indices of the search space.\n2. Enter a while loop as long as `left` is less than `right`.\n3. Calculate the midpoint `mid` using the formula `mid = left + (right - left) / 2`.\n4. Compare the value at index `mid` with the value at index `right` to determine which half of the array contains the minimum element.\n - If `nums[mid] > nums[right]`, it means the minimum element lies in the right half of the array. Update `left = mid + 1` to search in the right half.\n - Otherwise, the minimum element lies in the left half of the array, including the `mid` index. Update `right = mid` to search in the left half.\n5. Repeat steps 3-4 until the search space is narrowed down to a single element, i.e., `left >= right`.\n6. Return the value at `nums[left]` as the minimum element.\n\n# **Complexity:**\n- Time Complexity: The binary search approach has a time complexity of O(log n), where n is the size of the input array `nums`. The search space is halved in each iteration, leading to efficient searching.\n- Space Complexity: The code has a space complexity of O(1) as it uses a constant amount of extra space for the variables `left`, `right`, and `mid`. No additional data structures are used that scale with the input size.\n\n# C++\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int left = 0;\n int right = nums.size() - 1;\n\n while (left < right) {\n int mid = left + (right - left) / 2;\n\n if (nums[mid] > nums[right]) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return nums[left];\n }\n};\n\n```\n# Java\n```\nclass Solution {\n public int findMin(int[] nums) {\n int left = 0;\n int right = nums.length - 1;\n\n while (left < right) {\n int mid = left + (right - left) / 2;\n\n if (nums[mid] > nums[right]) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return nums[left];\n }\n}\n```\n# Python\n```\nclass Solution(object):\n def findMin(self, nums):\n left = 0\n right = len(nums) - 1\n\n while left < right:\n mid = left + (right - left) / 2\n\n if nums[mid] > nums[right]:\n left = mid + 1\n else:\n right = mid\n\n return nums[left]\n\n\n```\n# JavaScript\n```\nvar findMin = function(nums) {\n let left = 0;\n let right = nums.length - 1;\n\n while (left < right) {\n let mid = left + Math.floor((right - left) / 2);\n\n if (nums[mid] > nums[right]) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return nums[left];\n};\n\n```
| 22 | 1 |
['Python', 'C++', 'Java', 'JavaScript']
| 5 |
find-minimum-in-rotated-sorted-array
|
4 Solutions Including Divide-and-Conquer, Binary Search (+ Follow-Up)
|
4-solutions-including-divide-and-conquer-ll58
|
Solutions for 153 (no duplicate): link\n\nReference: LeetCode\nDifficulty: Hard\n\n## Problem\n\n> Suppose an array sorted in ascending order is rotated at some
|
junhaowanggg
|
NORMAL
|
2020-04-16T22:41:50.228932+00:00
|
2020-04-16T22:41:50.228969+00:00
| 2,767 | false |
Solutions for 153 (no duplicate): [link](https://www.junhaow.com/lc/problems/binary-search/rotated-sorted-array/153_find-minimum-in-rotated-sorted-array.html)\n\nReference: [LeetCode](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array-ii/)\nDifficulty: <span class="red">Hard</span>\n\n## Problem\n\n> Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.\n\n> (i.e., `[0,1,2,4,5,6,7]` might become `[4,5,6,7,0,1,2]`).\n\n> Find the minimum element.\n\n> You may assume duplicate exists in the array.\n\n**Example:** \n\n```cpp\nInput: [3,4,5,1,2] \nOutput: 1\n\nInput: [2,2,2,0,1]\nOutput: 0\n\nInput: [3,3,3,3]\nOutput: 3\n\nInput: [3,6,3]\nOutput: 3\n\nInput: [3,1,3]\nOutput: 1\n```\n\n**Follow-up Questions:**\n\n- Would allow duplicates affect the run-time complexity? How and why?\n\n\n## Analysis\n\nSorting & Brute-Force as in 153.\n\n### Divide & Conquer\n\nReference: [Huahua](https://www.youtube.com/watch?v=P4r7mF1Jd50&list=PLLuMmzMTgVK5DkeNodml9CHCW4BGxpci7&index=11&t=0s)\n\n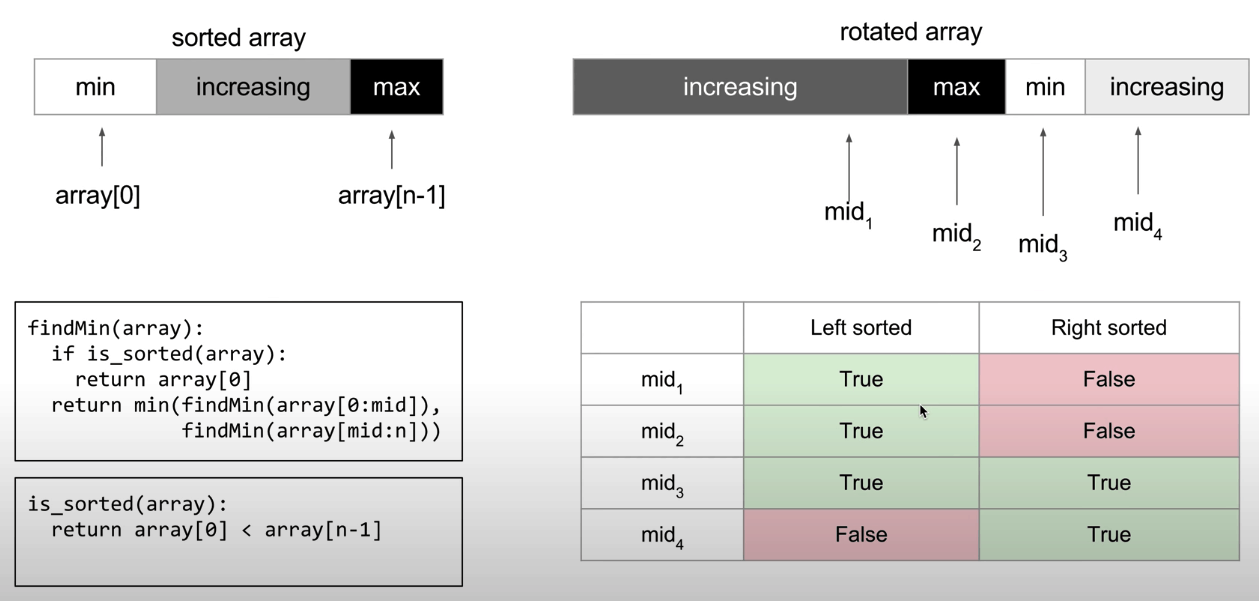\n\nIn the `mid3` case, the result could be calculated in `O(1)`.\n\n**Note:** Duplicates affect the run-time complexity. Consider the following case:\n\n\n\n```cpp\npublic:\n int findMin(vector<int>& nums)\n {\n return findMin(nums, 0, nums.size() - 1);\n }\n\nprivate:\n int findMin(const vector<int>& nums, int lo, int hi)\n {\n // only one element\n if (lo == hi) \n return nums[lo];\n\n if (isSorted(nums, lo, hi)) \n return nums[lo];\n \n int mid = lo + (hi - lo) / 2;\n int left = findMin(nums, lo, mid);\n int right = findMin(nums, mid + 1, hi);\n return min(left, right);\n }\n\n bool isSorted(const vector<int>& nums, int lo, int hi)\n {\n return nums[lo] < nums[hi]; // must be < (<= will fail in the case [3, 1, 3])\n }\n```\n\n**Time:** `O(\\log{N})`\n- False: `T(N) = 2T(N/2) = O(N)` \u274C\n - At each level, at least one side could be done in `O(1)`.\n- True: `T(N) = O(1) + T(N/2) = O(\\log{N})`\n\n**Space:** `O(\\log{N})`\n\n\n\n### Binary Search\n\n\nThe basic idea is that if `nums[mid] >= nums[lo]` we assure that the inflection point is on the right part.\n\nHowever, unlike the solution in 153, we need 3 cases:\n\n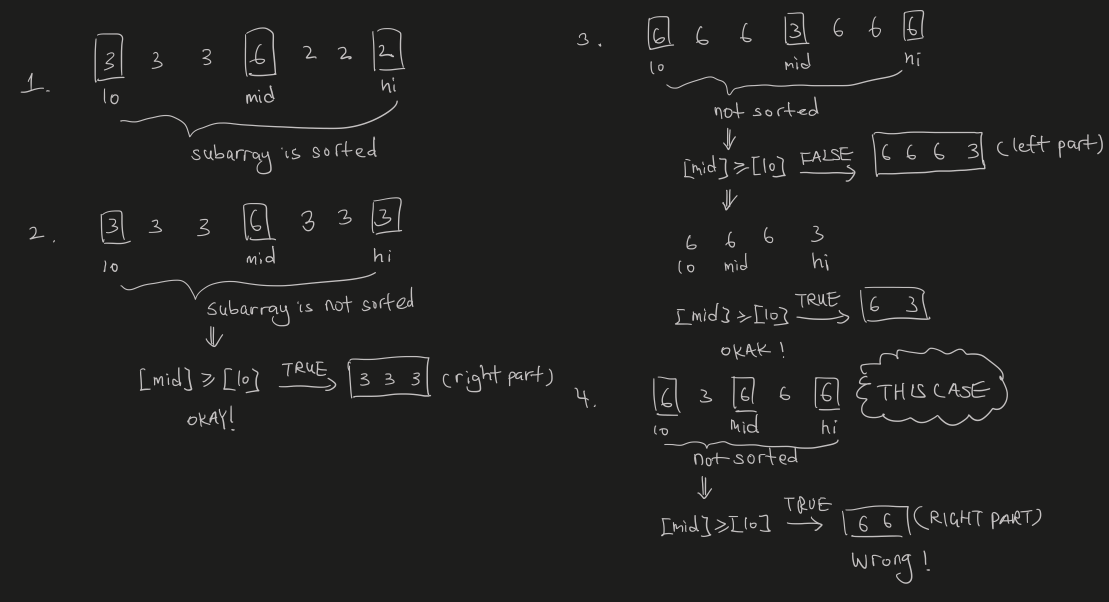\n\nRecursion:\n\n```cpp\npublic:\n int findMin(vector<int>& nums)\n {\n return findMin(nums, 0, nums.size() - 1);\n }\n\nprivate:\n int findMin(const vector<int>& nums, int lo, int hi)\n {\n // only one element\n if (lo == hi) \n return nums[lo];\n \n // the subarray is sorted\n if (nums[lo] < nums[hi])\n return nums[lo];\n \n int mid = lo + (hi - lo) / 2;\n\n // changes here --> 3 cases\n if (nums[mid] > nums[lo])\n {\n return findMin(nums, mid + 1, hi);\n }\n else if (nums[mid] < nums[lo])\n {\n return findMin(nums, lo, mid);\n }\n else // nums[mid] == nums[lo]\n {\n return min(findMin(nums, mid + 1, hi), findMin(nums, lo, mid));\n }\n }\n```\n\nIteration:\n\nInvalid!\n\n```cpp\npublic:\n int findMin(vector<int>& nums)\n {\n int lo = 0;\n int hi = nums.size() - 1;\n // stops when there is only one element\n // in other words, it makes sure that there are at least 2 elements\n while (lo < hi)\n {\n if (nums[lo] < nums[hi]) return nums[lo];\n \n int mid = lo + (hi - lo) / 2;\n if (nums[mid] > nums[lo])\n {\n lo = mid + 1;\n }\n else if (nums[mid] > nums[lo])\n {\n hi = mid;\n }\n else\n {\n // ???\n }\n }\n return nums[lo];\n }\n```\n\n**Time:** `O(\\log{N})`\n- In the worst case scenario it would become `O(N)`.\n\n**Space:** `O(\\log{N})`\n\n\n
| 21 | 0 |
['Binary Search', 'Divide and Conquer', 'Recursion', 'C', 'Binary Tree', 'C++']
| 3 |
find-minimum-in-rotated-sorted-array
|
7-Line O(LogN) Solution
|
7-line-ologn-solution-by-lestrois-6szs
|
public int FindMin(int[] nums) {\n int left = 0, right = nums.Length - 1, mid = 0;\n while(left < right){\n mid = (left + right) >> 1;\
|
lestrois
|
NORMAL
|
2015-07-13T21:00:59+00:00
|
2015-07-13T21:00:59+00:00
| 4,427 | false |
public int FindMin(int[] nums) {\n int left = 0, right = nums.Length - 1, mid = 0;\n while(left < right){\n mid = (left + right) >> 1;\n if(nums[mid] > nums[right]) left = mid + 1;\n else right = mid;\n }\n return nums[right];\n }
| 21 | 1 |
['Divide and Conquer']
| 6 |
find-minimum-in-rotated-sorted-array
|
【Video】Use part of input array to compare numbers.
|
video-use-part-of-input-array-to-compare-uopd
|
Intuition\nUse part of input array to compare numbers.\n\n# Solution Video\n\nhttps://youtu.be/JiNsSV16vLU\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subs
|
niits
|
NORMAL
|
2024-11-10T17:27:21.114958+00:00
|
2024-11-10T17:27:21.114992+00:00
| 2,119 | false |
# Intuition\nUse part of input array to compare numbers.\n\n# Solution Video\n\nhttps://youtu.be/JiNsSV16vLU\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 10,666\nThank you for your support!\n\n---\n\n# Approach\nThe description says "You must write an algorithm that runs in $$O(log n)$$ time.", so we will solve this question with `Binary Search`.\n\n```\nInput: nums = [3,4,5,1,2]\n```\nLet me put left, right and middle pointer.\n\n```\n[3,4,5,1,2]\n L M R\n```\nTypical Binary Search is like this.\n\n---\n\n\nIf a middle number is greater than a target number, we move `right` to `middle - 1`. On the other hand if the middle number is less than the target number, we will move `left` to `middle + 1`.\n\n**Binary search assumes that the input is sorted.**\n\n---\n\nThe target number for this question is a minimum number in the input, but problem here is that input array is rorated a few times.\n\n### How can we decide to move left or right pointer?\n\nIt\'s tough to think about whole array but part of array is still sorted in ascending order, even if the input is rotated.\n\nFor example,\n\n```\n[0,1,2,3,4,5]\n\u2193\n[4,5,0,1,2,3]\n```\nRotated twice. Between `4` and `5`, they are sorted and between `0` and `3`, they are also sorted. We will use those parts of array.\n\nLet\'s go back to main story.\n\nMy strategy is to compare middle number with right number. In this case, `5` and `2`.\n\n```\n[3,4,5,1,2]\n L M R\n```\n`5` is greater than `2`. That means we don\'t know how many numbers we have on the right side of the middle number, but we can say the numbers return to the minimum value and then begin to increase again on the right side of the middle number.\n\nTo prove that, let\'s think about this example quickly.\n\n```\n[1,2,3,4,5]\n L M R\n```\nIn this case, `3` is less than `5`. **That means minimum number is definitely on the left side of the middle number. That\'s because input array is sorted and the last number(= right number) is greater than middle number. We are sure that the numbers increase from middle to right.**\n\nLet\'s go back to main story again.\n\n```\n[3,4,5,1,2]\n L M R\n```\nMiddle number is greater than right number, so we can say at some point, the numbers return to minimum value. That\'s why we should move the left pointer to `middle pointer + 1`.\n\n```\n[3,4,5,1,2]\n M L R\n```\n\nNext, middle pointer should be...\n\n```\n[3,4,5,1,2]\n L R\n M\n```\n\nCompare `1` with `2`. The `middle` number is less than the `right` number, so we are sure that the minimum number is on the left of the middle number.\n\nThere is one point when we move right pointer.\n\n---\n\n\u2B50\uFE0F Points\n\nWhen we move `right` pointer to left side, we will update `right` pointer with `middle pointer`. On the other hand when we move `left` pointer, we will update `left` pointer with `middle pointer + 1`.\n\nWhy? Let\'s think about this case.\n\n```\n[1,2,3,4,5]\n L M R\n```\nCompare `3` with `5`. We will move the `right` pointer to left side. In this case, we only know that the middle number is smaller than the right number, so **the middle number could still be the minimum value.** \n\n```\n[3,4,5,1,2]\n L M R\n```\n\nIn this case, since the middle number is greater than the right number, **it\u2019s impossible for the middle number to be the minimum value.** That\'s why we can update `left` pointer with `middle pointer + 1`.\n\n---\n\nLet\'s go back to main story again.\n\nIn this case, we will update `right` pointer with `middle` pointer.\n\n```\n[3,4,5,1,2]\n L R\n M\n\n\u2193\n\n[3,4,5,1,2]\n L \n M\n R\n```\nNow `L == R`. We stop itertaion.\n\n```\nreturn 1(= left number or right number)\n```\n\n---\n\nhttps://youtu.be/bU_dXCOWHls\n\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n \n left = 0\n right = len(nums) - 1\n\n while left < right:\n mid = (left + right) // 2\n\n if nums[mid] <= nums[right]:\n right = mid\n else:\n left = mid + 1\n \n return nums[left]\n```\n```javascript []\nvar findMin = function(nums) {\n let left = 0;\n let right = nums.length - 1;\n\n while (left < right) {\n const mid = Math.floor((left + right) / 2);\n\n if (nums[mid] <= nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left]; \n};\n```\n```java []\nclass Solution {\n public int findMin(int[] nums) {\n int left = 0;\n int right = nums.length - 1;\n\n while (left < right) {\n int mid = left + (right - left) / 2;\n\n if (nums[mid] <= nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left]; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int left = 0;\n int right = nums.size() - 1;\n\n while (left < right) {\n int mid = left + (right - left) / 2;\n\n if (nums[mid] <= nums[right]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n\n return nums[left]; \n }\n};\n```\n\n# Step by Step Algorithm\n\n1. **Initialize Pointers**\n\n ```python\n left = 0\n right = len(nums) - 1\n ```\n\n - We define two pointers, `left` and `right`.\n - `left` starts at the beginning of the array (`0`), and `right` starts at the last index (`len(nums) - 1`).\n - The goal is to narrow down the range between `left` and `right` until we find the minimum element.\n\n2. **Binary Search Loop**\n\n ```python\n while left < right:\n ```\n\n - We enter a loop that continues as long as `left` is less than `right`.\n - This loop performs a binary search to locate the minimum value in the rotated sorted array.\n\n3. **Calculate Midpoint**\n\n ```python\n mid = (left + right) // 2\n ```\n\n - We calculate the midpoint `mid` by taking the integer division of `(left + right) / 2`.\n - `mid` represents the middle index of the current subarray defined by `left` and `right`.\n\n4. **Compare Midpoint with Right Element**\n\n ```python\n if nums[mid] <= nums[right]:\n right = mid\n ```\n\n - If the element at `mid` is less than or equal to the element at `right`, this means the minimum element could be at `mid` or to its left (in the left half of the current subarray).\n - We update `right` to `mid`, effectively discarding the right half of the array in the next iteration.\n\n5. **Move Left Pointer**\n\n ```python\n else:\n left = mid + 1\n ```\n\n - If `nums[mid]` is greater than `nums[right]`, this means the minimum element must be in the right half of the current subarray.\n - We update `left` to `mid + 1`, moving it to the right half of the array for the next iteration.\n\n6. **Return Minimum Element**\n\n ```python\n return nums[left]\n ```\n\n - Once the loop exits (when `left == right`), both `left` and `right` will be pointing to the minimum element in the array.\n - We return `nums[left]` as the minimum value.\n\n\n---\n\nThank you for reading my post.\n\n##### \u2B50\uFE0F Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n##### \u2B50\uFE0F Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n##### \u2B50\uFE0F Related Video\n#33 Search in Rotated Sorted Array\n\nhttps://youtu.be/dO9OZJP_Hm8
| 20 | 0 |
['C++', 'Java', 'Python3', 'JavaScript']
| 1 |
find-minimum-in-rotated-sorted-array
|
100% BEATS optimized Java Solutions🔥|| Clean and easy to understand code|| look at once
|
100-beats-optimized-java-solutions-clean-1qna
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n# simple binary search\
|
L005er22
|
NORMAL
|
2023-03-27T14:30:47.872864+00:00
|
2023-03-27T14:30:47.872903+00:00
| 2,374 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n# ***simple binary search***\n# Complexity\n- Time complexity: O(logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findMin(int[] nums) {\n\n int start = 0, end = nums.length-1;\n\n while(start < end){\n\n int mid = (start+end) / 2;\n if(mid > 0 && nums[mid] < nums[mid-1])\n return nums[mid];\n if(nums[start] <= nums[mid] && nums[mid] > nums[end])\n start = mid + 1;\n else\n end = mid - 1;\n }\n return nums[start];\n }\n}\n```\nplease upvote this for better solution of other questions\n
| 19 | 0 |
['Two Pointers', 'Binary Search', 'Java']
| 4 |
find-minimum-in-rotated-sorted-array
|
✅ C++ | No Tension | Pure Standard Binary Search | Most intuitive | very clean
|
c-no-tension-pure-standard-binary-search-6pl5
|
Runtime : 7ms\nClean and very simple \n\nExplanation : \n1. If the nums[mid] is in the left hand side, then it must be greater than the smallest number in the
|
HustlerNitin
|
NORMAL
|
2022-06-23T07:03:56.003235+00:00
|
2022-11-13T13:48:30.827949+00:00
| 1,780 | false |
**Runtime : 7ms**\nClean and very simple \n\n**Explanation :** \n1. If the `nums[mid]` is in the **left hand side**, then it must be greater than the smallest number in the left hand side, i.e. `nums[0]`. That is `nums[0] <= nums[mid]`. Then we know the minimum number must in the `right side` of mid. So move `low` to `mid + 1`\n\n2. If the `nums[mid]` is in the **right hand side**, then it must be no greater than the smallest number in the left hand side, i.e. `nums[0]`. That is `nums[0] > nums[mid]`. Then we know the minimum number must in the `left side of mid`. So move `high` to `mid-1`.\n\n**Dry run on below 2 test cases, after this you will be crystal clear with my approach**\nEx.1\n`Input: nums = [4,5,6,7,0,1,2]`\n`Output: 0`\n\nEx.2\n`Input: nums = [2,1]`\n`Output: 1`\n\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n \n\t\t// corner case\n\t\tif(nums.size()==1) return nums[0];\n\t\n // If the array is already sorted then return first element\n if(nums[0] < nums[nums.size()-1])\n return nums[0];\n \n // Find the Pivot element\n int low=0;\n int high=nums.size()-1;\n \n while(low<=high)\n {\n int mid=low+(high-low)/2;\n if(nums[0] <= nums[mid]) \n {\n low=mid+1;\n }\n else\n {\n high=mid-1;\n }\n }\n return nums[low];\n }\n};\n```\n*Thanks for upvoting !*
| 18 | 0 |
['Binary Search', 'C', 'C++']
| 5 |
find-minimum-in-rotated-sorted-array
|
Simple Binary Search
|
simple-binary-search-by-loickenleetcode-8mob
|
\n def findMin(self, nums: List[int]) -> int:\n lo, hi = 0, len(nums)-1\n while lo < hi:\n mid = (lo+hi)//2\n if nums[mid
|
loickenleetcode
|
NORMAL
|
2019-10-04T07:55:00.302647+00:00
|
2019-10-04T07:55:30.098416+00:00
| 2,701 | false |
```\n def findMin(self, nums: List[int]) -> int:\n lo, hi = 0, len(nums)-1\n while lo < hi:\n mid = (lo+hi)//2\n if nums[mid] > nums[hi]:\n lo = mid+1\n else:\n hi = mid\n return nums[lo]\n```
| 18 | 0 |
['Python']
| 4 |
find-minimum-in-rotated-sorted-array
|
C++ binary search sol
|
c-binary-search-sol-by-reetisharma-nc5n
|
\n \n int findMin(vector<int>& nums) {\n \n int l = 0,r=nums.size()-1,n=nums.size();\n int mid,prev,next;\n \n whi
|
reetisharma
|
NORMAL
|
2021-04-06T18:07:11.716260+00:00
|
2021-04-06T18:07:11.716292+00:00
| 1,379 | false |
```\n \n int findMin(vector<int>& nums) {\n \n int l = 0,r=nums.size()-1,n=nums.size();\n int mid,prev,next;\n \n while(l<=r){\n \n mid = l + (r-l)/2;\n prev = (mid + n - 1)%n;\n next = (mid+1)%n;\n \n if(nums[mid]<=nums[prev] && nums[mid]<=nums[next])\n return nums[mid];\n else if(nums[mid]>nums[r])\n l = mid+1;\n else\n r = mid-1;\n }\n return -1;\n }\n```
| 17 | 0 |
['Binary Search', 'C']
| 4 |
find-minimum-in-rotated-sorted-array
|
Beginner friendly C++ Binary Search solution - O(logN)
|
beginner-friendly-c-binary-search-soluti-b7ee
|
Sorted array after rotation will have 2 parts , both sorted in ascending order.\n For eg: [1,2,3,4,5] after rotating 2 times will become [4,5,1,2,3]. Here fi
|
priyal04
|
NORMAL
|
2021-10-23T10:01:40.918265+00:00
|
2021-10-23T10:01:40.918295+00:00
| 1,099 | false |
* Sorted array after rotation will have 2 parts , both sorted in ascending order.\n For eg: [1,2,3,4,5] after rotating 2 times will become [4,5,1,2,3]. Here first part is [4,5] and second part is [1,2,3]. \n* Basically we have to find first element of second part. \n* It might also be possible that after several rotations we might get sorted array again. To handle this we\'ll first check if first element is samller than the last element. If it is so then the array is sorted and will return first element.\n* We can apply modified version of binary search to solve this question.\n* We will first find mid , which is (start+end)/2. Then we\'ll check whether our mid lies in the first part or second.\n* If nums[mid] >= nums[0] then mid lies in first part otherwise in second part.\n* If our mid lies in first part then we will make start = mid +1 (since our ans always lies in second part).\n* If it lies in second part then will update our ans and make end = mid - 1.\n\n```\nint findMin(vector<int>& nums) {\n int n = nums.size();\n \n\t\t//if size of array is one\n if(n==1)\n return nums[0];\n \n //if array is sorted then first element is smallest\n if(nums[0] < nums[n-1])\n return nums[0];\n \n int start = 0;\n int end = n-1;\n \n int ans = INT_MAX;\n while(start <= end){\n \n int mid = (start + end) / 2;\n\t\t\t\n\t\t\t//if mid is in first part of array\n if(nums[mid] >= nums[0])\n start = mid +1;\n \n else\n {\n ans = min(ans , nums[mid]);\n end = mid - 1;\n }\n }\n return ans;\n }\n```\n\nTime Complexity : O(logn)\n\n***If you like the solution please upvote!***
| 16 | 0 |
['C', 'Binary Tree']
| 2 |
find-minimum-in-rotated-sorted-array
|
Java | TC: O(logN) | SC: O(1) | Optimal Binary Search with Early Exit
|
java-tc-ologn-sc-o1-optimal-binary-searc-1n0v
|
java\n/**\n * Modified Binary Search\n *\n * Time Complexity: O(log N)\n *\n * Space Complexity: O(1)\n *\n * N = Length of the input array.\n */\nclass Solutio
|
NarutoBaryonMode
|
NORMAL
|
2021-10-19T07:03:10.407469+00:00
|
2021-10-19T07:10:49.160980+00:00
| 1,188 | false |
```java\n/**\n * Modified Binary Search\n *\n * Time Complexity: O(log N)\n *\n * Space Complexity: O(1)\n *\n * N = Length of the input array.\n */\nclass Solution {\n public int findMin(int[] nums) {\n if (nums == null || nums.length == 0) {\n throw new IllegalArgumentException("Input is invalid");\n }\n\n int len = nums.length;\n if (len == 1 || nums[0] < nums[len - 1]) {\n return nums[0];\n }\n if (len == 2) {\n return Math.min(nums[0], nums[1]);\n }\n\n int start = 0;\n int end = len - 1;\n\n while (start < end) {\n if (nums[start] < nums[end]) {\n return nums[start];\n }\n\n int mid = start + (end - start) / 2;\n if (nums[mid] <= nums[end]) {\n end = mid;\n } else {\n start = mid + 1;\n }\n }\n\n return nums[start];\n }\n}\n```\n\n---\n\nSolutions to other Rotated Sorted Array questions on LeetCode:\n- [33. Search in Rotated Sorted Array](https://leetcode.com/problems/search-in-rotated-sorted-array/discuss/1529302/Java-or-TC:-O(logN)-or-SC:-O(1)-or-Modified-Binary-Search-optimal-solution)\n- [81. Search in Rotated Sorted Array II](https://leetcode.com/problems/search-in-rotated-sorted-array-ii/discuss/1529305/Java-or-TC:-O(N2)-or-SC:-O(1)-or-Modified-Binary-Search-optimal-solution)\n- [154. Find Minimum in Rotated Sorted Array II + FollowUp](https://leetcode.com/problems/find-minimum-in-rotated-sorted-array-ii/discuss/1529323/Java-or-TC:-O(N2)-or-SC:-O(1)-or-Optimal-Binary-Search-w-Early-Exit-and-FollowUp)\n
| 15 | 0 |
['Array', 'Binary Tree', 'Java']
| 2 |
find-minimum-in-rotated-sorted-array
|
✅Accepted beats 100% || Java / C || Solution
|
accepted-beats-100-java-c-solution-by-th-d17c
|
Complexity\n- Time complexity: O(log n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:\n Add your space complexity here, e.g. O(n) \n\n# JAV
|
thilaknv
|
NORMAL
|
2023-03-09T15:55:30.329503+00:00
|
2024-05-09T11:56:43.020054+00:00
| 1,844 | false |
# Complexity\n- Time complexity: **O(log n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# JAVA :-\n -- | Details | --\n--- | --- | ---:\n**Runtime** | 1ms | Beats **100%**\n**Memory** | 40MB | Beats **20%**\n```\nclass Solution {\n public int findMin(int[] A) {\n final int N = A.length;\n if(N == 1) return A[0];\n int start = 0, end = N-1, mid;\n while(start < end){\n mid = (start+end) / 2;\n if(mid > 0 && A[mid] < A[mid-1]) return A[mid];\n if(A[start] <= A[mid] && A[mid] > A[end]) start = mid + 1;\n else end = mid - 1;\n }\n return A[start];\n }\n}\n```\n# C :-\n -- | Details | --\n--- | --- | ---:\n**Runtime** | 1ms | Beats **100%**\n**Memory** | 6MB | Beats **30%**\n```\nint findMin(int* A, int N){\n if(N == 1) return A[0];\n int start = 0, end = N-1, mid;\n while(start < end){\n mid = (start+end) / 2;\n if(mid > 0 && A[mid] < A[mid-1]) return A[mid];\n if(A[start] <= A[mid] && A[mid] > A[end]) start = mid + 1;\n else end = mid - 1;\n }\n return A[start];\n}\n```\n## Please UPVOTE : |\n
| 12 | 0 |
['Array', 'Binary Search', 'C', 'Java']
| 3 |
find-minimum-in-rotated-sorted-array
|
Python - O(logn) - Detailed Explanation
|
python-ologn-detailed-explanation-by-nad-mpdo
|
Idea:\n\nWe have an array that have been sorted at some index unknown to us, let\'s call this index the inflection point (IP).\nSide note: You can solve all the
|
nadaralp
|
NORMAL
|
2020-10-15T05:30:25.173101+00:00
|
2020-10-15T05:30:25.173132+00:00
| 1,827 | false |
#### Idea:\n\nWe have an array that have been sorted at some index unknown to us, let\'s call this index the `inflection point (IP)`.\n**Side note: You can solve all the rotated array questions using inflection point technique... good for interviews, I\'ve been asked this question in an onsite interview**\n\nWe can identify the IP as: **The only place where arr[IP] > arr[IP + 1] and arr[IP] > arr[IP - 1]**. Basically the only element which is bigger than both left and right elements.\nLet\'s take the following array as an example:\n`[4, 5, 0, 1, 2, 3]`.\n\nBased on the characteristics above, we can conclude that `5` is the IP.\nIn addition, we can see that elements from index `0...IP [0, IP]` and `[IP + 1, n ]` are always increasing, from this we can infer that is it enough for us to compare `min(arr[0], arr[IP + 1])` for our answer.\n\n**Edge case**: no inflection point, IP will be the last index. So if IP == n - 1 just return arr[0]\n\n#### Algorithm:\n\n```\nclass Solution:\n def get_inflection_point(self, A):\n n = len(A)\n left, right = 0, n - 1\n \n while left <= right:\n mid = left + (right - left) // 2\n if mid == n - 1 or A[mid] > A[mid + 1]:\n return mid\n \n # inflection point to right\n if A[mid] >= A[left]:\n left = mid + 1\n else:\n right = mid - 1\n \n return left\n \n def findMin(self, A: List[int]) -> int:\n n = len(A)\n IP = self.get_inflection_point(A)\n if IP == n - 1:\n return A[0]\n \n return min(A[0], A[IP + 1])\n \n```
| 12 | 0 |
['Binary Tree', 'Python']
| 3 |
find-minimum-in-rotated-sorted-array
|
Binary search template solution | Intuition Explained in detail | Video solution
|
binary-search-template-solution-intuitio-r36s
|
Intuition\n Describe your first thoughts on how to solve this problem. \nhey every one i, have made video playlist for binary search where i discuss a template
|
_code_concepts_
|
NORMAL
|
2023-07-18T09:05:59.708815+00:00
|
2023-07-22T13:05:48.057167+00:00
| 1,164 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nhey every one i, have made video playlist for binary search where i discuss a template solution and intuition behind it, this template solution will be very useful as this will help you solve many other questions in binary search this question is the part of that playlist:\n\nVideo link for question: https://youtu.be/PJpYFuUVI48\n\nPlaylist ink: \nhttps://youtube.com/playlist?list=PLICVjZ3X1AcYYdde4GTp79zfdp_VACSkX\n\n# Code\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int left=0;\n int right=nums.size()-1;\n while(left<right){\n int mid= left + (right-left)/2;\n if(nums[mid]<= nums[right]){\n right=mid;\n }\n else{\n left=mid+1;\n }\n }\n return nums[left];\n }\n};\n```
| 11 | 0 |
['C++']
| 2 |
find-minimum-in-rotated-sorted-array
|
Binary Search[Java] - 0ms - 100%Beats
|
binary-searchjava-0ms-100beats-by-vinith-farm
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vinith_1420
|
NORMAL
|
2022-12-22T15:42:00.808899+00:00
|
2022-12-22T15:42:00.809012+00:00
| 1,481 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findMin(int[] nums) {\n int start = 0, end = nums.length - 1;\n while(start < end)\n {\n int mid = start + (end -start) / 2;\n if(nums[mid] > nums[end])\n start = mid + 1 ;\n \n if(nums[mid] < nums[end])\n end = mid ;\n }\n return nums[start];\n }\n}\n```
| 10 | 0 |
['Java']
| 1 |
find-minimum-in-rotated-sorted-array
|
Easy C++ solution
|
easy-c-solution-by-hirakmondal2000-hrqi
|
Considering the first element of the vector as the minimum value, we start the binary search.\nNow, if v[mid] < min it means the right side of mid is sorted and
|
hirakmondal2000
|
NORMAL
|
2022-02-12T13:46:18.757289+00:00
|
2022-02-12T20:12:45.298749+00:00
| 249 | false |
Considering the first element of the vector as the minimum value, we start the binary search.\nNow, if ```v[mid] < min``` it means the right side of ```mid``` is sorted and the minimum value must be at the left side or ```mid``` is the minimum value. So we set ```min = v[mid];``` and continue searching on the left side.\nAnd if not then it means the left side of ```mid``` is sorted and we need to search on the rights side.\n\n```\nclass Solution {\npublic:\n int findMin(vector<int>& v) \n {\n int min = v[0];\n int low = 0;\n int high = v.size() - 1;\n while(low <= high)\n {\n int mid = low + (high - low) / 2;\n if(v[mid] < min)\n {\n min = v[mid];\n high = mid - 1;\n }\n else\n low = mid + 1; \n }\n return min;\n }\n}\n```
| 10 | 0 |
['Binary Tree']
| 2 |
find-minimum-in-rotated-sorted-array
|
153. Find Minimum in Rotated Sorted Array
|
153-find-minimum-in-rotated-sorted-array-wphc
|
\n\n int lo = 0, hi = nums.size() - 1; \n\t int Mn = 1e5;\n while (lo <= hi)\n {\n int m = lo + (hi - lo) / 2;\n\n i
|
phoenix2000
|
NORMAL
|
2021-11-28T09:00:15.147843+00:00
|
2021-11-28T09:00:15.147870+00:00
| 306 | false |
\n\n int lo = 0, hi = nums.size() - 1; \n\t int Mn = 1e5;\n while (lo <= hi)\n {\n int m = lo + (hi - lo) / 2;\n\n if(nums[0] > nums[nums.size()-1]){\n if(nums[m] >= nums[0]){\n lo = m + 1;\n }\n else\n {\n hi = m - 1;\n }\n Mn = min(Mn, nums[m]);\n }\n else\n { // when array is sorted in increasing order\n return nums[0];\n }\n }\n\n return Mn;\n }
| 10 | 0 |
['Array', 'Binary Tree']
| 5 |
find-minimum-in-rotated-sorted-array
|
Go Binary Search Solution
|
go-binary-search-solution-by-evleria-b1ke
|
\nfunc findMin(nums []int) int {\n\tleft, right := 0, len(nums)-1\n\tfor left < right {\n\t\tmid := (left + right) / 2\n\t\tif nums[mid] > nums[right] {\n\t\t\t
|
evleria
|
NORMAL
|
2021-08-31T20:31:26.403903+00:00
|
2021-08-31T20:31:26.403935+00:00
| 907 | false |
```\nfunc findMin(nums []int) int {\n\tleft, right := 0, len(nums)-1\n\tfor left < right {\n\t\tmid := (left + right) / 2\n\t\tif nums[mid] > nums[right] {\n\t\t\tleft = mid + 1\n\t\t} else {\n\t\t\tright = mid\n\t\t}\n\t}\n\n\treturn nums[left]\n}\n```
| 10 | 0 |
['Go']
| 2 |
find-minimum-in-rotated-sorted-array
|
Simple C++ solution beats 100% (cartoon included :)
|
simple-c-solution-beats-100-cartoon-incl-d06y
|
There are a lot of binary search solutions. However, I found that a simple linear search solution seems to be just as fast for the given test cases. Logic is as
|
hckrtst
|
NORMAL
|
2018-07-28T22:41:55.797370+00:00
|
2018-10-13T07:51:20.709964+00:00
| 884 | false |
There are a lot of binary search solutions. However, I found that a simple linear search solution seems to be just as fast for the given test cases. Logic is as follows:\n\n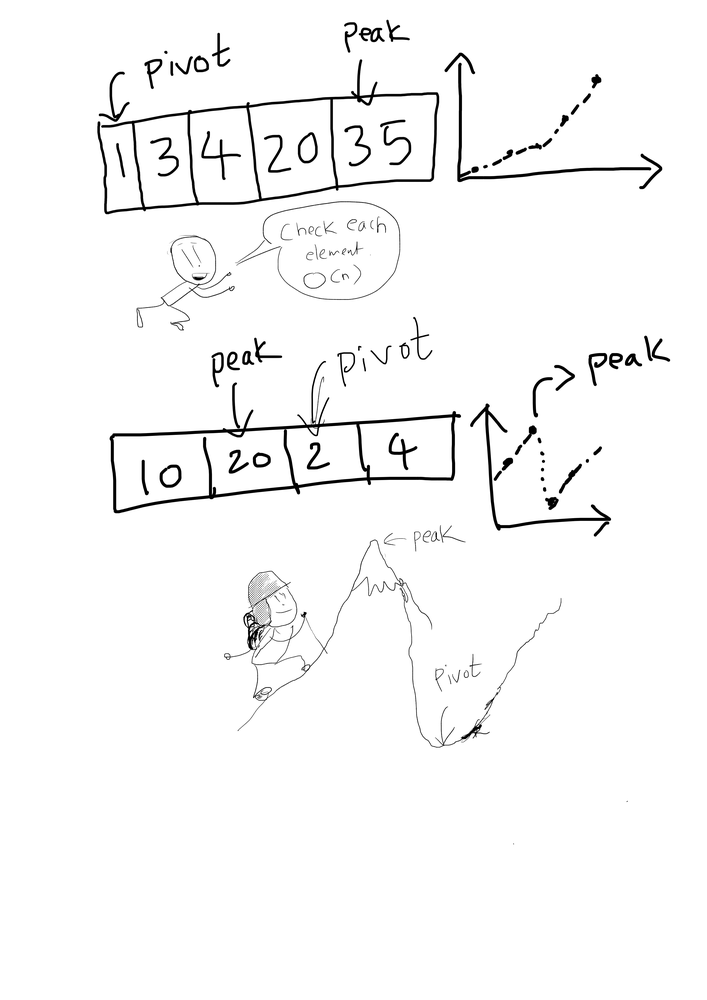\n\n\nCode below:\n\n```cpp\nint findMin(vector<int>& nums) {\n int min = nums[0];\n for (int i = 0; i < nums.size(); i++) {\n if ((i < nums.size() - 1) &&\n nums[i] > nums[i+1]) {\n min = nums[i+1];\n break;\n } \n }\n return min; \n}\n\n```
| 10 | 4 |
[]
| 2 |
find-minimum-in-rotated-sorted-array
|
C++ two-pointer solution
|
c-two-pointer-solution-by-oldcodingfarme-w0mm
|
\n int findMin(vector& nums) {\n int l = 0, r = nums.size()-1;\n while (l < r) {\n int mid = (r-l)/2 + l;\n if (nums[mid]
|
oldcodingfarmer
|
NORMAL
|
2015-11-18T21:22:15+00:00
|
2020-10-16T04:09:00.902380+00:00
| 2,274 | false |
\n int findMin(vector<int>& nums) {\n int l = 0, r = nums.size()-1;\n while (l < r) {\n int mid = (r-l)/2 + l;\n if (nums[mid] < nums[r])\n r = mid;\n else\n l = mid + 1;\n }\n return nums[l];\n }
| 10 | 1 |
['Two Pointers', 'C++']
| 4 |
find-minimum-in-rotated-sorted-array
|
SIMPLE JAVASCRIPT✅EASY EXPLANATION✅TUTORIAL✅O(logn)TIME✅97.48%BEATS✅[47ms]
|
simple-javascripteasy-explanationtutoria-nogn
|
\n\n\n# How code works:\n\n /-----------------------------\\\n | |\nInput: [4, 5, 6, 7, 0, 1, 2, 3]\n |
|
ikboljonme
|
NORMAL
|
2023-04-07T23:40:45.131626+00:00
|
2023-04-07T23:40:45.131660+00:00
| 851 | false |
\n\n\n# How code works:\n```\n /-----------------------------\\\n | |\nInput: [4, 5, 6, 7, 0, 1, 2, 3]\n | |\n \\-----------------------------/\n \n /-----------------------------\\\n | |\nleft: 0 right: 7\n | |\n \\-----------------------------/\n \n /---------------------\\\n | |\nmid: 3 nums[mid]: 7\n | |\n \\---------------------/\n \nSince nums[mid] > nums[right], we move left pointer to mid+1\n \n /-----------------------------\\\n | |\nInput: [4, 5, 6, 7, 0, 1, 2, 3]\n | |\n \\--------------/\n \n /-----------------------------\\\n | |\nleft: 4 right: 7\n | |\n \\-----------------------------/\n \n /---------------------\\\n | |\nmid: 5 nums[mid]: 1\n | |\n \\---------------------/\n \nSince nums[mid] < nums[right], we move right pointer to mid\n\n /-----------------------------\\\n | |\nInput: [4, 5, 6, 7, 0, 1, 2, 3]\n | |\n \\--------/\n \n /-----------------------------\\\n | |\nleft: 4 right: 5\n | |\n \\-----------------------------/\n \n /---------------------\\\n | |\nmid: 4 nums[mid]: 0\n | |\n \\---------------------/\n \nSince nums[mid] < nums[right], we move right pointer to mid\n\n /-----------------------------\\\n | |\nInput: [4, 5, 6, 7, 0, 1, 2, 3]\n | |\n \\--/\n \n /-----------------------------\\\n | |\nleft: 4 right: 4\n | |\n \\-----------------------------/\n \nSince left === right, we have found the minimum element: nums[left] (which is 0 in this case)\n\n```\n# Explanation\n1. It initializes two pointers left and right to the first and last indices of the array, respectively.\n\n2. The function enters a while loop that runs as long as left is less than right.\n\n3. Inside the while loop, the function calculates the middle index of the current range using the formula mid = Math.floor((left + right) / 2).\n\n4. The function checks whether the value at the middle index nums[mid] is greater than the value at the right index nums[right].\n\n5. If the value at the middle index is greater than the value at the right index, then the minimum element must be in the right half of the current range, so the left pointer is updated to mid + 1.\n\n6. If the value at the middle index is not greater than the value at the right index, then the minimum element must be in the left half of the current range, so the right pointer is updated to mid.\n\n7. The while loop continues until the range is reduced to a single element, at which point left and right point to the same index, and the minimum element is simply nums[left].\n\n8. Finally, the function returns the minimum element of the array.\n# Complexity\n- Time complexity:\nIt is O(log N), where N is the number of elements in the input array. This is because at each step of the binary search, the size of the search space is halved.\n\n- Space complexity:\nIt is O(1), which means that the amount of memory used by the algorithm is constant and does not depend on the size of the input array. This is because the algorithm only uses a few variables to keep track of the search space and does not create any additional data structures.\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findMin = function (nums) {\n let left = 0,\n right = nums.length - 1;\n\n while (left < right) {\n let mid = Math.floor((left + right) / 2);\n if (nums[mid] > nums[right]) left = mid + 1;\n else right = mid;\n }\n return nums[left];\n};\n\n```
| 9 | 0 |
['JavaScript']
| 2 |
find-minimum-in-rotated-sorted-array
|
Java Solution | Fastest and Easiest solution on the internet!
|
java-solution-fastest-and-easiest-soluti-17r9
|
\'\'\'\n\t\t\n\tclass Solution {\n\t\tpublic int findMin(int[] nums) {\n \n\t\tint start = 0;\n int end = nums.length -1;\n \n wh
|
shridipdas
|
NORMAL
|
2022-10-09T12:24:38.362963+00:00
|
2022-10-30T17:54:30.409936+00:00
| 1,275 | false |
\'\'\'\n\t\t\n\tclass Solution {\n\t\tpublic int findMin(int[] nums) {\n \n\t\tint start = 0;\n int end = nums.length -1;\n \n while (start <= end) {\n int mid = start + (end - start)/2;\n\t\t\t\t\n if (mid < end && nums[mid] > nums[mid + 1])\n return nums[mid + 1]; // greater index holds the min element in the array\n if (start < mid && nums[mid - 1] > nums[mid] )\n return nums[mid]; // greater index holds the min element in the array\n\t\t\t\t\t\n\t\t\t\tif (nums[start] > nums[mid]) // search in the left half \n end = mid - 1;\n else // search in the right half\n start = mid + 1;\n } \n return nums[0];\n\t\t}\n\t}\n\'\'\'\t\n*Logic : Return nums[pivot + 1] or return nums[0] if array is sorted.*\n\nTime complexity - O(logn)\nSpace complexity - O(1)\n\n\n1. Apply Binary Search for best time complexity of O(logn).\n2. Find and return nums[pivot + 1]\n3. If no pivot exists, array is sorted, simply return the first element of the array.\n\n\nWhat is this pivot?\nIt is the index where the existing element and the next element do not follow the order of the array, if its ascending then the element at pivot index and pivot + 1 index will be descending and vice versa.\n\nIt is usually the index of the largest element in asc rotated sorted array and index of the smallest number in desc rotated sorted array.\nFor example in\n\'\'\'\n\t\t\n\t\t// rotated asc array\n\t\tarrary1 = {3, 4, 5, 1, 2} \n\t\t// pivot index is 3 where the largest element lies.\n\t\t\n\t\t// rotated desc array\n\t\tarray2 = {7, 6, 10, 9, 8}\n\t\t// pivot index is 1 where the smallest element lies.\n\'\'\'\nConsider a given array\n\'\'\'\n\t\t\t\n\tint arr[] = {4,5,6,7,0,1,2}\n\t// here pivot is the 3rd index\n\t// the minimum element is next the pivot index i.e 4th index and element is 0 which is the minimum\n\tint arr2[] = {1, 2, 3, 4, 5}\n\t// here we do not have a pivot, array is sorted just return the first element i.e. 1 which is the minimum.\n\'\'\'\n\nNow lets find the pivot and return the next element after the pivot index as this will be the minimum element in the array.\n\n4 Cases to find pivot index\n\n\'\'\'\n\t\t\t\n\tif nums[mid] > nums[mid +1]\n\t\treturn nums[mid + 1]; // since nums[pivot + 1] is the minimum element in the array\n\tif nums[mid - 1] > nums[mid]\n\t\treturn nums[mid];\n\tif nums[start] > nums[mid] // search in the left half\n\t\tend = mid - 1;\n\telse // search in the right half\n\t\tstart = mid + 1;\n\'\'\'\n\nWe can solve this question even in linear time, there is no harm in giving it a try.\nNote ** Linear Search vs Binary Search-\n\n**For every million comparisions in linear search there is only 19 comparisions in binary search in worst case senarios. Binary Search is very efficient specially with greater i/p size.**\n\n\'\'\'\n\t\n\tpublic class Main{\n\t\tpublic int findMin(int[] nums) {\n\t\t\t\n\t\t\tfor (int i = 0; i < nums.length; i++) {\n\t\t\t\tif (nums[i] > nums[i+1]) { // checking for flaws ie different order.\n\t\t\t\t\treturn nums[i+1]; // min element lie after the max element\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn nums[0]; // if array is not rotated\n\t\t}\n\t}\n\t\n\'\'\'\n\n*Logic - Iterate through the array try to find an anomaly and return the i + 1 index which holds the min element in the array.*\nTime Complexity - O(n)\nSpace Complexity - O(1)\n**********************************************\n\nConsider to upvote, if you found it helpful :}**\n\nHappy Coding!!\n\n\n\n
| 9 | 0 |
['Binary Tree', 'Java']
| 3 |
find-minimum-in-rotated-sorted-array
|
C++|| 4 Ms Easy Solution explained by Aditya Verma ji
|
c-4-ms-easy-solution-explained-by-aditya-2l1k
|
\n \n\t\n\t/Solution explained by aditya verma:\n\tCode explanation:\n\tSince our aim is to find the element in a rotated sorted array... the code when done
|
avinashyerra
|
NORMAL
|
2022-08-03T16:00:16.306910+00:00
|
2022-08-03T17:47:41.975205+00:00
| 666 | false |
\n \n\t\n\t/*Solution explained by aditya verma:\n\tCode explanation:\n\tSince our aim is to find the element in a rotated sorted array... the code when done by \n\tsorting and returning the first element will also get accepted or traversing the vector and \n\treturning the minimum will also get accepted but the complexities will be O(nlogn) and \n\tO(n) respectively. But we have to write a solution of O(logn) time complexity....\n\tSo here we are comparing the mid with its previous and next element (so when a element with \n\tminimum value should be less than both the next and previous if that is the case we will return \n\tthe mid or else as we can see in video we have to move to unsorted side so compare the mid with \n\tits start if nums[start]<=nums[mid] we will move to the other side or else if \n\tnums[mid]<=nums[end] so move to the area of [start.....mid-1].\n\t*/\n\t/*****but aditya ji forgot to mention this point that is if nums[start]<nums[end] that is vector\n\tis already sorted we return the first element as it will be the minimum.***/\n\t/*So when this condition is added the solution will get accepted and its time complexity will be\n\tO(logn)*/\n\t\n\tint n=nums.size();\n int start=0;\n int end=n-1;\t\n while(start<=end){\n if(nums[start]<nums[end]) return nums[start];\n int mid=start+(end-start)/2;\n int next=(mid+1)%n;\n int prev=(mid-1+n)%n;\n if(nums[mid]<=nums[end] && nums[mid]<=nums[prev]){\n return nums[mid];\n }\n if(nums[start]<=nums[mid]){\n start=mid+1;\n }\n if(nums[mid]<=nums[end]){\n end=mid-1;\n }\n }\n return 0;\n \n /*THANKS FOR YOUR VIEW*/
| 9 | 0 |
['Binary Search', 'C']
| 4 |
find-minimum-in-rotated-sorted-array
|
Easiest and best C++ solution : beats 100% submissions
|
easiest-and-best-c-solution-beats-100-su-fhjd
|
\n int findMin(vector<int>& nums) {\n int s = 0;\n int e = nums.size()-1;\n int mid;\n \n while(s<=e){\n mid = (s+
|
aditya_kumar2699
|
NORMAL
|
2021-05-14T19:58:42.987515+00:00
|
2021-05-14T20:31:20.944415+00:00
| 1,133 | false |
```\n int findMin(vector<int>& nums) {\n int s = 0;\n int e = nums.size()-1;\n int mid;\n \n while(s<=e){\n mid = (s+e)/2;\n \n if(nums[mid] >= nums[e]){\n s = mid+1;\n }\n else{\n e = mid;\n }\n }\n return nums[mid];\n \n }\n```\t
| 9 | 2 |
['C', 'Binary Tree', 'C++']
| 0 |
find-minimum-in-rotated-sorted-array
|
Find Minimum in Rotated Sorted Array - Java Solution (Beats 100%)
|
find-minimum-in-rotated-sorted-array-jav-tux3
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAs the given array (with unique elements) is rotated k (unknown) times and it\'s sorted
|
Naveen-NaS
|
NORMAL
|
2024-01-07T12:59:47.101696+00:00
|
2024-01-07T12:59:47.101771+00:00
| 1,569 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs the given array (with **unique** elements) is rotated k (unknown) times and it\'s sorted in non-decreasing order, which means there must exist a single element where it becomes the greater than the last element of Array. Taking this observation into consideration, I employed binary search to ascertain the minimum element. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach adeptly utilizes binary search to identify the rotation point in a rotated sorted array with unique elements. By recognizing the crucial point where an element surpasses the last one, my algorithm efficiently adjusts the search range to pinpoint the minimum element, ensuring a time complexity of O(log n).\nThe steps incorporated in my approach are as follows :\n\n- "start" is initialized to the beginning of the array (0).\n"end" is initialized to the end of the array (nums.length - 1).\n\n- The while loop continues to run until the "start" index is less than or equal to the "end" index. Within the loop, the middle index is calculated, and subsequently, a check for the minimum element is performed.\n\n- We check if mid is greater than 0 and if nums[mid] is less than nums[mid - 1]. If this condition is true, it means we\'ve found the minimum element, and return nums[mid].\n- If the above condition is not true, then we updates the search range at last and continues the searching. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**The time complexity is O(log n)**, where "n" is the length of the input array. This is because the binary search approach efficiently reduces the search space in each iteration.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**The space complexity is O(1)** since the algorithm uses a constant amount of extra space for variables like "start," "end," and "mid," regardless of the size of the input array.\n# Code\n```\nclass Solution {\n public int findMin(int[] nums) {\n int start = 0;\n int end = nums.length - 1;\n\n while (start <= end) {\n int mid = start + (end - start) / 2;\n\n if (mid > 0 && nums[mid] < nums[mid - 1]) {\n return nums[mid];\n } else if (nums[mid] > nums[end]) {\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n return nums[start];\n }\n}\n\n```
| 8 | 0 |
['Java']
| 6 |
find-minimum-in-rotated-sorted-array
|
Easy Code |fuck that algorithms do as u like
|
easy-code-fuck-that-algorithms-do-as-u-l-6bs7
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shitoncoding
|
NORMAL
|
2023-09-19T05:39:42.018377+00:00
|
2023-09-19T05:39:42.018412+00:00
| 652 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def findMin(self, nums):\n nums.sort()\n return(nums[0])\n```
| 8 | 0 |
['Python']
| 9 |
find-minimum-in-rotated-sorted-array
|
Most optimal solution using binary search | C++ and JAVA code
|
most-optimal-solution-using-binary-searc-c2qj
|
\n\n# Approach\nIdentify the sorted half from the array, pickup the smallest element from that half, update the answer if it is smaller than the answer, then el
|
priyanshu11_
|
NORMAL
|
2023-08-06T07:04:55.076989+00:00
|
2023-08-06T07:04:55.077019+00:00
| 1,351 | false |
\n\n# Approach\nIdentify the sorted half from the array, pickup the smallest element from that half, update the answer if it is smaller than the answer, then eliminate that half. Repeat this until the search space gets exhausted.\n\n# Complexity\n- Time complexity:\nO(log(n))\n\n- Space complexity:\nO(1)\n\n# C++ Code\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int low = 0, high = nums.size()-1, ans = INT_MAX;\n while(low<=high) {\n int mid = (low+high)/2;\n if(nums[low]<=nums[mid]) {\n ans = min(ans, nums[low]);\n low = mid+1;\n } else {\n ans = min(ans, nums[mid]);\n high = mid-1;\n }\n }\n return ans;\n }\n};\n```\n# JAVA Code\n```\npublic class Solution {\n public int findMin(int[] nums) {\n int low = 0, high = nums.length - 1, ans = Integer.MAX_VALUE;\n while (low <= high) {\n int mid = (low + high) / 2;\n if (nums[low] <= nums[mid]) {\n ans = Math.min(ans, nums[low]);\n low = mid + 1;\n } else {\n ans = Math.min(ans, nums[mid]);\n high = mid - 1;\n }\n }\n return ans;\n }\n}\n```\n
| 8 | 0 |
['Array', 'Binary Search', 'C++', 'Java']
| 0 |
find-minimum-in-rotated-sorted-array
|
153: Beats 91.70% Solution with step by step explanation
|
153-beats-9170-solution-with-step-by-ste-ucvt
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nThis solution also uses binary search to find the minimum element in the
|
Marlen09
|
NORMAL
|
2023-02-20T04:19:44.728852+00:00
|
2023-02-20T04:19:44.728893+00:00
| 4,313 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis solution also uses binary search to find the minimum element in the rotated sorted array. It initializes two pointers, left and right, to the beginning and end of the array, respectively. It then repeatedly compares the element at the midpoint of the array to the element at the end of the array, and updates the pointers accordingly until the minimum element is found.\n\nThe time complexity of this solution is O(log n), since binary search is used. The space complexity is O(1), since only constant space is used.\n\n# Complexity\n- Time complexity:\nBeats\nBeats\n55.81%\n\n- Space complexity:\nBeats\n55.81%\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n left, right = 0, len(nums) - 1\n while left < right:\n mid = left + (right - left) // 2\n if nums[mid] > nums[right]:\n left = mid + 1\n else:\n right = mid\n return nums[left]\n\n```
| 8 | 0 |
['Array', 'Binary Search', 'Python', 'Python3']
| 2 |
find-minimum-in-rotated-sorted-array
|
✅☑️ Easy C++ solution || Binary Search || Linear Search || Brute Force -> Optimize.
|
easy-c-solution-binary-search-linear-sea-6dun
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe can Solved this question using Two approach.\n\n1. Using Linear Search (Brute Force)
|
its_vishal_7575
|
NORMAL
|
2023-02-04T20:43:07.902387+00:00
|
2023-02-05T07:52:35.083715+00:00
| 1,505 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can Solved this question using Two approach.\n\n1. Using Linear Search (Brute Force).\n2. Using Binary Search (Optimize).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can easily understand the All the approaches by seeing the code which is easy to understand with comments.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity is given in code comment.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity is given in code comment.\n\n# Code\n```\n/*\n\n Time Complexity : O(N), because we traversed over all the elements in the array, which has allowed us to\n achieve a linear time complexity.\n\n Space Complexity : O(1), the algorithm itself takes constant space but the program as a whole takes linear\n space because of storing the input array.\n\n Using Array + Linear Search. \n\n*/\n\n\n/***************************************** Approach 1 First Code *****************************************/\n\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int n = nums.size();\n int minimum = nums[0];\n for(int i=1; i<n; i++){\n minimum = min(nums[i], minimum);\n }\n return minimum;\n }\n};\n\n\n\n\n\n\n/***************************************** Approach 1 Second Code *****************************************/\n\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int n = nums.size();\n for(int i=0; i<n-1; i++){\n if(nums[i] > nums[i+1]){\n return nums[i+1];\n }\n }\n return nums[0];\n }\n};\n\n\n\n\n\n\n/*\n\n Time Complexity : O(log N) where N is the number of elements in the input array. Here we used binary search\n which takes logarithmic time complexity. All of this possible because the array was initially sorted.\n\n Space Complexity : O(1), this approach takes also constant time but the program as a whole takes O(N) space\n because of the space required to store the input.\n\n Using Array + Binary Search.\n\n*/\n\n\n/***************************************** Approach 2 First Code *****************************************/\n\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int low = 0;\n int high = nums.size()-1;\n while(low < high){\n int mid = low + (high-low)/2;\n if(nums[mid] < nums[high]){\n high = mid;\n }\n else{\n low = mid+1;\n }\n }\n return nums[low];\n }\n};\n```
| 8 | 0 |
['Array', 'Binary Search', 'C++']
| 0 |
find-minimum-in-rotated-sorted-array
|
Best O(LogN) Solution
|
best-ologn-solution-by-kumar21ayush03-5diq
|
Approach 1\nSorting\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1) \n\n# Code\n\nclass Solution {\npublic:\n int findMin(vector<i
|
kumar21ayush03
|
NORMAL
|
2023-01-26T14:21:40.553449+00:00
|
2023-01-26T14:21:40.553484+00:00
| 658 | false |
# Approach 1\nSorting\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n sort (nums.begin(), nums.end());\n return nums[0];\n }\n};\n```\n# Approach 2\nLinear Search\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int minVal = nums[0];\n for (int i = 1; i < nums.size(); i++)\n minVal = min (nums[i], minVal);\n return minVal;\n }\n};\n```\n\n# Approach 3\nBinary Search\n\n# Complexity\n- Time complexity:\n$$O(logn)$$\n\n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int n = nums.size();\n if (n == 1)\n return nums[0];\n if (nums[0] < nums[n - 1])\n return nums[0];\n int low = 0, high = n - 1;\n while (low <= high) {\n int mid = (low + high) / 2;\n if (nums[mid] > nums[mid + 1])\n return nums[mid + 1];\n if (nums[mid] < nums[mid - 1])\n return nums[mid]; \n if (nums[low] < nums[mid])\n low = mid + 1;\n else if (nums[high] > nums[mid])\n high = mid - 1;\n }\n return -1;\n }\n};\n```
| 8 | 0 |
['C++']
| 2 |
find-minimum-in-rotated-sorted-array
|
📌 Python3 simple naive solution with binary search
|
python3-simple-naive-solution-with-binar-ujwd
|
\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n start = 0\n end = len(nums) - 1\n \n if(nums[start] <= nums[end]
|
dark_wolf_jss
|
NORMAL
|
2022-06-29T00:05:43.237151+00:00
|
2022-06-29T00:05:43.237194+00:00
| 1,206 | false |
```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n start = 0\n end = len(nums) - 1\n \n if(nums[start] <= nums[end]):\n return nums[0]\n \n while start <= end:\n mid = (start + end) // 2\n \n if(nums[mid] > nums[mid+1]):\n return nums[mid+1]\n \n if(nums[mid-1] > nums[mid]):\n return nums[mid]\n \n if(nums[mid] > nums[0]):\n start = mid + 1\n else:\n end = mid - 1\n \n return nums[start]\n```
| 8 | 0 |
['Binary Search', 'Python3']
| 0 |
find-minimum-in-rotated-sorted-array
|
✅Find Minimum in Rotated Sorted Array || W/ Approach || C++ | JAVA | Python
|
find-minimum-in-rotated-sorted-array-w-a-9za7
|
Idea\n\n We basically need to find the smallest element\nWe can do that by binary search as follows:\n Binary search, left (Starting) = 0, right (Last element)
|
Maango16
|
NORMAL
|
2021-08-31T13:02:17.835965+00:00
|
2021-08-31T13:19:19.544214+00:00
| 578 | false |
**Idea**\n\n* We basically need to find the smallest element\nWe can do that by binary search as follows:\n* Binary search, left (Starting) = 0, right (Last element) = n-1\n* `mid = left + (right - left) / 2 // Or (Left + Right)/2` \n* If `nums[left] > nums[right]`, then `nums[left]` is the minimum (Basically, after completing the iteration or on not fullfillment of the condition, we will reach here. Else we continue traversing)\n* Else, traverse\n\t* If `nums[mid] > nums[right]` then search on the right side, because smaller elements are in the right side\n\t* Else search on the left side.\n\n**SOLUTION**\n`In C++`\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int left = 0 , right = nums.size()-1 ;\n if (!right) // Case of single element\n return nums[0] ;\n while (left < right)\n {\n int mid = left + (right - left) / 2;\n if (nums[left] < nums[right]) \n return nums[left]; // Smaller element\n else if (nums[mid] > nums[right]) \n left = mid + 1; // Check on right\n else \n right = mid; // Check on left\n }\n return nums[left];\n }\n};\n```\n`In JAVA`\n```\nclass Solution {\n public int findMin(int[] nums) {\n int left = 0;\n int right = nums.length - 1;\n \n while(left < right){\n int mid = left + (right - left) /2;\n \n if(nums[mid] > nums[right])\n {\n left = mid + 1;\n }\n else if(nums[mid] < nums[right])\n {\n right = mid;\n }\n else\n {\n return nums[right];\n }\n }\n return nums[left];\n }\n}\n```\n`In Python`\n```\nclass Solution(object):\n def findMin(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n left, right = 0, len(nums)-1\n while left < right:\n mid = (left + right) // 2\n if nums[mid] > nums[right]:\n left = mid + 1\n else:\n right = mid\n return nums[left]\n```\n**TIME COMPLEXITY - O(logN)**\nIf you want to try a harder problem of a similar type, try out [33. Search in Rotated Sorted Array](https://leetcode.com/problems/search-in-rotated-sorted-array/).
| 8 | 4 |
[]
| 1 |
find-minimum-in-rotated-sorted-array
|
JAVA Binary Search Easy-to-understand|| faster than 100%
|
java-binary-search-easy-to-understand-fa-7snl
|
Solution 1:\n\nclass Solution {\n public int findMin(int[] nums) {\n int low = 0;\n int high = nums.length-1;\n \n while(low < h
|
rohitkumarsingh369
|
NORMAL
|
2021-08-31T10:44:52.292376+00:00
|
2021-08-31T11:02:10.813434+00:00
| 887 | false |
**Solution 1:**\n```\nclass Solution {\n public int findMin(int[] nums) {\n int low = 0;\n int high = nums.length-1;\n \n while(low < high){\n \n int mid = low + (high-low) / 2;\n if(nums[mid] < nums[high])\n high = mid;\n else \n low = mid+1;\n \n }\n return nums[low];\n }\n}\n```\n\n**Solution 2 :**\n\n```\nclass Solution {\n public int findMin(int[] nums) {\n int low=0;\n int high=nums.length-1;\n while(low < high)\n {\n int mid = low + (high - low) / 2;\n if (nums[mid] ==nums[high])\n high--;\n\n else if(nums[mid] > nums[high])\n low = mid + 1;\n else\n high = mid;\n }\n return nums[high];\n }\n}\n```
| 8 | 0 |
['Binary Tree', 'Java']
| 0 |
find-minimum-in-rotated-sorted-array
|
Clear Python 3 solution faster than 93%
|
clear-python-3-solution-faster-than-93-b-a5n8
|
\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n low = 0\n high = len(nums) - 1\n while low <= high:\n mid =
|
swap24
|
NORMAL
|
2020-07-27T06:40:55.210678+00:00
|
2020-07-27T06:40:55.210728+00:00
| 2,051 | false |
```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n low = 0\n high = len(nums) - 1\n while low <= high:\n mid = low + (high - low) // 2\n ele = nums[mid]\n if ele > nums[high]:\n low = mid + 1\n elif mid == 0 or nums[mid - 1] > nums[mid]:\n return nums[mid]\n else:\n high = mid - 1\n```
| 8 | 1 |
['Binary Tree', 'Python', 'Python3']
| 2 |
find-minimum-in-rotated-sorted-array
|
5 lines C++ implementation
|
5-lines-c-implementation-by-rainbowsecre-a04j
|
class Solution {\n public:\n int findMin(vector<int>& nums) {\n int start=0, end=nums.size()-1;\n while(end>start){\n
|
rainbowsecret
|
NORMAL
|
2016-02-25T02:11:07+00:00
|
2016-02-25T02:11:07+00:00
| 1,213 | false |
class Solution {\n public:\n int findMin(vector<int>& nums) {\n int start=0, end=nums.size()-1;\n while(end>start){\n int mid=start+(end-start)/2;\n if(nums[mid]<nums[end]) end=mid;\n else start=mid+1;\n }\n return nums[start];\n }\n };
| 8 | 0 |
[]
| 0 |
find-minimum-in-rotated-sorted-array
|
Must Read Binary Search Pattern
|
must-read-binary-search-pattern-by-dixon-vx9w
|
Search in Rotated Sorted Array\n81. Search in Rotated Sorted Array II\n153. Find Minimum in Rotated Sorted Array\n\n# Code\n\n\nclass Solution {\n public sta
|
Dixon_N
|
NORMAL
|
2024-07-14T13:00:14.401025+00:00
|
2024-07-14T13:00:14.401057+00:00
| 2,158 | false |
33. Search in Rotated Sorted Array\n81. Search in Rotated Sorted Array II\n153. Find Minimum in Rotated Sorted Array\n\n# Code\n```\n\nclass Solution {\n public static int findMin(int[] arr) {\n int low = 0, high = arr.length - 1;\n int ans = Integer.MAX_VALUE;\n while (low <= high) {\n int mid = (low + high) / 2;\n\n // Search space is already sorted,\n // then arr[low] will always be\n // the minimum in that search space:\n if (arr[low] <= arr[high]) {\n ans = Math.min(ans, arr[low]);\n break;\n }\n\n // If left part is sorted:\n if (arr[low] <= arr[mid]) {\n // Keep the minimum:\n ans = Math.min(ans, arr[low]);\n\n // Eliminate left half:\n low = mid + 1;\n\n } else { // If right part is sorted:\n\n // Keep the minimum:\n ans = Math.min(ans, arr[mid]);\n\n // Eliminate right half:\n high = mid - 1;\n }\n }\n return ans;\n }\n}\n\n\n```
| 7 | 0 |
['Java']
| 5 |
find-minimum-in-rotated-sorted-array
|
approach one O(log n)
|
approach-one-olog-n-by-malarupucharansai-17ww
|
Intuition:we solve this by appliying binary search technique\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nif the arr[0] is less
|
MalarupuCharanSai
|
NORMAL
|
2024-02-14T13:39:09.212480+00:00
|
2024-02-14T13:39:09.212511+00:00
| 2,883 | false |
# Intuition:we solve this by appliying binary search technique\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nif the arr[0] is less then arr[len(arr)-1] then it is already in sorted order \nso return arr[0]\nelse:\nperform binary search and find the min using while until left<right\n1)find mid if the arr[mid-1]>arr[mid] then in sorted array of rotation arr[mid] is the min of all\n2)if arr[mid+1] is less than mid then the arr[mid+1] is the small\n3) perform the binary search until we return the ans or left>right\n4)if we did not get it by using arr[mid] take a minn variable and assing the min values to it in the while loop (arr[mid] value in iterations is lesss than minn)\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(log N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n left=0\n right=len(nums)-1\n minn=nums[0]\n if nums[0]<=nums[right]:\n return nums[0]\n while True:\n if left>=right:\n return minn\n mid=(left+right)//2\n if(nums[mid]<minn):\n minn=nums[mid]\n if nums[mid+1]<nums[mid]:\n return nums[mid+1]\n if (nums[mid-1]>nums[mid]):\n return nums[mid]\n if nums[mid]>nums[right]:\n left=mid+1\n if nums[mid]<nums[right]:\n right=mid-1\n \n\n \n \n\n```
| 7 | 0 |
['Python3']
| 5 |
find-minimum-in-rotated-sorted-array
|
Easy and simple Approach | Beats 100%
|
easy-and-simple-approach-beats-100-by-ka-6xvh
|
Intuition\nThe problem asks to find the minimum element in a rotated sorted array. The idea is to use binary search to efficiently find the minimum element. The
|
kanishakpranjal
|
NORMAL
|
2024-01-28T05:41:11.978044+00:00
|
2024-01-28T05:41:11.978075+00:00
| 1,135 | false |
# Intuition\nThe problem asks to find the minimum element in a rotated sorted array. The idea is to use binary search to efficiently find the minimum element. The key observation is that the minimum element will always be on the side where the rotation occurred. By comparing the middle element with the end element, we can determine which side to search.\n\n# Approach\nThe approach is to use binary search to iteratively narrow down the search space. We maintain two pointers, `start` and `end`, representing the current search range. In each iteration, we calculate the middle index (`mid`) and compare the value at `mid` with the value at `end`.\n\n- If `nums[mid] > nums[end]`, it means the minimum element is on the right side of `mid`, so we update `start = mid + 1`.\n- If `nums[mid] <= nums[end]`, it means the minimum element is on the left side of `mid` or could be `mid` itself, so we update `end = mid`.\n\nWe continue this process until `start` is equal to `end`, and at that point, we have found the minimum element.\n\n# Complexity\n- Time complexity: $$O(\\log n)$$ - Binary search is used, which halves the search space in each iteration.\n- Space complexity: $$O(1)$$ - Constant space is used as we only have a few variables.\n\n# Code\n```java\nclass Solution {\n public int findMin(int[] nums) {\n int start = 0;\n int end = nums.length - 1;\n\n while (start < end) {\n int mid = start + (end - start) / 2;\n if (nums[mid] > nums[end]) {\n start = mid + 1;\n } else {\n end = mid;\n }\n }\n return nums[start];\n }\n}\n```\n\nThe provided code implements the described approach and efficiently finds the minimum element in the rotated sorted array.
| 7 | 0 |
['Java']
| 3 |
find-minimum-in-rotated-sorted-array
|
✅✅Beats 99% | O(log N) | Python Solution (using binary search)
|
beats-99-olog-n-python-solution-using-bi-imrl
|
Intuition\nThe goal is to find the minimum element in a rotated sorted array. We can use a binary search approach to efficiently locate the minimum element.\n\n
|
monster0Freason
|
NORMAL
|
2023-10-14T07:04:16.679148+00:00
|
2023-10-15T15:03:18.184670+00:00
| 1,196 | false |
# Intuition\nThe goal is to find the minimum element in a rotated sorted array. We can use a binary search approach to efficiently locate the minimum element.\n\n# Approach\n1. Initialize the `ans` variable with the first element of the array `nums`.\n\n2. Set two pointers, `low` and `high`, to the start and end of the array, respectively.\n\n3. Check if the array is already sorted in ascending order by comparing the elements at the low and high indices. If it is sorted, return the first element, which is the minimum.\n\n4. Perform a binary search by looping while `low` is less than or equal to `high`.\n\n5. Within the loop:\n - Check if the array is sorted by comparing the elements at the low and high indices. If it is sorted, update `ans` with the minimum of the current `ans` and `nums[low]` and break out of the loop.\n\n - Calculate the middle index `mid` as the average of `low` and `high`.\n\n - Update `ans` with the minimum of the current `ans` and `nums[mid]`.\n\n - Determine if the pivot point (where rotation occurs) is in the right half of the array. If `nums[mid]` is greater than or equal to `nums[low]`, set `low` to `mid + 1`. Otherwise, set `high` to `mid - 1`.\n\n6. Return the final value of `ans`, which is the minimum element in the rotated sorted array.\n\n# Complexity\n- Time complexity: The binary search approach has a time complexity of O(log N), where N is the size of the input array `nums`.\n- Space complexity: The space complexity is O(1) as we only use a few variables for tracking and no additional data structures.\n\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n ans = nums[0]\n low, high = 0, len(nums) - 1\n\n if nums[low] < nums[high]:\n return nums[low]\n\n while low <= high:\n if nums[low] < nums[high]:\n ans = min(ans, nums[low])\n break\n \n mid = (low + high) // 2\n ans = min(ans, nums[mid])\n\n \n if nums[mid] >= nums[low]:\n low = mid + 1\n else:\n high = mid - 1\n\n return ans\n\n```\n\n# Please upvote the solution if you understood it.\n\n
| 7 | 0 |
['Binary Search', 'Python3']
| 1 |
find-minimum-in-rotated-sorted-array
|
JAVA | Binary Search
|
java-binary-search-by-akash2377-oyrr
|
\nclass Solution {\n public int findMin(int[] nums) {\n int n = nums.length;\n int start = 0;\n int end = n-1;\n while(start<=end
|
Akash2377
|
NORMAL
|
2022-09-27T07:04:53.081241+00:00
|
2022-09-27T07:04:53.081281+00:00
| 1,081 | false |
```\nclass Solution {\n public int findMin(int[] nums) {\n int n = nums.length;\n int start = 0;\n int end = n-1;\n while(start<=end){\n int mid = start + (end-start)/2;\n if(nums[mid]<nums[end]){\n end = mid;\n }else{\n start = mid+1;\n }\n }\n return nums[end];\n }\n}\n```
| 7 | 0 |
['Binary Tree', 'Java']
| 2 |
find-minimum-in-rotated-sorted-array
|
✅ C++ || 4 SOLUTIONS || T.C. : O(logn), S.C.: O(1)
|
c-4-solutions-tc-ologn-sc-o1-by-9tin_bit-zga9
|
\u2705 APPROACH 1:\n\n1. TIME COMPLEXITY : O(logn)\n2. SPACE COMPLEXITY : O(1)\n\n# BINARY SEARCH SOLUTION\n\n\nint findMin(vector<int>& nums) {\n int
|
rab8it
|
NORMAL
|
2022-06-04T04:33:29.868700+00:00
|
2022-06-04T04:41:04.521262+00:00
| 474 | false |
* \u2705 ***APPROACH 1:***\n\n**1. TIME COMPLEXITY : O(logn)\n2. SPACE COMPLEXITY : O(1)**\n\n# **BINARY SEARCH SOLUTION**\n\n```\nint findMin(vector<int>& nums) {\n int left=0,right=nums.size()-1;\n \n while(left<right){\n int mid=left+(right-left)/2;\n\n if(nums[mid]>nums[right])left=mid+1; // in this case we assure the minimum is in the right side\n else right=mid; // in this case we assure the minimum is in the left side\n }\n return nums[left];\n }\n```\n\n* ***\u2705 APPROACH 2 :***\n\n**1. TIME COMPLEXITY : O(n)\n2. SPACE COMPLEXITY : O(1)**\n\n# **SIMPLE TRAVERSAL**\n\n```\nint findMin(vector<int>& nums) {\n int ans=INT_MAX;\n for(int i=0;i<nums.size();i++){\n ans=min(ans,nums[i]);\n }\n return ans;\n }\n```\n\n* ***\u2705APPROACH 3 :***\n\n**1. TIME COMPLEXITY : O(n)\n2. SPACE COMPLEXITY : O(1)**\n\n# **TRAVERSE FROM END**\n\n```\nint findMin(vector<int>& nums) {\n \n for(int i=nums.size()-1;i>0;i--){\n if(nums[i]<nums[i-1])return nums[i];\n }\n return nums[0];\n }\n```\n\n* ***\u2705APPROACH 4 :***\n\n**1. TIME COMPLEXITY : O(nlogn)\n2. SPACE COMPLEXITY : O(1)**\n\n# **SORTING**\n\n```\nint findMin(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n return nums[0];\n }\n```\n\n\n\n\n\uD83D\uDE4C\uD83D\uDE4C HAPPY CODING !!
| 7 | 0 |
['Binary Search', 'C', 'Binary Tree', 'C++']
| 0 |
find-minimum-in-rotated-sorted-array
|
Binary Search | O(log n) runtime & O(1) space
|
binary-search-olog-n-runtime-o1-space-by-f4yk
|
\nclass Solution {\n /**\n * find the pivot in the sorted array. Find the middle index of the array. We can compare the\n * middle index elemen
|
lowkeyish
|
NORMAL
|
2022-05-05T08:56:40.884850+00:00
|
2022-05-05T08:56:40.884882+00:00
| 219 | false |
```\nclass Solution {\n /**\n * find the pivot in the sorted array. Find the middle index of the array. We can compare the\n * middle index element with either the previous element and next element and see if the pivot is\n * present there. If mid is greater than next, mid is the pivot. If the prev is greater than mid,\n * prev is the pivot.\n * <p>\n * If both cases are failed, the pivot will either be in the left half or the right half. Compare\n * the leftmost element in the partition with the mid-element. If mid is greater, the first half\n * is in ascending order and the pivot will be in the latter half. So, ignore the first and\n * consider just the latter half. Else, vice versa\n */\n public int findMin(int[] nums) {\n int pivot = findPivot(nums, 0, nums.length - 1);\n return pivot == -1 ? nums[0] : nums[pivot + 1];\n }\n \n private int findPivot(int[] nums, int left, int right) {\n if (left > right) return -1;\n int mid = (left + right) / 2;\n if (mid < right && nums[mid] > nums[mid + 1])\n return mid;\n else if (mid > left && nums[mid - 1] > nums[mid])\n return mid - 1;\n \n if (nums[left] > nums[mid])\n return findPivot(nums, left, mid - 1);\n else\n return findPivot(nums, mid + 1, right);\n }\n}\n```
| 7 | 0 |
['Binary Tree', 'Java']
| 0 |
find-minimum-in-rotated-sorted-array
|
[C++] Binary Search | 100% FASTER
|
c-binary-search-100-faster-by-vishal_sen-mr8e
|
Please upvote if it helped you.\n\t\n\tclass Solution {\n\tpublic:\n\t\tint findMin(vector& nums) {\n\n\t\t\tint first = 0; \n\t\t\tint last = nums.size() - 1;
|
vishal_sengar_dtu
|
NORMAL
|
2021-08-12T10:44:17.126809+00:00
|
2021-08-12T11:01:15.431514+00:00
| 220 | false |
Please upvote if it helped you.\n\t\n\tclass Solution {\n\tpublic:\n\t\tint findMin(vector<int>& nums) {\n\n\t\t\tint first = 0; \n\t\t\tint last = nums.size() - 1; \n\t\t\tint ans = INT_MAX; \n\n\t\t\twhile(first <= last){\n\n\t\t\t\tint mid = first + (last - first) / 2; \n\n\t\t\t\tif(ans >= nums[mid]) ans = nums[mid]; \n\n\t\t\t\tif(nums[mid] > nums[last]) first = mid + 1; \n\n\t\t\t\telse last = mid - 1; \n\t\t\t}\n\n\t\t\treturn ans; \n\t\t}\n\t};\nThank You !!
| 7 | 0 |
[]
| 1 |
find-minimum-in-rotated-sorted-array
|
Binary Search
|
binary-search-by-gracemeng-5yu2
|
\nclass Solution {\n public int findMin(int[] nums) {\n int left = 0, right = nums.length - 1;\n while (left < right) {\n if (nums[l
|
gracemeng
|
NORMAL
|
2018-09-08T07:03:23.280899+00:00
|
2020-05-04T16:17:15.868325+00:00
| 681 | false |
```\nclass Solution {\n public int findMin(int[] nums) {\n int left = 0, right = nums.length - 1;\n while (left < right) {\n if (nums[left] < nums[right]) { // Sorted as a whole\n return nums[left];\n }\n int mid = left + (right - left) / 2;\n if (nums[mid] > nums[right]) { // Unsorted right half\n left = mid + 1;\n } else { // Unsorted left half\n left++;\n right = mid;\n }\n }\n return nums[left];\n }\n}\n```
| 7 | 0 |
[]
| 1 |
find-minimum-in-rotated-sorted-array
|
4ms C++ binary search solution with short explanation
|
4ms-c-binary-search-solution-with-short-k71u1
|
The idea is to binary search for the minimum. If the midpoint of an interval is larger than the right endpoint, the minimum must be in the right half of the int
|
deck
|
NORMAL
|
2015-06-14T05:53:52+00:00
|
2015-06-14T05:53:52+00:00
| 805 | false |
The idea is to binary search for the minimum. If the midpoint of an interval is larger than the right endpoint, the minimum must be in the right half of the interval. If not, the minimum is in the left half, but may be the midpoint itself (so we keep the midpoint in the active search interval in this case).\n\n class Solution {\n public:\n int findMin(vector<int> &num) {\n int L = 0, U = num.size() - 1;\n while (L < U) {\n int M = L + (U - L) / 2;\n if (num[M] > num[U]) {\n L = M + 1;\n } else {\n U = M;\n }\n }\n return num[L];\n }\n };
| 7 | 0 |
['C++']
| 1 |
find-minimum-in-rotated-sorted-array
|
[Animated Video] Simple, visual solution
|
animated-video-simple-visual-solution-by-8ubk
|
CodeInMotion ResourcesEvery Leetcode Pattern You Need To Knowhttps://www.blog.codeinmotion.io/p/leetcode-patternsBlind 75 Animated Playlisthttps://www.youtube.c
|
codeinmotion
|
NORMAL
|
2025-01-07T23:05:58.309915+00:00
|
2025-01-07T23:05:58.309915+00:00
| 462 | false |

# *CodeInMotion Resources*
## Every Leetcode Pattern You Need To Know
https://www.blog.codeinmotion.io/p/leetcode-patterns
## Blind 75 Animated Playlist
https://www.youtube.com/playlist?list=PLHm8nzcbp3_19DiTlDg8QYvR-hN5jzPCp
## Subscribe to YouTube
https://www.youtube.com/@CodeInMotion-IO?sub_confirmation=1
---
## Animated Video
https://youtu.be/5AM_xIetqvQ
## Intuition
Rotating a sorted array means that some pivot splits the array into two sorted subarrays. Our goal is to find the smallest element, which effectively is the pivot point. The key observation is that the smallest element is always on the “lesser” side during the rotation. By leveraging binary search and comparing elements with the right boundary, we can discard half of the search space at a time until we narrow down to the minimum element.
## Approach
1. Initialize two pointers, **left** at index 0 and **right** at the end of the array.
2. While **left** is less than **right**:
- Compute **mid** as the average of **left** and **right**.
- If the **nums[mid]** is less than or equal to **nums[right]**, it means the minimum could be at **mid** or to the left of **mid**, so set **right = mid**.
- Otherwise, it means the minimum is to the right of **mid**, so set **left = mid + 1**.
3. Once the loop finishes, the **left** pointer will be pointing to the minimum element. Return **nums[left]**.
## Complexity
- Time complexity: $$O(\log n)$$
- Space complexity: $$O(1)$$
## Code
```Python []
class Solution:
def findMin(self, nums: List[int]) -> int:
left, right = 0, len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] <= nums[right]:
right = mid
else:
left = mid + 1
return nums[left]
```
```Java []
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] <= nums[right]) {
right = mid;
} else {
left = mid + 1;
}
}
return nums[left];
}
}
```
```JavaScript []
/**
* @param {number[]} nums
* @return {number}
*/
var findMin = function(nums) {
let left = 0, right = nums.length - 1;
while (left < right) {
let mid = Math.floor(left + (right - left) / 2);
if (nums[mid] <= nums[right]) {
right = mid;
} else {
left = mid + 1;
}
}
return nums[left];
};
```
```C# []
public class Solution {
public int FindMin(int[] nums) {
int left = 0;
int right = nums.Length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] <= nums[right]) {
right = mid;
} else {
left = mid + 1;
}
}
return nums[left];
}
}
```
```C++ []
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] <= nums[right]) {
right = mid;
} else {
left = mid + 1;
}
}
return nums[left];
}
};
```
```Go []
func findMin(nums []int) int {
left, right := 0, len(nums) - 1
for left < right {
mid := left + (right - left) / 2
if nums[mid] <= nums[right] {
right = mid
} else {
left = mid + 1
}
}
return nums[left]
}
```
### Please thumbs up on the bottom-left corner!<br>It motivates me to create more solutions and videos for you!

| 6 | 0 |
['Array', 'Binary Search', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#']
| 0 |
find-minimum-in-rotated-sorted-array
|
Short and simple solution || Fully explained || Beats 100%
|
short-and-simple-solution-fully-explaine-m6ey
|
(Please upvote\uD83D\uDE00 Thank\'s!)\n# Intuition\nYou can look at it like this:\nWe are looking for the beginning of the lower part of the numbers.\nAt first
|
yosefper
|
NORMAL
|
2024-06-20T10:47:36.305920+00:00
|
2024-06-20T10:48:34.561975+00:00
| 312 | false |
##### (Please upvote\uD83D\uDE00 Thank\'s!)\n# Intuition\nYou can look at it like this:\nWe are looking for the **beginning of the lower part** of the numbers.\nAt first we choose the middle of the array, and check whether the part from it to the **right** is arranged in ascending order.\nIf so, this means that the minimal number is either the first number in this part, or it is in the second part, so we will change **right** to be the first number in this part, because we no longer have anything to check in the part between the original **right** and the **middle**.\nIf not, this means that the lowest number is indeed inside this part, so we will make **left** the first number of this part, because we no longer have anything to check the part between the original **left** and the **middle**.\nWhen we reach a situation where left and right are equal, it means that we have reached exactly the lowest number in the lowest part of the array, which is the minimum number we wanted.\n\n# Complexity\n- Time complexity:\n$$O(log(n))$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\n public int findMin(int[] nums) {\n \n int left = 0, right = nums.length -1, middle;\n\n while(left < right){\n middle = (left + right) / 2;\n if(nums[middle] < nums[right]) right = middle;\n else left = middle + 1;\n }\n\n return nums[left];\n }\n}\n```\n{:style=\'width:300px\'}
| 6 | 0 |
['Array', 'Binary Search', 'Java']
| 1 |
find-minimum-in-rotated-sorted-array
|
🚀 100% | 0 ms 👏🏻 | Simple solution with explanation using binary search
|
100-0-ms-simple-solution-with-explanatio-6if9
|
Intuition\nThe intuition behind this solution is to use binary search to find the minimum element in the rotated array. By comparing the middle element with the
|
shadsheikh
|
NORMAL
|
2024-01-16T20:19:39.594693+00:00
|
2024-01-17T07:10:12.735216+00:00
| 1,494 | false |
# Intuition\nThe intuition behind this solution is to use binary search to find the minimum element in the rotated array. By comparing the middle element with the element at the end of the array, we can determine which half of the array to focus on.\n\n# Approach\n1. Initialize two pointers, start at the beginning of the array and end at the end of the array.\n2. Use a while loop to iterate until start is less than end.\n3. Calculate the middle index mid.\n4. If the element at mid is greater than the element at end, set start to mid + 1 (as the minimum element is on the right side).\n5. If the element at mid is less than or equal to the element at end, set end to mid (as the minimum element is on the left side or is the element at mid).\n6. Continue the loop until start equals end.\n7. Return the value of nums[start] as it represents the minimum element.\n\n# Complexity\n- Time complexity: O(log(n))\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int start=0,end=nums.size()-1;\n \n while(start<end){\n int mid=start+(end-start)/2;\n if(nums[mid]>nums[end]) start = mid+1;\n else end = mid;\n }\n\n return nums[start];\n }\n};\n```
| 6 | 0 |
['Binary Search', 'C++']
| 1 |
find-minimum-in-rotated-sorted-array
|
✅Beats 100% || Easy || Binary Search || C++
|
beats-100-easy-binary-search-c-by-nikhil-6i4v
|
\n\n# Code\n\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n //using log n algo(binary search)\n\n int low=0;\n int high
|
nikhil_120
|
NORMAL
|
2023-07-02T09:00:11.172142+00:00
|
2023-07-02T09:01:09.087622+00:00
| 1,390 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n //using log n algo(binary search)\n\n int low=0;\n int high=nums.size()-1;\n int ans=INT_MAX;\n while(low<=high){\n int mid=low+(high-low)/2;\n if(nums[mid]>=nums[low]){// means left half is sorted\n ans=min(ans,nums[low]); //storing the minimum \n low=mid+1; //eleminating left half\n }\n else{ //else right half is sorted\n ans=min(ans,nums[mid]);// storing the minimum\n high=mid-1;\n }\n }\n return ans;\n }\n};\n```
| 6 | 0 |
['C++']
| 0 |
find-minimum-in-rotated-sorted-array
|
Easiest Solution in leetcode #Python3
|
easiest-solution-in-leetcode-python3-by-0n32g
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Mohammad_tanveer
|
NORMAL
|
2023-04-03T13:48:26.027778+00:00
|
2023-04-03T13:48:26.027808+00:00
| 1,324 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMin(self, nums: List[int]) -> int:\n low=0\n high=len(nums)-1\n while low<high:\n mid=(low+high)//2\n if nums[mid]>nums[high]:\n low=mid+1\n else:\n high=mid\n return nums[low]\n \n```
| 6 | 0 |
['Python3']
| 0 |
find-minimum-in-rotated-sorted-array
|
0 ms 🔥 simple 6 lines C++ code -- beats 100%
|
0-ms-simple-6-lines-c-code-beats-100-by-wuphx
|
\u2764\uFE0FUPVOTE!\n# Complexity\n- Time complexity: O(LogN)\n\n- Space complexity: O(1)\n\n# Code\n\nclass Solution {\npublic:\n int findMin(vector<int>& n
|
AD44
|
NORMAL
|
2022-10-28T06:50:54.802173+00:00
|
2022-10-28T06:50:54.802197+00:00
| 745 | false |
**\u2764\uFE0FUPVOTE!**\n# Complexity\n- Time complexity: O(LogN)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int findMin(vector<int>& nums) {\n int start = 0,end = nums.size()-1; \n while(start<end)\n { \n int mid = (start + end)/2;\n if(nums[mid]>nums[end]) start = mid+1; \n else end = mid; \n } \n return nums[start];\n }\n};\n```
| 6 | 0 |
['C++']
| 2 |
find-minimum-in-rotated-sorted-array
|
TypeScript/JavaScript Binary Search
|
typescriptjavascript-binary-search-by-si-mec5
|
Since we\'re dealing with a sorted array problem and the description explicitly tells us to solve in O(logn) time, we should immediately think of trying to use
|
SigmaSum
|
NORMAL
|
2021-10-23T05:12:54.737187+00:00
|
2021-10-23T05:13:15.205472+00:00
| 1,078 | false |
Since we\'re dealing with a sorted array problem and the description explicitly tells us to solve in O(logn) time, we should immediately think of trying to use binary search. The trick is we need to modify binary search since in this case we\'re not looking for a specific target.\n\nKnowing that modified binary search is a possible solution, we can use a small example such as [2,3,1] and see what information we can gain from the mid point. In this case, we see that the array has been rotated twice and the midpoint value is three. From this, we can see that if the midpoint is greater than the value at the rightPointer, then the array has been rotated with the minimum value somewhere to the right of the mid point. So we can update left to equal mid + 1, since we no longer want to consider the mid point and want to look on the right half of the array. If however we have the example [3, 1, 2], our mid point value is 1 which is less than the rightPointer, so the right side of the array is properly sorted and the mid point value is the minimum of the right side of the array, so we want to keep it in the solution space as a possible minimum value. Therefore we set the right equal to mid. When we break out of this loop, the left index will point to the minimum value. \n```\nfunction findMin(nums: number[]): number {\n if(nums.length === 1){\n return nums[0];\n }\n \n let left = 0;\n let right = nums.length - 1;\n \n while(left < right){\n const mid = left + Math.floor((right - left) / 2);\n \n if(nums[mid] > nums[right]){\n left = mid + 1;\n }\n else {\n right = mid;\n }\n }\n \n return nums[left];\n};\n```
| 6 | 0 |
['Binary Search', 'TypeScript', 'JavaScript']
| 2 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.