question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
sort-array-by-parity-ii | [C++] Two Pointers || Inplace || O(n) time | c-two-pointers-inplace-on-time-by-manish-dghf | \nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n for(int i=0,j=0;i<nums.size();){\n\t\t\t// If we get an odd numbe | manishbishnoi897 | NORMAL | 2021-09-28T11:07:35.292274+00:00 | 2021-09-28T11:07:35.292305+00:00 | 145 | false | ```\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n for(int i=0,j=0;i<nums.size();){\n\t\t\t// If we get an odd number or an even number which is already processed then leave that number \n if(nums[i]&1 || (i<j && !(i&1))){ \n i++;\n }\n else{\n swap(nums[i],nums[j]); // Placing even numbers at their right place. By doing this, the odd numbers will come in their place automatically\n j+=2;\n }\n }\n return nums;\n }\n};\n``` | 3 | 0 | ['Two Pointers', 'C'] | 1 |
sort-array-by-parity-ii | c++ EASY SOLUTION | c-easy-solution-by-bholanathbarik9748-c345 | class Solution\n{\npublic:\n\n vector sortArrayByParityII(vector &nums)\n {\n vector v;\n vector v1;\n vector v2;\n\n for (int | bholanathbarik9748 | NORMAL | 2021-09-28T10:03:21.768227+00:00 | 2021-09-28T10:06:57.004864+00:00 | 101 | false | class Solution\n{\npublic:\n\n vector<int> sortArrayByParityII(vector<int> &nums)\n {\n vector<int> v;\n vector<int> v1;\n vector<int> v2;\n\n for (int i = 0; i < nums.size(); i++)\n {\n if (nums[i] & 1)\n {\n v2.push_back(nums[i]);\n }\n else\n {\n v1.push_back(nums[i]);\n }\n }\n\n for (int i = 0; i < nums.size() / 2; i++)\n {\n v.push_back(v1[i]);\n v.push_back(v2[i]);\n }\n return v;\n }\n}; | 3 | 1 | [] | 1 |
sort-array-by-parity-ii | Sort Array By Parity II | Inplace | O(n) time | C++ | sort-array-by-parity-ii-inplace-on-time-il4fk | explanation:\nfor every no. there are two possibilities: either its correct on its position or not correct.\nalso as there are equal no. of odd and even nos, so | saleemkhan086 | NORMAL | 2021-09-28T09:13:43.723263+00:00 | 2021-09-28T09:13:43.723308+00:00 | 308 | false | explanation:\nfor every no. there are two possibilities: either its correct on its position or not correct.\nalso as there are equal no. of odd and even nos, so for every incorrect odd, there will be one incorrect even and vice-versa.\n\nSo we will just keep two pointers : one for odd positions and one for even positions.\nIgnore those which are already at correct position.\nSwap those which are at incorrect.\n\n```\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n \n int i=0;\n int j=1;\n \n while(i<nums.size() && j<nums.size())\n {\n while(i<nums.size() && nums[i]%2==0)\n i+=2;\n while(j<nums.size() && nums[j]%2==1)\n j+=2;\n \n if(i<nums.size() && j<nums.size())\n {\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n \n }\n return nums;\n }\n};\n``` | 3 | 1 | ['C'] | 0 |
sort-array-by-parity-ii | C++ solution | Two pointer | In-place | c-solution-two-pointer-in-place-by-perfe-ujun | \nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n int evenPointer = 0, oddPointer = 1;\n while(evenPointer < | perfei | NORMAL | 2021-07-13T15:06:19.637308+00:00 | 2021-07-13T15:06:19.637356+00:00 | 175 | false | ```\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n int evenPointer = 0, oddPointer = 1;\n while(evenPointer < nums.size() && oddPointer <nums.size()){\n if(nums[evenPointer] %2 == 1 && nums[oddPointer]%2==0){\n swap(nums[evenPointer],nums[oddPointer]);\n evenPointer+=2;\n oddPointer+=2;\n continue;\n }\n if(nums[evenPointer]%2==0){\n evenPointer+=2;\n }\n if(nums[oddPointer]%2==1){\n oddPointer+=2;\n }\n }\n return nums;\n }\n};\n``` | 3 | 0 | ['Two Pointers', 'C'] | 0 |
sort-array-by-parity-ii | Python 3 two pointers O(n) | python-3-two-pointers-on-by-gravizapa-mqpb | \nclass Solution:\n def sortArrayByParityII(self, A: List[int]) -> List[int]:\n\t\tans = [None] * len(A)\n\t\tk = 0\n\t\tt = 1\n\t\tfor i in A:\n\t\t\tif i % | Gravizapa | NORMAL | 2021-01-05T21:02:19.380268+00:00 | 2021-01-05T21:03:18.664529+00:00 | 561 | false | ```\nclass Solution:\n def sortArrayByParityII(self, A: List[int]) -> List[int]:\n\t\tans = [None] * len(A)\n\t\tk = 0\n\t\tt = 1\n\t\tfor i in A:\n\t\t\tif i % 2 == 0:\n\t\t\t\tans[k] = i\n\t\t\t\tk += 2\n\t\t\telse:\n\t\t\t\tans[t] = i\n\t\t\t\tt += 2\n\t\treturn ans\n``` | 3 | 0 | ['Python', 'Python3'] | 0 |
sort-array-by-parity-ii | [c++] easy and fast | c-easy-and-fast-by-sanjeev1709912-ulyl | Please upvote my solution if you like it\n\n\'\'\'\nclass Solution {\npublic:\n\n vector sortArrayByParityII(vector& A) {\n int n=A.size();\n v | sanjeev1709912 | NORMAL | 2020-08-17T15:01:08.818854+00:00 | 2020-08-20T13:38:27.595766+00:00 | 395 | false | **Please upvote my solution if you like it**\n\n\'\'\'\nclass Solution {\npublic:\n\n vector<int> sortArrayByParityII(vector<int>& A) {\n int n=A.size();\n vector<int>ans(n);\n int ec=0,oc=1;\n for(int i=0;i<n;i++)\n {\n if(A[i]%2==0)\n {\n ans[ec]=A[i];\n ec+=2;\n }\n else\n {\n ans[oc]=A[i];\n oc+=2;\n }\n }\n return ans;\n }\n};\n\'\'\' | 3 | 1 | ['Two Pointers', 'C', 'C++'] | 1 |
sort-array-by-parity-ii | c++ o(n) solution | c-on-solution-by-elisheva-xxpa | \n\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& A) {\n int i,even=0,odd=1;\n vector<int> B(A.size());\n for | elisheva_ | NORMAL | 2020-08-01T22:32:41.234679+00:00 | 2020-08-01T22:40:19.747739+00:00 | 110 | false | ```\n\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& A) {\n int i,even=0,odd=1;\n vector<int> B(A.size());\n for(i=0;i<A.size();i++)\n {\n if((A[i]%2)==0)\n {\n B[even]=A[i];\n even+=2;\n } \n else\n {\n B[odd]=A[i];\n odd+=2; \n }\n }\n return B;\n }\n};\n``` | 3 | 0 | [] | 1 |
sort-array-by-parity-ii | Javascript - Simple using filter | javascript-simple-using-filter-by-jamieh-wa46 | \nvar sortArrayByParityII = function(A) {\n let evenNums = A.filter((i) => i % 2 === 0);\n let oddNums = A.filter((i) => i % 2 !== 0);\n \n let res | jamiehsmith | NORMAL | 2020-07-25T21:07:38.013084+00:00 | 2020-07-25T21:07:38.013124+00:00 | 376 | false | ```\nvar sortArrayByParityII = function(A) {\n let evenNums = A.filter((i) => i % 2 === 0);\n let oddNums = A.filter((i) => i % 2 !== 0);\n \n let res = [];\n for (let i = 0; i < A.length / 2; i++) {\n res.push(evenNums[i], oddNums[i]);\n }\n \n return res;\n};\n```\n\nStats:\nRuntime: 100 ms, faster than 88.97% of JavaScript online submissions for Sort Array By Parity II.\nMemory Usage: 44.3 MB, less than 12.50% of JavaScript online submissions for Sort Array By Parity II. | 3 | 0 | ['JavaScript'] | 0 |
sort-array-by-parity-ii | Efficient Python solution with generator | efficient-python-solution-with-generator-6r6z | We only need to check every other element for violating the problem statement invariant. If that happens, we can use generator to find matching pair to swap and | mereck | NORMAL | 2019-06-09T15:55:16.603054+00:00 | 2019-06-09T16:22:31.121028+00:00 | 109 | false | We only need to check every other element for violating the problem statement invariant. If that happens, we can use generator to find matching pair to swap and to also pick up where we left off on next mismatch.\n\n```\ndef sortArrayByParityII(self, A: List[int]) -> List[int]:\n\t\n def gen_odd():\n for j in range(1, len(A), 2):\n if not A[j] % 2: yield j\n\n odd = gen_odd()\n for i in range(0,len(A),2):\n if A[i] % 2:\n j = next(odd)\n A[i], A[j] = A[j], A[i]\n\n return A\n``` | 3 | 0 | [] | 2 |
sort-array-by-parity-ii | Java Solutions | java-solutions-by-pratik_patil-qw9f | Solution 1:\n\nTime complexity: O(n)\nSpace complexity: O(1)\n\n\nclass Solution \n{\n public int[] sortArrayByParityII(int[] A) \n {\n int i = 0;\ | pratik_patil | NORMAL | 2019-01-22T17:25:47.628547+00:00 | 2019-01-22T17:25:47.628606+00:00 | 204 | false | **Solution 1:**\n\nTime complexity: `O(n)`\nSpace complexity: `O(1)`\n\n```\nclass Solution \n{\n public int[] sortArrayByParityII(int[] A) \n {\n int i = 0;\n int j = 1;\n \n while(i < A.length && j < A.length)\n {\n while(i < A.length && A[i] % 2 == 0) i += 2;\n while(j < A.length && A[j] % 2 == 1) j += 2;\n \n if(i < A.length && j < A.length)\n swap(A, i, j);\n }\n return A;\n }\n \n private void swap(int[] A, int i, int j)\n {\n int temp = A[i];\n A[i] = A[j];\n A[j] = temp;\n }\n}\n```\n\n**Solution 2:**\n\nTime complexity: `O(n)`\nSpace complexity: `O(1)`\n\n```\nclass Solution \n{\n public int[] sortArrayByParityII(int[] A) \n {\n int evenIndex = 0;\n int oddIndex = A.length - 1;\n \n while(evenIndex < A.length && oddIndex > 0)\n {\n if(A[evenIndex] % 2 > A[oddIndex] % 2)\n swap(A, evenIndex, oddIndex);\n \n if(A[evenIndex] % 2 == 0) evenIndex += 2;\n if(A[oddIndex] % 2 == 1) oddIndex -= 2;\n }\n return A;\n }\n \n private void swap(int[] A, int i, int j)\n {\n int temp = A[i];\n A[i] = A[j];\n A[j] = temp;\n }\n}\n``` | 3 | 0 | [] | 0 |
sort-array-by-parity-ii | C solution | c-solution-by-zhaoyaqiong-et4b | \nint *sortArrayByParityII(int const *A, int ASize, int *returnSize) {\n int odd = 1, even = 0;\n int *ret = (int *) malloc(sizeof(int) * (*returnSize = A | zhaoyaqiong | NORMAL | 2018-12-13T03:32:09.339028+00:00 | 2018-12-13T03:32:09.339101+00:00 | 293 | false | ```\nint *sortArrayByParityII(int const *A, int ASize, int *returnSize) {\n int odd = 1, even = 0;\n int *ret = (int *) malloc(sizeof(int) * (*returnSize = ASize));\n for (int i = 0; i < *returnSize; ++i) {\n if (A[i] % 2 == 0) {\n ret[even] = A[i];\n even += 2;\n } else {\n ret[odd] = A[i];\n odd += 2;\n }\n }\n return ret;\n}\n``` | 3 | 0 | [] | 0 |
sort-array-by-parity-ii | Kotlin solution | kotlin-solution-by-huangdachuan-r2hi | \nclass Solution {\n fun sortArrayByParityII(A: IntArray): IntArray {\n val even = A.filter { it % 2 == 0 }\n val odd = A.filter { it % 2 == 1 | huangdachuan | NORMAL | 2018-10-18T04:36:52.960965+00:00 | 2018-10-19T01:17:53.894855+00:00 | 96 | false | ```\nclass Solution {\n fun sortArrayByParityII(A: IntArray): IntArray {\n val even = A.filter { it % 2 == 0 }\n val odd = A.filter { it % 2 == 1 }\n return even.zip(odd).flatMap { listOf(it.first, it.second) }.toIntArray()\n }\n}\n``` | 3 | 1 | [] | 0 |
sort-array-by-parity-ii | Two Pointer Solution [Java] Optimal Space and Optimal Runtime | two-pointer-solution-java-optimal-space-sotph | \nclass Solution {\n public int[] sortArrayByParityII(int[] A) {\n int odd = 1;\n int even = 0;\n \n while (even < A.length && od | eddiecarrillo | NORMAL | 2018-10-14T03:01:16.907793+00:00 | 2018-10-14T18:34:22.228710+00:00 | 513 | false | ```\nclass Solution {\n public int[] sortArrayByParityII(int[] A) {\n int odd = 1;\n int even = 0;\n \n while (even < A.length && odd < A.length){\n while (odd < A.length && A[odd] % 2 == 1) odd +=2;\n while (even < A.length && A[even] % 2 == 0) even += 2;\n \n if (even < A.length && odd < A.length){\n swap(A, even, odd);\n even += 2;\n odd += 2;\n }\n }\n \n return A;\n \n }\n \n void swap(int[] A, int a, int b){\n int temp = A[a];\n A[a] = A[b];\n A[b] = temp;\n }\n \n \n \n \n}\n``` | 3 | 2 | [] | 1 |
sort-array-by-parity-ii | very easy approach, beats 98 % | very-easy-approach-beats-98-by-aashna_sa-wwem | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Aashna_Sahu001 | NORMAL | 2025-03-24T20:37:18.170953+00:00 | 2025-03-24T20:37:18.170953+00:00 | 183 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int[] sortArrayByParityII(int[] nums) {
int ans [] = new int[nums.length];
int evenIndex = 0;
int oddIndex = 1;
for(int i : nums){
if(i % 2 == 0 ){
ans[evenIndex] = i;
evenIndex += 2;
}
if(i % 2 == 1){
ans[oddIndex] = i;
oddIndex += 2;
}
}
return ans;
}
}
``` | 2 | 0 | ['Java'] | 1 |
sort-array-by-parity-ii | simple answer 🙂 | simple-answer-by-sriharshavarthm-kp23 | IntuitionMY friend's intution (Rohithkumar_kr);[https://leetcode.com/u/Rohithkumar_kr/]he got banned later...Approachsimple approachComplexity
Time complexity: | SriHarshavarthM | NORMAL | 2025-03-18T07:34:11.857874+00:00 | 2025-03-18T07:35:02.607793+00:00 | 215 | false | # Intuition
MY friend's intution (Rohithkumar_kr);[https://leetcode.com/u/Rohithkumar_kr/]
he got banned later...
# Approach
simple approach
# Complexity
- Time complexity:
0ms
- Space complexity:
beats 50%
# Code
```cpp []
class Solution {
public:
vector<int> sortArrayByParityII(vector<int>& nums) {
vector<int> even, odd , ans;
for(int i : nums){
if(i%2==0) even.push_back(i);
if(i%2!=0) odd.push_back(i);
}
for(int i =0;i< even.size();i++){
ans.push_back(even[i]);
ans.push_back(odd[i]);
}
return ans;
}
};
``` | 2 | 0 | ['C++'] | 1 |
sort-array-by-parity-ii | Beats 95% | 3 ms | Efficient Solution 🦾🦾 | beats-95-3-ms-efficient-solution-by-shiv-bpx1 | Code | ShivankDXD | NORMAL | 2025-01-30T19:53:09.795584+00:00 | 2025-01-30T19:53:09.795584+00:00 | 242 | false |
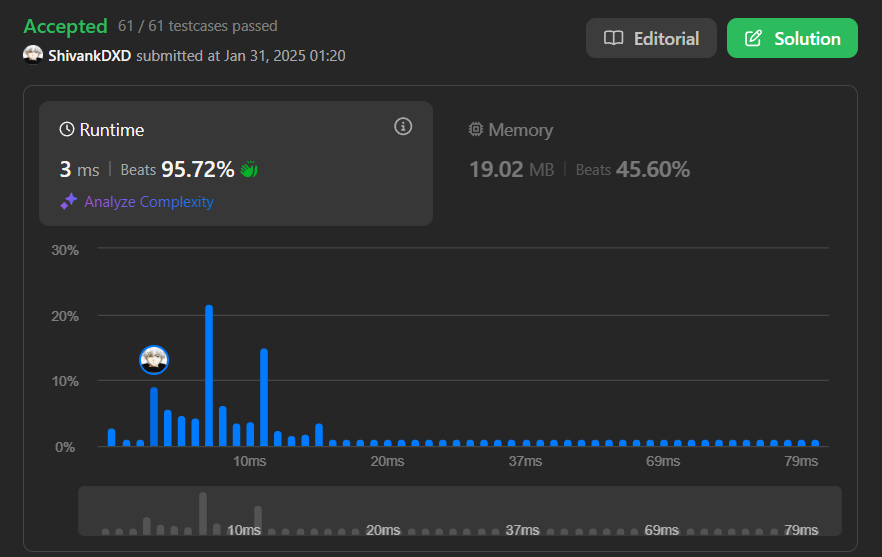
# Code
```python3 []
class Solution:
def sortArrayByParityII(self, nums: List[int]) -> List[int]:
even_index, odd_index = 0, 1
n = len(nums)
while even_index < n and odd_index < n:
if nums[even_index] % 2 == 0:
even_index += 2
elif nums[odd_index] % 2 == 1:
odd_index += 2
else:
nums[even_index], nums[odd_index] = nums[odd_index], nums[even_index]
even_index += 2
odd_index += 2
return nums
``` | 2 | 0 | ['Python3'] | 0 |
sort-array-by-parity-ii | 2ms in java very easiest code 😊. | 2ms-in-java-very-easiest-code-by-galani_-zhcl | Code | Galani_jenis | NORMAL | 2025-01-10T07:27:14.529753+00:00 | 2025-01-10T07:27:14.529753+00:00 | 280 | false | 
# Code
```java []
class Solution {
public int[] sortArrayByParityII(int[] nums) {
int[] arr = new int[nums.length];
short e = 0, o = 1;
for (int num : nums) {
if (num % 2 == 0){
arr[e] = num;
e += 2;
}else {
arr[o] = num;
o += 2;
}
}
return arr;
}
}
``` | 2 | 0 | ['Java'] | 0 |
sort-array-by-parity-ii | Easy JAVA Solution that beats 99.70%|| Two Pointer Approach.||Beginner Friendly | easy-java-solution-that-beats-9970-two-p-o098 | IntuitionThe problem requires alternating even and odd numbers in the array. Since there are equal counts of even and odd numbers (as guaranteed by the problem) | virajodedra04 | NORMAL | 2024-12-21T06:20:44.231426+00:00 | 2024-12-21T06:20:44.231426+00:00 | 424 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires alternating even and odd numbers in the array. Since there are equal counts of even and odd numbers (as guaranteed by the problem), we can:
- Separate the even and odd numbers.
- Rebuild the array by placing even numbers at even indices and odd numbers at odd indices.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Separate Even and Odd Numbers:
- Traverse the array once, collecting even numbers in one array and odd numbers in another.
2. Rebuild the Original Array:
- Use two separate indices, one for even numbers and one for odd numbers.
- Place the numbers alternately in the original array based on their
respective parity positions (even or odd).
# Complexity
- Time complexity: O(n).
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n).
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int[] sortArrayByParityII(int[] nums) {
int n = nums.length;
int[] even = new int[n / 2];
int[] odd = new int[n / 2];
// Fill even and odd arrays
int evenIndex = 0, oddIndex = 0;
for (int i = 0; i < n; i++) {
if (nums[i] % 2 == 0) {
even[evenIndex++] = nums[i];
} else {
odd[oddIndex++] = nums[i];
}
}
// Rebuild nums array with alternating even and odd numbers
evenIndex = 0;
oddIndex = 0;
for (int i = 0; i < n; i++) {
if (i % 2 == 0) {
nums[i] = even[evenIndex++];
} else {
nums[i] = odd[oddIndex++];
}
}
return nums;
}
}
```

| 2 | 0 | ['Two Pointers', 'Java'] | 0 |
sort-array-by-parity-ii | SIMPLE TWO-POINTER C++ COMMENTED SOLUTION | simple-two-pointer-c-commented-solution-21uuu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Jeffrin2005 | NORMAL | 2024-07-20T13:00:08.980122+00:00 | 2024-08-04T17:23:51.342410+00:00 | 120 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:o(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:o(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution {\npublic:\n/*\n // Example dry run with nums = [5, 2, 4, 7]:\n // Initial state: nums = [5, 2, 4, 7], i = 0, j = 1\n // First iteration: i = 0 (5 is odd), j = 1 (2 is even), swap -> nums = [2, 5, 4, 7]\n // i moves to 2, j moves to 3\n // Second iteration: i = 2 (4 is even), j = 3 (7 is odd), no swap needed\n // i moves out of bounds, loop exits\n // Final state: nums = [2, 5, 4, 7]\n*/\n std::vector<int> sortArrayByParityII(std::vector<int>& nums) {\n int n = nums.size();\n int i = 0; // even indices\n int j = 1; // odd indices\n while (i < n && j < n) {\n if (nums[i] % 2 == 0){\n i += 2;// Move to the next even index\n }else if (nums[j] % 2 == 1){\n j+=2; // Move to the next odd index\n }else{\n swap(nums[i], nums[j]); \n i+=2;\n j+=2;\n }\n }\n \n\n return nums;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
sort-array-by-parity-ii | c++ optimal easy to understand code | c-optimal-easy-to-understand-code-by-poo-hezc | \n\n# Approach\n- In This first we have to make an array named "ans" where we stor the sorted rearranged array.\n- then here we initialized two indexes"posindex | pooja-panday | NORMAL | 2024-07-16T16:17:35.783204+00:00 | 2024-07-16T16:17:35.783242+00:00 | 116 | false | \n\n# Approach\n- In This first we have to make an array named "ans" where we stor the sorted rearranged array.\n- then here we initialized two indexes"posindex=0" which starts from 0 and negindex=1 which start from 1 \n- after iterating if the number is even set it on posindex and increment it by 2 same as for negative index.\n- then at last return the array ans; \n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n int n=nums.size();\n vector<int>ans(n,0);\n int evenindex=0,oddindex=1;\n for(int i=0;i<n;i++){\n if(nums[i]%2==0){\n ans[evenindex]=nums[i];\n evenindex+=2;\n }\n else{\n ans[oddindex]=nums[i];\n oddindex+=2;\n }\n }\n \n return ans;\n \n \n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
sort-array-by-parity-ii | 🔢 5. 2 Easy Solutions !! || Concise & Clean Codes ! || C++ Code Reference ! | 5-2-easy-solutions-concise-clean-codes-c-ngg1 | 2 Approaches !! \ncpp [Approach 1]\n\n vector<int> sortArrayByParityII(vector<int>& A) {\n \n int i=0, j=1, n=A.size();\n\n while(i<n && | Amanzm00 | NORMAL | 2024-07-12T05:32:48.472784+00:00 | 2024-07-12T05:32:48.472816+00:00 | 78 | false | ## 2 Approaches !! \n```cpp [Approach 1]\n\n vector<int> sortArrayByParityII(vector<int>& A) {\n \n int i=0, j=1, n=A.size();\n\n while(i<n && j<n)\n {\n if(A[i]%2==0) i+=2;\n else if (A[j]&1) j+=2;\n else swap(A[i],A[j]);\n }\n\n return A;\n }\n\n\n```\n```cpp [Approach 2]\n\n vector<int> sortArrayByParityII(vector<int>& A) {\n\n int i=0, j=1, n=A.size();\n\n while(1)\n {\n while(i<n && A[i]%2==0) i+=2;\n while (j<n && A[j]&1) j+=2;\n\n if(i>n || j>n) return A;\n swap(A[i],A[j]);\n }\n }\n\n\n```\n\n\n---\n# *Guy\'s Upvote Pleasee !!* \n\n\n# ***(\u02E3\u203F\u02E3 \u035C)***\n\n\n | 2 | 0 | ['Array', 'Two Pointers', 'Sorting', 'C++'] | 0 |
sort-array-by-parity-ii | Java Solution beats 99% ;) | java-solution-beats-99-by-aditya_narayan-uxgh | Intuition\nImagine you have a group of children standing in a line, and you want to arrange them such that every child in an even position (0, 2, 4, ...) is wea | Aditya_Narayan_Pandey | NORMAL | 2024-06-27T17:53:09.704569+00:00 | 2024-06-27T17:53:09.704603+00:00 | 792 | false | # Intuition\nImagine you have a group of children standing in a line, and you want to arrange them such that every child in an even position (0, 2, 4, ...) is wearing a red shirt and every child in an odd position (1, 3, 5, ...) is wearing a blue shirt. However, right now the children are standing in a random order, and you need to rearrange them according to the shirt color rule.\n\nHere\u2019s how you can accomplish this task in a structured way:\n\n # Initialization:\n\n### You start with two pointers: \np1 at position 0 (the first position) and p2 at position 1 (the second position). These pointers will help you find and fix misplaced children.\n### Scanning and Fixing Misplacements:\n\nYou begin to move p1 through the line, but only at even positions (0, 2, 4, ...), checking if the child in that position is wearing a red shirt.\n\nSimilarly, you move p2 through the line, but only at odd positions (1, 3, 5, ...), checking if the child in that position is wearing a blue shirt.\n\nIf p1 finds a child at an even position who is not wearing a red shirt, it stops.\n\nIf p2 finds a child at an odd position who is not wearing a blue shirt, it stops.\n\n### Swapping Misplaced Children:\n\nOnce both p1 and p2 have stopped (both found misplacements), you swap the children at these positions. This exchange corrects the order for both the even and odd positions.\nContinuing the Process:\n\nYou continue this process until one of the pointers goes beyond the end of the line, meaning you\'ve checked all the positions.\nBy following this method, you ensure that every child at an even position wears a red shirt, and every child at an odd position wears a blue shirt. \nLet\'s look at the code implementing this:\n\n# Code\n```\nclass Solution {\n public int[] sortArrayByParityII(int[] nums) {\n int p1=0;\n int p2=1;\n int n=nums.length;\n while(p1<n && p2<n){\n while(p1<n && nums[p1]%2==0)p1+=2;\n while(p2<n && nums[p2]%2!=0)p2+=2;\n if(p1>=n || p2>=n)break;\n int x=nums[p1];\n nums[p1]=nums[p2];\n nums[p2]=x;\n }\n return nums;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
sort-array-by-parity-ii | ✅ Easy C++ Solution | easy-c-solution-by-moheat-hu2g | Code\n\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n int even = 0;\n int odd = 1;\n int n = nums.s | moheat | NORMAL | 2024-04-29T05:41:57.149581+00:00 | 2024-04-29T05:41:57.149612+00:00 | 49 | false | # Code\n```\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n int even = 0;\n int odd = 1;\n int n = nums.size();\n vector<int> v(n);\n for(int i=0;i<n;i++)\n {\n if(nums[i] % 2 == 0)\n {\n v[even] = nums[i];\n even = even + 2;\n }\n else\n {\n v[odd] = nums[i];\n odd = odd + 2;\n }\n }\n return v;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
sort-array-by-parity-ii | Vector use || 97% T.C || CPP | vector-use-97-tc-cpp-by-ganesh_ag10-se37 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ganesh_ag10 | NORMAL | 2024-04-18T15:28:14.388440+00:00 | 2024-04-18T15:28:14.388475+00:00 | 1,033 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n vector<int> v1,v2;\n for(int i=0;i<nums.size();i++)\n {\n if(nums[i]%2==0)\n v2.push_back(nums[i]);\n else\n v1.push_back(nums[i]);\n }\n int l1=0,l2=0;\n for(int i=0;i<nums.size();i++)\n {\n if(i%2==0)\n nums[i]=v2[l2++];\n else\n nums[i]=v1[l1++];\n }\n\n return nums;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
sort-array-by-parity-ii | C++ | Easy Solution | c-easy-solution-by-dhruvp0105-kcml | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dhruvp0105 | NORMAL | 2023-07-07T18:42:53.979593+00:00 | 2023-07-07T18:42:53.979623+00:00 | 249 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sortArrayByParityII(vector<int>& nums) {\n \n vector<int> ans(nums.size(),0);\n int even=0;\n int odd=1;\n\n cout<<"Hello";\n for(int i=0;i<nums.size();i++){\n if(nums[i] % 2==0){\n ans[even]=nums[i];\n if(even+2 <= nums.size()-1){\n even+=2;\n }\n // cout<<ans[i]<<" ";\n }\n else{\n ans[odd]=nums[i];\n if(odd+2 <= nums.size()-1){\n odd+=2;\n }\n // cout<<ans[i]<<" ";\n }\n }\n\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
smallest-integer-divisible-by-k | Python O(K) with Detailed Explanations | python-ok-with-detailed-explanations-by-je7x1 | For a given K, we evaluate 1 % K, 11 % K, 111 % K, ..., 11...1 (K \'1\'s) % K. \n If any remainder is 0, then the current number is the smallest integer divisib | infinute | NORMAL | 2019-03-24T04:03:09.610054+00:00 | 2019-03-24T04:03:09.610098+00:00 | 8,963 | false | For a given K, we evaluate `1 % K, 11 % K, 111 % K, ..., 11...1 (K \'1\'s) % K`. \n* If any remainder is 0, then the current number is the smallest integer divisible by `K`. \n* If none of the remainders is 0, then at some point, there must be some duplicate remainders (due to [Pigeonhole principle](https://en.wikipedia.org/wiki/Pigeonhole_principle)), as the `K` remainders can only take at most `K-1` different values excluding 0. In this case, no number with the pattern 1...1 is divisible by `K`. This is because once a remainder has a duplicate, the next remainder will be in a loop, as the previous remainder determines the next_mod, i.e., `next_mod = (10 * prev_mod + 1) % K`. Therefore, we will never see remainder==0.\n\nA simple example is when K is 6. Once we see 1111 % 6 = 1, we immediately know 11111 % 6 will be 5, since 1 % 6 = 1 and 11 % 6 = 5. Therefore, there will be no such number that is divisible by 6.\n* 1 % 6 = 1\n* 11 % 6 = 5\n* 111 % 6 = 3\n* 1111 % 6 = 1\n* 11111 % 6 = 5\n* 111111 % 6 = 3\n\nAlso, it is easy to see that for any number whose last digit is not in `{1, 3, 7, 9}`, we should return `-1`.\n```\nclass Solution:\n def smallestRepunitDivByK(self, K: int) -> int:\n if K % 10 not in {1, 3, 7, 9}: return -1\n mod, mod_set = 0, set()\n for length in range(1, K + 1):\n mod = (10 * mod + 1) % K\n if mod == 0: return length\n if mod in mod_set: return -1\n mod_set.add(mod)\n return -1\n``` | 182 | 5 | ['Hash Table', 'Python'] | 17 |
smallest-integer-divisible-by-k | [Java/C++/Python] O(1) Space with Proves of Pigeon Holes | javacpython-o1-space-with-proves-of-pige-1vdu | Intuition:\nLet\'s say the final result has N digits of 1. \nIf N exist, N <= K, just do a brute force check.\nAlso if K % 2 == 0, return -1, because 111....11 | lee215 | NORMAL | 2019-03-24T03:06:42.329245+00:00 | 2019-03-24T03:06:42.329273+00:00 | 13,989 | false | ## **Intuition**:\nLet\'s say the final result has `N` digits of 1. \nIf `N` exist, `N <= K`, just do a brute force check.\nAlso if `K % 2 == 0`, return -1, because 111....11 can\'t be even.\nAlso if `K % 5 == 0`, return -1, because 111....11 can\'t end with 0 or 5.\n<br>\n\n\n## **Explanation**\nFor different `N`, we calculate the remainder of mod `K`.\nIt has to use the remainder for these two reason:\n\n1. Integer overflow\n2. The division operation for big integers, is **NOT** `O(1)`, it\'s actually depends on the number of digits..\n\n\n## **Prove**\n\nWhy 5 is a corner case? It has a reason and we can find it.\nAssume that `N = 1` to `N = K`, if there isn\'t `111...11 % K == 0`\nThere are at most `K - 1` different remainders: `1, 2, .... K - 1`.\n\nSo this is a pigeon holes problem:\nThere must be at least 2 same remainders.\n\n\nAssume that,\n`f(N) \u2261 f(M)`, `N > M`\n`f(N - M) * 10 ^ M \u2261 0`\n`10 ^ M \u2261 0, mod K`\nso that K has factor 2 or factor 5.\n\n\nProof by contradiction\uFF0C\n`If (K % 2 == 0 || K % 5 == 0) return -1;`\notherwise, there must be a solution `N <= K`.\n\n## **Time Complexity**:\nTime `O(K)`, Space `O(1)`\n\n<br>\n\n**Java:**\n```\n public int smallestRepunitDivByK(int K) {\n if (K % 2 == 0 || K % 5 == 0) return -1;\n int r = 0;\n for (int N = 1; N <= K; ++N) {\n r = (r * 10 + 1) % K;\n if (r == 0) return N;\n }\n return -1;\n }\n```\n\n**C++:**\n```\n int smallestRepunitDivByK(int K) {\n for (int r = 0, N = 1; N <= K; ++N)\n if ((r = (r * 10 + 1) % K) == 0)\n return N;\n return -1;\n }\n```\n\n**Python:**\n```\n def smallestRepunitDivByK(self, K):\n if K % 2 == 0 or K % 5 == 0: return -1\n r = 0\n for N in xrange(1, K + 1):\n r = (r * 10 + 1) % K\n if not r: return N\n```\n | 154 | 10 | [] | 22 |
smallest-integer-divisible-by-k | Proof: we only need to consider the first K candidates in [1, 11, 111, 1111, ...] | proof-we-only-need-to-consider-the-first-8v9t | This problem is the second problem from Leetcode Contest 129. Among all the top-25 ranked participants, only 10 of them bounded their loop in K iterations. Thus | starsthu2016 | NORMAL | 2019-03-24T04:29:07.585319+00:00 | 2019-03-24T04:29:07.585353+00:00 | 5,467 | false | This problem is the second problem from Leetcode Contest 129. Among all the top-25 ranked participants, only 10 of them bounded their loop in K iterations. Thus, we have the strong motivation to mathematically prove the title of this post and bound our execution in K iterations. Otherwise, most people basically set an upper bound as 10^5 according to the note or just write a "while True" loop.\n\nIf this is true, the code in Python can be very elegant like this.\n```\ndef smallestRepunitDivByK(self, K: int) -> int: \n if K % 2 ==0 or K % 5==0:\n return -1 \n module = 1\n for Ndigits in range(1, K+1):\n if module % K == 0:\n return Ndigits\n module = (module * 10 + 1) % K\n return 1234567890 # This line never executes\n```\nProof:\nIt is obvious that if K is the multiple of 2 or multiple of 5, N is definitely not multiple of K because the ones digit of N is 1. Thus, return -1 for this case.\n\nIf K is neither multiple of 2 nor multiple of 5, we have this theorem. \n\nTheorem: there must be one number from the K-long candidates list [1, 11, 111, ..., 111..111(with K ones)], which is the multiple of K. \n\nWhy? Let\'s think in the opposite way. Is it possible that none of the K candidates is the multiple of K?\n\nIf true, then the module of these K candidate numbers (mod K) must be in [1, .., K-1] (K-1 possible module values). Thus, there must be 2 candidate numbers with the same module. Let\'s denote these two numbers as N_i with i ones, and N_j with j ones and i<j.\n\nThus N_j-N_i = 1111...1000...0 with (j-i) ones and i zeros. N_j-N_i = 111..11 (j-i ones) * 100000..000 (i zeros). We know that N_i and N_j have the same module of K. Then N_j-N_i is the multiple of K. However, 100000..000 (i zeros) does not contain any factors of K (K is neither multiple of 2 nor multiple of 5). Thus, 111..11 (j-i ones) is the multiple of K. This is contradictory to our assumption that all K candidates including 111..11 (j-i ones) are not multiple of K.\n\nFinally, we know that there is at least one number, from the first K candidates, which is the multiple of K. | 132 | 2 | [] | 17 |
smallest-integer-divisible-by-k | ✅ [C++/Java/Python] 5 lines || Image Explain || Beginner Friendly | cjavapython-5-lines-image-explain-beginn-fl74 | PLEASE UPVOTE if you like \uD83D\uDE01 If you have any question, feel free to ask. \n Inspired by the Theorem\n\t A fraction is either a finite decimal or an in | linfq | NORMAL | 2021-12-30T02:34:59.425716+00:00 | 2021-12-30T14:02:17.625655+00:00 | 3,992 | false | **PLEASE UPVOTE if you like** \uD83D\uDE01 **If you have any question, feel free to ask.** \n* Inspired by the Theorem\n\t* A fraction is either a finite decimal or an infinite loop decimal\n\t\t* 3 / 5 = 0.6\n\t\t* 2 / 7. = 0.**285714** 285714 2857...\n\t* Furthermore the length of the loop does not exceed the denominator.\n\t\t* because 0 <= remainder < denominator\n* Different from appending 0 to continue dividing when the fraction has a remainder, we append 1. But the state transition of remainder and divisor is similar.\n\t* **once the remainder repeats, in other word the loop starts that means it cannot be divisible**.\n* `if k % 2 == 0 or k % 5 == 0: return -1` trick can save a little time\n* when we code, we can either stop at repeated remainder or stop after k transfers.\n\t* stop at repeated remainder, we need to record the previous remainders, so the Space Complexity is O(k), but can save a little time\n\t* stop after k transfers, we can reduce the **Space Complexity to O(1)**\n\t* **Time Complexity** of both solutions above is **O(k)**, because 0 <= remainder < k, according to the **Pigeonhole Theorem**\n\t\n* It may be better to understand this problem from the perspective of state transition\n\t* we directly define the remainder as the state\n\t* The stop condition is that the remainder is 0, so 0 is the stop state.\n\t* `k = 7` can stop after 6 transfers, so we `return 6`\n\n\t\t\n\n\t* `k = 12` enters the loop and won\'t stop, so we `return -1`\n\n\t\t\n\n\n```\nTime Complexity:O(k)\nSpace Complexity:O(k)\n```\n\n**Python**\n```\nclass Solution(object):\n def smallestRepunitDivByK(self, k):\n # if k % 2 == 0 or k % 5 == 0: return -1 # this trick may save a little time\n hit, n, ans = [False] * k, 0, 0\n while True: # at most k times, because 0 <= remainder < k\n ans, n = ans + 1, (n * 10 + 1) % k # we only focus on whether to divide, so we only need to keep the remainder.\n if n == 0: return ans # can be divisible\n if hit[n]: return -1 # the remainder of the division repeats, so it starts to loop that means it cannot be divisible.\n hit[n] = True\n```\n**C++**\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n // if (k % 2 == 0 || k % 5 == 0) return -1; // this trick may save a little time\n int n = 0, ans = 0;\n bool *hit = new bool[k]; \n for (int i = 0; i < k; i ++) hit[i] = false;\n while (true) { // at most k times, because 0 <= remainder < k\n ++ ans;\n n = (n * 10 + 1) % k; // we only focus on whether to divide, so we only need to keep the remainder.\n if (n == 0) return ans; // can be divisible\n if (hit[n]) return -1; // the remainder of the division repeats, so it starts to loop that means it cannot be divisible.\n hit[n] = true;\n }\n }\n};\n```\n**Java**\n```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n // if (k % 2 == 0 || k % 5 == 0) return -1; // this trick may save a little time\n boolean[] hit = new boolean[k];\n int n = 0, ans = 0;\n while (true) { // at most k times, because 0 <= remainder < k\n ++ ans;\n n = (n * 10 + 1) % k; // we only focus on whether to divide, so we only need to keep the remainder.\n if (n == 0) return ans; // can be divisible\n if (hit[n]) return -1; // the remainder of the division repeats, so it starts to loop that means it cannot be divisible.\n hit[n] = true;\n }\n }\n}\n```\n\n\n```\nTime Complexity:O(k)\nSpace Complexity:O(1)\n```\n\n**Python**\n```\nclass Solution(object):\n def smallestRepunitDivByK(self, k):\n # if k % 2 == 0 or k % 5 == 0: return -1 # this trick may save a little time\n n = 0\n for i in range(k): # at most k times, because 0 <= remainder < k\n n = (n * 10 + 1) % k # we only focus on whether to divide, so we only need to keep the remainder.\n if n == 0: return i + 1 # i started from 0, so before return it should be added 1\n return -1 # If it had not stop after k transfers, it must enter the loop, and it won\'t stop.\n```\n**C++**\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n\t\t// if (k % 2 == 0 || k % 5 == 0) return -1; // this trick may save a little time\n int n = 0;\n for (int i = 0; i < k; i++) { // at most k times, because 0 <= remainder < k\n n = (n * 10 + 1) % k; // we only focus on whether to divide, so we only need to keep the remainder.\n if (n == 0) return i + 1; // i started from 0, so before return it should be added 1\n }\n return -1; // If it had not stop after k transfers, it must enter the loop, and it won\'t stop.\n }\n};\n```\n**Java**\n```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n\t\t// if (k % 2 == 0 || k % 5 == 0) return -1; // this trick may save a little time\n int n = 0;\n for (int i = 0; i < k; i ++) { // at most k times, because 0 <= remainder < k\n n = (n * 10 + 1) % k; // we only focus on whether to divide, so we only need to keep the remainder.\n if (n == 0) return i + 1; // i started from 0, so before return it should be added 1\n }\n return -1; // If it had not stop after k transfers, it must enter the loop, and it won\'t stop.\n }\n}\n```\n\n**PLEASE UPVOTE if you like** \uD83D\uDE01 **If you have any question, feel free to ask.** | 82 | 1 | ['C', 'Python', 'Java'] | 10 |
smallest-integer-divisible-by-k | ✅ [C++/Python] Simple Solution w/ Explanation | Brute+ Optimizations w/ Math & Pigeonhole | cpython-simple-solution-w-explanation-br-49il | We are given an integer k and we need to find the length of smallest integer n which is divisible by k. Return -1 if no such n exists.\n\n----\n\n\u2714\uFE0F S | archit91 | NORMAL | 2021-12-30T07:08:49.906311+00:00 | 2021-12-30T07:30:56.341577+00:00 | 2,033 | false | We are given an integer `k` and we need to find the length of smallest integer `n` which is divisible by `k`. Return -1 if no such `n` exists.\n\n----\n\n\u2714\uFE0F ***Solution - I (Brute-Force w/ some Math to avoid Overflow)***\n\nTo start, we can see that the problem can be divided into two cases -\n* **`n` exists such that `n % k == 0`**: \n\t* Starting with `n = 1`, we can simply keep appending 1 at its end till we dont get `n % k == 0`. \n\t* We are given that **`n` may not fit in 64-bit integers**. So simply looping till we dont get `n % k == 0` may work in languages supporting big integers and maybe for other languages you can even maintain string & write custom division function for long integer string division, but it will be very inefficient.\n\t* Let remainder `R1 = n1 % k`. If `R1 != 0`, then the next `n2` after appending 1 would be `n1 * 10 + 1`. \n\t We then have: \n\t\t ```python\n\t\t => R2 = n2 % k \n\t\t => R2 = (n1 * 10 + 1) % k ... [ putting in value of n2 ]\n\t\t => R2 = [(n1 % k) * (10 % k)] % k + 1 % k ... [ modulo property ]\n\t\t => R2 = [R1 * (10 % k)] % k + 1 % k ... [ \u2235 R1 = n1 % k ]\n\t\t => R2 = (R1 * 10 + 1) % k\n\t\t ```\n\t* Thus, we can **use previous remainder `R`, append `1` to its end, then take its mod `k` and use it in the next iteration**. This avoids overflow and is more efficient than keep appending 1 at the end of `n` itself (doing `n % k` is not O(1) operation for big integers even in langauge that support it).\n\t* Finally at some point, we find `n % k == 0` at which point we will return the iteration count as the answer (since we were adding only 1 digit at each iteration).\n\n* **no such `n` exists**:\n\t* If no `n` exists such that `n % k == 0`, then we need to find a way to see it and not get caught in infinite loop\n\t* Since there\'s a **finite number of possible remainders** for a given input `k`, if no `n` exist, then the same remainder is bound to repeat again sometime.\n\t* Thus, if a remainder occurs again, we can directly `return -1` because in this case no `n` exist and we will just keep going in inifite loop.\n\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n int n = 1, R;\n unordered_set<int> seen;\n for(int i = 1; ; i++) {\n R = n % k; // find remainder\n if(R == 0) return i; // if R == 0, we found the required n, returns its length\n\t\t\tif(seen.count(R)) return -1; // seen again? no n exists, so return -1\n seen.insert(R); // mark as seen\n n = R * 10 + 1; // update n for next iteration\n }\n return -1;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n n, seen, i = 1, set(), 1\n while True:\n R = n % k\n if R == 0: return i\n if R in seen: return -1\n seen.add(R)\n n = R * 10 + 1\n i += 1\n```\n\n***Time Complexity :*** `O(K)`, We keep iterating till we either find `n % k == 0` or a repeated remainder. In the worst case, we find all possible `k` remainder before returning final result which requires `O(k)` time\n***Space Complexity :*** `O(K)`, for storing `seen` remainders\n\n---\n\n\u2714\uFE0F ***Solution - II (Optimization w/ Math & Pigeonhole Principle)***\n\nWe can further optimize the solution by using the **[pigeonhole principle](https://en.wikipedia.org/wiki/Pigeonhole_principle)** which states that if there are `n` items to be placed in `m` places with `n > m`, then atleast one place must contain more than 1 item. In this case, we have `k` possible remainders from `0 to k-1`. So, when we try to place remainder `R` into `seen` for more than `k` times, we will definitely find a duplicate. Thus, we can optimize on space by simply iterating `k` times and if we dont find a `R == 0`, then we will return -1 at the end (since `R` must have or will repeat from that point).\n\nFurthermore, we can see that since `n` consists only of `1`s, the answer will never exist in the cases where `k` is divisible by `2` or `5`. This is because a number `n` ending with 1 can never be divisible by an integer `k` which is even (`k % 2 == 0`) or ending with 5 (`k % 5 == 0`).\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(k % 2 == 0 or k % 5 == 0) return -1;\n int n = 1, R;\n for(int i = 1; i <= k ; i++) {\n R = n % k; \n if(R == 0) return i; \n n = R * 10 + 1; \n }\n return -1;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if k % 2 == 0 or k % 5 == 0: return -1\n n = 1\n for i in range(k):\n R = n % k\n if R == 0: return i+1\n n = R * 10 + 1\n```\n\n***Time Complexity :*** `O(K)`\n***Space Complexity :*** `O(1)`\n\n---\n---\n\n\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, please do comment below \uD83D\uDC47 \n\n---\n---\n | 64 | 3 | [] | 5 |
smallest-integer-divisible-by-k | C++ EASY TO SOLVE || Everything you need to Know from Intuitions till Proofs | c-easy-to-solve-everything-you-need-to-k-k4s3 | Everything you need to Know from all the Intuitions till Proofs\n> At start let\'s reframe the question for better understanding .\nSo the question is we are g | Cosmic_Phantom | NORMAL | 2021-12-30T13:41:50.003817+00:00 | 2024-08-23T02:28:35.486962+00:00 | 2,433 | false | # **Everything you need to Know from all the Intuitions till Proofs**\n> **At start let\'s reframe the question for better understanding .**\nSo the question is we are given a number `K` , check every `N` until the solution is found or no solution exists.\nWe can start N with the first one that is greater than or equal to K.\nSo in simple words we need to find a integer `N` where `N` can be 1 , 11, 111, 1111, 1111....1 and we can say `N` is a integer which is made up of 1\'s and `K` is the input number that should divide `N`\n***\n**For example:-**\n```\nInput: k = 3 \nSo N can be:\n1 ->1/3 N is not divisible by K\n11 ->11/3 N is not divisible by K\n111->111/3 N is divisble by k\nso the answer is the length of N(111) i.e 3\nOutput: 3\t\t\t\n```\n***\n\n**1st Intuition:-**\nAfter understanding the question one thing is clear that at every iteration we need to append 1 to the previous `N` i.e <mark>1 =append 1->11 =append 1-> 111 =append 1->1111....</mark> and this goes on till we get a `N` which is divisble by `K` .\n***\n**2nd Intuition:-**\nAfter some brainstorming and getting bald by finding this intuition :) I got this 2nd intuition that if we need to append a digit to a number by 1 digit, the easiest way is to multiply it by 10 .Let me explain this in a more clear way.\n```\nso let\'s say you have a number 123 \nThe number of digits it has is 3\nNow if we multiply it by 10 =>123 * 10 = 1230\nyup, we successfully added a digit easily by multiplying it by 10 so now the total number of digits are 4 .\n```\nThe above intuition will help us to get the N as 1 ,11 ,111 ,1111 .... \nFinally some joy, as we are getting close to result.\n***\n**3rd Intuition :-**\n* Now the question arises that we can add a 0 easily at the end to increase the number of digits but how to add a specific digit at end (in our case instead of 0\'s we need 1\'s) !???\nOkkk , so let\'s take the same number 123 . let\'s say this time we want to append a digit 2 instead of 0 .\n\n<mark>An observation we all know:-If we are appending a single digit to a number it increases the value of the last digit of the original number by the same amount\n123[N] +2[single digit] = 125 [final number]\nso we can see that in N we addded a digit 2 and the final number is incremented by 2\n</mark>\n***\n**4th Intuition:-**\n* Now let\'s see how can we conclude the answer for how to append a specific digit at end (in our case instead of 0\'s we need 1\'s) !???\n* **So in conclusion,** to append a specific digit at the end of a number, we first multiply it by 10 (freeing up the last digit slot) and then add the digit that we want to append.\n\n**Let\'s take a example:-**\n```\nLet\'s say we want to append 2 at the end of 123\n\nn*10 = 1230(slot freed)\nn*10 + 2 = 1232 (Number 2 appended).\nNot gonna lie that was cool :)\n```\n***\n**Final Intution:-**\n* After understanding the above 4 intuitons we\'ve understood now how to append a digit at the end of a number. Let us see how can we generate the sequence 1, 11, 111, ....111...11 using the above Intuitions.\n\n**So now we need to append 1\'s as we increment our sequence**\n\nSo, Let\'s start out with num = 1 and repeatedly do num = num * 10 + 1, then in every iteration we\'ll get a new number with a digit 1 appended and in the end we will get the above sequence.\n\n1 * 10 + 1 = 11\n11 * 10 + 1 = 111\n111 * 10 + 1 = 1111\n1111 * 10 + 1 = 11111\n11111 * 10 + 1 = 111111\n1111111 * 10 +1 =1111111\n***\n**The rise of a new issue :(**\n* We can get the remainder directly from N by N % K and move on to the next N by N = N * 10 + 1.\nBut but there is a issue when N will soon be overflow since max integer in cpp/java is +2,147,483,647, which means the max N is 1,111,111,111 .\n* So instead of creating whole new numbers every time we will just use the remainder of the next N with the previous reminder\n\n**So how do we do it ????**\nBy the rules of modular arithmetic (a * b + c) mod m is same as ((a * b) % m + c % m) % m.THINK!!!\n\n**Let\'s see the proof of the above statement:-**\n```\nHere is a rule to get the remainder of the next N with the previous remainder.\nN = m * k + r ......*where r is n % k and m is modulo*\n10 * N + 1 = 10 * (m * k + r) + 1\n10 * N+ 1 = 10 * m * k + 10 * r + 1\n(10 * N + 1) % k = (10 * m * k + 10 * r + 1) % k\n(10 * N + 1) % k = (10 * r + 1) % k // (10 * m * k) % k = 0\n```\nSo whatever N is, (10 * n + 1) % k equals to (10 * r + 1) % k, where r is n % k. So that\'s why we only need to keep the remainder and thus the issue get\'s resolved .\n***\n\n*This was tough not gonna lie, now i can die happily :))*\n**Code:-**\n```\nclass Solution {\npublic: \n int smallestRepunitDivByK(int K) {\n for (int r = 0, N = 1; N <= K; ++N)\n if ((r = (r * 10 + 1) % K) == 0)\n return N;\n return -1;\n }\n};\n```\n\n**Time Complexity:-** `O(K) `\n**Space Complexity:-** `O(1)`\n\n*** | 60 | 6 | ['Math', 'C', 'C++'] | 10 |
smallest-integer-divisible-by-k | Detailed Explanation using Modular Arithmetic | detailed-explanation-using-modular-arith-0565 | Modular Arithmetic\n First, let us see how to compute powers of 10 modulo m, where m is any given number.\n---\n Use the fact that a*b % m = ( a%m * b%m ) % m\n | just__a__visitor | NORMAL | 2019-03-24T04:46:43.509599+00:00 | 2019-03-24T04:46:43.509664+00:00 | 3,466 | false | **Modular Arithmetic**\n* First, let us see how to compute powers of 10 modulo `m`, where `m` is any given number.\n---\n* Use the fact that `a*b % m = ( a%m * b%m ) % m`\n* 10<sup>n</sup> = 10<sup>n-1</sup> * 10. This implies that 10<sup>n</sup> % m = ( 10<sup>n-1</sup>%m * 10%m )%m.\n---\n**Conclusion**\n* If we denote the remainder of 10<sup>n-1</sup> as `prevRem`, then the remainder of 10<sup>n</sup> is nothing but `(prevRem * 10%m )%m`\nIn this manner, we can calculate all powers of 10 in the modular arithmetic of `m`.\n---\n**Intuition**\n* Recall that a number with digits `abc` can be represented as `100a + 10b + c`.\n* Similarly, a number with digits `abcdef` can be represented as `10000a + 1000b + 100c + 10d + e`. \n* This leads us to the fact that a number containing only the digit 1 can be represented as 1 + 10 + 100 + 1000 + ... 10<sup>maxPower</sup>\n* What would the length of such a number be? As can be clearly observed, `1` = 10<sup>0</sup>, `11` = 1 + 10<sup>1</sup>, \n `111` = 1 + 10<sup>1</sup> + 10<sup>2</sup>, `1111` = 1 + 10<sup>1</sup> + 10<sup>2</sup> + 10<sup>3</sup>.\n Therefore, for a general setting, the length is `maxPower + 1`.\n---\n**Computing 1111.....111 modulo `m`**\n* As we\'ve seen above 111...11 = 1 + 10 + 100 + 1000 + ... 10<sup>maxPower</sup>.\n* Use the fact that `(a + b)%m = (a%m + b%m) %m `\n* Therefore, in the modular arithemtic, the number 111...11 can be derived by taking the modulo of powers of 10 (by the previous technique) and then summing it up by the above rule.\n---\n\nSo far, we have seen how to generate the powers of 10 modulo `m` and how to determine the length of the number in the particular representation.\nUsing the above technique, we can generate all the numbers which contain only the digits 1 in the modular arithemetic of `m`. Now, since the desired number\nis divisible by `m`, therefore we need to see if we can generate `0` in the modular arithmetic of `m`.\n---\n---\n\n**Algorithm**\n* If `k` is a multiple of `2` or `5`, the answer would be `-1`, since the remainder can never be zero. (Why?). This happens because every multiple of a number\n which is multiple of 2 or 5 is divisible by 2 or 5, hence they can\'t end in a stream of ones.\n * Initialize `prevRem` to 1. Start the iterations. In each iteration, generate 10<sup>power</sup> in the modular arithmetic and accumulate the sum (also in modular arithemetic) and check if you\'ve reached zero or not.\n * Use the previously derived formula to obtain the next remainder and add it to the sum. If the sum becomes `0`, we have found the answer.\n * As soon as sum becomes zero, determine the length of the number (as described above) and return the length.\n \n ---\n **Upper Bound**\n * The upper bound on the length can be derived in an elegant manner using Pigeon hole principle. Refer to this [post](https://leetcode.com/problems/smallest-integer-divisible-by-k/discuss/260916/proof-we-only-need-to-consider-the-first-k-candidates-in-1-11-111-1111/253036)\n---\n```\nclass Solution \n{\npublic:\n int smallestRepunitDivByK(int k);\n};\n\nint Solution :: smallestRepunitDivByK(int k)\n{\n\tif(k%2==0 || k%5==0) return -1;\n int prevRem=1, newRem, sum=0;\n int maxLength = 100000;\n for(int power=0; power<maxLength; power++)\n {\n newRem = (prevRem * 10%k)%k;\n sum = (sum + newRem)%k;\n prevRem = newRem;\n if(sum==0) return power+1;\n }\n return -1;\n}\n``` | 45 | 4 | [] | 2 |
smallest-integer-divisible-by-k | [Python] Math, Pigeon holes, explained | python-math-pigeon-holes-explained-by-db-4pwu | First of all, let us notice, that if number is divisible by 2 or by 5, then we need to return -1 immediatly, because number ending with 1 can not divide by 2 or | dbabichev | NORMAL | 2020-11-25T09:00:18.521643+00:00 | 2020-11-25T09:00:18.521672+00:00 | 1,393 | false | First of all, let us notice, that if number is divisible by `2` or by `5`, then we need to return `-1` immediatly, because number ending with `1` can not divide by `2` or `5`. From now on we assume, that `K` is not divisible by `2` or `5`. Let us consider numbers:\n\n`1`\n`11`\n`111`\n...\n`111...111`,\n\nwhere were have `K` ones in the last group. Then, there can be only two cases:\n1. All reminders of given numbers when we divide by `K` are different.\n2. Some two reminders are equal.\n\nIn the first case, we have `K` numbers and also `K` possible reminders and they are all different, it means, that one of them will be equal to `0`.\n\nIn the second case, two numbers have the same reminder, let us say number `11...1111` with `a` ones and `111...11111` with `b` ones, where `b > a`. Then, difference of these two numbers will be divisible by `K`. What is the difference? It is number `11...1100...000` with `b-a` ones and `a` zeroes at the end. We already mentioned that `K` is not divisible by `2` or `5` and it follows, that `11...111` divisible by `K` now, where we have `b-a` ones.\n\nSo, we proved the following statements: **if K not divisible by 2 and 5, then N <= K**. What we need to do now is just iterate through numbers and stop when we find number divisible by `K`. To simplify our cumputation, we notice, that each next number is previous multiplied by `10` plus `1`.\n\n**Complexity**: time complexity is `O(n)`, space is `O(1)`.\n\n```\nclass Solution(object):\n def smallestRepunitDivByK(self, K):\n if K % 2 == 0 or K % 5 == 0: return -1\n rem, steps = 1, 1\n while rem % K != 0:\n rem = (rem*10 + 1) % K\n steps += 1\n return steps\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 37 | 11 | ['Math'] | 3 |
smallest-integer-divisible-by-k | [Python3] ✔️ Less Math, More Intuition ✔️ | 2 Accepted Solutions | Intuitive | python3-less-math-more-intuition-2-accep-vh04 | Important: A number containing only 1s cannot be divisible by 2 or 5. You can easily convince yourself that this is true since:\n A number divisble by 2 can onl | PatrickOweijane | NORMAL | 2021-12-30T01:39:06.965263+00:00 | 2021-12-30T02:11:38.577558+00:00 | 2,464 | false | **Important**: A number containing only `1`s cannot be divisible by `2` or `5`. You can easily convince yourself that this is true since:\n* A number divisble by 2 can only end with `0`, `2`, `4`, `6`, or `8`.\n* A number divisble by 5 can only end with `0`, or `5`.\n\n\u2714\uFE0F **[Accepted] First Approach:** *Making use of Python Big Integer*\nHere, we solve the problem as if overflow does not exist. In fact, Python supports arbitrarily large numbers. However, this comes at the cost of speed/memory, but anyways this is the naive way of doing it:\n```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if not k % 2 or not k % 5: return -1\n n = length = 1\n while True:\n if not n % k: return length\n length += 1\n n = 10*n + 1\n```\n\n\u2714\uFE0F **[Accepted] Second Approach:** *Using some math*\nTo improve that, the trick to avoid overflow is that we only need to store the remainder. A small proof for that can be found below:\n\n1. At every iteration, `n = kq + r` for some quotient `q` and remainder `r`.\n2. Therefore, `10*n + 1` = `10(kq + r) + 1` = `10kq + 10r + 1`.\n3. `10kq` is divisible by `k`, so for `10*n + 1` to be divisible by `k`, it all depends on if `10r + 1` is divisible by `k`.\n4. Therefore, we only have to keep track of `r`!\n\n```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if not k % 2 or not k % 5: return -1\n r = length = 1\n while True:\n r = r % k\n if not r: return length\n length += 1\n r = 10*r + 1\n``` | 32 | 5 | ['Math', 'Python', 'Python3'] | 4 |
smallest-integer-divisible-by-k | Smallest Integer Divisible by K | smallest-integer-divisible-by-k-by-alpeo-z9q0 | Given a positive integer K, we must find the length of the smallest positive integer N such that N is divisible by K, and N only contains the digit 1. If there | alpeople | NORMAL | 2020-11-25T17:15:22.667097+00:00 | 2020-11-25T17:16:35.647770+00:00 | 1,289 | false | Given a positive integer `K`, we must find the *length* of the smallest positive integer `N` such that `N` is divisible by `K`, and `N` only contains the digit `1`. If there is no such `N`, return `-1`. Therefore the following constraints must be met.\n\n* `N % K == 0`\n* length of `N` is minimized\n* `N` only contains the digit `1`\n\nThe first important item to note is that `N` may not fit into a 64-bit signed integer. This means that we can not simply iterate though the possible values of `N` and mod `K`. \n\nTo find a way to reduce the problem, lets take the example of `K=3`. The value `3` has the following possible remainders when dividing.\n\n| 0 | 1 | 2 |\n|:-:|:-:|:-:|\n\nNow, lets find the value of `N` by brute-force. In the table below, we can see that the condition `N % K == 0` is first met with the value of `111`. More interestingly, we can see that the pattern `1 -> 2 -> 0` repeats. \n\n| N | 1 | 11 | 111 | 1111 | 11111 | 111111\n|:---:|:-:|:--:|:---:|:----:|:-----:|:-----:|\n| N%K | 1 | 2 | 0 | 1 | 2 | 0 |\n\nNow, lets take a look at the example `K=6`. We can see that there are a finite number of possible remainders for any value mod `K` and that we only need to iterate thought the sequence of remainders *once* to find that `N` is not divisible by `K`.\n\n| 0 | 1 | 2 | 3 | 4 | 5 |\n|:-:|:-:|:-:|:-:|:-:|:-:|\n\n| N | 1 | 11 | 111 | 1111 | 11111 | 111111 | 1111111 |\n|:---:|:-:|:--:|:---:|:----:|:-----:|:------:|:-------:|\n| N%K | 1 | 5 | 3 | 1 | 5 | 3 | 1 |\n\nThe final piece that we must solve is how to calculate the `N%K` sequence: how to find the next remainder. We can\'t go though the values of `N` because it might not fit in a 64-bit integer. Let take a look at how we would calculate the next value of `N` and go from there. \n\n\n`N next = (N * 10) + 1` : the next value of `N` `1 -> 11 -> 111 ...`\n`remainder = N%K` : the remainder\n\n`(N next)%K = ((N * 10) + 1)%K` : we can mod both sides of our next remainder equation \n`(N next)%K = ((N * 10)%K + 1%K)%K` : the equation can then be rearranged. "It is useful to know that modulos can be taken anywhere in the calculation if it involves only addition and multiplication." *[- duke-cps102](http://db.cs.duke.edu/courses/cps102/spring10/Lectures/L-04.pdf)*\n`(N next)%K = ((N * 10)%K + 1)%K` : `1` mod anything is `1`\n`(N next)%K = ((N * 10)%K + 1)%K` : `1` mod anything is `1`\n**`remainder next = (remainder*10 + 1) %K`** : knowing that `N%K` is our remainder, we have now have a general equation that can find our next remainder value without knowing the value of `N`.\n\n```\ndef smallestRepunitDivByK(self, K: int) -> int:\n r = 0\n for c in range(1, K+1):\n r = (r*10 + 1)%K\n if r == 0: return c\n return -1\n```\n\nThe runtime of this solution is **`O(K)`**. \nThe space complexity is **`O(1)`**. | 20 | 0 | ['Python3'] | 3 |
smallest-integer-divisible-by-k | java solution with explanation | java-solution-with-explanation-by-keerth-s7ux | \nclass Solution {\n public int smallestRepunitDivByK(int k) {\n if(k%2==0 || k%5==0)\n return -1;\n int rem=0;//to calculate previo | keerthy0212 | NORMAL | 2021-12-30T04:20:36.961195+00:00 | 2021-12-30T04:20:36.961235+00:00 | 1,104 | false | ```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n if(k%2==0 || k%5==0)\n return -1;\n int rem=0;//to calculate previous rem\n for(int i=1;i<=k;i++)\n {\n rem=(rem*10+1)%k;\n if(rem==0)\n return i;\n }\n \n return -1;\n }\n}\n```\n\n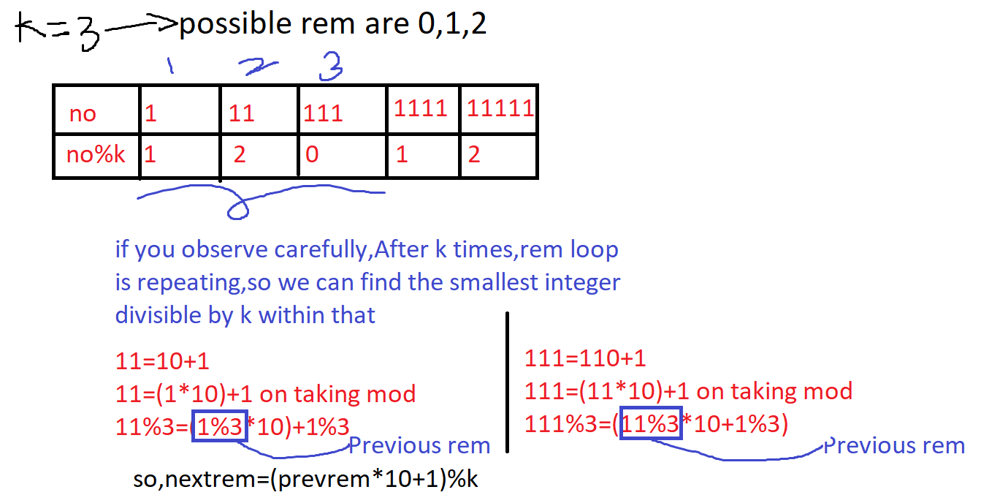\n | 17 | 4 | ['Java'] | 2 |
smallest-integer-divisible-by-k | Explanation for why new_remainder = (old_remainder * 10 + 1)%K | explanation-for-why-new_remainder-old_re-z43t | Edit\nI explain two methods below, but at the bottom there\'s also a TL;DR version if that\'s what suits you.\n\n\nThis post is just an explanation to why\nnew_ | TheJesterKing | NORMAL | 2020-11-26T18:04:09.287198+00:00 | 2021-12-30T09:47:36.147036+00:00 | 514 | false | ## Edit\nI explain two methods below, but at the bottom there\'s also a TL;DR version if that\'s what suits you.\n<hr>\n\nThis post is just an explanation to why\n`new_remainder = ((old_remainder * 10) + 1) % K`\nis the same as\n`new_remainder = ((old_number * 10) + 1) % K`\n\nI will write \n`((old_remainder * 10) + 1) % K`\nas \n` (old_remainder * 10 + 1) % K`\nfrom now as it\'s more succinct and means the same thing.\n\nSo this was pretty confusing for me, and I\'ve found atleast two easy ways to understand why this is true, there are other ways too but they were a bit beyond me and these two seem the simplest to grasp.\n<br>\n## The first method:\nThis is kind of straightforward, we just express numbers in a manner that makes the relation obvious.\n\nSo notice that every number `x` can be written as `aK + b`, \nwhere `a` is `x//K` and `b` is`x%K`.\n\nNow let\'s begin, `1 = aK+b`. So `1%K` is `b`.\n\nNext, we\'d want to find out 11%K.\nGenerally, you\'d do `next_remainder = (old_number * 10 + 1) % K`\n(Because old_number * 10 + 1 gives you the next number, 1\\*10 + 1 = 11, 11\\*10+1 = 111, so on..)\n\nAnd the natural way to do this would be `11 % K = (1 * 10 + 1) % K`\nAnd then for 111, we\'d do 111 % K = (11 * 10 + 1) % K\nFor 1111, we\'d do 1111 % K = (111 * 10 + 1) % K.\nHowever, this is bad because it\'ll lead to an overflow very soon.\n\nNow let\'s try to use the fact that `1 = aK + b`\n\nSo to find out 11%K :\n\n`11 % K = ((aK + b) * 10 + 1) % K`\n=> `11 % K = (10aK + 10b + 1) % K`\nbut `10aK` is a multiple of `K`, so we can just get rid of that\n(Example, 3 % 10, (10 + 3) % 10, (100 + 3) % 10, (1000 + 3) % 10 all evaluate to 3)\n=> `11 % K = (10b + 1) % K`\n\nAnd voila, `b` was our remainder earlier (remember, `1%K` is `b` as we saw above).\n\nLet\'s do this for 111 just so that we\'re sure we get it.\n\nSo `11 = cK + d`. Notice `d` is the remainder, `11%K = d`\n`111 % K = ((cK + d) * 10 + 1) % K`\n=> `111 % K = (10cK + 10d+ 1) % K`\n=> `111 % K = (10d + 1) % K`\nand `d` was again the remainder we had when we divided 11 by K.\n\nSo from this, it\'s easy to observe that \n`new_remainder % K = (10 * old_remainder + 1) % K`\n\nHopefully that made sense but if it didn\'t, here\'s another way\n<br>\n## The second method:\n\nHere we make use of two modular arithmetic rules:\n1) ` (a + b) % m = (a%m + b%m) % m`\n2) `(a * b) % m = (a%m * b%m) % m`\n\nNow we have `new_number = old_number * 10 + 1`\nie `m = n * 10 + 1`\nthen `m % K = (n * 10 + 1) % K`\n\nNow let\'s focus on the right hand side, `(n * 10 + 1) % K`\n\nlet `n * 10` be denoted by `a`, and `1` be denoted by `b`,\nthen `(n * 10 + 1) % K` can be represented as `(a + b) % K`.\nAnd we saw above that ` (a + b) % K = (a%K + b%K) % K`.\n\nSo we have `(n * 10 + 1) % K` = `((n * 10)%K + 1%K)) % K`.\nNow` (n * 10)%K` can be simplified using rule 2 from above as\n`(n%K * 10%K) % K`\n\nSo finally, we get \n`(n*10 + 1)%K = ((n%K * 10%K)%K + 1%K)%K`\nwhich using rule 1(stated the other way around) can be simplified to \n`(n*10 + 1)%K = (n%K * 10%K + 1%K)%K`\nwhich further reduces to \n`(n*10 + 1)%K = (n%K * 10 + 1)%K`\n(because if we allow K to be 1, then it trivially reduces to (0 * 0 + 0)%1 which is 0, \nand if we allow K to be a multiple of 10, it simply boils down to (n%10 * 0 + 1)%10 which is 1)\n \nSo notice that `(n*10 + 1)%K = (n%K * 10 + 1)%K` which shows that you can simply replace `n` by `n%K`, \nthat is replace `old_number` by `old_number%K`, essentially leading to\n`new_remainder % K = (10 * old_remainder + 1) % K`\n\nI hope that helps.<hr>\n\n## Edit\nI came back to the problem a year later, today. I had forgotten everything and had to re-derive the solution, then noticed I had written this post a year ago(26 Novemeber 2020), haha.\nJust want to give a TL;DR version of the way I derived it today(30 December 2021), just the way I worked it out on paper without any words.. just in case that\'s something that helps it to click if the two methods above didn\'t.\n\nNeed to show that \n`[(n%k)*10 + 1] %k == (n*10 + 1) %k`\n\n```[(n%k)*10 + 1] %k```\n`-> [ { (n%k) * 10 }%k + 1%k] %k` \nbecause (a+b)%m = (a%m + b%m)%m\n\n`-> [ { (n%k%k) * 10%k }%k +1%k] %k`\nbecause (a\\*b)%m = (a%m * b%m)%m\n\n`-> [ {n%k * 10%k}%k + 1%k] %k`\nbecase a%m%m = a%m\n\n`-> [ {n*10}%k + 1%k] %k`\nbecause (a%m * b%m)%m = (a\\*b)%m\n\n`-> [n*10 + 1] %k`\nbecause 1%k is 1 for all k != 1. \n(And if k is 1, the whole thing evaluates to 0 anyway so it\'s fine)\n\nSo `[(n%k)*10 + 1] %k == (n*10 + 1) %k` | 16 | 0 | [] | 4 |
smallest-integer-divisible-by-k | 0 ms C++ solution with explanation | 0-ms-c-solution-with-explanation-by-rtf1-yeq3 | Explanation:\nFirst, you should be able to convince yourself that if K is even or divisible by 5, then no multiple of K can end in 1.\nWhat\'s perhaps not obvio | rtf121 | NORMAL | 2019-07-13T22:03:26.096955+00:00 | 2019-07-13T22:08:04.314583+00:00 | 1,097 | false | Explanation:\nFirst, you should be able to convince yourself that if K is even or divisible by 5, then no multiple of K can end in 1.\nWhat\'s perhaps not obvious is that if K is not even or divisible by 5, then there must be a solution. Here\'s a nice way to see it:\n\nLet n_1 = 1, n_2 = 11, n_3 = 111, etc. Note that n_i is a multiple of K if and only if ( n_i % K == 0 ) .\n\nAs we look at all the terms in this sequence taken modulo K, since the sequence is infinitely long but there are only finitely many residue classes mod K, we must eventually repeat some value. Say, (n_i % K == n_j % K ), where i and j are distinct positive integers.\n\nThen (n_i - n_j % K == 0). But if you look at these numbers, you get something like (11111111-111 % K == 0), i.e. (11111000 % K == 0). Since we\'ve already checked that K has no factor of 2 or 5, this implies that (11111 % K == 0).\n\nI want to make sure you don\'t confuse this logic with the code below. This reasoning is only to justify that there is some solution. In the actual code, we don\'t need to carry out this same logic. We can just look for the first n_i whose value mod K is 0, and because of the argument above we know that this search will terminate (in fact, we know it will terminate after K or fewer steps, since it will take at most K+1 steps to repeat a value mod K).\n\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n if ((K%2 == 0) or (K%5 == 0))\n return -1;\n \n int currentLength = 1;\n int currentModulus = currentLength % K;\n \n while (currentModulus != 0)\n {\n currentModulus *= 10;\n currentModulus += 1;\n currentModulus = currentModulus % K;\n currentLength += 1; \n }\n return currentLength; \n }\n};\n``` | 16 | 0 | [] | 1 |
smallest-integer-divisible-by-k | C++ 3 lines, O(K) | O(1) | c-3-lines-ok-o1-by-votrubac-542p | Intuition\nWe can do a long division until our modulo is zero. If the number is not divisible, at some point we will encountered a modulo that we have seen befo | votrubac | NORMAL | 2019-03-24T04:07:58.367209+00:00 | 2019-03-24T04:07:58.367248+00:00 | 1,551 | false | # Intuition\nWe can do a long division until our modulo is zero. If the number is not divisible, at some point we will encountered a modulo that we have seen before.\n# O(K) Memory Solution\nFor every digit, we track modulo ```m``` and add one more ```1``` (```(m % K) * 10 + 1```). We can ignore division results for this problem.\nTrack all moduli in ```seen``` and stop if the value has been seen before (in other words, we detected a loop).\nIf we ever seen ```m == 0```, then the integer is divisible, and number of digits is number of different moduli we encountered.\n```\nint smallestRepunitDivByK(int K) {\n vector<bool> seen(K);\n for (int m = 1; !seen[m % K]; m = (m % K) * 10 + 1) seen[m % K] = true;\n return seen[0] ? count_if(begin(seen), end(seen), [](bool s) { return s; }) : -1;\n}\n```\n## Complexity Analysis\nRuntime: O(K). We can have maximum K moduli before we enter a loop.\nMemory: O(K). We need to track K moduli.\n# Constant Memory Solution\nAlternativelly, we can just always perform up to K iterations and check if our modulo ```m``` is zero. As the solution above demonstrates, we need maximum K steps to find a solution or we enter a loop.\n```\nint smallestRepunitDivByK(int K) {\n for (int m = 1, N = 1 % K; N <= K; m = (m * 10 + 1) % K, ++N)\n if (m == 0) return N;\n return -1;\n}\n```\n## Complexity Analysis\nRuntime: O(K). We perform maximum K iterations.\nMemory: O(1).\n | 15 | 3 | [] | 2 |
smallest-integer-divisible-by-k | java 1ms modular solution with explanation | java-1ms-modular-solution-with-explanati-sfki | At first, if K ends with digit {0, 2, 4, 5, 6, 8}, i.e., K can be divided by 2 or 5, we can\'t find such integer.\nIf not, a intuitive idea is initiating the ta | pangeneral | NORMAL | 2019-04-16T01:34:47.138722+00:00 | 2019-04-16T01:34:47.138792+00:00 | 918 | false | At first, if ```K``` ends with digit {0, 2, 4, 5, 6, 8}, i.e., ```K``` can be divided by 2 or 5, we can\'t find such integer.\nIf not, a intuitive idea is initiating the target integer ```number``` to 1 and keep the operation ```number = number * 10 + 1``` until ```n``` can be divide by ```K```. However, if ```K``` is very large, ```number``` will overflow.\nHere, we need to make use of the characteristics of modular arithmetic:\n1. ```(a + b) % k = (a % k + b % k) % k```\n2. ```(a * b) % k = ( (a % k) * (b % k)) % k```\nAssume the smallest number is ```m = n * 10 + 1```, then ```(n * 10 + 1) % K = 0```, which means ```((n % K) * (10 % k) + 1 % K ) % K = 0```. Therefore, we can replace ```number``` with ```number % K``` to calculate the smallest number.\n```\npublic int smallestRepunitDivByK(int K) {\n\tif( K % 2 == 0 || K % 5 == 0 )\n\t\treturn -1;\n\tint base = 1, number = 1;\n\twhile( number % K != 0 ) {\n\t\tnumber = (number * 10 + 1) % K;\n\t\tbase++;\n\t}\n\treturn base;\n}\n``` | 13 | 0 | ['Java'] | 0 |
smallest-integer-divisible-by-k | [C++] Simple Short Explanation | No Pigeon Holes | c-simple-short-explanation-no-pigeon-hol-liyf | Explanation - \n\nSince the series is 1, 11, 111, 1111, ... so the Next_Num = Prev10+1;\n\nNow using some modulo property.\nLet say remainder from prev is - \nA | luci3fr | NORMAL | 2020-11-25T16:15:54.497148+00:00 | 2020-11-26T04:00:26.797057+00:00 | 726 | false | Explanation - \n\nSince the series is 1, 11, 111, 1111, ... so the Next_Num = Prev*10+1;\n\nNow using some modulo property.\nLet say remainder from prev is - \nA = Prev%K;\nB = Next%K \n= (Prev * 10 + 1)%K \n= ( (Prev * 10)%K + 1%K )%K\n= ( ( (Prev%K) * (10%K) )%K + 1%K )%K \n=( ( A * (10%K) )%K + 1%K )%K\n=( ( A * 10 )%K + 1%K )%K\n=(A*10+1)%K --- Equation #1\n\nAlso to note that if we reach a remainder(X) which we have already seen, then same steps will be repeated and we will again reach X if we proceed ahead. This means we will never reach remainder = 0 and move infinitely in cycle. So keep track of what all remainder we have seen so far in set or array, whichever way you prefer.\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n unordered_set<int>st; // to keep track of remainders we have seen so far\n int rem=1%K; // Series start with 1\n while(rem!=0 && st.find(rem)==st.end()){\n st.insert(rem);\n rem=(rem*10+1)%K; // From Equation #1 above\n }\n \n if(rem==0)\n return st.size()+1; // Set has all the intermediate remainders we got before we reach zero, so answer is one more than size of set\n \n return -1;\n }\n};\n``` | 12 | 2 | ['C'] | 4 |
smallest-integer-divisible-by-k | Very short and clear explanation O(K) (also 2 lines[Java/C++/C#/JavaScript/PHP]). | very-short-and-clear-explanation-ok-also-8tqf | We\'re interested a % K == 0, for a=1,11,111,.. Next element a = (a*10+1)%K, notice that this is a function of one value that maps a value of (0 to K-1) to a v | zed_b | NORMAL | 2019-03-25T14:41:37.239912+00:00 | 2019-03-25T14:41:37.239951+00:00 | 1,121 | false | We\'re interested a % K == 0, for a=1,11,111,.. Next element ```a = (a*10+1)%K```, notice that this is a function of one value that maps a value of (0 to K-1) to a value of (0 to K-1). So, if after K runs we haven\'t seen 0, it means we have seen another value (0,K-1) twice, which means we\'ve already are in a loop between those two occurances, and if 0 hasn\'t occured, it never will.\n\n```C++\n// C++, Java, C, C#\nfor(int i=1,a=0;i<=K;i++) if((a=(a*10+1)%K)==0)return i;\nreturn -1;\n```\n```JavaScript\n// Let it be JavaScript\nfor(let i=1,a=0;i<=K;i++) if((a=(a*10+1)%K)==0)return i;\nreturn -1;\n```\n```PHP\n// PHP $$$\nfor($i=1,$a=0;$i<=$K;$i++) if(($a=($a*10+1)%$K)==0)return $i;\nreturn -1;\n```\n```Python\n# Python is too line verbose\na = 0\nfor i in range(1,K+1):\n\ta=(a*10+1)%K\n\tif a==0:\n\t\treturn i\nreturn -1\n``` | 11 | 1 | [] | 3 |
smallest-integer-divisible-by-k | C++ | easy | c-easy-by-sonusharmahbllhb-03qc | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n int ans=1;\n int num=0;\n while(ans<100000){\n num=num*10+ | sonusharmahbllhb | NORMAL | 2021-08-30T13:45:45.110194+00:00 | 2021-08-30T13:45:45.110226+00:00 | 568 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n int ans=1;\n int num=0;\n while(ans<100000){\n num=num*10+1;\n if(num>=k) num=num%k;\n if(num==0) return ans;\n ans++;\n }\n return -1;\n }\n};\n``` | 8 | 0 | ['C', 'C++'] | 1 |
smallest-integer-divisible-by-k | Smallest Integer Divisible by K || C++ || 100% FAST | smallest-integer-divisible-by-k-c-100-fa-lzcp | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n int num=0;\n for(int i=1;i<=K;i++)\n {\n num=(num*10)%K+1; | ayushidoshi56 | NORMAL | 2020-11-25T10:47:35.484975+00:00 | 2020-11-25T10:47:35.485011+00:00 | 335 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n int num=0;\n for(int i=1;i<=K;i++)\n {\n num=(num*10)%K+1;\n if(num%K==0)\n {\n return i;\n }\n }\n return -1;\n }\n};\n``` | 6 | 1 | [] | 4 |
smallest-integer-divisible-by-k | Efficient Solution using modulo-arithmetic: Consider Only (1, 3, 7, 9) as unit digit-> | efficient-solution-using-modulo-arithmet-8sn6 | We know that the number with unit digit of 0, 2, 4, 5, 6, 8 never gives least significant digit as 1 so we have to return -1 in these cases. \nonly we have to | mdcse | NORMAL | 2022-02-14T15:16:04.661361+00:00 | 2022-02-14T15:16:41.706113+00:00 | 117 | false | We know that the number with **unit digit of 0, 2, 4, 5, 6, 8 never gives least significant digit as 1 so we have to return -1** in these cases. \nonly we have to consider the number whith least significant digit **1, 3, 7, 9.**\nTry to under stand the problem by spliting it in least significant digit as 1, 3, 7, 9.\nthen only go to Solution part.\nand if you like this approach then **please upvote it.**\n\n\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) \n {\n if(k%10==1 || k%10==3 || k%10==7 || k%10==9)\n {\n int x=0, count=0;\n while(1)\n {\n count++;\n x=((10 * x)%k +1 )%k;\n if(!x)return count;\n }\n }\n \n return -1;\n }\n};\n```\n\n\n\n | 4 | 0 | ['C'] | 0 |
smallest-integer-divisible-by-k | [Java Solution, Faster than 100%] Easy understand with pigeonhole principle | java-solution-faster-than-100-easy-under-zxqe | We start with a math problem, which can be easily proved by the Pigeonhole principle: \nGiven a positive k such as gcd(k, 10) = 1. Prove that there is a positiv | khanhba | NORMAL | 2021-12-30T15:09:10.460741+00:00 | 2021-12-30T15:28:41.652084+00:00 | 230 | false | We start with **a math problem**, which can be easily proved by the Pigeonhole principle: \nGiven a positive k such as gcd(k, 10) = 1. Prove that there is a positive integer n with all digits equal to 1 such that: n is divisible by k. \n\nWe can easily see that by Pigeonhole principle: in k + 1 numbers 1, 11, 111, ..., 111..1 (k + 1 digts 1) \n-> there will be two number that has the same remainder when divided by k, for example, 11...1 (p digits 1) and 11...1 (q digits 1) ( p > q). \nThen, (111...1 - 111...1) % k = 0 or 11...1 * 10^q % k = 0. So 11...1 (p - q digit 1) % k = 0 (because gcd(k, 10) = 1)\n\n**So back to origin problem**, we can easily find the smallest integer n by a loop from 1 to k + 1, each time we will recalculate the remainder of the current number divided by k, and return the result when remainder = 0. The solution is only **O(k)** time complexity. \nDon\'t forget to check ***if (k, 10) != 1*** we will not have any solution. (because an integer n is divisible by 2 must be even and divisible by 5 must have end digit is 0 or 5). \n\n```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n if(k % 2 == 0 || k % 5 == 0) {\n return -1;\n }\n int ans = 1, cur = 1;\n for(int i = 1; i <= k + 1; i++) {\n if(cur % k == 0) {\n return ans; \n }\n ans++; cur = (cur * 10 + 1) % k;\n }\n return ans;\n }\n}\n``` | 4 | 0 | ['Math'] | 0 |
smallest-integer-divisible-by-k | C++ | Math | Clear Code with Explanation | c-math-clear-code-with-explanation-by-si-n20i | 1015. Smallest Integer Divisible by K\n\nAn intuitive solution is to check the number one by one.\ncpp\nint n = 1, len = 1;\nwhile (n % k != 0)\n len += 1, n | sinkinben | NORMAL | 2021-12-30T05:34:07.504715+00:00 | 2021-12-30T05:34:07.504752+00:00 | 549 | false | **1015. Smallest Integer Divisible by K**\n\nAn intuitive solution is to check the number one by one.\n```cpp\nint n = 1, len = 1;\nwhile (n % k != 0)\n len += 1, n = n * 10 + 1;\nreturn len\n```\n\nHowever, there are two problems in this intuitive solution:\n+ `n` may overflow `INTMAX`, hence we should use the remainer of `n % k` as the next value to be checked.\n+ such `n` which satisfy `n % k == 0` may not exist.\n\nTo fix 1st issue:\n```cpp\nint n = 1, len = 1;\nwhile (n % k != 0)\n len += 1, n = (n * 10 + 1) % k;\nreturn len\n```\n\nAnd based on this code, we can infer that `n` may have `k` different values at most.\n\nTo fix 2nd issue, we can try to check each possible value of `n` (which means we would try `k` times at most.)\n\nSince `n = (n * 10 + 1) % k`, it\'s sure that the remainer is different after each step of loop.\n\n```cpp\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if ((k & 1) == 0) return -1;\n int len = 1, n = 1;\n for (int i = 1; i <= k; ++i)\n {\n if (n % k == 0) return len;\n n = (n * 10 + 1) % k, len += 1;\n }\n return -1;\n }\n};\n```\n | 4 | 0 | ['C'] | 1 |
smallest-integer-divisible-by-k | Intution for 'cycle of remainders': 11 % 6 == 11111 % 6 == 11111111 % 6 == 3 | intution-for-cycle-of-remainders-11-6-11-995v | While I had a gut feeling about the cyclic repetition of remainders, I had a hard time coming up with a proof (and thereby an efficient solution). While all the | celmar_stone | NORMAL | 2020-11-28T08:03:38.616091+00:00 | 2020-11-29T05:21:27.282091+00:00 | 250 | false | While I had a gut feeling about the cyclic repetition of remainders, I had a hard time coming up with a proof (and thereby an efficient solution). While all the info is already there between other comments and the solution, I hope that the intution below helps.\n\nGiven a solution exists, finding it is not that hard: we keep creating the next larger number consisting of only \'1\'s and checking if it divides K without remainder:\n```python\ndef find_sol(K):\n\tn = count = 1\n\twhile True:\n\t remainder = n % K\n\t\tif remainder == 0:\n\t\t break\n\t\tn = 10 * n + 1\n\t\tcount += 1\t\n\treturn count\n```\n\nThe key question is: does a solution exist? Observations:\n* A multiple of an even number can never be an odd number --> K has to be odd\n* A similar case can be made for muliples of 5: they can only end in \'5\' or \'0\'\n\nFor numbers ending in 1, 3, 7, and 9, we have to think of something else. By the pigeonhole principle, it is clear that taking a series of numbers modulo K can only have K distinct remainders: remainder in [0..K-1].\nBut: how to prove that, as soon as we see a duplicate remainder, we actually have entered a **cycle of remainders**? Differently put: how can we prove that the **next remainder only depends on the previous remainder**, and not on the actual number \'n\'? Concretely:\n> Why does 11 % 6 == 11111 % 6 == 11111111 % 6 == 3?\n\nAll it really takes, is to look at two consecutive remainders with the equations already used in the code above:\n* Relation between \'n\' and the remainder: `n = x * k + rem`\n* Next number n: `next_n = 10 * n + 1`\n* the next remainder is calculated by: `next_rem = next_n % k`\n\nNow substitute the equations into one another:\n```python\nnext_rem = next_n % k\n = (10 * n + 1) % k\n = (10 * (x * k + rem) + 1) % k\n\t\t = ((10 * x * k) % k + (10 * rem) % k + 1 % k) % k # distributive property of modulo\n\t\t = (10 * rem) % k + 1 # any multiple of k is 0 when taken modulo k\n```\n\nSo, a future remainder depends only on the previous remainder, not on the actual value of n. Therefore: as soon as we see a remainder for the second time, we have entered a cycle.\nThis has the further benefit of making our code much more efficient, since we don\'t have to use any numbers larger than K:\n\n```python\nclass Solution:\n def smallestRepunitDivByK(self, K: int) -> int:\n if K % 2 == 0 or K % 5 == 0:\n return -1 # multiples of 2, 4, 5, 6, 8 can never end with digit 1\n \n remainder = 0\n for cnt in range(1, K+1):\n remainder = (10 * remainder + 1) % K\n if remainder == 0:\n return cnt\n return -1\n```\n\n**Analysis**\nO(K) time: at most K operations that take O(1) each\nO(1) space\n\n | 4 | 0 | ['Python3'] | 1 |
smallest-integer-divisible-by-k | JavaScript Solution | javascript-solution-by-dingyangf911-xtox | ```\nvar smallestRepunitDivByK = function(K) {\n let count = 1\n let start = 1\n let set = new Set()\n while (start) {\n let r = start % K\n | dingyangf911 | NORMAL | 2020-11-25T15:09:09.154987+00:00 | 2020-11-25T15:09:09.155027+00:00 | 248 | false | ```\nvar smallestRepunitDivByK = function(K) {\n let count = 1\n let start = 1\n let set = new Set()\n while (start) {\n let r = start % K\n if ( r === 0 ) {\n break\n }\n if ( set.has(r) === true ) {\n return -1\n } else {\n set.add(r)\n start = r * 10 + 1\n count++\n }\n \n }\n return count\n}; | 4 | 0 | ['JavaScript'] | 0 |
smallest-integer-divisible-by-k | Python | python-by-gsan-l76j | The Pigeonhole Principle from the other solutions also apply here: If we don\'t have the remainder 0 after k iterations (k iterations counted inside the last wh | gsan | NORMAL | 2020-11-25T09:15:26.634598+00:00 | 2020-11-25T23:25:08.411949+00:00 | 233 | false | The Pigeonhole Principle from the other solutions also apply here: If we don\'t have the remainder `0` after `k` iterations (`k` iterations counted inside the last while-loop) we have `k` spaces for `k-1` candidates and we will get a duplicate.\n\n```python\nclass Solution:\n def smallestRepunitDivByK(self, k):\n #start from n\n n = 1\n while n<k: \n n = 10*n + 1\n #set of remainders\n rm = set()\n while True:\n if n%k==0:\n return len(str(n))\n if n%k in rm:\n return -1\n rm.add(n%k)\n n = 10*n + 1\n``` | 4 | 0 | [] | 0 |
smallest-integer-divisible-by-k | C# HashSet | c-hashset-by-serpol-5v6p | \npublic int SmallestRepunitDivByK(int K) {\n int res = 1;\n int len = 1;\n HashSet<int> rests = new HashSet<int>();\n while(true) {\n res %= | serpol | NORMAL | 2019-03-28T15:04:53.467105+00:00 | 2019-03-28T15:04:53.467169+00:00 | 226 | false | ```\npublic int SmallestRepunitDivByK(int K) {\n int res = 1;\n int len = 1;\n HashSet<int> rests = new HashSet<int>();\n while(true) {\n res %= K;\n if(res == 0) return len;\n if(rests.Contains(res)) return -1;\n rests.Add(res);\n len++;\n res *= 10;\n res += 1;\n }\n}\n``` | 4 | 1 | [] | 0 |
smallest-integer-divisible-by-k | 🔥Easiest & Best Solution in 5 Lines 💯 | easiest-best-solution-in-5-lines-by-no_o-7nhd | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | No_one_can_stop_me | NORMAL | 2023-04-11T01:42:47.151913+00:00 | 2023-04-11T01:43:17.802488+00:00 | 151 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(k)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nPlssssss Up Vote! -> \uD83D\uDE2D\n# Code\n```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n int remainder = 0;\n for (int length_N = 1; length_N <= k; length_N++) {\n remainder = (remainder * 10 + 1) % k;\n if (remainder == 0) return length_N;\n }\n return -1;\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
smallest-integer-divisible-by-k | Smallest Integer Divisible by K | Java | O(n) | 85% faster | | smallest-integer-divisible-by-k-java-on-isurq | class Solution {\n\n public int smallestRepunitDivByK(int k) {\n if (k % 2 == 0 || k % 5 == 0) return -1;\n int remainder = 0;\n for (in | abhishekjha786 | NORMAL | 2021-12-30T18:10:05.891179+00:00 | 2021-12-30T18:10:05.891218+00:00 | 54 | false | class Solution {\n\n public int smallestRepunitDivByK(int k) {\n if (k % 2 == 0 || k % 5 == 0) return -1;\n int remainder = 0;\n for (int i = 1; i <= k; i++) {\n remainder = (remainder * 10 + 1) % k;\n if (remainder == 0) return i;\n }\n return -1;\n }\n}\n**Please help to UPVOTE if this post is useful for you.\nIf you have any questions, feel free to comment below.\nHAPPY CODING :)\nLOVE CODING :)** | 3 | 1 | ['Math'] | 0 |
smallest-integer-divisible-by-k | [Java - C++ - C - C# - JavaScript] easy o(1) space | java-c-c-c-javascript-easy-o1-space-by-z-w88m | if you like it pls upvote\n\nJava\n\nclass Solution {\n public int smallestRepunitDivByK(int K) {\n if (K % 2 == 0 || K % 5 == 0) return -1;\n | zeldox | NORMAL | 2020-11-25T12:24:48.135705+00:00 | 2020-11-25T12:25:52.468781+00:00 | 170 | false | if you like it pls upvote\n\nJava\n```\nclass Solution {\n public int smallestRepunitDivByK(int K) {\n if (K % 2 == 0 || K % 5 == 0) return -1;\n int r = 0;\n for (int N = 1; N <= K; N++) {\n r = (r * 10 + 1) % K;\n if (r == 0) return N;\n }\n return -1;\n }\n}\n```\n\nC++\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n if (K % 2 == 0 || K % 5 == 0) return -1;\n int r = 0;\n for (int N = 1; N <= K; N++) {\n r = (r * 10 + 1) % K;\n if (r == 0) return N;\n }\n return -1;\n }\n};\n```\n\nC\n```\nint smallestRepunitDivByK(int K){\n\tif (K % 2 == 0 || K % 5 == 0) return -1;\n int r = 0;\n for (int N = 1; N <= K; N++) {\n r = (r * 10 + 1) % K;\n if (r == 0) return N;\n }\n return -1;\n}\n```\n\nC#\n```\npublic class Solution {\n public int SmallestRepunitDivByK(int K) {\n if (K % 2 == 0 || K % 5 == 0) return -1;\n int r = 0;\n for (int N = 1; N <= K; N++) {\n r = (r * 10 + 1) % K;\n if (r == 0) return N;\n }\n return -1;\n }\n}\n```\n\nJavaScript\n```\nvar smallestRepunitDivByK = function(K) {\n if (K % 2 == 0 || K % 5 == 0) return -1;\n var r = 0;\n for (var N = 1; N <= K; N++) {\n r = (r * 10 + 1) % K;\n if (r == 0) return N;\n }\n return -1;\n};\n``` | 3 | 0 | ['C', 'Java', 'JavaScript'] | 0 |
smallest-integer-divisible-by-k | C++ Simplest and Shortest Solution, 0 ms faster than 100% | c-simplest-and-shortest-solution-0-ms-fa-8k32 | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n if (K % 2 == 0) // Always false when K is even\n return -1;\n \n | yehudisk | NORMAL | 2020-11-25T08:11:24.928561+00:00 | 2020-11-25T08:11:24.928601+00:00 | 122 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n if (K % 2 == 0) // Always false when K is even\n return -1;\n \n int num = 1, res = 1;\n \n while (num % K) {\n num = (num * 10 + 1) % K;\n res++;\n if (res > K)\n return -1;\n }\n return res;\n }\n};\n```\n**Like it? please upvote...** | 3 | 2 | ['C'] | 0 |
smallest-integer-divisible-by-k | Python | Easy Understanding | While Loop | Brute Force | 1988ms) | python-easy-understanding-while-loop-bru-u6vk | ```class Solution:\n def smallestRepunitDivByK(self, K: int) -> int:\n if K%2==0 or K%5==0:\n return -1\n i=1\n c=1\n | ishaan-s1 | NORMAL | 2020-10-15T13:36:18.088508+00:00 | 2020-10-15T13:36:18.088542+00:00 | 103 | false | ```class Solution:\n def smallestRepunitDivByK(self, K: int) -> int:\n if K%2==0 or K%5==0:\n return -1\n i=1\n c=1\n while True:\n if i%K==0:\n return c\n i=10*i+1\n c+=1\n#1*10+1=11, 11*10+1=111, 111*10+1=1111 ....... | 3 | 1 | [] | 1 |
smallest-integer-divisible-by-k | c++ solution , beats 100% | c-solution-beats-100-by-goyalanshul809-wv8v | class Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n \n int i =0;\n if(k%2==0 || k%5==0)\n return -1;\n in | goyalanshul809 | NORMAL | 2020-08-17T05:38:05.592420+00:00 | 2020-08-17T05:38:05.592460+00:00 | 179 | false | class Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n \n int i =0;\n if(k%2==0 || k%5==0)\n return -1;\n int mod = 0;\n while(true)\n {\n mod = (mod*10 + 1)%k;\n i++;\n if(mod==0)\n return i;\n \n }\n return -1 ;\n }\n}; | 3 | 0 | [] | 0 |
smallest-integer-divisible-by-k | [Java/C++] Find 111....11 divisible by K | javac-find-11111-divisible-by-k-by-hamle-uxfg | Intuition and Algorithm\n\nIf W = 11\u2026\u202611 have t ones\nThen W * 10 +1 will have t + 1 ones\n\nLet\u2019s create every number modulus K\n\nWe know:\ | hamlet_fiis | NORMAL | 2019-03-24T04:03:02.733776+00:00 | 2019-03-24T04:03:02.733834+00:00 | 381 | false | <strong>Intuition and Algorithm</strong>\n\nIf <code>W = 11\u2026\u202611</code> have <code>t</code> ones\nThen <code>W * 10 +1 </code> will have <code>t + 1</code> ones\n\nLet\u2019s create every number modulus <code>K</code>\n\nWe know:\n* <code> (A*B+C)%K</code> = <code> (A%K * B%K + C%K) %K</code>\n\nIt is only necessary to iterate <code>K</code> times because we get a distinct result in each iteration, if the module is <code>0</code> then the number of iterations is the answer.\n\n<b>C++</b>\n<code>\n\n\tclass Solution {\n\tpublic:\n\t\tint smallestRepunitDivByK(int K) {\n\t\t\tfor(int i=1,val=1; i<=K; i++){\n\t\t\t\tif(val % K == 0) return i;\n\t\t\t\tval = (val*10 + 1)%K;\n\t\t\t} \n\t\t\treturn -1;\n\t\t}\n\t};\n</code>\n\n<b>Java</b>\n<code>\n\n\tclass Solution {\n\t\tpublic int smallestRepunitDivByK(int K) {\n\t\t\tfor(int i=1,val=1; i<=K; i++){\n\t\t\t\tif(val % K == 0) return i;\n\t\t\t\tval = (val*10 + 1)%K;\n\t\t\t} \n\t\t\treturn -1;\n\t\t}\n\t}\n</code>\n\nA small improvement is to validate if there is a loop.\n\n<b>C++</b>\n<code>\n\n\tclass Solution {\n\tpublic:\n\t\tint smallestRepunitDivByK(int K) {\n\t\t\tunordered_set<int>S;\n \n\t\t\tfor(int i=1,val=1; i<=K; i++){\n\t\t\t\tif(val % K == 0) return i;\n\t\t\t\tif(S.find(val%K) != S.end())return -1; //exists a loop\n\t\t\t\tval = (val*10 + 1)%K;\n\t\t\t}\n \n\t\t\treturn -1;\n\t\t}\n\t};\n</code> | 3 | 1 | [] | 0 |
smallest-integer-divisible-by-k | ✅💯🔥Simple Code🚀📌|| 🔥✔️Easy to understand🎯 || 🎓🧠Beats 100%🔥|| Beginner friendly💀💯 | simple-code-easy-to-understand-beats-100-wz7w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | atishayj4in | NORMAL | 2024-07-28T21:09:57.927539+00:00 | 2024-08-01T19:45:27.445316+00:00 | 139 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n// //////////////////ATISHAY\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ \\\\\n// \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\JAIN////////////////// \\\\\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n if (k%2==0 || k%5==0){\n return -1;\n }\n int ans = 0;\n for (int n=1; n<=k; n++) {\n ans = (ans*10+1)%k;\n if (ans==0){\n return n;\n }\n }\n return -1;\n }\n}\n```\n | 2 | 0 | ['Hash Table', 'Math', 'C', 'Python', 'C++', 'Java'] | 1 |
smallest-integer-divisible-by-k | ✅100% faster C++ Code O(1) space ✅ | 100-faster-c-code-o1-space-by-daveak-prkn | \n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n \n int smallestRepunitDivByK(int k) {\n | DaveAk | NORMAL | 2023-05-06T19:55:53.913881+00:00 | 2023-05-06T19:55:53.913921+00:00 | 363 | false | \n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n \n int smallestRepunitDivByK(int k) {\n int m=k;\n if(k%2==0 || k%5==0)return -1;\n int digits=0,c=0;\n m=k;\n while(m!=0)m=m/10,digits=digits*10+1,c++;\n \n int rem=(digits%k);\n while(rem!=0){\n c++;\n rem=rem*10+1;\n rem=rem%k;\n }\n return c;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
smallest-integer-divisible-by-k | Easiest C code 100%beats | easiest-c-code-100beats-by-karan_kumar19-d5dg | \n# Code\n\nint smallestRepunitDivByK(int k){\nint karan=1;\nint j=0;\nfor(int i=1;i<=k;i++)\n{\nj++;\nif(karan%k==0)\nreturn j;\nelse\nkaran=(karan*10+1)%k;\n} | Karan_kumar19 | NORMAL | 2022-11-16T18:00:10.731654+00:00 | 2022-11-16T18:00:10.731684+00:00 | 190 | false | \n# Code\n```\nint smallestRepunitDivByK(int k){\nint karan=1;\nint j=0;\nfor(int i=1;i<=k;i++)\n{\nj++;\nif(karan%k==0)\nreturn j;\nelse\nkaran=(karan*10+1)%k;\n}\nreturn -1;\n}\n``` | 2 | 0 | ['C'] | 1 |
smallest-integer-divisible-by-k | ✅Easiest & Short Code in C++||O(1)SC✅✅ | easiest-short-code-in-co1sc-by-adish_21-5dx4 | Complexity\n- Time complexity:\nO(k)\n\n- Space complexity:\nO(1)\n\n# Code\nPlease upvote if u liked my Solution\uD83D\uDE42\n\nclass Solution {\npublic:\n | aDish_21 | NORMAL | 2022-10-20T04:23:36.137375+00:00 | 2022-10-20T04:23:36.137420+00:00 | 1,332 | false | # Complexity\n- Time complexity:\nO(k)\n\n- Space complexity:\nO(1)\n\n# Code\n**Please upvote if u liked my Solution**\uD83D\uDE42\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if((k & 1)==0 || k==5)\n return -1;\n int n=0;\n for(int i=0;i<k;i++){\n n = (n * 10) % k + (1 % k); //using the modulo property i.e ((a*b)+c)%k == ((a*b)%k + c%k)%k\n if(n % k == 0)\n return i+1;\n }\n return -1;\n }\n};\n``` | 2 | 0 | ['Math', 'C++'] | 0 |
smallest-integer-divisible-by-k | C++ || 0ms Solution | c-0ms-solution-by-khwaja_abdul_samad-won7 | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n \n if(k % 2 == 0 || k%5 == 0)\n return -1;\n \n int | Khwaja_Abdul_Samad | NORMAL | 2022-08-21T06:57:00.915351+00:00 | 2022-08-21T06:57:00.915552+00:00 | 282 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n \n if(k % 2 == 0 || k%5 == 0)\n return -1;\n \n int num = 0;\n int count = 0;\n \n while(count<k)\n {\n count++;\n \n num = (num * 10 + 1)%k;\n //cout<<num<<endl;\n if(num%k == 0)\n return count;\n }\n \n return -1;\n }\n};\n``` | 2 | 0 | ['C'] | 0 |
smallest-integer-divisible-by-k | java solution | java-solution-by-mmk0077-3rdk | \nclass Solution {\n public int smallestRepunitDivByK(int k) {\n int n=0;\n if(k%2==0 || k%5==0)\n return -1;\n int i=1;\n | MMK0077 | NORMAL | 2022-01-02T08:21:51.510247+00:00 | 2022-01-02T08:21:51.510276+00:00 | 181 | false | ```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n int n=0;\n if(k%2==0 || k%5==0)\n return -1;\n int i=1;\n while(i<=k){\n n=(n*10+1)%k; /*its used to get next remainder*/\n if(n==0){\n return i;\n }\n i++; /*counting length of n*/\n }\n return -1;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
smallest-integer-divisible-by-k | Some Exploration on Euler's Totient Function, The Carmichael Function and Modulus Order | some-exploration-on-eulers-totient-funct-61oa | Happy New Year!\n\nI have to thank @cjj9000 for providing me the direction which ultimately led to this interesting exploration. I initiall thought this could b | jingminz | NORMAL | 2022-01-01T07:01:16.095530+00:00 | 2022-01-01T07:06:31.521005+00:00 | 571 | false | Happy New Year!\n\nI have to thank @cjj9000 for providing me the direction which ultimately led to this interesting exploration. I initiall thought this could be broken into 3 steps and the question could be solved analytically instead of iteratively. However, it turned out to be more challenging than I initially thought and we would still require a tiny bit iteration on a few candidates to find the final ansnwer. Maybe someone can take it from here and further update the alternative solution.\n\nBelow is my initial thought process and exploration (again, thanks to @cjj9000 for the hint on Euler\'s Totient Function)\n\t\t\t\n### Step 1: Reframing the problem\nProblem 1015 is asking us to find the smallest `111...111` (of **m** digits) that is divisible by `k`, which is equivalent to finding the smallest `999...999` (of **m** digits) that is divisible by `9k`, which is then equivalent to finding the smallest **m** such that `10 ** m - 1` is divisible by `9k`, or `mod(10 ** m, 9k) == 1`.\n\nHere, we can immediately see that if `k % 2 == 0 or k % 5 == 0`, then `mod(10 ** m, 9k) == 1` will never happen. Written in Python\n\n```python\nif k % 2 == 0 or k % 5 == 0:\n\treturn -1\n```\n\n**Actually, here we can already have a solution that is based on** `mod(10 ** m, 9k) == 1`. Below is the Python code. O(n) time complexity and O(1) space complexity. Although similar to the popular solution, the perspective is different\n* Solution 1\n\t```python\n\tclass Solution:\n\t\tdef smallestRepunitDivByK(self, k: int) -> int:\n\t\t\tif k % 2 == 0 or k % 5 == 0:\n\t\t\t\treturn -1\n\n\t\t\tif k == 1:\n\t\t\t\treturn 1\n\n\t\t\ti, k = 1, k * 9\n\t\t\tremainder = 10 % k\n\t\t\twhile remainder != 1:\n\t\t\t\tremainder = remainder * 10 % k\n\t\t\t\ti += 1\n\t\t\treturn i\n\t```\n\n### Step 2: Prime Factorization and Euler\'s Totient Function\n\t\nPostiive integers `a` and `b` are coprime or relatively prime when the highest common factor between them is `1`, such as 3 and 4. And when `a` and `b` are relatively prime, Euler\'s Theorem says that there existing a function `phi(b)` such that `mod(a ** phi(b), b) == 1` and this function is called Euler\'s Totient Function and it has a explicit structure to construct. Replacing `a` with `10` and `b` with `9k`, it seems like we can leverage this theorem to our benefits. From here, we have two subproblems: \n\n**1**. In order to utilize totient function, we need to make sure the *relatively prime* requirement is satisfied. This is not hard to prove: because `10` and `9` are relatively prime, and `k` does not have either 2 or 5 as prime factors which are the only non-trivial factors `10` has, and therefore, `10` and `9k` are relatively prime. QED - **also notice that this gurantees that there will be a solution to the problem as long as k is coprime to 10**\n\n**2**. Even if we can find `phi(9k)` which should be straightforward, it doesn\'t guarantee that this number is the **m** we are looking for. Potentially, it could be a number larger than **m**. For instance, `111` (3 digits) is the smallest `111...111` number that is divisible by `k = 3` but `111 * 1000 + 111 == 111111` (6 digits) is also divisible by 3. Our goal is to go from `phi(9k)` and somehow find the smallest **m**\n\nBefore we proceed to the next step, I would like to describe what `phi(b)` looks like. You can find more details [here on wiki](https://en.wikipedia.org/wiki/Euler%27s_totient_function). \n* Given `b`\'s prime factorization as `b == (p1 ** r1) * (p2 ** r2) * (p3 ** r3) ...` where `p1`, `p2`, `p3`, etc. are prime numbers and `r1`, `r2`, `r3`, etc. are their respective powers, then `phi(b)` can be constructed as `phi(b) == (p1 ** (r1 - 1)) * (p1 - 1) * (p2 ** (r2 - 1) * (p2 - 1)) ...` An easy way to understand totient function is that for each prime factor `p{i}` of `b`, we replace one instance of `p{i}` with it\'s adjacent coprime number `p{i} - 1`. A simple example for b == 36 is illustrated below\n\t* prime factorization of 36 is (`2` ** 2) * (`3` ** 2)\n\t* it\'s totient number is (`2` ** 1) * (`2` - 1) * (`3` ** 1) * (`3` - 1), which is 12\n\nHere are the functions for prime factorization and totien number calculation in Python. We use dictionary to store the factorization results. Notice that the time complexity of `prime_factorization()` and `totient` offsets each other\n```python\n\tdef prime_factorization(num):\n\t\t"""\n\t\tO(n) worst case time complexity if num is a prime number\n\t\t"""\n\t\tp, num = 2, num\n\t\tans = defaultdict(int)\n\t\twhile num != 1:\n\t\t\twhile num % p == 0:\n\t\t\t\tans[p] += 1\n\t\t\t\tnum /= p\n\t\t\tp += 1\n\t\treturn ans\n\n\tdef totient(p_factors):\n\t\t"""\n\t\tO(n) time complexity where n is number of unique prime factors\n\t\t"""\n\t\treturn reduce(lambda x, y: x * (y[0] ** (y[1] -1) * (y[0] - 1)), p_factors.items(), 1)\n```\n\n### Step 3 Going from `phi(9k)` to **m**\nNow that we got `M` (a.k.a `phi(9k)`), and based on Euler\'s theorem we know that `mod(10 ** M, 9k) == 1`, then the next question is to find if `M` == **m**, or if there\'s a certain relationship between them. Actually, we can prove that `M` has to be a multiple of **m**, or equivalently, **m** is a factor or divisor of `M`, because:\n* First, it is easy to have an intuition that `mod((10 ** m) ** n, 9k) == 1` because of power rule. Then we just need to prove that `M` has to be a multiple of **m**\n* Assuming `M > m` and `mod(M, m) == c` where `0 < c < m`, then we can reconstruct `111...111` (`M` digits) into `111...111000...000` (`M` digits in total with **m** trailing `0`s)+ `111...111` (**m** digits). Because we know both numbers are divisible by `k` and therefore `111...111000...000` has to be divisible by `k`. But we also know that `1000...000` (**m** trailing `0`s) is relatively prime to `k`, and this gives us that `111...111` (`M` - **m** digits) has to be divisible by `k`. Repeatedly, because of `mod(M, m) == c`, we have `111...111` (c digits) has to be divisiable by `k` where `c < m`, thus contradicting to the assumption that **m** is the smallest number of digits. \n\n\tTherefore, **m** is a factor of `M`. QED\n\nThen the question becomes clear: we need to factorize `M` and find the minium factor **m** such that `mod(10 ** m, 9k) == 1`. Essentially, the work we\'ve done so far is to significantly reduce the possible values of **m**. One interesting finding is that\n* If `k` is a prime number, then **m** is a factor of `k - 1`. This is easy to see from the construction of totien function\n* Additionally, there would be at most `k` - 1 distint remainders so we shouldn\'t care about `M`\'s factors that are larger than `k` - 1\n\nSo now, it looks like the only piece left is to construct all the factors of `M` that are leq `k` - 1 and iterate through them low to high to see which one has `mod(10 ** i, k) == 1`. There are a few tricks when dealing with modular exponentiation so it\'s memory efficient and computationally fast. In fact, Python\'s `pow()` already has it built in so we can leverage that. Therefore, we have the below alternative *solution* ~ 90ms (note, `k_tot = self.totient(p_factors)` can be replaced by `k_tot = self.carmichael(p_factors)` to further reduce runtime to ~60ms)\n* *Solution 2*?\n\t```python\n\tclass Solution:\n\t\tdef smallestRepunitDivByK(self, k: int) -> int:\n\t\t\tif k % 2 == 0 or k % 5 == 0:\n\t\t\t\treturn -1\n\n\t\t\tif k == 1:\n\t\t\t\treturn 1\n\n\t\t\t# Step 2\n\t\t\tp_factors = self.prime_factorization(k * 9)\n\t\t\tk_tot = self.totient(p_factors)\n\n\t\t\t# Step 3\n\t\t\tp_factors_tot = self.prime_factorization(k_tot)\n\t\t\tcandidates = self.all_factors(p_factors_tot)\n\n\t\t\tfor l in candidates:\n\t\t\t\tif pow(10, l, 9 * k) == 1:\n\t\t\t\t\treturn l\n\n\t\tdef prime_factorization(self, num):\n\t\t\tp, num = 2, num\n\t\t\tans = defaultdict(int)\n\t\t\twhile num != 1:\n\t\t\t\twhile num % p == 0:\n\t\t\t\t\tans[p] += 1\n\t\t\t\t\tnum /= p\n\t\t\t\tp += 1\n\t\t\treturn ans\n\n\t\tdef totient(self, p_factors):\n\t\t\treturn reduce(lambda x, y: x * (y[0] ** (y[1] -1) * (y[0] - 1)), p_factors.items(), 1)\n\n\t\tdef all_factors(self, p_factors):\n\t\t\tblocks = [[k ** i for i in range(p_factors[k] + 1)] for k in p_factors]\n\t\t\twhile len(blocks) > 1:\n\t\t\t\tb1, b2 = blocks.pop(), blocks.pop()\n\t\t\t\tb3 = [v1 * v2 for v1 in b1 for v2 in b2]\n\t\t\t\tblocks.append(b3)\n\t\t\treturn sorted(blocks[0])[1:]\n\t```\n\n### A few words\nHonestly, I didn\'t find the solution 2 that exciting because at the end, we still need iterating `pow()` on a few candidates to find the final result. The hard question here is:\n* Given positive integers `a` and `b`, where `a` and `b` are mutually prime, can we analytically find the smallest number **m** such that `mod(a ** m, b) == 1`\n* In fact, **m** is called the order of `a` modulo `b`. However, I didn\'t find an analytical formula to compute the order given arbitrary coprime `a` and `b` \n* But at least, the Carmichael Function `lambda` can help us further narrow down the range from using totient function `phi`. Specifically, `lambda` is the smallest integer such that\n\t* `lambda` <= `phi` and `lambda | phi`\n\t* `mod(a ** lambda(b), b) == 1` for any coprime `a` where 1 < `a` < `b`\n\t* Although it could provide a much smaller range, we still have to iterate through to find out the final answer\n\t* 2 Python implementations of the Carmichael Function\n\t```python\n\t# Mine\n\tdef carmichael(self, p_factors):\n\t\tcar_factors = []\n\t\tfor k, p in p_factors.items():\n\t\t\tif k == 2 and p > 2:\n\t\t\t\tcar_factors.append(self.prime_factorization(self.totient({k: p}) // 2))\n\t\t\telse:\n\t\t\t\tcar_factors.append(self.prime_factorization(self.totient({k: p})))\n\t\tlcm = defaultdict(int) \n\t\tfor factors in car_factors:\n\t\t\tfor k, p in factors.items():\n\t\t\t\tlcm[k] = max(lcm[k], p)\n\t\treturn reduce(lambda x, y: x * y[0] ** y[1], lcm.items(), 1)\n\t\t\n\t\t# Internet - slow when n > 100 but looks cool\n\t\tf=lambda n,k=1:1-any(a**-~k*~-a**k%n for a in range(n))or-~f(n,k+1)\n\t```\n* Why not we just use `pow()` to brute force it, knowing that `pow()` has a very efficient implementation of modular operation?\n\t*Solution 3*? ~220ms\n\t```python\n\tclass Solution:\n\t\tdef smallestRepunitDivByK(self, k: int) -> int:\n\t\t\tif k % 2 == 0 or k % 5 == 0:\n\t\t\t\treturn -1\n\n\t\t\tif k == 1:\n\t\t\t\treturn 1\n\n\t\t\tfor l in range(1, k + 1):\n\t\t\t\tif pow(10, l, 9 * k) == 1:\n\t\t\t\t\treturn l\n\t```\n* [reference1](https://www.math.sinica.edu.tw/www/file_upload/summer/crypt2017/data/2015/[20150707][carmichael].pdf)\n* [reference2](https://en.wikipedia.org/wiki/Euler%27s_totient_function)\n* [reference3](https://en.wikipedia.org/wiki/Carmichael_function)\n* [reference4](https://en.wikipedia.org/wiki/Modular_arithmetic)\n* [reference5](https://math.stackexchange.com/questions/1025578/is-there-a-better-way-of-finding-the-order-of-a-number-modulo-n)\n\n\n\n | 2 | 0 | [] | 0 |
smallest-integer-divisible-by-k | [JavaScript] 1015. Smallest Integer Divisible by K | javascript-1015-smallest-integer-divisib-9w6p | ---\n\nHope it is simple to understand.\n\n---\n\n\nvar smallestRepunitDivByK = function (k) {\n let count = 0;\n let n = 0;\n while (count < k) {\n | pgmreddy | NORMAL | 2021-12-30T13:20:36.655905+00:00 | 2021-12-31T02:53:51.887887+00:00 | 167 | false | ---\n\nHope it is simple to understand.\n\n---\n\n```\nvar smallestRepunitDivByK = function (k) {\n let count = 0;\n let n = 0;\n while (count < k) {\n count++;\n n = n * 10 + 1; // 1, 11, 111, 1111, 11111 ..\n n = n % k; // because for example 27%3 === 3%3 + 18%3\n if (n === 0) return count;\n }\n return -1;\n};\n```\n\n---\n | 2 | 0 | ['JavaScript'] | 0 |
smallest-integer-divisible-by-k | Easy Python Solution | easy-python-solution-by-vistrit-6boz | \ndef smallestRepunitDivByK(self, k: int) -> int:\n n=0\n for i in range(1,k+1):\n n=(n*10+1)%k\n if not n: return i\n | vistrit | NORMAL | 2021-12-30T08:31:22.227997+00:00 | 2021-12-30T08:31:22.228039+00:00 | 290 | false | ```\ndef smallestRepunitDivByK(self, k: int) -> int:\n n=0\n for i in range(1,k+1):\n n=(n*10+1)%k\n if not n: return i\n return -1\n``` | 2 | 0 | ['Python', 'Python3'] | 0 |
smallest-integer-divisible-by-k | Python Easy Solution | python-easy-solution-by-aditigarg_28-zs6i | ```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if k%2==0 or k%5==0: return -1\n i=0\n d=1\n while i<=10 | aditigarg_28 | NORMAL | 2021-12-30T08:15:47.460867+00:00 | 2021-12-30T08:15:47.460904+00:00 | 104 | false | ```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if k%2==0 or k%5==0: return -1\n i=0\n d=1\n while i<=100000:\n if d%k==0:\n return i+1\n d=(d*10)+1\n i+=1\n return -1\n \n \n | 2 | 0 | [] | 0 |
smallest-integer-divisible-by-k | c++ solution | c-solution-by-dilipsuthar60-23qp | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int K)\n {\n long long sum=1;\n for(int i=1;i<=K;i++)\n {\n if(su | dilipsuthar17 | NORMAL | 2021-12-30T04:52:07.162435+00:00 | 2021-12-30T04:52:07.162486+00:00 | 306 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K)\n {\n long long sum=1;\n for(int i=1;i<=K;i++)\n {\n if(sum%K==0)\n {\n return i;\n }\n sum=(sum*10+1)%K;\n }\n return -1;\n }\n};\n``` | 2 | 0 | ['Math', 'C', 'C++'] | 0 |
smallest-integer-divisible-by-k | Solution with explanation | solution-with-explanation-by-dhiru634-mk4o | Why using remainder again and again?\n\t let a be some number\n\tand a % k = rem \n\tnow when to the next number since rem != 0 we have \n\tb = 10 * a + 1\n\ta | dhiru634 | NORMAL | 2021-12-30T03:32:36.026437+00:00 | 2021-12-30T06:21:27.103786+00:00 | 272 | false | * **Why using remainder again and again?**\n\t let **a** be some number\n\tand **a % k = rem** \n\tnow when to the next number since rem != 0 we have \n\t**b = 10 * a + 1**\n\tand \n\t**b % K = (10 * a + 1)%k**\n\tNow,\n\t **(10 * a + 1)%k**\n\t**= (10 % k) * (a % k) + 1 % k**\n\t**= rem * (10 % k) + 1 % K**\n\tsince [ **rem < k** ] so, **[rem = rem % k**]\n\t**= (rem % k) * (10 % K) + 1 % k**\n\t**= (rem * 10) % K + 1 % 10**\n\t**= (rem * 10 + 1) % k**\n* **Why loop is repeated only K times ?**\n\t* We are keeping track of the remainder that has come, and it is obvious that if the remainder is repeated then we do not have the number.\n\t* Now suppose we do not get any repeated remainder with each iteration then after K iteration all the remainders will have come and in the (K+1)th iteration we will see repetition and exit and return -1.\n\t* And if we see repetition in less than K repetition then also we will exit returning -1.\n\t* so in any case the loop will run at max of K times\n\t\n```\npublic class SmallestIntegerDivisibleByK {\n// Taking k length array since there can be atMax k remainders\n\tpublic int smallestRepunitDivByK(int k) {\n\t\tint[] rem = new int[k];\n\t\tint num = 1;\n\t\tint length =1;\n\t\twhile(num%k!=0 && rem[num%k]!=1){\n\t\t\tint remainder = num%k;\n\t\t\tnum = remainder * 10 + 1;\n\t\t\tlength++;\n\t\t\trem[remainder] = 1;\n\n\t\t}\n\t\tif(num%k == 0) return length;\n\t\telse return -1;\n\t}\n}\n\n```\n**Do upvote if you like the solution. Thanks!!** | 2 | 0 | ['Math', 'Java'] | 0 |
smallest-integer-divisible-by-k | Using while loop and hashmap in Python | using-while-loop-and-hashmap-in-python-b-om6g | \nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n #edge case\n\t\tif k % 2 == 0 or k % 5 == 0: return -1\n\t\t\n\t\t#keep track of | kryuki | NORMAL | 2021-12-30T02:15:55.858190+00:00 | 2021-12-30T02:15:55.858232+00:00 | 213 | false | ```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n #edge case\n\t\tif k % 2 == 0 or k % 5 == 0: return -1\n\t\t\n\t\t#keep track of the remainder\n remain, length = 0, 0\n found_so_far = set()\n while remain not in found_so_far:\n found_so_far.add(remain)\n remain = (remain * 10 + 1) % k\n length += 1\n return length if remain == 0 else -1\n``` | 2 | 0 | ['Python', 'Python3'] | 0 |
smallest-integer-divisible-by-k | ✅ [Solution] Swift: Smallest Integer Divisible by K (+ test cases) | solution-swift-smallest-integer-divisibl-ima6 | swift\nclass Solution {\n func smallestRepunitDivByK(_ k: Int) -> Int {\n guard !(k % 2 == 0 || k % 5 == 0) else { return -1 }\n guard k != 1 e | AsahiOcean | NORMAL | 2021-12-30T01:45:44.873953+00:00 | 2021-12-30T01:45:44.873997+00:00 | 894 | false | ```swift\nclass Solution {\n func smallestRepunitDivByK(_ k: Int) -> Int {\n guard !(k % 2 == 0 || k % 5 == 0) else { return -1 }\n guard k != 1 else { return 1 }\n var length = 1\n var temp = 1\n while temp != 0 {\n temp = (temp * 10 + 1) % k\n length += 1\n }\n return length\n }\n}\n```\n\n---\n\n<details>\n<summary>\n<img src="https://git.io/JDblm" height="24">\n<b>TEST CASES</b>\n</summary>\n\n<pre>\n<b>Result:</b> Executed 3 tests, with 0 failures (0 unexpected) in 0.008 (0.009) seconds\n</pre>\n\n```swift\nimport XCTest\n\nclass Tests: XCTestCase {\n \n private let solution = Solution()\n \n func test0() {\n let value = solution.smallestRepunitDivByK(1)\n XCTAssertEqual(value, 1)\n }\n func test1() {\n let value = solution.smallestRepunitDivByK(2)\n XCTAssertEqual(value, -1)\n }\n func test3() {\n let value = solution.smallestRepunitDivByK(3)\n XCTAssertEqual(value, 3)\n }\n}\n```\n</details> | 2 | 0 | ['Swift'] | 0 |
smallest-integer-divisible-by-k | C++ 4 Lines O(K) Time | O(1) Space | c-4-lines-ok-time-o1-space-by-aarjav20-ax00 | \nint smallestRepunitDivByK(int K) {\n int r=0;\n for(int i=1;i<=K;i++)\n {\n r=(r*10+1)%K;\n if(r==0) return i; \n | aarjav20 | NORMAL | 2021-03-14T18:38:47.595164+00:00 | 2021-03-14T18:38:47.595210+00:00 | 187 | false | ```\nint smallestRepunitDivByK(int K) {\n int r=0;\n for(int i=1;i<=K;i++)\n {\n r=(r*10+1)%K;\n if(r==0) return i; \n }\n return -1; }\n``` | 2 | 0 | [] | 0 |
smallest-integer-divisible-by-k | Solution using memoization of remainders | solution-using-memoization-of-remainders-6fci | We can simply memonize the remainders and check to see if we already have got this remainder. If we have already got this remainder, this means that we are stuc | rockr8938 | NORMAL | 2020-11-29T21:16:07.965552+00:00 | 2020-11-29T21:16:45.827965+00:00 | 82 | false | We can simply memonize the remainders and check to see if we already have got this remainder. If we have already got this remainder, this means that we are stuck in infinte loop, so break out and return -1;\n\n```\nclass Solution {\npublic:\n bool dp[100005];\n int smallestRepunitDivByK(int K) {\n memset(dp,0,sizeof(dp));\n int len =1;\n int last_rem=0;\n \n \n while(true)\n {\n last_rem =(last_rem*10 + 1)%K;\n if(last_rem==0)\n return len;\n if(dp[last_rem])\n break;\n dp[last_rem]=1;\n len++;\n }\n return -1;\n }\n};\n``` | 2 | 0 | ['Memoization', 'C++'] | 0 |
smallest-integer-divisible-by-k | [Java] 1ms Pigeonhole Division w/ Explanation | java-1ms-pigeonhole-division-w-explanati-sn8x | \nclass Solution {\n public int smallestRepunitDivByK(int K) {\n if(K%2 ==0 || K % 5 == 0){\n return -1;\n } else {\n int | allenjue | NORMAL | 2020-11-25T19:19:23.448364+00:00 | 2020-11-26T00:21:03.243673+00:00 | 110 | false | ```\nclass Solution {\n public int smallestRepunitDivByK(int K) {\n if(K%2 ==0 || K % 5 == 0){\n return -1;\n } else {\n int remainder = 0;\n for(int length = 1; length <= K; length++){\n remainder = (remainder*10 + 1) % K;\n if(remainder == 0)\n return length;\n }\n }\n return -1;\n }\n}\n```\n**PROBLEM OVERVIEW**\nWe are given a number whose digits only contain `1`. We are also given a divisor K, and need to find the length of the "N" (basically how many digits) until it is divisible by K.\n\n**SOLUTION ASSESSMENT**\nSince the digit ends in a 1:\n* Any even number is impossible because any mulitple of an even number is even (!=1)\n* 5 is impossible because all final digits of any multiple of 5 are 0 or 5.\n\nGreat! We cut the number of possibilities by 60%.\n\nNext, we may notice that for every increase of 1, 11, 111, ...,etc, the pattern may be modeled by\n* (current* 10) + 1\n* However, there is a warning that there may be `overflow,` even with a 64-bit signed number\n\nSo how can we work our way around this?\n\nWe can use the modulo operator and divide the number everytime there is a chance to. By doing so, we are essentially doing **long-division with the digits that we have, and the modulo operator does the task of "carrying over" the remainder.**\n\nSee *Quotient Remainder Theorem* [https://www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/the-quotient-remainder-theorem]\n\n**WORKED EXAMPLE**\nGIven K=3\n1. remainder = (0 + 1) % 3 = 1\n2. remainder = (10 * 1 + 1) % 3 = 2\n3. remainder = (2 * 1 + 1) % 3 = 0\n4. since remainder == 0, and it took 3 steps, the length = 3\n\nNow, here\'s the pigeonhole algorithm part. As we iterate from N = 1,11,111,..., etc, we are increasing the length by 1 each time. However, we **cannot have a length longer than K**. As we iterate from length 1 -> K, we have all the possible lengths; the pigeonhole principle asserts that there are at most K unique remainders. So if we iterate beyond K times, it is guaranteed that the remainder repeats, and there is not need to coninue searching.\n\n**TIME COMPLEXITY**\nO(N) - Iterates at most from 1->K. Note: K iterations is worst case.\n**SPACE COMPLEXITY**\nO(1) \n\n | 2 | 0 | ['Java'] | 0 |
smallest-integer-divisible-by-k | Swift Solution (Beats 100%) | swift-solution-beats-100-by-jtbergman-r9fk | Solution 1: Using Remainder Set\nIn this solution, we iterate through 1, 11, 111, ... and stop either when num = 0 in which case num % K == 0 or we stop when we | jtbergman | NORMAL | 2020-11-25T15:09:56.608736+00:00 | 2020-11-25T15:09:56.608772+00:00 | 100 | false | **Solution 1: Using Remainder Set**\nIn this solution, we iterate through `1, 11, 111, ...` and stop either when `num = 0` in which case `num % K == 0` or we stop when we have seen `num` before. This means that there is no number for which `num % K == 0` so we should return -1. \n```swift \nfunc smallestRepunitDivByK(_ K: Int) -> Int {\n var length = 0 \n var num = 0\n var seen = Set<Int>()\n\n repeat {\n seen.insert(num) \n num = ((num * 10) + 1) % K \n length += 1\n } while num != 0 && !seen.contains(num)\n\n return (num == 0) ? length : -1\n}\n```\n\n**Solution 2: Pigeonhole Principle**\nThere are `k` possible remainders for `num % k`. For example, if `k = 2` the possible remainders are `0, 1`. Therefore, by the pigeonhole principle, after performing `k` iterations either a remainder will repeat or we will find a number such that `num % k == 0`. \n```swift \nfunc smallestRepunitDivByK(_ K: Int) -> Int {\n var length = 0 \n var num = 0\n\n for _ in 0 ..< K {\n num = ((num * 10) + 1) % K \n length += 1\n if num == 0 { return length }\n }\n\n return -1\n}\n```\n\n**Solution 3: Performance Improvement**\nWe will combine solution 2 with a speed up covering lots of `K`. If the given `K` is divisible by either 2 or 5, then the solution will be `-1`. This is because dividing a number ending with 1 by a multiple of 2 or 5 will always have a remainder of 1.\n```swift \nfunc smallestRepunitDivByK(_ K: Int) -> Int {\n if K % 2 == 0 || K % 5 == 0 { return -1 }\n var length = 0 \n var num = 0\n\n for _ in 0 ..< K {\n num = ((num * 10) + 1) % K \n length += 1\n if num == 0 { return length }\n }\n\n return -1\n}\n```\n | 2 | 0 | [] | 0 |
smallest-integer-divisible-by-k | Rust solution | rust-solution-by-sugyan-yc9s | rust\nimpl Solution {\n pub fn smallest_repunit_div_by_k(k: i32) -> i32 {\n let mut m = 0;\n for i in 1..=k {\n m = (m * 10 + 1) % k | sugyan | NORMAL | 2020-11-25T11:55:51.770440+00:00 | 2020-11-25T11:55:51.770467+00:00 | 61 | false | ```rust\nimpl Solution {\n pub fn smallest_repunit_div_by_k(k: i32) -> i32 {\n let mut m = 0;\n for i in 1..=k {\n m = (m * 10 + 1) % k;\n if m == 0 {\n return i;\n }\n }\n -1\n }\n}\n``` | 2 | 0 | ['Rust'] | 0 |
smallest-integer-divisible-by-k | c++(0ms 100%) iteratively and math (with comments) | c0ms-100-iteratively-and-math-with-comme-zl6a | we understand that : if our last digit in our number K is 0.2.4.5.6.8 we will answer -1(this obviously )\n 2. in other case we understand that we always have an | zx007pi | NORMAL | 2020-11-25T10:24:14.852913+00:00 | 2021-12-30T19:07:24.183561+00:00 | 402 | false | 1. we understand that : if our last digit in our number K is 0.2.4.5.6.8 we will answer -1(this obviously )\n 2. in other case we understand that we always have answer and that answer we can image as sequense of digit 1(N). what we say about our number N ? first - we absolutelly understand that number will have common divider with our number K. second - but our number N we can imagine as sum, where sum we can transform into this : 1 * first_digit + 10 * second_digit + 100 * third_digit and so etc. third - if our N have common divider consecuently our sum have too. and we can apply **chinese remainder theorem.** \n3. we will summarize our remainders and check sum%K if we have 0, we have answer.\n4. we can have next remainder if we multiply previous remainder and 10 and take mod from that number and K\n\n\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n if(K%2 == 0 || K%5 == 0) return -1;\n int rez = 1; //number of digits 1 in our answer\n int remainder = 1; //first remainder\n int total = 1; // summe of our remainders\n while(total%K != 0){\n rez++;\n remainder = (remainder*10)%K;\n total = (total + remainder)%K;\n }\n return rez;\n }\n};\n```\n\n**or such :**\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n if(K%2 == 0 || K%5 == 0) return -1;\n int rez = 1, rem = 1, tot = 1; \n for(;tot%K != 0 ; rez++, rem = rem*10%K,tot = (tot + rem)%K);\n return rez;\n }\n};\n```\n**or such :**\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n int a = 1; \n for(int r = 1, t = 1; t%K != 0 && a <= K; a++, t += (r = r*10%K));\n return a > K ? -1 : a;\n }\n};\n``` | 2 | 0 | ['C', 'C++'] | 1 |
smallest-integer-divisible-by-k | [Python3] group theory | python3-group-theory-by-nicku5011-8ace | Write [(N+1) many 1s]111....1 = (10^(N+1) - 1)/9 (simple geometric series expansion)\n\nIt is easy to see that there exists N such that K divides (10^(N+1) - 1) | nicku5011 | NORMAL | 2020-10-18T13:00:14.344249+00:00 | 2021-09-20T11:39:26.884423+00:00 | 199 | false | Write [(N+1) many 1s]111....1 = (10^(N+1) - 1)/9 (simple geometric series expansion)\n\nIt is easy to see that there exists N such that K divides (10^(N+1) - 1)/9 if and only if 10^(N+1) = 1 (mod 9K), i.e. 10^(N+1) is the identity in the multiplicative group Z_{9K}\\*. Z_{9K}\\* consists of elements coprime with 9K. Hence the algorithm returns -1 if gcd(10,9K) != 1\n\nIf gcd(10,9K) = 1, then the group action f(x) = 10x acts transitively on Z_{9K}\\* and we know that the answer is the size of the orbit of 1 under f.\n\n```\nclass Solution:\n def gcd(self, a: int, b: int) -> int:\n if(b == 1):\n return a\n else:\n return gcd(b, a%b)\n \n def smallestRepunitDivByK(self, K: int) -> int:\n D = 9*K\n g = self.gcd(10, D)\n \n if g != 1:\n return -1\n \n else:\n k = 1\n current = 1\n \n while True:\n current = current*10 % D\n if current == 1:\n return k\n else:\n k += 1\n``` | 2 | 0 | [] | 0 |
smallest-integer-divisible-by-k | JavaScript Clean Solution Beat 100% | javascript-clean-solution-beat-100-by-co-lifo | javascript\nvar smallestRepunitDivByK = function(K) {\n if(!(K%2) || !(K%5)) return -1; // short circuit\n \n let len = 0, val = 0, loop = 100000;\n | control_the_narrative | NORMAL | 2020-08-11T22:52:03.527136+00:00 | 2020-08-11T22:52:03.527263+00:00 | 189 | false | ```javascript\nvar smallestRepunitDivByK = function(K) {\n if(!(K%2) || !(K%5)) return -1; // short circuit\n \n let len = 0, val = 0, loop = 100000;\n \n while(loop--) {\n val = (val*10 + 1) % K; \n len++\n if(!val) return len;\n }\n};\n``` | 2 | 0 | ['JavaScript'] | 0 |
smallest-integer-divisible-by-k | Java solution with simple intuition | java-solution-with-simple-intuition-by-a-h1td | \nclass Solution {\n public int smallestRepunitDivByK(int K) {\n // Obviously if last digit is 1, then K can never be a factor of 2 or 5\n if ( | ankit2grover | NORMAL | 2019-03-24T18:43:47.993933+00:00 | 2019-03-24T18:43:47.993967+00:00 | 287 | false | ```\nclass Solution {\n public int smallestRepunitDivByK(int K) {\n // Obviously if last digit is 1, then K can never be a factor of 2 or 5\n if ((K % 2 == 0) || (K % 5 == 0)) {\n return -1;\n } \n // Remainder that will be added to next 1\n int rem = 0;\n // keep track of length of 1\n int count = 1;\n int value = 1;\n // Make sure that first number to try divisible should be greater than K\n while (value < K) {\n value = Integer.parseInt(value + "1");\n ++count;\n }\n // As we know remaining nubers are only odd and not factor of 2 or 5 then definitely all other numbers are valid.\n while (value % K != 0) {\n rem = value % K;\n value = Integer.parseInt(rem + "1");\n ++count;\n }\n return count;\n }\n}\n``` | 2 | 0 | [] | 0 |
smallest-integer-divisible-by-k | Golang O(K)/O(1) and O(K)/O(K) | golang-oko1-and-okok-by-andrew18-gn2n | Time: O(K), Space: O(K)\n\n\nfunc smallestRepunitDivByK(K int) int {\n m := make(map[int]bool)\n n := 0\n for i := 1; ; i++ {\n n = n*10 + 1\n | andrew18 | NORMAL | 2019-03-24T05:28:44.955069+00:00 | 2019-03-24T05:28:44.955115+00:00 | 110 | false | Time: O(K), Space: O(K)\n\n```\nfunc smallestRepunitDivByK(K int) int {\n m := make(map[int]bool)\n n := 0\n for i := 1; ; i++ {\n n = n*10 + 1\n n = n%K\n if n == 0 { return i }\n if m[n] { return -1 }\n m[n] = true\n }\n}\n```\n\nTime: O(K), Space: O(1)\n```\nfunc smallestRepunitDivByK(K int) int {\n for n, i := 0, 1; i<=K; i++ {\n n = n*10 + 1\n n = n%K\n if n == 0 { return i }\n }\n return -1\n}\n```\n | 2 | 0 | ['Hash Table', 'Go'] | 0 |
smallest-integer-divisible-by-k | C++ O(sqrt(k)) Beats 100% | c-osqrtk-beats-100-by-firelion8798-gu8w | Approach\n Describe your approach to solving the problem. \nSuppose $n$ consists of $m$ digits. Then, $n = 1 + 10 + \cdots + 10^{m - 1} = \frac{10^m - 1}{9}$. T | firelion8798 | NORMAL | 2024-02-29T02:11:27.605198+00:00 | 2024-02-29T02:18:14.944197+00:00 | 40 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nSuppose $n$ consists of $m$ digits. Then, $n = 1 + 10 + \\cdots + 10^{m - 1} = \\frac{10^m - 1}{9}$. The necessary and sufficient condition is therefore $10^m \\equiv 1 \\ (\\mathrm{mod}\\ 9k)$. If $\\gcd(k, 10) = 1$ (in other words, $k$ is not divisble by $2$ or $5$), then such an $m$ must exist by Euler\'s theorem; otherwise, we immediately return $-1$.\n\nWe can use the baby-step giant-step algorithm to compute $m$ in time $\\mathcal{O}(\\sqrt{k})$. \nIf you\'re not familiar with it, we write $m = Sa - b$ for some $a > 0$ and $0 \\leq b < S$, where $S$ is the square root of our modulus (in this case, $9k$). Then, $10^{Sa - b} \\equiv 1 \\ (\\mathrm{mod}\\ 9k) \\implies 10^{Sa} \\equiv 10^{b} \\ (\\mathrm{mod} \\ 9k)$, so we can compute all values of $10^b$, store them in a hashmap, and find the first collision when iterating through values of $10^{Sa}$ in increasing order. Since $m \\leq \\Phi(9k) < 9k - 1$, we will need at most $\\mathcal{O}(\\sqrt{k})$ steps to get our answer.\n\n# Complexity\n- Time complexity: $\\mathcal{O}(\\sqrt{k})$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $\\mathcal{O}(\\sqrt{k})$\n\n# Code\n```\nclass Solution {\n inline int discrete_log(int x, int M) {\n int S = (int)sqrt(M);\n unordered_map<int, int> rhs_powers;\n\n for (int i = 0, p = 1; i < S; ++i) { \n rhs_powers[p] = i;\n p = (long long)p * x % M;\n }\n\n int pow_xs = 1;\n for (int i = 1; i <= S; ++i) {\n pow_xs = (long long)pow_xs * x % M;\n }\n\n for (int i = S, p = pow_xs;; i += S) {\n if (rhs_powers.count(p % M)) return i - rhs_powers[p % M];\n p = ((long long)p * pow_xs) % M;\n }\n }\npublic:\n int smallestRepunitDivByK(int k) {\n if (k % 2 == 0 || k % 5 == 0) return -1;\n return k == 1 ? 1 : discrete_log(10, 9 * k);\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
smallest-integer-divisible-by-k | Best Java Solution || Beats 95% | best-java-solution-beats-95-by-ravikumar-lmry | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2023-09-24T15:17:00.857810+00:00 | 2023-09-24T15:17:00.857828+00:00 | 263 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n int prev = 0;\n\n if(k%2==0 || k%5==0) return -1;\n\n for(int i=1; i<=k; i++){\n prev = (prev*10+1)%k;\n if(prev == 0) return i;\n }\n return -1;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
smallest-integer-divisible-by-k | 80% beats best solution | 80-beats-best-solution-by-re_cur_sion-n52f | \n\n# Approach\n Describe your approach to solving the problem. \nWe have make a vairable n as we know the number only contain 1 ,\nmake a for loop from 1 to k | re_cur_sion | NORMAL | 2023-07-04T06:53:11.913696+00:00 | 2023-07-04T06:53:11.913715+00:00 | 20 | false | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe have make a vairable n as we know the number only contain 1 ,\nmake a for loop from 1 to k then in a variable p make 1,11,and so on till the length of k. \nNow if p % n is equal to 0 then we just return the length else we return -1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n int n =0;\n int p = 0;\n for(int i=1;i<=k;i++){\n p = n*10+1;\n n = p%k;\n if(n==0){\n return i;\n }\n }\n\n return -1;\n \n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
smallest-integer-divisible-by-k | Solution | solution-by-deleted_user-0gvd | C++ []\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n for (int r=0,N=1;N<=k;N++) {\n if ((r=(r*10+1)%k)==0) {\n | deleted_user | NORMAL | 2023-05-21T07:22:40.690124+00:00 | 2023-05-21T07:34:51.617187+00:00 | 815 | false | ```C++ []\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n for (int r=0,N=1;N<=k;N++) {\n if ((r=(r*10+1)%k)==0) {\n return N;\n }\n }\n return -1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if k%2==0 or k%5==0:\n return -1\n else:\n cur = 1\n res = 1\n while cur%k!=0:\n cur = (10*cur+1)%k\n res += 1\n return res\n```\n\n```Java []\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n if (k % 2 == 0 || k % 5 == 0) return -1;\n \n int phi = get_euler(k * 9);\n int res = phi;\n for (int i = 1; i <= phi / i; i++) {\n if (phi % i == 0) {\n if (qmi(10, i, 9 * k) == 1) return i;\n if (qmi(10, phi / i, 9 * k) == 1) res = Math.min(res, phi / i);\n }\n }\n return res;\n }\n private int get_euler(int x) {\n int res = x;\n for (int i = 2; i <= x / i; i++) {\n if (x % i == 0) {\n res = res / i * (i - 1);\n while (x % i == 0) x /= i;\n }\n }\n if (x > 1) res = res / x * (x - 1);\n return res;\n }\n private long qmi(long a, long k, long p) {\n long res = 1;\n while (k > 0) {\n if ((k & 1) == 1) res = res * a % p;\n a = a * a % p;\n k >>= 1;\n }\n return res;\n }\n}\n``` | 1 | 0 | ['C++', 'Java', 'Python3'] | 0 |
smallest-integer-divisible-by-k | C++ Easy and simple solution | c-easy-and-simple-solution-by-ayushluthr-va1x | Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F\n# Co | ayushluthra62 | NORMAL | 2023-05-09T20:28:11.335988+00:00 | 2023-05-09T20:28:11.336029+00:00 | 178 | false | ***Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F***\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(1)\n\n# Code\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n int count=1;\n if(k%2==0|| k%5==0) return -1;\n if(k==1)return 1;\n int ans=1;\n int rem=1;\n while(rem!=0){\n ans=rem*10+1;\n rem=ans%k;\n count++;\n }\n return count;\n }\n};\n\n```\n***Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F*** | 1 | 0 | ['Hash Table', 'C++'] | 0 |
smallest-integer-divisible-by-k | Easy Understandable Code | c++ | easy-understandable-code-c-by-yash04147-08gp | \n\'\'\'\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(k==1) return 1;\n if(k%2==0 || k%5==0) return -1;\n int re | yash04147 | NORMAL | 2022-11-08T19:44:19.466940+00:00 | 2022-11-08T19:44:19.466980+00:00 | 26 | false | ```\n\'\'\'\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(k==1) return 1;\n if(k%2==0 || k%5==0) return -1;\n int rem = 0;\n for(int i = 1; i<=k ;i++){\n rem = (rem*10+1)%k;\n if(rem == 0){\n return i;\n }\n }\n return -1;\n }\n};\n\'\'\'\n``` | 1 | 0 | ['Math', 'C'] | 0 |
smallest-integer-divisible-by-k | JAVA | Two solutions | java-two-solutions-by-sourin_bruh-6byg | Please Upvote !!! (\u25E0\u203F\u25E0)\n\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n if (k % 2 == 0 || k % 5 == 0) return -1;\n | sourin_bruh | NORMAL | 2022-09-30T14:55:44.628504+00:00 | 2022-09-30T14:55:44.628550+00:00 | 119 | false | ### ***Please Upvote !!!*** **(\u25E0\u203F\u25E0)**\n```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n if (k % 2 == 0 || k % 5 == 0) return -1;\n int n = 1, len = 1;\n\n while (n % k != 0) {\n n = (n * 10 + 1) % k;\n len++;\n }\n\n return len;\n }\n}\n\n// TC: O(k)\n```\n#### OR\n```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n if (k % 2 == 0 || k % 5 == 0) return -1;\n int rem = 0;\n\n for (int len = 1; len <= k; len++) {\n rem = (rem * 10 + 1) % k;\n if (rem == 0) return len;\n }\n\n return -1;\n }\n}\n\n// O(k)\n``` | 1 | 0 | ['Java'] | 0 |
smallest-integer-divisible-by-k | [C++] O(1) Space , Deriving Formula | c-o1-space-deriving-formula-by-kevinujun-jmpv | Code is reffered from lee215\nIt is pretty much clear that we don\'t have to look further if k is divisible by 2 or 5 since 1, 11, 111 can not be divided by 2 o | kevinujunior | NORMAL | 2022-09-14T05:39:28.793541+00:00 | 2022-09-14T05:41:21.399266+00:00 | 130 | false | Code is reffered from [lee215](https://leetcode.com/lee215/)\nIt is pretty much clear that we don\'t have to look further if k is divisible by 2 or 5 since 1, 11, 111 can not be divided by 2 or 5, otherwise there exist a solution\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(k%2==0|| k%5==0) return -1;\n \n for(int N=1,r=0;N<=k;N++){ \n // let\'s 1111 = a+b\n // 1111 = 1110 + 1\n // 1111%k = (1110%k + 1%k)%k\n // 1111%k = (1110%k + 1)%k\n // 1111%k = (111%k*10 +1)%k\n // now 111%k is the rem of last 111\n\t\t\t// 1111%k = (r*10 + 1)%k\n // here r is the previous remainder\n r = (r*10+1)%k;\n if(r==0) return N;\n }\n return 0;\n }\n};\n\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | C++ easy solution | c-easy-solution-by-gopijada55-qwes | class Solution {\n# public:\n int smallestRepunitDivByK(int k) {\n if(k%2==0 ||k%5==0){\n return -1;\n } \n unordered_mapm;\n | gopijada55 | NORMAL | 2022-08-13T14:04:27.212507+00:00 | 2022-08-13T14:05:49.807917+00:00 | 61 | false | class Solution {\n# public:\n int smallestRepunitDivByK(int k) {\n if(k%2==0 ||k%5==0){\n return -1;\n } \n unordered_map<int,int>m;\n m[1]++;\n int x=1;\n while(x<k){\n x*=10;\n m[1]++;\n x++;\n }\n while(x!=0){\n x-=k;\n while(x!=0 && x<k){\n x*=10;\n m[1]++;\n x++; \n }\n }\n return m[1];\n }\n}; | 1 | 0 | ['Math'] | 0 |
smallest-integer-divisible-by-k | Easy C++ Solution..... Just 5 lines of Code | easy-c-solution-just-5-lines-of-code-by-jqc6o | class Solution {\npublic:\n\n int smallestRepunitDivByK(int k) {\n if(k%5==0 or k%2==0) return -1;\n int rem=0;\n for(int i= 1; i<=k; | pankaj_sharma001 | NORMAL | 2022-06-01T14:04:40.577187+00:00 | 2022-06-01T14:04:40.577225+00:00 | 212 | false | class Solution {\npublic:\n\n int smallestRepunitDivByK(int k) {\n if(k%5==0 or k%2==0) return -1;\n int rem=0;\n for(int i= 1; i<=k;i++){\n rem = (rem*10+1)%k;\n if(rem==0) return i;\n }\n return -1;\n }\n}; | 1 | 0 | ['Math', 'C', 'C++'] | 0 |
smallest-integer-divisible-by-k | 0ms || 100%faster || CPP || Logical || Only take care of higher numbers via modulus | 0ms-100faster-cpp-logical-only-take-care-sh70 | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(k%2==0 || k%5==0) return -1;\n long long int s=1,pp=0,cnt=0;\n whil | PeeroNappper | NORMAL | 2022-04-13T13:50:16.594119+00:00 | 2022-04-13T13:51:02.094140+00:00 | 87 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(k%2==0 || k%5==0) return -1;\n long long int s=1,pp=0,cnt=0;\n while(s){\n pp=(pp*10)%k+1;\n if(pp%k==0) return cnt+1;\n cnt++;\n }\n return -1;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
smallest-integer-divisible-by-k | Python modulo approach with mathematical proof | python-modulo-approach-with-mathematical-bg9s | Key observation: \n\t if k is divisible by 2 or 5, there is no way 11....1 can be divisible by k, because anything that can be divided by 2 must be even at last | ironmask | NORMAL | 2022-01-30T09:00:08.704046+00:00 | 2022-01-30T09:03:10.122578+00:00 | 122 | false | Key observation: \n\t* if k is divisible by 2 or 5, there is no way 11....1 can be divisible by k, because anything that can be divided by 2 must be even at last digit, and by 5 must end with either 0 or 5;\n\t* otherwise, k can divide 11...1. There is no need to check for repeated modulo to detect cycle because there will be no cycle. The proof below was quoted from @DBabichev with his post: https://leetcode.com/problems/smallest-integer-divisible-by-k/discuss/948435/Python-Math-Pigeon-holes-explained\n\t* to avoid overflow when 11.111 is too big, another observation is that the next sequence of 1s are basically (previousNumber*10+1)%k = ((previousQuotient*k+previousMod)*10+1)%k == (previousMod*10+1)%k\n```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n #R1D12I8C0X9=T30 : modulo\n m,l=1%k,1\n seen=set()\n while True:\n if m==0:\n return l\n elif (m*10+1)%k in seen:\n return -1\n m,l=(m*10+1)%k,l+1\n seen.add(m)\n \n def smallestRepunitDivByK(self, k: int) -> int:\n m,seen=0,set()\n for i in range(k):\n m=(m*10+1)%k\n if m in seen:\n return -1\n if m==0:\n return i+1\n seen.add(m)\n \n def smallestRepunitDivByK(self, k: int) -> int: # no need to check dup, if there is a repeated modulo, there exists a 111...111 that is divisible by k\n \'\'\'\n Proof using Pigeon hole theorem, copied from @DBabichev with his post: https://leetcode.com/problems/smallest-integer-divisible-by-k/discuss/948435/Python-Math-Pigeon-holes-explained\n First of all, let us notice, that if number is divisible by 2 or by 5, then we need to return -1 immediatly, because number ending with 1 can not divide by 2 or 5. From now on we assume, that K is not divisible by 2 or 5. Let us consider numbers:\n\n1\n11\n111\n...\n111...111,\n\nwhere were have K ones in the last group. Then, there can be only two cases:\n\nAll reminders of given numbers when we divide by K are different.\nSome two reminders are equal.\nIn the first case, we have K numbers and also K possible reminders and they are all different, it means, that one of them will be equal to 0.\n\nIn the second case, two numbers have the same reminder, let us say number 11...1111 with a ones and 111...11111 with b ones, where b > a. Then, difference of these two numbers will be divisible by K. What is the difference? It is number 11...1100...000 with b-a ones and a zeroes at the end. We already mentioned that K is not divisible by 2 or 5 and it follows, that 11...111 divisible by K now, where we have b-a ones.\n\nSo, we proved the following statements: if K not divisible by 2 and 5, then N <= K where N is the number of how many 1s. What we need to do now is just iterate through numbers and stop when we find number divisible by K. To simplify our cumputation, we notice, that each next number is previous multiplied by 10 plus 1.\n \'\'\'\n if k%2==0 or k%5==0:\n return -1\n m=0\n for i in range(k):\n m=(m*10+1)%k\n if m==0:\n return i+1\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | 100% faster kotlin easy solution | 100-faster-kotlin-easy-solution-by-sahil-my4r | ```\nclass Solution {\n fun smallestRepunitDivByK(k: Int): Int {\n if(k%2==0||k%5==0) return -1\n var a=0\n for(i in 1..k){\n | Sahil14_11 | NORMAL | 2021-12-30T16:48:51.332602+00:00 | 2021-12-30T16:48:51.332646+00:00 | 40 | false | ```\nclass Solution {\n fun smallestRepunitDivByK(k: Int): Int {\n if(k%2==0||k%5==0) return -1\n var a=0\n for(i in 1..k){\n a=(a*10+1)\n if(a%k==0){\n return i\n } \n a%=k\n }\n return -1\n }\n} | 1 | 0 | ['Kotlin'] | 0 |
smallest-integer-divisible-by-k | Python Simple Solution O(k) Time, O(1) Space w/ Explanation | python-simple-solution-ok-time-o1-space-nz7xu | When you run through the multiples of the prime numbers from 1 to 9, you\'ll notice that 2 and 5 don\'t have any muliples that end in 1. The reason for this is | user5061gb | NORMAL | 2021-12-30T11:20:04.439232+00:00 | 2021-12-30T11:20:04.439276+00:00 | 88 | false | When you run through the multiples of the prime numbers from 1 to 9, you\'ll notice that 2 and 5 don\'t have any muliples that end in 1. The reason for this is that a number that is of the form 111...111 = 10^n + 10^(n-1) + ... + 1. The modulus of a sum is the sum of moduluses and since 2 divides 10 and 5 divides 10, 111...111 mod 10 = 1. Hence, we can immediately rule out all numbers that have 2 and 5 in their prime factorization.\n\nThe rest is simply using the modular property that the modulus of a sum or product is the same as the sum/product of the moduluses.\nFor instance, let\'s use 7 as an example:\n1 mod 7 = 1. Ok so 7 needs more 1\'s. To add a 1, we multiply by 10 and add 1 => 1 * 10 + 1 = 11. Then, we can check if 11 mod 7 is 0. No it isn\'t so we need to add another 1. However, since we\'re only dealing with moduluses, we can use the property descriped above and only store the remainder: 1 * 10 + 1 = 1 mod 7 * 10 mod 7 + 1 mod 7 = 4. So now, our currect remainder is 4. When we multiply by 10 and add 1 again to append the next digit, aka 1 * 100 + 1 * 10 + 1, we can use our previous remainder. This is because 1 * 100 + 1 * 10 + 1 = 10 * (1 * 10 + 1) + 1. Taking the modulus of that, 10 mod 7 * (previous remainder) + 1 mod 7 = (3 * 4 + 1) mod 7 = 6. Essentially, all we\'re doing is using the previous remainder to compute the next one.\n\n```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if k % 2 == 0 or k % 5 == 0: return -1\n \n digits, rem = 1, 1\n while rem % k != 0:\n rem = (rem % k) * (10 % k) + 1\n digits += 1\n \n return digits | 1 | 0 | ['Math', 'Python'] | 0 |
smallest-integer-divisible-by-k | C++||Brute using set||Critical Observation | cbrute-using-setcritical-observation-by-g2umb | To understand the approach you can head over to this post \n\nSo,this problem will be done in a brute way where we will check the remainders (num%k), where num | puspendudas2002 | NORMAL | 2021-12-30T10:32:00.122116+00:00 | 2021-12-30T10:33:41.352445+00:00 | 58 | false | ***To understand the approach you can head over to*** [this post](https://leetcode.com/problems/smallest-integer-divisible-by-k/discuss/1655732/C%2B%2BJavaPython-5-lines-oror-Image-Explain-oror-Beginner-Friendly) \n\n`So,this problem will be done in a brute way where we will check the remainders (num%k), where num will start from 1,11,111,....so on untill we get the (num%k==0 or simply the num gets divisble by k)`\n\n`If you have understand the approach how the problem is needed to be done,one problem is still there that we cannot update the num since num can go beyond 64-bit signed integer, so we need to update num%k `\n\n```\nEg:-11%k can be written as ((1%k)*10+1)%k,\n 111%k can be written as ((11%k)*10+1)%k,\n\t so on....\n```\n\n***Code:-***\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n int num=1%k,sz=1; //taking num as as the remainer of first possible case of 1 and sz to keep the track of current number of digits \n set<int> m; //to store the remainders\n while(num){\n if(m.count(num)) //to check if a repeated remainder is inserted\n return -1;\n m.insert(num);\n sz++;\n num*=10; //\n num++; //increasing the number by 1 digit by appending 1\n num%=k; //\n }\n return sz; //returning the number of digits when num becomes 0\n }\n};\n```\n***T.C.:-O(k)*** | 1 | 0 | ['Ordered Set'] | 0 |
smallest-integer-divisible-by-k | C++ || 100% FAST || CLEAN CODE | c-100-fast-clean-code-by-easy_coder-ty52 | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n // edge case\n \n if(k % 2 == 0 || k % 5 == 0) return -1;\n | Easy_coder | NORMAL | 2021-12-30T06:00:58.799126+00:00 | 2021-12-30T06:00:58.799176+00:00 | 72 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n // edge case\n \n if(k % 2 == 0 || k % 5 == 0) return -1;\n \n int n = 1;\n int len = 1;\n \n while(n % k !=0 ){\n n = (n * 10 + 1) % k;\n len++;\n }\n \n return len;\n }\n}; | 1 | 0 | ['Math', 'C'] | 0 |
smallest-integer-divisible-by-k | ✅ [C++] Simple Solution || Easy-Understanding | c-simple-solution-easy-understanding-by-dpd6e | \n\n\n\nint smallestRepunitDivByK(int k)\n{\n if(k%2==0 || k%5==0) return -1;\n int ans=1;\n int remainder=1;\n int total=1;\n while(total%k!=0)\n { | Nazim173 | NORMAL | 2021-12-30T06:00:10.505267+00:00 | 2021-12-30T06:00:10.505314+00:00 | 33 | false | \n\n\n```\nint smallestRepunitDivByK(int k)\n{\n if(k%2==0 || k%5==0) return -1;\n int ans=1;\n int remainder=1;\n int total=1;\n while(total%k!=0)\n {\n ans++;\n remainder=(remainder*10)%k;\n total=(total+remainder)%k;\n }\n return ans;\n}\n```\n\n`Vote plz.. vro :|` | 1 | 0 | ['C'] | 0 |
smallest-integer-divisible-by-k | C++ | SC: O(N), TC: O(N) | Explained Code | c-sc-on-tc-on-explained-code-by-kshitijs-ok7x | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n /*\n Here, for example n = 1111, and k = 7\n so, if the remainder of | kshitijSinha | NORMAL | 2021-12-30T05:25:33.436659+00:00 | 2021-12-30T05:25:33.444077+00:00 | 44 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n /*\n Here, for example n = 1111, and k = 7\n so, if the remainder of 1111 / 7 = 5\n then (5*10)%7 + 1 == 11111 % 7\n LHS = 50%7 + 1 = 2\n RHS = 2\n \n Q: How do we know that there will be no \'n\' divisible by \'k\'?\n A: If we find a cycle, if same remainder is repeated, that means we will always get the same result in a cycle\n */\n int i = 1;\n int count = 1;\n unordered_set<int> uSetAlreadyRemainderFound;\n do{\n if(i%k == 0)\n return count;\n if(uSetAlreadyRemainderFound.find(i%k) != uSetAlreadyRemainderFound.end())\n return -1;\n uSetAlreadyRemainderFound.insert(i%k);\n i = (i%k * 10)%k + 1;\n count++;\n }while(1);\n return -1;\n }\n};\n``` | 1 | 0 | ['C'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.