question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
smallest-integer-divisible-by-k | Javascript Solution Time O(n) and time O(n), 100% better Memory Usage | javascript-solution-time-on-and-time-on-7aupq | \n/**\n * @param {number} k\n * @return {number}\n */\nvar smallestRepunitDivByK = function(k) {\n if( 1 > k > 1e6 ) return -1;\n let val = 0;\n for (l | akashmdev | NORMAL | 2021-12-30T05:07:12.893177+00:00 | 2021-12-30T05:07:12.893221+00:00 | 102 | false | ```\n/**\n * @param {number} k\n * @return {number}\n */\nvar smallestRepunitDivByK = function(k) {\n if( 1 > k > 1e6 ) return -1;\n let val = 0;\n for (let i = 1; i < 1e6; i++) {\n val = (val * 10 + 1) % k;\n if (val === 0) return i;\n }\n return -1;\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
smallest-integer-divisible-by-k | [C++] Simplest Intuitive Solution | Faster than 100% | c-simplest-intuitive-solution-faster-tha-sue8 | APPROACH : \n We know that any such number with 1 in all digits doesn\'t exist for k=2 or k=5.\n Therefore any multiple of 2 or 5 also don\'t divide any such nu | Mythri_Kaulwar | NORMAL | 2021-12-30T04:13:07.183523+00:00 | 2021-12-30T04:32:13.130224+00:00 | 161 | false | **APPROACH :** \n* We know that any such number with ```1``` in all digits doesn\'t exist for ```k=2``` or ```k=5```.\n* Therefore any multiple of ```2``` or ```5``` also don\'t divide any such number. \n* So if ```k``` is divisible by either ```2``` or ```5```, we return ```-1```;\n* For any other ```k```, we initialize ```n=1``` and ```length=1``` (stores the length of such number) and we loop (we do ```n=n*10+1``` & ```length++``` )until we find such number that\'s divisible by ```k``` (```n%k == 0```)\n* But soon, it will cause integer overflow if we keep storing ```n```. So instead we store the remainder that\'s obtained when we divide ```n``` with ```k```. Why? \n\n**Why do we store the remainders modulo ```k``` ?**\nThe reason is simple : \n* For every iteration, ```n = kQ + r``` , for some quotient ```Q``` and remainder ```r```.\n* The above equation can be written as : ```(n*10 + 1) = (kQ + r)*10 + 1```\n* So ```n*10 + 1 = kQ*10 + (r*10 + 1)```. \n* ```kQ*10``` is divisible by ```k```. So for ```n*10 + 1``` to be divisible by ```k```, ```r*10 + 1``` should be divisible by ```k```. \n\n**Time Complexity :** O(k) \n\n**Space Complexity :** O(1)\n\n**Code :**\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(!(k%2) || !(k%5)) return -1;\n \n auto r = 1, length = 1;\n while(true){\n r = r%k;\n if(!r) return length;\n r = r*10 + 1;\n length++;\n }\n }\n};\n```\n\n\n | 1 | 0 | ['C', 'C++'] | 0 |
smallest-integer-divisible-by-k | Python Solution (Weird case) | python-solution-weird-case-by-shivi127-8how | ```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if k%10==0 or k%5==0:\n return -1\n\n num = 1\n coun | shivi127 | NORMAL | 2021-12-30T04:05:27.124815+00:00 | 2021-12-30T04:05:36.891761+00:00 | 68 | false | ```\nclass Solution:\n def smallestRepunitDivByK(self, k: int) -> int:\n if k%10==0 or k%5==0:\n return -1\n\n num = 1\n count = 0\n while num%k!=0:\n num = num*10+1\n count+=1\n \n return count+1\n\t | 1 | 1 | ['Python'] | 1 |
smallest-integer-divisible-by-k | [Rust] Not optimal, but reasoned this one out | rust-not-optimal-but-reasoned-this-one-o-4bnc | From other posts, I see that it turns out that "if a number is not divisible by 2 or 5, then it is a divisor of some repunit". Knowing this you can optimize my | quintic | NORMAL | 2021-12-30T02:30:44.981931+00:00 | 2021-12-30T02:30:44.981974+00:00 | 82 | false | From other posts, I see that it turns out that "if a number is not divisible by 2 or 5, then it is a divisor of some repunit". Knowing this you can optimize my solution quite a bit, but this was fun anyway.\n\nSince I didn\'t know the above, what I noticed is that I can write a repunit as follows.\n\n```\nn = 10^(i -1) + 10^(i - 2) + ... + 10 + 1\n```\n\nNow if I use Euclid\'s algorithm on `n` to divide by some number `k` I get \n\n```\nn = (q_(i - 1) * k + r_(i - 1)) + ... + (q_1 * k + r_1) + (q_0 * k + r_0)\n```\n\nNow we see that if `k` divides the sum of the `r_i` then `k` divides `n`, which is the same as saying\nthe sum is 0 mod k.\n\nNow the algoirhtm I came up with is to compute `r_i` sequentually, and sum them up mod k. If this is zero, return\nthe number of `r_i` that I computed. However, if we every see a sum of `r_i` repeat, then it\'s sort of like long division where we have a repeating pattern, so we can safely reason that we will never find a sum that is 0 mod k.\n\nLastly, we have to ensure that we will always either run into a 0 or a repeating pattern. We can guarantee that since we are doing this math mod k, and so there are only a finite number of sums mod k that we can compute. Thus pidgenhole principle says if we don\'t find a zero, we will find a repeat.\n\n```rust\nuse std::collections::HashSet;\n\npub struct Solution {}\n\nimpl Solution {\n pub fn smallest_repunit_div_by_k(k: i32) -> i32 {\n let mut seen = HashSet::new();\n let mut n = 1;\n let mut r = 1 % k;\n let mut sum = r;\n loop {\n if sum == 0 {\n return n;\n } else if seen.contains(&sum) {\n return -1;\n }\n seen.insert(sum);\n r = (10 * r) % k;\n sum = (sum + r) % k;\n n += 1;\n }\n }\n}\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | JAVA - O(K) - compute and space | java-ok-compute-and-space-by-venkim-xfkq | If k is even or is a multiple, it will never divide a number ending in 1. So, we can immediately rule those out and return -1. \n Since remainders at some po | venkim | NORMAL | 2021-12-30T02:11:39.768146+00:00 | 2021-12-30T02:12:53.187120+00:00 | 54 | false | If k is even or is a multiple, it will never divide a number ending in 1. So, we can immediately rule those out and return -1. \n Since remainders at some point starts repeating, we can use that information to keep only remainders and the moment we start seeing a reminder that has already seen, we can stop and decide we will not find a number 111....1 that is divisible by k. So, we generate val * 10 + 1 with existing val. \n\nif val = k \\* factor + rem; then we can safely keep only the remainder and ignore the k\\*factor since k\\*factor % k = 0. So, we only keep track of remainders and keep a Set of remainders.. \n\n```\nclass Solution {\n public int smallestRepunitDivByK(int k) {\n // multiples of 2 and 5 never end with 1\n if (k % 2 ==0 || k % 5 == 0)\n return -1;\n \n Set<Integer> seen = new HashSet<>();\n int rslt = 1, val = 0;\n while (seen.add(val)){\n val = (val*10 + 1) % k;\n if (val == 0){\n return rslt;\n }\n rslt++;\n }\n return -1;\n }\n}\n``` | 1 | 1 | [] | 0 |
smallest-integer-divisible-by-k | 【Java】An easy Solution By using the knowledge points that primary school students understand | java-an-easy-solution-by-using-the-knowl-7cfa | Cycle to find the right X:\n\njava\n//Here is the idea of problem solving\n\nint x = 1\n\nint ans = 1;\n\nwhile (x % K != 0) {\n\tx = x * 10 + 1;\n\t++ans;\n}\n | Haruko386 | NORMAL | 2021-12-30T00:27:36.168707+00:00 | 2021-12-30T00:27:36.168743+00:00 | 215 | false | Cycle to find the right X:\n\n```java\n//Here is the idea of problem solving\n\nint x = 1\n\nint ans = 1;\n\nwhile (x % K != 0) {\n\tx = x * 10 + 1;\n\t++ans;\n}\n```\n\nIt will overflow here, so it is changed to X % = k; x = x * 10 + 1;\n\nPossibility of dead circulation\n\nIt\'s actually a multiple of 2 and 5. At this time, 10 can be divided and needs to be excluded\n\nSolution \n```java\nclass Solution {\n public int smallestRepunitDivByK(int K) {\n if (K % 2 == 0 || K % 5 == 0)\n return -1;\n int i = 1;\n for (int n = 1; n % K != 0; i++) {\n n %= K;\n n = n * 10 + 1;\n }\n return i;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
smallest-integer-divisible-by-k | C++ || CLEAN CODE || WITH PROPER EXPLANATION | c-clean-code-with-proper-explanation-by-vsihr | class Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n \n /\n \n We have to solve the question using two key problems ans ther | anu_2021 | NORMAL | 2021-10-22T07:35:03.577336+00:00 | 2021-10-22T07:35:03.577381+00:00 | 128 | false | class Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n \n /*\n \n We have to solve the question using two key problems ans there solutions .........\n \n Problem....(a) As n may not fit in a 64 bit signed integer.\n \n Problem....(b) There is no info about the maximum length of n until which we should check for.\n \n \n Solution....(a) We have to use the property i.e A number X is divisible by K if and only if sum of remainders all the digits of X by K is also divisible by K .\n \n Example (1): X=111 is divisible by K=3 \n \n digits of 111 : 1,1,1 now (1%3)=1 , (1%3)=1 ,(1%3)=1\n \n sum of those remainders (1+1+1)=3 which is divisible by K=3\n \n \n Solution....(b) Notice that if N does not exist, Our codes\'s (See below) while-loop will continue endlessly. However, the possible values of remainder are limited -- ranging from 0 to K-1. Therefore, if the while-loop continues forever, the remainder repeats after every certain period . Also, if remainder repeats, then it gets into a loop. Hence, the while-loop is endless if and only if the remainder repeats.\n \n As rem=(X%K) and rem should be lie between [0,K-1] .\n \n */\n \n int i=0,n=0;\n \n while(i++<=k){\n \n n=(n*10+1)%k;\n \n if(n==0){\n return i;\n }\n \n }\n \n return -1;\n \n }\n}; | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | Go | go-by-dynasty919-dm4w | \nfunc smallestRepunitDivByK(k int) int {\n res := 1\n n := 1 % k\n set := make(map[int]bool)\n set[n] = true\n for n != 0 {\n n = (n * 10 | dynasty919 | NORMAL | 2021-06-05T17:28:42.956838+00:00 | 2021-06-05T17:28:42.956869+00:00 | 65 | false | ```\nfunc smallestRepunitDivByK(k int) int {\n res := 1\n n := 1 % k\n set := make(map[int]bool)\n set[n] = true\n for n != 0 {\n n = (n * 10 + 1) % k\n if set[n] {\n return -1\n }\n set[n] = true\n res++\n }\n return res\n}\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | javascript 240ms | javascript-240ms-by-henrychen222-lkpt | \nconst smallestRepunitDivByK = (k) => {\n let remain = 0;\n for (let i = 1; i < 1e6; i++) {\n remain = (remain * 10 + 1) % k;\n if (remain | henrychen222 | NORMAL | 2021-03-13T22:24:50.677233+00:00 | 2021-03-13T22:24:50.677282+00:00 | 157 | false | ```\nconst smallestRepunitDivByK = (k) => {\n let remain = 0;\n for (let i = 1; i < 1e6; i++) {\n remain = (remain * 10 + 1) % k;\n if (remain == 0) return i;\n }\n return -1;\n};\n``` | 1 | 1 | ['JavaScript'] | 1 |
smallest-integer-divisible-by-k | Generate the quotient | generate-the-quotient-by-madno-ag46 | One can generate the quotient digits from least significant to most significant, because the problem has a recursive substructure.\n\nTo find K*Y=1111, we decom | madno | NORMAL | 2020-12-10T19:38:23.546227+00:00 | 2020-12-10T20:04:17.134101+00:00 | 174 | false | One can generate the quotient digits from least significant to most significant, because the problem has a recursive substructure.\n\nTo find ```K*Y=1111```, we decompose Y into its digits say ```abcd```\n\n```\nK*abcd = 1111\nK*10*abc +K*d-1 = 1110, and K*d has to end with 1, so move the one from right to left\nK*10*abc +rest(d) = 1110, we can simplify by introducing rest(d) = K*d-1, where rest(d) is divisible by 10\nK*abc +rest(d)/10 = 111\nK*10*ab +K*c+rest(d)/10-1 = 110, rest(c,d)=K*c+rest(d)/10-1, and rest(c,d) is divisible by 10\nK*ab +rest(c,d)/10 = 11\nK*a +rest(b,c,d)/10 = 1\n rest(a,b,c,d) = 0\n```\nIn general ```rest(next) = K*nextDigit + rest(previous)/10 - 1``` where rest ends with 0,\nand we can search for the unique nextDigit between ```0...9``` making rest ending in 0,\nsince every other part of the equation is known (```rest(previous)``` was recursively calculated,\nwith the base case 0).\n\n\n\n```\nclass Solution {\n //111=37*3\n //K*d+(K*j+(K*i-1)/10-1)/10 = 1\n // (3*3+(3*7-1)/10-1)/10\n public int smallestRepunitDivByK(int K) {\n if (K==1) return 1;\n int len = 1;\n var quotient = new StringBuilder();\n for(long rest = 0; rest != 10; ++len){\n boolean match = false;\n for(int digit = 0; digit <= 9; ++digit){\n if ((K*digit+rest/10)%10 == 1){\n rest = K*digit+rest/10-1;\n match = true;\n quotient.append((char)(digit+\'0\'));\n break;\n }\n }\n if (!match) return -1;\n }\n System.out.println(quotient.reverse());\n return len;\n }\n}\n``` | 1 | 0 | ['Math', 'Greedy', 'Java'] | 0 |
smallest-integer-divisible-by-k | [Kotlin] Simple solution, explained | kotlin-simple-solution-explained-by-jani-u2od | The key to understanding the solution (and hint given), is to understand why using the remainder R to get to the next number to test can be used in place of N, | janinbv | NORMAL | 2020-11-26T07:44:42.334289+00:00 | 2020-11-26T07:46:05.237821+00:00 | 51 | false | The key to understanding the solution (and hint given), is to understand why using the remainder R to get to the next number to test can be used in place of N, where N is 1, 11, 111, and so on. So instead of using N * 10 + 1, we can use R * 10 + 1.\n\nAssume that taking modulo K of N gives remainder R. N then equals K * x + R (x is N / K integer value, we don\'t really care what its value is). \nThe next number to test is ((K * x + R) * 10 + 1). \nUsing the distributive property for multiplication, this is equivalent to ((K * x * 10) + (R * 10) + 1).\nTaking modulo K of the next number is ((K * x * 10) + (R * 10) + 1) % K\nUsing the distributive property for modulo, this is equivalen to ( (K * x * 10) % K + (R * 10) % K + 1 % K) % K\n(The last %K is appended in case the separate remainders added together exceed K)\nSince (K * x * 10) % K is always 0, (clearly evenly divisible by K), this can be reduced to:\n( (R * 10) % K + 1 % K) % K\nUsing the distributive property again, this time to combine items, we have (R * 10 + 1) % K\n\nThis is why, in the end, we can use (R * 10 + 1) % K for each iteration. Since the remainder is always less than K, we will never overflow like we would if we keep multiplying by 10 and adding 1.\n\nFinally, any number divisible by 2 (even), or 5 (which ends in 5 or 0), can never be evenly divided into a number that is all ones, so those can be easily eliminated at the start. It turns all other numbers have a solution, so no check is required to avoid an endless loop.\n\n```\n fun smallestRepunitDivByK(K: Int): Int {\n if (K % 2 == 0 || K % 5 == 0) {\n return -1\n }\n var n = 1\n var len = 1\n while(n % K != 0) {\n n = (n * 10 + 1) % K\n len++\n }\n return len\n }\n | 1 | 0 | ['Math', 'Kotlin'] | 2 |
smallest-integer-divisible-by-k | [Ruby] O(k) | ruby-ok-by-mistersky-trfd | \n# @param {Integer} k\n# @return {Integer}\ndef smallest_repunit_div_by_k(k)\n return -1 unless [1, 3, 7, 9].include?(k%10)\n \n mod = 0\n mod_set = Set.ne | mistersky | NORMAL | 2020-11-25T21:06:06.950395+00:00 | 2020-11-25T21:06:06.950436+00:00 | 49 | false | ```\n# @param {Integer} k\n# @return {Integer}\ndef smallest_repunit_div_by_k(k)\n return -1 unless [1, 3, 7, 9].include?(k%10)\n \n mod = 0\n mod_set = Set.new\n \n (1..k).each do |length|\n mod = (10*mod + 1)%k\n\n return length if mod == 0\n return -1 if mod_set.include?(mod)\n\n mod_set << mod\n end\n \n -1\nend\n``` | 1 | 0 | ['Ruby'] | 0 |
smallest-integer-divisible-by-k | Smallest Int Divisible by K | C++ | 100% fast | smallest-int-divisible-by-k-c-100-fast-b-cgen | first we rule out 2 obvious cases where K will never divide into n, where n is a number consisting of only 1s.\n\n1. When K is divisible by 2, because for any n | junyanbill | NORMAL | 2020-11-25T19:50:35.088229+00:00 | 2020-11-25T20:45:08.048469+00:00 | 96 | false | first we rule out 2 obvious cases where K will never divide into n, where n is a number consisting of only 1s.\n\n1. When K is divisible by 2, because for any number (a) to be divisible by another number (b), it logically follows that a must be also divisible by divisors of b. And any n will never be divisible by 2.\n2. When K is divisible by 5, reason same as 2.\n\nWith these eliminated we have removed a huge number of potential Ks, leaving only those that end with 1, 3, 7, or 9.\n\nNow we perform division just like how you would on paper, by dividing the remainder. This way the program never has integer overflow. \ne.g. to divide 13 into 111111 we:\n\tfirst digit: divide 1 by 13= 0, remainder 1.\n\tsecond digit: multiply remainder of 1 by 10, plus 1=11, divide by 13 = 0, remainder of 11.\n\tthird digit: multiply remainder of 11 by 10, plus 1=111, divide by 13= 8, remainder of 7,\n\tfourth digit: multiply remainder of 7 by 10, plus 1=71, divide by 13= 5, remainder of 6,\n\tfifth digit: multiply remainder of 6 by 10, plus 1=61, divide by 13=4, remainder of 9,\n\tsixth digit: multiply remainder of 9 by 10, plus 1=91, divide by 13=7, remainder of 0.\n\nAnd you can see that the pattern is clear, the remainder rolls upwards until the remainder is the divisor itself, or it rolls over the size of the divisor, which restarts the pattern from the beginning. Logically this makes sense, as whenever the remainder is larger than the divisor that means you can divide into the number 1 more time.\n\nHere this property can be used to set the limit that when reached, means it is clear that K will never divide into n.\n```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n if (K%2==0||K%5==0)\n return -1;\n\n int temp=0;\n for(int i=1;i<=K;i++)\n {\n temp=(temp*10)%K+1;\n if(temp%K==0)\n {\n return i;\n }\n }\n return -1;\n\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
smallest-integer-divisible-by-k | [C++] From failed solution to a successful one | c-from-failed-solution-to-a-successful-o-f1ts | \n/*\nIntuition: For Example 3: K = 3\nm=\n1\n11\n111\nThis is brute-froce search the anwser. You will encounter overflow soon. What really matter is remainer o | codedayday | NORMAL | 2020-11-25T15:56:46.134216+00:00 | 2020-11-25T16:09:24.303803+00:00 | 93 | false | ```\n/*\nIntuition: For Example 3: K = 3\nm=\n1\n11\n111\nThis is brute-froce search the anwser. You will encounter overflow soon. What really matter is remainer of mod(m, K);\nFor example, 111 % 3 is same as 21 % 3. How do we get it? (111 - 3 * someInterger) % 3 is same as 111 % 3. If someInterger = 30, then 21 % 3 == 111 % 3\nThat is a straighforward example why we can find the answer by working on remainder instead of growing 111...1 sequence. \n\nFOr the proposed solution is:\nm=\n1\n2\n0\n\n\n*/\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n\t // N is the remainder, which must be in the range of between 1%K and K\n for (int m = 1, N = 1 % K; N <= K; m = (m * 10 + 1) % K, ++N)\n if (m == 0) return N;\n return -1;\n }\n};\n\n```\nReferece:\n[1] https://leetcode.com/problems/smallest-integer-divisible-by-k/discuss/260887/C%2B%2B-3-lines-O(K)-or-O(1) | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | Python Simple Solutiom | python-simple-solutiom-by-lokeshsk1-gu55 | \nclass Solution:\n def smallestRepunitDivByK(self, K):\n if K % 2 == 0 or K % 5 == 0:\n return -1\n r = 0\n for N in range( | lokeshsk1 | NORMAL | 2020-11-25T14:31:45.578151+00:00 | 2020-11-25T14:31:45.578193+00:00 | 206 | false | ```\nclass Solution:\n def smallestRepunitDivByK(self, K):\n if K % 2 == 0 or K % 5 == 0:\n return -1\n r = 0\n for N in range(1, K + 1):\n r = (r * 10 + 1) % K\n if r==0:\n return N\n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
smallest-integer-divisible-by-k | Java easy peasy | java-easy-peasy-by-rahul_20-a6jg | \nclass Solution {\n public int func(int k)\n {\n int temp=1;\n for(int i=1;i<100001;i++)\n {\n if(temp%k==0)\n | rahul_20 | NORMAL | 2020-11-25T12:00:28.919161+00:00 | 2020-11-25T12:00:28.919189+00:00 | 113 | false | ```\nclass Solution {\n public int func(int k)\n {\n int temp=1;\n for(int i=1;i<100001;i++)\n {\n if(temp%k==0)\n {\n return i;\n }\n int mod=temp%k;\n temp=mod*10+1;\n }\n return -1;\n }\n \n public int smallestRepunitDivByK(int K) {\n \n if((K & 1)==1)\n {\n return func(K);\n }\n return -1;\n \n }\n}\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | C# Simple Time = Space = O(n) Soln | c-simple-time-space-on-soln-by-harsh007k-lt8b | \n\npublic class Solution {\n // Time O(n) || Space O(N)\n public int SmallestRepunitDivByK(int K) {\n if (K % 2 == 0) return -1;\n int rema | harsh007kumar | NORMAL | 2020-11-25T11:08:51.015745+00:00 | 2020-11-25T11:08:51.015785+00:00 | 48 | false | \n```\npublic class Solution {\n // Time O(n) || Space O(N)\n public int SmallestRepunitDivByK(int K) {\n if (K % 2 == 0) return -1;\n int remainder = 0;\n int count = 0;\n HashSet<int> set = new HashSet<int>(100);\n while (true)\n {\n remainder = (remainder * 10 + 1) % K;\n if (remainder == 0) return count + 1;\n ++count;\n \n // seen this remainder before than break the loop\n if (set.Contains(remainder)) break;\n // else add this remainder to the set\n else set.Add(remainder);\n }\n return -1;\n }\n}\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | Python O(K) by simulation [w/ Comment] | python-ok-by-simulation-w-comment-by-bri-23vr | Python O(K) by simulation \n\n---\n\nImplementation\n\n\nclass Solution:\n def smallestRepunitDivByK(self, K: int) -> int:\n \n\n if (K % 2 == | brianchiang_tw | NORMAL | 2020-11-25T08:32:43.368294+00:00 | 2020-11-25T08:32:43.368334+00:00 | 116 | false | Python O(K) by simulation \n\n---\n\n**Implementation**\n\n```\nclass Solution:\n def smallestRepunitDivByK(self, K: int) -> int:\n \n\n if (K % 2 == 0) or (K % 5 == 0):\n \n # Quick response on special cases\n # 11111...1 is always not divisible by 2 and by 5\n return -1\n \n \n # initialization\n remainder = 0\n \n # scan for each sequence 111...1 with length N\n for N in range(1, K+1):\n \n # update remainder on modulo K\n remainder = (remainder * 10 + 1) % K \n \n if remainder == 0:\n return N\n \n``` | 1 | 0 | ['Math', 'Simulation', 'Python', 'Python3'] | 1 |
smallest-integer-divisible-by-k | Python with modular arithmetic | python-with-modular-arithmetic-by-tonymo-d1tw | If x mod k = a, when x * y + c mod k = (a * y + c) mod k\nSo we can do the while loop as follow\nhttps://en.wikipedia.org/wiki/Modular_arithmetic\n\nclass Solut | tonymok97 | NORMAL | 2020-11-25T08:11:49.950162+00:00 | 2020-11-25T08:13:51.178291+00:00 | 98 | false | If x mod k = a, when x * y + c mod k = (a * y + c) mod k\nSo we can do the while loop as follow\nhttps://en.wikipedia.org/wiki/Modular_arithmetic\n```\nclass Solution(object):\n def smallestRepunitDivByK(self, K):\n seen = set()\n curr_mod = 1 % K\n length = 1\n while(curr_mod not in seen):\n seen.add(curr_mod)\n if curr_mod == 0:\n return length\n # update if it does not satisfy\n curr_mod = (curr_mod * 10 + 1) % K\n length += 1\n return -1\n```\n\nHowever, with the python infinite numbering system, you can also do brute force with higher complexity\n```\nclass Solution(object):\n def smallestRepunitDivByK(self, K):\n seen = set()\n curr = 1 \n length = 1\n while((curr % K) not in seen):\n seen.add(curr % K)\n if curr % K == 0:\n return length\n # update if it does not satisfy\n curr = curr * 10 + 1\n length += 1\n return -1\n``` | 1 | 1 | [] | 0 |
smallest-integer-divisible-by-k | C++ | [99%, 100% memory] | 10-liner | Crispy AF | c-99-100-memory-10-liner-crispy-af-by-aj-o2u1 | \nclass Solution {\nprivate:\n int done[100005];\npublic:\n int smallestRepunitDivByK(int K) {\n long long x = 0;\n memset(done, 0, sizeof(d | ajinkya1p3 | NORMAL | 2020-11-25T08:09:00.223481+00:00 | 2020-11-25T08:14:42.782726+00:00 | 58 | false | ```\nclass Solution {\nprivate:\n int done[100005];\npublic:\n int smallestRepunitDivByK(int K) {\n long long x = 0;\n memset(done, 0, sizeof(done));\n \n for (int i=1; ; i++) {\n x = (x * 10 + 1) % K;\n \n if (x == 0) {\n return i;\n } else if (done[x]) {\n return -1;\n }\n \n done[x] = 1;\n }\n }\n};\n```\n\nExplanation -\n\n1. Calculate 1, 11, 111, 1111,..... modulo K\n2. If remainder becomes 0, return length. If remainder repeats, return -1\n3. ???\n4. Profit! \uD83E\uDD19\n\nAs always,\n\uD83E\uDD19 Stay crispy guys \uD83E\uDD19 | 1 | 1 | [] | 1 |
smallest-integer-divisible-by-k | Nice number theory question | nice-number-theory-question-by-huangdach-wouq | \n/// If k is a multiple of 2 or 5, we cannot find such \'ans = 1..1\' such that\n/// ans is divisible by k because it\'s impossible for ans to have factor of 2 | huangdachuan | NORMAL | 2020-08-16T23:13:49.357282+00:00 | 2020-08-16T23:13:49.357331+00:00 | 141 | false | ```\n/// If k is a multiple of 2 or 5, we cannot find such \'ans = 1..1\' such that\n/// ans is divisible by k because it\'s impossible for ans to have factor of 2 nor 5.\n/// Otherwise we claim during 1, 11, 111, 1...1 (k ones), there must be one number\n/// that is divisible by K. Proof by contradiction: if no such number, then for these\n/// k numbers, no number\'s module is 0. For the remaining choices 1, 2, 3, ... k -1,\n/// by Pigeonhole principle, there must be two numbers that share the same module.\n/// These two numbers x and y (x < y) has a diff y - x that has some zeroes as suffix.\n/// In other words, if x is i\'s ones, y is j\'s ones (i < j), then y - x = (j-i) ones * 10e(i),\n/// the 10e(i) part can only provide 2 and 5 factors, which is not divisible by k.\n/// So (j-i) ones is divisible by k, but j - i < k, so contradiction.\nclass Solution {\npublic:\n int smallestRepunitDivByK(int K) {\n if (K % 2 == 0 || K % 5 == 0) {\n return -1;\n }\n int module = 0;\n for (int i = 1; i <= K; ++i) {\n module = (10 * module + 1) % K;\n if (module == 0) {\n return i;\n }\n }\n return -1;\n }\n};\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | c++ solution 100% | c-solution-100-by-harshitata404-deiv | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if((!(k%2))||!(k%5))return -1;\n int r=1,l=1;\n while(r%k){\n | harshitata404 | NORMAL | 2020-06-12T13:42:45.585935+00:00 | 2020-06-12T13:42:45.585976+00:00 | 158 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if((!(k%2))||!(k%5))return -1;\n int r=1,l=1;\n while(r%k){\n r%=k;\n l++;\n r=r*10+1;\n }\n return l;\n }\n};\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | python 3 easy to understand | python-3-easy-to-understand-by-wdiii-i83s | \nclass Solution:\n def smallestRepunitDivByK(self, K: int) -> int:\n if K%2==0 or K%5==0:\n return -1\n start=1\n while star | wdiii | NORMAL | 2020-06-10T18:48:57.478884+00:00 | 2020-06-10T18:48:57.478938+00:00 | 167 | false | ```\nclass Solution:\n def smallestRepunitDivByK(self, K: int) -> int:\n if K%2==0 or K%5==0:\n return -1\n start=1\n while start%K!=0:\n start=start*10+1\n return len(str(start))\n``` | 1 | 0 | [] | 0 |
smallest-integer-divisible-by-k | simple c++ solution | simple-c-solution-by-bannag-wynf | \nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(k%2==0 || k%5==0) return -1;\n if(k==1) return 1;\n set<int> hash; | bannag | NORMAL | 2020-05-28T03:04:52.805680+00:00 | 2020-05-28T03:04:52.805729+00:00 | 122 | false | ```\nclass Solution {\npublic:\n int smallestRepunitDivByK(int k) {\n if(k%2==0 || k%5==0) return -1;\n if(k==1) return 1;\n set<int> hash;\n long long val=1;\n long long modulo=0;\n int l=1;\n while(1){\n if(val % k==0){\n return l;\n }else if(hash.count(val %k)){\n return -1;\n }else{\n hash.insert(val%k);\n }\n l+=1;\n val = val*(10%k) +1;\n val = val%k;\n }\n return -1;\n }\n};\n``` | 1 | 0 | [] | 0 |
check-array-formation-through-concatenation | Python 5 lines - hashmap | python-5-lines-hashmap-by-eric496-mp7n | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n mp = {x[0]: x for x in pieces}\n res = []\n | eric496 | NORMAL | 2020-11-01T04:01:49.892066+00:00 | 2020-11-01T04:04:48.039396+00:00 | 8,045 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n mp = {x[0]: x for x in pieces}\n res = []\n \n for num in arr:\n res += mp.get(num, [])\n \n return res == arr\n``` | 127 | 4 | [] | 15 |
check-array-formation-through-concatenation | C++ Track First Elements | c-track-first-elements-by-votrubac-ndcx | Since all elements are unique, we can map the first element in pieces to the piece position. Then, we just check if we have the right piece, and if so - try to | votrubac | NORMAL | 2020-11-01T22:43:49.908218+00:00 | 2020-11-02T18:37:34.606722+00:00 | 6,108 | false | Since all elements are unique, we can map the first element in `pieces` to the piece position. Then, we just check if we have the right piece, and if so - try to fit it.\n\nAs values are within [0..100], we can use an array instead of a hashmap.\n\n```cpp\nbool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n vector<int> ps(101, -1);\n for (int i = 0; i < pieces.size(); ++i)\n ps[pieces[i][0]] = i;\n for (int i = 0; i < arr.size(); ) {\n int p = ps[arr[i]], j = 0;\n if (p == -1)\n return false;\n while (j < pieces[p].size())\n if (arr[i++] != pieces[p][j++])\n return false;\n }\n return true;\n}\n``` | 104 | 3 | [] | 12 |
check-array-formation-through-concatenation | [Python] 2 Solutions, explained | python-2-solutions-explained-by-dbabiche-98cp | Solution 1, using strings\n\nImagine, that we have array [3, 4, 18, 6, 8] and pieces [4, 18], [6, 8], [3]. Let us create strings from original string and from p | dbabichev | NORMAL | 2021-01-01T10:55:56.573073+00:00 | 2021-01-01T10:55:56.573107+00:00 | 3,261 | false | ### Solution 1, using strings\n\nImagine, that we have array `[3, 4, 18, 6, 8]` and pieces `[4, 18]`, `[6, 8]`, `[3]`. Let us create strings from original string and from parts in the following way: `!3!4!18!6!8!` for `arr` and `!4!18!`, `!6!8!` and `!3!` for pieces. Then what we need to check is just if all of our pieces are substrings of first string. We can state this, because all numbers are different.\n\n**Complexity**: time complexity is `O(n^2)` to check all substrings and space is `O(n)`.\n\n```\nclass Solution:\n def canFormArray(self, arr, pieces):\n arr_str = "!".join(map(str, arr)) + "!"\n return all("!".join(map(str, p)) + "!" in arr_str for p in pieces)\n```\n\n### Solution 2, using hash table.\n\n Let us create correspondences `d` between each start of piece and the whole piece. Then we iterate over our `arr` and for each number check if we have piece starting with this number: if we have, we add it to constructed list, if not, add nothing. In this way, each what is constucted in the end equal to `arr` if and only if answer for our problem is `True`. Why though? Imagine `[1, 2, 3, 4, 5]` and pieces `[1, 2]` and `[3, 4, 5]`. Then we go element by element and have `[1, 2] + [] + [3, 4, 5] + []`. Imagine now, that we have pieces `[1, 2]` and `[4, 5]`. Then what will be reconstructed is `[1, 2] + [] + [] + [4, 5] + []`.\n \n **Complexity**: time and space complexity is `O(n)`.\n\n```\nclass Solution:\n def canFormArray(self, arr, pieces):\n d = {x[0]: x for x in pieces}\n return list(chain(*[d.get(num, []) for num in arr])) == arr\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 61 | 10 | [] | 8 |
check-array-formation-through-concatenation | C++ Easy solution using maps | c-easy-solution-using-maps-by-aparna_g-h17b | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n map<int,vector<int>> mp; \n // map the 1st e | aparna_g | NORMAL | 2021-01-01T08:17:35.090587+00:00 | 2021-01-01T08:17:35.090621+00:00 | 3,470 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n map<int,vector<int>> mp; \n // map the 1st element in pieces[i] to pieces[i]\n for(auto p:pieces) \n mp[p[0]] = p;\n vector<int> result;\n for(auto a:arr) {\n if(mp.find(a)!=mp.end()) \n result.insert(result.end(),mp[a].begin(),mp[a].end());\n }\n return result ==arr;\n }\n};\n```\n***Happy New Year :-)*** | 51 | 7 | ['C', 'C++'] | 9 |
check-array-formation-through-concatenation | JAVA 1ms using StringBuilder easy to understand | java-1ms-using-stringbuilder-easy-to-und-v6d1 | \n\n\n\n\n\n\n\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n StringBuilder sb = new StringBuilder();\n for(int | manjumallesh | NORMAL | 2020-11-01T10:08:34.157985+00:00 | 2021-05-08T06:31:20.914053+00:00 | 3,603 | false | \n\n\n\n\n\n\n```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n StringBuilder sb = new StringBuilder();\n for(int x : arr){\n\t\t\tsb.append("#");\n sb.append(x);\n sb.append("#");\n }\n for(int i = 0; i < pieces.length; i++){\n StringBuilder res = new StringBuilder();\n for(int j = 0; j < pieces[i].length; j++){\n\t\t\t\tres.append("#");\n res.append(pieces[i][j]);\n res.append("#");\n }\n if(!sb.toString().contains(res.toString())){\n return false;\n }\n }\n return true;\n }\n}\n```\n_Please_ *upvote* _if you like it_ | 45 | 3 | [] | 14 |
check-array-formation-through-concatenation | "Python" easy explanation blackboard | python-easy-explanation-blackboard-by-ha-3fmk | Simple and easy python3 solution\n The approch is well explained in the below image*\n\n\n\n\n\nclass Solution:\n def canFormArray(self, arr: List[int], piec | harish_sahu | NORMAL | 2021-01-01T08:40:35.722083+00:00 | 2021-01-01T08:42:23.528254+00:00 | 2,523 | false | * **Simple and easy python3 solution**\n* **The approch is well explained in the below image**\n\n\n\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n keys, ans = {}, []\n for piece in pieces:\n keys[piece[0]] = piece\n for a in arr:\n if a in keys:\n ans.extend(keys[a])\n return \'\'.join(map(str, arr)) == \'\'.join(map(str, ans))\n``` | 37 | 4 | ['Python', 'Python3'] | 7 |
check-array-formation-through-concatenation | JAVA | ~O(n) 0ms runtime | with Explanation | java-on-0ms-runtime-with-explanation-by-csqdq | Idea:\nStore the pieces in such a way that each array piece is linked and first element of each piece should be accessible in O(1) time. Hence using a HashMap. | suraj008 | NORMAL | 2021-01-01T10:08:24.730573+00:00 | 2021-05-07T08:10:54.657368+00:00 | 2,792 | false | Idea:\nStore the pieces in such a way that each array piece is linked and first element of each piece should be accessible in O(1) time. Hence using a HashMap. Then, traverse the arr and check if each value exits as a key (rest of the values in the arraylist of each key will be indexed over & checked in for loop)\neg: \n```\narr = [91,4,64,8,78,2], pieces = [[78,2],[4,64,8],[91]]\nHashMap:\n78-> [78,2]\n4-> [4,64,8]\n91-> [91]\n\n[91,4,64,8,78,2] (91 exists as a key and [91] an array of values)\n ^ \n[91,4,64,8,78,2] (4 exists as a key and [4,64,8] an array of values)\n ^ * *\n[91,4,64,8,78,2] (78 exists as a key and [78,2] an array of values )\n\t\t ^ * \n```\t\t \n```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n HashMap<Integer,int[]> hm = new HashMap();\n for(int[] list:pieces)\n hm.put(list[0],list);\n \n int index = 0;\n while(index<arr.length){\n if(!hm.containsKey(arr[index]))\n return false;\n \n int[] list = hm.get(arr[index]);\n for(int val:list){\n if(index>=arr.length || val!=arr[index])\n return false;\n index++;\n }\n }\n return true;\n }\n}\n```\n | 33 | 3 | ['Java'] | 5 |
check-array-formation-through-concatenation | [Python] HashMap Solution O(N) + Follow up question | python-hashmap-solution-on-follow-up-que-2yl6 | Problem 1: Special Constraint\n- The integers in arr are distinct.\n- The integers in pieces are distinct (i.e., If we flatten pieces in a 1D array, all the int | hiepit | NORMAL | 2021-06-02T07:03:31.757858+00:00 | 2021-06-02T07:13:19.556806+00:00 | 461 | false | **Problem 1: Special Constraint**\n- The integers in `arr` are **distinct**.\n- The integers in `pieces` are **distinct** (i.e., If we flatten pieces in a 1D array, all the integers in this array are **distinct**).\n- `sum(pieces[i].length) == arr.length`.\n\n```python\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n map = dict()\n for p in pieces:\n map[p[0]] = p\n\n n = len(arr)\n i = 0\n while i < n:\n if arr[i] not in map:\n return False\n p = map[arr[i]]\n if arr[i:i + len(p)] != p:\n return False\n i += len(p)\n return True\n```\n\n**Complexity**\n- Time: `O(N)`, where `N` is number of elements in array `arr`.\n- Space: `O(N)`\n\n\n**Problem 2: Follow up question**\n- The integers in `arr` can be **duplicated**.\n- The integers in `pieces` can be **duplicated**.\n- `sum(pieces[i].length) != arr.length`.\n\n**Example 1:**\nInput: arr = [4,91,4,64,78], pieces = [[78],[4],[4,64],[91]]\nOutput: true\n\n**Example 2:**\nInput: arr = [4,91,4,64,78], pieces = [[78],[4],[4,64],[91], [5]]\nOutput: false\n\n```python\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n pieces.sort(key=lambda x: -len(x)) # Sort by decreasing order of length of pieces to avoid \n # case an bigger array contains another array, but bigger array is processed later\n\n m = sum(len(p) for p in pieces)\n seen = set()\n\n n = len(arr)\n i = 0\n while i < n:\n good = False\n for j, p in enumerate(pieces):\n if j in seen: continue\n if arr[i:i + len(p)] == p:\n good = True\n i += len(p)\n seen.add(j)\n break\n if not good: return False\n return i == m\n```\n\nComplexity:\n- Time: `O(NlogN + N*M)`, where `N` is number of elements in array `arr`, `M` is number of elements in `pieces` after flat into 1D.\n- Space: `O(M)` | 21 | 9 | [] | 0 |
check-array-formation-through-concatenation | Python O(n) by dictionary [w/ Comment] | python-on-by-dictionary-w-comment-by-bri-6li5 | Python O(n) by dictionary\n\n---\n\nImplementation:\n\n\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n | brianchiang_tw | NORMAL | 2020-11-02T04:10:05.689821+00:00 | 2020-11-02T04:10:05.689875+00:00 | 1,742 | false | Python O(n) by dictionary\n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n \n ## dictionary\n # key: head number of piece\n # value: all number of single piece\n mapping = { piece[0]: piece for piece in pieces }\n \n result = []\n \n # try to make array from pieces\n for number in arr:\n \n result += mapping.get( number, [] )\n \n # check they are the same or not\n return result == arr\n```\n\n---\n\nReference:\n\n[1] [Python official docs about dictionary.get( ..., default value)](https://docs.python.org/3/library/stdtypes.html#dict.get)\n | 16 | 1 | ['Iterator', 'Python', 'Python3'] | 6 |
check-array-formation-through-concatenation | [Python3] 2-line O(N) | python3-2-line-on-by-ye15-nmtk | Algo\nWe can leverage on the fact that the integers in pieces are distinct and define a mapping mp to map from the first element of piece to piece. Then, we cou | ye15 | NORMAL | 2020-11-01T04:00:57.544216+00:00 | 2020-11-01T16:06:17.850946+00:00 | 1,204 | false | Algo\nWe can leverage on the fact that the integers in `pieces` are distinct and define a mapping `mp` to map from the first element of piece to piece. Then, we could linearly scan `arr` and check if what\'s in arr `arr[i:i+len(mp[x])]` is the same as the one in piece `mp[x]`. \n\nImplementation\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n mp = {x[0]: x for x in pieces}\n i = 0\n while i < len(arr): \n if (x := arr[i]) not in mp or mp[x] != arr[i:i+len(mp[x])]: return False \n i += len(mp[x])\n return True \n```\n\nEdited on 11/01/2020 \nAdding a 2-line implementation \n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n mp = {x[0]: x for x in pieces}\n return sum((mp.get(x, []) for x in arr), []) == arr\n```\n\nAnalysis\nTime complexity `O(N)`\nSpace complexity `O(N)` | 14 | 2 | ['Python3'] | 3 |
check-array-formation-through-concatenation | brute force | c++ | unordered_map | brute-force-c-unordered_map-by-supreet_t-olx9 | \n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n unordered_map<int,vector<int>> m;\n \n for(int i=0 | supreet_thakur | NORMAL | 2020-11-01T10:15:50.883544+00:00 | 2020-11-01T10:15:50.883577+00:00 | 773 | false | ```\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n unordered_map<int,vector<int>> m;\n \n for(int i=0;i<pieces.size();i++)\n {\n m[pieces[i][0]] = pieces[i];\n }\n \n for(int i=0;i<arr.size();)\n {\n if(m.find(arr[i])==m.end())\n return false;\n \n vector<int> temp = m[arr[i]];\n \n for(int j=0;j<temp.size();j++,i++)\n {\n if(arr[i]!=temp[j])\n return false;\n }\n }\n \n return true;\n }\n``` | 10 | 2 | [] | 0 |
check-array-formation-through-concatenation | JAVA 1ms memory 100%, o(n), 7 lines | java-1ms-memory-100-on-7-lines-by-grant_-ylne | \nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n Map<Integer, Integer> map = new HashMap();\n for (int i = 0; i | grant_lian | NORMAL | 2020-11-01T04:08:28.907143+00:00 | 2020-11-04T00:39:55.170789+00:00 | 942 | false | ```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n Map<Integer, Integer> map = new HashMap();\n for (int i = 0; i < arr.length; i++) map.put(arr[i], i);\n for (int[] piece: pieces) {\n if (!map.containsKey(piece[0])) return false;\n for (int i = 0; i < piece.length - 1; i++)\n if (map.getOrDefault(piece[i], Integer.MIN_VALUE) + 1 != map.getOrDefault(piece[i + 1], Integer.MIN_VALUE)) return false;\n }\n return true;\n }\n}\n``` | 10 | 7 | [] | 0 |
check-array-formation-through-concatenation | [Java] Easy to Understand O(n) Solution | java-easy-to-understand-on-solution-by-a-1e6l | This is a easy problem but it is a liitle bit tricky. To solve this problem, we will need to:\n1. Compare the number from pieces to arr to make your life easier | admin007 | NORMAL | 2021-01-01T19:56:00.271063+00:00 | 2021-01-01T19:56:16.698939+00:00 | 501 | false | This is a easy problem but it is a liitle bit tricky. To solve this problem, we will need to:\n1. Compare the number **from pieces to arr** to make your life easier.\n2. **If we cannot find the number in arr, return false immediately.**\n3. If we find this number in arr, we also need to **do further checking if the current piece\'s length longer than one**. So we will check whether *map.get(p[i]) == ++index;*.\n4. If all cases are valid, finally we will return the answer as true.\n```\n public boolean canFormArray(int[] arr, int[][] pieces) {\n if (arr.length == 0)\n return true;\n Map<Integer, Integer> map = new HashMap<>(); // value to index in arr.\n for (int i = 0; i < arr.length; i++) {\n map.put(arr[i], i);\n }\n for (int[] p : pieces) {\n if (!map.containsKey(p[0])) return false;\n int index = map.get(p[0]);\n for (int i = 1; i < p.length; i++) { // if current piece\'s length > 1, we do further check.\n if (!map.containsKey(p[i]) || map.get(p[i]) != ++index) return false;\n }\n }\n return true;\n }\n``` | 8 | 1 | [] | 0 |
check-array-formation-through-concatenation | Java- HashMap- 1ms- Easy to Understand Solution | java-hashmap-1ms-easy-to-understand-solu-apqu | \npublic boolean canFormArray(int[] arr, int[][] pieces) {\n Map<Integer, Integer> positionMap = new HashMap<>();\n\t\t#Store positions of all the elemen | rishabhsairawat | NORMAL | 2020-11-11T08:01:59.455158+00:00 | 2020-12-03T10:39:56.292668+00:00 | 590 | false | ```\npublic boolean canFormArray(int[] arr, int[][] pieces) {\n Map<Integer, Integer> positionMap = new HashMap<>();\n\t\t#Store positions of all the elements of arr\n for(int i = 0; i < arr.length; i++)\n positionMap.put(arr[i], i);\n\n for(int[] piece: pieces){\n\t\t\t#First element does not have any position in original arr\n if(!positionMap.containsKey(piece[0])) return false;\n for(int i = 1; i < piece.length; i++) {\n\t\t\t\t#Whether element exists in original arr and appears next to the previous element\n if(!positionMap.containsKey(piece[i])) return false;\n if(positionMap.get(piece[i]) - positionMap.get(piece[i-1]) != 1) return false;\n }\n }\n\n return true;\n}\n``` | 8 | 1 | ['Java'] | 4 |
check-array-formation-through-concatenation | [C++] Array-based Solution Explained, 100% Time, ~75% Space | c-array-based-solution-explained-100-tim-0iz5 | As a little forenote, this problem might be solved using a hashamp (like an unordered_map in C++) to keep track of where is each piece that starts with a given | ajna | NORMAL | 2021-01-01T15:02:33.404429+00:00 | 2021-01-01T15:02:33.404464+00:00 | 1,058 | false | As a little forenote, this problem might be solved using a hashamp (like an `unordered_map` in C++) to keep track of where is each piece that starts with a given number, but given the very limited range (`1 - 100`) and the vastly superior performance of an array, \xE7a va sans dire what I decided to pick.\n\nSo, in order to start our to verify if we can effectively assemble all the vectors in `pieces`, we will first of all create an array of integers called `startAt`, with size `101` (so that we can accept indexes up to `100`, leaving index `0` unused instead of have to subtract `1` for each access later) and then initialise it with all its cell to be `== -1`.\n\nOn another loop, we will take each subvector in `pieces` and store its index in the cell of `startAt` matching its first element - so, for example, if `pieces` was `{{26, 35, 81}, {6, 14, 51}, {8, 72}}` we will store `0`, `1` and `2` in the cells with index `26`, `6` and `8` respectively.\n\nTime now for our main loop!\n\nIn it we will parse with pointer `i` through `arr` and\n* first of all if we have a chunk position stored in `startAt` - if not, we can confidently return `false`;\n* otherwise we know we have one valid chunk, so we parse through all of it to check if each single element matches in exactly that order:\n\t* for a mismatch we again return `false`;\n\t* for a match we go on, increasing `i` accordingly.\n\nIf we managed to come out of the main loop, it means all the elements in `arr` were parsed successfully composing all the element in `pieces`, so we can return `true` ;)\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n int startAt[101];\n // populating startAt\n for (int i = 1; i < 101; i++) startAt[i] = -1;\n for (int i = 0, len = pieces.size(); i < len; i++) {\n startAt[pieces[i][0]] = i;\n }\n // parsing arr\n for (int i = 0, len = arr.size(); i < len;) {\n // checking if we do not have a matching chunk\n if (startAt[arr[i]] == -1) return false;\n // verifying the whole chunk matches\n for (int n: pieces[startAt[arr[i]]]) {\n if (n != arr[i]) return false;\n i++;\n }\n }\n return true;\n }\n};\n``` | 7 | 0 | ['C', 'C++'] | 2 |
check-array-formation-through-concatenation | C++ Super Easy and Short Solution | c-super-easy-and-short-solution-by-yehud-5ns0 | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int, vector<int> > m;\n for (a | yehudisk | NORMAL | 2020-12-20T20:00:33.466296+00:00 | 2020-12-20T20:00:33.466341+00:00 | 563 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int, vector<int> > m;\n for (auto p : pieces)\n m[p[0]] = p;\n \n vector<int> res;\n for (auto a : arr) {\n if (m.find(a) != m.end())\n res.insert(res.end(), m[a].begin(), m[a].end());\n }\n \n return arr == res;\n }\n};\n```\n**Like it? please upvote...** | 7 | 0 | ['C'] | 1 |
check-array-formation-through-concatenation | simple and easy solution with javascript | simple-and-easy-solution-with-javascript-1x84 | here\'s my simple solution,if there is any suggestion for improvement or a better solution,feel free to share it in the comment section below \n\n\nvar canFormA | armageddon2033 | NORMAL | 2020-11-01T04:15:22.112235+00:00 | 2020-11-04T18:18:10.697716+00:00 | 1,079 | false | here\'s my simple solution,if there is any suggestion for improvement or a better solution,feel free to share it in the comment section below \n\n```\nvar canFormArray = function(arr, pieces) {\n\tlet total = "";\n arr=arr.join("");\n for (let i = 0; i < pieces.length; i++) {\n pieces[i] = pieces[i].join("");\n total += pieces[i];\n if (arr.indexOf(pieces[i]) == -1) return false;\n }\n return total.length == arr.length;\n};\n``` | 7 | 1 | ['JavaScript'] | 5 |
check-array-formation-through-concatenation | c++ solution using set and vector<int> | c-solution-using-set-and-vectorint-by-di-0dc7 | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& p) \n {\n set<vector<int>>s;\n for(auto &it:p)\n | dilipsuthar17 | NORMAL | 2021-04-23T10:19:20.061596+00:00 | 2021-04-23T10:19:20.061630+00:00 | 276 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& p) \n {\n set<vector<int>>s;\n for(auto &it:p)\n {\n s.insert(it);\n }\n vector<int>v;\n for(int i=0;i<arr.size();i++)\n {\n v.push_back(arr[i]);\n if(s.count(v))\n {\n v.clear();\n }\n }\n return v.size()==0;\n }\n};\n``` | 6 | 0 | ['C', 'Ordered Set', 'C++'] | 0 |
check-array-formation-through-concatenation | C++ Smart | O(N) | Explained | c-smart-on-explained-by-absomani-y0w8 | There are lot of helpful constraints in the problem like :\n Length of array would be equal to sum of all the lengths of pieces.\n Distinct elements in array\n | absomani | NORMAL | 2020-11-05T08:21:33.012612+00:00 | 2020-11-05T08:21:33.012646+00:00 | 773 | false | There are lot of helpful constraints in the problem like :\n* Length of array would be equal to sum of all the lengths of pieces.\n* Distinct elements in array\n* Distinct elements in pieces\n* Re-ordering not allowed\n\nBased on this, you can think smartly and consider ``pieces`` as a treatment and ``arr`` as the control i.e. Pieces as hypothesis and Arr as reference.\n\n* Now you can have a Hash Map that only tracks the first element of each of the pieces against which you have the entire piece. For a key value pair, <K, V> , K is ``piece[0]`` and value is ``piece`` where ``piece`` is some ``pieces[i]`` for ```i >= 0 and i < N ```\n* We would now traverse the ``arr`` doing the following checks:\n\t* If the present value is not present in our hash-map, then we wont be able to solve the problem because reordering is not allowed.\n\t* If the present value is present, then we map the subarray against what is stored in the hashmap against the present value.\n\t* Finally, if we are able to match all such instances, there is an ordering possible.\n\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n int N = arr.size();\n unordered_map<int,vector<int>> Mp;\n for(auto &piece: pieces)\n Mp[piece[0]] = piece;\n int idx = 0;\n while(idx < N) {\n int val = arr[idx];\n if(!Mp.count(val))\n return false;\n for(auto &piece_val : Mp[val])\n {\n if(idx == N)\n return false;\n if(piece_val != arr[idx++])\n return false;\n }\n }\n return idx == N;\n }\n};\n``` | 6 | 2 | ['C'] | 1 |
check-array-formation-through-concatenation | Python3 hashmap-based solution - Check Array Formation Though Concatenation | python3-hashmap-based-solution-check-arr-5v5x | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n d = {p[0]: p for p in pieces}\n i = 0\n w | r0bertz | NORMAL | 2020-11-02T08:45:14.766757+00:00 | 2020-11-02T08:45:14.766802+00:00 | 409 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n d = {p[0]: p for p in pieces}\n i = 0\n while i < len(arr):\n if arr[i] not in d or len(arr) - i < len(d[arr[i]]) or arr[i: i+len(d[arr[i]])] != d[arr[i]]:\n return False\n i += len(d[arr[i]])\n return True \n``` | 6 | 1 | ['Python', 'Python3'] | 0 |
check-array-formation-through-concatenation | Easy C++ solution | easy-c-solution-by-imran2018wahid-j3js | \nclass Solution \n{\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) \n {\n // First I\'m storing the indexes of the ve | imran2018wahid | NORMAL | 2021-04-08T07:05:37.921659+00:00 | 2021-04-08T07:06:23.804662+00:00 | 362 | false | ```\nclass Solution \n{\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) \n {\n // First I\'m storing the indexes of the vectors of pieces in a map with a key equals to the first value in that vector.\n unordered_map<int,int>m;\n for(int i=0;i<pieces.size();i++)\n {\n m[pieces[i][0]]=i;\n }\n int i=0;\n while(i<arr.size())\n {\n //If any element of arr is absent in pieces then return false\n if(m.find(arr[i])==m.end())\n {\n return false;\n }\n // Otherwise pick up that vector whose first element is arr[i]\n // and compare all the elements of that selected vector with \n // the elements of arr. If in the mean time any mismatch occurs\n // simply return false.\n else\n {\n int j=0;\n vector<int>tmp=pieces[m[arr[i]]];\n while(i<arr.size() && j<tmp.size())\n {\n if(arr[i]!=tmp[j])\n {\n return false;\n }\n i++;\n j++;\n }\n }\n }\n return true;\n }\n};\n``` | 5 | 0 | ['C'] | 3 |
check-array-formation-through-concatenation | Java beats 100% (no hashmap) | java-beats-100-no-hashmap-by-rahulj18-bz0y | \nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n int i = 0;\n while (i < arr.length) {\n int v = arr[ | rahulj18 | NORMAL | 2021-01-02T04:53:42.554505+00:00 | 2021-01-02T04:54:15.096903+00:00 | 337 | false | ```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n int i = 0;\n while (i < arr.length) {\n int v = arr[i];\n int[] p = find(v, pieces);\n if (p == null) return false;\n int k = 0;\n while (k < p.length && arr[i++] == p[k++]);\n if (k != p.length) return false;\n }\n return true;\n }\n \n private int[] find(int v, int[][] pieces) {\n for (int i = 0; i < pieces.length; i++) {\n if (v == pieces[i][0]) return pieces[i];\n }\n return null;\n }\n}\n``` | 5 | 1 | ['Java'] | 1 |
check-array-formation-through-concatenation | [Python] Simple O(n) solution based on the hints | python-simple-on-solution-based-on-the-h-sx1p | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for i, piece in enumerate(pieces):\n for j,n | kevinzzz666 | NORMAL | 2021-01-01T17:57:55.143051+00:00 | 2021-01-01T18:08:52.692804+00:00 | 457 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for i, piece in enumerate(pieces):\n for j,num in enumerate(piece):\n try: pieces[i][j] = arr.index(num)\n except: return False\n \n pieces.sort()\n \n return [i for i in range(len(arr))] == [x for piece in pieces for x in piece]\n\t\t## or use list(chain(*[piece for piece in pieces]))\n```\n\n\n\nNote: All the following steps are based on the assumption of all the numbers being distinct.\n* Step 1: for each number in each piece of the pieces, ***try*** to locate its **index** in the target array. If failed, then return ***False***\n* Step 2: ***sort*** the **index** pieces\n* Step 3: ***chain*** the sorted **index** pieces (I used list comprehensions, but you can use chain) to see if it matches the target **index** list, which is [0, 1, 2, ..., len(arr)-1]\n\n# Happy New Year! | 5 | 1 | ['Python', 'Python3'] | 1 |
check-array-formation-through-concatenation | [Java] O(n) | java-on-by-66brother-akuj | Explanation:\n1. first, all elements are distinct (if not, this problem becomes more harder)\n2. for each array in the pieces array, all of those elements shoul | 66brother | NORMAL | 2020-11-01T07:21:11.099618+00:00 | 2020-11-01T07:57:23.399485+00:00 | 505 | false | Explanation:\n1. first, all elements are distinct (if not, this problem becomes more harder)\n2. for each array in the pieces array, all of those elements should be adjecent in the A array(since all of them are unique), then we can rearrange them\n3. We should also do addtional check if the numbers of elemens in pieces is equal to A and if all of them are identical\n\n```\nclass Solution {\n public boolean canFormArray(int[] A, int[][] pieces) {\n int n=0;\n Map<Integer,Integer>map=new HashMap<>();\n for(int i=0;i<A.length;i++){\n map.put(A[i],i);\n }\n \n for(int pair[]:pieces){\n n+=pair.length;\n if(!map.containsKey(pair[0]))return false;\n for(int i=1;i<pair.length;i++){\n if(!map.containsKey(pair[i]))return false;\n int index1=map.get(pair[i]);\n int index2=map.get(pair[i-1]);\n if(index1-index2!=1)return false;\n }\n }\n if(n!=map.size())return false;\n return true;\n }\n}\n``` | 5 | 2 | [] | 1 |
check-array-formation-through-concatenation | Java 1 ms solution with explanation | java-1-ms-solution-with-explanation-by-g-05ah | \n1. Store array element, index mapping in a hashmap.\n2. Iterate through the pieces array, \n\t2.1 if length of piece is 1 and the element is contained in hash | govi92 | NORMAL | 2020-11-01T06:42:27.494559+00:00 | 2020-11-01T06:43:40.170801+00:00 | 255 | false | \n1. Store array element, index mapping in a hashmap.\n2. Iterate through the pieces array, \n\t2.1 if length of piece is 1 and the element is contained in hashmap, *continue*\n\t2.2 else if length is more than 1 and first element is contained in hashmap, iterate through rest of the elements of the piece. If index of each in the hashmap is not 1 more than the index of the previous *return false*\n\t2.3 else *return false*\n3. Return true (if we reach here, we have verified the index in the hashmap so that we can reconstruct the array with the pieces)\n\n\n```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n \n Map<Integer, Integer> map = new HashMap<>();\n for(int i=0;i<arr.length;i++)\n {\n map.put(arr[i], i);\n }\n \n for(int[] piece : pieces)\n {\n if(piece.length==1 && map.containsKey(piece[0]))\n continue;\n else if(piece.length>1 && map.containsKey(piece[0]))\n {\n int cur = map.get(piece[0]);\n for(int j=1;j<piece.length;j++)\n {\n cur++;\n if(map.containsKey(piece[j]) && cur!=map.get(piece[j]))\n return false;\n }\n }\n else\n return false;\n }\n return true;\n }\n}\n``` | 5 | 2 | [] | 2 |
check-array-formation-through-concatenation | [Kotlin] Simple Traversal | kotlin-simple-traversal-by-parassidhu-cn2y | I am updating my solution with the help of @pgmreddy, @binlei and this.\n\nIdea: \n- We traverse over pieces and map the first element of each inner array to th | parassidhu | NORMAL | 2020-11-01T04:09:07.666925+00:00 | 2020-11-01T09:44:23.918683+00:00 | 460 | false | I am updating my solution with the help of @pgmreddy, @binlei and [this](https://leetcode.com/problems/check-array-formation-through-concatenation/discuss/918408/python-5-lines-hashmap/).\n\n**Idea:** \n- We traverse over `pieces` and map the first element of each inner array to the array itself.\n- We then create another array of same size as `arr` and would fill it with data in next step\n- We now traverse over `arr` and find the element in our map. If we find it, we put the whole array to our result array\n- In the end we match if our `result` array has the same contents as `arr`\n\n\n**Example:**\nLet\'s take an example:\n`arr = [91,4,64,78]` and `pieces = [[78],[4,64],[91]]`\n\nStep 1 would produce a map like this:\n78 -> [78]\n4 -> [4, 64]\n91 -> [91]\n\nStep 2: We create array of size 4: `[0, 0, 0 ,0]`\n\nStep 3: Traversing `arr`:\n- Find 91 in map. Found. `result` -> `[91, 0, 0, 0]`\n- Find 4 in the map. Found. `result` -> `[91, 4, 64, 0]`\n- Find 64 in the map. Not Found. `result` -> `[91, 4, 64, 0]`\n- Find 78 in the map. Found. `result` -> `[91, 4, 64, 78]`\n\nSince `arr == result` content-wise, we return true. To test another case, try to make `[4, 64]` as `[64, 4]` in the above example and check.\n\n```\nfun canFormArray(arr: IntArray, pieces: Array<IntArray>): Boolean {\n val map = hashMapOf<Int, IntArray>()\n \n for (piece in pieces) {\n map[piece[0]] = piece // Mapping first element to inner array\n }\n \n val result = IntArray(arr.size)\n var i = 0\n \n for (num in arr) {\n if (map.containsKey(num)) { // Found the element. Now we\'ll add all its inner array\'s elements to result array\n for (p in map[num]!!) {\n result[i++] = p\n }\n }\n }\n \n return arr.contentEquals(result)\n }\n``` | 5 | 2 | ['Kotlin'] | 1 |
check-array-formation-through-concatenation | C++ | 4-lines | c-4-lines-by-sanjiv27-0cyr | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& A, vector<vector<int>>& P) {\n for(vector v: P){\n auto it = search(A.begin(), | sanjiv27 | NORMAL | 2021-06-11T22:40:37.709264+00:00 | 2021-06-11T22:40:37.709292+00:00 | 179 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& A, vector<vector<int>>& P) {\n for(vector v: P){\n auto it = search(A.begin(),A.end(),v.begin(),v.end());\n if(it==A.end()) return 0;\n }\n return 1;\n }\n};\n``` | 4 | 0 | [] | 0 |
check-array-formation-through-concatenation | Check Array Formation Through Concatenation | Java | check-array-formation-through-concatenat-duif | Explanation:\nStep 1:\nCreate a HashMap. Since we cannot change the order of the pieces, we are concerned only about the first element of every piece. So the ke | deleted_user | NORMAL | 2021-01-01T11:03:45.582726+00:00 | 2021-01-01T11:03:45.582767+00:00 | 417 | false | **Explanation**:\n**Step 1:**\nCreate a HashMap. Since we cannot change the order of the pieces, we are concerned only about the first element of every piece. So the key for the hashmap will be the first element of every piece, and the value would be the array itself. \n\n**Step 2:**\nIterate through the ***arr*** array. If the HashMap does not have any of the arr elements as its key, it means we cannot concatenate. Return False. If an element is matched with the Key, iterate through the array associated with the key. \n\n```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n HashMap <Integer, int []> hashMap = new HashMap <>();\n \n for (int [] piece : pieces) {\n hashMap.put (piece [0], piece);\n }\n \n int index = 0;\n while (index < arr.length) {\n if (hashMap.containsKey (arr [index])) {\n int [] temp = hashMap.get (arr [index]);\n for (int inIndex = 0; inIndex < temp.length; inIndex++) {\n if (temp [inIndex] != arr [index]) {\n return false;\n }\n index++;\n }\n }\n else {\n return false;\n }\n }\n return true;\n }\n}\n```\n\nTime Complexity: O (n + s)\nn = Number of elements in arr\ns = Number of elements in Pieces | 4 | 1 | [] | 1 |
check-array-formation-through-concatenation | [C++] O(n), clean code and easy to understand. | c-on-clean-code-and-easy-to-understand-b-g6it | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int, int> mp;\n \n for | lovebaonvwu | NORMAL | 2020-11-01T09:50:19.964673+00:00 | 2020-11-01T09:50:19.964708+00:00 | 303 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int, int> mp;\n \n for (int i = 0; i < pieces.size(); ++i) {\n mp[pieces[i][0]] = i;\n }\n \n for (int i = 0; i < arr.size();) {\n if (mp.find(arr[i]) == mp.end()) {\n return false;\n }\n \n auto piece = pieces[mp[arr[i]]];\n \n for (int j = 0; j < piece.size(); ++j, ++i) {\n if (arr[i] != piece[j]) {\n return false;\n }\n }\n }\n \n return true;\n }\n};\n``` | 4 | 1 | [] | 1 |
check-array-formation-through-concatenation | python simple 36ms O(n) well commented | python-simple-36ms-on-well-commented-by-n4bo7 | from collections import defaultdict\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n\t\n #creating the ha | manojc_raavi | NORMAL | 2020-11-01T05:57:36.092919+00:00 | 2020-11-01T05:57:36.092954+00:00 | 225 | false | from collections import defaultdict\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n\t\n #creating the hash map\n dic=defaultdict(int)\n \n #mapping index of that element to element\n for i,ele in enumerate(arr):dic[ele]=i\n \n #traversing through pieces\n for i in pieces:\n \n #calculating its length and initializing , index variable to -1\n n=len(i);ind=-1\n \n #traversing through elemnt array in pieces\n for j in range(n):\n #if the element was not in arr we can directly return False\n if i[j] not in dic:\n return False\n else:\n #if it is not the first element\n if ind!=-1:\n \n #if the element was not sucessor of the previous element in the arr then return False\n if ind+1!=dic[i[j]]:\n return False\n \n #assigning the new index to the index variable\n ind=dic[i[j]]\n #if no case fails then return True\n return True\n \n | 4 | 0 | ['Python3'] | 0 |
check-array-formation-through-concatenation | Check Array Formation Through Concatenation Solution in C++ | check-array-formation-through-concatenat-ugj9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | The_Kunal_Singh | NORMAL | 2023-05-10T03:21:00.542850+00:00 | 2023-05-10T03:21:00.542880+00:00 | 281 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n^3)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n int i, j, k, flag=0, element_present=0;\n for(i=0 ; i<pieces.size() ; i++)\n {\n flag=0;\n for(j=0 ; j<pieces[i].size() ; j++)\n {\n if(flag==0)\n {\n for(k=0 ; k<arr.size() ; k++)\n {\n if(pieces[i][j]==arr[k])\n {\n flag=1;\n element_present=1;\n break;\n }\n }\n if(flag==0)\n return false;\n }\n else if(pieces[i][j]!=arr[k])\n {\n return false;\n }\n k++;\n }\n }\n if(element_present==0)\n return false;\n return true;\n }\n};\n```\n\n | 3 | 0 | ['C++'] | 1 |
check-array-formation-through-concatenation | Check Array Formation Through Concatenation : C++ Solution | check-array-formation-through-concatenat-k5o7 | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n vector<int> v(101,-1);\n for(int i=0;i<piece | isimran18 | NORMAL | 2021-01-01T11:20:41.089703+00:00 | 2021-01-01T11:20:41.089741+00:00 | 299 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n vector<int> v(101,-1);\n for(int i=0;i<pieces.size();i++)\n v[pieces[i][0]] = i;\n for(int i=0;i<arr.size();){\n int p = v[arr[i]], j=0;\n if(p==-1)\n return false;\n while(j<pieces[p].size()){\n if(arr[i++]!=pieces[p][j++])\n return false;\n }\n }\n return true;\n }\n};\n``` | 3 | 1 | [] | 0 |
check-array-formation-through-concatenation | [JS] JavaScript 1 Liner (Short, with and without RegExp) | js-javascript-1-liner-short-with-and-wit-e9cp | just for fun\n\nvar canFormArray = function(arr, pieces) {\n return pieces.map(String).every((s) => new RegExp(`(^|,)${s}(,|$)`).test(arr.join()));\n};\n\nor | easyandme | NORMAL | 2020-12-04T05:03:04.863737+00:00 | 2020-12-05T17:41:10.890266+00:00 | 209 | false | just for fun\n```\nvar canFormArray = function(arr, pieces) {\n return pieces.map(String).every((s) => new RegExp(`(^|,)${s}(,|$)`).test(arr.join()));\n};\n```\nor use `reduce` (a bit worse)\n```\nvar canFormArray = function(arr, pieces) {\n return pieces.map(String).reduce((a, b) => new RegExp(`(^|,)${b}(,|$)`).test(arr.join()) ? a && true : false, true);\n};\n```\nor remove the slow `RegExp`\n```\nvar canFormArray = function(arr, pieces) {\n return pieces.every((p) => p.toString() === arr.slice(arr.indexOf(p[0]), arr.indexOf(p[0]) + p.length).toString());\n};\n``` | 3 | 0 | [] | 0 |
check-array-formation-through-concatenation | short and fast ^^ | short-and-fast-by-andrii_khlevniuk-d4eo | \nbool canFormArray(vector<int>& a, vector<vector<int>>& p)\n{\n\tunordered_map<char, char> m;\n\tfor(char i{0}; i<size(p); m[p[i][0]] = i, i++);\n\n\tfor(char | andrii_khlevniuk | NORMAL | 2020-11-02T02:19:55.566227+00:00 | 2020-11-02T16:53:49.154728+00:00 | 371 | false | ```\nbool canFormArray(vector<int>& a, vector<vector<int>>& p)\n{\n\tunordered_map<char, char> m;\n\tfor(char i{0}; i<size(p); m[p[i][0]] = i, i++);\n\n\tfor(char i{0}; i<size(a); i += size(p[m[a[i]]]))\n\t\tif(m.find(a[i])==m.end() or size(p[m[a[i]]])+i>size(a) or !equal(begin(p[m[a[i]]]), end(p[m[a[i]]]), begin(a)+i)) return false;\n\n\treturn true;\n}\n```\nor\n```\nbool canFormArray(vector<int>& a, vector<vector<int>>& p)\n{\n\tchar m[101]{0};\n\tfor(char i{0}; i<size(p); m[p[i][0]] = i+1, ++i);\n\n\tfor(char i{0}; i<size(a); i += size(p[m[a[i]]-1]))\n\t\tif(!m[a[i]] or size(p[m[a[i]]-1])+i>size(a) or !equal(begin(p[m[a[i]]-1]), end(p[m[a[i]]-1]), begin(a)+i)) return false;\n\n\treturn true;\n}\n```\nor\n```\nbool canFormArray(vector<int>& a, vector<vector<int>>& p)\n{\n\tvector m(101,-1);\n\tfor(char i{0}; i<size(p); m[p[i][0]] = i, ++i);\n\n\tvector<int> b;\n\tfor(char i{0}, j{0}; i<size(a) and (j = m[a[i]])+1; i += size(p[j]))\n\t\tcopy(p[j].begin(), p[j].end(), back_inserter(b));\n\n\treturn a==b;\n}\n```\n | 3 | 1 | ['C', 'C++'] | 0 |
check-array-formation-through-concatenation | [Java] Simple solution with O(n + m) time and O(m) space | java-simple-solution-with-on-m-time-and-m3gyi | \nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n Map<Integer, int[]> map = new HashMap<>();\n for (int[] piece : | roka | NORMAL | 2020-11-01T07:18:39.265641+00:00 | 2020-11-01T07:18:39.265682+00:00 | 174 | false | ```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n Map<Integer, int[]> map = new HashMap<>();\n for (int[] piece : pieces) {\n map.put(piece[0], piece);\n }\n \n int idx = 0;\n while (idx < arr.length) {\n int[] piece = map.get(arr[idx]);\n if (piece == null) return false;\n \n for (int j = 0; j < piece.length; j++, idx++) {\n if (piece[j] != arr[idx]) {\n return false;\n }\n }\n }\n \n return true;\n }\n}\n``` | 3 | 0 | [] | 1 |
check-array-formation-through-concatenation | python easy solution | python-easy-solution-by-akaghosting-x7vh | \tclass Solution:\n\t\tdef canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n\t\t\tfor i in pieces:\n\t\t\t\tif i[0] not in arr:\n\t\t\t\t\t | akaghosting | NORMAL | 2020-11-01T05:55:29.658875+00:00 | 2020-11-01T05:55:29.658905+00:00 | 170 | false | \tclass Solution:\n\t\tdef canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n\t\t\tfor i in pieces:\n\t\t\t\tif i[0] not in arr:\n\t\t\t\t\treturn False\n\t\t\t\tidx = arr.index(i[0])\n\t\t\t\tif arr[idx:idx + len(i)] != i:\n\t\t\t\t\treturn False\n\t\t\treturn True | 3 | 0 | [] | 0 |
check-array-formation-through-concatenation | C# The array has distinct numbers - this is important | c-the-array-has-distinct-numbers-this-is-7iiv | Oct. 31, 2020\n\nShare my solution written in the contest. \n\npublic class Solution {\n public bool CanFormArray(int[] arr, int[][] pieces) {\n var l | jianminchen | NORMAL | 2020-11-01T05:09:54.783863+00:00 | 2020-11-01T05:09:54.783895+00:00 | 161 | false | Oct. 31, 2020\n\nShare my solution written in the contest. \n```\npublic class Solution {\n public bool CanFormArray(int[] arr, int[][] pieces) {\n var length = arr.Length;\n var rows = pieces.Length; \n \n \n var map = new Dictionary<int, int>();\n for(int i = 0; i < rows; i++)\n {\n map.Add(pieces[i][0], i);\n }\n \n int index = 0;\n while(index < length)\n {\n var current = arr[index];\n if(!map.ContainsKey(current))\n return false; \n var value = map[current];\n foreach(var item in pieces[value])\n {\n if(arr[index] != item)\n return false;\n index++;\n }\n }\n \n return index == length; \n }\n}\n``` | 3 | 0 | [] | 1 |
check-array-formation-through-concatenation | [ Go ] Using map | go-using-map-by-haladonu-l2mi | Idea is to store the first element of piece as key and other elements as value in the map and then use this information to validate the piece order in the given | haladonu | NORMAL | 2020-11-01T04:32:59.313195+00:00 | 2020-11-01T04:32:59.313241+00:00 | 166 | false | Idea is to store the first element of piece as key and other elements as value in the map and then use this information to validate the piece order in the given array\n\n```\nfunc canFormArray(arr []int, pieces [][]int) bool {\n m := make(map[int][]int)\n \n for _, p := range pieces {\n m[p[0]] = p[1:]\n }\n \n for i :=0; i < len(arr); {\n piece, ok := m[arr[i]]\n \n if !ok {\n return false\n }\n \n i++\n for _, p := range piece {\n if p != arr[i] {\n return false\n }\n i++\n }\n }\n \n return true\n}\n``` | 3 | 0 | ['Go'] | 0 |
check-array-formation-through-concatenation | Simple java code 0 ms beats 100 % | simple-java-code-0-ms-beats-100-by-arobh-bxi9 | Complexity\n\n# Code\n\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n int[] map = new int[101];\n for (int i = | Arobh | NORMAL | 2024-03-21T13:40:17.266160+00:00 | 2024-03-21T13:40:17.266196+00:00 | 178 | false | # Complexity\n\n# Code\n```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n int[] map = new int[101];\n for (int i = 0; i < arr.length; i++) {\n map[arr[i]] = i+1;\n }\n for (int[] piece: pieces) {\n for (int j = 0; j < piece.length; j++) {\n if (map[piece[j]] == 0 || map[piece[j]] - map[piece[0]] != j) {\n return false;\n }\n }\n }\n return true;\n }\n}\n``` | 2 | 0 | ['Array', 'Hash Table', 'Java'] | 0 |
check-array-formation-through-concatenation | c++ | easy | fast | c-easy-fast-by-venomhighs7-9du5 | \n\n# Code\n\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n\n unordered_map <int, int> mp;\n | venomhighs7 | NORMAL | 2022-11-16T04:29:10.397952+00:00 | 2022-11-16T04:29:10.397994+00:00 | 997 | false | \n\n# Code\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n\n unordered_map <int, int> mp;\n \n for(int i = 0; i<arr.size(); i++){\n \n mp[arr[i]] = i;\n \n }\n \n int temp = -1;\n unordered_map <int, int> :: iterator map_it;\n for(auto it : pieces){\n \n for(auto pr : it){\n \n if(mp.find(pr) != mp.end()){\n if(temp == -1){\n map_it = mp.find(pr);\n temp = map_it -> second; \n }\n map_it = mp.find(pr);\n if(temp++ != map_it -> second) return false; \n }\n else return false;\n }\n temp = -1;\n }\n return true;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
check-array-formation-through-concatenation | C++ | c-by-rony_the_loser-8bks | (```) class Solution {\npublic:\n bool canFormArray(vector& arr, vector>& pieces) {\n \n unordered_map> mp;\n \n for(auto x: piec | Algo_wizard2020 | NORMAL | 2022-07-25T11:50:08.644832+00:00 | 2022-07-25T11:50:08.644872+00:00 | 193 | false | (```) class Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n unordered_map<int,vector<int>> mp;\n \n for(auto x: pieces)\n {\n mp[x[0]] = x;\n }\n \n vector<int> res;\n \n for(auto x: arr)\n {\n if(mp.find(x) != mp.end()) \n {\n res.insert(res.end(), mp[x].begin(),mp[x].end());\n }\n }\n \n return res == arr;\n }\n}; | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | C++ | O(N) | Unordered_map Solution | c-on-unordered_map-solution-by-harshv251-2akv | Please upvote if this helped :) Cheers\n\nFirst map all arr elements to its indexes in unordered map.\nMake a temp variable to store index.\nIterate first vecto | harshv2511 | NORMAL | 2022-07-24T17:42:09.129443+00:00 | 2022-07-28T17:08:47.933839+00:00 | 282 | false | **Please upvote if this helped :) Cheers**\n\nFirst map all arr elements to its indexes in unordered map.\nMake a temp variable to store index.\nIterate first vector of pieces, say [2, 3, 4, 5].\nuse find function find 2 in hashmap and map iterator to find index 2 is mapped to. Store that index in temp. do temp++. \nThen look for 3. if index mapped with 3 is equal to temp them continue. Otherwise return false.\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n // TC : O(N) + O(N) making hasmap + iterating pieces\n // SC : O(N) hashmap\n \n unordered_map <int, int> mp;\n \n for(int i = 0; i<arr.size(); i++){\n \n mp[arr[i]] = i;\n \n }\n \n int temp = -1;\n unordered_map <int, int> :: iterator map_it;\n for(auto it : pieces){\n \n for(auto pr : it){\n \n if(mp.find(pr) != mp.end()){\n if(temp == -1){\n map_it = mp.find(pr);\n temp = map_it -> second; \n }\n map_it = mp.find(pr);\n if(temp++ != map_it -> second) return false; \n }\n else return false;\n }\n temp = -1;\n }\n return true;\n }\n};\n``` | 2 | 0 | ['C', 'C++'] | 0 |
check-array-formation-through-concatenation | [JS] Using Hashmap - O(n) time and space | js-using-hashmap-on-time-and-space-by-wi-wd7x | \nvar canFormArray = function(arr, pieces) {\n\t// create map of pieces with key as first element of a piece to the piece\n const map = new Map(); // O(n)\n | wintryleo | NORMAL | 2021-08-22T18:19:44.426564+00:00 | 2021-08-22T18:19:44.426619+00:00 | 272 | false | ```\nvar canFormArray = function(arr, pieces) {\n\t// create map of pieces with key as first element of a piece to the piece\n const map = new Map(); // O(n)\n pieces.forEach(piece => map.set(piece[0], piece)); // O(n)\n\t\n\t// traverse through the array, check if there is any piece starting with it (ordering within piece should be same)\n\t// if piece exist, traverse through the array and piece parallely and\n\t// check if the elements match.\n\t// when piece is traversed completely, look for another piece and follow the same \n for(let idx = 0; idx < arr.length;) { // O(n)\n\t\t// exit case 1: no piece with current element\n if(!map.has(arr[idx])) { // O(1)\n return false;\n }\n const piece = map.get(arr[idx]); // O(1)\n let pIdx = 0;\n while(pIdx < piece.length) { // max - O(n)\n\t\t\t// exit case 2: while traversing, the piece and array index values mismatch\n if(piece[pIdx] !== arr[idx]) {\n return false;\n }\n ++pIdx;\n ++idx;\n }\n }\n\t// exit case 3: checked for all the elements in the array and matches it with pieces, so return true\n return true;\n};\n```\nTime Complexity = O(n)\nSpace Complexity = O(n) | 2 | 0 | ['JavaScript'] | 0 |
check-array-formation-through-concatenation | Python3 Intuitive solution by hash map | python3-intuitive-solution-by-hash-map-b-6kz6 | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n dic = {}\n for piece in pieces:\n dic | georgeqz | NORMAL | 2021-05-28T20:18:52.656226+00:00 | 2021-06-07T20:21:59.214308+00:00 | 188 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n dic = {}\n for piece in pieces:\n dic[piece[0]] = piece\n idx = 0\n while idx < len(arr):\n key = arr[idx]\n if key in dic:\n if arr[idx: idx + len(dic[key])] == dic[key]:\n idx += len(dic[key])\n else:\n return False\n else:\n return False\n return True\n``` | 2 | 0 | ['Python', 'Python3'] | 0 |
check-array-formation-through-concatenation | Simple C++ Solution | ( with video ) | simple-c-solution-with-video-by-f2016941-9kcx | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n int n=arr.size();\n vector<int>check(n,0);\n | f2016941 | NORMAL | 2021-04-30T11:35:56.671856+00:00 | 2021-04-30T11:35:56.671887+00:00 | 185 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n int n=arr.size();\n vector<int>check(n,0);\n for(auto i : pieces){\n bool placed=false;\n for(int j=0;j<n;j++){\n if(i[0]==arr[j] && check[j]==0){\n bool ok=true;\n for(int k=0;k<(int)i.size();k++){\n if(j+k<n && i[k]==arr[j+k] && check[j+k]==0) continue;\n else ok=false;\n }\n if(ok){\n for(int k=0;k<(int)i.size();k++) check[j+k]=1;\n placed=true;\n }\n }\n if(placed) break;\n }\n if(placed==false) return false;\n }\n return true;-\n }\n};\n``` | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | [Python] Faster than 99% | python-faster-than-99-by-fooman-x718 | Really simple, and breaks early increasing efficiency\n\n\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n | FooMan | NORMAL | 2021-03-31T03:05:50.255549+00:00 | 2021-03-31T03:05:50.255594+00:00 | 215 | false | Really simple, and breaks early increasing efficiency\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n p = {val[0]: val for val in pieces}\n \n i = 0\n while i < len(arr):\n if arr[i] in p:\n for val in p[arr[i]]:\n if i == len(arr) or arr[i] != val:\n return False\n i += 1\n else:\n return False\n \n return True\n``` | 2 | 0 | ['Python', 'Python3'] | 0 |
check-array-formation-through-concatenation | Java | Arrays | Beats 100% | java-arrays-beats-100-by-vvgusser-vrwf | \nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n var cache = new int[101];\n Arrays.fill(cache, -1);\n\n | vvgusser | NORMAL | 2021-03-24T21:19:25.835674+00:00 | 2021-03-24T21:19:25.835704+00:00 | 387 | false | ```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n var cache = new int[101];\n Arrays.fill(cache, -1);\n\n int n = arr.length;\n\n // fill cache with element indexes\n for (int i = 0; i < n; i++) {\n cache[arr[i]] = i;\n }\n\n for (var piece : pieces) {\n var nextExpected = cache[piece[0]];\n\n for (var el : piece) {\n if (cache[el] == -1 || cache[el] != nextExpected)\n return false;\n\n nextExpected = cache[el] + 1;\n }\n }\n\n return true; \n }\n}\n``` | 2 | 0 | ['Array', 'Java'] | 0 |
check-array-formation-through-concatenation | Python3 simple solution by two approaches | python3-simple-solution-by-two-approache-f636 | This approach may be wrong but it clears all test cases\n\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n | EklavyaJoshi | NORMAL | 2021-03-06T04:12:41.838112+00:00 | 2021-03-06T04:17:09.169623+00:00 | 108 | false | This approach may be wrong but it clears all test cases\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n s = \'\'.join(map(str, arr))\n for i in pieces:\n if \'\'.join(map(str, i)) not in s or not i[0] in arr:\n return False\n return True\n```\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for i in pieces:\n if i[0] not in arr:\n return False\n pieces.sort(key=lambda a:arr.index(a[0]))\n res = []\n for i in pieces:\n res += i\n return True if res == arr else False\n```\n**If you like the solution, please vote for this** | 2 | 0 | ['Python3'] | 0 |
check-array-formation-through-concatenation | C beats 88%, O(n) solution Explained | c-beats-88-on-solution-explained-by-nich-si03 | Solution\nc\nbool canFormArray(int* arr, int arrSize, int** pieces, int piecesSize, int* piecesColSize){\n\n int pmap[101]; \n for(int i=0; i<piecesSiz | nichyjt | NORMAL | 2021-02-12T13:25:15.253175+00:00 | 2021-03-18T12:15:39.339123+00:00 | 109 | false | ### Solution\n```c\nbool canFormArray(int* arr, int arrSize, int** pieces, int piecesSize, int* piecesColSize){\n\n int pmap[101]; \n for(int i=0; i<piecesSize; ++i){\n int j=0;\n while(j<piecesColSize[i]){\n if(j-1<0){\n // First (and possibly only) value, has no previous neighbour\n pmap[pieces[i][j]] = -1;\n }else{ \n pmap[pieces[i][j]] = pieces[i][j-1];\n }\n ++j;\n }\n }\n \n // Check if value exists and is piece-togetherable \n for(int i=0; i<arrSize; ++i){\n if(pmap[arr[i]]==0){\n return false;\n }\n // has a neighbour. peek one value back and check equality\n if(pmap[arr[i]]>0){\n if(i==0 || arr[i-1]!=pmap[arr[i]]) return false;\n }\n }\n return true; \n}\n```\n### Explanation\nThis algorithm uses a mapping technique and passes through the arrays twice.\n\nThe first `for` loop tracks occurences for every value in `pieces`, where the index of the mapping array, `pmap`, relates to the value of the element in `pieces`.\n\nIf the element is part of a `piece` with more than one element, we set the value of the element in `pmap` to be the previous element in `piece`. This is used later on to verify that the multi-element `pieces[i]` can actually be used to form `arr` without rearranging the elems in `pieces[i]`.\n\nThe second loop basically checks that:\n1. The element exists (note: unless assigned, the \'default\' initialisation for an int array is `0`.)\n2. As mentioned earlier, `pieces[i]` need not be rearranged.\n | 2 | 0 | ['C'] | 0 |
check-array-formation-through-concatenation | Python solution | python-solution-by-vikram006-g55w | \ndef canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for piece in pieces:\n if piece[0] not in arr:\n r | vikram006 | NORMAL | 2021-01-10T19:25:22.861407+00:00 | 2021-01-10T19:25:22.861490+00:00 | 314 | false | ```\ndef canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for piece in pieces:\n if piece[0] not in arr:\n return False\n pieces.sort(key = lambda a: arr.index(a[0]))\n ans = []\n for piece in pieces:\n ans += piece\n return True if ans == arr else False\n```\n\nWould really appreciate your suggestions on improving my solution. | 2 | 1 | ['Python', 'Python3'] | 0 |
check-array-formation-through-concatenation | Standard Java Solution | standard-java-solution-by-sriharik-qq3k | Theory\nThere are several brute force solutions to this, but the optimal solution will take both linear time and space. We want to take advantage of the fact th | sriharik | NORMAL | 2021-01-02T01:21:43.437465+00:00 | 2021-01-02T01:21:43.437489+00:00 | 102 | false | ### Theory\nThere are several brute force solutions to this, but the optimal solution will take both linear time and space. We want to take advantage of the fact that the `peices` array will have only distinct integers. I chose to keep a mapping from the first element of the array, to the entire array reference. Then we need to go over the original array, and see if that reference is in the map, if it is, then check each element in our reference to our original array, then continue the loop.\n\n### Solution\n```\n public boolean canFormArray(int[] arr, int[][] pieces) {\n Map<Integer, int[]> map = new HashMap<>();\n for (int[] p : pieces)\n map.put(p[0], p);\n \n int i = 0;\n while (i < arr.length) {\n if (!map.containsKey(arr[i])) return false;\n int[] part = map.get(arr[i]);\n for (int j = 0; j < part.length; j++) {\n if (part[j] != arr[i]) return false;\n i++;\n }\n }\n return true;\n }\n``` | 2 | 0 | [] | 1 |
check-array-formation-through-concatenation | Python two solutions, one two-liner | python-two-solutions-one-two-liner-by-po-42s8 | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n table = {l[0] : l for l in pieces}\n cur = 0\n | pony1999 | NORMAL | 2021-01-01T21:35:39.266302+00:00 | 2021-01-01T21:35:39.266342+00:00 | 150 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n table = {l[0] : l for l in pieces}\n cur = 0\n while cur < len(arr):\n if (arr[cur] not in table or arr[cur:cur + len(table[arr[cur]])] != table[arr[cur]]): return False\n cur += len(table[arr[cur]])\n return True\n```\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n table = {l[0] : l for l in pieces}\n return arr == list(chain(*[table[n] for n in arr if n in table]))\n``` | 2 | 0 | ['Python'] | 0 |
check-array-formation-through-concatenation | Using MCM | using-mcm-by-mandh_budhi_huon_me-rpzr | \nclass Solution {\n int dp[101][101];\n bool cal(int i , int j,vector<int>&a,map<vector<int>,int>&m)\n {\n if(i>j) return true;\n int &a | karan_kaira | NORMAL | 2021-01-01T17:33:25.829114+00:00 | 2021-01-01T17:33:25.829211+00:00 | 923 | false | ```\nclass Solution {\n int dp[101][101];\n bool cal(int i , int j,vector<int>&a,map<vector<int>,int>&m)\n {\n if(i>j) return true;\n int &ans = dp[i][j];\n if(ans!=-1) return ans;\n vector<int> cur;\n ans = false;\n for(int k = i ; k <= j ; k ++ )\n {\n cur.push_back(a[k]);\n if(m[cur]==false) continue;\n if(cal(k+1,j,a,m)) return ans = true;\n }\n return ans;\n }\npublic:\n bool canFormArray(vector<int>& a, vector<vector<int>>& p) {\n map<vector<int>,int> m ;\n for(auto ele : p) m[ele] = 1;\n memset(dp,-1,sizeof(dp));\n return cal(0,a.size()-1,a,m);\n }\n};\n``` | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | [Java, C++] Brute force, HashMap and Binary Search | java-c-brute-force-hashmap-and-binary-se-trxf | Brute Force\n\n\nSince the input size is small, brute force works.\n Keep a pointer arrPt to keep track of our progress in arr. If it reaches the end of arr, it | jamweg22 | NORMAL | 2021-01-01T14:05:20.155410+00:00 | 2021-01-01T14:08:43.431803+00:00 | 97 | false | ### Brute Force\n\n\nSince the input size is small, brute force works.\n* Keep a pointer `arrPt` to keep track of our progress in `arr`. If it reaches the end of `arr`, it means `arr` can be formed by concatenating the subarrays in `pieces`.\n* We have to find the subarray in `pieces` starting with the element pointed by `arrPt`. If not found, we can immediately return `false`. Otherwise, iterate over the subarray found, and check if subsequent elements are matching the ones in `arr` \n\n\n#### Java\n\n\n```java\npublic boolean canFormArray(int[] arr, int[][] pieces) {\n\tfinal int len = arr.length;\n\t\n\tint arrPt = 0;\n\t\n\twhile (arrPt < len) {\n\t\tint prior = arrPt;\n\t\t\n\t\tfor (int[] piece: pieces) {\n\t\t\t//\tFound the subpiece starting with the element in arr\n\t\t\tif (piece[0] == arr[arrPt] ) {\n\t\t\t\t//\tIterate through the elements in subpiece, checking if it matches the order in arr\n\t\t\t\tfor(int i: piece) if (i != arr[arrPt++] ) return false;\n\t\t\t\t//\tAll elements in subpiece matches. Break out of the loop\n\t\t\t\tbreak;\n\t\t\t}\n\t\t}\n\t\t//\tIf the pointer doesn\'t move after searching for subarray,\n\t\t//\tit means subarray not found. Return false.\n\t\tif (prior == arrPt) return false;\n\t}\n\treturn true;\n}\n```\n\n\n#### C++\n\n\n```cpp\nbool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n\tconst int len = arr.size();\n\n\tint arrPt = 0;\n\n\twhile (arrPt < len) {\n\t\tint prior = arrPt;\n\n\t\tfor (auto& piece : pieces) {\n\t\t\t//\tFound the subpiece starting with the element in arr\n\t\t\tif (piece[0] == arr[arrPt]) {\n\t\t\t\t//\tIterate through the elements in subpiece, checking if it matches the order in arr\n\t\t\t\tfor (int i : piece) if (i != arr[arrPt++]) return false;\n\t\t\t\t//\tAll elements in subpiece matches. Break out of the loop\n\t\t\t\tbreak;\n\t\t\t}\n\t\t}\n\t\t//\tIf the pointer doesn\'t move after searching for subarray,\n\t\t//\tit means subarray not found. Return false.\n\t\tif (prior == arrPt) return false;\n\t}\n\treturn true;\n}\n```\n\n---\n\n### Hash Map\n\n\n* Instead of having to iterate through the `pieces` array everytime to look for the subpiece stating with element pointed by `arrPt`, we can use extra space to be able to retrieve the subpiece in O(1) time.\n* Since the input size is small, we can just use an array in place of `Hashmap` or `unordered_map`.\n\n\n#### Java\n\n\n```java\npublic boolean canFormArray(int[] arr, int[][] pieces) {\n\tfinal int len = arr.length;\n\n\tint[][] map = new int[101][];\n\tfor (int[] p: pieces) map[ p[0] ] = p;\n\n\tint arrPt = 0;\n\n\twhile (arrPt < len) {\n\t\t//\tNo subpiece starts with the element currently pointed in arr.\n\t\tif (map[ arr[arrPt] ] == null) return false;\n\n\t\t//\tOtherwise iterate through the subpiece, checking each element one by one\n\t\tfor (int i: map[ arr[arrPt]] )\n\t\t\tif ( arr[arrPt++] != i) return false;\n\t}\n\n\treturn true;\t\n}\n```\n\n\n#### C++ (Using unordered_map)\n\n\n```cpp\nbool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n\tconst int len = arr.size();\n\n\tunordered_map<int, vector<int>*> map;\n\tfor (auto& piece : pieces)\n\t\tmap[piece[0]] = &piece;\n\n\tint arrPt = 0;\n\n\twhile (arrPt < len) {\n\t\tauto found = map.find(arr[arrPt]);\n\t\tif (found == map.end()) return false;\n\n\t\tfor (int i : *(found->second)) {\n\t\t\tif (arr[arrPt++] != i) return false;\n\t\t}\n\t}\n\n\treturn true;\n}\n```\n\n---\n\n### Binary Search\n\n* By sorting the `pieces` based on the subarray\'s first element, we can now perform binary search whenever we want to search for subarray.\n\n#### Java\n\n```java\npublic boolean canFormArray(int[]arr, int[][] pieces) {\n\tArrays.sort( pieces, (x,y)-> {\n\t\treturn x[0] - y[0];\n\t});\n\n\tfinal int len = arr.length;\n\tint arrPt = 0;\n\n\twhile (arrPt < len) {\n\t\tint[] res = binarySearch( pieces, arr[arrPt] );\n\t\tif (res == null) return false;\t\t//\tNot found. Return false\n\n\t\tfor (int i: res)\n\t\t\tif (i != arr[arrPt++] ) return false;\n\t}\n\treturn true;\n}\n\nprivate int[] binarySearch(int[][] pieces, int val) {\n\tint left = 0;\n\tint right = pieces.length - 1;\n\n\twhile (left < right) {\n\t\tint mid = left + (right - left) / 2;\n\n\t\tif (pieces[mid][0] < val) \n\t\t\tleft = mid + 1;\n\t\telse right = mid;\n\t}\n\n\t//\tIf the subpiece is not what we looking for, return null\n\treturn pieces[left][0] == val? pieces[left]: null;\n}\n```\n\n#### C++\n\n```cpp\nbool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n\tsort(pieces.begin(), pieces.end(), [](auto& x, auto& y)->bool {\n\t\treturn x[0] - y[0] < 0;\n\t});\n\n\tconst int len = arr.size();\n\tint arrPt = 0;\n\n\twhile (arrPt < len) {\n\t\tauto res = binarySearch(pieces, arr[arrPt]);\n\t\tif (!res) return false;\n\n\t\tfor (int i : *res ) {\n\t\t\tif (i != arr[arrPt++]) return false;\n\t\t}\n\t}\n\treturn true;\n}\nvector<int>* binarySearch(vector<vector<int>>& pieces, int val) {\n\tint left = 0;\n\tint right = pieces.size() - 1;\n\n\twhile (left < right) {\n\t\tint mid = left + (right - left) / 2;\n\n\t\tif (pieces[mid][0] < val)\n\t\t\tleft = mid + 1;\n\t\telse right = mid;\n\t}\n\n\treturn pieces[left][0] == val ? &pieces[left] : nullptr ;\n}\n```\n | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | Simple and Easy to understand solution using Hashmap / Dictionary with comments | simple-and-easy-to-understand-solution-u-edtf | in C#, Dictionary is similar to HashMap in Java. \n\n\npublic class CheckArrayFormationThroughConcatenationSolution\n{\n public bool CanFormArray(int[] arr, | spartan9595 | NORMAL | 2021-01-01T11:01:43.508694+00:00 | 2021-01-01T11:03:39.202543+00:00 | 96 | false | in C#, Dictionary is similar to HashMap in Java. \n\n```\npublic class CheckArrayFormationThroughConcatenationSolution\n{\n public bool CanFormArray(int[] arr, int[][] pieces)\n {\n //Store all the first values, row number in Dictionary for the pieces array.\n Dictionary<int, int> values = new Dictionary<int, int>();\n for (int i = 0; i < pieces.Length; i++)\n {\n values.Add(pieces[i][0], i);\n }\n\n for (int i = 0; i < arr.Length;)\n {\n int val = arr[i];\n //Check if you have found the value from the hashmap.\n if (values.ContainsKey(val))\n {\n int index = values[val];\n //once you found the index value for that element iterate over the inner elements of pieces[index] array\n for (int j = 0; j < pieces[index].Length; j++)\n {\n //at any point if you have not found the element matching with arr[] array just return false otherwise increment i.\n if (arr[i] != pieces[index][j])\n {\n return false;\n }\n\n i++;\n }\n }\n //If you have not found then you can return false as we didn\'t find the required element\n else\n {\n return false;\n }\n }\n\n return true;\n }\n}\n```\n\nLet me know if you have any doubts.\nhttps://github.com/pankajrathi95/DS-Algo/tree/master/src/LeetCode/30DayLeetCodeChallenge-Jan2021 | 2 | 0 | ['Array'] | 1 |
check-array-formation-through-concatenation | O(nlogn) solution based on sorting in golang | onlogn-solution-based-on-sorting-in-gola-ge3t | golang\nfunc canFormArray(arr []int, pieces [][]int) bool {\n sort.Slice(pieces, func(i, j int) bool {\n return pieces[i][0] < pieces[j][0]\n })\n | chia13 | NORMAL | 2021-01-01T10:39:15.952296+00:00 | 2021-01-01T10:39:27.206994+00:00 | 80 | false | ```golang\nfunc canFormArray(arr []int, pieces [][]int) bool {\n sort.Slice(pieces, func(i, j int) bool {\n return pieces[i][0] < pieces[j][0]\n })\n left := 0\n for left < len(arr) {\n j := sort.Search(len(pieces), func(j int) bool {\n return pieces[j][0] >= arr[left]\n })\n if j == len(pieces) || left + len(pieces[j]) > len(arr) {\n return false\n } \n for i := 0; i < len(pieces[j]); i++ {\n if arr[left] != pieces[j][i] {\n return false\n }\n left++\n }\n }\n return true\n}\n``` | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | 100% faster c++ | 100-faster-c-by-ankgupta1147-mri3 | class Solution {\npublic:\n bool canFormArray(vector& arr, vector>& pieces) {\n \n int N = arr.size();\n int M = pieces.size();\n | ankgupta1147 | NORMAL | 2021-01-01T09:39:17.202482+00:00 | 2021-01-01T09:39:17.202511+00:00 | 113 | false | class Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n int N = arr.size();\n int M = pieces.size();\n \n if(N == 0 || M == 0)\n return (N == 0);\n \n unordered_map<int, int> mp;\n int idx = 0;\n \n for(auto vec : pieces)\n mp[vec[0]] = idx++;\n \n idx = 0;\n while(idx < N)\n {\n if(mp.find(arr[idx]) != mp.end())\n { \n for(auto ele : pieces[mp[arr[idx]]])\n {\n if(ele == arr[idx])\n idx++;\n else\n return false;\n }\n }\n else\n return false;\n }\n \n return idx == N;\n }\n}; | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | Python Easy Solution ( While and For loop) | python-easy-solution-while-and-for-loop-3uq10 | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n cnt=0\n j=0\n while j<len(arr):\n | saisathwik1999 | NORMAL | 2020-12-28T08:28:11.480098+00:00 | 2020-12-28T08:28:11.480182+00:00 | 218 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n cnt=0\n j=0\n while j<len(arr):\n inc=0\n for i in pieces:\n l=len(i)\n if arr[j:j+l]==i:\n cnt+=l\n j+=l\n inc+=1\n if not inc:\n j+=1 \n return cnt==len(arr) | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | Simple & Easy Solution by Python 3 | simple-easy-solution-by-python-3-by-jame-w5y5 | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for piece in pieces:\n if piece[0] not in ar | jamesujeon | NORMAL | 2020-12-03T14:03:02.940738+00:00 | 2020-12-03T14:03:02.940781+00:00 | 266 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for piece in pieces:\n if piece[0] not in arr:\n return False\n index = arr.index(piece[0])\n if arr[index:index + len(piece)] != piece:\n return False\n return True\n``` | 2 | 0 | ['Python3'] | 2 |
check-array-formation-through-concatenation | C++ Easy to understand String Concat and Find | c-easy-to-understand-string-concat-and-f-4edr | Simple Idea:\n\nGiven by constraints that all elements are distinct and the number of elements will be the same we can concatenate the elements in first string | t_rex | NORMAL | 2020-11-13T12:19:49.677296+00:00 | 2020-11-13T12:19:49.677335+00:00 | 155 | false | Simple Idea:\n\nGiven by constraints that all elements are **distinct** and the number of elements will be the same we can concatenate the elements in first string and then compare if all pieces can be found in this string.\n\nThe only case left to handle is:\narr : [85,15]\npieces : [[85][1]]\n\nHere number of elements are the same and both are present in original text BUT they are not the same.\nFor this case we must check the size of both the strings.\n\n\n\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n string a="";\n string b="";\n int s1 = 0;int s2=0;\n bool flag =true;\n \n //concatenate arr into one single string\n // [48,18,16] -> "481816"\n for(int i =0;i<arr.size();i++){\n a += to_string(arr[i]);\n }\n \n // track the length of the converted string\n s1 = a.size();\n \n //loop through all parts of pieces and concatenate each item\n //then check if you can find that in the original string\n for(int i =0;i<pieces.size();i++){\n \n for(int j =0;j<pieces[i].size();j++){\n b += to_string(pieces[i][j]);\n }\n \n // if not found that means break and return false\n if(a.find(b)==string::npos){\n flag =false;\n break;\n }\n \n //keep adding and tracking length of all the strings in pieces.\n s2 += b.size();\n b="";\n }\n \n /**\n\t\tif both strings add up to same length, and have same number of \n\t\telements(constraint) and we find through above process that all elements in\n\t\tpieces are present in original text then return true, else false.\n\t\t**/\n return flag&&(s1==s2);\n }\n | 2 | 0 | ['String', 'C'] | 0 |
check-array-formation-through-concatenation | JAVA | 0 ms | java-0-ms-by-wilsoncursino-lu5m | \nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n for(int[] p: pieces) \n\t\t\tif(!contains(arr, p)) \n\t\t\t\treturn f | wilsoncursino | NORMAL | 2020-11-06T23:34:09.968416+00:00 | 2020-11-06T23:34:09.968449+00:00 | 170 | false | ```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n for(int[] p: pieces) \n\t\t\tif(!contains(arr, p)) \n\t\t\t\treturn false;\n return true;\n }\n boolean contains(int[] a, int[] b){\n int i = 0;\n int j = 0;\n while(i < a.length && a[i] != b[j]) i++;\n while(i < a.length && j < b.length && a[i] == b[j]){\n i++;\n j++;\n }\n return j == b.length;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
check-array-formation-through-concatenation | C++ SIMPLE EASY SOLUTION | c-simple-easy-solution-by-chase_master_k-038d | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n int n=arr.size();\n unordered_map<int,int> m | chase_master_kohli | NORMAL | 2020-11-03T17:25:52.637370+00:00 | 2020-11-03T17:25:52.637404+00:00 | 187 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n int n=arr.size();\n unordered_map<int,int> m;\n for(int i=0;i<n;i++){\n m[arr[i]]=i;\n }\n n=pieces.size();\n for(int i=0;i<n;i++){\n int nn=pieces[i].size();\n for(int j=0;j<nn-1;j++){\n int x=pieces[i][j];\n int y=pieces[i][j+1];\n if(m.count(x)==0 || m.count(y)==0)\n return false;\n if(m[y]-m[x] != 1)\n return false;\n m[x]=-1;\n }\n if(m.count(pieces[i][nn-1])==0)\n return false;\n m[pieces[i][nn-1]]=-1;\n }\n for(auto x:m)\n if(x.second!=-1)\n return false;\n return true;\n }\n};\n``` | 2 | 1 | [] | 0 |
check-array-formation-through-concatenation | C++: 100% time, 100 % memory | c-100-time-100-memory-by-huimingzhou-x1l5 | cpp\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int, int> mp;\n for (int i | huimingzhou | NORMAL | 2020-11-01T23:05:26.140962+00:00 | 2020-11-01T23:05:26.141010+00:00 | 71 | false | ```cpp\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int, int> mp;\n for (int i = 0; i < pieces.size(); ++i) {\n mp[pieces[i][0]] = i;\n }\n \n int ind = 0;\n while (ind < arr.size()) {\n int p = mp[arr[ind]];\n for (int& x : pieces[p]) {\n if (x == arr[ind]) {\n if (++ind == arr.size()) break;\n } else {\n return false;\n }\n }\n }\n return true;\n }\n};\n``` | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | Java HashMap O(N) | java-hashmap-on-by-motorix-6dx0 | Use a hashmap to keep track of (head of a piece, the whole piece).\n2. Traverse every element in arr and compare every element with those in pieces.\n\n\n pu | motorix | NORMAL | 2020-11-01T22:30:52.348271+00:00 | 2020-11-01T22:34:43.117931+00:00 | 90 | false | 1. Use a hashmap to keep track of ```(head of a piece, the whole piece)```.\n2. Traverse every element in ```arr``` and compare every element with those in ```pieces```.\n\n```\n public boolean canFormArray(int[] arr, int[][] pieces) {\n HashMap<Integer, int[]> map = new HashMap<>();\n for(int i = 0; i < pieces.length; i++) {\n map.put(pieces[i][0], pieces[i]);\n }\n for(int i = 0; i < arr.length;) {\n if(!map.containsKey(arr[i])) return false;\n int[] p = map.get(arr[i]);\n for(int j = 0; j < p.length; j++, i++) {\n if(arr[i] != p[j]) return false;\n }\n }\n return true;\n }\n```\n\nTime: ```O(N)```, ```N``` is the length of ```arr```\nSpace: ```O(M)```, ```M``` is the length of ```pieces``` | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | simple C++ 100%/100% | simple-c-100100-by-cdkr-qjrn | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n unordered_map<int, vector<int>*> m;\n | cdkr | NORMAL | 2020-11-01T19:20:53.735422+00:00 | 2020-11-01T19:20:53.735464+00:00 | 49 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n unordered_map<int, vector<int>*> m;\n \n for(auto& p : pieces) {\n m[p[0]] = &p;\n }\n \n for(int i = 0; i < arr.size();) {\n\n auto p = m[arr[i]];\n\n if(!p || !equal(p->begin(), p->end(), arr.begin() + i)) return false;\n\n i += p->size();\n }\n return true;\n }\n};\n``` | 2 | 0 | [] | 1 |
check-array-formation-through-concatenation | Rust O(n) HashMap | rust-on-hashmap-by-grs-7ks5 | \nuse std::collections::HashMap;\n\nimpl Solution {\n pub fn can_form_array(arr: Vec<i32>, pieces: Vec<Vec<i32>>) -> bool {\n let mut pieces_map: Hash | grs | NORMAL | 2020-11-01T18:14:56.428215+00:00 | 2020-11-01T18:14:56.428262+00:00 | 51 | false | ```\nuse std::collections::HashMap;\n\nimpl Solution {\n pub fn can_form_array(arr: Vec<i32>, pieces: Vec<Vec<i32>>) -> bool {\n let mut pieces_map: HashMap<i32, &Vec<i32>> = HashMap::new();\n for piece_arr in &pieces {\n pieces_map.insert(piece_arr[0], piece_arr);\n }\n \n let mut i = 0;\n while i < arr.len() {\n match pieces_map.get(&arr[i]) {\n Some(piece_arr) => {\n let mut piece_len = piece_arr.len();\n if i + piece_len > arr.len() || &arr[i..i + piece_len] != &piece_arr[..] {\n return false;\n }\n i += piece_arr.len();\n }\n None => {\n return false;\n }\n }\n }\n \n return true;\n }\n}\n``` | 2 | 0 | [] | 1 |
check-array-formation-through-concatenation | c++ bucket sort | c-bucket-sort-by-michelusa-ibbf | Since values are limited, we can use bucket sort to index the ranges by the first element each.\nElement index zero (first element of indexes array) indicates " | michelusa | NORMAL | 2020-11-01T17:05:30.384901+00:00 | 2020-11-01T17:05:30.384932+00:00 | 138 | false | Since values are limited, we can use bucket sort to index the ranges by the first element each.\nElement index zero (first element of indexes array) indicates "not found".\n\n```\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n array<size_t, 101> indexes = {};\n \n for (auto pit = cbegin(pieces); pit != cend(pieces); ++pit) {\n indexes[pit->front()] = distance(cbegin(pieces), pit) + 1;\n }\n for (auto it = cbegin(arr); it != cend(arr); ++it) {\n const auto idx = indexes[*it];\n if (idx) {\n const auto& piece = pieces[idx - 1];\n //compare remaining member of this piece to arr content\n for (auto j = 1; j < piece.size(); ++j) {\n ++it;\n if (piece[j] != *it)\n return false;\n }\n } else\n return false;\n }\n return true;\n } | 2 | 0 | ['C'] | 0 |
check-array-formation-through-concatenation | ⭐️ [ Kt, Js, Py3, Cpp ] 🎯 Do we "have" what we "need"? | kt-js-py3-cpp-do-we-have-what-we-need-by-9x65 | Solution #1: Map\n\nReturn true if and only if we can make what we need from what we have via a map m which stores the first value A[0] of each array "piece" A | claytonjwong | NORMAL | 2020-11-01T16:28:42.133396+00:00 | 2021-01-01T16:01:34.637415+00:00 | 89 | false | **Solution #1: Map**\n\nReturn `true` if and only if we can `make` what we `need` from what we `have` via a map `m` which stores the first value `A[0]` of each array "piece" `A` which we `have`.\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun canFormArray(need: IntArray, have: Array<IntArray>): Boolean {\n var m = mutableMapOf<Int, Int>()\n var make = mutableListOf<Int>()\n have.forEachIndexed { i, A -> m[A[0]] = i }\n var i = 0\n var N = need.size\n while (i < N) {\n if (!m.contains(need[i]))\n return false\n var j = m[need[i]]!!\n make.addAll(have[j].toList())\n i += have[j].size\n }\n return need.toList() == make\n }\n}\n```\n\n*Javascript*\n```\nlet canFormArray = (need, have, m = new Map(), make = []) => {\n have.forEach((A, i) => m.set(A[0], i));\n let i = 0,\n N = need.length;\n while (i < N) {\n if (!m.has(need[i]))\n return false;\n let j = m.get(need[i]);\n make.push(...have[j]);\n i += have[j].length;\n }\n return _.zip(need, make).every(pair => pair[0] == pair[1]);\n};\n```\n\n*Python3*\n```\nclass Solution:\n def canFormArray(self, need: List[int], have: List[List[int]]) -> bool:\n m = {A[0]: i for i, A in enumerate(have)}\n make = []\n i = 0\n N = len(need)\n while i < N:\n if need[i] not in m:\n return False\n j = m[need[i]]\n make.extend(have[j].copy())\n i += len(have[j])\n return need == make\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n using Map = unordered_map<int, int>;\n bool canFormArray(VI& need, VVI& have, Map m = {}, VI make = {}) {\n for (auto i{ 0 }; i < have.size(); ++i)\n m[have[i][0]] = i;\n int i = 0,\n N = need.size();\n while (i < N) {\n if (m.find(need[i]) == m.end())\n return false;\n auto j = m[need[i]];\n make.insert(make.end(), have[j].begin(), have[j].end());\n i += have[j].size();\n }\n return need == make;\n }\n};\n```\n\n---\n\n**Solution #2: Queue**\n\nUse a queue `q` to store matching candidate pieces from what we `have` compared to what we `need`. Return `true` if and only if we `have` what we `need`.\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun canFormArray(need: IntArray, have: Array<IntArray>): Boolean {\n var q: Queue<Int> = LinkedList<Int>()\n for (i in 0 until need.size) {\n var x = need[i]\n if (0 < q.size) {\n if (x != q.peek())\n return false\n q.poll()\n continue\n }\n var found = false\n for (j in 0 until have.size) {\n if (x == have[j][0]) {\n found = true\n for (k in 1 until have[j].size)\n q.add(have[j][k])\n break\n }\n }\n if (!found)\n return false\n }\n return true\n }\n}\n```\n\n*Javascript*\n```\nlet canFormArray = (need, have, q = []) => {\n for (let x of need) {\n if (q.length) {\n if (x != q[0])\n return false;\n q.shift();\n continue;\n }\n let found = false;\n for (let piece of have) {\n if (x == piece[0]) {\n q.push(...piece.slice(1, piece.length));\n found = true;\n break;\n }\n }\n if (!found)\n return false;\n }\n return true;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def canFormArray(self, need: List[int], have: List[List[int]]) -> bool:\n q = deque()\n for x in need:\n if q:\n if x != q[0]:\n return False\n q.popleft()\n continue\n found = False\n for piece in have:\n if x == piece[0]:\n found = True\n q.extend(piece[1:])\n break\n if not found:\n return False\n return True\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n using Queue = queue<int>;\n bool canFormArray(VI& need, VVI& have, Queue q = {}) {\n for (auto x: need) {\n if (q.size()) {\n if (x != q.front())\n return false;\n q.pop();\n continue;\n }\n auto found{ false };\n for (auto& piece: have) {\n if (x == piece[0]) {\n found = true;\n for (auto i{ 1 }; i < piece.size(); q.push(piece[i++]));\n break;\n }\n }\n if (!found)\n return false;\n }\n return true;\n }\n};\n``` | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | [Python3] Straight-forward comparision based solution + early Termination [Time: O(n^2) Space: O(1)] | python3-straight-forward-comparision-bas-2kz1 | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n #checks if each array in pieces is valid array or not \ | fox6 | NORMAL | 2020-11-01T16:07:28.882063+00:00 | 2020-11-02T13:44:14.360635+00:00 | 122 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n #checks if each array in pieces is valid array or not \n def helper(arr, test):\n start = None\n try:\n start = arr.index(test[0])\n except:\n return False\n\n i = 0\n while i < len(test):\n if i + start == len(arr) or test[i] != arr[i+start]:\n return False\n i+=1\n\n return True\n \n \n if len(arr) != sum([len(a) for a in pieces]) : return False\n for test in pieces:\n if helper(arr, test) == False: return False\n\n return True\n``` | 2 | 0 | ['Python'] | 0 |
check-array-formation-through-concatenation | Kotlin 2 lines - sort | kotlin-2-lines-sort-by-joy32812-bmcw | sort pieces by first integer index in arr\n2. flat pieces, check if two lists are equal\n\n\nfun canFormArray(arr: IntArray, pieces: Array<IntArray>): Boolean { | joy32812 | NORMAL | 2020-11-01T11:21:47.699846+00:00 | 2020-11-01T11:21:47.699885+00:00 | 122 | false | 1. sort pieces by first integer index in arr\n2. flat pieces, check if two lists are equal\n\n```\nfun canFormArray(arr: IntArray, pieces: Array<IntArray>): Boolean {\n pieces.sortBy { p -> arr.indexOfFirst { it == p[0] } }\n return arr.toList().equals(pieces.flatMap { it.toList() })\n}\n``` | 2 | 1 | [] | 1 |
check-array-formation-through-concatenation | [[ NO LOOPS ]] 2-Line Python Solution | no-loops-2-line-python-solution-by-code_-q71x | \n def canFormArray(self, arr, pieces):\n kv = {e[0]: e for e in pieces}\n return arr == list(itertools.chain(*[ kv.get(e, []) for e in arr]))\ | code_report | NORMAL | 2020-11-01T05:01:47.137163+00:00 | 2020-11-01T05:02:06.771515+00:00 | 160 | false | ```\n def canFormArray(self, arr, pieces):\n kv = {e[0]: e for e in pieces}\n return arr == list(itertools.chain(*[ kv.get(e, []) for e in arr]))\n``` | 2 | 1 | ['Python'] | 0 |
check-array-formation-through-concatenation | Python easy solution iterative (100% faster) | python-easy-solution-iterative-100-faste-rbir | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for p in pieces:\n if p[0] not in arr:\n | kimchi_boy | NORMAL | 2020-11-01T04:46:41.919630+00:00 | 2020-11-01T04:46:41.919660+00:00 | 131 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n for p in pieces:\n if p[0] not in arr:\n return False\n if len(p) > 1:\n i = 0\n j = arr.index(p[i])\n while True:\n if i == len(p):\n break\n if j == len(arr) or arr[j] != p[i]:\n return False\n else:\n i += 1\n arr.remove(arr[j])\n \n return True\n``` | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | Java Using HashMap O(N) | java-using-hashmap-on-by-elizyu-xvt6 | Explanation: We can use HashMap to record indexes, and as long as the indexes are in the same order as how it is presented in the piece, it works.\n@pgmreddy th | elizyu | NORMAL | 2020-11-01T04:17:03.828828+00:00 | 2020-11-02T16:33:52.597572+00:00 | 301 | false | Explanation: We can use HashMap to record indexes, and as long as the indexes are in the same order as how it is presented in the piece, it works.\n@pgmreddy thank you for the test case - I have updated the code and added comment for the line I have edited!\n```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n if(pieces == null || pieces.length == 0) return false;\n HashMap<Integer, Integer> map = new HashMap<>();\n for(int i = 0; i < arr.length; i++) {\n map.put(arr[i], i);\n }\n int prev;\n for(int[] piece : pieces){\n prev = -1;\n for(int num : piece){\n if(!map.containsKey(num)) return false;\n if(prev != -1){\n if(map.get(num) != prev + 1) return false; // the next number in the piece must also be the next number in the target array\n }\n prev = map.get(num);\n }\n }\n return true;\n }\n}\n```\n\nFeel free to leave comments or advice and Upvote for others to see!\nThanks!! | 2 | 0 | ['Java'] | 0 |
check-array-formation-through-concatenation | Swift | Using Dictionary | swift-using-dictionary-by-jayantsogikar-dpw1 | \nfunc canFormArray(_ arr: [Int], _ pieces: [[Int]]) -> Bool {\n var dict : [Int:Int] = [:]\n for i in 0..<pieces.count{\n dict[pieces[i][0]] = i\n | jayantsogikar | NORMAL | 2020-11-01T04:06:31.635161+00:00 | 2020-11-01T04:06:31.635212+00:00 | 154 | false | ```\nfunc canFormArray(_ arr: [Int], _ pieces: [[Int]]) -> Bool {\n var dict : [Int:Int] = [:]\n for i in 0..<pieces.count{\n dict[pieces[i][0]] = i\n }\n var i = 0\n while i < arr.count{\n if dict[arr[i]] == nil{\n return false\n }\n let a = pieces[dict[arr[i]]!]\n for j in 0..<a.count{\n if arr[i] != a[j]{\n return false\n }\n i += 1\n }\n }\n return true\n}\n``` | 2 | 0 | ['Swift'] | 0 |
check-array-formation-through-concatenation | C++ easy solution using hash_map | c-easy-solution-using-hash_map-by-yipman-zsox | map[arr[i]] - 1: the current vector in pieces, visited[map[arr[i]] - 1]: the current number in pieces[i]\nmap: key is the number in vector> pieces, value is the | yipman | NORMAL | 2020-11-01T04:03:46.293349+00:00 | 2020-11-01T04:17:49.610046+00:00 | 223 | false | map[arr[i]] - 1: the current vector in pieces, visited[map[arr[i]] - 1]: the current number in pieces[i]\nmap<int, int>: key is the number in vector<vector<int>> pieces, value is the position in vector<vector<int>> pieces.\nvector< >visited: the position of every vector pieces[i] in vector<vector<int>>pieces visited.\nUsing hash_map, we can easily find the corresponding position of number arr[i] in hash_map. Every time when arr[i] is visited, we find the item in pieces, and push the next item to hash_map and map[arr[i]]=0, like popping it out. \n```\nbool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int, int> map;\n int m = (int)arr.size(), n = (int)pieces.size();\n vector<int> visited(n, 0);\n for (int i = 0; i < n; i++) {\n map[pieces[i][0]] = i + 1;\n visited[i]++;\n }\n for (int i = 0; i < m; i++) {\n if (!map[arr[i]]) return false;\n int piecePos = map[arr[i]] - 1, piecesInPos = visited[piecePos];\n if (piecesInPos < pieces[piecePos].size()) {\n map[pieces[piecePos][piecesInPos]] = piecePos + 1;\n visited[piecePos]++;\n }\n map[arr[i]] = 0;\n }\n return true;\n} | 2 | 0 | [] | 0 |
check-array-formation-through-concatenation | 🧠 Can You Form the Array? Use This Simple Map Trick to Solve It Instantly! | can-you-form-the-array-use-this-simple-m-4xwd | IntuitionWe want to check if we can form arr by concatenating subarrays from pieces in any order, while preserving the internal order of elements in each piece. | loginov-kirill | NORMAL | 2025-04-02T08:12:33.270219+00:00 | 2025-04-02T08:12:33.270219+00:00 | 1,036 | false |
### Intuition
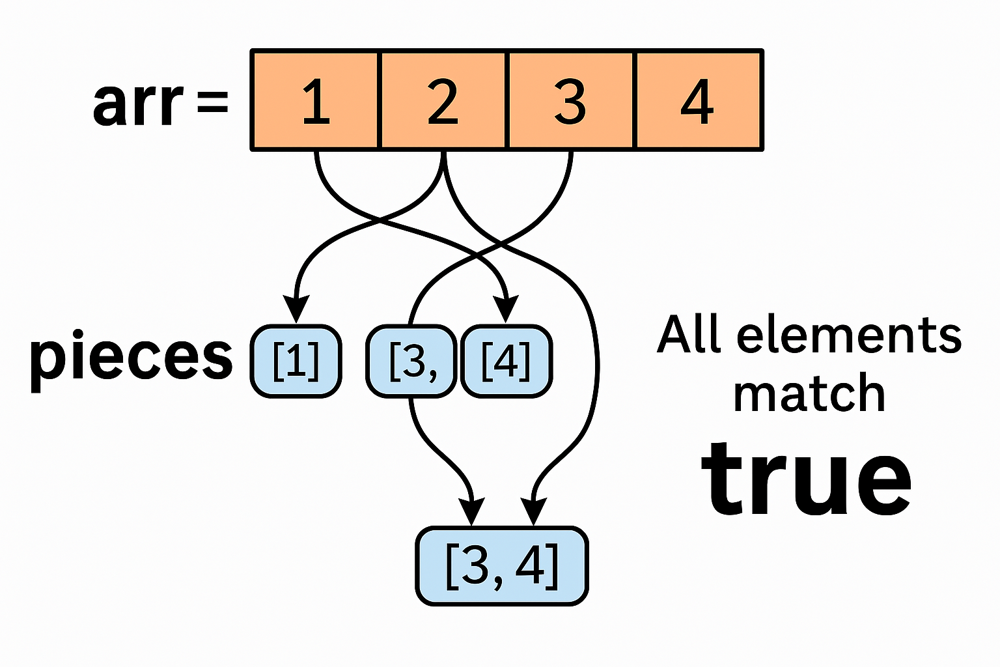
We want to check if we can form `arr` by concatenating subarrays from `pieces` in any order, while preserving the **internal order** of elements in each piece.
---
### Approach
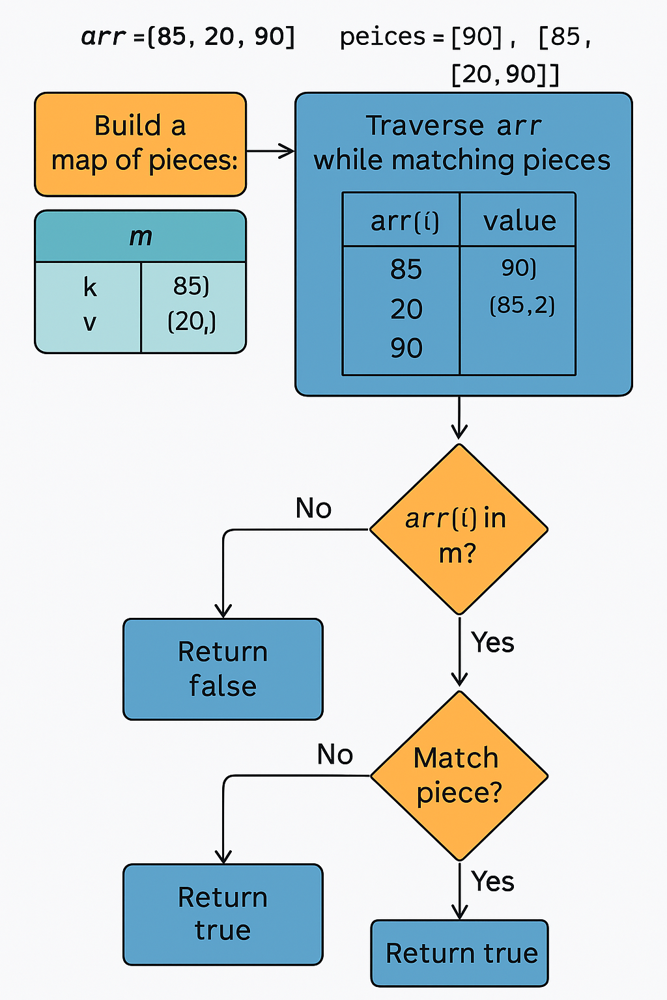
1. Build a hash map where the key is the first number of each piece, and the value is the piece itself.
2. Traverse through `arr`, and at each index:
- Check if `arr[i]` is the start of any piece.
- If yes, match the full piece against the next elements in `arr`.
- If any mismatch happens — return `false`.
3. If everything matches perfectly — return `true`.
This greedy matching uses constant-time lookup for pieces.
---
### Complexity
**Time Complexity:**
- ( O(n) ) — one pass through `arr`, each `piece` used once
**Space Complexity:**
- ( O(p) ) — `p = number of pieces` stored in hash map
---
### Code
```python []
class Solution(object):
def canFormArray(self, arr, pieces):
m = {p[0]: p for p in pieces}
i = 0
while i < len(arr):
if arr[i] not in m:
return False
p = m[arr[i]]
for num in p:
if i >= len(arr) or arr[i] != num:
return False
i += 1
return True
```
```javascript []
function canFormArray(arr, pieces) {
const m = new Map();
for (const p of pieces) m.set(p[0], p);
for (let i = 0; i < arr.length;) {
const p = m.get(arr[i]);
if (!p) return false;
for (let j = 0; j < p.length; j++) {
if (arr[i + j] !== p[j]) return false;
}
i += p.length;
}
return true;
}
```
<img src="https://assets.leetcode.com/users/images/b91de711-43d7-4838-aabe-07852c019a4d_1743313174.0180438.webp" width="270"/>
| 1 | 0 | ['Array', 'Hash Table', 'Python', 'JavaScript'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.