question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
check-array-formation-through-concatenation | Hash Map Solution | hash-map-solution-by-tlecodes-3jwy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | tlecodes | NORMAL | 2024-08-09T11:08:11.511930+00:00 | 2024-08-09T11:08:11.511956+00:00 | 161 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int, vector<int>> mapPieces;\n int index = 0, n = arr.size();\n for (auto it : pieces) {\n mapPieces[it[0]] = it;\n }\n while (index < n) {\n if (mapPieces.find(arr[index]) == mapPieces.end()) {\n return false;\n }\n auto piece = mapPieces[arr[index]];\n for (int x : piece) {\n if (x != arr[index]) {\n return false;\n }\n index++;\n }\n }\n return true;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
check-array-formation-through-concatenation | C# Linq One-liner | c-linq-one-liner-by-ilya-a-f-9qqe | \npublic class Solution\n{\n public bool CanFormArray(int[] arr, int[][] pieces) => pieces\n .OrderBy(p => Array.IndexOf(arr, p[0]))\n .SelectM | ilya-a-f | NORMAL | 2024-04-05T01:08:14.084444+00:00 | 2024-04-05T13:25:21.522829+00:00 | 15 | false | ```\npublic class Solution\n{\n public bool CanFormArray(int[] arr, int[][] pieces) => pieces\n .OrderBy(p => Array.IndexOf(arr, p[0]))\n .SelectMany(p => p)\n .SequenceEqual(arr);\n}\n```\n```\npublic class Solution\n{\n public bool CanFormArray(int[] arr, int[][] pieces)\n {\n var dic = pieces.ToDictionary(p => p[0]);\n return arr.SelectMany(a => dic.GetValueOrDefault(a, [])).SequenceEqual(arr);\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
check-array-formation-through-concatenation | Solution with Hash +90% | solution-with-hash-90-by-fredo30400-coje | javascript []\nvar canFormArray = function(arr, pieces) {\n let arr2 = [];\n let d = new Map();\n for(let t of pieces){d.set(t[0],t);}\n for(let t o | fredo30400 | NORMAL | 2023-11-28T21:45:27.560800+00:00 | 2023-11-28T21:45:27.560825+00:00 | 176 | false | ```javascript []\nvar canFormArray = function(arr, pieces) {\n let arr2 = [];\n let d = new Map();\n for(let t of pieces){d.set(t[0],t);}\n for(let t of arr){\n if (d.has(t)){arr2 = arr2.concat(d.get(t));}\n }\n return JSON.stringify(arr2)==JSON.stringify(arr);\n};\n```\n```java []\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n int[] arr2 = new int[arr.length];\n int index = 0;\n Map<Integer,int[]> d = new HashMap<>();\n for(int[] t:pieces){d.put(t[0],t);}\n for(int t:arr){\n if (d.containsKey(t)){\n int i=0;\n for(;i<d.get(t).length;i++){\n arr2[index+i] = d.get(t)[i];}\n index += i;\n }\n }\n return Arrays.equals(arr,arr2);\n }\n}\n```\n```ruby []\ndef can_form_array(arr, pieces)\n arr2 = []\n d = {}\n pieces.each{|t| d[t[0]]=t}\n arr.each{|t|\n arr2 += d[t] if d.key?(t)\n }\n return arr2==arr\nend\n```\n | 1 | 0 | ['Java', 'Ruby', 'JavaScript'] | 0 |
check-array-formation-through-concatenation | simple code made using dict and beat 90% | simple-code-made-using-dict-and-beat-90-xy5rk | \n\n# Code\n\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n \n ## create a dictionary\n # | hrishikeshprasadc | NORMAL | 2023-10-16T04:30:35.053395+00:00 | 2023-10-16T04:30:35.053419+00:00 | 150 | false | \n\n# Code\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n \n ## create a dictionary\n # key: head number of piece\n # value: all number of single piece\n mapping = { piece[0]: piece for piece in pieces }\n \n result = []\n \n # try to make array from pieces\n for number in arr:\n \n result += mapping.get( number, [] )\n \n # check they are the same or not\n return result == arr\n``` | 1 | 0 | ['Python3'] | 1 |
check-array-formation-through-concatenation | c++ || MAP || easy | c-map-easy-by-shradhaydham24-4aqd | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shradhaydham24 | NORMAL | 2023-09-02T19:30:42.981419+00:00 | 2023-09-02T19:30:42.981438+00:00 | 466 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) \n {\n map<int,vector<int>> mp; \n for(auto i:pieces) \n mp[i[0]] = i;\n vector<int> result;\n for(auto a:arr) \n {\n if(mp.find(a)!=mp.end()) \n result.insert(result.end(),mp[a].begin(),mp[a].end());\n }\n return result ==arr;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
check-array-formation-through-concatenation | ✅✅ Python | 2 Different Approaches ✅✅ | python-2-different-approaches-by-vinnisn-61cv | Approach 1: Hashmap\n\n\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n d = {pair[0]: pair for pair in p | vinnisnx | NORMAL | 2023-08-28T17:35:20.435115+00:00 | 2023-08-28T17:35:37.041396+00:00 | 17 | false | # Approach 1: Hashmap\n\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n d = {pair[0]: pair for pair in pieces}\n i = 0\n while i < len(arr):\n if (arr[i] in d) and (arr[i:(n:=len(d[arr[i]]))+i] == d[arr[i]]):\n i += n\n else:\n return False\n return True\n\n```\n# Approach 2: Iteration through **"pieces"**\n```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n prev = 0\n for i, num in enumerate(arr):\n if arr[prev:i+1] in pieces:\n prev = i+1\n return prev == len(arr)\n\n``` | 1 | 0 | ['Array', 'Hash Table', 'Python3'] | 0 |
check-array-formation-through-concatenation | Java | Easy solution | java-easy-solution-by-aziizpc-gu3l | class Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n\n String s = "";\n Map myMap = new HashMap();\n\n for (int | aziizpc | NORMAL | 2023-04-05T10:20:46.500192+00:00 | 2023-04-05T10:21:16.898502+00:00 | 713 | false | class Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n\n String s = "";\n Map<Integer, int[]> myMap = new HashMap<Integer, int[]>();\n\n for (int i = 0 ; i < pieces.length ; i++){\n myMap.put(pieces[i][0], pieces[i]);\n }\n\n for (int i = 0 ; i < arr.length ; i++){\n if (myMap.containsKey(arr[i])){\n s = s + ", " + Arrays.toString(myMap.get(arr[i]));\n i = i + (myMap.get(arr[i]).length) - 1;\n }\n else return false;\n }\n\n s = "[" + s.replaceAll("\\\\[|\\\\]", "").replaceAll("^, ", "") + "]";\n return Arrays.toString(arr).equals(s); \n }\n} | 1 | 0 | ['Java'] | 0 |
check-array-formation-through-concatenation | C++/Python Solution | cpython-solution-by-arpit3043-c6gc | C++\nRuntime: 8 ms, faster than 58.49% of C++ online submissions for Check Array Formation Through Concatenation.\nMemory Usage: 10.2 MB, less than 76.10% of C+ | arpit3043 | NORMAL | 2022-09-03T08:59:20.750371+00:00 | 2022-09-03T08:59:20.750404+00:00 | 872 | false | ### C++\n**Runtime: 8 ms, faster than 58.49% of C++ online submissions for Check Array Formation Through Concatenation.\nMemory Usage: 10.2 MB, less than 76.10% of C++ online submissions for Check Array Formation Through Concatenation.**\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) \n {\n vector<int> ps(101,-1);\n for(int i=0;i<pieces.size();i++)\n {\n ps[pieces[i][0]]=i;\n }\n for(int i=0;i<arr.size();)\n {\n int p=ps[arr[i]];\n if(p==-1)\n {\n return false;\n }\n for(int j=0;j<pieces[p].size();j++)\n {\n if(pieces[p][j]!=arr[i++])\n return false;\n }\n }\n return true;\n \n }\n};\n```\n\n### Python\n```\nclass Solution:\n def canFormArray(self, arr, pieces):\n d = {x[0]: x for x in pieces}\n return list(chain(*[d.get(num, []) for num in arr])) == arr\n``` | 1 | 0 | ['C', 'Python', 'C++', 'Python3'] | 1 |
check-array-formation-through-concatenation | C++ solution with map | c-solution-with-map-by-osmanay-34aq | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n map<int,vector<int>> m;\n \n | osmanay | NORMAL | 2022-08-15T21:59:21.282625+00:00 | 2022-08-15T21:59:21.282661+00:00 | 98 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n map<int,vector<int>> m;\n \n for(auto p:pieces){\n m[p[0]] = p;\n }\n vector<int> res;\n \n for(int num:arr)\n if(m.count(num))\n res.insert(res.end(),m[num].begin(),m[num].end());\n\n return res == arr;\n \n }\n};\n``` | 1 | 0 | [] | 0 |
check-array-formation-through-concatenation | C++||Hash map||Easy to Understand | chash-mapeasy-to-understand-by-return_7-acl3 | ```\nclass Solution {\npublic:\n bool canFormArray(vector& arr, vector>& pieces) \n {\n vector ps(101,-1);\n for(int i=0;i<pieces.size();i++ | return_7 | NORMAL | 2022-08-03T08:20:57.494660+00:00 | 2022-08-03T08:20:57.494691+00:00 | 173 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) \n {\n vector<int> ps(101,-1);\n for(int i=0;i<pieces.size();i++)\n {\n ps[pieces[i][0]]=i;\n }\n for(int i=0;i<arr.size();)\n {\n int p=ps[arr[i]];\n if(p==-1)\n {\n return false;\n }\n for(int j=0;j<pieces[p].size();j++)\n {\n if(pieces[p][j]!=arr[i++])\n return false;\n }\n }\n return true;\n \n }\n};\n//if you like the solution plz upvote. | 1 | 0 | ['C'] | 0 |
check-array-formation-through-concatenation | Python (48 ms, 83.84 %, 13.8 MB, 76.12 %) | python-48-ms-8384-138-mb-7612-by-takeich-s2df | Cleanup solution from https://leetcode.com/problems/check-array-formation-through-concatenation/discuss/2356869/Python-3-Easy-solution\npython\nclass Solution:\ | TakeIchiru | NORMAL | 2022-08-02T09:22:46.693216+00:00 | 2022-08-02T09:22:46.693258+00:00 | 52 | false | Cleanup solution from https://leetcode.com/problems/check-array-formation-through-concatenation/discuss/2356869/Python-3-Easy-solution\n``` python\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n hashmap = {piece[0]: piece for piece in pieces} \n \n size: int = len(arr)\n i = 0 \n while i < size:\n if arr[i] not in hashmap:\n return False\n lis = hashmap[arr[i]]\n for l in lis:\n if l != arr[i]:\n return False\n i += 1\n\n return True\n``` | 1 | 0 | [] | 0 |
check-array-formation-through-concatenation | Python 3 Easy solution | python-3-easy-solution-by-goh29932-hizl | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n hashmap = {}\n for i in range(len(pieces)):\n | goh29932 | NORMAL | 2022-07-30T20:14:21.778889+00:00 | 2022-07-30T20:14:21.778928+00:00 | 228 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n hashmap = {}\n for i in range(len(pieces)):\n hashmap[pieces[i][0]] = pieces[i]\n print(hashmap) \n i = 0 \n while i<len(arr):\n if arr[i] not in hashmap.keys():\n return False\n \n else:\n lis = hashmap[arr[i]]\n \n for j in range(len(lis)):\n \n if lis[j] != arr[i]:\n return False\n i += 1\n \n return True\n\n\n``` | 1 | 0 | ['Python'] | 1 |
check-array-formation-through-concatenation | simple python loop | simple-python-loop-by-ashok0888-vdzt | \ndef canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n res=[]\n for j in range(len(arr)):\n for i in | ashok0888 | NORMAL | 2022-06-30T06:20:59.803357+00:00 | 2022-06-30T06:24:49.934994+00:00 | 54 | false | ```\ndef canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n res=[]\n for j in range(len(arr)):\n for i in range(len(pieces)):\n if arr[j]==pieces[i][0]:\n res=res+pieces[i]\n return res==arr\n``` | 1 | 0 | [] | 0 |
check-array-formation-through-concatenation | 📌Fastest Java☕ solution using hashmap | fastest-java-solution-using-hashmap-by-s-8ieo | ```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n HashMap hmap = new HashMap<>();\n for(int piece[]:pieces)\n | saurabh_173 | NORMAL | 2022-05-30T16:44:14.405554+00:00 | 2022-05-30T16:44:14.405585+00:00 | 228 | false | ```\nclass Solution {\n public boolean canFormArray(int[] arr, int[][] pieces) {\n HashMap<Integer,int[]> hmap = new HashMap<>();\n for(int piece[]:pieces)\n hmap.put(piece[0],piece);\n int i=0;\n while(i<arr.length)\n {\n if(!hmap.containsKey(arr[i]))\n return false;\n int list[] = hmap.get(arr[i]);\n for(int k:list)\n {\n if(i>=arr.length || k!=arr[i])\n return false;\n i++;\n }\n }\n return true;\n }\n} | 1 | 0 | ['Java'] | 1 |
check-array-formation-through-concatenation | Java | Easy to Understand | java-easy-to-understand-by-pagalpanda-uqqg | \n\tpublic boolean canFormArray(int[] arr, int[][] pieces) {\n StringBuilder sb = new StringBuilder();\n for(int a : arr) \n sb.append( | pagalpanda | NORMAL | 2022-05-13T01:57:16.603553+00:00 | 2022-05-13T01:57:16.603590+00:00 | 114 | false | ```\n\tpublic boolean canFormArray(int[] arr, int[][] pieces) {\n StringBuilder sb = new StringBuilder();\n for(int a : arr) \n sb.append("#").append(a).append("#");\n \n String str = sb.toString();\n for(int piece[] : pieces) {\n StringBuilder p = new StringBuilder();\n for(int item : piece) \n p.append("#").append(item).append("#");\n \n if(!str.contains(p.toString())) return false;\n }\n return true;\n }\n``` | 1 | 0 | ['Java'] | 0 |
check-array-formation-through-concatenation | C++ and C# | c-and-c-by-shaunrd0-807o | Both solutions use same concept; For-each array in pieces, check that all elements appear in the same order within arr.\nSince the problem indicates values are | shaunrd0 | NORMAL | 2022-05-09T14:53:43.334710+00:00 | 2022-05-09T14:53:43.334738+00:00 | 85 | false | Both solutions use same concept; For-each array in `pieces`, check that all elements appear in the same order within `arr`.\nSince the problem indicates values are distinct, we don\'t need to worry about duplicates. The problem also says that the sum of all array lengths in `pieces` is equal to the length of `arr`, so we don\'t need to worry about left over elements in `pieces`. \n\nC++\n\n```C++\nclass Solution {\n public:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n for (int row = 0; row < pieces.size(); row++) {\n auto it = std::find(begin(arr), end(arr), pieces[row][0]);\n for (int col = 0; col < pieces[row].size(); col++) {\n if (it == end(arr)) return false;\n if (*(it++) != pieces[row][col]) return false;\n }\n }\n return true;\n }\n};\n```\n\nC#\n\n```C#\npublic class Solution {\n public bool CanFormArray(int[] arr, int[][] pieces) {\n for (int row = 0; row < pieces.Length; row++) {\n int found = Array.IndexOf(arr, pieces[row][0]);\n for (int col = 0; col < pieces[row].Length; col++) {\n if (found == -1 || found >= arr.Length) return false;\n if (arr[found++] != pieces[row][col]) return false;\n }\n }\n return true;\n }\n}\n``` | 1 | 0 | ['C'] | 0 |
check-array-formation-through-concatenation | C++ || Using set || Simple & concise solution | c-using-set-simple-concise-solution-by-m-mj8q | Please upvote if you liked my approach :)\n\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& p) \n {\n set<vec | markrash4 | NORMAL | 2022-02-27T14:03:23.693128+00:00 | 2022-02-27T14:03:23.693159+00:00 | 96 | false | **Please upvote if you liked my approach :)**\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& p) \n {\n set<vector<int> > s;\n \n for(auto it:p)\n s.insert(it);\n \n vector<int> v;\n \n for(auto a:arr)\n {\n v.push_back(a);\n \n if(s.count(v))\n v.clear();\n }\n \n return v.size() == 0;\n }\n};\n``` | 1 | 0 | ['C', 'Ordered Set', 'C++'] | 0 |
check-array-formation-through-concatenation | C++ 100% , Time complexity O(NLogN). Using Hash Map. | c-100-time-complexity-onlogn-using-hash-07b0g | \n\n\n\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& p) {\n int sum_p =0;\n map<int,vector<int>> mp;\n | aash1999 | NORMAL | 2021-12-31T13:28:15.612926+00:00 | 2021-12-31T13:28:15.612963+00:00 | 201 | false | \n\n```\n\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& p) {\n int sum_p =0;\n map<int,vector<int>> mp;\n \n for(int i =0 ;i <p.size() ;i++){\n mp.insert(pair<int,vector<int>>(p[i][0],p[i]));\n }\n int index =0 ;\n int key = arr[0];\n if(mp.find(key) == mp.end())return false;\n \n for(int i=0; i< arr.size() ; i++){\n if(index == mp[key].size()){\n index =0 ;\n key = arr[i];\n }\n if(mp.find(key) == mp.end())return false;\n if(mp[key][index] != arr[i])return false;\n ++index;\n \n }\n \n return true;\n \n }\n};\n\n``` | 1 | 0 | [] | 0 |
check-array-formation-through-concatenation | C++ STL solution using binary search [4ms] | c-stl-solution-using-binary-search-4ms-b-x0v0 | \nclass Solution {\n public:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces)\n {\n\t\t// let n = size(arr) and m = size(pieces)\n | hrishikesh_deshpande | NORMAL | 2021-11-14T15:41:24.871040+00:00 | 2021-11-14T15:56:51.247394+00:00 | 163 | false | ```\nclass Solution {\n public:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces)\n {\n\t\t// let n = size(arr) and m = size(pieces)\n sort(begin(pieces), end(pieces)); // O(m log m)\n auto it = cbegin(arr);\n while (it != cend(arr)) { // O(n)\n const auto lb = lower_bound(cbegin(pieces), cend(pieces), *it,\n [](const auto& v, const auto& i) { return v.front() < i; }); // O(log m)\n if (lb == cend(pieces) ||\n !equal(lb->cbegin(), lb->cend(), it)) break; // O(min(size(piece),n)) worst case \n\n it += lb->size();\n }\n return it == cend(arr);\n }\n};\n```\n**If you have any doubts or suggestions, please feel free to comment.\nIf you find this solution useful, you know where the upvote is :)** | 1 | 0 | ['C', 'Binary Tree', 'C++'] | 0 |
check-array-formation-through-concatenation | C++|| EASY TO UNDERSTAND || FAST and EFFICIENT || maps | c-easy-to-understand-fast-and-efficient-su6nh | Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are alwa | aarindey | NORMAL | 2021-10-19T21:29:16.674416+00:00 | 2021-10-19T21:29:16.674444+00:00 | 108 | false | **Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome**\n```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n unordered_map<int,vector<int>> mp;\n for(vector<int> p:pieces)\n {\n mp[p[0]]=p;\n }\n int i=0;\n while(i<arr.size())\n {\n if(mp.find(arr[i])!=mp.end())\n {\n vector<int> piece=mp[arr[i]];\n for(int j=0;j<piece.size();j++)\n {\n if(arr[i]==piece[j])\n i++;\n else\n return false;\n }\n }\n else\n {\n return false;\n }\n }\n return true;\n }\n};\n``` | 1 | 0 | [] | 0 |
check-array-formation-through-concatenation | Python the most optimal solution: O(n) time, O(n) space with hashmap | python-the-most-optimal-solution-on-time-hwzp | \nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n res = []\n \n n = len(arr)\n indexe | byuns9334 | NORMAL | 2021-10-11T07:56:01.150309+00:00 | 2021-10-11T07:56:01.150343+00:00 | 141 | false | ```\nclass Solution:\n def canFormArray(self, arr: List[int], pieces: List[List[int]]) -> bool:\n res = []\n \n n = len(arr)\n indexes = {}\n for i in range(len(pieces)):\n indexes[pieces[i][0]] = i \n idx = 0 \n while idx < n:\n if arr[idx] not in indexes:\n return False\n item = pieces[indexes[arr[idx]]]\n for j in range(len(item)):\n if arr[idx+j] != item[j]:\n return False\n else:\n res.append(item[j])\n idx += len(item)\n return True\n \n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
check-array-formation-through-concatenation | C++ Runtime 0ms | c-runtime-0ms-by-tanwi_agrawal-yg8u | \nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n map<int,int>mp;\n for(int i=0;i<ar | tanwi_agrawal | NORMAL | 2021-08-20T09:08:43.743522+00:00 | 2021-08-20T09:08:43.743559+00:00 | 130 | false | ```\nclass Solution {\npublic:\n bool canFormArray(vector<int>& arr, vector<vector<int>>& pieces) {\n \n map<int,int>mp;\n for(int i=0;i<arr.size();i++)\n {\n mp.insert({arr[i],i});\n }\n for(int i=0;i<pieces.size();i++)\n {\n int index=0;\n for(int j=0;j<pieces[i].size();j++)\n {\n if(mp.find(pieces[i][j])==mp.end())\n return false;\n else\n {\n if(j==0)\n index=mp[pieces[i][0]]+1;\n else if(mp[pieces[i][j]]==index)\n index=mp[pieces[i][j]]+1;\n else\n return false;\n }\n }\n }\n return true;\n \n }\n};\n``` | 1 | 0 | [] | 0 |
check-array-formation-through-concatenation | Kotlin 1 line | kotlin-1-line-by-georgcantor-co4x | \nfun canFormArray(\n a: IntArray,\n p: Array<IntArray>\n) = p.sortedBy { a.indexOf(it.first()) }.map { it.map { it } }.flatten() == a.toList()\n | GeorgCantor | NORMAL | 2021-07-19T18:12:01.895948+00:00 | 2021-07-19T18:14:35.785478+00:00 | 100 | false | ```\nfun canFormArray(\n a: IntArray,\n p: Array<IntArray>\n) = p.sortedBy { a.indexOf(it.first()) }.map { it.map { it } }.flatten() == a.toList()\n``` | 1 | 0 | ['Kotlin'] | 1 |
house-robber-iii | Step by step tackling of the problem | step-by-step-tackling-of-the-problem-by-0a1on | Step I -- Think naively\n\nAt first glance, the problem exhibits the feature of "optimal substructure": if we want to rob maximum amount of money from current b | fun4leetcode | NORMAL | 2016-03-13T19:04:05+00:00 | 2019-11-08T17:46:02.650690+00:00 | 141,203 | false | **Step I -- Think naively**\n\nAt first glance, the problem exhibits the feature of "optimal substructure": if we want to rob maximum amount of money from current binary tree (rooted at `root`), we surely hope that we can do the same to its left and right subtrees. \n\nSo going along this line, let\'s define the function `rob(root)` which will return the maximum amount of money that we can rob for the binary tree rooted at `root`; the key now is to construct the solution to the original problem from solutions to its subproblems, i.e., how to get `rob(root)` from `rob(root.left), rob(root.right), ...` etc.\n\nApparently the analyses above suggest a recursive solution. And for recursion, it\'s always worthwhile figuring out the following two properties:\n\n 1. Termination condition: when do we know the answer to `rob(root)` without any calculation? Of course when the tree is empty ---- we\'ve got nothing to rob so the amount of money is zero.\n\n 2. Recurrence relation: i.e., how to get `rob(root)` from `rob(root.left), rob(root.right), ...` etc. From the point of view of the tree root, there are only two scenarios at the end: `root` is robbed or is not. If it is, due to the constraint that "we cannot rob any two directly-linked houses", the next level of subtrees that are available would be the four "**grandchild-subtrees**" (`root.left.left, root.left.right, root.right.left, root.right.right`). However if `root` is not robbed, the next level of available subtrees would just be the two "**child-subtrees**" (`root.left, root.right`). We only need to choose the scenario which yields the larger amount of money.\n\nHere is the program for the ideas above:\n\n public int rob(TreeNode root) {\n if (root == null) return 0;\n \n int val = 0;\n \n if (root.left != null) {\n val += rob(root.left.left) + rob(root.left.right);\n }\n \n if (root.right != null) {\n val += rob(root.right.left) + rob(root.right.right);\n }\n \n return Math.max(val + root.val, rob(root.left) + rob(root.right));\n }\n\nHowever the solution runs very slowly (`1186 ms`) and barely got accepted (the time complexity turns out to be exponential, see my [comments](https://discuss.leetcode.com/topic/39834/step-by-step-tackling-of-the-problem/26?page=2) below).\n\n---\n\n**Step II -- Think one step further**\n\nIn step `I`, we only considered the aspect of "optimal substructure", but think little about the possibilities of overlapping of the subproblems. For example, to obtain `rob(root)`, we need `rob(root.left), rob(root.right), rob(root.left.left), rob(root.left.right), rob(root.right.left), rob(root.right.right)`; but to get `rob(root.left)`, we also need `rob(root.left.left), rob(root.left.right)`, similarly for `rob(root.right)`. The naive solution above computed these subproblems repeatedly, which resulted in bad time performance. Now if you recall the two conditions for dynamic programming (DP): "**optimal substructure**" + "**overlapping of subproblems**", we actually have a DP problem. A naive way to implement DP here is to use a hash map to record the results for visited subtrees. \n\nAnd here is the improved solution:\n\n public int rob(TreeNode root) {\n return robSub(root, new HashMap<>());\n }\n \n private int robSub(TreeNode root, Map<TreeNode, Integer> map) {\n if (root == null) return 0;\n if (map.containsKey(root)) return map.get(root);\n \n int val = 0;\n \n if (root.left != null) {\n val += robSub(root.left.left, map) + robSub(root.left.right, map);\n }\n \n if (root.right != null) {\n val += robSub(root.right.left, map) + robSub(root.right.right, map);\n }\n \n val = Math.max(val + root.val, robSub(root.left, map) + robSub(root.right, map));\n map.put(root, val);\n \n return val;\n }\n\nThe runtime is sharply reduced to `9 ms`, at the expense of `O(n)` space cost (`n` is the total number of nodes; stack cost for recursion is not counted).\n\n---\n\n**Step III -- Think one step back**\n\nIn step `I`, we defined our problem as `rob(root)`, which will yield the maximum amount of money that can be robbed of the binary tree rooted at `root`. This leads to the DP problem summarized in step `II`. \n\nNow let\'s take one step back and ask why we have overlapping subproblems. If you trace all the way back to the beginning, you\'ll find the answer lies in the way how we have defined `rob(root)`. As I mentioned, for each tree root, there are two scenarios: it is robbed or is not. `rob(root)` does not distinguish between these two cases, so "information is lost as the recursion goes deeper and deeper", which results in repeated subproblems.\n\nIf we were able to maintain the information about the two scenarios for each tree root, let\'s see how it plays out. Redefine `rob(root)` as a new function which will return an array of two elements, the first element of which denotes the maximum amount of money that can be robbed if `root` is **not robbed**, while the second element signifies the maximum amount of money robbed if it is **robbed**. \n\nLet\'s relate `rob(root)` to `rob(root.left)` and `rob(root.right)...`, etc. For the 1st element of `rob(root)`, we only need to sum up the larger elements of `rob(root.left)` and `rob(root.right)`, respectively, since `root` is not robbed and we are free to rob its left and right subtrees. For the 2nd element of `rob(root)`, however, we only need to add up the 1st elements of `rob(root.left)` and `rob(root.right)`, respectively, plus the value robbed from `root` itself, since in this case it\'s guaranteed that we cannot rob the nodes of `root.left` and `root.right`. \n\nAs you can see, by keeping track of the information of both scenarios, we decoupled the subproblems and the solution essentially boiled down to a greedy one. Here is the program:\n\n public int rob(TreeNode root) {\n int[] res = robSub(root);\n return Math.max(res[0], res[1]);\n }\n \n private int[] robSub(TreeNode root) {\n if (root == null) return new int[2];\n \n int[] left = robSub(root.left);\n int[] right = robSub(root.right);\n int[] res = new int[2];\n\n res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);\n res[1] = root.val + left[0] + right[0];\n \n return res;\n } | 4,407 | 3 | [] | 284 |
house-robber-iii | Simple C++ solution | simple-c-solution-by-espuer-ugnw | /**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * | espuer | NORMAL | 2016-03-24T19:44:28+00:00 | 2018-08-12T22:26:52.121897+00:00 | 32,495 | false | /**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\n class Solution {\n public:\n int tryRob(TreeNode* root, int& l, int& r) {\n if (!root)\n return 0;\n \n int ll = 0, lr = 0, rl = 0, rr = 0;\n l = tryRob(root->left, ll, lr);\n r = tryRob(root->right, rl, rr);\n \n return max(root->val + ll + lr + rl + rr, l + r);\n }\n \n int rob(TreeNode* root) {\n int l, r;\n return tryRob(root, l, r);\n }\n };\n\nBasically you want to compare which one is bigger between 1) you + sum of your grandchildren and 2) sum of your children. Personally I like my solution better than the most voted solution because I don't need complex data structures like map. | 286 | 5 | [] | 23 |
house-robber-iii | Easy understanding solution with dfs | easy-understanding-solution-with-dfs-by-1tqxw | dfs all the nodes of the tree, each node return two number, int[] num, num[0] is the max value while rob this node, num[1] is max value while not rob this value | jiangbowei2010 | NORMAL | 2016-03-12T00:08:53+00:00 | 2018-10-23T23:33:43.224514+00:00 | 43,890 | false | dfs all the nodes of the tree, each node return two number, int[] num, num[0] is the max value while rob this node, num[1] is max value while not rob this value. Current node return value only depend on its children's value. Transform function should be very easy to understand.\n\n public class Solution {\n public int rob(TreeNode root) {\n int[] num = dfs(root);\n return Math.max(num[0], num[1]);\n }\n private int[] dfs(TreeNode x) {\n if (x == null) return new int[2];\n int[] left = dfs(x.left);\n int[] right = dfs(x.right);\n int[] res = new int[2];\n res[0] = left[1] + right[1] + x.val;\n res[1] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);\n return res;\n }\n } | 254 | 18 | ['Java'] | 25 |
house-robber-iii | Python O(n) code: Optimized for Readability | python-on-code-optimized-for-readability-i908 | Implementing the decoupled recursive approach detailed here\n\n\nclass Solution(object):\n def rob(self, root):\n """\n :type root: TreeNode\n | wayne-x | NORMAL | 2016-10-04T06:05:57.129000+00:00 | 2018-10-01T06:17:29.537060+00:00 | 13,654 | false | Implementing the decoupled recursive approach detailed [here](https://discuss.leetcode.com/topic/39834/step-by-step-tackling-of-the-problem)\n\n```\nclass Solution(object):\n def rob(self, root):\n """\n :type root: TreeNode\n :rtype: int\n """\n def superrob(node):\n # returns tuple of size two (now, later)\n # now: max money earned if input node is robbed\n # later: max money earned if input node is not robbed\n \n # base case\n if not node: return (0, 0)\n \n # get values\n left, right = superrob(node.left), superrob(node.right)\n \n # rob now\n now = node.val + left[1] + right[1]\n \n # rob later\n later = max(left) + max(right)\n \n return (now, later)\n \n return max(superrob(root))\n``` | 173 | 0 | [] | 14 |
house-robber-iii | ✅ [C++/Python] Simple Solutions w/ Explanation | Optimization from Brute-Force to DP to Optimized DP | cpython-simple-solutions-w-explanation-o-vwdd | We are given a binary tree consisting of houses. We need to find maximum loot that we can get without robbing two directly linked houses\n\n---\n\n \u274C Solut | archit91 | NORMAL | 2021-12-05T06:18:26.430091+00:00 | 2021-12-05T06:42:35.100666+00:00 | 10,334 | false | We are given a binary tree consisting of houses. We need to find maximum loot that we can get without robbing two directly linked houses\n\n---\n\n \u274C ***Solution - I (Brute-Force)***\n\nLet\'s try to solve this starting with brute-force.\n\n* At each house/node of the tree, we have the choice to either rob it or not to rob it\n* If we rob the current node, we cannot rob the left or right child of the current node\n* If we dont rob the current node, we can move to the left and right nodes and rob them\n* We choose the option which yields us the maximum loot\n\nWe can implement this in two ways- \n1. In 1st implementation below, I have used a boolean `canRob` variable denoting whether we can rob the current node or not. Each time we move to child nodes with `canRob` parameter set to true or false depending on whether the current node was robbed or not.\n2. In the 2nd implementation, we never move to directly linked nodes when we rob the current node. So we can either not rob the current node, or we can rob it and move to both child nodes of `root -> left` and `root -> right` if they exists.\n\nI found 1st version a bit simpler but the 2nd version will be better for optimization into `dp`.\n\n### **C++**\n> *1st Implementation*\n```cpp\nclass Solution {\npublic:\n int rob(TreeNode* root, bool canRob = true) {\n if(!root) return 0;\n int dontRob = rob(root -> left, true) + rob(root -> right, true);\n int robRoot = canRob ? root -> val + rob(root -> left, false) + rob(root -> right, false) : -1;\n return max(dontRob, robRoot);\n }\n};\n```\n\n> *2nd Implementation*\n```cpp\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n if(!root) return 0;\n int dontRob = rob(root -> left) + rob(root -> right), robRoot = root -> val;\n if(root -> left) robRoot += rob(root -> left -> left) + rob(root -> left -> right);\n if(root -> right) robRoot += rob(root -> right -> left) + rob(root -> right -> right);\n return max(dontRob, robRoot);\n }\n};\n```\n\n>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> <hr> \n\n### **Python**\n> *1st Implmentation*\n```python\nclass Solution:\n def rob(self, root, canRob = True):\n if not root: return 0\n dont_rob = self.rob(root.left, True) + self.rob(root.right, True)\n rob_root = root.val + self.rob(root.left, False) + self.rob(root.right, False) if canRob else -1\n return max(dont_rob, rob_root)\n```\n\n> *2nd Implemtation*\n```python\nclass Solution:\n def rob(self, root):\n if not root: return 0\n dont_rob, rob_root = self.rob(root.left) + self.rob(root.right), root.val\n if root.left: rob_root += self.rob(root.left.left) + self.rob(root.left.right)\n if root.right: rob_root += self.rob(root.right.left) + self.rob(root.right.right)\n return max(dont_rob, rob_root)\n```\n\n***Time Complexity :*** <code>O(2<sup>N</sup>)</code>, where `N` is the number of nodes in the tree. \n***Space Complexity :*** `O(H)`, where `H` is the height of the tree. `H` is the max recursion depth & thus `O(H)` space is required by recursive stack. It is `O(N)` in case of skewed tree and `O(logN)` in case of balanced binary tree.\n\n\n---\n\n \u2714\uFE0F ***Solution - II (Dynamic Programming)***\n\nDrawing out the recursion tree, we can see that there are multiple repeated computations taking place. But call to `rob()` with same parameters should always give us the same result which is maximum possible loot that we can get starting from that node. So, instead of doing repeated computations over and over again, we can simply save the result for a given state of function and directly return the same result when repeated call is made. \n\nHere, for the 1st case, we use a `dp` hashmap where `dp[node][canRob]` denotes the maximum possible loot that we can get starting from `node` in the tree & `canRob` denotes whether it can be robbed or not. Note that in this case we needed to save the complete state of function into `dp` which includes `canRob` parameter as well.\nSimilarly, for 2nd case, we use `dp` hashmap where `dp[node]` denotes the maximum possible loot that we can get starting from `node` in the tree.\n\n### **C++**\n> *1st Implementation*\n```cpp\nclass Solution {\npublic:\n unordered_map<TreeNode*, vector<int>> dp;\n int rob(TreeNode* root, bool canRob = true) {\n if(!root) return 0;\n if(dp.count(root) && dp[root][canRob] != -1) return dp[root][canRob];\n dp[root] = {-1,-1};\n int dontRob = rob(root -> left, true) + rob(root -> right, true);\n int robRoot = canRob ? root -> val + rob(root -> left, false) + rob(root -> right, false) : -1;\n return dp[root][canRob] = max(dontRob, robRoot);\n }\n};\n```\n\n> *2nd Implementation*\n```cpp\nclass Solution {\npublic:\n unordered_map<TreeNode*, int> dp;\n int rob(TreeNode* root) {\n if(!root) return 0;\n if(dp.count(root)) return dp[root];\n int dontRob = rob(root -> left) + rob(root -> right), robRoot = root -> val;\n if(root -> left) robRoot += rob(root -> left -> left) + rob(root -> left -> right);\n if(root -> right) robRoot += rob(root -> right -> left) + rob(root -> right -> right);\n return dp[root] = max(dontRob, robRoot);\n }\n};\n```\n\n### **Python**\n> *1st Implementation*\n```python\nclass Solution:\n @cache\n def rob(self, root, canRob = True):\n if not root: return 0\n dont_rob = self.rob(root.left, True) + self.rob(root.right, True)\n rob_root = root.val + self.rob(root.left, False) + self.rob(root.right, False) if canRob else -1\n return max(dont_rob, rob_root)\n```\n\n> *2nd Implemtation*\n```python\nclass Solution:\n @cache\n def rob(self, root):\n if not root: return 0\n dont_rob, rob_root = self.rob(root.left) + self.rob(root.right), root.val\n if root.left: rob_root += self.rob(root.left.left) + self.rob(root.left.right)\n if root.right: rob_root += self.rob(root.right.left) + self.rob(root.right.right)\n return max(dont_rob, rob_root)\n```\n\n***Time Complexity :*** <code>O(N)</code>, we calculate `dp[node]` for each of `N` nodes in the tree only once.\n***Space Complexity :*** `O(N)`, required for maintaining `dp`\n\n---\n\n \u2714\uFE0F ***Solution - III (Space-Optimized Dynamic Programming)***\n\nIn the above solutions, we recursed for both cases when current node was robbed and current node wasn\'t robbed and depending on the result from both cases, we decided which one to choose. This led to separate dfs calls with multiple states, one with current node\'s state as being robbed and other one with the state being not robbed. This required us memoize the results to avoid repeated calls to a node\'s state which was already calculated in one of earlier dfs call.\n\nGoing a slightly different route, instead of doing separate calls, we just make a single dfs call to left and right child nodes (without differentiating the state of current node) and return the results for both the cases of the child nodes being robbed and not robbed. We can then calculate the result for current node for -\n * state when **current node is robbed** which will be equal to current node\'s value + sum of result of child nodes not being robbed.\n * state when **current node is NOT robbed** which will be equal to sum of result of child nodes in their maximum loot state (i.e, for each child node, choose its state of either being robbed or not robbed, whichever gave maximum loot).\n\nTo summarize, this approach issues a single dfs call down till the leaf node and from there it propagates upwards the value of **1.** maximum loot when child node is not robbed and, **2.** maximum loot when child node is robbed. This allows us to calculate result for both states of current node being robbed and not being robbed without the need of memoizing the results for child nodes.\n\n### **C++**\n```cpp\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n auto ans = dfs(root);\n return max(ans.first, ans.second);\n }\n pair<int, int> dfs(TreeNode* root) {\n if(!root) return {0, 0};\n auto [leftDontRob, leftRob] = dfs(root -> left);\n auto [rightDontRob, rightRob] = dfs(root -> right);\n return {\n max(leftDontRob, leftRob) + max(rightDontRob, rightRob),\n root -> val + leftDontRob + rightDontRob\n };\n }\n};\n```\n\n### **Python**\n```python\nclass Solution:\n def rob(self, root):\n def dfs(root):\n if not root: return (0, 0)\n L, R = dfs(root.left), dfs(root.right)\n return (max(L) + max(R), root.val + L[0] + R[0])\n return max(dfs(root))\n```\n\n***Time Complexity :*** <code>O(N)</code>\n***Space Complexity :*** `O(H)`, required for recursive stack\n\n---\n---\n\n\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, comment below \uD83D\uDC47 \n\n---\n---\n | 163 | 4 | [] | 12 |
house-robber-iii | [Python3] Dynamic Programming + Depth First Search | python3-dynamic-programming-depth-first-kw12c | we construct a dp tree, each node in dp tree represents [rob the current node how much you gain, skip the current node how much you gain]\n dp_node[0] =[rob the | zhanweiting | NORMAL | 2019-09-06T19:51:01.402294+00:00 | 2020-04-09T04:40:59.333645+00:00 | 11,841 | false | * we construct a dp tree, each node in dp tree represents [rob the current node how much you gain, skip the current node how much you gain]\n dp_node[0] =[rob the current node how much you gain]\n dp_node[1] =[skip the current node how much you gain]\n* we start the stolen from the leaf: Depth First Search\n* for each node you have 2 opitions:\n\toption 1: rob the node, then you can\'t rob the child of the node.\n\t\t\t\t\tdp_node[0] = node.val + dp_node.left[1] +dp_node.right[1]\n\toption 2: skip the node, then you can rob or skip the child of the node. \n\t\t\t\t\tdp_node[1] = dp_node.left[0] + dp_node.right[0]\n* \tthe maximum of gain of the node depents on max(dp_node[0],dp_node[1])\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n """\n Input: [3,4,5,1,3,null,1]\n input tree dp tree:\n 3 [3+3+1,4+5]\n / \\ / \\\n 4 5 [4,3] [5,1]\n / \\ \\ / \\ \\\n 1 2 1 [1,0] [2,0] [1,0]\n / \\ / \\ / \\\n [0,0] [0,0] [0,0] [0,0] [0,0] [0,0]\n \n """\n def rob(self, root: TreeNode) -> int:\n return max(self.dfs(root))\n \n def dfs(self, root: TreeNode):\n if not root:\n return (0, 0)\n left = self.dfs(root.left)\n right = self.dfs(root.right)\n return (root.val + left[1] + right[1], max(left[0], left[1]) + max(right[0], right[1]))\n``` | 139 | 2 | ['Dynamic Programming', 'Depth-First Search', 'Python', 'Python3'] | 9 |
house-robber-iii | Easy to understand(java) | easy-to-understandjava-by-siyuan10-2d84 | public class Solution {\n \n public int rob(TreeNode root) {\n if (root == null) return 0;\n return Math.max(robInclude(root), robExclude(ro | siyuan10 | NORMAL | 2016-03-13T23:05:29+00:00 | 2018-10-09T18:15:28.709300+00:00 | 11,892 | false | public class Solution {\n \n public int rob(TreeNode root) {\n if (root == null) return 0;\n return Math.max(robInclude(root), robExclude(root));\n }\n \n public int robInclude(TreeNode node) {\n if(node == null) return 0;\n return robExclude(node.left) + robExclude(node.right) + node.val;\n }\n \n public int robExclude(TreeNode node) {\n if(node == null) return 0;\n return rob(node.left) + rob(node.right);\n }\n} | 127 | 4 | [] | 20 |
house-robber-iii | C++ | with and without memo | Detailed explaination | c-with-and-without-memo-detailed-explain-d185 | So, robber is active again , let\'s see how we can calculate an efficient robbery !!\n\nThis again is a classic DFS problem where we have to look out for the re | priyam_vd | NORMAL | 2021-12-05T02:18:11.648468+00:00 | 2023-02-13T11:50:51.345472+00:00 | 7,774 | false | So, robber is active again , let\'s see how we can calculate an efficient robbery !!\n\nThis again is a classic **DFS** problem where we have to look out for the recurrence relation and think dynamically ... The houses are present in the form of binary tree and if we are at the root_house then we have two choices :: \n**/a. to the rob the root house and skip it\'s children and move on to root\'s grandchildren.../** OR **/b. to skip this house and move on to left and right_subtree, with the hope that it will yeild better result./**\n * In case robber is robbing the *root_house*, maximum money he is gonna rob == **root->val + answer(root->left->left + root->left->right + root->right->left + root->right->right)**{as then these nodes are gonna be the grandchildren of curr_root (in case they exist)}..\n * In case he is not robbing the *root_house*, maximum money he gonna rob == **answer(root->left + root->right)**.\n * And Final answer == **max(root_included, root_excluded)**\n * We are ready with the approach , just need to write base case and do recursion calls and then some calculations ... But before blindly making recursion calls , we should check out if we are calling on the same node multiple times or not !! If multiple calls on same is done, then Time Complexity would get screwed and we will have to memoize the solution !!\n * \n * Here , in this example we can see that::\n * When we include(root) , then it calls on (nodes with value 1,3 and 1) .... And when node with the value 4 will be the root and we will be excluding it , then it will call on those same nodes with value(1 and 3).... So memoization would be perfect way to go for this problem.....\n * **Now we know, what calls to make , what calculation to do and we also know that we need to memoize**.... So here is the code for that !!!\n \n\n### Solution 1 ... with MEMO \n```\nclass Solution {\n\nprivate:\n unordered_map<TreeNode*,int>memo;\n int helper(TreeNode* root) {\n if (root == NULL) return 0;\n \n if (memo.count(root)){\n return memo[root];\n } \n \n int ans_including_root = root->val;\n \n if (root->left != NULL) {\n ans_including_root += helper(root->left->left) + helper(root->left->right);\n }\n \n if (root->right != NULL) {\n ans_including_root += helper(root->right->left) + helper(root->right->right);\n }\n \n int ans_excluding_root = helper(root->left) + helper(root->right);\n \n int ans = max(ans_including_root , ans_excluding_root);\n \n memo[root]=ans;\n \n return ans;\n }\n \npublic:\n int rob(TreeNode* root) {\n return helper(root);\n } \n};\n```\n\nIt\'s a good solution to come up with ... But why to use memo when we can have a better solution without it ? \n* Why was the memoization needed ? Because we were going Top Down and we weren\'t sure whether to include the root_house at that instance or not .... So , we were making recursion calls for both cases , which led to the complication of situation and we had to cover it up with the map !!\n* So , instead of going that Top-down way , let\'s try going the deepest and then while returning back, we will decide whether to choose that house or not !\n* **We will return the Pair here, {case_when_curr_root_is_chosen, case_when_not_chosen}** ... \n * Let\'s assume any particular node (H), gets the answer from it\'s left child as {a,b} and right child as{x,y} ....\n * So , b is the case when H->left was not included and y is the case when H->right was not included... So, if we are gonna rob the House (H) , then total money we can get, p == **H->val +y+b**\n * And when House will be not robbed then maximum money robbed, q == **max(a,b) + max(x,y)**..... and what this node H will return is {p,q}\n \n \n### Solution 2 -- without memo\n```\nclass Solution {\nprivate:\n pair<int,int> max_money_robbed(TreeNode* root){\n \n if(root==NULL)return {0,0};\n \n pair<int,int>left = max_money_robbed(root->left);\n pair<int,int>right = max_money_robbed(root->right);\n \n int root_house_robbed = left.second + right.second + root->val;\n int root_house_not_robbed = max(left.first,left.second)+ max(right.first,right.second);\n \n pair<int,int>ans;\n \n ans.first = root_house_robbed, ans.second = root_house_not_robbed;\n \n return ans;\n \n }\npublic:\n int rob(TreeNode* root) {\n pair<int,int>result = max_money_robbed(root);\n return max(result.first,result.second);\n }\n};\n\n**If you reached here, Thanks for giving it a read !!**\n \n\n\n \n | 118 | 6 | ['Dynamic Programming', 'Tree', 'Memoization', 'C'] | 7 |
house-robber-iii | JAVA | 3 Approaches | Recursion | DP | Greedy | Detailed Explanation | java-3-approaches-recursion-dp-greedy-de-tvu9 | Intution: Since we have to start with root and we can\'t rob two directly-linked houses. We have two cases:\n Case1: If we rob the root node - Then we can\'t ro | Chaitanya1706 | NORMAL | 2021-12-05T01:56:50.451961+00:00 | 2021-12-05T02:12:12.478446+00:00 | 9,616 | false | **Intution:** Since we have to start with root and we can\'t rob two directly-linked houses. We have two cases:\n* **Case1:** If we rob the root node - Then we can\'t rob the child nodes of root but we can rob the 4 grandchildren of the root (i.e., root.left.left, root.left.right, root.right.left, root.right.right).\n* **Case2:** If we don\'t rob the root node - Then we can rob the 2 children of root (i.e., root.left, root.right).\nAnd our answer will be maximum of the two cases.\nFor Example:\n ```\n1.) 3 2.) 3\n / \\ / \\\n 2 3 4 5\n \\ \\ / \\ / \n 3 1 1 3 1\n\tHere rob the root node and its grandchildren Here better will be to rob the child nodes of \n\ti.e., (3+3+1) = 7 root i.e., (4+5)=9. \n\tHere Case1 will give 5(2+3) < 7 Here Case2 will give 8(3+1+3+1) < 9\n```\nNow after all the discussion lets start with approach starting from recursion and will optimize as much possible.\n\n**Approach1: Recursive (TLE)**\nT.C : O(2^n)\nS.C : O(1) (ignoring stack memory used for recursion)\n```\nclass Solution{\n public int rob(TreeNode root) {\n if (root == null) return 0;\n\n int ans = 0;\n\t\t\n\t\t// max value from left grandchildren\n if (root.left != null) {\n ans += rob(root.left.left) + rob(root.left.right);\n }\n\t\t\n\t\t// max value from right grandchildren\n if (root.right != null) {\n ans += rob(root.right.left) + rob(root.right.right);\n }\n\n return Math.max(ans + root.val, rob(root.left) + rob(root.right)); //(Case1,Case2)\n }\n}\n```\n\n**Approach2: Rucrsion Using HashMap**\nT.C : O(n)\nS.C. : O(n)\n**Explanation:** If you observe the recursive approach we have overlapping subproblems like for root node we are calling on its grandchildren (root.left.left, root.left.right, root.right.left, root.right.right) and when we are on child node of root (root.left, root.right) then again we will need the data of those four nodes so again calling on it. So here you have **Recusrion+Overlapping SubProblems** which can make you think of DP Approach.\nSo what we are doing is just store the calculated answer for each node int the HashMap and if we need the value for that node again at any point we will just do the map.get(node) and get the value. Rest Recursive logic is absolutely same.\n```\nclass Solution{\n public int rob(TreeNode root) {\n return rob(root, new HashMap<>());\n }\n\n public int rob(TreeNode root, Map<TreeNode, Integer> map) {\n \n if (root == null) return 0;\n\n if (map.containsKey(root)) return map.get(root);\n\n int ans = 0;\n\n if (root.left != null) {\n ans += rob(root.left.left, map) + rob(root.left.right, map);\n }\n\n if (root.right != null) {\n ans += rob(root.right.left, map) + rob(root.right.right, map);\n }\n\n ans = Math.max(ans + root.val, rob(root.left, map) + rob(root.right, map));\n map.put(root, ans);\n\n return ans;\n }\n}\n```\n\n**Approach3: Greedy Approach** \nT.C. : O(n)\nS.C. : O(1)\n**Explanation:** Since we can now say that for each node we need only two data is required that is what will be the max value if that node is robbed and whats the max value if the node is not robbed.\nSo why not just keep the array of two elements of which first element have the data if that node is not robbed and second element has the data if that node is robbed.\nSo at last we have to return max of first and second element data stored for root. And this makes it a greedy approach.\n\n**More Explanation:** So in the below code how we are filling ans[0] and ans[1]:\n1.) Since ans[0] will have the value if root is not robbed, so we are concerned just about the root.left and root.right data which is in left and right array. Now we want max value so we need to check both Cases for both left and right that which Case will give max value \n* left[0],right[0] -> indicates that while calculating, left and right node were not robbed and it has value from its child nodes \n* left[1],right[1] -> indicates that left and right were robbed so they have data from their grandchildren also.\nAnd we need max of the two cases for both left and right.\n\n2.) Now ans[1] will have the value if root is robbed then we can\'t rob root\'s children but we can can rob its grandchildren and left[0] and right[0] have data in which left and right were not robbed that is root\'s children were not robbed. So our value will be root.val + left[0] + right[0].\nAnd at last max of ans[0] and ans[1] will be answer.\n```\nclass Solution {\n public int rob(TreeNode root) {\n int ans[] = robHouse(root);\n return Math.max(ans[0],ans[1]);\n }\n \n public int[] robHouse(TreeNode root){\n if(root==null){\n return new int[2];\n }\n \n int left[] = robHouse(root.left);\n int right[] = robHouse(root.right);\n \n int ans[] = new int[2];\n \n ans[0] = Math.max(left[0],left[1])+Math.max(right[0],right[1]);\n ans[1] = root.val+left[0]+right[0];\n \n return ans;\n }\n}\n```\n \n* I hope the explanation helped you...Thanks!! | 114 | 2 | ['Greedy', 'Recursion', 'Java'] | 9 |
house-robber-iii | Simple C++ DFS Solution | simple-c-dfs-solution-by-balajanovski-swpz | The general idea here is that at each node you have two choices. \nYou can either decide to rob that node, or skip it.\nFrom this central idea, we can derive th | balajanovski | NORMAL | 2020-01-20T06:19:30.149063+00:00 | 2020-01-20T21:16:13.710481+00:00 | 5,900 | false | The general idea here is that at each node you have two choices. \nYou can either decide to rob that node, or skip it.\nFrom this central idea, we can derive the following logic.\n\nAt each node, we return the possibilities if we had decided to rob that node, or if we had decided to skip it (this is represented in the structure RobbedRoot).\n\nTo find out the maximum stolen money if the robber had decided to steal from the current node, we must skip the left and right nodes.\n`int robThisNode = root->val + robLeft.skippedRoot + robRight.skippedRoot;`\nThis is so that we do not trip the alarms of two adjacent house nodes.\n\nHowever, if we decide to skip the current node, we have two options for the left and right sides.\nWe can now rob the left and/or right node, as our skipping of the current node means that we won\'t trip the alarm.\nBut we can also decide to skip the left and/or right node.\n\nThis is because greedily robbing the node just because you have the option to does not guarantee that you will make the maximum profit, as by robbing a node, you could block off an adjacent higher value node which could lead to a higher profit.\n\nFor example in:\n\n```cpp\n/*\n4\n \\\n\t 1\n\t\t \\\n\t\t 2\n\t\t\t \\\n\t\t\t\t3\n*/\n```\n\t\t\t\t\nDeciding to rob 2, after skipping 1, blocks off the more profitable 3.\nSo, we also need to take into account the cases for skipping the left and right nodes as well.\n\nHence:\n`int skipThisNode = max(robLeft.robbedRoot, robLeft.skippedRoot) + max(robRight.robbedRoot, robRight.skippedRoot);`\n\nHence, the final code:\n\n```cpp\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\n\nstruct RobbedRoot {\n int robbedRoot;\n int skippedRoot;\n};\n\nclass Solution {\nprivate:\n RobbedRoot robDFS(TreeNode* root) {\n if (root == nullptr) {\n return RobbedRoot{0, 0};\n }\n \n RobbedRoot robLeft = robDFS(root->left);\n RobbedRoot robRight = robDFS(root->right);\n \n int robThisNode = root->val + robLeft.skippedRoot + robRight.skippedRoot;\n int skipThisNode = max(robLeft.robbedRoot, robLeft.skippedRoot) + max(robRight.robbedRoot, robRight.skippedRoot);\n \n return RobbedRoot{robThisNode, skipThisNode};\n }\npublic:\n int rob(TreeNode* root) {\n RobbedRoot finalState = robDFS(root);\n \n return max(finalState.robbedRoot, finalState.skippedRoot);\n }\n};\n``` | 49 | 1 | ['C', 'C++'] | 5 |
house-robber-iii | [Python] very short dfs, explained | python-very-short-dfs-explained-by-dbabi-gv8p | If you already solved House Robber I or II, you probably aware, that this problem is about dp. However, let us look at it from a bit different point of view, it | dbabichev | NORMAL | 2020-11-23T08:20:38.479261+00:00 | 2020-11-23T13:20:00.188210+00:00 | 1,932 | false | If you already solved House Robber I or II, you probably aware, that this problem is about dp. However, let us look at it from a bit different point of view, it will be much easier to digest: let us use dfs and for each node we will keep two values:\n1. Maximum gain we can get if we already visited all subtree given node, if we rob given node.\n2. Maximum gain, we can get if we already visited all subtree given node, if we do not rob given node.\n\nHow we can find it, using recursion now?\nImagine, that we have `node` and `L` and `R` are left and right children. Then:\n1. If we rob given node, than we can not rob children, so answer will be `node.val + L[1] + R[1]`\n2. If we do not rob house, we have two options for `L` and two options for `R`, and we choose the best ones, so we have `max(L) + max(R)`.\n\n**Complexity**: time complexity is `O(n)`, because we visit all our tree. Space complexity is `O(h)`, because we use recursion.\n\n```\nclass Solution:\n def rob(self, root):\n def dfs(node):\n if not node: return [0, 0]\n L = dfs(node.left)\n R = dfs(node.right)\n return [node.val + L[1] + R[1], max(L) + max(R)]\n \n return max(dfs(root))\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 46 | 6 | ['Depth-First Search'] | 2 |
house-robber-iii | C++, JAVA, PYTHON & explanation | c-java-python-explanation-by-chellya-eee3 | Let \n\nf1(node) be the value of maximum money we can rob from the subtree with node as root ( we can rob node if necessary).\n\nf2(node) be the value of maximu | chellya | NORMAL | 2016-03-12T06:38:22+00:00 | 2018-10-13T19:07:10.661476+00:00 | 11,907 | false | Let \n\n`f1(node)` be the value of maximum money we can rob from the subtree with `node` as root ( we can rob `node` if necessary).\n\n`f2(node)` be the value of maximum money we can rob from the subtree with `node` as root but without robbing `node`. \n\nThen we have \n\n`f2(node) = f1(node.left) + f1(node.right)` and \n\n`f1(node) = max( f2(node.left)+f2(node.right)+node.value, f2(node) )`.\n\n# C++\n\n class Solution {\n public:\n int rob(TreeNode* root) {\n return robDFS(root).second;\n }\n pair<int, int> robDFS(TreeNode* node){\n if( !node) return make_pair(0,0);\n auto l = robDFS(node->left);\n auto r = robDFS(node->right);\n int f2 = l.second + r.second;\n int f1 = max(f2, l.first + r.first + node->val);\n return make_pair(f2, f1);\n }\n };\n\n\n# JAVA\n\n public class Solution {\n public int rob(TreeNode root) {\n return robDFS(root)[1];\n }\n int[] robDFS(TreeNode node){\n int [] res = new int[2];\n if(node==null) return res;\n int [] l = robDFS(node.left);\n int [] r = robDFS(node.right);\n res[0] = l[1] + r[1];\n res[1] = Math.max(res[0], l[0] + r[0] + node.val);\n return res;\n }\n }\n\n# PYTHON\n\n class Solution(object):\n def rob(self, root):\n return self.robDFS(root)[1];\n def robDFS(self,node):\n if node is None:\n return (0,0)\n l = self.robDFS(node.left)\n r = self.robDFS(node.right)\n return (l[1] + r[1], max(l[1] + r[1], l[0] + r[0] + node.val)) | 45 | 1 | [] | 7 |
house-robber-iii | 1ms Java Solution | 1ms-java-solution-by-kkklll-rhft | public int rob(TreeNode root) {\n int[] maxVal = dpRob(root);\n return Math.max(maxVal[0], maxVal[1]);\n }\n \n public int[] dpRob(TreeNo | kkklll | NORMAL | 2016-04-01T22:36:00+00:00 | 2016-04-01T22:36:00+00:00 | 7,336 | false | public int rob(TreeNode root) {\n int[] maxVal = dpRob(root);\n return Math.max(maxVal[0], maxVal[1]);\n }\n \n public int[] dpRob(TreeNode root) {\n if (root == null) {\n return new int[]{0, 0};\n } else {\n int[] maxVal = new int[2];//maxVal[0] store the max value without robing current node, maxVal[1] store the max value with robing current node,\n int[] leftMax = dpRob(root.left);\n int[] rightMax = dpRob(root.right);\n maxVal[0] = Math.max(leftMax[0], leftMax[1]) + Math.max(rightMax[0], rightMax[1]);\n maxVal[1] = leftMax[0] + rightMax[0] + root.val;\n return maxVal;\n }\n } | 34 | 0 | [] | 10 |
house-robber-iii | Python - Human Readable Code - 6 lines | python-human-readable-code-6-lines-by-pr-4sms | This return statement should help ypu understand - \nreturn (root.val + without_l + without_r, max(with_l, without_l) + max(with_r, without_r))\n\n\n def rob | pratikjain227 | NORMAL | 2020-01-22T06:20:27.991633+00:00 | 2020-01-22T06:20:27.991681+00:00 | 2,249 | false | This return statement should help ypu understand - \n`return (root.val + without_l + without_r, max(with_l, without_l) + max(with_r, without_r))`\n\n```\n def rob(self, root):\n def with_without_rob(root):\n\n if root :\n with_l, without_l = with_without_rob(root.left)\n with_r, without_r = with_without_rob(root.right) \n return (root.val + without_l + without_r, max(with_l, without_l) + max(with_r, without_r))\n return (0, 0)\n \n return max(with_without_rob(root))\n``` | 32 | 0 | ['Recursion', 'Python'] | 2 |
house-robber-iii | ✅INTUITIVE| Detailed Explanation| C++ O(n) Recursion+Memo | intuitive-detailed-explanation-c-on-recu-no5x | Explanation:\n\nWe know that we cant choose consecutive nodes in a tree thus this leaves us with 2 options when we reach a node-\n1)Include that node and then i | pranavs036 | NORMAL | 2021-12-05T10:56:10.591991+00:00 | 2021-12-05T10:57:28.572101+00:00 | 3,686 | false | **Explanation**:\n\nWe know that we cant choose consecutive nodes in a tree thus this leaves us with 2 options when we reach a node-\n1)**Include that node** and then include its **grandchildren** ( that are root->left->left, root->left->right and root->right->left,root->right->right) in this way we dont select any connected nodes.\n2)**Dont** include the node and return the sum of maximum values of its **children** that are the left and right subtrees i.e. call our function on root->left and root->right\n\nNow if we write a purely recursive function for this it **will result in a TLE** as we will call the function on a node many times ( granchildren of our current node will also be the future children of the left and right subtrees) thus we use memoization.\nWe simply use an unordered map with key as TreeNode* and value as int to maintain the memo.\n\n``` \nclass Solution {\n int max_num=INT_MIN;\npublic:\n \n unordered_map<TreeNode*,int>umap;\n int helper(TreeNode*root){\n \n if(root==NULL)return 0;\n if(umap[root])return umap[root];\n int left_max=0;\n int right_max=0;\n if(root->left){\n left_max=helper(root->left->left)+helper(root->left->right);\n }\n if(root->right){\n right_max=helper(root->right->left)+helper(root->right->right);\n }\n \n return umap[root]=max(root->val+left_max+right_max,helper(root->left)+helper(root->right));\n \n \n }\n\n \n int rob(TreeNode* root) {\n return helper(root);\n }\n};\n``` | 30 | 2 | ['Recursion', 'Memoization', 'C'] | 1 |
house-robber-iii | C++ Brute Force --> Optimized DP Solutions || Explained | c-brute-force-optimized-dp-solutions-exp-3jed | Approach:\n\n if we rob the ith level then we can\'t rob the i+1 th level and hence we move to the (i+2)th level\n\t ans = root->val + rob(root->left->left) + r | anis23 | NORMAL | 2022-08-08T17:43:45.279173+00:00 | 2022-08-08T17:43:45.279212+00:00 | 1,254 | false | **Approach:**\n\n* if we rob the ith level then we can\'t rob the i+1 th level and hence we move to the (i+2)th level\n\t* ```ans = root->val + rob(root->left->left) + rob(root->left->right) + rob(root->right->left) + rob(root->right->right)```\n* if we don\'t rob the ith level then we move to the (i+1)th level\n\t* ```ans = rob(root->left) + rob(root->right)```\n* final ans will be the maximum of above two cases\n\n\n**Brute force:**\n\n```\nclass Solution\n{\npublic:\n int rob(TreeNode *root)\n {\n if (root == NULL)\n return 0;\n int val = 0;\n if (root->left != NULL)\n val += rob(root->left->left) + rob(root->left->right);\n if (root->right != NULL)\n val += rob(root->right->left) + rob(root->right->right);\n int notrob = rob(root->left) + rob(root->right);\n int rob = val + root->val;\n return max(notrob, rob);\n }\n};\n```\n\n* we can observe that there are some repetitive calls in the above code and that\'s why it gives TLE\n* so we can just store the optimal answer we get for each node in a map\n* return the value if it has been already computed\n* otherwise follow the same approach\n* in the below code,\n\t* x = notrob case\n\t* y = rob the root case\n\n\n\n**DP**\n\n```\nclass Solution\n{\npublic:\n unordered_map<TreeNode *, int> mp;\n int rob(TreeNode *root)\n {\n if (root == NULL)\n return 0;\n if (mp.find(root) != mp.end())\n return mp[root];\n mp[root] = -1;\n int x = rob(root->left) + rob(root->right);\n int y = root->val;\n if (root->left != NULL)\n y += rob(root->left->left) + rob(root->left->right);\n if (root->right != NULL)\n y += rob(root->right->left) + rob(root->right->right);\n mp[root] = max(x, y);\n return mp[root];\n }\n};\n```\n\n* we can see that we only have two options at each node either rob the node or not\n* if we rob the root\n\t* then we don\'t want to rob the left and right child\n\t* ```ans = root->val + leftnotrob+ rightnotrob```\n* if we don\'t rob the root\n\t* we will check what\'s the best case for the left and right child, whether to rob them or not\n\t* ```ans = max(leftnotrob, leftrob) + max(rightnotrob, rightrob```\n* store these values in a pair to handle repetitive calls\n* ```pair = {notrob,rob}```\n\n\n**DP-space optimized:**\n\n```\nclass Solution\n{\npublic:\n unordered_map<TreeNode *, int> mp;\n int rob(TreeNode *root)\n {\n if (root == NULL)\n return 0;\n auto ans = dfs(root);\n return max(ans.first, ans.second);\n }\n pair<int, int> dfs(TreeNode *root)\n {\n if (root == NULL)\n return {0, 0};\n auto [leftnotrob, leftrob] = dfs(root->left);\n auto [rightnotrob, rightrob] = dfs(root->right);\n int notrob = max(leftnotrob, leftrob) + max(rightnotrob, rightrob);\n int rob = root->val + leftnotrob + rightnotrob;\n return {notrob, rob};\n }\n};\n``` | 18 | 0 | ['Dynamic Programming', 'Depth-First Search', 'Recursion', 'Memoization', 'C', 'C++'] | 1 |
house-robber-iii | My 12ms C++ solution | my-12ms-c-solution-by-leop-mbcr | \n\n int rob(TreeNode node, int& lm, int& rm) {\n if (!node) return 0;\n int lm1 = 0, lm2 = 0, rm1 = 0, rm2 = 0;\n \n lm = rob( | leop | NORMAL | 2016-03-23T16:20:59+00:00 | 2018-10-15T11:15:37.163054+00:00 | 3,532 | false | \n\n int rob(TreeNode* node, int& lm, int& rm) {\n if (!node) return 0;\n int lm1 = 0, lm2 = 0, rm1 = 0, rm2 = 0;\n \n lm = rob(node->left, lm1, rm1);\n rm = rob(node->right, lm2, rm2);\n \n return max(node->val + lm1 + rm1 + lm2 + rm2, lm + rm);\n }\n\n int rob(TreeNode* root) {\n int res = 0;\n int lm = 0, rm = 0;\n res = rob(root, lm, rm);\n return res;\n }\n\n - **lm** is the max rob value of node->left\n - **rm** is the max rob value of node->right\n - **lm1** is the max rob value of node->left->left (Same as **lm2**)\n - **rm1** is the max rob value of node->left->right (Same as **rm2**)\n - So the max rob value of node is the max value between **(lm + rm)** and **(node->val + lm1 + lm2 + rm1 + rm2)** | 18 | 0 | ['C++'] | 1 |
house-robber-iii | [C++] DFS/DP Recursive Memoised Solution Explained, ~85% Time, ~40% Space | c-dfsdp-recursive-memoised-solution-expl-trdx | Neat one that had me think for a moment and try a wrong approach first (see last bit of the code); then I opted to go for a simpler solution and I solved it in | ajna | NORMAL | 2020-11-23T12:58:23.591284+00:00 | 2020-11-24T01:19:17.037214+00:00 | 2,540 | false | Neat one that had me think for a moment and try a wrong approach first (see last bit of the code); then I opted to go for a simpler solution and I solved it in one line.\n\nAt each iteration, we will first of all check if we have `root` and:\n* if not, we of course return `0`;\n* if yes, then we compute the max between:\n\t* the current value (`root->val`) + the recursive calls to `rob` passing each of its grandchildren (if any, `0` otherwise);\n\t* the sum of the recursive calls to `rob` passing it its direct children `root->left` and `root->right` (again if any, `0` otherwise).\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n return root ? max(root->val + (root->left ? rob(root->left->left) + rob(root->left->right) : 0) + (root->right ? rob(root->right->left) + rob(root->right->right) : 0), rob(root->left) + rob(root->right)) : 0;\n }\n};\n```\n\nSame code, expanded on more lines for better readability:\n\n```cpp\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n return root ? max(\n // current value plus values of the grandchildren (if any, 0 otherwise)\n root->val\n + (root->left ? rob(root->left->left) + rob(root->left->right) : 0)\n + (root->right ? rob(root->right->left) + rob(root->right->right) : 0),\n // values of the direct children (if any, 0 otherwise)\n rob(root->left) + rob(root->right)\n ) : 0;\n }\n};\n```\n\nWhich times out, so memoisation time it is - same logic, but wrapped through a helper function that checks if we already had a result computed in the hashmap `memo` for that specific node - if so we return it, if not we compute and store it:\n\n```cpp\nclass Solution {\npublic:\n unordered_map<TreeNode*, int> memo;\n int memoisedRob(TreeNode* root) {\n return memo.find(root) != end(memo) ? memo[root] : memo[root] = rob(root);\n }\n int rob(TreeNode* root) {\n return root ? max(root->val + (root->left ? memoisedRob(root->left->left) + memoisedRob(root->left->right) : 0) + (root->right ? memoisedRob(root->right->left) + memoisedRob(root->right->right) : 0), memoisedRob(root->left) + memoisedRob(root->right)) : 0;\n }\n};\n```\n\nAnd just for the chronicles, my first BFS-based attempt, making the wrong assumption that proceeding by layers and applying the formula from the other problems was what was needed to solve this problem - regrettably it works only with very short trees:\n\n```cpp\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n // aufwiedersehen, edge case\n if (!root) return 0;\n // support variables\n vector<int> houseRows;\n int len = 1, dp[3];\n TreeNode *curr;\n queue<TreeNode*> q;\n q.push(root);\n // BFSing our way into getting the cumulative values of each row\n while (len) {\n houseRows.push_back(0);\n while (len--) {\n // extracting the front of the queue\n curr = q.front();\n q.pop();\n // increasing the matching row in houseRows\n houseRows.back() += curr->val;\n // adding possible children to q\n if (curr->left) q.push(curr->left);\n if (curr->right) q.push(curr->right);\n }\n len = q.size();\n }\n // recycling len - bad practice in production and interviews, but we are stingy here\n len = houseRows.size();\n dp[0] = houseRows[0];\n dp[1] = max(houseRows[0], houseRows[1]);\n dp[2] = max(houseRows[2] + dp[0], dp[1]);\n for (int n: dp) cout << n << \' \';\n for (int i = 3; i < len; i++) {\n dp[i % 3] = max(dp[(i - 1) % 3], max(dp[(i - 3) % 3], dp[(i - 2) % 3]) + houseRows[i]);\n }\n return dp[--len % 3];\n }\n};\n``` | 16 | 2 | ['Dynamic Programming', 'Depth-First Search', 'Recursion', 'Memoization', 'C', 'C++'] | 1 |
house-robber-iii | Don't think about level order traversal | dont-think-about-level-order-traversal-b-dmg4 | Don\'t be fooled by the example testcases.\n\nlook at this--> [2,1,3,null,4] ans =7;\n```\t\t\n\t\t2\n\t1 3\n4\t\n\nans = 4+3\n\n//LOL | roshitkhare | NORMAL | 2022-04-28T19:32:05.638941+00:00 | 2022-04-28T19:32:05.638982+00:00 | 267 | false | Don\'t be fooled by the example testcases.\n\nlook at this--> [2,1,3,null,4] ans =7;\n```\t\t\n\t\t2\n\t1 3\n4\t\n\nans = 4+3\n\n//LOL | 15 | 0 | [] | 1 |
house-robber-iii | JavaScript with explaination | javascript-with-explaination-by-0618-v82h | As most of the tree problems, recurssion is the easiest way to start.\nThen, we need to figure out what we want to get from each of the node.\nWe want to know t | 0618 | NORMAL | 2019-09-19T02:36:43.256127+00:00 | 2019-09-19T02:36:43.256180+00:00 | 1,381 | false | As most of the tree problems, recurssion is the easiest way to start.\nThen, we need to figure out what we want to get from each of the node.\nWe want to know the max value we can get if we rob it or not, `[rob, not]`.\nIf the node is a leaf, it\'s `[0,0]`,\nif it\'s not a leaf:\n1. if we rob it, then we can\'t rob its leaves.\n2. if we do not rob it, then we need to find the max from the combinations of the leaves. \n\n```\nvar rob = function(root) {\n function helper(node){\n if(!node) return [0,0];\n const [lr,ln] = helper(node.left);\n const [rr, rn] = helper(node.right);\n return [node.val + ln + rn, Math.max(lr+rr, ln+rn, lr+rn, ln+rr)];\n }\n \n return Math.max(...helper(root));\n};\n``` | 15 | 1 | ['Dynamic Programming', 'JavaScript'] | 0 |
house-robber-iii | Python solution beats 100 % inspired by the top post | python-solution-beats-100-inspired-by-th-uzh9 | \nclass Solution:\n def rob(self, root):\n def dfs(node):\n if not node: return 0, 0\n l, r = dfs(node.left), dfs(node.right)\n | cenkay | NORMAL | 2018-07-31T22:43:23.087384+00:00 | 2018-08-09T00:55:44.075085+00:00 | 2,217 | false | ```\nclass Solution:\n def rob(self, root):\n def dfs(node):\n if not node: return 0, 0\n l, r = dfs(node.left), dfs(node.right)\n return max(l) + max(r), node.val + l[0] + r[0]\n return max(dfs(root))\n``` | 15 | 0 | [] | 3 |
house-robber-iii | My simple Java recursive solution | my-simple-java-recursive-solution-by-chu-w9qi | public class Solution {\n public int rob(TreeNode root) {\n if(root==null) return 0;\n if(root.left==null&&root.right==null) return | chuqi | NORMAL | 2016-05-15T22:50:04+00:00 | 2018-09-09T06:52:41.034014+00:00 | 3,267 | false | public class Solution {\n public int rob(TreeNode root) {\n if(root==null) return 0;\n if(root.left==null&&root.right==null) return root.val;\n \n int left=0, right=0;\n int subleft=0, subright=0;\n \n if(root.left!=null){\n left=rob(root.left);\n subleft=rob(root.left.left)+rob(root.left.right);\n }\n \n if(root.right!=null){\n right=rob(root.right);\n subright=rob(root.right.left)+rob(root.right.right);\n }\n \n int sum1=left+right;\n int sum2=subleft+subright+root.val;\n \n return (sum1>sum2)?sum1:sum2;\n }\n} | 15 | 3 | [] | 6 |
house-robber-iii | c++ || Recursive + Memoization | c-recursive-memoization-by-beast_123-anty | C++\nWhen I started out doing Programming I used to find this question the most difficult. But Today I did It Without any Difficuty. Practice + Consistency + H | Beast_123 | NORMAL | 2021-10-10T03:48:24.497709+00:00 | 2021-10-10T03:48:24.497741+00:00 | 684 | false | **C++**\nWhen I started out doing Programming I used to find this question the most difficult. But Today I did It Without any Difficuty. Practice + Consistency + Hard Work Can Change Everything. Good Luck.\n\n**Recursive Solution** ---->> This Gives TLE;\n```\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n if(!root) return 0;\n int self = root->val;\n if(root->left) self += (rob(root->left->left) + rob(root->left->right));\n if(root->right) self += (rob(root->right->left) + rob(root->right->right));\n int nself = (rob(root->left) + rob(root->right));\n return max(self ,nself); \n }\n};\n````\n**After Memoization** \n```\nclass Solution {\npublic:\n unordered_map<TreeNode*,int> m;\n int rob(TreeNode* root) {\n if(m.count(root)) return m[root];\n if(!root) return 0;\n int self = root->val;\n if(root->left) self += (rob(root->left->left) + rob(root->left->right));\n if(root->right) self += (rob(root->right->left) + rob(root->right->right));\n int nself = (rob(root->left) + rob(root->right));\n m[root] = max(self ,nself);\n return m[root];\n }\n};\n```\n**IF YOU FIND THIS HELPFUL DO UPVOTE!!** | 14 | 0 | ['Dynamic Programming', 'Tree', 'Recursion', 'C'] | 1 |
house-robber-iii | [Java] From Recursive TLE to DP Memoization AC in 4 lines | java-from-recursive-tle-to-dp-memoizatio-4wlx | \nclass Solution {\n public int rob(TreeNode root) {\n if (root == null)\n return 0; \n \n int robCurrent = root.val;\n | ihavehiddenmyid | NORMAL | 2021-10-08T07:56:06.752862+00:00 | 2021-10-08T07:57:45.118649+00:00 | 1,224 | false | ```\nclass Solution {\n public int rob(TreeNode root) {\n if (root == null)\n return 0; \n \n int robCurrent = root.val;\n if (root.left != null)\n robCurrent += rob(root.left.left) + rob(root.left.right);\n if (root.right != null)\n robCurrent += rob(root.right.left) + rob(root.right.right);\n \n int doNotRobCurrent = 0;\n doNotRobCurrent += rob(root.left) + rob(root.right);\n \n int res = Math.max(robCurrent, doNotRobCurrent);\n return res; \n }\n}\n```\n\n```\nclass Solution {\n private HashMap<TreeNode, Integer> dp = new HashMap<>(); // Line 1\n \n public int rob(TreeNode root) {\n if (root == null)\n return 0; \n \n if (dp.containsKey(root)) // Line 2\n return dp.get(root); // Line 3\n \n int robCurrent = root.val;\n if (root.left != null)\n robCurrent += rob(root.left.left) + rob(root.left.right);\n if (root.right != null)\n robCurrent += rob(root.right.left) + rob(root.right.right);\n \n int doNotRobCurrent = 0;\n doNotRobCurrent += rob(root.left) + rob(root.right);\n \n int res = Math.max(robCurrent, doNotRobCurrent);\n dp.put(root, res); // Line 4\n return res;\n }\n}\n``` | 14 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Java'] | 4 |
house-robber-iii | C++: O(n) Simple recursion (Choosing vs Not choosing) | c-on-simple-recursion-choosing-vs-not-ch-gfz2 | Approach: DFS on Tree\n On each node, Recursively store what value it would have if you choose vs not choosing it. Store both values :)\n If you choose current | abhi_dtu2014 | NORMAL | 2020-06-29T16:44:17.937312+00:00 | 2020-06-29T16:53:07.066871+00:00 | 1,066 | false | **Approach: DFS on Tree**\n* On each node, Recursively store what value it would have if you choose vs not choosing it. Store both values :)\n* If you choose current node, then you will have to add child node\'s not_choose values.\n* If you don\'t choose current node, then you can add maximum of child node\'s choose, not_choose values.\n\n```\nclass Solution {\npublic:\n pair<int,int> findMaxMoney (TreeNode* root) {\n if (!root) return {0, 0};\n int choose, not_choose;\n pair<int,int> left = findMaxMoney(root->left);\n pair<int,int> right = findMaxMoney(root->right);\n choose = root->val + left.second+right.second;\n not_choose = max(left.first, left.second) + \n max(right.first, right.second);\n return {choose, not_choose};\n }\n int rob(TreeNode* root) {\n pair<int,int> maxValue = findMaxMoney(root);\n return max(maxValue.first, maxValue.second); \n }\n};\n``` | 13 | 0 | ['Recursion', 'C'] | 1 |
house-robber-iii | 12ms C++ dfs solution | 12ms-c-dfs-solution-by-xiaohui5319-s1tf | //max_include_root = root->val + max_donot_include_root_left + max_donnot_include_root_right\n //max_donot_include_root = max(max_include_root_left, max_donn | xiaohui5319 | NORMAL | 2016-03-20T22:49:07+00:00 | 2016-03-20T22:49:07+00:00 | 2,357 | false | //max_include_root = root->val + max_donot_include_root_left + max_donnot_include_root_right\n //max_donot_include_root = max(max_include_root_left, max_donnot_include_root_left) + max(max_include_root_right, max_donnot_include_root_right)\n \n class Solution {\n public:\n int rob(TreeNode* root) {\n int max_include_root = 0;\n int max_donnot_include_root = 0;\n return dfs(root, max_include_root, max_donnot_include_root);\n }\n \n int dfs(TreeNode* root, int& max_include_root, int& max_donnot_include_root) {\n if (root == NULL) {\n max_include_root = 0;\n max_donnot_include_root = 0;\n return 0;\n }\n int max_donnot_include_root_left = 0;\n int max_donnot_include_root_right = 0;\n\n int max_include_root_left = 0;\n int max_include_root_right = 0;\n\n int max_left = dfs(root->left, max_include_root_left, max_donnot_include_root_left);\n int max_right = dfs(root->right, max_include_root_right, max_donnot_include_root_right);\n\n max_include_root = root->val + max_donnot_include_root_left + max_donnot_include_root_right;\n max_donnot_include_root = max_left + max_right;\n\n return max(max_include_root, max_donnot_include_root);\n }\n }; | 13 | 0 | ['Depth-First Search', 'C++'] | 1 |
house-robber-iii | 6-line simple Python solution using DFS | 6-line-simple-python-solution-using-dfs-dkep9 | The dfs function returns an array, the first element means the maximum if we include the value of the current node, and the second element means the maximum if | feather | NORMAL | 2016-04-15T04:20:44+00:00 | 2016-04-15T04:20:44+00:00 | 2,379 | false | The dfs function returns an array, the first element means the maximum if we include the value of the current node, and the second element means the maximum if we exclude the value of the current node.\n\n So in the return statement, as the first element, we include the value of the current node, and we should exclude the left and right children, so we add the second element from the result of left and right children. The second element has 4 conditions, we can include the left child and include the right child, include the left child and exclude the right child..., so we return the maximum of them.\n\n # Definition for a binary tree node.\n # class TreeNode(object):\n # def __init__(self, x):\n # self.val = x\n # self.left = None\n # self.right = None\n \n class Solution(object):\n def rob(self, root):\n """\n :type root: TreeNode\n :rtype: int\n """\n def dfs(node):\n if not node:\n return [0, 0]\n left, right = dfs(node.left), dfs(node.right)\n return [node.val+left[1]+right[1], max([left[0]+right[0], left[0]+right[1], left[1]+right[0], left[1]+right[1]])]\n \n return max(dfs(root)) | 13 | 1 | ['Python'] | 3 |
house-robber-iii | ✅ C++ | Step by step Recusion --> memoization | Easy to undestand | c-step-by-step-recusion-memoization-easy-48ro | There are two case possible :\n1. * You can pick the current root\n\t\tif you pick the current root you cannot pick its immediate children.\n\t\t so you will fi | jitenp549 | NORMAL | 2021-12-05T05:28:40.732510+00:00 | 2021-12-05T05:28:40.732572+00:00 | 475 | false | There are two case possible :\n1. * **You can pick the current root**\n\t\t*if you pick the current root you cannot pick its immediate children.\n\t\t* so you will find if we can pick grand children if exists i.e. \n\t\t\t* root->left->left, \n\t\t\t* root->left->right, \n\t\t\t* root->right->left,\n\t\t\t* root->right-.right\n2. * **if you dont pick the current root**\n\t\t* you can pick its children i.e \n\t\t\t* root->left,\n\t\t\t* root->right\n3. **determine from which path you are getting maximum**\n\n***Recusive Approach : -***\n```\n int rob(TreeNode* root) {\n \n if(!root) return 0;\n \n int include = root->val;\n if(root->left) include += rob(root->left->left) + rob(root->left->right);\n if(root->right) include += rob(root->right->left) + rob(root->right->right);\n \n int exclude = rob(root->left) + rob(root->right);\n \n return max(include, exclude);\n \n \n }\n```\n\n***Memoization : -***\n```\nunordered_map<TreeNode*, int> dp;\n int rob(TreeNode* root) {\n \n if(!root) return 0;\n \n if(dp[root]) return dp[root];\n \n int include = root->val;\n if(root->left) include += rob(root->left->left) + rob(root->left->right);\n if(root->right) include += rob(root->right->left) + rob(root->right->right);\n \n int exclude = rob(root->left) + rob(root->right);\n \n return dp[root] = max(include, exclude);\n \n }\n```\n\n**Make sure to give it a upvote if you find it helpful\n<Happy Coding/>** | 12 | 0 | ['Dynamic Programming', 'Recursion'] | 0 |
house-robber-iii | [C++] |Depth First Search | DP with explaination | c-depth-first-search-dp-with-explainatio-rpqd | We construct a dp tree.\nEach node (dp_node) in this dp tree is an array of two elements:\ndp_node = [your gain when you ROB the current node, your gain when yo | sonugiri | NORMAL | 2020-05-15T22:58:52.907117+00:00 | 2020-05-15T22:58:52.907150+00:00 | 395 | false | We construct a dp tree.\nEach node (dp_node) in this dp tree is an array of two elements:\ndp_node = [your gain when you ROB the current node, your gain when you SKIP the current node]\ndp_node[0] =[your gain when you ROB the current node]\ndp_node[1] =[your gain when you SKIP the current node]\n\nwe start by scanning from the leaf: Depth First Search\n**For each node you have 2 options:\noption 1: ROB the node, then you can\'t rob the child/children of the node.\ndp_node[0] = node.val + dp_node.left[1] + dp_node.right[1]\noption 2: SKIP the node, then you can ROB or SKIP the child/children of the node.\ndp_node[1] = max(dp_node.left[0], dp_node.left[1]) + max(dp_node.right[0], dp_node.right[1])**\n\nthe maximum of gain of the node\n\n```\n Input: [3,4,5,1,3,null,1]\n input tree dp tree:\n 3 [3+3+1,4+5]\n / \\ / \\\n 4 5 [4,3] [5,1]\n / \\ \\ / \\ \\\n 1 2 1 [1,0] [2,0] [1,0]\n / \\ / \\ / \\\n [0,0] [0,0] [0,0] [0,0] [0,0] [0,0]\n \n``` \n\n```\npair<int,int> helper( TreeNode *node ) {\n\tif( !node ) return {0, 0};\n\n\tauto l = helper( node->left );\n\tauto r = helper( node->right );\n\tint withNode = node->val + l.second + r.second;\n\tint withoutNode = max( r.first, r.second ) + max( l.first, l.second ); \n\treturn { withNode, withoutNode };\n}\n\nint rob( TreeNode* root ) {\n\tauto res = helper( root );\n\treturn max( res.first, res.second );\n}\n```\n | 11 | 0 | [] | 0 |
house-robber-iii | C++ || Easy || DP || Recursion + Memoization | c-easy-dp-recursion-memoization-by-dsa_c-arg9 | \n// T.C. -> O(N)\n// S.C. -> O(N) [Recursion auxillary stack space] + O(N) [Unordered Map]\nclass Solution {\npublic:\n unordered_map<TreeNode*,int> mp;\n | konarksharmaa | NORMAL | 2022-09-07T11:33:34.526249+00:00 | 2022-09-07T11:33:34.526298+00:00 | 1,237 | false | ```\n// T.C. -> O(N)\n// S.C. -> O(N) [Recursion auxillary stack space] + O(N) [Unordered Map]\nclass Solution {\npublic:\n unordered_map<TreeNode*,int> mp;\n int rob(TreeNode* root) {\n if(root == NULL)return 0;\n if(mp.count(root)) return mp[root];\n int sum1 = root->val;\n \n if(root->left != NULL){\n sum1 += rob(root->left->left);\n sum1 += rob(root->left->right);\n }\n \n if(root->right != NULL){\n sum1 += rob(root->right->left);\n sum1 += rob(root->right->right);\n }\n int sum2 = rob(root->left) + rob(root->right);\n return mp[root] = max(sum1,sum2);\n }\n};\n``` | 10 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 0 |
house-robber-iii | Dp on Binary Trees | Learn How to Tackle such Problems | 95% Faster | dp-on-binary-trees-learn-how-to-tackle-s-dhz9 | Approach:-\n The Thief cannot choose the two adjacent nodes right?\n Also, If we know the maximum amount the thief can stole for the child and grand child nodes | sunny_38 | NORMAL | 2021-12-05T06:03:14.656527+00:00 | 2021-12-05T09:47:02.305615+00:00 | 634 | false | **Approach:-**\n* The Thief *cannot choose the two adjacent nodes* right?\n* Also, If we know the maximum amount the thief can stole for the child and grand child nodes of current node, we can answer the maximum amount for current node also...Guess Why? [Think for above condition].\n* Since, *If we choose current node into our answer*, we cannot take the child nodes of the current node right? Hence, **we\'d be looking for maximum answer we can get with grand child nodes**.\n* When *we don\'t choose current node into our answer*, **we would look for maximum answer for left as well as right child nodes**.\n* **dp[node v] = max(root->val + dp[left grand child of v] + dp[right grand child of v] , dp[left child of v] + dp[right child of v] )** is the dp relation.\n* Wait, How we would maintain an array in binary tree?, If you\'d notice we want only values for child nodes and grand child nodes right?\n* So, we would maintain a **pair<int,int>** for every node **{max ans child nodes, max ans for grand child nodes}** and recursively calculate answer for every node.\n\n```\nclass Solution {\npublic:\n // TIME COMPLEXITY:- O(N)\n // SPACE COMPLEXITY:- O(1) [neglecting the extra space due to recursion stack]\n pair<int,int> findMax(TreeNode* root){\n if(!root)\n return {0,0};\n pair<int,int> l = findMax(root->left); // {max ans for left child, max ans for left grand child}\n pair<int,int> r = findMax(root->right); // {max ans for right child, max ans for right grand child}\n return {max(root->val+l.second+r.second,l.first+r.first),l.first+r.first}; // either choose the current node or go with the grand child nodes\n }\n int rob(TreeNode* root) {\n return findMax(root).first; // answer will be the max ans for current node\n }\n};\n```\n\n**Don\'t forget to Upvote!** | 10 | 2 | [] | 0 |
house-robber-iii | Recursive Logic Python3 5 Lines of Code | recursive-logic-python3-5-lines-of-code-wvh52 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | GANJINAVEEN | NORMAL | 2023-03-16T03:27:57.276510+00:00 | 2023-03-16T03:27:57.276541+00:00 | 1,294 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n def dfs(root):\n if not root: return [0,0]\n leftpair,rightpair=dfs(root.left),dfs(root.right)\n withroot,without=root.val+leftpair[1]+rightpair[1],max(leftpair)+max(rightpair)\n return [withroot,without]\n return max(dfs(root))\n #please upvote me it would encourage me alot\n\n \n``` | 9 | 0 | ['Python3'] | 0 |
house-robber-iii | 5 line C++ solution using memoization | 5-line-c-solution-using-memoization-by-s-ygq5 | \nunordered_map<TreeNode *,int> map;\n int rob(TreeNode* root) \n {\n if(!root)\n return 0;\n if(map.count(root))\n re | sriu1 | NORMAL | 2020-08-25T13:52:45.559920+00:00 | 2020-08-25T13:55:33.163170+00:00 | 876 | false | ```\nunordered_map<TreeNode *,int> map;\n int rob(TreeNode* root) \n {\n if(!root)\n return 0;\n if(map.count(root))\n return map[root];\n int total=0;\n if(root->left)\n total+= rob(root->left->left)+rob(root->left->right);\n if(root->right)\n total+=rob(root->right->left)+rob(root->right->right);\n \n return map[root]=max(root->val+total,rob(root->left)+rob(root->right));\n \n }\n``` | 9 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 1 |
house-robber-iii | 337: Solution with step by step explanation | 337-solution-with-step-by-step-explanati-bngo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nThe problem can be solved using a recursive approach. We can traverse the | Marlen09 | NORMAL | 2023-03-01T18:19:28.479514+00:00 | 2023-03-01T18:19:28.479566+00:00 | 1,567 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe problem can be solved using a recursive approach. We can traverse the binary tree in a post-order traversal. At each node, we need to decide whether to rob the node or not.\n\nLet\'s define a helper function dfs which returns two values - robThis and notRobThis. robThis represents the maximum amount that can be robbed if we choose to rob the current node, and notRobThis represents the maximum amount that can be robbed if we choose not to rob the current node.\n\nTo calculate robThis, we need to add the value of the current node and the value of the grandchildren nodes (the nodes which are two levels below the current node) to notRobGrandChildren. To calculate notRobThis, we need to add the maximum of robGrandChildren and notRobGrandChildren.\n\nThe base case for the recursion is when the node is None, in which case we return (0, 0).\n\nAt the root node, we need to return the maximum of robThis and notRobThis.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n # Define the helper function\n def dfs(node):\n # Base case: if the node is None, return (0, 0)\n if not node:\n return (0, 0)\n \n # Recursive case: calculate the values for the left and right subtrees\n left_rob, left_not_rob = dfs(node.left)\n right_rob, right_not_rob = dfs(node.right)\n \n # Calculate the values for the current node\n rob_this = node.val + left_not_rob + right_not_rob\n not_rob_this = max(left_rob, left_not_rob) + max(right_rob, right_not_rob)\n \n # Return the values for the current node\n return (rob_this, not_rob_this)\n \n # Call the helper function on the root node and return the maximum value\n return max(dfs(root))\n\n``` | 8 | 0 | ['Dynamic Programming', 'Tree', 'Depth-First Search', 'Python', 'Python3'] | 2 |
house-robber-iii | C++ | Simple Solution | c-simple-solution-by-noobmaster101-2bnp | \nclass Solution {\npublic:\n vector<int> helper(TreeNode* root){\n if(!root) return {0, 0, 0};\n \n vector<int> temp = {0, 0, 0};\n | noobmaster101 | NORMAL | 2020-09-08T04:12:49.396498+00:00 | 2020-09-08T04:12:49.396528+00:00 | 271 | false | ```\nclass Solution {\npublic:\n vector<int> helper(TreeNode* root){\n if(!root) return {0, 0, 0};\n \n vector<int> temp = {0, 0, 0};\n \n vector<int> l = helper(root->left);\n vector<int> r = helper(root->right);\n \n temp[1] = max(l[1]+r[1], root->val+l[0]+l[2]+r[0]+r[2]);\n temp[0] = l[1];\n temp[2] = r[1];\n \n return temp;\n }\n \n int rob(TreeNode* root) {\n vector<int> temp = helper(root);\n return temp[1];\n }\n};\n``` | 8 | 1 | [] | 1 |
house-robber-iii | Best Python Solution (Clean, Explained) | best-python-solution-clean-explained-by-21fg6 | Explaination\nI learn the answer from @realisking, I couldn\'t come up with such elegant solution myself.\n\nOn every node we got two option, to rob or not to r | christopherwu0529 | NORMAL | 2019-06-30T03:50:21.658024+00:00 | 2019-06-30T03:55:57.418839+00:00 | 526 | false | # Explaination\nI learn the answer from @realisking, I couldn\'t come up with such elegant solution myself.\n\nOn every node we got two option, to rob or not to rob\n* To rob this node, then we cannot rob our left and right child, so the max value would be the total of\n * value of this node\n * the max value from left child, when we not rob the left child\n * the max value from right child, when we not rob the right child\n* Not to rob this node, means that we can either rob or not rob our left and right child, so the max value would be the total of\n * 0, because we choose not to rob this node\n * the max of `rob the left child` and `not rob the left child`\n * the max of `rob the right child` and `not rob the right child`\n\n`get_max_value(node)` returns the `max value when we rob this node` and `max value when we not rob this node` on each node.\nSo we get the max from the two returns from `get_max_value(root)`\n\nThe time complexity is `O(LogN)`, because we keep calling `get_max_value()` until the very bottom of the tree.\nThe space complexity is `O(LogN)`, too. Even we only use `O(1)` of space on every `get_max_value()`\nBut we used `LogN` level of recursion. `N` is the number of houses.\n\n# Code\n```\nclass Solution(object):\n def rob(self, root):\n def get_max_value(node):\n if node is None: return 0, 0\n left_rob, left_not_rob = get_max_value(node.left)\n right_rob, right_not_rob = get_max_value(node.right)\n\n rob = node.val+left_not_rob+right_not_rob\n not_rob = max(left_rob, left_not_rob)+max(right_rob, right_not_rob)\n\n return rob, not_rob\n\n return max(get_max_value(root))\n```\n\n# More Resource\nI really take time tried to make the best solution or explaination. \nBecause I wanted to help others like me. \nIf you like my answer, a star on [GitHub](https://github.com/wuduhren/leetcode-python) means a lot to me. \nhttps://github.com/wuduhren/leetcode-python | 8 | 0 | [] | 2 |
house-robber-iii | Complex Numbers | complex-numbers-by-stefanpochmann-omxe | Solution:\n\n def rob(self, root):\n def rob(root):\n if not root:\n return 0\n z = root.val * 1j + rob(root.left | stefanpochmann | NORMAL | 2016-03-12T08:47:41+00:00 | 2016-03-12T08:47:41+00:00 | 777 | false | **Solution:**\n\n def rob(self, root):\n def rob(root):\n if not root:\n return 0\n z = root.val * 1j + rob(root.left) + rob(root.right)\n return max(z.real, z.imag) + z.real * 1j\n return int(rob(root).real)\n\nThe helper function returns a complex number. The real part tells, well, the real answer (maximum amount with or without robbing the (sub)tree's root). The imaginary part tells the maximum amount without robbing the root. (But in the temporary variable `z`, the real part is the amount without the root and the imaginary part is the amount with the root.)\n\n---\n\n**Shorter version:**\n\n def rob(self, root):\n def rob(root):\n z = root.val * 1j + rob(root.left) + rob(root.right) if root else 0\n return max(z.real, z.imag) + z.real * 1j\n return int(rob(root).real)\n\n---\n\n**Tuple version:**\n\nHere the helper returns a tuple, first element being the real answer and second element being the without-root answer. Variables "y/n" mean yes/no, telling whether the subtree's root might be robbed.\n\n def rob(self, root):\n def rob(root):\n if not root:\n return 0, 0\n y, n = rob(root.left)\n Y, N = rob(root.right)\n return max(root.val + n + N, y + Y), y + Y\n return rob(root)[0]\n\nA variation:\n\n def rob(self, root):\n def rob(root):\n if not root:\n return 0, 0\n y, n = map(sum, zip(rob(root.left), rob(root.right)))\n return max(root.val + n, y), y\n return rob(root)[0]\n\nAnother:\n\n def rob(self, root):\n def rob(root):\n y, n = map(sum, zip(rob(root.left), rob(root.right), (0, root.val))) if root else (0, 0)\n return max(y, n), y\n return rob(root)[0] | 8 | 0 | ['Python'] | 0 |
house-robber-iii | Easy 4 lines C++ DFS | easy-4-lines-c-dfs-by-zefengsong-1emq | 4 lines brute force, 1656ms.\n\n int rob(TreeNode* root) {\n return DFS(root, true);\n }\n \n int DFS(TreeNode* root, bool canRob){\n | zefengsong | NORMAL | 2017-08-04T08:35:02.886000+00:00 | 2017-08-04T08:35:02.886000+00:00 | 976 | false | 4 lines brute force, 1656ms.\n```\n int rob(TreeNode* root) {\n return DFS(root, true);\n }\n \n int DFS(TreeNode* root, bool canRob){\n if(!root) return 0;\n int noRob = DFS(root->left, true) + DFS(root->right, true);\n return canRob ? max(root->val + DFS(root->left, false) + DFS(root->right, false), noRob) : noRob;\n }\n```\nHere is a greedy one, 22ms.\n**idea:**\nEach node only has 2 status, be robbed or not.\nStore amount of money under 2 status into a vector<int>v(2).\nv[0]: it's not robbed.\nv[1]: it's robbed.\n```\n int rob(TreeNode* root) {\n auto res = DFS(root);\n return max(res[0], res[1]);\n }\n \n vector<int> DFS(TreeNode* root){\n if(!root) return {0,0};\n auto left = DFS(root->left);\n auto right = DFS(root->right);\n vector<int>res(2);\n res[0] = max(left[0], left[1]) + max(right[0], right[1]);\n res[1] = root->val + left[0] + right[0];\n return res;\n }\n``` | 8 | 0 | ['Depth-First Search', 'C++'] | 0 |
house-robber-iii | ✅Accepted| | ✅Easy solution || ✅Short & Simple || ✅Best Method | accepted-easy-solution-short-simple-best-1c10 | \n# Code\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode( | sanjaydwk8 | NORMAL | 2023-01-17T06:15:13.250996+00:00 | 2023-01-17T06:15:13.251034+00:00 | 1,066 | false | \n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n pair<int, int> solve(TreeNode* t)\n {\n if(t==NULL)\n return {0,0};\n auto p1=solve(t->left);\n auto p2=solve(t->right);\n pair<int, int> p;\n p.first=t->val+p1.second+p2.second;\n p.second=max(p1.first, p1.second)+max(p2.first, p2.second);\n return p;\n }\n int rob(TreeNode* root) {\n auto p= solve(root);\n return max(p.first, p.second);\n }\n};\n```\nPlease **UPVOTE** if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!! | 7 | 0 | ['C++'] | 0 |
house-robber-iii | Very Simple and Intuitive C++ Dp solution | very-simple-and-intuitive-c-dp-solution-0mriw | We basically have two cases:\n1. Take the root\n2. Don\'t take the root\n\nFor CASE I, we take the root and all the left and right children of root->left and ro | i_am_shm | NORMAL | 2022-10-11T14:46:25.817761+00:00 | 2022-10-11T14:48:00.751753+00:00 | 1,267 | false | We basically have two cases:\n**1. Take the root\n2. Don\'t take the root**\n\nFor **CASE I**, we take the root and all the left and right children of root->left and root->right i.e.,\nresult = root+(root->left->left)+(root->left->right)+(root->right->left)+(root->right->right)\n**Note**: We can\'t take (root->left) and (root->right) if we take the root node\n\nFor **CASE II**, we can break it into two sub cases:\ni) Take root->left\nii) Take root->right\n\nFor CASE i) we take (root->left) + max ((root->right), (root->right->left)+(root->right->right))\nFor CASE ii) we take (root->right) + max ((root->left), (root->left->left)+(root->left->right))\n\nAt the end, we take max of all these results and return it\n\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n unordered_map<TreeNode*,int>mp;\n int solve(TreeNode* root){\n //base case\n if(!root)return 0;\n if(mp.count(root))return mp[root];\n int l=solve(root->left);\n int r=solve(root->right);\n int ll=0,lr=0,rl=0,rr=0;\n if(root->left){\n ll=solve(root->left->left);\n lr=solve(root->left->right);\n }\n if(root->right){\n rl=solve(root->right->left);\n rr=solve(root->right->right);\n }\n int val=root->val;\n int lmx=ll+lr;\n int rmx=rl+rr;\n //if we take the root node\n int t1=val+lmx+rmx;\n //if we take the left child of root\n int t2=l+max(r,rmx);\n //if we take the right child of root\n int t3=r+max(l,lmx);\n //take maximum of all the cases and memoize\n mp[root]=max(t1,max(t2,t3));\n return mp[root];\n }\n int rob(TreeNode* root) {\n return solve(root);\n }\n};\n``` | 7 | 0 | ['Dynamic Programming', 'Depth-First Search', 'Memoization', 'C'] | 0 |
house-robber-iii | Java simple recursive solution with explanation. | java-simple-recursive-solution-with-expl-t7dd | We can think in terms of the choices the robber has to make at every node.\n\n\n public int rob(TreeNode root) {\n return rob(root, false);\n }\n\n | garvij | NORMAL | 2020-11-23T21:34:08.234384+00:00 | 2020-11-23T21:34:54.149443+00:00 | 650 | false | We can think in terms of the choices the robber has to make at every node.\n\n```\n public int rob(TreeNode root) {\n return rob(root, false);\n }\n\n public int rob(TreeNode root, boolean isParentRobbed) {\n\n if (root == null) {\n return 0;\n }\n\n // if the parent house is robbed, the current house CANNOT be robbed\n if (isParentRobbed) {\n return rob(root.left, false) + rob(root.right, false);\n }\n\n // the robber has two options\n // 1. DO NOT rob the current house\n // 2. rob the current house\n // we need the maximum profit of the two choices\n return Math.max(rob(root.left, false) + rob(root.right, false), // DON\'T rob\n root.val + rob(root.left, true) + rob(root.right, true)); // rob\n\n }\n\n``` | 7 | 1 | ['Recursion', 'Java'] | 4 |
house-robber-iii | Simple Solution with Diagrams in Video - JavaScript, C++, Java, Python | simple-solution-with-diagrams-in-video-j-clzu | Video\nPlease upvote here so others save time too!\n\nLike the video on YouTube if you found it useful\n\nClick here to subscribe on YouTube:\nhttps://www.youtu | danieloi | NORMAL | 2024-11-04T10:53:02.612930+00:00 | 2024-11-04T10:53:02.612954+00:00 | 1,103 | false | # Video\nPlease upvote here so others save time too!\n\nLike the video on YouTube if you found it useful\n\nClick here to subscribe on YouTube:\nhttps://www.youtube.com/@mayowadan?sub_confirmation=1\n\nThanks!\n\nhttps://youtu.be/Yf9kCchl7No?si=Okmp9Wir2xZyjP3J\n\n```Javascript []\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n */\n/**\n * @param {TreeNode} root\n * @return {number}\n */\nvar rob = function (root) {\n // Returns maximum value from the pair: [includeRoot,\n // excludeRoot]\n const result = heist(root);\n return Math.max(result[0], result[1]);\n};\n\nfunction heist(root) {\n // Empty tree case\n if (root === null) {\n return [0, 0];\n }\n // Recursively calculating the maximum amount that can\n // be robbed from the left subtree of the root\n const leftSubtree = heist(root.left);\n // Recursively calculating the maximum amount that can\n // be robbed from the right subtree of the root\n const rightSubtree = heist(root.right);\n // includeRoot contains the maximum amount of money\n // that can be robbed with the parent node included\n const includeRoot =\n root.val + leftSubtree[1] + rightSubtree[1];\n // excludeRoot contains the maximum amount of money\n // that can be robbed with the parent node excluded\n const excludeRoot =\n Math.max(leftSubtree[0], leftSubtree[1]) +\n Math.max(rightSubtree[0], rightSubtree[1]);\n\n return [includeRoot, excludeRoot];\n}\n```\n```Python []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\n\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n # Returns maximum value from the pair: [includeRoot, excludeRoot]\n result = self.heist(root)\n return max(result[0], result[1])\n\n def heist(self, root: Optional[TreeNode]) -> List[int]:\n # Empty tree case\n if root is None:\n return [0, 0]\n\n # Recursively calculating the maximum amount that can be robbed\n # from the left subtree of the root\n leftSubtree = self.heist(root.left)\n\n # Recursively calculating the maximum amount that can be \n # robbed from the right subtree of the root\n rightSubtree = self.heist(root.right)\n\n # includeRoot contains the maximum amount of money that can be\n # robbed with the parent node included\n includeRoot = root.val + leftSubtree[1] + rightSubtree[1]\n\n # excludeRoot contains the maximum amount of money that can be\n # robbed with the parent node excluded\n excludeRoot = max(leftSubtree[0], leftSubtree[1]) + max(\n rightSubtree[0], rightSubtree[1]\n )\n\n return [includeRoot, excludeRoot]\n```\n```Java []\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\n\nclass Solution {\n public int rob(TreeNode root) {\n // Returns maximum value from the pair: [includeRoot, excludeRoot]\n int[] result = heist(root);\n return Math.max(result[0], result[1]);\n }\n\n private int[] heist(TreeNode root) {\n // Empty tree case\n if (root == null) {\n return new int[] { 0, 0 };\n }\n\n // Recursively calculating the maximum amount that can be robbed from the left\n // subtree of the root\n int[] leftSubtree = heist(root.left);\n\n // Recursively calculating the maximum amount that can be robbed from the right\n // subtree of the root\n int[] rightSubtree = heist(root.right);\n\n // includeRoot contains the maximum amount of money that can be robbed with the\n // parent node included\n int includeRoot = root.val + leftSubtree[1] + rightSubtree[1];\n\n // excludeRoot contains the maximum amount of money that can be robbed with the\n // parent node excluded\n int excludeRoot = Math.max(leftSubtree[0], leftSubtree[1]) + Math.max(rightSubtree[0], rightSubtree[1]);\n\n return new int[] { includeRoot, excludeRoot };\n }\n}\n```\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),\n * right(right) {}\n * };\n */\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n // Returns maximum value from the pair: {includeRoot, excludeRoot}\n vector<int> result = heist(root);\n return max(result[0], result[1]);\n }\n\nprivate:\n vector<int> heist(TreeNode* root) {\n // Empty tree case\n if (root == nullptr) {\n return {0, 0};\n }\n\n // Recursively calculating the maximum amount that can be robbed from\n // the left subtree of the root\n vector<int> leftSubtree = heist(root->left);\n\n // Recursively calculating the maximum amount that can be robbed from\n // the right subtree of the root\n vector<int> rightSubtree = heist(root->right);\n\n // includeRoot contains the maximum amount of money that can be robbed\n // with the parent node included\n int includeRoot = root->val + leftSubtree[1] + rightSubtree[1];\n\n // excludeRoot contains the maximum amount of money that can be robbed\n // with the parent node excluded\n int excludeRoot = max(leftSubtree[0], leftSubtree[1]) +\n max(rightSubtree[0], rightSubtree[1]);\n\n return {includeRoot, excludeRoot};\n }\n};\n``` | 6 | 0 | ['Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
house-robber-iii | Beats 90% O(N) time ✅✅ | beats-90-on-time-by-zenitsu02-fwtf | Approach\nApproach is written in the code in the form of comments just go through them and dry run once , i gaurentee you will understand the logic... I can als | Zenitsu02 | NORMAL | 2023-05-24T14:00:51.397109+00:00 | 2023-05-24T14:00:51.397155+00:00 | 1,033 | false | # Approach\nApproach is written in the code in the form of comments just go through them and dry run once , i gaurentee you will understand the logic... I can also explain the logic in brief \nSo here goes the logic , when we add the root data then we can\'t add the adjacent values so we will skip them and when we will not add the root data then we have choice whether we want to add adjacent values or not...\n\n# Complexity\n\n- Time complexity: O(N) as we are traversing all the nodes only once\n\n- Space complexity: O(height of tree)\n\n# **If you liked the solution then pls upvote the solution \uD83E\uDD79**\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n\n pair<int,int> solve(TreeNode *root){\n // base case\n if(root == NULL){\n return {0,0};\n }\n\n // left part ki call\n pair<int,int> leftAns = solve(root->left);\n\n // right part ki call\n pair<int,int> rightAns = solve(root->right);\n\n // creating final ans \n pair<int,int>ans;\n\n // jab humne root ke data koh include kara, toh adjacent koh pick nhi kr skte\n ans.first = root->val + leftAns.second + rightAns.second;\n\n // jab humne root ke data koh include nhi kara \n ans.second = max(leftAns.first, leftAns.second) + max(rightAns.first, rightAns.second);\n\n return ans;\n }\n\n\n int rob(TreeNode* root) {\n // we can think of this problem ans we want to add the root value or not\n pair<int,int>ans = solve(root);\n return max(ans.first, ans.second);\n }\n};\n``` | 6 | 0 | ['C++'] | 1 |
house-robber-iii | recursive approach + memoization | recursive-approach-memoization-by-droj-bbun | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | droj | NORMAL | 2022-11-19T14:09:55.047168+00:00 | 2022-11-19T14:09:55.047209+00:00 | 2,279 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\ndef fun(flg,root,memo):\n if(root==None):\n return 0\n if((root,flg) in memo):\n return memo[(root,flg)]\n if(flg==1):\n a=fun(0,root.left,memo)+fun(0,root.right,memo)\n memo[(root,flg)]=a\n return a\n a=fun(0,root.left,memo)+fun(0,root.right,memo)\n b=fun(1,root.left,memo)+fun(1,root.right,memo)+root.val\n x=max(a,b)\n memo[(root,flg)]=x\n return x\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n memo={}\n return(fun(0,root,memo))\n``` | 6 | 0 | ['Recursion', 'Python', 'Python3'] | 1 |
house-robber-iii | Some Intuition With Pictures, - May be this could help | some-intuition-with-pictures-may-be-this-56c4 | Some intution\n\n\n\nQuestion That we have\n What if we select this node? What Options Do we have? \n If we dont select this node then what could be the answer | RohanPrakash | NORMAL | 2021-03-18T21:58:16.105092+00:00 | 2021-03-18T22:21:06.243574+00:00 | 261 | false | Some intution\n\n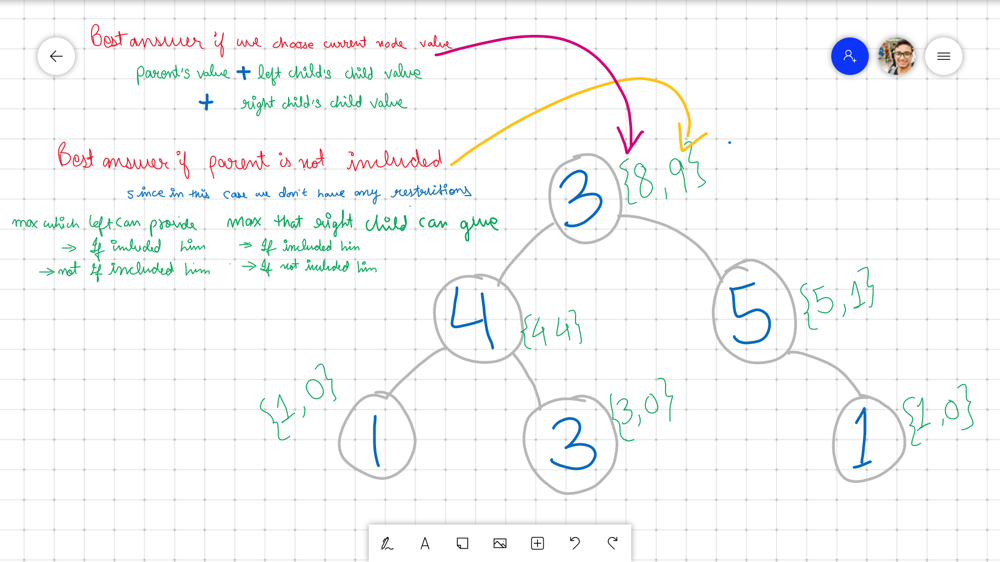\n\n**Question That we have**\n* What if we select this node? What Options Do we have? \n* If we dont select this node then what could be the answer at this Point\n* If we select this node then how do we get the answers for child nodes ? \n\n\nLets find answers to these two questions. Lets us ask Child nodes the best possible solutions if we want to include the Immediate child\'s value.\nOr if we skip then what is the best possible answers that we can get. Let\'s ask them.\n\n* Now Assume Child Node responds with his best answers for \n{ if we his (child\'s) value , If we dont Include ie we skip }\n\n\n```\npair<int,int> sub(TreeNode *root)\n {\n if(!root)\n return {0,0};\n \n pair<int,int> leftChildAnswer = sub(root->left);\n pair<int,int> rightChildAnswer= sub(root->right);\n \n int best_If_ParentValueIncluded = root->val + leftChildAnswer.second + rightChildAnswer.second;\n\n int best_If_ParentValueNotIncluded = max(rightChildAnswer.first , rightChildAnswer.second)\n + max(leftChildAnswer.first , leftChildAnswer.second);\n \n return {best_If_ParentValueIncluded , best_If_ParentValueNotIncluded};\n }\n \n int rob(TreeNode* root) \n {\n pair<int,int> ans = sub(root);\n return max(ans.first , ans.second);\n }\n``` | 6 | 0 | [] | 2 |
house-robber-iii | Beats 100% Java Easy Solution DP | beats-100-java-easy-solution-dp-by-onefi-pen3 | \nclass Solution {\n public int rob(TreeNode root) {\n if(root == null)\n return 0;\n int[] result = helper(root);\n return M | onefineday01 | NORMAL | 2020-04-13T07:16:15.093247+00:00 | 2020-04-13T07:16:15.093297+00:00 | 1,069 | false | ```\nclass Solution {\n public int rob(TreeNode root) {\n if(root == null)\n return 0;\n int[] result = helper(root);\n return Math.max(result[0], result[1]);\n }\n public int[] helper(TreeNode root){\n if(root == null){\n int[] result = {0, 0};\n return result;\n }\n int[] result = new int[2];\n int[] left = helper(root.left);\n int[] right = helper (root.right);\n result[0] = root.val + left[1] + right[1];\n result[1] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);\n return result;\n }\n}\n``` | 6 | 0 | ['Dynamic Programming', 'Tree', 'Depth-First Search', 'Recursion', 'Java'] | 1 |
house-robber-iii | CPP | EASY | 1 LINE | 100 % BEATS | RECURSION | cpp-easy-1-line-100-beats-recursion-by-h-n4eq | \n// In pair, returning take this value and not taking connected values or not taking this value and taking connected values.\nint rob(TreeNode* root) {\n\tretu | hidden13 | NORMAL | 2019-10-14T17:30:58.103222+00:00 | 2019-10-14T17:30:58.103258+00:00 | 617 | false | ```\n// In pair, returning take this value and not taking connected values or not taking this value and taking connected values.\nint rob(TreeNode* root) {\n\treturn robMax(root).first;\n}\n\npair<int, int> robMax(TreeNode* root){\n\tif(!root) return {0, 0};\n\n\tpair<int, int> right = robMax(root->right);\n\tpair<int, int> left = robMax(root->left);\n\n\treturn {max(root->val + right.second + left.second, right.first + left.first), right.first + left.first};\n}\n``` | 6 | 0 | ['Recursion', 'C++'] | 1 |
house-robber-iii | Complexity of Naive Recursion | complexity-of-naive-recursion-by-agade-effu | In this popular forum thread the author claims that the complexity of the naive recursion is exponential:\n\n"The time complexity for the naive recursion in ste | agade | NORMAL | 2019-08-31T18:25:33.964414+00:00 | 2019-08-31T20:33:59.133460+00:00 | 178 | false | In [this](https://leetcode.com/problems/house-robber-iii/discuss/79330/Step-by-step-tackling-of-the-problem) popular forum thread the author claims that the complexity of the naive recursion is exponential:\n\n"The time complexity for the naive recursion in step I is indeed exponential. For each tree node tn at depth d, let T(d) be the number of times the rob function will be called on it. Then we have T(d) = T(d - 1) + T(d - 2). This is because rob will be called on tn either from its parent (at depth d - 1) or its grandparent (at depth d - 2), according to its definition. Note T(0) = T(1) = 1, i.e., rob will be called only once for the tree root and its two child nodes. Therefore T(d) will essentially be the (d+1)-th Fibonacci number (starting from 1), which grows exponentially (more info can be found here)."\n\nThere is discussion in the comments about it actually being O(N^2) because the d (tree depth) in the T(d) above, scales logarithmically with the number of nodes. The author is right that in the worst case it scales exponentially. But for a balanced tree the scaling is indeed polynomial but not O(N^2) as I thought. I figured there was a 4 way branching so 4^log(N)->N^2. Empirically I find ~O(N^1.68157) for a perfectly balanced tree.\n\nI imagine the ~1.68157 corresponds to 1+log2(\u03C6) (\u03C6=(1+sqrt(5))/2) because the scaling of T(d) is \u03C6^d=\u03C6^log2(N)=2^(log2(N)log2(\u03C6))=N^log2(\u03C6). As the definition of T(d) was the number of calls per node at depth d we still have to multiply by N (half the nodes are at the leaves) to obtain N^(1+log2(\u03C6))=N^(1.694...) which my empirical result would hopefully converge to if I let it run longer.\n\n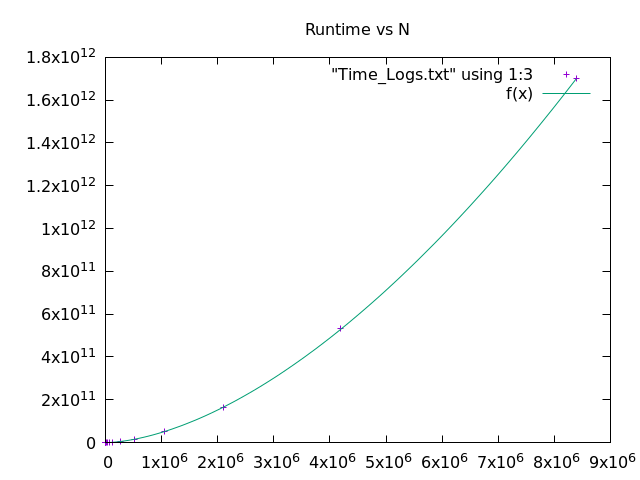\n\nLocal code\n```\n#include <iostream>\n#include <fstream>\n#include <chrono>\n#include <random>\nusing namespace std;\nusing namespace std::chrono;\n\ndefault_random_engine generator(system_clock::now().time_since_epoch().count());\nuniform_int_distribution<int> Val_Generator(0,25);\n\nstruct TreeNode{\n\tint val;\n\tTreeNode *left,*right;\n\tTreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n};\n\nint rob(const TreeNode *root,const bool can_take){\n\tif(root==nullptr){\n\t\treturn 0;\n\t}\n\tif(can_take){\n\t\treturn max(root->val+rob(root->left,false)+rob(root->right,false),rob(root->left,true)+rob(root->right,true));\n\t}\n\telse{\n\t\treturn rob(root->left,true)+rob(root->right,true);\n\t}\n}\nint rob(const TreeNode* root){\n if(root==nullptr){\n\t\treturn 0;\n\t}\n\treturn rob(root,true);\n}\n\nvoid Add_Leaves(TreeNode *root){\n\tif(root->left!=nullptr){ //root->right is automatically not null because we only use balanced trees\n\t\tAdd_Leaves(root->left);\n\t\tAdd_Leaves(root->right);\n\t}\n\telse{\n\t\troot->left=new TreeNode(Val_Generator(generator));\n\t\troot->right=new TreeNode(Val_Generator(generator));\n\t}\n}\n\nint main(){\n\tTreeNode *root=new TreeNode(Val_Generator(generator));\n\tofstream Timing_File("Time_Logs.txt",ios::trunc);\n\tfor(int depth{1};depth<25;++depth){\n\t\ttime_point<high_resolution_clock> start{high_resolution_clock::now()};\n\t\trob(root);\n\t\tTiming_File << pow(2.0,depth-1) << " " << depth << " " << (high_resolution_clock::now()-start).count() << endl;\n\t\tAdd_Leaves(root);\n\t}\n}\n```\nMakefile\n```\nall:\n\tg++ Local.cpp -o Local -std=c++17 -O3 -march=native -g\n```\nGnuplot script\n```\nset terminal pngcairo\nset output \'Timing_vs_N.png\'\nset title \'Runtime vs N\'\n\na=1\nc=2\nf(x)= a*x**c\nfit f(x) "Time_Logs.txt" using 1:3 via a,c\n\nplot "Time_Logs.txt" using 1:3,\\\n\tf(x)\n``` | 6 | 0 | [] | 1 |
house-robber-iii | 12 ms C++ solution | 12-ms-c-solution-by-ttang2009-jpdd | class Solution {\n public:\n \tint rob(TreeNode* root) \n \t{\n \t\tint mt, ms;\n \t\trob(root, mt, ms);\n \t\treturn max(mt, ms);\n \t}\n | ttang2009 | NORMAL | 2016-03-12T02:08:44+00:00 | 2016-03-12T02:08:44+00:00 | 863 | false | class Solution {\n public:\n \tint rob(TreeNode* root) \n \t{\n \t\tint mt, ms;\n \t\trob(root, mt, ms);\n \t\treturn max(mt, ms);\n \t}\n \n \tvoid rob(TreeNode* node, int& mt, int& ms)\n \t{\n \t\tmt = ms = 0;\n \t\tif (!node) return;\n \n \t\tint mtl, mtr, msl, msr;\n \t\trob(node->left, mtl, msl);\n \t\trob(node->right, mtr, msr);\n \n \t\tmt = msl + msr + node->val;\n \t\tms = max(mtl, msl) + max(mtr, msr);\n \t\treturn;\n \t}\n }; | 6 | 2 | [] | 0 |
house-robber-iii | BEATS 100.00% runtime and 99.54% memory!🔥🔥🔥 Intuitive and efficient solution! 😎🤑 | beats-10000-runtime-and-9954-memory-intu-qt1f | IntuitionAt each node, we can either rob it or don't rob it.If we rob the node, we get node.val, but we can't rob the children of the node, but we can rob the c | bufferjjh | NORMAL | 2025-03-12T17:47:20.370350+00:00 | 2025-03-17T22:42:25.694449+00:00 | 418 | false | 
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
At each node, we can either rob it or don't rob it.
If we rob the node, we get $node.val$, but we can't rob the children of the node, but we can rob the children of the children (since they are not direct connections) 😈.
If we don't rob the node, we can rob both of its children 😈!
# Approach
<!-- Describe your approach to solving the problem. -->
Using the intuition above, we take the max of both cases. But wait...🤔, the only recursive calls made are $rob(root.left)$ and $rob(root.right)$. That's because we store the value of $rob(node)$ in $node.val$ after we're done with that node, so we can get the value of, for example, $rob(node.left)$ by just getting $node.left.val$🔥. This makes our solution fast and memory efficient. Note: This is why we call $rob(root.left)$ and $rob(root.right)$ at the beginning.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(n)$ since each node is visited once.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(1)$ since we don't use any auxillary collections.
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int rob(TreeNode root) {
if (root == null) {
return 0;
}
rob(root.left);
rob(root.right);
int robThisNode = root.val;
int dontRobThisNode = 0;
if (root.left != null) {
dontRobThisNode += root.left.val;
if (root.left.left != null) {
robThisNode += root.left.left.val;
}
if (root.left.right != null) {
robThisNode += root.left.right.val;
}
}
if (root.right != null) {
dontRobThisNode += root.right.val;
if (root.right.left != null) {
robThisNode += root.right.left.val;
}
if (root.right.right != null) {
robThisNode += root.right.right.val;
}
}
root.val = Math.max(robThisNode, dontRobThisNode);
return root.val;
}
}
``` | 5 | 0 | ['Java'] | 1 |
house-robber-iii | easy recursive solution in c++ | easy-recursive-solution-in-c-by-yash_jai-ah4t | Intuition\n Describe your first thoughts on how to solve this problem. \nwe have to find the max sum possible of all the non adjacent values in the tree\n# Appr | yash_jain26 | NORMAL | 2023-08-24T18:09:16.265524+00:00 | 2023-08-24T18:09:16.265542+00:00 | 561 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe have to find the max sum possible of all the non adjacent values in the tree\n# Approach\n<!-- Describe your approach to solving the problem. -->\nto do this we will use recursion and store two piece of values one will be the sum if that node is used and one if that node is not used.\nif that node is used then we cant take the values of its child so we will add the values when its chil node is not used. when that node is not considered then we can either take its child node or not so we will store the max of the both case. answer will be max of both the values.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n pair<int,int> solve(TreeNode* root){\n if(root == NULL){\n return {0,0};\n }\n\n pair<int,int> left = solve(root->left);\n pair<int,int> right = solve(root->right);\n\n pair<int,int> temp;\n temp.first = root->val + left.second + right.second;\n temp.second = max(left.first,left.second) + max(right.first,right.second);\n\n return temp;\n }\n\n int rob(TreeNode* root) {\n pair<int,int> ans = solve(root);\n return max(ans.first,ans.second);\n }\n};\n``` | 5 | 0 | ['Tree', 'Recursion', 'Binary Tree', 'C++'] | 1 |
house-robber-iii | Easy C++ Solution using C++ | easy-c-solution-using-c-by-2005115-e6zd | \n# Approach\nThe solve function takes a TreeNode* representing the root of a binary tree and returns a pair of integers. The pair contains two values: the maxi | 2005115 | NORMAL | 2023-07-11T07:08:13.458565+00:00 | 2023-07-11T07:08:13.458588+00:00 | 731 | false | \n# Approach\nThe solve function takes a TreeNode* representing the root of a binary tree and returns a pair of integers. The pair contains two values: the maximum amount of money that can be robbed from the subtree rooted at root if root is included, and the maximum amount of money that can be robbed if root is not included.\n\nInside the solve function, the base case is checked first. If the root is NULL, indicating an empty subtree, a pair of zeros is returned.\n\nRecursively, the solve function is called for the left and right subtrees, and their results are stored in the left and right pairs.\n\nA new pair result is created to store the maximum amounts of money for the current subtree. The first value of result is calculated by adding the value of root->val (the money in the current house) to the sums of the second values from the left and right pairs (representing the maximum amounts when root is not included).\n\nThe second value of result is calculated by taking the maximum of the first and second values from the left pair and adding it to the maximum of the first and second values from the right pair.\n\nFinally, the maximum value between the first and second values of result is returned as the maximum amount of money that can be robbed.\n\nIn the rob function, the solve function is called for the root node, and the maximum of the first and second values from the returned pair is returned as the maximum amount of money that can be robbed from the entire binary tree.\n<!-- Describe your approach to solving the problem. -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\npair<int,int >solve(TreeNode* root)\n{\n if(root==NULL)\n {\n pair<int,int>p=make_pair(0,0);\n return p;\n }\n pair<int,int>left=solve(root->left);\n pair<int,int>right=solve(root->right);\n pair<int,int > result;\n result.first=root->val+left.second+right.second;\n result.second=max(left.first,left.second)+max(right.first,right.second);\n return {result.first,result.second};\n\n}\n int rob(TreeNode* root)\n {\n pair<int,int>n=solve(root);\n return max(n.first, n.second);\n }\n};\n``` | 5 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'C++'] | 1 |
house-robber-iii | dp soln✅ | step-by-step-easy-video-explanation👁️ | O(n)🔥| | dp-soln-step-by-step-easy-video-explanat-8fx7 | Challenge Company 4 : Flipkart\n#ReviseWithArsh #6Companies30Days Challenge 2023\nQ15. House Robber - Very Imp.\n\nhttps://youtu.be/vOJXQ_mKFoQ\nIf you found th | nandini-gangrade | NORMAL | 2023-01-17T23:08:02.930761+00:00 | 2023-01-18T14:26:27.393956+00:00 | 983 | false | ***Challenge Company 4 : Flipkart\n#ReviseWithArsh #6Companies30Days Challenge 2023\nQ15. House Robber - Very Imp.***\n\nhttps://youtu.be/vOJXQ_mKFoQ\n***If you found this video helpful, please consider supporting the hard work behind it. Your support would be greatly appreciated^_^***\n\n# Intuition\nDynamic Programming.\n\n# Approach\nThe key idea is to use recursion to break the problem down into subproblems and to use memoization to avoid redundant computation.\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution {\npublic:\n unordered_map<TreeNode*, int> lookup; // create a lookup table to store the results of subproblems\n int rob(TreeNode* root) {\n return helper(root);\n }\n int helper(TreeNode* node) {\n if (!node) // if the input node is null, return 0\n return 0;\n if (lookup.count(node)) // if the result is already in the lookup table, return the value stored in the lookup table\n return lookup[node];\n int left = helper(node->left); // calculate the maximum amount of money that can be robbed from the left subtree\n int right = helper(node->right); // calculate the maximum amount of money that can be robbed from the right subtree\n int left_grandchild = helper(node->left ? node->left->left : nullptr) + helper(node->left ? node->left->right : nullptr);\n // calculate the maximum amount of money that can be robbed from the left subtree\'s grandchild\n int right_grandchild = helper(node->right ? node->right->left : nullptr) + helper(node->right ? node->right->right : nullptr);\n // calculate the maximum amount of money that can be robbed from the right subtree\'s grandchild\n int result = max(node->val + left_grandchild + right_grandchild, left + right);\n // To avoid alerting the police, the thief cannot rob both the current node and its immediate children.\n // Therefore, the maximum amount of money that can be robbed from the current node is the maximum of the following two options:\n // 1. The maximum amount of money that can be robbed from the left subtree + the maximum amount of money that can be robbed from the right subtree.\n // 2. The value of the current node + the maximum amount of money that can be robbed from the left subtree\'s grandchild + the maximum amount of money that can be robbed from the right subtree\'s grandchild.\n lookup[node] = result; // store the result in the lookup table\n return result;\n }\n};\n\n```\n\n\n | 5 | 0 | ['Dynamic Programming', 'Tree', 'Recursion', 'C++'] | 0 |
house-robber-iii | DP solution Python | dp-solution-python-by-kryuki-dr8w | \nfrom collections import defaultdict\n\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n def rec(node, depth):\n if not | kryuki | NORMAL | 2021-12-05T02:01:13.355748+00:00 | 2021-12-06T06:38:03.540925+00:00 | 749 | false | ```\nfrom collections import defaultdict\n\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n def rec(node, depth):\n if not node:\n return\n layer_dict[depth].append(node)\n rec(node.left, depth + 1)\n rec(node.right, depth + 1)\n \n #get layer dict\n layer_dict = defaultdict(list)\n rec(root, 0)\n \n #dp\n dp_use, dp_no_use = {None : 0}, {None : 0}\n \n for layer in range(max(layer_dict.keys()), -1, -1):\n for u in layer_dict[layer]:\n dp_use[u] = dp_no_use[u.left] + dp_no_use[u.right] + u.val\n dp_no_use[u] = max(dp_use[u.left], dp_no_use[u.left]) + max(dp_use[u.right], dp_no_use[u.right])\n \n return max(dp_use[root], dp_no_use[root])\n``` | 5 | 0 | ['Dynamic Programming', 'Python', 'Python3'] | 1 |
house-robber-iii | c++ faster 100% space 100% | c-faster-100-space-100-by-leetcoder10086-0qve | we define function rob return the maximum amount of money.\nAnd It will automatically contact the police if two directly-linked houses were broken into on the s | leetcoder10086 | NORMAL | 2021-11-02T22:42:53.920172+00:00 | 2022-05-23T15:20:09.879777+00:00 | 340 | false | we define function rob return the maximum amount of money.\n**And It will automatically contact the police if two directly-linked houses were broken into on the same night.**\n\nit means that if we choose the value of current node we cannot choose the value of beside node.\nso the ans = max(current->val + (**the largest amount of money without choosing the beside node**), **the largest amount of money without choosing the current node**);\n\nhow can we find the **the largest amount of money without choosing the beside node**?\nfor example, if the current node is the root,\n**the largest amount of money without choosing the beside node** = rob(current->left->left) + rob(current->left->right) + rob(current->right->left) + rob(current->right->right)\n= 3 + 1 = 4.\n\n**how can we simplify it?**\nwhen backtracking, we can use variable sum to store the sum of rob(current->left) and rob(current->right).\nand when it backtrack to the parent node, current = parent node. \nAnd sum = (rob(current->left->left) + rob(current->left->right)) \nor (rob(current->left->left) + rob(current->left->right)).\n\nso when it backtrack to the parent node, we use preSum to store **the largest amount of money without choosing the beside node**.\nAnd the end we return max(root->val + preSum, sum).\n\n\n```\nclass Solution {\npublic:\n int sum = 0;\n int rob(TreeNode* root) {\n if(!root){\n sum = 0;\n return 0;\n }\n int l = rob(root->left);\n int preSum = sum;\n int r = rob(root->right);\n preSum += sum;\n sum = l + r;\n return max(root->val + preSum, sum);\n }\n};\n``` | 5 | 0 | ['Dynamic Programming', 'C'] | 1 |
house-robber-iii | C++ Solution || Using Unordered map | c-solution-using-unordered-map-by-kannu_-kt25 | \nclass Solution {\npublic:\n unordered_map<TreeNode*, int>mp;\n int rob(TreeNode* root) {\n if(root == NULL) return 0;\n if(mp.find(root) ! | kannu_priya | NORMAL | 2021-04-26T10:58:59.849804+00:00 | 2021-04-26T11:00:11.694108+00:00 | 435 | false | ```\nclass Solution {\npublic:\n unordered_map<TreeNode*, int>mp;\n int rob(TreeNode* root) {\n if(root == NULL) return 0;\n if(mp.find(root) != mp.end()) return mp[root];\n \n int total = 0;\n if(root->left) total += (rob(root->left->left) + rob(root->left->right));\n if(root->right) total += (rob(root->right->left) + rob(root->right->right));\n return mp[root] = max((root->val+total), (rob(root->left)+rob(root->right)));\n }\n};\n``` | 5 | 1 | ['C', 'C++'] | 1 |
house-robber-iii | Python 3 | DFS, Backtracking | Explanation | python-3-dfs-backtracking-explanation-by-yclt | Explanation\n- It\'s a tree, there is an implied recursion relation between each layer\n- Two options:\n\t- Take value in current node, then the direct children | idontknoooo | NORMAL | 2020-09-30T22:18:29.907908+00:00 | 2020-09-30T22:18:29.907955+00:00 | 756 | false | ### Explanation\n- It\'s a tree, there is an implied recursion relation between each layer\n- Two options:\n\t- Take value in current node, then the direct children node can\'t be taken, but we can take the maximum below its direct children\n\t- Don\'t take value in current node, then we take the maximum below current node\n- Return the maximum of root can get\n### Implementation\n```\nclass Solution:\n def rob(self, root: TreeNode) -> int:\n def dfs(node):\n if not node: return 0, 0\n left, right = dfs(node.left), dfs(node.right)\n v_take = node.val + left[1] + right[1]\n v_not_take = max(left) + max(right)\n return v_take, v_not_take\n return max(dfs(root))\n```\nHere is a 1-liner in Python 3.8\n```\nclass Solution:\n def rob(self, root: TreeNode) -> int:\n def dfs(node):\n return (node.val + (left:=dfs(node.left))[1] + (right:=dfs(node.right))[1], max(left) + max(right)) if node else (0, 0)\n return max(dfs(root))\n``` | 5 | 0 | ['Backtracking', 'Depth-First Search', 'Python', 'Python3'] | 1 |
house-robber-iii | Java | postorder | 0 ms 100% faster | java-postorder-0-ms-100-faster-by-0401mc-qiu1 | So the idea here is to keep track of the sum with including the current node and without including the current node. \n\n\tpublic int rob(TreeNode root) {\n | 0401mc | NORMAL | 2020-03-22T16:30:32.452723+00:00 | 2020-03-22T16:48:04.837814+00:00 | 298 | false | So the idea here is to keep track of the sum **with** including the current node and **without** including the current node. \n\n\tpublic int rob(TreeNode root) {\n if (root == null) return 0;\n int[] res = postOrder(root);\n return Math.max(res[0], res[1]);\n }\n \n private int[] postOrder(TreeNode node) {\n\t\tif (node == null) return new int[2];\n int[] l = postOrder(node.left);\n int[] r = postOrder(node.right);\n\n int with = node.val + l[1] + r[1];\n int without = Math.max(l[0], l[1]) + Math.max(r[0], r[1]);\n\n return new int[]{with, without};\n } | 5 | 0 | [] | 1 |
house-robber-iii | Java DP with explanation | java-dp-with-explanation-by-algopirate-8nj6 | \nclass Solution {\n // using DFS and backtracking; bottom to top\n // at certain point/node, this is how we determine the max\n // There are a couple | algopirate | NORMAL | 2020-01-15T01:58:57.479828+00:00 | 2020-01-15T01:58:57.479861+00:00 | 319 | false | ```\nclass Solution {\n // using DFS and backtracking; bottom to top\n // at certain point/node, this is how we determine the max\n // There are a couple of cases at this node \n // 1. if we consider to rob this node: max is current root.val + the value get from \n // robbing both its grandchildren \n // 2. if we consider not to rob: max is the sum of both its left child sum and its right \n // sum if exists \n // finally, we take the max and return and of course store the result into hashmap for \n // future use\n \n public int DFS(TreeNode root, HashMap<TreeNode, Integer>map){\n if(root == null) return 0;\n \n // if this root has been visited and the max has been calculated, return immediately\n if(map.containsKey(root)) return map.get(root);\n \n int result = 0;\n // say we rob the current root, we will also rob its both grandchildren\n // below is to rob its left child\'s both children\n if(root.left != null)\n result += DFS(root.left.left, map) + DFS(root.left.right, map); \n // below is to rob its right child\'s both children\n if(root.right != null)\n result += DFS(root.right.left, map) + DFS(root.right.right, map);\n \n // the sum we get from result will be compared to just robbing its left and right child \n result = Math.max(result + root.val, DFS(root.left, map)+DFS(root.right, map));\n map.put(root, result);\n return result;\n \n }\n public int rob(TreeNode root) {\n return DFS(root, new HashMap<TreeNode, Integer>());\n }\n}\n``` | 5 | 0 | [] | 0 |
house-robber-iii | Java clean solution with recursion and map as cache | java-clean-solution-with-recursion-and-m-g5us | ```\n private Map map = new HashMap<>();\n \n public int rob(TreeNode root) {\n if (map.containsKey(root)) {\n return map.get(root);\ | zuihulu | NORMAL | 2019-06-08T02:33:02.420728+00:00 | 2019-06-08T02:33:02.420784+00:00 | 436 | false | ```\n private Map<TreeNode, Integer> map = new HashMap<>();\n \n public int rob(TreeNode root) {\n if (map.containsKey(root)) {\n return map.get(root);\n }\n \n int result = Math.max(robFrom(root), robNext(root));\n map.put(root, result);\n return result;\n }\n \n private int robFrom(TreeNode node) {\n if (node == null) {\n return 0;\n }\n \n return node.val + robNext(node.left) + robNext(node.right);\n }\n \n private int robNext(TreeNode node) {\n if (node == null) {\n return 0;\n }\n \n return rob(node.left) + rob(node.right);\n }\n} | 5 | 0 | [] | 1 |
house-robber-iii | C++, DFS using unordered_map clean solution | c-dfs-using-unordered_map-clean-solution-72ql | class Solution {\npublic:\n \n unordered_mapm;\n \n int func(TreeNode root) {\n \n if(!root) return 0;\n \n int child=0, | naman_nm | NORMAL | 2019-05-31T17:06:19.363174+00:00 | 2019-05-31T17:06:19.363223+00:00 | 527 | false | class Solution {\npublic:\n \n unordered_map<TreeNode*, int>m;\n \n int func(TreeNode* root) {\n \n if(!root) return 0;\n \n int child=0, grandchild=0;\n \n child = func(root->left);\n child += func(root->right);\n \n if(root->left)\n {\n grandchild = m[root->left->left];\n grandchild += m[root->left->right];\n }\n if(root->right)\n {\n grandchild += m[root->right->left];\n grandchild += m[root->right->right];\n } \n \n m[root] = max(root->val + grandchild , child); \n return m[root]; \n }\n \n int rob(TreeNode* root) {\n \n m.clear();\n if(!root)\n return 0;\n \n return func(root);\n }\n}; | 5 | 0 | ['C++'] | 1 |
house-robber-iii | Java solution | java-solution-by-wuruoye-12bl | \u9898\u76EE\u4E3A\uFF1A\u6709\u5F88\u591A\u4E92\u76F8\u8FDE\u63A5\u7684\u623F\u95F4\uFF0C\u8FD9\u4E9B\u623F\u95F4\u6B63\u597D\u8FDE\u6210\u4E00\u68F5\u4E8C\u53 | wuruoye | NORMAL | 2019-02-23T08:55:59.757832+00:00 | 2019-02-23T08:55:59.757895+00:00 | 407 | false | \u9898\u76EE\u4E3A\uFF1A\u6709\u5F88\u591A\u4E92\u76F8\u8FDE\u63A5\u7684\u623F\u95F4\uFF0C\u8FD9\u4E9B\u623F\u95F4\u6B63\u597D\u8FDE\u6210\u4E00\u68F5\u4E8C\u53C9\u6811\u7684\u6837\u5B50\uFF0C\u5C0F\u5077\u9700\u8981\u4ECE\u8FD9\u68F5\u6811\u7684\u6839\u7ED3\u70B9\u623F\u95F4\u51FA\u53D1\u5F00\u59CB\u5077\u4E1C\u897F\u3002\u4E3A\u4E86\u4E0D\u88AB\u6293\u4F4F\uFF0C\u5C0F\u5077\u4E0D\u80FD\u5077\u76F8\u8FDE\u7684\u4E24\u4E2A\u623F\u95F4\u3002\n\n\u4E8E\u662F\uFF0C\u6709\u8FD9\u4E48\u4E24\u4E2A\u8981\u6C42\uFF1A\n\n1. \u5982\u679C\u5F53\u524D\u7ED3\u70B9\u7684\u7236\u7ED3\u70B9\u6CA1\u6709\u88AB\u5077\uFF0C\u90A3\u4E48\u5F53\u524D\u7ED3\u70B9\u53EF\u5077\u53EF\u4E0D\u5077\n2. \u5982\u679C\u5F53\u524D\u7ED3\u70B9\u7684\u7236\u7ED3\u70B9\u88AB\u5077\u4E86\uFF0C\u90A3\u4E48\u5F53\u524D\u7ED3\u70B9\u4E0D\u53EF\u5077\n\n\u6240\u4EE5\uFF0C\u5F53\u4ECE\u6839\u7ED3\u70B9\u5224\u65AD\u5F00\u59CB\u7684\u65F6\u5019\uFF0C\u6709\uFF1A\n\n1. \u5982\u679C\u5077\u5F53\u524D\u7ED3\u70B9\uFF0C\u90A3\u4E48\u4E0B\u9762\u80FD\u5077\u7684\u53EA\u80FD\u662F\u81EA\u5DF1\u7684\u5B59\u5B50\u7ED3\u70B9\n2. \u5982\u679C\u4E0D\u5077\u5F53\u524D\u7ED3\u70B9\uFF0C\u90A3\u4E48\u4E0B\u9762\u53EF\u4EE5\u5077\u81EA\u5DF1\u7684\u5B69\u5B50\u7ED3\u70B9\n\n\u4EE3\u7801\u5982\u4E0B\uFF1A\n\n public static int rob(TreeNode node) {\n if (node == null) return 0;\n int max = rob(node.left) + rob(node.right);\n int m = node.val;\n if (node.left != null) {\n m += rob(node.left.left) + rob(node.left.right);\n }\n if (node.right != null) {\n m += rob(node.right.left) + rob(node.right.right);\n }\n max = Math.max(max, m);\n return max;\n }\n\n\u5728\u8FD9\u79CD\u65B9\u6CD5\u4E2D\u53EF\u4EE5\u770B\u5230\uFF0C\u4ECE\u7ED3\u70B9 node \u6709\u4E24\u6761\u7EBF\uFF0C\u5206\u522B\u662F\u8D70\u5411 node \u7684\u5B50\u7ED3\u70B9\u548C\u5B59\u5B50\u7ED3\u70B9\uFF0C\u8FD9\u5C31\u5BFC\u81F4\u4E00\u4E2A\u95EE\u9898\uFF1A\u4F1A\u4EA7\u751F\u91CD\u590D\u8BA1\u7B97\u3002\u6BD4\u5982\uFF0C\u5BF9\u4E8E\u4ECE node \u7ED3\u70B9\u5230\u5B83\u7684\u5B59\u5B50\u7ED3\u70B9\uFF0C\u53EF\u4EE5\u6709\u4E24\u79CD\u65B9\u5F0F\uFF1Anode -> \u5B59\u5B50\u548Cnode -> \u5B69\u5B50 -> \u5B69\u5B50\u3002\u4ECE\u4E24\u6761\u8DEF\u5927\u5230\u8FBE\u540C\u4E00\u7ED3\u70B9\uFF0C\u5C31\u662F\u8BF4\u4F1A\u4ECE\u4E24\u4E2A\u9012\u5F52\u51FD\u6570\u5206\u522B\u8FDB\u5165 node \u7684\u5B59\u5B50\u7ED3\u70B9\uFF0C\u90A3\u4E48\u52BF\u5FC5\u4F1A\u8BA1\u7B97\u4E24\u6B21\u8FD9\u4E2A\u7ED3\u70B9\u7684\u89E3\u3002\n\n\u6240\u4EE5\u9700\u8981\u91C7\u53D6\u4E00\u5B9A\u7684\u63AA\u65BD\uFF0C\u4F7F\u5F97\u91CD\u590D\u8FDB\u5165\u540C\u4E00\u7ED3\u70B9\u7684\u65F6\u5019\u907F\u514D\u91CD\u590D\u8BA1\u7B97\uFF0C\u5373\u4F7F\u7528\u7F13\u5B58\uFF1A\n\n public static int rob(TreeNode root) {\n return rob(root, new HashMap<>());\n }\n private static int rob(TreeNode node, Map<TreeNode, Integer> saved) {\n if (node == null) return 0;\n if (saved.containsKey(node)) return saved.get(node);\n int max = rob(node.left, saved) + rob(node.right, saved);\n int m = node.val;\n if (node.left != null) {\n m += rob(node.left.left, saved) + rob(node.left.right, saved);\n }\n if (node.right != null) {\n m += rob(node.right.left, saved) + rob(node.right.right, saved);\n }\n max = Math.max(max, m);\n saved.put(node, max);\n return max;\n }\n\n\u4F7F\u7528\u4E00\u4E2A HashMap \u4FDD\u5B58\u5DF2\u7ECF\u6C42\u89E3\u8FC7\u7684\u7ED3\u70B9\uFF0C\u5C31\u662F\u4E00\u79CD\u7F13\u5B58\u7684\u601D\u60F3\u3002\n\n\u518D\u770B\u672C\u65B9\u6CD5\u7684\u7F3A\u9677\uFF0C\u8FD9\u662F\u4E00\u79CD\u201C\u8DF3\u8DC3\u5F0F\u201D\u7684\u89E3\u6CD5\uFF0C\u4ECE\u4E00\u4E2A\u7ED3\u70B9\u51FA\u53D1\u5230\u53E6\u4E00\u4E2A\u7ED3\u70B9\uFF0C\u4F1A\u6709\u591A\u6761\u8DEF\u5F84\uFF0C\u800C\u591A\u6761\u8DEF\u5F84\u4F1A\u5BFC\u81F4\u91CD\u590D\u8BA1\u7B97\uFF0C\u90A3\u4E48\u5982\u679C\u80FD\u4F7F\u5B83\u4E0D\u518D\u8DF3\u8DC3\uFF0C\u53EA\u80FD\u4E00\u6B65\u4E00\u6B65\u5F80\u4E0B\u8D70\u7684\u8BDD\uFF0C\u8FD9\u4E2A\u91CD\u590D\u8BA1\u7B97\u4E5F\u5C31\u4E0D\u590D\u5B58\u5728\u4E86\u3002\n\n\u5982\u4F55\u6539\u8FDB\uFF1F\u5C0F\u5077\u5BF9\u4E8E\u6BCF\u4E2A\u7ED3\u70B9\u6709\u4E24\u79CD\u5904\u7406\uFF1A\u5077\u6216\u4E0D\u5077\u3002\n\n1. \u5982\u679C\u5C0F\u5077\u5077\u4E86\u5F53\u524D\u7ED3\u70B9\uFF0C\u90A3\u4E48\u5B83\u7684\u5B50\u7ED3\u70B9\u4E0D\u80FD\u5077\n2. \u5982\u679C\u5C0F\u5077\u4E0D\u5077\u5F53\u524D\u7ED3\u70B9\uFF0C\u90A3\u4E48\u5B50\u7ED3\u70B9\u53EF\u4EE5\u5077\uFF0C\u4E5F\u53EF\u4EE5\u4E0D\u5077\uFF08\u53D6\u5176\u4E2D\u8F83\u5927\u7684\u5373\u53EF\uFF09\n\n\u8FD9\u6B21\u7684\u6761\u4EF6\u597D\u50CF\u4E0E\u4E0A\u9762\u7684\u6761\u4EF6\u4E00\u6837\uFF0C\u4F46\u662F\u8FD8\u662F\u6709\u533A\u522B\u7684\uFF0C\u90A3\u4E2A\u6D89\u53CA\u5230\u4E86\u5B59\u5B50\u7ED3\u70B9\uFF0C\u800C\u8FD9\u4E2A\uFF0C\u53EA\u6D89\u53CA\u5230\u5B69\u5B50\uFF0C\u5982\u679C\u4E0A\u9762\u90A3\u4E2A\u662F\u201C\u8DF3\u8DC3\u5F0F\u201D\u7684\uFF0C\u90A3\u4E48\u8FD9\u4E2A\u5C31\u662F\u201C\u6B65\u8FDB\u5F0F\u201D\u7684\u3002\u5F53\u4E00\u4E2A\u7ED3\u70B9\u7684\u89E3\uFF0C\u53EA\u4E0E\u5B83\u7684\u5B69\u5B50\u7ED3\u70B9\u6709\u5173\u65F6\uFF0C\u8FD9\u4E2A\u95EE\u9898\u5C31\u53D8\u5F97\u7B80\u5355\u4E86\u3002\u5982\u4E0B\uFF1A\n\n public static int rob(TreeNode root) {\n int[] rob = max(root);\n return Math.max(rob[0], rob[1]);\n }\n private static int[] max(TreeNode node) {\n if (node == null) {\n return new int[]{0, 0};\n }\n int[] rob = new int[2];\n int[] left = max(node.left);\n int[] right = max(node.right);\n rob[0] = left[1] + right[1] + node.val;\n rob[1] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);\n return rob;\n }\n\n\u51FD\u6570rob\u8FD4\u56DE\u4E86\u4E00\u4E2A\u6570\u7EC4\uFF0C\u6570\u7EC4\u7684\u7B2C\u4E00\u4E2A\u6570\u662F\u5077\u4E86\u5F53\u524D\u7ED3\u70B9\u7684\u89E3\uFF0C\u7B2C\u4E8C\u4E2A\u6570\u662F\u4E0D\u5077\u5F53\u524D\u7ED3\u70B9\u7684\u89E3\uFF0C\u90A3\u4E48\u5BF9\u4E8E\u4E00\u4E2A\u7ED3\u70B9 node \u6765\u8BF4\uFF0C\u5B83\u53EA\u8981\u77E5\u9053\u4E86\u5B83\u7684\u5DE6\u53F3\u5B69\u5B50\u7ED3\u70B9\u7684\u8FD9\u6837\u4E00\u4E2A\u6570\u7EC4\uFF0C\u5C31\u53EF\u4EE5\u6839\u636E\u4E0A\u9762\u90A3\u4E2A\u6761\u4EF6\u6C42\u51FA\u5F53\u524D\u7ED3\u70B9\u7684\u6700\u4F18\u89E3\uFF0C\u56E0\u4E3A\u6CA1\u6709\u4E86\u8DF3\u8DC3\u8BBF\u95EE\uFF0C\u6240\u6709\u7684\u7ED3\u70B9\u53EA\u4F1A\u8BBF\u95EE\u5230\u4E00\u904D\u3002\n | 5 | 1 | [] | 3 |
house-robber-iii | Python 3 iterative and recursive solution | python-3-iterative-and-recursive-solutio-jwop | \n# the value in the couple is (yesrob, norob)\n# yesrob is the max amount with robbing the current node\n# norob is the max amount without robbing the current | luffyzhou | NORMAL | 2018-05-15T06:52:44.254947+00:00 | 2018-05-15T06:52:44.254947+00:00 | 439 | false | ```\n# the value in the couple is (yesrob, norob)\n# yesrob is the max amount with robbing the current node\n# norob is the max amount without robbing the current node\nclass Solution_iterative_postorder:\n def rob(self, root):\n stack = [(0, root)]\n d = {None: (0, 0)}\n while stack:\n seen, node = stack.pop()\n if node is None:\n continue\n if not seen:\n stack.extend([(1, node), (0, node.right), (0, node.left)])\n else:\n yesrob = d[node.left][1] + d[node.right][1] + node.val\n norob = max(d[node.left]) + max(d[node.right])\n d[node] = (yesrob, norob)\n return max(d[root])\n\n\nclass Solution_recursive:\n def rob(self, root):\n """\n :type root: TreeNode\n :rtype: int\n """\n def couple(root):\n if root is None:\n return (0, 0)\n left = couple(root.left)\n right = couple(root.right)\n return (left[1] + right[1] + root.val, max(left) + max(right))\n\n return max(couple(root))\n``` | 5 | 0 | [] | 1 |
house-robber-iii | 14ms java solution | 14ms-java-solution-by-larrywang2014-c6hg | public int rob(TreeNode root) {\n Map<TreeNode, Integer> include = new HashMap<>();\n Map<TreeNode, Integer> exclude = new HashMap<>();\n | larrywang2014 | NORMAL | 2016-03-12T00:34:16+00:00 | 2016-03-12T00:34:16+00:00 | 735 | false | public int rob(TreeNode root) {\n Map<TreeNode, Integer> include = new HashMap<>();\n Map<TreeNode, Integer> exclude = new HashMap<>();\n return helper(root, false, exclude, include);\n }\n \n private int helper(TreeNode cur, boolean parentRobbed, Map<TreeNode, Integer> exclude, Map<TreeNode, Integer> include)\n {\n if (cur == null)\n {\n return 0;\n }\n \n int ret = Integer.MIN_VALUE;\n \n int leftMax = 0;\n int rightMax = 0;\n \n // do not rob the current house\n // ------------------------------------ \n if (!exclude.containsKey(cur))\n {\n leftMax = helper(cur.left, false, exclude, include);\n rightMax = helper(cur.right, false, exclude, include);\n exclude.put(cur, leftMax + rightMax);\n }\n ret = Math.max(ret, exclude.get(cur));\n \n // if parent house is not robbed, rob the current house\n // ------------------------------------------------------------------\n if (!parentRobbed)\n {\n // rob the current house\n // ----------------------------\n if (!include.containsKey(cur))\n {\n leftMax = helper(cur.left, true, exclude, include);\n rightMax = helper(cur.right, true, exclude, include);\n include.put(cur, cur.val + leftMax + rightMax);\n }\n ret = Math.max(ret, include.get(cur));\n }\n \n return ret;\n } | 5 | 1 | [] | 0 |
house-robber-iii | 2ms Java AC O(n) solution | 2ms-java-ac-on-solution-by-aicp7-cm7u | The idea is for each node, we have a associated Point. Point's x represents the MAX value for taking this node. Point's y is the MAX value for not taking this n | aicp7 | NORMAL | 2016-03-19T00:34:06+00:00 | 2016-03-19T00:34:06+00:00 | 1,377 | false | The idea is for each node, we have a associated Point. Point's x represents the MAX value for taking this node. Point's y is the MAX value for not taking this node. The program will go from bottom to top and keep updating until root. \n\n\n public class Solution {\n public int rob(TreeNode root) {\n return robHelp(root).x;\n }\n public Point robHelp(TreeNode root) {\n if (root == null) {\n return new Point(0, 0);\n }\n Point leftPoint = robHelp(root.left);\n Point rightPoint = robHelp(root.right);\n \n return new Point(Math.max(root.val + leftPoint.y + rightPoint.y, leftPoint.x + rightPoint.x), leftPoint.x + rightPoint.x);\n }\n } | 5 | 0 | [] | 0 |
house-robber-iii | Java DP solution with explanation | java-dp-solution-with-explanation-by-coo-c8tf | /**\n * Let S(k, r) represent the state of robbed money, where k is current node and r is whether to rob k (=1) or not (=0),\n * therefore, S(k, r) can | cooniur | NORMAL | 2016-05-19T09:03:54+00:00 | 2016-05-19T09:03:54+00:00 | 1,330 | false | /**\n * Let S(k, r) represent the state of robbed money, where k is current node and r is whether to rob k (=1) or not (=0),\n * therefore, S(k, r) can be read as "the amount of money can be robbed at node k, either to rob k (r=1) or not to rob k (r=0)"\n *\n * Then, the state can be calculated via:\n * S(k,0) = max{S(k.left, 0), S(k.left, 1)} + max{S(k.right, 0), S(k.right, 1)}\n * S(k,1) = k.val + S(k.left, 0) + S(k.right, 0)\n * \n * Finally, the max amount of money can be robbed at root node is max{S(root,0), S(root,1)}\n */\n public class Solution {\n \n private Map<TreeNode, Integer> rob = new HashMap<>();\n private Map<TreeNode, Integer> norob = new HashMap<>();\n \n public int rob(TreeNode root) {\n return Math.max(robHelper(root, true), robHelper(root, false));\n }\n \n private int robHelper(TreeNode root, boolean robRoot) {\n if (root == null) {\n return 0;\n }\n \n if (robRoot) {\n if (rob.containsKey(root)) {\n // Solved case\n return rob.get(root);\n } else {\n int money = root.val + robHelper(root.left, false) + robHelper(root.right, false);\n rob.put(root, money);\n return money;\n }\n } else {\n if (norob.containsKey(root)) {\n // Solved case\n return norob.get(root);\n } else {\n int leftMax = Math.max(robHelper(root.left, false), robHelper(root.left, true));\n int rightMax = Math.max(robHelper(root.right, false), robHelper(root.right, true));\n int money = leftMax + rightMax;\n norob.put(root, money);\n return money;\n }\n }\n }\n } | 5 | 0 | ['Dynamic Programming', 'Java'] | 0 |
house-robber-iii | Simple C++ solution | DP | recursion | Memoization | simple-c-solution-dp-recursion-memoizati-w3qo | Intuition\nAs we need to find the maximum sum of the nodes of the tree which are not directly linked, we can use a DFS traversal. And if we decide to pick a nod | saurabhdamle11 | NORMAL | 2024-08-02T07:10:16.531508+00:00 | 2024-08-02T09:06:08.541443+00:00 | 895 | false | # Intuition\nAs we need to find the maximum sum of the nodes of the tree which are not directly linked, we can use a DFS traversal. And if we decide to pick a node, then we will have to skip its child nodes and consider the grandchild nodes. If we decide not to pick a node, then we can pick its child nodes.\n\n# Approach\n1. For every recursive call, check the following\n2. If the node does not exist, return 0.\n3. If we have already calculated the amount if we decide to pick up a node, return the value from the map.\n4. For the 1st scenario of picking the node, add the node value to a variable called pick. If its grandchildren exist, then recursively call the function for them and add the value to pick variable.\n5. For the 2nd scenario of not picking the current node, set a variable not_pick to 0. If its child nodes exist, then recursively call the function for them and add the value to not_pick variable.\n6. return the max of pick and not_pick. And also update the map of current node with the max.\n\n# Complexity\n\n### Time complexity\nO(n)\n\n### Space complexity\nO(n)\n\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n\n int solve(TreeNode* node,unordered_map<TreeNode*,int>& dp){\n if(!node){return 0;}\n int pick = node->val;\n if(dp.find(node)!=dp.end()){return dp[node];}\n if(node->left && node->left->left){pick+=solve(node->left->left,dp);}\n if(node->left && node->left->right){pick+=solve(node->left->right,dp);}\n if(node->right && node->right->left){pick+=solve(node->right->left,dp);}\n if(node->right && node->right->right){pick+=solve(node->right->right,dp);}\n int not_pick = 0;\n if(node->left){not_pick+=solve(node->left,dp);}\n if(node->right){not_pick+=solve(node->right,dp);}\n return dp[node]=max(pick,not_pick);\n }\n\n int rob(TreeNode* root) {\n unordered_map<TreeNode*,int> dp;\n return solve(root,dp);\n }\n};\n``` | 4 | 0 | ['Dynamic Programming', 'Tree', 'Depth-First Search', 'Memoization', 'Binary Tree', 'C++'] | 2 |
house-robber-iii | C++ | Space optimized approach | c-space-optimized-approach-by-virtual91-ta7q | \nclass Solution {\npublic:\n // Time complexity - O(N)\n // vector<int> of size = 2 where -> [pick, not pick]\n vector<int> traverser(TreeNode* curr){ | Virtual91 | NORMAL | 2022-11-24T14:35:52.563101+00:00 | 2022-11-24T14:35:52.563141+00:00 | 974 | false | ```\nclass Solution {\npublic:\n // Time complexity - O(N)\n // vector<int> of size = 2 where -> [pick, not pick]\n vector<int> traverser(TreeNode* curr){\n if(!curr){\n return {0, 0};\n }\n \n vector<int>l, r, t;\n l = traverser(curr->left);\n r = traverser(curr->right);\n \n t.push_back( l[1] + r[1] + curr->val );\n t.push_back( max(l[0], l[1]) + max(r[0], r[1]) );\n \n return t;\n }\n int rob(TreeNode* root) {\n vector<int>holder = traverser(root);\n return max(holder[0], holder[1]);\n }\n};\n``` | 4 | 0 | ['Depth-First Search', 'C++'] | 0 |
house-robber-iii | Concise C++ DP DFS Solution | concise-c-dp-dfs-solution-by-amitpandey3-t7ab | \nclass Solution {\npublic:\n pair<int, int> dfs(TreeNode* root) {\n if(!root) return {0, 0};\n auto [leftDontRob, leftRob] = dfs(root -> lef | AmitPandey31 | NORMAL | 2022-08-31T18:00:35.307874+00:00 | 2022-09-01T07:45:35.609751+00:00 | 382 | false | ```\nclass Solution {\npublic:\n pair<int, int> dfs(TreeNode* root) {\n if(!root) return {0, 0};\n auto [leftDontRob, leftRob] = dfs(root -> left);\n auto [rightDontRob, rightRob] = dfs(root -> right);\n return {\n max(leftDontRob, leftRob) + max(rightDontRob, rightRob),\n root -> val + leftDontRob + rightDontRob\n };\n }\n int rob(TreeNode* root) {\n auto ans = dfs(root);\n return max(ans.first, ans.second);\n }\n};\n```\n**Please Upvote\nthank you!!** | 4 | 0 | ['Dynamic Programming', 'Depth-First Search', 'C', 'C++'] | 0 |
house-robber-iii | ✅ Simplest solution ever on Dynamic Programming | simplest-solution-ever-on-dynamic-progra-157r | /\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() : val(0), left | Deepak_38 | NORMAL | 2022-07-13T13:27:01.839062+00:00 | 2022-07-13T13:27:01.839087+00:00 | 242 | false | /**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic: \n unordered_map<TreeNode*, int> map;\n \n int rob(TreeNode* root) {\n \n if(root==NULL) return 0;\n \n if(map.count(root)) return map[root];\n \n int sum=0;\n \n if(root->left)\n sum+=rob(root->left->left)+rob(root->left->right);\n if(root->right)\n sum+=rob(root->right->left)+rob(root->right->right);\n \n return map[root]=max(root->val+sum,rob(root->left)+rob(root->right)); \n }\n};\n\n\n | 4 | 0 | ['Dynamic Programming', 'C', 'C++'] | 0 |
house-robber-iii | Easy understanding with comments - Java | easy-understanding-with-comments-java-by-eq7z | \nclass Solution {\n public int rob(TreeNode root) {\n if(root == null)\n return 0;\n \n //maintain this to avoid repetitive | v_suresh | NORMAL | 2022-03-29T08:16:58.640576+00:00 | 2022-04-02T23:48:52.172896+00:00 | 522 | false | ```\nclass Solution {\n public int rob(TreeNode root) {\n if(root == null)\n return 0;\n \n //maintain this to avoid repetitive subproblem calculations\n HashMap<TreeNode, Integer> memo = new HashMap<>();\n return robRecursive(root, memo);\n }\n \n public int robRecursive(TreeNode node, HashMap<TreeNode, Integer> memo){\n if(node == null)\n return 0;\n \n //If already calculated, return the result for that node\n if(memo.containsKey(node))\n return memo.get(node);\n \n // Selecting current house and skipping it\'s children if children is not NULL, call its grand children instead, if children is NULL, take 0\n int robCurrentHouse = node.val +\n (node.left == null? 0: robRecursive(node.left.left, memo) + robRecursive(node.left.right,memo)) +\n (node.right == null? 0: robRecursive(node.right.left, memo) + robRecursive(node.right.right,memo));\n \n //If we are skipping current house, lets consider it\'s children\n int skipCurrentHouse = robRecursive(node.left, memo) + robRecursive(node.right, memo);\n \n //Add the newly calculated amount to the respective node on the map\n memo.put(node, Math.max(robCurrentHouse, skipCurrentHouse));\n \n return Math.max(robCurrentHouse, skipCurrentHouse);\n }\n}\n``` | 4 | 0 | ['Memoization', 'Java'] | 1 |
house-robber-iii | ✅Simple approach ,fast and explained (WITH PICTURES) | simple-approach-fast-and-explained-with-t85v6 | Simple Approach:-\nAs theif cannot enter two directly connected house, so he cannot enter root and its children. So, he has only two options :\n1. Either he ent | piyush_krs | NORMAL | 2021-12-05T18:20:30.245959+00:00 | 2022-06-17T10:10:39.038591+00:00 | 128 | false | ***Simple Approach:-***\nAs theif cannot enter two directly connected house, so he cannot enter root and its children. So, he has only two options :\n1. Either he enter the **root and its grandchildren**.\n2. Or he enter the **children only**.\n\nLets write the recursive solution.\n\nWe will use pair (**pair<int,int> t**) to store answer :\n1. **root value**+**sum of grandchildren** in **t.first** and\n2. **sum of children** in **t.second**\n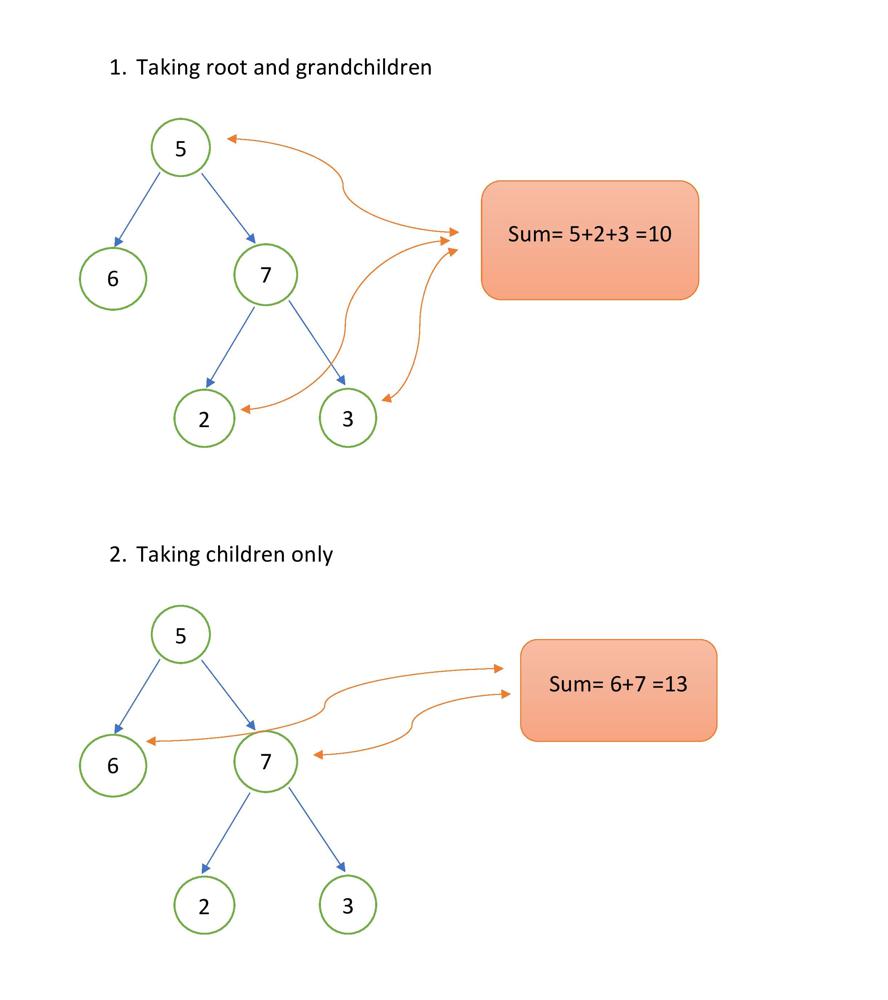\n\n\n```\nclass Solution {\npublic:\n \n pair<int,int> solve(TreeNode* root){\n if(root == NULL)\n return {0,0};\n \n pair<int,int> l = solve(root->left);\n pair<int,int> r = solve(root->right);\n \n pair<int,int> t;\n \n //here l.second + r.second = Sum of grandchildren and l.first + r.first = Sum of children\n //t.first contains maxmium money theif can rob till this house(node)\n t.first = max(root->val + l.second + r.second, l.first + r.first);\n \n //t.second contains the sum of children\n t.second = l.first + r.first;\n \n return t;\n }\n \n int rob(TreeNode* root) {\n return solve(root).first;\n }\n};\n```\n Thanks for reading : ) | 4 | 0 | ['Depth-First Search'] | 0 |
house-robber-iii | Discussion on Approach - Can we do this with level order traversal ? | discussion-on-approach-can-we-do-this-wi-d5ii | Hey,\n\nI was working on this solution. my approach was to solve this with level order traversal. However it seems to be not possible with that approch. but i w | imminal35 | NORMAL | 2021-12-05T10:48:01.821613+00:00 | 2021-12-05T10:52:51.811158+00:00 | 836 | false | Hey,\n\nI was working on this solution. my approach was to solve this with level order traversal. However it seems to be not possible with that approch. but i would like to hear/thoughts/suggestions from you all. \n\nmy approch was:\n1. Traverse the tree level wise.\n2. Put values into 1 D (sum of particular level) array now problem reduced to find maximum sum by skipping alternate values. \n\nChallange : How it\'s possibe to implement a solution which involves kth level value + some nth level value in solution.\n\nLooking forward to some amazing answers on this. Thanks \n\nIn case you want my solution (Not passed) \n```\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n vector<int> vect;\n queue<TreeNode*> q;\n if(root==NULL) return 0;\n q.push(root);\n while(q.size()>0){\n int n = q.size();\n vector<int> t;\n for(int i=0;i<n;i++){\n TreeNode* temp = q.front();\n q.pop();\n t.push_back(temp->val);\n if(temp->left) q.push(temp->left);\n if(temp->right) q.push(temp->right);\n }\n int temp = 0;\n for(auto item : t) temp+=item;\n vect.push_back(temp);\n temp = 0;\n }\n int odd = 0 , even =0 , finalAns = vect[0];\n for(int i=0;i<vect.size();i++){\n for(int k=i+2;k<vect.size();k+=2){\n odd += vect[k];\n }\n for(int k=i+3;k<vect.size();k+=2){\n even = vect[k];\n }\n if(odd+vect[i] >finalAns){\n finalAns = odd+vect[i];\n }\n if(even+vect[i] > finalAns){\n finalAns = even+vect[i];\n }\n odd = 0;\n even = 0;\n }\n return finalAns;\n }\n};\n``` | 4 | 0 | ['Breadth-First Search', 'Recursion', 'C', 'Iterator', 'C++'] | 4 |
house-robber-iii | Easy Intuitive Recursion Python | easy-intuitive-recursion-python-by-vivek-z3ct | Each Node in the tree has two options:\n\n1. \tNot Contribute to the max sum (money) in which case we just call the recursive function for left and right child | vivekaditya8 | NORMAL | 2021-12-05T09:09:59.384261+00:00 | 2021-12-05T09:18:23.270097+00:00 | 298 | false | Each Node in the tree has **two** options:\n\n1. \t**Not Contribute** to the max sum (money) in which case we just call the recursive function for left and right child and add them.\n\n```\n"""\ncond1 = self.rob(root.left)+self.rob(root.right)\n"""\n```\n\n2. \t**Contribute** to the max sum in which case we cannot select the immediate two childs of the node (as per the question constraints direct links cannot be added). In this case we add **the contribution of the current node** and **call the function on the four grandchildren of that node** and add all the four grandchildren sum. \n```\n"""\ncond2 = root.val + (self.rob(root.left.left)+self.rob(root.left.right)+self.rob(root.right.left)+self.rob(root.right.right)\n"""\n```\n\nGet the max of above conditions will be the answer.\n```\n"""\nreturn max(cond1,cond2)\n"""\n```\n\n\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n \n def rob(self, root: Optional[TreeNode]) -> int:\n \n# """\n# Base Condtions\n# """\n if(not root):\n return 0\n elif(not root.left and not root.right):\n return root.val\n # """\n # if only left child is present. cond2 will not contain grandchildren of right ones\n # cond1 will be as simple as just calling on left node;; no adding with right node required.\n # """\n elif(not root.right):\n cond1 = self.rob(root.left)\n cond2 = root.val+self.rob(root.left.left)+self.rob(root.left.right)\n max_money = max(cond1,cond2)\n # """\n # If only right child is present ; similar as above explaination\n # """\n elif(not root.left):\n cond1 = self.rob(root.right)\n cond2 = root.val+self.rob(root.right.left)+self.rob(root.right.right)\n max_money = max(cond1,cond2)\n \n else:\n \n cond1 = self.rob(root.left)+self.rob(root.right)\n cond2 = root.val + (self.rob(root.left.left)+self.rob(root.left.right)+self.rob(root.right.left)+self.rob(root.right.right))\n max_money = max(cond1,cond2)\n \n return max_money\n```\n\n**Inorder to optimise** the above Solution simply **use a dictionary** to store the sum value of a node so that it is not calculated again in recursive calls:\n\nOptimised code : (Same as Above; just added a dictionary)\n\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n d = {}\n def rob(self, root: Optional[TreeNode]) -> int:\n \n# """\n# Base Condtions\n# """\n if(not root):\n return 0\n \n elif(Solution.d.get(root) != None):\n return Solution.d[root]\n \n elif(not root.left and not root.right):\n return root.val\n # """\n # if only left child is present. cond2 will not contain grandchildren of right ones\n # cond1 will be as simple as just calling on left node;; no adding with right node required.\n # """\n elif(not root.right):\n cond1 = self.rob(root.left)\n cond2 = root.val+self.rob(root.left.left)+self.rob(root.left.right)\n max_money = max(cond1,cond2)\n # """\n # If only right child is present ; similar as above explaination\n # """\n elif(not root.left):\n cond1 = self.rob(root.right)\n cond2 = root.val+self.rob(root.right.left)+self.rob(root.right.right)\n max_money = max(cond1,cond2)\n \n else:\n \n cond1 = self.rob(root.left)+self.rob(root.right)\n cond2 = root.val + (self.rob(root.left.left)+self.rob(root.left.right)+self.rob(root.right.left)+self.rob(root.right.right))\n max_money = max(cond1,cond2)\n \n Solution.d[root] = max_money\n \n return max_money\n``` | 4 | 0 | ['Recursion', 'Binary Tree', 'Python'] | 0 |
house-robber-iii | C++ DP | c-dp-by-cqbaoyi-k8ub | This is a straightforwad DP problem. \nThe helper function returns a pair of {the best result of the subtree if root is robbed, the best result of the subtree i | cqbaoyi | NORMAL | 2021-08-28T02:27:55.342730+00:00 | 2021-08-28T02:27:55.342762+00:00 | 516 | false | This is a straightforwad DP problem. \nThe `helper` function returns a pair of `{the best result of the subtree if root is robbed, the best result of the subtree if root is not robbed}`.\n\nTime complexity `O(n)`\nSpace complexity `O(n)` (considering the call stack)\n\n```\n pair<int, int> helper(TreeNode* root)\n {\n if (!root)\n return {0, 0};\n auto l = helper(root->left);\n auto r = helper(root->right);\n int cur_not_rob = max(l.first, l.second) + max(r.first, r.second);\n int cur_rob = l.second + r.second + root->val;\n return {cur_rob, cur_not_rob};\n }\n \n int rob(TreeNode* root) {\n auto res = helper(root);\n return max(res.first, res.second);\n }\n``` | 4 | 0 | ['Dynamic Programming', 'Tree', 'C'] | 2 |
house-robber-iii | [C++] Easy to Understand DP solution | Clean and consize | c-easy-to-understand-dp-solution-clean-a-3j3g | Please upvote if it helps!\n\n#define mp make_pair\nclass Solution {\n map<pair<TreeNode*,int>, int> m;\npublic:\n int func(TreeNode* root, int f)\n {\ | somurogers | NORMAL | 2021-06-22T02:42:31.145106+00:00 | 2021-06-22T02:42:31.145146+00:00 | 238 | false | Please upvote if it helps!\n```\n#define mp make_pair\nclass Solution {\n map<pair<TreeNode*,int>, int> m;\npublic:\n int func(TreeNode* root, int f)\n {\n if(!root)\n return 0;\n \n if(m[mp(root,f)]!=0)\n return m[mp(root,f)];\n \n int ans = func(root->left, 0) + func(root->right, 0);\n if(f==0)\n {\n ans = max(ans, root->val+func(root->left,1) + func(root->right,1));\n }\n return m[mp(root,f)] = ans;\n }\n \n int rob(TreeNode* root) {\n if(!root)\n return 0;\n int ans = func(root,0);\n return ans;\n }\n};\n``` | 4 | 1 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 0 |
house-robber-iii | JAVA | Simple and Easy Solution | Using pair Class | java-simple-and-easy-solution-using-pair-i45j | Do vote up if you like it :)\n\nclass Solution {\n \n class Pair{\n int withRob;\n int withoutRob;\n \n public Pair(int withRo | nknidhi321 | NORMAL | 2021-06-02T07:10:18.546206+00:00 | 2021-06-02T07:10:18.546252+00:00 | 96 | false | **Do vote up if you like it :)**\n```\nclass Solution {\n \n class Pair{\n int withRob;\n int withoutRob;\n \n public Pair(int withRob, int withoutRob){\n this.withRob = withRob;\n this.withoutRob = withoutRob;\n }\n }\n \n public int rob(TreeNode root) {\n Pair obj = robHelper(root);\n return Math.max(obj.withRob, obj.withoutRob);\n }\n \n public Pair robHelper(TreeNode root){\n if(root == null)\n return new Pair(0, 0);\n \n Pair leftObj = robHelper(root.left);\n Pair rightObj = robHelper(root.right);\n \n int withRob = leftObj.withoutRob + rightObj.withoutRob + root.val;\n int withoutRob = Math.max(leftObj.withRob, leftObj.withoutRob) + Math.max(rightObj.withRob, rightObj.withoutRob);\n \n return new Pair(withRob, withoutRob);\n }\n \n}\n``` | 4 | 0 | [] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.