question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
house-robber-iii | Simple Java Recursion+Memoization solution | simple-java-recursionmemoization-solutio-cknk | Time O(n) | Space O(n)\n DP on trees\n \twe can choose b/w grandchildren+parent or children\n\n\n HashMap<TreeNode, Integer> map=new HashMap<>();\n public | shahbaz_07 | NORMAL | 2020-11-28T20:22:25.230768+00:00 | 2020-11-28T20:22:25.230799+00:00 | 331 | false | * Time O(n) | Space O(n)\n* DP on trees\n* \twe can choose b/w grandchildren+parent or children\n```\n\n HashMap<TreeNode, Integer> map=new HashMap<>();\n public int rob(TreeNode root) {\n //we can choose b/w grandchildren+parent or children\n if(root==null)return 0;\n \n if(map.containsKey(root)) return map.get(root);\n \n int total=0;\n \n if(root.left!=null)\n total+=rob(root.left.left)+rob(root.left.right);\n \n if(root.right!=null)\n total+=rob(root.right.left)+rob(root.right.right);\n \n int profit= Math.max((root.val +total), rob(root.left) + rob(root.right));\n \n map.put(root, profit);\n return profit;\n }\n``` | 4 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 0 |
house-robber-iii | [Python 3] Explained Solution (video + code) | python-3-explained-solution-video-code-b-b4gq | \nhttps://www.youtube.com/watch?v=mSzz_bZUVCQ\n\nclass Solution:\n def rob(self, root: TreeNode) -> int:\n @lru_cache(None)\n \n def hel | spec_he123 | NORMAL | 2020-11-23T16:25:53.990575+00:00 | 2020-11-23T16:25:53.990610+00:00 | 409 | false | [](https://www.youtube.com/watch?v=mSzz_bZUVCQ)\nhttps://www.youtube.com/watch?v=mSzz_bZUVCQ\n```\nclass Solution:\n def rob(self, root: TreeNode) -> int:\n @lru_cache(None)\n \n def helper(node, parent_stolen):\n if not node:\n return 0\n \n if parent_stolen:\n # we did steal from parent\n # the only option is to not steal since we stole from the parent\n return helper(node.left, False) + helper(node.right, False)\n\n else:\n # we did NOT steal parent\n # Given a choice to choose b/w stealing or not stealing\n # stealing at the current node\n steal = node.val + helper(node.left, True) + helper(node.right, True)\n \n # NOT stealing current node\n not_stealing = helper(node.left, False) + helper(node.right, False)\n \n return max(steal, not_stealing)\n \n return helper(root, False)\n``` | 4 | 0 | ['Recursion', 'Python', 'Python3'] | 0 |
house-robber-iii | Rust dfs solution | rust-dfs-solution-by-sugyan-0ex6 | rust\nuse std::rc::Rc;\nuse std::cell::RefCell;\nimpl Solution {\n pub fn rob(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {\n let ret = Solution::dfs( | sugyan | NORMAL | 2020-11-23T13:25:07.751543+00:00 | 2020-11-23T13:25:07.751574+00:00 | 144 | false | ```rust\nuse std::rc::Rc;\nuse std::cell::RefCell;\nimpl Solution {\n pub fn rob(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {\n let ret = Solution::dfs(&root);\n std::cmp::max(ret.0, ret.1)\n }\n fn dfs(node: &Option<Rc<RefCell<TreeNode>>>) -> (i32, i32) {\n if let Some(n) = node {\n let l = Solution::dfs(&n.borrow().left);\n let r = Solution::dfs(&n.borrow().right);\n (\n n.borrow().val + l.1 + r.1,\n std::cmp::max(l.0, l.1) + std::cmp::max(r.0, r.1),\n )\n } else {\n (0, 0)\n }\n }\n}\n``` | 4 | 0 | ['Depth-First Search', 'Rust'] | 0 |
house-robber-iii | JavaScript recursion solution | javascript-recursion-solution-by-sao_mai-jlwq | Max at root is either the sum of max left subtree and max right subtree, or the sum of the root with max of left subtree children and max of right subtree child | sao_mai | NORMAL | 2020-10-18T20:46:36.520827+00:00 | 2020-10-18T20:46:36.520868+00:00 | 426 | false | Max at root is either the sum of max left subtree and max right subtree, or the sum of the root with max of left subtree children and max of right subtree children. The key here is that you want to return both the max at the root and the max of its children in the helper method.\n```\n/**\n * Definition for a binary tree node.\n * function TreeNode(val, left, right) {\n * this.val = (val===undefined ? 0 : val)\n * this.left = (left===undefined ? null : left)\n * this.right = (right===undefined ? null : right)\n * }\n */\n/**\n * @param {TreeNode} root\n * @return {number}\n */\nvar rob = function(root) {\n return helper(root)[0];\n};\n\nfunction helper(root){\n if(root == null) return [0, 0];\n const left = helper(root.left);\n const right = helper(root.right);\n const currMax = Math.max(left[0] + right[0], root.val + left[1] + right[1]);\n const childrenMax = left[0] + right[0]; \n return [currMax, childrenMax];\n}\n``` | 4 | 0 | ['Recursion', 'JavaScript'] | 0 |
house-robber-iii | Python DP Soln | python-dp-soln-by-srajsonu-12pj | \nclass Solution:\n def dp(self, root, dp):\n if not root: return 0\n if root in dp:\n return dp[root]\n \n val = 0\n | srajsonu | NORMAL | 2020-08-21T05:42:25.021440+00:00 | 2020-08-21T05:42:25.021482+00:00 | 302 | false | ```\nclass Solution:\n def dp(self, root, dp):\n if not root: return 0\n if root in dp:\n return dp[root]\n \n val = 0\n if root.left:\n val += self.dp(root.left.left, dp) + self.dp(root.left.right, dp)\n \n if root.right:\n val += self.dp(root.right.left, dp) + self.dp(root.right.right, dp)\n \n val = max(val + root.val, self.dp(root.left, dp) + self.dp(root.right, dp))\n dp[root] = val\n return val\n \n def rob(self, root: TreeNode) -> int:\n dp = {}\n return self.dp(root, dp)\n``` | 4 | 0 | ['Memoization', 'Python'] | 2 |
house-robber-iii | GOOGLE INTERVIEW QUESTION | DP | INTUITIVE EXPLANATION !! | google-interview-question-dp-intuitive-e-4dq4 | It is same as the question https://leetcode.com/problems/house-robber/ but now we have to steal in a Binary Tree. At that question We have used our DP as maxim | prajwalpant15 | NORMAL | 2020-08-06T13:18:30.606542+00:00 | 2020-08-06T13:27:01.800466+00:00 | 365 | false | It is same as the question https://leetcode.com/problems/house-robber/ but now we have to steal in a Binary Tree. At that question We have used our DP as maximum profit at ith index if we pick value at ith index or we do not pick the value at ith index.\n\nHere We have to use the same Dp state but we have to use it to Every Node in the tree. At Every Node we can store the maximum profit till that node if we rob the node or if we donot rob it.\n\nSo you have to store a pair at every Node pair is like ** <max profit if we robNode , max profit if we doNotRob> \n**\n**Crux: If you are robbing the currNode you cant rob the childrens.\nif you choose to rob the currNode\nmaxProfit if we ROB currNode=currNodeVal+maxSumOfleftChild when we dont rob it +maxSumOfrightChild when we dont rob it.\nbecause you cant rob the childrens if you rob the currNode**\n\n**If you choose to not rob the currNode then \nmaxProfit if we doNotROB currNode=maxFromLeftPair+maxFromRightPair\nbecause if you are not robbing the current node then you can make any choice from the childrens you can rob the childrens or you dont its your wish so you have to return max from left child pair and from right child pair and add them.**\n\n```\nclass Solution\n{\n \npublic:\n pair<int,int> topDownDp(TreeNode* root)\n {\n if(root==NULL) return {0,0};\n \n pair<int,int> fromLeft=topDownDp(root->left);\n pair<int,int> fromRight=topDownDp(root->right);\n \n \n int robNode=root->val+fromLeft.second+fromRight.second;\n int doNotRob=max(fromLeft.first,fromLeft.second)+max(fromRight.first,fromRight.second);\n \n return {robNode,doNotRob};\n }\n\n int rob(TreeNode* root) \n {\n pair<int,int> choices=topDownDp(root);\n return max(choices.first,choices.second); \n }\n\n}; | 4 | 0 | [] | 1 |
house-robber-iii | Python Intuitive O(n) solution | python-intuitive-on-solution-by-bovinova-jmlf | For each node, compute the maximum money whether choosing the node or not.\n```\nclass Solution:\n def rob(self, root: TreeNode) -> int:\n \n d | bovinovain | NORMAL | 2020-08-05T21:53:40.098658+00:00 | 2020-08-05T21:53:40.098693+00:00 | 172 | false | For each node, compute the maximum money whether choosing the node or not.\n```\nclass Solution:\n def rob(self, root: TreeNode) -> int:\n \n def check(root): \n\t\t# return a tuple (choosing the root, not choosing the root)\n if not root:\n return (0,0)\n left = check(root.left)\n right = check(root.right)\n return (root.val + left[1] + right[1], max(left) + max(right))\n \n return max(check(root))\n\t\t | 4 | 0 | [] | 1 |
house-robber-iii | C++ DP solution with a vector to store two states | c-dp-solution-with-a-vector-to-store-two-gh65 | In this code, at every node, it returns a vector storing two states : rob this node or not rob\nres[0] means the max value I can get from the botton if I rob th | AL2O3_yhl | NORMAL | 2020-05-23T16:48:00.676603+00:00 | 2020-05-23T16:48:00.676648+00:00 | 364 | false | In this code, at every node, it returns a vector storing two states : rob this node or not rob\nres[0] means the max value I can get from the botton **if I rob this node**\nres[1] means the max value I can get from the botton **if I don\'t rob this node**\nTime O(n) the recu will visit every node\nSpace O(1n) every node takes O(1) space\n```\nclass Solution {\npublic:\n int rob(TreeNode* root) {\n if(!root) return 0;\n vector<int> res = robHelper(root);\n return max(res[0], res[1]);\n }\n vector<int> robHelper(TreeNode* root){\n vector<int> res(2, 0);\n if(!root) return res;\n if(root->left == root->right){\n res[0] = root->val;\n return res;\n } \n vector<int> l = robHelper(root->left);\n vector<int> r = robHelper(root->right);\n res[0] = l[1] + r[1] + root->val;\n res[1] = max(max(l[1] + r[1], l[0] + r[0]), max(l[1] + r[0], l[0] + r[1]));\n return res;\n }\n};\n``` | 4 | 0 | ['Dynamic Programming', 'C', 'C++'] | 1 |
house-robber-iii | [Python] DFS solution with explanations | python-dfs-solution-with-explanations-by-shy4 | Explanations:\nFor each node, the robber can either rob this node and leave out the consecutive left and right nodes, or he/she can not rob this node and try ou | codingasiangirll | NORMAL | 2020-05-06T18:34:23.652639+00:00 | 2020-05-06T18:36:28.303121+00:00 | 112 | false | **Explanations**:\nFor each node, the robber can either rob this node and leave out the consecutive left and right nodes, or he/she can not rob this node and try out different combinations to find the max value that he/she can rob. The combinations include rob 1. both left and right nodes, 2. rob only left node and not rob the right one, 3. rob only right node and not rob the left one, 4. rob neither of the left or right nodes. \n`_rob` function will return the two scenario for each node.\nIn the end, return the mac value.\n\n**Complexcity**: Time O(N), N is the number of nodes. Space O(1).\n```\nclass Solution:\n def rob(self, root: TreeNode) -> int:\n def _rob(node):\n if not node: return 0, 0\n left, left_no = _rob(node.left)\n right, right_no = _rob(node.right)\n cur = node.val + left_no + right_no\n no = max(left + right, left + right_no, left_no + right, left_no + right_no)\n return cur, no\n return max(_rob(root))\n``` | 4 | 0 | [] | 0 |
house-robber-iii | Go 4ms very simple | go-4ms-very-simple-by-tjucoder-wg43 | go\nfunc rob(root *TreeNode) int {\n\treturn max(robber(root))\n}\n\nfunc robber(node *TreeNode) (int, int) {\n\tif node == nil {\n\t\treturn 0, 0\n\t}\n\tgold | tjucoder | NORMAL | 2020-04-07T13:19:11.066108+00:00 | 2020-04-07T13:19:11.066145+00:00 | 242 | false | ```go\nfunc rob(root *TreeNode) int {\n\treturn max(robber(root))\n}\n\nfunc robber(node *TreeNode) (int, int) {\n\tif node == nil {\n\t\treturn 0, 0\n\t}\n\tgold := node.Val\n\tl1, l2 := robber(node.Left)\n\tr1, r2 := robber(node.Right)\n\tc1 := gold + l2 + r2\n\tc2 := max(l1, l2) + max(r1, r2)\n\treturn c1, c2\n}\n\nfunc max(values ...int) int {\n\tmaxValue := math.MinInt32\n\tfor _, v := range values {\n\t\tif v > maxValue {\n\t\t\tmaxValue = v\n\t\t}\n\t}\n\treturn maxValue\n}\n``` | 4 | 0 | ['Go'] | 0 |
house-robber-iii | Linear time -- Python | linear-time-python-by-ht_wang-tint | Same logic as House Robber\n\ndef rob(self, root):\n """\n :type root: TreeNode\n :rtype: int\n """\n def helper(root):\n | ht_wang | NORMAL | 2019-11-30T01:04:26.466300+00:00 | 2019-11-30T18:46:09.732396+00:00 | 474 | false | Same logic as [House Robber](https://leetcode.com/problems/house-robber/discuss/440346/python-constant-space-O(N))\n```\ndef rob(self, root):\n """\n :type root: TreeNode\n :rtype: int\n """\n def helper(root):\n if not root:\n return 0, 0 \n \n l_prev, l_rob = helper(root.left)\n r_prev, r_rob = helper(root.right)\n \n prev = max([l_prev+r_prev, l_rob+r_rob, l_prev+r_rob, l_rob+r_prev])\n rob = l_prev+r_prev+root.val\n return prev, rob\n return max(helper(root))\n``` | 4 | 0 | [] | 1 |
house-robber-iii | Java bottom-up and top-down solutions using DP | java-bottom-up-and-top-down-solutions-us-54w9 | The naive solution is straightforward, just traverse the tree and in each node, we either take it or not. If we take it, we cannot take its children, if not ta | yfcheng | NORMAL | 2016-03-12T01:44:25+00:00 | 2016-03-12T01:44:25+00:00 | 1,287 | false | The naive solution is straightforward, just traverse the tree and in each node, we either take it or not. If we take it, we cannot take its children, if not take, we can take either or both of the children. This will cause TLE due to extra calculation. Since this is a house robber problem, DP is the first come to mind for optimization. There are two ways to work with this problem. The top-down is the most intuitive one for me, as follows. Used two map, hasRoot and noRoot, since we need to keep track of the result for either rob the house or not. \n\nThe second approach is bottom-up. It is not very intuitive for a tree. But one can think about post-order traversal. We traverse the left and the right child and return some necessary result, and then process the root. First, what do we need the child to return? So from the first solution, we can see that we either rob a house or not, so the child needs to return two values, *rob* or *no rob* for the root. Here we can just use an int array to keep the two values. `// traverse the tree int[] left = helper(curr.left); int[] right = helper(curr.right);` Here left[0] represents robbing root node, left[1] not robbing. \n\nThen we do stuff for the root node. We need an int array again to save its result. We either rob root, and take the `left[1]` and `right[1]` and add root value to it, or we don't rob root, and take the largest one for left and right. In the end, we just return res. \n\nHere are two solutions, hope it helps!\n\n\nTop-down approach:\n\n Map<TreeNode, Integer> hasRoot = new HashMap<>();\n Map<TreeNode, Integer> noRoot = new HashMap<>();\n public int rob(TreeNode root) {\n if (root == null) {\n return 0;\n }\n int max = Math.max(helper(root, true), helper(root, false));\n return max;\n }\n \n private int helper(TreeNode root, boolean canrob) {\n if (root == null) {\n return 0;\n }\n int res = 0;\n if (canrob) {\n // check the hasRoot map for previous calculated\n if(hasRoot.containsKey(root)) {\n return hasRoot.get(root);\n }\n res = Math.max(helper(root.left, false) + helper(root.right, false) + root.val, helper(root.left, true) + helper(root.right, true));\n hasRoot.put(root, res);\n } else {\n // check the noRoot map\n if(noRoot.containsKey(root)) {\n return noRoot.get(root);\n }\n res = helper(root.left, true) + helper(root.right, true);\n noRoot.put(root, res);\n }\n return res;\n }\n\n\nBottom-up:\n\n // bottom-up solution\n public int rob(TreeNode root) {\n int[] num = helper(root);\n // nums[0] includes root, nums[1] excludes root\n return Math.max(num[0], num[1]);\n }\n private int[] helper(TreeNode curr) {\n if (curr == null) {\n return new int[2];\n }\n // traverse the tree\n int[] left = helper(curr.left);\n int[] right = helper(curr.right);\n \n // do stuff\n \n int[] res = new int[2];\n // case 1: add root value, so exclude both left and right\n res[0] = left[1] + right[1] + curr.val; \n // case 2: exclued root value, get max from both left child and right child\n res[1] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]); \n \n // done stuff\n \n return res;\n } | 4 | 0 | [] | 1 |
house-robber-iii | Simple 1ms Java solution with easy comments | simple-1ms-java-solution-with-easy-comme-xfzh | /*\n \u5411\u5de6\u53f3\u4e24\u8fb9\u8981\u6570\u636e, \u9010\u5c42\u5411\u4e0a\u8fd4\u56de\u3002\n \u8fd4\u56de\u7684\u662fint[2] result.\n | mach7 | NORMAL | 2016-03-12T21:28:09+00:00 | 2016-03-12T21:28:09+00:00 | 634 | false | /*\n \u5411\u5de6\u53f3\u4e24\u8fb9\u8981\u6570\u636e, \u9010\u5c42\u5411\u4e0a\u8fd4\u56de\u3002\n \u8fd4\u56de\u7684\u662fint[2] result.\n result[0] -- \u62a2\u5f53\u524droot\u6240\u80fd\u5f97\u7684\u6700\u5927\u503c\u3002\n result[1] -- \u4e0d\u62a2\u5f53\u524droot\u6240\u80fd\u5f97\u7684\u6700\u5927\u503c\u3002\n */\n public class Solution {\n public int rob(TreeNode root) {\n int[] result = findMax(root);\n return Math.max(result[0], result[1]);\n }\n \n // returns int[2] result. \n // result[0] -- max value robbing current root; result[1] -- max value without robbing current root.\n private int[] findMax(TreeNode root) {\n if (root == null) {\n return new int[] {0, 0};\n }\n int[] left = findMax(root.left);\n int[] right = findMax(root.right);\n int result0 = root.val + left[1] + right[1]; // rob current root\n int result1 = Math.max(left[0], left[1]) + Math.max(right[0], right[1]); // not rob current root\n return new int[] {result0, result1};\n }\n } | 4 | 1 | [] | 0 |
house-robber-iii | 6-line Python solution, return (subtree max money if not rob this node, subtree max money) | 6-line-python-solution-return-subtree-ma-r719 | def rob(self, root):\n def dfs(node):\n # return (subtree max money if not rob this node, subtree max money)\n if not node: return | kitt | NORMAL | 2016-03-21T16:59:12+00:00 | 2016-03-21T16:59:12+00:00 | 1,224 | false | def rob(self, root):\n def dfs(node):\n # return (subtree max money if not rob this node, subtree max money)\n if not node: return 0, 0\n max_l_ignore, max_l = dfs(node.left)\n max_r_ignore, max_r = dfs(node.right)\n return max_l + max_r, max(max_l + max_r, node.val + max_l_ignore + max_r_ignore)\n\n return dfs(root)[1] | 4 | 0 | ['Depth-First Search', 'Python'] | 1 |
house-robber-iii | Two solutions with Java (1 ms) | two-solutions-with-java-1-ms-by-skoy12-n7qw | public int rob(TreeNode root) {\n if(root==null) return 0;\n rob1(root);\n return root.val;\n }\n public int rob1(TreeNode root){\n | skoy12 | NORMAL | 2016-04-24T11:45:37+00:00 | 2016-04-24T11:45:37+00:00 | 1,333 | false | public int rob(TreeNode root) {\n if(root==null) return 0;\n rob1(root);\n return root.val;\n }\n public int rob1(TreeNode root){\n if(root==null) return 0;\n int pre=0;\n root.val+=rob1(root.left)+rob1(root.right);\n if(root.left!=null) pre+=root.left.val;\n if(root.right!=null) pre+=root.right.val;\n root.val=Math.max(pre,root.val);\n return pre;\n }\nThe other solution need extra class:\n\n class Profit{\n int preprofit;\n int maxprofit;\n Profit(int pre,int max){\n preprofit=pre;\n maxprofit=max;\n }\n }\n public class Solution {\n public int rob(TreeNode root ) {\n return rob1(root).maxprofit;\n }\n public Profit rob1(TreeNode root){\n if (root == null) return new Profit(0, 0);\n int pre = 0, max = root.val;\n Profit left = rob1(root.left), right = rob1(root.right);\n max += left.preprofit + right.preprofit;\n pre = left.maxprofit + right.maxprofit;\n max = Math.max(pre,max);\n return new Profit(pre,max);\n }\n } | 4 | 2 | [] | 5 |
house-robber-iii | C++ implementation refer to @fun4LeetCode | c-implementation-refer-to-fun4leetcode-b-lpkb | First naive Solution \n\n class Solution {\n public:\n int rob(TreeNode root) {\n if(root == NULL) return 0;\n int val = 0;\ | rainbowsecret | NORMAL | 2016-03-20T09:40:58+00:00 | 2016-03-20T09:40:58+00:00 | 998 | false | First naive Solution \n\n class Solution {\n public:\n int rob(TreeNode* root) {\n if(root == NULL) return 0;\n int val = 0;\n if(root->left) {\n val += rob(root->left->left) + rob(root->left->right);\n }\n if(root->right) {\n val += rob(root->right->left) + rob(root->right->right);\n }\n return max(val + root->val, rob(root->left) + rob(root->right));\n }\n };\n\nSecond, use the dict to record the sub-problem information method\n\n class Solution {\n public:\n int rob(TreeNode* root) {\n unordered_map<TreeNode*, int> dict;\n return help(root, dict);\n }\n \n int help(TreeNode* root, unordered_map<TreeNode*, int>& dict) {\n if(root == NULL) return 0;\n if(dict.find(root)!=dict.end()) return dict[root];\n int val = 0;\n if(root->left != NULL) {\n val += help(root->left->left, dict) + help(root->left->right, dict);\n }\n if(root->right != NULL) {\n val += help(root->right->left, dict) + help(root->right->right, dict);\n }\n val = max(val + root->val, help(root->left, dict) + help(root->right, dict));\n dict[root] = val;\n return val;\n }\n };\n\nThird Solution is optimized a bit :\n\n class Solution {\n public:\n int rob(TreeNode* root) {\n vector<int> result = help(root);\n return max(result[0], result[1]);\n }\n /**\n * result[0] : record the max sum exclude the root value\n * result[1] : record the max sum include the root value\n **/\n vector<int> help(TreeNode* root) {\n vector<int> result(2, 0);\n if(!root) {\n return result;\n }\n vector<int> left = help(root->left);\n vector<int> right = help(root->right);\n /** root excluded : so we can include the child or not **/\n result[0] = max(left[0], left[1]) + max(right[0], right[1]);\n /** root included : so must exclude the child **/\n result[1] = root->val + left[0] + right[0];\n return result;\n }\n }; | 4 | 0 | [] | 2 |
house-robber-iii | Short Python solution | short-python-solution-by-dimal97psn-nc24 | class Solution(object):\n def rob(self, root):\n def solve(root):\n if not root:\n return 0, 0\n | dimal97psn | NORMAL | 2016-06-29T03:32:20+00:00 | 2016-06-29T03:32:20+00:00 | 1,089 | false | class Solution(object):\n def rob(self, root):\n def solve(root):\n if not root:\n return 0, 0\n left, right = solve(root.left), solve(root.right)\n return (root.val + left[1] + right[1]), (max(left) + max(right))\n return max(solve(root)) | 4 | 0 | ['Python'] | 1 |
house-robber-iii | ✅ Easy to Understand | Recursion with Memorization | DP | Detailed Video Explanation🔥 | easy-to-understand-recursion-with-memori-i33e | IntuitionThe problem is a variation of the House Robber problem but applied to a binary tree. Since we cannot rob two directly linked houses (nodes), we must ma | sahilpcs | NORMAL | 2025-03-15T10:12:49.588469+00:00 | 2025-03-15T10:13:17.028329+00:00 | 507 | false | # Intuition
The problem is a variation of the House Robber problem but applied to a binary tree. Since we cannot rob two directly linked houses (nodes), we must make an optimal choice at each node to maximize the robbed amount. The key observation is that for each node, we have two choices: either rob it and skip its children or skip it and consider robbing its children.
# Approach
We use a recursive approach with memoization to avoid redundant computations.
1. Define a recursive function that takes a node and a boolean flag (`probbed`) indicating whether the parent node was robbed.
2. If the node is null, return 0 (base case).
3. Use a HashMap (`dp`) to store results to prevent recomputation.
4. If the current node is not robbed, we can include its value and call the function on its grandchildren.
5. If we skip the current node, we call the function on its immediate children.
6. The result for each node is the maximum of these two options.
# Complexity
- Time complexity:
- Since we process each node once and use memoization, the time complexity is $$O(n)$$ where $$n$$ is the number of nodes in the tree.
- Space complexity:
- The recursive call stack takes $$O(h)$$ space, where $$h$$ is the height of the tree. In the worst case (skewed tree), $$h = O(n)$$. The HashMap also takes $$O(n)$$ space for memoization. Therefore, the overall space complexity is $$O(n)$$.
# Code
```java []
class Solution {
// HashMap to store computed results for each TreeNode to avoid recomputation (memoization)
Map<TreeNode, Integer[]> dp;
public int rob(TreeNode root) {
dp = new HashMap(); // Initialize the memoization map
return sol(root, false); // Start the recursive function with root and 'false' (not robbed)
}
// Recursive function to determine the maximum money that can be robbed
private int sol(TreeNode root, boolean probbed){
if(root == null) // Base case: if the node is null, return 0
return 0;
// Store computed values for both states (robbed or not) to optimize recursion
dp.putIfAbsent(root, new Integer[2]);
if(dp.get(root)[probbed ? 1 : 0] != null) // If already computed, return cached result
return dp.get(root)[probbed ? 1 : 0];
int one = 0;
// Case 1: If the current node is NOT robbed in the previous step, we can rob it
if(!probbed){
one = root.val + sol(root.left, true) + sol(root.right, true);
}
// Case 2: Skip robbing the current node and explore the next level of children
int two = sol(root.left, false) + sol(root.right, false);
// Store the maximum value from both choices in the memoization map and return it
return dp.get(root)[probbed ? 1 : 0] = Math.max(one, two);
}
}
```
https://youtu.be/xZYVvph1I-I | 3 | 0 | ['Dynamic Programming', 'Tree', 'Depth-First Search', 'Binary Tree', 'Java'] | 1 |
house-robber-iii | Easy approach | easy-approach-by-kadir3-u9cz | Intuitionits very effective solution and easy to understand. (first time posting solution)Approachusing dynamic programming to calculate each nodesComplexity
T | Kadir3 | NORMAL | 2025-01-29T07:12:56.421737+00:00 | 2025-01-29T07:12:56.421737+00:00 | 514 | false | # Intuition
its very effective solution and easy to understand. (first time posting solution)
# Approach
using dynamic programming to calculate each nodes
# Complexity
- Time complexity:
Its very fast
- Space complexity:
idk
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
pair<int,int> rec(TreeNode* root){
pair<int,int> x={0,0},y={0,0},z={0,0};
if (root->left==NULL && root->right==NULL) {z.first=root->val; return z;}
if (root->left!=NULL){ x=rec(root->left);}
if (root->right!=NULL){ y=rec(root->right);}
z.first=x.second+y.second+root->val;
z.second=max(x.first,x.second)+max(y.first,y.second);
return z;
}
int rob(TreeNode* root) {
auto k=rec(root);
return max(k.first,k.second);
}
};
``` | 3 | 0 | ['Dynamic Programming', 'C++'] | 2 |
house-robber-iii | Let's rob the Houses 🏠 | Simple and Easy Solution ✅✅ | Recursion + Memoization ✅ | lets-rob-the-houses-simple-and-easy-solu-sq8z | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves determining the maximum amount of money that can be robbed from a | its_kartike | NORMAL | 2024-08-13T09:00:16.569125+00:00 | 2024-08-13T09:00:16.569156+00:00 | 356 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves determining the maximum amount of money that can be robbed from a binary tree of houses without robbing two directly connected houses. My initial thought is to use dynamic programming to track the maximum value that can be obtained at each node, considering two cases: robbing the current house or not robbing it.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Recursive Function with Memoization**: We define a recursive function `doingRobbery` that calculates the maximum amount of money that can be robbed starting from the current node (`curr`).\n - If we rob the current node, we cannot rob its immediate children, so we consider the values of its grandchildren.\n - If we do not rob the current node, we can choose to rob or not rob its immediate children, so we take the maximum value for each child.\n - We store the results in a map (`ump`) to avoid redundant calculations (memoization).\n2. **Base Cases**: If the current node is `nullptr`, return 0. If the node has already been processed, return the stored result.\n3. **Rob or Not Rob**: For each node, calculate the maximum money that can be robbed by either robbing the current node or not robbing it. The final result is the maximum of these two values.\n4. **Main Function**: The `rob` function starts the process from the root node, using the helper function `doingRobbery` to determine the maximum amount that can be robbed.\n\n# Complexity\n- **Time complexity**: \n - The time complexity is $$O(n)$$, where $$n$$ is the number of nodes in the tree. This is because each node is processed only once, and memoization ensures that we do not recompute the results for any node.\n\n- **Space complexity**: \n - The space complexity is $$O(n)$$ due to the recursion stack and the unordered map used for memoization, where $$n$$ is the number of nodes in the tree.\n\n# Code\n```cpp []\nclass Solution {\n int doingRobbery(TreeNode *curr, unordered_map<TreeNode *, int> &ump){\n if(curr == nullptr) return 0;\n if(ump.find(curr) != ump.end()) return ump[curr];\n\n // Rob the current node\n int robbed = curr->val + \n ((curr->left) ? (doingRobbery(curr->left->left, ump) + doingRobbery(curr->left->right, ump)) : 0) + \n ((curr->right) ? (doingRobbery(curr->right->left, ump) + doingRobbery(curr->right->right, ump)) : 0);\n\n // Do not rob the current node\n int notRobbed = doingRobbery(curr->left, ump) + doingRobbery(curr->right, ump);\n\n // Store the result in the map and return the maximum of both scenarios\n return ump[curr] = max(robbed, notRobbed);\n }\n\npublic:\n int rob(TreeNode* root) {\n unordered_map<TreeNode *, int> ump;\n return doingRobbery(root, ump);\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Tree', 'Recursion', 'Memoization', 'C++'] | 0 |
house-robber-iii | [Python3] Easy to understand | Recursive Post-order | Linear time & space | python3-easy-to-understand-recursive-pos-9b19 | Intuition\nAt each node, we either need to consider the node iteslf or its children.\n\n# Approach\nFrom each node, return the max we can get by including the n | open_sourcerer_ | NORMAL | 2023-09-17T20:43:50.845298+00:00 | 2023-09-17T20:43:50.845321+00:00 | 398 | false | # Intuition\nAt each node, we either need to consider the node iteslf or its children.\n\n# Approach\nFrom each node, return the max we can get by including the node and also max without the node.\n\n1. For base cases (Leaf node\'s Null children), return `[0, 0]`\n2. With postorder traversal, at each node up in recusrsion calculate the following and return:\n\n```\nwithCurrentNode = node.val + leftSubtreeMaxWithoutRoot + rightSubtreeMaxWithoutRoot\n\nwithoutCurrentNode = max(leftSubtreeMaxWithRoot, leftSubtreeMaxWithoutRoot) + max(rightSubtreeMaxWithRoot, rightSubtreeMaxWithoutRoot)\n```\n\n# Complexity\n- Time complexity:\nO(N) - We need to look at all the nodes once\n- Space complexity:\nO(H) Space - H being the height of the tree. For an unbalanced tree, this will be O(N) Space. The space is for maintaining the call stack\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def rob(self, root: Optional[TreeNode]) -> int:\n\n def postorder(root):\n if not root:\n return [0, 0] # [ withRoot, withoutRoot ]\n \n left = postorder(root.left)\n right = postorder(root.right)\n\n withRoot = root.val + left [1] + right[1]\n withoutRoot = max(left) + max(right)\n return [withRoot, withoutRoot]\n \n return max(postorder(root))\n``` | 3 | 0 | ['Python3'] | 0 |
house-robber-iii | NeetCode solution|| Clean code | neetcode-solution-clean-code-by-jain_06_-feg1 | \n# Code\n\nclass Solution {\npublic:\n\n pair<int,int> helper(TreeNode* root){\n if(root == NULL) return {0,0};\n\n pair<int,int> left1 = help | jain_06_07 | NORMAL | 2023-07-14T10:13:09.177567+00:00 | 2023-07-14T10:13:09.177584+00:00 | 394 | false | \n# Code\n```\nclass Solution {\npublic:\n\n pair<int,int> helper(TreeNode* root){\n if(root == NULL) return {0,0};\n\n pair<int,int> left1 = helper(root->left);\n pair<int,int> right1 = helper(root->right);\n\n int with = root->val + left1.second + right1.second ;\n int without = max(left1.first, left1.second) + max(right1.first, right1.second);\n\n return {with, without};\n }\n int rob(TreeNode* root) {\n pair<int,int> ans = helper(root);\n return max(ans.first, ans.second);\n }\n};\n``` | 3 | 0 | ['C++'] | 1 |
maximum-path-quality-of-a-graph | [Python] short dfs, explained | python-short-dfs-explained-by-dbabichev-n3c6 | Key to success in this problem is to read problem constraints carefully: I spend like 10 minutes before I understand that problem can be solved using very simpl | dbabichev | NORMAL | 2021-11-07T04:00:45.482990+00:00 | 2021-11-07T04:00:45.483025+00:00 | 8,055 | false | Key to success in this problem is to read problem constraints carefully: I spend like 10 minutes before I understand that problem can be solved using very simple dfs. Why? Because it is given that `maxTime <= 100` and `time_j >= 10`. It means that we can make no more than `10` steps in our graph! So, all we need to do is to run `dfs(node, visited, gain, cost)`, where:\n\n1. `node` is current node we are in.\n2. `visited` is set of visited nodes: we need to keep set, because we count visitet nodes only once.\n3. `gain` is total gain we have so far.\n4. `cost` is how much time we still have.\n\n#### Complexity\nWe have at most `10` steps, and it is also given that each node have at most degree `4`, so in total we can make no more than `4^10` states. That is why we will not get TLE.\n\n#### Code\n```python\nclass Solution:\n def maximalPathQuality(self, values, E, maxTime):\n G = defaultdict(list)\n for x, y, w in E:\n G[x].append((y, w))\n G[y].append((x, w))\n \n def dfs(node, visited, gain, cost):\n if node == 0: self.ans = max(self.ans, gain)\n for neib, w in G[node]:\n if w <= cost:\n dfs(neib, visited | set([neib]), gain + (neib not in visited) * values[neib], cost - w)\n\n self.ans = 0\n dfs(0, set([0]), values[0], maxTime)\n return self.ans\n```\n\nIf you have any questoins, feel free to ask. If you like the solution and explanation, please **upvote!** | 130 | 4 | ['Depth-First Search'] | 15 |
maximum-path-quality-of-a-graph | Simple DFS solution (C++) | simple-dfs-solution-c-by-byte_walker-nme8 | We will do DFS in this problem. We have the condition here that we can visit a node any number of times but we shall add its value only once for that path for t | Byte_Walker | NORMAL | 2021-11-07T04:03:57.490926+00:00 | 2021-11-07T05:44:47.091319+00:00 | 7,268 | false | We will do DFS in this problem. We have the condition here that we can visit a node any number of times but we shall add its value only once for that path for the calculation of its quality. \n\nSo, we would require a visited array which would keep track of the visited nodes so that we do not add its value again into the quality score. \n\nHere, we are doing DFS and we increase the count of that node in visited array indicating how many times we have visited that node. If its being visited for the first time, we add its value to our sum. After we have processed all its neighbours, we then mark the current node as unvisited i.e. we reduce the count of that node from the visited array. \n\nWe do not use a boolean visited array since if we go that way we would not be able to track visited properly since if we turn visited back to false after processing its neighbours, it would mean we treat that node as non visited even if its been visited multiple times before. To account for that, we use counter based visited array which increases or decreases the visited count thus serving its purpose.\n\nThe code provided below is self explanatory and I am sure you would be able to understand it easily.\n\n```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size();\n int res = values[0];\n vector<vector<pair<int,int>>> graph(n);\n for(int i=0;i<edges.size();i++)\n {\n graph[edges[i][0]].push_back({edges[i][1], edges[i][2]});\n graph[edges[i][1]].push_back({edges[i][0], edges[i][2]});\n }\n \n vector<int> visited(n, 0);\n dfs(graph, values, visited, res, 0, 0, 0, maxTime);\n return res;\n }\n \n void dfs(vector<vector<pair<int,int>>>& graph, vector<int>& values, vector<int>& visited, int& res, int node, int score, int time, int& maxTime)\n {\n if(time > maxTime)\n return;\n \n if(visited[node] == 0)\n score += values[node];\n \n \xA0 \xA0 \xA0 \xA0visited[node]++;\n\t\t\n \xA0 \xA0 \xA0\n \xA0 \xA0 \xA0 \xA0if(node == 0)\n res = max(res, score);\n \n for(auto it : graph[node])\n {\n int neigh = it.first;\n int newTime = time + it.second;\n dfs(graph, values, visited, res, neigh, score, newTime, maxTime);\n }\n \n visited[node]--;\n }\n};\n```\n | 99 | 1 | ['Depth-First Search', 'C', 'C++'] | 16 |
maximum-path-quality-of-a-graph | [Python] Concise DFS | python-concise-dfs-by-lee215-poie | Python\npy\n def maximalPathQuality(self, A, edges, maxTime):\n G = collections.defaultdict(dict)\n for i, j, t in edges:\n G[i][j] | lee215 | NORMAL | 2021-11-07T04:50:19.381026+00:00 | 2021-11-07T04:50:19.381056+00:00 | 4,944 | false | **Python**\n```py\n def maximalPathQuality(self, A, edges, maxTime):\n G = collections.defaultdict(dict)\n for i, j, t in edges:\n G[i][j] = G[j][i] = t\n\n def dfs(i, seen, time):\n res = sum(A[j] for j in seen) if i == 0 else 0\n for j in G[i]:\n if time >= G[i][j]:\n res = max(res, dfs(j, seen | {j}, time - G[i][j]))\n return res\n\n return dfs(0, {0}, maxTime)\n``` | 40 | 1 | [] | 9 |
maximum-path-quality-of-a-graph | Java DFS O(2^20) with explanation | java-dfs-o220-with-explanation-by-hdchen-saon | I spent a few minutes but I can\'t come out a workable solution until I read the constraints very carefully.\n\nAnalysis\n1. 10 <= time[j], maxTime <= 100 By th | hdchen | NORMAL | 2021-11-07T05:42:59.077988+00:00 | 2021-11-07T05:47:03.882305+00:00 | 4,072 | false | I spent a few minutes but I can\'t come out a workable solution until I read the constraints very carefully.\n\n**Analysis**\n1. `10 <= time[j], maxTime <= 100` By this constraint, there are at most 10 nodes in a path.\n2. There are at most `four` edges connected to each node\n3. Based on the aforementioned constraints, the brute force approach runs in O(4^10) = O(2^20) which is sufficient to pass the tests.\n\n```\nclass Solution {\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n int n = values.length;\n List<int[]>[] adj = new List[n];\n for (int i = 0; i < n; ++i) adj[i] = new LinkedList();\n for (int[] e : edges) {\n int i = e[0], j = e[1], t = e[2];\n adj[i].add(new int[]{j, t});\n adj[j].add(new int[]{i, t});\n }\n int[] res = new int[1];\n int[] seen = new int[n];\n seen[0]++;\n dfs(adj, 0, values, maxTime, seen, res, values[0]);\n return res[0];\n }\n private void dfs(List<int[]>[] adj, int src, int[] values, int maxTime, int[] seen, int[] res, int sum) {\n if (0 == src) {\n res[0] = Math.max(res[0], sum);\n }\n if (0 > maxTime) return;\n for (int[] data : adj[src]) {\n int dst = data[0], t = data[1];\n if (0 > maxTime - t) continue;\n seen[dst]++;\n dfs(adj, dst, values, maxTime - t, seen, res, sum + (1 == seen[dst] ? values[dst] : 0));\n seen[dst]--;\n }\n }\n}\n``` | 25 | 1 | ['Depth-First Search', 'Java'] | 5 |
maximum-path-quality-of-a-graph | Plain DFS | plain-dfs-by-votrubac-99xt | Perhaps this problem would be more interesting if we have more nodes, or max time is not limited to 100.\n\nHere, we first build an adjacency list, and then run | votrubac | NORMAL | 2021-11-07T04:02:08.079831+00:00 | 2021-11-07T04:08:39.112416+00:00 | 4,430 | false | Perhaps this problem would be more interesting if we have more nodes, or max time is not limited to `100`.\n\nHere, we first build an adjacency list, and then run DFS, subtracting time and tracking the current value.\n\nThe visited array helps us determine when a node is visited for the first time. We add the node value when we visit the node for the first time.\n\n**C++**\n```cpp\nint max_val = 0;\nint dfs(vector<vector<pair<int, int>>> &al, vector<int> &vis, vector<int>& vals, int i, int time, int val) {\n val += (++vis[i] == 1) ? vals[i] : 0;\n if (i == 0)\n max_val = max(max_val, val);\n for (auto [j, t] : al[i])\n if (time - t >= 0)\n dfs(al, vis, vals, j, time - t, val);\n --vis[i];\n return max_val;\n}\nint maximalPathQuality(vector<int>& vals, vector<vector<int>>& edges, int maxTime) {\n vector<vector<pair<int, int>>> al(vals.size());\n vector<int> vis(vals.size());\n for (auto &e : edges) {\n al[e[0]].push_back({e[1], e[2]});\n al[e[1]].push_back({e[0], e[2]});\n }\n return dfs(al, vis, vals, 0, maxTime, 0);\n}\n``` | 25 | 0 | [] | 5 |
maximum-path-quality-of-a-graph | python | BFS | 99.33% | commented | python-bfs-9933-commented-by-hanjo108-fm9i | Hello, just wrote this and wanted to checkout other\'s solution, and I couldn\'t find fast BFS solutions, so I am just sharing my code.\n\nI wonder how can I no | hanjo108 | NORMAL | 2022-04-20T05:50:24.474835+00:00 | 2022-04-20T06:01:57.193806+00:00 | 1,174 | false | Hello, just wrote this and wanted to checkout other\'s solution, and I couldn\'t find fast BFS solutions, so I am just sharing my code.\n\nI wonder how can I not keeping copy of set every append to queue. Please **any suggest** will be appreciated\n\n**Thought process:**\n1. build undirected graph\n2. start BFS from 0 with (current vertex / time taken so far / quality collected so far / used vertext so far for this path)\n3. **Memoization** here which let you stop if current vertext can\'t give you better result extremely accelerate the whole algorithm\n4. Also if the time taken so far is more than the limit, no need to proceed\n5. If we are at node \'0\' then let\'s keep the maximum quality points collected so far\n6. quality will only be updated if has not been collected for the path. I am copying the set to use for new path. (like I said, any suggestion to use instead of this is big thanks)\n\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph = defaultdict(list)\n\t\t# build graph\n for edge in edges:\n graph[edge[0]].append((edge[1], edge[2]))\n graph[edge[1]].append((edge[0], edge[2]))\n \n q = deque()\n q.append((0, 0, values[0], set([0])))\n cache = {}\n maxPoint = 0\n\t\t\n while q:\n currV, currTime, currPoints, currSet = q.popleft()\n if currV in cache:\n\t\t\t\t# if vertex has been visited, and if the previousTime is \n\t\t\t\t# less or equal to current time but current points is lower?\n\t\t\t\t# then this path can\'t give us better quality so stop proceeding.\n prevTime, prevPoints = cache[currV]\n if prevTime <= currTime and prevPoints > currPoints:\n continue\n cache[currV] = (currTime, currPoints)\n\t\t\t# can\'t go over the maxTime limit\n if currTime > maxTime:\n continue\n\t\t\t# collect maxPoint only if current vertex is 0\n if currV == 0:\n maxPoint = max(maxPoint, currPoints)\n for neigh, neighTime in graph[currV]:\n newSet = currSet.copy()\n\t\t\t\t# collects quality only if not collected before\n if neigh not in currSet:\n newSet.add(neigh)\n newPoint = currPoints + values[neigh]\n else:\n newPoint = currPoints\n q.append((neigh, currTime + neighTime, newPoint, newSet))\n return maxPoint\n```\n\n\n\n**Please correct me if I am wrong !\nPlease UPVOTE if you find this solution helpful !\nHappy algo!**\n | 15 | 0 | ['Breadth-First Search', 'Memoization', 'Python'] | 3 |
maximum-path-quality-of-a-graph | Python | Top 99.6%, 196ms | DFS + Caching + Dijkstra | python-top-996-196ms-dfs-caching-dijkstr-fkvj | Initially, we can just write a DFS. Something like this:\n\n\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTi | float4 | NORMAL | 2021-11-17T21:07:51.400099+00:00 | 2021-11-17T21:08:34.026575+00:00 | 1,453 | false | Initially, we can just write a DFS. Something like this:\n\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n neighbours = defaultdict(list)\n for v,w,t in edges:\n neighbours[v].append((w,t))\n neighbours[w].append((v,t))\n \n def dfs(time, quality, visited, node):\n q = quality if node == 0 else -float("inf")\n for nb,t in neighbours[node]:\n if time+t <= maxTime:\n res = dfs(time+t, quality, visited | set([nb]), nb)\n q = max(q, res if nb in visited else res+values[nb])\n return q\n \n return dfs(0, values[0], set([0]), 0)\n```\n\nThis code is already fast enough to get an `Accepted`, but it takes 2912ms.\n\nWe can speed this up by adding some caching. We can use `@cache` from `functools` to do this. However, `@cache` requires that all function parameters, in this case `time`, `quality`, `visited`, `node`, are hashable types, and `visited` is a set and therefore not hashable. We can fix this by using an int to store the visited nodes. Ints are hashable, and thus we can use caching now. The dfs now looks like this:\n\n```\n @cache\n def dfs(time, quality, visited, node):\n q = quality if node == 0 else -float("inf")\n for nb,t in neighbours[node]:\n if time+t <= maxTime:\n res = dfs(time+t, quality, visited | (1<<nb), nb)\n q = max(q, res if (visited >> nb) & 1 else res+values[nb])\n return q\n \n return dfs(0, values[0], 1, 0)\n```\n\nThis code brings us down from 2912ms to 296ms, which was faster than 96.89% of sumissions. We can still speed it up further though. Observe the following lines from the dfs:\n\n```\n for nb,t in neighbours[node]:\n if time+t <= maxTime:\n```\n\nWe have this `if`-statement because we only want to recurse to neighbours that we can reach within `maxTime` seconds. However, note that if we go to such a neighbour, we *also* have to be able to go all the way back to our end node, node 0, within `maxTime`. Therefore, we can change it to:\n\n```\n for nb,t in neighbours[node]:\n if time+t+timeFrom0ToNb <= maxTime:\n```\n\nWe can use Dijkstras algorithm to calculate `timeFrom0ToNb` for all nodes in the graph. We then arrive at the final submission:\n\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n neighbours = defaultdict(list)\n for v,w,t in edges:\n neighbours[v].append((w,t))\n neighbours[w].append((v,t))\n \n times = defaultdict(lambda: float("inf"))\n q = [(0, 0)]\n while len(q):\n time, node = heappop(q)\n if times[(node,0)] == float("inf"):\n times[(node,0)] = time\n for nb,t in neighbours[node]:\n if time+t <= maxTime//2 and times[(nb,0)] == float("inf"):\n heappush(q, (time+t, nb))\n \n @cache\n def dfs(time, quality, visited, node):\n q = quality if node == 0 else -float("inf")\n for nb,t in neighbours[node]:\n if time+t+times[(nb,0)] <= maxTime:\n res = dfs(time+t, quality, visited | (1<<nb), nb)\n q = max(q, res if (visited >> nb) & 1 else res+values[nb])\n return q\n \n return dfs(0, values[0], 1, 0)\n```\n\nThis submission took 196ms, and was faster than 99.6% of submissions. | 13 | 0 | ['Dynamic Programming', 'Depth-First Search'] | 1 |
maximum-path-quality-of-a-graph | Java | DFS | java-dfs-by-pagalpanda-ooa6 | \n\tpublic int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n List<List<int[]>> adjList = new ArrayList();\n for(int i : values) | pagalpanda | NORMAL | 2021-11-16T13:39:27.528284+00:00 | 2021-11-16T13:39:27.528310+00:00 | 1,527 | false | ```\n\tpublic int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n List<List<int[]>> adjList = new ArrayList();\n for(int i : values) {\n adjList.add(new ArrayList());\n }\n \n for(int edge[] : edges) {\n adjList.get(edge[0]).add(new int[] {edge[1], edge[2]});\n adjList.get(edge[1]).add(new int[] {edge[0], edge[2]});\n }\n int[] visited = new int[values.length];\n solve(values, adjList, visited, 0, maxTime, 0, 0);\n return ans;\n }\n int ans;\n \n void solve(int[] values, List<List<int[]>> adjList, int[] visited, int node, int maxTime, int currTime, int score) {\n if(currTime > maxTime) {\n return;\n }\n if(visited[node] == 0) {\n score += values[node];\n }\n \n if(node == 0) {\n ans = Math.max(ans, score);\n }\n \n visited[node]++;\n \n for(int[] v : adjList.get(node)) {\n solve(values, adjList, visited, v[0], maxTime, currTime + v[1], score);\n }\n \n visited[node]--;\n }\n``` | 11 | 0 | ['Backtracking', 'Depth-First Search', 'Java'] | 3 |
maximum-path-quality-of-a-graph | Python3 || dfs w/ mask || T/S: 67% / 79% | python3-dfs-w-mask-ts-67-79-by-spaulding-e705 | Here\'s the plan:\n\n1. We construct the graph with weights\n\n2. We recursively dfs-traverse the graph, and we keep track of the time and quality as we move fr | Spaulding_ | NORMAL | 2024-09-21T21:29:00.383574+00:00 | 2024-09-21T21:30:07.287834+00:00 | 175 | false | Here\'s the plan:\n\n1. We construct the graph with weights\n\n2. We recursively dfs-traverse the graph, and we keep track of the time and quality as we move from node to node.\n3. We use a mask to determine whether we have visited the present node on this dfs; if not, we can increase the quality.\n4. If we traverse back to the zero-node, we update the maximum quality as necessary.\n\n```python3 []\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n\n def dfs(node:int, prev_qual:int, prev_time:int, prev_mask:int)-> None:\n \n if node == 0: \n self.maxQuality = max(self.maxQuality, prev_qual)\n \n for nxt, wgt in graph[node]:\n if wgt > prev_time: continue\n\n if prev_mask & (1<< nxt): qual = prev_qual\n else: qual = prev_qual + values[nxt]\n\n mask = prev_mask | (1<< nxt)\n time = prev_time - wgt\n\n dfs(nxt, qual, time, mask)\n\n return\n\n\n self.maxQuality = 0\n graph = defaultdict(list)\n\n for u, v, wgt in edges:\n graph[u].append((v, wgt))\n graph[v].append((u, wgt))\n \n dfs(0, values[0], maxTime, 1)\n return self.maxQuality \n```\n[https://leetcode.com/problems/maximum-path-quality-of-a-graph/submissions/1397820301/](https://leetcode.com/problems/maximum-path-quality-of-a-graph/submissions/1397820301/)\n\n\nI could be wrong, but I think that time complexity is *O*(2^*N*) and space complexity is *O*(*N*), in which *N* ~ the number of nodes in reach of the zero node within `maxTime`. (The constraints limit this quantity to no greater than 10--this fact allows the code to be a little generous with time.) | 10 | 0 | ['Python3'] | 1 |
maximum-path-quality-of-a-graph | Backtracking + DFS Based Approach || C++ Clean Code | backtracking-dfs-based-approach-c-clean-sog9l | Code : \n\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n \n int n = valu | i_quasar | NORMAL | 2021-11-21T16:25:30.629246+00:00 | 2021-11-25T15:26:26.757733+00:00 | 1,068 | false | # Code : \n```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n \n int n = values.size();\n \n vector<vector<pair<int, int>>> adj(n);\n \n for(auto& edge : edges) {\n adj[edge[0]].push_back({edge[1], edge[2]});\n adj[edge[1]].push_back({edge[0], edge[2]});\n }\n \n vector<int> vis(n, 0); \n return explorePaths(adj, values, vis, 0, values[0], maxTime);\n }\n\t\n int explorePaths(vector<vector<pair<int, int>>>& adj, vector<int>& values, vector<int>& vis, int node, int quality, int time) {\n \n int maxQuality = 0;\n \n if(node == 0) maxQuality = max(maxQuality, quality);\n \n vis[node]++;\n \n for(auto& [adjnode, wt] : adj[node]) {\n if(wt <= time)\n {\n int val = quality + (vis[adjnode] ? 0 : values[adjnode]);\n maxQuality = max(maxQuality, explorePaths(adj, values, vis, adjnode, val, time - wt));\n }\n }\n \n vis[node]--;\n \n return maxQuality;\n }\n};\n```\n\n***If you find this helpful, do give it a like :)*** | 9 | 2 | ['Backtracking', 'Depth-First Search', 'Graph', 'C'] | 0 |
maximum-path-quality-of-a-graph | C++ DFS | c-dfs-by-lzl124631x-v4yj | See my latest update in repo LeetCode\n## Solution 1. DFS\n\nSince 10 <= timej, maxTime <= 100, the path at most have 10 edges. Since each node at most has 4 ed | lzl124631x | NORMAL | 2021-11-07T04:01:40.785036+00:00 | 2021-11-09T19:43:27.649527+00:00 | 1,294 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n## Solution 1. DFS\n\nSince `10 <= timej, maxTime <= 100`, the path at most have `10` edges. Since each node at most has `4` edges, the maximum number of possible paths is `4^10 ~= 1e6`, so a brute force DFS should work.\n\n```cpp\n// OJ: https://leetcode.com/problems/maximum-path-quality-of-a-graph/\n// Author: github.com/lzl124631x\n// Time: O(4^10)\n// Space: O(V + E)\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& V, vector<vector<int>>& E, int maxTime) {\n int N = V.size();\n vector<vector<pair<int, int>>> G(N); // build graph\n for (auto &e : E) {\n int u = e[0], v = e[1], c = e[2];\n G[u].emplace_back(v, c);\n G[v].emplace_back(u, c);\n }\n vector<int> cnt(N); // `cnt[u]` is the number of times we\'ve visted node `u` in the current path\n int ans = 0;\n function<void(int, int, int)> dfs = [&](int u, int val, int time) {\n if (cnt[u] == 0) val += V[u];\n cnt[u]++;\n if (u == 0) ans = max(ans, val); // Only update answer if the current node is `0`.\n for (auto &[v, c] : G[u]) {\n if (time + c > maxTime) continue; // if the current time + the edge time is greater than maxTime, skip\n dfs(v, val, time + c);\n }\n cnt[u]--;\n };\n dfs(0, 0, 0);\n return ans;\n }\n};\n```\n\nOr we can optionally add Dijkstra to backtrack earlier.\n\n```cpp\n// OJ: https://leetcode.com/problems/maximum-path-quality-of-a-graph/\n// Author: github.com/lzl124631x\n// Time: O(ElogE + 4^10)\n// Space: O(V + E)\nclass Solution {\n typedef array<int, 2> T;\npublic:\n int maximalPathQuality(vector<int>& V, vector<vector<int>>& E, int maxTime) {\n int N = V.size();\n vector<vector<array<int, 2>>> G(N); // build graph\n for (auto &e : E) {\n int u = e[0], v = e[1], c = e[2];\n G[u].push_back({v, c});\n G[v].push_back({u, c});\n }\n priority_queue<T, vector<T>, greater<T>> pq; // use Dijkstra to find the shortest distance from node 0 to all other nodes.\n vector<int> dist(N, INT_MAX);\n dist[0] = 0;\n pq.push({0, 0});\n while (pq.size()) {\n auto [d, u] = pq.top();\n pq.pop();\n if (d > dist[u]) continue;\n for (auto &[v, c] : G[u]) {\n if (dist[v] > dist[u] + c) {\n dist[v] = dist[u] + c;\n pq.push({dist[v], v});\n }\n }\n }\n vector<int> cnt(N); // `cnt[u]` is the number of times we\'ve visted node `u` in the current path\n int ans = 0;\n function<void(int, int, int)> dfs = [&](int u, int val, int time) {\n if (cnt[u] == 0) val += V[u];\n cnt[u]++;\n if (u == 0) ans = max(ans, val); // Only update answer if the current node is `0`.\n for (auto &[v, c] : G[u]) {\n if (time + c + dist[v] > maxTime) continue; // if the current time + the edge time + dist[u] is greater than maxTime, skip\n dfs(v, val, time + c);\n }\n cnt[u]--;\n };\n dfs(0, 0, 0);\n return ans;\n }\n};\n``` | 9 | 0 | [] | 2 |
maximum-path-quality-of-a-graph | Java dfs | java-dfs-by-shufflemix-x0z3 | ```java\nclass Solution {\n public class Node {\n int id;\n int value;\n List edges;\n public Node(int id, int value) {\n | shufflemix | NORMAL | 2021-11-07T04:01:36.980854+00:00 | 2021-11-07T04:01:36.980922+00:00 | 1,485 | false | ```java\nclass Solution {\n public class Node {\n int id;\n int value;\n List<Edge> edges;\n public Node(int id, int value) {\n this.id = id;\n this.value = value;\n edges = new ArrayList<>();\n }\n }\n \n public class Edge {\n int id1;\n int id2;\n int cost;\n public Edge(int id1, int id2, int cost) {\n this.id1 = id1;\n this.id2 = id2;\n this.cost = cost;\n }\n }\n \n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n List<Node> nodes = new ArrayList<>();\n for (int i = 0; i < values.length; i++) {\n nodes.add(new Node(i, values[i]));\n }\n \n for (int[] edge : edges) {\n Edge e = new Edge(edge[0], edge[1], edge[2]);\n nodes.get(edge[0]).edges.add(e);\n nodes.get(edge[1]).edges.add(e);\n }\n \n for (Node node : nodes) {\n Collections.sort(node.edges, (e1, e2) -> {\n return e1.cost - e2.cost;\n });\n }\n \n Set<Integer> qualityAdded = new HashSet<>();\n qualityAdded.add(0);\n return visit(nodes, 0, qualityAdded, maxTime, nodes.get(0).value, 0);\n }\n \n private int visit(List<Node> nodes, int curId, Set<Integer> qualityAdded, int maxTime, int quality, int time) { \n if (time > maxTime) {\n return Integer.MIN_VALUE;\n }\n \n int maxQuality = Integer.MIN_VALUE;\n if (curId == 0 && time <= maxTime) {\n maxQuality = Math.max(maxQuality, quality);\n }\n \n for (Edge edge : nodes.get(curId).edges) {\n if (time + edge.cost > maxTime) {\n break;\n }\n \n int nbrId = edge.id1 != curId ? edge.id1 : edge.id2;\n boolean hasAdded = qualityAdded.contains(nbrId);\n qualityAdded.add(nbrId);\n int newQuality = hasAdded ? quality : quality + nodes.get(nbrId).value;\n maxQuality = Math.max(maxQuality, visit(nodes, nbrId, qualityAdded, maxTime, newQuality, time + edge.cost));\n if (!hasAdded) {\n qualityAdded.remove(nbrId);\n }\n }\n \n return maxQuality;\n }\n} | 8 | 0 | [] | 1 |
maximum-path-quality-of-a-graph | 💥💥 Beats 100% on runtime and memory [EXPLAINED] | beats-100-on-runtime-and-memory-explaine-p427 | Intuition\nFinding the best route through a graph, maximizing the quality of the path while staying within a specified travel time. Each node has a value that c | r9n | NORMAL | 2024-10-28T05:40:33.365555+00:00 | 2024-10-28T05:40:33.365613+00:00 | 100 | false | # Intuition\nFinding the best route through a graph, maximizing the quality of the path while staying within a specified travel time. Each node has a value that contributes to the total quality, and the goal is to visit nodes strategically to collect the highest possible quality without exceeding the time limit.\n\n# Approach\nUse a backtracking technique to explore all possible paths from the starting node, keeping track of the current travel time and quality, and updating the maximum quality whenever you return to the starting node.\n\n# Complexity\n- Time complexity:\nO(2^N), where N is the number of nodes, because each node can either be included in a path or not, creating many combinations.\n\n- Space complexity:\nO(N), due to the storage required for the recursive call stack and tracking visited nodes.\n\n# Code\n```typescript []\n// Define a type for the graph node structure\ntype TGraphNode = {\n aNodes: number[]; // Array of connected nodes\n aTimes: number[]; // Array of times to reach connected nodes\n};\n\n/**\n * Builds a graph represented as an array of nodes from given edges.\n * @param {number} n - The number of nodes in the graph.\n * @param {[number, number, number?][]} edges - An array of edges, where each edge is defined by [u, v, t].\n * @returns {TGraphNode[]} - An array of graph nodes where each node contains its connections and travel times.\n */\nfunction buildGraph(n: number, edges: [number, number, number?][]): TGraphNode[] {\n // Initialize the nodes array\n const nodes: TGraphNode[] = [];\n for (let i = 0; i < n; i++) {\n nodes.push({ aNodes: [], aTimes: [] });\n }\n\n // Loop through each edge to build the graph\n const m = edges.length;\n for (let i = 0; i < m; i++) {\n const [u, v, t] = edges[i]; // Destructure the edge\n nodes[u].aNodes.push(v); // Add node v to u\'s adjacency list\n nodes[u].aTimes.push(t!); // Add travel time to u\'s adjacency list (using \'!\' for undefined)\n nodes[v].aNodes.push(u); // Add node u to v\'s adjacency list\n nodes[v].aTimes.push(t!); // Add travel time to v\'s adjacency list (using \'!\' for undefined)\n }\n\n return nodes; // Return the constructed graph\n}\n\n// Array to track the number of times each node is visited\nconst curUseds = new Uint8Array(1000);\n\n/**\n * Calculates the maximum path quality of a graph within a given time limit.\n * @param {number[]} values - An array of values associated with each node.\n * @param {[number, number, number][]} edges - An array of edges representing connections and their travel times.\n * @param {number} maxTime - The maximum allowed time for a path.\n * @returns {number} - The maximum quality of a valid path.\n */\nvar maximalPathQuality = function (values: number[], edges: [number, number, number][], maxTime: number): number {\n const n = values.length; // Number of nodes\n const g = buildGraph(n, edges); // Build the graph\n\n let curTime = 0; // Current travel time\n let curQual = 0; // Current path quality\n let res = 0; // Resulting maximum quality\n curUseds.fill(0, 0, n); // Reset usage tracker\n\n // Backtracking function to explore paths\n function bt(u: number) {\n if (!curUseds[u]) curQual += values[u]; // Add value if it\'s the first visit\n ++curUseds[u]; // Increment visit count\n\n if (u === 0) res = Math.max(res, curQual); // Update result if back at start\n\n const { aNodes, aTimes } = g[u]; // Get neighbors and travel times\n\n // Explore all connected nodes\n for (let i = 0; i < aNodes.length; ++i) {\n if (aTimes[i] + curTime <= maxTime) { // Check if the path is within time limit\n curTime += aTimes[i]; // Update current time\n bt(aNodes[i]); // Recur for the next node\n curTime -= aTimes[i]; // Backtrack time\n }\n }\n\n --curUseds[u]; // Decrement visit count\n if (!curUseds[u]) curQual -= values[u]; // Remove value if it was the last visit\n }\n\n bt(0); // Start backtracking from node 0\n return res; // Return the maximum quality found\n};\n\n\n``` | 7 | 0 | ['Array', 'Backtracking', 'Graph', 'TypeScript'] | 0 |
maximum-path-quality-of-a-graph | [Python] DFS and BFS solution | python-dfs-and-bfs-solution-by-nightybea-23pa | DFS solution:\npython\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n ans = 0\n | nightybear | NORMAL | 2021-11-07T06:43:52.499813+00:00 | 2021-11-07T06:43:52.499847+00:00 | 1,025 | false | DFS solution:\n```python\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n ans = 0\n graph = collections.defaultdict(dict)\n for u, v, t in edges:\n graph[u][v] = t\n graph[v][u] = t\n \n def dfs(curr, visited, score, cost):\n if curr == 0:\n nonlocal ans\n ans = max(ans, score)\n \n for nxt, time in graph[curr].items():\n if time <= cost:\n dfs(nxt, visited|set([nxt]), score+values[nxt]*(nxt not in visited), cost-time)\n \n dfs(0, set([0]), values[0], maxTime)\n return ans\n```\n\nBFS solution\n```python\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n ans = 0\n graph = collections.defaultdict(dict)\n for u,v,t in edges:\n graph[u][v] = t\n graph[v][u] = t\n \n # node, cost, visited, score\n q = collections.deque([(0, maxTime, set([0]), values[0])])\n while q:\n curr, cost, visited, score = q.popleft()\n if curr == 0:\n ans = max(ans, score)\n for nxt, time in graph[curr].items():\n if time > cost:\n continue\n q.append((nxt, cost-time, visited|set([nxt]), score + values[nxt]*(nxt not in visited)))\n\n return ans\n``` | 5 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Python', 'Python3'] | 1 |
maximum-path-quality-of-a-graph | [JavaScript] Simple DFS | javascript-simple-dfs-by-stevenkinouye-0poq | javascript\nvar maximalPathQuality = function(values, edges, maxTime) {\n const adjacencyList = values.map(() => []);\n for (const [node1, node2, time] of | stevenkinouye | NORMAL | 2021-11-07T04:01:04.341916+00:00 | 2021-11-07T04:01:49.453579+00:00 | 336 | false | ```javascript\nvar maximalPathQuality = function(values, edges, maxTime) {\n const adjacencyList = values.map(() => []);\n for (const [node1, node2, time] of edges) {\n adjacencyList[node1].push([node2, time]);\n adjacencyList[node2].push([node1, time]);\n }\n \n const dfs = (node, quality, time, seen) => {\n // if we returned back to the 0 node, then we log it as a valid value\n let best = node === 0 ? quality : 0;\n \n // try to visit all the neighboring nodes within the maxTime\n // given while recording the max\n for (const [neighbor, routeTime] of adjacencyList[node]) {\n const totalTime = time + routeTime;\n if (totalTime > maxTime) continue;\n if (seen.has(neighbor)) {\n best = Math.max(best, \n dfs(neighbor, quality, totalTime, seen));\n } else {\n seen.add(neighbor);\n best = Math.max(best, \n dfs(neighbor, quality + values[neighbor], totalTime, seen));\n seen.delete(neighbor);\n }\n }\n return best;\n }\n return dfs(0, values[0], 0, new Set([0]));\n};\n```\n | 5 | 0 | ['Depth-First Search', 'JavaScript'] | 2 |
maximum-path-quality-of-a-graph | Naive DFS, backtrack, simple but my internet went off | naive-dfs-backtrack-simple-but-my-intern-y6sh | Let\'s go directly to the data size, time >= 10 and maxTime <= 100. We will let it traverse at most 10 steps from 0. \nThe sentence, at most four edges for each | ch-yyk | NORMAL | 2021-11-07T04:10:23.433518+00:00 | 2021-11-07T08:27:00.428846+00:00 | 605 | false | Let\'s go directly to the data size, `time >= 10` and `maxTime <= 100`. We will let it traverse at most 10 steps from 0. \nThe sentence, `at most four edges for each node`, indicate that we will have at most 4^10 steps to move in total which is\naround 10^6 to 10^7 steps. So searching in a brute force way should work on LeetCode...\n\nI use backtrack here as it\'s easier to mark qualities from unique nodes.\n\n```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n // 10 steps at most, 4 directions at most -> 4 ^ 10 -> 2 ^ 20\n this->maxTime = maxTime;\n this->n = values.size();\n visited = vector<int>(1000, 0);\n vector<vector<pair<int,int>>> graph(n);\n for(vector<int>& vec : edges) {\n graph[vec[0]].emplace_back(vec[1], vec[2]);\n graph[vec[1]].emplace_back(vec[0], vec[2]);\n }\n \n // run backtracking\n visited[0] = 1;\n backtrack(graph, values, 0, values[0], 0);\n return res;\n }\nprivate:\n int res = 0;\n int maxTime, n;\n vector<int> visited;\n void backtrack(vector<vector<pair<int,int>>>& graph, vector<int>& values, int curr, int quality, int time) { \n if(curr == 0) {\n res = max(quality, res);\n }\n for(auto [v, t] : graph[curr]) {\n if(time + t > maxTime) continue;\n if(visited[v] > 0) // visited\n backtrack(graph, values, v, quality, time + t); \n else {\n visited[v] = 1;\n backtrack(graph, values, v, quality + values[v], time + t);\n visited[v] = 0;\n }\n } \n }\n};\n``` | 4 | 0 | [] | 1 |
maximum-path-quality-of-a-graph | python super easy to understand dfs | python-super-easy-to-understand-dfs-by-h-3qjj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | harrychen1995 | NORMAL | 2023-10-30T14:47:47.267258+00:00 | 2023-10-30T14:47:47.267291+00:00 | 301 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n \n \n graph = collections.defaultdict(set)\n time = {}\n for a, b, t in edges:\n time[(a,b)] = t\n time[(b,a)] = t\n graph[a].add(b)\n graph[b].add(a)\n ans = 0\n def dfs(root, t, visit, s):\n if t > maxTime:\n return\n if root == 0:\n nonlocal ans\n ans = max(ans, s)\n \n visit.add(root)\n for v in graph[root]:\n if v not in visit:\n dfs(v, t+time[(root,v)], set(visit), s+values[v])\n else:\n dfs(v,t+time[(root,v)], set(visit), s)\n \n \n dfs(0, 0, set(), values[0])\n return ans\n\n\n\n\n``` | 3 | 0 | ['Depth-First Search', 'Python3'] | 1 |
maximum-path-quality-of-a-graph | DFS || BACKTRACKING || C++ || EASY TO UNDERSTAND 60% FASTER SOLUTION | dfs-backtracking-c-easy-to-understand-60-jz38 | \nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size();\n | abhay_12345 | NORMAL | 2023-02-03T17:40:47.629027+00:00 | 2023-02-03T17:40:47.629062+00:00 | 873 | false | ```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size();\n int res = values[0];\n vector<vector<pair<int,int>>> graph(n);\n for(int i=0;i<edges.size();i++)\n {\n graph[edges[i][0]].push_back({edges[i][1], edges[i][2]});\n graph[edges[i][1]].push_back({edges[i][0], edges[i][2]});\n }\n \n vector<int> visited(n, 0);\n dfs(graph, values, visited, res, 0, 0, 0, maxTime);\n return res;\n }\n \n void dfs(vector<vector<pair<int,int>>>& graph, vector<int>& values, vector<int>& visited, int& res, int node, int score, int time, int& maxTime)\n {\n if(time > maxTime)\n return;\n \n if(visited[node] == 0)\n score += values[node];\n \n visited[node]++;\n\t\t\n \n if(node == 0)\n res = max(res, score);\n \n for(auto it : graph[node])\n {\n int neigh = it.first;\n int newTime = time + it.second;\n dfs(graph, values, visited, res, neigh, score, newTime, maxTime);\n }\n \n visited[node]--;\n }\n};\n``` | 2 | 0 | ['Backtracking', 'Depth-First Search', 'Graph', 'C', 'C++'] | 1 |
maximum-path-quality-of-a-graph | [Java/C++] dfs with optimization | javac-dfs-with-optimization-by-quantumin-3jrd | A straightforward idea is to try all paths from node 0 and calculate the max path quality for paths also end with node 0.\n\nOne optimization we can add is: onc | quantuminfo | NORMAL | 2021-11-07T04:00:37.384118+00:00 | 2021-11-07T04:00:37.384148+00:00 | 385 | false | A straightforward idea is to try all paths from node `0` and calculate the `max path quality` for paths also end with node `0`.\n\nOne **optimization** we can add is: once we cannot return back to node `0`, we stop. The `min_time` required from any node to node `0` can be pre-computed using *Dijkstra algorithm*.\n\n**Time complexity**: `O(4^10)`\n\n**Note the constraints**: `10 <= time_j, maxTime <= 100` and There are at most **four** edges connected to each node..\nIt means the max levels of `dfs` search is `10`, and at each level we have maximum of `4` neighbouring nodes to try. \nSo the time complexity is: `O(4^10)`.\n\n**Java solution**\n```\npublic int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n final int N = values.length;\n List<List<int[]>> map = new ArrayList<>();\n for (int i = 0; i < N; i++) {\n map.add(new ArrayList<>());\n }\n for (int[] e : edges) {\n map.get(e[0]).add(new int[]{e[1], e[2]});\n map.get(e[1]).add(new int[]{e[0], e[2]});\n }\n \n int[] minTimeToZero = bfs(map, N);\n Set<Integer> visited = new HashSet<>();\n visited.add(0);\n int[] res = new int[]{0};\n dfs(map, minTimeToZero, N, values, 0, maxTime, visited, res);\n return res[0];\n}\n\nprivate void dfs(List<List<int[]>> map, int[] minTimeToZero, int N, int[] values, int cur, int maxTime, Set<Integer> visited, int[] res) {\n if (cur == 0) {\n int sum = 0;\n for (int i : visited) {\n sum += values[i];\n }\n res[0] = Math.max(res[0], sum);\n }\n \n for (int[] nei : map.get(cur)) {\n if (minTimeToZero[nei[0]] + nei[1] <= maxTime) {\n boolean added = visited.add(nei[0]);\n dfs(map, minTimeToZero, N, values, nei[0], maxTime - nei[1], visited, res);\n if (added) {\n visited.remove(nei[0]);\n }\n }\n }\n}\n\nprivate int[] bfs(List<List<int[]>> map, int N) {\n int[] minTimeToZero = new int[N];\n Arrays.fill(minTimeToZero, Integer.MAX_VALUE);\n PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> Integer.compare(a[1], b[1]));\n q.offer(new int[]{0, 0});\n minTimeToZero[0] = 0;\n while (!q.isEmpty()) {\n int[] cur = q.poll();\n if (cur[1] > minTimeToZero[cur[0]]) {\n continue;\n }\n for (int[] nei : map.get(cur[0])) {\n if (nei[1] + cur[1] < minTimeToZero[nei[0]]) {\n minTimeToZero[nei[0]] = nei[1] + cur[1];\n q.offer(new int[]{nei[0], nei[1] + cur[1]});\n }\n }\n }\n return minTimeToZero;\n}\n```\n\n**C++ solution**\n```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n const int N = values.size();\n vector<unordered_map<int, int>> mp(N, unordered_map<int, int>());\n for (const auto& e : edges) {\n mp[e[0]][e[1]] = e[2];\n mp[e[1]][e[0]] = e[2];\n }\n vector<int> min_time0 = bfs(mp, N);\n unordered_set<int> visited;\n visited.insert(0);\n int res = 0;\n dfs(mp, min_time0, values, 0, maxTime, visited, res);\n return res;\n }\nprivate:\n void dfs(const vector<unordered_map<int, int>>& mp, const vector<int>& min_time0, const vector<int>& values, \n int cur, int max_time, unordered_set<int>& visited, int& res) {\n if (cur == 0) {\n int sum = 0;\n for (int i : visited) {\n sum += values[i];\n }\n res = max(sum, res);\n }\n \n for (const auto& [next, time] : mp[cur]) {\n if (time + min_time0[next] <= max_time) {\n bool added = visited.count(next) == 0;\n visited.insert(next);\n dfs(mp, min_time0, values, next, max_time - time, visited, res);\n if (added) {\n visited.erase(next);\n }\n }\n }\n }\n \n vector<int> bfs(const vector<unordered_map<int, int>>& mp, const int N) {\n vector<int> min_time0(N, INT_MAX);\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> min_heap;\n min_heap.push({0, 0});\n min_time0[0] = 0;\n while (!min_heap.empty()) {\n pair cur = min_heap.top();\n min_heap.pop();\n for (const auto& [next, time] : mp[cur.second]) {\n if (time + cur.first < min_time0[next]) {\n min_time0[next] = time + cur.first;\n min_heap.push({time + cur.first, next});\n }\n }\n }\n return min_time0;\n }\n};\n``` | 3 | 0 | [] | 1 |
maximum-path-quality-of-a-graph | Python | Easy | Graph | Maximum Path Quality of a Graph | python-easy-graph-maximum-path-quality-o-xap7 | \nsee the Successfully Accepted Submission\nPython\nclass Solution:\n def maximalPathQuality(self, values, edges, maxTime):\n n = len(values)\n | Khosiyat | NORMAL | 2023-10-11T15:15:40.166161+00:00 | 2023-10-11T15:15:40.166182+00:00 | 95 | false | \n[see the Successfully Accepted Submission](https://leetcode.com/submissions/detail/1071689029/)\n```Python\nclass Solution:\n def maximalPathQuality(self, values, edges, maxTime):\n n = len(values)\n adj = [[] for _ in range(n)]\n\n # Create an adjacency list to represent the graph with edges and time values.\n for e in edges:\n i, j, t = e[0], e[1], e[2]\n adj[i].append((j, t))\n adj[j].append((i, t))\n\n res = [0]\n seen = [0] * n\n seen[0] += 1\n # Start DFS traversal from node 0 with initial score values[0].\n self.dfs(adj, 0, values, maxTime, seen, res, values[0])\n return res[0]\n\n def dfs(self, adj, src, values, maxTime, seen, res, score):\n # If we return to the source node (node 0), update the result with the maximum score.\n if src == 0:\n res[0] = max(res[0], score)\n\n # If we run out of time, return.\n if maxTime < 0:\n return\n\n # Iterate through adjacent nodes.\n for data in adj[src]:\n dst, t = data[0], data[1]\n\n # If we have enough time to reach the destination node, continue DFS.\n if maxTime - t < 0:\n continue\n\n seen[dst] += 1\n # Continue DFS to the destination node with updated score and remaining time.\n self.dfs(adj, dst, values, maxTime - t, seen, res, score + (values[dst] if seen[dst] == 1 else 0))\n seen[dst] -= 1\n```\n\n\n\n | 2 | 0 | ['Graph', 'Python'] | 0 |
maximum-path-quality-of-a-graph | BFS 177ms Beats 100.00%of users with Python3 | bfs-177ms-beats-10000of-users-with-pytho-98q7 | Intuition\nGraph question - first think about using BFS\n\n# Approach\nBFS\n\n# Complexity\n\n\n# Code\n\nclass Solution:\n def maximalPathQuality(self, valu | cherrychoco | NORMAL | 2023-07-18T22:42:45.050634+00:00 | 2023-07-21T20:32:04.853032+00:00 | 345 | false | # Intuition\nGraph question - first think about using BFS\n\n# Approach\nBFS\n\n# Complexity\n\n\n# Code\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n\n graph = collections.defaultdict(list)\n for u, v, t in edges :\n graph[u].append((v,t))\n graph[v].append((u,t))\n\n queue = collections.deque([(0, 0, values[0], [0])]) # (node, time, totalVal, path)\n valList = [(-1,-1)]*len(values)\n valList[0] = (values[0], 0)\n output = 0\n while queue :\n node, curTime, curVal, visited = queue.popleft()\n if node == 0 :\n output = max(output, curVal)\n for nxt, t in graph[node] :\n if curTime + t > maxTime :\n continue\n nxtVal = curVal\n if nxt not in visited:\n nxtVal += values[nxt]\n #This is the condition that significantly reduces the runtime\n if curTime+t >= valList[nxt][1] and nxtVal < valList[nxt][0] :\n continue\n queue.append((nxt, curTime+t, nxtVal, visited + [nxt]))\n valList[nxt] = (nxtVal, curTime+t)\n return output\n\n``` | 2 | 0 | ['Breadth-First Search', 'Python', 'Python3'] | 0 |
maximum-path-quality-of-a-graph | DFS || BACKTRACKING || C++ || EASY TO UNDERSTAND 60% FASTER SOLUTION | dfs-backtracking-c-easy-to-understand-60-sg7i | \nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size();\n | abhay_12345 | NORMAL | 2023-02-03T17:39:03.938361+00:00 | 2023-02-03T17:39:03.938404+00:00 | 627 | false | ```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size();\n int res = values[0];\n vector<vector<pair<int,int>>> graph(n);\n for(int i=0;i<edges.size();i++)\n {\n graph[edges[i][0]].push_back({edges[i][1], edges[i][2]});\n graph[edges[i][1]].push_back({edges[i][0], edges[i][2]});\n }\n \n vector<int> visited(n, 0);\n dfs(graph, values, visited, res, 0, 0, 0, maxTime);\n return res;\n }\n \n void dfs(vector<vector<pair<int,int>>>& graph, vector<int>& values, vector<int>& visited, int& res, int node, int score, int time, int& maxTime)\n {\n if(time > maxTime)\n return;\n \n if(visited[node] == 0)\n score += values[node];\n \n visited[node]++;\n\t\t\n \n if(node == 0)\n res = max(res, score);\n \n for(auto it : graph[node])\n {\n int neigh = it.first;\n int newTime = time + it.second;\n dfs(graph, values, visited, res, neigh, score, newTime, maxTime);\n }\n \n visited[node]--;\n }\n};\n``` | 2 | 0 | ['Backtracking', 'Depth-First Search', 'Graph', 'C', 'C++'] | 0 |
maximum-path-quality-of-a-graph | Simple Java Backtracking Solution | simple-java-backtracking-solution-by-syc-0esl | \nclass Solution {\n int res = 0;\n\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n Map<Integer, Map<Integer, Integer | sycmtic | NORMAL | 2023-01-14T22:40:44.799161+00:00 | 2023-01-14T22:40:44.799197+00:00 | 194 | false | ```\nclass Solution {\n int res = 0;\n\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n Map<Integer, Map<Integer, Integer>> map = new HashMap<>();\n int n = values.length;\n for (int i = 0; i < n; i++) map.put(i, new HashMap<>());\n for (int[] edge : edges) {\n map.get(edge[0]).put(edge[1], edge[2]);\n map.get(edge[1]).put(edge[0], edge[2]);\n }\n Map<Integer, Integer> visited = new HashMap<Integer, Integer>();\n visited.put(0, 1);\n dfs(0, maxTime, values[0], visited, values, map);\n return res;\n }\n\n public void dfs(int cur, int time, int value, Map<Integer, Integer> visited, int[] values, Map<Integer, Map<Integer, Integer>> map) {\n if (cur == 0) {\n res = Math.max(res, value);\n }\n for (Map.Entry<Integer, Integer> entry : map.get(cur).entrySet()) {\n if (time < entry.getValue()) continue;\n if (!visited.containsKey(entry.getKey())) value += values[entry.getKey()];\n visited.put(entry.getKey(), visited.getOrDefault(entry.getKey(), 0) + 1);\n dfs(entry.getKey(), time - entry.getValue(), value, visited, values, map);\n visited.put(entry.getKey(), visited.getOrDefault(entry.getKey(), 0) - 1);\n if (visited.get(entry.getKey()) == 0) {\n visited.remove(entry.getKey());\n value -= values[entry.getKey()];\n }\n }\n }\n}\n``` | 2 | 0 | ['Backtracking', 'Graph', 'Java'] | 0 |
maximum-path-quality-of-a-graph | dfs brute force | dfs-brute-force-by-beermario-lrej | python\n\'\'\'\ndfs, brute force\nO(4^n), O(4^n)\n\'\'\'\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: | beermario | NORMAL | 2022-08-05T09:12:28.288451+00:00 | 2022-08-05T09:12:28.288480+00:00 | 334 | false | ```python\n\'\'\'\ndfs, brute force\nO(4^n), O(4^n)\n\'\'\'\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph = collections.defaultdict(list)\n for u, v, time in edges:\n graph[u].append((v, time))\n graph[v].append((u, time))\n \n max_quality = 0\n visited = {0}\n def dfs(node, visited, quality, time_left):\n nonlocal max_quality\n \n if node == 0:\n max_quality = max(max_quality, quality)\n \n for neighbor, time in graph[node]:\n if time <= time_left:\n if neighbor in visited:\n dfs(neighbor, visited, quality, time_left - time)\n else:\n visited.add(neighbor)\n dfs(neighbor, visited, quality + values[neighbor], time_left - time)\n visited.remove(neighbor)\n \n dfs(0, visited, values[0], maxTime)\n return max_quality\n``` | 2 | 0 | ['Depth-First Search'] | 0 |
maximum-path-quality-of-a-graph | Max Simplified Backtracking Cpp 👨💻 | max-simplified-backtracking-cpp-by-conve-afrv | Why Backtracking ?\nBecause we got at most 4 children of a node and no need of worrying out infinite recursive call as your DFS tree is bounded by the maxTime. | ConvexChull | NORMAL | 2022-07-07T18:29:07.891037+00:00 | 2022-07-07T18:31:50.058108+00:00 | 378 | false | # Why Backtracking ?\nBecause we got at most 4 children of a node and no need of worrying out infinite recursive call as your DFS tree is bounded by the maxTime. Also look at constraints backtracking seems good bet.\n# Logic \n* Basically if you somehow were able reach to the node 0 then you should update the sum you have with answer , this will be always valid as we have a conditional check " if(currTime+child.second<=maxTime)" while traversing. Thus we reach next recursive call only when our currTime is <=maxTime.\n\n* If the node\'s frequency is one then this means that it was visited the very first time and we can add its value to our sum variable.\n\n* Before recursive call pops off the stack undo our work by decrementing node from hashmap (Essence of Backtracking ).\n\n```\n int ans=INT_MIN;// global variable\n\n void dfs(vector<int>& values,vector<pair<int,int>> adj[],int& maxTime,int currTime,unordered_map<int,int>& frequency,int node,int sum)\n {\n frequency[node]++;// in both cases if visited before or first time increment its frequency\n \n if(frequency[node]==1)// visited first time\n sum+=values[node];\n \n if(node==0)// arrived at destination aka node 0\n ans=max(ans,sum);\n \n for(auto child:adj[node])// exploring children\n {\n if(currTime+child.second<=maxTime)// validation check\n dfs(values,adj,maxTime,currTime+child.second,frequency,child.first,sum); \n }\n \n if(--frequency[node]==0)frequency.erase(node);// backtrack from this node\n }\n \n \n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n \n int n=values.size();\n \n vector<pair<int,int>> adj[n];\n \n for(auto a:edges)\n {\n adj[a[0]].push_back({a[1],a[2]});\n adj[a[1]].push_back({a[0],a[2]});// dont forget this undirected graph is given\n }\n \n unordered_map<int,int> frequency;\n \n dfs(values,adj,maxTime,0,frequency,0,0);\n \n return ans;\n \n }\n```\n\n**The graph may not be connected**. This is just given to confuse us we only care about the component in which node 0 lies. No need to bother about the other components as we have to reach back to node 0. | 2 | 0 | ['Backtracking', 'C++'] | 1 |
maximum-path-quality-of-a-graph | (C++) 2065. Maximum Path Quality of a Graph | c-2065-maximum-path-quality-of-a-graph-b-nn26 | Based on @votrubac\'s solution\n\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n | qeetcode | NORMAL | 2021-11-07T22:23:05.527911+00:00 | 2021-11-07T22:23:23.380609+00:00 | 339 | false | Based on @votrubac\'s solution\n```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size(); \n vector<vector<pair<int, int>>> graph(n); \n for (auto& x : edges) {\n graph[x[0]].emplace_back(x[1], x[2]); \n graph[x[1]].emplace_back(x[0], x[2]); \n }\n \n int ans = 0; \n vector<int> freq(n); freq[0] = 1; \n \n function<void(int, int, int)> fn = [&](int u, int time, int val) {\n if (u == 0) ans = max(ans, val); \n for (auto& [v, t] : graph[u]) \n if (time + t <= maxTime) {\n if (++freq[v] == 1) fn(v, time+t, val + values[v]); \n else fn(v, time+t, val); \n --freq[v]; \n }\n }; \n \n fn(0, 0, values[0]); \n return ans; \n }\n};\n``` | 2 | 0 | ['C'] | 1 |
maximum-path-quality-of-a-graph | Java DFS Solution | java-dfs-solution-by-jackyzhang98-hbzz | Classic DFS. Since we can visit a node many times, it is necessary to keep its frequency in a hashmap. The code should explains itself.\n\nclass Solution {\n | jackyzhang98 | NORMAL | 2021-11-07T04:29:49.906057+00:00 | 2021-11-07T04:29:49.906086+00:00 | 331 | false | Classic DFS. Since we can visit a node many times, it is necessary to keep its frequency in a hashmap. The code should explains itself.\n```\nclass Solution {\n Map<Integer, List<Pair<Integer, Integer>>> map = new HashMap<>(); // source, dest, time\n int max = 0;\n int[] values;\n \n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n this.values = values;\n \n // construct map\n for (int[] edge : edges) {\n int v1 = edge[0];\n int v2 = edge[1];\n int time = edge[2];\n \n insert(v1, new Pair(v2, time));\n insert(v2, new Pair(v1, time));\n }\n \n // use hashmap to record the path\n Map<Integer, Integer> freq = new HashMap<>();\n freq.put(0, 1);\n dfs(0, maxTime, 0, freq);\n \n return max;\n }\n \n private void insert(int key, Pair<Integer, Integer> pair) {\n if (!map.containsKey(key)) {\n map.put(key, new ArrayList<>());\n }\n map.get(key).add(pair);\n }\n \n private void dfs(int root, int maxTime, int currTime, Map<Integer, Integer> freq) {\n if (currTime > maxTime) {\n return;\n }\n if (root == 0) {\n max = Math.max(max, computeValues(freq));\n }\n \n List<Pair<Integer, Integer>> neighbors = map.get(root);\n \n if (neighbors != null) {\n for (Pair<Integer, Integer> pair : neighbors) {\n int n_idx = pair.getKey();\n int n_time = pair.getValue();\n \n freq.put(n_idx, freq.getOrDefault(n_idx, 0) + 1);\n dfs(n_idx, maxTime, currTime + n_time, freq);\n freq.put(n_idx, freq.get(n_idx) - 1);\n \n // remember to remove the node if its frequency is 0\n if (freq.get(n_idx) == 0) {\n freq.remove(n_idx);\n }\n }\n }\n }\n \n private int computeValues(Map<Integer, Integer> freq) {\n int sum = 0;\n \n for (int idx : freq.keySet()) {\n sum += values[idx];\n }\n \n return sum;\n }\n}\n``` | 2 | 0 | [] | 0 |
maximum-path-quality-of-a-graph | weak testcase | weak-testcase-by-ankitsingh9164-cba0 | [0,32,43,1000]\n[[0,1,10],[1,3,10],[2,3,35],[0,2,10]]\n 49\n \n [0,32,43,1000]\n[[0,2,10],[0,1,10],[1,3,10],[2,3,35]]\n 49\n \nit\'s giving wrong ans on my code | ankitsingh9164 | NORMAL | 2021-11-07T04:03:54.359713+00:00 | 2021-11-07T04:05:04.197597+00:00 | 211 | false | [0,32,43,1000]\n[[0,1,10],[1,3,10],[2,3,35],[0,2,10]]\n 49\n \n [0,32,43,1000]\n[[0,2,10],[0,1,10],[1,3,10],[2,3,35]]\n 49\n \nit\'s giving wrong ans on my code but still it passed internal testcase\n\n`\n ArrayList<int[]> tree[];\n\t \n\t public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n int n=values.length;\n tree=new ArrayList[n];\n for (int i = 0; i <n; i++) {\n tree[i]=new ArrayList<>();\n }\n\n for (int x[]:edges) {\n tree[x[0]].add(new int[]{x[1],x[2]});\n tree[x[1]].add(new int[]{x[0],x[2]});\n }\n int m[]=new int[n];\n Queue<Node> q=new LinkedList<>();\n q.add(new Node(0,0,values[0],new HashSet<>()));\n int max=0;\n while (!q.isEmpty()){\n Node c=q.remove();\n int time=c.time;\n if(m[c.node]>c.val) continue;\n m[c.node]=c.val;\n if (c.node==0){\n max=Math.max(max,c.val);\n \n }\n\n for (int x[]:tree[c.node]) {\n int newval=c.val;\n if (!c.vis.contains(x[0])){\n newval+=values[x[0]];\n }\n if (time+x[1]>maxTime) continue;\n\n q.add(new Node(\n x[0],time+x[1],newval,c.vis\n ));\n }\n }\n return max;\n }\n static class Node{\n int node;\n int time;\n int val;\n\n public Node(int node, int time, int val, HashSet<Integer> x) {\n this.node = node;\n this.time = time;\n this.val = val;\n vis.addAll(x);\n vis.add(node);\n }\n\n HashSet<Integer> vis=new HashSet<>();\n\n }\n\n` | 2 | 0 | [] | 1 |
maximum-path-quality-of-a-graph | [Python3] iterative dfs | python3-iterative-dfs-by-ye15-0efr | Please check out this commit for solutions of weekly 266. \n\n\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], max | ye15 | NORMAL | 2021-11-07T04:02:00.111791+00:00 | 2021-11-07T05:11:25.635188+00:00 | 566 | false | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/6b6e6b9115d2b659e68dcf3ea8e21befefaae16c) for solutions of weekly 266. \n\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph = [[] for _ in values]\n for u, v, t in edges: \n graph[u].append((v, t))\n graph[v].append((u, t))\n \n ans = 0 \n stack = [(0, values[0], 0, 1)]\n while stack: \n time, val, u, mask = stack.pop()\n if u == 0: ans = max(ans, val)\n for v, t in graph[u]: \n if time + t <= maxTime: \n if not mask & 1<<v: stack.append((time+t, val+values[v], v, mask ^ 1<<v))\n else: stack.append((time+t, val, v, mask))\n return ans \n``` | 2 | 0 | ['Python3'] | 1 |
maximum-path-quality-of-a-graph | Simple C Solution using DFS | simple-c-solution-using-dfs-by-sahnasere-zroq | Code\n\n#define max(a,b) (a > b ? a : b)\n\nstruct ht_map{\n struct ht_map* next;\n int adj;\n int time;\n};\n\nvoid find_path_dfs(struct ht_map** time | sahnaseredini | NORMAL | 2024-04-06T18:47:23.935318+00:00 | 2024-04-06T18:47:23.935340+00:00 | 14 | false | # Code\n```\n#define max(a,b) (a > b ? a : b)\n\nstruct ht_map{\n struct ht_map* next;\n int adj;\n int time;\n};\n\nvoid find_path_dfs(struct ht_map** times, int* values, int size, int* visited, int* out, int max, int i, int time, int max_time){\n if(time > max_time)\n return;\n if(visited[i] == 0)\n max += values[i];\n\n int j;\n\n if(i == 0){\n *out = max(*out, max);\n }\n\n visited[i]++;\n if(times[i]){\n struct ht_map *current = times[i];\n while(current){\n j = current->adj;\n int new_time = time + current->time;\n find_path_dfs(times, values, size, visited, out, max, j, new_time, max_time);\n current = current->next;\n }\n }\n visited[i]--;\n}\n\nint maximalPathQuality(int* values, int valuesSize, int** edges, int edgesSize, int* edgesColSize, int maxTime) {\n if (valuesSize == 1){\n return values[0];\n }\n int* out = malloc(sizeof(int));\n *out = 0;\n struct ht_map** times = malloc(valuesSize * sizeof(struct ht_map*));\n int* visited = malloc(valuesSize * sizeof(int));\n int i, j;\n for (i = 0; i < valuesSize; i++){\n times[i] = NULL;\n visited[i] = 0;\n }\n \n for (i = 0; i < edgesSize; i++){\n struct ht_map *ins1, *ins2;\n int src = edges[i][0];\n int dst = edges[i][1];\n int time = edges[i][2];\n\n ins1 = malloc(sizeof(struct ht_map));\n ins1->adj = dst;\n ins1->time = time;\n ins1->next = times[src];\n times[src] = ins1;\n \n ins2 = malloc(sizeof(struct ht_map));\n ins2->adj = src;\n ins2->time = time;\n ins2->next = times[dst];\n times[dst] = ins2;\n }\n\n find_path_dfs(times, values, valuesSize, visited, out, 0, 0, 0, maxTime);\n\n return *out;\n}\n``` | 1 | 0 | ['Array', 'Backtracking', 'Graph', 'C'] | 0 |
maximum-path-quality-of-a-graph | Beats 95%, DFS with Memoization, (bitwise operator explainer) | beats-95-dfs-with-memoization-bitwise-op-jaje | Intuition\nSince you\'re allowed to revisit nodes, you can\'t use previously visited nodes to avoid loops, instead you have to use the time_left to avoid loops, | Yowfat | NORMAL | 2024-04-02T19:37:06.884363+00:00 | 2024-04-02T19:58:51.529760+00:00 | 56 | false | # Intuition\nSince you\'re allowed to revisit nodes, you can\'t use previously visited nodes to avoid loops, instead you have to use the time_left to avoid loops,\nhowever, if you\'ve previously visited this node, you can\'t add it\'s value to the answer, so you still need to keep track of previously visited\n\n# Approach\nWe first create a better way to access the graph by connecting all edges in a dictionary\n\nThen we use dfs to traverse the graph, I use bitwise operators and masking because it can keep track of visited nodes while being hashable (for the lru_cache).\n\nIf you\'re back at the origin node (0), then we check if this answer is larger than what we\'ve seen previously \n\nwe go through each of the neighbors of the node, if the cost of going there is less than the time we have left, we visit it, \n\nwe check if the neighbor has been visited via & operator in the mask\n\nif it has been visited, the neighbor\'s value is 0, otherwise we just keep the neighbor\'s value.\n\n## THE MEAT of bitwise operators and masking\nwe can use bitwise operators to track visited nodes, \nif a node has been visited we can mark it as 1\n\nie: 0010001 means, nodes 0 and nodes 4 has been visited \nbecause position 0 and position 4 in reverse is 1\n\n### Marking a node as visited\n#### we can use the | (or) operator\nin python 1 << 4 just means 1000 (1 at the 4th reversed pos)\nwe can mark a node 3 as visited by doing \nmask = 1 << 3 | mask because if mask is 10001\nthe | (or) will compare 100 and 10001 and will create a new mask with 1\nin every pos where there is a 1 in either mask\n\n### checking if a node has been visited previously\n##### **We can use the & (and) operator**\n1 << 4 means 8 which is 1000 when in binary\n**1 << 4 & 9 (1001) = True**\n because both 1000 and 1001 have 1 in the 4th position\n\nwe then update the mask with an | operator and dfs with the neighbor, remembering to use the updated mask and updating the cost, as well as adding the neighbor\'s value to the current value\n\n\n# Complexity\n- Time complexity:\nO(N or Time_left / cost of edges) we may revisit nodes, but we will only loop till we get to 0 time left\n\n- Space complexity:\nO(edges) we create a map of the edges\n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n edge_map = defaultdict(dict)\n # create a O(1) access for all edges, both ways since it\'s undirected\n for i, j, cost in edges:\n edge_map[i][j] = cost\n edge_map[j][i] = cost \n\n #original answer is just the value of node(0)\n ans = values[0]\n\n #lru cache for easy memoing \n @lru_cache(None)\n def dfs(node, value, mask, time_left):\n #if we\'re at the origin, we check if the value exceeds our old answer\n if node == 0:\n nonlocal ans\n ans = max(ans, value)\n\n for neighbor in edge_map[node]:\n cost = edge_map[node][neighbor]\n #if we have enough time left for this path\n if cost <= time_left:\n neighbor_value = 0 if mask & (1 << neighbor) else values[neighbor]\n dfs(neighbor, value + neighbor_value, mask | (1 << neighbor), time_left - cost)\n\n dfs(0, values[0], 1, maxTime)\n return ans\n\n\n``` | 1 | 0 | ['Python3'] | 1 |
maximum-path-quality-of-a-graph | Very easy DFS code | Beginner friendly | very-easy-dfs-code-beginner-friendly-by-y1q1b | \nclass Solution {\npublic:\n int maxi=-1;\n void solve(unordered_map<int,vector<pair<int,int>>> &m,vector<int> &temp, int node,int t,bool &f,vector<int>& | looserboy | NORMAL | 2023-10-28T06:49:54.738616+00:00 | 2023-10-28T06:49:54.738648+00:00 | 802 | false | ```\nclass Solution {\npublic:\n int maxi=-1;\n void solve(unordered_map<int,vector<pair<int,int>>> &m,vector<int> &temp, int node,int t,bool &f,vector<int>& v){\n if(t<0) return;\n if(node==0&&f&&t>=0){\n int tp=0;\n vector<int> vis(v.size(),0);\n for(auto it: temp){\n if(!vis[it]) {tp+=v[it];vis[it]=1;}\n }\n maxi=max(maxi,tp);\n }\n f=1;\n for(auto i:m[node]){\n temp.push_back(node);\n solve(m,temp,i.first,t-i.second,f,v);\n temp.pop_back();\n }\n }\n int maximalPathQuality(vector<int>& v, vector<vector<int>>& e, int t) {\n unordered_map<int,vector<pair<int,int>>> m;\n for(auto i: e){\n m[i[0]].push_back({i[1],i[2]});\n m[i[1]].push_back({i[0],i[2]});\n }\n vector<int> temp;\n bool f=0;\n solve(m,temp,0,t,f,v);\n if(maxi==-1) return v[0];\n return maxi;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'Depth-First Search', 'Graph', 'Recursion', 'C'] | 1 |
maximum-path-quality-of-a-graph | Simple easy to understand | simple-easy-to-understand-by-raj_tirtha-7s1j | Code\n\nclass Solution {\npublic:\n int ans=0;\n void dfs(int node,int maxTime,vector<int> &vis,vector<vector<pair<int,int>>> &adj,int &sum,vector<int> &v | raj_tirtha | NORMAL | 2023-08-24T05:07:00.896643+00:00 | 2023-08-24T05:07:00.896662+00:00 | 77 | false | # Code\n```\nclass Solution {\npublic:\n int ans=0;\n void dfs(int node,int maxTime,vector<int> &vis,vector<vector<pair<int,int>>> &adj,int &sum,vector<int> &values){\n vis[node]++;\n if(vis[node]==1) sum+=values[node];\n if(node==0) ans=max(ans,sum);\n for(auto it:adj[node]){\n if(it.second<=maxTime){\n dfs(it.first,maxTime-it.second,vis,adj,sum,values);\n }\n }\n vis[node]--;\n if(vis[node]==0) sum-=values[node];\n }\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n=values.size();\n vector<vector<pair<int,int>>> adj(n);\n for(int i=0;i<edges.size();i++){\n int u=edges[i][0],v=edges[i][1],wt=edges[i][2];\n adj[u].push_back({v,wt});\n adj[v].push_back({u,wt});\n }\n vector<int> vis(n,0);\n int sum=0;\n dfs(0,maxTime,vis,adj,sum,values);\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
maximum-path-quality-of-a-graph | (Here's my Journey) Beats 80% | heres-my-journey-beats-80-by-pathetik_co-u53r | Intuition\n Describe your first thoughts on how to solve this problem. \n\nThese kinds of problem are not very common , as normally the composer tries to make a | pathetik_coder | NORMAL | 2023-05-01T21:15:01.340670+00:00 | 2023-05-01T21:15:01.340725+00:00 | 58 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThese kinds of problem are not very common , as normally the composer tries to make a problem interesting by mixing the use of differnt algorithm or making a different version of algorithm .\nBut in this question It was just constraints Hell.\n\nWhich took a hell lot of time to resolve.\n\nAnd one more thing it\'s not easy to calculate time complexity for such problems , I just gave it a go and thankfully it got accepted.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. Just go through all possible which can start and also ent at 0 , but keep track of the visited node as they will be counted only once.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int ans;\n vector<vector<pair<int , int>>> edges;\n vector<int> vis;\n\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edgess, int maxTime) {\n \n int n = values.size();\n edges.resize(n);\n vis.resize(n);\n\n ans = 0;\n\n\n for(auto vec : edgess) {\n edges[vec[0]].push_back({vec[1] , vec[2]});\n edges[vec[1]].push_back({vec[0] , vec[2]});\n }\n dfs(0 , 0 , values[0] , maxTime , values);\n\n return ans;\n\n }\n\n void dfs(int node , int curr_time , int curr_sum , int mx_time , vector<int> &vals) {\n \n if(node == 0) {\n ans = max(ans , curr_sum);\n }\n\n vis[node]++;\n\n for(auto [next , time] : edges[node]) {\n if(curr_time + time > mx_time) continue;\n dfs(next , curr_time + time , curr_sum + (vis[next] ? 0 : vals[next]) , mx_time , vals);\n }\n\n vis[node]--;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
maximum-path-quality-of-a-graph | Python BackTrack | python-backtrack-by-zzjoshua-001n | \nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n \n ans, res = values[0], 0\ | zzjoshua | NORMAL | 2022-11-15T21:28:35.574986+00:00 | 2022-11-15T21:28:35.575010+00:00 | 78 | false | ```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n \n ans, res = values[0], 0\n nodes = defaultdict(list)\n for x,y,c in edges:\n nodes[x].append((y, c))\n nodes[y].append((x, c))\n\n def backtrack(visit, time, value):\n nonlocal res\n x = visit[-1]\n if value > res and x == 0:\n res = value\n \n for y,c in nodes[x]:\n if c + time <= maxTime:\n total = value + values[y] if y not in visit else value\n visit.append(y)\n backtrack(visit, c + time, total)\n visit.pop()\n \n backtrack([0], 0 , values[0])\n return res \n \n``` | 1 | 0 | ['Backtracking', 'Python'] | 0 |
maximum-path-quality-of-a-graph | [Python] Commented DFS Solution | Concise | python-commented-dfs-solution-concise-by-1mw7 | \nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n # Creating an adjaceny list \n | ParthRohilla | NORMAL | 2022-11-09T12:42:55.350167+00:00 | 2022-11-09T12:42:55.350199+00:00 | 366 | false | ```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n # Creating an adjaceny list \n G = defaultdict(list)\n for u,v,w in edges:\n G[u].append([v,w])\n G[v].append([u,w])\n \n def dfs(current, path, left):\n # We calculate the total path quality when we reach Node 0\n # So the most trivial case would be when we just call dfs() the first time\n # Later on, if we end up tracking back to Node 0 Again, we have a candidate for a "valid path"\n # So we add up values for all the nodes in the set\n # We continue our dfs() until we have some time left\n if current == 0:\n tmp = 0\n for node in path:\n tmp += values[node]\n self.best = max(self.best, tmp)\n # Moving to neighbour nodes and calling dfs() until time left\n for nei, wei in G[current]:\n if wei <= left:\n dfs(nei, {nei} | path, left - wei)\n \n self.best = 0\n # Calling helper dfs() method\n # arguments signify : current node, current path set, time left \n dfs(0, {0}, maxTime)\n return self.best\n``` | 1 | 0 | ['Depth-First Search', 'Python'] | 1 |
maximum-path-quality-of-a-graph | BFS | bfs-by-pranvpable-pgv7 | \nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph = defaultdict(list)\n | pranvpable | NORMAL | 2022-11-03T14:03:14.262921+00:00 | 2022-11-03T14:03:14.262961+00:00 | 91 | false | ```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph = defaultdict(list)\n \n for u,v,time in edges:\n graph[u].append([v,time])\n graph[v].append([u,time])\n \n seen = set()\n seen.add(0)\n queue = deque([(0,0,seen)])\n answer = values[0]\n memo = {}\n while queue:\n time, node, seen = queue.popleft()\n currPoints = sum(values[i] for i in seen)\n if node in memo:\n prevTime, prevPoints = memo[node]\n if prevTime <= time and prevPoints > currPoints:\n continue\n memo[node] = (time, currPoints)\n \n if time > maxTime:\n continue\n if node == 0:\n answer = max(answer, currPoints)\n \n for nei,val in graph[node]:\n queue.append((time+val,nei,seen | {nei}))\n \n return answer\n``` | 1 | 0 | ['Breadth-First Search'] | 0 |
maximum-path-quality-of-a-graph | [C++] Super Short Solution !!! | c-super-short-solution-by-kylewzk-ze8h | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kylewzk | NORMAL | 2022-10-08T05:48:32.931058+00:00 | 2022-10-08T05:48:32.931104+00:00 | 67 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& v, vector<vector<int>>& e, int m) {\n int res = 0, seen[1001]{};\n vector<pair<int, int>> g[1001];\n for(auto & i : e) {\n g[i[0]].push_back({i[1], i[2]});\n g[i[1]].push_back({i[0], i[2]});\n }\n auto dfs = [&](auto&& self, int n, int t, int cur) {\n if(t < 0) return;\n if(!seen[n]) cur += v[n];\n if(n == 0) res = max(cur, res);\n seen[n]++;\n for(auto & c : g[n]) self(self, c.first, t-c.second, cur);\n seen[n]--;\n };\n dfs(dfs, 0, m, 0);\n return res;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
maximum-path-quality-of-a-graph | [Python 3] DFS+BackTrack | python-3-dfsbacktrack-by-gabhay-heoz | \tclass Solution:\n\t\tdef maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n\t\t\tn=len(values)\n\t\t\tG=[[] for _ in | gabhay | NORMAL | 2022-08-02T12:08:01.888539+00:00 | 2022-08-02T12:10:56.953097+00:00 | 138 | false | \tclass Solution:\n\t\tdef maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n\t\t\tn=len(values)\n\t\t\tG=[[] for _ in range(n)]\n\t\t\tfor u,v,t in edges:\n\t\t\t\tG[u].append([v,t])\n\t\t\t\tG[v].append([u,t])\n\t\t\tself.res=0\n\t\t\tdef dfs(node,time,path,val):\n\t\t\t\tif node==0:\n\t\t\t\t\tself.res=max(self.res,val)\n\t\t\t\tfor child,t in G[node]:\n\t\t\t\t\tif time+t<=maxTime\n\t\t\t\t\t\tif child in path:\n\t\t\t\t\t\t\tdfs(child,time+t,path,val)\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\tpath.add(child)\n\t\t\t\t\t\t\tdfs(child,time+t,path,val+values[child])\n\t\t\t\t\t\t\tpath.remove(child)\n\t\t\tdfs(0,0,set([0]),values[0])\n\t\t\treturn self.res | 1 | 0 | [] | 0 |
maximum-path-quality-of-a-graph | [Python] DFS Recursive | python-dfs-recursive-by-happysde-apu1 | \nclass Solution:\n \n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n d = defaultdict(list)\n | happysde | NORMAL | 2022-06-27T22:15:53.469773+00:00 | 2022-06-27T22:15:53.469811+00:00 | 152 | false | ```\nclass Solution:\n \n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n d = defaultdict(list)\n n = len(values)\n \n for edge in edges:\n d[edge[0]].append([edge[1], edge[2]])\n d[edge[1]].append([edge[0], edge[2]])\n \n visited = [0]*n\n ans = 0\n \n def dfs(node, curTime, total):\n nonlocal ans\n if curTime > maxTime:\n return\n \n if visited[node] == 0:\n total+= values[node]\n \n if node == 0:\n if total > ans:\n ans = total\n \n visited[node] += 1\n \n for vertex, time in d[node]:\n dfs(vertex, curTime + time, total)\n \n visited[node] -= 1\n \n dfs(0, 0, 0)\n return ans\n``` | 1 | 0 | ['Depth-First Search', 'Recursion', 'Python3'] | 1 |
maximum-path-quality-of-a-graph | Python || DFS with just 3 Dimensions || Using Node Traversal Count to stop | python-dfs-with-just-3-dimensions-using-2as69 | Its mentioned that : There are at most four edges connected to each node.\nSo I have implemented a map to store how many times a node has been traversed.\nI bre | subin_nair | NORMAL | 2022-06-16T13:08:50.525978+00:00 | 2022-06-16T19:39:10.126970+00:00 | 187 | false | Its mentioned that : `There are at most four edges connected to each node.`\nSo I have implemented a map to store how many times a `node` has been traversed.\nI break the `dfs` process when the a node has been traversed for the `5th` time. \nThis is because **`nodes should be traversed back and forth for a max of 4 times coz it can have only 4 edges max`**\nHence the dfs gets stopped from running infinitely like `node0->node1->node0->node1.....`.\nAlso we break when the cumulatime `time` taken exceeds the `maxTime`.\nWhenever we reach node 0 , we store the total quality value `qual` so far in `sol`\n\n```py\nclass Solution:\n def maximalPathQuality(self, quality: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph, sol = defaultdict(list), []\n sol = []\n for x, y, time in edges:\n graph[x].append((y, time))\n graph[y].append((x, time))\n\n def dfs(node, time, qual):\n if node == 0: sol.append(qual)\n new_qual = qual\n for nxt_node, nxt_time in graph[node]:\n if time + nxt_time <= maxTime:\n if vis[nxt_node] + 1 >= 5: return -inf\n vis[nxt_node] += 1\n new_qual = max(dfs(nxt_node, nxt_time + time, qual + quality[nxt_node] * (vis[nxt_node] == 1)), new_qual)\n vis[nxt_node] -= 1\n return new_qual\n\n vis = defaultdict(int, {0: 1})\n dfs(0, 0, quality[0])\n return max(sol)\n```\n\n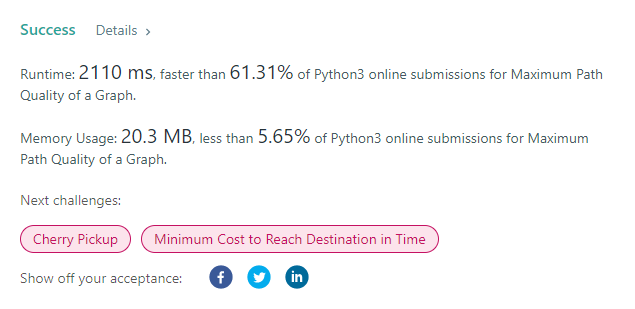\n\n\n\n\n**Happy Coding !!**\n\nIn case of any questions, feel free to ask. | 1 | 0 | ['Depth-First Search', 'Python'] | 1 |
maximum-path-quality-of-a-graph | C++ || DFS || Easy to understand | c-dfs-easy-to-understand-by-iota_2010-0nbe | \nclass Solution {\npublic:\n int rec(vector<int>& values, vector<vector<pair<int,int>>>& vec, int maxt,int x)\n {\n int ans=INT_MIN;\n if(x | iota_2010 | NORMAL | 2022-05-25T21:45:25.538870+00:00 | 2022-05-25T21:45:25.538907+00:00 | 119 | false | ```\nclass Solution {\npublic:\n int rec(vector<int>& values, vector<vector<pair<int,int>>>& vec, int maxt,int x)\n {\n int ans=INT_MIN;\n if(x==0)\n ans=0;\n for(int i=0;i<vec[x].size();i++)\n {\n int a=vec[x][i].first,b=vec[x][i].second;\n if(b<=maxt)\n {\n int v=values[a];\n values[a]=0;\n int p=rec(values,vec,maxt-b,a);\n if(p!=INT_MIN)\n ans=max(ans,p+v);\n values[a]=v;\n }\n }\n return ans;\n }\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxt) {\n int trav=0;\n vector<vector<pair<int,int>>> vec(values.size()+5);\n for(int i=0;i<edges.size();i++)\n {\n int a=edges[i][0],b=edges[i][1],c=edges[i][2];\n vec[a].push_back({b,c});\n vec[b].push_back({a,c});\n }\n int v=values[0];\n values[0]=0;\n return rec(values,vec,maxt,0)+v; \n }\n};\n``` | 1 | 0 | ['Backtracking', 'Depth-First Search', 'C', 'C++'] | 0 |
maximum-path-quality-of-a-graph | Python 🐍 DFS recursive with cache and frozen set | python-dfs-recursive-with-cache-and-froz-2fg6 | Idea inspired from @float4, using cashe to speed up the dfs so it\'s do any unnecessary recalucations that were made before, however as cache doesn\'t work with | injysarhan | NORMAL | 2022-02-02T09:08:41.215088+00:00 | 2022-02-02T09:08:41.215121+00:00 | 242 | false | Idea inspired from @float4, using cashe to speed up the dfs so it\'s do any unnecessary recalucations that were made before, however as cache doesn\'t work with sets and maps, had to use a immuatble version of set --> [frozenset](https://www.programiz.com/python-programming/methods/built-in/frozenset) \n\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph=defaultdict(list)\n \n for in_,out,cost in edges:\n graph[in_].append((out,cost))\n graph[out].append((in_,cost))\n \n \n self.max_res=0\n @cache\n def dfs(node,time,val,seen):\n \n if node==0:\n self.max_res=max(self.max_res,val)\n \n for neigh,t in graph[node]:\n if time+t>maxTime:\n continue\n dfs(neigh, time+t, val+(neigh not in seen) * values[neigh], seen | frozenset([neigh]) )\n dfs(0,0,values[0],frozenset([0]))\n return self.max_res\n``` | 1 | 0 | ['Depth-First Search', 'Python'] | 0 |
maximum-path-quality-of-a-graph | DFS || C++ || Easy To Understand | dfs-c-easy-to-understand-by-vineetjai-a93a | \nclass Solution {\n vector<vector<pair<int,int>>> grp;\n int ans;\n void dfs(int u,int cost,int gain,vector<int>& values,vector<int> &vis){\n i | vineetjai | NORMAL | 2021-12-29T07:21:14.101035+00:00 | 2021-12-29T07:21:14.101077+00:00 | 359 | false | ```\nclass Solution {\n vector<vector<pair<int,int>>> grp;\n int ans;\n void dfs(int u,int cost,int gain,vector<int>& values,vector<int> &vis){\n if(!vis[u]) gain+=values[u];\n if(u==0) ans=max(ans,gain);\n vis[u]++; \n for(auto j:grp[u])\n if(j.second<=cost) dfs(j.first,cost-j.second,gain,values,vis);\n vis[u]--;\n }\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n=values.size();\n grp.clear();\n ans=0;\n grp=vector<vector<pair<int,int>>> (n);\n for(auto &i:edges){\n grp[i[0]].push_back({i[1],i[2]});\n grp[i[1]].push_back({i[0],i[2]});\n }\n vector<int> vis(n,0);\n dfs(0,maxTime,0,values,vis);\n return ans;\n }\n};\n```\n\nPassed in 128 ms. | 1 | 0 | ['Depth-First Search', 'C'] | 1 |
maximum-path-quality-of-a-graph | [Python] memoized DFS | python-memoized-dfs-by-mars_congressiona-kcna | Like many other solutions, in order to memoize the backtracking, we can use a bitmask, i.e. an int holding (2**n)-1 bits. I write out as functions what we need | Mars_Congressional_Republic | NORMAL | 2021-12-04T20:58:23.981319+00:00 | 2021-12-04T20:58:23.981349+00:00 | 167 | false | Like many other solutions, in order to memoize the backtracking, we can use a bitmask, i.e. an int holding (2**n)-1 bits. I write out as functions what we need to do to a bitmask in order to run the DFS successfully\n\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n\n n = len(values)\n #values is values of ith node\n graph = defaultdict(list)\n for src, dest, time in edges:\n graph[src].append((dest,time))\n graph[dest].append((src, time))\n\n self.ansr = 0\n # let\'s make visited a bitmask...\n # bitmask will be 2**n-1\n #bitmask starts at one\n def set_ith_bit(x, i):\n return (1<<i)|x\n \n def unset_ith_bit(x, i):\n return ~(1<<i) & x\n \n def check_ith_bit(x,i):\n return (x >> i) & 1\n \n @lru_cache(None)\n def backtrack(node = 0, curTime = 0, visited = 1, curval = values[0]):\n if(curTime > maxTime):\n return\n for v,time in graph[node]:\n if(curTime+time<=maxTime): \n \n backtrack(v, curTime+time, set_ith_bit(visited, v), curval+values[v] if not check_ith_bit(visited,v) else curval)\n if(node == 0):\n \n self.ansr = max(self.ansr, curval)#max(self.ansr, (sum([values[i] for i in range(n) if visited[i]>0])))\n #print(self.ansr)\n return\n backtrack()\n return self.ansr\n\t\t\n``` | 1 | 1 | [] | 0 |
maximum-path-quality-of-a-graph | c++ dfs | c-dfs-by-nitesh_nitp-oz8s | long long int max(long long int ans,long long int sum)\n{\n return ans>=sum?ans:sum;\n}\nvoid fun(int a,vector>>& g,vector& values,int maxTime,long long int | nitesh_nitp | NORMAL | 2021-11-12T13:03:21.041018+00:00 | 2021-11-12T13:03:21.041051+00:00 | 152 | false | long long int max(long long int ans,long long int sum)\n{\n return ans>=sum?ans:sum;\n}\nvoid fun(int a,vector<vector<pair<int,int>>>& g,vector<int>& values,int maxTime,long long int & sum,int & time,long long int & ans)\n{\n if(a==0) { ans=max(ans,sum); }\n for(auto x : g[a])\n {\n if((time+x.second)<=maxTime)\n {\n sum=sum+values[x.first];\n int temp=values[x.first];\n values[x.first]=0;\n time=time+x.second;\n fun(x.first,g,values,maxTime,sum,time,ans);\n time=time-x.second;\n sum=sum-temp;\n values[x.first]=temp;\n }\n }\n}\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) { \n long long int ans=INT_MIN;\n int n=values.size();\n vector<vector<pair<int,int>>> g(n);\n for(auto x : edges)\n {\n g[x[0]].push_back(make_pair(x[1],x[2]));\n g[x[1]].push_back(make_pair(x[0],x[2]));\n }\n ans=max(ans,values[0]); long long int sum=values[0]; int time=0; values[0]=0;\n fun(0,g,values,maxTime,sum,time,ans);\n return ans;\n }\n}; | 1 | 0 | [] | 0 |
maximum-path-quality-of-a-graph | [Scala] Functional no vars DFS solution | scala-functional-no-vars-dfs-solution-by-ul7q | \n def maximalPathQuality(values: Array[Int], edges: Array[Array[Int]], maxTime: Int): Int = {\n val adjList = edges.foldLeft(Map.empty[Int, Seq[(Int, Int)] | cosminci | NORMAL | 2021-11-11T15:38:12.079567+00:00 | 2022-03-02T21:29:37.031373+00:00 | 55 | false | ```\n def maximalPathQuality(values: Array[Int], edges: Array[Array[Int]], maxTime: Int): Int = {\n val adjList = edges.foldLeft(Map.empty[Int, Seq[(Int, Int)]].withDefaultValue(Seq.empty)) {\n case (adj, Array(n1, n2, cost)) =>\n adj\n .updated(n1, adj(n1) :+ (n2, cost))\n .updated(n2, adj(n2) :+ (n1, cost))\n }\n\n def dfs(node: Int, visited: Set[Int], quality: Int, budget: Int): Int =\n adjList(node)\n .collect {\n case (next, cost) if (cost <= budget) =>\n val nextQuality = Option.when(!visited.contains(next))(values(next)).getOrElse(0)\n dfs(next, visited + next, quality + nextQuality, budget - cost)\n }\n .appendedAll(Option.when(node == 0)(quality))\n .maxOption\n .getOrElse(0)\n\n dfs(node = 0, visited = Set(0), quality = values.head, budget = maxTime)\n }\n``` | 1 | 0 | ['Depth-First Search'] | 0 |
maximum-path-quality-of-a-graph | [JAVA] Modified DFS + visited | java-modified-dfs-visited-by-rico_13-vcwj | ```\nclass Solution {\n int maxq=0;\n public void helper(List[] graph ,int si,int ql,int vis[],int time,int []values){\n if(time<0) return;\n | Rico_13 | NORMAL | 2021-11-07T20:57:47.808538+00:00 | 2021-11-07T20:57:47.808584+00:00 | 125 | false | ```\nclass Solution {\n int maxq=0;\n public void helper(List<int[]>[] graph ,int si,int ql,int vis[],int time,int []values){\n if(time<0) return;\n vis[si]++;\n if(vis[si]==1) ql+=values[si];\n \n if(si==0 && time>=0) maxq=Math.max(maxq,ql);\n \n \n \n for(int []a:graph[si]){\n int v=a[0];\n int vtime=a[1];\n \n \n helper(graph,v,ql,vis,time-vtime,values);\n }\n vis[si]--;\n }\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n int n=values.length;\n// {node,time} for every node in the neighbor\n List<int[]>[] graph=new ArrayList[n];\n for(int i=0;i<n;i++){\n graph[i]=new ArrayList<>();\n }\n \n for(int a[]:edges){\n int u=a[0];\n int v=a[1];\n int t=a[2];\n \n graph[u].add(new int[]{v,t});\n graph[v].add(new int[]{u,t});\n }\n int vis[]=new int[n];\n \n helper(graph,0,0,vis,maxTime,values);\n \n return maxq;\n \n }\n} | 1 | 1 | ['Backtracking', 'Java'] | 0 |
maximum-path-quality-of-a-graph | Never use Map if you can use array in Java on LeetCode | never-use-map-if-you-can-use-array-in-ja-4a83 | Just backtracking solution for Q4, but I use Map<Integer, Integer> visited, then I get a TLE, after the contest, I tried int[] visited, and AC.\n\n\nTLE code\n\ | toffeelu | NORMAL | 2021-11-07T07:10:10.999421+00:00 | 2021-11-07T07:10:31.533575+00:00 | 141 | false | Just backtracking solution for Q4, but I use `Map<Integer, Integer> visited`, then I get a TLE, after the contest, I tried `int[] visited`, and AC.\n\n\nTLE code\n```\nclass Solution {\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n int n = values.length;\n Map<Integer, Map<Integer, Integer>> edgeMap = new HashMap<>();\n for(int[] edge: edges){\n edgeMap.putIfAbsent(edge[0], new HashMap<>());\n edgeMap.get(edge[0]).put(edge[1], edge[2]);\n edgeMap.putIfAbsent(edge[1], new HashMap<>());\n edgeMap.get(edge[1]).put(edge[0], edge[2]);\n }\n Map<Integer, Integer> visited = new HashMap<>();\n visited.put(0, 1);\n backtrack(values, edgeMap, visited, 0, 0, maxTime, values[0]);\n return res;\n }\n \n int res = 0;\n \n void backtrack(int[] values, Map<Integer, Map<Integer, Integer>> edgeMap, Map<Integer, Integer> visited, int cur, int time, int maxTime, int gain){\n if(time > maxTime){\n return;\n }\n if(cur == 0){\n res = Math.max(res, gain);\n }\n if(!edgeMap.containsKey(cur)){\n return;\n }\n for(int next: edgeMap.get(cur).keySet()){\n int cost = edgeMap.get(cur).get(next);\n int value = visited.containsKey(next) ? 0 : values[next];\n visited.put(next, visited.getOrDefault(next, 0) + 1);\n backtrack(values, edgeMap, visited, next, time + cost, maxTime, gain + value);\n visited.put(next, visited.get(next) - 1);\n if(visited.get(next) == 0){\n visited.remove(next);\n }\n }\n return;\n }\n}\n``` | 1 | 0 | [] | 3 |
maximum-path-quality-of-a-graph | Java DFS solution | java-dfs-solution-by-nehakothari-v7sw | Inspiration from @votrubac \'s Plain DFS solution :\nhttps://leetcode.com/problems/maximum-path-quality-of-a-graph/discuss/1563744/Plain-DFS\n\n\nclass Solution | nehakothari | NORMAL | 2021-11-07T06:11:18.317857+00:00 | 2021-11-07T06:11:18.317889+00:00 | 102 | false | Inspiration from @votrubac \'s Plain DFS solution :\nhttps://leetcode.com/problems/maximum-path-quality-of-a-graph/discuss/1563744/Plain-DFS\n\n```\nclass Solution {\n \n int result = 0;\n List<List<int[]>> graph = new ArrayList<>();\n int[] values;\n int[] visited;\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n \n int vertices = values.length;\n this.values = values;\n \n visited = new int[vertices];\n \n \n for (int i = 0; i < vertices; i++) {\n graph.add(new ArrayList<>());\n \n }\n \n for (int i = 0; i < edges.length; i++) { \n \n int v1 = edges[i][0];\n int v2 = edges[i][1];\n int w = edges[i][2]; \n \n graph.get(v1).add(new int[]{v2, w});\n graph.get(v2).add(new int[]{v1, w});\n }\n \n dfs(0, visited, 0, maxTime);\n return result;\n \n }\n \n public void dfs(int node, int[] visited, int gain, int cost) {\n \n if (visited[node] == 0) {\n gain += values[node];\n }\n visited[node]++;\n \n if (node == 0) {\n result = Math.max(result, gain);\n }\n \n for (int[] n : graph.get(node)) {\n \n int neighbour = n[0];\n int w = n[1];\n \n if (w <= cost) {\n \n dfs(neighbour, visited, gain, cost - w);\n \n }\n }\n visited[node]--;\n }\n}\n\n``` | 1 | 0 | [] | 0 |
maximum-path-quality-of-a-graph | Java | backtracking | Concise | O(4^10) | java-backtracking-concise-o410-by-tyro-e4nz | Backtracking with the length of the paths limited to 10 at most. The branch factor is 4. So Time O(4^10).\n\n\nclass Solution {\n Map<Integer, Map<Integer, I | tyro | NORMAL | 2021-11-07T05:42:35.216046+00:00 | 2021-11-07T05:51:54.754014+00:00 | 349 | false | Backtracking with the length of the paths limited to 10 at most. The branch factor is 4. So Time O(4^10).\n\n```\nclass Solution {\n Map<Integer, Map<Integer, Integer> > g = new HashMap();\n int res = 0;\n int[] values;\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n this.values = values;\n for(int[] e : edges) {\n int u = e[0], v = e[1], t = e[2];\n g.computeIfAbsent(u, x -> new HashMap()).put(v, t);\n g.computeIfAbsent(v, x -> new HashMap()).put(u, t);\n }\n dfs(new ArrayList(), 0, maxTime, 0);\n return res;\n }\n void dfs(List<Integer> path, int cur, int maxTime, int time) {\n path.add(cur);\n if(cur == 0) {\n int tmp = 0;\n Set<Integer> hs = new HashSet();\n for(int i : path) {\n if(hs.add(i)) tmp += values[i];\n }\n res = Math.max(res, tmp);\n }\n for(var en : g.getOrDefault(cur, new HashMap<>()).entrySet()) {\n int nei = en.getKey(), t = en.getValue();\n if(t + time > maxTime) continue;\n dfs(path, nei, maxTime, t + time);\n }\n path.remove(path.size() - 1);\n }\n}\n``` | 1 | 0 | ['Backtracking', 'Depth-First Search', 'Java'] | 0 |
maximum-path-quality-of-a-graph | [C++] DFS | c-dfs-by-ericyxing-hvnn | Logical Thinking\nSince each node\'s value can be added only once, we\'d better use Depth-First Search to solve this problem. So we start from node 0, and try a | EricYXing | NORMAL | 2021-11-07T05:14:26.718260+00:00 | 2021-11-07T05:14:26.718304+00:00 | 176 | false | <strong>Logical Thinking</strong>\n<p>Since each node\'s value can be added only once, we\'d better use <strong>Depth-First Search</strong> to solve this problem. So we start from node <code>0</code>, and try all possible paths (edges can be used more than once). Each time we come to a new node which is not counted before, update the current quality with its value. Whenever we come back to node <code>0</code>, update the answer with current quality. If current time is larger than the maximal time, stop the current path and try the next one.</p>\n\n\n<strong>C++</strong>\n\n```\n// Topic : 2065. Maximum Path Quality of a Graph (https://leetcode.com/problems/maximum-path-quality-of-a-graph/)\n// Author : YCX\n// Time : O(max<int>(M + N, T / minE))\n// Space : O(M + N)\n\n\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n unordered_map<int, vector<pair<int, int>>> connect;\n for (auto e : edges)\n {\n connect[e[0]].push_back({e[1], e[2]});\n connect[e[1]].push_back({e[0], e[2]});\n }\n int n = values.size(), ans = 0;\n vector<int> cal(n, 0);\n cal[0] = 1;\n dfs(0, connect, cal, values, values[0], maxTime, 0, ans);\n return ans;\n }\n \nprivate: \n void dfs(int start, unordered_map<int, vector<pair<int, int>>>& connect, vector<int>& cal, vector<int>& values, int curQuality, int maxTime, int curTime, int& ans)\n {\n if (curTime > maxTime)\n return;\n if (start == 0)\n ans = max<int>(ans, curQuality);\n for (auto i : connect[start])\n {\n if (cal[i.first] == 0)\n {\n cal[i.first] = 1;\n dfs(i.first, connect, cal, values, curQuality + values[i.first], maxTime, curTime + i.second, ans);\n cal[i.first] = 0;\n }\n else\n dfs(i.first, connect, cal, values, curQuality, maxTime, curTime + i.second, ans);\n }\n }\n};\n```\n | 1 | 0 | ['Depth-First Search', 'C'] | 0 |
maximum-path-quality-of-a-graph | Easy understanding java code (Plain DFS) | easy-understanding-java-code-plain-dfs-b-dy1z | \nclass Solution {\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n int n = values.length;\n int[] res = new int[] | Ramsey0704 | NORMAL | 2021-11-07T04:50:25.970236+00:00 | 2021-11-07T04:50:25.970266+00:00 | 112 | false | ```\nclass Solution {\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n int n = values.length;\n int[] res = new int[]{Integer.MIN_VALUE};\n List<List<int[]>> graph = buildGraph(n, edges);\n Set<Integer> visited = new HashSet<>();\n visited.add(0);\n helper(graph, values, 0, 0, maxTime, visited, res);\n return res[0];\n }\n private void helper(List<List<int[]>> graph, int[] values, int curNode, int curTime, int maxTime, Set<Integer> visited, int[] res) {\n if (curTime > maxTime) {\n return;\n }\n if (curNode == 0) {\n int tmp = 0;\n for (int key : visited) {\n tmp += values[key];\n }\n res[0] = Math.max(res[0], tmp);\n }\n for (int[] info : graph.get(curNode)) {\n int neiborNode = info[0];\n int neiborTimeCost = info[1];\n boolean flag = visited.add(neiborNode);\n helper(graph, values, neiborNode, curTime + neiborTimeCost, maxTime, visited, res);\n if (flag) {\n visited.remove(neiborNode);\n }\n }\n }\n private List<List<int[]>> buildGraph(int n, int[][] edges) {\n List<List<int[]>> graph = new ArrayList<>();\n for (int i = 0; i < n; i++) {\n graph.add(new ArrayList<>());\n }\n for (int[] e : edges) {\n graph.get(e[0]).add(new int[]{e[1], e[2]});\n graph.get(e[1]).add(new int[]{e[0], e[2]});\n }\n return graph;\n }\n}\n``` | 1 | 0 | [] | 0 |
maximum-path-quality-of-a-graph | I have one conjecture, need some1 to prove (for optimal pruning during DFS search) | i-have-one-conjecture-need-some1-to-prov-mi79 | Hi, my statement is that:\n\n\n"This path(or at least one of the best path) won\'t contain duplicate directional edge. "\n\n\nI mean it can contain 0->1 and 1- | a_pinterest_employee | NORMAL | 2021-11-07T04:11:34.747658+00:00 | 2021-11-10T20:14:04.554672+00:00 | 213 | false | Hi, my statement is that:\n\n```\n"This path(or at least one of the best path) won\'t contain duplicate directional edge. "\n```\n\nI mean it can contain 0->1 and 1->0, but it won\'t contian two 0->1. | 1 | 0 | [] | 4 |
maximum-path-quality-of-a-graph | Python Simple Dijkstra | python-simple-dijkstra-by-kodewithklossy-sswg | \nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph = defaultdict(dict) # dict o | kodewithklossy | NORMAL | 2021-11-07T04:07:33.028458+00:00 | 2021-11-07T04:07:33.028497+00:00 | 260 | false | ```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n graph = defaultdict(dict) # dict of dict to store weights\n pq = []\n res = 0\n\n heapq.heappush(pq, (-values[0], 0, 0, {0})) # quality, time, index, nodes\n\n for i in range(len(edges)):\n u, v, w = edges[i]\n graph[u][v] = w\n graph[v][u] = w\n\n while pq:\n top = heapq.heappop(pq)\n u = top[2]\n if u == 0:\n res = max(res, -top[0])\n for v in graph[u]:\n time = top[1] + graph[u][v]\n nodes = top[3].copy()\n if time <= maxTime:\n if v in nodes:\n heapq.heappush(pq, (top[0], time, v, nodes))\n else:\n nodes.add(v)\n heapq.heappush(pq, (top[0] - values[v], time, v, nodes))\n\n return res\n``` | 1 | 0 | [] | 1 |
maximum-path-quality-of-a-graph | [Python] simple brute-force DFS | O(4^10) | python-simple-brute-force-dfs-o410-by-go-la9n | We can just DFS / backtrack the graph starting from the initial node in the simplistic way. Cyclic paths are allowed because visited nodes are not filtered out | gowe | NORMAL | 2021-11-07T04:00:55.849087+00:00 | 2021-11-07T04:00:55.849148+00:00 | 187 | false | We can just DFS / backtrack the graph starting from the initial node in the simplistic way. Cyclic paths are allowed because visited nodes are not filtered out as they are in typical graph traversal. There won\'t be stack overflow since the constraints on input are pretty small. \n\n> There are *at most four* edges connected to each node.\n\nFor every nodes, we have at most four neighbours to traverse.\n\n> `10 <= timej, maxTime <= 100`\n\n`maxTime / time_j <= 10` and hence the maximum path length is at most `10`.\n\nAt each DFS/backtracking level, we have at most 4 sub-functions to call. And the depths of DFS/backtracking are at most `10`. So we have `T = O(4^10) = O(2^20)`, which is reasonble to get accepted.\n\n\n```python\n\nfrom collections import defaultdict, Counter\n\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n g = defaultdict(dict) # construct the graph\n for a, b, t in edges:\n g[a][b] = t\n g[b][a] = t\n \n mpq = pq = 0 # global maximal path quality, path quality of the current path\n remaining_time = maxTime\n visited = Counter() # nodes of the current path\n def backtrack(node):\n nonlocal pq, mpq, remaining_time\n visited[node] += 1\n if visited[node] == 1: # one more unique node\n pq += values[node] # update path quality\n if node == 0: # path is valid (from 0 to 0)\n mpq = max(mpq, pq) # update maximal path quality\n for neigh, time in g[node].items():\n if remaining_time >= time:\n remaining_time -= time\n backtrack(neigh)\n remaining_time += time\n visited[node] -= 1\n if visited[node] == 0:\n del visited[node]\n pq -= values[node]\n backtrack(0)\n return mpq\n``` | 1 | 0 | [] | 0 |
maximum-path-quality-of-a-graph | Java DFS - key is to flip the newVisit | java-dfs-key-is-to-flip-the-newvisit-by-bus82 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | yyy0755 | NORMAL | 2025-03-25T06:26:41.341232+00:00 | 2025-03-25T06:26:41.341232+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
private int ans;
private List<int[]>[] graph;
private int[] values;
public int maximalPathQuality(int[] values, int[][] E, int maxTime) {
int n = values.length;
this.values = values;
// Build the graph (undirected)
graph = new ArrayList[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int[] edge : E) {
int u = edge[0], v = edge[1], w = edge[2];
graph[u].add(new int[]{v, w});
graph[v].add(new int[]{u, w});
}
ans = 0;
// visited[i] is true if node i has been visited in the current path
boolean[] visited = new boolean[n];
visited[0] = true; // Start at node 0
dfs(0, values[0], maxTime, visited);
return ans;
}
private void dfs(int node, int gain, int timeLeft, boolean[] visited) {
// Whenever we return to node 0, update our answer
if (node == 0) {
ans = Math.max(ans, gain);
}
// Explore all neighbors of the current node
for (int[] edge : graph[node]) {
int neib = edge[0], cost = edge[1];
if (cost <= timeLeft) {
boolean newVisit = false;
// Only add the neighbor's value if it's the first time visiting it
if (!visited[neib]) {
newVisit = true;
visited[neib] = true;
}
dfs(neib, gain + (newVisit ? values[neib] : 0), timeLeft - cost, visited);
// Backtrack: if we marked neib as newly visited in this call, unmark it
if (newVisit) {
visited[neib] = false;
}
}
}
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-path-quality-of-a-graph | Python3 - BFS Solution - Beats 98% | python3-bfs-solution-beats-98-by-aaron_m-tx0b | Code | aaron_mathis | NORMAL | 2025-02-23T18:37:40.415245+00:00 | 2025-02-23T18:37:40.415245+00:00 | 7 | false | # Code
```python3 []
class Solution:
def maximalPathQuality(self, nodeValues: List[int], edges: List[List[int]], maxAllowedTime: int) -> int:
# Build the adjacency list representation of the graph
graph = defaultdict(list)
for startNode, endNode, travelTime in edges:
graph[startNode].append((endNode, travelTime))
graph[endNode].append((startNode, travelTime))
# Initialize the queue for BFS traversal
# (currentNode, currentTime, pathValueSum, visitedNodes)
bfsQueue = deque([(0, 0, nodeValues[0], [0])])
# Stores (maxValueReached, minTimeReached) for each node
nodeVisitInfo = [(-1, -1)] * len(nodeValues)
nodeVisitInfo[0] = (nodeValues[0], 0)
maxPathQuality = 0 # Stores the maximum path quality found
while bfsQueue:
currentNode, elapsedTime, currentPathValue, visitedNodes = bfsQueue.popleft()
# If we return to node 0, update max path quality
if currentNode == 0:
maxPathQuality = max(maxPathQuality, currentPathValue)
# Explore neighbors of the current node
for neighborNode, travelTime in graph[currentNode]:
if elapsedTime + travelTime > maxAllowedTime:
continue # Skip if time exceeds the allowed limit
newPathValue = currentPathValue
if neighborNode not in visitedNodes:
newPathValue += nodeValues[neighborNode] # Add value only if first visit
# Optimization: Skip paths that are worse than already found ones
if elapsedTime + travelTime >= nodeVisitInfo[neighborNode][1] and newPathValue < nodeVisitInfo[neighborNode][0]:
continue
# Append the new path to the queue
bfsQueue.append((neighborNode, elapsedTime + travelTime, newPathValue, visitedNodes + [neighborNode]))
# Update node visit information with the best value and earliest time
nodeVisitInfo[neighborNode] = (newPathValue, elapsedTime + travelTime)
return maxPathQuality
``` | 0 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Python3'] | 0 |
maximum-path-quality-of-a-graph | Working BFS. | working-bfs-by-woekspace-v4k7 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | woekspace | NORMAL | 2025-01-24T08:31:45.733601+00:00 | 2025-01-24T08:31:45.733601+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges,
int maxTime) {
int n = values.size();
vector<pair<int, int>> adj[n];
for (int i = 0; i < edges.size(); i++) {
int u = edges[i][0];
int v = edges[i][1];
int w = edges[i][2];
adj[u].push_back({v, w});
adj[v].push_back({u, w});
}
set<pair<int, pair<int, set<int>>>> q;
q.insert({0, {0, {0}}});
set<set<int>> anspth;
while (!q.empty()) {
auto it = *(q.begin());
int curt = it.first;
int node = it.second.first;
set<int> curpath = it.second.second;
q.erase(it);
if (node == 0) {
anspth.insert(curpath);
}
for (auto nbg : adj[node]) {
int nbgnode = nbg.first;
int delt = nbg.second;
int newt = curt + delt;
if (newt <= maxTime) {
bool ok = 0;
if (curpath.find(nbgnode) != curpath.end()) {
ok = 1;
}
curpath.insert(nbgnode);
q.insert({newt, {nbgnode, curpath}});
if (ok == 0) {
curpath.erase(nbgnode);
}
}
}
}
int ans = 0;
for (auto it : anspth) {
int temp = 0;
for (auto it2 : it) {
temp += values[it2];
}
ans = max(ans, temp);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-path-quality-of-a-graph | Python Hard | python-hard-by-lucasschnee-r2lk | null | lucasschnee | NORMAL | 2025-01-17T16:03:02.929882+00:00 | 2025-01-17T16:03:02.929882+00:00 | 17 | false | ```python3 []
class Solution:
def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:
'''
2000 edges
There are at most four edges connected to each node.
we want to maximize score
score is sum of unique nodes
simple dp
except how do we keep
'''
lookup = defaultdict(list)
for u, v, w in edges:
lookup[u].append((v, w))
lookup[v].append((u, w))
INF = 10 ** 10
@cache
def calc(node, time, mask):
best = -INF
if node == 0:
best = 0
for v, w in lookup[node]:
if w <= time:
if (1 << v) & mask:
best = max(best, calc(v, time - w, mask))
else:
best = max(best, calc(v, time - w, (1 << v) | mask) + values[v])
return best
return calc(0, maxTime, 1) + values[0]
``` | 0 | 0 | ['Python3'] | 0 |
maximum-path-quality-of-a-graph | 2065. Maximum Path Quality of a Graph | 2065-maximum-path-quality-of-a-graph-by-5taqm | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-17T15:47:17.521104+00:00 | 2025-01-17T15:47:17.521104+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
from collections import defaultdict, deque
class Solution:
def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:
graph = defaultdict(list)
for u, v, time in edges:
graph[u].append((v, time))
graph[v].append((u, time))
queue = deque([(0, 0, values[0], {0})]) # node, time spent, quality, visited nodes
state_cache = {}
max_result = 0
while queue:
node, time_spent, quality, visited_nodes = queue.popleft()
if node in state_cache:
prev_time, prev_quality = state_cache[node]
if prev_time <= time_spent and prev_quality >= quality:
continue
state_cache[node] = (time_spent, quality)
if time_spent > maxTime:
continue
if node == 0:
max_result = max(max_result, quality)
for neighbor, travel_time in graph[node]:
new_visited_nodes = visited_nodes.copy()
if neighbor not in visited_nodes:
new_visited_nodes.add(neighbor)
new_quality = quality + values[neighbor]
else:
new_quality = quality
queue.append((neighbor, time_spent + travel_time, new_quality, new_visited_nodes))
return max_result
``` | 0 | 0 | ['Python3'] | 0 |
maximum-path-quality-of-a-graph | Java DFS | Just dont add cycle check that we do in regular DFS | java-dfs-just-dont-add-cycle-check-that-i270z | IntuitionApproachComplexity
Time complexity:
O(V+E)
Space complexity:
Code | saptarshichatterjee1 | NORMAL | 2024-12-17T15:11:49.389569+00:00 | 2024-12-17T15:11:49.389569+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(V+E)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n\n int maxQ= 0;\n\n public void dfs(HashMap<Integer, List<int[]>> adj, int maxTime, Set<Integer> qualities, int quality, int time, int thzNode, int[] values){\n if(time > maxTime) return;\n if(thzNode == 0) maxQ = Math.max(maxQ, quality);\n if(adj.get(thzNode) == null) return;\n //DFS but just dont check for if already visisted\n for(int[] eachConnect : adj.get(thzNode)){\n int addedQ = quality;\n boolean added = false;\n if(!qualities.contains(eachConnect[0])){ //Dont take same Node twice for Quality\n added =true;\n qualities.add(eachConnect[0]);\n addedQ += values[eachConnect[0]];\n }\n dfs(adj, maxTime, qualities, addedQ,time + eachConnect[1], eachConnect[0], values);\n if(added) qualities.remove(eachConnect[0]);\n }\n }\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n HashMap<Integer, List<int[]>> adj = new HashMap();\n for(int[] edge : edges){\n List<int[]> exist1 = adj.getOrDefault(edge[0], new ArrayList<int[]>());\n List<int[]> exist2 = adj.getOrDefault(edge[1], new ArrayList<int[]>());\n //Adj list has List< [connectedNode, PathVal] .. >\n exist1.add(new int[]{edge[1], edge[2]});\n exist2.add(new int[]{edge[0], edge[2]});\n adj.put(edge[0], exist1);\n adj.put(edge[1], exist2);\n }\n Set<Integer> qualities = new HashSet();\n qualities.add(0);\n dfs(adj, maxTime, qualities,values[0], 0, 0, values);\n return maxQ;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
maximum-path-quality-of-a-graph | Maximum Path Quality of a Graph | maximum-path-quality-of-a-graph-by-naeem-2sbh | IntuitionApproachit's pretty much straightforward. i am keeping track of frequency of node in my path in the visited array. keeping track of time while doing DF | Naeem_ABD | NORMAL | 2024-12-17T06:57:33.214146+00:00 | 2024-12-17T06:57:33.214146+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nit\'s pretty much straightforward. i am keeping track of frequency of node in my path in the visited array. keeping track of time while doing DFS. calling recursive call if only the time + time of that edge is less than or equal to the limit.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int time = 0;\n int ans = INT_MIN;\n\n void solve( int i , int quality , vector<int>& val \n , vector<vector<pair<int,int>>>& adj , vector<int>& visited , int maxi )\n {\n visited[i]++;\n if( visited[i] == 1 )\n {\n quality = quality + val[i];\n }\n\n if( i == 0 )\n {\n ans = max( ans , quality );\n }\n\n for( auto it : adj[i] )\n {\n if( time + it.second <= maxi )\n {\n time = time + it.second;\n solve( it.first , quality , val , adj , visited , maxi );\n time = time - it.second;\n }\n }\n\n visited[i]--;\n }\n\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) \n {\n int n = values.size();\n vector<int> visited(n,0);\n\n vector<vector<pair<int,int>>> adj(n);\n for(auto e : edges)\n {\n adj[e[0]].push_back({e[1],e[2]});\n adj[e[1]].push_back({e[0],e[2]});\n }\n\n solve(0,0,values,adj,visited,maxTime);\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-path-quality-of-a-graph | ✅BFS + BitMagic || python | bfs-bitmagic-python-by-darkenigma-r93k | Code | darkenigma | NORMAL | 2024-12-16T00:56:29.914721+00:00 | 2024-12-16T00:56:29.914721+00:00 | 4 | false | \n# Code\n```python3 []\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n n=len(values)\n gra=[[] for i in range(n)]\n for a,b,time in edges:\n gra[a].append([b,time])\n gra[b].append([a,time])\n\n q=deque()\n q.append([0,0,1,values[0]])\n ans=0\n while(len(q)):\n t,i,s,val=q.popleft()\n # if(t>maxTime):continue\n if(i==0):\n ans=max(ans,val)\n for a,b in gra[i]:\n if(t+b<=maxTime):\n if(s&(1<<a)):\n q.append([t+b,a,s,val])\n else:\n q.append([t+b,a,s|(1<<a),val+values[a]])\n\n return ans\n \n``` | 0 | 0 | ['Array', 'Graph', 'Python3'] | 0 |
maximum-path-quality-of-a-graph | Dijskra (beat 95%) | dijskra-beat-95-by-fredzqm-uddt | Code\njava []\nclass Solution {\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n Node[] nodes = new Node[values.length];\ | fredzqm | NORMAL | 2024-12-09T00:38:28.586735+00:00 | 2024-12-09T00:38:28.586773+00:00 | 18 | false | # Code\n```java []\nclass Solution {\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n Node[] nodes = new Node[values.length];\n for (int i = 0; i < values.length; i++) {\n nodes[i] = new Node(i, values[i]);\n }\n for (int[] e: edges) {\n Node a = nodes[e[0]], b = nodes[e[1]];\n a.edges.put(b, e[2]);\n b.edges.put(a, e[2]);\n }\n\n int maxQuality = 0;\n PriorityQueue<Path> pq = new PriorityQueue<>();\n pq.add(new Path(nodes[0]));\n while (!pq.isEmpty()) {\n Path p = pq.poll();\n if (!p.to.foundNodeSet.add(p.visitedNodes)) {\n continue;\n }\n if (p.to == nodes[0]) {\n int sum = 0;\n for (Node n: p.visitedNodes) sum += n.value;\n maxQuality = Math.max(maxQuality, sum);\n }\n for (Map.Entry<Node, Integer> e: p.to.edges.entrySet()) {\n Node to = e.getKey();\n int len = p.len + e.getValue();\n if (len > maxTime) continue;\n Path np = new Path(p, to, len);\n pq.add(np);\n }\n }\n return maxQuality;\n }\n\n static class Node {\n int idx, value;\n Map<Node, Integer> edges = new HashMap<>();\n Set<Set<Node>> foundNodeSet = new HashSet<>();\n\n public Node(int i, int v) {\n idx = i; value = v;\n }\n\n public String toString() {\n return String.format("(%d %d)", idx, value);\n }\n }\n\n static class Path implements Comparable<Path>{\n int len;\n Node to;\n Set<Node> visitedNodes;\n\n public Path(Node zero) {\n this.to = zero;\n this.visitedNodes = Set.of(zero);\n }\n\n public Path(Path prev, Node to, int len) {\n this.to = to;\n this.len = len;\n this.visitedNodes = new HashSet<>(prev.visitedNodes);\n this.visitedNodes.add(to);\n }\n\n public int compareTo(Path p) {\n return len - p.len;\n }\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
maximum-path-quality-of-a-graph | maximum-path-quality-of-a-graph - Java Solution | maximum-path-quality-of-a-graph-java-sol-m2g9 | \n\n# Code\njava []\nclass Solution {\n HashMap<Integer,List<int[]>> graph;\n int result=0;\n public int maximalPathQuality(int[] values, int[][] edges | himashusharma | NORMAL | 2024-11-14T07:29:54.068179+00:00 | 2024-11-14T07:29:54.068220+00:00 | 9 | false | \n\n# Code\n```java []\nclass Solution {\n HashMap<Integer,List<int[]>> graph;\n int result=0;\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n graph=new HashMap<>();\n for(int[] i:edges){\n graph.computeIfAbsent(i[0],k->new ArrayList<>()).add(new int[]{i[1],i[2]});\n graph.computeIfAbsent(i[1],k->new ArrayList<>()).add(new int[]{i[0],i[2]});\n }\n backtrack(values,new int[values.length],0,0,0,maxTime);\n return result;\n }\n private void backtrack(int[] values,int[] visited,int idx,int time,int value,int maxTime){\n if(time>maxTime){\n return;\n }\n if(visited[idx]==0){\n value+=values[idx];\n }\n if(idx==0){\n result=Math.max(result,value);\n }\n visited[idx]++;\n for(int[] i:graph.getOrDefault(idx,new ArrayList<>())){\n backtrack(values,visited,i[0],time+i[1],value,maxTime);\n }\n visited[idx]--;\n }\n}\n``` | 0 | 0 | ['Array', 'Backtracking', 'Graph', 'Java'] | 0 |
maximum-path-quality-of-a-graph | Python (Simple Backtracking) | python-simple-backtracking-by-rnotappl-nn29 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2024-11-01T16:51:43.856798+00:00 | 2024-11-01T16:51:43.856840+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maximalPathQuality(self, values, edges, maxTime):\n n, self.max_val, graph = len(values), 0, defaultdict(list)\n\n for u,v,t in edges:\n graph[u].append((v,t))\n graph[v].append((u,t))\n\n def backtrack(node,values,total,time):\n if node == 0 and time <= maxTime:\n self.max_val = max(self.max_val,total)\n\n for neighbor,t in graph[node]:\n if time + t <= maxTime:\n val = values[neighbor]\n values[neighbor] = 0 \n backtrack(neighbor,values,total+val,time+t)\n values[neighbor] = val\n\n val = values[0]\n values[0] = 0\n backtrack(0,values,val,0)\n return self.max_val\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-path-quality-of-a-graph | 2065. Maximum Path Quality of a Graph.cpp | 2065-maximum-path-quality-of-a-graphcpp-cx9u6 | Code\n\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size(); \n | 202021ganesh | NORMAL | 2024-10-29T10:54:48.933522+00:00 | 2024-10-29T10:54:48.933540+00:00 | 2 | false | **Code**\n```\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size(); \n vector<vector<pair<int, int>>> graph(n); \n for (auto& x : edges) {\n graph[x[0]].emplace_back(x[1], x[2]); \n graph[x[1]].emplace_back(x[0], x[2]); \n }\n \n int ans = 0; \n vector<int> freq(n); freq[0] = 1; \n \n function<void(int, int, int)> fn = [&](int u, int time, int val) {\n if (u == 0) ans = max(ans, val); \n for (auto& [v, t] : graph[u]) \n if (time + t <= maxTime) {\n if (++freq[v] == 1) fn(v, time+t, val + values[v]); \n else fn(v, time+t, val); \n --freq[v]; \n }\n }; \n \n fn(0, 0, values[0]); \n return ans; \n }\n};\n``` | 0 | 0 | ['C'] | 0 |
maximum-path-quality-of-a-graph | Python3 Djikstra+Backtracking (For somewhat tighter constraints) | python3-djikstrabacktracking-for-somewha-dos4 | Use Djikstra to find the shortest distance to come back to 0 for every node. This shortest distance will be used as a pruning/terminating condition while backtr | vintersosa | NORMAL | 2024-10-08T06:50:39.158988+00:00 | 2024-10-08T06:50:39.159031+00:00 | 3 | false | Use Djikstra to find the shortest distance to come back to 0 for every node. This shortest distance will be used as a pruning/terminating condition while backtracking.\n\n\nTC: 4^maxTime (though will be reduced due to pruning and for this question it will always be less than 4^10 as maxTime is 100 at maximum and every edge is 10 at minimum)\n\n# Code\n```python3 []\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n \n graph = defaultdict(list)\n for x,y,time in edges:\n graph[x].append((y, time))\n graph[y].append((x, time))\n\n n = len(values)\n best_dist = [inf]*n\n best_dist[0] = 0\n heap = [(0,0)]\n while heap:\n val, node = heapq.heappop(heap)\n if val>best_dist[node]:\n continue\n for ne, t in graph[node]:\n nval = t+val\n if best_dist[ne]<=nval:\n continue\n best_dist[ne]=nval\n heapq.heappush(heap, (nval, ne))\n \n visited = set()\n def backtrack(node, rem):\n \n res = 0\n for ne, time in graph[node]:\n if best_dist[ne]+time>rem:\n continue\n if ne in visited:\n res = max(res, backtrack(ne, rem-time))\n else:\n visited.add(ne)\n res = max(res, values[ne]+backtrack(ne, rem-time))\n visited.remove(ne)\n return res\n visited.add(0)\n return values[0]+backtrack(0, maxTime)\n\n\n\n\n \n``` | 0 | 0 | ['Python3'] | 0 |
maximum-path-quality-of-a-graph | C# DFS with Backtracking Solution | c-dfs-with-backtracking-solution-by-getr-m3sd | Intuition\n- Describe your first thoughts on how to solve this problem. Graph Traversal: Since the problem involves finding paths from node 0 back to node 0, a | GetRid | NORMAL | 2024-10-02T15:41:32.388229+00:00 | 2024-10-02T15:41:32.388268+00:00 | 10 | false | # Intuition\n- <!-- Describe your first thoughts on how to solve this problem. -->Graph Traversal: Since the problem involves finding paths from node 0 back to node 0, a natural way to explore the graph is using DFS. DFS allows us to explore all possible paths while keeping track of the time taken.\n\n- Maximizing Quality: The quality of a path is determined by the sum of the values of unique nodes visited. Therefore, we need to ensure that each node is only added to the total quality once, even if it is revisited later.\n\n- Backtracking: To explore different paths, backtracking is essential. After exploring a particular path, we need to "unvisit" nodes and undo any changes made to the current quality. This allows us to try other paths that might lead to better results.\n\n- Pruning Paths: Since we are constrained by the maximum allowed time (maxTime), we prune paths that exceed the allowed time by returning early from the DFS function.\n\n- Tracking Visits: The visited array tracks how many times a node has been visited. This is important for determining whether a node\u2019s value should be added to the current quality when visiting it for the first time.\n___\n\n# Approach\n<!-- Describe your approach to solving the problem. -->// Build the Graph: Represent the graph using an adjacency list for efficient traversal.\n// Depth-First Search (DFS): Implement a DFS starting from node 0. Keep track of:\n// *Time Used: Total time taken so far.\n// *Current Quality: Sum of unique node values visited.\n// *Visited Nodes: An array to track whether a node has been visited to prevent adding its value multiple times.\n// Backtracking: Since nodes and edges can be revisited, we need to backtrack after exploring each path to reset the state for the next path.\n// Prune Paths Exceeding maxTime: If the time used exceeds maxTime, we prune that path.\n// Update Maximum Quality: Whenever we return to node 0, we check if the current quality is greater than the maximum found so far.\n___\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(V + E), where \'V\' is the number of vertices (nodes) in the graph. and \'E\' is the number of edges.\n___\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(V + E), primarily due to the space required for the recursion stack in the DFS, The visited array to track visited nodes, and the adjacency list, which takes O(V + E) space.\n___\n\n# Code\n```csharp []\npublic class Solution {\n int maxQuality;\n int[] values;\n List<(int neighbor, int time)>[] adjList;\n int[] visited;\n int maxTime;\n public int MaximalPathQuality(int[] values, int[][] edges, int maxTime) {\n this.values = values;\n this.maxTime = maxTime;\n int n = values.Length;\n adjList = new List<(int, int)>[n];\n for(int i = 0; i < n; i++) adjList[i] = new List<(int, int)>();\n foreach(var edge in edges) {\n int u = edge[0];\n int v = edge[1];\n int time = edge[2];\n adjList[u].Add((v, time));\n adjList[v].Add((u, time));\n }\n visited = new int[n];\n int currentQuality = values[0];\n visited[0] = 1;\n maxQuality = values[0];\n dfs(0, 0, currentQuality);\n return maxQuality;\n }\n void dfs(int node, int timeUsed, int currentQuality) {\n if(timeUsed > maxTime) return;\n if(node == 0) {\n if(currentQuality > maxQuality) maxQuality = currentQuality;\n }\n foreach(var (neighbor, time) in adjList[node]) {\n int newTimeUsed = timeUsed + time;\n if(newTimeUsed > maxTime) continue;\n bool firstVisit = visited[neighbor] == 0;\n if(firstVisit) currentQuality += values[neighbor];\n visited[neighbor]++;\n dfs(neighbor, newTimeUsed, currentQuality);\n visited[neighbor]--;\n if(firstVisit) currentQuality -= values[neighbor];\n }\n }\n}\n``` | 0 | 0 | ['Array', 'Backtracking', 'Graph', 'C#'] | 0 |
maximum-path-quality-of-a-graph | Java BFS with DP | java-bfs-with-dp-by-shandlikamal248-mqcx | Intuition\nBFS with dp\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. | shandlikamal248 | NORMAL | 2024-09-18T16:52:24.458864+00:00 | 2024-09-18T16:52:24.458897+00:00 | 12 | false | # Intuition\nBFS with dp\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n class Node {\n int num;\n int time;\n int quality;\n HashSet<Integer> set;\n Node(int a,int b,int c, HashSet<Integer> s){\n num = a;\n time= b;\n quality=c;\n set=s;\n }\n }\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n int n = values.length;\n HashMap<Integer,ArrayList<int[]>> graph = new HashMap<>();\n for(int i=0;i<n;i++){\n graph.put(i,new ArrayList<>());\n }\n for(int i=0;i<edges.length;i++){\n ArrayList<int[]> arr = graph.get(edges[i][0]);\n arr.add(new int[]{edges[i][1],edges[i][2]});\n\n arr = graph.get(edges[i][1]);\n arr.add(new int[]{edges[i][0],edges[i][2]});\n }\n HashMap<Integer,int[]> visited = new HashMap<>();\n \n Queue<Node> pq = new LinkedList<>();\n HashSet<Integer> set = new HashSet<>();\n set.add(0);\n pq.add(new Node(0,0,values[0],set));\n int maxQuality=Integer.MIN_VALUE;\n while(!pq.isEmpty()){\n\n Node ele= pq.poll();\n if(visited.containsKey(ele.num)){\n int[] dp = visited.get(ele.num);\n if(dp[0]<= ele.time && dp[1]> ele.quality){\n continue;\n }\n }\n visited.put(ele.num,new int[]{ele.time,ele.quality});\n if(ele.num==0){\n maxQuality=Math.max(maxQuality,ele.quality);\n }\n for(int[]child:graph.get(ele.num)){\n HashSet<Integer> newSet = (HashSet)ele.set.clone();\n int newQuality = ele.quality;\n if(ele.time+child[1]<=maxTime){\n if(!newSet.contains(child[0])){\n newSet.add(child[0]);\n newQuality+= values[child[0]];\n }\n \n pq.add(new Node(child[0],ele.time+child[1], newQuality, newSet));\n }\n }\n }\n return maxQuality;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
maximum-path-quality-of-a-graph | Easy CPP Solution Beats 90% users | easy-cpp-solution-beats-90-users-by-king-nzt3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kingsenior | NORMAL | 2024-09-16T20:58:13.065718+00:00 | 2024-09-16T20:58:13.065741+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<vector<pair<int,int>>> adj;\n vector<int> best;\n void dfs(int rt,int time,int ans,int k,vector<int>& values,vector<int>& vis){\n int f=0;\n if(vis[rt]==0) f=1;\n int has = vis[rt]==0 ? values[rt] : 0;\n vis[rt] = 1;\n \n for(auto v:adj[rt]){\n int ch = v.first;\n int t = v.second;\n if(time+t<=k){\n dfs(ch,time+t,ans+has,k,values,vis);\n }\n }\n if(f)vis[rt] = 0;\n best[rt] = max(best[rt],ans+has);\n }\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n=values.size();\n adj = vector<vector<pair<int,int>>> (n);\n best = vector<int>(n,0);\n for(auto e:edges){\n int u=e[0];\n int v=e[1];\n int t=e[2];\n adj[u].push_back({v,t});\n adj[v].push_back({u,t});\n }\n vector<int> vis(n,0);\n dfs(0,0,0,maxTime,values,vis);\n return best[0];\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-path-quality-of-a-graph | C++ Solution | c-solution-by-mayank71203-13p2 | Code\ncpp []\nclass Solution {\nprivate:\n int n,res, maxiTime;\npublic:\n void dfs(vector<int>& values, vector<vector<pair<int,int>>>& graph,int node, in | mayank71203 | NORMAL | 2024-09-10T21:01:50.626224+00:00 | 2024-09-10T21:01:50.626261+00:00 | 4 | false | # Code\n```cpp []\nclass Solution {\nprivate:\n int n,res, maxiTime;\npublic:\n void dfs(vector<int>& values, vector<vector<pair<int,int>>>& graph,int node, int time, int curr){\n if(time > maxiTime){\n return ;\n }\n\n int oldValue = values[node];\n curr += oldValue;\n values[node] = 0;\n \n if(node == 0){\n res = max(res,curr);\n }\n\n for(int i = 0; i< graph[node].size(); i++){\n dfs(values, graph, graph[node][i].first, time + graph[node][i].second, curr);\n }\n\n values[node] = oldValue;\n }\n\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n n = values.size();\n maxiTime = maxTime;\n // creating graph.\n vector<vector<pair<int,int>>> graph(n);\n for(int i = 0; i < edges.size(); i++){\n graph[edges[i][0]].push_back({edges[i][1],edges[i][2]});\n graph[edges[i][1]].push_back({edges[i][0],edges[i][2]});\n }\n\n res = 0;\n dfs(values, graph, 0, 0, 0);\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-path-quality-of-a-graph | Maximum Path Quality of a Graph | maximum-path-quality-of-a-graph-by-shalu-prc1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Shaludroid | NORMAL | 2024-09-09T19:36:16.292932+00:00 | 2024-09-09T19:36:16.292969+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nimport java.util.*;\n\nclass Solution {\n private int maxQuality = 0;\n\n public int maximalPathQuality(int[] values, int[][] edges, int maxTime) {\n // Step 1: Build the graph\n Map<Integer, List<int[]>> graph = new HashMap<>();\n for (int[] edge : edges) {\n graph.computeIfAbsent(edge[0], k -> new ArrayList<>()).add(new int[]{edge[1], edge[2]});\n graph.computeIfAbsent(edge[1], k -> new ArrayList<>()).add(new int[]{edge[0], edge[2]});\n }\n\n // Step 2: Initialize visited array to track how many times we visited each node\n int[] visited = new int[values.length];\n\n // Step 3: Start DFS from node 0 with time 0 and quality = values[0] (since we start at node 0)\n dfs(graph, values, visited, 0, 0, values[0], maxTime);\n\n return maxQuality;\n }\n\n private void dfs(Map<Integer, List<int[]>> graph, int[] values, int[] visited, int node, int time, int quality, int maxTime) {\n // Step 4: If we are back at node 0, update the maximum quality\n if (node == 0) {\n maxQuality = Math.max(maxQuality, quality);\n }\n\n // Mark this node as visited\n visited[node]++;\n\n // Step 5: Explore all neighboring nodes\n for (int[] neighbor : graph.getOrDefault(node, new ArrayList<>())) {\n int nextNode = neighbor[0];\n int travelTime = neighbor[1];\n\n // If the travel time exceeds the maximum allowed time, skip this path\n if (time + travelTime > maxTime) continue;\n\n // Calculate the new quality if it\'s the first time visiting this node\n int newQuality = quality;\n if (visited[nextNode] == 0) {\n newQuality += values[nextNode];\n }\n\n // Continue DFS from the next node\n dfs(graph, values, visited, nextNode, time + travelTime, newQuality, maxTime);\n }\n\n // Backtrack: unmark this node as visited\n visited[node]--;\n }\n}\n\n``` | 0 | 0 | ['Java'] | 0 |
maximum-path-quality-of-a-graph | Backtracking in Graph with Comments | backtracking-in-graph-with-comments-by-s-7ihp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | stalebii | NORMAL | 2024-09-08T18:20:24.855500+00:00 | 2024-09-08T18:20:24.855539+00:00 | 16 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n * (2^n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:\n def dfs(curr, quality, remain):\n nonlocal res\n\n # base; stop as the current path is not feasible\n if remain < 0:\n return \n\n # action; at node 0, update the res\n if curr == 0:\n res = max(res, quality)\n\n for neigh, time in adj[curr]:\n # update possible remain value\n new_remain = remain - time\n\n # neigh never seen before\n if neigh not in visited:\n\n # mark as seen\n visited.add(neigh)\n\n new_quality = quality + values[neigh]\n\n # recur on neigh\n dfs(neigh, new_quality, new_remain)\n\n # revert back seen\n visited.remove(neigh)\n \n # neigh seen before\n else:\n # recur on neigh\n dfs(neigh, quality, new_remain)\n \n # 1. build a bidirectional adjacency list\n adj = defaultdict(list)\n for src, des, time in edges:\n adj[src] += [(des, time)]\n adj[des] += [(src, time)]\n \n res = 0 \n\n # 2. mark node 0 as seen\n visited = set([0]) # trace back the visited nodes\n\n # 3. run dfs starting at node 0\n dfs(0, values[0], maxTime)\n\n return res\n``` | 0 | 0 | ['Array', 'Backtracking', 'Depth-First Search', 'Graph', 'Recursion', 'Python', 'Python3'] | 0 |
maximum-path-quality-of-a-graph | Easy DFS solution | easy-dfs-solution-by-vikash_kumar_dsa2-0q4b | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vikash_kumar_dsa2 | NORMAL | 2024-09-01T14:51:07.110806+00:00 | 2024-09-01T14:51:07.110831+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int ans = -1;\n void dfs(unordered_map<int,vector<pair<int,int>>> &adj,vector<int> &values,vector<int> &temp,int node,bool isFirst,int maxTime){\n if(maxTime < 0){\n return;\n }\n if(node == 0 && isFirst && maxTime >= 0){\n int sum = 0;\n vector<int> vis(values.size(),0);\n for(auto val : temp){\n if(!vis[val]){\n sum += values[val];\n vis[val] = 1;\n }\n }\n ans = max(ans,sum);\n }\n isFirst = true;\n for(auto val : adj[node]){\n temp.push_back(node);\n dfs(adj,values,temp,val.first,isFirst,maxTime-val.second);\n temp.pop_back();\n }\n }\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n unordered_map<int,vector<pair<int,int>>> adj;\n for(int i = 0;i<edges.size();i++){\n adj[edges[i][0]].push_back({edges[i][1],edges[i][2]});\n adj[edges[i][1]].push_back({edges[i][0],edges[i][2]});\n }\n vector<int> temp;\n bool isFirst = false;\n dfs(adj,values,temp,0,isFirst,maxTime);\n if(ans == -1){\n return values[0];\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-path-quality-of-a-graph | The only Difficulty you might face. | the-only-difficulty-you-might-face-by-pa-mxfv | Intuition\nThe only difficulty you might face in this question is on deciding how to maintain the visited state. \n\n# Code\ncpp []\nclass Solution {\npublic:\n | payadikishan | NORMAL | 2024-08-28T01:13:47.269756+00:00 | 2024-08-28T01:13:47.269786+00:00 | 39 | false | # Intuition\nThe only difficulty you might face in this question is on deciding how to maintain the visited state. \n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {\n int n = values.size();\n int res = values[0];\n vector<vector<pair<int,int>>> graph(n);\n for(int i=0;i<edges.size();i++)\n {\n graph[edges[i][0]].push_back({edges[i][1], edges[i][2]});\n graph[edges[i][1]].push_back({edges[i][0], edges[i][2]});\n }\n \n vector<int> visited(n, 0);\n dfs(graph, values, visited, res, 0, 0, 0, maxTime);\n return res;\n }\n \n void dfs(vector<vector<pair<int,int>>>& graph, vector<int>& values, vector<int>& visited, int& res, int node, int score, int time, int& maxTime)\n {\n if(time > maxTime)\n return;\n \n if(visited[node] == 0)\n score += values[node];\n \n visited[node]++;\n\t\t\n \n if(node == 0)\n res = max(res, score);\n \n for(auto it : graph[node])\n {\n int neigh = it.first;\n int newTime = time + it.second;\n dfs(graph, values, visited, res, neigh, score, newTime, maxTime);\n }\n \n visited[node]--;\n }\n};\n/*For every path there should be a seperate visited array. This was thing to understand If its being visited for the first time, we add its value to our sum. After we have processed all its neighbours, we then mark the current node as unvisited i.e. we reduce the count of that node from the visited array.*/\n``` | 0 | 0 | ['C++'] | 1 |
maximum-path-quality-of-a-graph | Python 3: FT 94%: Modified Dijkstra, Hard to Solve, but Surprisingly Straightforward To Code Up | python-3-ft-94-modified-dijkstra-hard-to-ichv | Intuition\n\nThe tough part of this problem IMO is convincing yourself that whatever algorithm you come up with won\'t give you TLE.\n\nA big part of that is to | biggestchungus | NORMAL | 2024-08-25T05:41:20.741356+00:00 | 2024-08-25T05:42:26.896084+00:00 | 13 | false | # Intuition\n\nThe tough part of this problem IMO is convincing yourself that whatever algorithm you come up with won\'t give you TLE.\n\nA big part of that is to notice that\n* the minimum `time` between any two edges is `10` or more\n* and the `maxTime` is at most 100\n* therefore each path can have at most 11 nodes in it, 9 other than 0\n\nAlso notice that there are at most four edges.\n\nSo a worst-case-ish scenario is where `0` is connected to four other nodes that are cheap, and those four are connected each to three more, and so on.\n\nThe total paths would be `4 ** 10` because there are 10 choices, or about 1e6 paths. That\'s on the cusp of TLE but slightly below.\n\nThen don\'t forget that\n* 4 choices per path is the absolute worst case, most of the time we\'ll have many fewer\n* the fact we must start and end at 0 means that only four nodes connect to zero, and the penultimate node in the loop back to zero must also be one of these nodes, which limits the number of paths we\'ll explore\n* and also we can recognize that **if we have several ways to visit nodes `{n1, n2, ..., nk}` ending with a certain node `n_i`, only the shortest one will give the best answer in general**\n* therefore to have `1e6` unique paths we\'d need a lot more than "just" 1e3 nodes\n\nAll of these will conspire to reduce the number of paths we explore.\n\n# Modified Dijkstra\n\nThe key insight is the bolded statement above:\n* suppose we have some set `vis` of visited nodes for some path\n* and that path ends at `u`\n* then we only want to explore more nodes from the *shortest* path for `(vis, u)`\n\nTherefore we want to pop `(vis, u)` combinations in order by total time taken. That way we only explore (or "relax" in graph terminology) from each set of nodes and origin once, with the minimum time.\n\n**This is what Dijkstra\'s algorithm does.** It pops paths in order by min cost (time in this case), and we only relax from the minimum time for each state.\n\n# Approach\n\nFor Dijkstra we need to\n* record the minimum time for each `(vis, u)` combination\n * one option is to use a bit set for `vis` and an int for `u`, but there are 1000 nodes so the bit set would have `O(n)` memory. Yikes.\n * another option is to **use a `frozenset` of the visited nodes** so that we get `O(1)` memory used to mark each node, `O(1)` lookup, and still be able to hash it\n * note that `set` is NOT hashable since it\'s mutable. `frozenset`s are immutable and thus hashable; this is the main reason they exist in Python\n* also have a heap of `(totalTime, currentNode, visitedNodes)`\n * this is a mean heap by `totalTime` ascending\n\nWhat I implement in the code is the "poor man\'s Python version" of Dijkstra.\n* we use a heap as a priority queue\n* priority queues don\'t support decreasing the key of an arbitrary element, so we don\'t. If we find a new best time for `(vis, u)` we just push the new `(newBestTime, vis, u)` to the heap.\n* therefore we have a quick "if this isn\'t the best time, then this element is stale and was superceded by a better time, so skip this element" check\n\nThe consequence is `O(E)` memory use instead of `O(V)`.\n\nIf you want `O(V)` you MUST use a "priority queue" that supports updating the priority of elements. Common options include\n* a custom data structure where you can reduce the key, such as a custom heap implementation where you record the current index in the heap of each element. That way you can change the priority, then repair the heap starting at that element\'s current location\n* a combination of a tree set and a hash set\n * if you find a new state `(vis, u)` and the new time is lower, then\n * remove `(time, vis, u)` from the tree set to remove the old entry\n * add `(time, vis, u)` to the tree set\n * and now you can have just one entry in the tree set for each `(vis, u)` AND do updates and pop the min element in `log(entries)` time\n\n# Complexity\n\n- Time complexity: roughly `O(4**(maxTime/time) * maxTime/time * log(4**(maxTime/time)) * maxTime/time)` in the absolute worst case where we have a ton of nodes, they all have four edges, and all edges have the same value of time. Anything else (e.g. some edges having large `time` values) will reduce the complexity.\n - we can travel over `maxTime/time` edges so that\'s the max number of nodes in the path plus one\n - for each node in the path there are at most 4 destination nodes to choose from\n - the heap we have will have roughly `4**(maxTime/time) * maxTime/time` entries in it. The first part is the number of paths, and the second part is because we include the time of each endpoint as well; if it\'s a ring of `k` nodes that takes `totalTime` to visit then we\'ll have `(vis, u)` with the same `totalTime` for all `k` nodes in the ring\n\n- Space complexity: same as time? idk the complexity analysis for this is hard\n\n# Code\n```python3 []\nclass Solution:\n def maximalPathQuality(self, values: List[int], edges: List[List[int]], T: int) -> int:\n # undir graph nodes 0..n-1\n # edges are [u, v, time]..\n # takes time to go between u and v\n \n N = len(values)\n\n # valid path takes up to maxTime seconds\n # quality of path is the sum of values of unique nodes on the path\n\n # return max quality of any path\n\n # 1000 nodes, at most 2000 edges\n\n # at most 4 edges of any node\n\n #### what about all paths of length 0? just nodes\n # all paths of length 1: a node and another node\n\n # all paths of length L:\n # if I have paths of length L1 ending at u\n # and paths of length L2 ending at v\n # and u--v has dist L3\n # then that contributes to L=L1+L2+L3\n\n # but all paths is a huge number of paths\n # and all pairwise interactions might matter\n\n #################\n\n # time, maxTime in 10..100 so we can visit at most 11 total nodes\n #\n # so the Dijkstra or SPFA-like algo should work well here\n\n adj = [[] for _ in range(N)]\n\n for u, v, t in edges:\n if t > T: continue\n adj[u].append((v, t))\n adj[v].append((u, t))\n\n # points only depend on unique nodes\n # > so we only care about uniques, duh\n # > and the time required\n # > connectivity is about where we are currently b/c path must be connected\n\n min_time = {(frozenset([0]), 0): 0} # visited, currNode\n \n pq = [(0, 0, frozenset([0]))] # time, currNode, visited\n while pq:\n time, u, visited = heappop(pq)\n\n if min_time[(visited, u)] > time: continue # stale entry\n\n for v, t in adj[u]:\n vis_v = visited | {v}\n t_v = time + t\n\n if t_v > T or t_v >= min_time.get((vis_v, v), math.inf): continue\n\n min_time[(vis_v, v)] = t_v\n heappush(pq, (t_v, v, vis_v))\n\n return max(sum(values[v] for v in visited) for visited, v in min_time if v == 0)\n``` | 0 | 0 | ['Python3'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.