question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
vowels-of-all-substrings | [Java] Simple Solution with Approach | java-simple-solution-with-approach-by-sv-hzoe | Consider an string - axexixoxu\n\n\n\n\n\n\nclass Solution {\n public long countVowels(String word) {\n \n char[] arr = word.toCharArray();\n | svmgarg | NORMAL | 2021-12-31T06:48:06.953431+00:00 | 2021-12-31T06:49:16.983483+00:00 | 109 | false | Consider an string - axexixoxu\n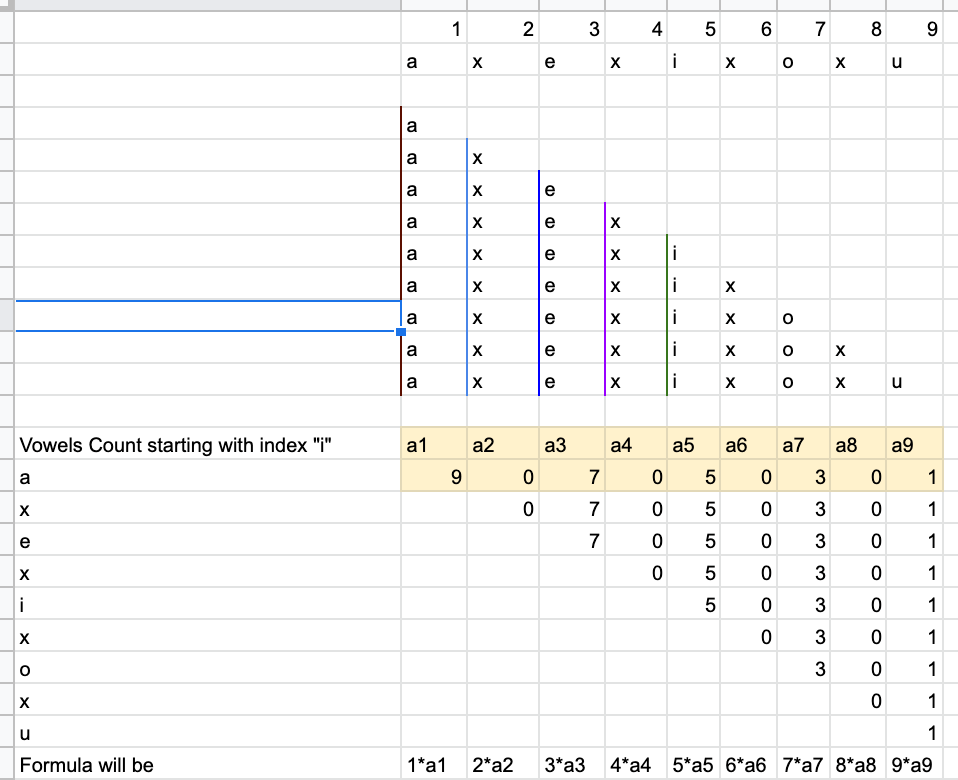\n\n\n\n```\n\nclass Solution {\n public long countVowels(String word) {\n \n char[] arr = word.toCharArray();\n int n = arr.length;\n \n long result = 0L;\n for(int i=0; i<n; i++){\n if(isVowel(arr[i])){\n result = result + (n-i)*(i+1L);\n }\n }\n \n \n return result;\n }\n \n public boolean isVowel(char c){\n return (c == \'a\' || c == \'e\' || c == \'i\' || c == \'o\' || c == \'u\');\n }\n}\n``` | 1 | 0 | [] | 1 |
vowels-of-all-substrings | C++ easy solution using maths | c-easy-solution-using-maths-by-hunny123-ojd9 | class Solution {\npublic:\n long long countVowels(string s) {\n long long res=0;\n for(int i=0;i<s.length();i++)\n\n {\n if(s | hunny123 | NORMAL | 2021-12-26T17:28:05.911423+00:00 | 2021-12-26T17:28:05.911472+00:00 | 96 | false | class Solution {\npublic:\n long long countVowels(string s) {\n long long res=0;\n for(int i=0;i<s.length();i++)\n\n {\n if(s[i]==\'a\'||s[i]==\'e\'||s[i]==\'o\'||s[i]==\'u\'||s[i]==\'i\')\n {\n res=res+(s.length()-i)*(i+1);\n }\n \n }\n return res;\n \n }\n}; | 1 | 0 | [] | 0 |
vowels-of-all-substrings | Faster || C++ || O(N) || Using map only | faster-c-on-using-map-only-by-shubhamp07-cyfp | ```\nclass Solution {\npublic:\n long long countVowels(string word) {\n \n long long int ans = 0; //This will be the final answer\n \n | shubhamp07 | NORMAL | 2021-11-21T09:24:14.954299+00:00 | 2021-11-21T09:24:34.762568+00:00 | 134 | false | ```\nclass Solution {\npublic:\n long long countVowels(string word) {\n \n long long int ans = 0; //This will be the final answer\n \n unordered_map<char , int > mp; // Unordered map of char to int\n \n mp[\'a\']=1; mp[\'e\']=1; mp[\'i\']=1; mp[\'o\']=1; mp[\'u\']=1;\n \n int n = word.size(); // Size of the word\n \n for(int i=0;i<word.size();i++)\n {\n if(mp.count(word[i])){ // Checking if current character is vowel or not\n \n long long int val = (long long)(i+1)*(n-i); // Contribution of given character\n ans += val; // Incrementing the final answer\n } \n }\n \n return ans; // Returning the final answer\n }\n}; | 1 | 0 | [] | 0 |
vowels-of-all-substrings | C++ Easy Solution | c-easy-solution-by-urveshgodhani-6esf | \t\tlong long count = 0;\n long long ans = 0;\n \n for(int i = 0 ; i < word.size() ; i++)\n {\n if(word[i] == \'a\' || wo | urveshgodhani | NORMAL | 2021-11-16T04:53:29.807005+00:00 | 2021-11-16T04:53:29.807053+00:00 | 153 | false | \t\tlong long count = 0;\n long long ans = 0;\n \n for(int i = 0 ; i < word.size() ; i++)\n {\n if(word[i] == \'a\' || word[i] == \'e\' || word[i] == \'i\' || word[i] == \'o\' || word[i] == \'u\')\n count += (i+1);\n \n ans += count;\n }\n \n return ans; | 1 | 0 | ['C', 'C++'] | 0 |
vowels-of-all-substrings | C++ o(n) simple solution using concept of Arithmetic Progression | c-on-simple-solution-using-concept-of-ar-5mcj | \tclass Solution {\n\tpublic:\n\t\tlong long a, res;\n\t\tlong long count(long long &a, long long &n){\n\t\t\treturn (n(2a+(n-1)*-2))/2;\n\t\t}\n\t\tlong long c | gauravchaurasia1704 | NORMAL | 2021-11-15T14:00:27.492032+00:00 | 2021-11-15T14:00:27.492059+00:00 | 102 | false | \tclass Solution {\n\tpublic:\n\t\tlong long a, res;\n\t\tlong long count(long long &a, long long &n){\n\t\t\treturn (n*(2*a+(n-1)*-2))/2;\n\t\t}\n\t\tlong long countVowels(string &word) {\n\t\t\tres = 0;\n\t\t\ta=word.size();\n\t\t\tfor(long long i=1; i<=word.size(); i++){\n\t\t\t\tif(word[i-1] == \'a\' || word[i-1] == \'e\' || word[i-1] == \'i\' || word[i-1] == \'o\' || word[i-1] == \'u\')\n\t\t\t\t\tres += count(a, i);\n\t\t\t}\n\t\t\treturn res;\n\t\t}\n\t}; | 1 | 1 | [] | 0 |
vowels-of-all-substrings | Java O(N) Solution with 1-D dp | java-on-solution-with-1-d-dp-by-joejoe33-i8zo | \nclass Solution {\n private boolean isVowelChar(char c) {\n return c==\'a\' || c==\'e\' || c==\'i\' || c==\'o\' || c==\'u\';\n }\n public long | joejoe3333 | NORMAL | 2021-11-13T21:42:11.133384+00:00 | 2021-11-13T21:42:11.133426+00:00 | 122 | false | ```\nclass Solution {\n private boolean isVowelChar(char c) {\n return c==\'a\' || c==\'e\' || c==\'i\' || c==\'o\' || c==\'u\';\n }\n public long countVowels(String word) {\n if (word == null || word.length() == 0) {\n return 0L;\n }\n // create 1 dp array\n long[] countVowelsToIndex = new long[word.length()]; \n // this indicates total number of vowels of all substrings that end at index i\n // set initial value\n countVowelsToIndex[0] = isVowelChar(word.charAt(0)) ? 1 : 0;\n // now fill in the dp\n long res = 0L;\n res += countVowelsToIndex[0];\n for (int i=1; i < word.length(); i++) {\n // check if current character is vowel\n long cnt=0L;\n if (isVowelChar(word.charAt(i))) {\n // case 1: the current char is a vowel\n // first add result from last index\n cnt += countVowelsToIndex[i-1]; \n // then add total number of chars count from [0,i], that is i+1\n cnt += (i+1);\n } else {\n // case 2 : not a vowel\n // just add result from last index\n cnt += countVowelsToIndex[i-1];\n }\n countVowelsToIndex[i] = cnt;\n res += countVowelsToIndex[i];\n } // time=O(N), space=O(N)\n return res;\n }\n}\n``` | 1 | 0 | [] | 0 |
vowels-of-all-substrings | C++|| Observation Based Solution||TC: O(n) and SC: O(1) | c-observation-based-solutiontc-on-and-sc-gw35 | ```\nclass Solution {\npublic:\n long long countVowels(string word) {\n \n long long ans =0;\n int n =word.size();\n for(int i=0;i<n | Kishan_Srivastava | NORMAL | 2021-11-09T13:13:52.038049+00:00 | 2021-11-09T13:13:52.038093+00:00 | 58 | false | ```\nclass Solution {\npublic:\n long long countVowels(string word) {\n \n long long ans =0;\n int n =word.size();\n for(int i=0;i<n;i+=1)\n { \n // if ith index has vowel\n // then that vowel is in (i+1)*(n-i) substrings\n if(word[i]==\'a\' or word[i]==\'e\' or word[i]==\'i\' or word[i]==\'o\' or word[i]==\'u\')\n ans+=(long long)(i+1)*(long long)(n-i);\n \n }\n \n return ans;\n }\n};\n\n | 1 | 0 | [] | 1 |
vowels-of-all-substrings | Golang very simple O(n) solution | golang-very-simple-on-solution-by-tjucod-9heo | go\nfunc countVowels(word string) int64 {\n vowel := int64(0)\n magic := int64(0)\n for i, v := range word {\n switch v {\n case \'a\', \ | tjucoder | NORMAL | 2021-11-08T15:30:43.195961+00:00 | 2021-11-08T15:30:43.195995+00:00 | 75 | false | ```go\nfunc countVowels(word string) int64 {\n vowel := int64(0)\n magic := int64(0)\n for i, v := range word {\n switch v {\n case \'a\', \'e\', \'i\', \'o\', \'u\':\n magic += int64(i) + 1\n }\n vowel += magic\n }\n return vowel\n}\n``` | 1 | 0 | ['Go'] | 0 |
vowels-of-all-substrings | C# Clear Solution with Explanation | c-clear-solution-with-explanation-by-aip-nvie | My way to come up with the formula:\n\nWord: abcdef\n\nPossible substrings:\na ab abc abcd abcde abcdef\nb bc bcd bcde bcdef\nc cd cde cdef\nd de def\ne ef\nf\n | AIP | NORMAL | 2021-11-08T13:32:32.021920+00:00 | 2021-11-08T13:35:24.428045+00:00 | 90 | false | **My way to come up with the formula:**\n```\nWord: abcdef\n\nPossible substrings:\na ab abc abcd abcde abcdef\nb bc bcd bcde bcdef\nc cd cde cdef\nd de def\ne ef\nf\n\nWordLength = 6\nword[0] a: 6 (6 substrings in a first row)\nword[1] b: 5 + 5 (5 substrings in a first row and 5 substrings in a second row)\nword[2] c: 4 + 4 + 4 \nword[3] d: 3 + 3 + 3 + 3\nword[4] e: 2 + 2 + 2 + 2 + 2\nword[5] f: 1 + 1 + 1 + 1 + 1 + 1\n...\nword[i] : (WordLength - i) * (i+1) // count of elements in a row * count of groups\n```\n\n**Solution:**\n```\n\tprivate readonly char[] Vowels = new char[] {\'a\', \'e\', \'i\', \'o\', \'u\'};\n \n\tpublic long CountVowels2(string word) {\n long result = 0;\n long wordLength = word.Length;\n for (int i=0; i<wordLength; i++) {\n if (Vowels.Contains(word[i])) \n result += (wordLength - i) * (i+1);\n }\n return result;\n }\n``` | 1 | 0 | [] | 0 |
vowels-of-all-substrings | O(n) time, O(1) solution [C++] | on-time-o1-solution-c-by-mandysingh150-t75b | Faster than 100%, O(n) time, O(1) space\n\nEvery vowel character will occur in (i+1) * (size-i) substrings, where i is the index of the vowel character in strin | mandysingh150 | NORMAL | 2021-11-08T06:31:56.161543+00:00 | 2021-11-08T06:34:11.159075+00:00 | 32 | false | **Faster than 100%, O(n) time, O(1) space**\n\nEvery vowel character will occur in **(i+1) * (size-i)** substrings, where **i** is the index of the vowel character in string.\n```\nclass Solution {\npublic:\n bool isVowel(char ch) {\n return ch==\'a\' or ch==\'e\' or ch==\'i\' or ch==\'o\' or ch==\'u\';\n }\n long long countVowels(string word) {\n long long ans = 0;\n for(int i=0 ; i<word.size() ; ++i)\n if(isVowel(word[i]))\n ans += (i+1)*(word.size()-i);\n return ans;\n }\n};\n``` | 1 | 0 | [] | 0 |
vowels-of-all-substrings | 2063. Vowels of All Substrings||C++||with Explanation | 2063-vowels-of-all-substringscwith-expla-jg8z | Logic-\nWeight that char (at index i), Ci is contributing is given by, \n= Number of substrings containing that index char (if Ci is vowel)\n =0 (otherwise if | guptasim8 | NORMAL | 2021-11-08T06:02:50.083668+00:00 | 2021-11-08T06:02:50.083703+00:00 | 179 | false | Logic-\nWeight that char (at index i), Ci is contributing is given by, \n= Number of substrings containing that index char (if Ci is vowel)\n =0 (otherwise if char Ci is not a vowel)\n \nThe total sum of the number of vowels (\'a\', \'e\', \'i\', \'o\', and \'u\') in every substring of word will be equal to the sum of weight contributed by each character.\nSo,\n**Number of substrings containing that index i char (if Ci is vowel)= (no of prefix substrings+ no of suffix substrings -1)+ (no of prefix substrings * no of suffix substrings )**\nHere, \n(no of prefix substrings+ no of suffix substrings +1 )=n\n\nSo, we can say ,\n**Number of substrings containing that index i char (if Ci is vowel)=n+ (no of prefix substrings * no of suffix substrings )**\n\n\nEg |"bcaxy"|=5\ncalculating weight contributed to sum by char a=>\n* prefix- |bc|=2, prefix strings ending with a= {ca,bca}=2\n* suffix=|xy|=2, suffix strings starting with a= {ax,axy}=2\n* {a}=1\n* sum of above 3 terms=2+2+1=5=n\n* substrings having char a in middle(having both a part of prefix substring and suffix substring=\n2*2=4\n{cax,caxy,bcax,bcaxy}\nans=n+2*2=5+2*2=9\n\n```\n long long countVowels(string word) {\n int n=word.size();\n long long sum=0;\n for(int j=0;j<n;j++){\n if(word[j]==\'a\'||word[j]==\'e\'||word[j]==\'i\'||word[j]==\'o\'||word[j]==\'u\'){\n if(j==0||j==n-1){\n sum+=n;\n }\n else\n sum+= n+((long long)j)*(n-j-1);\n }\n }\n return sum;\n }\n``` | 1 | 0 | ['C', 'C++'] | 0 |
vowels-of-all-substrings | (C++) 2063. Vowels of All Substrings | c-2063-vowels-of-all-substrings-by-qeetc-764q | \n\nclass Solution {\npublic:\n long long countVowels(string word) {\n long ans = 0; \n string vowel = "aeiou"; \n for (long i = 0; i < | qeetcode | NORMAL | 2021-11-07T21:51:43.516561+00:00 | 2021-11-07T21:51:43.516590+00:00 | 45 | false | \n```\nclass Solution {\npublic:\n long long countVowels(string word) {\n long ans = 0; \n string vowel = "aeiou"; \n for (long i = 0; i < word.size(); ++i) \n if (vowel.find(word[i]) != string::npos)\n ans += (i+1)*(word.size()-i); \n return ans; \n }\n};\n``` | 1 | 0 | ['C'] | 0 |
vowels-of-all-substrings | Javascript easy solution. O(n) | javascript-easy-solution-on-by-jupiterjw-qapz | \n// Save vowels in a set\nconst VOWELS = new Set([\'a\', \'e\', \'i\', \'o\', \'u\']);\n\n/**\n * @param {string} word\n * @return {number}\n */\nconst countVo | JupiterJW | NORMAL | 2021-11-07T19:59:30.151060+00:00 | 2021-11-07T20:03:41.315804+00:00 | 149 | false | ```\n// Save vowels in a set\nconst VOWELS = new Set([\'a\', \'e\', \'i\', \'o\', \'u\']);\n\n/**\n * @param {string} word\n * @return {number}\n */\nconst countVowels = function(word) {\n let count = 0;\n\n const length = word.length;\n // Return diretly if the word is empty\n if (!length) {\n return count;\n }\n\n \n for (let i = 0; i < length; i += 1) {\n\t // Continue if current letter is not a vowel\n if (!VOWELS.has(word[i])) {\n continue;\n }\n\n const left = i;\n const right = length - 1 - i;\n\t // Otherwise calculate how many substrings it appears in and add the number to the count\n count += length + left * right;\n }\n\n return count;\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
vowels-of-all-substrings | ✔Simple and Short || C++ Approach | simple-and-short-c-approach-by-sarvesh_2-9k10 | bool check(char x){\n \n \n if(x==\'a\' || x==\'e\' || x==\'i\' || x==\'o\' || x==\'u\') return true;\n else return false;\n }\n | sarvesh_2-1 | NORMAL | 2021-11-07T19:48:18.843448+00:00 | 2021-11-07T19:48:18.843530+00:00 | 57 | false | bool check(char x){\n \n \n if(x==\'a\' || x==\'e\' || x==\'i\' || x==\'o\' || x==\'u\') return true;\n else return false;\n }\n long long countVowels(string word) {\n \n long long ans=0;\n \n \n for(int i=0;i<word.size();i++)\n {\n \n if(check(word[i])){\n ans+=((i+1)*(word.size() -i));\n }\n }\n return ans;\n }```\n\n``` | 1 | 0 | ['C', 'C++'] | 0 |
vowels-of-all-substrings | C++||Very Short Solution|| One optimized solution but still TLE|| | cvery-short-solution-one-optimized-solut-ppkf | \t//Use of Little Math\n\tclass Solution {\n\tpublic:\n long long countVowels(string word) {\n double count=0;\n double n=word.size();\n | kundankumar4348 | NORMAL | 2021-11-07T16:13:34.856314+00:00 | 2021-11-07T16:13:34.856361+00:00 | 44 | false | \t//Use of Little Math\n\tclass Solution {\n\tpublic:\n long long countVowels(string word) {\n double count=0;\n double n=word.size();\n for(double i=0;i<n;++i){\n if(word[i]==\'a\' || word[i]==\'e\'||word[i]==\'i\'||word[i]==\'o\'||word[i]==\'u\')\n count+=((i+1)*(n-i));\n }\n return count;\n\t\t}\n\t};\n\t\n\t//Optimized Solution But still got TLE\n\t\n\tclass Solution {\n\tpublic:\n long long countVowels(string word) {\n unordered_map<char,int> m1;\n m1[\'a\']=1;\n m1[\'e\']=1;\n m1[\'i\']=1;\n m1[\'o\']=1;\n m1[\'u\']=1; \n //count//lastIndex\n vector<pair<int,int>> v;\n double ans=0;\n for(int i=0;i<word.size();++i){\n int len=v.size();\n vector<pair<int,int>> temp;\n for(int j=0;j<len;++j){\n //if(v[j].second==i-1){\n if(m1.find(word[i])!=m1.end()){\n int count=v[j].first+1;\n int lastIndex=i;\n ans+=count;\n temp.push_back({count,lastIndex});\n } else{\n int count=v[j].first;\n int lastIndex=i;\n ans+=count;\n temp.push_back({count,lastIndex});\n }\n }\n if(m1.find(word[i])!=m1.end()){\n temp.push_back({1,i});\n ans++;\n }\n else temp.push_back({0,i});\n v=temp;\n }\n return ans;\n }\n\t}; | 1 | 0 | [] | 1 |
vowels-of-all-substrings | [Python 3] two prefix sums | python-3-two-prefix-sums-by-chestnut8901-4hrn | ```\nclass Solution:\n def countVowels(self, word: str) -> int:\n n = len(word)\n \n # mark vowel\n # \'aba\' vowels = [1, 0, 1]\ | chestnut890123 | NORMAL | 2021-11-07T16:06:21.690376+00:00 | 2021-11-07T16:06:21.690410+00:00 | 121 | false | ```\nclass Solution:\n def countVowels(self, word: str) -> int:\n n = len(word)\n \n # mark vowel\n # \'aba\' vowels = [1, 0, 1]\n vowels = list(map(lambda x: int(x in \'aeiou\'), word))\n \n # add vowel count in each substring\n # acc = [0, 1, 1, 2]\n acc = list(accumulate(vowels, initial=0))\n \n # add up vowel count\n # acc2 = [0, 1, 2, 4]\n acc2 = list(accumulate(acc))\n\n \n ans = 0\n for i in range(n+1):\n # add up accumulative vowel count in substring start from index i\n ans += acc2[-1] - acc2[i]\n # subtract previous vowel counts from current substrings\n if i > 0:\n ans -= (acc[i-1]) * (len(acc2) - i)\n \n return ans | 1 | 0 | ['Prefix Sum', 'Python', 'Python3'] | 0 |
vowels-of-all-substrings | easy solution using (size -i)*(i+1) || C++ | easy-solution-using-size-ii1-c-by-gravit-982e | \nclass Solution {\npublic:\n long long countVowels(string s) {\n long long n = s.length();\n long long sum = 0;\n for (long long i = 0; | gravity2000 | NORMAL | 2021-11-07T07:49:41.672225+00:00 | 2021-11-07T07:49:41.672256+00:00 | 57 | false | ```\nclass Solution {\npublic:\n long long countVowels(string s) {\n long long n = s.length();\n long long sum = 0;\n for (long long i = 0; i < n; i++)\n if (s[i] == \'a\' || s[i] == \'e\' || s[i] == \'i\' || s[i] == \'o\' || s[i] == \'u\')\n sum += (n-i)*(i+1);\n return sum;\n }\n};\n``` | 1 | 1 | ['C'] | 0 |
vowels-of-all-substrings | [Java] Easy Solution O(n) with Explanation | java-easy-solution-on-with-explanation-b-xa80 | To find number of substrings which have a vowel at index i:\n\n\t\t\tsubstrings ending with index i: i\n\t\t\tsubstrings starting with index i | ippilimahesh1999 | NORMAL | 2021-11-07T06:49:16.506415+00:00 | 2021-11-07T06:49:16.506460+00:00 | 158 | false | To find number of substrings which have a vowel at index i:\n\n\t\t\tsubstrings ending with index i: i\n\t\t\tsubstrings starting with index i: n - i\n\t\t\tsubstrings contains index i in the middle: i * (n - i - 1) \n\t\t\t\n\t\t\tSo total will be addition of all : i + (n-i) + (i*(n-i-1)) \n\t\t\t\nSolution:\n```\npublic long countVowels(String word) {\n long n = (long)word.length();\n long ans = 0;\n for (int i=0; i<n; i++) {\n char c = word.charAt(i);\n if ("aeiou".indexOf(c) >= 0) {\n ans += i;\n ans += (n - i);\n ans += i * (n - i - 1);\n }\n }\n return ans;\n}\n``` | 1 | 0 | ['Java'] | 1 |
vowels-of-all-substrings | Simple java single pass DP O(n) | simple-java-single-pass-dp-on-by-seqquoi-ixvn | \n\n\npublic long countVowels(String word) {\n long cnt = 0;\n int n = word.length();\n long dp[] = new long[n+1];\n Set<Character> | seqquoia | NORMAL | 2021-11-07T06:48:01.714832+00:00 | 2021-11-07T06:48:01.714873+00:00 | 242 | false | \n\n```\npublic long countVowels(String word) {\n long cnt = 0;\n int n = word.length();\n long dp[] = new long[n+1];\n Set<Character> vowels = new HashSet<Character>();\n vowels.add(\'a\');vowels.add(\'e\');vowels.add(\'i\');vowels.add(\'o\');vowels.add(\'u\'); \n \n for (int i=1; i<n+1; i++) {\n if (vowels.contains(word.charAt(i-1))) {\n dp[i] = i + dp[i-1];\n } else {\n dp[i] = dp[i-1];\n }\n cnt+=dp[i];\n }\n \n return cnt;\n }\n\t``` | 1 | 1 | ['String', 'Dynamic Programming', 'Java'] | 0 |
vowels-of-all-substrings | Can anyone explain my approach:)..Easy O(n) simplest solution.(Python) | can-anyone-explain-my-approacheasy-on-si-zkc1 | \n\t\n c=0\n ans=0\n for i in range(len(word)):\n if word[i] in [\'a\',\'e\',\'i\',\'o\',\'u\']:\n c+=1 # fo | athulzkrish | NORMAL | 2021-11-07T04:49:51.227539+00:00 | 2021-11-07T04:49:51.227582+00:00 | 90 | false | \n\t\n c=0\n ans=0\n for i in range(len(word)):\n if word[i] in [\'a\',\'e\',\'i\',\'o\',\'u\']:\n c+=1 # for all substrings from this point, vowels accumulated\n c+=i # for all substrings till this point, the count of vowel is accumulated\n ans+=c\n return ans\n\t\t\n\t\t#Comment down a good explanation for this code please.\n \n\t\t | 1 | 0 | ['Python'] | 1 |
vowels-of-all-substrings | [Python3] greedy 1-line O(N) | python3-greedy-1-line-on-by-ye15-qwaw | Please check out this commit for solutions of weekly 266. \n\n\nclass Solution:\n def countVowels(self, word: str) -> int:\n return sum((i+1)*(len(wor | ye15 | NORMAL | 2021-11-07T04:23:03.580501+00:00 | 2021-11-07T05:11:30.898902+00:00 | 124 | false | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/6b6e6b9115d2b659e68dcf3ea8e21befefaae16c) for solutions of weekly 266. \n\n```\nclass Solution:\n def countVowels(self, word: str) -> int:\n return sum((i+1)*(len(word)-i) for i, x in enumerate(word) if x in "aeiou")\n``` | 1 | 1 | ['Python3'] | 0 |
vowels-of-all-substrings | C++|| O(n) || explained | c-on-explained-by-ygehi9527-8ll5 | Idea: The idea is to use a prefix sum array-based technique where we store the occurrences of each character in all the substrings concatenated. \n\nclass Solut | ygehi9527 | NORMAL | 2021-11-07T04:08:13.423753+00:00 | 2021-11-07T07:02:39.616053+00:00 | 127 | false | Idea: The idea is to use a prefix sum array-based technique where we store the occurrences of each character in all the substrings concatenated. \n```\nclass Solution {\npublic:\n long long countVowels(string s) {\n long long n = s.length();\n vector<long long> v;\n\n for (long long i = 0; i < n; i++) {\n // No. of occurrences of 0th character\n // in all the substrings\n if (i == 0)\n v.push_back(n);\n else\n // No. of occurrences of the ith character\n // in all the substrings\n\t\t\t//For each of the following characters, we store the no. of substrings starting with that character + the number of //substrings formed by the previous characters containing this character \u2013 the number of substrings formed by the previous //characters only.\n v.push_back((n - i) + v[i - 1] - i);\n }\n\n long long sum = 0;\n for (int i = 0; i < n; i++)\n if (s[i] == \'a\' || s[i] == \'e\' || s[i] == \'i\'\n || s[i] == \'o\' || s[i] == \'u\')\n sum += v[i];\n // Return the total sum\n // of occurrences of vowels\n return sum;\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 1 |
maximum-compatibility-score-sum | Backtracking with STL | 10 lines of code | C++ | backtracking-with-stl-10-lines-of-code-c-7n5v | As constraints 1 <= m, n <= 8 are very small, we can easily get our answer by evaluating all possible combinations. \nTo generate all possible combinations of | av1shek | NORMAL | 2021-07-25T04:06:37.883365+00:00 | 2021-07-25T04:06:37.883409+00:00 | 7,114 | false | As constraints ```1 <= m, n <= 8``` are very small, we can easily get our answer by evaluating all possible combinations. \nTo generate all possible combinations of students and mentors, we can shuffle any one of them in all possible way.\n\nIn below code i m trying to shuffle students, but shuffling of vector can be costly so I have shuffled their index and evaluated their responses by using shuffled index.\n\n**C++ code:**\n```\nint maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n\tint ans = 0;\n\tvector<int> pos;\n\tfor(int i=0;i<students.size();i++) pos.push_back(i);\n\tdo{\n\t\tint curr = 0;\n\t\tfor(int i = 0;i<students.size(); i++)\n\t\t\tfor(int j=0;j<students[pos[i]].size();j++)\n\t\t\t\tcurr += (students[pos[i]][j] == mentors[i][j]);\n\t\tans = max(ans, curr);\n\t} while(next_permutation(pos.begin(), pos.end()) );\n\treturn ans;\n}\n``` | 86 | 6 | [] | 19 |
maximum-compatibility-score-sum | [Java] || Backtracking || Easy to Understand | java-backtracking-easy-to-understand-by-li3qd | \t\n\tclass Solution {\n\t\tint max;\n\t\tpublic int maxCompatibilitySum(int[][] students, int[][] mentors) {\n\t\t\tboolean[] visited = new boolean[students.le | Vishnu_Jupiter | NORMAL | 2021-07-25T04:12:41.257837+00:00 | 2021-11-18T12:24:46.502030+00:00 | 5,081 | false | \t\n\tclass Solution {\n\t\tint max;\n\t\tpublic int maxCompatibilitySum(int[][] students, int[][] mentors) {\n\t\t\tboolean[] visited = new boolean[students.length];\n\t\t\thelper(visited, students, mentors, 0, 0);\n\t\t\treturn max;\n\t\t}\n\t\tpublic void helper(boolean[] visited, int[][] students, int[][] mentors, int pos, int score){\n\t\t\tif(pos >= students.length){\n\t\t\t\tmax = Math.max(max, score);\n\t\t\t\treturn;\n\t\t\t}\n\t\t\tfor(int i = 0; i < mentors.length; i++)\n\t\t\t\tif(!visited[i]){\n\t\t\t\t\tvisited[i] = true;\n\t\t\t\t\thelper(visited, students, mentors, pos + 1, score + score(students[pos], mentors[i]));\n\t\t\t\t\tvisited[i] = false;\n\t\t\t\t}\n\t\t}\n\t\tpublic int score(int[] a, int[] b){\n\t\t\tint count = 0;\n\n\t\t\tfor(int i = 0; i < b.length; i++)\n\t\t\t\tif(a[i] == b[i]) count += 1;\n\t\t\treturn count;\n\t\t}\n\t} | 67 | 2 | ['Backtracking', 'Java'] | 17 |
maximum-compatibility-score-sum | [C++] DP + Bitmask | 4ms | c-dp-bitmask-4ms-by-divyanshu1-mf7l | Time Complexity: O((2^n)*n*m)\n\n\n\nint dp[300]; //dp-array\nclass Solution {\npublic:\n int solve(vector<int> &a, vector<int> &b, int i, int mask, int | divyanshu1 | NORMAL | 2021-07-25T04:01:19.793394+00:00 | 2021-09-22T00:06:03.172079+00:00 | 5,719 | false | Time Complexity: `O((2^n)*n*m)`\n\n```\n\nint dp[300]; //dp-array\nclass Solution {\npublic:\n int solve(vector<int> &a, vector<int> &b, int i, int mask, int n, int m){\n if(i>=n){\n return 0;\n }\n if(dp[mask]!=-1){\n return dp[mask];\n }\n int ans=0;\n for(int k=0; k<n; k++){ //for each mentor\n if((mask&(1<<k))){ //check if mentor has not chosen yet\n int new_mask=mask^(1<<k);\n \n int current_ans=0;\n for(int x=0; x<m; x++){\n if((a[i]&(1<<x)) == (b[k]&(1<<x))){ //if xth bit of student and mentor is same, increase the answer\n current_ans++;\n }\n }\n ans=max(ans, current_ans + solve(a, b, i+1, new_mask, n, m) );\n }\n }\n return dp[mask]=ans;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& s, vector<vector<int>>& mr){\n int n = s.size();\n int m = s[0].size();\n vector<int> a, b;\n //convert to decimal e.g. [1,1,0] = 6\n for(auto v: s){ //for students array\n int x=0;\n for(int i=0; i<m; i++){\n x+=(v[i]<<((m-i)-1));\n }\n a.push_back(x);\n }\n \n for(auto v: mr){ //for mentor array\n int x=0;\n for(int i=0; i<m; i++){\n x+=(v[i]<<((m-i)-1));\n }\n b.push_back(x);\n }\n \n int mask = pow(2, n)-1; //all set bit 1 -> mentor not chosen, 0 -> mentor chosen\n //initialise dp array with -1\n for(int j=0; j<=mask; j++){\n dp[j]=-1;\n }\n \n return solve(a, b, 0, mask, n, m);\n }\n};\n\n```\n\n*If you like the solution, please **Upvote** \uD83D\uDC4D!!*\n\n***Similar concept problem*** : [1879. Minimum XOR Sum of Two Arrays](https://leetcode.com/problems/minimum-xor-sum-of-two-arrays/discuss/1238778/c-bitmaskdp) | 60 | 8 | [] | 6 |
maximum-compatibility-score-sum | C++ Brute force DFS | c-brute-force-dfs-by-lzl124631x-sgow | See my latest update in repo LeetCode\n\n## Solution 1. Brute Force (DFS)\n\nThe brute force solution is generating all the permuntations of the mentors and cal | lzl124631x | NORMAL | 2021-07-25T04:01:50.614797+00:00 | 2021-07-25T04:13:07.988131+00:00 | 3,137 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Brute Force (DFS)\n\nThe brute force solution is generating all the permuntations of the mentors and calculate the score of this permutation and the students.\n\nThe permutation generation process with DFS takes `O(M! * M)` time and calculating the score takes `O(N)` time, so the overall time complexity is `O(M! * MN)`.\n\nSince `M` and `N` are at most `8` and `8! * 8^2 = 2,580,480 ~= 2.6e6`, such solution should be able to pass.\n\n```cpp\n// OJ: https://leetcode.com/contest/weekly-contest-251/problems/maximum-compatibility-score-sum/\n// Author: github.com/lzl124631x\n// Time: O(M! * MN)\n// Space: O(N)\nclass Solution {\n int used[9] = {}, ans = 0, m, n;\n void dfs(vector<vector<int>>& S, vector<vector<int>>& M, int i, int score) {\n if (i == m) {\n ans = max(ans, score);\n return;\n }\n for (int j = 0; j < m; ++j) {\n if (used[j]) continue;\n used[j] = 1;\n int s = 0;\n for (int k = 0; k < n; ++k) s += S[i][k] == M[j][k]; // calculate the compatibility score of student `i` and mentor `j`.\n dfs(S, M, i + 1, score + s);\n used[j] = 0;\n }\n }\npublic:\n int maxCompatibilitySum(vector<vector<int>>& S, vector<vector<int>>& M) {\n m = S.size(), n = S[0].size();\n dfs(S, M, 0, 0);\n return ans;\n }\n};\n``` | 32 | 5 | [] | 7 |
maximum-compatibility-score-sum | [C++] Backtracking Solution | c-backtracking-solution-by-manishbishnoi-kzxm | \nclass Solution {\n // Calculating compatibility scores of ith student and jth mentor\n int cal(int i,int j,vector<vector<int>>& arr1,vector<vector<int>> | manishbishnoi897 | NORMAL | 2021-07-25T04:03:33.466450+00:00 | 2021-07-25T04:05:58.542661+00:00 | 2,219 | false | ```\nclass Solution {\n // Calculating compatibility scores of ith student and jth mentor\n int cal(int i,int j,vector<vector<int>>& arr1,vector<vector<int>>& arr2){\n int cnt=0;\n for(int k=0;k<arr1[0].size();k++){\n if(arr1[i][k]==arr2[j][k]){\n cnt++;\n }\n }\n return cnt;\n }\n \n int helper(int i,int m,vector<vector<int>>& arr1,vector<vector<int>>& arr2,vector<bool>& vis){\n if(i==m){\n return 0;\n }\n int ans = 0;\n for(int j=0;j<m;j++){\n if(!vis[j]){\n vis[j]=1;\n ans = max(ans,cal(i,j,arr1,arr2) + helper(i+1,m,arr1,arr2,vis));\n vis[j]=0; // Backtracking\n }\n }\n return ans;\n }\n \npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m = students.size();\n vector<bool> vis(m,0); // To keep track of which mentor is already paired up\n return helper(0,m,students,mentors,vis);\n }\n};\n```\n**Hit upvote if you like :)** | 26 | 3 | ['Backtracking', 'C'] | 2 |
maximum-compatibility-score-sum | [Python3] permutations | python3-permutations-by-ye15-ucw2 | Approach 1 - brute force\n\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n m = len(stu | ye15 | NORMAL | 2021-07-25T04:01:47.612282+00:00 | 2021-07-26T18:12:14.887824+00:00 | 2,339 | false | **Approach 1 - brute force**\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n m = len(students)\n \n score = [[0]*m for _ in range(m)]\n for i in range(m): \n for j in range(m): \n score[i][j] = sum(x == y for x, y in zip(students[i], mentors[j]))\n \n ans = 0 \n for perm in permutations(range(m)): \n ans = max(ans, sum(score[i][j] for i, j in zip(perm, range(m))))\n return ans \n```\n\nEdited on 7/26/2021\n**Approach 2 - dp**\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n m = len(students)\n \n score = [[0]*m for _ in range(m)]\n for i in range(m): \n for j in range(m): \n score[i][j] = sum(x == y for x, y in zip(students[i], mentors[j]))\n \n @cache \n def fn(mask, j): \n """Return max score of assigning students in mask to first j mentors."""\n ans = 0 \n for i in range(m): \n if not mask & (1<<i): \n ans = max(ans, fn(mask^(1<<i), j-1) + score[i][j])\n return ans \n \n return fn(1<<m, m-1)\n``` | 26 | 4 | ['Python3'] | 3 |
maximum-compatibility-score-sum | Mask DP | mask-dp-by-votrubac-jj2s | With m and n constrained to 8, it\'s feasible to just check all permutations.\n \nWe just check all possible assignments for each student i, using mask to track | votrubac | NORMAL | 2021-07-25T04:01:14.536236+00:00 | 2021-07-25T05:51:32.976298+00:00 | 3,345 | false | With `m` and `n` constrained to `8`, it\'s feasible to just check all permutations.\n \nWe just check all possible assignments for each student `i`, using `mask` to track mentors that have been assigned. We track and return the maximum score.\n \nTo speed things up, we can use memoisation, where we store interim results for each `i` and `mask`.\n\n**C++**\n```cpp\nint dp[256] = {[0 ... 255] = -1};\nint maxCompatibilitySum(vector<vector<int>>& s, vector<vector<int>>& m, int i = 0, int mask = 0) {\n if (i == s.size())\n return 0;\n if (dp[mask] < 0)\n for (int j = 0; j < m.size(); ++j) {\n if ((mask & (1 << j)) == 0)\n dp[mask] = max(dp[mask], \n inner_product(begin(s[i]), end(s[i]), begin(m[j]), 0, plus<int>(), equal_to<int>())\n + maxCompatibilitySum(s, m, i + 1, mask + (1 << j)));\n }\n return dp[mask];\n}\n``` | 21 | 2 | [] | 10 |
maximum-compatibility-score-sum | [Javascript] Optimal Hungarian Algorithm in O(m*m*n) | javascript-optimal-hungarian-algorithm-i-l0db | Intuition:\n\nThis may strike one as a bipartite graph problem, where the nodes of the left part are the students and the nodes of the right part are the mentor | George_Chrysochoou | NORMAL | 2021-07-25T09:49:23.618006+00:00 | 2021-07-25T09:50:07.172193+00:00 | 1,542 | false | **Intuition**:\n\nThis may strike one as a bipartite graph problem, where the nodes of the left part are the students and the nodes of the right part are the mentors. Each node on the left is connected with every node on the right, with a cost equal to the count of the same answers for the student and each mentor respectively. Essentially we want to make an assignment such that the total cost is maximized. This is known as the assignment problem, and the fastest way of solving such a problem is the Kuhn Munkres algorithm, better known as the Hungarian algorithm. There are a ton of resources online for studying the Hungarian algorithm but I am not going to delve into its theory here, as it\'s quite lengthy. \n\nIn any way, the assignment problem can be solved with easier ( yet less optimal complexity-wise) algorithms like Ford Fulkerson, and Hopcroft Karp.\n\n**Process**\n\nI first create an adjacency list between the students and the mentors, where A[i][j]= - (the count of the same answers of student i and mentor j).\nThe assignment problem is used to minimize the total cost, so in order to maximize it I need the edges to be negative.\nI then execute the Hungarian algorithm and return the negative result. \n```\nlet HunFast=(GRAPH)=>{\n let a=[...Array(GRAPH.length)].map((d,i)=>[...GRAPH[i]])\n let A=(len)=>[...Array(len)].map(d=>0)\n a.unshift(A(a[0].length))\n for(let i=0;i< a.length;i++)\n a[i].unshift(0)\n let n=a.length-1,m=a[0].length-1,u=A(n+1), v=A(m+1), p=A(m+1), way=A(m+1);\n for (let i=1; i<=n; i++) {\n p[0] = i;\n var j0 = 0,minv=A(m+1).map(d=>Infinity),used=A(m+1).map(d=>false)\n do {\n used[j0] = true;\n var i0 = p[j0] , delta = Infinity, j1;\n for (let j=1; j<=m;j++)\n if (!used[j]) {\n let cur = a[i0][j]-u[i0]-v[j];\n if (cur < minv[j])\n minv[j] = cur, way[j] = j0;\n if (minv[j] < delta)\n delta = minv[j], j1 = j;\n }\n for (let j=0; j<=m;j++)\n if (used[j])\n u[p[j]] += delta, v[j] -= delta;\n else\n minv[j] -= delta;\n j0 = j1;\n } while (p[j0] != 0);\n do {\n let j1 = way[j0];\n p[j0] = p[j1],j0 = j1\n } while (j0);\n }\n return -v[0]\n}\nvar maxCompatibilitySum = function(S, M) {\n let m=S.length, A=[...Array(m)].map(d=>[...Array(m)])\n for(let i=0;i<m;i++ )\n for(let j=0;j<m;j++)\n A[i][j]=-S[i].reduce((a,c,k)=> a+ Number(c===M[j][k]),0)\n return -HunFast(A)\n};\n\n``` | 13 | 0 | ['Graph', 'JavaScript'] | 3 |
maximum-compatibility-score-sum | Classical Dijkstra in Python with clear explanation (Similar with 1066) | classical-dijkstra-in-python-with-clear-0yqmx | This questions is similar to 1066. Campus Bike II. Please also refer to my post: Classical Dijkstra in Python with clear explanation\n\nWorkers -> Students, Bik | Lunius | NORMAL | 2021-07-25T04:09:24.737016+00:00 | 2021-07-28T00:43:12.191419+00:00 | 936 | false | This questions is similar to [1066. Campus Bike II](https://leetcode.com/problems/campus-bikes-ii/). Please also refer to my post: [Classical Dijkstra in Python with clear explanation](https://leetcode.com/problems/campus-bikes-ii/discuss/478958/classical-dijkstra-in-python-with-clear-explanation)\n\n`Workers` -> `Students`, `Bikes` -> `Mentors`, Manhattan distance -> Hamming distance \n\nHere I reimplemented the same idea with a classical Dijkstra algorithm with explanations, for those who are interested in this classical algorithm. \n\nThe code basically performs a state-based search, with certain kinds of `state` space and `cost`, with an `initial state` and a `termination condition`: \n\n`state` : a scheme of mentor assignment for the first `i` students, which can be denoted as a tuple (number of assigned students, status of all mentors). The status of all students can be denoted in multiple ways, here we use a bit string. (e.g. total 4 mentors, the first taken while the rest 3 available, \'1000\')\n\n`cost` : total sum of Hanmming distances between the students and mentors assigned following a scheme.\n\n`initial state`: no students assigned any mentor, all mentors are in available status. (e.g. (0, \'0000\'))\n\n`termination condition`: each student assigned a mentor. Since Dijkstra algorithm guarantees optimal cost when a node is closed, as well as BFS, so we can terminate the search when a scheme appears with last student assigned a mentor. \n\nThe final results is `m*n - total sum of Hamming distances`.\n\nHere is the code: \n\n```\nimport heapq\nfrom collections import defaultdict\n\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n m, n = len(students), len(students[0])\n def hamming(student, mentor):\n return sum([int(student[i] != mentor[i]) for i in range(n)])\n \n pq = [(0, 0, \'0\'*m)] # state: (n-comp_score aka Hamming distance, number of assigned students, mentor status)\n optimal = defaultdict(lambda:float(\'inf\'))\n \n while pq: # O(V)\n cost, i, mentor_status = heapq.heappop(pq) # O(logV)\n \n # early stopping with termination condition \n if i == m:\n return m * n - cost\n \n # generate successors. The next student to be assigned is at index i\n for j, mentor in enumerate(mentors): # O(m)\n if mentor_status[j] != \'1\':\n new_cost = cost + hamming(students[i], mentor)\n new_mentor_status = mentor_status[:j] + \'1\' + mentor_status[j+1:]\n \n # update optimal cost if a new successor appears with lower cost to the same node\n if new_cost < optimal[(i+1, new_mentor_status)]:\n optimal[(i+1, new_mentor_status)] = new_cost\n heapq.heappush(pq, (new_cost, i+1, new_mentor_status)) # O(logV)\n \n return 0\n```\n\n**Complexity**\nGiven `V` is the number of vertices, `E` is the number of edges in the graph, the time complexity of Dijkstra with min Heap is `O(V*logV + V*E/V*logV) = O((V+E)logV)`. Here the `O(E/V)` denotes the average number of neighbors of a vertex, where the neighbors of each vertices is stored in an adjacency list. In this problem, the average number of neighbors of a vertex is bounded by `O(m)`, since at each step we are looking for a mentor for the next step. \n\nSo the time complexity becomes: `O(V*logV + V*m*logV) = O(V(m+1)logV) = O(mVlogV)`, where `V`, the number of vertices, is bounded by O(`m!`), the number of permutations of `m` students, becasue each vertex denotes one possible way to assign at most `m`students to at most `m` mentors. And further more, `O(m!) <= O(m^m)`, so the time complexity is bounded as `<= O(m^(m+2)*log(m))`. | 11 | 0 | ['Python'] | 2 |
maximum-compatibility-score-sum | (JAVA)DP + Bitmasking | 2ms | javadp-bitmasking-2ms-by-ashuman231-6l8w | \nTimeComplexity : (m * 2 ^ m) * n\nSpace Complexity: m * (2 ^ m)\n\n```\nclass Solution {\n\n\tstatic int dp[][] = null;\n\tstatic int all_visited = 0;\n\tint | ashuman231 | NORMAL | 2021-07-25T04:04:38.608668+00:00 | 2021-07-25T07:54:22.116923+00:00 | 1,028 | false | \nTimeComplexity : (m * 2 ^ m) * n\nSpace Complexity: m * (2 ^ m)\n\n```\nclass Solution {\n\n\tstatic int dp[][] = null;\n\tstatic int all_visited = 0;\n\tint fun(int pos, int mask, int[][] students, int[][] mentors, int m, int n) {\n\n\n\t\tif (mask == all_visited) {\n\t\t\tdp[pos][mask] = 0;\n\t\t\treturn 0;\n\t\t}\n\n\t\tif (dp[pos][mask] != -1)\n\t\t\treturn dp[pos][mask];\n\n\n\t\tint max1 = 0;\n\t\tfor (int i = 0; i < m; i++) { // try to find best matching between student and mentor\n\n\t\t\tif ((mask & (1 << i)) == 0) {\n\n\t\t\t\tint cal = 0; // used for calculating how many answers matched in student and mentor\n\t\t\t\tfor (int k = 0; k < n; k++) {\n\t\t\t\t\tif (students[pos][k] == mentors[i][k])\n\t\t\t\t\t\tcal++;\n\t\t\t\t}\n\n\t\t\t\tmax1 = Math.max(max1, cal + fun(pos + 1, (mask | (1 << i)), students, mentors, m, n));\n\t\t\t}\n\t\t}\n\n\t\tdp[pos][mask] = max1;\n\t\treturn max1;\n\t}\n\n\n\tpublic int maxCompatibilitySum(int[][] students, int[][] mentors) {\n\n\n\t\tint m = students.length;\n\t\tint n = students[0].length;\n\t\tall_visited = (1 << m) - 1; // to mark that all students all matched with all mentors\n\t\tdp = new int[m + 1][1 << (m + 1)];\n\n\t\tfor (int i = 0; i < dp.length; i++) {\n\t\t\tfor (int j = 0; j < dp[0].length; j++)\n\t\t\t\tdp[i][j] = -1; // for marked all as unvisited/uncalculated\n\t\t}\n\n\t\treturn fun(0, 0, students, mentors, m, n);\n\t}\n | 11 | 3 | [] | 0 |
maximum-compatibility-score-sum | [C++] OPTIMIZED Backtracking solution; Include Complexity Analysis; Beats 100% | c-optimized-backtracking-solution-includ-r5uo | \nint res;\n\nvoid backtracking(vector<vector<int>> &vec, int pos, vector<int> &visited, int count) {\n\tif (pos == vec.size()) {\n\t\tres = max(res, count);\n\ | brandonbai | NORMAL | 2021-07-25T04:02:28.858386+00:00 | 2021-07-25T04:55:05.313583+00:00 | 694 | false | ```\nint res;\n\nvoid backtracking(vector<vector<int>> &vec, int pos, vector<int> &visited, int count) {\n\tif (pos == vec.size()) {\n\t\tres = max(res, count);\n\t\treturn;\n\t}\n\tfor (int i = 0; i < vec.size() ; i++) {\n\t\tif (visited[i] == 1)\n\t\t\tcontinue;\n\t\tvisited[i] = 1;\n\t\tbacktracking(vec, pos + 1, visited, count + vec[pos][i]);\n\t\tvisited[i] = 0;\n\t}\n}\n\nint maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n\tres = 0;\n\tvector<vector<int>> sVec (students.size(), vector<int> (mentors.size(), 0));\n\tfor (int i = 0; i < students.size(); i++) {\n\t\tfor (int j = 0; j < mentors.size(); j++) {\n\t\t\tint score(0); \n\t\t\tfor (int n = 0; n < students[0].size(); n++) {\n\t\t\t\tif (students[i][n] == mentors[j][n])\n\t\t\t\t\tscore++;\n\t\t\t}\n\t\t\tsVec[i][j] = score;\n\t\t}\n\t}\n\tvector<int> visited (mentors.size(), 0);\n\tbacktracking(sVec, 0, visited, 0);\n\treturn res;\n}\n```\n\t\nUsing backtracking to try out all the possibilities is intuitive. However, the total complexity and possibilities will be O(m! * n) \n(Imagine there are 4 students, 4 mentors and 2 questions. Student[0] can try 4 mentors; student[1] can try 3 mentors\u2026\u2026 And each pair takes O(n) to get the sum of compatibility score.)\n\n\n\n\nTherefore, we can generate a matrix of size m by m, called sVec.\nsVec[i][j] represents compatibility score of student[i] and mentor[j]. Using such a 2D vector, we could cut the backtracking time complexity to O(m!), because we don\u2019t have to iterate the n questions and calculate the score again. Calculate the matrix takes O(m*m*n); Backtracking takes O(m!). The final time complexity will be O(m*m*n + m!), which is equivalent to O(m!).\n\n | 10 | 2 | [] | 5 |
maximum-compatibility-score-sum | dp+bitmask => 100%fast c++ | dpbitmask-100fast-c-by-__hokaage-ub1a | \tclass Solution {\n\tpublic:\n\t\tint dp[15][5000],m;\n \n int sol(vector&stud,vector&ment,int i,int mask){\n //cout<<"here\n";\n if(i>=siz | __hokaage__ | NORMAL | 2021-07-25T04:24:05.505977+00:00 | 2021-07-25T04:26:33.886917+00:00 | 589 | false | \tclass Solution {\n\tpublic:\n\t\tint dp[15][5000],m;\n \n int sol(vector<int>&stud,vector<int>&ment,int i,int mask){\n //cout<<"here\\n";\n if(i>=size(stud))\n return 0;\n \n if(dp[i][mask]!=-1)\n return dp[i][mask];\n \n int ans=0,score;\n for (int j=0;j<size(ment);++j) {\n if ((mask>>j)&1) \n continue;\n score = m-__builtin_popcount(stud[i]^ment[j]);\n //cout<<score<<" "<<m<<\'\\n\';\n ans=max(ans,score+sol(stud,ment,i+1,mask|(1<<j)));\n }\n return dp[i][mask]=ans;\n }\n \n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n m = size(students[0]);\n \n memset(dp,-1,sizeof dp);\n vector<int>stud,ment;\n int x;\n \n for (int i=0;i<size(students);++i){\n //cout<<"here\\n";\n x=0;\n for (int b:students[i]){\n x+=b;\n x<<=1;\n }\n x>>=1;\n stud.push_back(x);\n x=0;\n for (int b:mentors[i]){\n x+=b;\n x<<=1;\n }\n x>>=1;\n ment.push_back(x);\n }\n \n \n return sol(stud,ment,0,0);\n }\n\t}; | 9 | 3 | [] | 5 |
maximum-compatibility-score-sum | Python Backtracking | python-backtracking-by-theonepieceisreal-32hu | ```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n n = len(students)\n \n | theonepieceisreal | NORMAL | 2021-07-25T04:11:48.047753+00:00 | 2021-07-25T04:11:48.047779+00:00 | 753 | false | ```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n n = len(students)\n \n def dfs(i, used, score):\n if i == n: return score\n \n res = float(-inf)\n \n for j, mentor in enumerate(mentors):\n if j in used: continue\n \n ss = sum(int(a == b) for a, b in zip(students[i], mentor))\n used.add(j)\n score += ss\n \n res = max(res, dfs(i + 1, used, score))\n\n used.remove(j)\n score -= ss\n \n return res\n \n return dfs(0, set(), 0)\n | 9 | 0 | [] | 2 |
maximum-compatibility-score-sum | Python3. Straightforward top down dp | python3-straightforward-top-down-dp-by-y-jj2c | \nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n pair_score = defaultdict(int)\n | yaroslav-repeta | NORMAL | 2021-07-25T04:03:49.109818+00:00 | 2021-07-25T04:03:49.109862+00:00 | 763 | false | ```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n pair_score = defaultdict(int)\n n = len(students)\n\n # build compatibilty score for every possible student-mentor pair\n for i in range(n):\n for j in range(n):\n pair_score[i, j] = sum(s_ans == m_ans for s_ans, m_ans in zip(students[i], mentors[j]))\n \n # try to pair student[i] with every unused mentor\n # mentor[j] is unused if \'j\'th bit in mask is \'1\'\n @cache\n def dfs(i, mask):\n if i == len(students):\n return 0\n return max(dfs(i + 1, mask - (1 << j)) + pair_score[i, j] for j in range(n) if (1 << j) & mask)\n \n return dfs(0, (1 << len(students)) - 1)\n``` | 9 | 1 | [] | 1 |
maximum-compatibility-score-sum | C++ | DP | BITMASKING | Beats 95% | c-dp-bitmasking-beats-95-by-wayward_blue-88bt | \nclass Solution {\npublic:\n int dp[8][1<<8];\n int ans = 0;\n int dfs(vector<vector<int>>& students, vector<vector<int>>&mentors, int idx, int mask){ | wayward_blue | NORMAL | 2022-03-10T11:33:49.496174+00:00 | 2022-03-10T11:33:49.496211+00:00 | 344 | false | ```\nclass Solution {\npublic:\n int dp[8][1<<8];\n int ans = 0;\n int dfs(vector<vector<int>>& students, vector<vector<int>>&mentors, int idx, int mask){\n if(idx == students.size()) return 0;\n if(dp[idx][mask]!=-1)return dp[idx][mask]; \n int ans = 0;\n for(int i = 0; i < mentors.size(); i++){\n if(mask&(1<<i)) continue;\n int marks = 0;\n for(int j = 0; j < students[0].size(); j++){\n if(students[idx][j]==mentors[i][j])marks++;\n }\n ans=max(ans,marks + dfs(students, mentors, idx+1, mask|1<<i));\n }\n return dp[idx][mask]=ans;\n }\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n memset(dp,-1,sizeof(dp));\n return dfs(students, mentors, 0, 0);\n }\n};\n``` | 6 | 1 | ['Dynamic Programming', 'C', 'Bitmask'] | 1 |
maximum-compatibility-score-sum | [python] Simple solution using itertools.permutations() | python-simple-solution-using-itertoolspe-ius7 | Since this was originally a contest problem, we want to find a solution that\'s simple to code.\n\nFirst thing to do is look at the constraints and when we do w | kosievdmerwe | NORMAL | 2021-07-25T04:21:36.662453+00:00 | 2021-07-28T16:25:24.270532+00:00 | 547 | false | Since this was originally a contest problem, we want to find a solution that\'s simple to code.\n\nFirst thing to do is look at the constraints and when we do we notice that both m and n are at most 8. When the constraints are this small (less than 10/11) this means we can likely use a factorial time solution (or a polynomial solution with a high power.)\n\nAnd 8! is only 40k, so we can just try all pairings of mentor and student, since there are 8! of them.\n\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n ans = 0\n for perm in itertools.permutations(range(len(students))):\n cur = 0\n for i in range(len(students)):\n for j in range(len(students[0])):\n cur += 1 if students[i][j] == mentors[perm[i]][j] else 0\n ans = max(ans, cur)\n return ans\n```\n\nThis uses `O(m! * n * m)` time and the extra memory use is `O(m)`.\n\n### Bonus One-Line version\nGranted it\'s split over multiple lines for readabilty.\n\nThe one trick I use is that `sum(array_of_bools)` returns the number of `True`s in the array.\n\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n return max(\n sum(\n students[i][j] == mentors[perm[i]][j]\n for i in range(len(students)) \n for j in range(len(students[0]))\n ) \n for perm in itertools.permutations(range(len(students)))\n )\n``` | 6 | 0 | ['Python'] | 0 |
maximum-compatibility-score-sum | C++ simple dp solution | c-simple-dp-solution-by-santhan_ch-gfdg | \n\n\nclass Solution {\npublic:\n int dp[10];\n int comp(vector<vector<int>>& students, vector<vector<int>>& mentors,int i,int j){\n int k,l,count=0 | santhan_ch | NORMAL | 2021-07-25T04:01:00.453136+00:00 | 2021-09-13T16:01:14.500588+00:00 | 440 | false | \n\n```\nclass Solution {\npublic:\n int dp[10];\n int comp(vector<vector<int>>& students, vector<vector<int>>& mentors,int i,int j){\n int k,l,count=0;\n for( k=0;k<students[i].size();k++){\n if(students[i][k]==mentors[j][k])\n count++;\n }\n return count;\n }\n int find(vector<vector<int>>& students, vector<vector<int>>& mentors,int ind){\n if(ind==students.size())\n return 0;\n int ans=-1;\n \n for(int j=0;j<students.size();j++){\n if(dp[j]==0){\n dp[j]=1;\n ans=max(comp(students,mentors,ind,j)+find(students,mentors,ind+1),ans);\n dp[j]=0;\n }\n }\n return ans;\n }\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n return find(students,mentors,0);\n \n }\n};\n``` | 6 | 0 | [] | 1 |
maximum-compatibility-score-sum | [Python3] Bitmask DP - Detailed Explanation | python3-bitmask-dp-detailed-explanation-00ayw | Intuition\n- Each student we try all possible mentor left. the total score of current student i depend on the choice of the previous mentor choice of student i | dolong2110 | NORMAL | 2024-09-12T15:02:03.594944+00:00 | 2024-09-12T15:02:03.594986+00:00 | 314 | false | # Intuition\n- Each student we try all possible mentor left. the total score of current student `i` depend on the choice of the previous mentor choice of student `i - 1`. It means we have explore all possible cases and which are overlap in states and find the maximum of score -> the signal of DP\n- `m` and `n` is very small which we can save the states in bit number.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**1. Initialization:**\n- `m, n = len(students), len(students[0])`: Calculates the number of students (m) and the number of preferences per individual `n`.\n**2. Dynamic Programming (Top-Down Approach):**\n- `@cache`: This decorator is used to memoize the dp function, avoiding redundant calculations.\n- `def dp(student: int, mentor: int) -> int:`: Defines the recursive dp function.\n - `if student == m: return 0`: If all students have been assigned, return 0 as there are no more assignments to make.\n - `res = 0`: Initializes the maximum compatibility sum to 0.\n - `for i in range(m):`: Iterates through all mentors.\n - `if mentor & (1 << i): continue`: Checks if the current mentor has already been assigned. If so, skip it.\n - `score = sum(1 for j in range(n) if students[student][j] == mentors[i][j])`: Calculates the compatibility score between the current student and mentor.\n - `res = max(res, score + dp(student + 1, mentor | (1 << i)))`: Recursively calculates the maximum compatibility sum by assigning the current mentor to the student and exploring the remaining assignments.\n - `return res`: Returns the maximum compatibility sum for the current state.\n- `return dp(0, 0)`: Calls the dp function with initial values of 0 for the current student and mentor indices, starting the dynamic programming process.\n\n**3. Explanation:**\n- The `dp` function uses a top-down dynamic programming approach to efficiently calculate the maximum compatibility sum.\n- The state of the assignment is represented by the `student` and `mentor` indices, and the bitmask `mentor` is used to keep track of assigned mentors.\n- The `dp` function recursively explores different combinations of mentor assignments, calculating the compatibility score for each combination and updating the maximum result.\n- The memoization decorator ensures that the `dp` function avoids recalculating results for the same state, improving efficiency.\n- The final result is the maximum compatibility sum obtained by considering all possible assignments.\n\n\n# Complexity\n- Time complexity: $$O(M * 2 ^ M * M * N)$$ ~ $$O(M ^ 2 * 2 ^ M * N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(M * 2 ^ M)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n m, n = len(students), len(students[0])\n @cache\n def dp(student: int, mentor: int) -> int:\n if student == m: return 0\n res = 0\n for i in range(m):\n if mentor & (1 << i): continue\n score = sum(1 for j in range(n) if students[student][j] == mentors[i][j])\n res = max(res, score + dp(student + 1, mentor | (1 << i)))\n return res\n return dp(0, 0)\n``` | 5 | 0 | ['Array', 'Dynamic Programming', 'Backtracking', 'Bit Manipulation', 'Bitmask', 'Python3'] | 0 |
maximum-compatibility-score-sum | Go solution with backtracking | go-solution-with-backtracking-by-tuanbie-6pqj | \nfunc maxCompatibilitySum(students [][]int, mentors [][]int) int {\n result, m, mentorVisit := int(0), len(students), make([]bool, len(students))\n \n | tuanbieber | NORMAL | 2022-09-03T14:24:35.226766+00:00 | 2022-09-03T14:26:12.898029+00:00 | 468 | false | ```\nfunc maxCompatibilitySum(students [][]int, mentors [][]int) int {\n result, m, mentorVisit := int(0), len(students), make([]bool, len(students))\n \n var backtrack func(int, int)\n backtrack = func(index int, currentCompatibility int) {\n if index == m {\n result = max(result, currentCompatibility)\n return\n }\n \n for i := 0; i < m; i++ {\n if mentorVisit[i] == false {\n mentorVisit[i] = true\n backtrack(index + 1, currentCompatibility + getCompatibility(students[index], mentors[i])) \n mentorVisit[i] = false\n } \n }\n }\n \n backtrack(0, 0)\n \n return result\n}\n\nfunc getCompatibility(sAnswers, mAnswers []int) int {\n sum := 0\n \n for i := 0; i < len(sAnswers); i++ {\n if sAnswers[i] == mAnswers[i] {\n sum++\n }\n }\n \n return sum\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n \n return b\n}\n``` | 5 | 0 | ['Backtracking', 'Recursion', 'Go'] | 1 |
maximum-compatibility-score-sum | C++ | Recursive DP | Bitmasking | 3ms | 10 MB | Beats 99.62% | c-recursive-dp-bitmasking-3ms-10-mb-beat-nerq | \n\n\nint score[8][8];\nint dp[8][1<<8];\nint n;\nint backtrack(int i, int mask){\n\tif(i==n) return 0;\n\tif(dp[i][mask]!=-1) return dp[i][mask];\n\tint ret=IN | raiaankur1 | NORMAL | 2022-06-28T19:01:43.169557+00:00 | 2022-06-28T19:01:43.169610+00:00 | 514 | false | \n\n```\nint score[8][8];\nint dp[8][1<<8];\nint n;\nint backtrack(int i, int mask){\n\tif(i==n) return 0;\n\tif(dp[i][mask]!=-1) return dp[i][mask];\n\tint ret=INT_MIN;\n\tfor(int j=0; j<n; j++)\n\t\tif(mask&(1<<j))\n\t\tret = max(ret, score[i][j] + backtrack(i+1, mask^(1<<j)));\n\treturn dp[i][mask] = ret;\n}\nint maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n\tmemset(dp, -1, sizeof dp);\n\tmemset(score, 0, sizeof score);\n\tn=students.size();\n\tfor(int i=0; i<n; i++)\n\t\tfor(int j=0; j<n; j++)\n\t\t\tfor(int k=0; k<students[0].size(); k++)\n\t\t\t\tscore[i][j] += students[i][k]==mentors[j][k];\n\treturn backtrack(0, (1<<n)-1); //start with 1st student; with all the mentors available to assign\n//(1<<n-1 has all the n bits ON)\n}\n/*\nHint:\n\tSimilar to job assignment problem.\n*/\n```\n\nThanks \u270C | 4 | 0 | ['Dynamic Programming', 'Recursion', 'C', 'Bitmask', 'C++'] | 1 |
maximum-compatibility-score-sum | C++ || Backtracking || Commented || faster than 100% | c-backtracking-commented-faster-than-100-a9ag | For every student try to pair it with every mentor, and for all these combinations, save the maximum resultant.\n\nclass Solution {\npublic:\n \nvoid find(ve | sahiltuli_31 | NORMAL | 2021-07-25T05:52:41.775786+00:00 | 2021-07-25T05:56:56.730908+00:00 | 296 | false | For every student try to pair it with every mentor, and for all these combinations, save the maximum resultant.\n```\nclass Solution {\npublic:\n \nvoid find(vector<vector<int> > &students,vector<vector<int >> &mentors,int st,int n,vector<int> &used,int &temp,int &ans)\n{\n if(st == n)\n {\n ans = max(ans,temp);\n return;\n }\n \n for(int i = 0 ;i < n;i++)\n {\n if(used[i] == 0)//got a mentor thats still free, so pair it\n {\n used[i] = 1;\n int score = 0;\n for(int j = 0 ;j < students[st].size();j++)\n {\n if(students[st][j] == mentors[i][j])\n score++;\n }\n temp += score;//add the score\n find(students,mentors,st+1,n,used,temp,ans);//recur for remaining students\n used[i] = 0;//backtrack\n temp -= score;\n }\n }\n}\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n \n int n = students.size();\n vector<int> used(n,0);//to keep track of fee mentors\n int temp = 0;//temp ans for a specific combination\n int i = 0;//start with the first student\n int ans = 0;//final ans\n find(students,mentors,i,n,used,temp,ans);\n return ans;\n \n }\n};\n```\nConsider Upvoting ..!!!! | 4 | 0 | ['Backtracking', 'C++'] | 0 |
maximum-compatibility-score-sum | Very simple c++ code with all possible combinations. Simply use of stl. | very-simple-c-code-with-all-possible-com-xi18 | \n// As m and n are too small so that we can check every possible combination.\n// As it hard to shuffle complete so just use their indexes. And with stl functi | abaddu_21 | NORMAL | 2021-07-25T04:37:14.084606+00:00 | 2021-07-25T05:08:46.270608+00:00 | 346 | false | ```\n// As m and n are too small so that we can check every possible combination.\n// As it hard to shuffle complete so just use their indexes. And with stl function permutation\n// check ans with next permutation. Continue till all permutation done.\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& stud, vector<vector<int>>& ment) {\n int r=stud.size(),c=stud[0].size(),ans=0,i=0;\n vector<int> idx;\n while(i<r)\n {\n idx.push_back(i);\n i++;\n }\n do\n {\n int curr=0;\n i=0;\n while(i<r)\n {\n int j=0;\n while(j<c)\n {\n curr+=(stud[idx[i]][j]==ment[i][j]);\n j++;\n }\n i++;\n }\n ans=max(ans,curr);\n }while(next_permutation(idx.begin(),idx.end()));\n return ans;\n }\n};\n``` | 4 | 0 | ['C'] | 1 |
maximum-compatibility-score-sum | DP with Bitmasking Easy Intuititive || C++ | dp-with-bitmasking-easy-intuititive-c-by-p5xz | Explanation and intuition :\n At first, the noticing fact are the problem contraints. Both m and n are less than or equals to 8.\n Also, we have to keep a track | dikbhranto_dishari | NORMAL | 2023-06-13T03:25:05.810662+00:00 | 2023-06-13T03:26:34.987681+00:00 | 227 | false | **Explanation and intuition** :\n* At first, the noticing fact are the problem contraints. Both m and n are less than or equals to 8.\n* Also, we have to keep a track of the subset from the mentors array who have been already assigned to a particular student (can be done in the other way too).\n* Thus, these facts enhance our idea that we can use DP with bitmasks. \n* At first, make two vectors to store for each student and mentor their answer sum in decimal (as n<=8, the number will definitely fit in int).\n* e.g., [1,0,1,0,0] for a student turns 16+4=20\n* For a mentor with [1,0,0,0,1], the sum is 16+1=17\n* Thus, doing ```__builtin_popcount``` of XOR of the two sums, we get number of different bits. So just subtract it from n to get the compatibility score !\n\n* Now, coming to DP, let we will be assigning each student a particular mentor one by one. \n* Thus, f(index,mentors) -> max compatibility score for assigning students from index till end when the mentors present in "mentors" have already been assigned. \n* Let, mentor 1,2,5 have been assigned among 5 mentors. We can keep track using mask 10011 having set bits indicating the already assigned mentors (starting from right, 0-based indexing)\n* Thus, state change from index to index+1 happens ->\n\t\tFrom 1 to m, when that bit of the mask is unset. We just set it, add the compatibility score and call for next index.\n\t\tFinally, we take the max of all the sums !\n\t\t\n\t**The code :**\n\t\n\t```class Solution {\npublic:\n \n int dp[9][1<<8];\n \n int f(vector<int> &s_sum, vector<int> &t_sum, int index, int mask, int m, int n){\n // from this index with mask \'mask\', find the max result\n \n if (index==m){\n return 0;\n }\n \n if (dp[index][mask]!=-1) return dp[index][mask];\n \n int ans=0;\n \n for (int j=0;j<m;j++){\n // which teacher\n if (mask & (1<<j)) continue;\n // mask set\n \n int s_score=s_sum[index];\n int t_score=t_sum[j];\n int temp=s_score^t_score;\n int to_add=n-(__builtin_popcount(temp));\n // number of same bits\n \n ans=max(ans, to_add + f(s_sum, t_sum, index+1, mask|(1<<j), m, n));\n }\n \n return dp[index][mask]=ans;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m=students.size();\n int n=students[0].size();\n \n vector<int> s_sum(m,0);\n for (int i=0;i<m;i++){\n int sum=0;\n for (int j=0;j<n;j++){\n sum=sum*2;\n sum+=students[i][j];\n }\n s_sum[i]=sum;\n }\n // [6,5,1] for example 1\n \n vector<int> t_sum(m,0);\n for (int i=0;i<m;i++){\n int sum=0;\n for (int j=0;j<n;j++){\n sum*=2;\n sum+=mentors[i][j];\n }\n t_sum[i]=sum;\n }\n // [4,1,6] for example 1\n \n memset(dp,-1,sizeof(dp));\n \n int res=f(s_sum,t_sum,0,0,m,n);\n \n return res;\n }\n};```\n\n**Time complexity** :\n\nTime complexity in DP : No. of states * transition time between states \n\nHere, no. of states = No. of indices * Total possible mask size\n\t\t\t\t\t\t\t= m*(2^m)\nTransition time is in order of O(m), basically work done in each state\n\nPrecomputation time of binary to decimal conversion : O(m*n)\n\nThus total complexity : O(m*n) + O((m^2) * (2^m)) = O(m^2 * 2^m)\n\n**Hope you like it !** | 3 | 0 | ['Dynamic Programming', 'C++'] | 1 |
maximum-compatibility-score-sum | Permutations | Backtracking | C++ | permutations-backtracking-c-by-tusharbha-9wpe | \nclass Solution {\n void dfs(int i, int n, int m, vector<vector<int>>& students, vector<vector<int>>& mentors, int &ans) {\n if(i == n) {\n | TusharBhart | NORMAL | 2023-03-20T15:12:37.023390+00:00 | 2023-03-20T15:12:37.023420+00:00 | 914 | false | ```\nclass Solution {\n void dfs(int i, int n, int m, vector<vector<int>>& students, vector<vector<int>>& mentors, int &ans) {\n if(i == n) {\n int cnt = 0;\n for(int j=0; j<n; j++) {\n for(int k=0; k<m; k++) cnt += students[j][k] == mentors[j][k];\n }\n ans = max(ans, cnt);\n return;\n }\n for(int j=i; j<n; j++) {\n swap(students[i],students[j]);\n dfs(i + 1, n, m, students, mentors, ans);\n swap(students[i],students[j]);\n }\n }\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n = students.size(), m = students[0].size(), ans = 0;\n dfs(0, n, m, students, mentors, ans);\n return ans;\n }\n};\n``` | 3 | 0 | ['Backtracking', 'C++'] | 0 |
maximum-compatibility-score-sum | c++ | easy | short | c-easy-short-by-akshat0610-rars | \nclass Solution {\npublic:\n int ans=INT_MIN;\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) \n {\n int | akshat0610 | NORMAL | 2022-10-21T08:51:13.435902+00:00 | 2022-10-21T08:51:13.435940+00:00 | 757 | false | ```\nclass Solution {\npublic:\n int ans=INT_MIN;\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) \n {\n int idx=0;\n int n=students.size();\n vector<bool>vis(n,false);\n int currscore=0;\n fun(idx,students,mentors,n,vis,currscore);\n return ans;\n } //student //mentor\n void fun(int idx,vector<vector<int>>&student,vector<vector<int>>&mentor,int &n,vector<bool>&vis,int currscore)\n {\n //base\n if(idx >= n)\n {\n if(currscore > ans)\n {\n ans=currscore;\n }\n return;\n }\n //for the curr ith studen we have the choise for all the mentors\n //we will try to match the curr student with every mentor individulally\n //so to avoid the clash in matching we will make that mentor visited after considerration and will run the loop from the starting\n //we have choise of m mentors\n for(int i=0;i<n;i++)\n {\n if(vis[i]==true)\n {\n continue;\n }\n else if(vis[i]==false) //then only we can match the ith student with the curr mentor\n {\n vis[i]=true; //making the curr mentor vis as it got matched now with curr ith student\n int temp = match(student[idx],mentor[i]); \t \t\t\n fun(idx+1,student,mentor,n,vis,currscore+temp);\n vis[i]=false; //backtracking\n }\n }\n }\n int match(vector<int>&student,vector<int>&mentor)\n {\n int n=student.size();\n int count=0;\n\n for(int i=0;i<n;i++)\n {\n if(student[i]==mentor[i])\n {\n count++;\n }\n }\n return count;\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Backtracking', 'Depth-First Search', 'Recursion', 'C', 'C++'] | 1 |
maximum-compatibility-score-sum | C++||Backtracking ||Recursive||Easy to Understand | cbacktracking-recursiveeasy-to-understan-1k1d | ```\nclass Solution {\npublic:\n int ans=0;\n void backtrack(vector>& students, vector>& mentors,int idx,int curr_res,vector &vis)\n {\n if(idx> | return_7 | NORMAL | 2022-07-16T06:23:10.504286+00:00 | 2022-07-16T06:23:10.504320+00:00 | 322 | false | ```\nclass Solution {\npublic:\n int ans=0;\n void backtrack(vector<vector<int>>& students, vector<vector<int>>& mentors,int idx,int curr_res,vector<int> &vis)\n {\n if(idx>=mentors.size())\n {\n ans=max(ans,curr_res);\n return ;\n }\n for(int i=0;i<students.size();i++)\n {\n if(vis[i]!=0)\n continue;\n int temp=0;\n vis[i]=1;\n for(int j=0;j<students[i].size();j++)\n {\n if(students[i][j]==mentors[idx][j])\n {\n temp++;\n }\n }\n backtrack(students,mentors,idx+1,curr_res+temp,vis);\n vis[i]=0;\n }\n }\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors)\n {\n vector<int> vis(students.size(),0);\n backtrack(students,mentors,0,0,vis);\n return ans;\n \n \n }\n};\n// if you like the solution plz upvote. | 3 | 0 | ['Backtracking', 'Recursion', 'C'] | 0 |
maximum-compatibility-score-sum | [Python] | python-by-rahulranjan95-iwiz | \nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n res = [-1]\n visited = [False] | rahulranjan95 | NORMAL | 2021-09-03T05:48:54.844241+00:00 | 2021-09-03T05:49:39.674474+00:00 | 353 | false | ```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n res = [-1]\n visited = [False]*len(students)\n #ssf ===> score so far\n #res ==> final result. It is a list as it acts as a global variable\n #idx ====> index over students array.\n self.maxCompatibilityUtil(students,mentors,0,visited,res,0)\n return res[0]\n \n \n def maxCompatibilityUtil(self,students,mentors,ssf,visited,res,idx):\n if idx==len(students):\n res[0] = max(res[0],ssf)\n return \n \n for i in range(len(mentors)):\n if visited[i]==False:\n visited[i]=True\n temp = 0\n for j in range(len(mentors[i])):\n if mentors[i][j]==students[idx][j]:\n temp = temp+1\n self.maxCompatibilityUtil(students,mentors,ssf+temp,visited,res,idx+1)\n visited[i]=False\n\t\t\t\t\n\t```\n\t\nWe have to check for every student-mentor pair. \nCan someone please tell me how to post any image? Or maybe some tool that can help me draw and post on leetcode. With Euler tree, this can be understood pretty easily. | 3 | 0 | ['Backtracking', 'Recursion', 'Python', 'Python3'] | 0 |
maximum-compatibility-score-sum | [C++] Backtracking Solution, faster than 100% | c-backtracking-solution-faster-than-100-w1ra1 | The idea is simple :-\n1) I made a 2D matrix of size MM for every possible combination.\n2) then find "Maximum sum of a Matrix where each value is from a unique | shubhamrgh | NORMAL | 2021-07-25T10:28:01.552117+00:00 | 2021-07-25T10:45:25.437150+00:00 | 242 | false | The idea is simple :-\n1) I made a 2D matrix of size M*M for every possible combination.\n2) then find "Maximum sum of a Matrix where each value is from a unique row and column".\n\n```\nclass Solution {\npublic:\n vector<int> col;\n int mx = INT32_MIN;\n void maxSum(int n, vector<vector<int>> &matrix, int idx, int sum)\n {\n if (idx == n)\n {\n mx = max(mx, sum);\n return;\n }\n for (int i = 0; i < n; i++)\n {\n if (!col[i])\n {\n col[i] = true;\n maxSum(n, matrix, idx + 1, sum + matrix[idx][i]);\n col[i] = false;\n }\n }\n }\n void fillMatrix(vector<int>&s,vector<int>&m, int i, int j, vector<vector<int>>&matrix)\n {\n int x = 0;\n for(int k = 0; k<s.size(); k++)\n {\n if(s[k]==m[k])\n x++;\n }\n matrix[i][j] = x;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m = students.size();\n vector<vector<int>>matrix(m,vector<int>(m,0));\n for(int i = 0; i<m; i++)\n {\n for(int j = 0; j<m; j++)\n {\n fillMatrix(students[i],mentors[j], i, j, matrix);\n }\n }\n col.assign(m, false);\n maxSum(m, matrix, 0, 0);\n return mx;\n }\n};\n```\n\n\n**Upvote if you like!!!** | 3 | 0 | ['Backtracking', 'C'] | 0 |
maximum-compatibility-score-sum | Naive Brute Force Using next_permutation(68ms) | naive-brute-force-using-next_permutation-dwom | Here is a pretty naive implementation ,hope it helps\n```\nclass Solution {\npublic:\n int maxCompatibilitySum(vector>& student, vector>& mentors) {\n | amardeepganguly | NORMAL | 2021-07-25T04:05:53.569214+00:00 | 2021-07-25T04:09:48.491328+00:00 | 189 | false | Here is a pretty naive implementation ,hope it helps\n```\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& student, vector<vector<int>>& mentors) {\n int m=student.size();\n int n=student[0].size();\n //This matrix com stores the compatibility score between i th student and jth mentor\n int com[m][m];\n memset(com,0,sizeof com);\n //We fill out every student-teacher compatibility scores\n for(int i=0;i<m;i++)\n for(int j=0;j<m;j++)\n {\n int res=0;\n for(int k=0;k<n;k++)\n {\n res+=(student[i][k]==mentors[j][k]);\n }\n com[i][j]=res;\n }\n //allot vector is used to assign students to mentors in such a way that every student is assigned to one teacher\n //We try out every such possibility using next_permutation\n //For example if we have 5 students initially the allot=[0,1,2,3,4]\n //which means ith student is assigned to allot[i] teacher \n \n vector<int> allot;\n for(int i=0;i<m;i++) allot.push_back(i);\n int ans=0;\n for(int i=0;i<m;i++) ans+=(com[i][allot[i]]);\n //Here we check every possible assignment of m students to m teachers\n do{ int temp=0;\n for(int i=0;i<m;i++) temp+=(com[i][allot[i]]);\n ans=max(ans,temp);\n \n }while(next_permutation(allot.begin(),allot.end()));\n return ans;\n \n }\n} | 3 | 0 | ['C'] | 1 |
maximum-compatibility-score-sum | Java | Simple DFS | Check all permutations | java-simple-dfs-check-all-permutations-b-tzlx | \nclass Solution {\n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n return dfs(students,mentors,new boolean[mentors.length],0); | Sans26 | NORMAL | 2021-07-25T04:02:49.234844+00:00 | 2021-07-25T04:03:46.893483+00:00 | 599 | false | ```\nclass Solution {\n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n return dfs(students,mentors,new boolean[mentors.length],0);\n }\n int dfs(int[][] s,int[][] m,boolean[] b,int o){\n int sum=0;\n if(o==s.length){\n return 0;\n }\n for(int i=0; i<m.length; i++){\n if(b[i]){\n continue;\n }\n int ss=0;\n for(int j=0; j<m[0].length; j++){\n if(s[o][j]==m[i][j]){\n ss++;\n }\n }\n b[i]=true;\n sum=Math.max(sum,ss+dfs(s,m,b,o+1));\n b[i]=false;\n }\n return sum;\n }\n}\n``` | 3 | 1 | ['Depth-First Search', 'Java'] | 0 |
maximum-compatibility-score-sum | [c++] next_permutation solution. | c-next_permutation-solution-by-mahmoud_w-fkpu | \'\'\'\n\nclass Solution {\npublic:\n int maxCompatibilitySum(vector>& students, vector>& mentors) {\n\t\n int m = students.size() ; // number o | Mahmoud_Warrak | NORMAL | 2021-07-25T04:02:13.304232+00:00 | 2021-07-25T04:10:03.344784+00:00 | 268 | false | \'\'\'\n\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n\t\n int m = students.size() ; // number of students\n int n = students[0].size() ; // number of questions\n int chos[m] ; // this array select mentors to students\n iota( chos , chos+m , 0 ) ; // fill every mentor with the opposite student\n ll ans = 0 , curans = 0 ; \n do{\n curans = 0 ;\n for ( int i = 0 ; i < m ; i ++ ){\n for ( int j = 0 ; j < n ; j ++ ){\n curans += ( students[i][j] == mentors[chos[i]][j] ) ; // add one if they are equal\n }\n }\n ans = max ( ans , curans ) ; // if the current answer larger than the answer \n // make the answer equals the current answer \n }while ( next_permutation(chos , chos+m ) ) ; // keep track all the permutations of chos\n return ans ;\n }\n};\n\'\'\'\nfill free to ask any questions. | 3 | 1 | [] | 0 |
maximum-compatibility-score-sum | Bitmask DP | JAVA | bitmask-dp-java-by-drashta01-uqkj | \n\nclass Solution {\n Integer[][]dp;\n int m, n;\n int[][] S;\n int[][] M;\n public int maxCompatibilitySum(int[][] students, int[][] mentors) { | drashta01 | NORMAL | 2021-07-25T04:00:54.630249+00:00 | 2021-07-25T04:00:54.630294+00:00 | 234 | false | ```\n\nclass Solution {\n Integer[][]dp;\n int m, n;\n int[][] S;\n int[][] M;\n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n m = students.length;\n n = students[0].length;\n S = students;\n M = mentors;\n dp = new Integer[m][1 << 8];\n return dfs(0, 0);\n }\n\n // m : no of students\n // n : no of Questions\n public int dfs(int i, int mask){\n if(i == m)\n return 0;\n \n if(dp[i][mask] != null) return dp[i][mask];\n \n int maxScore = 0;\n for (int j = 0; j < m; j++){\n if((mask & (1 << j)) == 0){\n int score = 0;\n for (int k = 0; k < n; k++){\n score += S[i][k] == M[j][k] ? 1 : 0;\n }\n score += dfs(i + 1, mask | (1 << j));\n maxScore = Math.max(maxScore, score);\n }\n }\n dp[i][mask] = maxScore;\n return maxScore;\n }\n}\n``` | 3 | 0 | [] | 0 |
maximum-compatibility-score-sum | Unlock the Secret to Maximizing Compatibility Scores with This Genius Algorithm! 🚀🔥 | unlock-the-secret-to-maximizing-compatib-pfo0 | IntuitionThe problem requires finding the best pairing between students and mentors to maximize the compatibility score.
Since the number of students/mentors is | ishaan2003 | NORMAL | 2025-02-28T13:38:04.004561+00:00 | 2025-02-28T13:38:04.004561+00:00 | 115 | false | # Intuition
The problem requires finding the best pairing between students and mentors to maximize the compatibility score.
Since the number of students/mentors is small (≤ 8), we can use backtracking to explore all possible assignments efficiently.
# Approach
1. Use backtracking to generate all permutations of student-to-mentor pairings.
2. Calculate the compatibility score for each assignment by comparing corresponding answers.
3. Keep track of the maximum compatibility score found.
4. Recursively explore all possible assignments while marking mentors as used and backtracking.
# Complexity
- Time complexity:
Since we are generating all permutations of students to mentors, the worst case complexity is **O(n!)**.
Each permutation takes **O(n²)** to compute the compatibility score, so the final complexity is **O(n! * n²)**.
- Space complexity:
**O(n)** for recursion depth in the worst case (n students).
**O(n²)** for storing the input.
Overall, **O(n²)**.
# Code
```cpp []
class Solution {
public:
int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {
int ans = 0;
h(students,mentors,0,0,ans);
return ans;
}
private:
void h(vector<vector<int>>& students, vector<vector<int>>& mentors,int i,int com,int& ans){
if(i >= students.size()){
// updating ans to the max compatibility score
ans = max(ans,com);
return;
}
// checking compability of i'th student with each mentor
for(int j = 0;j < mentors.size();j++){
// cout << com << " ";
if(mentors[j].size()){
int c = compatibility(i,j, students,mentors);
vector<int> temp = mentors[j];
mentors[j] = {};
h(students,mentors,i+1, com+c,ans);
mentors[j] = temp; // backtracking
}
}
}
// finding the compatibility score
int compatibility(int i,int j,vector<vector<int>>& students, vector<vector<int>>& mentors){
int count = 0;
for(int x=0;x < students[i].size();x++){
if(students[i][x] == mentors[j][x]) count++;
}
return count;
}
};
``` | 2 | 0 | ['C++'] | 0 |
maximum-compatibility-score-sum | Backtracking + Recursive Approach with Detail Explanation || Beginner Friendly | backtracking-recursive-approach-with-det-6nbn | Code\n\nclass Solution {\n int max;\n\n private void solveBacktrack(int[][] students, int[][] mentors, int pos, int score, boolean[] vis) {\n // Ba | Shree_Govind_Jee | NORMAL | 2024-02-01T16:17:56.264306+00:00 | 2024-02-01T16:17:56.264341+00:00 | 314 | false | # Code\n```\nclass Solution {\n int max;\n\n private void solveBacktrack(int[][] students, int[][] mentors, int pos, int score, boolean[] vis) {\n // Base Case\n if (pos >= students.length) {\n max = Math.max(max, score);\n return;\n }\n\n // Recursive Approach Start....\n for (int i = 0; i < mentors.length; i++) {\n if (!vis[i]){\n vis[i] = true;\n solveBacktrack(students, mentors, pos + 1, score + helper(students[pos], mentors[i]), vis);\n\n // BackTrack....\n vis[i] = false;\n }\n }\n }\n\n private int helper(int[] student, int[] mentor) {\n int count = 0;\n for (int i = 0; i < mentor.length; i++) {\n if (student[i] == mentor[i])\n count++;\n }\n return count;\n }\n\n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n boolean[] vis = new boolean[students.length];\n solveBacktrack(students, mentors, 0, 0, vis);\n return max;\n }\n}\n``` | 2 | 0 | ['Array', 'Dynamic Programming', 'Backtracking', 'Bit Manipulation', 'Recursion', 'Bitmask', 'Java'] | 0 |
maximum-compatibility-score-sum | Recursion Solution | recursion-solution-by-20ce01050-m7t6 | Intuition\nInitially, I considered a greedy approach for solving the problem, where I would always chreoose the maximum compatibility score. However, I realized | 20ce01050 | NORMAL | 2023-09-15T08:34:13.948071+00:00 | 2023-09-15T08:34:13.948099+00:00 | 135 | false | # Intuition\nInitially, I considered a greedy approach for solving the problem, where I would always chreoose the maximum compatibility score. However, I realized that this approach may not yield the correct result. Instead, I decided to adopt a recursive approach to solve the problem.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe code finds the maximum compatibility sum between students and mentors by exploring all possible pairings using a recursive approach. It calculates compatibility scores for each pairing and tracks visited mentors to ensure each student gets paired only once. The maximum score is returned as the result. \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N^2 * M)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int f(vector<vector<pair<int, int>>> &pq, int index, vector<int>& visited) {\n if (index == pq.size()) {\n return 0;\n }\n int score = 0;\n for (int i = 0; i < pq[index].size(); i++) {\n if (visited[i] != 1) {\n visited[i] = 1;\n score = max(score, pq[index][i].second + f(pq, index + 1, visited));\n visited[i] = 0; \n }\n }\n return score;\n }\n\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n = students.size();\n int m = students[0].size();\n vector<vector<pair<int, int>>> pq(n);\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n int score = 0;\n for (int k = 0; k < m; k++) {\n if (students[i][k] == mentors[j][k]) {\n score++;\n }\n }\n pq[i].push_back({j, score});\n }\n }\n vector<int> visited(n, 0);\n return f(pq, 0, visited);\n }\n};\n\n``` | 2 | 0 | ['Recursion', 'C++'] | 0 |
maximum-compatibility-score-sum | Easy C++ Solution || Bitmask + DP || 100% Faster ✔✔ | easy-c-solution-bitmask-dp-100-faster-by-ytck | \n\n# Code\n\nclass Solution {\npublic:\n int dp[8][256];\n int calcSum(vector<int> &v1,vector<int> &v2){\n int cnt=0;\n for(int i=0;i<v1.si | mamatva004 | NORMAL | 2023-06-19T13:56:53.296861+00:00 | 2023-06-19T13:56:53.296889+00:00 | 755 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int dp[8][256];\n int calcSum(vector<int> &v1,vector<int> &v2){\n int cnt=0;\n for(int i=0;i<v1.size();i++) cnt+=(v1[i]==v2[i]);\n return cnt;\n }\n int help(int idx,int mask, vector<vector<int>>& students, vector<vector<int>>& mentors,int m){\n if(idx==m) return 0;\n if(dp[idx][mask]!=-1) return dp[idx][mask];\n int sum=0;\n for(int i=0;i<m;i++){\n if(mask&(1<<i)){\n sum=max(sum,calcSum(students[idx],mentors[i])+help(idx+1,mask^(1<<i),students,mentors,m));\n }\n }\n return dp[idx][mask]=sum;\n }\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m=students.size();\n memset(dp,-1,sizeof dp);\n return help(0,(1<<m)-1,students,mentors,m);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Bitmask', 'C++'] | 1 |
maximum-compatibility-score-sum | Easy Brute Force Accepted | easy-brute-force-accepted-by-sanket_jadh-ha1e | ```\nclass Solution {\npublic:\n int count(int i,int j,vector>&s,vector>&m){\n int ct=0;\n for(int k=0;k<s[i].size();k++){\n if(s[i] | Sanket_Jadhav | NORMAL | 2022-08-20T06:32:35.065432+00:00 | 2022-08-20T06:32:35.065458+00:00 | 376 | false | ```\nclass Solution {\npublic:\n int count(int i,int j,vector<vector<int>>&s,vector<vector<int>>&m){\n int ct=0;\n for(int k=0;k<s[i].size();k++){\n if(s[i][k]==m[j][k])ct++;\n }\n \n return ct;\n }\n \n int func(int i,vector<int>&vis,vector<vector<int>>&st,vector<vector<int>>&men){\n if(i==st.size())return 0;\n \n int ans=0;\n for(int j=0;j<vis.size();j++){\n int comp=0;\n if(!vis[j]){\n vis[j]=1;\n comp=count(i,j,st,men)+func(i+1,vis,st,men);\n \n vis[j]=0;\n }\n ans=max(ans,comp);\n }\n \n return ans;\n }\n \n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n \n int n=students.size(),m=students[0].size();\n vector<int>vis(n);\n \n return func(0,vis,students,mentors);\n }\n}; | 2 | 0 | ['Recursion', 'C++'] | 0 |
maximum-compatibility-score-sum | [C++] : From Backtracking to DP + Bit masking | c-from-backtracking-to-dp-bit-masking-by-0430 | Approch 1 : Using Backtracking\n\nclass Solution {\npublic:\n \n int calculate_score(vector<int> &a, vector<int> &b)\n {\n int ans = 0;\n | zanhd | NORMAL | 2022-04-09T17:03:56.295620+00:00 | 2022-04-10T14:23:19.827575+00:00 | 166 | false | Approch 1 : Using Backtracking\n```\nclass Solution {\npublic:\n \n int calculate_score(vector<int> &a, vector<int> &b)\n {\n int ans = 0;\n for(int i = 0; i < a.size(); i++)\n {\n ans += (a[i] == b[i]);\n }\n return ans;\n }\n \n int mx_sum(int i, vector<bool> used, vector<vector<int>> &score, int n,int m)\n {\n if(i >= n) return 0;\n int ans = 0;\n for(int j = 0; j < m; j++)\n {\n if(used[j]) continue;\n used[j] = 1;\n ans = max(ans, score[i][j] + mx_sum(i + 1, used, score, n, m));\n used[j] = 0;\n }\n return ans;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) \n {\n int n = students.size();\n int m = mentors.size();\n \n vector<vector<int>> score(n, vector<int> (m, 0));\n \n for(int i = 0; i < n; i++)\n for(int j = 0; j < m; j++)\n score[i][j] = calculate_score(students[i], mentors[j]);\n \n vector<bool> used(m, 0);\n return mx_sum(0, used, score, n, m);\n }\n \n};\n```\n\nApproach 2 : Using DP + mask (using mask to replace used and to memoize results)\n```\nconst int N = 9;\nint dp[N][1 << 8];\nclass Solution {\npublic:\n \n int calculate_score(vector<int> &a, vector<int> &b)\n {\n int ans = 0;\n for(int i = 0; i < a.size(); i++)\n {\n ans += (a[i] == b[i]);\n }\n return ans;\n }\n \n int mx_sum(int i, int mask, vector<vector<int>> &score, int n,int m)\n {\n if(i >= n) return 0;\n \n if(dp[i][mask] != -1) return dp[i][mask];\n \n int ans = 0;\n for(int j = 0; j < m; j++)\n {\n if(mask & (1 << j)) continue;\n ans = max(ans, score[i][j] + mx_sum(i + 1, mask + (1 << j), score, n, m));\n }\n return dp[i][mask] = ans;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) \n {\n int n = students.size();\n int m = mentors.size();\n \n vector<vector<int>> score(n, vector<int> (m, 0));\n \n for(int i = 0; i < n; i++)\n for(int j = 0; j < m; j++)\n score[i][j] = calculate_score(students[i], mentors[j]);\n \n //global\n for(int i = 0; i < N; i++)\n for(int j = 0; j < (1 << 8); j++)\n dp[i][j] = -1;\n \n int mask = 0;\n return mx_sum(0, mask, score, n, m);\n }\n \n};\n``` | 2 | 0 | ['Backtracking'] | 1 |
maximum-compatibility-score-sum | Python 3, one line | python-3-one-line-by-l1ne-p2lu | There\'s only a max of 8 students and mentors, so we can just try every permutation. Easy peasy.\n\npython\nclass Solution:\n def maxCompatibilitySum(self, S, | l1ne | NORMAL | 2021-08-15T05:28:28.691075+00:00 | 2021-08-15T05:30:12.362933+00:00 | 192 | false | There\'s only a max of 8 students and mentors, so we can just try every permutation. Easy peasy.\n\n```python\nclass Solution:\n def maxCompatibilitySum(self, S, M):\n return max(sum(sum(map(eq, *z)) for z in zip(S, P)) for P in permutations(M))\n``` | 2 | 0 | [] | 1 |
maximum-compatibility-score-sum | Python Bitmask Memoization Solution | python-bitmask-memoization-solution-by-2-dwe0 | \nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n n = len(students)\n m = len(st | 2019csb1077 | NORMAL | 2021-08-14T05:15:27.249710+00:00 | 2021-08-14T05:15:27.249745+00:00 | 117 | false | ```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n n = len(students)\n m = len(students[0])\n full = 1<<n\n dp = [[-1 for i in range(full)] for j in range(n)]\n def rec(mentorMask, studentIndex):\n if mentorMask==full-1 or studentIndex==n:\n return 0\n if dp[studentIndex][mentorMask]!=-1:\n return dp[studentIndex][mentorMask]\n ans = 0\n for j in range(n):\n if mentorMask&(1<<j)==0:\n score = 0\n for i in range(m):\n if students[studentIndex][i]==mentors[j][i]:\n score+=1 \n ans = max(ans, score + rec(mentorMask^(1<<j), studentIndex+1))\n dp[studentIndex][mentorMask] = ans\n return ans\n return rec(0,0)\n``` | 2 | 0 | [] | 0 |
maximum-compatibility-score-sum | [C++] STL - next_permutation() | c-stl-next_permutation-by-harshit_2000-7quv | The brute force solution is generating all the permuntations of the students and calculates the score of this permutation and the students.\nTime Complexity : O | harshit_2000 | NORMAL | 2021-08-07T06:27:41.290523+00:00 | 2021-08-07T06:27:41.290569+00:00 | 140 | false | The brute force solution is generating all the permuntations of the students and calculates the score of this permutation and the students.\nTime Complexity : ``` O(n! * nm) ``` **n!** for permutations and **nm** for calculating score.\nSince , ``` n, m <= 8 ``` and ``` 8! * 8 * 8 == 2,580,480 ``` which should pass.\n\n```\nclass Solution {\npublic:\n int factorial(int n){\n vector<int> arr(n + 1);\n arr[0] = 1;\n arr[1] = 1;\n for (int i = 2; i <= n; i++){\n arr[i] = arr[i - 1] * i;\n }\n return arr[n];\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int max_ = 0, curr_max = 0;\n int row = students.size(), col = students[0].size();\n int total_permutations = factorial(row);\n for (int k = 0; k < total_permutations; k++){\n \n next_permutation(students.begin(), students.end());\n curr_max = 0;\n \n for (int i = 0; i < row; i++){\n for (int j = 0; j < col; j++){\n if (mentors[i][j] == students[i][j]) curr_max++;\n }\n }\n \n max_ = max(max_ , curr_max);\n }\n return max_;\n }\n};\n``` | 2 | 0 | [] | 1 |
maximum-compatibility-score-sum | Python - Simple DFS solution | python-simple-dfs-solution-by-ajith6198-gy21 | \nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n \n n, m = len(students), len(s | ajith6198 | NORMAL | 2021-08-03T04:30:57.256693+00:00 | 2021-08-03T04:31:15.605250+00:00 | 368 | false | ```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n \n n, m = len(students), len(students[0])\n out = []\n\t\t\n def dfs(i, used, score):\n \n if i == n:\n out.append(score)\n return\n \n for mentor in range(n):\n if str(mentor) not in used:\n curr = sum(a==b for a, b in zip(students[i], mentors[mentor]))\n dfs(i+1, used+str(mentor), score+curr)\n \n dfs(0, \'\', 0)\n return max(out)\n``` | 2 | 0 | ['Depth-First Search', 'Python'] | 2 |
maximum-compatibility-score-sum | C++ with comments #bitmask #DP #easy | c-with-comments-bitmask-dp-easy-by-elcam-43rx | \n int dp[9][265];\n\t// function to calculate value for some matrix a of students and other matrix b of mentors --- \n\t\t\t\t\t// a == students[i] && b | elcamino10 | NORMAL | 2021-07-28T13:22:49.576573+00:00 | 2021-07-28T13:26:32.593618+00:00 | 141 | false | ```\n int dp[9][265];\n\t// function to calculate value for some matrix a of students and other matrix b of mentors --- \n\t\t\t\t\t// a == students[i] && b == mentors[j] \n int ch(vector<int> a, vector<int> b){\n int n=a.size(),ans=0;\n for(int i=0;i<n;i++){\n if(a[i]==b[i])\n ans++;\n }\n return ans;\n }\n int fun(vector<vector<int>>& students, vector<vector<int>>& mentors,int j,int mask){\n int n=mentors.size();\n if(j<0)\n return 0;\n\t\t\t// normal dp condition \n if(dp[j][mask]!=-1)\n return dp[j][mask];\n\t\t\t// we will traverse for element and check the score for each students[i] and mentors[j] \n\t\t\t// and choose if and only if i is not taken already which is represented by the mask\n for(int i=0;i<n;i++){\n\t\t// this is checking condition to check if i was already taken or not. \n\t\t// eg. is mask was 6 then its binary representation is 110 and we want to check if i==2 is present or not \n\t\t// i.e is there 1 at the 2nd index from right. hence we take & of 110 and 100(1<< i )\n if(mask&(1<<i)){\n dp[j][mask]=max(dp[j][mask],ch(students[i],mentors[j])+fun(students,mentors,j-1,mask^(1<<i)));\n\t\t\t\t// because we are now using the i th array of students we have to mark its index in the mask as 0 --- \n\t\t\t\t// mask^(1<<i) converts the index at i position to 0 \n }\n }\n return dp[j][mask];\n }\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n=mentors.size();\n memset(dp,-1,sizeof dp);\n\t\t// initially all the indices (i.e n indices) of mask should be set to 1 hence the -1\n int mask=pow(2,n)-1;\n return fun(students,mentors,n-1,mask);\n }\n``` | 2 | 0 | ['Dynamic Programming', 'Bitmask'] | 2 |
maximum-compatibility-score-sum | 1ms 100% JAVA BackTracking + BitMask solution | 1ms-100-java-backtracking-bitmask-soluti-fpli | \n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n int n = students.length;\n return helper(0, 0, students, m | chenzuojing | NORMAL | 2021-07-28T01:13:42.186439+00:00 | 2021-07-28T01:13:59.966478+00:00 | 115 | false | ```\n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n int n = students.length;\n return helper(0, 0, students, mentors, new Integer[n][1 << n]);\n }\n\n\n private int helper(int pos, int mask, int[][] students, int[][] mentors, Integer[][] memo) {\n int n = students.length;\n if (mask == (1 << n) - 1)\n return 0;\n if (memo[pos][mask] != null)\n return memo[pos][mask];\n\n int maxScore = 0;\n for (int i = 0; i < n; i++) {\n if ((mask & (1 << i)) == 0) {\n int score = getScore(students[pos], mentors[i]);\n maxScore = Math.max(maxScore, score + helper(pos + 1, (mask | (1 << i)), students, mentors, memo));\n }\n }\n\n return memo[pos][mask] = maxScore;\n }\n\n private int getScore(int[] a, int[] b) {\n int count = 0;\n for (int i = 0; i < b.length; i++)\n if (a[i] == b[i]) count++;\n return count;\n }\n``` | 2 | 0 | [] | 1 |
maximum-compatibility-score-sum | C++ Solution using Permutation | c-solution-using-permutation-by-smritina-ig0j | \nclass Solution {\npublic:\n int cal(vector<vector<int>> &mentors, vector<vector<int>> &students)\n {\n int n=students.size(),m=students[0].size(),s | smritinaik1421 | NORMAL | 2021-07-27T10:17:39.431256+00:00 | 2021-07-27T10:17:39.431299+00:00 | 91 | false | ```\nclass Solution {\npublic:\n int cal(vector<vector<int>> &mentors, vector<vector<int>> &students)\n {\n int n=students.size(),m=students[0].size(),sum=0;\n \n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n sum+=(students[i][j]==mentors[i][j])?1:0;\n }\n }\n \n return sum;\n }\n \n int permutation(vector<vector<int>>&mentors, vector<vector<int>>&students, int index, int maxSum)\n {\n if(index==mentors.size())\n {\n maxSum=max(maxSum,cal(mentors,students));\n return maxSum;\n }\n \n for(int i=index;i<mentors.size();i++)\n {\n swap(mentors[i],mentors[index]);\n \n maxSum=max(maxSum,permutation(mentors,students,index+1,maxSum));\n \n swap(mentors[i],mentors[index]);\n }\n \n return maxSum;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n=students.size(),maxSum=INT_MIN;\n \n maxSum=permutation(mentors,students,0,maxSum);\n \n return maxSum;\n }\n};\n``` | 2 | 0 | [] | 1 |
maximum-compatibility-score-sum | C++ | Backtracking | Beginner friendly | c-backtracking-beginner-friendly-by-yash-agnv | Since constraints were very small\n\nm == students.length == mentors.length\nn == students[i].length == mentors[j].length\n1 <= m, n <= 8\nstudents[i][k] is eit | yashporwal11 | NORMAL | 2021-07-27T07:31:56.559528+00:00 | 2021-07-30T16:06:48.022747+00:00 | 123 | false | Since constraints were very small\n```\nm == students.length == mentors.length\nn == students[i].length == mentors[j].length\n1 <= m, n <= 8\nstudents[i][k] is either 0 or 1.\nmentors[j][k] is either 0 or 1.\n```\n\nthat\'s why I decided to go with the backtracking approach.\n\n```\nclass Solution {\npublic:\n\t// to calculate score of the student-mentor pair\n int score(vector<int>&s, vector<int>&m){\n int cnt=0;\n for(int i=0;i<s.size();i++){\n if(s[i]==m[i]) cnt++;\n }\n return cnt;\n }\n \n int solve(vector<vector<int>>& s, vector<vector<int>>& m, int student, int sz, vector<bool>&vis){\n \xA0 \xA0 \xA0 \xA0if(student==sz) return 0; // if all pairs are done\n int ans=0;\n for(int i=0;i<sz;i++){\n if(!vis[i]){\n vis[i]=1;\n ans=max(ans,score(s[student],m[i])+solve(s,m,student+1,sz,vis)); // pass next student(student+1)\n vis[i]=0;\n }\n }\n return ans;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& s, vector<vector<int>>& m) {\n int ans=0;\n vector<bool>vis(m.size(),0); // to keep track of already selected mentors\n for(int i=0;i<m.size();i++){\n vis[i]=1; // select ith mentor\n ans=max(ans,score(s[0],m[i])+solve(s,m,1,s.size(),vis)); // calculate score of student and selected mentor and then solve for other pairs\n vis[i]=0; // deselect(backtrack)\n }\n return ans;\n }\n};\n``` | 2 | 0 | [] | 2 |
maximum-compatibility-score-sum | C++ | Faster than 100% | Backtracking and Bit Mask | Comments Added | c-faster-than-100-backtracking-and-bit-m-vkks | We calculate compatibility between every student and mentor. Since the number of mentors and students are capped at 8, we can check every possible combination o | kaushal7797 | NORMAL | 2021-07-25T18:10:20.391607+00:00 | 2021-07-25T18:10:20.391654+00:00 | 71 | false | We calculate compatibility between every student and mentor. Since the number of mentors and students are capped at 8, we can check every possible combination of mentor and student. To keep a track of mentor assigned to student, we use bit masking.\n\nRefer to the code below for the above approach - \n\n```\nclass Solution {\npublic:\n vector<vector<int>> v;\n int n;\n int res=0;\n \n\t// function to calucate compatibility between two vectors.\n int compat(vector<int> a, vector<int> b) {\n int ans = 0;\n for(int i=0 ; i<a.size() ; i++) {\n if(a[i]==b[i]) ans++;\n }\n return ans;\n }\n \n void check(int idx, int bits, int sum) {\n // if all students have been assinged a mentor, check whether resultant sum is maximum.\n\t if(idx==n) {\n res = max(res,sum);\n }\n \n for(int i=0 ; i<n ; i++) {\n // select an unassigned mentor \n\t\t\tif(bits & 1<<i) {\n\t\t\t // mark mentor as assigned\n bits = (bits ^ (1<<i));\n sum = sum + v[idx][i];\n // recur for next student\n\t\t\t\tcheck(idx+1,bits,sum);\n\t\t\t\t// backtrack\n sum = sum - v[idx][i];\n bits = bits | 1<<i;\n }\n }\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n vector<vector<int>> temp (8, vector<int> (8,0));\n v = temp;\n n = students.size();\n \n\t\t// vector v store the compatibility between each student mentor pair.\n\t\tfor(int i=0 ; i<students.size() ; i++) {\n for(int j=0 ; j<mentors.size() ; j++) {\n v[i][j] = compat(students[i], mentors[j]);\n }\n }\n\t\t// the bit value is intialized at 255 as 255 = "11111111" in binary.\n check(0,255,0);\n return res;\n }\n};\n``` | 2 | 0 | [] | 0 |
maximum-compatibility-score-sum | My very slow (4224ms!!) brute force (Python) | my-very-slow-4224ms-brute-force-python-b-hkcx | This is my very slow, but lovely brute force solution.\nIt\'s so straightforward, so I think it\'s self-explanatory.\n\n\nfrom itertools import permutations\n\n | kryuki | NORMAL | 2021-07-25T05:40:41.366353+00:00 | 2021-08-02T21:41:37.569402+00:00 | 42 | false | This is my very slow, but lovely brute force solution.\nIt\'s so straightforward, so I think it\'s self-explanatory.\n\n```\nfrom itertools import permutations\n\nclass Solution:\n def maxCompatibilitySum(self, students, mentors) -> int:\n def calc(lst1, lst2):\n res = 0\n for num1, num2 in zip(lst1, lst2):\n res += num1 == num2\n return res\n\n R = len(students)\n all_pairs = list(permutations(range(R)))\n\n res = 0\n for pair in all_pairs:\n score = 0\n for idx1, idx2 in enumerate(pair):\n score += calc(students[idx1], mentors[idx2])\n res = max(res, score)\n return res\n``` | 2 | 0 | [] | 0 |
maximum-compatibility-score-sum | Easy | Backtracking Solution | easy-backtracking-solution-by-kritikpanc-v5gm | \n\t class Solution {\n\t\t public:\n\t\t\tvoid sol( vector>& arr ,unordered_set&vis , int row , int count , int &ans){\n\t\t\t\tif(row == arr.size()){\n\t\t\t | kritikpancholi | NORMAL | 2021-07-25T04:03:01.148370+00:00 | 2021-07-25T04:03:01.148402+00:00 | 178 | false | \n\t class Solution {\n\t\t public:\n\t\t\tvoid sol( vector<vector<int>>& arr ,unordered_set<int>&vis , int row , int count , int &ans){\n\t\t\t\tif(row == arr.size()){\n\t\t\t\t\tans = max(count ,ans );\n\t\t\t\t\treturn ; \n \n }\n \n for(int i = 0;i<arr[0].size();i++){\n if(vis.count(i)){\n continue ;\n }else {\n \n vis.insert(i);\n sol(arr,vis , row+1,count + arr[row][i],ans );\n vis.erase(i);\n }\n }\n \n }\n \n int maxCompatibilitySum(vector<vector<int>>& s, vector<vector<int>>& m) {\n vector<vector<int>>arr(s.size(),vector<int>(m.size())) ;\n for(int i = 0;i<s.size();i++){\n \n for(int j = 0;j<m.size();j++){\n int val = 0 ;\n \n for(int k = 0 ;k<s[0].size();k++ ){\n if(m[i][k] == s[j][k]){\n val++;\n } \n }\n arr[i][j] = val ;\n }\n }\n // for checking visited column\n unordered_set<int>vis ; \n \n int ans = 0 ;\n sol(arr,vis,0,0,ans);\n return ans ;\n \n }};\n | 2 | 1 | [] | 0 |
maximum-compatibility-score-sum | Backtracking with Dp and Bit Manipulation || explanation in comments || C++ | backtracking-with-dp-and-bit-manipulatio-ytm4 | \nclass Solution {\npublic:\n int dp[10][18000];\n int helper(int idx,int taken,vector<vector<int>>& student,vector<vector<int>>& mentor)\n {\n | tejpratapp468 | NORMAL | 2021-07-25T04:02:23.280881+00:00 | 2021-07-25T04:06:21.364571+00:00 | 129 | false | ```\nclass Solution {\npublic:\n int dp[10][18000];\n int helper(int idx,int taken,vector<vector<int>>& student,vector<vector<int>>& mentor)\n {\n if(idx>=student.size()) return 0;\n if(dp[idx][taken]!=-1) return dp[idx][taken];\n int ans=-1e8;\n for(int i=0;i<student.size();i++)\n {\n //taken will tell us about the indexes that have been taken, e.g. taken=000101 in bit reprenstation tells index 0 and 2 have been taken\n if(taken&(1<<i)) continue; //if this index is already taken then continue\n taken^=(1<<i); //take the current index ,xor will set the bit at index i\n int curr=0;\n for(int k=0;k<student[idx].size();k++){ //calculate current score\n if(student[idx][k]==mentor[i][k]) curr++;\n }\n ans=max(ans,(curr)+helper(idx+1,taken,student,mentor));//take maximum of all possibilities\n taken^=(1<<i); //backtrack the previous taken index, xor will reset the bit at index i\n }\n return dp[idx][taken]=ans;\n }\n int maxCompatibilitySum(vector<vector<int>>& student, vector<vector<int>>& mentor) {\n int n=student.size();int q=student[0].size();\n memset(dp,-1,sizeof(dp));\n int ans=helper(0,0,student,mentor);\n return ans;\n }\n};\n``` | 2 | 1 | [] | 0 |
maximum-compatibility-score-sum | Permutation of `m`, with explanation | permutation-of-m-with-explanation-by-ryz-0ctw | Thought process:\nFind match of students and mentors is the same as keep students in original order, but match them with permutated mentors order.\ni.e. m = 3, | ryz | NORMAL | 2021-07-25T04:02:21.853964+00:00 | 2021-07-25T04:11:21.607613+00:00 | 162 | false | Thought process:\nFind match of students and mentors is the same as keep students in original order, but match them with permutated mentors order.\ni.e. m = 3, perms = [[0, 1, 2], [0, 2, 1], [1, 0, 2], [1, 2, 0], [2, 1, 0], [2, 0, 1]]\n\nTime: O(m! + m!*n*m)\nSpace: O(m!)\n\n```\nclass Solution(object):\n def maxCompatibilitySum(self, students, mentors):\n\t\tm = len(students)\n n = len(students[0])\n ori = [i for i in range(m)]\n perms = []\n def perm(ori, i):\n if i == len(ori): \n perms.append(ori[:])\n return\n for j in range(i, len(ori)):\n ori[j], ori[i] = ori[i], ori[j]\n perm(ori, i+1)\n ori[j], ori[i] = ori[i], ori[j]\n perm(ori, 0)\n res = 0\n for p in perms:\n cur = 0\n for i in range(m):\n match = p[i]\n for j in range(n):\n cur += 1 if students[i][j] == mentors[match][j] else 0\n res = max(res, cur)\n return res | 2 | 0 | [] | 0 |
maximum-compatibility-score-sum | Backtracking | Easy to Understand | backtracking-easy-to-understand-by-ghozt-1l8e | Code | ghozt777 | NORMAL | 2025-03-05T13:12:53.528680+00:00 | 2025-03-05T13:13:42.388467+00:00 | 83 | false | # Code
```cpp []
class Solution {
int cal_max_score(vector<vector<int>> &scores, int i = 0){
static unordered_set<int> used_mentors ;
if(i >= scores.size()) return 0 ;
int res = 0 ;
for(int j = 0 ; j < scores[i].size() ; j++){
if(used_mentors.find(j) != used_mentors.end()) continue ;
used_mentors.insert(j) ;
int curr = scores[i][j] ;
res = max(res,curr+cal_max_score(scores,i+1)) ;
used_mentors.erase(j) ;
}
return res ;
}
public:
int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {
int n = students.size() ;
vector<vector<int>> scores(n,vector<int>(n,0)) ;
// generate student - mentor score values
for(int s = 0 ; s < n ; s++){
for(int m = 0 ; m < n ; m++){
for(int j = 0 ; j < students[0].size() ; j++){
scores[s][m] += students[s][j] == mentors[m][j] ;
}
}
}
// try every student - mentor combination
return cal_max_score(scores) ;
}
};
``` | 1 | 0 | ['Backtracking', 'C++'] | 0 |
maximum-compatibility-score-sum | Python 3: TC O(m 2**m), SC O(2**m): DFS+BT optimized to DFS+Caching | python-3-tc-om-2m-sc-o2m-dfsbt-optimized-rg4r | Intuition\n\n## Brute Force\n\nThe brute force answer to pretty much all "what\'s the best matching?" problems is to literally try all possible pairings, with D | biggestchungus | NORMAL | 2024-08-01T23:58:24.437952+00:00 | 2024-08-01T23:58:24.437980+00:00 | 53 | false | # Intuition\n\n## Brute Force\n\nThe brute force answer to pretty much all "what\'s the best matching?" problems is to literally try all possible pairings, with DFS + backtracking. It works pretty well.\n\nDFS + backtracking is a very good technique to know really well. It shows up in a lot of problems. And learning it improves your command of recursion and stack entry/exit operations which makes you better at related algorithms too.\n\nThe complexity is\n* for student `0` we consider all mentors `j in 0..m-1`, `m` choices\n * for student `1` we consider all mentors `j\' != j`, `m-1` choices\n * for student `2` we consider all mentors `j\'\' != j, j\'`, `m-2` choices\n * ... etc.\n\nAnd so the cost is `O(m!)` stack frames. Tack on another factor of `m` because we iterate through the `m` mentors to find the ones that are free. (this can be optimized, but it\'s a bit tricky, involves Yates-shuffle-like operation you have to invert, yikes) \n\n## Optimization: Identify and Cache Repeated Subproblems\n\nAt first glance it doesn\'t look like there are repeated subproblems.\n\nBut matching problems often do have repeated subproblems when we\'re maximizng a sum, or another operation that commutes.\n\nSuppose we match student `0` with mentor `0` at the top level of DFS+BT, and then match student `1` with mentor `1`. Then we\'ll find the best matches of students 2+ with mentors 2+.\n\nIn another DFS+BT branch we\'ll match student `0` with mentor `1`, and match student `1` with mentor `0`. Then we\'ll find the best matches of students 2+ with mentors 2+.\n\nSame subproblem! The shared problem is we just need the *sum* of compatibilities over students `i:` with each subset of remaining mentors `j`. Sum commutes so we don\'t care about the order. We can sum from students 0..m-1 as done in DFS+BT... or we can sum from the last student backward, getting the best answer for `i:` and some set of available mentors `avail` by\n* iterating through the mentors\n* if mentor `j` is availble, then the score could be `compats[i][j]` plus the best possible compatibility of `i+1:` with `avail - {j}`\n\nSo the way to optimize is to **DFS + caching, with arguments `i` and `avail` as a set of items.**\n\nWe can\'t hash sets in Python because sets are mutable, but there are two alternatives:\n* brute force: use a `frozenset`, designed for exactly this situation\n* clever: **use a bit set, aka an integer where the bit `1 << j` indicates if `j` is available**\n\n# Complexity\n- Time complexity: `O(m 2**m)`\n - for DFS + caching we sum up the operations per stack frame across all stack frames we cache\n - for `i==0` no mentors are taken yet, so there are `m choose 0` configurations of `avail`\n - for `i==1`, one mentor is taken; there are `m choose 1` possible `avail` values\n - for `i`, `i` mentors are taken with `m choose i` possible\n - so the sum of cached states is `m choose 0 + m choose 1 + ... == 2**m`\n - to compute each cached state, we iterate over the `m` mentors to see if they\'re available. Therefore it\'s `O(m * 2**m)`\n - we can be a bit faster by iterating only over the set bits, so the work would be `O(m*(m choose 0) + (m-1)*(m choose 1) + (m-2)*(m choose 2) + ...)` ... which is still `O(m * 2**m)`\n - the first half of those terms have a prefactor of at least `m/2`\n - and the sum `(m choose 0) + .. + (m choose m//2)` is order half of `2**m` because the terms are symmetric, `m choose i == m choose (m-i)`\n - so we have at least `O(m/2 * 2**(m-1))` operations\n - that simplifies to `O(m * 2**m / 4) = O(m * 2**m)`\n\n- Space complexity: `O(2**m)`, which is the number of cached states (see above)\n\nThe sum of all subsets of `m` elements is `2**m`, a fact you can basically just memorize. Therefore most "cache the answer for each subset" has a memory complexity of `2**m` and a time complexity of at *least* `2**m`.\n\n# Code\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n # n questions, answers 0 or 1\n # m students 0..m-1\n # m mentors\n\n # student and mentors answered same questions of length n\n\n m = len(students)\n n = len(students[0])\n\n # compat between student i and mentor j: total indices where students[i] == mentors[j], i.e. num q\'s answered the same\n\n # maximize the sum of compat. scores\n\n # m,n <= 8\n\n # DFS + BT?\n\n # wlog each student i gets matched with a mentor j\n\n # accelerate a bit by precomputing the compatibilities\n compats = [[0]*m for _ in range(m)]\n for i in range(m):\n for j in range(m):\n compats[i][j] = sum(a == b for a, b in zip(students[i], mentors[j]))\n\n # mentor_avail = [True]*m\n # max_compat = 0 # TODO: early pruning\n # def pair(i: int, compat: int):\n # nonlocal max_compat\n \n # if i == m:\n # max_compat = max(max_compat, compat)\n # else:\n # for j in range(m):\n # if not mentor_avail[j]: continue\n\n # mentor_avail[j] = False\n # pair(i+1, compat + compats[i][j])\n # mentor_avail[j] = True\n\n # def pair(0, 0)\n\n # return max_avail\n\n # complexity: worst case we try all m pairings for student 0\n # and for each, all m-1 pairings for student 1, etc.\n # for 8!\n\n # better: we could record the max compatibility for students i: with a specific subset of mentors still available\n # because we just need the total compatibility, not the details of the matching once we\'re done\n #\n # so for each i there would be m choose (m-i) == m choose i ways to have remaining items, only distinct subsets give different answers\n # and thus it\'s the sum of m choose i over all i, aka 2**m which is a lot better than m!\n\n ALL = (1 << m) - 1\n @cache\n def maxCompat(i: int, avail: int) -> int:\n if i == m: return 0\n\n ans = 0\n for j in range(m):\n b = 1 << j\n if avail & b:\n # mentor is available: get max score where we bind i to j and continue with i+1 and remaining mentors\n ans = max(ans, compats[i][j] + maxCompat(i+1, avail ^ b))\n\n return ans\n\n return maxCompat(0, ALL)\n``` | 1 | 0 | ['Python3'] | 1 |
maximum-compatibility-score-sum | No Bitmask, No DP, No Recursion, Just Pure Permutation (as given in hints) | no-bitmask-no-dp-no-recursion-just-pure-5eki5 | This is a tricky problem since one doesn\'t (at least I) think about permutations when dealing with variations. However, proceedings on the lines of "Minimum Fa | miho_nishizumi | NORMAL | 2024-05-02T14:44:08.653398+00:00 | 2024-05-03T17:02:19.149198+00:00 | 136 | false | This is a tricky problem since one doesn\'t (at least I) think about permutations when dealing with variations. However, proceedings on the lines of "[Minimum Falling Path Sum II](https://leetcode.com/problems/minimum-falling-path-sum-ii/)" encounters failure, as additional data structures make the intermittently-working program more complex, thereby depicting the complexity of the problem. It is not surprising, that the worst case for this problem corresponds to finding maximum path in a `8x8` matrix with each selected column not to be chosen again.\n\n```\nclass Solution {\npublic:\n template<typename incoming, typename outgoing>\n void load(incoming &in, outgoing &out) {\n for(typename incoming::value_type &s: in) {\n int res = 0, e = 0;\n while(not s.empty()) {\n res += s.back() * (std::pow(2, e)); s.pop_back();\n ++e;\n }\n out.push_front(res);\n }\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int const n = students.size(), m = students[0].size();\n std::deque<int> g, h;\n load(students, g); load(mentors, h);\n std::sort(g.begin(), g.end());\n int ans = 0;\n std::function<int(int, int)> get_value = [&](int a, int b) {\n int res = a ^ b, diff = 0;\n while(res) {\n res = res & (res - 1);\n diff += 1;\n }\n return m - diff;\n };\n \n do {\n int res = 0;\n for(int i = 0; i < n; ++i) {\n res += get_value(g[i], h[i]);\n }\n ans = std::max(res, ans);\n } while(std::next_permutation(g.begin(), g.end()));\n \n return ans;\n }\n};\n```\n\n | 1 | 0 | ['C', 'Probability and Statistics'] | 1 |
maximum-compatibility-score-sum | My simple Dp+Bitmask Memoized Solution--Self Explanatory code | my-simple-dpbitmask-memoized-solution-se-8vm7 | \n\n# Code\n\nclass Solution {\npublic:\nint dp[10][1024];\nint compat(vector<int>&s,vector<int>&m){\n int res=0;\n for(int i=0;i<s.size();i++){\n | shashank290604 | NORMAL | 2023-10-14T23:20:10.578988+00:00 | 2023-10-14T23:20:10.579016+00:00 | 126 | false | \n\n# Code\n```\nclass Solution {\npublic:\nint dp[10][1024];\nint compat(vector<int>&s,vector<int>&m){\n int res=0;\n for(int i=0;i<s.size();i++){\n if(s[i]==m[i])res++;\n }\n return res;\n}\nint rec(vector<vector<int>>& students, vector<vector<int>>& mentors,int ind,int mask){\nif(ind>=students.size())return 0;\nif(dp[ind][mask]!=-1)return dp[ind][mask];\nint ans=0;\nfor(int i=0;i<mentors.size();i++){\n // if mentor is not taken then set the mentor\n if(( mask &(1<<i))==0){\nint newmask=(mask|(1<<i));\nans=max(ans,compat(students[ind],mentors[i])+rec(students,mentors,ind+1,newmask));\n }\n\n}\nreturn dp[ind][mask]=ans;\n}\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\nmemset(dp,-1,sizeof(dp));\n return rec(students,mentors,0,0);\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
maximum-compatibility-score-sum | ✅✔️Easy to understand C++ Solution using Backtracking ✈️✈️✈️✈️✈️ | easy-to-understand-c-solution-using-back-atr9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ajay_1134 | NORMAL | 2023-07-07T06:28:31.902093+00:00 | 2023-07-07T06:28:31.902117+00:00 | 289 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int ans = 0;\n int score(vector<int>&v1, vector<int>&v2, int m){\n int cnt = 0;\n for(int i=0; i<m; i++){\n cnt += (v1[i] == v2[i]);\n }\n return cnt;\n }\n void solve(int idx, vector<int>&arr, vector<vector<int>>& ss , vector<vector<int>>& mrs, int n, int m){\n if(idx == arr.size()){\n int sum = 0;\n for(int i=0; i<n; i++){\n sum += score(ss[i],mrs[arr[i]],m);\n }\n ans = max(ans,sum);\n return;\n }\n for(int i=idx; i<arr.size(); i++){\n swap(arr[idx],arr[i]);\n solve(idx+1,arr,ss,mrs,n,m);\n swap(arr[idx],arr[i]);\n }\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n = students.size();\n int m = students[0].size();\n vector<int>arr(n);\n for(int i=0; i<n; i++) arr[i] = i;\n solve(0,arr,students,mentors,n,m);\n return ans;\n }\n};\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'Backtracking', 'C++'] | 0 |
maximum-compatibility-score-sum | Python, brute force dfs/bitmask dp solution with explanation | python-brute-force-dfsbitmask-dp-solutio-453n | backtrack (permutation)\nlist all permutation of student to enumearte all of student-teacher pairs.\n### python\npython\n\'\'\'\nPrecalculate the score for each | shun6096tw | NORMAL | 2023-03-17T07:15:32.441583+00:00 | 2023-09-11T07:56:36.492255+00:00 | 43 | false | ### backtrack (permutation)\nlist all permutation of student to enumearte all of student-teacher pairs.\n### python\n```python\n\'\'\'\nPrecalculate the score for each student-teacher pairing, and enumerate all of the pairing using permutation to find max score\ntc is O(n * (m^2) + m * m!), sc is O(m^2)\n\'\'\'\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n backtrack = []\n ans = 0\n scores = [[0] * len(students) for _ in range(len(students))]\n for i, vec_i in enumerate(students):\n for j, vec_j in enumerate(mentors):\n scores[i][j] = sum(x == y for x, y in zip(vec_i, vec_j))\n def dfs(used_st):\n if len(backtrack) == len(students):\n nonlocal ans\n ans = max(ans, sum(scores[backtrack[i]][i] for i in range(len(students))))\n return\n \n for i in range(len(students)):\n if used_st >> i & 1: continue\n backtrack.append(i)\n dfs(used_st | (1 << i))\n backtrack.pop()\n dfs(0)\n return ans\n```\n\n### c++\n```cpp\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int size = students.size();\n vector<vector<int>> scores (size, vector<int>(size));\n for (int i = 0; i < size; i+=1) {\n for (int j = 0, sub; j < size; j+=1) {\n sub = 0;\n for (int k = 0; k < students[0].size(); k+=1)\n sub += (students[i][k] == mentors[j][k]);\n scores[i][j] = sub;\n }\n }\n vector<int> backtrack;\n int ans = 0;\n function<void(int)> dfs = [&] (int used) {\n if (backtrack.size() == size) {\n int sub = 0;\n for (int i = 0; i < size; i+=1)\n sub += scores[backtrack[i]][i];\n if (sub > ans) ans = sub;\n return;\n }\n for (int i = 0; i < size; i+=1) {\n if (used >> i & 1) continue;\n backtrack.emplace_back(i);\n dfs(used | (1 << i));\n backtrack.pop_back();\n }\n };\n dfs(0);\n return ans;\n }\n};\n```\n\n### bitmask dp\ndp[mask] is max score of matched some , a bit of 1 means a student is matched.\ncount how many matched student in mask = cnt,\nfor each matched students in mask,\nwe try to match cnt-th mentor with a matched student and calculate score.\n\ndp[mask] = max(dp[mask], dp[mask ^ (1 << j)] + scores[j][cnt-1]),\nwhere j is a matched student.\n\ntc is O(n * 2 ^n), sc is O(2^n + n* n).\n\n### python\n```python\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n size = len(students)\n scores = [[0] * size for _ in range(size)]\n for i, vec_i in enumerate(students):\n for j, vec_j in enumerate(mentors):\n scores[i][j] = sum(x == y for x, y in zip(vec_i, vec_j))\n dp = [0] * (1 << size)\n for mask in range(1, 1 << size):\n cnt = sum(mask >> j & 1 for j in range(size))\n for j in range(size):\n if mask >> j & 1:\n dp[mask] = max(dp[mask], dp[mask ^ (1 << j)] + scores[j][cnt-1])\n return dp[(1 << size) - 1]\n```\n\n### c++\n```cpp\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int size = students.size();\n vector<vector<int>> scores (size, vector<int>(size));\n for (int i = 0; i < size; i+=1) {\n for (int j = 0, sub; j < size; j+=1) {\n sub = 0;\n for (int k = 0; k < students[0].size(); k+=1)\n sub += (students[i][k] == mentors[j][k]);\n scores[i][j] = sub;\n }\n }\n vector<int> dp (1 << size);\n for (int mask = 1, cnt; mask < 1 << size; mask+=1) {\n cnt = 0;\n for (int j = 0; j < size; j+=1) cnt += mask >> j & 1;\n for (int j = 0; j < size; j+=1) {\n if (mask >> j & 1)\n dp[mask] = max(dp[mask], dp[mask ^ (1 << j)] + scores[j][cnt-1]);\n }\n }\n return dp[(1 << size) - 1];\n }\n};\n``` | 1 | 0 | ['Backtracking', 'C', 'Bitmask', 'Python'] | 0 |
maximum-compatibility-score-sum | c++ | easy | short | c-easy-short-by-venomhighs7-4964 | \n# Code\n\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n\tint ans = 0;\n\tvector<int> | venomhighs7 | NORMAL | 2022-10-14T04:13:30.643782+00:00 | 2022-10-14T04:13:30.643839+00:00 | 197 | false | \n# Code\n```\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n\tint ans = 0;\n\tvector<int> pos;\n\tfor(int i=0;i<students.size();i++) pos.push_back(i);\n\tdo{\n\t\tint curr = 0;\n\t\tfor(int i = 0;i<students.size(); i++)\n\t\t\tfor(int j=0;j<students[pos[i]].size();j++)\n\t\t\t\tcurr += (students[pos[i]][j] == mentors[i][j]);\n\t\tans = max(ans, curr);\n\t} while(next_permutation(pos.begin(), pos.end()) );\n\treturn ans;\n}\n};\n``` | 1 | 1 | ['C++'] | 0 |
maximum-compatibility-score-sum | ✅✅C++ || Permutation || Easy to Understand || Backtracking | c-permutation-easy-to-understand-backtra-eidy | \nclass Solution {\npublic:\n vector<int>visited;\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n | tamim447 | NORMAL | 2022-09-30T15:48:09.784692+00:00 | 2022-11-01T16:34:16.503739+00:00 | 356 | false | ```\nclass Solution {\npublic:\n vector<int>visited;\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n = students.size();\n int m = students[0].size();\n visited.resize(n+1, 0);\n return permutation(students, mentors, 0, n, m);\n }\n int permutation(vector<vector<int>>& students, vector<vector<int>>& mentors, int pos, int n, int m) {\n if(pos>=n) {\n return 0;\n }\n int mx = 0;\n for(int i=0; i<n; i++) {\n if(!visited[i]) {\n int cnt = 0;\n for(int j = 0; j < m; j++) {\n if(students[pos][j] == mentors[i][j]) cnt++;\n }\n visited[i] = 1;\n mx = max(mx, cnt+permutation(students, mentors, pos+1, n, m));\n visited[i] = 0;\n }\n }\n return mx;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'C'] | 1 |
maximum-compatibility-score-sum | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-51m6 | Backtracking\n\n Time Complexity :- O(N * N!)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n \n int calculate(vector<vector<int>>& students | __KR_SHANU_IITG | NORMAL | 2022-09-12T06:45:42.812487+00:00 | 2022-09-12T06:45:42.812530+00:00 | 441 | false | * ***Backtracking***\n\n* ***Time Complexity :- O(N * N!)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n \n int calculate(vector<vector<int>>& students, vector<vector<int>>& mentors, vector<int>& arr)\n {\n int n = students.size();\n \n // find the compatability for curr_combination\n \n int sum = 0;\n \n for(int i = 0; i < n; i++)\n { \n for(int j = 0; j < students[i].size(); j++)\n {\n if(students[i][j] == mentors[arr[i]][j])\n sum++;\n }\n }\n \n return sum;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n \n int n = students.size();\n \n // store the indexo of all mentors into array\n \n vector<int> arr(n);\n \n for(int i = 0; i < n; i++)\n {\n arr[i] = i;\n }\n \n int maxi = INT_MIN;\n \n // for every combination of mentor find the comapatability and take maximum of it\n \n do\n {\n // calculate compatability\n \n int ans = calculate(students, mentors, arr);\n \n // update maxi\n \n maxi = max(maxi, ans);\n }\n \n while(next_permutation(arr.begin(), arr.end()));\n \n return maxi;\n }\n};\n``` | 1 | 0 | ['Backtracking', 'C', 'C++'] | 0 |
maximum-compatibility-score-sum | Easy recursion+bitmask+memoization | easy-recursionbitmaskmemoization-by-aksh-52z7 | \nclass Solution {\npublic:\n int dp[9][1<<9];\n int n,m;\n int maxCompatibilitySum(vector<vector<int>>& s, vector<vector<int>>& ma) {\n m=s.siz | akshatsaxena2017 | NORMAL | 2022-08-08T06:22:34.791542+00:00 | 2022-08-08T06:22:34.791582+00:00 | 117 | false | ```\nclass Solution {\npublic:\n int dp[9][1<<9];\n int n,m;\n int maxCompatibilitySum(vector<vector<int>>& s, vector<vector<int>>& ma) {\n m=s.size(),n=ma[0].size();\n memset(dp,-1,sizeof(dp));\n return fun(m,0,s,ma);\n }\n int fun(int i,int mask,vector<vector<int>>& s,vector<vector<int>>& ma){\n if(i==0){\n return 0;\n }\n if(dp[i][mask]!=-1) return dp[i][mask];\n int ans=0;\n vector<int>temp=s[i-1];\n for(int j=0;j<m;j++){\n int mask1=mask&(1<<j);\n if(!mask1){\n int sum=0;\n for(int p=0;p<n;p++) sum+=(ma[j][p]==temp[p]);\n ans=max(ans,sum+fun(i-1,mask|(1<<j),s,ma));\n }\n }\n return dp[i][mask]=ans;\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'C'] | 0 |
maximum-compatibility-score-sum | Easy to Understand C++ solution | easy-to-understand-c-solution-by-ishank1-0261 | \nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n \n vector<int> stuMask;\ | ishank193aggarwal | NORMAL | 2022-07-07T17:23:32.402273+00:00 | 2022-07-07T17:23:32.402342+00:00 | 59 | false | ```\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n \n vector<int> stuMask;\n vector<int> menMask;\n \n for(int i=0;i<students.size();i++){\n int mask=0;\n for(int j=0;j<students[i].size();j++){\n if(students[i][j]==1)\n mask=mask|(1<<j);\n }\n stuMask.push_back(mask);\n }\n \n for(int i=0;i<mentors.size();i++){\n int mask=0;\n for(int j=0;j<mentors[i].size();j++){\n if(mentors[i][j]==1)\n mask=mask|(1<<j);\n }\n menMask.push_back(mask);\n }\n \n vector<vector<int>> dp(students.size(),vector<int>(mentors.size(),0));\n for(int i=0;i<stuMask.size();i++){\n for(int j=0;j<menMask.size();j++){\n int val=0;\n for(int k=0;k<students[0].size();k++){\n if((stuMask[i]&(1<<k)) == (menMask[j]&(1<<k))){\n val++;\n }\n }\n dp[i][j]=val;\n }\n }\n \n int ans=0;\n vector<bool> stuVisited(students.size(),false);\n helper(dp,ans,0,stuVisited,0);\n return ans;\n }\n \n void helper(vector<vector<int>> &dp,int &ans,int val,vector<bool> &stuVisited,int idx){\n \n if(idx==stuVisited.size()){\n ans=max(ans,val);\n return;\n }\n \n for(int i=0;i<stuVisited.size();i++){\n if(!stuVisited[i]){\n stuVisited[i]=true;\n helper(dp,ans,val+dp[i][idx],stuVisited,idx+1);\n stuVisited[i]=false;\n }\n }\n }\n};\n``` | 1 | 0 | [] | 0 |
maximum-compatibility-score-sum | C++ || DP+Bitmask | c-dpbitmask-by-m_sahil_kumar-gbht | \nclass Solution {\npublic:\n int dp[9][(1<<8)+1];\n int n,m;\n\n int rec(int lev,int mask,vector<vector<int>>& st, vector<vector<int>>& mt){\n | M_sahil_kumar | NORMAL | 2022-06-21T11:47:18.446500+00:00 | 2022-06-21T11:47:18.446541+00:00 | 88 | false | ```\nclass Solution {\npublic:\n int dp[9][(1<<8)+1];\n int n,m;\n\n int rec(int lev,int mask,vector<vector<int>>& st, vector<vector<int>>& mt){\n if(lev==n) return 0;\n if(dp[lev][mask]!=-1) return dp[lev][mask];\n int ans=0;\n for(int i=0;i<n;i++){\n \n if(!(mask&(1<<i))){\n int score=0;\n for(int j=0;j<m;j++){score+=(st[lev][j]==mt[i][j]);}\n ans=max(ans,score+rec(lev+1,mask|(1<<i),st,mt));\n }\n }\n return dp[lev][mask]=ans;\n }\n int maxCompatibilitySum(vector<vector<int>>& st, vector<vector<int>>& mt) {\n n=st.size();\n m=st[0].size();\n memset(dp,-1,sizeof(dp));\n return rec(0,0,st,mt);\n }\n};``` | 1 | 0 | ['Dynamic Programming', 'Bitmask'] | 0 |
maximum-compatibility-score-sum | [Python] DP bitmask with explanation (faster than 92%) | python-dp-bitmask-with-explanation-faste-xf4n | Solution from @ye15 https://leetcode.com/problems/maximum-compatibility-score-sum/discuss/1360746/Python3-permutations\n\nBut I use dp dict instead of python @c | woflow | NORMAL | 2022-04-07T07:30:54.260183+00:00 | 2022-04-07T07:43:47.258459+00:00 | 107 | false | Solution from @ye15 https://leetcode.com/problems/maximum-compatibility-score-sum/discuss/1360746/Python3-permutations\n\nBut I use dp dict instead of python @cache decorator.\nIt took me a while to understand the solution. So I want to write an explantaion to save some time for other.\n\nFirst step is easy. Calculate the score for all pairs of student and mentor.\n\nBut trying all the permutations is tricky.\nBecause the total number of students is m. 1 <= m <= 8.\nWe can use integer instead of bit. Max mask is 1 << 8 == 256\n\n**For example:**\n\nn = 3\nMask 000 means three students are not assigned.\nMask 100 means student 2 is assigned.\n\nSo basically assign all possible students to mentor 2 and then mentor 1 and then mentor 0.\nUse mask to record the visited concept of DFS.\nUse dp to record the calculated result for same input.\n\n**Most tricky parts:**\n\nif not (mask & (1 << i)):\nIf student i is not assigned.\n\nmask ^ (1<<i) \nFlip the bit to 1. Mark the student assigned.\n\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n m = len(students)\n score = [[0] * m for _ in range(m)]\n\t\t\n\t\t# Calculate the score for all pairs of student and mentor\n for i in range(m): \n for j in range(m): \n score[i][j] = sum(x == y for x, y in zip(students[i], mentors[j]))\n \n\t\t# Memorize the max result for same input (mask, j)\n dp = {}\n\t\t\n\t\t# Find all possible student i. Assign student i to mentor j.\n\t\t# Mask is used to record assigned students.\n def assign(mask, j): \n\t\t\t# This if can be removed. Assign function will stop when all students are assigned.\n\t\t\t# But it\'s easier to understand.\n\t\t\tif j < 0:\n\t\t\t\treturn 0\n\t\t\t# Mask, j calculated. Return the result from dp dict.\n if (mask,j) in dp:\n return dp[(mask,j)]\n\t\t\t\t\n ans = 0\n for i in range(m): \n\t\t\t\t# Find all unassigned students\n if not (mask & (1<<i)): \n\t\t\t\t\t# Flip the unassigned student index to 1 in mask\n\t\t\t\t\t# Assign student i to mentor j\n ans = max(ans, assign(mask ^ (1 << i), j - 1) + score[i][j])\n dp[(mask,j)] = ans \n return ans \n \n return assign(0, m-1)\n``` | 1 | 0 | ['Dynamic Programming', 'Bitmask'] | 0 |
maximum-compatibility-score-sum | C++ solution with explanation faster than 80% | c-solution-with-explanation-faster-than-d6ckr | \n//We have m different students and m different mentors. So, there are m! different ways of mapping students\n//with the mentors. This is what I\'ve done and a | Ani2424 | NORMAL | 2022-02-17T16:00:59.468423+00:00 | 2022-02-22T06:54:41.021725+00:00 | 88 | false | ```\n//We have m different students and m different mentors. So, there are m! different ways of mapping students\n//with the mentors. This is what I\'ve done and at last took the maximum of it. This is kind of brute force but \n//before that I converted every row to a binary number because bitwise operations are very fast\n\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m = students.size();\n int n = students[0].size();\n \n /*Converting the 2D vector to a 1D vector*/\n vector<int> st(m);\n vector<int> me(m);\n for(int i=0; i<m; i++){\n int num1 = 0, num2 = 0;\n for(int j=0; j<n; j++){\n num1*=2;\n num1+=students[i][j];\n num2*=2;\n num2+=mentors[i][j];\n }\n st[i] = num1; //student\n me[i] = num2; //mentor\n }\n /*I\'ve converted every row to a number whose binary representation is same as that of the row*/\n \n vector<int> perm(m); //created an array to map students to mentors\n for(int i=0; i<m; i++) perm[i] = i; //first permutation -> 0,1,2,3,...,m\n int res = 0; //result = maximum of all scores obtained from m! different permutations (or mappings)\n do{\n //this is a permutation\n int score = 0;\n for(int i=0; i<m; i++){\n int k = st[i]^me[perm[i]]; //xor between student and mentor will turn OFF matching bits\n //there are n bits in total and suppose p out of them are not matching\n //so the score = (n-p)\n score+=(n - __builtin_popcount(k));\n //__builtin_popcount(...) is an inbuilt function to count the number of ON bits in a number\n }\n res = max(score, res);\n }\n while(next_permutation(perm.begin(), perm.end())); //we iterate to the next permutation (or mapping)\n \n return res;\n }\n};\n``` | 1 | 0 | [] | 1 |
maximum-compatibility-score-sum | [C++] Recursion + Memorization beats 93% | c-recursion-memorization-beats-93-by-ilo-xdh8 | Time Complexity: O((2^m)nm)\nHelper function if not skipped takes O(mn) and will only be called 2^m times. \n\nclass Solution {\npublic: \n int helper(vec | ilovehawthorn | NORMAL | 2022-02-01T07:25:29.735071+00:00 | 2022-02-01T07:31:49.003908+00:00 | 163 | false | Time Complexity: O((2^m)*n*m)\nHelper function if not skipped takes O(mn) and will only be called 2^m times. \n```\nclass Solution {\npublic: \n int helper(vector<vector<int>>& s, vector<vector<int>>& me, int mask, vector<int>& dp){\n int idx = bitset<8>(mask).count(), m = s.size(), n = s[0].size();\n if(idx>=m) return 0;\n if(dp[mask]!=-1) return dp[mask];\n int ans=0;\n for(int i=0; i<m; i++){\n if(mask&(1<<i))continue;\n int cnt=0;\n for(int j=0; j<n; j++){\n if(s[idx][j]==me[i][j]) cnt++;\n }\n ans=max(ans,cnt+helper(s, me, mask|(1<<i), dp));\n }\n return dp[mask]=ans;\n }\n \n int maxCompatibilitySum(vector<vector<int>>& s, vector<vector<int>>& me) {\n vector<int> dp(256/*2^8*/, -1);\n return helper(s, me, 0, dp);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization', 'C'] | 0 |
maximum-compatibility-score-sum | Backtracking solution || C++ || Easy to understand | backtracking-solution-c-easy-to-understa-7ne0 | ```\nclass Solution {\npublic:\n int check(vector&student,vector&mentor){\n int i=0,sum=0;\n while(i<student.size()){\n if(student[i | Sarthak2512 | NORMAL | 2021-12-27T12:15:14.538793+00:00 | 2021-12-27T12:15:14.538817+00:00 | 113 | false | ```\nclass Solution {\npublic:\n int check(vector<int>&student,vector<int>&mentor){\n int i=0,sum=0;\n while(i<student.size()){\n if(student[i]==mentor[i])sum++;\n i++;\n }\n return sum;\n }\n void solve(vector<vector<int>>&students,vector<vector<int>>&mentors,int sum,int i, int &max_compat){\n if(i==students.size()){\n max_compat=fmax(sum,max_compat);\n return;\n }\n int n=students.size();\n for(int j=i;j<n;j++){\n swap(mentors[i],mentors[j]);\n solve(students,mentors,sum+check(students[i],mentors[i]),i+1,max_compat);\n swap(mentors[i],mentors[j]);\n }\n return;\n }\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int max_compat=0;\n solve(students,mentors,0,0,max_compat);\n return max_compat;\n }\n}; | 1 | 0 | ['Backtracking', 'C'] | 0 |
maximum-compatibility-score-sum | C++ | next_permutation | c-next_permutation-by-magzhan-z5jn | \n\tint maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int maxScore = 0;\n \n vector<int> studentId, | magzhan | NORMAL | 2021-10-27T00:15:22.465431+00:00 | 2021-10-27T00:15:22.465469+00:00 | 106 | false | ```\n\tint maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int maxScore = 0;\n \n vector<int> studentId, mentorId;\n for (int i = 0; i < students.size(); i++) {\n studentId.push_back(i);\n mentorId.push_back(i);\n }\n \n int n = mentors[0].size();\n int maxSum = 0;\n \n do {\n int sum = 0;\n for (int j = 0; j < mentorId.size(); j++) {\n int cnt = 0;\n for (int k = 0; k < n; k++) {\n if (mentors[mentorId[j]][k] == students[studentId[j]][k]) {\n cnt++;\n }\n }\n sum += cnt;\n }\n if (maxSum < sum) {\n maxSum = sum;\n }\n \n } while (next_permutation(studentId.begin(), studentId.end()));\n \n return maxSum;\n }\n``` | 1 | 0 | [] | 0 |
maximum-compatibility-score-sum | DP + Bitmask | 0ms Solution | With complete explanation | dp-bitmask-0ms-solution-with-complete-ex-dbd4 | Here in this problem out of all the combinations between students and mentor, we have to find the optimal combination in which the score is maximum.\n\nTo do so | n19 | NORMAL | 2021-08-31T10:35:01.771104+00:00 | 2021-08-31T10:35:38.238952+00:00 | 148 | false | Here in this problem out of all the combinations between students and mentor, we have to find the optimal combination in which the score is maximum.\n\nTo do so we can use recursion to explore all the combinations.\nNow, while doing this we need to maintain track of all the mentors which have already been assigned to students, so that the new student look for only the remaining mentors.\n\nWe can easily acheive this using the visited array, by marking the mentors already assigned, but due to constraints being small we can instead easily use an integer whose ith bit will denote whether the ith mentor is aready assigned or not.\n\nTo faster up the recursion we can use memoisation on the mask, and **i need not be included in the dp** as from the mask we can easily determin the i by looking at the number of set bits.\n\nAlso finding the score between student[a] and mentor[b] takes O(n) time we can do precomputations to already store the result in DP[i][j] which denote the score between student[i] and mentor[j].\n\n```\nclass Solution {\n int DP[8][8];\n int dp[256] = {[0 ... 255] = -1};\n int getMaxCompatibility(int i, int mask, vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m = students.size(), n = students[0].size();\n \n if (i == m) return 0;\n if (dp[mask] != -1) return dp[mask];\n \n int score = 0;\n for(int j = 0;j<m;j++) {\n if ((mask & (1 << j)) == 0) {\n score = max(score, DP[i][j] + getMaxCompatibility(i+1, mask + (1 << j), students, mentors));\n }\n }\n \n return dp[mask] = score;\n }\n \n \npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m = students.size(), n = students[0].size();\n\t\t\n for(int i = 0;i<m;i++) {\n for(int j = 0;j<m;j++) {\n int sc = 0;\n for(int k = 0;k<n;k++) {\n sc += (students[i][k] == mentors[j][k] ? 1 : 0);\n }\n DP[i][j] = sc;\n }\n }\n \n return getMaxCompatibility(0, 0, students, mentors);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Bitmask'] | 0 |
maximum-compatibility-score-sum | SIMPLE & EASY JAVA Solution | simple-easy-java-solution-by-dyanjno123-irsk | \nclass Solution {\n\tint ans;\n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n int[][] arr = new int[students.length][students | Dyanjno123 | NORMAL | 2021-08-04T03:31:36.647184+00:00 | 2021-08-04T03:31:36.647252+00:00 | 178 | false | ```\nclass Solution {\n\tint ans;\n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n int[][] arr = new int[students.length][students.length];\n for(int i = 0; i < students.length; i++) {\n \tfor(int j = 0; j < mentors.length; j++) {\n \t\tarr[i][j] = find(students[i], mentors[j]);\n \t}\n }\n ans = 0;\n boolean[] check = new boolean[mentors.length];\n pair(0, students.length, check, arr, 0);\n return ans;\n }\n \n public void pair(int ssf, int tc, boolean[] check, int[][] arr, int sum) {\n \tif(ssf == tc) {\n \t\tif(sum > ans)\n \t\t\tans = sum;\n \t\treturn;\n \t}\n \tfor(int i = 0; i < check.length; i++) {\n \t\tif(check[i] == false) {\n \t\t\tcheck[i] = true;\n \t\t\tpair(ssf + 1, tc, check, arr, sum + arr[ssf][i]);\n \t\t\tcheck[i] = false;\n \t\t}\n \t}\n }\n \n public int find(int[] stu, int[] men) {\n \tint ans = 0;\n \tfor(int i = 0; i < stu.length; i++)\n \t\tif(stu[i] == men[i])\n \t\t\tans++;\n \treturn ans;\n }\n}\n``` | 1 | 1 | ['Backtracking', 'Java'] | 0 |
maximum-compatibility-score-sum | Scala. Extremely simple, easy to understand and ineffective | scala-extremely-simple-easy-to-understan-hvlv | \n def maxCompatibilitySum(students: Array[Array[Int]], mentors: Array[Array[Int]]): Int =\n search(students.toList, mentors.toSet)\n\n def search(students | nikiforo | NORMAL | 2021-08-01T10:16:02.691145+00:00 | 2021-08-01T10:16:02.691191+00:00 | 82 | false | ```\n def maxCompatibilitySum(students: Array[Array[Int]], mentors: Array[Array[Int]]): Int =\n search(students.toList, mentors.toSet)\n\n def search(students: List[Array[Int]], mentors: Set[Array[Int]]): Int =\n students match {\n case Nil => 0\n case s :: tail => mentors.map(m => compatibility(s, m) + search(tail, mentors - m)).max\n }\n\n def compatibility(s: Array[Int], m: Array[Int]): Int = s.zip(m).count { case(s, m) => s == m } \n ``` | 1 | 0 | [] | 1 |
maximum-compatibility-score-sum | C# DSF Solution 100%, 120ms, 25MB | c-dsf-solution-100-120ms-25mb-by-robl123-y8hd | public class Solution {\n public int MaxCompatibilitySum(int[][] students, int[][] mentors) \n {\n int rows = students.Length;\n int co | robl123 | NORMAL | 2021-07-30T19:10:50.959221+00:00 | 2021-07-30T19:10:50.959257+00:00 | 103 | false | ```public class Solution {\n public int MaxCompatibilitySum(int[][] students, int[][] mentors) \n {\n int rows = students.Length;\n int cols = students[0].Length;\n\n int[,] compatability = new int[rows, rows];\n\n for (int i = 0; i < rows; i++) //student\n {\n int[] s = students[i];\n for (int j = 0; j < rows; j++) //mentor\n {\n int[] t = mentors[j];\n\n int comp = 0;\n for (int k = 0; k < cols; k++)\n {\n if (s[k] == t[k]) comp++;\n }\n\n compatability[i, j] = comp;\n }\n }\n\n int maxsum = 0;\n return MaxCompatibilitySumDFS(compatability, 0, new bool[rows], ref maxsum, 0);\n }\n \n public int MaxCompatibilitySumDFS(int[,] compatability, int i, bool[] visited, ref int maxsum, int sum)\n {\n int n = compatability.GetLength(0);\n \n maxsum = Math.Max(sum, maxsum);\n if (i >= n) return maxsum;\n\n for (int j = 0; j < n; j++)\n {\n if (visited[j]) continue;\n int sum1 = sum + compatability[i, j]; \n visited[j]=true;\n maxsum = MaxCompatibilitySumDFS(compatability, i + 1, visited, ref maxsum, sum1);\n visited[j] = false;\n }\n\n return maxsum;\n }\n}``` | 1 | 0 | [] | 0 |
maximum-compatibility-score-sum | C++ Easy Brute Force || Using XOR property | c-easy-brute-force-using-xor-property-by-6774 | \nint maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n = students.size(), m = students[0].size();\n // n | anshjain18 | NORMAL | 2021-07-30T18:10:05.595254+00:00 | 2021-07-30T18:10:05.595306+00:00 | 140 | false | ```\nint maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int n = students.size(), m = students[0].size();\n // n = number of students, m = number of questions\n vector<int> st(n), men(n);\n for(int i = 0; i < n; ++i) {\n int num1 = 0, num2 = 0;\n for(int j = 0; j < m; ++j) {\n if(students[i][j]) num1 += (1 << (m - 1 - j));\n if(mentors[i][j]) num2 += (1 << (m - 1 - j));\n }\n st[i] = num1; men[i] = num2;\n }\n vector<int> perm(n);\n int ans = 0;\n iota(perm.begin(), perm.end(), 0);\n do {\n int cur_score = 0;\n for(int i = 0; i < n; ++i) {\n int cur = st[i] ^ men[perm[i]];\n cur_score += m - __builtin_popcount(cur);\n \n }\n ans = max(ans, cur_score);\n }\n while(next_permutation(perm.begin(), perm.end()));\n return ans;\n }\n\t``` | 1 | 0 | [] | 1 |
maximum-compatibility-score-sum | Simple C++ Sol { Backtracking } | simple-c-sol-backtracking-by-_mrvariable-h7we | \nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int res = INT_MIN, n = students | _MrVariable | NORMAL | 2021-07-28T07:18:58.672991+00:00 | 2021-07-28T07:18:58.673025+00:00 | 97 | false | ```\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int res = INT_MIN, n = students.size(), m = students[0].size();\n \n vector<bool> visited(n, false);\n f(0, 0,students, mentors, visited, res, n, m);\n \n return res;\n }\n \n void f(int start, int sum, vector<vector<int> > &students, vector<vector<int> >&mentors, vector<bool> &visited, int &res, int n, int m) {\n if(start == n) {\n res = max(res, sum);\n return;\n }\n \n for(int i = 0; i < n; i++) {\n if(!visited[i]) {\n int count = 0;\n for(int j = 0; j < m; j++) {\n if(students[start][j] == mentors[i][j])\n count++;\n }\n visited[i] = true;\n f(start+1, sum+count, students, mentors, visited, res, n, m);\n visited[i] = false;\n }\n }\n }\n};\n``` | 1 | 0 | [] | 0 |
maximum-compatibility-score-sum | With Bitmasking | with-bitmasking-by-mit1234-yx6n | \nclass Solution {\n int dp[10][1<<10];\npublic:\n int check(vector<vector<int>>&st,vector<vector<int>>&mt,int i,int j)\n {\n int ans=0;\n | mit1234 | NORMAL | 2021-07-27T13:40:21.134893+00:00 | 2021-07-27T13:40:21.134936+00:00 | 52 | false | ```\nclass Solution {\n int dp[10][1<<10];\npublic:\n int check(vector<vector<int>>&st,vector<vector<int>>&mt,int i,int j)\n {\n int ans=0;\n \n for(int k=0;k<st[i].size();k++)\n {\n if(st[i][k]==mt[j][k])\n {\n ans++;\n }\n }\n return ans;\n }\n int get(vector<vector<int>>&st,vector<vector<int>>&mt,int index,int mask)\n {\n if(mask==0||(index>st.size()))\n {\n return 0;\n }\n if(dp[index][mask]!=-1)\n {\n return dp[index][mask];\n }\n int ans=0;\n for(int i=0;i<mt.size();i++)\n {\n if(mask&(1<<i))\n {\n int res=check(st,mt,index,i)+get(st,mt,index+1,mask^(1<<i));\n ans=max(ans,res);\n }\n }\n return dp[index][mask]=ans;\n }\n int maxCompatibilitySum(vector<vector<int>>& st, vector<vector<int>>& me) {\n \n int n=st.size();\n int m=me.size();\n int mask=(1<<m)-1;\n memset(dp,-1,sizeof(dp));\n return get(st,me,0,mask);\n }\n};\n``` | 1 | 0 | [] | 0 |
maximum-compatibility-score-sum | 3-line Python | 3-line-python-by-maristie-cvqz | An alternative optimization is to decorate function score() with @cache to avoid duplicated computations.\n\npython\n def maxCompatibilitySum(self, students: | maristie | NORMAL | 2021-07-27T06:59:03.616223+00:00 | 2021-07-27T10:20:42.627542+00:00 | 91 | false | An alternative optimization is to decorate function `score()` with `@cache` to avoid duplicated computations.\n\n```python\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n def score(s_id: int, m_id: int) -> int:\n return sum(map(lambda x, y: 1^x^y, students[s_id], mentors[m_id]))\n return max(sum(score(i, j) for i, j in enumerate(p)) for p in permutations(range(len(students))))\n``` | 1 | 0 | [] | 0 |
maximum-compatibility-score-sum | (C++) 1947. Maximum Compatibility Score Sum | c-1947-maximum-compatibility-score-sum-b-h758 | \n\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m = students.size(), n = | qeetcode | NORMAL | 2021-07-26T17:55:30.327109+00:00 | 2021-07-26T17:55:30.327151+00:00 | 124 | false | \n```\nclass Solution {\npublic:\n int maxCompatibilitySum(vector<vector<int>>& students, vector<vector<int>>& mentors) {\n int m = students.size(), n = students[0].size(); \n vector<vector<int>> score(m, vector<int>(m)); \n for (int i = 0; i < m; ++i) \n for (int j = 0; j < m; ++j) \n for (int k = 0; k < n; ++k) \n if (students[i][k] == mentors[j][k]) ++score[i][j]; \n \n vector<int> dp(1 << m); \n for (int mask = 0; mask < (1 << m); ++mask) {\n int i = __builtin_popcount(mask); \n for (int j = 0; j < m; ++j) \n if (!(mask & (1 << j))) \n dp[mask^(1 << j)] = max(dp[mask^(1 << j)], dp[mask] + score[i][j]); \n }\n return dp.back(); \n }\n};\n``` | 1 | 1 | ['C'] | 0 |
maximum-compatibility-score-sum | Java - 74 ms - permutation - beats 100% time and 100% memory | java-74-ms-permutation-beats-100-time-an-8946 | \nclass Solution {\n private int max;\n \n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n max = 0;\n permute(stude | cpp_to_java | NORMAL | 2021-07-26T05:11:30.237782+00:00 | 2021-07-26T05:11:59.041979+00:00 | 51 | false | ```\nclass Solution {\n private int max;\n \n public int maxCompatibilitySum(int[][] students, int[][] mentors) {\n max = 0;\n permute(students, mentors, 0, students.length);\n return max;\n }\n \n private void permute(int[][] students, int[][] mentors, int index, int N){\n if(index == N){\n int score = 0;\n for(int i = 0; i < N; i++){\n score += compatibility(students[i], mentors[i]);\n }\n \n max = Math.max(max, score);\n }else{\n for(int i = index; i < N; i++){\n swap(students, index, i);\n permute(students, mentors, index + 1, N);\n swap(students, index, i);\n }\n }\n }\n \n private void swap(int[][] students, int i, int j){\n int[] temp = students[i];\n students[i] = students[j];\n students[j] = temp;\n }\n \n private int compatibility(int[] a, int[] b){\n int i, N = a.length;\n int sum = 0;\n \n for(i = 0; i < N; i++){\n if(a[i] == b[i]){\n ++sum;\n }\n }\n \n return sum;\n }\n}\n``` | 1 | 0 | [] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.