question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
new-21-game | Would someone help me out? example3 case failed. | would-someone-help-me-out-example3-case-wt2pd | My intuitive idea is that \nstep1, get the total number ways (TOTAL) to get score>=K;\nstep2, and get the total number ways (COUNT)to get score <=N\nand result | beyourself | NORMAL | 2018-05-20T06:33:51.931499+00:00 | 2018-05-20T06:33:51.931499+00:00 | 370 | false | My intuitive idea is that \nstep1, get the total number ways (TOTAL) to get score>=K;\nstep2, and get the total number ways (COUNT)to get score <=N\nand resulting probability is(TOTAL / COUNT).\nHere is my brute-force code(I think memorization could be applied...let us just ignore it. Just focus on the correctness of my intutive idea)\n\t\t\n\tint count = 0;\n\tpublic double new21Game(int N, int K, int W) {\n\t\tif (N == 0) {\n\t\t\treturn 0.0;\n\t\t}\n\t\tint total = dfs(0, K, W, N, );\n\t\treturn count * 1.0 / total;\n\t}\n\t\t//Definition: what is the total ways of ending the game when the current sum is "total" and //the numberwe could draw is [1, W].\n\tprivate int dfs(int curSum, int K, int W, int N) {\n\t\t\t//Base case.\n\t\t\tif (curSum >= K) {\n\t\t\t\tif (curSum <= N) {\n\t\t\t\t\tcount++;\n\t\t\t\t}\n\t\t\t\treturn 1;\n\t\t\t}\n\n\t\t\t//Recursive case.\n\t\t\tint count = 0;\n\t\t\tfor (int i = 1; i <= W; i++) {\n\t\t\t\tcount += dfs(curSum + i, K, W, N);\n\t\t\t}\n\t\t\treturn count;\n\t}\n\t\t\n\t\t\nthe result for ex. 3 is:\nInput:\n21\n17\n10\nOutput:\n0.55218\nExpected:\n0.73278\n\t\t | 1 | 0 | [] | 1 |
new-21-game | Python O(n) solution | python-on-solution-by-hexadecimal-cl59 | It took me more than 30 minutes to figure out why I was "wrong" at Example 3...\n```class Solution:\n def new21Game(self, N, K, W):\n """\n :ty | hexadecimal | NORMAL | 2018-05-20T03:24:33.266090+00:00 | 2018-05-20T03:24:33.266090+00:00 | 751 | false | It took me more than 30 minutes to figure out why I was "wrong" at Example 3...\n```class Solution:\n def new21Game(self, N, K, W):\n """\n :type N: int\n :type K: int\n :type W: int\n :rtype: float\n """\n d=[0]*(K+max(W,N)+10)\n for i in range(K,N+1):\n d[i]=1\n ms=N-K+1\n for i in range(K-1,-1,-1):\n d[i]=ms/W\n ms+=d[i]-d[i+W]\n return d[0] | 1 | 0 | [] | 1 |
finding-mk-average | C++ Balance 3 Multisets | c-balance-3-multisets-by-votrubac-h1z3 | A bit lengthy; the idea is to keep track of the left, mid, and right sets. When removing or adding numbers, we reballance these sets so that the size of left an | votrubac | NORMAL | 2021-04-11T05:30:25.568829+00:00 | 2021-04-11T05:47:30.701111+00:00 | 10,569 | false | A bit lengthy; the idea is to keep track of the `left`, `mid`, and `right` sets. When removing or adding numbers, we reballance these sets so that the size of `left` and `right` stays `k`.\n\nAlso, we keep track of `sum` for elements in `mid`. That way, the calculate function is O(1).\n \nFinally, to track the current `m` numbers, we use a circular array of size `m`.\n\n```cpp\nint m = 0, k = 0, sz = 0, pos = 0;\nlong sum = 0;\nvector<int> v;\nmultiset<int> left, mid, right;\nvoid remove(int n) {\n if (n <= *rbegin(left))\n left.erase(left.find(n));\n else if (n <= *rbegin(mid)) {\n auto it = mid.find(n); \n sum -= *it;\n mid.erase(it);\n }\n else\n right.erase(right.find(n));\n if (left.size() < k) {\n left.insert(*begin(mid));\n sum -= *begin(mid);\n mid.erase(begin(mid));\n }\n if (mid.size() < sz) {\n mid.insert(*begin(right));\n sum += *begin(right);\n right.erase(begin(right));\n }\n}\nvoid add(int n) {\n left.insert(n);\n if (left.size() > k) {\n auto it = prev(end(left));\n mid.insert(*it);\n sum += *it;\n left.erase(it);\n }\n if (mid.size() > sz) {\n auto it = prev(end(mid));\n sum -= *it;\n right.insert(*it);\n mid.erase(it);\n }\n}\nMKAverage(int m, int k) : m(m), k(k), sz(m - 2 * k) {\n v = vector<int>(m);\n}\nvoid addElement(int num) {\n if (pos >= m)\n remove(v[pos % m]);\n add(num);\n v[pos++ % m] = num;\n}\nint calculateMKAverage() {\n if (pos < m)\n return -1;\n return sum / sz;\n}\n``` | 127 | 1 | [] | 21 |
finding-mk-average | Java O(logN), O(1) time. beat 100%. SortedList implementation. | java-ologn-o1-time-beat-100-sortedlist-i-qcxc | Java doesn\'t has SortedList like python. So manually implemented one.\nThe idea is to maintain 3 SortedList. Every time when add new element, remove old elemen | allenlipeng47 | NORMAL | 2021-04-11T07:28:14.797017+00:00 | 2021-04-11T07:31:30.663106+00:00 | 4,791 | false | Java doesn\'t has ```SortedList``` like python. So manually implemented one.\nThe idea is to maintain 3 SortedList. Every time when add new element, remove old element, keep 3 ```SortedList``` size as required.\nTotal size of ```l1```, ```l2```, ```l3``` is ```m```, ```l1```, ```l3``` has length of ```k```\n```\npublic class MKAverage {\n\n int m, k;\n Deque<Integer> queue = new ArrayDeque();\n SortedList l1 = new SortedList();\n SortedList l2 = new SortedList();\n SortedList l3 = new SortedList();\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n\n public void addElement(int num) {\n queue.addLast(num);\n // add in the proper place\n if (l1.isEmpty() || num <= l1.getLast()) {\n l1.add(num);\n } else if (l2.isEmpty() || num <= l2.getLast()) {\n l2.add(num);\n } else {\n l3.add(num);\n }\n if (queue.size() > m) {\n int removedElement = queue.removeFirst();\n // remove in the proper place\n if (l1.contains(removedElement)) {\n l1.remove(removedElement);\n } else if (l2.contains(removedElement)) {\n l2.remove(removedElement);\n } else {\n l3.remove(removedElement);\n }\n }\n\t\t// adjust size of l1, l2, l3\n if (l1.size > k) {\n l2.add(l1.removeLast());\n } else if (l1.size < k && !l2.isEmpty()) {\n l1.add(l2.removeFirst());\n }\n if (l2.size > m - k - k) {\n l3.add(l2.removeLast());\n } else if (l2.size < m - k - k && !l3.isEmpty()) {\n l2.add(l3.removeFirst());\n }\n }\n\n public int calculateMKAverage() {\n if (l1.size + l2.size + l3.size < m) {\n return -1;\n }\n return (int)Math.floor((double)(l2.sum) / (l2.size));\n }\n\n static class SortedList {\n long sum;\n int size;\n TreeMap<Integer, Integer> tm = new TreeMap<>();\n\n public void add(int n) {\n tm.put(n, tm.getOrDefault(n, 0) + 1);\n sum += n;\n size++;\n }\n\n public boolean isEmpty() {\n return size == 0;\n }\n\n public boolean contains(int n) {\n return tm.containsKey(n);\n }\n\n public void remove(int n) {\n if (!tm.containsKey(n)) {\n return;\n }\n int count = tm.get(n);\n sum -= n;\n size--;\n if (count == 1) {\n tm.remove(n);\n } else {\n tm.put(n, count - 1);\n }\n }\n\n public int removeLast() {\n Map.Entry<Integer, Integer> lastEntry = tm.lastEntry();\n if (lastEntry.getValue() == 1) {\n tm.remove(lastEntry.getKey());\n } else {\n tm.put(lastEntry.getKey(), lastEntry.getValue() - 1);\n }\n sum -= lastEntry.getKey();\n size--;\n return lastEntry.getKey();\n }\n\n public int removeFirst() {\n Map.Entry<Integer, Integer> firstEntry = tm.firstEntry();\n if (firstEntry.getValue() == 1) {\n tm.remove(firstEntry.getKey());\n } else {\n tm.put(firstEntry.getKey(), firstEntry.getValue() - 1);\n }\n sum -= firstEntry.getKey();\n size--;\n return firstEntry.getKey();\n }\n\n public int getLast() {\n return tm.lastKey();\n }\n\n public int getFirst() {\n return tm.firstKey();\n }\n }\n\t\n}\n``` | 69 | 0 | [] | 3 |
finding-mk-average | Python3 solution w/ SortedList, O(logM) add, O(1) calculate | python3-solution-w-sortedlist-ologm-add-gao8n | python3 doesn\'t have a built-in order statistic tree or even a basic BST and that may be why sortedcontainers is one of the few third-party libraries allowed.\ | chuan-chih | NORMAL | 2021-04-11T04:35:31.428924+00:00 | 2021-04-11T04:45:46.451031+00:00 | 5,218 | false | python3 doesn\'t have a built-in [order statistic tree](https://en.wikipedia.org/wiki/Order_statistic_tree) or even a basic BST and that may be why `sortedcontainers` is one of the few third-party libraries allowed.\n\nAnyway, with a [SortedList](http://www.grantjenks.com/docs/sortedcontainers/sortedlist.html) this solution is conceptually simple. I use both a deque and a SortedList to keep track of the last m numbers, FIFO. It\'s trivial to maintain the total sum of them. To maintain the sum of the smallest/largest k numbers, we examine the index at which the new number will be inserted into the SortedList and the index at which the oldest number will be removed from the SortedList. If the new number to be inserted will become one of the smallest/largest k numbers, we add it to self.first_k/self.last_k and subtract out the current kth smallest/largest number. The operation for removing the oldest number is similar but the reverse. The only gotcha is the off-by-1 error.\n\n```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m, k\n self.deque = collections.deque()\n self.sl = SortedList()\n self.total = self.first_k = self.last_k = 0\n\n def addElement(self, num: int) -> None:\n self.total += num\n self.deque.append(num)\n index = self.sl.bisect_left(num)\n if index < self.k:\n self.first_k += num\n if len(self.sl) >= self.k:\n self.first_k -= self.sl[self.k - 1]\n if index >= len(self.sl) + 1 - self.k:\n self.last_k += num\n if len(self.sl) >= self.k:\n self.last_k -= self.sl[-self.k]\n self.sl.add(num)\n if len(self.deque) > self.m:\n num = self.deque.popleft()\n self.total -= num\n index = self.sl.index(num)\n if index < self.k:\n self.first_k -= num\n self.first_k += self.sl[self.k]\n elif index >= len(self.sl) - self.k:\n self.last_k -= num\n self.last_k += self.sl[-self.k - 1]\n self.sl.remove(num)\n\n def calculateMKAverage(self) -> int:\n if len(self.sl) < self.m:\n return -1\n return (self.total - self.first_k - self.last_k) // (self.m - 2 * self.k)\n```\n\nTime complexity: O(logM) add due to operations on the SortedList (essentially an [order statistic tree](https://en.wikipedia.org/wiki/Order_statistic_tree)). O(1) calculate is trivial.\nSpace complexity: O(M) due to the deque and SortedList. | 60 | 1 | ['Queue', 'Python3'] | 8 |
finding-mk-average | Clean Java with 3 TreeMaps | clean-java-with-3-treemaps-by-fang2018-ldg8 | Sadly, there isn\'t a built-in multiset in Java, therefore we have to play around with treemap. \n\nclass MKAverage {\n TreeMap<Integer, Integer> top = new T | fang2018 | NORMAL | 2021-04-11T05:43:08.802309+00:00 | 2021-04-11T05:48:04.995994+00:00 | 4,696 | false | Sadly, there isn\'t a built-in multiset in Java, therefore we have to play around with treemap. \n```\nclass MKAverage {\n TreeMap<Integer, Integer> top = new TreeMap<>(), middle = new TreeMap<>(), bottom = new TreeMap<>();\n Queue<Integer> q = new LinkedList<>();\n long middleSum;\n int m, k;\n int countTop, countBottom;\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n if (q.size() == m) {\n int pop = q.poll();\n if (top.containsKey(pop)) { // delete item in top, if present\n remove(top, pop); \n countTop--;\n } else if (middle.containsKey(pop)) { // delete item in bottom, if present\n remove(middle, pop);\n middleSum -= pop;\n } else { // delete item in bottom, if present\n remove(bottom, pop); \n countBottom--;\n }\n } \n // insert to middle first\n add(middle, num);\n q.offer(num);\n middleSum += num;\n // move item from middle to top, to fill k slots\n while (countTop < k && !middle.isEmpty()) {\n countTop++;\n middleSum -= middle.lastKey();\n add(top, remove(middle, middle.lastKey()));\n }\n // rebalance middle and top\n while (!middle.isEmpty() && !top.isEmpty() && top.firstKey() < middle.lastKey()) {\n middleSum += top.firstKey();\n add(middle, remove(top, top.firstKey()));\n middleSum -= middle.lastKey();\n add(top, remove(middle, middle.lastKey()));\n }\n // move item from middle to bottom, to fill k slots\n while (countBottom < k && !middle.isEmpty()) {\n countBottom++;\n middleSum -= middle.firstKey();\n add(bottom, remove(middle, middle.firstKey()));\n }\n // rebalance middle and bottom\n while (!middle.isEmpty() && !bottom.isEmpty() && bottom.lastKey() > middle.firstKey()) {\n middleSum += bottom.lastKey();\n add(middle, remove(bottom, bottom.lastKey()));\n middleSum -= middle.firstKey();\n add(bottom, remove(middle, middle.firstKey()));\n }\n }\n \n \n private int remove(TreeMap<Integer, Integer> tm, int num) {\n tm.put(num, tm.get(num) - 1);\n if (tm.get(num) == 0) tm.remove(num); \n return num;\n }\n \n private void add(TreeMap<Integer, Integer> tm, int num) {\n tm.put(num, tm.getOrDefault(num, 0) + 1);\n }\n \n public int calculateMKAverage() {\n return q.size() == m ? (int)(middleSum / (m - 2 * k)) : -1;\n }\n}\n``` | 53 | 1 | [] | 12 |
finding-mk-average | [Python3] Fenwick tree | python3-fenwick-tree-by-ye15-7n7f | \n\nclass Fenwick: \n\n def __init__(self, n: int):\n self.nums = [0]*(n+1)\n\n def sum(self, k: int) -> int: \n k += 1\n ans = 0\n | ye15 | NORMAL | 2021-04-11T04:01:41.449823+00:00 | 2021-04-11T04:01:41.449850+00:00 | 6,647 | false | \n```\nclass Fenwick: \n\n def __init__(self, n: int):\n self.nums = [0]*(n+1)\n\n def sum(self, k: int) -> int: \n k += 1\n ans = 0\n while k:\n ans += self.nums[k]\n k &= k-1 # unset last set bit \n return ans\n\n def add(self, k: int, x: int) -> None: \n k += 1\n while k < len(self.nums): \n self.nums[k] += x\n k += k & -k \n\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k \n self.data = deque()\n self.value = Fenwick(10**5+1)\n self.index = Fenwick(10**5+1)\n\n def addElement(self, num: int) -> None:\n self.data.append(num)\n self.value.add(num, num)\n self.index.add(num, 1)\n if len(self.data) > self.m: \n num = self.data.popleft()\n self.value.add(num, -num)\n self.index.add(num, -1)\n\n def _getindex(self, k): \n lo, hi = 0, 10**5 + 1\n while lo < hi: \n mid = lo + hi >> 1\n if self.index.sum(mid) < k: lo = mid + 1\n else: hi = mid\n return lo \n \n def calculateMKAverage(self) -> int:\n if len(self.data) < self.m: return -1 \n lo = self._getindex(self.k)\n hi = self._getindex(self.m-self.k)\n ans = self.value.sum(hi) - self.value.sum(lo)\n ans += (self.index.sum(lo) - self.k) * lo\n ans -= (self.index.sum(hi) - (self.m-self.k)) * hi\n return ans // (self.m - 2*self.k)\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 53 | 2 | ['Python3'] | 7 |
finding-mk-average | C++ 3 multisets | c-3-multisets-by-lzl124631x-hhar | See my latest update in repo LeetCode\n\n## Solution 1. 3 Multisets\n\n Use 3 multiset<int> to track the top k, bottom k and middle elements.\n Use queue<int> q | lzl124631x | NORMAL | 2021-04-11T04:00:52.940852+00:00 | 2021-04-12T04:24:14.305750+00:00 | 3,331 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. 3 Multisets\n\n* Use 3 `multiset<int>` to track the top `k`, bottom `k` and middle elements.\n* Use `queue<int> q` to track the current `m` numbers.\n* Use `sum` to track the sum of numbers in `mid`.\n\nPlease see comments as explanations.\n\n```cpp\n// OJ: https://leetcode.com/contest/weekly-contest-236/problems/finding-mk-average/\n// Author: github.com/lzl124631x\n// Time: \n// MKAverage: O(1)\n// addElement: O(logM)\n// calculateMKAverage: O(1)\n// Space: O(M)\nclass MKAverage {\n multiset<int> top, bot, mid;\n queue<int> q;\n long sum = 0, m, k;\npublic:\n MKAverage(int m, int k) : m(m), k(k) {}\n \n void addElement(int n) {\n if (q.size() < m) mid.insert(n); // when there are less than `m` numbers, always insert into `mid`.\n q.push(n);\n if (q.size() == m) {\n // when we reached exactly `m` numbers, we nudge numbers from `mid` to `top` and `bot`, and calculate `sum`.\n for (int i = 0; i < k; ++i) {\n bot.insert(*mid.begin());\n mid.erase(mid.begin());\n }\n for (int i = 0; i < k; ++i) {\n top.insert(*mid.rbegin());\n mid.erase(prev(mid.end()));\n }\n for (int x : mid) sum += x;\n } else if (q.size() > m) {\n // when we\'ve seen more than `m` numbers. We first add the new number `n` to where it should belong.\n // If we add `n` to `top` or `bot`, we balance them with `mid` to make sure `top` and `bot` have exactly `k` numbers\n if (n < *bot.rbegin()) {\n bot.insert(n);\n int x = *bot.rbegin();\n bot.erase(prev(bot.end()));\n mid.insert(x);\n sum += x; \n } else if (n > *top.begin()) {\n top.insert(n);\n int x = *top.begin();\n top.erase(top.begin());\n mid.insert(x);\n sum += x;\n } else {\n mid.insert(n);\n sum += n;\n }\n // Then we remove the number `rm` that is no longer one of the latest `m` numbers.\n int rm = q.front();\n q.pop();\n auto it = mid.find(rm);\n if (it != mid.end()) { // first try removing from `mid`, then `top` or `bot`.\n mid.erase(it);\n sum -= rm;\n } else {\n it = top.find(rm);\n if (it != top.end()) {\n top.erase(it);\n } else {\n bot.erase(bot.find(rm));\n }\n }\n // Lastly, balance `top` and `bot` if needed\n if (bot.size() < k) {\n int x = *mid.begin();\n bot.insert(x);\n mid.erase(mid.begin());\n sum -= x;\n } else if (top.size() < k) {\n int x = *mid.rbegin();\n top.insert(x);\n mid.erase(prev(mid.end()));\n sum -= x;\n }\n }\n }\n \n int calculateMKAverage() {\n return q.size() == m ? (sum / (m - 2 * k)) : -1;\n }\n};\n``` | 42 | 2 | [] | 3 |
finding-mk-average | [Python] 4 heaps, one list, O(n log n), explained | python-4-heaps-one-list-on-log-n-explain-394b | The idea is similar to problem 480. Sliding Window Median, here we also have sliding window, but we need to find not median, but some other statistics: sum of s | dbabichev | NORMAL | 2021-04-11T21:49:18.183373+00:00 | 2021-04-15T09:08:34.447190+00:00 | 3,583 | false | The idea is similar to problem **480. Sliding Window Median**, here we also have sliding window, but we need to find not median, but some other statistics: sum of some middle elements in sorted window. Imagine for the purpose of example that `m = 7` and `k = 2`. Then we have widow of size `7`: `a1 < a2 < a3 < a4 < a5 < a6 < a7` and we need to evaluate the sum of `3` numbers `a3 + a4 + a5`. Let us solve two problems: evaluate `a1 + a2 + a3 + a4 + a5` and then substitute `a1 + a2`. How we are going to evaluate sum `a1 + a2` for example?\n\nThe idea is to keep `2` heaps: one for smallest `2` numbers in sliding window and another is for the `5` biggest numbers. We do it in very similar way as problem **480**, however we need to also evaluate sums. The trick is to use lazy deletion from heap, that is sometimes it happen, that there are some old elements in our window we need to be deleted later. If you know what is lazy deletion from heap, I think you got the idea, if not, please google it. The difficult part is how to update sum in heap as well, we need to do it carefully, because we have lazy updates, we need to make sure when we add or delete element, that it is element which will not be lazy update.\n\nFinally, we need to solve two separate problems: one for parts with sizes `2 vs 5` and another with sizes `5 vs 2`. Also I use trick where I fill heap with zeroes at first, so no need to check case when we do not have enough elements it parts.\n\n#### Complexity\nTime complexity is `O(n log n)`, where `n` is total number of calls of `addElement`. Space complexity is `O(n)`.\n\n```\nclass MKAverage:\n def __init__(self, m: int, k: int):\n self.m, self.k = m, k\n self.arr = [0]*m\n self.lh1, self.rh1 = self.heap_init(m, k)\n self.lh2, self.rh2 = self.heap_init(m, m - k)\n self.score = 0\n \n def heap_init(self, p1, p2):\n h1 = [(0, i) for i in range(p1-p2, p1)]\n h2 = [(0, i) for i in range(p1-p2)]\n heapq.heapify(h1)\n heapq.heapify(h2)\n return (h1, h2)\n \n def update(self, lh, rh, m, k, num):\n score, T = 0, len(self.arr)\n if num > rh[0][0]:\n heappush(rh, (num, T)) \n if self.arr[T - m] <= rh[0][0]:\n if rh[0][1] >= T - m: score += rh[0][0]\n score -= self.arr[T - m]\n heappush(lh, (-rh[0][0], rh[0][1]))\n heappop(rh)\n else:\n heappush(lh, (-num, T)) \n score += num\n if self.arr[T - m] >= rh[0][0]: \n heappush(rh, (-lh[0][0], lh[0][1]))\n q = heappop(lh)\n score += q[0]\n else:\n score -= self.arr[T - m]\n\n while lh and lh[0][1] <= T - m: heappop(lh) # lazy-deletion\n while rh and rh[0][1] <= T - m: heappop(rh) # lazy-deletion\n return score\n \n def addElement(self, num):\n t1 = self.update(self.lh1, self.rh1, self.m, self.k, num)\n t2 = self.update(self.lh2, self.rh2, self.m, self.m - self.k, num)\n self.arr.append(num)\n self.score += (t2 - t1)\n \n def calculateMKAverage(self):\n if len(self.arr) < 2*self.m: return -1\n return self.score//(self.m - 2*self.k)\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 38 | 0 | ['Heap (Priority Queue)'] | 7 |
finding-mk-average | Java one treemap and deque solution | java-one-treemap-and-deque-solution-by-t-e17q | Maintain a deque so we can remove the m+1 element. Maintain current sum and tot elements.\n- Keep a treemap and remove m+1 element on each add.\n- To compute av | techguy | NORMAL | 2021-08-19T16:10:43.335224+00:00 | 2021-08-19T16:11:14.309944+00:00 | 637 | false | - Maintain a deque so we can remove the `m+1` element. Maintain current sum and tot elements.\n- Keep a treemap and remove `m+1` element on each `add`.\n- To compute avg get low `k` elements, and top `k` elements, and subtract from current sum.\n\n```\nclass MKAverage {\n\n int tot = 0;\n int sum = 0;\n int m = 0;\n int k = 0;\n \n TreeMap<Integer, Integer> map = new TreeMap<>();\n Deque<Integer> deque = new ArrayDeque<>();\n \n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n deque.offerLast(num);\n map.put(num, map.getOrDefault(num, 0)+1);\n sum += num;\n tot++;\n if (tot > m) {\n int v = deque.pollFirst();\n sum -= v;\n tot--;\n int tot = map.get(v);\n if (tot == 1) map.remove(v);\n else map.put(v, tot-1);\n }\n \n }\n \n public int calculateMKAverage() {\n if (tot < m) return -1;\n int totLess = k;\n int s = sum;\n for (Map.Entry<Integer, Integer> e : map.entrySet()) {\n if (totLess == 0) break;\n int v = Math.min(totLess, e.getValue());\n s -= e.getKey()*v;\n totLess -= v;\n }\n \n totLess = k;\n for (Map.Entry<Integer, Integer> e : map.descendingMap().entrySet()) {\n if (totLess == 0) break;\n int v = Math.min(totLess, e.getValue());\n s -= e.getKey()*v;\n totLess -= v;\n }\n \n return s/(tot-2*k);\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 17 | 0 | [] | 7 |
finding-mk-average | Java | Queue + TreeMap | Explained, Example | java-queue-treemap-explained-example-by-0b4dl | Haven\'t seen this in the comments so I\'ll just go ahead with some bullet points.\n\n We need to be able to access the first and last k elements (of the last m | ig-rib | NORMAL | 2022-11-26T22:56:34.738264+00:00 | 2022-11-26T22:56:34.738291+00:00 | 912 | false | Haven\'t seen this in the comments so I\'ll just go ahead with some bullet points.\n\n* We need to be able to access the first and last k elements (of the last m elements) of the stream. If there was something as a SortedQueue in Java it would be cool, but there isn\'t, so **TreeMap** was all I could come up with, in order to manage the repeated elements correctly. This TreeMap will preserve the natural order of the last m elements of the stream.\n\n\n* We\'re gonna keep track of the **totalSum** of the last m elements of the stream.\n\n* We need to keep the last m elements of the Stream. We\'ll use a **queue** to do this. As soon as the queue has more than m elements, we push the first one out and subtract it from the total sum. We also reduce its count from the TreeMap (and delete the key if its count becomes 0).\n\n\n* In order to subtract the first and last k elements, we literally just have to get that info from the TreeMap. In a SortedList, we would do an iteration for the first k and one for the last k, subtract the sum of those from the totalSum. Here we have to be more careful with how we advance through the keys, since they\'re grouped by counts.\n\n* Next, just take the average, which is **(totalSum - sumOfExtremes) / (m - 2 * k)**\n\nExample:\n\n```\nM = 5, K = 2\nStream:\n[17612, 74607, 8272, 33433, 8272, 64938, [Takes average], 99741]\n\nObserve, when the average is taken, our q is like\nQ = [ 8272, 33433, 8272, 64938, 99741 ]\n\nOur Tree Map is (, in order):\n[ 8272 --> 2, 33433 -> 1, 64938 --> 1, 99741 --> 1 ]\n\nGetting the sum of\n* The first two elements: 8272 + 8272 = 16544\n* The last two elements: 64938 + 99741 = 164679\n\nFinally getting the average:\n\n(totalSum - sumOfExtremes) / (m - 2*k) = (214656 - 181223) / (5 - 2 * 2) = 33433 / 1 = 33433\n```\n\n\nThis is not the fastest implementation but the one I first came up with. It\'s giving me something between top 45% and top 80% regarding times.\n\n**Time Complexity:** **`O(NlogN)`**, N being the size of the stream.\n**Space Complexity:** **`O(M)`**\n\n```\nclass MKAverage {\n\n private TreeMap<Integer, Integer> counts;\n private Deque<Integer> stream;\n private int m;\n private int k;\n private int totalSum = 0;\n private int totalSize = 0;\n \n \n public MKAverage(int m, int k) {\n counts = new TreeMap<>();\n stream = new LinkedList<>();\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n totalSum += num;\n totalSize++;\n stream.add(num);\n if (stream.size() > m) {\n Integer key = stream.removeFirst();\n counts.put(key, counts.get(key) - 1);\n totalSum -= key;\n if (counts.get(key) == 0) counts.remove(key);\n }\n counts.put(num, counts.getOrDefault(num, 0) + 1);\n }\n \n public int calculateMKAverage() {\n if (totalSize < m) return -1;\n \n int key = counts.firstKey();\n int lastKey = counts.lastKey();\n int kSmall = k, kLarge = k;\n\n int extremeSum = 0;\n\n System.out.println(counts.toString());\n \n while (kSmall > 0) {\n int toSubtractSmall = Math.min(kSmall, counts.get(key));\n kSmall -= toSubtractSmall;\n extremeSum += key * toSubtractSmall;\n System.out.println(key + toSubtractSmall);\n if (toSubtractSmall == counts.get(key)) key = counts.higherKey(key);\n }\n\n while (kLarge > 0) {\n int toSubtractLarge = Math.min(kLarge, counts.get(lastKey));\n kLarge -= toSubtractLarge;\n extremeSum += lastKey * toSubtractLarge;\n System.out.println(lastKey + toSubtractLarge);\n if (toSubtractLarge == counts.get(lastKey)) lastKey = counts.lowerKey(lastKey);\n }\n \n int ret = (totalSum - extremeSum) / (m - 2 * k);\n \n return ret;\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 15 | 0 | ['Tree', 'Queue', 'Java'] | 2 |
finding-mk-average | Java Solution | PriorityQueue + Lazy Deletion | O(log M) add, O(1) calculate | Detailed Explanations | java-solution-priorityqueue-lazy-deletio-hlod | The structure of this solution may be a little complex, but easy to understand. Here, I keep 4 priority_queues to record the smallest k elements, (m -k2) elment | cdhcs1516 | NORMAL | 2021-04-11T05:12:45.990856+00:00 | 2021-04-11T05:13:39.533382+00:00 | 2,878 | false | The structure of this solution may be a little complex, but easy to understand. Here, I keep 4 priority_queues to record the smallest k elements, (m -k*2) elments in middle window and the largest k elements. For each operation, I just need to check which priority_queue the queue_in number and queue_out number locates, and conduct the transmission process. Here is a demonstration figure for this solution.\n\nSince priority_queue cannot directly delete a specific element, here I employ a lazy deletetion technique. Everytime I want to delete an element from a priority_queue, I use a hash table to record the elements required to delete. When I want to poll an element from such priority_queue, I would first do the deletion process if the top element of such priority_queue is contained in the delete table.\n\nHere take the sample example to explaine the process.\nInput\n["MKAverage", "addElement", "addElement", "calculateMKAverage", "addElement", "calculateMKAverage", "addElement", "addElement", "addElement", "calculateMKAverage"]\n[[3, 1], [3], [1], [], [10], [], [5], [5], [5], []]\nOutput\n[null, null, null, -1, null, 3, null, null, null, 5]\nSteps:\n1. Initial: left_maxHeap: [], middle_minHeap: [], middle_maxHeap: [], right_minHeap: [], sum : 0, vals_queue: []\n2. Add 3: left_maxHeap: [], middle_minHeap: [], middle_maxHeap: [], right_minHeap: [], sum : 0, vals_queue: [3]\n3. Add 1: left_maxHeap: [], middle_minHeap: [], middle_maxHeap: [], right_minHeap: [], sum : 0, vals_queue: [3, 1]\n4. Calculate: Since size(vals_queue) < m, return -1;\n5. Add 1: left_maxHeap: [], middle_minHeap: [], middle_maxHeap: [], right_minHeap: [], sum : 0, vals_queue: [3, 1, 10]\n\t* Since size(vals_queue) == m, initialize all the priority_queues. left_maxHeap: [1], middle_minHeap: [3], middle_maxHeap: [3], right_minHeap: [10], sum : 3, vals_queue: [3, 1, 10]\n6. Calculate: return sum / (m - 2k) = 3\n7. Add 5: vals_queue: [3, 1, 10, 5]. Required to poll 3 from left.\n\t* \tPoll 3: Since 3 is located in middle priority_queue, just delete it from middle_minHeap and middle_maxHeap. Update the sum = 0.\n\t* \tAdd 5: Since 5 is also located in middle priority_queue, just add it to middle_minHeap and middle_maxHeap. Update the sum = 5.\n\t* \tleft_maxHeap: [1], middle_minHeap: [5], middle_maxHeap: [5], right_minHeap: [10], vals_queue: [1, 10, 5], sum: 5.\n8. Add 5: vals_queue: [1, 10, 5, 5]. Required to poll 1 from left.\n\t* Poll 1: Since 1 is located in left priority_queue, delete it from left priority_queue and transmit the smallest value from middle_minHeap to the left priority_queue. Here remember this value also needed to be deleted from the middle_maxHeap to syncronize. Update the sum = 0.\n\t* Add 5: Since 5 is located in left priority_queue, first transmit the largest value from left priority_queue to the middle priority_queues and add 5 to the left priority_queue. Update the sum = 5.\n\t* left_maxHeap: [5], middle_minHeap: [5], middle_maxHeap: [5], right_minHeap: [10], vals_queue: [10, 5, 5], sum: 5.\n9. Add 5: vals_queue: [10, 5, 5, 5]. Required to poll 10 from left.\n\t* Poll 10: Since 10 is located in right priority_queue, delete it from right priority_queue and transmit the largest value from middle_maxHeap to the right priority_queue. Here remember this value also needed to be deleted from the middle_minHeap to syncronize. Update the sum = 0.\n\t* Add 5: Since 5 is located in left (right, either is ok) priority_queue, first transmit the largest value from left priority_queue to the middle priority_queues and add 5 to the left priority_queue. Update the sum = 5.\n\t* left_maxHeap: [5], middle_minHeap: [5], middle_maxHeap: [5], right_minHeap: [5], vals_queue: [5, 5, 5], sum: 5.\n10. Calculate: return sum / (m - 2k) = 5\n\nFor each add operation (despite the initialization), I do 2 priority_queue manipulation process which would cost O(log m) time. The lazy deletion process can be amortized to all add operations which should only cost O(1) time in average.\nFor each calculation operation, it cost O(1) time.\n\nIt it helps you, please upvote. Thanks!\n\n```java\nclass MKAverage {\n PriorityQueue<Integer> left = new PriorityQueue<>((a, b) -> b - a);\n PriorityQueue<Integer> right = new PriorityQueue<>((a, b) -> a - b);\n PriorityQueue<Integer> minMiddle = new PriorityQueue<>((a, b) -> a - b);\n PriorityQueue<Integer> maxMiddle = new PriorityQueue<>((a, b) -> b - a);\n Queue<Integer> vals = new LinkedList<>();\n Map<Integer, Integer> deleteLeft = new HashMap<>(), deleteRight = new HashMap<>(), deleteMinMiddle = new HashMap<>(), deleteMaxMiddle = new HashMap<>();\n \n long sum;\n int m, k;\n boolean flag;\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n sum = 0;\n flag = false;\n }\n \n public void addElement(int num) {\n vals.offer(num);\n \n if (!flag && vals.size() == m) {\n initialize();\n flag = true;\n }\n else if (flag) {\n int lv = vals.poll();\n update(left, deleteLeft);\n update(right, deleteRight);\n if (!left.isEmpty() && left.peek() >= lv) {\n update(minMiddle, deleteMinMiddle);\n int v = minMiddle.poll();\n deleteMaxMiddle.put(v, deleteMaxMiddle.getOrDefault(v, 0) + 1);\n left.offer(v);\n deleteLeft.put(lv, deleteLeft.getOrDefault(lv, 0) + 1);\n sum -= v;\n }\n else if (!right.isEmpty() && right.peek() <= lv) {\n update(maxMiddle, deleteMaxMiddle);\n int v = maxMiddle.poll();\n deleteMinMiddle.put(v, deleteMinMiddle.getOrDefault(v, 0) + 1);\n right.offer(v);\n deleteRight.put(lv, deleteRight.getOrDefault(lv, 0) + 1);\n sum -= v;\n }\n else {\n deleteMinMiddle.put(lv, deleteMinMiddle.getOrDefault(lv, 0) + 1);\n deleteMaxMiddle.put(lv, deleteMaxMiddle.getOrDefault(lv, 0) + 1);\n sum -= lv;\n }\n \n update(left, deleteLeft);\n update(right, deleteRight);\n if (!left.isEmpty() && left.peek() >= num) {\n int v = left.poll();\n minMiddle.offer(v);\n maxMiddle.offer(v);\n left.offer(num);\n sum += v;\n }\n else if (!right.isEmpty() && right.peek() <= num) {\n int v = right.poll();\n minMiddle.offer(v);\n maxMiddle.offer(v);\n right.offer(num);\n sum += v;\n }\n else {\n minMiddle.offer(num);\n maxMiddle.offer(num);\n sum += num;\n }\n }\n }\n \n public int calculateMKAverage() {\n // System.out.println(sum);\n return flag? (int)(sum / (m - 2 * k)) : -1;\n }\n \n private void initialize() {\n int i;\n for (i = 0; i < m; ++i) {\n int v = vals.poll();\n minMiddle.offer(v);\n maxMiddle.offer(v);\n sum += v;\n vals.offer(v);\n }\n i = 0;\n while (i < k) {\n update(minMiddle, deleteMinMiddle);\n int v = minMiddle.poll();\n left.offer(v);\n deleteMaxMiddle.put(v, deleteMaxMiddle.getOrDefault(v, 0) + 1);\n sum -= v;\n i ++;\n }\n \n i = 0;\n while (i < k) {\n update(maxMiddle, deleteMaxMiddle);\n int v = maxMiddle.poll();\n right.offer(v);\n deleteMinMiddle.put(v, deleteMinMiddle.getOrDefault(v, 0) + 1);\n sum -= v;\n i ++;\n }\n }\n \n private void update(PriorityQueue<Integer> pq, Map<Integer, Integer> delete) {\n while (!pq.isEmpty() && delete.containsKey(pq.peek()) && delete.get(pq.peek()) > 0) {\n int v = pq.poll();\n delete.put(v, delete.get(v) - 1);\n if (delete.get(v) == 0)\n delete.remove(v);\n }\n }\n}\n``` | 14 | 3 | ['Hash Table', 'Heap (Priority Queue)', 'Java'] | 3 |
finding-mk-average | C++ and multisets | c-and-multisets-by-motorbreathing-m1ko | \nclass MKAverage {\n queue<int> q;\n multiset<int> minheap;\n multiset<int> midheap;\n multiset<int> maxheap;\n int m;\n int k;\n int coun | motorbreathing | NORMAL | 2022-06-18T10:27:24.879887+00:00 | 2022-06-18T10:27:24.879927+00:00 | 589 | false | ```\nclass MKAverage {\n queue<int> q;\n multiset<int> minheap;\n multiset<int> midheap;\n multiset<int> maxheap;\n int m;\n int k;\n int count;\n long sum;\npublic:\n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n count = 0;\n sum = 0;\n }\n \n void addElement(int num) {\n count++;\n q.push(num);\n int x = q.front();\n if (count > m) {\n q.pop();\n if (maxheap.count(x)) {\n maxheap.erase(maxheap.find(x));\n int v = *midheap.begin();\n maxheap.insert(v);\n sum -= v;\n midheap.erase(midheap.find(v));\n } else if (minheap.count(x)) {\n minheap.erase(minheap.find(x));\n int v = *midheap.rbegin();\n sum -= v;\n minheap.insert(v);\n midheap.erase(midheap.find(v));\n } else {\n sum -= x;\n midheap.erase(midheap.find(x));\n }\n }\n maxheap.insert(num);\n if (maxheap.size() > k) {\n int v = *maxheap.rbegin();\n maxheap.erase(maxheap.find(v));\n minheap.insert(v);\n if (minheap.size() > k) {\n v = *minheap.begin();\n minheap.erase(minheap.begin());\n midheap.insert(v);\n sum += v;\n }\n }\n }\n \n int calculateMKAverage() {\n if (count < m)\n return -1;\n return sum / midheap.size();\n }\n};\n``` | 12 | 0 | [] | 1 |
finding-mk-average | [Java] Fenwick Tree + BinarySearch | java-fenwick-tree-binarysearch-by-66brot-mj54 | Idea : \n1. We can have a queue to maintain m elements\n2. Use two Fenwick tree, 1 for count and 1 for prefix sum\n3. Do 2 times binary search for the first k e | 66brother | NORMAL | 2021-04-11T04:01:16.968660+00:00 | 2021-04-12T06:57:39.638150+00:00 | 1,555 | false | Idea : \n1. We can have a queue to maintain m elements\n2. Use two Fenwick tree, 1 for count and 1 for prefix sum\n3. Do 2 times binary search for the first k elements and the last k elements by using the count from our first fenwick tree\n4. We can get the sum by subtrating the sum of first k elements and sum of last k element by using our second fenwick tree\n\n```\nclass MKAverage {\n Queue<Integer>q=new LinkedList<>();\n int m,k;\n FenWick fen1;\n FenWick fen2;\n int cnt[]=new int[100010];\n long sum=0;\n public MKAverage(int m, int k) {\n this.m=m;\n this.k=k;\n long A[]=new long[100010];\n long B[]=new long[100010];\n fen1=new FenWick(A);\n fen2=new FenWick(B);\n }\n \n public void addElement(int num) {\n q.add(num);\n sum+=num;\n fen1.update(num,1);\n fen2.update(num,num);\n cnt[num]++;\n }\n \n public int calculateMKAverage() {\n if(q.size()<m)return -1;\n while(q.size()>m){\n int peek=q.poll();\n cnt[peek]--;\n sum-=peek;\n fen1.update(peek,-1);\n fen2.update(peek,-peek);\n }\n \n \n \n int l=0,r=cnt.length-1;\n int pos1=-1,pos2=-1;\n while(l<=r){//binary search for the first k (there may be duplicated)\n int mid=l+(r-l)/2;\n long count=fen1.sumRange(0,mid);\n if(count>=k){\n pos1=mid;\n r=mid-1;\n }\n else{\n l=mid+1;\n }\n }\n \n \n \n l=0;r=cnt.length-1;\n while(l<=r){//binary search for the last k (there may be duplicated)\n int mid=l+(r-l)/2;\n long count=fen1.sumRange(mid,cnt.length-1);\n if(count>=k){\n pos2=mid;\n l=mid+1;\n }\n else{\n r=mid-1;\n }\n }\n \n \n \n long sum1=fen2.sumRange(0,pos1);\n long sum2=fen2.sumRange(pos2,cnt.length-1);\n long cnt1=fen1.sumRange(0,pos1);\n long cnt2=fen1.sumRange(pos2,cnt.length-1);\n \n if(cnt1>k){\n sum1-=(pos1*(cnt1-k));\n }\n if(cnt2>k){\n sum2-=(pos2*(cnt2-k));\n }\n long remain=sum-sum1-sum2;\n return (int)(remain/(m-2*k));\n }\n}\n\nclass FenWick {\n long tree[];//1-index based\n long A[];\n long arr[];\n public FenWick(long[] A) {\n this.A=A;\n arr=new long[A.length];\n tree=new long[A.length+1];\n }\n \n public void update(int i, int val) {\n arr[i]+=val;\n i++;\n while(i<tree.length){\n tree[i]+=val;\n i+=(i&-i);\n }\n }\n \n public long sumRange(int i, int j) {\n return pre(j+1)-pre(i);\n }\n \n public long pre(int i){\n long sum=0;\n while(i>0){\n sum+=tree[i];\n i-=(i&-i);\n }\n return sum;\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n\n/*\n ;\\\n |\' \\\n _ ; : ;\n / `-. /: : |\n | ,-.`-. ,\': : |\n \\ : `. `. ,\'-. : |\n \\ ; ; `-.__,\' `-.|\n \\ ; ; ::: ,::\'`:. `.\n \\ `-. : ` :. `. \\\n \\ \\ , ; ,: (\\\n \\ :., :. ,\'o)): ` `-.\n ,/,\' ;\' ,::"\'`.`---\' `. `-._\n ,/ : ; \'" `;\' ,--`.\n ;/ :; ; ,:\' ( ,:)\n ,.,:. ; ,:., ,-._ `. \\""\'/\n \'::\' `:\'` ,\'( \\`._____.-\'"\'\n ;, ; `. `. `._`-. \\\\\n ;:. ;: `-._`-.\\ \\`.\n \'`:. : |\' `. `\\ ) \\\n -hrr- ` ;: | `--\\__,\'\n \'` ,\'\n ,-\'\n\n\n free bug dog\n*/\n``` | 12 | 0 | [] | 3 |
finding-mk-average | [Python] SortedList solution | python-sortedlist-solution-by-oystermax-3n8f | There is a sortedcontainers package for Python (link), which I think is a good alternative for red-black tree or ordered map for python players.\nUsing SortedLi | oystermax | NORMAL | 2021-05-25T21:59:37.099283+00:00 | 2021-06-01T22:06:26.116785+00:00 | 914 | false | There is a `sortedcontainers` package for Python ([link](http://www.grantjenks.com/docs/sortedcontainers/index.html)), which I think is a good alternative for red-black tree or ordered map for python players.\nUsing `SortedList`, it takes `~ O(logn)` time for both remove and insert. (Since `SortedList` is based on list of list, instead of tree structure, the time cost is not exactly `O(logn)`)\n\n```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n MAX_NUM = 10 ** 5\n def __init__(self, m: int, k: int):\n \n self.m = m\n self.k = k\n \n # sorted list\n self.sl = SortedList([0] * m)\n\t\t# sum of k smallest elements\n self.sum_k = 0\n\t\t# sum of m - k smallest elements\n self.sum_m_k = 0\n \n # queue for the last M elements if the stream\n self.q = deque([0] * m)\n \n def addElement(self, num: int) -> None:\n # Time: O(logm)\n\t\t\n m, k, q, sl = self.m, self.k, self.q, self.sl \n \n # update q\n q.append(num)\n old = q.popleft()\n \n # remove the old num\n r = sl.bisect_right(old)\n\t\t# maintain sum_k\n if r <= k:\n self.sum_k -= old\n self.sum_k += sl[k]\n\t\t# maintain sum_m_k\n if r <= m - k:\n self.sum_m_k -= old\n self.sum_m_k += sl[m-k]\n # remove the old num\n sl.remove(old)\n \n # add the new num\n r = sl.bisect_right(num)\n if r < k:\n self.sum_k -= sl[k-1]\n self.sum_k += num\n if r < m - k:\n self.sum_m_k -= sl[m - k - 1]\n self.sum_m_k += num\n \n sl.add(num)\n \n return\n\n def calculateMKAverage(self) -> int:\n\t\t# Time: O(1)\n if self.sl[0] == 0:\n return -1\n return (self.sum_m_k - self.sum_k) // (self.m - self.k * 2)\n``` | 11 | 0 | ['Python'] | 1 |
finding-mk-average | python | 100% faster | bst solution explained | python-100-faster-bst-solution-explained-7bpn | So the challenge here is how can we quickly sum the k-largest and k-smallest elements, and I want to talk about how I did that with a binary search tree. The ke | queenTau | NORMAL | 2021-08-07T01:40:20.002017+00:00 | 2021-08-07T19:11:12.392861+00:00 | 899 | false | So the challenge here is how can we quickly sum the k-largest and k-smallest elements, and I want to talk about how I did that with a binary search tree. The key idea was to store the number of items in each sub-tree, as well as the sum of all the items in each sub tree. By storing the size of each node it becomes possible to determine if the ith smallest node is to the left of the current node, at the current node, or to the right of the current node. This means the ith smallest node can be found in a single trip down the tree. Because the sums are stored, we can also choose to sum elements which are smaller or larger than the target as we go (without having to actually traverse the tree).\n\nThe other aspects of my algorithm are fairly straightforward. I used a deque to store the last m elements in the stream, and an integer to store the sliding window sum for all of the last m elements. This means that to compute the average I have to subtract the sum of the k largest/smallest elements from the sliding window sum, and then divide by the number of elements (which is pre-computed since it\'s a constant). Whenever I add/remove an element to/from the queue I also/remove add it to/from the tree and update the sum, with different cases to handle when the tree is null, when the queue isn\'t full.\n\nBST Height (n is the number of nodes in the tree): \nBest : O(logn)\nAverage : O(logn)\nWorst : O(n)\n\nBST Runtimes (h is the height of the tree):\n\\_\\_init\\_\\_ : O(1)\ninsert/remove : O(h)\nklargets/ksmallest : O(h)\n\nMKAverage Runtimes:\n\\_\\_init\\_\\_ : O(1)\naddElement : O(h)\ncalculateMKAverage : O(h)\n\nBest Performance: 864 ms/49.3 MB : 100%/98%\n\nA more complete version of the binary search tree is below the code for this puzzle.\n\'\'\'\n\n\t#Binary Search Tree\n\tclass Node:\n\t\t#Create a Node\n\t\tdef __init__(self, val:int) -> None:\n\t\t\t"""Create a New Binary Search Tree Node"""\n\t\t\tself.val = val\n\t\t\tself.sum = val\n\t\t\tself.size = 1\n\t\t\tself.count = 1\n\t\t\tself.left = None\n\t\t\tself.right = None\n\t\t\n\t\t#Add a Node to the Tree\n\t\tdef insert(self, val:int) -> None:\n\t\t\t"""Add a Value to the Tree"""\n\t\t\t#Update the Size/Sum\n\t\t\tself.size += 1\n\t\t\tself.sum += val\n\t\t\t\n\t\t\t#Check the Case\n\t\t\tif val < self.val:\n\t\t\t\t#Check the Left Node\n\t\t\t\tif self.left:\n\t\t\t\t\t#Recurse\n\t\t\t\t\tself.left.insert(val)\n\t\t\t\telse:\n\t\t\t\t\t#Make a New Node\n\t\t\t\t\tself.left = Node(val)\n\t\t\telif val > self.val:\n\t\t\t\t#Check the Right Node\n\t\t\t\tif self.right:\n\t\t\t\t\t#Recurse\n\t\t\t\t\tself.right.insert(val)\n\t\t\t\telse:\n\t\t\t\t\t#Make a New Node\n\t\t\t\t\tself.right = Node(val)\n\t\t\telse:\n\t\t\t\t#Increment the Count\n\t\t\t\tself.count += 1\n\n\t\t#Remove a Node from the Tree (Safetys Removed)\n\t\tdef remove(self, val:int) -> None:\n\t\t\t"""Remove a Value From the Tree"""\n\t\t\t#Update the Size/Sum\n\t\t\tself.size -= 1\n\t\t\tself.sum -= val\n\t\t\t\n\t\t\t#Check the Case\n\t\t\tif val < self.val:\n\t\t\t\t#Recurse Left\n\t\t\t\treturn self.left.remove(val)\n\t\t\telif val > self.val:\n\t\t\t\t#Recurse Right\n\t\t\t\treturn self.right.remove(val)\n\t\t\telse:\n\t\t\t\t#Decrement the Count\n\t\t\t\tself.count -= 1\n\n\t\t#Sum the k Smallest Numbers\n\t\tdef ksmallest(self, k:int) -> int:\n\t\t\t"""Efficiently Sum the k Smallest Values in the Tree"""\n\t\t\t#Check the Left Branch\n\t\t\ts = 0\n\t\t\tif self.left:\n\t\t\t\t#Check the Case\n\t\t\t\tif k <= self.left.size:\n\t\t\t\t\t#Recurse Left\n\t\t\t\t\treturn self.left.ksmallest(k)\n\t\t\t\telse:\n\t\t\t\t\t#Update k/s\n\t\t\t\t\tk -= self.left.size\n\t\t\t\t\ts = self.left.sum\n\n\t\t\t#Check the Current Value\n\t\t\tif k <= self.count:\n\t\t\t\treturn s + k*self.val\n\t\t\telif self.right:\n\t\t\t\t#Recurse Right\n\t\t\t\treturn s + self.count*self.val + self.right.ksmallest(k - self.count)\n\t\t\telse:\n\t\t\t\t#Return Search Failure\n\t\t\t\treturn None\n\n\tclass MKAverage:\n\t\tdef __init__(self, m: int, k: int):\n\t\t\tself.k = k\n\t\t\tself.l = m - k\n\t\t\tself.m = m\n\t\t\tself.n = self.m - 2*self.k\n\t\t\tself.window = deque()\n\t\t\tself.tree = None\n\n\t\tdef addElement(self, num: int) -> None:\n\t\t\t#Check the Case\n\t\t\tif len(self.window) == self.m:\n\t\t\t\t#Remove the Previous Number from the Window/Tree\n\t\t\t\tself.tree.remove(self.window.popleft())\n\n\t\t\t\t#Add the New Number to the Window/Tree\n\t\t\t\tself.window.append(num)\n\t\t\t\tself.tree.insert(num)\n\t\t\telif self.window:\n\t\t\t\t#Add the New Number to the Window/Tree\n\t\t\t\tself.window.append(num)\n\t\t\t\tself.tree.insert(num)\n\t\t\telse:\n\t\t\t\t#Make a New Tree\n\t\t\t\tself.window.append(num)\n\t\t\t\tself.tree = Node(num)\n\n\t\tdef calculateMKAverage(self) -> int:\n\t\t\t#Check the Window\n\t\t\tif len(self.window) < self.m:\n\t\t\t\treturn -1\n\t\t\telse:\n\t\t\t\t#Compute Return the Average\n\t\t\t\treturn (self.tree.ksmallest(self.l) - self.tree.ksmallest(self.k))//self.n\n\'\'\'\n\nHere is my binary search tree class as it exists on my computer!\n\n\'\'\'\n\n #Binary Search Tree\n class Node:\n #Create a Node\n def __init__(self, val:int) -> None:\n """Create a New Binary Search Tree Node"""\n self.val = val\n self.sum = val\n self.size = 1\n self.count = 1\n self.left = None\n self.right = None\n \n #Get the Size of the Tree\n def __len__(self) -> int:\n """Return the Number of Items in the Tree"""\n return self.size\n \n #Search for an Item (Index Validity Guaranteed)\n def find(self, i:int):\n """Find and Return the Node at Index i\n \n It also returns an index describing which version of the \n current node was returned.\n \n If i is not a valid index then it returns None (but still \n does a non-trivial amount of work to figure that out, so \n be cautious when using this)\n """\n #Check the Left Branch\n if self.left:\n #Check the Case\n if i < self.left.size:\n #Recurse Left\n return self.left.find(i)\n else:\n #Update i\n i -= self.left.size\n \n #Check the Current Value\n if i < self.count:\n return self, i\n elif self.right:\n #Recurse Right\n return self.right.find(i - self.count)\n else:\n #Return Search Failure\n return None\n \n #Find the ith Smallest Element\n def __getitem__(self, i:int) -> int:\n """Get and Return the Value of the Node at Index i"""\n #Check i\n if i < -self.size or i >= self.size:\n #Index Out of Range\n return None\n elif i >= 0:\n #Find the Index Recursively\n return self.find(i)[0].val\n else:\n #Find the Index Recursively\n return self.find(self.size + i)[0].val\n \n #Count the Number of Occurences of an Item in the Tree\n def Count(self, val:int) -> int:\n #Check the Case\n if val == self.val:\n #Return the Count\n return self.count\n elif val < self.val:\n #Recurse Left\n return self.left.Count(val) if self.left else 0\n else:\n #Recurse Right\n return self.right.Count(val) if self.right else 0\n \n #Check if an Item is in the Tree\n def __contains__(self, val:int) -> bool:\n """Check Whether a Value is in the Tree"""\n return self.Count(val) > 0\n \n #Find the Minimum Item\n def getMin(self) -> int:\n """Returns the Minimum Value in the Tree"""\n return self[0]\n \n #Find the Maximum Item\n def getMax(self) -> int:\n """Returns the Maximum Valud in the Tree"""\n return self[-1]\n \n #Find the Median\n def median(self) -> float:\n """Returns the Median Value in the Tree"""\n #Check the Case\n if self.size%2:\n #The Median is a Single Item\n return self[self.size//2]\n else:\n #Find the Larger Item\n node, i = self.find(self.size//2)\n \n #Check the Case\n if i > 0:\n #The Median is Already Found\n return node.val\n elif node.left and node.left.size:\n #Get the Largest Value from the Left\n return (node.val + node.left[-1])/2\n else:\n #Do a Separate Search\n return (node.val + self[self.size//2 - 1])/2\n \n #Find the Average\n def mean(self) -> float:\n """Returns the Average Value in the Tree"""\n return self.sum/self.size\n \n #Add a Node to the Tree\n def insert(self, val:int) -> None:\n """Add a Value to the Tree"""\n #Check the Case\n self.size += 1\n self.sum += val\n if val < self.val:\n #Check the Left Node\n if self.left:\n #Recurse\n self.left.insert(val)\n else:\n #Make a New Node\n self.left = Node(val)\n elif val > self.val:\n #Check the Right Node\n if self.right:\n #Recurse\n self.right.insert(val)\n else:\n #Make a New Node\n self.right = Node(val)\n else:\n #Increment the Count\n self.count += 1\n \n #Remove a Node from the Tree\n def remove(self, val:int) -> bool:\n """Remove a Value From the Tree"""\n #Check the Case\n if val < self.val:\n #Check the Left Node\n if self.left and self.left.remove(val):\n #Decrement the Sum/Size\n self.sum -= val\n self.size -= 1\n \n #Return Success\n return True\n else:\n #The Node Wasn\'t Found\n return False\n elif val > self.val:\n #Check the Right Node\n if self.right and self.right.remove(val):\n #Decrement the Sum/Size\n self.sum -= val\n self.size -= 1\n \n #Return Success\n return True\n else:\n #The Node Wasn\'t Found\n return False\n else:\n #Check the Count\n if self.count:\n #Decrement the Count, Sum, and Size\n self.count -= 1\n self.sum -= val\n self.size -= 1\n \n #Return Success\n return True\n else:\n #Return Failure\n return False\n \n #Pop an Item at a Specified Index\n def pop(self, i:int) -> int:\n """Remove and Return the Item at Index i"""\n #Check i\n if i < 0 or i >= self.size:\n #Return Search Failure\n return None\n \n #Update the Size\n self.size -= 1\n \n #Check the Left Branch\n if self.left:\n #Check the Case\n if i < self.left.size:\n #Recurse Left\n val = self.left.pop(i)\n \n #Update the Sum\n self.sum -= val\n \n #Return the Value\n return val\n else:\n #Update i\n i -= self.left.size\n \n #Check the Current Value\n if i < self.count:\n #Update the Count/Sum\n self.count -= 1\n self.sum -= self.val\n \n #Return the Value\n return self.val\n else:\n #Recurse Right\n val = self.right.pop(i - self.count)\n \n #Update the Sum\n self.sum -= val\n \n #Return the Value\n return val\n \n #Yield Nodes in Increasing Order\n def increasing(self, unique:bool = False) -> int:\n """Yield the Values of the Tree in Increasing Order"""\n #Check the Left Node\n if self.left:\n #Recurse\n yield from self.left.increasing(unique)\n \n #Yield the Current Node\n if unique:\n yield self.val, self.count\n else:\n yield from (self.val for i in range(self.count))\n \n #Check the Right Node\n if self.right:\n #Recurse\n yield from self.right.increasing(unique)\n \n #Make the Tree Iterable\n def __iter__(self):\n return self.increasing()\n \n #Yield Nodes in Decreasing Order\n def decreasing(self, unique:bool = False) -> int:\n """Yield the Values in the Tree in Decreasing Order"""\n #Check the Right Node\n if self.right:\n #Recurse\n yield from self.right.decreasing(unique)\n \n #Yield the Current Node\n if unique:\n yield self.val, self.count\n else:\n yield from (self.val for i in range(self.count))\n \n #Check the Left Node\n if self.left:\n #Recurse\n yield from self.left.decreasing(unique)\n \n #Sum the k Largest Numbers\n def klargest(self, k:int) -> int:\n """Efficiently Sum the k Largest Values in the Tree"""\n #Check the Right Branch\n s = 0\n if self.right:\n #Check the Case\n if k <= self.right.size:\n #Recurse Left\n return self.right.klargest(k)\n else:\n #Update k/s\n k -= self.right.size\n s = self.right.sum\n \n #Check the Current Value\n if k <= self.count:\n return s + k*self.val\n elif self.left:\n #Recurse Left\n return s + self.count*self.val + self.left.klargest(k - self.count)\n else:\n #Return Search Failure\n return None\n \n #Sum the k Smallest Numbers\n def ksmallest(self, k:int) -> int:\n """Efficiently Sum the k Smallest Values in the Tree"""\n #Check the Left Branch\n s = 0\n if self.left:\n #Check the Case\n if k <= self.left.size:\n #Recurse Left\n return self.left.ksmallest(k)\n else:\n #Update k/s\n k -= self.left.size\n s = self.left.sum\n \n #Check the Current Value\n if k <= self.count:\n return s + k*self.val\n elif self.right:\n #Recurse Right\n return s + self.count*self.val + self.right.ksmallest(k - self.count)\n else:\n #Return Search Failure\n return None\n\'\'\' | 10 | 0 | ['Binary Search Tree', 'Python'] | 2 |
finding-mk-average | Python [short solution] | python-short-solution-by-gsan-5g05 | Warning: As the wonderful test cases have been updated, now the code gets TLE.\n\nThis one is slightly outlandish as I use the SortedList from sortedcontainers | gsan | NORMAL | 2021-04-11T04:01:35.464062+00:00 | 2021-04-15T09:23:08.974367+00:00 | 1,090 | false | **Warning: As the wonderful test cases have been updated, now the code gets TLE.**\n\nThis one is slightly outlandish as I use the `SortedList` from `sortedcontainers` class - it\'s not part of standard library. With that said this container proves useful in several questions, such as "1649. Create Sorted Array through Instructions".\n\nAnyway, `SortedList` insertions are, well, sorted. So at any time you can find the desired average simply by `sum(self.slist[self.k:-self.k]) // (self.m - 2*self.k)`. We use a queue to keep the least recently used entries and remove when necessary. For that purpose the built-in removel tool of `SortedList` is fast.\n\n```python\nimport collections\nimport sortedcontainers\nclass MKAverage:\n def __init__(self, m, k):\n self.m = m\n self.k = k\n self.que = collections.deque([])\n self.slist = sortedcontainers.SortedList()\n \n\n def addElement(self, num):\n self.que.append(num)\n self.slist.add(num)\n if len(self.que) > self.m:\n lru = self.que.popleft()\n self.slist.remove(lru)\n\n \n def calculateMKAverage(self):\n if len(self.que) < self.m:\n return -1\n return sum(self.slist[self.k:-self.k]) // (self.m - 2*self.k)\n``` | 10 | 1 | [] | 3 |
finding-mk-average | C++ 2 methods (Segment Tree && heaps) | c-2-methods-segment-tree-heaps-by-tom072-d0cp | The core of this problem is:\n\n> How to find the sum of the smallest/biggest 1~k th numbers in an array?\n\nSegment tree can do this in O(nlogn) time.\n\nWe ca | tom0727 | NORMAL | 2021-04-11T06:08:34.454442+00:00 | 2021-04-11T13:19:03.264614+00:00 | 823 | false | The core of this problem is:\n\n> How to find the sum of the smallest/biggest 1~k th numbers in an array?\n\nSegment tree can do this in `O(nlogn)` time.\n\nWe can keep a segment tree which stores the information about: "For a given value x, how many x are there in the array?".\n\nFor example the current array is `[3,1,10,5,5]`, then the tree node for value `5` will have a `cnt = 2`. To further speed up the code, we can keep an extra `sum` in the tree node. \n\nTo be more precise, if a tree node tells about the information of `[l,r]`, then the `cnt` and `sum` implies:\n`cnt` is the number of elements `x`, where `l <= x <= r`.\n`sum` is the **sum of elements** `x`, where `l <= x <= r`.\n\nNow we can easily query about the sum of first `k-th` smallest and biggest elements. \n\n<hr>\n\n```cpp\n#define maxn (100005<<2)\n#define ll long long\nstruct node {\n int cnt;\n ll sum;\n} tr[maxn];\n\nvoid push_up(int cur) {\n tr[cur].cnt = tr[cur<<1].cnt + tr[cur<<1|1].cnt;\n tr[cur].sum = tr[cur<<1].sum + tr[cur<<1|1].sum;\n}\n\nvoid update(int cur, int l, int r, int p, int x) {\n if (l == r) {\n tr[cur].sum += (ll)(x * p);\n tr[cur].cnt += x;\n return;\n }\n int mid = (l+r) >> 1;\n if (p <= mid) update(cur<<1, l, mid, p, x);\n else update(cur<<1|1, mid+1, r, p, x);\n push_up(cur);\n}\n\n// return the sum of the smallest 1~kth numbers\nll query_small(int cur, int l, int r, int k) {\n if (k <= 0) return 0;\n if (tr[cur].cnt <= k) return tr[cur].sum;\n if (l == r) {\n return (ll)(l) * (ll)(k); // for example [5,5,5], k = 1, only return 5, not 15\n }\n int mid = (l+r) >> 1;\n ll res = 0;\n res += query_small(cur<<1, l, mid, k);\n res += query_small(cur<<1|1, mid+1, r, k-tr[cur<<1].cnt);\n return res;\n}\n\n// return the sum of the biggest 1~kth numbers\nll query_big(int cur, int l, int r, int k) {\n if (k <= 0) return 0;\n if (tr[cur].cnt <= k) return tr[cur].sum;\n if (l == r) {\n return (ll)(l) * (ll)(k); // for example [5,5,5], k = 1, only return 5, not 15\n }\n int mid = (l+r) >> 1;\n ll res = 0;\n res += query_big(cur<<1, l, mid, k-tr[cur<<1|1].cnt);\n res += query_big(cur<<1|1, mid+1, r, k);\n return res;\n}\n\nclass MKAverage {\npublic:\n int m,k;\n vector<int> vec;\n ll sum = 0;\n int de;\n \n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n de = m-2*k;\n memset(tr, 0, sizeof(tr));\n }\n \n void addElement(int num) {\n vec.push_back(num);\n sum += (ll)(num);\n int n = vec.size();\n update(1, 1, 1e5, num, 1);\n \n if (n > m) {\n int cur = vec[n-m-1];\n sum -= cur;\n update(1, 1, 1e5, cur, -1);\n }\n }\n \n int calculateMKAverage() {\n if (vec.size() < m) return -1;\n ll res = query_small(1, 1, 1e5, k) + query_big(1, 1, 1e5, k);\n return (sum - res) / de;\n }\n};\n```\n\n<hr>\n\nSome sidenotes:\n\nSegment tree can also solve the following problems:\n\n1. Find the `k` th smallest element in an array.\n2. Find the number of pairs `(i,j)` such that `arr[i] > arr[j]`.\n3. Find the maximum **unique** element in a sliding window. (https://codeforces.com/problemset/problem/69/E).\n\nPlease see my blog (Chinese only) for Segment tree: https://tom0727.gitee.io/post/035-%E6%9D%83%E5%80%BC%E7%BA%BF%E6%AE%B5%E6%A0%91/\n\nIf you are interested, you can also learn about **Persistent Segment Tree**, which can solve problems like:\n\n1. Find the `k` th smallest element in **any segment** of an array.\n2. Answer queries about **any history version** of an array.\n3. Find the **LCM** of any segments of an array. (https://codeforces.com/problemset/problem/1422/F)\n4. In a **tree (n vertices, n-1 edges, connected graph)**, where every edge has a weight, find the `k`th smallest weight in the shortest path between `u,v`.\n\nPlease see my blog (Chinese only) for Persistent Segment tree: https://tom0727.gitee.io/post/036-%E4%B8%BB%E5%B8%AD%E6%A0%91/\n\n\n\n<hr>\n\nThe second method is using 3 heaps. Others have explained that solution well enough. I will only post my code here:\n\n```cpp\nclass MKAverage {\npublic:\n #define ll long long\n int m,k;\n vector<int> vec;\n multiset<int> small, mid, big;\n ll sum = 0;\n int de;\n \n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n de = m-2*k;\n }\n\t\n void addElement(int num) {\n vec.push_back(num);\n sum += (ll)(num);\n mid.insert(num);\n int n = vec.size();\n if (n < m) return;\n \n if (n == m) {\n for (int i = 0; i < k; i++) {\n auto itr = prev(mid.end());\n int cur = *itr;\n big.insert(cur);\n mid.erase(itr);\n sum -= cur;\n }\n for (int i = 0; i < k; i++) {\n auto itr = mid.begin();\n int cur = *itr;\n small.insert(cur);\n mid.erase(itr);\n sum -= cur;\n }\n return;\n }\n \n \n if (n > m) {\n int cur = vec[n-m-1];\n if (small.count(cur)) {\n small.erase(small.find(cur));\n } else if (big.count(cur)) {\n big.erase(big.find(cur));\n } else if (mid.count(cur)) {\n sum -= cur;\n mid.erase(mid.find(cur));\n }\n }\n \n if (small.size() < k) {\n auto itr = mid.begin();\n int cur = *itr;\n sum -= cur;\n small.insert(cur);\n mid.erase(itr);\n }\n if (big.size() < k) {\n auto itr = prev(mid.end());\n int cur = *itr;\n sum -= cur;\n big.insert(cur);\n mid.erase(itr);\n }\n \n while (*prev(small.end()) > *mid.begin()) {\n auto itr1 = prev(small.end());\n auto itr2 = mid.begin();\n int cur1 = *itr1, cur2 = *itr2;\n small.erase(itr1); mid.erase(itr2);\n small.insert(cur2); mid.insert(cur1);\n sum -= cur2, sum += cur1;\n }\n \n while (*big.begin() < *prev(mid.end())) {\n auto itr1 = big.begin();\n auto itr2 = prev(mid.end());\n int cur1 = *itr1, cur2 = *itr2;\n big.erase(itr1); mid.erase(itr2);\n big.insert(cur2); mid.insert(cur1);\n sum -= cur2, sum += cur1;\n }\n }\n \n int calculateMKAverage() {\n if (vec.size() < m) return -1;\n return sum / de;\n }\n};\n```\n | 9 | 1 | [] | 0 |
finding-mk-average | [Java] Elegant O(log M)-add O(1)-avg TreeSet Solution | java-elegant-olog-m-add-o1-avg-treeset-s-1f02 | Thanks to the suggestion by @anindya-saha; Here is a very elegant Solution. The solution works great in these questions: \n 295. Find Median from Data Stream\n | xieyun95 | NORMAL | 2021-05-22T06:57:24.519303+00:00 | 2021-06-02T04:27:57.662087+00:00 | 1,006 | false | Thanks to the suggestion by @anindya-saha; Here is a very elegant Solution. The solution works great in these questions: \n* [295. Find Median from Data Stream](https://leetcode.com/problems/find-median-from-data-stream/discuss/1246287/Java-clean-O(logN)-TreeSet-Solution-oror-with-comments)\n* [1825. Finding MK Average](https://leetcode.com/problems/finding-mk-average/discuss/1222887/Java-Elegant-O(log-M)-add-O(1)-avg-TreeSet-Solution)\n```\nclass MKAverage {\n class Node implements Comparable<Node> {\n int val;\n int time;\n \n Node(int val, int time) {\n this.val = val;\n this.time = time;\n }\n \n @Override\n public int compareTo(Node other) {\n return (this.val != other.val ? this.val - other.val \n : this.time - other.time);\n }\n }\n \n private TreeSet<Node> set = new TreeSet<>(); // natural order\n private Deque<Node> queue = new LinkedList<>();\n private Node kLeft;\n private Node kRight;\n \n private int m, k;\n \n private int time = 0;\n private int sum = 0;\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n Node node = new Node(num, time++);\n\n addNode(node);\n removeNode();\n \n if (time == m) init();\n }\n \n private void init() {\n int i = 0;\n for (Node node : set) {\n if (i < k-1);\n else if (i == k-1) kLeft = node;\n else if (i < m-k) sum += node.val;\n else if (i == m-k) {\n kRight = node;\n return;\n }\n \n i++;\n }\n return;\n }\n \n private void addNode(Node node) {\n queue.offerLast(node);\n set.add(node);\n \n if (queue.size() <= m) return;\n \n if (node.compareTo(kLeft) < 0) {\n sum += kLeft.val;\n kLeft = set.lower(kLeft);\n } else if (node.compareTo(kRight) > 0) {\n sum += kRight.val;\n kRight = set.higher(kRight);\n } else {\n sum += node.val;\n } \n }\n \n private void removeNode() {\n if (queue.size() <= m) return;\n \n Node node = queue.pollFirst();\n \n if (node.compareTo(kLeft) <= 0) {\n kLeft = set.higher(kLeft);\n sum -= kLeft.val;\n } else if (node.compareTo(kRight) >= 0) {\n kRight = set.lower(kRight);\n sum -= kRight.val;\n } else {\n sum -= node.val;\n }\n \n set.remove(node);\n }\n \n public int calculateMKAverage() {\n return (queue.size() < m ? -1 : sum / (m - 2 * k));\n }\n}\n```\n\n**Original Post:** \n```\nclass MKAverage {\n class Node {\n int val;\n int time;\n Node(int val, int time) {\n this.val = val;\n this.time = time;\n }\n }\n \n private TreeSet<Node> set; \n private Deque<Node> queue;\n private Node kLeft;\n private Node kRight;\n \n int m;\n int k;\n \n int time;\n int sum;\n\n public MKAverage(int m, int k) {\n this.set = new TreeSet<>((a,b) -> (a.val != b.val) ? a.val - b.val : a.time - b.time);\n this.queue = new LinkedList<>();\n this.m = m;\n this.k = k;\n \n this.time = 0;\n this.sum = 0;\n }\n \n public void addElement(int num) {\n Node node = new Node(num, time++);\n\n addNode(node);\n removeNode();\n \n if (time == m) init();\n }\n \n private void init() {\n int i = 0;\n for (Node node : set) {\n if (i < k-1);\n else if (i == k-1) kLeft = node;\n else if (i < m-k) sum += node.val;\n else if (i == m-k) {\n kRight = node;\n return;\n }\n \n i++;\n }\n return;\n }\n \n private void addNode(Node node) {\n queue.offerLast(node);\n set.add(node);\n \n if (queue.size() <= m) return;\n \n if (node.val < kLeft.val) {\n sum += kLeft.val;\n kLeft = set.lower(kLeft);\n } else if (node.val >= kRight.val) {\n sum += kRight.val;\n kRight = set.higher(kRight);\n } else {\n sum += node.val;\n } \n }\n \n private void removeNode() {\n if (queue.size() <= m) return;\n \n Node node = queue.pollFirst();\n \n if (node.val < kLeft.val || (node.val == kLeft.val && node.time <= kLeft.time)) {\n kLeft = set.higher(kLeft);\n sum -= kLeft.val;\n } else if (node.val > kRight.val || (node.val == kRight.val && node.time >= kRight.time)) {\n kRight = set.lower(kRight);\n sum -= kRight.val;\n } else {\n sum -= node.val;\n }\n \n set.remove(node);\n }\n \n public int calculateMKAverage() {\n return (queue.size() < m ? -1 : sum / (m - 2 * k));\n }\n}\n``` | 8 | 0 | ['Tree', 'Ordered Set', 'Java'] | 4 |
finding-mk-average | Simple 97.11% O(n log n) Python3 solution with queue, map and two pointers | simple-9711-on-log-n-python3-solution-wi-vp11 | Hey guys, this is my first time posting here and english is not my first language, hopefully i can be clear but i think the code is simple enough\n \n\n# Intuit | user8889zs | NORMAL | 2024-04-30T02:16:09.100674+00:00 | 2024-04-30T02:16:09.100693+00:00 | 806 | false | Hey guys, this is my first time posting here and english is not my first language, hopefully i can be clear but i think the code is simple enough\n \n\n# Intuition\nAt first it did it the brute force way, just adding the elements to a first in, first out queue and keeping a separate count and sum but it would exceed the maximum time alloted. Then i had the idea to keep count of how many times each element appeared in the queue with a map, since for the average calculation we would have to sort it anyway to remove the k greater and smaller elements. this also helped with the sorting because then we dont need to sort the full queue, only one of each unique element.\n\n# Approach\nFirst we create a queue, a counter and a map. We use the queue so we know wich element is the oldest one added, the counter is so we dont need to run through the queue to know if we exceed the size, and we\'ll use the map later to calculate the average.\n```\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.queue = collections.deque()\n self.count = 0\n self.quantities = {} def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.queue = collections.deque()\n self.count = 0\n self.quantities = {}\n```\nWhen we add a new element, we keep count of how many of those elements are in the queue using the map. if the queue is bigger than m, we remove the older element of the queue and then update it\'s counter\n```\n def addElement(self, num: int) -> None:\n self.queue.append(num)\n self.quantities[num] = self.quantities[num] + 1 if num in self.quantities else 1\n if self.count >= self.m:\n first = self.queue.popleft()\n self.quantities[first] -= 1\n else:\n self.count += 1\n \n```\nNow to calculate the average. here, **we sort the map keys so we know the order of the elements in the queue, and remove the k largest and smaller elements from the map counter, not the queue**.\n```\ndef calculateMKAverage(self) -> int:\n if self.count < self.m:\n return -1\n #the order of unique elements in the queue, we know the quantity on the map\n _list = sorted(self.quantities.keys())\n #we keep the original queue intact for later operations\n copy = self.quantities.copy()\n #how many largest and smaller elements we should remove from each end\n removeLeft = removeRight = self.k\n #where we\'ll start removing them\n pointerLeft = 0\n pointerRight = len(_list)-1\n```\n We keep going from left to right and from right to left until we\'ve removed k elements from both ends, and them we calculate the sum and the average\n```\nwhile removeLeft > 0:\n leftmostKey = _list[pointerLeft]\n if copy[leftmostKey] >= removeLeft:\n copy[leftmostKey] -= removeLeft\n removeLeft = 0\n else:\n removeLeft -= copy[leftmostKey]\n copy[leftmostKey] = 0 \n pointerLeft += 1\n \n while removeRight > 0:\n rightmostKey = _list[pointerRight]\n if copy[rightmostKey] >= removeRight:\n copy[rightmostKey] -= removeRight\n removeRight = 0\n else:\n removeRight -= copy[rightmostKey]\n copy[rightmostKey] = 0\n pointerRight -= 1\n \n total_sum = count = 0\n for k in copy:\n total_sum += k*copy[k]\n count += copy[k]\n return math.floor(total_sum/count)\n```\n\n# Complexity\n- Time complexity: $$O(n log n)$$\n Overall complexity is dictated by sorting the unique elements of the queue using the map keys, so it becomes $$O(n log n)$$ where $$n$$ is the number of **unique** elements in the queue. \n\n- Space complexity:$$O(m)$$\n $$m$$ is both the maximum size of the queue and the maximum size of the map if every element is unique (i.e.: there are no repeated elements)\n\n\n# Full Code\n```\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.queue = collections.deque()\n self.count = 0\n self.quantities = {}\n\n def addElement(self, num: int) -> None:\n if self.count >= self.m:\n first = self.queue.popleft()\n self.quantities[first] -= 1\n else:\n self.count += 1\n self.queue.append(num)\n self.quantities[num] = self.quantities[num] + 1 if num in self.quantities else 1\n\n\n \n\n def calculateMKAverage(self) -> int:\n if self.count < self.m:\n return -1\n _list = sorted(self.quantities.keys())\n copy = self.quantities.copy()\n removeLeft = removeRight = self.k\n pointerLeft = 0\n pointerRight = len(_list)-1\n while removeLeft > 0:\n leftmostKey = _list[pointerLeft]\n if copy[leftmostKey] >= removeLeft:\n copy[leftmostKey] -= removeLeft\n removeLeft = 0\n else:\n removeLeft -= copy[leftmostKey]\n copy[leftmostKey] = 0 \n pointerLeft += 1\n \n while removeRight > 0:\n rightmostKey = _list[pointerRight]\n if copy[rightmostKey] >= removeRight:\n copy[rightmostKey] -= removeRight\n removeRight = 0\n else:\n removeRight -= copy[rightmostKey]\n copy[rightmostKey] = 0\n pointerRight -= 1\n \n total_sum = count = 0\n for k in copy:\n total_sum += k*copy[k]\n count += copy[k]\n return math.floor(total_sum/count)\n```\nHope it was clear guys! bye | 7 | 0 | ['Python3'] | 1 |
finding-mk-average | C++ Easy Deque + Ordered Map [Add O(logM) Avg O(K) Space O(M)] | c-easy-deque-ordered-map-add-ologm-avg-o-mcud | Idea\n##### addElement\n- Use a deque to keep track of the last m elements.\n- Use a ordered map to store the m elements in order.\n- Use a varaiable sum to sum | carbonk | NORMAL | 2021-05-19T07:54:58.633229+00:00 | 2021-05-20T01:47:52.892989+00:00 | 350 | false | ### Idea\n##### addElement\n- Use a deque to keep track of the last m elements.\n- Use a ordered map to store the m elements in order.\n- Use a varaiable sum to sum all m elements\n\n#### calculateMKAverage\n- We iterate through the first K and last K elements in ordered map, and subtract them from sum. And calculate the average.\n\n### Time Complexity\nTime:\n- addElement O(logM)\n- calculateMKAverage O(K)\n\nSpace:\n- O(M)\n\n### Code\n```cpp\nclass MKAverage {\npublic:\n MKAverage(int m, int k): m(m), k(k) {\n \n }\n \n void addElement(int num) {\n //O(logN)\n dq.push_back(num);\n mp[num]++;\n sum+=num;\n if(dq.size()>m) {\n //if there are more then m elements, remove the first element.\n //from deque and mp.\n int front = dq.front();\n mp[front]--;\n sum-=front;\n if(mp[front]==0) mp.erase(front);\n dq.pop_front();\n }\n }\n \n int calculateMKAverage() {\n //O(K)\n if(dq.size()<m) return -1;\n long long int temp_sum = sum;\n \n //normal order: remove smallest k number from sum\n int temp_k = k;\n for(auto it = mp.begin(); it!=mp.end(); it++){\n if(temp_k >= it->second){\n temp_sum -= it->first*it->second;\n temp_k-=it->second;\n }\n else{\n temp_sum -= it->first*temp_k;\n break;\n }\n }\n \n //reverse order: remove largest k number from sum\n temp_k = k;\n for(auto it = mp.rbegin(); it!=mp.rend(); it++){\n if(temp_k >= it->second){\n temp_sum -= it->first*it->second;\n temp_k-=it->second;\n }\n else{\n temp_sum -= it->first*temp_k;\n break;\n }\n }\n \n return temp_sum/(m-2*k);\n }\nprivate:\n const int m = 0;\n const int k = 0;\n deque<int> dq; //used for keeping only m elements\n map<int, int> mp; //act as an sorted array\n long long int sum = 0; //the sum of current m numbers.\n};\n``` | 7 | 0 | [] | 2 |
finding-mk-average | Binary Indexed Trees (BIT or Fenwick tree) + Binary lifting (logN Time Complexity) | binary-indexed-trees-bit-or-fenwick-tree-xjnk | ref: https://leetcode-cn.com/circle/article/OeMXPy/\nTwo properties of BIT:\n(1) nodes[i] or sums[i] manages the sum in the range nums[i - i & (-i), i - 1].\ne. | longhun | NORMAL | 2021-04-14T09:06:24.895436+00:00 | 2021-10-04T00:00:48.357012+00:00 | 1,045 | false | ref: https://leetcode-cn.com/circle/article/OeMXPy/\nTwo properties of BIT:\n(1) nodes[i] or sums[i] manages the sum in the range nums[i - i & (-i), i - 1].\ne.g.\nnodes[4] = nums[0] + nums[1] + nums[2] + nums[3]\nnodes[6] = nums[4] + nums[5]\n(2) parent(i) = i + i&(-i)\n\nAssuming we have added nums[0], ..., nums[7] to our tree. \nThe following figure illustrates how BIT works.\n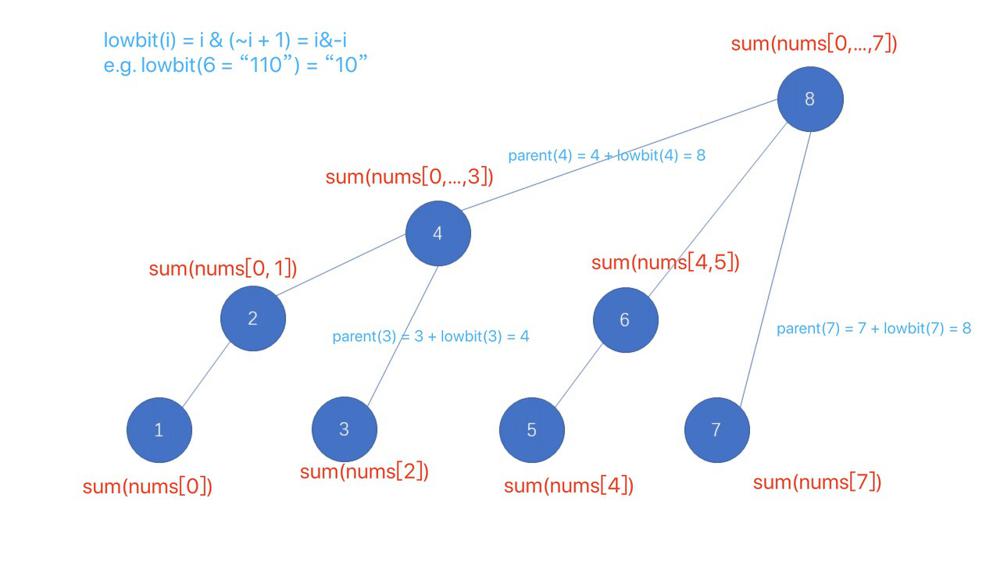\n\nref: https://leetcode.com/problems/finding-mk-average/discuss/1152438/Python3-Fenwick-tree\nref: https://codeforces.com/blog/entry/61364\n[Tutorial] Searching Binary Indexed Tree in O(log(N)) using Binary Lifting\nmake use of binary lifting to achieve O(log(N)) for search_low_boundary\nWhat is binary lifting?\nIn binary lifting, a value is increased (or lifted) by powers of 2,\nstarting with the highest possible power of 2 = 2^\u230Alog(N)\u230B, down to the lowest power, 2^0.\n\nHow binary lifting is used?\nWe are trying to find pos, which is the position of lower bound of v in prefix sums array,\nwhere v is the value we are searching for.\nSo, we initialize pos = 0 and set each bit of pos, from most significant bit to least significant bit.\nWhenever a bit is set to 1, the value of pos increases (or lifts).\nWhile increasing or lifting pos, we make sure that prefix sum till pos should be less than v,\nfor which we maintain the prefix sum and update it whenever we increase or lift pos.\n\n\nTime:\n addElement: O(logN)\n N is the parameter of addElement\n calculateMKAverage: O(logM)\n M is the max_num = 10^5\n search_low_boundary takes O(logM)\n each BinaryIndexTree.query takes O(logM) and there are four queries in total.\nSpace: O(M)\n M is the max_num = 10^5\n \nSimilar Questions:\n307. Range Sum Query - Mutable\n308. Range Sum Query 2D - Mutable\n1619. Mean of Array After Removing Some Elements\n1825. Finding MK Average\n\n\n```\n\nimport math\nfrom collections import deque\n\n\nclass BinaryIndexTree:\n def __init__(self, n: int):\n self.leng = n + 1\n """\n i is the number, nodes[i] = sum(nums[i - i & (-i), i - 1]), \n nums is the original array\n e.g.: https://pic.leetcode-cn.com/755dd21358e8cd6ac39c85bdbaa67188dcf67dad7bd8c32d4ad777c1f376ff08-binaryindexedtreeexpandedtreewithinfo.gif\n """\n self.nodes = [0] * self.leng\n\n def query(self, i: int) -> int:\n """\n i is a number\n return the sum of numbers that is less than or equal to,\n which is equivalent to the sum of logN ranges (\u7B49\u4E8Ei\u4EE3\u8868\u7684logi\u4E2A\u533A\u95F4\u7684\u603B\u548C\u3002)\n """\n ans = 0\n while i:\n ans += self.nodes[i]\n i -= i & -i # remove the lowbit of i\n return ans\n\n def update(self, i: int, delta: int) -> None:\n while i < self.leng:\n self.nodes[i] += delta\n # parent(i) = i + i&(-i), i&(-i) is the lowbit of i,\n # e.g. i = 10, 10 = (1100)2, lowbit(1100_2) = 100_2\n i += i & -i\n\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n """\n Constraints:\n 3 <= m <= 105\n 1 <= k*2 < m\n 1 <= num <= 105\n At most 105 calls will be made to addElement and calculateMKAverage.\n """\n self.max_num = 10 ** 5\n self.m = m\n self.k = k\n # self.queue_len_limit = m - 2 * k\n self.queue = deque([])\n """\n self.value_tree.query(num) = the sum of the number which <= num\n self.count_tree.query(num) = the count of the number which <=num\n """\n self.value_tree = BinaryIndexTree(self.max_num)\n self.count_tree = BinaryIndexTree(self.max_num)\n\n self.remaining_cnt = m - 2 * k\n self.MKAverage = None # avoid repetitive computing for MKAverage\n\n def addElement(self, num: int) -> None:\n self.value_tree.update(num, num)\n self.count_tree.update(num, 1)\n self.queue.append(num)\n if len(self.queue) > self.m:\n removed_num = self.queue.popleft()\n self.value_tree.update(removed_num, -removed_num)\n self.count_tree.update(removed_num, -1)\n\n self.MKAverage = None # avoid recomputing MKAverage if no new number added\n\n def search_low_boundary(self, count: int) -> int:\n """\n search the minimum num that makes self.count_tree.query(num) >= count\n \u5373self.queue\u4E2D\u5C0F\u4E8E\u7B49\u4E8Enum\u7684\u6570\u81F3\u5C11\u6709count\u4E2A\n e.g, input 1,\n self.value_tree.nodes = [0, 1, 3, 3, 10, 5, 11, 7, 36]\n self.count_tree.nodes = [0, 1, 2, 1, 4, 1, 2, 1, 8]\n self.max_num = 8\n i, low_boundary_num, prefix_sum\n 3, 0, 0\n 2, 0, 0\n 1, 2, 2\n 0, 2, 2\n\n low_boundary_num = 2, low_boundary_num + 1 = 3,\n so search_low_boundary(3) = 3 means the minimum num that makes self.count_tree.query(num) >= 3\n """\n # there are prefix_sum numbers that are less than count\n low_boundary_num, prefix_sum = 0, 0\n # self.max_num + 1 \u662Fself.count_tree.sums\u7684\u957F\u5EA6\n for i in range(int(math.log2(self.max_num + 1)), -1, -1):\n low_boundary_num2 = low_boundary_num + (1 << i)\n # print(i, low_boundary_num, prefix_sum, low_boundary_num2)\n\n if low_boundary_num2 <= self.max_num and prefix_sum + self.count_tree.nodes[low_boundary_num2] < count:\n prefix_sum += self.count_tree.nodes[low_boundary_num2]\n low_boundary_num = low_boundary_num2\n\n # +1 because \'low_boundary_num\' will have position of largest value less than \'count\'\n return low_boundary_num + 1\n\n def calculateMKAverage(self) -> int:\n if len(self.queue) < self.m:\n return -1\n if self.MKAverage is not None:\n return self.MKAverage\n low_num, high_num = self.search_low_boundary(self.k), self.search_low_boundary(self.m - self.k)\n num_sum = self.value_tree.query(high_num) - self.value_tree.query(low_num)\n """\n https://leetcode.com/problems/finding-mk-average/discuss/1152438/Python3-Fenwick-tree/903394\n Because probably there are more than k number that is less than or equal to low_num, \n and there are more than m-k number that is less than or equal to high_num, we have to make some adjustments.\n \u5373\u6709\u7684\u6570\u591A\u51CF\u4E86, \u6709\u7684\u6570\u5C11\u51CF\u4E86\u3002\u9700\u8981\u91CD\u65B0\u8C03\u6574\n e.g. m = 6, k = 2, nums = [1,2,2,3,3,4]\n prefix_sum = [0,1,3,5,6] prefix_sum[i] \u8868\u793A <= i\u7684\u6570\u7684\u4E2A\u6570\n k1 = k, k2 = m - k = 4\n -> prefix_sum[lo=2]=3>=k1=2\n -> prefix_sum[hi=3]=5>=k2=4\n -> values_tree.query(hi)-values_tree.query(lo) = sum([1,2,2,3,3]) - sum([1,2,2]) = sum([3,3])\n But the actual solution here is sum([2,3]), we need to remove a 3 and add back a 2.\n """\n num_sum += (self.count_tree.query(low_num) - self.k) * low_num\n num_sum -= (self.count_tree.query(high_num) - (self.m - self.k)) * high_num\n\n # rounded down to the nearest integer\n self.MKAverage = num_sum // self.remaining_cnt\n return self.MKAverage\n```\n | 7 | 0 | [] | 2 |
finding-mk-average | Don't use SortedList in interviews. Three MinMaxHeap. Add: O(logM + log(M-2K)), Calc:O(1). Beats 96% | dont-use-sortedlist-in-interviews-three-9woll | Intuition\n Describe your first thoughts on how to solve this problem. \nIn the inteview, usually we cannot use SortedList which is not in standard libraries. D | four_points | NORMAL | 2024-05-15T16:47:00.906908+00:00 | 2024-05-15T16:53:10.453506+00:00 | 1,387 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn the inteview, usually we cannot use SortedList which is not in standard libraries. Doublecheck your goal, passing interviews or just solving leetcode?\n\n# Approach\nSplit data into 3 parts. And make each part as MinMaxHeap so that we can get pop min/max values by average O(logN).\nMinMaxHeap can be written with lazy deletion.\nCodes are long but must be faily easy.\n\n# Complexity\n- Time complexity:\nAddElement: O(logM + log(M-2K))\nCalculateMKAverage: O(1)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nfrom heapq import heappush, heappop\nfrom collections import deque\nclass MinMaxHeap:\n def __init__(self):\n self.minheap = []\n self.maxheap = []\n self.mindeletings = []\n self.maxdeletings = []\n self.len = 0\n self.sum = 0\n\n def push(self, val):\n heappush(self.minheap, val)\n heappush(self.maxheap, -val)\n self.len += 1\n self.sum += val\n\n def pop_min(self):\n self.balance_min()\n val = heappop(self.minheap)\n \n heappush(self.maxdeletings, -val)\n self.len -= 1\n self.sum -= val\n return val\n\n def pop_max(self):\n self.balance_max()\n val = -heappop(self.maxheap)\n\n heappush(self.mindeletings, val)\n self.len -= 1\n self.sum -= val\n return val\n \n def min(self):\n self.balance_min()\n if len(self.minheap) == 0:\n return 10000000\n return self.minheap[0]\n\n def max(self):\n self.balance_max()\n if len(self.maxheap) == 0:\n return -10000000\n return -self.maxheap[0]\n\n def balance_min(self):\n while len(self.mindeletings) > 0 and self.minheap[0] == self.mindeletings[0]:\n heappop(self.mindeletings)\n heappop(self.minheap)\n \n def balance_max(self):\n while len(self.maxdeletings) > 0 and self.maxheap[0] == self.maxdeletings[0]:\n heappop(self.maxdeletings)\n heappop(self.maxheap)\n\n def delete(self, val): # doesn\'t care if it exits\n heappush(self.mindeletings, val)\n heappush(self.maxdeletings, -val)\n self.len -= 1\n self.sum -= val\n\nclass MKAverage:\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.ar = deque()\n self.p1 = MinMaxHeap()\n self.p2 = MinMaxHeap()\n self.p3 = MinMaxHeap()\n\n def addElement(self, num: int) -> None:\n if len(self.ar) < self.m:\n self.ar.append(num)\n if len(self.ar) == self.m: # initialize\n sorted_ar = sorted(self.ar)\n for i in range(self.m):\n if i < self.k:\n self.p1.push(sorted_ar[i])\n elif i < self.m - self.k:\n self.p2.push(sorted_ar[i])\n else:\n self.p3.push(sorted_ar[i])\n return\n \n # handle ar\n val = self.ar.popleft()\n self.ar.append(num)\n\n # delete from p1, p2, or p3\n if val <= self.p1.max():\n self.p1.delete(val)\n elif val <= self.p2.max():\n self.p2.delete(val)\n else:\n self.p3.delete(val)\n\n # push to p1, p2, or p3\n if num < self.p1.max():\n self.p1.push(num)\n elif num <= self.p2.max():\n self.p2.push(num)\n else:\n self.p3.push(num)\n\n # rebalance\n if self.p1.len > self.k:\n self.p2.push(self.p1.pop_max())\n if self.p3.len > self.k:\n self.p2.push(self.p3.pop_min())\n\n if self.p2.len > self.m - 2 * self.k:\n if self.p1.len < self.k:\n self.p1.push(self.p2.pop_min())\n if self.p3.len < self.k:\n self.p3.push(self.p2.pop_max()) \n\n def calculateMKAverage(self) -> int:\n if len(self.ar) < self.m:\n return -1\n return self.p2.sum // self.p2.len\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 6 | 0 | ['Heap (Priority Queue)', 'Python3'] | 5 |
finding-mk-average | Java TreeSet | Easy to Understand | java-treeset-easy-to-understand-by-mayan-18ax | \nclass MKAverage {\n TreeSet<Long> small, medium, large;\n Queue<Long> queue;\n long sum = 0;\n int m, k, total;\n long ind = 0;\n public MKA | mayank12559 | NORMAL | 2021-04-11T05:04:25.556288+00:00 | 2021-04-11T07:19:59.021625+00:00 | 883 | false | ```\nclass MKAverage {\n TreeSet<Long> small, medium, large;\n Queue<Long> queue;\n long sum = 0;\n int m, k, total;\n long ind = 0;\n public MKAverage(int m, int k) {\n queue = new ArrayDeque();\n small = new TreeSet();\n large = new TreeSet();\n medium = new TreeSet();\n this.m = m;\n this.k = k;\n total = m - 2*k;\n }\n \n // each operation at O(logn)\n public void addElement(int num) {\n ind ++;\n long n = num*1000000L+ind;\n if(queue.size() < m){\n queue.add(n);\n \n //one time operation - O(nlogn)\n if(queue.size() == m){\n List<Long> al = new ArrayList(queue);\n Collections.sort(al);\n for(int i=0;i<k;i++){\n small.add(al.get(i));\n }\n for(int i=k;i<al.size()-k;i++){\n sum += al.get(i);\n medium.add(al.get(i));\n }\n for(int i=al.size()-k;i<al.size();i++){\n large.add(al.get(i));\n }\n }\n }else{\n long val = queue.poll();\n queue.add(n);\n \n long mFirst = medium.first();\n long mLast = medium.last();\n if(medium.contains(val)){\n medium.remove(val);\n sum -= val;\n }else if(small.contains(val)){\n small.remove(val);\n }else{\n large.remove(val);\n }\n \n if(n < mFirst){\n small.add(n);\n }else if(n > mFirst && n < mLast){\n medium.add(n);\n sum += n;\n }else{\n large.add(n);\n }\n \n if(large.size() == k+1){\n long largeFirst = large.first();\n large.remove(largeFirst);\n medium.add(largeFirst);\n sum += largeFirst;\n }\n if(small.size() == k+1){\n long smallLast = small.last();\n small.remove(smallLast);\n medium.add(smallLast);\n sum += smallLast;\n }\n if(small.size() == k-1){\n long mediumFirst = medium.first();\n small.add(mediumFirst);\n medium.remove(mediumFirst);\n sum -= mediumFirst;\n }\n if(large.size() == k-1){\n long mediumLast = medium.last();\n medium.remove(mediumLast);\n large.add(mediumLast);\n sum -= mediumLast;\n }\n }\n }\n \n public int calculateMKAverage() {\n if(queue.size() < m){\n return -1;\n }\n return (int)(sum/(1000000L*total)); \n }\n}\n``` | 6 | 0 | [] | 1 |
finding-mk-average | Simple and easy to understand | simple-and-easy-to-understand-by-sachint-4om0 | Intuition\n1. use List to maintain the order\n2. Use Treemap to maintain the sorted order \n3. In add method check the size and take action accordingly \n4. In | sachintech | NORMAL | 2024-03-08T18:43:40.452320+00:00 | 2024-03-08T18:43:40.452341+00:00 | 389 | false | # Intuition\n1. use List to maintain the order\n2. Use Treemap to maintain the sorted order \n3. In add method check the size and take action accordingly \n4. In calculate method skip first k elament and last k element \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- addElement(int num)= O(log n)\n- calculateMKAverage() = O(m * log n)\n\n- Space complexity:\n- O(m) \n\n# Code\n```\n\nclass MKAverage {\n private int m, k;\n private List<Integer> stream;\n private TreeMap<Integer, Integer> minMap;\n private long sum;\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n this.stream = new ArrayList<>();\n this.minMap = new TreeMap<>(); \n this.sum = 0;\n }\n\n public void addElement(int num) {\n stream.add(num);\n sum +=num;\n minMap.put(num, minMap.getOrDefault(num, 0)+1);\n\n if(stream.size()>m){\n int val = stream.get(0);\n sum -=val;\n \n int count = minMap.get(val);\n if(count==1)\n minMap.remove(val);\n else minMap.put(val,count-1);\n \n stream.remove(0);\n }\n }\n\n\n public int calculateMKAverage() {\n if (stream.size() < m) {\n return -1;\n }\n\n long excludeSum=0;\n\n int counter =0;\n int last = m-k;\n for(int key : minMap.keySet()){\n int count = minMap.get(key);\n while(count>0){\n if(counter<k || counter>=last)\n excludeSum += key;\n count--;\n counter++;\n }\n \n }\n\n return (int) ((sum - excludeSum) / (m - 2 * k));\n }\n\n\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 5 | 0 | ['Java'] | 1 |
finding-mk-average | Python3 Keeping Three Containers For Small/Middle/Large Values (Runtime 98%, Memory 94%) | python3-keeping-three-containers-for-sma-fdoq | Intuition\nSince this data structure deals only with the last m elements from a data stream, it\'s natural to use a deque that only stores the latest m elements | hoyyang | NORMAL | 2023-08-20T20:39:24.189812+00:00 | 2023-08-20T20:39:24.189837+00:00 | 663 | false | # Intuition\nSince this data structure deals only with the last m elements from a data stream, it\'s natural to use a deque that only stores the latest m elements (*self.container*). The first solution I came up was precisely that, as can be seen from the commented data block. \n\nIn that straight-forward approach, whenever a valid "calculateMKAverage" query is sent, we will sort *self.container* ad hoc in order to preserve the order of the data stream from sorting. It\'s pretty obvious why that approach is unfeasible with larger m, as each sort operation is an $$O(m log m)$$ operation. I tried implementing a basic cache that only gets refreshed when the data is changed, and the newly added value does not equal to the removed value. This however is inadequate for this question. It was this tinkering with cache that led me to the solution that I finally came up with\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe use *self.container* to keep track of the data stream order, and use three separate sorted containers (*self.smallest, self.middle, self.largest*) to keep track of the minimum/maximum-k elements, and the m-2k elements in the middle. \nUsing SortedList provides many crucial advantages for our purpose:\n1. The sorted nature of the elements means that add, delete and membership operations benefit from binary search algorithm (which is natively provided by the SortedList). As can be seen on https://grantjenks.com/docs/sortedcontainers/sortedlist.html, add, remove and pop operations only have $$O(log(k))$$ time complexity on SortedList\n2. Because the three containers are separately sorted, moving between smallest/middle and largest/middle becomes very easy: we know that it must happen at their respective ends (for example, when a new added value is smaller than existing values in the smallest container, it will naturally be sorted to take the index of middle[0], and the element that no longer is the smallest would sit at the index of smallest[-1] after we move the new value into the smallest container)\n3. Sorting operations have the average time complexity of $$O(n log n)$$. This means that doing a lump-sum sorting of the entire container will certainly be less efficient than doing three sortings of smaller containers($$max(O(klogk), O((m-2k)log(m-2k))$$). What\'s more, by using SortedList we aren\'t even doing a complete sorting each time! A full sorting only happens when we initialize the three containers, and all subsequent operations involve the adding and deleting of single elements, which are $$O(log(k))$$ operations.\n\nThe other optimization is keeping a running sum instead of calculating the sum of *self.middle* every time when average is queried. With any addition and deletion of element it will only impact the running_sum in 2 ways:\n1. When an element is put in the *self.middle* (either as a new element, or moving from the extremes), we add it to the running sum\n2. When an element is removed from *self.middle* (either directly removed, or moving to the extremes), we subtract it from the running sum.\n\n\nLet\'s break down what happens when a new element(*num*) gets added:\n\n1. When the container has not reached m, we simply appended *num* at the end of *self.container*. If after appending it we have reached the target size of m, we initialize the partition of values into *self.smallest, self.middle, self.largest*, and calculate the initial running sum *self.mid_sum*\n\n2. For any subsequent data stream, it will be pushed onto *self.container*, and the oldest one gets popped. After keeping track of stream order with this deque, we move our attention to how this will impact the three containers (Tip: *smallest[-1] == max(smallest), largest[0] == min(largest)*):\n- If both the popped element and the added element belong to the middle container, we don\'t have to worry about anything else: we delete the old value and add the new value to our running sum\n- If the popped element is from the middle, and the added element goes to the extremes, we will check where it will actually go to (*num_small = num<= self.smallest[-1]*). Remember, since only the k number of extreme values get discarded, after adding a new element it will now contain k+1 elements, with the one at their respective end (*max(smallest) and min(largest)*) disqualified and moved back to the middle. We then adjust the running sum based on which one moved into and which one moved out of the midle\n- If the popped element is from the extremes, we will first put the new element in the middle, and move min(middle) or max(middle) to the side the of extreme that has its element just popped. **And here\'s a pitfall: the new value can potentially update the other extreme.** Here\'s the debugging log when you didn\'t check for that: As you can see, we didn\'t check if 64938 can update the largest, resulting in 64938 incorrectly placed in the middle.\n\n```\nSortedList([8272]) SortedList([15456]) SortedList([33433])\nContainer before adding: deque([8272, 33433, 15456])\nPopped: 8272 Num: 64938\nSortedList([15456]) SortedList([64938]) SortedList([33433])\n\n```\n\n- Solving the above mentioned bug is easy: it doesn\'t hurt if we simply try to update the other extreme by moving the potential update candidate there, and pulling back the disqualified one! If the new value doesn\'t update it, nothing happens since they\'ll be pulled back, but if it does, then it will correctly update it.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(log k)$$ for *addElement* since each time it only involves a handful of operations involving adding and removing values from three SortedList.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m)$$, since we store a m-sized deque and a partition of that deque, with total size of 2m\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# from collections import deque\n\n\n# class MKAverage:\n# container = None\n# m = None\n# k = None\n# cached = None\n# def __init__(self, m: int, k: int):\n# self.container = deque()\n# self.m = m\n# self.k = k\n# self.cached = None\n\n# def addElement(self, num: int) -> None:\n# popped = None\n# if len(self.container) < self.m:\n# self.container.append(num)\n# else:\n# popped = self.container.popleft()\n# self.container.append(num)\n# if popped != num:\n# self.cached = None\n\n# def calculateMKAverage(self) -> int:\n# if len(self.container) < self.m:\n# return -1\n# if self.cached is not None:\n# return self.cached\n# m = self.m\n# k = self.k\n# self.cached = int(sum(sorted(self.container)[k:m-k])/(m-2*k))\n# return self.cached\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n\n\nfrom collections import deque\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n\n def __init__(self, m: int, k: int):\n self.smallest = SortedList()\n self.middle = SortedList()\n self.largest = SortedList()\n self.container = deque()\n self.mid_sum = None\n self.m = m\n self.k = k\n \n \n\n def addElement(self, num: int) -> None:\n if len(self.container) < self.m:\n self.container.append(num)\n if len(self.container) == self.m:\n #initializing partition when first filled\n sorted_result = sorted(self.container)\n self.smallest = SortedList(sorted_result[:self.k])\n self.middle = SortedList(sorted_result[self.k:self.m-self.k])\n self.largest = SortedList(sorted_result[-self.k:])\n self.mid_sum = sum(self.middle)\n else:\n #print ("Container before adding:", self.container)\n popped = self.container.popleft()\n self.container.append(num)\n #print ("Popped:", popped, "Num:", num)\n # if popped from middle and added to middle, don\'t worry about anything\n if self.smallest[-1]<popped<self.largest[0] and self.smallest[-1]<num<self.largest[0]:\n self.mid_sum+=num-popped\n self.middle.add(num)\n self.middle.remove(popped)\n\n \n # if popped from the middle and added to the extremes, update corresponding container\n elif self.smallest[-1]<popped<self.largest[0]:\n self.middle.remove(popped)\n # where should num go\n num_small = num<= self.smallest[-1]\n if num_small:\n self.smallest.add(num)\n # element that moved to the middle\n moved = self.smallest.pop()\n else:\n self.largest.add(num)\n # element that moved to the middle\n moved = self.largest.pop(0)\n self.middle.add(moved)\n self.mid_sum += moved-popped\n \n # if popped from the extremes, first putting the new number in the middle, then move\n # popped from smallest\n elif popped<= self.smallest[-1]:\n self.smallest.remove(popped)\n self.middle.add(num)\n # smallest in the middle moved to smallest container\n moved = self.middle.pop(0)\n self.smallest.add(moved)\n # First adding num to middle, then moving moved from middle\n self.mid_sum += num-moved\n # Updating the largest container\n # moving max(middle) to largest\n moved = self.middle.pop()\n self.mid_sum -= moved\n self.largest.add(moved)\n # moving min(largest) to middle\n moved = self.largest.pop(0)\n self.mid_sum += moved\n self.middle.add(moved)\n \n elif popped>= self.largest[0]:\n self.largest.remove(popped)\n self.middle.add(num)\n # largest in the middle moved to largest container\n moved = self.middle.pop()\n self.largest.add(moved)\n # First adding num to middle, then moving moved from middle\n self.mid_sum += num-moved\n # Updating the smallest container\n # moving min(middle) to smallest\n moved = self.middle.pop(0)\n self.mid_sum -= moved\n self.smallest.add(moved)\n # moving max(smallest) to middle\n moved = self.smallest.pop()\n self.mid_sum += moved\n self.middle.add(moved)\n\n \n #print (self.smallest, self.middle, self.largest)\n\n def calculateMKAverage(self) -> int:\n if len(self.container) < self.m:\n return -1\n return self.mid_sum // (self.m - 2* self.k)\n``` | 5 | 0 | ['Python3'] | 1 |
finding-mk-average | [Python3] 1-SortedList + Queue with a thought process. | python3-1-sortedlist-queue-with-a-though-2zam | Intuition\n To manage current m values, we can use a queue.\n But if we sort and count the middle sum on every insertion, A single Insertion will take O(MlogM) | asayu123 | NORMAL | 2022-11-08T06:14:45.990291+00:00 | 2022-11-08T06:32:46.861819+00:00 | 504 | false | **Intuition**\n* To manage current m values, we can use a queue.\n* But if we sort and count the middle sum on every insertion, A single Insertion will take O(MlogM) time, O(TM log M) as total where M is the number of elements in the window, T is the total stream elements. \n\n* So we can use the following ideas.\n\t* Idea1: Use TreeSet to keep M elements sorted.\n\t* Idea2: Incrementally update the middle value\'s sum rather than scanning multiple elements every time.\n\n**Algorithm**\n* The key part is how we can incrementally update the middle sum. We can divide the sorted list into 3 partitions like the following.\n```\n # Array: [A | B | C] \n\t\t# : A -> k-smallest values. B -> middle values. C-> k-largest values.\n\t\t# Index range\n\t\t# [0..k-1 | k ... m-k-1 | m-k .. m-1]\n```\n\n* And when we remove staled element from the sorted list, there are 3 possible patterns.\n\n```\n# If we remove element from C -> that does not affect the middle sum.\n# from B -> we lose that value, C\'s left most value become B\'s right most value so add that value to the middle sum.\n# from A -> we lose B\'s leftmost value and obtain C\'s leftmost value to the middle sum, since they are pushed to left.\n```\n\n* Then when we add a new value to the sorted list, there are also 3 possible patterns.\n\n```\n# If we insert element to C -> that does not affect the middle sum.\n# B -> we need to add that value, and lost B\'s rightmost value since it will be pushed to C.\n# A -> we need to add A\'s rightmost value to the middle sum and subtract B\'s rightmost value from the middle sum since they are pushed to right.\n```\n\n* An edge case you need to consider is that the sorted list contains multiple possible values. We need to use the same rule between insertion/deletion, for now, I use bisect_right method so that we can always manipulate the rightmost value.\n\n* When we remove/add elements to sorted list, we can update the middle sum based on its deletion/insertion index.\n\n**Code Example**\n```\nfrom sortedcontainers import SortedList\nfrom collections import deque\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.middleSum = 0\n self.queue = deque()\n self.sortedValues = SortedList()\n self.m = m\n self.k = k \n\n def addElement(self, num: int) -> None: # Total O(mlogm)\n # [A | B | C]\n # [0..k-1 | k m-k-1 | m-k .. m-1]\n # A -> k-smallest B-> middle C-> k-largest\n\n if len(self.queue) < self.m: \n self.queue.append(num)\n self.sortedValues.add(num)\n\t\t # This initialization will be triggered only once when the queue size become m-1 to m.\n if len(self.queue) == self.m: # O(mlogm) for initialization.\n self.middleSum = sum(self.sortedValues[self.k:(self.m - self.k)])\n return\n \n # After the queue size become m, each Operation cost is O(logm)\n remove_val = self.queue.popleft()\n \n # Phase1: Remove\n removal_idx = self.sortedValues.bisect_right(remove_val) - 1 # pick right most element.\n if removal_idx < self.k: # on A\n self.middleSum -= self.sortedValues[self.k] # leftmost B\n self.middleSum += self.sortedValues[self.m - self.k] # leftmost C\n elif removal_idx > self.m - self.k - 1: # on C\n pass\n else: # on B\n self.middleSum -= remove_val\n self.middleSum += self.sortedValues[self.m - self.k] # leftmost C\n \n self.sortedValues.remove(remove_val)\n \n # Phase2: Insert\n self.queue.append(num)\n \n insertion_idx = self.sortedValues.bisect_right(num)\n if insertion_idx < self.k: # on A\n self.middleSum += self.sortedValues[self.k - 1] # rightmost A\n self.middleSum -= self.sortedValues[self.m - self.k - 1] # rightmost B\n elif insertion_idx > self.m - self.k - 1: # on C\n pass\n else: # on B\n self.middleSum += num\n self.middleSum -= self.sortedValues[self.m - self.k - 1] # rightmost B\n \n self.sortedValues.add(num) \n\n def calculateMKAverage(self) -> int: # O(1)\n if len(self.queue) < self.m:\n return -1\n return self.middleSum // (self.m - (2 * self.k))\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n```\n\n**Complexity Analysis**\n\nTime:\n* Total O(TlogM) # T = Total elements in a stream. M = Total elements in a window.\n\t* Initialization: O(MlogM)\n\t* Insertion: O(logM)\n\t* Query: O(1)\n\nMemory:\n* O(M) for queue / sorted list\n\n**Runtime History**\n* Runtime: 3212 ms, faster than 48.67% of Python3 online submissions for Finding MK Average.\n* Memory Usage: 49.6 MB, less than 74.34% of Python3 online submissions for Finding MK Average.\n\n\n\n\n | 5 | 0 | ['Queue', 'Python3'] | 0 |
finding-mk-average | Python3 simple solution | python3-simple-solution-by-mnikitin-uebx | \nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.values = [0] * m\n self.m = m\n self.k = k\n self.idx = 0\n\n | mnikitin | NORMAL | 2021-04-11T04:01:23.443245+00:00 | 2021-04-11T04:04:48.105554+00:00 | 397 | false | ```\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.values = [0] * m\n self.m = m\n self.k = k\n self.idx = 0\n\n def addElement(self, num: int) -> None:\n self.values[self.idx % self.m] = num\n self.idx += 1\n\n def calculateMKAverage(self) -> int:\n if self.idx < self.m:\n return -1\n values = sorted(self.values)[self.k : -self.k]\n return int(sum(values) / len(values))\n``` | 5 | 5 | [] | 5 |
finding-mk-average | Easy to Understand With Examples using Three TreeSet | easy-to-understand-with-examples-using-t-vwob | Intuition\n\nLet\'s walk through the intuition behind this solution with a concrete example. Suppose we\'re given m = 5 and k = 1, and we start receiving a stre | najimali | NORMAL | 2024-04-08T15:50:08.992380+00:00 | 2024-04-08T15:50:08.992408+00:00 | 405 | false | # Intuition\n\nLet\'s walk through the intuition behind this solution with a concrete example. Suppose we\'re given `m = 5` and `k = 1`, and we start receiving a stream of integers.\n\n### Initial Stream: `[3, 1, 10, 7, 2]`\n\n- Our objective is to calculate the MKAverage for the last `m = 5` elements in the stream, after removing the smallest `k = 1` and largest `k = 1` elements.\n\n#### Step 1: Add Elements to the Stream\n- As elements `3, 1, 10, 7, 2` are added to the stream, they\'re also added to the `middles` set since we haven\'t reached `m` elements yet.\n\n#### Step 2: Calculate MKAverage\n- Once we reach `m` elements, we calculate the MKAverage:\n 1. Remove the smallest `k` and largest `k` elements: remove `1` and `10`.\n 2. Calculate the average of the remaining: `(3 + 7 + 2) / 3 = 4`.\n\n### Adding Another Element: Stream becomes `[3, 1, 10, 7, 2, 5]`\n- Now, we exceed `m` elements. The oldest element (`3`) must be considered for removal.\n\n#### Handling the New Element\n- The new element `5` is added, and we need to maintain our sets according to the rules:\n 1. **If adding to `middles` directly:** We ensure the sets `smaller` and `larger` are properly populated with the smallest and largest `k` elements, respectively.\n 2. **Adjustment:** Since `3` (the oldest) is removed, we check where it belonged (in this case, it was part of `middles`). We then adjust the sets to ensure they still contain correct elements. In this scenario, we might find no need to adjust since `5` fits into `middles` directly.\n \n#### Recalculate MKAverage\n- Now, the stream considered for MKAverage is `[1, 10, 7, 2, 5]`.\n 1. Remove smallest `k=1` (`1`) and largest `k=1` (`10`).\n 2. Calculate the average of `[7, 2, 5]`: `(7 + 2 + 5) / 3 = 4.66`, rounded down to `4`.\n\n### Why This Works\n- **Efficiency:** This approach avoids recalculating from scratch for each new element or MKAverage calculation. By maintaining the sets, we can quickly adjust to new elements and efficiently calculate the MKAverage.\n- **Dynamic Adjustments:** As new elements come in, we dynamically adjust which elements belong in the smallest, middle, and largest sets. This flexibility ensures we always have the correct elements for calculating the MKAverage, even as the stream changes.\n\nThis example highlights how we manage a stream of data in an efficient and dynamic manner, allowing for quick updates and calculations without needing to sort or fully re-evaluate the data set with each new element or calculation request.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe solution uses three instances of a custom MultiSet class to manage the smallest, middle, and largest elements and their sums. The MultiSet class uses a TreeSet to maintain sorted order of elements, allowing for efficient retrieval and removal of the smallest and largest elements. This class also tracks the sum of the elements it contains, which is crucial for calculating the average.\n\n**Initialization**: When an MKAverage object is created, the sizes of the three multisets are initialized based on the given m and k. The queue holds the last m elements of the stream.\n\n**Adding an Element**: Each new element is added to a queue to ensure we only consider the last m elements and to the middles set initially. If the queue exceeds m elements, the oldest element is removed, and adjustments are made among the three multisets to maintain their size constraints and sort order. This involves moving elements between the sets based on their values to ensure smaller and larger always contain the smallest and largest k elements, respectively.\n\n**Calculating MKAverage**: If there are fewer than m elements in the stream, the method returns -1. Otherwise, the MKAverage is calculated by dividing the sum of the middles set by its size (which is m - 2k).\n\n# Complexity\n- Time Compexity - O(logM)\n\n- Space complexity: - O(M)\n\n\n# Code\n```\nclass MKAverage {\n Queue<Node> queue = new LinkedList<>();\n int containerSize = 0;\n MultiSet smaller = new MultiSet();\n MultiSet middles = new MultiSet();\n MultiSet larger = new MultiSet();\n int index = 0;\n \n public MKAverage(int m, int k) {\n this.index = 0;\n this.containerSize = m;\n queue.clear();\n\n smaller.clear();\n smaller.setMaxSize(k);\n \n larger.clear();\n larger.setMaxSize(k);\n \n middles.clear();\n middles.setMaxSize(k);\n }\n\n public void addElement(int num) {\n Node newNode = new Node(num,index++);\n queue.add(newNode);\n middles.add(newNode);\n if(queue.size() < containerSize) return;\n if(queue.size() == containerSize){\n while(smaller.size() < smaller.getMaxSize()){\n smaller.add(middles.pollFirst());\n }\n while(larger.size() < larger.getMaxSize()){\n larger.add(middles.pollLast());\n }\n return;\n }\n \n Node lastNode = queue.poll();\n if(smaller.contains(lastNode)){\n smaller.remove(lastNode);\n smaller.add(middles.pollFirst());\n } else if(larger.contains(lastNode)){\n larger.remove(lastNode);\n larger.add(middles.pollLast());\n } else middles.remove(lastNode);\n\n if(smaller.lastValue() > middles.firstValue()){\n smaller.add(middles.pollFirst());\n middles.add(smaller.pollLast());\n } else if(larger.firstValue() < middles.lastValue()){\n larger.add(middles.pollLast());\n middles.add(larger.pollFirst());\n }\n }\n void print(){\n System.out.println("smaller "+ smaller);\n System.out.println("middles "+ middles);\n System.out.println("larger "+ larger);\n System.out.println();\n }\n public int calculateMKAverage() {\n if(queue.size() < containerSize) return -1;\n int deno = containerSize - (2 * smaller.getMaxSize());\n return middles.getSum()/deno;\n }\n\n}\nclass Node {\n int val;\n int index;\n Node(int val, int index) {\n this.val = val;\n this.index = index;\n }\n @Override\n public String toString(){\n return val +" -> "+index;\n }\n }\nclass MultiSet{\n private int sum;\n private int maxSize;\n private TreeSet<Node> set;\n\n MultiSet(){\n sum = 0;\n set = new TreeSet<Node>((first, second) -> {\n if(first.val == second.val) return first.index - second.index;\n return first.val - second.val;\n });\n }\n void setMaxSize(int maxSize){\n this.maxSize = maxSize;\n }\n int getMaxSize(){\n return maxSize;\n }\n void clear(){\n set.clear();\n }\n int lastValue(){\n return set.last().val;\n }\n int firstValue(){\n return set.first().val;\n }\n void add(Node node){\n sum+=node.val;\n set.add(node);\n }\n void remove(Node node){\n sum-=node.val;\n set.remove(node);\n }\n Node pollFirst(){\n Node node = set.pollFirst();\n sum-=node.val;\n return node;\n }\n Node pollLast(){\n Node node = set.pollLast();\n sum-=node.val;\n return node;\n }\n int getSum(){\n return sum;\n }\n int size(){\n return set.size();\n }\n boolean contains(Node node){\n return set.contains(node);\n }\n\n @Override\n public String toString(){\n return set.toString();\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
finding-mk-average | Solution using BST. Easy to understand | solution-using-bst-easy-to-understand-by-6vlp | Intuition\nUse BST as we are keeping track of sorted items. \n\n# Approach\nThere can be multiple approaches to solve this problem. Let me describe three approa | patel_manish | NORMAL | 2023-12-04T10:09:03.532851+00:00 | 2023-12-04T10:09:03.532885+00:00 | 405 | false | # Intuition\nUse BST as we are keeping track of sorted items. \n\n# Approach\nThere can be multiple approaches to solve this problem. Let me describe three approaches (note that first two approaches lead to TLE here):\n\n1. Brute force: We can do exactly as the problem says. Maintain a list of all elements. When an add operation comes, append to the list. When a get avg operation comes, slice out last "m" elements, sort the m elements, slice out m-2k elements from middle and return the average of this m-2k elements.\n\nTime complexity of this approach:\nFor One Add: O(1)\nFor One Get: O( m + m log m + (m-2k) ) = O( mlog m)\n\n2. Use two hashmaps: Instead of sorting m elements and slicing out m-2k elements we can maintain sliding window of last m elements using a queue. When adding a new element if the queue size becomes greater than m remove the leftmost element from queue. When calculating the average, construct a min-heap and max-heap of size k and keep track of cumulative sum of these m elements. Then sum of m-2k elements = cumulative_sum-(sum of elements from min heap) - (sum of elements from max heap)\n\nTime complexity:\nOne Get: O( m log k)\n\n3. Use BST: Since we need a sorted list of m elements, we can use a BST for it. For Add operation, add the new element to BST and remove the first element that went out of sliding window of size m. \n\nFor Get operation, get the middle m-2k elements and return the average. However if you do this naively you will get TLE. Instead keep a track of cumulative sum and subtract the sum of k elements from this cumulative sum and then get the average\n\nTC : \nOne Add: (log m)\nOne Get: O(k)\n\n```\nimport sortedcontainers\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.all_elements = []\n self.bst = sortedcontainers.SortedList()\n self.m = m\n self.k = k\n self.m_sum = 0\n\n def addElement(self, num: int) -> None:\n self.all_elements.append(num)\n self.m_sum += num\n self.bst.add(num)\n if len(self.bst) == self.m+1:\n self.bst.remove(self.all_elements[-(self.m+1)])\n self.m_sum -= self.all_elements[-(self.m+1)]\n \n \n\n def calculateMKAverage(self) -> int:\n if len(self.all_elements) < self.m:\n return -1\n min_sum = sum(self.bst[:self.k])\n max_sum = sum(self.bst[-self.k:])\n return (self.m_sum-min_sum-max_sum) // (self.m-2*self.k)\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 4 | 0 | ['Python3'] | 1 |
finding-mk-average | My Intuitive C++ Solution, to solve most of streaming data Problem | my-intuitive-c-solution-to-solve-most-of-v7m1 | Intuition\n Describe your first thoughts on how to solve this problem. \nIf you have solved other streaming data related problem. You can build this solution ba | khalid007 | NORMAL | 2023-09-02T13:41:14.839036+00:00 | 2023-09-02T14:18:51.522108+00:00 | 636 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf you have solved other streaming data related problem. You can build this solution based on the solution of other similar problems. One such problem is median in a streaming data. \n\n# Approach\nFor this you have to keep in mind few things : \n\n1. Queue maintaining order of inputs, so that when the size of queue is m, you can easily remove the stale value.\n2. Maintain three multiset to track the lowest K, top K and mid elements.\n3. Balance the sizes of each multiset at every insertion.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(log(m))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MKAverage {\n int total;\n int m;\n int k;\n queue<int> recentData;\n multiset<int, greater<int>> smallestK;\n multiset<int> greatestK;\n multiset<int> midElements;\n long midSum;\npublic:\n MKAverage(int m, int k) {\n total = 0;\n this->m = m;\n this->k = k;\n midSum = 0;\n }\n\n // 1. < k elements;\n // 2. > k & < 2k elements;\n // 3. > 2k & < m elements;\n // 4. > m elements;\n void addElement(int num) {\n // If we have already m data in queue then remove the stale data\n if(total == m) {\n int stale = recentData.front();\n\n recentData.pop();\n recentData.push(num);\n\n // Remove the stale value from the appropriate set containing the value\n if(greatestK.find(stale) != greatestK.end()) {\n greatestK.erase(greatestK.find(stale));\n }\n else if(smallestK.find(stale) != smallestK.end()) {\n smallestK.erase(smallestK.find(stale));\n }\n else {\n // If the value in middle set, update midSum\n midElements.erase(midElements.find(stale));\n midSum -= stale;\n }\n total--;\n }\n else {\n recentData.push(num);\n }\n\n\n if(total < k) {\n greatestK.insert(num);\n }\n else if(total < 2*k) {\n greatestK.insert(num);\n int smaller = *greatestK.begin();\n smallestK.insert(smaller);\n greatestK.erase(greatestK.begin());\n }\n else if(total < m) {\n // Insert from Greater to Smaller\n greatestK.insert(num);\n int smaller = *greatestK.begin();\n greatestK.erase(greatestK.begin());\n midElements.insert(smaller);\n\n // Add smaller value of top k to midSum\n midSum += smaller;\n smaller = *midElements.begin();\n midElements.erase(midElements.begin());\n // Remove the smaller value of mid elements to midSum\n midSum -= smaller;\n smallestK.insert(smaller);\n\n // Now Balance the size\n if(smallestK.size() > k) {\n int greater = *smallestK.begin();\n smallestK.erase(smallestK.begin());\n\n midElements.insert(greater);\n midSum += greater;\n\n if(midElements.size() > m - 2*k) {\n auto ptr = midElements.end();\n greater = *(--ptr);\n midElements.erase(ptr);\n midSum -= greater;\n greatestK.insert(greater);\n }\n }\n }\n\n total++;\n }\n \n int calculateMKAverage() {\n if(total < m) {\n return -1;\n }\n else {\n return midSum/(m-2*k);\n }\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 4 | 0 | ['Queue', 'Heap (Priority Queue)', 'Data Stream', 'Ordered Set', 'C++'] | 0 |
finding-mk-average | JAVA EASY SOLUTION || TREEMAP || QUEUE | java-easy-solution-treemap-queue-by-anik-td25 | \nclass MKAverage {\n\n int sum,total,m,k;\n\n TreeMap<Integer,Integer> map=new TreeMap<>();\n Queue<Integer> queue=new LinkedList<>();\n public MKAve | aniket7419 | NORMAL | 2022-02-03T07:59:52.873856+00:00 | 2022-02-03T07:59:52.873901+00:00 | 302 | false | ```\nclass MKAverage {\n\n int sum,total,m,k;\n\n TreeMap<Integer,Integer> map=new TreeMap<>();\n Queue<Integer> queue=new LinkedList<>();\n public MKAverage(int m, int k) {\n\n this.m=m;\n this.k=k;\n }\n\n public void addElement(int num) {\n\n total++;\n sum+=num;\n queue.add(num);\n map.put(num,map.getOrDefault(num,0)+1);\n if (total>m){\n total--;\n int first=queue.poll();\n sum-=first;\n if (map.get(first)==1)\n map.remove(first);\n else map.put(first,map.get(first)-1);\n\n }\n\n\n }\n\n public int calculateMKAverage() {\n\n if (total<m) return -1;\n\n int count=k;\n int temp_sum=sum;\n for (Map.Entry<Integer,Integer> entry:map.entrySet()){\n if (count==0) break;\n int val=entry.getValue();\n int key=entry.getKey();\n int min=Math.min(count,val);\n count-=min;\n temp_sum-=min*key;\n\n }\n count=k;\n for (Map.Entry<Integer,Integer> entry:map.descendingMap().entrySet()){\n if (count==0) break;\n int val=entry.getValue();\n int key=entry.getKey();\n int min=Math.min(count,val);\n count-=min;\n temp_sum-=min*key;\n }\n\n\n return temp_sum/(m-2*k);\n }\n}\n``` | 4 | 0 | [] | 1 |
finding-mk-average | Clean Solution using three TreeMaps | Easy to understand | clean-solution-using-three-treemaps-easy-so9h | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kesarwaniankit4812 | NORMAL | 2024-04-15T19:26:12.550348+00:00 | 2024-04-15T19:26:12.550404+00:00 | 842 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n$$O(log(n))$$ for *addElement*\n$$O(1)$$ for *calculateMKAverage*\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MKAverage {\n \n int m;\n int k;\n TreeMap<Integer, Integer> lowBucket;\n TreeMap<Integer, Integer> midBucket;\n TreeMap<Integer, Integer> highBucket;\n int midBucketSum;\n int lowBucketSize;\n int highBucketSize;\n\n Deque<Integer> stream = new ArrayDeque<>();\n\n public MKAverage(int m, int k) {\n lowBucket = new TreeMap<>();\n midBucket = new TreeMap<>();\n highBucket = new TreeMap<>();\n\n midBucketSum = 0;\n lowBucketSize = 0;\n highBucketSize = 0;\n\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n if (lowBucket.isEmpty() || num <= lowBucket.lastKey()) {\n lowBucket.merge(num, 1, Integer::sum);\n lowBucketSize++;\n } else if (highBucket.isEmpty() || num >= highBucket.firstKey()) {\n highBucket.merge(num, 1, Integer::sum);\n highBucketSize++;\n } else {\n midBucket.merge(num, 1, Integer::sum);\n midBucketSum += num;\n }\n\n stream.offer(num);\n\n if (stream.size() > m) {\n int oldestNum = stream.poll();\n\n if (lowBucket.containsKey(oldestNum)) {\n if (lowBucket.merge(oldestNum, -1, Integer::sum) == 0) {\n lowBucket.remove(oldestNum);\n }\n lowBucketSize--;\n } else if (highBucket.containsKey(oldestNum)) {\n if (highBucket.merge(oldestNum, -1, Integer::sum) == 0) {\n highBucket.remove(oldestNum);\n }\n highBucketSize--;\n } else {\n if (midBucket.merge(oldestNum, -1, Integer::sum) == 0) {\n midBucket.remove(oldestNum);\n }\n midBucketSum -= oldestNum;\n }\n }\n\n balanceBucket();\n }\n \n public int calculateMKAverage() {\n if (stream.size() < m) {\n return -1;\n }\n\n return (int) (midBucketSum / (m - 2 * k));\n }\n\n private void balanceBucket() {\n // Move element from low to middle\n while (lowBucketSize > k) {\n int element = lowBucket.lastKey();\n if (lowBucket.merge(element, -1, Integer::sum) == 0) {\n lowBucket.remove(element);\n }\n\n midBucket.merge(element, 1, Integer::sum);\n midBucketSum += element;\n\n lowBucketSize--;\n }\n\n // Move element from high to middle\n while (highBucketSize > k) {\n int element = highBucket.firstKey();\n if (highBucket.merge(element, -1, Integer::sum) == 0) {\n highBucket.remove(element);\n }\n\n midBucket.merge(element, 1, Integer::sum);\n midBucketSum += element;\n\n highBucketSize--;\n }\n\n // Move element from middle to low\n while (lowBucketSize < k && !midBucket.isEmpty()) {\n int element = midBucket.firstKey();\n if (midBucket.merge(element, -1, Integer::sum) == 0) {\n midBucket.remove(element);\n }\n midBucketSum -= element;\n\n lowBucket.merge(element, 1, Integer::sum);\n lowBucketSize++;\n }\n\n // Move element from middle to high\n while (highBucketSize < k && !midBucket.isEmpty()) {\n int element = midBucket.lastKey();\n if (midBucket.merge(element, -1, Integer::sum) == 0) {\n midBucket.remove(element);\n }\n midBucketSum -= element;\n\n highBucket.merge(element, 1, Integer::sum);\n highBucketSize++;\n }\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 3 | 0 | ['Java'] | 0 |
finding-mk-average | C++ Solution Using Only 1 Multiset | c-solution-using-only-1-multiset-by-sequ-i9my | Intuition\nmost solutions use 3 multisets, but actually 1 is enough.\n\nBasically we need a queue of size m to support the sliding window. We also want the elem | sequoia18 | NORMAL | 2024-01-14T21:34:24.375248+00:00 | 2024-08-11T12:42:37.803466+00:00 | 445 | false | # Intuition\nmost solutions use 3 multisets, but actually 1 is enough.\n\nBasically we need a queue of size `m` to support the sliding window. We also want the elements inside the window to be sorted so that we can get the middle elements. To support this, We use another multiset (C++ STL\'s implementation of binary search tree) to maintain the queue elements\' order.\n\n# Approach\n\nFirst trick is that we store the multiset\'s iterator in the queue so that we can remove an element both from the queue and multiset easily.\n\nSecond trick is that we store the `start` and `end` iterator of the multiset pointing to the `k`th and `n-k`th (0-indexed) element of the sliding window. We always keep this invariant by updating `start` and `end` when we insert/delete from the sliding window.\n\nThe hard part is how to update `start` and `end` correctly. Imaging the follwing sorted list represented by the multiset (m = 10, k = 2)\n\n```\n[1,2,2,3,4,5,5,6]\n ^ ^\n start end\n```\n\nIf there are elements of same value in the sorted list, c++ multiset guaranteeds to insert the new element to the end of the range. So if a 5 is to be inserted, it will be inserted after the last 5 (the 5 right before 6). c++ multiset also guarantees that the first element in the range of same values will be removed when we delete. E.g. if we remove 5 from the sliding window, it is the first 5 (the 5 right after 4) that is to be removed. This helps produce the following update logic:\n\n- when insert: we move `start` left if `num < *start`, we move `end` right if `num >= *end`\n- when delete: we move `start` right if `num <= *start`. The tricky part is in `end`, in addition to move `end` left when `num > *end`, we also have to move `end` left if `num == *end` and `end` points to the first number in the range (when we delete 5 in the case above).\n\nFinally we keep and update the sum of middle elements in each `addElement` to make `calculateMKAverage` constant time.\n\n\n# Complexity\n\n- Time complexity: `addElement` $$O(log(m))$$, `calculateMKAverage` $$O(1)$$\n- Space complexity: $$O(m)$$\n\n\n# Code\n\n```\nclass MKAverage {\n multiset<int> mset_;\n multiset<int>::iterator start_, end_;\n long long total_ = 0;\n\n queue<multiset<int>::iterator> que_;\n\n int m_, k_;\npublic:\n MKAverage(int m, int k) {\n m_ = m;\n k_ = k;\n }\n \n void addElement(int num) {\n auto it = mset_.insert(num);\n que_.push(it);\n if (que_.size() <= 2 * k_) {\n return;\n }\n // first time reaching 2k + 1 elements, initialize start,\n // end and total\n if (que_.size() == 2 * k_ + 1) {\n start_ = mset_.begin();\n for (int i = 0; i < k_; ++i) {\n ++start_;\n }\n end_ = start_;\n total_ = *start_;\n return;\n }\n // push, keep the invariant that start and end point to\n // the kth and (n-k)th elements\n if (num < *start_) {\n total_ += *(--start_);\n } else if (num >= *end_) {\n total_ += *(++end_);\n } else {\n total_ += num;\n }\n // pop, keep the invariant as well, special logic for end\n if (que_.size() > m_) {\n auto remove = que_.front();\n if (*remove <= *start_) {\n total_ -= *(start_++);\n } else if (*remove > *end_ || remove == end_) {\n total_ -= *(end_--);\n } else {\n total_ -= *remove;\n }\n mset_.erase(que_.front());\n que_.pop();\n }\n }\n \n int calculateMKAverage() {\n return que_.size() < m_ ? -1 : total_ / (m_ - 2 * k_); \n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 3 | 0 | ['C++'] | 2 |
finding-mk-average | [C++] Modular Code With 3 Maps | O(Log(N)) Time | c-modular-code-with-3-maps-ologn-time-by-zsyv | \n/* \n Time: addElement: O(logm) | calculateMKAverage: O(1)\n Space: O(m)\n Tag: TreeMap, Sorting, Queue\n Difficulty: H\n*/\n\nclass MKAverage {\n | meKabhi | NORMAL | 2022-07-06T22:42:00.887535+00:00 | 2022-07-06T22:42:00.887563+00:00 | 871 | false | ```\n/* \n Time: addElement: O(logm) | calculateMKAverage: O(1)\n Space: O(m)\n Tag: TreeMap, Sorting, Queue\n Difficulty: H\n*/\n\nclass MKAverage {\n map<int, int> left, middle, right;\n queue<int> q;\n int sizeofLeft, sizeofMiddle, sizeofRight;\n int k;\n long long mkSum;\n int m;\n\n void addToSet1(int num) {\n left[num]++;\n sizeofLeft++;\n }\n\n void deleteFromSet1(int num) {\n left[num]--;\n if (left[num] == 0) left.erase(num);\n sizeofLeft--;\n }\n\n void addToSet2(int num) {\n middle[num]++;\n sizeofMiddle++;\n mkSum += num;\n }\n\n void deleteFromSet2(int num) {\n middle[num]--;\n if (middle[num] == 0) middle.erase(num);\n sizeofMiddle--;\n mkSum -= num;\n }\n\n void addToSet3(int num) {\n right[num]++;\n sizeofRight++;\n }\n\n void deleteFromSet3(int num) {\n right[num]--;\n if (right[num] == 0) right.erase(num);\n sizeofRight--;\n }\n\npublic:\n MKAverage(int m, int k) {\n sizeofLeft = 0, sizeofMiddle = 0, sizeofRight = 0;\n mkSum = 0;\n this->k = k;\n this->m = m;\n }\n\n void addElement(int num) {\n if (sizeofLeft < k) {\n addToSet1(num);\n q.push(num);\n } else if (sizeofMiddle < (m - (2 * k))) {\n int lastEle = prev(left.end())->first;\n if (num >= lastEle) {\n addToSet2(num);\n } else {\n deleteFromSet1(lastEle);\n addToSet1(num);\n addToSet2(lastEle);\n }\n q.push(num);\n } else if (sizeofRight < k) {\n int last1 = prev(left.end())->first;\n int last2 = prev(middle.end())->first;\n if (num >= last1 && num >= last2) {\n addToSet3(num);\n } else if (num >= last1 && num < last2) {\n deleteFromSet2(last2);\n addToSet2(num);\n addToSet3(last2);\n } else {\n deleteFromSet2(last2);\n addToSet3(last2);\n deleteFromSet1(last1);\n addToSet2(last1);\n addToSet1(num);\n }\n q.push(num);\n } else {\n int toErase = q.front();\n q.pop();\n int first3 = right.begin()->first;\n int first2 = middle.begin()->first;\n int first1 = left.begin()->first;\n\n if (toErase >= first3) {\n deleteFromSet3(toErase);\n } else if (toErase >= first2) {\n deleteFromSet3(first3);\n deleteFromSet2(toErase);\n addToSet2(first3);\n } else {\n deleteFromSet3(first3);\n deleteFromSet2(first2);\n deleteFromSet1(toErase);\n addToSet1(first2);\n addToSet2(first3);\n }\n addElement(num);\n }\n }\n\n int calculateMKAverage() {\n if (q.size() < m) return -1;\n return mkSum / (m - (2 * k));\n }\n};\n``` | 3 | 0 | ['Tree', 'Queue', 'C', 'Sorting', 'C++'] | 1 |
finding-mk-average | c++(404ms 78%) queue and set | c404ms-78-queue-and-set-by-zx007pi-fg9w | Runtime: 404 ms, faster than 78.26% of C++ online submissions for Finding MK Average.\nMemory Usage: 146 MB, less than 62.50% of C++ online submissions for Find | zx007pi | NORMAL | 2021-09-24T06:25:17.468251+00:00 | 2021-09-24T06:43:45.194789+00:00 | 672 | false | Runtime: 404 ms, faster than 78.26% of C++ online submissions for Finding MK Average.\nMemory Usage: 146 MB, less than 62.50% of C++ online submissions for Finding MK Average.\n**General idea :**\n**1.** create queue with current of elements {element, id of element in stream} \n**2.** while size of queue less than **m** only put elements in queue\n**3.** one time whan size of queue will be equal **m** sort all elements from queue and put all elements into 3 sets : **mini** , **midi**, **maxi** , where mini contain first k elements, midi - next n( n = m - k - k) elements and maxi contain last k elements. And calculate sum of **midi** elements\n\n**from step 3 will repeat :**\n**1** delete old element from queue and from mini or midi or maxi\n**2** after deleting always will be reconstruct our mini, midi and maxi in such manner : mini - k elements, midi - n-1 elements and maxi - k elements (will support mini and maxi with maximal size)\n**3** put new element into mini , midi or maxi (for all theese steps recalculate sum)\n```\nclass MKAverage {\npublic:\n set<pair<int,int>> mini,midi,maxi;\n queue<pair<int,int>> q;\n int id, k, n, m, lim, sum;\n \n MKAverage(int m, int k) {\n sum = id = 0, this->k = k, this->m = m, n = m - k - k, lim = m + 1; \n }\n \n void addElement(int num) {\n q.push({num, ++id});\n \n if(q.size() == lim){\n auto p = q.front(); q.pop();\n \n if(mini.count(p)) mini.erase(p); //delete old\n else if(maxi.count(p)) maxi.erase(p);\n else midi.erase(p), sum -= p.first;\n \n if(mini.size() != k){ //replace\n mini.insert(*midi.begin()), sum -= midi.begin()->first;\n midi.erase(*midi.begin());\n }\n else if(maxi.size() != k){\n maxi.insert(*midi.rbegin()), sum -= midi.rbegin()->first;\n midi.erase(*midi.rbegin());\n }\n \n if(num >= mini.rbegin()->first && num <= maxi.begin()->first) midi.insert({num, id}), sum += num; //insert new\n else if(num < mini.rbegin()->first){\n sum += mini.rbegin()->first;\n midi.insert(*mini.rbegin());\n mini.erase(*mini.rbegin());\n mini.insert({num, id});\n }else {\n sum += maxi.begin()->first;\n midi.insert(*maxi.begin());\n maxi.erase(*maxi.begin());\n maxi.insert({num, id});\n } \n }\n else if(q.size() == m){\n vector<pair<int,int>>v(m);\n \n for(int i = 0; i != m; i++){\n q.push(v[i] = q.front()); q.pop();\n }\n \n sort(v.begin(), v.end());\n int i = 0;\n while(i != k) mini.insert(v[i++]);\n for(int l = k + n; i != l; i++) midi.insert(v[i]), sum += v[i].first;\n while(i != m) maxi.insert(v[i++]);\n }\n }\n \n int calculateMKAverage() {\n return q.size() == m ? sum / n : -1; \n }\n};\n``` | 3 | 0 | ['C', 'C++'] | 0 |
finding-mk-average | Java | Just one TreeSet | add O(logM) avg O(1) | java-just-one-treeset-add-ologm-avg-o1-b-ihak | Last m stream elements are kept sorted using TreeSet. First K and Last K elements are identified by remembering the edge elements, and updated with each additio | prezes | NORMAL | 2021-05-19T21:46:23.236922+00:00 | 2021-05-19T22:14:30.095741+00:00 | 287 | false | Last m stream elements are kept sorted using TreeSet. First K and Last K elements are identified by remembering the edge elements, and updated with each addition (with O(logM)). Sum of m-2k "middle" elements is updated with each addition (and used to calculate average in O(1)). \nDuplicate elements are distinguished using a "timestamp" (here we can use just a simple serial integer, since number of calls to addElement <= 10^5)\n\nMore comments inline.\n```\nclass MKAverage {\n private TreeSet<Pair<Integer, Integer>> order= new TreeSet<>((a,b)->{\n int diff= a.getKey()-b.getKey();\n return diff!=0 ? diff : a.getValue()-b.getValue();\n });\n private LinkedList<Pair<Integer, Integer>> stream= new LinkedList<>();\n private Pair<Integer, Integer> kLeft= null, kRight= null;\n private int m, k;\n private int serial= 0; // "timestamp"\n private int midSum= 0, midSize= 0;\n\n public MKAverage(int m, int k) {\n this.m= m;\n this.k= k;\n this.midSize= m-2*k;\n }\n \n private void init(){\n // one off once we reach the size of m\n // find kLeft and kRight elements (NOT in midSum)\n // calculate initial midSum\n int i=0;\n for(Pair<Integer,Integer> elt:order){\n if(i<k-1);\n else if(i==k-1) kLeft= elt;\n else if(i<m-k) midSum+= elt.getKey();\n else if(i==m-k){kRight= elt; break;}\n i++;\n }\n }\n \n public void addElement(int num) {\n Pair<Integer, Integer> addElt= new Pair<>(num, serial++);\n stream.addLast(addElt);\n add(addElt);\n if(stream.size()==m)\n init();\n else if(stream.size() > m)\n remove(stream.removeFirst());\n }\n \n private void add(Pair<Integer, Integer> elt){\n if(order.size()<m){\n order.add(elt); \n return;\n }\n // compare new elt with kLeft and kRight\n int eltKey= elt.getKey(), kLeftKey= kLeft.getKey(), kRightKey= kRight.getKey();\n order.add(elt);\n if(eltKey < kLeftKey){\n // add to left k and move kLeftKey to previous, \n // adding kLeft to midSum\n midSum+= kLeftKey;\n // finding the elt immediately before the current kLeft\n kLeft= order.floor(new Pair(kLeftKey, kLeft.getValue()-1));\n }else if(eltKey < kRightKey){\n // add to midSum, no change to kLeft or kRight\n midSum+= eltKey;\n }else{\n // add to right k and move kRightKey to next\n // adding kRight to midSum\n midSum+= kRightKey;\n // finding the elt immediately after the current kRight\n kRight= order.ceiling(new Pair(kRightKey, kRight.getValue()+1));\n }\n }\n \n private void remove(Pair<Integer, Integer> elt){\n // compare the elt being removed with kLeft and kRight\n int eltKey= elt.getKey(), kLeftKey= kLeft.getKey(), kRightKey= kRight.getKey();\n order.remove(elt);\n if(eltKey <= kLeftKey){\n // remove elt from left k and move kLeftKey to next, \n // finding the elt immediately after the current kLeft\n kLeft= order.ceiling(new Pair(kLeftKey, kLeft.getValue()+1));\n // removing the new kLeft from midSum\n midSum-= kLeft.getKey();\n }else if(eltKey < kRightKey){\n // remove from midSum, no change to kLeft or kRight\n midSum-= eltKey;\n }else{\n // remove from right k and move kRightKey to previous\n // finding the elt immediately before the current kRight\n kRight= order.floor(new Pair(kRightKey, kRight.getValue()-1));\n // removing the new kRight from midSum\n midSum-= kRight.getKey();\n }\n } \n \n public int calculateMKAverage() {\n return stream.size()==m ? midSum/midSize : -1;\n }\n} | 3 | 0 | [] | 0 |
finding-mk-average | Java O(1) Calcualte, O(log(m)) add. Three MultiSet | java-o1-calcualte-ologm-add-three-multis-f1f7 | Should be short if Java has a native MultiSet implement as Guava TreeMultiSet\n\nclass MKAverage {\n private MultiTreeSet bottom = new MultiTreeSet();\n p | janevans | NORMAL | 2021-04-11T04:27:44.097496+00:00 | 2021-04-11T04:27:44.097521+00:00 | 266 | false | Should be short if Java has a native MultiSet implement as [Guava TreeMultiSet](https://guava.dev/releases/21.0/api/docs/com/google/common/collect/TreeMultiset.html)\n```\nclass MKAverage {\n private MultiTreeSet bottom = new MultiTreeSet();\n private MultiTreeSet middle = new MultiTreeSet();\n private MultiTreeSet top = new MultiTreeSet(); \n private int m, k;\n private LinkedList<Integer> elements = new LinkedList<>();\n private long sum = 0;\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n elements.add(num);\n bottom.add(num); // blindly add to bottom\n\t\t// remove the element from the corresponding stack\n if (elements.size() > m) {\n int removed = elements.removeFirst();\n if (bottom.contains(removed)) {\n bottom.remove(removed);\n } else if (middle.contains(removed)) {\n middle.remove(removed);\n sum -= removed;\n } else if (top.contains(removed)) {\n top.remove(removed);\n }\n }\n if (elements.size() == m) {\n\t\t // once we reach m, bottom can only be >= k (because each call, we add 1 element to bottom, and remove at most 1 element from it)\n while (bottom.total > k) {\n int element = bottom.pollLast();\n middle.add(element);\n sum += element;\n }\n\t\t\t// fix size of middle stack\n while (middle.total > m - 2*k) {\n int element = middle.pollLast();\n top.add(element);\n sum -= element;\n }\n // fix ordering of bottom-middle stack\n while (bottom.getLast() > middle.getFirst()) {\n int e1 = middle.pollFirst();\n int e2 = bottom.pollLast();\n middle.add(e2);\n bottom.add(e1);\n sum = sum - e1 + e2;\n }\n // fix ordering of middle-top stack\n while (middle.getLast() > top.getFirst()) {\n int e1 = top.pollFirst();\n int e2 = middle.pollLast();\n middle.add(e1);\n top.add(e2);\n sum = sum + e1 - e2;\n }\n }\n }\n \n public int calculateMKAverage() {\n return elements.size() == m ? (int)(sum/(m - 2*k)) : -1;\n }\n \n static class MultiTreeSet {\n private TreeMap<Integer, Integer> map = new TreeMap<Integer, Integer>();\n private int total = 0;\n \n public void add(int val) {\n int count = map.getOrDefault(val, 0) + 1;\n map.put(val, count);\n total++;\n }\n \n public void remove(int val) {\n int count = map.get(val);\n if (count == 1) map.remove(val);\n else map.put(val, count-1);\n total--;\n }\n \n public boolean contains(int val) {\n return map.containsKey(val);\n }\n \n public int getFirst() {\n return map.firstKey();\n }\n \n public int getLast() {\n return map.lastKey();\n }\n \n public int pollFirst() {\n int first = map.firstKey();\n remove(first);\n return first;\n }\n \n public int pollLast() {\n int last = map.lastKey();\n remove(last);\n return last;\n }\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 3 | 1 | [] | 1 |
finding-mk-average | Queue + Multiset | C++ | Simple Solution | queue-multiset-c-simple-solution-by-void-np39 | \nclass MKAverage {\npublic:\n \n queue<int> q;\n multiset<int> mk;\n int total;\n int kt;\n MKAverage(int m, int k) {\n total = m;\n | voidp | NORMAL | 2021-04-11T04:05:04.830718+00:00 | 2021-04-11T04:05:04.830743+00:00 | 197 | false | ```\nclass MKAverage {\npublic:\n \n queue<int> q;\n multiset<int> mk;\n int total;\n int kt;\n MKAverage(int m, int k) {\n total = m;\n kt = k;\n }\n \n void addElement(int num) {\n \n if(q.size() == total){\n int e = q.front();\n q.pop();\n auto it = mk.find(e);\n mk.erase(it); \n }\n \n q.push(num);\n mk.insert(num); \n }\n \n int calculateMKAverage() {\n \n if(q.size() < total)\n return -1;\n \n long long sum = 0;\n int counts = total - 2*kt;\n int a = counts;\n int t = 0;\n auto it = mk.begin();\n while(t < kt){\n it++;\n t++; \n }\n \n \n while(counts){\n sum += *it;\n it++;\n counts--;\n }\n \n \n return sum/a;\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n ``` | 3 | 4 | [] | 1 |
finding-mk-average | C++ | Multiset Solution | c-multiset-solution-by-kena7-4h3f | Code | kenA7 | NORMAL | 2025-04-05T07:12:45.795287+00:00 | 2025-04-05T07:12:45.795287+00:00 | 51 | false |
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
class MKAverage {
public:
multiset<int> left, right, mid;
deque<int> dq;
long m, k, sum, midSize;
MKAverage(int m, int k) {
this->m = m;
this->k = k;
sum = 0;
midSize = m - 2 * k;
}
void remove(int x) {
auto it = right.find(x);
if (it != right.end()) {
right.erase(it);
return;
}
else
{
auto rit=right.begin();
mid.insert(*rit);
sum+=*rit;
right.erase(rit);
}
it = mid.find(x);
if (it != mid.end()) {
sum -= x;
mid.erase(it);
return;
}
else
{
auto mit=mid.begin();
left.insert(*mit);
sum-=*mit;
mid.erase(mit);
}
it = left.find(x);
left.erase(it);
}
void add(int x) {
left.insert(x);
if (left.size() > k) {
auto it = prev(left.end());
mid.insert(*it);
sum += *it;
left.erase(it);
}
if (mid.size() > midSize) {
auto it = prev(mid.end());
right.insert(*it);
sum -= *it;
mid.erase(it);
}
}
void addElement(int num) {
if (dq.size() == m) {
remove(dq.front());
dq.pop_front();
}
dq.push_back(num);
add(num);
}
int calculateMKAverage() {
if (dq.size() < m)
return -1;
return sum / midSize;
}
};
``` | 2 | 0 | ['C++'] | 0 |
finding-mk-average | Using min-max heaps: beats 90% time / 100% memory | using-min-max-heaps-beats-90-time-100-me-rit9 | Intuition\nThe goal hele is to prvide a way of querying for some statistics over the sorted order of a dynamic set of elements - the previous m values at the mo | pefreis | NORMAL | 2024-06-07T12:46:25.764886+00:00 | 2024-06-07T21:47:45.672610+00:00 | 440 | false | # Intuition\nThe goal hele is to prvide a way of querying for some statistics over the sorted order of a dynamic set of elements - the previous $$m$$ values at the moment we are queried. Obviously, this can be accomplished by sorting the set of previous $$m$$ items each time we are queried, but in order to be efficient, the solution must maintain these elements (somewhat) sorted.\n\nNote that items that came before the previous $$m$$ elements should not be taken into consideration anymore, so we also have to handle their expiration appropriately.\n\n# Approach\nIn first place, a queue (`q`) is used to keep track of the previous $$m$$ values received from stream.\n\nFor keeping the $$m - 2k$$ middle elements of sorted order, this solution used a simple (not optimal) implementation of min-max heaps (`mid`). Also, the sum of these elements is stored and continuously updated so that **querying operation** takes $$O(1)$$ time to compute the average.\n\nFinally, to handle the expiration of values, other two min-max heaps (`l` and `r`) are maintained for the lowest and highest $$k$$ values. Also, the values are stored along with a `heapId` and indices (min and max) for locating it in the heap where it currently belongs.\n\nWith these in place, every time a new value is received, we first check if the queue is at its capacity, in which case the first entry in the queue must be expired. Then the new entry is inserted both in the queue and in the heaps.\n\nNote that whenever we expire an entry or insert a new one into the heaps, they must be "rebalanced" to keep their size. Since min-max heaps are employed, this can be easily done by removing the lowest (or highest) value from a heap and pushing it to the neighboring heap.\n\n# Complexity\n- Time complexity:\n$$O(M)$$ for `Constructor`, since we preallocate an array of size $$m$$ when creating the slice `q`.\n$$O(logM)$$ for each `AddElement` operation.\n$$O(1)$$ for each `CalculateMKAverage` operation.\n\n- Space complexity:\n$$O(M+2M)$$, being $$O(M)$$ for the queue and $$O(2M)$$ for the whole set of heaps.\n\n# Code\n```\nimport (\n "container/heap"\n)\n\ntype MKNode struct {\n val int\n heapId int\n minIdx, maxIdx int\n}\n\ntype MKMinHeap []*MKNode\ntype MKMaxHeap []*MKNode\n\nfunc (h MKMinHeap) Len() int { return len(h) }\nfunc (h MKMaxHeap) Len() int { return len(h) }\nfunc (h MKMinHeap) Less(i, j int) bool { return h[i].val < h[j].val }\nfunc (h MKMaxHeap) Less(i, j int) bool { return h[i].val > h[j].val }\nfunc (h MKMinHeap) Swap(i, j int) {\n h[i], h[j] = h[j], h[i]\n h[i].minIdx = i\n h[j].minIdx = j\n}\nfunc (h MKMaxHeap) Swap(i, j int) {\n h[i], h[j] = h[j], h[i]\n h[i].maxIdx = i\n h[j].maxIdx = j\n}\nfunc (h *MKMinHeap) Push(v any) {\n n := len(*h)\n node := v.(*MKNode)\n node.minIdx = n\n *h = append(*h, node)\n}\nfunc (h *MKMaxHeap) Push(v any) {\n n := len(*h)\n node := v.(*MKNode)\n node.maxIdx = n\n *h = append(*h, node)\n}\nfunc (h *MKMinHeap) Pop() any {\n tmp := *h\n size := len(tmp)\n node := tmp[size-1]\n node.minIdx = -1\n tmp[size-1] = nil\n *h = tmp[:size-1]\n return node\n}\nfunc (h *MKMaxHeap) Pop() any {\n tmp := *h\n size := len(tmp)\n node := tmp[size-1]\n node.maxIdx = -1\n tmp[size-1] = nil\n *h = tmp[:size-1]\n return node\n}\n\ntype MKHeap interface {\n Len() int\n Min() *MKNode\n Max() *MKNode\n PopMin() *MKNode\n PopMax() *MKNode\n Push(n *MKNode)\n Remove(minIdx int)\n}\n\ntype mkHeap struct {\n id int\n minHeap MKMinHeap\n maxHeap MKMaxHeap\n}\n\nfunc NewMKHeap(id int) MKHeap {\n minHeap := MKMinHeap{}\n heap.Init(&minHeap)\n maxHeap := MKMaxHeap{}\n heap.Init(&maxHeap)\n return &mkHeap{id, minHeap, maxHeap}\n}\n\nfunc (h *mkHeap) Len() int { return h.minHeap.Len() }\nfunc (h *mkHeap) Min() *MKNode { return h.minHeap[0] }\nfunc (h *mkHeap) Max() *MKNode { return h.maxHeap[0] }\nfunc (h *mkHeap) PopMin() *MKNode {\n n := heap.Pop(&h.minHeap).(*MKNode)\n heap.Remove(&h.maxHeap, n.maxIdx)\n n.maxIdx = -1\n n.heapId = -1\n return n\n}\nfunc (h *mkHeap) PopMax() *MKNode {\n n := heap.Pop(&h.maxHeap).(*MKNode)\n heap.Remove(&h.minHeap, n.minIdx)\n n.minIdx = -1\n n.heapId = -1\n return n\n}\nfunc (h *mkHeap) Push(n *MKNode) {\n n.heapId = h.id\n heap.Push(&h.minHeap, n)\n heap.Push(&h.maxHeap, n)\n}\nfunc (h *mkHeap) Remove(minIdx int) {\n n := heap.Remove(&h.minHeap, minIdx).(*MKNode)\n n.minIdx = -1\n heap.Remove(&h.maxHeap, n.maxIdx)\n n.maxIdx = -1\n n.heapId = -1\n}\n\ntype MKAverage struct {\n m, k int\n q []*MKNode\n l, mid, r MKHeap\n midSum int\n}\n\nfunc Constructor(m int, k int) MKAverage {\n q := make([]*MKNode, 0, m)\n l := NewMKHeap(0)\n mid := NewMKHeap(1)\n r := NewMKHeap(2)\n return MKAverage{m, k, q, l, mid, r, 0}\n}\n\nfunc (this *MKAverage) AddElement(num int) {\n if len(this.q) == this.m {\n this.expire()\n }\n newNode := &MKNode{val: num}\n this.q = append(this.q, newNode)\n this.r.Push(newNode)\n for this.r.Len() > this.k {\n n := this.r.PopMin()\n this.mid.Push(n)\n this.midSum += n.val\n }\n for this.mid.Len() > (this.m-2*this.k) {\n n := this.mid.PopMin()\n this.midSum -= n.val\n this.l.Push(n)\n }\n}\n\nfunc (this *MKAverage) CalculateMKAverage() int {\n if len(this.q) < this.m {\n return -1\n }\n return int(this.midSum / (this.m-2*this.k))\n}\n\nfunc (this *MKAverage) expire() {\n expired := this.q[0]\n if expired.heapId == 2 {\n this.r.Remove(expired.minIdx)\n n := this.l.PopMax()\n this.mid.Push(n)\n this.midSum += n.val\n n = this.mid.PopMax()\n this.midSum -= n.val\n this.r.Push(n)\n } else if expired.heapId == 1 {\n this.mid.Remove(expired.minIdx)\n this.midSum -= expired.val\n n := this.l.PopMax()\n this.mid.Push(n)\n this.midSum += n.val\n } else {\n this.l.Remove(expired.minIdx)\n }\n this.q[0] = nil\n this.q = this.q[1:]\n}\n\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * obj := Constructor(m, k);\n * obj.AddElement(num);\n * param_2 := obj.CalculateMKAverage();\n */\n``` | 2 | 0 | ['Queue', 'Heap (Priority Queue)', 'Data Stream', 'Go'] | 0 |
finding-mk-average | 3 Sorted collections approach in C# | 3-sorted-collections-approach-in-c-by-ar-3ccp | Intuition\n\nWe need to maintain 3 sorted sequences. \n\nThe tricky part is, there is no good way to represent sorted Sequences in C#, so we will create one.\n\ | artbidn | NORMAL | 2024-03-24T02:07:04.908062+00:00 | 2024-03-24T02:07:04.908099+00:00 | 212 | false | # Intuition\n\nWe need to maintain 3 sorted sequences. \n\nThe tricky part is, there is no good way to represent sorted Sequences in C#, so we will create one.\n\n# Approach\n\nOne thing should be obvious. At first, we are just adding elements to a sequence, but eventually we first need to \'pop\' the oldest adding element. You can either use Queue or LinkedList or circle array implementation, whatever you find easiest.\n\nRemoving an element procedure:\n1. Find a collection with the element and delete the element from it.\n2. Rebalance the left collection to contain k elements and mid collection to contain m - 2 * k elements. The right collection will then always end up with k elements.\n\nAdding an element procedure: \n\n1. Add to the left.\n2. If left size is larger than k, move largest element to mid\n3. If mid dize is larger than m - 2 * k, move largest element to right.\n\nWhenever an element enters or leaves the mid collection, we add/subtract its value from the sum.\n\nIn C#, SortedSet is nice because it has O(1) Min/Max fields. But it can only contain unique elements.\n\nTo mitigate that, we can combine it with a Dictionary to keep track of element counts. \n\n# Code\n```\npublic class MKAverage {\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n\n midSize = m - 2 * k;\n window = new int[m];\n index = 0;\n left = new CustomSortedList();\n mid = new CustomSortedList();\n right = new CustomSortedList();\n }\n \n public void AddElement(int num) {\n var realIndex = index % m;\n if (index >= m) {\n var old = window[realIndex];\n Remove(old);\n }\n\n Add(num);\n window[realIndex] = num;\n index++;\n }\n\n private void Remove(int n) {\n if (n <= left.Max) {\n left.Remove(n);\n }\n else if (n <= mid.Max) {\n mid.Remove(n);\n sum -= n;\n }\n else {\n right.Remove(n);\n }\n\n if (left.Count < k) {\n var moved = Move(mid, left, true);\n sum -= moved;\n }\n\n if (mid.Count < midSize) {\n var moved = Move(right, mid, true);\n sum += moved;\n }\n }\n\n private int Move(CustomSortedList from, CustomSortedList to, bool min) {\n var n = min ? from.Min : from.Max;\n from.Remove(n);\n to.Add(n);\n return n; \n }\n\n private void Add(int n) {\n left.Add(n);\n\n if (left.Count > k) {\n var moved = Move(left, mid, false);\n sum += moved;\n }\n\n if (mid.Count > midSize) {\n var moved = Move(mid, right, false);\n sum -= moved;\n }\n }\n \n public int CalculateMKAverage() {\n return (index < m) ? -1 : sum / midSize; \n }\n\n private int midSize;\n private int index;\n private int[] window;\n private int sum;\n\n private CustomSortedList left;\n private CustomSortedList mid;\n private CustomSortedList right;\n\n private class CustomSortedList {\n public CustomSortedList() {\n counts = new Dictionary<int, int>();\n set = new SortedSet<int>();\n }\n\n public void Add(int n) {\n if (counts.ContainsKey(n)) {\n counts[n]++;\n }\n else {\n counts[n] = 1;\n set.Add(n);\n }\n\n Count++;\n }\n\n public void Remove(int n) {\n if (!counts.TryGetValue(n, out var count)) {\n return;\n }\n\n if (count > 1) {\n counts[n] -= 1;\n }\n else {\n counts.Remove(n);\n set.Remove(n);\n }\n\n Count--;\n }\n\n public int Count {get; private set; } \n\n public int Max => set.Max;\n public int Min => set.Min;\n\n private Dictionary<int, int> counts;\n private SortedSet<int> set;\n }\n\n private int m;\n private int k;\n}\n\n``` | 2 | 0 | ['C#'] | 1 |
finding-mk-average | Multiset | Java | O(NlogM) time | O(M) space | multiset-java-onlogm-time-om-space-by-go-i19x | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nUsed three MultiSet to track the state of the elements added.\nsmallest - | govindarajss | NORMAL | 2024-03-11T03:28:17.850925+00:00 | 2024-03-11T03:28:17.850970+00:00 | 377 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nUsed three MultiSet to track the state of the elements added.\nsmallest - tracks the smallest k elemtns in the current window\nlargest - tracks the smallest k elemtns in the current window\nothers - tracks the rest of the elements\n\nUsed a FIFO queue to track the order of elements added.\n\nAlgorithm:\n**addElement**\n1) Remove the element not in the m-window if necessary from the multi-sets\n2) Add element to the fifo queue\n3) Add element to the state (multi-sets)\n\n# Complexity\n- Time complexity:\naddElement: O(log(m))\ncalculateMKAverage: O(1)\n\n- Space complexity:\nO(m)\n\n# Code\n```\nclass MKAverage {\n MultiSet smallest = new MultiSet();\n MultiSet largest = new MultiSet();\n MultiSet others = new MultiSet();\n\n Queue<Integer> queue = new LinkedList<>();\n\n final int m;\n final int k;\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n queue.offer(num);\n\n // remove\n if (queue.size() > m) {\n if (queue.peek() < others.getFirst()) {\n smallest.remove(queue.poll());\n } else if (queue.peek() > others.getLast()) {\n largest.remove(queue.poll());\n } else {\n others.remove(queue.poll());\n }\n }\n\n others.add(num);\n\n if (smallest.size() < k || smallest.getLast() > others.getFirst()) {\n smallest.add(others.pollFirst());\n if (smallest.size() > k) {\n others.add(smallest.pollLast());\n }\n }\n\n if (others.isEmpty()) {\n return;\n }\n\n if (largest.size() < k || largest.getFirst() < others.getLast()) {\n largest.add(others.pollLast());\n if (largest.size() > k) {\n others.add(largest.pollFirst());\n }\n }\n }\n \n public int calculateMKAverage() {\n if (queue.size() < m) {\n return -1;\n }\n return others.avg();\n }\n}\n\nclass MultiSet {\n TreeMap<Integer, Integer> elements = new TreeMap<>();\n int size = 0;\n long total = 0L;\n\n void add(int num) {\n elements.put(num, elements.getOrDefault(num, 0) + 1);\n size++;\n total += num;\n }\n\n int pollFirst() {\n int k = elements.firstKey();\n remove(k);\n return k;\n }\n\n int pollLast() {\n int k = elements.lastKey();\n remove(k);\n return k;\n }\n\n int getFirst() {\n return elements.firstKey();\n }\n\n int getLast() {\n return elements.lastKey();\n }\n\n int size() {\n return size;\n }\n\n boolean isEmpty() {\n return elements.isEmpty();\n }\n\n void remove(int num) {\n // assumption: the key is present\n int v = elements.get(num) - 1;\n if (v == 0) {\n elements.remove(num);\n } else {\n elements.put(num, elements.get(num) - 1);\n }\n size--;\n total -= num;\n }\n\n int avg() {\n return (int) (total / size);\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 2 | 0 | ['Java'] | 0 |
finding-mk-average | Python SortedList | python-sortedlist-by-nblam1994-3lli | Complexity\n- Time complexity: O(NlogN)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(N)\n Add your space complexity here, e.g. O(n) \n\n | nblam1994 | NORMAL | 2024-01-14T04:57:26.538704+00:00 | 2024-01-14T04:57:26.538735+00:00 | 388 | false | # Complexity\n- Time complexity: O(NlogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom sortedcontainers import SortedList\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.queue = deque([])\n self.sorted_list = SortedList()\n self.m = m\n self.k = k\n \n def addElement(self, num: int) -> None:\n if len(self.queue) >= self.m: \n val = self.queue.popleft()\n self.sorted_list.remove(val)\n self.queue.append(num)\n self.sorted_list.add(num)\n \n def calculateMKAverage(self) -> int:\n if len(self.queue) < self.m: return -1\n # print(self.sorted_list)\n return sum(\n self.sorted_list[self.k: len(self.sorted_list) - self.k]\n ) // (self.m - self.k * 2)\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 2 | 0 | ['Python3'] | 0 |
finding-mk-average | Easy to Understand 3 Multisets Approach | easy-to-understand-3-multisets-approach-xcqw8 | Approach:\nIn this problem we will be using SlidingWindow and Multiset so solve this problem.\nFor SlidingWindow we are using a queue stream and 3 Multisets kBo | badhansen | NORMAL | 2024-01-01T23:15:59.675137+00:00 | 2024-01-01T23:15:59.675161+00:00 | 871 | false | ### Approach:\nIn this problem we will be using **SlidingWindow** and **Multiset** so solve this problem.\nFor **SlidingWindow** we are using a `queue` `stream` and 3 **Multisets** `kBottom`, `middle` and `kTop` track the three buckets:\n\n**We will divide the 3 bucket as:**\n1. Bottom `K` numbers, MIDDLE numbers `(M - 2 * K)`, top `K` numbers\n\t`// also tracking numbers come in and leave.`\n `// also tracking the sum of the MIDDLE bucket.`\n2. At some point of time, all the buckets will all be satistified our first requirement and we need to add a new number.\n\ti) i.e. `K` bottom numbers, `MIDDLE` numbers, `K` top numbers -> a new number come in\n\tii) Then we need to remove a number because of the sliding window moves\n\tiii) When a number is being removed, the we have to maintain the three buckets like this way \n\tiv) i.e. to be `K` numbers, `MIDDLE` numbers, `K-1` numbers. \n\tv) First we will remove from the last bucket then middle and very last from the first bucket.\n \n3. After that, we will add the new elemment into the bottom bucket. So it becomes `K+1` numbers, MIDDLE numbers,` K-1` numbers. \n4. We remove the biggest value from the botton bucket and add it to the MIDDLE bucket. So it becomes `K` nums, `MIDDLE+1` nums, `K-1` nums.\n5. We then remove the biggest value from the `MIDDLE` bucket and add it to the top bucket\n6. So again, the three buckets become as approach described.\n\n**Time and Space Complexity:**\n\nTime Complexity: \nAdding and removing from a `queue` is constant `O(1)` time complexity and Inserting, erasing, and finding from `multiset` is `O(log n)`. \nso `addElement()` will be `O(log m)` and `calculateMKAverage()` will be `O(1)`\n\nSpace Complexity:\nAt most `m` elements will be present so space complexity will be `O(m)`.\n\n```\nenum class Positions {\n kBottom = 0,\n kMiddle,\n kTop,\n};\n\nclass MKAverage {\nprivate:\n int m, k;\n long long sum;\n \n queue<int> stream;\n multiset<int> kBottom;\n multiset<int> middle;\n multiset<int> kTop;\npublic:\n MKAverage(int m, int k) {\n this->m = m, this->k = k;\n sum = 0;\n }\n \n void addElement(int num) {\n stream.push(num);\n \n if (stream.size() > m) {\n int removedValue = stream.front();\n stream.pop();\n if (kTop.find(removedValue) != kTop.end()) {\n removingValue(removedValue, Positions::kTop);\n } else if (middle.find(removedValue) != middle.end()) {\n removingValue(removedValue, Positions::kMiddle);\n int value = removeSmallest(kTop);\n addingValue(value, Positions::kMiddle);\n } else {\n removingValue(removedValue, Positions::kBottom);\n int value = removeSmallest(kTop);\n addingValue(value, Positions::kMiddle);\n \n value = removeSmallest(middle);\n sum -= value; // Already removed the value so don\'t calling the removingValue function, just decrement the value from sum\n addingValue(value, Positions::kBottom);\n }\n }\n \n add(num);\n }\n \n int calculateMKAverage() {\n if (stream.size() < m) {\n return -1;\n }\n return sum / (int)middle.size();\n }\nprivate:\n void add(int num) {\n addingValue(num, Positions::kBottom);\n if (kBottom.size() > k) {\n int value = removeLargest(kBottom);\n addingValue(value, Positions::kMiddle);\n if (middle.size() > m - 2 * k) {\n value = removeLargest(middle);\n sum -= value; // For middle as we have already deleted the value from the set, so we are not calling the removingValue function\n addingValue(value, Positions::kTop);\n }\n }\n }\n void addingValue(int value, enum Positions pos) {\n switch (pos) {\n case Positions::kBottom:\n kBottom.insert(value);\n break;\n case Positions::kMiddle:\n middle.insert(value);\n sum += value;\n break;\n case Positions::kTop:\n kTop.insert(value);\n break;\n }\n }\n void removingValue(int value, enum Positions pos) {\n switch (pos) {\n case Positions::kBottom:\n kBottom.erase(kBottom.find(value));\n break;\n case Positions::kMiddle:\n middle.erase(middle.find(value));\n sum -= value;\n break;\n case Positions::kTop:\n kTop.erase(kTop.find(value));\n break;\n }\n }\n int removeSmallest(multiset<int>& set) {\n auto smallest = set.begin();\n int result = *smallest;\n set.erase(smallest);\n return result;\n }\n int removeLargest(multiset<int>& set) {\n auto largest = --set.end();\n int result = *largest;\n set.erase(largest);\n return result;\n }\n};\n ``` | 2 | 0 | ['Queue', 'C', 'C++'] | 0 |
finding-mk-average | Python, Binary search and double-ended queue. Showing clear thread of thoughts | python-binary-search-and-double-ended-qu-xqya | Intuition\n\nThought 1: We start from the naive solution\n Idea: Keep a container of m elements (data structure: double-ended queue, probably a doubly-linked li | qihangyao | NORMAL | 2023-11-10T17:35:20.614836+00:00 | 2023-11-10T17:35:20.614857+00:00 | 67 | false | # Intuition\n\nThought 1: We start from the naive solution\n* Idea: Keep a container of m elements (data structure: double-ended queue, probably a doubly-linked list in exact implementation)\n* AddElement -> cost O(1)\n* calculateMKAverage -> sort (O(m log m)))\n\nThought 2: Can we do better for calculate MKAverage?\n* Idea: Keep an additional structure, which is sorted\n* AddElement -> find the element to remove O(log m), add the element O(log m).\n(Note: Actually I noticed that cPython list is not a implementation that allows us to insert/remove an element in constant time. An exact data structure suitable would be a binary search tree.)\n* calculateMKAverage -> O(m)\n\nThought 3: MKAverage is still slower than adding element. Can we do even better for calulating MKAverage?\n* Idea: Keep a value of the sum of the elements qualified. Update the sum everytime we add an element.\n\n# Approach\n\nHow do we do even better for calculating MKAverage?\n1. when we remove an element A, if A\n - if among smallest (largest) k, we reduce sum by k+1 smallest (largest) value.\n - if not, we reduce sum by A.\n2. when we add an element B, if B\n - if among smallest (largest) k, we add to sum the k+1 smallest (largest) value.\n - if not, we add B to sum.\n* AddElement -> Still O(log m), as the additional overhead is constant.\n* calculateMKAverage -> O(1).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n* AddElement -> Still O(log m), as the additional overhead is constant.\n* calculateMKAverage -> O(1).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n* O(m) for the deque and sorted list that we keep.\n\n# Code\n```\nimport bisect\nfrom collections import deque\n\nclass MKAverage:\n\n # Naive\n # Keep a container of m elements (data structure: doubl-ended queue)\n # AddElement -> cost O(1)\n # calculateMKAverage -> sort (O(m log m)))\n\n # Can we do better for calculate MKAverage?\n # Keep an additional structure, which is sorted\n # AddElement -> find the element to remove O(log m), add the element O(log m)\n # calculateMKAverage -> O(m)\n\n # Can we do even better for calulating MKAverage?\n # Keep a value of the sum of the elements qualified.\n # Update the average everytime we add an element.\n # How to?\n # 1. when we remove an element A, if A\n # - if among smallest (largest) k, we reduce sum by k+1 smallest (largest) value.\n # - if not, we reduce sum by A\n # 2. when we add an element B, if B\n # - if among smallest (largest) k, we add to sum the k+1 smallest (largest) value.\n # - if not, we add B to sum.\n # calculateMKAverage -> O(1)\n\n def __init__(self, m: int, k: int):\n\n self.m = m\n self.k = k\n\n self.deque = deque()\n self.sorted = list()\n self.total = 0\n \n\n def addElement(self, num: int) -> None:\n\n if len(self.deque) < self.m:\n self.deque.append(num)\n bisect.insort(self.sorted, num)\n if len(self.deque) == self.m:\n self.total = sum(self.sorted[self.k:-self.k]) \n else:\n # remove element\n v = self.deque.popleft()\n index = bisect.bisect_left(self.sorted, v)\n if index < self.k:\n self.total -= self.sorted[self.k]\n elif index >= self.m - self.k:\n self.total -= self.sorted[-self.k-1]\n else:\n self.total -= v\n self.sorted.pop(index)\n\n # add element\n self.deque.append(num)\n index = bisect.bisect_left(self.sorted, num)\n self.sorted.insert(index, num)\n if index < self.k:\n self.total += self.sorted[self.k]\n elif index >= self.m - self.k:\n self.total += self.sorted[-self.k - 1]\n else:\n self.total += num\n\n\n def calculateMKAverage(self) -> int:\n\n if len(self.deque) < self.m:\n return - 1\n\n return int(self.total / (self.m - 2 * self.k) )\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 2 | 0 | ['Python3'] | 0 |
finding-mk-average | c++ solution | c-solution-by-dilipsuthar60-r3o3 | \nclass MKAverage\n{\n public:\n multiset<int> left, mid, right;\n int k;\n int m;\n long long sum;\n queue<int> q;\n MKAverage(int mt, | dilipsuthar17 | NORMAL | 2022-06-19T18:10:31.830632+00:00 | 2022-06-19T18:10:31.830679+00:00 | 689 | false | ```\nclass MKAverage\n{\n public:\n multiset<int> left, mid, right;\n int k;\n int m;\n long long sum;\n queue<int> q;\n MKAverage(int mt, int kt)\n {\n sum = 0;\n m = mt;\n k = kt;\n }\n void remove()\n {\n int val = q.front();\n q.pop();\n if (val <= *left.rbegin())\n {\n left.erase(left.find(val));\n left.insert(*mid.begin());\n sum -= *mid.begin();\n mid.erase(mid.begin());\n }\n else if (val >= *right.begin())\n {\n right.erase(right.find(val));\n right.insert(*mid.rbegin());\n sum -= *mid.rbegin();\n mid.erase(--mid.end());\n }\n else\n {\n sum -= val;\n mid.erase(mid.find(val));\n }\n }\n void add(int val)\n {\n q.push(val);\n if (mid.size() == 0)\n {\n if (q.size() == m)\n {\n queue<int> nq = q;\n vector<int> v;\n while (nq.size())\n {\n v.push_back(nq.front());\n nq.pop();\n }\n sort(v.begin(), v.end());\n for (int i = 0; i < m; i++)\n {\n if (i < k)\n {\n left.insert(v[i]);\n }\n else if (i > m - 1 - k)\n {\n right.insert(v[i]);\n }\n else\n {\n mid.insert(v[i]);\n sum += v[i];\n }\n }\n }\n }\n else if (val<*left.rbegin())\n {\n int curr = *left.rbegin();\n left.insert(val);\n mid.insert(curr);\n left.erase(--left.end());\n sum += curr;\n }\n else if (val > *right.begin())\n {\n int curr = *right.begin();\n right.erase(right.begin());\n right.insert(val);\n sum += curr;\n mid.insert(curr);\n }\n else\n {\n sum += val;\n mid.insert(val);\n }\n }\n void addElement(int num)\n {\n add(num);\n if (q.size() > m)\n {\n remove();\n }\n }\n\n int calculateMKAverage()\n {\n if (q.size() < m)\n {\n return -1;\n }\n return sum / mid.size();\n }\n};\n``` | 2 | 0 | ['C', 'C++'] | 0 |
finding-mk-average | [C++] simple solution using sorted map faster than 98% | c-simple-solution-using-sorted-map-faste-jm73 | \nclass MKAverage {\npublic:\n vector<int> items;\n map<int,int> lastM;\n int m,k,s,e;\n long total;\n \n MKAverage(int m, int k) {\n t | ltbtb_rise | NORMAL | 2021-09-22T13:06:10.925831+00:00 | 2021-09-22T13:21:53.536565+00:00 | 309 | false | ```\nclass MKAverage {\npublic:\n vector<int> items;\n map<int,int> lastM;\n int m,k,s,e;\n long total;\n \n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n s = 0;\n e = 0;\n total = 0;\n }\n \n\t// O(logM)\n void addElement(int num) {\n items.push_back(num);\n lastM[num]++;\n total += num;\n e++;\n \n if(e-s>m) \n {\n if(--lastM[items[s]] == 0) lastM.erase(items[s]);\n total -= items[s++];\n }\n }\n \n\t// O(K)\n int calculateMKAverage() {\n if(e - s < m) return -1;\n int n = k, minVal = 0, maxVal = 0;\n auto itr = lastM.begin();\n while(n>0) \n {\n minVal += itr->first * min(itr->second, n);\n n -= min(itr->second, n);\n if(n > 0)\n {\n itr++;\n }\n }\n \n auto _itr = lastM.rbegin();\n n = k;\n while(n>0) \n {\n maxVal += _itr->first * min(_itr->second, n);\n n -= min(_itr->second, n);\n if(n > 0)\n {\n _itr++;\n }\n }\n \n return (total - minVal - maxVal) / (m-2*k);\n }\n};\n``` | 2 | 1 | [] | 1 |
finding-mk-average | What should I do when meeting this question in interview - A step by step guide | what-should-i-do-when-meeting-this-quest-5twc | Code first.\n\nclass MultiMap {\n public TreeMap<Integer, Integer> map;\n private int cnt = 0;\n private double sum = 0.0;\n \n public MultiMap() | hammer001 | NORMAL | 2021-08-22T06:43:28.586133+00:00 | 2021-08-22T06:43:28.586163+00:00 | 260 | false | Code first.\n```\nclass MultiMap {\n public TreeMap<Integer, Integer> map;\n private int cnt = 0;\n private double sum = 0.0;\n \n public MultiMap() {\n this.map = new TreeMap<>();\n }\n \n public void add(Integer key) {\n this.cnt ++;\n this.sum += key;\n this.map.put(key, this.map.getOrDefault(key, 0) + 1);\n }\n \n public boolean containsKey(Integer key) {\n return this.map.getOrDefault(key, 0) > 0;\n }\n \n public void remove(Integer key) {\n if (!this.map.containsKey(key)) {\n return;\n }\n \n this.cnt --;\n this.sum -= key;\n this.map.put(key, this.map.get(key)-1);\n \n if (this.map.get(key) == 0) {\n this.map.remove(key);\n }\n }\n \n public Integer getMin() {\n return this.map.firstKey();\n }\n \n public Integer getMax() {\n return this.map.lastKey();\n }\n \n public int avg() {\n return (int)(this.sum/this.cnt);\n }\n \n public int size() {\n return this.cnt;\n }\n}\n\nclass TripleMap {\n public MultiMap small;\n public MultiMap mid;\n public MultiMap big;\n private int m;\n private int k;\n \n public TripleMap(int m, int k) {\n this.small = new MultiMap();\n this.mid = new MultiMap();\n this.big = new MultiMap();\n this.m = m;\n this.k = k;\n }\n \n public void add(int num) {\n if (mid.size() == 0) {\n mid.add(num);\n return;\n }\n \n if (num < mid.getMin()) {\n small.add(num);\n } else if (num > mid.getMax()) {\n big.add(num);\n } else {\n mid.add(num);\n }\n \n this.balance();\n }\n \n private void balance() {\n int size = small.size() + mid.size() + big.size();\n \n if (size < m) {\n return;\n }\n \n while (small.size() > k) {\n int victim = small.getMax();\n small.remove(victim);\n mid.add(victim);\n }\n \n while (big.size() > k) {\n int victim = big.getMin();\n big.remove(victim);\n mid.add(victim);\n }\n \n while (small.size() < k) {\n int victim = mid.getMin();\n mid.remove(victim);\n small.add(victim);\n }\n \n while (big.size() < k) {\n int victim = mid.getMax();\n mid.remove(victim);\n big.add(victim);\n }\n }\n \n public void remove(int num) {\n if (small.containsKey(num)) {\n small.remove(num);\n } else if (mid.containsKey(num)) {\n mid.remove(num);\n } else if (big.containsKey(num)) {\n big.remove(num);\n }\n \n this.balance();\n }\n \n public int avg() {\n return this.mid.avg();\n }\n}\n\nclass MKAverage {\n private TripleMap map;\n private Queue<Integer> q;\n private int m;\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.map = new TripleMap(m, k);\n this.q = new LinkedList<Integer>();\n }\n \n public void addElement(int num) {\n this.q.add(num);\n this.map.add(num);\n \n if (this.q.size() > m) {\n int victim = this.q.remove();\n this.map.remove(victim);\n }\n }\n \n public int calculateMKAverage() {\n if (this.q.size() < m) {\n return -1;\n }\n \n return this.map.avg();\n }\n}\n```\n\nLong code, and nearly un-implementable during a 1-hour interview. \n\nThe trick is: define the interface, implement the core logic, and implement the interface when having time. I define 2 extra classes in this solution `TripleMap` and `MultiMap`. During an intervew, you can call out these 2 data structure, and define the function signature first. Then, write down the MKAverage first without implementing the functions in `TripleMap` and `MultiMap`.\n\nLike below\n\n```\nclass MultiMap {\n public void add(Integer key) {\n }\n \n public boolean containsKey(Integer key) {\n }\n \n public void remove(Integer key) {\n }\n \n public Integer getMin() {\n }\n \n public Integer getMax() {\n }\n \n public int avg() {\n }\n \n public int size() {\n }\n}\n\nclass TripleMap {\n public MultiMap small;\n public MultiMap mid;\n public MultiMap big;\n private int m;\n private int k;\n \n public void add(int num) {\n }\n\n public void remove(int num) {\n }\n \n public int avg() {\n }\n}\n\nclass MKAverage {\n private TripleMap map;\n private Queue<Integer> q;\n private int m;\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.map = new TripleMap(m, k);\n this.q = new LinkedList<Integer>();\n }\n \n public void addElement(int num) {\n this.q.add(num);\n this.map.add(num);\n \n if (this.q.size() > m) {\n int victim = this.q.remove();\n this.map.remove(victim);\n }\n }\n \n public int calculateMKAverage() {\n if (this.q.size() < m) {\n return -1;\n }\n \n return this.map.avg();\n }\n}\n```\n\nThen, walk through the core algorithm with your interviewer. And start to implement the 2 classes | 2 | 1 | [] | 1 |
finding-mk-average | C++ TreeMap+Queue | c-treemapqueue-by-verdict_ac-qfgn | \nclass MKAverage {\npublic:\n map<int,int>record;\n long long total;\n queue<int>q;\n int m;\n int k;\n MKAverage(int m, int k) {\n th | Verdict_AC | NORMAL | 2021-06-06T13:44:09.819221+00:00 | 2021-06-06T13:44:09.819266+00:00 | 243 | false | ```\nclass MKAverage {\npublic:\n map<int,int>record;\n long long total;\n queue<int>q;\n int m;\n int k;\n MKAverage(int m, int k) {\n this->m=m;\n this->k=k;\n total=0;\n }\n \n void addElement(int num) {\n q.push(num);\n total+=(long long)num;\n record[num]++;\n if(q.size()>m)\n {\n int nums=q.front();\n q.pop();\n total-=nums;\n record[nums]--;\n if(record[nums]==0)record.erase(nums);\n }\n return;\n }\n \n int calculateMKAverage() {\n if(q.size()<m)return -1;\n long long sum=total;\n cout << sum << endl;\n int count=k;\n for(auto &x:record)\n {\n int nums=x.first;\n int times=x.second;\n if(times<=count)\n {\n count-=times;\n sum-=(long long)nums*times;\n }else\n {\n sum-=(long long)nums*count;\n count=0;\n }\n if(count==0)break;\n }\n count=k;\n for(auto x=record.rbegin();x!=record.rend();x++)\n {\n int nums=x->first;\n int times=x->second;\n if(x->second<=count)\n {\n count-=x->second;\n sum-=(long long)nums*x->second;\n }else\n {\n sum-=(long long)nums*count;\n count=0;\n }\n if(count==0)break;\n }\n return sum/(long long)(m-k*2);\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 2 | 0 | ['Tree', 'Queue'] | 0 |
finding-mk-average | [Java] 3 TreeSets + 1 Queue, clear and easy-to-write code | java-3-treesets-1-queue-clear-and-easy-t-nttj | Similar problems\nThis problem is a variant of\n- 295. Find Median from Data Stream\n- 480. Sliding Window Median\n\nAnd I strongly suggest you read this post, | maristie | NORMAL | 2021-06-05T03:33:38.617653+00:00 | 2021-06-05T03:43:48.602190+00:00 | 198 | false | ## Similar problems\nThis problem is a variant of\n- [295. Find Median from Data Stream](https://leetcode.com/problems/find-median-from-data-stream/)\n- [480. Sliding Window Median](https://leetcode.com/problems/sliding-window-median/)\n\nAnd I strongly suggest you read [this post](https://leetcode.com/problems/sliding-window-median/discuss/96346/), which shows an elegant way to rebalance between disjoint sorted sets.\n\n## Intuition\n\nLet\'s get back to this problem. We\'re asked to maintain the last `m` elements of a stream, while return its average excluding top `k` and bottom `k` elements. It\'s easy to infer that some kind of sorted set data structure should be used, and logarithmic maintenance time is required.\n\n### Difficulties\n\nThe major difficulties include\n1. How to maintain a dynamic sorted set in the first place\n2. How to distinguish the top `k` and bottom `k` elements from the candidates for MK average\n\nFor 1, C++ users are lucky since there is built-in multiset. However, it\'s not difficult to implement one in Java. The key is to differentiate between elements with the same value, which can be done using a logical counter incrementing by 1, and this assigned unique identifier can be stored with the value. Several lines of code should suffice to define such a class and corresponding comparator (or alternatively the `Comparable` interface).\n\nFor 2, similar to the aforementioned problems, we can use multiple disjoint dynamic sorted sets to distinguish between and maintain subsets of a population. In particular, a top `k` set, a bottom `k` set and a window of candidates for evaluation of MK average should be identified in this problem. Thus 3 multisets are needed. In addition, we should be able to remove expired elements, which can be done by recording the entry order of elements with a single queue.\n\n### Invariant Maintenance\n\nThe most complicated part is maintain the invariant that\n> Top `k` set and bottom `k` set contain the corresponding top or bottom `k` elements, while the remaining set contains the `m - 2k` elements left.\n\nAgain, I would recommend you reading the post above to learn about the intuition to rebalance between multiple sorted sets. The most important part is to define a **balancing operation**.\n\n## Implementation\n\n```java\nclass MKAverage {\n static class Element {\n int id;\n int val;\n \n Element(int id, int val) {\n this.id = id;\n this.val = val;\n }\n }\n \n int m;\n int k;\n int size = 0;\n int sum = 0;\n Comparator<Element> cmp = Comparator.<Element>comparingInt(e -> e.val).thenComparingInt(e -> e.id);\n TreeSet<Element> window = new TreeSet<>(cmp);\n TreeSet<Element> topK = new TreeSet<>(cmp);\n TreeSet<Element> bottomK = new TreeSet<>(cmp);\n Queue<Element> queue = new ArrayDeque<Element>();\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n var element = new Element(size++, num);\n queue.offer(element);\n window.add(element);\n sum += num;\n \n if (size == m) {\n while (window.size() > m - 2 * k) {\n balance();\n }\n } else if (size > m) {\n if (window.last().val > topK.first().val) {\n move(window, topK);\n } else {\n move(window, bottomK);\n } \n var toRemove = queue.poll();\n topK.remove(toRemove);\n bottomK.remove(toRemove);\n if (window.remove(toRemove)) {\n sum -= toRemove.val;\n }\n balance();\n }\n }\n \n private void move(TreeSet<Element> from, TreeSet<Element> to) {\n var element = (from == topK || to == bottomK) ? from.pollFirst() : from.pollLast();\n to.add(element);\n sum += to == window ? element.val : -element.val;\n }\n \n private void balance() {\n if (topK.size() > k) {\n move(topK, window);\n } else if (bottomK.size() > k) {\n move(bottomK, window);\n }\n \n if (topK.size() < k) {\n move(window, topK);\n } else if (bottomK.size() < k) {\n move(window, bottomK);\n }\n }\n \n public int calculateMKAverage() {\n return size < m ? -1 : sum / (m - 2 * k);\n }\n}\n``` | 2 | 0 | [] | 0 |
finding-mk-average | C++ Intuitive Fenwick Tree Solution O(N * (logN)^2) w/explanation | c-intuitive-fenwick-tree-solution-on-log-00hd | First of all we only need to maintain a windows of size m at any point, so we maintain a queue for storing the numbers. \n\nFor MK Avg calculation, the whole se | varkey98 | NORMAL | 2021-04-14T18:05:57.380014+00:00 | 2021-04-14T18:07:47.632042+00:00 | 363 | false | First of all we only need to maintain a windows of size m at any point, so we maintain a queue for storing the numbers. \n\nFor MK Avg calculation, the whole search space of ```[1,10^5]``` is used for each testcase. \nI used 2 Fenwick Trees, for finding the sum of a given range in ```O(logN)``` time, the first tree is used.\n\nBut how to find the range?\nThere comes the second tree. We maintain a tree for getting the count of numbers upto a given number optimally. Then again, what we can do with a mere count? So, we do a search for the number from both the start and end to find the right value at which our wanted window for the answer starts and ends. Since we are searching in the space of ```[1,10^5]```, we can do a binary search for these 2 errands. \n\nSo if we know the boundary values, we can simply find the sum of all the elements, currently in our queue, which lie within these 2 values. \n\nOne last thing, when we update our queue, we update both our trees also, because we only want to search among the numbers which are currently in window of length ```m```.\n\nOne final optimization, if the starting and ending values occur more than once and we don\'t need all of them, for the given solution, I did a linear search. For that also a binary search can e done thus obtaining the mentioned complexity. That fragment of code is given in the comments.\n\n```\nclass FenwickTree\n{\npublic:\n\tvector<long> tree;\n\tlong sum=0;\n\tFenwickTree(int n)\n\t{\n\t\ttree.resize(n+1);\n\t}\n\tvoid update(int i,int val)\n\t{\n\t\twhile(i<tree.size())\n\t\t{\n\t\t\ttree[i]+=val;\n\t\t\ti+=i&(-i);\n\t\t}\n\t\tsum+=val;\n\t}\n\tint query(int i)\n\t{\n\t\tint ret=0;\n\t\twhile(i)\n\t\t{\n\t\t\tret+=tree[i];\n\t\t\ti=i&(i-1);\n\t\t}\n\t\treturn ret;\n\t}\n\tvoid append(int i)\n\t{\n\t\tint parent=tree.size();\n\t\tparent=parent&(parent-1);\n\t\tsum+=i;\n\t\ttree.push_back(sum-query(parent));\n\t}\n\tint binarySearch(int target)\n\t{\n\t\tint start=1,end=tree.size()-1;\n\t\twhile(start<end)\n\t\t{\n\t\t\tint q=start+(end-start)/2;\n\t\t\tint temp=query(q);\n\t\t\tif(temp>=target)\n\t\t\t\tend=q;\n\t\t\telse start=q+1;\n\t\t}\n\t\treturn end;\n\t}\n};\nclass MKAverage \n{\npublic:\n\tFenwickTree* sum=new FenwickTree(100000);\n\tFenwickTree* count = new FenwickTree(100000);\n\tint m,k;\n\tqueue<int> q;\n MKAverage(int x, int y) \n {\n m=x;\n k=y;\n }\n \n void addElement(int num) \n {\n q.push(num);\n if(q.size()>m)\n {\n \tint temp=q.front();\n \tcount->update(temp,-1);\n \tsum->update(temp,-temp);\n \tq.pop();\n }\n count->update(num,1);\n sum->update(num,num);\n }\n \n int calculateMKAverage() \n {\n if(q.size()<m)\n \treturn -1;\n int temp=count->sum;\n int first=count->binarySearch(k),last=count->binarySearch(temp-k);\n int firstCount=count->query(first),lastCount=count->query(last);\n int firstSum=sum->query(first),lastSum=sum->query(last);\n while(firstCount-->k)\n \tfirstSum-=first;\n while(lastCount-->temp-k)\n \tlastSum-=last;\n return (lastSum-firstSum)/(m-2*k);\n }\n};\n``` | 2 | 0 | ['C', 'Binary Tree'] | 2 |
finding-mk-average | Java BIT/Fenwick 60ms | java-bitfenwick-60ms-by-zoro406-zpzs | \nclass MKAverage {\n Deque<Integer> queue;\n Bit countBit;\n Bit valueBit;\n int m;\n int k;\n public MKAverage(int m, int k) {\n queu | zoro406 | NORMAL | 2021-04-13T07:47:01.072246+00:00 | 2021-04-13T07:50:53.811197+00:00 | 316 | false | ```\nclass MKAverage {\n Deque<Integer> queue;\n Bit countBit;\n Bit valueBit;\n int m;\n int k;\n public MKAverage(int m, int k) {\n queue = new ArrayDeque();\n countBit = new Bit(100001);\n valueBit = new Bit(100001);\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n queue.addLast(num);\n countBit.add(num, 1);\n valueBit.add(num, num);\n if(queue.size()>m)\n {\n var polledNum = queue.pollFirst();\n countBit.add(polledNum, -1);\n valueBit.add(polledNum, -polledNum);\n }\n }\n \n public int calculateMKAverage() {\n if(queue.size() < m)\n return -1;\n \n\t\t// Get first k elements index\n var left = binarySearch(k);\n\t\t\n\t\t// Get last k elements index\n var right = binarySearch(m-k);\n \n // Ex: [5 5 5] \n // left and right are equal, so difference is 0. What this means is the answer is at either left or right.\n // Using the countBit we can calculate the correct sum at index left.\n // Thats why we also have to do step 1 and step 2. \n long result = valueBit.sum(right) - valueBit.sum(left); \n \n result += (countBit.sum(left) - k)*left; // step 1\n result -= (countBit.sum(right) - m + k)*right; // step 2\n \n return (int)(result/(m-2*k));\n }\n \n public int binarySearch(int val)\n {\n int l = 0;\n int r = 100001;\n while(l<r)\n {\n int mid = l + (r-l)/2;\n if(countBit.sum(mid) < val)\n l = mid + 1;\n else \n r = mid;\n }\n \n return l;\n }\n \n \n class Bit\n {\n\t // Use long because the sum can exceed Integer.MAX_VALUE\n long[] bit;\n public Bit(int size)\n {\n\t\t\t// 1-indexed\n bit = new long[size+1];\n }\n \n public void add(int num, int value)\n { \n num += 1;\n while(num < bit.length)\n {\n bit[num] += value; \n num += num & (-num);\n }\n }\n \n public long sum(int num)\n {\n long s = 0;\n num += 1;\n while(num>0)\n {\n s += bit[num];\n num &= num-1;\n }\n \n return s;\n }\n }\n}\n``` | 2 | 0 | [] | 0 |
finding-mk-average | Naive Java solution with 2 PQs + TreeMap, probably will be TLE soon though | naive-java-solution-with-2-pqs-treemap-p-ctfj | Comments are in line.\n\nI expect this to be TLE soon with more test cases added, but I find this to be naive enough so sharing it.\n\n\nclass MKAverage {\n | kwi_t | NORMAL | 2021-04-11T05:00:29.811527+00:00 | 2021-04-11T05:04:27.378976+00:00 | 212 | false | Comments are in line.\n\nI expect this to be TLE soon with more test cases added, but I find this to be naive enough so sharing it.\n\n```\nclass MKAverage {\n int m;\n int k;\n List<Integer> lastM; // Record last m numbers, ordered by when they were added. This is for removing number.\n TreeMap<Integer, Integer> middle; // Record the numbers in the middle. Remains empty until we have more than 2*k numbers.\n PriorityQueue<Integer> smallerK;\n long smallerSum;\n PriorityQueue<Integer> largerK;\n long largerSum;\n long sum;\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n lastM = new ArrayList<>();\n middle = new TreeMap<>();\n smallerK = new PriorityQueue<>((a, b) -> b - a);\n smallerSum = 0;\n largerK = new PriorityQueue<>();\n largerSum = 0;\n sum = 0;\n }\n \n public void addElement(int num) {\n /**\n\t\t * First, check if need to remove number.\n\t\t * If yes, remove it from the head of lastM and update total sum.\n\t\t * Also check if need to remove it from middle M, smaller K or larger K, and update smaller sum and larger sum.\n\t\t */\n if (lastM.size() == m) {\n int toRemove = lastM.remove(0);\n sum -= toRemove;\n if (middle.containsKey(toRemove)) {\n middle.put(toRemove, middle.get(toRemove) - 1);\n if (middle.get(toRemove) == 0) {\n middle.remove(toRemove);\n }\n }\n \n if (toRemove <= smallerK.peek()) {\n smallerK.remove(toRemove);\n smallerSum -= toRemove;\n int toOffer = middle.firstKey();\n middle.put(toOffer, middle.get(toOffer) - 1);\n if (middle.get(toOffer) == 0) {\n middle.remove(toOffer);\n }\n smallerK.offer(toOffer);\n smallerSum += toOffer;\n } else if (toRemove >= largerK.peek()) {\n largerK.remove(toRemove);\n largerSum -= toRemove;\n int toOffer = middle.lastKey();\n middle.put(toOffer, middle.get(toOffer) - 1);\n if (middle.get(toOffer) == 0) {\n middle.remove(toOffer);\n }\n largerK.offer(toOffer);\n largerSum += toOffer;\n }\n }\n \n\t\t/**\n\t\t * Add it to the tail of lastM, and update total sum.\n\t\t * Set the number to add to middle m to just be the current num for now, this might change if num is put into either smaller/larger half.\n\t\t */\n lastM.add(num);\n int addToMiddle = num;\n sum += num;\n if (smallerK.size() < k) {\n\t\t /**\n\t\t\t * Don\'t have k numbers yet, simply add the number to both halves and update smaller and larger sum.\n\t\t\t */\n smallerK.offer(num);\n smallerSum += num;\n largerK.offer(num);\n largerSum += num;\n } else {\n\t\t /**\n\t\t\t * Have more than k numbers, check whether to put the number to smaller k or larger k.\n\t\t\t * \n\t\t\t * The reason to do both check is that when we don\'t have 2*k numbers, the two halves will overlap,\n\t\t\t * the number may still need to be in both halves.\n\t\t\t * \n\t\t\t * Update the eventual number to be added to middle m.\n\t\t\t */\n if (num <= smallerK.peek()) {\n addToMiddle = smallerK.poll();\n smallerSum -= addToMiddle;\n smallerK.offer(num);\n smallerSum += num;\n }\n \n if (num >= largerK.peek()) {\n addToMiddle = largerK.poll();\n largerSum -= addToMiddle;\n largerK.offer(num);\n largerSum += num;\n }\n }\n \n\t\t/**\n\t\t * Finally, only add to middle m if we have more than 2*k numbers.\n\t\t */\n if (lastM.size() > 2 * k) {\n middle.put(addToMiddle, middle.getOrDefault(addToMiddle, 0) + 1);\n }\n }\n \n public int calculateMKAverage() {\n if (lastM.size() != m) {\n return -1;\n }\n \n return (int) ((sum - smallerSum - largerSum) / (m - 2 * k));\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 2 | 0 | [] | 1 |
finding-mk-average | [C++]Fenwick Tree Solution. | cfenwick-tree-solution-by-waluigi120-0zmk | The idea for the problem is to maintain a data structure so that it can list the first k numbers\' sum and last k numbers\' sum quickly. It will also have the c | waluigi120 | NORMAL | 2021-04-11T04:06:29.673018+00:00 | 2021-04-11T04:06:29.673055+00:00 | 380 | false | The idea for the problem is to maintain a data structure so that it can list the first k numbers\' sum and last k numbers\' sum quickly. It will also have the capability of counting how many elements there are between specific range of the values. The data structure has the aformentioned abilities is a Fenwick Tree. You can have the implementation of a segment tree as well. But it will overcomplicate the issue.\n\nHow do we find the sum of first k elements? Essentially, whenever a new element flies in, we have a sliding window to window out an element that is out of the last m elements. We can use -1 and -value on the Fenwick tree to undo its effect. \n\nNow, we want to find the first k elements\' sum. We can use binary search to find the value such that the sum of the occurence of values less than a given value x is less than k, and we will have to find the first spot such property violated.\n\nWe just need to do some simple math to figure out what exactly the sum of the first k elements will be given the value of the violator and the value of the sum before the violator. And we will get the first k elements\' sum.\n\nFor the last k elements, it works the same.\n\nMy code is written in cLay, a transpiler written by LayCurse. For accessing it, you can either visit his yukicoder page or you can visit the link here: [LayCurse\'s Blog](http://rsujskf.s602.xrea.com/)\n\n```\n#define main dummy_main\n{}\n#undef main\n\nconst int MN = 1d5+10;\nclass MKAverage {\npublic:\n int m, k, size, a[MN];\n fenwick<ll> tr[2];\n\n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n this->size = 0;\n dummy_main();\n rep(i,0,2){\n tr[i].walloc(MN);\n tr[i].init(MN);\n }\n }\n \n void addElement(int num) {\n int & x = this->size;\n if( x >= m){\n tr[0].add(a[x-m], -1);\n tr[1].add(a[x-m], -a[x-m]);\n }\n a[x] = num;\n tr[0].add(num, 1);\n tr[1].add(num, num); \n ++x; \n }\n \n int calculateMKAverage() {\n // tr[0].range(0, x);\n // tr[0].range(x,1d5+2);\n if(size < m) return -1;\n auto u =bsearch_max[int, x, 0, 1d5+2] (tr[0].range(0,x) <= k);\n u = max(u-2,0);\n while(tr[0].range(0,u) <= k) ++u;\n --u;\n auto v = tr[0].range(0,u);\n auto vv = k-v;\n auto lowex = vv*(u+1) + tr[1].range(0,u);\n //part one\n\n auto uu = bsearch_min[int, x, 0, 1d5+2] (tr[0].range(x,1d5+2) <= k);\n uu = min(uu+2,1d5+2);\n while(tr[0].range(uu, 1d5+2) <= k) --uu;\n ++uu;\n auto vvv = tr[0].range(uu, 1d5+2);\n auto vx = k-vvv;\n auto upperx = vx * (uu-1)+tr[1].range(uu, 1d5+2);\n auto whole = tr[1].range(0,1d5+2);\n return (whole-upperx-lowex)/(m-2*k);\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n\n\n// void main(){\n\n// MKAverage mk(3,1);\n// mk.addElement(3);\n// mk.addElement(1);\n// wt( mk.calculateMKAverage());\n// mk.addElement(10);\n// wt(mk.calculateMKAverage());\n// mk.addElement(5);\n// mk.addElement(5);\n// mk.addElement(5);\n// __asm int 3;\n// wt(mk.calculateMKAverage());\n// }\n``` | 2 | 0 | [] | 0 |
finding-mk-average | Multiset | Queue O(logn) Time complexity | multiset-queue-ologn-time-complexity-by-adxtx | Intuition\n- Try to visualize it what are our requirements.\n- Firstly we need to maintain a window of size m so that only latest m elements are considered.\n- | yash559 | NORMAL | 2024-10-06T19:31:14.268419+00:00 | 2024-10-06T19:31:14.268441+00:00 | 113 | false | # Intuition\n- Try to visualize it what are our requirements.\n- Firstly we need to maintain a **window of size m** so that only latest m elements are considered.\n- Which data structure can we think of? yes it\'s **queue** when size exceeds m just pop oldest value and insert latest value.\n- Now our main aim is to actually get the sum also by excluding the **k largest and smallest elements in window**.\n- Now we need the ordering to be sorted right, and a window of m size need to be maintained.\n- Again which data structure comes to your brain? it\'s **priority queue.**\n- but we need smallest and largest values right, also we need to keep track of sum.\n- Now, to find and remove element in priority queue is difficult think of other data structure which works similar to priority queue but also allows you to find the element quicker.\n- Yes, it\'s **Multiset** which stores elements in sorted order and duplicates are also maintained.\n- Now, we create **3 multisets** one is **low of size k mid of size m-2k and high of k**.\n- We keep track of sum of mid multiset for average.\n# Insertion\n- Whenever we try to insert a new value, we will first insert it into **low** if it\'s size exceeds k then we take out the **largest value** in low and insert it into **mid**.\n- Then if size of mid exceeds **m-2k** then take the **largest of mid** and insert it into high.\n- high doesn\'t necessarily have to be of **k size**.\n- while modifying mid set keep track of summation of elements in mid.\n# Deletion\n- We have to remove the oldest value which is popped out by queue from multisets.\n- Firstly, we have to find out in which multiset the value lies.\n- If it is in **low** then we erase it, not size of low is imbalanced, to balance it we take the lowest value from mid and insert it to low.\n- Now, mid size if imbalanced( < m-2k) then we take smallest from high and insert it into mid and erase it from high.\n- Now, if the value is present in **mid** then erase it from mid and take the lowest value from high and insert it into mid, maintain sum of mid accordingly.\n- Now, if the value is present in **high** we remove it. now balancing is done.\n\n# Complexity\n- Time complexity: $$O(logn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass MKAverage {\npublic:\n multiset<long long> low, mid, high;\n long long midSum = 0;\n long long totalcount = 0;\n queue<long long> que;\n int m,k;\n bool removeFromSet(multiset<long long> &se, long long num) {\n auto iter = se.find(num);\n if(iter == se.end()) return false;\n se.erase(iter);\n return true;\n }\n void remove(int num) {\n if(removeFromSet(low, num)) {\n //mid to low\n int element = *mid.begin();\n low.insert(element);\n midSum -= element;\n mid.erase(mid.find(element));\n //high to mid\n element = *high.begin();\n midSum += element;\n mid.insert(element);\n high.erase(high.find(element));\n }\n else if(removeFromSet(mid, num)) {\n //high to mid\n midSum -= num;\n int element = *high.begin();\n midSum += element;\n mid.insert(element);\n high.erase(high.find(element));\n }\n else {\n removeFromSet(high, num);\n }\n }\n\n void insert_val(int num) {\n low.insert(num);\n if(low.size() > k) {\n int element = *low.rbegin();\n low.erase(low.find(element));\n midSum += element;\n mid.insert(element);\n }\n if(mid.size() > m - 2*k) {\n int element = *mid.rbegin();\n midSum -= element;\n mid.erase(mid.find(element));\n high.insert(element);\n }\n }\n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n }\n \n void addElement(int num) {\n que.push(num);\n insert_val(num);\n totalcount++;\n if(totalcount > m) {\n int n = que.front();\n remove(n);\n que.pop();\n totalcount--;\n }\n cout << midSum << endl;\n }\n \n int calculateMKAverage() {\n if(totalcount < m) return -1;\n return midSum / (m - 2*k);\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 1 | 0 | ['C++'] | 0 |
finding-mk-average | Java Queue & TreeMap Solution | java-queue-treemap-solution-by-fireonser-mjkv | Intuition\n Describe your first thoughts on how to solve this problem. \nWe need last m elements -> we use queue to record last m elements\nWe need to remove k | fireonserver | NORMAL | 2024-08-22T16:22:49.162137+00:00 | 2024-08-22T16:22:49.162166+00:00 | 43 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need last m elements -> we use queue to record last m elements\nWe need to remove k smallest and k largest\n1. total number of elements to be added is m - 2 * k\n2. Use TreeMap to remove k smallest\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAdd\n1. Whenever we add a number, we check if the size of the queue is larger than m. If the size is larger than m, we remove the first element in the queue.\n2. Meanwhile we maintain our TreeMap\n\nQuery\n1. Main 2 fields, one is how many ksmallest we have skipped, the other is how many elements we have added.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * log n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m)\n# Code\n```java []\nclass MKAverage {\n int m, k;\n Queue<Integer> q;\n TreeMap<Integer, Integer> tm; \n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n q = new ArrayDeque<>();\n tm = new TreeMap<>();\n }\n \n public void addElement(int num) {\n q.offer(num);\n tm.put(num, tm.getOrDefault(num, 0) + 1);\n if (q.size() > m) {\n int polled = q.poll();\n int count = tm.get(polled);\n if (count == 1) \n tm.remove(polled);\n else\n tm.put(polled, count - 1);\n } \n }\n \n public int calculateMKAverage() {\n if (q.size() < m) return -1;\n long sum = 0;\n int added = 0;\n int ksmall = 0;\n int total = m - (2 * k);\n for (int i : tm.keySet()) {\n int count = tm.get(i);\n int remove = Math.min(k - ksmall, count);\n ksmall += remove;\n count -= remove;\n int add = Math.min(total - added, count);\n sum += i * add;\n added += add;\n if (added == total) break;\n }\n return (int) sum / (m - 2 * k);\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 1 | 0 | ['Java'] | 1 |
finding-mk-average | C++| Multisets | c-multisets-by-chandrasekhar_n-6inm | Intuition\nUse a Queue to strore elements from the Q, max size of the Q should be m. Use 3 multisets, 1 for smallest K elements, second set for for M-2K mid ele | Chandrasekhar_N | NORMAL | 2024-08-14T12:25:03.228207+00:00 | 2024-08-14T12:25:03.228236+00:00 | 83 | false | # Intuition\nUse a Queue to strore elements from the Q, max size of the Q should be m. Use 3 multisets, 1 for smallest K elements, second set for for M-2K mid elements, third set for largest K elements. For every element added, pop Q front if its size > m and then update the sets and sum \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MKAverage {\npublic:\n queue<int> mQ;\n multiset<int> left;\n multiset<int> center;\n multiset<int> right;\n int M;\n int K;\n long int mSum;\n bool mFlag;\n vector<int> mArr;\n int mSize;\n MKAverage(int m, int k) {\n M = m;\n K = k;\n mSum = 0;\n mFlag = false;\n mSize = (M-2*K);\n }\n \n void removeFromSet(int num) {\n if (left.find(num) != left.end()) {\n left.erase(left.find(num));\n int val = *center.begin();\n center.erase(center.find(val));\n mSum -= val;\n left.insert(val);\n val = *right.begin();\n mSum += val;\n center.insert(val);\n right.erase(right.find(val));\n\n } else if (center.find(num) != center.end()) {\n center.erase(center.find(num));\n mSum -= num;\n int val = *right.begin();\n mSum += val;\n center.insert(val);\n right.erase(right.find(val));\n\n } else {\n right.erase(right.find(num));\n }\n }\n\n void addToSet(int num) {\n left.insert(num);\n if(left.size()>K) {\n int val = *left.rbegin();\n left.erase(left.find(val));\n center.insert(val);\n mSum += val;\n }\n\n if(center.size()>mSize) {\n int val = *center.rbegin();\n mSum -= val;\n center.erase(center.find(val));\n right.insert(val);\n }\n }\n\n void addElement(int num) {\n mQ.push(num);\n if(mQ.size()>M) {\n //Remove front element from Q and from the liar\n int val = mQ.front();\n mQ.pop();\n removeFromSet(val);\n }\n //Add num to set\n addToSet(num);\n }\n \n int calculateMKAverage() {\n if(mQ.size()<M)\n return -1;\n\n return mSum/mSize;\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 1 | 0 | ['C++'] | 1 |
finding-mk-average | Using multiset iterators | using-multiset-iterators-by-miguel-l-ata9 | Intuition\n Describe your first thoughts on how to solve this problem. \nKeep elements in a sorted container to easily exclude the k lowest and highest by keepi | miguel-l | NORMAL | 2024-07-13T17:34:33.676905+00:00 | 2024-07-13T17:34:33.676940+00:00 | 73 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nKeep elements in a sorted container to easily exclude the k lowest and highest by keeping track of the sum. Use a queue and some pointers to keep the container updated.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse a multiset to keep track of the m valid elements.\nWhile building, when there are finally m elements, initialize pointers to point to the kth lowest and kth highest element and adjust the sum.\nAs we add and remove elements, maintain the correct pointer position and sum.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\naddElement: $$O(log m)$$\ncalculateMKAverage: $$O(1)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(m)$$\n# Code\n```\nclass MKAverage {\n int m, k;\n int64_t sum = 0;\n std::multiset<int> data;\n decltype(data)::iterator lo, hi;\n std::queue<decltype(data)::iterator> q;\npublic:\n MKAverage(int m, int k) : m{m}, k{k} {\n\n }\n \n void addElement(int num) {\n q.push(data.insert(num));\n\n if (q.size() < m) {\n sum += num;\n return;\n }\n else if (q.size() == m) {\n sum += num;\n lo = data.begin(), hi = std::prev(data.end());\n sum -= *lo + *hi;\n for (int i = 1; i < k; ++i)\n lo = std::next(lo),\n hi = std::prev(hi),\n sum -= *lo + *hi;\n return;\n }\n\n // Adjust for the entering number\n if (num >= *hi)\n sum += *hi, hi = std::next(hi);\n else if (num < *lo)\n sum += *lo, lo = std::prev(lo);\n else\n sum += num;\n\n // Adjust for the leaving number\n if (q.front() == hi || *q.front() > *hi)\n hi = std::prev(hi), sum -= *hi;\n else if (q.front() == lo || *q.front() <= *lo)\n lo = std::next(lo), sum -= *lo;\n else\n sum -= *q.front();\n\n data.erase(q.front());\n q.pop();\n }\n \n int calculateMKAverage() {\n if (q.size() < m)\n return -1;\n\n return sum / (m - 2 * k);\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 1 | 0 | ['C++'] | 0 |
finding-mk-average | C++ Simple *ONE* Map & deque | c-simple-one-map-deque-by-vishnum1998-xmr9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nUse one map which store | vishnum1998 | NORMAL | 2024-07-03T16:12:58.359652+00:00 | 2024-07-03T16:12:58.359698+00:00 | 85 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse one map which stores the key and count. It auoto sorts the data.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\ncalculateMKAverage: O(k)\naddElement: O(m)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m)\n# Code\n```\n#include <ranges>\nclass MKAverage {\npublic:\n deque<int> q;\n map<int,int> m;\n int M,K;\n long total=0;\n MKAverage(int m, int k) {\n this->M=m;\n this->K=k;\n }\n \n void addElement(int num) {\n q.push_back(num);\n m[num]++;\n total+=num;\n if(q.size()>M){\n m[q.front()]--;\n if(m[q.front()]==0)\n m.erase(q.front());\n total-=q.front();\n q.pop_front();\n\n }\n }\n \n int calculateMKAverage() {\n if(q.size()<M)\n return -1;\n int j=K;\n int toRemove=0,toRemoveR=0;;\n for(auto & [k, v]:m){\n if(j>v){\n toRemove+=k*v;\n j-=v;\n continue;\n }else{\n toRemove+=k*j;\n break;\n }\n\n }\n j=K;\n for (auto & [k, v] : m | std::views::reverse){\n if(j>v){\n toRemoveR+=k*v;\n j-=v;\n continue;\n }else{\n toRemoveR+=k*j;\n break;\n }\n } \n return (total - toRemove - toRemoveR) / (M-2*K);\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 1 | 0 | ['C++'] | 0 |
finding-mk-average | Java, Design a class to store sorted nums with duplicates | java-design-a-class-to-store-sorted-nums-x4ic | Intuition\nIf we implement a brute force solution, we will make the following observations:\n1. We need to store only m recent numbers of stream\n2. If the numb | Vladislav-Sidorovich | NORMAL | 2024-06-13T10:51:44.608319+00:00 | 2024-06-13T10:51:44.608338+00:00 | 40 | false | # Intuition\nIf we implement a brute force solution, we will make the following observations:\n1. We need to store only `m` recent numbers of stream\n2. If the numbers will be sorted we in consant time may remove `k` smalles/biggest numbers\n3. We may keep track of `sum` of `[k+1, m-k-2]` sorted numbers\n\nTaking into account the observation above the problem is reduce to the following:\n1. Split `m` numbers into 3 sorted parts of sizes `k`, `m-2*k`, `k`\n2. Add and remove numbers to the collections\n3. Keep the collections balanced\n4. Collections **must** support dupplicate numbers, so we can\'t use `TreeSet`\n\n# Approach\nLet\'s use `TreeMap<val, count>` to solve the problem of duplicate numbers in `TreeSet`. \nLet\'s deisgin a class `SortedList` with required operations and delegate the most work to that class.\n`SortedList` should support the following operations:\n1. add number\n2. remove number\n3. min/max number\n4. size\n5. avg value\n\n# Complexity\n- Time complexity: \n--`max of O(log k) and O(log m-2k)` - add element\n-- `O(1)` - avg\n\n- Space complexity: `O(m)`\n\n# Code\n```\nclass MKAverage {\n private final int m;\n private final int k;\n private final int midSize;\n\n // keep track queue of size m\n private final LinkedList<Integer> queue = new LinkedList<>();\n\n // keep nums sorted in 3 parts: [mins, mids, maxs]\n private final SortedList mins = new SortedList();\n private final SortedList mids = new SortedList();\n private final SortedList maxs = new SortedList();\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n this.midSize = m - 2*k;\n }\n\n // add to sorted collection\n // remove the oldest element\n // adjust 3 sorted sub collections [0,k] [k+1, m-k-2] [m-k-1, m-1]\n public void addElement(int num) {\n queue.add(num);\n if (queue.size() > m && queue.peek() == num) { //no rebalance required\n queue.poll();\n return;\n }\n\n //do rebalance\n addToSorted(num);\n\n if (queue.size() > m) {\n removeFromSorted(queue.poll());\n }\n }\n\n private void removeFromSorted(int toDel) {\n if (maxs.contains(toDel)) { // maxs has +1 in size\n maxs.remove(toDel);\n return;\n }\n mids.add(maxs.min());\n maxs.remove(maxs.min());\n\n if (mids.contains(toDel)) { // mids has +1 in size\n mids.remove(toDel);\n return;\n }\n mins.add(mids.min());\n mids.remove(mids.min());\n\n // mis has +1 in size\n mins.remove(toDel);\n }\n\n private void addToSorted(int num) {\n mins.add(num);\n adjustToSize(mins, mids, k); // size k | mins -> mids\n adjustToSize(mids, maxs, midSize); // size m - 2*k | mids -> maxs\n //maxs may have k+1 size\n }\n\n private void adjustToSize(SortedList low, SortedList big, int size) {\n if (low.size() > size) {\n big.add(low.max());\n low.remove(low.max());\n }\n }\n\n public int calculateMKAverage() {\n if (queue.size() < m) {\n return -1;\n }\n return mids.avg();\n }\n\n private static class SortedList {\n private TreeMap<Integer, Integer> vals = new TreeMap<>();\n private int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;\n private int size;\n private long totalSum;\n\n void add(int num) {\n vals.put(num, vals.getOrDefault(num, 0) + 1);\n min = Math.min(min, num);\n max = Math.max(max, num);\n\n totalSum += num;\n size++;\n }\n\n void remove(int num) {\n int count = vals.getOrDefault(num, 0);\n if (count > 0) {\n size--;\n totalSum -= num;\n\n if (count == 1) {\n vals.remove(num);\n\n if (min == num) {\n min = vals.firstKey();\n }\n if (max == num) {\n max = vals.lastKey();\n }\n } else {\n vals.put(num, count - 1);\n }\n }\n }\n\n boolean contains(int num) {\n return vals.containsKey(num);\n }\n\n int avg() {\n return (int) (totalSum / size);\n }\n\n int min() {\n return min;\n }\n int max() {\n return max;\n }\n\n int size() {\n return size;\n }\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 1 | 0 | ['Queue', 'Ordered Map', 'Java'] | 0 |
finding-mk-average | heap | bst | heap-bst-by-hzhaoc-csbm | heap with lazy update 700ms\n\npython\nclass MKAverage:\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.lh1, self | hzhaoc | NORMAL | 2024-01-31T04:21:41.655027+00:00 | 2024-01-31T04:21:41.655055+00:00 | 196 | false | # heap with lazy update 700ms\n\n```python\nclass MKAverage:\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.lh1, self.rh1 = [(0, i) for i in range(m-k)], [(0, i) for i in range(m-k, m)]\n self.lh2, self.rh2 = [(0, i) for i in range(k)], [(0, i) for i in range(k, m)]\n for h in [self.lh1, self.rh1, self.lh2, self.rh2]:\n heapq.heapify(h)\n self.dq = deque([0 for i in range(m)])\n self.s = 0\n self.i = m-1\n\n def addElement(self, v):\n self.i += 1\n l1 = self.add(self.lh1, self.rh1, v, self.i)\n l2 = self.add(self.lh2, self.rh2, v, self.i)\n self.dq.popleft()\n self.dq.append(v)\n self.s += l1 - l2\n # print(\'add\', v)\n # print(\'lh1\', self.lh1)\n # print(\'rh1\', self.rh1)\n # print(\'lh2\', self.lh2)\n # print(\'rh2\', self.rh2)\n # print(\'s\', self.s)\n\n def add(self, lh, rh, v, i):\n m = self.m\n k = self.k\n dq = self.dq\n s = 0\n\n prev = dq[0]\n if v >= rh[0][0]: \n # new v adds to rh\n heapq.heappush(rh, (v, i))\n if prev <= -lh[0][0]:\n # old v rmvs from lh, move smallest from rh to lh for balancing\n _v, _i = heapq.heappop(rh)\n heapq.heappush(lh, (-_v, _i))\n s += _v\n s -= prev\n else:\n # old v rmvs from rh. do nothing\n pass\n else:\n # new v adds to lh\n heapq.heappush(lh, (-v, i))\n s += v\n if prev > -lh[0][0]:\n # old v rmvs from rh, move biggest from lh to rh for balancing\n _v, _i = heapq.heappop(lh)\n heapq.heappush(rh, (-_v, _i))\n s -= -_v\n else:\n # old v rmvs from lh\n s -= prev\n\n while lh and lh[0][1] <= i - m:\n heapq.heappop(lh)\n while rh and rh[0][1] <= i - m:\n heapq.heappop(rh)\n return s\n \n def calculateMKAverage(self):\n if self.i < 2*self.m - 1:\n return -1\n return self.s // (self.m - self.k*2)\n```\n\n# balanced BST (sortedList), 950ms\n```python\nclass MKAverage:\n def __init__(self, m: int, k: int):\n from sortedcontainers import SortedList\n self.sl = SortedList()\n self.s = 0\n self.l = 0\n self.r = 0\n self.dq = deque()\n self.m = m\n self.k = k\n\n def addElement(self, v: int) -> None:\n # O(logm)\n dq = self.dq\n sl = self.sl\n\n if len(dq) == self.m:\n prev = dq.popleft()\n self.s -= prev\n\n i = sl.index(prev)\n if i >= self.m - self.k:\n self.r -= prev\n self.r += sl[-self.k-1]\n if i <= self.k-1:\n self.l -= prev\n self.l += sl[self.k]\n sl.remove(prev)\n\n self.s += v\n dq.append(v)\n \n sl.add(v)\n i = sl.bisect_left(v)\n if i >= len(sl) - self.k:\n self.r += v\n if len(sl) >= self.k+1:\n self.r -= sl[-self.k-1]\n\n i = sl.bisect_right(v) - 1\n if i <= self.k - 1:\n self.l += v\n if len(sl) >= self.k+1:\n self.l -= sl[self.k]\n\n def calculateMKAverage(self) -> int:\n # O(1)\n if len(self.dq) < self.m:\n return -1\n v = self.s - self.l - self.r\n n = self.m - self.k - self.k\n v = v // n\n return v\n``` | 1 | 0 | ['Binary Search Tree', 'Heap (Priority Queue)', 'Python3'] | 0 |
finding-mk-average | 3 TreeMaps (Clean Code) | 3-treemaps-clean-code-by-khamidjon-n0xi | Intuition\nThe idea is to have 3 treemaps tl, tm and th. For lowest k (tl), highest k (th) and all others (tm). The trick is we need to balance the maps when an | khamidjon | NORMAL | 2023-12-29T23:38:37.234088+00:00 | 2023-12-29T23:39:29.764893+00:00 | 142 | false | # Intuition\nThe idea is to have 3 treemaps **tl**, **tm** and **th**. For lowest k (tl), highest k (th) and all others (tm). The trick is we need to balance the maps when an element is added/removed. \n\n\n# Code\n```\nclass MKAverage {\n int mx = (int)2e5, mn = 0, i = 0, m, k;\n long sm = 0l;\n TreeMap<Integer, Integer> tl = new TreeMap(), tm = new TreeMap(), th = new TreeMap(); \n HashMap<Integer, Integer> ind = new HashMap();\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n \n public void addElement(int num) {\n addNewNum(num);\n if(i > m) removeOldNum();\n }\n \n public int calculateMKAverage() {\n return i >= m ? (int)(sm / ((m - 2 * k)*1l)) : -1;\n }\n\n void addNewNum(int num){\n ind.put(i++, num);\n add(tl, num);\n if(i <= k) return;\n int v1 = removeHighest(tl);\n \n add(tm, v1);\n int v2 = removeHighest(tm);\n sm += v1 - v2;\n\n add(th, v2);\n if(i <= 2*k) return;\n int v3 = removeLowest(th);\n\n add(tm, v3);\n sm += v3;\n }\n\n void removeOldNum() {\n int prev = ind.get(i - m - 1);\n\n if(tl.get(prev) != null){\n remove(tl, prev);\n int low = removeLowest(tm);\n sm -= low;\n add(tl, low);\n } else if (th.get(prev) != null){\n remove(th, prev);\n int high = removeHighest(tm);\n sm -= high;\n add(th, high);\n } else {\n remove(tm, prev);\n sm -= prev;\n }\n\n ind.remove(i - m - 1);\n }\n\n void remove(Map<Integer, Integer> tree, int val) {\n tree.put(val, tree.getOrDefault(val, 0) - 1);\n if(tree.get(val) == 0) tree.remove(val);\n }\n\n void add(Map<Integer, Integer> tree, int val){\n tree.put(val, tree.getOrDefault(val, 0) + 1);\n }\n\n int removeLowest(TreeMap<Integer, Integer> tree){\n int low = tree.ceilingKey(mn);\n tree.put(low, tree.get(low) - 1);\n if(tree.get(low) == 0) tree.remove(low);\n return low;\n }\n\n int removeHighest(TreeMap<Integer, Integer> tree){\n int high = tree.floorKey(mx);\n tree.put(high, tree.get(high) - 1);\n if(tree.get(high) == 0) tree.remove(high);\n return high;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
finding-mk-average | 3 multiset and a queue | 3-multiset-and-a-queue-by-pranavgaur2000-mcxc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | pranavgaur2000 | NORMAL | 2023-12-23T16:37:47.513188+00:00 | 2023-12-23T16:37:47.513208+00:00 | 450 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n For average: O(1)\n For insert: O(log(m))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m)\n\n# Code\n```\nclass MKAverage {\n multiset<int> low, mid, high;\n int m, k;\n long long midSum;\n int totalElements;\n queue<int> q;\n\n bool removeFromSet(int num, multiset<int> &s) {\n auto it = s.find(num);\n if(it != s.end()) {\n s.erase(it);\n return true;\n }\n return false;\n }\n\n void remove(int num) {\n if(removeFromSet(num, low)) {\n int element = *mid.begin();\n mid.erase(mid.find(element));\n midSum -= element;\n low.insert(element);\n element = *high.begin();\n mid.insert(element);\n midSum += element;\n high.erase(high.find(element));\n }\n else if(removeFromSet(num, mid)) {\n midSum -= num;\n int element = *high.begin();\n mid.insert(element);\n midSum += element;\n high.erase(high.find(element));\n return;\n }\n else removeFromSet(num, high);\n }\n\n void addUtil(int num) {\n low.insert(num);\n if(low.size() > k) {\n int element = *low.rbegin();\n low.erase(low.find(element));\n mid.insert(element);\n midSum += element;\n }\n if(mid.size() > m - 2*k) {\n int element = *mid.rbegin();\n mid.erase(mid.find(element));\n high.insert(element);\n midSum -= element;\n }\n }\n\npublic:\n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n midSum = 0;\n totalElements = 0;\n }\n\n \n void addElement(int num) {\n totalElements++;\n if(totalElements > m) {\n int element = q.front();\n q.pop();\n remove(element);\n totalElements--;\n }\n\n q.push(num);\n addUtil(num);\n }\n \n int calculateMKAverage() {\n if(totalElements < m) return -1;\n return midSum / (m - 2*k);\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n \n 8272\n 33433\n 15456\n */\n``` | 1 | 0 | ['C++'] | 0 |
finding-mk-average | A sub optimal solution which is possible to code fully in an interview | a-sub-optimal-solution-which-is-possible-i02y | Intuition\n Describe your first thoughts on how to solve this problem. \nWhile solving the problem I got the intuition to maintain three heaps, or dividing an a | user7030K | NORMAL | 2023-11-24T15:57:53.793234+00:00 | 2023-11-24T15:57:53.793268+00:00 | 330 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhile solving the problem I got the intuition to maintain three heaps, or dividing an array to three parts and keeping sum of these tree parts and update if any element is added or deleted from each. But I was finding it very difficult to convert my intuition into code in a time bound manner. \nSo I thought if it were an interview, rather than ending up not coding anything to achieve O(1) sum, I may very well code out a non optimal solution. If someone else is also feeling lost and demotivated looking at all the other solutions, here is one which gets accepted, even if not the best! :) Hope it gives you the moral boost to have patience and understand the optimal one, as I am going to do now. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nMaintain a deque to act as a FIFO container to tell us the relevant m elements. We store the number as entry. Whenever we have more than m elements, we discard that number from sortedlist. This setup is very similar to an LRU cache. \nTo calculate the average, I go sub optimal and directly take sum of middle m-2k elements. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nPush and pop into a deque is O(1). For sorted list insertion and deletion is O(logn). We will keep max m elements in the list at a time, so O(logm). The biggest bottleneck on time is calculation of sum which is O(m-2k) Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m) for the sorted list. Also O(m) for the deque().\n# Code\n```\nfrom sortedcontainers import SortedList\nclass MKAverage(object):\n\n def __init__(self, m, k):\n """\n :type m: int\n :type k: int\n """\n self.m = m \n self.k = k \n self.elements = SortedList()\n self.deque = deque() \n\n def addElement(self, num):\n """\n :type num: int\n :rtype: None\n """\n if len(self.elements) >= self.m:\n oldNum = self.deque.popleft()\n self.elements.discard(oldNum)\n # idx = bisect.bisect_left(self.elements, num)\n self.elements.add(num)\n self.deque.append(num)\n\n def calculateMKAverage(self):\n """\n :rtype: int\n """\n if len(self.elements) < self.m:\n return -1 \n Leftover = self.elements[self.k:-self.k]\n return int(sum(Leftover)/len(Leftover))\n \n\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 1 | 0 | ['Doubly-Linked List', 'Python'] | 1 |
finding-mk-average | Straight forward solution | straight-forward-solution-by-ogoyal-hbzn | Intuition\nTo compute the MKAverage, we need a rolling window of the last m numbers and an efficient way to exclude the smallest and largest k numbers. A deque | ogoyal | NORMAL | 2023-11-06T00:53:55.739611+00:00 | 2023-11-06T00:53:55.739632+00:00 | 38 | false | # Intuition\nTo compute the MKAverage, we need a rolling window of the last m numbers and an efficient way to exclude the smallest and largest k numbers. A deque is suitable for the rolling window, and a Counter can efficiently track number frequencies.\n\n# Approach\n1. Initialization: Use a deque to maintain the last m numbers and a Counter for their frequencies. Track the sum of middle numbers with middle_sum.\n2. addElement: On new number addition, if deque is full, remove the oldest number. Update deque and Counter. If deque has m numbers, compute the middle_sum by deducting the smallest and largest k values.\n3. calculateMKAverage: If deque size is less than m, return -1. Otherwise, return middle_sum divided by (m - 2 * k).\n\n# Complexity\n- Time complexity:\naddElement is O(m log m) due to sorting. calculateMKAverage is O(1).\n\n- Space complexity:\nThe deque will hold at most m elements and the counter will hold, in the worst case, m unique elements. This gives a space complexity of O(m).\n\n# Code\n```\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m, k\n self.queue = deque()\n self.counter = Counter()\n self.middle_sum = 0\n self.qlen = 0\n\n def addElement(self, num: int) -> None:\n # If m numbers already in queue, remove the leftmost number\n if len(self.queue) == self.m:\n old = self.queue.popleft()\n self.counter[old] -= 1\n if self.counter[old] == 0:\n del self.counter[old]\n else:\n self.qlen += 1\n\n self.queue.append(num)\n self.counter[num] += 1\n\n # If m numbers in the queue, recompute the middle_sum\n if len(self.queue) == self.m:\n self.middle_sum = sum(num * count for num, count in self.counter.items())\n sorted_items = sorted(self.counter.items())\n \n # Deduct smallest k\n c = 0\n remain = self.k\n while remain:\n if sorted_items[c][1] >= remain:\n self.middle_sum -= (sorted_items[c][0] * remain)\n break\n else:\n self.middle_sum -= (sorted_items[c][0] * sorted_items[c][1])\n remain -= sorted_items[c][1]\n c += 1\n\n # Deduct largest k\n c = -1\n remain = self.k\n while remain:\n if sorted_items[c][1] >= remain:\n self.middle_sum -= (sorted_items[c][0] * remain)\n break\n else:\n self.middle_sum -= (sorted_items[c][0] * sorted_items[c][1])\n remain -= sorted_items[c][1]\n c -= 1\n\n def calculateMKAverage(self) -> int:\n if self.qlen < self.m:\n return -1\n return self.middle_sum // (self.m - 2 * self.k)\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 1 | 0 | ['Python3'] | 0 |
finding-mk-average | Best Java Solution || Beats 100% | best-java-solution-beats-100-by-ravikuma-5tpr | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2023-10-08T19:22:46.478973+00:00 | 2023-10-08T19:22:46.478991+00:00 | 591 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MKAverage {\n\n private int m;\n private int k;\n private int size = 0;\n private long sum = 0L;\n\n private Queue<Integer> q = new ArrayDeque<>(m);\n private TreeMap<Integer, Integer> left = new TreeMap<>();\n private TreeMap<Integer, Integer> middle = new TreeMap<>();\n private TreeMap<Integer, Integer> right = new TreeMap<>();\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n }\n\n private void removeOne(TreeMap<Integer, Integer> map, int num) {\n Integer rmCount = map.get(num);\n if (rmCount.equals(1)) {\n map.remove(num);\n } else {\n map.put(num, rmCount - 1);\n }\n }\n\n private void edgeFix(TreeMap<Integer, Integer> prev, TreeMap<Integer, Integer> next) {\n if (next.firstKey() < prev.lastKey()) {\n Integer nextKey = next.firstKey();\n Integer nextCount = next.get(nextKey);\n Integer prevKey = prev.lastKey();\n Integer prevCount = prev.get(prevKey);\n if (prevCount.equals(1)) {\n prev.remove(prevKey);\n } else {\n prev.put(prevKey, prevCount - 1);\n }\n prev.put(nextKey, prev.getOrDefault(nextKey, 0) + 1);\n if (nextCount.equals(1)) {\n next.remove(nextKey);\n } else {\n next.put(nextKey, nextCount - 1);\n }\n next.put(prevKey, next.getOrDefault(prevKey, 0) + 1);\n if (prev == middle) {\n sum = sum - prevKey + nextKey;\n }\n if (next == middle) {\n sum = sum - nextKey + prevKey;\n }\n }\n }\n\n public void addElement(int num) {\n q.offer(num);\n // all full\n if (size == m) {\n Integer rm = q.poll();\n // remove and add the same value, no need to change\n if (rm == num) {\n return;\n }\n // the position of the value removed\n boolean removeLeft = false;\n boolean removeRight = false;\n TreeMap<Integer, Integer> rmMap = null;\n if (rm >= middle.firstKey() && rm <= middle.lastKey()) {\n removeOne(middle, rm);\n sum = sum - rm;\n } else if (rm <= left.lastKey()) {\n removeLeft = true;\n removeOne(left, rm);\n } else if (rm >= right.firstKey()) {\n removeRight = true;\n removeOne(right, rm);\n }\n // insert new value into middle first \n middle.put(num, middle.getOrDefault(num, 0) + 1);\n sum = sum + num;\n // update values\n if (removeLeft) {\n Integer moveKey = middle.firstKey();\n removeOne(middle, moveKey);\n sum = sum - moveKey;\n left.put(moveKey, left.getOrDefault(moveKey, 0) + 1);\n } else if (removeRight) {\n Integer moveKey = middle.lastKey();\n removeOne(middle, moveKey);\n sum = sum - moveKey;\n right.put(moveKey, right.getOrDefault(moveKey, 0) + 1);\n }\n edgeFix(middle, right);\n edgeFix(left, middle);\n return;\n }\n // if not full\n // left not full\n if (size < k) {\n left.put(num, left.getOrDefault(num, 0) + 1);\n } else {\n // left is full\n Integer maxLeft = left.lastKey();\n // num is in left\n if (num < maxLeft) {\n left.put(num, left.getOrDefault(num, 0) + 1);\n Integer maxLeftCount = left.get(maxLeft);\n if (maxLeftCount == 1) {\n left.remove(maxLeft);\n } else {\n left.put(maxLeft, maxLeftCount - 1);\n }\n num = maxLeft;\n }\n // right not full\n if (size < k + k) {\n right.put(num, right.getOrDefault(num, 0) + 1);\n } else {\n // num is in right\n Integer minRight = right.firstKey();\n if (num > minRight) {\n right.put(num, right.getOrDefault(num, 0) + 1);\n Integer minRightCount = right.get(minRight);\n if (minRightCount == 1) {\n right.remove(minRight);\n } else {\n right.put(minRight, minRightCount - 1);\n }\n num = minRight;\n }\n // middle is not full\n middle.put(num, middle.getOrDefault(num, 0) + 1);\n sum += num;\n }\n }\n size++;\n }\n\n public int calculateMKAverage() {\n if (size < m) {\n return -1;\n }\n return (int) (sum / (size - k - k));\n }\n}\n\n\n\n\n\n/*\n\n// this code is correct and T.C = O(logn);\n but it gives wrong answer for 16/17 cases even my output and the expected output both are same\n\nclass MKAverage {\n\n ArrayList<Integer> arr;\n int m;\n int k;\n int sum;\n\n PriorityQueue<Integer> min = new PriorityQueue<>();\n PriorityQueue<Integer> max = new PriorityQueue<>(Comparator.reverseOrder());\n\n\n public MKAverage(int M, int K) {\n arr = new ArrayList<>();\n m=M;\n k=K;\n sum=0;\n }\n \n public void addElement(int num) {\n if(arr.size()<m){\n arr.add(num);\n sum+=num;\n min.add(num);\n max.add(num);\n } \n else{\n int a = arr.get(0);\n sum = sum-a;\n arr.remove(0);\n arr.add(arr.size(),num);\n sum=sum+num;\n min.remove(a);\n max.remove(a);\n min.add(num);\n max.add(num);\n }\n \n }\n \n public int calculateMKAverage() {\n\n if(arr.size()<m) return -1;\n \n\n int a = min.peek();\n int b = max.peek();\n return (sum-a-b)/(m-2);\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 1 | 0 | ['Java'] | 2 |
finding-mk-average | Python SortedList - intuitive logic and explanation | python-sortedlist-intuitive-logic-and-ex-gntm | Algorithm:\n1. Maintaina queue for keeping items in stream order and 3 sorted lists - lesser, mid and greater for keeping track of the k lesser items, k greater | subhashgo | NORMAL | 2023-10-05T01:28:12.571050+00:00 | 2023-10-05T01:28:12.571078+00:00 | 39 | false | Algorithm:\n1. Maintaina queue for keeping items in stream order and 3 sorted lists - lesser, mid and greater for keeping track of the k lesser items, k greater items and m-2k selected items that need to be averaged\n2. When the stream size exceeds m, we need to remove the oldest entry from the stream i.e. the first entry\n\ta. This entry could be in the lesser, mid or greater lists. We simply try each of them. This is ok because we will be balancing their size while adding the new item\n3. Just add the item to the queue and also to the greater list. \n\ta. Then, trickle down the first entry in the greater list to the mid list and similarly from the mid list to the lesser list. \n\tb, Then, if the lesser list size is greater than k, bubble up the last entry to the mid list and similarly from the mid list to the greater list\n\tc. The trickling down ensures that a global sorting order is maintained across the 3 lists and the bubbling up ensures that their sizes remain balanced\n4. For each change in the mid list, keep `self.sum` updated\n5. Return `self.sum` divided by m - 2k as the average\n\n```\nfrom sortedcontainers import SortedList\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.stream = []\n self.lesser = SortedList()\n self.mid = SortedList()\n self.greater = SortedList()\n self.m = m\n self.k = k\n self.sum = 0 \n\n def addElement(self, num: int) -> None:\n self.stream.append(num)\n \n if len(self.stream) > self.m:\n # remove oldest entry from stream\n old = self.stream.pop(0)\n \n # the oldest entry could be anywhere in the 3 sorted lists\n if old in self.lesser:\n self.lesser.remove(old)\n elif old in self.mid:\n self.mid.remove(old)\n self.sum -= old\n else:\n self.greater.remove(old)\n \n # always add new entry to the greatest list\n # and let it trickle down to mid and lowest lists\n self.greater.add(num)\n extra = self.greater.pop(0)\n self.mid.add(extra)\n self.sum += extra\n extra = self.mid.pop(0)\n self.sum -= extra\n self.lesser.add(extra)\n \n # if lesser list has more than k entries,\n # bubble up last entry to mid\n if len(self.lesser) > self.k:\n extra = self.lesser.pop()\n self.mid.add(extra)\n self.sum += extra\n \n # if mid list has more than m - 2k entries,\n # bubble up last entry to greatest\n if len(self.mid) > self.m - 2 * self.k:\n extra = self.mid.pop()\n self.sum -= extra\n self.greater.add(extra)\n \n\n def calculateMKAverage(self) -> int:\n if len(self.stream) < self.m:\n return -1\n return self.sum // (self.m - 2*self.k)\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
finding-mk-average | Python3 1 SortedList solution & C++ 3 set solution | python3-1-sortedlist-solution-c-3-set-so-b5ua | Intuition\r\n Describe your first thoughts on how to solve this problem. \r\nThis is a very nice problem to test your ability to analyze what data structure is | huikinglam02 | NORMAL | 2023-07-25T06:25:38.081260+00:00 | 2023-07-26T02:07:08.212241+00:00 | 37 | false | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nThis is a very nice problem to test your ability to analyze what data structure is needed, how to design a working system, what data structure different languages provides and their limitations.\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\nIf you use Python, the sortedcontainer modules will do this very simplistically, because it can both bisect and arrive at element by index in log(N) time.\r\nI tried looking up documentation of C# sorted set, Microsoft so far does not support giving you the iterator inside a sorted set. So you cannot solve the problem in C#.\r\nFor C++, 3 std::set would suffice.\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n$$O(n log n)$$\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n$$O(n)$$\r\n# Code\r\nPython3:\r\n```\r\nfrom collections import deque\r\nimport sortedcontainers\r\nclass MKAverage:\r\n \'\'\'\r\n Break down the task in hand:\r\n We want to keep m last numbers in check, have these numbers sorted, such that the top and bottom k elements can be accessed quickly. \r\n But we also want to update the tree regularly. We cannot afford to calculate the largest and smallest k - sums every time a query is make, so we need to maintain the left and right sums. \r\n When a new number nums[i] comes in, we first find where is nums[i - m]. This node we must remove. We identify if it is in the left and right k sums, and if so, deduct it from the sums. Note that we also need to add the kth smallest element and the m - k th smallest element. Also, we need to deduct it from the total sum.\r\n Then we insert nums[i]. We first ask where the insertion position should be, and update the two k sums and totalSum in similar manner as before\r\n\r\n When calculateMKAverage is called, we just return (totalSum - leftkSum - rightkSum) // (m - 2 * k)\r\n \'\'\'\r\n def __init__(self, m: int, k: int):\r\n self.tree = sortedcontainers.SortedList()\r\n self.Total = 0\r\n self.leftSum = 0\r\n self.rightSum = 0\r\n self.index = -1\r\n self.m = m\r\n self.k = k\r\n self.dq = deque()\r\n \r\n def deleteNode(self, num, ind):\r\n treeIndex = self.tree.index([num, ind])\r\n if treeIndex < self.k:\r\n self.leftSum -= num\r\n self.leftSum += self.tree[self.k][0]\r\n if len(self.dq) + 1 - treeIndex <= self.k:\r\n self.rightSum -= num\r\n self.rightSum += self.tree[len(self.dq) + 1 - self.k - 1][0]\r\n self.tree.remove([num, ind])\r\n self.Total -= num\r\n \r\n def insertNode(self, num, ind):\r\n self.tree.add([num, ind])\r\n treeIndex = self.tree.bisect_left([num, ind])\r\n if treeIndex < self.k:\r\n self.leftSum += num\r\n if len(self.dq) > self.k:\r\n self.leftSum -= self.tree[self.k][0]\r\n if len(self.dq) - treeIndex <= self.k:\r\n self.rightSum += num\r\n if len(self.dq) > self.k:\r\n self.rightSum -= self.tree[len(self.dq) - self.k - 1][0]\r\n self.Total += num\r\n \r\n def addElement(self, num: int) -> None:\r\n self.index += 1\r\n if len(self.dq) == self.m:\r\n value, index = self.dq.popleft()\r\n self.deleteNode(value, index)\r\n self.dq.append([num, self.index])\r\n self.insertNode(num, self.index)\r\n\r\n def calculateMKAverage(self) -> int:\r\n return -1 if len(self.tree) < self.m else (self.Total - self.leftSum - self.rightSum) // (self.m - 2 * self.k)\r\n\r\n# Your MKAverage object will be instantiated and called as such:\r\n# obj = MKAverage(m, k)\r\n# obj.addElement(num)\r\n# param_2 = obj.calculateMKAverage()\r\n```\r\nC++:\r\n```\r\n#include <queue>\r\n#include <set>\r\nusing namespace std;\r\n\r\nclass MKAverage {\r\n/*\r\n We use two sets of size k and one set of size m to store the nodes. When we delete a previous node, we first check if it is in the left and right trees. If so, update the trees.\r\n*/\r\nprivate:\r\n set<pair<int, int>> tree;\r\n set<pair<int, int>> left;\r\n set<pair<int, int>> right;\r\n long long Total;\r\n long long leftSum;\r\n long long rightSum;\r\n int index;\r\n int m;\r\n int k;\r\n queue<pair<int, int>> q;\r\n\r\n void deleteNode(int num, int index)\r\n {\r\n pair<int, int> nodeToRemove = make_pair(num, index);\r\n if (left.find(nodeToRemove) != left.end())\r\n {\r\n pair<int, int> nodeToInsert = *next(tree.find(*left.rbegin()), 1);\r\n left.insert(nodeToInsert);\r\n leftSum -= (long long)num;\r\n leftSum += (long long)nodeToInsert.first;\r\n left.erase(nodeToRemove);\r\n }\r\n if (right.find(nodeToRemove) != right.end())\r\n {\r\n pair<int, int> nodeToInsert = *prev(tree.find(*right.begin()), 1);\r\n right.insert(nodeToInsert);\r\n rightSum -= (long long)num;\r\n rightSum += (long long)nodeToInsert.first;\r\n right.erase(nodeToRemove);\r\n }\r\n\r\n tree.erase(nodeToRemove);\r\n Total -= (long long)num;\r\n }\r\n\r\n void insertNode(int num, int index)\r\n {\r\n pair<int, int> nodeToInsert = make_pair(num, index);\r\n if (left.size() < k || left.lower_bound(nodeToInsert) != left.end())\r\n {\r\n if (left.size() == k)\r\n {\r\n pair<int, int> nodeToRemove = *left.rbegin();\r\n left.erase(nodeToRemove);\r\n leftSum -= (long long)nodeToRemove.first; \r\n }\r\n left.insert(nodeToInsert);\r\n leftSum += (long long)num;\r\n \r\n }\r\n if (right.size() < k || right.upper_bound(nodeToInsert) != right.begin())\r\n {\r\n if (right.size() == k)\r\n {\r\n pair<int, int> nodeToRemove = *right.begin();\r\n right.erase(nodeToRemove);\r\n rightSum -= (long long)nodeToRemove.first; \r\n }\r\n right.insert(nodeToInsert);\r\n rightSum += (long long)num; \r\n }\r\n\r\n tree.insert(nodeToInsert);\r\n Total += (long long)num;\r\n }\r\n\r\npublic:\r\n MKAverage(int m, int k) {\r\n tree = set<pair<int, int>>{};\r\n left = set<pair<int, int>>{};\r\n right = set<pair<int, int>>{};\r\n q = queue<pair<int, int>>{};\r\n Total = (long long)0;\r\n leftSum = (long long)0;\r\n rightSum = (long long)0;\r\n index = -1;\r\n this->m = m;\r\n this->k = k;\r\n }\r\n\r\n void addElement(int num) {\r\n index++;\r\n if (q.size() == m)\r\n {\r\n pair<int, int> element = q.front();\r\n q.pop();\r\n deleteNode(element.first, element.second);\r\n }\r\n q.push(make_pair(num, index));\r\n insertNode(num, index);\r\n }\r\n\r\n int calculateMKAverage() {\r\n return tree.size() < m ? -1 : (Total - leftSum - rightSum) / (long long)(m - 2 * k);\r\n }\r\n};\r\n``` | 1 | 0 | ['C++', 'Python3'] | 0 |
finding-mk-average | Python (Simple Deque + SortedList) | python-simple-deque-sortedlist-by-rnotap-65xy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2023-04-23T17:32:40.344789+00:00 | 2023-04-23T17:32:40.344822+00:00 | 65 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MKAverage:\n\n def __init__(self, m, k):\n from sortedcontainers import SortedList\n self.m = m\n self.k = k\n self.ans = deque()\n self.res = SortedList()\n self.total = 0\n\n def addElement(self, num):\n self.ans.append(num)\n self.res.add(num)\n self.total += num\n\n if len(self.ans) > self.m:\n x = self.ans.popleft()\n self.res.remove(x)\n self.total -= x\n\n def calculateMKAverage(self):\n if len(self.ans) < self.m:\n return -1\n else:\n remove = sum(self.res[:self.k]) + sum(self.res[-self.k:])\n\n return int((self.total-remove)/(self.m-2*self.k))\n\n \n``` | 1 | 0 | ['Python3'] | 1 |
finding-mk-average | C# Ordered Set + Queue | c-ordered-set-queue-by-justunderdog-ypkl | Complexity\n- Time complexity:\n - MKAverage(int m, int k): O(1)\n\n - AddElement(int num):\n - count < m: O(1)\n - count == m: O(k + mlogm) | justunderdog | NORMAL | 2022-11-19T16:19:58.370762+00:00 | 2022-11-19T16:19:58.370791+00:00 | 125 | false | # Complexity\n- Time complexity:\n - MKAverage(int m, int k): $$O(1)$$\n\n - AddElement(int num):\n - count < m: $$O(1)$$\n - count == m: $$O(k + mlogm)$$\n - count > m: $$O(logm)$$\n - CalculateMKAverage(): $$O(1)$$\n\n- Space complexity: $$O(m)$$\n\n# Code\n```\npublic class MKAverage\n{\n private readonly int m;\n private readonly int k;\n\n private readonly Queue<int> q;\n private readonly List<int> stream;\n\n private long sum;\n private long s1;\n private long s2;\n\n public MKAverage(int m, int k)\n {\n this.m = m;\n this.k = k;\n\n q = new Queue<int>();\n stream = new List<int>();\n\n sum = 0;\n s1 = 0;\n s2 = 0;\n }\n\n public void AddElement(int num)\n {\n q.Enqueue(num);\n\n if (stream.Count < m)\n {\n stream.Add(num);\n\n if (stream.Count == m)\n {\n stream.Sort();\n\n for (int i = 0; i < k; i++)\n {\n s1 += stream[i];\n s2 += stream[m - 1 - i];\n }\n }\n }\n else\n {\n InsertElement(num);\n DeleteElement();\n }\n\n sum += num;\n }\n\n private void InsertElement(int num)\n {\n int index = stream.BinarySearch(num);\n if (index < 0)\n {\n index = ~index;\n }\n\n stream.Insert(index, num);\n\n if (index < k)\n {\n s1 -= stream[k];\n s1 += num;\n }\n if (index > m - k)\n {\n s2 -= stream[m - k];\n s2 += num;\n }\n }\n\n private void DeleteElement()\n {\n int num = q.Dequeue();\n int index = stream.BinarySearch(num);\n\n if (index < k)\n {\n s1 += stream[k];\n s1 -= num;\n }\n if (index > m - k)\n {\n s2 += stream[m - k];\n s2 -= num;\n }\n\n stream.RemoveAt(index);\n sum -= num;\n }\n\n public int CalculateMKAverage()\n {\n if (stream.Count < m)\n {\n return -1;\n }\n\n return (int)((sum - s1 - s2) / (m - 2 * k));\n }\n}\n``` | 1 | 0 | ['Queue', 'Ordered Set', 'C#'] | 1 |
finding-mk-average | Python: Faster than 100% using 1 hash | python-faster-than-100-using-1-hash-by-t-psyk | Algorithm is fairly straightforward. Keep track of the m window with a hash. Use hash to find MK Average. Ran 4x. Faster than 100% each time and 100% less memor | trolleysunrise | NORMAL | 2022-08-31T02:45:28.208125+00:00 | 2022-08-31T02:46:48.046031+00:00 | 169 | false | Algorithm is fairly straightforward. Keep track of the m window with a hash. Use hash to find MK Average. Ran 4x. Faster than 100% each time and 100% less memory 3x (89% the other).\n\nMore Details:\n\nOn insert\n1. Increment the counter for the newest number in the hash.\n2. If we\'ve already added m elements to the hash, decrement the counter for the oldest element.\n3. Clean up unnecessary keys\n\nCalculating Average\nHash already contains exactly the m window as (k,v) where sum of values == m.\n1. Sort the keys. Keys represent the numbers in the m window.\n2. Loop through the keys from both sides simultaneously; decreasing the values of endpoints until only middle keys have v > 0.\n3. Instead of adding every number in the m window, take the product sum of k,v to save on operations. Skip the multiplication for kth largest and smallest elements in the hash.\n4. Return the average\n\nCode\n```\nclass MKAverage(object):\n\n def __init__(self, m, k):\n """\n :type m: int\n :type k: int\n """\n self.m = m\n self.k = k\n self.values = []\n self.holder = {}\n\n def addElement(self, num):\n """\n :type num: int\n :rtype: None\n """\n self.values.append(num)\n self.holder[num] = 1 if num not in self.holder else self.holder[num] + 1\n if len(self.values) > self.m:\n val = self.values[-self.m-1]\n if self.holder[val] == 1:\n del(self.holder[val])\n else:\n self.holder[val] -= 1\n\n def calculateMKAverage(self):\n """\n :rtype: int\n """\n if len(self.values) < self.m:\n return -1\n \n kbegin,kend = self.k,self.k\n workingcopy = self.holder.copy()\n sortedkeys = sorted(self.holder.keys())\n\n for i,x in enumerate(sortedkeys):\n \n if kbegin <= 0 and kend <= 0: break\n \n if kbegin < workingcopy[x] and kbegin > 0:\n workingcopy[x] -= kbegin\n kbegin = 0\n elif kbegin >= workingcopy[x]:\n kbegin -= workingcopy[x]\n workingcopy[x] = 0\n \n if kend < workingcopy[sortedkeys[-i-1]] and kend > 0:\n workingcopy[sortedkeys[-i-1]] -= kend\n kend = 0\n elif kend >= workingcopy[sortedkeys[-i-1]]:\n kend -= workingcopy[sortedkeys[-i-1]]\n workingcopy[sortedkeys[-i-1]] = 0\n \n nums = [ k*workingcopy[k] for k in workingcopy if workingcopy[k] > 0]\n \n return sum(nums)//(self.m-self.k*2)\n \n | 1 | 0 | ['Python'] | 0 |
finding-mk-average | Python Solution SortedList | python-solution-sortedlist-by-user6397p-wxny | \nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.arr = SortedList()\n self.m = m\n | user6397p | NORMAL | 2022-08-14T15:09:15.669749+00:00 | 2022-08-14T15:09:15.669791+00:00 | 358 | false | ```\nfrom sortedcontainers import SortedList\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.arr = SortedList()\n self.m = m\n self.k = k\n self.q = deque()\n self.total = None\n\n def addElement(self, num: int) -> None:\n self.q.append(num)\n m = self.m\n k = self.k\n if len(self.q) > m:\n val = self.q.popleft() \n ind1 = self.arr.bisect_left(val)\n ind2 = self.arr.bisect_right(val)\n left, right, mid = False, False, False\n kth, mth = self.arr[k], self.arr[m - k - 1]\n if k <= ind1 < m - k or k <= ind2 - 1 < m - k or (ind1 <= k and m - k <= ind2 - 1 < m):\n mid = True\n elif ind1 < k:\n left = True\n elif ind2 - 1 >= m - k:\n right = True \n \n self.arr.remove(val)\n ind1 = self.arr.bisect_left(num)\n ind2 = self.arr.bisect_right(num) \n self.arr.add(num) \n \n if k <= ind1 < m - k or k <= ind2 < m - k or (ind1 <= k and m - k <= ind2 < m):\n if mid:\n self.total += num - val\n if left:\n self.total += num - kth\n if right:\n self.total += num - mth\n elif ind1 < k:\n if mid:\n self.total += self.arr[k] - val\n if left:\n pass\n if right:\n self.total += self.arr[k] - mth\n elif ind2 >= m - k:\n if mid:\n self.total += self.arr[m - k - 1] - val\n if left:\n self.total += self.arr[m - k - 1] - kth\n if right:\n pass\n else:\n self.arr.add(num)\n if self.total is None and len(self.arr) == self.m:\n self.total = sum(self.arr[k:m-k])\n \n\n def calculateMKAverage(self) -> int:\n if len(self.arr) < self.m:\n return -1\n \n return int(self.total / (self.m - 2 * self.k))\n``` | 1 | 0 | ['Binary Search Tree', 'Python3'] | 0 |
finding-mk-average | Segment Tree Solution | segment-tree-solution-by-i_see_you-wsqs | \nclass MKAverage {\npublic:\n #define LL long long\n struct node {\n int frq;\n LL sum;\n \n node() { frq = 0; sum = 0; }\n | i_see_you | NORMAL | 2022-05-20T23:31:29.837833+00:00 | 2022-05-20T23:31:29.837864+00:00 | 153 | false | ```\nclass MKAverage {\npublic:\n #define LL long long\n struct node {\n int frq;\n LL sum;\n \n node() { frq = 0; sum = 0; }\n node(int _frq, LL _sum): frq(_frq), sum(_sum) {}\n };\n \n node Tree[100005 * 4];\n const int limit = 100000;\n\n \n node merge_segments(const node &lf, const node &rt) {\n return node(lf.frq + rt.frq, lf.sum + rt.sum);\n }\n \n void update(int node, int b, int e, int pos, int add) {\n if (b == e) {\n Tree[node].frq += add;\n Tree[node].sum += (add * pos);\n return ;\n }\n int mid = (b + e) >> 1;\n int lf = node << 1;\n int rt = lf | 1;\n \n if (pos <= mid) update(lf, b, mid, pos, add);\n else update(rt, mid + 1, e, pos, add);\n \n Tree[node] = merge_segments(Tree[lf], Tree[rt]);\n }\n \n \n LL get_left_kth_sum(int node, int b, int e, int kth) {\n if (kth <= 0) return 0;\n if (kth >= Tree[node].frq) return Tree[node].sum;\n if (b == e) {\n return kth * 1LL * b;\n }\n \n int mid = (b + e) >> 1;\n int lf = node << 1;\n int rt = lf | 1;\n \n return get_left_kth_sum(lf, b, mid, kth) + get_left_kth_sum(rt, mid + 1, e, kth - Tree[lf].frq);\n }\n \n LL get_right_kth_sum(int node, int b, int e, int kth) {\n if (kth <= 0) return 0;\n if (kth >= Tree[node].frq) return Tree[node].sum;\n if (b == e) {\n return kth * 1LL * b;\n }\n \n int mid = (b + e) >> 1;\n int lf = node << 1;\n int rt = lf | 1;\n \n return get_right_kth_sum(lf, b, mid, kth - Tree[rt].frq) + get_right_kth_sum(rt, mid + 1, e, kth);\n }\n \n int M, K;\n queue <int> window;\n\n MKAverage(int m, int k) {\n M = m;\n K = k;\n }\n \n void addElement(int num) {\n window.push(num);\n update(1, 0, limit, num, +1);\n \n if (window.size() > M) {\n update(1, 0, limit, window.front(), -1);\n window.pop();\n }\n \n }\n \n int calculateMKAverage() {\n if (window.size() < M) return -1;\n LL total = Tree[1].sum;\n LL left_k_sum = get_left_kth_sum(1, 0, limit, K);\n LL right_k_sum = get_right_kth_sum(1, 0, limit, K);\n \n \n return (total - left_k_sum - right_k_sum) / (M - 2 * K);\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 1 | 0 | [] | 0 |
finding-mk-average | Python | Window + SortedList | O(nlogn) | python-window-sortedlist-onlogn-by-aryon-d5aa | addElement: O(log n)\ncalculateMKAverage: O(1)\n```\nfrom sortedcontainers import SortedList\nfrom collections import deque\n\nclass MKAverage:\n\n def init( | aryonbe | NORMAL | 2022-05-14T07:30:32.717303+00:00 | 2022-05-14T07:34:40.380864+00:00 | 294 | false | addElement: O(log n)\ncalculateMKAverage: O(1)\n```\nfrom sortedcontainers import SortedList\nfrom collections import deque\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.sl = SortedList()\n self.window = deque()\n self.sum = 0\n\n def addElement(self, num: int) -> None:\n if len(self.sl) < self.m:\n self.window.append(num)\n self.sl.add(num)\n if len(self.sl) == self.m:\n self.sum = sum(self.sl[self.k:-self.k])\n else:\n v = self.window.popleft()\n self.window.append(num)\n i = self.sl.bisect_left(v)\n j = self.sl.bisect_left(num)\n if 0<=i<self.k:\n if self.k < j:\n self.sum -= self.sl[self.k]\n if j <= self.m - self.k:\n self.sum += num\n else:\n self.sum += self.sl[self.m-self.k]\n elif self.k <= i < self.m - self.k:\n self.sum -= v\n if 0<= j < self.k:\n self.sum += self.sl[self.k-1]\n elif self.k <= j <= self.m-self.k:\n self.sum += num\n else:\n self.sum += self.sl[self.m-self.k]\n else:\n if j < self.m - self.k:\n self.sum -= self.sl[self.m-self.k-1]\n if self.k <= j:\n self.sum += num\n else:\n self.sum += self.sl[self.k-1]\n self.sl.remove(v)\n self.sl.add(num)\n\n def calculateMKAverage(self) -> int:\n if len(self.sl) < self.m:\n return -1\n return self.sum//(self.m-2*self.k)\n \n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage() | 1 | 0 | ['Python'] | 0 |
finding-mk-average | c++ bst + queue | c-bst-queue-by-taho2509-d6kl | The idea is to have addElement and calculateMKAverage both in O(log m), although it still is O(m) in the worst case: a left only(or right only) childs tree.\n\n | taho2509 | NORMAL | 2022-03-09T01:49:11.874616+00:00 | 2022-03-09T01:49:11.874647+00:00 | 289 | false | The idea is to have addElement and calculateMKAverage both in O(log m), although it still is O(m) in the worst case: a left only(or right only) childs tree.\n\n```\nclass BST {\n struct node {\n int data;\n node* left;\n node* right;\n int lCount;\n int rCount;\n int lsum;\n int rsum;\n int multiplicity;\n };\n\n node* insert(int x, node* t) {\n if(t == NULL)\n {\n t = new node;\n t->data = x;\n t->lCount = 0;\n t->rCount = 0;\n t->lsum = 0;\n t->rsum = 0;\n t->multiplicity = 1;\n t->left = t->right = NULL;\n }\n else if(x < t->data)\n {\n t->lCount++;\n t->lsum += x;\n t->left = insert(x, t->left);\n }\n else if(x > t->data)\n {\n t->rCount++;\n t->rsum += x;\n t->right = insert(x, t->right);\n } else {\n t->multiplicity++;\n }\n return t;\n }\n\n node* findMin(node* t) {\n if(t == NULL)\n return NULL;\n else if(t->left == NULL)\n return t;\n else\n return findMin(t->left);\n }\n \n node* fullRemove(int x, node* t, int qt, int sr) {\n node* temp;\n\n // Element not found\n if(t == NULL)\n return NULL;\n\n // Searching for element\n else if(x < t->data) {\n t->lCount-=qt;\n t->lsum -= sr;\n t->left = fullRemove(x, t->left, qt,sr);\n }\n else if(x > t->data) {\n t->rCount-=qt;\n t->rsum -= sr;\n t->right = fullRemove(x, t->right, qt,sr);\n }\n\n // Element found\n // With one or zero child\n else\n {\n temp = t;\n if(t->left == NULL)\n t = t->right;\n else if(t->right == NULL)\n t = t->left;\n delete temp;\n }\n\n return t;\n }\n\n node* remove(int x, node* t) {\n node* temp;\n\n // Element not found\n if(t == NULL)\n return NULL;\n\n // Searching for element\n else if(x < t->data) {\n t->lCount--;\n t->lsum -= x;\n t->left = remove(x, t->left);\n }\n else if(x > t->data) {\n t->rCount--;\n t->rsum -= x;\n t->right = remove(x, t->right);\n }\n\n // Element found\n // repeated\n else if(t->multiplicity > 1) {\n t->multiplicity--;\n }\n // With 2 children\n else if(t->left && t->right)\n {\n temp = findMin(t->right);\n t->data = temp->data;\n t->rCount-=temp->multiplicity;\n t->rsum -= t->data*temp->multiplicity;\n t->right = fullRemove(t->data, t->right,temp->multiplicity,t->data*temp->multiplicity);\n }\n // With one or zero child\n else\n {\n temp = t;\n if(t->left == NULL)\n t = t->right;\n else if(t->right == NULL)\n t = t->left;\n delete temp;\n }\n if(t == NULL)\n return t;\n\n return t;\n }\n \n node* root;\n void kSmallestSumRec(node *root, int k , int &temp_sum) {\n if (root == NULL)\n return ;\n\n // if we fount k smallest element then break the function\n if ((root->lCount + root->multiplicity) == k) {\n temp_sum += root->data*root->multiplicity + root->lsum ;\n return ;\n }\n\n else if (k > root->lCount)\n {\n // store sum of all element smaller than current root ;\n temp_sum += root->lsum;\n k -= root->lCount;\n \n if(root->multiplicity >= k) {\n temp_sum += root->data*k;\n return;\n } else {\n temp_sum += root->data*root->multiplicity;\n k -= root->multiplicity;\n }\n \n kSmallestSumRec(root->right , k , temp_sum);\n }\n else // call left sub-tree\n kSmallestSumRec(root->left , k , temp_sum );\n }\n \n void kGreatestSumRec(node *root, int k , int &temp_sum) {\n if (root == NULL)\n return ;\n\n // if we fount k smallest element then break the function\n if ((root->rCount + root->multiplicity) == k) {\n temp_sum += root->data*root->multiplicity + root->rsum ;\n return ;\n }\n\n else if (k > root->rCount)\n {\n temp_sum += root->rsum;\n k -= root->rCount;\n \n if(root->multiplicity >= k) {\n temp_sum += root->data*k;\n return;\n } else {\n temp_sum += root->data*root->multiplicity;\n k -= root->multiplicity;\n }\n\n kGreatestSumRec(root->left, k , temp_sum);\n }\n else // call left sub-tree\n kGreatestSumRec(root->right, k , temp_sum);\n }\n\n public:\n BST() {\n root = NULL;\n }\n\n void insert(int x) {\n root = insert(x, root);\n }\n\n void remove(int x) {\n root = remove(x, root);\n }\n\n int kElementSum(int k) {\n int sum = 0;\n kSmallestSumRec(root, k, sum);\n kGreatestSumRec(root, k, sum);\n return sum;\n }\n};\n\nclass MKAverage {\n long long sum;\n queue<int> elements;\n int m;\n int k;\n BST* tree;\npublic:\n MKAverage(int m, int k):m(m), k(k), sum(0) {\n tree = new BST();\n }\n \n void addElement(int num) {\n if(elements.size() == m) {\n sum = sum - elements.front();\n tree->remove(elements.front());\n elements.pop();\n }\n\n sum = sum + num;\n tree->insert(num);\n elements.push(num);\n }\n \n int calculateMKAverage() {\n if(elements.size() < m) return -1;\n \n return (sum - tree->kElementSum(k))/(m - 2*k);\n }\n};\n``` | 1 | 0 | ['Binary Search Tree', 'Queue', 'C'] | 0 |
finding-mk-average | Python using SortedList add in O(N) calculate in O(1) | python-using-sortedlist-add-in-on-calcul-q4c2 | Use 3 SortedList left, mid, right to maintain the smallest k elements, mid part and the biggest k elements seperately. \nWe can do insert, delete, search operat | utada | NORMAL | 2021-09-16T17:56:21.038392+00:00 | 2021-09-16T17:56:21.038441+00:00 | 243 | false | Use 3 SortedList `left`, `mid`, `right` to maintain the smallest k elements, mid part and the biggest k elements seperately. \nWe can do insert, delete, search operations in SortedList in O(logN). It\'s somehow like TreeSet/TreeMap in Java(but SortedList can store duplicate elements) and MultiSet in C++.\n```\nfrom sortedcontainers import SortedList\nclass MKAverage:\n # T:O(1) for calculateMKAverage O(Log(N)) for addElement\n def __init__(self, m: int, k: int):\n self.queue = collections.deque();\n self.m = m\n self.k = k\n self.N = m-2*k #numbers needed to calculate MKAve\n self.sum = 0\n self.left = SortedList()\n self.mid = SortedList()\n self.right = SortedList()\n\n def addElement(self, num: int) -> None:\n if (len(self.queue)==self.m):\n self.remove(self.queue[0])\n self.queue.popleft()\n self.queue.append(num)\n self.add(num)\n\n def calculateMKAverage(self) -> int:\n if len(self.queue)<self.m:\n return -1\n else:\n return self.sum//self.N\n def add(self, x):\n self.left.add(x)\n if len(self.left)>self.k:\n mxLeft = self.left.pop()\n self.sum+=mxLeft\n self.mid.add(mxLeft)\n if len(self.mid)>self.N:\n mxMid = self.mid.pop()\n self.sum-=mxMid\n self.right.add(mxMid)\n \n def remove(self, x):\n if x<=self.left[-1]:\n self.left.remove(x)\n elif x<=self.mid[-1]:\n self.sum-=x\n self.mid.remove(x)\n else:\n self.right.remove(x)\n if len(self.left)<self.k:\n mnMid = self.mid.pop(0)\n self.sum-=mnMid\n self.left.add(mnMid)\n if len(self.mid)<self.N:\n mnRight = self.right.pop(0)\n self.sum+=mnRight\n self.mid.add(mnRight)\n``` | 1 | 0 | [] | 2 |
finding-mk-average | 4 Heaps, 1 Queue / List | 50.00% speed | 4-heaps-1-queue-list-5000-speed-by-odani-9itc | This solution is referenced from C++ 3 multisets by Izl124631x\nI don\'t know how to implement ordered set with duplicates in javascript, or lazy update / delet | odaniel | NORMAL | 2021-07-03T02:37:11.803442+00:00 | 2021-07-04T04:15:52.757782+00:00 | 454 | false | This solution is referenced from [C++ 3 multisets by Izl124631x](https://leetcode.com/problems/finding-mk-average/discuss/1152418/C%2B%2B-3-multisets)\nI don\'t know how to implement `ordered set` with `duplicates` in `javascript`, or `lazy update / delete` in `Heap`\nSo I will just implement and use `Heap` in a intuitive way, it\'s mostly sufficient, since solution using `multiset` are dealing mostly `min` and `max` of the `Heap`\n\nThe idea is to have 3 balanced `Heap` , and 1 copy `Heap`\n* `Left Heap`, storing smallest `k`s, implemented in `Max Heap`\n* `Mid Heap`, storing numbers which forms actual sum, implemented in `Min Heap`\n* `Mid Copy Heap`, this is redundant `Heap`, which is just to get the `max` of `Mid Min Heap`, this follows every action of `Mid Min Heap` when adding an element. This obviusly needs to improve, since it\'s waste of memory. But you would notice in my solution below, I didn\'t have this, instead I just use `O(m)` to get the `max`. I\'m lazy to copy paste.\n* `Right Heap`, storing largest `k`s, implemented in `Min Heap`\n\nSo this way, the four `Heap`s form a `Moving Window` and could transfer `min` and `max` between each other, please refer to `Leetcode 480 Sliding Window Median` for similar idea\n\nNote: for the `queue`, I\'m lazy to implement the `Queue` with `LinkedList`, instead I just use `array.shift`\n```\nclass MKAverage {\n constructor(m, k) {\n this.m = m;\n this.k = k;\n this.sum = 0;\n this.left = new Heap((a, b) => a > b);\n this.mid = new Heap((a, b) => a < b)\n this.right = new Heap((a, b) => a < b)\n this.q = [];\n }\n \n addElement(num) {\n\n // add new num\n if (this.q.length < this.m) {\n this.mid.push(num);\n }\n this.q.push(num);\n if (this.q.length === this.m) {\n for (let i = 0; i < this.k; ++i) {\n this.left.push(this.mid.pop());\n }\n for (let i = 0; i < this.k; ++i) {\n this.right.push(this.mid.popMax());\n }\n this.sum += this.mid.sum\n } else if (this.q.length > this.m) {\n if (num < this.left.top()) {\n this.left.push(num);\n const value = this.left.pop();\n this.mid.push(value);\n this.sum += value; \n } else if (num > this.right.top()) {\n this.right.push(num);\n const value = this.right.pop();\n this.mid.push(value);\n this.sum += value;\n } else {\n this.mid.push(num)\n this.sum += num;\n }\n \n // remove old num\n const value = this.q.shift();\n if (this.mid.has(value)) {\n this.mid.remove(value);\n this.sum -= value;\n } else if (this.right.has(value)) {\n this.right.remove(value)\n } else {\n this.left.remove(value)\n }\n\n // balance three heaps\n if (this.left.size < this.k) {\n const value = this.mid.pop();\n this.left.push(value);\n this.sum -= value;\n } else if (this.right.size < this.k) {\n const value = this.mid.popMax();\n this.right.push(value);\n this.sum -= value;\n }\n }\n }\n \n calculateMKAverage() {\n return this.q.length === this.m ? Math.trunc(this.sum / (this.m - 2 * this.k)) : -1;\n }\n};\n\nclass Heap {\n constructor(compare) {\n this.store = [];\n this.compare = compare;\n this.index = {};\n }\n \n top() {\n return this.store[0];\n }\n \n get size() {\n return this.store.length;\n }\n \n isEmpty() {\n return this.size === 0;\n }\n\n has(value) {\n return Boolean(this.index[value] && this.index[value].size)\n }\n \n push(value) {\n this.store.push(value);\n const i = this.store.length - 1;\n if (!this.index[value]) this.index[value] = new Set([i]);\n else this.index[value].add(i)\n this.heapifyUp(i);\n }\n \n remove(value) {\n const i = this.index[value].values().next().value;\n this.index[value].delete(i);\n if (i === this.store.length - 1) return this.store.pop();\n this.store[i] = this.store.pop()\n this.index[this.store[i]].delete(this.store.length);\n this.index[this.store[i]].add(i);\n this.heapifyDown(this.heapifyUp(i));\n }\n\n popMax() {\n const max = Math.max(...this.store);\n this.remove(max);\n return max;\n }\n\n get sum() {\n return this.store.reduce((p, c) => p + c, 0);\n }\n \n pop() {\n const value = this.store[0];\n this.index[value].delete(0);\n if (this.store.length < 2) return this.store.pop();\n this.store[0] = this.store.pop();\n this.index[this.store[0]].delete(this.store.length);\n this.index[this.store[0]].add(0);\n this.heapifyDown(0);\n return value;\n }\n \n heapifyDown(parent) {\n const childs = [1,2].map((n) => parent * 2 + n).filter((n) => n < this.store.length);\n let child = childs[0];\n if (childs[1] && this.compare(this.store[childs[1]], this.store[child])) {\n child = childs[1];\n }\n if (child && this.compare(this.store[child], this.store[parent])) {\n const childVal = this.store[child];\n const parentVal = this.store[parent];\n this.store[child] = parentVal;\n this.store[parent] = childVal;\n this.index[childVal].delete(child);\n this.index[childVal].add(parent);\n this.index[parentVal].delete(parent);\n this.index[parentVal].add(child);\n return this.heapifyDown(child);\n }\n return parent;\n }\n \n heapifyUp(child) {\n const parent = Math.floor((child - 1) / 2);\n if (child && this.compare(this.store[child], this.store[parent])) {\n const childVal = this.store[child];\n const parentVal = this.store[parent];\n this.store[child] = parentVal;\n this.store[parent] = childVal;\n this.index[childVal].delete(child);\n this.index[childVal].add(parent);\n this.index[parentVal].delete(parent);\n this.index[parentVal].add(child);\n return this.heapifyUp(parent);\n }\n return child;\n }\n}\n``` | 1 | 0 | ['Heap (Priority Queue)', 'JavaScript'] | 1 |
finding-mk-average | [Python] Queue and Binary Search, add O(log m), average O(1) | python-queue-and-binary-search-add-olog-837av | \nimport bisect\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.list = [] ##Used as a sorted | rajat499 | NORMAL | 2021-05-17T20:33:04.300331+00:00 | 2021-05-17T20:33:04.300371+00:00 | 275 | false | ```\nimport bisect\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.list = [] ##Used as a sorted list. Elements are sorted in non decreasing order\n self.added = [] ##Used as a queue\n self.sum = None\n\t\t\n def addElement(self, num: int) -> None:\n ln = len(self.list)\n if ln < self.m:\n self.added.append(num)\n index = bisect.bisect_right(self.list, num)\n self.list.insert(index, num)\n if len(self.list) == self.m:\n self.sum = sum(self.list[self.k:self.m-self.k])\n else:\n\t\t\t## Pop the element to get the last m-1 elements added\n x = self.added.pop(0)\n self.added.append(num)\n pop_index = bisect.bisect_left(self.list, x)\n if pop_index<self.k:\n self.sum -= self.list[self.k]\n elif pop_index >= self.m-self.k:\n self.sum -= self.list[self.m-self.k-1]\n else:\n self.sum -= x\n self.list.pop(pop_index)\n\t\t\t\n\t\t\t##Get the index of the new element to be added in the sorted list\n add_index = bisect.bisect_right(self.list, num)\n self.list.insert(add_index, num)\n if add_index<self.k:\n self.sum += self.list[self.k]\n elif add_index >= self.m-self.k:\n self.sum += self.list[self.m-self.k-1]\n else:\n self.sum += num\n\n def calculateMKAverage(self) -> int:\n if len(self.list)<self.m:\n return -1\n else:\n return self.sum//(self.m - 2*self.k)\n``` | 1 | 0 | [] | 2 |
finding-mk-average | Multiset Approach Easy to Understand | multiset-approach-easy-to-understand-by-3hm5e | \n#define ll long long int\nclass MKAverage {\n ll m,k,tot,midsum;\n queue<ll> dq;\n multiset<ll> low,mid,high;\npublic:\n MKAverage(int M, int K) { | ojha1111pk | NORMAL | 2021-04-25T14:35:23.113112+00:00 | 2021-04-25T14:35:23.113146+00:00 | 607 | false | ```\n#define ll long long int\nclass MKAverage {\n ll m,k,tot,midsum;\n queue<ll> dq;\n multiset<ll> low,mid,high;\npublic:\n MKAverage(int M, int K) {\n low.clear(); // store k smallest numbers in latest stream of m numbers\n high.clear();// stores k largest numbers in latest stream of m numbers\n mid.clear(); // stores the remaining numbers of the curr stream of numbers\n midsum=0; // sum of elements in middle midset\n m=M;\n tot=0; // intialized tot number of elements\n k=K;\n }\n \n void addElement(int num) {\n\t\t// push the current element into queue\n dq.push(num);\n\t\t// if number of elements < k then insert into smaller set only\n if(low.size()<k)\n low.insert(num);\n \n else{\n\t\t\t// initiallly we only fill low and high multisets\n if(high.size()<k){\n auto it=low.end();\n --it;\n // if given element is greater than current max of all k smallest\n if(*it<=num)\n high.insert(num); // insert into high multiset\n else{\n\t\t\t\t\t// else insert new element into low and max from low into high multiset\n int val=*it;\n low.erase(it);\n high.insert(val);\n low.insert(num);\n }\n }\n // if tot >= 2*k\n\t\t\t// now we need to insert elements into middle set depending upon the following conditions\n else{\n auto it=low.end();\n --it;\n auto it2=high.begin();\n\t\t\t\t// if current number is one of the smallest then insert into low\n\t\t\t\t// insert the max of low into middle set\n if(num<*it){\n ll val=*it;\n low.erase(it);\n mid.insert(val);\n midsum+=val;\n low.insert(num);\n }\n \n\t\t\t\t// if curr number is one of the k largest put into high\n\t\t\t\t// put the smallest from high into middle set\n else if(num>*it2){\n ll val=*it2;\n high.erase(it2);\n mid.insert(val);\n midsum+=val;\n high.insert(num);\n }\n \n\t\t\t\t// if curr number itself lies in middle set inherently\n else{\n mid.insert(num);\n midsum+=num;\n }\n\t\t\t\t\n\t\t\t\t// if we have more than m elements we need to remove the oldest element from front of queue\n\t\t\t\t// we search for that element in three sets and do the needful maintainigng the size of low and high always equal to k\n if(dq.size()==m+1){\n ll f=dq.front();\n dq.pop();\n\t\t\t\t\t// if element in middle then delete from middle set and just be done with it\n if(mid.find(f)!=mid.end()){\n mid.erase(mid.find(f));\n midsum-=f;\n }\n\t\t\t\t\t// deletion from low decreases its size so need to insert one of the smaller element from middle set\n else if(low.find(f)!=low.end()){\n low.erase(low.find(f));\n auto it=mid.begin();\n ll val=*it;\n midsum-=val;\n mid.erase(it);\n low.insert(val);\n }\n\t\t\t\t\t// deletion from high reduces its size so we insert the max from middle into high set\n else{\n high.erase(high.find(f));\n auto it=mid.end();\n --it;\n ll val=*it;\n mid.erase(it);\n midsum-=val;\n high.insert(val);\n }\n } \n }\n }\n } \n \n int calculateMKAverage() {\n ll ls=low.size(),ms=mid.size(),hs=high.size();\n tot=ls+ms+hs;\n\t\t// if tot size < m\n if(tot<m)\n return -1;\n\t\t// calculating the average\n ll mss=mid.size();\n ll ans=(midsum)/mss;\n return ans;\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 0 |
finding-mk-average | Help needed , last test case giving TLE | help-needed-last-test-case-giving-tle-by-mv73 | \nclass MKAverage {\npublic:\n int m,k;\n int temp;\n multiset<int,greater<int>> s;\n vector<int> v;\n \n MKAverage(int m, int k) {\n t | sai_prasad_07 | NORMAL | 2021-04-13T16:26:03.238714+00:00 | 2021-04-13T16:26:03.238746+00:00 | 103 | false | ```\nclass MKAverage {\npublic:\n int m,k;\n int temp;\n multiset<int,greater<int>> s;\n vector<int> v;\n \n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n v.clear();\n temp = 0;\n }\n \n void addElement(int num) {\n v.push_back(num);\n if(s.size()<m){\n s.insert(num);\n }else{\n s.erase(s.lower_bound(v[temp]));\n temp++;\n s.insert(num);\n }\n }\n \n int calculateMKAverage() {\n if(s.size()<m) return -1;\n vector<int> arr;\n for(auto it:s){\n arr.push_back(it);\n }\n long long ress=0;\n long long count = 0;\n int i=k;\n for(int j=k;j<arr.size();j++){\n i++;\n if(i>k && i<=(m-k)){\n ress+=arr[j];\n count++;\n }\n if(i>(m-k)) break;\n }\n int res = ress/count ;\n return res;\n }\n};\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage* obj = new MKAverage(m, k);\n * obj->addElement(num);\n * int param_2 = obj->calculateMKAverage();\n */\n``` | 1 | 0 | [] | 1 |
finding-mk-average | [Javascript] 2 Segment Trees + Divide and Conquer | javascript-2-segment-trees-divide-and-co-q2c0 | \nThe main idea is to create two seperate segment trees. One will store the count of the elements up to a specific element. So for example if the elements 1,2, | George_Chrysochoou | NORMAL | 2021-04-13T13:37:25.574998+00:00 | 2021-04-15T05:06:42.354343+00:00 | 255 | false | \nThe main idea is to create two seperate segment trees. One will store the count of the elements up to a specific element. So for example if the elements 1,2, 3, 3, 4, 4 are given then it ll look sth like\n\n0 1 2 3 4 \n**0 1 2 4 5** <=cumulative counts up to a specific element (think prefix sums [0,i] )\n\nThe other segment tree will store the sum of the given elements. So in the previous example:\n0 1 2 3 4 \n**0 1 3 9 17** <=cumualtive sum of given elements\n\nWhat I intend to do is always maintain m values in those trees, namely the m last elements. \nIf I can achieve that, then the required MK average boils down to calculating the average of the inbetween range of elements.\n\nLet us denote with S and E the start and the end of my required window after we removed the first and last K elements. \nIn order to find those two indices, we ll have to use Divide and Conquer on the segment tree queries of the first segment tree. The whole idea is creating the function seachPrefixIndex(x) that recursively finds the leftmost index where the prefix[0,i]>=x\n\n\n\nSince we know that my window will begin after I removed the first k elements, S will start from the k+1-th element. But the thing is that a given prefix may not contain the value k+1 per se. That would mean that I have multiple occurences of a value. \nIn the first example, if I wanted to remove k=2 elements, then i\'d have to search for (k+1=3), but as you can see there is no such value inside the Index segment tree values. That\'s because we have two occurences of the element 3 and as such the prefix is 4 instead of 3. So we ll have to adjust the divide and conquer method to search for the leftmost occurence of any value>=k+1 . \nOnce we find said index we ll have to take the (last) prefix[0:index]-k elements. \nThe same idea goes for the E (end) index of my window. Once a new element is given, we roll the whole thing by removing the earliest( first) element that was given. \n\n```\n\nclass ArraySegTree{\n // Array to perfrom operations on, range query operation, PointUpdate operation\n constructor(A,op=(a,b)=>a+b,upOp=(a,b)=>a+b,opSentinel=0){\n this.n=A.length,this.t=[...Array(4*this.n+1)],this.op=op,this.upOp=upOp,this.opSentinel=opSentinel\n //root\'s idx =1\n this.build(A,1,0,this.n-1)\n }\n left=x=>this.t[2*x];right=x=>this.t[2*x+1]\n build(A,idx,left,right){\n if(left==right)\n return this.t[idx]=A[left]\n let mid=(left+right)>>1\n this.build(A,2*idx,left,mid) //go left\n this.build(A,2*idx+1,mid+1,right) //go right\n this.t[idx]=this.op(this.left(idx),this.right(idx)) //merge\n }\n //just specify l,r on actual queries\n //Here queries use the actul indices of the starting array A, so rangeQuery(0,n-1) returns the whole array\n rangeQuery=(l,r,tl=0,tr=this.n-1,idx=1)=>{\n if(l>r)\n return this.opSentinel\n if(l===tl&&r===tr)\n return this.t[idx]\n let mid=(tl+tr)>>1\n return this.op(\n this.rangeQuery(l,Math.min(r,mid),tl,mid,idx*2),\n this.rangeQuery(Math.max(l,mid+1),r,mid+1,tr,idx*2+1)\n ) \n }\n //just specify arrIdx,newVal on actual pointUpdates\n pointUpdate=(arrIdx,newVal,tl=0,tr=this.n-1,idx=1)=>{\n if(tl==tr)\n return this.t[idx]=this.upOp(this.t[idx],newVal)\n let mid=(tl+tr)>>1\n if(arrIdx<=mid)\n this.pointUpdate(arrIdx,newVal,tl,mid,2*idx)\n else\n this.pointUpdate(arrIdx,newVal,mid+1,tr,2*idx+1)\n this.t[idx]=this.op(this.left(idx),this.right(idx))\n }\n seachPrefixIndex=(x,start=0,end=this.n-1)=>{\n let s=this.rangeQuery(start,end)\n if(s<x)\n return -1\n if(start===end)\n return start\n let mid=start+end>>1,left=this.rangeQuery(start,mid)\n if( left>=x)\n return this.seachPrefixIndex(x,start,mid)\n else\n return this.seachPrefixIndex(x-left,mid+1,end)\n }\n}\n\nvar MKAverage = function(m, k) {\n this.A=[],this.m=m,this.k=k,this.div=m-2*k\n this.S1=new ArraySegTree([...Array(1e5+2)].map(d=>0))//indices\n this.S2=new ArraySegTree([...Array(1e5+2)].map(d=>0))//sums\n};\n\n/** \n * @param {number} num\n * @return {void}\n */\nMKAverage.prototype.addElement = function(num) {\n this.A.push(num)\n this.S1.pointUpdate(num,1)\n this.S2.pointUpdate(num,num)\n if(this.A.length>this.m){\n let z=this.A.shift()\n this.S1.pointUpdate(z,-1)\n this.S2.pointUpdate(z,-z)\n }\n};\n\n/**\n * @return {number}\n */\nMKAverage.prototype.calculateMKAverage = function() {\n if(this.A.length<this.m)\n return -1\n \n let S=this.S1.seachPrefixIndex(this.k+1),\n count1=this.S1.rangeQuery(0,S),\n take=(count1-this.k)*S\n \n let E=this.S1.seachPrefixIndex(this.m-this.k),\n count2=this.S1.rangeQuery(0,E),\n remove=(count2-this.m+this.k)*E\n \n let midSum=this.S2.rangeQuery(S+1,E)\n return (take+midSum-remove)/this.div>>0\n};\n``` | 1 | 0 | ['Tree', 'JavaScript'] | 0 |
finding-mk-average | Java clean code with MinMaxHeap implementation. | java-clean-code-with-minmaxheap-implemen-rhhx | O(logN) for addElement\nO(1) for calculateMKAverage\n\nclass MKAverage {\n int m , k;\n LinkedList<Integer> q = new LinkedList<>();\n MinMaxQ head = ne | yubad2000 | NORMAL | 2021-04-12T21:20:43.001467+00:00 | 2021-04-12T21:20:43.001510+00:00 | 238 | false | O(logN) for addElement\nO(1) for calculateMKAverage\n```\nclass MKAverage {\n int m , k;\n LinkedList<Integer> q = new LinkedList<>();\n MinMaxQ head = new MinMaxQ();\n MinMaxQ body = new MinMaxQ();\n MinMaxQ tail = new MinMaxQ();\n \n public MKAverage(int m, int k) {\n this.m=m;\n this.k=k;\n }\n \n public void addElement(int num) {\n if (q.size()==m) {\n int pre = q.poll();\n if (tail.contains(pre)) {\n tail.remove(pre);\n } else if (body.contains(pre)) {\n body.remove(pre);\n body.add(tail.pollMin());\n } else if (head.contains(pre)){\n head.remove(pre);\n body.add(tail.pollMin());\n head.add(body.pollMin());\n }\n }\n \n head.add(num);\n if (head.count>k) {\n body.add(head.pollMax());\n if (body.count>(m-2*k)) \n tail.add(body.pollMax());\n }\n q.offer(num);\n }\n \n public int calculateMKAverage() {\n if (q.size()<m) return -1; \n return (int)Math.floor(body.sum/(m-2*k));\n }\n \n class MinMaxQ {\n int count = 0;\n long sum = 0;\n TreeMap<Integer, Integer> map = new TreeMap<>();\n Integer min() { return map.firstKey();}\n Integer max() { return map.lastKey();}\n int count() { return count;}\n long sum() { return sum;}\n boolean contains(int num) { return map.containsKey(num);}\n boolean isEmpty(){ return map.isEmpty();}\n \n int add(int num) {\n map.merge(num, 1, (a,b)->a+b);\n sum+=num;\n return ++count;\n }\n \n Integer pollMin() {\n Integer min = this.min();\n if (min!=null) remove(min);\n return min;\n }\n \n Integer pollMax() {\n Integer max = this.max();\n if (max!=null) remove(max);\n return max;\n }\n \n boolean remove(int num) {\n if (!map.containsKey(num)) return false;\n map.merge(num, -1, (a,b)->a+b);\n if (map.get(num)==0) \n map.remove(num);\n count--;\n sum-=num;\n return true;\n }\n }\n}\n``` | 1 | 0 | [] | 0 |
finding-mk-average | [Java] Fenwick Tree + Binary Search, O(logN) for both addElement & calculateMKAverage | java-fenwick-tree-binary-search-ologn-fo-7qqq | \n// Time complexity : O(logN)\n// Space complexity : O(N)\n// N is the possible max value in stream, which is 100000 based on the description\n\nclass MKAverag | feng4 | NORMAL | 2021-04-12T18:31:14.540621+00:00 | 2021-04-12T18:31:14.540668+00:00 | 187 | false | ```\n// Time complexity : O(logN)\n// Space complexity : O(N)\n// N is the possible max value in stream, which is 100000 based on the description\n\nclass MKAverage {\n \n private int LIMIT = 100000;\n \n int m, k;\n long sum;\n Queue<Integer> q;\n BIT bit1, bit2;\n\n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n sum = 0;\n q = new LinkedList<>();\n bit1 = new BIT(LIMIT + 1);\n bit2 = new BIT(LIMIT + 1);\n }\n \n public void addElement(int num) {\n q.offer(num);\n bit1.update(num, 1);\n bit2.update(num, num);\n sum += num;\n \n if (q.size() > m) {\n int r = q.poll();\n bit1.update(r, -1);\n bit2.update(r, -r);\n sum -= r;\n }\n }\n \n public int calculateMKAverage() {\n if (q.size() < m) return -1;\n \n long lSum = findKSmallest(),\n rSum = findKLargest();\n\n return (int)((sum - lSum -rSum) / (m - 2 * k));\n \n }\n \n private long rangQuery(BIT bit, int hig, int low) {\n return bit.query(hig) - bit.query(low - 1);\n }\n \n private long findKSmallest() {\n int l = 1, r = LIMIT, number = -1;\n while (l + 1 < r) {\n int m = l + (r - l) / 2;\n long count = rangQuery(bit1, m, 1);\n if (count >= k) r = m;\n else l = m;\n }\n \n if (rangQuery(bit1, l, 1) >= k) number = l;\n else number = r;\n \n long cnt = rangQuery(bit1, number, 1),\n sum = rangQuery(bit2, number, 1);\n \n return removeMoreThanK(sum, cnt, number);\n }\n \n private long findKLargest() {\n int l = 1, r = LIMIT, number = -1;\n while (l + 1 < r) {\n int m = l + (r - l) / 2;\n long count = rangQuery(bit1, LIMIT, m);\n if (count >= k) l = m;\n else r = m;\n }\n \n if (rangQuery(bit1, LIMIT, r) >= k) number = r;\n else number = l;\n \n long cnt = rangQuery(bit1, LIMIT, number),\n sum = rangQuery(bit2, LIMIT, number);\n \n return removeMoreThanK(sum, cnt, number);\n }\n \n private long removeMoreThanK(long sum, long cnt, int number) {\n if (cnt > k) {\n return sum - (cnt - k) * number;\n }\n return sum;\n }\n \n class BIT {\n long[] array;\n \n BIT(int size) {\n array = new long[size];\n }\n \n public void update(int ind, int v) {\n while (ind < array.length) {\n array[ind] += v;\n ind += ind & -ind;\n }\n }\n \n public long query(int ind) {\n long res = 0;\n while (ind > 0) {\n res += array[ind];\n ind -= ind & -ind;\n }\n return res;\n }\n }\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * MKAverage obj = new MKAverage(m, k);\n * obj.addElement(num);\n * int param_2 = obj.calculateMKAverage();\n */\n``` | 1 | 0 | [] | 0 |
finding-mk-average | [Python 3] O(logm) LazySumHeap and PartitionSum | python-3-ologm-lazysumheap-and-partition-sd2a | \nclass LazySumHeap:\n \n def __init__(self, key):\n self.heap = []\n self.key = key\n self.c = Counter()\n self.sz = 0\n | serdes | NORMAL | 2021-04-12T04:04:25.648120+00:00 | 2021-04-12T04:04:25.648163+00:00 | 115 | false | ```\nclass LazySumHeap:\n \n def __init__(self, key):\n self.heap = []\n self.key = key\n self.c = Counter()\n self.sz = 0\n self.sum = 0\n \n def __len__(self):\n return self.sz\n \n def clean(self):\n while self.heap and not self.c[self.heap[0][2]]:\n heappop(self.heap)\n \n def peek(self):\n self.clean()\n return self.heap[0][2]\n \n def pop(self):\n self.clean()\n \n ret = heappop(self.heap)[2]\n \n self.c[ret] -= 1\n self.sz -= 1\n self.sum -= ret\n \n return ret\n \n def remove(self, x):\n self.c[x] -= 1\n self.sz -= 1\n self.sum -= x\n \n def push(self, x):\n \n entry = [self.key(x), id(x), x]\n \n heappush(self.heap, entry)\n \n self.c[x] += 1\n self.sz += 1\n self.sum += x\n \n \nclass PartitionSum:\n \n # lowest <= k elements\n def __init__(self, k):\n self.k = k\n self.lo = LazySumHeap(lambda x:-x)\n self.hi = LazySumHeap(lambda x:x)\n \n def rebalance(self):\n \n while len(self.lo) > self.k:\n self.hi.push(self.lo.pop())\n \n while self.hi and len(self.lo) < self.k:\n self.lo.push(self.hi.pop())\n \n def add(self, x):\n \n if not self.hi or (self.hi and x < self.hi.peek()):\n self.lo.push(x)\n else:\n self.hi.push(x)\n\n self.rebalance()\n \n def remove(self, x):\n \n if x <= self.lo.peek():\n self.lo.remove(x)\n else:\n self.hi.remove(x)\n \n self.rebalance()\n\n\nclass MKAverage:\n\n def __init__(self, M: int, K: int):\n global m,k,q,lo,hi\n \n m = M\n k = K\n \n q = deque()\n \n lo = PartitionSum(k)\n hi = PartitionSum(m-k)\n \n\n def addElement(self, x: int) -> None:\n global m,k,q,lo,hi\n \n if len(q) <= m-1:\n q.append(x)\n lo.add(x)\n hi.add(x)\n \n else:\n \n y = q.popleft()\n lo.remove(y)\n hi.remove(y)\n \n q.append(x)\n lo.add(x)\n hi.add(x)\n\n def calculateMKAverage(self) -> int:\n global m,k,q,lo,hi\n \n if len(q) < m:\n return -1\n else:\n return (lo.hi.sum - hi.hi.sum) // (m-k-k)\n``` | 1 | 0 | [] | 0 |
finding-mk-average | Python3 SortedList | python3-sortedlist-by-gautamsw51-50ka | Create a SortedList srr and an array arr.\narr contains all elements in the order they are inserted.\nsrr contains last m elements of arr in sorted order.\nmids | gautamsw51 | NORMAL | 2021-04-11T17:54:48.575413+00:00 | 2021-04-11T17:54:48.575443+00:00 | 136 | false | Create a SortedList srr and an array arr.\narr contains all elements in the order they are inserted.\nsrr contains last m elements of arr in sorted order.\nmidsum is the sum of elements of srr excluding 1st k and last k elements.\nWhile taking average size would be n = m - 2 * k\nwhenever a new element has to be inserted, remove (arr.length-m)th element from srr,\ndo this operation while keeping track of midsum so that complexity for addElement() is log(n).\ninserpos() used to determine at what position will a new elemet get inserted when added to srr.\n```\nfrom sortedcontainers import SortedList\nclass MKAverage:\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.arr = []\n self.srr = SortedList([])\n self.midsum = 0\n self.n = self.m - 2*self.k\n def insertpos(self, x: int) -> int:\n l = 0\n r = self.m-1\n if x<=self.srr[0]:\n return 0\n if x>=self.srr[-1]:\n return self.m\n while l<=r:\n m = (l+r)//2\n if self.srr[m]<x and (m+1==len(self.srr) or self.srr[m+1]>=x):\n return m+1\n elif self.srr[m]<x:\n l = m + 1\n else:\n r = m - 1\n return -1\n def addElement(self, x: int) -> None:\n self.arr.append(x)\n if len(self.arr)==self.m:\n arr = sorted(self.arr)\n for i in range(self.k):\n self.srr.add(arr[i])\n for i in range(self.k, self.m-self.k):\n self.srr.add(arr[i])\n self.midsum += arr[i]\n for i in range(self.m-self.k, self.m):\n self.srr.add(arr[i])\n if len(self.arr)<=self.m:\n return\n rem = self.arr[-self.m-1]\n if rem<=self.srr[self.k-1]:\n self.srr.remove(rem)\n ip = self.insertpos(x)\n if ip>=self.k and ip<=self.m-self.k-1:\n self.midsum += x - self.srr[self.k-1]\n elif ip>self.m-self.k-1:\n self.midsum += self.srr[self.m-self.k-1] - self.srr[self.k-1]\n self.srr.add(x)\n elif rem<=self.srr[self.m-self.k-1]:\n self.srr.remove(rem)\n ip = self.insertpos(x)\n self.midsum -= rem\n if ip<self.k:\n self.midsum += self.srr[self.k-1]\n elif ip>=self.k and ip<=self.m-self.k-1:\n self.midsum += x\n else:\n self.midsum += self.srr[self.m-self.k-1]\n self.srr.add(x)\n else:\n self.srr.remove(rem)\n ip = self.insertpos(x)\n if ip<self.k:\n self.midsum += self.srr[self.k-1] - self.srr[self.m-self.k-1]\n elif ip>=self.k and ip<=self.m-self.k-1:\n self.midsum += x - self.srr[self.m-self.k-1]\n self.srr.add(x)\n def calculateMKAverage(self) -> int:\n if len(self.arr)<self.m:\n return -1\n else:\n return self.midsum//self.n\n``` | 1 | 0 | [] | 0 |
finding-mk-average | C++ Balance 3 Multisets/Heaps | c-balance-3-multisetsheaps-by-subhaj-m7je | Have 3 multisets: first multiset, middle multiset, last multiset.\n\nWe can limit the elements under consideration to \'m\'. Because we are always interested i | subhaj | NORMAL | 2021-04-11T12:04:15.812086+00:00 | 2021-04-11T12:23:30.452805+00:00 | 183 | false | Have 3 multisets: f*irst multiset, middle multiset, last multiset.*\n\nWe can limit the elements under consideration to \'m\'. Because we are always interested in last m elements from the numbers stream. \nThe first multiset will contain first K smallest elements. and the last multiset will contain last K elements. \nThe middle multiset will contain *m - 2K* elements. (i.e we don\'t have to remove K smaller element and K larger elements from the stream to calculate average ).\n\nIf less than \'m\' elements are processed in the number stream, the average will always be -1.\nSo we arrive at the following property which we will keep satisfying when more than \'m\' elemens are processed. \n**Property 1: At any given point, first.size() + middle.size() + last.size() should be equal to m**\n\nAlso have a queue or a vector to track the last element which is to be removed. \nWhen less than m elements are processed, push the element to the queue as well as to the middle multiset. \n\nWhen exactly m elemens are processed, then relalace the multisets in the following manner.\n\tAdd the first k elements from the middle multiset to the first multiset. \n\tAdd the last k elements form the middle multiset to the last multiset. \n\t\n```\n\t int count = 0;\n\t\twhile(count < k)\n\t\t{\n\t\t\tfirst.insert(*middle.begin());\n\t\t\tmiddle.erase(middle.begin());\n\n\t\t\tlast.insert(*middle.rbegin());\n\t\t\tmiddle.erase(prev(middle.end()));\n\t\t\tcount++;\n\t\t}\n```\n\nNow all the multisets are balanced, When a new element is encountered, \nFirst add the element to the middle multiset. \nWe also need to remove the first element from the queue and from one of the multisets (we need to look for the multisets one by one where the element exists) to satisfy **property 1** \nFind the multiset where the element exists and , then -\tRemove the element from the multiset and Adjust the multisets. \n\nAdjusting the multisets:\n*Both the first multiset and last multiset should have K elements.*\n\nif first multiset is having less than K elements, then adjust with middle multiset, so that first multiset will have K elements. \nif last multiset is haveing less than K elements, then adjust with middle multiset, so that last multiset will have K elements.\n```\nwhile(first.size() < k)\n{\n\tfirst.insert(*middle.begin());\n\tmiddle.erase(middle.begin());\n}\n\nwhile(last.size() < k)\n{\n\tlast.insert(*prev(middle.end()));\n\tmiddle.erase(prev(middle.end()));\n} \n```\n*Since multisets are sorted in nature, the last element in first multiset should be less than or equal to the first element of the middle multiset. \nSimilarly the last element of the middle multiset should be less than or equal to the first element of the last multiset.*\n\nIf the above property is not satisfied, we make adjustments to the multisets. \n```\n while(*last.begin() < *prev(middle.end()))\n {\n middle.insert(*last.begin());\n last.erase(last.begin());\n \n last.insert(*prev(middle.end()));\n middle.erase(prev(middle.end()));\n } \n\n while(*prev(first.end()) > *middle.begin())\n {\n middle.insert(*prev(first.end()));\n first.erase(prev(first.end()));\n \n first.insert(*middle.begin());\n middle.erase(middle.begin());\n }\n```\n\nHow to calculate the MK Average ?\nWe can add all the element in the middle multiset, and return the average. This approach will have linear complexity. \n\n*We can calculate MK Average in constant time by keeping a running sum of elements in the middle multiset.*\n\ni.e. whenever an element is removed from the middle multiset, we subtract the element from the sum. Similarly when an element is added to the middle multiset, we add the element to the sum. When ```calculateMKAverage``` function is called we simply return \n```\nreturn q.size() < m ? -1 : sum/middle.size(); // sum is the running sum of elements in middle multiset.\n```\n\nFull code:\n```\nclass MKAverage {\n \n private:\n void adjustHeaps(multiset<int>& first, multiset<int>& middle, multiset<int>& last)\n {\n while(first.size() < k)\n {\n first.insert(*middle.begin());\n sum -= *middle.begin();\n middle.erase(middle.begin());\n }\n \n while(last.size() < k)\n {\n last.insert(*prev(middle.end()));\n sum -= *prev(middle.end());\n middle.erase(prev(middle.end()));\n } \n \n while(*last.begin() < *prev(middle.end()))\n {\n middle.insert(*last.begin());\n sum += *last.begin();\n last.erase(last.begin());\n \n last.insert(*prev(middle.end()));\n sum -= *prev(middle.end());\n middle.erase(prev(middle.end()));\n } \n\n while(*prev(first.end()) > *middle.begin())\n {\n sum += *prev(first.end());\n middle.insert(*prev(first.end()));\n first.erase(prev(first.end()));\n \n first.insert(*middle.begin());\n sum -= *middle.begin();\n middle.erase(middle.begin());\n }\n }\npublic:\n int m,k;\n long long sum = 0;\n multiset<int> first, last, middle;\n queue<int> q;\n \n MKAverage(int m, int k) {\n this->m = m;\n this->k = k;\n }\n \n void addElement(int num) {\n if(q.size() < m-1)\n {\n middle.insert(num);\n q.push(num);\n }\n else if(q.size() == m-1)\n {\n auto f = middle.begin();\n auto l = middle.rbegin();\n q.push(num);\n middle.insert(num);\n int count = 0;\n while(count < k)\n {\n first.insert(*middle.begin());\n middle.erase(middle.begin());\n \n last.insert(*middle.rbegin());\n middle.erase(prev(middle.end()));\n \n count++;\n }\n for(auto i : middle) sum += i;\n }\n else\n {\n q.push(num);\n auto elem = q.front();\n q.pop();\n middle.insert(num);\n sum += num;\n \n if(first.find(elem)!= first.end()){\n first.erase(first.find(elem)); \n adjustHeaps(first, middle, last);\n }\n \n else if(middle.find(elem) != middle.end())\n {\n sum -= elem;\n middle.erase(middle.find(elem));\n adjustHeaps(first, middle, last);\n }\n \n else if(last.find(elem)!= last.end())\n {\n last.erase(last.find(elem)); \n adjustHeaps(first, middle, last);\n }\n }\n }\n \n int calculateMKAverage() {\n return q.size() < m ? -1 : sum/middle.size();\n }\n};\n``` | 1 | 0 | [] | 0 |
finding-mk-average | c++ BIT | 300 ms | c-bit-300-ms-by-cxky-7pvk | I had similar idea just with @ye15. So I posted c++ version here\n\nclass MKAverage {\npublic:\n int m, k;\n deque<int> dq;\n long sum[100003], cnt[100 | cxky | NORMAL | 2021-04-11T11:39:35.700293+00:00 | 2021-04-11T11:49:27.469771+00:00 | 408 | false | I had similar idea just with @ye15. So I posted c++ version here\n```\nclass MKAverage {\npublic:\n int m, k;\n deque<int> dq;\n long sum[100003], cnt[100003];\n MKAverage(int m, int k) {\n memset(sum, 0, sizeof(sum));\n this->m = m, this->k = k;\n }\n void update(int num, int val) {\n int u = val / num;\n num += 1;\n while (num < 100002) {\n cnt[num] += u;\n sum[num] += val;\n num += num & -num;\n }\n }\n long get(long BIT[],int x) {\n long res = 0;\n x += 1;\n while (x) {\n res += BIT[x];\n x -= x & -x;\n }\n return res;\n }\n void addElement(int num) {\n dq.push_back(num);\n update(num, num);\n if (dq.size() > m) {\n update(dq.front(), -dq.front());\n dq.pop_front();\n }\n }\n int searchIndex(int kk) { // binary search\n int low = 0, high = 1e5 + 1;\n while (low < high) {\n int mid = high + low >> 1;\n if (get(cnt, mid) < kk) low = mid + 1;\n else high = mid;\n }\n return low;\n }\n int calculateMKAverage() {\n if (dq.size() < m)\n return -1;\n int low = searchIndex(k);\n int high = searchIndex(m - k);\n long ans = get(sum, high) - get(sum, low);\n ans += (get(cnt, low) - k) * low;\n ans -= (get(cnt, high) - (m - k)) * high;\n return ans / (m - 2 * k);\n }\n};\n``` | 1 | 0 | ['C', 'Binary Tree'] | 1 |
finding-mk-average | [C++] three multisets | c-three-multisets-by-sky_io-tcmv | idea\n\n store the last m elements in three sets: L, M, R, the sum of elements in M is S\n\n every time we add a new element, besides an insertion operation, we | sky_io | NORMAL | 2021-04-11T06:16:05.323195+00:00 | 2021-04-11T06:17:08.962821+00:00 | 113 | false | ## idea\n\n* store the last m elements in three sets: `L, M, R`, the sum of elements in M is `S`\n\n* every time we add a new element, besides an insertion operation, we may also need to erase one extra element.\n\n* after the insertion and erasion, adjust L, M; adjust M, R\n\n\t(I added an `int adjust(multiset<int> &a, multiset<int> &b, int n)` function to make set `a`\'s size <= n, and return the difference of sum(a) after the adjustment.)\n\t\n## code\n```c++\ntypedef long long ll;\nclass MKAverage {\nprivate:\n int m, mm, K;\n vector<int> A;\n multiset<int> L, M, R;\n ll S;\npublic:\n MKAverage(int m, int k): m(m), mm(m - 2*k), K(k), S(0) {}\n\n int adjust(multiset<int> &a, multiset<int> &b, int n) {\n int diff = 0; // sum(a) diff\n if (a.size() < n) {\n if (!b.empty()) {\n auto it = b.begin();\n diff += *it;\n a.insert(*it);\n b.erase(it);\n }\n } else if (a.size() > n) {\n auto it = a.rbegin();\n diff -= *it;\n b.insert(*it);\n a.erase(prev(a.end()));\n }\n return diff;\n }\n \n void addElement(int num) {\n A.push_back(num);\n if (L.empty() || *L.rbegin() >= num) {\n L.insert(num);\n } else if (M.empty() || *M.rbegin() >= num) {\n M.insert(num);\n S += num;\n } else {\n R.insert(num);\n }\n if (A.size() > m) {\n int v = A[A.size() - 1 - m];\n if (v <= *L.rbegin()) {\n L.erase(L.find(v));\n } else if (v <= *M.rbegin()) {\n M.erase(M.find(v));\n S -= v;\n } else {\n R.erase(R.find(v));\n }\n }\n S -= adjust(L, M, K);\n S += adjust(M, R, mm);\n }\n \n int calculateMKAverage() {\n if (A.size() < m) return -1;\n return S / mm;\n }\n};\n``` | 1 | 0 | [] | 0 |
finding-mk-average | [Python3] Deque and SortedList | python3-deque-and-sortedlist-by-grokus-az1m | ```\nfrom sortedcontainers import SortedList\n\n\nclass MKAverage:\n\n def init(self, m: int, k: int):\n self.m = m\n self.k = k\n self. | grokus | NORMAL | 2021-04-11T04:41:12.607797+00:00 | 2021-04-11T04:41:12.607824+00:00 | 140 | false | ```\nfrom sortedcontainers import SortedList\n\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.m = m\n self.k = k\n self.q = deque()\n self.mid = SortedList()\n self.total = 0\n\n def addElement(self, num: int) -> None:\n self.q.append(num)\n self.mid.add(num)\n self.total += num\n if len(self.q) > self.m:\n x = self.q.popleft()\n self.mid.remove(x)\n self.total -= x\n\n def calculateMKAverage(self) -> int:\n if len(self.q) < self.m:\n return -1\n remove = sum(self.mid[:self.k]) + sum(self.mid[-self.k:])\n return int((self.total - remove) / (self.m - self.k * 2))\n | 1 | 0 | [] | 0 |
finding-mk-average | [C#] solution O(M^2) using List | c-solution-om2-using-list-by-micromax-pqym | C# does not have any sorted tree classes that allow duplicate elements. So fast workaround is maintain a sorted List with small optimization for large M.\n\nWe | micromax | NORMAL | 2021-04-11T04:15:06.897912+00:00 | 2021-04-11T06:29:52.120651+00:00 | 124 | false | C# does not have any sorted tree classes that allow duplicate elements. So fast workaround is maintain a sorted List with small optimization for large M.\n\nWe maintain sorted list of all nums in current sliding window. To maintain expiration of numbers in sliding window we can use queue.\nWhen new number arrives we do two actions:\n1) binarysearch and remove expiring number. Adjust average value. Time is O(logM + M) but usually less\n2) binarysearch and insert new number. Adjust average value. Time is O(logM + M) but usually less\n\nRuntime is ~1.6sec so it barely makes a cut. But its fast and easy implementation if you not comfortable with implementing Trees on your own.\n\n```\npublic class MKAverage {\n private Queue<int> window = new Queue<int>();\n private List<int> sorted;\n private int lowIdx;\n private int highIdx;\n private int m;\n private int k;\n private long currSum = 0;\n \n public MKAverage(int m, int k) {\n this.m = m;\n this.k = k;\n lowIdx = k;\n highIdx = m - k - 1;\n sorted = new List<int>(m);\n }\n \n public void AddElement(int num) {\n var sCount = sorted.Count;\n if (window.Count == m){\n var t = window.Dequeue();\n var tIdx = sorted.BinarySearch(t);\n if (tIdx <= lowIdx){\n currSum -= sorted[lowIdx];\n currSum += sorted[highIdx + 1];\n } else if (tIdx <= highIdx){\n currSum -= t;\n currSum += sorted[highIdx + 1]; \n }\n\n sorted.RemoveAt(tIdx);\n }\n \n \n if (sCount < m - 1){\n\t\t // no need to sort untill M elements are in the window\n sorted.Add(num);\n } else if (sCount == m - 1){\n\t\t // when first time hitting M elements in window we sort List from here on we maintain sorted order\n sorted.Add(num);\n sorted.Sort();\n for(var i = lowIdx; i <= highIdx; i++){\n currSum += sorted[i];\n }\n } else{\n var numIdx = sorted.BinarySearch(num);\n numIdx = numIdx < 0 ? ~numIdx : numIdx;\n sorted.Insert(numIdx, num); \n if (numIdx <= lowIdx){\n currSum -= sorted[highIdx+1];\n currSum += sorted[lowIdx];\n } else if (numIdx <= highIdx){\n currSum -= sorted[highIdx+1];\n currSum += num;\n }\n }\n \n window.Enqueue(num);\n \n }\n \n public int CalculateMKAverage() {\n return sorted.Count < m ? -1 : (int)(currSum/(m-k-k));\n }\n}\n\n``` | 1 | 0 | [] | 0 |
finding-mk-average | debug avl tree - python3 (not a solution) | debug-avl-tree-python3-not-a-solution-by-e1fq | i did not get it during the contest using the following avl tree structure (which should be more sophisticated than a preorder traversal but i ran out of time), | mikeyliu | NORMAL | 2021-04-11T04:13:51.903254+00:00 | 2021-04-11T04:15:02.755236+00:00 | 95 | false | i did not get it during the contest using the following avl tree structure (which should be more sophisticated than a preorder traversal but i ran out of time), any idea on what went wrong? the avl tree is from geeks4geeks.\n```\nclass TreeNode:\n def __init__(self, val):\n self.val = val\n self.left = None\n self.right = None\n self.height = 1\n \n \n# AVL tree class which supports insertion,\n# deletion operations\nclass AVL_Tree:\n \n def insert(self, root, key):\n \n # Step 1 - Perform normal BST\n if not root:\n return TreeNode(key)\n elif key < root.val:\n root.left = self.insert(root.left, key)\n else:\n root.right = self.insert(root.right, key)\n \n # Step 2 - Update the height of the \n # ancestor node\n root.height = 1 + max(self.getHeight(root.left),\n self.getHeight(root.right))\n \n # Step 3 - Get the balance factor\n balance = self.getBalance(root)\n \n # Step 4 - If the node is unbalanced,\n # then try out the 4 cases\n # Case 1 - Left Left\n if balance > 1 and key < root.left.val:\n return self.rightRotate(root)\n \n # Case 2 - Right Right\n if balance < -1 and key > root.right.val:\n return self.leftRotate(root)\n \n # Case 3 - Left Right\n if balance > 1 and key > root.left.val:\n root.left = self.leftRotate(root.left)\n return self.rightRotate(root)\n \n # Case 4 - Right Left\n if balance < -1 and key < root.right.val:\n root.right = self.rightRotate(root.right)\n return self.leftRotate(root)\n \n return root\n \n # Recursive function to delete a node with\n # given key from subtree with given root.\n # It returns root of the modified subtree.\n def delete(self, root, key):\n \n # Step 1 - Perform standard BST delete\n if not root:\n return root\n \n elif key < root.val:\n root.left = self.delete(root.left, key)\n \n elif key > root.val:\n root.right = self.delete(root.right, key)\n \n else:\n if root.left is None:\n temp = root.right\n root = None\n return temp\n \n elif root.right is None:\n temp = root.left\n root = None\n return temp\n \n temp = self.getMinValueNode(root.right)\n root.val = temp.val\n root.right = self.delete(root.right,\n temp.val)\n \n # If the tree has only one node,\n # simply return it\n if root is None:\n return root\n \n # Step 2 - Update the height of the \n # ancestor node\n root.height = 1 + max(self.getHeight(root.left),\n self.getHeight(root.right))\n \n # Step 3 - Get the balance factor\n balance = self.getBalance(root)\n \n # Step 4 - If the node is unbalanced, \n # then try out the 4 cases\n # Case 1 - Left Left\n if balance > 1 and self.getBalance(root.left) >= 0:\n return self.rightRotate(root)\n \n # Case 2 - Right Right\n if balance < -1 and self.getBalance(root.right) <= 0:\n return self.leftRotate(root)\n \n # Case 3 - Left Right\n if balance > 1 and self.getBalance(root.left) < 0:\n root.left = self.leftRotate(root.left)\n return self.rightRotate(root)\n \n # Case 4 - Right Left\n if balance < -1 and self.getBalance(root.right) > 0:\n root.right = self.rightRotate(root.right)\n return self.leftRotate(root)\n \n return root\n \n def leftRotate(self, z):\n \n y = z.right\n T2 = y.left\n \n # Perform rotation\n y.left = z\n z.right = T2\n \n # Update heights\n z.height = 1 + max(self.getHeight(z.left), \n self.getHeight(z.right))\n y.height = 1 + max(self.getHeight(y.left), \n self.getHeight(y.right))\n \n # Return the new root\n return y\n \n def rightRotate(self, z):\n \n y = z.left\n T3 = y.right\n \n # Perform rotation\n y.right = z\n z.left = T3\n \n # Update heights\n z.height = 1 + max(self.getHeight(z.left),\n self.getHeight(z.right))\n y.height = 1 + max(self.getHeight(y.left),\n self.getHeight(y.right))\n \n # Return the new root\n return y\n \n def getHeight(self, root):\n if not root:\n return 0\n \n return root.height\n \n def getBalance(self, root):\n if not root:\n return 0\n \n return self.getHeight(root.left) - self.getHeight(root.right)\n \n def getMinValueNode(self, root):\n if root is None or root.left is None:\n return root\n \n return self.getMinValueNode(root.left)\n \n def preOrder(self, root):\n if not root:\n return []\n ans=[]\n ans.extend(self.preOrder(root.left))\n ans.append(root.val)\n \n ans.extend(self.preOrder(root.right))\n return ans\n\n\nclass MKAverage:\n\n def __init__(self, m: int, k: int):\n self.stream=[]\n self.tree=AVL_Tree()\n self.root=None\n self.m=m\n self.k=k\n\n def addElement(self, num: int) -> None:\n \n #maintain tree\n self.root=self.tree.insert(self.root,num)\n if len(self.stream)>self.m:\n self.root=self.tree.delete(self.root,self.stream[-self.m])\n \n #maintain stream\n self.stream.append(num)\n\n def calculateMKAverage(self) -> int:\n if len(self.stream)<self.m:\n return -1\n orderlist=self.tree.preOrder(self.root)\n sellist=orderlist[self.k:-self.k]\n return int(sum(sellist)/len(sellist))\n\n\n# Your MKAverage object will be instantiated and called as such:\n# obj = MKAverage(m, k)\n# obj.addElement(num)\n# param_2 = obj.calculateMKAverage()\n```\n\n | 1 | 0 | [] | 1 |
finding-mk-average | Python SortedList and Deque | python-sortedlist-and-deque-by-vlee-786a | \nimport collections\nimport math\nimport statistics\nfrom typing import Deque\n\nimport sortedcontainers\n\n\nclass MKAverage:\n def __init__(self, m: int, | vlee | NORMAL | 2021-04-11T04:03:05.435967+00:00 | 2021-04-11T04:03:05.435994+00:00 | 309 | false | ```\nimport collections\nimport math\nimport statistics\nfrom typing import Deque\n\nimport sortedcontainers\n\n\nclass MKAverage:\n def __init__(self, m: int, k: int):\n self.m: int = m\n self.k: int = k\n self.sl = sortedcontainers.SortedList()\n self.dq: Deque[int] = collections.deque()\n\n def addElement(self, num: int) -> None:\n self.sl.add(num)\n self.dq.append(num)\n if len(self.dq) > self.m:\n item: int = self.dq.popleft()\n self.sl.remove(item)\n\n def calculateMKAverage(self) -> int:\n if len(self.dq) < self.m:\n return -1\n mean = statistics.mean(self.sl[self.k:-self.k])\n return math.floor(mean)\n``` | 1 | 1 | ['Queue', 'Python3'] | 1 |
finding-mk-average | Java TreeMap and Queue | java-treemap-and-queue-by-disha-mdfc | IntuitionSince it needs elements to be in sorted order so that the largest and smallest k elements can be ignored, and there can also be duplicate elements, we | disha | NORMAL | 2025-03-08T17:07:42.801886+00:00 | 2025-03-08T17:07:42.801886+00:00 | 9 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Since it needs elements to be in sorted order so that the largest and smallest k elements can be ignored, and there can also be duplicate elements, we will use TreeMap.
And in order to remove oldest element when more than m elements are inserted, we use Queue to store the elements.
# Approach
<!-- Describe your approach to solving the problem. -->
While inserting, check if the queue size is already equal to m.
If yes, remove the first element in the Queue, and reduce the count of the element in the treemap, if the count reduces to zero, remove the key altogether.
While calculating average, loop over treemap elements. Following scenarios can occur:
- previous elements count + current element count <= k : It means this element is not to be added in the sum
- k < previous elements count + current element count <= m - k :
- If k > previous elements count : Remove k - prev count from current element count to be added. As this count lies in k smallest elements
- previous elements count + current element count > m - k :
- If k > previous elements count : Remove k - prev count from current element count to be added. As this count lies in k smallest elements
- Remove (prev count + current element count) - (m - k) from the current element count to be added. As this count lies in k largest elements
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(m)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(m)
# Code
```java []
class MKAverage {
Map<Integer, Integer> numCounts;
Queue<Integer> elements;
int numElements;
int m, k;
public MKAverage(int m, int k) {
numCounts = new TreeMap<>();
elements = new LinkedList<>();
numElements = 0;
this.m = m;
this.k = k;
}
public void addElement(int num) {
if(numElements == m) {
int old = elements.poll();
numCounts.put(old, numCounts.get(old) - 1);
if(numCounts.get(old) == 0) numCounts.remove(old);
numElements--;
}
elements.add(num);
numCounts.put(num, numCounts.getOrDefault(num, 0)+1);
numElements++;
}
public int calculateMKAverage() {
if(numElements < m) return -1;
int freqSum = 0;
int numSum = 0;
for(Map.Entry<Integer, Integer> entry: numCounts.entrySet()) {
int num = entry.getKey();
int numCount = entry.getValue();
int count = numCount;
if(freqSum + numCount > k) {
if(freqSum + numCount <= m - k){
if(k > freqSum) count -= k - freqSum;
numSum += count*num;
} else {
if(k > freqSum) count -= k - freqSum;
count -= freqSum + numCount - (m - k);
numSum += count*num;
}
}
freqSum += numCount;
if(freqSum >= m - k) break;
}
return numSum/(m - (2*k));
}
}
/**
* Your MKAverage object will be instantiated and called as such:
* MKAverage obj = new MKAverage(m, k);
* obj.addElement(num);
* int param_2 = obj.calculateMKAverage();
*/
``` | 0 | 0 | ['Java'] | 0 |
finding-mk-average | Short Interview friendly solution - Accepted | short-interview-friendly-solution-accept-2mcd | Intuition
Use SortedList to keep track of sorted elements in window whenever a new element is added.
Calculate the average in current window and return answer. | nishantapatil3 | NORMAL | 2025-02-19T07:22:24.744343+00:00 | 2025-02-19T07:22:24.744343+00:00 | 20 | false | # Intuition
1. Use SortedList to keep track of sorted elements in window whenever a new element is added.
2. Calculate the average in current window and return answer.
# Complexity
- Time complexity: O(log m)
- Space complexity: O(m)
# Code
```python3 []
class MKAverage:
def __init__(self, m: int, k: int):
self.m = m
self.k = k
self.window = deque()
self.sorted_list = SortedList()
def addElement(self, num: int) -> None:
self.window.append(num)
self.sorted_list.add(num)
if len(self.window) > self.m:
old = self.window.popleft()
self.sorted_list.remove(old)
def calculateMKAverage(self) -> int:
n = len(self.window)
if n < self.m:
return -1
# remove k smallest and k largest
arr = self.sorted_list[self.k : -self.k]
return sum(arr) // len(arr)
# Your MKAverage object will be instantiated and called as such:
# obj = MKAverage(m, k)
# obj.addElement(num)
# param_2 = obj.calculateMKAverage()
``` | 0 | 0 | ['Python3'] | 0 |
finding-mk-average | ◈ Python ◈ Ordered Set ◈ Data Stream ◈ Design | python-ordered-set-data-stream-design-by-cfrx | Glossary:
m: The number of most recent elements to consider.
k: The number of smallest and largest elements to exclude.
arr: The array storing all added numbers | zurcalled_suruat | NORMAL | 2025-02-12T06:42:40.729458+00:00 | 2025-02-12T07:20:22.121590+00:00 | 7 | false | Glossary:
- $m$: The number of most recent elements to consider.
- $k$: The number of smallest and largest elements to exclude.
- $arr$: The array storing all added numbers.
- $ss$: The sorted set storing the last $m$ elements.
- $ix$: The index of the last added element in $arr$.
- $sm$: The sum of the elements in the middle range (excluding the smallest $k$ and largest $k$ elements).
- $ix_{start}$: The starting index of the middle range in $ss$.
- $ix_{end}$: The ending index of the middle range in $ss$.
- $S$: Small element
- $M$: Middle element
- $L$: Large element
- $|ss|$: Size of the sorted set $ss$
Mathematical Intuition:
The problem requires calculating the moving average of the last $m$ numbers, excluding the $k$ smallest and $k$ largest elements. We maintain a sorted set $ss$ containing at most the last $m$ added numbers. The core idea is to efficiently update the sum $sm$ of the elements used for the average calculation.
Imagine ss divided into three sections as shown in the figure 'Three sections of sorted set ss':
```
Three sections of sorted set ss
+-----------+-----------+-----------+
| Small | Middle | Large |
| k=3 | m-2k | k=3 |
+-----------+-----------+-----------+
```
1. **`get_ss_ix_range_considered()`**: This function determines the indices in $ss$ that correspond to the elements used for calculating the average. Since we exclude the $k$ smallest and $k$ largest, the relevant range is from index $k$ to $|ss| - k - 1$. If the size of $ss$ is less than or equal to $2k$, there are no elements in the middle range, and the function returns `None`.
2. **`remove_ix_arr(ix_arr)`**: This function removes the element at index `ix_arr` from the considered set. It finds the corresponding element in $ss$ and removes it. The crucial part is updating $sm$. We determine the position of the removed element within $ss$ and the before and after states of the sorted set as shown in the figures 'Removing from Small (Remove S1)', 'Removing from Large (Remove L1)', and 'Removing from Middle (Remove M1)':
```
Removing from Small (Remove S1)
0 k=3 m-k=7 m-1=9
ss: [S][S][S]...[M][M][M]...[L][L][L] (Before)
^
|
Removed
0 k=3 m-k=7 m-1=9
ss: [S][S][M]...[M][M]...[L][L][L] (After)
sm: (Adjust sm - a Middle element became Small)
Removing from Large (Remove L1)
0 k=3 m-k=7 m-1=9
ss: [S][S][S]...[M][M][M]...[L][L][L] (Before)
^
|
Removed
0 k=3 m-k=7 m-1=9
ss: [S][S][S]...[M][M]...[M][L][L] (After)
sm: (Adjust sm if the element moving into Large was previously contributing to the sum)
Removing from Middle (Remove M1)
0 k=3 m-k=7 m-1=9
ss: [S][S][S]...[M][M][M]...[L][L][L] (Before)
^
|
Removed
0 k=3 m-k=7 m-1=9
ss: [S][S][S]...[M][M]...[L][L][L] (After)
sm: (Subtract M1 from sm)
```
3. **`add_ix_arr(ix_arr)`**: This function adds the element at index `ix_arr` to the considered set. It adds the element to $ss$. Then we determine the position of the newly added element within $ss$ and the before and after states of the sorted set as shown in the figures 'Adding to Small (Add S4)', 'Adding to Large (Add L4)', and 'Adding to Middle (Add M2)':
```
Adding to Small (Add S4)
0 k m-k m-1
ss: [S][S][S]...[M][M][M]...[L][L][L] (Before)
^
|
Add
ss: [S][S][S]...[S][M][M][M]...[L][L][L] (After)
sm: (Adjust sm - a Middle element became Small)
Adding to Large (Add L4)
0 k m-k m-1
ss: [S][S][S]...[M][M][M]...[L][L][L] (Before)
^
|
Add
ss: [S][S][S]...[M][M][M][L]...[L][L][L] (After)
sm: (Adjust sm - a Middle element became Large)
Adding to Middle (Add M2)
0 k m-k m-1
ss: [S][S][S]...[M][M][M]...[L][L][L] (Before)
sm: (Sum of elements in the Middle section)
ss: [S][S][S]...[M][M][M][M]...[L][L][L] (After)
sm: (Add M2 to sm)
```
4. **`addElement(num)`**: This function adds a new number to the data structure. First, it removes the oldest element if the size of $ss$ has reached $m$. Then, it adds the new number and updates $ss$ and $sm$ using `add_ix_arr()`.
5. **`calculateMKAverage()`**: This function calculates the MKAverage. It checks if there are enough elements ($|ss| \ge m$). If not, it returns -1. Otherwise, it calculates the average by dividing $sm$ by the number of elements in the middle range ($|ss| - 2k$).
Mathematical Proof of Correctness:
The correctness hinges on the proper maintenance of $ss$ and $sm$. $ss$ always contains the last $m$ elements in sorted order. $sm$ represents the sum of the middle elements. `remove_ix_arr` and `add_ix_arr` correctly update $sm$ based on the position of the added/removed element in $ss$. `addElement` ensures that only the last $m$ elements are considered. `calculateMKAverage` uses the correctly maintained $sm$ and the size of the middle range to compute the average.
Algorithm:
1. Maintain a sorted set $ss$ of the last $m$ elements.
2. Maintain the sum $sm$ of the middle elements (excluding the $k$ smallest and $k$ largest).
3. `addElement(num)`:
a. If $|ss| \ge m$, remove the oldest element from $ss$ and update $sm$.
b. Add $num$ to $ss$.
c. Update $sm$ based on the position of $num$ in $ss$.
4. `calculateMKAverage()`:
a. If $|ss| < m$, return -1.
b. Calculate the average: $\lfloor \frac{sm}{m - 2k} \rfloor$.
Time and Space Complexity:
Time Complexity:
- `addElement()`: $O(\log m)$ for adding/removing from the sorted set.
- `calculateMKAverage()`: $O(1)$.
Overall per operation: $O(\log m)$
Space Complexity: $O(m)$ to store the sorted set.
# Code
```python3 []
from sortedcontainers import SortedSet as SS
import math
class MKAverage:
def __init__(self, m: int, k: int):
self.arr = []
self.ss = SS()
self.ix = -1
self.m = m
self.k = k
self.sm = 0 # sum of coinsidered elements
assert self.m > 0
assert self.m > (self.k * 2)
print(f"m,k {m,k}")
def get_ss_ix_range_considered(self):
if(
(len(self.ss) <= 2 * self.k)
):
return None, None
ix_start = self.k
ix_end = len(self.ss)-self.k -1
return ix_start, ix_end
def remove_ix_arr(self, ix_arr):
assert 0 <= ix_arr < len(self.arr)
item_to_remove = (self.arr[ix_arr],ix_arr)
# update sum of considered numbers
# consider the last m numbers in three intervals (1-based indexing) stored in the sorted set self.ss
# [ ... ][ k+1 ... m-k ][ ... ]
# [ I ][ II ][ III ]
# Intervals - I, III are filled first , in a balanced way
# Only once I, III are filled with each k elements does II start getting populated
# If any element trying to be removed from in I , I pulls leftmost element from II
# Then any element trying to be removed in III , III pulls rightmost element from II
# If removed number is in I -> -ss[ix_start] ( interval - I will suck up ix_start )
# If removed number is in II -> +ss[ix_ss_new]
# If removed number is in III , +ss[ix_end] ( interval - |I will suck up ix_start )
ix_ss_item_to_remove = self.ss.index(item_to_remove)
ix_start,ix_end = self.get_ss_ix_range_considered()
if(None in [ix_start,ix_end]):
# there are less than 2 * k elements in self.ss so no elements in interval - II
pass
elif(ix_ss_item_to_remove<ix_start):
self.sm += -self.ss[ix_start][0]
elif(ix_start<=ix_ss_item_to_remove<=ix_end):
self.sm += -self.ss[ix_ss_item_to_remove][0]
elif(ix_end<ix_ss_item_to_remove):
self.sm += -self.ss[ix_end][0]
pass
self.ss.remove(item_to_remove)
def add_ix_arr(self, ix_arr):
assert 0 <= ix_arr < len(self.arr)
item_to_add = (self.arr[ix_arr],ix_arr)
# update sum of considered numbers
# consider the last m numbers in three intervals (1-based indexing) stored in the sorted set self.ss
# [ ... ][ k+1 ... m-k ][ ... ]
# [ I ][ II ][ III ]
# Intervals - I, III are filled first , in a balanced way
# Only once I, III are filled with each k elements does II start getting populated
# Then any element trying to land in I , it pushes its rightmost element to II
# Then any element trying to land in III , it pushes its leftmost element to II
# If new number is in I -> +ss[ix_start] ( interval - I will push up ix_start to interval - II )
# If new number is in II -> +ss[ix_ss_new]
# If new number is in III , +ss[ix_end] ( interval - III will push up ix_end to interval - II )
self.ss.add(item_to_add)
assert len(self.ss) <= self.m
ix_ss_item_to_add = self.ss.index(item_to_add)
ix_start,ix_end = self.get_ss_ix_range_considered()
if(None in [ix_start,ix_end]):
# there are less than 2 * k elements in self.ss so any new elements will move to interval I or III and there will be no change in interval - II
pass
elif(ix_ss_item_to_add<ix_start):
self.sm += self.ss[ix_start][0]
elif(ix_start<=ix_ss_item_to_add<=ix_end):
self.sm += self.ss[ix_ss_item_to_add][0]
elif(ix_end<ix_ss_item_to_add):
self.sm += self.ss[ix_end][0]
pass
def addElement(self, num: int) -> None:
assert len(self.ss) <= self.m
# 1. remove index that has become stale (only consider last m elements as per P.S.)
while(len(self.ss) >= self.m ):
ix_arr_to_remove = self.ix - (self.m -1)
self.remove_ix_arr(ix_arr_to_remove)
# 2.add new number
self.ix +=1
self.arr.append(num)
self.add_ix_arr(self.ix)
# print(f"+{num} | sm={self.sm}, ss={self.ss} , considered ixs={self.get_ss_ix_range_considered()}")
def calculateMKAverage(self) -> int:
if(len(self.ss) < self.m):
return -1
ix_start,ix_end = self.get_ss_ix_range_considered()
if(None in [ix_start,ix_end]):
return -1
avg = math.floor(self.sm / (ix_end +1 - ix_start))
return avg
# Your MKAverage object will be instantiated and called as such:
# obj = MKAverage(m, k)
# obj.addElement(num)
# param_2 = obj.calculateMKAverage()
``` | 0 | 0 | ['Design', 'Data Stream', 'Ordered Set', 'Python3'] | 0 |
finding-mk-average | TreeMap + Queue | treemap-queue-by-up41guy-ldnt | https://carefree-ladka.github.io/js.enigma/docs/DSA/TreeMap
https://carefree-ladka.github.io/js.enigma/docs/DSA/TreeSet
https://carefree-ladka.github.io/js.enig | Cx1z0 | NORMAL | 2025-01-14T16:44:55.779807+00:00 | 2025-01-14T16:44:55.779807+00:00 | 11 | false | https://carefree-ladka.github.io/js.enigma/docs/DSA/TreeMap
https://carefree-ladka.github.io/js.enigma/docs/DSA/TreeSet
https://carefree-ladka.github.io/js.enigma/docs/DSA/SortedList
and many more ... . I built this site to revsie topics for last minute .
The implementation is quite efficient
---
```javascript []
class TreeNode {
constructor(key, value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
this.height = 1;
}
}
class TreeMap {
constructor() {
this.root = null;
this.size = 0;
}
// Get height of node
#getHeight(node) {
return node ? node.height : 0;
}
// Get balance factor
#getBalance(node) {
return node ? this.#getHeight(node.left) - this.#getHeight(node.right) : 0;
}
// Right rotation
#rightRotate(y) {
const x = y.left;
const T2 = x.right;
x.right = y;
y.left = T2;
y.height = Math.max(this.#getHeight(y.left), this.#getHeight(y.right)) + 1;
x.height = Math.max(this.#getHeight(x.left), this.#getHeight(x.right)) + 1;
return x;
}
// Left rotation
#leftRotate(x) {
const y = x.right;
const T2 = y.left;
y.left = x;
x.right = T2;
x.height = Math.max(this.#getHeight(x.left), this.#getHeight(x.right)) + 1;
y.height = Math.max(this.#getHeight(y.left), this.#getHeight(y.right)) + 1;
return y;
}
// Insert a key-value pair
put(key, value) {
this.root = this.#put(this.root, key, value);
return this;
}
#put(node, key, value) {
if (!node) {
this.size++;
return new TreeNode(key, value);
}
if (key < node.key) {
node.left = this.#put(node.left, key, value);
} else if (key > node.key) {
node.right = this.#put(node.right, key, value);
} else {
node.value = value; // Update value if key exists
return node;
}
node.height = Math.max(this.#getHeight(node.left), this.#getHeight(node.right)) + 1;
const balance = this.#getBalance(node);
// Left Left Case
if (balance > 1 && key < node.left.key) {
return this.#rightRotate(node);
}
// Right Right Case
if (balance < -1 && key > node.right.key) {
return this.#leftRotate(node);
}
// Left Right Case
if (balance > 1 && key > node.left.key) {
node.left = this.#leftRotate(node.left);
return this.#rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node.right.key) {
node.right = this.#rightRotate(node.right);
return this.#leftRotate(node);
}
return node;
}
// Get value by key
get(key) {
const node = this.#get(this.root, key);
return node ? node.value : undefined;
}
#get(node, key) {
if (!node) return null;
if (key === node.key) return node;
return key < node.key ? this.#get(node.left, key) : this.#get(node.right, key);
}
// Remove key-value pair
remove(key) {
const hasKey = this.has(key);
if (hasKey) {
this.root = this.#remove(this.root, key);
this.size--;
}
return hasKey;
}
#remove(node, key) {
if (!node) return null;
if (key < node.key) {
node.left = this.#remove(node.left, key);
} else if (key > node.key) {
node.right = this.#remove(node.right, key);
} else {
if (!node.left || !node.right) {
return node.left || node.right;
}
const successor = this.#getMin(node.right);
node.key = successor.key;
node.value = successor.value;
node.right = this.#remove(node.right, successor.key);
}
node.height = Math.max(this.#getHeight(node.left), this.#getHeight(node.right)) + 1;
const balance = this.#getBalance(node);
// Rebalance after removal
if (balance > 1 && this.#getBalance(node.left) >= 0) {
return this.#rightRotate(node);
}
if (balance > 1 && this.#getBalance(node.left) < 0) {
node.left = this.#leftRotate(node.left);
return this.#rightRotate(node);
}
if (balance < -1 && this.#getBalance(node.right) <= 0) {
return this.#leftRotate(node);
}
if (balance < -1 && this.#getBalance(node.right) > 0) {
node.right = this.#rightRotate(node.right);
return this.#leftRotate(node);
}
return node;
}
// Check if key exists
has(key) {
return this.#get(this.root, key) !== null;
}
// Get minimum key
firstKey() {
if (!this.root) return undefined;
return this.#getMin(this.root).key;
}
// Get maximum key
lastKey() {
if (!this.root) return undefined;
return this.#getMax(this.root).key;
}
#getMin(node) {
while (node.left) {
node = node.left;
}
return node;
}
#getMax(node) {
while (node.right) {
node = node.right;
}
return node;
}
// Get first key greater than or equal to given key
ceilingKey(key) {
let node = this.root;
let ceiling = null;
while (node) {
if (key === node.key) {
return key;
}
if (key < node.key) {
ceiling = node.key;
node = node.left;
} else {
node = node.right;
}
}
return ceiling;
}
// Get last key less than or equal to given key
floorKey(key) {
let node = this.root;
let floor = null;
while (node) {
if (key === node.key) {
return key;
}
if (key < node.key) {
node = node.left;
} else {
floor = node.key;
node = node.right;
}
}
return floor;
}
// Clear all entries
clear() {
this.root = null;
this.size = 0;
}
// Get size of tree
getSize() {
return this.size;
}
// Check if tree is empty
isEmpty() {
return this.size === 0;
}
// Get all keys in order
keys() {
const result = [];
this.#inorderTraversal(this.root, node => result.push(node.key));
return result;
}
// Get all values in order of keys
values() {
const result = [];
this.#inorderTraversal(this.root, node => result.push(node.value));
return result;
}
// Get all entries in order
entries() {
const result = [];
this.#inorderTraversal(this.root, node => result.push([node.key, node.value]));
return result;
}
#inorderTraversal(node, callback) {
if (node) {
this.#inorderTraversal(node.left, callback);
callback(node);
this.#inorderTraversal(node.right, callback);
}
}
}
class MKAverage {
constructor(m, k) {
// Initialize parameters
this.m = m;
this.k = k;
this.total = 0;
// Queue to maintain the last m elements
this.queue = [];
// TreeMap to maintain sorted elements with their frequencies
this.countMap = new TreeMap();
}
addElement(num) {
this.queue.push(num);
this.#addToMap(num);
// Remove oldest element if window size exceeds m
if (this.queue.length > this.m) {
const oldNum = this.queue[this.queue.length - this.m - 1];
this.#removeFromMap(oldNum);
}
}
// Helper method to add number to TreeMap
#addToMap(num) {
const count = this.countMap.get(num) || 0;
this.countMap.put(num, count + 1);
this.total += num;
}
// Helper method to remove number from TreeMap
#removeFromMap(num) {
const count = this.countMap.get(num);
if (count === 1) {
this.countMap.remove(num);
} else {
this.countMap.put(num, count - 1);
}
this.total -= num;
}
calculateMKAverage() {
// Return -1 if we don't have enough elements
if (this.queue.length < this.m) {
return -1;
}
let remainSum = this.total;
let remainCount = this.m;
let currentK = this.k;
// Remove k smallest elements
const entries = this.countMap.entries();
let i = 0;
while (currentK > 0 && i < entries.length) {
const [num, count] = entries[i];
const toRemove = Math.min(currentK, count);
remainSum -= num * toRemove;
remainCount -= toRemove;
currentK -= toRemove;
i++;
}
// Remove k largest elements
currentK = this.k;
i = entries.length - 1;
while (currentK > 0 && i >= 0) {
const [num, count] = entries[i];
const toRemove = Math.min(currentK, count);
remainSum -= num * toRemove;
remainCount -= toRemove;
currentK -= toRemove;
i--;
}
// Calculate average of remaining elements
return Math.floor(remainSum / remainCount);
}
}
``` | 0 | 0 | ['Design', 'Queue', 'Data Stream', 'Ordered Set', 'JavaScript'] | 0 |
finding-mk-average | 4 heaps python solution | 4-heaps-python-solution-by-user0549z-nqxn | \n# Approach\nUse 4 heaps\n max heap for lowwer k elements\n max and max heaps for middle elements\n min heap for higher k elements\n\n\n# Complexity\n addEleme | user0549Z | NORMAL | 2024-11-19T14:19:05.384756+00:00 | 2024-11-19T14:19:05.384793+00:00 | 24 | false | \n# Approach\nUse 4 heaps\n* max heap for lowwer k elements\n* max and max heaps for middle elements\n* min heap for higher k elements\n\n\n# Complexity\n* addElement - O(log(n))\n* calculateMKAverage - O(1)\n\n- Space complexity:\n* for heaps = 4*O(m)\n* for presence checker map = 3*O(m)\n* sor stack = O(m)\n* Total - 8*O(m)\n\n# Code\n```python3 []\nfrom collections import deque\nfrom collections import defaultdict as dd\nimport heapq\nclass MKAverage:\n m,k = 0,0\n pres_in_lower_k = dd(int)\n pres_in_higher_k = dd(int)\n pres_in_middle = dd(int)\n\n elements_in_middle = 0\n elements_in_lower_k = 0\n elements_in_higher_k = 0\n\n lower_k_max_heap = []\n higher_k_min_heap = []\n middle_min_heap = []\n middle_max_heap = []\n\n middle_sum = 0\n\n s = deque()\n\n def __init__(self, m: int, k: int):\n self.m, self.k = m,k\n\n self.pres_in_lower_k = dd(int)\n self.pres_in_higher_k = dd(int)\n self.pres_in_middle = dd(int)\n\n self.elements_in_middle = 0\n self.elements_in_lower_k = 0\n self.elements_in_higher_k = 0\n\n self.lower_k_max_heap = []\n self.higher_k_min_heap = []\n self.middle_min_heap = []\n self.middle_max_heap = []\n\n self.middle_sum = 0\n self.s = deque()\n\n def addInitialElements(self,num):\n heapq.heappush(self.lower_k_max_heap, -num)\n self.elements_in_lower_k+=1\n self.pres_in_lower_k[num] += 1\n\n if self.elements_in_lower_k>self.k:\n # remove from lower k elements\n top = -heapq.heappop(self.lower_k_max_heap)\n self.elements_in_lower_k -= 1\n self.pres_in_lower_k[top] -= 1\n\n # add in upper k elements\n heapq.heappush(self.middle_min_heap, top)\n heapq.heappush(self.middle_max_heap, -top)\n self.elements_in_middle+=1\n self.pres_in_middle[top] += 1\n self.middle_sum += top\n\n if self.elements_in_middle > self.m - (2*self.k):\n\n #remove from middle\n middle_top = -heapq.heappop(self.middle_max_heap)\n self.elements_in_middle-=1\n self.pres_in_middle[middle_top] -= 1\n self.middle_sum -= middle_top\n\n #add in higher queue\n heapq.heappush(self.higher_k_min_heap, middle_top)\n self.pres_in_higher_k[middle_top] += 1\n self.elements_in_higher_k += 1\n\n def addElementAndBalanceHeap(self,num): \n # print("val",num)\n # self.print_data()\n heapq.heappush(self.lower_k_max_heap, -num)\n self.elements_in_lower_k+=1\n self.pres_in_lower_k[num] += 1\n\n if self.elements_in_lower_k > self.k:\n top = -heapq.heappop(self.lower_k_max_heap)\n self.elements_in_lower_k -= 1\n self.pres_in_lower_k[top] -= 1\n\n heapq.heappush(self.middle_min_heap, top)\n heapq.heappush(self.middle_max_heap, -top)\n self.elements_in_middle+=1\n self.pres_in_middle[top] += 1\n self.middle_sum += top\n\n self.sanitize_heap()\n if self.lower_k_max_heap and self.middle_min_heap and -self.lower_k_max_heap[0]>self.middle_min_heap[0]:\n lower_max, middle_min = -heapq.heappop(self.lower_k_max_heap),heapq.heappop(self.middle_min_heap)\n heapq.heappush(self.lower_k_max_heap, -middle_min)\n heapq.heappush(self.middle_min_heap, lower_max)\n heapq.heappush(self.middle_max_heap, -lower_max)\n self.pres_in_middle[middle_min] -= 1\n self.pres_in_middle[lower_max] += 1\n self.pres_in_lower_k[middle_min] += 1\n self.pres_in_lower_k[lower_max] -= 1\n self.middle_sum += lower_max - middle_min\n\n self.sanitize_heap()\n\n if self.elements_in_middle > self.m - (2*self.k):\n middle_top = -heapq.heappop(self.middle_max_heap)\n self.elements_in_middle -= 1\n self.pres_in_middle[middle_top] -= 1\n self.middle_sum -= middle_top\n\n heapq.heappush(self.higher_k_min_heap, middle_top)\n self.pres_in_higher_k[middle_top] += 1\n self.elements_in_higher_k += 1\n\n self.sanitize_heap()\n\n if self.middle_max_heap and self.higher_k_min_heap and -self.middle_max_heap[0]>self.higher_k_min_heap[0]:\n middle_max, higher_min = -heapq.heappop(self.middle_max_heap),heapq.heappop(self.higher_k_min_heap)\n heapq.heappush(self.middle_max_heap, -higher_min)\n heapq.heappush(self.middle_min_heap, higher_min)\n heapq.heappush(self.higher_k_min_heap, middle_max)\n self.pres_in_middle[middle_max] -= 1\n self.pres_in_middle[higher_min] += 1\n self.pres_in_higher_k[middle_max] += 1\n self.pres_in_higher_k[higher_min] -= 1\n self.middle_sum += higher_min - middle_max\n # print("after") \n # self.print_data()\n\n\n def remove_element(self):\n element_to_be_removed = self.s.popleft()\n # element poped from lower k elements\n if self.lower_k_max_heap and -self.lower_k_max_heap[0] >= element_to_be_removed:\n self.elements_in_lower_k-=1\n self.pres_in_lower_k[element_to_be_removed] -= 1\n return\n \n if self.middle_max_heap and -self.middle_max_heap[0] >= element_to_be_removed:\n self.elements_in_middle-=1\n self.pres_in_middle[element_to_be_removed] -= 1\n self.middle_sum -= element_to_be_removed\n return \n\n self.pres_in_higher_k[element_to_be_removed] -= 1\n self.elements_in_higher_k -= 1\n \n\n\n\n\n\n def addElement(self, num: int) -> None:\n self.s.append(num)\n if self.elements_in_middle + self.elements_in_lower_k + self.elements_in_higher_k < self.m:\n self.addInitialElements(num)\n return\n self.sanitize_heap()\n self.remove_element()\n self.sanitize_heap()\n self.addElementAndBalanceHeap(num)\n \n\n\n\n\n\n\n \n\n \n\n def calculateMKAverage(self) -> int:\n if self.elements_in_middle + self.elements_in_lower_k + self.elements_in_higher_k < self.m:\n return -1\n\n return self.middle_sum//(self.m-(2*self.k))\n \n def sanitize_heap(self):\n while self.lower_k_max_heap and self.pres_in_lower_k[-self.lower_k_max_heap[0]] == 0:\n heapq.heappop(self.lower_k_max_heap)\n\n while self.middle_max_heap and self.pres_in_middle[-self.middle_max_heap[0]] == 0:\n heapq.heappop(self.middle_max_heap)\n \n while self.middle_min_heap and self.pres_in_middle[self.middle_min_heap[0]] == 0:\n heapq.heappop(self.middle_min_heap)\n \n while self.higher_k_min_heap and self.pres_in_higher_k[self.higher_k_min_heap[0]] == 0:\n heapq.heappop(self.higher_k_min_heap)\n\n def print_data(self):\n print(" lower ")\n print(self.pres_in_lower_k,self.elements_in_lower_k)\n print(self.lower_k_max_heap)\n print(" middle ")\n print(self.pres_in_middle,self.elements_in_middle)\n print(self.middle_min_heap, self.middle_max_heap)\n print(self.middle_sum)\n print("last")\n print(self.pres_in_higher_k,self.elements_in_higher_k)\n print(self.higher_k_min_heap)\n print()\n print()\n``` | 0 | 0 | ['Python3'] | 0 |
finding-mk-average | 1825. Finding MK Average.cpp | 1825-finding-mk-averagecpp-by-202021gane-mwkr | Code\n\nclass MKAverage {\npublic:\n set<pair<int, int>, greater<>>MaxHeap;\n set<pair<int, int>>MinHeap;\n set<pair<int, int>>MidHeap;\n queue<int> | 202021ganesh | NORMAL | 2024-10-16T10:24:03.846104+00:00 | 2024-10-16T10:24:03.846128+00:00 | 10 | false | **Code**\n```\nclass MKAverage {\npublic:\n set<pair<int, int>, greater<>>MaxHeap;\n set<pair<int, int>>MinHeap;\n set<pair<int, int>>MidHeap;\n queue<int>vals;\n int M, K;\n int count;\n long long Sum;\n int midLength;\n MKAverage(int m, int k) {\n M = m;\n K = k;\n Sum = 0L;\n count = 0;\n midLength = M - 2 * K;\n }\n void addElement(int num) {\n count++;\n vals.push(num);\n if (count > M)\n {\n pair<int, int> target = { vals.front(),count - M };\n vals.pop();\n if (MaxHeap.find(target) != MaxHeap.end())\n {\n MaxHeap.erase(target);\n MaxHeap.insert(*MidHeap.begin());\n Sum -= (*MidHeap.begin()).first;\n MidHeap.erase(MidHeap.begin());\n }\n else if (MinHeap.find(target) != MinHeap.end())\n {\n MinHeap.erase(target);\n MinHeap.insert(*MidHeap.rbegin());\n Sum -= (*MidHeap.rbegin()).first;\n MidHeap.erase(*MidHeap.rbegin());\n } \n else\n {\n Sum -= target.first;\n MidHeap.erase(MidHeap.find(target));\n }\n }\n MaxHeap.insert({ num,count });\n if (MaxHeap.size() > K)\n {\n auto maxVal = *MaxHeap.begin();\n MaxHeap.erase(MaxHeap.begin());\n MinHeap.insert(maxVal); \n if (MinHeap.size() > K)\n {\n auto minVal = *MinHeap.begin();\n MinHeap.erase(MinHeap.begin());\n MidHeap.insert(minVal);\n Sum += minVal.first;\n }\n }\n\n }\n int calculateMKAverage() {\n if (count < M) return -1;\n else return Sum / midLength;\n }\n};\n``` | 0 | 0 | ['C'] | 0 |
finding-mk-average | scala SortedSet | scala-sortedset-by-vititov-3h4k | scala []\nclass MKAverage(_m: Int, _k: Int) {\n import scala.util.chaining._\n import collection.mutable\n val (lo,mid,hi) = (mutable.TreeSet.empty[(Int,Int) | vititov | NORMAL | 2024-10-14T00:03:38.197446+00:00 | 2024-10-14T00:03:38.197465+00:00 | 3 | false | ```scala []\nclass MKAverage(_m: Int, _k: Int) {\n import scala.util.chaining._\n import collection.mutable\n val (lo,mid,hi) = (mutable.TreeSet.empty[(Int,Int)],mutable.TreeSet.empty[(Int,Int)],mutable.TreeSet.empty[(Int,Int)])\n val q = mutable.Queue.empty[(Int,Int)]\n var (sumMid,i) = (0,0)\n def toLo():Unit = mid.head.pipe{case a@(v,_) => lo += a; sumMid -= v; mid -= a}\n def fromLo():Unit = lo.last.pipe{case a@(v,_) => mid += a; sumMid += v; lo -= a}\n def toHi():Unit = mid.last.pipe{case a@(v,_) => hi += a; sumMid -= v; mid -= a}\n def fromHi():Unit = hi.head.pipe{case a@(v,_) => mid += a; sumMid += v; hi -= a}\n def addElement(num: Int): Unit = {\n i+=1\n val pair = (num,i)\n q.addOne(pair); mid += pair; sumMid += pair._1\n if(i == _m) Iterator.range(0,_k).foreach{_ => toLo(); toHi()}\n else if(i > _m) {\n fromLo(); fromHi(); toLo(); toHi();\n val h = q.dequeue()\n if(hi.contains(h)) { hi -= h; toHi()}\n else if(lo.contains(h)) { lo -= h; toLo()}\n else {mid -= h; sumMid -= h._1}\n }\n }\n def calculateMKAverage(): Int = if(i<_m) -1 else sumMid / mid.size\n}\n\n/**\n * Your MKAverage object will be instantiated and called as such:\n * val obj = new MKAverage(m, k)\n * obj.addElement(num)\n * val param_2 = obj.calculateMKAverage()\n */\n``` | 0 | 0 | ['Design', 'Queue', 'Data Stream', 'Ordered Set', 'Scala'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.