question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
time-needed-to-buy-tickets | Swift solution | swift-solution-by-azm819-xb7r | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | azm819 | NORMAL | 2024-04-09T06:49:59.195554+00:00 | 2024-04-09T06:49:59.195609+00:00 | 62 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n func timeRequiredToBuy(_ tickets: [Int], _ k: Int) -> Int {\n var result = 0\n for i in 0 ..< k {\n result += min(tickets[i], tickets[k])\n }\n result += tickets[k]\n for i in k + 1 ..< tickets.count {\n result += min(tickets[i], tickets[k] - 1)\n }\n return result\n }\n}\n``` | 2 | 0 | ['Array', 'Queue', 'Swift', 'Simulation'] | 1 |
time-needed-to-buy-tickets | c++ || optimal approach || O(n) | c-optimal-approach-on-by-ankitsingh07s-z6sa | image.png\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Comp | ankitsingh07s | NORMAL | 2024-04-09T06:48:21.530165+00:00 | 2024-04-09T06:48:21.530199+00:00 | 1 | false | image.png\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int timeRequiredToBuy(vector<int>& tickets, int k) {\n int ans=0;\n\n for(int i=0 ; i<tickets.size() ; i++){\n if(i<=k){\n ans += min(tickets[i] , tickets[k]);\n }\n else{\n ans += min(tickets[i] , tickets[k] - 1);\n }\n } \n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
time-needed-to-buy-tickets | ✅100% || Easy Solution🔥With explanation🔥||Beginner Friendly | 100-easy-solutionwith-explanationbeginne-9sle | Intuition\nTo solve this problem, we need to calculate the time required to buy tickets given a specific index \'k\'. The idea is to iterate through the tickets | ranjan_rr | NORMAL | 2024-04-09T06:41:26.670920+00:00 | 2024-04-09T06:41:26.670943+00:00 | 25 | false | # Intuition\n**To solve this problem, we need to calculate the time required to buy tickets given a specific index \'**k**\'. The idea is to iterate through the tickets array and sum up the values, then calculate the number of elements bigger than the **k-th** element that occur after it, as these elements will not decrease in the last round. Subtracting this count from the total sum gives us the final answer.**\n\n# Approach\n1.Initialize variables \'**sum\'** to store the sum of all elements in the tickets array and \'**bigger\'** to count the number of elements bigger than the k-th element that occur after it.\n2.Iterate through the tickets array and update \'sum\' and \'**bigger\'** accordingly.\n3.Calculate the time required to buy tickets by summing up the minimum of temp and \'**tickets[i]**\' for each element in the array.\n4.Subtract the count of \'**bigger**\' from the calculated answer to get the final result.\nReturn the final answer.\n\n# Complexity\n#### - Time complexity:\n**O(n)**, where n is the size of the tickets array. We iterate through the array once to calculate the sum and count the number of elements bigger than the k-th element.\n\n#### - Space complexity:\n**O(1)**, as we use only a constant amount of extra space for storing variables.\n\n# Code\n```\nclass Solution {\npublic:\n int timeRequiredToBuy(vector<int>& tickets, int k) {\n int sum = 0,bigger = 0;//bigger: Number of bigger elements than kth element which are coming after it.\n //the bigger elements after kth element will not get decreament in the last round as the kth element becomes 0.\n for(int i = 0;i < tickets.size();i++)\n {\n sum += tickets[i];\n\n if(i > k && (tickets[i] >= tickets[k]))\n {\n bigger++;\n }\n }\n \n int temp = tickets[k],ans = 0;\n\n for(int i = 0;i < tickets.size();i++)\n {\n ans += min(temp,tickets[i]);//whichever is small will be added\n }\n \n return (ans - bigger);//decreament number of bigger elements from the ans\n \n }\n};\n``` | 2 | 0 | ['Array', 'Greedy', 'Counting', 'C++'] | 0 |
new-21-game | One Pass DP O(N) | one-pass-dp-on-by-lee215-jtiq | Intuition:\nThe same problems as "Climbing Stairs" or "Fibo Sequence".\n\n## Explanation:\ndp[i] is the probability that we get points i at some moment.\nIn ano | lee215 | NORMAL | 2018-05-20T03:25:37.797325+00:00 | 2019-10-22T17:06:57.725045+00:00 | 47,263 | false | ## **Intuition**:\nThe same problems as "Climbing Stairs" or "Fibo Sequence".\n\n## **Explanation**:\n`dp[i]` is the probability that we get points `i` at some moment.\nIn another word:\n`1 - dp[i]`is the probability that we skip the points `i`.\n\nThe do equation is that:\n`dp[i] = sum(last W dp values) / W`\n\nTo get `Wsum = sum(last W dp values)`,\nwe can maintain a sliding window with size at most `W`.\n<br>\n\n## **Time Complexity**:\nTime `O(N)`\nSpace `O(N)`, can be improve to `O(W)`\n<br>\n\n**C++:**\n```cpp\n double new21Game(int N, int K, int W) {\n if (K == 0 || N >= K + W) return 1.0;\n vector<double> dp(N + 1);\n dp[0] = 1.0;\n double Wsum = 1.0, res = 0.0;\n for (int i = 1; i <= N; ++i) {\n dp[i] = Wsum / W;\n if (i < K) Wsum += dp[i]; else res += dp[i];\n if (i - W >= 0) Wsum -= dp[i - W];\n }\n return res;\n }\n```\n\n**Java:**\n```java\n public double new21Game(int N, int K, int W) {\n if (K == 0 || N >= K + W) return 1;\n double dp[] = new double[N + 1], Wsum = 1, res = 0;\n dp[0] = 1;\n for (int i = 1; i <= N; ++i) {\n dp[i] = Wsum / W;\n if (i < K) Wsum += dp[i]; else res += dp[i];\n if (i - W >= 0) Wsum -= dp[i - W];\n }\n return res;\n }\n```\n**Python:**\n```py\n def new21Game(self, N, K, W):\n if K == 0 or N >= K + W: return 1\n dp = [1.0] + [0.0] * N\n Wsum = 1.0\n for i in range(1, N + 1):\n dp[i] = Wsum / W\n if i < K: Wsum += dp[i]\n if i - W >= 0: Wsum -= dp[i - W]\n return sum(dp[K:])\n``` | 428 | 27 | [] | 55 |
new-21-game | Logical Thinking | logical-thinking-by-gracemeng-1shr | Game rule is as follows\n\npoint 0 initially\nwhile (point < K) {\n draw w from [1, W] randomly \n point += w\n}\nprobability(point <= N) ?\n\n> Let\'s o | gracemeng | NORMAL | 2019-01-29T17:26:54.484807+00:00 | 2019-01-29T17:26:54.484867+00:00 | 15,217 | false | >**Game rule** is as follows\n```\npoint 0 initially\nwhile (point < K) {\n draw w from [1, W] randomly \n point += w\n}\nprobability(point <= N) ?\n```\n> **Let\'s observe that**\n```\npoint total range [0, K + W - 1]\n```\n> we define `probability[i]` as probability to get i points\nsince all start with point 0 => `probability[0] = 1`\n\n>**Probability transition:**\n```\nBefore we reach point `i`, we draw `w`, i.e., our last point is `i - w` \n\nprobability to get i points = sum(probability to get i - w points * 1 / W) for w can be any of [1, W]\nwhere 0 <= i - w < K\n```\n\n> target probability = sum of prabability to get points [K, N]\n\n> **Note**\n> \n> If K = 10, W = 10\n>draw 1, then 9, probability is P(1) * P(9) = 0.1 * 0.1 = 0.01\n>draw 10, probability is P(10) = 0.1.\n>\n> (1, 9) and (10) can\'t be simply regarded as combination candidates for they don\'t share the same probability.\n\n****\n```\n public double new21Game(int N, int K, int W) {\n // Corner cases.\n if (K == 0) return 1;\n \n int maxPoint = K + W - 1;\n // probability[i] is probability of getting point i.\n double[] probability = new double[maxPoint + 1];\n \n probability[0] = 1;\n for (int i = 1; i <= maxPoint; i++) {\n for (int w = 1; w <= W; w++) {\n if (i - w >= 0 && i - w < K)\n probability[i] += probability[i - w] * 1 / W;\n }\n }\n \n double targetProbability = 0; // Probability of N or less points.\n for (int i = K; i <= N; i++) {\n targetProbability += probability[i];\n }\n \n return targetProbability;\n }\n```\n**(\u4EBA \u2022\u0348\u1D17\u2022\u0348)** Thanks for voting! | 229 | 9 | [] | 19 |
new-21-game | My take on how to reach at Solution | my-take-on-how-to-reach-at-solution-by-c-erld | Firstly, observe that when Alice is done playing, her points can be in range [K, K+W-1]. She can\'t get past K+W because she stops playing when she is at K or m | cooldown | NORMAL | 2018-05-20T17:18:23.380778+00:00 | 2018-10-22T22:43:01.039861+00:00 | 11,495 | false | Firstly, observe that when Alice is done playing, her points can be in range [K, K+W-1]. She can\'t get past K+W because she stops playing when she is at K or more.\n\nNow, we will see how to find the probabilities to stay in the positions in the above range and store them in p[] array.\n\nWe need to know the probabilities of all elems in range [0,K] first. From there we can calculate for elems in range (K, K+W-1]\n\nFor positions x <= K,\np[x] = (p[x-1] + p[x-2] + ..... + p[x-W]) * (1/W); (Probabilities of previous possible positions to get to x, multiplied by probability of choosing an elem to get to x)\n\nFor implementation, we can keep track past values using a single variable. For each new positions, we will subtract p[x-W-1] and add p[x-1]. Look at implementation below\n\nFor positions x > K,\np[x] = (p[K-1] + p[K-2] + .... + p[x - W]) * 1/W; (Since, we can\'t/shouldn\'t reach x from >= K positions)\n\n\'\'\'\npublic double new21Game(int N, int K, int W) {\n \n if(N >= K+W-1) return 1.0; // all possibilities of positions after alice stops playing are from [K, K+W-1]\n \n double p[] = new double[K+W];\n double prob = 1/(W+0.0); // single elem probability\n \n double prev = 0;\n \n p[0] = 1; // Since we start from 0, initialize it to 1\n \n\t //Until K\n for(int i = 1; i <= K; i++) {\n prev = prev - (i-W-1 >= 0 ? p[i - W -1] : 0) + p[i-1];\n p[i] = prev*prob;\n }\n \n double req = p[K];\n \n\t // From K+1, we don\'t add the p[i-1] term here as it is >= K\n for(int i = K+1; i <= N; i++) {\n prev = prev - (i-W-1 >= 0 ? p[i - W -1] : 0);\n p[i] = prev * prob;\n req += p[i];\n //System.out.println(p[i]);\n }\n \n return req;\n }\n\'\'\'\n\nPlease comment below, if you didn\'t understand something. I will try to clarify.\n | 164 | 3 | [] | 15 |
new-21-game | Java O(K + W) DP solution with explanation | java-ok-w-dp-solution-with-explanation-b-ptgc | Firstly I came up with a basic DP solution which cost O((K + W) * W) time and it runs TLE:\n\n\nclass Solution {\n public double new21Game(int N, int K, int | wangzi6147 | NORMAL | 2018-05-20T03:49:36.088634+00:00 | 2018-10-17T05:12:27.747424+00:00 | 12,681 | false | Firstly I came up with a basic DP solution which cost `O((K + W) * W)` time and it runs TLE:\n\n```\nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (K == 0) {\n return 1;\n }\n int max = K + W - 1;\n double[] dp = new double[max + 1];\n dp[0] = 1;\n for (int i = 1; i <= max; i++) {\n for (int j = 1; j <= W; j++) {\n if (i - j >= 0 && i - j < K) {\n dp[i] += dp[i - j] / W;\n }\n }\n }\n double result = 0;\n for (int i = K; i <= N; i++) {\n result += dp[i];\n }\n return result;\n }\n}\n```\n\nThen I realize that the transition equation `dp[i] = (dp[i - W] + dp[i - W + 1] + ... + dp[i - 1]) / W` could be simplified to `dp[i] = (sum[i - 1] - sum[i - W - 1]) / W`.\n\nFurthermore, if we use `dp[i]` to directly represent the `sum[i]`, we can get `dp[i] = dp[i - 1] + (dp[i - 1] - dp[i - W - 1]) / W`. This equation takes us to the final `O(K + W)` solution. Just take care with the beginning and the end of the array.\n\n```\nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (K == 0) {\n return 1;\n }\n int max = K + W - 1;\n double[] dp = new double[max + 1];\n dp[0] = 1;\n for (int i = 1; i <= max; i++) {\n dp[i] = dp[i - 1];\n if (i <= W) {\n dp[i] += dp[i - 1] / W;\n } else {\n dp[i] += (dp[i - 1] - dp[i - W - 1]) / W;\n }\n if (i > K) {\n dp[i] -= (dp[i - 1] - dp[K - 1]) / W;\n }\n }\n return dp[N] - dp[K - 1];\n }\n}\n```\n | 114 | 1 | [] | 22 |
new-21-game | Python 3 - Memorize DFS from O(KW+W) to O(K + W) | python-3-memorize-dfs-from-okww-to-ok-w-mutin | Intuiatively, we can generate the following equation:\n#### F(x) = (F(x+1) + F(x+2) + ... + F(x+W)) / W\nWhere F(x) is the prob that we will eventually have <= | vividlau | NORMAL | 2019-01-18T05:03:38.493188+00:00 | 2021-01-14T03:01:24.975728+00:00 | 4,184 | false | Intuiatively, we can generate the following equation:\n#### F(x) = (F(x+1) + F(x+2) + ... + F(x+W)) / W\nWhere F(x) is the prob that we will eventually have <= N points when we have x points.\nWe will stop picking when we have >= K points, so the exit of the recursion is `cur >= K`.\nThere are K+W states in total and for each state < K, we spend O(W) (the for loop) to generate the prob, therefore O(KW+W) in total.\n```\nclass Solution:\n def new21Game(self, N, K, W):\n """\n :type N: int\n :type K: int\n :type W: int\n :rtype: float\n """\n return self.dfs(N, K, W, 0, {})\n \n def dfs(self, N, K, W, cur, memo):\n \n if cur >= K:\n return 1.0 if cur <= N else 0\n \n if cur in memo:\n return memo[cur]\n \n prob = 0\n \n for i in range(1, W+1):\n prob += self.dfs(N, K, W, cur+i, memo)\n \n prob /= W\n \n memo[cur] = prob\n \n return prob\n```\n\nHowever, do we really need a for loop to get the prob?\nSince \n#### F(x) = (F(x+1) + F(x+2) + ... + F(x+W)) / W\n#### F(x+1) = (F(x+2) + F(x+3) + ... + F(x+1+W)) / W\nAfter a substraction, we have \n#### F(x) = F(x+1) - 1/W * (F(x+1+W) - F(x+1))\nIn this case, we get our prob at **points = x** by a simple substraction which is O(1).\nHere we still have K + W states so the time complexity should be O(K+W).\n\n\n### But Wait...\nWhy does the exit or the base case of the recursion change..?\nThat\'s because the expression \n#### F(x) = F(x+1) - 1/W * (F(x+1+W) - F(x+1))\nrelies on the fact that for every F(x), we have:\n#### F(x) = (F(x+1) + F(x+2) + ... + F(x+W)) / W\nBut that is not true. \n#### In fact, when x = K, F(x) = either 1 or 0, but not (F(x+1) + ... + F(x+W)) / W\nSince the rule does not apply for F(K), we can not use the formula to calculate F(K-1)....\nAnd that is why we modify the base case here.\nAt x = K-1, only one more pick left, therefore we have two cases:\n\n1. N-(K-1) >= W, which means we pick all 1 to W safely.\n2. N-(K-1) < W, means that some of the numbers will make our points > N. Then we can only pick N-(K-1) from 1 to W.\n\nThe prob is therefore ```min(N-K+1, W) / W```\n```\nclass Solution:\n def new21Game(self, N, K, W):\n """\n :type N: int\n :type K: int\n :type W: int\n :rtype: float\n """\n return self.dfs(N, K, W, 0, {})\n \n def dfs(self, N, K, W, cur, memo):\n \n if cur == K-1:\n return min(N-K+1, W) / W\n if cur > N:\n return 0\n elif cur >= K:\n return 1.0\n \n if cur in memo:\n return memo[cur]\n \n prob = self.dfs(N, K, W, cur+1, memo) - (self.dfs(N, K, W, cur+1+W, memo) - self.dfs(N, K, W, cur+1, memo)) / W\n \n memo[cur] = prob\n \n return prob\n``` | 68 | 3 | [] | 9 |
new-21-game | Image Explanation🏆- [Complete Intuition - Maths, Probability, DP, Sliding Window] - C++/Java/Python | image-explanation-complete-intuition-mat-ts4n | Video Solution (Aryan Mittal) - Link in LeetCode Profile\nNew 21 Game by Aryan Mittal\n\n\n\n# Approach & Intution\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n# Code | aryan_0077 | NORMAL | 2023-05-25T04:12:39.306700+00:00 | 2023-05-25T04:24:27.428828+00:00 | 16,632 | false | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`New 21 Game` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n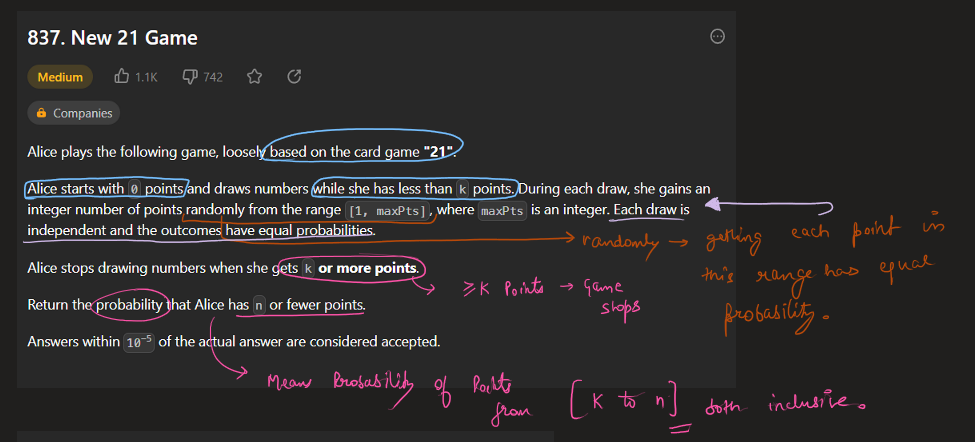\n\n\n\n\n\n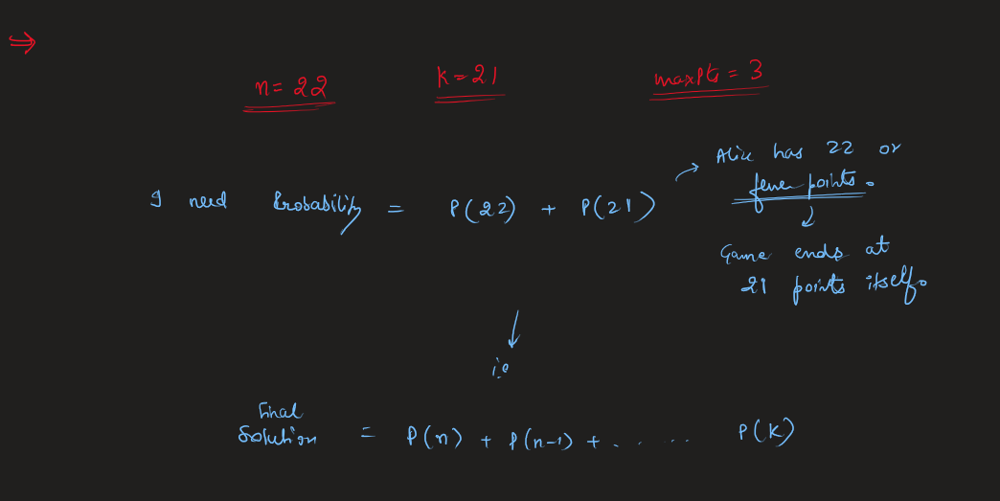\n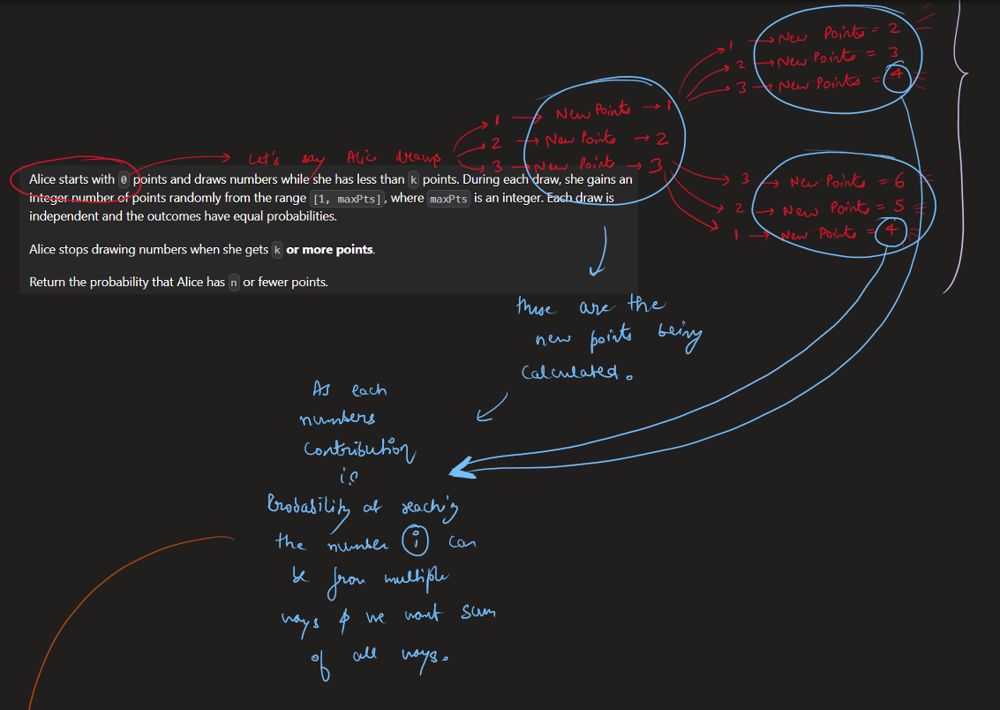\n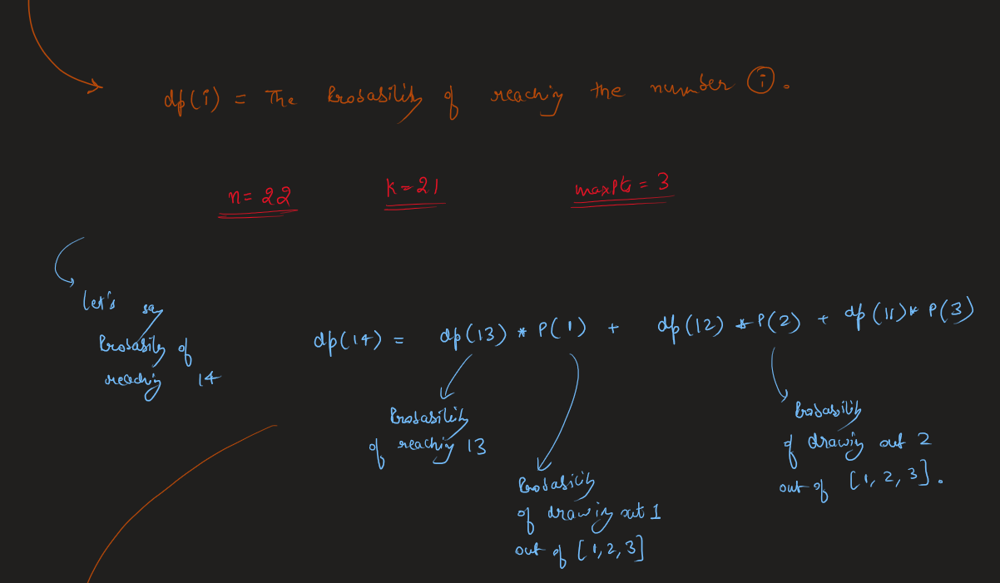\n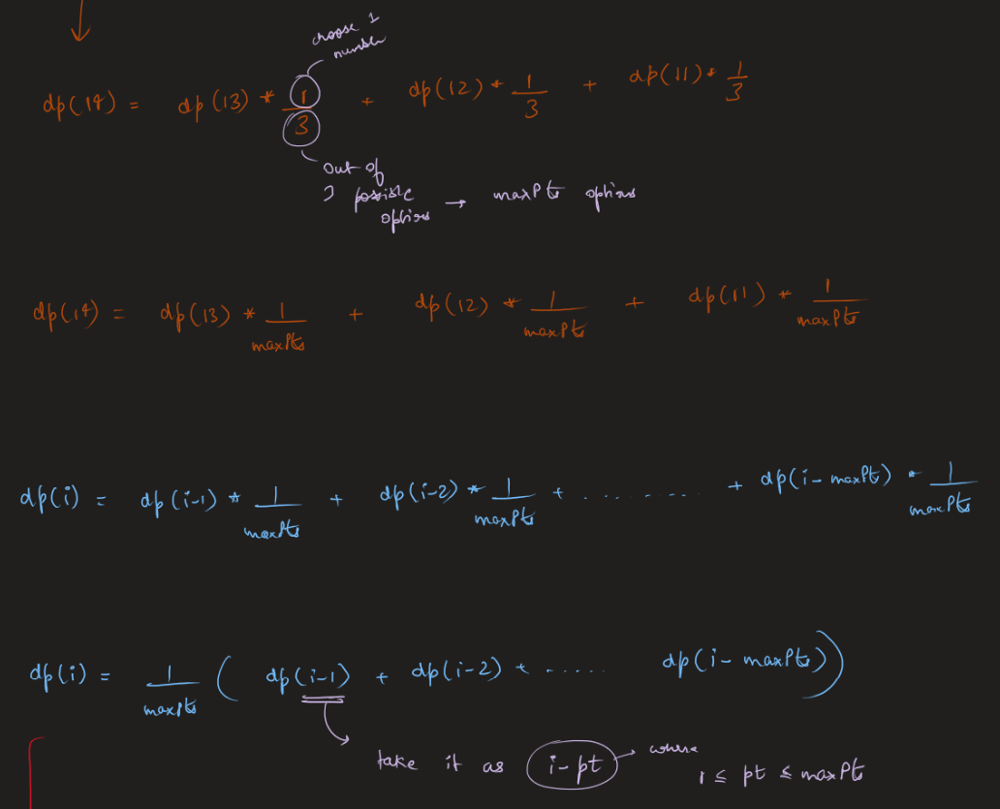\n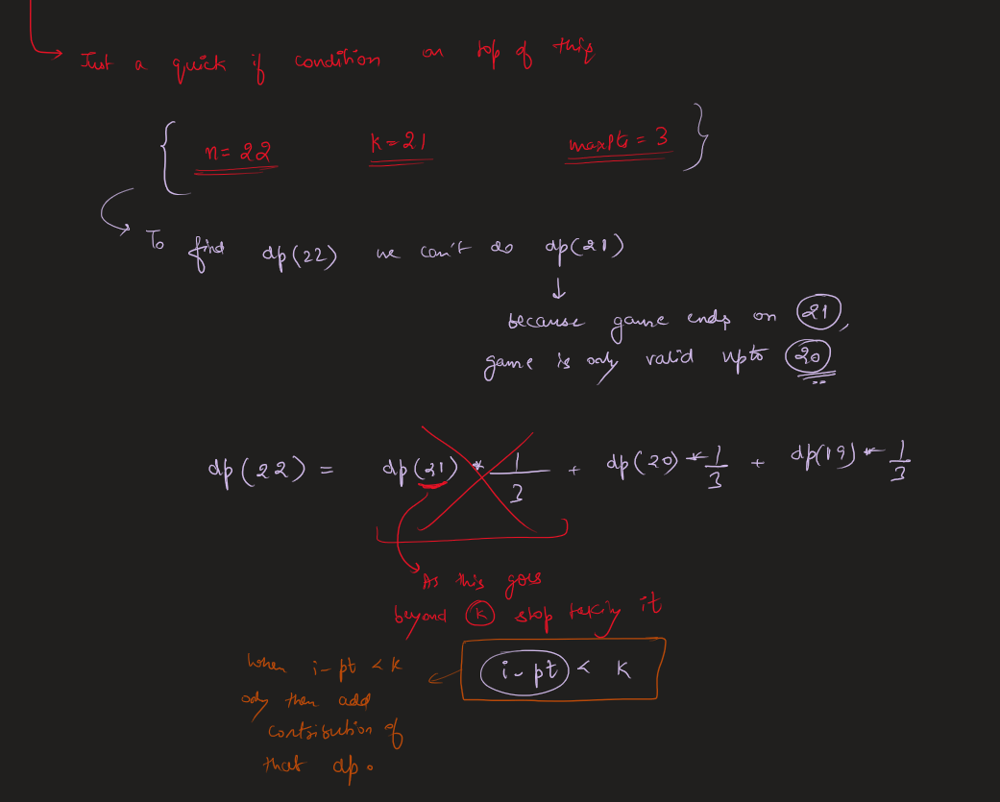\n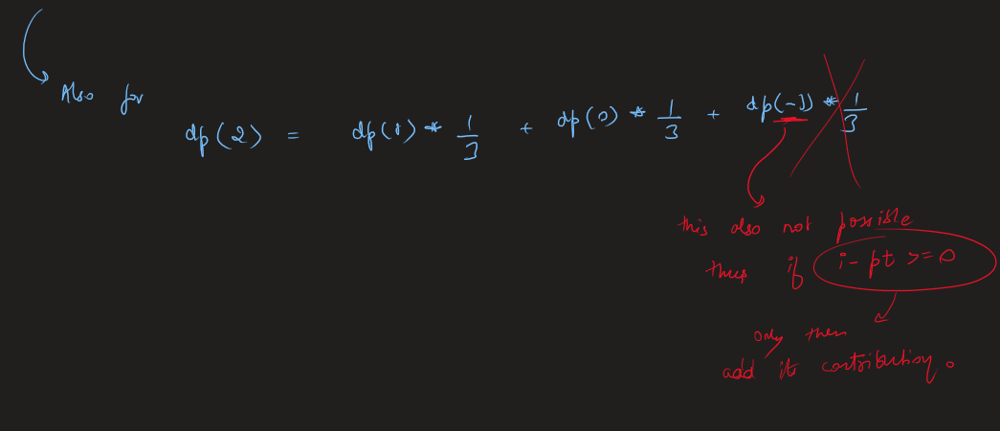\n\n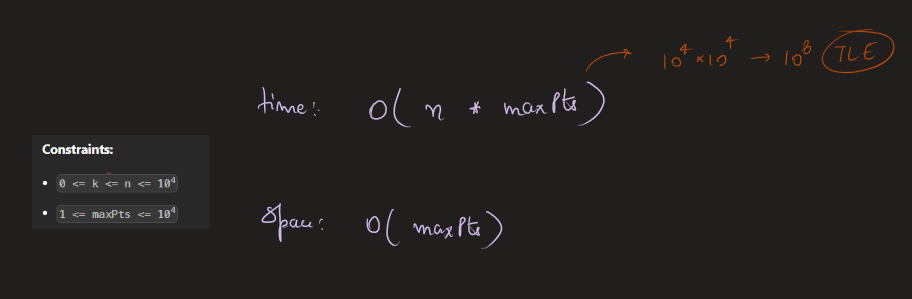\n\n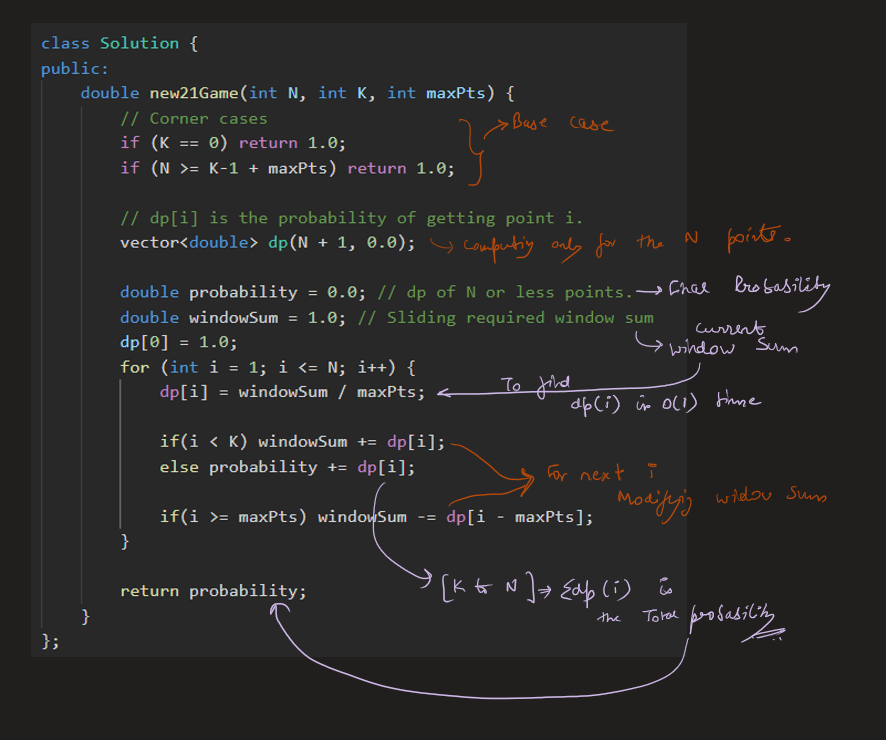\n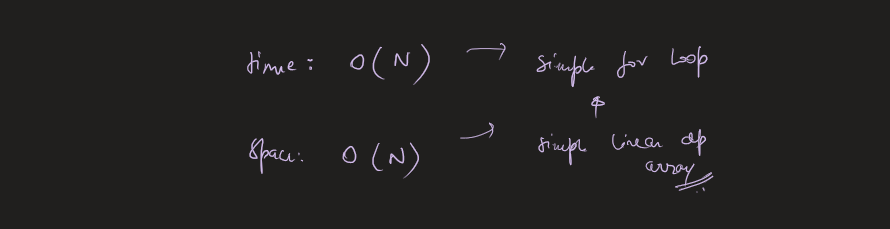\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n double new21Game(int N, int K, int maxPts) {\n // Corner cases\n if (K == 0) return 1.0;\n if (N >= K-1 + maxPts) return 1.0;\n\n // dp[i] is the probability of getting point i.\n vector<double> dp(N + 1, 0.0);\n\n double probability = 0.0; // dp of N or less points.\n double windowSum = 1.0; // Sliding required window sum\n dp[0] = 1.0;\n for (int i = 1; i <= N; i++) {\n dp[i] = windowSum / maxPts;\n\n if(i < K) windowSum += dp[i];\n else probability += dp[i];\n \n if(i >= maxPts) windowSum -= dp[i - maxPts];\n }\n\n return probability;\n }\n};\n```\n```Java []\nclass Solution {\n public double new21Game(int N, int K, int maxPts) {\n // Corner cases\n if (K == 0) return 1.0;\n if (N >= K - 1 + maxPts) return 1.0;\n\n // dp[i] is the probability of getting point i.\n double[] dp = new double[N + 1];\n Arrays.fill(dp, 0.0);\n\n double probability = 0.0; // dp of N or less points.\n double windowSum = 1.0; // Sliding required window sum\n dp[0] = 1.0;\n for (int i = 1; i <= N; i++) {\n dp[i] = windowSum / maxPts;\n\n if (i < K) windowSum += dp[i];\n else probability += dp[i];\n\n if (i >= maxPts) windowSum -= dp[i - maxPts];\n }\n\n return probability;\n }\n}\n```\n```Python []\nclass Solution:\n def new21Game(self, N, K, maxPts):\n # Corner cases\n if K == 0:\n return 1.0\n if N >= K - 1 + maxPts:\n return 1.0\n\n # dp[i] is the probability of getting point i.\n dp = [0.0] * (N + 1)\n\n probability = 0.0 # dp of N or less points.\n windowSum = 1.0 # Sliding required window sum\n dp[0] = 1.0\n for i in range(1, N + 1):\n dp[i] = windowSum / maxPts\n\n if i < K:\n windowSum += dp[i]\n else:\n probability += dp[i]\n\n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n\n return probability\n``` | 62 | 1 | ['Math', 'Dynamic Programming', 'C++', 'Java', 'Python3'] | 6 |
new-21-game | Python DP, iterate on points rather than draw count. Should be a "hard" problem | python-dp-iterate-on-points-rather-than-bi5sk | dp(n) means the probability getting point "n" at any count of draws. \ne.g. when random number is 1~3, we have:\ndp(n)=dp(n-3)\(1/3)+dp(n-2)\(1/3)+dp(n-1)\*(1/3 | yuanzhi247012 | NORMAL | 2019-11-26T05:28:31.755083+00:00 | 2019-11-26T05:31:36.932245+00:00 | 2,488 | false | dp(n) means the probability getting point "n" at any count of draws. \ne.g. when random number is 1~3, we have:\ndp(n)=dp(n-3)\\*(1/3)+dp(n-2)\\*(1/3)+dp(n-1)\\*(1/3)\nAnd this kind of sum can be optimized using sliding window sum.\n\nWe cannot iterate DP on draw count, because it is hard to decide when to stop iterating. Instead we iterate on the obtained point, because each point can be obtained by the dp value of previous points. \n\nThis problem should be "hard" rather than "medium".\n\n```\n def new21Game(self, N: int, K: int, W: int) -> float:\n if K==0 or K-1+W<=N:\n return 1\n dp=[1]+[0]*N\n cursum=1\n for i in range(1,N+1):\n # dp[i]=sum(dp[max(0,i-W):min(i,K)])*(1/W)\n dp[i]=cursum*(1/W)\n if i<K:\n cursum+=dp[i]\n if i>=W:\n cursum-=dp[i-W]\n return sum(dp[K:])\n``` | 48 | 0 | [] | 3 |
new-21-game | Intuition on why counting is incorrect | intuition-on-why-counting-is-incorrect-b-d3vq | When we are counting the number of ways of reaching score >= K and dividing it by the number of ways when score >=K and score <N , we are assuming that the prob | hindustani_bhau | NORMAL | 2020-09-14T18:22:20.710140+00:00 | 2020-09-14T18:22:20.710205+00:00 | 1,682 | false | When we are counting the number of ways of reaching ```score >= K ``` and dividing it by the number of ways when ```score >=K and score <N``` , we are assuming that the probability of reaching each of those scores by different paths is the same.\n\nLet\'s say ```W = 10```\nFor example, to reach score 3, we can have multiple paths:\n1, 1, 1\n1, 2\n2, 1\n3\n\nP(1, 1, 1) = 0.1 * 0.1 * 0.1\nP(1, 2) = 0.1 * 0.1\nP(2, 1) = 0.1 * 0.1\nP(3) = 0.1\n\nSo, the probabilities are all different. When we are counting the number of ways of reaching 3, we are ignoring the fact that the probability of reaching it is different by different paths.\n\nHope this gives a slight bit of intuition. | 44 | 0 | [] | 4 |
new-21-game | Can someone explain why counting number of ways to get to X approach doesn't give correct answer?? | can-someone-explain-why-counting-number-m3yst | I understand it\'s not efficient and sufferes from extreme complexity. BUT I was wondering if someone can tell me why I don\'t get the correct answer for Exampl | edaengineer | NORMAL | 2018-05-20T05:38:51.527002+00:00 | 2018-05-20T05:38:51.527002+00:00 | 2,380 | false | I understand it\'s not efficient and sufferes from extreme complexity. **BUT I was wondering if someone can tell me why I don\'t get the correct answer for Example-3 using this approach???**\n\nYour answer 0.55218, Expected Output: 0.73278\n\nways[X] shows the number of ways to get to X points\ntotal: total number of ways to get to >= K points\n\nSo the answer should be Sum of (1) and (2):\n\n1) Probability of getting X points (ways[X]/total) * (ways to go from X to between K and N, which is equal to (N-K+1))\nAdd these for X from N-W to K-1.\n\n2) Probability of getting X points (ways[X]/total) * (Ways to go between K and less than N)\nAdd these for X from K-W to N-W-1.\n\n\n\n\n```\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n // N=21; K=17; W=10;\n ways.assign(N+W, 0);\n if (N-K >= W-1) return 1;\n total = 0;\n \n countWays(0, K, W);\n double res=0.0, tmp=0.0;\n for (int i=K-1; i>= K-W+1 && i >=0 && i >= N-W; i--) {\n tmp += ((1.0*ways[i])/total) * ((double)N-K+1);\n }\n for (int i=N-W-1; i>= K-W && i >=0; i--) {\n tmp += ((1.0*ways[i])/total) * ((double)i+W-K+1);\n }\n return tmp;\n }\n \n void countWays(int cur, int K, int W) {\n ways[cur]++;\n if (cur >= K) {\n total++;\n return;\n }\n for (int i=1; i<=W; i++) {\n countWays(cur+i, K, W);\n }\n }\n vector<int> ways;\n int total;\n};\n\n``` | 26 | 0 | [] | 8 |
new-21-game | A setp by setp explanation | a-setp-by-setp-explanation-by-zhjy23212-alyo | This question takes me a while to understand what this means.\n\nAfter struggled for a while, I would like to post how I understand if you are confused about wh | zhjy23212 | NORMAL | 2019-09-10T05:15:11.996883+00:00 | 2019-09-10T05:15:44.795110+00:00 | 2,943 | false | This question takes me a while to understand what this means.\n\nAfter struggled for a while, I would like to post how I understand if you are confused about what happened even after reading some of the solutions posted here.\n\nTake one example first: \n\nN = 12, W = 10, K = 10\n\nThe stop range for the game is [10, 10 + 10 -1] which is [K, K + W -1]\n\ndp[i] means if the target K is set to this one what is the possiblty to be <=N\n\nFor i <= W\ndp[0] = 1.0 for sure\n\ndp[1] = 1.0 / W because one of W chance we get 1\n\ndp[2] = dp[1] / W + 1 / W we have 2 ways to get 2 here, 1 + 1 and 0 + 2\n\ndp[3] = dp[2] / W + 1 / W\n\nand so on, we can see this is a GP until i reach W, so dp[i] = (dp[i-1] + 1.0) / 2\n\nTo reach value i which is bigger than W, you must start from some previous value i in range [i - w, i - 1], so the possibilty smaller than that is not possible\n\nFor example i = 11, previous value range is [1, 10], but there is no such part of 1/W because no value of single draw can be > W, so we don\'t do the addition here. Instead, we need to reduce the change of value 1 after move to next value\n\ndp[11] = dp[1] + dp[2] ... + dp[10]\n\ndp[12] = dp[2] + d[3] ... + dp[10]\n\nEverytime we move to the next, get rid of the leftmost value.\n\nThe function stops at reach N.\n\nHere we use a Wsum to carry the sum to the next dp everytime.\n\nAnd the values end in range\n[10, min(10 + 10 -1, N)] will be the result\n\nHope this helps.\n\n```\nclass Solution:\n """\n @param N: int\n @param K: int\n @param W: int\n @return: the probability\n """\n def new21Game(self, N, K, W):\n # Write your code here.\n if K == 0 or N >= K + W: \n return 1.0\n dp = [1.0] + [0.0] * N\n Wsum = 1.0\n for i in range(1, N + 1):\n dp[i] = Wsum / W\n if i < K: \n Wsum += dp[i]\n if i - W >= 0: \n Wsum -= dp[i - W]\n return sum(dp[K:])\n```\n | 20 | 0 | ['Dynamic Programming', 'Python3'] | 4 |
new-21-game | Python🔥Java🔥C++🔥Simple Solution🔥Easy to Understand | pythonjavacsimple-solutioneasy-to-unders-njrd | !! BIG ANNOUNCEMENT !!\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies relat | techwired8 | NORMAL | 2023-05-25T01:23:25.122407+00:00 | 2023-05-25T01:26:48.894278+00:00 | 9,182 | false | **!! BIG ANNOUNCEMENT !!**\nI am currently Giving away my premium content well-structured assignments and study materials to clear interviews at top companies related to computer science and data science to my current Subscribers. This is only for first 10,000 Subscribers. **DON\'T FORGET** to Subscribe\n\n# Search \uD83D\uDC49 `Tech Wired Leetcode` to Subscribe\n\n# or\n\n\n# Click the Link in my Profile\n# Approach:\n\n- If the minimum target points K is 0 or the maximum total points N is greater than or equal to K + W, it is guaranteed to win, so return 1.0.\n- Create a dp array of size N + 1 to store the probabilities. \n- Initialize all elements to 0.0, except dp[0] which is set to 1.0.\n- Initialize windowSum to 1.0 to keep track of the sum of the previous maxPts probabilities.\n- Initialize probability to 0.0 to store the final probability of winning.\n- Iterate from 1 to N and calculate the probabilities using dynamic programming:\n- Update dp[i] as windowSum / maxPts.\n- If i is less than K, add dp[i] to windowSum.\n- If i is greater than or equal to K, add dp[i] to probability.\n- If i - maxPts is greater than or equal to 0, subtract dp[i - maxPts] from windowSum.\n- Return probability as the result.\n# Intuition:\n\n- We can think of the game as a series of draws, where at each draw we can draw any number from 1 to maxPts with equal probability.\n- To calculate the probability of winning, we use dynamic programming to keep track of the probabilities for each point.\n- Starting from point 0, we calculate the probabilities for each subsequent point up to N.\n- At each point i, the probability of reaching that point is the sum of probabilities from the previous maxPts points divided by maxPts.\n- If the current point i is less than K, we add the probability to the windowSum to keep track of the sum of previous probabilities.\n- If the current point i is greater than or equal to K, we add the probability to the probability variable, which represents the final probability of winning.\n- We maintain a sliding window of size maxPts to efficiently calculate the probabilities, removing the probability of the point that falls outside the window and adding the probability of the current point.\n- Finally, we return the probability as the result, which represents the probability of winning the game.\n\n```Python []\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k == 0 or n >= k + maxPts:\n return 1.0\n \n windowSum = 1.0\n probability = 0.0\n \n dp = [0.0] * (n + 1)\n dp[0] = 1.0\n \n for i in range(1, n + 1):\n dp[i] = windowSum / maxPts\n \n if i < k:\n windowSum += dp[i]\n else:\n probability += dp[i]\n \n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n \n return probability\n```\n```Java []\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n \n double windowSum = 1.0;\n double probability = 0.0;\n \n double[] dp = new double[n + 1];\n dp[0] = 1.0;\n \n for (int i = 1; i <= n; i++) {\n dp[i] = windowSum / maxPts;\n \n if (i < k) {\n windowSum += dp[i];\n } else {\n probability += dp[i];\n }\n \n if (i >= maxPts) {\n windowSum -= dp[i - maxPts];\n }\n }\n \n return probability;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n \n double windowSum = 1.0;\n double probability = 0.0;\n \n vector<double> dp(n + 1, 0.0);\n dp[0] = 1.0;\n \n for (int i = 1; i <= n; i++) {\n dp[i] = windowSum / maxPts;\n \n if (i < k) {\n windowSum += dp[i];\n } else {\n probability += dp[i];\n }\n \n if (i >= maxPts) {\n windowSum -= dp[i - maxPts];\n }\n }\n \n return probability;\n }\n};\n\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D | 17 | 2 | ['Dynamic Programming', 'C++', 'Java', 'Python3'] | 2 |
new-21-game | 🏆C++ || DP + Sliding Window | c-dp-sliding-window-by-chiikuu-i98f | Code\n\nclass Solution {\npublic:\n double new21Game(int n, int k, int mp) {\n if(k==0 || n>k+mp)return 1;\n vector<double>dp(n+1,0.0);\n | CHIIKUU | NORMAL | 2023-05-25T08:04:52.420513+00:00 | 2023-05-25T08:04:52.420544+00:00 | 1,526 | false | # Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int mp) {\n if(k==0 || n>k+mp)return 1;\n vector<double>dp(n+1,0.0);\n dp[0]=1;\n double ans=0.0;\n double ps=1;\n for(int i=1;i<=n;i++){\n dp[i] = ps/mp;\n if(i<k)ps += dp[i];\n else ans += ps/mp;\n if(i-mp>=0)ps -= dp[i-mp];\n }\n return ans;\n }\n};\n```\n\n | 13 | 1 | ['C++'] | 0 |
new-21-game | C++ || Bottom Up DP || O(N) || Beats 100% | c-bottom-up-dp-on-beats-100-by-mukuldev0-4v7q | If points are curr then probability at this stage depends on curr+1,curr+2,....., curr+maxPts.\nProbability for curr will then be the sum of all these elements | MukulDev007 | NORMAL | 2023-05-25T07:58:20.414790+00:00 | 2023-05-25T07:58:20.414839+00:00 | 904 | false | If points are curr then probability at this stage depends on curr+1,curr+2,....., curr+maxPts.\nProbability for curr will then be the sum of all these elements divided my maxPts.\nThe base case will be when points are greater or equal to k, where if points are less than or equal to n then probability at this stage would be 1.\n\nI started with top down DP.\n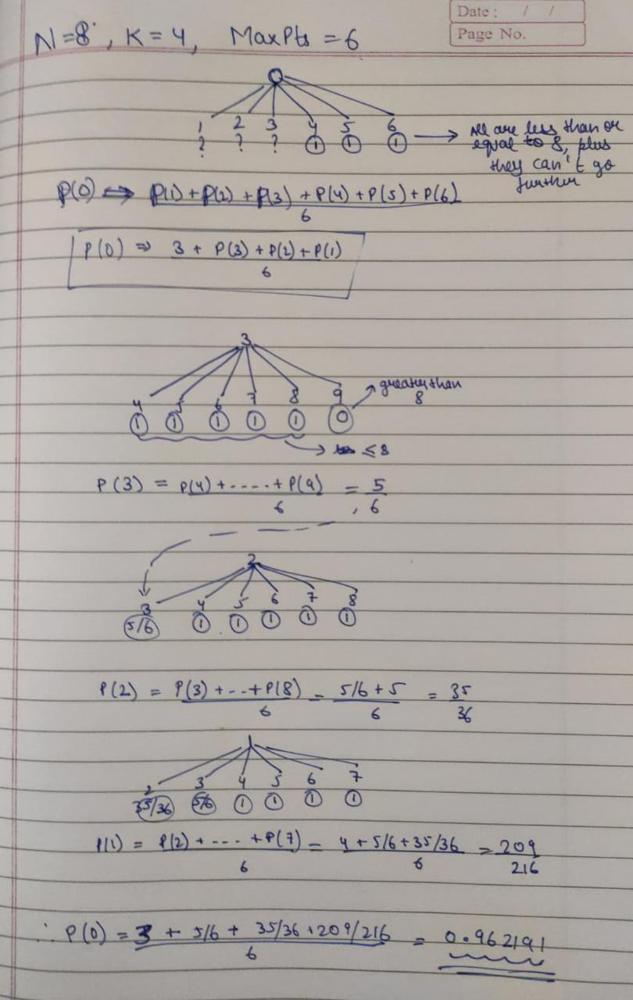\n(I know the first tree that i should have explored should be 1 then 2 then 3 but it was too long to represent)\n# Code (TopDown - Gives TLE )\n```\nclass Solution {\npublic:\n double game(int curr,int k,int n,int maxPts,vector<double>&dp){\n if(curr>=k) return curr<=n;\n if(dp[curr]!=-1) return dp[curr];\n double sum = 0;\n for(int i=1;i<=maxPts;i++){\n sum+=game(curr+i,k,n,maxPts,dp);\n }\n return dp[curr] = sum/maxPts;\n \n }\n double new21Game(int n, int k, int maxPts) {\n vector<double> dp(n,-1.0);\n return game(0,k,n,maxPts,dp);\n }\n};\n```\nThis can be easily converted to Bottom Up. i\'th element depends on the sum of i+1,i+2,...,i+maxPts divided by maxPts. Base case would be similar to TopDown. But it will still give TLE.\nI think the reason is that the summing part takes linear time. If there was some way to make it somehow constant. Then i saw the tag "Sliding window".\nIf we know the sum of a window, we can get sum of next window by subtracting the last element of window and add the new element to it. Time to math.\n\n\nNow we just need to make the initial window and we can apply this relation.\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if(n==0 || k==0 ) return 1.0;\n vector<double> dp(k+maxPts+1,0);\n double sum = 0;\n //Dealing with base case when points greater than k\n for(int i=0;i<maxPts;i++){\n dp[k+i] = (k+i)<=n;\n //Calculating the initial window\n sum+=dp[k+i];\n }\n //Initial window value\n dp[k-1] = sum/maxPts;\n\n //Calculating other probabilities using the relation\n for(int i=k-2;i>=0;i--){\n dp[i] = dp[i+1] + ((dp[i+1] - dp[i+maxPts+1])/maxPts);\n }\n return dp[0];\n }\n};\n```\n\n\nDo upvote if this solution seemed helpful. | 13 | 0 | ['Math', 'Dynamic Programming', 'Memoization', 'Sliding Window', 'C++'] | 2 |
new-21-game | ✅ 0ms | ✨ O(N) O(maxPts) | 🏆 Most Efficient Solution | 👍 Simplest Code with Circular Buffer | 0ms-on-omaxpts-most-efficient-solution-s-pgtx | Intuition\n Describe your first thoughts on how to solve this problem. \n## Probability Analysis\nWhen Alice has x points and she tries next round, the probabil | hero080 | NORMAL | 2023-05-25T05:07:06.684784+00:00 | 2023-05-25T05:21:55.264092+00:00 | 3,260 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n## Probability Analysis\nWhen Alice has x points and she tries next round, the probability of getting y points that round is:\n\n$$P(x \\rightarrow y | x) = 1 / L$$ if $x < k$ and $y \\in [x + 1, x + L]$\nwhere $L$ is `maxPts` and $x \\rightarrow y$ means the event of getting x points first then immediately getting y points after.\n\nUsing the conditional probability formula we have:\n\n$$P(x \\rightarrow y) = P(x \\rightarrow y | x) * P(x)$$\n\nIf we think this backwards, then the probability of getting x points is:\n\n$$\nP(x) = \\sum_{i= 1}^L P((x - i) \\rightarrow x)\n = \\sum_{i= 1}^L P((x - i) \\rightarrow x | x - i) * P(x - i) \\\\\n = \\sum_{i=1}^L \\frac{1}{L} P(x - i)\n = \\frac{1}{L} \\sum_{i=1}^L P(x - i)\n$$\nThe above formula assumes $x \\le k$ and uses the convention $P(x) = 0$ for $x < 0$ to simply things.\n\nBecause Alice stops playing once she got $k$ or more points, we only need to modify the above recursive relation slightly:\n\n$$P(x) = \\frac{1}{L} \\sum_{i=x - k + 1}^L P(x - i)$$ for $x \\ge k$\n\n## Dynamic Programming and Sliding Window\nWe can easily calculate each $P(x)$ using simple **dynamic programming** and a **sliding window** tech.\n\nFor example, when $L = 4$:\n$$P(27) = \\frac{1}{4} (P(26) + P(25) + P(24) + P(23)) = S_{26}/4$$\nThen next we update our window sum $S$ by:\n$$S_{27} = S_{26} + P(27) - P(23) $$\nand so on.\n\nFor the case when $x \\ge k$ the sliding window shrinks only.\n\n## Special Cases\n\n### Stops at Zero\nWhen $k = 0$ there is no round at all and we simply return `1` since we are promised that $n \\ge k$.\n\n### Sliding Window too Small\nWhen $k - 1 + L <= n$, there is no way for Alice to get points more than $n$ directly from $x < k$. In this case we simply return `1` and no further calculation needed.\n\n### Sliding Window too Big\nWhen $1 + L >= n$\nIn this case the sliding window\'s "tail" is negative index. While the **Circular Buffer** optimization below handles negative index well and this special case will work just fine, we can nevertheless use a more efficient algorithm for this special case.\n\nSimplify the summation boundary of our previous formula:\n\n$$\nP(x) = \\frac{1}{L} \\sum_{i=0}^{x - 1} P(i) = \\frac{1}{L} S_{x-1}\n\\Rightarrow S_x = S_{x - 1} + P(x) = (1 + \\frac{1}{L}) S_{x - 1}\n$$\nwhere $1 \\le x \\le k$\n\nIf we define $\\alpha = (1 + \\frac{1}{L})$ we get a nice result for $S_x$:\n$$S_x = \\alpha^{x - 1}$$ for $x \\le k$\n\nand then:\n$$P(x) = \\frac{1}{L} S_{k-1} = \\frac{1}{L} \\alpha^{k-1}$$ for $x \\ge k$\n\nNotice that the probability we are looking for is the sum of these between $[k, n]$ and since they are *all the same*, we simply get:\n$$P = \\frac{1}{L} \\alpha^{k-1} (n - k + 1)$$\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe use a circular buffer to store the last $L + 1$ probability data.\nWe use a sliding window to keep updating the last one.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$\\Theta(N)$$ normally.\n$$\\Theta(1)$$ for the first two special cases.\n$$\\Theta(\\log k)$$ for the last case.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$\\Theta(L)$$ normally (in this case we have $L \\le N$).\n$$\\Theta(1)$$ for the first two special cases.\n$$\\Theta(1)$$ for the last case (in this case when $L > N$).\nwhere $L$ is the `maxPts`\n\n\n# Code\n```\n\ntemplate <typename T>\nclass CircularBuffer {\n public:\n explicit CircularBuffer(int min_size) : data_(1 << BitLen(min_size)), mask_(data_.size() - 1) {}\n\n static constexpr int BitLen(int min_size) {\n return 32 - __builtin_clz(min_size);\n }\n\n T& operator[](int index) {\n return data_[index & mask_];\n }\n\n const T& operator[](int index) const {\n return data_[index & mask_];\n }\n\n int Capacity() const {\n return data_.size();\n }\n\n int mask() const { return mask_; }\n\n private:\n std::vector<T> data_;\n const uint mask_;\n};\n\nclass Solution {\n public:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n - k + 1 >= maxPts) {\n return 1;\n }\n const double kFactor = 1.0 / maxPts;\n if (maxPts + 1 >= n) {\n return std::pow(1 + kFactor, k - 1) / maxPts * (n - k + 1);\n }\n\n CircularBuffer<double> dp(maxPts + 1);\n dp[0] = 1;\n double sum = 1;\n for (int i = 1; i < k; ++i) {\n dp[i] = sum * kFactor;\n sum += dp[i] - dp[i - maxPts];\n }\n double answer = 0;\n for (int i = k; i <= n; ++i) {\n answer += sum * kFactor;\n sum -= dp[i - maxPts];\n }\n return answer;\n }\n};\n``` | 13 | 0 | ['Math', 'Dynamic Programming', 'Sliding Window', 'Probability and Statistics', 'C++'] | 5 |
new-21-game | Easy to understand Java solution with probability calculation examples | easy-to-understand-java-solution-with-pr-hehp | \nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (N >= K + W - 1)\n return 1.0;\n\n double[] p = new double[ | silvercenturion | NORMAL | 2021-06-05T16:22:17.633395+00:00 | 2021-06-05T16:34:25.488519+00:00 | 1,617 | false | ```\nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (N >= K + W - 1)\n return 1.0;\n\n double[] p = new double[N + 1];\n\n // p[i] = probability of being able to sum up to i\n // eg:\n // W = 5 i.e cards = 1, 2, 3, 4, 5\n // 1/W = probability of picking any one of the above to make sum = i\n // p[3] = (p[2] + p[1] + p[0]) * 1/W\n // if we look closely here we will be either picking 1, 2 or 3 to make our\n // sum 3 for p[2] will pick 1, for p[1] pick 2 and p[0] pick 3. Cannot go\n // for the whole range till 5 because p[3 - 3] is the last number in the\n // range that has a probability\n // similaryly\n // p[6] = (p[5] + p[4] + p[3] + p[2] + p[1]) * 1/W\n // lets say we have K = 7 and N = 10 in that case\n // for i <= K\n // p[i] = (p[i - 1] + p[i - 2] + p[i - 3] + ... p[i - W]) * 1 / W\n // If we look closely here we are kind of moving in a sliding window\n // for eg. for p[6] the sum of previous numbers will be \n // p[5] + p[4] + p[3] + p[2] + p[1]\n // and for p[7] previous sum will be\n // p[6] + p[5] + p[4] + p[3] + p[2]\n // we only need the sum of numbers within the range W before i\n // therefore we added p[7 - 1] = p[6] and removed p[7 - 1 - W] = p[6 - 5] = [1]\n p[0] = 1.0;\n\n double prev = 0.0;\n // for all i <= k\n for (int i = 1; i <= K; i++) {\n // add previously calculated p and remove last element\n // in prev which will be out of the window if it exits\n // eg for i = 6, add p[5] to running sum and remove\n // p[5 - W] since i = 6, p[6 - 1 - W]\n prev += p[i - 1] - ((i - W - 1) >= 0 ? p[i - 1 - W]: 0);\n p[i] = prev * 1 / (W * 1.0);\n }\n\n double res = p[K];\n // for all i > K\n // Also notice here\n // consider the same eg W = 5, K = 7, N = 10\n // sum for p[8] = p[7] + p[6] + p[5] + p[4] + p[3]\n // sum for p[9] = p[7] + p[6] + p[5] + p[4]\n // sum for p[10] = p[7] + p[6] + p[5]\n // we do not add up the values of p[9] and p[8]\n // Which means we stop at p[9] or p[8] if we ever pick\n // 2 after having sum = 6 or 3 after sum = 6\n for (int i = K + 1; i < N + 1; i++) {\n // we just remove the last element and not add the i - 1st\n // element because we have already passed K and we do not \n // need previously calculated values, we just remove the ones\n // that go out of our current i\'s range\n prev -= (i - 1 - W >= 0 ? p[i - 1 - W] : 0);\n p[i] = prev * 1 / (W * 1.0);\n res += p[i];\n }\n\n\t\treturn res;\n }\n\n}\n``` | 13 | 1 | [] | 4 |
new-21-game | [C++] One solution and two optimization with explanation | c-one-solution-and-two-optimization-with-gezo | The idea:\nAs always, try to think recursively first, let P(i) return the probability of reaching i. Through the description of the question, we can deduce that | haoran_xu | NORMAL | 2021-06-13T11:08:58.684368+00:00 | 2021-06-13T11:11:40.183460+00:00 | 926 | false | The idea:\nAs always, try to think recursively first, let `P(i)` return the probability of reaching `i`. Through the description of the question, we can deduce that `P(i) = P(i - 1) / maxpts + P(i - 2) / maxpts + ... + P(i - maxpts) / maxpts` where `0 <= i - whatever < k`. For the final answer all we need to do is just add up `P(k) + P(k + 1) + ... + P(n)`. Great! Let us implement this.\n\nImplementation 1:\n```\nclass Solution {\n vector<double> mem;\n double P(int i, int k, int maxPts) {\n if(mem[i] != -1) {\n return mem[i];\n }\n \n mem[i] = 0;\n for(int j = 1; j <= maxPts; j++) {\n if(i - j >= 0 && i - j < k) mem[i] += P(i - j, k, maxPts) / maxPts;\n }\n \n return mem[i];\n }\n \npublic:\n double new21Game(int n, int k, int maxPts) {\n if(k == 0 || k + maxPts <= n) return 1;\n mem = vector<double>(n + 1, -1);\n mem[0] = 1;\n double ret = 0;\n for(int i = k; i <= n; i++) {\n ret += P(i, k, maxPts);\n }\n \n return ret;\n }\n};\n```\nThis solution works for most test cases, but eventually TLE. Hmmmm, before we start optimizing, let us first analyze the time complexity to have a basic idea of the upper bound we want to beat. There are a total of `n` unique cases, each case takes an average `O(n)`, this gives us the time complexity of `O(n^2)`\n\nOptimization 1(dp):\nOk, maybe we timed out because recursion calls takes slightly more time. I doubt it but you never know with leetcode. As with most memorization solutions, we can change this to a bottom up DP solution. \n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n vector<double> dp(n + 1, 0);\n double prob = 1.0/maxPts;\n dp[0] = 1;\n for(int i = 0; i < k; i++) {\n double add = dp[i] * prob;\n for(int j = i + 1; j <= n && j - i <= maxPts; j++) {\n dp[j] += add;\n }\n }\n \n double sum = 0;\n for(int i = k; i <= n; i++) {\n sum += dp[i];\n }\n \n return sum;\n }\n};\n```\nNoticed that I changed a couple of things, instead of finding the solution backwards, we add to the solutions to the right of us. This actually does not change our recurrence relationship, I just find this way of implementation easier to write. The time complexity is still the same but we got rid of recursion so let us press submit and...TLE.\n\nOpimization 2(dp + sliding window):\nLet us revisit our recurrence relationship again...this is why I always love to write down the reccurence relationship before implementation just so that if we need to optimize we can look back to find some ideas from it. To remind you, our reccurence relationship is `P(i) = P(i - 1) / maxpts + P(i - 2) / maxpts + ... + P(i - maxpts) / maxpts`. Let\'s so some algebraic manipulation and get `P(i) = P(i - 1) / maxpts + P(i - 2) / maxpts + ... + P(i - maxpts) / maxpts = (P(i - 1) + P(i - 2) + ... + P(i - maxpts)) / maxpts`. Whenever you see this continuous pattern (aka subarrays) you should think sliding window. We are essentially getting the sum of an atmost `maxpts` sized sliding window and then dividing it by `maxpts`. Due to the nature of sliding window, we can reduce the running time to `O(n)`! Nice, let us implement.\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if(k == 0 || k + maxPts <= n) return 1.0;\n vector<double> dp(n + 1, 0);\n dp[0] = 1;\n int j = 0;\n int i = 0;\n double wsum = 0, res = 0;\n while(j <= n) {\n if(j < k) wsum += dp[j++];\n else res += dp[j++];\n if(j - i > maxPts) {\n wsum -= dp[i++];\n }\n \n if(j <= n) dp[j] = wsum / maxPts;\n }\n \n return res;\n }\n};\n```\nFinally, not more TLE. As before the time complexity is `O(n)` and the space complexity is `O(n)`. | 10 | 0 | [] | 0 |
new-21-game | [Python/C++] Posterior probability + climbing stairs | pythonc-posterior-probability-climbing-s-l6oa | The question ask us to play a game:\n\nlet X = 0\nwhile X <= K:\n\tX += draw a sample from W, where W = [1, 10]\n\nand figure out that, at the end of the game, | ftliao | NORMAL | 2020-07-01T11:45:36.148484+00:00 | 2020-07-01T12:24:30.127428+00:00 | 975 | false | The question ask us to play a game:\n```\nlet X = 0\nwhile X <= K:\n\tX += draw a sample from W, where W = [1, 10]\n```\nand figure out that, at the end of the game, what\'s the probability \n```\nP( X \u2264 N | X \u2265 K) \uFF1F\n```\n\nFor each probablity X = i, it is the relation:\n```\nP( X = i ) = P( X = i - 1) + P ( X = i - 2 ) + .... P ( X = i - W ), where i > W\n```\n\nFor example, \n```\nP( X = 0 ) = 1 # Initial state, no need to draw cards\nP( X = 1 ) = 1/W # Only 1 out of W chance in getting X = 1\nP( X = 2 ) = 1/W + 1/W^2 # We can draw a 2 or two 1s.\nP( X = 3 ) = 1/W + 1/W^2 + 1/W^2 + 1/W^3 # We can draw a 3, a (2,1), a (1,2), and two 1s. \nP (X = 4 ) = ( P( X = 3 ) + P( X = 2 ) ) / W\n.etc\n```\n\nThe above sequence is similar to climbing stairs or Fibo series, except, this time, we would be updating probabilities.\n\nThus, we can represent the above probabilities with an array of length ```N + 1``` and add up the probabilities between ```[K, N]```. \n\n\n**Python**\n```\nclass Solution:\n def new21Game(self, N: int, K: int, W: int) -> float:\n if K == 0 or N >= K + W:\n return 1\n \n dp = [1] + [0] * N\n res = 0\n wsum = 1.0\n for i in range(1, N+1):\n dp[i] = wsum / W\n if i < K:\n wsum += dp[i]\n else:\n res += dp[i]\n \n if i - W >= 0:\n wsum -= dp[i-W]\n \n return res\n```\n\n**C++**\n```\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n if(K == 0 or N >= K + W)\n return 1;\n \n vector<double> dp(N + 1, 0);\n dp[0] = 1;\n \n double wsum = 1.0;\n double res = 0;\n for(int i=1; i<N+1; i++) {\n dp[i] = wsum / double(W);\n if(i < K)\n wsum += dp[i];\n else\n res += dp[i];\n \n if(i-W >= 0)\n wsum -= dp[i-W];\n }\n \n return res;\n }\n};\n```\n | 10 | 0 | [] | 2 |
new-21-game | C++ 12ms O(K+W) solution with explanation | c-12ms-okw-solution-with-explanation-by-spap5 | First, the destination conditional probability is P(<=N | >= K) which equals to P(<= N && >= K) / P(>=K).\n\nWithout limitations, \nP(x) = 1 / w * (P(x - 1) + P | zhoubowei | NORMAL | 2018-05-20T15:17:41.517980+00:00 | 2018-09-18T11:36:37.453659+00:00 | 2,567 | false | First, the destination conditional probability is **P(<=N | >= K)** which equals to **P(<= N && >= K) / P(>=K)**.\n\nWithout limitations, \nP(x) = 1 / w * (P(x - 1) + P(x - 2) +... + P(x-w)) \n= 1 / w * sumP(x - w, x - 1)\n= **1 / w * sumP(lb, ub)**.\nHere, P(x) means the probability of becoming x points after some draws.\nlb, ub means lower bound and upper bound.\n\nBut there are some limitations to lb and ub:\n1. **lb >= 0** (let P(0) = 1)\n2. **ub <= K - 1**, because when you have K points or more, you cannot draw a new card.\n\nTo calculate all the P()s is very time-consuming, thus we can use the cumulative sum technique.\n\nFinally, \nP(<= N && >= K) = sumP(K, N), and\nP(>= K) = sumP(K, +\u221E).\nIn fact, when x > K + W - 1, P(x) = 0, thus sumP(K, +\u221E) = sumP(K, K + W - 1);\nAlso, sumP(K, N) = sumP(K, min(N, K + W - 1))\n\nHere is my code:\n\n```\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n vector<double> sum(K + W); // cumulative sum\n sum[0] = 1;\n for (int i = 1; i <= K + W - 1; i++) {\n int t = min(i - 1, K - 1);\n if (i <= W) {\n sum[i] = sum[i - 1] + sum[t] / W;\n } else {\n sum[i] = sum[i - 1] + max((sum[t] - sum[i - W - 1]) / W, 0.0);\n }\n }\n double result = (sum[min(N, K + W - 1)] - sum[K - 1]) / (sum[K + W - 1] - sum[K - 1]);\n return result;\n }\n};\n``` | 10 | 0 | [] | 3 |
new-21-game | Diagram & Image Explaination🥇 C++ Full Optimized🔥 DP | Well Explained | diagram-image-explaination-c-full-optimi-dxs7 | Diagram\n Describe your first thoughts on how to solve this problem. \n\n\n# Approach\n Describe your approach to solving the problem. \nCheck if Alice can alwa | 7mm | NORMAL | 2023-05-25T00:01:36.385657+00:00 | 2023-05-25T00:09:01.595553+00:00 | 3,386 | false | # Diagram\n<!-- Describe your first thoughts on how to solve this problem. -->\n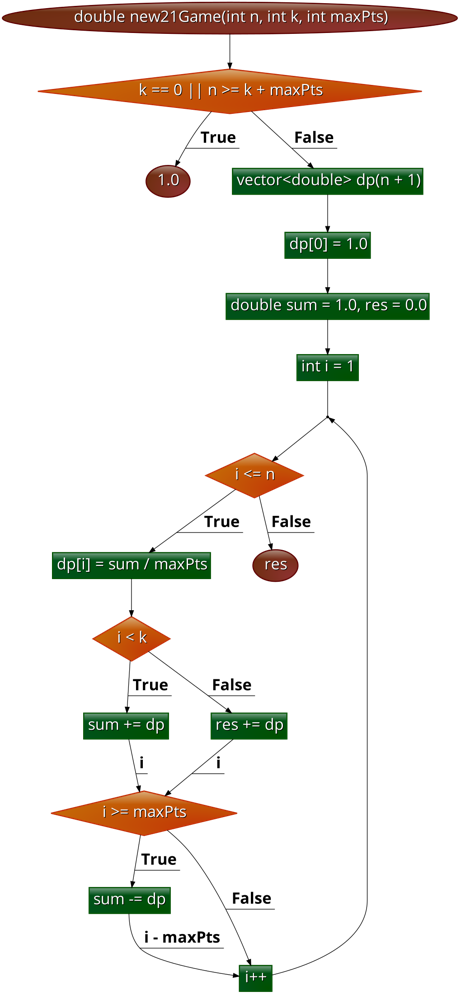\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCheck if Alice can always get k or more points. If so, return 1.0.\n\nCreate a vector dp of size n + 1 to store the probabilities of getting each point from 0 to n. Initialize dp[0] = 1.0.\n\nInitialize two variables, sum and res, to keep track of the sum of probabilities and the final result, respectively. Set sum = 1.0.\n\nLoop over all possible points from 1 to n. For each point i, calculate the probability of getting that point by taking the sum of the probabilities of getting the previous maxPts points and dividing by maxPts.\n\nIf i < k, add the probability of getting i points to sum.\n\nIf i >= k, add the probability of getting i points to res.\n\nUpdate sum by subtracting the probability of getting the point i - maxPts.\n\nReturn the value of res, which represents the probability of getting n or fewer points in the game.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * maxPts) \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n vector<double> dp(n + 1);\n dp[0] = 1.0;\n double sum = 1.0, res = 0.0;\n for (int i = 1; i <= n; i++) {\n dp[i] = sum / maxPts;\n if (i < k) {\n sum += dp[i];\n } else {\n res += dp[i];\n }\n if (i >= maxPts) {\n sum -= dp[i - maxPts];\n }\n }\n return res;\n }\n};\n\n```\n\n | 9 | 1 | ['Dynamic Programming', 'Sliding Window', 'C++', 'Java', 'Python3'] | 4 |
new-21-game | C++ solution using dp | c-solution-using-dp-by-maitreya47-poh8 | We store the probability of every state, i.e. probability of getting 2, 3, etc at any point- in our dp vector. Realise that play will stop at k, so atmax the pl | maitreya47 | NORMAL | 2021-06-21T03:30:02.765884+00:00 | 2021-06-21T03:30:02.765929+00:00 | 1,491 | false | We store the probability of every state, i.e. probability of getting 2, 3, etc at any point- in our dp vector. Realise that play will stop at k, so atmax the player will draw is (k-1) + maxPts, so we are guaranteed to get anything <= k-1-maxPts. We start with zero points so probability of ending up with 0 points also = 1. After checking k, we set dp[0] = 1 (for same reason as stated).\nNow comes the tricky part, we iterate for i=0 to n and in each iteration update the dp[i+1] (hence go until <n, as we need to update upto dp[n].\nIn each iteration, check if \'i\' is <k, if it is add its value in sum and calcuate dp[i+1] = sum/maxPts.\nThis is done because we are checking how many ways are present to reach that state. For example:\nf(1)- only one possible way- from f(0) draw card=1\nf(2)- two ways, either draw card=2 from f(0) or draw card=1 from f(1)\nhence we keep adding the dp[i] and atlast divide it with maxPts as we can only draw card between range [1, maxPts].\nNow, if i>=maxPts, we need to subtract dp[i-maxPts] from it- take this example, we have maxPts=5, hence we can draw any card [1, 2, 3, 4, 5] with equal probability. Now if we need to calculate f(7)\nf(7) = f(6) (after this draw 1) + f(5) (after this draw 2)+ f(4) (after this draw 3)+ f(3) (after this draw 4)+ f(2) (after this draw 5), no other states possible that can reach f(7) in 1 step. Hence, if our current sum contains value of dp[1] (f(1)), that needs to subtracted from sum. \nAtlast, add all the probabilities of states that are possible stopping values, i.e. we can stop at k, k+1, or anything else upto n (remember we checked n>=k-1+maxPts at the start). Now the summation of this probabilities will be our answer.\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if(k==0 || n>=k+maxPts-1)\n return (double) 1;\n vector<double> dp(n+1);\n dp[0]=1;\n double sum = 0;\n for(int i=0; i<n; i++)\n {\n if(i<k)\n sum+=dp[i]; // reach f(2) by directly drawing f(2) or f(1) and f(1) \n if(i>=maxPts)\n sum-=dp[i-maxPts];\n \n dp[i+1] = sum/maxPts;\n }\n double ret = 0;\n for(int i=k; i<=n; i++)\n ret+=dp[i];\n return ret;\n }\n};\n``` | 8 | 0 | ['Dynamic Programming', 'C', 'C++'] | 3 |
new-21-game | Java Solution for New 21 Game Problem | java-solution-for-new-21-game-problem-by-1sch | Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal is to calculate the probability that Alice has n or fewer points. To achieve t | Aman_Raj_Sinha | NORMAL | 2023-05-25T03:53:42.314754+00:00 | 2023-05-25T03:53:42.314836+00:00 | 1,820 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to calculate the probability that Alice has n or fewer points. To achieve this, we can consider the probability at each point and use dynamic programming to build up the probabilities iteratively.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. First, we handle the base cases. If k is 0 or if n is greater than or equal to k + maxPts, Alice will always stop drawing after the first round and have a probability of 1.0 to have n or fewer points.\n1. We create an array dp to store the probabilities for each possible number of points.\n1. Initialize dp[0] to 1.0, indicating that Alice starts with 0 points.\n1. We use a sliding window approach to calculate the probabilities iteratively. We maintain a windowSum variable that represents the sum of probabilities within the window of size maxPts.\n1. Iterate from 1 to n and calculate dp[i] as windowSum / maxPts since each draw has equal probabilities.\n1. If i is less than k, we update windowSum by adding dp[i] since we can continue drawing.\n1. Otherwise, if i is greater than or equal to k, we update probability by adding dp[i] since Alice has stopped drawing at this point.\n1. We adjust the windowSum by subtracting the probability that falls outside the window, i.e., dp[i - maxPts], if it exists.\n1. Finally, we return the calculated probability.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the solution is O(n) because we iterate from 1 to n to calculate the probabilities.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) because we use an array dp of size n+1 to store the probabilities.\n\n# Code\n```\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts)\n return 1.0;\n \n double[] dp = new double[n + 1];\n double windowSum = 1.0;\n double probability = 0.0;\n \n dp[0] = 1.0;\n \n for (int i = 1; i <= n; i++) {\n dp[i] = windowSum / maxPts;\n \n if (i < k)\n windowSum += dp[i];\n else\n probability += dp[i];\n \n if (i - maxPts >= 0)\n windowSum -= dp[i - maxPts];\n }\n \n return probability;\n }\n}\n``` | 7 | 0 | ['Java'] | 0 |
new-21-game | Swift: New 21 Game (+ Test Cases) | swift-new-21-game-test-cases-by-asahioce-8ap4 | swift\nclass Solution {\n func new21Game(_ n: Int, _ k: Int, _ maxPts: Int) -> Double {\n guard k != 0 && n < (k + maxPts) else { return 1.0 }\n | AsahiOcean | NORMAL | 2021-06-02T23:55:27.057712+00:00 | 2021-06-02T23:55:27.057742+00:00 | 687 | false | ```swift\nclass Solution {\n func new21Game(_ n: Int, _ k: Int, _ maxPts: Int) -> Double {\n guard k != 0 && n < (k + maxPts) else { return 1.0 }\n var dp = [Double](repeating: 0, count: n+1)\n dp[0] = 1.0\n var result = 0.0, val = 1.0\n for i in 1...n {\n dp[i] = val / Double(maxPts)\n i < k ? (val += dp[i]) : (result += dp[i])\n if i - maxPts >= 0 { val -= dp[i - maxPts] }\n }\n return result\n }\n}\n```\n\n```swift\nimport XCTest\n\n// Executed 3 tests, with 0 failures (0 unexpected) in 0.006 (0.007) seconds\n// In the examples for the task the values seem to have been rounded up\n\nclass Tests: XCTestCase {\n private let s = Solution()\n func test1() {\n XCTAssertEqual(s.new21Game(10, 1, 10), 0.9999999999999999) // 1.00000\n }\n func test2() {\n XCTAssertEqual(s.new21Game(6, 1, 10), 0.60000)\n }\n func test3() {\n XCTAssertEqual(s.new21Game(21, 17, 10), 0.7327777870686082) // 0.73278\n }\n}\n\nTests.defaultTestSuite.run()\n``` | 7 | 1 | ['Swift'] | 0 |
new-21-game | 👨💻 Easy Approach | C++ | O(N) | easy-approach-c-on-by-anuj_10-evyq | Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve the problem, we can use dynamic programming to calculate the probability that | anuj_10 | NORMAL | 2023-05-25T05:29:06.722160+00:00 | 2023-05-25T05:29:06.722185+00:00 | 922 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve the problem, we can use dynamic programming to calculate the probability that Alice has n or fewer points. We can define a dynamic programming array dp of size n + 1, where dp[i] represents the probability of having i or fewer points.\n\nWe can initialize dp[0] to 1, as Alice starts with 0 points. Then we can iterate from 1 to n and calculate dp[i] based on the previous probabilities.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Create a dynamic programming array dp of size n + 1 to store the probabilities.\n- Initialize dp[0] to 1, as Alice starts with 0 points.\n- Initialize probability variable to 0 to keep track of the total probability of having n or fewer points.\n- Initialize point variable to 1, as the probability of starting with 0 points is 1.\n- Iterate from 1 to n and calculate dp[i] based on the previous probabilities:\n- Set dp[i] to point / maxPts, as the probability of gaining i points is equal to the probability of gaining i-1 points divided by maxPts.\n- If i is less than k, add dp[i] to point to keep track of the total probability of having less than k points.\n- If i is greater than or equal to k, add dp[i] to probability to keep track of the total probability of having k or fewer points.\n- If i - maxPts is greater than or equal to 0, subtract dp[i - maxPts] from point to account for the points that can no longer be obtained.\n- Return probability, which represents the probability that Alice has n or fewer points.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts)\n return 1.0;\n vector<double> dp(n + 1);\n double point = 1.0, probability = 0.0;\n dp[0] = 1.0;\n for (int i = 1; i <= n; i++) {\n dp[i] = point / maxPts;\n if (i < k)\n point += dp[i];\n else\n probability += dp[i];\n if (i - maxPts >= 0)\n point -= dp[i - maxPts];\n }\n return probability;\n }\n};\n```\n\n# An Upvote will be encouraging \uD83D\uDC4D\n | 6 | 0 | ['Dynamic Programming', 'C++'] | 0 |
new-21-game | Taking recursion solution to linear solution | taking-recursion-solution-to-linear-solu-d783 | step 1 wirte recursion solution\n\n\ndouble solver(int n, int k, int mp,int sr, vector<double>&dp)\n {\n if(sr>=k)\n return sr<=n?1:0;\n | vikassingh2810 | NORMAL | 2022-06-10T17:31:04.236856+00:00 | 2022-06-10T17:32:24.247131+00:00 | 599 | false | step 1 wirte recursion solution\n\n```\ndouble solver(int n, int k, int mp,int sr, vector<double>&dp)\n {\n if(sr>=k)\n return sr<=n?1:0;\n \n if(dp[sr]!=-1)\n return dp[sr];\n \n double ans=0;\n for(int i=1;i<=mp;i++)\n {\n ans+=solver(n,k,mp,sr+i,dp);\n }\n \n return dp[sr]=(double)ans/mp;\n }\n double new21Game(int n, int k, int mp) {\n \n vector<double>dp(k+mp,-1.00);\n \n return solver(n,k,mp,0,dp);\n }\n```\n\n\n\nstep 2 wirte array dp from above recursion\n\n```\ndouble new21Game(int n, int k, int mp) {\n\n\t double dp[k+mp];\n\n for(int i=k+mp-1;i>=k;i--)\n {\n\t if(i<=n)\n\t\t dp[i]=1;\n\t else\n\t\t dp[i]=0;\n }\n\n for(int i=k-1;i>=0;i--)\n {\n\t double ans=0;\n\n\t for(int j=1;j<=mp;j++)\n\t {\n\t\t ans+=dp[i+j];\n\t }\n\n\t dp[i]=ans/mp;\n } \n\n\treturn dp[0];\n\n\t\t\t\t}\n```\n\n\n\nstep 3 realizing that the value inside j loop can be calculated be prefix sum or sliding window;\t\n```\ndouble new21Game(int n, int k, int mp) {\n\n double dp[k+mp];\n\n\tdouble sum=0;\n\n for(int i=k+mp-1;i>=k;i--)\n {\n\t if(i<=n)\n\t\t dp[i]=1;\n\t else\n\t\t dp[i]=0;\n\n\t sum+=dp[i];\n }\n\n\n for(int i=k-1;i>=0;i--)\n {\n\n\t dp[i]=sum/mp;\n\n\t sum+=dp[i];\n\t sum-=dp[i+mp];\n } \n\n\treturn dp[0];\n}\n\n```\n\n | 6 | 0 | ['Dynamic Programming'] | 1 |
new-21-game | [Python3] top-down & bottom-up dp | python3-top-down-bottom-up-dp-by-ye15-lnkj | Algo \nDefine fn(n) as the probability of points between K and N, i.e. [K, N] given existing point n. Then, \n\n1) if n < K, fn(n) = 1/W*(fn(n+1) + fn(n+2) + .. | ye15 | NORMAL | 2020-11-16T20:08:10.628759+00:00 | 2021-05-13T17:30:37.239301+00:00 | 1,075 | false | Algo \nDefine `fn(n)` as the probability of points between `K` and `N`, i.e. `[K, N]` given existing point `n`. Then, \n\n1) if `n < K`, `fn(n) = 1/W*(fn(n+1) + fn(n+2) + ... + fn(n+W))`;\n2) if `K <= n <= N`, `fn(n) = 1`;\n3) if `N < n`, `fn(n) = 0`. \n\nTrick: if `n+1 < K`, then from \n`fn(n) = 1/W*(fn(n+1) + fn(n+2) + ... + fn(n+W))`\n`fn(n+1) = 1/W*(fn(n+2) + fn(n+3) + ... + fn(n+W+1))`\none can derive `fn(n) = (1+W)/W*fn(n) - 1/W*fn(n+W+1)`. When `n+1 == K`, this trick cannot be applied as the relationship of `fn(n+1) = 1/W*(fn(n+2) + ...)` doesn\'t hold in general. \n\nTop-down implementation (244ms, 5.39%)\n```\nclass Solution:\n def new21Game(self, N: int, K: int, W: int) -> float:\n \n @lru_cache(None)\n def fn(n): \n """Return prob of of points between K and N given current point n."""\n if N < n: return 0\n if K <= n: return 1\n if n+1 < K: return (1+W)/W*fn(n+1) - 1/W*fn(n+W+1)\n return 1/W*sum(fn(n+i) for i in range(1, W+1))\n \n return fn(0)\n```\n\nBottom-up implementation (52ms, 99.67%)\n```\nclass Solution:\n def new21Game(self, N: int, K: int, W: int) -> float:\n ans = [0]*K + [1]*(N-K+1) + [0]*W\n val = sum(ans[K:K+W])\n for i in reversed(range(K)): \n ans[i] = val/W\n val += ans[i] - ans[i+W]\n return ans[0]\n``` | 6 | 0 | ['Python3'] | 2 |
new-21-game | Python 12-line code||rolling sum | python-12-line-coderolling-sum-by-gulugu-kq43 | \nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if n >= k - 1 + maxPts: return 1 #the last possible stop-point is k-1 | gulugulugulugulu | NORMAL | 2022-04-10T21:24:02.888959+00:00 | 2022-04-10T21:24:02.888994+00:00 | 884 | false | ```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if n >= k - 1 + maxPts: return 1 #the last possible stop-point is k-1, if we roll a maxPts and it will end within n, that means anyway it will end within n with prob 1, there is no need to continue\n dp = [0] * (n + 1) #dp[i] is the probability we reach point i. As we care what\'s the probability within n, at most we need dp to calculate from 1 to n\n dp[0], curSum = 1, 0 #dp[0] is the probability we reach 0. As we start with 0, we have a probability of 1 reaching 0\n for i in range(1, n + 1):\n if i - 1 < k: # when the previous point hasn\'t reached k, that means we can still continue to roll, and we\'ll add that point. Otherwise, when i - 1 already reaches k, then the game stops and we cannot reach status i from i - 1 (we cannot pick any more number)\n curSum += dp[i - 1]\n if i - 1 >= maxPts: # we can only reach point i from point i - 1, i - 2, ..., i - maxPts. and hence when we calculate point i, we need to make sure the previous points outside of the range drops out\n curSum -= dp[i - 1 - maxPts]\n dp[i] = curSum / maxPts\n return sum(dp[k:]) # we calculate all the probabilities that we land in point k, point k + 1, until point n\n``` | 5 | 0 | ['Python', 'Python3'] | 0 |
new-21-game | O(N) java solution with explanation | on-java-solution-with-explanation-by-utt-ldrq | \tlet prob[i] denote the probability of reaching the point i\n w is the maximum coin which we can draw\n\n the probability of drawing each coin is equal, | uttu_dce | NORMAL | 2021-11-27T20:08:43.728058+00:00 | 2021-11-27T20:08:55.008605+00:00 | 687 | false | \tlet prob[i] denote the probability of reaching the point i\n w is the maximum coin which we can draw\n\n the probability of drawing each coin is equal, so the probability of drawing each coin in 1/w\n \n if we want to know the probability of drawing 14, then we can do it as follows\n prob[13] * probabilityOfDrawing(1) + prob[12]*probabilityOfDrawing(2) + prob[11]*probabilityOfDrawing(3) + prob[10]*probabilityOfDrawing(4) ...\n\n but all the values probabilityOfDrawing(1) = probabilityOfDrawing(2) = probabilityOfDrawing(3) = probabilityOfDrawing(4) .. = 1/w;\n so in general \n prob[n] = (prob[m-1] + prob[m-2] + prob[m-3] + prob[m-4] + ... prob[m-w]) / (w); [taking out that term common]\n so if we observe, we are calculating the sum of the previous w elements\n\n but here there is one edge case \n for example if we are finding prob[21], then we will do something like this:\n\n if (k = 17)\n prob[21] = prob[20] * probabilityOfDrawing(1) + ....\n\n here in this case, we will never draw 1 after we have reached 20 (remember, the game ends as soon as we touch k or we cross k, so as the sum has already crossed k in this case, we will not draw anything from here)\n\n so while we are calculating the sum of the previous w elements, any element i, which is greater than k will not be considered, because we will never make a jump from that point\n\n we use sliding window for keeping track of the the sum of previous w values\n\n and at the end, we calculate prob[k] + prob[k+1] + .... prob[n] (because we wanted probabolity that the final answer is between k to n)\n\n\n```\nclass Solution {\n public double new21Game(int n, int k, int w) {\n \n if(n >= k + w || k == 0 ) return 1.0 ;\n \n double[] dp = new double[n+1];\n dp[0] = 1.0;\n\n double res = 0.0;\n double runningSum = dp[0];\n\n for(int i=1; i<=n; i++) {\n \n // at this point, i assume that i have with me the sum of the previous w elements\n dp[i] = (runningSum * 1.0) / (w);\n \n // if the element we are trying to add is less than k, only then we will add\n if(i < k) {\n runningSum+=dp[i];\n } else {\n // in case the current i is greater than k we will add it to our answer because at the end we need the sum of dp values from k to n\n res+=dp[i];\n }\n\n if(i - w >= 0) {\n // adjust the tail end\n runningSum-=dp[i-w];\n }\n \n }\n\n return res;\n }\n}\n``` | 5 | 0 | [] | 0 |
new-21-game | Monte Carlo Simulations | monte-carlo-simulations-by-sebastienp-zy7q | Disclaimer: this solution does not pass the test as the required precision is 10^-5, but for real applications, it gives quite a interesting insight. Also this | sebastienp | NORMAL | 2020-07-08T15:09:45.291693+00:00 | 2020-07-13T05:41:27.553027+00:00 | 1,231 | false | Disclaimer: this solution does not pass the test as the required precision is 10^-5, but for real applications, it gives quite a interesting insight. Also this is more a solution towards statistics than Software Engineer. Nonetheless, I think it\'s interesting to know different approaches:\n\n```\nimport random\nclass Solution:\n def new21Game(self, N: int, K: int, W: int) -> float:\n """\n Start with 0 points. \n Draws points uniformly distributed in [1, W] while total points < K \n \n\t\tMore specifically we are looking for "the probability that she has N or less points"\n\t\tLet\'s call X the random variable that takes 2 values {Alice has points <=N, Alice has points >N}. This is a Bernouilli random variable with parameter p (p being the value we are trying to find).\n\t\tProbability(Alice has points <= N) = p\n\t\tProbability(Alice has points > N) = 1 - p\n\t\tThe Law of large number tell us that the empirical mean ((x1 + x2 + ... + xn) / n) converges to the expected value as n goes to infinity.\n\t\tThe expected value of a Bernouilli random variable is exaclty what the parameter p is\n\t\tMonte Carlo Simulations give us an approximation of the expected value:\n\t\t(Provided that the numbers of simulation is big enough cf Law of large numbers)\n """\n def simulation(N, K, W):\n points = 0\n while points < K:\n points += random.randint(1, W)\n if points <= N:\n return 1\n return 0\n \n sample_size = 100000\n total_time_points_smallest_than_N = 0\n for i in range(sample_size):\n total_time_points_smallest_than_N += simulation(N, K, W)\n return total_time_points_smallest_than_N / sample_size\n \n```\n\nRuntime: ~ O(sample_size * K)\nSpace: ~ O(1)\n\n\n\nTop Down Recursion with Memoization:\n\n```\ndef helper(N: int, K: int, W: int, P: int, memo: dict) -> float:\n\tif P in memo.keys():\n\t\treturn memo[P]\n\tif P < K:\n\t\tres = []\n\t\tfor new_point in range(1, W+1):\n\t\t\tres.append(helper(N, K, W, P + new_point, memo))\n\t\tmemo[P] = sum(res) / W\n\telse:\n\t\tmemo[P] = 1.0 if P <= N else 0.0\n\n\treturn memo[P]\n\nreturn helper(N, K, W, 0, {})\n```\n | 5 | 0 | [] | 2 |
new-21-game | C++ DP O(K) time and space | c-dp-ok-time-and-space-by-alreadydone-s8ho | Build an array dp such that dp[i] == new21Game(N-K+i+1, i+1, W), so that dp[K-1] == new21Game(N,K,W).\ndp[i] can be computed from dp[i-1], ..., dp[i-W] because | alreadydone | NORMAL | 2019-05-28T05:26:45.594748+00:00 | 2019-05-28T05:26:45.594792+00:00 | 665 | false | Build an array dp such that `dp[i] == new21Game(N-K+i+1, i+1, W)`, so that `dp[K-1] == new21Game(N,K,W)`.\n`dp[i]` can be computed from `dp[i-1], ..., dp[i-W]` because of the following formula:\n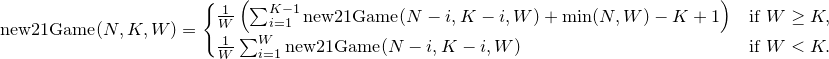\nThis is because:\nFrom the initial state 0, we have 1/W probability jumping to each state between 1 and W. If W >= K, then W-K+1 of these states are terminal (>=K), and min(W,N)-K+1 of them lie between K and N, yielding a probability of (min(W,N)-K+1)/W.\nFor any of remaining states `i` that is between 1 and K-1, we consider its probability of being <= N when first reaching a state that is >=K. But that is same as the probability of being <= N-i when first reaching a state that is >=K-i, which is `new21Game(N-i,K-i,W)`.\n\nIn the code below, `total` denotes the running summations in the above formula.\n\nRuntime: 4 ms, faster than 97.62% of C++ online submissions for New 21 Game.\nMemory Usage: 10.9 MB, less than 88.89% of C++ online submissions for New 21 Game.\n```\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n if (K == 0) return 1.0;\n vector<double> dp(K);\n auto total = 0.0;\n for (auto i = 0; i < K; ++i) {\n if (i < W) dp[i] = (total + min(N-K+1,W-i)) / W;\n else dp[i] = total / W, total -= dp[i-W];\n total += dp[i];\n }\n return dp[K-1];\n }\n};\n``` | 5 | 0 | [] | 0 |
new-21-game | C++ top-bottom solution | c-top-bottom-solution-by-zackyne-ffyz | according to the solution:\n\nf(x) = 1/W [f(x + 1) + f(x + 2) + ... + f(x + W)] (1)\nf(x - 1) = 1/W [f(x) + f(x + 1) + ... + f(x + W - 1)] (2)\n | zackyne | NORMAL | 2019-04-20T15:27:24.437453+00:00 | 2019-04-20T15:27:24.437496+00:00 | 407 | false | according to the solution:\n\nf(x) = 1/W *[f(x + 1) + f(x + 2) + ... + f(x + W)] (1)\nf(x - 1) = 1/W *[f(x) + f(x + 1) + ... + f(x + W - 1)] (2)\n\n(2) - (1), we can get :\nf(x - 1) = f(x) - 1/W *[f(x + W) - f(x) (3)\n\nbut in (3) equation, the x must less than K - 1, this is very important.\n\n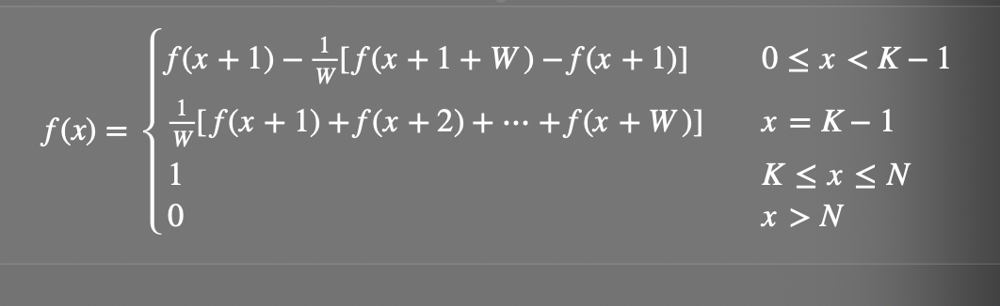\n\n\n```c++\nclass Solution {\n int N;\n int K;\n int W;\n double fk;\n vector<double> cache;\npublic:\n double new21Game(int N, int K, int W) {\n this->N = N;\n this->K = K;\n this->W = W;\n fk = 1.0 / W * (min(N - K + 1, W));\n cache = vector<double>(K + W, -1);\n return f(0);\n }\n \n double f(int x) {\n if (x == K - 1) {\n return fk;\n }\n \n if (x >= K && x <= N) {\n return 1.0;\n }\n \n if (x > N) {\n return 0;\n }\n \n if (cache[x] != -1) {\n return cache[x];\n }\n \n double ans = f(x + 1) - 1.0 / W * (f(x + 1 + W) - f(x + 1));\n cache[x] = ans;\n return ans;\n } \n};\n``` | 5 | 1 | [] | 1 |
new-21-game | O(N) dp solution from uwi, with explanation | on-dp-solution-from-uwi-with-explanation-djbf | A intuitive idea is simply use dp[i] as the probability to reach i, dp[i]=probability[i].\n\nThen dp[i]=sum(dp[i-j]) for j in [1, W], but this causes O(KW) comp | luckypants | NORMAL | 2018-05-20T03:18:53.456090+00:00 | 2018-05-20T03:18:53.456090+00:00 | 1,594 | false | A intuitive idea is simply use `dp[i]` as the probability to reach `i`, `dp[i]=probability[i]`.\n\nThen `dp[i]=sum(dp[i-j]) for j in [1, W]`, but this causes O(KW) complexity.\n\nIn uwi\'s code, \n\n`dp[i]` is the prefix for numbers larger than or equal to i, so `probability[i]=sum(dp[:i+1])`\n\nLet\'s use `p[i]` for `probability[i]`.\n\nIn this case,\n\n**the initial situation** is `p[0]=1, p[i]=0 for i>0`, so `dp[0]=1, dp[1]=-1`\n**the recursive formula** at `i` is to update `p[i+1:i+W+1]` only, so set `dp[i+1]+=p[i]/W, dp[i+W+1]-=p[i]/W`, and `p[i]` is maintained in the code as `val`.\n\nSo just add `val` for `i in range(K, N+1)`.\n\nHere is my python version:\n\n```\nclass Solution:\n def new21Game(self, N, K, W):\n dp = [0]*(N+3)\n dp[0] = 1\n dp[1] = -1\n val = 0\n \n for i in range(K):\n val += dp[i]\n if i+1<=N:\n dp[i+1] += val/W\n if i+W+1<=N:\n dp[i+W+1] -= val/W\n ret = 0\n for i in range(K, N+1):\n val += dp[i]\n ret += val\n\n return ret\n``` | 5 | 0 | [] | 0 |
new-21-game | Java Solution | Memoization->Bottom Up->Optimization | 3 step optimization for acceptance | 3 ms | java-solution-memoization-bottom-up-opti-perp | Approach\nFor complete acceptance of the solution 3 step process is given below where first we make a recusion along with memoization(gives TLE) then optimising | adarsh-mishra27 | NORMAL | 2023-05-25T15:39:20.729436+00:00 | 2023-05-25T15:42:31.587955+00:00 | 715 | false | # Approach\nFor complete acceptance of the solution 3 step process is given below where first we make a recusion along with memoization(gives TLE) then optimising it further using bottom-up iterative approach(gives TLE) then finally applying sliding window in iterative code for most optimized solution!\n\n# Code \nStep 1:\n```\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(k==0 || n>=k-1+maxPts) return 1.0;\n dp=new Double[n+maxPts+1];\n double prob=(double)1/(double)maxPts; //probability of occurence of each number between [1, maxPts]\n return util(n, k, prob, 0, maxPts);\n }\n private Double dp[];\n private double util(int n, int k, double prob, int cur, int max) {\n if(cur>n) {\n return 0.0;\n }\n if(cur>=k) {\n return 1.0;\n } \n if(dp[cur]!=null) return dp[cur];\n double sum=0.0;\n for(int i=1;i<=max;i++) {\n double ret=util(n, k, prob, cur+i, max);\n sum+=(prob * ret);\n }\n return dp[cur]=sum;\n }\n}\n```\n\nStep 2:\n```\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(k==0 || n>=k-1+maxPts) return 1.0;\n double dp[]=new double[n+1];\n double prob=(double)1/(double)maxPts;\n for(int i=n;i>0;i--) {\n if(i>=k) {\n dp[i]=1.0;\n }\n for(int j=1;j<=maxPts;j++) {\n if(i-j>=0) {\n dp[i-j]+=prob*dp[i];\n }\n }\n }\n return dp[0];\n }\n}\n```\n\nStep 3:\n```\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(k==0 || n>=k+maxPts-1) return 1.0;\n double dp[]=new double[n+maxPts];\n double prob=(double)1/(double)maxPts;\n double sum=0.0;\n int j=k-1+maxPts;\n for(int i=n;i>=0;i--) {\n if(i>=k) {\n dp[i]=1.0;\n }\n else {\n dp[i]+=prob*sum;\n if(j-i==maxPts) {\n sum-=dp[j--];\n }\n }\n sum+=dp[i];\n }\n return dp[0];\n }\n}\n```\n\n | 4 | 0 | ['Dynamic Programming', 'Memoization', 'Sliding Window', 'Probability and Statistics', 'Java'] | 2 |
new-21-game | Math solution: O(k) time, O(maxPts) space, explained | math-solution-ok-time-omaxpts-space-expl-yrgw | Explanation\nHere we\'ll call maxPts a dice, since it is essentially one. (Yep, 1d10000 would make a big die, not for a casual DnD game).\n\nImagine Alice getti | VladimirTheLeet | NORMAL | 2023-05-25T03:44:41.122538+00:00 | 2023-05-27T19:36:41.440616+00:00 | 533 | false | # Explanation\n*Here we\'ll call `maxPts` a dice, since it is essentially one. (Yep, 1d10000 would make a big die, not for a casual DnD game).*\n\nImagine Alice getting points as traverse through the integers left to right, from 0 to the values of k and n.\n\n\u2026\u2007$k-2$\u2007\u2007\u2007$k-1$\u2007\u2007\u2007**k\u2007\u2007\u2007\u2026\u2007\u2007\u2007n**\u2007\u2007\u2007$n+1$\u2007\u2026 \n\nThe numbers above represent possible points scores during the game. Take a look at the bolded interval \u2013 that\'s where Alice needs to land for a win. Less than $k$ means the game would still go on, and scores more than $n$ would be a bust. The count of integers on that interval (including borders) is $n - k + 1$, denote this number as $winLength$.\n\nLet\'s think about possible situations where Alice can get into it on her next move. Obviously, she is somewhere in the range of $dice$ points before $k$, (no below that, or even the maximum dice roll would not be enough, and no further, since then the game is already over). Denote Alice\'s current position (i.e. her score) as $cur$. What is the chance that her next turn will bring her to the winning score? Since all dice rolls are of equal probability, the odds are as follows:\n\n*(the count of positions inside the winning interval that are reachable with the die roll) / (the count of all possible positions after the move)*\n\nThe divisor is not difficult to determine \u2013 $dice$ possible roll values mean $dice$ possible outcomes. What can be said about the divisible? Since we are at position $cur$, the farthest reachable point is $cur + dice$. If it lies inside the interval, then the number of reachable positions between it and $k$ is equal to **(cur + dice) - k + 1**. This is almost a ready value for the divisor, we only need to consider possible constraints and boundary cases. Obviously, the number of reachable values in an interval cannot be greater than the interval itself. Hence, the upper bound for it is $n - k + 1$, i.e. **winLength**. Indeed, if the current position and the size of the dice allow, we can hit any point in the interval, no more than that. The lower bound will be **0** \u2013 if we are far on the left, with a small dice it may not be possible to reach the interval at all. This restriction extends the scope of the resulting formula as far to the left as we wish, i.e. all the way to zero.\n\nSo! We got the formula for **probability of hitting the win on the next move**: min((n - k + 1), max(0, cur + dice - k + 1)) / dice, or simply put, **clamp(0, (cur + dice - k + 1), winLength) / dice** and we know that it is valid for any score $cur$.\n\nLets consider the case where Alice is one point before $k$, i.e. $cur = k - 1$. The game will end on the following turn in any event, and the chance to win is $clamp(0, dice, winLength) / dice$. Lets call it $Chance_{k-1}$.\nNow we consider the position $$cur = k - 2$$. The chance to get from there directly into the winning interval is still determined by the formula. However, now there is an additional possibility that we will hit $$k - 1$$ first, and the game will continue. The probability of hitting it (as well as any position in the range of the dice roll) is $$1/dice$$. If we get there, we already know the probability of winning from here, it\'s $$Chance_{k-1}$$. Thus, the value $$Chance_{k-2}$$ of winning for position $$k-2$$ is equal to the probability of getting right into the interval + the odds of landing on $$k - 1$$, multiplied by the probability of winning it: $Chance_{k-2} = clamp(0, dice - 1, winLength) / dice + (1 / dice) * Chance_{k-1} = (clamp(0, dice - 1, winLength) + Chance_{k-1}) / dice$.\nLets examine the preceding position as well, $cur=k-3$. There are now two possible positions ahead before the winning interval, for each of them the probability of victory has already been calculated, and the chance of hitting each on the current turn is equal to $1/dice$. So, $Chance_{k-3} = (clamp(0, dice - 2, winLength) + Chance_{k-1} + Chance_{k-2}) / dice$.\nLet\'s move on like that until we reach the starting position of zero points and write out the values in order, so that the sequence rule is clear:\n\n$Chance_{k-1} = clamp(0, dice, winLength) / (dice)$\n$Chance_{k-2} = (clamp(0, dice - 1, winLength) + Chance_{k-1}) / dice$\n$Chance_{k-3} = (clamp(0, dice - 2, winLength) + Chance_{k-1} + Chance_{k-2}) / dice$\n\u2026\n$Chance_{(k-1)-i} = (clamp(0, dice - i, winLength) + \\sum_{j=1}^{min(i, dice)}Chance_{k-j}) / dice$\n\nWhy the sum is limited to no more than $dice$ of previous Chances and not all of them? Remember, as previously stated: "the probability of hitting any position *in the dice roll range* is $1/dice$". As we examine the points more and more to the left, the positions go out of range of the die roll, become unreachable, and the probability of hitting them on the next turn is zero, contributing nothing to the overall chance.\n\n*Math is over, congratulations to all who\'ve made it through to this point.*\n\n# Approach\nSo, we apply the formula derived above to calculate the odds of winning, sequentially from a score of $k-1$ downto $0$ in the dynamic programming manner. We are changing `i` from `0` to `k-1` inclusive, thus getting the calculation of $Chance_{k-1}$ at the first iteration and $Chance_{0}$ at the last iteration \u2013 the probability of winning for the starting 0 points, which is what we need.\n\nDuring the iterations we use the Queue with max size of $dice$ as a sliding window to the last $dice$ calculated chances and update the computed sum of said chances as we go, by adding newly obtained and subtracting the oldest, $(dice+1)$-th one.\n\n\n# Complexity\n- Time complexity: $\u0398(k)$\n$k$ iterations, no more, no less.\n- Space complexity: $\u0398(min(k, maxPts))$\nJust the queue holding up to maxPts of elements, and a couple of variables.\n\n```swift []\nclass Solution {\n func new21Game(_ n: Int, _ k: Int, _ maxPointsPerDraw: Int) -> Double\n {\n let dice = Double(maxPointsPerDraw), winLength = Double(n - k + 1)\n \n // already won or interval is so big we can\'t miss it\n if k == 0 || winLength >= dice { return 1.0 }\n\n var chance = 0.0\n var lastChances = Queue<Double>()\n var lastChancesSum = 0.0\n for i in 0..<k\n {\n chance = (clamp(mn: 0.0, dice - Double(i), mx: winLength) + lastChancesSum) / dice\n lastChancesSum += chance\n lastChances.enqueue(chance)\n if lastChances.count > maxPointsPerDraw {\n lastChancesSum -= lastChances.dequeue()!\n }\n }\n return chance\n }\n}\n\nclass Queue<T>\n{\n var isEmpty: Bool { head == nil }\n private(set) var count: Int = 0\n\n func enqueue(_ val: T)\n {\n if let node = tail {\n node.next = getNode(val)\n tail = node.next\n }\n else {\n head = getNode(val)\n tail = head\n }\n count += 1\n }\n func enqueue<S>(_ s: S) where S : Sequence, S.Element == T {\n s.forEach { element in enqueue(element) }\n }\n\n func dequeue() -> T?\n {\n if let node = head {\n head = node.next\n if head == nil { tail = nil } \n count -= 1 \n defer { node.next = nil; node.val = nil; nodeCache.append(node) }\n return node.val\n }\n else { return nil }\n }\n\n private var head: QueueNode?\n private var tail: QueueNode?\n private var nodeCache: [QueueNode] = []\n private func getNode(_ val: T) -> QueueNode {\n if let node = nodeCache.popLast() {\n node.val = val; return node\n }\n else { return QueueNode(val) } \n }\n\n private class QueueNode {\n var next: QueueNode?\n var val: T!\n init(_ val: T) { self.val = val }\n }\n}\n\nfunc clamp<T: Comparable>(mn: T, _ value: T, mx: T) -> T {\n return min(max(value, mn), mx)\n}\n```\n```cpp []\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts)\n {\n double dice = maxPts, winLength = n - k + 1;\n \n // already won or interval is so big we can\'t miss it\n if ( k == 0 || winLength >= dice ) { return 1; }\n\n double chance = 0, lastChancesSum = 0;\n queue<double> lastChances;\n\n for (int i = 0; i < k; i++)\n {\n chance = (clamp(dice - i, 0.0, winLength) + lastChancesSum) / dice;\n lastChancesSum += chance;\n lastChances.push(chance);\n if (lastChances.size() > dice) {\n lastChancesSum -= lastChances.front();\n lastChances.pop();\n }\n }\n return chance;\n }\n};\n```\n```java []\nclass Solution {\n public double new21Game(int n, int k, int maxPts)\n {\n double dice = maxPts, winLength = n - k + 1;\n\n // already won or interval is so big we can\'t miss it\n if ( k == 0 || winLength >= dice ) { return 1; }\n\n double chance = 0, lastChancesSum = 0;\n Queue<Double> lastChances = new LinkedList<>();\n \n for (int i = 0; i < k; i++)\n {\n chance = (clamp(dice - i, 0.0, winLength) + lastChancesSum) / dice;\n lastChancesSum += chance;\n lastChances.add(chance);\n if (lastChances.size() > dice) {\n lastChancesSum -= lastChances.remove();\n }\n }\n return chance;\n }\n\n static double clamp(double val, double min, double max) {\n return Math.max(min, Math.min(max, val));\n }\n}\n```\n```python3 []\nfrom queue import Queue\nclass Solution:\n def new21Game(self, n: int, k: int, dice: int) -> float:\n winLength = n - k + 1\n\n # if already won or interval is so big we can\'t miss it\n if k == 0 or winLength >= dice:\n return 1.0\n\n chance = 0.0; lastChancesSum = 0.0\n lastChances = Queue(maxsize = dice + 1)\n\n for i in range(k):\n chance = (clamp(dice - i, 0.0, winLength) + lastChancesSum) / dice\n lastChancesSum += chance\n lastChances.put(chance)\n if lastChances.full():\n lastChancesSum -= lastChances.get()\n\n return chance\n \ndef clamp(value, lower, upper):\n return lower if value < lower else upper if value > upper else value\n``` | 4 | 0 | ['Math', 'Dynamic Programming', 'Swift', 'Sliding Window', 'Probability and Statistics'] | 0 |
new-21-game | Easy DP solution ✅✅ | easy-dp-solution-by-zenitsu02-mcl9 | \n# Approach\nCheck if Alice can always get k or more points. If so, return 1.0.\n\nCreate a vector dp of size n + 1 to store the probabilities of getting each | Zenitsu02 | NORMAL | 2023-05-25T00:55:30.908562+00:00 | 2023-05-25T00:55:30.908588+00:00 | 1,398 | false | \n# Approach\nCheck if Alice can always get k or more points. If so, return 1.0.\n\nCreate a vector dp of size n + 1 to store the probabilities of getting each point from 0 to n. Initialize dp[0] = 1.0.\n\nInitialize two variables,sum and res, to keep track of the sum of probabilities and the final result, respectively. Set sum = 1.0.\n\nLoop over all possible points from 1 to n. For each point i, calculate the probability of getting that point by taking the sum of the probabilities of getting the previous maxPts points and dividing by maxPts.\n\nIf i < k, add the probability of getting i points to sum.\n\nIf i >= k, add the probability of getting i points to res.\n\nUpdate sum by subtracting the probability of getting the point i - maxPts.\n\nReturn the value of res, which represents the probability of getting n or fewer points in the game.\n\n# **Pls Upvote the solution if Helpful \uD83E\uDD79 **\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n vector<double> dp(n + 1);\n dp[0] = 1.0;\n double sum = 1.0, res = 0.0;\n for (int i = 1; i <= n; i++) {\n dp[i] = sum / maxPts;\n if (i < k) {\n sum += dp[i];\n } else {\n res += dp[i];\n }\n if (i >= maxPts) {\n sum -= dp[i - maxPts];\n }\n }\n return res;\n }\n};\n``` | 4 | 0 | ['C++'] | 1 |
new-21-game | Recursion with memoization TLE, O(n^2), then optimization to iterative sliding window | recursion-with-memoization-tle-on2-then-otcka | \nclass Solution:\n """\n Recursive solution: Begin with cur_points.\n If cur_points<k, play next round:\n For each draw from 1 to maxPts:\n | zhangvict | NORMAL | 2022-01-10T23:30:26.528184+00:00 | 2022-01-11T00:14:04.350456+00:00 | 481 | false | ```\nclass Solution:\n """\n Recursive solution: Begin with cur_points.\n If cur_points<k, play next round:\n For each draw from 1 to maxPts:\n play the next round with draw points. Find the probability of winning from that many points. Divide by maxPts.\n \n Add the weighted probabilites together to get final result.\n \n Base case is:\n when cur_points>n, the probabilty is 0\n elif cur_points>=k, probability is 1.\n \n \n There are multiple ways to reach a new threshold, e.g. for threshold n-2 by drawing 1 twice or by drawing 2 once, so we memoize the solution.\n """\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n memo=dict()\n \n def prob(cur_points): #probability of winning starting from cur_points\n if cur_points>n:\n memo[cur_points]=0\n elif cur_points>=k:\n memo[cur_points]=1\n if cur_points in memo:\n return memo[cur_points]\n \n output=0\n for next_draw in range(1,maxPts+1):\n next_prob=prob(cur_points+next_draw)\n output+=next_prob/maxPts\n \n memo[cur_points]=output\n return output\n \n return prob(0)\n```\n\n```\nclass Solution:\n """\n Recursive solution: O(n*max_pts)\n Begin with cur_points.\n If cur_points<k, play next round:\n For each draw from 1 to maxPts:\n play the next round with draw points. Find the probability of winning from that many points. Divide by maxPts.\n \n Add the weighted probabilites together to get final result.\n \n Base case is:\n when cur_points>n, the probabilty is 0\n elif cur_points>=k, probability is 1.\n \n There are multiple ways to reach a new threshold, e.g. for threshold n-2 by drawing 1 twice or by drawing 2 once, so we memoize the solution.\n \n Optmization to iterative solution:\n let dp[i] be the probability of winning from i points. It is initialized as:\n \n dp[i]=1 for i =k,...,n\n dp[i]=0 for i=n+1,...,k+max_pts-1 (if k+max_pts<=n+1, probability of winning is everywhere 1)\n 0--------k---n---\n ---------[--max_pts-]\n \n we have an expression:\n dp[k-1]=(n+1-k)/max_pts\n dp[i-1]=dp[i]+dp[i]/max_pts-dp[i+max_pts+1]/max_pts\n \n Alternatively, we can keep track of the current sum of the probabilities cur_sum\n """\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k-1+maxPts<=n:\n return 1.0\n \n dp=[0 for _ in range(k+maxPts)]\n \n for i in range(k,n+1):\n dp[i]=1\n cur_sum=n-k+1\n for i in range(k-1,-1,-1):\n dp[i]=cur_sum/maxPts\n cur_sum=cur_sum+dp[i]-dp[i+maxPts]\n return dp[0]\n``` | 4 | 0 | [] | 1 |
new-21-game | My attempt at making sense | my-attempt-at-making-sense-by-sumondutta-8tu0 | \n\t i) [1...,w] is the range the value that can be drawn in a single draw\n\t ii) the game stops as soon as sum of all values drawn becomes k or more.\n\t | sumondutta | NORMAL | 2021-11-14T00:04:49.609446+00:00 | 2021-11-14T01:55:40.496232+00:00 | 317 | false | 1. \n\t i) [1...,w] is the range the value that can be drawn in a single draw\n\t ii) the game stops as soon as **sum** of all values drawn becomes k or more.\n\t iii) the goal is to find the probability that the **sum** is n or less at the end of the game. Let\'s call it sol(n).\n2. The game does not stop until the sum is atleast k. It\'s not possible for sum to be less than k at the end of the game. If n<k then sol(n)=0\n3. The maximum sum at the end of the game can be (k-1)+w. This is because the maximum sum that can be reached without ending the game is k-1. Having reached this point you can make only another draw and pick a maxium of w in that draw.\n4. if n> (k-1)+w then sol(n)=1\n5. The range of values at the end of the game is [k,..,k-1+w]\n6. sol(n)= P(k)+P(k+1)+...+P(n) , where P(x)= probability of the sum at the end of the game being x.\n7. useful math formula: If probability of event x is px and probability of event y is py, then probility of x happening after y is py * px.\n8. Probability of sum=0 at the begining of the game is 1\n9. Probability of sum=1 after any draw is probability of sum=0 prior to the draw multiplied by probability of picking 1 in the current draw\n10. \n\tprob(x)= probability of sum being x after current draw \n\tc(x) = probability of drawing x in current draw\n\tprob(0)=1\n\tprob(1) = prob(0) * c(1)\n\tprob(2)= prob(1) * c(1) + prob(0) * c(2)\n\tprob(3) = prob(2) * c(1) + prob(1) * c(2) + prob(0) * c(3)\n11. c(x) = probability of drawing x in current draw = 1/w \n12. prob(3) = ( prob(2) + prob(1) + prob(0) )/w\n13. prob(x) = ( prob(xMaxPriorSum)+....+ prob(xMinPriorSum) )/w, max sum prior to current draw = xMaxPriorSum , min sum prior to current draw = xMinPriorSum to make the new sum x\n14. Generally xMaxPriorSum will increase with x and xMinPriorSum will remain zero\n15. Because of the constraints in the problem the above will not be the case\n16. xMaxPriorSum will not grow beyond k-1. If xMaxPriorSum had been k , the game would have ended\n17. Since the maxium value you can get from the current draw is w, xMinPriorSum=x-w \n18. dp[i] = probability that sum after current draw would be x. \n19. w=4, k=3, n=7\n\t\t dp[0]=prob(0)\n\t\t dp[1]= prob(0) * c(1)\n\t\t dp[2] = prob(1) * c(1) + prob(0) * c(2) , dp[x] = prob(xMaxPriorSum) * c(x-xMaxPriorSum)+ ..... + prob(xMinPriorSum) * c(x-MinPriorSum)\n\t\t dp[3] = prob(2) * c(1) + prob(1) * c(2) + prob(0) * c(3)\n\t\t dp[4] = prob(2) * c(2) + prob(1) * c(3) + prob(0) * c(4) , notice that xMaxPriorSum did not increase with x as x=k-1\n\t\t dp[5] = prob(2) * c(3) + prob(1) * c(4) ,xMinPriorSum increased as current draw value can\'t exceed 4\n\t\t dp[6] = prob(2) * c(4)\n\t\t dp[7] = 0\n20. dp[7] is not our sol(7). The sol(n) = sum(dp[3],..,dp[7])\n21. Remember c(x) = 1/w for all value of x. Therefore, the value of dp[x] can be derived from the value of dp[x-1]\n22. w=4, k=3, n=7\n\t\t dp[0]=1\n\t\t dp[1]= prob(0) /w\n\t\t dp[2] = (prob(1) + prob(0))/w , dp[x] = (prob(xMaxPriorSum)+ ... + prob(xMinPriorSum) )/w\n\t\t dp[3] = (prob(2) + prob(1) + prob(0)) /w \n\t\t dp[4] = (prob(2) + prob(1) + prob(0))/w , notice that xMaxPriorSum did not increase with x as x=k-1\n\t\t dp[5] = (prob(2) + prob(1) )/w ,xMinPriorSum increased as current draw value can\'t exceed 4\n\t\t dp[6] = prob(2) /w\n\t\t dp[7] = 0\n23. For each x the value of xMaxPriorSum and xMinPriorSum has to be adjusted if necessary and the value of ( prob(xMaxPriorSum)+....+ prob(xMinPriorSum) ) has to be dtermined. Lets call it dpSum. dpSum is then divied by w to get dp[x]\n25. remember ( prob(xMaxPriorSum)+....+ prob(xMinPriorSum) ) = dpSum . It\'s a variable, it changes with x. \n24. By leveraging dynamic programming dp[x] can be determined by the following way:\n\t\tadd dp[x-1] to the dpSum if x<k\n\t\tif x >= w, subtract dp[x-w] from dpSum\n dp[x] = dpSum/w\n\nThe code can be found here: https://leetcode.com/problems/new-21-game/discuss/132334/One-Pass-DP-O(N)\t\t \n\t\t \n\t \n\t | 4 | 0 | [] | 0 |
new-21-game | C++ bottom-up DP solution | c-bottom-up-dp-solution-by-ianchew-lgis | \nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n // Max score is K + W - 1 points.\n const int last_score = min(N, K + W | ianchew | NORMAL | 2020-05-02T22:32:39.402074+00:00 | 2020-05-02T22:32:39.402123+00:00 | 603 | false | ```\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n // Max score is K + W - 1 points.\n const int last_score = min(N, K + W - 1);\n // dp[n] is the probability that score n will be reached at some point.\n std::vector<double> dp(last_score + 2);\n // Since the game starts at score 0, dp[0] is 100%.\n dp[0] = 1.0;\n // dp[n] = sum(dp from n-W to n-1)/W, since we can reach score n by being\n // at score n-1 and drawing a 1, or being at score n-2 and drawing a 2, and\n // so on. The chance of being at score n-i and drawing an i is dp[n-i]/W.\n // However, if we\'ve stopped drawing, then we need to sum from n-W to K-1.\n // So properly, dp[n] = sum(dp from max(n-W, 0) to min(n-1, K))/W.\n \n // wsum, the windowed sum, is the sum or the last W elements, or properly\n // sum(dp from max(n-W, 0) to min(n-1, K)). The next element is wsum/W.\n double wsum = 0.0;\n \n for (int i=0; i <= last_score; ++i) { // Windowed.\n if (i < K) {\n // Only add to wsum if we\'re still drawing.\n wsum += dp[i];\n }\n if (i - W >= 0) {\n // Delete last element from window.\n wsum -= dp[i - W];\n }\n dp[i+1] = wsum/W;\n }\n \n // The final result is the sum of dp in range [K, N], since the set of\n // possible end scores are K to K + W - 1, (as such the sum of dp from K\n // to K + W - 1 should be 1.0 if we actually computed the whole vector) and\n // we\'re looking for the chance of ending up with a score below or equal to N.\n // Therefore, the chance of getting N or less points is the chance of ending\n // at K (dp[K]), plus the chance of ending at K+1, and so on up to N.\n return std::accumulate(dp.begin()+K, dp.begin()+N+1, 0.0);\n }\n};\n``` | 4 | 0 | ['Dynamic Programming', 'C'] | 0 |
new-21-game | Simple C++ solution using DP (tabulation) method | simple-c-solution-using-dp-tabulation-me-kkkp | Intuition\nThe intuition behind this solution is to use dynamic programming to calculate the probabilities of achieving different scores in the New 21 Game. The | priyam05soni | NORMAL | 2023-05-25T06:41:50.228381+00:00 | 2023-05-25T06:41:50.228403+00:00 | 658 | false | # Intuition\nThe intuition behind this solution is to use dynamic programming to calculate the probabilities of achieving different scores in the New 21 Game. The algorithm iteratively calculates the probabilities and keeps track of the cumulative sum.\n\n# Approach\n- The game has three parameters: \'n\' represents the maximum total points that can be obtained, \'k\' is the target score to reach or exceed, and \'maxPts\' is the maximum number of points that can be drawn in a single turn.\n\n- If \'k\' is zero or if \'n\' is greater than or equal to \'k + maxPts\', it means we can achieve the target score \'k\' or higher with certainty. In this case, we return 1.0, indicating a 100% chance of winning.\n\n- We create a dynamic programming array \'dp\' of size \'n + 1\'. Each element \'dp[i]\' represents the probability of getting \'i\' points.\n\n- We initialize \'currSum\' to 1.0, representing the probability of starting with 0 points. \'ans\' is initialized to 0.0, which will store the final answer.\n\n- We set \'dp[0]\' to 1.0 because the probability of starting with 0 points is 100%.\n\n- We iterate from 1 to \'n\' and calculate the probability for each \'i\':\n\n a. \'dp[i]\' is set to \'currSum\' divided by \'maxPts\'. This represents the probability of getting \'i\' points in the current turn.\n\n b. If \'i\' is less than \'k\', we update \'currSum\' by adding \'dp[i]\'. This accounts for the current turn\'s points and adds it to the cumulative sum.\n\n c. If \'i\' is greater than or equal to \'k\', we add \'dp[i]\' to \'ans\'. This keeps track of the probability of achieving \'k\' or more points.\n\n d. If the index \'i - maxPts\' is greater than or equal to 0, it means that the \'maxPts\' points drawn \'maxPts\' turns ago are no longer in play. So, we subtract \'dp[i - maxPts]\' from \'currSum\' to update the cumulative sum accordingly.\n\n- After the iteration, \'ans\' will contain the probability of reaching or exceeding the target score \'k\' with the given constraints.\n\n- Finally, we return \'ans\', which represents the probability of winning the New 21 Game.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is O(n), where n is the maximum total points that can be obtained.\n\n- Space complexity:\nThe space complexity of this solution is O(n).\ndyn\n\n\n\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n vector<double> dp(n + 1);\n double currSum = 1.0;\n double ans = 0.0;\n\n dp[0] = 1.0;\n\n for (int i = 1; i < n+1; i++) {\n\n dp[i] = currSum / maxPts;\n\n if (i < k) \n currSum += dp[i];\n\n else \n ans += dp[i];\n \n if (i - maxPts >= 0) \n currSum -= dp[i - maxPts];\n \n }\n\n return ans;\n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'C++'] | 0 |
new-21-game | [ C++ ] [ Dynamic Programming ] [ Commented Solution ] | c-dynamic-programming-commented-solution-lso5 | Code\n\nclass Solution {\n public:\n double new21Game(int n, int k, int maxPts) {\n // When the game ends, the point is in [k..k - 1 + maxPts]\n // P = | Sosuke23 | NORMAL | 2023-05-25T02:05:10.516572+00:00 | 2023-05-25T02:05:10.516601+00:00 | 1,236 | false | # Code\n```\nclass Solution {\n public:\n double new21Game(int n, int k, int maxPts) {\n // When the game ends, the point is in [k..k - 1 + maxPts]\n // P = 1, if n >= k - 1 + maxPts\n // P = 0, if n < k (note the constraints already have k <= n)\n if (k == 0 || n >= k - 1 + maxPts)\n return 1.0;\n\n double ans = 0.0;\n vector<double> dp(n + 1); // dp[i] := prob to have i points\n dp[0] = 1.0;\n double windowSum = dp[0]; // P(i - 1) + P(i - 2) + ... + P(i - maxPts)\n\n for (int i = 1; i <= n; ++i) {\n // The prob to get point i is\n // P(i) = [P(i - 1) + P(i - 2) + ... + P(i - maxPts)] / maxPts\n dp[i] = windowSum / maxPts;\n if (i < k)\n windowSum += dp[i];\n else // The game ends\n ans += dp[i];\n if (i - maxPts >= 0)\n windowSum -= dp[i - maxPts];\n }\n\n return ans;\n }\n};\n\n``` | 3 | 0 | ['C++'] | 0 |
new-21-game | Can anyone help me explain my TLE code with memorization? | can-anyone-help-me-explain-my-tle-code-w-u1ba | I just use a map to store each K and corresponding probability.\nEach time I try a num in range[1,W]\nI think in this way, no duplicate dfs will be calculated a | codoge1 | NORMAL | 2018-05-20T04:12:49.713971+00:00 | 2018-10-03T13:41:17.171538+00:00 | 606 | false | I just use a map to store each K and corresponding probability.\nEach time I try a num in range[1,W]\nI think in this way, no duplicate dfs will be calculated and it should be similar to dp solution.\nCan anyone tell how this can be slower than dp...? It cannot pass all the test cases.\n\nclass Solution {\n Map<Integer, Double> map; //record K\n public double new21Game(int N, int K, int W) {\n map = new HashMap<>();\n return dfs(N, K, W);\n }\n \n public double dfs(int N, int K, int W) {\n if (map.containsKey(K)) {\n return map.get(K);\n }\n if (K <= 0) {\n if (N >= 0) {\n return 1.0;\n }\n return 0.0;\n }\n double p = 0.0;\n for (int i = W; i >= 1; i--) {\n p = p + dfs(N - i, K - i, W) / W;\n }\n map.put(K, p);\n return p;\n }\n}\n | 3 | 0 | [] | 2 |
new-21-game | Naive DFS to Sliding Window step by step intuitive conversion giving O(k+m) TC | naive-dfs-to-sliding-window-step-by-step-6umk | This problem can be naively solved using a DFS DP solution:\n\nclass Solution:\n def new21Game(self, n: int, k: int, m: int) -> float:\n @cache\n | boriswilliams | NORMAL | 2024-08-18T16:11:37.048062+00:00 | 2024-08-19T10:50:40.646641+00:00 | 40 | false | This problem can be naively solved using a DFS DP solution:\n```\nclass Solution:\n def new21Game(self, n: int, k: int, m: int) -> float:\n @cache\n def f(p):\n if p >= k:\n return 1 if p <= n else 0\n return sum(f(p+i) for i in range(1, m+1))/m\n return f(0)\n```\nIt can then be converted into a DP array solution:\n```\nclass Solution:\n def new21Game(self, n: int, k: int, m: int) -> float:\n dp = [1]*(k+m)\n for i in range(k+m-1, n, -1):\n dp[i] = 0\n for i in range(k-1, -1, -1):\n dp[i] = sum(dp[i+1:i+m+1])/m\n return dp[0]\n```\nWe can now see there is opportunity to optimise our solution using the Sliding Window pattern:\n```\nclass Solution:\n def new21Game(self, n: int, k: int, m: int) -> float:\n dp = [1]*(k+m)\n for i in range(k+m-1, n, -1):\n dp[i] = 0\n x = sum(dp[k:k+m])\n for i in range(k-1, -1, -1):\n dp[i] = x/m\n x += dp[i] - dp[i+m]\n return dp[0]\n```\nTime complexity: worst case: $$O(k+m)$$\nSpace complexity: $$O(k+m)$$ | 2 | 0 | ['Python3'] | 0 |
new-21-game | [Simple] Beat 100% + explanation | simple-beat-100-explanation-by-aleclc-knh2 | \n\nclass Solution:\n # In each draw, prob is based on last maxPts draws\n # So we can use a sliding window starting at 1..=maxPts\n def new21Game(self | AlecLC | NORMAL | 2023-07-28T20:40:15.571831+00:00 | 2023-07-28T21:06:20.115837+00:00 | 49 | false | \n```\nclass Solution:\n # In each draw, prob is based on last maxPts draws\n # So we can use a sliding window starting at 1..=maxPts\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if not k:\n return 1\n\n # dp[i] = probability of getting i points at any point in the game\n dp = [0.0] * (n+1)\n dp[0] = 1\n\n # cumulative probability of all states that can reach i \u2014 starts at 1 bc dp[0]=1\n # represents the sum of a sliding window\n prob_of_previous_states = 1\n\n for i in range(1, n+1):\n # prob of drawing num = sum_allprevs(prob of reaching prev state + 1/maxpts)\n # = prob of all prev states * 1/maxPts\n dp[i] = prob_of_previous_states / maxPts\n\n # if A continues drawing, we add the current entry to the cumulative sum\n if i < k:\n prob_of_previous_states += dp[i]\n\n # If A continues drawing, we subtract the out of range entry from the cumulative sum\n # This is because that entry cannot reach the next value\n if 0 <= i - maxPts < k:\n prob_of_previous_states -= dp[i - maxPts]\n\n\n # we want the probability that the final score is n or fewer\n # because she stops drawing at k, this is equivalent to the probability that the final score is in [k, n]\n # in other words, we want sum(dp[i]) | k \u2264 i \u2264 n\n # dp is already upper bounded by n, so sum(dp[k:]) is our answer\n return sum(dp[k:])\n```\n | 2 | 0 | ['Dynamic Programming', 'Sliding Window', 'Python3'] | 0 |
new-21-game | New 21 Game || C++ || DP || DSA | new-21-game-c-dp-dsa-by-rajivraj841311-m0w2 | Intuition\n Describe your first thoughts on how to solve this problem. \n Concept of Dynamic programming is used to solve this problem.\n\n# Approach\n Describe | rajivraj841311 | NORMAL | 2023-05-25T17:53:24.973208+00:00 | 2023-05-25T17:53:24.973249+00:00 | 294 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n* Concept of Dynamic programming is used to solve this problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n* O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n* O(N)\n\n# Code\n```\nclass Solution {\n public:\n double new21Game(int n, int k, int maxPts) {\n // When the game ends, the point is in [k..k - 1 + maxPts]\n // P = 1, if n >= k - 1 + maxPts\n // P = 0, if n < k (note the constraints already have k <= n)\n if (k == 0 || n >= k - 1 + maxPts)\n return 1.0;\n\n double answer = 0.0;\n vector<double> dp(n + 1); // dp[i] := prob to have i points\n dp[0] = 1.0;\n double windowSum = dp[0]; // P(i - 1) + P(i - 2) + ... + P(i - maxPts)\n\n for (int i = 1; i <= n; ++i) {\n // The prob to get point i is\n // P(i) = [P(i - 1) + P(i - 2) + ... + P(i - maxPts)] / maxPts\n dp[i] = windowSum / maxPts;\n if (i < k)\n windowSum += dp[i];\n else // The game ends\n answer += dp[i];\n if (i - maxPts >= 0)\n windowSum -= dp[i - maxPts];\n }\n\n return answer;\n }\n};\n\n``` | 2 | 0 | ['C++'] | 0 |
new-21-game | Give it 2 hours . TRY it yourself for logic building from scratch ! ✔🐱🏍🙌 | give-it-2-hours-try-it-yourself-for-logi-pcnv | Intuition\n##### Build-up for the game :-\n\nIn this game, Alice starts with 0 points and draws numbers randomly. She wants to know the chance of having n or fe | Ayush_Singh_610 | NORMAL | 2023-05-25T17:24:04.012304+00:00 | 2023-05-25T17:24:04.012344+00:00 | 280 | false | # Intuition\n##### Build-up for the game :-\n\nIn this game, Alice starts with 0 points and draws numbers randomly. She wants to know the chance of having `n` or fewer points at the end.\n\nTo figure this out, we can use a trick called "counting." We start counting from 0 and keep track of the chance of having each number of points. \n\nWe use a list to remember the chances. At the beginning, the chance of having 0 points is 100% or 1.0. Then we look at the next number, 1, and think about how we can get there. We can get to 1 point by drawing a number from 1 to `maxPts`. We calculate the chances of each of those possibilities and add them up. \n\nNext, we move on to the number 2 and do the same thing. We consider all the ways to get to 2 points, based on the chances we already calculated for the previous numbers.\n\nWe keep doing this for each number up to `n`, using the chances we already know to figure out the chances for the next number.\n\nFinally, we add up all the chances from `k` to `n` to find the overall chance of having `n` or fewer points.\n\nSo, in simple terms, we\'re just counting and keeping track of the chances of having different numbers of points. We use the chances we already calculated to find the chances for the next numbers. By adding up all the chances, we get the answer Alice is looking for.\n\n----\n##### More Intuition in technical terms now :- \n\nIn this game, Alice starts with 0 points and draws numbers randomly until she reaches a certain number of points called `k`. We want to know the probability of Alice having `n` or fewer points at the end of the game.\n\nTo solve this problem, we can use a technique called Dynamic Programming, or DP for short. DP is like a special way of solving problems where we break down a big problem into smaller, easier-to-solve subproblems.\n\nIn this case, we can think of the problem like a puzzle. We start with the smallest subproblem: what is the probability of having 0 points? Since Alice starts with 0 points, the probability is 100% or 1.0.\n\nThen, we move on to the next subproblem: what is the probability of having 1 point? To solve this, we look at all the ways Alice can get 1 point. She can draw a number from 1 to `maxPts`, so we need to consider all those possibilities and calculate the probabilities. Once we know the probabilities of having 0 and 1 point, we can calculate the probability of having 2 points by adding up the probabilities of getting to 2 from the previous points (0 and 1).\n\nWe keep doing this for all the points up to `n`. Each time, we use the probabilities we already calculated for the previous points to calculate the probability for the current point. This is why we use a list or array called `dp` to store the probabilities. `dp` stands for "dynamic programming".\n\nBy building up the probabilities step by step, using the probabilities we already know, we can finally find the probability of having `n` or fewer points.\n\nSo, in summary, we use dynamic programming (DP) to solve this problem because it helps us break down the big problem into smaller, easier-to-solve subproblems. We calculate the probabilities for each point by using the probabilities we already calculated for the previous points. This way, we can find the final probability we\'re looking for.\n\n----\n##### Maths :-\n\nCertainly! Let\'s denote the probability that Alice has exactly `i` points as `P[i]`. We want to calculate the probability that Alice has `n` or fewer points, which can be expressed as:\n\n> P(n) = P[0] + P[1] + P[2] + ... + P[n]\n\nTo calculate `P[i]`, we can use dynamic programming and break it down into subproblems. Here\'s the recursive equation:\n\n> P[i] = (P[i-1] + P[i-2] + ... + P[i-maxPts]) / maxPts\n\nThe above equation states that the probability of having `i` points is equal to the sum of probabilities of reaching the current point from the previous `maxPts` points, divided by `maxPts`. This is because in each draw, Alice gains an integer number of points randomly from the range [1, maxPts] with equal probabilities.\n\nTo calculate `P[i]`, we iterate from 1 to `n` and use the above equation to fill in the probabilities in a dynamic programming array or list. We initialize `P[0] = 1` since Alice starts with 0 points. Then, we calculate `P[1]` using the equation, followed by `P[2]`, and so on, until we reach `P[n]`. Finally, we sum up the probabilities from `P[k]` to `P[n]` to obtain the desired probability.\n\nBy using dynamic programming, we avoid recalculating the same probabilities multiple times, leading to an efficient solution to the problem.\n\n----\n##### Intuition for the code :-\nThe given code calculates the probability that Alice will have `n` or fewer points in the game, where Alice starts with 0 points and draws numbers randomly until she reaches `k` or more points.\n\nHere\'s the intuition behind the code:\n\n1. First, the code checks for a special case where `k` is 0 or `n` is greater than or equal to `k + maxPts`. In these cases, it means that Alice is guaranteed to have `n` or fewer points, so the probability is 1.0. The code returns 1.0 in these cases.\n\n2. If the special cases don\'t apply, the code proceeds to calculate the probability using dynamic programming.\n\n3. A list `dp` is initialized with `n + 1` elements, representing the probabilities of having each number of points from 0 to `n`. All elements are initially set to 0.0, except for `dp[0]`, which is set to 1.0 since Alice starts with 0 points.\n\n4. The loop iterates from 1 to `n`, and for each index `i`, it calculates the probability `dp[i]` of having `i` or fewer points.\n\n5. The probability `dp[i]` is calculated by summing the probabilities of getting to `i` from the previous points. The probability of getting to `i` is equal to the sum of the probabilities of getting to `i - 1`, `i - 2`, ..., `i - maxPts`, divided by `maxPts`.\n\n6. The variable `_sum` is used to keep track of the cumulative sum of probabilities. It is initialized to 1.0 since `dp[0] = 1.0`.\n\n7. Within the loop, if `i` is less than `k`, the current probability `dp[i]` is added to `_sum` to update the cumulative sum.\n\n8. If `i - maxPts` is greater than or equal to 0, it means that the window of the previous `maxPts` probabilities has shifted, so the probability at `i - maxPts` is subtracted from `_sum` to keep the sliding window of size `maxPts` in the cumulative sum.\n\n9. After the loop, the final probability of winning is calculated by summing the probabilities starting from index `k` to the end of the list (`sum(dp[k:])`) since Alice stops drawing numbers when she reaches `k` or more points.\n\nThe code uses dynamic programming to efficiently calculate the probabilities by reusing the results of previous calculations. By iterating through the indices and updating the probabilities based on the previous results, it builds up the probability distribution for the desired range of points. \n\n# Approach\n\nIn this version, the circular buffer is replaced with a simple list `dp`, which stores the probabilities.\n\nHere\'s an explanation of the changes:\n\n1. The `if` condition `n >= k + maxPts` is used to determine whether the probability of winning is guaranteed to be 1. If true, the function directly returns 1.0.\n\n2. Instead of using a circular buffer, a regular list `dp` of size `n + 1` is initialized with all elements set to 0.0. The element `dp[0]` is set to 1.0 to represent the initial probability.\n\n3. The variable `_sum` is used to keep track of the cumulative sum of probabilities. It is initialized to 1.0.\n\n4. The loop iterates from 1 to `n`, and at each iteration, the probability for the current index `i` is calculated as `_sum / maxPts`. The `_sum` is divided by `maxPts` because there are `maxPts` possible outcomes, each with an equal probability of occurring.\n\n5. If `i` is less than `k`, the current probability `dp[i]` is added to `_sum` to update the cumulative sum.\n\n6. If `i - maxPts` is greater than or equal to 0, the probability `dp[i - maxPts]` is subtracted from `_sum` to keep the sliding window of size `maxPts` in the cumulative sum.\n\n7. After the loop, the final probability of winning is calculated by summing the probabilities starting from index `k` to the end of the list (`sum(dp[k:])`) and returned.\n\nThis version eliminates the need for a circular buffer and simplifies the code while maintaining efficiency.\n\n# Complexity\n- **Time complexity** : $$O(n)$$, here n is the value given as input.\n- **Space complexity** : $$O(n)$$, w here n is the value given as input. This is because the code uses a list `dp` of size `n + 1` to store the probabilities for each number of points from 0 to n.\n\nThe loop that iterates from 1 to n has a time complexity of $$O(n)$$. Within the loop, the calculations involve accessing elements of the `dp` list, which has a constant time complexity. Overall, the time complexity of the code is determined by the loop, resulting in $$O(n)$$.\n\nSimilarly, the space complexity is determined by the `dp` list, which has a size of n + 1. Therefore, the space complexity of the code is $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n \'\'\'\n if k == 0 or n >= k + maxPts:\n return 1\n \n windowSum = 1\n probability = 0\n \n dp = [0] * (n + 1)\n dp[0] = 1\n \n for i in range(1, n + 1):\n dp[i] = windowSum / maxPts\n \n if i < k:\n windowSum += dp[i]\n else:\n probability += dp[i]\n \n if i >= maxPts:\n windowSum -= dp[i - maxPts]\n \n return probability\n \'\'\'\n\n# MLE\n\'\'\'\nclass CircularBuffer:\n def __init__(self, min_size):\n self.data = [None] * (1 << self.bit_len(min_size))\n self.mask = len(self.data) - 1\n\n @staticmethod\n def bit_len(min_size):\n return 32 - min_size.bit_length()\n\n def __getitem__(self, index):\n return self.data[index & self.mask]\n\n def __setitem__(self, index, value):\n self.data[index & self.mask] = value\n\n def capacity(self):\n return len(self.data)\n\n def get_mask(self):\n return self.mask\n\nclass Solution:\n def new21Game(self, n, k, maxPts):\n if k == 0 or n - k + 1 >= maxPts:\n return 1.0\n\n kFactor = 1.0 / maxPts\n if maxPts + 1 >= n:\n return pow(1 + kFactor, k - 1) / maxPts * (n - k + 1)\n\n dp = CircularBuffer(maxPts + 1)\n dp[0] = 1.0\n _sum = 1.0\n for i in range(1, k):\n dp[i] = _sum * kFactor\n _sum += dp[i] - dp[i - maxPts]\n\n answer = 0.0\n for i in range(k, n + 1):\n answer += _sum * kFactor\n _sum -= dp[i - maxPts]\n\n return answer\n\'\'\'\n\n# Efficient Solution:-\nclass Solution:\n def new21Game(self, n, k, maxPts):\n if k == 0 or n >= k + maxPts:\n return 1.0\n\n dp = [0.0] * (n + 1)\n dp[0] = 1.0\n _sum = 1.0\n for i in range(1, n + 1):\n dp[i] = _sum / maxPts\n if i < k:\n _sum += dp[i]\n if i - maxPts >= 0:\n _sum -= dp[i - maxPts]\n\n return sum(dp[k:])\n\n``` | 2 | 1 | ['Math', 'Dynamic Programming', 'Sliding Window', 'Probability and Statistics', 'Python3'] | 0 |
new-21-game | Mathematical Intuition (Very Easy) || O(N) Time Complexity || O(N) Space Complexity | mathematical-intuition-very-easy-on-time-8vuw | Mathematical Intuition\n Describe your first thoughts on how to solve this problem. \nSince we can draw a number $a_i \leq maxPts$ any number of time before get | psycho0_0 | NORMAL | 2023-05-25T14:10:59.779359+00:00 | 2023-05-25T14:27:37.209378+00:00 | 446 | false | # Mathematical Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince we can draw a number $a_i \\leq maxPts$ any number of time before getting $k \\leq \\sum_{i=1}^{N} a_i \\leq n $. We can reframe the problem in the following way: \nGiven list of numbers $a_i$ where $ 1 \\leq a_i \\leq maxPts $ where $i \\in Z+$ . We want to find sum of $P(\\sum_{i=1}^{N} a_i = K)$ where k <=K <= n. [ note: N is not contrained here]. \n \nWe can write $P(\\sum_{i=1}^{N} a_i = K) = \\sum_{z=1}^{maxpts} P(\\sum_{i=1}^{N-1} a_i = K-z) P(a_N = z)$ where for K-z < 0 probability is also zero.\n\nWe know that $P(a_N = Z) = 1/maxPts$ [$\\because$ all values are equiprobable] so $P(\\sum_{i=1}^{N} a_i = K) = 1/maxPts * \\sum_{z=1}^{maxpts} P(\\sum_{i=1}^{N-1} a_i = K-z)$\nSince N is not contrained here So we will omit N from equation and focus on probability where sum of any number of integers is equal to K so $dp[K] = P(\\sum_{i} a_i = K)$ \n\nWe can write above equation as $dp[k] = 1/maxpts * \\sum_{z=1}^{maxpts} dp[K-z]$. Here dp[K-z] = 0 if K-z < 0 or K-z > k \n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to simply code the last equation and sum the probabilities from k to n in \'dp\' array. Now the problem can be solved using dp.\n# Complexity\n- Time complexity: O(n) if we use sliding window to compute the sum $\\sum_{z=1}^{maxpts} dp[K-z]$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n /**** MATHS *******/\n // Given k <= \\sum_{i=1}^{N} a_i <= n [ note: N is not contrained here]\n // We want to find P(\\sum_{i=1}^{N} a_i = K) where k <=K <= n\n \n // Now we can write P(\\sum_{i=1}^{N} a_i = K) = \\sum_{z=1}^{maxpts} P(\\sum_{i=1}^{N-1} a_i = K-z) P(a_N = z)\n\n // We know that P(a_N = Z) = 1/maxPts [all values are equiprobable]\n\n // so P(\\sum_{i=1}^{N} a_i = K) = 1/maxPts * \\sum_{z=1}^{maxpts} P(\\sum_{i=1}^{N} a_i = K-z)\n // Since N is not contrained here So we will consider N = inf which will cover all the probability where sum of any number of integers is equal to K\n\n // so dp[K] = P(\\sum_{i} a_i = K) \n\n // We can write above equation as dp[k] = 1/maxpts * \\sum_{z=1}^{maxpts} dp[K-z]\n // Here dp[K-z] = 0 if K-z < 0 or K-z > k \n\n double dp[] = new double[n+1];\n dp[0]=1.0;\n double windowSum = 0;\n for(int i=1;i<=n;i++){\n /** Commented code is bit slow. We can implement the same using sliding window as well */\n // for(int j = Math.max(0,i-maxPts);j<Math.min(i,k);j++){\n // dp[i] += dp[j];\n // }\n // dp[i] /=maxPts;\n if(i-1 < k){\n windowSum += dp[i-1];\n }\n if(i-maxPts-1>=0 && i-maxPts-1 < k ){\n windowSum -= dp[i-maxPts-1];\n }\n dp[i] = windowSum/maxPts;\n }\n double sum=0;\n for(int i=k;i<=n;i++){\n sum+=dp[i];\n }\n return sum;\n }\n}\n``` | 2 | 0 | ['Math', 'Dynamic Programming', 'Sliding Window', 'Java'] | 0 |
new-21-game | C++||DP||Sliding window || Beats 100%||Most Optimized | cdpsliding-window-beats-100most-optimize-aam7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | coder_shailesh411 | NORMAL | 2023-05-25T08:35:27.085074+00:00 | 2023-05-25T08:35:27.085105+00:00 | 575 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if(k==0 || n>=k+maxPts)return 1.0;\n\n vector<double>dp(n+1);\n dp[0]=1.0;\n\n double currsum=1.0;\n double ans=0.0;\n for(int i=1;i<n+1;i++){\n dp[i]=currsum/maxPts;\n if(i<k){\n currsum += dp[i];\n }else ans+= dp[i];\n\n if(i>=maxPts){\n currsum-= dp[i-maxPts];\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Sliding Window', 'C++'] | 0 |
new-21-game | DP of O(n) | dp-of-on-by-xatcher-rclc | Intuition\nUsing probability and sliding window with DP\n\n# Approach\nWithin code\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# C | xatcher | NORMAL | 2023-05-25T05:42:41.603769+00:00 | 2023-05-25T05:42:41.603812+00:00 | 247 | false | # Intuition\nUsing probability and sliding window with DP\n\n# Approach\nWithin code\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int N, int K, int maxPts) {\n // Corner cases\n if (K == 0) return 1.0;\n if (N >= K-1 + maxPts) return 1.0;\n\n // dp[i] is the probability of getting point i.\n vector<double> dp(N + 1, 0.0);\n\n double probability = 0.0; // dp of N or less points.\n double windowSum = 1.0; // Sliding required window sum\n dp[0] = 1.0;\n for (int i = 1; i <= N; i++) {\n dp[i] = windowSum / maxPts;\n //probability of getting ith point is more than i/max as we have more than on draws to get points and we are taking sum of all the previous probabilities to add as the new chances then dibide total by max\n\n if(i < K) windowSum += dp[i];\n else probability += dp[i];\n \n if(i >= maxPts) windowSum -= dp[i - maxPts];\n }\n\n return probability;\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Sliding Window', 'Probability and Statistics', 'C++'] | 0 |
new-21-game | Easy and simple solution in JavaScript. Almost like editorial but in JS :) | easy-and-simple-solution-in-javascript-a-rczz | Please upvote\n# Code\n\n/**\n * @param {number} n\n * @param {number} k\n * @param {number} maxPts\n * @return {number}\n */\n function new21Game(n, k, maxP | AzamatAbduvohidov | NORMAL | 2023-05-25T04:16:13.414747+00:00 | 2023-05-25T04:16:13.414778+00:00 | 1,166 | false | # Please upvote\n# Code\n```\n/**\n * @param {number} n\n * @param {number} k\n * @param {number} maxPts\n * @return {number}\n */\n function new21Game(n, k, maxPts) {\n let dp = new Array(n+1);\n dp[0] = 1;\n s = k > 0 ? 1 : 0;\n for (let i = 1; i <= n; i++) {\n dp[i] = s / maxPts;\n if (i < k) {\n s += dp[i];\n }\n if (i - maxPts >= 0 && i - maxPts < k) {\n s -= dp[i - maxPts];\n }\n }\n let ans = 0;\n for (let i = k; i <= n; i++) {\n ans += dp[i];\n }\n return ans;\n }\n``` | 2 | 0 | ['JavaScript'] | 0 |
new-21-game | Easy & More Optimized JavaScript Solution Using Dynamic Programming | easy-more-optimized-javascript-solution-igx5e | Time complexity:\n Add your time complexity here, e.g. O(n) \n O(n)\n\n# Space complexity:\n Add your space complexity here, e.g. O(n) \n O(n)\n\n# Code\n | RockstarPabitra | NORMAL | 2023-05-25T02:50:23.712441+00:00 | 2023-05-25T02:50:23.712492+00:00 | 307 | false | # Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n# Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n# Code\n```\n/**\n * @param {number} n\n * @param {number} k\n * @param {number} maxPts\n * @return {number}\n */\nvar new21Game = function(n, k, maxPts) {\n if (k == 0 || n >= k + maxPts) return 1.0;\n let sum = 1.0;\n let result = 0.0;\n let dp = new Array(n + 1);\n dp[0] = 1.0;\n for (let i = 1; i <= n; i++) {\n dp[i] = sum / maxPts;\n if (i < k) sum += dp[i];\n else result += dp[i];\n if (i - maxPts >= 0) sum -= dp[i - maxPts];\n }\n return result;\n};\n``` | 2 | 0 | ['Math', 'Dynamic Programming', 'Sliding Window', 'Probability and Statistics', 'JavaScript'] | 0 |
new-21-game | [Ruby] Reverse solution, with image examplanation step by step | ruby-reverse-solution-with-image-exampla-45jp | Intuition\n\nSupposing $n = 5, k = 4, maxPts = 5$.\n\nwe use an array result[] to represent:\n\n\n result[x] := The probability that we finally have less or eq | hegwin | NORMAL | 2023-01-15T17:18:44.541510+00:00 | 2023-01-15T17:19:44.366034+00:00 | 142 | false | # Intuition\n\nSupposing $n = 5, k = 4, maxPts = 5$.\n\nwe use an array `result[]` to represent:\n\n```\n result[x] := The probability that we finally have less or equal than n points \n when we currently have x points in hand\n and we draw cards till we have k points\n```\n\nBy that definition:\n 1. When we have $4$ points, we can not draw any more, and the probability having less or equal than $5$ points is $1.0$\n 2. When we have $5$ points, we can not draw any more, and the probability having less or equal than $5$ points is $1.0$\n 3. When we have $6$ points, we can not draw any more, and the probability having less or equal than $5$ points is $0.0$\n 4. ...\n\nLet\'s puts this in the image below:\n\n\n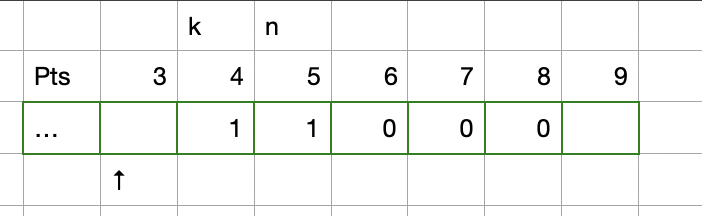\n\nWhat will happen when we have 3 points in hand?\n\n1. We have $1/5$ probability to get 1 point and reach $4$;\n2. We have $1/5$ probability to get 2 points and reach $5$;\n3. We have $1/5$ probability to get `3/4/5` points and reach `6/7/8`, but already goes over 5;\n\nBy this we get:\n\n$$\nresult[3] = \\frac{1}{5} \\times result[4] + \\frac{1}{5} \\times result[5] + ... + \\frac{1}{5} \\times result[8]\n\n= \\frac{1}{5} \\times (result[4]+result[5]+ result[6] + result[7] + result[8])\n$$\n\n```\nresult[3] = 0.4\n```\n\n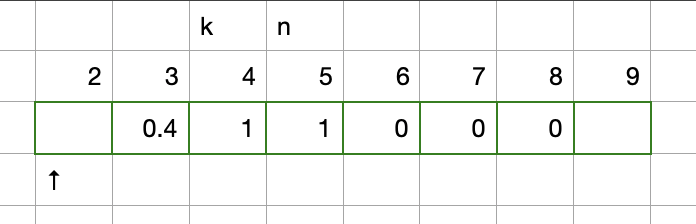\n\nThen let\'s have look at `result[2]`:\n\n1. We have `1/5` chance to to 3 (calculated in previous step);\n2. We have `1/5` chance to go to either 4 or 5 (got by definition);\n3. We have `1/5` chance to go to either 6 or 7 (got by definition);\n\n$$\nresult[2] = \\frac{1}{5} \\times (result[3]+result[4]+ result[5] + result[6] + result[7])\n$$\n\n```\nresult[2] = 0.48\n```\n\nAnd loop until we get to result[0]:\n\n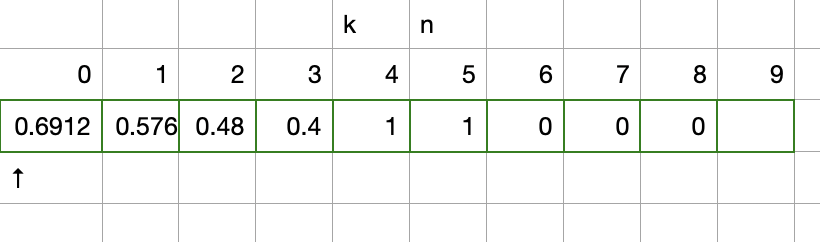\n\nAs we\'ve defined, `result[0]` represents *the probability we will have less than or equal to n points when we have 0 points in hand, we continue drawing until we have at least k points*.\n\nThat\'s the answer.\n\n\n# Complexity\n- Time complexity: $$O(k+n)$$\n\n- Space complexity: $$O(k+maxPts)$$\n\n# Code\n```\n# @param {Integer} n\n# @param {Integer} k\n# @param {Integer} max_pts\n# @return {Float}\ndef new21_game(n, k, max_pts)\n return 1 if k - 1 + max_pts <= n # We can never reach n when we stop at k\n\n result = Array.new(k + max_pts, 0.0)\n\n k.upto(n) do |i|\n result[i] = 1\n end\n\n sum = result[k...(k+max_pts)].sum\n\n (k-1).downto(0) do |i|\n result[i] = sum / max_pts\n sum += result[i] - result[i+max_pts]\n end\n\n result[0]\nend\n``` | 2 | 0 | ['Math', 'Dynamic Programming', 'Sliding Window', 'Ruby'] | 1 |
new-21-game | DP and Probability || Explaination || ✔ | dp-and-probability-explaination-by-athar-kkhx | -> Solution is inspired from https://leetcode.com/problems/new-21-game/discuss/132334/One-Pass-DP-O(N) and https://leetcode.com/problems/new-21-game/discuss/228 | athar_mohammad | NORMAL | 2022-08-05T13:48:20.421624+00:00 | 2022-08-05T14:09:18.235643+00:00 | 543 | false | -> Solution is inspired from https://leetcode.com/problems/new-21-game/discuss/132334/One-Pass-DP-O(N) and https://leetcode.com/problems/new-21-game/discuss/228406/Logical-Thinkingsolution \n```\nclass Solution {\n \npublic:\n double new21Game(int n, int k, int maxPts) {\n if(n >= k+maxPts || k == 0)return 1;\n vector<double>dp(n+1);\n dp[0] = 1.0;\n double ans = 0,window_sum = 1;\n // prob(i) = prob(i-maxpts)*1/maxpts + prob(i-maxpts+1)*1/(maxpts+1) + ...\n // since we can only draw a number from 1 to maxpts so to get i points we first reach i-maxpts or i-maxpts+1 or ...\n // after that we draw some number between 1 to maxpts which would have prob of 1/maxpts \n // now this formula can be tranformed into a formula with sum as\n // prob(i) = (prob(i-maxpts)+prob(i-maxpts+1)+...)/maxpts\n // so we can maintain probabilty sum of the window and start adding probabilty for number between k and n as \n // probabilty of numbers less than k can only be used for window_sum and we will not be adding probability of \n // points that are greater than equal to k as we would stop there we would only be adding their probabily using \n // the probability of all points less than i and inside the window of maxpts\n for(int i = 1; i<=n;i++){\n dp[i] = (window_sum/(double)maxPts);\n if(i < k)window_sum+=dp[i];\n else ans += dp[i];\n if(i >= maxPts)window_sum -= dp[i-maxPts];\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Dynamic Programming'] | 0 |
new-21-game | DP solution with Go (and explanation) | dp-solution-with-go-and-explanation-by-m-4qru | Let\'s take n = 21, k = 17, maxPts = 10 as an example\n\nThe finish state would be from 17 to 26 (as 16 will continue, and maximum draw will be 10)\n\nIf you\'r | marc000 | NORMAL | 2022-03-04T07:55:52.390650+00:00 | 2022-03-27T17:33:25.610358+00:00 | 211 | false | Let\'s take n = 21, k = 17, maxPts = 10 as an example\n\nThe finish state would be from 17 to 26 (as 16 will continue, and maximum draw will be 10)\n\nIf you\'re currently in 16, what\'s the probability your final result less than n (21)? \nIt should be 0.5, as you can draw 1,2,3,4,5. So, 5 / 10 = 0.5 as P(16)\n\nIf you\'re currently in 15, what\'s the probability your final result less than n (21)? \nit\'s when you draw 1 and then draw again and final result less than 21 which is the question above)\n when you draw 2, 3, 4, 5, 6\nP(15) = 1/10 * P(16) + 1/10 * P(17) + 1/10 * P(18) ... + 1/10 * P(21) \n(P(17) to P(21) are all equal to 1 )\n\nSo the generalization\nP(i) is the probably that you\'re currently with i points, and your final result less than n\nP(i) = 1/maxPts * ( P(i+1) + P(i+2) ... + P(i + maxPts) )\n\nWe start from P(k) and compute all the way to P(0) and P(0) is your answer\n\nwe need P[k + maxPts] size at most\nand in computation for P(i), we need Sum(P(i+1) to P(i+maxPts)), so we maintain\na sum. \n\nIn each iteration: \nP(i) = Sum / maxPts\nSum -= P(i+maxPts) // pop last element \nSum += P(i)\n\nThe Implementation\n```\nfunc new21Game(n int, k int, maxPts int) float64 {\n // if n is big, then from dp[k] to dp[k-1+maxPts] should be 1, rest are zero \n // if maxPts is big, then from dp[k] to dp[n] will be 1, rest are zero \n // we don\'t need to record zeros\n dp := make([]float64, min(n + 1, k + maxPts))\n \n // dp[i] = 1/maxPts * (dp[i+1] + dp[i+2] + dp[i+3] ... dp[i+maxPts])\n // so we maintain sum = dp[i+1] ... dp[i+maxPts]\n sum := 0.0 \n for i := k; i <= min(n, k - 1 + maxPts); i++ {\n dp[i] = 1.0\n sum += dp[i]\n }\n \n for i := k - 1; i >= 0; i-- {\n dp[i] = sum / float64(maxPts)\n \n // remove the last element dp[i+maxPts] \n // or if maxPts is too large, then it should be 0, we just ignore it\n if i + maxPts < len(dp) {\n sum -= dp[i+maxPts]\n } \n sum += dp[i] \n }\n \n return dp[0]\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n \n return b\n}\n``` | 2 | 0 | [] | 1 |
new-21-game | C++ Brute and Optimal Approaches | c-brute-and-optimal-approaches-by-trinit-lxpf | Approach 1: TLE but is useful to understand the intuition\n\n// basically we ll have to find the probability of alice getting\n// a number between [k...n]. beca | trinity_06 | NORMAL | 2021-10-17T18:46:12.910811+00:00 | 2021-10-17T18:46:12.910860+00:00 | 384 | false | Approach 1: TLE but is useful to understand the intuition\n```\n// basically we ll have to find the probability of alice getting\n// a number between [k...n]. because we dont stop drawing until we reach k\n\n// current_prob[i]->denotes the probability of reaching the number i\n\n//note that 2 events are occuring together\n//1. probability of reaching i-1\n//2. probability of picking 1\n// current_prob[i]=current_prob[i-1].P(1) + current_prob[i-2].P(2) + current_prob[i-3].P(3)\n// +......+current_prob[i-maxPts].P(maxPts)\n \n// P(1)=(1/maxPts)\n// P(2)=1/maxPts\n\n// current_prob[i]=current_prob[i-1].(1/maxPts) + current_prob[i-2].(1/maxPts) + current_prob[i-3].(1/maxPts)\n// +......+current_prob[i-maxPts].(1/maxPts)\n \n// max range of the solution:\n// k->k-1+maxPts\n// we cannot consider a number which is greater than the threshold: i-j>k\n// Example:\n// n=21\n// k=18\n// current_prob[21]=(current_prob[20]+current_prob[19]+current_prob[18])X + current_prob[17]\n\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if(k==0)\n return 1.0;\n int maxRange=k-1+maxPts;\n vector<double>current_prob(maxRange+1,0);\n current_prob[0]=1.0;\n for(int i=1;i<=maxRange;i++){\n for(int j=0;j<=maxPts;j++){\n if(i-j>=0 && i-j<k){\n current_prob[i]+=current_prob[i-j]/(double)maxPts;\n }\n }\n }\n double ans=0;\n for(int i=k;i<=n;i++){\n ans+=current_prob[i];\n }\n return ans;\n }\n};\n```\n2. Optimised Code Using Sliding Window\n```C++\n// optimised idea:\n// dp[14]=c.(dp[13]+dp[12]+......+dp[8])\n// dp[15]=c.(dp[14]+dp[13]+......+dp[9])\n\n//sliding window\n\n\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if(k==0||n>=k+maxPts)\n return 1.0;\n int maxRange=k-1+maxPts;\n vector<double>current_prob(maxRange+1,0);\n current_prob[0]=1.0;\n double runningsum=current_prob[0];\n double result=0.0;\n for(int i=1;i<=n;i++){\n current_prob[i]=runningsum/(double)maxPts;\n \n //handle the front end of the running sum\n if(i<k){\n runningsum+=current_prob[i];\n }\n else\n result+=current_prob[i];\n //tail end of the running sum\n if(i-maxPts>=0){\n runningsum-=current_prob[i-maxPts];\n }\n }\n \n return result;\n }\n};\n``` | 2 | 0 | [] | 0 |
new-21-game | c++ back to front, sliding window | c-back-to-front-sliding-window-by-liqt20-i1es | \ndouble new21Game(int n, int k, int maxPts) {\n int maxScore = k - 1 + maxPts;\n if (maxScore <= n) {\n return 1.0;\n }\n | liqt20 | NORMAL | 2021-09-22T23:48:06.206858+00:00 | 2021-09-22T23:48:06.206906+00:00 | 351 | false | ```\ndouble new21Game(int n, int k, int maxPts) {\n int maxScore = k - 1 + maxPts;\n if (maxScore <= n) {\n return 1.0;\n }\n vector<double> dp(k + maxPts, 0);\n for(int i = k; i <= n; i++) {\n dp[i] = 1.0;\n }\n double sum = n - k + 1;\n for(int i = k-1; i >= 0; i--) {\n dp[i] = sum / maxPts;\n sum = sum + dp[i] - dp[i + maxPts];\n }\n return dp[0];\n }\n``` | 2 | 0 | [] | 0 |
new-21-game | Javascript solution O(N) with explanation (and math proof) | javascript-solution-on-with-explanation-182i1 | Based on Lee\'s post: https://leetcode.com/problems/new-21-game/discuss/132334/One-Pass-DP-O(N), I figured out a way to understand the solution. Hopefully you f | 6117392 | NORMAL | 2021-05-29T00:05:28.517127+00:00 | 2021-05-29T00:11:16.222690+00:00 | 827 | false | Based on Lee\'s post: https://leetcode.com/problems/new-21-game/discuss/132334/One-Pass-DP-O(N), I figured out a way to understand the solution. Hopefully you find the thought process to be intuitive.\n\nAssume we have:\n```\nmax = 10, k = 12, n = 15\n```\nSince max is 10, probability of drawing any card is `0.1`.\n\nThe DP array, or I\'ll call it `P[i]` below, contains probability of reaching sum `i` at some point of the game.\n\n===== Let\'s list out P0 to P15 one by one... =====\n\nNote: below 3 cases are not mutually exclusive. Also k can be smaller than max, but the logic won\'t change.\n\nCase 1:\nif i <= k, always add 1.1P(i-1) to P(i). Proof:\n```\nP0 = 1 // initialization\nP1 = 0.1 // getting card 1\'s chance is 0.1\nP2 = 0.1P1 + 0.1P0 = 1.1P1 // chance of getting card 1 then 1 again is 0.1P1, chance of getting card 2 is 0.1P0, adding them together we have 1.1P1\nP3 = 0.1P2 + 0.1P1 + 0.1P0 = 1.1P2 // same, getting card 2 then 1, or, getting card 1 then 2, or, getting card 3\n...\n...\nP10 = 1.1P9 // i reaches max\n```\n\nCase 2:\nif i > max, remove 0.1P(i - max - 1) from P(i). This is essentially a sliding window problem:\n```\nP11 = 0.1P10 + 0.1P9 + ... + 0.1P1 = 1.1P10 - 0.1P0\nP12 = 0.1P11 + 0.1P10 + ... + 0.1P2 = 1.1P11 - 0.1P1 // no more P1 because getting sum1 requires we draw card 11 - impossible\n```\n\nCase 3:\nif i > k, sliding window\'s right stops growing, meaning always add P(i-1) instead of 1.1P(i-1) to P(i):\n```\nP13 = 0.1P11 + 0.1P10 + ... + 0.1P3 = P12 - 0.1P2 // no longer add 0.1P12, because reaching 12 ends the game. Sliding window\'s left stops at 0.1P11\nP14 = P13 - 0.1P3 // remember to keep removing 0.1P3 as i=14 satisfies both case 2 and case 3\n```\n\nCode:\n```\nvar new21Game = function(n, k, maxPts) {\n if (k+maxPts <= n || k===0) return 1;\n\n let dp = [];\n dp[0] = 1;\n dp[1] = 1/maxPts;\n \n for (let i = 2; i <= n; i++) {\n dp[i] = 0;\n \n if (i <= k) {\n dp[i] = (1 + 1/maxPts) * dp[i-1];\n } else {\n dp[i] = dp[i-1];\n }\n if (i > maxPts) {\n dp[i] -= dp[i-maxPts-1] / maxPts;\n }\n }\n \n return dp.reduce((acc, cur, idx) => {\n if (idx >= k) {\n acc += cur;\n }\n return acc;\n }, 0)\n};\n```\n | 2 | 0 | ['Math', 'Dynamic Programming', 'Sliding Window', 'JavaScript'] | 1 |
new-21-game | [Java] Clean O(K + W)-Time O(W)-Space Solution || with comments | java-clean-ok-w-time-ow-space-solution-w-jr1e | The most basic solution, though TLE, explains everything clearer: \n\n\nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (K == 0 | xieyun95 | NORMAL | 2021-04-30T02:59:19.648844+00:00 | 2021-04-30T02:59:19.648884+00:00 | 650 | false | The most basic solution, though TLE, explains everything clearer: \n\n```\nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (K == 0) return 1.0;\n \n // dp[i] : prob of getting no more than N points when starting with i points\n double[] dp = new double[K];\n \n for (int i = K-1; i >= 0; i--) {\n for (int p = i + 1; p <= i + W; p++) {\n if (p > N) {\n dp[i] += 0.0;\n } else if (p >= K) {\n dp[i] += 1.0;\n } else {\n dp[i] += dp[p];\n }\n }\n \n dp[i] /= W;\n }\n \n return dp[0];\n }\n}\n```\n\nWe can easily optimize the solution above to: \n```\nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (K == 0) return 1.0;\n \n Deque<Double> queue = new LinkedList<>();\n double sum = 0.0;\n for (int i = K; i < K + W; i++) {\n double prob = (i <= N) ? 1.0 : 0.0;\n queue.offerLast(prob);\n sum += prob;\n }\n \n \n for (int i = K - 1; i >= 0; i--) {\n double prob = sum / W;\n sum = sum - queue.pollLast() + prob;\n queue.offerFirst(prob);\n }\n \n return queue.peekFirst();\n }\n}\n``` | 2 | 1 | ['Dynamic Programming', 'Queue', 'Java'] | 0 |
new-21-game | Python DP linear time clear deduction based on equation | python-dp-linear-time-clear-deduction-ba-dz1t | Update: now the description has been updated, the same approach still applies. It is actually using sliding window implicitly. Suppose dp[i] represents the prob | workcool | NORMAL | 2021-03-17T04:35:23.122544+00:00 | 2023-05-25T05:16:01.987289+00:00 | 633 | false | *Update: now the description has been updated, the same approach still applies. It is actually using sliding window implicitly. Suppose dp[i] represents the prob with start with i points.*\nThen \n\n dp[i] = 1/maxPts * (dp[i+1] + dp[i+2] + ... + dp[i+maxPts])\ndp[i+1] = 1/maxPts * ( dp[i+2] + ... + dp[i+maxPts] + dp[i+maxPts + 1])\n\n*It is obvious that if we do dp backward, moving from i+1 to i, most of the elments in the sliding window keep the same, except the first and last elements. That\'s where sliding window comes in.*\n\n*A more straightforward way is to just calculate dp[i+1] - dp[i], then it tells formula for dp[i], which can be directly used in code (this is a useful trick: simplify dp equations by looking at difference, which implicitly utilizing sliding window); below old post shows this approach. Both approaches actually the same in essence.*\n\nBased on the solution, \n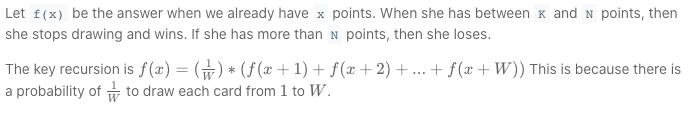\nNote that this holds only for x < K (for x>= K we can preset the value to 1.0 or 0.0).\nI got TLE by only using the above recursion function.\nActually based on it we have\nf(x) - f(x-1) = 1/W * ( f(x+W) - f(x) ), holds for x < K.\nthat is:\nf(x-1) = f(x) - 1/W( f(x+W) - f(x) ), for x < K.\n\nBased on this recurision relationship, we can directly have the following solution, without using any other variables or sliding windows.\n\n```\nclass Solution:\n def new21Game(self, N: int, K: int, W: int) -> float:\n if K == 0:\n return 1.0\n \n # dp[i] = 1/W * dp[i+j] for j in range [1, W]\n \n dp = [0] * (K + W)\n for i in range(K, N+1):\n dp[i] = 1.0 \n \n # note that dp[K-1] need to compute seperately\n for i in range(1, W+1):\n dp[K-1] += 1/W * dp[K-1+i]\n \n\t\t# starting from K-2, since the recusion needs x < K, and here x is i+1, so i < K-1\n for i in range(K-2, -1, -1):\n dp[i] = dp[i+1] - 1/W * (dp[i+1+W]-dp[i+1])\n \n return dp[0] | 2 | 0 | ['Dynamic Programming', 'Sliding Window', 'Python3'] | 1 |
new-21-game | C++ Solution, use queue | c-solution-use-queue-by-woshiyuanlei-qyuu | \nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n if(K == 0 || W == 1) return 1.0;\n double res = 0;\n double sum | woshiyuanlei | NORMAL | 2021-03-02T07:04:56.079723+00:00 | 2021-03-02T07:04:56.079766+00:00 | 264 | false | ```\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n if(K == 0 || W == 1) return 1.0;\n double res = 0;\n double sum = 1.0;\n queue<double> q;\n for(int i = 1; i < W; i++) q.push(0);\n q.push(1.0);\n for(int i = 1; i < K; i++) {\n q.push(sum / W);\n sum += sum / W;\n if(q.size() > W) {\n sum -= q.front();\n q.pop();\n }\n }\n for(int i = K; i <= N && q.size(); i++) {\n res += sum / W;\n sum -= q.front();\n q.pop();\n }\n return res;\n }\n};\n``` | 2 | 0 | [] | 0 |
new-21-game | Fast 8-line JAVA O(N) solution | fast-8-line-java-on-solution-by-legendar-0ju2 | dp[i] stores possibility of getting i.\n\n\n public double new21Game(int N, int K, int W) {\n if (K == 0) return 1.0;\n double[] dp = new doubl | legendaryengineer | NORMAL | 2020-04-24T22:50:01.325158+00:00 | 2020-05-01T00:02:19.410753+00:00 | 331 | false | dp[i] stores possibility of getting i.\n\n```\n public double new21Game(int N, int K, int W) {\n if (K == 0) return 1.0;\n double[] dp = new double[K + W];\n dp[0] = 1.0;\n for (int i = 1; i <= Math.min(N, K + W - 1); i++) {\n double pos = dp[Math.min(i - 1, K - 1)] - (i - W - 1 >= 0 ? dp[i - W - 1] : 0);\n dp[i] = pos / W + dp[i - 1];\n }\n return dp[N] - dp[K - 1];\n }\n```\n\nbased on TLE solution:\n\n```\n public double new21Game(int N, int K, int W) {\n double[] dp = new double[K + W];\n dp[0] = 1.0;\n for (int i = 1; i <= Math.min(N, K + W - 1); i++) {\n double pos = 0;\n for (int j = Math.max(0, i - W); j <= Math.min(i - 1, K - 1); j++) {\n pos += dp[j];\n }\n dp[i] = pos / W;\n }\n double res = 0;\n for (int i = K; i <= Math.min(N, K + W - 1); i++) {\n res += dp[i];\n }\n return res;\n }\n``` | 2 | 2 | [] | 0 |
new-21-game | Javascript - DP | javascript-dp-by-denzel777-3d2p | \nconst new21Game = (N, K, W) => {\n if (K === 0 || N >= K + W) return 1;\n\n let sum = 1;\n let ans = 0;\n const dp = [];\n dp[0] = 1;\n\n for (let i = 1 | denzel777 | NORMAL | 2019-10-16T21:36:46.405895+00:00 | 2019-10-16T21:36:46.405942+00:00 | 211 | false | ```\nconst new21Game = (N, K, W) => {\n if (K === 0 || N >= K + W) return 1;\n\n let sum = 1;\n let ans = 0;\n const dp = [];\n dp[0] = 1;\n\n for (let i = 1; i <= N; i++) {\n dp[i] = sum / W;\n\n if (i < K) {\n sum = sum + dp[i];\n } else {\n ans = ans + dp[i];\n }\n\n if (i - W >= 0) {\n sum = sum - dp[i - W];\n }\n }\n\n return ans;\n};\n``` | 2 | 2 | [] | 0 |
new-21-game | Java - DP - 3 ms, faster than 98.51% - 35.5 MB, less than 24.32% | java-dp-3-ms-faster-than-9851-355-mb-les-bz01 | \nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (K == 0 || K + W <= N) {\n return 1;\n }\n if (N < K | woshilxd912 | NORMAL | 2019-06-20T03:36:37.999971+00:00 | 2019-06-20T03:36:38.000013+00:00 | 583 | false | ```\nclass Solution {\n public double new21Game(int N, int K, int W) {\n if (K == 0 || K + W <= N) {\n return 1;\n }\n if (N < K) {\n return 0;\n }\n double base = 1.0 / W;\n double[] dp = new double[N + 1];\n double sum = 0;\n double res = 0;\n for (int i = 1; i <= N; ++i) {\n dp[i] = sum * base + (i <= W ? base : 0);\n if (i < K) {\n sum += dp[i];\n }\n if (i > W) {\n sum -= dp[i - W];\n }\n if (i >= K) {\n res += dp[i];\n }\n }\n return res;\n }\n}\n``` | 2 | 0 | [] | 2 |
new-21-game | Sliding window + DP | sliding-window-dp-by-yuxiong-u42z | """\nSliding window + DP\nRunning Time: O(N)\n\nDefine dp[i] = probability of getting i points\nOptimal Substructure:\n\t\t\n dp[x] = 1/W * dp[x-1] + 1/W * d | yuxiong | NORMAL | 2018-11-11T18:11:16.978840+00:00 | 2018-11-11T18:11:16.978878+00:00 | 982 | false | """\nSliding window + DP\nRunning Time: O(N)\n\nDefine dp[i] = probability of getting i points\nOptimal Substructure:\n\t\t\n dp[x] = 1/W * dp[x-1] + 1/W * dp[x-2] + 1/W * dp[x-3] + ... + 1/W * dp[x-W]\n Or: dp[x] = 1/W * (dp[x-1] + dp[x-2] + dp[x-3] + ... + dp[x-W])\n\nSo with dp[0]=1, our base case, we can keep the running_sum = dp[x-1] + dp[x-2] + dp[x-3] + ... + dp[x-W] to calculate dp[x].\n\nNote: When x >= K, Alice stops drawing numbers. So no y > x can be formed from x.\n So we don\'t include dp[x] into the running_sum when x >= K.\n"""\n```\nclass Solution:\n def new21Game(self, N, K, W):\n # Corner cases:\n if K == 0: return 1\n if N == 0: return 0\n if K > N: return 0\n \n dp = [0] * (N + 1) # dp[i] means the probability with i points\n dp[0] = 1\n \n # The running sum of the sliding window\n running_sum = 1\n p1 = 0\n for p2 in range(1, N + 1):\n if p2 - p1 > W:\n running_sum -= dp[p1]\n p1 += 1\n dp[p2] = running_sum * (1/W)\n\n if p2 < K: running_sum += dp[p2] # When x >= K, Alice stops drawing numbers. So no y > x can be formed from x.\n return sum(dp[K:N+1])\n``` | 2 | 0 | [] | 1 |
new-21-game | C++ Beats 100% DP with Simple Explanation | c-beats-100-dp-with-simple-explanation-b-8jhn | Approach\nIt\'s fairly clear this question will have to be DP, since it\'s similar to \'count number of ways to reach i\', but instead we\'re counting the proba | tangd6 | NORMAL | 2023-12-12T03:01:15.776757+00:00 | 2023-12-12T03:01:15.776790+00:00 | 1,001 | false | # Approach\nIt\'s fairly clear this question will have to be DP, since it\'s similar to \'count number of ways to reach i\', but instead we\'re counting the probabilities to reach i. So our dp will be\n\ndp[i] = probability of reaching i. (not quite, but it\'s a good way to think about it)\n\nTherefore, our solution will be the sum of all dp[k..n] probabilities, since we are going to overshoot k every time! We shouldn\'t count any numbers before k since those are not numbers we are going to END on.\n\nNow the way to do is to just have a DP state where we calculate the probabilities forward from the state we are currently on. E.g. if I am on number i with probability 0.5, I know there is a 0.5 * (1/maxPts) probability that any of the 1..maxPts numbers ahead of me will be chosen. \n\nTo set dp[i + 1..maxPts] we can either use a loop in O(n), or use a line sweep in O(1). Of course, we choose the faster one.\n\nThen just keep a running prefix sum and when you are on i, that running sum will be the probability of dp[i]. So dp[i] isn\'t the probability, it\'s the line sweep array, which is close enough :)\n\nNote: we set dp[0] = 1.0, dp[1] = -1.0 because we will always start from 0, so it\'s 100%. The -1 is to reduce the probability back down after we propagate the probability of 0 onwards.\n\n# Code\n```\nclass Solution {\npublic:\n static constexpr int mx = (int)1e4 + 5;\n double dp[mx];\n double new21Game(int n, int k, int maxPts) {\n dp[0] = 1.0;\n dp[1] = -1.0;\n double run = 0;\n for (int i = 0; i < k; i++) {\n run += dp[i];\n if (i+1 <= n) dp[i+1] += run / maxPts;\n if (i+maxPts+1 <= n) dp[i+maxPts+1] -= run / maxPts;\n }\n double ans = 0;\n for (int i = k; i <= n; i++) {\n run += dp[i];\n ans += run;\n }\n return ans;\n }\n};\n\n``` | 1 | 0 | ['C++'] | 0 |
new-21-game | Python | DP | Explained | python-dp-explained-by-dinar-r9m1 | The solution:\n\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k == 0:\n return 1\n dp = [1] + [ | dinar | NORMAL | 2023-05-30T14:44:10.765006+00:00 | 2023-05-30T14:44:10.765033+00:00 | 43 | false | **The solution**:\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k == 0:\n return 1\n dp = [1] + [0] * n\n s = 1\n for i in range(1, n + 1):\n if i - maxPts >= k:\n break\n dp[i] = s / maxPts\n if i - maxPts >= 0:\n s -= dp[i - maxPts]\n if i < k:\n s += dp[i]\n return sum(dp[k:])\n```\n\n**Explanation:**\nThe given solution uses dynamic programming to calculate the probability that Alice has n or fewer points in the game. Let\'s break down the logic step by step:\n\n1. Initialize the probability array `dp` with `dp[0] = 1` (Alice starts with 0 points) and all other elements as 0. This array will store the probabilities of having a certain number of points.\n\n2. Initialize the sum variable `s` to 1. `s` represents the cumulative probability of reaching the current point.\n\n3. Iterate over the range from 1 to n+1 (inclusive) to calculate the probabilities for each possible point value.\n\n4. Check if the current point value minus the maximum points `maxPts` is greater than or equal to k. If so, break the loop because Alice can already achieve k or more points, and there is no need to calculate further.\n\n5. Calculate the probability `dp[i]` for the current point value. It is the sum of the probabilities of reaching the previous `maxPts` points, divided by `maxPts` (since each draw has equal probabilities).\n\n6. If the current point value minus `maxPts` is greater than or equal to 0, subtract the probability `dp[i - maxPts]` from the sum `s`. This step ensures that the sum `s` only contains the probabilities of the last `maxPts` points.\n\n7. If the current point value is less than k, add the probability `dp[i]` to the sum `s`. This step updates the cumulative probability `s` with the current point\'s probability.\n\n8. After the loop, return the sum of probabilities from index k to the end of the `dp` array. This represents the probability that Alice has n or fewer points.\n\nThe time complexity of this solution is O(n) because we iterate over the range from 1 to n+1. The space complexity is also O(n) because we use the `dp` array to store the probabilities of each point value. | 1 | 0 | ['Dynamic Programming', 'Python'] | 0 |
new-21-game | Java very easy solution | java-very-easy-solution-by-abhineshchand-94oe | Intuition\n Describe your first thoughts on how to solve this problem. \n- First of all what is this :P. First find the person who created this question and giv | abhineshchandra1234 | NORMAL | 2023-05-25T20:25:25.662645+00:00 | 2023-05-25T20:25:25.662704+00:00 | 117 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- First of all what is this :P. First find the person who created this question and give my blessings also.\n- We will solve this problem using dp\n- The questions says alice has to start from 0 points and she can pick any points from 1 to W.\n- If the score ie points sum exceed k she has to stop picking coins.\n- Now we have to return probabilty for the score<=n.\n- Max score she can reach is k-1 + W\n- Suppose she is at k-1 score if she picks 1 point she will reach k and she cannot pick anymore. if she picks W point she will reach k-1 + W and she cannot pick anymore.\n- Input: `n = 21`, `k = 17`, `maxPts = 10`\n- `d[21]` is the probality to reach `21` score.\n- we can reach `d[21]` from `d[11]` by picking max point `10`.\n- It covers cond `i-W>=0` and make our calculation easier\n- `d[21] = d[20]*p(1) + d[19]*p(2) + d[18]*p(3) +.. +d[11]*p(10)`\n- since all have equal probability\n- `d[21] = d[20]*1/W + d[19]*1/W +.. +d[11]*1/W`\n- `d[21] = 1/W*(d[20]+ d[19]+.. +d[11])`\n- Now alice is not allowed to pick points above score k\n- so we will remove `dp[17] to dp[20]`\n- this covers cond `i<k`\n- so our result will be `d[21] = 1/W*(d[16]+ d[15]+.. +d[11])`\n- till k-1 alice has the option to pick points so we will build our sum but from k or above alice cannot pick anymore points and we will remove extra sum.\n- `c = 1/W`\n- `D[16] start = c * (D[6] + D[7] +..+D[15]) = c*D[15]`\n- `D[16] end = c * (D[7]+ D[8]+..+D[15]) = c*(D[15]-D[6])`\n- `D[17] start = c * (D[7] +D[8]+..+D[16]) = c*D[16]`\n- `D[17] end = c * (D[8]+D[9]+..+D[16]) = c*(D[16]-D[7])`\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public double new21Game(int n, int k, int W) {\n \n if(k==0 || n>=k+W)\n return 1;\n double dp[] = new double[n+1], Wsum=1, res=0;\n dp[0] = 1;\n for(int i=1; i<=n; i++) {\n dp[i] = Wsum/W;\n if(i<k)\n Wsum += dp[i];\n else\n res += dp[i];\n \n if(i-W>=0)\n Wsum -= dp[i-W];\n }\n return res;\n }\n}\n``` | 1 | 0 | ['Math', 'Dynamic Programming', 'Sliding Window', 'Probability and Statistics', 'Java'] | 1 |
new-21-game | Java Easy Solution | java-easy-solution-by-prerna__02-skuq | \n\n# Code\n\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(k==0) return 1.00;\n if(k==1 && maxPts<=n) return 1.0 | prerna__02 | NORMAL | 2023-05-25T19:12:24.070580+00:00 | 2023-05-25T19:12:24.070624+00:00 | 257 | false | \n\n# Code\n```\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(k==0) return 1.00;\n if(k==1 && maxPts<=n) return 1.00;\n double dp[] = new double[n+1];\n dp[0] = 1.00;\n double prev=0.00;\n for(int i=1; i<=n; i++){\n if((i-maxPts-1)>=0){\n prev-=dp[i-1-maxPts];\n }\n if((i-1)<k){\n prev+=dp[i-1];\n }\n dp[i]=prev/maxPts; \n }\n\n double res = 0.00;\n for(int i=k; i<=n; i++){\n res+=dp[i];\n }\n return res; \n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
new-21-game | Python Easy Solution | python-easy-solution-by-celestial2897-vkpj | Code\n\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n dp = [1.0] + [0] * n\n Wsum = 1.0\n if k == 0 or | celestial2897 | NORMAL | 2023-05-25T18:58:37.246406+00:00 | 2023-05-25T18:58:37.246444+00:00 | 371 | false | # Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n dp = [1.0] + [0] * n\n Wsum = 1.0\n if k == 0 or n >= k + maxPts:\n return 1\n for i in range(1, n+1):\n dp[i] = Wsum/maxPts\n if i < k:\n Wsum += dp[i]\n if i >= maxPts:\n Wsum -= dp[i-maxPts]\n return sum(dp[k:])\n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
new-21-game | 837. New 21 Game || Java | 837-new-21-game-java-by-arpary-cmrt | \nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(k==0||n>=k+maxPts)\n return 1;\n double dp[]=new doubl | ArpAry | NORMAL | 2023-05-25T17:32:18.703661+00:00 | 2023-05-25T17:32:18.703705+00:00 | 61 | false | ```\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(k==0||n>=k+maxPts)\n return 1;\n double dp[]=new double[n+1];\n Arrays.fill(dp,0.0);\n dp[0]=1;\n double cur_sum=dp[0];\n for(int i=1;i<=n;i++)\n {\n dp[i]=cur_sum/(double)maxPts;\n if(i<k)\n cur_sum+=dp[i];\n if(i>=maxPts)\n cur_sum-=dp[i-maxPts];\n }\n double ans=0;\n for(int i=k;i<=n;i++)\n ans+=dp[i];\n return ans;\n }\n}\n``` | 1 | 0 | [] | 0 |
new-21-game | ✅ Intuitive solution – even if you're bad at Dynamic Programming | intuitive-solution-even-if-youre-bad-at-dlj33 | Intuition\nI thought it was much more intuitive to take this problem backwards.\n\nLet\'s say that maxPts = 6, k = 5, and n = 7.\n\nThat means that Alice rolls | elliotfiske | NORMAL | 2023-05-25T17:26:36.372592+00:00 | 2023-05-25T17:38:01.057187+00:00 | 121 | false | # Intuition\nI thought it was much more intuitive to take this problem *backwards*.\n\nLet\'s say that `maxPts = 6`, `k = 5`, and `n = 7`.\n\nThat means that Alice rolls a dice each turn, and if her total ends up between 5 and 7 she wins. Any higher than 7 and she loses.\n\nThis smells like dynamic programming, so let\'s see if we can find an easy solution for some given input.\n\nIf Alice had exactly 4 points, we know that she will only roll the dice 1 more time. If she rolls `[1, 2, 3]`, she wins, and if she rolls `[4, 5, 6]`, she loses. So the chance of her winning from 4 points is `0.5`.\n\nHow can we generalize this? My solution was to consider the base cases - if Alice has 5 points, she\'s already won, so the chance of her winning is `1.0`. If she has 8 points, she\'s already lost, so the chance of her winning is `0.0`.\n\nLet\'s make a number line:\n```\nAlice\'s points: 0 1 2 3 4 5 6 7 8 9 10\nChance to win: ? ? ? ? 0.5 1 1 1 0 0 0\n```\n\nYou\'ll notice that when Alice has 4 points, she has an equal chance of landing on any of the numbers from 5 => 10 on her next roll. Therefore, we can take the average of the probability of the values from 5 => 10 to find her chance of winning when she\'s at 4 points.\n\nWe find that `average([1, 1, 1, 0, 0, 0]) = 0.5`, which lines up with our intuition before.\n\nThen, we can do the same thing for 3 points. She has a 1/6 chance of rolling a 1, bringing her total to 4, which we know will end up with her having a 0.5 chance to win. If she rolls `[2, 3, 4]`, she\'ll win, and if she rolls `[5, 6]`, she loses.\n\nSo, we can say that her total chance of winning at 3 points is \n```\n1/6 * (0.5 + 1 + 1 + 1 + 0 + 0) = 0.583\n```\n\nWe put this into the list of probabilities, and can now work our way backwards all the way to 0 points, which will be the answer (her chance of winning at the very start of the game).\n\n# Approach\nFor my solution, I initialized an array like `[1, 1, 1, 0, 0, 0]`, then calculated the probability for the next lowest value. We don\'t need to remember more values outside of our 6-length window, so we can just push the new value into the beginning of the array and pop the oldest value off the end.\n\nWe also need to account for some edge cases \u2013 if `k == 0`, Alice already wins without rolling anything, so we return `1.0`.\n\nAlso, if our "window" to win is big enough, we also can immediately return `1.0`. For instance, if we\'re rolling a dice and we have to hit between 3 and 13, we know that we\'ll never "bust" and go over 13.\n\n# Complexity\n- Time complexity:\n`O(n)`\n\n- Space complexity:\n`O(maxPts)`\n\n# Code\n```\nclass Solution {\n func new21Game(_ n: Int, _ k: Int, _ maxPts: Int) -> Double {\n if k == 0 { return 1.0 }\n if n - k >= maxPts { return 1.0 }\n\n let goodRollCount = n - k + 1\n var chances = [Double](repeating: 1, count: goodRollCount)\n + [Double](repeating: 0, count: maxPts - goodRollCount)\n\n var result = 0.0\n var sum = chances.reduce(0) { $0 + $1 }\n\n for _ in 0..<k {\n result = sum / Double(chances.count)\n sum -= chances.popLast()!\n sum += result\n chances.insert(result, at: 0)\n }\n\n return result\n }\n}\n``` | 1 | 0 | ['Swift'] | 1 |
new-21-game | Rust dp solution | rust-dp-solution-by-arbuztw-hp9w | \nimpl Solution {\n pub fn new21_game(n: i32, k: i32, max_pts: i32) -> f64 {\n let (n, k, max_pts) = (n as usize, k as usize, max_pts as usize);\n | arbuztw | NORMAL | 2023-05-25T17:21:05.518273+00:00 | 2023-05-25T17:21:05.518306+00:00 | 184 | false | ```\nimpl Solution {\n pub fn new21_game(n: i32, k: i32, max_pts: i32) -> f64 {\n let (n, k, max_pts) = (n as usize, k as usize, max_pts as usize);\n let total_max_pts = k + max_pts;\n let mut dp: Vec<f64> = Vec::with_capacity(total_max_pts);\n let mut sum: f64 = 0.0;\n dp.push(1.0);\n for i in 1..total_max_pts {\n if i < k + 1 {\n sum += dp[i-1];\n }\n if i > max_pts {\n sum -= dp[i-max_pts-1];\n }\n dp.push(sum / max_pts as f64);\n }\n dp.into_iter().take(n+1).skip(k).sum()\n }\n}\n```\n | 1 | 0 | ['Dynamic Programming', 'Rust'] | 0 |
new-21-game | C++ Dynamic Programming with Sliding window O(n) | c-dynamic-programming-with-sliding-windo-1s5f | \n# Code\n\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if(k==0 || n>= k+maxPts)\n return 1.0;\n vector<double> d | vmalik25 | NORMAL | 2023-05-25T15:43:17.090633+00:00 | 2023-05-25T15:43:17.090673+00:00 | 50 | false | \n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if(k==0 || n>= k+maxPts)\n return 1.0;\n vector<double> dp(n + 1, 0.0);\n double winsum=0;\n \n for(int i=k;i<k+maxPts;++i){\n if (i<=n){\n winsum+=1;\n dp[i]=1.0;\n }\n }\n for(int i=k-1;i>=0;--i){\n double remove=0.0;\n dp[i]=winsum*(1.0/maxPts);\n if(i+maxPts<=n){\n remove=dp[i+maxPts];\n }\n winsum+=dp[i]-remove;\n }\n return dp[0];\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Sliding Window', 'C++'] | 0 |
new-21-game | Simple C++ Solution | simple-c-solution-by-divyanshu_singh_cs-3id9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Divyanshu_singh_cs | NORMAL | 2023-05-25T13:25:35.673859+00:00 | 2023-05-25T13:25:35.673903+00:00 | 104 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int N, int K, int maxPts) {\n \n if (K == 0) return 1.0;\n if (N >= K-1 + maxPts) return 1.0;\n\n \n vector<double> dp(N + 1, 0.0);\n\n double probability = 0.0; \n double windowSum = 1.0; \n dp[0] = 1.0;\n for (int i = 1; i <= N; i++) {\n dp[i] = windowSum / maxPts;\n\n if(i < K) windowSum += dp[i];\n else probability += dp[i];\n \n if(i >= maxPts) windowSum -= dp[i - maxPts];\n }\n\n return probability;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
new-21-game | C++ EASY SOLUTION || DYNAMIC PROGRAMMING. | c-easy-solution-dynamic-programming-by-a-cdvi | \n\n# Code\n\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n\n if (k == 0 || n >= k + maxPts) {\n return 1.0 | ayush_0204 | NORMAL | 2023-05-25T08:09:33.596329+00:00 | 2023-05-25T08:09:33.596354+00:00 | 25 | false | \n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n\n if (k == 0 || n >= k + maxPts) {\n return 1.0;\n }\n vector<double> dp(n + 1);\n double currSum = 1.0;\n double ans = 0.0;\n\n dp[0] = 1.0;\n\n for (int i = 1; i < n+1; i++) {\n\n dp[i] = currSum / maxPts;\n\n if (i < k) \n currSum += dp[i];\n\n else \n ans += dp[i];\n \n if (i - maxPts >= 0) \n currSum -= dp[i - maxPts];\n \n }\n\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
new-21-game | New 21 Game 100% Beats | new-21-game-100-beats-by-prayas_saxena-hxr8 | 100% Beats\n# Code\n\npublic class Solution {\n public double New21Game(int n, int k, int maxPts) {\n if(k==0||n>=k+maxPts){\n return 1.0;\ | prayas_saxena | NORMAL | 2023-05-25T06:36:57.115860+00:00 | 2023-05-25T06:36:57.115900+00:00 | 568 | false | **100% Beats**\n# Code\n```\npublic class Solution {\n public double New21Game(int n, int k, int maxPts) {\n if(k==0||n>=k+maxPts){\n return 1.0;\n }\n double[] arr=new double[n+1];\n double Sum=1.0, result=0.0;\n arr[0]=1;\n for(int i =1;i<arr.Length;i++){\n arr[i]=Sum/maxPts;\n if(i<k){\n Sum+=arr[i];\n }\n else{\n result+=arr[i]; \n }\n if(i-maxPts>=0){\n Sum=Sum-arr[i-maxPts];\n }\n }\n return result;\n }\n}\n``` | 1 | 0 | ['Math', 'Probability and Statistics', 'C#'] | 0 |
new-21-game | simple python code using hashmap | simple-python-code-using-hashmap-by-nand-tlvo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Nandagopal26 | NORMAL | 2023-05-25T06:17:35.297537+00:00 | 2023-05-25T06:17:35.297572+00:00 | 1,235 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k==0:\n return 1.0\n\n windowsum=0\n for i in range(k,k + maxPts):\n windowsum+= 1 if i<=n else 0\n\n dp={}\n for i in range(k-1,-1,-1):\n dp[i]=windowsum/maxPts\n remove=0\n if i+maxPts<=n:\n remove=dp.get(i+maxPts,1)\n windowsum+= dp[i]-remove\n return dp[0] \n``` | 1 | 0 | ['Python3'] | 1 |
new-21-game | Solution in C++ | solution-in-c-by-ashish_madhup-vr0s | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ashish_madhup | NORMAL | 2023-05-25T05:13:58.325652+00:00 | 2023-05-25T05:13:58.325695+00:00 | 489 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) \n {\n if (k == 0 || n >= k + maxPts - 1) return 1.0;\n vector<double> dp(n + 1);\n dp[0] = 1.0;\n double W = 1.0, res = 0.0;\n for (int i = 1; i <= n; ++i) \n {\n dp[i] = W / maxPts;\n if (i < k) W += dp[i];\n else res += dp[i];\n if (i - maxPts >= 0) W -= dp[i - maxPts];\n }\n return res;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
new-21-game | 837. New 21 Game, Daily LeetCoding Challenge | 837-new-21-game-daily-leetcoding-challen-istx | \nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k==0 || n>=k+maxPts) return 1.0;\n vector<double>dp(n+1,0);\n | pspraneetsehra08 | NORMAL | 2023-05-25T04:01:39.476053+00:00 | 2023-05-25T04:01:39.476123+00:00 | 22 | false | ```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k==0 || n>=k+maxPts) return 1.0;\n vector<double>dp(n+1,0);\n dp[0]=1.0;\n double result=0;\n double runningSum=dp[0];\n for (int i=1;i<=n;i++)\n {\n dp[i]=runningSum/(double)maxPts;\n if (i<k)\n {\n runningSum+=dp[i];\n }\n else{\n result+=dp[i];\n }\n if (i-maxPts>=0)\n runningSum-=dp[i-maxPts];\n }\n return result;\n\n }\n};\n``` | 1 | 0 | [] | 0 |
new-21-game | C++ | c-by-david500-tu5c | While Alice has less than k, she will keep drawing. On the last turn, k-1, she could draw the maximum number, maxPts (w), so the maximum she can ever draw is k- | david500 | NORMAL | 2023-05-25T04:00:54.370696+00:00 | 2023-05-25T04:00:54.370729+00:00 | 242 | false | While Alice has less than k, she will keep drawing. On the last turn, k-1, she could draw the maximum number, maxPts (w), so the maximum she can ever draw is k-1+w.\n\nIf n is >= k-1+w, then it will always be true.\n\nWe can have a dp of 0 -> k+w-1, where dp[i] gives the probability that we can i or less.\n\ndp[0] is the base case, we start with 0, so the probabiltiy is 100%.\n\nAt dp[1], we have 1/w chance to draw a 1.\nAt dp[8], we have:\n dp[1] chance to draw a 1, then 1/w chance to draw a 7 to make it 8. \n dp[2] chance to draw a 2, then 1/w chance to draw a 6 to make it 8.\n ...\n dp[7] chance to draw a 7, then 1/w chance to draw a 1 to make it 8.\n + drawing an 8 to make 8.\nSo formula become dp[0] * 1/w, dp[1] * 1/w + dp[2] * 1/w + dp[3] * 1/w ....\nOr, (dp[0], dp[1] + dp[2] + dp[3] ... dp[7]) * 1/w.\n\nKeep in mind we only go back max w steps, as that is that maximum points we can draw.\n\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int w) {\n if (n >= k+w-1) return 1.0;\n vector<double> dp(k+w);\n dp[0] = 1;\n double p = 1/(double)w;\n\n double cur = 0;\n for (int i = 1; i <= k; i++) {\n if (i-w-1 >= 0) cur -= dp[i-w-1];\n cur += dp[i-1];\n dp[i] = cur * p;\n }\n double ans = dp[k];\n\n for (int i = k+1; i <= n; i++) {\n if (i-w-1 >= 0) cur -= dp[i-w-1];\n dp[i] = cur * p;\n ans += dp[i];\n }\n\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
new-21-game | Python3 Solution | python3-solution-by-motaharozzaman1996-1thz | \n\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k==0 or n>=k+maxPts:\n return 1\n\n dp=[1.0]+[ | Motaharozzaman1996 | NORMAL | 2023-05-25T03:11:43.491005+00:00 | 2023-05-25T03:11:43.491031+00:00 | 1,248 | false | \n```\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n if k==0 or n>=k+maxPts:\n return 1\n\n dp=[1.0]+[0.0]*n\n maxPts_sum=1.0\n for i in range(1,n+1):\n dp[i]=maxPts_sum/maxPts\n if i<k:\n maxPts_sum+=dp[i]\n\n if i-maxPts>=0:\n maxPts_sum-=dp[i-maxPts]\n\n\n return sum(dp[k:]) \n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
new-21-game | C# using DP + sliding window | c-using-dp-sliding-window-by-dmitriy-mak-9q6w | Approach\n- To calculate the probability of winning, we can use DP (dynamic programming) to keep track of the probabilities for each point.\n- Use sliding windo | dmitriy-maksimov | NORMAL | 2023-05-25T03:03:47.730294+00:00 | 2023-05-25T03:03:47.730334+00:00 | 210 | false | # Approach\n- To calculate the probability of winning, we can use DP (dynamic programming) to keep track of the probabilities for each point.\n- Use sliding window `windowSum` to efficiently calculate probabilities.\n- Calculate the probabilities. `dp[0]` is `1.0`. For each point `i` ($$1..n$$), the probability of reaching that point is the sum of probabilities from the previous `maxPts` points divided by `maxPts`.\n- If `i` is less than `k`, we add the probability to the `windowSum` to keep sum of previous probabilities.\n- If `i` is `>= k`, we add the probability to `probability` variable.\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\npublic class Solution\n{\n public double New21Game(int n, int k, int maxPts)\n {\n if (k == 0 || n >= k + maxPts)\n {\n return 1.0;\n }\n\n var windowSum = 1.0;\n var probability = 0.0;\n\n var dp = new double[n + 1];\n dp[0] = 1.0;\n\n for (var i = 1; i <= n; i++)\n {\n dp[i] = windowSum / maxPts;\n\n if (i < k)\n {\n windowSum += dp[i];\n }\n else\n {\n probability += dp[i];\n }\n\n if (i >= maxPts)\n {\n windowSum -= dp[i - maxPts];\n }\n }\n\n return probability;\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
new-21-game | ✅ O(n) Easy Solution Explained | on-easy-solution-explained-by-eleev-ojst | Approach\nThis solution applies dynamic programming to calculate the probability of Alice reaching a specific score. Initializing a DP array with the certainty | eleev | NORMAL | 2023-05-25T00:22:27.905071+00:00 | 2023-05-25T00:52:36.800121+00:00 | 115 | false | # Approach\nThis solution applies dynamic programming to calculate the probability of Alice reaching a specific score. Initializing a DP array with the certainty of 0 points (probability of 1), it iteratively builds probabilities for scores from 1 to `n` by averaging the last `maxPtsd` scores.\n\nA `sum` variable tracks the sum of recent probabilities. When the score reaches Alice\'s stopping point `k`, these probabilities contribute to the final result.\n\nTo maintain `sum`, the solution deducts the probability of scores \'maxPtsd\' behind once exceeding `maxPtsd`. This guarantees `sum` only contains recent probabilities.\n\nUltimately, the solution provides the combined probability of Alice achieving `n` or less points, by summing probabilities from `k` to `n`.\n\n# Time Complexity\n**O(n)**\nThe runtime complexity for this solution is `O(n)`, where n is the maximum possible points Alice can achieve. This is because we are iterating over each point from 0 to n exactly once to build our dynamic programming array.\n\n# Space complexity\n**O(n)**\nThe space complexity is also `O(n)` due to the storage needed for the dynamic programming array that stores the probability for each point from 0 to n.\n\n# Solution\n```\nclass Solution {\n func new21Game(_ n: Int, _ k: Int, _ maxPts: Int) -> Double {\n if k == 0 || n >= k + maxPts { return 1.0 }\n\n var dp = [Double](repeating: 0, count: n + 1)\n dp[0] = 1.0\n var sum = 1.0, res = 0.0\n let maxPtsd = Double(maxPts)\n\n for i in 1...n {\n dp[i] = sum / maxPtsd\n i < k ? (sum += dp[i]) : (res += dp[i])\n i - maxPts >= 0 ? (sum -= dp[i - maxPts]) : ()\n }\n\n return res\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Swift', 'Probability and Statistics'] | 0 |
new-21-game | 🗓️ Daily LeetCoding Challenge May, Day 25 | daily-leetcoding-challenge-may-day-25-by-mlmy | This problem is the Daily LeetCoding Challenge for May, Day 25. Feel free to share anything related to this problem here! You can ask questions, discuss what yo | leetcode | OFFICIAL | 2023-05-25T00:00:17.688939+00:00 | 2023-05-25T00:00:17.689017+00:00 | 3,376 | false | This problem is the Daily LeetCoding Challenge for May, Day 25.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/new-21-game/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 1 approach in the official solution</summary>
**Approach 1:** Dynamic Programming
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br> | 1 | 0 | [] | 7 |
new-21-game | Solution | solution-by-deleted_user-q6yu | C++ []\nclass Solution {\npublic:\n double new21Game(int n, int k, int mx) {\n if (k == 0 || n >= k + mx) return 1.0;\n vector<double> dp(n+1); | deleted_user | NORMAL | 2023-05-05T13:13:21.069771+00:00 | 2023-05-05T13:57:46.069176+00:00 | 963 | false | ```C++ []\nclass Solution {\npublic:\n double new21Game(int n, int k, int mx) {\n if (k == 0 || n >= k + mx) return 1.0;\n vector<double> dp(n+1);\n dp[0] = 1.0;\n double pref = 1.0;\n double res = 0.0; \n for (int i = 1; i <= n; i++){\n dp[i] = pref / mx;\n if (i < k) pref += dp[i];\n if (i >= mx && i < k + mx) pref -= dp[i - mx];\n if (i >= k) res += dp[i];\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n dp = [1.0] + [0] * n\n Wsum = 1.0\n if k == 0 or n >= k + maxPts:\n return 1\n for i in range(1, n+1):\n dp[i] = Wsum/maxPts\n if i < k:\n Wsum += dp[i]\n if i >= maxPts:\n Wsum -= dp[i-maxPts]\n return sum(dp[k:])\n```\n\n```Java []\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(n>=k+maxPts-1){\n return 1;\n }\n double[] dp =new double[k+maxPts];\n double p=1/(maxPts+0.0);\n dp[0]=1;\n double prev =0;\n for(int i=1;i<=k;i++){\n prev = prev -(i-maxPts-1>=0?dp[i-maxPts-1]:0)+dp[i-1];\n dp[i]=prev*p;\n }\n double res = dp[k];\n for(int i=k+1;i<=n;i++){\n prev = prev -(i-maxPts-1>=0?dp[i-maxPts-1]:0);\n dp[i]=prev*p;\n res+=dp[i];\n }\n return res;\n }\n}\n```\n | 1 | 0 | ['C++', 'Java', 'Python3'] | 0 |
new-21-game | Java solution using dp | java-solution-using-dp-by-rishabhk02-mknd | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rishabhk02 | NORMAL | 2023-01-19T08:35:11.153227+00:00 | 2023-01-19T08:35:11.153259+00:00 | 553 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public double new21Game(int n, int k, int maxPts) {\n if(k==0) return 1.00;\n if(k==1 && maxPts<=n) return 1.00;\n double dp[] = new double[n+1];\n dp[0] = 1.00;\n double prev=0.00;\n for(int i=1; i<=n; i++){\n if((i-maxPts-1)>=0){\n prev-=dp[i-1-maxPts];\n }\n if((i-1)<k){\n prev+=dp[i-1];\n }\n dp[i]=prev/maxPts; \n }\n\n double res = 0.00;\n for(int i=k; i<=n; i++){\n res+=dp[i];\n }\n return res; \n }\n}\n\n// 12\n// k =\n// 1\n// maxPts =\n// 10\n``` | 1 | 0 | ['Java'] | 0 |
new-21-game | Fast C++ O(n) solution | fast-c-on-solution-by-obose-wt06 | Intuition\n Describe your first thoughts on how to solve this problem. \nMy first thought was to use dynamic programming to approach this problem. \n# Approach\ | Obose | NORMAL | 2023-01-17T19:55:11.755221+00:00 | 2023-01-17T19:55:11.755268+00:00 | 658 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first thought was to use dynamic programming to approach this problem. \n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use an array of doubles, dp, to store the probability that we reach each score. We can start with dp[0] = 1.0, indicating that the probability of reaching the score 0 is 1.0. For all the scores between 0 and k, we can use the probability of reaching any score i-j, where j is the points we get on the turn (j <= maxPts), to calculate the probability of reaching score i using dynamic programming.\n\nWe can also use a sliding window technique to keep track of the cumulative probability of reaching scores between i and i - maxPts. We can add the probability of reaching the current score to this window and subtract the probability of reaching the score i - maxPts from the window. This will help us to keep track of the cumulative probability of reaching scores between i and i - maxPts.\n\nFinally, for all the scores between k and n, we can calculate the probability of reaching this score by adding the probability of reaching any score i-j, where j is the points we get on the turn (j <= maxPts). The sum of all these probabilities will be the final answer.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(n), where n is the target score. This is because we iterate over all the scores between 0 and n and calculate the probability of reaching each score.\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this solution is O(n), where n is the target score. This is because we use an array of size n to store the probability of reaching each score.\n# Code\n```\nclass Solution {\npublic:\n double new21Game(int n, int k, int maxPts) {\n if (k == 0 || n >= k + maxPts - 1) return 1.0;\n vector<double> dp(n + 1);\n dp[0] = 1.0;\n double W = 1.0, res = 0.0;\n for (int i = 1; i <= n; ++i) {\n dp[i] = W / maxPts;\n if (i < k) W += dp[i];\n else res += dp[i];\n if (i - maxPts >= 0) W -= dp[i - maxPts];\n }\n return res;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
new-21-game | Python DP solution explained | python-dp-solution-explained-by-evilgeni-ygxm | python\n"""\nThis code gives TLE but is easier to explaine, see the second code below for a no-TLE version\n"""\nclass Solution:\n def new21Game(self, n: int | evilgenius | NORMAL | 2022-02-07T23:14:52.961231+00:00 | 2022-02-07T23:15:15.963535+00:00 | 526 | false | ```python\n"""\nThis code gives TLE but is easier to explaine, see the second code below for a no-TLE version\n"""\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n\t\t# each index in dp stores the probability that, starting from this index, the final points <= n\n dp=[0]*(k+1)\n\t\t# if we start from k, we do not have the next draw, and the result is always <= n\n dp[k]=1\n for idx in range(k-1,-1,-1):\n\t\t\t# two cases, 1) jumps to a next point that is <= k, then we can use the probability at the next point\n for right in range(idx+1,min(k+1,idx+maxPts+1)):\n dp[idx]+=dp[right]/maxPts\n \n\t\t\t# 2) jumps to range (k, n]\n if idx+maxPts>k:\n dp[idx]+=(min(idx+maxPts,n)-k)/maxPts\n \n return dp[0]\n```\n\n```python\n"""\nThis version optimizes the sum and avoids TLE.\n"""\nclass Solution:\n def new21Game(self, n: int, k: int, maxPts: int) -> float:\n dp=[0]*(k+1)\n dp[k]=1\n\t\t# keep track of the sum of dp from index to end\n sum_to_end=[0]*(len(dp)+1)\n sum_to_end[-2]=1\n \n for idx in range(k-1,-1,-1):\n\t\t\t# use the difference of sum instead\n dp[idx]+= (sum_to_end[idx+1]-sum_to_end[min(k+1,idx+maxPts+1)])/maxPts\n \n if idx+maxPts>k:\n dp[idx]+=(min(idx+maxPts,n)-k)/maxPts\n \n sum_to_end[idx]=sum_to_end[idx+1]+dp[idx]\n \n return dp[0]\n``` | 1 | 0 | ['Math', 'Dynamic Programming', 'Python'] | 0 |
new-21-game | C++ Easy to Understand Dynamic programming (Recursive memoized TLE solution also included) | c-easy-to-understand-dynamic-programming-h5cc | DP\n\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n vector<double> dp(N+1,0);dp[0]=1;\n double sum=0;\n for(int | pjdope | NORMAL | 2020-09-14T22:08:41.014185+00:00 | 2020-09-14T22:08:41.014214+00:00 | 533 | false | DP\n```\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n vector<double> dp(N+1,0);dp[0]=1;\n double sum=0;\n for(int i=1;i<=N;i++)\n {\n if(i-1<K)\n sum+=dp[i-1];\n if(i-W-1>=0)\n sum-=dp[i-W-1];\n dp[i]=(double)(sum*((double)1.0/W));\n }\n double ans=0;\n for(int i=0;i<=N;i++)\n {\n if(i>=K)\n ans+=dp[i];\n }\n return ans;\n }\n};\n```\nThis version gives TLE\n```\nclass Solution {\npublic:int n;\n vector<double> dp;\n double solve(int sum,int k,int W)\n {\n if(sum>=k)\n {\n if(sum<=n)\n return 1.0;\n else\n return 0.0;\n }\n if(dp[sum]!=-1)return dp[sum];\n double x=0;\n for(int i=1;i<=W;i++)\n {\n if(sum+i>=k and sum+i>n)break;\n x+=(double)1/W * solve(sum+i,k,W);\n }\n return dp[sum]=x;\n }\n double new21Game(int N, int K, int W) {\n n=N;\n dp=vector<double>(K,-1);\n return solve(0,K,W);\n }\n};\n \n ``` | 1 | 0 | [] | 1 |
new-21-game | c# dp | c-dp-by-lchunlosaltos-wuxr | ```\nlearn from this java solution\nhttps://leetcode.com/problems/new-21-game/discuss/723643/Java-DP-%2B-Sliding-Window\npublic double New21Game(int N, int K, i | lchunlosaltos | NORMAL | 2020-07-08T22:17:47.922285+00:00 | 2020-07-08T22:21:12.171973+00:00 | 137 | false | ```\nlearn from this java solution\nhttps://leetcode.com/problems/new-21-game/discuss/723643/Java-DP-%2B-Sliding-Window\npublic double New21Game(int N, int K, int W) {\n //N = target let\'s say 21;\n //K = is stop point; 17;\n //W = num range 1..W; 1..10;\n if (N>=K-1+W) return 1.0;\n if (N < K) return 0.0;\n if (K == 0) return 1.0;\n double[] dp = new double[N+1];\n dp[0] = 1.0;\n double prob = 1.0/(double)W;\n //dp[i] = 1/w(dp[i-1]+dp[i-2]+... dp[i-w]);\n //the probability of getting at i is the sum of probability from previous i-1 to i-w time 1/w\n double sum=1.0;\n for(int i = 1; i <= N; i++)\n {\n dp[i] = prob * sum; // i = 1 to 10; = prob (1/10)\n if (i < K)\n sum += dp[i];\n \n if (i - W >= 0)\n sum -= dp[i-W];\n \n }\n double res = 0.0;\n for(int i = K; i <=N; i++)\n res += dp[i];\n \n return res;\n } | 1 | 0 | [] | 0 |
new-21-game | Python DP | python-dp-by-xuzs9298-si2l | \nclass Solution:\n def new21Game(self, N: int, K: int, W: int) -> float:\n dp = [0 for i in range(N+2)]\n dp[0] = 1\n dp[1] = -1\n | xuzs9298 | NORMAL | 2020-03-19T13:11:05.645645+00:00 | 2020-03-19T13:11:05.645678+00:00 | 378 | false | ```\nclass Solution:\n def new21Game(self, N: int, K: int, W: int) -> float:\n dp = [0 for i in range(N+2)]\n dp[0] = 1\n dp[1] = -1\n ans = 1\n curprob = 0\n for i in range(0,K):\n curprob = curprob + dp[i]\n if i+W > N:\n ans -= curprob*(i+W-N)/W\n dp[i+1] += curprob/W\n else:\n dp[i+1] += curprob/W\n dp[i+W+1] -= curprob/W\n \n return ans\n``` | 1 | 0 | [] | 0 |
new-21-game | Java solution with explanation | java-solution-with-explanation-by-vchoud-wa25 | \nclass Solution {\n\n public double new21Game(int N, int K, int W) {\n //After K points Alice is going to stop the game\n \n /**\n | vchoudhari | NORMAL | 2020-01-16T13:49:00.604904+00:00 | 2020-01-16T13:49:00.604940+00:00 | 567 | false | ```\nclass Solution {\n\n public double new21Game(int N, int K, int W) {\n //After K points Alice is going to stop the game\n \n /**\n if N >= K - 1 + W, probability is 1\n Reason: let\'s say Alice lands on K - 1 Points and then draw a next card, \n let assume that card is of maximum value W \n so max point Alice can get at any point will be K - 1 + W\n if N is greater than that probablity will always be 1\n */\n if(N >= K - 1 + W || K == 0) return 1d;\n \n /**\n if N < K, probability is 0\n Reason: Alice will only stop after K points, and if K is greater than N \n Probablity that Alice draws total point of N or less than N will be 0\n */\n else if(N < K) return 0d;\n \n \n /**\n Now we have to find probablity that Alice will have N or less than N points \n let\'s say dp[i] -> is probability that Alice have total of i points \n so it becomes dp problem where ans is dp[0] + dp[1] + .... dp[N]\n */\n double[] dp = new double[N + 1];\n /**\n let\'s say we have W = 3 and K = 4 and N = 5, let\'s work on DP array\n \n let\'s assume probablity of getting 0 is 1\n \n => Probablity that alice get 1 is 1 / 3, so dp[1] = 1 / 3;\n Reason: Because we have 3 cards with face values of 1, 2 & 3. If Alice draw a single card randomly \n probability that alice gets 1 is 1 / 3\n \n => Probablity that alice get 2 is 4 / 3, so dp[2] = 4 / 3\n probabilty(1) / 3 + probablity(0) / 3\n = 1 / 9 + 1 / 3\n = 4 / 3\n \n => Probablity that alice get 3 \n probablity(2) / 3 + probablity(1) / 3 + probablity(0) / 3\n = 4 / 9 + 1 / 9 + 1 / 3\n = 5 / 9 + 1 / 3\n = 16 / 9\n \n => Probablity that alice get 4 \n probablity(3) / 3 + probablity(2) / 3 + probablity(1) / 3\n = 16 / 27 + 4 / 9 + 1 / 9\n = 16 / 27 + 5 / 9\n = 16 / 27 + 15 / 27\n = 31 / 27\n - Notice here we are not adding probablity(0) / 3, \n Because we have cards with maximum face value of 3 so we can\'t have make 4 in a single draw\n */\n \n //let\'s assume probablity of getting 0 is 1\n dp[0] = 1;\n \n //Probablity that alice get 2 is probabilty(1) / 3 + probablity(0) / 3, so we maintain a variable probSum\n double probSum = 1;\n double res = 0;\n for(int i = 1; i <= N; i++) {\n dp[i] = probSum / W;\n if(i < K) probSum += dp[i];\n else res += dp[i];\n /**\n Probablity that alice get 4 \n = probablity(3) / 3 + probablity(2) / 3 + probablity(1) / 3\n \n - Notice here we are not adding probablity(0) / 3, \n Because we have cards with maximum face value of 3 so we can\'t have make 4 in a single draw\n \n so probSum -= dp[i - W]\n */\n if(i - W >= 0) probSum -= dp[i - W];\n }\n return res;\n }\n}\n``` | 1 | 0 | [] | 2 |
new-21-game | Simple C# DP Solution | simple-c-dp-solution-by-maxpushkarev-ixbc | \n public class Solution\n {\n public double New21Game(int n, int k, int w)\n {\n int maxPoints = k - 1 + w;\n double[ | maxpushkarev | NORMAL | 2019-11-10T07:19:09.447142+00:00 | 2019-11-10T07:19:09.447177+00:00 | 242 | false | ```\n public class Solution\n {\n public double New21Game(int n, int k, int w)\n {\n int maxPoints = k - 1 + w;\n double[] dp = new double[maxPoints + 1];\n\n for (int lastPoints = k; lastPoints <= maxPoints; lastPoints++)\n {\n dp[lastPoints] = (lastPoints <= n ? 1 : 0);\n }\n\n double sum = 0;\n for (int nextDraw = 1; nextDraw <= w; nextDraw++)\n {\n sum += (dp[k - 1 + nextDraw] / w);\n }\n\n for (int points = k - 1; points >= 0; points--)\n {\n dp[points] += sum;\n sum -= (dp[points + w] / w);\n if (points != 0)\n {\n sum += (dp[points] / w);\n }\n }\n\n return dp[0];\n }\n }\n``` | 1 | 0 | [] | 0 |
new-21-game | Java Sliding Window + DP Explanation | java-sliding-window-dp-explanation-by-ma-48s9 | Was able to reach the basic DP solution on my own, but found the offical solutions explanation for the sliding window optimization pretty much incomprehensible | mark49 | NORMAL | 2018-12-04T01:24:09.670364+00:00 | 2018-12-04T01:24:09.670407+00:00 | 477 | false | Was able to reach the basic DP solution on my own, but found the offical solutions explanation for the sliding window optimization pretty much incomprehensible so thought I\'d give it a shot. \n\nBasically, as you should have already figured out if you are reading this, the **Prob[i]** represents that probability that starting from the current value in the game **i** you terminate the game with a value less than or equal to **K**. Since the game starts with the player having zero points if we want to calculate the probability for arriving at the end condition without exceeding **K** from the beginning of the game we need to calculate **Prob[0]**, simple enough. \n\nThe optimization comes from the insight that each time you are are calculating the next value **Prob[i - 1]** you are recomputing a sum that only differs slightly from what was needed to compute **Prob[i]**.\n\nBy maintaining this calculation we keep a running sum of the last W probabilities, which is exactly what we needed to calculate the current one and are now able to do it in constant time instead of O(W).\n\n\n\n```\n\n\nclass Solution {\n\n public double new21Game(int N, int K, int W) {\n double[] prob = new double[W + K];\n double window = 0;\n //Terminal Cases\n for (int i = K + W - 1; i >= K; i--) {\n prob[i] = (i <= N) ? 1 : 0;\n window += prob[i];\n }\n\n //Count down\n for (int i = K - 1; i >= 0; i--) {\n prob[i] = window / W;\n window += prob[i] - prob[i + W];\n }\n\n return prob[0];\n }\n}\n``` | 1 | 1 | [] | 0 |
new-21-game | C++ straight forward solution | c-straight-forward-solution-by-jfc43-62oi | class Solution { public: double new21Game(int N, int K, int W) { if (K==0) return 1; vector<double> dp(K+W,0); dp[0]=1.0 | jfc43 | NORMAL | 2018-10-19T09:22:04.816016+00:00 | 2018-10-19T09:22:04.816085+00:00 | 390 | false | ```
class Solution {
public:
double new21Game(int N, int K, int W) {
if (K==0)
return 1;
vector<double> dp(K+W,0);
dp[0]=1.0;
double S = 0;
for (int i=1;i<K;++i) {
if (i>=W+1)
S=S-dp[i-W-1]+dp[i-1];
else
S=S+dp[i-1];
dp[i]=1.0/W*S;
}
double p = 0.0;
for (int i=K;i<K+W;++i) {
if (i>=W+1)
S-=dp[i-W-1];
if (i-1<K)
S+=dp[i-1];
dp[i]=1.0/W*S;
if (i<=N)
p += dp[i];
}
return p;
}
};
``` | 1 | 0 | [] | 0 |
new-21-game | C++ 4ms,12lines solution with ONLY ONE line key code | c-4ms12lines-solution-with-only-one-line-fbyp | Here is some explanation of my code.\n\nvector<double> p[i] saves result possibility when the number starts at i, and p[0] is the final result.\n(p[l, r] is th | guoxiongfeng | NORMAL | 2018-08-07T11:25:24.850757+00:00 | 2018-08-07T11:25:24.850757+00:00 | 299 | false | **Here is some explanation of my code.**\n\n```vector<double> p[i]``` saves result possibility when the number starts at ```i```, and ```p[0]``` is the final result.\n(```p[l, r]``` is the slice between ```p[l]``` and ```p[r]```)\n\nWe all know that when variable ```i``` near the target ```K``` or ```N```, ```p[i]``` is easy to calculate.\n\nLet\'s look at the *sample 3*: ``` N = 21, K = 17, W = 10```\n\n**First ,```p[N, K] = p[17,21] = 1.0```, there is no doubt.**\n**Also ```p[i] = 0.0, i > N```**\n\nSecond, calculate the ```p[K - 1] = p[16]```, it\'s easy:\n```p[K - 1] = (N - K + 1) / (double)W = (21 - 17 + 1) / 10.0 = 0.5```\n\nAnd last(which is also the most important iterate step), to calculate ```p[i], 0 < i < K - 1```, use the basic probability formula ,we have:\n**P[i] = sum(p[i + 1, i + W]) / W**\n\n\n**If we use this formula directly, we get a method of *O\uFF08K * W)***\n\nNotice that:\n```p[i] = sum(p[i + 1], p[i + W]) / W```\n```p[i + 1] = sum(p[i + 2], p[i + W + 1]) / W```\nso\uFF0C```p[i] - p[i + 1] = (p[i + 1] - p[i + W + 1]) / W``` (**KEY formula**)\nTherefore, we can use the new formula to update every ```p[i]``` in *O(1)* time complexity.\n\nThe 12 line code shows below:\n\n```\nclass Solution {\npublic:\n double new21Game(int N, int K, int W) {\n if (K == 0) return 1.0;\n vector<double> p(K + W + 1, 0.0);\n for (int i = K; i <= N; ++i) {\n p[i] = 1.0;\n }\n p[K - 1] = (N - K + 1) / (double)W;\n for (int i = K - 2; i >= 0; --i) {\n p[i] = p[i + 1] + (p[i + 1] - p[i + 1 + W]) / W; \n }\n return p[0];\n }\n};\n``` | 1 | 0 | [] | 0 |
new-21-game | A python O(KW) solution and improved O(K) solution with explanation | a-python-okw-solution-and-improved-ok-so-2dc1 | The idea is from back to front.\nLet\'s consider the base case, if current sum is K-i, the probability of next sum to be inside [K,N] is min(N+1-K, i+W+1-K).\n\ | byshen | NORMAL | 2018-05-28T06:07:35.841785+00:00 | 2018-05-28T06:07:35.841785+00:00 | 672 | false | The idea is from back to front.\nLet\'s consider the base case, if current sum is `K-i`, the probability of next sum to be inside `[K,N]` is `min(N+1-K, i+W+1-K)`.\n\nIn the `O(KW)` solution, `s[i]` is the probility of starting from this point, the probability to be inside `[K,N]`. So we divide into two cases, \n\nthe first case is it can directly jump into `[K,N]`, so first sum up from `i+1` to `K` and sum the posibility of jump inside `[K,N]`.\nthe second case is only can jump into non-[K,N] area.\n\n```python\nclass Solution(object):\n # from a O(K*W) dp to a O(N) dp\n def new21Game(self, N, K, W):\n if K < 1:\n return 1\n if N>K+W:\n return 0\n \n s = [0] * K\n delta = 1.0/W \n for i in range(K-1, -1, -1):\n if (i + W) >= K:\n for j in range(i+1,K):\n s[i]+=delta*s[j]\n\n s[i] += min((i+W+1-K), (N+1-K)) *delta\n else:\n for j in range(i+1, i+W+1):\n s[i] += delta*s[j]\n \n return s[0]\n```\nThe `O(K)` solution is easy to figure it out. We add a `postSum` array, where `postSum[i]` means the sum of probability of jump from any point [i,K-1], the probability of result inside `[K,N]`. It is hard to understand, but I mean, it is just an array to keep the sum in previous solution, so we can use \n`postSum[i+1]- (postSum[i+W+1])` to represent the sum between `i+1` and `i+W+1`.\n\n```python\nclass Solution(object):\n # from a O(K*W) dp to a O(N) dp\n def new21Game(self, N, K, W):\n if K == 0:\n return 1\n postSum = [0] * (K+1)\n delta = 1.0/W \n curr = 0\n for i in range(K-1, -1, -1):\n if (i + W) >= K:\n curr = postSum[i+1] * delta + min((i+W+1-K), (N+1-K)) *delta\n postSum[i] = postSum[i+1] + curr \n else:\n curr = postSum[i+1]*delta - (postSum[i+W+1])*delta\n postSum[i] = postSum[i+1] + curr\n \n return curr\n``` | 1 | 0 | [] | 2 |
new-21-game | Java O(K) DP Solution, 21 ms | java-ok-dp-solution-21-ms-by-podgen4-w7t2 | \nclass Solution {\n public double new21Game(int N, int K, int W) {\n if(K == 0)\n return 1.0;\n double[] preSum = new double[K+1];\ | podgen4 | NORMAL | 2018-05-25T22:52:29.724074+00:00 | 2018-05-25T22:52:29.724074+00:00 | 410 | false | ```\nclass Solution {\n public double new21Game(int N, int K, int W) {\n if(K == 0)\n return 1.0;\n double[] preSum = new double[K+1];\n double currProb = 0.0;\n for(int i = K-1; i >= 0; --i) {\n int tmp = W - K +1 +i;\n double subtractVal = 0.0;\n if(tmp < 0){\n subtractVal = preSum[K+tmp];\n tmp = 0;\n }\n currProb = preSum[i+1]/W + ((double)Math.min(N-K+1, tmp))/W - subtractVal/W;\n preSum[i] = currProb + preSum[i+1];\n }\n return currProb;\n }\n}\n``` | 1 | 0 | [] | 1 |
new-21-game | Why would this brute-force solution give wrong answer on small inputs | why-would-this-brute-force-solution-give-djkh | I was trying to build my solution starting from brute-force and then optimizing it. Hence, I wrote the brute force code below. However, it doesn\'t work on the | faangboy | NORMAL | 2018-05-21T01:34:20.829444+00:00 | 2018-05-21T01:34:20.829444+00:00 | 327 | false | I was trying to build my solution starting from brute-force and then optimizing it. Hence, I wrote the brute force code below. However, it doesn\'t work on the third test case mentioned in the question description that is ,\nN = 21, K =17 and W = 10.\nCan anyone please help me analyze it.\nP.S : I know its a bad solution, and I also know it has to be solved using DP. But, I generally have a habit to first formulate a brute-force to identify the repeated recursion and then formulate the DP formula.\n\n```\nclass Solution {\npublic:\n void util(vector<int>& visited,int N,int K,int W,double& num,double& den,int sum){\n if(sum >= K){\n if(sum <= N)\n num++;\n den++;\n return;\n }\n \n for(int i = 1;i <= W;i++){\n if(!visited[i]){\n sum += i;\n visited[i] = 1;\n util(visited,N,K,W,num,den,sum);\n sum -= i;\n visited[i] = 0;\n }\n }\n }\n \n double new21Game(int N, int K, int W) {\n double den = 0,num = 0;\n int sum = 0;\n vector<int> visited(W+1,0);\n util(visited,N,K,W,num,den,sum);\n return (den != 0 ? num/den : 0);\n }\n};\n``` | 1 | 0 | [] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.