question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
construct-the-minimum-bitwise-array-i | C# Linq 1 line | c-linq-1-line-by-gbamqzkdyg-xgij | Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\ncsharp []\npublic class Solution {\n public int[] MinBitwiseArray(IList<int> num | gbamqzkdyg | NORMAL | 2024-10-14T08:13:32.961343+00:00 | 2024-10-14T08:13:32.961377+00:00 | 7 | false | # Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```csharp []\npublic class Solution {\n public int[] MinBitwiseArray(IList<int> nums) => nums.Select(num => num % 2 == 0 ? -1 : num - ((num + 1) & (-num - 1)) / 2).ToArray();\n}\n``` | 0 | 0 | ['C#'] | 0 |
construct-the-minimum-bitwise-array-i | brute force | brute-force-by-user5285zn-jiuu | \nrust []\nfn f(x: i32) -> i32 {\n for y in 1..x {\n if (y | (y+1)) as i32 == x {return y}\n }\n -1\n}\nimpl Solution {\n pub fn min_bitwise | user5285Zn | NORMAL | 2024-10-14T04:56:38.174853+00:00 | 2024-10-14T04:56:38.174888+00:00 | 1 | false | \n```rust []\nfn f(x: i32) -> i32 {\n for y in 1..x {\n if (y | (y+1)) as i32 == x {return y}\n }\n -1\n}\nimpl Solution {\n pub fn min_bitwise_array(nums: Vec<i32>) -> Vec<i32> {\n nums.into_iter().map(f).collect()\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
construct-the-minimum-bitwise-array-i | Min Bitwise Array - JS | min-bitwise-array-js-by-zemamba-g5ft | javascript []\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar minBitwiseArray = function(nums) {\n ans = []\n for (let i = 0; i < nums.le | zemamba | NORMAL | 2024-10-13T20:29:29.510840+00:00 | 2024-10-13T20:29:29.510867+00:00 | 5 | false | ```javascript []\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar minBitwiseArray = function(nums) {\n ans = []\n for (let i = 0; i < nums.length; i++) {\n for (let j = 1; j < nums[i]; j++) {\n if ((j | (j + 1)) == nums[i]) {\n ans.push(j)\n break\n }\n }\n if (!ans[i]) ans.push(-1)\n }\n\n return ans\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
construct-the-minimum-bitwise-array-i | See the python solution | see-the-python-solution-by-testcasefail-cg2p | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | TestCaseFail | NORMAL | 2024-10-13T18:25:11.429933+00:00 | 2024-10-13T18:25:11.429953+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n ans = []\n for num in nums:\n found = False\n for candidate in range(num): \n if candidate | (candidate + 1) == num:\n ans.append(candidate)\n found = True\n break\n if not found:\n ans.append(-1)\n \n return ans\n``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | C++ Solution | c-solution-by-user1122v-2dv8 | \n# Code\ncpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n for(int i = 0; i < nums.size(); i++){\n in | user1122v | NORMAL | 2024-10-13T17:56:40.686586+00:00 | 2024-10-13T17:56:40.686628+00:00 | 9 | false | \n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n for(int i = 0; i < nums.size(); i++){\n int flag = 0;\n for(int j = 1; j < nums[i]; j++){\n if((j | (j + 1)) == nums[i]){\n nums[i] = j;\n flag = 1;\n break;\n }\n }\n if(!flag) nums[i] = -1;\n }\n return nums;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | [C++/Java/Python] DP Solution O(N^2) | cjavapython-dp-solution-on2-by-lee215-gmg2 | Intuition\ndp[i][j] means the number of possible permutations of first i + 1 digits,\nwhere the i + 1th digit is j + 1th smallest in the rest of unused digits.\ | lee215 | NORMAL | 2018-09-09T03:11:12.918248+00:00 | 2020-01-31T07:54:49.540221+00:00 | 19,948 | false | # Intuition\n`dp[i][j]` means the number of possible permutations of first `i + 1` digits,\nwhere the `i + 1`th digit is `j + 1`th smallest in the rest of unused digits.\n\n\nOk, may not make sense ... Let\'s see the following diagram.\n\n\nI take the example of `S = "DID"`.\nIn the parenthesis, I list all possible permutations.\n\nThe permutation can start from `1, 2, 3, 4`.\nSo `dp[0][0] = dp[0][1] = dp[0][2] = dp[0][3] = 1`.\n\nWe decrese from the first digit to the second,\nthe down arrow show the all possibile decresing pathes.\n\nThe same, because we increase from the second digit to the third,\nthe up arrow show the all possibile increasing pathes.\n\n`dp[2][1] = 5`, mean the number of permutations\nwhere the third digitis the second smallest of the rest.\nWe have 413,314,214,423,324.\nFow example 413, where 2,3 are left and 3 the second smallest of them.\n<br>\n\n# Explanation\nAs shown in the diagram,\nfor "I", we calculate prefix sum of the array,\nfor "D", we calculate sufixsum of the array.\n<br>\n\n# Complexity\nTime `O(N^2)`\nSpace `O(N^2)`\n<br>\n\n**C++:**\n```cpp\n int numPermsDISequence(string S) {\n int n = S.length(), mod = 1e9 + 7;\n vector<vector<int>> dp(n + 1, vector<int>(n + 1));\n for (int j = 0; j <= n; j++) dp[0][j] = 1;\n for (int i = 0; i < n; i++)\n if (S[i] == \'I\')\n for (int j = 0, cur = 0; j < n - i; j++)\n dp[i + 1][j] = cur = (cur + dp[i][j]) % mod;\n else\n for (int j = n - i - 1, cur = 0; j >= 0; j--)\n dp[i + 1][j] = cur = (cur + dp[i][j + 1]) % mod;\n return dp[n][0];\n }\n```\n\n**Java:**\n```java\n public int numPermsDISequence(String S) {\n int n = S.length(), mod = (int)1e9 + 7;\n int[][] dp = new int[n + 1][n + 1];\n for (int j = 0; j <= n; j++) dp[0][j] = 1;\n for (int i = 0; i < n; i++)\n if (S.charAt(i) == \'I\')\n for (int j = 0, cur = 0; j < n - i; j++)\n dp[i + 1][j] = cur = (cur + dp[i][j]) % mod;\n else\n for (int j = n - i - 1, cur = 0; j >= 0; j--)\n dp[i + 1][j] = cur = (cur + dp[i][j + 1]) % mod;\n return dp[n][0];\n }\n```\n\n# Solution 2:\nNow as we did for every DP, make it 1D dp.\nTime `O(N^2)`\nSpace `O(N)`\n\n**C++:**\n```cpp\n int numPermsDISequence(string S) {\n int n = S.length(), mod = 1e9 + 7;\n vector<int> dp(n + 1, 1), dp2(n);\n for (int i = 0; i < n; dp = dp2, i++) {\n if (S[i] == \'I\')\n for (int j = 0, cur = 0; j < n - i; j++)\n dp2[j] = cur = (cur + dp[j]) % mod;\n else\n for (int j = n - i - 1, cur = 0; j >= 0; j--)\n dp2[j] = cur = (cur + dp[j + 1]) % mod;\n }\n return dp[0];\n }\n```\n\n**Java:**\n```java\n public int numPermsDISequence(String S) {\n int n = S.length(), mod = (int)1e9 + 7;\n int[] dp = new int[n + 1], dp2 = new int[n];;\n for (int j = 0; j <= n; j++) dp[j] = 1;\n for (int i = 0; i < n; i++) {\n if (S.charAt(i) == \'I\')\n for (int j = 0, cur = 0; j < n - i; j++)\n dp2[j] = cur = (cur + dp[j]) % mod;\n else\n for (int j = n - i - 1, cur = 0; j >= 0; j--)\n dp2[j] = cur = (cur + dp[j + 1]) % mod;\n dp = Arrays.copyOf(dp2, n);\n }\n return dp[0];\n }\n```\n\n**Python2**\n```py\n def numPermsDISequence(self, S):\n dp = [1] * (len(S) + 1)\n for c in S:\n if c == "I":\n dp = dp[:-1]\n for i in range(1, len(dp)):\n dp[i] += dp[i - 1]\n else:\n dp = dp[1:]\n for i in range(len(dp) - 1)[::-1]:\n dp[i] += dp[i + 1]\n return dp[0] % (10**9 + 7)\n```\n**Python3**\n```py\n def numPermsDISequence(self, S):\n dp = [1] * (len(S) + 1)\n for a, b in zip(\'I\' + S, S):\n dp = list(itertools.accumulate(dp[:-1] if a == b else dp[-1:0:-1]))\n return dp[0] % (10**9 + 7)\n``` | 288 | 9 | [] | 49 |
valid-permutations-for-di-sequence | Easy-to-understand solution with detailed explanation | easy-to-understand-solution-with-detaile-jmb5 | \nBefore diving into the state transition function, let us first start with a simple example.\n\n### 1. a simple example\n\nIn the following discussion, for sim | wxd_sjtu | NORMAL | 2018-11-23T07:57:21.259281+00:00 | 2018-11-23T07:57:21.259326+00:00 | 7,633 | false | \nBefore diving into the state transition function, let us first start with a simple example.\n\n### 1. a simple example\n\nIn the following discussion, for simplification, I will use both notation DI-seq and DI-rule instead of DI sequence.\n\nConsider a permutation 1032, which is based on a DI-seq "DID", how to use it to construct a new instance ending at **2** and based on DI-seq "DID**D**"?\n\n**Method**:\nstep 1.\nfor the original permutation `1032`, we add 1 to the digits *that are larger than or equal to* **2**.\n```C++\n1032->1043\n ^^\n```\n\nstep 2.\nthen directly append **2** to `1043`, i.e., 1043 -> 1043**2**\n\n**Remark on step 1**:\n(1) By performing add operation, 2 in the original permutation now becomes 3, and thus there is no duplicate element for the new arrival **2**.\n(2) More importantly, such operation on the digits **will not break the original DI-rule**. e.g., 1043 still keeps its old DI-rule, i.e., "DID". The proof is straight-forward, you can validate yourself.\n\nNow a new permutation with DI-rule "DID**D**" and ending at **2** has been constructed from 1032, namely 1043**2**.\n\n\nWith the same spirit, using 1032("DID"), we can construct instances with DI-rule "DID**D**": 2043**1**(ending with **1**), 2143**0**(ending with **0**).\n(Note that the instance(based on "DID**D**") which ends with 3 can not be constructed.)\n\n\n\nSimilarly, from 1032("DID"), we can construct instances with DI-rule "DID**I**": 10423(ending with **3**), 10324(ending with **4**).\n(Note that the instance(based on "DID**I**") which ends with 1 or 2 can not be constructed.)\n\n\n\n### 2. state transition function\n\nWith the example above in mind, the transition function seems to be clear.\n\nGiven a string DI-seq S, let `dp[i][j]` represents the number of permutation of number `0, 1, ... , i`, satisfying DI-rule S.substr(0, i), and ending with digit `j`.\n\n\n```C++\nif(S[i-1] == \'D\')\n dp[i][j] = dp[i-1][j] + dp[i-1][j+1] + ... + dp[i-1][i-1]\n\nif(S[i-1] == \'I\') \n dp[i][j] = dp[i-1][0] + dp[i-1][1] + ... + dp[i-1][j-1]\n```\n\n\n\n\n### 3. Solution\n\n```C++\nlass Solution {\npublic:\n int numPermsDISequence(string S) {\n int n = S.size(), m = 1e9 + 7;\n vector<vector<int>> dp(n+1, vector<int>(n+1, 0));\n dp[0][0] = 1;\n for(int i = 1; i <= n; i++)\n for(int j = 0; j <= i; j++)\n if(S[i-1] == \'D\')\n for(int k = j; k <= i-1; k++)\n dp[i][j] = dp[i][j]%m + dp[i-1][k]%m;\n else\n for(int k = 0; k <= j-1; k++)\n dp[i][j] = dp[i][j]%m + dp[i-1][k]%m;\n int res = 0;\n for(int i = 0; i <= n; i++)\n res = res%m + dp[n][i]%m;\n return res%m;\n }\n};\n```\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n | 164 | 2 | [] | 19 |
valid-permutations-for-di-sequence | Top-down with Memo -> Bottom-up DP -> N^3 DP -> N^2 DP -> O(N) space | top-down-with-memo-bottom-up-dp-n3-dp-n2-f8t1 | Top-down with Memo:\n\nDefinition: helper(String s, Map<String, Long> map): Answer to s.\n\nIntuition: Insert the largest number into appropriate postion.\n\neg | wangzi6147 | NORMAL | 2018-09-09T22:02:54.189890+00:00 | 2018-10-18T02:01:41.061592+00:00 | 5,593 | false | **Top-down with Memo:**\n\nDefinition: `helper(String s, Map<String, Long> map)`: Answer to `s`.\n\nIntuition: Insert the largest number into appropriate postion.\n\neg. `s=\'IIDD\'`, we can only insert `4` between `I` and `D`. We break the remained numbers `0, 1, 2, 3` into two groups both with the size of 2. We have `C(4, 2)` possible combinations. Then `helper("IIDD") = helper("I") * helper("D") * C(4, 2)`.\n\nTricky: How to calculate `C(n, k) % M`? I referred a method using *Pascal Triangle* from [here](https://www.geeksforgeeks.org/compute-ncr-p-set-1-introduction-and-dynamic-programming-solution/). (This part makes this method ugly and lengthy, anybody has better approaches?)\n\nTime complexity: `O(n^4)` in my implementation, however could improve to `O(n^3)`.\n\nCode:\n\n```\nclass Solution {\n private int M = (int)1e9 + 7;\n private int[][] nCkMemo;\n public int numPermsDISequence(String S) {\n int n = S.length();\n nCkMemo = new int[n + 1][n + 1];\n return (int)helper(S, new HashMap<>());\n }\n private long helper(String s, Map<String, Long> map) {\n if (s.equals("")) {\n return 1;\n }\n if (map.containsKey(s)) {\n return map.get(s);\n }\n long result = 0;\n int n = s.length();\n if (s.charAt(0) == \'D\') {\n result += helper(s.substring(1), map);\n result %= M;\n }\n if (s.charAt(n - 1) == \'I\') {\n result += helper(s.substring(0, n - 1), map);\n result %= M;\n }\n for (int i = 1; i < n; i++) {\n if (s.charAt(i - 1) == \'I\' && s.charAt(i) == \'D\') {\n long left = helper(s.substring(0, i - 1), map);\n long right = helper(s.substring(i + 1), map);\n result += (((left * right) % M) * nCk(n, i)) % M;\n result %= M;\n }\n }\n map.put(s, result);\n return result;\n }\n private int nCk(int n, int k) {\n if (k == 0 || k == n) {\n return 1;\n }\n if (nCkMemo[n][k] == 0) {\n nCkMemo[n][k] = (nCk(n - 1, k) + nCk(n - 1, k - 1)) % M;\n }\n return nCkMemo[n][k];\n }\n}\n```\n\n**Bottom-up DP:**\n\nSame idea with the Top-down. `dp[i][j]` represent the answer of `s.substring(i, j)`. Just a Bottom-up implementation:\n\nTime complexity: `O(n^3)`\n\n```\nclass Solution {\n private int M = (int)1e9 + 7;\n public int numPermsDISequence(String S) {\n int n = S.length();\n long[][] dp = new long[n + 1][n + 1];\n int[][] nCkMemo = new int[n + 1][n + 1];\n for (int i = 0; i <= n; i++) {\n dp[i][i] = 1;\n }\n for (int len = 1; len <= n; len++) {\n for (int i = 0; i <= n - len; i++) {\n int j = i + len;\n if (S.charAt(i) == \'D\') {\n dp[i][j] += dp[i + 1][j];\n dp[i][j] %= M;\n }\n for (int k = i + 1; k < j; k++) {\n if (S.charAt(k - 1) == \'I\' && S.charAt(k) == \'D\') {\n dp[i][j] += (((dp[i][k - 1] * dp[k + 1][j]) % M) * nCk(len, k - i, nCkMemo)) % M;\n dp[i][j] %= M;\n }\n }\n if (S.charAt(j - 1) == \'I\') {\n dp[i][j] += dp[i][j - 1];\n dp[i][j] %= M;\n }\n }\n }\n return (int)dp[0][n];\n }\n private int nCk(int n, int k, int[][] nCkMemo) {\n if (k == 0 || k == n) {\n return 1;\n }\n if (nCkMemo[n][k] == 0) {\n nCkMemo[n][k] = (nCk(n - 1, k, nCkMemo) + nCk(n - 1, k - 1, nCkMemo)) % M;\n }\n return nCkMemo[n][k];\n }\n}\n```\n\n**N^3 DP:**\n\nLet\'s change the definition of `dp` matrix to make the calculation simple: let\'s say `dp[i][j]` represents the number of permutation of number `0, 1, ... , i` which ends with `j`. Also, it represents the answer of `s.substring(0, i)` which ends with `j`.\nWe will have two conditions: \n\n1. `s.charAt(i - 1) == \'I\'`: In this case, `dp[i][j] = sum(dp[i - 1][0], dp[i - 1][1], ... , dp[i - 1][j - 1])`.\n2. `s.charAt(i - 1) == \'D\'`: In this case, `dp[i][j] = sum(dp[i - 1][j], dp[i - 1][j + 1], ... , dp[i - 1][i - 1])`.\n\nImagine each time when appending the `j` to the previous permutations, you have to **add 1 to each number in the previous permutation which is greater than or equals to `j`**. In this way, we keep the orders and counts of previous permutations and cumulate.\n\neg. We already have permutation `(1, 0, 3, 2)`. We are trying to append `2`. Now the `(1, 0, 3, 2)` changes to `(1, 0, 4, 3)` then appended with a `2`. We have `(1, 0, 4, 3, 2)`. Although the values change but the order and count don\'t change.\n\nTime complexity: `O(n^3)`\n\nCode:\n\n```\nclass Solution {\n public int numPermsDISequence(String S) {\n int n = S.length(), M = (int)1e9 + 7;\n int[][] dp = new int[n + 1][n + 1];\n dp[0][0] = 1;\n for (int i = 1; i <= n; i++) {\n for (int j = 0; j <= i; j++) {\n if (S.charAt(i - 1) == \'D\') {\n for (int k = j; k < i; k++) {\n dp[i][j] += dp[i - 1][k];\n dp[i][j] %= M;\n }\n } else {\n for (int k = 0; k < j; k++) {\n dp[i][j] += dp[i - 1][k];\n dp[i][j] %= M;\n }\n }\n }\n }\n int result = 0;\n for (int j = 0; j <= n; j++) {\n result += dp[n][j];\n result %= M;\n }\n return result;\n }\n}\n```\n\n **N^2 DP:**\n \n Notice that in the previous method, we are actually calculate the **prefix sum** and **suffix sum** in the two conditions:\n \n1. `s.charAt(i - 1) == \'I\'`: In this case, `dp[i][j] = sum[i - 1][j - 1]`.\n2. `s.charAt(i - 1) == \'D\'`: In this case, `dp[i][j] = sum[i - 1][i - 1] - sum[i - 1][j - 1]`.\n\nWe can define `dp[i][j]` as `sum(dp[i][0], dp[i][1], ... dp[i][j])` which is `sum[i][j]`.\n\nTime complexity: `O(n^2)`\n\nCode:\n\n```\nclass Solution {\n public int numPermsDISequence(String S) {\n int n = S.length(), M = (int)1e9 + 7;\n int[][] dp = new int[n + 1][n + 1];\n Arrays.fill(dp[0], 1);\n for (int i = 1; i <= n; i++) {\n for (int j = 0; j <= i; j++) {\n dp[i][j] = j == 0 ? 0 : dp[i][j - 1];\n if (S.charAt(i - 1) == \'D\') {\n dp[i][j] += (dp[i - 1][i - 1] - (j == 0 ? 0 : dp[i - 1][j - 1])) % M;\n if (dp[i][j] < 0) {\n dp[i][j] += M;\n }\n } else {\n dp[i][j] += j == 0 ? 0 : dp[i - 1][j - 1];\n }\n dp[i][j] %= M;\n }\n }\n return dp[n][n];\n }\n}\n```\n\n**O(N) space:**\n\nPrevious solution could be optimized to `O(n)` space.\n\nTime complexity: `O(n^2)`. Space complexity: `O(n)`.\n\n```\nclass Solution {\n public int numPermsDISequence(String S) {\n int n = S.length(), M = (int)1e9 + 7;\n int[] dp = new int[n + 1];\n Arrays.fill(dp, 1);\n for (int i = 1; i <= n; i++) {\n int[] temp = new int[n + 1];\n for (int j = 0; j <= i; j++) {\n temp[j] = j == 0 ? 0 : temp[j - 1];\n if (S.charAt(i - 1) == \'D\') {\n temp[j] += (dp[i - 1] - (j == 0 ? 0 : dp[j - 1])) % M;\n if (temp[j] < 0) {\n temp[j] += M;\n }\n } else {\n temp[j] += j == 0 ? 0 : dp[j - 1];\n }\n temp[j] %= M;\n }\n dp = temp;\n }\n return dp[n];\n }\n}\n```\n | 38 | 1 | [] | 6 |
valid-permutations-for-di-sequence | Share my O(N^3) => O(N^2) C++ DP solution. Including the thoughts of improvement. | share-my-on3-on2-c-dp-solution-including-lsv6 | Came up with the original idea during contest, so might not be the best. But it works.\nc++\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n | xidui | NORMAL | 2018-09-09T03:20:21.534047+00:00 | 2018-10-17T13:58:10.604683+00:00 | 3,498 | false | Came up with the original idea during contest, so might not be the best. But it works.\n```c++\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int N = S.length() + 1;\n int MOD = 1e9 + 7;\n // dp[i][j] number of permutation whose length is i and end with j\n int dp[202][202] = {};\n dp[1][1] = 1;\n for (int i = 2; i <= N; ++i) {\n // length is i\n for (int j = 1; j <= i; ++j) {\n // end with j\n if (S[i - 2] == \'D\') {\n // decrease to j\n // add all string with length i - 1 and last digit is greater than or equal to j\n for (int k = j; k <= i; ++k) {\n dp[i][j] = (dp[i][j] + dp[i-1][k]) % MOD;\n }\n } else {\n // increase to j\n // add all string with length i - 1 and last digit is smaller than j\n for (int k = 1; k < j; ++k) {\n dp[i][j] = (dp[i][j] + dp[i-1][k]) % MOD;\n }\n }\n }\n }\n int ans = 0;\n for (int i = 1; i <= N; ++i) ans = (ans + dp[N][i]) % MOD;\n return ans;\n }\n};\n```\n\n**UPDATE 9/9/2018**:\nThanks to `@chosun1`, I used prefix sum to save the result which reduce the complexity to O(N ^ 2). There is no need to keep a separate 2d array for prefix sum, just change the definition of dp array is fine. Here is the updated code, it is even shorter.\n\n`dp[i][j]` means number of permutation whose length is `i` and end with **at most** `j`.\n\nLet\'s say the current position of DI sequence is `\'D\'`, \nSo, `dp[i][j] = dp[i][j-1] + X`, where `X` is number of permutations whose length is `i` and end exactly with `j`. We can calculate it by adding number of permutations whose length is `i-1` and end with `{j, j+1, ..., i-1}`, because they will satisfy the condition of "decreasing to j". (*Wait! Wait! Why start with j not j + 1?, see the bolded explaination below.*)\nAccording to the definition of dp array, we can get `X = dp[i-1][i-1] - dp[i-1][j-1]`.\n\nIf the DI sequence is `\'I\'`, it\'s similiar.\n\n**So, why start with j, not j + 1, since the sequence is decreasing to j?**\n`Thought Experiment`: In the sequence with length of `i-1`, the largest number in this sequence should be `i-1`. However, when we are dealing with length `i` and end with `j`, the previous sequence has already another `j` and we should also add `i` to the sequence. What we can do is, **add one to all those numbers greater than or equal to j**. This operation will make the largest number to be `i` without breaking the sequence property, also, it will free the `j` so that we can use it at the end of the sequence. By this thought experiment, we can easily get the result of `X`. For example, if the sequence is `{3,4,1,2,5}` and we want to expand it to be of length 6 and end with 3. We first make it to be `{3->4,4->5,1,2,5->6}`, and then, add 3 to the end of the sequence.\n\n```c++\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int N = S.length() + 1;\n int MOD = 1e9 + 7;\n // dp[i][j] means number of permutation whose length is i and end with at most j.\n int dp[202][202] = {};\n dp[1][1] = 1;\n for (int i = 2; i <= N; ++i) {\n // length is i\n for (int j = 1; j <= i; ++j) {\n // end with j\n if (S[i - 2] == \'D\') {\n // decrease to j\n dp[i][j] = (dp[i][j-1] + (dp[i-1][i-1] - dp[i-1][j-1]) % MOD) % MOD;\n } else {\n // increase to j\n dp[i][j] = (dp[i][j-1] + (dp[i-1][j-1] - dp[i-1][0]) % MOD) % MOD;\n }\n }\n }\n return (dp[N][N] + MOD) % MOD;\n }\n};\n``` | 25 | 1 | [] | 6 |
valid-permutations-for-di-sequence | How to define the DP states (with clear picture explanation) | how-to-define-the-dp-states-with-clear-p-2w5m | When I tried to understand lee215\'s solution, I got stuck. Then I redescribe this process to better understand the whole process. Credits go to lee215. \nThe | liketheflower | NORMAL | 2020-07-02T03:46:16.981643+00:00 | 2021-06-17T18:54:53.931041+00:00 | 2,190 | false | When I tried to understand lee215\'s [solution](https://leetcode.com/problems/valid-permutations-for-di-sequence/discuss/168278/C++JavaPython-DP-Solution-O(N2)), I got stuck. Then I redescribe this process to better understand the whole process. Credits go to lee215. \nThe intuition is: given a string s, results of the number of permutations for the following strings are the same.\n```\n0,1,2\n1,2,3\n1,2,4\n```\n\nBased on this observation, we can use the index of the sorted unused digits to aggregate the results.\nI am going to improve the illustration and also state definition.\nDefine the state of DP[i][j] as:\n- i is the digit index.\n- j is the **index** of current digit from sorted(current digit + remaining digits).\n\nThe reason we define j in this way is:\nAll the following will have the same results based on the same string S.\n```\n0, 1,2\n1,2,3\n1,2,4\n```\nWe can use index to have an unified representation.\n```\n0, 1, 2 -> 0, 1, 2\n1, 2, 3 -> 0, 1, 2\n1, 2, 4 -> 0, 1, 2\n```\nAfter figuring out this, the transitions can be shown as below:\n\n\nMore detail can be found [Here.](https://medium.com/@jim.morris.shen/hard-dp-77774c6a4695?source=friends_link&sk=d901fef6067a08fdbb184acfdeb8cf5e)\n\nAfter figuring out the state transitions, then the code is pretty simple.\nif "D": postfix sum\nif \'I\': prefix sum\n```\n/*\njimmy shen\nTime complexity: O(n^2)\nSpace complexity: O(n)\n*/\n\nint MOD = 1e9+7;\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int N = S.size();\n vector<int> dp(N+1, 1);\n for (int i=1;i<N+1;++i){\n int M = (N+1)-i;\n vector<int> new_dp(M, 0);\n if (S[i-1]==\'D\'){\n //postfix sum\n for (int j=dp.size()-2;j>=0;--j){\n dp[j] += dp[j+1]; \n if (dp[j]>=MOD)dp[j] %= MOD;\n }\n for (int j=0;j<M;++j){\n new_dp[j] = dp[j+1];\n }\n }\n else{\n //prefix sum\n for (int j=1;j<dp.size();++j){\n dp[j] += dp[j-1]; \n if (dp[j]>=MOD)dp[j] %= MOD;\n }\n for (int j=0;j<M;++j){\n new_dp[j] = dp[j];\n }\n }\n dp = new_dp;\n }\n int ret = 0;\n for (int i=0;i<dp.size();++i){\n ret+=dp[i];\n if (ret>=MOD)ret %= MOD;}\n return ret;\n }\n};\n``` | 21 | 2 | [] | 4 |
valid-permutations-for-di-sequence | Python DP approach (+ some Explanation) | python-dp-approach-some-explanation-by-w-1io4 | Most of us here are preparing for programming Interviews and those interviews have a threshold of about 45 minutes, and you have to come-up with an approach, wr | wizard_ | NORMAL | 2020-06-27T06:31:12.855432+00:00 | 2020-06-27T06:31:12.855480+00:00 | 888 | false | Most of us here are preparing for programming Interviews and those interviews have a threshold of about 45 minutes, and you have to come-up with an approach, write code, and explain. If you spend some time on the discuss section, you will realize there are some awesome solutions, which take you more than an interview-time to understand, let alone to come-up and code it. You may probably not hit the cool greedy solution, or the most optimized DP within time (though with time you will improve) but you should first practice to be able to solve the problem **within time**.\nIt is often helpful to keep a timer of 45 minutes to solve these problems, even if you are not able to solve it you will get enough understanding to explain your approaches and why those won\'t work out? Then move to discuss sections and try to understand a solution in 10-20 minutes. If you are able to understand in this time, you can code in the remaining time.\n\nSo, the following is what I came up within ~45 minutes:\nThis problem clearly speaks for a Dynamic Programmic approach. \nYou can imagine a state graph, \n* last state can have any values between [0, n]\n* if the last step was \'D\', the previous state can have only a higher value than what at the last state. Similarly, a lower value if step was \'I\'.\n* and the combination should be unique.\n\nThe third point, required some book-keeping of what numbers have appeared already. And I started out with a solution to keep the mask (as a tuple) (which as you may already know, won\'t work). After much brainstorming, I realized that it is not required to keep the details of which numbers (specifically) have appeared. It would just suffice to keep the details of the number of numbers haven\'t appeared and how many of them are lower (or higher) than the last number.\n\n```python\nclass Solution:\n def numPermsDISequence(self, S: str) -> int:\n N = len(S)\n MOD = 10**9 + 7\n \n @lru_cache(None)\n def dp(i, less, more):\n res = 0\n if(i < 0): return 1\n if(less + more == 0): return 0\n if(S[i] == \'I\'):\n for k in range(less):\n res = (res + dp(i-1, k, less - k -1 + more)) % MOD\n elif(S[i] == \'D\'):\n for k in range(more):\n res = (res + dp(i-1, less + k, more - k - 1)) % MOD\n return res\n \n return sum(dp(N-1, k, N-k) for k in range(N+1)) % MOD\n``` | 17 | 1 | [] | 1 |
valid-permutations-for-di-sequence | Python O(N^3)/O(N^2) time O(N) space DP solution with clear explanation (no "relative rank" stuff) | python-on3on2-time-on-space-dp-solution-atmk5 | Since I didn\'t understand the relative rank stuff, I found this problem to be quite confusing until I saw this thread:\nhttps://leetcode.com/problems/valid-per | wynning | NORMAL | 2018-10-27T23:35:39.578844+00:00 | 2018-10-27T23:35:39.578883+00:00 | 1,096 | false | Since I didn\'t understand the relative rank stuff, I found this problem to be quite confusing until I saw this thread:\nhttps://leetcode.com/problems/valid-permutations-for-di-sequence/discuss/169126/Visualization-Key-to-the-DP-solution:-imagine-cutting-a-piece-of-paper-and-separating-the-halves\n\n**Property: If we increment elements that are greater than or equal to a certain value the D or I property will not be broken, as this only makes "larger" elements even larger.**\n\nFrom this point, it is easier to see where the dynamic programming essence comes in. Basically the number of solutions with length i depends on, and can be derived from, the number of solutions with length i-1, as follows:\n\n We increment all elements that are greater than or equal to 0, and see if we can append 0 to the end of the sequence.\n We increment all elements that are greater than or equal to 1, and see if we can append 1 to the end of the sequence.\n ...\n We increment all elements that are greater than or equal to i, and see if we can append i to the end of the sequence.\n\n**Therefore, we only care about the last number of each existing valid permutation.**\n\nFor each j in the range (0, i), we want to find the number of valid permutations of len i ending in j. \n* When placing j following a decreasing instruction \'D\', we want the last number in the existing permutation to have a higher value. \n* When placing j following an increasing instruction \'I\', we want the last number in the existing permutation to have a lower value. \n\nWe use two DP arrays of len(S)+1, dp and dp2. We swap dp and dp2 at the end of each step.\n\n**D:** 10\nThe only valid permutation for \'D\' is 10.\n* solutions ending with 0: 1\n* solutions ending with 1: 0\n\n**DI:** 102, 201\nWe want the last number in each existing permutation to have a lower value than j.\n* \\# solutions ending with 0: 0\nWe cannot add a 0 to any existing valid permutation, since the only valid permutation for \'D\' is 10.\n* \\# solutions ending with 1: dp2[1] = dp[0], which is 1\nWe have 1 solution ending with a 0 we can add a 0 to, since we want the last number in the permutation to have a lower value.\n* \\# solutions ending with 2: dp2[2] = dp[0] + dp[1], which is 1\nWe have 1 solution ending with a 0 we can add a 2 to, since we want the last number in the permutation to have a lower value.\n\n**DID:** 5 permutations\nWe want the last number in each existing permutation to have a higher value than j. \n* \\# of solutions ending with 0: dp[0] + dp[1] + dp[2] = 2\nWe increment all elements in 102, 201 that are >= 0 to get 213 and 312, which we can add a 0 to.\n* \\# solutions ending with 1: dp[1] + dp[2] = 2\nWe increment all elements in 102, 201 that are >= 1 to get 203 and 302, which we can add a 1 to.\n* \\# solutions ending with 2: dp[2] = 1\nSimilarly, the permutation 102 becomes 103, which we can add a 2 to.\n* \\# solutions ending with 3: 0\n\n**DIDI:** 16 permutations\nFrom this point onward, only the number of permutations is listed for the sake of brevity.\n\nsolutions ending with 0: 0\nsolutions ending with 1: 2 (dp[0])\nsolutions ending with 2: 4 (dp[0] + dp[1])\nsolutions ending with 3: 5 (dp[0] + dp[1] + dp[2])\nsolutions ending with 4: 5 (dp[0] + dp[1] + dp[2] + dp[3])\n\nNow let\'s see the two different outcomes for adding an I or D to that sequence:\n\n**DIDID:** 61 permutations\nsolutions ending with 0: 16 (dp[0] + dp[1] + dp[2] + dp[3] + dp[4])\nsolutions ending with 1: 16 (dp[1] + dp[2] + dp[3] + dp[4])\nsolutions ending with 2: 14 (dp[2] + dp[3] + dp[4])\nsolutions ending with 3: 10 (dp[3] + dp[4])\nsolutions ending with 4: 5 (dp[4])\nsolutions ending with 5: 0\n\n**DIDII:** 35 permutations\nsolutions ending with 0: 0 \nsolutions ending with 1: 0 (dp[0])\nsolutions ending with 2: 2 (dp[0] + dp[1])\nsolutions ending with 3: 6 (dp[0] + dp[1] + dp[2])\nsolutions ending with 4: 11 (dp[0] + dp[1] + dp[2] + dp[3])\nsolutions ending with 5: 16 (dp[0] + dp[1] + dp[2] + dp[3] + dp[4])\n\nYou might be able to notice a pattern here:\nWhen placing j following a decreasing instruction \'D\', then dp2[j] = sum of dp[j] to dp[i-1]\nWhen placing j following an increasing instruction \'I\', then dp2[j] = sum of dp[0] to dp[j-1]\n\nTherefore:\n\n```\nclass Solution(object):\n def numPermsDISequence(self, S):\n """\n :type S: str\n :rtype: int\n """\n dp = [1 for c in range(len(S)+1)]\n dp2 = [0 for c in range(len(S)+1)]\n \n for i in range(1, len(S) + 1):\n if S[i-1] == \'D\':\n for j in range(i+1):\n dp2[j] = sum(dp[j:i])\n else:\n for j in range(i+1):\n dp2[j] = sum(dp[:j])\n dp, dp2 = dp2, dp\n \n return sum(dp) % 1000000007\n```\n\t\t\n\t\t\nThis solution is O(n^3)\nInstead of having to use sum() each inner loop, you can calculate prefix/suffix sums in order to bring the runtime down to O(n^2) | 10 | 1 | [] | 2 |
valid-permutations-for-di-sequence | Why Backtracking + Memoization is working ?? | why-backtracking-memoization-is-working-ac2j0 | To all Coders of the Leetcode Community this post needs to be addressed \nwhy this solution is working ??\n```\nclass Solution {\npublic:\n \n int mod = 1 | njcoder | NORMAL | 2022-07-06T14:04:29.998988+00:00 | 2022-07-06T14:04:50.661159+00:00 | 889 | false | To all Coders of the Leetcode Community this post needs to be addressed \nwhy this solution is working ??\n```\nclass Solution {\npublic:\n \n int mod = 1e9 + 7;\n \n int n;\n \n vector<int> vis;\n \n int dp[202][202];\n \n long long func(int i,int j,string &s){\n if(i == n) return 1;\n if(dp[i][j] != -1) return dp[i][j];\n long long ans=0;\n if(s[i] == \'D\'){\n \n for(int k=j-1;k>=0;k--){\n if(vis[k] == false){\n vis[k] = true;\n long long tmp = func(i+1,k,s);\n ans += tmp;\n ans%=mod;\n vis[k] = false;\n }\n }\n }else{\n for(int k=j+1;k<=n;k++){\n if(vis[k] == false){\n vis[k] = true;\n long long tmp = func(i+1,k,s);\n ans += tmp;\n ans%=mod;\n vis[k] = false;\n }\n }\n }\n \n return dp[i][j] = ans;\n \n }\n \n int numPermsDISequence(string s) {\n \n n = s.size();\n memset(dp,-1,sizeof(dp));\n \n vis = vector<int> (n+1,false);\n \n long long ans = 0;\n for(int i=0;i<=n;i++){\n vis[i] = true;\n long long tmp = func(0,i,s);\n ans += tmp;\n ans%=mod;\n vis[i] = false;\n }\n \n return ans;\n \n }\n}; | 9 | 1 | [] | 1 |
valid-permutations-for-di-sequence | C++ | Memoization | Backtracking | Easy | c-memoization-backtracking-easy-by-vaibh-qv4e | \nclass Solution {\npublic:\n int vis[201];\n long long int dp[202][202];\n int mod=1000000007;\n int util(string &s,int index,int prev){\n i | vaibhavagrwal | NORMAL | 2021-06-20T17:04:28.950693+00:00 | 2021-06-20T17:04:28.950739+00:00 | 1,437 | false | ```\nclass Solution {\npublic:\n int vis[201];\n long long int dp[202][202];\n int mod=1000000007;\n int util(string &s,int index,int prev){\n if(index==s.size()) return 1;\n \n if(dp[index][prev]!=-1) return dp[index][prev];\n \n long long int cnt=0;\n if(s[index]==\'D\'){\n for(int i=0;i<prev;i++){\n if(vis[i]==0){\n vis[i]=1;\n cnt+=(util(s,index+1,i))%mod;\n vis[i]=0;\n }\n } \n }\n else{\n for(int i=prev+1;i<=s.size();i++){\n if(vis[i]==0){\n vis[i]=1;\n cnt+=(util(s,index+1,i))%mod;\n vis[i]=0;\n }\n }\n }\n return dp[index][prev]=cnt%mod;\n }\n int numPermsDISequence(string s) {\n long long int cnt=0;\n memset(vis,0,sizeof(vis));\n memset(dp,-1,sizeof(dp));\n for(int i=0;i<=s.size();i++){\n vis[i]=1;\n cnt+=(util(s,0,i))%mod;\n vis[i]=0;\n }\n return cnt%mod;\n }\n};\n``` | 7 | 0 | ['Dynamic Programming', 'Backtracking', 'Memoization', 'C'] | 3 |
valid-permutations-for-di-sequence | C++ Soln || BackTracking + DP | c-soln-backtracking-dp-by-mitedyna-mo08 | \n#define mod 1000000007;\nclass Solution {\npublic:\n vector<int> vis;\n int dp[201][202];\n int sol(string &s, int ind, int prev){\n if(ind==s | mitedyna | NORMAL | 2021-06-04T21:54:43.898302+00:00 | 2021-06-04T21:54:43.898341+00:00 | 949 | false | ```\n#define mod 1000000007;\nclass Solution {\npublic:\n vector<int> vis;\n int dp[201][202];\n int sol(string &s, int ind, int prev){\n if(ind==s.length()+1){return 1;}\n if(dp[ind][prev+1]!=-1)return dp[ind][prev+1];\n long ans=0;\n for(int i=0;i<=s.length();i++){\n if(vis[i]!=0)continue;\n if(prev!=-1){\n if(s[ind-1]==\'D\'){\n if(i>prev)break;\n vis[i]=1;\n ans+=sol(s,ind+1,i);\n vis[i]=0;\n }\n else{\n if(i<prev)continue;\n vis[i]=1;\n ans+=sol(s, ind+1,i);\n vis[i]=0;\n }\n }\n else {\n vis[i]=1;\n ans+=sol(s, ind+1, i);\n vis[i]=0;\n }\n \n }\n return dp[ind][prev+1]=ans%mod;\n }\n int numPermsDISequence(string s) {\n memset(dp,-1,sizeof dp);\n vis.resize(s.length()+1,0);\n return sol(s,0,-1);\n }\n};\n``` | 6 | 1 | ['Dynamic Programming', 'Backtracking', 'C'] | 2 |
valid-permutations-for-di-sequence | DP O(N^2), Space O(N), With intuitive walkthrough about how to derive it. | dp-on2-space-on-with-intuitive-walkthrou-tkaa | Knowing that we only have to figure out how many permutaitons there are, I stopped thinking about index orders, and instead thought about paths.\n\nConceptually | johnb003 | NORMAL | 2020-10-04T04:51:45.745883+00:00 | 2020-10-04T04:51:45.745957+00:00 | 689 | false | Knowing that we only have to figure out how many permutaitons there are, I stopped thinking about index orders, and instead thought about paths.\n\nConceptually, with D alone there\'s only one path.\n\n```\n * \n \\\n * (ending)\n ```\n \n If we do DI, then the up path can end either between the existing two nodes, or at the top:\n\n```\n0: * (ending)\n1: * /\n \\ /\n2: *\n\n0: *\n1: \\ *(ending)\n \\ /\n2: *\n```\n\nThe way I began to represent this is the number of paths that END at a given index.\nD: [0, 1]\nDI: [1, 1, 0]\n\nNow, for DID, we should think about continuing the path that ends at index 0 and 1. Since it will have to go down from there, we\'ll add an index and consider the number of places the current paths can go. When there are more than just 1 paths ending at an index, we\'ll need to preserve the increasing possibilities, so I\'m using variables instead of 1 to show how it should work.\n\n```\n0: x |\n1: y |\n2: z |\n3: | (add an index)\n\n// add x to all of the indices below it.\n// add y to all of the indices below it.\n// etc. for each index i from 1..n\n// x = 1, y = 1, z = 0\n0: x |\n1: y | x\n2: z | x y\n3: | x y z\n\n0: 1 | -> 0\n1: 1 | 1 -> 1\n2: 0 | 1 1 -> 2\n3: | 1 1 -> 2\n```\n\nSo DID = [0, 1, 2, 2] (The sum of these = 5)\n\nNow lets take it one step further for each direction to watch how it evolves:\n\n```\nDIDD:\n0: 0 | -> 0\n1: 1 | -> 0\n2: 2 | 1 -> 1\n3: 2 | 1 2 -> 3\n4: | 1 2 2 -> 5\n\nDIDI:\n0: 0 | 2 2 1 | 5\n1: 1 | 2 2 1 | 5\n2: 2 | 2 2 | 4\n3: 2 | 2 | 2\n4: 0 | | 0\n```\n\nFor increasing the end paths, we have to first imagine shifting all of the indices up (down visually in my ascii art) by one and inserting a new index at 0 => [0 0 1 2 2]. Then accumulating each index to the indices before it. However, we don\'t actually have shift all the data, we can just modify where we read the array from. That\'s why it\'s depicted above as adding the number of ending paths to all of the rows ABOVE OR EQUAL to that index.\n\nNow, at this point, we can look for patterns.\nOne thing I spotted was this:\n```\n0: 0 | 2 2 1 | 5\n1: 1 | 2 2 1 | 5\n2: 2 | 2 2 | 4\n3: 2 | 2 | 2\n4: 0 | | 0\n-------------------\n 2*4 +\n\t 2*3 +\n\t\t 1*2 +\n\t\t 0*1\n```\nWhich, does give us the answer, but alas isn\'t that useful for determining the next incremental step.\nSo instead looking at each row rather than each column, we can see that "2 2 1" from the previous array is present, at index 0 and 1.\nAnd it\'s essentially a running sum from back to front.\n\nSo now we can translate that into an algorithm to compute each index:\nSo, for the case of "I":\n\nassuming we index into the string with k, S[k] == "I":\nn = k+1\n\n\t// sum from n-1 to 0\n\t// writing from n-1 to 0\n\tdp[n] = 0;\n\tfor (int i = n-1; i >= 0; i--) {\n\t\tdp[i] = (dp[i+1] + dp[i]) % m;\n\t}\n\nNow lets look at D again:\n\n DIDD:\n\t0: 0 | -> 0\n\t1: 1 | -> 0\n\t2: 2 | 1 -> 1\n\t3: 2 | 2 1 -> 3\n\t4: | 2 2 1 -> 5\n\nIndex 4 shows [2 2 1], and index 3 shows [2 1], so spotting the pattern, just like in the increasing case, we can accumulate the values from the previous step and store them, but this time we need to iterate through the array in the forwards direction when accumulating.\n \n\t// sum from 0 to n-1\n\t// writing from 1 to n\n\t//sum = dp[0];\n\tint saved = dp[0];\n\tdp[0] = 0;\n\tfor (int i = 1; i <= n; i++) {\n\t\tint t = dp[i];\n\t\tdp[i] = (dp[i-1] + saved) % m;\n\t\tsaved = t;\n\t}\n\nI\'m having to use some temporary values so I can modify the same array, since we need to iterate through it forward and shift it at the same time.\n\nHere\'s the full solution:\n\n int numPermsDISequence(string s) {\n int m = 1000000007;\n // make the buffer:\n int dp[s.size()+1];\n dp[0] = 1;\n \n int sum = 0;\n for (int k = 0; k < s.size(); k++) {\n int n = k+1;\n if (s[k] == \'D\') {\n // sum from 0 to n-1\n // writing to 1 to n\n //sum = dp[0];\n int saved = dp[0];\n dp[0] = 0;\n for (int i = 1; i <= n; i++) {\n int t = dp[i];\n dp[i] = (dp[i-1] + saved) % m;\n saved = t;\n }\n } else {\n // sum from n-1 to 0\n // writing from n-1 to 0\n dp[n] = 0;\n for (int i = n-1; i >= 0; i--) {\n dp[i] = (dp[i+1] + dp[i]) % m;\n }\n }\n }\n sum = 0;\n for (int i = 0; i <= s.size(); i++) {\n sum = (sum + dp[i]) % m;\n }\n return sum;\n } | 6 | 1 | [] | 0 |
valid-permutations-for-di-sequence | Java DFS with memo | java-dfs-with-memo-by-mostlyjoking-thyy | \n\nclass Solution {\n private static int MOD = 1000000007;\n public int numPermsDISequence(String S) {\n int res = 0;\n Integer[][] dp = ne | mostlyjoking | NORMAL | 2020-05-25T20:03:00.952317+00:00 | 2020-05-25T20:03:00.952374+00:00 | 804 | false | \n```\nclass Solution {\n private static int MOD = 1000000007;\n public int numPermsDISequence(String S) {\n int res = 0;\n Integer[][] dp = new Integer[S.length() + 1][S.length() + 1];\n \n for (int i = 0; i <= S.length(); i++) {\n res += dfs(i, S.length() - i, dp, S, 0);\n res = res % MOD;\n }\n return res;\n }\n \n private int dfs(int higher, int lower, Integer[][] dp, String S, int index) {\n if (index == S.length()) {\n return 1;\n }\n int d = S.charAt(index) == \'D\' ? 1 : 0;\n if (dp[higher][lower] != null) {\n return dp[higher][lower];\n }\n int count = 0;\n if (d == 1) {\n if (lower > 0) {\n for (int i = 0; i < lower; i++) {\n count += dfs(higher + i, lower - (i + 1), dp, S, index + 1);\n count = count % MOD;\n }\n }\n } else {\n if (higher > 0) {\n for (int i = 0; i < higher; i++) {\n count += dfs(higher - (i + 1), lower + i, dp, S, index + 1);\n count = count % MOD;\n }\n }\n }\n dp[higher][lower] = count;\n return count;\n }\n}\n``` | 5 | 0 | [] | 3 |
valid-permutations-for-di-sequence | Java sol | java-sol-by-cuny-66brother-8i9i | \nclass Solution {\n int mod=1000000007;\n long dp[][];\n public int numPermsDISequence(String s) {//i: string index end: end with number end\n | CUNY-66brother | NORMAL | 2020-05-01T11:46:30.108331+00:00 | 2020-05-01T11:46:30.108365+00:00 | 625 | false | ```\nclass Solution {\n int mod=1000000007;\n long dp[][];\n public int numPermsDISequence(String s) {//i: string index end: end with number end\n int len=s.length();\n long res=0;\n dp=new long[len+1][len+1];\n dp[0][0]=1;\n for(int i=1;i<=s.length();i++){\n char c=s.charAt(i-1);\n for(int end=0;end<=i;end++){\n long val=0;\n if(c==\'D\'){\n for(int j=end;j<=i-1;j++){\n val+=dp[i-1][j];\n val%=mod;\n }\n }else{\n for(int j=0;j<end;j++){\n val+=dp[i-1][j];\n val%=mod;\n }\n }\n dp[i][end]=val;\n }\n }\n for(int i=0;i<dp[0].length;i++){\n res+=dp[len][i];\n res%=mod;\n }\n return (int)(res%mod);\n }\n}\n``` | 4 | 0 | [] | 0 |
valid-permutations-for-di-sequence | Backtracking to DP Java Solution | backtracking-to-dp-java-solution-by-nave-0fw0 | Idea\nWe will try all possibilities for all positions and backtracking when we can\'t go further. seen maintains the visited numbers in per recursion tree branc | naveen_kothamasu | NORMAL | 2019-05-10T01:11:45.153681+00:00 | 2019-05-10T01:16:08.057815+00:00 | 745 | false | **Idea**\nWe will try all possibilities for all positions and backtracking when we can\'t go further. `seen` maintains the visited numbers in per recursion tree branch.\n\n**Solution1** **TLE**\n```\nclass Solution {\n int[] seen = null;\n public int numPermsDISequence(String s) {\n seen = new int[s.length()+1];\n int count = 0;\n for(int i=0; i <= s.length(); i++) {\n seen[i] = 1;\n \tcount += numPerms(s, 0, i);\n seen[i] = 0;\n }\n return count;\n }\n private int numPerms(String s, int j, int p){\n if(j == s.length())\n return 1;\n char ch = s.charAt(j);\n int count = 0;\n if(ch == \'D\'){\n for(int i=p-1; i >= 0; i--){\n if(seen[i] == 1)\n continue;\n seen[i] = 1;\n count += numPerms(s, j+1, i);\n seen[i] = 0;\n }\n }else{\n for(int i=p+1; i <= s.length(); i++){\n if(seen[i] == 1)\n continue;\n seen[i] = 1;\n count += numPerms(s, j+1, i);\n seen[i] = 0;\n }\n }\n return count;\n }\n}\n```\n**Solution2** DP Memo for overlapping subproblems. `dp[j][p]` indicates number of permutations till `j`th char in `s` and for permutations ending with number `p` (`p` stands for parent in my recursion, since we are exploring the subtree rooted at `p` in the recursion call).\n```\nclass Solution {\n private static final int DIV = 1000000007;\n int[] seen = null;\n Integer[][] dp = null;\n public int numPermsDISequence(String s) {\n dp = new Integer[s.length()][s.length()+1];\n seen = new int[s.length()+1];\n int count = 0;\n for(int i=0; i <= s.length(); i++) {\n seen[i] = 1;\n \tcount = count % DIV + numPerms(s, 0, i) % DIV;\n seen[i] = 0;\n }\n return count % DIV;\n }\n private int numPerms(String s, int j, int p){\n if(j == s.length())\n return 1;\n if(dp[j][p] != null) return dp[j][p];\n char ch = s.charAt(j);\n int count = 0;\n if(ch == \'D\'){\n for(int i=p-1; i >= 0; i--){\n if(seen[i] == 1)\n continue;\n seen[i] = 1;\n count = count % DIV + numPerms(s, j+1, i) % DIV;\n seen[i] = 0;\n }\n }else{\n for(int i=p+1; i <= s.length(); i++){\n if(seen[i] == 1)\n continue;\n seen[i] = 1;\n count = count % DIV + numPerms(s, j+1, i) % DIV;\n seen[i] = 0;\n }\n }\n dp[j][p] = count % DIV;\n return dp[j][p];\n }\n}\n``` | 4 | 0 | [] | 1 |
valid-permutations-for-di-sequence | Backtracking+memoization is working . Why?? | backtrackingmemoization-is-working-why-b-9hjf | Doubt\n Since to decide a unique state , we need:\n\n 1.index at which we are currently in string s\n 2.previous element chosen\n | anupamraZ | NORMAL | 2023-04-08T04:56:30.258408+00:00 | 2023-04-08T04:56:30.258438+00:00 | 302 | false | # Doubt\n Since to decide a unique state , we need:\n\n 1.index at which we are currently in string s\n 2.previous element chosen\n 3.set of numbers that are used or left.Here vis vector.\n\n But i have done memoization over first two, but the soln is working.Can\'t understand why??\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n ll dp[202][202];\n ll mod=1e9+7;\nint fun(int ind,int prev,int n,string&s, vector<bool>&vis)\n{\n if(ind==s.size())\n {\n return 1;\n }\n\n if(dp[ind][prev]!=-1) return dp[ind][prev];\n int ans=0;\n if(s[ind]==\'D\')\n {\n for(int i=prev-1;i>=0;i--)\n {\n if(vis[i]==0)\n {\n vis[i]=1;\n ans+=fun(ind+1,i,n,s,vis);\n ans%=mod;\n vis[i]=0;\n }\n }\n }\n else if(s[ind]==\'I\')\n {\n for(int i=prev+1;i<=n;i++)\n {\n if(vis[i]==0)\n {\n vis[i]=1;\n ans+=fun(ind+1,i,n,s,vis);\n ans%=mod;\n vis[i]=0;\n }\n }\n }\n return dp[ind][prev]=ans;\n}\n\nint numPermsDISequence(string s) \n{\n memset(dp,-1,sizeof(dp));\n ll n=s.size();\n vector<bool>vis(n+1,0);\n int ans=0;\n for(int i=0;i<=n;i++)\n {\n vis[i]=1;\n ans+=fun(0,i,n,s,vis);\n ans%=mod;\n vis[i]=0;\n }\n //cout<<"ans="<<ans<<endl;\n return ans;\n}\n};\n``` | 3 | 0 | ['Backtracking', 'Memoization', 'C++'] | 0 |
valid-permutations-for-di-sequence | MEMO/C++ | memoc-by-anurag852001-3ew7 | \tclass Solution {\n\tpublic:\n int dp[201][201];\n int mod=1e9+7;\n int util(string &s,vector&visited,int curr,int index,int n){\n if(index==s. | anurag852001 | NORMAL | 2022-06-15T10:24:04.288640+00:00 | 2022-06-15T10:24:04.288686+00:00 | 794 | false | \tclass Solution {\n\tpublic:\n int dp[201][201];\n int mod=1e9+7;\n int util(string &s,vector<int>&visited,int curr,int index,int n){\n if(index==s.length())\n return 1;\n if(dp[curr][index]!=-1)\n return dp[curr][index];\n int res=0;\n visited[curr]=true;\n if(s[index]==\'I\'){\n for(int i=curr+1;i<=n;i++)\n if(!visited[i])\n res=(res+util(s,visited,i,index+1,n))%mod;\n \n }else{\n for(int i=curr-1;i>=0;i--)\n if(!visited[i])\n res=(res+util(s,visited,i,index+1,n))%mod;\n \n }\n visited[curr]=false;\n return dp[curr][index]=res;\n }\n int numPermsDISequence(string s) {\n memset(dp,-1,sizeof(dp));\n int n=s.length();\n vector<int>visited(n+1,false);\n int res=0;\n for(int i=0;i<=n;i++)\n res=(res+util(s,visited,i,0,n))%mod;\n return res;\n \n }\n\t}; | 3 | 0 | ['Dynamic Programming'] | 1 |
valid-permutations-for-di-sequence | Detailed explanation and intuition | detailed-explanation-and-intuition-by-se-4a7p | Intuition\n\nThe possible lengths of s, and the fact that there\'s a modulo involved, hints that were dealing with some sort of recursive function.\n\nIndeed, w | sebnyberg | NORMAL | 2022-11-05T14:51:59.733483+00:00 | 2022-11-05T15:03:13.975716+00:00 | 429 | false | # Intuition\n\nThe possible lengths of `s`, and the fact that there\'s a modulo involved, hints that were dealing with some sort of recursive function.\n\nIndeed, we have a very large number of alternatives for each step. For a 200 character string, there are 200 valid first choices to explore (some of which may later turn out to be invalid). Then, there\'s potentially 199 choices, and so on, yielding $\\textrm{O}(n!)$.\n\nThis tells us that we need to memoize each step somehow. For memoization to work, we must describe the state in such a way that the state space isn\'t too large.\n\nA naive first attempt at a state would be to store:\n\n1. $\\textrm{O}(n)$ - previously picked index\n2. $\\textrm{O}(n)$ - remaining string length\n3. $\\textrm{O}(n!)$ - set of remaining numbers\n\nClearly, (3) won\'t work.\n\nAt this point when you\'re stuck, it\'s good to write down some different examples and look for clues. Try moving from a massive `n` to the next step, like `n = 100` to `n = 99`. Try to move from `n = 1` to `n = 0`. Try the other direction, i.e. to introduce a new number to the set.\n\nFor me, the breakthrough was when I imagined the last step of a long series of changes that started with `n = 100`. What possible numbers could be left in the set?\n\n$$\n\\{ (0, 1), (0, 2), ..., (0, n) \\}\\\\\n\\{ (1, 0), (1, 2), ..., (1, n) \\}\\\\\n... \\\\\n\\{ (n, 0), (n, 1), ..., (n, n-1) \\}\\\\\n$$\n\nTo evaluate `\'D\'` or `\'I\'` with these pairs, it only mattered whether the pair was increasing or decreasing. In other words, we could reduce all these pairs to $(0, 1)$ or $(1, 0)$ and it would make no difference to the result.\n\nThis told me that the set could always contain the same numbers, i.e. from `0..n`. It was only the relative position of numbers that mattered.\n\n# Approach\n\nDue to the reasoning above, the set of possible choices is dependent only on the length of / position in `s` and the previously picked value `x`. This gives us a state space of $\\textrm{O}(n^2)$.\n\nOnce a valid current number is found, we pick it and continue evaluation. Since the set of numbers is reduced each turn, we must deduct 1 from number `y` when is larger than `x` (x is removed from the set).\n\nNote: it is trivial to change top-down to bottom-up, almost always at the expense of legibility. So I\'ll stick with top-down here.\n\n# Complexity\n\n- Time complexity: $\\textrm{O}(n^2)$\n- Space complexity: $\\textrm{O}(n^2)$\n\n# Code\n\n```go\nconst mod = 1e9 + 7\n\nfunc numPermsDISequence(s string) int {\n\tvar res int\n\tn := len(s)\n\tmem := make([][]int, n+1)\n\tfor i := range mem {\n\t\tmem[i] = make([]int, n+1)\n\t\tfor j := range mem[i] {\n\t\t\tmem[i][j] = -1\n\t\t}\n\t}\n\tfor i := 0; i <= n; i++ {\n\t\tres = (res + numPerms(mem, s, i)) % mod\n\t}\n\treturn res\n}\n\nfunc numPerms(mem [][]int, s string, x int) int {\n\tn := len(s)\n\tif mem[n][x] != -1 {\n\t\treturn mem[n][x]\n\t}\n\tif len(s) == 0 {\n\t\treturn 1\n\t}\n\tvar res int\n\tif s[0] == \'I\' {\n\t\tfor y := x + 1; y <= n; y++ {\n\t\t\tres = (res + numPerms(mem, s[1:], y-1)) % mod\n\t\t}\n\t} else {\n\t\tfor y := x - 1; y >= 0; y-- {\n\t\t\tres = (res + numPerms(mem, s[1:], y)) % mod\n\t\t}\n\t}\n\tmem[n][x] = res\n\treturn res\n}\n``` | 2 | 0 | ['Go'] | 0 |
valid-permutations-for-di-sequence | Python|DP|10 lines of code| Detailed comments | pythondp10-lines-of-code-detailed-commen-q6qd | ```\ndef numPermsDISequence(self, s: str) -> int:\n n = len(s)\n \n # len(dp) is the length of remaining unused set as remain_set\n | user5318zb | NORMAL | 2022-05-12T04:29:20.046687+00:00 | 2022-05-12T04:29:20.046727+00:00 | 528 | false | ```\ndef numPermsDISequence(self, s: str) -> int:\n n = len(s)\n \n # len(dp) is the length of remaining unused set as remain_set\n # dp[i] means the last digit of any permutation formed by used set is remain_set[i]\n # so, initially, remain_set = [0, 1, ..,n]\n # dp[i] = 1\n # so, the remain_set for dp[i] is [0, 1,..,i-1, i+1..n]\n # Two edge cases:\n # remain_set for dp[0] becomes [1, 2,..,n]\n # remain_set for dp[n] becomes [0, 1, 2,..,n-1]\n # for the new remain_set, dp\'s lenght becomes the length of new remain_set\n # let\'s create a new dp1 which depends on s[0]\n # if s[0] is \'I\',\n # dp1[0] = dp[0] + dp[1]\n # dp1[i] = dp[0] + dp[1] + ..+ dp[i]\n # if s[0] is \'D\',\n # dp1[len(remain_set)-1 # n-1] = dp[n]\n # dp1[i] = dp[i+1] + dp[i+2] + ..+ dp[n]\n dp = [1] * (n+1)\n for c in s:\n dp1 = [0]*(len(dp)-1)\n if c == "I":\n for i in range(len(dp1)):\n dp1[i] = sum(dp[:i+1])\n else:\n for i in range(len(dp1)-1, -1, -1):\n dp1[i] = sum(dp[i+1:])\n dp = dp1\n return dp[0] % (10**9 + 7) | 2 | 0 | [] | 0 |
valid-permutations-for-di-sequence | C++ | DFS + MEMO | c-dfs-memo-by-kumarabhi98-v0se | \nclass Solution {\npublic:\n int mod = 1e9+7;\n int dfs(vector<vector<int>> &dp,vector<bool> &vis,string &s,int in,int n,int last){\n if(in>=s.siz | kumarabhi98 | NORMAL | 2022-03-24T17:11:27.424880+00:00 | 2022-03-24T17:11:27.424923+00:00 | 575 | false | ```\nclass Solution {\npublic:\n int mod = 1e9+7;\n int dfs(vector<vector<int>> &dp,vector<bool> &vis,string &s,int in,int n,int last){\n if(in>=s.size()) return 1;\n if(dp[in][last]!=-1) return dp[in][last];\n if(s[in]==\'D\'){ \n long re = 0;\n for(int i = 0; i<last; ++i){\n if(vis[i]==1) continue;\n vis[i] = 1;\n int k = dfs(dp,vis,s,in+1,n,i);\n vis[i]=0;\n re = (re + k)%mod;\n }\n return dp[in][last] = (int)re;\n }\n else{\n long re = 0;\n for(int i = last+1; i<=s.size(); ++i){\n if(vis[i]==1) continue;\n vis[i] = 1;\n int k = dfs(dp,vis,s,in+1,n,i);\n vis[i]=0;\n re = (re + k)%mod;\n }\n return dp[in][last] = (int)re;\n }\n }\n int numPermsDISequence(string s) {\n int n = s.size(), i = 0; \n long re = 0;\n vector<vector<int>> dp(n+2,vector<int>(n+2,-1));\n vector<bool> vis(n+1,0);\n \n if(s[0]==\'D\') i++; \n for(;i<=n;i++){\n vis[i] = 1;\n re = (re + dfs(dp,vis,s,0,n,i))%mod;\n vis[i] = 0;\n }\n return (int)re;\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'C'] | 1 |
valid-permutations-for-di-sequence | Python3 divide and conquer solution, slightly quicker than official divide and conquer solution | python3-divide-and-conquer-solution-slig-apg8 | \nfrom functools import lru_cache\n\n\nclass Solution:\n def __init__(self):\n self.mod = 10 ** 9 + 7\n\n @lru_cache(maxsize=None)\n def nCk(sel | cava | NORMAL | 2019-12-04T07:19:37.417556+00:00 | 2019-12-04T07:19:37.417595+00:00 | 432 | false | ```\nfrom functools import lru_cache\n\n\nclass Solution:\n def __init__(self):\n self.mod = 10 ** 9 + 7\n\n @lru_cache(maxsize=None)\n def nCk(self, n, k):\n if k == 1: return n\n if k == 0 or n == k: return 1\n return self.nCk(n - 1, k - 1) + self.nCk(n - 1, k)\n\n @lru_cache(maxsize=None)\n def numPermsDISequence(self, s: str) -> int:\n if len(s) <= 1: return 1\n n = len(s) + 1\n ans = 0\n\t\t#Insert max number in every \'DI\' part, left and right part are choosed from left numbers\n for i in range(n - 1):\n if s[i:i + 2] == \'ID\': ans += self.nCk(n - 1, i + 1) * self.numPermsDISequence(s[:i]) * self.numPermsDISequence(s[i + 2:])\n\t\t#Insert max number at start position if s[0] == \'D\'\n if s[0] == \'D\': ans += self.numPermsDISequence(s[1: n - 1])\n\t\t#Same insert max number at end\n if s[n - 2] == \'I\': ans += self.numPermsDISequence(s[: n - 2])\n return ans % self.mod\n``` | 2 | 2 | ['Divide and Conquer', 'Python3'] | 1 |
valid-permutations-for-di-sequence | Python recursive solution(Time out and just for reference) | python-recursive-solutiontime-out-and-ju-gq2j | \nclass Solution(object):\n def numPermsDISequence(self, S):\n """\n :type S: str\n :rtype: int\n """\n n = len(S)\n | cslzy | NORMAL | 2018-09-09T09:46:46.356936+00:00 | 2018-10-18T02:34:32.677979+00:00 | 335 | false | ```\nclass Solution(object):\n def numPermsDISequence(self, S):\n """\n :type S: str\n :rtype: int\n """\n n = len(S)\n \n def helper(S, D, I):\n if S == \'\': return 1\n sign = S[0]\n S = S[1:]\n \n count = 0\n if sign == \'D\':\n for i, d in enumerate(D):\n count += helper(S, D[:i], D[i + 1:] + I)\n else:\n for i, d in enumerate(I):\n count += helper(S, D + I[:i], I[i + 1:])\n \n return count\n \n count = 0\n nums = [i for i in range(n + 1)]\n for i in range(n + 1):\n count += helper(S, nums[:i], nums[i + 1:])\n \n return count\n \n``` | 2 | 3 | [] | 0 |
valid-permutations-for-di-sequence | C++ || Bactracking || Memoization | c-bactracking-memoization-by-akash92-5blh | Intuition\n Describe your first thoughts on how to solve this problem. \nWe need to explore all possible combinations to get the total count of valid permutatio | akash92 | NORMAL | 2024-09-16T10:34:30.451733+00:00 | 2024-09-16T10:34:30.451756+00:00 | 246 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to explore all possible combinations to get the total count of valid permutations\nFor this we only need previous element and current index to decide current element\n\n# Complexity\n- Time complexity: $$O(n^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nconst int mod = 1e9+7;\nclass Solution {\n int n, vis[202], dp[202][202];\nprivate:\n int f(int prev, int len, string& s){\n if(len == n+1) return 1;\n if(dp[prev+1][len] != -1) return dp[prev+1][len];\n int ans = 0;\n if(prev == -1){\n for(int i=0; i<=n; i++){\n vis[i] = 1;\n ans = (ans + f(i,len+1,s))%mod;\n vis[i] = 0;\n }\n }\n else if(prev != -1 && s[len-1] == \'D\'){\n for(int i=0; i<prev; i++){\n if(!vis[i]){\n vis[i] = 1;\n ans = (ans + f(i,len+1,s))%mod;\n vis[i] = 0;\n }\n }\n }\n else if(prev != -1 && s[len-1] == \'I\'){\n for(int i=prev+1; i<=n; i++){\n if(!vis[i]){\n vis[i] = 1;\n ans = (ans + f(i,len+1,s))%mod;\n vis[i] = 0;\n }\n }\n }\n\n return dp[prev+1][len] = ans;\n }\npublic:\n int numPermsDISequence(string s) {\n n = s.size();\n memset(vis, 0, sizeof(vis));\n memset(dp, -1, sizeof(dp));\n return f(-1,0,s);\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | ✅Easiest Approach || RECURSIVE -> MEMOIZATION || Jai Shree Ram🚩🚩 | easiest-approach-recursive-memoization-j-8ylo | Approach and Intuition\n- Visualising all the possible permuations and returning only valid ones\n- Taking a prev value which checks the prev value taken , now | vermayugam_29 | NORMAL | 2024-04-28T19:38:35.017352+00:00 | 2024-04-28T19:38:35.017372+00:00 | 236 | false | # Approach and Intuition\n- Visualising all the possible permuations and returning only valid ones\n- Taking a prev value which checks the prev value taken , now if prev is -1 this means we can taking any integer .\n- If `s[i] == \'I\'` then we need to take only that element which is not visited yet and is `> than prev` one and vice versa for `s[i] == \'D\'`.\n- Our base case tells whether valid permutation is formed or not.\n- We have taken bool vis array because while one recursive call we do not want to repeat same elements and so we are marking vis elements and `backtracking` vis elements as not visited.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $O(N^3)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(N^2)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# RECURSIVE (TLE)\n```JAVA []\nclass Solution {\n boolean[] vis;\n int mod = (int)1e9+7;\n public int numPermsDISequence(String s) {\n vis = new boolean[s.length()+2];\n return solve(s,0,-1);\n }\n private int solve(String s,int idx,int prev){\n if(idx >= s.length()){\n return 1;\n }\n\n int cnt = 0;\n for(int i=0;i<=s.length();i++){\n if(!vis[i]){\n vis[i] = true;\n if(prev == -1){\n cnt = (cnt + solve(s,idx,i)) % mod;\n } else if((s.charAt(idx) == \'D\' && i < prev) \n || s.charAt(idx) == \'I\' && i > prev){\n cnt = (cnt + solve(s,idx+1,i)) % mod;\n }\n vis[i] = false;\n }\n }\n\n return cnt;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<bool> vis;\n int mod = (int)1e9+7;\n int n;\n int solve(string s,int idx,int prev){\n if(idx >= n){\n return 1;\n }\n\n int cnt = 0;\n for(int i=0;i<=n;i++){\n if(!vis[i]){\n vis[i] = true;\n if(prev == -1){\n cnt = (cnt + solve(s,idx,i)) % mod;\n } else if((s[idx] == \'D\' && i < prev) \n || s[idx] == \'I\' && i > prev){\n \n cnt = (cnt + solve(s,idx+1,i)) % mod;\n }\n vis[i] = false;\n }\n }\n\n return cnt;\n }\n int numPermsDISequence(string s) {\n n = s.size();\n vis = vector<bool> (n + 2 , false);\n return solve(s,0,-1);\n }\n};\n```\n```Python []\nclass Solution:\n def __init__(self):\n self.vis = []\n self.mod = int(1e9 + 7)\n self.n = 0\n\n def solve(self, s, idx, prev):\n if idx >= self.n:\n return 1\n\n cnt = 0\n for i in range(self.n + 1):\n if not self.vis[i]:\n self.vis[i] = True\n if prev == -1 or (s[idx] == \'D\' and i < prev) or (s[idx] == \'I\' and i > prev):\n cnt = (cnt + self.solve(s, idx + 1, i)) % self.mod\n self.vis[i] = False\n\n return cnt\n\n def numPermsDISequence(self, s: str) -> int:\n self.n = len(s)\n self.vis = [False] * (self.n + 2)\n return self.solve(s, 0, -1)\n\n```\n\n# MEMOIZATION\n```JAVA []\nclass Solution {\n boolean[] vis;\n Integer[][] memo;\n int mod = (int)1e9+7;\n public int numPermsDISequence(String s) {\n vis = new boolean[s.length()+2];\n memo = new Integer[s.length()][s.length()+3];\n return solve(s,0,-1);\n }\n private int solve(String s,int idx,int prev){\n if(idx >= s.length()){\n return 1;\n } else if(memo[idx][prev+1] != null){\n return memo[idx][prev+1];\n }\n\n int cnt = 0;\n for(int i=0;i<=s.length();i++){\n if(!vis[i]){\n vis[i] = true;\n if(prev == -1){\n cnt = (cnt + solve(s,idx,i)) % mod;\n } else if((s.charAt(idx) == \'D\' && i < prev) \n || s.charAt(idx) == \'I\' && i > prev){\n \n cnt = (cnt + solve(s,idx+1,i)) % mod;\n }\n vis[i] = false;\n }\n }\n\n return memo[idx][prev+1] = cnt;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<bool> vis;\n vector<vector<int>> dp;\n int mod = (int)1e9+7;\n int n;\n int solve(string s,int idx,int prev){\n if(idx >= n){\n return 1;\n } if(dp[idx][prev+1] != -1){\n return dp[idx][prev+1];\n }\n\n int cnt = 0;\n for(int i=0;i<=n;i++){\n if(!vis[i]){\n vis[i] = true;\n if(prev == -1){\n cnt = (cnt + solve(s,idx,i)) % mod;\n } else if((s[idx] == \'D\' && i < prev) \n || s[idx] == \'I\' && i > prev){\n \n cnt = (cnt + solve(s,idx+1,i)) % mod;\n }\n vis[i] = false;\n }\n }\n\n return dp[idx][prev+1] = cnt;\n }\n int numPermsDISequence(string s) {\n n = s.size();\n vis = vector<bool> (n + 2 , false);\n dp = vector<vector<int>> (n + 1 , vector<int>(n + 3, -1));\n return solve(s,0,-1);\n }\n};\n```\n```Python []\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n memo = {}\n vis = [False] * (len(s) + 2)\n mod = 10**9 + 7\n\n def solve(idx, prev):\n if idx >= len(s):\n return 1\n if (idx, prev) in memo:\n return memo[(idx, prev)]\n\n cnt = 0\n for i in range(len(s) + 1):\n if not vis[i]:\n vis[i] = True\n if prev == -1 or (s[idx] == \'D\' and i < prev) or (s[idx] == \'I\' and i > prev):\n cnt = (cnt + solve(idx + 1, i)) % mod\n vis[i] = False\n\n memo[(idx, prev)] = cnt\n return cnt\n\n return solve(0, -1)\n\n```\n\n | 1 | 1 | ['Dynamic Programming', 'Backtracking', 'Recursion', 'Python', 'C++', 'Java', 'Python3'] | 1 |
valid-permutations-for-di-sequence | explained why backtrack + memorization working | explained-why-backtrack-memorization-wor-hssz | why it works without explicitly saving the state of the visited array?\n\n\nWhen we backtrack and return from a recursive call, we reset _ visited[curr] to fals | demon_code | NORMAL | 2023-09-15T20:38:42.767177+00:00 | 2023-09-15T20:38:42.767205+00:00 | 404 | false | why it works without explicitly saving the state of the visited array?\n\n\nWhen we backtrack and return from a recursive call, we reset ```_ visited[curr] to false _``` which means that the state of visited is restored to what it was before the recursive call.\n\nThe memoization table dp is used to store and retrieve previously computed results for specific combinations of curr and index. This allows the algorithm to avoid redundant calculations and significantly improves its efficiency.\n\nIn summary, while the visited array is modified during the recursion, it is effectively reset to its original state when backtracking,``` _ thanks to the visited[curr] = false statement _ ``` \nThe state of visited is managed correctly within the recursive calls, and the memoization table dp ensures that previously computed results are reused to avoid unnecessary computations. This is why the algorithm works correctly without explicitly saving the state of the visited array.\n\n```\nclass Solution {\npublic:\n string s="";\n int n;\n int dp[203][203];\n int m=1e9+7;\n int solve(int idx,int prev, vector<int>&vis)\n {\n if(idx==n) return 1; \n if(dp[idx+1][prev+1]!=-1) return dp[idx+1][prev+1];\n long long ans=0;\n if(idx==-1)\n {\n for(int i=0; i<=n; i++) \n {\n vis[i]=1;\n ans+=solve(0,i,vis)%m;\n ans%=m;\n vis[i]=0;\n }\n }else\n {\n for(int i=0; i<=n; i++)\n {\n if(vis[i]==0 )\n {\n if(s[idx]==\'D\' &&i<prev)\n {\n vis[i]=1;\n ans+=solve(idx+1,i, vis)%m;\n ans%=m;\n vis[i]=0;\n }else if(s[idx]==\'I\' && i>prev)\n {\n vis[i]=1;\n ans+=solve(idx+1,i, vis)%m;\n ans%=m;\n vis[i]=0;\n }\n }\n }\n }\n return dp[idx+1][prev+1]=(int)ans;\n }\n \n int numPermsDISequence(string s1) \n {\n s=s1;\n n=s.size();\n vector<int> vis(n+1,0);\n memset(dp,-1,sizeof(dp));\n return solve(-1,-1,vis);\n }\n};\n\n\n``` | 1 | 0 | ['Backtracking', 'Memoization', 'C'] | 0 |
valid-permutations-for-di-sequence | Solution | solution-by-deleted_user-btew | C++ []\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int n = S.length(), mod = 1e9 + 7;\n vector<vector<int>> dp(n + 1, | deleted_user | NORMAL | 2023-05-11T22:05:47.224145+00:00 | 2023-05-11T22:18:32.504069+00:00 | 267 | false | ```C++ []\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int n = S.length(), mod = 1e9 + 7;\n vector<vector<int>> dp(n + 1, vector<int>(n + 1));\n for (int j = 0; j <= n; j++) dp[0][j] = 1;\n for (int i = 0; i < n; i++)\n if (S[i] == \'I\')\n for (int j = 0, cur = 0; j < n - i; j++)\n dp[i + 1][j] = cur = (cur + dp[i][j]) % mod;\n else\n for (int j = n - i - 1, cur = 0; j >= 0; j--)\n dp[i + 1][j] = cur = (cur + dp[i][j + 1]) % mod;\n return dp[n][0];\n }\n};\n```\n\n```Python3 []\nfrom itertools import accumulate\n\nclass Solution:\n def numPermsDISequence(self, S):\n dp = [1] * (len(S) + 1)\n for a, b in zip("I" + S, S):\n dp = list(accumulate(dp[:-1] if a == b else dp[-1:0:-1]))\n return dp[0] % (10**9 + 7)\n```\n\n```Java []\nclass Solution {\n\tpublic int numPermsDISequence(String s) {\n\t\tint length = s.length();\n\t\tint mod = 1000000007;\n\t\tint[] dp1 = new int[length + 1];\n\t\tint[] dp2 = new int[length];\n\t\tfor (int j = 0; j <= length; j++) {\n\t\t\tdp1[j] = 1;\n\t\t}\n\t\tfor (int i = 0; i < length; i++) {\n\t\t\tif (s.charAt(i) == \'I\') {\n\t\t\t\tfor (int j = 0, curr = 0; j < length - i; j++) {\n\t\t\t\t\tdp2[j] = curr = (curr + dp1[j]) % mod;\n\t\t\t\t}\n\t\t\t} else {\n\t\t\t\tfor (int j = length - i - 1, curr = 0; j >= 0; j--) {\n\t\t\t\t\tdp2[j] = curr = (curr + dp1[j + 1]) % mod;\n\t\t\t\t}\n\t\t\t}\n\t\t\tdp1 = Arrays.copyOf(dp2, length);\n\t\t}\n\t\treturn dp1[0];\n\t}\n}\n```\n | 1 | 1 | ['C++', 'Java', 'Python3'] | 0 |
valid-permutations-for-di-sequence | DP Solution | dp-solution-by-garima1501-3qr2 | To add a new character to a sequence we only have to consider the last element-\n\nLets say currently DID sequence is 1032- this can form\n\nDIDI - in cases whe | garima1501 | NORMAL | 2022-10-02T06:55:30.737862+00:00 | 2022-10-02T07:01:45.913923+00:00 | 386 | false | To add a new character to a sequence we only have to consider the last element-\n\nLets say currently DID sequence is 1032- this can form\n\nDIDI - in cases where we end with 3,4\nDIDD - in cases where we end with 0,1,2\n\nSo just use the last element value to create a new sequence.\n\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n mem=defaultdict(int)\n def dfs(i,val=0):\n if i==len(s):\n return 1\n if (i,val) in mem:\n return mem[i,val]\n p=0\n if s[i]=="D":\n for ind in range(0,val+1):\n p+=dfs(i+1,ind)%(10**9+7)\n else:\n for ind in range(val+1,i+2):\n p+=dfs(i+1,ind)%(10**9+7)\n mem[i,val]=p\n return p\n return dfs(0)\n ```\n\t\t\t\t | 1 | 0 | ['Python3'] | 0 |
valid-permutations-for-di-sequence | Python solution: tricky question | python-solution-tricky-question-by-huiki-6wb2 | \nclass Solution:\n # an implicit DP problem\n # For simplicity, let\'s consider the sequence "D"\n # So we have the sequences [0,1] to permute\n # | huikinglam02 | NORMAL | 2022-07-25T22:30:33.523858+00:00 | 2022-07-25T22:31:01.982591+00:00 | 244 | false | ```\nclass Solution:\n # an implicit DP problem\n # For simplicity, let\'s consider the sequence "D"\n # So we have the sequences [0,1] to permute\n # The valid permutation is [1,0]\n # Now let\'s go to "DI", we add the number 2\n # and let\'s separate the cases in which the sequence ends with different numbers\n # We see that 0 cannot be the end, because it cannot account for the I\n # We see that it can end with 1, by increasing every number larger than 1 by 1: [2, 0, 1]\n # We see the same applies for ending with 2: [1, 0, 2]\n # Now we consider the alternative "DD"\n # We see that we can get 0 to be the end by increasing all numbers larger or equal to 0 by 1: [2,1,0]\n # We cannot satisfy this for 1 and 2\n # Therefore, to solve the problem, we need to build the sequences from left to right\n # dp[i][j] = number of sequences that uses integers from [0,i] and ends with j\n # dp[0][0] = 1\n # If s = "D": dp[1][0] = dp[0][0] = 1; dp[1][1] = 0\n # If s = "I": dp[1][0] = 0; dp[1][1] = dp[0][0] = 1\n # If s = "DI": dp[2][0] = 0; dp[2][1] = dp[1][0] = 1; dp[2][2] = dp[1][0] + dp[1][1] = 1\n # If s = "DD": dp[2][0] = dp[1][0] + dp[1][1] = 1; dp[2][1] = dp[1][0] = 0; dp[2][2] = 0\n # If s = "DID": dp[3][0] = dp[2][0] + dp[2][1] + dp[2][2] = 0 + 1 + 1 = 2; dp[3][1] = dp[2][1] + dp[2][2] = 1 + 1 = 2; dp[3][2] = dp[2][2] = 1; dp[3][3] = 0\n # As we see we should calculate prefix sum or suffix sums according to whether the current character is "D" or "L" respectively to facilitate calculations\n def numPermsDISequence(self, s: str) -> int:\n prev, MOD = [1], pow(10,9) + 7\n for i, c in enumerate(s):\n if c == "D":\n prefix = [0]*(i+2)\n for j in range(1,i+2,1):\n prefix[j] = prefix[j-1] + prev[j-1]\n prefix[j] %= MOD\n #print("prefix = ", prefix)\n nxt = [0]*(i+2)\n for j in range(i+1):\n nxt[j] = prefix[i+1] - prefix[j]\n else:\n suffix = [0]*(i+2)\n for j in range(i,-1,-1):\n suffix[j] = suffix[j+1] + prev[j]\n suffix[j] %= MOD\n #print("suffix = ", suffix)\n nxt = [0]*(i+2)\n for j in range(1,i+2):\n nxt[j] = suffix[0] - suffix[j]\n prev = nxt[:]\n return sum(prev) % MOD\n``` | 1 | 0 | [] | 0 |
valid-permutations-for-di-sequence | Beats 100% Other's Solutions | beats-100-others-solutions-by-day_trippe-qzg3 | \nclass Solution:\n def numPermsDISequence(self, S: str) -> int:\n dp = [1] * (len(S) + 1)\n for a, b in zip(\'I\' + S, S):\n dp = l | Day_Tripper | NORMAL | 2022-07-17T06:54:39.101665+00:00 | 2022-07-17T06:54:39.101832+00:00 | 246 | false | ```\nclass Solution:\n def numPermsDISequence(self, S: str) -> int:\n dp = [1] * (len(S) + 1)\n for a, b in zip(\'I\' + S, S):\n dp = list(itertools.accumulate(dp[:-1] if a == b else dp[-1:0:-1]))\n return dp[0] % (10**9 + 7)\n``` | 1 | 0 | [] | 0 |
valid-permutations-for-di-sequence | [Python3] top-down dp | python3-top-down-dp-by-ye15-7hl9 | \n\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n \n @cache \n def fn(i, x): \n """Return number of valid | ye15 | NORMAL | 2021-06-09T20:27:53.897620+00:00 | 2021-06-09T20:27:53.897664+00:00 | 553 | false | \n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n \n @cache \n def fn(i, x): \n """Return number of valid permutation given x numbers smaller than previous one."""\n if i == len(s): return 1 \n if s[i] == "D": \n if x == 0: return 0 # cannot decrease\n return fn(i, x-1) + fn(i+1, x-1)\n else: \n if x == len(s)-i: return 0 # cannot increase \n return fn(i, x+1) + fn(i+1, x)\n \n return sum(fn(0, x) for x in range(len(s)+1)) % 1_000_000_007\n``` | 1 | 0 | ['Python3'] | 3 |
valid-permutations-for-di-sequence | Simple C++ solution | simple-c-solution-by-caspar-chen-hku-tnde | \nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int n = S.length(), mod = 1e9 + 7;\n vector<vector<int>> dp(n + 1, vector<in | caspar-chen-hku | NORMAL | 2020-05-22T09:43:41.729001+00:00 | 2020-05-22T09:43:41.729036+00:00 | 388 | false | ```\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int n = S.length(), mod = 1e9 + 7;\n vector<vector<int>> dp(n + 1, vector<int>(n + 1));\n for (int j = 0; j <= n; j++){\n dp[0][j] = 1;\n } \n for (int i = 0; i < n; i++){\n if (S[i] == \'I\'){\n for (int j = 0, cur = 0; j < n - i; j++)\n dp[i + 1][j] = cur = (cur + dp[i][j]) % mod;\n } else {\n for (int j = n - i - 1, cur = 0; j >= 0; j--)\n dp[i + 1][j] = cur = (cur + dp[i][j + 1]) % mod; \n }\n } \n return dp[n][0];\n }\n};\n``` | 1 | 0 | [] | 2 |
valid-permutations-for-di-sequence | C++ DP 100%/100% | c-dp-100100-by-tkwind-o8sp | I highly doubt if this is a real interview question or merely from contest, which adopts ideas/techniques in some fields. \n \nThe main challege to apply DP is | tkwind | NORMAL | 2020-01-26T00:12:13.521917+00:00 | 2020-01-26T00:14:24.060978+00:00 | 405 | false | I highly doubt if this is a real interview question or merely from contest, which adopts ideas/techniques in some fields. \n \nThe main challege to apply DP is the state space is too large, if remembering which numbers have been assigned. This challenge can be overcomed by using ranking. For people with background in discrete and combinatorics math, the idea is rather common. \n\nAlso, this problem requires some modeling technique commonly seen in optimal control/operations research. Dynamic programming models typically requires defining state and actions associated with the state. One can solve a DP model as a sequence of action choosing problems for each state. Another way is to regard state and action pair as a whole, and solve the DP by searching for the next state-and-actoin. As for which approach to take, it depends on specific problems. For this question, the latter one is more straightforward. \n\nTherefore, it is not a fair problem and should not be used in real interview. \n\n```\n int numPermsDISequence(string S) {\n const int M = 1e9 + 7, n = S.length(); \n vector<int> curr(n + 1, 1), next(n + 1, 0);\n for (int t = 0; t < n; ++t) {\n char c = S[t]; \n int sum = 0; \n if (c == \'D\') {\n for (int i = n - t - 1; i >=0; --i) {\n sum = (curr[i + 1]%M + sum%M)%M;\n next[i] = sum; \n }\n } else {\n for (int i = 0; i < n - t; ++i) {\n sum = (curr[i]%M + sum%M)%M; \n next[i] = sum; \n }\n }\n swap(curr, next); \n } \n return curr.front(); \n }\n``` | 1 | 0 | [] | 2 |
valid-permutations-for-di-sequence | [JAVA] DFS with memo | java-dfs-with-memo-by-flyflyflyalex-nseo | \'\'\'\n\n\tclass Solution {\n\t\tint MOD = (int)1e9 + 7;\n\t\tpublic int numPermsDISequence(String s) {\n\t\t\tif (s == null || s.length() == 0) {\n\t\t\t\tret | flyflyflyalex | NORMAL | 2020-01-16T22:58:10.285566+00:00 | 2020-01-28T00:26:05.587467+00:00 | 336 | false | \'\'\'\n\n\tclass Solution {\n\t\tint MOD = (int)1e9 + 7;\n\t\tpublic int numPermsDISequence(String s) {\n\t\t\tif (s == null || s.length() == 0) {\n\t\t\t\treturn 0;\n\t\t\t}\n\t\t\tSet<Integer> hashSet = new HashSet<>();\n\t\t\tfor (int i = 0; i <= s.length(); i++) {\n\t\t\t\thashSet.add(i);\n\t\t\t}\n\n\t\t\tlong result = helper(s, 0, hashSet, null, null, new boolean[s.length() + 1][s.length() + 1], new long[s.length() + 1][s.length() + 1]);\n\t\t\tSystem.out.println(result);\n\t\t\treturn (int)(result % MOD);\n\t\t}\n\n\t\tpublic long helper(String s, int startIndex, Set<Integer> hashSet, Integer lastNumber, Integer relativeIndex, boolean[][] visited, long[][] dp) {\n\t\t\tif (startIndex == s.length() + 1) {\n\t\t\t\treturn 1;\n\t\t\t}\n\t\t\tif (relativeIndex != null && visited[startIndex][relativeIndex]) {\n\t\t\t\treturn dp[startIndex][relativeIndex];\n\t\t\t}\n\n\t\t\tlong result = 0;\n\t\t\tint index = -1;\n\t\t\tPriorityQueue<Integer> pQueue = new PriorityQueue<Integer>(hashSet); \n\t\t\tfor (int i : pQueue) {\n\t\t\t\tindex++;\n\t\t\t\tif (startIndex != 0 && ((s.charAt(startIndex - 1) == \'D\' && i > lastNumber) || \n\t\t\t\t\t\t\t\t\t\t(s.charAt(startIndex - 1) == \'I\' && i < lastNumber))) {\n\t\t\t\t\tcontinue;\n\t\t\t\t}\n\t\t\t\thashSet.remove(i);\n\t\t\t\tresult += helper(s, startIndex + 1, hashSet, i, index, visited, dp);\n\t\t\t\tresult %= MOD;\n\t\t\t\thashSet.add(i);\n\t\t\t}\n\n\t\t\tif (relativeIndex != null) {\n\t\t\t\tvisited[startIndex][relativeIndex] = true;\n\t\t\t\tdp[startIndex][relativeIndex] = result;\n\t\t\t}\n\t\t\treturn result;\n\t\t}\n\t}\n\'\'\'\n\n | 1 | 0 | [] | 0 |
valid-permutations-for-di-sequence | Java Solution !!! | java-solution-by-kylewzk-f3i9 | \n public int numPermsDISequence(String S) {\n int len = S.length(), N = len + 1, mod = 1000000007;\n int[][] dp = new int[N+1][N];\n \n | kylewzk | NORMAL | 2019-03-18T05:44:24.123336+00:00 | 2019-03-18T05:44:24.123384+00:00 | 556 | false | ```\n public int numPermsDISequence(String S) {\n int len = S.length(), N = len + 1, mod = 1000000007;\n int[][] dp = new int[N+1][N];\n \n for(int i = 0; i < N; i++) dp[1][i] = 1;\n \n for(int i = 1; i <= len; i++) {\n if(S.charAt(i-1) == \'D\') for(int j = N - i -1; j >= 0; j--) dp[i+1][j] = (dp[i+1][j+1] + dp[i][j+1])%mod;\n else for(int j = 0; j <= N - i-1; j++) dp[i+1][j] = ((j > 0 ? dp[i+1][j-1] : 0) + dp[i][j])%mod;\n }\n \n return dp[N][0];\n }\n``` | 1 | 0 | [] | 0 |
valid-permutations-for-di-sequence | 10 lines C++, Time O(n^2), Space O(n), with remark | 10-lines-c-time-on2-space-on-with-remark-p266 | C++\n// K(s, x) = nums of perms with tail ranking x\n// K(s + \'I\') = K(s, x) + K(s, x+1) + ... + K(s, s.len)\n// K(s + \'D\') = K(s, 0) + K(s, 1) + ... + K(s, | pjincz | NORMAL | 2018-11-29T08:28:01.202452+00:00 | 2018-11-29T08:28:01.202511+00:00 | 450 | false | ```C++\n// K(s, x) = nums of perms with tail ranking x\n// K(s + \'I\') = K(s, x) + K(s, x+1) + ... + K(s, s.len)\n// K(s + \'D\') = K(s, 0) + K(s, 1) + ... + K(s, x - 1)\n\n// G(s, 0) = 0\n// G(s, x) = K(s, 0) + K(s, 1) + ... + K(s, x - 1)\n\n// K(s + \'I\') = K(s, x) + K(s, x+1) + ... + K(s, s.len) = G(s, s.len + 1) - G(s, x)\n// K(s + \'D\') = K(s, 0) + K(s, 1) + ... + K(s, x - 1) = G(s, x)\n\n// G(s, x + 1) = G(s, x) + K(s, x)\n\n\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n vector<int64_t> G = {0, 1};\n \n for (int s_len = 0; s_len < S.size(); ++s_len) {\n vector<int64_t> nG = {0};\n \n for (int x = 0; x <= s_len + 1; ++x) {\n int64_t k = S[s_len] == \'I\' ? G[s_len + 1] - G[x] : G[x];\n nG.push_back((nG.back() + k + 1000000007) % 1000000007);\n }\n \n G.swap(nG);\n }\n \n return G[S.size() + 1];\n }\n};\n``` | 1 | 1 | [] | 1 |
valid-permutations-for-di-sequence | C++ STL partial_sum, 0ms | c-stl-partial_sum-0ms-by-0xffffffff-9bma | class Solution {\n public:\n int numPermsDISequence(string S) {\n int n = S.size() + 1, d = 0, i = 0;\n vector<int> arr(n, 1);\n | 0xffffffff | NORMAL | 2018-09-09T23:32:58.083920+00:00 | 2018-09-17T08:21:41.759783+00:00 | 378 | false | class Solution {\n public:\n int numPermsDISequence(string S) {\n int n = S.size() + 1, d = 0, i = 0;\n vector<int> arr(n, 1);\n auto func = [](int a, int b) { return (a + b) % 1000000007; };\n for (char c : S) {\n if (c == \'D\') {\n ++d;\n partial_sum(arr.rbegin() + i, arr.rend() - d, arr.rbegin() + i, func);\n } else {\n ++i;\n partial_sum(arr.begin() + d, arr.end() - i, arr.begin() + d, func);\n }\n }\n return *(arr.begin() + d);\n }\n }; | 1 | 1 | [] | 1 |
valid-permutations-for-di-sequence | C++ O(n^2) solution with only one 1D array. Extremely intuitive detailed thought process | c-on2-solution-with-only-one-1d-array-ex-3wje | \nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int MOD = 1e9 + 7;\n deque<int> memo;\n memo.push_back(1);\n f | chenbai10 | NORMAL | 2018-09-09T06:04:04.474024+00:00 | 2018-09-09T06:04:04.474078+00:00 | 519 | false | ```\nclass Solution {\npublic:\n int numPermsDISequence(string S) {\n int MOD = 1e9 + 7;\n deque<int> memo;\n memo.push_back(1);\n for (int i = 0; i < S.size(); i++) {\n if (S[i] == \'D\') {\n memo.push_back(0);\n for (int j = i; j >= 0; j--) {\n memo[j] = (memo[j] + memo[j + 1]) % MOD;\n }\n } else {\n assert(S[i] == \'I\');\n memo.push_front(0);\n for (int j = 1; j <= i + 1; j++) {\n memo[j] = (memo[j] + memo[j - 1]) % MOD;\n }\n }\n }\n int sum = 0;\n for (int num: memo) {\n sum = (sum + num) % MOD;\n }\n return sum;\n }\n};\n```\n\nHow you derives the algorithm? Details below.\n\n# 1. Determine the parameters for DP\nLet\'s say you have already computed numPermsDISequence(3), can you compute numPermsDISequence(4)?\nWe examine a sequence in numPermsDISequence(3), denoted by [ o o o ]. Imagine there are three pointers pointing to each of the token here. So we want to insert an item into the sequence. Let\'s say S[4] = "D", how many ways can we insert the last item?\nObviously, this depend on where the last pointer is pointing to. Let\'s use bold token here to denote the item that the last of the 3 pointers points to, and "I" to denote how you insert the 4th item.\n[ **o** o o ] -> [ I **o** o o ] 1 way\n[o **o** o ] -> [ I o **o** o ] [ o I **o** o ] 2 ways\nso on so forth.\nObviously, the number of ways you can insert the 4th token is dependent on where the 3rd pointer points to. So we need another parameter for DP purpose, which is the index of the last element in the array.\n\n# 2. Derive recursive formula\nNow we have to start from scrach by redefining the function with an additional parameter we just described. Let\'s say we have numPermsDISequence(3, *j*) for *j* in 0~2, which returns the ways of constructing length=3 sequence whose last element is *j*. For simplicity, Let F(*j*)=numPermsDISequence(3, *j*) and F\'(*j*)=numPermsDISequence(4, *j*). How do we compute F\'(*j*)? Again, let\'s assume S[4] = "D".\n\nF\'(0) will produces a sequence of [ I o o o ]. In order for that to happen, the bolden o can be any of the tokens after I. So:\n\n[ I **o** o o ] [ I o **o** o ] [ I o o **o** ]\nF\'(0) = F(0) + F(1) + F(2)\n\nSimilarly, F\'(1) = F(1) + F(2), F\'(2) = F(2), F(3) = 0. Note that F(3) = 0 because there is no way you can produce [ o o o I ] no matter what.\nLet n = 4. You have F\'(j) = sum(F(k)) for k in j~n. To optimize sum computation, we simply compute from F\'(n) to F\'(0), because F\'(k - 1) = sum( j= k-1 to n) = sum( j = k to n ) + F(k - 1) = F\'(k) + F(k - 1)\nIf we already have an array that maintains [ F(0), F(1), F(2) ], for the decreasing case, we only need to append a "0" to the **end of the array**, and then recompute F(2) ~ F(0) from **right to left**.\n[ F(0), F(1), F(2), **F\'(3) = 0** ]\n[ F(0), F(1), **F\'(3) + F(2)**, 0 ]\n[ F(0), **F\'(2) + F(1)**, F\'(3) + F(2), 0 ]\n[ **F\'(1) + F(0)**, F\'(2) + F(1), F\'(3) + F(2), 0 ]\n\nWhen S[4] = "I". We simply mirror everything. We will push a 0 in the **start of the array** and then update sums from **left to right**.\n\nWe need a data structure to insert/remove an item at the beginning/end of array in O(1) time, and random access in O(1) time. Dynamic array will satisfy this requirement, which is deque in c++.\n\n# 3. Compute the result\n\nAt the end of the algorithm, numPermsDISequence(4) is simply ways of constructing arrays that the last element end in either 0, 1, 2 or 3. So result(4) = F\'(0) + F\'(1) + F\'(2) + F\'(3). We can use std::accumulate but due to the MOD requirement we have to compute it manually:( | 1 | 1 | [] | 1 |
valid-permutations-for-di-sequence | DP, DFS up and down | dp-dfs-up-and-down-by-luudanhhieu-6rjj | Approach
n := len(s), up + down + start = n
DP dp := make([][]int, n+1) caching for process at index start with up and down is meaning for total greater and les | luudanhhieu | NORMAL | 2025-04-04T16:14:58.540682+00:00 | 2025-04-04T16:14:58.540682+00:00 | 1 | false | # Approach
- `n := len(s)`, `up + down + start = n`
- DP `dp := make([][]int, n+1)` caching for process at index `start` with `up` and `down` is meaning for total greater and less than number is picking at index `start`.
# Complexity
- Time complexity:O(n^2)
- Space complexity:O(n^2)
# Code
```golang []
func numPermsDISequence(s string) int {
n := len(s)
dp := make([][]int, n+1)
for i := range dp {
dp[i] = make([]int, n+1)
for j := range dp[i] {
dp[i][j] = -1
}
}
rs := 0
for start := n - 1; start >= 0; start-- {
m := n - start
for i := 0; i <= m; i++ {
up := m - i
down := i
rsi := dfs(up, down, start, s, dp)
if start == 0 {
rs += rsi
rs %= 1000000007
}
}
}
return rs
}
func dfs(up, down, start int, s string, dp [][]int) int {
if start == len(s) {
return 1
}
rs := dp[up][down]
if rs != -1 {
return rs
}
rs = 0
if s[start] == 'I' && up > 0 {
for i := 1; i <= up; i++ {
rs += dfs(up-i, down+i-1, start+1, s, dp)
rs %= 1000000007
}
} else if s[start] == 'D' && down > 0 {
for i := 1; i <= down; i++ {
rs += dfs(up+i-1, down-i, start+1, s, dp)
rs %= 1000000007
}
}
dp[up][down] = rs
return rs
}
``` | 0 | 0 | ['Go'] | 0 |
valid-permutations-for-di-sequence | C++ dfs dp memo | c-dp-memo-by-user5976fh-8kpe | null | user5976fh | NORMAL | 2025-03-10T00:57:38.451127+00:00 | 2025-03-10T00:58:22.839421+00:00 | 8 | false | ```cpp []
class Solution {
public:
vector<vector<int>> dp;
const int m = 1e9 + 7;
string s;
int numPermsDISequence(string str) {
s = str;
int n = s.size();
dp.resize(n, vector<int>(n + 1, -1));
int ans = 0;
for (int i = 0; i <= n; ++i){
ans = (ans + dfs(0, i)) % m;
}
return ans;
}
int dfs(int i, int a){
if (i == s.size()) return 1;
if (dp[i][a] == -1) {
int b = s.size() - i - a;
long long ways = 0;
if (s[i] == 'I') {
for (int k = 1; k <= a; ++k) {
ways = (ways + dfs(i + 1, a - k)) % m;
}
} else {
for (int k = 1; k <= b; ++k) {
ways = (ways + dfs(i + 1, a + b - k)) % m;
}
}
dp[i][a] = ways;
}
return dp[i][a];
}
};
``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | Optimizing DI Sequence Permutations: A Python & C++ Dynamic Programming Solution 🚀🔥 | optimizing-di-sequence-permutations-a-py-m0od | Intuition 🤔The problem revolves around arranging a permutation of numbers based on D (descending) and I (ascending) constraints. Using dynamic programming, we c | py_rex_47 | NORMAL | 2025-02-09T13:33:17.837559+00:00 | 2025-02-09T13:33:17.837559+00:00 | 11 | false | # Intuition 🤔
The problem revolves around arranging a permutation of numbers based on `D` (descending) and `I` (ascending) constraints. Using dynamic programming, we can keep track of valid permutations for each step and build the solution iteratively.
# Approach 🛠️
- Use a 2D DP table, where `dp[i][j]` represents the number of ways to arrange the first `i` characters of the sequence, ending with the number `j`.
- Use prefix sums to efficiently compute cumulative sums required for `D` and `I` constraints:
1a. For `D` (descending), accumulate values for `indices k ≥ j`.
1b. For `I` (ascending), accumulate values for `indices k < j`.
- Iteratively fill the DP table, ensuring values remain within the modulo constraint 109 + 7109 + 7.
- The final result is the sum of all values in the last row of the DP table.
# Python Performance 🔥
# C++ Performance 📈
# Complexity ⏳
- Time complexity:`𝑂(𝑛2)`
t1. Outer loop iterates over n, inner loop computes prefix sums and fills dp.
- Space complexity: `𝑂(𝑛2)`
s1. Space used by the DP table.
# Code 🔍
```python []
class Solution(object):
def numPermsDISequence(self, s):
"""
:type s: str
:rtype: int
"""
n = len(s)
mod = 10**9 + 7
dp = [[0] * (n + 1) for _ in range(n + 1)]
dp[0][0] = 1
for i in range(1, n + 1):
prefix = [0] * (n + 1)
prefix[0] = dp[i-1][0]
for j in range(1, n + 1):
prefix[j] = (prefix[j-1] + dp[i-1][j]) % mod
for j in range(i + 1):
if s[i - 1] == 'D':
dp[i][j] = (prefix[i-1] - (prefix[j-1] if j > 0 else 0)) % mod
else:
dp[i][j] = (prefix[j-1] if j > 0 else 0) % mod
return sum(dp[n]) % mod
```
``` C++ []
class Solution {
public:
int numPermsDISequence(string s) {
int n = s.size();
const int mod = 1e9 + 7;
// Initialize DP table
vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0));
dp[0][0] = 1;
for (int i = 1; i <= n; ++i) {
// Precompute prefix sums for dp[i-1]
vector<int> prefix(n + 1, 0);
prefix[0] = dp[i - 1][0];
for (int j = 1; j <= n; ++j) {
prefix[j] = (prefix[j - 1] + dp[i - 1][j]) % mod;
}
for (int j = 0; j <= i; ++j) {
if (s[i - 1] == 'D') {
// Sum from dp[i-1][j] to dp[i-1][i-1] using prefix sum
dp[i][j] = (prefix[i - 1] - (j > 0 ? prefix[j - 1] : 0) + mod) % mod;
} else {
// Sum from dp[i-1][0] to dp[i-1][j-1] using prefix sum
dp[i][j] = (j > 0 ? prefix[j - 1] : 0) % mod;
}
}
}
// Return the total sum of the last row modulo 10^9 + 7
int result = 0;
for (int j = 0; j <= n; ++j) {
result = (result + dp[n][j]) % mod;
}
return result;
}
};
``` | 0 | 0 | ['String', 'Dynamic Programming', 'Python', 'C++', 'Python3'] | 0 |
valid-permutations-for-di-sequence | In depth explanation of relative ranking approach (Base case + State transition + Answer) . | in-depth-explanation-of-relative-ranking-dkpg | IntuitionFirstly, let's define the dp state and then understand its meaning in depth .
dp[i][j] here represents the number of ways to constuct the permutation u | _rkpro | NORMAL | 2025-01-25T04:24:13.556464+00:00 | 2025-01-25T04:24:13.556464+00:00 | 9 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Firstly, let's define the $$dp$$ state and then understand its meaning in depth .
$$dp[i][j]\ $$here represents the number of ways to constuct the permutation using numbers from $$0$$ to $$i$$ and the $$(i+1)^{th}$$ number of this permutation has the $$(j+1)^{th}$$ rank .
*Note that the $$(i+1)^{th}$$ number is not equal to $$(j+1)$$ but it is having $$(j+1)^{th}$$ rank in the current permutation. For example, in the permutation $$[ 2\ 4\ 3\ 0\ 1 ]$$, the rank of $$2$$ is $$1$$, the rank of $$4$$ is $$2$$, the rank of $$3$$ is also $$2$$, the rank of $$0$$ is $$1$$ and the rank of $$1$$ is also $$1$$.*
This means that there are $$j$$ elements smaller than the current element that have already occurred in the permutation before index $$i$$ .
# Approach
<!-- Describe your approach to solving the problem. -->
Now, let's understand the state transitions :
* When $$s_i = \ 'D'$$ then the previous index must be greater than the current index . Since the current element has a rank of $$(j+1)$$, therefore the previous element must have a rank equal to either $$(j+1)\ or\ (j+2)\ or ... or\ i$$ .
```
dp[i][j] = dp[i-1][j] + dp[i-1][j+1] + ... + dp[i-1][i-1]
```
* When $$s_i = \ 'I'$$ then the previous index must be lesser than the current index . Since the current element has a rank of $$(j+1)$$, therefore the previous element must have a rank equal to either $$1\ or\ 2\ or ... or\ (j-1)\ or\ j$$ .
```
dp[i][j] = dp[i-1][0] + dp[i-1][1] + ... + dp[i-1][j-1]
```
Now, let's see the base case :
When $$i=0$$ and $$j=0$$ then there can be only $$1$$ permutation possible which is equal to $$[ 0 ]$$ . Therefore, $$dp[0][0] = 1$$ .
Now, let's understand the way to obtain final answer.
The $$(n+1)^{th}$$ element of the permutation can have a rank of either $$1\ or\ 2\ or\ 3\ or\ ...\ or\ (n+1)$$ .
```
ans = dp[n][0] + dp[n][1] + dp[n][2] + ... + dp[n][n] .
```
# Complexity
- Time complexity: $$O(n^3)$$ .
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n^2)$$ .
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numPermsDISequence(string s) {
int n=(int)s.length(), mod=1e9+7;
vector<vector<int>> dp(n+1, vector<int> (n+1, -1));
for (int i=0; i<=n; i++) {
for (int j=0; j<=i; j++) {
if (i == 0) {
dp[i][j] = 1;
continue;
}
int total=0;
if (s.at(i-1) == 'D') {
for (int p=j; p<i; p++) {
int val = dp[i-1][p];
total = (total%mod + val%mod)%mod;
}
} else {
for (int p=0; p<j; p++) {
int val = dp[i-1][p];
total = (total%mod + val%mod)%mod;
}
}
dp[i][j] = total;
}
}
int ans=0;
for (int i=0; i<=n; i++) {
int val = dp[n][i];
ans = (ans%mod + val%mod)%mod;
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | DP - All possible permutations | dp-all-possible-permutations-by-vats_lc-mqxd | Code | vats_lc | NORMAL | 2025-01-04T13:30:31.666121+00:00 | 2025-01-04T13:30:31.666121+00:00 | 8 | false | # Code
```cpp []
const int MOD = 1e9 + 7;
class Solution {
public:
int getAns(int i, int n, char ch, int num, string& s, vector<int>& count,
vector<vector<int>>& dp) {
if (i == n) {
for (int j = 0; j <= n; j++)
if (count[j] == 1) {
if (ch == 'D' && num > j)
return 1;
if (ch == 'I' && num < j)
return 1;
return 0;
}
}
if (dp[i][num] != -1)
return dp[i][num];
int ans = 0;
if (ch == 'D') {
for (int j = 0; j <= num - 1; j++) {
if (count[j] > 0) {
count[j]--;
ans = (ans + getAns(i + 1, n, s[i], j, s, count, dp)) % MOD;
count[j]++;
}
}
} else {
for (int j = num + 1; j <= n; j++) {
if (count[j] > 0) {
count[j]--;
ans = (ans + getAns(i + 1, n, s[i], j, s, count, dp)) % MOD;
count[j]++;
}
}
}
return dp[i][num] = ans;
}
int numPermsDISequence(string s) {
int n = s.size();
vector<int> count(n + 1, 1);
vector<vector<int>> dp(n + 1, vector<int>(n + 1, -1));
char ch = s[0];
int ans = 0;
for (int i = 0; i <= n; i++) {
count[i]--;
ans = (ans + getAns(1, n, s[0], i, s, count, dp)) % MOD;
count[i]++;
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | 903. Valid Permutations for DI Sequence | 903-valid-permutations-for-di-sequence-b-cnlv | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-02T02:51:43.906811+00:00 | 2025-01-02T02:51:43.906811+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int numPermsDISequence(string s) {
int n = s.size(), mod = 1e9 + 7;
vector<int> dp(n + 1, 1), temp(n + 1);
for (int i = 1; i <= n; ++i) {
if (s[i - 1] == 'I') {
for (int j = 0, sum = 0; j <= n - i; ++j) {
sum = (sum + dp[j]) % mod;
temp[j] = sum;
}
} else {
for (int j = n - i, sum = 0; j >= 0; --j) {
sum = (sum + dp[j + 1]) % mod;
temp[j] = sum;
}
}
swap(dp, temp);
}
return dp[0];
}
};
``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | EASY DP || C++ || 👍✅ | easy-dp-c-by-athar4403-b1j8 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Athar4403 | NORMAL | 2024-10-18T05:10:59.441929+00:00 | 2024-10-18T05:10:59.441963+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N^3)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n #define ll long long\n const int mod = 1e9+7;\n int solve(int ind, int prev, string s, int n,vector<int>&vis,vector<vector<int>>&dp){\n if(ind>=n)return 1;\n if(dp[ind][prev]!=-1)return dp[ind][prev];\n\n ll ans=0;\n for(int i=0;i<=n;i++){\n if(i!=prev && vis[i]==0){\n if(s[ind]==\'D\' && i<prev){\n vis[i]=1;\n ans=(ans+solve(ind+1,i,s,n,vis,dp))%mod;\n vis[i]=0;\n }\n if(s[ind]==\'I\' && i>prev){\n vis[i]=1;\n ans= (ans+solve(ind+1,i,s,n,vis,dp))%mod;\n vis[i]=0;\n }\n }\n }\n return dp[ind][prev]=ans%mod;\n }\n int numPermsDISequence(string s) {\n \n int n = s.length();\n ll ans=0;\n vector<vector<int>>dp(n+1,vector<int>(n+1,-1));\n for(int i=0;i<=n;i++){\n vector<int>vis(n+2,0);\n vis[i]=1;\n \n ans= (ans+solve(0,i,s,n,vis, dp))%mod;\n }\n return ans;\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | 903. Valid Permutations for DI Sequence.cpp | 903-valid-permutations-for-di-sequencecp-5mdt | Code\n\nclass Solution {\npublic:\n int MOD = 1e9+7;\n long long dp[202][202];\n long long perms(string &s, int n, int pos, int prev, vector<bool> &vis | 202021ganesh | NORMAL | 2024-08-15T12:15:06.906799+00:00 | 2024-08-15T12:15:06.906831+00:00 | 4 | false | **Code**\n```\nclass Solution {\npublic:\n int MOD = 1e9+7;\n long long dp[202][202];\n long long perms(string &s, int n, int pos, int prev, vector<bool> &visited) {\n if(pos >= n) return 1; \n if(dp[pos][prev] != -1) return dp[pos][prev];\n long long ans = 0;\n for(int i=0;i<=n;i++) {\n if(!visited[i]) {\n if(s[pos] == \'D\' && prev > i) {\n visited[i] = true;\n ans = (ans + perms(s,n,pos+1,i,visited) % MOD) % MOD;\n visited[i] = false;\n }\n if(s[pos] == \'I\' && prev < i) {\n visited[i] = true;\n ans = (ans + perms(s,n,pos+1,i,visited) % MOD) % MOD;\n visited[i] = false;\n }\n }\n }\n return dp[pos][prev] = ans;\n }\n int numPermsDISequence(string s) {\n int n = s.length();\n long long ans = 0;\n memset(dp,-1,sizeof(dp));\n for(int i=0;i<=n;i++) {\n vector<bool> visited(n+1,false);\n visited[i] = true;\n ans = (ans + perms(s,n,0,i,visited) % MOD) % MOD;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C'] | 0 |
valid-permutations-for-di-sequence | Dynamic Programming O(n^3) Time Complexity | dynamic-programming-on3-time-complexity-0mxlu | Intuition\n- We can solve this using Dynamic Programming\n- we need to fix valid elements and at the need to check whether we can form a valid permutation or no | yash559 | NORMAL | 2024-08-15T01:36:32.380919+00:00 | 2024-08-15T01:36:32.380946+00:00 | 11 | false | # Intuition\n- We can solve this using Dynamic Programming\n- we need to fix valid elements and at the need to check whether we can form a valid permutation or not \n- if we can then add 1 and check for remaining combinations\n\n# Complexity\n- Time complexity: $$O(n^3)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n^2)$$ for dp\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int MOD = 1e9+7;\n long long dp[202][202];\n long long perms(string &s, int n, int pos, int prev, vector<bool> &visited) {\n if(pos >= n) return 1; // if you can reach till end then you have found one valid permutation\n if(dp[pos][prev] != -1) return dp[pos][prev];\n long long ans = 0;\n //we have to fix rest elements in permutation so we need to check all elements for next position\n for(int i=0;i<=n;i++) {\n //if it not visited\n if(!visited[i]) {\n //check whether current element satisfies these conditions\n if(s[pos] == \'D\' && prev > i) {\n visited[i] = true;\n //then consider it and go for next position and current will become previous\n ans = (ans + perms(s,n,pos+1,i,visited) % MOD) % MOD;\n\n //will backtracking make sure to revoke changes\n visited[i] = false;\n }\n if(s[pos] == \'I\' && prev < i) {\n visited[i] = true;\n ans = (ans + perms(s,n,pos+1,i,visited) % MOD) % MOD;\n visited[i] = false;\n }\n }\n }\n return dp[pos][prev] = ans;\n }\n int numPermsDISequence(string s) {\n int n = s.length();\n long long ans = 0;\n memset(dp,-1,sizeof(dp));\n //we need to fix the starting element in permutation and check how many \n //combinations are satisfied\n for(int i=0;i<=n;i++) {\n\n //visited array to keep track of not considering the element in permutation if it is\n //previously visited\n vector<bool> visited(n+1,false);\n visited[i] = true;\n //we need to consider pos and prev variables\n //pos to keep track of string s\n //prev to keep track of previously considered element\n ans = (ans + perms(s,n,0,i,visited) % MOD) % MOD;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | help me out please | help-me-out-please-by-lerno_breed-b9ij | \n Describe your first thoughts on how to solve this problem. \n## Why this is not working \n\n\n# Code\n\nclass Solution {\npublic:\n // Brute force\n in | lerno_breed | NORMAL | 2024-07-30T10:15:56.356722+00:00 | 2024-07-30T10:15:56.356757+00:00 | 5 | false | \n<!-- Describe your first thoughts on how to solve this problem. -->\n## Why this is not working \n\n\n# Code\n```\nclass Solution {\npublic:\n // Brute force\n int f(int i, string temp, int prev, string s) {\n int n = s.size();\n if (i == n) {\n \n for (int j = 0; j <= n; j++) {\n auto it = find(temp.begin(), temp.end(), j + \'0\');\n if (it == temp.end()) {\n if (s[i - 1] == \'D\' && j < prev) \n {\n return 1;\n }\n if (s[i - 1] == \'I\' && j > prev){\n return 1;\n }\n }\n }\n return 0;\n }\n int ct = 0;\n for (int j = 0; j <= n; j++) {\n auto it = find(temp.begin(), temp.end(), j + \'0\');\n if (it == temp.end()) {\n if (s[i] == \'D\' && j > prev) {\n temp.push_back(j + \'0\');\n ct += f(i + 1, temp, j, s);\n temp.pop_back();\n } else if (s[i] == \'I\' && j < prev) {\n temp.push_back(j + \'0\');\n ct += f(i + 1, temp, j, s);\n temp.pop_back();\n }\n }\n }\n return ct;\n }\n\n int numPermsDISequence(string s) {\n string temp = "";\n if (s[0] == \'D\') {\n return f(0, temp, 0, s);\n }\n\n return f(0, temp, s.size(), s);\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | Valid Permutation For DI sequence | valid-permutation-for-di-sequence-by-nae-iom0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Naeem_ABD | NORMAL | 2024-07-16T18:19:14.689998+00:00 | 2024-07-16T18:19:14.690034+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n mem=defaultdict(int)\n def dfs(i,val=0):\n if i==len(s):\n return 1\n if (i,val) in mem:\n return mem[i,val]\n p=0\n if s[i]=="D":\n for ind in range(0,val+1):\n p+=dfs(i+1,ind)%(10**9+7)\n else:\n for ind in range(val+1,i+2):\n p+=dfs(i+1,ind)%(10**9+7)\n mem[i,val]=p\n return p\n return dfs(0)\n``` | 0 | 0 | ['Python3'] | 0 |
valid-permutations-for-di-sequence | Extremely simple, clear & fast, 20 lines, Runtime: 100%, Memory: 100%, O(n²) | extremely-simple-clear-fast-20-lines-run-r9gq | Intuition & Approach\n Describe your first thoughts on how to solve this problem. \n\nInitially I struggled to find a good solution, calculating permutations is | FSGT | NORMAL | 2024-05-28T13:33:16.278833+00:00 | 2024-05-28T13:47:48.835918+00:00 | 15 | false | # Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nInitially I struggled to find a good solution, calculating permutations is very expensive, and with a complicated condition it would be difficult to reuse previously calculated permutations if I also need to keep track of which numbers I have used.\n\nHowever, after realizing that (for our conditions) the range [1,7,19] would be logically equivalent to the range [0,1,2], the problem could be simplified a lot by normalized all numbers after each removal. If I remove the element \'i\', and the next value should be smaller (\'D\'), I can specify that I will allow usage of all numbers from [0 <= x <= i-1], and if the next value should be bigger (\'I\'), I can specify that I only allow [i <= x <= totalNumbers].\n\nThis allows us to write a very basic memoization solution with time complexity O(n\xB2), using the two keys idx (numbers used) and i (previous number used) in two different layouts (increasing and decreasing), idx & i are both capped by n (length of s), O(n\xB2 + n\xB2) => O(n\xB2)\n\n\n\n\n\n# Complexity\n- Time complexity: O(n\xB2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n\xB2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int NumPermsDISequence(string s)\n => (int)NormalizedMemoization(s, 0, 0, s.Length, new Dictionary<(int,int,int), long>());\n\n public long NormalizedMemoization(string s, int idx, int min, int max, Dictionary<(int,int,int), long> memoization) {\n if (idx == s.Length)\n return min <= max ? 1 : 0;\n\n if (memoization.TryGetValue((idx,min,max), out var ways))\n return ways;\n\n for (int i = min; i <= max; i++) {\n if (s[idx] == \'D\') {\n ways += NormalizedMemoization(s, idx+1, 0, i-1, memoization);\n } else {\n ways += NormalizedMemoization(s, idx+1, i, s.Length - idx - 1, memoization);\n }\n }\n ways %= 1_000_000_007;\n memoization[(idx,min,max)] = ways;\n return ways;\n }\n}\n``` | 0 | 0 | ['Recursion', 'Memoization', 'C#'] | 0 |
valid-permutations-for-di-sequence | Combinatorics Approach 2x+ times faster than DP | combinatorics-approach-2x-times-faster-t-7t3h | Intuition\nFirst, we simplify the input into a series of transitions up and down by some amounts. III becomes a transition with +3 and DDDDD represents one with | jmavis | NORMAL | 2024-04-19T23:20:58.119763+00:00 | 2024-04-22T19:56:55.869807+00:00 | 9 | false | # Intuition\nFirst, we simplify the input into a series of transitions up and down by some amounts. III becomes a transition with +3 and DDDDD represents one with -4. Here is a representation of "DDIIIIDDD" with 3 transition points.\n\n\n\nThis approach is based on an important observation of the relation between the solution at transition i to i+1.\n \n\nTo get from T1 to T2 we would need to start with a value that could decrease by 2. T2 to T3 increase by 4 and T3 to End decrease by 3.\n \n\nWe have the numbers 0-9 to possibly insert at each transition point. We couldn\'t go from T1 to T2 starting with 0 or 1 because there aren\'t two numbers below those. We can only have a starting value at T1 in the range 2-9 that can get to T2. Let \u0394 = the number of elements needed to move from T[i] to T[i+1]. If T[i] is increasing then all \u0394 numbers selected must be greater than the transition\'s start and less than if the transition is down.\n\nFor T3 we can only get to the end with a starting value from 3-9. If we get to T3 with a valid combination of 0-9 then we have only 3 remaining.\n\nLet\'s see how many ways to get from T3 to the end from the starting value X with Y being all the combinations of 0-9.\nHere are a few:\nIf X is 7 and Y is [0,1,2] there is one way [2,1,0]\nIf X is 7 and Y is [0,5,6] there is one way [6,5,0]\nIf X is 6 and Y is [0,1,2] there is one way [2,1,0]\nif X is 3 and Y is [0,1,4] there are no ways because 4 cannot be placed to the right of T3\'s 3 starting point.\n\nYou can try this with every combination and we can see that as long as all in Y are less than X there is one possible path to the end. Otherwise, there are 0.\n\nHere we get our key insight. If we reach T3 with 3 numbers to the less than of T3\'s start the answer is always 1 else 0. **The starting value at T[i] doesn\'t matter!** The only thing that influences the result from point T3 is the number to the left of the starting point. Similarly, if T[i] is decreasing then the count to the right is the only thing that matters.\n\n\nLet\'s go one step further to T2. When arriving at T2 there will have been 2 numbers used to get so 7 values remaining to choose from. If we arrive at T2 with at least 4 values to the right we can get to T3 otherwise there are 0 ways. To move from T2 to T3 we will need to consume 4 values greater than T2\'s starts. But if we arrive at T3 with less than 3 to the left there are no solutions. If for example, we know T2 has 6 values to the right and 1 to the left. When we move from T2 consuming 4 of those right values how do we know what value T3 would start with and how many it has to the left or right?\n\n\n\n \n \n\nThere are 3 possibilities for the remaining 2 values to the right of T2:\n\n1. Both are to the right of T3\n\n2. One is left and one is right\n\n3. Both to the left of T3\n\n\n\n \n \n\nLooking at the cases from T3\'s perspective:\n\n1. We know T3 has 2 to the right and 1 to the left since T3 is greater than T2 and T2 is greater than the 1 to the left.\n\n2. Left = 2 and right = 1\n\n3. Left = 3 and right = 0\n\n \n\nHey, we know the answers to all of those cases! Only case 3 leaves us with a single possible combination. This means that at point T2 we need to select 4 numbers and have 2 still to the left of T3. Since T3 is the end point we can\'t select that and it consumes one of the 6 to the right of T2. Then we have to fill in 3 "slots" from 5 numbers. T2 _ _ _ T3\n\n \n\nHere is where combinatorics comes in. How many ways can we select 3 of the 5 numbers? That is expressed as 5 choose 3. Which can be calculated with a formula: Ck(n) = n!/(k!(n\u2212k)!) = 5!/(3!(5-3)!) = 10. We find there are 10 ways to go from T2 to T3 by choosing 4 numbers greater than T2\'s start that will give us the position where T3 has only 3 to the left. So for T2 with L = 1 R = 6 there are 10 solutions.\n\n \n\nNow we don\'t know at T2 that T3 L=3,R=0 is the only solution. So try the case where T3 is L=2R=1 for example. There are now only 4 numbers between T2 and T3 so there are 4 choose 3 = 4 ways to make this traversal. And 3 choose 3 = 1 ways for T3 at L0R2.\n\n \n\nThen the number of combinations for an increase from T2 to T3 with L=1 and R=6 = (5 choose 3) * T3(L3R0) + (4 choose 3) * T3(L2R1) + (3 choose 3) * T3(L1R2)\n\nEnding at the beginning, let\'s now look at T1 to T2 with the goal of T2 having L=1R=6. Since there are no values chosen to the left of T1 we have all 10 possible values to start with. Let\'s first try picking 8. This is T1 with L=8R=1. We are decreasing at T1 so we look to the left count. There are 8 and we need to choose 2 such that T2 has one to the left. Then there are 8 - (the value at T2 itself) - (the value to the left of T2) = 8-1-1 = 6 values to select from. Of those 6 values I need to choose 1. So there are 6 choose 1 = 6 ways to go from T1L=8R=1 to T2L=1R=6. And we know the result of that T2 state is 10. Since we have 6 ways to get to the 10 ways there are 60 solutions from T1L=8R=1. \n\n\n\nI want to take a step back and use actual numbers for demostration and proof this abstraction really works. We know of 0-9 that only "1" has one to the left so this is really about going from 8 -> ? -> 1 and how many ways are there to choose the middle such that it is less than 8 and greater than 1? [7,6,5,4,3,2] which is the 6 values we calculated. The only value possible in this scenario for T3L3R0 is 9. This path with the possible choices at each index then looks like this:\n\n\nHow can we be sure that we use each element only once? Here is a chart breaking down each index and what values could be inside it. Below each choice in black is the total in that range. In blue is the number in that range we know have been consumed, but not which specifically. Then below that is the remaining choices. When we reach that final index we know from the remaing values under 9 (0..8) there have been 8 consumed and there is only one value available. One we\'ve chosen it then we have chosen all and only once.\n\n\nYou can then pick any value in the range at each point and remove it from the future ranges. Until you cross off all of them. Here is one path way were I choose a value in a black circle at each index and remove it from the future values. I satisfy the value changes and only use each value once.\n\n\nA minor optimization is that since L+R+(the index of T[i])=size we can derive the available right from the available L at T[i]. With the formula R=size-L-(index of T[i]). Making only the number on the left needed as input.\n\n\nIn summary, the combinations at T[i] (L) to T[i+1] is the sum of every T[i+1] (L) * the combination of choices from L to (L+R-\u0394) if increasing and 0 to (L-\u0394) if decreasing. If we sum all T[0] for every L in 0 to size we get the number of valid permutations without any duplicates. Yay.\n\nI had a lot of fun on this and decided to make my first solution post. Constructive feedback is appreciated.\n\n \n\n# Approach:\n\nThe core functions numPermsDISequence, calcTransitionsFrom follow the above summary. The combinations calculation for each possible transition chooses with delta-1 and calculates the value to choose from as the delta + the index - 1. The -1 accounts for the ending value. Since our ranges spread out from the "center" point and delta away then each range gains an additional possible value at each step.\n\nSince the combinations calculations can take some computation I cache it even accross runs since x choose y is the same no matter what.\n\nFor calcCombinations(value, choose) I minimize the calculations required for the n!/(k!(n\u2212k)!) by selecting the smaller denominator and canceling out the pairs in the numerator.\n\nFor example 60 choose 6:\n60!/(6!(54!)) becomes (60*59*58*57*56*55)/(6*5*4*3*2*1)\n\nThen I use BigInteger to do the multiplication/division since the numerator could be very large.\n\n \n\n# Results:\n\nI will compare my combinatorics approach to the dynamic programming approach given in "numPermsDISequenceDP". Both of which pass.\n\n \n\nSince a big performance hit is calculating the combinations I run two types of tests. One with a fresh instance of Solution() each time and the second with a shared instance that has will calculate and cache the results as it goes.\n\n \nHere are the benchmark results for both approaches given the same input for each comparison.\n\n \n\n##### Test #1 Total time taken for 200 runs each with a random 500 length string:\n\n- No cache:\n - Combinatorics: 9873ms\n - DP: 24005ms\n - Improvement 14132ms\n\n- Caching:\n - Combinatorics: 9954ms\n - DP: 24317ms\n - Improvement: 14363ms\n\n \n\n##### Test #2 Total time taken to run a single 200 length test 200 times:\n\n- No cache:\n - Combinatorics: 842ms\n - DP: 1704ms\n - Improvement 862ms\n\n- Caching:\n - Combinatorics: 713ms\n - DP: 1699ms\n - Improvement 986ms\n\n\n##### Test #3 Total time taken for random strings with sizes from 1 to 1000:\n- Combinatorics: 100201ms\n- DP: 224077ms\n- Improvement 140,576ms\n\n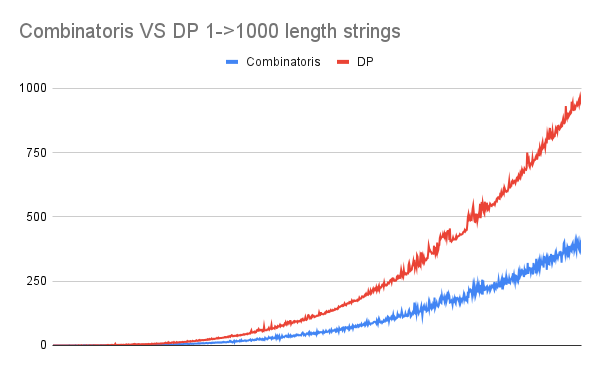\n\n \n\n# Complexity\n\n- Time complexity:\n\nIn the worst case # Transitions = n (ex: "IDIDID...")\n\nThen for each transition, we check all combinations possible which in the worst case is n again.\n\nSo the complexity is $$O(n*n)$$ same as the DP solution just a slower increase.\n\n \n\n- Space complexity:\n\nThe combination caching takes up a constant 200x200 Long\n\nThe transitions caching would be n * 200 Long\n\n \n\n# Code\n\n```\nclass Solution() {\n private val modulo: Long = 1000000007\n private val maxLength = 200\n private val combinationsCalculator = CombinationsCalculator(modulo, maxLength)\n fun numPermsDISequence(s: String): Int {\n if (s.length <= 1) return 1\n if (s.length > maxLength) throw IllegalArgumentException("Cannot exceed $maxLength max length")\n val transitions = parseTransitions(s)\n var perms: Long = 0\n\n for (i in 0..s.length) {\n val permsFor = calcTransitionsFrom(\n i,\n s.length,\n 0,\n transitions\n )\n perms = (perms + permsFor) % modulo\n }\n\n return perms.toInt()\n }\n\n private fun calcTransitionsFrom(\n availableLeft: Int,\n size: Int,\n transitionNumber: Int,\n transitions: Array<TransitionPoint>\n ): Long {\n if (transitionNumber == transitions.size) return 1\n val currentTransition = transitions[transitionNumber]\n val availableRight = size - availableLeft - currentTransition.spacesToLeft\n var result = currentTransition.getTransitionFor(availableLeft)\n if (result == null) {\n val nextPositions = currentTransition.nextPositions(availableLeft, availableRight)\n var sum = 0L\n nextPositions.forEachIndexed { index: Int, nextLeft: Int ->\n val nextStepTransitions = calcTransitionsFrom(\n nextLeft,\n size,\n transitionNumber + 1,\n transitions\n )\n if (nextStepTransitions != 0L) {\n val combinationsForRange = combinationsCalculator.combinations(\n currentTransition.toFill + index - 1,\n currentTransition.toFill - 1\n )\n sum =\n (sum + (combinationsForRange * nextStepTransitions) % modulo) % modulo\n }\n }\n currentTransition.setTransitionsFor(availableLeft, sum)\n result = sum\n }\n\n return result\n }\n\n private fun parseTransitions(s: String): Array<TransitionPoint> {\n val size = s.length+1\n var prev = 0\n var index = 1\n val result = mutableListOf<TransitionPoint>()\n\n while (index < s.length) {\n if (s[prev] != s[index]) {\n val delta = (index - prev) * if (s[index] == \'I\') -1 else 1\n result.add(TransitionPoint(delta, prev, size))\n prev = index\n }\n index++\n }\n val delta = (index - prev) * if (s[index - 1] == \'I\') 1 else -1\n result.add(TransitionPoint(delta, prev, size))\n result.add(TransitionPoint(0, index, size))\n return result.toTypedArray()\n }\n\n class CombinationsCalculator(modulus: Long, private val maxLength: Int) {\n private val combinationsCache: Array<Array<Long?>> =\n Array(maxLength) { Array(maxLength) { null } }\n private val modulo = modulus.toBigInteger()\n\n fun combinations(value: Int, choose: Int): Long {\n if (value < choose) return 0\n if (value == choose || choose == 0) return 1\n\n var result = combinationsCache[value][choose]\n if (result == null) {\n result = calcValueChoose(value, choose)\n combinationsCache[value][choose] = result\n }\n return result\n }\n\n private fun calcValueChoose(value: Int, choose: Int): Long {\n val minDivisor = minOf(choose, value - choose)\n val maxDivisor = maxOf(choose, value - choose)\n val divisors = (2..minDivisor).toList()\n val numerators = ((maxDivisor + 1)..value).toList()\n\n val numerator = multiplyBigInt(numerators)\n val denominator = multiplyBigInt(divisors)\n\n return ((numerator/denominator) % modulo).toLong()\n }\n\n private fun multiplyBigInt(values: List<Int>): BigInteger {\n var result = BigInteger("1")\n\n for (value in values) {\n result *= value.toBigInteger()\n }\n\n return result\n }\n }\n\n class TransitionPoint(val delta: Int, val spacesToLeft: Int, val size: Int) {\n private val transitionsFrom: Array<Long?> = Array(size) { null }\n val toFill = delta.absoluteValue\n private val isIncrease = delta >= 0\n\n fun getTransitionFor(availableToLeft: Int): Long? {\n return transitionsFrom[availableToLeft]\n }\n\n fun setTransitionsFor(availableToLeft: Int, transitions: Long) {\n transitionsFrom[availableToLeft] = transitions\n }\n\n fun nextPositions(availableLeft: Int, availableRight: Int): IntProgression {\n return if (isIncrease) {\n availableLeft..(availableLeft + availableRight - toFill)\n } else {\n (availableLeft - toFill) downTo 0\n }\n }\n }\n}\n``` | 0 | 0 | ['Kotlin'] | 0 |
valid-permutations-for-di-sequence | Python recursive solution, detailed explanation | python-recursive-solution-detailed-expla-adux | Intuition\nLooks like a DP problem, since sub problems are getting reused. \n\n# Approach\nWe just need to keep track of state of dp. i.e since we\'re only inte | lostguardian_01 | NORMAL | 2024-04-16T11:34:02.126842+00:00 | 2024-04-16T11:34:02.126863+00:00 | 15 | false | # Intuition\nLooks like a DP problem, since sub problems are getting reused. \n\n# Approach\nWe just need to keep track of state of dp. i.e since we\'re only interested in number of solutions, the numbers itself dont matter only the number of elements above and below out previous choice.\n \nState = (idx, u, b) \nidx = index in s\nu = no elements above prev\nb = no elements below prev\n\n# Complexity\n- Time complexity:\n$$O(N^3)$$ : no of state = N^2, time per state = N\n(since a is redundant, a = n-idx-b, we actually have only N^2 states and a can be removed. only added for simplicity of explanation)\n\n- Space complexity:\n$$O(N^3)$$ : same as above\n\n# Code\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n """\n 1) brute force: all possible perms and check if valid => n+1!*n (too big) \n 2) dynamic programming: since if we are at an idx i, the rest of the substring is getting repeated.\n state => (current idx of s, no. choices above prev, no. choices below prev)\n transition => case1: \'D\' we can choose any element from above choices. \n case2: \'I\' we can choose any element from below choices.\n """\n n = len(s)\n mod = 10**9+7\n ans = 0 \n @cache\n def rec(idx, a, b):\n # if it reaches end it means its a valid sequence (implicitly means a=0, b=0)\n if idx == n: return 1 \n # initialize valid sequences to 0 \n ret = 0 \n if s[idx] == \'D\':\n # if current idx is D, then we choose any element from the \'b\' elements below it.\n # correspondingly update a and b (elements above and below element we choose)\n for i in range(1,b+1):\n ret+=rec(idx+1, a+i-1, b-i)\n elif s[idx] == \'I\':\n for i in range(1,a+1):\n ret+=rec(idx+1, a-i, b+i-1)\n return ret%mod\n # we take first element as any of the 0 to n. and find for all starting elements. \n for i in range(n+1):\n ans = (ans + rec(0, n-i, i))%mod\n return ans\n``` | 0 | 0 | ['Python3'] | 0 |
valid-permutations-for-di-sequence | 👍Runtime 598 ms Beats 100.00% of users with Scala | runtime-598-ms-beats-10000-of-users-with-c0zh | Code\n\nobject Solution {\n def numPermsDISequence(s: String): Int = {\n val n = s.length()\n val dp = Array.ofDim[Int](n + 2, 2)\n val | pvt2024 | NORMAL | 2024-04-11T02:27:42.563647+00:00 | 2024-04-11T02:27:42.563666+00:00 | 1 | false | # Code\n```\nobject Solution {\n def numPermsDISequence(s: String): Int = {\n val n = s.length()\n val dp = Array.ofDim[Int](n + 2, 2)\n val mod = 1000000007\n dp(1)(0) = 1\n\n for (i <- 1 to n) {\n if (s.charAt(i - 1) == \'I\') {\n for (j <- 0 to i) dp(j + 1)(i & 1) = (dp(j)((i + 1) & 1) + dp(j)(i & 1)) % mod\n } else {\n for (j <- 0 to i) dp(j + 1)(i & 1) = ((dp(i)((i + 1) & 1) + mod - dp(j)((i + 1) & 1)) % mod + dp(j)(i & 1)) % mod\n }\n }\n\n dp(n + 1)(n & 1)\n }\n}\n``` | 0 | 0 | ['Scala'] | 0 |
valid-permutations-for-di-sequence | Solution Valid Permutations for DI Sequence | solution-valid-permutations-for-di-seque-6wj3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Suyono-Sukorame | NORMAL | 2024-03-03T13:57:50.479317+00:00 | 2024-03-03T13:57:50.479345+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n /**\n * @param String $s\n * @return Integer\n */\n function numPermsDISequence($s) {\n $mod = 1000000007;\n $n = strlen($s);\n \n $dp = array_fill(0, $n + 1, 1);\n \n for ($i = 0; $i < $n; $i++) {\n $next = array_fill(0, $n + 1, 0);\n if ($s[$i] == \'I\') {\n $sum = 0;\n for ($j = 0; $j < $n - $i; $j++) {\n $sum = ($sum + $dp[$j]) % $mod;\n $next[$j] = $sum;\n }\n } else {\n $sum = 0;\n for ($j = $n - $i - 1; $j >= 0; $j--) {\n $sum = ($sum + $dp[$j + 1]) % $mod;\n $next[$j] = $sum;\n }\n }\n $dp = $next;\n }\n \n return $dp[0];\n }\n}\n\n``` | 0 | 0 | ['PHP'] | 0 |
valid-permutations-for-di-sequence | The constraint is sort of too loose for backtracking to pass | the-constraint-is-sort-of-too-loose-for-3ouxc | Code\n\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n N = len(s)+1\n seen = set([])\n @cache\n def dp(i,prev): | MaxOrgus | NORMAL | 2024-02-27T04:15:46.468555+00:00 | 2024-02-27T04:15:46.468578+00:00 | 9 | false | # Code\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n N = len(s)+1\n seen = set([])\n @cache\n def dp(i,prev):\n if i == N-1:\n return 1\n res = 0\n if prev == -1:\n for k in range(N):\n seen.add(k)\n res += dp(i,k) % (10**9+7)\n seen.remove(k)\n elif s[i] == \'I\':\n for k in range(prev+1,N):\n if k not in seen:\n seen.add(k)\n res += dp(i+1,k) % (10**9+7) \n seen.remove(k)\n else:\n for k in range(prev):\n if k not in seen:\n seen.add(k)\n res += dp(i+1,k) % (10**9+7)\n seen.remove(k)\n return res % (10**9+7)\n \n\n \n return dp(0,-1) % (10**9+7)\n\n\n \n\n \n``` | 0 | 0 | ['Backtracking', 'Python3'] | 0 |
valid-permutations-for-di-sequence | revised_backtrack... | revised_backtrack-by-aman_17000s-flj2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | aman_17000s | NORMAL | 2024-02-24T10:48:51.642920+00:00 | 2024-02-24T10:48:51.642955+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string s="";\n int n;\n int dp[203][203];\n int m=1e9+7;\n int solve(int idx,int prev, vector<int>&vis)\n {\n if(idx==n) return 1; \n if(dp[idx+1][prev+1]!=-1) return dp[idx+1][prev+1];\n long long ans=0;\n if(idx==-1)\n {\n for(int i=0; i<=n; i++) \n {\n vis[i]=1;\n ans+=solve(0,i,vis)%m;\n ans%=m;\n vis[i]=0;\n }\n }else\n {\n for(int i=0; i<=n; i++)\n {\n if(vis[i]==0 )\n {\n if(s[idx]==\'D\' &&i<prev)\n {\n vis[i]=1;\n ans+=solve(idx+1,i, vis)%m;\n ans%=m;\n vis[i]=0;\n }else if(s[idx]==\'I\' && i>prev)\n {\n vis[i]=1;\n ans+=solve(idx+1,i, vis)%m;\n ans%=m;\n vis[i]=0;\n }\n }\n }\n }\n return dp[idx+1][prev+1]=(int)ans;\n }\n \n int numPermsDISequence(string s1) \n {\n s=s1;\n n=s.size();\n vector<int> vis(n+1,0);\n memset(dp,-1,sizeof(dp));\n return solve(-1,-1,vis);\n }\n};\n\n``` | 0 | 0 | ['Backtracking', 'C++'] | 0 |
valid-permutations-for-di-sequence | Dynamic Programming for Permutations with DI Sequence | dynamic-programming-for-permutations-wit-8p1r | Intuition\nThe problem involves finding the number of valid permutations based on a given string s, where \'I\' indicates that the next digit should be greater, | davitacols | NORMAL | 2024-02-23T21:38:03.963171+00:00 | 2024-02-23T21:38:03.963208+00:00 | 9 | false | # Intuition\nThe problem involves finding the number of valid permutations based on a given string `s`, where \'I\' indicates that the next digit should be greater, and \'D\' indicates that the next digit should be smaller. The intuition is to use dynamic programming to build a 2D array `dp` to keep track of the number of valid permutations for each length and ending digit.\n\n## Approach\n- Initialize a 2D array `dp` of size (n + 1) x (n + 1) to represent the number of valid permutations for each length and ending digit.\n- Initialize `dp[0][0]` to 1, as there is one valid permutation of length 0 (empty sequence) ending with digit 0.\n- Iterate through each character in the given string `s` and fill in the `dp` array based on the rules:\n - If the current character is \'I\', choose a digit greater than the previous one.\n - If the current character is \'D\', choose a digit smaller than the previous one.\n- The result is the sum of valid permutations for the last row of `dp` (length n) modulo 10^9 + 7.\n\n## Complexity\n- Time complexity: O(n^2), where n is the length of the given string. The nested loops iterate through each position in the 2D array.\n- Space complexity: O(n^2) due to the 2D array `dp` that stores the number of valid permutations for each length and ending digit.\n\n## Code\n```python\nclass Solution(object):\n def numPermsDISequence(self, s):\n """\n :type s: str\n :rtype: int\n """\n MOD = 10**9 + 7\n n = len(s)\n \n # dp[i][j]: Number of valid permutations of length i ending with digit j\n dp = [[0] * (n + 1) for _ in range(n + 1)]\n dp[0][0] = 1\n \n for i in range(1, n + 1):\n for j in range(i + 1):\n if s[i - 1] == \'I\':\n # If current character is \'I\', choose a digit greater than the previous one\n dp[i][j] = (dp[i][j] + sum(dp[i - 1][k] for k in range(j))) % MOD\n else:\n # If current character is \'D\', choose a digit smaller than the previous one\n dp[i][j] = (dp[i][j] + sum(dp[i - 1][k] for k in range(j, i))) % MOD\n \n return sum(dp[n]) % MOD\n\n# Example usage:\nsol = Solution()\n\n# Example 1\ns1 = "DID"\nresult1 = sol.numPermsDISequence(s1)\nprint(result1) # Output: 5\n\n# Example 2\ns2 = "D"\nresult2 = sol.numPermsDISequence(s2)\nprint(result2) # Output: 1\n | 0 | 0 | ['Python'] | 0 |
valid-permutations-for-di-sequence | Efficient JS solution - DP O(N^2) (Beat 100% time) | efficient-js-solution-dp-on2-beat-100-ti-7xdi | \n\nPro tip: Xi\xE8 \uD83D\uDC9C She\'s really cute tho.\n\n# Complexity\n- Time complexity: O(n^2)\n- Space complexity: O(n)\n\n# Code\njs\nlet MOD = 100000000 | CuteTN | NORMAL | 2024-01-30T02:33:17.476018+00:00 | 2024-01-30T02:33:17.476051+00:00 | 6 | false | \n\nPro tip: Xi\xE8 \uD83D\uDC9C She\'s really cute tho.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```js\nlet MOD = 1000000007;\nlet pre = new Uint32Array(201);\nlet cur = new Uint32Array(201);\n\n/**\n * @param {string} s\n * @return {number}\n */\nvar numPermsDISequence = function (s) {\n let n = s.length;\n cur.fill(0);\n cur[0] = 1;\n\n for (let i = 0; i < n; ++i) {\n let tem = pre;\n pre = cur;\n cur = tem;\n\n if (s[i] == "I") {\n let sum = pre[0];\n cur[0] = 0;\n for (let j = 1; j <= i + 1; ++j) {\n cur[j] = sum;\n sum = (sum + pre[j]) % MOD;\n }\n } else {\n let sum = 0;\n cur[i + 1] = 0;\n for (let j = i; j >= 0; --j) {\n sum = (sum + pre[j]) % MOD;\n cur[j] = sum;\n }\n }\n }\n\n let res = 0;\n for (let i = 0; i <= n; ++i) res = (res + cur[i]) % MOD;\n\n return res;\n};\n``` | 0 | 0 | ['Dynamic Programming', 'JavaScript'] | 0 |
valid-permutations-for-di-sequence | ✅ C++ Solution DP Memoization ✅ | c-solution-dp-memoization-by-atom-1-grrh | \n\n# Code\n\nclass Solution {\npublic:\n int mod = 1e9+7;\n int solve(int i,int ind, string &s,vector<int> &visited,vector<vector<int>> &dp){\n if | atom-1 | NORMAL | 2024-01-08T13:12:50.506281+00:00 | 2024-01-08T13:12:50.506318+00:00 | 76 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int mod = 1e9+7;\n int solve(int i,int ind, string &s,vector<int> &visited,vector<vector<int>> &dp){\n if(ind==s.size()) return 1;\n\n if(dp[i][ind]!=-1) return dp[i][ind];\n\n long long int ans = 0;\n if(s[ind]==\'I\'){\n for(int j=i+1;j<=s.size();j++){\n if(!visited[j]){\n visited[j]=1;\n ans = (ans+solve(j,ind+1,s,visited,dp)%mod)%mod;\n visited[j]=0;\n }\n }\n }\n else{\n for(int j=0;j<i;j++){\n if(!visited[j]){\n visited[j]=1;\n ans = (ans+solve(j,ind+1,s,visited,dp)%mod)%mod;\n visited[j]=0;\n }\n }\n }\n return dp[i][ind] = ans%mod;\n }\n int numPermsDISequence(string s) {\n int n=s.size();\n\n vector<vector<int>> dp(n+1,vector<int>(n+1,-1));\n vector<int> visited(n+1,0);\n int ans = 0;\n for(int i=0;i<=n;i++){\n visited[i]=1;\n ans = (ans+solve(i,0, s,visited,dp)%mod)%mod;\n visited[i]=0;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['String', 'Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 0 |
valid-permutations-for-di-sequence | python DP top down + backtracking | python-dp-top-down-backtracking-by-harry-nkyl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | harrychen1995 | NORMAL | 2023-11-21T16:09:23.367090+00:00 | 2023-11-21T16:09:23.367120+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n n = len(s) + 1\n \n\n visit = set()\n @functools.lru_cache(None)\n def dp(prev, j):\n \n if j == len(s):\n return 1\n ans = 0\n if prev == -1:\n for i in range(n):\n visit.add(i)\n ans += dp(i+1, 0)\n visit.remove(i)\n return ans\n if s[j] == "D":\n\n for i in range(prev-1):\n if i in visit:\n continue\n visit.add(i)\n ans += dp(i+1, j+1)\n visit.remove(i)\n else:\n for i in range(prev, n):\n if i in visit:\n continue\n visit.add(i)\n ans += dp(i+1, j+1)\n visit.remove(i)\n return ans\n \n return dp(-1, 0) % (10**9 + 7)\n\n\n\n\n``` | 0 | 0 | ['Dynamic Programming', 'Backtracking', 'Python3'] | 0 |
valid-permutations-for-di-sequence | Dynamic programming with top to down approach | dynamic-programming-with-top-to-down-app-qiso | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | geeknkta | NORMAL | 2023-11-01T06:58:44.300633+00:00 | 2023-11-01T06:58:44.300659+00:00 | 19 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long mod = 1000000007;\n int helper(int index, string s, vector<int>&visited, int currentElement, vector<vector<int> >&dp) {\n\n if(index == s.length()) {\n return 1;\n }\n\n if(dp[index][currentElement] != -1)\n return dp[index][currentElement];\n int ans = 0;\n\n for(int i=0; i<=s.length(); i++) {\n if(visited[i] == 0) {\n if(s[index] == \'D\' && currentElement > i || (s[index] == \'I\' && currentElement < i)) {\n visited[i] = 1;\n ans = (ans + helper(index+1, s, visited, i, dp) ) % mod;\n visited[i] = 0;\n }\n }\n }\n\n dp[index][currentElement] = ans;\n return ans;\n }\n int numPermsDISequence(string s) {\n int n = s.length();\n vector<int> visited(n+1, 0);\n vector<vector<int> > dp(n+1, vector<int>(n+1, -1));\n int ans = 0;\n for(int i=0; i<=n; i++) {\n visited[i] = 1;\n ans = (ans + helper(0, s, visited, i, dp))%mod;\n visited[i] = 0;\n } \n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | Dynamic programming with top to down approach | dynamic-programming-with-top-to-down-app-5qgp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | geeknkta | NORMAL | 2023-11-01T06:58:43.006844+00:00 | 2023-11-01T06:58:43.006871+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long mod = 1000000007;\n int helper(int index, string s, vector<int>&visited, int currentElement, vector<vector<int> >&dp) {\n\n if(index == s.length()) {\n return 1;\n }\n\n if(dp[index][currentElement] != -1)\n return dp[index][currentElement];\n int ans = 0;\n\n for(int i=0; i<=s.length(); i++) {\n if(visited[i] == 0) {\n if(s[index] == \'D\' && currentElement > i || (s[index] == \'I\' && currentElement < i)) {\n visited[i] = 1;\n ans = (ans + helper(index+1, s, visited, i, dp) ) % mod;\n visited[i] = 0;\n }\n }\n }\n\n dp[index][currentElement] = ans;\n return ans;\n }\n int numPermsDISequence(string s) {\n int n = s.length();\n vector<int> visited(n+1, 0);\n vector<vector<int> > dp(n+1, vector<int>(n+1, -1));\n int ans = 0;\n for(int i=0; i<=n; i++) {\n visited[i] = 1;\n ans = (ans + helper(0, s, visited, i, dp))%mod;\n visited[i] = 0;\n } \n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | java easy memoization after recursion | DP | java-easy-memoization-after-recursion-dp-hrn7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vishal_113 | NORMAL | 2023-10-25T18:53:49.482344+00:00 | 2023-10-25T18:53:49.482363+00:00 | 97 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int mod = 1000000007;\n public int numPermsDISequence(String s) {\n int n=s.length();\n int cnt=0;\n boolean check[]=new boolean[n+1];\n Integer dp[][]=new Integer[n+1][n+1];\n for(int i=0;i<=n;i++){\n check[i]=true;\n cnt+=fun(n-1,n,s.toCharArray(),i ,check, dp); cnt%=mod;\n check[i]=false;\n }\n return cnt%mod;\n }\n private int fun(int i, int n, char str[], int next,boolean check[], Integer dp[][]){\n if(i < 0)return 1;\n\n if(dp[i][next] != null)return dp[i][next]%mod;\n \n int count=0;\n for(int j=0;j<=n;j++){\n if(check[j])continue;\n if(str[i] == \'D\'){\n if(j > next){\n check[j]=true;\n count+=fun(i-1,n,str,j , check , dp); count%=mod;\n check[j]=false;\n }\n }else{\n if(j < next){\n check[j]=true;\n count+=fun(i-1,n,str,j, check , dp); count%=mod;\n check[j]=false;\n }\n }\n }\n\n return dp[i][next] = count%mod;\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 0 |
valid-permutations-for-di-sequence | simple easy to understand c++ solution | simple-easy-to-understand-c-solution-by-n5euk | class Solution {\npublic:\n int numPermsDISequence(string s) {\n constexpr int mod=1\'000\'000\'007;\n int n=s.length();\n vector>DP(n+1 | ar2609034 | NORMAL | 2023-10-17T14:07:23.286734+00:00 | 2023-10-17T14:07:23.286753+00:00 | 4 | false | class Solution {\npublic:\n int numPermsDISequence(string s) {\n constexpr int mod=1\'000\'000\'007;\n int n=s.length();\n vector<vector<int>>DP(n+1, vector<int>(n+1));\n for(int i=0;i<=n;++i){\n DP[0][i]=1;\n }\n for(int i=1;i<=n;++i){\n if(s[i-1]==\'I\'){\n int postsum=0;\n for(int j=n-i;j>=0;--j){\n postsum=(postsum+DP[i-1][j+1])%mod;\n DP[i][j]=postsum;\n }\n }else{\n int presum=0;\n for(int j=0;j<=n-i;++j){\n presum=(presum+DP[i-1][j])%mod;\n DP[i][j]=presum;\n }\n }\n }\n return DP[n][0];\n }\n}; | 0 | 0 | [] | 0 |
valid-permutations-for-di-sequence | Easiest Solution | easiest-solution-by-kunal7216-lnpl | \n\n# Code\njava []\nclass Solution {\n public int numPermsDISequence(String s) {\n\tint n = s.length();\n\tint[][] dp = new int [n+2][2];\n\tint mod = 10000 | Kunal7216 | NORMAL | 2023-09-24T15:44:42.358383+00:00 | 2023-09-24T15:44:42.358405+00:00 | 68 | false | \n\n# Code\n```java []\nclass Solution {\n public int numPermsDISequence(String s) {\n\tint n = s.length();\n\tint[][] dp = new int [n+2][2];\n\tint mod = 1000000007;\n\tdp[1][0] = 1;\n\tfor(int i = 1; i<=n; i++){\n\t\tif(s.charAt(i-1)==\'I\') {\n\t\t\tfor(int j = 0; j<=i; j++) dp[j+1][i&1]=(dp[j][(i+1)&1] + dp[j][i&1])%mod; \n\t\t} else {\n\t\t\tfor(int j = 0; j<=i; j++) dp[j+1][i&1]=((dp[i][(i+1)&1] + mod - dp[j][(i+1)&1])%mod + dp[j][i&1])%mod;\n\t\t} \n\t}\n\treturn dp[n+1][n&1];\n}\n}\n```\n```c++ []\nclass Solution {\npublic:\n int visited[201];\n int mod = 1e9+7;\n map<pair<int,int>,int>mp;\n int solve(int idx , int last,string &s){\n //base case\n if(idx<0)return 1;\n \n if(mp.count({idx,last}))\n return mp[{idx,last}];\n int ans = 0 ;\n \n //hash means any number can be insertd at last position\n if(s[idx]==\'#\'){\n for(int i=0;i<s.size();i++){\n if(!visited[i]){\n visited[i]=1;\n ans = (ans + solve(idx-1,i,s))%mod;\n visited[i]=0;\n }\n }\n }\n \n if(s[idx]==\'D\'){\n for(int i=last+1;i<s.size();i++){\n if(!visited[i]){\n visited[i]=1;\n ans = (ans + solve(idx-1,i,s))%mod;\n visited[i]=0;\n }\n } \n }\n \n if(s[idx]==\'I\'){\n for(int i=0;i<last;i++){\n if(!visited[i]){\n visited[i]=1;\n ans = (ans + solve(idx-1,i,s))%mod;\n visited[i]=0;\n }\n } \n }\n \n return mp[{idx,last}] = ans;\n \n }\n int numPermsDISequence(string s) {\n s.push_back(\'#\');\n int n=s.size();\n return solve(n-1,0,s);\n }\n};\n``` | 0 | 0 | ['C++', 'Java'] | 0 |
valid-permutations-for-di-sequence | Editorial-like solution, simple to understand with multiple approaches from Brute-force to optimal | editorial-like-solution-simple-to-unders-ee9v | The problem asks what is the number of valid permutations that follow a string of "DI" instructions, if a number i is used in a podition with \'D\' the next num | itaib2004 | NORMAL | 2023-08-02T09:38:37.534688+00:00 | 2023-08-02T09:38:37.534710+00:00 | 52 | false | The problem asks what is the number of valid permutations that follow a string of `"DI"` instructions, if a number `i` is used in a podition with `\'D\'` the next number must be in the range `0 <= j < i`, likewise if it\'s in an `\'I\'` position the next number must be `i < j <= n` where `n` is the length if the string provided, the hard part comes in that we cannot repeat the same number, so it seems (but turns out not to be the case) that we need to remember all the previous numbers to solve the problem, let\'s see how we might develop a solution.\n\n\n# Approach #1: Brute-Force\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe first thing that is recommended to be done in a complex problem like this one is to generate all possible solutions and discard the invalid ones, that can be done via backtracking, we define a helper function `backTrack` that keeps track of where in the string we are and what was the previous number used, and define a set `state` that contains all numbers previously used; at a given index position `i` we check for all numbers bigger/smaller than the previous number, if we can insert it into the permutation we add it to the stack, we we are done generating all it\'s sub-solutions we remove it from the set, (this can also be done with a stack, which may be faster).\nIf we reach `i == n` we finished generating a permutation and add `1` to our count (which I named `ans`).\n\n# Algorithm\n<!-- Describe your approach to solving the problem. -->\n1. Define a set/stack and a counter\n2. Define the `backTrack` function:\n2.1 If we reached the end, increase the counter\n2.2 If not, go through all numbers lower/higher than the previous number and check if they can be added, if yes then add the number tot the set, call `backTrack` with `i+1` and this added number, when the function returns, remove the number from the set\n3. Call `backTrack` for all possible starting number `0` to `n`\n\n# Complexity\n- Time complexity: $$O(n!)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nAt any index `i` we have `i` options to choose from in worst-case, since `n` can go up to `200` this will result in a TLE.\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe use a set/stack that will contain at most `n` numbers when a permutation is complete\n\n# Implementation (only python, sorry)\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n n = len(s)\n ans = [0]\n state = set()\n def backTrack(i, p):\n if i == n:\n ans[0] += 1\n return\n if s[i] == "I":\n for j in range(p+1, n+1):\n if j not in state:\n state.add(j)\n backTrack(i+1, j)\n state.remove(j)\n else:\n for j in range(0, p):\n if j not in state:\n state.add(j)\n backTrack(i+1, j)\n state.remove(j)\n return \n for i in range(n+1):\n state.add(i)\n backTrack(0, i)\n state.remove(i)\n return ans[0]%(10**9+7)\n```\n\n# Approach #2: Dynamic programming\n\n# Intuition\nThe previous solution was too slow to be accepted, we need to find a faster way to calculate the answer. We first note that we got asked the number of valid permutations, so maybe (for this problem to be possible, we definitely) we don\'t need to generate all possible permutations to know how many there are, usually we can break down a problem into sub-problems to generate an answer faster from solving sub-problems\nAt first it may look like this is impossible to do here, since at each index the number we choose will affect all the possible choices in the future, but remembering we only need to know the quantity we may wonder if maybe the quantities are not dependent directly on the number you choose to place, let\'s do a thought experiment, imagine instead of using the numbers `(1,2,3,4, ...)` to generate our permutatons we use `(1,1,1,1, ...)` only a bunch of ones, and when we use a number like `3` the whole thing turns into `(1,1,0,1, ...)` so we have a certain concept of "order" so that the problem is the same, now think about using `1` or `2` or `3`, in a given index `i` we would get accordingly `(0,1,1,1), (1,0,1,1), (1,1,0,1)` which are different, but look very similar! Why they all look so similar? because they all have the same idea of **relative ordering**, `1` is still smaller than `3` and `4` even when 2 is out of the equation and likewise for all the others, so if we only focus on the relative ordering of the numbers essentially all of the three sub-problems above are **identical**, so we can just represent them all as `(1,1,1)`.\nThis is still not the complete picture, we know that the `"ID"` will limit our choice of next number, so returning to the last example, if the digit is `\'I\'`, then in the case of choosing `1` we would have `(0,1,1,1)` and the next number could be any of the following ones, but if we chose `2` the the sub-problem is `(1,0,1,1)` and we can only choose as the next number the ones to the right of the new zero, likewise if it were a `\'D\'` it would be the ones to the left of the zero, with that in mind we can now define our dynamic programming sub-problem.\n\n`\ndp[i][j] = Solution to sub-problem s[i:n], if we can choose only ones bounded to the j\'th one\n`\n\nBy bounded I mean that if `s[i]` is `\'I\'` we can choose the ones from the `j` one to the right-end and if it is a `\'D\'` we can choose the ones from `j` one to the left-end.\nFor example `dp[2][3]` for the tuple `(1,1,1,1,1,1,1)` is the solution to the sub-string `s[2:n]` using at position `2` any one that is from the inclusive left/right (depending on `s[2]`) of the highlighted one in `(1,1,_1_,1,1)`, notice that the size of the tuple is smaller by 2 than the original because we zero\'ed two other ones in the original tuple, in general, if the original tuple is of size `n`, at index `i` the tuple will have size `n-i`.\n\nNow that we have a table, let\'s see how we can generate answers from sub-problems. The base case is very simple, `s[n-1]` is either `\'I\'` or `\'D\'` and the tuple is simply `(1,1)`, we can define the base cases as follows:\n```\nif s[n-1] == \'I\':\n #If we choose 1, then it is impossible to increase\n dp[n-1][0] = 1\n dp[n-1][1] = 0\nelif s[n-1] == \'D:\n #If we choose 0, then it is impossible to decrease\n dp[n-1][0] = 0\n dp[n-1][1] = 1\n```\nThis idea of choosing the highest number or the lowest, makes it impossible to continue will keep re-occurring in later cases too.\nFor an index `i < n-1` we know that if `s[i] == \'I\'` then the last number will have an answer of zero, if `s[i] == \'D\'` then the first number will have an answer of zero, in general `dp[i][j]\n` will have all the answers that were pre-calculated in that row `i` (from the definition of the dp) and will also contain all the possible answers of the sub-problem at the `i+1` using only one to the left/right of it, which in our table happens that answer turns out to be stored in `dp[i+1][j]` (you can convince yourself of that by imagining how removing a one from a tuple changes the absolute postion of each remaining one), so our final update step looks like this.\n\n```\nif s[n-1] == \'I\':\n if i == n-1:\n #If we choose 1, then it is impossible to increase\n dp[n-1][0] = 1\n dp[n-1][1] = 0\n else:\n if j == n-i:\n dp[i][j] = 0\n else:\n dp[i][j] = dp[i][j+1] + dp[i+1][j]\nelif s[n-1] == \'D:\n if i == n-1:\n #If we choose 0, then it is impossible to decrease\n dp[n-1][0] = 0\n dp[n-1][1] = 1\n else:\n if j == 0:\n dp[i][j] = 0\n else:\n dp[i][j] = dp[i][j-1] + dp[i+1][j]\n```\nPhew! That\'s a pretty complicated update step, make sure you understand it, before writing it down because later on it will get worse! Now at last all that\'s left to do is to write down the solution\n\n# Algorithm\n1. Define our table `dp`\n2. Go from the base case to the original case\n3. Update the table according to the update step\n4. return the `sum` of all possible start choices\n\n# Implementation (only python, sorry)\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n n = len(s)\n dp = [[None for j in range(n-i+1)] for i in range(n)]\n for j in range(n-1, 0-1, -1):\n if s[j] == "I":\n if j == n-1:\n dp[j][0] = 1\n dp[j][1] = 0\n else:\n dp[j][n-j] = 0\n for i in range((n-j)-1, 0-1, -1):\n dp[j][i] = dp[j+1][i]+dp[j][i+1]\n else:\n if j == n-1:\n dp[j][0] = 0\n dp[j][1] = 1\n else:\n dp[j][0] = 0\n for i in range(1, n-j+1):\n dp[j][i] = dp[j+1][i-1]+dp[j][i-1]\n return sum([dp[0][i] for i in range(n+1)])%(10**9+7)\n```\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nIt only takes $O(1)$ to calculate the update step, we have `n + n-1 + n-2 + ... ` entries in the table, so $n^2$ time to compute every entry.\n\n- Space complexity: $$O(n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe table has size $n^2$\n\n# Approach 3 DP + Double buffer\n\nWe notice that the update step only makes use of the last computed row and the current row being computed, so we can use two arrays and to calculate the whole ordeal, the space complexity will then be $O(n)$\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n n = len(s)\n dp = None\n for j in range(n-1, 0-1, -1):\n ndp = [None for i in range(n-j+1)]\n if s[j] == "I":\n if j == n-1:\n ndp[0] = 1\n ndp[1] = 0\n else:\n ndp[n-j] = 0\n for i in range((n-j)-1, 0-1, -1):\n ndp[i] = dp[i]+ndp[i+1]\n else:\n if j == n-1:\n ndp[0] = 0\n ndp[1] = 1\n else:\n ndp[0] = 0\n for i in range(1, n-j+1):\n ndp[i] = dp[i-1]+ndp[i-1]\n dp = ndp\n return sum(dp)%(10**9+7)\n```\n\n# Approach 4 Optimized memory\n\nWe can make a solution with only one array, first notice that the update step of `\'I\'` is fairly easy to adapt to one array since the base case is in a completely new index, but in the `\'D` case we need to update `i=0` so we set a variable `last` to remember the last value removed, but we need the last variable to update the next entry so we define an `nlast` to remember the variable that is about to be updated so that we can then update last with the value that was before the update, whew... (see the code, it\'s easier to understand)\n\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n n = len(s)\n dp = [0 for _ in range(n+1)]\n for j in range(n-1, 0-1, -1):\n if s[j] == "I":\n if j == n-1:\n dp[0] = 1\n dp[1] = 0\n else:\n dp[n-j] = 0\n for i in range((n-j)-1, 0-1, -1):\n dp[i] = dp[i]+dp[i+1]\n else:\n if j == n-1:\n dp[0] = 0\n dp[1] = 1\n else:\n last = dp[0]\n dp[0] = 0\n for i in range(1, n-j+1):\n nlast = dp[i]\n dp[i] = last+dp[i-1]\n last = nlast\n return sum(dp)%(10**9+7)\n```\n\nAny comments or improvements are appreciated, thank you for reading! | 0 | 0 | ['Python3'] | 0 |
valid-permutations-for-di-sequence | Simple C++ Solution | Dynamic Programming | Recursion | Memoization | simple-c-solution-dynamic-programming-re-55jb | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rj_9999 | NORMAL | 2023-07-07T10:03:50.466912+00:00 | 2023-07-07T10:03:50.466940+00:00 | 77 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint mod=1e9+7;\nlong long hope(int index,int prev,vector<int>&curr,vector<int>&visited,string &s,int &n,vector<vector<long long>>&dp){\n if(index>=s.length() && curr.size()==n+1)return 1;\n if(dp[index+1][prev+1]!=-1)return dp[index+1][prev+1];\n long long ans=0;\n if(index==-1){\n for(int i=0;i<=n;i++){\n curr.push_back(i);\n visited[i]=-1;\n ans=(ans%mod+hope(index+1,i,curr,visited,s,n,dp)%mod)%mod;\n curr.pop_back();\n visited[i]=0;\n }\n }\n else if(index!=-1){\n if(s[index]==\'I\'){\n int previous=prev;\n for(int i=previous+1;i<=n;i++){\n if(visited[i]!=-1){\n curr.push_back(i);\n visited[i]=-1;\n ans=(ans%mod+hope(index+1,i,curr,visited,s,n,dp)%mod)%mod;\n curr.pop_back();\n visited[i]=0;\n }\n }\n }\n else if(s[index]==\'D\'){\n int previous=prev;\n for(int i=0;i<previous;i++){\n if(visited[i]!=-1){\n curr.push_back(i);\n visited[i]=-1;\n ans=(ans%mod+hope(index+1,i,curr,visited,s,n,dp)%mod)%mod;\n curr.pop_back();\n visited[i]=0;\n }\n }\n }\n }\n return dp[index+1][prev+1]=ans%mod;\n}\n int numPermsDISequence(string s) {\n int n=s.length();\n vector<int>visited(s.length()+1,0);\n vector<int>curr;\n vector<vector<long long>>dp(202,vector<long long>(202,-1));\n long long fa=hope(-1,-1,curr,visited,s,n,dp)%mod;\n int answer=fa;\n return answer; \n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 1 |
valid-permutations-for-di-sequence | Scala solution | scala-solution-by-malovig-mu9v | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | malovig | NORMAL | 2023-06-13T14:55:04.926856+00:00 | 2023-06-13T14:55:04.926881+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nobject Solution {\n def numPermsDISequence(s: String): Int = {\n val n = s.length\n val dp = Array.ofDim[Int](n+2, 2)\n val mod = 1000000007\n dp(1)(0) = 1\n for (i <- 1 to n) \n if (s(i-1) == \'I\') for (j <- 0 to i) dp(j+1)(i%2) = (dp(j)((i+1)%2) + dp(j)(i%2)) % mod\n else for (j <- 0 to i) dp(j+1)(i%2) = ((dp(i)((i+1)%2) + mod - dp(j)((i+1)%2)) % mod + dp(j)(i%2)) % mod\n dp(n+1)(n%2)\n }\n}\n``` | 0 | 0 | ['Scala'] | 0 |
valid-permutations-for-di-sequence | c++ 3ms dp top down + prefix sum | c-3ms-dp-top-down-prefix-sum-by-vedantna-3sy3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vedantnaudiyal | NORMAL | 2023-04-29T11:54:37.331369+00:00 | 2023-04-29T11:54:37.331410+00:00 | 58 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint mod=1e9+7;\n int numPermsDISequence(string s) {\n int n=s.size();\n vector<vector<int>> dp(n+1,vector<int>(n+1));\n for(int i=0;i<=n;i++){\n dp[0][i]=1+i;\n }\n for(int i=1;i<=n;i++){\n for(int j=0;j<=n-i;j++){\n long long ans=0;\n if(s[i-1]==\'I\'){\n ans=dp[i-1][n+1-i]-dp[i-1][j];\n ans=(ans+mod)%mod;\n }\n else{\n ans+=1LL*dp[i-1][j];\n ans=(ans+mod)%mod;\n }\n if(j>0) ans+=dp[i][j-1];\n ans%=mod;\n dp[i][j]=ans;\n }\n }\n return dp[n][0];\n }\n};\n``` | 0 | 0 | ['C++'] | 1 |
valid-permutations-for-di-sequence | O(n^2) DP with O(n) space | on2-dp-with-on-space-by-xjpig-ebf6 | Intuition\n Describe your first thoughts on how to solve this problem. \n- dp[j] in the i-th round memorizes the number of permutations ends with j for s[0:i].\ | XJPIG | NORMAL | 2023-04-26T04:19:42.404935+00:00 | 2023-04-26T04:19:42.404964+00:00 | 28 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- dp[j] in the i-th round memorizes the number of permutations ends with j for s[0:i].\n\n- When s[i] is \'D\', update the ndp[j] with sum(dp[j:i]), which increases each element larger than j by one in the prefix.\n- When s[i] is \'I\', update ndp[j] with sum(dp[0:j-1]) while keeping the prefix.\n- Make use of the sum of prefix to get any sum(dp[j:i]) in $$O(1)$$\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numPermsDISequence(string s) {\n int n=s.size(),mod=1e9+7;\n vector<int> dp{1};\n for(int i=0;i<n;i++){\n vector<int> pre{0}; //pre[i]=sum(dp[0:i-1])\n int tmp=0;\n for(auto j:dp) pre.emplace_back((j+pre.back())%mod);\n vector<int> ndp;\n if(s[i]==\'D\') for(int j=0;j<=i+1;j++) ndp.emplace_back(pre.back()>pre[j]?pre.back()-pre[j]:pre.back()-(pre[j]-mod)); //sum(dp[j,i])\n else for(int j=0;j<=i+1;j++) ndp.emplace_back(pre[j]); //sum(dp[0],...,dp[j-1])\n dp=ndp;\n }\n int result=0;\n for(auto i:dp) result=(result+i)%mod;\n return result;\n }\n};\n\n\n``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | Python (Simple DP) | python-simple-dp-by-rnotappl-yy2k | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2023-02-25T13:29:51.610198+00:00 | 2023-02-25T13:29:51.610236+00:00 | 76 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numPermsDISequence(self, s):\n n, mod = len(s), 10**9+7\n\n @lru_cache(None)\n def dfs(i,val):\n if i == n:\n return 1\n\n if s[i] == "D":\n if val == 0: return 0\n return dfs(i,val-1) + dfs(i+1,val-1)\n\n if s[i] == "I":\n if val == n-i: return 0\n return dfs(i,val+1) + dfs(i+1,val)\n\n return sum([dfs(0,j) for j in range(n+1)])%mod\n \n``` | 0 | 0 | ['Python3'] | 0 |
valid-permutations-for-di-sequence | C++ Easy Solution✅|Using DP & Backtraking🔥|Optimal Solution | c-easy-solutionusing-dp-backtrakingoptim-8bda | \n\n# Complexity\n- Time complexity:O(NNN)\n\n- Space complexity:O(N*N)\n Add your space complexity here, e.g. O(n) \n\n# Code\n\nclass Solution {\npublic:\n | Jayesh_06 | NORMAL | 2023-02-18T06:40:56.343790+00:00 | 2023-02-18T06:40:56.343840+00:00 | 114 | false | \n\n# Complexity\n- Time complexity:O($$N*N*N$$)\n\n- Space complexity:O($$N*N$$)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int mod=1e9+7;\n //TC=O(N*N*N)\n //SC=O(N*N)\n int find(int ind,int pre,string& s,int n,vector<bool>& vis,vector<vector<int>>& dp){\n if(ind==n){\n return 1;\n }\n if(dp[ind][pre+1]!=-1){\n return dp[ind][pre+1];\n }\n int way1=0,way2=0;\n if(pre==-1){\n for(int i=0;i<=n;i++){\n if(!vis[i]){\n vis[i]=true;\n way1=(way1+find(ind,i,s,n,vis,dp))%mod;\n vis[i]=false;\n }\n }\n return way1%mod;\n }\n else{\n if(s[ind]==\'D\'){\n for(int i=0;i<=n;i++){\n if(i<pre){\n if(!vis[i]){\n vis[i]=true;\n way1=(way1+find(ind+1,i,s,n,vis,dp))%mod;\n vis[i]=false;\n }\n }\n }\n }else{\n for(int i=0;i<=n;i++){\n if(i>pre){\n if(!vis[i]){\n vis[i]=true;\n \n way2=(way2+find(ind+1,i,s,n,vis,dp))%mod;\n vis[i]=false;\n }\n }\n\n }\n }\n }\n return dp[ind][pre+1]=(way1+way2)%mod;\n }\n int numPermsDISequence(string s) {\n int n=s.size();\n vector<vector<int>> dp(n+1,vector<int>(n+2,-1));\n vector<bool> vis(n+1,false);\n return find(0,-1,s,n,vis,dp);\n }\n};\n```\n# AUTHOR:JAYESH BADGUJAR\n\n | 0 | 0 | ['Dynamic Programming', 'Backtracking', 'Memoization', 'C++'] | 0 |
valid-permutations-for-di-sequence | [Scala] Clean Functional DP | scala-clean-functional-dp-by-heavenwatch-qbwr | Let dp[i][j] be the number of permutations that s[i:] could form with the first number be the jth smallest candidate number.\n\nThen if s[i] == \'D\', because f | heavenwatcher | NORMAL | 2023-02-13T00:37:55.175611+00:00 | 2023-02-13T00:40:18.610089+00:00 | 19 | false | Let `dp[i][j]` be the number of permutations that `s[i:]` could form with the first number be the `j`th smallest candidate number.\n\nThen if `s[i] == \'D\'`, because for `dp[i][j]` we already choose the `j`th smallest possible value, we can only choose the candidate numbers before `j` for the `i+1`th position. So `dp[i][j] = dp[i + 1][0] + dp[i + 1][1] + ... + dp[i + 1][j - 1]`.\n\nThe same logic applies to the case when `s[i] == \'I`. We can choose the `j + 1`th, `j + 2`th... candidate value for position `i + 1`. Note that because `j`th value is taken, the `j + 1`th value in `i`\'s candidate numbers will be the `j`th value in `i+1`\'s candidate numbers. So `dp[i][j] = dp[i + 1][j] + dp[i + 1][j + 1] + ...`.\n\nBecause `dp[i][]` only depends on `dp[i + 1][]`, we can eliminate the first dimension of dp states to save some memory.\n```Scala\nobject Solution {\n def numPermsDISequence(s: String): Int = {\n val mod = (1e9 + 7).toInt\n def add(x: Int, y: Int) = ((x + y) % mod + mod) % mod\n\n s.reverse.foldLeft(Vector(1)) {\n case (dp, \'D\') => Vector.tabulate(dp.size + 1)(j => (0 until j).map(dp).fold(0)(add))\n case (dp, \'I\') => Vector.tabulate(dp.size + 1)(j => (j until dp.size).map(dp).fold(0)(add))\n case _ => null\n }.reduce(add)\n }\n}\n``` | 0 | 0 | [] | 0 |
valid-permutations-for-di-sequence | Easy C++ Beginner Friendly DP + Backtracking Solution | easy-c-beginner-friendly-dp-backtracking-zbfx | \n\n# Code\n\nclass Solution {\npublic:\n vector<int> vis;\n int dp[202][202];\n int mod = 1000000007;\n int recur(string &s, int i, int n,int idx){ | kartikdangi01 | NORMAL | 2023-01-24T17:36:34.157807+00:00 | 2023-01-24T17:36:34.157838+00:00 | 78 | false | \n\n# Code\n```\nclass Solution {\npublic:\n vector<int> vis;\n int dp[202][202];\n int mod = 1000000007;\n int recur(string &s, int i, int n,int idx){\n if(idx==n-1){\n return 1;\n }\n if(dp[idx][i]!=-1)\n return dp[idx][i];\n \n int res = 0;\n if(s[idx]==\'D\'){\n for(int j=i-1;j>=0;j--){\n if(vis[j]) continue;\n vis[j] = 1;\n res = (res + (recur(s,j,n,idx+1))%mod)%mod;\n vis[j] = 0; \n }\n }\n else{\n for(int j=i+1;j<n;j++){\n if(vis[j]) continue;\n vis[j] = 1;\n res = (res + (recur(s,j,n,idx+1))%mod)%mod;\n vis[j] = 0;\n }\n }\n return dp[idx][i] = res;\n }\n\n int numPermsDISequence(string s) {\n int n = s.size()+1;\n vis.resize(n,0);\n for(int i=0;i<202;i++){\n for(int j=0;j<202;j++){\n dp[i][j] = -1;\n }\n }\n int ans = 0;\n for(int i=0;i<n;i++){\n vis[i] = 1;\n ans = (ans + (recur(s,i,n,0))%mod)%mod;\n vis[i] = 0;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Backtracking', 'C++'] | 0 |
valid-permutations-for-di-sequence | C solution beats 100% | c-solution-beats-100-by-obose-v1fq | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is asking us to find the number of permutations of a string of length n tha | Obose | NORMAL | 2023-01-18T03:01:27.390736+00:00 | 2023-01-18T03:01:27.390773+00:00 | 51 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking us to find the number of permutations of a string of length n that satisfy the condition that the string only contains \'I\' and \'D\' and where \'I\' represents increasing and \'D\' represents decreasing.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use Dynamic Programming to solve this problem. We create a 2D array dp[n+1][n+1] where dp[i][j] represent the number of permutations of the first i characters that end with j \'I\'s.\n\nWe iterate through the string one character at a time, and for each character, we check if it is an \'I\' or a \'D\'. If it is an \'I\', we update dp[i][j] using dp[i-1][k] where k is from j to i-1. If it is a \'D\', we update dp[i][j] using dp[i-1][k] where k is from 0 to j-1.\n\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nint numPermsDISequence(char * s){\n int n = strlen(s), mod = 1e9 + 7;\n int dp[n + 1][n + 1];\n memset(dp, 0, sizeof(dp));\n dp[0][0] = 1;\n for (int i = 1; i <= n; i++)\n {\n for (int j = 0; j <= i; j++)\n {\n if (s[i - 1] == \'D\')\n for (int k = j; k < i; k++)\n dp[i][j] = (dp[i][j] + dp[i - 1][k]) % mod;\n else\n for (int k = 0; k < j; k++)\n dp[i][j] = (dp[i][j] + dp[i - 1][k]) % mod;\n }\n }\n int ans = 0;\n for (int i = 0; i <= n; i++)\n ans = (ans + dp[n][i]) % mod;\n return ans;\n}\n``` | 0 | 0 | ['C'] | 0 |
valid-permutations-for-di-sequence | Detailed comments for an O(N^2) solution | detailed-comments-for-an-on2-solution-by-czt0 | \n# Code\n\nclass Solution {\npublic:\n\n int numPermsDISequence(string s) {\n int N = s.size() + 1;\n vector<vector<int>> dp(N, vector<int>(N) | cal_apple | NORMAL | 2023-01-06T08:52:58.617419+00:00 | 2023-01-06T08:52:58.617454+00:00 | 55 | false | \n# Code\n```\nclass Solution {\npublic:\n\n int numPermsDISequence(string s) {\n int N = s.size() + 1;\n vector<vector<int>> dp(N, vector<int>(N));\n const int mod = 1e9 + 7;\n\n // dp[i][j] : answers for length=i+1 (using number [0,1,..,i]) that ends with j (j <= i)\n for (int j = 0; j < N; j++) {\n dp[0][j] = 1;\n }\n\n for (int i = 1; i < N; i++) {\n for (int j = 0; j <= i; j++) {\n // when we append j to the array, in order to avoid duplicate, by default, all the elements >= j in the previous array will automatically increment by one\n // e.g. [2, 1, 0] + [1] => [3, 2, 0, 1]\n\n if (s[i-1] == \'I\') {\n // dp[i][j] = dp[i-1][0] + dp[i-1][1] + .. dp[i-1][j-1]\n dp[i][j] = j ? dp[i-1][j-1] : 0;\n } else {\n // dp[i][j] = dp[i-1][j] + dp[i-1][j+1] + .. dp[i-1][i-1]\n dp[i][j] = dp[i-1][i-1] - (j ? dp[i-1][j-1] : 0);\n }\n }\n\n // change dp[i][j] to prefix sum so that we can have O(N^2) overall complexity instead of O(N^3)\n for (int j = 1; j <= i; j++) {\n dp[i][j] += dp[i][j-1];\n dp[i][j] %= mod;\n if (dp[i][j] < 0) {\n dp[i][j] += mod;\n }\n }\n }\n\n return dp[N-1][N-1];\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
valid-permutations-for-di-sequence | Just a runnable solution | just-a-runnable-solution-by-ssrlive-4e9e | Code\n\nimpl Solution {\n pub fn num_perms_di_sequence(s: String) -> i32 {\n let n = s.len();\n let m = 1_000_000_007;\n let mut dp = ve | ssrlive | NORMAL | 2023-01-03T07:31:48.025936+00:00 | 2023-01-03T07:31:48.025976+00:00 | 26 | false | # Code\n```\nimpl Solution {\n pub fn num_perms_di_sequence(s: String) -> i32 {\n let n = s.len();\n let m = 1_000_000_007;\n let mut dp = vec![vec![0; n + 1]; n + 1];\n dp[0][0] = 1;\n for i in 1..=n {\n for j in 0..=i {\n if s.chars().nth(i - 1).unwrap() == \'D\' {\n for k in j..=i - 1 {\n dp[i][j] = dp[i][j] % m + dp[i - 1][k] % m;\n }\n } else if j > 0 {\n for k in 0..=j - 1 {\n dp[i][j] = dp[i][j] % m + dp[i - 1][k] % m;\n }\n }\n }\n }\n let mut res = 0;\n for i in 0..=n {\n res = res % m + dp[n][i] % m;\n }\n (res % m) as _\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
valid-permutations-for-di-sequence | [Python3] | Top-Down DP O(N^2) | python3-top-down-dp-on2-by-swapnilsingh4-03vp | \nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n n,ans = len(s),0\n mod = 1_00_00_00_000 + 7\n memo = [[-1] * 201 for | swapnilsingh421 | NORMAL | 2022-12-16T12:44:38.593003+00:00 | 2022-12-16T12:44:38.593031+00:00 | 126 | false | ```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n n,ans = len(s),0\n mod = 1_00_00_00_000 + 7\n memo = [[-1] * 201 for i in range(201)]\n def dp(ind,prevNum):\n if ind < 0:\n return 1\n if memo[ind][prevNum] != -1:\n return memo[ind][prevNum]\n val = 0\n if s[ind] == \'D\':\n for more in range(prevNum+1,n+1):\n if more not in vis:\n vis.add(more)\n val += dp(ind-1,more)\n vis.remove(more)\n else:\n for less in range(prevNum):\n if less not in vis:\n vis.add(less)\n val += dp(ind-1,less)\n vis.remove(less)\n memo[ind][prevNum] = val\n return memo[ind][prevNum]\n for i in range(n+1):\n vis = set([i])\n ans += dp(n-1,i)\n return ans % mod\n \n``` | 0 | 0 | ['Dynamic Programming', 'Python', 'Python3'] | 0 |
valid-permutations-for-di-sequence | Python | Backtracking, works and easy to understand | python-backtracking-works-and-easy-to-un-qhda | python\nfrom functools import lru_cache\nclass Solution:\n def numPermsDISequence(self, s):\n return self.backtrack(s) % (10**9 + 7)\n\n def backtr | steve-jokes | NORMAL | 2022-11-30T06:50:18.097049+00:00 | 2022-11-30T06:50:18.097090+00:00 | 90 | false | ```python\nfrom functools import lru_cache\nclass Solution:\n def numPermsDISequence(self, s):\n return self.backtrack(s) % (10**9 + 7)\n\n def backtrack(self, s): # with pruning and memo\n L = len(s)\n nums = set(range(-1, L + 1)) # dummy -1 as \'pre\', only happens when idx == 0 (in which case we don\'t need var \'pre\')\n\n @lru_cache(None)\n def backtrack(idx, pre): # current index\n nums.remove(pre)\n\n cnt = 0\n if not nums: cnt = 1 # empty, it\'s a valid permutation\n elif idx == 0: cnt = sum(backtrack(idx + 1, num) for num in range(L + 1))\n elif s[idx - 1] == \'D\': cnt = sum(backtrack(idx + 1, num) for num in range(pre) if num in nums)\n elif s[idx - 1] == \'I\': cnt = sum(backtrack(idx + 1, num) for num in range(pre + 1, L + 1) if num in nums)\n\n nums.add(pre) # recover\n return cnt\n\n return backtrack(0, -1)\n``` | 0 | 0 | ['Backtracking', 'Memoization', 'Python'] | 0 |
valid-permutations-for-di-sequence | C++ || Backtracking + Memoization | c-backtracking-memoization-by-rohitraj13-seb1 | \nclass Solution {\npublic:\n int visited[201];\n int mod = 1e9+7;\n map<pair<int,int>,int>mp;\n int solve(int idx , int last,string &s){\n / | rohitraj13may1998 | NORMAL | 2022-11-07T16:31:02.168103+00:00 | 2022-11-07T16:31:02.168145+00:00 | 119 | false | ```\nclass Solution {\npublic:\n int visited[201];\n int mod = 1e9+7;\n map<pair<int,int>,int>mp;\n int solve(int idx , int last,string &s){\n //base case\n if(idx<0)return 1;\n \n if(mp.count({idx,last}))\n return mp[{idx,last}];\n int ans = 0 ;\n \n //hash means any number can be insertd at last position\n if(s[idx]==\'#\'){\n for(int i=0;i<s.size();i++){\n if(!visited[i]){\n visited[i]=1;\n ans = (ans + solve(idx-1,i,s))%mod;\n visited[i]=0;\n }\n }\n }\n \n if(s[idx]==\'D\'){\n for(int i=last+1;i<s.size();i++){\n if(!visited[i]){\n visited[i]=1;\n ans = (ans + solve(idx-1,i,s))%mod;\n visited[i]=0;\n }\n } \n }\n \n if(s[idx]==\'I\'){\n for(int i=0;i<last;i++){\n if(!visited[i]){\n visited[i]=1;\n ans = (ans + solve(idx-1,i,s))%mod;\n visited[i]=0;\n }\n } \n }\n \n return mp[{idx,last}] = ans;\n \n }\n int numPermsDISequence(string s) {\n s.push_back(\'#\');\n int n=s.size();\n return solve(n-1,0,s);\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Backtracking', 'Memoization', 'C++'] | 0 |
valid-permutations-for-di-sequence | js solution dp | js-solution-dp-by-renettadonathanrbo95-veuy | \nvar numPermsDISequence = function(s) {\n let mod = 10**9+7,res = 0\n const dp = new Array(s.length+1).fill().map(()=>new Array)\n dp[0][0]=1\n for | renettadonathanrbo95 | NORMAL | 2022-11-07T08:56:00.549537+00:00 | 2022-11-07T08:56:00.549584+00:00 | 39 | false | ```\nvar numPermsDISequence = function(s) {\n let mod = 10**9+7,res = 0\n const dp = new Array(s.length+1).fill().map(()=>new Array)\n dp[0][0]=1\n for(i=1;i<s.length+1;i++) {\n if(s[i-1]===\'D\') {\n dp[i][i]=0\n for(j=i-1;j>=0;j--) {\n dp[i][j]=(dp[i][j+1]+dp[i-1][j])%mod\n }\n } else {\n dp[i][0]=0\n for(j=1;j<=i;j++) {\n dp[i][j]=(dp[i][j-1]+dp[i-1][j-1])%mod\n }\n }\n }\n dp[s.length].map((e)=>{res+=e%mod})\n return res%mod\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
valid-permutations-for-di-sequence | [C++] Beginner Friendly, DP Solution | c-beginner-friendly-dp-solution-by-hardi-jrgs | \nclass Solution {\npublic:\n int mod=1000000007;\n int solve(string &s, int index, vector<bool> &vis, int last, vector<vector<int> > &dp){\n //if | hardikjain40153 | NORMAL | 2022-08-22T19:03:35.648661+00:00 | 2022-08-22T19:03:35.648708+00:00 | 214 | false | ```\nclass Solution {\npublic:\n int mod=1000000007;\n int solve(string &s, int index, vector<bool> &vis, int last, vector<vector<int> > &dp){\n //if we reach the last index, there will be single element left we can do this in one way.\n if(index == s.size()){\n return 1;\n }\n \n if(dp[index][last] != -1) return dp[index][last];\n \n //when we need less than last one\n long long cnt = 0;\n if(s[index] == \'D\'){\n for(int i=0; i<last; i++){\n if(vis[i]) continue;\n vis[i] = true;\n cnt+=(solve(s, index+1, vis, i, dp))%mod;\n vis[i] = false;\n }\n }\n \n //when we need greater than last one\n else{\n for(int i=last+1; i<=s.size(); i++){\n if(vis[i]) continue;\n vis[i] = true;\n cnt+=(solve(s, index+1, vis, i, dp))%mod;\n vis[i] = false;\n }\n }\n \n return dp[index][last] = cnt%mod;\n }\n int numPermsDISequence(string s) {\n vector<bool> vis(s.size()+1, false);\n vector<vector<int> > dp(s.size()+2, vector<int>(s.size()+2, -1));\n \n //start with any number at first position, then apply conditions in function\n long long cnt = 0;\n for(int i=0; i<=s.size(); i++){\n vis[i] = true;\n cnt+=(solve(s, 0, vis, i, dp))%mod;\n vis[i] = false;\n }\n \n return cnt%mod;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C'] | 0 |
valid-permutations-for-di-sequence | Java, time O(N^2), space O(N), 3ms=>2ms, dp[n+1] | java-time-on2-space-on-3ms2ms-dpn1-by-vk-7ss1 | \npublic int numPermsDISequence(String s) {\n\tint n = s.length();\n\tint[][] dp = new int [n+2][2];\n\tint mod = 1000000007;\n\tdp[1][0] = 1;\n\tfor(int i = 1; | vkochengin | NORMAL | 2022-08-19T18:55:26.868210+00:00 | 2022-08-20T07:51:42.833535+00:00 | 157 | false | ```\npublic int numPermsDISequence(String s) {\n\tint n = s.length();\n\tint[][] dp = new int [n+2][2];\n\tint mod = 1000000007;\n\tdp[1][0] = 1;\n\tfor(int i = 1; i<=n; i++){\n\t\tif(s.charAt(i-1)==\'I\') {\n\t\t\tfor(int j = 0; j<=i; j++) dp[j+1][i&1]=(dp[j][(i+1)&1] + dp[j][i&1])%mod; \n\t\t} else {\n\t\t\tfor(int j = 0; j<=i; j++) dp[j+1][i&1]=((dp[i][(i+1)&1] + mod - dp[j][(i+1)&1])%mod + dp[j][i&1])%mod;\n\t\t} \n\t}\n\treturn dp[n+1][n&1];\n}\n```\nfrom dp[][] to dp[]\n```\npublic int numPermsDISequence(String s) {\n\tint n = s.length();\n\tint mod = 1000000007;\n\tint[] dp = new int[n+1];\n\tdp[0] = 1;\n\tint c, sum,prev;\n\tfor(int i = 1; i<=n; i++){\n\t\tif(s.charAt(i-1)==\'I\') {\n\t\t\tsum = 0;\n\t\t\tfor(int j = 0; j<=i; j++){\n\t\t\t\tprev = sum;\n\t\t\t\tsum = (sum+dp[j])%mod;\n\t\t\t\tdp[j] = prev; \n\t\t\t} \n\t\t} else {\n\t\t\tc = dp[i-1]+mod;\n\t\t\tsum = c%mod;\n\t\t\tfor(int j = 0; j<=i; j++) {\n\t\t\t\tprev = sum;\n\t\t\t\tsum = (sum+(c-dp[j])%mod)%mod;\n\t\t\t\tdp[j] = prev; \n\t\t\t }\n\t\t} \n\t}\n\treturn dp[n]%mod;\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Java'] | 0 |
valid-permutations-for-di-sequence | python3 solution | python3-solution-by-daheofdiamond-zfc5 | Solution, requires a bit of observation\n\n\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n myStore = [1]\n \n for ind | daheofdiamond | NORMAL | 2022-07-30T00:23:07.200012+00:00 | 2022-07-30T00:23:07.200049+00:00 | 177 | false | Solution, requires a bit of observation\n\n```\nclass Solution:\n def numPermsDISequence(self, s: str) -> int:\n myStore = [1]\n \n for index, val in enumerate(s):\n if val == 0:\n continue\n temp = []\n for i in range(index + 2):\n if val == "I":\n curr = sum(myStore[i:])\n else:\n curr = sum(myStore[:i])\n temp.append(curr)\n myStore = temp\n return sum(myStore) % (10**9+7)\n```\n | 0 | 0 | ['Python3'] | 0 |
valid-permutations-for-di-sequence | JAVA Solution | java-solution-by-user6539fn-mioy | class Solution {\n private static final int mod = 1000000007;\n int[] seen = null;\n Integer[][] dp = null;\n public int numPermsDISequence(String s | user6539fn | NORMAL | 2022-07-29T07:26:55.530688+00:00 | 2022-07-29T07:26:55.530744+00:00 | 159 | false | class Solution {\n private static final int mod = 1000000007;\n int[] seen = null;\n Integer[][] dp = null;\n public int numPermsDISequence(String s) {\n dp = new Integer[s.length()][s.length()+1];\n seen = new int[s.length()+1];\n int count = 0;\n for(int i=0; i <= s.length(); i++) {\n seen[i] = 1;\n \tcount = count % mod + numPerms(s, 0, i) % mod;\n seen[i] = 0;\n }\n return count % mod;\n }\n private int numPerms(String s, int j, int p){\n if(j == s.length())\n return 1;\n if(dp[j][p] != null) return dp[j][p];\n char ch = s.charAt(j);\n int count = 0;\n if(ch == \'D\'){\n for(int i=p-1; i >= 0; i--){\n if(seen[i] == 1)\n continue;\n seen[i] = 1;\n count = count % mod + numPerms(s, j+1, i) % mod;\n seen[i] = 0;\n }\n }else{\n for(int i=p+1; i <= s.length(); i++){\n if(seen[i] == 1)\n continue;\n seen[i] = 1;\n count = count % mod + numPerms(s, j+1, i) % mod;\n seen[i] = 0;\n }\n }\n dp[j][p] = count % mod;\n return dp[j][p];\n }\n} | 0 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 0 |
valid-permutations-for-di-sequence | ANYONE CAN MODIFY THIS BFS approach with TLE? | anyone-can-modify-this-bfs-approach-with-cwhu | \nclass Solution {\npublic:\n int numPermsDISequence(string s) {\n int n=s.length();\n queue<pair<string,unordered_set<int>>> q;\n unord | Fullmetal_01 | NORMAL | 2022-07-06T12:47:49.126826+00:00 | 2022-07-07T05:52:07.527555+00:00 | 65 | false | ```\nclass Solution {\npublic:\n int numPermsDISequence(string s) {\n int n=s.length();\n queue<pair<string,unordered_set<int>>> q;\n unordered_set<int> v;\n string str="";\n for(int i=0;i<=n;++i)\n {\n str="";\n v.clear();\n str+=(i+\'0\');\n v.insert(i);\n q.push({str,v});\n }\n int i=0;\n unordered_set<string> visall;\n while(!q.empty())\n {\n int sz=q.size();\n if(i==n)\n {\n return q.size();\n }\n while(sz--)\n {\n auto temp=q.front();\n q.pop();\n if(visall.find(temp.first)!=visall.end())\n {\n continue;\n }\n if(s[i]==\'D\')\n {\n for(int j=temp.first.back()-\'0\'-1;j>=0;--j)\n {\n if(temp.second.find(j)==temp.second.end())\n {\n temp.first+=(j+\'0\');\n temp.second.insert(j);\n if(visall.find(temp.first)==visall.end())\n {\n q.push({temp.first,temp.second});\n }\n temp.second.erase(j);\n temp.first.pop_back();\n }\n }\n }\n else\n {\n for(int j=temp.first.back()-\'0\'+1;j<=n;++j)\n {\n if(temp.second.find(j)==temp.second.end())\n {\n temp.first+=(j+\'0\');\n temp.second.insert(j);\n if(visall.find(temp.first)==visall.end())\n {\n q.push({temp.first,temp.second});\n }\n temp.second.erase(j);\n temp.first.pop_back();\n }\n }\n }\n }\n i++;\n }\n return 0;\n }\n};\n``` | 0 | 0 | ['Breadth-First Search', 'C'] | 0 |
valid-permutations-for-di-sequence | C++ Easy | c-easy-by-subhrajit123-18b8 | class Solution {\npublic:\n int mod = 1e9 + 7;\n // unordered_setst;\n int perm(int i, int prev, int n, string &s, vector>&dp, vector&vis)\n {\n | Subhrajit123 | NORMAL | 2022-07-06T11:46:49.372375+00:00 | 2022-07-06T11:47:32.850386+00:00 | 262 | false | class Solution {\npublic:\n int mod = 1e9 + 7;\n // unordered_set<int>st;\n int perm(int i, int prev, int n, string &s, vector<vector<int>>&dp, vector<bool>&vis)\n {\n //cout<<"HERE"<<i<<"\\n";\n if(i<0)\n {\n return 1;\n }\n if(dp[i][prev] != -1)\n {\n return dp[i][prev];\n }\n \n int ways = 0;\n \n if(i == n)\n {\n for(int j=0; j<=n;j++)\n {\n int x = j;\n vis[x] = true;\n //cout<<x<<"\\n";\n ways = (ways + perm(i-1, x, n, s, dp, vis))%mod;\n //cout<<ways<<" "<<x<<"\\n";\n vis[x] = false;\n }\n }\n else\n {\n if(s[i] == \'D\')\n {\n for(int j=0; j<=n; j++)\n {\n if(vis[j] == true) continue;\n int x = j;\n if(prev < x)\n {\n vis[x] = true;\n ways = (ways + perm(i-1, x,n, s, dp, vis))%mod;\n vis[x] = false;\n }\n \n }\n }\n else\n {\n for(int j=0; j<=n; j++)\n {\n if(vis[j] == true) continue;\n int x = j;\n if(prev > x)\n {\n vis[x] = true;\n ways = (ways + perm(i-1, x,n, s, dp, vis))%mod;\n vis[x] = false;\n }\n }\n }\n }\n return dp[i][prev] = ways;\n }\n \n \n int numPermsDISequence(string s) {\n vector<bool>vis(s.size()+10, -1);\n for(int i=0; i<= s.size();i++)\n {\n vis[i] = false;\n //cout<<i<<"\\n";\n }\n vector<vector<int>>dp(s.size()+10, vector<int>(s.size()+10, -1));\n return perm(s.size(), s.size()+5, s.size(), s, dp, vis);\n return 0;\n }\n}; | 0 | 0 | ['Dynamic Programming', 'C'] | 0 |
valid-permutations-for-di-sequence | EASY C++ SOLUTION DP | RECURSION | MEMOIZATION | easy-c-solution-dp-recursion-memoization-f8ar | \nclass Solution {\npublic:\n \n int dp[201][201];\n int m = 1e9+7;\n int helper(string &s, int i, vector<bool> &visit, int start){\n if(i==s | jatinbansal1179 | NORMAL | 2022-07-06T11:15:27.397477+00:00 | 2022-07-06T11:15:27.397526+00:00 | 548 | false | ```\nclass Solution {\npublic:\n \n int dp[201][201];\n int m = 1e9+7;\n int helper(string &s, int i, vector<bool> &visit, int start){\n if(i==s.length()){\n return 1;\n }\n \n if(dp[i][start]!=-1){\n return dp[i][start];\n }\n if(s[i]==\'D\'){\n int ans = 0;\n for(int j = 0;j < start;j++){\n \n if(visit[j]==false){\n visit[j]=true;\n ans = (ans%m + helper(s,i+1,visit,j)%m)%m;\n visit[j]=false;\n }\n }\n return dp[i][start] = ans;\n }\n else{\n int ans = 0;\n for(int j = start+1;j <= s.length();j++){\n \n if(visit[j]==false){\n visit[j]=true;\n ans = (ans%m + helper(s,i+1,visit,j)%m)%m;\n visit[j]=false;\n }\n }\n return dp[i][start] = ans;\n }\n }\n \n \n int numPermsDISequence(string s) {\n vector<bool> visit(s.length()+1,false);\n int ans = 0;\n memset(dp,-1,sizeof(dp));\n for(int i = 0; i <= s.length();i++){\n visit[i]=true;\n \n ans = (ans%m + helper(s,0,visit,i)%m)%m;\n visit[i]=false;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 1 |
valid-permutations-for-di-sequence | Easy C++ Solution | easy-c-solution-by-abhi-1301-iwp0 | \nusing ll = long long;\n\nll dp[205][205];\nconst ll mod = 1e9 + 7;\nint n;\n\nll solve(int index, string &s, vector<int> &v, int piche)\n{\n if (index >= s | Abhi-1301 | NORMAL | 2022-07-06T10:10:12.451897+00:00 | 2022-07-06T10:10:12.451937+00:00 | 747 | false | ```\nusing ll = long long;\n\nll dp[205][205];\nconst ll mod = 1e9 + 7;\nint n;\n\nll solve(int index, string &s, vector<int> &v, int piche)\n{\n if (index >= s.size())\n return 1;\n\n if (dp[index][piche] != -1)\n return dp[index][piche];\n\n dp[index][piche] = 0;\n\n if (s[index] == \'D\')\n {\n for (int i = 0; i < piche; ++i)\n {\n if (v[i] == 0)\n {\n v[i] = 1;\n dp[index][piche] += solve(index + 1, s, v, i);\n dp[index][piche] %= mod;\n v[i] = 0;\n }\n }\n }\n else\n {\n for (int i = piche + 1; i < n + 1; ++i)\n {\n if (v[i] == 0)\n {\n v[i] = 1;\n dp[index][piche] += solve(index + 1, s, v, i);\n dp[index][piche] %= mod;\n v[i] = 0;\n }\n }\n }\n\n return dp[index][piche] %= mod;\n\n}\n\nclass Solution\n{\n public:\n int numPermsDISequence(string s)\n {\n memset(dp, -1, sizeof(dp));\n n=s.size();\n \n if(n==1)\n return 1;\n \n vector<int>v(n+1,0);\n \n ll ans=0;\n \n for(int i=0;i<=n;++i)\n {\n v[i]=1;\n ans+=solve(0,s,v,i);\n ans%=mod;\n v[i]=0;\n }\n return ans;\n \n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 2 |
valid-permutations-for-di-sequence | C# Solution | c-solution-by-rwdenier-iq42 | \n//This is based on a couple others..\n//I take no credit other than the obvious refactoring.\n//I deliberately chose the one that seemed easier to understand, | rwdenier | NORMAL | 2022-06-20T03:24:59.077889+00:00 | 2022-06-20T03:24:59.077929+00:00 | 93 | false | ```\n//This is based on a couple others..\n//I take no credit other than the obvious refactoring.\n//I deliberately chose the one that seemed easier to understand, not the fastest.\n\npublic class Solution \n{\n //Number of Permutations Table - Using long to avoid a lot of mod operations.\n long [,] np;\n int MOD;\n \n public void GetNumPermutationsEndingIn(int len, int end, int endStart, int endStop)\n {\n for(int k = endStart; k <= endStop; k++)\n {\n np[len,end] += np[len-1,k];\n }\n //This is just trying to keep the value from overflowing..\n if (np[len,end] > 0xFFFFFFFFFFFF)\n {\n np[len,end] = np[len,end]%this.MOD;\n }\n }\n \n public int NumPermsDISequence(string S) {\n int n = S.Length;\n this.MOD = 1000000000 + 7;\n this.np = new long[n+1,n+1];\n this.np[0,0] = 1;\n for(int len = 1; len <= n; len++)\n {\n for(int end = 0; end <= len; end++)\n {\n if(S[len-1] == \'D\')\n {\n //Here the transformation is to decrease. This means the previous MUST be bigger than this one.\n //The starting point is apparently end not end-1 here to also include the number of permutations frm the previous as a starting point. \n //The next np[len,end] is np[len-1,end] + np[len-1,end+1]... + np[len-1,len-1]\n GetNumPermutationsEndingIn(len,end, end/*prev end start*/, len-1/*prev end stop*/);\n }\n else\n {\n //The next np[len,end] is np[len-1,0] + np[len-1,1]... + np[len-1,end-1]\n GetNumPermutationsEndingIn(len,end, 0/*prev end start*/ , end-1/*prev end stop*/);\n }\n }\n }\n \n //To get the complete the complete set a simple sum is required.\n long res = 0;\n for(int i = 0; i <= n; i++)\n {\n res += np[n,i];\n }\n return (int)(res%MOD);\n }\n}\n``` | 0 | 0 | [] | 0 |
valid-permutations-for-di-sequence | 🔥 First Javascript Solution | first-javascript-solution-by-joenix-91z1 | \nfunction numPermsDISequence(s) {\n let mod = 1e9 + 7, dp = [[1], []], res = 0\n\n for (let i = 1; i <= S.length; i++) {\n for (let j = 0; j <= i; | joenix | NORMAL | 2022-05-19T11:46:56.339096+00:00 | 2022-05-19T11:46:56.339136+00:00 | 88 | false | ```\nfunction numPermsDISequence(s) {\n let mod = 1e9 + 7, dp = [[1], []], res = 0\n\n for (let i = 1; i <= S.length; i++) {\n for (let j = 0; j <= i; j++) {\n let l = 0, r = j\n if (s.charAt(i-1) === \'D\') {\n l = j, r = i\n }\n dp[1][j] = 0\n for (let k = l; k < r; k++) {\n dp[1][j] += dp[0][k]\n dp[1][j] %= mod\n }\n }\n [dp[0], dp[1]] = [dp[1], dp[0]]\n }\n\n for (let cnt of dp.shift()) {\n res += cnt\n res %= mod\n }\n return res\n}\n``` | 0 | 0 | ['JavaScript'] | 0 |
valid-permutations-for-di-sequence | C++ | Memoization solution | c-memoization-solution-by-diavolos-l3jb | ```\nclass Solution {\nprivate:\n int n,mod=1000000000+7;\n vector>mem;\n int solve(string &s,int index,int prev,vector&seen){\n if(index==n){\n | Diavolos | NORMAL | 2022-05-19T08:30:33.657073+00:00 | 2022-05-19T08:30:33.657114+00:00 | 692 | false | ```\nclass Solution {\nprivate:\n int n,mod=1000000000+7;\n vector<vector<int>>mem;\n int solve(string &s,int index,int prev,vector<bool>&seen){\n if(index==n){\n return 1;\n } else if(mem[index][prev]!=-1){\n return mem[index][prev];\n } else {\n int ans=0;\n if(s[index]==\'D\'){\n for(int i=0;i<prev;i++){\n if(!seen[i]){\n seen[i]=true;\n ans=(ans%mod+solve(s,index+1,i,seen)%mod)%mod;\n seen[i]=false;\n }\n }\n } else {\n for(int i=prev+1;i<=n;i++){\n if(!seen[i]){\n seen[i]=true;\n ans=(ans%mod+solve(s,index+1,i,seen)%mod)%mod;\n seen[i]=false;\n }\n }\n }\n return mem[index][prev]=ans;\n }\n }\npublic:\n int numPermsDISequence(string &s) {\n n=s.size();\n int ans=0;\n mem=vector<vector<int>>(n+1,vector<int>(n+1,-1));\n vector<bool>seen(n+1,false);\n for(int i=0;i<=n;i++){\n seen[i]=true;\n ans=(ans%mod+solve(s,0,i,seen)%mod)%mod;\n seen[i]=false;\n }\n return ans;\n }\n}; | 0 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 1 |
valid-permutations-for-di-sequence | PYTHON SOLUTION || EASY || EXPLAINED || DP || WELL WRITTTEN CODE|| | python-solution-easy-explained-dp-well-w-c30f | Try putting Value at the position keeping in mind that the current value should be increasing or decreasing \nTo check this check s[pos - 1] \nNow since we cann | reaper_27 | NORMAL | 2022-03-16T12:46:46.690586+00:00 | 2022-03-16T12:46:46.690613+00:00 | 456 | false | Try putting Value at the position keeping in mind that the current value should be increasing or decreasing \nTo check this check s[pos - 1] \nNow since we cannot repeat any digit we should use a dictionary to keep in check what value we used so far .\n\nOnce you find the no. of answer having index = i and last item = x , put it on dp\n\n\n\n\n\n```\nclass Solution:\n def recursion(self,idx,s,prev,limit,val,used):\n if idx == limit + 1:\n return 1\n if (idx,prev) in self.dp:return self.dp[(idx,prev)]\n start = 0 if s[idx-1] == \'D\' else prev + 1\n end = prev -1 if s[idx-1] == \'D\' else limit\n ans = 0\n for i in range(start,end+1):\n if i in used and used[i]==True:continue\n used[i] = True\n ans+=self.recursion(idx+1,s,i,limit,val+str(i),used)\n used[i] = False\n self.dp[(idx,prev)]=ans\n return ans\n def numPermsDISequence(self, s: str) -> int:\n limit = len(s)\n ans = 0\n self.dp = {}\n for i in range(limit+1):\n ans+= self.recursion(1,s,i,limit,str(i),{i:True})\n return ans%1000000007\n``` | 0 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Python', 'Python3'] | 1 |
valid-permutations-for-di-sequence | MEMOIZATION DP | memoization-dp-by-atharva20194080-jmgn | \nclass Solution {\npublic:\n int dp[203][203];\n int mod=1e9+7;\n int solve(int index , string& s, vector<int> & visited , int prev){\n if(inde | atharva20194080 | NORMAL | 2022-03-15T10:55:11.078320+00:00 | 2022-03-15T10:55:11.078347+00:00 | 177 | false | ```\nclass Solution {\npublic:\n int dp[203][203];\n int mod=1e9+7;\n int solve(int index , string& s, vector<int> & visited , int prev){\n if(index==s.size()) return 1;\n if(dp[index][prev]!=-1) return dp[index][prev];\n int n=s.size();\n long long temp=0;\n if(s[index]==\'D\'){\n //0 to prev-1\n for(int i=0;i<=prev-1;i++){\n if(visited[i]==0){\n visited[i]=1;\n temp=(temp%mod+(long long)solve(index+1,s,visited,i)%mod)%mod;\n\n visited[i]=0;\n }\n }\n }else {\n //prev+1 to n\n for(int i=prev+1;i<=n;i++){\n if(visited[i]==0){\n visited[i]=1;\n temp=(temp%mod+(long long)solve(index+1,s,visited,i)%mod)%mod;\n visited[i]=0;\n }\n }\n }\n return dp[index][prev]=temp;\n }\n int numPermsDISequence(string s) {\n memset(dp,-1,sizeof dp);\n int n=s.size();\n vector<int> visited(n+1,0);\n int count=0;\n for(int i=0;i<=n;i++){\n visited[i]=1;\n count= (count%mod+(long long)solve(0,s,visited,i)%mod)%mod;\n visited[i]=0;\n }\n return count;\n }\n};\n``` | 0 | 0 | [] | 1 |
valid-permutations-for-di-sequence | Compiling both O(n^2) approaches. | compiling-both-on2-approaches-by-josshei-92n4 | The first approach is based on this post by lee215.\n\nIn both the cases we are avoiding looping through the values already looped through by the previous eleme | jossheim | NORMAL | 2021-07-01T00:53:46.926865+00:00 | 2021-07-01T01:27:17.448990+00:00 | 422 | false | The first approach is based on [this](https://leetcode.com/problems/valid-permutations-for-di-sequence/discuss/168278/C%2B%2BJavaPython-DP-Solution-O(N2)) post by lee215.\n\nIn both the cases we are avoiding looping through the values already looped through by the previous element by just using the previous values to make it O(n^2) instead of O(n^3).\n```\n// Runtime: 4ms\nvoid firstApproach(string& s, int n, vvi&dp) {\n for (int i =0;i<=n;i++) dp[0][i] = 1;\n for (int i = 1;i<=n;i++) {\n if (s[i-1] == \'I\') {\n dp[i][0] = dp[i-1][0];\n for (int j=1;j<=n-i;j++) {\n dp[i][j] = (dp[i][j-1] + dp[i-1][j])%mod; // summing dp[i-1][0..j]\n }\n } else {\n dp[i][n-i] = dp[i-1][n-i+1];\n for (int j=n-i-1;j>=0;j--) {\n dp[i][j] = (dp[i][j+1] + dp[i-1][j+1])%mod; // summing dp[i-1][j+1...n-i+1]\n }\n }\n }\n }\n```\n\n\nThe second approach is based on the intuitions by wxd_sjtu [here](https://leetcode.com/problems/valid-permutations-for-di-sequence/discuss/196939/Easy-to-understand-solution-with-detailed-explanation), another great explanation by ariawynn [here](https://leetcode.com/problems/valid-permutations-for-di-sequence/discuss/186571/Python-O(N3)O(N2)-time-O(N)-space-DP-solution-with-clear-explanation-(no-%22relative-rank%22-stuff)).\nA great visualisation for this approach is also provided by quadpixels [here](https://leetcode.com/problems/valid-permutations-for-di-sequence/discuss/169126/Visualization-Key-to-the-DP-solution:-imagine-cutting-a-piece-of-paper-and-separating-the-halves)\n\n```\n// Runtime: 4ms\nvoid secondApproach(string& s, int n, vvi&dp) {\n for (int i=0;i<=n;i++) dp[0][i] = 1;\n for (int i = 1;i<=n;i++) {\n if (s[i-1] == \'I\') {\n dp[i][1] = dp[i-1][0];\n for (int j = 2;j<=i;j++) {\n dp[i][j] = (dp[i][j-1] + dp[i-1][j-1])%mod; // summing dp[i-1][0...j-1]\n } \n } else {\n dp[i][i-1] = dp[i-1][i-1];\n for (int j = i-2;j>=0;j--) {\n dp[i][j] = (dp[i][j+1] + dp[i-1][j])%mod; // summing dp[i-1][j...i-1]\n }\n }\n }\n }\n```\n\nBoilerplate:\n```\ntypedef vector<int> vi;\ntypedef vector<vi> vvi;\nint mod = 1e9+7;\nint numPermsDISequence(string& s) {\n\tint n = s.size();\n\tvvi dp = vvi(n+1, vi(n+1,0));\n\tfirstApproach(s, n, dp);\n\t//secondApproach(s, n, dp);\n\tint ans =0;\n\tfor (int i: dp[n]) ans = (ans + i)%mod;\n\treturn ans;\n}\n```\n\nJust a compilation, kudos to the original posters.\n | 0 | 0 | [] | 0 |
valid-permutations-for-di-sequence | C++ Easy | c-easy-by-aaditya-pal-ouzv | c++\nclass Solution {\npublic:\n int n;\n string s;\n int mod = 1e9 + 7;\n map<pair<int,int>,int>dp;\n int countways(int id,int prev,vector<bool> | aaditya-pal | NORMAL | 2021-05-29T20:35:28.717124+00:00 | 2021-05-29T20:35:28.717156+00:00 | 319 | false | ```c++\nclass Solution {\npublic:\n int n;\n string s;\n int mod = 1e9 + 7;\n map<pair<int,int>,int>dp;\n int countways(int id,int prev,vector<bool>&taken){\n\n if(id==n+1){\n return 1;\n }\n if(dp.find({id,prev})!=dp.end()) return dp[{id,prev}];\n int ans = 0;\n if(s[id-1]==\'D\'){\n for(int i = 0;i<=prev;i++){\n if(taken[i]==true) continue;\n taken[i] = true;\n ans+=countways(id+1,i,taken)%mod;\n ans%=mod;\n taken[i] = false;\n }\n }\n else{\n for(int i = prev+1;i<=n;i++){\n if(taken[i]==true) continue;\n taken[i] = true;\n ans+=countways(id+1,i,taken)%mod;\n ans%=mod;\n taken[i] = false;\n }\n }\n return dp[{id,prev}] = ans%mod;\n }\n int numPermsDISequence(string _s) {\n s = _s;\n n = s.size();\n vector<bool>taken(n+1,false);\n int ans = 0;\n for(int i = 0;i<=n;i++){\n taken[i] = true;\n ans+=countways(1,i,taken)%mod;\n ans%=mod;\n taken[i] = false;\n }\n return ans;\n }\n};\n``` | 0 | 0 | [] | 0 |
valid-permutations-for-di-sequence | Java - DP - O(N^3) | java-dp-on3-by-kataria_aakash-4kuh | \nclass Solution {\n int MOD = 1000000007;\n Map<Integer, Integer> cache;\n public int numPermsDISequence(String s) {\n cache = new HashMap<>(); | kataria_aakash | NORMAL | 2021-05-15T17:58:04.744129+00:00 | 2021-05-15T17:58:45.764806+00:00 | 237 | false | ```\nclass Solution {\n int MOD = 1000000007;\n Map<Integer, Integer> cache;\n public int numPermsDISequence(String s) {\n cache = new HashMap<>();\n return dpRec(s, 0, 0, s.length(), new boolean[s.length()+1]);\n }\n private int dpRec(String s, int i, int x, int y, boolean[] vis) {\n if(i == s.length()){\n int j;\n for(j = x; j <= y; j++) if(vis[j] == false) break;\n return (j <= y) ? 1 : 0;\n } \n int key = i*40000 + x*200 + y;\n if(cache.containsKey(key)) return cache.get(key);\n int count = 0;\n for(int j = x; j <= y; j++) {\n if(vis[j] == false) {\n vis[j] = true;\n count += (s.charAt(i) == \'D\') ? dpRec(s, i+1, 0, j-1, vis) : dpRec(s, i+1, j+1, s.length(), vis);\n count = count%MOD;\n vis[j] = false;\n }\n }\n cache.put(key, count);\n return count;\n }\n}\n``` | 0 | 0 | [] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.