question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
get-equal-substrings-within-budget | **Maximizing Equal Substrings Within a Given Cost Using Sliding Window Technique** | maximizing-equal-substrings-within-a-giv-1zyw | \n# Intuition\nWhen given two strings and a cost constraint, the problem essentially boils down to finding the longest substring that can be transformed within | kazakie96 | NORMAL | 2024-05-29T06:57:24.650654+00:00 | 2024-05-29T06:57:24.650676+00:00 | 3 | false | \n# Intuition\nWhen given two strings and a cost constraint, the problem essentially boils down to finding the longest substring that can be transformed within the given cost. My first thought was to use a sliding window approach. This method is efficient for problems involving subarrays or substrings and constraints, as it dynamically adjusts the window size to stay within the allowed cost.\n\n# Approach\nThe key idea is to maintain a window that keeps track of the total transformation cost. Here\'s a step-by-step breakdown:\n\n1. **Initialization**: We initialize several variables:\n - `n` to store the length of the strings.\n - `res` to store the maximum length of the valid substring.\n - `win` to store the current total cost within the window.\n - `l` as the left pointer of our sliding window.\n\n2. **Iterate with the Right Pointer**: We iterate through the string using a right pointer `r`.\n - For each character, we calculate the transformation cost to change `s[r]` to `t[r]` and add it to `win`.\n\n3. **Adjust the Window**: If the total cost `win` exceeds `maxCost`, we need to shrink the window from the left side to bring the cost back within the limit:\n - We do this by incrementing the left pointer `l` and subtracting the transformation cost of the character at the left pointer from `win`.\n\n4. **Update the Result**: After adjusting the window, we update `res` with the maximum length of the valid window (`r - l + 1`).\n\n5. **Return the Result**: Finally, we return the maximum length stored in `res`.\n\n\n\n# Complexity\n- **Time complexity**: The time complexity is $$O(n)$$ because we traverse the string once with the right pointer, and the left pointer also moves at most `n` times.\n- **Space complexity**: The space complexity is $$O(1)$$ as we use a constant amount of extra space regardless of the input size.\n\n**#SlidingWindow #Algorithm #StringManipulation #ComplexityAnalysis**\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int n = s.length(); // length of the strings\n int res = 0; // result to store the maximum length\n int win = 0; // variable to store the current total cost\n int l = 0; // left pointer of the sliding window\n\n // Iterate through the string with the right pointer r\n for(int r = 0; r < n; r++) {\n // Add the transformation cost for the current character\n win += Math.abs(s.charAt(r) - t.charAt(r));\n \n // If the current cost exceeds maxCost, adjust the left pointer\n while(win > maxCost) {\n win -= Math.abs(s.charAt(l) - t.charAt(l));\n l++;\n }\n \n // Update the result with the maximum length found\n res = Math.max(res, r - l + 1);\n }\n return res; // Return the result\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
get-equal-substrings-within-budget | Easy Sliding Window Solution | easy-sliding-window-solution-by-shivamkh-rf1w | \n# Code\n\nclass Solution {\npublic:\n static int equalSubstring(string& s, string& t, int maxCost) {\n const int n=s.size();\n int l=0, r;// | ShivamKhator | NORMAL | 2024-05-29T06:00:47.923191+00:00 | 2024-05-29T06:00:47.923209+00:00 | 7 | false | \n# Code\n```\nclass Solution {\npublic:\n static int equalSubstring(string& s, string& t, int maxCost) {\n const int n=s.size();\n int l=0, r;// 2 pointers\n int cost=0, len=0;\n\n // Initialize the window by moving r while cost<=maxCost\n for (r = 0; r < n; r++) {\n cost+=abs(s[r]-t[r]);\n if (cost>maxCost) {\n cost-=abs(s[r]-t[r]);\n break;\n }\n }\n\n // If the initial window exceeds the whole string\n if (r==n && cost<=maxCost) return n;\n \n len=r; //initial length for the valid window\n\n // Sliding the window\n for (; r<n; r++) {\n cost+=abs(s[r]-t[r]);\n while (cost > maxCost) {\n cost-=abs(s[l]-t[l]);\n l++;\n }\n len=max(len, r-l+1);\n }\n return len;\n }\n};\n\n\n\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n\n\n | 1 | 0 | ['String', 'Sliding Window', 'Prefix Sum', 'C++'] | 0 |
get-equal-substrings-within-budget | Sliding window | sliding-window-by-drgavrikov-in2z | Approach\n Describe your approach to solving the problem. \nUse the classic sliding window approach to solve this problem with two pointers (left pointer and ri | drgavrikov | NORMAL | 2024-05-28T22:34:29.691886+00:00 | 2024-05-28T22:46:28.504972+00:00 | 17 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nUse the classic sliding window approach to solve this problem with two pointers (left pointer and right pointer) to find the longest valid substring. \n\nIterate through the differences in ASCII values between corresponding characters of s and t with the right pointer to expand the window by adding the cost of the current character to currentCost. If current cost exceeds max cost, contract the window by moving the left pointer to the right and subtracting the cost of the character at the left pointer from current cost until current cost is within maxCost. Update maxLength with the length of the current valid window.\n\n# Complexity\n- Time complexity: $O(N)$ where $N$ is string length, because rightPointer increment each steps. \n\n- Space complexity: $O(1)$ additional memory\n\n# Code\n```\nclass Solution {\n fun equalSubstring(s: String, t: String, maxCost: Int): Int {\n var currentCost = 0\n var maxLength = 0\n var leftPointer = 0\n \n for (rightPointer in s.indices) {\n currentCost += abs(s[rightPointer] - t[rightPointer])\n while (leftPointer <= rightPointer && currentCost > maxCost) {\n currentCost -= abs(s[leftPointer] - t[leftPointer])\n leftPointer++\n }\n maxLength = max(maxLength, rightPointer - leftPointer + 1)\n }\n \n return maxLength\n }\n}\n```\n\nMost of my solutions are in [C++](https://github.com/drgavrikov/leetcode-cpp]) and [Kotlin](https://github.com/drgavrikov/leetcode-jvm) on my [Github](https://github.com/drgavrikov). | 1 | 0 | ['Sliding Window', 'Kotlin'] | 0 |
get-equal-substrings-within-budget | Kotlin. Beats 100% (150 ms). Sliding window + static "diffs" array | kotlin-beats-100-150-ms-sliding-window-s-7px3 | \n\n# Code\n\nclass Solution {\n fun equalSubstring(s: String, t: String, maxCost: Int): Int {\n for (i in 0 until s.length) {\n diffs[i] = | mobdev778 | NORMAL | 2024-05-28T21:04:19.163278+00:00 | 2024-05-28T21:04:19.163296+00:00 | 4 | false | \n\n# Code\n```\nclass Solution {\n fun equalSubstring(s: String, t: String, maxCost: Int): Int {\n for (i in 0 until s.length) {\n diffs[i] = Math.abs(s[i] - t[i])\n }\n var maxLen = -1\n var diff = 0\n var left = diff\n var right = left\n while (right < s.length) {\n diff += diffs[right]\n while (diff > maxCost) {\n diff -= diffs[left]\n left++\n }\n maxLen = Math.max(maxLen, -left + right)\n right++\n }\n return maxLen + 1\n }\n\n companion object {\n val diffs = IntArray(100_001)\n }\n}\n``` | 1 | 0 | ['Kotlin'] | 0 |
get-equal-substrings-within-budget | sliding window | sliding-window-by-mr_stark-ao5p | \nclass Solution {\npublic:\n int equalSubstring(string s, string t, int mc) {\n int i = 0;\n int j = 0;\n int n = s.length();\n | mr_stark | NORMAL | 2024-05-28T19:08:22.363085+00:00 | 2024-05-28T19:08:22.363110+00:00 | 14 | false | ```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int mc) {\n int i = 0;\n int j = 0;\n int n = s.length();\n int cc= 0,res = 0;\n while(j<n)\n {\n cc += abs(s[j]-t[j]);\n while(cc>mc)\n {\n cc -= (abs(s[i]-t[i]));\n i++;\n }\n res = max(res,j-i+1);\n j++;\n }\n \n return res;\n \n }\n};\n``` | 1 | 0 | ['C'] | 0 |
construct-the-minimum-bitwise-array-i | [Java/C++/Python] Low Bit, O(n) | javacpython-low-bit-on-by-lee215-on3s | Intuition\nans[i] OR (ans[i] + 1) == nums[i]\nans[i] and ans[i] + 1 are one odd and one even.\nnums[i] is an odd.\n\n\n# Explanation\n..0111 || (..0111 + 1) = | lee215 | NORMAL | 2024-10-12T17:29:49.389526+00:00 | 2024-10-14T03:10:02.060348+00:00 | 1,062 | false | # **Intuition**\n`ans[i] OR (ans[i] + 1) == nums[i]`\n`ans[i]` and `ans[i] + 1` are one odd and one even.\n`nums[i]` is an odd.\n<br>\n\n# **Explanation**\n`..0111 || (..0111 + 1) = ..1111`\nThe effect is that change the rightmost 0 to 1.\n\nFor each `a` in array `A`,\nfind the rightmost 0,\nand set the next bit from 1 to 0.\n\n`a + 1` will filp the 1-suffix to 0-suffix,\nand flip the rightmost 0 to 1.\n`a & -a` is a trick to get the rightmost 1.\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(n)` for result\n<br>\n\n**Java**\n```java\n public int[] minBitwiseArray(List<Integer> A) {\n int n = A.size(), res[] = new int[n];\n for (int i = 0; i < n; i++) {\n int a = A.get(i);\n if (A.get(i) % 2 == 0) {\n res[i] = -1;\n } else {\n res[i] = a - ((a + 1) & (-a - 1)) / 2;\n }\n }\n return res;\n }\n```\n\n**C++**\n```cpp\n vector<int> minBitwiseArray(vector<int>& A) {\n vector<int> res;\n for (int a : A) {\n if (a % 2 == 0) {\n res.push_back(-1);\n } else {\n res.push_back(a - ((a + 1) & (-a - 1)) / 2);\n }\n }\n return res;\n }\n```\n\n**Python**\n```py\n def minBitwiseArray(self, A: List[int]) -> List[int]:\n res = []\n for a in A:\n if a % 2 == 0:\n res.append(-1)\n else:\n res.append(a - ((a + 1) & (-a - 1)) // 2)\n return res\n```\n\n# More Bits Problem\n- 3315. [Construct the Minimum Bitwise Array II](https://leetcode.com/problems/construct-the-minimum-bitwise-array-ii/discuss/5904140/JavaC%2B%2BPython-Bit-O(n))\n- 3307. [Find the K-th Character in String Game II](https://leetcode.com/problems/find-the-k-th-character-in-string-game-ii/discuss/5846414)\n- 3304. [Find the K-th Character in String Game I](https://leetcode.com/problems/find-the-k-th-character-in-string-game-i/discuss/5846330/)\n\n | 14 | 0 | ['C', 'Python', 'Java'] | 2 |
construct-the-minimum-bitwise-array-i | Python3 || 11 lines, just odd numbers || T/S: 99% / 25% | python3-11-lines-just-odd-numbers-ts-99-jog3f | Here\'s the intuition:\n\nThe prime number condition is a red herring. The real condition is the elements of nums are odd integers (excepting of course, 2). Odd | Spaulding_ | NORMAL | 2024-10-12T17:23:49.583340+00:00 | 2024-10-16T21:37:11.677326+00:00 | 518 | false | Here\'s the intuition:\n\nThe *prime number* condition is a *red herring*. The real condition is the elements of `nums` are odd integers (excepting of course, 2). Odd numbers are either *4 mod 1* or *4 mod 3*. The *4 mod 1* case becomes trivial after analyzing some examples. The *4 mod 3* case requires a bit more investigation, but does have an intuitive answer as well.\n\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums):\n\n def helper(num):\n\n if num %4 == 1: # <-- 4 mod 1 case\n return num - 1 \n\n if num %4 == 3: # <-- 4 mod 3 case\n tmp = num\n for i in range(num.bit_length()):\n tmp //= 2\n if not tmp%2: break\n \n return num - (1<<i) \n\n return -1 # <-- just for num = 2\n\n\n return map(helper,nums)\n```\n```cpp []\n#include <vector>\n#include <cmath> // for bit_length\n\nclass Solution {\npublic:\n std::vector<int> minBitwiseArray(const std::vector<int>& nums) {\n std::vector<int> result;\n \n for (int num : nums) {\n result.push_back(helper(num));\n }\n \n return result;\n }\n \nprivate:\n int helper(int num) {\n if (num % 4 == 1) { // Case when num % 4 == 1\n return num - 1;\n }\n \n if (num % 4 == 3) { // Case when num % 4 == 3\n int tmp = num;\n for (int i = 0; i < (int)log2(num) + 1; ++i) {\n tmp /= 2;\n if (tmp % 2 == 0) {\n return num - (1 << i);\n }\n }\n }\n\n return -1; // Special case for num == 2\n }\n};\n\n```\n```java []\n\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n List<Integer> result = new ArrayList<>();\n for (int num : nums) {\n result.add(helper(num));}\n\n int[] arrayResult = new int[result.size()];\n for (int i = 0; i < result.size(); i++) {\n arrayResult[i] = result.get(i);}\n \n return arrayResult;}\n\n private int helper(int num) {\n if (num % 4 == 1) { // 4 mod 1 case\n return num - 1;\n }\n if (num % 4 == 3) { // 4 mod 3 case\n int tmp = num;\n int i = 0;\n while (tmp > 0) {\n tmp /= 2;\n if (tmp % 2 == 0) break;\n i++;}\n\n return num - (1 << i);}\n return -1; // just for num = 2\n }\n}\n```\n[https://leetcode.com/problems/construct-the-minimum-bitwise-array-i/submissions/1420194451/](https://leetcode.com/problems/construct-the-minimum-bitwise-array-i/submissions/1420194451/)\n\n\nI could be wrong, but I think that time complexity is *O*(*NB*) and space complexity is *O*(*N*), in which *N* ~ `len(nums)` and *B* ~ average bit length the elements in `nums`. | 13 | 0 | ['C++', 'Java', 'Python3'] | 0 |
construct-the-minimum-bitwise-array-i | Explained - Bit wise manipulation || Very simple and easy understand | explained-bit-wise-manipulation-very-sim-2g2q | \n# Intuition \n- By analysing few cases I observed following:\n - as all are prime except 2, all numbers are odd ( so the last bit is set)\n - as all numbers | kreakEmp | NORMAL | 2024-10-12T16:04:50.193936+00:00 | 2024-10-12T16:04:50.193973+00:00 | 1,854 | false | \n# Intuition \n- By analysing few cases I observed following:\n - as all are prime except 2, all numbers are odd ( so the last bit is set)\n - as all numbers are odd => trivial ans is n-1. Where n-1 one has last bit set to zero and (n-1) | n will be always eqaul to n\n - Now we need to optimise further to find a smaller number that satisfy given condition\n - if all bits are not set then the highest bit must be set in the answer as well.( the answer must be number whose largest bit is same as that of given number)\n\n- Finally concluded with the following two cases :\n 1. when all bits are one (that is the number is in the form n^2 -1 ) => then answer will be n/2\n 2. when all bits are not one => \n - then in the answer the highest bit must be set( Need to find the largest number less than current number which is a power of 2 and add this value to answer)\n - then set the highest bit to zero. ( subtract largest number less than current number which is smaller than 2)\n Other way of thinking this is => \n \nLets take an example of n = 13 ( 1101) and initialize ans with 0\nNow n is not a number whose all bits are set, so we remove the highest bit and the same is added to ans temporary variable.\nor you can think up lik find the largest number which is power of 2 and less than n (that is 8 here ) and subtract this from the number ( this will set the higest bit zero) and add this number to the ans as well.\nSo now n = 13 - 8 = 5 and ans = 0 + 8 = 8\n\nIn next iteration n = 5 is again not in the form which has all bits set, so we repeat above steps\nfind the largest power of 2 which is smaller than n = 5 that is 4\nNow subtract 4 from n and add it to the ans => n = 5 - 4 = 1 and ans = 8 + 4 = 12\n\nIn next iteration we find that n = 1 is in the form where all the bits are set. So we add n/2 to ans and set n to zero\nn = 0 and ans = 12 + 1/2 = 12\n \nHence here our answer is 12\n\n# Approach \n- Iterate over each number in the nums\n- if n is equal to 2 which is a even number and we will consider a special case here. So return the answer as -1\n- if not equal to 2 then do the following steps:\n - initialize temp answer sum to zero and copy value of n to a temp var t\n - now if t is greater than 0 then repeat :\n - if it is in the form where all bits are set(or we can check if n+1 is a power of 2 or not) then sum qill be equal to t/2 and set t to zero\n - if all bits are not set then find the largest number which is power of 2 and less than t. Add the number to sum and subtract it from t\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool isPowerOfTwo(int n) {\n return ((n & (n - 1)) == 0);\n }\n \n int largestPowerOfTwoLessThan(int n) {\n if (n <= 1) return 0;\n int exponent = floor(log2(n));\n return 1 << exponent; // Equivalent to pow(2, exponent)\n }\n \n vector<int> minBitwiseArray(vector<int>& nums) {\n vector<int> ans;\n for(auto n: nums){\n if(n == 2) ans.push_back(-1);\n else{\n int t = n, sum = 0;\n while(t > 0){\n if(isPowerOfTwo(t+1)){\n sum += t/2;\n t = 0;\n }else{\n int d = largestPowerOfTwoLessThan(t);\n sum += d;\n t -= d;\n }\n }\n ans.push_back(sum);\n }\n }\n return ans;\n }\n};\n```\n\n---\n\n\n<b>Here is an article of my interview experience - A Journey to FAANG Company, I recomand you to go through this to know which all resources I have used & how I cracked interview at Amazon:\nhttps://leetcode.com/discuss/interview-experience/3171859/Journey-to-a-FAANG-Company-Amazon-or-SDE2-(L5)-or-Bangalore-or-Oct-2022-Accepted\n\n--- | 12 | 0 | ['C++'] | 2 |
construct-the-minimum-bitwise-array-i | Easy Approach for Beginners | easy-approach-for-beginners-by-siddhuuse-wflm | Intuition \n Describe your first thoughts on how to solve this problem. \nGiven a list of numbers, the goal is to find the smallest integer \( j \) such that | siddhuuse | NORMAL | 2024-10-12T17:08:50.191086+00:00 | 2024-10-12T17:08:50.191114+00:00 | 451 | false | # Intuition \n<!-- Describe your first thoughts on how to solve this problem. --> \nGiven a list of numbers, the goal is to find the smallest integer \\( j \\) such that \\( j | (j + 1) = i \\) for each \\( i \\) in the input list. If no such \\( j \\) exists, we return -1 for that element. The bitwise OR operation between \\( j \\) and \\( j + 1 \\) is always greater than or equal to both \\( j \\) and \\( j + 1 \\). \n\n# Approach \n<!-- Describe your approach to solving the problem. --> \nFor each element \\( i \\) in the input list, we are looking for the smallest integer \\( j \\) such that \\( j | ( j + 1 ) = i \\). We do this because \\( j | ( j + 1 ) \\) is always greater than \\( j \\) and \\( j + 1 \\). This means that as we iterate from \\( j = 0 \\) up to \\( i - 1 \\), we will find a \\( j \\) that satisfies the condition or determine that no such \\( j \\) exists. If we find a valid \\( j \\), we append it to the answer list; otherwise, we append -1 if no valid \\( j \\) exists after checking all possibilities. \n\n# Complexity \n- **Time complexity:** \n $$O(n \\cdot m)$$ \n Where \\( n \\) is the length of the input list and \\( m \\) is the value of the largest element in the list. \n\n- **Space complexity:** \n $$O(n)$$ \n\n# Code \n```python3\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n ans = []\n for i in nums:\n for j in range(i):\n if j | (j + 1) == i:\n ans.append(j)\n break\n else:\n ans.append(-1)\n return ans\n | 9 | 0 | ['Array', 'Bit Manipulation', 'Python3'] | 1 |
construct-the-minimum-bitwise-array-i | 💖 [EASY] INTUITION & EXPLANATION | easy-intuition-explanation-by-ramitgangw-np5k | \n\n# \uD83D\uDC93**_PLEASE CONSIDER UPVOTING_**\uD83D\uDC93\n\n \n\n\n# \u2B50 Intuition\nTo construct the minimum bitwise array ans, we need to find the small | ramitgangwar | NORMAL | 2024-10-12T16:06:41.526945+00:00 | 2024-10-12T16:06:41.526979+00:00 | 533 | false | <div align="center">\n\n# \uD83D\uDC93**_PLEASE CONSIDER UPVOTING_**\uD83D\uDC93\n\n</div>\n\n***\n# \u2B50 Intuition\nTo construct the minimum bitwise array `ans`, we need to find the smallest integer `ans[i]` such that the bitwise OR of `ans[i]` and `ans[i] + 1` equals `nums[i]`. Since `nums[i]` is guaranteed to be a prime number, we can leverage the properties of prime numbers and binary representations to derive the solution efficiently.\n\n# \u2B50 Approach\n1. **Iterate through each element in `nums`**:\n - For each prime number `num`, we initialize `ans[i]` to `-1` to indicate that no valid number has been found yet.\n \n\n2. **Check possible values for `ans[i]`**:\n - We will iterate over possible values of `ans[i]` from `0` to `num - 1`.\n - For each possible value, we check if it satisfies the condition:\n \n ```\n possibleAns | (possibleAns + 1) == num\n ```\n - If a valid `possibleAns` is found, we set `ans[i]` to this value and break out of the loop.\n\n3. **Return the result**:\n - If no valid value is found, `ans[i]` remains `-1`, indicating it\'s not possible to construct such an integer for that index.\n\n# \u2B50 Complexity\n- **Time complexity:** \n The time complexity is $$O(n \\times m)$$, where $$n$$ is the number of elements in `arr` and $$m$$ is the maximum value in `arr`. This is because, for each number in `arr`, we might check all values from `0` to `num - 1` to find a valid `ans[i]`.\n\n- **Space complexity:** \n The space complexity is $$O(n)$$, where $$n$$ is the size of the input array, due to the array `ans` being used to store results.\n\n# \u2B50 Code\n```java []\nclass Solution { \n public int[] minBitwiseArray(List<Integer> arr) {\n int[] ans = new int[arr.size()];\n\n for (int i = 0; i < arr.size(); i++) {\n int num = arr.get(i);\n ans[i] = -1;\n for (int possibleAns = 0; possibleAns < num; possibleAns++) {\n if ((possibleAns | (possibleAns + 1)) == num) {\n ans[i] = possibleAns;\n break;\n }\n }\n }\n\n return ans; \n }\n}\n``` | 6 | 0 | ['Java'] | 1 |
construct-the-minimum-bitwise-array-i | Simple Java || C++ Code ☠️ | simple-java-c-code-by-abhinandannaik1717-tzaj | Code\njava []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int n = nums.size();\n int[] ans = new int[n];\n | abhinandannaik1717 | NORMAL | 2024-10-14T13:02:41.540525+00:00 | 2024-10-14T13:02:41.540550+00:00 | 217 | false | # Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int n = nums.size();\n int[] ans = new int[n];\n for(int i=0;i<n;i++){\n int a = nums.get(i);\n for(int j=0;j<a;j++){\n if((j | (j+1)) == a){\n ans[i] = j;\n break;\n }\n if(j == a-1){\n ans[i] = -1;\n } \n }\n }\n return ans;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n int n = nums.size();\n for(int i=0;i<n;i++){\n int a = nums[i];\n for(int j=0;j<a;j++){\n if((j | (j+1)) == a){\n nums[i] = j;\n break;\n }\n if(j == a-1){\n nums[i] = -1;\n } \n }\n }\n return nums;\n }\n};\n```\n\n\n\n### Explanation:\n\n\n\n1. **Initialization:**\n - You initialize the length `n` of the input list `nums` using `nums.size()`.\n - You create an integer array `ans` of size `n` to store the result for each number in the list.\n\n2. **Outer Loop:**\n - The outer loop iterates over each prime number in `nums`. For each prime number `a`, you attempt to find the smallest `j` such that the bitwise OR of `j` and `j + 1` equals `a`.\n\n3. **Inner Loop (Finding `j`):**\n - For each prime number `a`, you loop through all possible values of `j` from `0` to `a - 1`. The goal is to find the smallest `j` such that:\n ```\n j | (j + 1) == a\n ```\n - `j | (j + 1)` performs a bitwise OR between `j` and `j + 1`.\n - If this condition is satisfied, you store the value of `j` in `ans[i]` and immediately break out of the loop since you\'ve found the smallest `j`.\n\n4. **Handling Edge Cases (No Valid `j`):**\n - If you finish the inner loop without finding any valid `j`, meaning no value of `j` satisfies `j | (j + 1) == a`, then you set `ans[i]` to `-1`.\n - This ensures that when it\'s not possible to construct such a value, the result reflects that.\n\n5. **Return the Result:**\n - After processing all the prime numbers in `nums`, you return the `ans` array, which contains the smallest valid `j` for each prime number, or `-1` if no such `j` exists.\n\n#### Example Walkthrough:\n\n\n**Input:**\n```java\nnums = [5, 7, 11]\n```\n\n- **For `nums[0] = 5`:**\n - We iterate over `j = 0, 1, 2, 3, 4`:\n - `0 | (0 + 1) = 0 | 1 = 1`\n - `1 | (1 + 1) = 1 | 2 = 3`\n - `2 | (2 + 1) = 2 | 3 = 3`\n - `3 | (3 + 1) = 3 | 4 = 7`\n - **When `j = 4`:**\n - `4 | (4 + 1) = 4 | 5 = 5` (Condition satisfied)\n - So, `ans[0] = 4`.\n\n- **For `nums[1] = 7`:**\n - We iterate over `j = 0, 1, 2, 3, 4, 5, 6`:\n - `0 | (0 + 1) = 1`\n - `1 | (1 + 1) = 3`\n - `2 | (2 + 1) = 3`\n - `3 | (3 + 1) = 7` (Condition satisfied)\n - So, `ans[1] = 3`.\n\n- **For `nums[2] = 11`:**\n - We iterate over `j = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10`:\n - For each `j`, we do not find any value that satisfies `j | (j + 1) = 11`.\n - Therefore, `ans[2] = -1`.\n\n**Output:**\n```java\nans = [4, 3, -1]\n```\n\n### Time Complexity: **O(n * a)**\n\n### Space Complexity: \n- **O(n)** (for Java code) \n- **O(1)** (for C++ code) | 5 | 0 | ['C++', 'Java'] | 0 |
construct-the-minimum-bitwise-array-i | [Python3] Brute-Force -> Greedy - Detailed Solution | python3-brute-force-greedy-detailed-solu-y1a8 | Intuition\n Describe your first thoughts on how to solve this problem. \n- Using pen and draw some examples and recognized the pattern\n\n\nInput | Answer | Inp | dolong2110 | NORMAL | 2024-10-12T16:01:58.622170+00:00 | 2024-10-12T16:52:48.745616+00:00 | 193 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Using pen and draw some examples and recognized the pattern\n\n```\nInput | Answer | Input | Answer\n-------------------------------\n2 -1 10\n3 1 11 1\n5 4 101 100\n7 3 111 11\n11 9 1011 1001\n13 12 1101 1100\n17 16 10001 10000\n19 17 10011 10001\n31 15 11111 1111\n```\n\n- From the expamples I drawn It is recognized that the `answer` is the original number removing the most-left `1` bit of the continous 1 chain from starting from the right.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**`helper(num)` function:**\n\n**1. Base Case:**\n\n- `if num == 2: return -1`\n - This handles a specific case where the input number is 2. It directly returns -1 for this case. It seems like a special condition for this particular problem.\n\n**2. Binary Conversion:**\n\n- `bin_arr = [0] + list(map(int, bin(num)[2:]))`\n - `bin(num)` converts the integer num to its binary representation as a string (e.g., `bin(5)` returns `"0b101"`).\n- `[2:]` slices the string to remove the "0b" prefix.\n- `map(int, ...)` converts each character (\'1\' or \'0\') in the string to an integer.\n- `list(...)` creates a list of these integers.\n- `[0] + ...` adds a leading 0 to the list. This is likely done to handle potential edge cases during the bit manipulation later.\n\n**3. Bit Manipulation:**\n\n- `for i in range(len(bin_arr) - 1, -1, -1):`\n - This loop iterates through the `bin_arr` in reverse order (from the least significant bit to the most significant bit).\n - `if bin_arr[i] == 0:`\n - If a 0 bit is found:\n - `bin_arr[i + 1] = 0` : The next higher bit (to the left) is set to 0.\n - `break`: The loop terminates after this change.\n - This part seems to be designed to modify the binary representation in a specific way. It essentially finds the rightmost \'1\' bit and sets the bit to its left to \'0\'.\n \n**4. Decimal Conversion:**\n\n- `res = power = 0`\n - Initializes `res` (to store the result) and `power` (to keep track of the power of 2) to 0.\n- `for i in range(len(bin_arr) - 1, -1, -1):`\n - This loop iterates through the modified `bin_arr` in reverse order.\n - `res += bin_arr[i] * (2 ** power)`\n - This calculates the decimal value of each bit and adds it to `res`.\n - `res + bin_arr[i]`\n - `power += 1`\n - Increments the `power` for the next bit.\n- `return res`: Returns the calculated decimal value.\n\n**`minBitwiseArray(nums)` function:**\n\n- `return [helper(num) for num in nums]`\n - This uses list comprehension to apply the `helper` function to each number in the input list `nums` and returns a new list with the transformed values.\n\n**Overall, the code seems to be designed to:**\n\n1. Convert each number in the input list to its binary representation.\n2. Modify the binary representation by finding the rightmost \'1\' and setting the bit to its left to \'0\'.\n3. Convert the modified binary representation back to decimal.\n\n# Code\n##### 1. Brute-Force\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n def helper(num: int) -> int:\n for new_num in range(num):\n if new_num | (new_num + 1) == num: return new_num\n return -1\n \n return [helper(num) for num in nums]\n```\n\n- Time complexity: $$O(N * M)$$ with `N` is the number of number in `nums` and `M` is the number in `nums`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n##### 2. Greedy\n```\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n def helper(num: int) -> int:\n if num == 2: return -1\n bin_arr = [0] + list(map(int, bin(num)[2:]))\n for i in range(len(bin_arr) - 1, -1, -1):\n if bin_arr[i] == 0:\n bin_arr[i + 1] = 0\n break\n res = power = 0\n for i in range(len(bin_arr) - 1, -1, -1):\n res += bin_arr[i] * (2 ** power)\n res + bin_arr[i]\n power += 1\n return res\n \n return [helper(num) for num in nums]\n```\n- Time complexity: $$O(N * 32)$$ with `N` is the number of number in `nums` and `M` is the number in `nums`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 5 | 0 | ['Greedy', 'Bit Manipulation', 'Python3'] | 0 |
construct-the-minimum-bitwise-array-i | 💡Efficient Java Solution | O(n) time complexity | 100% Beat 💡 | efficient-java-solution-on-time-complexi-0yw6 | Intuition
Prime Numbers:
The list nums contains prime numbers. All primes except 2 are odd numbers, and the only even prime number is 2.
This observation is cr | princevanani9 | NORMAL | 2024-12-30T09:42:43.066929+00:00 | 2024-12-30T09:42:43.066929+00:00 | 150 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1. Prime Numbers:
- The list nums contains prime numbers. All primes except 2 are odd numbers, and the only even prime number is 2.
- This observation is critical because prime numbers, when written in binary, follow certain patterns.
2. Prime Numbers with All 1s in Binary:
- There is a special category of prime numbers that, when written in binary, consist entirely of 1s.
- Examples of such numbers include 3 (binary 11), 7 (binary 111), 31 (binary 11111), etc.
- These numbers are always of the form 2^k - 1 (i.e., one less than a power of 2).
3. Prime Numbers with Mixed Bits:
- Not all prime numbers are of the form 2^k - 1. Some prime numbers have a binary representation with at least one 0 bit.
- For example, 13 (binary 1101), 11 (binary 1011), etc., are prime but do not consist entirely of 1s in their binary form.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Handle Special Case for 2:
- If the number is 2, it is treated as a special case and can be skipped or handled separately (since it's the only even prime).
2. For Each Prime Number:
- Check if the number is of the form 2^k - 1:
- If so, reset the MSB (i.e., halve the number).
- For Other Numbers:
- Loop through the bits and find the next smallest valid number by resetting bits from LSB to MSB.
- Ensure that after resetting a bit, the condition temp1 | (temp1 + 1) == temp is satisfied.
3. Store the Result and move to the next number.
# Complexity
- Time complexity: O(n * 32)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int[] minBitwiseArray(List<Integer> nums) {
int [] ans= new int[nums.size()];
Arrays.fill(ans,-1);
for(int i=0;i<ans.length;i++){
int temp=nums.get(i);
int min=Integer.MAX_VALUE;
if( ((temp+1)& temp)!=0){
for(int j=0;j<32;j++){
if((temp & (1<<j))!=0){
int temp1=(temp & ~(1<<j));
if((temp1 | (temp1+1)) == temp){
min=Math.min(min,temp1);
}
}
}
if(min != Integer.MAX_VALUE )
ans[i]=min;
}
else{
int n= temp;
int position=-1;
while(n>0){
position++;
n=n>>1;
}
ans[i]= (temp & ~(1<< (position)));
}
}
return ans;
}
}
``` | 4 | 0 | ['Array', 'Bit Manipulation', 'Java'] | 0 |
construct-the-minimum-bitwise-array-i | Java Clean solution | 100% Beat | java-clean-solution-100-beat-by-shree_go-xmjt | Complexity\n- Time complexity:O(n^2)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co | Shree_Govind_Jee | NORMAL | 2024-10-12T16:03:54.540597+00:00 | 2024-10-12T16:03:54.540619+00:00 | 347 | false | # Complexity\n- Time complexity:$$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int n = nums.size();\n \n int[] ans = new int[n];\n for(int i=0; i<n; i++){\n for(int j=0; j<=nums.get(i); j++){\n if((j|(j+1))==nums.get(i)){\n ans[i]=j;\n break;\n }\n }\n if(ans[i]==0){\n ans[i]=-1;\n }\n }\n return ans;\n }\n}\n``` | 3 | 0 | ['Array', 'Math', 'Bit Manipulation', 'Bitmask', 'Java'] | 0 |
construct-the-minimum-bitwise-array-i | Easy linear O(n*31) solution ----> | easy-linear-on31-solution-by-be_fighter-v23y | Understanding the Problem:\n1. For each number in the array nums, you want to generate a new number that is the "minimum" possible based on certain bitwise oper | be_fighter | NORMAL | 2024-10-12T17:17:50.525481+00:00 | 2024-10-12T17:17:50.525515+00:00 | 105 | false | # Understanding the Problem:\n1. For each number in the array nums, you want to generate a new number that is the "minimum" possible based on certain bitwise operations.\n\n2. The exact property you\'re trying to maintain here is that if you modify a bit, you want the new number (newnum) to still be closely related to the original number num, specifically such that when you OR it with newnum + 1, it should give back the original number (num).\n\n# In other words:\n\n1. Key Insight: We are trying to find a way to unset one bit of the number while keeping a specific relationship with the original number intact.\n# Bitwise Thinking:\nTo develop this approach, let\'s think about how numbers work in binary:\n\n1. Each bit in a number represents a power of 2.\n2. By unsetting (turning off) a bit, you are effectively subtracting that power of 2 from the number.\n3. The goal is to find a way to unset a bit and create a new number that behaves predictably when you apply the bitwise OR with (newnum + 1).\n# Step-by-Step Approach:\n1. Loop Through Each Number:\nFor every number in nums, perform the following:\n\n\n\n\n2. You take each number (num) and initialize a flag to track whether you found a valid new number.\n\n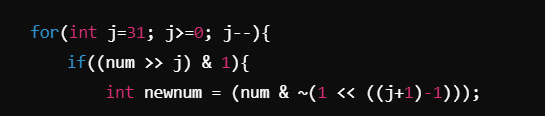\n\n3. You iterate through all the bits of num, starting from the most significant bit (bit 31, for a 32-bit integer).\n4. You check if the bit at position j is set (1), using (num >> j) & if it\'s set, this means you are allowed to try unsetting this bit.\nnewnum is created by unsetting the bit at position j using (num & ~(1 << ((j+1)-1))). This operation clears the bit at position j.\n\n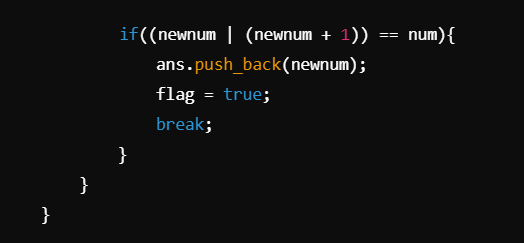\n\n\n5. After unsetting the bit, you check if this newnum satisfies the condition (newnum | (newnum + 1)) == num.\n6. This condition ensures that when you OR newnum with newnum + 1, you should get back the original number num. This helps maintain some structural similarity with the original number.\n7. If the condition is satisfied, newnum is valid, and you store it in ans and set the flag to true, indicating success for this number.\nYou then break out of the loop since you have already found the "minimum" number for this element.\n\n8. If no valid newnum is found (i.e., if flag remains false after trying all possible bit manipulations), you append -1 to the answer. This implies there\u2019s no valid number that satisfies the condition for that particular num.\n\n# Return the Result:\n1. Finally, after processing all numbers, the function returns the ans array, which contains the results of the bit manipulations for each number.\n\n# Why This Approach?\n1. Bitwise Manipulation: This approach leverages bitwise operations to explore different possibilities of "unsetting" bits in an attempt to minimize the number while maintaining a key property.\n2. Efficiency: By iterating through the bits starting from the most significant, it quickly finds a valid solution for each number (if it exists), thus avoiding unnecessary computations.\n\n# Complexity\n- Time complexity:\nO(N*31) as one outer loop and o(31) for traversing on bits\n\n- Space complexity:\nO(N)\n\n# code\n```C++ []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n \n int n=nums.size();\n vector<int>ans;\n \n for(int i=0;i<n;i++){\n\n bool flag=false;\n int num=nums[i];\n for(int j=31;j>=0;j--){\n\n if((num>>j)&1){\n int newnum=(num&~(1<<((j+1)-1)));\n if((newnum|(newnum+1))==num){\n ans.push_back(newnum);\n flag=true;\n break;\n }\n }\n }\n if(flag==false){\n ans.push_back(-1);\n }\n }\n return ans;\n }\n};\n```\n```java []\nimport java.util.*;\n\nclass Solution {\n public List<Integer> minBitwiseArray(int[] nums) {\n List<Integer> ans = new ArrayList<>();\n int n = nums.length;\n\n for (int i = 0; i < n; i++) {\n boolean flag = false;\n int num = nums[i];\n\n for (int j = 31; j >= 0; j--) {\n if ((num >> j & 1) == 1) {\n int newnum = (num & ~(1 << ((j + 1) - 1)));\n if ((newnum | (newnum + 1)) == num) {\n ans.add(newnum);\n flag = true;\n break;\n }\n }\n }\n if (!flag) {\n ans.add(-1);\n }\n }\n return ans;\n }\n\n\n```\n```python []\nclass Solution:\n def minBitwiseArray(self, nums):\n ans = []\n n = len(nums)\n\n for num in nums:\n flag = False\n for j in range(31, -1, -1):\n if (num >> j) & 1:\n newnum = (num & ~(1 << ((j + 1) - 1)))\n if (newnum | (newnum + 1)) == num:\n ans.append(newnum)\n flag = True\n break\n if not flag:\n ans.append(-1)\n \n return ans\n```\n```javascript []\nclass Solution {\n minBitwiseArray(nums) {\n let ans = [];\n let n = nums.length;\n\n for (let i = 0; i < n; i++) {\n let flag = false;\n let num = nums[i];\n\n for (let j = 31; j >= 0; j--) {\n if ((num >> j) & 1) {\n let newnum = (num & ~(1 << ((j + 1) - 1)));\n if ((newnum | (newnum + 1)) === num) {\n ans.push(newnum);\n flag = true;\n break;\n }\n }\n }\n if (!flag) {\n ans.push(-1);\n }\n }\n\n return ans;\n }\n}\n```\n\n | 2 | 0 | ['Array', 'Bit Manipulation', 'Bitmask', 'C++', 'Java', 'Python3', 'JavaScript'] | 1 |
construct-the-minimum-bitwise-array-i | Simple | Beats 100% | simple-beats-100-by-lokeshwar777-4o39 | Code\npython3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n res = []\n\n for num in nums:\n for i | lokeshwar777 | NORMAL | 2024-10-12T16:07:27.894191+00:00 | 2024-10-12T16:07:27.894214+00:00 | 139 | false | # Code\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n res = []\n\n for num in nums:\n for i in range(num):\n if i | (i+1) == num:\n res.append(i)\n break\n else:\n res.append(-1)\n \n\n return res\n``` | 2 | 0 | ['Python3'] | 1 |
construct-the-minimum-bitwise-array-i | brute force | brute-force-by-_dharamvir-cck0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | _dharamvir__ | NORMAL | 2024-10-12T16:02:00.432870+00:00 | 2024-10-12T16:02:00.432907+00:00 | 327 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n*1000)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n\n vector<int>ans(nums.size(),-1);\n\n for(int i=0;i<nums.size();i++){\n \n int num=nums[i];\n\n for(int j=1;j<num;j++){\n\n int check=j|(j+1);\n\n if(check==num){ans[i]=j;break;}\n\n }\n\n }\n \n return ans;\n \n }\n};\n``` | 2 | 0 | ['Array', 'C++'] | 0 |
construct-the-minimum-bitwise-array-i | C++ brute force, beats 100% time | c-brute-force-beats-100-by-amithm7-nq5f | Intuition & ApproachCheck for a number k = 0 to nums[i] - 1 with (k | k+1) == nums[i]. Exit loop on match since we want smallest k.Complexity
Time complexity: | amithm7 | NORMAL | 2025-02-01T06:27:07.915042+00:00 | 2025-02-01T06:28:31.138864+00:00 | 44 | false | # Intuition & Approach
Check for a number `k` = `0` to `nums[i] - 1` with `(k | k+1) == nums[i]`. Exit loop on match since we want smallest `k`.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
vector<int> minBitwiseArray(vector<int>& nums) {
int n = nums.size();
vector<int> ans(n, -1);
for (int i = 0; i < n; i++)
for (int k = 0; k < nums[i]; k++)
if ((k | k + 1) == nums[i]) {
ans[i] = k;
break;
}
return ans;
}
``` | 1 | 1 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | C++ in-place 100% | c-in-place-100-by-michelusa-9fj5 | \ncpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int> nums) const {\n \n for (int i = 0; i != nums.size(); ++i) {\n | michelusa | NORMAL | 2024-11-29T16:26:17.906077+00:00 | 2024-11-29T16:26:17.906112+00:00 | 28 | false | \n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int> nums) const {\n \n for (int i = 0; i != nums.size(); ++i) {\n int target = exchange(nums[i], -1); \n for (int val = 1; val != target; ++val) {\n if ((val | (val+ 1)) == target) {\n nums[i] = val;\n break;\n }\n } \n }\n return nums;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | C++ in-place | c-in-place-by-michelusa-twjc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | michelusa | NORMAL | 2024-11-29T16:15:32.428056+00:00 | 2024-11-29T16:15:32.428091+00:00 | 22 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int> nums) const {\n \n for (int i = 0; i != nums.size(); ++i) {\n int target = exchange(nums[i], -1); \n for (int val = 0; val != target; ++val) {\n if ((val | (val+ 1)) == target) {\n nums[i] = val;\n break;\n }\n } \n }\n return nums;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Finding the Largest Integer 𝑖 i Such That ( 𝑖 ∣ ( 𝑖 + 1 ) ) = 𝑎 (i∣(i+1))=a | finding-the-largest-integer-i-i-such-tha-pum8 | Intuition\nWe are given a list of integers, and for each integer, we need to find a value \( i \) such that when you perform the bitwise OR operation between \( | 204g1a0551 | NORMAL | 2024-11-13T10:19:14.455824+00:00 | 2024-11-13T10:19:14.455854+00:00 | 19 | false | ### Intuition\nWe are given a list of integers, and for each integer, we need to find a value \\( i \\) such that when you perform the bitwise OR operation between \\( i \\) and \\( i+1 \\), the result is equal to the original integer. The goal is to compute this value \\( i \\) for each element of the input list and return an array of these values.\n\n### Approach\n1. **Understanding the Problem**:\n - For each integer \\( a \\), we want to find the largest integer \\( i \\) such that the bitwise OR between \\( i \\) and \\( i+1 \\) results in \\( a \\).\n - To do this, for each integer \\( a \\), we will iterate through all possible values of \\( i \\) from \\( 0 \\) to \\( a-1 \\). For each \\( i \\), we check if \\( (i | (i + 1)) == a \\), and if it holds, we return \\( i \\).\n\n2. **Implementation Details**:\n - The `check()` method iterates from \\( 0 \\) to \\( a-1 \\), performing the bitwise OR between \\( i \\) and \\( i+1 \\) to see if it equals \\( a \\).\n - If such an \\( i \\) is found, return \\( i \\); otherwise, return -1 (although based on the problem setup, this case shouldn\'t occur).\n\n3. **Efficiency**:\n - The function `check(int a)` checks all integers from \\( 0 \\) to \\( a-1 \\), making the time complexity of each call \\( O(a) \\).\n - For each element in the list, we call `check()` once, so the overall time complexity is proportional to the sum of the sizes of the individual integers.\n\n### Complexity\n- **Time complexity**: \n - For each integer \\( a \\), the function `check()` iterates up to \\( a \\). Hence, for all integers in the list, the time complexity is roughly the sum of all values of \\( a \\). If the average value of \\( a \\) is \\( k \\), the total time complexity would be \\( O(k \\cdot n) \\), where \\( n \\) is the number of elements in the list.\n \n - In the worst case, if each integer is large, the time complexity becomes \\( O(a \\cdot n) \\), where \\( a \\) is the largest value in the list.\n\n- **Space complexity**:\n - The space complexity is \\( O(n) \\) because we store the result in an array of the same size as the input list.\n\n### Code\n```java\nimport java.util.List;\n\nclass Solution {\n public static int check(int a) {\n // Try all values of i from 0 to a-1\n for (int i = 0; i < a; i++) {\n // Check if (i | (i + 1)) is equal to a\n if ((i | (i + 1)) == a) {\n return i;\n }\n }\n // If no such i exists, return -1\n return -1;\n }\n\n public int[] minBitwiseArray(List<Integer> nums) {\n int[] arr = new int[nums.size()];\n // For each number in the input list, calculate the corresponding min value\n for (int i = 0; i < nums.size(); i++) {\n arr[i] = check(nums.get(i));\n }\n return arr;\n }\n}\n```\n\n### Explanation of the Code\n1. **`check(int a)`**: \n - This method takes an integer `a` and iterates from \\( i = 0 \\) to \\( i = a - 1 \\). For each \\( i \\), it checks if \\( (i | (i + 1)) == a \\). If such an \\( i \\) exists, it is returned.\n \n2. **`minBitwiseArray(List<Integer> nums)`**: \n - This method takes a list of integers `nums`. It creates an array `arr` of the same size as the list and fills it by calling `check()` on each element of the list. Finally, the array is returned.\n\n### Example\n```java\npublic class Main {\n public static void main(String[] args) {\n Solution sol = new Solution();\n List<Integer> nums = List.of(5, 7, 10);\n int[] result = sol.minBitwiseArray(nums);\n System.out.println(Arrays.toString(result)); // Output: [4, 6, 8]\n }\n}\n```\n\nFor `nums = [5, 7, 10]`:\n- For \\( 5 \\), \\( i = 4 \\) is the largest integer such that \\( (i | (i+1)) = 5 \\).\n- For \\( 7 \\), \\( i = 6 \\) is the largest integer such that \\( (i | (i+1)) = 7 \\).\n- For \\( 10 \\), \\( i = 8 \\) is the largest integer such that \\( (i | (i+1)) = 10 \\).\n\nThus, the output is `[4, 6, 8]`.\n\n### Optimization\n- The current approach checks every integer from 0 to \\( a-1 \\), which could be inefficient for large values of \\( a \\). A potential optimization could involve a more analytical approach, leveraging bitwise properties to directly find the correct \\( i \\) without iterating through all values. | 1 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | Clever Bitlogic with Rust | clever-bitlogic-with-rust-by-chrispls-xt2i | Intuition\nThe core idea here is to use the "+ 1" to cascade carry bits and restore a the highest bit of the original number it can. \n\n# Approach\n\nI\'ve don | chrispls | NORMAL | 2024-10-20T21:16:51.768592+00:00 | 2024-10-20T21:16:51.768621+00:00 | 9 | false | # Intuition\nThe core idea here is to use the "+ 1" to cascade carry bits and restore a the highest bit of the original number it can. \n\n# Approach\n\nI\'ve done my best to detail the workings in the code + debug logging.\nFirst off, if `num` is even, there\'s no way to encode it as `x | (x + 1)`. \n- If `x` is even, then `x + 1` is odd and their `|` is odd.\n- If `x` is odd, then `x + 1` is even and their `|` is odd.\nTherefor, all even numbers are immediately encoded as `-1` aka "cannot be done".\n\nNow we know that all other `num` values are odd, so they have one or more trailing ones in their binary representation:\n```\nnum => binary => tail\n 3 => 0b0011 => 0b11\n 5 => 0b0101 => 0b1\n 7 => 0b0111 => 0b111 \n911 => 0b11_1101_1111 => 0b01_1111\n```\n\nWe want to abuse that chain, to get get `ans[i] + 1` to always be a bit that\'s set in `num`, so that the `|` works. We do this by taking each "tail" and shortening it by one. Now when that tail is incremented, it carries into the highest bit of that initial tail.\n\nUsing `num=7`:\n- `7` in binary is `0b0111`\n- The tail is `0b111`, and there\'s nothing after the tail\n- We\'ll find the high bit of the tail by shifting right by 1 and incrementing to cause a carry:\n - `0b0111 >> 1 == 0b0011`\n - `0b0011 + 1 == 0b0100`\n - Which we see matches the `0b0111` tail we started with.\n- Now subtract off this high bit from our original number.\n- `7 - 0b0100 == 0b0111 - 0b0100 == 0b0011 == 3` \n- This is our answer for `7`: it should be encoded as `3`.\n- We can confirm by redoing our `ans[i]` math:\n - `3 + 1 == 4, 3 | 4 == 0b0011 | 0b0100 == 0b0111 == 7`\n\nThe code does this concisely with:\n```rust []\n// p is from `nums`\nlet half_p: i32 = p >> 1;\nreturn p - (1 << half_p.trailing_ones());\n```\n\nNote: If you don\'t use the full tail here, you get answers that work but they are not minimal! Using the full is necessary to get the smallest answer. On some observation, numbers with short enough tails don\'t make this distinction. (Try the above with `num=5`, for example.)\n\nI recommend doing a few by hand and comparing the debug output in the code below to better understand what\'s happening. It\'s a very clever trick I saw in a different write up here, but without much explanation. I hope this adds more context. :)\n\n# Complexity\n- Time complexity: $$O(n)$$, a fixed number of bit ops (all $$O(1)$$) per num in `nums`.\n - Note: If you do not have access to a hardware "count trailing ones" intrinsic, then this complexity worsens. Most CPUs support this, but how it gets exposed into higher langauges varies.\n Worst case, you need to write a $$O(b)$$ loop where $$b$$ is the number of bits in your integer *value*. Since the problem bounds this to ~1000, $$b$$ is never more than 10.\n- Space complexity: $$O(n)$$, a fixed amount of space per num in `nums`.\n\n# Code\n```rust []\nimpl Solution {\n pub fn min_bitwise_array(nums: Vec<i32>) -> Vec<i32> {\n nums.into_iter().map(min_bitwise).collect()\n }\n}\n\nfn min_bitwise(p: i32) -> i32 {\n if p % 2 == 0 {\n // (p | (p+1)) is always odd, so no even number can be expressed this way.\n -1\n } else {\n // The core idea here, is to find a run of 1s in the binary reprentation of \'p\'.\n // We\'ll then subtract off the top 1 in that string from \'p\'.\n // Any chain will give us a correct encoding, but we want the minimum value stored so that means the longest chain we can find.\n // Because we\'ll add 1 to this chain, we need it to be the longest chain of 1s from the least significant bit.\n // Consider 991:\n // 991 = 0b01111011111\n // ^___^ is our chain.\n // We want to subtract off the top of the chain, but one shorter so the +1 restores that upper bit. We\'ll use:\n // 991 >> 1 = 0b00111101111\n // Now we count the lower ones (4 long), and know the value to subtract out of \'p\':\n // 1 << 4\n // This ultimately lets the (ans[i] + 1) logic turn back into that upper bit, and get OR\'d into \'ans[i]\' and restore \'p\'!\n //\n // Fail a test to see detailed output:\n if cfg!(debug_assertions) {\n let x = " ";\n let xx = " ";\n let half_p = p >> 1;\n let hf_ct1 = half_p.trailing_ones();\n\n println!("min_bitwise({p}):");\n println!("{x}Consider:");\n println!("{x} {p:>3} = 0b{p:011b}");\n println!("{x} {} trailing ones", p.trailing_ones());\n\n println!("{x}Shift right once:");\n println!("{x} {half_p:>3} = 0b{half_p:011b}");\n println!("{x} {} trailing ones", hf_ct1);\n\n println!();\n println!("{xx}(1 << {hf_ct1}) = 0b{:011b}", 1 << hf_ct1);\n println!("{x} {p:>3} = 0b{p:011b}");\n\n println!("{x}Then");\n println!("{xx}{p} - (1 << {hf_ct1}) == 0b{:011b}", p - (1 << hf_ct1));\n\n println!("{x}and to piece it back together:");\n println!("{xx}0b{0:011b} ({p} - (1 << {hf_ct1}))", p - (1 << hf_ct1));\n println!("{x} + 0b{0:011b} ({0})", 1);\n println!("{x} ----------");\n println!(\n "{xx}0b{0:011b} ({p} - (1 << {hf_ct1}) + 1)",\n p - (1 << hf_ct1) + 1\n );\n println!("{x} | 0b{0:011b} ({0})", p);\n println!("{x} ----------");\n let sum = (p - (1 << hf_ct1)) | (p - (1 << hf_ct1) + 1);\n println!("{x} 0b{0:011b} ({0})", sum);\n\n println!();\n println!();\n }\n\n let half_p = p >> 1;\n p - (1 << half_p.trailing_ones())\n }\n}\n``` | 1 | 0 | ['Bit Manipulation', 'Rust'] | 0 |
construct-the-minimum-bitwise-array-i | 💡✅🔥 Bitwise operations with detailed explanation🔥 C++ Simple Solution 🔥 🧠Optimized ✅ | bitwise-operations-with-detailed-explana-jnko | \n\n## Problem Overview\n\nThe goal of this problem is to find a value x for each number in the array nums such that:\n\n1. \( x \) is a non-negative integer le | franesh | NORMAL | 2024-10-15T17:56:50.039621+00:00 | 2024-10-15T17:56:50.039659+00:00 | 36 | false | \n\n## Problem Overview\n\nThe goal of this problem is to find a value `x` for each number in the array `nums` such that:\n\n1. \\( x \\) is a non-negative integer less than the current number \\( \\text{num} \\).\n2. \\( x \\) should satisfy the equation \\( x \\text{ OR } (x + 1) = \\text{num} \\), where "OR" represents the bitwise OR operation.\n\nIf such an `x` exists, we should return that value for the current number. If not, we return `-1` for that number.\n\n---\n\n## Intuition\n\nBefore diving into the code, let\'s first break down the key idea behind the problem. The task is to find a number `x` such that when we perform a bitwise OR operation between `x` and `x+1`, the result is equal to a given number from the array. Bitwise operations can be a little tricky, but with some experimentation, we can find a pattern.\n\n### What is Bitwise OR?\n\nBitwise OR (`|`) compares each corresponding bit of two numbers. If either of the bits is `1`, the result is `1`. Otherwise, the result is `0`. For example:\n\n- \\( 5 = 101_2 \\) (binary representation)\n- \\( 6 = 110_2 \\)\n- \\( 5 \\text{ OR } 6 = 111_2 = 7 \\)\n\nThus, performing a bitwise OR on 5 and 6 gives 7.\n\n### What We Are Looking For\n\nWe want to find a number `x` such that \\( x \\text{ OR } (x + 1) = \\text{num} \\). For example:\n\n- If \\( \\text{num} = 7 \\), we need to find `x` such that \\( x \\text{ OR } (x + 1) = 7 \\).\n- We can try \\( x = 5 \\):\n - \\( 5 = 101_2 \\) (binary)\n - \\( 6 = 110_2 \\)\n - \\( 5 \\text{ OR } 6 = 111_2 = 7 \\), so `x = 5` works.\n\nOur task is to iterate over possible values of `x` for each number in the array `nums`, check the condition, and store the result.\n\n---\n\n## Approach\n\n### Step 1: Initialize a Result Vector\n\nWe need to return a vector of integers, where each entry corresponds to the smallest `x` for which \\( x \\text{ OR } (x + 1) = \\text{num} \\). So, we start by creating an empty vector `ans` that will hold these results.\n\n### Step 2: Iterate Over Each Number in `nums`\n\nWe need to process each number in the input array `nums`. For each number `num`, we try different values of `x` starting from `0` up to `num - 1`. We will check if \\( x \\text{ OR } (x + 1) \\) equals `num`.\n\n### Step 3: Find the Minimum Value of `x`\n\nFor each `num` in the array, we loop over all potential values of `x` from `0` to `num - 1`. We check if \\( x \\text{ OR } (x + 1) \\) equals `num`. If we find such an `x`, we store it in our result vector and stop the search for that `num`.\n\n### Step 4: Handle Cases Where No `x` is Found\n\nIf after trying all possible values of `x`, no suitable value is found, we append `-1` to the result vector. This indicates that no `x` satisfies the condition for that particular `num`.\n\n### Step 5: Return the Result\n\nAfter processing all numbers in `nums`, we return the result vector, which contains either the value of `x` or `-1` for each number.\n\n---\n\n## Code Explanation\n\n```cpp\n#include <vector> // Include the vector library\n\nusing namespace std; // Use the standard namespace\n\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n vector<int> ans; // Create a vector to store the results\n \n // Iterate over each number in the input array \'nums\'\n for (int num : nums) {\n bool found = false; // A flag to check if we find a valid \'x\'\n \n // Try different values of \'x\' starting from 0 up to \'num-1\'\n for (int x = 0; x < num; ++x) { // No need to check values greater than or equal to \'num\'\n \n // Check if the condition holds: x OR (x + 1) == num\n if ((x | (x + 1)) == num) {\n ans.push_back(x); // If condition is met, store \'x\' in the result vector\n found = true; // Set the flag to true as we found a valid \'x\'\n break; // Stop searching as we found the minimum \'x\'\n }\n }\n \n // If no such \'x\' was found, append -1 to the result vector\n if (!found) {\n ans.push_back(-1);\n }\n }\n \n return ans; // Return the result vector\n }\n};\n```\n\n---\n\n## Detailed Explanation\n\n1. **Include Necessary Libraries**:\n - We include the `vector` library since we need to return a vector containing the results.\n\n2. **Class Definition**:\n - The `Solution` class encapsulates our solution.\n\n3. **minBitwiseArray Function**:\n - **Input**: The function takes a vector of integers (`nums`) as input.\n - **Output**: It returns a vector of integers where each element corresponds to the minimum value of `x` (or `-1` if no valid `x` is found).\n\n4. **Vector Initialization**:\n - We create an empty vector `ans` that will store the result for each number in `nums`.\n\n5. **Loop Through Each Number**:\n - We iterate over the numbers in the array `nums`. For each number `num`, we initialize a flag `found` to `false`, indicating that we haven\'t found a valid `x` yet.\n \n6. **Inner Loop to Find `x`**:\n - For each `num`, we try different values of `x` from `0` to `num - 1`. If we find that \\( x \\text{ OR } (x + 1) = \\text{num} \\), we append `x` to `ans` and break out of the loop. If no such `x` is found after checking all possibilities, we append `-1` to `ans`.\n\n7. **Return the Result**:\n - After processing all the numbers, we return the vector `ans`, which contains either the minimum `x` or `-1` for each number in `nums`.\n\n---\n\n## Complexity Analysis\n\n### Time Complexity\n\n- The outer loop runs once for each element in the `nums` array. If there are `n` elements, this takes \\( O(n) \\) time.\n- For each number `num`, the inner loop runs at most `num` times, where `num` is the value of the current number. In the worst case, this could be \\( O(\\text{max}(nums)) \\) for each number.\n\nThus, the overall time complexity is:\n\n\\[ O(n \\cdot \\text{max}(nums)) \\]\n\nWhere `n` is the number of elements in `nums`, and `max(nums)` is the maximum value in the array.\n\n### Space Complexity\n\n- We use an additional vector `ans` to store the results, which has the same size as the input `nums` array. Therefore, the space complexity is \\( O(n) \\), where `n` is the number of elements in `nums`.\n\n---\n\n## Example Walkthrough\n\nLet\'s consider an example to understand the execution of the code.\n\n### Input:\n```cpp\nnums = [7, 5, 10]\n```\n\n### Process:\n\n1. **For `num = 7`:**\n - We try `x = 0`: \\( 0 \\text{ OR } 1 = 1 \\neq 7 \\).\n - We try `x = 1`: \\( 1 \\text{ OR } 2 = 3 \\neq 7 \\).\n - We try `x = 2`: \\( 2 \\text{ OR } 3 = 3 \\neq 7 \\).\n - We try `x = 3`: \\( 3 \\text{ OR } 4 = 7 = 7 \\). Success! So, we append `3` to `ans`.\n\n2. **For `num = 5`:**\n - We try `x = 0`: \\( 0 \\text{ OR } 1 = 1 \\neq 5 \\).\n - We try `x = 1`: \\( 1 \\text{ OR } 2 = 3 \\neq 5 \\).\n - We try `x = 2`: \\( 2 \\text{ OR } 3 = 3 \\neq 5 \\).\n - We try `x = 3`: \\( 3 \\text{ OR }\n\n 4 = 7 \\neq 5 \\). No valid `x`, so we append `-1`.\n\n3. **For `num = 10`:**\n - We try `x = 0` to `x = 8`: None of these work.\n - We try `x = 9`: \\( 9 \\text{ OR } 10 = 10 = 10 \\). Success! So, we append `9` to `ans`.\n\n### Output:\n```cpp\nans = [3, -1, 9]\n```\n\n---\n\n## Conclusion\n\nThis solution uses bitwise operations to solve the problem by finding the smallest `x` for which \\( x \\text{ OR } (x + 1) = \\text{num} \\). By iterating through possible values of `x`, we can efficiently find a result or determine if no solution exists for each number. | 1 | 0 | ['Array', 'Bit Manipulation', 'C++'] | 0 |
construct-the-minimum-bitwise-array-i | Simple C sol, Beats 100% :) | simple-c-sol-beats-100-by-user0490hi-xm65 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | user0490hI | NORMAL | 2024-10-14T13:50:43.631013+00:00 | 2024-10-14T13:50:43.631048+00:00 | 57 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* minBitwiseArray(int* nums, int numsSize, int* returnSize) {\n\nint *jvrc = (int *)malloc(numsSize * sizeof(int ));\n\nfor(int i = 0 ; i < numsSize ; i++)\n{\n int count = 0 ,tom = 0 , c = 0, z = 0 ;\n\n while(c < 1500)\n {\n int a = z|(z+1);\n if(a == nums[i])\n {\n printf("hi");\n jvrc[i] = z ;\n tom++;\n break;\n }\n c++;\n z++;\n }\n if(tom == 0)\n {\n jvrc[i] = -1;\n }\n\n}\n\n*returnSize = numsSize; \nreturn jvrc; \n}\n``` | 1 | 0 | ['C'] | 0 |
construct-the-minimum-bitwise-array-i | easy solution | easy-solution-by-leet1101-85t7 | Intuition\nWe need to find an integer ans[i] such that the bitwise OR of ans[i] and ans[i] + 1 is equal to nums[i] for each prime number in the input array nums | leet1101 | NORMAL | 2024-10-12T17:26:57.671750+00:00 | 2024-10-12T17:26:57.671768+00:00 | 159 | false | # Intuition\nWe need to find an integer `ans[i]` such that the bitwise OR of `ans[i]` and `ans[i] + 1` is equal to `nums[i]` for each prime number in the input array `nums`. The challenge is to minimize the value of `ans[i]` while ensuring this condition holds. If no such value of `ans[i]` exists, we return `-1`.\n\n# Approach\n1. For each element `nums[i]`, we iterate over possible values of `ans[i]`, checking if the condition `(ans[i] OR (ans[i] + 1)) == nums[i]` is satisfied.\n2. Start from 0 and go up to `nums[i]` because we want to minimize `ans[i]`. If we find such a value, we use it; otherwise, we return `-1` for that index.\n3. Store the results in an array `ans` and return it.\n\n# Complexity\n- **Time complexity**: \n $$O(n^2)$$ where $$n$$ is the size of the input array. For each element, we loop through all possible values up to `nums[i]`.\n \n- **Space complexity**: \n $$O(n)$$, which is the space needed to store the result array `ans`.\n\n# Code\n```cpp\nclass Solution {\npublic:\n int findOR(int n) {\n for (int i = 0; i <= n; i++) {\n if ((i | (i + 1)) == n) return i;\n }\n return -1;\n }\n\n vector<int> minBitwiseArray(vector<int>& nums) {\n vector<int> ans(nums.size());\n for (int i = 0; i < nums.size(); i++) {\n ans[i] = findOR(nums[i]);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | 💡✅🔥 Bitwise operations with detailed explanation | bitwise-operations-with-detailed-explana-9edp | Intuition\nObservations:\n- all prime numbers are odd (except 10_2), so numbers will always be like ...0111 or 111\n- simpliest answer is just num - 1, but we w | jekatigr | NORMAL | 2024-10-12T16:51:15.503147+00:00 | 2024-10-12T16:51:15.503184+00:00 | 58 | false | # Intuition\nObservations:\n- all prime numbers are odd (except $$10_2$$), so numbers will always be like `...0111` or `111`\n- simpliest answer is just `num - 1`, but we want to minimize it\n- it\'s easy to notice how to find an answer for a number with ones only (like `1111`). We just need to take a number without leading `1`:\n$$111_2 \\lor (111_2 + 1_2) = 111_2 \\lor 1000_2 = 1111_2$$\n- in the examples there is a case with `num = 11` ($$1011_2$$) and `ans = 9` ($$1001_2$$). Approach from the previous point is actually applicable here, just not with the leading `1` but with the rightest `1` before some `0`. For $$1011_2$$ it\'s the 3 digit or the second `1` from the right:\n$$1001_2 \\lor (1001_2 + 1_2) = 1001_2 \\lor 1010_2 = 1011_2$$\n\n# Approach\n1. count the number of trailing `1`\'s in a `num` before `0`\n2. answer will be the `num` without rigthest `1` so we can substruct `num` with $$2^{k-1}$$, where k = number of `1`\'s, for example:\n`num` = $$11_{10}$$ = $$1011_2$$, k = 2, `ans` = $$11_{10} - 2^{(2 - 1)}$$ = $$11 - 2 ^ 1$$= $$9$$.\n\nWe can use bitwise shift to make traversal on number binary representation easier.\n\n# Complexity\n- Time complexity:\n$$O(n * k)$$, where `n = nums.length` and `k` is a longest binary representation of a number.\n\n- Space complexity:\n$$O(1)$$ in case we don\'t count answer array, $$O(n)$$ otherwise.\n\n# Code\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar minBitwiseArray = function(nums) {\n const ans = [];\n\n for (const n of nums) {\n let num = n;\n let ones = 0;\n\n while(num > 0 && num % 2 === 1) {\n ones += 1;\n num >>= 1;\n }\n\n if (ones === 0) {\n ans.push(-1);\n\n continue;\n }\n\n ans.push(n - 2 ** (ones - 1));\n }\n\n return ans;\n};\n``` | 1 | 0 | ['Array', 'Math', 'Bit Manipulation', 'JavaScript'] | 0 |
construct-the-minimum-bitwise-array-i | Easy Java Solution || Beats 100% || | easy-java-solution-beats-100-by-gaganurs-6rei | \n\n# Code\njava []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int []output=new int[nums.size()];\n for(int i=0;i< | gaganursmg | NORMAL | 2024-10-12T16:03:37.361549+00:00 | 2024-10-12T16:03:37.361573+00:00 | 67 | false | \n\n# Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int []output=new int[nums.size()];\n for(int i=0;i<nums.size();i++){\n int num=nums.get(i);\n int sum=-1;\n int a=0;\n while(a<num){\n if((a | a+1)==nums.get(i)){\n sum=a;\n break;\n }\n a++;\n }\n output[i]=sum;\n } \n return output;\n }\n}\n```\n | 1 | 0 | ['Bit Manipulation', 'Java'] | 0 |
construct-the-minimum-bitwise-array-i | simple | simple-by-ryuji-2a1b | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | ryuji | NORMAL | 2025-03-30T21:19:17.695089+00:00 | 2025-03-30T21:19:17.695089+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```rust []
impl Solution {
pub fn min_bitwise_array(nums: Vec<i32>) -> Vec<i32> {
nums.iter()
.map(|&x| {
if x % 2 == 0 {
return -1;
}
for i in 1..x {
if (i | (i + 1)) == x {
return i;
}
}
-1
})
.collect()
}
}
``` | 0 | 0 | ['Rust'] | 0 |
construct-the-minimum-bitwise-array-i | Simple Swift Solution | simple-swift-solution-by-felisviridis-hwdo | Code | Felisviridis | NORMAL | 2025-03-27T09:34:22.899176+00:00 | 2025-03-27T09:34:22.899176+00:00 | 1 | false | 
# Code
```swift []
class Solution {
func minBitwiseArray(_ nums: [Int]) -> [Int] {
var result = [Int]()
for num in nums {
var found = false
for i in 0...num {
if i | (i + 1) == num {
result.append(i)
found = true
break
}
}
if !found {
result.append(-1)
}
}
return result
}
}
``` | 0 | 0 | ['Swift'] | 0 |
construct-the-minimum-bitwise-array-i | Java&JS&TS Solution (JW) | javajsts-solution-jw-by-specter01wj-c4yw | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | specter01wj | NORMAL | 2025-03-26T19:21:46.551987+00:00 | 2025-03-26T19:21:46.551987+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
public int[] minBitwiseArray(List<Integer> nums) {
int n = nums.size();
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
int num = nums.get(i);
boolean found = false;
for (int x = 0; x <= num; x++) {
if ((x | (x + 1)) == num) {
ans[i] = x;
found = true;
break;
}
}
if (!found) {
ans[i] = -1;
}
}
return ans;
}
```
```javascript []
var minBitwiseArray = function(nums) {
const ans = [];
for (let i = 0; i < nums.length; i++) {
let num = nums[i];
let found = false;
for (let x = 0; x <= num; x++) {
if ((x | (x + 1)) === num) {
ans.push(x);
found = true;
break;
}
}
if (!found) {
ans.push(-1);
}
}
return ans;
};
```
```typescript []
function minBitwiseArray(nums: number[]): number[] {
const ans: number[] = [];
for (let i = 0; i < nums.length; i++) {
const num = nums[i];
let found = false;
for (let x = 0; x <= num; x++) {
if ((x | (x + 1)) === num) {
ans.push(x);
found = true;
break;
}
}
if (!found) {
ans.push(-1);
}
}
return ans;
};
``` | 0 | 0 | ['Array', 'Bit Manipulation', 'Java', 'TypeScript', 'JavaScript'] | 0 |
construct-the-minimum-bitwise-array-i | C++ simple concept ,complexity - O(n^2), bit , beats 100% | c-simple-concept-complexity-on2-bit-beat-9crq | IntuitionApproach
starting inner loop from the nums[i]/2 because analysing showing that not any j is less than nums[i]/2 value except nums[i]==2
Complexity
Time | mihirbaraiya | NORMAL | 2025-03-14T06:06:40.232868+00:00 | 2025-03-14T06:06:40.232868+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
* starting inner loop from the nums[i]/2 because analysing showing that not any j is less than nums[i]/2 value except nums[i]==2
# Complexity
- Time complexity:O(n^2)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> minBitwiseArray(vector<int>& nums) {
int n= nums.size();
vector<int >ans;
for(int i=0;i<n;i++){
for(int j=nums[i]/2;j<nums[i];j++){
if((j|(j+1))==nums[i]){
ans.emplace_back(j);
break;
}
}
if(ans.size()!=i+1){
ans.emplace_back(-1);
}
}
return ans;
}
};
``` | 0 | 0 | ['Array', 'C++'] | 0 |
construct-the-minimum-bitwise-array-i | Easy to understand solution in Java. | easy-to-understand-solution-in-java-by-k-a5c5 | Complexity
Time complexity:
O(n * max_num)
(where max_num is the maximum value in the list nums).
Space complexity:
O(n)
Code | Khamdam | NORMAL | 2025-03-10T06:34:35.353090+00:00 | 2025-03-10T06:34:35.353090+00:00 | 3 | false | # Complexity
- Time complexity:
O(n * max_num)
*(where max_num is the maximum value in the list nums)*.
- Space complexity:
O(n)
# Code
```java []
class Solution {
public int[] minBitwiseArray(List<Integer> nums) {
int n = nums.size();
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[i] = -1;
int num = nums.get(i);
for (int j = 0; j < num; j++) {
if ((j | (j + 1)) == num) {
ans[i] = j;
break;
}
}
}
return ans;
}
}
``` | 0 | 0 | ['Array', 'Bit Manipulation', 'Java'] | 0 |
construct-the-minimum-bitwise-array-i | Iterative Bitwise Search | Dart Solution | Time O(n · m) | Space O(n) | iterative-bitwise-search-dart-solution-t-4rfz | ApproachThe solution processes each element in the input array and, for each element, finds the smallest candidate integer that satisfies a specific bitwise pro | user4343mG | NORMAL | 2025-03-03T05:54:18.933630+00:00 | 2025-03-03T05:54:18.933630+00:00 | 2 | false | ## Approach
The solution processes each element in the input array and, for each element, finds the smallest candidate integer that satisfies a specific bitwise property:
1. **Iterate Over the Input Array**:
For every number in the list, the algorithm attempts to find the smallest integer `j` such that the bitwise OR of `j` and `j + 1` equals that number.
2. **Bitwise Condition Check**:
For each candidate `j` from 1 up to the current number, the solution checks if
$$j \;OR\; (j+1) == \text{current number}$$
If the condition is met, `j` is added to the result, and the search continues with the next element.
3. **Handling No Valid Candidate**:
If no candidate satisfies the condition for an element, the solution appends `-1` to the result list.
4. **Final Result**:
Once all elements have been processed, the constructed list is returned.
## Complexity
- **Time complexity**: $$O(n \times m)$$
where $$ n $$ is the number of elements in the input array and $$ m $$ is the value of the current element in the worst case, since for each element the inner loop may iterate up to that number.
- **Space complexity**: $$O(n)$$
The algorithm uses additional space for the result list, which stores one integer per element in the input array.
# Code
```dart []
class Solution {
List<int> minBitwiseArray(List<int> nums) {
List<int> ans = [];
main:
for (var i = 0; i < nums.length; i++) {
for (var j = 1; j <= nums[i]; j++) {
if (j | (j + 1) == nums[i]) {
ans.add(j);
continue main;
}
}
ans.add(-1);
}
return ans;
}
}
``` | 0 | 0 | ['Dart'] | 0 |
construct-the-minimum-bitwise-array-i | Simple pattern based O(N) solution. Brute force is not needed. | simple-pattern-based-on-solution-brute-f-wwbu | IntuitionThe pattern is as follows:
'2' is the only prime number and hence, the result is -1
All other prime numbers apart from 2 are odd numbers i.e the lowest | night1coder | NORMAL | 2025-02-22T09:49:00.748558+00:00 | 2025-02-22T09:51:03.252736+00:00 | 3 | false | # Intuition
The pattern is as follows:
1. '2' is the only prime number and hence, the result is -1
2. All other prime numbers apart from 2 are odd numbers i.e the lowest bit is set.
3. The trivial ans is (num-1), but the question says to find the lowest possible answer.
4. Hence, we need to find the lowest one bit after the lowest zero bit and turn it off.
5. We need to turn it off because when we add 1, the carry of 1 will basically sit in the turned-off position.
# Approach
<!-- Describe your approach to solving the problem. -->
1. For every number, do the following
1. right shift the number until a zero is found in the lowest bit
2. increment a counter by 1
2. Now the counter says the number of bits until we find the lowest zeroth bit.
3. Now turn off the first one bit after the zeroth bit i.e num ^ (1 << (onebits -1));
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
TC - O(n)
Max we can go is 32 bit and the constraints are small.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
SC - O(n)
# Code
```java []
class Solution {
public int[] minBitwiseArray(List<Integer> nums) {
int n = nums.size();
int[] ans = new int[n];
int i=0;
for(int num: nums){
if(num == 2){
ans[i++] = -1;
continue;
}
int n1=num, onebits = 0;
while((n1 & 1) != 0){
onebits++;
n1>>=1;
}
ans[i++] = num ^ (1<< (onebits-1));
}
return ans;
}
}
``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | kFor=cache(lambda v:k) | kforcachelambda-vk-by-qulinxao-x4gz | null | qulinxao | NORMAL | 2025-02-20T06:07:50.088605+00:00 | 2025-02-20T06:07:50.088605+00:00 | 1 | false | ```python3 []
class Solution:
def minBitwiseArray(self, nums: List[int]) -> List[int]:
kFor=cache(lambda v:k)
k=-1;kFor(2)
for k in range(max(nums)):kFor(k|(k+1))
return [kFor(v)for v in nums]
``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | Pre-compute in the constructor | pre-compute-in-the-constructor-by-evgeny-6a1m | Code | evgenysh | NORMAL | 2025-02-09T16:16:01.729595+00:00 | 2025-02-09T16:16:01.729595+00:00 | 4 | false | # Code
```python3 []
class Solution:
def __init__(self, limit=1000):
self.min_or_input = dict()
# precompute the min bitwise inputs
for n in range(limit + 1):
val = n | (n + 1)
if val not in self.min_or_input:
self.min_or_input[val] = n
def minBitwiseArray(self, nums: List[int]) -> List[int]:
return [self.min_or_input.get(n, -1) for n in nums]
``` | 0 | 0 | ['Python3'] | 1 |
construct-the-minimum-bitwise-array-i | Easy Approach for Beginners 2.0 | easy-approach-for-beginners-20-by-vbarys-35e3 | IntuitionLets develop ideas from https://leetcode.com/problems/construct-the-minimum-bitwise-array-i/solutions/5904063/easy-approach-for-beginners/Thanks to @si | vbaryshev | NORMAL | 2025-02-06T09:19:03.665998+00:00 | 2025-02-06T09:20:11.077683+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Lets develop ideas from https://leetcode.com/problems/construct-the-minimum-bitwise-array-i/solutions/5904063/easy-approach-for-beginners/
Thanks to @siddhuuse (https://leetcode.com/u/siddhuuse/)
In a little clearer way, because flat is better than nested.
# Approach
<!-- Describe your approach to solving the problem. -->
Please don't forget that boolean operators and binary operators in python are different things. And they work differently. "OR" as boolean operator is not the same as binary or "|"
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n*m)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```python3 []
from typing import List
class Solution:
def compare(self, i: int) -> int:
for j in range(i):
if (j | j+1) == i:
return j
return -1
def minBitwiseArray(self, nums: List[int]) -> List[int]:
ans = []
for i in nums:
ans.append(self.compare(i))
return ans
``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | BEATS 100% || C++ || EASY | beats-100-c-easy-by-sakshishah11-p7u1 | Complexity
Time complexity: O(N^2)
Space complexity: O(1)
Code | SakshiShah11 | NORMAL | 2025-02-03T10:44:47.857365+00:00 | 2025-02-03T10:44:47.857365+00:00 | 6 | false |
# Complexity
- Time complexity: O(N^2)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> minBitwiseArray(vector<int>& nums) {
int n=nums.size();
vector<int> ans(n,-1);
for(int i=0;i<n;i++){
for(int j=0;j<nums[i];j++){
if((j| (j+1))==nums[i]){
ans[i]=j;
break;
}
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | [C++] Simple Solution | c-simple-solution-by-samuel3shin-2ufl | Code | Samuel3Shin | NORMAL | 2025-01-30T16:13:54.060449+00:00 | 2025-01-30T16:13:54.060449+00:00 | 4 | false | # Code
```cpp []
class Solution {
public:
vector<int> minBitwiseArray(vector<int>& A) {
int N = A.size();
vector<int> ans(N, -1);
for(int i=0; i<N; i++) {
for(int j=0; j<=A[i]; j++) {
if((j|(j+1)) == A[i]) {
ans[i] = j;
break;
}
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | The best solution!!! without native methods... | the-best-solution-without-native-methods-oae3 | IntuitionThe problem requires finding the smallest possible (ans[i]) such that ((ans[i] | (ans[i] + 1)) = nums[i]). If no such (ans[i]) exists, it should return | javid99999 | NORMAL | 2025-01-27T19:25:17.669262+00:00 | 2025-01-27T19:25:17.669262+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires finding the smallest possible \(ans[i]\) such that \((ans[i] | (ans[i] + 1)) = nums[i]\). If no such \(ans[i]\) exists, it should return \(-1\). The key insight is that for each \(nums[i]\), we can iterate through potential values for \(ans[i]\) starting from \(0\), and check the condition using bitwise operations.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Use a loop to iterate through the \(nums\) array.
2. Use a variable \(i\) to represent potential values of \(ans[i]\). Start \(i\) from \(0\) and increment until the condition \((i | (i + 1)) == nums[j]\) is satisfied.
3. If the condition is met, append \(i\) to the answer and move to the next \(nums[j]\).
4. If \(i\) reaches \(nums[j]\) without finding a valid \(ans[i]\), append \(-1\) to the answer and move to the next element.
5. Reset \(i\) by assigning \(-1\) to start fresh for the next \(nums[j]\).
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
The time complexity is \(O(n \cdot m)\), where \(n\) is the length of the \(nums\) array, and \(m\) is the maximum number of iterations needed to find a valid \(ans[i]\). Each element of \(nums\) requires checking potential \(ans[i]\) values up to a maximum.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
The space complexity is \(O(n)\), as the output array \(ans\) stores one value for each element in \(nums\).
# Code
```php []
class Solution {
/**
* @param Integer[] $nums
* @return Integer[]
*/
function minBitwiseArray($nums) {
$ans = [];
$j = 0;
$c = count($nums);
for($i = 0; $j < $c; $i++)
{
if(($i | ($i + 1)) == $nums[$j])
{
$ans[] = $i;
$j++;
$i = -1;
}
if($i == $nums[$j])
{
$ans[] = -1;
$j++;
$i = -1;
}
}
return $ans;
}
}
``` | 0 | 0 | ['PHP'] | 0 |
construct-the-minimum-bitwise-array-i | one pass bitwise. | one-pass-bitwise-by-rishiinsane-e7aw | IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(n)
Code | RishiINSANE | NORMAL | 2025-01-26T09:41:47.244906+00:00 | 2025-01-26T09:41:47.244906+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
vector<int> minBitwiseArray(vector<int>& nums) {
int n = nums.size();
vector<int> ans;
for (auto it : nums) {
if (it == 2)
ans.push_back(-1);
else {
int temp = it, val = 0;
while (temp > 0) {
if (allSetBits(temp)) {
val += temp / 2;
temp = 0;
} else {
int x = largestPowerOfTwoLessThan(temp);
temp -= x;
val += x;
}
}
ans.push_back(val);
}
}
return ans;
}
bool allSetBits(int n) { return ((n & (n + 1)) == 0); }
int largestPowerOfTwoLessThan(int n) {
if (n <= 1)
return 0;
int power = floor(log2(n));
return 1 << power;
}
};
``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Elixir - Bit manipulation | elixir-bit-manipulation-by-lykos_unleash-aezz | Complexity
Time complexity:
O(n)
Space complexity:
O(n)
Code | Lykos_unleashed | NORMAL | 2025-01-21T03:24:00.857130+00:00 | 2025-01-21T03:24:00.857130+00:00 | 4 | false | # Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```elixir []
defmodule Solution do
@spec min_bitwise_array(nums :: [integer]) :: [integer]
def min_bitwise_array(nums) do
for n <- nums do
cond do
n == 2 -> -1
Bitwise.band(n, n + 1) == 0 -> remove_msb(n)
true ->
least_zero_bit_pos = find_least_zero_bit_pos(n, 1)
mask = Bitwise.bsl(1, least_zero_bit_pos - 2)
Bitwise.bxor(n, mask)
end
end
end
defp no_of_bits(n) do
bits = :math.log2(n)
ceiled_bits = ceil(bits)
if bits == ceiled_bits, do: ceiled_bits + 1, else: ceiled_bits
end
defp remove_msb(n) do
no_of_bits = no_of_bits(n)
mask = Bitwise.bsl(1, no_of_bits - 1) - 1
Bitwise.band(n, mask)
end
defp find_least_zero_bit_pos(n, pos) do
if Bitwise.band(n, 1) == 0, do: pos, else: find_least_zero_bit_pos(Bitwise.bsr(n, 1), pos + 1)
end
end
``` | 0 | 0 | ['Elixir'] | 0 |
construct-the-minimum-bitwise-array-i | Easiest soln u will ever find | easiest-soln-u-will-ever-find-by-mamthan-tmv3 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | mamthanagaraju1 | NORMAL | 2025-01-15T07:39:05.582413+00:00 | 2025-01-15T07:39:05.582413+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> minBitwiseArray(vector<int>& nums) {
int n=nums.size();
vector<int>ans(n,-1);
for(int i=0;i<nums.size();i++){
for(int j=0;j<=nums[i];j++){//run till nums[i] value to find the j ==nums[i]
if((j|(j+1)) == nums[i]){//if found replace -1 with j
ans[i] = j;
break;
}
}
}
return ans;
}
};
```

| 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Simple C implement | simple-c-implement-by-ggandrew1218-iqi5 | Code | ggandrew1218 | NORMAL | 2025-01-13T13:02:03.008249+00:00 | 2025-01-13T13:02:03.008249+00:00 | 21 | false |
# Code
```c []
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* minBitwiseArray(int* nums, int numsSize, int* returnSize) {
int* ans = malloc(sizeof(int) * numsSize);
for(int i = 0; i < numsSize;i++)
{
//printf("Num : %d\n", nums[i]);
if( ((nums[i]+1) & nums[i]) == 0)
{
ans[i] = nums[i]>>1;
}
else
{
int tmp = nums[i];
int count = (tmp + 1) ^ tmp;
ans[i] = -1;
for(int j = 0; j < count;j++)
{
if( ( tmp | (tmp - 1)) == nums[i] )
{
ans[i] = tmp-1;
}
tmp--;
}
}
}
*returnSize = numsSize;
return ans;
}
``` | 0 | 0 | ['C'] | 0 |
construct-the-minimum-bitwise-array-i | Easy to understand | easy-to-understand-by-vedantkhapre-kd7a | IntuitionWe need to find the smallest integer x such that x | (x + 1) equals the prime number at each index of the array. If no such x exists, we return -1Appro | vedantkhapre | NORMAL | 2025-01-13T07:01:52.089118+00:00 | 2025-01-13T07:01:52.089118+00:00 | 4 | false | # Intuition
We need to find the smallest integer `x` such that `x | (x + 1)` equals the prime number at each index of the array. If no such `x` exists, we return `-1`
---
# **Approach**
1. Initialize an answer array `ans` with `-1` (because the default answer is `-1` if no valid `x` is found).
2. Loop through each prime number in `nums` and check values of `x` from `0` to that prime.
3. If `x | (x + 1)` equals the prime, store `x` in `ans[i]` and stop checking further.
4. Return the final array `ans`
# Code
```cpp []
class Solution {
public:
vector<int> minBitwiseArray(vector<int>& nums) {
vector<int> ans(nums.size(), -1); //set all values to -1 by default
for (int i = 0; i < nums.size(); i++) {
for (int x = 0; x <= nums[i]; x++) { // test values from 0 to nums[i]
if ((x | (x + 1)) == nums[i]) { //if condition is not satisfied ans[i] remains -1
ans[i] = x;
break;
}
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | C++ 0 ms | c-0-ms-by-eridanoy-fvsa | IntuitionApproach2 -> -1
other -> replace the one before the first zero with zeroComplexity
Time complexity:
Space complexity:
Code | eridanoy | NORMAL | 2025-01-11T14:28:59.769223+00:00 | 2025-01-11T14:28:59.769223+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
2 -> -1
other -> replace the one before the first zero with zero
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> minBitwiseArray(vector<int>& nums) {
constexpr int len = sizeof(int) * 8;
for_each(begin(nums), end(nums), [](auto& num) {
for(int i = 0; i < len; ++i) {
if(num & (1 << i)) continue;
i? num ^= 1 << (i - 1): num = -1;
break;
}
});
return nums;
}
};
``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | ☑️ Golang solution beats 100% | golang-solution-beats-100-by-codemonkey8-v2q6 | Code | CodeMonkey80s | NORMAL | 2025-01-11T03:44:02.552304+00:00 | 2025-01-11T03:44:02.552304+00:00 | 8 | false | # Code
```golang []
func minBitwiseArray(nums []int) []int {
find := func(n int) int {
for i := 0; i < n; i++ {
v := i | (i + 1)
if n == v {
return i
}
}
return -1
}
res := make([]int, len(nums))
for i, num := range nums {
res[i] = find(num)
}
return res
}
``` | 0 | 0 | ['Go'] | 0 |
construct-the-minimum-bitwise-array-i | 3314. Construct the Minimum Bitwise Array I | 3314-construct-the-minimum-bitwise-array-aida | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-08T08:15:40.198973+00:00 | 2025-01-08T08:15:40.198973+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minBitwiseArray(self, nums: List[int]) -> List[int]:
ans = []
for num in nums:
found = False
for candidate in range(num):
if (candidate | (candidate + 1)) == num:
ans.append(candidate)
found = True
break
if not found:
ans.append(-1)
return ans
``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | One Liner | one-liner-by-khaled-alomari-dlnb | Complexity
Time complexity:
O(n)
Space complexity:
O(1)
Code | khaled-alomari | NORMAL | 2024-12-30T20:50:52.212573+00:00 | 2024-12-30T20:50:52.212573+00:00 | 18 | false | # Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(1)$$
# Code
```javascript []
const minBitwiseArray = nums => nums.map(v => v === 2 ? -1 : (((-v - 2) ^ v) / 4) + v);
```
```typescript []
const minBitwiseArray = (nums: number[]) => nums.map((v) => v === 2 ? -1 : (((-v - 2) ^ v) / 4) + v);
``` | 0 | 0 | ['Math', 'Bit Manipulation', 'Bitmask', 'TypeScript', 'JavaScript'] | 0 |
construct-the-minimum-bitwise-array-i | BITWISE BEHAVIOUR (100%) java | bitwise-behaviour-100-java-by-prachikuma-77x0 | IntuitionConsider the binary number behaviour for a num to satisfy { ans[i] OR ans[i] + 1 = nums[i] }
CASE 1
nums[i] % 4 == 1 ie ending 01 eg 5,9,13,.. they al | PrachiKumari | NORMAL | 2024-12-30T06:40:39.587505+00:00 | 2024-12-30T06:40:39.587505+00:00 | 8 | false | # Intuition
Consider the binary number behaviour for a num to satisfy { ans[i] OR ans[i] + 1 = nums[i] }
***CASE 1***
- nums[i] % 4 == 1 ie ending 01 eg 5,9,13,.. they all ends
& for all of them ans = nums[i]-1 , eg nums[i] = 9, then smallest possible ans = 8 (8 OR (8+1) == 9)
***CASE 2***
- nums[i] % 4 ==3 ie ending 11 ed 7,11,15,19..
We need to adjust by subtracting the appropriate power of 2 based on the position of trailing 1s.
Eg : nums[i] = 7 then ans[i]= 3 (7-4)
nums[i] = 11 then ans[i] = 11-2
nums[i] = 15 then ans[i] = 11-8 = 7
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
// prims so positives
public int getValue(int num){
// 2 cases possible (num%4 == 1 , num%4== 3)
if (num%4 == 1){
return num-1;
}
if (num%4 == 3){
int temp = num;
int i=0;
while (temp >0){
temp /= 2;
if(temp%2 == 0) break;
i++;
}
return num - (1<<i);
}
return -1;
}
public int[] minBitwiseArray(List<Integer> nums) {
int n = nums.size();
int[] ans = new int[n];
for (int i = 0 ; i<n ;i++){
ans[i] = getValue(nums.get(i));
}
return ans;
}
}
``` | 0 | 0 | ['Bit Manipulation', 'Java'] | 0 |
construct-the-minimum-bitwise-array-i | Easy Java Solution | easy-java-solution-by-abhishekji66-zao2 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | abhishekji66 | NORMAL | 2024-12-27T10:07:24.990200+00:00 | 2024-12-27T10:07:24.990200+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int[] minBitwiseArray(List<Integer> nums) {
int[] a = new int[nums.size()];
for(int i=0;i<nums.size();i++){
int b = 1;
while(b<nums.get(i)){
if((b | (b+1)) == nums.get(i)){
a[i]=b;
break;
}
b++;
}
if(a[i]<=0) a[i]=-1;
}
return a;
}
}
``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | Worst solution ever (Must see) | worst-solution-ever-must-see-by-devansh_-wr79 | IntuitionApproachComplexity
Time complexity:O(n2)
Space complexity:O(1)
Code | devansh_1703 | NORMAL | 2024-12-24T16:38:57.338467+00:00 | 2024-12-24T16:38:57.338467+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:$$O(n^2)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int[] minBitwiseArray(List<Integer> lst) {
int[] ans=new int[lst.size()];
int add=-1,in=0;;
for(int n : lst){
add=-1;
for(int i=1;i<n;i++){
if(((i)|(i+1))==n){
add=i;
break;
}
}
ans[in++]=add;
}
return ans;
}
}
``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | Optimal C++ Solution Beats 100% | optimal-c-solution-beats-100-by-dakshg-2ny7 | Code\ncpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int> &nums) {\n int n = nums.size();\n vector<int> ans(n);\n\n | dakshg | NORMAL | 2024-12-05T03:30:15.643843+00:00 | 2024-12-05T03:30:15.643879+00:00 | 12 | false | # Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int> &nums) {\n int n = nums.size();\n vector<int> ans(n);\n\n for(int i = 0; i < n; ++i) {\n if(nums[i] == 2) {\n ans[i] = -1;\n continue;\n }\n\n int mask = 1;\n while(nums[i] & mask)\n mask <<= 1;\n \n mask >>= 1;\n ans[i] = nums[i] & ~mask;\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Beats 100% using bit manipulation | beats-100-using-bit-manipulation-by-gopi-a8m1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | gopigaurav | NORMAL | 2024-12-01T09:57:33.463434+00:00 | 2024-12-01T09:57:33.463469+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n\n # intuition is take the num and unset the leftmost bit untill u reach the 0\n\n # in the sense 1 0 0 1 1 here unset the 1 at position 2 from right\n # ie 1 0 0 0 1 and add +1 to this value and do OR between the two\n\n def fn(num):\n # traverse through the 32 bit number store the last_set_bit\n last_set_bit = 0\n for i in range(32):\n if num & (1 << i):\n last_set_bit = i\n else:\n break\n\n mask = (1 << last_set_bit)\n mask = ~mask & num\n return mask \n\n ans = []\n for num in nums:\n\n if num == 2:\n ans.append(-1)\n continue\n temp = fn(num)\n ans.append(temp)\n return ans\n \n``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | Rust/Python. Real linear solution with full explanation | rustpython-real-linear-solution-with-ful-5mqg | Intuition\n\nFirst we need to understand that the question asks to solve equation:\n\nx OR (x + 1) = y\n\nfor x. Here they have a strange requirement of y being | salvadordali | NORMAL | 2024-11-26T08:06:31.363891+00:00 | 2024-11-26T08:06:39.739515+00:00 | 6 | false | # Intuition\n\nFirst we need to understand that the question asks to solve equation:\n\n`x OR (x + 1) = y`\n\nfor `x`. Here they have a strange requirement of `y` being prime, but we later we will see that it is irrelevant. On top of this the `x` should be as small as possible.\n\n\nLets look at some number `10111001111` and after trying multiple numbers you can see that all you need is to find how many consequitive ones from the right do you have (in our case it is 4: `1111`) and remove the top one -> `0111`. So your number will be:\n\n```\n10111001111\n= \n10111000111 \nOR\n10111001000\n```\nIt is easily to see that this will work (when you have some ones at the end) as `1...1` or `1..1 + 1` will give you `11...1`.\n\nAs you see here it will work for any number and for even you never can find the solution.\n\n------\nSo we have the solution. Now we can easily implement this with a loop:\n\n```\n def find_x(self, y):\n if y % 2 == 0:\n return -1\n\n count, temp = 0, y\n while temp & 1:\n count += 1\n temp >>= 1\n\n mask = 1 << (count - 1)\n return y & ~mask\n```\n\nBut we do not want a loop. We need efficient binary operation. And you can achieve it with `x & ((x | ~(x + 1)) >> 1)`. This will work because:\n\n - `x + 1` changes your `1..1` to `10..0`\n - `!(x + 1)` inverts bits of that value\n - `(x | !(x + 1))` all trailing ones are still ones then zero and then once again\n - prev expression >> 2 just shifts one value to the right\n - x & prev expression gets you the number you want\n \n# Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(n)$\n\n# Code\n```python []\nclass Solution:\n\n def find_x(self, x):\n if x % 2 == 0:\n return -1\n return x & ((x | ~(x+1)) >> 1)\n\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n return [self.find_x(v) for v in nums] \n```\n```rust []\nimpl Solution {\n fn find_x(x: i32) -> i32 {\n if x % 2 == 0 {\n return -1;\n }\n x & ((x | !(x + 1)) >> 1)\n }\n\n fn min_bitwise_array(nums: Vec<i32>) -> Vec<i32> {\n nums.into_iter().map(|v| Self::find_x(v)).collect()\n }\n}\n```\n\n**BTW, rust has** `trailing_ones()` function so you can just do:\n\n`x & !(1 << (x.trailing_ones() - 1))`. But I am not sure what ASM code will it generate. So if Rust experts are here, can you tell if it gives an efficient implementation. | 0 | 0 | ['Python3', 'Rust'] | 0 |
construct-the-minimum-bitwise-array-i | Easy Java Solution | easy-java-solution-by-mayankbisht8630-max3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | MayankBisht8630 | NORMAL | 2024-11-23T16:25:56.545924+00:00 | 2024-11-23T16:25:56.545949+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int n = nums.size();\n \n int[] ans = new int[n];\n for(int i=0; i<n; i++){\n for(int j=0; j<=nums.get(i); j++){\n if((j|(j+1))==nums.get(i)){\n ans[i]=j;\n break;\n }\n }\n if(ans[i]==0){\n ans[i]=-1;\n }\n }\n return ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | 🟢🔴🟢 Beats 100.00%👏 Easiest Solution 🟢🔴🟢 | beats-10000-easiest-solution-by-develope-39ib | \nclass Solution {\n List<int> minBitwiseArray(List<int> nums) {\n\n List<int> ans = [];\n for(int i = 0; i < nums.length; i++){\n int prime = -1; | developerSajib88 | NORMAL | 2024-11-13T06:33:09.665383+00:00 | 2024-11-13T06:33:09.665411+00:00 | 25 | false | ```\nclass Solution {\n List<int> minBitwiseArray(List<int> nums) {\n\n List<int> ans = [];\n for(int i = 0; i < nums.length; i++){\n int prime = -1; \n for(int j = 1; j < nums[i]; j++){\n if(j | (j + 1) == nums[i]){\n prime = j;\n break;\n }\n }\n ans.add(prime);\n }\n return ans;\n \n }\n}\n``` | 0 | 0 | ['C', 'Python', 'C++', 'Java', 'JavaScript', 'C#', 'Dart'] | 0 |
construct-the-minimum-bitwise-array-i | Swift💯 | swift-by-upvotethispls-8xxe | Optimized Brute Force Search (accepted answer)\nOR-ing by (n+1) will never yield an even result, so if n is even (n&1==1), return -1. Otherwise brute force sear | UpvoteThisPls | NORMAL | 2024-11-13T00:09:36.171269+00:00 | 2024-11-13T00:09:36.171303+00:00 | 5 | false | **Optimized Brute Force Search (accepted answer)**\nOR-ing by (n+1) will never yield an even result, so if `n` is even (`n&1==1`), return -1. Otherwise brute force search from `n/2` on to find the smallest possible result. \n```\nclass Solution {\n func minBitwiseArray(_ nums: [Int]) -> [Int] {\n nums.map{ n in \n n&1 == 1 ? ((n/2)...).first{i in i|(i+1)==n}! : -1\n }\n }\n}\n``` | 0 | 0 | ['Swift'] | 0 |
construct-the-minimum-bitwise-array-i | Easy to UnderStand Beginner Friendly | easy-to-understand-beginner-friendly-by-5e06x | To address this problem, here\u2019s the breakdown:\n\n# Intuition\nThe goal is to transform each element of the array v by minimizing its binary representation | tinku_tries | NORMAL | 2024-11-11T09:51:29.239621+00:00 | 2024-11-11T09:51:29.239657+00:00 | 4 | false | To address this problem, here\u2019s the breakdown:\n\n# Intuition\nThe goal is to transform each element of the array `v` by minimizing its binary representation. For each element `v[i]`, if it is odd, we attempt to adjust it such that the resulting value retains as few high-value bits as possible while being slightly modified if necessary. This may involve clearing specific bits in a controlled way to achieve the minimal required configuration.\n\n# Approach\n1. **Helper Function `f`**: \n - This function minimizes a given integer `n` by selectively clearing one of the bits to create the smallest possible number that still closely resembles `n` in its binary structure.\n - We iterate through each bit of `n`. When we encounter the first unset bit (`0`), we adjust the last set bit (`1`) we added, which helps minimize the integer.\n \n2. **Main Transformation in `minBitwiseArray`**:\n - **Check Each Element**:\n - If `v[i]` is even, we skip it, as we only want to modify odd numbers.\n - For odd numbers:\n - If `v[i]` is a power of two minus one (e.g., `1, 3, 7, 15...`), its minimized value should be half of `v[i]` minus one (a straightforward case).\n - Otherwise, we use the `f` function to get a minimized version.\n - **Store Result**: We create an array `ans` to store the minimized results for each `v[i]`.\n\n# Complexity\n- **Time Complexity**: \n - Let `n` be the length of the input array `v`. For each odd element, we process its bits (approximately `O(log k)` for integer `k`).\n - Overall complexity is `O(nlog k)` in the worst case.\n\n- **Space Complexity**: \n - `O(n)` for storing the resulting minimized array.\n\n# Beats\n\n\n\n# Code\n```cpp\n#include <vector>\nusing namespace std;\n\nclass Solution {\npublic:\n // Helper function to minimize binary form of odd number `n`\n int f(int n) {\n int ans = 0, i = 0;\n bool flag = true;\n \n // Iterate through bits of `n` to minimize its value\n while(n) {\n if(n % 2) ans += 1 << i; // If bit is set, add it to `ans`\n else if(flag) {\n ans -= 1 << (i - 1); // Clear the last added bit to minimize\n flag = false;\n }\n i++;\n n /= 2;\n }\n return ans;\n }\n \n // Main function to transform array based on minimization rules\n vector<int> minBitwiseArray(vector<int>& v) {\n int n = v.size();\n vector<int> ans(n, -1); // Initialize results with `-1`\n \n // Process each element in the input vector\n for(int i = 0; i < n; i++) {\n if(v[i] % 2 == 0) continue; // Skip even numbers\n else if(((v[i] + 1) & (v[i])) == 0) // Special case for `2^k - 1`\n ans[i] = (v[i] - 1) / 2;\n else ans[i] = f(v[i]); // Use helper function for other odd numbers\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Array', 'Bit Manipulation', 'C++'] | 0 |
construct-the-minimum-bitwise-array-i | Short and Easy Solution ✅✅ | short-and-easy-solution-by-poojakapri252-y3av | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | poojakapri2529 | NORMAL | 2024-11-10T16:56:36.436376+00:00 | 2024-11-10T16:56:36.436412+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n vector<int>ans(nums.size(),-1);\n for(int i=0;i<nums.size();i++)\n {\n int num=nums[i];\n\n for(int j=1;j<num;j++)\n {\n int newans=j|(j+1);\n if(newans==num)\n { \n ans[i]=j;\n break;\n }\n\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Construct the Minimum bitwise array - python3 solution | construct-the-minimum-bitwise-array-pyth-y8hi | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ChaithraDee | NORMAL | 2024-11-10T14:54:25.382917+00:00 | 2024-11-10T14:54:25.382940+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n ans = []\n for i in nums:\n for j in range(i):\n if j | (j + 1) == i:\n ans.append(j)\n break\n else:\n ans.append(-1)\n return ans\n``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | C# brute force | c-brute-force-by-dmitriy-maksimov-v63c | Complexity\n- Time complexity: O(n \times 2^m)\n- Space complexity: O(n)\n\n# Code\ncsharp []\npublic class Solution\n{\n public int[] MinBitwiseArray(IList< | dmitriy-maksimov | NORMAL | 2024-11-10T08:06:19.051206+00:00 | 2024-11-10T08:06:19.051240+00:00 | 6 | false | # Complexity\n- Time complexity: $$O(n \\times 2^m)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```csharp []\npublic class Solution\n{\n public int[] MinBitwiseArray(IList<int> nums)\n {\n var result = Enumerable.Repeat(-1, nums.Count).ToArray();\n\n for (var i = 0; i < nums.Count; i++)\n {\n for (int j = 0; j < nums[i]; j++)\n {\n if ((j | (j + 1)) == nums[i])\n {\n result[i] = j;\n break;\n }\n }\n }\n\n return result;\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
construct-the-minimum-bitwise-array-i | ✅ Easy Rust Solution | easy-rust-solution-by-erikrios-01p5 | \nimpl Solution {\n pub fn min_bitwise_array(nums: Vec<i32>) -> Vec<i32> {\n let n = nums.len();\n\n let mut results = Vec::with_capacity(n);\n | erikrios | NORMAL | 2024-11-10T02:30:57.296787+00:00 | 2024-11-10T02:30:57.296810+00:00 | 1 | false | ```\nimpl Solution {\n pub fn min_bitwise_array(nums: Vec<i32>) -> Vec<i32> {\n let n = nums.len();\n\n let mut results = Vec::with_capacity(n);\n\n \'outer: for num in nums {\n for i in 0..num {\n if i | (i + 1) == num {\n results.push(i);\n continue \'outer;\n }\n }\n results.push(-1);\n }\n\n results\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
construct-the-minimum-bitwise-array-i | c++ 100% solution | c-100-solution-by-kartikbhutra02-ztt5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kartikbhutra02 | NORMAL | 2024-11-09T12:39:16.032589+00:00 | 2024-11-09T12:39:16.032625+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n int n = nums.size();\n vector <int> ans(n, -1);\n for(int i=0;i<n;i++) {\n if(nums[i] == 2) continue;\n ans[i] = nums[i]&(nums[i]+1) + (nums[i]^(nums[i]+1))/4;\n }\n return ans;\n }\n};\n\n``` | 0 | 0 | ['Bit Manipulation', 'C++'] | 0 |
construct-the-minimum-bitwise-array-i | Java Straightforward Solution | java-straightforward-solution-by-curenos-39pa | Code\njava []\nclass Solution {\n public int getKthElement(int n) {\n int res = -1;\n for (int i = 0; i <= 1000; i++)\n if ((i | (i + 1)) == n)\n | curenosm | NORMAL | 2024-11-09T00:51:16.617062+00:00 | 2024-11-09T00:51:16.617092+00:00 | 5 | false | # Code\n```java []\nclass Solution {\n public int getKthElement(int n) {\n int res = -1;\n for (int i = 0; i <= 1000; i++)\n if ((i | (i + 1)) == n)\n return i;\n return res;\n }\n\n public int[] minBitwiseArray(List<Integer> nums) {\n return IntStream.range(0, nums.size())\n .map(it -> getKthElement(nums.get(it)))\n .toArray();\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | Simple C++ Solution Beats 100% | simple-c-solution-beats-100-by-samarth_v-po5l | Code\ncpp []\nvector<int> minBitwiseArray(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans(n);\n for(int i=0;i<n;++i){\n | samarth_verma_007 | NORMAL | 2024-11-04T18:09:15.823378+00:00 | 2024-11-04T18:09:15.823420+00:00 | 5 | false | # Code\n```cpp []\nvector<int> minBitwiseArray(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans(n);\n for(int i=0;i<n;++i){\n if(nums[i]&1){\n int j=0;\n while(nums[i] & (1<<j)){\n ++j;\n }\n --j;\n ans[i]=(nums[i] & (~(1<<j)));\n }\n else ans[i]=-1;\n }\n\n return ans;\n}\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Easy Way Solution in c++ | easy-way-solution-in-c-by-ni30_rjpt-mdpy | Initialization of temp: Moved the initialization of temp outside the inner loop and set it to -1 by default.\nReadability: Improved formatting and variable nami | ni30_rjpt | NORMAL | 2024-11-03T13:41:49.765101+00:00 | 2024-11-03T13:41:49.765129+00:00 | 1 | false | Initialization of temp: Moved the initialization of temp outside the inner loop and set it to -1 by default.\nReadability: Improved formatting and variable naming for clarity.\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n int size = nums.size();\n\n for (int i = 0; i < size; i++) {\n int temp = -1; // Initialize temp here\n\n for (int j = 1; j < nums[i]; j++) {\n if ((j | (j + 1)) == nums[i]) {\n temp = j;\n break;\n }\n }\n nums[i] = temp; // Assign temp to nums[i] after the inner loop\n }\n\n return nums;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | GO | Brute Force | go-brute-force-by-2107mohitverma-bjnv | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | 2107mohitverma | NORMAL | 2024-10-31T04:00:37.509522+00:00 | 2024-10-31T04:00:37.509558+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc minBitwiseArray(nums []int) []int {\n\tn := len(nums)\n\tans := make([]int, n)\n\n\tfor idx := 0; idx < n; idx++ {\n\t\tfor num := 1; num <= nums[idx]; num++ {\n\t\t\tif num|(num+1) == nums[idx] {\n\t\t\t\tans[idx] = num\n\t\t\t\tbreak\n\t\t\t}\n\t\t}\n\t\tif ans[idx] == 0 {\n\t\t\tans[idx] = -1\n\t\t}\n\t}\n\n\treturn ans\n}\n``` | 0 | 0 | ['Go'] | 0 |
construct-the-minimum-bitwise-array-i | Brute force | brute-force-by-kinnar-rbn1 | Intuition\n Describe your first thoughts on how to solve this problem. \nAs the constraints has limited small value used brute force\n# Approach\n Describe your | Kinnar | NORMAL | 2024-10-29T13:51:39.003464+00:00 | 2024-10-29T13:51:39.003496+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs the constraints has limited small value used brute force\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBrute force\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n int n=nums.size();\n vector<int>ans(n);\n for(int i=0;i<n;i++){\n int m=nums[i];\n if(m==2)\n ans[i]=-1;\n else{\n for(int j=1;j<m;j++){\n if((j|(j+1))==m){\n ans[i]=j;\n break;\n }\n }\n }\n }return ans;\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Python 94%, Easy to Understand. Optimize the brutal force method | python-94-easy-to-understand-optimize-th-69c2 | Approach\n Describe your approach to solving the problem. \nStart with brutal force. Iterate from 1 to nums[i] for each number to find if there is a number that | user8139UI | NORMAL | 2024-10-26T07:19:28.097451+00:00 | 2024-10-26T07:19:28.097477+00:00 | 3 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nStart with brutal force. Iterate from 1 to nums[i] for each number to find if there is a number that satisfy the requirement. \nThen, after some thinking, I optimize the starting point from 1 to n = 2**(cnt-1)-2. Where cnt is the index of the leading "1" of nums[i] in binary. \n# Code\n```python []\nclass Solution(object):\n def minBitwiseArray(self, nums):\n ans = [-1]*len(nums)\n for i in range(len(nums)):\n n = nums[i]\n cnt = 0\n while n != 0:\n cnt += 1\n n = n >> 1\n n = 2**(cnt-1)-2\n while n < nums[i]:\n if n | n+1 == nums[i]:\n ans[i] = n\n break\n n+=1\n return ans\n \n``` | 0 | 0 | ['Python'] | 0 |
construct-the-minimum-bitwise-array-i | C Solution | c-solution-by-nosetup-xum2 | Intuition\n Describe your first thoughts on how to solve this problem. \nNeed to clarify the question.\n\nThis problem is looking for a same size array with new | nosetup | NORMAL | 2024-10-25T20:17:18.112674+00:00 | 2024-10-25T20:17:18.112691+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNeed to clarify the question.\n\nThis problem is looking for a same size array with new values that is\ngiven[i] = A, result[i] = B\nwhere,\nA = (B | B + 1)\nwe find individual \'B\' for each given.\nHere is a image showing A(orange) and B(green).\n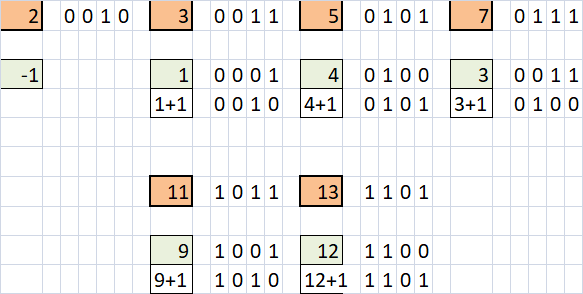\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOnly question is deciding what values to use for loop length.\nAs seen for example:\nLowest Value we can use is right shifted once.\n"given[j] >> 1"\ngiven[j] = 7 | 0111\nresult[j] = 3 | 0011\n\nMy initial loop used:\nfor (int j = nums[i]; j >= nums[i] / 2; j--)\n\nLater was updated to:\nfor (int j = nums[i] / 2; j <= nums[i]; j++)\n\nDifference is j++ can use a break for the first answer it finds, where j-- will need to always evaluate entire loop.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* minBitwiseArray(int* nums, int numsSize, int* returnSize) {\n\n returnSize[0] = numsSize;\n int* ans = malloc(numsSize * sizeof(int));\n\n for (int i = 0; i < numsSize; i++) {\n ans[i] = -1; \n for (int j = nums[i] / 2; j <= nums[i]; j++) {\n if ((j | j + 1) == nums[i]) {\n ans[i] = j;\n break;\n }\n }\n }\n return ans;\n}\n\n``` | 0 | 0 | ['C'] | 0 |
construct-the-minimum-bitwise-array-i | Solution with explanation | solution-with-explanation-by-angielf-78g9 | Approach\nThe key insight here is that x | (x + 1) will always be equal to num if and only if the least significant bit of num is 1. This is because x | (x + 1) | angielf | NORMAL | 2024-10-25T08:54:55.061357+00:00 | 2024-10-25T08:54:55.061384+00:00 | 6 | false | # Approach\nThe key insight here is that x | (x + 1) will always be equal to num if and only if the least significant bit of num is 1. This is because x | (x + 1) will always set the least significant bit of num to 1.\n\nBy iterating over each num and finding the smallest x that satisfies the condition, we can construct the result array.\n\n# Complexity\n- Time complexity:\n$$O(n*m)$$, where n is the length of the input list nums and m is the maximum value in nums. This is because for each number in nums, the function iterates up to that number to find a match.\n\n- Space complexity:\n$$O(n)$$, where n is the length of the input list nums. This is because the function creates a new list ans of the same length as nums to store the results.\n\n# Code\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n ans = []\n for num in nums:\n found = False\n for x in range(num):\n if (x | (x + 1)) == num:\n ans.append(x)\n found = True\n break\n if not found:\n ans.append(-1)\n return ans\n```\n``` javascript []\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar minBitwiseArray = function(nums) {\n const ans = [];\n for (const num of nums) {\n let found = false;\n for (let x = 0; x < num; x++) {\n if ((x | (x + 1)) === num) {\n ans.push(x);\n found = true;\n break;\n }\n }\n if (!found) {\n ans.push(-1);\n }\n }\n return ans;\n};\n```\n``` php []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer[]\n */\n function minBitwiseArray($nums) {\n $ans = [];\n foreach ($nums as $num) {\n $found = false;\n for ($x = 0; $x < $num; $x++) {\n if (($x | ($x + 1)) === $num) {\n $ans[] = $x;\n $found = true;\n break;\n }\n }\n if (!$found) {\n $ans[] = -1;\n }\n }\n return $ans;\n }\n}\n``` | 0 | 0 | ['Array', 'Bit Manipulation', 'PHP', 'Python3', 'JavaScript'] | 0 |
construct-the-minimum-bitwise-array-i | easy code | easy-code-by-npsy1811-aa5e | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | red_viper | NORMAL | 2024-10-25T07:07:39.521914+00:00 | 2024-10-25T07:07:39.521952+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n int size = nums.size(), temp;\n\n for( int i =0 ; i< size; i++)\n {\n for( int j =1 ; j< nums[i] ;j ++)\n {\n if( (j | (j+1)) == nums[i])\n {cout<< (j | (j+1)) <<" ";\n temp =j;\n break;}\n else temp = -1;\n }\n nums[i ] =temp;\n }\n\n return nums;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | ✅ C# | readable solution 🚅 faster than 95% | c-readable-solution-faster-than-95-by-th-8zd1 | \n\nDon\'t hesitate to suggest or ask bellow about something that you don\'t understand\n\ncsharp []\npublic class Solution {\n public int[] MinBitwiseArray( | Thanat05 | NORMAL | 2024-10-23T19:56:36.771614+00:00 | 2024-10-23T19:57:08.375034+00:00 | 9 | false | \n\n**Don\'t hesitate to suggest or ask bellow about something that you don\'t understand**\n\n```csharp []\npublic class Solution {\n public int[] MinBitwiseArray(IList<int> nums) {\n List<int> ls = new();\n foreach (int n in nums)\n {\n bool IsPrime = false;\n for (int i = 0; i < n; i++)\n {\n int ans = i | i + 1;\n if (n == ans)\n {\n IsPrime = true;\n ls.Add(i);\n break;\n }\n }\n if (!IsPrime)\n ls.Add(-1);\n }\n return ls.ToArray();\n }\n}\n```\n\nIf you like it don\'t forget to **upvote!** | 0 | 0 | ['C#'] | 0 |
construct-the-minimum-bitwise-array-i | Runtime: 0ms Beats 100.00% || C++ || Java || Python3 | runtime-0ms-beats-10000-c-java-python3-b-eule | cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n vector<int> ans;\n\n for(int num : nums) {\n | Deviant25 | NORMAL | 2024-10-23T12:20:15.414232+00:00 | 2024-10-23T12:20:15.414256+00:00 | 17 | false | ```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n vector<int> ans;\n\n for(int num : nums) {\n int ans_i = -1;\n\n for (int i = 0; i < num; ++i) {\n if ((i | (i + 1)) == num) {\n ans_i = i;\n break;\n }\n }\n ans.push_back(ans_i);\n }\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int n = nums.size();\n int[] ans = new int[n];\n\n for (int i = 0; i < n; i++) {\n int num = nums.get(i);\n ans[i] = -1;\n\n for (int j = 0; j < num; j++) {\n if ((j | (j + 1)) == num) {\n ans[i] = j;\n break;\n }\n }\n }\n return ans;\n }\n}\n```\n```Python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n ans = []\n\n for num in nums:\n ans_i = -1\n\n for i in range(num):\n if (i | (i + 1)) == num:\n ans_i = i\n break\n ans.append(ans_i)\n return ans\n``` | 0 | 0 | ['C++', 'Java', 'Python3'] | 0 |
construct-the-minimum-bitwise-array-i | Python3 | 4ms | Beats 99% | python3-4ms-beats-99-by-padth-u3hj | Code\npython3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n result = []\n\n for n in nums:\n if n | padth | NORMAL | 2024-10-23T04:11:27.478762+00:00 | 2024-10-23T04:11:27.478797+00:00 | 4 | false | # Code\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n result = []\n\n for n in nums:\n if n % 2 == 0:\n result.append(-1)\n continue\n\n i = 0\n while n & (1 << i) != 0:\n i += 1\n\n result.append((1 << (i - 1)) ^ n)\n\n return result\n``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | laziest brute force | laziest-brute-force-by-user5400vw-qv6h | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | user5400vw | NORMAL | 2024-10-23T04:08:54.305065+00:00 | 2024-10-23T04:08:54.305089+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```rust []\n\nimpl Solution {\n pub fn min_bitwise_array(nums: Vec<i32>) -> Vec<i32> {\n // brute force\n let mut res: Vec<i32> = vec![];\n for n in nums {\n // try all until sum goes over\n let mut found = false;\n for i in 0..n {\n let mut trial = i as i32 | (i+1) as i32;\n if (trial == n) {\n res.push(i);\n found = true;\n break\n }\n }\n if !found {\n res.push(-1);\n }\n\n }\n res\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
construct-the-minimum-bitwise-array-i | C Solution || Beats 99.12% | c-solution-beats-9912-by-heber_alturria-b3wq | c []\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* minBitwiseArray(int* nums, int numsSize, int* returnSize) {\n | Heber_Alturria | NORMAL | 2024-10-22T20:41:21.954307+00:00 | 2024-10-22T20:41:21.954333+00:00 | 5 | false | ```c []\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* minBitwiseArray(int* nums, int numsSize, int* returnSize) {\n int *result = calloc(numsSize, sizeof(int));\n *returnSize = numsSize;\n\n memset(result, -1, numsSize * sizeof(int));\n\n for (int i = 0; i < numsSize; i++) {\n for (int val = 0; val <= nums[i]; val++) {\n if ((val | (val + 1)) == nums[i]) {\n result[i] = val;\n break;\n }\n }\n }\n\n return result;\n}\n``` | 0 | 0 | ['Array', 'Bit Manipulation', 'C'] | 0 |
construct-the-minimum-bitwise-array-i | 100% Python 1 line solution Bit manipulation | 100-python-1-line-solution-bit-manipulat-7gj6 | \n\n# Intuition\nPerforming a bitwise OR with n and n+1 will fill the leftmost 0 in n. Therefore to get the lowest value of n where n OR (n+1) == v, we can repl | El1247 | NORMAL | 2024-10-21T14:08:28.385991+00:00 | 2024-10-21T14:08:28.386025+00:00 | 2 | false | \n\n# Intuition\nPerforming a bitwise OR with `n` and `n+1` will fill the leftmost `0` in `n`. Therefore to get the lowest value of `n` where `n OR (n+1) == v`, we can replace the highest consecutive `1` in `v` with a `0`. \n\nThe consecutive part refers to the unbroken stream of `1`\'s starting from the Least Significant Bit. For `7 == 0b0111` this would be the `1` next to the `0`, aka the second digit, or the value representing `4`. For `23 == 0b10111` the highest consecutive `1` is in the third position, again representing `4`.\n\nIf we replaced a higher, non-consecutive 1, then the addition of `n` and `n+1` would plug the lower `0`, and make a different number.\n\nIf there is a `0` in the very first bit, aka there is not an unbroken `1`, then a value of `-1` will have to be returned, as `n OR (n+1)` will always populate the `1`\'s column.\n\nTo calculate the position of the highest consecutive `1`, we can find the value of the lowest `0` and leftshift it by `1`. To find the value of the lowest `0`, we can `AND` the bitwise `NOT` of `n` with `n+1`. For the value of `v == 23` this would look like (`_` are for alignment padding):\n`23 ___ == 0b0000 0001 0111`\n`NOT 23 == 0b1111 1110 1000 == 23 ^ 0xFFF`\n`23 + 1 == 0b0000 0001 1000`\n`AND __ == 0b0000 0000 1000 == (23 ^ 0xFFF) & 23+1`\n`>> 1 _ == 0b0000 0000 0100 == ((23 ^ 0xFFF) & 23+1) >> 1`\n`v - n _== 0b0000 0001 0011 == 19`\n\nSubtracting this value from `v` gives us the minimum value of `n`.\n\n# Approach\nIterate through each element in the list. For each value:\n- Check if the there is a `1` in the `1`\'s column. If not, insert the value `-1` in the return array. As these are a list of primes, ignoring `2`, all primes will be odd, and therefor meet this condition. So this simply becomes a check to see if the value is equal to `2`.\n- Identify the value of the highest consecutive `1` using the above mentioned method of `(v ^ 0xFFF) & v+1)`.\n- Subtract this value from the target prime and store it in the return array. \n\n# Complexity\n- Time complexity:\nSimple bitwise operations are performed on each element in the list once: $$O(n)$$\n\n- Space complexity:\nThe return array needs to be of the same size of the input array, as well as constant space for performing bitwise operations: $$O(n)$$\n\n# Code\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n return [v - (((v^0xFFF) & v+1) >> 1) if v != 2 else -1 for v in nums ]\n``` | 0 | 0 | ['Bit Manipulation', 'Python3'] | 0 |
construct-the-minimum-bitwise-array-i | Simple Java Solution | simple-java-solution-by-prince_kumar1-htj7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | prince_kumar1 | NORMAL | 2024-10-20T10:27:47.680791+00:00 | 2024-10-20T10:27:47.680816+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n \n int []ans=new int[nums.size()];\n\n for(int i=0;i<nums.size();i++){\n\n int x=nums.get(i);\n int p=-1;\n\n for(int j=1;j<=x;j++){\n if((j|(j+1))==x){\n p=j;\n break;\n }\n }\n\n ans[i]=p;\n \n }\n\n return ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | Simple solution | simple-solution-by-liminghb123-ihbz | Intuition\n\n\n# Approach\n\n\n# Complexity\n- Time complexity:\nO(n*n)\n\n- Space complexity:\nO(n)\n\n# Code\ncpp []\nclass Solution {\npublic:\n vector<in | liminghb123 | NORMAL | 2024-10-20T02:32:03.143522+00:00 | 2024-10-20T02:32:03.143550+00:00 | 0 | false | # Intuition\n\n\n# Approach\n\n\n# Complexity\n- Time complexity:\nO(n*n)\n\n- Space complexity:\nO(n)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n vector<int> ans;\n\n for (int j = 0; j < nums.size(); j++)\n {\n for (int i = 0; i < nums[j]; i++)\n {\n if ((i | (i + 1)) == nums[j])\n {\n ans.push_back(i);\n break;\n }\n }\n if (ans.size() < (j+1))\n {\n ans.push_back(-1);\n }\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Python, brute force | python-brute-force-by-blue_sky5-foc3 | \nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n result = []\n for n in nums:\n for r in range(n):\n | blue_sky5 | NORMAL | 2024-10-19T17:52:03.644774+00:00 | 2024-10-19T17:52:03.644801+00:00 | 0 | false | ```\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n result = []\n for n in nums:\n for r in range(n):\n if r | (r + 1) == n:\n result.append(r)\n break\n else:\n result.append(-1)\n \n return result\n``` | 0 | 0 | [] | 0 |
construct-the-minimum-bitwise-array-i | Python Bruteforce | python-bruteforce-by-antarab-gq0l | \nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n res=[]\n for x in nums:\n if x%2==0:\n | antarab | NORMAL | 2024-10-19T16:37:28.267897+00:00 | 2024-10-19T16:37:28.267929+00:00 | 3 | false | ```\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n res=[]\n for x in nums:\n if x%2==0:\n res.append(-1)\n else:\n for y in range(1,x):\n if y | (y+1) ==x:\n res.append(y)\n break\n \n return res\n``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | One line solution. Bit manipulation. O(n) | one-line-solution-bit-manipulation-on-by-c4yu | \nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n return [(n&(n+1)) | ((~n&(n+1))//2-1) for n in nums]\n | xxxxkav | NORMAL | 2024-10-18T21:01:17.199300+00:00 | 2024-10-18T21:03:51.686299+00:00 | 7 | false | ```\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n return [(n&(n+1)) | ((~n&(n+1))//2-1) for n in nums]\n``` | 0 | 0 | ['Bit Manipulation', 'Python3'] | 0 |
construct-the-minimum-bitwise-array-i | TS Solution | ts-solution-by-ahmedhhamdy-x9ge | Create an array ans of the same length as nums, initialized with -1 (default value if no valid ans[i] is found).\n\nMain Loop:\n\nFor each element in nums, we t | ahmedhhamdy | NORMAL | 2024-10-18T14:10:40.710191+00:00 | 2024-10-18T14:10:40.710223+00:00 | 7 | false | Create an array ans of the same length as nums, initialized with -1 (default value if no valid ans[i] is found).\n\nMain Loop:\n\nFor each element in nums, we try to find the smallest x such that x | (x + 1) == nums[i].\nIf we find such a value, we update ans[i] and break out of the loop to move to the next index.\n\nThe condition \n\nx | (x + 1) == nums[i] checks if the bitwise OR of x and x + 1 equals the current number in nums.\n\n# Complexity\n- Time complexity: 6ms\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 52.76MB\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```typescript []\nfunction minBitwiseArray(nums: number[]): number[] {\n let ans = new Array(nums.length).fill(-1)\n \n for (let i = 0; i < nums.length; i++) {\n for (let x = 0; x < nums[i]; x++) {\n if ((x | (x + 1)) == nums[i]) {\n ans[i] = x\n break\n }\n }\n }\n return ans\n};\n\n``` | 0 | 0 | ['TypeScript'] | 0 |
construct-the-minimum-bitwise-array-i | Java, Easy And Optimized solution Using Bitwise Operator | java-easy-and-optimized-solution-using-b-cgog | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vipin_121 | NORMAL | 2024-10-18T09:44:26.506267+00:00 | 2024-10-18T09:44:26.506297+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int[] ans=new int[nums.size()];\n int n=nums.size();\n for(int i=0;i<n;i++){\n int sf=1;\n int no=nums.get(i);\n if(no==2){\n ans[i]=-1;\n continue;\n }\n while((no&sf)!=0){\n sf=sf<<1;\n }\n sf=sf>>1;\n ans[i]=no&~(sf);\n }\n return ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | C++ Easy Solution :-> | c-easy-solution-by-atchayasmail-141y | Intuition\n Describe your first thoughts on how to solve this problem. \nGet the largest 2\'s power within nums[i]\n\n# Approach\n Describe your approach to sol | atchayasmail | NORMAL | 2024-10-18T04:29:18.714769+00:00 | 2024-10-18T04:29:18.714805+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGet the largest 2\'s power within nums[i]\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTake largest 2\'s power as k and keep incrementing it till the OR condition satisfies.\n\n# Complexity\n- Time complexity: O(n*m), where m = nums[i]\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n\n vector<int> ans(nums.size());\n for (int i = 0; i < nums.size(); i++) {\n if (nums[i] % 2 == 0) {\n ans[i] = -1;\n continue;\n }\n int k = 1;\n while (k * 2 <= nums[i]) {\n k *= 2;\n }\n while (k < nums[i]) {\n\n int chk = k | k - 1;\n if (chk == nums[i]) {\n ans[i] = k - 1;\n break;\n }\n\n chk = k | k + 1;\n if (chk == nums[i]) {\n ans[i] = k;\n break;\n }\n k++;\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Solution | solution-by-hamzamks-qmc2 | \n\n# Code\njava []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int n = nums.size();\n int ans[] = new int[n];\n | hamzamks | NORMAL | 2024-10-17T11:51:55.121111+00:00 | 2024-10-17T11:51:55.121137+00:00 | 4 | false | \n\n# Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int n = nums.size();\n int ans[] = new int[n];\n // Initialize all elements to -1\n for (int i = 0; i < n; i++) {\n ans[i] = -1;\n }\n\n for (int i = 0; i < nums.size(); i++) {\n Integer val = nums.get(i);\n for (int j = 0; j <= val; j++) {\n if ((j | (j + 1)) == nums.get(i)) {\n ans[i] = j;\n break;\n }\n }\n\n }\n return ans ; \n\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | [C] | c-by-zhang_jiabo-05pf | C []\nint * minBitwiseArray(\n\tconst int * const nums,\n\tconst int numsLen,\n\n\tint * const pRetsLen //out\n){\n\t*pRetsLen = numsLen;\n\tint * const rets = | zhang_jiabo | NORMAL | 2024-10-17T07:52:15.398970+00:00 | 2024-10-17T07:52:15.398994+00:00 | 2 | false | ```C []\nint * minBitwiseArray(\n\tconst int * const nums,\n\tconst int numsLen,\n\n\tint * const pRetsLen //out\n){\n\t*pRetsLen = numsLen;\n\tint * const rets = (int *)malloc(sizeof (int) * *pRetsLen);\n\n\tfor (int i = 0; i < numsLen; i += 1){\n\t\tif (nums[i] % 2 == 0){\n\t\t\trets[i] = -1;\n\t\t\tcontinue;\n\t\t}\n\n\t\tint mask = 1;\n\t\twhile ( (nums[i] & (mask << 1)) != 0 ){\n\t\t\tmask <<= 1;\n\t\t}\n\n\t\trets[i] = nums[i] & ~mask;\n\t}\n\n\treturn rets;\n}\n``` | 0 | 0 | ['C'] | 0 |
construct-the-minimum-bitwise-array-i | 💯💯 Simple solution using for loop (easy to understand) | simple-solution-using-for-loop-easy-to-u-be8b | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | CvQArRopoq | NORMAL | 2024-10-16T22:40:25.439298+00:00 | 2024-10-16T22:40:25.439338+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int ans[]=new int[nums.size()];\n int val=0,x=0;\n for(int i : nums){\n boolean f=false;\n val=i;\n for(int j=0;j<i;j++){\n if((j | j+1) == val){\n f=true;\n ans[x++]=j;\n break;\n }\n }\n if(!f){\n ans[x++]=-1;\n }\n }\n return ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | Easy DP solution :) | easy-dp-solution-by-nomorenoove-e4i2 | \n\n# Code\ncpp []\nclass Solution {\n unordered_map<int, int> dp;\n\n int solve(int num){\n if(dp[num]) return dp[num];\n if(floor(log2(num | nomorenoove | NORMAL | 2024-10-16T21:10:31.595097+00:00 | 2024-10-16T21:10:31.595116+00:00 | 2 | false | \n\n# Code\n```cpp []\nclass Solution {\n unordered_map<int, int> dp;\n\n int solve(int num){\n if(dp[num]) return dp[num];\n if(floor(log2(num + 1)) == ceil(log2(num + 1))) return ((num + 1) / 2) - 1;\n\n int val = pow(2, (int)log2(num));\n\n return dp[num] = val + solve(num - val);\n }\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) {\n vector<int> ans;\n dp[1] = 0;\n\n for(auto it : nums){\n if(it == 2) ans.push_back(-1);\n else{\n ans.push_back(solve(it));\n }\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | Easy C++ Solution | easy-c-solution-by-mushahid3689-c09a | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | SyntaxTerror123 | NORMAL | 2024-10-16T07:55:41.164633+00:00 | 2024-10-16T07:55:41.164665+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> minBitwiseArray(vector<int>& nums) \n {\n \n vector<int>a;\n \n for(int i=0;i<nums.size();i++)\n {\n bool x = false;\n int m = 0;\n int n = 1;\n while(m<=nums[i] && n<=nums[i])\n {\n int z = m|n;\n if(z==nums[i])\n {\n a.push_back(m);\n x = true;\n break;\n }\n m++;\n n++;\n \n }\n if(!x)\n a.push_back(-1);\n \n }\n return a;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
construct-the-minimum-bitwise-array-i | 47 ms Beats 97.69% | Easy Bitmask Solution | 47-ms-beats-9769-easy-bitmask-solution-b-rgcu | Complexity\n- Time complexity: O(10n)\n\n- Space complexity: O(n)\n\n# Code\npython3 []\nclass Solution:\n def __init__(self):\n # n <= 1000 < 1024 == | user1043p | NORMAL | 2024-10-16T07:06:58.746389+00:00 | 2024-10-16T07:06:58.746406+00:00 | 8 | false | # Complexity\n- Time complexity: $$O(10n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python3 []\nclass Solution:\n def __init__(self):\n # n <= 1000 < 1024 == 2 ** 10\n self.masks = [0x0, 0x1, 0x3, 0x7, 0xf, 0x1f, 0x3f, 0x7f, 0xff, 0x1ff, 0x3ff]\n\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n ans = [-1] * len(nums)\n\n for i, x in enumerate(nums):\n if x == 2:\n continue\n for j in range(1, 10):\n if x & self.masks[j] and not x & (self.masks[j + 1] - self.masks[j]):\n ans[i] = x - (self.masks[j] - self.masks[j - 1])\n break\n\n return ans\n``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | Java Easy Solution | java-easy-solution-by-iamsd-q98y | Code\njava []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int len = nums.size();\n int[] ans = new int[len];\n | iamsd_ | NORMAL | 2024-10-15T06:16:08.818426+00:00 | 2024-10-15T06:16:08.818460+00:00 | 1 | false | # Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n int len = nums.size();\n int[] ans = new int[len];\n\n for (int i = 0; i < len; i++) {\n boolean flag = true;\n for (int j = 1; j < nums.get(i); j++) {\n if ((j | j + 1) == nums.get(i)) {\n ans[i] = j;\n flag = false;\n break;\n }\n }\n\n if (flag) {\n ans[i] = -1;\n }\n }\n\n return ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | [Python] brutal force solution that beat 90% | python-brutal-force-solution-that-beat-9-ycp3 | \nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n # build a map from value to index to easy access answer list\n n | wangw1025 | NORMAL | 2024-10-15T04:21:14.972141+00:00 | 2024-10-15T04:21:14.972175+00:00 | 5 | false | ```\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n # build a map from value to index to easy access answer list\n num_map = collections.defaultdict(list)\n for idx, n in enumerate(nums):\n num_map[n].append(idx)\n \n ans = [-1] * len(nums)\n max_num = max(nums)\n \n for i in range(1, max_num):\n val = i | (i + 1)\n if val in num_map and ans[num_map[val][0]] == -1:\n for tidx in num_map[val]:\n ans[tidx] = i\n \n return ans\n``` | 0 | 0 | ['Python3'] | 0 |
construct-the-minimum-bitwise-array-i | Java | java-by-sumeetrayat-snm9 | \n\n# Code\njava []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n\n\t\t\n\t\tint count=0;\n\t\tint ans[]= new int[nums.size()];\n\ | sumeetrayat | NORMAL | 2024-10-15T03:05:31.640444+00:00 | 2024-10-15T03:05:31.640469+00:00 | 4 | false | \n\n# Code\n```java []\nclass Solution {\n public int[] minBitwiseArray(List<Integer> nums) {\n\n\t\t\n\t\tint count=0;\n\t\tint ans[]= new int[nums.size()];\n\t\tfor (int i = 0; i<=nums.size()-1; i++) {\n\t\t\t\n\t\t\tfor (int j = 0; j<=nums.get(i); j++) {\n\t\t\t\t\n\t\t\t\tif((j | (j + 1)) == nums.get(i))\n\t\t\t\t{\n\t\t\t\t\tcount++;\n\t\t\t\t\tans[i]=j;\n\t\t\t\t\tbreak;\n\t\t\t\t}\n\t\t\t}\n\t\t\tif(count==0)\n\t\t\t{\n\t\t\t\tans[i]=-1;\n\t\t\t}\n\t\t\tcount=0;\n\t\t}\n return ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
construct-the-minimum-bitwise-array-i | Ruby one-liner, beats 100%/100% | ruby-one-liner-beats-100100-by-dnnx-wd9n | ruby []\n# @param {Integer[]} nums\n# @return {Integer[]}\ndef min_bitwise_array(nums)\n nums.map { |n| n == 2 ? -1 : n - (((n ^ (n + 1)) + 1) / 4) } \nend\n | dnnx | NORMAL | 2024-10-14T16:23:21.077297+00:00 | 2024-10-14T16:23:21.077328+00:00 | 4 | false | ```ruby []\n# @param {Integer[]} nums\n# @return {Integer[]}\ndef min_bitwise_array(nums)\n nums.map { |n| n == 2 ? -1 : n - (((n ^ (n + 1)) + 1) / 4) } \nend\n``` | 0 | 0 | ['Ruby'] | 0 |
construct-the-minimum-bitwise-array-i | [Python] Brute force | python-brute-force-by-pbelskiy-o0up | \nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n ans = []\n\n for n in nums:\n for x in range(n):\n | pbelskiy | NORMAL | 2024-10-14T12:58:00.631835+00:00 | 2024-10-14T12:58:00.631865+00:00 | 1 | false | ```\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n ans = []\n\n for n in nums:\n for x in range(n):\n if x | (x + 1) == n:\n ans.append(x)\n break\n else:\n ans.append(-1)\n\n return ans\n``` | 0 | 0 | ['Python'] | 0 |
construct-the-minimum-bitwise-array-i | Beats 100.00% | 1-liner | beats-10000-1-liner-by-nicholasgreenwood-ajki | \n\n\n\ntypescript []\nfunction minBitwiseArray(nums: number[]): number[] {\n return nums.map((num) => (num === 2 ? -1 : (((-num - 2) ^ num) >> 2) + num))\n}\n | NicholasGreenwood | NORMAL | 2024-10-14T11:15:52.143063+00:00 | 2024-10-18T14:08:44.343571+00:00 | 32 | false | \n\n\n\n```typescript []\nfunction minBitwiseArray(nums: number[]): number[] {\n return nums.map((num) => (num === 2 ? -1 : (((-num - 2) ^ num) >> 2) + num))\n}\n``` | 0 | 0 | ['TypeScript', 'JavaScript'] | 0 |
construct-the-minimum-bitwise-array-i | Easy | easy-by-shanku1999-1jz8 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shanku1999 | NORMAL | 2024-10-14T11:12:36.234485+00:00 | 2024-10-14T11:12:36.234513+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minBitwiseArray(self, nums: List[int]) -> List[int]:\n res=[]\n def getResult(n:int):\n for i in range(n):\n if i|(i+1)==n:\n return i\n break\n return -1\n return [getResult(num) for num in nums]\n \n``` | 0 | 0 | ['Python3'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.