question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-minimum-time-to-reach-last-room-ii | Slight Modification from part 1 of this question | slight-modification-from-part-1-of-this-hgy21 | Intuition\n Describe your first thoughts on how to solve this problem. \nIt says that you have alternating cost for between edges, so maybe keep track of a inde | yamuprajapati05 | NORMAL | 2024-11-04T06:40:09.576953+00:00 | 2024-11-04T06:40:09.576988+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt says that you have alternating cost for between edges, so maybe keep track of a index.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis will help to tell you whether this move will cost 1 or 2 based on the index.\n# Complexity\n- Time complexity: Same as part 1\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Same as part 1\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\n pair<int,int> dir[4] = { {0,1}, {1,0}, {0,-1}, {-1, 0} };\n\npublic:\n int minTimeToReach(vector<vector<int>>& m) {\n priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>> >q;\n int n = m.size();\n int cols = m[0].size();\n set<pair<int,int>>vis;\n\n // cost, nodei, nodej, move_idx\n q.push({0, 0, 0, 0});\n \n while(!q.empty()){\n auto p = q.top();\n int cost = p[0];\n int i = p[1];\n int j = p[2];\n int move_idx = p[3];\n q.pop();\n\n if(i==n-1 && j==cols-1){\n return cost;\n }\n\n for(auto [x,y] : dir){\n int newj = j+x;\n int newi = i+y;\n if(newj >= 0 && newj < cols && newi >= 0 && newi < n && !vis.count({newi, newj})){\n // this adder the part here that will tell us what to add, it will be chosen based on the move_idx.\n int adder = 2;\n if(move_idx % 2 == 0){\n adder = 1;\n }\n q.push({ max(cost+adder, m[newi][newj] + adder), newi, newj, move_idx+1 });\n vis.insert({newi, newj});\n }\n }\n\n } \n\n return -1;\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
find-minimum-time-to-reach-last-room-ii | JAVA solution | using Heap | java-solution-using-heap-by-chiranjeeb2-o2hz | The solution below is the extension of the simplified version of this problem \n\nhttps://leetcode.com/problems/find-minimum-time-to-reach-last-room-i/discuss/6 | chiranjeeb2 | NORMAL | 2024-11-03T23:21:18.435826+00:00 | 2024-11-03T23:26:52.239681+00:00 | 12 | false | The solution below is the extension of the simplified version of this problem \n\nhttps://leetcode.com/problems/find-minimum-time-to-reach-last-room-i/discuss/6003977/JAVA-Solution-or-using-heap\n\n```\npublic int minTimeToReach(int[][] moveTime) {\n int m = moveTime.length, n = moveTime[0].length;\n \n int[][] moves = {{0,1},{0,-1},{1,0},{-1,0}};\n \n PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> a[0] - b[0]);\n \n Integer[][] minTime = new Integer[m][n];\n \n // 0: min time sofar\n // 1: i co-ordinate \n // 2: j co-ordinate \n // 3: 1 - represnets odd position, 0 - represents even position \n pq.offer(new int[]{0,0,0,0});\n \n while(!pq.isEmpty()){\n int[] top = pq.poll();\n \n if(top[1] == m-1 && top[2] == n-1){\n return top[0];\n }\n \n if(minTime[top[1]][top[2]] != null && minTime[top[1]][top[2]] < top[0]){\n continue;\n }\n \n for(int[] move : moves){\n int x = move[0] + top[1], y = move[1] + top[2];\n \n if(x < 0 || x >= m || y < 0 || y >= n){\n continue;\n }\n \n // if cur is odd position then cost is 2 otherwise the cost is 1\n int nextMoveCost = Math.max(moveTime[x][y], top[0]) + (top[3] == 1 ? 2 : 1);\n \n if(minTime[x][y] == null || minTime[x][y] > nextMoveCost){\n minTime[x][y] = nextMoveCost;\n \n // if the current position is even then next position will be odd and vice versa\n pq.offer(new int[]{nextMoveCost, x, y, (top[3] == 1 ? 0 : 1)});\n }\n }\n }\n \n return -1;\n }\n\n``` | 0 | 0 | ['Heap (Priority Queue)', 'Java'] | 0 |
find-minimum-time-to-reach-last-room-ii | 🚀 C# Priority Queue with Memory Optimization for Pathfinding | c-priority-queue-with-memory-optimizatio-ptln | \n\n\n## Intuition:\nTo find the minimum time to reach the bottom-right corner of a grid while considering movement penalties, we can apply an optimized pathfin | ivanvinogradov207 | NORMAL | 2024-11-03T21:26:11.918535+00:00 | 2024-11-04T02:02:48.419213+00:00 | 16 | false | \n\n\n## Intuition:\nTo find the minimum time to reach the bottom-right corner of a grid while considering movement penalties, we can apply an optimized pathfinding algorithm using a priority queue. The idea is similar to Dijkstra\'s algorithm, where the goal is to explore paths in order of their minimal cumulative time.\n\n## Approach:\n1. **Priority Queue**: Use a priority queue to always explore the current minimum time path.\n2. **Memory Matrix**: Track the minimum time needed to reach each cell to avoid re-processing paths with higher times.\n3. **Directional Movement**: Use an array to define movement directions (up, down, left, right).\n4. **Double Step Logic**: Alternate movement cost between normal and "double step" as a strategic choice.\n5. **Termination**: Stop once the bottom-right corner is reached and update the minimum time.\n\n## Complexity:\n- **Time complexity**: \n $$O(n \\times m \\log(n \\times m))$$ due to the priority queue operations in a grid of size `n x m`.\n\n- **Space complexity**: \n $$O(n \\times m)$$ for the memory matrix and priority queue storage.\n\n# Code:\n```csharp []\npublic class Solution {\n \n public int MinTimeToReach(int[][] moveTime) \n {\n int n = moveTime.Length, m = moveTime[0].Length;\n\n var memory = new int[n,m];\n for (int i = 0; i < n; i++)\n for (int j = 0; j < m; j++)\n memory[i,j] = -1;\n\n var directions = new (int,int)[]\n {\n (0,1),\n (1,0),\n (-1,0),\n (0,-1)\n };\n\n var queue = new PriorityQueue<(int,int,bool),int>();\n queue.Enqueue((0,0,false),0);\n \n var minTime = int.MaxValue;\n\n while (queue.Count > 0)\n {\n if (queue.TryDequeue(out var current, out int time))\n {\n (int i, int j, bool doubleStep) = current;\n\n if (i == n-1 && j == m-1)\n {\n minTime = Math.Min(minTime, time);\n continue;\n }\n\n if (time >= minTime)\n continue;\n\n if (memory[i,j] >= 0 && memory[i,j] <= time)\n continue;\n\n memory[i,j] = time;\n\n foreach ((var xDir, var yDir) in directions)\n {\n int newI = i+xDir, newJ = j+yDir;\n if (newI < 0 || newI >= n || newJ < 0 || newJ >= m)\n continue;\n \n var newTime = Math.Max(moveTime[newI][newJ], time)+(doubleStep ? 2 : 1);\n if (newTime < minTime)\n queue.Enqueue((newI, newJ, !doubleStep),newTime);\n }\n }\n }\n\n return minTime;\n }\n}\n``` | 0 | 0 | ['Depth-First Search', 'Memoization', 'Queue', 'Heap (Priority Queue)', 'Shortest Path', 'C#'] | 0 |
find-minimum-time-to-reach-last-room-ii | Beats 100% ✅ ✅ | Dijkstra's | Heap 🌟 🌟 | beats-100-dijkstras-heap-by-ram_tanniru-m6o2 | Intuition\nThe problem resembles a shortest path problem where we need to reach the bottom-right corner of a grid with the minimum time cost. Since each cell ha | ram_tanniru | NORMAL | 2024-11-03T18:23:47.871003+00:00 | 2024-11-03T18:23:47.871033+00:00 | 19 | false | ### Intuition\nThe problem resembles a shortest path problem where we need to reach the bottom-right corner of a grid with the minimum time cost. Since each cell has a specific time to traverse, and there\'s a toggle condition affecting the time cost, Dijkstra\'s algorithm (minimum priority queue) is well-suited. We track the minimum time required to reach each cell with a certain state (`flag`), representing a two-state toggle.\n\n### Approach\n1. **Use a Priority Queue**: Initialize a priority queue to manage states efficiently by their minimum cumulative distance. Each entry in the queue will track `(current distance, x, y, flag)`.\n2. **Direction Array**: Define movement directions (right, down, left, up) to navigate the grid.\n3. **3D Visited Array**: Use a `boolean[][][]` array to record visited cells with two possible `flag` states, preventing redundant processing.\n4. **Dijkstra\u2019s Logic**:\n - Start from the top-left cell `(0, 0)` with an initial distance of `0` and `flag = true`.\n - At each cell, calculate the next possible distance based on the `flag` state:\n - If `flag` is `true`, add 1 to the distance and toggle `flag` to `false` for the next cell.\n - If `flag` is `false`, add 2 to the distance and toggle `flag` to `true` for the next cell.\n - Push these states to the priority queue, always prioritizing the least cumulative distance.\n - If the bottom-right cell is reached, return the distance.\n\n### Complexity\n- **Time Complexity**: \n Since we process each cell potentially with two states (`flag = true` or `false`), the complexity is approximately \\(O(n \\times m \\times \\log(n \\times m))\\), where `n` and `m` are the grid dimensions. The logarithmic factor arises from the priority queue operations.\n\n- **Space Complexity**: \n The space complexity is \\(O(n \\times m)\\), considering the `visited` array and the space used by the priority queue, which holds states for each cell.\n\n# Code\n```python3 []\nclass Solution:\n def minTimeToReach(self, moveTime: List[List[int]]) -> int:\n n,m = len(moveTime),len(moveTime[0])\n vis = [[False for i in range(m)] for j in range(n)]\n dir = [(0,1),(1,0),(-1,0),(0,-1)]\n pq = [(0,0,0,True)]\n while pq:\n dist,i,j,flag = heapq.heappop(pq)\n if i==n-1 and j==m-1:\n return dist\n for dx,dy in dir:\n x,y = i+dx,j+dy\n if 0<=x<n and 0<=y<m and not vis[x][y]:\n vis[x][y] = True\n if flag:\n newDist = max(dist+1,moveTime[x][y]+1)\n else:\n newDist = max(dist+2,moveTime[x][y]+2)\n heapq.heappush(pq,(newDist,x,y,not flag))\n return -1\n```\n```java []\nclass Tuple {\n int dist;\n int x;\n int y;\n boolean flag;\n Tuple(int dist,int x,int y,boolean flag){\n this.dist = dist;\n this.x = x;\n this.y = y;\n this.flag = flag;\n }\n}\nclass Solution {\n public int minTimeToReach(int[][] moveTime) {\n int n = moveTime.length;\n int m = moveTime[0].length;\n PriorityQueue<Tuple> pq = new PriorityQueue<>((a,b)->a.dist-b.dist);\n boolean[][] vis = new boolean[n][m];\n int[][] dir = {{0,1},{1,0},{-1,0},{0,-1}};\n pq.add(new Tuple(0,0,0,true));\n while(!pq.isEmpty()){\n Tuple t = pq.poll();\n int dist = t.dist;\n int i = t.x;\n int j = t.y;\n boolean flag = t.flag;\n if(i==n-1 && j==m-1) {\n return dist;\n }\n for (int[] d : dir) {\n int dx = d[0];\n int dy = d[1];\n int x = i+dx;\n int y = j+dy;\n int newDist;\n if(0<=x && x<n && 0<=y && y<m && !vis[x][y]) {\n vis[x][y] = true;\n if(flag) {\n newDist = Math.max(moveTime[x][y]+1,dist+1);\n pq.add(new Tuple(newDist,x,y,false));\n }\n else {\n newDist = Math.max(moveTime[x][y]+2,dist+2);\n pq.add(new Tuple(newDist,x,y,true));\n }\n }\n }\n }\n return -1;\n }\n}\n``` | 0 | 0 | ['Heap (Priority Queue)', 'Shortest Path', 'Java', 'Python3'] | 0 |
find-minimum-time-to-reach-last-room-ii | Python solution(Dijkstra) | python-solutiondijkstra-by-tzju4iid9i-dzd4 | Complexity\n- Time complexity: O(N*M(logNM))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(NM)\n Add your space complexity here, e.g. O(n) | TzjU4iID9I | NORMAL | 2024-11-03T17:46:25.465639+00:00 | 2024-11-03T17:46:25.465666+00:00 | 6 | false | # Complexity\n- Time complexity: O(N*M(logNM))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(NM)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minTimeToReach(self, moveTime: List[List[int]]) -> int:\n if not moveTime:\n return -1\n n, m = len(moveTime), len(moveTime[0])\n queue = [(0, 1, 0, 0)] # (arrivetime, step, row, col)\n visited = set((0, 0))\n\n while queue:\n time, step, r, c = heapq.heappop(queue)\n print(time, step, r, c)\n if r == n - 1 and c == m - 1:\n print(r, c)\n return time\n for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:\n nr, nc = r + dr, c + dc\n if 0 <= nr < n and 0 <= nc < m and (nr, nc) not in visited:\n visited.add((nr, nc))\n if step == 1:\n newtime = max(time, moveTime[nr][nc]) + 1\n heapq.heappush(queue, [newtime, 2, nr, nc])\n else:\n newtime = max(time, moveTime[nr][nc]) + 2\n heapq.heappush(queue, [newtime, 1, nr, nc])\n \n\n``` | 0 | 0 | ['Python3'] | 0 |
find-minimum-time-to-reach-last-room-ii | Same code as 3341 with only 1 change | Easy and beginner friendly | same-code-as-3341-with-only-1-change-eas-i0vz | \n# Code\ncpp []\nclass Solution {\npublic:\n int minTimeToReach(vector<vector<int>>& moveTime) {\n int row = moveTime.size();\n int col = move | AMANJOTSINGH14 | NORMAL | 2024-11-03T16:55:42.769868+00:00 | 2024-11-03T16:55:42.769896+00:00 | 10 | false | \n# Code\n```cpp []\nclass Solution {\npublic:\n int minTimeToReach(vector<vector<int>>& moveTime) {\n int row = moveTime.size();\n int col = moveTime[0].size();\n priority_queue<tuple<int, int, int,int>, vector<tuple<int, int, int,int>>,greater<tuple<int, int, int,int>>> pq;\n vector<vector<int>> times(row, vector<int>(col, INT_MAX));\n pq.push({0,0,0,0});\n vector<pair<int,int>> dir= {{0,1},{0,-1},{1,0},{-1,0}};\n while(!pq.empty()){\n auto [time, x, y,flip]=pq.top();\n pq.pop();\n if(x==row-1 && y==col-1) return time;\n int i=0;\n while(i<4){\n int newX= x+ dir[i].first;\n int newY = y+ dir[i].second;\n if(newX<row && newX>=0 && newY<col && newY>=0 && times[newX][newY]==INT_MAX){\n if(time>=moveTime[newX][newY]) times[newX][newY]=time+ flip%2+1;\n else times[newX][newY]=moveTime[newX][newY] +flip%2+1;\n pq.push({times[newX][newY],newX,newY,flip%2+1});\n }\n i++;\n }\n }\n return -1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
find-minimum-time-to-reach-last-room-ii | extended dijkstra | extended-dijkstra-by-joshuadlima-34r3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | joshuadlima | NORMAL | 2024-11-03T16:42:30.321768+00:00 | 2024-11-03T16:42:30.321788+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n * m * log(n * m))\n\n- Space complexity: O(n * m)\n\n# Code\n```cpp []\n#define ll long long\nclass Solution {\npublic:\n vector<pair<int, int>> edges = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n\n int minTimeToReach(vector<vector<int>>& moveTime) {\n int n = moveTime.size(), m = moveTime[0].size();\n\n set<vector<ll>> st;\n ll dist[n][m][2];\n for(int i = 0; i < n; i++)\n for(int j = 0; j < m; j++)\n for(int k = 0; k <= 1; k++)\n dist[i][j][k] = LLONG_MAX;\n \n vector<ll> temp = {0, 0, 0, 1};\n st.insert(temp), dist[0][0][1] = 0;\n \n while (!st.empty())\n {\n auto itr = st.begin();\n ll dis = (*itr)[0];\n pair<int, int> node = {(*itr)[1], (*itr)[2]};\n int currentCost = ((*itr)[3] == 0 ? 1 : 0);\n st.erase(itr);\n \n for (auto it : edges)\n {\n ll edgeWeight = -1;\n pair<int, int> adjNode = {-1, -1};\n\n if(it.first + node.first < n && it.first + node.first >= 0 && it.second + node.second < m && it.second + node.second >= 0)\n adjNode = {it.first + node.first, it.second + node.second}, edgeWeight = moveTime[it.first + node.first][it.second + node.second];\n else\n continue;\n \n \n if (max(dis + currentCost + 1, edgeWeight + currentCost + 1) < dist[adjNode.first][adjNode.second][currentCost])\n {\n if (dist[adjNode.first][adjNode.second][currentCost] != LLONG_MAX) // node is in set\n st.erase({dist[adjNode.first][adjNode.second][currentCost], adjNode.first, adjNode.second, currentCost});\n \n dist[adjNode.first][adjNode.second][currentCost] = max(dis + currentCost + 1, edgeWeight + currentCost + 1);\n st.insert({dist[adjNode.first][adjNode.second][currentCost], adjNode.first, adjNode.second, currentCost});\n }\n }\n }\n\n return min(dist[n - 1][m - 1][0], dist[n - 1][m - 1][1]);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
falling-squares | Easy Understood O(n^2) Solution with explanation | easy-understood-on2-solution-with-explan-us8x | The idea is quite simple, we use intervals to represent the square. the initial height we set to the square cur is pos[1]. That means we assume that all the squ | leuction | NORMAL | 2017-10-15T03:04:30.634000+00:00 | 2018-10-25T01:50:26.012499+00:00 | 10,226 | false | The idea is quite simple, we use intervals to represent the square. the initial height we set to the square `cur` is `pos[1]`. That means we assume that all the square will fall down to the land. we iterate the previous squares, check is there any square `i` beneath my `cur` square. If we found that we have squares `i` intersect with us, which means my current square will go above to that square `i`. My target is to find the highest square and put square `cur` onto square `i`, and set the height of the square `cur` as \n```java\ncur.height = cur.height + previousMaxHeight;\n``` \nActually, you do not need to use the interval class to be faster, I just use it to make my code cleaner\n\n```java\nclass Solution {\n private class Interval {\n int start, end, height;\n public Interval(int start, int end, int height) {\n this.start = start;\n this.end = end;\n this.height = height;\n }\n }\n public List<Integer> fallingSquares(int[][] positions) {\n List<Interval> intervals = new ArrayList<>();\n List<Integer> res = new ArrayList<>();\n int h = 0;\n for (int[] pos : positions) {\n Interval cur = new Interval(pos[0], pos[0] + pos[1] - 1, pos[1]);\n h = Math.max(h, getHeight(intervals, cur));\n res.add(h);\n }\n return res;\n }\n private int getHeight(List<Interval> intervals, Interval cur) {\n int preMaxHeight = 0;\n for (Interval i : intervals) {\n // Interval i does not intersect with cur\n if (i.end < cur.start) continue;\n if (i.start > cur.end) continue;\n // find the max height beneath cur\n preMaxHeight = Math.max(preMaxHeight, i.height);\n }\n cur.height += preMaxHeight;\n intervals.add(cur);\n return cur.height;\n }\n}\n``` | 96 | 1 | ['Java'] | 16 |
falling-squares | Treemap solution and Segment tree (Java) solution with lazy propagation and coordinates compression | treemap-solution-and-segment-tree-java-s-pmsc | Here is the link I refer to:\nhttps://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/\nhttps://leetcode.com/articles/falling-squares/\n\nI think the fir | britishorthair | NORMAL | 2018-01-28T00:42:53.703000+00:00 | 2018-09-30T00:24:33.983749+00:00 | 7,265 | false | Here is the link I refer to:\nhttps://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/\nhttps://leetcode.com/articles/falling-squares/\n\nI think the first link is pretty useful to help you understand the segment tree's basic and lazy propagation. The second link I really appreciate its systematic way to define the interface to solve this using different algorithm. However, the segment tree implementation is not well explained in the article (at least it's hard for me to understand).\nThus, I decided to post my Treemap solution, segment tree solution and segment tree solution with lazy propagation for future readers.\n\nTreeMap Solution: The basic idea here is pretty simple, for each square i, I will find all the maximum height from previously dropped squares range from floorKey(i_start) (inclusive) to end (exclusive), then I will update the height and delete all the old heights.\n```\nimport java.util.SortedMap;\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n List<Integer> res = new ArrayList<>();\n TreeMap<Integer, Integer> startHeight = new TreeMap<>();\n startHeight.put(0, 0); \n int max = 0;\n for (int[] pos : positions) {\n int start = pos[0], end = start + pos[1];\n Integer from = startHeight.floorKey(start);\n int height = startHeight.subMap(from, end).values().stream().max(Integer::compare).get() + pos[1];\n max = Math.max(height, max);\n res.add(max);\n // remove interval within [start, end)\n int lastHeight = startHeight.floorEntry(end).getValue();\n startHeight.put(start, height);\n startHeight.put(end, lastHeight);\n startHeight.keySet().removeAll(new HashSet<>(startHeight.subMap(start, false, end, false).keySet()));\n }\n return res;\n }\n}\n```\nSegment tree with coordinates compression: It's easy to understand if go through the links above.\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n int n = positions.length;\n Map<Integer, Integer> cc = coorCompression(positions);\n int best = 0;\n List<Integer> res = new ArrayList<>();\n SegmentTree tree = new SegmentTree(cc.size());\n for (int[] pos : positions) {\n int L = cc.get(pos[0]);\n int R = cc.get(pos[0] + pos[1] - 1);\n int h = tree.query(L, R) + pos[1];\n tree.update(L, R, h);\n best = Math.max(best, h);\n res.add(best);\n }\n return res;\n }\n \n private Map<Integer, Integer> coorCompression(int[][] positions) {\n Set<Integer> set = new HashSet<>();\n for (int[] pos : positions) {\n set.add(pos[0]);\n set.add(pos[0] + pos[1] - 1);\n }\n List<Integer> list = new ArrayList<>(set);\n Collections.sort(list);\n Map<Integer, Integer> map = new HashMap<>();\n int t = 0;\n for (int pos : list) map.put(pos, t++);\n return map;\n }\n \n class SegmentTree {\n int[] tree;\n int N;\n \n SegmentTree(int N) {\n this.N = N;\n int n = (1 << ((int) Math.ceil(Math.log(N) / Math.log(2)) + 1));\n tree = new int[n];\n }\n \n public int query(int L, int R) {\n return queryUtil(1, 0, N - 1, L, R);\n }\n \n private int queryUtil(int index, int s, int e, int L, int R) {\n // out of range\n if (s > e || s > R || e < L) {\n return 0;\n }\n // [L, R] cover [s, e]\n if (s >= L && e <= R) {\n return tree[index];\n }\n // Overlapped\n int mid = s + (e - s) / 2;\n return Math.max(queryUtil(2 * index, s, mid, L, R), queryUtil(2 * index + 1, mid + 1, e, L, R));\n }\n \n public void update(int L, int R, int h) {\n updateUtil(1, 0, N - 1, L, R, h);\n }\n \n private void updateUtil(int index, int s, int e, int L, int R, int h) {\n // out of range\n if (s > e || s > R || e < L) {\n return;\n }\n tree[index] = Math.max(tree[index], h);\n if (s != e) {\n int mid = s + (e - s) / 2;\n updateUtil(2 * index, s, mid, L, R, h);\n updateUtil(2 * index + 1, mid + 1, e, L, R, h);\n }\n }\n }\n}\n```\nSegment tree with lazy propagation and coordinates compression: This code is easy to add if you already got the code above.\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n int n = positions.length;\n Map<Integer, Integer> cc = coorCompression(positions);\n int best = 0;\n List<Integer> res = new ArrayList<>();\n SegmentTree tree = new SegmentTree(cc.size());\n for (int[] pos : positions) {\n int L = cc.get(pos[0]);\n int R = cc.get(pos[0] + pos[1] - 1);\n int h = tree.query(L, R) + pos[1];\n tree.update(L, R, h);\n best = Math.max(best, h);\n res.add(best);\n }\n return res;\n }\n \n private Map<Integer, Integer> coorCompression(int[][] positions) {\n Set<Integer> set = new HashSet<>();\n for (int[] pos : positions) {\n set.add(pos[0]);\n set.add(pos[0] + pos[1] - 1);\n }\n List<Integer> list = new ArrayList<>(set);\n Collections.sort(list);\n Map<Integer, Integer> map = new HashMap<>();\n int t = 0;\n for (int pos : list) map.put(pos, t++);\n return map;\n }\n \n class SegmentTree {\n int[] tree;\n int[] lazy;\n int N;\n \n SegmentTree(int N) {\n this.N = N;\n int n = (1 << ((int) Math.ceil(Math.log(N) / Math.log(2)) + 1));\n tree = new int[n];\n lazy = new int[n];\n }\n \n public int query(int L, int R) {\n return queryUtil(1, 0, N - 1, L, R);\n }\n \n private int queryUtil(int index, int s, int e, int L, int R) {\n if (lazy[index] != 0) {\n // apply lazy to node\n int update = lazy[index];\n lazy[index] = 0;\n tree[index] = Math.max(tree[index], update);\n // check if this is leaf\n if (s != e) {\n lazy[2 * index] = Math.max(lazy[2 * index], update);\n lazy[2 * index + 1] = Math.max(lazy[2 * index + 1], update);\n }\n }\n // out of range\n if (s > e || s > R || e < L) {\n return 0;\n }\n // [L, R] cover [s, e]\n if (s >= L && e <= R) {\n return tree[index];\n }\n // Overlapped\n int mid = s + (e - s) / 2;\n return Math.max(queryUtil(2 * index, s, mid, L, R), queryUtil(2 * index + 1, mid + 1, e, L, R));\n }\n \n public void update(int L, int R, int h) {\n updateUtil(1, 0, N - 1, L, R, h);\n }\n \n private void updateUtil(int index, int s, int e, int L, int R, int h) {\n if (lazy[index] != 0) {\n // apply lazy to node\n int update = lazy[index];\n lazy[index] = 0;\n tree[index] = Math.max(tree[index], update);\n // check if this is leaf\n if (s != e) {\n lazy[2 * index] = Math.max(lazy[2 * index], update);\n lazy[2 * index + 1] = Math.max(lazy[2 * index + 1], update);\n }\n }\n // out of range\n if (s > e || s > R || e < L) {\n return;\n }\n if (s >= L && e <= R) {\n tree[index] = Math.max(tree[index], h);\n if (s != e) {\n lazy[2 * index] = Math.max(lazy[2 * index], h);\n lazy[2 * index + 1] = Math.max(lazy[2 * index + 1], h);\n }\n return;\n }\n int mid = s + (e - s) / 2;\n updateUtil(2 * index, s, mid, L, R, h);\n updateUtil(2 * index + 1, mid + 1, e, L, R, h);\n tree[index] = Math.max(tree[2 * index], tree[2 * index + 1]);\n }\n }\n}\n``` | 70 | 1 | [] | 11 |
falling-squares | Easy and Concise Python Solution (97%) | easy-and-concise-python-solution-97-by-l-rx3z | I used two list to take note of the current state.\nIf you read question 218. The Skyline Problem, you will easily understand how I do this.\n\npos tracks the x | lee215 | NORMAL | 2017-10-15T03:18:19.858000+00:00 | 2018-10-12T18:03:48.384902+00:00 | 6,636 | false | I used two list to take note of the current state.\nIf you read question **218. The Skyline Problem**, you will easily understand how I do this.\n\n```pos``` tracks the x-coordinate of start points.\n```height``` tracks the y-coordinate of lines.\n\n \n\n````\ndef fallingSquares(self, positions):\n height = [0]\n pos = [0]\n res = []\n max_h = 0\n for left, side in positions:\n i = bisect.bisect_right(pos, left)\n j = bisect.bisect_left(pos, left + side)\n high = max(height[i - 1:j] or [0]) + side\n pos[i:j] = [left, left + side]\n height[i:j] = [high, height[j - 1]]\n max_h = max(max_h, high)\n res.append(max_h)\n return res | 52 | 2 | [] | 14 |
falling-squares | C++ O(nlogn) | c-onlogn-by-imrusty-b7lk | Similar to skyline concept, going from left to right the path is decomposed to consecutive segments, and each segment has a height. Each time we drop a new squa | imrusty | NORMAL | 2017-10-16T03:07:44.821000+00:00 | 2018-09-18T18:17:40.831226+00:00 | 3,532 | false | Similar to skyline concept, going from left to right the path is decomposed to consecutive segments, and each segment has a height. Each time we drop a new square, then update the level map by erasing & creating some new segments with possibly new height. There are at most 2n segments that are created / removed throughout the process, and the time complexity for each add/remove operation is O(log(n)).\n\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& p) {\n map<pair<int,int>, int> mp;\n mp[{0,1000000000}] = 0;\n vector<int> ans;\n int mx = 0;\n for (auto &v:p) {\n vector<vector<int>> toAdd;\n cout << endl;\n int len = v.second, a = v.first, b =v.first + v.second, h = 0;\n auto it = mp.upper_bound({a,a});\n if (it != mp.begin() && (--it)->first.second <= a) ++it;\n while (it != mp.end() && it->first.first <b) {\n if (a > it->first.first) toAdd.push_back({it->first.first,a,it->second});\n if (b < it->first.second) toAdd.push_back({b,it->first.second,it->second});\n h = max(h, it->second);\n it = mp.erase(it);\n }\n mp[{a,b}] = h + len;\n for (auto &t:toAdd) mp[{t[0],t[1]}] = t[2];\n mx = max(mx, h + len);\n ans.push_back(mx);\n }\n \n return ans;\n }\n};\n``` | 19 | 0 | [] | 8 |
falling-squares | Easy Understood TreeMap Solution | easy-understood-treemap-solution-by-liuk-1180 | The squares divide the number line into many segments with different heights. Therefore we can use a TreeMap to store the number line. The key is the starting p | liukx08 | NORMAL | 2017-10-17T01:57:35.736000+00:00 | 2018-10-10T06:18:27.132197+00:00 | 3,311 | false | The squares divide the number line into many segments with different heights. Therefore we can use a TreeMap to store the number line. The key is the starting point of each segment and the value is the height of the segment. For every new falling square (s, l), we update those segments between s and s + l.\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n List<Integer> list = new ArrayList<>();\n TreeMap<Integer, Integer> map = new TreeMap<>();\n\n // at first, there is only one segment starting from 0 with height 0\n map.put(0, 0);\n \n // The global max height is 0\n int max = 0;\n\n for(int[] position : positions) {\n\n // the new segment \n int start = position[0], end = start + position[1];\n\n // find the height among this range\n Integer key = map.floorKey(start);\n int h = map.get(key);\n key = map.higherKey(key);\n while(key != null && key < end) {\n h = Math.max(h, map.get(key));\n key = map.higherKey(key);\n }\n h += position[1];\n\n // update global max height\n max = Math.max(max, h);\n list.add(max);\n\n // update new segment and delete previous segments among the range\n int tail = map.floorEntry(end).getValue();\n map.put(start, h);\n map.put(end, tail);\n key = map.higherKey(start);\n while(key != null && key < end) {\n map.remove(key);\n key = map.higherKey(key);\n }\n }\n return list;\n }\n}\n``` | 16 | 0 | [] | 8 |
falling-squares | Java - keep it simple, beats 99.6% | java-keep-it-simple-beats-996-by-tsuvmxw-7pxd | So we have N squares, 2N end points, 2N-1 intervals. We want to update the heights of intervals covered by a new square. Intervals are fixed; no insertion, merg | tsuvmxwu | NORMAL | 2017-10-31T19:23:29.249000+00:00 | 2018-10-11T01:43:09.164849+00:00 | 1,668 | false | So we have N squares, 2N end points, 2N-1 intervals. We want to update the heights of intervals covered by a new square. Intervals are fixed; no insertion, merging etc. Sort and binary-search.\n\n```\n public List<Integer> fallingSquares(int[][] positions)\n {\n int[] ends = new int[positions.length*2];\n for(int i=0; i<positions.length; i++)\n {\n ends[i*2+0] = positions[i][0];\n ends[i*2+1] = positions[i][0]+positions[i][1];\n }\n Arrays.sort(ends);\n\n int[] ceilings = new int[ends.length-1];\n int maxAll = 0;\n ArrayList<Integer> results = new ArrayList<>();\n for(int i=0; i<positions.length; i++)\n {\n int X = positions[i][0];\n int x = Arrays.binarySearch(ends, X);\n assert x>=0;\n int maxCeiling = 0;\n int Y = X + positions[i][1];\n for(int y=x; ends[y]<Y; y++)\n maxCeiling = Math.max(maxCeiling, ceilings[y]);\n maxCeiling += (Y-X);\n for(int y=x; ends[y]<Y; y++)\n ceilings[y] = maxCeiling;\n maxAll = Math.max(maxAll, maxCeiling);\n results.add(maxAll);\n }\n return results;\n }\n``` | 14 | 0 | [] | 4 |
falling-squares | Segment tree with lazy propagation and coordinates compression | segment-tree-with-lazy-propagation-and-c-ljjo | Understand the problem first\nInput: positions = [[1, 2], [2, 3], [6, 1]]\nAnd it will look like below, so you can easily get the result: [2, 5, 5]\n\n\nWith th | suensky2014 | NORMAL | 2021-03-06T05:10:51.066880+00:00 | 2021-03-06T05:10:51.066915+00:00 | 1,174 | false | ## Understand the problem first\nInput: `positions = [[1, 2], [2, 3], [6, 1]]`\nAnd it will look like below, so you can easily get the result: `[2, 5, 5]`\n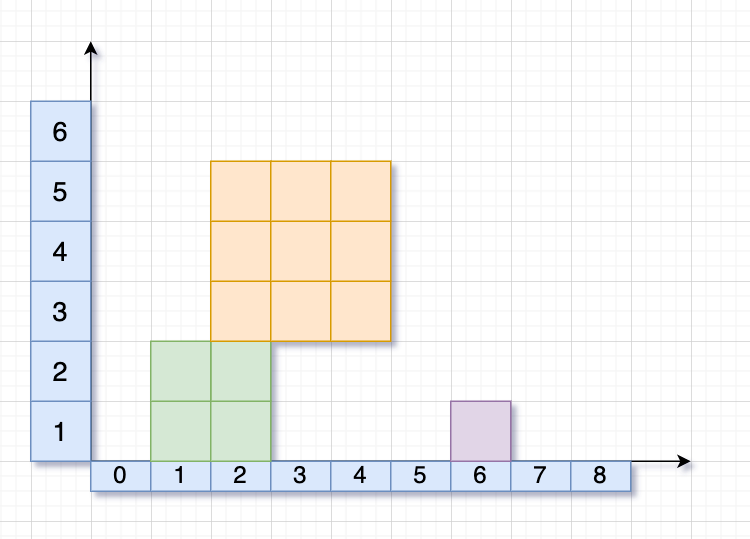\n\nWith that, we can come up with the straightforward `O(N^2)` solution:\n```java\npublic List<Integer> fallingSquares(int[][] positions) {\n int[] heights = new int[positions.length];\n\n List<Integer> ans = new ArrayList<>();\n int cur = 0;\n for (int i = 0; i < heights.length; ++i) {\n int left = positions[i][0];\n int size = positions[i][1];\n int right = left + size - 1;\n heights[i] += size;\n\n for (int j = i + 1; j < heights.length; ++j) {\n int left2 = positions[j][0];\n int size2 = positions[j][1];\n int right2 = left2 + size2 - 1;\n if (left2 <= right && right2 >= left) {\n heights[j] = Math.max(heights[i], heights[j]);\n }\n }\n cur = Math.max(cur, heights[i]);\n ans.add(cur);\n }\n return ans;\n }\n```\n\n## Segment tree with lazy propagation using array\nAn example of Segment tree:\n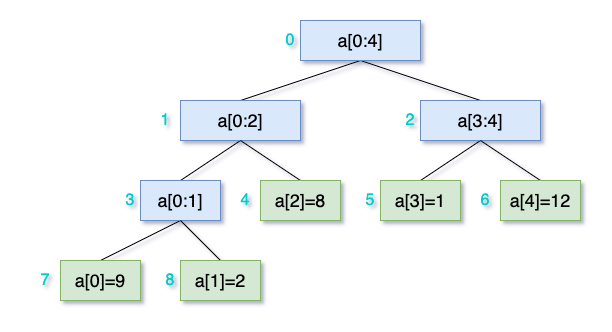\n\n```java\nclass SegmentTree {\n\tprivate int[] tree;\n\tprivate int[] lazy;\n\tprivate int n;\n\n\tpublic SegmentTree(int n) {\n\t\tthis.n = n;\n\t\tint len = (1 << (1 + (int)(Math.ceil(Math.log(n) / Math.log(2))))) - 1;\n\t\ttree = new int[len];\n\t\tlazy = new int[len];\n\t}\n\n\tpublic int query(int left, int right) {\n\t\treturn queryCore(left, right, 0, n - 1, 0);\n\t}\n\n\tpublic void update(int left, int right, int newVal) {\n\t\tupdateCore(left, right, 0, n - 1, 0, newVal);\n\t}\n\n\tprivate int queryCore(int left, int right, int segLeft, int segRight, int index) {\n\t\tif (lazy[index] != 0) {\n\t\t\t// Execute un-merged update.\n\t\t\texecute(index, lazy[index], segLeft, segRight);\n\t\t\t// Clear merged update.\n\t\t\tlazy[index] = 0;\n\t\t}\n\n\t\tif (left > segRight || right < segLeft) {\n\t\t\treturn 0;\n\t\t}\n\n\t\tif (left <= segLeft && segRight <= right) {\n\t\t\treturn tree[index];\n\t\t}\n\n\t\tint mid = getMid(segLeft, segRight);\n\t\treturn merge(queryCore(left, right, segLeft, mid, index * 2 + 1),\n\t\t\tqueryCore(left, right, mid + 1, segRight, index * 2 + 2));\n\t}\n\n\tprivate void updateCore(int left, int right,\n\t\t\t\t\t\t\tint segLeft, int segRight, int index, int newVal) {\n\t\tif (lazy[index] != 0) {\n\t\t\texecute(index, lazy[index], segLeft, segRight);\n\t\t\tlazy[index] = 0;\n\t\t}\n\n\t\tif (left > segRight || right < segLeft) {\n\t\t\treturn;\n\t\t}\n\n\t\tif (left <= segLeft && segRight <= right) {\n\t\t\t// Execute update for newVal.\n\t\t\texecute(index, newVal, segLeft, segRight);\n\t\t\treturn;\n\t\t}\n\n\t\tint mid = getMid(segLeft, segRight);\n\t\tupdateCore(left, right, segLeft, mid, index * 2 + 1, newVal);\n\t\tupdateCore(left, right, mid + 1, segRight, index * 2 + 2, newVal);\n\n\t\ttree[index] = merge(tree[index * 2 + 1], tree[index * 2 + 2]);\n\n\t}\n\n\tprivate void execute(int index, int update, int segLeft, int segRight) {\n\t\t// Apply the udpate.\n\t\ttree[index] = merge(tree[index], update);\n\t\tif (segLeft != segRight) {\n\t\t\t// Propagate the update to children.\n\t\t\tlazy[2 * index + 1] = merge(lazy[2 * index + 1], update);\n\t\t\tlazy[2 * index + 2] = merge(lazy[2 * index + 2], update);\n\t\t}\n\t}\n\n\tprivate int merge(int x, int y) {\n\t\treturn Math.max(x, y);\n\t}\n\n\tprivate int getMid(int left, int right) {\n\t\treturn left + (right - left) / 2;\n\t}\n}\n```\n\n## Segment tree with lazy propagation using binary tree\n```java\nclass SegmentTree {\n\tprivate Node root;\n\n\tpublic SegmentTree(int n) {\n\t\tthis.root = new Node(0, 0, n - 1);\n\t}\n\n\tpublic int query(int left, int right) {\n\t\treturn queryCore(left, right, root);\n\t}\n\n\tpublic void update(int left, int right, int newVal) {\n\t\tupdateCore(left, right, root, newVal);\n\t}\n\n\tprivate int queryCore(int left, int right, Node cur) {\n\t\tif (cur == null) {\n\t\t\treturn 0;\n\t\t}\n\n\t\tif (cur.lazyVal != 0) {\n\t\t\t// Execute un-merged update.\n\t\t\texecute(cur, cur.lazyVal);\n\t\t\t// Clear merged update.\n\t\t\tcur.lazyVal = 0;\n\t\t}\n\n\t\tif (left > cur.high || right < cur.low) {\n\t\t\treturn 0;\n\t\t}\n\n\t\tif (left <= cur.low && cur.high <= right) {\n\t\t\treturn cur.val;\n\t\t}\n\n\t\treturn merge(queryCore(left, right, cur.left),\n\t\t\tqueryCore(left, right, cur.right));\n\t}\n\n\tprivate void updateCore(int left, int right, Node cur, int newVal) {\n\t\tif (cur.lazyVal != 0) {\n\t\t\t// Execute un-merged update.\n\t\t\texecute(cur, cur.lazyVal);\n\t\t\t// Clear merged update.\n\t\t\tcur.lazyVal = 0;\n\t\t}\n\n\t\tif (left > cur.high || right < cur.low) {\n\t\t\treturn;\n\t\t}\n\n\t\tif (left <= cur.low && cur.high <= right) {\n\t\t\t// Execute update for newVal.\n\t\t\texecute(cur, newVal);\n\t\t\treturn;\n\t\t}\n\n\t\tint mid = getMid(cur.low, cur.high);\n\t\tif (cur.left == null) {\n\t\t\tcur.left = new Node(0, cur.low, mid);\n\t\t\tcur.right = new Node(0, mid + 1, cur.high);\n\t\t}\n\t\tupdateCore(left, right, cur.left, newVal);\n\t\tupdateCore(left, right, cur.right, newVal);\n\n\t\tcur.val = merge(cur.left.val, cur.right.val);\n\t}\n\n\tprivate void execute(Node cur, int update) {\n\t\t// Apply the udpate.\n\t\tcur.val = merge(cur.val, update);\n\t\tif (cur.low != cur.high) {\n\t\t\t// Propagate the update to children.\n\t\t\tif (cur.left == null) {\n\t\t\t\tint mid = getMid(cur.low, cur.high);\n\t\t\t\tcur.left = new Node(0, cur.low, mid);\n\t\t\t\tcur.right = new Node(0, mid + 1, cur.high);\n\t\t\t}\n\t\t\tcur.left.lazyVal = merge(cur.left.lazyVal, update);\n\t\t\tcur.right.lazyVal = merge(cur.right.lazyVal, update);\n\t\t}\n\t}\n\n\tprivate int merge(int x, int y) {\n\t\treturn Math.max(x, y);\n\t}\n\n\tprivate int getMid(int left, int right) {\n\t\treturn left + (right - left) / 2;\n\t}\n\n\tstatic class Node {\n\t\t// The value for range [low ... high].\n\t\tpublic int val;\n\t\tpublic int low;\n\t\tpublic int high;\n\t\t// The lazy update yet to apply.\n\t\tpublic int lazyVal;\n\t\tpublic Node left = null;\n\t\tpublic Node right = null;\n\n\t\tpublic Node(int val, int low, int high) {\n\t\t\tthis.val = val;\n\t\t\tthis.low = low;\n\t\t\tthis.high = high;\n\t\t\tthis.lazyVal = 0;\n\t\t}\n\t}\n}\n```\n\n## Coordinates compression\nExample: [1,2,6] -> [0,1,2]\n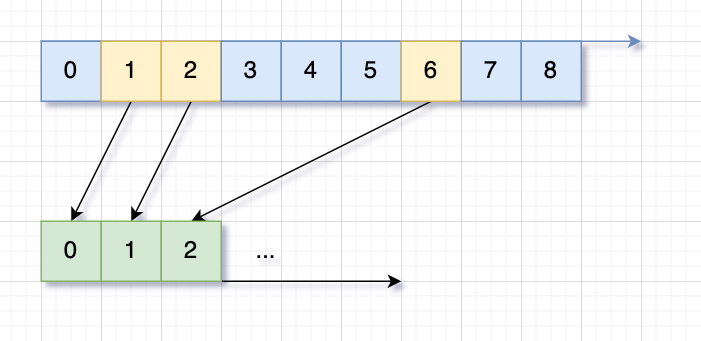\n\n```java\nMap<Integer, Integer> compressCoord(int[][] positions) {\n\tSet<Integer> points = new HashSet<>();\n\tfor (int[] pos : positions) {\n\t\tpoints.add(pos[0]);\n\t\tpoints.add(pos[0] + pos[1] - 1);\n\t}\n\n\tList<Integer> pointList = new ArrayList<>(points);\n\tCollections.sort(pointList);\n\n\tMap<Integer, Integer> coords = new HashMap<>();\n\tfor (int i = pointList.size() - 1; i >= 0; --i) {\n\t\tcoords.put(pointList.get(i), i);\n\t}\n\n\treturn coords;\n}\n```\n\n## Solution\nPut together, `SegmentTree` can be either of above.\n```java\npublic List<Integer> fallingSquares(int[][] positions) {\n\tMap<Integer, Integer> coords = compressCoord(positions);\n\n\tSegmentTree st = new SegmentTree(coords.size());\n\tList<Integer> ans = new ArrayList<>();\n\n\tint max = 0;\n\tfor (int[] pos : positions) {\n\t\tint left = coords.get(pos[0]);\n\t\tint right = coords.get(pos[0] + pos[1] - 1);\n\t\tint height = st.query(left, right) + pos[1];\n\t\tst.update(left, right, height);\n\n\t\tmax = Math.max(max, height);\n\t\tans.add(max);\n\t}\n\n\treturn ans;\n}\n```\n | 12 | 0 | [] | 4 |
falling-squares | C++ Segment Tree with range compression (easy & compact) | c-segment-tree-with-range-compression-ea-im0e | It is a good practice to use lazy propagation with range updates but since this problem has lesser number of points (1000), we can normally do it with segment t | leetcode07 | NORMAL | 2020-07-17T13:13:44.587899+00:00 | 2020-07-17T13:18:27.632288+00:00 | 1,058 | false | It is a good practice to use lazy propagation with range updates but since this problem has lesser number of points (1000), we can normally do it with segment tree and range compression (otherwise both memory and time exceeds). \n\nIf you are not good at segment trees please read the following artice: https://cp-algorithms.com/data_structures/segment_tree.html\n\n```\nclass Solution {\npublic:\n \n unordered_map<int, int> mp; //used for compression\n int tree[8000]; //tree[i] holds the maximum height for its corresponding range\n \n void update(int t, int low, int high, int i, int j, int h){\n if(i>j)\n return;\n if(low==high){\n tree[t]=h;\n return;\n }\n int mid=low+((high-low)/2);\n update(2*t, low, mid, i, min(mid, j), h);\n update(2*t+1, mid+1, high, max(mid+1, i), j, h);\n tree[t]=max(tree[2*t], tree[2*t+1]);\n }\n \n int query(int t, int low, int high, int i, int j){\n if(i>j)\n return -2e9;\n if(low==i && high==j)\n return tree[t];\n int mid=low+((high-low)/2);\n return max(query(2*t, low, mid, i, min(mid, j)), query(2*t+1, mid+1, high, max(mid+1, i), j));\n }\n \n vector<int> fallingSquares(vector<vector<int>>& positions) {\n set<int> s;\n memset(tree, 0, sizeof(tree));\n for(auto it: positions){\n s.insert(it[0]);\n s.insert(it[0]+it[1]-1);\n }\n int compressed=1, n=positions.size();\n vector<int> ans(n);\n for(auto it: s)\n mp[it]=compressed++;\n for(int i=0; i<n; i++){\n int start=positions[i][0], end=positions[i][1]+start-1, h=positions[i][1];\n int curr=query(1, 1, 2*n, mp[start], mp[end]), ncurr=curr+h;\n update(1, 1, 2*n, mp[start], mp[end], ncurr);\n ans[i]=tree[1]; //maximum height across all points till now\n }\n return ans;\n }\n};\n``` | 12 | 0 | [] | 1 |
falling-squares | Python 3 || 9 lines, bisect || T/S: 99% / 81% | python-3-9-lines-bisect-ts-99-81-by-spau-b3kw | \nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n\n def helper(box: List[int])->int:\n\n l, h = box\ | Spaulding_ | NORMAL | 2023-09-15T21:34:52.910832+00:00 | 2024-05-29T18:14:17.590275+00:00 | 507 | false | ```\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n\n def helper(box: List[int])->int:\n\n l, h = box\n r = l + h\n \n i, j = bisect_right(pos, l), bisect_left (pos, r)\n\n res = h + max(hgt[i-1:j], default = 0)\n pos[i:j], hgt[i:j] = [l, r], [res, hgt[j - 1]]\n\n return res\n\n \n hgt, pos, res, mx = [0], [0], [], 0\n \n return accumulate(map(helper, positions), max)\n```\n[https://leetcode.com/problems/falling-squares/submissions/1271687553/](https://leetcode.com/problems/falling-squares/submissions/1271687553/)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*log*N*) and space complexity is *O*(*N*), in which *N* ~ `len(positions)`. | 11 | 0 | ['Python3'] | 3 |
falling-squares | Python with dict, O(N^2) solution with comments | python-with-dict-on2-solution-with-comme-q5ij | \nclass Solution:\n def fallingSquares(self, positions):\n """\n :type positions: List[List[int]]\n :rtype: List[int]\n """\n | codercorgi | NORMAL | 2017-10-17T05:01:04.894000+00:00 | 2018-10-03T00:59:56.445702+00:00 | 1,049 | false | ```\nclass Solution:\n def fallingSquares(self, positions):\n """\n :type positions: List[List[int]]\n :rtype: List[int]\n """\n ans = []\n heights = {}\n for pos, side in positions:\n # finds nearby positions, if any\n left, right = pos, pos+side-1\n # compare to see if this block overlaps with L/R boundaries of existing blocks\n nearby = [key for key in heights.keys() if not (key[1] < pos or key[0] > right)]\n # finds height of block based on heights of existing and overlapping blocks\n if len(nearby) > 0:\n h = max(heights[key] for key in nearby) + side\n else:\n h = side\n # update the heights for left and right boundaries\n heights[(pos,right)] = h\n # add height to ans\n if len(ans) == 0:\n ans.append(h)\n else:\n ans.append(max(h,ans[-1]))\n return ans\n``` | 11 | 0 | [] | 4 |
falling-squares | Java 14ms, beats 99.38% using interval tree | java-14ms-beats-9938-using-interval-tree-yvd2 | java\nclass Solution {\n \n class Node {\n public int l;\n public int r;\n public int max;\n public int height;\n publi | zhewang711 | NORMAL | 2017-12-17T08:07:36.618000+00:00 | 2018-09-04T16:19:03.612324+00:00 | 1,836 | false | ```java\nclass Solution {\n \n class Node {\n public int l;\n public int r;\n public int max;\n public int height;\n public Node left;\n public Node right;\n \n public Node (int l, int r, int max, int height) {\n this.l = l;\n this.r = r;\n this.max = max;\n this.height = height;\n }\n }\n \n \n private boolean intersect(Node n, int l, int r) {\n if (r <= n.l || l >= n.r) {\n return false;\n }\n return true;\n }\n \n private Node insert(Node root, int l, int r, int height) {\n if (root == null) {\n return new Node(l, r, r, height);\n }\n \n if (l <= root.l) {\n root.left = insert(root.left, l, r, height);\n } else {\n // l > root.l\n root.right = insert(root.right, l, r, height);\n }\n root.max = Math.max(r, root.max);\n return root;\n }\n \n // return the max height for interval (l, r)\n private int maxHeight(Node root, int l, int r) {\n if (root == null || l >= root.max) {\n return 0;\n }\n \n int res = 0;\n if (intersect(root, l, r)) {\n res = root.height;\n }\n if (r > root.l) {\n res = Math.max(res, maxHeight(root.right, l, r));\n }\n res = Math.max(res, maxHeight(root.left, l, r));\n return res;\n }\n \n public List<Integer> fallingSquares(int[][] positions) {\n Node root = null;\n List<Integer> res = new ArrayList<>();\n int prev = 0;\n \n for (int i = 0; i < positions.length; ++i) {\n int l = positions[i][0];\n int r = positions[i][0] + positions[i][1];\n int currentHeight = maxHeight(root, l, r);\n root = insert(root, l, r, currentHeight + positions[i][1]);\n prev = Math.max(prev, currentHeight + positions[i][1]);\n res.add(prev);\n }\n \n return res;\n }\n}\n``` | 11 | 1 | [] | 3 |
falling-squares | O(nlogn) C++ Segment Tree | onlogn-c-segment-tree-by-sean-lan-uk23 | \nclass Solution {\npublic:\n int n;\n vector<int> height, lazy;\n\n void push_up(int i) {\n height[i] = max(height[i*2], height[i*2+1]);\n }\n\n void p | sean-lan | NORMAL | 2017-11-08T09:56:55.190000+00:00 | 2017-11-08T09:56:55.190000+00:00 | 1,627 | false | ```\nclass Solution {\npublic:\n int n;\n vector<int> height, lazy;\n\n void push_up(int i) {\n height[i] = max(height[i*2], height[i*2+1]);\n }\n\n void push_down(int i) {\n if (lazy[i]) {\n lazy[i*2] = lazy[i*2+1] = lazy[i];\n height[i*2] = height[i*2+1] = lazy[i];\n lazy[i] = 0;\n }\n }\n\n void update(int i, int l, int r, int L, int R, int val) {\n if (L <= l && r <= R) {\n height[i] = val;\n lazy[i] = val;\n return;\n }\n push_down(i);\n int mid = l + (r-l)/2;\n if (L < mid) update(i*2, l, mid, L, R, val);\n if (R > mid) update(i*2+1, mid, r, L, R, val);\n push_up(i);\n }\n\n int query(int i, int l, int r, int L, int R) {\n if (L <= l && r <= R) return height[i];\n push_down(i);\n int res = 0;;\n int mid = l + (r-l)/2;\n if (L < mid) res = max(res, query(i*2, l, mid, L, R));\n if (R > mid) res = max(res, query(i*2+1, mid, r, L, R));\n return res;\n }\n\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n vector<int> a;\n for (auto& p : positions) {\n a.push_back(p.first);\n a.push_back(p.first+p.second);\n }\n sort(a.begin(), a.end());\n n = unique(a.begin(), a.end()) - a.begin();\n a.resize(n);\n \n height.resize(n<<2, 0);\n lazy.resize(n<<2, 0);\n vector<int> res;\n for (auto& p : positions) {\n int l = lower_bound(a.begin(), a.end(), p.first) - a.begin();\n int r = lower_bound(a.begin(), a.end(), p.first+p.second) - a.begin();\n int maxh = query(1, 0, n, l, r);\n update(1, 0, n, l, r, maxh+p.second);\n res.push_back(query(1, 0, n, 0, n));\n }\n return res;\n }\n};\n``` | 10 | 0 | [] | 2 |
falling-squares | ✅✅Easy Readable c++ code || Segment Tree with lazy propagation || Cordinate Compression. | easy-readable-c-code-segment-tree-with-l-d0b5 | Intuition and Approach\n Describe your first thoughts on how to solve this problem. \nFirst of all, it will feel awkard and you might not get the intution of se | anupamraZ | NORMAL | 2023-06-19T13:49:06.035482+00:00 | 2023-06-19T13:49:06.035503+00:00 | 804 | false | # Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst of all, it will feel awkard and you might not get the intution of segment tree. But when you deminish 2D concept into 1D by replacing the height by values at in 1D. Then you will get idea of segment tree.\n\nFor a time being, forgot about cordinate compression. That is easiest part of this problem.\n\nThis figure in testcase-1 will diminish to:\n\n\nNow think it as range update and range query. Whenever a new square comes, it gets stacked and freezed over tallest stack in its range [l,r]. Just imagine like tetris game. Have you digested till now? If not, please use pen paper and visualize.\n\nso, what will be flow to solve the problem:\n For each query:\n 1.Query maximum height in range of upcoming square.\n 2.Update the value of all element in this range by \n`updatedVal=height of coming square+ maximum value earlier in that range.`\n 3. Then again query for maximum height in overall range [1,n].\n\n\nSo,let\'s know how to implement it:\nuse lazy propagation over segment tree for this.You can read it over [here.](https://cp-algorithms.com/data_structures/segment_tree.html#range-updates-lazy-propagation)\n\nUnder the topic given above in link, you will have two subsection:\n1. Addtion over segment/range [concentrate over why we mark lazy[0] after pushing for the node]\n2. Assignment over segment/range. [we will use this].\n since i am not using marked vector to track assignment (just to save space), i will use the fact that our height will never be -1, so i will just make lazy[node]=-1 after pushing/assignment for the node and whenever lazy[node]==-1, i will not update my node.\n```\nvoid push(int node)\n{\n if(lazy[node]!=-1)\n {\n tree[2*node] =tree[2*node+1]=lazy[node];\n lazy[2*node] = lazy[2*node+1]=lazy[node];\n lazy[node]=-1;\n }\n}\n```\n\nAfter that, it is as same as normal code for lazy propagation.\n\n**But you will ask, cordinates are order of 1e8**, so this will not work. So, use cordinate compression for that. Since ,maximum positions can be no more that 2*size of given vector,so we will only need some critical x cordinates.\n```\n unordered_map<int, int> index;\n set<int> sortedCoords;\n for (const auto& pos : positions) \n {\n sortedCoords.insert(pos[0]);\n sortedCoords.insert(pos[0] + pos[1] - 1);\n }\n int compressedIdx = 1;\n for (auto it:sortedCoords) \n {\n index[it] = compressedIdx;\n compressedIdx++;\n } \n\n```\n\n\n\nNaming of variables are as:\n- tl and tr are range of positions denoted by tree[node].\n- l and r are our given range of query.\n\nNote: I am using 1-based indexing in the following implementation.\n\n# Complexity\n- Time complexity: O(m * log(n)) where n= last compressed index and m=number of queries. As , we are using 2 query and 1 update per query.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1e5) as i am using a constant size tree and lazy.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n const static int N = 1e5 + 2;\nint INF = 1e9;\nint tree[4 * N], lazy[4 * N];\nvoid push(int node)\n{\n if(lazy[node]!=-1)\n {\n tree[2*node] =tree[2*node+1]=lazy[node];\n lazy[2*node] = lazy[2*node+1]=lazy[node];\n lazy[node]=-1;\n }\n}\nvoid update(int node, int tl, int tr, int l, int r, int updatedVal)\n{\n if (tl > tr)return;\n else if (l<=tl && tr <=r)\n {\n tree[node] = updatedVal;\n lazy[node] = updatedVal; // ye value update krni hai tl to tr segment of segment tree.\n }\n else if(tl==tr && (tl<l||tr>r)) return;\n else\n {\n push(node);\n int tm = (tl + tr) / 2;\n update(2*node, tl, tm, l,r, updatedVal);\n update(2*node + 1, tm + 1, tr,l, r, updatedVal);\n tree[node] = max(tree[2*node], tree[2*node+ 1]);\n }\n}\nint query(int node, int tl, int tr, int l, int r)\n{\n if (tl >tr)return -INF;\n if (l <= tl && tr <= r)return tree[node];\n if(tl==tr) return -INF;\n push(node);\n int tm = (tl + tr) / 2;\n int q1=query(2*node, tl, tm, l,r);\n int q2=query(2*node + 1, tm + 1, tr,l, r);\n return max(q1,q2);\n}\n\n vector<int> fallingSquares(vector<vector<int>>& positions) \n {\n memset(tree,0,sizeof(tree));\n memset(lazy,0,sizeof(lazy));\n memset(a,0,sizeof(a));\n\n unordered_map<int, int> index;\n set<int> sortedCoords;\n for (const auto& pos : positions) \n {\n sortedCoords.insert(pos[0]);\n sortedCoords.insert(pos[0] + pos[1] - 1);\n }\n int compressedIdx = 1;\n for (auto it:sortedCoords) \n {\n index[it] = compressedIdx;\n compressedIdx++;\n } \n int n= compressedIdx;\n int best = 0;\n vector<int> ans; \n for (const auto& pos : positions) \n {\n int l = index[pos[0]];\n int r = index[pos[0] + pos[1] - 1];\n int mxinlr=query(1,1,n,l,r);\n update(1,1,n,l,r,mxinlr+pos[1]);\n int temp=query(1,1,n,1,n);\n ans.push_back(temp);\n }\n return ans;\n }\n};\n``` | 9 | 0 | ['Segment Tree', 'C++'] | 3 |
falling-squares | Clean And Concise Lazy Propagation Segment Tree | clean-and-concise-lazy-propagation-segme-kego | \nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n SegmentNode root = new SegmentNode(0,Integer.MAX_VALUE,0);\n Li | gcl272633743 | NORMAL | 2020-01-31T13:31:13.961105+00:00 | 2020-01-31T13:31:13.961139+00:00 | 659 | false | ```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n SegmentNode root = new SegmentNode(0,Integer.MAX_VALUE,0);\n List<Integer> ans = new ArrayList<>();\n int max = 0;\n for(int[] p : positions){\n int left = p[0], height = p[1], right = left + height;\n int maxHeight = query(root, left, right) + height;\n max = Math.max(max,maxHeight);\n ans.add(max);\n add(root, left, right, maxHeight);\n }\n return ans;\n }\n public int query(SegmentNode root, int start, int end){\n if(start<=root.start && end>=root.end) return root.maxHeight;\n if(start>=root.end || end<=root.start) return 0;\n if (root.left==null) return root.maxHeight;\n int mid = root.start + (root.end - root.start) / 2;\n if (end <= mid) {\n return query(root.left, start, end);\n } else if (start >= mid) {\n return query(root.right, start, end);\n }\n return Math.max(query(root.left,start,mid),query(root.right,mid,end));\n }\n\n public void add(SegmentNode root, int start, int end, int maxHeight){\n if(start<=root.start && end>=root.end){\n root.maxHeight = maxHeight;\n root.left = null;\n root.right = null;\n return;\n }\n if(start>=root.end || root.start>=end) return;\n if(root.left==null){\n int mid = root.start + (root.end - root.start) / 2;\n root.left = new SegmentNode(root.start,mid,0);\n root.right = new SegmentNode(mid,root.end,0);\n }\n add(root.left,start,end,maxHeight);\n add(root.right,start,end,maxHeight);\n root.maxHeight = Math.max(root.left.maxHeight,root.right.maxHeight);\n }\n}\nclass SegmentNode{\n public SegmentNode left , right;\n public int start, end, maxHeight;\n public SegmentNode(int start, int end, int maxHeight){\n this.start = start;\n this.end = end;\n this.maxHeight = maxHeight;\n }\n}\n``` | 8 | 0 | ['Tree', 'Java'] | 1 |
falling-squares | C++, map with explanation, O(nlogn) solution 36ms | c-map-with-explanation-onlogn-solution-3-2cs5 | The idea is to store all non-overlapping intervals in a tree map, and to update the new height while adding new intervals into the map.\nThe interval is represe | zestypanda | NORMAL | 2017-10-15T04:29:35.357000+00:00 | 2017-10-15T04:29:35.357000+00:00 | 939 | false | The idea is to store all non-overlapping intervals in a tree map, and to update the new height while adding new intervals into the map.\nThe interval is represented by left bound l, right bound r, and height h. The format in the map is \n'''\ninvals[l] = {r, h};\n'''\nThe number of intervals in the map is at most 2n. The run time for search, insert and erase is O(nlogn) when adding n intervals. The iteration from iterator low to up seems time consuming, but all those intervals will be deleted after the loop. So the run time for this part in total is O(2n) because there are at most 2n intervals to delete.\n\nFor some reasons possibly related to Leetcode platform, the low and up iterators part is very sensitive to revision. I have another version "equal" to this one, but it results in undefined behavior/random output.\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n map<int, vector<int>> invals;\n int n = positions.size();\n vector<int> ht(n, 0);\n int l = positions[0].first, h = positions[0].second;\n ht[0] = h;\n invals[l] = {l+h, h};\n for (int i = 1; i < n; i++) {\n int h = drop(invals, positions[i]);\n ht[i] = max(h, ht[i-1]);\n }\n return ht;\n }\nprivate:\n // return the height of current square\n int drop(map<int, vector<int>>& invals, pair<int, int>& square) {\n int l = square.first, h = square.second, r = l+h, pre_ht = 0;\n auto low = invals.lower_bound(l), up = invals.lower_bound(r);\n // consider intervals in range [low-1, up) \n if (low != invals.begin()) low--;\n for (auto it = low; it != up; it++) \n if (it->second[0] > l) pre_ht = max(pre_ht, it->second[1]);\n // erase overlapping intervals, add current interval and update the interval at low and up-1\n int l1 = low->first, r1 = low->second[0], h1 = low->second[1], r2 = 0, h2 = 0;\n if (up != invals.begin()) {\n up--;\n r2 = up->second[0];\n h2 = up->second[1];\n up++;\n }\n invals.erase(low, up);\n invals[l] = {r, pre_ht+h};\n if (l1 < l) invals[l1] = {min(l, r1), h1};\n if (r2 > r) invals[r] = {r2, h2};\n return pre_ht+h;\n }\n};\n``` | 7 | 0 | [] | 4 |
falling-squares | C++ | segment tree | lazy propagations | O(n^2) |O(nlogn) | solution with Explanation | c-segment-tree-lazy-propagations-on2-onl-2o6t | So, here the heightOfSquare[i] will be max(heightOfSquare[j] where j < i and that are overlap with square[i] via x coordinate) + sideLength[i] (i.e. positions[i | ghoshashis545 | NORMAL | 2021-08-04T19:25:32.378322+00:00 | 2021-09-05T06:45:17.531356+00:00 | 628 | false | So, here the **heightOfSquare**[i] will be **max**(**heightOfSquare**[j] where j < i and that are overlap with **square**[i] via x coordinate) + **sideLength**[i] (i.e. **positions**[i][1]).\n\nBut, **results**[i] will be **max**(**prefixResult**,**heightOfSquare**[i]) because it may happen that tallest square is not i it\'s j where j < i.\n\n***Overlapping Conditions** :*\nleft and right point of ith box should be as follow ...\nleft(l) should be **positions**[i][0] (that given)\nright(r) should be **positions**[i][0] + **positions**[i][1] - **1** \nwe take **-1** because problem statement say that (A square brushing the left/right side of another square does not count as landing on it).\n\nyou can also take left and right points as (**positions**[i][0]+1) and (**positions**[i][0] + **positions**[i][1]) respectively.\n\nAs we know that a square box **i** placed top of another square **j** if and only if **(li-ri)** and **(lj-rj)** are overlap where, **li,ri** means left and right point of square **i**.\n \n1. li <= rj <= ri\n2. li <= lj <= ri\n3. li <= rj <= ri\n4. li <= lj <= ri\nIf any of the above condition is true then we can say that square_i(li-ri) and square_j(lj-rj) are ovelaps.\n```\nBrute Force Approach:\nvector<int> fallingSquares(vector<vector<int>>& positions) {\n vector<int>results;\n int n = (int)positions.size();\n auto check_overlap =[&](int i,int j){\n int li = positions[i][0];\n int ri = positions[i][0] + positions[i][1] - 1;\n int lj = positions[j][0];\n int rj = positions[j][0] + positions[j][1] - 1; \n return ((li <= lj && lj <= ri) or (li <= rj && rj <= ri) or (lj <= li && li <= rj) or (lj <= ri && ri <= rj));\n };\n \n vector<int>heightOfSquare(n,0);\n \n int prefixResult = 0;\n \n for(int i = 0; i < n; ++i){\n \n int sideLength = positions[i][1];\n int mxHeight = 0; \n for(int j = 0; j < i; ++j){\n if(check_overlap(i,j))\n mxHeight = max(mxHeight , heightOfSquare[j]);\n }\n \n heightOfSquare[i] = mxHeight + sideLength;\n \n prefixResult = max(prefixResult,heightOfSquare[i]);\n \n results.push_back(prefixResult);\n\n }\n return results;\n\t}\n\tTime : O(N^2)\n\tSpace : O(N)\n```\n\nNow we have to optimize this solution using lazy propagation and Co-ordinate compression technique.\n```\n// a = max(a,b);\nvoid umax(int &a,int b){\n a = max(a,b);\n}\nclass LaZy{\n vector<int>lazy,tree,a;\npublic:\n LaZy(int n){\n// initialization\n lazy.assign(4*n,0);\n tree.assign(4*n,0);\n }\n\n// update lazy\n void push(int nd,int ss,int se){\n int x = lazy[nd];\n// lazy value update \n if(x){\n umax(tree[nd],x);\n lazy[nd] = 0;\n }\n// not leaf node and lazy value of parent node updated\n if(ss != se and x){\n umax(lazy[2*nd],x);\n umax(lazy[2*nd+1],x);\n }\n }\n// update range (l,r) such that arr[i] = max(arr[i],val) for l <= i<= r.\n void update(int nd,int ss,int se,int l,int r,int val)\n {\n push(nd,ss,se);\n if(ss > r or se < l)\n return ;\n if(l <= ss and se <= r)\n {\n umax(lazy[nd],val);\n push(nd,ss,se); \n return;\n }\n int mid = (ss+se)/2;\n// call for left tree\n update(2*nd,ss,mid,l,r,val);\n// call for right tree\n update(2*nd+1,mid+1,se,l,r,val);\n// update current node value from it\'s subtree values. \n tree[nd] = max(tree[2*nd],tree[2*nd+1]);\n }\n \n// find maximum element in range(l,r) i.e. mx = max({arr[l],arr[l+1],arr[l+2]....arr[r]}) \n int query(int nd,int ss,int se,int l,int r)\n {\n \n push(nd,ss,se);\n if(ss > r or se < l)\n return 0;\n if(l <= ss and se <= r){\n return tree[nd];\n }\n int mid = (ss+se)/2; \n return max(query(2*nd,ss,mid,l,r),query(2*nd+1,mid+1,se,l,r));\n }\n};\n\n\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n\n // Now, as we can see that coordinate ranges is too large(10^8 + 10^6 + 1) that not fit in general array.\n// so we have to used coordinate compressions technique.\n \n\n// for storing index \n unordered_map<int,int>index;\n\n// storing elements in sorted order \n set<int>st;\n \n// As we know that a square box i placed top of another square j if and only if (li-ri) and (lj-rj) are overlap.\n \n// If ((li <= rj <= ri) or (li <= lj <= ri) or (li <= rj <= ri) or (li <= lj <= ri)) is true then we can see that square_i(li-ri) and square_j(lj-rj) are ovelaps.\n \n \n// so we can see that overlaping only depends on left and right points of the square not entire length of the square.\n \n for(int i = 0; i < (int)positions.size(); ++i){\n int l = positions[i][0];\n int r = positions[i][0] + positions[i][1] - 1;\n st.insert(l);\n st.insert(r); \n }\n \n \n// Now, here what I am doing that if the set contain st = {1,7,10,20} then we simple do that index[1] = 1 and index[7] = 2 and so on...\n \n int cnt = 0;\n// itterate over the set \n for(auto it : st)\n index[it] = ++cnt;\n \n// now we instantiated LaZy objects lz and passing size of the index(how many different indices are there).\n LaZy lz(cnt);\n \n// used for storing results. \n vector<int>results;\n\n// \n int prefixResult = 0;\n for(int i = 0; i < (int)positions.size(); ++i){\n int li = positions[i][0];\n int ri = positions[i][0] + positions[i][1] - 1;\n \n int index_li = index[li];\n int index_ri = index[ri];\n \n// Now, we find the square whose some part are in range (li-ri) because those squares are overlapping with current square_i.\n \n// so when we dropped square_i then height of the square_i will be max(the height of the square that are in range li-ri) + height of square_i.\n \n// so, here you might little bit confused that why I passing index_i and index_ri instead of passing li,ri.\n// so, the answer will be the value of li,ri are quite large that cann\'t fixed inarray so we passed index_li,index_ri. \n \n int height_i = lz.query(1,1,cnt,index_li,index_ri) + positions[i][1];\n \n// so, after placing the square at li-ri the height of the range li-ri will be changes and i.e. height_i. \n lz.update(1,1,cnt,index_li,index_ri,height_i);\n\n// It mights happen that tallest square present ouside of this range li-ri in this actual answer will be max(prefixResult,height_i).\n \n umax(prefixResult,height_i);\n \n// add results into the vector \n results.push_back(prefixResult);\n }\n return results;\n }\n};\nTime : O(nlogn)\nSpace : O(n)\n```\n | 6 | 1 | [] | 3 |
falling-squares | c++, map based short solution | c-map-based-short-solution-by-jadenpan-0nd4 | The running time complexity should be O(n\xb2), since the bottleneck is given by finding the maxHeight in certain range.\nIdea is simple, we use a map, and map[ | jadenpan | NORMAL | 2017-10-15T07:21:32.667000+00:00 | 2017-10-15T07:21:32.667000+00:00 | 1,702 | false | The running time complexity should be O(n\xb2), since the bottleneck is given by finding the maxHeight in certain range.\nIdea is simple, we use a map, and ```map[i] = h``` means, from ```i``` to next adjacent x-coordinate, inside this range, the height is ```h```.\nTo handle edge cases like adjacent squares, I applied STL functions, for left bound, we call ```upper_bound``` while for right bound, we call ```lower_bound```.\nSpecial thanks to @storypku for pointing out bad test cases like [[1,2],[2,3],[6,1],[3,3],[6,20]]\n\n```\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n map<int,int> mp = {{0,0}, {INT_MAX,0}};\n vector<int> res;\n int cur = 0;\n for(auto &p : positions){\n int l = p.first, r = p.first + p.second, h = p.second, maxH = 0;\n auto ptri = mp.upper_bound(l), ptrj = mp.lower_bound(r); // find range\n int tmp = ptrj->first == r? ptrj->second : (--ptrj)++->second; // tmp will be applied by new right bound \n for(auto i = --ptri; i != ptrj; ++i)\n maxH = max(maxH, i->second); // find biggest height\n mp.erase(++ptri, ptrj); // erase range\n mp[l] = h+maxH; // new left bound\n mp[r] = tmp; // new right bound\n cur = max(cur, mp[l]);\n res.push_back(cur);\n }\n return res;\n }\n``` | 6 | 1 | [] | 2 |
falling-squares | Python Diffenrent Concise Solutions | python-diffenrent-concise-solutions-by-g-psez | Thanks this great work : https://leetcode.com/articles/falling-squares/ \n\n\nApproach 1 :\njust like this article said , there are two operations: \n>update, w | gyh75520 | NORMAL | 2019-10-20T08:29:48.747310+00:00 | 2019-10-20T11:14:40.157677+00:00 | 474 | false | Thanks this great work : https://leetcode.com/articles/falling-squares/ \n\n\n**Approach 1 :**\njust like this article said , there are two operations: \n>update, which updates our notion of the board (number line) after dropping a square; \n>query, which finds the largest height in the current board on some interval.\n\nInstead of asking the question "what squares affect this query?", lets ask the question "what queries are affected by this square?"\n```python\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n max_h_of_p = [0]*len(positions)\n \n for i,(left,size) in enumerate(positions):\n right = left+size-1\n max_h_of_p[i] += size\n for offset,(left2,size2) in enumerate(positions[i+1:]):\n j = offset+i+1\n right2 = left2+size2-1\n if left2 <= right and left <= right2: # intersect\n max_h_of_p[j] = max(max_h_of_p[j], max_h_of_p[i])\n \n res = [] \n for h in max_h_of_p:\n res.append(max(res[-1],h)) if res else res.append(h)\n return res\n```\n-------------------------\n\n**Approach 2 :**\nSegment tree with coordinates compression\n```python\nclass SegmentTreeNode:\n def __init__(self, low, high):\n self.low = low\n self.high = high\n self.left = None\n self.right = None\n self.max = 0\n\nclass Solution: \n def _build(self, left, right):\n root = SegmentTreeNode(self.coords[left], self.coords[right])\n if left == right:\n return root\n \n mid = (left+right)//2\n root.left = self._build(left, mid)\n root.right = self._build(mid+1, right)\n return root\n \n def _update(self, root, lower, upper, val):\n if not root:\n return\n if lower <= root.high and root.low <= upper:# intersect\n root.max = val\n self._update(root.left, lower, upper, val)\n self._update(root.right, lower, upper, val)\n \n def _query(self, root, lower, upper):\n if lower <= root.low and root.high <= upper:\n return root.max\n if upper < root.low or root.high < lower:\n return 0\n return max(self._query(root.left, lower, upper), self._query(root.right, lower, upper))\n \n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n\t\t# coordinates compression\n coords = set()\n for left, size in positions:\n right = left+size-1\n coords.add(left)\n coords.add(right)\n self.coords = sorted(list(coords))\n root = self._build(0, len(self.coords)-1)\n \n res = []\n for left, size in positions:\n right = left+size-1\n h = self._query(root, left, right) + size\n res.append(max(res[-1],h)) if res else res.append(h)\n self._update(root, left, right, h)\n return res\n``` | 4 | 0 | ['Python3'] | 1 |
falling-squares | Java segment tree O(position.length * log(max_range)) | java-segment-tree-opositionlength-logmax-paf7 | My first segment tree ever.\n\n\n class SegNode {\n int left, mid, right;\n int max;\n boolean modified;\n SegNode leftChild, rig | qamichaelpeng | NORMAL | 2017-10-15T06:15:06.577000+00:00 | 2017-10-15T06:15:06.577000+00:00 | 1,213 | false | My first segment tree ever.\n```\n\n class SegNode {\n int left, mid, right;\n int max;\n boolean modified;\n SegNode leftChild, rightChild;\n SegNode(int left, int right, int max){\n this.left=left;\n this.right=right;\n this.mid=left+(right-left)/2;\n this.max=max;\n }\n int query(int left, int right){\n int ans;\n if ((left<=this.left&&right>=this.right)||this.leftChild==null){\n ans=this.max;\n }\n else {\n pushdown();\n ans = Integer.MIN_VALUE;\n if (left <= this.mid && this.leftChild != null)\n ans = Math.max(ans, leftChild.query(left, Math.min(this.mid, right)));\n if (right > this.mid && this.rightChild != null)\n ans = Math.max(ans, rightChild.query(Math.max(this.mid + 1, left), right));\n }\n// log.info("query on ({},{}) is {}, this.left, right, max: ({}, {}, {})", left, right, ans, this.left,this.right,this.max);\n return ans;\n }\n void pushdown(){\n if (this.leftChild!=null){\n if (this.modified) {\n this.leftChild.modified=true;\n this.leftChild.max=max;\n this.rightChild.modified=true;\n this.rightChild.max=max;\n }\n } else {\n this.leftChild=new SegNode(left, mid, max);\n this.rightChild=new SegNode(mid+1,right, max);\n\n }\n }\n\n void insert(int left, int right, int value){\n\n// log.info("insert {}, {}, {} on ({}, {})", left, right, value, this.left, this.right);\n if (left<=this.left && right>=this.right){\n if (value>this.max) {\n this.max = Math.max(this.max, value);\n modified=true;\n }\n\n } else {\n pushdown();\n if (left<=mid) this.leftChild.insert(left, Math.min(mid, right), value);\n if (right>mid)this.rightChild.insert(Math.max(mid+1, left), right, value);\n this.max=Math.max(this.leftChild.max, this.rightChild.max);\n modified=false;\n }\n }\n }\n\n public List<Integer> fallingSquares(int[][] positions) {\n List<Integer> ans=new ArrayList<>();\n int left=0, right=1_000_000_000;\n if (positions.length==0)return ans;\n SegNode root=new SegNode(left, right, 0);\n int oldPeek=0;\n for (int[] rec: positions){\n int curMax=root.query(rec[0], rec[0]+rec[1]-1);\n// log.info("curMax on ({},{}): {}", rec[0], rec[0]+rec[1]-1, curMax);\n\n int newMax=curMax+rec[1];\n oldPeek=Math.max(oldPeek, newMax);\n ans.add(oldPeek);\n root.insert(rec[0], rec[0]+rec[1]-1, newMax);\n }\n return ans;\n\n }\n``` | 4 | 1 | [] | 2 |
falling-squares | C++ O(n(log(n)) time O(n) space | c-onlogn-time-on-space-by-imrusty-80rj | Similar to skyline concept, going from left to right the path is decomposed to consecutive segments, and each segment has a height. Each time we drop a new squa | imrusty | NORMAL | 2017-10-16T03:07:03.540000+00:00 | 2017-10-16T03:07:03.540000+00:00 | 1,281 | false | Similar to skyline concept, going from left to right the path is decomposed to consecutive segments, and each segment has a height. Each time we drop a new square, then update the level map by erasing & creating some new segments with possibly new height. There are at most 2n segments that are created / removed throughout the process, and the time complexity for each add/remove operation is O(log(n)).\n\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& p) {\n map<pair<int,int>, int> mp;\n mp[{0,1000000000}] = 0;\n vector<int> ans;\n int mx = 0;\n for (auto &v:p) {\n vector<vector<int>> toAdd;\n cout << endl;\n int len = v.second, a = v.first, b =v.first + v.second, h = 0;\n auto it = mp.upper_bound({a,a});\n if (it != mp.begin() && (--it)->first.second <= a) ++it;\n while (it != mp.end() && it->first.first <b) {\n if (a > it->first.first) toAdd.push_back({it->first.first,a,it->second});\n if (b < it->first.second) toAdd.push_back({b,it->first.second,it->second});\n h = max(h, it->second);\n it = mp.erase(it);\n }\n mp[{a,b}] = h + len;\n for (auto &t:toAdd) mp[{t[0],t[1]}] = t[2];\n mx = max(mx, h + len);\n ans.push_back(mx);\n }\n \n return ans;\n }\n};\n``` | 4 | 0 | [] | 4 |
falling-squares | C++ coordinate compression | c-coordinate-compression-by-colinyoyo26-3hnt | \nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& ps) {\n set<int> sx;\n for (auto &p : ps) sx.emplace(p[0]), sx.em | colinyoyo26 | NORMAL | 2021-09-03T05:11:06.974756+00:00 | 2021-09-03T05:12:14.663191+00:00 | 163 | false | ```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& ps) {\n set<int> sx;\n for (auto &p : ps) sx.emplace(p[0]), sx.emplace(p[0] + p[1]);\n vector<int> x(sx.begin(), sx.end()), hs(x.size()), ans;\n unordered_map<int, int> idx;\n for (int i = 0; auto t : x) idx[t] = i++;\n for (int mh = 0; auto &p : ps) {\n int l = idx[p[0]], r = idx[p[0] + p[1]];\n int mx = *max_element(hs.begin() + l, hs.begin() + r);\n for (int i = l; i < r; i++) hs[i] = p[1] + mx;\n mh = max(mh, hs[l]);\n ans.emplace_back(mh);\n }\n return ans;\n }\n};\n``` | 3 | 0 | [] | 0 |
falling-squares | Segment Tree Lazy Propagation || O(nlog(n)) || C++ | segment-tree-lazy-propagation-onlogn-c-b-hfia | I used an unordered map as the container of the segment tree, whose expected complexity is O(1).\n\n\nvector<int> fallingSquares(vector<vector<int>>& p) {\n | NAHDI51 | NORMAL | 2021-07-22T15:45:52.105682+00:00 | 2021-07-22T15:48:19.000690+00:00 | 296 | false | I used an unordered map as the container of the segment tree, whose expected complexity is O(1).\n\n```\nvector<int> fallingSquares(vector<vector<int>>& p) {\n segment_tree seg((int)(1e8+1e6)+1); //Boundary position\n int mx = 0;\n vector<int> ans;\n for(int i = 0; i < p.size(); i++) {\n int h = p[i][1] + seg.query(p[i][0]+1, p[i][0] + p[i][1]);\n seg.update(p[i][0]+1, p[i][0]+p[i][1], h);\n mx = max(mx, h);\n ans.push_back(mx);\n }\n return ans;\n}\n```\nSegement Tree implementation:\n```\nclass segment_tree {\nunordered_map<unsigned int, int> seg;\nunordered_map<unsigned int, int> lazy;\n\nint size;\nbool invalid(int x, int y) {\n return x > y;\n}\nbool out_range(int a, int b, int x, int y) {\n return a > y || b < x;\n}\nbool in_range(int a, int b, int x, int y) {\n return a <= x && y <= b;\n}\nvoid propagate(int k, int x, int y, int val) {\n seg[k] = val;\n if(x != y)\n lazy[2*k] = val, lazy[2*k+1] = val;\n}\nvoid lazy_update(int k, int x, int y) {\n if(lazy[k]) {\n seg[k] = lazy[k];\n if(x != y)\n lazy[2*k] = lazy[k], lazy[2*k+1] = lazy[k];\n lazy[k] = 0;\n }\n}\npublic:\nsegment_tree(int n) {\n size = n+1;\n}\nvoid update(int l, int r, int val) {\n update(l, r, 1, 0, size-1, val);\n}\nvoid update(int a, int b, int k, int x, int y, int val) {\n if(invalid(x, y)) return;\n lazy_update(k, x, y);\n if(out_range(a, b, x, y)) return;\n if(in_range(a, b, x, y)) {propagate(k, x, y, val); return;}\n int d = (x+y) / 2;\n update(a, b, 2*k, x, d, val);\n update(a, b, 2*k+1, d+1, y, val);\n seg[k] = max(seg[2*k], seg[2*k+1]);\n}\nint query(int l, int r) {\n return query(l, r, 1, 0, size-1);\n}\nint query(int a, int b, int k, int x, int y) {\n if(invalid(x, y)) return INT_MIN;\n lazy_update(k, x, y);\n if(out_range(a, b, x, y)) return INT_MIN;\n if(in_range(a, b, x, y)) return seg[k];\n int d = (x+y)/2;\n return max(\n query(a, b, 2*k, x, d), \n query(a, b, 2*k+1, d+1, y)\n );\n}\n};\n``` | 3 | 0 | ['Tree', 'C'] | 0 |
falling-squares | [Java]Easy to understand plain segment tree | javaeasy-to-understand-plain-segment-tre-bb8i | \nclass Solution {\n class Node {\n int low, high;\n Node left, right;\n int val;\n public Node(int low, int high, int val) {\n | fang2018 | NORMAL | 2020-09-05T07:06:36.788386+00:00 | 2020-09-05T07:33:53.665661+00:00 | 187 | false | ```\nclass Solution {\n class Node {\n int low, high;\n Node left, right;\n int val;\n public Node(int low, int high, int val) {\n this.low = low;\n this.high = high;\n this.val = val;\n }\n @Override\n public String toString() {\n return low + " " + high + " " + val; \n }\n } \n Node root = new Node(0, 1000_000_10, 0);\n private int query(Node root, int l, int r) { \n if (l <= root.low && root.high <= r) {\n return root.val;\n } \n int mid = (root.low + root.high) / 2;\n int res = Integer.MIN_VALUE;\n if (root.left == null) root.left = new Node(root.low, mid, root.val);\n if (root.right == null) root.right = new Node(mid + 1, root.high, root.val);\n if (l <= mid) {\n res = Math.max(res, query(root.left, l, r));\n } \n if (r > mid) {\n res = Math.max(res, query(root.right, l, r));\n }\n return res;\n }\n private void update(Node root, int l, int r, int val) { \n if (l <= root.low && root.high <= r) {\n root.val = val;\n root.left = null;\n root.right = null;\n return;\n } \n int mid = (root.low + root.high) / 2;\n if (root.left == null) root.left = new Node(root.low, mid, root.val);\n if (root.right == null) root.right = new Node(mid + 1, root.high, root.val);\n if (l <= mid) {\n update(root.left, l, r, val);\n } \n if (r > mid) {\n update(root.right, l, r, val);\n } \n root.val = Math.max(root.left.val, root.right.val);\n }\n public List<Integer> fallingSquares(int[][] positions) {\n List<Integer> res = new ArrayList<>();\n int max = 0;\n for (int[] p : positions) {\n int val = query(root, p[0], p[0] + p[1] - 1);\n update(root, p[0], p[0] + p[1] - 1, p[1] + val);\n res.add(root.val);\n }\n return res;\n }\n}\n``` | 3 | 0 | [] | 0 |
falling-squares | C++ O(NlogN) TreeMap | c-onlogn-treemap-by-laseinefirenze-9fmh | In this question squares are only added without being removed, so a new, higher square will cover all squares under it. These squares are no longer needed to co | laseinefirenze | NORMAL | 2018-10-22T02:41:49.430750+00:00 | 2018-10-22T02:41:49.430832+00:00 | 390 | false | In this question squares are only added without being removed, so a new, higher square will cover all squares under it. These squares are no longer needed to consider, so we could just remove them from our records of heights. \nI used a ```TreeMap``` to record all useful heights. Every square adds 2 points to the record. Once a point is visited, it will be removed from the record, which gives us O(N) times for visiting. Searching the positions of new points takes O(logN), so the whole time complexity is O(NlogN).\n\n```C++\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n map<int, int> heights;\n heights[INT_MIN] = heights[INT_MAX] = 0;\n \n int maxh = 0;\n vector<int> res;\n for (auto p : positions) {\n int left = p.first, side = p.second, right = left + side;\n auto lt = --heights.upper_bound(left), rt = heights.lower_bound(right);\n int lh = 0, rh = 0;\n for (auto it = lt; it != rt; ) {\n rh = it->second;\n lh = max(lh, it->second);\n if (it == lt) it ++;\n else it = heights.erase(it);\n }\n lh += side;\n heights[left] = lh;\n heights[right] = rh;\n maxh = max(maxh, lh);\n res.push_back(maxh);\n }\n return res; \n }\n};\n``` | 3 | 0 | [] | 2 |
falling-squares | Python binary search 44ms | python-binary-search-44ms-by-kleedy-fz1v | \nclass Solution(object):\n def fallingSquares(self, positions):\n axis = [0, float(\'inf\')]\n heights = [0, 0]\n an = [0]\n for | kleedy | NORMAL | 2018-06-02T06:47:59.399013+00:00 | 2018-09-29T06:04:30.982828+00:00 | 486 | false | ```\nclass Solution(object):\n def fallingSquares(self, positions):\n axis = [0, float(\'inf\')]\n heights = [0, 0]\n an = [0]\n for left,length in positions:\n right = left + length\n idl = bisect.bisect_right(axis, left)\n idr = bisect.bisect_left(axis, right)\n \n h = max(heights[idl - 1: idr]) + length\n\n axis[idl: idr] = [left, right]\n heights[idl: idr] = [h, heights[idr - 1]]\n an.append(max(an[-1], h))\n\n return an[1:]\n``` | 3 | 0 | [] | 1 |
falling-squares | Python, O(n^2) solution, with explanation | python-on2-solution-with-explanation-by-6bihn | usesq to store information of squares. sq[i][0] is left edge, sq[i][1] is length, sq[i][2] is highest point. Everytime a new square falls, check if it has overl | bigbiang | NORMAL | 2017-10-15T03:34:06.529000+00:00 | 2017-10-15T03:34:06.529000+00:00 | 457 | false | use```sq``` to store information of squares. ```sq[i][0]``` is left edge, ```sq[i][1]``` is length, ```sq[i][2]``` is highest point. Everytime a new square falls, check if it has overlap with previous ```sq```, if so, add the largest ```sq[i][2]``` to its height.\n```\nclass Solution(object):\n def fallingSquares(self, positions):\n """\n :type positions: List[List[int]]\n :rtype: List[int]\n """\n if not positions:\n return []\n sq = [[positions[0][0], positions[0][1], positions[0][1]]]\n result = [positions[0][1]]\n max_h = result[0]\n for pos in positions[1: ]:\n h = pos[1]\n l = pos[0]\n add = 0\n for prev in sq:\n if not l >= prev[0] + prev[1] and not l + h <= prev[0]:\n add = max(add, prev[2])\n sq.append([l, h, h + add])\n max_h = max(max_h, h + add)\n result.append(max_h)\n return result\n``` | 3 | 2 | [] | 0 |
falling-squares | O(n^2) solution with explanation | on2-solution-with-explanation-by-yorkshi-57e0 | The height of the base of each box is the highest top of any other box already dropped that overlaps along the x-axis.\n\nSo for each box, we iterate over all p | yorkshire | NORMAL | 2017-10-15T03:43:04.449000+00:00 | 2017-10-15T03:43:04.449000+00:00 | 671 | false | The height of the base of each box is the highest top of any other box already dropped that overlaps along the x-axis.\n\nSo for each box, we iterate over all previously dropped boxes to find the base_height of the new box. The default is zero (ground level) if no overlaps are found.\nIf there is no overlap between a box and a previous box, then they are separate and will not stick, so the new box will not go on top of the previous box.\nIf there is overlap then the base_height of the new box will be the max of the previous base_height and height of the top of the previous box.\n\nStore the height of the new box as being base_height + side_length. Then append to the result the higher of the previous maximum height and this new box height. \n\n```\nclass Solution(object):\n def fallingSquares(self, positions):\n """\n :type positions: List[List[int]]\n :rtype: List[int]\n """\n heights, result = [], [] # heights is the top edge height for each box dropped\n highest = 0 # greatest height so far\n \n for i, position in enumerate(positions):\n\n left, side_length = position[0], position[1]\n \n base_height = 0 # default if no overlap with any boxes\n for j in range(i): # loop over all previously dropped boxes\n \n prev_left, prev_side = positions[j][0], positions[j][1] \n if (left + side_length <= prev_left) or (left >= prev_left + prev_side):\n continue # no overlap between this box and previous box\n base_height = max(base_height, heights[j])\n \n heights.append(base_height + side_length)\n highest = max(highest, heights[-1])\n result.append(highest)\n \n return result | 3 | 1 | ['Python'] | 1 |
falling-squares | Python Segment Tree with Lazy Propagation | python-segment-tree-with-lazy-propagatio-w01y | http://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/\n\n\nclass Solution:\n def fallingSquares(self, positions):\n """\n :type positi | notz22 | NORMAL | 2017-12-08T03:16:14.271000+00:00 | 2017-12-08T03:16:14.271000+00:00 | 493 | false | http://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/\n\n```\nclass Solution:\n def fallingSquares(self, positions):\n """\n :type positions: List[List[int]]\n :rtype: List[int]\n """\n # compress positions into consecutive indices\n all_pos = set()\n for p in positions:\n all_pos.add(p[0])\n all_pos.add(p[0] + p[1])\n \n pos_ind = {}\n for i, pos in enumerate(sorted(all_pos)):\n pos_ind[pos] = i\n \n n = len(pos_ind)\n segtree = [0] * (4 * n)\n lazy = [0] * (4 * n)\n \n def _insert(left, right, h, root, start, end):\n if lazy[root] != 0:\n if start != end:\n lazy[root*2] = max(lazy[root*2], lazy[root])\n lazy[root*2 + 1] = max(lazy[root*2+1], lazy[root])\n segtree[root] = max(segtree[root], lazy[root])\n lazy[root] = 0 \n \n if left > end or right < start:\n return\n \n if start == end:\n segtree[root] = max(segtree[root], h)\n return \n \n if left <= start and right >= end:\n segtree[root] = max(segtree[root], h)\n lazy[root*2] = max(lazy[root*2], h)\n lazy[root*2 + 1] = max(lazy[root*2+1], h)\n return\n \n mid = (start + end) // 2\n _insert(left, right, h, root*2, start, mid)\n _insert(left, right, h, root*2 + 1, mid + 1, end)\n segtree[root] = max(segtree[2*root], segtree[2*root + 1], h)\n return\n \n def _query(left, right, root, start, end):\n if lazy[root] != 0:\n if start != end:\n lazy[root*2] = max(lazy[root*2], lazy[root])\n lazy[root*2 + 1] = max(lazy[root*2+1], lazy[root])\n segtree[root] = max(segtree[root], lazy[root])\n lazy[root] = 0\n \n if left > end or right < start:\n return 0\n \n if start == end: \n return segtree[root]\n \n if left <= start and right >= end:\n return segtree[root]\n \n mid = (start + end) // 2\n return max(_query(left, right, root*2, start, mid), _query(left, right, root*2+1, mid + 1, end))\n \n def insert(left, right, h):\n _insert(left, right, h, 1, 0, n-1)\n \n def query(left, right):\n return _query(left, right, 1, 0, n-1)\n \n res = []\n accu_max = 0\n for p in positions:\n left_raw, h = p\n right_raw = left_raw + h\n left = pos_ind[left_raw]\n right = pos_ind[right_raw] - 1\n cur_max = query(left, right)\n new_max = cur_max + h\n accu_max = max(accu_max, new_max)\n res.append(accu_max)\n insert(left, right, new_max)\n return res\n``` | 3 | 0 | [] | 0 |
falling-squares | Lazy propagation | Point compression | Python | lazy-propagation-point-compression-pytho-z093 | Intuition\n Describe your first thoughts on how to solve this problem. \nRange update speaks segment tree.\n\n# Approach\n Describe your approach to solving the | tarushfx | NORMAL | 2024-01-19T16:21:41.090294+00:00 | 2024-01-19T16:21:41.090324+00:00 | 109 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRange update speaks segment tree.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Lazy propagation + Point compression**:\nUse max function instead of the regular addition function.\nAlso since the squares are going to be in an increasing order hence no need to worry about coming back and updating the parent. The parent will always be greater.\n\nPS: I am so proud of myself solving this on my first attempt, because this was my 1000th AC question and the hardest question I have solved on leetcode. Have a great day, cheers. :)\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import inf\n\n\nclass LazySegmentTree:\n def __init__(self, arr):\n self.arr = arr\n self.arr_size = len(arr)\n self.size = 4 * self.arr_size\n self.tree = [0] * self.size\n self.lazy = [0] * self.size\n self.build_tree(0, 0, self.arr_size - 1)\n\n def left_child(self, node):\n return 2 * node + 1\n\n def right_child(self, node):\n return 2 * node + 2\n\n def build_tree(self, node, start, end):\n if start == end:\n self.tree[node] = self.arr[start]\n return self.tree[node]\n mid = (start + end) // 2\n self.tree[node] = max(\n self.build_tree(self.left_child(node), start, mid),\n self.build_tree(self.right_child(node), mid + 1, end),\n )\n return self.tree[node]\n\n def update_diff(self, index, diff):\n self.update_helper(0, 0, self.arr_size - 1, index, index, diff)\n\n def update_range(self, left, right, value):\n self.update_helper(0, 0, self.arr_size - 1, left, right, value)\n\n def update_helper(self, node, start, end, left, right, diff):\n # Handle lazy propagation\n if self.lazy[node] != 0:\n self.tree[node] = max(self.tree[node], self.lazy[node])\n if start != end:\n self.lazy[self.left_child(node)] = self.lazy[node]\n self.lazy[self.right_child(node)] = self.lazy[node]\n self.lazy[node] = 0\n\n if start > right or end < left or start > end:\n return\n\n if start >= left and end <= right:\n self.tree[node] = diff\n if start != end:\n self.lazy[self.left_child(node)] = diff\n self.lazy[self.right_child(node)] = diff\n return\n\n mid = (start + end) // 2\n self.update_helper(self.left_child(node), start, mid, left, right, diff)\n self.update_helper(self.right_child(node), mid + 1, end, left, right, diff)\n self.tree[node] = max(\n self.tree[self.left_child(node)], self.tree[self.right_child(node)]\n )\n\n def query(self, left, right):\n return self.query_helper(0, 0, self.arr_size - 1, left, right)\n\n def query_helper(self, node, start, end, left, right):\n if self.lazy[node] != 0:\n self.tree[node] = max(self.tree[node], self.lazy[node])\n if start != end:\n self.lazy[self.left_child(node)] = self.lazy[node]\n self.lazy[self.right_child(node)] = self.lazy[node]\n self.lazy[node] = 0\n if start >= left and end <= right:\n return self.tree[node]\n\n if start > right or end < left:\n return 0\n\n mid = (start + end) // 2\n return max(\n self.query_helper(self.left_child(node), start, mid, left, right),\n self.query_helper(self.right_child(node), mid + 1, end, left, right),\n )\n\n\n\nclass Solution:\n def fallingSquares(self, positions):\n ans = []\n pos = set()\n for l, side in positions:\n pos.add(l)\n pos.add(l + side - 1)\n pos = sorted(list(pos))\n mp = {}\n for i, j in enumerate(pos):\n mp[j] = i\n n = len(pos)\n st = LazySegmentTree([0] * n)\n for l, side in positions:\n left, right = mp[l], mp[l + side - 1]\n mx = st.query(left, right)\n st.update_range(left, right, mx + side)\n ans.append(st.query(0, n - 1))\n return ans\n\n\n# S = Solution()\n# print(S.fallingSquares([[1, 2], [2, 3], [6, 1]]))\n# print(S.fallingSquares([[100, 100], [200, 100]]))\n\n``` | 2 | 0 | ['Segment Tree', 'Python3'] | 0 |
falling-squares | Solution | solution-by-deleted_user-wr9k | C++ []\n#include <vector>\n#include <algorithm>\n#include <iterator>\n\nstruct SegmentTree {\n\n SegmentTree(int n) : n(n) {\n size = 1;\n whil | deleted_user | NORMAL | 2023-04-20T12:29:29.066873+00:00 | 2023-04-20T13:48:12.825343+00:00 | 906 | false | ```C++ []\n#include <vector>\n#include <algorithm>\n#include <iterator>\n\nstruct SegmentTree {\n\n SegmentTree(int n) : n(n) {\n size = 1;\n while (size < n) {\n size <<= 1;\n }\n tree.resize(2*size);\n lazy.resize(2*size);\n }\n\n void add_range(int l, int r, int h) {\n l += size;\n r += size;\n\n tree[l] = max(tree[l], h);\n tree[r] = max(tree[r], h);\n if (l != r) {\n if (!(l & 1)) {\n lazy[l+1] = max(lazy[l-1], h);\n }\n if (r & 1) {\n lazy[r-1] = max(lazy[r-1], h);\n }\n }\n l >>= 1;\n r >>= 1;\n while (l != r) {\n tree[l] = max(tree[2*l], tree[2*l + 1]);\n tree[r] = max(tree[2*r], tree[2*r + 1]);\n if (l / 2 != r / 2) {\n if (!(l & 1)) {\n lazy[l+1] = max(lazy[l+1], h);\n }\n if (r & 1) {\n lazy[r-1] = max(lazy[r-1], h);\n }\n }\n l >>= 1;\n r >>= 1;\n }\n while (l > 0) {\n tree[l] = max(tree[2*l], tree[2*l + 1]);\n l >>= 1;\n }\n }\n int max_range(int l, int r) {\n l += size;\n r += size;\n\n int max_val = max(tree[l], tree[r]);\n while (l / 2 != r / 2) {\n if (!(l & 1)) {\n max_val = max(tree[l + 1], max_val);\n max_val = max(lazy[l + 1], max_val);\n }\n if (r & 1) {\n max_val = max(tree[r - 1], max_val);\n max_val = max(lazy[r - 1], max_val);\n }\n max_val = max(max_val, lazy[l]);\n max_val = max(max_val, lazy[r]);\n\n l >>= 1;\n r >>= 1;\n }\n max_val = max(max_val, lazy[r]);\n\n while (l / 2 > 0) {\n max_val = max(lazy[l], max_val);\n l >>= 1;\n }\n return max_val;\n }\n int global_max() {\n return max_range(0, n-1);\n }\n int size;\n int n;\n vector<int> tree;\n vector<int> lazy;\n};\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n \n vector<int> points;\n for (const auto& rect: positions) {\n points.push_back(rect[0]);\n points.push_back(rect[0] + rect[1] - 1);\n }\n sort(begin(points), end(points));\n auto new_end = unique(begin(points), end(points));\n points.resize(distance(begin(points), new_end));\n\n SegmentTree st(points.size());\n\n vector<int> results;\n\n int max_height = 0;\n for (const auto& rect: positions) {\n int x_1 = rect[0];\n int x_2 = rect[0] + rect[1] - 1;\n\n int l = distance(begin(points), lower_bound(begin(points), end(points), x_1));\n int r = distance(begin(points), lower_bound(begin(points), end(points), x_2));\n\n int cur_height = st.max_range(l, r);\n int new_height = rect[1] + cur_height;\n max_height = max(new_height, max_height);\n st.add_range(l, r, new_height);\n results.push_back(max_height);\n }\n return results;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n height = [0]\n pos = [0]\n res = []\n max_h = 0\n for left, side in positions:\n i = bisect.bisect_right(pos, left)\n j = bisect.bisect_left(pos, left + side)\n high = max(height[i - 1:j] or [0]) + side\n pos[i:j] = [left, left + side]\n height[i:j] = [high, height[j - 1]]\n max_h = max(max_h, high)\n res.append(max_h)\n return res\n```\n\n```Java []\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions)\n {\n int[] ends = new int[positions.length*2];\n for(int i=0; i<positions.length; i++)\n {\n ends[i*2+0] = positions[i][0];\n ends[i*2+1] = positions[i][0]+positions[i][1];\n }\n Arrays.sort(ends);\n\n int[] ceilings = new int[ends.length-1];\n int maxAll = 0;\n ArrayList<Integer> results = new ArrayList<>();\n for(int i=0; i<positions.length; i++)\n {\n int X = positions[i][0];\n int x = Arrays.binarySearch(ends, X);\n assert x>=0;\n int maxCeiling = 0;\n int Y = X + positions[i][1];\n for(int y=x; ends[y]<Y; y++)\n maxCeiling = Math.max(maxCeiling, ceilings[y]);\n maxCeiling += (Y-X);\n for(int y=x; ends[y]<Y; y++)\n ceilings[y] = maxCeiling;\n maxAll = Math.max(maxAll, maxCeiling);\n results.add(maxAll);\n }\n return results;\n }\n}\n```\n | 2 | 0 | ['C++', 'Java', 'Python3'] | 0 |
falling-squares | java solutions | java-solutions-by-infox_92-zjpg | \nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n int max = 0;\n List<Integer> result = new ArrayList<>();\n | Infox_92 | NORMAL | 2022-11-06T16:17:40.701918+00:00 | 2022-11-06T16:17:40.701991+00:00 | 571 | false | ```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n int max = 0;\n List<Integer> result = new ArrayList<>();\n TreeSet<Node> nodes = new TreeSet<>((n1, n2) -> n1.l - n2.l);\n // start position 0, height 0\n nodes.add(new Node(0, 0));\n for (int[] position : positions) {\n // failing square\n Node node = new Node(position[0], position[1]);\n // the right position\n int r = node.l+node.h;\n \n // find the node before the failing square\n Node floor = nodes.floor(node);\n \n // maxH is max height between node.l to r; will be add to node.h\n int maxH = floor.h;\n int preH = floor.h;\n if (floor.l == node.l) {\n floor.h = node.h;\n node = floor;\n } else nodes.add(node);\n \n Node prev = null;\n Node curr = nodes.higher(node);\n // iterate existing node till over the range of failing square\n while (curr != null && curr.l < r) {\n if (prev != null) nodes.remove(prev);\n preH = curr.h;\n maxH = Math.max(maxH, preH);\n prev = curr;\n curr = nodes.higher(curr);\n }\n \n if (prev != null) prev.l = r;\n \n node.h += maxH;\n nodes.add(new Node(r, preH));\n max = Math.max(max, node.h);\n result.add(max);\n }\n \n return result;\n }\n \n class Node {\n // start position\n int l;\n // height\n int h;\n public Node(int l, int h) {\n this.l = l;\n this.h = h;\n }\n }\n}\n``` | 2 | 0 | ['Java', 'JavaScript'] | 1 |
falling-squares | c++ | easy | short | c-easy-short-by-venomhighs7-pwg0 | \n# Code\n\nclass Solution {\npublic:\n unordered_map<int, int> mp; //used for compression\n int tree[8000]; //tree[i] holds the maximum height for its co | venomhighs7 | NORMAL | 2022-10-29T14:17:33.817598+00:00 | 2022-10-29T14:17:33.817641+00:00 | 710 | false | \n# Code\n```\nclass Solution {\npublic:\n unordered_map<int, int> mp; //used for compression\n int tree[8000]; //tree[i] holds the maximum height for its corresponding range\n \n void update(int t, int low, int high, int i, int j, int h){\n if(i>j)\n return;\n if(low==high){\n tree[t]=h;\n return;\n }\n int mid=low+((high-low)/2);\n update(2*t, low, mid, i, min(mid, j), h);\n update(2*t+1, mid+1, high, max(mid+1, i), j, h);\n tree[t]=max(tree[2*t], tree[2*t+1]);\n }\n \n int query(int t, int low, int high, int i, int j){\n if(i>j)\n return -2e9;\n if(low==i && high==j)\n return tree[t];\n int mid=low+((high-low)/2);\n return max(query(2*t, low, mid, i, min(mid, j)), query(2*t+1, mid+1, high, max(mid+1, i), j));\n }\n \n vector<int> fallingSquares(vector<vector<int>>& positions) {\n set<int> s;\n memset(tree, 0, sizeof(tree));\n for(auto it: positions){\n s.insert(it[0]);\n s.insert(it[0]+it[1]-1);\n }\n int compressed=1, n=positions.size();\n vector<int> ans(n);\n for(auto it: s)\n mp[it]=compressed++;\n for(int i=0; i<n; i++){\n int start=positions[i][0], end=positions[i][1]+start-1, h=positions[i][1];\n int curr=query(1, 1, 2*n, mp[start], mp[end]), ncurr=curr+h;\n update(1, 1, 2*n, mp[start], mp[end], ncurr);\n ans[i]=tree[1]; \n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
falling-squares | Python (dynamic) segment tree with Lazy-Propagation O(NLogN) | python-dynamic-segment-tree-with-lazy-pr-6uoh | I find solution 4 a little confusing. I have implemented a dynamic segment tree with Lazy-Propagation, inspired by @luxy622:\n\nfrom collections import defaultd | ginward | NORMAL | 2022-05-14T11:55:49.619008+00:00 | 2022-05-14T11:59:06.920429+00:00 | 212 | false | I find solution 4 a little confusing. I have implemented a dynamic segment tree with Lazy-Propagation, inspired by [@luxy622:](https://leetcode.com/problems/my-calendar-iii/discuss/214831/Python-13-Lines-Segment-Tree-with-Lazy-Propagation-O(1)-time)\n```\nfrom collections import defaultdict\nclass Solution:\n def query(self, start, end, left, right, ID):\n if right<start or left>end or left>right:\n return 0\n if left>=start and right<=end:\n return self.tree[ID]\n else:\n mid = (left+right)//2\n return max(self.lazy[ID], max(self.query(start, end, left, mid, 2*ID), self.query(start, end, mid+1, right, 2*ID+1)))\n\n def update(self, start, end, left, right, ID, height):\n if right<start or left>end or left>right:\n return\n if left>=start and right<=end:\n self.tree[ID] = max(height, self.tree[ID])\n self.lazy[ID] = max(height, self.lazy[ID])\n else:\n mid = (left+right)//2\n self.update(start, end, left, mid, 2*ID, height)\n self.update(start, end, mid+1, right, 2*ID+1, height)\n self.tree[ID] = max(self.lazy[ID], max(self.tree[2*ID], self.tree[2*ID+1]))\n \n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n coords = set()\n for left, size in positions:\n coords.add(left)\n coords.add(left + size - 1)\n index = {x: i for i, x in enumerate(sorted(coords))}\n best = 0\n res = []\n self.tree = defaultdict(int)\n self.lazy = defaultdict(int)\n for pos in positions:\n x, y = index[pos[0]], index[pos[0] + pos[1] - 1]\n h = pos[1] + self.query(x, y, 0, len(index), 1)\n best = max(h, best)\n self.update(x, y, 0, len(index), 1, h)\n res.append(best)\n return res\n``` | 2 | 0 | ['Tree'] | 0 |
falling-squares | Simple bruteforce solution C++ | simple-bruteforce-solution-c-by-hieudoan-0xd4 | The constraint is just small, who do you bother to use overkilled weapon like segment tree (ofcouse compression in advance)\n\nclass Solution {\npublic:\n ve | hieudoan190598 | NORMAL | 2022-03-24T06:59:11.385202+00:00 | 2022-03-24T06:59:11.385245+00:00 | 204 | false | The constraint is just small, who do you bother to use overkilled weapon like segment tree (ofcouse compression in advance)\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& a) {\n int n = a.size();\n vector<int> ans(n, 0);\n for(int i=0; i<n; i++) {\n ans[i] = a[i][1];\n int curL = a[i][0];\n int curR = a[i][1] + curL;\n for(int j=0; j<i; j++) {\n int L = a[j][0];\n int R = L + a[j][1];\n if (curL < R && curR > L) ans[i] = max(ans[i], a[i][1] + ans[j]);;\n }\n }\n for(int i=1; i<n; i++) ans[i] = max(ans[i], ans[i-1]);\n return ans;\n }\n};\n``` | 2 | 0 | [] | 1 |
falling-squares | C++ segment tree | c-segment-tree-by-vikassingh2810-ehuc | \nclass node\n{\n public:\n int hei,max_hei;\n int s,e;\n node* l;\n node* r;\n node(int s,int e):hei(0),max_hei(0),s(s),e(e),l(NULL),r(NULL)\n | vikassingh2810 | NORMAL | 2021-11-02T05:32:01.474714+00:00 | 2021-11-02T05:32:01.474741+00:00 | 190 | false | ```\nclass node\n{\n public:\n int hei,max_hei;\n int s,e;\n node* l;\n node* r;\n node(int s,int e):hei(0),max_hei(0),s(s),e(e),l(NULL),r(NULL)\n {}\n};\nclass Solution {\n \n public:\n node* build(vector<int>&nums,int s,int e)\n {\n if(s>=e)\n return NULL;\n if(e-s==1)\n return new node(nums[s],nums[e]);\n \n int mid=(s+e)/2;\n \n node* root=new node(nums[s],nums[e]);\n \n root->l=build(nums,s,mid);\n root->r=build(nums,mid,e);\n \n return root;\n }\n \n int find(node* root,int s,int e)\n {\n if(e<=root->s || s>=root->e)\n return INT_MIN;\n \n if(s<=root->s && e>=root->e)\n {\n return root->max_hei;\n }\n else\n {\n int l=find(root->l,s,e);\n int r=find(root->r,s,e);\n \n return max(root->hei,max(l,r));\n }\n }\n void update(node* root,int s,int e,int val)\n {\n \n if(e<=root->s || s>=root->e)\n return;\n \n if(s<=root->s && e>=root->e)\n {\n root->hei=val;\n root->max_hei=max(root->max_hei,root->hei);\n }\n else\n {\n update(root->l,s,e,val);\n update(root->r,s,e,val);\n root->max_hei=max(root->hei,max(root->l->max_hei,root->r->max_hei));\n }\n }\n \n vector<int> fallingSquares(vector<vector<int>>& rect){\n set<int>st;\n \n for(vector<int> &v:rect)\n { \n st.insert(v[0]); \n st.insert(v[1]+v[0]);\n } \n vector<int>x;\n for(auto &i:st)\n x.push_back(i);\n \n node* root=build(x,0,x.size()-1);\n vector<int>ans;\n for(auto & v:rect)\n {\n int val=0;\n int res=find(root,v[0],v[0]+v[1]);\n update(root,v[0],v[0]+v[1],res+v[1]);\n \n ans.push_back(root->max_hei);\n } \n return ans;\n }\n};\n``` | 2 | 0 | [] | 0 |
falling-squares | If you don't know segment trees or facing difficulty in understanding the solutions! | if-you-dont-know-segment-trees-or-facing-he3a | Being not very comfortable with advanced algorithms, I just tried to optimise my brute force solution by a method which is apparantly called \'Coordinate Compre | diggy26 | NORMAL | 2021-10-18T10:31:44.554865+00:00 | 2021-10-29T13:02:47.481027+00:00 | 214 | false | Being not very comfortable with advanced algorithms, I just tried to optimise my brute force solution by a method which is apparantly called \'Coordinate Compression\'. This solution beats 58% of submissions. Of course, there are better methods which works in O(n log(n)) but this solution would be a decent start if you are at beginner/intermediate level.\n\nI realised that only coordinates that affect my answer are the left and right ends (in x-axis) of the square. So, I tried to capture those end points uniquely and in ascending order using a set. Then I created a reference map which maps original point to the compressed point. Now, we are good to go. Find the maximum height in left to right limits, update the values in this range and save the value to ans array. \n\nHere\'s the code:\n\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n unordered_map<int,int> ref;\n unordered_map<int,int> m; //index, max height\n set<int> s;\n \n for(int i = 0; i<positions.size(); i++){\n s.insert(positions[i][0]); //left end\n s.insert(positions[i][0]+positions[i][1]-1); //right end\n }\n \n int mappedValue = 1;\n for(int originalValue : s){\n ref.insert({originalValue, mappedValue});\n mappedValue++;\n }\n \n vector<int> ans(positions.size());\n int mx = 0;\n \n for(int i = 0; i<positions.size(); i++){\n int left = ref[positions[i][0]];\n int right = ref[positions[i][0]+positions[i][1]-1];\n int len = positions[i][1];\n int prevMax = 0;\n \n for(int j = left; j<=right; j++){\n prevMax = max(prevMax, m[j]);\n }\n \n for(int j = left; j<=right; j++){\n m[j] = prevMax+len;\n }\n \n mx = max(mx, prevMax+len);\n ans[i] = mx;\n }\n \n return ans;\n }\n};\n``` | 2 | 0 | ['C'] | 1 |
falling-squares | [Java] Simple brute force solution, beats 71.5%T and 100%S | java-simple-brute-force-solution-beats-7-c8se | Runtime: 19 ms, faster than 71.50% of Java online submissions for Falling Squares.\nMemory Usage: 39.2 MB, less than 100.00% of Java online submissions for Fall | xiaoshuixin | NORMAL | 2020-11-20T09:16:50.875329+00:00 | 2020-11-20T09:16:50.875372+00:00 | 194 | false | Runtime: 19 ms, faster than 71.50% of Java online submissions for Falling Squares.\nMemory Usage: 39.2 MB, less than 100.00% of Java online submissions for Falling Squares.\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n int n = positions.length;\n int[] height = new int[n];\n int maxHeight = 0;\n ArrayList<Integer> res = new ArrayList<Integer>();\n for(int i = 0; i < n; i++){\n int left = positions[i][0];\n int right = positions[i][0] + positions[i][1];\n int h = 0;\n for(int j = 0; j < i; j++){\n int l = positions[j][0];\n int r = positions[j][0] + positions[j][1];\n if( !(right <= l || left >= r))\n h = Math.max(height[j],h);\n }\n height[i] = h + positions[i][1];\n maxHeight = Math.max(height[i],maxHeight);\n res.add(maxHeight);\n } \n return res; \n }\n}\n``` | 2 | 0 | [] | 2 |
falling-squares | Kotlin - Segment Tree, Binary Tree Implementation, with Lazy Propagation | kotlin-segment-tree-binary-tree-implemen-0t8h | \nclass Solution {\n fun fallingSquares(positions: Array<IntArray>): List<Int> {\n val root = SegmentTree()\n \n val ans = mutableListOf | idiotleon | NORMAL | 2020-11-16T03:07:44.029339+00:00 | 2020-11-16T03:17:58.109978+00:00 | 539 | false | ```\nclass Solution {\n fun fallingSquares(positions: Array<IntArray>): List<Int> {\n val root = SegmentTree()\n \n val ans = mutableListOf<Int>()\n var tallest = 0\n \n for((start, sideLen) in positions){\n val end = start + sideLen\n \n val height = root.query(start, end - 1) + sideLen\n \n root.update(start, end - 1, height)\n tallest = maxOf(tallest, height)\n \n ans.add(tallest)\n }\n \n return ans\n }\n \n private class SegmentTree {\n private companion object {\n private const val RANGE = 1e9.toInt() + 1\n }\n\n private val root = SegmentTreeNode(0, RANGE)\n\n fun update(rangeLo: Int, rangeHi: Int, value: Int) = update(rangeLo, rangeHi, value, root)\n fun query(rangeLo: Int, rangeHi: Int) = query(rangeLo, rangeHi, root)\n\n private fun update(rangeLo: Int, rangeHi: Int, value: Int, node: SegmentTreeNode?) {\n if (node == null) return\n if (rangeLo <= node.lo && node.hi <= rangeHi) {\n node.lazy += value\n }\n\n pushDown(node)\n\n // complete overlap or no overlap at all\n if (rangeLo <= node.lo && node.hi <= rangeHi || rangeHi < node.lo || rangeLo > node.hi) return\n\n update(rangeLo, rangeHi, value, node.left)\n update(rangeLo, rangeHi, value, node.right)\n\n node.max = maxOf(node.left!!.max, node.right!!.max)\n }\n\n private fun query(rangeLo: Int, rangeHi: Int, node: SegmentTreeNode?): Int {\n if (node == null) return 0\n pushDown(node)\n\n // no overlap\n if (rangeLo > node.hi || rangeHi < node.lo) return 0\n\n // complete overlap\n if (rangeLo <= node.lo && node.hi <= rangeHi) return node.max\n\n val leftMax = query(rangeLo, rangeHi, node.left)\n val rightMax = query(rangeLo, rangeHi, node.right)\n\n return maxOf(leftMax, rightMax)\n }\n\n private fun pushDown(node: SegmentTreeNode) {\n node.max = maxOf(node.max, node.lazy)\n\n if (node.lo != node.hi) {\n val mid = node.lo + (node.hi - node.lo) / 2\n\n if (node.left == null) {\n node.left = SegmentTreeNode(node.lo, mid)\n }\n\n if (node.right == null) {\n node.right = SegmentTreeNode(mid + 1, node.hi)\n }\n \n node.left!!.lazy = maxOf(node.left!!.lazy, node.lazy)\n node.right!!.lazy = maxOf(node.right!!.lazy, node.lazy)\n }\n\n node.lazy = 0\n }\n }\n\n private data class SegmentTreeNode(val lo: Int,\n val hi: Int,\n var max: Int = 0,\n var lazy: Int = 0,\n var left: SegmentTreeNode? = null,\n var right: SegmentTreeNode? = null)\n}\n```\n\n\nWith range compressed:\n```\nclass Solution {\n fun fallingSquares(positions: Array<IntArray>): List<Int> { \n val ranksMap = compressRange(positions)\n \n val root = SegmentTree()\n \n val ans = mutableListOf<Int>()\n var tallest = 0\n \n for((start, sideLen) in positions){\n val end = start + sideLen - 1\n \n val rangeLo = ranksMap[start]!!\n val rangeHi = ranksMap[end]!!\n \n val height = root.query(rangeLo, rangeHi) + sideLen\n \n root.update(rangeLo, rangeHi, height)\n tallest = maxOf(tallest, height)\n \n ans.add(tallest)\n }\n \n return ans\n }\n \n private fun compressRange(positions: Array<IntArray>): HashMap<Int, Int>{\n val coordSet = HashSet<Int>()\n for((start, sideLen) in positions){\n val end = start + sideLen - 1\n coordSet.add(start)\n coordSet.add(end)\n }\n val sortedCoords = coordSet.toMutableList().also{ it.sort() }\n \n var ranks = 1\n val ranksMap = HashMap<Int, Int>()\n for(coord in sortedCoords) ranksMap[coord] = ranks++\n \n return ranksMap\n }\n \n private class SegmentTree {\n private companion object {\n private const val RANGE = 1e9.toInt() + 1\n }\n\n private val root = SegmentTreeNode(0, RANGE)\n\n fun update(rangeLo: Int, rangeHi: Int, value: Int) = update(rangeLo, rangeHi, value, root)\n fun query(rangeLo: Int, rangeHi: Int) = query(rangeLo, rangeHi, root)\n\n private fun update(rangeLo: Int, rangeHi: Int, value: Int, node: SegmentTreeNode?) {\n if (node == null) return\n if (rangeLo <= node.lo && node.hi <= rangeHi) {\n node.lazy += value\n }\n\n pushDown(node)\n\n // complete overlap or no overlap at all\n if (rangeLo <= node.lo && node.hi <= rangeHi || rangeHi < node.lo || rangeLo > node.hi) return\n\n update(rangeLo, rangeHi, value, node.left)\n update(rangeLo, rangeHi, value, node.right)\n\n node.max = maxOf(node.left!!.max, node.right!!.max)\n }\n\n private fun query(rangeLo: Int, rangeHi: Int, node: SegmentTreeNode?): Int {\n if (node == null) return 0\n pushDown(node)\n\n // no overlap\n if (rangeLo > node.hi || rangeHi < node.lo) return 0\n\n // complete overlap\n if (rangeLo <= node.lo && node.hi <= rangeHi) return node.max\n\n val leftMax = query(rangeLo, rangeHi, node.left)\n val rightMax = query(rangeLo, rangeHi, node.right)\n\n return maxOf(leftMax, rightMax)\n }\n\n private fun pushDown(node: SegmentTreeNode) {\n node.max = maxOf(node.max, node.lazy)\n\n if (node.lo != node.hi) {\n val mid = node.lo + (node.hi - node.lo) / 2\n\n if (node.left == null) {\n node.left = SegmentTreeNode(node.lo, mid)\n }\n\n if (node.right == null) {\n node.right = SegmentTreeNode(mid + 1, node.hi)\n }\n \n node.left!!.lazy = maxOf(node.left!!.lazy, node.lazy)\n node.right!!.lazy = maxOf(node.right!!.lazy, node.lazy)\n }\n\n node.lazy = 0\n }\n }\n\n private data class SegmentTreeNode(val lo: Int,\n val hi: Int,\n var max: Int = 0,\n var lazy: Int = 0,\n var left: SegmentTreeNode? = null,\n var right: SegmentTreeNode? = null)\n}\n``` | 2 | 0 | ['Kotlin'] | 0 |
falling-squares | C++ O(nlog(n)) solution beats 95% | c-onlogn-solution-beats-95-by-gooong-wq05 | Hi, this is my concise and fast C++ solution based on set. We use this set to store the height of each interval and update iteratively.\n\n\nvector<int> falling | gooong | NORMAL | 2020-10-09T13:48:48.009600+00:00 | 2020-10-09T13:48:48.009633+00:00 | 206 | false | Hi, this is my concise and fast C++ solution based on `set`. We use this set to store the height of each interval and update iteratively.\n\n```\nvector<int> fallingSquares(vector<vector<int>>& positions) {\n\tvector<int> ret;\n\tmap<int, int> r2h; // right to height\n\tr2h[INT_MAX] = 0;\n\tint maxh = 0;\n\tfor(auto &position: positions){\n\t\tint l=position[0], d=position[1];\n\t\tint r = l + d;\n\t\tauto iter = r2h.upper_bound(l); // O(logn) operation for set\n\t\tint wh = iter->second;\n\t\tif(!r2h.count(l)) r2h[l] = wh;\n\t\twhile(iter->first<r){\n\t\t\t// Erase the interval that will be overlapped. Each interval will be erased at most once.\n\t\t\titer = r2h.erase(iter);\n\t\t\twh = max(wh, iter->second);\n\t\t}\n\t\t// update the height of current interval\n\t\tr2h[r] = wh + d;\n\t\tmaxh = max(maxh, wh+d);\n\t\tret.push_back(maxh);\n\t}\n\treturn ret;\n}\n``` | 2 | 3 | [] | 0 |
falling-squares | [Python] Segment Tree with LP | python-segment-tree-with-lp-by-zero_to_t-do9z | Idea: Denote N = number of squares; create 2 * N lines corresponding to left and right edges of every squares. These 2 * N lines define our 2 * N segments. Segm | zero_to_twelve | NORMAL | 2020-07-09T08:10:19.451681+00:00 | 2020-07-09T08:10:19.451718+00:00 | 192 | false | **Idea:** Denote N = number of squares; create 2 * N lines corresponding to left and right edges of every squares. These 2 * N lines define our 2 * N segments. Segment Tree serve to provide height of each segment.\nFor each incoming square, we use binary search to find its left edge and right edge, and update the height of corresponding segment. Update rule here is: new segment height = maximum old height of any point in segment + square side. Or in formula: <code>h(i, j) = max{ h(k, k) } + side</code> where <code> k in [i, j]</code>. We can query the segment tree to find <code>max{h(k, k)} </code> in <code>O(logN)</code>. Update the height in <code>O(logN)</code>. And finally we query the 0-th element of segment tree to find maximum height, this is also done in O(logN).\n\nThus overall time complexity is <code>O(NlogN)</code>. Auxiliary space is <code>O(N)</code>.\n```\nclass SegmentTree:\n def __init__(self, N):\n self.N = N\n self.st = [0] * 4 * N\n self.lazy = [0] * 4 * N\n def updateLazy(self, index, val, low, high):\n self.st[index] = val\n if low != high:\n self.lazy[2*index + 1] = val\n self.lazy[2*index + 2] = val\n self.lazy[index] = 0\n def updateRange(self, index, i, j, val, low, high):\n if low > j or high < i: \n return\n if self.lazy[index]:\n self.updateLazy(index, self.lazy[index], low, high)\n if i <= low and high <= j:\n self.updateLazy(index, val, low, high)\n return\n mid = (low + high)//2\n self.updateRange(2*index + 1, i, j, val, low, mid)\n self.updateRange(2*index + 2, i, j, val, mid + 1, high)\n self.st[index] = max(self.st[2*index + 1], self.st[2*index + 2])\n def queryRange(self, index, i, j, low, high):\n if low > j or high < i:\n return 0\n if self.lazy[index]:\n self.updateLazy(index, self.lazy[index], low, high)\n if i <= low and high <= j:\n return self.st[index]\n mid = (low + high)//2\n left = self.queryRange(2*index + 1, i, j, low, mid)\n right = self.queryRange(2*index + 2, i, j, mid + 1, high)\n return max(left, right)\n \nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n lines = []\n n = len(positions)\n for pos in positions:\n lines.append(pos[0])\n lines.append(pos[0] + pos[1])\n lines = sorted(lines)\n st = SegmentTree(2*n)\n res = []\n for pos in positions:\n start_idx = bisect.bisect_right(lines, pos[0])\n end_idx = bisect.bisect_left(lines, pos[0] + pos[1])\n maxHeight = st.queryRange(0, start_idx, end_idx, 0, 2*n - 1)\n st.updateRange(0, start_idx, end_idx, pos[1] + maxHeight, 0, 2*n - 1)\n res.append(st.st[0])\n return res\n``` | 2 | 0 | [] | 0 |
falling-squares | 3 Clean Incrementally Difficult Recursive Segment Tree (Simple, Compressed, Lazy) | 3-clean-incrementally-difficult-recursiv-iie0 | I try to code recursive segment trees instead of array-based ones since they are easier to understand. Even if they are a bit slower, they still easily meet the | thaicurry | NORMAL | 2020-06-10T08:00:10.681270+00:00 | 2020-06-10T15:05:44.035086+00:00 | 133 | false | I try to code recursive segment trees instead of array-based ones since they are easier to understand. Even if they are a bit slower, they still easily meet the time limit for LeetCode and programming interviews.\n\nHere, I have 3 steadily harder implementations of the Segment Tree so that it is easier to understand.\n\n**Simple Segment Tree (Memory Exceeded)**\nUnfortunately, the range of values here is 1e9 which means that this will take too much memory and time. But this is the best for initial debugging with small test-cases.\n\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n SegmentTree sg = new SegmentTree((int)1e4);\n int maxHeight = 0;\n List<Integer> output = new ArrayList<>();\n \n for (int[] position: positions) {\n int start = position[0];\n int end = position[0] + position[1] - 1;\n int heightInRange = sg.query(start, end);\n int updatedHeightInRange = heightInRange + position[1];\n maxHeight = Math.max(maxHeight, updatedHeightInRange);\n output.add(maxHeight);\n sg.update(start, end, updatedHeightInRange);\n }\n \n return output;\n \n }\n \n class SegmentTree {\n SegmentTreeNode root;\n \n public SegmentTree(int endIndex) {\n root = new SegmentTreeNode(0, endIndex);\n }\n \n public void update(int start, int end, int height) {\n for (int pos = start; pos <= end; pos++) {\n update(pos, height, root);\n }\n }\n \n private void update(int point, int height, SegmentTreeNode curr) {\n if (curr.start == curr.end) {\n curr.val = height;\n return;\n }\n \n int mid = curr.getMid();\n if (point <= mid) {\n update(point, height, curr.left);\n } else {\n update(point, height, curr.right);\n }\n \n curr.val = Math.max(curr.left.val, curr.right.val);\n }\n \n public int query(int start, int end) {\n return query(start, end, root);\n }\n \n \n private int query(int start, int end, SegmentTreeNode curr) {\n if (curr.start == curr.end) {\n return curr.val;\n } else if (curr.start == start && curr.end == end) {\n return curr.val;\n } else {\n int mid = curr.getMid();\n if (start >= mid + 1) {\n return query(start, end, curr.right);\n } else if (mid >= end) {\n return query(start, end, curr.left);\n } else {\n int leftVal = query(start, mid, curr.left);\n int rightVal = query(mid + 1, end, curr.right);\n return Math.max(leftVal, rightVal);\n }\n }\n }\n \n \n class SegmentTreeNode {\n int start;\n int end;\n int val;\n SegmentTreeNode left;\n SegmentTreeNode right;\n \n public SegmentTreeNode(int start, int end) {\n this.start = start;\n this.end = end;\n this.val = 0;\n if (start != end) {\n int mid = getMid();\n this.left = new SegmentTreeNode(start, mid);\n this.right = new SegmentTreeNode(mid + 1, end);\n } \n }\n \n public int getMid() {\n return start + (end - start) / 2;\n }\n \n }\n }\n}\n```\n\n**Compressed Co-ordinates (AC)**\nWe see that the actual number of points << range of points.\nThis is a hint that we can compress the range.\n\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n Map<Integer, Integer> index = getCompressedCoordinates(positions);\n SegmentTree sg = new SegmentTree(index.size() + 1);\n int maxHeight = 0;\n List<Integer> output = new ArrayList<>();\n \n for (int[] position: positions) {\n int start = index.get(position[0]);\n int end = index.get(position[0] + position[1] - 1);\n int heightInRange = sg.query(start, end);\n int updatedHeightInRange = heightInRange + position[1];\n maxHeight = Math.max(maxHeight, updatedHeightInRange);\n output.add(maxHeight);\n sg.update(start, end, updatedHeightInRange);\n }\n \n return output;\n \n }\n \n private Map<Integer, Integer> getCompressedCoordinates(int[][] positions) {\n Set<Integer> coords = new HashSet();\n coords.add(0);\n for (int[] pos: positions) {\n coords.add(pos[0]);\n coords.add(pos[0] + pos[1] - 1);\n }\n List<Integer> sortedCoords = new ArrayList(coords);\n Collections.sort(sortedCoords);\n\n Map<Integer, Integer> index = new HashMap();\n int t = 0;\n for (int coord: sortedCoords) index.put(coord, t++);\n return index;\n }\n \n class SegmentTree {\n SegmentTreeNode root;\n \n public SegmentTree(int endIndex) {\n root = new SegmentTreeNode(0, endIndex);\n }\n \n public void update(int start, int end, int height) {\n SegmentTree debug = this;\n for (int pos = start; pos <= end; pos++) {\n update(pos, height, root);\n }\n }\n \n private void update(int point, int height, SegmentTreeNode curr) {\n if (curr.start == curr.end) {\n curr.val = height;\n return;\n }\n \n int mid = curr.getMid();\n if (point <= mid) {\n update(point, height, curr.left);\n } else {\n update(point, height, curr.right);\n }\n \n curr.val = Math.max(curr.left.val, curr.right.val);\n }\n \n public int query(int start, int end) {\n SegmentTree debug = this;\n return query(start, end, root);\n }\n \n \n private int query(int start, int end, SegmentTreeNode curr) {\n if (curr.start == 0 && curr.end == 2) {\n int debug = 1;\n }\n if (curr.start == curr.end) {\n return curr.val;\n } else if (curr.start == start && curr.end == end) {\n return curr.val;\n } else {\n int mid = curr.getMid();\n if (start >= mid + 1) {\n return query(start, end, curr.right);\n } else if (mid >= end) {\n return query(start, end, curr.left);\n } else {\n int leftVal = query(start, mid, curr.left);\n int rightVal = query(mid + 1, end, curr.right);\n return Math.max(leftVal, rightVal);\n }\n }\n }\n \n class SegmentTreeNode {\n int start;\n int end;\n int val;\n SegmentTreeNode left;\n SegmentTreeNode right;\n \n public SegmentTreeNode(int start, int end) {\n this.start = start;\n this.end = end;\n this.val = 0;\n if (start != end) {\n int mid = getMid();\n this.left = new SegmentTreeNode(start, mid);\n this.right = new SegmentTreeNode(mid + 1, end);\n } \n }\n \n public int getMid() {\n return start + (end - start) / 2;\n }\n \n }\n }\n}\n```\n\n**Lazy Propagation (AC)**\n\nThis isn\'t as hard as it looks and it makes range updates much faster.\nYou are unlikely to need to code this end to end in an interview, but it is helpful to understand how the lazy function works and when we propagate it to the lower levels.\n\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n Map<Integer, Integer> index = getCompressedCoordinates(positions);\n SegmentTree sg = new SegmentTree(index.size() + 1);\n int maxHeight = 0;\n List<Integer> output = new ArrayList<>();\n \n for (int[] position: positions) {\n int start = index.get(position[0]);\n int end = index.get(position[0] + position[1] - 1);\n int heightInRange = sg.query(start, end);\n int updatedHeightInRange = heightInRange + position[1];\n maxHeight = Math.max(maxHeight, updatedHeightInRange);\n output.add(maxHeight);\n sg.update(start, end, updatedHeightInRange);\n }\n \n return output;\n \n }\n \n private Map<Integer, Integer> getCompressedCoordinates(int[][] positions) {\n Set<Integer> coords = new HashSet();\n coords.add(0);\n for (int[] pos: positions) {\n coords.add(pos[0]);\n coords.add(pos[0] + pos[1] - 1);\n }\n List<Integer> sortedCoords = new ArrayList(coords);\n Collections.sort(sortedCoords);\n\n Map<Integer, Integer> index = new HashMap();\n int t = 0;\n for (int coord: sortedCoords) index.put(coord, t++);\n return index;\n }\n \n class SegmentTree {\n SegmentTreeNode root;\n \n public SegmentTree(int endIndex) {\n root = new SegmentTreeNode(0, endIndex);\n }\n \n public void update(int start, int end, int height) {\n SegmentTree debug = this;\n for (int pos = start; pos <= end; pos++) {\n update(pos, height, root);\n }\n }\n \n private void update(int point, int height, SegmentTreeNode curr) {\n if (curr.start == curr.end) {\n curr.val = height;\n return;\n }\n \n int mid = curr.getMid();\n if (point <= mid) {\n update(point, height, curr.left);\n } else {\n update(point, height, curr.right);\n }\n \n curr.val = Math.max(curr.left.val, curr.right.val);\n }\n \n public int query(int start, int end) {\n SegmentTree debug = this;\n return query(start, end, root);\n }\n \n \n private int query(int start, int end, SegmentTreeNode curr) {\n if (curr.start == 0 && curr.end == 2) {\n int debug = 1;\n }\n if (curr.start == curr.end) {\n return curr.val;\n } else if (curr.start == start && curr.end == end) {\n return curr.val;\n } else {\n int mid = curr.getMid();\n if (start >= mid + 1) {\n return query(start, end, curr.right);\n } else if (mid >= end) {\n return query(start, end, curr.left);\n } else {\n int leftVal = query(start, mid, curr.left);\n int rightVal = query(mid + 1, end, curr.right);\n return Math.max(leftVal, rightVal);\n }\n }\n }\n \n class SegmentTreeNode {\n int start;\n int end;\n int val;\n SegmentTreeNode left;\n SegmentTreeNode right;\n \n public SegmentTreeNode(int start, int end) {\n this.start = start;\n this.end = end;\n this.val = 0;\n if (start != end) {\n int mid = getMid();\n this.left = new SegmentTreeNode(start, mid);\n this.right = new SegmentTreeNode(mid + 1, end);\n } \n }\n \n public int getMid() {\n return start + (end - start) / 2;\n }\n \n }\n }\n}\n``` | 2 | 1 | [] | 1 |
falling-squares | python3 bisect solution | python3-bisect-solution-by-butterfly-777-ku7h | ```\nfrom bisect import bisect_left as bl, bisect_right as br\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n | butterfly-777 | NORMAL | 2019-05-28T03:33:09.081574+00:00 | 2019-05-28T03:33:09.081626+00:00 | 149 | false | ```\nfrom bisect import bisect_left as bl, bisect_right as br\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n ans, xs, hs = [], [0], [0]\n for (x, h) in positions:\n i, j = br(xs, x), bl(xs, x+h)\n H = max(hs[max(i-1, 0):j], default = 0) + h\n xs[i:j] = [x, x + h]\n hs[i:j] = [H, hs[j - 1]]\n ans.append(H)\n if len(ans) > 1:\n ans[-1] = max(ans[-1], ans[-2])\n return ans | 2 | 0 | [] | 1 |
falling-squares | Java 44ms solution. Segment tree with lazy propagation | java-44ms-solution-segment-tree-with-laz-721u | \nclass Solution {\n public static class SegmentTree {\n TreeNode root;\n public class TreeNode {\n TreeNode left;\n Tree | zq670067 | NORMAL | 2018-10-23T18:58:11.402083+00:00 | 2018-10-23T18:58:11.402138+00:00 | 313 | false | ```\nclass Solution {\n public static class SegmentTree {\n TreeNode root;\n public class TreeNode {\n TreeNode left;\n TreeNode right;\n int leftBound;\n int rightBound;\n int lazy;\n int max;\n public TreeNode(int l,int r,int m) {\n leftBound = l;\n rightBound = r;\n lazy = 0;\n max = m;\n }\n public int getMid(){\n return leftBound + (rightBound-leftBound)/2;\n }\n public TreeNode getLeft() {\n if (left == null) left = new TreeNode(leftBound,getMid(),0);\n return left;\n }\n public TreeNode getRight() {\n if (right == null) right = new TreeNode(getMid()+1,rightBound,0);\n return right;\n }\n }\n public SegmentTree() {\n root = new TreeNode(0,Integer.MAX_VALUE,0);\n }\n public int getMax(){\n return root.max;\n }\n public TreeNode update(int l,int r,int val) {\n return update(root,l,r,val);\n }\n public TreeNode update(TreeNode node,int l,int r,int val) {\n if (node.lazy != 0) {\n node.max = node.lazy;\n if (node.leftBound != node.rightBound) {\n node.getLeft().lazy = node.lazy;\n node.getRight().lazy = node.lazy;\n }\n node.lazy = 0;\n }\n if(node.rightBound < node.leftBound || r < node.leftBound || l > node.rightBound) return node;\n if(node.leftBound >= l && node.rightBound <= r ) {\n node.max = val;\n if (node.leftBound != node.rightBound) {\n node.getLeft().lazy = val;\n node.getRight().lazy = val;\n }\n return node;\n }\n node.left = update(node.getLeft(),l,r,val);\n node.right = update(node.getRight(),l,r,val);\n node.max = Math.max(node.left.max,node.right.max);\n return node;\n }\n public int query(int l,int r) {\n return query(root,l,r);\n }\n public int query(TreeNode node,int l,int r) {\n if(node.rightBound < node.leftBound || r < node.leftBound || l > node.rightBound) return 0;\n if (node.lazy != 0) {\n node.max = node.lazy;\n if (node.leftBound != node.rightBound) {\n node.getLeft().lazy = node.lazy;\n node.getRight().lazy = node.lazy;\n }\n node.lazy = 0;\n }\n if(node.leftBound >= l && node.rightBound <= r ) return node.max;\n int q1 = query(node.getLeft(),l,r);\n int q2 = query(node.getRight(),l,r);\n return Math.max(q1,q2);\n }\n\n }\n public List<Integer> fallingSquares(int[][] positions) {\n List<Integer> res = new ArrayList<Integer>();\n SegmentTree segmentTree = new SegmentTree();\n for(int[] p: positions) {\n int h = segmentTree.query(p[0],p[0]+p[1]-1);\n segmentTree.update(p[0],p[0]+p[1]-1,h+p[1]);\n res.add(segmentTree.getMax());\n }\n return res;\n }\n \n}\n``` | 2 | 0 | [] | 1 |
falling-squares | Super Simple Java Solution - TreeSet with explanation | super-simple-java-solution-treeset-with-rvm45 | The solution is simple as follows:\n1- We need to records 3 things of each square: {start point, end point, current height}\nstart point is given;\nend point is | bmask | NORMAL | 2018-07-30T04:07:23.330291+00:00 | 2018-07-30T04:07:23.330291+00:00 | 211 | false | The solution is simple as follows:\n1- We need to records 3 things of each square: {start point, end point, current height}\nstart point is given;\nend point is : start+end-1;\ncurrent height is: if it lies on any square it will be baseSquareHeight+side_length otherwise it will be side_length\n2- Whenever a new square drops we need to find the highest dropped square which has some base in common with the new square. It is similar to finding two rectangle with common area. So the formula is:\nMath.max(new square start, dropped square start)<=Math.min(new square end, dropped square end)\n3- In case we have multiple dropped squares which have common area with the new square, choose the one with highest height.\n4- Then record the new square, and its height (if it lies on any square it will be baseSquareHeight+side_length otherwise it will be side_length)\n```\npublic List<Integer> fallingSquares(int[][] positions) { \n\t TreeSet<int[]> squares = new TreeSet<>(new Comparator<int[]>(){\n\t\t public int compare(int[] sqr1, int[] sqr2){\n\t\t\t return -(sqr1[2]-sqr2[2]); //highest squares at first\n\t\t }\n\t });\n\t List<Integer> result = new ArrayList<>();\n\t int maxHeight=-1;\n\t for(int[] position:positions){\n\t\t int start=position[0]; int end=position[0]+position[1]-1;\n\t\t int height=0;\n\t\t for(int[] square:squares){\n\t\t //find if the new square lies on any dropped square. If yes, pick the highest one\n\t\t\t if(Math.max(start, square[0])<=Math.min(end, square[1]) && height<square[2]) {height=square[2]; break;}\n\t\t }\n\t\t height+=position[1]; //baseSquareHeight+side_length\n\t\t maxHeight=Math.max(maxHeight, height);\n\t\t squares.add(new int[]{start,end,height});\n\t\t result.add(maxHeight);\n\t }\n\t \n return result;\n }\n``` | 2 | 0 | [] | 0 |
falling-squares | Simple and Fast c++ using interval tree, beat 99.99% | simple-and-fast-c-using-interval-tree-be-7k5t | // map means current height in interval\n// update by each position\n\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& positi | rico_cpp | NORMAL | 2018-06-28T01:25:17.729488+00:00 | 2018-06-28T01:25:17.729488+00:00 | 263 | false | // map <start, {end, height}> means current height in interval\n// update by each position\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n map<int, pair<int,int>> m;\n vector<int> res;\n int maxM = 0;\n for (const auto& p:positions)\n {\n int left = p.first, right = left+p.second;\n int curM = 0;\n auto it = m.upper_bound(left);\n if (it != m.begin())\n {\n --it;\n if (it->second.first <= left) ++it;\n }\n while (it != m.end() and it->first < right)\n {\n curM = max(curM, it->second.second); \n if (it->second.first > right)\n {\n m[right] = it->second;\n }\n if (it->first < left){\n it->second = {left, it->second.second};\n it++;\n }\n else m.erase(it++);\n }\n m[left] = {right, curM+p.second};\n maxM = max(maxM, curM+p.second);\n res.push_back(maxM);\n }\n return res;\n }\n};\n``` | 2 | 0 | [] | 0 |
falling-squares | Java ordered linked list, beat 100%, 11ms | java-ordered-linked-list-beat-100-11ms-b-2npu | \n class Node {\n int x, h;\n Node next;\n Node(int x, int h) {\n this.x = x;\n this.h = h;\n }\n }\n | iaming | NORMAL | 2017-10-29T21:02:14.871000+00:00 | 2017-10-29T21:02:14.871000+00:00 | 255 | false | ```\n class Node {\n int x, h;\n Node next;\n Node(int x, int h) {\n this.x = x;\n this.h = h;\n }\n }\n public List<Integer> fallingSquares(int[][] positions) {\n int n = positions.length, max = 0;\n List<Integer> ans = new ArrayList<>();\n Node head = new Node(0, 0);\n for (int[] p : positions) {\n Node prev = head;\n while (prev.next != null && prev.next.x < p[0]) {\n prev = prev.next;\n }\n int lasth = prev.h;\n int h = (prev.next == null || prev.next.x > p[0]) ? prev.h + p[1] : p[1];\n Node post = prev.next;\n while (post != null && post.x < p[0] + p[1]) {\n h = Math.max(h, post.h + p[1]);\n lasth = post.h;\n post = post.next;\n }\n Node cur = new Node(p[0], h);\n prev.next = cur;\n if (post == null || post.x > p[0] + p[1]) {\n cur.next = new Node(p[0] + p[1], lasth);\n cur = cur.next;\n }\n cur.next = post;\n max = Math.max(max, h);\n ans.add(max);\n }\n return ans;\n }\n``` | 2 | 0 | [] | 0 |
falling-squares | Easy AC SEGMENT TREE SOLUTION | easy-ac-segment-tree-solution-by-brutefo-q4c6 | Intuitionmy first thought is using segmenttree to save the status o every position but it's to large. So I decide to use Segment Tree MapApproachFirst I use Seg | BruteForceEnjoyer | NORMAL | 2025-02-18T03:45:49.600328+00:00 | 2025-02-18T03:45:49.600328+00:00 | 33 | false | # Intuition
my first thought is using segmenttree to save the status o every position but it's to large. So I decide to use Segment Tree Map
# Approach
First I use Segment Tree Map to save to height of every position we visited, i use lazy tree to make my programme faster, we just update the bigger node which include smaller node
# Code
```cpp []
class Solution {
public:
map < long long , long long > segment;
map < long long , long long > lazy;
void lazy_prog ( long long seed , long long low , long long high )
{
if ( lazy[seed] )
{
segment[seed] = lazy[seed];
if ( low != high )
{
lazy[seed*2+1] = lazy[seed];
lazy[seed*2+2] = lazy[seed];
}
lazy[seed] = 0;
}
}
long long findhighest ( long long seed , long long blow , long long bhigh , long long low , long long high )
{
lazy_prog ( seed , blow , bhigh );
if ( blow >= low && bhigh <= high ) return segment[seed];
if ( blow > high || bhigh < low ) return 0;
long long mid = ( blow + bhigh ) / 2;
return max ( findhighest( seed*2 + 1 , blow , mid , low , high )
, findhighest ( seed*2 + 2 , mid + 1, bhigh , low , high ) );
}
void add ( long long seed , long long blow , long long bhigh , long long low , long long high , long long key )
{
lazy_prog ( seed , blow , bhigh );
if ( blow >= low && bhigh <= high ){
segment[seed] = key;
lazy[seed] = key;
return;
}
if ( blow > high || bhigh < low ) return;
long long mid = ( blow + bhigh ) / 2;
add ( seed*2 + 1 , blow , mid , low , high , key );
add ( seed*2 + 2 , mid + 1 , bhigh , low , high , key );
segment[seed] = max(segment[seed*2+1] , segment[seed*2+2] );
}
vector<int> fallingSquares(vector<vector<int>>& positions) {
vector < int > result ;
long long l , r, height;
for ( int i = 0 ; i < positions.size() ; i ++ )
{
for ( int j = 0 ; j < 2 ; j ++ )
{
if ( j == 0 ) l = positions[i][j];
else {
r = l + positions[i][j] - 1;
height = positions[i][j];
}
}
long long highest = findhighest ( 0 , 0 , 101000005, l , r );
add ( 0 , 0 , 101000005, l , r, highest + height );
result.push_back(segment[0]);
}
return result ;
}
};
``` | 1 | 0 | ['Tree', 'Segment Tree', 'Recursion', 'C++'] | 0 |
falling-squares | Iterative Segment Tree | iterative-segment-tree-by-aryashp-9y8h | Segment Tree\nI used the iterative implemnetation of segment tree instead of recursive and coordinate compression by binary search\n\n# Complexity\n- Time compl | aryashp | NORMAL | 2023-04-02T19:38:51.224430+00:00 | 2023-04-02T19:38:51.224460+00:00 | 103 | false | # Segment Tree\nI used the iterative implemnetation of segment tree instead of recursive and coordinate compression by binary search\n\n# Complexity\n- Time complexity:\nO(n^2) as instead of performing Lazy Propagation, we can increase the elements falling in range of square edge one by one.\n\n# Code\n```\ntypedef long long ll;\nll N = (ll)1e5;\nll tree[(ll)2e5];\n\nvoid build(ll n)\n{\n for(int i=n-1; i>0; i--)\n {\n tree[i] = max(tree[i<<1], tree[i<<1|1]);\n }\n}\n\nvoid modify(ll p, ll val, ll n)\n{\n for(tree[p+=n] = val; p>1; p>>=1)\n {\n tree[p>>1] = max(tree[p], tree[p^1]);\n }\n}\n\nll query(ll l, ll r, ll n)\n{\n ll res = 0;\n for(l+=n, r+=n; l<r; l>>=1, r>>=1)\n {\n if(l&1) res = max(res, tree[l++]);\n if(r&1) res = max(res, tree[--r]);\n }\n return res;\n}\n\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n memset(tree,0,sizeof(tree));\n set<ll> id;\n vector<ll> idx;\n unordered_map<ll,ll> mp;\n for(ll i=0; i<positions.size(); i++)\n {\n id.insert(positions[i][0]);\n id.insert(positions[i][0]+positions[i][1]);\n }\n for(auto x:id) idx.push_back(x);\n ll n = idx.size();\n sort(idx.begin(), idx.end());\n vector<int> ans;\n for(ll i=0; i<positions.size(); i++)\n {\n ll l = lower_bound(idx.begin(), idx.end(), positions[i][0]) - idx.begin();\n ll r = lower_bound(idx.begin(), idx.end(), positions[i][0]+positions[i][1]) - idx.begin()-1;\n ll mx = query(l,r+1,n);\n for(ll j=l; j<=r; j++)\n {\n modify(j,mx+positions[i][1],n);\n }\n ans.push_back(query(0,n-1,n));\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Segment Tree', 'C++'] | 0 |
falling-squares | Easy Java Solution O(n^2) | easy-java-solution-on2-by-sabrinakundu77-txfe | Code\n\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n // create ans list\n List<Integer> ans = new ArrayList<>( | sabrinakundu777 | NORMAL | 2022-12-26T05:18:22.650551+00:00 | 2022-12-26T05:18:22.650596+00:00 | 112 | false | # Code\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n // create ans list\n List<Integer> ans = new ArrayList<>();\n // create list of intervals we\'ve already\n // visited\n List<int[]> checked = new ArrayList<>();\n // create 2d array of positions {x1, x2, height} \n // same as input in skyline problem #218\n int[][] skyline = new int[positions.length][3];\n for (int i = 0; i < skyline.length; i++) {\n skyline[i] = new int[]{positions[i][0], positions[i][0]+positions[i][1], positions[i][1]};\n }\n // initialize max to height of first square dropped\n int max = skyline[0][2];\n // add max to list at the same index as skyline\'s index\n ans.add(0, max);\n // add same square to checked list\n checked.add(skyline[0]);\n // iterate through the squares\n for (int i = 1; i < skyline.length; i++) {\n int preMax = 0;\n // iterate through checked squares\n for (int[] prev : checked) {\n // if checked square overlaps current square, \n // then compare it\'s height with current height \n // and assign result to preMax.\n if ((skyline[i][0] < prev[1]) && (skyline[i][1] > prev[0])) {\n preMax = Math.max(preMax, prev[2]);\n } \n }\n // add preMax to current square\'s height\n skyline[i][2] += preMax;\n // add square to checked list\n checked.add(skyline[i]);\n // compare square\'s new height to max height of all squares and change max\n max = Math.max(max, skyline[i][2]);\n // add the new max to ans list at same index as current square\'s index\n ans.add(i, max);\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
falling-squares | C# Dynamic Segment Tree (Online search) Beats 100% | c-dynamic-segment-tree-online-search-bea-sae6 | Code\n\npublic class Solution {\n public class Node{\n public int l, r, cnt, add;\n public Node(int l, int r, int cnt, int add){\n t | enze_zhang | NORMAL | 2022-10-22T09:02:47.709499+00:00 | 2022-10-22T09:02:47.709527+00:00 | 45 | false | # Code\n```\npublic class Solution {\n public class Node{\n public int l, r, cnt, add;\n public Node(int l, int r, int cnt, int add){\n this.l = l;\n this.r = r;\n this.cnt = cnt;\n this.add = add;\n }\n }\n\n const int N = (int)1e9 + 7, M = 100010;\n Node[] tr = new Node[M * 4];\n int pos = 1;\n public IList<int> FallingSquares(int[][] positions) {\n List<int> list = new();\n for(int i = 0; i < positions.Length; i++){\n int x = positions[i][0], len = positions[i][1];\n int res = Query(1, 1, N - 1, x, x + len - 1);\n Update(1, 1, N - 1 , x, x + len - 1, res + len);\n list.Add(Query(1, 1, N - 1, 1, N - 1));\n }\n return list.ToArray();\n }\n\n public void PushUp(int u){\n tr[u].cnt = Math.Max(tr[tr[u].l].cnt, tr[tr[u].r].cnt);\n }\n\n public void PushDown(int u){\n if(tr[u] == null) tr[u] = new Node(0, 0, 0, 0);\n if(tr[u].l == 0){\n tr[u].l = ++pos;\n tr[tr[u].l] = new Node(0, 0, 0, 0);\n }\n if(tr[u].r == 0){\n tr[u].r = ++pos;\n tr[tr[u].r] = new Node(0, 0, 0, 0);\n }\n if(tr[u].add == 0) return;\n\n tr[tr[u].l].add = tr[u].add;\n tr[tr[u].r].add = tr[u].add;\n\n tr[tr[u].l].cnt = tr[u].add;\n tr[tr[u].r].cnt = tr[u].add;\n tr[u].add = 0;\n }\n\n public void Update(int u, int lc, int rc, int l, int r, int d){\n if(l <= lc && rc <= r){\n tr[u].cnt = d;\n tr[u].add = d;\n return;\n }\n int mid = rc + lc >> 1;\n PushDown(u);\n if(l <= mid) Update(tr[u].l, lc, mid, l, r, d);\n if(r > mid) Update(tr[u].r, mid + 1, rc, l, r, d);\n PushUp(u);\n }\n\n public int Query(int u, int lc, int rc, int l, int r){\n if(l <= lc && rc <= r) return tr[u].cnt;\n int max = 0;\n PushDown(u);\n int mid = rc + lc >> 1;\n if(l <= mid) max = Query(tr[u].l, lc, mid, l, r);\n if(r > mid) max = Math.Max(max, Query(tr[u].r, mid + 1, rc, l, r));\n return max;\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
falling-squares | Python sorted list comments O(nlogn) | python-sorted-list-comments-onlogn-by-te-0ycn | I wrote this before looking at other people\'s solutions. It\'s definitely not the most concise, but I think it\'s logically clear what\'s happening. The commen | tet | NORMAL | 2022-09-04T08:47:40.332819+00:00 | 2022-09-04T08:47:40.332849+00:00 | 134 | false | I wrote this before looking at other people\'s solutions. It\'s definitely not the most concise, but I think it\'s logically clear what\'s happening. The comments explain everything but the strategy is to keep a list of ranges and find the tallest height of the ranges which intersect the shadow of the new square. While we find this height, we can simultaneously update/remove ranges to account for this new square. Any partially covered range gets chopped off at the corresponding edge of the new square. Any range that is completely covered by the square gets deleted. If the square is in the middle of a range, then the range gets cut off at the left side of the new square and a new range covers from the right side onward until the end of the original range.\n\n```\nfrom sortedcontainers import SortedList\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n # sorted list where value is a tuple of (leftside, length, height)\n # iterate through squares and find which ranges it intersects,\n # updating the ranges and tracking the highest point\n # add a new range with the appropriate height\n # if this height is greater than tallest, replace tallest.\n # append tallest to answer\n \n # add, del/pop, bisect, and __getitem__ are all O(log(n)) operations on SortedList\n # number of operations is bounded by c*n times where n is the length of positions and c is a constant\n # time complexity: O(n log(n))\n # space complexity: O(n)\n \n \n sl = SortedList()\n ans = []\n tallest = 0\n \n for left, length in positions:\n idx = sl.bisect_left((left, 0, 0))\n max_height = 0\n if idx > 0:\n # ls: left side, l: length, h: height\n ls, l, h = sl[idx-1]\n # left side of new square is within range\n if ls + l > left:\n max_height = h\n del sl[idx-1]\n sl.add((ls, left-ls, h))\n # new square is in middle of range\n if ls + l > left + length:\n sl.add((left+length, ls+l-(left+length), h))\n \n right = left + length\n # while right side of new square is to the right of left side of range\n # (should only run n times total since ranges are being compressed on each iteration)\n while idx < len(sl) and sl[idx][0] < right:\n ls, l, h = sl[idx]\n max_height = max(max_height, h)\n # new square completely covers range\n if ls + l <= right:\n sl.pop(idx)\n # new square covers left side of range\n else:\n del sl[idx]\n sl.add((right, ls + l - right, h))\n \n tallest = max(max_height+length, tallest)\n sl.add((left, length, max_height+length))\n ans.append(tallest)\n #print(sl)\n return ans\n\t``` | 1 | 0 | ['Python', 'Python3'] | 0 |
falling-squares | Java Solution - Segment Tree | java-solution-segment-tree-by-yihaoye-de32 | \nclass Solution {\n \n private Node root;\n \n public List<Integer> fallingSquares(int[][] positions) {\n // \u7EBF\u6BB5\u6811\n int | yihaoye | NORMAL | 2022-08-16T10:46:34.784306+00:00 | 2022-08-16T10:46:34.784332+00:00 | 253 | false | ```\nclass Solution {\n \n private Node root;\n \n public List<Integer> fallingSquares(int[][] positions) {\n // \u7EBF\u6BB5\u6811\n int max = (int) (1e9);\n root = new Node(0, max);\n List<Integer> res = new ArrayList<>();\n for (int[] position : positions) {\n int rangeMaxValue = query(root, position[0], position[0] + position[1] - 1);\n update(root, position[0], position[0] + position[1] - 1, rangeMaxValue + position[1]);\n int curGlobalMaxValue = query(root, 0, max);\n res.add(curGlobalMaxValue);\n }\n return res;\n }\n \n /**\n * \u7EBF\u6BB5\u6811\u7684\u7ED3\u70B9\n */\n class Node {\n private int leftX; // \u5DE6\u8303\u56F4\n private int rightX; // \u53F3\u8303\u56F4\n private int maxValue; // \u8303\u56F4\u5185\u7684\u6700\u5927\u503C\n private int lazy; // \u61D2\u6807\u8BB0\n Node leftChild, rightChild; // \u5DE6\u5B50\u6811\u548C\u53F3\u5B50\u6811\n\n public Node(int leftX, int rightX) {\n this.leftX = leftX;\n this.rightX = rightX;\n }\n }\n\n /**\n * \u533A\u95F4\u6C42\u503C\n *\n * @param root \u6811\u7684\u6839\n * @param left \u5DE6\u8FB9\u754C\n * @param right \u53F3\u8FB9\u754C\n */\n public int query(Node root, int left, int right) {\n // \u4E0D\u5728\u8303\u56F4\u5185 \u76F4\u63A5\u8FD4\u56DE\n if (root.rightX < left || right < root.leftX) {\n return 0;\n }\n // \u67E5\u8BE2\u7684\u533A\u95F4\u5305\u542B\u5F53\u524D\u7ED3\u70B9\n if (left <= root.leftX && root.rightX <= right) {\n return root.maxValue;\n } else {\n lazyCreate(root); // \u52A8\u6001\u5F00\u70B9\n pushDown(root); // \u4E0B\u4F20 lazy\n int l = query(root.leftChild, left, right); // \u6C42\u5DE6\u5B50\u6811\n int r = query(root.rightChild, left, right); // \u6C42\u53F3\u5B50\u6811\n return Math.max(l, r);\n }\n }\n\n /**\n * \u533A\u95F4\u66F4\u65B0\n *\n * @param root \u6811\u7684\u6839\n * @param left \u5DE6\u8FB9\u754C\n * @param right \u53F3\u8FB9\u754C\n * @param value \u66F4\u65B0\u503C\n */\n public void update(Node root, int left, int right, int value) {\n // \u4E0D\u5728\u8303\u56F4\u5185 \u76F4\u63A5\u8FD4\u56DE\n if (root.rightX < left || right < root.leftX) {\n return;\n }\n // \u4FEE\u6539\u7684\u533A\u95F4\u5305\u542B\u5F53\u524D\u7ED3\u70B9\n if (left <= root.leftX && root.rightX <= right) {\n root.maxValue = value;\n root.lazy = value;\n } else {\n lazyCreate(root); // \u52A8\u6001\u5F00\u70B9\n pushDown(root); // \u4E0B\u4F20 lazy\n update(root.leftChild, left, right, value); // \u66F4\u65B0\u5DE6\u5B50\u6811\n update(root.rightChild, left, right, value); // \u66F4\u65B0\u53F3\u5B50\u6811\n pushUp(root); // \u4E0A\u4F20\u7ED3\u679C\n }\n }\n\n /**\n * \u521B\u5EFA\u5DE6\u53F3\u5B50\u6811\n *\n * @param root\n */\n public void lazyCreate(Node root) {\n if (root.leftChild == null) {\n root.leftChild = new Node(root.leftX, root.leftX + (root.rightX - root.leftX) / 2);\n }\n if (root.rightChild == null) {\n root.rightChild = new Node(root.leftX + (root.rightX - root.leftX) / 2 + 1, root.rightX);\n }\n }\n\n /**\n * \u4E0B\u4F20 lazy\n *\n * @param root\n */\n public void pushDown(Node root) {\n if (root.lazy > 0) {\n root.leftChild.maxValue = root.lazy;\n root.leftChild.lazy = root.lazy;\n root.rightChild.maxValue = root.lazy;\n root.rightChild.lazy = root.lazy;\n root.lazy = 0;\n }\n }\n\n /**\n * \u4E0A\u4F20\u7ED3\u679C\n *\n * @param root\n */\n public void pushUp(Node root) {\n root.maxValue = Math.max(root.leftChild.maxValue, root.rightChild.maxValue);\n }\n}\n``` | 1 | 0 | [] | 0 |
falling-squares | [C++] O(n^2) explained with picture, beats 94% memory | c-on2-explained-with-picture-beats-94-me-sy9u | \n\n\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& pos) {\n int n = pos.size(); \n vector <int> h(n); //h[i | ivan-2727 | NORMAL | 2022-08-11T21:13:46.515449+00:00 | 2022-08-11T21:15:35.198587+00:00 | 338 | false | 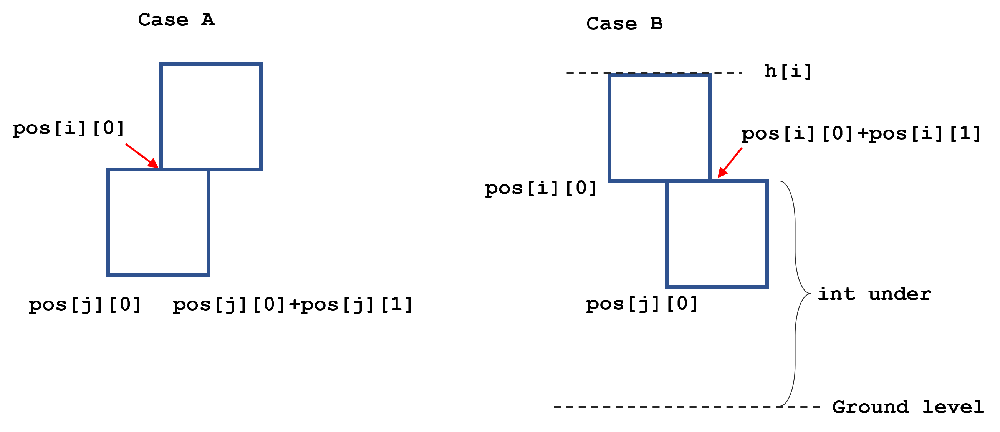\n\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& pos) {\n int n = pos.size(); \n vector <int> h(n); //h[i] means the height at which the top surface of i-th block ends up \n h[0] = pos[0][1]; //in the beginning it\'s obviously just the height of the first block because it is dropped at an empty surface\n vector <int> ans(1, h[0]); //and the first element of the answer is the same \n for (int i = 1; i < n; i++) {\n int under = 0; //the hight at which the i-th block will stop moving down. then h[i] = under + own height of the block\n for (int j = 0; j < i; j++) {\n bool ok = false; // check if there is any previous block under the i-th block\n if (pos[j][0] < pos[i][0]) { //if the j-th block is to the left from the left side of the i-th block \n if (pos[j][0] + pos[j][1] > pos[i][0]) ok = true; //it\'s right point must be to the right side to overlap (case A)\n }\n else { //if it\'s to the right, then it\'s left side should be to the left from the right side of the i-th block (case B)\n if (pos[j][0] < pos[i][0] + pos[i][1]) ok = true;\n }\n if (ok) under = max(under, h[j]);\n }\n h[i] = under + pos[i][1];\n ans.push_back(max(ans.back(), h[i])); \n }\n return ans; \n }\n};\n``` | 1 | 0 | ['Dynamic Programming'] | 0 |
falling-squares | C++ | Two Methods | Segment Tree + Discretization | Map | c-two-methods-segment-tree-discretizatio-tsd6 | Map: O(n^2)\nc++\nclass Solution {\n public:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n vector<int> ans;\n map<int, pair<int, int>> | xjdkc | NORMAL | 2022-05-27T22:10:08.083512+00:00 | 2022-05-27T22:17:55.103887+00:00 | 616 | false | * Map: O(n^2)\n```c++\nclass Solution {\n public:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n vector<int> ans;\n map<int, pair<int, int>> h;\n int max_height = 0;\n for (int i = 0; i < positions.size(); ++i) {\n int left = positions[i][0];\n int right = left + positions[i][1];\n int height = 0;\n for (auto& it : h) {\n if (it.first >= right) break;\n if (it.second.first > left) {\n height = max(height, it.second.second);\n }\n }\n height += positions[i][1];\n h[left] = {right, height};\n max_height = max(max_height, height);\n ans.push_back(max_height);\n }\n return ans;\n }\n};\n```\n\n* SegmentTree: O(nlogn)\n```c++\nclass Solution {\n public:\n // SegmentTree + Discretization\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n set<int> coords;\n for (int i = 0; i < positions.size(); ++i) {\n coords.insert(positions[i][0]);\n coords.insert(positions[i][0] + positions[i][1]);\n }\n\n int range = 0;\n unordered_map<int, int> h;\n for (auto& it : coords) {\n h[it] = ++range;\n }\n\n int max_height = 0;\n vector<int> ans;\n SegmentTree<STMax> st(range);\n ans.reserve(positions.size());\n for (int i = 0; i < positions.size(); ++i) {\n int left = positions[i][0];\n int right = positions[i][0] + positions[i][1];\n int height = st.query(h[left] + 1, h[right]) + positions[i][1];\n st.update(h[left] + 1, h[right], height);\n max_height = max(max_height, height);\n ans.push_back(max_height);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Tree', 'C', 'C++'] | 1 |
falling-squares | [Python3] brute-force | python3-brute-force-by-ye15-bwd4 | \n\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n ans = []\n for i, (x, l) in enumerate(positions): \n | ye15 | NORMAL | 2021-09-30T02:08:15.929811+00:00 | 2021-09-30T02:08:15.929866+00:00 | 139 | false | \n```\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n ans = []\n for i, (x, l) in enumerate(positions): \n val = 0\n for ii in range(i): \n xx, ll = positions[ii]\n if xx < x+l and x < xx+ll: val = max(val, ans[ii])\n ans.append(val + l)\n for i in range(1, len(ans)): ans[i] = max(ans[i-1], ans[i])\n return ans\n``` | 1 | 0 | ['Python3'] | 1 |
falling-squares | c++ map: maintain the disjoint intervals | c-map-maintain-the-disjoint-intervals-by-g5wb | \nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n map<pair<int, int>, int> i2h;\n int g_max = 0;\n | zlfzeng | NORMAL | 2021-07-26T01:39:33.776693+00:00 | 2021-08-02T02:41:35.776925+00:00 | 79 | false | ```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n map<pair<int, int>, int> i2h;\n int g_max = 0;\n vector<int> ret; \n for(auto &p: positions){\n int left = p[0];\n int size = p[1];\n int right = left + size;\n int height = size; \n \n auto it = i2h.lower_bound(make_pair(left , right));\n if(it != i2h.begin()){\n auto it2 = it;\n it2--;\n if(it2->first.second > left) {\n it = it2; \n }\n }\n \n int maxheight = 0;\n while(it != i2h.end()){\n if(it->first.first >= right) break;\n \n if(it->first.first < left) {\n i2h[make_pair(it->first.first, left)] = it->second; \n }\n if(it->first.second > right) {\n i2h[make_pair(right, it->first.second)] = it->second; \n }\n maxheight = max(maxheight, it->second);\n \n it = i2h.erase(it);\n \n }\n \n i2h[make_pair(left, right)] = maxheight + height; \n g_max = max(g_max, maxheight + height);\n ret.push_back(g_max);\n \n }\n return ret;\n }\n};\n``` | 1 | 0 | [] | 0 |
falling-squares | C++ easy peasy solution using unordered_map | c-easy-peasy-solution-using-unordered_ma-m0pf | Upvote if helpful :)\n\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n unordered_map<int,pair<int,int>> int | tarruuuu | NORMAL | 2021-06-17T05:03:55.587195+00:00 | 2021-06-17T05:03:55.587228+00:00 | 288 | false | Upvote if helpful :)\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n unordered_map<int,pair<int,int>> intervals;\n \n vector<int> output;\n int maxheight = 0;\n \n for(auto v:positions){\n int start = v[0];\n int end = v[0]+v[1];\n int height = v[1];\n \n int currmax = 0;\n for(auto i:intervals){\n if(i.second.first>=end || i.second.second<=start)\n continue;\n \n currmax = max(currmax,i.first);\n }\n int currheight = height+currmax;\n intervals[currheight] = {start,end};\n \n maxheight = max(currheight,maxheight);\n output.push_back(maxheight);\n }\n return output;\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 2 |
falling-squares | Python3 - beats 62.93% 296 ms - Using SortedList as BST and Defining an Ordering in Intervals | python3-beats-6293-296-ms-using-sortedli-h4ms | The approach is to maintain a sorted list of disjoint intervals, and their max height. \nTo do this I have defined an ordering in the intervals. Since brushing | ampl3t1m3 | NORMAL | 2021-05-06T21:13:42.411297+00:00 | 2021-05-06T21:13:42.411327+00:00 | 119 | false | The approach is to maintain a sorted list of disjoint intervals, and their max height. \nTo do this I have defined an ordering in the intervals. Since brushing off square sides is not allowed,\nan interval it1 is less than it2 if it1.end <= it1.start.\n(the height is of no consequence when deciding order)\n\nWhenever we see a new square, we extract all the intervals it intersects with\n(intersection is checked by overloading the eq operator). The part of the original square which lies outside the new square is cut out and saved back in the sorted list. After all intersections are processes, we add the current interval with its max height.\n\nHope the explanation is clear, else please let me know in the comments.\n\nTime complexity - Every time we see a square it may potentially intersect with L squares of size 1. Processing these squares requires Log(n) time due to property of SortedList BST. \n\nSo time complexity is O(NL Log(N))\n\n```\nfrom sortedcontainers import SortedList\n\nclass It:\n def __init__(self, start,end,h):\n self.start = start\n self.end = end\n self.h = h\n \n def __lt__(self, obj):\n return self.end <= obj.start\n \n def __gt__(self, obj):\n return self.start >= obj.end\n\n def __eq__(self, obj):\n return not (self.__lt__(obj) or self.__gt__(obj))\n\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n ans = []\n mx = 0\n \n sl = SortedList()\n \n for p in positions:\n \n new_square = It(p[0],p[0]+p[1],p[1])\n h = 0\n while new_square in sl:\n it = sl.pop(sl.index(new_square))\n h = max(h,it.h)\n if it.start < new_square.start:\n sl.add(It(it.start,new_square.start,it.h))\n if it.end > new_square.end:\n sl.add(It(new_square.end,it.end,it.h))\n\t\t\t\t\t\n new_square.h += h\n sl.add(new_square)\n mx = max(mx,new_square.h)\n ans.append(mx)\n \n return ans\n\n``` | 1 | 0 | [] | 1 |
falling-squares | [Java] brute force, most simple... | java-brute-force-most-simple-by-66brothe-rshq | \nclass Solution {\n public List<Integer> fallingSquares(int[][] A) {\n long max=0;\n List<Integer>res=new ArrayList<>();\n \n Lis | 66brother | NORMAL | 2020-09-20T23:07:50.604747+00:00 | 2020-09-20T23:07:50.604791+00:00 | 104 | false | ```\nclass Solution {\n public List<Integer> fallingSquares(int[][] A) {\n long max=0;\n List<Integer>res=new ArrayList<>();\n \n List<long[]>list=new ArrayList<>();\n list.add(new long[]{0,Integer.MAX_VALUE,0});\n \n //can not sort\n for(int i=0;i<A.length;i++){\n int pair[]=A[i];\n long len=pair[1];\n long l=pair[0],r=l+len-1;\n long m=0;\n \n for(long pos[]:list){\n if(pos[1]<l)continue;\n if(pos[0]>r)continue;\n m=Math.max(m,pos[2]+len);\n }\n list.add(new long[]{l,r,m});\n max=Math.max(max,m);\n res.add((int)(max));\n }\n return res;\n }\n}\n``` | 1 | 0 | [] | 0 |
falling-squares | C++ using map and emplace. | c-using-map-and-emplace-by-_chaitanya99-wsxt | \nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n map<int,int> count = {{-1,0}};\n int n = positions | _chaitanya99 | NORMAL | 2020-09-08T06:16:34.294359+00:00 | 2020-09-08T06:16:34.294401+00:00 | 141 | false | ```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n map<int,int> count = {{-1,0}};\n int n = positions.size();\n vector<int> ans;\n int res = 0;\n for(int i=0;i<n;i++) {\n auto ed = count.emplace(positions[i][0]+positions[i][1], (--count.upper_bound(positions[i][0]+positions[i][1]))->second);\n auto st = count.emplace(positions[i][0], (--count.upper_bound(positions[i][0]))->second);\n int add = 0;\n for(auto it = st.first;it!=ed.first;it++) {\n add = max(add, it->second);\n }\n for(auto it = st.first;it!=ed.first;it++) {\n it->second = add + positions[i][1];\n res = max(res, it->second);\n }\n \n ans.push_back(res);\n }\n return ans;\n }\n};\n``` | 1 | 0 | [] | 0 |
falling-squares | Evolve from intuition | evolve-from-intuition-by-yu6-bcme | O(n^2) Store the height of fallen squares as interval heights [left, right, height]. When a new square falls, we check intersection with existing intervals and | yu6 | NORMAL | 2020-08-29T22:41:12.285666+00:00 | 2020-08-29T22:48:30.028173+00:00 | 77 | false | 1. O(n^2) Store the height of fallen squares as interval heights [left, right, height]. When a new square falls, we check intersection with existing intervals and compute the height of the new interval. Existing interval height does not need to be updated because we are only interested in the max height. Outdated lower interval height does not impact computing the max height. The idea is from [@leuction](https://leetcode.com/problems/falling-squares/discuss/108766/Easy-Understood-O(n2)-Solution-with-explanation).\n```\n\tpublic List<Integer> fallingSquares(int[][] positions) {\n List<int[]> squares=new ArrayList<>();\n List<Integer> res=new ArrayList<>();\n for(int[] square:positions) {\n int[] fs=new int[]{square[0],square[0]+square[1],square[1]};\n int height=getHeight(fs,squares);\n res.add(height);\n squares.add(fs);\n } \n return res;\n }\n private int getHeight(int[] cur, List<int[]> squares) {\n int height=0, preMax=0;\n for(int[] square:squares) {\n preMax=Math.max(preMax,square[2]);\n if(square[0]>=cur[1]||square[1]<=cur[0]) continue;\n height=Math.max(height,square[2]);\n }\n return Math.max(preMax,cur[2]+=height);\n }\n```\n2. O(nlogn) Intuitively, there should be a way to store the intervals in binary search tree so that get is O(logn). The idea is to represent the outline of the squares the same way as in 218. The Skyline Problem. In the worset case, each point is added, visited and removed. The idea is from [@britishorthair](https://leetcode.com/problems/falling-squares/discuss/112678/Treemap-solution-and-Segment-tree-(Java)-solution-with-lazy-propagation-and-coordinates-compression).\n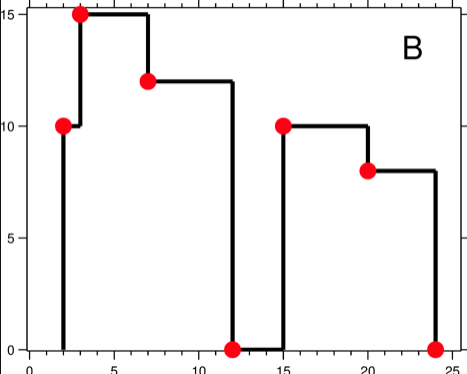\n\n\n```\n\tpublic List<Integer> fallingSquares(int[][] positions) {\n List<Integer> res=new ArrayList<>();\n TreeMap<Integer,Integer> tm=new TreeMap<>();\n tm.put(0,0);\n int max=0;\n for(int[] square:positions) {\n int start=square[0], end=square[0]+square[1];\n int left=tm.floorKey(start);\n Map<Integer,Integer> map=tm.subMap(left, end);\n int height=0;\n for(int h:map.values()) \n height=Math.max(h,height); \n height+=square[1];\n max=Math.max(max,height); \n res.add(max);\n int curHeight=tm.floorEntry(end).getValue();\n tm.put(start,height);\n tm.put(end, curHeight);\n tm.subMap(start,false,end,false).clear();\n } \n return res;\n }\n```\n | 1 | 0 | [] | 0 |
falling-squares | The Easiest Java Segmentation Tree with Lazy Propagation. | the-easiest-java-segmentation-tree-with-p13ve | \nclass Solution {\n class SegmentTree {\n Node root;\n public SegmentTree (int low, int high) {\n root = new Node(low, high);\n | fang2018 | NORMAL | 2020-07-29T18:26:00.618717+00:00 | 2020-07-29T19:29:49.551258+00:00 | 157 | false | ```\nclass Solution {\n class SegmentTree {\n Node root;\n public SegmentTree (int low, int high) {\n root = new Node(low, high);\n }\n public void update (int L, int R, Node node, int val) {\n if (L <= node.low && R >= node.high) {\n node.lazy = Math.max(node.lazy, val);\n } \n push(node);\n if ((L <= node.low && R >= node.high) || L > node.high || R < node.low) {\n return;\n } \n update(L, R, node.left, val);\n update(L, R, node.right, val);\n node.max = Math.max(node.left.max, node.right.max);\n } \n public int query (int L, int R, Node node) {\n push(node);\n if (L > node.high || R < node.low) return 0;\n if (L <= node.low && R >= node.high) return node.max;\n return Math.max(query(L, R, node.left), query(L, R, node.right));\n } \n public void push (Node node) {\n node.max = Math.max(node.max, node.lazy);\n if (node.low != node.high) {\n int mid = (node.low + node.high) / 2;\n if (node.left == null) {\n node.left = new Node(node.low, mid);\n } \n if (node.right == null) {\n node.right = new Node(mid + 1, node.high);\n } \n node.left.lazy = Math.max(node.left.lazy, node.lazy);\n node.right.lazy = Math.max(node.right.lazy, node.lazy);\n }\n node.lazy = 0;\n } \n }\n class Node {\n int low, high;\n int max, lazy;\n Node left, right;\n public Node (int low, int high) {\n this.low = low;\n this.high = high;\n }\n }\n public List<Integer> fallingSquares(int[][] positions) {\n List<Integer> res = new ArrayList<>();\n SegmentTree st = new SegmentTree(0, 110_000_000);\n int max = 0;\n for (int[] p : positions) {\n int s = p[0], e = p[0] + p[1] - 1;\n int tmp = st.query(s, e, st.root);\n st.update(s, e, st.root, tmp + p[1]);\n max = Math.max(max, st.root.max);\n res.add(max);\n }\n return res;\n }\n} \n``` | 1 | 0 | [] | 0 |
falling-squares | [Python] Segment Tree with coordinate compression | python-segment-tree-with-coordinate-comp-i59l | Similar to the techniques from https://codeforces.com/blog/entry/18051\n\npython\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> L | stwind | NORMAL | 2020-07-22T05:09:16.239303+00:00 | 2020-07-22T05:09:16.239353+00:00 | 181 | false | Similar to the techniques from https://codeforces.com/blog/entry/18051\n\n```python\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n V = set()\n for p, w in positions:\n V.add(p)\n V.add(p + w)\n rank = {x: i for i, x in enumerate(sorted(V))}\n \n s, n = len(rank), 1\n while n < s:\n n *= 2\n seg, lazy = [0] * (2 * n - 1), [0] * (2 * n - 1)\n \n def push(k, l, r):\n if lazy[k] < 0:\n return\n seg[k] = lazy[k]\n if k < n - 1:\n lazy[k * 2 + 1] = lazy[k]\n lazy[k * 2 + 2] = lazy[k]\n lazy[k] = -1\n \n def update(a, b, x, k=0, l=0, r=n):\n if b <= l or r <= a:\n return\n push(k, l, r)\n if a <= l and r <= b:\n lazy[k] = x\n push(k, l, r)\n else:\n m = (l + r) // 2\n update(a, b, x, k * 2 + 1, l, m)\n update(a, b, x, k * 2 + 2, m, r)\n seg[k] = max(seg[k * 2 + 1], seg[k * 2 + 2])\n \n def query(a, b, k=0, l=0, r=n):\n push(k, l, r)\n if b <= l or r <= a:\n return 0\n if a <= l and r <= b:\n return seg[k]\n m = (l + r) // 2\n left = query(a, b, 2 * k + 1, l, m)\n right = query(a, b, 2 * k + 2, m, r)\n return max(left, right)\n \n res, mx = [], 0\n for p, w in positions:\n rp, rw = rank[p], rank[p + w]\n mh = query(rp, rw) + w\n update(rp, rw, mh)\n mx = max(mx, mh)\n res.append(mx)\n return res\n``` | 1 | 0 | [] | 0 |
falling-squares | [Java] Standard TreeMap solution [Detailed] | java-standard-treemap-solution-detailed-iec5s | Save Pair(left, right) as key and height as value into TreeMap.\n\nPair start = map.lowerKey(p1);\nPair end = map.lowerKey(p2);\n\n1. Modify the end interval if | Aranne | NORMAL | 2020-06-18T04:16:02.663466+00:00 | 2020-06-18T04:16:02.663498+00:00 | 122 | false | Save `Pair(left, right)` as key and `height` as value into TreeMap.\n```\nPair start = map.lowerKey(p1);\nPair end = map.lowerKey(p2);\n```\n1. Modify the `end` interval if it intersects with `[left, right]`\n2. Modify the `start` interval if it intersects with `[left, right]`\n3. Seach in `subMap = map.subMap(p1, true, p2, false)` to find max height\n4. clear all intervals in range `[left, right]`\n5. put new range into map\n```\nclass Solution {\n class Pair {\n int left;\n int right;\n public Pair(int l, int r) {\n left = l;\n right = r;\n }\n public String toString() {\n return left +","+right;\n }\n }\n public List<Integer> fallingSquares(int[][] positions) {\n List<Integer> res = new ArrayList<>();\n TreeMap<Pair, Integer> map = new TreeMap<>((a, b) -> a.left - b.left);\n int max = 0;\n \n for (int[] square : positions) {\n int left = square[0];\n int right = square[0] + square[1];\n int height = square[1];\n Pair p1 = new Pair(left, 0);\n Pair p2 = new Pair(right, 0);\n \n int maxH = 0;\n Pair start = map.lowerKey(p1);\n Pair end = map.lowerKey(p2);\n \n if (end != null && end.right > right) { // change end before start\n int h = map.get(end);\n int r = end.right;\n maxH = Math.max(maxH, h); // compare with intersact range\n map.put(new Pair(right, r), h);\n }\n if (start != null && start.right > left) {\n int h = map.get(start); \n int l = start.left;\n maxH = Math.max(maxH, h); \n map.put(new Pair(l, left), h);\n }\n \n Map<Pair, Integer> submap = map.subMap(p1, true, p2, false);\n for (Pair key : submap.keySet()) {\n maxH = Math.max(maxH, map.get(key));\n }\n submap.clear(); // remove intervals in range\n \n int newH = height + maxH;\n map.put(new Pair(left, right), newH); // put new range\n \n max = Math.max(max, newH);\n res.add(max);\n } \n return res;\n }\n}\n``` | 1 | 0 | [] | 1 |
falling-squares | Accepted C# Solution with Segment Tree | accepted-c-solution-with-segment-tree-by-2xef | \n public class Solution\n {\n private class SegTree\n {\n public class Node\n {\n public readonly long | maxpushkarev | NORMAL | 2020-03-29T06:49:16.800900+00:00 | 2020-03-29T06:49:16.800939+00:00 | 131 | false | ```\n public class Solution\n {\n private class SegTree\n {\n public class Node\n {\n public readonly long Left;\n public readonly long Right;\n\n public Node(long left, long right)\n {\n Left = left;\n Right = right;\n }\n\n public Node LeftChild;\n public Node RightChild;\n public bool IsLeaf => LeftChild == null && RightChild == null;\n public long Max;\n }\n\n public readonly Node Root;\n\n public SegTree(long min, long max)\n {\n Root = new Node(min, max);\n }\n\n public long GetHeight(Node node, long from, long to)\n {\n if (from > node.Right || to < node.Left)\n {\n return 0;\n }\n\n if (node.IsLeaf)\n {\n return node.Max;\n }\n\n\n long leftCand = GetHeight(node.LeftChild, Math.Max(from, node.LeftChild.Left), Math.Min(to, node.LeftChild.Right));\n long rightCand = GetHeight(node.RightChild, Math.Max(from, node.RightChild.Left), Math.Min(to, node.RightChild.Right));\n\n return Math.Max(leftCand, rightCand);\n }\n\n public void Cover(Node node, long from, long to, long height)\n {\n if (from > node.Right || to < node.Left)\n {\n return;\n }\n\n if (node.Left == from && node.Right == to)\n {\n node.LeftChild = null;\n node.RightChild = null;\n node.Max = height;\n return;\n }\n\n if (node.Right == node.Left)\n {\n node.Max = height;\n return;\n }\n\n if (node.IsLeaf)\n {\n long mid = node.Left + (node.Right - node.Left) / 2;\n node.LeftChild = new Node(node.Left, mid);\n node.RightChild = new Node(mid + 1, node.Right);\n }\n\n Cover(node.LeftChild, Math.Max(from, node.LeftChild.Left), Math.Min(to, node.LeftChild.Right), height);\n Cover(node.RightChild, Math.Max(from, node.RightChild.Left), Math.Min(to, node.RightChild.Right), height);\n\n node.Max = Math.Max(node.LeftChild.Max, node.RightChild.Max);\n\n if (node.LeftChild != null && node.RightChild != null)\n {\n if (node.LeftChild.IsLeaf && node.RightChild.IsLeaf && node.LeftChild.Max == node.RightChild.Max)\n {\n //remove reduntant childs when parent interval is fully covered\n node.LeftChild = null;\n node.RightChild = null;\n }\n }\n }\n }\n\n\n public IList<int> FallingSquares(int[][] positions)\n {\n checked\n {\n long maxHeight = 0;\n IList<int> res = new List<int>(positions.Length);\n long min = int.MaxValue;\n long max = int.MinValue;\n\n foreach (var square in positions)\n {\n min = Math.Min(min, square[0]);\n max = Math.Max(max, (long) square[0] + square[1]);\n }\n\n SegTree tree = new SegTree(min, max);\n\n foreach (var square in positions)\n {\n long left = square[0];\n long size = square[1];\n long right = left + size - 1;\n\n var currentHeight = tree.GetHeight(tree.Root, left, right);\n currentHeight += size;\n tree.Cover(tree.Root, left, right, currentHeight);\n\n maxHeight = Math.Max(maxHeight, currentHeight);\n res.Add((int)maxHeight);\n }\n\n return res;\n }\n }\n }\n``` | 1 | 0 | ['Tree'] | 0 |
falling-squares | C# Solution | c-solution-by-leonhard_euler-j8do | \npublic class Solution \n{\n public IList<int> FallingSquares(int[][] positions) \n {\n var result = new List<int>();\n var intervals = new | Leonhard_Euler | NORMAL | 2019-08-02T05:44:50.174374+00:00 | 2019-08-02T05:44:50.174420+00:00 | 69 | false | ```\npublic class Solution \n{\n public IList<int> FallingSquares(int[][] positions) \n {\n var result = new List<int>();\n var intervals = new List<Interval>();\n int max = 0;\n foreach(var p in positions)\n {\n var interval = new Interval(p[0], p[0] + p[1] - 1, p[1]);\n max = Math.Max(max, InsertInterval(intervals, interval));\n result.Add(max);\n }\n \n return result;\n }\n \n private int InsertInterval(List<Interval> intervals, Interval interval)\n {\n int maxOverlappingHeight = 0;\n foreach(var i in intervals) {\n if (i.End < interval.Start) continue;\n if (i.Start > interval.End) continue;\n maxOverlappingHeight = Math.Max(maxOverlappingHeight, i.Height);\n }\n \n interval.Height += maxOverlappingHeight;\n intervals.Add(interval);\n return interval.Height;\n }\n}\n\npublic class Interval\n{\n public int Start;\n public int End;\n public int Height;\n public Interval(int s, int e, int h)\n {\n Start = s;\n End = e;\n Height = h;\n }\n}\n``` | 1 | 0 | [] | 0 |
falling-squares | python bisect, beat 82%, very similar to Calendar Three | python-bisect-beat-82-very-similar-to-ca-87qj | \n\n\nimport bisect\nimport collections\n\nclass Solution(object):\n def fallingSquares(self, positions):\n """\n :type positions: List[List[in | yjiang01 | NORMAL | 2019-06-04T08:23:11.988493+00:00 | 2019-06-04T08:23:11.988546+00:00 | 174 | false | \n\n```\nimport bisect\nimport collections\n\nclass Solution(object):\n def fallingSquares(self, positions):\n """\n :type positions: List[List[int]]\n :rtype: List[int]\n """\n \n max_height = collections.defaultdict(int)\n square_endpoints = []\n \n ans_max = 0\n ans = []\n for square in positions:\n left = square[0]\n right = left + square[1]\n \n if left not in max_height:\n bisect.insort(square_endpoints, left)\n if right not in max_height:\n bisect.insort(square_endpoints, right)\n \n left_idx = bisect.bisect_left(square_endpoints, left)\n right_idx = bisect.bisect_left(square_endpoints, right)\n \n if left not in max_height:\n if left_idx - 1 >= 0: \n max_height[left] = max_height[square_endpoints[left_idx-1]]\n else:\n max_height[left] = 0\n \n if right not in max_height:\n max_height[right] = max_height[square_endpoints[right_idx-1]]\n \n height = 0\n for i in range(left_idx, right_idx):\n height = max(max_height[square_endpoints[i]], height)\n \n for i in range(left_idx, right_idx):\n max_height[square_endpoints[i]] = height + square[1]\n \n ans_max = max(ans_max, max_height[left])\n ans.append(ans_max)\n \n return ans\n\t\t``` | 1 | 0 | [] | 0 |
falling-squares | short python with bisect | short-python-with-bisect-by-horizon1006-elak | ```\nclass Solution:\n def fallingSquares(self, positions):\n g ,MAX, ans= [(0,0),(1e9,0)], 0, []\n for i,side in positions:\n l = b | horizon1006 | NORMAL | 2019-01-14T12:00:34.929780+00:00 | 2019-01-14T12:00:34.929836+00:00 | 201 | false | ```\nclass Solution:\n def fallingSquares(self, positions):\n g ,MAX, ans= [(0,0),(1e9,0)], 0, []\n for i,side in positions:\n l = bisect.bisect(g,(i,0)) \n r = bisect.bisect_left(g,(i+side,0)) \n curr = max(g[k][1] for k in range(l-1,r))+side\n MAX = max(MAX,curr) \n ans += MAX, \n g[l:r] = [(i,curr),(i+side,g[r-1][1])] \n return ans\n | 1 | 0 | [] | 0 |
falling-squares | TreeMap solution | treemap-solution-by-maot1991-gy9p | TreeMap functions as the sorted map.\n\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n TreeMap<Integer, Integer> map = | maot1991 | NORMAL | 2018-09-21T21:14:41.383434+00:00 | 2018-09-21T21:14:41.383495+00:00 | 173 | false | TreeMap functions as the sorted map.\n```\nclass Solution {\n public List<Integer> fallingSquares(int[][] positions) {\n TreeMap<Integer, Integer> map = new TreeMap();\n map.put(0, 0);\n List<Integer> res = new ArrayList<Integer>();\n int heighest = 0;\n for (int i = 0; i < positions.length; i++){\n int baseLine = 0;\n int start = positions[i][0];\n int end = start + positions[i][1];\n int key = map.floorKey(start);\n int endValue = map.get(key);\n while (key < end){\n endValue = map.get(key);\n baseLine = Math.max(baseLine, map.getOrDefault(key, 0));\n if (key >= start) map.remove(key);\n if (map.ceilingKey(key+1) == null) break;\n else key = map.ceilingKey(key+1);\n }\n int newHeight = baseLine + positions[i][1];\n heighest = Math.max(newHeight, heighest);\n res.add(heighest);\n map.put(start, newHeight);\n map.put(end, endValue);\n }\n return res;\n }\n}\n``` | 1 | 0 | [] | 0 |
falling-squares | Short Java solution !!! | short-java-solution-by-kylewzk-bf6w | \n int max = Integer.MIN_VALUE;\n\t\t\n public List<Integer> fallingSquares(int[][] p) {\n List<int[]> list = new ArrayList<>();\n List<Inte | kylewzk | NORMAL | 2018-06-27T11:00:30.679334+00:00 | 2018-10-10T03:14:56.629909+00:00 | 272 | false | ```\n int max = Integer.MIN_VALUE;\n\t\t\n public List<Integer> fallingSquares(int[][] p) {\n List<int[]> list = new ArrayList<>();\n List<Integer> ans = new ArrayList<>();\n for (int[] s : p) {\n int[] node = new int[]{s[0], s[0] + s[1], s[1]};\n ans.add(getMax(list, node));\n }\n return ans;\n }\n \n private int getMax(List<int[]> list, int[] node) {\n int height = 0;\n for (int[] e : list) {\n if(e[0] >= node[1] || e[1] <= node[0]) continue;\n height = Math.max(height, e[2]);\n }\n node[2] += height;\n list.add(node);\n max = Math.max(max, node[2]);\n return max;\n }\n``` | 1 | 0 | [] | 1 |
falling-squares | Java BST O(nlogn) | java-bst-onlogn-by-octavila-e043 | ``` static class Segment{ int start, end, height; Segment(int s, int e, int h) { start = s; end = e; height = h; } } p | octavila | NORMAL | 2018-02-17T06:50:07.358275+00:00 | 2018-02-17T06:50:07.358275+00:00 | 180 | false | ```
static class Segment{
int start, end, height;
Segment(int s, int e, int h) {
start = s;
end = e;
height = h;
}
}
public List<Integer> fallingSquares(int[][] positions) {
List<Integer> res = new ArrayList<>();
TreeSet<Segment> bst = new TreeSet<>((s1, s2) -> Integer.compare(s1.start, s2.start));
int max = 0;
for(int[] p : positions) {
Segment current = new Segment(p[0], p[0] + p[1], p[1]);
Segment left = bst.lower(current);
if(left != null && left.end > current.start) {
bst.add(new Segment(current.start, left.end, left.height));
left.end = current.start;
}
Segment right = bst.lower(new Segment(current.end, 0, 0));
if(right != null && right.end > current.end)
bst.add(new Segment(current.end, right.end, right.height));
Set<Segment> sub = bst.subSet(current, true, new Segment(current.end, 0, 0), false);
for(Iterator<Segment> i = sub.iterator(); i.hasNext(); i.remove())
current.height = Math.max(current.height, i.next().height + p[1]);
bst.add(current);
res.add(max = Math.max(max, current.height));
}
return res;
}
``` | 1 | 0 | [] | 0 |
falling-squares | Discretization and ZKW segment tree(iterative segment tree) | discretization-and-zkw-segment-treeitera-vfkv | \nclass Solution {\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n //Discretization \n map<int,vector<int> >hash;\ | 1179729428 | NORMAL | 2018-02-04T03:39:30.595000+00:00 | 2018-02-04T03:39:30.595000+00:00 | 328 | false | ```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n //Discretization \n map<int,vector<int> >hash;\n vector<vector<int> >pos(positions.size(),vector<int>{0,-1,-1});//pos is the discretization of positions,pos[0] is the height of positions[i], [pos[1],pos[2]] is the discrete range of positions[i]\n for(int i=0;i<positions.size();i++){\n pos[i][0]=positions[i].second;\n int st=positions[i].first,en=positions[i].first+positions[i].second-1;\n if(hash.find(st)==hash.end())hash.emplace(st,vector<int>{i});\n else hash[st].push_back(i);\n if(hash.find(en)==hash.end())hash.emplace(en,vector<int>{i});\n else hash[en].push_back(i);\n }\n int i=0;\n for(auto p:hash){\n for(int j:p.second){\n if(pos[j][1]==-1)pos[j][1]=i;\n else pos[j][2]=i;\n }\n i++;\n }\n vector<int>res;\n int n=pow(2,ceil(log2(hash.size()+2))),m=0,f=1;\n vector<pair<int,int> >sgt(2*n-1,pair<int,int>(0,0));//iterative segment tree,pair.first is max height,pair.second is 'focused lazy value'(a lazy value not a mark,never push-down)\n for(auto v:pos){\n if(f){//first square\n for(int i=v[1]+n;i<=v[2]+n;i++)update_single(sgt,i,v[0]);\n f=0;m=v[0];\n res.push_back(m);\n }else{\n int mt=query_range(sgt,v[1]+n,v[2]+n)+v[0];//max height in [v[1],v[2]]\n update_range(sgt,v[1]+n,v[2]+n,mt);//update height in [v[1],v[2]] to mt\n m=max(m,mt);\n res.push_back(m);\n }\n }\n return res;\n }\n void update_single(vector<pair<int,int> >&sgt,int i,int v){\n for(;i>0;i=(i-1)/2)sgt[i].first=v;\n }\n int query_range(vector<pair<int,int> >&sgt,int i,int j){\n int st=i-1,en=j+1,ml=0,mr=0,fl=0,fr=0;\n for(;en-st>=1;st=(st-1)/2,en=(en-1)/2){\n if(sgt[st].second&&fl)ml=max(ml,sgt[st].second);\n if(en-st>1&&st%2){ml=max(ml,sgt[st+1].first);fl=1;}\n if(sgt[en].second&&fr)mr=max(mr,sgt[en].second);\n if(en-st>1&&en%2==0){mr=max(mr,sgt[en-1].first);fr=1;}\n } \n ml=max(ml,mr);\n for(;st>0;st=(st-1)/2){\n if(sgt[st].second)ml=max(ml,sgt[st].second);\n }\n return ml;\n }\n void update_range(vector<pair<int,int> >&sgt,int i,int j,int m){\n int st=i-1,en=j+1,fl=0,fr=0;\n for(;en-st>=1;st=(st-1)/2,en=(en-1)/2){\n if(st*2+1<sgt.size()&&fl)sgt[st].first=max(sgt[st*2+1].first,sgt[st*2+2].first);\n if(en-st>1&&st%2){sgt[st+1].first=m;sgt[st+1].second=m;fl=1;}\n if(en*2+1<sgt.size()&&fr)sgt[en].first=max(sgt[en*2+1].first,sgt[en*2+2].first);\n if(en-st>1&&en%2==0){sgt[en-1].first=m;sgt[en-1].second=m;fr=1;}\n }\n for(;st>0;st=(st-1)/2){\n sgt[st].first=max(sgt[st].first,max(sgt[st*2+1].first,sgt[st*2+2].first));\n } \n }};\n``` | 1 | 3 | [] | 0 |
falling-squares | C++ discretization + Segment Tree O(nlog(n)) time 29ms | c-discretization-segment-tree-onlogn-tim-gomj | \nclass Solution {\n vector<int> vec;\n int getId(int x) {\n return lower_bound(vec.begin(), vec.end(), x) - vec.begin() + 1;\n }\n int m;\n | szfck | NORMAL | 2017-10-15T15:11:28.659000+00:00 | 2017-10-15T15:11:28.659000+00:00 | 323 | false | ```\nclass Solution {\n vector<int> vec;\n int getId(int x) {\n return lower_bound(vec.begin(), vec.end(), x) - vec.begin() + 1;\n }\n int m;\n int seg[2005 * 4], lazy[2005 * 4];\n \n void build(int rt, int left, int right) {\n seg[rt] = 0, lazy[rt] = -1;\n if (left == right) return;\n int mid = (left + right) / 2;\n build(rt * 2, left, mid);\n build(rt * 2 + 1, mid + 1, right);\n }\n \n void add(int rt, int left, int right, int L, int R, int val) {\n if (L <= left && right <= R) {\n seg[rt] = lazy[rt] = val;\n return;\n }\n pushDown(rt, left, right);\n \n int mid = (left + right) / 2;\n \n if (L <= mid) add(rt * 2, left, mid, L, R, val);\n if (R > mid) add(rt * 2 + 1, mid + 1, right, L, R, val);\n \n seg[rt] = max(seg[rt * 2], seg[rt * 2 + 1]);\n }\n \n \n void pushDown(int rt, int left, int right) {\n // use lazy symbol to reduce the segment tree traverse, only update the son when needed\n if (lazy[rt] != -1) {\n seg[rt * 2] = lazy[rt * 2] = lazy[rt * 2 + 1] = seg[rt * 2 + 1] = lazy[rt];\n lazy[rt] = -1;\n }\n }\n \n int query(int rt, int left, int right, int L, int R) {\n if (L <= left && right <= R) {\n return seg[rt];\n }\n pushDown(rt, left, right);\n \n int mid = (left + right) / 2;\n \n int res = -1;\n if (L <= mid) res = max(res, query(rt * 2, left, mid, L, R));\n if (R > mid) res = max(res, query(rt * 2 + 1, mid + 1, right, L, R));\n \n return res;\n }\npublic:\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n int n = positions.size();\n \n for (int i = 0; i < n; i++) {\n vec.push_back(positions[i].first);\n vec.push_back(positions[i].first + positions[i].second - 1);\n }\n \n \n //discretization\n sort(vec.begin(), vec.end());\n vec.erase(unique(vec.begin(), vec.end()), vec.end());\n \n m = vec.size();\n \n //build tree\n build(1, 1, m);\n \n vector<int> res;\n int curMax = 0;\n \n //insert segment to tree and query\n for (int i = 0; i < n; i++) {\n \n //use discretization to reduce the size of segment tree\n int l = getId(positions[i].first);\n int r = getId(positions[i].first + positions[i].second - 1);\n \n \n // query the maxHeight from l to r\n int segMax = query(1, 1, m, l, r);\n \n int newHeight = segMax + positions[i].second;\n \n // add new height to segment tree from l to r\n add(1, 1, m, l, r, newHeight);\n \n curMax = max(curMax, newHeight);\n \n res.push_back(curMax);\n }\n \n return res;\n }\n};\n``` | 1 | 0 | [] | 0 |
falling-squares | [699. Falling Squares] C++ AC with brief explanation | 699-falling-squares-c-ac-with-brief-expl-j9xr | We should divide the whole interval of the positions into different pieces. Because if we directly consider each whole interval, like:\n\nfor this test case: | jasonshieh | NORMAL | 2017-10-16T00:39:18.618000+00:00 | 2017-10-16T00:39:18.618000+00:00 | 276 | false | We should divide the whole interval of the positions into different pieces. Because if we directly consider each whole interval, like:\n\nfor this test case: [[50,47],[95,48],[88,77],[84,3],[53,87],[98,79],[88,28],[13,22],[53,73],[85,55]], when we add [84,3] into our graph, the heigh is changed from 47 to 50 only for the interval [84->87], not the whole interval.\nSo from this, I think we should divide the whole interval by each start point and end point.\n\nIn order to distinguish the start point and end point, I add 0.5 to the start point. So each time we add a new interval, we can easily find out all shorter intervals it affects. By finding out the largest height at the affected interval, we can figure out the new height for this interval and the new largest height for the whole graph.\n\n\n class Solution {\n public:\n vector<int> fallingSquares(vector<pair<int, int>>& positions) {\n if(positions.empty()) return {};\n int n = positions.size();\n vector<int> res;\n vector<double> intervals;\n for(auto p : positions){\n intervals.push_back(p.first + 0.5);\n intervals.push_back((p.first + p.second)*1.0);\n }\n sort(intervals.begin(), intervals.end());\n unordered_map<string, int> mp;\n vector<int> height(intervals.size(), 0);\n for(int i = 0; i < intervals.size(); ++i){\n mp[to_string(intervals[i])] = i;\n }\n int glb_max = 0;\n for(int i = 0; i < n; ++i){\n int left = mp[to_string(positions[i].first + 0.5)];\n int right = mp[to_string(positions[i].first*1.0 + positions[i].second)];\n int cur_max = *max_element(height.begin() + left, height.begin() + right + 1);\n while(left <= right){\n height[left++] = cur_max + positions[i].second;\n }\n glb_max = max(glb_max, cur_max + positions[i].second);\n res.push_back(glb_max);\n }\n return res;\n }\n }; | 1 | 0 | [] | 0 |
falling-squares | 98% beat using Segment Tree | 98-beat-using-segment-tree-by-aviadblume-kj6j | IntuitionStore in a segment tree heights of left edges of each cube.
when adding a cube to the board, update all cubes in the x-range of the cube.ApproachComple | aviadblumen | NORMAL | 2025-03-20T20:16:52.887378+00:00 | 2025-03-20T20:16:52.887378+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Store in a segment tree heights of left edges of each cube.
when adding a cube to the board, update all cubes in the x-range of the cube.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
$$O(nlog(n))$$
- Space complexity:
$$O(n)$$
# Code
```cpp []
class SegmentTree {
vector<int> tree, lazy;
int size;
public:
SegmentTree(int n) {
size = n;
tree.assign(4 * n, 0);
lazy.assign(4 * n, 0);
}
void rangeUpdate(int node, int start, int end, int l, int r, int val) {
if (lazy[node] != 0) {
tree[node] = max(tree[node], lazy[node]);
if (start != end) {
lazy[2 * node + 1] = max(lazy[node],lazy[2 * node + 1]);
lazy[2 * node + 2] = max(lazy[node],lazy[2 * node + 2]);
}
lazy[node] = 0;
}
if (start > r || end < l) return;
if (start >= l && end <= r) {
tree[node] = max(tree[node],val);
if (start != end) {
lazy[2 * node + 1] = max(val,lazy[2 * node + 1]);
lazy[2 * node + 2] = max(val,lazy[2 * node + 2]);
}
return;
}
int mid = (start + end) / 2;
rangeUpdate(2 * node + 1, start, mid, l, r, val);
rangeUpdate(2 * node + 2, mid + 1, end, l, r, val);
tree[node] = max(tree[2 * node + 1],tree[2 * node + 2]);
}
int rangeQuery(int node, int start, int end, int l, int r) {
if (lazy[node] != 0) {
tree[node] = max(tree[node], lazy[node]);
if (start != end) {
lazy[2 * node + 1] = max(lazy[node],lazy[2 * node + 1]);
lazy[2 * node + 2] = max(lazy[node],lazy[2 * node + 2]);
}
lazy[node] = 0;
}
if (start > r || end < l) return 0;
if (start >= l && end <= r) return tree[node];
int mid = (start + end) / 2;
return max(rangeQuery(2 * node + 1, start, mid, l, r),
rangeQuery(2 * node + 2, mid + 1, end, l, r));
}
void update(int l, int r, int val) {
rangeUpdate(0, 0, size - 1, l, r, val);
}
int query(int l, int r) {
return rangeQuery(0, 0, size - 1, l, r);
}
};
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
vector<int> x_values;
for(auto& p:positions)
x_values.push_back(p[0]);
sort(x_values.begin(),x_values.end());
SegmentTree t(size(x_values));
vector<int> result;
for(auto& p:positions){
int x = p[0], cube_size = p[1];
int left_indx = lower_bound(x_values.begin(),x_values.end(),x)-x_values.begin();
int right_indx = lower_bound(x_values.begin(),x_values.end(),x+cube_size)-x_values.begin()-1;
int height = t.query(left_indx,right_indx) + cube_size;
t.update(left_indx,right_indx,height);
if (result.empty())
result.push_back(height);
else
result.push_back(max(height,result.back()));
}
return result;
}
};
``` | 0 | 0 | ['C++'] | 0 |
falling-squares | Easy to understand Segment Tree Code! | easy-to-understand-segment-tree-code-by-xcbvv | IntuitionIf you know about Segment Tree then the question is not hard at all. The challenge is to create the range with the commpresed indexes for the sqaures.A | Deepansh_1912 | NORMAL | 2025-03-13T07:51:03.220126+00:00 | 2025-03-13T07:51:03.220126+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
If you know about Segment Tree then the question is not hard at all. The challenge is to create the range with the commpresed indexes for the sqaures.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class SegTree{
vector<int>seg;
public:
SegTree(int n){
seg.resize(4*n+1, 0);
}
int query(int ind, int low, int high, int l, int h){
if(h<low || high<l) return 0;
if(low>=l && high<=h) return seg[ind];
int mid = (low + high)/2;
int left = query(2*ind+1, low, mid, l, h);
int right = query(2*ind+2, mid+1, high, l, h);
return max(left, right);
}
void update(int ind, int low, int high, int l, int h,int val){
if(h<low || l>high) return;
if(low == high){
seg[ind] = max(seg[ind], val);
return;
}
int mid = (low + high) /2;
update(2*ind+1, low, mid, l, h, val);
update(2*ind+2, mid+1, high, l, h, val);
seg[ind] = max(seg[2*ind+1], seg[2*ind+2]);
}
};
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
set<int>sortedCords;
map<int, int>mpp;
for(auto pos : positions){
sortedCords.insert(pos[0]);
sortedCords.insert(pos[0]+pos[1]-1);
}
int count = 1;
for(int cords : sortedCords){
mpp[cords] = count++;
}
int n = count;
SegTree ob(n);
vector<int>ans;
int maxi = 0;
for(auto& pos : positions){
int l = mpp[pos[0]];
int r = mpp[pos[0]+pos[1]-1];
int maxHeight = ob.query(0, 1, n, l, r);
ob.update(0, 1, n, l, r, maxHeight+pos[1]);
maxi = max(maxi , ob.query(0, 1, n, 1, n));
ans.push_back(maxi);
}
return ans;
}
};
``` | 0 | 0 | ['Segment Tree', 'Ordered Set', 'C++'] | 0 |
falling-squares | 🔷 Coordinate Compression for Falling Squares 🎯 | Beats 88% - Efficient Height Tracking | coordinate-compression-for-falling-squar-4480 | IntuitionThe problem requires tracking the maximum height of stacked squares at each step. My initial insight was that we only need to track height changes at t | holdmypotion | NORMAL | 2025-02-24T18:23:08.855194+00:00 | 2025-02-24T18:23:08.855194+00:00 | 6 | false | # Intuition
The problem requires tracking the maximum height of stacked squares at each step. My initial insight was that we only need to track height changes at the specific coordinates where squares begin and end. Since the actual positions can range up to 10^8, we can use coordinate compression to map these positions to a smaller range, making the problem more manageable.
# Approach
The solution uses coordinate compression to efficiently track heights across the board:
1. **Coordinate Compression**:
- Extract all unique coordinates where squares begin and end
- Sort these coordinates and map them to sequential indices
- This transforms the potentially large coordinate space into a compact array
2. **Height Tracking**:
- Initialize a heights array to track the height at each compressed coordinate
- For each square:
- Find the maximum height in the range the square will land on
- Calculate the new height by adding the square's size to this maximum
- Update all coordinates within the square's range with this new height
- Track the maximum height seen so far for the result
3. **Result Generation**:
- After processing each square, append the maximum height seen so far to the result
This approach elegantly handles the key challenge of efficiently representing a potentially sparse area where squares may land far apart from each other.
# Complexity
- Time complexity: **O(n²)**
- We process n squares
- For each square, we potentially need to update O(n) positions in the heights array
- Finding the maximum height in a range is also O(n) in the worst case
- Space complexity: **O(n)**
- We store at most 2n coordinates (each square contributes two coordinates)
- The heights array size is at most 2n
- The result array stores n heights
# Code
```python3 []
class Solution:
def fallingSquares(self, positions: List[List[int]]) -> List[int]:
coords = set()
for left, size in positions:
coords.add(left)
coords.add(left + size)
coord_map = {coord: idx for idx, coord in enumerate(sorted(coords))}
heights = [0] * len(coord_map)
result = []
max_height_so_far = 0
for left, size in positions:
left_idx = coord_map[left]
right_idx = coord_map[left + size]
current_max_height = max(heights[left_idx:right_idx])
new_height = current_max_height + size
for i in range(left_idx, right_idx):
heights[i] = new_height
max_height_so_far = max(max_height_so_far, new_height)
result.append(max_height_so_far)
return result
```
The key insight of this solution is recognizing that we only need to track heights at the specific coordinates where changes happen, rather than modeling the entire range. By compressing the coordinates, we transform a potentially sparse problem into a dense one that's easier to handle.
If you found this solution helpful, please consider upvoting! Happy coding! 💻 | 0 | 0 | ['Ordered Set', 'Python3'] | 0 |
falling-squares | O(n*n) calculate height of each square | onn-calculate-height-of-each-square-by-l-wohu | Intuition
Calculate height of each square
Compare and get result of "height of the current tallest stack of squares."
???? why this problem is hardComplexity
T | luudanhhieu | NORMAL | 2025-02-20T03:40:43.782453+00:00 | 2025-02-20T03:40:43.782453+00:00 | 2 | false | # Intuition
- Calculate height of each square
- Compare and get result of "height of the current tallest stack of squares."
???? why this problem is hard
# Complexity
- Time complexity: O(n*n)
- Space complexity:O(n)
# Code
```golang []
func fallingSquares(positions [][]int) []int {
rs := make([]int, 1)
rs[0] = positions[0][1]
for i := 1; i < len(positions); i++ {
mx := 0
for j := range rs {
if positions[j][0] < positions[i][0]+positions[i][1] && positions[j][1]+positions[j][0] > positions[i][0] {
mx = max(mx, rs[j])
}
}
rs = append(rs, positions[i][1]+mx)
}
for i := 1; i < len(rs); i++ {
if rs[i] < rs[i-1] {
rs[i] = rs[i-1]
}
}
return rs
}
``` | 0 | 0 | ['Go'] | 0 |
falling-squares | Rust Solution | Beats 100% | Segment Tree | rust-solution-beats-100-segment-tree-by-x7r94 | Approach
Build hashmap of actual position into index from left and right positions of every building.
For easy calculation, x inidx_to_x[idx] = xstands for[x, x | skygazer227 | NORMAL | 2025-02-20T03:32:37.181865+00:00 | 2025-02-20T03:32:37.181865+00:00 | 4 | false | # Approach
- Build hashmap of actual position into index from left and right positions of every building.
- For easy calculation, x in `idx_to_x[idx] = x` stands for `[x, x + 1]` line segment.
- For every iteration over buildings:
1. Query maximum height within range
2. Update height to `side_length + max_height` for range
3. Query maximum height for entire tree
# Complexity
- Time complexity: O(NlogN)
- Space complexity: O(N)
# Code
```rust []
use std::collections::HashMap;
struct SegmentTree {
data: Vec<i32>,
}
impl SegmentTree {
fn new(size: usize) -> Self {
Self {
data: vec![0; size],
}
}
fn query(&self, node: usize, start: usize, end: usize, left: usize, right: usize) -> i32 {
if left > end || right < start {
return -1;
}
if left <= start && end <= right {
return self.data[node];
}
let left_max = self.query(node * 2, start, (start + end) / 2, left, right);
let right_max = self.query(node * 2 + 1, (start + end) / 2 + 1, end, left, right);
left_max.max(right_max)
}
fn update(
&mut self,
node: usize,
start: usize,
end: usize,
left: usize,
right: usize,
height: i32,
) {
if left > end || right < start {
return;
}
if start == end {
self.data[node] = height;
return;
}
self.update(node * 2, start, (start + end) / 2, left, right, height);
self.update(
node * 2 + 1,
(start + end) / 2 + 1,
end,
left,
right,
height,
);
self.data[node] = self.data[node * 2].max(self.data[node * 2 + 1]);
}
}
impl Solution {
pub fn falling_squares(positions: Vec<Vec<i32>>) -> Vec<i32> {
let mut idx_to_x = positions
.iter()
.flat_map(|x| [x[0], x[0] + x[1] - 1])
.collect::<Vec<_>>();
idx_to_x.sort();
idx_to_x.dedup();
let x_to_idx = idx_to_x
.iter()
.enumerate()
.map(|(i, &x)| (x, i))
.collect::<HashMap<_, _>>();
let n = idx_to_x.len();
let mut tree = SegmentTree::new(4 * n);
let mut result = vec![];
for position in positions {
let (x, side_length) = (position[0], position[1]);
let (left, right) = (x_to_idx[&x], x_to_idx[&(x + side_length - 1)]);
let max_height = tree.query(1, 0, n - 1, left, right);
tree.update(1, 0, n - 1, left, right, side_length + max_height);
result.push(tree.query(1, 0, n - 1, 0, n - 1));
}
result
}
}
``` | 0 | 0 | ['Segment Tree', 'Rust'] | 0 |
falling-squares | Python Hard | python-hard-by-lucasschnee-xp7i | null | lucasschnee | NORMAL | 2025-02-11T17:38:53.288556+00:00 | 2025-02-11T17:38:53.288556+00:00 | 4 | false | ```python3 []
class Solution:
def fallingSquares(self, positions: List[List[int]]) -> List[int]:
prev = []
def overlap(l, r, left, right):
return not (r <= left or right <= l)
ans = []
mx = 0
for left, sideLength in positions:
right = left + sideLength
max_height = 0
for l, r, h in prev:
if overlap(l, r, left, right):
max_height = max(max_height, h)
max_height += sideLength
mx = max(mx, max_height)
prev.append((left, right, max_height))
ans.append(mx)
return ans
``` | 0 | 0 | ['Python3'] | 0 |
falling-squares | Segment Tree || Lazy Propagation || Coordinate Compression | segment-tree-lazy-propagation-coordinate-3hc6 | IntuitionSince the problem is kind of rnage update and query. It is very intuitive to think of Segment tree with Lazy propagation.ApproachBasically what we are | Mainamanhoon | NORMAL | 2025-01-15T10:15:09.214756+00:00 | 2025-01-15T10:15:09.214756+00:00 | 12 | false | # Intuition
Since the problem is kind of rnage update and query. It is very intuitive to think of Segment tree with Lazy propagation.
# Approach
Basically what we are doing is updating a range in every step. Along with the update we need to check is the square was already present the range we are about/going to update. so first of all perform a query in the range we are about to update. if a non-zero value is obtained, it is very obvious that the coming block is going to rest on an existing block(it will not land on the ground), hence we will add the integer we got from query to height of the square.
For example if a square of side h1 is falling in range l to r , we will firstly perform a query for range l to r (whether there is any square already lying in the range or not ). If a non zero value h2 is obtained from the query then we would have to update (h1+h2) to the range l to r.
# Complexity
- Time complexity: O(k⋅logk)+O(k⋅logn)
- Space complexity: 𝑂(𝑛+𝑘)
# Code
```cpp []
class Solution {
public:
vector<int>seg;
vector<int>lazy;
int n;
void updateRange(int node, int start, int end, int left, int right, int val){
if(lazy[node]){
seg[node] =lazy[node];
if(start!=end){
lazy[2*node+1] = lazy[node];
lazy[2*node+2] =lazy[node];
}
lazy[node]=0;
}
if(right<start || left>end || start>end) return;
if(left<=start && right>=end){
seg[node] =val;
if(start!=end){
lazy[2*node+2] = val;
lazy[2*node+1] = val;
}
return;
}
int mid = start+(end-start)/2;
updateRange(2*node+1,start,mid,left,right,val);
updateRange(2*node+2,mid+1,end,left,right,val);
seg[node]= max(seg[2*node+1],seg[2*node+2]);
}
int queryRange(int node, int start, int end, int left, int right){
if(start>end || start>right || end <left)return 0;
if(lazy[node]!=0){
seg[node] = lazy[node];
if(start!=end){
lazy[2*node+1]=lazy[node];
lazy[2*node+2] = lazy[node];
}
lazy[node]=0;
}
if(left<=start && end<=right) return seg[node];
int mid = start+(end-start)/2;
int q1 = queryRange(2*node+1,start,mid,left,right);
int q2 = queryRange(2*node+2,mid+1,end,left,right);
return max(q1,q2);
}
vector<int> fallingSquares(vector<vector<int>>& positions) {
vector<int> ac;
for(int i=0;i<positions.size();i++){
ac.push_back(positions[i][0]);
ac.push_back(positions[i][1]+positions[i][0]-1);
}
sort(ac.begin(),ac.end());
ac.erase(unique(ac.begin(),ac.end()), ac.end());
unordered_map<int, int> coordMap;
for (int i = 0; i < ac.size(); i++) {
coordMap[ac[i]] = i;
}
n = ac.size();
seg.resize(4*n,0);
lazy.resize(4*n,0);
vector<int>ans;
int temp =0;
for(auto& v: positions){
int hello = queryRange(0,0,n,coordMap[v[0]],coordMap[v[0]+v[1]-1]);
updateRange(0,0,n,coordMap[v[0]],coordMap[v[0]+v[1]-1],v[1]+hello);
ans.push_back(max(temp,queryRange(0,0,n,coordMap[v[0]],coordMap[v[0]+v[1]-1])));
temp = max(temp,ans.back());
}
return ans;
}
};
``` | 0 | 0 | ['Segment Tree', 'C++'] | 0 |
falling-squares | 699. Falling Squares | 699-falling-squares-by-g8xd0qpqty-t5zj | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2024-12-29T06:38:54.989258+00:00 | 2024-12-29T06:38:54.989258+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public List<Integer> fallingSquares(int[][] positions) {
int n = positions.length;
int[] maxHeights = new int[n];
List<Integer> result = new ArrayList<>();
for (int i = 0; i < n; i++) {
int xStart = positions[i][0];
int squareSize = positions[i][1];
int xEnd = xStart + squareSize;
maxHeights[i] += squareSize;
for (int j = i + 1; j < n; j++) {
int xStart2 = positions[j][0];
int squareSize2 = positions[j][1];
int xEnd2 = xStart2 + squareSize2;
if (xStart2 < xEnd && xStart < xEnd2) { // If squares overlap
maxHeights[j] = Math.max(maxHeights[j], maxHeights[i]);
}
}
}
int highest = -1;
for (int height : maxHeights) {
highest = Math.max(highest, height);
result.add(highest);
}
return result;
}
}
``` | 0 | 0 | ['Java'] | 0 |
falling-squares | Easy Soln | easy-soln-by-dicusa-zsbl | Intuition\nFor each square:\na. Find the maximum height of intersecting squares\nb. Calculate the height of the new square based on intersections\nc. Track the | dicusa | NORMAL | 2024-12-01T18:58:24.037633+00:00 | 2024-12-01T18:58:24.037681+00:00 | 8 | false | # Intuition\nFor each square:\na. Find the maximum height of intersecting squares\nb. Calculate the height of the new square based on intersections\nc. Track the overall maximum height\n\n# Approach\n1. Tracking intersections by checking x-coordinate ranges.\n2. Dynamically updating maximum height.\n3. Using set to store placed squares with their coordinates and heights.\n\n# Complexity\n- Time complexity:\n $$O(n\xB2)$$\n\n# Code\n```python3 []\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n heightSet=set() #(x1,x2,h)\n res=[]\n for x,h in positions:\n currHeight=0\n maxHeight=0\n x1,x2=x,x+h\n # print(x1,x2,heightSet)\n for s in heightSet:\n maxHeight=max(maxHeight,s[2])\n if not (s[1]<=x1 or s[0]>=x2):\n # print(f\'s1,s2={s[0]},{s[1]} | x1,x2={x1},{x2} | sH,h={s[2]},{h}\')\n currHeight = max(currHeight,s[2])\n heightSet.add((x1,x2,currHeight+h))\n res.append(max(currHeight+h,maxHeight))\n return res\n``` | 0 | 0 | ['Python3'] | 0 |
falling-squares | Breaking 2D into 1D Problem || Step by Step Lazy Propogation and Coordinate Compression | breaking-2d-into-1d-problem-step-by-step-oy2a | \n# Approach\nInstead of thinking of squares as $2-D$ figures, we can treat them as a line segment flattened into a $1-D$ plane holding a value which is equal t | math_pi | NORMAL | 2024-11-22T11:57:06.332605+00:00 | 2024-11-22T11:57:52.391931+00:00 | 12 | false | \n# Approach\nInstead of thinking of squares as $2-D$ figures, we can treat them as a line segment flattened into a $1-D$ plane holding a value which is equal to the side of the sqaure. *[See below image.]*\n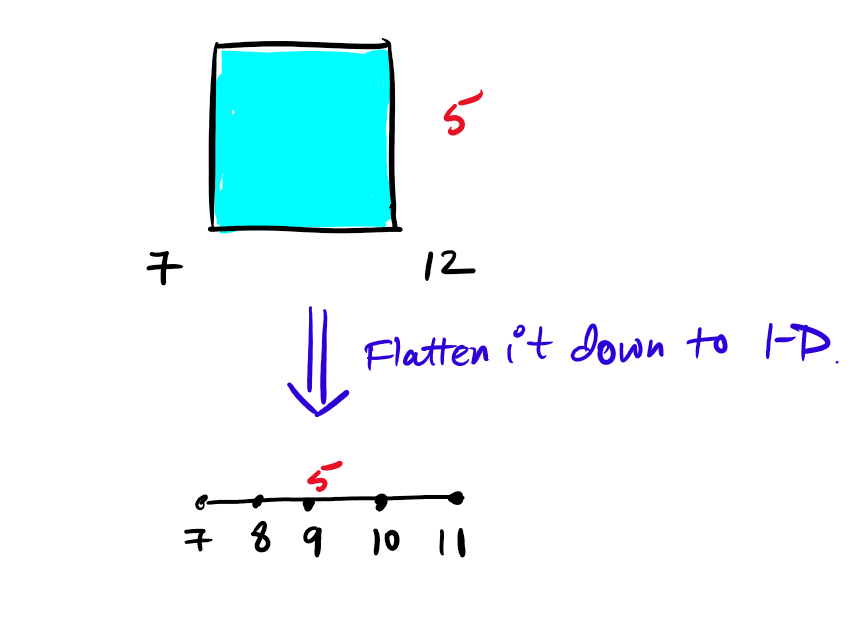\n\n\nIn order to make computations easier a square can be represented as two line segments covering **S =** ***(x[0], x[0]+x[1]-1)***. \n\nSo the problem is now converted to an easier familiar problem of assigning a value of *x[1]* to the range **S** and finding the maximum in the entire range from ***[1, max(x[0]+x[1])]***. This can be easily done via **Lazy Segment Tree**.\n\nBut there is one problem, since the coordinates can be of the order of *1e8*, storing them directly would lead to *memory limit exceed*. \n\nWe can ask ourselves: does the volume of the starting and ending points of range really matters? \nThe answer is no, it does not. What matters is the relative ordering of ranges, For this we can utilize a technique called **Coordinate Compression**. \n\nBy compressing the coordinates we can easily fit the points to a memory friendly limit.\n\nFor more info about Lazy Segment Tree: https://codeforces.com/edu/course/2/lesson/5/2\nFor more info about Coordinate Compression: https://usaco.guide/silver/sorting-custom\n\n\n# Complexity\n- Time complexity:\n$O(NlogN)$\n\n- Space complexity:\n$O(N)$\n\n# Code\n```cpp []\nstruct segTree {\n vector<long long> tr, op;\n int size;\n const long long NO_OPERATION = LLONG_MAX; \n const long long NULL_VALUE = 0; \n\n segTree(int n) {\n size = 1;\n while (size < n) size *= 2;\n tr.assign(size * 2, 0);\n op.assign(size * 2, NO_OPERATION);\n }\n\n long long calc_op(long long a, long long b) {\n return max(a, b);\n }\n\n long long modify_op(long long a, long long b, long long len) {\n return (b == NO_OPERATION) ? a : b;\n }\n\n void apply_op(long long &a, long long b, long long len) {\n a = modify_op(a, b, len);\n }\n\n void propagate(int v, int lx, int rx) {\n if (op[v] == NO_OPERATION || rx - lx == 1) return;\n int m = (lx + rx) / 2;\n apply_op(tr[2 * v + 1], op[v], m - lx);\n apply_op(op[2 * v + 1], op[v], 1);\n apply_op(tr[2 * v + 2], op[v], rx - m);\n apply_op(op[2 * v + 2], op[v], 1);\n op[v] = NO_OPERATION;\n }\n\n void build(int v, int lx, int rx, const vector<long long> &a) {\n if (rx - lx == 1) {\n if (lx < (int)a.size()) {\n tr[v] = a[lx];\n }\n return;\n }\n int m = (lx + rx) / 2;\n build(2 * v + 1, lx, m, a);\n build(2 * v + 2, m, rx, a);\n tr[v] = calc_op(tr[2 * v + 1], tr[2 * v + 2]);\n }\n\n void build(const vector<long long> &a) {\n build(0, 0, size, a);\n }\n\n void modify(int v, int lx, int rx, int l, int r, long long val) {\n propagate(v, lx, rx);\n if (rx <= l || lx >= r) return;\n if (lx >= l && rx <= r) {\n apply_op(tr[v], val, rx - lx);\n apply_op(op[v], val, 1);\n return;\n }\n int m = (lx + rx) / 2;\n modify(2 * v + 1, lx, m, l, r, val);\n modify(2 * v + 2, m, rx, l, r, val);\n tr[v] = calc_op(tr[2 * v + 1], tr[2 * v + 2]);\n }\n\n void modify(int l, int r, long long val) {\n modify(0, 0, size, l, r, val);\n }\n\n long long calc(int v, int lx, int rx, int l, int r) {\n propagate(v, lx, rx);\n if (rx <= l || lx >= r) return NULL_VALUE;\n if (lx >= l && rx <= r) return tr[v];\n int m = (lx + rx) / 2;\n long long s1 = calc(2 * v + 1, lx, m, l, r);\n long long s2 = calc(2 * v + 2, m, rx, l, r);\n return calc_op(s1, s2);\n }\n\n long long calc(int l, int r) {\n return calc(0, 0, size, l, r);\n }\n};\nclass Solution {\npublic:\n \n vector<int> fallingSquares(vector<vector<int>>& positions) {\n set<int> cord;\n for(auto &x: positions) {\n cord.insert(x[0]);\n cord.insert(x[0]+x[1]);\n }\n int id = 0;\n map<int, int> compress;\n for(auto x: cord) compress[x]=id++;\n segTree seg(id);\n vector<int> res;\n int mx = 0;\n for(auto &x: positions) {\n int l = compress[x[0]], r = compress[x[0]+x[1]]; \n int cur = seg.calc(l, r);\n seg.modify(l, r, cur+x[1]);\n res.push_back(seg.calc(0, id));\n }\n return res;\n }\n};\n``` | 0 | 0 | ['Hash Table', 'Segment Tree', 'Ordered Set', 'C++'] | 0 |
falling-squares | Simple python3 solution with comments | simple-python3-solution-with-comments-by-cbbc | Complexity\n- Time complexity: O(n \cdot \log(n)) \n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n) \n Add your space complexity here, e. | tigprog | NORMAL | 2024-11-05T13:38:01.265726+00:00 | 2024-11-05T13:38:01.265772+00:00 | 12 | false | # Complexity\n- Time complexity: $$O(n \\cdot \\log(n))$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def fallingSquares(self, positions: List[List[int]]) -> List[int]:\n data = SortedList()\n\n max_height = 0\n result = []\n\n for left, side_length in positions:\n u, v = left, left + side_length\n current_height = side_length\n\n index = data.bisect_left((u, u, 0))\n if index != 0:\n index -= 1\n \n while index != len(data):\n x, y, other_height = data[index]\n if y <= u: # old square is to the left of new square\n index += 1\n continue\n elif v <= x: # old square is to the right of new square\n break\n else: # old and new squares intersect\n current_height = max(current_height, side_length + other_height)\n data.pop(index)\n\n if x < u: # update left part of old square\n data.add((x, u, other_height))\n index += 1\n \n if v < y: # update right part of old square\n data.add((v, y, other_height))\n index += 1 \n \n data.add((u, v, current_height))\n \n max_height = max(max_height, current_height)\n result.append(max_height)\n \n return result\n``` | 0 | 0 | ['Greedy', 'Ordered Set', 'Python3'] | 0 |
falling-squares | TreeMap | treemap-by-sav20011962-7p1a | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nTreeMap: key - right border, value - pair(width, full height)\n# Complexi | sav20011962 | NORMAL | 2024-09-23T13:23:11.920299+00:00 | 2024-09-23T13:24:15.387949+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTreeMap: key - right border, value - pair(width, full height)\n# Complexity\n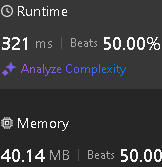\n# Code\n```kotlin []\nclass Solution {\n fun fallingSquares(positions: Array<IntArray>): List<Int> {\n val tree = TreeMap<Int, Pair<Int,Int>>() // key - right border, value - pair(width, full height)\n var rez : MutableList<Int> = mutableListOf()\n var max_height = 0\n for ((left,sideLength) in positions) {\n val sub = tree.tailMap(left+1) \n // i find cubes that fell earlier \n // with a right boundary greater \n // than the left boundary of the falling one.\n var tek_max_height = 0\n for ((pos,pair) in sub) {\n if (pos-pair.first<left+sideLength) \n // I check that the previously dropped cube \n // has a left boundary BEFORE \n // the right boundary of the current cube.\n tek_max_height = maxOf(tek_max_height,pair.second)\n }\n tree[left+sideLength] = Pair(sideLength,tek_max_height+sideLength)\n max_height = maxOf(max_height,tek_max_height+sideLength)\n rez.add(max_height)\n }\n return rez\n }\n}\n``` | 0 | 0 | ['Kotlin'] | 0 |
falling-squares | Optimized Approach with Binary Search | optimized-approach-with-binary-search-by-de93 | Intuition\nwe can use a greedy approach. Each square\'s height will depend on the heights of the squares already placed on the line. We maintain a list of the c | orel12 | NORMAL | 2024-09-02T20:09:31.133779+00:00 | 2024-09-02T20:09:31.133798+00:00 | 15 | false | # Intuition\nwe can use a greedy approach. Each square\'s height will depend on the heights of the squares already placed on the line. We maintain a list of the current heights and use binary search to efficiently find where each new square starts and ends relative to the squares already placed.\n\n# Approach\nWe maintain two lists: one for positions and another for heights. For each new square, we:\n1. Use binary search to find the range of existing squares it overlaps with.\n2. Calculate the new height based on the maximum height in that range.\n3. Insert the new position and height into our lists.\n4. Track and update the maximum height seen so far.\n\n# Complexity\n- Time complexity: $$O(n^2)$$ due to potentially checking all previous squares for each new square.\n- Space complexity: $$O(n)$$ for storing the positions and heights of the squares.\n\n\n# Code\n```python3 []\nclass Solution:\n def fallingSquares(self, positions):\n pos, height, res, max_h = [0], [0], [], 0\n for l, s in positions:\n i, j = bisect_right(pos, l), bisect_left(pos, l + s)\n h = max(height[i-1:j] or [0]) + s\n pos[i:j], height[i:j] = [l, l + s], [h, height[j-1]]\n res.append(max_h := max(max_h, h))\n return res\n\n``` | 0 | 0 | ['Python3'] | 0 |
falling-squares | Simple and short version of segment tree with lazy update | simple-and-short-version-of-segment-tree-eyem | Intuition\n Describe your first thoughts on how to solve this problem. \nI found the segment tree in the solutions are very long so that I update one with short | jesselee_leetcode | NORMAL | 2024-08-30T08:47:12.445478+00:00 | 2024-08-30T08:47:12.445512+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI found the segment tree in the solutions are very long so that I update one with short version. you can also change my segment tree code into template (I did so, lol).\n\nNOTE: when you want to use segment tree to solve other questions, remember update the max() part in LazySegmentTree\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- step1: query current result in the range\n- step2: add the new one\n- step3: update the tree\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass LazySegmentTree:\n\n def __init__(self):\n self.vals = Counter()\n self.lazy = Counter()\n\n\n def query(self, start, end, left, right, index):\n if start > right or end < left:\n return 0\n\n if start <= left <= right <= end:\n return self.vals[index]\n\n mid = (left + right) // 2\n left_value = self.query(start, end, left, mid, 2 * index)\n right_value = self.query(start, end, mid + 1, right, 2 * index + 1)\n return max(self.lazy[index], left_value, right_value)\n\n def update(self, start, end, left, right, index, value = 1):\n if start > right or end < left:\n return\n\n if start <= left and right <= end:\n self.vals[index] = max(self.vals[index], value)\n self.lazy[index] = max(self.lazy[index], value)\n else:\n mid = (left + right) // 2\n self.update(start, end, left, mid, index * 2, value)\n self.update(start, end, mid + 1, right, index * 2 + 1, value)\n\n self.vals[index] = max(self.lazy[index],\n self.vals[index * 2], self.vals[index * 2 + 1]\n )\n\n\n\n\nclass Solution:\n def fallingSquares(self, positions):\n\n\n sg_tree = LazySegmentTree()\n res = []\n res_max = 0\n for start, length in positions:\n end = start + length - 1\n current = sg_tree.query(start, end, 0, 10**9, 1)\n current_new = current + length\n \n sg_tree.update(start, end, 0, 10**9, 1, current_new)\n\n res_max = max(res_max, current_new)\n res.append(res_max)\n\n return res\n\n\n\n\n``` | 0 | 0 | ['Segment Tree', 'Python3'] | 0 |
falling-squares | ✅A COMMON IDEA,🧐 O(n^2) where n is critical points | a-common-idea-on2-where-n-is-critical-po-ye02 | Intuition\n Describe your first thoughts on how to solve this problem. \nwe will store height of every critical points of our block except at end ,this way we w | sameonall | NORMAL | 2024-08-15T18:21:19.945734+00:00 | 2024-08-15T18:21:19.945764+00:00 | 4 | false | ### Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwe will store height of every critical points of our block except at end ,this way we will always have height of every block with aleast one critical point and we can update height changes due to new blocks except by it end points.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#include <iostream>\n#include <vector>\n#include <set>\n#include <unordered_map>\n#include <algorithm>\n\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n set<int> points;\n for (auto& d : positions) {\n points.insert(d[0]);\n points.insert(d[0] + d[1]);\n }\n \n unordered_map<int, int> index;\n int n = 0;\n for (auto& ele : points) index[ele] = n++;\n \n vector<int> height(n, 0);\n vector<int> result;\n int maxHeight = 0;\n\n for (auto& p : positions) {\n int li = index[p[0]];\n int ri = index[p[0] + p[1]];\n int currHeight = 0;\n\n // Find the maximum height in the current interval [li, ri)\n for (int j = li; j < ri; j++) {\n currHeight = max(currHeight, height[j]);\n }\n\n // Update the height for the current interval [li, ri)\n for (int j = li; j < ri; j++) {\n height[j] = currHeight + p[1];\n }\n\n // Update the global maximum height and store the result\n maxHeight = max(maxHeight, currHeight + p[1]);\n result.push_back(maxHeight);\n }\n \n return result;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
falling-squares | C++ BST Solution detailed with comments | c-bst-solution-detailed-with-comments-by-7e8w | Approach\nWe can store closed-open intervals $[i,~j)$ in a BST such that\n\n a < b $\Leftrightarrow$ the whole a interval is to the left of b\n a > b $\Leftrigh | diegood12 | NORMAL | 2024-08-07T12:50:21.927929+00:00 | 2024-08-07T12:50:21.927961+00:00 | 15 | false | # Approach\nWe can store closed-open intervals $[i,~j)$ in a BST such that\n\n* `a < b` $\\Leftrightarrow$ the whole `a` interval is to the left of `b`\n* `a > b` $\\Leftrightarrow$ the whole `a` interval is to the right of `b`\n* `a == b` $\\Leftrightarrow$ `a` intercepts `b`\n\nDetails on how to do that are in the code and [my solution for 729. My Calendar I](https://leetcode.com/problems/my-calendar-i/solutions/5438715/just-use-a-set).\n\nBy addind a height to these intervals, we have rectangles.\n\nSo, for each step, we can take the lower bound and the upper bound of the new square to be added to find which rectangles intercepts with it. Then, we replace those with 3 rectangles:\n\n* the first one being the little tip that comes from the first intercepting rectangle\n* the second being a rectangle that have the width of the new square and the height of the heighest intercepting rectangle\n* The third being the little tip that comes from the last intercepting rectangle\n\nThe images represent this mechanism with some possible scenarios\n\n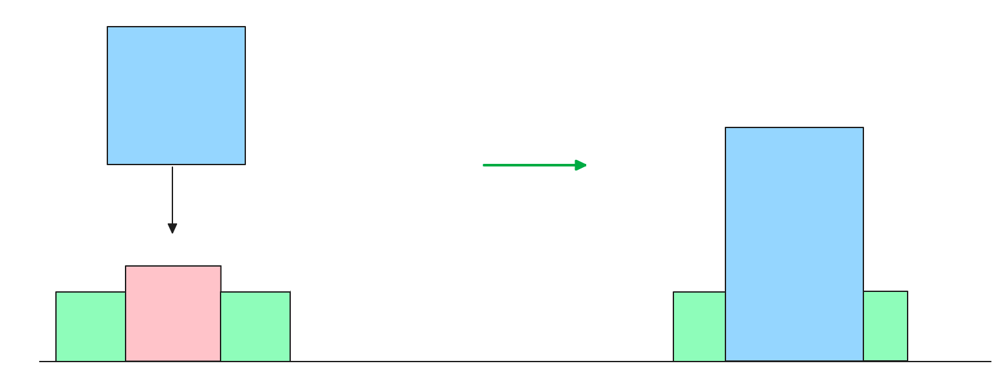\n\n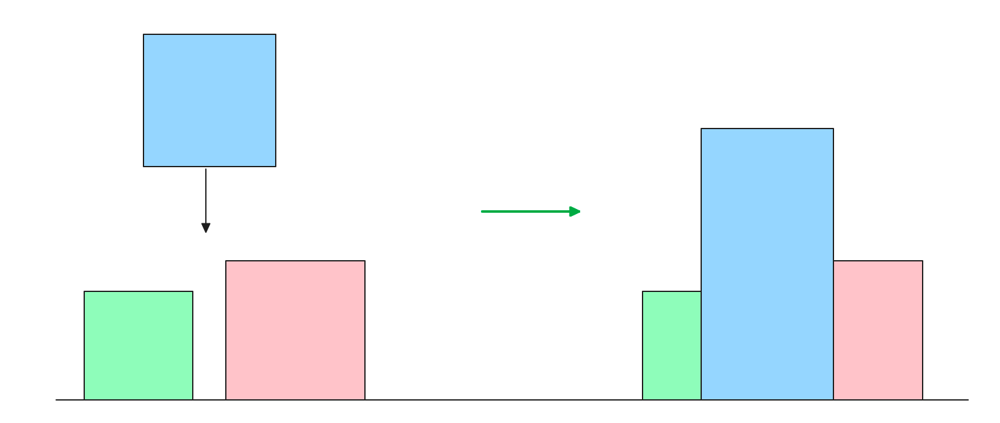\n\n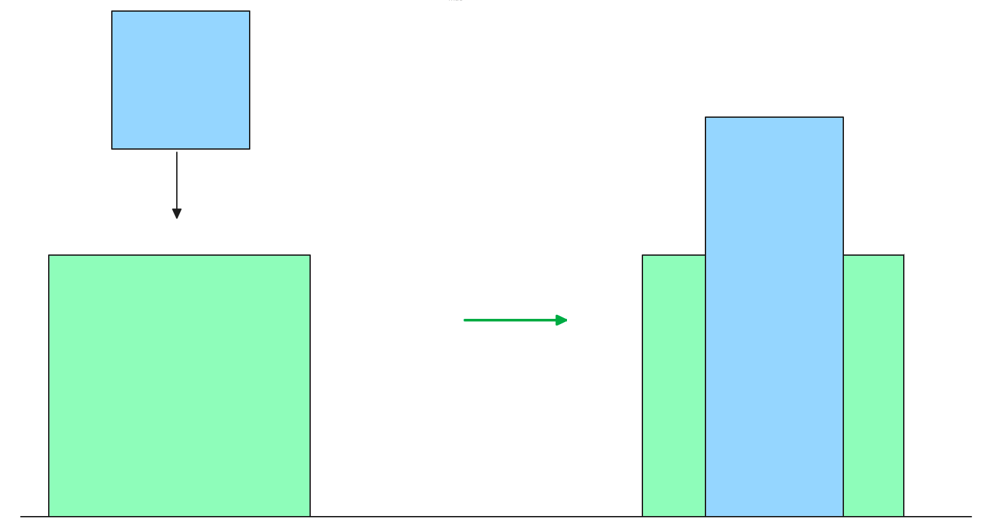\n\n\n# Complexity\n- Time complexity:\n$$O(n \\cdot \\log(n))$$ - we can find all intercepting rectangles in $O(\\log(n))$ time and we do this $n$ times.\nThe inner iteration is amortized $O(n)$, so we get $O(n\\cdot\\log(n))$ as our complexity.\n\n- Space complexity:\n$$O(n)$$ for the result array and $$O(n)$$ for the BST (worst case).\n\n# Code\n```\nclass Solution {\nprivate:\n struct Rect {\n int begin;\n int end;\n int height;\n };\n\n struct Compare {\n // this comparator is quite something...\n // with this, equality happens when an interval intersects another\n // considering an interval as [a, b)\n bool operator()(const Rect& a, const Rect& b) const {\n // scenarios:\n // a < b (the whole interval a is to the left of b):\n // [ ) | [ )\n // [ ) | [ )\n // a > b (the whole interval a is to the right of b):\n // [ ) | [ )\n // [ ) | [ )\n // a == b (a intersects b):\n // [ ) | [ ) \n // [ ) | [ )\n return a.end <= b.begin;\n }\n };\n\n typedef set<Rect, Compare> RectTree;\npublic:\n vector<int> fallingSquares(vector<vector<int>>& positions) {\n // with this bad boy, lookup is done in O(log(n)) time\n RectTree rects;\n\n vector<int> result;\n // this makes our .push_back\'s efficient\n result.reserve(positions.size());\n\n int max_height = 0;\n\n for (const auto& p: positions) {\n const int begin = p[0];\n const int end = p[0] + p[1];\n const int height = p[1];\n\n // this is the first rect in the tree that intercepts with our new rectangle\n const auto lb = rects.lower_bound({ begin, end, height });\n // and this is the first rect after ours that DOESN\'t intercept with it\n const auto ub = rects.upper_bound({ begin, end, height });\n\n int max_height_in_interval = 0;\n\n // so, we\'re gonna iterate over these elements, find the greatest height of them\n // and delete them\n for (auto it = lb; it != ub; ) {\n // since we\'re erasing the iterator from the tree, we must grab its information\n // (we\'ll need it later on this iteration)\n const auto [b, e, h] = *it;\n\n max_height_in_interval = max(max_height_in_interval, h);\n\n // we must grab the next iterator right away since we\'re modifying the tree\n // while iterating\n auto nxt = next(it);\n rects.erase(it);\n it = nxt;\n\n // if we find a rect that starts before our current rect begins\n // we must re-insert the little tip of the previous square\n if (b < begin) {\n rects.insert({ b, begin, h });\n }\n \n // same for a rect that ends after our current rect ends\n if (e > end) {\n rects.insert({ end, e, h });\n }\n }\n\n const int new_height = max_height_in_interval + height;\n\n // after deleting all intercepting rects, we have room for our new big rect\n rects.insert({ begin, end, new_height });\n\n // finally, we can update the result array\n result.push_back(max_height = max(max_height, new_height));\n }\n\n return result;\n }\n};\n\n``` | 0 | 0 | ['Binary Search Tree', 'Ordered Set', 'C++'] | 0 |
falling-squares | simplfy check every previous square, O(n^2) | simplfy-check-every-previous-square-on2-lbfhy | \n\nimpl Solution {\n pub fn falling_squares(xs: Vec<Vec<i32>>) -> Vec<i32> {\n let n = xs.len();\n let mut h = vec![0; n];\n let mut hh | user5285Zn | NORMAL | 2024-07-23T13:03:32.027918+00:00 | 2024-07-23T13:03:32.027964+00:00 | 2 | false | \n```\nimpl Solution {\n pub fn falling_squares(xs: Vec<Vec<i32>>) -> Vec<i32> {\n let n = xs.len();\n let mut h = vec![0; n];\n let mut hh = 0; \n let mut r = Vec::with_capacity(n);\n hh = 0;\n for i in 0..n {\n let x = xs[i][0];\n let s = xs[i][1];\n for j in 0..i {\n let y = xs[j][0];\n let z = xs[j][1];\n if (y <= x && x < y + z) || (y < x + s && x + s <= y + z) \n | (x <= y && y < x + s) || (x < y + z && y + z <= x + s) {\n h[i] = h[i].max(h[j])\n }\n }\n h[i] += s;\n hh = hh.max(h[i]);\n r.push(hh)\n }\n r\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
falling-squares | Beating 100% users in Runtime & Memory using PHP | beating-100-users-in-runtime-memory-usin-5qoh | Code\n\nclass Solution {\n function fallingSquares($positions) {\n $hgt = [0];\n $pos = [0];\n $res = [];\n $mx = 0;\n\n f | nishk2 | NORMAL | 2024-07-17T08:26:22.238615+00:00 | 2024-07-17T08:26:22.238644+00:00 | 1 | false | # Code\n```\nclass Solution {\n function fallingSquares($positions) {\n $hgt = [0];\n $pos = [0];\n $res = [];\n $mx = 0;\n\n foreach ($positions as $box) {\n $mx = max($mx, self::helper($box, $pos, $hgt));\n $res[] = $mx;\n }\n\n return $res;\n }\n\n private static function helper($box, &$pos, &$hgt) {\n list($l, $h) = $box;\n $r = $l + $h;\n\n $i = self::bisectRight($pos, $l);\n $j = self::bisectLeft($pos, $r);\n\n $maxHeight = 0;\n for ($k = $i - 1; $k < $j; $k++) {\n if (isset($hgt[$k]) && $hgt[$k] > $maxHeight) {\n $maxHeight = $hgt[$k];\n }\n }\n\n $res = $h + $maxHeight;\n array_splice($pos, $i, $j - $i, [$l, $r]);\n array_splice($hgt, $i, $j - $i, [$res, isset($hgt[$j - 1]) ? $hgt[$j - 1] : 0]);\n\n return $res;\n }\n\n private static function bisectRight($arr, $x) {\n $lo = 0;\n $hi = count($arr);\n while ($lo < $hi) {\n $mid = intval(($lo + $hi) / 2);\n if ($x < $arr[$mid]) {\n $hi = $mid;\n } else {\n $lo = $mid + 1;\n }\n }\n return $lo;\n }\n\n private static function bisectLeft($arr, $x) {\n $lo = 0;\n $hi = count($arr);\n while ($lo < $hi) {\n $mid = intval(($lo + $hi) / 2);\n if ($arr[$mid] < $x) {\n $lo = $mid + 1;\n } else {\n $hi = $mid;\n }\n }\n return $lo;\n }\n}\n``` | 0 | 0 | ['PHP'] | 0 |
falling-squares | C++ Clean Solution | Easy O(N^2) | c-clean-solution-easy-on2-by-mhasan01-1thg | Approach\n\nThe idea is that when we are putting the $i$-th square, we need to know the "highest" square that it will be put into.\n\nLet $h[i]$ be the height o | mhasan01 | NORMAL | 2024-07-02T18:34:15.936378+00:00 | 2024-07-02T18:34:15.936452+00:00 | 67 | false | # Approach\n\nThe idea is that when we are putting the $i$-th square, we need to know the "highest" square that it will be put into.\n\nLet $h[i]$ be the height of putting the $i$-th square, then initially $h[i]=p[i][1]$ which is the size of the square.\n\nNow we can find all $j < i$ such that $i-$th square overlaps with the $j$-th square, we will need to find the maximal $h[j]$\n\nNow $h[i]=\\max(h[i], h[j]+p[i][1)$ if we have found $j$\n\nWe can store the answer by keeping track of the maximal $h[i]$ from left to right. \n\n# Complexity\n- Time complexity: $O(N^2)$\n\n- Space complexity: $O(N)$\n\n## Note\n- There\'s a more optimal solution with $O(N \\log N)$ using Segment Tree Lazy Propagation\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> fallingSquares(vector<vector<int>>& p) {\n int n = (int) p.size();\n vector<int> ans(n);\n vector<int> h(n);\n int res = 0;\n for (int i = 0; i < n; i++) {\n h[i] = p[i][1];\n for (int j = 0; j < i; j++) {\n int li = p[i][0];\n int ri = li + p[i][1];\n int lj = p[j][0];\n int rj = lj + p[j][1];\n if (li >= lj) {\n swap(li, lj);\n swap(ri, rj);\n }\n if (li <= lj && lj < ri) {\n h[i] = max(h[i], h[j] + p[i][1]);\n }\n }\n res = max(res, h[i]);\n ans[i] = res;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.