question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
falling-squares | :: Kotlin :: Segment Tree Solution | kotlin-segment-tree-solution-by-znxkznxk-vmqt | \n\n# Code\n\nclass Solution {\n fun fallingSquares(positions: Array<IntArray>): List<Int> {\n val posToIdx = HashMap<Double, Int>()\n val pos | znxkznxk1030 | NORMAL | 2024-07-01T04:39:40.371766+00:00 | 2024-07-01T04:39:40.371795+00:00 | 2 | false | \n\n# Code\n```\nclass Solution {\n fun fallingSquares(positions: Array<IntArray>): List<Int> {\n val posToIdx = HashMap<Double, Int>()\n val pos = mutableListOf<Double>()\n\n for (position in positions) {\n pos.add(position[0].toDouble() + 0.1)\n pos.add((position[0] + position[1]).toDouble() - 0.1)\n }\n\n pos.sort()\n\n for (index in pos.indices) {\n val crd = pos[index]\n if (posToIdx.containsKey(crd)) continue\n posToIdx.put(crd, index)\n }\n\n val st = SegmentTree(pos.size * 2)\n val result = mutableListOf<Int>()\n var m = 0\n for (position in positions) {\n val u = posToIdx.getOrDefault(position[0].toDouble() + 0.1, -1)\n val v = posToIdx.getOrDefault((position[0] + position[1]).toDouble() - 0.1, -1)\n val l = position[1]\n\n val max = st.query(u, v)\n st.update(u, v, max + l)\n m = maxOf(m, max + l)\n result.add(m)\n }\n\n return result\n }\n}\n\nclass SegmentTree(val n: Int) {\n val tree = IntArray(n * 4)\n val lazy = IntArray(n * 4)\n\n fun update(l: Int, r: Int, value: Int) {\n update(0, 0, n - 1, l, r, value)\n }\n\n fun update(node: Int, start: Int, end: Int, l: Int, r: Int, value: Int) {\n if (start > end || start > r || end < l) return\n if (lazy[node] != 0) {\n tree[node] = maxOf(tree[node], lazy[node])\n if (start != end) {\n lazy[node * 2 + 1] = maxOf(lazy[node * 2 + 1], lazy[node])\n lazy[node * 2 + 2] = maxOf(lazy[node * 2 + 1], lazy[node])\n }\n lazy[node] = 0\n }\n\n if (l <= start && end <= r) {\n tree[node] = maxOf(tree[node], value)\n if (start != end) {\n lazy[2 * node + 1] = maxOf(lazy[node * 2 + 1], value)\n lazy[2 * node + 2] = maxOf(lazy[node * 2 + 1], value)\n }\n return\n }\n val mid = (start + end) / 2\n\n update(node * 2 + 1, start, mid, l, r, value)\n update(node * 2 + 2, mid + 1, end, l, r, value)\n\n tree[node] = maxOf(tree[node * 2 + 1], tree[node * 2 + 2])\n }\n\n fun query(l: Int, r: Int): Int {\n return query(0, 0, n - 1, l, r)\n }\n\n fun query(node: Int, start: Int, end: Int, l: Int, r: Int): Int {\n if (start > end || start > r || end < l) return Int.MIN_VALUE\n if (lazy[node] != 0) {\n tree[node] = maxOf(tree[node], lazy[node])\n if (start != end) {\n lazy[node * 2 + 1] = maxOf(lazy[node * 2 + 1], lazy[node])\n lazy[node * 2 + 2] = maxOf(lazy[node * 2 + 1], lazy[node])\n }\n lazy[node] = 0\n }\n\n if (l <= start && end <= r) {\n return tree[node]\n }\n val mid = (start + end) / 2\n val left = query(node * 2 + 1, start, mid, l, r)\n val right = query(node * 2 + 2, mid + 1, end, l, r)\n return maxOf(left, right)\n }\n}\n``` | 0 | 0 | ['Kotlin'] | 0 |
falling-squares | Lazy Segment tree || with index 1 | lazy-segment-tree-with-index-1-by-wolfes-i55a | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Wolfester | NORMAL | 2024-06-22T11:00:09.173188+00:00 | 2024-06-22T11:00:09.173214+00:00 | 16 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> \n\n# Code\n```\nclass Solution {\npublic:\n const static int N = 1e5 + 2;\n int INF = 1e9;\n int tree[4 * N], lazy[4 * N], a[4*N];\n\n void build(int v, int tl, int tr) {\n if (tl == tr) {\n tree[v] = a[tl];\n } else {\n int tm = (tl + tr) / 2;\n build(v*2+1, tl, tm);\n build(v*2+2, tm+1, tr);\n tree[v] = max(tree[v*2+1], tree[v*2 + 2]);\n }\n }\n\n\n void push(int node){\n if(lazy[node]!=-1){\n tree[2*node] = lazy[node];\n tree[2*node+1] = lazy[node];\n\n lazy[2*node] = lazy[node];\n lazy[2*node+1] = lazy[node];\n lazy[node] = -1;\n }\n }\n\n void update(int node, int tl, int tr, int l, int r, int updatedVal){\n if (tl > tr)return;\n else if (l<=tl && tr <=r){\n tree[node] = updatedVal;\n lazy[node] = updatedVal; // ye value update krni hai tl to tr segment of segment tree.\n }\n else if(tl==tr && (tl<l||tr>r)) return;\n else{\n push(node);\n int tm = (tl + tr) / 2;\n update(2*node, tl, tm, l,r, updatedVal);\n update(2*node + 1, tm + 1, tr,l, r, updatedVal);\n tree[node] = max(tree[2*node], tree[2*node+ 1]);\n }\n }\n\n\n int query(int node, int tl, int tr, int l, int r){\n if (tl >tr) return -INF;\n if (l <= tl && tr <= r) return tree[node];\n if(tl==tr) return -INF;\n\n push(node);\n int tm = (tl + tr) / 2;\n int q1=query(2*node, tl, tm, l,r);\n int q2=query(2*node + 1, tm + 1, tr,l, r);\n return max(q1,q2);\n }\n\n\n vector<int> fallingSquares(vector<vector<int>>& pos) {\n memset(tree,0,sizeof(tree));\n memset(lazy,0,sizeof(lazy));\n memset(a,0,sizeof(a));\n\n \n\n\n unordered_map<int,int> mp;\n set<int> st;\n for(auto x : pos){\n st.insert(x[0]);\n st.insert(x[0]+x[1]-1);\n }\n\n int idx = 1;\n for(auto x : st){\n mp[x] = idx;\n idx++;\n }\n\n int n = idx;\n build(1, 1, n);\n vector<int> ans;\n for(auto x : pos){\n int l = mp[x[0]];\n int r = mp[x[0]+x[1]-1];\n\n int mxi = query(1, 1, n, l, r);\n update(1, 1, n, l, r, mxi+x[1]);\n\n int temp = query(1,1,n,1,n);\n ans.push_back(temp);\n }\n\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
falling-squares | scala SortedMap | scala-sortedmap-by-vititov-k5ee | scala\nobject Solution {\n import collection.immutable.SortedMap\n def fallingSquares(positions: Array[Array[Int]]): List[Int] =\n positions.map(_.toList)\ | vititov | NORMAL | 2024-06-12T21:23:01.314656+00:00 | 2024-06-12T21:23:01.314676+00:00 | 1 | false | ```scala\nobject Solution {\n import collection.immutable.SortedMap\n def fallingSquares(positions: Array[Array[Int]]): List[Int] =\n positions.map(_.toList)\n .foldLeft((List(-1),SortedMap.empty[Int,(Int,Int)])){case ((l,aMap),p) =>\n lazy val y2 = aMap.maxBefore(p.head).filter{case (k,(len,_)) => k+len > p.head}.toList ++\n aMap.iteratorFrom(p.head).takeWhile(_._1 < p.sum)\n lazy val newHeight = y2.map(_._2._2).maxOption.getOrElse(0) + p.last\n lazy val newSegments = List(\n y2.headOption.map{case (k,(_,h)) => (k, (p.head - k,h))}\n .filterNot(x=>x._1<=0 || x._2._1<=0),\n Some(p.head,(p.last,newHeight)),\n y2.lastOption.map{case (k,(v,h)) => (p.sum, ((k+v)-p.sum,h))}\n .filterNot(x=>x._1<=0 || x._2._1<=0)\n ).flatten\n lazy val newMap = aMap -- y2.map(_._1) ++ newSegments\n ((l.head max newHeight) +: l, newMap )\n }._1.reverse.tail\n}\n``` | 0 | 0 | ['Ordered Map', 'Scala'] | 0 |
falling-squares | segment tree | segment-tree-by-moyinolorunpa-pcua | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | MoyinolorunPA | NORMAL | 2024-06-10T04:54:15.559280+00:00 | 2024-06-10T04:54:15.559327+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#from math import inf\n\n\nclass LazySegmentTree:\n def __init__(self, arr):\n self.arr = arr\n self.arr_size = len(arr)\n self.size = 4 * self.arr_size\n self.tree = [0] * self.size\n self.lazy = [0] * self.size\n self.build_tree(0, 0, self.arr_size - 1)\n\n def left_child(self, node):\n return 2 * node + 1\n\n def right_child(self, node):\n return 2 * node + 2\n\n def build_tree(self, node, start, end):\n mid = (start + end) // 2\n if start == mid == end: #. |\n self.tree[node] = self.arr[start] #. sme\n return self.tree[node]\n \n\n if start <= mid and start and mid < end or start+1 == end: # start != end: #. | |. # |. |. |\n self.tree[node] = max( # sm. e. # s m. e\n self.build_tree(self.left_child(node), start, mid),\n self.build_tree(self.right_child(node), mid + 1, end),\n )\n return self.tree[node]\n\n def update_diff(self, index, diff):\n self.update_helper(0, 0, self.arr_size - 1, index, index, diff)\n\n def update_range(self, left, right, value):\n self.update_helper(0, 0, self.arr_size - 1, left, right, value)\n\n def update_helper(self, node, start, end, left, right, diff):\n # Handle lazy propagation\n\n mid = (start + end) // 2\n\n\n if self.lazy[node] != 0:\n self.tree[node] = max(self.tree[node], self.lazy[node])\n if start <= mid and start and mid < end or start+1 == end : # start != end: #. | |. # |. |. |\n self.lazy[self.left_child(node)] = self.lazy[node] # sm. e #. s. m. e\n self.lazy[self.right_child(node)] = self.lazy[node]\n \n if start == mid == end: ###. |\n self.lazy[node] = 0 #. sme\n #. l r > s. e. #. s. e < l. r\n if start > right or end < left or start > end: #. |___|. |___|. #. |___|. |___|. \n return # \n #. l|___|r # l|___|r #. l|_______|r. #. l|___|r\n if start >= left and end <= right: # s|_______|e. # s|_______|e. #. s|_______|e. #. s|_________|e.\n self.tree[node] = diff\n if start < end and mid < end and start <= mid or start+1 == end :# start != end: # #. | |. # |. |. |\n self.lazy[self.left_child(node)] = diff # sm. e. #. s. m. e\n self.lazy[self.right_child(node)] = diff\n return\n\n \n if self.lazy[node] == 0: # xxxx \n self.update_helper(self.left_child(node), start, mid, left, right, diff)\n self.update_helper(self.right_child(node), mid + 1, end, left, right, diff)\n self.tree[node] = max(\n self.tree[self.left_child(node)], self.tree[self.right_child(node)]\n )\n\n def query(self, left, right):\n return self.query_helper(0, 0, self.arr_size - 1, left, right)\n\n def query_helper(self, node, start, end, left, right):\n \n mid = (start + end) // 2\n \n if self.lazy[node] != 0:\n self.tree[node] = max(self.tree[node], self.lazy[node])\n \n if start <= mid and start and mid < end or start+1 == end : # start != end: # #. | |. # |. |. |\n self.lazy[self.left_child(node)] = self.lazy[node] # sm. e #. s. m. e\n self.lazy[self.right_child(node)] = self.lazy[node]\n \n if start <= mid <= end: ####. |\n self.lazy[node] = 0 # sme\n\n if left <= start and end <= right: #. l|___|r # l|___|r #. l|_______|r. #. l|___|r\n return self.tree[node] # s|_______|e. # s|_______|e. #. s|_______|e. #. s|_________|e.\n\n if start > right or end < left:\n return 0\n\n \n return max(\n self.query_helper(self.left_child(node), start, mid, left, right),\n self.query_helper(self.right_child(node), mid + 1, end, left, right),\n )\n\n\n\nclass Solution(object):\n def fallingSquares(self, positions):\n ans = []\n pos = set()\n for l, side in positions:\n pos.add(l)\n pos.add(l + side - 1)\n pos = sorted(list(pos))\n mp = {}\n for i, j in enumerate(pos):\n mp[j] = i\n n = len(pos)\n st = LazySegmentTree([0] * n)\n for l, side in positions:\n left, right = mp[l], mp[l + side - 1]\n mx = st.query(left, right)\n st.update_range(left, right, mx + side)\n ans.append(st.query(0, n - 1))\n return ans\n\n\nS = Solution()\nprint(S.fallingSquares([[1, 2], [2, 3], [6, 1]]))\nprint(S.fallingSquares([[100, 100], [200, 100]]))\n\n"""\n[2, 5, 5]\n[100, 100]\n"""\n``` | 0 | 0 | ['Python'] | 0 |
falling-squares | Java || 5ms 100% || Fast. Use only arrays for compress and fall | java-5ms-100-fast-use-only-arrays-for-co-3wwv | Algorithm:\n1. Gather all of the left and right edge positions for all squares. For each edge position, save: the original x-position, the index into the posit | dudeandcat | NORMAL | 2024-05-16T23:38:45.192095+00:00 | 2024-05-17T00:14:20.583623+00:00 | 28 | false | **Algorithm:**\n1. **Gather** all of the left and right edge positions for all squares. For each edge position, save: the original x-position, the index into the `positions[][]` array for that square, and whether the saved position is a left or right edge of the square.\n2. **Sort** all the saved edge positions, which include original array index of the square, and whether the edge position is the left or right edge of a square.\n3. **Compress** the saved and sorted positions to new x-axis values, so that all possible new x-axis values are always at the left or right edge of a block. Calling them "blocks" now because after x-axis compression, they are no longer "squares". Since there is a maximum of 1000 squares, there will be a maximum of 2000 compressed positions, so all of the compressed positions can fit in a reasonable sized array.\n4. **Drop** the blocks in order. Use an array to represent all possible compressed x-axis positions, where the array contains the maximum height of blocks above each compressed position. For each block, search all x-axis compressed positions used by the block, to find what height the dropped block lands on. Then update the x-axis compressed positions for the block, to the top of the block after it lands. Save highest block after dropping each block.\n5. **Return** list of max heights after each dropped block.\n\n**---- Slower code but better programming practices ----**\nRuntimes of 9ms to 11ms, May 2024.\n```\nclass Solution {\n class SortPoint {\n int origPos;\n short index;\n boolean isRight;\n SortPoint(int origPos, int index, boolean isRight) {\n this.origPos = origPos;\n this.index = (short)index;\n this.isRight = isRight;\n }\n }\n \n public List<Integer> fallingSquares(int[][] positions) {\n int n = positions.length;\n\n // Gather all the edge-points from all of the squares, so we \n // can compress the left and right positions of the square \n // down into a more manageable range. \n final SortPoint[] points = new SortPoint[n * 2];\n int pointsIdx = 0;\n for (int i = 0; i < n; i++) {\n int[] square = positions[i];\n points[pointsIdx++] = new SortPoint(square[0], i, false);\n points[pointsIdx++] = new SortPoint(square[0] + square[1], i, true);\n }\n \n // Sort all the squares\' edge points in ascending position \n // order.\n Arrays.sort(points, (a, b) -> a.origPos - b.origPos);\n \n // Convert the sorted edge points to new compressed position \n // values. If adjacent sorted points have the same original \n // position values, then they are at the same new compressed \n // positions. Save the new left and right edge compressed \n // positions for each square.\n int newPos = -1;\n final int[] lefts = new int[n]; \n final int[] rights = new int[n];\n int prevPos = -1;\n for (SortPoint point : points) {\n if (point.origPos != prevPos) {\n newPos++;\n prevPos = point.origPos;\n }\n if (point.isRight)\n rights[point.index] = newPos;\n else\n lefts[point.index] = newPos;\n }\n\n // With the new compressed left and right edge positions for the \n // squares, loop to drop each square. For the new compressed \n // positions that are within the square, add the height of the square \n // to all of those x-axis positions, collecting any new highest values.\n int maxHeight = 0;\n final int[] xAxis = new int[newPos];\n List<Integer> result = new ArrayList(n);\n for (int i = 0; i < n; i++) { // Drop the boxes in order.\n int height = 0;\n for (int start = lefts[i], j = rights[i] - start; j > 0; j--)\n height = Math.max(height, xAxis[start++]);\n height += positions[i][1];\n maxHeight = Math.max(maxHeight, height);\n for (int start = lefts[i], j = rights[i] - start; j > 0; j--)\n xAxis[start++] = height;\n result.add(maxHeight);\n }\n \n return result;\n }\n}\n```\n**---- Faster code but bad programming practices ----**\nRuntimes of 5ms to 8ms, May 2024.\n```\nclass Solution {\n private static final int ORG_POS_SHIFT = 16;\n private static final int ORG_POS_MASK = 0xFFF_FFFF;\n private static final int IS_RIGHT_SHIFT = 12;\n private static final int IS_RIGHT_MASK = 0xF;\n private static final int IS_RIGHT = 1 << IS_RIGHT_SHIFT;\n private static final int IDX_SHIFT = 0;\n private static final int IDX_MASK = 0xFFF;\n \n public List<Integer> fallingSquares(int[][] positions) {\n int n = positions.length;\n\n // Gather all the edge-points from all of the squares, so we \n // can compress the left and right positions of the square \n // down into a more manageable range. The edge points of the \n // square are packed into the bits of a long, so the long \n // contains: 1) the original position in the most significant \n // bits so it will eventually be sorted by the original position, \n // 2) a boolean indicating if this position is for the right \n // edge of the square, and 3) the original index of the \n // square in the positions[] array.\n final long[] points = new long[n * 2];\n int pointsIdx = 0;\n for (int i = 0; i < n; i++) {\n int[] square = positions[i];\n points[pointsIdx++] = ((long)square[0] << ORG_POS_SHIFT) | i;\n points[pointsIdx++] = (((long)square[0] + square[1]) << ORG_POS_SHIFT) | \n i | IS_RIGHT;\n }\n \n // Sort all the squares\' edge points in ascending position \n // order.\n Arrays.sort(points);\n \n // Convert the sorted edge points to new compressed position \n // values. If adjacent sorted points have the same original \n // position values, then they are at the same new compressed \n // positions. Save the new left and right edge compressed \n // positions for each square.\n int newPos = -1;\n final int[] lefts = new int[n]; \n final int[] rights = new int[n];\n long endNewPos = -1;\n for (long point : points) {\n if (point > endNewPos) {\n newPos++;\n endNewPos = point | IS_RIGHT | IDX_MASK;\n }\n if ((point & IS_RIGHT) != 0)\n rights[(int)point & IDX_MASK] = newPos;\n else\n lefts[(int)point & IDX_MASK] = newPos;\n }\n\n // With the new compressed left and right edge positions for the \n // squares, loop to drop each square. For the new compressed \n // positions that are within the square, add the height of the square \n // to all of those x-axis positions, collecting any new highest values.\n int maxHeight = 0;\n final int[] xAxis = new int[newPos];\n List<Integer> result = new ArrayList(n);\n for (int i = 0; i < n; i++) { // Drop the boxes in succession \n int height = 0;\n for (int start = lefts[i], j = rights[i] - start; j > 0; j--)\n height = Math.max(height, xAxis[start++]);\n height += positions[i][1];\n maxHeight = Math.max(maxHeight, height);\n for (int start = lefts[i], j = rights[i] - start; j > 0; j--)\n xAxis[start++] = height;\n result.add(maxHeight);\n }\n \n return result;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
falling-squares | Simple TS | simple-ts-by-pailhead-194v | Intuition\nEach square landing should create an edge at some height, between two points that can catch the next square.\n\n# Approach\nKeep a list of edges that | pailhead | NORMAL | 2024-04-11T03:04:20.368648+00:00 | 2024-04-11T03:06:42.447814+00:00 | 6 | false | # Intuition\nEach square landing should create an edge at some height, between two points that can catch the next square.\n\n# Approach\nKeep a list of edges that represent left, right and height. \nFor each of the squares, find all the edges that overlap the bounds of the square. \nFind which edge from those results is the highest call this intersection.\nPut another edge square height above the found intersection.\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$ I think, since the edges grow towards N with each iteration\n\n- Space complexity:\n$$O(n)$$ Since we keep track of N edges. \n\n# Code\n```\nfunction fallingSquares(positions: number[][]): number[] {\n let maxHeight = 0\n const answer:number[] = []\n const edges:[number,number,number][] =[]\n while(positions.length){\n const [sLeft,sHeight] = positions.shift()\n const sRight = sLeft+sHeight\n let intersectionHeights:number[] = [0]\n let maxFoundHeight = 0\n for ( let i = edges.length -1; i >= 0 ; i--){\n const testEdge = edges[i]\n const [tl,tr,th] = testEdge\n if(!intersectEdges(tl,tr,sLeft,sRight)) continue\n intersectionHeights.push(th)\n maxFoundHeight = Math.max(maxFoundHeight,th)\n }\n const nextHeight = maxFoundHeight+sHeight\n maxHeight = Math.max(maxHeight,nextHeight)\n edges.push([sLeft,sRight,nextHeight])\n answer.push(maxHeight)\n }\n return answer\n};\n\nconst intersectEdges = (a:number,b:number,c:number,d:number)=>\n Math.min(b,d)-Math.max(a,c) > 0\n``` | 0 | 0 | ['TypeScript'] | 0 |
get-equal-substrings-within-budget | [Java/C++/Python] Sliding Window | javacpython-sliding-window-by-lee215-gcq6 | Intuition\nChange the input of string s and t into an array of difference.\nThen it\'s a standard sliding window problem.\n\n\n## Complexity\nTime O(N) for one | lee215 | NORMAL | 2019-09-29T04:01:58.917594+00:00 | 2019-09-29T07:05:53.272274+00:00 | 15,547 | false | ## **Intuition**\nChange the input of string `s` and `t` into an array of difference.\nThen it\'s a standard sliding window problem.\n<br>\n\n## **Complexity**\nTime `O(N)` for one pass\nSpace `O(1)`\n<br>\n\n**Java:**\n```java\n public int equalSubstring(String s, String t, int k) {\n int n = s.length(), i = 0, j;\n for (j = 0; j < n; ++j) {\n k -= Math.abs(s.charAt(j) - t.charAt(j));\n if (k < 0) {\n k += Math.abs(s.charAt(i) - t.charAt(i));\n ++i;\n }\n }\n return j - i;\n }\n```\n\n**C++:**\n```cpp\n int equalSubstring(string s, string t, int k) {\n int n = s.length(), i = 0, j;\n for (j = 0; j < n; ++j) {\n if ((k -= abs(s[j] - t[j])) < 0)\n k += abs(s[i] - t[i++]);\n }\n return j - i;\n }\n```\n\n**Python:**\n```python\n def equalSubstring(self, s, t, cost):\n i = 0\n for j in xrange(len(s)):\n cost -= abs(ord(s[j]) - ord(t[j]))\n if cost < 0:\n cost += abs(ord(s[i]) - ord(t[i]))\n i += 1\n return j - i + 1\n```\n | 172 | 8 | [] | 39 |
get-equal-substrings-within-budget | ✅97.44%🔥Easy solution🔥With explanation🔥 | 9744easy-solutionwith-explanation-by-mra-92yz | Intuition\n#### The problem requires finding the longest substring where the cost of converting it from s to t does not exceed maxCost. To achieve this, we can | MrAke | NORMAL | 2024-05-28T00:26:10.462586+00:00 | 2024-05-28T00:26:10.462613+00:00 | 21,595 | false | # Intuition\n#### The problem requires finding the longest substring where the cost of converting it from `s` to `t` does not exceed `maxCost`. To achieve this, we can utilize a sliding window approach to dynamically adjust the size of the substring while ensuring the cost constraint is respected.\n\n----\n\n# Approach\n### 1. Initialize Variables:\n - ##### `start` to mark the beginning of the sliding window.\n - ##### `current_cost` to keep track of the total transformation cost of the current window.\n - ##### `max_length` to store the maximum length of a valid window found.\n### 2. Iterate through the String:\n - ##### Use `end` as the current end of the window.\n - ##### For each character at `end`, compute the cost to convert `s[end]` to `t[end]` and add it to `current_cost`.\n\n### 3. Adjust the Window:\n\n - ##### If `current_cost` exceeds `maxCost`, increment `start` to shrink the window from the left, subtracting the cost of the character at `start` from `current_cost`, until the total cost is within the allowed limit.\n\n### 4. Update the Maximum Length:\n\n - ##### After adjusting the window, compare its size `(end - start + 1)` with `max_length` and update `max_length` if the current window is larger.\n\n### 5. Return the Result:\n- ##### The maximum valid window length found during the iteration is returned as the result.\n\n----\n\n# Complexity\n- ### Time complexity:\n#### $$O(n)$$, where n is the length of the string `s` (or `t`). This is because each character is processed at most twice (once when expanding the window and once when shrinking it).\n\n- ### Space complexity:\n#### $$O(1)$$, as we are using a constant amount of extra space regardless of the input size.\n---\n\n# Code\n```python []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n n = len(s)\n start = 0\n current_cost = 0\n max_length = 0\n\n for end in range(n):\n current_cost += abs(ord(s[end]) - ord(t[end]))\n\n while current_cost > maxCost:\n current_cost -= abs(ord(s[start]) - ord(t[start]))\n start += 1\n\n max_length = max(max_length, end - start + 1)\n \n return max_length\n```\n```C++ []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n = s.size();\n int start = 0;\n int current_cost = 0;\n int max_length = 0;\n\n for (int end = 0; end < n; ++end) {\n current_cost += abs(s[end] - t[end]);\n\n while (current_cost > maxCost) {\n current_cost -= abs(s[start] - t[start]);\n ++start;\n }\n\n max_length = max(max_length, end - start + 1);\n }\n\n return max_length;\n }\n};\n\n```\n```java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int n = s.length();\n int start = 0;\n int currentCost = 0;\n int maxLength = 0;\n\n for (int end = 0; end < n; ++end) {\n currentCost += Math.abs(s.charAt(end) - t.charAt(end));\n\n while (currentCost > maxCost) {\n currentCost -= Math.abs(s.charAt(start) - t.charAt(start));\n ++start;\n }\n\n maxLength = Math.max(maxLength, end - start + 1);\n }\n\n return maxLength;\n }\n}\n\n```\n```javascript []\nvar equalSubstring = function(s, t, maxCost) {\n let n = s.length;\n let start = 0;\n let currentCost = 0;\n let maxLength = 0;\n\n for (let end = 0; end < n; end++) {\n currentCost += Math.abs(s.charCodeAt(end) - t.charCodeAt(end));\n\n while (currentCost > maxCost) {\n currentCost -= Math.abs(s.charCodeAt(start) - t.charCodeAt(start));\n start++;\n }\n\n maxLength = Math.max(maxLength, end - start + 1);\n }\n\n return maxLength;\n};\n```\n```C# []\npublic class Solution {\n public int EqualSubstring(string s, string t, int maxCost) {\n int n = s.Length;\n int start = 0;\n int currentCost = 0;\n int maxLength = 0;\n\n for (int end = 0; end < n; ++end) {\n currentCost += Math.Abs(s[end] - t[end]);\n\n while (currentCost > maxCost) {\n currentCost -= Math.Abs(s[start] - t[start]);\n ++start;\n }\n\n maxLength = Math.Max(maxLength, end - start + 1);\n }\n\n return maxLength;\n }\n}\n\n```\n---\n\n\n\n | 105 | 6 | ['String', 'Sliding Window', 'Python', 'C++', 'Java', 'Python3', 'JavaScript', 'C#'] | 12 |
get-equal-substrings-within-budget | Java Sliding Window with Clear Explanation | java-sliding-window-with-clear-explanati-prff | Explanation:\n\nThe idea is that you want to convert one character to another in that same position i.e. s[i] to t[i] such that you form the longest contiguous | kkzeng | NORMAL | 2019-09-29T04:26:40.964616+00:00 | 2019-09-29T19:54:27.316251+00:00 | 4,244 | false | **Explanation:**\n\nThe idea is that you want to convert one character to another in that same position i.e. s[i] to t[i] such that you form the longest contiguous converted String.\n\nThere is just one key realization that you must make to solve this problem:\n\nYou need to realize that this problem can be reduced to finding the longest subarray such that the sum of the elements in that subarray is less than maxCost.\n\nThis is because you can generate an array `diff` such that `diff[i] = Math.abs(s[i] - t[i])` which is the cost of converting one character to another. You also want to find the maximum length substring that can be converted given the maxCost so this is equivalent to finding the longest subarray in `diff` which has sum of elements less than cost.\n\nFor this we can use a sliding window. We slide the `end` of the window to the right with each step. If the total sum exceeds the maxCost, we slide the `start` of the window to the right until the total sum inside the window is less than maxCosts. With each eligible window, we take the length and keep track of the maximum length.\n\nFor more info on sliding window: [Explanation](https://www.geeksforgeeks.org/window-sliding-technique/)\n\n**Code:**\n\n```\n\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n // Convert the problem into a min subarray problem\n int[] diff = new int[s.length()];\n for(int i = 0; i < s.length(); ++i) {\n int asciiS = s.charAt(i);\n int asciiT = t.charAt(i);\n diff[i] = Math.abs(asciiS - asciiT);\n }\n \n // Now find the longest subarray <= maxCost\n // all diff[i] >= 0 (non-negative)\n \n // Use sliding window?\n int maxLen = 0;\n int curCost = 0;\n int start = 0;\n \n for(int end = 0; end < diff.length; ++end) {\n curCost += diff[end];\n while(curCost > maxCost) {\n curCost -= diff[start];\n ++start;\n }\n maxLen = Math.max(maxLen, end - start + 1);\n }\n \n return maxLen;\n }\n}\n```\n\n`Time Complexity: O(N) where N is the length of strings s, t`\n`Space Complexity: O(N) for diff`\nNote: O(1) space can be achieved if we don\'t create the diff array - we can just get the values on the fly. | 57 | 2 | ['Java'] | 14 |
get-equal-substrings-within-budget | 🔥🔥 Diagrammatic Explanation 👁️👁️ | diagrammatic-explanation-by-hi-malik-jc93 | What the question is saying, we have two strings and have maxCost. Keep maxCost in your mind and tell, a big to big s string can be converted to t string. And i | hi-malik | NORMAL | 2024-05-28T00:26:14.570485+00:00 | 2024-05-28T00:26:14.570522+00:00 | 6,256 | false | What the question is saying, we have **two strings** and have **maxCost**. Keep **maxCost** in your mind and tell, a big to big **s** string can be converted to **t** string. And if we converted the whole string, how much will be the cost!\n\nLet\\s undrestand with an example;\n```\nInput: s = "abcd", t = "bcdf", maxCost = 3\nOutput: 3\n```\n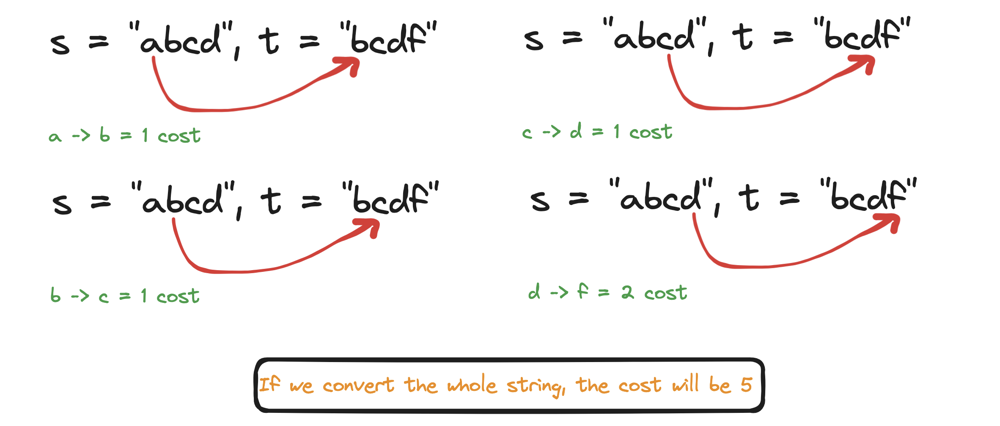\n\n> But, what the question is saying! We have to be in the **maxCost**\n> > What it saying is, get that string out! Which can be converted within the given **maxCost**\n\nSo, in the above example! **abc** length is **three** and it can be converted into **bcd** within this **maxCost**\n\n> But what if were unable to conert, then what will be! Let;s take one more example!\n\n```\nInput: s = "abcd", t = "acde", maxCost = 0\nOutput: 1\n```\n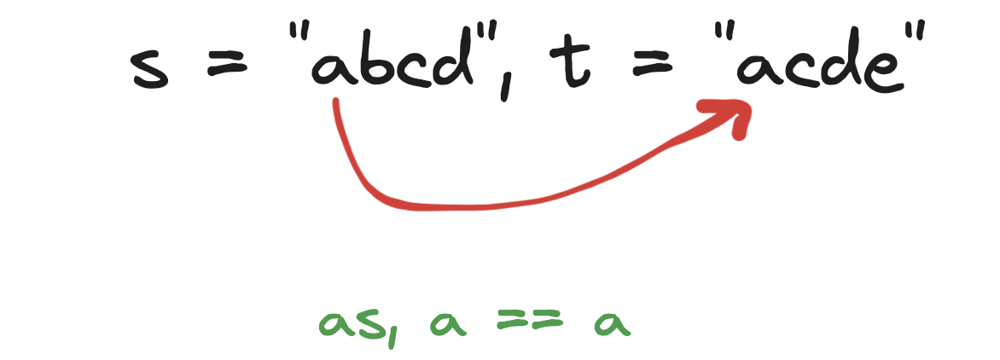\nNow, as **a == a** and how we got the **Output 1** because, we just have to get the length out from the string! How long a string can be converted and return it\'s length!\n\nSo, how we going to code is,\n\n1. Initialize `n` to the length of string `s`.\n2. Initialize `ans` to 0, which will hold the maximum length of the substring that can be changed within the given cost.\n3. Initialize `window` to 0, which will accumulate the cost of changing the substring from `s` to `t`.\n4. Initialize `left` to 0, which will be the starting index of the sliding window.\n5. Loop through the string using `right` as the ending index of the sliding window.\n6. Add the cost of changing `s[right]` to `t[right]` to `window`.\n7. If `window` exceeds `maxCost`, shrink the window from the left by subtracting the cost of changing `s[left]` to `t[left]` and incrementing `left`.\n8. Update `ans` with the maximum length of the substring found so far.\n9. Return the maximum length `ans`.\n\n```plaintext\nFunction equalSubstring(s, t, maxCost):\n n = length of s\n ans = 0\n window = 0\n left = 0\n\n For right from 0 to n - 1:\n window += absolute difference between ASCII values of s[right] and t[right]\n\n While window > maxCost:\n window -= absolute difference between ASCII values of s[left] and t[left]\n left += 1\n\n ans = maximum of ans and (right - left + 1)\n\n Return ans\n```\n\n**Let\'s Code it UP** *ladies n gentlemen*\n\n**C++**\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n = s.length();\n int ans = 0, window = 0, left = 0;\n for (int right = 0; right < n; right++) {\n window += abs(s[right] - t[right]);\n while (window > maxCost) {\n window -= abs(s[left] - t[left]);\n left++;\n }\n ans = max(ans, right - left + 1);\n }\n return ans;\n }\n};\n```\n**JAVA**\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int n = s.length();\n int ans = 0, window = 0, left = 0;\n for (int right = 0; right < n; right++) {\n window += Math.abs(s.charAt(right) - t.charAt(right));\n while (window > maxCost) {\n window -= Math.abs(s.charAt(left) - t.charAt(left));\n left++;\n }\n ans = Math.max(ans, right - left + 1);\n }\n return ans;\n }\n}\n```\n**PYTHON**\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n n = len(s)\n ans = 0\n window = 0\n left = 0\n \n for right in range(n):\n window += abs(ord(s[right]) - ord(t[right]))\n while window > maxCost:\n window -= abs(ord(s[left]) - ord(t[left]))\n left += 1\n ans = max(ans, right - left + 1)\n \n return ans\n```\n\n___\nComplexity Analysis\n\n___\n* **Time Complexity :-** BigO(N) \n* **Space Complexity :-** BigO(1) | 56 | 1 | ['C', 'Python', 'Java'] | 11 |
get-equal-substrings-within-budget | [C++] Sliding window O(n) & Prefix sum O(nlogn) implementations | c-sliding-window-on-prefix-sum-onlogn-im-fvsa | Observation\nSince we need to find the maximum substring that can be replaced we can actually breakdown this problem to an array of integers that represent the | phoenixdd | NORMAL | 2019-09-29T04:01:45.948903+00:00 | 2019-10-06T20:12:21.145749+00:00 | 3,986 | false | **Observation**\nSince we need to find the maximum substring that can be replaced we can actually breakdown this problem to an array of integers that represent the replacement cost of `s[i]` to `t[i]` and then find the maximum length of continuous integers in that array whose `sum <= maxCost`.\neg:\n`s = "aabcd"`\n`t = "zbdag"`\nThe array to find the maximum length on comes out to` [1,1,2,2,3]`.\n\nThis problem can now be solved in many ways, two of which are descibed below.\nSomewhat similar to `209. Minimum Size Subarray Sum`\n\n**Sliding window solution**\nIn general a sliding window is when we keep increasing the size of the window by increasing the right end to fit our goal, if it increases the goal we reduce the window by sliding the left end until it again fits the goal, this ensures that the maximum window size is attained.\n```c++\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) \n {\n int start=0,end=0,sum=0;\n while(end<s.length())\n {\n sum+=abs(s[end]-t[end++]);\n if(sum>maxCost)\n sum-=abs(s[start]-t[start++]);\n }\n return end-start;\n }\n};\n```\n\n**Complexity**\nTime: O(n). Since each element is added and removed once at max.\nSpace: O(1). Since we get the elemets of sum array on the fly.\n\n**Prefix sum slolution**\nHere we create an array of prefix sums that hold the sum of differences from `0` to `i`.\nAt every iteration of `i` we can find the continuous sum of `numbers <= maxCost` by binary searching the lowerbound of `prefixSum[i] - maxCost`.\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) \n {\n vector<int> prefixDiffSum(s.length()+1,0);\n int Max=0;\n for(int i=1;i<s.length()+1;i++)\n {\n prefixDiffSum[i]=prefixDiffSum[i-1]+abs(s[i-1]-t[i-1]); //Stores sum of differences from begining till i.\n Max=max(Max,i-(int)(lower_bound(prefixDiffSum.begin(),prefixDiffSum.begin()+i+1,prefixDiffSum[i]-maxCost)-prefixDiffSum.begin())); //Binary search to find start of the window that holds sum<=maxCost and ends with i.\n }\n return Max;\n }\n};\n```\n**Complexity**\nTime: O(nlogn). \nSpace: O(n). Storing prefix sums. | 51 | 2 | [] | 4 |
get-equal-substrings-within-budget | Sliding window vs Prefix sum+Binary search||0ms beats 100% | sliding-window-vs-prefix-sumbinary-searc-kghm | Intuition\n Describe your first thoughts on how to solve this problem. \nUse sliding window; it\'s a linear solution with O(1) space.\n\n2nd approach uses prefi | anwendeng | NORMAL | 2024-05-28T00:46:15.162432+00:00 | 2024-05-28T02:38:54.012864+00:00 | 4,650 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse sliding window; it\'s a linear solution with O(1) space.\n\n2nd approach uses prefix sum. Note that `cost[l...r]=sum[r+1]-sum[l]` where `sum` is 1-indexed prefix sums.\n\n3rd approach is a revision for the 2nd one, within the inner loop uses binary search to move l instead of moving l 1 by 1.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. set the 2 pointers `l=0,r=0` & `cost=0, len=0`\n2. Find the longest initial valid window by moving `r` while `cost<=maxCost`\n3. When `r==n && cost<=maxCost` return `n`\n4. Initialize `len=r`\n5. Use a nested loop to slide window; `cost+=abs(s[r]-t[r])`\n- in the inner loop proceed to find the next valid window\n```\n while (cost>maxCost) {\n cost-=abs(s[l]-t[l]);\n l++;//moving l \n```\n- update `len=max(len, r-l+1)`\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\nprefix sum: $O(n)$\n# Code||C++ 0ms beats 100%\n```\nclass Solution {\npublic:\n static int equalSubstring(string& s, string& t, int maxCost) {\n const int n=s.size();\n int l=0, r;// 2 pointers\n int cost=0, len=0;\n\n // Initialize the window by moving r while cost<=maxCost\n for (r = 0; r < n; r++) {\n cost+=abs(s[r]-t[r]);\n if (cost>maxCost) {\n cost-=abs(s[r]-t[r]);\n break;\n }\n }\n\n // If the initial window exceeds the whole string\n if (r==n && cost<=maxCost) return n;\n \n len=r; //initial length for the valid window\n\n // Sliding the window\n for (; r<n; r++) {\n cost+=abs(s[r]-t[r]);\n while (cost > maxCost) {\n cost-=abs(s[l]-t[l]);\n l++;\n }\n len=max(len, r-l+1);\n }\n return len;\n }\n};\n\n\n\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# C++ prefix sum||0ms beats 100%\n```\nclass Solution {\npublic:\n static int equalSubstring(string& s, string& t, int maxCost) {\n const int n=s.size();\n vector<int> sum(n+1, 0);// 1-indexed prefix sum\n for(int i=0; i<n; i++)\n sum[i+1]=sum[i]+abs(s[i]-t[i]);\n \n int l=0, r, len=0;\n for(r=0; r<n; r++){\n int cost=sum[r+1]-sum[l];\n while (cost> maxCost) {\n cost=sum[r+1]-sum[++l];\n }\n len=max(len, r-l+1);\n }\n return len;\n }\n};\n\n\n```\n# 3rd C++ using Prefix sum + binary search\n```\nclass Solution {\npublic:\n static int equalSubstring(string& s, string& t, int maxCost) {\n const int n=s.size();\n vector<int> sum(n+1, 0);// 1-indexed prefix sum\n for(int i=0; i<n; i++)\n sum[i+1]=sum[i]+abs(s[i]-t[i]);\n \n int l=0, r, len=0;\n for(r=0; r<n; r++){\n int cost=sum[r+1]-sum[l];\n if (cost> maxCost) {\n //Use binary search to move l\n l=lower_bound(sum.begin()+(l+1), sum.end(), cost-maxCost)-sum.begin();\n cost=sum[r+1]-sum[l];\n }\n len=max(len, r-l+1);\n }\n return len;\n }\n};\n\n``` | 39 | 3 | ['Binary Search', 'Sliding Window', 'Prefix Sum', 'C++'] | 8 |
get-equal-substrings-within-budget | Standard Python moving window (similar problems listed) | standard-python-moving-window-similar-pr-w6iy | Please see and vote for my solutions for these similar problems.\n1208. Get Equal Substrings Within Budget\n3. Longest Substring Without Repeating Characters\n1 | otoc | NORMAL | 2019-09-29T04:12:23.004153+00:00 | 2019-09-29T04:21:47.175296+00:00 | 1,875 | false | Please see and vote for my solutions for these similar problems.\n[1208. Get Equal Substrings Within Budget](https://leetcode.com/problems/get-equal-substrings-within-budget/discuss/392901/Simple-Python-moving-window)\n[3. Longest Substring Without Repeating Characters](https://leetcode.com/problems/longest-substring-without-repeating-characters/discuss/348137/Simple-Python-two-pointer-solution-(52ms-beat-97.94))\n[159. Longest Substring with At Most Two Distinct Characters](https://leetcode.com/problems/longest-substring-with-at-most-two-distinct-characters/discuss/348157/Simple-Python-two-pointer-solution)\n[340. Longest Substring with At Most K Distinct Characters](https://leetcode.com/problems/longest-substring-with-at-most-k-distinct-characters/discuss/348216/Simple-Python-two-pointer-solution-(72-ms-beat-94.93))\n[992. Subarrays with K Different Integers](https://leetcode.com/problems/subarrays-with-k-different-integers/discuss/348984/Different-Python-two-pointer-solutions)\n[424. Longest Repeating Character Replacement](https://leetcode.com/problems/longest-repeating-character-replacement/discuss/363071/Simple-Python-two-pointer-solution)\n[209. Minimum Size Subarray Sum](https://leetcode.com/problems/minimum-size-subarray-sum/discuss/344476/Simple-Python-two-pointer-solution)\n[713. Subarray Product Less Than K](https://leetcode.com/problems/subarray-product-less-than-k/discuss/344245/Simple-Python-solution-(beat-94.59))\n[76. Minimum Window Substring](https://leetcode.com/problems/minimum-window-substring/discuss/344533/Simple-Python-two-pointer-solution)\n\n```\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n n = len(s)\n cost = 0\n left = 0\n max_len = 0\n for right in range(n):\n cost += abs(ord(s[right]) - ord(t[right]))\n while cost > maxCost:\n cost -= abs(ord(s[left]) - ord(t[left]))\n left += 1\n max_len = max(max_len, right - left + 1)\n return max_len\n``` | 36 | 0 | [] | 3 |
get-equal-substrings-within-budget | C++/Java Sliding Window O(n) | O(1) | cjava-sliding-window-on-o1-by-votrubac-er3l | Intuition\nInstead of two string, we can imagine an array of the same size with absolute differences. Then, the problem is to find the longest subarray with the | votrubac | NORMAL | 2019-09-29T04:03:48.007478+00:00 | 2019-09-29T05:02:57.349724+00:00 | 2,588 | false | # Intuition\nInstead of two string, we can imagine an array of the same size with absolute differences. Then, the problem is to find the longest subarray with the sum not exceeding ```maxCost```.\n# Sliding Window\nWe can use a sliding window technique when we move right ```i``` pointer and decrease ```maxCost```, and increment left ```j``` pointer, increasing ```maxCost``` if it is negative.\n\nThen, the difference ```i - j``` is our answer.\n### C++\n```\nint equalSubstring(string s, string t, int maxCost) {\n auto i = 0, j = 0;\n while (i < s.size()) {\n maxCost -= abs(s[i] - t[i++]);\n if (maxCost < 0) maxCost += abs(s[j] - t[j++]);\n }\n return i - j;\n}\n```\n### Java\n```\npublic int equalSubstring(String s, String t, int maxCost) {\n int i = 0, j = 0;\n while (i < s.length()) {\n maxCost -= Math.abs(s.charAt(i) - t.charAt(i++));\n if (maxCost < 0) maxCost += Math.abs(s.charAt(j) - t.charAt(j++));\n }\n return i - j;\n}\n```\n# Complexity Analysis\nTime: O(n)\nMemory: O(1) | 34 | 1 | [] | 3 |
get-equal-substrings-within-budget | ✅Detailed Explanation🔥2 Approaches🔥🔥Extremely Simple and effective🔥🔥🔥 Beginner-friendly🔥 | detailed-explanation2-approachesextremel-b5xy | \uD83C\uDFAFProblem Explanation:\nYou are given two strings s and t and integer maxCost. You want to return maximum length of substring from s such that you nee | heir-of-god | NORMAL | 2024-05-28T05:42:33.700104+00:00 | 2024-05-28T06:47:41.944540+00:00 | 1,852 | false | # \uD83C\uDFAFProblem Explanation:\nYou are given two strings ```s``` and ```t``` and integer ```maxCost```. You want to return maximum length of substring from ```s``` such that you need up to ```maxCost``` cost to change it.\n- "cost" is absolute ASCII difference between s[i] and t[i]\n- Substring is a contiguous sequence of characters within a string\n\n# \uD83D\uDCE5Input:\n- String ```s``` which we have initally\n- String ```t``` to which we want to transform ```s```\n- Integer ```maxCost``` which represents maximum cost of changing substring\n\n# \uD83D\uDCE4Output:\nThe maximum possible length of substring we can change for ```cost <= maxCost```\n\n# \uD83E\uDDE0 Approach 1: Sliding Window \n\n# \uD83E\uDD14 Intuition\nI don\'t know why but it seems to me that in case of that problem to come up with optimized solution is much easier than to come up with relatively slow one.\n- First key point you want to understand that, in fact, we just not interested in strings ```s``` and ```t``` at all. We can compute some array like ```delta``` and just forget about those strings because what we really are interested in is just differences between ```s[i]``` and ```t[i]``` for every ```i```.\n- So, it really comes down to finding the largest sublist of elements in the list such that the sum of the elements does not exceed ```maxCost```, which is actually the very standard sliding window problem.\n- Let\'s move on to the code, and then to a more complex, but less effective solution.\n\n# \uD83D\uDCBB Coding \nAs was said earlier we will use Sliding window approach for this problem\n- Initialize ```res``` variable which will contain maximum length of substring we\'ve found, ```cur_start``` variable which store current start of substring (since our sliding window will have dynamic size) and ```cur_cost``` variable which just store the cost of current substring\n- We want to iterate through every ```last_ind``` and apply this operations on every step:\n - Add new element to the sliding window\n - While our ```cur_cost``` is greater than ```maxCost``` move left pointer to the right so decreasing the size of the window and total cost of the substring.\n - If length of current valid window is greater than maximum length we\'ve seen so far update it \n- Return result which is stored in ```res```\n\n# \uD83D\uDCD2 Complexity\n- \u23F0 Time complexity: O(n), every element in array will be called at most twice so this is O(2n) => O(n)\n- \uD83E\uDDFA Space complexity: O(1), since no extra space is used\n\n# \uD83E\uDDD1\u200D\uD83D\uDCBB Code\n``` python []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n res: int = 0\n cur_cost: int = 0\n cur_start: int = 0\n\n for last_ind in range(len(s)):\n cur_cost += abs(ord(s[last_ind]) - ord(t[last_ind]))\n\n while cur_cost > maxCost:\n cur_cost -= abs(ord(s[cur_start]) - ord(t[cur_start]))\n cur_start += 1\n\n if last_ind - cur_start + 1 > res:\n res = last_ind - cur_start + 1\n\n return res\n```\n``` C++ []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int res = 0;\n int cur_cost = 0;\n int cur_start = 0;\n\n for (int last_ind = 0; last_ind < s.size(); last_ind++) {\n cur_cost += abs(s[last_ind] - t[last_ind]);\n\n while (cur_cost > maxCost) {\n cur_cost -= abs(s[cur_start] - t[cur_start]);\n cur_start++;\n }\n\n if (last_ind - cur_start + 1 > res) {\n res = last_ind - cur_start + 1;\n }\n }\n\n return res;\n }\n};\n```\n``` JavaScript []\nvar equalSubstring = function(s, t, maxCost) {\n let res = 0;\n let cur_cost = 0;\n let cur_start = 0;\n\n for (let last_ind = 0; last_ind < s.length; last_ind++) {\n cur_cost += Math.abs(s.charCodeAt(last_ind) - t.charCodeAt(last_ind));\n\n while (cur_cost > maxCost) {\n cur_cost -= Math.abs(s.charCodeAt(cur_start) - t.charCodeAt(cur_start));\n cur_start++;\n }\n\n if (last_ind - cur_start + 1 > res) {\n res = last_ind - cur_start + 1;\n }\n }\n\n return res;\n};\n```\n``` Java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int res = 0;\n int cur_cost = 0;\n int cur_start = 0;\n\n for (int last_ind = 0; last_ind < s.length(); last_ind++) {\n cur_cost += Math.abs(s.charAt(last_ind) - t.charAt(last_ind));\n\n while (cur_cost > maxCost) {\n cur_cost -= Math.abs(s.charAt(cur_start) - t.charAt(cur_start));\n cur_start++;\n }\n\n if (last_ind - cur_start + 1 > res) {\n res = last_ind - cur_start + 1;\n }\n }\n\n return res;\n }\n}\n```\n``` C []\nint equalSubstring(char* s, char* t, int maxCost) {\n int res = 0;\n int cur_cost = 0;\n int cur_start = 0;\n\n for (int last_ind = 0; last_ind < strlen(s); last_ind++) {\n cur_cost += abs(s[last_ind] - t[last_ind]);\n\n while (cur_cost > maxCost) {\n cur_cost -= abs(s[cur_start] - t[cur_start]);\n cur_start++;\n }\n\n if (last_ind - cur_start + 1 > res) {\n res = last_ind - cur_start + 1;\n }\n }\n\n return res;\n}\n```\n\n\n# \uD83E\uDDE0 Approach 2: Prefix sum and binary search\n\n# \uD83E\uDD14 Intuition\nThis approach is quite harder to come up with or implement but it\'s big advantage to know different approaches to the same problem.\n- Unlike the previous solution, this time let\u2019s actually define an array that will store the cost to change one letter to another, but at the same time we want to store not just one cost, but a prefix sum in order to effectively find the cost of the current substring.\n- We will iterate through every possible ```right_index``` and call binary search on ```costs[right_index] - maxCost``` in order to find the most left index where we can put our pointer left so that s[left:right] has cost less than or equal to maxCost\n\n# \uD83D\uDCBB Coding \n- Initialize preffix sum array ```costs``` and calculate it with loop\n- Write ```binary_search``` function which will return not whether element exist in array but the left most index from where we can start to fit ```maxCost``` (so we need to return mid + 1, because index mid will contain index to where we can put this new sum and so value which is actually is our substring will be 1 index right)\n- Iterate through every possible ```right``` index and call binary search to find most left index, calculate new length and update result\n### [Here\'s vizualization on example](https://pythontutor.com/render.html#code=class%20Solution%3A%0A%20%20%20%20def%20equalSubstring%28self,%20s%3A%20str,%20t%3A%20str,%20maxCost%3A%20int%29%20-%3E%20int%3A%0A%20%20%20%20%20%20%20%20costs%3A%20list%5Bint%5D%20%3D%20%5B0%20for%20_%20in%20range%28len%28s%29%20%2B%201%29%5D%0A%20%20%20%20%20%20%20%20for%20ind%20in%20range%281,%20len%28s%29%20%2B%201%29%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20costs%5Bind%5D%20%3D%20costs%5Bind%20-%201%5D%20%2B%20abs%28ord%28s%5Bind%20-%201%5D%29%20-%20ord%28t%5Bind%20-%201%5D%29%29%0A%0A%20%20%20%20%20%20%20%20res%3A%20int%20%3D%200%0A%0A%20%20%20%20%20%20%20%20for%20right_index%20in%20range%281,%20len%28costs%29%29%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20min_left%3A%20int%20%3D%20self.binary_search%28costs,%20costs%5Bright_index%5D%20-%20maxCost%29%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20right_index%20-%20min_left%20%3E%20res%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20res%20%3D%20right_index%20-%20min_left%0A%0A%20%20%20%20%20%20%20%20return%20res%0A%0A%20%20%20%20def%20binary_search%28self,%20arr,%20x%29%20-%3E%20int%3A%0A%20%20%20%20%20%20%20%20lo%3A%20int%20%3D%200%0A%20%20%20%20%20%20%20%20hi%3A%20int%20%3D%20len%28arr%29%20-%201%0A%20%20%20%20%20%20%20%20while%20lo%20%3C%20hi%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20mid%3A%20int%20%3D%20%28lo%20%2B%20hi%29%20//%202%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20arr%5Bmid%5D%20%3C%20x%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20lo%20%3D%20mid%20%2B%201%0A%20%20%20%20%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20hi%20%3D%20mid%0A%20%20%20%20%20%20%20%20return%20lo%0A%0As%20%3D%20Solution%28%29%0As.equalSubstring%28%22abcd%22,%20%22bcdf%22,%203%29&cumulative=false&curInstr=109&heapPrimitives=nevernest&mode=display&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false) how this works, you can check it if you want.\n\n\n# \uD83D\uDCD2 Complexity\n- \u23F0 Time complexity: O(n logn), we call binary search for every character in s which is O(n) * O(logn) = O(n logn)\n- \uD83E\uDDFA Space complexity: O(n) since we creating array ```costs``` of size n\n\n# \uD83E\uDDD1\u200D\uD83D\uDCBB Code\n``` python []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n costs: list[int] = [0 for _ in range(len(s) + 1)]\n for ind in range(1, len(s) + 1):\n costs[ind] = costs[ind - 1] + abs(ord(s[ind - 1]) - ord(t[ind - 1]))\n\n res: int = 0\n\n for right_index in range(1, len(costs)):\n min_left: int = self.binary_search(costs, costs[right_index] - maxCost)\n if right_index - min_left > res:\n res = right_index - min_left\n\n return res\n\n def binary_search(self, arr, x) -> int:\n lo: int = 0\n hi: int = len(arr) - 1\n while lo < hi:\n mid: int = (lo + hi) // 2\n if arr[mid] < x:\n lo = mid + 1\n else:\n hi = mid\n return lo\n```\n``` C++ []\nclass Solution {\npublic:\n int binary_search(const vector<int>& arr, int x) {\n int lo = 0;\n int hi = arr.size() - 1;\n while (lo < hi) {\n int mid = (lo + hi) / 2;\n if (arr[mid] < x) {\n lo = mid + 1;\n } else {\n hi = mid;\n }\n }\n return lo;\n }\n\n int equalSubstring(string s, string t, int maxCost) {\n int len = s.size();\n vector<int> costs(len + 1, 0);\n for (int ind = 1; ind <= len; ind++) {\n costs[ind] = costs[ind - 1] + abs(s[ind - 1] - t[ind - 1]);\n }\n\n int res = 0;\n\n for (int right_index = 1; right_index <= len; right_index++) {\n int min_left = binary_search(costs, costs[right_index] - maxCost);\n if (right_index - min_left > res) {\n res = right_index - min_left;\n }\n }\n\n return res;\n }\n};\n```\n``` JavaScript []\nvar binarySearch = function(arr, x) {\n let lo = 0;\n let hi = arr.length - 1;\n while (lo < hi) {\n let mid = Math.floor((lo + hi) / 2);\n if (arr[mid] < x) {\n lo = mid + 1;\n } else {\n hi = mid;\n }\n }\n return lo;\n};\n\nvar equalSubstring = function(s, t, maxCost) {\n let len = s.length;\n let costs = new Array(len + 1).fill(0);\n for (let ind = 1; ind <= len; ind++) {\n costs[ind] = costs[ind - 1] + Math.abs(s.charCodeAt(ind - 1) - t.charCodeAt(ind - 1));\n }\n\n let res = 0;\n\n for (let right_index = 1; right_index <= len; right_index++) {\n let min_left = binarySearch(costs, costs[right_index] - maxCost);\n if (right_index - min_left > res) {\n res = right_index - min_left;\n }\n }\n\n return res;\n};\n```\n``` Java []\nclass Solution {\n private int binarySearch(int[] arr, int x) {\n int lo = 0;\n int hi = arr.length - 1;\n while (lo < hi) {\n int mid = (lo + hi) / 2;\n if (arr[mid] < x) {\n lo = mid + 1;\n } else {\n hi = mid;\n }\n }\n return lo;\n }\n\n public int equalSubstring(String s, String t, int maxCost) {\n int len = s.length();\n int[] costs = new int[len + 1];\n costs[0] = 0;\n for (int ind = 1; ind <= len; ind++) {\n costs[ind] = costs[ind - 1] + Math.abs(s.charAt(ind - 1) - t.charAt(ind - 1));\n }\n\n int res = 0;\n\n for (int right_index = 1; right_index <= len; right_index++) {\n int min_left = binarySearch(costs, costs[right_index] - maxCost);\n if (right_index - min_left > res) {\n res = right_index - min_left;\n }\n }\n\n return res;\n }\n}\n```\n``` C []\nint binary_search(int* arr, int len, int x) {\n int lo = 0;\n int hi = len - 1;\n while (lo < hi) {\n int mid = (lo + hi) / 2;\n if (arr[mid] < x) {\n lo = mid + 1;\n } else {\n hi = mid;\n }\n }\n return lo;\n}\n\nint equalSubstring(char* s, char* t, int maxCost) {\n int len = strlen(s);\n int* costs = (int*)malloc((len + 1) * sizeof(int));\n costs[0] = 0;\n for (int ind = 1; ind <= len; ind++) {\n costs[ind] = costs[ind - 1] + abs(s[ind - 1] - t[ind - 1]);\n }\n\n int res = 0;\n\n for (int right_index = 1; right_index <= len; right_index++) {\n int min_left = binary_search(costs, len + 1, costs[right_index] - maxCost);\n if (right_index - min_left > res) {\n res = right_index - min_left;\n }\n }\n\n free(costs);\n return res;\n}\n```\n\n## \uD83D\uDCA1I encourage you to check out [my profile](https://leetcode.com/heir-of-god/) and [Project-S](https://github.com/Heir-of-God/Project-S) project for detailed explanations and code for different problems (not only Leetcode). Happy coding and learning! \uD83D\uDCDA\n\n### Please consider *upvote* because I try really hard not just to put here my code and rewrite testcase to show that it works but explain you WHY it works and HOW. Thank you\u2764\uFE0F\n\n## If you have any doubts or questions feel free to ask them in comments. I will be glad to help you with understanding\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\n\n\n | 26 | 7 | ['String', 'Binary Search', 'C', 'Sliding Window', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 12 |
get-equal-substrings-within-budget | [Java/Python 3] Sliding window space O(1) w/ brief explanation and analysis. | javapython-3-sliding-window-space-o1-w-b-acpl | Maintain a window and keep accumulating the cost on hi end; if the cost is higher than maxCost, then shrink widow by removing element from lo end; \n2. Update t | rock | NORMAL | 2019-09-29T04:02:23.316633+00:00 | 2019-09-30T07:44:48.502713+00:00 | 1,140 | false | 1. Maintain a window and keep accumulating the cost on `hi` end; if the cost is higher than `maxCost`, then shrink widow by removing element from `lo` end; \n2. Update the max window `width` during each iteration.\n\n```\n public int equalSubstring(String s, String t, int maxCost) {\n int width = 0;\n for (int hi = 0, lo = -1; hi < s.length(); ++hi) {\n maxCost -= Math.abs(s.charAt(hi) - t.charAt(hi));\n if (maxCost < 0) {\n ++lo;\n maxCost += Math.abs(s.charAt(lo) - t.charAt(lo));\n }\n width = Math.max(width, hi - lo);\n }\n return width;\n }\n```\n```\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n width, lo = 0, -1\n for hi in range(len(s)):\n maxCost -= abs(ord(s[hi]) - ord(t[hi]))\n if maxCost < 0:\n lo += 1\n maxCost += abs(ord(s[lo]) - ord(t[lo]))\n width = max(width, hi - lo)\n return width\n```\n**Analysis:**\n\nTime: O(n), space: O(1), where n = s.length(). | 18 | 2 | [] | 5 |
get-equal-substrings-within-budget | c++ || easiest | c-easiest-by-rajat_gupta-74xf | \nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n\t\n int n=s.size(),arr[n];\n\t\t\n for(int i=0;i<n;i++)\n | rajat_gupta_ | NORMAL | 2021-05-10T18:10:16.673295+00:00 | 2021-05-10T18:10:16.673342+00:00 | 1,083 | false | ```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n\t\n int n=s.size(),arr[n];\n\t\t\n for(int i=0;i<n;i++)\n arr[i]=abs(s[i]-t[i]);\n \n int cost=0,start=0,maxlen=INT_MIN;\n\t\t\n for(int i=0;i<n;i++){\n cost+=arr[i];\n \n while(cost>maxCost)\n cost-=arr[start++];\n \n maxlen=max(maxlen,i-start+1);\n }\n return maxlen;\n }\n};\n```\n**Feel free to ask any question in the comment section.**\nI hope that you\'ve found the solution useful.\nIn that case, **please do upvote and encourage me** to on my quest to document all leetcode problems\uD83D\uDE03\nHappy Coding :)\n | 13 | 0 | ['C', 'C++'] | 4 |
get-equal-substrings-within-budget | Python || Easy Clean Solution. Sliding Window. | python-easy-clean-solution-sliding-windo-w5ik | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | dilmurat-aliev | NORMAL | 2023-09-07T13:14:56.647787+00:00 | 2023-09-07T13:14:56.647811+00:00 | 605 | false | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n left = ans = curr = 0\n for i in range(len(s)):\n curr += abs(ord(s[i]) - ord(t[i]))\n while curr > maxCost:\n curr -= abs(ord(s[left]) - ord(t[left]))\n left += 1\n ans = max(ans, i - left + 1)\n return ans\n```\n\n | 12 | 0 | ['String', 'Sliding Window', 'Python3'] | 3 |
get-equal-substrings-within-budget | Easy PrefSum + BinarySearch O(NLogN) | easy-prefsum-binarysearch-onlogn-by-upad-gpcc | Intuition\nThe intution came to me when i was solving the question i saw i needed to find a substring sum which leads me to this size or less.\n# Approach\nMade | upadhyayabhi0107 | NORMAL | 2022-12-20T15:09:28.416814+00:00 | 2022-12-20T15:09:28.416851+00:00 | 1,074 | false | # Intuition\nThe intution came to me when i was solving the question i saw i needed to find a substring sum which leads me to this size or less.\n# Approach\nMade a prefix sum to calculate sum/change cost in O(1)\nThen i searched substring of size k which satisfy the value and then if it satisfied i searched for higher values otherwise lesser size.\n# Complexity\n- Time complexity:O(NLogN)\n\n- Space complexity:O(N)\n\n# Code\n```\nclass Solution {\npublic:\n bool check(vector<int>& pref , int cost , int mid){\n int l = 0 , r = mid;\n int flag = false;\n while(r < pref.size()){\n int sum = pref[r] - pref[l];\n if(sum <= cost){\n flag = true;\n break;\n }\n l++;\n r++;\n }\n return flag;\n }\n int equalSubstring(string s, string t, int cost) {\n int n = s.size();\n vector<int> pref(n + 1 , 0);\n for(int i = 1 ; i <= n ; i++){\n pref[i] = pref[i-1] + abs((s[i - 1] - \'a\') - (t[i - 1] - \'a\'));\n }\n int l = 0 , h = s.size()+1;\n int ans = 0;\n while(l <= h){\n int mid = l + (h - l)/2;\n if(check(pref , cost , mid)){\n ans = mid ;\n l = mid + 1;\n }\n else{\n h = mid - 1;\n }\n }\n return ans;\n }\n};\n``` | 12 | 0 | ['Binary Search', 'Prefix Sum', 'C++'] | 3 |
get-equal-substrings-within-budget | Python Solution with explanation | python-solution-with-explanation-by-a_bs-9cx1 | Intuition\n\nThe problem asks us to find the longest substring where we can change characters in the first string (s) to make it equal to the second string (t) | 20250406.A_BS | NORMAL | 2024-05-28T02:36:01.820770+00:00 | 2024-05-28T02:36:01.820790+00:00 | 389 | false | ## Intuition\n\nThe problem asks us to find the longest substring where we can change characters in the first string (s) to make it equal to the second string (t) within a given cost limit (maxCost). We can solve this using a sliding window approach.\n\n## Approach\n\n1. We\'ll use two pointers: `start` and `end`. `start` will mark the beginning of the current window in string `s`, and `end` will iterate through `s`.\n2. At each step, we\'ll calculate the cost of making the characters at `s[end]` and `t[end]` equal. This cost is the absolute difference between their ASCII values.\n3. We\'ll keep track of the total cost (`current_cost`) for the current window.\n4. If `current_cost` exceeds `maxCost`, we need to reduce the cost. We\'ll achieve this by moving the `start` pointer forward, effectively shrinking the window and removing characters from `s`. We\'ll update `current_cost` accordingly.\n5. As we iterate through `s`, we\'ll keep track of the maximum length (`max_length`) of a valid substring encountered so far.\n\n## Complexity\n\n* **Time complexity:** O(n), where n is the length of the strings. We iterate through each character in `s` at most once.\n* **Space complexity:** O(1). We only use constant extra space for variables like `start`, `end`, `current_cost`, and `max_length`.\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n start = 0\n current_cost = 0\n max_length = 0\n\n for end in range(len(s)):\n # Calculate the cost to change s[end] to t[end]\n current_cost += abs(ord(s[end]) - ord(t[end]))\n\n # If the current cost exceeds maxCost, move the start pointer to reduce the cost\n while current_cost > maxCost:\n current_cost -= abs(ord(s[start]) - ord(t[start]))\n start += 1\n\n # Calculate the maximum length of the valid window\n max_length = max(max_length, end - start + 1)\n \n return max_length\n\n```\n\n## Code Review\n\nThe provided code accurately implements the described approach. Here\'s a breakdown:\n\n1. It initializes `start`, `current_cost`, and `max_length`.\n2. The loop iterates through `s` using `end` as the pointer.\n3. Inside the loop:\n - It calculates the cost for the current characters `s[end]` and `t[end]`.\n - It checks if `current_cost` exceeds `maxCost`. If yes, it shrinks the window by moving `start` forward and updates `current_cost`.\n4. Finally, it updates `max_length` if the current window length (`end - start + 1`) is greater.\n5. The function returns `max_length`, which represents the longest valid substring.\n | 10 | 0 | ['Python3'] | 2 |
get-equal-substrings-within-budget | ✅Detailed Explanation💯Beats 100%🔥Sliding Window (+Optimised)🔥1 & 2 pass solutions🔥O(n), O(1)🔥 | detailed-explanationbeats-100sliding-win-sf70 | \nSubmission Link\n> Don\'t mind leetcode submission rating too much, its very random.\n\n# \uD83C\uDFAF Problem Explanation:\nWe are given two strings s and t | Saketh3011 | NORMAL | 2024-05-28T02:06:10.187170+00:00 | 2024-05-28T17:50:26.483293+00:00 | 1,756 | false | \n[Submission Link](https://leetcode.com/problems/get-equal-substrings-within-budget/submissions/1269912694?envType=daily-question&envId=2024-05-28)\n> Don\'t mind leetcode submission rating too much, its very random.\n\n# \uD83C\uDFAF Problem Explanation:\nWe are given two strings `s` and `t` of the same length and a number `maxCost`. The goal is to change `s` to `t` character by character. Changing the `s[i]` to `t[i]` costs the absolute difference between their ASCII values. We need to find the longest substring of `s` that you can change to match `t` without the total cost exceeding `maxCost`. If we can\'t change any substring within the cost, return 0.\n\n## \uD83D\uDD0D Methods To Solve This Problem:\nThis post covers the following approaches:\n1. Sliding Window, 2 pass.\n2. Optimised Sliding Window, 1 pass \uD83D\uDD25.\n\n---\n\n# Method 1: Sliding Window\n\n## \uD83E\uDD14 Intuition:\n- This is classic sliding window question. To solve this problem think of using a sliding window. \n- Imagine you have a window that you slide from right over the strings `s` and `t` to keep track of the cost of changing characters within that window. \n- If the cost exceeds `maxCost`, you shrink the window from the left side until the cost is manageable again. This way, you can efficiently find the longest substring that fits within the allowed cost.\n\n\n\n## \uD83E\uDDE0 Approach:\n1. **Set Up Pointers and Variables**:\n - Use two pointers, `l` (left) and `r` (right), to represent the current window.\n - Initialize `cost` to 0 to keep track of the current window\'s conversion cost.\n - Initialize `result` to 0 to store the maximum length of a valid substring found.\n\n2. **Expand the Window**:\n - Iterate through the string using the right pointer `r`.\n - For each character, calculate the cost of changing `s[r]` to `t[r]` and add it to `cost`.\n\n3. **Shrink the Window**:\n - If `cost` exceeds `maxCost`, move the left pointer `l` to the right to reduce the window size. Subtract the cost of changing `s[l]` to `t[l]` from `cost`.\n\n4. **Update the Result**:\n - After adjusting the window, update `result` with the maximum length of the current valid window.\n\n5. **Return the Result**:\n - Finally, return the maximum length of the substring that can be changed within the given cost constraint.\n\n## \u2699\uFE0F Dry Run:\n##### Input: s = "abcd", t = "bcdf", maxCost = 3\n| Iteration | Window | l | r | Sliding Window | abs(s[r] - t[r]) | cost | result |\n|:---------:|:---------:|:---:|:---:|:--------------------------:|:----------------:|:------:|:-----------------------:|\n| 1 | Expanding | 0 | 0 | "***a***bcd" "***b***cdf" | 1 (\'a\'-\'b\') | 1 | `max(0, 0 - 0 + 1)` = 1 |\n| 2 | Expanding | 0 | 1 | "***ab***cd" "***bc***df" | 1 (\'b\'-\'c\') | 2 | `max(1, 1 - 0 + 1)` = 2 |\n| 3 | Expanding | 0 | 2 | "***abc***d" "***bcd***f" | 1 (\'c\'-\'d\') | 3 | `max(2, 2 - 0 + 1)` = 3 |\n| 4 | Expanding | 0 | 3 | "***abcd***" "***bcdf***" | 2 (\'d\'-\'f\') | 5 | Cost exceeds maxCost |\n| 4 | Shrinking | 1 | 3 | "a***bcd***" "b***cdf***" | -1 (\'a\'-\'b\') | 4 | Cost exceeds maxCost |\n| 4 | Shrinking | 2 | 3 | "ab***cd***" "bc***df***" | -1 (\'b\'-\'c\') | 3 | `max(3, 3 - 2 + 1)` = 3 |\n##### Output: result = 3\n\n\n## \uD83D\uDCD2 Complexity:\n- \u23F0 Time complexity: $$O(n)$$. Each character in the string is processed at most twice, once by the right pointer and once by the left pointer. Thus 2 pass solution.\n- \uD83E\uDDFA Space complexity: $$O(1)$$. No additional space is used.\n\n## \uD83E\uDDD1\u200D\uD83D\uDCBB Code\n``` python []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n l, cost = 0, 0\n result = 0\n\n for r in range(len(s)):\n cost += abs(ord(s[r]) - ord(t[r]))\n\n while cost > maxCost:\n cost -= abs(ord(s[l]) - ord(t[l]))\n l += 1\n\n result = max(result, r - l + 1)\n \n return result\n```\n``` java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int l = 0, cost = 0, result = 0;\n\n for (int r = 0; r < s.length(); r++) {\n cost += Math.abs(s.charAt(r) - t.charAt(r));\n\n while (cost > maxCost) {\n cost -= Math.abs(s.charAt(l) - t.charAt(l));\n l++;\n }\n\n result = Math.max(result, r - l + 1);\n }\n\n return result;\n }\n}\n```\n``` cpp []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int l = 0, cost = 0, result = 0;\n\n for (int r = 0; r < s.length(); r++) {\n cost += abs(s[r] - t[r]);\n\n while (cost > maxCost) {\n cost -= abs(s[l] - t[l]);\n l++;\n }\n\n result = max(result, r - l + 1);\n }\n\n return result;\n }\n};\n```\n``` javascript []\nvar equalSubstring = function(s, t, maxCost) {\n let l = 0, cost = 0, result = 0;\n\n for (let r = 0; r < s.length; r++) {\n cost += Math.abs(s.charCodeAt(r) - t.charCodeAt(r));\n\n while (cost > maxCost) {\n cost -= Math.abs(s.charCodeAt(l) - t.charCodeAt(l));\n l++;\n }\n\n result = Math.max(result, r - l + 1);\n }\n\n return result;\n};\n```\n\n---\n\n\n# Method 2: Optimised Sliding Window [1 Pass]\uD83D\uDD25BEST\uD83D\uDD25\n\n## \uD83E\uDD14 Intuition:\nIn the above approach we were making a note of `result`. Do we really have to do that?\nWe only need max length. We can expand sliding window as before and when we have to shrinking window, lets just shrinking it by 1 `l++` maintaining max length. `l` will incremented for each `r` increment when `cost` is not satisfied, in case `cost` is satisfied `r` is incremented and l remains stationary, increasing window length.\n\n## \uD83E\uDDE0 Approach:\n1. **Set Up Pointers and Variables**:\n - Use two pointers, `l` (left) and `r` (right), to represent the current window.\n - Instead of initializing `cost` and `result`, we directly update `maxCost` as we iterate through the string.\n\n2. **Expand and Shrink the Window**:\n - Iterate through the string using the right pointer `r`.\n - For each character, subtract the cost of changing `s[r]` to `t[r]` from `maxCost`.\n - If `maxCost` becomes negative, indicating that the current window exceeds the cost constraint, move the left pointer `l` to the right to shrink the window. Add the cost of changing `s[l]` to `t[l]` back to `maxCost`.\n\n3. **Update the Result**:\n - Keep track of the maximum length of the valid window (`r - l + 1`).\n\n4. **Return the Result**:\n - Finally, return the maximum length of the substring that can be changed within the given cost constraint.\n\n\n\n## \u2699\uFE0F Dry Run:\n##### Inputs: s = "abcd", t = "bcdf", maxCost = 3\n| Iteration | Window | l | r | Sliding Window | abs(s[r] - t[r]) | maxCost | r - l |\n|:---------:|:---------:|:-----:|:-----:|:-----------------------------:|:----------------:|:---------:|:-----------:|\n| 1 | Expanding | 0 | 0 | "***a***bcd" "***b***cdf" | 1 (\'a\'-\'b\') | 2 | 1 |\n| 2 | Expanding | 0 | 1 | "***ab***cd" "***bc***df" | 1 (\'b\'-\'c\') | 1 | 2 |\n| 3 | Expanding | 0 | 2 | "***abc***d" "***bcd***f" | 1 (\'c\'-\'d\') | 0 | 3 |\n| 4 | Expanding | 0 | 3 | "***abcd***" "***bcdf***" | 2 (\'d\'-\'f\') | -2 | Cost exceeds maxCost |\n| 4 | Shrinking | 1 | 3 | "a***bcd***" "b***cdf***" | -1 (\'a\'-\'b\') | -1 | Cost exceeds maxCost |\n##### Output: result = 3\n\n\n## \uD83D\uDCD2 Complexity:\n- \u23F0 Time complexity: $$O(n)$$. Each character in the string is processed at most once, once by the right pointer and left pointer is constant. Thus 1 pass solution.\n- \uD83E\uDDFA Space complexity: $$O(1)$$. No additional space is used.\n\n## \uD83E\uDDD1\u200D\uD83D\uDCBB Code\n``` python []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n l = 0\n for r in range(len(s)):\n maxCost -= abs(ord(s[r]) - ord(t[r]))\n if maxCost < 0:\n maxCost += abs(ord(s[l]) - ord(t[l]))\n l += 1\n\n return r - l + 1\n```\n``` java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int l = 0, r;\n for (r = 0; r < s.length(); r++) {\n maxCost -= Math.abs(s.charAt(r) - t.charAt(r));\n if (maxCost < 0)\n maxCost += Math.abs(s.charAt(l) - t.charAt(l++));\n }\n return r - l;\n }\n}\n```\n``` cpp []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int l = 0, r;\n for (r = 0; r < s.length(); r++) {\n maxCost -= abs(s[r] - t[r]);\n if (maxCost < 0)\n maxCost += abs(s[l] - t[l++]);\n }\n return r - l;\n }\n};\n```\n``` javascript []\nvar equalSubstring = function(s, t, maxCost) {\n let l = 0, r;\n for (r = 0; r < s.length; r++) {\n maxCost -= Math.abs(s.charCodeAt(r) - t.charCodeAt(r));\n if (maxCost < 0)\n maxCost += Math.abs(s.charCodeAt(l) - t.charCodeAt(l++));\n }\n return r - l;\n};\n```\n\n---\n# Please consider giving an Upvote!\n | 10 | 0 | ['String', 'Sliding Window', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 5 |
get-equal-substrings-within-budget | JAVA ( Sliding Window ) | java-sliding-window-by-infox_92-z7mr | class Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n // Convert the problem into a min subarray problem\n int[] di | Infox_92 | NORMAL | 2022-10-25T17:49:14.197105+00:00 | 2022-10-25T17:49:14.197148+00:00 | 583 | false | class Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n // Convert the problem into a min subarray problem\n int[] diff = new int[s.length()];\n for(int i = 0; i < s.length(); ++i) {\n int asciiS = s.charAt(i);\n int asciiT = t.charAt(i);\n diff[i] = Math.abs(asciiS - asciiT);\n }\n \n // Now find the longest subarray <= maxCost\n // all diff[i] >= 0 (non-negative)\n \n // Use sliding window?\n int maxLen = 0;\n int curCost = 0;\n int start = 0;\n \n for(int end = 0; end < diff.length; ++end) {\n curCost += diff[end];\n while(curCost > maxCost) {\n curCost -= diff[start];\n ++start;\n }\n maxLen = Math.max(maxLen, end - start + 1);\n }\n \n return maxLen;\n }\n} | 10 | 0 | [] | 1 |
get-equal-substrings-within-budget | C++ Sliding Window (+ Cheat Sheet) | c-sliding-window-cheat-sheet-by-lzl12463-barf | See my latest update in repo LeetCode\n\n## Solution 1. Sliding Window\n\nCheck out "C++ Maximum Sliding Window Cheatsheet Template!".\n\nShrinkable Sliding Win | lzl124631x | NORMAL | 2021-10-19T06:13:57.959135+00:00 | 2021-10-19T06:13:57.959177+00:00 | 3,566 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Sliding Window\n\nCheck out "[C++ Maximum Sliding Window Cheatsheet Template!](https://leetcode.com/problems/frequency-of-the-most-frequent-element/discuss/1175088/C%2B%2B-Maximum-Sliding-Window-Cheatsheet-Template!)".\n\nShrinkable Sliding Window:\n\n```cpp\n// OJ: https://leetcode.com/problems/get-equal-substrings-within-budget/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(1)\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int i = 0, j = 0, N = s.size(), cost = 0, ans = 0;\n for (; j < N; ++j) {\n cost += abs(s[j] - t[j]);\n for (; cost > maxCost; ++i) cost -= abs(s[i] - t[i]);\n ans = max(ans, j - i + 1);\n }\n return ans;\n }\n};\n```\n\nNon-shrinkable Sliding Window:\n\n```cpp\n// OJ: https://leetcode.com/problems/get-equal-substrings-within-budget/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(1)\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int i = 0, j = 0, N = s.size(), cost = 0;\n for (; j < N; ++j) {\n cost += abs(s[j] - t[j]);\n if (cost > maxCost) {\n cost -= abs(s[i] - t[i]);\n ++i;\n }\n }\n return j - i;\n }\n};\n```\n | 10 | 0 | [] | 2 |
get-equal-substrings-within-budget | [Java] Simple Sliding Window, 10 lines code, Time O(N), Space O(1) | java-simple-sliding-window-10-lines-code-05cy | java\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int l = 0, r = 0, n = s.length(), cost = 0, ans = 0;\n | hiepit | NORMAL | 2019-09-29T04:25:43.150086+00:00 | 2019-09-29T04:34:54.117194+00:00 | 705 | false | ```java\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int l = 0, r = 0, n = s.length(), cost = 0, ans = 0;\n while (r < n) {\n cost += Math.abs(s.charAt(r) - t.charAt(r));\n while (cost > maxCost) {\n cost -= Math.abs(s.charAt(l) - t.charAt(l));\n l++;\n }\n ans = Math.max(ans, r - l + 1);\n r++;\n }\n return ans;\n }\n}\n``` | 10 | 0 | ['Java'] | 3 |
get-equal-substrings-within-budget | [JavaScript] Easy to understand - 2 solutions | javascript-easy-to-understand-2-solution-1ddu | SOLUTION 1\n\nWe use the sliding window to solve it. The left and right means both edges of the window.\n\nSo, we could meet 2 situations when we move the right | poppinlp | NORMAL | 2019-09-29T06:15:54.824917+00:00 | 2020-05-12T10:18:58.449052+00:00 | 526 | false | ## SOLUTION 1\n\nWe use the sliding window to solve it. The `left` and `right` means both edges of the window.\n\nSo, we could meet 2 situations when we move the right edge from start to end:\n\n- The cost is less than `maxCost`: we could update the max length;\n- The cost is bigger than `maxCost`: we need to move the left edge to reduce cost.\n\nHere\'s the code:\n\n```js\nconst equalSubstring = (s, t, maxCost) => {\n let max = 0;\n for (let left = -1, right = 0; right < s.length; ++right) {\n maxCost -= Math.abs(s.charCodeAt(right) - t.charCodeAt(right));\n if (maxCost >= 0) {\n right - left > max && (max = right - left);\n } else {\n while (maxCost < 0) {\n ++left;\n maxCost += Math.abs(s.charCodeAt(left) - t.charCodeAt(left));\n }\n }\n }\n return max;\n};\n```\n\n## SOLUTION 2\n\nHere\'s a more concise version of solution 1.\n\nWe move the right edge step by step just like solution 1. But the key point is that we also move the left edge step by step if it\'s necessary.\n\nBut why? It\'s pretty easy to find out that the window could be invalidated.\n\nLet\'s see, first of all, we only need to find out the longest substring which means we don\'t care about the others.\n\nThen, if we have a substring right now. There are only 2 situations:\n\n- We could find a longer one: the window will be validated naturally when we meet the longer one.\n- It\'s the longest one: we got the longest length even the current window may not be validated.\n\nSo, according to this, we could get this code:\n\n```js\nconst equalSubstring = (s, t, maxCost) => {\n let left = -1;\n for (let right = 0; right < s.length; ++right) {\n maxCost -= Math.abs(s.charCodeAt(right) - t.charCodeAt(right));\n if (maxCost < 0) {\n ++left;\n maxCost += Math.abs(s.charCodeAt(left) - t.charCodeAt(left));\n }\n }\n return s.length - left - 1;\n};\n | 8 | 0 | ['JavaScript'] | 2 |
get-equal-substrings-within-budget | ✅ ⬆️ Sliding Window | Prefix Sum | Binary Search 🔥🔥 [Java] | sliding-window-prefix-sum-binary-search-350y0 | Binary Search\nTC: O(nlogn)\nSC: O(n)\n\npublic int equalSubstring(String s, String t, int maxCost) {\n int[] costs = new int[s.length() + 1]; // to i | sandeepk97 | NORMAL | 2024-05-28T00:45:21.455665+00:00 | 2024-05-28T00:50:32.286511+00:00 | 822 | false | **Binary Search**\nTC: O(nlogn)\nSC: O(n)\n```\npublic int equalSubstring(String s, String t, int maxCost) {\n int[] costs = new int[s.length() + 1]; // to include 0\n for (int i = 1; i <= s.length(); ++i) {\n costs[i] = Math.abs(s.charAt(i - 1) - t.charAt(i - 1));\n }\n\n int res = 0;\n\n for (int i = 1; i < costs.length; ++i) {\n\n costs[i] += costs[i - 1];\n int j = Arrays.binarySearch(costs, costs[i] - maxCost);\n if (j < 0) {\n j = -j - 1;\n }\n res = Math.max(res, i - j);\n }\n\n return res;\n }\n```\n\n**Sliding Window**\nTC: O(n)\nSC: O(1)\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int N = s.length();\n \n int maxLen = 0;\n // Starting index of the current substring\n int start = 0;\n // Cost of converting the current substring in s to t\n int currCost = 0;\n \n for (int i = 0; i < N; i++) {\n // Add the current index to the substring\n currCost += Math.abs(s.charAt(i) - t.charAt(i));\n \n // Remove the indices from the left end till the cost becomes less than allowed\n while (currCost > maxCost) {\n currCost -= Math.abs(s.charAt(start) - t.charAt(start));\n start++;\n }\n \n maxLen = Math.max(maxLen, i - start + 1);\n }\n \n return maxLen;\n }\n}\n```\n\n\n\n**Please Upvote** | 7 | 1 | ['Binary Tree', 'Prefix Sum', 'Java'] | 7 |
get-equal-substrings-within-budget | Java | Sliding Window | 15 lines | Clean code | java-sliding-window-15-lines-clean-code-pobgk | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | judgementdey | NORMAL | 2024-05-28T00:17:45.415965+00:00 | 2024-05-28T18:02:04.226291+00:00 | 624 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n var len = 0;\n var cost = 0;\n var i = 0;\n var j = 0;\n\n while (j < s.length()) {\n if (cost <= maxCost) {\n cost += Math.abs(s.charAt(j) - t.charAt(j));\n j++;\n }\n while (cost > maxCost) {\n cost -= Math.abs(s.charAt(i) - t.charAt(i));\n i++;\n }\n len = Math.max(len, j-i);\n }\n return len;\n }\n}\n```\nIf you like my solution, please upvote it! | 6 | 1 | ['String', 'Sliding Window', 'Java'] | 3 |
get-equal-substrings-within-budget | simplest C++ | simplest-c-by-naman238-mtd8 | \nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n vector<int> v(t.size());\n for(int i=0;i<t.size();i++)\n | naman238 | NORMAL | 2020-06-19T17:43:01.026931+00:00 | 2020-06-19T17:43:01.026980+00:00 | 307 | false | ```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n vector<int> v(t.size());\n for(int i=0;i<t.size();i++)\n {\n v[i]=abs(t[i]-s[i]);\n }\n int ans=0;\n int i=0;\n int j=0;\n int k=maxCost;\n while(i<t.size())\n {\n k-=v[i];\n while(k<0)\n {\n k+=v[j];\n j++;\n }\n ans=max(ans,i-j+1);\n i++;\n }\n return ans;\n }\n};\n``` | 6 | 0 | [] | 1 |
get-equal-substrings-within-budget | Two pointers simple explanation with clean code | two-pointers-simple-explanation-with-cle-66lm | Intuition\n- We can store difference of each character from two strings in a separate list. \n- Now our problem statemenet reduces to find maximum number of ele | anupsingh556 | NORMAL | 2024-05-28T06:53:42.259419+00:00 | 2024-05-28T06:53:42.259436+00:00 | 690 | false | # Intuition\n- We can store difference of each character from two strings in a separate list. \n- Now our problem statemenet reduces to find maximum number of elements you can pick such that their sum does not exceed m we can use sliding window to solve this\n- Instead of storing difference in a separate list we can find this inline saving us extra space\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- We use `beg` as first pointer of elements and `sum` will store sum of all elements till `res` will have maximum elements\n- Maintain two pointers `beg` and `i` add current difference to sum\n- Now move `beg` till the sum is greater than `m` so that the subsequence is valid\n- update result if this subsequence has more elements than res\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n) we doing single pass on our list only\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: Constant Space no extra space needed\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int m) {\n int res = 0,beg=0,sum=0;\n for(int i=0;i<s.size();i++) {\n sum+=abs(s[i]-t[i]);\n while(sum>m) {\n sum-=abs(s[beg]-t[beg]);\n beg++;\n }\n res = max(res, i-beg+1);\n }\n return res;\n }\n};\n``` | 5 | 0 | ['C++'] | 2 |
get-equal-substrings-within-budget | [Python3] Sliding Window - Two ways to implement - Easy to Understand | python3-sliding-window-two-ways-to-imple-pgpm | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dolong2110 | NORMAL | 2023-04-27T17:47:06.595242+00:00 | 2023-04-27T17:47:06.595274+00:00 | 1,146 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n res = 0\n i = j = cost = 0\n while j < len(s):\n cost += abs(ord(s[j]) - ord(t[j]))\n while cost > maxCost:\n cost -= abs(ord(s[i]) - ord(t[i]))\n i += 1\n res = max(res, j - i + 1)\n j += 1\n return res\n```\n\n\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n res = 0\n i = j = cost = 0\n while j < len(s):\n cost += abs(ord(s[j]) - ord(t[j]))\n if cost > maxCost:\n cost -= abs(ord(s[i]) - ord(t[i]))\n i += 1\n j += 1\n return j - i\n``` | 5 | 0 | ['Sliding Window', 'Python3'] | 1 |
get-equal-substrings-within-budget | python | easy | | python-easy-by-abhishen99-apc9 | \nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n \n cost=0\n l=0\n ans=0\n for r in ra | Abhishen99 | NORMAL | 2021-07-03T16:02:16.236365+00:00 | 2021-07-03T16:02:16.236395+00:00 | 711 | false | ```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n \n cost=0\n l=0\n ans=0\n for r in range(len(s)):\n \n cost+= abs(ord(s[r])-ord(t[r]))\n while cost > maxCost:\n cost -= abs(ord(s[l]) - ord(t[l]))\n l+=1\n ans=max(ans, r-l+1)\n return ans\n \n \n \n \n``` | 5 | 0 | ['Python', 'Python3'] | 2 |
get-equal-substrings-within-budget | C++ Subarrray Sum Very Easy to Understand. O(N) | c-subarrray-sum-very-easy-to-understand-5bm2q | \nWe can visualise this problem as we have to maximise the length of the substring we can change in string a to string b such that it never exceeds maximum_cos | 0nurag | NORMAL | 2020-12-03T12:33:56.935431+00:00 | 2020-12-03T12:33:56.935475+00:00 | 264 | false | \nWe can visualise this problem as we have to maximise the length of the substring we can change in string a to string b such that it never exceeds maximum_cost.\n\nIt is like having a **Maximum Size Subarray Sum with sum less than k.**\n\nAlgorithm\n1. For each index (0 to n) , take absolute difference of string s and t at index i. and increase our cost\n\t\t\t**cost = cost + abs(s[i] - t[i]);**\t\t\t\n2. Till cost is greater than maximumCost, Just Take a counter at index j = 0, and till i increment j and decrease the cost difference at that index j.\n3. Take the maximum of (i - j + 1).\n\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n \n int i = 0, j =0, cost = 0, maxm = INT_MIN;\n \n for(i = 0; i < s.size(); i++)\n {\n cost += abs(s[i] - t[i]);\n \n if(cost > maxCost) \n {\n while(j <= i and cost > maxCost)\n {\n int prevCost = abs(s[j] - t[j]);\n cost = cost - prevCost;\n j++;\n }\n }\n \n maxm = max(maxm, i - j + 1);\n }\n return (maxm == INT_MIN) ? 0 : maxm;\n }\n};\n``` | 5 | 0 | [] | 2 |
get-equal-substrings-within-budget | Easy to understand solution. Beginner friendly solution. O(n) Time Complexity. | easy-to-understand-solution-beginner-fri-syxk | Intuition\n Describe your first thoughts on how to solve this problem. \n1. Cost Calculation: Calculate the cost to transform each character of s to t. This giv | ShivaanjayNarula | NORMAL | 2024-07-03T00:51:25.234475+00:00 | 2024-07-03T00:51:25.234520+00:00 | 15 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. **Cost Calculation:** Calculate the cost to transform each character of s to t. This gives us the cost array.\n\n2. **Prefix Sum:** Use the prefix sum array to quickly compute the total cost of any substring.\n\n3. **Binary Search:** Use binary search to efficiently find the maximum length of the substring that can be transformed within the given cost.\n\n4. **Sliding Window Check:** For each potential length found via binary search, use the prefix sum to check if there exists a valid substring of that length.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Calculate the Cost Array:**\nFirst, we calculate the cost array where each element represents the cost of changing s[i] to t[i]\n```\nvector<int> cost(n, 0);\nfor(int i = 0; i < n; i++) {\n cost[i] = abs(s[i] - t[i]);\n}\n\n```\n2. **Calculate the Prefix Sum Array:**\nNext, we create a prefix sum array to efficiently calculate the sum of costs for any substring.\n```\nvector<int> prefixSum(n + 1, 0);\nfor(int i = 1; i <= n; i++) {\n prefixSum[i] = prefixSum[i - 1] + cost[i - 1];\n}\n\n```\n3. **Binary Search for the Maximum Length:**\nWe use binary search to find the maximum length of the substring that satisfies the cost condition. \nThe idea is to check for each possible length mid if there exists a substring of this length whose total transformation cost is within maxCost.\n```\nint left = 0;\nint right = n;\nint ans = 0;\nwhile (left <= right) {\n int mid = (left + right) / 2;\n if (check(prefixSum, maxCost, mid)) {\n ans = mid;\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n}\n\n```\n4. **Check Function:**\nThe check function verifies if there is any substring of length mid whose transformation cost does not exceed maxCost.\nThis is done by iterating over the prefix sum array and calculating the cost for each possible substring of length mid.\n```\nbool check(vector<int> &prefixSum, int maxCost, int mid) {\n for (int i = 0; i + mid < prefixSum.size(); i++) {\n if (prefixSum[i + mid] - prefixSum[i] <= maxCost) {\n return true;\n }\n }\n return false;\n}\n```\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Please upvote my solution, if found helpful. I am literally crying right now.\n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n = s.size();\n vector<int> cost(n, 0);\n for(int i = 0; i < n; i++)\n {\n cost[i] = abs(s[i] - t[i]);\n }\n vector<int> prefixSum(n+1, 0);\n for(int i = 1; i <= n; i++)\n {\n prefixSum[i] = prefixSum[i-1] + cost[i-1];\n }\n int left = 0;\n int right = n;\n int ans = 0;\n while(left <= right)\n {\n int mid = (left + right) / 2;\n if(check(prefixSum, maxCost, mid))\n {\n ans = mid;\n left = mid + 1;\n }\n else\n {\n right = mid - 1;\n }\n }\n return ans;\n }\n bool check(vector<int> &prefixSum, int maxCost, int mid)\n {\n for(int i = 0; i + mid < prefixSum.size(); i++)\n {\n if(prefixSum[i+mid] - prefixSum[i] <= maxCost)\n {\n return true;\n }\n }\n return false;\n }\n};\n``` | 4 | 0 | ['Binary Search', 'Recursion', 'Sliding Window', 'Prefix Sum', 'C++'] | 0 |
get-equal-substrings-within-budget | ✅EASY AND SIMPLE SOLUTION✅ | easy-and-simple-solution-by-deleted_user-vhdc | \n\n# Code\n\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int start = 0;\n int cost = 0;\n int m | deleted_user | NORMAL | 2024-05-28T18:14:23.850304+00:00 | 2024-05-28T18:14:23.850333+00:00 | 56 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int start = 0;\n int cost = 0;\n int max_length = 0;\n\n for (int i = 0; i < s.size(); i++) {\n cost = cost + abs(s[i] - t[i]);\n\n while (cost > maxCost) {\n cost = cost - abs(s[start] - t[start]);\n start++;\n }\n\n max_length = max(max_length, i - start + 1);\n }\n\n return max_length;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
get-equal-substrings-within-budget | JAVA Solution Explained in HINDI | java-solution-explained-in-hindi-by-the_-a5dw | https://youtu.be/h__hozHfOy0\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote | The_elite | NORMAL | 2024-05-28T14:39:03.281324+00:00 | 2024-05-28T14:39:03.281357+00:00 | 183 | false | https://youtu.be/h__hozHfOy0\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\n# Subscribe:- [ReelCoding](https://www.youtube.com/@reelcoding?sub_confirmation=1)\n\nSubscribe Goal:- 400\nCurrent Subscriber:- 395\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int n = s.length();\n int i = 0, j = 0, ans = 0, curCost = 0;\n\n while (j < n) {\n curCost += Math.abs(t.charAt(j) - s.charAt(j));\n while (i < n && curCost > maxCost) {\n curCost -= Math.abs(t.charAt(i) - s.charAt(i));\n i++;\n }\n ans = Math.max(ans, j - i + 1);\n j++;\n }\n\n return ans;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
get-equal-substrings-within-budget | Bests over 98.7% users.... You can rely on this code which is self explanatory | bests-over-987-users-you-can-rely-on-thi-dyo3 | \n\n# Code\n\n\n\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n n = len(s)\n start = 0\n current_co | Aim_High_212 | NORMAL | 2024-05-28T02:12:16.997447+00:00 | 2024-05-28T02:12:16.997486+00:00 | 20 | false | \n\n# Code\n```\n\n\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n n = len(s)\n start = 0\n current_cost = 0\n max_length = 0\n\n for end in range(n):\n current_cost += abs(ord(s[end]) - ord(t[end]))\n\n while current_cost > maxCost:\n current_cost -= abs(ord(s[start]) - ord(t[start]))\n start += 1\n\n max_length = max(max_length, end - start + 1)\n \n return max_length\n \n``` | 4 | 0 | ['C', 'Python', 'Java', 'Python3'] | 0 |
get-equal-substrings-within-budget | Very fast easy to understand solution | very-fast-easy-to-understand-solution-by-vfou | \n public int equalSubstring(String s1, String s2, int maxCost) {\n int []arr = new int[s1.length()];\n for(int i=0;i<s1.length();i++){\n | sk944795 | NORMAL | 2022-08-13T08:19:15.501612+00:00 | 2022-08-13T08:19:15.501642+00:00 | 475 | false | ```\n public int equalSubstring(String s1, String s2, int maxCost) {\n int []arr = new int[s1.length()];\n for(int i=0;i<s1.length();i++){\n arr[i] = Math.abs(s1.charAt(i)-s2.charAt(i)); \n }\n int i=0,j=0,sum=0,max=0;\n\n while(i<arr.length && j<arr.length){\n sum += arr[j++];\n if(sum<=maxCost){\n max = Math.max(max,j-i);\n }else{\n while(sum>maxCost){\n sum -= arr[i++];\n }\n }\n }\n return max;\n }\n``` | 4 | 0 | ['Sliding Window', 'Java'] | 1 |
get-equal-substrings-within-budget | Java sliding window | java-sliding-window-by-hobiter-bzer | \n public int equalSubstring(String s, String t, int maxCost) {\n int res = 0, n = s.length();\n for (int r = 0, l = 0, diff = 0; r < n; r++) { | hobiter | NORMAL | 2020-07-18T00:04:36.502251+00:00 | 2020-07-18T00:04:36.502286+00:00 | 179 | false | ```\n public int equalSubstring(String s, String t, int maxCost) {\n int res = 0, n = s.length();\n for (int r = 0, l = 0, diff = 0; r < n; r++) {\n diff += Math.abs(s.charAt(r) - t.charAt(r));\n while (diff > maxCost) {\n diff -= Math.abs(s.charAt(l) - t.charAt(l++));\n }\n res = Math.max(r - l + 1, res);\n }\n return res;\n }\n``` | 4 | 0 | [] | 1 |
get-equal-substrings-within-budget | ✅ Beats 100% | ✅ Working 25.10.2024 | beats-100-working-25102024-by-piotr_mami-piti | python3 []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n # Get length of input strings (they are guaranteed to b | Piotr_Maminski | NORMAL | 2024-10-25T00:01:19.171608+00:00 | 2024-10-25T00:02:43.971315+00:00 | 93 | false | ```python3 []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n # Get length of input strings (they are guaranteed to be equal length)\n n = len(s)\n \n # Create array of transformation costs between characters at each position\n # ord() converts character to ASCII value, abs() gets positive difference\n costs = [abs(ord(s[i]) - ord(t[i])) for i in range(n)]\n \n # Initialize variables for sliding window approach:\n curr_sum = 0 # Tracks current cost within window\n max_length = 0 # Stores maximum valid window length found\n left = 0 # Left pointer of sliding window\n \n # Right pointer moves through string, expanding window\n for right in range(n):\n # Add cost of new character to window sum\n curr_sum += costs[right]\n \n # If window cost exceeds maxCost, shrink window from left\n # until we\'re back under maxCost\n while curr_sum > maxCost and left <= right:\n curr_sum -= costs[left]\n left += 1\n \n # Current window is valid, update max_length if current window is larger\n # Window size is (right - left + 1)\n max_length = max(max_length, right - left + 1)\n \n # Return the length of longest valid substring found\n return max_length\n```\n```cpp []\nclass Solution {\npublic:\n // Function to find the longest substring that can be transformed within maxCost\n static int equalSubstring(string& s, string& t, int maxCost) {\n // Length of input strings\n const int n = s.size();\n \n // Two pointers for sliding window\n int l = 0, r;\n \n // Track current cost and max length found\n int cost = 0, len = 0;\n\n // First pass: Try to include as many characters as possible from start\n for (r = 0; r < n; r++) {\n // Add cost of transforming current character\n cost += abs(s[r]-t[r]);\n \n // If cost exceeds maxCost, undo last addition and break\n if (cost > maxCost) {\n cost -= abs(s[r]-t[r]);\n break;\n }\n }\n\n // If we reached end of string and cost is acceptable,\n // entire string can be transformed\n if (r == n && cost <= maxCost) return n;\n \n // Store the length of first valid window\n len = r;\n\n // Second pass: Sliding window approach\n for (; r < n; r++) {\n // Add cost of including new character\n cost += abs(s[r]-t[r]);\n \n // While cost exceeds maxCost, shrink window from left\n while (cost > maxCost) {\n cost -= abs(s[l]-t[l]);\n l++;\n }\n \n // Update maximum length if current window is larger\n len = max(len, r-l+1);\n }\n \n return len;\n }\n};\n\n// Lambda function for I/O optimization\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n```java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n // Length of input strings\n final int n = s.length();\n \n // Two pointers for sliding window\n int l = 0, r;\n \n // Track current cost and max length found\n int cost = 0, len = 0;\n \n // First pass: Try to include as many characters as possible from start\n for (r = 0; r < n; r++) {\n // Add cost of transforming current character\n cost += Math.abs(s.charAt(r) - t.charAt(r));\n \n // If cost exceeds maxCost, undo last addition and break\n if (cost > maxCost) {\n cost -= Math.abs(s.charAt(r) - t.charAt(r));\n break;\n }\n }\n \n // If we reached end of string and cost is acceptable,\n // entire string can be transformed\n if (r == n && cost <= maxCost) return n;\n \n // Store the length of first valid window\n len = r;\n \n // Second pass: Sliding window approach\n for (; r < n; r++) {\n // Add cost of including new character\n cost += Math.abs(s.charAt(r) - t.charAt(r));\n \n // While cost exceeds maxCost, shrink window from left\n while (cost > maxCost) {\n cost -= Math.abs(s.charAt(l) - t.charAt(l));\n l++;\n }\n \n // Update maximum length if current window is larger\n len = Math.max(len, r - l + 1);\n }\n \n return len;\n }\n}\n```\n```csharp []\npublic class Solution {\n public int EqualSubstring(string s, string t, int maxCost) {\n // Length of input strings\n int n = s.Length;\n \n // Two pointers for sliding window\n int l = 0, r;\n \n // Track current cost and max length found\n int cost = 0, len = 0;\n \n // First pass: Try to include as many characters as possible from start\n for (r = 0; r < n; r++) {\n // Add cost of transforming current character\n cost += Math.Abs(s[r] - t[r]);\n \n // If cost exceeds maxCost, undo last addition and break\n if (cost > maxCost) {\n cost -= Math.Abs(s[r] - t[r]);\n break;\n }\n }\n \n // If we reached end of string and cost is acceptable,\n // entire string can be transformed\n if (r == n && cost <= maxCost) return n;\n \n // Store the length of first valid window\n len = r;\n \n // Second pass: Sliding window approach\n for (; r < n; r++) {\n // Add cost of including new character\n cost += Math.Abs(s[r] - t[r]);\n \n // While cost exceeds maxCost, shrink window from left\n while (cost > maxCost) {\n cost -= Math.Abs(s[l] - t[l]);\n l++;\n }\n \n // Update maximum length if current window is larger\n len = Math.Max(len, r - l + 1);\n }\n \n return len;\n }\n}\n```\n```golang []\npackage solution\n\ntype Solution struct{}\n\nfunc (s *Solution) equalSubstring(s string, t string, maxCost int) int {\n n := len(s)\n l, r := 0, 0\n cost := 0\n length := 0\n\n // First pass: Try to include as many characters as possible from start\n for r = 0; r < n; r++ {\n cost += abs(int(s[r]) - int(t[r]))\n \n if cost > maxCost {\n cost -= abs(int(s[r]) - int(t[r]))\n break\n }\n }\n\n if r == n && cost <= maxCost {\n return n\n }\n \n length = r\n\n // Second pass: Sliding window approach\n for ; r < n; r++ {\n cost += abs(int(s[r]) - int(t[r]))\n \n for cost > maxCost {\n cost -= abs(int(s[l]) - int(t[l]))\n l++\n }\n \n if r-l+1 > length {\n length = r - l + 1\n }\n }\n \n return length\n}\n\nfunc abs(x int) int {\n if x < 0 {\n return -x\n }\n return x\n}\n```\n```php []\nclass Solution {\n /**\n * @param String $s\n * @param String $t\n * @param Integer $maxCost\n * @return Integer\n */\n function equalSubstring($s, $t, $maxCost) {\n // Length of input strings\n $n = strlen($s);\n \n // Two pointers for sliding window\n $l = 0;\n \n // Track current cost and max length found\n $cost = 0;\n $len = 0;\n \n // First pass: Try to include as many characters as possible from start\n for ($r = 0; $r < $n; $r++) {\n // Add cost of transforming current character\n $cost += abs(ord($s[$r]) - ord($t[$r]));\n \n // If cost exceeds maxCost, undo last addition and break\n if ($cost > $maxCost) {\n $cost -= abs(ord($s[$r]) - ord($t[$r]));\n break;\n }\n }\n \n // If we reached end of string and cost is acceptable,\n // entire string can be transformed\n if ($r == $n && $cost <= $maxCost) return $n;\n \n // Store the length of first valid window\n $len = $r;\n \n // Second pass: Sliding window approach\n for (; $r < $n; $r++) {\n // Add cost of including new character\n $cost += abs(ord($s[$r]) - ord($t[$r]));\n \n // While cost exceeds maxCost, shrink window from left\n while ($cost > $maxCost) {\n $cost -= abs(ord($s[$l]) - ord($t[$l]));\n $l++;\n }\n \n // Update maximum length if current window is larger\n $len = max($len, $r - $l + 1);\n }\n \n return $len;\n }\n}\n```\n### Complexity \n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n | 3 | 0 | ['PHP', 'C++', 'Java', 'Go', 'Python3', 'C#'] | 0 |
get-equal-substrings-within-budget | Simple || Sliding Window Solution || Python | simple-sliding-window-solution-python-by-4cvi | \n# Approach\nThe approach is to find the longest substring in string s that can be transformed into a substring in string t while keeping the total transformat | kunaljs | NORMAL | 2024-05-28T08:29:06.553191+00:00 | 2024-05-28T08:29:06.553212+00:00 | 234 | false | \n# Approach\nThe approach is to find the longest substring in string `s` that can be transformed into a substring in string `t` while keeping the total transformation cost within a specified limit.\n\nIt does this by comparing characters in both strings and calculating the cost of transforming each character. Then, it moves through the string, adjusting the window of characters being considered, until it finds the longest substring that meets the cost constraint. Finally, it returns the length of this longest substring.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n def getCost(char1, char2):\n return abs(ord(char1)-ord(char2))\n \n l, r = 0, 0\n n = len(s)\n ans = 0\n while r<n:\n maxCost -= getCost(s[r], t[r])\n while l<=r and maxCost<0:\n maxCost += getCost(s[l], t[l])\n l += 1\n ans = max(ans, (r-l+1))\n r += 1\n return ans\n\n\n\n``` | 3 | 0 | ['Two Pointers', 'Sliding Window', 'Python3'] | 4 |
get-equal-substrings-within-budget | Python | Sliding Window | python-sliding-window-by-khosiyat-kpf5 | see the Successfully Accepted Submission\n\n# Code\n\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n start = 0\n | Khosiyat | NORMAL | 2024-05-28T05:36:19.938315+00:00 | 2024-05-28T05:36:19.938333+00:00 | 281 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/get-equal-substrings-within-budget/submissions/1270083696/?source=submission-ac)\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n start = 0\n currentCost = 0\n maxLength = 0\n \n for end in range(len(s)):\n currentCost += abs(ord(s[end]) - ord(t[end]))\n \n while currentCost > maxCost:\n currentCost -= abs(ord(s[start]) - ord(t[start]))\n start += 1\n \n maxLength = max(maxLength, end - start + 1)\n \n return maxLength\n\n```\n\n### Initialize Variables\n\n- `start` to keep track of the start of the current window.\n- `currentCost` to keep track of the cost of transforming the current window substring.\n- `maxLength` to store the maximum length of a valid substring.\n\n### Sliding Window\n\n1. Iterate through each character of the strings `s` and `t` using an index `end`.\n2. For each character, calculate the transformation cost `|s[end] - t[end]|` and add it to `currentCost`.\n3. If `currentCost` exceeds `maxCost`, shrink the window from the left by incrementing `start` until `currentCost` is less than or equal to `maxCost`.\n4. Update `maxLength` with the size of the current window (`end - start + 1`) if it is greater than the previously recorded `maxLength`.\n\n### Edge Cases\n\n- If `maxCost` is zero, the algorithm should still handle it correctly, as any cost greater than zero will automatically shrink the window to ensure the current cost is zero or less.\n\n\n | 3 | 0 | ['Python3'] | 0 |
get-equal-substrings-within-budget | Easiest, Understandable C++ Solution with intuition, approach, complexities and code | easiest-understandable-c-solution-with-i-tqti | Intuition\n Describe your first thoughts on how to solve this problem. \nAs question telling us to deal with costs as difference of ascii value of corresponding | itssme_jai | NORMAL | 2024-05-28T05:20:04.682611+00:00 | 2024-05-28T05:20:04.682631+00:00 | 362 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs question telling us to deal with costs as difference of ascii value of corresponding characters of s and t, so we will deal with that way only\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nnow first of all we will find cost of characters. lets say we have abcd and acde for that costs will be 0,1,1,1.\n\nas we can se a pattern that it is a problem of sliding window\nnow we will apply that method to find a subarray(substring) that best satisfy required condition of maxCost.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n=s.size();\n \n //abcd and acde\n // 0,1,1,1 \n int i=0, j=0, ans=0,sum=0;\n while(j<n){\n\n sum+=abs(int(s[j])-int (t[j]));\n\n if(sum<=maxCost){\n ans=max(j-i+1,ans);\n \n }\n\n else {\n while(sum>maxCost && i<=j){\n sum= sum-abs(int(s[i])-int (t[i]));\n i++;\n }\n }\n j++;\n\n }\n\n return ans; \n }\n};\n``` | 3 | 0 | ['Sliding Window', 'C++'] | 1 |
get-equal-substrings-within-budget | Easy C++ Solution | Binary Search | Prefix Sum | Beats 100 💯✅ | easy-c-solution-binary-search-prefix-sum-hfnj | Intuition and Approach\n\nThe goal is to find the longest substring of equal length in s and t such that the sum of the absolute differences of corresponding ch | shobhitkushwaha1406 | NORMAL | 2024-05-28T01:07:50.570116+00:00 | 2024-05-28T01:07:50.570134+00:00 | 286 | false | ## Intuition and Approach\n\nThe goal is to find the longest substring of equal length in `s` and `t` such that the sum of the absolute differences of corresponding characters in this substring is less than or equal to `cost`.\n\n### Steps:\n1. **Precompute the Prefix Sum Array**: Compute a prefix sum array where each element at index `i` represents the cumulative cost of transforming the substring `s[0:i-1]` to `t[0:i-1]`.\n2. **Binary Search**: Use binary search to determine the maximum length of the substring that satisfies the cost constraint.\n3. **Sliding Window Technique**: For each mid value in binary search, use a sliding window to check if there exists a valid substring of that length where the sum of the differences is less than or equal to `cost`.\n\n### Detailed Explanation:\n1. **Prefix Sum Calculation**: This helps in efficiently calculating the sum of differences for any substring.\n2. **Binary Search on Length**: Since we are looking for the maximum length, binary search helps in reducing the search space efficiently.\n3. **Sliding Window within Binary Search**: For each midpoint, use a sliding window to check if a valid substring of that length exists.\n\n### Complexity:\n- **Time Complexity**: `O(n log n)`\n - Calculating the prefix sum takes `O(n)`.\n - The binary search runs in `O(log n)` iterations, and in each iteration, the sliding window check takes `O(n)`.\n- **Space Complexity**: `O(n)` for the prefix sum array.\n\n```cpp\nclass Solution {\npublic:\n bool check(vector<int>& pref, int cost, int mid) {\n int l = 0, r = mid;\n while (r < pref.size()) {\n int sum = pref[r] - pref[l];\n if (sum <= cost) {\n return true;\n }\n l++;\n r++;\n }\n return false;\n }\n\n int equalSubstring(string s, string t, int cost) {\n int n = s.size();\n vector<int> pref(n + 1, 0);\n for (int i = 1; i <= n; i++) {\n pref[i] = pref[i - 1] + abs(s[i - 1] - t[i - 1]);\n }\n\n int l = 0, h = n;\n int ans = 0;\n while (l <= h) {\n int mid = l + (h - l) / 2;\n if (check(pref, cost, mid)) {\n ans = mid;\n l = mid + 1;\n } else {\n h = mid - 1;\n }\n }\n return ans;\n }\n};\n | 3 | 0 | ['Array', 'Binary Search', 'Prefix Sum', 'C++'] | 2 |
get-equal-substrings-within-budget | 💯✅🔥Easy Java Solution|| 12 ms ||≧◠‿◠≦✌ | easy-java-solution-12-ms-_-by-suyalneera-ut7s | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is about finding the maximum length of a substring in s that is equal to th | suyalneeraj09 | NORMAL | 2024-05-28T00:35:38.246548+00:00 | 2024-05-28T00:41:34.498793+00:00 | 315 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about finding the maximum length of a substring in s that is equal to the corresponding substring in t and the sum of the absolute differences between characters in the two substrings does not exceed maxCost.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is to maintain a prefix sum array prefixDiffSum where prefixDiffSum[i] stores the sum of absolute differences between characters in s and t from the beginning to the i-th character. Then, for each character in s, we perform a binary search to find the maximum length of a substring that ends at the current character and has a sum of absolute differences not exceeding maxCost.\n# Complexity\n- Time complexity:O(n log n), where n is the length of the strings s and t. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n), where n is the length of the strings s and t\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int[] prefixDiffSum = new int[s.length() + 1];\n int Max = 0;\n for (int i = 1; i < s.length() + 1; i++) {\n prefixDiffSum[i] = prefixDiffSum[i - 1] + Math.abs(s.charAt(i - 1) - t.charAt(i - 1)); // Stores sum of differences from beginning till i\n int start = 0;\n int end = i;\n while (start <= end) {\n int mid = start + (end - start) / 2;\n if (prefixDiffSum[i] - prefixDiffSum[mid] <= maxCost) {\n Max = Math.max(Max, i - mid);\n end = mid - 1;\n } else {\n start = mid + 1;\n }\n }\n }\n return Max;\n }\n}\n```\n\n | 3 | 0 | ['String', 'Sliding Window', 'String Matching', 'Java'] | 5 |
get-equal-substrings-within-budget | Sliding Window Solution || JAVA ;) | sliding-window-solution-java-by-kshitij_-g2p3 | \n\n# Code\n\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int maxLen =0;\n int n = s.length();\n i | Kshitij_Pandey | NORMAL | 2023-02-07T11:42:42.722172+00:00 | 2023-02-07T11:42:42.722224+00:00 | 74 | false | \n\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int maxLen =0;\n int n = s.length();\n int j=0;\n int currCost=0;\n\n for(int i=0; i<n; i++){\n //getting elemnts from the window\n char c1 = s.charAt(i);\n char c2 = t.charAt(i);\n currCost += getCost(c1,c2);\n while(maxCost < currCost){\n //removing elements from the window\n char c3 = s.charAt(j);\n char c4 = t.charAt(j);\n int costReduce = getCost(c3, c4);\n currCost -= costReduce;\n j++;\n }\n maxLen = Math.max(maxLen, i-j+1);\n }\n return maxLen;\n }\n private int getCost(char c1, char c2){\n int val1 = c1-\'a\';\n int val2 = c2-\'a\';\n int ans = val1-val2;\n return Math.abs(ans);\n }\n}\n``` | 3 | 0 | ['Java'] | 1 |
get-equal-substrings-within-budget | [C++] - Sliding Window standard problem | c-sliding-window-standard-problem-by-mor-1z6g | \nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int currCost=0;\n int len=s.length();\n int low=0; | morning_coder | NORMAL | 2021-04-23T03:47:04.375887+00:00 | 2021-04-23T03:47:04.375929+00:00 | 333 | false | ```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int currCost=0;\n int len=s.length();\n int low=0;\n int max_len=0;\n \n for(int i=0;i<len;i++){\n currCost+=abs(s[i]-t[i]);\n \n while(low<=i && currCost>maxCost){\n currCost-=abs(s[low]-t[low]);\n low++;\n } \n max_len=max(max_len,i-low+1);\n }\n return max_len;\n }\n \n};\n``` | 3 | 0 | ['C', 'Sliding Window', 'C++'] | 1 |
get-equal-substrings-within-budget | Java Sliding Window | java-sliding-window-by-wushangzhen-4x42 | \nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int l = 0;\n int r = 0;\n int max = 0;\n whil | wushangzhen | NORMAL | 2019-09-29T04:03:28.612604+00:00 | 2019-09-29T04:03:28.612656+00:00 | 279 | false | ```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int l = 0;\n int r = 0;\n int max = 0;\n while (r < s.length()) {\n maxCost -= Math.abs(s.charAt(r) - t.charAt(r));\n r++;\n if (maxCost >= 0) {\n max = Math.max(max, r - l);\n }\n while (maxCost < 0) {\n maxCost += Math.abs(s.charAt(l) - t.charAt(l));\n l++;\n }\n }\n return max;\n }\n}\n``` | 3 | 1 | [] | 2 |
get-equal-substrings-within-budget | Simple Approach : ) | simple-approach-by-adi_blessed-6upq | IntuitionThe problem requires us to find the maximum length of a substring that can be transformed from string 's' to string 't 'with a given maximum cost. The | Adi_blessed | NORMAL | 2025-01-16T07:08:28.458922+00:00 | 2025-01-16T07:08:28.458922+00:00 | 21 | false | # Intuition
The problem requires us to find the maximum length of a substring that can be transformed from string 's' to string 't 'with a given maximum cost. The cost is defined as the sum of the absolute differences between the ASCII values of the characters in the two strings at the same positions.
# Approach
Sliding Window Technique: We will use a sliding window approach to keep track of the current substring we are considering.
Cost Calculation: As we iterate through the characters of the strings, we will calculate the cost of transforming the substring from s to t.
Adjusting the Window: If the cost exceeds maxCost, we will move the start of the window forward to reduce the cost until it is within the allowed limit.
Max Length Tracking: Throughout the process, we will keep track of the maximum length of the valid substring found.
# Complexity
- Time complexity:
O(n)), where (n) is the length of the strings. We traverse the strings once.
- Space complexity:
(O(1)), as we are using a constant amount of extra space.
# Code
```python3 []
class Solution:
def equalSubstring(self, s: str, t: str, maxCost: int) -> int:
n = 0 # Start of the sliding window
newCost = 0 # Current cost of the substring
maxLength = 0 # Maximum length of valid substring found
# Iterate through each character in the strings
for i in range(len(s)):
# Calculate the cost of transforming s[i] to t[i]
newCost += abs(ord(s[i]) - ord(t[i]))
# If the cost exceeds maxCost, move the start of the window
while newCost > maxCost:
newCost -= abs(ord(s[n]) - ord(t[n])) # Remove the cost of the character at the start of the window
n += 1 # Move the start of the window forward
# Update the maximum length of the valid substring
maxLength = max(maxLength, i - n + 1)
return maxLength # Return the maximum length found
``` | 2 | 0 | ['Python3'] | 0 |
get-equal-substrings-within-budget | Very Easy to Understand Python Solution (Sliding Window Approach) | very-easy-to-understand-python-solution-us4q6 | Approach
💡 Approach: Sliding Window
We use the sliding window technique to efficiently find the longest substring that can be modified within the given cost.
St | Vinit_K_P | NORMAL | 2025-01-09T04:31:50.229458+00:00 | 2025-01-09T04:31:50.229458+00:00 | 31 | false | # Approach
- 💡 **Approach: Sliding Window**
We use the sliding window technique to efficiently find the longest substring that can be modified within the given cost.
**Steps:**
- Calculate the Cost Array:
Compute the difference in ASCII values for corresponding characters of s and t to form the cost array.
**Sliding Window Logic:**
1) Maintain two pointers: left (start of the window) and right (end of the window).
2) Expand the window by incrementing right and adding cost[right] to the current_cost.
3) If current_cost exceeds maxCost, shrink the window by incrementing left and subtracting cost[left] from current_cost.
**Track Maximum Length:**
Keep updating the maximum length of the valid substring (right - left + 1) during the process.
# Complexity
# - Time complexity:
**Cost Calculation:** O(n), where n is the length of the string.
**Sliding Window Traversal:** O(n), as both left and right pointers traverse the string at most once.
**Total:** O(n).
# - Space complexity:
**Cost Array:** O(n) to store the absolute differences.
**Total:** O(n).
# Code
```python3 []
class Solution:
def equalSubstring(self, s: str, t: str, maxCost: int) -> int:
cost= [abs(ord(s[i]) - ord(t[i])) for i in range(len(s))]
i = 0
curr_cst = 0
max_len = 0
for j in range(len(s)):
curr_cst += cost[j]
if curr_cst > maxCost:
curr_cst -= cost[i]
i+=1
max_len = max(max_len, j-i+1)
return max_len
``` | 2 | 0 | ['Python3'] | 0 |
get-equal-substrings-within-budget | 💯🔥Constant space O(1)🎉||✅ DRY RUN || ♻️ Step wise explanation || 2 Approach💥|| 4 Lang Solution | constant-space-o1-dry-run-step-wise-expl-cd21 | Screenshot \uD83C\uDF89 \n\n\n\n\n# Intuition \uD83E\uDD14\n Describe your first thoughts on how to solve this problem. \n Given--> \n \n 1 Two string | Prakhar-002 | NORMAL | 2024-05-29T01:50:47.409274+00:00 | 2024-05-29T01:50:47.409295+00:00 | 34 | false | # Screenshot \uD83C\uDF89 \n\n\n\n\n# Intuition \uD83E\uDD14\n<!-- Describe your first thoughts on how to solve this problem. -->\n `Given`--> \n \n 1 Two string name (s) And (t) with same length\n\n 2 And a maxCost which tells us cost\n\n---\n\n `Que description` -->\n\n we have to maximize the length of subStr and return the len of str\n\n1. `subString` must be `same for both` the given subString\n\n2. we can `change the chars of s` to **match** the `of t\'s subString` \n\n3. And we need to `maximize` this subString length\n\n4. Now catch is the `cost of changing a cha`r of a s is -->\n\n5. `Absolute diff of ascii value of char of t - char of s at Ith pos`\n \n6. ``` java\n Math.abs(t.charAt(i) - s.charAt(i)) --> BY JAVA\n ```\n\n7. And we `can\'t afford cost above given maxCost`\n---\n `Ex 1`\n\n s = "abcd" & t = "bcdf" maxCost = 3\n\n Ans = 3 because "abc" can be change to "bcd" \n\n \'b\' - \'a\' == 1\n \'c\' - \'b\' == 1 => Total cost == 3 equal to maxCost\n \'d\' - \'c\' == 1\n\n`I guess all of you got the idea`\n\n\n# Approach \uD83D\uDE0D\n<!-- Describe your approach to solving the problem. -->\n\n Approach is simple and we\'ll use no space nothing at all\n\n`First Approach` \n\n## 1. Brute force Approach \uD83D\uDE0F\n\n 1. Make a array of all the abs diff of char at ith for s and t \n\n 2. And then check for the subArrays if they fit in our solution or not \n\n \uD83E\uDD70 I can weste your time to continue this appproch \n\n But i don\'t wanna weste your time so \n\n let\'s jump to our main sol\n\n `Second Approach` \n\n\n## 2. No Extra space Approach \uD83D\uDE80\uD83D\uDE80\n\n 1. Take two pointer Left assign with 0 and right for loop\n\n 2. We\'ll go in whole string // In any string length\n\n 3. and store the cost of each time one char change\n\n 4. and add to our curCost from right pointer \n\n 5. If at some pos our curCost > maxCost \n\n 6. inc our left pointer and dec the values from left in curCost\n\n 7. store the max of subStringlen from (right - left + 1) and (Itself)\n\n# Under Stand with code \uD83E\uDEF0\n\n LET\'s understand with code first then `we will dry run this`\n\n`Step 1` **make variables**\n\n``` PYTHON []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n curCost = 0\n subStringLen = 0\n\n l = 0 # left \n```\n```JAVA []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int curCost = 0;\n int subStringLen = 0;\n\n int left = 0;\n\n```\n```JAVASCRIPT []\nvar equalSubstring = function (s, t, maxCost) {\n let curCost = 0\n let subStringLen = 0\n\n let left = 0\n```\n```C []\nint equalSubstring(char* s, char* t, int maxCost) {\n int curCost = 0;\n int subStringLen = 0;\n\n int left = 0;\n\n```\n`Step 2` **Apply loop and extract our cost of each index**\n\n- Becaue we `extract the diff at same time` \n- that\'s `why we don\'t need arr`\n\n``` PYTHON []\n \n for right in range(len(s)): \n curCost += abs(ord(s[right]) - ord(t[right]))\n\n```\n```JAVA []\n for (int right = 0; right < s.length(); right++) {\n curCost += Math.abs(s.charAt(right) - t.charAt(right));\n\n }\n\n```\n```JAVASCRIPT []\n for (let right = 0; right < s.length; right++) {\n curCost += Math.abs(\n s.charAt(right).charCodeAt(0) - \n t.charAt(right).charCodeAt(0)\n );\n```\n```C []\n for (int right = 0; right < strlen(s); right++) {\n curCost += abs(s[right] - t[right]);\n\n }\n\n```\n\n`Step 3` **subtract starting value if curCost > maxCost** \n\n- We\'ll apply `while loop for this` and `inc our left pointer`\n\n``` PYTHON []\n\n while curCost > maxCost:\n curCost -= abs(ord(s[left]) - ord(t[l]))\n\n lelf += 1\n```\n```JAVA []\n\n while (curCost > maxCost) {\n curCost -= Math.abs(s.charAt(left) - t.charAt(left));\n left++;\n }\n\n```\n```JAVASCRIPT []\n\n while (curCost > maxCost) {\n curCost -= Math.abs(s.charAt(left).charCodeAt(0) - t.charAt(left).charCodeAt(0));\n\n left++;\n }\n```\n```C []\n\n while (curCost > maxCost) {\n curCost -= abs(s[left] - t[left]);\n left++;\n }\n```\n\n`Step 4` Now `Store the max len` and return it\n\n We will count our len in the loop and return to main fun\n\n``` PYTHON []\n \n subStringLen = max(subStringLen, r - l + 1)\n\n return subStringLen\n```\n```JAVA []\n subStringLen = Math.max(subStringLen, right - left + 1);\n }\n\n return subStringLen;\n }\n}\n\n```\n```JAVASCRIPT []\n subStringLen = Math.max(subStringLen, right - left + 1);\n }\n\n return subStringLen;\n};\n```\n```C []\n \n subStringLen = fmax(subStringLen, right - left + 1);\n }\n\n return subStringLen;\n}\n\n``` \n\n# DRY RUN \u2622\uFE0F\n\n `Taking same example` \n\n---\n\n\n `Ex`\n\n s = "abcd" & t = "bcdf" maxCost = 3\n\n subStrinLen = 0\n\n\n\n```\nIn the loop \ns = "abcd" \n ^ l = 0 \n curCost = 1 subStrinLen = 1\n | r = 0 \n```\n\n```\nIn the loop\ns = "abcd" \n ^ l = 0 \n curCost = 2 subStrinLen = 2\n ^ \n | r = 1 \n```\n```\nIn for the loop\ns = "abcd" \n ^ l = 0 \n curCost = 3 subStrinLen = 3\n ^ \n | r = 2 \n```\n\n```\nIn for the loop\ns = "abcd" \n ^ l = 0 \n curCost = 5 subStrinLen = 3\n ^ \n | r = 3 \n\n In while loop \n s = "abcd" \n ^ l = 1 \n curCost = 5 - 1 = 4 subStrinLen = 3\n ^ \n | r = 3 \n ```\n \n In while loop \n s = "abcd" \n ^ l = 2 \n curCost = 4 - 1 = 3 subStrinLen = 3\n ^ \n | r = 3 \n ```\n \n```\n Loop Ended Max length == subStringLen \n\n---\n\n# Complexity \u2603\uFE0F\n- Time complexity: $$O(n)$$ \u267B\uFE0F\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$ \uD83D\uDD25\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n# Code \uD83D\uDC96\n``` PYTHON []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n curCost = 0\n subStringLen = 0\n\n l = 0 # left \n\n for r in range(len(s)): # r == right pointer\n curCost += abs(ord(s[r]) - ord(t[r]))\n\n while curCost > maxCost:\n curCost -= abs(ord(s[l]) - ord(t[l]))\n\n l += 1\n\n subStringLen = max(subStringLen, r - l + 1)\n\n return subStringLen\n```\n```JAVA []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int curCost = 0;\n int subStringLen = 0;\n\n int left = 0;\n\n for (int right = 0; right < s.length(); right++) {\n curCost += Math.abs(s.charAt(right) - t.charAt(right));\n\n while (curCost > maxCost) {\n curCost -= Math.abs(s.charAt(left) - t.charAt(left));\n left++;\n }\n\n subStringLen = Math.max(subStringLen, right - left + 1);\n }\n\n return subStringLen;\n }\n}\n```\n```JAVASCRIPT []\nvar equalSubstring = function (s, t, maxCost) {\n let curCost = 0\n let subStringLen = 0\n\n let left = 0\n\n for (let right = 0; right < s.length; right++) {\n curCost += Math.abs(s.charAt(right).charCodeAt(0) - t.charAt(right).charCodeAt(0));\n\n while (curCost > maxCost) {\n curCost -= Math.abs(s.charAt(left).charCodeAt(0) - t.charAt(left).charCodeAt(0));\n\n left++;\n }\n\n subStringLen = Math.max(subStringLen, right - left + 1);\n }\n\n return subStringLen;\n};\n```\n```C []\nint equalSubstring(char* s, char* t, int maxCost) {\n int curCost = 0;\n int subStringLen = 0;\n\n int left = 0;\n\n for (int right = 0; right < strlen(s); right++) {\n curCost += abs(s[right] - t[right]);\n\n while (curCost > maxCost) {\n curCost -= abs(s[left] - t[left]);\n left++;\n }\n\n subStringLen = fmax(subStringLen, right - left + 1);\n }\n\n return subStringLen;\n}\n```\n\n\n | 2 | 0 | ['String', 'Binary Search', 'C', 'Sliding Window', 'Prefix Sum', 'Java', 'Python3', 'JavaScript'] | 1 |
get-equal-substrings-within-budget | simple and easy Sliding Window solution 😍❤️🔥 | simple-and-easy-sliding-window-solution-qflkm | if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) \n {\n | shishirRsiam | NORMAL | 2024-05-28T19:17:35.675591+00:00 | 2024-05-28T19:17:35.675607+00:00 | 51 | false | # if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) \n {\n int i = 0, j = 0;\n int ans = 0, cost = 0, n = s.size();\n while(j<n)\n {\n cost += abs(s[j] - t[j++]);\n while(cost > maxCost) cost -= abs(s[i] - t[i++]);\n ans = max(ans, j-i);\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['String', 'Sliding Window', 'C++'] | 4 |
get-equal-substrings-within-budget | Easy approach||Best Solution | easy-approachbest-solution-by-singhpayal-1pod | Intuition\nSimple intuition was to form a vector to store individual cost of each characters of string and then simply apply sliding window to find largest suba | payalsingh2212 | NORMAL | 2024-05-28T17:38:47.027277+00:00 | 2024-05-28T17:38:47.027311+00:00 | 30 | false | # Intuition\nSimple intuition was to form a vector to store individual cost of each characters of string and then simply apply sliding window to find largest subarray\n\n# Approach\n1) vector to store abs(s[i]-t[i]);\n2) sliding window (;D)\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity:O(n)\n\n# Code\n```\nclass Solution {\npublic:\n\n/*Don\'t get scared from the below function .Incase u r not getting\nwatch youtube tutorial on sliding window and with simple logic u \nwill be able to solve on your own and please upvote :_; */\nint largestSubarraySumLessThan(vector<int>& nums, int target) {\n int n = nums.size();\n int start = 0, end = 0, sum = 0;\n int maxLength = 0;\n\n while (end < n) {\n sum += nums[end];\n \n while (sum > target && start <= end) {\n sum -= nums[start];\n start++;\n }\n\n maxLength = max(maxLength, end - start + 1);\n end++;\n }\n\n return maxLength;\n}\n int equalSubstring(string s, string t, int maxCost) {\n int N=s.size();\n vector<int>vec(N);\n for(int i=0;i<s.size();i++){\n vec[i]=abs(s[i]-t[i]);\n }\n int ans=largestSubarraySumLessThan(vec, maxCost) ;\n\n return ans; // and please upvote\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
get-equal-substrings-within-budget | Easy C++ Sliding Window Solution⭐💯 | easy-c-sliding-window-solution-by-_risha-tywe | Longest Substring with a Maximum Cost\n\n## Intuition\nTo find the longest substring where the sum of absolute differences between corresponding characters of t | _Rishabh_96 | NORMAL | 2024-05-28T17:24:52.607411+00:00 | 2024-05-28T17:24:52.607440+00:00 | 14 | false | # Longest Substring with a Maximum Cost\n\n## Intuition\nTo find the longest substring where the sum of absolute differences between corresponding characters of two strings `s` and `t` does not exceed a given `maxCost`, we can use a sliding window approach. This technique allows us to efficiently manage the range of characters we are considering by expanding and contracting the window based on the cost constraints.\n\n## Approach\n1. Initialize two pointers `start` and `end` to mark the bounds of the sliding window. Also, initialize a variable `sum` to keep track of the current cost.\n2. Expand the window by moving the `end` pointer from left to right.\n3. For each character, calculate the absolute difference between the characters in `s` and `t` at the `end` pointer and add it to `sum`.\n4. If `sum` exceeds `maxCost`, contract the window from the left by moving the `start` pointer to the right and subtracting the corresponding difference from `sum`.\n5. The length of the current valid window is `end - start`. Keep track of the maximum length encountered.\n6. Continue this process until the `end` pointer reaches the end of the string `s`.\n\n## Complexity\n- **Time Complexity:** \\(O(n)\\) where \\(n\\) is the length of the string `s`. This is because each character is processed at most twice (once when expanding the window and once when contracting it).\n- **Space Complexity:** \\(O(1)\\) because we only use a fixed amount of extra space.\n\n## Code\n```cpp\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int start = 0, end = 0, sum = 0;\n\n while (end < s.length()) {\n sum += abs(s[end] - t[end]);\n end++;\n\n if (sum > maxCost) {\n sum -= abs(s[start] - t[start]);\n start++;\n }\n }\n\n return end - start;\n }\n};\n | 2 | 0 | ['String', 'Sliding Window', 'C++'] | 0 |
get-equal-substrings-within-budget | EXPLAINED WELLL | explained-welll-by-nurliaidin-fqo9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. Compute Differences: | Nurliaidin | NORMAL | 2024-05-28T15:40:33.265297+00:00 | 2024-05-28T15:40:33.265320+00:00 | 73 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Compute Differences:** Iterate over each character of strings `s` and `t` simultaneously. For each index `i`, calculate the difference between the character codes of `s[i]` and `t[i]`, storing these differences in an array arr.\n2. **Initialize Sliding Window**: Use two pointers,`left` and `right`, to create a sliding window over the array`arr`. Initialize a `count` to keep track of the count of subsets that meet your criteria (define what criteria you are using, e.g., subsets with a sum greater than a certain value). \n3. **Sliding Window Logic:** Move the `right` pointer to expand the window and include more elements. Update the `count` based on whether the current window meets your criteria. If the window becomes invalid (e.g., the sum exceeds a threshold), move the `left` pointer to reduce the window size until it becomes valid again.\n4. **Track Maximum Count:** Throughout the sliding window process, keep track of the maximum value of the `count`. This maximum value represents the result you are seeking.\n5. **Return Result:** After the sliding window has processed the entire array, return the maximum value recorded.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n``` javascript []\nvar equalSubstring = function(s, t, maxCost) {\n let n = s.length;\n let arr = new Array(n);\n\n let left=0, right=0;\n let count = 0, calc = 0;\n let res = 0;\n while(right < n) {\n arr[right] = Math.abs(t[right].charCodeAt(0) - s[right].charCodeAt(0));\n count++;\n calc += arr[right];\n while(maxCost < calc) {\n calc -= arr[left];\n count--;\n left++;\n }\n res = Math.max(res, count);\n right++;\n }\n return res;\n};\n```\n``` cpp []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n = s.size();\n int arr[n];\n int left=0, right=0;\n int count = 0, calc = 0;\n int res = 0;\n while(right < n) {\n arr[right] = abs(t[right] - s[right]);\n count++;\n calc += arr[right];\n while(maxCost < calc) {\n calc -= arr[left];\n count--;\n left++;\n }\n res = max(res, count);\n right++;\n }\n return res;\n }\n};\n``` | 2 | 0 | ['String', 'Sliding Window', 'C++', 'JavaScript'] | 2 |
get-equal-substrings-within-budget | Easy to Understand | Simple | Clean | Crisp Code | Beats 90% | C++ | Java | Python | Kotlin | easy-to-understand-simple-clean-crisp-co-zx6j | Problem Statement\n Describe your first thoughts on how to solve this problem. \nGiven 2 strings. Find the longest possible Substring in both of them which can | Don007 | NORMAL | 2024-05-28T15:34:41.485922+00:00 | 2024-05-28T15:34:41.485942+00:00 | 157 | false | # Problem Statement\n<!-- Describe your first thoughts on how to solve this problem. -->\nGiven 2 strings. Find the longest possible Substring in both of them which can be same after applying some operations on String **s** less than **maxCost**.\n\n# Intuition and Approach\n<!-- Describe your approach to solving the problem. -->\nHere, We need to find the **Longest Possible Substring** which is present in both the Strings **s** and **t**. \n\nSo, If we think greedily then we will try to perform all operations which are having the least cost over the complete string in order to **Maximize** the Number of Operations Performed on the String **s**. But, it doesn\'t ensures that the **Resulting string** will be having the **Longest Possible Substring** present in it.\n\nDifference is states as the Difference of ASCII values of Characters at Specific Index\n\nGiven Below Example for Better Understanding\ns = "abcd"\nt = "bdfc"\nmaxCost = 3\n\nTotal Difference At Corresponding Indices are\n```\nfor i in range(0,len(s)):\n abs( s[i] - t[i] )\n```\nThereFore, \n$$[abs(s[0] - t[0]), abs(s[1] - t[1]), abs(s[2] - t[2]), abs(s[3] - t[3]) ] = [1, 2, 3, 1] $$\n\n##### If Greedily is Considered,\n\nThen, we will First make 1st index equal for both strings with cost 1.\nRemaining Cost = 3 - 1 = 2\nAfter Operation Strings\ns = "bbcd"\nt = "bdfc"\n\nNow, we will make operations at last index equal for both strings with cost 1.\nRemaining Cost = 2 - 1 = 1\nAfter Operation Strings\ns = "bbcc"\nt = "bdfc"\n\nNow, We can not make any further operations on String **s** with Cost = 1.\n\nHere, Total Longest Possible Substring of Equal Length in Strings **s** and **t** are 1.\n\ns = "abcd"\nt = "bdfc"\n\nAfter Applying 2 Continuous Operations from index 1\ns = "bdcd"\nt = "bdfc"\nRemaining Cost = 3 - 1(1st index) - 2(2nd index) = 0\nLongest Possible Substring = 2\n\nIf we Start Performing Operations from index 2 by Skipping index 1\ns = "adcd"\ng = "bdfc"\nRemaining Cost = 3 - 2(2nd index) = 1\nNow further No More Operations can be performed\nLongest Possible Substring = 1\n\nSimilarly, for index 3 and index 4\ns = "abfd"\nt = "bdfc"\nRemaining Cost = 3 - 3(3rd index) = 0\nLongest Possible Substring = 1\n\ns = "abcc"\nt = "bdfc"\nRemaining Cost = 3 - 1(4th index) = 2\nLongest Possible Substring = 1\n\nTherefore, If we apply Operations at indexes 1 and 2, which is equal to the total maxCost = 3, We can obtain a string of length 2, which is **greater than** the Total Longest Possible Substring Obtained from the Greedy Approach.\n\nFrom this we Understand that \n***All Operations that are to be performed on the string **s** should be consecutive.***\n\nIn order to Perform Operation on string **s** consecutively we can use 2 pointers i and j in which we will iterate index j from index i until we get a sum which is greater than to maxCost from index i. We will iterate index i from 0 to n\n***Note - Index i is taken into consideration here***\n```\nwhile ( j < len(s) and sum >= maxCost ):\n j += 1\n```\n\nAt the arrival of such an index when sum becomes greater than maxCost we can store the difference of indices into result.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n = s.size();\n vector<int> pref(n);\n for ( int i = 0 ; i < n ; i++ ) {\n pref[i] = ( i - 1 >= 0 ? pref[i-1] : 0 ) + abs(s[i]-t[i]);\n // std::cout << pref[i] << " ";\n }\n int ans = 0;\n for ( int i = 0 ; i < n ; i++ ) {\n int sum = ( i - 1 >= 0 ? pref[i-1] : 0 ) + maxCost;\n int u = upper_bound(pref.begin(),pref.end(),sum) - pref.begin();\n ans = std::max({ ans, u-i });\n }\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int[] pref = new int[s.length()];\n for ( int i = 0 ; i < s.length() ; i++ ) {\n pref[i] = Math.abs( ((int)s.charAt(i)) - ((int)t.charAt(i)) );\n if ( i > 0 ) {\n pref[i] += pref[i-1];\n }\n }\n int ans = 0, j = 0;\n for ( int i = 0 ; i < s.length() ; i++ ) {\n int curr = maxCost;\n if ( i - 1 >= 0 ) {\n curr += pref[i-1];\n }\n while ( j < s.length() && curr >= pref[j] ) {\n j++;\n }\n ans = Math.max( ans, j - i );\n }\n return ans;\n }\n}\n```\n```Python []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n pref = []\n for i in range(0,len(s)):\n pref.append(abs( ord(s[i]) - ord(t[i]) ))\n if ( len(pref) > 1 ):\n pref[-1] += pref[-2]\n ans, j = 0, 0\n for i in range(0,len(s)):\n curr = maxCost\n if ( i - 1 >= 0 ):\n curr += pref[i-1]\n while ( j < len(s) and curr >= pref[j] ):\n j += 1\n ans = max( ans, j - i )\n return ans\n```\n```Kotlin []\nimport kotlin.math.abs\nclass Solution {\n fun equalSubstring(s: String,t: String,maxCost: Int): Int {\n var ans: Int = 0;\n var pref = IntArray(s.length);\n for (item in s.indices) {\n pref[item] = abs(s[item] - t[item])\n if ( item > 0 ) {\n pref[item] += pref[item-1];\n }\n }\n var j:Int = 0\n for (i in 0..<s.length) {\n var sum:Int = maxCost;\n if ( i - 1 >= 0 ) {\n sum += pref[i-1]\n }\n while ( j < s.length && sum >= pref[j] ) {\n j += 1\n }\n ans = max( ans, j - i );\n }\n return ans\n }\n}\n```\n# **Please Upvote.** \n# **If You Liked, Understood the Solution.**\n# Thanks For Reading | 2 | 0 | ['Array', 'Two Pointers', 'String', 'Binary Search', 'Sliding Window', 'Prefix Sum', 'C++', 'Java', 'Python3', 'Kotlin'] | 0 |
get-equal-substrings-within-budget | Easy Sliding Window | easy-sliding-window-by-anshubaloria123-xf0w | Intuition\n Describe your first thoughts on how to solve this problem. \nsliding window\n\n# Approach\n Describe your approach to solving the problem. keep addi | anshubaloria123 | NORMAL | 2024-05-28T10:35:19.456398+00:00 | 2024-05-28T10:35:19.456417+00:00 | 24 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nsliding window\n\n# Approach\n<!-- Describe your approach to solving the problem. -->keep adding the current difference value until it is less then max value once it cross , then increse the previous pointer till it is less then max value and in each iteration take out the maximum result\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n\nPLEASE UPVOTE MY SOLUTION\n\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int n = s.length();\n int start = 0;\n int currentCost = 0;\n int maxLength = 0;\n\n for (int end = 0; end < n; ++end) {\n currentCost += Math.abs(s.charAt(end) - t.charAt(end));\n\n while (currentCost > maxCost) {\n currentCost -= Math.abs(s.charAt(start) - t.charAt(start));\n ++start;\n }\n\n maxLength = Math.max(maxLength, end - start + 1);\n }\n\n return maxLength;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
get-equal-substrings-within-budget | Simple Two Pointer Approach!! | simple-two-pointer-approach-by-tsahu9461-kbrn | Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Code\n\nclass Solution {\npublic:\n int equ | tsahu9461 | NORMAL | 2024-05-28T07:46:35.789833+00:00 | 2024-05-28T07:46:35.789866+00:00 | 5 | false | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int left = 0; //to keep track of the first element in every substring\n int right = 0; // to keep track of current element\n int maxLen = 0;\n int n = s.size();\n int cost = 0;\n while(right < n){\n cost += abs((s[right] - \'0\') - (t[right] - \'0\'));\n while(cost > maxCost){ //if cost exceeds shrink the window\n cost -= abs((s[left] - \'0\') - (t[left] - \'0\'));\n left++;\n }\n maxLen = max(maxLen, right - left + 1); //update maxLen\n right++;\n }\n return maxLen;\n }\n};\n``` | 2 | 0 | ['Array', 'Two Pointers', 'Sliding Window', 'C++'] | 1 |
get-equal-substrings-within-budget | EASY WINDOW MAKINS SOLUTION || IN DEPTH APPROACH . | easy-window-makins-solution-in-depth-app-4e36 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n- You have two strings s and t of the same length.\n- There\'s a cost associated with | Abhishekkant135 | NORMAL | 2024-05-28T07:15:30.914598+00:00 | 2024-05-28T07:15:30.914614+00:00 | 47 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n- You have two strings `s` and `t` of the same length.\n- There\'s a cost associated with changing a character in `s` to the corresponding character in `t`. The cost is the absolute difference between their ASCII values.\n- The code finds the maximum length of a substring in `s` that can be transformed to the same substring in `t` with a total cost less than or equal to `maxCost`.\n\n**Nutshell:**\n\n- The code employs a sliding window approach with two pointers `i` and `j`. It keeps track of the current cost within the window and expands the window as long as the cost is within the limit. It shrinks the window from the left side if the cost exceeds the limit.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n\n\n\n**Steps:**\n\n1. **Initialization:**\n - `int i = 0, j = 0, ans = 0;`: Initializes `i` and `j` as pointers to the beginning of both strings (`s` and `t`) and `ans` to store the maximum length found so far.\n\n2. **Sliding Window Loop:**\n - `while (j < s.length()) {`: Continues the loop as long as the right pointer `j` is within the bounds of `s` (not reaching the end).\n - **Expanding the Window:**\n - `while (j < s.length() && maxCost >= 0) {`: This loop expands the window by incrementing `j` as long as the cost stays within the limit (`maxCost` is non-negative).\n - `maxCost = maxCost - (Math.abs(s.charAt(j) - t.charAt(j)));`: Calculates the cost for including the character at index `j` in the window. It subtracts the absolute difference between the characters at `j` in `s` and `t` from the remaining `maxCost`.\n - **Update Maximum Length:**\n - `if (maxCost >= 0) {`: If the cost remains non-negative after including the character at `j`, it signifies a valid substring within the window.\n - `ans = Math.max(ans, j - i + 1);`: Updates `ans` with the maximum length encountered so far. Here, `j - i + 1` represents the current window length.\n - Increments `j` to move the right pointer and explore the next character.\n - **Shrinking the Window (if Cost Exceeds Limit):**\n - `while (maxCost < 0) {`: This loop shrinks the window from the left side (incrementing `i`) as long as the cost exceeds the limit (`maxCost` is negative).\n - `maxCost = maxCost + (Math.abs(s.charAt(i) - t.charAt(i)));`: Calculates the cost for removing the character at index `i` from the window. It adds the absolute difference between the characters at `i` in `s` and `t` to the current `maxCost`.\n - Increments `i` to move the left pointer and adjust the window.\n\n3. **Return Result:**\n - After the loop exits, `ans` holds the maximum length of a valid substring found within the cost limit.\n - `return ans;`: Returns the calculated maximum length.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int i=0;\n int j=0;\n int ans=0;\n while(j<s.length()){\n while(j<s.length() && maxCost>=0){\n maxCost=maxCost-(Math.abs(s.charAt(j)-t.charAt(j)));\n if(maxCost>=0){\n ans=Math.max(ans,j-i+1);\n }\n j++;\n }\n \n while(maxCost<0){\n maxCost=maxCost+(Math.abs(s.charAt(i)-t.charAt(i)));\n i++;\n }\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Sliding Window', 'Java'] | 0 |
get-equal-substrings-within-budget | Simple Solution using Sliding Window - Beats 100% T.C O(N) | simple-solution-using-sliding-window-bea-yuer | Intuition\n Describe your first thoughts on how to solve this problem. \nWe want to find the longest substring in s such that changing it to match t costs no mo | nobody_me | NORMAL | 2024-05-28T06:09:18.733758+00:00 | 2024-05-28T06:09:18.733774+00:00 | 61 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want to find the longest substring in s such that changing it to match t costs no more than maxCost. The cost of changing a character `s[i]` to `t[i]` is the absolute difference `abs(s[i] - t[i])`\n\n# Sliding Window Approach\n<!-- Describe your approach to solving the problem. -->\n1. Imagine you have a window that starts at the beginning of the string s.\n1. You keep expanding this window to include more characters until the total cost of changes exceeds maxCost.\n1. If the cost becomes too high, you start moving the start of the window forward to reduce the cost.\n1. Throughout this process, you keep track of the maximum length of any valid window (substring) found.\n\n- `j` to mark the start of the current window.\n- `count` to count the number of characters in the current window.\n- `sum` to keep track of the total cost of converting the current window.\n- `maxcount` to store the maximum length of a valid window found.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int j = 0, count = 0,sum = 0, maxcount = 0;\n for(int i=0;i<s.size();i++)\n {\n sum+=abs(s[i]-t[i]);\n count++;\n while(sum>maxCost && j<s.size())\n {\n sum-=abs(s[j]-t[j]);\n count--;\n j++;\n }\n maxcount = max(maxcount,count);\n }\n return maxcount;\n }\n};\n``` | 2 | 0 | ['Two Pointers', 'String', 'Sliding Window', 'Prefix Sum', 'C++'] | 1 |
get-equal-substrings-within-budget | Use Sliding Window To Get Maximum Window Size | Java | C++ | use-sliding-window-to-get-maximum-window-pwtk | Intuition, approach, and complexity discussed in video solution in detail\nhttps://youtu.be/gJQsXRKX7bI\n# Code\nC++\n\nclass Solution {\npublic:\n int equal | Lazy_Potato_ | NORMAL | 2024-05-28T05:28:48.190585+00:00 | 2024-05-28T05:28:48.190601+00:00 | 150 | false | # Intuition, approach, and complexity discussed in video solution in detail\nhttps://youtu.be/gJQsXRKX7bI\n# Code\nC++\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int leftPtr = 0, size = s.size(), rightPtr = 0;\n int currCost = 0, maxLen = 0;\n while(rightPtr < size){\n currCost += abs(s[rightPtr] - t[rightPtr]);\n if(currCost > maxCost){\n while(leftPtr <= rightPtr && currCost > maxCost){\n currCost -= abs(s[leftPtr] - t[leftPtr]);\n leftPtr++;\n }\n }\n if(leftPtr <= rightPtr){\n maxLen = max(maxLen, rightPtr - leftPtr + 1);\n }\n rightPtr++;\n } \n return maxLen;\n }\n};\n```\nJava\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int leftPtr = 0, size = s.length(), rightPtr = 0;\n int currCost = 0, maxLen = 0;\n \n while (rightPtr < size) {\n currCost += Math.abs(s.charAt(rightPtr) - t.charAt(rightPtr));\n \n if (currCost > maxCost) {\n while (leftPtr <= rightPtr && currCost > maxCost) {\n currCost -= Math.abs(s.charAt(leftPtr) - t.charAt(leftPtr));\n leftPtr++;\n }\n }\n \n if (leftPtr <= rightPtr) {\n maxLen = Math.max(maxLen, rightPtr - leftPtr + 1);\n }\n \n rightPtr++;\n }\n \n return maxLen;\n }\n}\n\n``` | 2 | 0 | ['String', 'Sliding Window', 'C++', 'Java'] | 1 |
get-equal-substrings-within-budget | C# Solution for Get Equal Substrings Within Budget Problem | c-solution-for-get-equal-substrings-with-sqpd | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind using a prefix sum array and binary search is to efficiently calcu | Aman_Raj_Sinha | NORMAL | 2024-05-28T04:27:18.565294+00:00 | 2024-05-28T04:27:18.565311+00:00 | 98 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind using a prefix sum array and binary search is to efficiently calculate the cost of transforming any substring of s to t and then use binary search to find the maximum length of a valid substring within the given cost constraint. By precomputing the prefix sums, we can quickly determine the cost of any substring in constant time, and binary search helps in efficiently finding the maximum length.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tCalculate Transformation Costs:\n\t\u2022\tCompute the absolute differences between corresponding characters in s and t and store these costs in an array called cost.\n2.\tPrefix Sum Array:\n\t\u2022\tConstruct a prefix sum array, prefixSum, where each element at index i represents the total cost to transform the substring from the start of the string to the i-th character.\n3.\tBinary Search for Maximum Length:\n\t\u2022\tFor each starting index i of a substring in s, use binary search to find the farthest ending index j such that the total transformation cost from i to j is within maxCost.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tPreprocessing Costs and Prefix Sum: O(n)\n\u2022\tCalculating the cost array and the prefixSum array each takes O(n) time.\n\u2022\tFinding Maximum Length: O(n \\log n)\n\u2022\tFor each starting position, we perform a binary search to find the maximum valid ending position, which takes O(\\log n). Since we do this for each of the n starting positions, the total time is O(n \\log n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tSpace for Arrays: O(n)\n\t\u2022\tWe use two additional arrays, cost and prefixSum, each of size n.\n\n# Code\n```\npublic class Solution {\n public int EqualSubstring(string s, string t, int maxCost) {\n int n = s.Length;\n int[] cost = new int[n];\n for (int i = 0; i < n; i++) {\n cost[i] = Math.Abs(s[i] - t[i]);\n }\n \n int[] prefixSum = new int[n + 1];\n for (int i = 0; i < n; i++) {\n prefixSum[i + 1] = prefixSum[i] + cost[i];\n }\n \n int maxLength = 0;\n for (int i = 0; i < n; i++) {\n int low = i, high = n;\n while (low < high) {\n int mid = (low + high + 1) / 2;\n if (prefixSum[mid] - prefixSum[i] <= maxCost) {\n low = mid;\n } else {\n high = mid - 1;\n }\n }\n maxLength = Math.Max(maxLength, low - i);\n }\n \n return maxLength;\n }\n}\n``` | 2 | 0 | ['C#'] | 1 |
get-equal-substrings-within-budget | Sliding Window 2 Approaches | sliding-window-2-approaches-by-himanshum-hsxu | Sliding window with Prefix sum\n# Code\n\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n=s.length();\n | himanshumude01 | NORMAL | 2024-05-28T04:21:33.860953+00:00 | 2024-05-28T04:21:33.860979+00:00 | 37 | false | # Sliding window with Prefix sum\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n=s.length();\n vector<int>pref(n,0);\n pref[0]=abs(s[0]-t[0]);\n for(int i=1;i<n;i++)\n {\n pref[i]=pref[i-1]+abs(s[i]-t[i]);\n }\n // Why do we need this step \uD83E\uDD14? Can you answer it ?\n pref.insert(pref.begin(),0);\n int cost=0,maxLen=0;\n for(int i=0,j=0;j<n+1;j++)\n {\n cost=pref[j]-pref[i];\n while(i<j and cost>maxCost)\n {\n i++;\n cost=pref[j]-pref[i];\n }\n maxLen=max(maxLen,j-i);\n }\n\n return maxLen;\n }\n};\n```\n\n# Space Optimized Sliding Window\n\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n=s.length();\n int cost=0,maxLen=0;\n for(int i=0,j=0;j<n;j++)\n {\n cost+=abs(s[j]-t[j]);\n while(i<=j and cost>maxCost)\n {\n cost-=abs(s[i]-t[i]);\n i++;\n }\n maxLen=max(maxLen,j-i+1);\n }\n\n return maxLen;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
get-equal-substrings-within-budget | Binary Search + Sliding Window (MENTOSS ZINDAGIIIIII) | binary-search-sliding-window-mentoss-zin-jlcq | \n\n# Complexity\n- Time complexity:O(n*log(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O( | TechTinkerer | NORMAL | 2024-05-28T04:13:54.361750+00:00 | 2024-05-28T04:13:54.361782+00:00 | 47 | false | \n\n# Complexity\n- Time complexity:O(n*log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool check(int wins,vector<int>&v,int maxcost){\n int i=0,j=0;\n int n=v.size();\n int sum=0;\n while(j<n){\n sum+=v[j];\n\n if(j-i+1<wins)\n j++;\n\n else{\n if(sum<=maxcost)\n return true;\n\n sum-=v[i];\n j++;\n i++;\n }\n }\n\n return false;\n }\n int equalSubstring(string s, string t, int maxCost) {\n int n=s.size();\n vector<int> v;\n for(int i=0;i<n;i++){\n v.push_back(abs(s[i]-t[i]));\n }\n\n int lo=0,hi=n;\n int ans=0;\n while(lo<=hi){\n int mid=(lo+hi)/2;\n\n if(check(mid,v,maxCost)){\n ans=mid;\n lo=mid+1;\n }\n else hi=mid-1;\n }\n\n return ans;\n\n }\n};\n``` | 1 | 0 | ['Binary Search', 'Sliding Window', 'C++'] | 0 |
get-equal-substrings-within-budget | 🏆💢💯 Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅💥🔥💫Explained☠💥🔥 Beats 💯 | faster-lesser-cpython3javacpythonexplain-0xt0 | Intuition\n\n\nC++ []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int l = 0, curr = 0, cnt = 0;\n for | Edwards310 | NORMAL | 2024-05-28T03:49:55.002160+00:00 | 2024-05-28T03:49:55.002183+00:00 | 62 | false | # Intuition\n\n\n```C++ []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int l = 0, curr = 0, cnt = 0;\n for (int r = 0; s[r]; r++) {\n curr += abs(s[r] - t[r]);\n while (curr > maxCost) {\n curr -= abs(s[l] - t[l]);\n l++;\n }\n cnt = max(cnt, (r - l + 1));\n }\n return cnt;\n }\n};\n```\n```python3 []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n l, curr = 0, 0\n res = 0\n \n for r in range(len(s)):\n curr += abs(ord(s[r]) - ord(t[r]))\n while curr > maxCost:\n curr -= abs(ord(s[l]) - ord(t[l]))\n l += 1\n res = max(res, (r - l + 1))\n return res\n```\n```C []\nint equalSubstring(char* s, char* t, int maxCost) {\n int l = 0, curr = 0, cnt = 0;\n for (int r = 0; s[r]; r++) {\n curr += fabs(s[r] - t[r]);\n while (curr > maxCost) {\n curr -= fabs(s[l] - t[l]);\n l++;\n }\n cnt = fmax(cnt, (r - l + 1));\n }\n return cnt;\n}\n```\n```Java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int l = 0, curr = 0, cnt = 0;\n for (int r = 0; r < s.length(); r++) {\n curr += Math.abs(s.charAt(r) - t.charAt(r));\n while (curr > maxCost) {\n curr -= Math.abs(s.charAt(l) - t.charAt(l));\n l++;\n }\n cnt = Math.max(cnt, (r - l + 1));\n }\n return cnt;\n }\n}\n```\n```python []\nclass Solution(object):\n def equalSubstring(self, s, t, maxCost):\n """\n :type s: str\n :type t: str\n :type maxCost: int\n :rtype: int\n """\n n = len(s)\n cost = [abs(ord(s[i]) - ord(t[i])) for i in range(n)]\n \n left = 0\n total_cost = 0\n max_length = 0\n \n for right in range(n):\n total_cost += cost[right]\n \n while total_cost > maxCost:\n total_cost -= cost[left]\n left += 1\n \n max_length = max(max_length, right - left + 1)\n \n return max_length\n```\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int l = 0, curr = 0, cnt = 0;\n for (int r = 0; r < s.length(); r++) {\n curr += Math.abs(s.charAt(r) - t.charAt(r));\n while (curr > maxCost) {\n curr -= Math.abs(s.charAt(l) - t.charAt(l));\n l++;\n }\n cnt = Math.max(cnt, (r - l + 1));\n }\n return cnt;\n }\n}\n```\n\n | 2 | 0 | ['String', 'Binary Search', 'C', 'Sliding Window', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3', 'C#'] | 0 |
get-equal-substrings-within-budget | 💯✅🔥Easy ☕Java☕ Solution|| 7 ms ||≧◠‿◠≦✌ | easy-java-solution-7-ms-_-by-sreehithsan-7sbz | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is essentially about finding the longest substring in "s" that can be trans | sreehithsanam | NORMAL | 2024-05-28T03:01:11.147093+00:00 | 2024-05-28T03:01:11.147118+00:00 | 2 | false | # *Intuition*\n<!-- Describe your first thoughts on how to solve this problem. -->\n*The problem is essentially about finding the longest substring in "s" that can be transformed into the corresponding substring in "t" with a limited cost. The cost is defined as the sum of the absolute differences of the ASCII values of corresponding characters. To solve this, we can use the sliding window technique which helps in maintaining a window that adjusts based on the cost constraint.*\n\n# *Approach*\n<!-- Describe your approach to solving the problem. -->\n1. *Sliding Window Technique:*\n\n- *We maintain two pointers (slow and fast) that represent the current window in s.*\n- *We start with both pointers at the beginning and expand the fast pointer to include more characters until the cost exceeds maxCost.*\n- *If the cost exceeds maxCost, we increment the slow pointer to reduce the window size and thereby reduce the cost.*\n- *During this process, we keep track of the maximum window size that satisfies the cost constraint.*\n2. *Cost Calculation:*\n\n- *The cost is updated dynamically as the window expands or shrinks.*\n- *When fast pointer moves forward, we add the cost of the new character.*\n- *When slow pointer moves forward, we subtract the cost of the character that is left behind.*\n# *Complexity*\n- *Time complexity:*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n*The time complexity is $$O(n$$), where n is the length of the strings s and t. Each character is processed at most twice, once when the fast pointer moves and once when the slow pointer moves.*\n- *Space complexity:* \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n*The space complexity is $$O(1)$$ because we only use a fixed amount of extra space for variables such as pointers and the cost accumulator.*\n# *Code*\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int slow = -1, fast = 0; \n int n = s.length(),res = 0,cost = Math.abs(s.charAt(fast)-t.charAt(fast));\n boolean flag = true;\n while(slow<=fast&&fast<n){\n if(cost<=maxCost){\n res = Math.max(res,fast-slow);\n fast++;\n if(fast==n) break;\n cost+=Math.abs(s.charAt(fast)-t.charAt(fast));\n continue;\n }\n if(cost>maxCost){\n slow++;\n cost-=Math.abs(s.charAt(slow)-t.charAt(slow));\n continue;\n }\n }\n return res;\n }\n}\n```\n\n\n | 2 | 0 | ['String', 'Sliding Window', 'Java'] | 0 |
get-equal-substrings-within-budget | [C++] Binary Search the Maximum Length | c-binary-search-the-maximum-length-by-aw-cb1h | Intuition\n Describe your first thoughts on how to solve this problem. \n- Define a boolean function check(length) that can check if there exists a substring wi | pepe-the-frog | NORMAL | 2024-05-28T01:43:21.434637+00:00 | 2024-05-28T01:43:21.434659+00:00 | 339 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Define a boolean function `check(length)` that can check if there exists a substring with `length` meets the condition\n- The `check(length)` is a function like this:\n - `f(0) = true`, `f(1) = true`, ... `f(x) = true`, `f(x + 1) = false`, ...\n- We can find the `x` using the binary search\n - `f(x)` is the right-most true value\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- calculate the prefix sum to get the cost of `s.substr(i, length)`\n- binary search the maximum length\n - check if there exists a substring meets the condition\n\n# Complexity\n- Time complexity: $$O(n\\times{\\log{n}})$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // time/space: O(nlogn)/O(n)\n int equalSubstring(string s, string t, int maxCost) {\n // calculate the prefix sum to get the cost of `s.substr(i, length)`\n int n = s.size();\n vector<int> prefix(n + 1, 0);\n for (int i = 0; i < n; i++) prefix[i + 1] = prefix[i] + abs(s[i] - t[i]);\n\n // binary search the maximum length\n int l = 0, r = n;\n while (l < r) {\n int m = l + (r - l + 1) / 2;\n if (check(n, prefix, maxCost, m)) l = m;\n else r = m - 1;\n }\n return l;\n }\nprivate:\n // check if there exists a substring meets the condition\n bool check(int n, vector<int>& prefix, int maxCost, int length) {\n for (int i = 0; (i + length) <= n; i++) {\n int cost = prefix[i + length] - prefix[i];\n if (cost <= maxCost) return true;\n }\n return false;\n }\n};\n``` | 2 | 0 | ['C++'] | 3 |
get-equal-substrings-within-budget | Sliding Window Technique || beats 93% users with C++ & 85% with java || python3 || typescript | sliding-window-technique-beats-93-users-pi8gx | Approach\nSliding Window Technique\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Explanation\n1. Initialize Variables:\n\n- n: Lengt | SanketSawant18 | NORMAL | 2024-05-28T00:51:32.547067+00:00 | 2024-05-28T00:51:32.547102+00:00 | 238 | false | # Approach\nSliding Window Technique\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Explanation\n1. **Initialize Variables:**\n\n- n: Length of the strings s and t.\n- maxLength: To store the maximum length of the valid substring found.\n- currentCost: To track the total cost of the current window.\n- left: The left pointer of the sliding window.\n2. **Expand the Window:**\n\n- Iterate through the string s using the right pointer.\n- For each character at position right, calculate the cost to change s.charAt(right) to t.charAt(right) and add it to currentCost.\n3. **Shrink the Window if Needed:**\n\n- If currentCost exceeds maxCost, increment the left pointer to reduce the window size until currentCost is less than or equal to maxCost.\n4. **Update Maximum Length:**\n\n- For each valid window, update maxLength with the size of the current window, which is right - left + 1.\n5. **Return Result:**\n\n- Finally, return maxLength, which holds the maximum length of the substring that can be transformed within the given cost.\n\n---\n\n```java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int n = s.length();\n int maxLength = 0;\n int currentCost = 0;\n int left = 0;\n \n for (int right = 0; right < n; right++) {\n // Calculate the cost of changing s[right] to t[right]\n currentCost += Math.abs(s.charAt(right) - t.charAt(right));\n \n // While currentCost exceeds maxCost, move the left pointer to the right\n while (currentCost > maxCost) {\n currentCost -= Math.abs(s.charAt(left) - t.charAt(left));\n left++;\n }\n \n // Update the maximum length of the substring found so far\n maxLength = Math.max(maxLength, right - left + 1);\n }\n \n return maxLength;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n = s.length();\n int maxLength = 0;\n int currentCost = 0;\n int left = 0;\n\n for (int right = 0; right < n; right++) {\n // Calculate the cost of changing s[right] to t[right]\n currentCost += abs(s[right] - t[right]);\n\n // While currentCost exceeds maxCost, move the left pointer to the right\n while (currentCost > maxCost) {\n currentCost -= abs(s[left] - t[left]);\n left++;\n }\n\n // Update the maximum length of the substring found so far\n maxLength = max(maxLength, right - left + 1);\n }\n\n return maxLength;\n }\n};\n\n```\n```python3 []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n n = len(s)\n max_length = 0\n current_cost = 0\n left = 0\n \n for right in range(n):\n # Calculate the cost of changing s[right] to t[right]\n current_cost += abs(ord(s[right]) - ord(t[right]))\n \n # While current_cost exceeds maxCost, move the left pointer to the right\n while current_cost > maxCost:\n current_cost -= abs(ord(s[left]) - ord(t[left]))\n left += 1\n \n # Update the maximum length of the substring found so far\n max_length = max(max_length, right - left + 1)\n \n return max_length\n\n```\n```Typescript []\nfunction equalSubstring(s: string, t: string, maxCost: number): number {\n let n = s.length;\n let maxLength = 0;\n let currentCost = 0;\n let left = 0;\n\n for (let right = 0; right < n; right++) {\n // Calculate the cost of changing s[right] to t[right]\n currentCost += Math.abs(s.charCodeAt(right) - t.charCodeAt(right));\n\n // While currentCost exceeds maxCost, move the left pointer to the right\n while (currentCost > maxCost) {\n currentCost -= Math.abs(s.charCodeAt(left) - t.charCodeAt(left));\n left++;\n }\n\n // Update the maximum length of the substring found so far\n maxLength = Math.max(maxLength, right - left + 1);\n }\n\n return maxLength;\n}\n\n```\n | 2 | 0 | ['String', 'Sliding Window', 'C++', 'Java', 'TypeScript', 'Python3'] | 1 |
get-equal-substrings-within-budget | Python3 || O(n) and O(1) TIME AND SPACE || May 28 2024 Daily | python3-on-and-o1-time-and-space-may-28-fou5j | Intuition\nThe problem requires finding the maximum length of a substring in string s that can be transformed into the corresponding substring in string t with | praneelpa | NORMAL | 2024-05-28T00:04:31.198443+00:00 | 2024-05-28T00:04:31.198461+00:00 | 140 | false | # Intuition\nThe problem requires finding the maximum length of a substring in string s that can be transformed into the corresponding substring in string t with a cost less than or equal to maxCost. We can approach this problem using a sliding window technique.\n\n# Approach\nSliding Window: Initialize two pointers i and j at the start of s. Use these pointers to define a window that represents the current substring being considered.\nCost Calculation: Iterate through the characters of s and t within the window. Calculate the cost of transforming s[i] to t[i] using the absolute difference of their ASCII values.\nCost Constraint Check: If the cost exceeds maxCost, move the window by incrementing j and adjusting the cost accordingly until the cost constraint is satisfied again.\nTrack Maximum Length: Keep track of the maximum length of the substring that satisfies the cost constraint throughout the iterations.\nReturn Result: After iterating through the entire string s, return the maximum length of the substring that satisfies the cost constraint.\n\n# Complexity\n- Time complexity:\n The algorithm traverses the entire strings s and t once, so the time complexity is $$O(n)$$ where $$n$$ is the length of the strings.\n\n- Space complexity:\nThe algorithm uses only a constant amount of extra space, so the space complexity is $$O(1)$$\n\n# Code\n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n j = 0\n for i in range(len(s)):\n maxCost -= abs(ord(s[i]) - ord(t[i]))\n if maxCost < 0:\n maxCost += abs(ord(s[j]) - ord(t[j]))\n j += 1\n\n return len(s) - j\n``` | 2 | 0 | ['Python3'] | 1 |
get-equal-substrings-within-budget | Sliding window & Two Pointers Pattern | sliding-window-two-pointers-pattern-by-d-wqo3 | \n# Code\n\n// Exact same as some problem add it for reference\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n\n in | Dixon_N | NORMAL | 2024-05-20T02:09:52.692431+00:00 | 2024-05-20T02:09:52.692460+00:00 | 29 | false | \n# Code\n```\n// Exact same as some problem add it for reference\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n\n int maxLength=0,left=0,right=0;\n int n=s.length();\n\n while(right<n){\n\n int diff = Math.abs(s.charAt(right)-t.charAt(right));\n maxCost-=diff;\n while(maxCost<0){\n int leftDifference = Math.abs(s.charAt(left)-t.charAt(left));\n maxCost+=leftDifference;\n left++;\n }\n if(maxCost>=0) maxLength = Math.max(maxLength,right-left+1);\n right++;\n }\n return maxLength;\n \n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
get-equal-substrings-within-budget | C++ || easy | c-easy-by-shradhaydham24-sm83 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shradhaydham24 | NORMAL | 2023-07-16T15:42:44.164231+00:00 | 2023-07-16T15:42:44.164251+00:00 | 235 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) \n {\n int n=s.length();\n int i=0,j=0,ans=0,cost=0;\n for(;j<n;j++)\n {\n cost+=abs(s[j]-t[j]);\n for(;cost>maxCost;i++)\n cost-=abs(s[i]-t[i]);\n ans=max(ans,j-i+1);\n } \n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
get-equal-substrings-within-budget | Very Simple, C++ Longest Sub-Array Sum ✅✅ | very-simple-c-longest-sub-array-sum-by-d-dd18 | if it Helps You. Please UpVote Me...! \u2764\n# Approach\n Describe your approach to solving the problem. \n\nApproach is Simple But we have to change the probl | Deepak_5910 | NORMAL | 2023-06-13T09:50:46.760021+00:00 | 2023-06-13T09:50:46.760045+00:00 | 273 | false | # if it Helps You. Please UpVote Me...! \u2764\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nApproach is Simple But we have to change the problem Statement to **Longest Sub-Array with Sum <=K.**\n\n**Just Follow the Below Points to change the Problem Statement:-**\n1. Calculate the absolute Cost for Each Character and store it to the new Cost Vector.\n2. Now Calculate the Longest Sub-Array With Sum <= k.\n\n**EX:- S = "abc" and t = "bcd"\ncost[0] = abs(s[0]-t[0]) = 1\ncost[1] = abs(s[1]-t[1]) = 1\ncost[2] = abs(s[2]-t[2]) = 1**\n\n**Cost[] = {1,1,1} maxcost = 2 Now find the Longest SubSub-Array with Sum<=2.**\n\n\n\n\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxcost) {\n\n int n = s.size(),sum = 0,ans = 0;\n vector<int>cost(n,0);\n\n for(int i = 0;i<n;i++)\n cost[i] = abs(s[i]-t[i]);\n\n queue<int> q;\n\t for(int i=0;i<n;i++)\n\t {\n\t if(sum+cost[i]<=maxcost)\n\t {\n\t sum+=cost[i];\n\t q.push(cost[i]);\n\t if(ans<q.size())\n\t ans=q.size();\n\t }\n\t else if(q.size()>0)\n\t {\n\t sum-=q.front();\n\t q.pop();\n\t i--;\n\t }\n\t }\n\n return ans;\n \n }\n};\n```\n\n | 2 | 0 | ['Sliding Window', 'Prefix Sum', 'C++'] | 1 |
get-equal-substrings-within-budget | ✅✅C++ USING SLIDING WINDOW|| EASY TO UNDERSTAND✅✅ | c-using-sliding-window-easy-to-understan-rszg | \nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxc) {\n int sum=0,i=0,j=0,ans=0;\n while(j<s.size())\n {\n | Satyam_9766 | NORMAL | 2023-04-22T11:53:53.885859+00:00 | 2023-04-22T11:53:53.885892+00:00 | 278 | false | ```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxc) {\n int sum=0,i=0,j=0,ans=0;\n while(j<s.size())\n {\n int a = s[j]-\'a\';\n int b = t[j]-\'a\';\n sum+= abs(a-b);\n if(sum<=maxc)\n {\n j++;\n ans = max(ans,(j-i));\n }\n else if(maxc<sum)\n {\n while(maxc<sum)\n {\n int x = s[i]-\'a\';\n int y = t[i]-\'a\';\n sum-=abs(x-y);\n i++;\n }\n j++;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C', 'C++'] | 0 |
get-equal-substrings-within-budget | Php | Beats 100% Runtime and memory | php-beats-100-runtime-and-memory-by-kaur-17n7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kaursanampreet | NORMAL | 2023-04-02T04:42:19.309087+00:00 | 2023-04-02T04:42:19.309120+00:00 | 219 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n /**\n * @param String $s\n * @param String $t\n * @param Integer $maxCost\n * @return Integer\n */\n function equalSubstring($s, $t, $maxCost) {\n $left = $currCost = $ans = 0;\n for ($i = 0; $i < strlen($s); $i++) {\n $currCost += abs(ord($s[$i]) - ord($t[$i]));\n while($currCost > $maxCost) {\n $currCost -= abs(ord($s[$left]) - ord($t[$left]));\n $left++;\n }\n $ans = max($ans, $i - $left + 1);\n }\n return $ans;\n }\n}\n``` | 2 | 0 | ['PHP'] | 1 |
get-equal-substrings-within-budget | ✅ C++ || 3 Lines only || Sliding window | c-3-lines-only-sliding-window-by-t86-rmwb | c++\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost, int res = 0) {\n for (int i = 0, left = 0, counting = 0; i < cost | t86 | NORMAL | 2023-01-11T23:57:19.951261+00:00 | 2023-03-24T20:12:18.610082+00:00 | 139 | false | ```c++\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost, int res = 0) {\n for (int i = 0, left = 0, counting = 0; i < cost.size(); i++) {\n counting += abs(s[i] - t[i]);\n while (counting > maxCost) counting -= cost[left++];\n res = max(res, i - left + 1);\n }\n return res;\n }\n};\n```\n\n**For more solutions, check out this \uD83C\uDFC6 [GITHUB REPOSITORY](https://github.com/MuhtasimTanmoy/playground) with over 1500+ solutions.** | 2 | 1 | [] | 0 |
get-equal-substrings-within-budget | [C++/Python] | Sliding window | cpython-sliding-window-by-tusharbhart-b6xm | C++\n\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int ans = 0, c = maxCost, i = 0, j = 0;\n\n for(int | TusharBhart | NORMAL | 2022-10-02T17:34:09.945253+00:00 | 2022-10-02T17:34:09.945298+00:00 | 548 | false | # C++\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int ans = 0, c = maxCost, i = 0, j = 0;\n\n for(int j=0; j<s.size(); j++) {\n c -= abs(s[j] - t[j]);\n if(c >= 0) ans = max(ans, j - i + 1);\n else c += abs(s[i] - t[i]), i++;\n }\n return ans;\n }\n};\n```\n\n# Python\n```\nclass Solution(object):\n def equalSubstring(self, s, t, maxCost):\n ans, i, c = 0, 0, maxCost\n\n for j in range(len(s)):\n c -= abs(ord(s[j]) - ord(t[j]))\n if c >= 0: ans = max(ans, j - i + 1)\n else:\n c += abs(ord(s[i]) - ord(t[i]))\n i += 1\n \n return ans\n```\n | 2 | 0 | ['Sliding Window', 'Python', 'C++'] | 1 |
get-equal-substrings-within-budget | python solution with sliding window | python-solution-with-sliding-window-by-d-4jcy | \n\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n if maxCost == 0 and s!=t:\n return 1\n res = | derrickyu | NORMAL | 2022-09-19T08:12:37.848842+00:00 | 2022-09-19T08:12:37.848877+00:00 | 412 | false | \n```\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n if maxCost == 0 and s!=t:\n return 1\n res = 0\n m={\'a\':1,\'b\':2,\'c\':3,\'d\':4,\'e\':5,\'f\':6,\'g\':7,\'h\':8,\'i\':9,\'j\':10,\'k\':11,\'l\':12,\'m\':13,\'n\':14,\'o\':15,\'p\':16,\'q\':17,\'r\':18,\'s\':19,\'t\':20,\'u\':21,\'v\':22,\'w\':23,\'x\':24,\'y\':25,\'z\':26}\n l1=[]\n l2=[]\n for k in range(len(s)):\n l1.append(m[s[k]])\n l2.append(m[t[k]])\n l = 0\n for r in range(len(s)):\n maxCost -= (abs(l2[r]-l1[r]))\n if maxCost < 0:\n maxCost += (abs(l2[l]-l1[l]))\n l += 1\n return r-l+1\n \n```\n | 2 | 0 | ['Sliding Window', 'Python'] | 1 |
get-equal-substrings-within-budget | C# Solution | Time: O(n), Memory: O(1) | Easy to understand, Sliding window | c-solution-time-on-memory-o1-easy-to-und-2e57 | C#\npublic class Solution {\n public int EqualSubstring(string s, string t, int maxCost) {\n int cost = 0, start = 0, end = 0;\n while (end < s | tonytroeff | NORMAL | 2022-08-22T06:37:27.230215+00:00 | 2022-08-22T06:37:27.230255+00:00 | 265 | false | ```C#\npublic class Solution {\n public int EqualSubstring(string s, string t, int maxCost) {\n int cost = 0, start = 0, end = 0;\n while (end < s.Length) {\n cost += Math.Abs(s[end] - t[end]);\n if (cost > maxCost) {\n cost -= Math.Abs(s[start] - t[start]);\n start++;\n }\n \n end++;\n }\n \n return end - start;\n }\n}\n``` | 2 | 0 | ['Sliding Window'] | 1 |
get-equal-substrings-within-budget | C++ | Sliding Window | Template | Easy | c-sliding-window-template-easy-by-jaidee-5xpb | Do upvote if it helps! :)\n\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n=s.size();\n vector<int>dif | jaideep_ankur | NORMAL | 2022-02-05T17:44:30.569365+00:00 | 2022-02-05T17:44:30.569403+00:00 | 144 | false | **Do upvote if it helps! :)**\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n=s.size();\n vector<int>diff(n,0);\n for(int i=0;i<n;i++){\n diff[i]=abs((s[i]-\'a\')-(t[i]-\'a\'));\n }\n int res=0,left=0,k=maxCost,sum=0;\n for(int i=0;i<n;i++){\n sum+=diff[i];\n if(sum>k){\n sum-=diff[left];\n left++;\n }\n res=max(res,i-left+1);\n }\n return res;\n }\n};\n``` | 2 | 0 | ['C', 'Sliding Window'] | 1 |
get-equal-substrings-within-budget | Java || Sliding Window || T.C - O(n) S.C - O(1) | java-sliding-window-tc-on-sc-o1-by-legen-qs2r | \n public int equalSubstring(String s, String t, int maxCost) {\n\n\t\tint len = s.length(), max = 0, idx1 = -1, idx2 = 0, cost = 0;\n\n\t\twhile (idx2 < len | LegendaryCoder | NORMAL | 2021-04-19T17:59:30.195133+00:00 | 2021-04-19T17:59:30.195180+00:00 | 36 | false | \n public int equalSubstring(String s, String t, int maxCost) {\n\n\t\tint len = s.length(), max = 0, idx1 = -1, idx2 = 0, cost = 0;\n\n\t\twhile (idx2 < len) {\n\n\t\t\twhile (idx2 < len) {\n\t\t\t\tcost += Math.abs(s.charAt(idx2) - t.charAt(idx2));\n\t\t\t\tif (cost <= maxCost) {\n\t\t\t\t\tif (idx2 - idx1 > max)\n\t\t\t\t\t\tmax = idx2 - idx1;\n\t\t\t\t\tidx2++;\n\t\t\t\t} else {\n\t\t\t\t\tidx2++;\n\t\t\t\t\tbreak;\n\t\t\t\t}\n\t\t\t}\n\n\t\t\twhile (idx1 < idx2) {\n\t\t\t\tidx1++;\n\t\t\t\tcost -= Math.abs(s.charAt(idx1) - t.charAt(idx1));\n\t\t\t\tif (cost <= maxCost)\n\t\t\t\t\tbreak;\n\t\t\t}\n\n\t\t}\n\n\t\treturn max;\n\t} | 2 | 1 | [] | 0 |
get-equal-substrings-within-budget | Binary Search + sliding window | binary-search-sliding-window-by-just_mik-9fp0 | \nbool fun(int len,string s,string t,int maxcost,int n)\n {\n int temp=0,cost=0;\n for(int i=0;i<n;i++)\n {\n cost+=(abs((s[i | just_miku | NORMAL | 2020-10-13T05:26:06.000752+00:00 | 2020-10-13T05:26:06.000800+00:00 | 124 | false | ```\nbool fun(int len,string s,string t,int maxcost,int n)\n {\n int temp=0,cost=0;\n for(int i=0;i<n;i++)\n {\n cost+=(abs((s[i]-\'a\')-(t[i]-\'a\')));\n }\n for(int i=n;i<len;i++)\n {\n if(cost<=maxcost) return(1);\n cost+=(abs((s[i]-\'a\')-(t[i]-\'a\')));\n cost-=(abs((s[i-n]-\'a\')-(t[i-n]-\'a\')));\n }\n if(cost<=maxcost) return(1);\n return(0);\n }\n \n \n \n int equalSubstring(string s, string t, int maxCost)\n {\n int len1=s.size();\n int lo=0,hi=len1;\n int ans=0;\n while(hi>=lo)\n {\n int mid=(lo+hi)/2;\n if(fun(len1,s,t,maxCost,mid)) \n {\n ans=mid;\n lo=mid+1;\n }\n else hi=mid-1;\n }\n return(ans);\n }\n``` | 2 | 1 | ['Sliding Window', 'Binary Tree'] | 1 |
get-equal-substrings-within-budget | C# - Sliding window - easy & efficient code | c-sliding-window-easy-efficient-code-by-60sp1 | Please upvote and comment if you like the solution!\n```\n public int EqualSubstring(string s, string t, int maxCost) {\n\tint n = s.Length, left = 0, window = | stack_360 | NORMAL | 2020-08-15T19:45:36.263135+00:00 | 2020-08-15T19:58:15.433637+00:00 | 72 | false | Please upvote and comment if you like the solution!\n```\n public int EqualSubstring(string s, string t, int maxCost) {\n\tint n = s.Length, left = 0, window = 0, ans = int.MinValue;\n\tint[] cost = new int[n];\n\tfor (int right = 0; right < n; right++)\n\t{\n\t\tcost[right] = Math.Abs(s[right] - t[right]);\n\t\twindow += cost[right];\n\n\t\twhile (window > maxCost)\n\t\t\twindow -= cost[left++];\n\n\t\tans = Math.Max(ans, right - left + 1);\n\t}\n\treturn ans;\n } | 2 | 0 | [] | 0 |
get-equal-substrings-within-budget | C++: Sliding Window || O(n) Solution | c-sliding-window-on-solution-by-bingabid-1lfk | ```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n = s.length();\n int left=0,right=0,ans=0,cost=0; | bingabid | NORMAL | 2020-06-16T06:11:17.424813+00:00 | 2020-06-16T06:11:17.424860+00:00 | 101 | false | ```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int n = s.length();\n int left=0,right=0,ans=0,cost=0;\n while(right<n){\n cost= cost + abs(s[right]-t[right]);\n while(cost>maxCost){\n cost= cost - abs(s[left]-t[left]);\n left++;\n }\n ans = max(ans,right-left+1);\n right++;\n }\n return ans;\n }\n}; | 2 | 0 | [] | 0 |
get-equal-substrings-within-budget | C++ | Sliding Window Standard Problem | O(n) | c-sliding-window-standard-problem-on-by-sbfsy | Intuition:\n\nTrack using two pointers and keep on adding the cost in variable and keep on increasing the window towards right.\nOnce the variable value exceed | wh0ami | NORMAL | 2020-05-28T19:17:08.277610+00:00 | 2020-05-28T19:17:08.277649+00:00 | 108 | false | **Intuition:**\n\nTrack using two pointers and keep on adding the cost in variable and keep on increasing the window towards right.\nOnce the variable value exceed maxcost, reduce the window size from left.\n\n**Solution:**\n\n```\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n \n int n = s.length();\n \n int i = 0, j = 0, d = 0, res = 0;\n for (i = 0; i < n; i++) {\n d += abs(s[i] - t[i]);\n while (j < n && d > maxCost) {\n d -= abs(s[j] - t[j]);\n j++;\n }\n res = max(res, i-j+1);\n }\n \n return res;\n }\n};\n``` | 2 | 0 | [] | 0 |
get-equal-substrings-within-budget | [java] simple solution based on two pointers | java-simple-solution-based-on-two-pointe-v1ml | \nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n if(maxCost < 0 || s == null || t == null || s.length() != t.length | liyun1988 | NORMAL | 2019-09-29T05:49:38.924707+00:00 | 2019-09-29T05:49:38.924762+00:00 | 132 | false | ```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n if(maxCost < 0 || s == null || t == null || s.length() != t.length() || s.length() == 0) {\n return 0;\n }\n \n int[] diffs = new int[s.length()];\n int left = 0, cost = 0, maxLen = 0;\n for(int i = 0; i < s.length(); ++i) {\n diffs[i] = Math.abs((int)s.charAt(i) - (int)t.charAt(i));\n if(diffs[i] > maxCost) {\n left = i+1;\n cost = 0;\n } else {\n cost += diffs[i];\n\t\t\t\t// can use binary search to speed it up\n while(left <= i && cost > maxCost) {\n cost -= diffs[left];\n ++left;\n }\n }\n \n maxLen = Math.max(maxLen, i - left + 1);\n }\n \n return maxLen;\n }\n}\n``` | 2 | 0 | [] | 0 |
get-equal-substrings-within-budget | Two Pointer | Simple Solution | Time O(n), Space O(n) | two-pointer-simple-solution-time-on-spac-a2q2 | ```\n public int equalSubstring(String s, String t, int maxCost) {\n int l = s.length();\n int[] nums = new int[l];\n for(int i=0; i<s.l | popeye_the_sailort | NORMAL | 2019-09-29T04:01:51.759344+00:00 | 2019-09-29T04:01:51.759396+00:00 | 256 | false | ```\n public int equalSubstring(String s, String t, int maxCost) {\n int l = s.length();\n int[] nums = new int[l];\n for(int i=0; i<s.length(); ++i) {\n nums[i] = Math.abs(s.charAt(i) - t.charAt(i));\n }\n int len = 0;\n int sum = 0;\n for(int i=0, j=0; i<l; ++i) {\n sum += nums[i];\n while (j<=i && sum > maxCost) {\n sum -= nums[j++];\n }\n len = Math.max(len, i-j+1);\n }\n return len;\n } | 2 | 1 | [] | 1 |
get-equal-substrings-within-budget | Sliding window || Java || Easy || 🚀🚀 || 🔥🔥 | sliding-window-java-easy-by-vermaanshul9-ruof | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | vermaanshul975 | NORMAL | 2025-03-23T07:32:41.195534+00:00 | 2025-03-23T07:32:41.195534+00:00 | 17 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int equalSubstring(String s, String t, int maxCost) {
int n = s.length();
int l = 0;
int r= 0;
int cost = 0;
int ans =0;
while(r<n){
int a = s.charAt(r);
int b = t.charAt(r);
cost += Math.abs(a-b);
while(cost>maxCost){
cost -= Math.abs(s.charAt(l) - t.charAt(l));
l++;
}
ans = Math.max(ans,r-l+1);
r++;
}
return ans;
}
}
``` | 1 | 0 | ['Java'] | 0 |
get-equal-substrings-within-budget | Simple C++ Solution || Sliding window || C++ | simple-c-solution-sliding-window-c-by-ab-5e2g | IntuitionWe want to find the maximum length of a substring where the total transformation cost from s[i] to t[i] is less than or equal to maxCost.
If the cost e | Abhinandanpatil02 | NORMAL | 2025-03-18T07:19:07.911699+00:00 | 2025-03-18T07:19:07.911699+00:00 | 17 | false | ---
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We want to find the **maximum length of a substring** where the **total transformation cost from `s[i]` to `t[i]` is less than or equal to `maxCost`**.
If the cost exceeds `maxCost`, we need to **remove characters from the start of the current window** (sliding window technique).
---
# Approach
<!-- Describe your approach to solving the problem. -->
1. First, calculate a `cost` array which stores `abs(s[i] - t[i])` for each index.
2. Use **two pointers `i` (right) and `j` (left)** to maintain a sliding window.
3. Expand the right pointer `i`, and keep track of the total cost `c` and length `cnt` of current window.
4. If total cost exceeds `maxCost`, **shrink the window from the left** by increasing `j` and updating `c` and `cnt`.
5. Keep updating `len` with the maximum value of `cnt`.
---
# Example:
Let’s take this example:
`s = "abcd"`, `t = "bcdf"`, `maxCost = 3`
| Index | s[i] | t[i] | cost[i] = abs(s[i] - t[i]) | Window (i to j) | Total Cost | Comment |
|-------|------|------|-----------------------------|------------------|-------------|--------------------------------|
| 0 | a | b | 1 | 0 to 0 | 1 | Within maxCost |
| 1 | b | c | 1 | 0 to 1 | 2 | Within maxCost |
| 2 | c | d | 1 | 0 to 2 | 3 | Exactly maxCost |
| 3 | d | f | 2 | 0 to 3 | 5 | Cost > maxCost → Remove cost[0] (1) |
| | | | | 1 to 3 | 4 | Still > maxCost → Remove cost[1] (1) |
| | | | | 2 to 3 | 3 | Now valid |
Final Answer = Max length = **2** (from index 2 to 3)
---
### Complexity
- **Time complexity:**
$$O(n)$$
- One pass over the array for building cost.
- One pass for sliding window traversal.
- **Space complexity:**
$$O(n)$$
- Extra space used for the `cost` array.
---
# Code
```cpp []
class Solution {
public:
int equalSubstring(string s, string t, int maxCost) {
int n=s.length();
vector<int>cost;
for(int i=0;i<n;i++){
cost.push_back(abs(s[i]-t[i]));
}
int len=0,c=0;
int cnt=0;
int j=0;
for(int i=0;i<n;i++){
c+=cost[i];
cnt++;
if(c>maxCost){
c-=cost[j];
j++;
cnt--;
}
len=max(len,cnt);
}
return len;
}
};
``` | 1 | 0 | ['C++'] | 0 |
get-equal-substrings-within-budget | Easy to Understand || Sliding Window & 2 Pointers || C++ || Java || Python || Javascript | easy-to-understand-sliding-window-2-poin-ddbi | Complexity
Time complexity:
O(n)
Space complexity:
O(1)
Code | rajshingala | NORMAL | 2025-03-12T16:47:44.358500+00:00 | 2025-03-12T16:47:44.358500+00:00 | 26 | false | # Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(1)$$
# Code
```cpp []
class Solution {
public:
int equalSubstring(string s, string t, int maxCost) {
int n = s.length();
int l = 0;
int r = 0;
int cost = 0;
int maxLen = 0;
while(r < n) {
cost += abs(int(s[r]) - int(t[r]));
while(cost > maxCost) {
cost -= abs(int(s[l]) - int(t[l]));
l++;
}
maxLen = max(maxLen, r-l+1);
r++;
}
return maxLen;
}
};
```
```Java []
class Solution {
public int equalSubstring(String s, String t, int maxCost) {
int n = s.length();
int l = 0, r = 0, cost = 0, maxLen = 0;
while (r < n) {
cost += Math.abs(s.charAt(r) - t.charAt(r));
while (cost > maxCost) {
cost -= Math.abs(s.charAt(l) - t.charAt(l));
l++;
}
maxLen = Math.max(maxLen, r - l + 1);
r++;
}
return maxLen;
}
}
```
```python []
class Solution(object):
def equalSubstring(self, s, t, maxCost):
"""
:type s: str
:type t: str
:type maxCost: int
:rtype: int
"""
n = len(s)
l = r = cost = maxLen = 0
while r < n:
cost += abs(ord(s[r]) - ord(t[r]))
while cost > maxCost:
cost -= abs(ord(s[l]) - ord(t[l]))
l += 1
maxLen = max(maxLen, r - l + 1)
r += 1
return maxLen
```
```javascript []
/**
* @param {string} s
* @param {string} t
* @param {number} maxCost
* @return {number}
*/
var equalSubstring = function(s, t, maxCost) {
let n = s.length;
let l = 0, r = 0, cost = 0, maxLen = 0;
while (r < n) {
cost += Math.abs(s.charCodeAt(r) - t.charCodeAt(r));
while (cost > maxCost) {
cost -= Math.abs(s.charCodeAt(l) - t.charCodeAt(l));
l++;
}
maxLen = Math.max(maxLen, r - l + 1);
r++;
}
return maxLen;
};
``` | 1 | 0 | ['Two Pointers', 'Sliding Window', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
get-equal-substrings-within-budget | C# | c-by-adchoudhary-mffo | Code | adchoudhary | NORMAL | 2025-03-11T04:00:29.042359+00:00 | 2025-03-11T04:00:29.042359+00:00 | 3 | false | # Code
```csharp []
public class Solution {
public int EqualSubstring(string s, string t, int maxCost)
{
int N = s.Length;
int maxLen = 0;
// Starting index of the current substring
int start = 0;
// Cost of converting the current substring in s to t
int currCost = 0;
for (int i = 0; i < N; i++)
{
// Add the current index to the substring
currCost += Math.Abs(s[i] - t[i]);
// Remove the indices from the left end till the cost becomes less than allowed
while (currCost > maxCost)
{
currCost -= Math.Abs(s[start] - t[start]);
start++;
}
maxLen = Math.Max(maxLen, i - start + 1);
}
return maxLen;
}
}
``` | 1 | 0 | ['C#'] | 0 |
get-equal-substrings-within-budget | Sliding window solution using Python3!! | sliding-window-solution-using-python3-by-6sd0 | Intuition
The goal is to find the maximum length of a contiguous substring of s that can be changed to its corresponding substring in t without the total cost | Sivamani_R | NORMAL | 2025-03-09T12:31:11.847835+00:00 | 2025-03-09T12:31:11.847835+00:00 | 17 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1. ***The goal is to find the maximum length of a contiguous substring of*** `s` ***that can be changed to its corresponding substring in*** `t` ***without the total cost exceeding*** `maxCost`.
1. ***Changing a character*** `s[i]` ***to*** `t[i]` ***costs*** `abs(ord(s[i]) - ord(t[i]))`. ***So, we're essentially trying to find the longest window (substring) where the sum of these costs ≤ maxCost.***
1. ***This type of problem maps perfectly to a [Variable Sliding Window](https://www.codeintuition.io/courses/array/tFob_VIXJQJ8bUN3hlSMB) pattern, where we adjust the window boundaries dynamically based on whether the cost stays within the budget.***
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Use two pointers** `l` **and** `r` **to define a sliding window. Both start at index 0.**
1. **As you iterate through the string using** `r` **(right pointer), calculate the cost of changing** `s[r]` **to** `t[r]` **and accumulate it in** `val`**.**
1. **If the total cost** `val` **becomes greater than** `maxCost`**, shrink the window from the left** `(l += 1)` **and subtract the cost of** `s[l] - t[l]` **from** `val`**, until the window becomes valid again (i.e.,** `val <= maxCost`**).**
1. **At every step, update the result** `res` **with the maximum window length found so far** `(r - l + 1)`**.**
1. **Continue until the end of the string.**
# Complexity
##### - Time complexity:$$O(n)$$
- Each character is visited at most twice — once by the right pointer r and once by the left pointer l. So it's a linear-time solution.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
##### - Space complexity:$$O(1)$$
- No extra space is used apart from a few variables. Cost is calculated on-the-fly — no need to store cost arrays.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def equalSubstring(self, s: str, t: str, maxCost: int) -> int:
res,n=0,len(s)
l,r=0,0
val=0
while r<n:
val+=abs(ord(s[r])-ord(t[r]))
if val<=maxCost:
res=max(res,r-l+1)
else:
while val>maxCost:
val-=abs(ord(s[l])-ord(t[l]))
l+=1
r+=1
return res
```

| 1 | 0 | ['String', 'Sliding Window', 'Python3'] | 0 |
get-equal-substrings-within-budget | Short code. One pass. Beats 100%. | short-code-one-pass-beats-100-by-rickien-iu15 | IntuitionMaintain the maximum result found up to the ith charactor.ApproachWhen adding the cost of changing the ith charactor, check the accumulated cost, if sm | rickienol | NORMAL | 2025-03-07T04:04:55.605776+00:00 | 2025-03-07T04:04:55.605776+00:00 | 15 | false | # Intuition
Maintain the maximum result found up to the ith charactor.
# Approach
When adding the cost of changing the ith charactor, check the accumulated cost, if small enough, increase result by 1; otherwise, keep the result unchanged, and remove the cost from the first of the current window (the (i-res)th charactor).
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(1)$$
# Code
```cpp []
class Solution {
public:
int equalSubstring(string s, string t, int maxCost) {
int res = 0;
int accum = 0;
for (int i=0; i<s.size(); i++) {
accum += abs(s[i]-t[i]);
if (accum<=maxCost) {
res++;
} else {
accum -= abs(s[i-res]-t[i-res]);
}
}
return res;
}
};
``` | 1 | 0 | ['C++'] | 0 |
get-equal-substrings-within-budget | Easy Java Solution || Beats 98% of Java Users . | easy-java-solution-beats-98-of-java-user-wl7e | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | zzzz9 | NORMAL | 2025-02-12T16:35:19.476277+00:00 | 2025-02-12T16:35:19.476277+00:00 | 26 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int equalSubstring(String s, String t, int maxCost) {
int n = s.length() ;
int[] costs = new int[n] ;
for( int i=0 ; i<n ; ++i ){
costs[i] = Math.abs( s.charAt(i) - t.charAt(i) ) ;
}
int rs = 0 ;
int start = 0 ;
int curr = 0 ;
for( int i=0 ; i<n ; ++i ){
curr += costs[i] ;
while( curr > maxCost ){
curr -= costs[ start++ ] ;
}
rs = Math.max( rs , i - start + 1 ) ;
}
return rs ;
}
}
``` | 1 | 0 | ['String', 'Sliding Window', 'Prefix Sum', 'Java'] | 0 |
get-equal-substrings-within-budget | Python, Sliding Window, T=O(n), S=O(1) | python-sliding-window-ton-so1-by-aakarsh-rxcd | Intuition
This problem can be solved by Sliding Window approach, as maximum length of substring is asked.
Idea is to keep expanding the window to right in each | Aakarsh-Lohani | NORMAL | 2025-01-14T18:47:57.029419+00:00 | 2025-01-14T18:49:28.020440+00:00 | 19 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1. This problem can be solved by Sliding Window approach, as maximum length of substring is asked.
2. Idea is to keep expanding the window to right in each step and shrinking it from left, if it exceeds the maxCost.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Initialize the left and right to 0.(tracking the window)
2. Run 'for' loop to expand the window , with 'right' as the loop variable.
3. Add the cost to currCost.
4. If the CurrCost exceeds the maxCost , shrink the window by reducing cost by left index and incrementing left variable, until it satisfies the condition.
5. Update the maxLen variable as current left,right (window) is a candidate window.
6. Return the maxLen variable.
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def equalSubstring(self, s: str, t: str, maxCost: int) -> int:
maxLen=0
left,right=0,0
currCost=0
for right in range(len(s)):
currCost+=abs(ord(s[right])-ord(t[right]))
while currCost>maxCost:
currCost-=abs(ord(s[left])-ord(t[left]))
left+=1
maxLen=max(right-left+1,maxLen)
return maxLen
``` | 1 | 0 | ['String', 'Sliding Window', 'Python3'] | 0 |
get-equal-substrings-within-budget | Simple O(n) | simple-on-by-sansk_ritu-0q5k | IntuitionThe cost is defined by diff of chars at corresponding index of both the strings.ApproachCalculate cost of each index by taking difference and store the | Sansk_Ritu | NORMAL | 2024-12-26T14:38:46.030633+00:00 | 2024-12-26T14:38:46.030633+00:00 | 18 | false | # Intuition
The cost is defined by diff of chars at corresponding index of both the strings.
# Approach
Calculate cost of each index by taking difference and store them in a vector. Now in the vector, look for longest subset with sum less than or equal to maxCost.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n) -> for storing cost at all indices
# Code
```cpp []
class Solution {
public:
int equalSubstring(string s, string t, int maxCost) {
vector<int> cost (s.size());
for (int i=0; i<s.size(); i++){
int diff = abs (s[i]-t[i]);
cost[i] = diff;
}
int start =0;
int curr =0;
int ans =0;
for (int i =0; i<cost.size(); i++){
curr += cost[i];
if (curr<=maxCost){
ans = max(ans, i-start+1);
}
if (curr>maxCost){
while (start<cost.size() && curr>maxCost){
curr -= cost[start];
start++;
}
}
}
return ans;
}
};
``` | 1 | 0 | ['Sliding Window', 'C++'] | 0 |
get-equal-substrings-within-budget | Beats 100% users🔥 | Approach explained✅ | Well-commented code | beats-100-users-approach-explained-well-ntbad | Approach\n- Use two pointers (start and end) to represent the current window.\n- Expand the window by moving the end pointer and calculate the cost of transform | sleekGeek28 | NORMAL | 2024-12-05T16:18:55.538543+00:00 | 2024-12-05T16:18:55.538581+00:00 | 19 | false | # Approach\n- Use two pointers (start and end) to represent the current window.\n- Expand the window by moving the end pointer and calculate the cost of transforming the substring `s[start:end]`into `t[start:end]`.\n- If the total cost exceeds maxCost, shrink the window by moving the start pointer and reducing the cost accordingly.\n- Track the maximum length of a valid substring during the process.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int start = 0; // Left pointer for the sliding window\n int cost = 0; // Current transformation cost\n int len = 0; // Maximum length of a valid substring\n\n for (int end = 0; end < s.size(); end++) {\n // Add the transformation cost for the current character\n cost += abs(s[end] - t[end]);\n\n // Shrink the window if the cost exceeds maxCost\n while (cost > maxCost) {\n cost -= abs(s[start] - t[start]); // Reduce cost\n start++; // Move the start pointer\n }\n\n // Update the maximum length of the valid substring\n len = max(len, end - start + 1);\n }\n\n return len;\n }\n};\n``` | 1 | 0 | ['String', 'Sliding Window', 'C++'] | 1 |
get-equal-substrings-within-budget | Must Watch✅💯Easiest Sliding Window Approach With Detailed Explanation💯✅ | must-watcheasiest-sliding-window-approac-nzxi | Intuition\n- Given two strings s and t of equal length, and an integer maxCost, the task is to find the maximum length of a substring that can be made equal to | Ajay_Kartheek | NORMAL | 2024-09-11T20:47:24.892317+00:00 | 2024-09-11T20:47:24.892346+00:00 | 3 | false | # Intuition\n- Given two strings s and t of equal length, and an integer maxCost, the task is to find the maximum length of a substring that can be made equal to the corresponding substring of t by changing characters in s, where the cost of changing a character is the absolute difference between their ASCII values. The total cost of changes must not exceed maxCost.\n\n# Approach\n1. Sliding Window Technique:\n\n - We use a sliding window to keep track of the current substring being compared between s and t.\nThe idea is to maintain a window of characters from s and check the cost of converting this substring into the corresponding characters in t.\n\n - We expand the window by adding characters from s and calculating the transformation cost between s and t. If the cost exceeds maxCost, we shrink the window from the left.\n\n2. Window Adjustment:\n\n - For each character at index j in s, we calculate the difference with t[j] and add it to the current window cost.\nIf the window cost exceeds maxCost, we shrink the window from the left by incrementing the starting index i and reducing the cost accordingly.\n\n3. Max Length Update:\n\n - While maintaining the sliding window, we keep track of the maximum length of the substring that satisfies the condition (where the total transformation cost does not exceed maxCost).\n\n# Complexity\n- Time complexity:\nO(n) where n is the length of the strings s and t. Each character is processed once as part of the sliding window, resulting in linear time complexity.\n\n- Space complexity:\nO(1) as the algorithm uses only a few extra variables (for tracking the indices and cost), and the space used does not depend on the size of the input strings.\n# Code\n```python3 []\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n i = 0\n curr_wind = 0 # Initialize window cost\n max_length = 0 # Store maximum valid substring length\n \n for j in range(len(s)): # Iterate over each character in the string\n # Add cost of current character difference to window\n curr_wind += abs(ord(s[j]) - ord(t[j]))\n \n # If window cost exceeds maxCost, shrink the window\n while curr_wind > maxCost:\n curr_wind -= abs(ord(s[i]) - ord(t[i])) # Remove cost of leftmost character\n i += 1 # Move the start of the window to the right\n \n # Update maximum length of valid window\n max_length = max(max_length, j - i + 1)\n \n return max_length \n```\n```Java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int i = 0, currWind = 0, maxLength = 0;\n \n for (int j = 0; j < s.length(); j++) {\n // Add the cost of transforming s[j] to t[j] to the current window\n currWind += Math.abs(s.charAt(j) - t.charAt(j));\n \n // If the current window cost exceeds maxCost, shrink the window from the left\n while (currWind > maxCost) {\n currWind -= Math.abs(s.charAt(i) - t.charAt(i));\n i++;\n }\n \n // Update the maximum length of a valid substring\n maxLength = Math.max(maxLength, j - i + 1);\n }\n \n return maxLength;\n }\n}\n \n```\n```C++ []\nclass Solution {\npublic:\n int equalSubstring(string s, string t, int maxCost) {\n int i = 0, currWind = 0, maxLength = 0;\n \n for (int j = 0; j < s.length(); j++) {\n // Add the cost of transforming s[j] to t[j] to the current window\n currWind += abs(s[j] - t[j]);\n \n // If the current window cost exceeds maxCost, shrink the window from the left\n while (currWind > maxCost) {\n currWind -= abs(s[i] - t[i]);\n i++;\n }\n \n // Update the maximum length of a valid substring\n maxLength = max(maxLength, j - i + 1);\n }\n \n return maxLength;\n }\n};\n \n``` | 1 | 0 | ['String', 'Sliding Window', 'C++', 'Java', 'Python3'] | 0 |
get-equal-substrings-within-budget | Java O(N) Soln | Beats 99.3% in TC | Good Readability | Beginner's Friendly | java-on-soln-beats-993-in-tc-good-readab-of1y | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | karan_s01 | NORMAL | 2024-08-26T16:27:49.532466+00:00 | 2024-08-26T16:28:18.411870+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity : O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int[] cost = new int[s.length()];\n for (int i=0 ; i<cost.length ; i++){\n int temp = s.charAt(i) - t.charAt(i);\n if (temp<0){\n temp = -temp;\n }\n cost[i] = temp;\n }\n\n if (cost.length == 1){\n if (cost[0] <= maxCost){\n return 1;\n }\n return 0;\n }\n\n int start = 0;\n int currCost = 0;\n int maxLength = 0;\n\n for (int end = 0; end < cost.length; end++) {\n currCost += cost[end];\n\n while (currCost > maxCost && start <= end) {\n currCost -= cost[start];\n start++;\n }\n\n maxLength = Math.max(maxLength, end - start + 1);\n }\n\n return maxLength;\n }\n}\n```\n# ---------------------------------------------------------\n# .......................Don\'t forget to upvote.......................\n# --------------------------------------------------------- | 1 | 0 | ['String', 'Sliding Window', 'Java'] | 0 |
get-equal-substrings-within-budget | 💯Beats 97%💯 Faster✅ Sliding Window 🔥🎯Java☕ | beats-97-faster-sliding-window-java-by-v-j1yv | Intuition\nTo find the maximum length of a substring that can be transformed within a given cost, we can utilize a sliding window approach. By maintaining a win | vanshtrivedi12345 | NORMAL | 2024-06-01T11:00:40.758693+00:00 | 2024-06-01T11:00:40.758736+00:00 | 1 | false | # Intuition\nTo find the maximum length of a substring that can be transformed within a given cost, we can utilize a sliding window approach. By maintaining a window with two pointers, we can efficiently calculate the cost of transforming the substring and adjust the window size to maximize the length without exceeding the given cost.\n\n# Approach\n1. Calculate Differences:\n\nFirst, compute the absolute differences between corresponding characters of the strings s and t. Store these differences in an array arr.\n\n2. Sliding Window:\n\n- Initialize two pointers, l and r, both starting at the beginning of the array.\n- Use a variable sum to keep track of the current transformation cost of the substring within the window [l, r].\n- Expand the window by moving r to the right and adding the difference to sum as long as the sum does not exceed maxCost.\n- If the sum exceeds maxCost, shrink the window by moving l to the right and subtracting the corresponding difference from sum.\nKeep track of the maximum length of the window that satisfies the condition.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n\n# Code\n```\nclass Solution {\n public int equalSubstring(String s, String t, int maxCost) {\n int n=s.length();\n int arr[]=new int[n];\n for(int i=0;i<n;i++)\n {\n arr[i]=Math.abs(s.charAt(i)-t.charAt(i));\n\n }\n int count=-1;\n int sum=0;\n int l=0;\n int r=0;\n \n while(l<=n-1)\n { \n \n if(r<n&&sum+arr[r]<=maxCost)\n {\n sum=sum+arr[r];\n int c=r-l+1;\n count = (c > count) ? c : count;\n r++;\n }\n else\n {\n sum=sum-arr[l];\n l++;\n }\n\n }\n return count;\n }\n}\n```\n | 1 | 0 | ['Java'] | 0 |
get-equal-substrings-within-budget | Python 3 solution (sliding window) | python-3-solution-sliding-window-by-iloa-dbgs | Code\npy\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n costs = [abs(ord(a) - ord(b)) for a, b in zip(s, t)]\n | iloabachie | NORMAL | 2024-05-31T19:03:21.520996+00:00 | 2024-05-31T19:03:21.521028+00:00 | 1 | false | # Code\n```py\nclass Solution:\n def equalSubstring(self, s: str, t: str, maxCost: int) -> int:\n costs = [abs(ord(a) - ord(b)) for a, b in zip(s, t)]\n left = result = total = 0\n for right in range(len(costs)):\n total += costs[right]\n while left <= right and total > maxCost:\n total -= costs[left]\n left += 1\n if result < (new := right - left + 1):\n result = new\n return result \n``` | 1 | 0 | ['Python3'] | 0 |
get-equal-substrings-within-budget | Simple and easy solution with comments ✅✅ | simple-and-easy-solution-with-comments-b-an5j | Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | vaibhav2112 | NORMAL | 2024-05-30T15:13:59.902314+00:00 | 2024-05-30T15:13:59.902348+00:00 | 0 | false | # Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n // Method 1 - Sliding window\n // TC = O(N), SC = O(1)\n int equalSubstring(string s, string t, int maxCost) {\n int ans = 0, i = 0, j = 0, n = s.length(), diff = 0;\n\n while(j < n){\n // calculate difference\n diff = diff + abs(s[j] - t[j]);\n\n // if diff <= maxCost then store ans\n if(diff <= maxCost){\n ans = max(ans, (j-i+1));\n j++;\n }\n // else increment i till diff > maxCost\n else{\n while(diff > maxCost){\n diff = diff - abs(s[i] - t[i]);\n i++;\n }\n j++;\n }\n }\n\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.