question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-or | Focus on the largest bit | focus-on-the-largest-bit-by-abc32-swlt | Intuition\n Describe your first thoughts on how to solve this problem. \nDoing *2 is the same as shifting left (<<1). Here, we will focus on the maximum bit (=l | abc32 | NORMAL | 2024-01-04T08:36:33.964590+00:00 | 2024-01-04T08:36:33.964610+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDoing *2 is the same as shifting left (<<1). Here, we will focus on the maximum bit (=l). To maximize the answer, we need to make at least l as large as possible. If you think about it that way, it turns out that it\'s best to shift a single element k times. This is because if we operate k-1 times on nums[i] and once on nums[j], if we instead operate k times on nums[i], we get l+=1.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\ntypedef long long ll;\nclass Solution {\npublic:\n long long maximumOr(vector<int>& nums, int k) {\n int n=nums.size();\n vector<ll>l(n+1),r(n+1);\n for(int i=0;i<n-1;i++){\n l[i+1]|=l[i]|nums[i];\n }\n for(int i=n-1;i>=1;i--){\n r[i-1]|=r[i]|nums[i];\n }\n ll ans=0;\n for(int i=0;i<n;i++){\n ll tmp=l[i]|r[i]|((ll)nums[i]<<k);\n ans=max(ans,tmp);\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | KMP | kmp-by-votrubac-kg3h | Intuition: if we match right-to-left, we can greedily take the largest prefix in words that is also a suffix in target.\n> It can be proven by a contradiction. | votrubac | NORMAL | 2024-09-15T04:00:48.455411+00:00 | 2024-09-15T20:39:58.468552+00:00 | 2,668 | false | **Intuition:** if we match right-to-left, we can greedily take the largest prefix in `words` that is also a suffix in `target`.\n> It can be proven by a contradiction. As a quick example, say we matched two prefixes ["abc]["def"].\n> - If there is a longer second prefix, e.g. ["ab]["cdef"], picking it will never make the result worse.\n> - However, if we use a shorter second prefix, e.g. ["abc]?["ef"], the result *could* become worse.\n\n\nNow, the trick is how to find the largest prefix/suffix efficiently.\n\nFor that, we employ the KMP algorithm. The prefix function for `words[i] + "#" + target` returns the prefix array.\n\nThe corresponding element of that array shows the longest suffix that is also a prefix.\n\n> We track the maximum prefix/suffix size for each position in `target` using the `ps` array. \n\nThe `prefix_function` method is taken as-is from the CP-A web site.\n\n**Complexity Analysis**\n- Time: O(n + k * m), where n is len(words), m is len(target) and k is the number of words.\n- Memory: O(n + k * m)\n\n**C++**\n```cpp \nvector<int> prefix_function(const string &s) {\n int n = (int)s.length();\n vector<int> pi(n);\n for (int i = 1; i < n; i++) {\n int j = pi[i-1];\n while (j > 0 && s[i] != s[j])\n j = pi[j-1];\n if (s[i] == s[j])\n j++;\n pi[i] = j;\n }\n return pi;\n} \nint minValidStrings(vector<string>& words, string target) {\n vector<int> ps(target.size() + 1);\n for (const auto &w : words) {\n auto pi = prefix_function(w + "#" + target);\n for (int i = 1; i <= target.size(); ++i)\n ps[i] = max(ps[i], pi[w.size() + i]);\n }\n int len = target.size(), res = 0;\n for (; len && ps[len]; ++res)\n len -= ps[len];\n return len == 0 ? res : -1;\n}\n``` | 49 | 0 | ['C'] | 11 |
minimum-number-of-valid-strings-to-form-target-ii | easy solutions | z-algorithm | c++ | greedy | easy-solutions-z-algorithm-c-greedy-by-r-5h7c | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nuse z-algothm to calcul | rishendra2003 | NORMAL | 2024-09-15T04:17:45.000373+00:00 | 2024-09-15T04:32:31.239866+00:00 | 1,287 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nuse z-algothm to calculate the longest substring of target that begins at position k and is a prefix of any word in words and it is stored in array match then use greedy algorithm to calculate minimum steps\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minValidStrings(vector<string>& words, string target) {\n int n = target.size();\n vector<int> match(n, 0);\n for (auto& word : words) {\n string s = word + "#" + target;\n int excess = word.size() + 1;\n int nn = s.size();\n // z-algorithm\n vector<int> z(nn);\n int x = 0, y = 0;\n for (int i = 1; i < nn; i++) {\n z[i] = max(0, min(z[i - x], y - i + 1));\n while (i + z[i] < nn && s[z[i]] == s[i + z[i]]) {\n x = i;\n y = i + z[i];\n z[i]++;\n }\n if (i >= excess && z[i] > 0)\n match[i - excess] = max(match[i - excess], z[i]);\n }\n }\n // greedy algorithm\n int steps =0,currend=0,farthest=0;\n for(int i=0; i<n; i++){\n farthest = max(farthest, i+match[i]);\n if(i==currend){\n steps++;\n currend =farthest;\n if(currend>=n) break;\n }\n }\n // if we can\'t form the target\n if(currend<n) return -1;\n return steps;\n }\n};\n``` | 16 | 1 | ['Greedy', 'C++'] | 2 |
minimum-number-of-valid-strings-to-form-target-ii | 2 Approaches with O(m + n) | dp[i] <= dp[j] for i <= j | 2-approaches-with-om-n-dpi-dpj-for-i-j-b-az31 | Approach 1: Aho-Corasick + DP + Greedy\n## Idea\n- dp[i] stores the answer for target[...i]\n- Important observation: dp[i] <= dp[j] for i <= j\n - Why ? Becau | lone17 | NORMAL | 2024-09-15T04:29:50.970287+00:00 | 2024-09-27T20:56:51.782931+00:00 | 897 | false | # Approach 1: Aho-Corasick + DP + Greedy\n## Idea\n- `dp[i]` stores the answer for `target[...i]`\n- **Important observation**: `dp[i] <= dp[j] for i <= j`\n - Why ? Because `target[i...j]` is also a combination of prefixes of `words`.\n - If this is not clear to you, @votrubac has a nice explanation in his [solution](https://leetcode.com/problems/minimum-number-of-valid-strings-to-form-target-ii/solutions/5788346/kmp). Please check it out.\n- So for each position `i`, we just need to find the longest suffix of `target[...i]` which is also a prefix of `words`. The Aho-Corasick algorithm on Trie allows us to do that.\n - For more details about Aho-Corasick, see:\n - [Aho-Corasick algorithm - Algorithms for Competitive Programming](https://cp-algorithms.com/string/aho_corasick.html)\n - https://web.stanford.edu/class/archive/cs/cs166/cs166.1166/lectures/02/Slides02.pdf \n - Basically, it is a general case of KMP on a set of patterns. \n\n## Complexity\n- Time complexity: $$O(m + n)$$\n - $$O(m)$$ for building the trie with $$m$$ being the total words length\n - $$O(n)$$ for calculating the dp with $$n$$ being the length of `target`\n\n- Space complexity: $$O(m + n)$$\n - $$O(m)$$ for the trie\n - $$O(n)$$ for the dp array \n - The dp can be done in $$O(1)$$ space, making the overal space complexity $$O(m)$$. See below for details.\n\n\n\n\n\n\n# Approach 2: Rolling Hash + Sliding Window + DP + Greedy\n## Idea\n- Same dp array as above.\n- **We make another important observation**: \n - If the longest match for `dp[r]` starts from `l`\n - then the longest match for `dp[r + 1]` cannot starts before `l`\n\n## Complexity\n- Time complexity: $$O(n + m)$$\n - Compute the rolling hash for all possible prefix, this is $$O(m)$$\n - Perform sliding window to find the longest postfix matched at each position, this is $$O(n)$$\n- Space complexity: $$O(m + n)$$\n - $$O(m)$$ for storing all the prefix hashes\n - $$O(n)$$ for the dp array\n - The dp can be done in $$O(1)$$ space, making the overal space complexity $$O(m)$$. See below for details.\n\nNote: This takes significantly less space than approach 1, this could be that the Trie is expensive to store, or maybe it\'s just that my poor implementation of Aho-Corasick is poor.\n\n\n## An even faster implementation\nIf you don\'t like the `PolynomialRollingHash` class and want to implement rolling hash directly to get the best speed possible, I also got you covered. Please check the 3rd code tab.\n\n\n\n# Making the space complexity O(m)\nAs suggested by @zsq007 in his [comment](https://leetcode.com/problems/minimum-number-of-valid-strings-to-form-target-ii/solutions/5788552/2-approaches-with-om-n-dpi-dpj-for-i-j/comments/2632054), the dp part can be done in $$O(1)$$ space.\n\nThe idea is, it\'s observed that the dp array would consists of spans of equal numbers, e.g. `1112222223444...`\n \n=> So we can just keep track of when `l` moves to a new span, no need to store the whole dp array.\n\nThe code for rolling hash with $$O(m)$$ space is included in the 4th code tab. Note that this can also be applied for the Aho-Corasick approach, but I leave it as an excercise for the reader.\n\n\n\n# Code\n```python [AhoCorasick]\nclass AhoCorasick:\n def __init__(self, patterns: List[str]):\n self.trie = dict()\n self.vocab = set(\'qwertyuiopasdfghjklzxcvbnm\')\n root = self.trie\n root[\'parent\'] = None\n root[\'$\'] = 0 # len at root\n\n # build the trie\n for p in patterns:\n cur = root\n l = 0\n for c in p:\n if c not in cur:\n cur[c] = {\'parent\': cur}\n cur = cur[c]\n l += 1\n # store the length at every prefix\n cur[\'$\'] = l\n\n # construct suffix\n # refer to these materials for more details about AhoCorasick\n # - https://cp-algorithms.com/string/aho_corasick.html\n # - https://web.stanford.edu/class/archive/cs/cs166/cs166.1166/lectures/02/Slides02.pdf \n parent = None\n root[\'suffix\'] = None\n q = deque([root])\n while q:\n for _ in range(len(q)):\n cur = q.popleft()\n for c, child in cur.items():\n if c not in self.vocab:\n continue\n\n suffix = cur[\'suffix\']\n while suffix and c not in suffix:\n suffix = suffix[\'suffix\']\n if suffix:\n child[\'suffix\'] = suffix[c]\n else:\n child[\'suffix\'] = root\n\n q.append(child)\n\n\n def match(self, target: str):\n cur = self.trie\n for c in target:\n while c not in cur and cur[\'suffix\']:\n cur = cur[\'suffix\']\n\n if c in cur:\n cur = cur[c]\n\n # the first match that ends at each position (which is also the longest)\n yield cur[\'$\']\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n trie = AhoCorasick(words)\n \n n = len(target)\n i = 0\n dp = [inf] * n + [0] # 0 at the end as the sentinel value\n for m in trie.match(target):\n # only consider the longest match\n # because dp[i] <= dp[j] for i <= j\n dp[i] = min(dp[i], dp[i - m] + 1)\n\n # early stop when there can\'t be any match\n if dp[i] == inf:\n return -1\n i += 1\n \n return dp[-2]\n```\n\n```python [Rolling Hash + Sliding Window]\nclass PolynomialRollingHash:\n M = 10**9 + 9\n P = 31 # 31, 53, 29791, 11111, 111111\n P_INV = pow(P, M - 2, M)\n POWS = [1]\n\n def __init__(self, sequence=""):\n self.sequence = deque()\n self.hash = 0\n for element in sequence:\n self.append(element)\n\n def get_pow(self, i) -> int:\n while len(self.POWS) <= i:\n self.POWS.append(self.POWS[-1] * self.P % self.M)\n\n return self.POWS[i]\n\n def encode(self, element) -> int:\n """\n Encode a single element\n\n Note: avoid producing an encoding of 0.\n E.g. a -> 0 then the hashes for a, aa, aaa, ... are all 0.\n """\n\n # for lower-cased str inputs\n return ord(element) - 96\n\n def appendleft(self, element) -> int:\n x = self.encode(element)\n p = self.get_pow(len(self.sequence))\n self.sequence.appendleft(element)\n\n self.hash = (x * p + self.hash) % self.M\n\n return self.hash\n\n def popleft(self) -> int:\n element = self.sequence.popleft()\n x = self.encode(element)\n p = self.get_pow(len(self.sequence))\n\n self.hash = (self.hash - x * p) % self.M\n\n return self.hash\n\n def append(self, element) -> int:\n x = self.encode(element)\n self.sequence.append(element)\n\n self.hash = (self.hash * self.P + x) % self.M\n\n return self.hash\n\n def pop(self) -> int:\n element = self.sequence.pop()\n x = self.encode(element)\n\n self.hash = ((self.hash - x) * self.P_INV) % self.M\n\n return self.hash\n\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n # compute the hash for all prefix\n prefixes = set()\n for w in words:\n hasher = PolynomialRollingHash()\n for c in w:\n hasher.append(c)\n prefixes.add(hasher.hash)\n \n n = len(target)\n dp = [inf] * n + [0] # 0 at the end as the sentinel value\n\n """\n Important observation:\n \n If longest match at dp[r] starts at l \n then longest match at dp[r + 1] cannot starts before l\n\n Thus a sliding window is applicable here.\n """\n\n l = 0\n hasher = PolynomialRollingHash()\n for r in range(n):\n # expand the window one step to the right\n hasher.append(target[r])\n\n # shrink the window from the left until found a valid prefix\n h = hasher.hash\n while l <= r and h not in prefixes:\n h = hasher.popleft()\n l += 1\n\n # early stop if no valid prefix found\n if l > r:\n return -1\n\n # update the dp\n dp[r] = dp[l - 1] + 1\n \n return dp[-2]\n```\n\n```python [Even faster]\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n p = 31 # 31, 53, 29791, 11111, 111111\n M = 10**9 + 7\n power = [1]\n\n n = len(target)\n for _ in range(n + 1):\n power.append((power[-1] * p) % M)\n\n # compute the hash for all prefix\n prefixes = set()\n for w in words:\n m = len(w)\n h = 0\n for c in w:\n h = (h * p + (ord(c) - 96)) % M\n prefixes.add(h)\n \n dp = [inf] * n + [0] # 0 at the end as the sentinel value\n\n """\n Important observation:\n \n If longest match at dp[r] starts at l \n then longest match at dp[r + 1] cannot starts before l\n\n Thus a sliding window is applicable here.\n """\n\n h = 0\n l = 0\n for r in range(n):\n # expand the window one step to the right\n h = (h * p + (ord(target[r]) - 96)) % M\n\n # shrink the window from the left until found a valid prefix\n while l <= r and h not in prefixes:\n x = ord(target[l]) - 96\n h = (h - (x * power[r - l])) % M\n l += 1\n\n # early stop if no valid prefix found\n if l > r:\n return -1\n\n # update the dp\n dp[r] = dp[l - 1] + 1\n \n return dp[-2]\n```\n\n```python [O(m) space]\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n p = 53 # 31, 53, 29791, 11111, 111111\n M = 10**9 + 7\n power = [1]\n\n n = len(target)\n for _ in range(n + 1):\n power.append((power[-1] * p) % M)\n\n # compute the hash for all prefix\n prefixes = set()\n for w in words:\n m = len(w)\n h = 0\n for c in w:\n h = (h * p + (ord(c) - 96)) % M\n prefixes.add(h)\n \n\n """\n Important observation:\n \n - If longest match at dp[r] starts at l \n then longest match at dp[r + 1] cannot starts before l\n\n => Thus a sliding window is applicable here.\n\n - Additionally, the dp array will consists of spans of equal numbers, e.g. 1112222223444...\n => So we can just keep track when l move to a new span, no need to store the whole dp array.\n """\n\n h = 0\n l = 0\n span_start = 0\n ans = 1\n for r in range(n):\n # expand the window one step to the right\n h = (h * p + (ord(target[r]) - 96)) % M\n\n # shrink the window from the left until found a valid prefix\n while l <= r and h not in prefixes:\n x = ord(target[l]) - 96\n h = (h - (x * power[r - l])) % M\n l += 1\n\n # early stop if no valid prefix found\n if l > r:\n return -1\n\n # when l moves to a new span is also when r starts the next span\n if l > span_start:\n ans += 1\n span_start = r\n \n return ans\n```\n\n*This problem helped me reach Guardian after 2 years of practicing.* | 15 | 0 | ['Dynamic Programming', 'Greedy', 'Trie', 'Sliding Window', 'Rolling Hash', 'Python3'] | 8 |
minimum-number-of-valid-strings-to-form-target-ii | [Python3] kmp + dp | python3-kmp-dp-by-ye15-shkh | \npython\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target)\n vals = [set() for _ in range(n | ye15 | NORMAL | 2024-09-15T04:01:08.262574+00:00 | 2024-09-16T22:35:32.538324+00:00 | 971 | false | \n```python\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target)\n vals = [set() for _ in range(n)]\n \n def kmp(pattern, text):\n k = 0\n lps = [0] \n for i in range(1, len(pattern)):\n while k and pattern[k] != pattern[i]: k = lps[k-1]\n if pattern[k] == pattern[i]: k += 1\n lps.append(k)\n k = 0\n ans = []\n for i, ch in enumerate(text): \n while k and (k == len(pattern) or pattern[k] != ch): k = lps[k-1]\n if pattern[k] == ch: k += 1\n ans.append(k)\n return ans\n\n for word in words: \n cand = kmp(word, target)\n for i, k in enumerate(cand): \n if k: vals[i].add(k)\n dp = [inf]*(n+1)\n dp[n] = 0 \n for i in range(n-1, -1, -1): \n for k in vals[i]:\n dp[i-k+1] = min(dp[i-k+1], 1 + dp[i+1])\n return dp[0] if dp[0] < inf else -1\n```\n\nAdding solution via Aho-Corasick algo \n```\nclass AhoCorasick:\n def __init__(self):\n self.root = {"parent": None, "suffix": None, "$": 0}\n \n def build(self, patterns: List[str]): \n for pattern in patterns:\n node = self.root\n size = 0\n for ch in pattern:\n if ch not in node: node[ch] = {"parent": node}\n node = node[ch]\n size += 1\n node["$"] = size\n queue = deque([self.root])\n while queue:\n for _ in range(len(queue)):\n node = queue.popleft()\n for ch, child in node.items():\n if ch not in ("parent", "suffix", "$"): \n suffix = node["suffix"]\n while suffix and ch not in suffix: suffix = suffix["suffix"]\n if suffix: child["suffix"] = suffix[ch]\n else: child["suffix"] = self.root\n queue.append(child)\n\n def match(self, text: str):\n ans = []\n node = self.root\n for ch in text:\n while ch not in node and node["suffix"]:\n node = node["suffix"]\n if ch in node: node = node[ch]\n ans.append(node["$"])\n return ans \n \n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target)\n trie = AhoCorasick()\n trie.build(words)\n dp = [inf]*(n+1)\n dp[n] = 0\n for i, x in reversed(list(enumerate(trie.match(target)))):\n if x == 0: return -1 \n dp[i+1-x] = min(dp[i+1-x], dp[i+1] + 1)\n return dp[0] \n``` | 12 | 0 | ['Python3'] | 4 |
minimum-number-of-valid-strings-to-form-target-ii | Video Explanation - 2 Approaches[Z-Algorithm & Hashing] (Complete journey starting from brute force) | video-explanation-2-approachesz-algorith-w7n3 | Explanation\n\nClick here for the video\n\n# Code\ncpp []\nstruct SegTree {\npublic:\n \n SegTree (int _n) : n (_n) {\n tree.resize(4*n, 1e9);\n }\ | codingmohan | NORMAL | 2024-09-15T07:18:57.902395+00:00 | 2024-09-15T07:18:57.902417+00:00 | 367 | false | # Explanation\n\n[Click here for the video](https://youtu.be/SWhyXCNdb0o)\n\n# Code\n```cpp []\nstruct SegTree {\npublic:\n \n SegTree (int _n) : n (_n) {\n tree.resize(4*n, 1e9);\n }\n \n int query (int x, int y) {\n return query (x, y, 0, n-1, 0);\n }\n \n void update (int ind, int val) {\n update (ind, val, 0, n-1, 0);\n }\n \nprivate:\n \n vector<int> tree;\n int n;\n \n int query (int x, int y, int l, int r, int i) {\n if (r < x || l > y) return 1e9;\n if (l >= x && r <= y) return tree[i];\n \n int m = (l+r) >> 1;\n return min(\n query (x, y, l, m, i*2+1),\n query (x, y, m+1, r, i*2+2)\n );\n }\n \n void update (int ind, int val, int l, int r, int i) {\n if (l == r) {\n tree[i] = val;\n return;\n }\n \n int m = (l+r) >> 1;\n if (m >= ind) update (ind, val, l, m, i*2+1);\n else update (ind, val, m+1, r, i*2+2);\n \n tree[i] = min(tree[i*2+1], tree[i*2+2]);\n }\n};\n\n\nclass Solution {\n \n vector<int> z_function(string s) {\n int n = s.size();\n vector<int> z(n);\n int l = 0, r = 0;\n for(int i = 1; i < n; i++) {\n if(i < r) {\n z[i] = min(r - i, z[i - l]);\n }\n while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n z[i]++;\n }\n if(i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n return z;\n }\n \n vector<int> longest_match;\n\n void AmmendLongestMatch (const string& word, const string& target) {\n string s = word + "$" + target;\n vector<int> z = z_function(s);\n \n for (int i = 0; i < target.length(); i ++) {\n longest_match[i] = max (longest_match[i], z[i+word.length()+1]);\n }\n }\n \npublic:\n int minValidStrings(vector<string>& words, string target) {\n longest_match.clear();\n longest_match.resize(target.length(), 0);\n \n for (auto w: words) AmmendLongestMatch (w, target);\n \n int n = target.size();\n SegTree max_len_tree(n+1);\n max_len_tree.update(n, 0);\n \n for (int j = n-1; j >= 0; j --) {\n int len = longest_match[j];\n if (len == 0) continue;\n \n int max_len = 1 + max_len_tree.query (j+1, j+len);\n max_len_tree.update (j, max_len); \n }\n \n int ans = max_len_tree.query(0, 0);\n if (ans == 1e9) ans = -1;\n return ans;\n }\n};\n\n/*\n#define pii pair<int, int>\n#define F first\n#define S second\n\nconst int N = 5e4+1;\nconst int P = 31;\nconst int M = 1e9+7;\n\nconst int INF = 1e9;\n\ntypedef long long int ll;\n\nclass Solution {\n \n vector<ll> p_pow;\n vector<ll> inv_p_pow;\n \n // a^b % M\n ll FastPower (ll a, ll b) {\n ll ans = 1;\n while (b) {\n if (b&1) ans = (ans * a) % M;\n a = (a*a) % M;\n b /= 2;\n }\n return ans;\n }\n \n void ComputePower() {\n if (!p_pow.empty()) return;\n \n p_pow.resize(N, 1);\n for (int i = 1; i < N; i ++)\n p_pow[i] = (p_pow[i-1] * P) % M;\n \n inv_p_pow.resize(N, 1);\n \n inv_p_pow[N-1] = FastPower (p_pow[N-1], M-2);\n for (int i = N-2; i > 0; i --)\n inv_p_pow[i] = (inv_p_pow[i+1] * P) % M;\n }\n \n vector<ll> HashIt (const string& s) {\n int S = s.size();\n vector<ll> prefix_hash(S+1, 0);\n\n for (int i = 1; i <= S; i++) {\n ll cur = (p_pow[i] * (s[i-1]-\'a\'+1)) % M;\n prefix_hash[i] = (prefix_hash[i-1] + cur) % M;\n }\n return prefix_hash;\n }\n \n inline ll HashOfRange (int l, int r, vector<ll>& prefix_hash) { \n ll hash = (prefix_hash[r] - prefix_hash[l-1] + M) % M;\n return (hash * inv_p_pow[l-1]) % M;\n }\n \n int LongestMatching (int st, vector<ll>& prefix_hash_target, unordered_map<int, int>& hash_and_len) {\n int l = st, r = prefix_hash_target.size() - 1;\n \n while (l < r) {\n int m = (l+r) >> 1;\n int hash = HashOfRange (st, m+1, prefix_hash_target);\n \n auto it = hash_and_len.find(hash);\n if (it == hash_and_len.end()) r = m;\n else l = m+1;\n }\n \n int len = r - st + 1;\n int hash = HashOfRange (st, l, prefix_hash_target);\n if (hash_and_len.find(hash) == hash_and_len.end()) len--;\n return len;\n }\n \npublic:\n int minValidStrings(vector<string>& words, string target) {\n ComputePower();\n \n unordered_map<int, int> hash_and_len;\n for (auto w : words) {\n vector<ll> hash = HashIt(w);\n for (int l = 1; l < hash.size(); l ++) hash_and_len[hash[l]] = l;\n }\n \n int n = target.size();\n SegTree max_len_tree(n+2);\n max_len_tree.update(n+1, 0);\n \n vector<ll> prefix_hash_target = HashIt(target);\n \n for (int j = n; j > 0; j --) {\n int len = LongestMatching (j, prefix_hash_target, hash_and_len);\n if (len == 0) continue;\n \n int max_len = 1 + max_len_tree.query (j+1, j+len);\n max_len_tree.update (j, max_len); \n }\n \n int ans = max_len_tree.query(1, 1);\n if (ans == 1e9) ans = -1;\n return ans;\n }\n};\n*/\n``` | 9 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | String Hashing + Binary Search to find longest match | string-hashing-binary-search-to-find-lon-vlkj | \nfrom collections import defaultdict\n\nclass SHash:\n def __init__(self, input_string: str):\n self.input_string = input_string\n self.prime1 | theabbie | NORMAL | 2024-09-15T04:00:49.640853+00:00 | 2024-09-15T04:00:49.640885+00:00 | 663 | false | ```\nfrom collections import defaultdict\n\nclass SHash:\n def __init__(self, input_string: str):\n self.input_string = input_string\n self.prime1 = 31\n self.prime2 = 37\n self.mod1 = 10**9 + 7\n self.mod2 = 10**9 + 9\n self.precompute_hashes()\n \n def precompute_hashes(self):\n n = len(self.input_string)\n self.hash1 = [0] * (n + 1)\n self.hash2 = [0] * (n + 1)\n self.pow1 = [1] * (n + 1)\n self.pow2 = [1] * (n + 1)\n \n for i in range(n):\n self.hash1[i + 1] = (self.hash1[i] * self.prime1 + ord(self.input_string[i])) % self.mod1\n self.hash2[i + 1] = (self.hash2[i] * self.prime2 + ord(self.input_string[i])) % self.mod2\n self.pow1[i + 1] = (self.pow1[i] * self.prime1) % self.mod1\n self.pow2[i + 1] = (self.pow2[i] * self.prime2) % self.mod2\n \n def hash(self, start: int, end: int):\n hash_val1 = (self.hash1[end + 1] - self.hash1[start] * self.pow1[end - start + 1]) % self.mod1\n hash_val2 = (self.hash2[end + 1] - self.hash2[start] * self.pow2[end - start + 1]) % self.mod2\n \n return (hash_val1, hash_val2)\n \nclass SegmentTree:\n def __init__(self, data, default=float(\'inf\'), func=min):\n self._default = default\n self._func = func\n self._len = len(data)\n self._size = _size = 1 << (self._len - 1).bit_length()\n\n self.data = [default] * (2 * _size)\n self.data[_size:_size + self._len] = data\n for i in reversed(range(_size)):\n self.data[i] = func(self.data[i + i], self.data[i + i + 1])\n\n def __delitem__(self, idx):\n self[idx] = self._default\n\n def __getitem__(self, idx):\n return self.data[idx + self._size]\n\n def __setitem__(self, idx, value):\n idx += self._size\n self.data[idx] = value\n idx >>= 1\n while idx:\n self.data[idx] = self._func(self.data[2 * idx], self.data[2 * idx + 1])\n idx >>= 1\n\n def __len__(self):\n return self._len\n\n def query(self, start, stop):\n start += self._size\n stop += self._size\n\n res_left = res_right = self._default\n while start < stop:\n if start & 1:\n res_left = self._func(res_left, self.data[start])\n start += 1\n if stop & 1:\n stop -= 1\n res_right = self._func(self.data[stop], res_right)\n start >>= 1\n stop >>= 1\n\n return self._func(res_left, res_right)\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target)\n dp = SegmentTree([float(\'inf\')] * (n + 1))\n dp[n] = 0\n groups = defaultdict(set)\n for w in words:\n shash = SHash(w)\n m = len(w)\n for l in range(1, m + 1):\n groups[l].add(shash.hash(0, l - 1))\n shash = SHash(target)\n for i in range(n - 1, -1, -1):\n beg = 1\n end = n - i\n while beg <= end:\n mid = (beg + end) // 2\n if shash.hash(i, i + mid - 1) in groups[mid]:\n beg = mid + 1\n else:\n end = mid - 1\n if beg - 1 > 0:\n dp[i] = min(dp[i], 1 + dp.query(i + 1, i + beg))\n if dp[0] == float(\'inf\'):\n return -1\n return dp[0]\n``` | 6 | 0 | ['Python'] | 3 |
minimum-number-of-valid-strings-to-form-target-ii | [Python3/ C++] KMP + Greedy - Simple Solutions | python3-c-kmp-greedy-simple-solutions-by-7hy4 | Intuition\n- Inspired from this post\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem | dolong2110 | NORMAL | 2024-09-22T04:08:28.704356+00:00 | 2024-09-22T04:08:28.704377+00:00 | 245 | false | # Intuition\n- Inspired from this [post](https://leetcode.com/problems/minimum-number-of-valid-strings-to-form-target-ii/solutions/5788346/kmp/)\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n##### 1. KMP + Greedy\n```python3 []\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n def prefix_function(s: str) -> List[int]:\n n = len(s)\n lps = [0 for _ in range(n)]\n for i in range(1, n):\n j = lps[i - 1]\n while j > 0 and s[i] != s[j]: j = lps[j - 1]\n if s[i] == s[j]: j += 1\n lps[i] = j\n return lps\n \n l = len(target)\n ps = [0 for _ in range(l + 1)]\n for word in words:\n lps = prefix_function(word + "#" + target)\n for i in range(1, l + 1):\n ps[i] = max(ps[i], lps[len(word) + i])\n res = 0\n while l and ps[l]:\n l -= ps[l]\n res += 1\n return res if l == 0 else -1\n```\n```C++ []\nvector<int> prefix_function(const string &s) {\n int n = (int)s.length();\n vector<int> pi(n);\n for (int i = 1; i < n; i++) {\n int j = pi[i-1];\n while (j > 0 && s[i] != s[j])\n j = pi[j-1];\n if (s[i] == s[j])\n j++;\n pi[i] = j;\n }\n return pi;\n} \nint minValidStrings(vector<string>& words, string target) {\n vector<int> ps(target.size() + 1);\n for (const auto &w : words) {\n auto pi = prefix_function(w + "#" + target);\n for (int i = 1; i <= target.size(); ++i)\n ps[i] = max(ps[i], pi[w.size() + i]);\n }\n int len = target.size(), res = 0;\n for (; len && ps[len]; ++res)\n len -= ps[len];\n return len == 0 ? res : -1;\n}\n``` | 4 | 0 | ['Array', 'String', 'Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | z-function + Jump game II | z-function-jump-game-ii-by-dmitrii_bokov-sd5v | Approach\nLet\'s find for each index of target maximum prefix length in words. It\'s easy to do using z-function. Then it\'s exactly jump game II https://leetco | dmitrii_bokovikov | NORMAL | 2024-09-15T15:25:47.548829+00:00 | 2024-09-15T15:39:16.000649+00:00 | 107 | false | # Approach\nLet\'s find for each index of target maximum prefix length in words. It\'s easy to do using z-function. Then it\'s exactly jump game II https://leetcode.com/problems/jump-game-ii/description/\n\n```cpp []\n vector<int> zFunction(string_view s) {\n int n = size(s);\n vector<int> z(n);\n for (int i = 1, l = 0, r = 0; i < n; ++i) {\n if (i <= r) {\n z[i] = min(r - i + 1, z[i - l]);\n }\n while (i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n ++z[i];\n }\n if (i + z[i] - 1 > r) {\n l = i, r = i + z[i] - 1;\n }\n }\n return z;\n }\n\n int jump(vector<int>& nums) {\n int ans = 0;\n for (int l = 0, r = 0, n = size(nums); r < n; ++ans) {\n int farthest = r;\n for (int i = l; i <= r; ++i) {\n farthest = max(farthest, nums[i] + i);\n }\n if (farthest == r) {\n return -1;\n }\n l = r;\n r = farthest;\n }\n return ans;\n }\n\n int minValidStrings(vector<string>& words, string t) {\n const int n = size(t);\n vector<int> prefixes(n);\n for (const auto& w: words) {\n const auto z = zFunction(w + \'#\' + t);\n for (int i = size(w) + 1; i < size(z); ++i) {\n prefixes[i - size(w) - 1] = max(prefixes[i - size(w) - 1], z[i]);\n }\n }\n return jump(prefixes);\n }\n``` | 4 | 0 | ['C++'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | KMP Algo | kmp-algo-by-ashishpatel17-t7bp | Intuition\nUse kmp to find the target string from backwards . We will check the longest common prefix from the words that matches with the target from the last | AshishPatel17 | NORMAL | 2024-09-15T07:50:15.248887+00:00 | 2024-09-15T07:50:15.248909+00:00 | 144 | false | # Intuition\nUse kmp to find the target string from backwards . We will check the longest common prefix from the words that matches with the target from the last . \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n\n5*1e6\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int>find(string ashu)\n {\n int n = ashu.size();\n vector<int>lps(n , 0);\n int j =0 ;\n int i =1 ;\n while(i < n )\n {\n if(ashu[i] == ashu[j])\n {\n j++;\n lps[i] = j;\n i++;\n }\n else\n {\n if(j!=0)\n {\n j = lps[j-1];\n }\n else{\n lps[i] = 0;\n i++;\n }\n }\n }\n return lps;\n }\n int minValidStrings(vector<string>& words, string target) {\n int n = words.size();\n vector<vector<int>>ashu;\n for(auto i : words)\n {\n ashu.push_back(find(i + "#" + target));\n }\n int len = target.size();\n int match =0 ;\n while(len > 0)\n {\n int ans = 0 ;\n for(int i = 0 ; i < n ; i++)\n {\n ans = max(ans , ashu[i][words[i].size() + len]);\n }\n if(ans == 0)return -1;\n match++;\n len -= ans ;\n }\n return match;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | 🔥Z-Function boils to Min Jumps II Easy Short Fast | Comments | C++ | z-function-boils-to-min-jumps-ii-easy-sh-1qlw | Complexity\nn = words.length(), t = target.length(), K = len of each words\n- Time complexity: O(n * (K+t))\n\n- Space complexity: O(n)\n##### This solution is | bramar2 | NORMAL | 2024-09-15T05:55:15.469506+00:00 | 2024-09-15T06:52:32.047084+00:00 | 187 | false | # Complexity\n`n = words.length(), t = target.length(), K = len of each words`\n- Time complexity: $$O(n * (K+t))$$\n\n- Space complexity: $$O(n)$$\n##### This solution is very close to the optimal solution and very fast considering the small size of the code for this solution.\n\n*Only with fast-IO and no other optimizations to the below code. Some inlining and unnecessary if-statements may improve the time.\n# Code\nThere is also the clean C++ code thats very short with no comments (relative to other sols).\n\n\n```cpp []\n#include <bits/stdc++.h>\nusing namespace std;\nvector<int> z_function(string s) {\n // Source: cp-algorithms dot com/string/z-function.html\n int n = s.size();\n vector<int> z(n);\n int l = 0, r = 0;\n for(int i = 1; i < n; i++) {\n if(i < r) {\n z[i] = min(r - i, z[i - l]);\n }\n while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n z[i]++;\n }\n if(i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n return z;\n}\nclass Solution {\n\npublic:\n //Solution for leetcode dot com/problems/jump-game-ii/description/\n int jump(vector<int>& nums) {\n int size = (int) nums.size();\n if(size == 1) return 0;\n vector<long long> minJumps(size, INT_MAX); // minJumps[i] is the min num of jumps to get to nums[i]\n minJumps[0] = 0;\n for(int i = 0; i < size; i++) {\n // No check for minJumps[i] == INT_MAX because the test cases are generated such that you can reach nums[n-1]\n for(int j = min(i + nums[i], size - 1); j > i; j--) {\n if(minJumps[j] <= minJumps[i] + 1) {\n break; // because then everything below is ALSO better/equal to this current permutation\n }else minJumps[j] = minJumps[i] + 1;\n }\n }\n return minJumps[size - 1];\n }\n int minValidStrings(vector<string>& words, string target) {\n int n = words.size();\n vector<int> match(target.size(), 0);\n // match[i] will be the longest match starting at index i using Any word.\n // So for example with target = "abcde", and words = ["bcd"]\n // match = {0, 3, 0, 0, 0}\n for(string& word : words) {\n string comb = word + "!" + target;\n vector<int> z = z_function(comb); // We use the z function\n // Definition of Z[i]:\n // (from cp-algorithms)\n // z[i] = the length of the longest string that is, at the same time, a prefix of $s$\u200A\n // and a prefix of the suffix of `s` starting at `i`.\n for(int i = 0; i < target.size(); i++) {\n // z[n + j + 1]\n // we notice comb[n+i+1] = target[i], because n is word.length and 1 for the separator \'!\'\n // that means z[n+i+1] = longest string that matches\n // : words[0...X-1] [prefix of comb]\n // : target[j...j+(X-1)] (which is target starting from index j) [suffix of comb]\n // X is the possible values, then Z[n+i+1] = max(all X that matches)\n // in other words, it is the longest string that can be matched\n // using this word at index j\n\n // Example: target = "abacda", word = "acb"\n // match {0, 0, 0, 0, 0, 0} ->\n // {\n // 1 [match \'a\'],\n // 0 [no match],\n // 2 [match \'ac\'],\n // 0 [no match],\n // 0 [no match],\n // 1 [match \'a\']\n // }\n match[i] = max(match[i], z[word.length() + i + 1]);\n }\n }\n // match[i] will be the longest length we can match from i\n // In other words, we can jump either from j= 0 --> match[i]\n // to match[i+j] using one operation/string\n\n match.push_back(0); // We add extra \'0\' for the end result (where everything is concatenated).\n int ans = jump(match);\n return ans >= INT_MAX ? -1 : ans;\n }\n};\n```\n```cpp [Clean C++]\n#include <bits/stdc++.h>\nusing namespace std;\nvector<int> z_function(string s) {\n int n = s.size();\n vector<int> z(n);\n int l = 0, r = 0;\n for(int i = 1; i < n; i++) {\n if(i < r) {\n z[i] = min(r - i, z[i - l]);\n }\n while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n z[i]++;\n }\n if(i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n return z;\n}\nclass Solution {\npublic:\n int jump(vector<int>& nums) {\n int size = (int) nums.size();\n if(size == 1) return 0;\n vector<long long> minJumps(size, INT_MAX);\n minJumps[0] = 0;\n for(int i = 0; i < size; i++) {\n for(int j = min(i + nums[i], size - 1); j > i; j--) {\n if(minJumps[j] <= minJumps[i] + 1) {\n break;\n }else minJumps[j] = minJumps[i] + 1;\n }\n }\n return minJumps[size - 1];\n }\n int minValidStrings(vector<string>& words, string target) {\n int n = words.size();\n vector<int> match(target.size(), 0);\n for(string& word : words) {\n string comb = word + "!" + target;\n vector<int> z = z_function(comb);\n for(int i = 0; i < target.size(); i++) {\n match[i] = max(match[i], z[word.length() + i + 1]);\n }\n }\n match.push_back(0);\n int ans = jump(match);\n return ans >= INT_MAX ? -1 : ans;\n }\n};\n```\n```cpp [Optimized (kinda)]\n// 98ms beats 85.71%, 14.96 MB beats 100.00%\n#include <bits/stdc++.h>\nusing namespace std;\nclass Solution {public: int minValidStrings(const vector<string>& words, const string& target) { return 0; }};\nauto init = ([]() -> char {\n ios_base::sync_with_stdio(0);\n ios::sync_with_stdio(false);\n cout.tie(nullptr);\n cin.tie(nullptr);\n char c[100][100\'002];\n int cl[101], z[100\'002], match[50\'002];\n ofstream out("user.out");\n int i, j, n, t, k, l, r, cc, nr, f, a, ff; char b;\n string line;\n while(getline(cin, line)) {\n for(j = 0, i = 2, n = line.length(), cl[0] = 0; i < n; i++)\n if(line[i] == \'"\') {\n cl[++j] = 0;\n i += 2;\n }else c[j][cl[j]++] = line[i];\n cin >> b; getline(cin, line); t = line.size()-1;\n for(i = 0; i <= t; i++)\n match[i] = 0;\n match[t+1]=0;\n while(j--) {\n c[j][cl[j]] = \'!\';\n for(k = 0; k < t; k++)\n c[j][cl[j]+k+1] = line[k];\n for(z[0] = 0, i = 1, l = 0, r = 0, cc = cl[j] + t + 1; i < cc && !(z[i]=0); i++) {\n if(i < r)\n z[i] = min(r-i, z[i-l]);\n while(i + z[i] < cc && c[j][z[i]] == c[j][i + z[i]])\n z[i]++;\n if(i + z[i] > r)\n l = i, r = i + z[i];\n }\n for(k = t; k --> 0;)\n if(z[cl[j] + k + 1] > match[k])\n match[k] = z[cl[j] + k + 1];\n }\n nr = f = a = 0;\n while(f < t && a <= t) { // credit: @niits\n for(ff = 0, i = nr; i <= f; i++) {\n if(i + match[i] > ff) ff = i + match[i];\n }\n nr = f+1, f = ff, a++;\n }\n out << (a <= t ? a : -1) << \'\\n\';\n }\n out.flush();\n exit(0);\n return 1;\n})();\n``` | 3 | 0 | ['String', 'Dynamic Programming', 'String Matching', 'C++'] | 2 |
minimum-number-of-valid-strings-to-form-target-ii | Easy Java Solution | Beginner Friendly | easy-java-solution-beginner-friendly-by-4yfwo | Intuition\nTo solve the problem of finding the minimum number of valid strings required to construct a target string, we need to determine how each word from th | Ram4366 | NORMAL | 2024-09-15T04:44:54.949300+00:00 | 2024-09-15T04:44:54.949349+00:00 | 340 | false | # Intuition\nTo solve the problem of finding the minimum number of valid strings required to construct a target string, we need to determine how each word from the list can contribute to forming the target. The goal is to efficiently track the minimum number of words needed through dynamic programming (DP). The problem essentially boils down to a variant of the "minimum number of coins" problem, where the "coins" are the valid strings and the "amount" is the target string.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Preprocessing Matches:\n\n- For each word in the list, use the Knuth-Morris-Pratt (KMP) algorithm to determine all the positions in the target string where each word can match.\n- This preprocessing will help us quickly find where each word can be placed within the target string.\n2. Dynamic Programming (DP) Table:\n- Use a DP array where dp[i] represents the minimum number of words needed to form the substring target[0:i].\n- Initialize dp[0] = 0 because zero words are needed to form an empty string.\n- For each position i in the target, update the DP table based on the matches found during preprocessing. If a word can match starting at position i, update the DP value for the end of that match position.\n3. Result:\n\n- The value dp[n] (where n is the length of the target string) will give us the minimum number of words needed to form the entire target. If dp[n] remains as Integer.MAX_VALUE, it means it\u2019s impossible to form the target with the given words.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n## Time complexity: $$O(m * n + n * k)$$,\nwhere:\n- $$O(m * n)$$ is the time complexity for preprocessing each word using the KMP algorithm, where m is the length of a word and n is the length of the target string.\n- $$O(n * k)$$ is the time complexity for updating the DP table, where k is the number of matches found for each position in the target.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n## Space complexity: $$O(n + m * k)$$, \nwhere:\n- $$O(n)$$ is for the DP array.\n- $$O(m * k)$$ is for storing the matches found, where m is the length of the words and k is the number of matches.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minValidStrings(String[] words, String target) {\n int n = target.length();\n int[] dp = new int[n + 1];\n Arrays.fill(dp, Integer.MAX_VALUE);\n dp[0] = 0;\n\n List<List<Integer>> matches = new ArrayList<>(n);\n for (int i = 0; i < n; i++) {\n matches.add(new ArrayList<>());\n }\n char[] targetChars = target.toCharArray();\n for (String word : words) {\n char[] wordChars = word.toCharArray();\n int m = wordChars.length;\n int[] pi = new int[m];\n for (int i = 1, j = 0; i < m; i++) {\n while (j > 0 && wordChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (wordChars[i] == wordChars[j]) {\n j++;\n }\n pi[i] = j;\n }\n\n for (int i = 0, j = 0; i < n; i++) {\n while (j > 0 && targetChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (targetChars[i] == wordChars[j]) {\n j++;\n }\n if (j > 0) {\n matches.get(i - j + 1).add(j);\n if (j == m) {\n j = pi[j - 1]; \n }\n }\n }\n }\n for (int i = 0; i < n; i++) {\n if (dp[i] == Integer.MAX_VALUE) continue;\n for (int len : matches.get(i)) {\n if (i + len <= n) {\n dp[i + len] = Math.min(dp[i + len], dp[i] + 1);\n }\n }\n }\n return dp[n] == Integer.MAX_VALUE ? -1 : dp[n];\n }\n}\n``` | 3 | 0 | ['Java'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | Java Solution Beats 100% KMP | java-solution-beats-100-kmp-by-shaurya_m-7jyp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Shaurya_Malhan | NORMAL | 2024-09-16T10:39:53.980243+00:00 | 2024-09-16T10:39:53.980270+00:00 | 55 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minValidStrings(String[] words, String target) {\n int m = target.length();\n int n = words.length;\n ArrayList<int[]> arr = new ArrayList<>();\n for(int i = 0; i < n; i++) {\n StringBuilder sb = new StringBuilder();\n sb.append(words[i]);\n sb.append(\'#\');\n sb.append(target);\n int[] lps = new int[words[i].length() + m + 1];\n kmp(lps, sb.toString());\n arr.add(lps);\n }\n int total = 0;\n int i = m - 1;\n while(i >= 0) {\n int mm = 0;\n for(int j = 0; j < n; j++) {\n mm = Math.max(mm, arr.get(j)[words[j].length() + 1 + i]);\n }\n if(mm == 0) return -1;\n i -= mm;\n total++;\n }\n return total;\n }\n public static void kmp(int[] lps, String s) {\n int length = 0;\n int i = 1;\n while (i < s.length()) {\n if (s.charAt(i) == s.charAt(length)) {\n length++;\n lps[i] = length;\n i++;\n } else {\n if (length != 0) {\n length = lps[length - 1];\n } else {\n lps[i] = 0;\n i++;\n }\n }\n }\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | (Officially intended approach) Trie + Double Rolling Hash + Lazy Segment tree + Binary search + DP | officially-intended-approach-trie-double-lbth | Intuition\n# Approach\n\n- Idea is quite simple. For all prefix that exist in words, generate a hash value. (double hash)\n- Now DP[j] = min(DP[j],DP[i-1]+1) fo | l_returns | NORMAL | 2024-09-15T04:02:43.006874+00:00 | 2024-09-15T04:24:06.676928+00:00 | 604 | false | # Intuition\n# Approach\n\n- Idea is quite simple. For all prefix that exist in words, generate a hash value. (double hash)\n- Now `DP[j] = min(DP[j],DP[i-1]+1)` for all j such that `targert[i:j]` is one of the prefix of given words.\n- We build a rolling hash to query hash of `targert[i:j]` in O(1)\n- Then we find longest string starting at index i, which is present in given words. Using binary search. \n- `update(DP[i], DP[j])` as minimum of `DP[i-1]+1` where j is longest prefix present in words. Using lazy segment tree\n\n\n# Complexity\n- Time complexity:\n`O(sum(words) + len(target)*log(target))`\n\n- Space complexity:\n`O(26*sum(words) + len(target))`\n\n# Code\n```cpp []\n#include <iostream>\n#include <vector>\n#include <string>\n#include <unordered_set>\n#include <unordered_map>\n#include <memory>\n#include <limits.h>\n#include <functional>\n\n#define ll long long\n\nusing namespace std;\n\n// Hash function for pair<int, int>\nstruct pair_hash {\n template <class T1, class T2>\n std::size_t operator()(const std::pair<T1, T2>& p) const {\n auto h1 = std::hash<T1>{}(p.first);\n auto h2 = std::hash<T2>{}(p.second);\n return h1 ^ h2; // or use boost::hash_combine for better hash distribution\n }\n};\n\nclass TrieNode {\npublic:\n unordered_map<char, TrieNode*> children;\n bool isEndOfWord;\n\n TrieNode() : isEndOfWord(false) {}\n};\n\nclass Trie {\npublic:\n TrieNode* root;\n \n Trie() {\n root = new TrieNode();\n }\n\n ~Trie() {\n deleteTrie(root);\n }\n\n void deleteTrie(TrieNode* node) {\n if (node == nullptr) return;\n for (auto& pair : node->children) {\n deleteTrie(pair.second);\n }\n delete node;\n }\n\n void insert(const string& word) {\n TrieNode* current = root;\n for (char ch : word) {\n if (current->children.find(ch) == current->children.end()) {\n current->children[ch] = new TrieNode();\n }\n current = current->children[ch];\n }\n current->isEndOfWord = true;\n }\n\n void dfs(TrieNode* node, pair<int, int> hash, int base1, int base2, int mod1, int mod2, unordered_set<pair<int, int>, pair_hash>& hashSet) {\n if (node == nullptr) return;\n hashSet.insert(hash);\n\n for (auto& pair : node->children) {\n char ch = pair.first;\n TrieNode* child = pair.second;\n int newHash1 = ((ll)hash.first * base1 + (ch - \'a\' + 1)) % mod1;\n int newHash2 = ((ll)hash.second * base2 + (ch - \'a\' + 1)) % mod2;\n dfs(child, {newHash1, newHash2}, base1, base2, mod1, mod2, hashSet);\n }\n }\n\n void generatePrefixHashes(int base1, int base2, int mod1, int mod2, unordered_set<pair<int, int>, pair_hash>& hashSet) {\n dfs(root, {0, 0}, base1, base2, mod1, mod2, hashSet);\n }\n};\n\nclass RollingHash {\npublic:\n vector<pair<int, int>> hashArray;\n vector<pair<int, int>> powerArray;\n int base1, base2;\n int mod1, mod2;\n \n RollingHash(const string& s, int base1, int base2, int mod1, int mod2) \n : base1(base1), base2(base2), mod1(mod1), mod2(mod2) {\n int n = s.size();\n hashArray.resize(n + 1, {0, 0});\n powerArray.resize(n + 1, {1, 1});\n\n for (int i = 0; i < n; ++i) {\n hashArray[i + 1].first = ((ll)hashArray[i].first * base1 + (s[i] - \'a\' + 1)) % mod1;\n hashArray[i + 1].second = ((ll)hashArray[i].second * base2 + (s[i] - \'a\' + 1)) % mod2;\n powerArray[i + 1].first = ((ll)powerArray[i].first * base1) % mod1;\n powerArray[i + 1].second = ((ll)powerArray[i].second * base2) % mod2;\n }\n }\n\n pair<int, int> getHash(int i, int j) {\n int hash1 = ((ll)hashArray[j].first - ((ll)hashArray[i - 1].first * powerArray[j - i + 1].first) % mod1 + mod1) % mod1;\n int hash2 = ((ll)hashArray[j].second - ((ll)hashArray[i - 1].second * powerArray[j - i + 1].second) % mod2 + mod2) % mod2;\n return {hash1, hash2};\n }\n};\n\nclass SegmentTree {\nprivate:\n vector<int> tree;\n vector<int> lazy;\n int n;\n\n void buildTree(const vector<int>& arr, int node, int start, int end) {\n if (start == end) {\n tree[node] = arr[start];\n } else {\n int mid = (start + end) / 2;\n buildTree(arr, 2 * node + 1, start, mid);\n buildTree(arr, 2 * node + 2, mid + 1, end);\n tree[node] = min(tree[2 * node + 1], tree[2 * node + 2]);\n }\n }\n\n void push(int node, int start, int end) {\n if (lazy[node] != INT_MAX) {\n tree[node] = min(tree[node], lazy[node]);\n if (start != end) {\n lazy[2 * node + 1] = min(lazy[2 * node + 1], lazy[node]);\n lazy[2 * node + 2] = min(lazy[2 * node + 2], lazy[node]);\n }\n lazy[node] = INT_MAX;\n }\n }\n\n void updateRange(int node, int start, int end, int l, int r, int value) {\n push(node, start, end);\n if (start > r || end < l) return;\n if (start >= l && end <= r) {\n tree[node] = min(tree[node], value);\n if (start != end) {\n lazy[2 * node + 1] = min(lazy[2 * node + 1], value);\n lazy[2 * node + 2] = min(lazy[2 * node + 2], value);\n }\n return;\n }\n int mid = (start + end) / 2;\n updateRange(2 * node + 1, start, mid, l, r, value);\n updateRange(2 * node + 2, mid + 1, end, l, r, value);\n tree[node] = min(tree[2 * node + 1], tree[2 * node + 2]);\n }\n\n int query(int node, int start, int end, int idx) {\n push(node, start, end);\n if (start == end) {\n return tree[node];\n }\n int mid = (start + end) / 2;\n if (idx <= mid) {\n return query(2 * node + 1, start, mid, idx);\n } else {\n return query(2 * node + 2, mid + 1, end, idx);\n }\n }\n\npublic:\n SegmentTree(const vector<int>& arr) {\n n = arr.size();\n tree.resize(4 * n);\n lazy.resize(4 * n, INT_MAX);\n buildTree(arr, 0, 0, n - 1);\n }\n\n void updateRange(int l, int r, int value) {\n updateRange(0, 0, n - 1, l, r, value);\n }\n\n int query(int idx) {\n return query(0, 0, n - 1, idx);\n }\n};\n\nclass Solution {\npublic:\n int minValidStrings(vector<string>& words, string target) {\n unique_ptr<Trie> t = make_unique<Trie>();\n for (const string& s : words) {\n t->insert(s);\n }\n \n unordered_set<pair<int, int>, pair_hash> hashSet;\n int base1 = 31;\n int base2 = 53;\n int mod1 = 1000000007;\n int mod2 = 1000000009;\n t->generatePrefixHashes(base1, base2, mod1, mod2, hashSet);\n\n RollingHash rh(target, base1, base2, mod1, mod2);\n int n = target.size();\n vector<int> dp(n + 1, n + 1);\n dp[0] = 0;\n SegmentTree st(dp);\n\n for (int i = 0; i < n; ++i) {\n int s = i - 1, e = n - 1;\n while (s < e) {\n int m = (s + e + 1) / 2;\n auto [hash1, hash2] = rh.getHash(i + 1, m + 1);\n if (hashSet.find({hash1, hash2}) != hashSet.end()) {\n s = m;\n } else {\n e = m - 1;\n }\n }\n if (s == i - 1) continue;\n st.updateRange(i + 1, s + 1, st.query(i) + 1);\n }\n \n int result = st.query(n);\n return result == n + 1 ? -1 : result;\n }\n};\n\n``` | 2 | 0 | ['C++'] | 6 |
minimum-number-of-valid-strings-to-form-target-ii | Rabin-Karp Hash Function + Modular Arithmetic + Prefix Sum + Binary Search + Segment Tree | rabin-karp-hash-function-modular-arithme-oujr | Intuition\n Describe your first thoughts on how to solve this problem. \n- Let $dp[i]$ be the minimum cost to form the prefix of length $i$ of target.\n- Use Ra | azizkaz | NORMAL | 2024-09-17T17:00:30.528342+00:00 | 2024-09-17T17:00:30.528377+00:00 | 49 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Let $dp[i]$ be the minimum cost to form the prefix of length $i$ of target.\n- Use Rabin-Karp to hash every prefix of the $words$ and store it in a HashSet.\n- Use prefix sum to hash every prefix of the $target$ string\n- Use Binary search to find the longest substring starting at index $i$ ($target[i..j]$) that has a hash present in the HashSet.\n- Use Segment Tree to update $dp[i..j]$\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nRabin-Karp Hash Function + Modular Arithmetic + Prefix Sum + Binary Search + Segment Tree\n\n# Complexity\n- Time complexity: $O(m*l + n*logn)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(m*l + n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwhere $m$ is the length of the $words$ array, $l$ is the maximum length of the string in the $words$ array, and $n$ is the length of the $target$ string\n\n# Code\n```rust []\nuse std::collections::HashSet;\n\nconst MOD: i128 = 1000000000000000007;\n\nimpl Solution {\n pub fn min_valid_strings(words: Vec<String>, target: String) -> i32 {\n let mut h = HashSet::new(); \n\n for w in words {\n let mut s = 0;\n\n for c in w.chars() {\n s = (27*s + (c as u8 - b\'a\' + 1) as i128) % MOD;\n h.insert(s);\n }\n }\n\n let n = target.len();\n let b = target.as_bytes();\n\n let mut p = vec![0; n];\n let mut ht = vec![0; n];\n\n let mut s = 0;\n\n for i in 0..n { \n s = (27*s + (b[i] - b\'a\' + 1) as i128) % MOD;\n\n if i == 0 {\n p[i] = 1;\n } else {\n p[i] = (27*p[i-1]) % MOD;\n }\n\n ht[i] = s; \n }\n\n let l = Self::search(0, &h, &ht, &p);\n\n if l == 0 {\n return -1;\n }\n\n if l == n {\n return 1;\n } \n\n let mut t = vec![0; 2*n + 1];\n\n for i in 0..n+1 {\n t[i+n] = i32::MAX;\n }\n\n for i in (2..t.len()).step_by(2).rev() {\n t[(i-1)/2] = t[i].min(t[i-1]);\n } \n\n Self::set(0, 1, n + 1, &mut t);\n Self::set(l, 2, n + 1, &mut t);\n\n for i in 1..n {\n let c = Self::min(i, n, n + 1, &t);\n\n if c == i32::MAX {\n return -1;\n }\n\n let l = Self::search(i, &h, &ht, &p);\n\n if i + l == n {\n Self::set(n, c, n + 1, &mut t);\n } else {\n let pc = Self::min(i + l, i + l, n + 1, &t);\n\n if pc > c + 1 {\n Self::set(i + l, c + 1, n + 1, &mut t);\n }\n }\n }\n\n let c = Self::min(n, n, n + 1, &t);\n\n if c == i32::MAX {-1} else {c}\n } \n\n pub fn search(i: usize, h: &HashSet<i128>, ht: &Vec<i128>, p: &Vec<i128>) -> usize {\n let n = ht.len();\n\n let mut l = 0;\n let mut r = n - i;\n\n while l < r {\n let m = (l + r + 1)/2;\n\n let mut hc = ht[i+m-1]; \n\n if i > 0 {\n hc = (hc + MOD - (ht[i-1]*p[m]) % MOD) % MOD;\n } \n\n if h.contains(&hc) {\n l = m;\n } else {\n r = m - 1;\n }\n }\n\n l\n }\n\n pub fn min(mut i: usize, mut j: usize, n: usize, t: &Vec<i32>) -> i32 {\n i += n;\n j += n;\n\n let mut r = i32::MAX;\n\n while i <= j {\n if i % 2 == 1 {\n r = r.min(t[i-1]);\n i += 1;\n } \n \n if j % 2 == 0 {\n r = r.min(t[j-1]);\n j -= 1;\n }\n\n i /= 2;\n j /= 2;\n }\n\n r\n } \n\n pub fn set(mut k: usize, v: i32, n: usize, t: &mut Vec<i32>) {\n k += n;\n\n t[k-1] = v;\n\n k /= 2;\n\n while k >= 1 {\n t[k-1] = t[2*k-1].min(t[2*k]);\n\n k /= 2;\n }\n } \n}\n``` | 1 | 0 | ['Math', 'Binary Search', 'Segment Tree', 'Hash Function', 'Prefix Sum', 'Rust'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | [Python3] KMP + Greedy O(M*N + M*K) FULL EXPLANATION W/ Proof | python3-kmp-greedy-omn-mk-full-explanati-puhz | Intuition\n Describe your first thoughts on how to solve this problem. \n\nApplying two formal proofs of contradiction lead us to our greedy solution: Take the | anguerrera1 | NORMAL | 2024-09-16T15:48:43.449567+00:00 | 2024-09-16T15:48:43.449599+00:00 | 54 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nApplying two formal proofs of contradiction lead us to our greedy solution: Take the maximum amount of steps that we can at any given step. This is a loose proof, but the main ideas of the proofs are below.\n\n\n**Proof of Optimality & Correctness:**\n(This is best seen with a visualization, and in the following explanation assume we are traversing the array from right to left)\n\nAssume there was some solution that decides to take a shorter prefix step than the maximum possible at a given index. Our greedy algorithm with take one step from index i to index X. The "optimal" algorithm takes a smaller step from index i to index Y > X. \n\n**Case 1)** From index X, we can\'t take any steps backward. \n\nOur greedy algorithm will reach index X and return -1, since we we can\'t construct the target string. Supposedly, the "optimal" solution is able to reach end from a larger index. However, any solution that reaches the end, will use the prefix arr[:X]. We assumed there is no prefix arr[:X], because our initial assumption was that there was no solution and that we can\'t take any steps backward. This is a proof by contradiction, therefore our algorithm will find a solution.\n\nNow we show that our algorithm produces the optimal solution.\n\n**Case 2)** From index X, we can take steps backwards, and assume that both greedy and optimal algorithms find a solution (from case 1). \n\nAssume that we can reach the final index (or any index before X) in fewer steps by taking a step to index Y > X (taking a smaller than maximum jump). Our greedy algorithm reaches index X in one step. The "optimal algorithm" must take a series of steps to overcome the path in index X. However, the "optimal" algorithm will reach index X at some point in the solution. It will "pass by" index X in 2 or greater steps. If the greedy solution simply "followed" this optimal solution, because any prefix in arr[:X] is of course available for both algorithms, by immediately taking a step and ending and starting at the same positions as the "optimal" algorithm, the greedy algorithm would reach the final index in fewer or equal steps than the optimal algorithm, no matter what. Therefore, our "optimal" solution can never do better than our greedy solution. \n\nNote that this problem structure is unique, and lends itself to a greedy solution. However, other similar problem such as Word Break (LC 139), must consider every possible starting word at every index, since we cannot be greedy. Taking a smaller word might lead to a correct solution, because taking a larger word might not lead to matching a smaller word earlier on. At each index, we don\'t have the same set of choices across all words. As in, we don\'t have the choice of just choosing prefixes.\n\nIt is extremely unique and at first slightly non-intuitive why this is the case, but after thinking about this problem for a while, having the choice to take prefixes of words at every single index lends us to a greedy solution. If we couldn\'t take prefixes of words, and instead had to take whole words, then this would become Word Break which needs DP.\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDefine a KMP helper function, I highly suggest watching Neetcode\'s video on find the first occurence in string problem if you have never seen the KMP algorithm before. If you haven\'t seen the KMP algorithm before, this problem is likely not the best instroduction to it. \n\nThe KMP algorithm produces a "suffix" table after we have matched our pattern lps data structure with our target string. This "suffix" table tell us how many steps before the current index match a prefix available to us. And this is exactly what we need. We consider the maximum steps or maximum jump that we can take at each index across all words, and go for it. If we ever reach a point where we can\'t jump, then we return -1. The proof for this case is above.\n# Complexity\n- Time complexity: O(M*(N+K))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nM represents the # of words\nK is the longest length of a word in words\nN is the length of the target string\n\n- Space complexity: O(N + K)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThis is for the LPS and suffix tables.\n\n# Code\n```python3 []\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n def kmp(pattern, target):\n n, m = len(pattern), len(target)\n lps = [0]*n\n j,i = 0,1\n while i < n:\n while j and pattern[j] != pattern[i]:\n j = lps[j-1]\n if pattern[j] == pattern[i]:\n j += 1\n lps[i] = j\n else:\n lps[i] = 0\n i += 1\n\n res = [0]*m\n i,j = 0,0\n while i < m:\n while j and (j == n or pattern[j] != target[i]):\n j = lps[j-1]\n if pattern[j] == target[i]:\n j += 1\n res[i] = j\n else:\n res[i] = 0\n i += 1\n return res\n \n m = len(target)\n option = [0]*m\n for word in words:\n arr = kmp(word, target)\n for i,j in enumerate(arr):\n option[i] = max(option[i], j)\n i = m-1\n steps = 0\n while i > -1:\n if option[i] == 0:\n return -1\n i -= option[i]\n steps += 1\n return steps\n \n \n \n``` | 1 | 0 | ['Python3'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | Z-Function boils to Min Jumps II Easy Short Fast | Comments | C++ | z-function-boils-to-min-jumps-ii-easy-sh-roin | Complexity\nn = words.length(), t = target.length(), K = len of each words\n- Time complexity: O(n * (K+t))\n\n- Space complexity: O(n)\n##### This solution is | bramar2 | NORMAL | 2024-09-15T05:04:16.338734+00:00 | 2024-09-15T05:45:55.081482+00:00 | 8 | false | # Complexity\n`n = words.length(), t = target.length(), K = len of each words`\n- Time complexity: $$O(n * (K+t))$$\n\n- Space complexity: $$O(n)$$\n##### This solution is very close to the optimal solution and very fast considering the small size of the code for this solution.\n\n*Only with fast-IO and no other optimizations to the below code. Some inlining and unnecessary if-statements may improve the time.\n# Code\nThere is also the clean C++ code thats very short with no comments (relative to other sols).\n\n\n```cpp []\n#include <bits/stdc++.h>\nusing namespace std;\nvector<int> z_function(string s) {\n // Source: https://cp-algorithms.com/string/z-function.html\n int n = s.size();\n vector<int> z(n);\n int l = 0, r = 0;\n for(int i = 1; i < n; i++) {\n if(i < r) {\n z[i] = min(r - i, z[i - l]);\n }\n while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n z[i]++;\n }\n if(i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n return z;\n}\nclass Solution {\n\npublic:\n //Solution for https://leetcode.com/problems/jump-game-ii/description/\n int jump(vector<int>& nums) {\n int size = (int) nums.size();\n if(size == 1) return 0;\n vector<long long> minJumps(size, INT_MAX); // minJumps[i] is the min num of jumps to get to nums[i]\n minJumps[0] = 0;\n for(int i = 0; i < size; i++) {\n // No check for minJumps[i] == INT_MAX because the test cases are generated such that you can reach nums[n-1]\n for(int j = min(i + nums[i], size - 1); j > i; j--) {\n if(minJumps[j] <= minJumps[i] + 1) {\n break; // because then everything below is ALSO better/equal to this current permutation\n }else minJumps[j] = minJumps[i] + 1;\n }\n }\n return minJumps[size - 1];\n }\n int minValidStrings(vector<string>& words, string target) {\n int n = words.size();\n vector<int> match(target.size(), 0);\n // match[i] will be the longest match starting at index i using Any word.\n // So for example with target = "abcde", and words = ["bcd"]\n // match = {0, 3, 0, 0, 0}\n for(string& word : words) {\n string comb = word + "!" + target;\n vector<int> z = z_function(comb); // We use the z function\n // Definition of Z[i]:\n // (from cp-algorithms)\n // z[i] = the length of the longest string that is, at the same time, a prefix of $s$\u200A\n // and a prefix of the suffix of `s` starting at `i`.\n for(int i = 0; i < target.size(); i++) {\n // z[n + j + 1]\n // we notice comb[n+i+1] = target[i], because n is word.length and 1 for the separator \'!\'\n // that means z[n+i+1] = longest string that matches\n // : words[0...X-1] [prefix of comb]\n // : target[j...j+(X-1)] (which is target starting from index j) [suffix of comb]\n // X is the possible values, then Z[n+i+1] = max(all X that matches)\n // in other words, it is the longest string that can be matched\n // using this word at index j\n\n // Example: target = "abacda", word = "acb"\n // match {0, 0, 0, 0, 0, 0} ->\n // {\n // 1 [match \'a\'],\n // 0 [no match],\n // 2 [match \'ac\'],\n // 0 [no match],\n // 0 [no match],\n // 1 [match \'a\']\n // }\n match[i] = max(match[i], z[word.length() + i + 1]);\n }\n }\n // match[i] will be the longest length we can match from i\n // In other words, we can jump either from j= 0 --> match[i]\n // to match[i+j] using one operation/string\n\n match.push_back(0); // We add extra \'0\' for the end result (where everything is concatenated).\n int ans = jump(match);\n return ans >= INT_MAX ? -1 : ans;\n }\n};\n```\n```cpp [Clean C++]\n#include <bits/stdc++.h>\nusing namespace std;\nvector<int> z_function(string s) {\n int n = s.size();\n vector<int> z(n);\n int l = 0, r = 0;\n for(int i = 1; i < n; i++) {\n if(i < r) {\n z[i] = min(r - i, z[i - l]);\n }\n while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n z[i]++;\n }\n if(i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n return z;\n}\nclass Solution {\npublic:\n int jump(vector<int>& nums) {\n int size = (int) nums.size();\n if(size == 1) return 0;\n vector<long long> minJumps(size, INT_MAX);\n minJumps[0] = 0;\n for(int i = 0; i < size; i++) {\n for(int j = min(i + nums[i], size - 1); j > i; j--) {\n if(minJumps[j] <= minJumps[i] + 1) {\n break;\n }else minJumps[j] = minJumps[i] + 1;\n }\n }\n return minJumps[size - 1];\n }\n int minValidStrings(vector<string>& words, string target) {\n int n = words.size();\n vector<int> match(target.size(), 0);\n for(string& word : words) {\n string comb = word + "!" + target;\n vector<int> z = z_function(comb);\n for(int i = 0; i < target.size(); i++) {\n match[i] = max(match[i], z[word.length() + i + 1]);\n }\n }\n match.push_back(0);\n int ans = jump(match);\n return ans >= INT_MAX ? -1 : ans;\n }\n};\n``` | 1 | 0 | ['String', 'Dynamic Programming', 'String Matching', 'C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | 💠 Rolling Greedy Polynomial Hashing Explanation - II | rolling-greedy-polynomial-hashing-explan-1p26 | Intro \nThis problem is about breaking a target string into valid substrings, where each substring must match a prefix of some word in a list. After trying ever | subhanjan33 | NORMAL | 2024-09-15T04:23:22.834269+00:00 | 2024-09-15T04:40:38.895450+00:00 | 65 | false | # Intro \nThis problem is about breaking a target string into valid substrings, where each substring must match a prefix of some word in a list. After trying everything I moved towards efficient prefix checking, and a rolling hash approach. Hashing allows us to quickly verify if a substring matches any valid prefix in the word list.\n\n# Approach\n1. **Hashing Words:** \n - First, precompute the rolling hash values for all prefixes of each word in the `words` list. Using a polynomial rolling hash function with a prime modulus and random base ensures minimal hash collisions.\n - These hash values are stored in a set for fast lookups.\n\n2. **Hashing Target:**\n - Next, compute the rolling hash for every prefix of the `target` string. This allows us to efficiently calculate the hash for any substring in constant time.\n\n3. **Greedy Splitting:**\n - Then try to split the target string into the maximum possible number of valid substrings. For each position in the target string, we use a sliding window approach and binary search to find the farthest valid substring that matches any prefix hash from the words.\n - If a valid substring is found, we advance the window and continue the process. If no valid substring can be found, it\u2019s impossible to fully split the target, and we return `-1`.\n\n# Complexity\n- **Time complexity:** \n - Precomputing the hash values for each word and the target string takes $$O(m \\times k + n)$$ where:\n - $$m$$ is the number of words.\n - $$k$$ is the average length of a word.\n - $$n$$ is the length of the target string.\n - For each valid split attempt, we do binary search, making the overall complexity approximately $$O(n \\log n)$$ in the worst case.\n \n Hence, the total complexity is roughly $$O(m \\times k + n \\log n)$$.\n\n- **Space complexity:**\n - Storing the hash values for prefixes of each word and the target string takes $$O(m \\times k + n)$$.\n\n# Code\n```python3 []\n# Weelky Q4 - Minimum Number of Valid Strings to Form Target II\n\n# set up --> base value & modulo for polynomial rolling hash\npw = random.randint(100, 200) # base --> hashing\nmod = random.getrandbits(40) # large prime- like mod to avoid collisions\n\n# precompute powers of pw modulo mod\npowers = [1]\nfor _ in range(10**5):\n powers.append(powers[-1] * pw % mod)\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target) # len of target string\n\n # S1: precompute hash values for -- all prefixes of every word in \'words\'\n word_hashes = set() # set to store all possible hash values for word prefixes\n for word in words:\n current_hash = 0\n for char in word:\n # calc rolling hash for each prefix of the word\n current_hash = (current_hash * pw + ord(char)) % mod\n word_hashes.add(current_hash) # store hash of the current prefix\n\n # S2: precompute prefix hashes for -- target string\n target_hashes = [0] # target_hashes[i] will store hash of target[:i]\n for char in target:\n # compute rolling hash for each prefix of the target\n target_hashes.append((target_hashes[-1] * pw + ord(char)) % mod)\n\n # S3: greedily split target into max number of valid substrings\n left = right = 0 # L n R pointers for current window in the target\n split_count = 0 # counter for the num of valid substrings used\n \n while right < n: # while --> haven\'t reached the end of the target string\n max_right = right # this will track the farthest we can extend the current valid substring\n \n # try to extend the substring from each starting point between L and R\n for i in range(left, right + 1):\n low, high = i, n - 1\n # binary search for the farthest valid substring starting at index `i`\n while low <= high:\n mid = (low + high) // 2\n # calc the hash for the substring target[i:mid+1]\n current_hash = (target_hashes[mid + 1] - target_hashes[i] * powers[mid + 1 - i] % mod) % mod\n if current_hash in word_hashes:\n low = mid + 1 # valid substring found, try to extend further\n else:\n high = mid - 1 # invalid, shrink the window\n\n # update max_right --> farthest valid match found\n max_right = max(max_right, high + 1)\n\n # if no extension is possible, target cannot be fully split into valid words\n if max_right == right:\n return -1\n\n # move the window forward to the next unmatched part of the target\n left, right = right + 1, max_right\n split_count += 1 # used one valid substring to cover part of the target\n \n return split_count # finally\n\n``` | 1 | 0 | ['Math', 'Greedy', 'Rolling Hash', 'Python3'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | [**ONLY WORKS IN PYTHON**] DP + Sliding Window | only-works-in-python-dp-sliding-window-b-y9xq | Note: This DP + Sliding Window solution works only in Python and not in other languages. See below for more details.\n\n# Intuition\nThe problem involves partit | kimjiwook129 | NORMAL | 2024-09-15T04:07:25.732955+00:00 | 2024-09-15T15:32:59.368954+00:00 | 217 | false | **Note**: This DP + Sliding Window solution works only in Python and not in other languages. [See below](#additional-insight-on-why-this-is-not-tle) for more details.\n\n# Intuition\nThe problem involves partitioning the target string into the minimum number of valid substrings, where each substring must match the prefix of any word in the given words list.\n\nThe dynamic programming (dp) array helps track the minimum number of substrings needed to form the target up to each position. \n\nA sliding window (left and right) is used to explore all possible substrings within the target, ensuring that each substring is valid according to the list of words.\n\n# Approach\n- Sliding Window: Use two pointers (left and right) to explore substrings in target. Adjust left until the substring target[left:right + 1] is a valid prefix in words.\n\n- Update DP: For each valid substring found, update the dp array to track the minimum number of valid substrings needed to reach the current position.\n\n- Expand Window: Increment right to continue expanding the window and check the next substring in the target. Return dp[-1] as the result.\n\n# Complexity\n- Time complexity: $$O(N^2M)$$ where N is the length of target and M is the number of words. The nested loop results from checking substrings within the target, and the prefix search in words contributes to the overall complexity.\n\n- Space complexity: $$O(N)$$ where N is the length of target\n\n# Additional Insight on Why This is not TLE\n\nThe solution\'s time complexity of $$O(N^2M)$$, might suggest it could run into a Time Limit Exceeded (TLE) error. However, the code works efficiently in Python due to the language\'s optimized string matching.\n\nThanks to **@lone17** for this insight:\n> The code works in Python because string matching in Python is absurdly well optimized, it basically has a bunch of caching under the hood for quick string matching. (Side fact, the authors of Python did this because they observed that string matching is one of the most used operation in Python)\n\nAs a result, this DP + Sliding Window approach is feasible in Python but might not perform as well in other languages that lack such string matching optimizations.\n\n\n# Code\n```python3 []\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n dp = [0] * len(target)\n\n def search(prefix):\n for word in words:\n if word.startswith(prefix): return True\n return False \n\n left, right = 0, 0\n \n for i in range(len(target)):\n while not search(target[left:right + 1]) and left <= right: left += 1\n \n if left > right: return -1\n\n substrLen = right - left + 1\n dp[i] = 1 if i < substrLen else dp[i - substrLen] + 1\n\n right += 1\n\n return dp[-1]\n``` | 1 | 0 | ['Dynamic Programming', 'Sliding Window', 'Python3'] | 5 |
minimum-number-of-valid-strings-to-form-target-ii | Simple KMP Algorithm + DP || LPS Array || Beats 100% | simple-kmp-algorithm-dp-lps-array-beats-ki21c | Complexity\n- Time complexity:O(nm)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n|words|+m)\n Add your space complexity here, e.g. O(n) | dubeyad2003 | NORMAL | 2024-09-15T04:05:34.640568+00:00 | 2024-09-15T04:05:34.640606+00:00 | 206 | false | # Complexity\n- Time complexity:$$O(n*m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n*|words|+m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> LPS(string& s){\n int n = s.size();\n vector<int> lps(n, 0);\n int i = 1, prev = 0;\n while(i < n){\n if(s[i] == s[prev]){\n prev++;\n lps[i] = prev;\n i++;\n }else{\n if(prev > 0){\n prev = lps[prev-1];\n }else{\n lps[i] = 0;\n i++;\n }\n }\n }\n return lps;\n }\n vector <int> search(string p, string t)\n {\n string ns = p + "#" + t;\n vector<int> lps = LPS(ns);\n vector<int> ans;\n int n = p.size();\n for(int i=n+1; i<lps.size(); i++){\n ans.push_back(i-n-lps[i]);\n }\n return ans;\n }\n int minValidStrings(vector<string>& w, string t) {\n int n = w.size();\n vector<vector<int>> arr(n);\n for(int i=0; i<n; i++){\n arr[i] = search(w[i], t);\n }\n int m = t.size();\n vector<int> dp(m+1, 1e9);\n dp[0] = 0;\n for(int i=0; i<m; i++){\n for(int j=0; j<n; j++){\n dp[i+1] = min(dp[i+1], dp[arr[j][i]] + 1);\n }\n }\n if(dp[m] == 1e9) return -1;\n return dp[m];\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Aho Corsack | Python 3 | aho-corsack-python-3-by-chrehall68-fx3d | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | chrehall68 | NORMAL | 2024-09-15T04:00:54.758306+00:00 | 2024-09-15T04:00:54.758341+00:00 | 279 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nfrom typing import List\nfrom collections import deque\n\n\ndef to_idx(s: str):\n return ord(s) - ord("a")\n\n\nclass Trie:\n def __init__(self, depth=0):\n self.is_end = False\n self.depth = depth\n self.stored_words = [] # added for quick recovery of what this trie represents\n self.d = [None for _ in range(26)]\n self.failure_to = None # added for aho corasick\n\n def insert(self, string: str, idx: int):\n if idx == len(string):\n self.is_end = True\n self.stored_words.append(string)\n else:\n tmp = to_idx(string[idx])\n if self.d[tmp] is None:\n self.d[tmp] = Trie(self.depth + 1)\n self.d[tmp].insert(string, idx + 1)\n\n def __str__(self):\n return str(self.d) + str(self.is_end) + str(self.stored_words)\n\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n # trie\n t = Trie()\n for word in words:\n t.insert(word, 0)\n # aho corasick\n # build failure graph\n # start with everything connected to root\n q = deque()\n for i in range(len(t.d)):\n if t.d[i] is not None: # this is a valid connection\n # first, set the node to fail towards the root\n t.d[i].failure_to = t # fail to root\n q.append(t.d[i]) # explore it soon\n # also set root to loop back to itself to prevent infinite recursion\n # when trying to look for a success\n for i in range(len(t.d)):\n if t.d[i] is None:\n t.d[i] = t\n\n # then, just bfs\n while len(q) > 0:\n subtree = q.popleft()\n\n for i in range(len(subtree.d)):\n if subtree.d[i] is not None: # is a valid connection\n # add it to the queue\n q.append(subtree.d[i])\n\n # figure out where this new node should fail to\n # by exploring until something succeeds\n tmp = subtree.failure_to\n while tmp.d[i] is None: # while this is still a failure, go back\n tmp = tmp.failure_to\n # finally, store this\n subtree.d[i].failure_to = tmp.d[i]\n # and store any words this may entail\n subtree.d[i].stored_words.extend(tmp.d[i].stored_words)\n\n # min times[i] = min_times to create a length i string\n min_times = [float("inf") for _ in range(len(target) + 1)]\n min_times[0] = 0 # length 0 costs 0\n cur = t\n for i in range(1, len(target) + 1):\n # advance to next state\n tmp = cur.d[to_idx(target[i - 1])]\n if tmp is not None:\n cur = tmp\n else:\n while cur.failure_to.d[to_idx(target[i - 1])] is None:\n cur = cur.failure_to\n cur = cur.failure_to.d[to_idx(target[i - 1])]\n\n # just use the depth\n min_times[i] = min_times[i - cur.depth] + 1\n # print("at", target[i - 1], "have depth", cur.depth)\n # for el in cur.stored_words:\n # print(el, "depth", cur.depth)\n\n if min_times[-1] == float("inf"):\n return -1\n return min_times[-1]\n\n\n``` | 1 | 0 | ['Python3'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | Using kmp to store all the length of prefix and then dp | using-kmp-to-store-all-the-length-of-pre-irc7 | null | risabhuchiha | NORMAL | 2025-03-31T05:07:47.913314+00:00 | 2025-03-31T05:07:47.913314+00:00 | 2 | false |
```java []
class Solution {
Integer[] dp;
public int minValidStrings(String[] words, String target) {
int n = target.length();
dp=new Integer[target.length()];
// Arrays.fill(dp, Integer.MAX_VALUE);
//dp[0] = 0;
List<List<Integer>> matches = new ArrayList<>(n);
for (int i = 0; i < n; i++) {
matches.add(new ArrayList<>());
}
char[] targetChars = target.toCharArray();
for (String word : words) {
char[] wordChars = word.toCharArray();
//System.out.println(words);
int m = wordChars.length;
int[] pi = new int[m];
for (int i = 1, j = 0; i < m; i++) {
while (j > 0 && wordChars[i] != wordChars[j]) {
j = pi[j - 1];
}
if (wordChars[i] == wordChars[j]) {
j++;
}
pi[i] = j;
}
for (int i = 0, j = 0; i < n; i++) {
while (j > 0 && targetChars[i] != wordChars[j]) {
j = pi[j - 1];
}
if (targetChars[i] == wordChars[j]) {
j++;
}
if (j > 0) {
matches.get(i - j + 1).add(j);
if (j == m) {
j = pi[j - 1];
}
}
}
}
int ans=f(0,matches,words);
if(ans>=Integer.MAX_VALUE/10)return -1;
return ans;
}
public int f(int idx,List<List<Integer>> matches,String[]words){
if(idx>=matches.size())return 0;
if(dp[idx]!=null)return dp[idx];
int ans=Integer.MAX_VALUE/10;
for(int len:matches.get(idx)){
ans=Math.min(ans,1+f(idx+len,matches,words));
}
// ans=Math.min(ans,f(idx+1,matches));
return dp[idx]=ans;
}
}
``` | 0 | 0 | ['Java'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Rolling hash + sliding window + DP: $O(n+\sum l_i)$ solution (With rigorous correctness proof) | rolling-hash-sliding-window-dynamic-prog-bnc9 | Intuition and Approachn,∑li in title refers to the length of target and the total length of all words in words respectively.Approach 1: Using trie + dynamic pr | manishad119 | NORMAL | 2025-03-15T00:19:26.888248+00:00 | 2025-03-16T18:14:15.590144+00:00 | 3 | false | # Intuition and Approach
<!-- Describe your first thoughts on how to solve this problem. -->
$n,\sum l_i$ in title refers to the length of `target` and the total length of all words in words respectively.
## Approach 1: Using trie + dynamic programming (Correct but inefficient )
I had not looked at hint or even the topics before I started this approach. I knew it wouldn't be efficient enough but it was my solution. A fairly straight forward method.
1. Build a trie using all words in `words`.
2. INITIALIZE `min_valid_prefix` where `min_valid_prefix[i]` should hold the minimum number of valid prefixes that can be concatenated to form `target[0...i]` i.e `i+1` length prefix of target
3. FOR `i` from 0 to length of `target`-1
4. IF `i-1` has not been updated, it means there is no way to build `target[0..i-1]` with valid prefixes. return -1 immediately
5. OTHERWISE, ASSIGN `j`=`i`
6. Start at the root of trie
7. WHILE `j` < length of `target` AND we are in a valid node of trie
8. MOVE to `target[j]` in trie if `target[j]` is a child of current node and update `min_valid_prefix[j]` to the minimum of `min_valid_prefix[j]` and (`min_valid_prefix[i-1] + 1` or 1 if `i` is 0) OTHERWISE break out of WHILE.
9. INCREMENT `j`
10. END WHILE
11. END FOR `i`
Time complexity is $O(nl)$ where $n$ is the length of target and $l$ is the length of longest word in `words` in worst case
I knew I would get TLE but I could build a reasonably efficient algorithm that works correctly without even looking at the topic.
At this point, I decided to take a look at the topics. I saw rolling hash. I had done rolling hash before but it never crossed my mind to use it for this problem before. It was when I thought maybe I could solve it using rolling hash + sliding window + DP. Never looked at the hint until I completed it.
## Approach 2: Rolling hash + DP + sliding window:
Rolling hash algorith
Assign a=1, b=2 and so on....
rolling for string $s = c_1c_2c_3..c_n$
is $c_1 * 27^{n-1} + c_2 * 27^{n-2}..+ c_n * 27^0$ reduced module $m$ where $m$ is some prime number. To minimize chances of a hash collision i.e. a substring in `target` that has the same hash as some valid prefix in `words` but are not the same, I used three different rolling hashes, calculated the same way, but with three different modulo, specifically Mersenne primes $2^{19}-1$, $2^{31}-1$, $2^{61}-1$ but for simplicity I pretend I used only one for pseudocode
ALGORITHM:
1. BUILD a hash set of rolling hashes using all prefixes of all words in `words`. It can be done efficiently with $O(\sum l_i)$ where $l_i$ is the length of `word[i]`. Lookup and addition can be done in $O(1)$ amortized time
2. PRECALCULATE $27^i$ reduced modulo a prime $m$ for all $0\le i \le l$ where $l$ is the length of longest word
3. INITIALIZE `min_valid_prefix` which has the same meaning as in my previous approach
4. INITIALIZE `i` to 0
5. INITIALIZE `window_rolling_hash` to 0
6. FOR `j` in `0` to length of `target` - 1
7. UPDATE `window_rolling_hash` by adding `target[j]` to current window
8. WHILE `window_rolling_hash` IS NOT in the set of rolling hashes and `i` $\le$ `j`
9. UPDATE `window_rolling_hash` to remove `target[i]` from current window and increment `i`. For quick substraction use precalculated $27^{j-i}$ from 2.
10. END WHILE
11. IF `i` goes beyond `j` there is no way to form `target[0..j]` using valid prefixes so entire `target` can also not be built like that. RETURN -1 immediately
12. OTHERWISE SET `min_valid_prefix[j] = 1 + min_valid_prefix[i-1]` OR 1 if `i` is 0
13. END FOR
14. RETURN the last value in `min_valid_prefix`
Unlike our previous approach, here we do not consider all possible sub-strings, so we could still be skeptical that it gives the correct answer. It is not immediately clearly why this algorithm is correct. So let's go for a rigorous proof that this algorithm is correct. For simplicity of proof, we assume that no collision can occur.
We can see that we advance $j$ as long as current window is a valid prefix. We advance $i$ when our current window is not a valid prefix
Define $O_0 = 0$ for initialization.
Recursive equation , $O_i = MIN_{l=0}^{i-1}{O_l} + 1$ for $i > 0$
### Lemma 1: Suppose that $O_n$ be the minimum number of valid strings to form $n$ length valid prefix of `target`. Then $O_{i+1} \ge O_i$ for all $i$
For simplicity, we ignore the scenario where a `target` cannot be constructed using valid strings which is an undefined case.
suppose we have some $i$ such that $O_{i+1} < O_i$
$O_{i}$
$O_i = 1$ if `target[0..i-1]` is a valid prefix which is the smallest it can be so `target[0..i-1]` cannot be a valid prefix itself.
Because, $O_{i+1} < O_i$, it's optimal value could not be $O_{i+1} = O_i + 1$. Therefore optimal value is $O_{i+1} = O_l + 1$ for some $0 \le l < i$.
Any prefix of a valid prefix is also a valid prefix, so if `target[l..i]` is a valid prefix then so is `target[l..l]`, `target[l..l+1]` and so on. Therefore `target[l..i]` is also a valid prefix. Since, $l < i$, and `target[l..i]` is a valid prefix, it must have ben considered in computation of $O_i$. Therefore, $O_i \le O_l + 1 = O_{i+1}$ which is a contradiction.
### Lemma 2: Array `min_valid_prefix` is non-decreasing
PROOF:
`min_valid_prefix[i]` holds $O_{i+1}$. Since, $O$ is a non-decreasing sequence, array `min_valid_prefix` must also be non-decreasing during the execution. Let's prove this as step 1.
Again, let's assume that `target` cn really be constructed using valid strings.
Therefore, `min_valid_prefix[0]` is always 1 because when `j=0` and `target[0..0]` is a valid substring, `i` must also be 0. This is because $i$ must be less than or equal to $j$, and $i$ goes beyond $j$ we return -1 immediately.
Likewise `min_valid_prefix[1]` is either 1 or 2 because $i$ is either 0 or 1 when $j=1$. Since `min_valid_prefix[1]` is greater than or equal to `min_valid_prefix[0]`,we have established a base condition. Suppose that `min_valid_prefix[i]` $\ge$ `min_valid_prefix[i-1]` holds for all $i \le k$.
Consider the course of execution of program when $j=k+1$. Suppose value of $i$ at that point of execution is $l$ where `target[l..k+1]` is valid string. At that point, the program assigns `min_valid_prefix[l-1] + 1` (OR just `1` if $l=0$). Before that point, the program should have also reached $j=k$. Suppose that the value of $i$ at the point of execution is $l'$ such that `target[l'...k]` is a valid string. Program assigns `min_valid_prefix[k] = min_valid_prefix[l'-1] + 1` (OR just `1`) Here, $0\le l \le k+1$ Therefore $l-1 \le k$. Since, $i$ never decreases, and $i=l'$ is reached before $i=l$, we can conclude that $l' \le l$. Putting it together, $l'-1 \le l-1 \le k$. By prior assumption, we have `min_valid_prefix[l'-1] + 1` $\le$ `min_valid_prefix[l-1] + 1`. Therefore, `min_valid_prefix[k]` $\le$ `min_valid_prefix[k +1]`.
PROVED BY INDUCTION
### Lemma 3: Suppose that `target[i..j]` which is a valid prefix found in current window during program execution. Then, there exists no $i' < i$ such that `target[i'..j]` is a valid prefix
Proof:
SUPPOSE that such an $i'$ exists. Then `target[i'..j']` is a valid prefix for all $i' \le j' \le j$
During the course of execution of program, we would return immediately if $i'$ went past the value of $j$. Suppose that the value of $j$ when $i$ becomes $i'$ is $j'$. Since, $i'$ could not have gone beyond $j'$, we can conclude that $i' \le j' \le j$.
As we have established that `target[i'..j']` is a valid prefix, the program will to advance $j$ for next iteration. Because, `target[i'..j'']` is a valid prefix for all $j' \le j'' \le j$, we never advance $i$ until we reach $j$ in current window. Since the current window is still a valid prefix, we advance $j$ to $j+1$. Therefore, the window `target[i..j]` would never be encountered during the execution of program which contradicts our assumption.
### Lemma 4: Suppose that `target[i..j]` in current window is a valid prefix. We update `min_valid_prefix[j]` as `min_valid_prefix[i-1] + 1` before advancing $i$. This `min_valid_prefix[j]` is the optimal value
Proof:
We have already established that no $i' < i$ exists such that `target[i'..j]` is a valid prefix. suppose that there exists $i' > i$ such that `target[i'..j]`. We never consider such $i'$ during the execution. However since `min_valid` is non-decreasing `min_valid_prefix[i'-1]` $\ge$ `min_valid_prefix[i-1]`. If `i` is 0, then `min_valid_prefix[j]` is 1 which is the most optimal. And for every $i' > i$, `min_valid_prefix[i'-1] + 1` $\ge$ `min_valid[i'] + 1` so we do not need to consider such $i'$.
Proving these three lemmas proves that our sliding window + rolling hash + DP approach gives the optimal answer.
Final Note: Unmatching rolling hash can rule out an answer but the converse is not true. For this approach, we do not verify that the subtring is actually correct for a rolling hash match, otherwise it would still cause TLE in many custom made test cases.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(n + \sum l_i)$ where $l_i$ is the length of each word
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(n + \sum l_i)$. DP table and the set of rolling hashes
# Code
```python3 []
class Solution:
def minValidStrings(self, words: List[str], target: str) -> int:
# # A less efficient approach using dynamic programming, (only one I can think of right now)
# # with complexity O(m * n) where n is len(target) and m is the length of longest word in words
# for i in range(len(target)):
# # To start from i, we should be able to form target[0..i-1] with valid concatenations
# # if it is impossible to form any prefix of target that way it is impossible to form
# # target that way
# if i == 0 or min_valid[i-1] != -1:
# start = root
# j = i
# while j < len(target) and start is not None:
# start = start.get_child(target[j])
# if start is not None:
# # prefix found
# n_valid_suggest = 1 if i==0 else min_valid[i-1] + 1
# if min_valid[j] == -1 or min_valid[j] > n_valid_suggest:
# min_valid[j] = n_valid_suggest
# j += 1
# #print(min_valid)
# else:
# return -1
# return min_valid[-1]
# Attempt 2 using rolling hash, I haven'r checked hint yet
# Assume that ho rolling hash collision will ever occur.
# I will use it modulo a 64 bit prime number
# check the length of longest word in words
l_l = max([len(word) for word in words])
# I will use 3 different modulo (3 mersenne primes)
# to calculate 3 different rolling hashes all within 64 bit
modulos = (int(pow(2, 19)-1), int(pow(2, 31)-1) , int(pow(2, 61)-1))
# precalculate 27^l for l from 1 to l_1
powers_27 = [None]*(l_l + 1)
powers_27[0] = (1,1,1)
for i in range(1, l_l + 1):
(p1, p2, p3) = powers_27[i-1]
(m1,m2,m3) = modulos
powers_27[i] = ((p1*27)%m1, (p2*27)%m2, (p3*27)%m3)
# build a set to add every prefix in words. I will calculate 4 rolling hashes
# for 4 different modulo
rolling_hashes = set()
for word in words:
rolling_hash = (0,0,0)
for ch in word:
(h1, h2, h3) = rolling_hash
(m1,m2,m3) = modulos
n_c = ord(ch) - 96
rolling_hash = ((h1 * 27 + n_c) % m1,(h2 * 27 + n_c) % m2, (h3 * 27 + n_c) % m3)
rolling_hashes.add(rolling_hash)
# set window of i to j in target
# we can add and remove a character from the window and calculate rolling hash of current window
# efficiently
i=0
min_valid = [0]*len(target)
# min_valid is the number of valid prefixes that can be concatenated together to form target[0...i]
window_rolling_hash = (0,0,0)
(m1,m2,m3) = modulos
for j in range(len(target)):
# update window rolling hash after adding target[i] to current window
h1,h2,h3 = window_rolling_hash
n_c = ord(target[j]) - 96
window_rolling_hash = ((h1*27 + n_c)%m1, (h2*27 + n_c)%m2, (h3*27 + n_c)%m3)
# keep updating i as as long as the window of target[i..j] is not a valid prefix
while window_rolling_hash not in rolling_hashes and i <= j:
# advance i to get the window in range
n_c = ord(target[i]) - 96
p1,p2,p3 = powers_27[j-i]
# remove target[i] from the window and update window rolling hash
(h1,h2,h3) = window_rolling_hash
window_rolling_hash = (h1 - p1 * n_c + m1)%m1, (h2 - p2 * n_c + m2)%m2, (h3 - p3 * n_c + m3)%m3
i += 1
# if i goes beyond j there is no way to build target[0..j] with valid prefixes
if i > j:
return -1
if i==0:
min_valid[j] = 1
else:
min_valid[j] = 1 + min_valid[i-1]
return min_valid[-1]
``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | KMP | kmp-by-linda2024-oung | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | linda2024 | NORMAL | 2025-03-14T02:25:39.557430+00:00 | 2025-03-14T02:25:39.557430+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
private int[] PrefixTarget(string s)
{
int len = s.Length;
int[] preArr = new int[len];
for(int i = 1; i < len; i++)
{
int j = preArr[i-1];
while(j > 0 && s[i] != s[j])
{
j = preArr[j-1];
}
if(s[i] == s[j])
j++;
preArr[i] = j;
}
return preArr;
}
public int MinValidStrings(string[] words, string target) {
int len = words.Length, lenT = target.Length;
int[] dist = new int[lenT+1];
foreach(string w in words)
{
int[] preArr = PrefixTarget(w+"#"+target);
int wLen = w.Length;
for(int i = 1; i <= lenT; i++)
{
dist[i] = Math.Max(dist[i], preArr[wLen+i]);
}
}
int curLen = lenT, res = 0;
while(curLen > 0 && dist[curLen] > 0)
{
curLen -= dist[curLen];
res++;
}
return curLen == 0 ? res : -1;
}
}
``` | 0 | 0 | ['C#'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | DP + BFS [ EXPLAINED] | dp-bfs-explained-by-r9n-qe6l | IntuitionFigure out how many valid strings can be formed from the given words to match the target string. We try to break down the target by matching parts of i | r9n | NORMAL | 2025-02-05T07:34:20.513453+00:00 | 2025-02-05T07:34:20.513453+00:00 | 6 | false | # Intuition
Figure out how many valid strings can be formed from the given words to match the target string. We try to break down the target by matching parts of it using each word, calculating the longest possible match for each position of the target. We use the Knuth-Morris-Pratt (KMP) algorithm to help with efficient string matching and track the longest prefix-suffix using an array.
# Approach
We concatenate each word with the target, calculate the KMP table (LPS array), and for each position in the target, we check the maximum match length we can achieve using the words. We keep track of the number of jumps needed to cover the target.
# Complexity
- Time complexity:
O(n * m), where n is the number of words and m is the length of the target string. This is because we process each word and calculate its longest prefix-suffix array, which takes O(m) time per word.
- Space complexity:
O(n * (m + k)), where n is the number of words, m is the length of the target string, and k is the average length of the words. This is because we store the LPS arrays for each word combined with the target string.
# Code
```kotlin []
class Solution {
// Function to calculate the minimum number of valid strings
fun minValidStrings(words: Array<String>, target: String): Int {
val targetLength = target.length
val wordsCount = words.size
val lpsArrayList = mutableListOf<IntArray>()
// Process each word, compute its LPS (Longest Prefix Suffix) array
for (word in words) {
val combinedString = StringBuilder().apply {
append(word)
append('#') // Separator between word and target
append(target)
}.toString()
// LPS array will store the length of the longest prefix suffix at each index
val lps = IntArray(word.length + targetLength + 1)
kmp(lps, combinedString) // Compute KMP (Knuth-Morris-Pratt) for the combined string
lpsArrayList.add(lps) // Add the LPS array to the list
}
var total = 0
var i = targetLength - 1
// Iterate over the target from the end and try to match substrings
while (i >= 0) {
var maxMatch = 0
// For each word, find the maximum match length for the target
for (j in 0 until wordsCount) {
maxMatch = maxOf(maxMatch, lpsArrayList[j][words[j].length + 1 + i])
}
// If no match is found, return -1
if (maxMatch == 0) return -1
i -= maxMatch // Move the target index backward by the matched length
total++ // Increment the total number of valid strings
}
return total // Return the total number of valid strings
}
// KMP algorithm to compute the LPS (Longest Prefix Suffix) array
fun kmp(lps: IntArray, s: String) {
var length = 0
var i = 1
// Traverse the string and build the LPS array
while (i < s.length) {
if (s[i] == s[length]) {
length++
lps[i] = length // Store the length of the longest prefix suffix at index i
i++
} else {
if (length != 0) {
// If mismatch happens, fall back to the last valid LPS length
length = lps[length - 1]
} else {
lps[i] = 0 // No valid prefix-suffix match, set to 0
i++
}
}
}
}
}
``` | 0 | 0 | ['Array', 'Math', 'Binary Search', 'Dynamic Programming', 'Breadth-First Search', 'Segment Tree', 'Rolling Hash', 'String Matching', 'Hash Function', 'Kotlin'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | scala z-function + jump game ii | z-function-jump-game-ii-by-vititov-t9qw | scala version of @dmitrii_bokovikov approach https://leetcode.com/problems/minimum-number-of-valid-strings-to-form-target-ii/solutions/5790939/z-function-jump-g | vititov | NORMAL | 2025-01-11T22:03:20.480130+00:00 | 2025-01-11T22:04:24.262650+00:00 | 1 | false | scala version of @dmitrii_bokovikov approach https://leetcode.com/problems/minimum-number-of-valid-strings-to-form-target-ii/solutions/5790939/z-function-jump-game-ii/
z-function to find target maximum prefix length in words,
then jump game ii: https://leetcode.com/problems/jump-game-ii/
```scala []
object Solution {
import util.chaining.scalaUtilChainingOps
def minValidStrings(words: Array[String], target: String): Int =
lazy val zmx = words.iterator.foldLeft(Map.empty[Int,Int]){case (mx,w) =>
lazy val s = s"$w#$target."
Iterator.range(1,s.length).foldLeft(((0,0),Map(0->0),mx)){case (((l,r),z,mx),i) =>
lazy val zi0 = if(i<r) (r-i) min z.getOrElse(i-l,0) else 0
lazy val zi1 = zi0 + (Iterator.range(zi0,s.length-i)
.takeWhile(zi => s(zi) == s(i+zi)).map(_ + 1)).length
lazy val j = i-(w.length+1)
lazy val mx1 = if(j<0) mx else mx.updatedWith(j){_.orElse(Some(0)).map(_ max zi1)}
(if (i+zi1>r) (i,i+zi1) else (l,r), z + (i -> zi1), mx1)
}._3
}
lazy val l0 = List.range(0,target.length+1).map(i => (zmx(i)+i,i))
if(l0.length==1) (l0.head._1-l0.head._2)*2-1
else (List.unfold((0,l0.head,l0.tail)){case (acc,d0,l) =>
Option.when(l.nonEmpty){
lazy val (t,d) = l.span(_._2 <= d0._1)
if(d0._1 == d0._2) ((-1,(acc,d0,l)),(-1,(-1,-1),l.empty))
else ((acc+1,(acc,d0,l)),(acc+1,t.maxByOption(_._1).getOrElse(0,0),d))
}
}).last._1
}
``` | 0 | 0 | ['String', 'Greedy', 'Scala'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | [Python3] Z-function + BFS | python3-z-function-bfs-by-deimvis-xoiv | Intuition\nIf for each $i$ we know the "longest jump" we can make s.t. $\text{target}[i:i+\text{longest\_jump}] == \text{prefix of some word}$ then it\'s a grap | deimvis | NORMAL | 2024-11-29T12:33:52.068789+00:00 | 2024-11-29T12:34:38.323878+00:00 | 3 | false | # Intuition\nIf for each $i$ we know the "longest jump" we can make s.t. $\\text{target}[i:i+\\text{longest\\_jump}] == \\text{prefix of some word}$ then it\'s a graph problem where each $i$ is a node and there is an edge from $i$ to each of $[i+1, \\text{longest\\_jump}]$ nodes\n\n# Approach\n\n* Calculate the "longest jumps" efficiently using z-function\n* Calculate the shortest path using BFS\n\n# Complexity\n- Time complexity: $$ ( len(\\text{words}) \\times (\\text{max\\_word\\_length}+len(\\text{target})) ) $$\n\n- Space complexity: $$ sizeof(\\text{words}) + sizeof(\\text{target}) $$\n\n# Code\n```python3 []\n# https://cp-algorithms.com/string/z-function.html\n"""\nz_function returns an array of size len(s):\narray[i] = max(sz) s.t. s[:sz] == s[i:i+sz]\n"""\ndef z_function(s):\n n = len(s)\n z = [0] * n\n l = r = 0\n for i in range(1, n):\n if i < r:\n z[i] = min(z[i - l], r - i)\n while i + z[i] < n and s[i + z[i]] == s[z[i]]:\n z[i] += 1\n if i + z[i] > r:\n l = i\n r = i + z[i]\n return z\n\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target)\n\n # z function \u2014 O( len(words) x (max_word_length+len(target)) )\n # maxjump[i] = max(j) s.t. target[i:j] is a prefix of some word\n maxjump = [i for i in range(n)]\n for w in words:\n z = z_function(w + "$" + target)\n for i in range(n):\n maxjump[i] = max(maxjump[i], i + z[len(w) + 1 + i])\n\n # bfs \u2014 O( len(target) )\n q = [0]\n maxseen = 0\n step = 0\n while len(q) > 0:\n newq = []\n for i in q:\n for j in range(maxseen + 1, maxjump[i] + 1):\n if j == len(target):\n return step + 1\n newq.append(j)\n maxseen = j\n step += 1\n q = newq\n return -1\n\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Explained Aho-Corasick + greedy, 61ms beat 100% | explained-aho-corasick-greedy-61ms-beat-qp6am | Here\'s a concise description of the solution, focusing on the key invariants:\n\n# Intuition\nAho-Corasick algorithm can efficiently find, for each position in | ivangnilomedov | NORMAL | 2024-11-08T14:25:37.926201+00:00 | 2024-11-08T14:25:37.926233+00:00 | 11 | false | Here\'s a concise description of the solution, focusing on the key invariants:\n\n# Intuition\nAho-Corasick algorithm can efficiently find, for each position in the target string, the longest preceding substring that is a valid prefix of a word in words.\n\n# Approach\nThe main steps of the approach are:\n\n1. **Construct the Aho-Corasick Trie**:\n - The trie structure represents all the words in the `words` array.\n - The `fail` pointers form a directed acyclic graph (DAG) that allows efficient traversal of the trie.\n\n2. **Compute the Longest Indexed Suffix**: Using the constructed trie, the solution computes the length of the longest valid preceding substring for each index in the target string.\n\n3. **Determine the Minimum Number of Valid Strings**:\nThe solution uses a greedy approach. The key insight is that the minimum number of valid strings required can be computed by iterating through the target string from right to left and subtracting the length of the longest valid prefix that ends at each position.\n\nSpecifically, the solution does the following:\n\n1. Iterate through the target string from right to left.\n2. At each index `i`, the length of the longest valid prefix that ends at that index is given by `lis[i]`. \n3. If `lis[i]` is 0, it means there is no valid prefix that can be used to form the target string, so the solution returns -1 (indicating it\'s not possible to form the target).\n4. Otherwise, the solution subtracts `lis[i]` from the current index `i`, and increments the count of valid strings required.\n\nThis greedy approach is optimal because if there were a more optimal solution that requires fewer valid strings, then there must be some rightmost position in the target string where the two solutions differ. At that position, the non-greedy solution would have a longer valid prefix than the greedy solution, which would contradict the optimality of the non-greedy solution.\n\n# Complexity\n- Time complexity: $$O(|target|)$$\n - The time complexity of this final step is linear in the length of the target string, as it performs a single pass through the target string and performs constant-time operations at each index.\n\n- Space complexity: $$O(|target|)$$\n - The space required is proportional to the length of the target string, as it uses the `lis` vector computed in the previous step.\n\n# Complexity\n- Time complexity: $$O(|target| + \\sum_{w \\in words} |w|)$$\n - The time to construct the Aho-Corasick trie is $$O(\\sum_{w \\in words} |w|)$$.\n - The time to compute the longest indexed suffix is $$O(|target|)$$.\n\n- Space complexity: $$O(\\sum_{w \\in words} |w|)$$\n - The space required to store the Aho-Corasick trie is proportional to the total length of all the words in the `words` array.\n\n# Code\n```cpp []\nclass CarassiusTrie {\nprivate:\n /** The Aho-Corasick algorithm maintains two key invariants:\n * 1. The trie structure represents all the words in the `words` array.\n * 2. The `fail` pointers that allows efficient traversal of the trie. */\n struct Node {\n Node** child = nullptr;\n Node* fail = nullptr;\n int len;\n Node(int len = 0) : len(len) {}\n Node* set_len(int len) {\n this->len = len;\n return this;\n }\n Node* operator[] (char c, vector<Node>& buf, int& nxb) {\n if (!child[c])\n child[c] = buf[nxb++].set_len(len + 1);\n return child[c];\n }\n };\n\npublic:\n CarassiusTrie(const vector<string>& words, const string& target)\n : buf(accumulate(words.begin(), words.end(), 1,\n [](int acc, const string& s) { return acc + s.length(); })) {\n minch = numeric_limits<char>::max();\n char maxch = numeric_limits<char>::min();\n for (char c : target) {\n minch = min(minch, c);\n maxch = max(maxch, c);\n }\n for (const string& w : words) for (char c : w) {\n minch = min(minch, c);\n maxch = max(maxch, c);\n }\n alp_size = maxch - minch + 1;\n child_buf.resize(alp_size * buf.size());\n for (int i = 0; i < buf.size(); ++i)\n buf[i].child = &child_buf[i * alp_size];\n\n root = &buf[nxb++];\n for (const string& w : words)\n index(w);\n populate_fail();\n }\n\n vector<int> compute_longest_indexed_suffix(const string& t) {\n const int L = t.length();\n vector<int> lis(L);\n transform(\n t.begin(), t.end(), lis.begin(),\n [n = this->root, this](char c) mutable {\n c -= minch;\n while (n != this->root && !n->child[c])\n n = n->fail;\n if (n->child[c])\n n = n->child[c];\n return n->len;\n });\n return lis;\n }\n\nprivate:\n Node* root;\n\n vector<Node> buf;\n int nxb = 0;\n\n char minch;\n int alp_size;\n vector<Node*> child_buf;\n\n void index(const string& t) {\n Node* n = root;\n for (char c : t)\n n = (*n)[c - minch, buf, nxb];\n }\n\n void populate_fail() {\n root->fail = root;\n queue<Node*> q;\n for (char c = 0; c < alp_size; ++c) if (root->child[c]) {\n root->child[c]->fail = root;\n q.push(root->child[c]);\n }\n while (!q.empty()) {\n Node* n = q.front();\n q.pop();\n for (char c = 0; c < alp_size; ++c) if (n->child[c]) {\n Node* f = n->fail;\n while (f != root && !f->child[c])\n f = f->fail;\n n->child[c]->fail = f->child[c] ? f->child[c] : root;\n q.push(n->child[c]);\n }\n }\n }\n};\n\nclass Solution {\npublic:\n int minValidStrings(const vector<string>& words, const string& target) {\n CarassiusTrie caras(words, target);\n const vector<int> lis(caras.compute_longest_indexed_suffix(target));\n int res = 0;\n for (int l = target.length(); l > 0;) {\n if (lis[l - 1] == 0) return -1;\n l -= lis[l - 1];\n ++res;\n }\n return res;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Segement Tree + KMP +Dyanamic Programming | segement-tree-kmp-dyanamic-programming-b-obu0 | W=words.length();\nWi=words[i].length();\nT=target.length()\n\n# Complexity\n- Time complexity:O(sum(Wi)+W*T+Tlog(T))\n Add your time complexity here, e.g. O(n) | TechTinkerer | NORMAL | 2024-11-06T17:07:30.632493+00:00 | 2024-11-06T17:07:30.632543+00:00 | 14 | false | W=words.length();\nWi=words[i].length();\nT=target.length()\n\n# Complexity\n- Time complexity:O(sum(Wi)+W*T+Tlog(T))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(T + max(Wi))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass SegmentTree{\n \nvector<int> sgtree;\n\n public:\n \n SegmentTree(int n){\n sgtree.resize(4*n+1);\n \n \n }\n \n \n void build(int index,int low,int high,vector<int> &arr){\n if(low==high){\n sgtree[index]=arr[low];\n return ;\n }\n \n int mid=(low+high)/2;\n \n build(2*index+1,low,mid,arr);\n build(2*index+2,mid+1,high,arr);\n \n sgtree[index]=min(sgtree[2*index+1],sgtree[2*index+2]);\n \n \n }\n \n int query(int index,int low,int high,int l,int h){\n if(low>h||l>high)\n return 1e6;\n \n else if(l<=low&&high<=h)\n return sgtree[index];\n \n \n else{\n int mid=(low+high)/2;\n \n return min(query(2*index+1,low,mid,l,h),query(2*index+2,mid+1,high,l,h));\n }\n }\n \n void update(int index,int low,int high,int i,int val){\n if(low==high){\n sgtree[index]=val;\n return ;\n }\n \n int mid=(low+high)/2;\n \n if(i<=mid)\n update(2*index+1,low,mid,i,val);\n \n else\n update(2*index+2,mid+1,high,i,val);\n \n sgtree[index]=min(sgtree[2*index+1],sgtree[2*index+2]);\n }\n};\nclass Solution {\npublic:\n vector<int> getlps(string s){\n int m=s.size();\n\n int i=1;\n vector<int> lps(m,0);\n int len=0;\n\n lps[0]=0;\n while(i<m){\n if(s[i]==s[len]){\n len++;\n lps[i]=len;\n i++;\n }\n else{\n if(len>0){\n len=lps[len-1];\n }\n else{\n lps[i]=0;\n i++;\n }\n }\n }\n\n return lps;\n }\n int minValidStrings(vector<string>& words, string target) {\n\n int m=target.size();\n vector<int> v(m,0);\n for(auto i:words){\n auto lps=getlps(i+"#"+target);\n // for(auto i:lps)\n // cout<<i<<" ";\n // cout<<endl;\n for(int j=0;j<m;j++){\n v[j]=max(v[j],lps[j+(int)i.size()+1]);\n }\n }\n\n // for(auto i:v)\n // cout<<i<<" ";\n // cout<<endl;\n\n vector<int> dp(m+1,1e6);\n\n dp[0]=0;\n\n SegmentTree sg(m+1);\n\n sg.build(0,0,m,dp);\n\n for(int i=1;i<=m;i++){\n int len=v[i-1];\n\n int mini=sg.query(0,0,m,i-len,i-1);\n\n dp[i]=1+mini;\n\n sg.update(0,0,m,i,dp[i]);\n }\n\n return (dp[m]>=1e6)?-1:dp[m];\n }\n};\n``` | 0 | 0 | ['String', 'Dynamic Programming', 'Segment Tree', 'String Matching', 'C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Z-algorithm +DP + Segment Tree | z-algorithm-dp-segment-tree-by-techtinke-hwpk | W=words.length();\nWi=words[i].length();\nT=target.length()\n\n# Complexity\n- Time complexity:O(sum(Wi)+W*T+Tlog(T))\n Add your time complexity here, e.g. O(n) | TechTinkerer | NORMAL | 2024-11-06T16:08:48.207269+00:00 | 2024-11-06T16:08:48.207298+00:00 | 14 | false | W=words.length();\nWi=words[i].length();\nT=target.length()\n\n# Complexity\n- Time complexity:O(sum(Wi)+W*T+Tlog(T))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(T + max(Wi))\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass SegmentTree{\n public: \nvector<int> sgtree;\n\n \n \n SegmentTree(int n){\n sgtree.resize(4*n+1);\n \n \n }\n \n \n void build(int index,int low,int high,vector<int> &arr){\n if(low==high){\n sgtree[index]=arr[low];\n return ;\n }\n \n int mid=(low+high)/2;\n \n build(2*index+1,low,mid,arr);\n build(2*index+2,mid+1,high,arr);\n \n sgtree[index]=min(sgtree[2*index+1],sgtree[2*index+2]);\n \n \n }\n \n int query(int index,int low,int high,int l,int h){\n if(l>h)\n return 1e6;\n if(low>h||l>high)\n return 1e6;\n \n else if(l<=low&&high<=h)\n return sgtree[index];\n \n \n else{\n int mid=(low+high)/2;\n \n return min(query(2*index+1,low,mid,l,h),query(2*index+2,mid+1,high,l,h));\n }\n }\n \n void update(int index,int low,int high,int i,int val){\n if(low==high){\n sgtree[index]=val;\n return ;\n }\n \n int mid=(low+high)/2;\n \n if(i<=mid)\n update(2*index+1,low,mid,i,val);\n \n else\n update(2*index+2,mid+1,high,i,val);\n \n sgtree[index]=min(sgtree[2*index+1],sgtree[2*index+2]);\n }\n};\nclass Solution {\npublic:\n vector<int> zfunction(string s){\n int n=s.size();\n vector<int> z(n,0);\n\n int l=0,r=0;\n\n for(int i=1;i<n;i++){\n z[i]=max(0,min(z[i-l],r-i+1));\n\n while(s[z[i]]==s[z[i]+i])\n z[i]++;\n\n if(i+z[i]-1>r){\n l=i;\n r=i+z[i]-1;\n }\n }\n\n return z;\n }\n int minValidStrings(vector<string>& words, string target) {\n \n int m=target.size();\n\n vector<int> v(m,0);\n\n for(auto &i:words){\n\n int n=i.size();\n auto z=zfunction(i+"%"+target);\n\n for(int j=n+1,k=0;j<z.size();j++,k++){\n v[k]=max(v[k],z[j]);\n }\n\n }\n\n \n\n vector<int> dp(m+1,1e6);\n\n SegmentTree sg(m+1);\n dp[m]=0;\n sg.build(0,0,m,dp);\n\n \n\n for(int i=m-1;i>=0;i--){\n int len=v[i];\n\n int mini=sg.query(0,0,m,i+1,i+len);\n\n dp[i]=1+mini;\n\n sg.update(0,0,m,i,dp[i]);\n }\n\n \n\n return (dp[0]>=1e6)?-1:dp[0];\n\n\n }\n};\n``` | 0 | 0 | ['String', 'Dynamic Programming', 'Segment Tree', 'String Matching', 'C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Aho-Corasick 35 lines | aho-corasick-35-lines-by-nguyenquocthao0-7u2u | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | nguyenquocthao00 | NORMAL | 2024-10-24T13:17:22.377726+00:00 | 2024-10-24T13:17:22.377747+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Trie:\n def __init__(self):\n self.c=defaultdict(Trie)\n self.i=0\n self.prev=None\n def add(self, w):\n cur=self\n for i,ch in enumerate(w):\n cur=cur.c[ch]\n cur.i=i+1\n def next(self, ch):\n if ch in self.c: return self.c[ch]\n if not self.prev: return self\n return self.prev.next(ch)\n def aho_corasick(self):\n dq=deque((self, y) for y in self.c.values())\n while dq:\n x,y = dq.popleft()\n y.prev=x\n for ch in y.c: dq.append((x.next(ch), y.c[ch]))\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n trie=Trie()\n for w in words: trie.add(w)\n trie.aho_corasick()\n n=len(target)\n pre=[0]*n\n for i,ch in enumerate(target):\n trie=trie.next(ch)\n pre[i]=trie.i\n res,i=0, n-1\n while i>=0:\n if pre[i]==0: return -1\n res,i=res+1, i-pre[i]\n return res\n \n``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Hashing || Binary Search || Segment Tree || Lazy Propagation | hashing-binary-search-segment-tree-lazy-qw0j0 | Approach\nthere are following things which need to be done here:\n1. String matching with polynomial Hashing.\n2. Lazy Propagation for Range Minimum Query.\n3. | anandlm12 | NORMAL | 2024-10-05T15:27:58.546933+00:00 | 2024-10-05T15:27:58.546956+00:00 | 15 | false | # Approach\nthere are following things which need to be done here:\n1. String matching with polynomial Hashing.\n2. Lazy Propagation for Range Minimum Query.\n3. Binary Search.\n\n\nLets start with the String Matching code.\nHere I create a class were we are gonna check whether the substring of target matches with any prefix present in the array of strings \'words\'.\nFirstly create hash value of all prefix of each string in words and store it in a unordered_map and check wheather the hash value of a given substring of target present into that map or not.\n \nNow coming to the binary search part.\nIf I\'m on the ith index then will find the largest index till when prefix present suppose that index is j.\n\nThen for each index between [i, j] I will update each of with 1 + (minimum number of valid strings that can be concatenated till index (i - 1)).\n\nAnd finally return minimum value at n - 1.\n\n# Complexity\n- Time complexity:\nHashingTime = min(n, words[i] * words[i].size());\noverall = min(n * logn, HashingTime)\n\n# Code\n```cpp []\nconst int inf = 2e9;\nclass Hashing{\n long long p;\n int N, mod, length;\n vector<long long> power;\n vector<long long> hashString;\n unordered_map<long long, bool> hashPresent;\npublic:\n Hashing(){}\n Hashing(int N, int length, int mod, long long p) {\n this-> p = p;\n this-> N = N;\n this-> mod = mod;\n this->length = length;\n power.resize(N + 1);\n hashString.resize(length + 1);\n }\n void init(string& s, vector<string> words) {\n power[0] = 1;\n for(int i = 1; i <= N; i++) {\n power[i] = (power[i - 1] % mod * p % mod) % mod;\n }\n for(int i = 1; i <= length; i++) {\n hashString[i] = (hashString[i - 1] % mod + (power[i] * 1LL * (s[i - 1] - \'a\' + 1)) % mod) % mod;\n }\n for(int i = 0; i < words.size(); i++) {\n string temp = words[i];\n long long hashValue = 0;\n for(int i = 1; i <= (int) temp.size(); i++) {\n hashValue = (hashValue % mod + power[i] * 1LL * (temp[i - 1] - \'a\' + 1) % mod) % mod;\n hashPresent[(hashValue % mod * power[N] % mod) % mod] = true;\n }\n }\n }\n bool foundString(int i, int j) {\n long long hash = ((hashString[j + 1] - hashString[i] + mod) % mod * power[N - i] % mod) % mod;\n return (hashPresent.find(hash) != hashPresent.end());\n }\n};\n\nclass SegmentTree {\n int n;\n vector<int> seg, lazy;\n \n void propagate(int ind, int st, int en) {\n if (lazy[ind] != inf) {\n seg[ind] = min(seg[ind], lazy[ind]);\n \n if (st != en) { \n lazy[2 * ind + 1] = min(lazy[2 * ind + 1], lazy[ind]);\n lazy[2 * ind + 2] = min(lazy[2 * ind + 2], lazy[ind]);\n }\n \n lazy[ind] = inf;\n }\n }\n \npublic:\n SegmentTree(int _n) : n(_n) {\n seg.resize(4 * n, inf);\n lazy.resize(4 * n, inf);\n }\n \n void rangeUpdate(int ind, int st, int en, int l, int r, int val) {\n propagate(ind, st, en);\n \n if (st > r || en < l) return;\n \n if (st >= l && en <= r) {\n lazy[ind] = min(lazy[ind], val);\n propagate(ind, st, en);\n return;\n }\n \n int mid = (st + en) >> 1;\n rangeUpdate(2 * ind + 1, st, mid, l, r, val);\n rangeUpdate(2 * ind + 2, mid + 1, en, l, r, val);\n \n seg[ind] = min(seg[2 * ind + 1], seg[2 * ind + 2]);\n }\n \n int query(int ind, int st, int en, int l, int r) {\n if (st > r || en < l) return inf;\n \n propagate(ind, st, en);\n \n if (st >= l && en <= r) {\n return seg[ind];\n }\n \n int mid = (st + en) >> 1;\n return min(query(2 * ind + 1, st, mid, l, r), query(2 * ind + 2, mid + 1, en, l, r));\n }\n \n void update(int l, int r, int val) {\n rangeUpdate(0, 0, n - 1, l, r, val);\n }\n \n int query(int l, int r) {\n return query(0, 0, n - 1, l, r);\n }\n};\n\nclass Solution {\npublic:\n const static int N = 1e5;\n Hashing* hasher1;\n Hashing* hasher2;\n int minValidStrings(vector<string>& words, string target) {\n int n = target.size();\n hasher1 = new Hashing(N, n, 1e9 + 7, 29);\n hasher2 = new Hashing(N, n, 1e9 + 9, 31);\n hasher1->init(target, words);\n hasher2->init(target, words);\n \n SegmentTree S(n);\n \n for(int i = 0; i < n; i++) {\n int index = -1;\n int l = i, h = n - 1;\n while(l <= h) {\n int mid = (l + h) >> 1;\n if(hasher1->foundString(i, mid) && hasher2->foundString(i, mid)) {\n index = mid;\n l = mid + 1;\n }\n else {\n h = mid - 1;\n }\n }\n if(index == -1) continue;\n int minTillNow = (i == 0 ? 0 : S.query(i - 1, i - 1));\n S.update(i, index, minTillNow + 1);\n }\n int result = S.query(n - 1, n - 1);\n delete hasher1;\n delete hasher2;\n return (result == inf ? -1 : result);\n }\n};\n``` | 0 | 0 | ['Binary Search', 'Segment Tree', 'Rolling Hash', 'C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Python || Rolling Hashing ||faster than 96% | python-rolling-hashing-faster-than-96-by-h5pq | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vilaparthibhaskar | NORMAL | 2024-09-27T00:22:44.266109+00:00 | 2024-09-27T00:22:44.266149+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(N)\n\n# Code\n```python3 []\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n d, prime = 256, 1000000007\n pow_d = [1] * (len(target) + 1)\n for i in range(1, len(pow_d)):\n pow_d[i] = (pow_d[i - 1] * d) % prime\n h = set()\n for i in words:\n th = 0\n for j in i:\n th = (d * th + ord(j)) % prime\n h.add(th)\n dp = [math.inf] * len(target)\n i = 0\n th = 0\n l = 0\n while i < len(target):\n th = (d * th + ord(target[i])) % prime\n if th in h:\n dp[i] = 1 + (dp[l - 1] if l - 1 >= 0 else 0)\n else:\n while l < i:\n temp = pow_d[i - l]\n th = (th - ord(target[l]) * temp) % prime\n l += 1\n if th in h:\n dp[i] = 1 + (dp[l - 1] if l - 1 >= 0 else 0)\n break\n i += 1\n return (dp[-1] if dp[-1] != math.inf else -1)\n\n\n\n\n \n\n\n\n\n \n``` | 0 | 0 | ['Array', 'String', 'Dynamic Programming', 'Rolling Hash', 'Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Test a code. | test-a-code-by-ssrlive-tjlk | \nrust []\nimpl Solution {\n pub fn min_valid_strings(words: Vec<String>, target: String) -> i32 {\n let mut ps = vec![0; target.len() + 1];\n | ssrlive | NORMAL | 2024-09-26T08:46:30.740350+00:00 | 2024-09-26T08:46:30.740369+00:00 | 2 | false | \n```rust []\nimpl Solution {\n pub fn min_valid_strings(words: Vec<String>, target: String) -> i32 {\n let mut ps = vec![0; target.len() + 1];\n for w in words.iter() {\n let pi = Self::prefix_function(&format!("{}#{}", w, target));\n for i in 1..=target.len() {\n ps[i] = ps[i].max(pi[w.len() + i]);\n }\n }\n let mut len = target.len() as i32;\n let mut res = 0;\n while len > 0 && ps[len as usize] > 0 {\n res += 1;\n len -= ps[len as usize];\n }\n if len == 0 {\n res\n } else {\n -1\n }\n }\n\n fn prefix_function(s: &str) -> Vec<i32> {\n let s = s.as_bytes();\n let n = s.len();\n let mut pi = vec![0_i32; n];\n let mut i = 1;\n while i < n {\n let mut j = pi[i - 1];\n while j > 0 && s[i] != s[j as usize] {\n j = pi[(j - 1) as usize];\n }\n if s[i] == s[j as usize] {\n j += 1;\n }\n pi[i] = j;\n i += 1;\n }\n pi\n }\n}\n\n``` | 0 | 0 | ['Rust'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Z function optimization | z-function-optimization-by-go_net_shaw-tph6 | Intuition\nJust an string optimization problem\n Describe your first thoughts on how to solve this problem. \n\n # Approach \n Describe your approach to solving | go_net_shaw | NORMAL | 2024-09-21T23:14:19.227193+00:00 | 2024-09-21T23:14:19.227212+00:00 | 15 | false | # Intuition\nJust an string optimization problem\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(sumOfWords + target*countWords)= O(10^5+5$*$10^6)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(target+length of word)=O(10^5)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {//3:46am\npublic:\nvector<int> zfn(string s){\n// cout<<s<<endl;\nint n=s.size();\nvector<int>z(n,0);\n z[0]=s.size();\n \n int l=0,r=0;\n int i=1;\n while(i<n){\n if(r>=i){\n z[i]=min(r-i+1,z[i-l]);\n }\n while(i+z[i]<n&&s[z[i]]==s[i+z[i]]) z[i]++;\n\n if(i+z[i]-1>r) {\n l=i;\n r=i+z[i]-1;\n }\n i++;\n }\n return z;\n}\nint fn(vector<int>v){\n int n=v.size();\n int ans=0; int i=0;\n int last=0,nextLast=0;\n if(v[0]==0)return -1;\n while(last<=n-1){\n\n while(i<=last){\n nextLast=max(nextLast,i+v[i]);i++;\n }\n if(nextLast==last)return -1;\n ans++;\n \n last=nextLast;\n nextLast=0;\n }\n // if(last==n-1)ans++;\n return ans;\n}\n\n\n int minValidStrings(vector<string>& words, string target) {\n int n=target.size();\n vector<int>pre(n,0);\n for(auto w:words){\n string s=w+"#"+target;\n vector<int>z=zfn(s);\n \n for(int i=w.size()+1;i<z.size();i++){\n \n pre[i-w.size()-1]=max(pre[i-w.size()-1],z[i]);\n }\n \n }\n // for(auto it:pre)cout<<it<<" ";cout<<endl;\n return fn(pre);\n }\n};\n``` | 0 | 0 | ['String', 'Rolling Hash', 'C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | KMP + DP | kmp-dp-by-bora_marian-5jmu | Compute the KMP suffix length as prefix for the concatenation: (word + "#" + target) and check for target\'s suffixes which is the length of prefix.\nFor KMP ex | bora_marian | NORMAL | 2024-09-21T13:27:35.332281+00:00 | 2024-09-22T06:42:19.627928+00:00 | 11 | false | Compute the KMP suffix length as prefix for the concatenation: (word + "#" + target) and check for target\'s suffixes which is the length of prefix.\nFor KMP explanation refer to Tushar Roy\'s video: [https://www.youtube.com/watch?v=GTJr8OvyEVQ](https://www.youtube.com/watch?v=GTJr8OvyEVQ)\n$$dp[i]$$ represents the minimum number of \'good\' strings up to position \uD835\uDC56\n$$dp[i] = dp[i - l] + 1$$, where \uD835\uDC59 is the length of the word\'s prefix that matches the target\'s suffix ending at position \uD835\uDC56.\n\n\uD83D\uDCAA\uD83D\uDE80Keep leetcoding! Keep improving!\n# Code\n```csharp []\npublic class Solution {\n public int MinValidStrings(string[] words, string target) \n {\n int nt = target.Length;\n int[] dp = new int[nt + 1];\n HashSet<int>[] preLengths = new HashSet<int>[nt + 1];\n for (int i = 0; i <= nt; i++) \n {\n dp[i] = nt + 1;\n preLengths[i] = new HashSet<int>();\n }\n\n dp[0] = 0;\n foreach(var word in words) \n {\n StringBuilder sb = new StringBuilder(word);\n sb.Append("#");\n sb.Append(target);\n var lpsConcat = CalculateSuffixAsPrefixKMP(sb.ToString()); \n for (int i = 0; i < nt; i++) \n { \n int posInConcat = word.Length + i + 1; \n if (lpsConcat[posInConcat] > 0) \n { \n preLengths[i].Add(lpsConcat[posInConcat]);\n } \n }\n }\n \n for (int i = 0; i < nt; i++) \n {\n foreach(var len in preLengths[i]) \n {\n dp[i + 1] = Math.Min(dp[i + 1 - len] + 1, dp[i+1]);\n }\n }\n \n return dp[nt] > nt ? -1 : dp[nt];\n }\n\n public int[] CalculateSuffixAsPrefixKMP(string s) \n {\n int n = s.Length;\n int[] lps = new int[n];\n lps[0] = 0;\n for (int i = 1; i < n; i++) \n {\n int t = lps[i-1];\n \n while (t > 0 && s[i] != s[t])\n t = lps[t-1];\n if (s[i] == s[t])\n t++;\n lps[i] = t;\n }\n return lps;\n }\n}\npublic class DescendingComparer : IComparer<int>\n{\n public int Compare(int x, int y)\n {\n return y.CompareTo(x);\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Simple Clean Solution using KMP | simple-clean-solution-using-kmp-by-amit1-wnf8 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Amit130 | NORMAL | 2024-09-21T13:13:36.100424+00:00 | 2024-09-21T13:13:36.100444+00:00 | 15 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ~O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minValidStrings(vector<string>& words, string target) {\n int len = target.length();\n int n = words.size();\n vector<vector<int>> lps(n);\n for(int i=0;i<n;i++){\n vector<int> temp(words[i].length()+len+1);\n calcLps(temp,words[i]+\'#\'+target);\n lps[i]=temp;\n }\n int ans=0;\n while(len>0){\n int jump = 0;\n for(int i=0;i<words.size();i++){\n int currIndex = words[i].length()+len;\n jump=max(jump,lps[i][currIndex]);\n }\n ans++;\n if(jump==0){\n return -1;\n }\n len-=jump;\n }\n return ans;\n }\n\n void calcLps(vector<int>& ans,string pattern){\n int len=0;\n int i=1;\n while(i<pattern.length()){\n if(pattern[i]==pattern[len]){\n len++;\n ans[i]=len;\n i++;\n } else {\n if(len==0){\n ans[i]=0;\n i++;\n } else {\n len=ans[len-1];\n }\n }\n }\n return;\n }\n};\n\n\n\n/*\n\na a b c d a b c\ni\n\npattern : a\nlength: 1\n\n\n\n\n*/\n``` | 0 | 0 | ['Array', 'String', 'C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Z - function + segment Tree | z-function-segment-tree-by-_alphaorionis-x0bf | Approach\nZ -Function and Segment Tree\n\n# Code\ncpp []\nusing ll = long long;\nvector<int> z_function(string s) {\n int n = s.size();\n vector<int> z(n) | _alphaorionis_ | NORMAL | 2024-09-21T12:06:38.933292+00:00 | 2024-09-21T12:06:38.933315+00:00 | 12 | false | # Approach\nZ -Function and Segment Tree\n\n# Code\n```cpp []\nusing ll = long long;\nvector<int> z_function(string s) {\n int n = s.size();\n vector<int> z(n);\n int l = 0, r = 0;\n for(int i = 1; i < n; i++) {\n if(i < r) {\n z[i] = min(r - i, z[i - l]);\n }\n while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n z[i]++;\n }\n if(i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n return z;\n}\nconst int MX =2e5+1;\narray<int,4*MX> t;\nvoid update(int v,int tl,int tr,int pos,int val){\n if(tl==tr) {\n t[v] = min(t[v],val);\n return;\n }\n int tm = (tl+tr)>>1;\n if(pos<=tm) update(v<<1,tl,tm,pos,val);\n else update(v<<1|1,tm+1,tr,pos,val);\n t[v] = min(t[v<<1],t[v<<1|1]);\n}\nint query(int v,int tl,int tr,int l,int r){\n if(l>r) return 1e9;\n if(r<tl or tr<l){\n return 1e9;\n }\n if(l<=tl and tr<=r){\n return t[v];\n }\n int tm = (tl+tr)>>1;\n return min(query(v<<1,tl,tm,l,r),query(v<<1|1,tm+1,tr,l,r));\n}\nvoid build(){\n for(int i=0;i<4*MX;i++) t[i] =1e9;\n}\nclass Solution {\npublic:\n int minValidStrings(vector<string>& words, string target) {\n int n = target.size();\n vector<int> match(n);\n for(auto g:words){\n auto res = z_function(g+"#"+target);\n vector<int> clean(res.begin()+g.size()+1,res.end());\n for(int i=0;i<n;i++){\n match[i]=max(match[i],clean[i]);\n }\n }\n build();\n update(1,0,n,n,0);\n for(int i=n-1;i>=0;i--){\n int m = match[i];\n int q = query(1,0,n,i+1,i+match[i]);\n update(1,0,n,i,q+1);\n }\n int res = query(1,0,n,0,0);\n return res == 1e9 ? -1 : res;\n }\n};\n``` | 0 | 0 | ['C++'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | 3292. Minimum Number of Valid Strings to Form Target II | 3292-minimum-number-of-valid-strings-to-mhlkr | \n# Code\njava []\nclass Solution {\n public int minValidStrings(String[] words, String target) {\n int n = target.length();\n int[] dp = new i | Amitv28242 | NORMAL | 2024-09-20T13:16:27.751942+00:00 | 2024-09-20T13:16:27.751980+00:00 | 23 | false | \n# Code\n```java []\nclass Solution {\n public int minValidStrings(String[] words, String target) {\n int n = target.length();\n int[] dp = new int[n + 1];\n Arrays.fill(dp, Integer.MAX_VALUE);\n dp[0] = 0;\n\n List<List<Integer>> matches = new ArrayList<>(n);\n for (int i = 0; i < n; i++) {\n matches.add(new ArrayList<>());\n }\n char[] targetChars = target.toCharArray();\n for (String word : words) {\n char[] wordChars = word.toCharArray();\n int m = wordChars.length;\n int[] pi = new int[m];\n for (int i = 1, j = 0; i < m; i++) {\n while (j > 0 && wordChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (wordChars[i] == wordChars[j]) {\n j++;\n }\n pi[i] = j;\n }\n\n for (int i = 0, j = 0; i < n; i++) {\n while (j > 0 && targetChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (targetChars[i] == wordChars[j]) {\n j++;\n }\n if (j > 0) {\n matches.get(i - j + 1).add(j);\n if (j == m) {\n j = pi[j - 1]; \n }\n }\n }\n }\n for (int i = 0; i < n; i++) {\n if (dp[i] == Integer.MAX_VALUE) continue;\n for (int len : matches.get(i)) {\n if (i + len <= n) {\n dp[i + len] = Math.min(dp[i + len], dp[i] + 1);\n }\n }\n }\n return dp[n] == Integer.MAX_VALUE ? -1 : dp[n];\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Java'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Easy Java Solution | easy-java-solution-by-danish_jamil-361s | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Danish_Jamil | NORMAL | 2024-09-20T06:19:00.475380+00:00 | 2024-09-20T06:19:00.475410+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minValidStrings(String[] words, String target) {\n int n = target.length();\n int[] dp = new int[n + 1];\n Arrays.fill(dp, Integer.MAX_VALUE);\n dp[0] = 0;\n\n List<List<Integer>> matches = new ArrayList<>(n);\n for (int i = 0; i < n; i++) {\n matches.add(new ArrayList<>());\n }\n char[] targetChars = target.toCharArray();\n for (String word : words) {\n char[] wordChars = word.toCharArray();\n int m = wordChars.length;\n int[] pi = new int[m];\n for (int i = 1, j = 0; i < m; i++) {\n while (j > 0 && wordChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (wordChars[i] == wordChars[j]) {\n j++;\n }\n pi[i] = j;\n }\n\n for (int i = 0, j = 0; i < n; i++) {\n while (j > 0 && targetChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (targetChars[i] == wordChars[j]) {\n j++;\n }\n if (j > 0) {\n matches.get(i - j + 1).add(j);\n if (j == m) {\n j = pi[j - 1]; \n }\n }\n }\n }\n for (int i = 0; i < n; i++) {\n if (dp[i] == Integer.MAX_VALUE) continue;\n for (int len : matches.get(i)) {\n if (i + len <= n) {\n dp[i + len] = Math.min(dp[i + len], dp[i] + 1);\n }\n }\n }\n return dp[n] == Integer.MAX_VALUE ? -1 : dp[n];\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | StringHash + one extra question | stringhash-one-extra-question-by-xktz-fovz | Code is at the end.\n\nQuestion itself is pretty straight forward, either KMP or string hash + binary search to find the maximum common prefix, and do some clas | xktz | NORMAL | 2024-09-20T01:15:17.982992+00:00 | 2024-09-20T01:15:17.983022+00:00 | 1 | false | Code is at the end.\n\nQuestion itself is pretty straight forward, either KMP or string hash + binary search to find the maximum common prefix, and do some classical dp, for a common prefix start at $i$ with length $1..T$ where $T$ is the maximum possible common prefix, do the following operation, let $u \\in 1..T$:\n\n$$\ndp[i + u] \\gets \\min(dp[i+u], dp[i] + 1)\n$$\n\nAnd everything is fine. So we only need to range update $1..T$. There are a million ways to do that. My code uses some priority queue but one can always give up using extra brain and throw a segment tree with lazy prop on it. Complexity is obviously $O(n \\log n)$ for some $n$ which is at most sum of all sizes.\n\n---\n\n**A far more interesting extension of question question is following:**\n\nWhat if the question gives like this:\n\n$$\nwords.size() \\leq 1e5, \\sum_{w \\in words} |w| \\leq 2e5\n$$\n\nEvery other situation are the same.\n\nHow do you get the correct answer in appropriate time?\n\nAnswer: use square root decomp. Let $S = \\sum_{w \\in words} |w| \\leq 2e5$. Split $words$ into set $A, B$. Where:\n\n$$\nA = \\{w : |w| \\leq \\sqrt{S}\\}, B = words \\setminus A\n$$\n\nThen, build a trie on $A$. We know this trie only depths $\\sqrt{S}$ at most. For $B$, string hash or KMP or something. We know $|B| \\leq \\sqrt{S}$ also.\n\nThen we can find $T$ in $O(\\sqrt S)$ time . Overall complexity is $O(n \\sqrt{S} + S)$.\n\n---\n\n\n```\ntypedef long long ll;\n\nconstexpr ll BASE = 31, MOD = 1e9 + 7;\nconstexpr ll BASE1 = 31, MOD1 = 1e9 + 7;\n\nconstexpr ll MAXN = 5e4 + 5;\n\nll ps[MAXN * 2];\n\nbool gened = false;\n\nvoid genps() {\n if (gened) return;\n gened = true;\n ps[0] = 1;\n for (ll i = 1; i < MAXN * 2; i ++) {\n ps[i] = ps[i - 1] * BASE % MOD;\n }\n}\n\nll TMP[MAXN * 4];\nll TMPALLOC;\n\nll *tmpalloc(ll T) {\n ll *a = TMP + TMPALLOC;\n TMPALLOC += (T + 1);\n return a;\n}\n\n\nvoid loadhash(ll *a, string &s) {\n ll M = s.size();\n s = " " + s;\n a[0] = 0;\n for (ll i = 1; i <= M; i ++) {\n a[i] = (a[i - 1] * BASE1 + s[i] - \'a\' + 1) % MOD1;\n }\n}\n\nusing larr = ll*;\n\nlarr hshs[MAXN];\nll szs[MAXN];\nll targhash[MAXN];\n\nll query(ll *a, ll l, ll r) {\n return (a[r] - a[l - 1] * ps[r - l + 1] % MOD1 + MOD1) % MOD1;\n}\n\nll lensame(ll *a, ll starta, ll enda, ll *b, ll startb, ll endb) {\n if (query(a, starta, starta) != query(b, startb, startb)) {\n return 0;\n }\n ll lo = 1, hi = min(enda - starta + 1, endb - startb + 1);\n while (lo < hi) {\n ll mid = (lo + hi + 1) >> 1;\n if (query(a, starta, starta + mid - 1) == query(b, startb, startb + mid - 1)) {\n lo = mid;\n } else {\n hi = mid - 1;\n }\n }\n return lo;\n}\n\nll N, M;\nmultiset<ll> mxs;\nll dp[MAXN];\n\nclass Solution {\npublic:\n int minValidStrings(vector<string>& words, string target) {\n TMPALLOC = 0;\n genps();\n N = target.size(), M = words.size();\n for (ll i = 0; i < M; i ++) {\n hshs[i] = tmpalloc(words[i].size());\n szs[i] = words[i].size();\n loadhash(hshs[i], words[i]);\n }\n loadhash(targhash, target);\n\n priority_queue<pair<ll, ll>, vector<pair<ll,ll>>, greater<>> pq;\n\n \n mxs.clear();\n // handle zero case\n {\n ll zmx = 0;\n for (ll i = 0; i < M; i ++) {\n zmx = max(zmx, lensame(hshs[i], 1, szs[i], targhash, 1, N));\n }\n if (zmx == 0) {\n return -1;\n }\n dp[0] = 0;\n pq.push({zmx, 1});\n mxs.insert(1);\n }\n\n for (ll i = 1; i <= N; i ++) {\n while (!pq.empty() && pq.top().first < i) {\n auto [j, v] = pq.top();\n pq.pop();\n mxs.erase(mxs.find(v));\n }\n\n if (mxs.empty()) {\n return -1;\n }\n\n dp[i] = *mxs.begin();\n\n {\n ll zmx = 0;\n for (ll j = 0; j < M; j ++) {\n zmx = max(zmx, lensame(hshs[j], 1, szs[j], targhash, i + 1, N));\n }\n if (zmx == 0) {\n continue;\n }\n pq.push({i + zmx, dp[i] + 1});\n mxs.insert(dp[i] + 1);\n }\n }\n return dp[N];\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | [Python3] Sliding Window + DP | python3-sliding-window-dp-by-liuyunjiaha-w6cy | Intuition\n Describe your first thoughts on how to solve this problem. \n\nExpand the right side of window when prefix is valid, otherwise expand the left side. | liuyunjiahang | NORMAL | 2024-09-20T00:16:54.745039+00:00 | 2024-09-20T00:16:54.745066+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nExpand the right side of window when `prefix is valid`, otherwise expand the left side.\n\nStore the computation result with dp, `dp[right] = dp[left] + 1`\n\n# Code\n```python3 []\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n left = 0\n right = 1\n n = len(target)\n dp = [0] * (n + 1)\n\n while right <= n:\n if left == right:\n return -1\n if self.isValidPrefix(words, target[left:right]): \n dp[right] = dp[left] + 1\n right += 1\n else:\n left += 1\n return dp[-1]\n\n\n def isValidPrefix(self, words, prefix):\n for word in words:\n if word.startswith(prefix):\n return True\n return False\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Golang Aho Corasick DP | golang-aho-corasick-dp-by-harshawasthi90-ttgp | Aho Corasick\n\npackage main\n\nvar dp [5e4 + 1]int\n\nfunc minValidStrings(words []string, target string) int {\n\tn := len(target)\n\troot := buildTrie(words) | harshawasthi90 | NORMAL | 2024-09-18T20:59:19.409956+00:00 | 2024-09-18T22:54:38.408314+00:00 | 13 | false | # Aho Corasick\n```\npackage main\n\nvar dp [5e4 + 1]int\n\nfunc minValidStrings(words []string, target string) int {\n\tn := len(target)\n\troot := buildTrie(words)\n\tcomputeSuffix(root)\n\n\tcurrent := root\n\tfor i := 1; i <= len(target); i++ {\n\t\tch := target[i-1] - \'a\'\n\n\t\tfor current.child[ch] == nil && root != current {\n\t\t\tcurrent = current.suffix\n\t\t}\n\n\t\tcurrent = current.child[ch]\n\t\tif current == nil {\n\t\t\treturn -1\n\t\t}\n\n\t\t// Longest suffix in target[:i] that is prefix in Trie\n\t\tsuffixLength := current.length\n\n\t\tdp[i] = 1 + dp[i-suffixLength]\n\t}\n\n\treturn dp[n]\n}\n\ntype Trie struct {\n\tchild []*Trie\n\tsuffix *Trie\n\tlength int\n}\n\nfunc NewTrie() *Trie {\n\treturn &Trie{child: make([]*Trie, 26)}\n}\n\nfunc buildTrie(words []string) *Trie {\n\troot := NewTrie()\n\tfor _, word := range words {\n\t\tcurrent := root\n\t\tl := 0\n\t\tfor _, ch := range word {\n\t\t\tch = ch - \'a\'\n\t\t\tif current.child[ch] == nil {\n\t\t\t\tcurrent.child[ch] = NewTrie()\n\t\t\t}\n\t\t\tl++\n\t\t\tcurrent = current.child[ch]\n\t\t\tcurrent.length = l\n\t\t}\n\t}\n\treturn root\n}\n\nfunc computeSuffix(root *Trie) {\n\troot.suffix = root\n\tqueue := []*Trie{root}\n\n\tfor len(queue) > 0 {\n\t\tparent := queue[0]\n\t\tqueue = queue[1:]\n\n\t\tfor i := 0; i < 26; i++ {\n\t\t\tchild := parent.child[i]\n\t\t\tif child == nil {\n\t\t\t\tcontinue\n\t\t\t}\n\t\t\ts := parent.suffix\n\t\t\tfor s != root && s.child[i] == nil {\n\t\t\t\ts = s.suffix\n\t\t\t}\n\t\t\tif s.child[i] != nil && parent != root {\n\t\t\t\tchild.suffix = s.child[i]\n\t\t\t} else {\n\t\t\t\tchild.suffix = root\n\t\t\t}\n\t\t\tqueue = append(queue, child)\n\t\t}\n\t}\n}\n\n```\n\n\n---\n\n# Max LPS\n\n```\npackage main\n\nvar dp [5e4 + 1]int\nvar lps [1e5 + 2]int\n\nfunc minValidStrings(words []string, target string) int {\n\tn := len(target)\n\tmaxPrefix := make([]int, n)\n\n\tfor _, word := range words {\n\t\tmaxLps(maxPrefix, word, target)\n\t}\n\n\tfor i := 1; i <= n; i++ {\n\t\tprev := i - maxPrefix[i-1]\n\t\tif prev == i {\n\t\t\treturn -1\n\t\t}\n\t\tdp[i] = 1 + dp[prev]\n\t}\n\n\treturn dp[n]\n}\n\nfunc maxLps(maxPrefix []int, word string, target string) {\n\tl1 := len(word)\n\tstr := word + "$" + target\n\n\tfor i := 1; i < len(str); i++ {\n\t\tlps[i] = lps[i-1]\n\t\tfor lps[i] != 0 && str[i] != str[lps[i]] {\n\t\t\tlps[i] = lps[lps[i]-1]\n\t\t}\n\t\tif str[i] == str[lps[i]] {\n\t\t\tlps[i]++\n\t\t}\n\t}\n\n\tfor i := 0; i < len(target); i++ {\n\t\tmaxPrefix[i] = max(maxPrefix[i], lps[i+l1+1])\n\t}\n}\n\n\n\n\n``` | 0 | 0 | ['Go'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | simple cpp | simple-cpp-by-varun_ea-ulow | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Varun_EA | NORMAL | 2024-09-18T14:29:49.537805+00:00 | 2024-09-18T14:29:49.537846+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nstruct SegTree {\npublic:\n \n SegTree (int _n) : n (_n) {\n tree.resize(4*n, 1e9);\n }\n \n int query (int x, int y) {\n return query (x, y, 0, n-1, 0);\n }\n \n void update (int ind, int val) {\n update (ind, val, 0, n-1, 0);\n }\n \nprivate:\n \n vector<int> tree;\n int n;\n \n int query (int x, int y, int l, int r, int i) {\n if (r < x || l > y) return 1e9;\n if (l >= x && r <= y) return tree[i];\n \n int m = (l+r) >> 1;\n return min(\n query (x, y, l, m, i*2+1),\n query (x, y, m+1, r, i*2+2)\n );\n }\n \n void update (int ind, int val, int l, int r, int i) {\n if (l == r) {\n tree[i] = val;\n return;\n }\n \n int m = (l+r) >> 1;\n if (m >= ind) update (ind, val, l, m, i*2+1);\n else update (ind, val, m+1, r, i*2+2);\n \n tree[i] = min(tree[i*2+1], tree[i*2+2]);\n }\n};\n\n\nclass Solution {\n \n vector<int> z_function(string s) {\n int n = s.size();\n vector<int> z(n);\n int l = 0, r = 0;\n for(int i = 1; i < n; i++) {\n if(i < r) {\n z[i] = min(r - i, z[i - l]);\n }\n while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n z[i]++;\n }\n if(i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n return z;\n }\n \n vector<int> longest_match;\n\n void AmmendLongestMatch (const string& word, const string& target) {\n string s = word + "$" + target;\n vector<int> z = z_function(s);\n \n for (int i = 0; i < target.length(); i ++) {\n longest_match[i] = max (longest_match[i], z[i+word.length()+1]);\n }\n }\n \npublic:\n int minValidStrings(vector<string>& words, string target) {\n longest_match.clear();\n longest_match.resize(target.length(), 0);\n \n for (auto w: words) AmmendLongestMatch (w, target);\n \n int n = target.size();\n SegTree max_len_tree(n+1);\n max_len_tree.update(n, 0);\n \n for (int j = n-1; j >= 0; j --) {\n int len = longest_match[j];\n if (len == 0) continue;\n \n int max_len = 1 + max_len_tree.query (j+1, j+len);\n max_len_tree.update (j, max_len); \n }\n \n int ans = max_len_tree.query(0, 0);\n if (ans == 1e9) ans = -1;\n return ans;\n }\n};\n\n/*\n#define pii pair<int, int>\n#define F first\n#define S second\n\nconst int N = 5e4+1;\nconst int P = 31;\nconst int M = 1e9+7;\n\nconst int INF = 1e9;\n\ntypedef long long int ll;\n\nclass Solution {\n \n vector<ll> p_pow;\n vector<ll> inv_p_pow;\n \n // a^b % M\n ll FastPower (ll a, ll b) {\n ll ans = 1;\n while (b) {\n if (b&1) ans = (ans * a) % M;\n a = (a*a) % M;\n b /= 2;\n }\n return ans;\n }\n \n void ComputePower() {\n if (!p_pow.empty()) return;\n \n p_pow.resize(N, 1);\n for (int i = 1; i < N; i ++)\n p_pow[i] = (p_pow[i-1] * P) % M;\n \n inv_p_pow.resize(N, 1);\n \n inv_p_pow[N-1] = FastPower (p_pow[N-1], M-2);\n for (int i = N-2; i > 0; i --)\n inv_p_pow[i] = (inv_p_pow[i+1] * P) % M;\n }\n \n vector<ll> HashIt (const string& s) {\n int S = s.size();\n vector<ll> prefix_hash(S+1, 0);\n\n for (int i = 1; i <= S; i++) {\n ll cur = (p_pow[i] * (s[i-1]-\'a\'+1)) % M;\n prefix_hash[i] = (prefix_hash[i-1] + cur) % M;\n }\n return prefix_hash;\n }\n \n inline ll HashOfRange (int l, int r, vector<ll>& prefix_hash) { \n ll hash = (prefix_hash[r] - prefix_hash[l-1] + M) % M;\n return (hash * inv_p_pow[l-1]) % M;\n }\n \n int LongestMatching (int st, vector<ll>& prefix_hash_target, unordered_map<int, int>& hash_and_len) {\n int l = st, r = prefix_hash_target.size() - 1;\n \n while (l < r) {\n int m = (l+r) >> 1;\n int hash = HashOfRange (st, m+1, prefix_hash_target);\n \n auto it = hash_and_len.find(hash);\n if (it == hash_and_len.end()) r = m;\n else l = m+1;\n }\n \n int len = r - st + 1;\n int hash = HashOfRange (st, l, prefix_hash_target);\n if (hash_and_len.find(hash) == hash_and_len.end()) len--;\n return len;\n }\n \npublic:\n int minValidStrings(vector<string>& words, string target) {\n ComputePower();\n \n unordered_map<int, int> hash_and_len;\n for (auto w : words) {\n vector<ll> hash = HashIt(w);\n for (int l = 1; l < hash.size(); l ++) hash_and_len[hash[l]] = l;\n }\n \n int n = target.size();\n SegTree max_len_tree(n+2);\n max_len_tree.update(n+1, 0);\n \n vector<ll> prefix_hash_target = HashIt(target);\n \n for (int j = n; j > 0; j --) {\n int len = LongestMatching (j, prefix_hash_target, hash_and_len);\n if (len == 0) continue;\n \n int max_len = 1 + max_len_tree.query (j+1, j+len);\n max_len_tree.update (j, max_len); \n }\n \n int ans = max_len_tree.query(1, 1);\n if (ans == 1e9) ans = -1;\n return ans;\n }\n};\n*/\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | KMP + INTERVAL OVERLAPING | kmp-interval-overlaping-by-vikassingh281-kux4 | Intuition\nThe task involves finding the minimum number of words from a list that, when concatenated or overlapped, can cover a target string. The solution uses | vikassingh2810 | NORMAL | 2024-09-18T07:24:14.050369+00:00 | 2024-09-18T07:27:09.409041+00:00 | 8 | false | # Intuition\nThe task involves finding the minimum number of words from a list that, when concatenated or overlapped, can cover a target string. The solution uses the KMP (Knuth-Morris-Pratt) string matching algorithm to efficiently search for all the occurrences of each word in the target string. Then, it handles interval overlapping to determine the minimum number of word fragments required to cover the entire target string.\n\n# Approach\nLPS (Longest Prefix Suffix) Calculation:\n\nFirst, we preprocess each word in the list using the LPS array from the KMP algorithm. The LPS array helps to skip unnecessary comparisons during the string matching process.\nMatching words to the target:\n\nFor each word in the list, we use the KMP algorithm to find its occurrences in the target string. Every time a match is found or the pattern can\'t we match any further we save interval (index on target), in which some prefix of patter was matched , we record its start and end positions in an interval.\nHandling Interval Overlapping:\n\nOnce we have all the intervals (start and end positions of matched word fragments), we sort them based on their starting positions. Then, we try to cover the target string by merging these intervals, aiming to minimize the number of word fragments used to cover the entire target.\nFinal Result:\n\nThe algorithm traverses through the intervals and checks if it\'s possible to cover the entire target string with them. If yes, it returns the minimum number of fragments needed. Otherwise, it returns -1 indicating it\'s impossible to cover the target string.\n# Complexity\n# Time Complexity:\n\nPreprocessing (LPS array calculation) for each word takes O(m) where m is the length of the word.\nMatching each word with the target string takes O(n) where n is the length of the target string.\nSorting the intervals takes O(k log k) where k is the number of intervals.\nOverall time complexity: O(n * m + k log k).\nSpace Complexity:\n\nStoring LPS arrays for each word takes O(n * m).\nStoring intervals takes O(k), where k is the number of matches.\nOverall space complexity: O(n * m + k).\n\n# Code\n```cpp []\nclass Solution {\npublic:\n // Function to calculate the LPS array for a given string using KMP preprocessing\n void lpscal(string& s, vector<int> lps[], int n) {\n int m = s.size();\n int i = 0; // Length of the previous longest prefix suffix\n lps[n].resize(m, 0); // Initialize LPS array for this word\n lps[n][0] = 0; // LPS of first character is always 0\n int j = 1; // Start from the second character\n\n // Build the LPS array\n while (j < m) {\n if (s[i] == s[j]) {\n i++; // Increase the prefix length\n lps[n][j] = i; // Assign LPS value\n j++;\n } else if (i != 0)\n i = lps[n][i - 1]; // Move to the last matched prefix\n else\n j++;\n }\n }\n\n // Function to find matches of word \'p\' in the target \'t\' using the LPS array\n void match(string& p, string& t, vector<int> lps[], int x, vector<vector<int>>& inter) {\n int n = t.size();\n int m = p.size();\n int i = 0; // Pointer for target string\n int j = 0; // Pointer for word string\n\n // Perform the matching\n while (i < n) {\n if (t[i] == p[j]) {\n i++;\n j++;\n } else {\n // When mismatch occurs, update the pointers\n if (j != 0) {\n inter.push_back({i - j, i - 1}); // Store the match interval\n j = lps[x][j - 1]; // Jump to the previous LPS value\n } else\n i++;\n }\n\n // If a full match of word \'p\' is found\n if (j == m) {\n inter.push_back({i - j, i - 1}); // Store the interval\n j = lps[x][j - 1]; // Jump to the next possible match\n }\n }\n\n // If some part of the word is still matched at the end of the target string\n if (j != m && i - 1 >= i - j)\n inter.push_back({i - j, i - 1});\n }\n\n // Main function to find the minimum number of words to cover the target string\n int minValidStrings(vector<string>& words, string target) {\n int n = words.size();\n vector<int> lps[n]; // LPS arrays for each word\n\n // Preprocess all words and compute their LPS arrays\n for (int i = 0; i < n; i++) {\n lpscal(words[i], lps, i);\n }\n\n vector<vector<int>> inter; // Store intervals of matches (start, end)\n\n // Find matching intervals for each word in the target string\n for (int i = 0; i < n; i++) {\n match(words[i], target, lps, i, inter);\n }\n\n // Sort intervals based on their start positions\n sort(inter.begin(), inter.end(), [](vector<int>& a, vector<int>& b) {\n return a[0] < b[0];\n });\n\n int ans = 0; // Store the answer (minimum number of words)\n int end = -1; // Track the last covered position in the target\n int k = inter.size();\n int t = target.size();\n\n // If no intervals are found, return -1\n if (k == 0)\n return -1;\n\n int i = 0;\n\n // Try to cover the entire target using the intervals\n while (i < k && end < t - 1) {\n int j = i;\n int temp = -1; // Track the farthest position we can cover\n while (j < k && inter[j][0] <= end + 1) {\n temp = max(temp, inter[j][1]);\n j++;\n }\n\n // If no further progress can be made, return -1\n if (temp == -1)\n return -1;\n\n ans++; // Increment the count of words used\n end = temp; // Update the last covered position\n i = j; // Move to the next interval\n }\n\n // Return the result if the target is fully covered, else return -1\n return end >= t - 1 ? ans : -1;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | JAVA | java-by-abhiguptanitb-29mf | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | abhiguptanitb | NORMAL | 2024-09-18T02:39:41.829604+00:00 | 2024-09-18T02:39:41.829631+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minValidStrings(String[] words, String target) {\n int n = target.length();\n int[] dp = new int[n + 1];\n Arrays.fill(dp, Integer.MAX_VALUE);\n dp[0] = 0;\n\n List<List<Integer>> matches = new ArrayList<>(n);\n for (int i = 0; i < n; i++) {\n matches.add(new ArrayList<>());\n }\n char[] targetChars = target.toCharArray();\n for (String word : words) {\n char[] wordChars = word.toCharArray();\n int m = wordChars.length;\n int[] pi = new int[m];\n for (int i = 1, j = 0; i < m; i++) {\n while (j > 0 && wordChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (wordChars[i] == wordChars[j]) {\n j++;\n }\n pi[i] = j;\n }\n\n for (int i = 0, j = 0; i < n; i++) {\n while (j > 0 && targetChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (targetChars[i] == wordChars[j]) {\n j++;\n }\n if (j > 0) {\n matches.get(i - j + 1).add(j);\n if (j == m) {\n j = pi[j - 1]; \n }\n }\n }\n }\n for (int i = 0; i < n; i++) {\n if (dp[i] == Integer.MAX_VALUE) continue;\n for (int len : matches.get(i)) {\n if (i + len <= n) {\n dp[i + len] = Math.min(dp[i + len], dp[i] + 1);\n }\n }\n }\n return dp[n] == Integer.MAX_VALUE ? -1 : dp[n];\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Using z-function | using-z-function-by-nguyenquocthao00-27y3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | nguyenquocthao00 | NORMAL | 2024-09-18T01:41:46.319745+00:00 | 2024-09-18T01:41:46.319767+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n=len(target)\n data=[0]*n\n def process(w):\n z,l,r = [0]*(len(w)+1), 0, 0\n for i in range(1, len(w)):\n z[i]=max(0, min(r-i, z[i-l]))\n while i+z[i]<len(w) and w[i+z[i]]==w[z[i]]: z[i]+=1\n if i+z[i]>=r: l,r=i,i+z[i]\n l,r=0,0\n for i in range(n):\n zv = max(0, min(r-i, z[i-l]))\n while i+zv<n and zv<len(w) and target[i+zv]==w[zv]: zv+=1\n if i+zv>=r: l,r=i,i+zv\n data[i]=max(data[i], zv)\n for w in words: process(w)\n res,curmax, nextmax=0,0,0\n for i,v in enumerate(data):\n if nextmax<i: return -1\n nextmax=max(nextmax, i+v)\n if curmax==i: res,curmax=res+1, nextmax\n if nextmax<n: return -1\n return res\n\n \n``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | How I think about this. Z function and sliding window. | how-i-think-about-this-z-function-and-sl-k9b7 | Intuition\nDisclaimer: This is code from another solution. i am just providing my views on the intuition i got after reading it, and steps to solve it yourself. | Fustigate | NORMAL | 2024-09-17T22:06:45.124950+00:00 | 2024-09-17T22:06:45.124980+00:00 | 8 | false | # Intuition\nDisclaimer: This is code from another solution. i am just providing my views on the intuition i got after reading it, and steps to solve it yourself.\n\nFirst, understand the z function. Know what the z function aims to calculate (the max len of prefix overlap of s[i:] and s).\n\nNow, to solve this problem, the first step is to calculate the maximum index we can hop to from every character of s. A hop just means "take a prefix of a word that overlaps with the prefix of target and move the pointer at target to the next character not seen yet". A really clever way is to use the z function, with input of every string as word#target (# can be substituted for any other character that wont exist in word or target). With this trick, the z function will calculate the max length of overlap of every suffix of target with the word. We are using max() in the code for updating the dp array because we want the farthest point we can hop to from the index after considering all words.\n\nThe last operation is to use a sliding window (two pointers) technique to find the minimum number of hops.\n\nIn summary, we use the z function to find the farthest index we can hop to from each index in target, and use a sliding window to find the result.\n\n# Code\n```python\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n \n def Z_function(s):\n n = len(s)\n Z = [0] * n\n l = r = 0\n for i in range(1, n):\n if i < r:\n Z[i] = min(Z[i - l], r - i)\n while i + Z[i] < n and s[Z[i]] == s[i + Z[i]]:\n Z[i] += 1\n if i + Z[i] > r:\n l = i\n r = i + Z[i]\n return Z\n \n n = len(target)\n dp = [0] * n\n for word in words:\n Z_arr = Z_function(word + \'#\' + target)\n offset = len(word) + 1\n for i in range(n):\n dp[i] = max(dp[i], Z_arr[i + offset])\n\n l = r = 0\n hops = 0\n while r < n:\n max_reach = 0\n for i in range(l, r + 1):\n max_reach = max(max_reach, i + dp[i])\n if max_reach == 0: # we cannot go further\n return -1\n l = r + 1\n r = max_reach\n hops += 1\n return hops\n \n``` | 0 | 0 | ['Sliding Window', 'Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | binary search on robin-karp substring hash while doing Dynamic Programming | binary-search-on-robin-karp-substring-ha-uo5k | Intuition\n\nWe can get to a result if we travarse the given "target" from the end and build a bottom-up memoization table we call "memo".\n\nAnd our result wil | kamanashisroy | NORMAL | 2024-09-17T20:33:19.373154+00:00 | 2024-09-17T20:33:19.373212+00:00 | 26 | false | # Intuition\n\nWe can get to a result if we travarse the given "target" from the end and build a bottom-up memoization table we call "memo".\n\nAnd our result will be at the beginning "memo[0]".\n```\nfor i in range(len(target)-1,-1,-1):\n memo[i] = memo[i+longest match] + 1\nreturn memo[0] if memo[0] < N else -1\n```\n\nBut finding the longest match can be naive if we go through all the words to check for best match.\n\nInstead we can do binary search while checking if it is "possible" to find match of substring.\n\n```\nlo = pos\nhi = len(target)-1\nwhile lo<hi:\n mid = (lo+hi)>>1\n if not possible(pos,mid+1):\n hi = mid-1\n else:\n if mid == lo:\n break\n lo = mid\n# found best match in \nif hi >= pos:\n if possible(pos,hi+1):\n lo = hi\nlo = max(lo,pos)\nif not possible(pos,lo+1):\n continue\n```\n\n\n# Approach\n\nAs discussed above we traversed the given "target" from the end, while building a memoization table "memo".\n\nWe used rolling hash `RKSubstringHash` to quickly get the hash of a substring.\n\nWe used a set called `lookup` to see if the substring hash is there as prefix in the words. \n\nFinally to get the minimum cost, we used a `SegmentTreeRMQ` to `queryMax()` the best value in the substring range. \n\n# Complexity\n- Time complexity:\n\n`O(N*log(100))`\n\n- Space complexity:\n`O(N*log(N))`\n\n# Code\n```python3 []\n\nPRIME1 = 31\nPRIME2 = 1000000007\nclass RKHash:\n def __init__(self):\n self.val = 0\n self.sz = 0\n self.mul = 1\n \n def append(self, intval):\n self.val *= PRIME1\n self.val += intval+1\n self.val %= PRIME2\n self.sz += 1\n self.mul *= PRIME1\n self.mul %= PRIME2\n \n def prepend(self, intval):\n self.val += (intval+1)*self.mul\n self.val %= PRIME2\n self.sz += 1\n self.mul *= PRIME1\n self.mul %= PRIME2\n \n def __hash__(self):\n return (self.val,self.sz)\n \n def key(self):\n return (self.val,self.sz)\n\n def copy(self):\n ret = RKHash()\n ret.val = self.val\n ret.sz = self.sz\n ret.mul = self.mul\n return ret\n \n def test(self):\n sample = [1,2,3,4,5]\n rk1,rk2 = RKHash(),RKHash()\n for x in sample:\n rk1.append(x)\n for x in reversed(sample):\n rk2.prepend(x)\n assert(rk1.val == rk2.val)\n assert(rk1.sz == rk2.sz)\n\nclass RKSubstringHash:\n def __init__(self, given):\n self.N = len(given) \n self.rkprefix = [0]*self.N\n self.rkmul = [0]*self.N\n rk = RKHash()\n for i,x in enumerate(given):\n rk.append(x)\n self.rkprefix[i] = rk.key()\n self.rkmul[i] = rk.mul\n\n self.rksuffix = [0]*self.N\n rk = RKHash()\n for i in range(self.N-1,-1,-1):\n rk.prepend(given[i])\n self.rksuffix[i] = rk.key()\n \n def test_substring(self, given, beg:int,end:int):\n assert(beg<end)\n rk = RKHash()\n for i in range(beg,end):\n rk.append(given[i])\n #print(self.rksuffix)\n subkey = self.substring(beg,end)\n print(beg,end,\'test_substring\', given[beg:end] , rk.key(), subkey)\n assert(rk.key() == subkey)\n \n def substring(self, beg:int,end:int):\n assert(beg<end)\n if end >= self.N:\n #print(\'substring returning suffix\', self.rksuffix)\n return self.rksuffix[beg]\n if 0 == beg:\n return self.rkprefix[end-1]\n \n eprefix = self.rkprefix[end-1][0]\n bprefix = self.rkprefix[beg-1][0]\n bprefix *= self.rkmul[end-beg-1]\n bprefix %= PRIME2\n rval = (eprefix-bprefix)%PRIME2\n return (rval,end-beg)\n\nclass SegmentTreeRMQ:\n \'\'\'\n segment_tree.py file is part of Algosnippet.\n Algosnippet is a collection of practice data-structures and algorithms\n Copyright (C) 2024 Kamanashis Roy\n Algosnippet is free software: you can redistribute it and/or modify\n it under the terms of the GNU General Public License as published by\n the Free Software Foundation, either version 3 of the License, or\n (at your option) any later version.\n Algosnippet is distributed in the hope that it will be useful,\n but WITHOUT ANY WARRANTY; without even the implied warranty of\n MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the\n GNU General Public License for more details.\n You should have received a copy of the GNU General Public License\n along with Algosnippet. If not, see <https://www.gnu.org/licenses/>.\n \'\'\'\n\n def __init__(self, Ngiven:int, defaultVal:int = -1):\n depth = 0\n while (1<<depth) < Ngiven:\n depth += 1\n\n INFLO = (defaultVal,-1)\n self.N = 1<<depth\n self.nodes = [ INFLO for _ in range((self.N<<1)+2)]\n self.rightMost = [ i for i in range((self.N<<1)+2)]\n self.leftMost = [ i for i in range((self.N<<1)+2)]\n # N = 4\n # [ filler 0 ] [ root Node 1 ] 2 3 [ Internal nodes 4 5 6 7 ] [ Leaves 8 9 10 11 12 13 14 15 ]\n for i in range(self.N-1,0,-1):\n self.leftMost[i] = self.leftMost[i<<1]\n self.rightMost[i] = self.rightMost[(i<<1)+1]\n\n def fill(self,aNums):\n assert((self.N+len(aNums)-1) < len(self.nodes))\n for i,x in enumerate(aNums):\n self.nodes[i+self.N] = (x,i)\n \n for i in range(self.N-1,0,-1):\n self.nodes[i] = max(self.nodes[i<<1],self.nodes[(i<<1)+1])\n\n def __setitem__(self, i:int, givenVal:int) -> None:\n \'\'\'\n Procedure\n =========\n - sets the value at the leaf\n - go up towards the root and update the maximum value\n \'\'\'\n assert((self.N+i) < len(self.nodes))\n curr = self.N+i\n val = (givenVal,i)\n if val <= self.nodes[curr]:\n return # do not update\n self.nodes[curr] = val\n while curr > 1:\n # get parent\n parent = curr >> 1\n if self.nodes[parent] >= val:\n break # do not update\n self.nodes[parent] = val\n curr = parent\n\n def __getitem__(self, i:int) -> int:\n assert((self.N+i) < len(self.nodes))\n return self.nodes[self.N+i]\n \n def queryMaxAll(self):\n return self.nodes[1]\n \n def queryMaxLeft(self, i:int) -> int:\n \'\'\'\n Return the max score saved in range of [0,i] inclusive\n \'\'\'\n curr = self.N+i\n result = self.nodes[curr]\n path = []\n while curr > 1:\n parent = curr >> 1\n path.append((parent,curr&1))\n curr = parent\n\n while path:\n curr,odd = path.pop()\n if odd:\n # when we are going for right child\n # take best result from left\n left = curr<<1\n result = max(result, self.nodes[left])\n else:\n # when we are going for left chld, we cannot take memo\n pass\n return result\n \n def queryMax(self, givenLeft, givenRight, defaultVal = None):\n \'\'\'\n Return the maximum value between beg and end\n \'\'\'\n assert(givenLeft <= givenRight)\n assert((self.N+givenRight) < len(self.nodes))\n \n ret = max(self.nodes[self.N+givenLeft],self.nodes[self.N+givenRight])\n if defaultVal is not None:\n ret = max((defaultVal,-1),ret)\n stack = [1]\n while stack:\n cur = stack.pop()\n for child in (cur<<1,(cur<<1)+1):\n rightMost = self.rightMost[child]\n if rightMost < (self.N+givenLeft):\n continue\n leftMost = self.leftMost[child]\n if leftMost > (self.N+givenRight):\n continue\n\n if rightMost <= (self.N+givenRight) and leftMost >= (self.N+givenLeft):\n ret = max(ret,self.nodes[child])\n continue\n \n if defaultVal is not None and self.nodes[child][0] <= defaultVal:\n continue\n\n stack.append(child)\n \n return ret\n\n def printNodes(self, beg,end):\n print(self.nodes[self.N+beg:self.N+end])\n\nclass PrefixTrie:\n def __init__(self, val, rk = None):\n self.val = val\n self.children = [None]*26\n if rk is None:\n self.rk = RKHash()\n else:\n self.rk = rk.copy()\n if val is not None:\n self.rk.append(val)\n\n def __getitem__(self, i):\n return self.children[i]\n\n def __setitem__(self, i, val):\n self.children[i] = val\n\n def add(self, given):\n cur = self\n ORDA = ord(\'a\')\n for x in given:\n xval = ord(x)-ORDA\n if cur[xval] is None:\n cur[xval] = PrefixTrie(xval, cur.rk)\n cur = cur[xval]\n\n def find(self, given, beg):\n cur = self\n ORDA = ord(\'a\')\n gn = len(given)\n for i in range(beg,gn):\n xval = ord(given[i])-ORDA\n if cur[xval] is None:\n return\n yield i+1,cur[xval].rk\n cur = cur[xval]\n\n def getHashes(self, output):\n assert( (self.rk.val,self.rk.sz) not in output)\n output[(self.rk.val,self.rk.sz)] = self\n for x in self.children:\n if x is not None:\n x.getHashes(output)\n \ndef strToAscii(given):\n ORDA = ord(\'a\')\n ret = []\n for x in given:\n xval = ord(x)-ORDA\n ret.append(xval)\n return ret\n\nclass Solution:\n def minValidStrings(self, words: List[str], givenTarget: str) -> int:\n N = len(givenTarget)\n target = strToAscii(givenTarget)\n\n lookup = set()\n for w in words:\n rk = RKHash()\n wi = strToAscii(w)\n for x in wi:\n rk.append(x)\n lookup.add(rk.key())\n \n INF = float(\'Inf\')\n NINF = float(\'-Inf\')\n\n subLookup = RKSubstringHash(target)\n\n def possible(beg,end):\n assert(beg<end)\n #subLookup.test_substring(target, beg, end)\n hcode = subLookup.substring(beg,end)\n if hcode in lookup:\n return True\n return False\n\n memo = SegmentTreeRMQ(N+2,NINF)\n memo[N] = 0\n prevHash = RKHash()\n prevHash.test()\n ORDA = ord(\'a\')\n for pos in range(len(target)-1,-1,-1):\n\n lo = pos\n hi = len(target)-1\n while lo<hi:\n mid = (lo+hi)>>1\n if not possible(pos,mid+1):\n hi = mid-1\n else:\n if mid == lo:\n break\n lo = mid\n # found best match in \n if hi >= pos:\n if possible(pos,hi+1):\n lo = hi\n lo = max(lo,pos)\n if not possible(pos,lo+1):\n continue\n #print(pos, \'best match\', givenTarget[pos:lo+1])\n # longest possible prefix match is at lo\n # find the minimum value in range pos and lo\n if lo == pos: # single character match\n memo[pos] = memo[pos+1][0]-1\n continue\n loc = memo.queryMax(pos+1,lo+1)\n #memo.printNodes(0,N+1)\n #print(pos+1,lo+1, \'queryMax\', loc)\n if loc[1] != -1:\n memo[pos] = loc[0]-1\n\n memo.printNodes(0,N+1)\n result = memo[0]\n result = -result[0]\n if result > N:\n return -1\n return result\n``` | 0 | 0 | ['Binary Search', 'Dynamic Programming', 'Segment Tree', 'Rolling Hash', 'Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | gpt-o1-mini | gpt-o1-mini-by-leet4jin-danu | Intro\n\ngpt-o1-mini generator\n\n\n\n\n# Code\nc []\nint minValidStrings(char** words, int wordsSize, char* target) {\n int lenTarget = strlen(target);\n | leet4jin | NORMAL | 2024-09-17T13:25:16.899601+00:00 | 2024-09-17T13:25:16.899643+00:00 | 18 | false | # Intro\n\ngpt-o1-mini generator\n\n\n\n\n# Code\n```c []\nint minValidStrings(char** words, int wordsSize, char* target) {\n int lenTarget = strlen(target);\n // Using uint16_t for best to store prefix lengths efficiently\n uint16_t best[lenTarget];\n memset(best, 0, lenTarget * sizeof(uint16_t));\n \n // Find the length of the longest word to allocate kmp array on the stack once\n int lenLongestWord = 0;\n for (int i = 0; i < wordsSize; i++) {\n int lenWord = strlen(words[i]);\n if (lenWord > lenLongestWord) lenLongestWord = lenWord;\n }\n \n // Allocate kmp array on the stack\n uint16_t kmp[lenLongestWord + 1];\n \n for (int w = 0; w < wordsSize; w++) {\n char* word = words[w];\n int lenWord = strlen(word);\n \n // Build KMP failure function for the current word\n kmp[0] = 0;\n int j = 0;\n for (int i = 1; i < lenWord; i++) {\n while (j > 0 && word[i] != word[j]) {\n j = kmp[j - 1];\n }\n if (word[i] == word[j]) {\n j++;\n }\n kmp[i] = j;\n }\n \n // Perform KMP search to find prefixes in the target\n j = 0;\n for (int i = 0; i < lenTarget;) {\n if (word[j] == target[i]) {\n j++;\n i++;\n if (j > best[i - 1]) {\n best[i - 1] = j;\n }\n if (j == lenWord) {\n j = kmp[j - 1];\n }\n } else {\n if (j > 0) {\n j = kmp[j - 1];\n } else {\n i++;\n }\n }\n }\n }\n \n // Greedy approach to determine the minimum number of valid strings\n int steps = 0;\n int pos = lenTarget;\n while (pos > 0) {\n if (best[pos - 1] == 0) {\n return -1;\n }\n pos -= best[pos - 1];\n steps++;\n }\n \n return steps;\n}\n``` | 0 | 0 | ['C'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | Z function + jump game ii | z-function-jump-game-ii-by-alkhanzi-nlq4 | Approach\nWe have a target string and a list of words. We want to find the length of the maximum prefix match in our given words and the substring starting here | alkhanzi | NORMAL | 2024-09-17T09:38:38.395710+00:00 | 2024-09-17T09:38:38.395749+00:00 | 15 | false | # Approach\nWe have a target string and a list of words. We want to find the length of the maximum prefix match in our given words and the substring starting here `target[i:]`. If we have the maximum prefix match array then this problem reduces to [Jump game II](https://leetcode.com/problems/jump-game-ii/description/).\n\nFor [part 1](https://leetcode.com/problems/minimum-number-of-valid-strings-to-form-target-i/description/) of this problem, we can build a `trie` from our list of words and do a maximum possible trie matching at every index. This `trie` approach is too slow for this problem. A more efficient way to calculate this is via [Z-functions](https://cp-algorithms.com/string/z-function.html).\n\nFinally we find the minimum number of valid strings (or minimum jumps till end) using a greedy 1D BFS approach. For more details about this check this [solution](https://leetcode.com/problems/jump-game-ii/solutions/18014/concise-o-n-one-loop-java-solution-based-on-greedy/) or this [video](https://www.youtube.com/watch?v=dJ7sWiOoK7g&ab_channel=NeetCode).\n\n\n# Complexity\nTime complexity:\n - Z-function is linear with input. But we call it once per word.\n`O(m * (n + w))` where n = len(target), m = num words, w = avg. word length\n\n - 1D BFS is linear 1 pass.\n`O(n)`\n\nSpace complexity:\n`O(n + w)` for Z-function and `O(n)` for dp array.\n\n# Code\n```python3 []\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n \n def Z_function(s):\n n = len(s)\n Z = [0] * n\n l = r = 0\n for i in range(1, n):\n if i < r:\n Z[i] = min(Z[i - l], r - i)\n while i + Z[i] < n and s[Z[i]] == s[i + Z[i]]:\n Z[i] += 1\n if i + Z[i] > r:\n l = i\n r = i + Z[i]\n return Z\n \n n = len(target)\n dp = [0] * n\n for word in words:\n Z_arr = Z_function(word + \'#\' + target)\n offset = len(word) + 1\n for i in range(n):\n dp[i] = max(dp[i], Z_arr[i + offset])\n\n l = r = 0\n hops = 0\n while r < n:\n max_reach = 0\n for i in range(l, r + 1):\n max_reach = max(max_reach, i + dp[i])\n if max_reach == 0: # we cannot go further\n return -1\n l = r + 1\n r = max_reach\n hops += 1\n return hops\n \n``` | 0 | 0 | ['Dynamic Programming', 'Breadth-First Search', 'String Matching', 'Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | [Greedy] String Hashing + Binary Search + Segment Tree. Passes both easy and hard versions. | greedy-string-hashing-binary-search-segm-3ogd | Intuition\n- Greedy strategy works: Take the longest suffix of target which is also a prefix of some word and continue the process.\n\n- Example:\n - words = [ | astronom1cal | NORMAL | 2024-09-17T08:07:56.118137+00:00 | 2024-09-17T08:07:56.118169+00:00 | 13 | false | # Intuition\n- Greedy strategy works: Take the longest suffix of `target` which is also a prefix of some `word` and continue the process.\n\n- Example:\n - `words = ["abc","aaaaa","bcdef"], target = "aabcdabc"`\n - `abc` is longest suffix from `target` which is also a prefix.\n`target` now becomes `aabcd`.\n - `bcd` is longest suffix from `target` which is also a prefix.\n`target` now becomes `aa`.\n - `aa` is longest suffix from `target` which is also a prefix.\n`target` now becomes `""`.\n - Thus, the answer is 3. You can easily prove that this greedy strategy always gives us the best answer.\n\n# Approach\n- `n` is the length of `target`.\n- `m` is the size of the words array.\n- `w` is the maximum word length of any word in the array.\n- Use double base primes for string hashing.\n\n## Step by step solving this problem:\n - Generate hash values for all prefixes of all words.\n - Generate hash values for all prefixes of `target`.\n - Now, for every `i` from `0` to `n - 1`, find the maximum index from `i` such that the substring in `[i, idx]` is valid (basically the longest substring starting from i, which is a valid substring).\n`ending_index = idx, starting_index = i`.\n - Store these `(ending_index, starting_index)` pairs in a set of pairs.\nLet the size of the set of pairs be `N`.\n - Sort them in ascending order by the ending_index.\n - Build a Segment Tree based on the starting indices.\nThis helps in finding the `min_starting_index` whose `end_index is >= idx `\n( for some index `idx`).\n\n - Now, we can start finding the longest suffix which is also a prefix.\n - To do that, find the first index in `end_indices` that is `>=` our current string\'s end index (which is `R`). Call it `idx`.\n - Now check if `idx` exists. If it doesn\'t, return -1.\n - Query the Segment Tree in range `[idx, N - 1]` to find the `min_starting_index`.\n - Check if the `min_starting_index is <= R`. If not, return -1.\n - If everything\'s good, we have successfully found the longest prefix which is also a suffix. Now set `R to min_starting_index - 1` and continue the process. \n# Complexity\n- Time complexity:\n`O(n.log(n).log(n))`\n\n- Space complexity:\n`O(n)`\n\n# Code\n```cpp []\n#include <iostream>\n#include <cstdlib>\n#include <ctime>\n#include <climits>\n#include <numeric>\n#include <iomanip>\n#include <fstream>\n#include <string>\n#include <algorithm>\n#include <cmath>\n#include <bitset>\n#include <utility>\n#include <array>\n#include <vector>\n#include <deque>\n#include <forward_list>\n#include <list>\n#include <set>\n#include <unordered_set>\n#include <map>\n#include <unordered_map>\n#include <stack>\n#include <queue>\n#include <functional>\n#include <random>\n#include <chrono>\n#include <ranges>\n#include <ext/pb_ds/assoc_container.hpp>\n\nusing namespace __gnu_pbds;\ntemplate <typename T>\nusing ordered_set = tree<T, null_type, std::less<T>, rb_tree_tag, tree_order_statistics_node_update>;\ntemplate <typename T>\nusing ordered_multiset = tree<std::pair<T, T>, null_type, std::less<std::pair<T, T>>, rb_tree_tag, tree_order_statistics_node_update>;\n\nusing ll = long long;\nusing ld = long double;\nusing namespace std;\n\npair<ll, ll> extended_euclidean(ll a, ll b)\n{\n if (b == 0)\n {\n return {1, 0};\n }\n\n auto [x, y] = extended_euclidean(b, a % b);\n\n return {y, x - y * (a / b)};\n}\n\nll modinv(ll a, ll m)\n{\n ll x = extended_euclidean(a, m).first;\n\n return (x % m + m) % m;\n}\n\nclass SegmentTree\n{\nprivate:\n ll n;\n vector<ll> tree;\n\n void build(vector<ll> &arr, ll u, ll l, ll r)\n {\n if (l == r)\n {\n tree[u] = arr[l];\n }\n\n else\n {\n ll mid = (l + r) / 2;\n build(arr, 2 * u, l, mid);\n build(arr, 2 * u + 1, mid + 1, r);\n tree[u] = min(tree[2 * u], tree[2 * u + 1]);\n }\n }\n\npublic:\n SegmentTree(vector<ll> &arr)\n {\n n = (ll)arr.size();\n tree.resize(4 * n);\n\n if (n != 0)\n {\n build(arr, 1, 0, n - 1);\n }\n }\n\n ll query(ll ql, ll qr, ll l = 0, ll r = -1, ll u = 1)\n {\n if (r == -1)\n {\n r = n - 1;\n }\n\n if (l == ql && r == qr)\n {\n return tree[u];\n }\n\n else\n {\n ll mid = (l + r) / 2;\n\n if (ql >= l && qr <= mid)\n {\n return query(ql, qr, l, mid, 2 * u);\n }\n\n else if (ql >= mid + 1 && qr <= r)\n {\n return query(ql, qr, mid + 1, r, 2 * u + 1);\n }\n\n else\n {\n return min(query(ql, mid, l, mid, 2 * u), query(mid + 1, qr, mid + 1, r, 2 * u + 1));\n }\n }\n }\n};\n\nclass Solution\n{\npublic:\n int minValidStrings(vector<string> &words, string target)\n {\n ll n = (ll)target.length();\n const ll p1 = 31;\n const ll p2 = 37;\n const ll m = 1e9 + 7;\n\n vector<ll> p1_pow(50000), p2_pow(50000);\n p1_pow[0] = 1;\n p2_pow[0] = 1;\n\n for (ll i = 1; i < 50000; i++)\n {\n p1_pow[i] = (p1_pow[i - 1] * p1) % m;\n p2_pow[i] = (p2_pow[i - 1] * p2) % m;\n }\n\n set<pair<ll, ll>> hashes;\n\n for (auto &word : words)\n {\n ll hash_value1 = 0, hash_value2 = 0;\n\n for (ll i = 0; i < (ll)word.size(); i++)\n {\n hash_value1 = (hash_value1 + (word[i] - \'a\' + 1) * p1_pow[i]) % m;\n hash_value2 = (hash_value2 + (word[i] - \'a\' + 1) * p2_pow[i]) % m;\n hashes.insert({hash_value1, hash_value2});\n }\n }\n\n vector<ll> prefix_hash1(n), prefix_hash2(n);\n\n for (ll i = 0; i < n; i++)\n {\n prefix_hash1[i] = (((i == 0) ? 0 : prefix_hash1[i - 1]) + (target[i] - \'a\' + 1) * p1_pow[i]) % m;\n prefix_hash2[i] = (((i == 0) ? 0 : prefix_hash2[i - 1]) + (target[i] - \'a\' + 1) * p2_pow[i]) % m;\n }\n\n vector<pair<ll, ll>> pairs;\n\n for (ll i = 0; i < n; i++)\n {\n ll low = i, high = n - 1;\n ll end_idx = -1;\n\n while (low <= high)\n {\n ll mid = (low + high) / 2;\n\n ll hash_0_to_mid1 = prefix_hash1[mid];\n ll hash_0_to_mid2 = prefix_hash2[mid];\n ll hash_0_to_iminus11 = ((i == 0) ? 0 : prefix_hash1[i - 1]);\n ll hash_0_to_iminus12 = ((i == 0) ? 0 : prefix_hash2[i - 1]);\n ll p1_inv = modinv(p1_pow[i], m);\n ll p2_inv = modinv(p2_pow[i], m);\n\n ll hash_value1 = (((hash_0_to_mid1 - hash_0_to_iminus11 + m) % m) * p1_inv) % m;\n ll hash_value2 = (((hash_0_to_mid2 - hash_0_to_iminus12 + m) % m) * p2_inv) % m;\n\n if (hashes.contains({hash_value1, hash_value2}))\n {\n low = mid + 1;\n end_idx = mid;\n }\n\n else\n {\n high = mid - 1;\n }\n }\n\n if (end_idx != -1)\n {\n pairs.emplace_back(end_idx, i);\n }\n }\n\n ranges::sort(pairs);\n\n vector<ll> end_idxs, start_idxs;\n\n for (auto &[en, st] : pairs)\n {\n end_idxs.push_back(en);\n start_idxs.push_back(st);\n }\n\n SegmentTree tree(start_idxs);\n ll R = n - 1;\n ll N = (ll)end_idxs.size();\n ll ans = 0;\n\n while (R >= 0)\n {\n auto it = lower_bound(end_idxs.begin(), end_idxs.end(), R);\n\n if (it == end_idxs.end())\n {\n return -1;\n }\n\n ll idx = it - end_idxs.begin();\n ll min_starting_point = tree.query(idx, N - 1);\n\n if (min_starting_point > R)\n {\n return -1;\n }\n\n ans++;\n R = min_starting_point - 1;\n }\n\n return ans;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | gpt-o1 generate code. | gpt-o1-generate-code-by-leet4jin-zml8 | Intro\ngpt-o1 generate code.\n\n# Code\nc []\nint minValidStrings(char** words, int wordsSize, char* target) {\n int lenTarget = strlen(target);\n int *be | leet4jin | NORMAL | 2024-09-17T06:32:53.859944+00:00 | 2024-09-17T06:32:53.859987+00:00 | 7 | false | # Intro\ngpt-o1 generate code.\n\n# Code\n```c []\nint minValidStrings(char** words, int wordsSize, char* target) {\n int lenTarget = strlen(target);\n int *best = (int *)calloc(lenTarget, sizeof(int));\n\n for (int w = 0; w < wordsSize; w++) {\n char *word = words[w];\n int lenWord = strlen(word);\n int *kmp = (int *)malloc(lenWord * sizeof(int));\n kmp[0] = 0;\n int j = 0;\n for (int i = 1; i < lenWord; i++) {\n while (j > 0 && word[i] != word[j])\n j = kmp[j - 1];\n if (word[i] == word[j])\n j++;\n kmp[i] = j;\n }\n j = 0;\n for (int i = 0; i < lenTarget; ) {\n if (word[j] == target[i]) {\n j++; i++;\n if (j > best[i - 1])\n best[i - 1] = j;\n if (j == lenWord)\n j = kmp[j - 1];\n } else {\n if (j > 0)\n j = kmp[j - 1];\n else\n i++;\n }\n }\n free(kmp);\n }\n int steps = 0, pos = lenTarget;\n while (pos > 0) {\n if (best[pos - 1] == 0) {\n free(best);\n return -1;\n }\n pos -= best[pos - 1];\n steps++;\n }\n free(best);\n return steps;\n}\n``` | 0 | 0 | ['C'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Python KMP | python-kmp-by-pchen36-56q5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | pchen36 | NORMAL | 2024-09-17T04:49:52.507950+00:00 | 2024-09-17T04:49:52.507986+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(m*n) # m: len(words), n: len(target)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m+n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n #KMP \n #idea: picking up the longest suffix of target in prefix of words will get the minimum number of valid prefixes\n n = len(target)\n dp = [0]*n #store the longest length of suffix until i\n ans = 0\n def create_LPS(s):\n m = len(s)\n LPS = [0]*m\n l, r = 0, 1\n while r < m:\n if s[l] == s[r]:\n l += 1\n LPS[r] = l\n r += 1\n else:\n if l == 0:\n r += 1\n else:\n l = LPS[l-1]\n return LPS\n\n for word in words:\n l_w = len(word)\n LPS = create_LPS(word+\'#\'+target)\n for i in range(n):\n dp[i] = max(dp[i], LPS[l_w+1+i])\n #print(dp)\n length = n\n while length > 0 and dp[length-1] > 0:\n ans += 1\n length -= dp[length-1]\n return ans if length == 0 else -1\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Easy Explanation of KMP approach✔✔🙌 beats 💯 %. | easy-explanation-of-kmp-approach-beats-b-zwnk | Intuition\nMake use of KMP algorithm to reduce time complexity to avoid TLE.\n\n# Approach\nAs the constraints are pretty high here as compared to its first par | dhimanrishabh414 | NORMAL | 2024-09-16T19:23:52.272806+00:00 | 2024-09-16T19:33:09.630968+00:00 | 37 | false | # Intuition\nMake use of KMP algorithm to reduce time complexity to avoid **TLE**.\n\n# Approach\nAs the constraints are pretty high here as compared to its first part, we nee to think of an approach which can be solved in time complexity below O(n^2). Where comes a concept of **KMP** algorithm. where we kind of precomputes the lps(**longest prefix sufix**) which helps in utilizing this lps information further and solve the problem. \n\n# Complexity\n- Time complexity: O(O(sum(word lengths) + ("#" used) + (length of words) * target length) + O(target length * length of words)) => max(O(n+100+100 * m) , O(m * 100)) ~ **O(n+m)**;\n\n- Space complexity: O(sum(word lengths) + ("#" used) + (length of words) * target length) => O(n+100+100 * m) ~ **O(n+m)**; \n\n# Code\n```java []\nclass Solution {\n private int[] kmp(String s){\n int n = s.length();\n int lps[] = new int[n];\n int pL = 0;\n \n int i = 1;\n while(i<n){\n if(s.charAt(i) == s.charAt(pL)){\n lps[i] = pL + 1;\n pL = lps[i];\n i++;\n }\n else {\n if(pL == 0){\n lps[i] = 0;\n i++;\n }\n else{\n pL = lps[pL-1]; \n }\n }\n }\n\n return lps;\n }\n\n\n public int minValidStrings(String[] words, String target) {\n List<int[]> arr = new ArrayList();\n for(String word : words)arr.add(kmp(word+"#"+target));\n int res = 0;\n int i = target.length()-1;\n \n while(i >= 0){\n int maxLen = 0;\n for(int j=0;j<words.length;j++){\n maxLen = Math.max(maxLen, arr.get(j)[words[j].length() + 1 + i]);\n }\n if(maxLen == 0)return -1;\n i -= maxLen;\n res++;\n }\n\n return res;\n }\n}\n``` | 0 | 0 | ['Two Pointers', 'String', 'String Matching', 'Java'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | KMP + BFS | kmp-bfs-by-xxxxkav-dueo | \nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n \n def kmp(sub_s, s):\n k, n, pref = 0, len(sub_s), | xxxxkav | NORMAL | 2024-09-16T19:21:33.806855+00:00 | 2024-09-16T19:21:44.881330+00:00 | 4 | false | ```\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n \n def kmp(sub_s, s):\n k, n, pref = 0, len(sub_s), [0]\n for i in range(1, n):\n while k and sub_s[k] != sub_s[i]:\n k = pref[k-1]\n if sub_s[k] == sub_s[i]:\n k += 1\n pref.append(k)\n k, ans = 0, []\n for i, ch in enumerate(s):\n while k and sub_s[k] != ch:\n k = pref[k-1]\n if sub_s[k] == ch:\n k += 1 \n ans.append(i-k+1)\n if k == n:\n k = pref[k-1]\n return ans\n\n n, graph = len(target), defaultdict(set)\n for word in words: \n for v, u in enumerate(kmp(word, target), 1):\n if u != v:\n graph[u].add(v)\n \n queue, visited = [0], [0] * n\n step, visited[0] = 1, 1\n while queue:\n new_queue = []\n for u in queue:\n for v in graph[u]:\n if v == n:\n return step\n if not visited[v]:\n new_queue.append(v)\n visited[v] = 1\n queue = new_queue\n step += 1 \n return -1 \n``` | 0 | 0 | ['Breadth-First Search', 'Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | short kmp + greedy solution | short-kmp-greedy-solution-by-vincent_gre-ttig | \ndef minValidStrings(self, words: List[str], tar: str) -> int:\n def kmp(strs):\n s, dp = strs+\'|\'+tar, [0]*(len(strs)+len(tar)+1)\n for i i | vincent_great | NORMAL | 2024-09-16T02:52:01.417715+00:00 | 2024-09-16T05:45:56.930668+00:00 | 15 | false | ```\ndef minValidStrings(self, words: List[str], tar: str) -> int:\n def kmp(strs):\n s, dp = strs+\'|\'+tar, [0]*(len(strs)+len(tar)+1)\n for i in range(1, len(s)):\n k = dp[i-1]\n while k and s[i]!=s[k]:\n k = dp[k-1]\n dp[i] = k+(s[i]==s[k])\n return dp[len(strs):]\n\n dp, p = [0]+[inf]*len(tar), [0]*(len(tar)+1)\n for w in words:\n p = [max(i, j) for i, j in zip(p, kmp(w))]\n for i in range(1, len(tar)+1):\n if i-p[i]>=0:\n dp[i] = min(dp[i], dp[i-p[i]]+1)\n return dp[-1] if dp[-1]<inf else -1\n``` | 0 | 0 | [] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | non-dp solution, ~20 lines, 76 ms, 11.72 MB | non-dp-solution-20-lines-76-ms-1172-mb-b-ca9q | Complexity\nLet w = length of longest word, k = number of words, m = total length of words, n = length of target.\n- Time complexity: O(m + n * k)\n- Space comp | llllvvuu | NORMAL | 2024-09-15T23:09:18.261401+00:00 | 2024-09-15T23:15:18.097297+00:00 | 15 | false | # Complexity\nLet w = length of longest word, k = number of words, m = total length of words, n = length of target.\n- Time complexity: O(m + n * k)\n- Space complexity: O(w + n)\n\nNote that n * k and m are both ~5,000,000. If n * k were much bigger than m, then the following solution would be better: https://leetcode.com/problems/minimum-number-of-valid-strings-to-form-target-ii/solutions/5789605/c-simplest-and-shortest-solution-two-pointer-and-rolling-hash-only-no-trees-tries-kmp-z-etc/\n\n# Code\n```c []\nint minValidStrings(char** words, int wordsSize, char* target) {\n int lenLongestWord = 0, len = strlen(target), steps = 0;\n for (int i = 0; i < wordsSize; i++) {\n int lenWord = strlen(words[i]);\n if (lenWord > lenLongestWord) lenLongestWord = lenWord;\n }\n int kmp[lenLongestWord + 1], best[len];\n memset(best, 0, len * sizeof(int));\n\n for (int i = 0; i < wordsSize; i++) { // KMP\n const char *word = words[i];\n kmp[0] = 0;\n for (int j = 0, k = 1; word[k];) {\n if (word[k] == word[j]) kmp[k++] = j++ + 1;\n else if (j) j = kmp[j - 1];\n else kmp[k++] = 0;\n }\n for (int j = 0, k = 0; target[k];) {\n if (target[k] == word[j]) {\n best[k] = best[k] > j + 1 ? best[k] : j + 1;\n k++; j++;\n } else if (j) j = kmp[j - 1];\n else k++;\n }\n }\n\n for (int remaining = len; remaining; steps++) { // greedy\n if (!best[remaining - 1]) return -1;\n remaining -= best[remaining - 1];\n }\n return steps;\n}\n``` | 0 | 0 | ['Greedy', 'C', 'String Matching'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | kmp | kmp-by-phi9t-iq1w | \n## Intuition\n\nWhen faced with this problem, the first thought is to determine how to effectively break down the target string into substrings that match the | phi9t | NORMAL | 2024-09-15T18:48:25.884348+00:00 | 2024-09-15T18:49:02.055226+00:00 | 10 | false | \n## Intuition\n\nWhen faced with this problem, the first thought is to determine how to effectively break down the target string into substrings that match the words in the provided list. A naive approach might involve trying all possible combinations of words, but this quickly becomes infeasible due to the exponential number of possibilities, especially with longer target strings.\n\nTo optimize, we can leverage the **Knuth-Morris-Pratt (KMP) algorithm** for efficient substring matching. By pre-processing each word to build a KMP table, we can rapidly identify how each word contributes to constructing the target string. This approach allows us to dynamically determine the minimum number of operations (i.e., word selections) required to build the target incrementally.\n\n---\n\n## Approach\n\nThe problem can be approached using dynamic programming combined with efficient string matching techniques. Here\'s a step-by-step breakdown of the strategy:\n\n1. **KMP Table Construction for Each Word:**\n - For each word in `words`, build its KMP table. The KMP table helps in identifying the longest prefix of the word that matches a suffix of the current target substring. This is crucial for overlapping matches, ensuring we don\'t miss potential matches that can reduce the number of operations.\n\n2. **Building Match Tables:**\n - Using the KMP tables, construct a match table for each word against the entire target string. This table records, for each position in the target, the length of the prefix of the word that matches the target up to that position.\n\n3. **Dynamic Programming to Determine Minimum Operations:**\n - Initialize a dynamic programming (DP) table `tbl_min_ops`, where `tbl_min_ops[i]` represents the minimum number of operations needed to construct the target string up to the `i-th` character.\n - Iterate through each character in the target string. For each position, consider all words and update the DP table based on the match tables. If a word matches a substring ending at the current position, update the minimum operations accordingly.\n - If no word matches at a particular position, it\'s impossible to form the target, and the function returns `-1`.\n\n4. **Final Result:**\n - After processing the entire target string, the last entry in the DP table will hold the minimum number of operations required to form the target. If it\'s not possible, `-1` is returned.\n\nThis method ensures that we efficiently explore all possible word matches while minimizing redundant computations, thanks to the preprocessing done by the KMP algorithm.\n\n---\n\n## Code\n\nHere\'s the Python implementation of the described approach:\n\n```python\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n DEBUG_VIZ = False\n\n def build_kmp_table(word):\n tbl = [0] * len(word)\n for i in range(1, len(word)):\n tgt = word[i]\n l = tbl[i - 1]\n while l > 0 and word[l] != tgt:\n l = tbl[l - 1]\n if word[l] == tgt:\n l += 1\n tbl[i] = l\n return tbl\n\n def build_match_table(word, kmp_tbl):\n tbl = []\n l = 0\n for ch in target:\n if l == len(word):\n l = kmp_tbl[l - 1]\n while l > 0 and word[l] != ch:\n l = kmp_tbl[l - 1]\n if word[l] == ch:\n l += 1\n tbl.append(l)\n return tbl\n\n match_tbl_list = []\n for word in words:\n kmp_tbl = build_kmp_table(word)\n match_tbl = build_match_table(word, kmp_tbl)\n match_tbl_list.append(match_tbl)\n if DEBUG_VIZ:\n print(f"===== {word}")\n for i, l in enumerate(match_tbl):\n print(f"-- idx = {i}, prefix_len = {l}: {word} vs {target}")\n print(f" : {word[:l]}")\n matching = "." * (i - l + 1) + target[(i - l + 1) : (i + 1)]\n print(f" : {matching}")\n\n tbl_min_ops = [0]\n for i, ch in enumerate(target):\n min_ops = None\n for match_tbl in match_tbl_list:\n l = match_tbl[i]\n if l == 0:\n continue\n curr = tbl_min_ops[i + 1 - l] + 1\n if min_ops is None:\n min_ops = curr\n else:\n min_ops = min(curr, min_ops)\n if min_ops is None:\n return -1\n tbl_min_ops.append(min_ops)\n \n return tbl_min_ops[-1]\n```\n\n | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | String Hash+Binary Search+BST(std::Map) | string-hashbinary-searchbststdmap-by-don-p970 | Complexity\n\n- n=target.length,m=sum(words.length)\n\n- Time complexity: O(m+n \log(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(m) | dongdozizi | NORMAL | 2024-09-15T18:35:17.222262+00:00 | 2024-09-15T18:35:17.222290+00:00 | 13 | false | # Complexity\n\n- $$n=target.length,m=sum(words.length)$$\n\n- Time complexity: $$O(m+n \\log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n\n\nclass Solution {\npublic:\n typedef long long ll;\n vector<unordered_set<ll>> mp[2];\n ll max_l=0;\n ll base = 131;\n ll mod[2]={998244353,1000000007};\n vector<ll> hast[2];\n vector<ll> pow[2];\n\n void get_hash(string s,int id) {\n ll ans=0;\n for(int i=0;i<s.size();i++){\n ans=(ans*base+(ll)s[i])%mod[id];\n mp[id][i+1].insert(ans);\n }\n }\n void get_hash(string s){\n get_hash(s,0);get_hash(s,1);\n }\n\n void build_hast(string s,int id){\n hast[id][0]=0;\n for(ll i=0;i<s.size();i++){\n hast[id][i+1]=(hast[id][i]*base+s[i])%mod[id];\n }\n }\n void build_hast(string s){\n build_hast(s,0);build_hast(s,1);\n }\n\n ll get_hast(int l,int r,int id){\n return ((hast[id][r+1]-hast[id][l]*pow[id][r-l+1])%mod[id]+mod[id])%mod[id];\n }\n\n bool check(int st,int m){\n if(m==0) return true;\n return mp[0][m].count(get_hast(st,st+m-1,0))&&\n mp[1][m].count(get_hast(st,st+m-1,1));\n }\n\n int calc(int st,int l,int r){\n int m=(l+r)/2;\n if(l+1>=r){\n if(check(st,r)){\n return r;\n }\n else{\n return r-1;\n }\n }\n if(check(st,m)) return calc(st,m,r);\n else return calc(st,l,m-1);\n }\n vector<int> vec[50005];\n int minValidStrings(vector<string>& words, string t) {\n max_l=t.size();\n for(int i=0;i<words.size();i++){\n max_l=max((ll)words[i].size(),max_l);\n }\n for(int i=0;i<2;i++){\n mp[i].resize(max_l+10);\n hast[i].resize(max_l+10);\n pow[i].resize(max_l+10);\n }\n for(int i=0;i<2;i++){\n pow[i][0]=1;\n for(int j=1;j<=max_l;j++){\n pow[i][j]=pow[i][j-1]*base%mod[i];\n }\n }\n for(int i=0;i<words.size();i++){\n get_hash(words[i]);\n }\n int n=t.size();\n build_hast(t);\n\n vector<int> dp(n+1,1000000000);\n dp[0]=0;\n map<int,int> mp1;\n\n for(int i=0;i<n;i++){\n pair<int,int> pp;\n pp.first=dp[i]+1,pp.second=calc(i,0,n-i); \n if(pp.second==0&&mp1.size()==0) return -1;\n if(pp.second!=0){\n pp.second=i+pp.second;\n vec[pp.second].push_back(pp.first);\n mp1[pp.first]++;\n }\n dp[i+1]=mp1.begin()->first;\n for(int j=0;j<vec[i+1].size();j++){\n mp1[vec[i+1][j]]--;\n if(mp1[vec[i+1][j]]==0) mp1.erase(vec[i+1][j]);\n }\n }\n return dp[n];\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | JAVA || Beats 100% || String Hashing + DP | java-beats-100-string-hashing-dp-by-jai_-e0tj | Intuition\n Describe your first thoughts on how to solve this problem. \nSum of all strings length <= 10^5 so we would hash all strings and store all prefix of | jai_hanumant | NORMAL | 2024-09-15T17:34:52.515272+00:00 | 2024-09-15T17:34:52.515296+00:00 | 40 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSum of all strings length <= 10^5 so we would hash all strings and store all prefix of each string in HashSet<Index> set, then apply dp.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nin function \'fun\', firstly find maximum length that can be found from ith position using binary seach on length and checking its hash value in HashSet<Index> set.\n\nLet max length = yaha that means using one operation we can go from i to any position x <= yaha then finding required operations from x.\n\nConcept of limit : just to reduce time complexity -> limit indicates that minimum position we would travel to avoid multiple unnecessary function calls. eg-> suppose we can go from 1 to x <= 5 then from 2 we would see positions > 5.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public static long mod = (long) 1e9 + 7;\n public static long base[] = { 4441, 7817 };\n\n public static long[] get_hash(String s) {\n long h[] = { 0, 0 };\n for (int i = 0; i < s.length(); i++) {\n h = add(multiply(base, h), s.charAt(i));\n }\n return h;\n }\n\n public static long[] multiply(long a[], long b[]) {\n return new long[] { (a[0] * b[0]) % mod, (a[1] * b[1]) % mod };\n }\n\n public static long[] add(long a[], long b) {\n return new long[] { (a[0] + b) % mod, (a[1] + b) % mod };\n }\n\n // create an object of hsh & initialise it in main method.\n static class hsh {\n int n;\n String s;\n long pre[][], pp[][];\n\n void init(String S,HashSet<Index>set) {\n s = S;\n n = s.length();\n pp = new long[n + 1][2];\n pre = new long[n + 1][2];\n pp[0] = new long[] { 1, 1 };\n for (int i = 0; i < n; i++) {\n pre[i + 1][0] = ((pre[i][0] * base[0]) % mod + s.charAt(i)) % mod;\n pre[i + 1][1] = ((pre[i][1] * base[1]) % mod + s.charAt(i)) % mod;\n set.add(new Index((pre[i+1][0]+mod)%mod,(pre[i+1][1]+mod)%mod));\n if (i > 0) {\n pp[i][0] = (pp[i - 1][0] * base[0]) % mod;\n pp[i][1] = (pp[i - 1][1] * base[1]) % mod;\n }\n }\n }\n\n // returns hash of a substring (l,r) in O(1)\n // l -> inclusive, r -> exclusive\n long[] get(int s, int e) {\n return new long[] { (pre[e][0] - (pre[s][0] * pp[e - s][0]) % mod + mod) % mod,\n (pre[e][1] - (pre[s][1] * pp[e - s][1]) % mod + mod) % mod };\n }\n }\n\n public static int dp[];\n\n public static int fun( hsh ths, int i,int limit) {\n if (i >= tlen) {\n return 0;\n }\n if (dp[i] != -1) {\n return dp[i];\n }\n int ans = (int)Math.pow(10,7);\n int st = i;\n // while (st < tlen) {\n int low = 1, high = tlen - st;// length pr binary search\n int yaha = -1;\n while (low <= high) {\n int mid = (low + high) / 2;\n long tmp[]=ths.get(st,st+mid);\n if(set.contains(new Index(tmp[0],tmp[1]))){\n low = mid + 1;\n yaha = mid;\n } else {\n high = mid - 1;\n }\n }\n if (yaha == -1) {\n return (int)Math.pow(10,7);\n } else {\n for (int k = limit; k <= yaha; k++) {\n ans = Math.min(ans, 1 + fun( ths, i + k,Math.max(yaha-k,1)));\n }\n }\n\n // }\n return dp[i] = ans;\n }\n public static HashSet<Index> set;\n public static int tlen;\n public static int minValidStrings(String[] words, String target) {\n int n = words.length;\n set=new HashSet<>();\n for (int i = 0; i < n; i++) {\n hsh hs = new hsh();\n hs.init(words[i],set);\n }\n HashSet<Index>dontuse=new HashSet<>();\n hsh ths = new hsh();\n ths.init(target,dontuse);\n tlen = target.length();\n dp = new int[tlen + 1];\n Arrays.fill(dp, -1);\n int aa1=fun( ths, 0,1);\n if(aa1==(int)Math.pow(10,7)){\n aa1=-1;\n }\n return aa1;\n }\n\n // ----------------\n public static class Index {\n\n private long x;\n private long y;\n\n public Index(long x, long y) {\n this.x = x;\n this.y = y;\n }\n\n @Override\n public int hashCode() {\n return (int)(this.x ^ this.y);\n }\n\n @Override\n public boolean equals(Object obj) {\n if (this == obj)\n return true;\n if (obj == null)\n return false;\n if (getClass() != obj.getClass())\n return false;\n Index other = (Index) obj;\n if (x != other.x)\n return false;\n if (y != other.y)\n return false;\n return true;\n }\n }\n // -------------------------\n\n}\n``` | 0 | 0 | ['Java'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | minimum-number-of-valid-strings-to-form-target-ii | minimum-number-of-valid-strings-to-form-j6054 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | goseotaxi | NORMAL | 2024-09-15T17:06:27.968606+00:00 | 2024-09-15T17:06:27.968647+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc minValidStrings(words []string, target string) int {\n n := len(target)\n match := make([]int, n)\n\n for _, word := range words {\n s := word + "#" + target\n excess := len(word) + 1\n nn := len(s)\n z := make([]int, nn)\n x, y := 0, 0\n\n for i := 1; i < nn; i++ {\n if i <= y {\n z[i] = min(y - i + 1, z[i - x])\n }\n for i+z[i] < nn && s[z[i]] == s[i+z[i]] {\n z[i]++\n }\n if i+z[i]-1 > y {\n x = i\n y = i + z[i] - 1\n }\n if i >= excess && z[i] > 0 {\n pos := i - excess\n if match[pos] < z[i] {\n match[pos] = z[i]\n }\n }\n }\n }\n\n // \u0416\u0430\u0434\u043D\u044B\u0439 \u0430\u043B\u0433\u043E\u0440\u0438\u0442\u043C\n steps := 0\n currEnd := 0\n farthest := 0\n\n for i := 0; i < n; i++ {\n if i+match[i] > farthest {\n farthest = i + match[i]\n }\n if i == currEnd {\n if farthest <= i {\n return -1\n }\n steps++\n currEnd = farthest\n if currEnd >= n {\n break\n }\n }\n }\n\n if currEnd < n {\n return -1\n }\n return steps\n}\n\nfunc min(a, b int) int {\n if a < b {\n return a\n }\n return b\n}\n``` | 0 | 0 | ['Go'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Alternative solution with hashing and seg tree beats 95% + approach | alternative-solution-with-hashing-and-se-c34t | Intuition\nLet dp[i] represent the result for the prefix of length i in the target word. We will hash all possible prefixes that can be used from the vector wor | viksolve | NORMAL | 2024-09-15T14:26:37.755599+00:00 | 2024-09-15T14:26:37.755633+00:00 | 12 | false | # Intuition\nLet dp[i] represent the result for the prefix of length i in the target word. We will hash all possible prefixes that can be used from the vector words.\n\n# Approach\nIn the segment tree, let\'s store the minimum result we can achieve for a given prefix. If we reach that prefix during the loop, we will binary search the maximum length by which we can extend from index i and update the results in the segment tree accordingly\n\n# Complexity\nw=words.length()\nz=words[i].length();\n- Time complexity:\nO(n*logn+w*z)\n\n- Space complexity:\no(n+w*z)\n\n# Code\n```cpp []\ntypedef long long ll;\nconst int MOD1 = 1e9 + 7;\nconst int MOD2 = 1e9 + 9;\nconst int st1 = 139;\nconst int st2 = 137;\nconst int N = 5e4 + 5;\nbool calc=false;\nll pot1[N], pot2[N], h1[N], h2[N];\n//segment tree start\nint d[N*4], push[N*4];\nvoid add(int x, int var){\n if(d[x]>var) d[x]=var;\n if(!push[x]||push[x]>var) push[x]=var;\n}\nvoid pushuj(int x){\n if(!push[x]) return;\n add(x*2, push[x]);\n add(x*2+1, push[x]);\n push[x]=0;\n}\nvoid build(int x, int l, int r){\n if(l==r){\n if(l==1) d[x]=0;\n else d[x]=1e9;\n return;\n }\n pushuj(x);\n int sr=(l+r)/2;\n build(x*2, l, sr);\n build(x*2+1, sr+1, r);\n d[x]=min(d[x*2], d[x*2+1]);\n}\nvoid update(int x, int l, int r, int a, int b, int var){\n if(a<=l&&r<=b){\n add(x, var);\n return;\n }\n pushuj(x);\n int sr=(l+r)/2;\n if(a<=sr) update(x*2, l, sr, a, b, var);\n if(sr<b) update(x*2+1, sr+1, r, a, b, var);\n d[x]=min(d[x*2], d[x*2+1]);\n}\nint query(int x, int l, int r, int a, int b){\n if(a<=l&&r<=b){\n return d[x];\n }\n pushuj(x);\n int res=1e9;\n int sr=(l+r)/2;\n if(a<=sr) res=min(res, query(x*2, l, sr, a, b));\n if(sr<b) res=min(res, query(x*2+1, sr+1, r, a, b));\n d[x]=min(d[x*2], d[x*2+1]);\n return res;\n}\n//segment tree end\nvoid pre(){\n calc=true;\n pot1[0]=pot2[0]=1;\n for(int i=1;i<N;i++){\n pot1[i]=(pot1[i-1]*st1)%MOD1;\n pot2[i]=(pot2[i-1]*st2)%MOD2;\n }\n}\npair<int, int> get(int a, int b) { //get hash from target\n ll hash1 = (h1[a] - (h1[b+1] * pot1[b-a+1]) % MOD1 + MOD1) % MOD1;\n ll hash2 = (h2[a] - (h2[b+1] * pot2[b-a+1]) % MOD2 + MOD2) % MOD2;\n return {hash1, hash2};\n}\nstruct pair_hash { //hash function for unordered_set\n template <class T1, class T2>\n std::size_t operator() (const std::pair<T1, T2>& pair) const {\n return std::hash<T1>()(pair.first) ^ std::hash<T2>()(pair.second);\n }\n};\nclass Solution {\npublic:\n int minValidStrings(vector<string>& words, string target) {\n unordered_set<pair<int, int>, pair_hash> zb;\n if(!calc) pre();\n for(auto &s : words){//hashing all prefixes\n int m=s.size();\n ll hash1=0, hash2=0;\n for(int i=0;i<m;i++){\n hash1=(hash1+pot1[i]*s[i])%MOD1;\n hash2=(hash2+pot2[i]*s[i])%MOD2;\n zb.insert({hash1, hash2});\n }\n }\n target=".."+target;\n int n=target.size(), rozm=1;\n while(rozm<n){\n rozm<<=1;\n }\n build(1, 1, rozm);\n vector<int> dp(n+1, 1e9);\n dp[1]=0;\n h1[n+1]=h2[n+1]=h1[0]=h2[0]=0;\n for(int i=n;i>=1;i--){//hash target\n h1[i]=(h1[i+1]*st1+target[i])%MOD1;\n h2[i]=(h2[i+1]*st2+target[i])%MOD2;\n }\n for(int i=1;i<n-1;i++){\n dp[i]=query(1, 1, rozm, i, i);\n if(dp[i]==1e9) continue;\n int l=i+1, r=n-1, res=0;\n while(l<=r){//get maximum length\n int sr=(l+r)/2;\n if(zb.find(get(i+1, sr))!=zb.end()){\n res=max(res, sr);\n l=sr+1;\n }\n else r=sr-1;\n }\n if(!res) continue;\n update(1, 1, rozm, i+1, res, dp[i]+1);\n }\n dp[n-1]=query(1, 1, rozm, n-1, n-1);\n return (dp[n-1]==1e9) ? -1 : dp[n-1];\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Solution using dp + segment tree + binary search | solution-using-dp-segment-tree-binary-se-lx1i | \n\n# Code\ncpp []\nclass Hash{\n private:\n const long long mod1=999999929;\n const long long mod2=999999937;\n const long long mod3=(long long)(1e | rishichowdhury711 | NORMAL | 2024-09-15T13:26:57.051015+00:00 | 2024-09-15T13:26:57.051053+00:00 | 47 | false | \n\n# Code\n```cpp []\nclass Hash{\n private:\n const long long mod1=999999929;\n const long long mod2=999999937;\n const long long mod3=(long long)(1e15)+7;\n \n const long long p1=1001; // should be greater than the length of the string;\n const long long p2=1003; // should be greater than the length of the string;\n \n const long long p3=99911; // should be greater than the length of the string;\n \n public:\n vector<long long>pref1;\n vector<long long>pref2;\n vector<long long>base_pow1;\n vector<long long>base_pow2; \n string s;\n long long n;\n \n Hash(const string &a)\n {\n s=a;\n n=s.length();\n pref1.assign(n+1,0);\n pref2.assign(n+1,0);\n base_pow1.assign(n+1,0);\n base_pow2.assign(n+1,0);\n build();\n }\n void build()\n {\n base_pow1[0]=1;\n \n base_pow2[0]=1;\n pref1[0]=1;\n pref2[0]=1;\n \n for(long long i=1;i<=n;i++)\n {\n base_pow1[i]=(base_pow1[i-1]*p1)%mod1;\n base_pow2[i]=(base_pow2[i-1]*p2)%mod2;\n \n pref1[i]=((pref1[i-1]*p1)%mod1+s[i-1]+997)%mod1;\n \n pref2[i]=((pref2[i-1]*p2)%mod2+s[i-1]+997)%mod2;\n }\n \n }\n \n long long getHash(long long l,long long r)\n {\n long long h1=pref1[r+1];\n \n h1-=(pref1[l]*base_pow1[r-l+1])%mod1;\n h1=(h1%mod1+mod1)%mod1;\n \n long long h2=pref2[r+1];\n \n h2-=(pref2[l]*base_pow2[r-l+1])%mod2;\n \n h2=(h2%mod2+mod2)%mod2;\n \n long long h3=((h1*p3)%mod3+h2)%mod3;\n \n return h3;\n }\n};\nclass SegmentTree{\n private:\n vector<long long>tree;\n long long n;\n vector<long long>arr;\n public:\n SegmentTree(vector<long long>&a)\n {\n arr=a;\n n=(long long)a.size();\n tree.assign(4*n+1,0);\n // cout<<n<<endl;\n build(0,n-1,0);\n }\n\n void build(long long ss,long long se,long long si)\n {\n if(ss==se)\n {\n tree[si]=arr[se];\n return;\n }\n\n long long mid=(ss+se)/2;\n build(ss,mid,2*si+1);\n build(mid+1,se,2*si+2);\n tree[si]=min(tree[2*si+1],tree[2*si+2]);\n }\n\n void update(long long ss,long long se,long long si,long long idx,long long val)\n {\n if(ss==se)\n {\n tree[si]=val;\n return;\n }\n\n long long mid=(ss+se)/2;\n if(idx<=mid)\n {\n update(ss,mid,2*si+1,idx,val);\n }\n else\n {\n update(mid+1,se,2*si+2,idx,val);\n }\n tree[si]=min(tree[2*si+1],tree[2*si+2]);\n }\n\n long long query(long long ss,long long se,long long si,long long l,long long r)\n {\n if(ss>=l && se<=r)\n {\n return tree[si];\n }\n\n if(ss>r || se<l)\n return (long long)(1e9);\n\n long long mid=(ss+se)/2;\n\n return min(query(ss,mid,2*si+1,l,r),query(mid+1,se,2*si+2,l,r));\n }\n\n long long make_query(long long l,long long r)\n {\n return query(0,n-1,0,l,r);\n }\n\n void make_update(long long idx,long long val)\n {\n update(0,n-1,0,idx,val);\n }\n\n};\nclass Solution {\npublic:\n int minValidStrings(vector<string>& words, string target) {\n Hash ht(target);\n long long n=(long long)words.size();\n set<long long>s;\n for(long long i=0;i<n;i++)\n {\n Hash h(words[i]);\n long long len=words[i].length();\n for(long long j=0;j<len;j++)\n {\n s.insert(h.getHash(0,j));\n }\n }\n\n long long count=0;\n long long m=target.length();\n vector<long long>dp(m+1,(long long)(1e9));\n\n function<long long(long long)>f=[&](long long i)->long long{\n long long low=i;\n long long high=m-1;\n long long res=-1;\n while(low<=high)\n {\n long long mid=(low+high)/2;\n if(s.find(ht.getHash(i,mid))!=s.end())\n {\n res=mid;\n low=mid+1;\n }\n else\n {\n high=mid-1;\n }\n }\n return res;\n };\n dp[m]=0;\n if(s.find(ht.getHash(m-1,m-1))!=s.end())\n dp[m-1]=1;\n SegmentTree sgt(dp);\n for(long long i=m-2;i>=0;i--)\n {\n long long j=f(i);\n if(j==-1)\n continue;\n dp[i]=min(dp[i],sgt.make_query(i+1,j+1)+1);\n sgt.make_update(i,dp[i]);\n }\n if(dp[0]==(long long)(1e9))\n return -1;\n return dp[0];\n\n }\n};\n``` | 0 | 0 | ['Binary Search', 'Dynamic Programming', 'Greedy', 'Segment Tree', 'Rolling Hash', 'C++'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | KMP + Greedy (interval schedule) | kmp-greedy-interval-schedule-by-ashishku-zkt2 | Intuition\nWe need to find the minimum prefix-concatenation. The order or the specific way to achieve this is not required. For each point, we need to determine | Ashishkumanar | NORMAL | 2024-09-15T11:35:01.829200+00:00 | 2024-09-15T11:35:01.829225+00:00 | 50 | false | # Intuition\nWe need to find the minimum prefix-concatenation. The order or the specific way to achieve this is not required. For each point, we need to determine the maximum distance it can travel according to the prefix rule. We can use the KMP algorithm for each word to calculate this maximum distance. Once we know the distance it can travel, we can convert the problem into an interval scheduling problem, where overlaps are allowed.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: o(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: o(m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> dp,cnt;\n unordered_map<char,vector<int>> map;\n int m,n;\n int minValidStrings(vector<string>& w, string t) {\n m=t.size();\n n=w.size();\n dp.resize(m+1,INT_MAX);cnt.resize(m,0);\n dp[m]=0;\n for(int i1=0;i1<n;i1++){\n string s=w[i1];\n vector<int> a(s.size(),0),b(m,0);\n kmp_int(s,a);\n int i=0,j=0;\n while(i<m){\n if(t[i]==s[j]){\n b[i]=j+1;\n int k=i+1-b[i];\n cnt[k]=max(cnt[k],b[i]);\n j++;\n if(j==s.size()) j=a[j-1];\n i++;\n }else if(j!=0) j=a[j-1];\n else i++;\n }\n }\n int count=0,l=0,r=0;\n //greedy aproach\n while(l<m){\n r=max(r,l+cnt[l]);\n if(r<=l) return -1;\n int mx=0;\n while(l<r){\n if(l+cnt[l]>r) mx= max(mx,l+cnt[l]);\n l++;\n }\n l=r;\n r=mx;\n count++;\n }\n\n if(l!=m) return -1;\n return count;\n }\n //kmp is answer\n void kmp_int(string s,vector<int>&a){\n int i=1,j=0;\n while(i<s.size()){\n if(s.at(i)==s.at(j)){\n a[i]=j+1;\n j++;\n i++;\n }else if(j!=0) j=a[j-1];\n else i++;\n }\n }\n};\n``` | 0 | 0 | ['C++'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | My Solutions | my-solutions-by-hope_ma-2e2a | 1. Use the z-function\n\n/**\n * Time Complexity: O(n_characters + n_words * n_target)\n * Space Complexity: O(n_word + n_target)\n * where `n_characters` is th | hope_ma | NORMAL | 2024-09-15T11:31:49.252692+00:00 | 2024-09-16T14:02:19.581771+00:00 | 4 | false | **1. Use the `z-function`**\n```\n/**\n * Time Complexity: O(n_characters + n_words * n_target)\n * Space Complexity: O(n_word + n_target)\n * where `n_characters` is the sum of the length of each string of the vector `words`\n * `n_word` is the maximum length of the strings of the vector `words`\n * `n_words` is the length of the vector `words`\n * `n_target` is the length of the string `target`\n */\nclass Solution {\n public:\n int minValidStrings(const vector<string> &words, const string &target) {\n constexpr char separator = \'#\';\n const int n_target = static_cast<int>(target.size());\n int jump[n_target];\n memset(jump, 0, sizeof(jump));\n for (const string &word : words) {\n const int n_word = static_cast<int>(word.size());\n const string s(word + separator + target);\n const int n = static_cast<int>(s.size());\n int z[n];\n memset(z, 0, sizeof(z));\n int l = 0;\n int r = 0;\n for (int i = 1; i < n; ++i) {\n if (i < r) {\n z[i] = min(z[i - l], r - i);\n }\n for (; i + z[i] < n && s[i + z[i]] == s[z[i]]; ++z[i]) {\n }\n if (i > n_word) {\n jump[i - n_word - 1] = max(jump[i - n_word - 1], z[i]);\n }\n if (i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n }\n\n int ret = 0;\n for (int max_reach = 0, next_max_reach = 0, i = 0; i < n_target && max_reach < n_target; ++i) {\n next_max_reach = max(next_max_reach, i + jump[i]);\n if (i == max_reach) {\n if (next_max_reach == max_reach) {\n ret = -1;\n break;\n }\n ++ret;\n max_reach = next_max_reach;\n }\n }\n return ret;\n }\n};\n```\n**2. Use the `KMP` algorithm**\n```\n/**\n * Time Complexity: O(n_characters + n_words * n_target)\n * Space Complexity: O(n_word + n_target)\n * where `n_characters` is the sum of the length of each string of the vector `words`\n * `n_word` is the maximum length of the strings of the vector `words`\n * `n_words` is the length of the vector `words`\n * `n_target` is the length of the string `target`\n */\nclass Solution {\n public:\n int minValidStrings(const vector<string> &words, const string &target) {\n constexpr char separator = \'#\';\n const int n_target = static_cast<int>(target.size());\n int jump[n_target];\n memset(jump, 0, sizeof(jump));\n for (const string &word : words) {\n const int n_word = static_cast<int>(word.size());\n const string s(word + separator + target);\n const int n = static_cast<int>(s.size());\n int next[n + 1];\n memset(next, 0, sizeof(next));\n next[0] = -1;\n int i = 0;\n int j = -1;\n while (i < n) {\n if (j == -1 || s[i] == s[j]) {\n ++i;\n ++j;\n next[i] = j;\n } else {\n j = next[j];\n }\n }\n for (int i = 1; i < n_target + 1; ++i) {\n const int length = max(0, next[n_word + 1 + i]);\n if (length != 0) {\n jump[i - length] = max(jump[i - length], length);\n }\n }\n }\n\n int ret = 0;\n for (int max_reach = 0, next_max_reach = 0, i = 0; i < n_target && max_reach < n_target; ++i) {\n next_max_reach = max(next_max_reach, i + jump[i]);\n if (i == max_reach) {\n if (next_max_reach == max_reach) {\n ret = -1;\n break;\n }\n ++ret;\n max_reach = next_max_reach;\n }\n }\n return ret;\n }\n};\n```\n**3. Use the `Aho-Corasick Automation`**\n```\n/**\n * Time Complexity: O(n_characters + n_target)\n * Space Complexity: O(n_characters + n_target)\n * where `n_characters` is the sum of the length of each string of the vector `words`\n * `n_target` is the length of the string `target`\n */\nclass Solution {\n private:\n static constexpr int letters = 26;\n static constexpr char a = \'a\';\n \n class AcaNode {\n public:\n AcaNode() : children_{}, fail_{}, depth_{} {\n }\n \n ~AcaNode() {\n for (AcaNode * const child : children_) {\n delete child;\n }\n }\n \n AcaNode* get_or_create_child(const char c) {\n AcaNode *&ret = children_[c - a];\n if (ret == nullptr) {\n ret = new AcaNode();\n }\n return ret;\n }\n \n AcaNode* get_child(const char c) const {\n return children_[c - a];\n }\n \n AcaNode* fail() const {\n return fail_;\n }\n \n void set_fail(AcaNode * const fail) {\n fail_ = fail;\n }\n \n int depth() const {\n return depth_;\n }\n \n void set_depth(const int depth) {\n depth_ = depth;\n }\n \n private:\n AcaNode *children_[letters];\n AcaNode *fail_;\n int depth_;\n };\n \n class AhoCorasickAutomation {\n public:\n AhoCorasickAutomation(const vector<string> &words) : root_{} {\n build(words);\n }\n \n vector<int> get_jump(const string &target) {\n const int n = static_cast<int>(target.size());\n vector<int> ret(n);\n AcaNode *node = &root_;\n for (int i = 0; i < n; ++i) {\n AcaNode *next_node = node->get_child(target[i]);\n while (next_node == nullptr && node != &root_) {\n node = node->fail();\n next_node = node->get_child(target[i]);\n }\n node = next_node;\n if (node == nullptr) {\n node = &root_;\n } else {\n ret[i - node->depth() + 1] = node->depth();\n }\n }\n return ret;\n }\n \n private:\n void build(const vector<string> &words) {\n for (const string &word : words) {\n AcaNode *node = &root_;\n const int n_word = static_cast<int>(word.size());\n for (int i = 0; i < n_word; ++i) {\n node = node->get_or_create_child(word[i]);\n node->set_depth(i + 1);\n }\n }\n \n queue<AcaNode *> q({&root_});\n while (!q.empty()) {\n AcaNode * const node = q.front();\n q.pop();\n \n for (int letter = 0; letter < letters; ++letter) {\n const char c = a + letter;\n AcaNode * const child = node->get_child(c);\n if (child == nullptr) {\n continue;\n }\n \n AcaNode *parent = node;\n for (;\n parent->fail() != nullptr && child->fail() == nullptr;\n parent = parent->fail()) {\n AcaNode *target = parent->fail()->get_child(c);\n if (target != nullptr) {\n child->set_fail(target);\n }\n }\n if (child->fail() == nullptr) {\n child->set_fail(&root_);\n }\n q.emplace(child);\n }\n }\n \n root_.set_fail(&root_);\n }\n \n AcaNode root_;\n };\n \n public:\n int minValidStrings(const vector<string> &words, const string &target) {\n const int n_target = static_cast<int>(target.size());\n AhoCorasickAutomation aca(words);\n const vector<int> jump = aca.get_jump(target);\n int ret = 0;\n for (int max_reach = 0, next_max_reach = 0, i = 0; i < n_target && max_reach < n_target; ++i) {\n next_max_reach = max(next_max_reach, i + jump[i]);\n if (i == max_reach) {\n if (next_max_reach == max_reach) {\n ret = -1;\n break;\n }\n ++ret;\n max_reach = next_max_reach;\n }\n }\n return ret;\n }\n};\n``` | 0 | 0 | [] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | BES PYTHON SOLUTION WITH 1639MS OF RUNTIME ! | bes-python-solution-with-1639ms-of-runti-eigk | \n# Code\npython3 []\nfrom typing import List\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target)\ | rishabnotfound | NORMAL | 2024-09-15T09:45:52.223810+00:00 | 2024-09-15T09:45:52.223838+00:00 | 11 | false | \n# Code\n```python3 []\nfrom typing import List\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target)\n dp = [0] * n\n\n # Function to check if any word starts with the given prefix\n def hasPrefix(pref):\n return any(w.startswith(pref) for w in words)\n\n l, r = 0, 0 # Left and right pointers for window in target\n\n for i in range(n):\n # Move left pointer to maintain valid prefix window\n while not hasPrefix(target[l:r + 1]) and l <= r:\n l += 1\n \n # If no valid prefix found, return -1\n if l > r:\n return -1\n\n # Calculate the length of the valid substring\n substr_len = r - l + 1\n\n # Update dp with the minimum number of valid substrings\n dp[i] = 1 if i < substr_len else dp[i - substr_len] + 1\n\n # Move the right pointer\n r += 1\n\n return dp[-1] # Return the result for the entire target string\n\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | C, simple/short solution 185 ms w/ two pointer and rolling hash only | c-simpleshort-solution-185-ms-w-two-poin-f74r | Let n = length of target, m = total length of words.\n\n# Intuition\nWe sort the list of prefix hashes of words in O(m * log m) time. This allows us to binary s | llllvvuu | NORMAL | 2024-09-15T09:01:08.769291+00:00 | 2024-09-15T23:20:47.830068+00:00 | 39 | false | Let n = length of target, m = total length of words.\n\n# Intuition\nWe sort the list of prefix hashes of `words` in O(m * log m) time. This allows us to binary search in O(log m) time, for any `i, j`, whether `target[i..j]` is a word prefix (recall that hash of `target[i..j]` is updated in O(1) time when incrementing `i` or `j`).\n\n(note: a HashSet or Bloom filter could be used for the above step to get O(1) amortized average. but these are more tedious to tune from scratch in C)\n\nLet `dp[j]` be the solution for `target[..j]`. We use the greedy algorithm for `dp[j]`; that is, we take the longest word prefix `target[i..j]`. To see why this works, we need to understand why `target[k..j]` with `k > i` cannot be better. This is because any solution for `target[k:]` can be truncated to `target[i:]`.\n\nTo track `target[i..j]`, we can use two-pointer technique `i <= j`. This works since `target[i..j+1]` can only be a word prefix if `target[i..j]` is a word prefix, therefore we can increment `i` monotonically and it will always track the longest word prefix for `j`.\n\nFinally, `dp[j] = dp[i - 1] + 1` and the answer is `dp[-1]`.\n\n# Complexity\n- Time complexity: O((m + n) * log m)\n- Space complexity: O(n + m)\n\n# Code\n```c []\n#define M1 (1000000007LL)\n#define M2 (1000000009LL)\n#define P (31LL)\n\nint cmp_u128(const void *a, const void *b) {\n const uint64_t *ua = (const uint64_t*)a;\n const uint64_t *ub = (const uint64_t*)b;\n \n if (ua[0] < ub[0]) return -1;\n if (ua[0] > ub[0]) return 1;\n if (ua[1] < ub[1]) return -1;\n if (ua[1] > ub[1]) return 1;\n return 0;\n}\n\nint find_u128(uint64_t *arr, int n, uint64_t *h) {\n int left = 0, right = n - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n int cmp = cmp_u128(&arr[mid * 2], h);\n if (cmp == 0) return mid;\n if (cmp < 0) left = mid + 1;\n else right = mid - 1;\n }\n return -1;\n}\n\nint minValidStrings(char** words, int wordsSize, char* target) {\n uint64_t h[2] = {0}, l = 0, r = 0, nHashes = 0, n = strlen(target), m = 0;\n for (int i = 0; i < wordsSize; i++) m += strlen(words[i]);\n uint64_t p1[n + 1], p2[n + 1], prefixHashes[m * 2], dp[n];\n for (int i = 0; i < wordsSize; i++) {\n h[0] = h[1] = 0;\n for (char *c = words[i]; *c; c++) {\n h[0] = (h[0] * P + (*c - \'a\' + 1)) % M1;\n h[1] = (h[1] * P + (*c - \'a\' + 1)) % M2;\n prefixHashes[2 * nHashes] = h[0];\n prefixHashes[2 * nHashes++ + 1] = h[1];\n }\n }\n qsort(prefixHashes, nHashes, 2 * sizeof(uint64_t), cmp_u128);\n h[0] = h[1] = 0;\n p1[0] = p2[0] = 1;\n for (char *c = target; *c; c++, r++) {\n p1[r + 1] = (p1[r] * P) % M1;\n p2[r + 1] = (p2[r] * P) % M2;\n h[0] = (h[0] * P + (*c - \'a\' + 1)) % M1;\n h[1] = (h[1] * P + (*c - \'a\' + 1)) % M2;\n for (; find_u128(prefixHashes, nHashes, h) == -1; l++) {\n if (l == r) return -1;\n h[0] = (h[0] + (M1 - p1[r - l]) * (target[l] - \'a\' + 1)) % M1;\n h[1] = (h[1] + (M2 - p2[r - l]) * (target[l] - \'a\' + 1)) % M2;\n }\n dp[r] = l == 0 ? 1 : 1 + dp[l - 1];\n }\n return r == 0 ? -1 : dp[r - 1];\n}\n``` | 0 | 0 | ['Two Pointers', 'Binary Search', 'Dynamic Programming', 'Greedy', 'C', 'Rolling Hash', 'Sorting'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Easy Solution | easy-solution-by-sandy141-310u | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Sandy141 | NORMAL | 2024-09-15T05:44:53.931723+00:00 | 2024-09-15T05:44:53.931747+00:00 | 18 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\npw = random.randint(100, 200)\nmod = random.getrandbits(40)\n\npws = [1]\nfor _ in range(10 ** 5):\n pws.append(pws[-1] * pw % mod)\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n n = len(target)\n \n vis = set()\n for w in words:\n x = 0\n for c in w:\n x = (x * pw + ord(c)) % mod\n vis.add(x)\n \n acc = [0]\n for c in target:\n acc.append((acc[-1] * pw + ord(c)) % mod)\n \n l = r = 0\n cnt = 0\n while r < n:\n nr = r\n for i in range(l, r + 1):\n left, right = i, n - 1\n while left <= right:\n mid = (left + right) // 2\n if (acc[mid+1] - acc[i] * pws[mid+1-i] % mod) % mod in vis:\n left = mid + 1\n else:\n right = mid - 1\n if right + 1 > nr:\n nr = right + 1\n mid = right\n if nr == r: return -1\n l, r = r + 1, nr\n cnt += 1\n return cnt\n \n``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | [Python 3] string hashing + greedy / sliding window, <400ms O(m+n) linear time / space | python-3-string-hashing-greedy-sliding-w-fbyb | Intuition\n Describe your first thoughts on how to solve this problem. \nThis is similar to a frog jumping forward in a sequence of stones. At the beginning, th | zzjjbb | NORMAL | 2024-09-15T05:38:52.480060+00:00 | 2024-09-15T05:38:52.480088+00:00 | 22 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is similar to a frog jumping forward in a sequence of stones. At the beginning, the frog is on `target[0]`, and it can jump from `i` to `j` if `target[i:j]` is valid. Also, it\'s easy to prove that the minimum step to reach `target[i]` is non-decreasing. Then, we only need to test the farthest letter it can reach in each step, and we get the answer when it reaches the end.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst, we should know that hashing a string costs linear time to it\'s length, and the hash value of it\'s substring can be calculated in $O(1)$ time similar to the prefix sum technique. We store the hash of all prefix of words (valid strings) in a set, and also store the hash of all prefix of target in a list.\n\nThen, we can start "jumping". In each round `i`, `range(frm, to)` means the indices it can reach with at least `i` jumps. Since the farthest position with `i` jumps is monotinic, we can use a sliding window as the range of substring for each valid test, which ensures linear time complexity.\n\n# Complexity\n`m = sum(words[i].length), n = target.length`\n- Time complexity:\n $O(m+n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n $O(m+n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\n# pre-calculate all pow(B, i, M) with linear time\nB = 131\nM = 212370440130137957\nPBM = []\nh = 1\nfor i in range(60_000):\n PBM.append(h)\n h = h * B % M\n\nclass Solution:\n def minValidStrings(self, words: List[str], target: str) -> int:\n # Calculate hash from left to right\n # Example: hash(\'abc\') = (a * B ** 2 + b * B **1 + c * B ** 0) % M\n # Suffix hash: hash(s2) = (hash(s1 + s2) - hash(s1) * B ** len(s2)) % M\n valid_h = set()\n for w in words:\n h = 0\n for c in w:\n h = (h * B + ord(c)) % M\n valid_h.add(h)\n \n target_h = [0] # Exclusive indexing: target_h[i] = hash(target[:i])\n h = 0\n for c in target:\n h = (h * B + ord(c)) % M\n target_h.append(h)\n \n def has_sub(l, r): # test whether target[l:r] is valid\n return (target_h[r] - target_h[l] * PBM[r - l]) % M in valid_h\n\n frm, to = 0, 1 # First str must start with target[0:1]\n n = len(target)\n for ans in count(1):\n new_to = to\n for i in range(frm, to):\n # If target[:x] can be matched, next string can start with target[x],\n # or in other words, the right boundary of next round can be x + 1\n while has_sub(i, new_to):\n if new_to == n:\n return ans\n new_to += 1\n if new_to == to: # no update means failed\n return -1\n frm, to = to, new_to\n \n``` | 0 | 0 | ['Python3'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | don't do this... O(nlog^2n) | dont-do-this-onlog2n-by-jwseph-ocks | Cyclic suffix array. I guess this would be faster if the 100 limit wasn\'t there...\n# Code\ncpp []\n#define all(v) begin(v), end(v)\n\ntemplate<class T>\nstruc | jwseph | NORMAL | 2024-09-15T04:48:00.715692+00:00 | 2024-09-15T04:50:10.631077+00:00 | 50 | false | - Cyclic suffix array. I guess this would be faster if the 100 limit wasn\'t there...\n# Code\n```cpp []\n#define all(v) begin(v), end(v)\n\ntemplate<class T>\nstruct Tree {\n static constexpr T def = INT_MAX;\n T f(T a, T b) { return min(a, b); }\n vector<T> t; int n;\n Tree(int n): t(2*n, def), n(n) {}\n void update(int i, T v) {\n for (t[i += n] = v; i /= 2;) t[i] = f(t[i*2], t[i*2+1]);\n }\n T query(int l, int r) {\n T al = def, ar = def;\n for (l += n, r += n; l < r; l /= 2, r /= 2) {\n if (l&1) al = f(al, t[l++]);\n if (r&1) ar = f(t[--r], ar);\n }\n return f(al, ar);\n }\n};\n\nstruct SuffixArray { // TODO: UPDATE TO USE willy108 VERS https://pastebin.com/JEAuS8a2\n string str; int n;\n vector<int> sa, isa;\n Tree<int> lcp;\n SuffixArray(string str_): str(str_+\'$\'), n(str.size()), sa(n), isa(n), lcp(n-1) {\n // sa has size sz(S)+1, starts with sz(S)\n iota(all(sa), 0);\n sort(all(sa), [&](int i, int j) { return str[i] < str[j]; });\n for (int i = 1; i < n; ++i) {\n int l = sa[i-1], r = sa[i];\n isa[r] = i > 1 && str[l] == str[r] ? isa[l] : i;\n }\n for (int k = 1; k < n; k *= 2) {\n // currently sorted by first k chars\n vector<int> s(sa), is(isa), pos(n);\n iota(all(pos), 0);\n for (int t: s) {\n int T = t-k; // verify that nothing goes out of bounds\n if (T >= 0) sa[pos[isa[T]]++] = T;\n }\n for (int i = 1; i < n; ++i) {\n int l = sa[i-1], r = sa[i];\n isa[r] = is[l] == is[r] && is[l+k] == is[r+k] ? isa[l] : i;\n }\n }\n int k = 0; // Kasai\'s Algo\n for (int r = 0; r < n-1; ++r) {\n int l = sa[isa[r]-1];\n while (l+k < n-1 && str[l+k] == str[r+k]) ++k;\n lcp.update(isa[r]-1, k);\n if (k) k--;\n }\n\t\t// if we cut off first chars of two strings\n\t\t// with lcp k then remaining portions still have lcp k-1\n }\n int getLCP(int i, int j) {\n if (i == j) return n-1-i;\n int l = isa[i], r = isa[j];\n if (l > r) swap(l, r);\n return lcp.query(l, r);\n }\n};\n\nclass Solution {\npublic:\n int minValidStrings(vector<string>& words, string s) {\n int INF = 1000000;\n string big;\n vector<int> pos;\n for (auto& w: words) {\n pos.push_back(big.size());\n big += w;\n }\n int start = big.size();\n big += s;\n SuffixArray sa(big);\n\n int m = words.size();\n int n = s.size();\n vector<int> idx;\n for (int i = 0; i < m; ++i) idx.push_back(i);\n sort(idx.begin(), idx.end(), [&](int i, int j) {\n int lcp = sa.getLCP(pos[i], pos[j]);\n int sz = min<int>(words[i].size(), words[j].size());\n if (lcp >= sz) return words[i].size() < words[j].size();\n return words[i][lcp] < words[j][lcp];\n });\n\n // for (int i = 0; i < m; ++i) {\n // cout << "> " << words[idx[i]] << endl;\n // }\n\n Tree<int> dp(n+2);\n for (int i = 0; i < n+2; ++i) dp.update(i, INF);\n dp.update(n, 0);\n for (int i = n-1; i >= 0; --i) {\n \n int l = 0, r = m-1;\n while (l < r) {\n int h = (l+r)/2;\n int lcp = sa.getLCP(pos[idx[h]], start+i);\n int sz = min<int>(words[idx[h]].size(), n-i);\n if (lcp >= sz || words[idx[h]][lcp] < s[i+lcp]) l = h+1;\n else r = h;\n }\n // cout << "searching for: " << s.substr(i) << " and found l=" << l << endl;\n // for (int h = 0; h < m; ++h) {\n // int lcp = sa.getLCP(pos[idx[h]], start+i);\n // int sz = min<int>(words[idx[h]].size(), n-i);\n // cout << ((lcp >= sz || words[idx[h]][lcp] < s[i+lcp]) ? "YES" : "NO" )<< " lcp=" << lcp << " sz=" << sz << endl;\n // }\n \n int lcp = min(sa.getLCP(pos[idx[l]], start+i), min<int>(words[idx[l]].size(), n-i));\n if (l) {\n l--;\n lcp = max(lcp, min(sa.getLCP(pos[idx[l]], start+i), min<int>(words[idx[l]].size(), n-i)));\n\n }\n\n dp.update(i, dp.query(i, i+lcp+1) + 1);\n }\n int res = dp.query(0, 1);\n // cout << "RES" << endl;\n // for (int i = 0; i <= n; ++i) {\n // cout << dp.query(i, i+1) << \' \';\n // }\n // cout << endl;\n return res < INF ? res : -1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | DP + Z-Function + Segment Tree | dp-z-function-segment-tree-by-then00bpro-pmbj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | then00bprogrammer | NORMAL | 2024-09-15T04:28:14.564334+00:00 | 2024-09-15T04:28:14.564357+00:00 | 64 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- n = len(target)\nO(len(words) * n + sum(words[i]) + n * logn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nusing ll = long long;\n\nstruct Node {\n ll min;\n \n Node() {\n min =0;\n }\n};\n\nclass SegmentTree {\npublic:\n vector<Node> segTree;\n\n SegmentTree(vector<ll> &arr) {\n ll n = arr.size();\n segTree.resize(4 * n + 1);\n build(0, 0, n - 1, arr);\n }\n\n void build(ll ind, ll low, ll high, vector<ll> &arr) {\n if (low == high) {\n segTree[ind].min = arr[low];\n return;\n }\n ll mid = low + (high - low) / 2;\n build(2 * ind + 1, low, mid, arr);\n build(2 * ind + 2, mid + 1, high, arr);\n segTree[ind].min = min(segTree[2 * ind + 1].min , segTree[2 * ind + 2].min);\n }\n\n void update(ll ind, ll low, ll high, ll i, ll val) {\n if (low == high) {\n segTree[ind].min = val;\n return;\n }\n ll mid = (low + high) >> 1;\n if (i <= mid) {\n update(2 * ind + 1, low, mid, i, val);\n }\n else {\n update(2 * ind + 2, mid + 1, high, i, val);\n }\n segTree[ind].min = min(segTree[2 * ind + 1].min , segTree[2 * ind + 2].min);\n }\n\n ll query(ll ind, ll low, ll high, ll l, ll r) {\n if (low > r || high < l || low > high) return 1e9;\n\n if (low >= l && high <= r) return segTree[ind].min;\n\n ll mid = (low + high) >> 1;\n ll left = query(2 * ind + 1, low, mid, l, r);\n ll right = query(2 * ind + 2, mid + 1, high, l, r);\n return min(left, right);\n }\n};\n\n\nclass Solution {\nprivate:\n vector<ll> z_function(string s) {\n ll n = s.size();\n vector<ll> z(n);\n ll l = 0, r = 0;\n for(ll i = 1; i < n; i++) {\n if(i < r) {\n z[i] = min(r - i, z[i - l]);\n }\n while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {\n z[i]++;\n }\n if(i + z[i] > r) {\n l = i;\n r = i + z[i];\n }\n }\n return z;\n }\n ll dfs(ll i, vector<ll> &match) {\n if(i>=match.size()) return 0;\n ll n = match.size();\n ll m = match[i];\n ll res=1e9;\n for(ll j=1;j<=m;j++) res=min(res,1+dfs(i+j,match));\n return res;\n }\npublic:\n int minValidStrings(vector<string>& words, string target) {\n ll m = words.size();\n ll n = target.size();\n vector <ll> match(n);\n for(ll i=0;i<m;i++) {\n string s = words[i] + "#" + target;\n vector <ll> z = z_function(s);\n vector <ll> t;\n for(ll j=words[i].size()+1;j<s.size();j++) {\n t.push_back(z[j]);\n }\n for(ll k=0;k<t.size();k++) {\n match[k]=max(match[k],t[k]);\n }\n }\n vector <ll> dp(n,1e9);\n SegmentTree sgt(dp);\n for(ll i=n-1;i>=0;i--) {\n ll m = match[i];\n if(m==0) continue;\n ll q = sgt.query(0, 0, n-1, min(i+1,n-1),min(i+m,n-1));\n if(q==1e9) {\n if(i+m>=n) {\n dp[i]=1;\n sgt.update(0,0,n-1,i,1);\n } \n }\n else {\n if(i+m>=n) {\n dp[i]=1;\n sgt.update(0,0,n-1,i,1);\n }\n else {\n dp[i]=1+q;\n sgt.update(0,0,n-1,i,1+q);\n }\n }\n }\n return dp[0]==1e9?-1:dp[0];\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'Segment Tree', 'C++'] | 1 |
minimum-number-of-valid-strings-to-form-target-ii | JS [ Realized it can be solved by KMP after the contest ] | js-realized-it-can-be-solved-by-kmp-afte-f4bz | Code\njavascript []\n/* -------------------------------------------------------- */\n/* ( The Authentic JS CodeBuff ) \t\t\t\t | Manu-Bharadwaj-BN | NORMAL | 2024-09-15T04:19:30.335369+00:00 | 2024-09-15T04:19:30.335395+00:00 | 29 | false | # Code\n```javascript []\n/* -------------------------------------------------------- */\n/* ( The Authentic JS CodeBuff ) \t\t\t\t \n ___ _ _ _ \n | _ ) |_ __ _ _ _ __ _ __| |_ __ ____ _ (_)\n | _ \\ \' \\/ _` | \'_/ _` / _` \\ V V / _` || |\n |___/_||_\\__,_|_| \\__,_\\__,_|\\_/\\_/\\__,_|/ |\n |__/ \n */\n/* --------------------------------------------------------- */\n/* Youtube: https://youtube.com/@code-with-Bharadwaj */\n/* Portfolio:https://manu-bharadwaj-portfolio.vercel.app/ */\n/* ----------------------------------------------------------- */\n\nvar findPattern = function(text, pattern) {\n let textLen = text.length;\n let patternLen = pattern.length;\n let suffixArr = new Array(patternLen).fill(0);\n for (let idx = 1; idx < patternLen; idx++) {\n let prevMatch = suffixArr[idx - 1];\n while (prevMatch > 0 && pattern[prevMatch] !== pattern[idx]) {\n prevMatch = suffixArr[prevMatch - 1];\n }\n suffixArr[idx] = prevMatch + +(pattern[prevMatch] === pattern[idx]);\n }\n\n let matchLengths = new Array(textLen).fill(0);\n matchLengths[0] = +(text[0] === pattern[0]);\n for (let idx = 1; idx < textLen; idx++) {\n let prevMatch = matchLengths[idx - 1];\n while (prevMatch > 0 && text[idx] !== pattern[prevMatch]) {\n prevMatch = suffixArr[prevMatch - 1];\n }\n matchLengths[idx] = prevMatch + +(text[idx] === pattern[prevMatch]);\n }\n return matchLengths;\n};\n\nvar minValidStrings = function(vocab, targetStr) {\n let targetLen = targetStr.length;\n let vocabSize = vocab.length;\n let stepTracker = new Array(targetLen + 1).fill(10 ** 9);\n stepTracker[0] = 0;\n\n let lookupMap = Array.from({ length: targetLen }).map(_ => new Set());\n for (let word of vocab) {\n let matches = findPattern(targetStr, word);\n for (let idx = 0; idx < matches.length; idx++) {\n if (matches[idx] > 0) {\n lookupMap[idx].add(matches[idx]);\n }\n }\n }\n\n for (let idx = 0; idx < targetLen; idx++) {\n let matchSet = lookupMap[idx];\n for (let matchLength of matchSet) {\n stepTracker[idx + 1] = Math.min(stepTracker[idx + 1], stepTracker[idx + 1 - matchLength] + 1);\n }\n }\n\n return stepTracker[targetLen] === 10 ** 9 ? -1 : stepTracker[targetLen];\n};\n\n``` | 0 | 0 | ['JavaScript'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Solution | solution-by-shikharcookies-7q9i | \n\n# Code\njava []\nclass Solution {\n public int minValidStrings(String[] words, String target) {\n int n = target.length();\n int[] dp = new | shikharcookies | NORMAL | 2024-09-15T04:04:22.817843+00:00 | 2024-09-15T04:04:22.817872+00:00 | 63 | false | \n\n# Code\n```java []\nclass Solution {\n public int minValidStrings(String[] words, String target) {\n int n = target.length();\n int[] dp = new int[n + 1];\n Arrays.fill(dp, Integer.MAX_VALUE);\n dp[0] = 0;\n\n List<List<Integer>> matches = new ArrayList<>(n);\n for (int i = 0; i < n; i++) {\n matches.add(new ArrayList<>());\n }\n char[] targetChars = target.toCharArray();\n for (String word : words) {\n char[] wordChars = word.toCharArray();\n int m = wordChars.length;\n int[] pi = new int[m];\n for (int i = 1, j = 0; i < m; i++) {\n while (j > 0 && wordChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (wordChars[i] == wordChars[j]) {\n j++;\n }\n pi[i] = j;\n }\n\n for (int i = 0, j = 0; i < n; i++) {\n while (j > 0 && targetChars[i] != wordChars[j]) {\n j = pi[j - 1];\n }\n if (targetChars[i] == wordChars[j]) {\n j++;\n }\n if (j > 0) {\n matches.get(i - j + 1).add(j);\n if (j == m) {\n j = pi[j - 1]; \n }\n }\n }\n }\n for (int i = 0; i < n; i++) {\n if (dp[i] == Integer.MAX_VALUE) continue;\n for (int len : matches.get(i)) {\n if (i + len <= n) {\n dp[i + len] = Math.min(dp[i + len], dp[i] + 1);\n }\n }\n }\n return dp[n] == Integer.MAX_VALUE ? -1 : dp[n];\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
minimum-number-of-valid-strings-to-form-target-ii | Segment Tree DP + Rolling Hash & Binary Search Update | segment-tree-dp-rolling-hash-binary-sear-1mnq | Approach\n\nWe compute the rolling hash for everything in words as well as target. Let dp[i] be the minimum amount of strings to make target[i..target.length-1] | CelonyMire | NORMAL | 2024-09-15T04:01:13.076364+00:00 | 2024-09-15T16:25:59.056147+00:00 | 210 | false | # Approach\n\nWe compute the rolling hash for everything in $$words$$ as well as $$target$$. Let $$dp[i]$$ be the minimum amount of strings to make $$target[i..target.length-1]$$. We need to update the DP in an efficient way.\n\nFor each $$i \\ s.t. \\ 0<=i<|target|$$, let $$r$$ be the maximum number of characters starting at $$target[i]$$ that matches some prefix of a word in $$words$$. We can take the minimum DP value in $$dp[i+1..i+r]$$ (by using a range query structure).\n\nWe can compute $$r$$ by going through all the words for a fixed $$dp[i]$$, then we can apply binary search for the length of the current word. We can use rolling hash to speed up the substring comparison.\n\n#### Time Complexity: $$O(|target|*|words|*log(|words|))$$\n\n---\n\n# Explained Solution\n\n```cpp []\nstruct rolling_hash {\n static constexpr unsigned long long M = (1ULL << 61) - 1, P = 257;\n inline static vector<unsigned long long> p = vector<unsigned long long>{1};\n vector<unsigned long long> h;\n rolling_hash(const string &s) {\n int n = s.size();\n h.resize(n + 1);\n for (unsigned long long i = p.size(), pp = p.back(); i <= n; i++)\n p.push_back(pp = __uint128_t(pp) * P % M);\n for (int i = n - 1; i >= 0; i--)\n h[i] = (s[i] + __uint128_t(h[i + 1]) * P % M) % M;\n }\n unsigned long long hash(int l, int r) {\n return (h[l] - __uint128_t(h[r + 1]) * p[r - l + 1] % M + M) % M;\n }\n};\n\ntemplate <typename T, typename A, typename C, typename C2 = C, typename F = identity>\nstruct segment_tree {\n vector<T> tree;\n A apply;\n C combine;\n C2 query_combine;\n F query_fn;\n segment_tree(int n, T v, A apply, C combine, C2 query_combine = {}, F query_fn = {}) : tree(2 * n, v), apply(apply), combine(combine), query_combine(query_combine), query_fn(query_fn) {\n for (int i = n - 1; i > 0; --i)\n tree[i] = combine(tree[i << 1], tree[i << 1 | 1]);\n }\n template <typename... Args>\n void update(int i, Args &&...args) {\n int n = tree.size() >> 1;\n for (apply(tree[i += n], std::forward<Args>(args)...); i >>= 1;)\n tree[i] = combine(tree[i << 1], tree[i << 1 | 1]);\n }\n template <typename R = T, typename... Args>\n R query(int l, int r, R ans = {}, Args &&...args) { // [l, r)\n int n = tree.size() >> 1;\n auto ansl = ans, ansr = ans;\n for (l += n, r += n; l < r; l >>= 1, r >>= 1) {\n if (l & 1)\n ansl = query_combine(ansl, query_fn(tree[l++], std::forward<Args>(args)...));\n if (r & 1)\n ansr = query_combine(query_fn(tree[--r], std::forward<Args>(args)...), ansr);\n }\n return query_combine(ansl, ansr);\n }\n};\n\nclass Solution {\npublic:\n int minValidStrings(vector<string> &w, string t) {\n int n = w.size(), m = t.size();\n rolling_hash rh_t(t);\n vector<rolling_hash> rh_w;\n for (int i = 0; i < n; i++) {\n rh_w.emplace_back(w[i]);\n }\n auto apply = [](int &x, int y) {\n x = min(x, y);\n };\n auto comb = [](int x, int y) {\n return min(x, y);\n };\n segment_tree dp(m + 1, (int)1e9, apply, comb);\n dp.update(m, 0);\n for (int i = m - 1; i >= 0; i--) {\n int r = 0;\n for (int j = 0; j < n; j++) {\n int lb = 0, rb = min((int)w[j].size(), m - i) + 1;\n while (rb - lb > 1) {\n int mb = (lb + rb) / 2;\n if (rh_w[j].hash(0, mb - 1) == rh_t.hash(i, i + mb - 1)) {\n r = max(r, mb);\n lb = mb;\n } else {\n rb = mb;\n }\n }\n }\n dp.update(i, dp.query(i, i + r + 1, (int)1e9) + 1);\n }\n int x = dp.query(0, 1, (int)1e9);\n return x == 1e9 ? -1 : x;\n }\n};\n```\n\n---\n\n# Optimal Solution\n\n```cpp\nstruct rolling_hash {\n static constexpr uint64_t M = (1ULL << 61) - 1, P = 257;\n inline static vector<uint64_t> p = vector<uint64_t>{1};\n vector<uint64_t> h;\n rolling_hash(const string &s) {\n int n = s.size();\n h.resize(n + 1);\n for (uint64_t i = p.size(), pp = p.back(); i <= n; i++)\n p.push_back(pp = __uint128_t(pp) * P % M);\n for (int i = n - 1; i >= 0; i--)\n h[i] = (s[i] + __uint128_t(h[i + 1]) * P % M) % M;\n }\n uint64_t hash(int l, int r) {\n return (h[l] - __uint128_t(h[r + 1]) * p[r - l + 1] % M + M) % M;\n }\n};\n\nclass Solution {\npublic:\n int minValidStrings(vector<string> &w, string t) {\n int n = w.size(), m = t.size();\n unordered_set<uint64_t> hs;\n for (int i = 0; i < n; i++) {\n rolling_hash rh(w[i]);\n for (int j = 0; j < w[i].size(); j++) {\n hs.insert(rh.hash(0, j));\n }\n }\n rolling_hash rh(t);\n vector z(m, 0);\n for (int i = 0, j = 0; i < m; i++) {\n for (j = max(j, i); j < m && hs.count(rh.hash(i, j)); j++) {\n }\n z[i] = hs.count(rh.hash(i, j - 1)) ? j - i : 0;\n }\n int ans = 0, next = 0, far = 0;\n for (int i = 0; i <= next && far < m;) {\n int i2 = i;\n for (; i <= next; i++) {\n far = max(far, i + z[i]);\n }\n if (far <= next) {\n return -1;\n }\n next = far;\n ans++;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Binary Search', 'Dynamic Programming', 'Segment Tree', 'Rolling Hash', 'C++'] | 1 |
swap-adjacent-in-lr-string | Simple Java one pass O(n) solution with explaination | simple-java-one-pass-on-solution-with-ex-o7xo | The idea is simple. Just get the non-X characters and compare the positions of them.\n\nclass Solution {\n public boolean canTransform(String start, String e | samuel_ji | NORMAL | 2018-02-04T21:23:00.743000+00:00 | 2018-10-25T05:13:51.142953+00:00 | 34,069 | false | The idea is simple. Just get the non-X characters and compare the positions of them.\n```\nclass Solution {\n public boolean canTransform(String start, String end) {\n if (!start.replace("X", "").equals(end.replace("X", "")))\n return false;\n \n int p1 = 0;\n int p2 = 0;\n \n while(p1 < start.length() && p2 < end.length()){\n \n // get the non-X positions of 2 strings\n while(p1 < start.length() && start.charAt(p1) == 'X'){\n p1++;\n }\n while(p2 < end.length() && end.charAt(p2) == 'X'){\n p2++;\n }\n \n //if both of the pointers reach the end the strings are transformable\n if(p1 == start.length() && p2 == end.length()){\n return true;\n }\n // if only one of the pointer reach the end they are not transformable\n if(p1 == start.length() || p2 == end.length()){\n return false;\n }\n \n if(start.charAt(p1) != end.charAt(p2)){\n return false;\n }\n // if the character is 'L', it can only be moved to the left. p1 should be greater or equal to p2.\n if(start.charAt(p1) == 'L' && p2 > p1){\n return false;\n }\n // if the character is 'R', it can only be moved to the right. p2 should be greater or equal to p1.\n if(start.charAt(p1) == 'R' && p1 > p2){\n return false;\n }\n p1++;\n p2++;\n }\n return true;\n }\n \n}\n``` | 322 | 6 | [] | 43 |
swap-adjacent-in-lr-string | Easy-to-understand explanation with PICTURE | easy-to-understand-explanation-with-pict-kl3g | \nBetter formatted original blog post here\n\n## Key observations:\nThere are three kinds of characters, \u2018L\u2019, \u2018R\u2019, \u2018X\u2019.\nReplacing | higherbro | NORMAL | 2020-10-01T04:34:07.717551+00:00 | 2020-10-08T04:36:12.357380+00:00 | 13,144 | false | \n[Better formatted original blog post here](https://medium.com/@algo.monster.hello/leetcode-777-swap-adjacent-in-lr-string-google-interview-question-3574d2c77d19)\n\n## Key observations:\nThere are three kinds of characters, \u2018L\u2019, \u2018R\u2019, \u2018X\u2019.\nReplacing XL with LX = move L to the left by one\nReplacing RX with XR = move R to the right by one\nIf we remove all the X in both strings, the resulting strings should be the same.\n## Additional observations:\nSince a move always involves X, an L or R cannot move through another L or R.\nSince an L can only move to the right, for each occurrence of L in the start string, its position should be to the same or to the left of its corresponding L in the end string.\n\n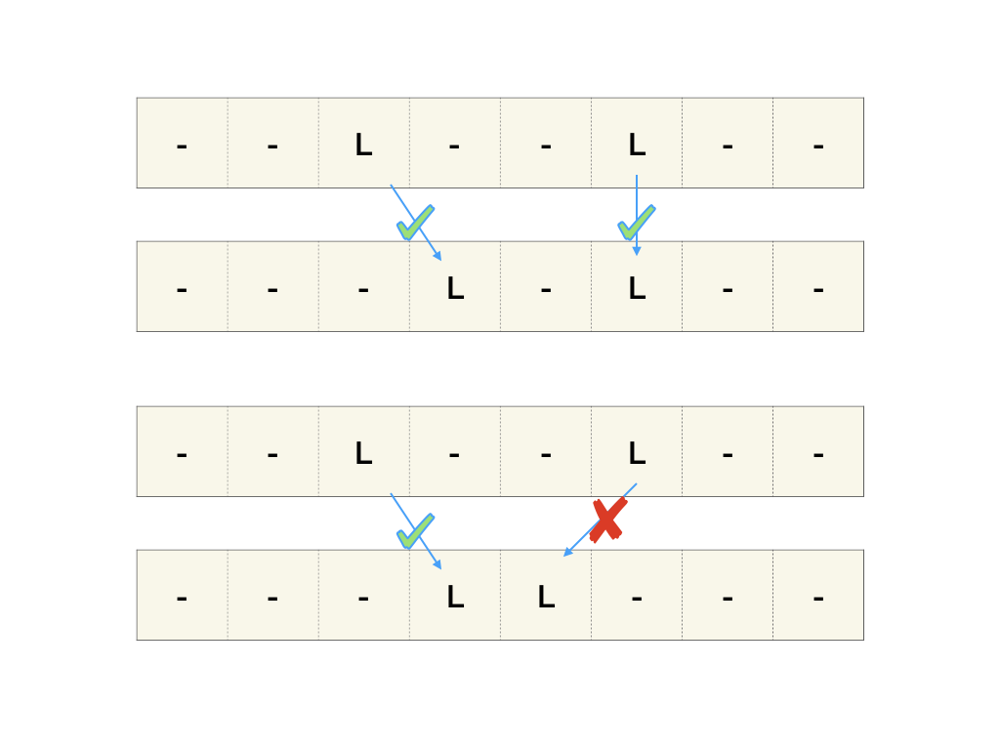\n\nAnd vice versa for the R characters.\n\n## Implementation\n\nWe first compare two strings with X removed. This checks relative position between Ls and Rs are correct.\n\nThen we find the indices for each occurence of L and check the condition in the above figure. Then we do the same for R.\n\n```python\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n if len(start) != len(end): return False\n \n # check L R orders are the same\n if start.replace(\'X\',\'\') != end.replace(\'X\', \'\'): return False\n \n n = len(start)\n Lstart = [i for i in range(n) if start[i] == \'L\']\n Lend = [i for i in range(n) if end[i] == \'L\']\n \n Rstart = [i for i in range(n) if start[i] == \'R\']\n Rend = [i for i in range(n) if end[i] == \'R\']\n\t\t# check L positions are correct\n for i, j in zip(Lstart, Lend):\n if i < j:\n return False\n \n # check R positions are correct\n for i, j in zip(Rstart, Rend):\n if i > j:\n return False\n \n return True\n```\n\n[Better formatted original post and solutions and patterns ](https://medium.com/@algo.monster.hello/leetcode-777-swap-adjacent-in-lr-string-google-interview-question-3574d2c77d19) | 209 | 4 | ['Python'] | 12 |
swap-adjacent-in-lr-string | C++ with explanation, O(n), 14ms | c-with-explanation-on-14ms-by-zestypanda-6uvf | First, check the sequence of L and R in start and end is the same;\nSecond, index of L in start should be >= index of corresponding L in end, while index of R < | zestypanda | NORMAL | 2018-02-04T16:54:59.267000+00:00 | 2018-09-22T02:19:24.657068+00:00 | 7,871 | false | First, check the sequence of L and R in start and end is the same;\nSecond, index of L in start should be >= index of corresponding L in end, while index of R <= corresponding index.\n```\nclass Solution {\npublic:\n bool canTransform(string start, string end) {\n int n = start.size();\n string s1, s2;\n for (int i = 0; i < n; ++i) \n if (start[i] != 'X') s1 += start[i];\n for (int i = 0; i < n; ++i) \n if (end[i] != 'X') s2 += end[i];\n if (s1 != s2) return false;\n for (int i = 0, j = 0; i < n && j < n;) {\n if (start[i] == 'X') \n i++;\n else if (end[j] == 'X') \n j++;\n else {\n if ((start[i] == 'L' && i < j) || (start[i] == 'R' && i > j)) return false;\n i++;\n j++;\n }\n }\n return true;\n }\n};\n``` | 76 | 5 | [] | 5 |
swap-adjacent-in-lr-string | [Python] Check their positions - with Picture - Clean & Concise | python-check-their-positions-with-pictur-bx0u | Key observations:\n- There are three kinds of characters, L, R, X.\n- Replacing XL with LX = move L to the left by one.\n- Replacing RX with XR = move R to the | hiepit | NORMAL | 2021-10-23T16:55:11.265687+00:00 | 2021-10-24T05:01:19.448116+00:00 | 4,909 | false | **Key observations:**\n- There are three kinds of characters, `L`, `R`, `X`.\n- Replacing `XL` with `LX` = move `L` to the left by one.\n- Replacing `RX` with `XR` = move `R` to the right by one.\n- If we remove all the `X` in both strings, the resulting strings should be the same.\n\n**Additional observations:**\n- Since a move always involves `X`, an `L` or `R` cannot move through another `L` or `R`.\n- Since an `L` can only move to the right, for each occurrence of `L` in the start string, its position should be to the same or to the left of its corresponding `L` in the end string.\n\n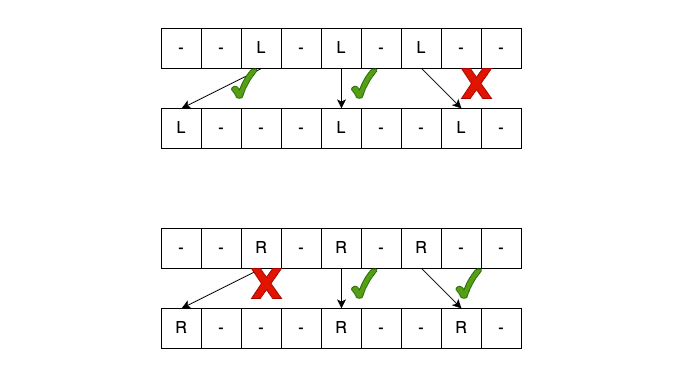\n\n\n```python\nclass Solution:\n def canTransform(self, start: str, end: str) -> bool:\n # L, R orders must be the same\n if start.replace("X", "") != end.replace("X", ""):\n return False\n \n n = len(start)\n startL = [i for i in range(n) if start[i] == \'L\']\n endL = [i for i in range(n) if end[i] == \'L\']\n startR = [i for i in range(n) if start[i] == \'R\']\n endR = [i for i in range(n) if end[i] == \'R\']\n \n for i, j in zip(startL, endL):\n if i < j:\n return False\n \n for i, j in zip(startR, endR):\n if i > j:\n return False\n \n return True\n```\nComplexity:\n- Time: `O(N)`, where `N <= 10^4` is length of `start` or `end` string.\n- Space: `O(N)`\n\nNote: This post is written based on this **[Easy-to-understand explanation with PICTURE](https://leetcode.com/problems/swap-adjacent-in-lr-string/discuss/873004/Easy-to-understand-explanation-with-PICTURE)** post. | 64 | 2 | [] | 3 |
swap-adjacent-in-lr-string | [Explained] Python simple and concise solution | explained-python-simple-and-concise-solu-9y1i | IDEA: \n1. As \'L\' and \'R\' are only swapped with \'X\', thus if we take out all \'X\'s from both start and end strings, the remaining strings should have the | h_cong | NORMAL | 2020-11-29T22:24:14.893387+00:00 | 2020-11-29T22:34:36.316829+00:00 | 2,058 | false | IDEA: \n1. As \'L\' and \'R\' are only swapped with \'X\', thus if we take out all \'X\'s from both start and end strings, the remaining strings should have the following properties:\n\ta. same total length.\n\tb. same number and order w.r.t. \'L\' and \'R\'.\n2. As len(start) = len(end) is given in the problem description, this means the number of \'X\' in both string should be the same as well considering the point above. \n3. We use two pointers one for the start string, one for the end string. When start pointer is pointing to the ```nth``` non-\'X\' char, the char that the end pointer is pointing to the ```nth``` non-\'X\' char should be the same, i.e. if the char in start string is a \'L\', the end pointer should be pointing to a \'L\' as well.\n4. As \'L\' can only move to the left of its index in start string, when we go through two strings using two pointers, the pointer index in the end string for ```nth``` \'L\' should be only smaller or equal than the pointer index pointing to the ```nth``` \'L\' in the start string. Same idea for \'R\', except now the end pointer index should be equal or larger than the start pointer index.\n5. Time complexity: O(n) where n is the length of the start string. As we only go through it once. ```.count()``` is a O(n) as well. Space Complexity: O(1). Constant spaces used for variables. \n\n```\ndef canTransform(self, start: str, end: str) -> bool:\n if start.count(\'X\') != end.count(\'X\'): \n return False\n \n n = len(start)\n i = j = 0\n \n while i < n and j < n: \n if start[i] == \'X\': \n i += 1\n continue\n if end[j] == \'X\':\n j += 1\n continue\n \n if start[i] != end[j]: return False\n if start[i] == \'L\' and i < j: return False\n if start[i] == \'R\' and i > j: return False\n \n i += 1\n j += 1\n \n return True\n``` | 52 | 0 | ['Python'] | 6 |
swap-adjacent-in-lr-string | Python simple solution, 3 lines O(n) | python-simple-solution-3-lines-on-by-yan-4z7j | The idea it to compare 'L' position in start is greater than or equal to that in end, also 'R' position in start is less than or equal to that in end.\n\nThe re | yanzhan2 | NORMAL | 2018-02-04T08:54:16.823000+00:00 | 2018-10-17T17:02:48.063849+00:00 | 8,593 | false | The idea it to compare 'L' position in start is greater than or equal to that in end, also 'R' position in start is less than or equal to that in end.\n\nThe reason is 'L' can move left when 'X' exists before, and 'R' can move right when 'X' exists after, and 'L' and 'R' cannot cross each other, so we do not care about 'X'.\n```\nclass Solution:\n def canTransform(self, start, end):\n """\n :type start: str\n :type end: str\n :rtype: bool\n """\n s = [(c, i) for i, c in enumerate(start) if c == 'L' or c == 'R']\n e = [(c, i) for i, c in enumerate(end) if c == 'L' or c == 'R']\n return len(s) == len(e) and all(c1 == c2 and (i1 >= i2 and c1 == 'L' or i1 <= i2 and c1 == 'R') for (c1, i1), (c2, i2) in zip(s,e))\n``` | 49 | 5 | [] | 7 |
swap-adjacent-in-lr-string | Simple Java Solution | simple-java-solution-by-bix-qe02 | public boolean canTransform(String start, String end) {\n int r = 0, l = 0;\n for (int i = 0; i< start.length(); i++){\n if (start.char | bix | NORMAL | 2018-02-10T09:22:34.261000+00:00 | 2018-10-17T17:03:44.281890+00:00 | 6,735 | false | public boolean canTransform(String start, String end) {\n int r = 0, l = 0;\n for (int i = 0; i< start.length(); i++){\n if (start.charAt(i) == \'R\'){ r++; l = 0;}\n if (end.charAt(i) == \'R\') { r--; l = 0;}\n if (end.charAt(i) == \'L\') { l++; r = 0;}\n if (start.charAt(i) == \'L\') { l--; r = 0;}\n if (l < 0 || r < 0) return false;\n }\n\n if (l != 0 || r != 0) return false;\n return true;\n }\n | 35 | 8 | [] | 13 |
swap-adjacent-in-lr-string | Explanation and java solution | explanation-and-java-solution-by-yihangd-cj9d | The solution is simple and similar to others, but more detailed explanation is needed.\n\nIn fact, "R" can move to the right until it is blocked by "L" while "L | yihangd | NORMAL | 2018-07-10T10:52:29.539342+00:00 | 2019-08-05T03:46:00.984542+00:00 | 3,544 | false | The solution is simple and similar to others, but more detailed explanation is needed.\n\nIn fact, "R" can move to the right until it is blocked by "L" while "L" can move to the left until it is blocked by "R". \n\nWe may count the number of "L" and "R" as follows. There are several principles during the loop:\n\n1. the value of `l` could be zero and negative, but not positive. This is becasue "L" could move to the left, so "L" may appear earlier in `end` than that in `start`. So once find `l > 0`, we may return false;\n2. the value of `r` could be zero and positive, but not negative. The reasons are similar to the one above. So once find`r < 0`, we may return false;\n3. When `l < 0`, `r` must be zero. This is because when `l < 0`, it means that one "L" appears earlier in `end`, and all "R"s before the current "L" in `end` should have also been visited in `start` (this is because "R" could only remove to the right).\n4. When `r > 0`, `l` must be zero. Reasons are similar.\n```java\nclass Solution {\n public boolean canTransform(String start, String end) {\n int l = 0, r = 0;\n for (int i = 0; i < start.length(); i++) {\n if (start.charAt(i) == \'L\') l++;\n if (start.charAt(i) == \'R\') r++;\n if (end.charAt(i) == \'L\') l--;\n if (end.charAt(i) == \'R\') r --;\n \n if (l > 0 || r < 0 || ( l < 0 && r != 0) || (r > 0 && l != 0)) return false;\n }\n \n return l == 0 && r == 0;\n }\n}\n``` | 33 | 2 | [] | 10 |
swap-adjacent-in-lr-string | Python O(n) two pointers with comments faster than 99% | python-on-two-pointers-with-comments-fas-xhql | The key is to figure out that we can ignore the Xs, but the relative position of the Ls and Rs must be equal in both strings. \n\nSo think of it as if the Ls ca | dkaifazhe | NORMAL | 2022-03-27T12:29:33.653923+00:00 | 2022-03-27T16:30:23.175579+00:00 | 2,025 | false | The key is to figure out that we can ignore the `X`s, but the relative position of the `L`s and `R`s must be equal in both strings. \n\nSo think of it as if the `L`s can only "move" backwards:\n```\nstart: XXXXL\n <--L\nend: LXXXX\n```\nand the `R`s can only "move" forward:\n```\nstart: RXXXX\n R-->\nend: XXXXR\n```\nSo we can scan the characters, skipping the `X`s, verifying that the next non-X character is equal in both strings. Later we have to make sure that:\n* If the current character is `L`, the index in `start` must be greater or equal to the index in `end` (can only "move" backwards in the `start` string).\n* If the current character is `R`, the index in `start` must be smaller or equal to the index in `end` (can only "move" forward in the `start` string).\n\nTime complexity: O(n)\nSpace complexity: O(1)\n\n```\n i = j = 0\n n = len(start)\n while i < n or j < n:\n \n # Skip "X" chars\n while i < n and start[i] == "X":\n i += 1\n while j < n and end[j] == "X":\n j += 1\n \n # Reached the end of only one string\n if i != j and (i == n or j == n):\n return False\n \n # Reached the end of both strings\n if i == j and i == n:\n return True\n \n # After skipping the Xs, the characters\n # in both strings must be equal\n if start[i] != end[j]:\n return False\n \n # "L" can only move backwards,\n # so if the current chars are "L",\n # the index of `end` must be less or equal\n # to the index of `start`\n if start[i] == "L" and j > i:\n return False\n \n # "R" can only move forward,\n # so if the current chars are "R",\n # the index of `end` must be greater or equal\n # to the index of `start`\n if start[i] == "R" and j < i:\n return False\n \n i += 1\n j += 1\n \n return True\n``` | 31 | 0 | ['Two Pointers', 'Python'] | 3 |
swap-adjacent-in-lr-string | Java Easy to Understand with Pictures | java-easy-to-understand-with-pictures-by-r6pg | \n\nFrom the above image it can be observed that \n Both start and end have same number of L and R .\n Length of start and end are same.\n XL transforming to LX | ethanhunt1084 | NORMAL | 2021-11-11T07:52:55.301462+00:00 | 2021-11-11T09:45:01.494687+00:00 | 2,722 | false | 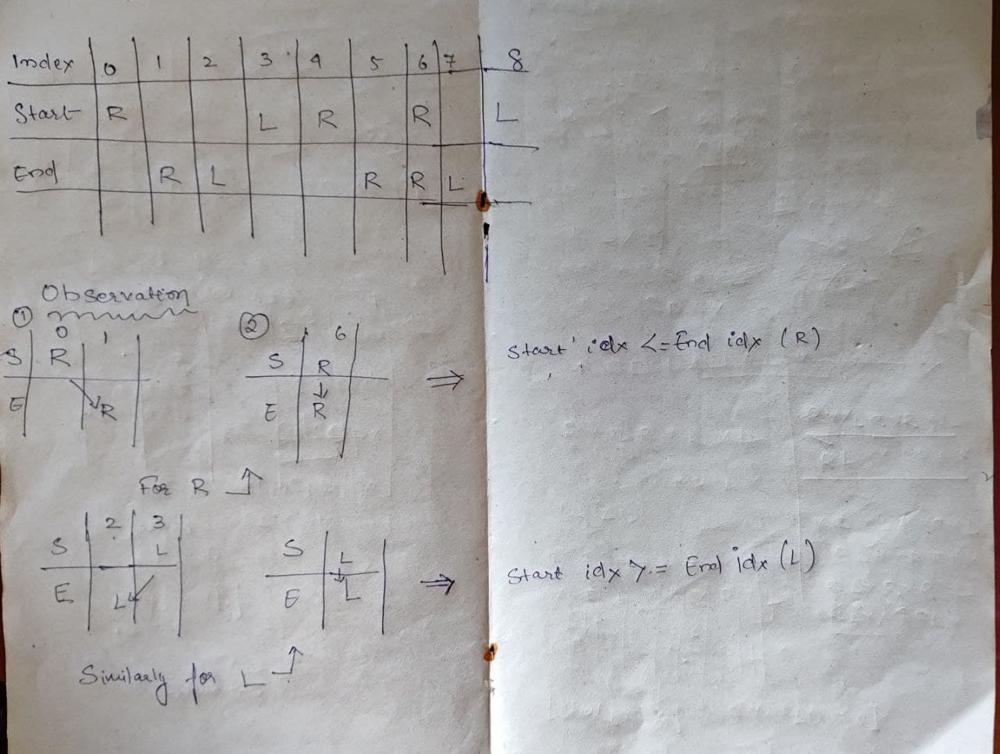\n<br/>\nFrom the above image it can be observed that \n* Both start and end have same number of L and R .\n* Length of start and end are same.\n* XL transforming to LX , means it either stays in the same start index or is less than that of its start index in the end.\n* Similarly RX transforming to XR , means it either stays in the same start index or is greater than that of its start index in the end.\n\n<br/>\n** JAVA**\n\n```\nclass Solution {\n public boolean canTransform(String start, String end) {\n\t\n\t//Checking if the number of L and R are equal without X in start and end\n if(!start.replace("X","").equals(end.replace("X",""))) return false;\n\t\t\n\t//Checking if length of start and end are different\n if(start.length()>end.length() || end.length()>start.length()) return false;\n \n //Making Arraylist for storing indices of L and R in both start and end\n\t\t\n ArrayList<Integer> lstart = new ArrayList<>(); \n ArrayList<Integer> lend = new ArrayList<>(); \n ArrayList<Integer> rstart = new ArrayList<>(); \n ArrayList<Integer> rend = new ArrayList<>(); \n \n\t\t//Iterating over start and storing L and R indices in their respective ArrayList\n for(int i=0;i<start.length();i++){\n if(start.charAt(i)==\'L\') lstart.add(i);\n if(start.charAt(i)==\'R\') rstart.add(i);\n\t\t\n\t\t//Iterating over end and storing L and R indices in their respective ArrayList\n }\n for(int i=0;i<end.length();i++){\n if(end.charAt(i)==\'L\') lend.add(i);\n if(end.charAt(i)==\'R\') rend.add(i);\n\n }\n \n //Taking two pointers and checking the condition which violates the rules\n\t\t\n\t\t//For L\n int i=0,j=0;\n while(i<lstart.size() && j<lend.size()){\n if (lend.get(j)>lstart.get(i)) return false; //index in start should be less than or equal to index in end \n i++;\n j++;\n }\n \n\t\t//For R\n i=0;j=0;\n while(i<rstart.size() && j<rend.size()){\n if (rend.get(j)<rstart.get(i)) return false; //index in start should be greater than or equal to index in end \n i++;\n j++;\n }\n \n return true;\n }\n}\n``` | 26 | 0 | ['Java'] | 5 |
swap-adjacent-in-lr-string | Imagine R and L as walker | imagine-r-and-l-as-walker-by-shawyoungta-svs5 | This is actually a good quesion. Why does everybody donw vote it. We can imagine R as the walker who can only walk right, and L as the walker who can only walk | shawyoungtang | NORMAL | 2018-04-28T02:10:14.225892+00:00 | 2018-04-28T02:10:14.225892+00:00 | 1,624 | false | This is actually a good quesion. Why does everybody donw vote it. We can imagine R as the walker who can only walk right, and L as the walker who can only walk left. X is the empty space that walkers can pass through\n```\nclass Solution {\n public boolean canTransform(String start, String end) {\n int i = 0, j = 0;\n if(start.length() != end.length()) return false;\n while(i < start.length() && j < end.length()){\n while(i < start.length() && start.charAt(i) == \'X\') ++i;\n while(j < end.length() && end.charAt(j) == \'X\') ++j;\n if(i == start.length() || j == end.length()) break;\n if(start.charAt(i) != end.charAt(j)) return false;\n if(start.charAt(i) == \'R\' && i > j) return false;\n else if(start.charAt(i) == \'L\' && i < j) return false;\n ++i;\n ++j;\n }\n while(i < start.length() && start.charAt(i) == \'X\') ++i;\n while(j < end.length() && end.charAt(j) == \'X\') ++j;\n return i == j;\n }\n}\n``` | 26 | 3 | [] | 1 |
swap-adjacent-in-lr-string | [C++] one pass - time:O(n) space:O(1) (with explanation) | c-one-pass-timeon-spaceo1-with-explanati-hw2y | Here I translate \'X\' to \'.\' for understanding more easily.\n\n\nstart = "R..LR.R.L"\nend = ".RL..RRL."\n\nFrom the above example, we can find some rules f | julianakuei | NORMAL | 2022-01-20T14:42:40.328739+00:00 | 2022-01-20T14:48:56.495637+00:00 | 1,440 | false | Here I translate \'X\' to \'.\' for understanding more easily.\n\n```\nstart = "R..LR.R.L"\nend = ".RL..RRL."\n```\nFrom the above example, we can find some rules for \'L\' and \'R\':\n\n**1. "*XL*" to "*LX*": L only go left\n2. "*RX*" to "*XR*": R only go right\n3. L and R cannot change their order**\n\nFor example, if we have "XXXXXXXL" and finally we may get the result "LXXXXXXX".\n###### -----------------------------------------------------------------\nWe only need to check the "L" and "R" position in two string.\nUsing two pointer `i` and `j` to keep comparing:\n1. skip \'X\', make sure `start[i]` and `end[j]` is the same \n2. \'R\' position in `start` is smaller than `end`\n3. \'L\' position in `start` is larger than `end`\n\n```\nclass Solution {\npublic:\n bool canTransform(string start, string end) {\n \n int i=0, j=0;\n while(i<start.size() && j<end.size()) {\n \n while(start[i]==\'X\') i++;\n while(end[j]==\'X\') j++;\n \n if(start[i]!=end[j]) return false;\n if(start[i]==\'R\' && i>j) return false;\n if(start[i]==\'L\' && i<j) return false;\n i++; j++;\n }\n while(i<start.size() && start[i]==\'X\') i++;\n while(j<end.size() && end[j]==\'X\') j++;\n return i==j;\n }\n};\n```\n | 18 | 0 | ['C'] | 1 |
swap-adjacent-in-lr-string | [C++] Simple subsequence matching with position constraint. | c-simple-subsequence-matching-with-posit-8079 | We see that L can move backwards and R can move forwards. So we can first see if subsequence that contains only L & R is the same for start and end. If so, we c | facelessvoid | NORMAL | 2018-02-04T04:10:10.166000+00:00 | 2018-02-04T04:10:10.166000+00:00 | 3,639 | false | We see that L can move backwards and R can move forwards. So we can first see if subsequence that contains only L & R is the same for start and end. If so, we can compare the corresponding positions of L and R. \nFor L in start it need to be somewhere ahead of corresponding L in end (since L can only move backwards).\nFor R in start, it needs to be somewhere behind of corresponding R in end.\n\n```\n bool canTransform(string start, string end) {\n int n=start.size();\n assert(n == end.size());\n\t// --Check for anagrams.\n int lcnt = 0, rcnt = 0;\n for(int i=0;i<n;i++){\n if(start[i] == \'L\') ++lcnt;\n else if(start[i] == \'R\') ++rcnt;\n if(end[i] == \'L\') --lcnt;\n else if(end[i] == \'R\') --rcnt;\n }\n if(lcnt || rcnt) return false;\n \n int i=0,j=0;\n while(j < n && i < n){\n while(j < n && end[j] == \'X\') ++j;\n while(i < n && start[i] == \'X\') ++i;\n if(i==n&&j==n) break;\n if(i==n || j==n || start[i] != end[j]) return false;\n if(start[i] == \'R\' && i > j) return false;\n else if(start[i] == \'L\' && i < j) return false;\n ++i; ++j;\n }\n \n return true;\n }\n``` | 17 | 2 | [] | 7 |
swap-adjacent-in-lr-string | Java Easy Understanding with explanation | java-easy-understanding-with-explanation-441r | (i) First, \'L\' cannot swap to left of \'R\', and \'R\' cannot swap to right of \'L\'. So we remove all \'X\' in both start and end to find if all \'L\' and \' | Ouyang2021 | NORMAL | 2022-06-12T22:55:20.483276+00:00 | 2022-06-12T22:55:20.483304+00:00 | 1,196 | false | (i) First, \'L\' cannot swap to left of \'R\', and \'R\' cannot swap to right of \'L\'. So we remove all \'X\' in both `start` and `end` to find if all \'L\' and \'R\' in the same order. If not, return false.\n\n(ii) Second, let\'s look at this pair:\n\tstart: "LXX"\n\tend: "XXL"\n\tAfter removing all \'X\', this pair can pass the first condition. But `start` can\'t transfer to `end`. The problem is the positon of \'L\' in `start` is more left than the \'L\' in `end` (\'L\' can only go to left side, can\'t go right). So we go through two strings(from `0` to `start.length()`), to make sure every \'L\' comes earlier in `end`. \n\tFor \'R\', make sure every \'R\' comes earlier in `start`. \n```\npublic boolean canTransform(String start, String end) {\n\t// First, remove all \'X\', and compare if they equal.\n\tStringBuffer s = new StringBuffer();\n\tStringBuffer e = new StringBuffer();\n\tfor (char c : start.toCharArray()) {\n\t\tif (c != \'X\') {\n\t\t\ts.append(c);\n\t\t}\n\t}\n\tfor (char c : end.toCharArray()) {\n\t\tif (c != \'X\') {\n\t\t\te.append(c);\n\t\t}\n\t}\n\tif (!s.toString().equals(e.toString()))\n\t\treturn false;\n\t// check R\n\t// form i to start.length(), \n\t// if R found in start count++, \n\t// if R found in end count--, \n\t// if count comes to negative, that means \'R\' is in more left position in end, so \'R\' can\'t move from start to end.\n\tint count = 0;\n\tfor (int i = 0; i < start.length(); i++) {\n\t\tif (start.charAt(i) == \'R\') {\n\t\t\tcount++;\n\t\t}\n\t\telse if (end.charAt(i) == \'R\') {\n\t\t\tcount--;\n\t\t}\n\t\tif (count < 0) {\n\t\t\treturn false;\n\t\t}\n\t}\n\t// check L\n\t// same with checking \'R\', only difference is: \n\t// to ensure every \'L\' comes first in end.\n\tcount = 0;\n\tfor (int i = 0; i < start.length(); i++) {\n\t\tif (end.charAt(i) == \'L\') {\n\t\t\tcount++;\n\t\t}\n\t\telse if (start.charAt(i) == \'L\') {\n\t\t\tcount--;\n\t\t}\n\t\tif (count < 0) {\n\t\t\treturn false;\n\t\t}\n\t}\n\treturn true;\n}\n```\n\nIt is easy to understand, if it helps, upvote please! \n^_^\n | 13 | 0 | ['Java'] | 3 |
swap-adjacent-in-lr-string | Javascript O(n) Time, O(1) Space Simple | javascript-on-time-o1-space-simple-by-c3-asbx | Intuition\n\n1. We cannot move Rs and Ls past eachother. \n2. We cannot move Rs to the left.\n3. We cannot move Ls to the right.\n\njavascript\n/**\n * @param { | c3mohamn | NORMAL | 2022-06-01T06:33:47.338566+00:00 | 2022-06-03T03:57:16.138578+00:00 | 610 | false | #### Intuition\n\n1. We cannot move Rs and Ls past eachother. \n2. We cannot move Rs to the left.\n3. We cannot move Ls to the right.\n\n```javascript\n/**\n * @param {string} start\n * @param {string} end\n * @return {boolean}\n */\nvar canTransform = function(start, end) {\n let i = 0;\n let j = 0;\n \n while (i < start.length || j < end.length) {\n if (start[i] === \'X\') {\n i++;\n continue;\n }\n \n if (end[j] === \'X\') {\n j++;\n continue;\n }\n \n\t\t// Breaking (1)\n if (start[i] !== end[j]) return false;\n \n\t\t// Breaking (2)\n if (start[i] === \'R\' && i > j) return false;\n\t\t\n\t\t// Breaking (3)\n if (start[i] === \'L\' && j > i) return false;\n \n i++;\n j++;\n }\n \n return true;\n};\n```\n\nExample:\n\nstart: XXRLX\nend: XXLRX\n\nThis breaks (1) because the first non-X we find in start and end respectively will be R and L. We will never be able to swap R and L.\n\nstart: XXRXX\nend: XRXXX\n\nThis breaks (2) because the index of the start R is greater than the index of end R. We can only move R to the right.\n\nstart: XXLXX\nend: XXXLX\n\nThis breaks (3) because the index of the start L is less than the index of end L. We can only move L to the left.\n\nThere are implicit swapping rules and we just ensure that those rules are followed. | 12 | 1 | ['TypeScript', 'JavaScript'] | 4 |
swap-adjacent-in-lr-string | Java simple idea and clean code O(n) Time, O(1) Space | java-simple-idea-and-clean-code-on-time-3ig49 | I found the brilliant idea and clean code at here, so I share it.\nThe key observations are same with problem\'s hint:\n- Think of the L and R as people on a ho | p89 | NORMAL | 2022-01-15T15:53:15.542984+00:00 | 2022-01-15T15:53:15.543008+00:00 | 891 | false | I found the brilliant idea and clean code at [here](https://gist.github.com/wangming2046/b5ac650ac565c0e37fd5886b68339201), so I share it.\nThe key observations are same with problem\'s hint:\n- Think of the L and R as people on a horizontal line, where X is a space.\n- L can only go to left spaces, R can only go to right spaces and the people can\'t cross each other.\n\nAssume the index of **first** `L` character in `start` string is `i`, we iterate `end` string to find index `j` of **first** `L` character in `end`.\nWe can only convert `start` to `end` if `i <= j`, otherwise it\'s impossible.\nFor example: the following case is okay\nstart = ".....L.."\nend = "..L....."\n\nThe same thinking when met `R` character in `start`, but because `R` can only go to right spaces, we can only convert `start` to `end` if `i >= j`.\n\nThen, continue iterate `start` string and do same logic.\n\nAlgorithm:\n- Define `j` pointer for `end` string.\n- Iterate `start` string.\n - When met `L` in `start` string, increase `j` until `end.charAt(j) == \'L\'`, if `j > i` return false\n - When met `R` in `start` string, increase `j` until `end.charAt(j) == \'R\'`, if `j < i` return false\n\nImplementation:\n\n```java\nclass Solution {\n \n public boolean canTransform(String start, String end) {\n \n if (start.replace("X", "").length() != end.replace("X", "").length()) {\n return false;\n }\n \n int len = start.length();\n int j = 0;\n for (int i = 0; i < len; i++) {\n \n if (start.charAt(i) == \'L\') {\n // find the next \'L\' position in "end"\n while (j < len && end.charAt(j) != \'L\') j += 1;\n \n // index of next \'L\' in "end" > index of \'L\' in "start", it\'s impossible to convert start to end.\n // For example:\n // start = "..L...."\n // end = "....L.."\n if (j > i) return false;\n \n j += 1;\n } \n \n if (start.charAt(i) == \'R\') {\n // find the next \'R\' position in "end"\n while (j < len && end.charAt(j) != \'R\') j += 1;\n \n // index of next \'R\' in "end" < index of \'R\' in "start", it\'s impossible to convert start to end.\n // For example:\n // start = "....R..."\n // end = "..R....."\n if (j < i) return false;\n \n j += 1;\n } \n }\n \n return true;\n }\n}\n``` | 9 | 1 | ['Two Pointers', 'Java'] | 1 |
swap-adjacent-in-lr-string | Short & Concise | C++ | short-concise-c-by-tusharbhart-zgs9 | \nclass Solution {\npublic:\n bool canTransform(string s, string e) {\n int i = 0, j = 0, n = s.size(), m = e.size();\n while(i < n || j < m) { | TusharBhart | NORMAL | 2022-12-29T14:20:00.807079+00:00 | 2022-12-29T14:20:00.807123+00:00 | 1,385 | false | ```\nclass Solution {\npublic:\n bool canTransform(string s, string e) {\n int i = 0, j = 0, n = s.size(), m = e.size();\n while(i < n || j < m) {\n while(s[i] == \'X\') i++;\n while(e[j] == \'X\') j++;\n\n if(s[i] != e[j]) return false;\n if(s[i] == \'R\' && i > j) return false;\n if(s[i] == \'L\' && i < j) return false; \n i++, j++;\n }\n return true;\n }\n};\n``` | 8 | 0 | ['Two Pointers', 'C++'] | 2 |
swap-adjacent-in-lr-string | Easy-understanding Java solution | easy-understanding-java-solution-by-adaz-25f3 | \nclass Solution {\n public boolean canTransform(String start, String end) {\n char[] s = start.toCharArray();\n char[] e = end.toCharArray();\ | adazhang | NORMAL | 2018-02-05T21:48:53.544000+00:00 | 2018-02-05T21:48:53.544000+00:00 | 1,799 | false | ```\nclass Solution {\n public boolean canTransform(String start, String end) {\n char[] s = start.toCharArray();\n char[] e = end.toCharArray();\n if (s.length != e.length) return false;\n for (int i = 0; i < s.length; i++) {\n if (s[i] == e[i]) continue;\n if (s[i] != 'X' && e[i] != 'X') return false;\n if (s[i] == 'L' && e[i] == 'X') return false;\n if (s[i] == 'X' && e[i] == 'R') return false;\n if (s[i] == 'R' && e[i] == 'X') {\n int nextR = findNext(s, i+1, 'X', 'R');\n if (nextR == -1) return false;\n else swap(s, i, nextR);\n } else if (s[i] == 'X' && e[i] == 'L') {\n int nextL = findNext(s, i+1, 'L', 'X');\n if (nextL == -1) return false;\n else swap(s, i, nextL);\n }\n \n }\n return true;\n }\n private int findNext(char[] s, int startIdx, char target, char skip) {\n for (int i = startIdx; i < s.length; i++) {\n if (s[i] == target) return i;\n else if (s[i] == skip) continue;\n else return -1;\n }\n return -1;\n }\n private void swap(char[] s, int i, int j) {\n char tmp = s[i];\n s[i] = s[j];\n s[j] = tmp;\n }\n}\n``` | 8 | 0 | [] | 1 |
swap-adjacent-in-lr-string | My Java Solution with my understanding as comments | my-java-solution-with-my-understanding-a-sxqu | \nclass Solution {\n public boolean canTransform(String start, String end) {\n // if there are no X, then the two string must be equal\n if (!s | vrohith | NORMAL | 2021-04-15T17:41:33.798543+00:00 | 2021-04-15T17:41:33.798586+00:00 | 845 | false | ```\nclass Solution {\n public boolean canTransform(String start, String end) {\n // if there are no X, then the two string must be equal\n if (!start.replace("X", "").equals(end.replace("X", "")))\n return false;\n int pointer1 = 0;\n int pointer2 = 0;\n while (pointer1 < start.length() && pointer2 < end.length()) {\n // increment p1 and p2 whenever we see X from the position\n // this is to get the nonX positions\n while (pointer1 < start.length() && start.charAt(pointer1) == \'X\') {\n pointer1 += 1;\n }\n while (pointer2 < end.length() && end.charAt(pointer2) == \'X\') {\n pointer2 += 1;\n }\n // if both the pointer reaches the end of the strings, then we can return true.\n // if only one of the pointer reaches the end of the strings, then we can return false\n if (pointer1 == start.length() && pointer2 == end.length())\n return true;\n if (pointer1 == start.length() || pointer2 == end.length())\n return false;\n // if the characyer at respective pointer1 and pointer2 of start and end is not equal, then we cannot transform\n if (start.charAt(pointer1) != end.charAt(pointer2))\n return false;\n // if the pointer1 at the start points to the \'L\' and pointer2 > pointer1 return false\n // this is because L can be only moved to the left and pointer1 must be > pointer2\n // if the pointer2 at the end points to the \'R\' and pointer1 > pointer2 return false\n // this is because R can be only moved to the right and pointer2 must be > pointer1\n if (start.charAt(pointer1) == \'L\' && pointer2 > pointer1)\n return false;\n if (end.charAt(pointer2) == \'R\' && pointer1 > pointer2)\n return false;\n pointer1 += 1;\n pointer2 += 1;\n }\n return true;\n }\n}\n``` | 7 | 0 | ['String', 'Java'] | 0 |
swap-adjacent-in-lr-string | 2 ways to solve this problem: DFS or 2 pointers - Easy to understand solution | 2-ways-to-solve-this-problem-dfs-or-2-po-sidn | Solution 1 (Time Limit Exceeded): Simply DFS, we iterate through all the possible next moves with the current LR string and perform the check, but this solution | betrumi | NORMAL | 2019-02-16T09:13:24.393990+00:00 | 2019-02-16T09:13:24.394029+00:00 | 1,259 | false | **Solution 1 (Time Limit Exceeded)**: Simply DFS, we iterate through all the possible next moves with the current LR string and perform the check, but this solution will cause Time Limit Exceeded:\n```java\nclass Solution {\n public boolean canTransform(String start, String end) {\n Map<String, List<String>> map = new HashMap<>();\n return search(start, end, map);\n }\n \n boolean search(String cur, String end, Map<String, List<String>> map) {\n if (cur.equals(end)) return true;\n List<String> states;\n if (map.containsKey(cur)) states = map.get(cur);\n else {\n states = getAllStates(cur);\n map.put(cur, states);\n }\n for (String s : states) {\n if (search(s, end, map)) return true;\n }\n return false;\n }\n \n List<String> getAllStates(String s) {\n List<String> states = new ArrayList<>();\n for (int i = 0;i < s.length() - 1;i++) {\n String ss = s.substring(i, i + 2);\n if (ss.equals("XL")) {\n String newS = s.substring(0, i) + "LX" + s.substring(i + 2, s.length());\n states.add(newS);\n }\n \n if (ss.equals("RX")) {\n String newS = s.substring(0, i) + "XR" + s.substring(i + 2, s.length());\n states.add(newS);\n }\n }\n return states;\n }\n}\n```\n\n**Solution 2 (Accepted)**: Simply use 2 pointers `i, j` to iterate through each character `ci, cj` of both strings one by one:\n- If `ci == \'X\' or cj == \'X\'`, increment `i` or `j`\n- If `ci != cj`, return `false`\n- Else, we will have `ci == cj`, at this step, need to check:\n\t- If `ci == \'L\'`, then we must have `i >= j`, otherwise return `false`\n\t- If `ci == \'R\'`, then we must have `j >= i`, otherwise return `false`\n\nKeep looping to the end of both strings and return `true` at the end of the function.\n```java\nclass Solution {\n public boolean canTransform(String start, String end) {\n if (start.length() != end.length()) return false;\n int n = start.length();\n int i = 0, j = 0;\n while (i < n && j < n) {\n while (i < n && start.charAt(i) == \'X\') i++;\n while (j < n && end.charAt(j) == \'X\') j++;\n if (i == n || j == n) break;\n char s = start.charAt(i);\n char e = end.charAt(j);\n if (s != e) return false;\n if (s == \'L\' && i < j) return false;\n if (s == \'R\' && i > j) return false;\n i++;\n j++;\n }\n if (i < n) {\n if (start.charAt(i) != \'X\') return false;\n i++;\n }\n if (j < n) {\n if (end.charAt(j) != \'X\') return false;\n j++;\n }\n return true;\n }\n}\n``` | 7 | 0 | [] | 3 |
swap-adjacent-in-lr-string | \u3010Simple Python (1 Scan, O(1) space)\u3011 | u3010simple-python-1-scan-o1-spaceu3011-07xnb | Actually two scans....\n```\nclass Solution(object):\n def canTransform(self, start, end):\n """\n :type start: str\n :type end: str\n | weidairpi | NORMAL | 2018-02-04T17:59:32.031000+00:00 | 2018-02-04T17:59:32.031000+00:00 | 1,148 | false | Actually two scans....\n```\nclass Solution(object):\n def canTransform(self, start, end):\n """\n :type start: str\n :type end: str\n :rtype: bool\n """\n if start.replace('X','')!=end.replace('X',''): return False\n\n l1=l2=r1=r2=0\n for v1,v2 in zip(start,end):\n if v1=='L': l1+=1\n elif v1=='R': r1+=1\n if v2=='L': l2+=1\n elif v2=='R': r2+=1\n if l1>l2 or r1<r2: return False\n return True | 7 | 0 | [] | 2 |
swap-adjacent-in-lr-string | CPP | Two Pointers | O(N) | WithExplaination | cpp-two-pointers-on-withexplaination-by-x60up | Observations\n\nLets take an example to understand solution:\n1. XXXXXXL\nWe can replace \'XL\' with XXXXXLX. Again doing this we can obtain XXXXLXX. Which show | CodeWithNamit | NORMAL | 2022-04-16T06:09:32.316510+00:00 | 2022-04-22T19:30:54.991083+00:00 | 324 | false | **Observations**\n\nLets take an example to understand solution:\n1. XXXXXXL\nWe can replace \'XL\' with XXXXXLX. Again doing this we can obtain XXXXLXX. Which shows we can move L in left. \nNote: We are able to move L in left as long as there is no R in left side of L.\n\n2. On a similar note we can say R can be moved to right until we have L following R.\n\n**Conclusion**\n\na. L can not cross R and R cannot cross L i.e. Order of LR in original and final string should be same.\nb. R in final string can be at position >= what it was before in original string. It cannot go in left.\nc. L in final string can be at position <= what is was before in original string. It cannot go in right.\n\n```\nclass Solution {\npublic:\n bool canTransform(string start, string end) { \n \n int len = start.length();\n int i=0,j=0;\n \n while(i<len && j<len){\n while(start[i]==\'X\'){\n i++;\n }\n while(end[j]==\'X\'){\n j++;\n }\n if(start[i]!=end[j]){\n return false;\n }\n if(start[i]==\'R\' && j<i){\n return false;\n }\n if(start[i]==\'L\' && j>i){\n return false;\n }\n i++;j++;\n }\n \n while(i<len && start[i]==\'X\'){\n i++;\n }\n while(j<len && end[j]==\'X\'){\n j++;\n }\n if(i<len || j<len){\n return false;\n }\n return true;\n }\n};\n\n```\n\n\nPlease upvote incase you find my explaination useful. | 6 | 0 | ['Two Pointers', 'String'] | 0 |
swap-adjacent-in-lr-string | Clean Python Solution (Self-Explained, Easy to Understand) | clean-python-solution-self-explained-eas-p5tp | python\n"""\n1. Check if the sequence of L and R are the same.\n2. Check if the index of L in the "start" are larger than index of the L in the "end", since L c | christopherwu0529 | NORMAL | 2022-02-21T04:17:17.872619+00:00 | 2022-02-21T04:17:17.872665+00:00 | 231 | false | ```python\n"""\n1. Check if the sequence of L and R are the same.\n2. Check if the index of L in the "start" are larger than index of the L in the "end", since L can only move left.\n3. Check if the index of R in the "start" are smaller than index of the R in the "end", since R can only move left.\n"""\nclass Solution(object):\n def canTransform(self, start, end):\n if len(start)!=len(end): return False\n if start.replace(\'X\', \'\')!=end.replace(\'X\', \'\'): return False #[1]\n \n\t\t#[2]\n startLIndex = [i for i, c in enumerate(start) if c==\'L\']\n endLIndex = [i for i, c in enumerate(end) if c==\'L\']\n for i in xrange(len(startLIndex)):\n if startLIndex[i]<endLIndex[i]:\n return False\n \n\t\t#[3]\n startRIndex = [i for i, c in enumerate(start) if c==\'R\']\n endRIndex = [i for i, c in enumerate(end) if c==\'R\']\n for i in xrange(len(startRIndex)):\n if startRIndex[i]>endRIndex[i]:\n return False\n \n return True\n\t\t\n"""\nFor interview preparation, similar problems, check out my GitHub.\nIt took me a lots of time to make the solution. Becuase I want to help others like me.\nPlease give me a star if you like it. Means a lot to me.\nhttps://github.com/wuduhren/leetcode-python\n"""\n``` | 6 | 0 | [] | 0 |
swap-adjacent-in-lr-string | Easy C++ O(n) solution with explanation | easy-c-on-solution-with-explanation-by-d-6wkn | NOTE:\n - In the given string start, L can move to the left but can\'t pass through R, R can move to the right but can\'t pass through L. Basically, there are 4 | dim_sum | NORMAL | 2018-07-13T23:38:27.142774+00:00 | 2020-06-27T23:56:29.190775+00:00 | 739 | false | NOTE:\n - In the given string `start`, `L` can move to the left but can\'t pass through `R`, `R` can move to the right but can\'t pass through `L`. Basically, there are 4 situations (when `start[i] != \'X\'` and `end[j] != \'X\'`):\n - `start[i] != end[j]` return `false`, cause `L` and `R` can\'t pass through each other.\n - `start[i] == \'L\' && j > i ` return `false`, cause `L` can\'t move to the right.\n - `start[i] == \'R\' && j < i` return `false` cause `R` can\'t move to the left.\n\n```\nclass Solution {\npublic:\n bool canTransform(string start, string end) {\n int i = 0, j = 0;\n for (; i < start.size() && j < end.size();) {\n if (start[i] == \'X\') i++;\n if (end[j] == \'X\') j++;\n \n if (start[i] != \'X\' && end[j] != \'X\') {\n if (start[i] != end[j]) return false;\n else if (start[i] == \'L\' && j > i) return false;\n else if (start[i] == \'R\' && j < i) return false;\n else i++, j++;\n }\n }\n \n while (i < start.size()) {\n if (start[i++] != \'X\') return false;\n }\n \n while (j < end.size()) {\n if (end[j++] != \'X\') return false;\n }\n \n return true;\n }\n};\n``` | 6 | 0 | [] | 1 |
swap-adjacent-in-lr-string | ✅ One Line Solution | one-line-solution-by-mikposp-v4vg | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)Code #1Time complexity: O(n). Space complexity: O(1) | MikPosp | NORMAL | 2025-02-14T12:55:57.775953+00:00 | 2025-02-14T12:59:55.656894+00:00 | 326 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)
# Code #1
Time complexity: $$O(n)$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def canChange(self, s: str, t: str) -> bool:
return (f:=lambda q:(p for p in enumerate(q) if p[1]!='X')) and all(c==w and (i<=j,i>=j)[c=='L'] for (i,c),(j,w) in zip_longest(f(s),f(t),fillvalue=(0,'')))
```
<!--
# Code #1.1
Time complexity: $$O(n)$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def canChange(self, s: str, t: str) -> bool:
return (f:=lambda q:(p for p in enumerate(q) if p[1]!='_')) and all((c==w)*(i<=j,i>=j)[c=='L'] for (i,c),(j,w) in zip_longest(f(s),f(t),fillvalue=(0,0)))
```
-->
# Code #2
Time complexity: $$O(n)$$. Space complexity: $$O(n)$$.
```python3
class Solution:
def canChange(self, s: str, t: str) -> bool:
return re.sub('X','',s)==re.sub('X','',t) and (f:=lambda q,s,t:min(accumulate((c==q)-(w==q) for c,w in zip(s,t)))>=0)('R',s,t) and f('L',s[::-1],t[::-1])
```
---
See also similar solution: [2337. Move Pieces to Obtain a String](https://leetcode.com/problems/move-pieces-to-obtain-a-string/solutions/6115924/one-line-solution/)
---
(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not claimed to be 'true' oneliners - please, remind about drawbacks only if you know how to make it better) | 5 | 1 | ['Two Pointers', 'String', 'Python', 'Python3'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.