question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-operations-to-make-all-array-elements-equal | C++ | 95% Fast | With best explanation | c-95-fast-with-best-explanation-by-vaibh-m3hi | Intuition\nDivide nums into 2 subarray\nsuppose we have nums = [2,6,8] and we need to find operations for query [5]. \nJust find elements that are greater than | VAIBHAV_SHORAN | NORMAL | 2023-03-30T18:19:11.555074+00:00 | 2023-03-30T18:20:57.070796+00:00 | 190 | false | # Intuition\nDivide nums into 2 subarray\nsuppose we have nums = [2,6,8] and we need to find operations for query [5]. \nJust find elements that are greater than 5 and that are lower than it. Here, [6,8] are greater and [2] is lower.\n\nFor greater, sum of these elements is 6+8 = 14. We need to bring these 2 elements equal to 5. Then there sum would be 10. That means we need to perform 14-10 = 4 operations.\n\nFor lower element, current sum is 2. We need to make it 5. That means we need (5 - 2) = 3 operations.\n\n# Approach\nUse prefix sum to fetch sum in O(1)\nFind lenght of subarrays using binary search(upper_bound)\n\n# Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(), nums.end());\n vector<long long> sum;\n \n // Prefix Sum\n long long sumi = 0;\n for(auto &i : nums){\n sumi += i;\n sum.push_back(sumi);\n }\n\n vector<long long> ans;\n\n for(auto &i : queries){\n long long cnt = 0;\n\n // Length of bigger elements subarray\n long long bigger = upper_bound(nums.begin(), nums.end(), i) - nums.begin();\n bigger = nums.size() - bigger;\n\n // Lenght of smaller elements subarray\n long long shorter = nums.size() - bigger - 1;\n while(shorter >= 0 && nums[shorter] == i) shorter--;\n shorter = shorter + 1;\n\n // Sum of greater and smaller elements\n long long leftSum = 0, rightSum = 0;\n if(shorter > 0) leftSum = sum[shorter-1];\n if(bigger > 0){\n rightSum = sum.back();\n if(bigger != nums.size()) rightSum -= sum[nums.size() - bigger - 1];\n }\n\n cnt += rightSum - (bigger * i);\n cnt += (shorter * i) - leftSum;\n\n ans.push_back(cnt);\n }\n\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Optimized Java solution || Binary Search || Prefix Sum | optimized-java-solution-binary-search-pr-wnt6 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | i_am_sumon | NORMAL | 2023-03-28T16:12:44.863708+00:00 | 2023-04-01T22:27:50.725304+00:00 | 675 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(q*log(n))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] q) {\n int n = nums.length;\n Arrays.sort(nums);\n \n List<Long> ans = new ArrayList<>();\n\n long[] prefix = new long[n+1];\n for(int i = 1; i <= n; i++) {\n prefix[i] = prefix[i-1] + nums[i-1];\n }\n\n for(int val : q) {\n int i = Arrays.binarySearch(nums, val);\n if(i < 0) i = -(i + 1);\n ans.add(1L * val * (2*i-n) + prefix[n] - 2 * prefix[i]);\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'Java'] | 2 |
minimum-operations-to-make-all-array-elements-equal | Easy solution in python-3 | easy-solution-in-python-3-by-pradyumna14-liy4 | Intuition\nIt can be solved using naive approach in O(n^2) time complexity, which includes one outer for loop for iterating in queries list and the inner outer | PRADYUMNA14 | NORMAL | 2023-03-28T09:49:53.145033+00:00 | 2023-03-28T09:50:59.725846+00:00 | 404 | false | # Intuition\nIt can be solved using naive approach in O(n^2) time complexity, which includes one outer for loop for iterating in queries list and the inner outer loop for calculating the sum (as shown) in \'nums\' list. Since, this solution is not optimal, we have to reduce the time complexity further.\n# Naive approach:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n ans=[]\n for i in range(len(queries)):\n summ=0\n for j in range(0,len(nums)):\n summ+=abs(nums[j]-queries[i])\n ans.append(summ)\n return(ans)\n\n# Approach\nTo reduce the T.C, the other possible methods for getting the summ varibale should be either O(log(n)) or O(1). Since we know that, if we make a prefix sum array, we can retrieve sum in O(1) only, we have used that here.\nThe reason for using binary search here is: If we can get the index of a number (say i), we can get the sum of elements upto the \'i\'th index using prefix_sum array(that too in O(1) time).\n# Complexity\n- Time complexity:\nO(nlog(n))\n\n- Space complexity:\nO(n) for the extra array that i took (arr)\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n n=len(nums)\n nums.sort()\n arr=nums.copy()\n for i in range(1,len(nums)): #Prefix_sum\n nums[i]+=nums[i-1]\n \n\n def binary_search(nums,x):\n start=0\n end=len(nums)-1 \n while(start<=end):\n mid=(start+end)//2\n if(nums[mid]==x):\n return(mid)\n elif(nums[mid]>x):\n end=mid-1\n else:\n start=mid+1 \n return(start)\n \n\n ans=[]\n for i in range(0,len(queries)):\n summ=0\n index=binary_search(arr,queries[i]) #to get the index\n if(index==0):\n summ=nums[-1]-(n*queries[i])\n else:\n summ=(index*queries[i])-(nums[index-1]) #for summ of elements before index\n summ+=(nums[-1]-nums[index-1])-((n-index)*queries[i]) #for summ of elements after index\n ans.append(summ)\n return(ans)\n``` | 2 | 0 | ['Binary Search', 'Sorting', 'Prefix Sum', 'Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | [Entire thought Process + Intuition, Binary Search + Prefix Sum Approach] | entire-thought-process-intuition-binary-2jzvf | Intuition\n\n * Let\'s try, to to make some observations:\n\n Input: nums = [3,1,6,8], queries = [1,5]\n Output: [14, 10]\n \n queires[0] = 1, an | _LearnToCode_ | NORMAL | 2023-03-27T07:44:48.970661+00:00 | 2023-03-27T07:44:48.970693+00:00 | 122 | false | # Intuition\n\n * Let\'s try, to to make some observations:\n\n Input: nums = [3,1,6,8], queries = [1,5]\n Output: [14, 10]\n \n queires[0] = 1, ans = 14, \n answer 14 can be easily compute as (total_sum_of_nums - nums_size * queries[0]) -> (18 - 4 * 1) -> 14\n\n queries[1] = 5, ans = 10, \n but the above point is NOT always valid for all "i"th queries.\n \n For example here, (18 - 4 * 5) -> -2 \n \n #1 -ve is indicating that we\'ve to add some more items on couple of indices.\n \n #2 -ve answer also indicating that some of the elements in "nums" are lesser than "queries[i]"\n \n #3 Also total_sum of array(nums) doesn\'t give us the information about the elements that\n are at different indices in "nums" array.\n \n #4 From [3, 1, 6, 8], queries[1] = 5, this thought is came from Obs#2\n \n Q: all the elements that are smaller(or equal can be added here)\n than (5 : current ith query) would contribute how much in our final answer?\n \n A: (count_of_elements * queries[i] - sum_of_all_those_elements)\n \n for example, here for the 1st query:\n \n cont_of_elements = 2 -> {1, 3} -> [1 & 3 are smaller than 5]\n \n contribution = (2 * 5 - (1 + 3)) = 6\n \n \n Similarly, total contribution of elements in our final answer from\n elements larger than queries[i] can be given as:\n \n contribution = (sum_of_all_such_elements - count_of_such_elements * queries[i])\n \n contribution = ((6 + 8) - (2 * 5)) -> (14 - 10) -> 4\n \n \n now add the contributions = (6 + 4) -> 10 [final answer for 1st query]\n \n \n * Counting part can be efficiently computed using "Binary Search" and for getting a sum of elements\n for any sub-array can be easily computed in O(1) with the help of "prefix-sum" array.\n - But "Binary Search" can be applied only in monotonic data, hence sorting required.\n \n \n +++ Now, I got the approach. Excellent man :).\n\n# Complexity\n- Time complexity: O(N + N * log(N)) -> O(N * log(N))\n- Space complexity: O(N)\n\n# Code\n```\n\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] queries) {\n Arrays.sort(nums);\n \n int N = nums.length;\n long[] prefixSum = new long[N];\n \n for(int i = 0; i < N; i += 1) {\n if(i == 0) prefixSum[i] = nums[i];\n else {\n prefixSum[i] = prefixSum[i - 1] + nums[i];\n }\n }\n \n List<Long> answer = new ArrayList<>();\n \n for(int i = 0; i < queries.length; i += 1) {\n int queryEle = queries[i];\n int idx = upperBound(nums, queryEle);\n if(idx == N) {\n answer.add(((N * 1L * queryEle) - prefixSum[N - 1]));\n } else {\n long contri1 = (prefixSum[N - 1] - prefixSum[idx] + nums[idx]) - (N - idx) * 1L * queryEle; // for larger > queries[i]\n long contri2 = 0;\n if(idx != 0) \n contri2 = (idx * 1L * queryEle) - (prefixSum[idx - 1] - prefixSum[0] + nums[0]); // for smaller <= queries[i]\n answer.add((contri1 + contri2));\n }\n }\n \n return answer;\n }\n \n // returns the first index (idx) such that nums[idx] > target\n private int upperBound(int[] nums, int target) {\n int left = 0, right = nums.length - 1;\n while(left <= right) {\n int mid = left + (right - left) / 2;\n if(nums[mid] <= target)\n left = mid + 1;\n else\n right = mid - 1;\n }\n return left;\n }\n}\n``` | 2 | 0 | ['Binary Search', 'Prefix Sum', 'Java'] | 1 |
minimum-operations-to-make-all-array-elements-equal | 📌📌 C++ || Sorting || Prefix Sum || Binary Search || Faster || Easy To Understand 🤷♂️🤷♂️ | c-sorting-prefix-sum-binary-search-faste-fg8x | Using Sorting && Binary Search\n\n Time Complexity :- O(NlogN)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n \n vector<long long> minOpera | __KR_SHANU_IITG | NORMAL | 2023-03-27T06:07:54.976390+00:00 | 2023-03-27T06:07:54.976435+00:00 | 266 | false | * ***Using Sorting && Binary Search***\n\n* ***Time Complexity :- O(NlogN)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n \n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n \n int n = nums.size();\n \n int m = queries.size();\n \n // sort the nums\n \n sort(nums.begin(), nums.end());\n \n // find the prefix sum array\n \n vector<long long> prefix(n, 0);\n \n prefix[0] = nums[0];\n \n for(int i = 1; i < n; i++)\n {\n prefix[i] = nums[i] + prefix[i - 1];\n }\n \n long long total_sum = prefix[n - 1];\n \n vector<long long> ans(m);\n \n for(int i = 0; i < m; i++)\n {\n long long min_op = 0;\n \n int tar = queries[i];\n \n // find the index of the upper bound of tar\n \n int idx = upper_bound(nums.begin(), nums.end(), tar) - nums.begin();\n \n // cal. the operations required till idx - 1\n \n long long left_sum = 0;\n \n if(idx > 0)\n {\n left_sum += prefix[idx - 1];\n }\n \n long long left_req_sum = (long long) tar * (long long) idx;\n \n min_op += abs(left_req_sum - left_sum);\n \n // cal. the operations required from idx to n - 1\n \n long long right_sum = total_sum;\n \n if(idx > 0)\n {\n right_sum -= prefix[idx - 1];\n }\n \n long long right_req_sum = (long long) (n - idx) * (long long) tar;\n \n min_op += abs(right_sum - right_req_sum);\n \n ans[i] = min_op;\n }\n \n return ans;\n }\n};\n``` | 2 | 0 | ['Binary Search', 'C', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | 💯🔥Best Code in C++ || BinarySearch🔥 || Sorting✅ || PrefixSum💯 | best-code-in-c-binarysearch-sorting-pref-27bj | Complexity\n- Time complexity:\nO(mlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n### Please Upvote if u liked my Solution\uD83E\uDD17\n\nclass Solution {\npubli | aDish_21 | NORMAL | 2023-03-26T08:40:21.776404+00:00 | 2023-03-26T08:40:21.776444+00:00 | 122 | false | # Complexity\n- Time complexity:\nO(mlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n### Please Upvote if u liked my Solution\uD83E\uDD17\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n int n=nums.size(),m=queries.size();\n long long pSum=0;\n sort(nums.begin(),nums.end());\n vector<long long> prefixSum(n),ans;\n for(int i=0;i<n;i++){\n pSum+=nums[i];\n prefixSum[i]=pSum;\n }\n for(auto it:queries){\n auto ub=upper_bound(nums.begin(),nums.end(),it);\n int ind=ub-nums.begin();\n long long minOper=0, req_sum=0, curr_sum;\n if(ind>0){\n req_sum = (long)it * ind, curr_sum = prefixSum[ind-1];\n minOper = req_sum - curr_sum;\n }\n req_sum = (long)it * (n-ind), curr_sum = (ind>0)? (prefixSum[n-1]-prefixSum[ind-1]) : prefixSum[n-1];\n minOper += curr_sum - req_sum;\n ans.push_back(minOper);\n }\n return ans;\n }\n};\n```\n\n | 2 | 0 | ['Binary Search', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | python3 Solution | python3-solution-by-motaharozzaman1996-1gik | \n\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n n=len(nums)\n prefix=[0 | Motaharozzaman1996 | NORMAL | 2023-03-26T06:39:49.813491+00:00 | 2023-03-26T06:39:49.813535+00:00 | 1,274 | false | \n```\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n n=len(nums)\n prefix=[0]+list(accumulate(nums))\n ans=[]\n for x in queries:\n i=bisect_left(nums,x)\n ans.append(x*(2*i-n)+prefix[n]-2*prefix[i])\n\n return ans \n``` | 2 | 0 | ['Python', 'Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Java || Sorting + Prefix Sum + Binary Search | java-sorting-prefix-sum-binary-search-by-pdyv | Complexity\n- Time complexity: O((m+n)logn)\n\n- Space complexity: O(n)\n\n## Code\njava []\nclass Solution {\n public List<Long> minOperations(int[] nums, i | nishant7372 | NORMAL | 2023-03-26T05:34:19.890228+00:00 | 2023-03-26T05:46:43.010329+00:00 | 400 | false | ## Complexity\n- Time complexity: O((m+n)logn)\n\n- Space complexity: O(n)\n\n## Code\n``` java []\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] queries) {\n Arrays.sort(nums);\n List<Long> list = new ArrayList<>();\n long[] prefix = new long[nums.length+2]; // taking prefix[0] an prefix[prefix.length-1] as 0 to avoid Index Out Of Bound\n long sum=0;\n for(int i=0;i<nums.length;i++){\n sum+=nums[i];\n prefix[i+1]=sum;\n }\n for(int x:queries){\n int idx = Arrays.binarySearch(nums,x);\n if(idx<0){\n idx = -1*(idx+2);\n }\n list.add(((long)(idx+1)*x - prefix[idx+1]) + ((prefix[prefix.length-2] - prefix[idx+1]) - (long)(nums.length - idx - 1)*x));\n }\n return list;\n }\n}\n``` | 2 | 0 | ['Binary Search', 'Sorting', 'Prefix Sum', 'Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | [Javascript] Sorting, Binary Search & Prefix Sum | javascript-sorting-binary-search-prefix-t2qez | Solution: Sorting, Binary Search & Prefix Sum\n\n1. Sort nums in asc order.\n2. Get the prefix sum from the left and right of nums.\n3. For each query, binary s | anna-hcj | NORMAL | 2023-03-26T04:00:46.081719+00:00 | 2023-03-26T04:00:46.081764+00:00 | 325 | false | **Solution: Sorting, Binary Search & Prefix Sum**\n\n1. Sort nums in asc order.\n2. Get the prefix sum from the left and right of nums.\n3. For each query, binary search for the split point - the first element where `nums[i] >= query`\n From there, we can calculate the absolute difference of the two segments of nums.\n Segment one: `query * i - leftSum[i - 1]`\n Segment two: `rightSum[i] - query * (n - i)`\n\n`n = length of nums`, `m = number of queries`\nTime Complexity: `O(n log(n) + m log(n))`\nSpace Complexity: `O(n + m)`\n```\nvar minOperations = function(nums, queries) {\n nums.sort((a, b) => a - b);\n let n = nums.length;\n let left = [...nums], right = [...nums];\n for (let i = 1; i < n; i++) left[i] += left[i - 1];\n for (let i = n - 2; i >= 0; i--) right[i] += right[i + 1];\n let ans = [];\n for (let query of queries) {\n let splitIndex = getSplitIndex(query);\n let leftDiff = splitIndex > 0 ? query * splitIndex - left[splitIndex - 1] : 0;\n let rightDiff = splitIndex < n ? right[splitIndex] - query * (n - splitIndex) : 0;\n ans.push(leftDiff + rightDiff);\n }\n return ans;\n \n function getSplitIndex(query) {\n let low = 0, high = n - 1;\n while (low < high) {\n let mid = Math.floor((low + high) / 2);\n if (nums[mid] >= query) high = mid;\n else low = mid + 1;\n }\n return nums[low] >= query ? low : n;\n }\n};\n``` | 2 | 0 | ['JavaScript'] | 1 |
minimum-operations-to-make-all-array-elements-equal | Easy to Understand ! Beginners Friendly | easy-to-understand-beginners-friendly-by-gt43 | IntuitionApproachFor Each query find the last index of that element in the nums .
The Elements left side of that index are smaller than Query[i] they should be | jayprakash00012 | NORMAL | 2025-03-26T09:00:31.491373+00:00 | 2025-03-26T09:00:31.491373+00:00 | 91 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
For Each query find the last index of that element in the nums .
The Elements left side of that index are smaller than Query[i] they should be increased
The Elements right side of that index are greater than Query[i] they should be decreased
Edge case-- idx==0 || idx==n
# Complexity
- Time complexity: O(Max(Nlogn,Mlogn))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
vector<long long> ans;
long long n=nums.size();
int m=queries.size();
sort(nums.begin(),nums.end());
vector<long long> prefixsum(n,0);
long long pre=0;
for(int i=0;i<n;i++){
pre+=nums[i];
prefixsum[i]=pre;
}
for(int i=0;i<m;i++){
long long idx=lower_bound(nums.begin(),nums.end(),queries[i]+1)-nums.begin();
long long g=queries[i];
if(idx==n || idx==0){
long long k=abs(n*g-prefixsum[n-1]);
ans.push_back(k);
continue;
}
idx=idx-1;
long long a=g*(idx+1)-prefixsum[idx];
a+=(prefixsum[n-1]-prefixsum[idx])-(n-idx-1)*g;
ans.push_back(a);
}
return ans;
}
};
``` | 1 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | prefix sum | prefix-sum-by-remedydev-98a5 | Approach\nWe build a prefix sum of differences so we can tell in constant time how many operations needed for sub array for a query\n \nexample: [1,3,4, 6, 8]\ | remedydev | NORMAL | 2023-11-16T03:43:55.336109+00:00 | 2023-11-16T03:43:55.336138+00:00 | 35 | false | # Approach\nWe build a prefix sum of differences so we can tell in constant time how many operations needed for sub array for a query\n ```\nexample: [1,3,4, 6, 8]\n prefix: 0 2 5 10 17\n```\nwe build posfix sum difference as well in order to tell in O(1) time amount of operations needed from left to right indexes\nThen we run binary search to find a splitting index for a query and run a calculation \n\n# Complexity\n- Time complexity:\n$$O(NLogM)$$ N-size of queries, M-size of nums\n\n- Space complexity:\n$$O(2n)$$\n\n# Code\n``` \nvar minOperations = function(nums, queries) {\n nums.sort((a,b)=>a-b);\n const pref=[0], post=Array(nums.length).fill().map(v=>0);\n \n for(let i=1;i<nums.length;i++){\n pref[i]=pref[i-1]+(nums[i]-nums[0]);\n }\n\n for(let i=nums.length-2;i>=0;i--){\n post[i]=post[i+1]+(nums[nums.length-1]-nums[i]);\n }\n \n // get total operations from left to right\n const getOpsPref=(l,r,q)=>{\n if(l>r) return 0;\n const pivot = q-nums[0];\n return pivot+( (pivot*r) - pref[r]);\n }\n\n // get total operations from right to left\n const getOpsPost=(l,r,q)=>{\n if(l>r) return 0;\n const pivot = Math.abs(q-nums[nums.length-1]);\n return pivot+( (pivot*(r-l)) - post[l]);\n }\n\n let ans=[];\n\n // Binary search\n for(const q of queries){\n let l=0, r=nums.length-1, split=-1;\n while(l<=r){\n const mid=Math.trunc((l+r)/2);\n if(nums[mid]<=q){\n split=mid;\n l=mid+1;\n }else{\n r=mid-1;\n }\n }\n const leftOperations = getOpsPref(0,split,q);\n const rightOperations = getOpsPost(split+1,nums.length-1,q);\n ans.push(leftOperations+rightOperations);\n }\n\n return ans;\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Rust, Python. (n + m) log n. Detailed explanation with math | rust-python-n-m-log-n-detailed-explanati-6b3g | Intuition\nLets look how to address this for one query and the value is $v$.\n\n- If the numbers are below $v$. Then the results are $v - a_1 + v - a_2 + ... v | salvadordali | NORMAL | 2023-05-02T00:55:15.330741+00:00 | 2023-05-02T00:55:15.330776+00:00 | 61 | false | # Intuition\nLets look how to address this for one query and the value is $v$.\n\n- If the numbers are below $v$. Then the results are $v - a_1 + v - a_2 + ... v - a_n = v \\cdot n - \\sum_{i=1}^{n} a_i $\n- If the numbers are above $v$. With similar logic, results are $\\sum_{i=1}^{n} a_i - v \\cdot n$\n\nSo we need to find how many numbers are below and above the $v$ and prefix sums to be able to quickly find sums. To be do both of those efficiently you need to sort array of numbers.\n\nAfter the sorting you will have:\n\n$a_1, a_2, ..., a_k$ **v** $a_{k + 1}, ..., a_n$\n\nThe result is:\n\n$v \\cdot k - \\sum_{i=1}^{k} a_i + s - \\sum_{i=1}^{k} a_i - v\\cdot n + v \\cdot k = s + 2 vk -vn - 2 \\sum_{i=1}^{k} a_i = s + v (2k - n) - 2 \\sum_{i=1}^{k} a_i$\n\nThe value of `s` is a full sum: `prefix[-1]`. The value of sum is `prefix[k]`. \n\n# Complexity\n- Time complexity: $O((n + m) \\log n)$\n- Space complexity: $O(n)$\n\n\n```Rust []\nimpl Solution {\n pub fn min_operations(mut nums: Vec<i32>, queries: Vec<i32>) -> Vec<i64> {\n nums.sort_unstable();\n let n = nums.len();\n\n let mut prefix: Vec<i64> = vec![0; n + 1];\n for i in 0 .. n {\n prefix[i + 1] = prefix[i] + nums[i] as i64;\n }\n\n let mut res: Vec<i64> = vec![0; queries.len()];\n for i in 0 .. queries.len() {\n let k = match nums.binary_search(&queries[i]) {\n Err(k) => k,\n Ok(k) => k,\n };\n res[i] = prefix[n] + (queries[i] as i64) * (2 * k - n) as i64 - 2 * prefix[k];\n }\n\n return res;\n }\n}\n```\n```python []\nfrom bisect import bisect_right\n\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n\n n = len(nums)\n prefix = [0] * (n + 1)\n for i, v in enumerate(nums):\n prefix[i + 1] = prefix[i] + v\n\n res, s = [0] * len(queries), prefix[-1]\n for i, v in enumerate(queries):\n k = bisect_right(nums, v)\n res[i] = s + v * (2 * k - n) - 2 * prefix[k]\n \n return res\n```\n\n\nQuestion to rust pro (this is my first weeks, so not so fluent). Is there a way to combine two arms in match (err/ok)?\n | 1 | 0 | ['Math', 'Python', 'Rust'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Swift | Prefix Sum + Binary Search | swift-prefix-sum-binary-search-by-upvote-n1vi | Prefix Sum + Binary Search (accepted answer)\n\nclass Solution {\n func minOperations(_ nums: [Int], _ queries: [Int]) -> [Int] {\n let nums = nums.so | UpvoteThisPls | NORMAL | 2023-04-08T23:45:53.447729+00:00 | 2023-04-08T23:45:53.447773+00:00 | 25 | false | **Prefix Sum + Binary Search (accepted answer)**\n```\nclass Solution {\n func minOperations(_ nums: [Int], _ queries: [Int]) -> [Int] {\n let nums = nums.sorted()\n let prefixSums = nums.reduce(into: [0]) { $0.append($1 + $0.last!) }\n \n return queries.map { q in \n var (left, right) = (0, nums.count)\n while left < right {\n let mid = (left+right)/2\n (left, right) = nums[mid] > q ? (left, mid) : (mid+1, right)\n }\n let totalAmountBelowAverage = q * left - prefixSums[left]\n let totalAmountAboveAverage = prefixSums.last! - prefixSums[left] - q * (nums.count - left) \n return totalAmountBelowAverage + totalAmountAboveAverage\n }\n }\n}\n``` | 1 | 0 | ['Swift'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Magical Formula lol | O(nlogn) | Binary Search | Prefix Sum | magical-formula-lol-onlogn-binary-search-u04l | // Intuition behind this is to isolate numbers less than queries[i] and number greater or equal to queries[i] and then perform this magical formula\n // ans | aryan_sri123 | NORMAL | 2023-03-27T10:13:55.621697+00:00 | 2023-03-27T10:14:42.916414+00:00 | 16 | false | // Intuition behind this is to isolate numbers less than queries[i] and number greater or equal to queries[i] and then perform this magical formula\n // ans[i] = (idx*x-res[idx-1]) + res[n-1]-res[idx-1]-x*n-idx --> key formula I derived (all terms are used in code)\n\t// 1,3,6,8 \n // 1,4,10,18 -> prefix sum array\n // check for 5\n // lower bound of 5 will give us index 2\n\t// Then apply this formula, think of it and you will get to know why I isolated numbers greater than queries[i] and less than queries[i] seprately\n \n\t\n\t\n\t\tclass Solution {\n\t\tpublic:\n\t\t\t\tvector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n\t\t\t\tsort(nums.begin(),nums.end());\n\t\t\t\tint n =nums.size();\n\t\t\t\tvector<long long> sumarray(n);\n\t\t\t\tlong long sum=0;\n\t\t\t\tfor(int i=0;i<n;i++){\n\t\t\t\t\tsum+=nums[i];\n\t\t\t\t\tsumarray[i] = sum;\n\t\t\t\t}\n\t\t\t\tlong long q = queries.size();\n\t\t\t\tvector<long long> ans(q);\n\t\t\t\tfor(int i=0;i<q;i++){\n\t\t\t\t\tlong long x = queries[i];\n\t\t\t\t\tlong long idx = lower_bound(nums.begin(),nums.end(),x)-nums.begin();\n\t\t\t\t\tif(idx == 0 || idx == n ) ans[i] = abs(n*x - sumarray[n-1] );\n\t\t\t\t\telse ans[i] = (idx*x - sumarray[idx-1] ) + sumarray[n-1]-sumarray[idx-1]-x*(n-idx);\n\t\t\t\t}\n\t\t\t\treturn ans;\n\t\t\t}\n\t\t}; | 1 | 0 | ['Binary Search', 'C', 'Prefix Sum'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Golang 156 ms 10.9 MB | golang-156-ms-109-mb-by-maxhero90-rmip | Complexity\n- Time complexity: O((n+m)*logn)\n- Space complexity: O(n+m)\n# Code\n\nfunc minOperations(nums []int, queries []int) []int64 {\n\tn := len(nums)\n\ | maxhero90 | NORMAL | 2023-03-27T09:22:15.111101+00:00 | 2023-03-27T09:23:41.505039+00:00 | 55 | false | # Complexity\n- Time complexity: $$O((n+m)*logn)$$\n- Space complexity: $$O(n+m)$$\n# Code\n```\nfunc minOperations(nums []int, queries []int) []int64 {\n\tn := len(nums)\n\tsort.Ints(nums)\n\tprefixSums := make([]int, n)\n\tprefixSums[0] = nums[0]\n\tfor i := 1; i < n; i++ {\n\t\tprefixSums[i] = prefixSums[i-1] + nums[i]\n\t}\n\tresult := make([]int64, len(queries))\n\tfor i, query := range queries {\n\t\tidx := sort.SearchInts(nums, query)\n\t\tif idx == 0 {\n\t\t\tresult[i] = int64(prefixSums[n-1] - query*n)\n\t\t} else {\n\t\t\tresult[i] = int64(prefixSums[n-1] - query*(n-idx) + query*idx - prefixSums[idx-1]<<1)\n\t\t}\n\t}\n\treturn result\n}\n``` | 1 | 0 | ['Go'] | 0 |
minimum-operations-to-make-all-array-elements-equal | C++, prefix sum | c-prefix-sum-by-gyokuro123-2krx | \n# Code\n\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(), nums.end());\n | gyokuro123 | NORMAL | 2023-03-27T03:26:46.286732+00:00 | 2023-03-27T03:26:46.286769+00:00 | 30 | false | \n# Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(), nums.end());\n vector<long long> sums(nums.size(), 0);\n sums[0] = nums[0];\n for(int i = 1; i < nums.size(); i++) sums[i] = nums[i] + sums[i-1];\n vector<long long> ans(queries.size(), 0);\n for(int i = 0; i < queries.size(); i++){\n auto it = upper_bound(nums.begin(), nums.end(), queries[i]);\n long long index = (int)(it - nums.begin());\n long long v1 = queries[i] * index;\n long long v2 = queries[i] * (nums.size()-index);\n long long res1 = 0;\n if(index != 0) res1 = v1 - sums[index - 1];\n long long res2 = 0;\n if(index == 0) res2 = sums[sums.size()-1] - v2;\n else if(index != nums.size()) res2 = sums[sums.size()-1] - sums[index - 1] - v2;\n ans[i] = res1 + res2;\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Sort | Binary Search | sort-binary-search-by-ajayc1007-zhvb | Intuition\nBrute force will give TLE. Look for a pivot from where either we only need to increment or decrement.\n\n# Approach\nCarefully note that the answer d | ajayc1007 | NORMAL | 2023-03-26T19:04:19.974647+00:00 | 2023-03-26T19:04:19.974677+00:00 | 346 | false | # Intuition\nBrute force will give TLE. Look for a pivot from where either we only need to increment or decrement.\n\n# Approach\nCarefully note that the answer does not depend on the order of the elements. In such a case, we can utilize binary search to identify a pivot 1) before which all elements are smaller 2) after which all elements are bigger. For binary, we first need to sort it.\nOnce completed, our answer will be sum of both the above cases using pattern.\n\n# Complexity\n- Time complexity: $$O(mlog(n))$$ , where m is no. of queries.\n\n# Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n vector<long long> prefix(n + 1);\n for (int i=0;i<n;++i) {\n prefix[i+1] = prefix[i] + (long long)nums[i];\n }\n vector<long long> ans;\n for (auto &query : queries) {\n int left = 0, right = n;\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (query < nums[mid]) {\n right = mid;\n }\n else {\n left = mid + 1;\n }\n }\n long long inc = (long long)query * left - prefix[left];\n long long dec = prefix[n] - prefix[left] - (long long)query * (n - left);\n ans.push_back(inc + dec);\n }\n return ans; \n }\n};\n``` | 1 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Sorting+Prefix Sum + Binary Search | sortingprefix-sum-binary-search-by-pande-bczc | Intuition\nIntuition is we need to make all element equal to given target and there is time constraint to we need to think like number of elements that are goin | Pandeyji_1999 | NORMAL | 2023-03-26T14:13:49.904887+00:00 | 2023-03-26T14:13:49.904923+00:00 | 306 | false | # Intuition\nIntuition is we need to make all element equal to given target and there is time constraint to we need to think like number of elements that are going to be increase i.e number which is less than target and decrease the number which is greater than the target.\n\n# Approach\nAs going on each index will lead to TLE so to optimize this ,sort the array and now we can find index till that we need to increase and after that we need to decrease.For this purpose I used lower bound.Now to count the step I use prefix sum .To avoid runtime error ,use long long.\n\n# Complexity\n- Time complexity:\nO(n*log(n))-for sorting\nO(n)-for prefix sum\nO(n*(log(n)))-for quering \n\n- Space complexity:\nO(n)-for prefix sum\n\n# Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n int n=nums.size();\n vector<long long >ans;\n sort(nums.begin(),nums.end());\n vector<long long >prefix(n);\n prefix[0]=nums[0];\n for(int i=1;i<n;i++)prefix[i]=nums[i]+prefix[i-1];\n \n for(auto x:queries)\n {\n long long target=x;\n long long l=0,h=n-1;\n long long idx=lower_bound(nums.begin(),nums.end(),target)-nums.begin();\n if(idx<n)\n {\n if(nums[idx]>target )idx--;\n }\n else idx--;\n \n // cout<<idx<<endl;\n if(idx<0)\n {\n long long rest=prefix[n-1]-(n)*target;\n ans.push_back(rest);\n }\n else\n {\n long long cnt=(idx+1)*(1ll)*target-prefix[idx];\n long long rest=prefix[n-1]-prefix[idx]-(n-idx-1)*target;\n long long res=cnt+rest;\n ans.push_back(res);\n }\n \n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Binary Search', 'Sorting', 'Prefix Sum'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Easy Solution using Prefix Sum + lower bound + upper bound | easy-solution-using-prefix-sum-lower-bou-fbm8 | Code\n\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n \n vector<long long> ans;\n | baquer | NORMAL | 2023-03-26T08:30:08.368056+00:00 | 2023-03-26T08:30:08.368102+00:00 | 201 | false | # Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n \n vector<long long> ans;\n int n = nums.size();\n sort(nums.begin(), nums.end());\n\n // Ye brute force hai.\n\n // for(int i = 0; i < queries.size(); i++) {\n // long long temp = 0;\n // for(int j = 0; j < nums.size(); j++) {\n // temp += abs(nums[j] - queries[i]);\n // }\n // ans.push_back(temp);\n // }\n\n // Prefix nikal lo pahle\n vector<long long> prefix(n+1);\n prefix[0] = 0;\n long long sum = 0;\n for(int i = 0; i < nums.size(); i++) {\n sum += nums[i];\n prefix[i+1] = sum;\n }\n\n for(auto q: queries) {\n\n \n long long lb = lower_bound(nums.begin(), nums.end(), q) - nums.begin() - 1;\n // lb pe -1 kia hai kyuni ye equal ya usse bada element ka pointer\n // return karta hai to mujhe usse niche wala chaiye, to agr equal \n // hua to -1 karu ga aur agr bada hua to -1 karu ga usse niche jane k\n // liye\n long long ub = upper_bound(nums.begin(), nums.end(), q) - nums.begin();\n long long left = 0;\n if(lb != -1) {\n left += (q*(lb+1)) - (prefix[lb+1] - prefix[0]);\n }\n long long right = 0;\n if(ub != n) {\n right += (prefix[n] - prefix[ub]) - (q*(n-ub));\n } \n ans.push_back(left+right);\n }\n return ans; \n }\n};\n``` | 1 | 0 | ['Binary Search', 'Prefix Sum', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | c++ solution | c-solution-by-dilipsuthar60-fkxv | \nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& q) \n {\n sort(nums.begin(),nums.end());\n int | dilipsuthar17 | NORMAL | 2023-03-26T07:02:39.413723+00:00 | 2023-03-26T07:02:39.413762+00:00 | 110 | false | ```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& q) \n {\n sort(nums.begin(),nums.end());\n int n=nums.size();\n vector<long long>ans;\n long long total=accumulate(nums.begin(),nums.end(),0ll);\n vector<long long>temp(n+1);\n for(int i=0;i<n;i++)\n {\n temp[i+1]=temp[i]+nums[i]; \n }\n for(int i=0;i<q.size();i++)\n {\n int index=lower_bound(nums.begin(),nums.end(),q[i])-nums.begin();\n long long left_sum=1ll*q[i]*(index)-temp[index];\n long long right_sum=(total-temp[index])-1ll*q[i]*(n-index);\n ans.push_back(left_sum+right_sum);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C', 'Binary Tree', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Easy C++ | easy-c-by-avatsal38-6s1d | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | avatsal38 | NORMAL | 2023-03-26T06:15:47.163663+00:00 | 2023-03-26T06:15:47.163711+00:00 | 146 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n #define ll long long int\n vector<long long> minOperations(vector<int>& a, vector<int>& q) {\n sort(a.begin(),a.end());\n int n=a.size();\n ll pre[n],suf[n];\n pre[0]=a[0],suf[n-1]=a[n-1];\n for(int i=1;i<n;i++)pre[i]=pre[i-1]+a[i];\n for(int i=n-2;i>=0;i--)suf[i]=suf[i+1]+a[i];\n vector<ll> ans;\n for(int i=0;i<q.size();i++)\n {\n ll no=q[i];\n ll s=upper_bound(a.begin(),a.end(),no)-a.begin();\n if(s==0)ans.push_back(suf[s]-(n-s)*no);\n else if(s==n)ans.push_back(no*s-pre[s-1]);\n else ans.push_back(no*s-pre[s-1]+suf[s]-(n-s)*no);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Sorting +Prefix Sum + BinarySearch, JAVA, attention the overflow | sorting-prefix-sum-binarysearch-java-att-g0p3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | tendencymilk | NORMAL | 2023-03-26T05:04:33.080055+00:00 | 2023-03-26T05:04:33.080097+00:00 | 208 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] queries) {\n List<Long> res = new ArrayList<>();\n int n = nums.length;\n long[] record = new long[n];\n Arrays.sort(nums); \n record[0] = nums[0];\n for(int i = 1; i < n; i++){\n record[i] = record[i-1] + nums[i];\n }\n \n \n for(int i = 0; i < queries.length; i++){\n long cur = 0;\n int tmp = search(nums, queries[i]);\n if(tmp == -1)tmp = 0;\n cur += Math.abs(record[tmp] - (long)queries[i] * (tmp+1));\n cur += Math.abs(record[n-1] - record[tmp] - (long)queries[i] * (n-tmp-1)); \n res.add(cur);\n }\n return res;\n }\n \n public int search(int[] arr, int target){\n int left = 0, right = arr.length - 1;\n while (left <= right) {\n int mid = left + (right-left) / 2;\n \n if (arr[mid] == target) {\n return mid;\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n return right;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | C++ Easy Solution | Binary Search + Sorting | O(NlongN) | c-easy-solution-binary-search-sorting-on-vp9j | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | manishk4514 | NORMAL | 2023-03-26T04:53:45.368695+00:00 | 2023-03-26T04:53:45.368726+00:00 | 155 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n vector<long long> res;\n \n static int next(vector<int>& arr, int target) {\n int start = 0, end = arr.size() - 1;\n if (end == 0) return -1;\n if (target > arr[end]) return end;\n\n int ans = -1;\n while (start <= end) {\n int mid = start + (end - start) / 2; // avoid overflow\n if (arr[mid] >= target) {\n end = mid - 1;\n } else {\n ans = mid;\n start = mid + 1;\n }\n }\n return ans;\n }\n \n void helper(vector<int>& nums, vector<long long>& prefix, int k) {\n int n = nums.size();\n int left = 0;\n int right = nums.size() - 1;\n int pos = next(nums, k);\n \n long long currRes = (pos == -1 ? 0 : abs(((pos + 1LL) * (long long)k) - prefix[pos])) * 1LL;\n long long nextSum = (pos == -1 ? prefix[n - 1] : prefix[n - 1] - prefix[pos]) * 1LL;\n long long total = (pos == -1 ? (long long)k * (n) : (long long)k * ((n - 1) - pos)) * 1LL;\n res.push_back(currRes + abs(total - nextSum));\n }\n \npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n int n = nums.size();\n int m = queries.size();\n sort(nums.begin(), nums.end());\n \n vector<long long> prefix(n);\n long long sum = 0LL;\n for(int i = 0; i < n; i++){\n sum += (long long)nums[i]; // cast to long long to avoid overflow\n prefix[i] = sum * 1LL;\n }\n \n for(int i = 0; i < m; i++){\n helper(nums, prefix, queries[i]);\n }\n return res;\n }\n};\n\n``` | 1 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Runtime 235 ms Beats 100% | runtime-235-ms-beats-100-by-akshat0610-kmds | Code\n\n#pragma GCC optimize("Ofast","inline","fast-math","unroll-loops","no-stack-protector")\n#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx, | akshat0610 | NORMAL | 2023-03-26T04:43:46.474363+00:00 | 2023-03-26T04:43:46.474427+00:00 | 126 | false | # Code\n```\n#pragma GCC optimize("Ofast","inline","fast-math","unroll-loops","no-stack-protector")\n#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,tune=native","f16c")\n\nstatic int fast_io = []() \n{ \n std::ios::sync_with_stdio(false); \n cin.tie(nullptr); \n cout.tie(nullptr); \n return 0; \n}();\n\n#ifdef LOCAL\n freopen("input.txt", "r" , stdin);\n freopen("output.txt", "w", stdout);\n#endif\n\nclass Solution \n{\npublic:\n vector<long long int>prefix;\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) \n\t{\n\t\t //to perform the binary search on the array we need to sort the array\n\t\t sort(nums.begin() , nums.end());\n\t\t \n //first of all we need to do the preprocessing of the nums \n\t\t for(int i=0;i<nums.size();i++)\n\t\t {\n\t\t if(prefix.size() == 0)\n\t\t\t {\n\t\t\t prefix.push_back(nums[i]);\n\t\t\t }\t\n\t\t\t else\n\t\t\t {\n\t\t\t \tlong long int sum = 0LL + prefix.back() + nums[i];\n\t\t\t \tprefix.push_back(sum);\n\t\t\t }\n\t\t }\n\t\t \n\t\t //processing the each query \n\t\t vector<long long int>ans;\n\t\t for(int i=0;i<queries.size();i++)\n\t\t {\n\t\t \n\t\t \t int ele = queries[i];\n\t\t long long int val = binary_search_(ele,nums);\t\n\t\t ans.push_back(val);\n\t\t } \n\t\t return ans;\n }\n long long int binary_search_(int &ele,vector<int>&nums)\n {\n \tint start = 0;\n \tint end = nums.size()-1;\n \tint pos = -1;\n \t\n \twhile(start <= end)\n \t{\n \t\tlong long int mid = (start + ((end - start)/2));\n \t\t\n \t\t//we need to find the last pos of the ele in the nums\n \t if(nums[mid] == ele)\n\t\t\t{\n\t\t\t pos = mid;\n\t\t\t\tstart = mid+1;\t\n\t\t\t}\t\n\t\t\telse if(ele > nums[mid])\n\t\t\t{\n\t\t\t\tstart = mid+1;\n\t\t\t}\n\t\t\telse if(ele < nums[mid])\n\t\t\t{\n\t\t\t\tend = mid-1;\n\t\t\t}\n\t\t}\n\t\t\n\t\tif(pos == -1)\n\t\t{\n\t\t\tlong long int ans = 0;\n\t\t\tif(start>=0 and start<nums.size())\n\t\t\t{\n\t\t\t long long int bigger = 0LL + ((nums.size()-1) - start + 1);\t\n\t\t\t long long int sum = prefix[prefix.size()+-1];\n\t\t\t \n\t\t\t if(start > 0) sum = sum - prefix[start-1];\n\t\t\t \n\t\t\t long long int val = (sum - (bigger*ele));\n\t\t\t \n\t\t\t ans = ans + 0LL + val;\n\t\t\t}\n\t\t\tif((end>=0 and end<nums.size()))\n\t\t\t{\n\t\t\t\t//taking out the smaller elements \n\t\t\t long long int smaller = 0LL + (end - 0 + 1);\t\n\t\t\t long long int sum = 0LL + prefix[end];\n\t\t\t\tlong long int val = 0LL + ((smaller*ele) - sum); \n\t\t\t ans = ans + 0LL + val;\n\t\t\t}\n\t\t\t\n\t\t\treturn ans;\n\t\t}\n\t\telse if(pos != -1)\n\t\t{\t \n\t\t \n\t\t long long int ans = 0;\n\t\t \n\t\t long long int smaller = 0LL + pos - 0 + 1;\n\t\t \n\t\t //if(ele == 1) cout<<"smaller = "<<smaller<<endl;\n\t\t \n\t\t \n\t\t if(smaller > 0)\n\t\t {\n\t\t \t\n\t\t\t \n\t\t long long int sum = 0LL + prefix[pos];\n\t\t long long int val1 = 0LL + ((smaller*ele) - sum); \n\t\t \n\t\t ans = ans + 0LL + val1;\n\t\t \n\t\t }\n\t\t \n\t\t \n\t\t long long int bigger = 0LL + ((nums.size()-1) - (pos+1) + 1);\n\t\t \n\t\t //if(ele == 1) cout<<"bigger = "<<bigger<<endl;\n\t\t \n\t\t if(bigger > 0)\n\t\t {\n\t\t \t\n\t\t long long int sum = 0LL + prefix[prefix.size()-1];\n\t\t \n\t\t if(pos+1-1 >= 0) sum = sum - prefix[pos+1-1];\n\t\t long long int val2 = (sum - (bigger*ele));\n\t\t \n\t\t \n\t\t \n\t\t ans = ans + 0LL + val2;\n\t\t }\n\t\t //cout<<"ans = "<<ans<<endl;\n\t\t return ans; \n\t\t}\n\t\treturn 0;\n\t}\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Binary Search + Prefix Sum | binary-search-prefix-sum-by-rishabhsingh-wrk8 | \nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n \n int n = size(nums);\n sort | Rishabhsinghal12 | NORMAL | 2023-03-26T04:10:57.639772+00:00 | 2023-03-26T04:10:57.639819+00:00 | 87 | false | ```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n \n int n = size(nums);\n sort(begin(nums), end(nums));\n \n vector<long long> pre(n);\n \n pre[0] = nums[0];\n \n for(int i = 1; i < n; i++) {\n pre[i] = 0LL + pre[i-1] + nums[i];\n }\n \n int m = size(queries);\n vector<long long> res;\n \n for(int i = 0; i < m; i++) {\n long long val = queries[i];\n \n int lb = (upper_bound(begin(nums), end(nums),val) - begin(nums));\n \n lb--;\n // cout << lb << \' \';\n long long ans = 0;\n if(lb != -1 and lb < n) {\n long long sum = 1LL * val * (lb+1);\n ans += 0LL + abs(sum - pre[lb]);\n }\n long long rem;\n if(lb == -1)rem = n;\n else rem = n-lb-1;\n \n if(rem) {\n long long sum = 1LL * val * rem;\n long long sums;\n if(lb == -1)sums = pre[n-1];\n else\n sums = 0LL + pre[n-1] - pre[lb];\n \n ans += 0LL + abs(sum - sums);\n }\n res.push_back(ans);\n \n }\n \n return res;\n }\n};\n``` | 1 | 0 | ['Binary Search', 'C', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | NLogN | Easy Solution | nlogn-easy-solution-by-yigitozcelep-gem6 | For each query target in queries, the solution performs binary search on the sorted array nums to find the index i such that nums[i] is the smallest element gre | Yigitozcelep | NORMAL | 2023-03-26T04:01:16.528644+00:00 | 2023-03-26T04:02:08.145454+00:00 | 213 | false | For each query target in queries, the solution performs binary search on the sorted array nums to find the index i such that nums[i] is the smallest element greater than or equal to the target. It then calculates the sum of the following two parts:\n\nThe total number of operations required to make the first i elements of nums equal to target. This is calculated as i * target - prefix[i-1] where prefix[i-1] represents the sum of the first i-1 elements of nums.\n\nThe total number of operations required to make the last n-i elements of nums equal to target. This is calculated as (prefix[n-1] - prefix[i-1]) - (n - i) * target where prefix[n-1] - prefix[i-1] represents the sum of the last n-i elements of nums.\n \n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n prefix = []\n nums.sort()\n prev = 0\n for num in nums:\n prev += num\n prefix.append(prev)\n \n data = []\n for target in queries:\n i = 0\n k = len(prefix)\n tot = 0\n while i < k:\n j = (i + k) // 2\n if nums[j] > target: k = j\n else: i = j + 1\n \n backs = prefix[i - 1] if i != 0 else 0\n tot += i * target - backs\n tot += (prefix[-1] - backs) - (len(nums) - i) * target\n data.append(tot)\n \n return data\n``` | 1 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Java solution | java-solution-by-yashhi_01-adfu | Code | yashhi_01 | NORMAL | 2025-04-09T13:23:52.632860+00:00 | 2025-04-09T13:23:52.632860+00:00 | 2 | false |
# Code
```java []
class Solution {
public int binarySearch(int[] nums, int k){
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < k) left = mid + 1;
else right = mid;
}
return left;
}
public List<Long> minOperations(int[] nums, int[] queries) {
//Initializations
int n = nums.length;
List<Long> result = new ArrayList<>();
//sort numbers
Arrays.sort(nums);
//Calculate prefix sum
long[] prefixSum = new long[nums.length];
prefixSum[0] = nums[0];
for(int i = 1 ; i < nums.length ; i++){
prefixSum[i] = prefixSum[i-1] + nums[i];
}
//Apply binary search for each query to get the mid index
for(int query : queries){
long sum = 0;
int index = binarySearch(nums, query);
if(index > 0){
sum += (long) query * index - prefixSum[index - 1];
}
if(index < n){
sum += (prefixSum[n - 1] - (index == 0 ? 0 : prefixSum[index - 1])) - (long) query * (n - index);
}
result.add(sum);
}
return result;
}
}
``` | 0 | 0 | ['Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Java prefixSum + binarySearch | java-prefixsum-binarysearch-by-54v-ag8t | IntuitionIf j numbers in nums that are smaller than query[i] then number of increments = query[i] * j - sum of smaller numbersIf k numbers in nums thare are gre | 54v | NORMAL | 2025-04-08T23:54:52.760057+00:00 | 2025-04-08T23:54:52.760057+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
If j numbers in nums that are smaller than query[i] then number of increments = query[i] * j - sum of smaller numbers
If k numbers in nums thare are greater than query[i] then number of decrements = sum of larger nums - query[i] * k
sum of numbers smaller than query of i = prefixSum[i]
sum of numbers larger than queries of i = prefixSum[nums.length] - prefixSum[i]
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(nlogn + qlogq)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n)
# Code
```java []
class Solution {
public List<Long> minOperations(int[] nums, int[] queries) {
int n = nums.length;
Arrays.sort(nums);
long[] prefixSum = new long[n + 1];
List<Long> res = new ArrayList<>();
for (int i = 0; i < n; i++) {
prefixSum[i + 1] = prefixSum[i] + nums[i];
}
for (int q = 0; q < queries.length; q++) {
int targetIndex = binarySearch(nums, queries[q]);
long leftChanges = (long)queries[q] * targetIndex - prefixSum[targetIndex];
long rightChanges = (prefixSum[n] - prefixSum[targetIndex]) - (long)queries[q] * (n - targetIndex);
res.add(rightChanges + leftChanges);
}
return res;
}
private static int binarySearch(int[] arr, int target) {
int low = 0, high = arr.length;
while (low < high) {
int mid = low + (high - low) / 2;
if (arr[mid] <= target) {
low = mid + 1;
} else {
high = mid;
}
}
return low;
}
}
``` | 0 | 0 | ['Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | solution using prefix sum | solution-using-prefix-sum-by-binod24-7wec | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | binod24 | NORMAL | 2025-03-30T12:06:04.873863+00:00 | 2025-03-30T12:06:04.873863+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
int n = nums.size();
vector<long long> ans;
vector<long long> preSum(n+1);
sort(nums.begin(), nums.end());
preSum[0] = nums[0];
for(int i= 1; i<n; i++){
preSum[i] = preSum[i-1] + nums[i];
}
preSum.insert(preSum.begin(), 0);
for(long long q : queries){
auto iter = upper_bound(nums.begin(), nums.end(), q);
int index = iter - nums.begin();
//cout<<"index=>"<<index<<endl;
long long left = index*q - preSum[index];
long long right = preSum[n] - preSum[index] - (n-index)*q;
//cout<<"n=>"<<n<<" preSum[n]=>"<<preSum[n]<<" preSum[index]=>"<<preSum[index]<<endl;
//cout<<"left=>"<<left<<" right=>"<<right<<endl;
ans.push_back(left+right);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Beats 90% of Coders || Best Solution || Pre Sum technique used | beats-90-of-coders-best-solution-pre-sum-f3ts | Code | Deepanshu_Rathore | NORMAL | 2025-03-28T04:24:14.031189+00:00 | 2025-03-28T04:24:14.031189+00:00 | 2 | false | # Code
```cpp []
class Solution {
public:
vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
sort(nums.begin(), nums.end());
int n = nums.size();
vector<long long> preSum(n+1, 0);
for(int i=0; i<n; ++i) {
preSum[i+1] = preSum[i] + nums[i];
}
vector<long long> ans;
for(int q: queries) {
int idx = lower_bound(nums.begin(), nums.end(), q) - nums.begin();
long long leftSum = preSum[idx];
long long rightSum = preSum[n] - preSum[idx];
long long leftOp = (1LL * idx * q) - leftSum;
long long rightOp = rightSum - (1LL * (n-idx) * q);
ans.push_back(leftOp + rightOp);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | 100% || C++ | 100-c-by-giri_69-anjt | Intuitionfor a query q, there are some elements smaller than q denoted as leftsum rest are called rightsum. Find teh sum of both of the valuesApproachComplexity | giri_69 | NORMAL | 2025-03-23T08:00:27.754316+00:00 | 2025-03-23T08:00:27.754316+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
for a query `q`, there are some elements smaller than `q` denoted as `leftsum` rest are called `rightsum`. Find teh sum of both of the values
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
int n=nums.size();
vector <long long int> ans;
sort(nums.begin(),nums.end());
vector <long long int> prefix(nums.size(),0);
prefix[0]=nums[0];
for(int i=1;i<nums.size();i++){
prefix[i] = prefix[i-1] + nums[i];
}
for(auto &q:queries){
long long greater=lower_bound(nums.begin(),nums.end(),q)-nums.begin();
long long leftSum=(greater>0)?(q*1LL*greater-prefix[greater-1]):0;
long long rightSum=(greater<n)?((prefix[n-1]-(greater>0?prefix[greater-1]:0))-q*1LL*(n-greater)):0;
ans.push_back(leftSum+rightSum);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | intuitive bisect solution | intuitive-bisect-solution-by-owenwu4-eats | Intuitionuse binary search to sum up the elements that are not equal to the current - you know bisect will give you right half elements are greater than current | owenwu4 | NORMAL | 2025-02-26T00:16:37.969510+00:00 | 2025-02-26T00:16:37.969510+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
use binary search to sum up the elements that are not equal to the current - you know bisect will give you right half elements are greater than current and left are less than, so you can leverage this
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:
nums.sort()
res = []
p = list(itertools.accumulate(nums))
n = len(nums)
for q in queries:
l = bisect_left(nums, q)
r = bisect_right(nums, q)
now = 0
if l > 0:
high = q * l
now += (high - p[l - 1])
if r < n:
low = q * (n - r)
if r <= 0:
high = p[-1]
else:
high = p[-1] - p[r - 1]
now += (high - low)
res.append(now)
return res
``` | 0 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Ugly looking but easy to understand C++ Binary search solution | ugly-looking-but-easy-to-understand-c-bi-bqgp | Code | amogh007 | NORMAL | 2025-02-22T01:20:45.849390+00:00 | 2025-02-22T01:20:45.849390+00:00 | 5 | false |
# Code
```cpp []
class Solution {
public:
vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
vector<long long>prefix(nums.size(), 0);
vector<long long>result;
sort(nums.begin(), nums.end());
for (int i = 1; i < nums.size(); i++) {
prefix[i] = prefix[i - 1] + nums[i - 1];
}
for(int i = 0; i < queries.size(); i++) {
long long num = queries[i];
auto index = lower_bound(nums.begin(), nums.end(), num);
int idx = index - nums.begin();
int size = nums.size();
if (idx == size) {
result.push_back((size * num) - prefix[size - 1] - nums[size - 1]);
continue;
}
long long sum_to_left = prefix[idx];
long long sum_to_right = prefix[size - 1] - prefix[idx] + nums[size - 1];
cout <<sum_to_left << " "<<sum_to_right<<endl;
long long rem_left_sum = (num * idx) - sum_to_left;
long long rem_right_sum = sum_to_right - (num * (nums.size() - idx));
result.push_back(rem_left_sum + rem_right_sum);
}
return result;
}
};
``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | prefix sum and binary search | prefix-sum-and-binary-search-by-johnchen-34b6 | Intuitionsort the nums, then do prefix sum.find the position of each query, the left part would be query * number of left - sum of left, the right part would be | johnchen | NORMAL | 2025-02-20T15:48:16.537962+00:00 | 2025-02-20T15:48:16.537962+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
sort the nums, then do prefix sum.
find the position of each query, the left part would be query * number of left - sum of left, the right part would be sum of right - query * number of right
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(nlog(n)) + O(m * log(n))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n + 1)
# Code
```cpp []
class Solution {
public:
vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
sort(nums.begin(), nums.end());
const int m = nums.size();
vector<long long> sum(m + 1);
for (int i = 0; i < m; ++ i)
sum[i + 1] = sum[i] + nums[i];
const int n = queries.size();
vector<long long> res(n);
for (int i = 0; i < n; ++ i)
{
const auto it = upper_bound(nums.cbegin(), nums.cend(), queries[i]);
const int index = distance(nums.cbegin(), it) + 1;
const long long left = static_cast<long long>(queries[i]) * (index - 1) - sum[index - 1];
const long long right = sum.back() - sum[index - 1] - static_cast<long long>(queries[i]) * (m - index + 1);
res[i] = left + right;
}
return res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Presum + BinarySearch | presum-binarysearch-by-wesleyzhouwj-99oy | IntuitionUsing Presum and Binary searchApproachComplexity
Time complexity: NlogN + MlogN (N is length of nums, M is length of queries)
Space complexity:
O(N)
C | wesleyzhouwj | NORMAL | 2025-02-07T05:16:24.029290+00:00 | 2025-02-07T05:16:24.029290+00:00 | 7 | false | # Intuition
Using Presum and Binary search
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: NlogN + MlogN (N is length of nums, M is length of queries)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
O(N)
# Code
```java []
class Solution {
public List<Long> minOperations(int[] nums, int[] queries) {
List<Long>res = new ArrayList<>();
Arrays.sort(nums);
long[] preSum = new long[nums.length];
long sum = 0l;
int len = nums.length;
for(int i=0;i<nums.length;i++){
sum += nums[i];
preSum[i] = sum;
}
for(int query: queries){
int pos = getPos(nums, query);
if(pos == -1 || pos == 0){
long count = preSum[nums.length-1] - len * (long)query;
res.add(count);
}else if(pos == nums.length){
long count = len * (long)query - preSum[nums.length-1];
res.add(count);
}else{
long count = ((long)query * pos - preSum[pos-1]) + ((preSum[nums.length-1] - preSum[pos-1]) - (long)query * (len - pos));
res.add(count);
}
}
return res;
}
private int getPos(int[] nums, int target){
int left = 0, right = nums.length-1;
while(left <= right){
int mid = left + (right - left)/2;
if(nums[mid] <= target){
left = mid+1;
}else{
right = mid-1;
}
}
return left;
}
}
``` | 0 | 0 | ['Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | You shall never get it | you-shall-never-get-it-by-sidsredhar27-5nda | Code | sidsredhar27 | NORMAL | 2025-02-04T11:42:29.991887+00:00 | 2025-02-04T11:42:29.991887+00:00 | 12 | false | # Code
```python3 []
from typing import List
class Solution:
def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:
nums.sort()
res = []
prefix = [0]
for i in nums:
prefix.append(prefix[-1] + i)
def getindex(num):
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < num:
left = mid + 1
else:
right = mid - 1
return left
for number in queries:
index = getindex(number)
left_sum = number * index - prefix[index]
right_sum = (prefix[-1] - prefix[index]) - number * (len(nums) - index)
res.append(left_sum + right_sum)
return res
``` | 0 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Simple math method | simple-math-method-by-sidsredhar27-zv2i | Code | sidsredhar27 | NORMAL | 2025-02-04T11:41:44.435541+00:00 | 2025-02-04T11:41:44.435541+00:00 | 8 | false | # Code
```python3 []
from typing import List
class Solution:
def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:
nums.sort()
res = []
prefix = [0]
for i in nums:
prefix.append(prefix[-1] + i)
def getindex(num):
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < num:
left = mid + 1
else:
right = mid - 1
return left
for number in queries:
index = getindex(number)
left_sum = number * index - prefix[index]
right_sum = (prefix[-1] - prefix[index]) - number * (len(nums) - index)
res.append(left_sum + right_sum)
return res
``` | 0 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | 2602. Minimum Operations to Make All Array Elements Equal | 2602-minimum-operations-to-make-all-arra-jhck | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-19T04:50:39.267141+00:00 | 2025-01-19T04:50:39.267141+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
sort(nums.begin(), nums.end());
vector<long long> prefixSum(nums.size() + 1, 0);
for (int i = 0; i < nums.size(); ++i) {
prefixSum[i + 1] = prefixSum[i] + nums[i];
}
vector<long long> result;
for (int target : queries) {
int idx = lower_bound(nums.begin(), nums.end(), target) - nums.begin();
long long left = (long long)target * idx - prefixSum[idx];
long long right = prefixSum[nums.size()] - prefixSum[idx] - (long long)target * (nums.size() - idx);
result.push_back(left + right);
}
return result;
}
};
``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Simple PrefixSum and BinarySearch | simple-prefixsum-and-binarysearch-by-sri-2mcg | IntuitionThe problem involves calculating the minimum number of operations needed to make all elements in the array nums equal to each query value in the querie | srirammente | NORMAL | 2025-01-14T10:23:11.149540+00:00 | 2025-01-14T10:23:11.149540+00:00 | 12 | false | # Intuition
The problem involves calculating the minimum number of operations needed to make all elements in the array nums equal to each query value in the queries array. Since operations involve incrementing or decrementing elements by 1, we can simplify the calculation by pre-sorting the array and using a prefix sum to quickly compute the number of operations for each query.
# Approach
1. Sorting: First, sort the nums array. This helps in efficiently finding the elements that are less than or equal to each query using binary search.
1. Prefix Sum: Compute a prefix sum array (arr) where arr[i] holds the sum of the first i elements of nums. This allows quick calculation of sums of subarrays, which is needed to calculate the number of operations.
1. Binary Search: For each query, use binary search to find the largest index where the element in nums is less than or equal to the query value. This index divides the array into two parts:
- Elements less than or equal to the query.
- Elements greater than the query.
1. Calculating Operations:
- Left part: The number of operations to convert the first part of the array to the query value is the difference between the sum of this part and the total sum if all elements were equal to the query.
- Right part: Similarly, calculate the number of operations for the second part.
- The total number of operations for each query is the sum of the operations for both parts.
1. Store Results: For each query, store the computed operations in a list and return this list at the end.
# Complexity
- Time complexity:
- Sorting the array takes O(nlogn).
- Constructing the prefix sum array takes O(n).
- For each query, binary search takes O(logn) and calculating the operations takes O(1).
- If there are m queries, the total time complexity is O(nlogn+mlogn).
- Space complexity:
The space complexity is O(n) for the prefix sum array and O(m) for storing the results, which gives an overall space complexity of O(n+m).
# Code
```java []
class Solution {
public List<Long> minOperations(int[] nums, int[] queries) {
Arrays.sort(nums);
int n = nums.length;
long[] arr = new long[n + 1];
for (int i = 0; i < n; i++) {
arr[i + 1] = arr[i] + nums[i];
}
List<Long> list = new ArrayList<>();
for (int query : queries) {
int index = binarySearch(nums, query);
long left = (long) index * query - arr[index];
long right = (arr[n] - arr[index]) - (long) (n - index) * query;
list.add(left + right);
}
return list;
}
private static int binarySearch(int[] nums, int query) {
int low = 0, high = nums.length;
while (low < high) {
int mid = (low + high) / 2;
if (nums[mid] <= query) {
low = mid + 1;
} else {
high = mid;
}
}
return low;
}
}
``` | 0 | 0 | ['Binary Search', 'Sorting', 'Prefix Sum', 'Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Sort + Prefix Sum + Binary Search | sort-prefix-sum-binary-search-by-up41guy-xzsw | null | Cx1z0 | NORMAL | 2025-01-04T04:08:58.474837+00:00 | 2025-01-04T04:17:17.604891+00:00 | 7 | false | ```javascript []
var minOperations = function (nums, queries) {
const sorted = nums.toSorted((a, b) => a - b);
const n = sorted.length;
// Build prefix sums
const sums = [0];
for (let i = 0; i < n; i++) sums.push(sums[i] + sorted[i]);
// Find position using binary search
const findPos = (target) => {
let left = 0, right = n;
while (left < right) {
const mid = (left + right) >> 1;
sorted[mid] < target ? left = mid + 1 : right = mid;
}
return left;
};
return queries.map(target => {
const pos = findPos(target);
return Number(BigInt(target * (2 * pos - n)) - BigInt(2 * sums[pos]) + BigInt(sums[n]));
});
};
``` | 0 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'JavaScript'] | 0 |
minimum-operations-to-make-all-array-elements-equal | BEATS 63% using prefixSumm & binarySearch | beats-63-using-prefixsumm-binarysearch-b-lj5r | Code | alexander_sergeev | NORMAL | 2024-12-26T20:25:26.065808+00:00 | 2024-12-26T20:25:26.065808+00:00 | 9 | false | # Code
```java []
class Solution {
public List<Long> minOperations(int[] nums, int[] queries) {
int n = nums.length;
Arrays.sort(nums);
long[] prefixArr = new long[n + 1];
for (int i = 0; i < n; i++) {
prefixArr[i + 1] = nums[i] + prefixArr[i];
}
List<Long> result = new ArrayList<>();
for (int target : queries) {
int left = 0;
int right = n - 1;
while (left < right) {
int mid = (left + right) / 2;
if (nums[mid] >= target + 1) {
right = mid;
} else left = mid + 1;
}
long posDiff = Math.abs(nums[left] - target);
long beforePos = (long) target * (left) - prefixArr[left];
long afterPos = (prefixArr[n] - prefixArr[left + 1]) - (long) target * (n - left - 1);
result.add(posDiff + beforePos + afterPos);
}
return result;
}
}
``` | 0 | 0 | ['Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Easy | easy-by-rifatt-oq78 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Rifatt | NORMAL | 2024-12-22T20:40:14.788938+00:00 | 2024-12-22T20:40:14.788938+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
vector<long long> ans;
int n=nums.size();
sort(nums.begin(),nums.end());
vector<long long> prefixSum(n+1,0);
for(int i=1;i<=n;i++){
prefixSum[i]=prefixSum[i-1]+nums[i-1];
}
for(auto it:queries){
auto idx=upper_bound(nums.begin(),nums.end(),it)-nums.begin();
long long left=idx*it-prefixSum[idx];
long long right=(prefixSum[n]-prefixSum[idx])-(n-idx)*it;
ans.push_back(left+right);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Absolute PreBinaryS | absolute-prebinarys-by-tonitannoury01-lxl4 | IntuitionApproachComplexity
Time complexity:
O(nlog(n))
Space complexity:
O(n)
Code | tonitannoury01 | NORMAL | 2024-12-22T14:46:43.195436+00:00 | 2024-12-22T14:46:43.195436+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(nlog(n))
- Space complexity:
O(n)
# Code
```javascript []
/**
* @param {number[]} nums
* @param {number[]} queries
* @return {number[]}
*/
var minOperations = function (nums, queries) {
nums.sort((a, b) => a - b);
let pre = [];
let sum = 0;
let res = [];
for (let n of nums) {
sum += n;
pre.push(sum);
}
for (let q of queries) {
let left = 0;
let right = nums.length;
let pivot;
while (left < right) {
let mid = Math.floor((left + right) / 2);
if (nums[mid] > q) {
right = mid;
} else {
left = mid + 1;
}
}
let t1 = q * left;
let t2 = q * (nums.length - left);
let c1 = pre[left - 1] || 0;
let c2 = pre[pre.length - 1] - (pre[left - 1] || 0);
res.push(Math.abs(t1 - c1) + Math.abs(t2 - c2));
}
return res;
};
``` | 0 | 0 | ['JavaScript'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Easy solution using Binary Search | easy-solution-using-binary-search-by-_jy-gqvk | Code\njava []\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] q) {\n Arrays.sort(nums);\n List<Long> ans = new ArrayList< | _jyoti_geek | NORMAL | 2024-11-28T14:51:50.851292+00:00 | 2024-11-28T14:51:50.851320+00:00 | 7 | false | # Code\n```java []\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] q) {\n Arrays.sort(nums);\n List<Long> ans = new ArrayList<>();\n int n = nums.length;\n int m = q.length;\n long[] pre = new long[n];\n pre[0] = nums[0];\n for(int i=1;i<n;i++){\n pre[i] = pre[i-1]+nums[i];\n }\n\n for(int i=0;i<m;i++){\n int query = q[i];\n\n int idx = helper(nums, query);\n if(idx==n){\n ans.add((n*1L*query)-pre[n-1]);\n }else{\n long right = (pre[n-1]-pre[idx]+nums[idx])-(n-idx)*1L*query;\n long left = 0;\n if(idx!=0){\n left = (idx*1L*query)-(pre[idx-1]-pre[0]+nums[0]);\n }\n ans.add(left + right);\n }\n }\n return ans;\n }\n\n public int helper(int[] nums, int target){\n int low = 0, high = nums.length-1;\n\n while(low<=high){\n int mid = low+(high-low)/2;\n\n if(nums[mid]<=target){\n low = mid+1;\n }else{\n high = mid-1;\n }\n }\n return low;\n }\n}\n``` | 0 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | scala solution | scala-solution-by-vititov-rrul | scala []\nobject Solution {\n def minOperations(nums: Array[Int], queries: Array[Int]): List[Long] = {\n val sorted = nums.to(Vector).map(_.toLong).sorted\n | vititov | NORMAL | 2024-10-14T15:06:17.711713+00:00 | 2024-10-14T15:06:17.711737+00:00 | 0 | false | ```scala []\nobject Solution {\n def minOperations(nums: Array[Int], queries: Array[Int]): List[Long] = {\n val sorted = nums.to(Vector).map(_.toLong).sorted\n val pfx = sorted.iterator.drop(1).scanLeft((sorted.head,0L,1)){case ((last,sum,cnt), num) =>\n (num,sum+(num-last).abs*cnt,cnt+1)\n }.to(Vector)\n val sfx = sorted.reverseIterator.drop(1).scanLeft((sorted.last,0L,1)){case ((last,sum,cnt), num) =>\n (num,sum+(num-last).abs*cnt,cnt+1)\n }.to(Vector).reverse\n queries.toList.map(_.toLong).map{q =>\n val (y0,y1) = (\n pfx.search((q,Long.MinValue,Int.MinValue)).insertionPoint,\n sfx.search((q,Long.MaxValue,Int.MaxValue)).insertionPoint)\n if(y0!=y1) pfx(y0)._2 + sfx(y1-1)._2\n else if(y0==sfx.size) pfx.last._2 + (q-pfx.last._1).abs*pfx.last._3\n else if(y0==0) sfx.head._2 + (sfx.head._1-q).abs*sfx.head._3\n else pfx(y0-1)._2 + (q-pfx(y0-1)._1)*pfx(y0-1)._3 + sfx(y1)._2 +(sfx(y1)._1-q)*sfx(y1)._3\n }\n }\n}\n``` | 0 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'Scala'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Python3 Combine { sorting, binary search, prefix sums } O(nlgn) + O(qlgn) time O(N) Space Iterative | python3-combine-sorting-binary-search-pr-3bqu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | 2018hsridhar | NORMAL | 2024-10-11T01:50:12.104522+00:00 | 2024-10-11T01:50:12.104553+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\n\'\'\'\nURL := https://leetcode.com/problems/minimum-operations-to-make-all-array-elements-equal/description/\n2602. Minimum Operations to Make All Array Elements Equal\n\nCategories : Sort, Greedy, Binary Search, Arithemtic, Counting\n\nComplexity\nN := len(nums) and Q := len(queries)\nT = O(NlgN) + O(QlgN)\nS = O(Q) ( Explicit ) O(1) ( Implicit )\n\n20 minutes and passed :-)\ndo better with prefix sums?\nCorrect but TLE -> we\'re gonna need prefix summations now :-) \n\'\'\'\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n m = len(nums)\n answer = [0 for idx in range(len(queries))]\n prefixSums = [0 for idx in range(len(nums))]\n prefixSumsRight = [0 for idx in range(len(nums))]\n runSum = 0\n for index, num in enumerate(nums):\n runSum += num\n prefixSums[index] = runSum\n\n runSum = 0\n for index, num in reversed(list(enumerate(nums))):\n runSum += num\n prefixSumsRight[index] = runSum\n\n for index, query in enumerate(queries):\n deltaLower = 0\n deltaUpper = 0\n lowerSum = 0\n upperSum = 0\n\n lowerIdx = self.bSearchLower(nums, query)\n if(lowerIdx != -1):\n lowerSum = prefixSums[lowerIdx]\n lowerEqual = query * (lowerIdx + 1)\n deltaLower = abs(lowerEqual - lowerSum)\n\n upperIdx = self.bSearchUpper(nums, query)\n if(upperIdx != -1):\n upperSum = prefixSumsRight[upperIdx]\n upperEqual = query * (len(nums) - upperIdx)\n deltaUpper = abs(upperEqual - upperSum)\n\n curProblem = deltaLower + deltaUpper\n answer[index] = curProblem\n return answer\n\n def bSearchLower(self, nums: List[int], query:int) -> int:\n targetIdx = -1\n low = 0\n high = len(nums) - 1\n while(low <= high):\n mid = floor((low + high) * 0.5)\n val = nums[mid]\n if(val <= query):\n if(mid >= targetIdx):\n targetIdx = mid\n low = mid + 1\n elif(val > query):\n high = mid - 1\n return targetIdx\n \n def bSearchUpper(self, nums: List[int], query:int) -> int:\n targetIdx = float(\'inf\')\n low = 0\n high = len(nums) - 1\n while(low <= high):\n mid = floor((low + high) * 0.5)\n val = nums[mid]\n if(val > query):\n if(mid <= targetIdx):\n targetIdx = mid\n high = mid - 1\n elif(val <= query):\n low = mid + 1\n if(targetIdx == float(\'inf\')):\n targetIdx = -1\n return targetIdx\n \n\n \n\n \n``` | 0 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | [Java] Prefix Sums + Binary Search | easy | java-prefix-sums-binary-search-easy-by-j-cip5 | Code\njava []\nclass Solution {\n private int n;\n public List<Long> minOperations(int[] nums, int[] queries) {\n List<Long> res = new ArrayList<>( | jsanchez78 | NORMAL | 2024-10-08T15:55:33.573058+00:00 | 2024-10-08T15:55:33.573087+00:00 | 7 | false | # Code\n```java []\nclass Solution {\n private int n;\n public List<Long> minOperations(int[] nums, int[] queries) {\n List<Long> res = new ArrayList<>();\n Arrays.sort(nums);\n // Init prefixSums\n this.n = nums.length;\n long[] prefix = new long[n + 1];\n for(int i = 1; i <= n; i++)\n prefix[i] = prefix[i - 1] + nums[i - 1];\n\n for(int query: queries){\n // Binary search\n int pivot = binarySearch(nums, query);\n long increase = pivot * (1L * query) - prefix[pivot];\n long decrease = prefix[n] - prefix[pivot] - ((n - pivot) * 1L * query);\n res.add(increase + decrease);\n }\n return res;\n }\n int binarySearch(int arr[], int x){\n int lo = 0, hi = n;\n while(lo < hi){\n int m = lo + ((hi - lo) >> 1);\n if (arr[m] < x)\n lo = m + 1;\n else\n hi = m;\n }\n return lo;\n }\n}\n``` | 0 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | sorting, prefix sum, binary search Python solution | sorting-prefix-sum-binary-search-python-kh0bn | Intuition\nOnce nums is sorted, we can find a dividing point for each querie using binary search. Then, the left side of nums is less than the querie and the ri | jbak | NORMAL | 2024-10-04T23:01:16.753433+00:00 | 2024-10-04T23:01:16.753454+00:00 | 24 | false | # Intuition\nOnce `nums` is sorted, we can find a dividing point for each querie using binary search. Then, the left side of `nums` is less than the querie and the right side of `nums` is greater than the querie. Using prefix sum hashmap, we can calculate the difference easily.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nsorting, prefix sum, binary search\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: `O(n log n + m log n)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n prefix_hash = {-1: 0} # index: prefix sum\n presum = 0\n n = len(nums)\n for idx, num in enumerate(nums):\n presum += num\n prefix_hash[idx] = presum\n \n ans = []\n for q in queries:\n # print(bisect_left(nums, q))\n dividing_idx = bisect_left(nums, q)\n left_side = (q * dividing_idx - prefix_hash[dividing_idx - 1])\n right_side = (prefix_hash[n-1] - prefix_hash[dividing_idx-1] - q * (n - dividing_idx))\n ans.append(left_side + right_side)\n\n return ans\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | C++ Solution || Sorting || Lower Bound || Prefix Sum | c-solution-sorting-lower-bound-prefix-su-oqlf | \ncpp []\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n // Sort the array\n sort(num | Vaibhav_Arya007 | NORMAL | 2024-09-29T19:08:17.209648+00:00 | 2024-09-29T19:08:17.209676+00:00 | 5 | false | \n```cpp []\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n // Sort the array\n sort(nums.begin(), nums.end());\n \n // Precompute the prefix sum\n int n = nums.size();\n vector<long long> prefixSum(n + 1, 0); // Use long long for prefixSum\n for (int i = 1; i <= n; i++) {\n prefixSum[i] = prefixSum[i - 1] + nums[i - 1];\n }\n\n vector<long long> ans(queries.size());\n\n // For each query, calculate the required number of operations\n for (int i = 0; i < queries.size(); i++) {\n int q = queries[i];\n \n // Find the position where nums[pos] > q using binary search\n int pos = lower_bound(nums.begin(), nums.end(), q) - nums.begin();\n \n // Left part: nums[0 ... pos-1] are less than or equal to q\n long long leftSum =(long long) q * pos - prefixSum[pos];\n \n // Right part: nums[pos ... n-1] are greater than q\n long long rightSum = (prefixSum[n] - prefixSum[pos]) - (long long)q * (n - pos);\n \n // Total number of operations for this query\n ans[i] = leftSum + rightSum;\n }\n\n return ans;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | O(mlogn) solution C++|| beats 85% | omlogn-solution-c-beats-85-by-krishnakan-yjpi | Intuition\n Describe your first thoughts on how to solve this problem. \nintuition was to find a pattern and generalize it.\n\n# Approach\n Describe your approa | krishnakant_1 | NORMAL | 2024-09-22T20:28:23.303012+00:00 | 2024-09-22T20:28:23.303050+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nintuition was to find a pattern and generalize it.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI find a number just greater than the query element and calculate the left side contribution, that is difference we need to increase the numbers in left by, to make it equal to query[i], similarly for right elements and add them up to get res[i].\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(mlog(n))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n+m)\n\n# Code\n```cpp []\nclass Solution {\n #define ll long long\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n int n = nums.size();\n int m = queries.size();\n vector<ll> res(m);\n\n sort(nums.begin(), nums.end());\n vector<ll> prefix(n);\n prefix[0] = nums[0];\n for (int i = 1; i < n; i++) {\n prefix[i] = prefix[i - 1] + nums[i];\n }\n\n for (int i = 0; i < m; i++) {\n int query = queries[i];\n int pivot = getJustBiggerIndex(nums, query);\n \n // Left side contribution (elements <= query)\n ll leftSum = (pivot > 0) ? prefix[pivot - 1] : 0;\n ll leftCount = pivot;\n ll leftOperations = query * leftCount - leftSum;\n\n // Right side contribution (elements > query)\n ll rightSum = (pivot < n) ? prefix[n - 1] - leftSum : 0;\n ll rightCount = n - leftCount;\n ll rightOperations = rightSum - query * rightCount;\n\n res[i] = leftOperations + rightOperations;\n }\n\n return res;\n }\n\n int getJustBiggerIndex(vector<int>& nums, int query) {\n int i = 0, j = nums.size() - 1;\n while (i <= j) {\n int mid = i + (j - i) / 2;\n if (nums[mid] <= query) {\n i = mid + 1;\n } else {\n j = mid - 1;\n }\n }\n return i;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | easy line by line cpp code | easy-line-by-line-cpp-code-by-varun_b_v-wqrb | \n# Code\ncpp []\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(begin(nums), end(nums) | Varun_B_V | NORMAL | 2024-09-22T12:26:04.929264+00:00 | 2024-09-22T12:26:04.929302+00:00 | 3 | false | \n# Code\n```cpp []\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(begin(nums), end(nums)); // Sort nums\n int n = nums.size();\n\n // Create prefix sum array\n vector<long long> ps(n, 0);\n ps[0] = nums[0];\n for (int i = 1; i < n; i++) {\n ps[i] = ps[i - 1] + nums[i];\n }\n\n vector<long long> ans;\n for (int x : queries) {\n int idx = lower_bound(nums.begin(), nums.end(), x) - nums.begin();\n \n // Case when idx == 0 (all elements are greater than x)\n long long leftSum = (idx > 0) ? ps[idx - 1] : 0;\n long long rightSum = ps[n - 1] - leftSum;\n\n long long leftOps = (idx > 0) ? (1LL * x * idx - leftSum) : 0;\n long long rightOps = (idx < n) ? (rightSum - 1LL * x * (n - idx)) : 0;\n\n ans.push_back(leftOps + rightOps);\n }\n\n return ans;\n }\n};\n\n``` | 0 | 0 | ['Binary Search', 'Prefix Sum', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | c++ solution | c-solution-by-dilipsuthar60-l0re | \nclass Solution {\npublic:\n int getLowerBound(vector<int>&nums, int value){\n int size=nums.size();\n int left=0,right=size-1,mid=0,index=siz | dilipsuthar17 | NORMAL | 2024-09-13T18:32:12.846664+00:00 | 2024-09-13T18:32:12.846699+00:00 | 1 | false | ```\nclass Solution {\npublic:\n int getLowerBound(vector<int>&nums, int value){\n int size=nums.size();\n int left=0,right=size-1,mid=0,index=size;\n while(left<=right){\n mid=(left+right)/2;\n if(nums[mid]>value){\n index=mid;\n right=mid-1;\n }\n else{\n left=mid+1;\n }\n }\n return index;\n }\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n int n=nums.size();\n sort(nums.begin(),nums.end());\n vector<long long>prefix(n+1,0);\n for(int i=0;i<n;i++){\n prefix[i+1]=prefix[i]+nums[i];\n }\n vector<long long>ans;\n for(auto &value:queries){\n long long index=getLowerBound(nums,value);\n long long leftSum = value*index - (prefix[index]-prefix[0]);\n long long rightSum = (prefix.back()-prefix[index]) - value*(n-index);\n ans.push_back(leftSum+rightSum);\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Simple binary search | simple-binary-search-by-risabhuchiha-njoi | \njava []\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] queries) {\n List<Long>ans=new ArrayList<>();\n Arrays.sort(nums) | risabhuchiha | NORMAL | 2024-09-12T21:41:56.308704+00:00 | 2024-09-12T21:41:56.308751+00:00 | 4 | false | \n```java []\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] queries) {\n List<Long>ans=new ArrayList<>();\n Arrays.sort(nums);\n long[]pre=new long[nums.length];\n pre[0]=nums[0];\n for(int i=1;i<pre.length;i++){\n pre[i]=pre[i-1]+nums[i];\n } \n for(int i=0;i<queries.length;i++){\n int x=queries[i];\n int l=f1(x,nums);\n int r=f2(x,nums);\n // System.out.println(l+" "+r);\n \n long aa=(long)x*(l+1)-(l==-1?0:pre[l])+pre[nums.length-1]-(r==0?0:pre[r-1])-(long)x*(nums.length-r);\n ans.add(aa);\n }\n return ans;\n }\n public int f1(int t,int[]a){\n int l=0;\n int r=a.length-1;\n int ans=-1;\n while(l<=r){\n int m=(l+r)/2;\n if(a[m]<t){\n ans=m;\n l=m+1;\n }\n else{\n r=m-1;\n }\n }\n return ans;\n }\n public int f2(int t,int[]a){\n int l=0;\n int r=a.length-1;\n int ans=a.length;\n while(l<=r){\n int m=(l+r)/2;\n if(a[m]>t){\n ans=m;\n r=m-1;\n }\n else{\n l=m+1;\n }\n }\n return ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Prefix sum + Binary search. 6 lines | prefix-sum-binary-search-6-lines-by-xxxx-fqsf | python3 []\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n pref = [*accumulate(nu | xxxxkav | NORMAL | 2024-09-11T17:36:51.763182+00:00 | 2024-09-11T17:37:05.672518+00:00 | 37 | false | ```python3 []\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n pref = [*accumulate(nums, initial = 0)]\n ans, n = [], len(nums)\n for q in queries:\n i = bisect_left(nums, q)\n ans.append((q*i - pref[i])*2 + pref[-1] - q*n) #(q*i - pref[i]) + (pref[-1]-pref[i] - q*(n-i))\n return ans\n``` | 0 | 0 | ['Binary Search', 'Prefix Sum', 'Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | python dynamic programming using left and right sums | python-dynamic-programming-using-left-an-xg83 | Intuition\nLet n = size of nums and m = size of queries. Brute force is O(n*m) but it is too slow to pass the tests. If we sort nums the problem is easier to gr | ie334 | NORMAL | 2024-08-20T04:11:30.918351+00:00 | 2024-08-20T04:11:30.918382+00:00 | 4 | false | # Intuition\nLet n = size of nums and m = size of queries. Brute force is O(n*m) but it is too slow to pass the tests. If we sort nums the problem is easier to grasp. Now for any q in queries we know things bigger than q need to be reduced to q. So use binary search on the sorted nums to find how many such elements are there and the required # of operations.\n\n# Approach\nFollow intuition and precompute left and right sums. lsums[i] = sum of elements in nums[j] where j is < i. Similarly rsums[i] = sum of elements in nums[j] where j >= i\n\n# Complexity\n- Time complexity:\nn = size of nums\nm = size of queries\n\nnlog(n) to sort nums\nn to find lsums and rsums\nfor each query we do log(n) binary search nlog(n)\n\n= O (nlog(n) + mlog(n))\n\n- Space complexity:\nO(n + m)\n\n# Code\n```python3 []\nimport bisect\n\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n n = len(nums)\n m = len(queries)\n lsums = [0 for i in range(n + 1)]\n rsums = [0 for i in range(n + 1)]\n s = sum(nums)\n r = 0\n nums = sorted(nums)\n for i in range(n):\n rsums[i] = s - r\n lsums[i] = r\n r += nums[i]\n lsums[n] = s\n rsums[n] = 0\n\n ops = [0 for i in range(m)]\n for j in range(m):\n q = queries[j]\n i = bisect.bisect_left(nums, q)\n ops[j] = rsums[i] - (n - i) * q + i * q - lsums[i]\n return ops\n\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Prefix Sum + Binary Search | Detailed Explanation | Python3 | prefix-sum-binary-search-detailed-explan-3vgc | Intuition\nWe have to equalize left and right sums based on where the desired value of all elements should be. This equalization point is a dividing index which | wavejumper45 | NORMAL | 2024-08-09T11:25:29.181635+00:00 | 2024-08-09T11:25:29.181660+00:00 | 36 | false | # Intuition\nWe have to equalize left and right sums based on where the desired value of all elements should be. This equalization point is a dividing index which can be rapidly found if the nums list is pre-sorted, using binary search. The accumulated sums (prefix sum) can be stored for all queries so it does not have to be re-computed. The tricky parts are the edge cases which are not so hard when you think it through.\n\n# Approach\nSo, pre-sort the list using Python3 List sort() method (timsort O(n log n)). Use itertools.accumulate to create a prefix sum. We want to 0 pad this (add a 0 at the start) so we don\'t have to offset the bisect indexes. Bisect right is what we want. When we are equalizing to a value that already exists, the index which is returned points just past the end of the value. With the 0-padding, this becomes the index of the prefix sum which includes the last value which is <= the desired. The edge case with bisect is that it points to len(arr). When this happens, we would get out of bounds, so need to test if that is the case and offset it by -1. At that point it would correspond to the left sum equaling again the last value which is <= the desired. It is trivial to then get the right sum, which is just the last element of the prefix array (equal to the sum of the entire array) subtracted by the left sum. Then, avoid dealing with floats (if you divided the left / right sums by the number of their elements) by just multiplying the number of elements in the left / right sections of the array by the desired value. By then subtracting from this the current sums of the left / right sections, you get the number of increment / decrement operations you need to equalize the entire array.\n\nThen just do this for each q in queries, append to a ret list, and return that list at the end.\n\n# Complexity\n- Time complexity:\n$$O(n\\ log\\ n)$$ - for time growth relative to the size of the array, Python\'s built in timsort and bisect binary search for each q in queries are of equal complexity (linearithmic)\n\n- Space complexity:\n$$O(n)$$ - for prefix array\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n n = len(nums)\n prefix = [0] + list(itertools.accumulate(nums))\n ret = []\n for q in queries:\n dividingIndex = bisect.bisect_right(nums, q)\n\n if dividingIndex == n:\n dividingIndex -= 1\n\n leftSum = prefix[dividingIndex]\n leftNumberElem = dividingIndex\n\n rightSum = prefix[-1] - leftSum\n rightNumberElem = n - dividingIndex\n\n leftDelta = abs(leftNumberElem * q - leftSum)\n rightDelta = abs(rightNumberElem * q - rightSum)\n\n ret.append(leftDelta + rightDelta)\n return ret\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Easy, Beginner-Friendly - Beats 100% | easy-beginner-friendly-beats-100-by-rich-50ta | \nclass Solution {\n public List<Long> minOperations(int[] nums, int[] queries) {\n int n = nums.length;\n Arrays.sort(nums);\n long[] s | RichardLeee | NORMAL | 2024-08-01T10:56:04.689685+00:00 | 2024-08-01T10:56:04.689713+00:00 | 25 | false | ```\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] queries) {\n int n = nums.length;\n Arrays.sort(nums);\n long[] sum = new long[n + 1];\n for (int i = 0; i < n; i++) {\n sum[i + 1] = sum[i] + nums[i];\n }\n \n List<Long> list = new ArrayList();\n for (int q : queries) {\n int lower = lowerBound(nums, q);\n long res = 0;\n res += (long) (lower - 0 + 1) * q - sum[lower + 1];\n res += sum[n] - sum[lower + 1] - (long) (n - 1 - lower) * q;\n list.add(res);\n }\n \n return list;\n }\n \n public int lowerBound(int[] nums, int q) {\n int l = 0, r = nums.length - 1;\n while (l <= r) {\n int m = l + r >> 1;\n if (nums[m] <= q) {\n l = m + 1;\n } else {\n r = m - 1; \n }\n }\n \n return r;\n }\n}\n\n//tc: O(nlogn)\n//sc: O(n)\n``` | 0 | 0 | ['Binary Search', 'Prefix Sum', 'Java'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Kotlin beats 100% | kotlin-beats-100-by-usernamectrlc-rwr1 | Intuition\n Describe your first thoughts on how to solve this problem. \nsort nums in order to break sort nums into 2 part. \nfirst part that every element is l | usernamectrlc | NORMAL | 2024-07-21T21:38:40.939876+00:00 | 2024-07-21T21:38:40.939907+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nsort nums in order to break sort nums into 2 part. \nfirst part that every element is less than current query \nsecond part that every element is equal or more than current querry\n\nuse binary search to find the first index that element is equal or more than the querry \n\nAfter that use presum left and presum right to calculate the final answer\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n fun minOperations(nums: IntArray, queries: IntArray): List<Long> {\n nums.sort()\n val preSum = LongArray(nums.size + 1)\n\n nums.forEachIndexed { i, number ->\n preSum[i + 1] = preSum[i] + number\n }\n\n val res = mutableListOf<Long>()\n val n = nums.size\n val maxNum = nums.maxOrNull() ?: 0\n\n queries.forEach { query ->\n if (query > maxNum) {\n res.add(query.toLong() * n - preSum.last())\n } else {\n val index = binarySearch(nums, query)\n val leftSum = preSum[index]\n val rightSum = preSum.last() - preSum[index]\n val leftOps = query.toLong() * index - leftSum\n val rightOps = rightSum - query.toLong() * (n - index)\n res.add(leftOps + rightOps)\n }\n }\n\n return res\n }\n\n private fun binarySearch(nums: IntArray, target: Int): Int {\n var left = 0\n var right = nums.size\n\n while (left < right) {\n val mid = left + (right - left) / 2\n if (nums[mid] < target) {\n left = mid + 1\n } else {\n right = mid\n }\n }\n\n return left\n }\n}\n\n``` | 0 | 0 | ['Binary Search', 'Sorting', 'Prefix Sum', 'Kotlin'] | 0 |
minimum-operations-to-make-all-array-elements-equal | C++ solution | c-solution-by-siddhantnigam-0z4t | Code\n\ntypedef long long ll;\n\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.be | siddhantnigam | NORMAL | 2024-07-15T12:57:19.661921+00:00 | 2024-07-15T12:57:19.661954+00:00 | 2 | false | # Code\n```\ntypedef long long ll;\n\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(), nums.end());\n\n ll n = nums.size();\n vector<ll> pref(n);\n pref[0] = nums[0];\n for(int i=1; i<n; i++)\n pref[i] = pref[i - 1] + nums[i];\n\n vector<ll> suff(n);\n suff.back() = nums.back();\n for(int i=n-2; i>=0; i--)\n suff[i] = nums[i] + suff[i + 1];\n\n vector<ll> res(queries.size());\n for(ll i=0; i<queries.size(); i++) {\n ll l = lower_bound(nums.begin(), nums.end(), queries[i]) - nums.begin();\n if(l > 0)\n res[i] = (queries[i] * l) - pref[l - 1];\n ll h = upper_bound(nums.begin(), nums.end(), queries[i]) - nums.begin();\n if(h < n)\n res[i] += suff[h] - (queries[i] * (n - h)); \n }\n\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | C++ || SORTING || LOWER BOUND || Binary Search || Prefix Sum + BRUTE FORCE | c-sorting-lower-bound-binary-search-pref-y3v8 | \n\n# Complexity\n- Time complexity:\nO(m)+O(nlogN)+O(mlogN)\nFor brute force : O(mn)\n\n- Space complexity:\nO(m)\n\n# Code\n\nclass Solution {\npublic:\n#defi | ayush089 | NORMAL | 2024-07-02T11:52:09.079312+00:00 | 2024-07-02T11:52:09.079337+00:00 | 8 | false | \n\n# Complexity\n- Time complexity:\nO(m)+O(nlogN)+O(mlogN)\nFor brute force : O(mn)\n\n- Space complexity:\nO(m)\n\n# Code\n```\nclass Solution {\npublic:\n#define ll long long\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n // BRUTE\n // ll n = nums.size();\n // ll m = queries.size();\n // vector<ll> ans(m, 0);\n // for (ll i = 0; i < m; i++) {\n // ll data = queries[i];\n // ll change = 0;\n // for (ll j = 0; j < n; j++) {\n // change += abs(nums[j] - data);\n // }\n // ans[i] = change;\n // }\n // return ans;\n sort(nums.begin(), nums.end());\n ll n = nums.size();\n ll m = queries.size();\n vector<ll> prefix(n), ans(m);\n prefix[0] = nums[0];\n for (ll i = 1; i < n; i++) {\n prefix[i] = prefix[i - 1] + nums[i];\n }\n for (ll i = 0; i < m; i++) {\n ll res = 0;\n ll data = queries[i];\n int lb = lower_bound(nums.begin(), nums.end(), data) - nums.begin();\n if (lb > 0) {\n res += data * lb - prefix[lb - 1];\n }\n\n if (lb < n) {\n res += (prefix[n - 1] - (lb > 0 ? prefix[lb - 1] : 0)) -\n (n - lb) * data;\n }\n\n ans[i] = res;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | 🐱👓Simple and easy to understandable approach ✨ || Full Explanation with example | simple-and-easy-to-understandable-approa-95qp | Intuition\n Describe your first thoughts on how to solve this problem. \n\nOur basic intituion is, if we have to reach to y from x (knowing x <= y) considering | ravi_thakur_ | NORMAL | 2024-06-29T14:19:11.331810+00:00 | 2024-06-29T14:19:11.331850+00:00 | 69 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nOur basic intituion is, if we have to reach to `y` from `x` (knowing x <= y) considering doing one operation at a time. Then, total operation will be `y-x`. and from `x` and `z` to `y` (knowing x, z <= y), the total operation will be `y-x` and `y-z` and the combined total operation will be `2y - (x + z)`.\n\nFor Example, we have `nums = [1, 2, 3, 4, 5]` and `queries = [4]`.\nSo, we reach to 4 from 1 in 3 steps, from 2 in 2 steps, from 3 in 1 steps, from 4 in 0 steps and from 5 in 1 steps.\n\nTherefore, total operations will be 7.\n\n\nNow to reach to 4 from 1, 2, 3 the combined total operation will be `3 * 4 - (1 + 2 + 3) = 6` and from 4 and 5 combined total operation is `(4 + 5) - 2 * 4 = 1`\n\nThe formula is `n x target - (sum of all elements)` if all elements are less than equal to target. and `(sum of all elements) - n x target` if all elements greater than equal to target, where _n_ is no of elements\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSort the `nums` array. And find the [`prefixSum`](https://leetcode.com/problems/running-sum-of-1d-array/description/) for the sorted `nums` array.\n\nNow iterate over the `queries` list. and find the optimal position for each query in sorted `nums` list (say `idx`) using binary search.\n\nif `idx == n` or `idx == 0`: add `abs(query * n - prefixSum[n-1])` to your `ans` array.\nelse: calculate the total operation for the left side of `idx` _i.e.,_ `abs(prefixSum[idx-1] - query * idx)` and total operation for the right side (from `idx` to `n-1`) _i.e.,_ `abs(query * (n-idx) - (prefixSum[n-1] - prefixSum[idx-1]))`, add them and append them in your `ans` array.\n\nNow `return ans`\n \n# Complexity\n- Time complexity: $O(n + (m+n) log(n))$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n\n nums.sort()\n n = len(nums)\n\n prefixSum = []\n for num in nums:\n if not prefixSum:\n prefixSum.append(num)\n continue\n last = prefixSum[-1]\n prefixSum.append(num + last)\n\n ans = []\n for query in queries:\n tmp = 0\n\n idx = self.positionInSortedArray(nums, query)\n if idx == n or idx == 0:\n tmp += abs(query * n - prefixSum[n - 1])\n elif 0 < idx < n:\n temp = query * (n-idx)\n # left\n tmp += abs(query * idx - prefixSum[idx - 1])\n # right\n tmp += abs(query * (n - idx) - (prefixSum[n - 1] - prefixSum[idx - 1]))\n\n ans.append(tmp)\n\n return ans\n\n def positionInSortedArray(self, arr: List[int], k: int) -> int:\n\n low, high = 0, len(arr)\n\n while low < high:\n\n mid = (low + high) // 2\n if arr[mid] == k:\n return mid\n elif arr[mid] > k:\n high = mid\n else:\n low = mid + 1\n\n return (low + high) // 2\n``` | 0 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | C++ | Prefix Sum | Binary Search | Sorting | Math | c-prefix-sum-binary-search-sorting-math-gdl5c | Code\n\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(),nums.end());\n | MrChromatic | NORMAL | 2024-06-27T02:57:23.687182+00:00 | 2024-06-27T02:57:23.687230+00:00 | 3 | false | # Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(),nums.end());\n int n=nums.size();\n vector<long long> pref(n,0);\n pref[0]=nums[0];\n for(int i=1;i<n;i++)\n pref[i]=nums[i]+pref[i-1];\n vector<long long> ans;\n for(long long q:queries){\n int ind=upper_bound(nums.begin(),nums.end(),q)-nums.begin();\n long long diff=0;\n if(ind-1>=0){\n diff+=q*ind-pref[ind-1];\n diff+=pref[n-1]-pref[ind-1]-(n-ind)*q;\n }\n else\n diff+=pref[n-1]-n*q;\n ans.push_back(diff);\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Math', 'Binary Search', 'Prefix Sum', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Python3 solution using prefix sum and binary search | python3-solution-using-prefix-sum-and-bi-iaon | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ryderwang | NORMAL | 2024-06-13T00:30:47.873877+00:00 | 2024-06-13T00:30:47.873894+00:00 | 38 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n nums.sort()\n prefix_sum = []\n su = 0\n for i in nums:\n su += i\n prefix_sum.append(su)\n res = []\n for cur in queries:\n ind = self.binary_search(cur, nums)\n if nums[ind] > cur:\n before = 0\n ind -= 1\n else:\n before = prefix_sum[ind]\n after = prefix_sum[-1] - before\n before_dis = cur * (ind + 1) - before\n after_dis = after - cur * (len(nums) - ind - 1)\n res.append(before_dis + after_dis)\n return res\n \n def binary_search(self, cur: int, nums: List[int]) -> int:\n start = 0\n end = len(nums) - 1\n while start + 1 < end:\n mid = start + (end - start) // 2\n if nums[mid] == cur:\n return mid\n elif nums[mid] > cur:\n end = mid\n else:\n start = mid\n if nums[end] < cur:\n return end\n return start\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | This solution is very beginner friendly. | this-solution-is-very-beginner-friendly-xznwj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | HellishAbhi | NORMAL | 2024-06-11T10:49:14.483036+00:00 | 2024-06-11T10:49:14.483074+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums,vector<int>& queries) {\n vector<long long> answer;\n int n = nums.size();\n vector<long long> presum(n);\n\n long long inc = 0;\n long long dec = 0;\n long long value = 0;\n\n sort(nums.begin(), nums.end());\n\n presum[0] = nums[0];\n for(int i = 1; i < n; i++){\n presum[i] = presum[i-1] + nums[i];\n }\n\n for(auto q : queries){\n int s = 0;\n int e = n-1;\n int mid;\n value = q;\n\n while(s <= e){\n mid = s + (e-s)/2;\n if(nums[mid] <= value){\n s = mid+1;\n }\n else{\n e = mid-1;\n }\n }\n\n inc = 0;\n dec = 0;\n\n if(s > 0){\n inc = abs((value * s) - presum[s-1]);\n }\n \n if(s == 0){\n dec = abs(value*n - presum[n-1]);\n }\n else{\n dec = abs((value * (n-s)) - (presum[n-1]-presum[s-1]));\n }\n\n answer.push_back(inc + dec);\n }\n return answer;\n }\n};\n```\n\nPlease upvote my solution and share it. | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | C# Binary Search | c-binary-search-by-ilya-a-f-cuw1 | csharp\npublic class Solution\n{\n public IList<long> MinOperations(int[] nums, int[] queries)\n {\n Array.Sort(nums);\n\n var sum = 0L;\n | ilya-a-f | NORMAL | 2024-06-03T19:57:31.064929+00:00 | 2024-06-03T19:57:31.064947+00:00 | 22 | false | ```csharp\npublic class Solution\n{\n public IList<long> MinOperations(int[] nums, int[] queries)\n {\n Array.Sort(nums);\n\n var sum = 0L;\n var prefix = Array.ConvertAll(nums, num => sum += num);\n\n return Array.ConvertAll(queries, query =>\n {\n var index = Array.BinarySearch(nums, query);\n var upperBound = Math.Abs(index + 1);\n\n var ops = prefix[^1];\n ops += query * ( 2L * upperBound - nums.Length);\n ops -= 2L * prefix.ElementAtOrDefault(upperBound - 1);\n return ops;\n });\n }\n}\n``` | 0 | 0 | ['Binary Search', 'C#'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Sorting || Prefix sum|| (nlogn) | sorting-prefix-sum-nlogn-by-kishansingh1-hupy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kishansingh1 | NORMAL | 2024-06-03T18:18:51.607624+00:00 | 2024-06-03T18:18:51.607655+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(nlog( n))$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n int n=nums.size();\n sort(nums.begin(),nums.end());\n vector<long long>presum;\n long long sum=0;\n presum.push_back(sum);\n for(auto it:nums)\n {\n sum+=it;\n presum.push_back(sum);\n }\n int m=presum.size();\n vector<long long >ans;\n for(int i=0;i<queries.size();i++){\n int ind= lower_bound(nums.begin(),nums.end(),queries[i])-nums.begin();\n cout<<ind<<endl;\n if(ind==0){\n long long sum=presum[m-1]-presum[0];\n long long req=static_cast<long long>(queries[i])*(n-ind);\n ans.push_back(sum-req);\n }\n else if(ind==n){\n long long req=static_cast<long long>(queries[i])*n;\n long long sum=presum[m-1];\n ans.push_back(req-sum);\n }\n else {\n long long sum1=static_cast<long long> (queries[i])*(ind)-presum[ind];\n long long sum2= presum[m-1]-presum[ind]-static_cast<long long>(queries[i])*(n-ind);\n ans.push_back(sum1+sum2);\n\n }\n }\n\n return ans;\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | c++ code | c-code-by-vikasverma_12-h8fh | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Vikasverma_12 | NORMAL | 2024-05-30T09:00:57.813386+00:00 | 2024-05-30T09:00:57.813415+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n long long n=nums.size();\n sort(nums.begin(),nums.end());\n vector<long long > pre(n+1,0);\n for(int i=0;i<n;i++){\n pre[i+1]=pre[i]+nums[i];\n }\n \n vector<long long > ans;\n for(auto it:queries){\n long long l=lower_bound(nums.begin(),nums.end(),it)-nums.begin();\n long long up=upper_bound(nums.begin(),nums.end(),it)-nums.begin();\n long long val=it*l-(pre[l]-pre[0]);\n if(up!=n){\n val+=(pre[n]-pre[up])-it*(n-up);\n }\n ans.push_back(val);\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Ez solution | ez-solution-by-ayushprakash-ehqf | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | AyushPrakash_ | NORMAL | 2024-05-29T16:39:18.470512+00:00 | 2024-05-29T16:39:18.470530+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:M*log(N) \n- no of queries == M and length of array is N\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n #define ll long long \n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(),nums.end());\n int n = nums.size();\n vector<ll> ps(n+1,0);\n\n for(int i = 0 ;i<n;i++){\n ps[i+1] += nums[i]+ps[i];\n }\n nums.insert(nums.begin(),0);\n n++;\n vector<ll> ans ;\n for(auto q : queries){\n ll llind = lower_bound(nums.begin(),nums.end(),q)-nums.begin()-1;\n ll uind = upper_bound(nums.begin(),nums.end(),q)-nums.begin();\n ll val = q*llind -( ps[llind] -ps[0]);\n if(uind!=n){\n val +=( ps[n-1] - ps[uind-1] )- q*(n-uind);\n }\n ans.push_back(val);\n }\n return ans; \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | JAVA Solution | java-solution-by-anurag0608-oxa2 | Intuition\nThere are already good solutions posted under solutions section. But I felt there are fewer good java solution. So posting it here.\n\n# Complexity\n | anurag0608 | NORMAL | 2024-05-28T21:28:16.726382+00:00 | 2024-05-28T21:28:16.726399+00:00 | 34 | false | # Intuition\nThere are already good solutions posted under solutions section. But I felt there are fewer good java solution. So posting it here.\n\n# Complexity\n- Time complexity: $$O(mlogn)$$, where m is query length and n is the size of array nums.\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\n public List<Long> minOperations(int[] nums, int[] queries) {\n Arrays.sort(nums);\n int n = nums.length;\n long[] pSum = new long[n+1];\n for(int i=1;i<=n;i++){\n pSum[i]+=pSum[i-1]+nums[i-1];\n }\n List<Long> ans = new ArrayList<>();\n for(int i=0;i<queries.length;i++){\n int[] smaller = howManySmaller(nums, queries[i]), \n larger = howManyGreater(nums, queries[i]);\n // smaller incs, larger decr\n long ops = 0;\n if(smaller[1]!=-1){\n ops = (long)((long)queries[i]*smaller[0] - pSum[smaller[1]+1]);\n }\n if(larger[1]!=-1){\n ops+= (long)(pSum[n] - pSum[larger[1]] - (long)queries[i]*larger[0]);\n }\n ans.add(ops);\n }\n return ans;\n }\n private int[] howManySmaller(int[] nums, int x){\n int l = -1, r = nums.length-1;\n while(l<r){\n int mid = r+(l-r)/2;\n if(nums[mid] >= x){\n r = mid-1;\n }else{\n l = mid;\n }\n }\n if(l < 0){\n return new int[]{0, -1};\n }\n return new int[]{l+1, l};\n }\n private int[] howManyGreater(int[] nums, int x){\n int l = 0, r = nums.length;\n while(l<r){\n int mid = l+(r-l)/2;\n if(nums[mid] <= x){\n l = mid+1;\n }else{\n r = mid;\n }\n }\n if(l >= nums.length){\n return new int[]{0, -1};\n }\n return new int[]{nums.length-l, l};\n }\n \n}\n// 1 3 6 8\n\n// q = 1\n\n\n``` | 0 | 0 | ['Binary Search', 'Sorting', 'Prefix Sum', 'Java'] | 1 |
minimum-operations-to-make-all-array-elements-equal | beats 90% at speed, 42ms, O(nlogn + n + m) time | beats-90-at-speed-42ms-onlogn-n-m-time-b-s0iu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | SingSongZepf | NORMAL | 2024-05-22T10:05:19.116687+00:00 | 2024-05-22T10:05:19.116720+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimpl Solution {\n\tpub fn min_operations(mut nums: Vec<i32>, queries: Vec<i32>) -> Vec<i64> {\n\t\tnums.sort_unstable(); // O(nlogn)\n\t\tlet (nl, ql) = (nums.len(), queries.len());\n\t\tlet mut prefix_sums: Vec<i64> = Vec::with_capacity(nl);\n\t\tnums.iter().fold(0i64, |acc, &val| {\n\t\t\tprefix_sums.push(acc + val as i64);\n\t\t\tacc + val as i64\n\t\t}); // O(n)\n\t\tqueries.iter().fold(Vec::<i64>::with_capacity(ql), |mut acc, &q| {\n\t\t\tif let Some(idx) = Self::find_index(&nums, q) {\n\t\t\t\tacc.push(((idx << 1) as i64 + 2 - nl as i64) * q as i64 - 2 * prefix_sums[idx] + prefix_sums[nl-1]);\n\t\t\t\tacc\n\t\t\t} else {\n\t\t\t\tacc.push(prefix_sums[nl-1] - nl as i64 * q as i64);\n\t\t\t\tacc\n\t\t\t}\n\t\t})\n\t}\n\tfn find_index(nums: &Vec<i32>, n: i32) -> Option<usize> {\n\t\tlet mut result: Option<usize> = None;\n\t\tlet mut low: i32 = 0;\n\t\tlet mut high: i32 = nums.len() as i32 - 1;\n\t\twhile low <= high {\n\t\t\tlet mid = low + (high - low) / 2;\n\t\t\tif nums[mid as usize] < n {\n\t\t\t\tresult = Some(mid as usize);\n\t\t\t\tlow = mid + 1;\n\t\t\t} else {\n\t\t\t\thigh = mid - 1;\n\t\t\t}\n\t\t}\n\t\tresult\n\t}\n}\n\n``` | 0 | 0 | ['Rust'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Python3 O(N + MlogN) Solution (no bisect tricks) | python3-on-mlogn-solution-no-bisect-tric-3v3w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\n# Complexity\n- Time complexity: O(N +MlogN)\n- Space complexity: O(N)\ | ihateinterviews | NORMAL | 2024-05-20T03:22:36.084441+00:00 | 2024-05-20T03:22:36.084457+00:00 | 47 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n# Complexity\n- Time complexity: O(N +MlogN)\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int], queries: List[int]) -> List[int]:\n answer = []\n nums.sort()\n leftSums = [0] * len(nums)\n rightSums = [0] * len(nums)\n\n leftSums[0] = nums[0]\n for i in range(1, len(nums)):\n leftSums[i] = leftSums[i - 1] + nums[i]\n\n rightSums[len(rightSums) - 1] = nums[-1]\n for i in range(len(nums) - 2, -1, -1):\n rightSums[i] = rightSums[i + 1] + nums[i]\n\n for n in queries:\n # Binary search to find i where nums[i] <= n\n left = 0\n right = len(nums) - 1\n closest = -1\n while left <= right:\n mid = (left + right) // 2\n if nums[mid] <= n:\n closest = mid\n left = mid + 1\n else:\n right = mid - 1\n\n smaller, larger = 0, 0\n if closest >= 0:\n smaller = abs(leftSums[closest] - (n * (closest + 1)))\n if closest + 1 < len(nums):\n larger = abs((len(nums) - closest - 1) * n - rightSums[closest + 1])\n\n answer.append(smaller + larger)\n\n return answer\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Easy sol^n | easy-soln-by-singhgolu933600-p61w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | singhgolu933600 | NORMAL | 2024-05-09T11:00:40.461066+00:00 | 2024-05-09T11:00:40.461099+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n sort(nums.begin(),nums.end());\n vector<long long>ans;\n vector<long long>sum(nums.size(),0);\n sum[0]=nums[0];\n for(int i=1;i<nums.size();i++)\n {\n sum[i]=sum[i-1]+nums[i];\n }\n for(int i=0;i<queries.size();i++)\n {\n int index=-1;\n int s=0;\n int e=nums.size()-1;\n int mid=s+(e-s)/2;\n while(s<=e)\n {\n if(nums[mid]==queries[i])\n {\n index=mid;\n break;\n }\n else if(nums[mid]>queries[i])\n {\n e=mid-1;\n }\n else\n {\n index=mid;\n s=mid+1;\n }\n mid=s+(e-s)/2;\n }\n long long left=1;\n long long right=1;\n index++;\n left=((long long)queries[i])*index;\n right=((long long)queries[i])*(nums.size()-index);\n index--;\n if(index!=-1)\n {\n left=left-sum[index];\n right=(sum[nums.size()-1]-sum[index])-right;\n }\n else\n {\n left=0;\n right=sum[nums.size()-1]-right;\n }\n ans.push_back(left+right);\n } \n return ans;\n }\n};\n``` | 0 | 0 | ['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
minimum-operations-to-make-all-array-elements-equal | beat 100% memory | beat-100-memory-by-lordemilio-kycp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | LordEmilio | NORMAL | 2024-04-18T16:26:29.485662+00:00 | 2024-04-18T16:26:29.485692+00:00 | 33 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def minOperations(self, nums, queries):\n nums.sort() # Sort the numbers once\n numsLen = len(nums)\n prefix_sums = [0] * (numsLen + 1)\n\n # Compute prefix sums for absolute differences\n for i in range(1, numsLen + 1):\n prefix_sums[i] = prefix_sums[i - 1] + nums[i - 1]\n\n output = []\n for query in queries:\n if query >= nums[-1]:\n # Calculate directly since all nums are less than or equal to query\n output.append(sum(query - num for num in nums))\n else:\n # Use binary search to find the split point\n l, r = 0, numsLen - 1\n while l <= r:\n mid = (l + r) // 2\n if nums[mid] > query:\n r = mid - 1\n else:\n l = mid + 1\n\n # l is now the count of numbers <= query\n sum_lower = l * query - prefix_sums[l] # Sum for numbers <= query\n sum_higher = (prefix_sums[numsLen] - prefix_sums[l]) - (numsLen - l) * query # Sum for numbers > query\n output.append(sum_lower + sum_higher)\n\n return output\n\n``` | 0 | 0 | ['Python'] | 0 |
minimum-operations-to-make-all-array-elements-equal | Prefix Sum + Binary Search || C++ Solution | prefix-sum-binary-search-c-solution-by-l-g5m1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Last_Of_UsOO | NORMAL | 2024-04-09T05:27:22.642936+00:00 | 2024-04-09T05:27:22.642985+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n Time Complexity : O(Nlog(N))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n Space Complexity : O(N);\n\n# Code\n```\nstatic auto fastio = []() {\n std::ios_base::sync_with_stdio(false);\n std::cin.tie(nullptr);\n std::cout.tie(nullptr);\n};\n\nclass Solution {\npublic:\n vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {\n fastio();\n int n = nums.size();\n int m = queries.size();\n sort(nums.begin(), nums.end());\n vector<long long> prefix_sum;\n prefix_sum.push_back(nums[0]);\n for (int i = 1; i < n; i++) {\n prefix_sum.push_back(prefix_sum.back() + nums[i]);\n }\n vector<long long> result;\n for (int i = 0; i < m; i++) {\n long long val = queries[i];\n int val_lb =\n lower_bound(nums.begin(), nums.end(), val) - nums.begin();\n long long sum, req;\n if (val_lb == n) {\n sum = prefix_sum[val_lb - 1];\n req = val * n;\n result.push_back(req - sum);\n } else if (val_lb == 0) {\n (sum, req) = {0};\n // cout << sum << " " << req << endl;\n if (nums[val_lb] == queries[i]) {\n sum = prefix_sum[n - 1] - prefix_sum[0];\n req = val * (n - 1);\n } else {\n sum = prefix_sum[n - 1];\n req = val * (n);\n }\n result.push_back(sum - req);\n } else {\n if (nums[val_lb] == queries[i]) {\n if (val_lb == n - 1) {\n sum = prefix_sum[val_lb - 1];\n req = val * (n - 1);\n result.push_back(req - sum);\n } else {\n sum = (val * (val_lb)) - prefix_sum[val_lb - 1];\n sum += prefix_sum[n - 1] - prefix_sum[val_lb] -\n (val * (n - 1 - val_lb));\n result.push_back(sum);\n }\n } else {\n sum = (val * (val_lb)) - prefix_sum[val_lb - 1];\n sum += (prefix_sum[n - 1] - prefix_sum[val_lb - 1]) -\n (val * (n - val_lb));\n result.push_back(sum);\n }\n }\n }\n return result;\n }\n};\n``` | 0 | 0 | ['Binary Search', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
maximum-difference-score-in-a-grid | [Java/C++/Python] DP, Minimum on Top-Left | javacpython-dp-minimum-on-top-left-by-le-7zk7 | Intuition\nMove from c1 to ck with path c1,c2,..,ck,\nres = (c2 - c1) + (c3 - c2) + .... = ck - c1\n\n\n# Explanation\nTo calculate the best score ending at a c | lee215 | NORMAL | 2024-05-12T04:05:12.446881+00:00 | 2024-05-12T05:16:21.905611+00:00 | 6,521 | false | # **Intuition**\nMove from `c1` to `ck` with path `c1,c2,..,ck`,\n`res = (c2 - c1) + (c3 - c2) + .... = ck - c1`\n<br>\n\n# **Explanation**\nTo calculate the best score ending at a cell `ck`,\njust need to find out the minimum `c1` on its top left area.\n\nTo do this, we can define `dp[i][j]` as the minimum in `A[i][j]` and its top-left.\n`dp[i][j] = min(A[i][j], dp[i-1][j], dp[i][j-1]))`\n\nInstead of create an array for DP,\nwe can also do it in-palce of `A`,\nto same some codes and spaces.\n<br>\n\n# **Complexity**\nTime `O(mn)`\nSpace `O(1)`\n<br>\n\n**Java**\n```java\n public int maxScore(List<List<Integer>> A) {\n int res = -1000_000, m = A.size(), n = A.get(0).size();\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int pre = Math.min(\n i > 0 ? A.get(i - 1).get(j) : 1000_000,\n j > 0 ? A.get(i).get(j - 1) : 1000_000\n );\n res = Math.max(res, A.get(i).get(j) - pre);\n if (pre < A.get(i).get(j)) {\n A.get(i).set(j, pre);\n }\n }\n }\n return res;\n }\n```\n**C++**\n```cpp\n int maxScore(vector<vector<int>>& A) {\n int res = -1e6, m = A.size(), n = A[0].size();\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int pre = min(i > 0 ? A[i - 1][j] : 1e6, j > 0 ? A[i][j - 1] : 1e6);\n res = max(res, A[i][j] - pre);\n A[i][j] = min(A[i][j], pre);\n }\n }\n return res;\n }\n```\n\n**Python**\n```py\n def maxScore(self, A: List[List[int]]) -> int:\n res, m, n = -inf, len(A), len(A[0])\n for i in range(m):\n for j in range(n):\n pre = min(A[i-1][j] if i else inf, A[i][j-1] if j else inf)\n res = max(res, A[i][j] - pre)\n A[i][j] = min(A[i][j], pre)\n return res\n```\n\n<br>\n\n# More DP problems\nHere is small DP problem list.\nGood luck and have fun.\n- 3148. [Maximum Difference Score in a Grid](https://leetcode.com/problems/maximum-difference-score-in-a-grid/discuss/5145704/JavaC%2B%2BPython-Minimum-on-Top-Left)\n- 3147. [Taking Maximum Energy From the Mystic Dungeon](https://leetcode.com/problems/taking-maximum-energy-from-the-mystic-dungeon/discuss/5145723/JavaC%2B%2BPython-DP)\n- 2920. [Maximum Points After Collecting Coins From All Nodes](https://leetcode.com/problems/maximum-points-after-collecting-coins-from-all-nodes/discuss/4220643/JavaC%2B%2BPython-DP)\n- 2919. [Minimum Increment Operations to Make Array Beautiful](https://leetcode.com/problems/minimum-increment-operations-to-make-array-beautiful/discuss/4220717/JavaC%2B%2BPython-Easy-and-Concise-DP-O(1)-Space)\n- 2896. [Apply Operations to Make Two Strings Equal](https://leetcode.com/problems/apply-operations-to-make-two-strings-equal/discuss/4144041/JavaC%2B%2BPython-DP-One-Pass-O(1)-Space)\n- 2830. [Maximize the Profit as the Salesman](https://leetcode.com/problems/maximize-the-profit-as-the-salesman/discuss/3934188/JavaC%2B%2BPython-DP)\n- 2008. [Maximum Earnings From Taxi](https://leetcode.com/problems/maximum-earnings-from-taxi/discuss/1470941/JavaC%2B%2BPython-DP-solution)\n- 1751. [Maximum Number of Events That Can Be Attended II](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended-ii/discuss/1052581/Python-DP)\n- 1235. [Maximum Profit in Job Scheduling](https://leetcode.com/problems/maximum-profit-in-job-scheduling/discuss/409009/Python-DP-Solution)\n | 101 | 1 | ['C', 'Python', 'Java'] | 15 |
maximum-difference-score-in-a-grid | Explained - Find min upto that cell and take diff | explained-find-min-upto-that-cell-and-ta-iq4k | Intuition\n- Need to find the min max, such that min item cell should be towards left and top of the max item cell.\n\n# Approach\n- Keep tracking the smallest | kreakEmp | NORMAL | 2024-05-12T04:01:07.787783+00:00 | 2024-05-12T05:28:49.745028+00:00 | 3,024 | false | # Intuition\n- Need to find the min max, such that min item cell should be towards left and top of the max item cell.\n\n# Approach\n- Keep tracking the smallest number till the current cell torards its left and towards its top.\n- Consider the current cell as the max item and take diff. Keep tracking the max diff\n\n# Complexity\n- Time complexity: O(N.N)\n\n- Space complexity: O(1)\n\n# Code\n```\nint maxScore(vector<vector<int>>& grid) {\n int ans = INT_MIN;\n for(int i = 0; i < grid.size(); ++i){\n for(int j = 0; j < grid[0].size(); ++j){\n int mn = INT_MAX;\n if(i == 0 && j == 0) continue;\n if(i != 0) mn = min(mn, grid[i-1][j]);\n if(j != 0) mn = min(mn, grid[i][j-1]);\n ans = max(ans, grid[i][j] - mn);\n grid[i][j] = min(grid[i][j], mn);\n }\n }\n return ans;\n}\n```\n\n\n---\n\n<b>Here is an article of my last interview experience - A Journey to FAANG Company, I recomand you to go through this to know which all resources I have used & how I cracked interview at Amazon:\nhttps://leetcode.com/discuss/interview-experience/3171859/Journey-to-a-FAANG-Company-Amazon-or-SDE2-(L5)-or-Bangalore-or-Oct-2022-Accepted\n\n--- | 39 | 4 | ['C++'] | 6 |
maximum-difference-score-in-a-grid | [C++] with Picture Explanation, DP | c-with-picture-explanation-dp-by-subbuff-mrj9 | Intuition\nThe short simple answer to this problem is that the answer is almost equal to the max value in the matrix minus the minimum value in the matrix.\nHow | SubBuffer | NORMAL | 2024-05-12T04:02:09.286396+00:00 | 2024-07-15T20:24:09.531493+00:00 | 2,652 | false | # Intuition\nThe short simple answer to this problem is that the answer is almost equal to the max value in the matrix minus the minimum value in the matrix.\nHowever, obviously there is more to this.\nLet\'s show why the above is true to a good extent.\nImagine the value in grid[i+k][j+t] (such that t,k>0) is larger than grid[i][j]. Then it will be easy to see **the path is irrelevant**. Thus, since there is always a path between the smallest value and the larger value, we should be good to calulate this value.\n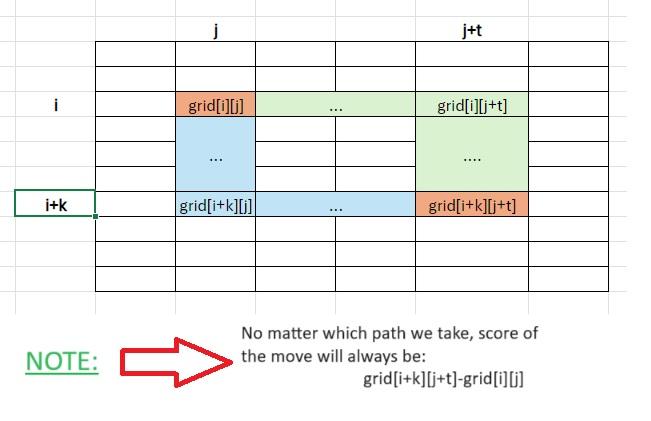\nNote that, not always the largest value will be in the bottom right and the smallest value in the upper left matrices. Thus, we need to do a **Dynamic Programming** with memorization approach. Some folks do it inplace, I rather do it in a different matrix. Depends on your preference (and space requirement).\n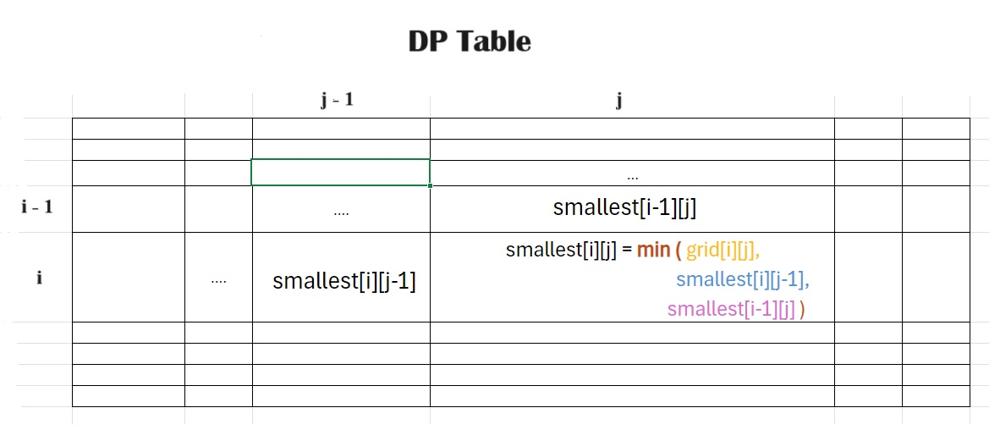\n\n\n\n\n# Approach\n**Case 1 (Non-Descending matrix):** So we can reach to grid[i+k][j] with `grid[i+k][j]-grid[i][j]`; and then to grid[i+k][j+t] with `grid[i+k][j+t]-grid[i+k][j]` \nso the entire move will be equal to = `grid[i+k][j+t]-grid[i][j]` \nThus, we see that for each grid[i+k][j+t] that we end the path, we just need to know **where the starting point was** (which will be the *smallest* value in the *upper left* matrix of a grid point).\n\n**Case 2 (Descending matrix):** Because the problem states that there needs to be *at least one move*, there is this exception that we need to keep track of whether all the values are in descending order or not. In this case, memorize the difference of the smallest value seen in the **upper left matrix** and the grid[i][j] value. At the end, check for descending case, and if so, output the seen minimum diff.\n\n# Complexity\n- Time complexity: \nO(m*n)\n\n- Space complexity:\nO(m*n)\n\n# Code\n```\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n vector<vector<int>> smallest ((int)grid.size(),vector<int>((int)grid[0].size(),0)); // DP matrix to determine the smallest value \n // between coordinates [0][0] and [i][j]\n smallest[0][0] = grid[0][0];\n int minDiffIfAllDesc = INT_MIN; // We return the diff if the matrix is all descending\n bool allDescending = true; // Initially assume the matrix is all descending\n \n // fill the first column of smallest\n for(int i = 1;i<grid.size();i++){\n if (allDescending && smallest[i-1][0]<=grid[i][0]){\n allDescending = false;\n }else{\n minDiffIfAllDesc = max(minDiffIfAllDesc, grid[i][0] - smallest[i-1][0]); // update for allDescending\n }\n smallest[i][0] = min(smallest[i-1][0],grid[i][0]);\n }\n\n // fill the first row of smallest\n for(int j = 1;j<grid[0].size();j++){ \n if (allDescending && smallest[0][j-1]<=grid[0][j]){\n allDescending = false;\n }else{\n minDiffIfAllDesc = max(minDiffIfAllDesc, grid[0][j] - smallest[0][j-1]); // update\n }\n smallest[0][j] = min(smallest[0][j-1],grid[0][j]);\n }\n\n // fill the rest of the smallest dp matrix\n for(int i = 1;i<grid.size();i++){\n for(int j = 1;j<grid[0].size();j++){\n smallest[i][j] = min(smallest[i-1][j],smallest[i][j-1]);\n if (allDescending && smallest[i][j]<=grid[i][j]){\n allDescending = false;\n }else{\n minDiffIfAllDesc = max(minDiffIfAllDesc, grid[i][j] - smallest[i][j]); // update\n }\n smallest[i][j] = min(smallest[i][j],grid[i][j]);\n } \n }\n\n if (allDescending){\n return minDiffIfAllDesc; // this is when matrix is all descending\n }\n\n // We return the mmax value if the matrix is NOT all descending\n int mmax = INT_MIN; \n for(int i = 0;i<grid.size();i++){\n for(int j = 0;j<grid[0].size();j++){\n mmax = max(mmax,grid[i][j]-smallest[i][j]); \n } \n }\n return mmax;\n }\n};\n``` | 18 | 0 | ['C++'] | 2 |
maximum-difference-score-in-a-grid | Simple java solution | simple-java-solution-by-siddhant_1602-s09e | Complexity\n- Time complexity: O(mn)\n\n- Space complexity: O(mn)\n\n# Code\n\nclass Solution {\n public int maxScore(List<List<Integer>> grid) {\n in | Siddhant_1602 | NORMAL | 2024-05-12T04:04:46.545459+00:00 | 2024-05-12T04:06:47.096760+00:00 | 806 | false | # Complexity\n- Time complexity: $$O(m*n)$$\n\n- Space complexity: $$O(m*n)$$\n\n# Code\n```\nclass Solution {\n public int maxScore(List<List<Integer>> grid) {\n int m = grid.size(), n = grid.get(0).size();\n int ans[][] = new int[m][n];\n ans[m-1][n-1] = grid.get(m-1).get(n-1);\n for(int i=n-2;i>=0;i--)\n {\n ans[m-1][i]=Math.max(ans[m-1][i+1],grid.get(m-1).get(i));\n }\n for(int i=m-2;i>=0;i--)\n {\n ans[i][n-1]=Math.max(ans[i+1][n-1], grid.get(i).get(n-1));\n }\n for(int i=m-2;i>=0;i--)\n {\n for (int j=n-2;j>=0;j--)\n {\n ans[i][j] = Math.max(grid.get(i).get(j), Math.max(ans[i+1][j], ans[i][j+1]));\n }\n }\n int count = Integer.MIN_VALUE;\n for(int i=0;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(i+1<m)\n {\n count=Math.max(count, ans[i+1][j]-grid.get(i).get(j));\n }\n if(j+1<n)\n {\n count=Math.max(count, ans[i][j+1]-grid.get(i).get(j));\n }\n \n }\n }\n return count;\n }\n}\n``` | 17 | 1 | ['Java'] | 1 |
maximum-difference-score-in-a-grid | C++ || NO DP || NO RECURSION || NEXT GREATER ELEMENT MATRIX || Beginner Friendly | c-no-dp-no-recursion-next-greater-elemen-q0r4 | First read the question 2-3 times(iff necessary) to get the basic understanding of question.\n\nHint: try to look different ways to get the answer ( I personall | int_float_double | NORMAL | 2024-05-16T17:41:54.448801+00:00 | 2024-05-16T18:23:46.364413+00:00 | 261 | false | ## **First read the question 2-3 times(iff necessary) to get the basic understanding of question.**\n\n**Hint:** try to look different ways to get the answer ( I personally suggest using pen and paper )\n\n\n\n**Explaination:** lets say you are at position (0,1) with value "5" and you want to find the max difference by traversing right and down only (not necessarily to adjacent element), just look for maximum element in submatrix of (0,1) excluding element at (0,1) lets say you find max element at (2,2) with value "14" now conclude that no matter what path you choose to reach (2,2) the sum of difference always gonna be (14-5)=9. then just use next greater elemnt technique to precompute the max element of every submatrix and find the answer !\n\n\n\nCode: \n```\n#pragma GCC optimize("fast")\nstatic auto _ = [] () {ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);return 0;}();\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int n=grid.size();\n int m=grid[0].size();\n int mr[n][m],mc[n][m];\n for(int i=0;i<n;i++){\n int ma=0;\n for(int j=m-1;j>=0;j--){\n ma=max(grid[i][j],ma);\n mr[i][j]=ma;\n }\n }\n for(int j=0;j<m;j++){\n int ma=0;\n for(int i=n-1;i>=0;i--){\n ma=max(mr[i][j],ma);\n mc[i][j]=ma;\n }\n }\n int ans=INT_MIN;\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n int a=-1,b=-1;\n if(i+1<n){\n a=mc[i+1][j];\n }\n if(j+1<m){\n b=mc[i][j+1];\n }\n if(a>-1 || b>-1){\n ans=max(ans,max(a,b)-grid[i][j]);\n }\n }\n }\n return ans;\n }\n};\n```\n\n\n\nAn Upvote will be appreciated \uD83C\uDF89 !!!\nCheers\uD83E\uDD42 | 14 | 0 | ['C', 'Matrix'] | 0 |
maximum-difference-score-in-a-grid | Track Previous Min | track-previous-min-by-votrubac-7sz9 | The path in the grid does not matter; the result is the difference between the first and last element.\n\nSo, we track the previously seen minimum element (to t | votrubac | NORMAL | 2024-05-12T05:07:51.693056+00:00 | 2024-05-12T05:07:51.693082+00:00 | 566 | false | The path in the grid does not matter; the result is the difference between the first and last element.\n\nSo, we track the previously seen minimum element (to the left or above) of the current cell `g[i][j]` in `prev_min[j]`. \n\n**C++**\n```cpp\nint maxScore(vector<vector<int>>& g) {\n int m = g.size(), n = g[0].size(), res = INT_MIN;\n vector<int> min_j(n, INT_MAX);\n for (int i = 0; i < m; ++i)\n for (int j = 0; j < n; ++j) {\n if (j > 0)\n min_j[j] = min(min_j[j], min_j[j - 1]);\n res = max(res, g[i][j] - min_j[j]);\n min_j[j] = min(min_j[j], g[i][j]);\n }\n return res;\n}\n``` | 13 | 1 | ['C'] | 2 |
maximum-difference-score-in-a-grid | Simple || DP || Tabulation 🔥🔥 | simple-dp-tabulation-by-harsh_padsala_26-36ci | Intuition\nThis is the first ever DP problem i could solved in live contest so i feel i should share to everyone\n\nIntuition was so simple we want to start fro | Harsh_Padsala_265 | NORMAL | 2024-05-12T05:40:43.687511+00:00 | 2024-05-16T03:42:13.579006+00:00 | 748 | false | # Intuition\nThis is the first ever DP problem i could solved in live contest so i feel i should share to everyone\n\nIntuition was so simple we want to start from cell from where we can maximise output. after starting from one cell , we only have three choice either right or down or none of them.\n\nSo i found that storing the maximum value from bottom right corner to top left corner will be helpful to find maximum value.\n\nat each cell ,value of current cell in dp depends of max(dp[right],dp[left]) as well as difference between current cell value and either (right or bottom ) cell value.\n\noutput will be the max value of DP array.\n\n# Approach\n1. Initialization:\n\n- The dp array is initialized to store the maximum score that can be achieved starting from each cell in the grid.\n- Each cell of dp represents the maximum score achievable from that cell to the bottom-right corner of the grid.\n\n2. Traversal from Bottom-right to Top-left:\n\n- We traverse the grid in reverse order, starting from the bottom-right corner (n-1, m-1) and moving towards the top-left corner (0, 0).\n- This traversal direction allows us to compute the maximum score from each cell by considering the scores of the cells below and to the right of the current cell.\n\n3. Score Calculation:\n\n- For each cell (i, j), we calculate the potential scores of moving down (a) and moving right (b).\n- We also calculate the difference in values between the current cell and the adjacent cells (c and d), as they contribute to the score of the current move.\n- The score of moving from (i, j) to (i+1, j) is grid[i+1][j] - grid[i][j] + dp[i+1][j].\n- The score of moving from (i, j) to (i, j+1) is grid[i][j+1] - grid[i][j] + dp[i][j+1].\n- We take the maximum of these potential scores (a and b) along with the maximum difference in cell values (c and d) and assign it to dp[i][j]. This ensures that we consider the maximum score achievable from the current cell.\n\n4. Updating Maximum Score:\n\n- We update the maximum score ans by taking the maximum of the current dp[i][j] value and the existing ans.\n\n5. Return Maximum Score:\n\n- Finally, we return the maximum score ans, which represents the maximum total score achievable starting from any cell in the grid.\n\n# Complexity\n- Time complexity:\nO( N * M ) | N = number of row | M = number of column\n\n- Space complexity:\nO( N * M ) | N = number of row | M = number of column\n\n```python []\nclass Solution(object):\n def maxScore(self, grid):\n n = len(grid)\n m = len(grid[0])\n dp = []\n\n for k in range(n+1):\n dp.append([0 for l in range(m+1)])\n\n ans = float(\'-inf\')\n for i in range(n-1,-1,-1):\n for j in range(m-1,-1,-1):\n a, b , c , d = float(\'-inf\'), float(\'-inf\') , float(\'-inf\') ,float(\'-inf\')\n if i+1<n:\n a = (grid[i+1][j]-grid[i][j]+dp[i+1][j])\n c = grid[i+1][j]-grid[i][j]\n if j+1<m:\n b = (grid[i][j+1]-grid[i][j]+dp[i][j+1])\n d = grid[i][j+1]-grid[i][j]\n \n\n dp[i][j] = max(a,b,max(c,d))\n ans = max(ans,dp[i][j])\n \n return ans\n \n\n \n```\n```java []\nclass Solution {\n public int maxScore(List<List<Integer>> grid) {\n int n = grid.size();\n int m = grid.get(0).size();\n int[][] dp = new int[n][m];\n int ans = Integer.MIN_VALUE;\n for (int i = n - 1; i >= 0; i--) {\n for (int j = m - 1; j >= 0; j--) {\n if (i == n - 1 && j == m - 1)\n continue;\n int a = Integer.MIN_VALUE, b = Integer.MIN_VALUE, c = Integer.MIN_VALUE, d = Integer.MIN_VALUE;\n if (i + 1 < n) {\n a = (grid.get(i + 1).get(j) - grid.get(i).get(j)) + dp[i + 1][j];\n b = grid.get(i + 1).get(j) - grid.get(i).get(j);\n }\n if (j + 1 < m) {\n c = (grid.get(i).get(j + 1) - grid.get(i).get(j)) + dp[i][j + 1];\n d = grid.get(i).get(j + 1) - grid.get(i).get(j);\n }\n dp[i][j] = Math.max(Math.max(a, b), Math.max(c, d));\n ans = Math.max(ans, dp[i][j]);\n }\n\n }\n return ans;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n vector<vector<int>> dp(n, vector<int>(m));\n int ans = INT_MIN;\n for (int i = n - 1; i >= 0; i--) {\n for (int j = m - 1; j >= 0; j--) {\n if (i == n - 1 && j == m - 1)\n continue;\n int a = INT_MIN, b = INT_MIN, c = INT_MIN, d = INT_MIN;\n if (i + 1 < n) {\n a = (grid[i + 1][j] - grid[i][j]) + dp[i + 1][j];\n b = grid[i + 1][j] - grid[i][j];\n }\n if (j + 1 < m) {\n c = (grid[i][j + 1] - grid[i][j]) + dp[i][j + 1];\n d = grid[i][j + 1] - grid[i][j];\n }\n dp[i][j] = max(max(a, b), max(c, d));\n ans = max(ans, dp[i][j]);\n }\n }\n return ans;\n }\n};\n```\n\nhelper blog : https://leetcode.com/discuss/study-guide/1965086/How-to-practice-for-2200%2B-rating-in-LC\n\n\n\n\n | 10 | 0 | ['Dynamic Programming', 'Python', 'C++', 'Java'] | 1 |
maximum-difference-score-in-a-grid | Python 3 || 8 lines, padded grid || T/S: 86% / 61% | python-3-8-lines-padded-grid-ts-86-61-by-aa6b | Here\'s the plan:\n1. We pad grid with a top-row and a left-column of inf to avoid checking for edge cases. (Illustrated below with input from Example 1)\n\n | Spaulding_ | NORMAL | 2024-05-13T17:44:36.708274+00:00 | 2024-05-24T01:57:15.979309+00:00 | 222 | false | Here\'s the plan:\n1. We pad `grid` with a top-row and a left-column of `inf` to avoid checking for edge cases. (Illustrated below with input from *Example 1*)\n```\n [inf, inf, inf, inf, inf]\n [inf, 9, 5, 7, 3 ]\n [inf, 8, 9, 6, 1 ]\n [inf, 6, 7, 14, 3 ]\n [inf, 2, 5, 3, 1 ]\n```\n2. We iterate through `grid` upper-left to bottom-right, and we use `grid` to keep track of the optimum scores:\n```\n [inf, inf, inf, inf, inf]\n [inf, 9, 5, 5, 3 ]\n [inf, 8, 5, 5, 1 ]\n [inf, 6, 5, 5, 1 ]\n [inf, 2, 2, 2, 1 ]\n\n```\nCODE:\n```\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n\n ans, m, n = -inf, len(grid), len(grid[0])\n grid = [[inf]*n] + grid\n grid = [[inf]+row for row in grid]\n # for row in grid: print(row)\n \n for row, col in product(range(m), range(n)):\n mn = min(grid[row][col+1], grid[row+1][col])\n ans = max(ans, grid[row+1][col+1] - mn)\n grid[row+1][col+1] = min(grid[row+1][col+1], mn)\n # for row in grid: print(row)\n \n return ans\n```\n[https://leetcode.com/problems/maximum-difference-score-in-a-grid/submissions/1257127827/](https://leetcode.com/problems/maximum-difference-score-in-a-grid/submissions/1257127827/)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*MN*) and space complexity is *O*(*MN*), in which *M* ~ `m` and *N* ~ `n`. | 9 | 0 | ['Python3'] | 1 |
maximum-difference-score-in-a-grid | Video Explanation [Optimising N*M*(N+M) solution step by step to N*M] | video-explanation-optimising-nmnm-soluti-dfj8 | Explanation\n\nClick here for the video\n\n# Code\n\ntypedef long long int ll;\n\nconst ll INF = 1e18;\n\nclass Solution {\n vector<vector<ll>> dp;\n vect | codingmohan | NORMAL | 2024-05-12T06:21:22.975026+00:00 | 2024-05-12T06:21:22.975054+00:00 | 283 | false | # Explanation\n\n[Click here for the video](https://youtu.be/pF3XT6cDHpU)\n\n# Code\n```\ntypedef long long int ll;\n\nconst ll INF = 1e18;\n\nclass Solution {\n vector<vector<ll>> dp;\n vector<vector<int>> grid;\n int rows, cols;\n \n /*\n ll MaxScore (int r, int c) {\n if (r == rows-1 && c == cols-1) return -INF;\n \n ll& ans = dp[r][c];\n if (ans != -INF) return ans;\n \n for (int rgt = c+1; rgt < cols; rgt ++) {\n ans = max(ans, (ll)grid[r][rgt] - grid[r][c] + max(0LL, MaxScore(r, rgt)));\n }\n for (int dwn = r+1; dwn < rows; dwn ++) {\n ans = max(ans, (ll)grid[dwn][c] - grid[r][c] + max(0LL, MaxScore(dwn, c)));\n }\n return ans;\n } \n */\n \npublic:\n \n /*\n int maxScore(vector<vector<int>>& _grid) {\n grid = _grid;\n rows = grid.size();\n cols = grid[0].size();\n \n dp.clear();\n dp.resize (rows+1, vector<ll>(cols+1, -INF));\n \n ll ans = -INF;\n for (int r = 0; r < rows; r ++)\n for (int c = 0; c < cols; c++) ans = max(ans, MaxScore(r, c));\n return ans;\n }\n */\n \n int maxScore(vector<vector<int>>& grid) {\n int rows = grid.size();\n int cols = grid[0].size();\n \n vector<vector<ll>> max_val (rows+1, vector<ll>(cols+1, INT_MIN));\n vector<vector<ll>> max_rgt (rows+1, vector<ll>(cols+1, INT_MIN));\n vector<vector<ll>> max_dwn (rows+1, vector<ll>(cols+1, INT_MIN));\n \n for (int c = cols-1; c >= 0; c --) {\n for (int r = rows-1; r >= 0; r --) { \n max_val[r][c] = max ({max_rgt[r][c+1], max_dwn[r+1][c]}) - grid[r][c];\n max_rgt[r][c] = max ({max_rgt[r][c+1], grid[r][c] + max_val[r][c], (ll)grid[r][c]});\n max_dwn[r][c] = max ({max_dwn[r+1][c], grid[r][c] + max_val[r][c], (ll)grid[r][c]});\n }\n }\n \n ll ans = -1e18;\n for (auto r: max_val)\n for (auto c: r) ans = max(ans, c);\n return ans;\n }\n};\n``` | 7 | 0 | ['C++'] | 0 |
maximum-difference-score-in-a-grid | 🧐Begginner and Advanced versions 🛀 Clean Code 🪟 Clear explanation ⁉️ Q&A👊 Beat 100% 🥁 | begginner-and-advanced-versions-clean-co-ch1l | \n\n\n# What\'s the short version of your solution?\n\nFor each number in the matrix, you just need to compare it with only one number: the smallest number for | navid | NORMAL | 2024-05-12T04:01:48.011171+00:00 | 2024-05-12T06:27:23.722789+00:00 | 567 | false | \n\n\n# What\'s the short version of your solution?\n\nFor each number in the matrix, you just need to compare it with only one number: the smallest number for which a move could be possible. Then you can simply find the difference and compare it to the max score.\n\n# Why is the example comparing multiple jumps?\nThe question is trying to trick you.\n\nYou don\'t need to be worried about comparing every single element with other elements. \n\n# What if I am the current element?\n\nIf you know which element is the smallest element that could jump to you (`currentMin`), all you need to do is find the difference between yourself and `currentMin` to find the `currentScore`. \n\n# But how can I find the currentMin?\n\nI\'ll let you know, but be patient: one step at a time. \n\nFor now, let\'s assume your `leftNeighbor` has stored the `currentMin` for itself. Also assume it\'s the case for your `topNeighbor`. So the `currentMin` will be the minimum of those.\n\n# Why?\n\nBecause anyone who could jump on you (no pun intended), could jump on either your `leftNeighbor` or your `topNeighbor`. \n\n# How to store the minimum value for the beginner version?\n \nYou can have another matrix (a two-dimentional array) for storing the minimum element that you (as the current element) could see (including yourself).\n\n# How should I find the max score?\n\nYou can keep a variable called `maxScore`. Every time you find the `currentScore` for yourself (as the current elemenet) you simply update the `maxScore`.\n\n# What\'s the time complexity?\nYou visit each element only once, so it will be the size of the input array: O(m * n)\n\n# What\'s the space complexity for the beginner version?\nFor every element of the input array, you need to store the minimum element that could reach that element with a jump (including itself). So you need space equal to the size of the input which is: O(m * n)\n\n\n\n# Code\n```\n public int maxScore(List<List<Integer>> grid) {\n int length = grid.size();\n int width = grid.get(0).size();\n int[][] minArray = new int[length][width];\n minArray[0][0] = grid.get(0).get(0);\n int maxScore = Integer.MIN_VALUE;\n \n for (int i = 1; i < length; i++) {\n Integer currentValue = grid.get(i).get(0);\n int leftNeighbor = minArray[i - 1][0];\n int currentScore = currentValue - leftNeighbor;\n maxScore = Math.max(maxScore, currentScore);\n minArray[i][0] = Math.min(currentValue, leftNeighbor);\n }\n\n for (int j = 1; j < width; j++) {\n Integer currentValue = grid.get(0).get(j);\n int topNeighbor = minArray[0][j - 1];\n int currentScore = currentValue - topNeighbor;\n maxScore = Math.max(maxScore, currentScore);\n minArray[0][j] = Math.min(currentValue, topNeighbor);\n }\n\n for (int i = 1; i < length; i++) {\n for (int j = 1; j < width; j++) {\n int leftNeighbor = minArray[i][j - 1];\n int topNeighbor = minArray[i - 1][j];\n int currentMin = Math.min(leftNeighbor, topNeighbor);\n int currentScore = grid.get(i).get(j) - currentMin;\n maxScore = Math.max(maxScore, currentScore);\n minArray[i][j] = Math.min(grid.get(i).get(j), currentMin);\n }\n }\n return maxScore;\n }\n```\n\n# Can we solve it in O(n^2) and O(1) space?\n\nAsk your interviewer first: is it ok if I manipulate the input?\n\nIn that case, after we read the information for each element and updated the `maxScore`, we don\'t need that value anymore so we can use that space to save the `currentMinIncludingMyself` for future use.\n\n# Can you also get rid of the first 2 for loops?\n\nOnly because you asked:\n```\n\n public int maxScore(List<List<Integer>> grid) {\n int m = grid.size();\n int n = grid.get(0).size();\n int maxScore = Integer.MIN_VALUE;\n\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n int leftNeighbor = j == 0 ? Integer.MAX_VALUE : grid.get(i).get(j - 1);\n int topNeighbor = i == 0 ? Integer.MAX_VALUE : grid.get(i - 1).get(j);\n int currentMin = Math.min(leftNeighbor, topNeighbor);\n int currentScore = grid.get(i).get(j) - currentMin;\n maxScore = Math.max(maxScore, currentScore);\n int currentMinIncludingMyself = Math.min(grid.get(i).get(j), currentMin);\n grid.get(i).set(j, currentMinIncludingMyself);\n }\n }\n return maxScore;\n }\n```\n\n\n# Awesome, Last question: How can I upvote this post?\nIt\'s very challenging. I couldn\'t figure it out yet.\n\n | 6 | 1 | ['Java'] | 1 |
maximum-difference-score-in-a-grid | 🔥Clean Code💯 with Best Explanation🔥||⚡BottomUP DP🌟 | clean-code-with-best-explanationbottomup-tl7q | Here if u will observe carefully then u will find that for each starting cell there is no need to take choice for all the below rows as well as right columns be | aDish_21 | NORMAL | 2024-05-12T15:30:30.634667+00:00 | 2024-05-12T15:36:38.436137+00:00 | 190 | false | ### Here if u will observe carefully then u will find that for each starting cell there is no need to take choice for all the below rows as well as right columns because the best score for a particular starting cell will always be equal to the maximum difference between the final ending cell & the starting cell as because all the intermediate cells will be cancelled out(as we know that starting cell value is fixed so to bring max difference we have to find the final cell having the max value). \n## ***The Search Space for final ending cell is as follows:-***\n`Suppose if the coordinates of the starting cell is (i, j) then the final cell coordinates (x, y) range will be x >=i && x < m whereas y >= j && y < n`\n\n## *Prove of how intermediates cells values are cancelled out:-*\n## Suppose value of any particular starting cell is c1 & that of final ending cell be c5 then the intermediates cells values will be c2, c3, c4 & so the score for that particular path will be `(c2 - c1) + (c3 - c2) + (c4 - c3) + (c5 - c4)` = c5 - c1 (all others cancel each other\uD83D\uDE01). Hence Proved.\n\n# Now observe my code carefully u will get it 100%.\n## `For any query u can comment below, I will surely ans it\uD83E\uDD17`\n\n## Connect with me on LinkedIN : https://www.linkedin.com/in/aditya-jhunjhunwala-51b586195/\n\n# Complexity\n```\n- Time complexity:\nO(m * n)\n\n- Space complexity:\nO(1)\n```\n\n# Code\n## Please Upvote if it helps\uD83E\uDD17\n```\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size(), ans = INT_MIN;\n for(int i = m - 1 ; i >= 0 ; i--){\n for(int j = n - 1 ; j >= 0 ; j--){\n if(i == m - 1 && j == n - 1)\n continue;\n int maxi = INT_MIN;\n if(i != m - 1)\n maxi = max(maxi, grid[i + 1][j]);\n if(j != n - 1)\n maxi = max(maxi, grid[i][j + 1]);\n ans = max(ans, maxi - grid[i][j]);\n grid[i][j] = max(maxi, grid[i][j]);\n }\n }\n return ans;\n }\n};\n``` | 5 | 0 | ['Dynamic Programming', 'Greedy', 'C++'] | 0 |
maximum-difference-score-in-a-grid | Easy memoization approach || C++ 🔥🔥 | easy-memoization-approach-c-by-abhinav_s-ttfo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n1. solvemaxScore Func | Abhinav_Shakya | NORMAL | 2024-05-12T05:22:25.223168+00:00 | 2024-05-12T06:08:59.980953+00:00 | 402 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. **solvemaxScore Function**: This function is a helper function that uses recursion and dynamic programming to solve the problem.\n\n - It takes four parameters: `grid` (the 2D grid), `i` and `j` (the current cell coordinates), and `dp` (a 2D array for memoization).\n - If `i` or `j` is out of the grid\'s bounds, it returns `INT_MIN` (the smallest possible integer), indicating an invalid state.\n - If the current cell `(i, j)` has been visited before (i.e., `dp[i][j]` is not `INT_MIN`), it returns the stored value.\n - It calculates two possible scores `take1` and `take2` for the two possible moves: moving right to `(i, j+1)` and moving down to `(i+1, j)`. The score for a move is calculated as the difference between the value of the destination cell and the current cell, plus the maximum score that can be obtained from the destination cell (if it\'s positive).\n - It stores the maximum of `take1` and `take2` in `dp[i][j]` and returns this value.\n\n2. **maxScore Function**: This is the main function that solves the problem.\n\n - It initializes the `dp` array (`fvalue`) with `INT_MIN`.\n - It calls the `solvemaxScore` function to calculate the maximum score from the top-left corner `(0, 0)`.\n - It then iterates over the `dp` array to find the maximum score among all cells and returns this value.\n\nThe code uses `INT_MIN` as a special value to indicate that a cell in the `dp` array has not been visited yet, and also as an initial value for the maximum score. The `maxScore` function returns the maximum score that can be obtained by moving from the top-left corner to the bottom-right corner of the grid, according to the rules defined in the `solvemaxScore` function.\n\n\n\n\n# Complexity\n- Time complexity:O(m*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(m*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n \n int solvemaxScore(vector<vector<int>>&grid , int i, int j, vector<vector<int>>&dp)\n {\n if(i>=grid.size() || j>=grid[0].size())\n {\n return INT_MIN;\n }\n \n if(dp[i][j]!=INT_MIN)\n {\n return dp[i][j];\n }\n \n int ans = INT_MIN;\n int take1=INT_MIN,take2=INT_MIN;\n \n if(i+1<grid.size())\n {\n take2 = grid[i+1][j] - grid[i][j] + max(0, solvemaxScore(grid,i+1,j,dp));\n // cout<<"take2 "<<"{i,j}"<<i<<","<<j<<" "<<take2<<endl;\n }\n if(j+1<grid[0].size())\n {\n take1 = grid[i][j+1] - grid[i][j] + max(0,solvemaxScore(grid,i,j+1,dp));\n // cout<<"take1 "<<"{i,j}"<<i<<","<<j<<" "<<take1<<endl;\n }\n \n \n dp[i][j] = max(take1,take2);\n return dp[i][j];\n }\n \n int maxScore(vector<vector<int>>& grid) {\n int r = grid.size();\n int c = grid[0].size();\n int maxi=INT_MIN;\n\n vector<vector<int>>fvalue(grid.size()+1,vector<int>(grid[0].size()+1,INT_MIN));\n int ans = solvemaxScore(grid,0,0,fvalue);\n \n int ans1 = INT_MIN;\n //here we are finding the maximum value from the dp ans storing it in the answer (ans1)\n for(int i=0;i<fvalue.size();i++)\n {\n for(int j=0;j<fvalue[0].size();j++)\n {\n ans1=max(ans1,fvalue[i][j]);\n }\n // cout<<endl;\n }\n\n return ans1;\n \n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
maximum-difference-score-in-a-grid | C++ || Recursion + Memoization || Beginner Friendly 🔥✅💯🤩 | c-recursion-memoization-beginner-friendl-c0m5 | \n\n# Code\n\nclass Solution {\npublic:\n int solve(int i, int j, vector<vector<int>>& grid, vector<vector<int>>& dp) {\n if (i >= grid.size() || j >= | _kvschandra_2234 | NORMAL | 2024-05-12T05:00:28.688685+00:00 | 2024-05-12T07:38:18.623688+00:00 | 1,608 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int solve(int i, int j, vector<vector<int>>& grid, vector<vector<int>>& dp) {\n if (i >= grid.size() || j >= grid[0].size()) return 0;\n if (dp[i][j] != -1) return dp[i][j];\n\n int pick1 = INT_MIN, pick2 = INT_MIN;\n if (i + 1 < grid.size()) pick1 = grid[i + 1][j] - grid[i][j] + solve(i + 1, j, grid, dp);\n if (j + 1 < grid[0].size()) pick2 = grid[i][j + 1] - grid[i][j] + solve(i, j + 1, grid, dp);\n\n dp[i][j] = max(0, max(pick1, pick2));\n return dp[i][j];\n }\n\n int maxScore(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n vector<vector<int>> dp(m, vector<int>(n, -1));\n int maxi = INT_MIN;\n int maxi1 = INT_MIN;\n for(int i = 0; i < m; i++) {\n for(int j = 0; j < n; j++) {\n maxi = max(maxi, solve(i, j, grid, dp));\n if(i+1 < m) maxi1 = max(maxi1, grid[i+1][j] - grid[i][j]);\n if(j+1 < n) maxi1 = max(maxi1, grid[i][j+1] - grid[i][j]);\n }\n }\n if(maxi == 0) return maxi1;\n return maxi;\n }\n};\n``` | 5 | 1 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 1 |
maximum-difference-score-in-a-grid | Easiest Python Solution 100% Beat - O(m*n) Time and O(1) Extra Space | easiest-python-solution-100-beat-omn-tim-qgrf | Intuition\nThe first thing to notice is that the maximum score can always come from a single move. Consider the case we have a maximum score with multiple moves | rohanvedula | NORMAL | 2024-05-15T14:38:42.955640+00:00 | 2024-05-15T14:38:42.955691+00:00 | 156 | false | # Intuition\nThe first thing to notice is that the maximum score can always come from a single move. Consider the case we have a maximum score with multiple moves. Let\'s assume that it start\'s with a value $$v_1$$ and ends with a value $$v_n$$. We know that the score of the path is $$v_1 - v_n$$ and as a part of going from start to end, we have to go through $$v_1 \\to v_2 \\to \\ldots \\to v_{n-1} \\to v_n$$. We know that by the conditions in the problem, all $$v_i$$ must be the the bottom and right $$v_1$$. Therefore, we have a path with an equivalent score that is $$v_1 \\to v_n$$. \n\n# Approach\nGiven the inuition described above, for each cell in the matrix, if we can store what the minimum value is to the top and left of any cell, we can calculate the maximum score using the current cell value and the minimum value. We can do this using a DP approach where we check the cell directly upwards and leftwards of any cell. Since we can reuse the original grid array, we use no extra space. \n\n# Complexity\n- Time complexity: $$O(n \\times m)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n m = len(grid)\n n = len(grid[0])\n ans = float(\'-inf\')\n\n for i in range(m):\n for k in range(n):\n min_at_pos = min(grid[i-1][k] if i!=0 else float(\'inf\'), grid[i][k-1] if k!=0 else float(\'inf\'))\n t = grid[i][k]\n ans = max(ans, grid[i][k]-min_at_pos)\n grid[i][k] = min(min_at_pos, t)\n\n return ans\n``` | 4 | 0 | ['Dynamic Programming', 'Matrix', 'Python', 'Python3'] | 1 |
maximum-difference-score-in-a-grid | C++ Solution | Dp Recursion + Memoization and Tabulation bottom up | c-solution-dp-recursion-memoization-and-31d7t | Tried solving the question using recursion and memoization in contest but two test cases were giving tle. Anyone have any suggetion to optimize the recusive dp | Abhishek_499 | NORMAL | 2024-05-12T05:12:38.489741+00:00 | 2024-05-12T05:12:38.489770+00:00 | 185 | false | Tried solving the question using recursion and memoization in contest but two test cases were giving tle. Anyone have any suggetion to optimize the recusive dp code please suggest.\n\n\nTried solving using tabulation bottom up dp and it passed all the test cases\n\n\nCode 1 ----> Recursion + Memoization\nCode 2 -----> Tabulation Bottom Up\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\nCode 1:\n# Code\n```\nclass Solution {\npublic:\n int m, n;\n int helper(vector<vector<int>>& grid, int row, int col, vector<vector<int>>& dp){\n if(row>=m or col>=n)\n return 0;\n \n \n if(dp[row][col]!=-1)\n return dp[row][col];\n \n int res=INT_MIN/2;\n \n for(int i=row+1;i<m;i++){\n int a=grid[i][col]-grid[row][col];\n res=max(res, a);\n int b=helper(grid, i, col, dp);\n \n if(a>0 and b>0){\n res=max(res, a+b);\n }\n }\n \n for(int i=col+1;i<n;i++){\n int a=grid[row][i]-grid[row][col];\n res=max(res, a);\n int b=helper(grid, row, i, dp);\n \n if(a>0 and b>0){\n res=max(res, a+b);\n }\n }\n \n return dp[row][col]=res;\n }\n int maxScore(vector<vector<int>>& grid) {\n \n \n m=grid.size();\n n=grid[0].size();\n vector<vector<int>> dp(m+1, vector<int>(n+1, -1));\n \n int res=INT_MIN;\n \n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(i==m-1 and j==n-1)\n continue;\n int a=helper(grid, i, j, dp);\n res=max(a, res);\n }\n }\n \n return res;\n \n }\n};\n\n\n```\nCode 2:\n\n\n```\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int m=grid.size();\n int n=grid[0].size();\n\n\n vector<vector<int>> dp(m, vector<int>(n, INT_MIN));\n\n\n dp[0][0]=grid[0][0];\n\n\n // dp[m-1][n-2]=grid[m-1][n-1]-grid[m-1][n-2];\n // dp[m-2][n-1]=grid[m-1][n-1]-grid[m-2][n-1];\n\n\n int curr=grid[0][0];\n int res=INT_MIN;\n\n\n for(int i=1;i<m;i++){\n dp[i][0]=max(dp[i][0], grid[i][0]-curr);\n curr=min(grid[i][0], curr);\n res=max(res, dp[i][0]);\n }\n\n\n curr=grid[0][0];\n for(int i=1;i<n;i++){\n dp[0][i]=max(dp[0][i], grid[0][i]-curr);\n curr=min(grid[0][i], curr);\n res=max(res, dp[0][i]);\n }\n\n\n\n\n for(int i=1;i<m;i++){\n for(int j=1;j<n;j++){\n int col = grid[i][j] - grid[i][j-1];\n int row= grid[i][j] - grid[i-1][j];\n \n dp[i][j] = max(dp[i][j], max(col,row));\n dp[i][j] = max(dp[i][j], max(col+dp[i][j-1], row+dp[i-1][j] ));\n \n res = max(res,dp[i][j]);\n }\n }\n\n\n return res;\n }\n};\n\n\n``` | 4 | 0 | ['C++'] | 1 |
maximum-difference-score-in-a-grid | Java - Extended Brute Force Solution | java-extended-brute-force-solution-by-ia-sdnm | \nclass Solution {\n private Integer dp[][];\n public int maxScore(List<List<Integer>> grid) {\n int row = grid.size();\n int col = grid.get | iamvineettiwari | NORMAL | 2024-05-12T04:24:18.640413+00:00 | 2024-05-12T04:56:51.338529+00:00 | 316 | false | ```\nclass Solution {\n private Integer dp[][];\n public int maxScore(List<List<Integer>> grid) {\n int row = grid.size();\n int col = grid.get(0).size();\n dp = new Integer[row][col];\n\n int max = Integer.MIN_VALUE;\n\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n int maxR = getMax(grid, i, j + 1);\n int maxD = getMax(grid, i + 1, j);\n int current = grid.get(i).get(j);\n\n max = Math.max(max, Math.max(maxR - current, maxD - current));\n }\n }\n\n return max;\n }\n \n private int getMax(List<List<Integer>> grid, int row, int col) {\n if (row >= grid.size() || col >= grid.get(row).size()) {\n return (int) -(1e6);\n }\n\n if (dp[row][col] != null) {\n return dp[row][col];\n }\n \n int moveRight = getMax(grid, row, col + 1);\n int moveDown = getMax(grid, row + 1, col);\n int current = grid.get(row).get(col);\n \n return dp[row][col] = Math.max(current, Math.max(moveRight,moveDown));\n }\n \n}\n``` | 4 | 0 | ['Recursion', 'Memoization', 'Java'] | 3 |
maximum-difference-score-in-a-grid | Cleanest Memoization JAVA code you will ever see || CLEAN CODE || | cleanest-memoization-java-code-you-will-5pbh4 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Akshatjain_ | NORMAL | 2024-06-06T11:16:33.289194+00:00 | 2024-06-06T11:16:33.289226+00:00 | 105 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxScore(List<List<Integer>> grid) {\n Integer [][] dp = new Integer[grid.size()][grid.get(0).size()];\n int ans = (int)(-1e9);\n //Calling from every cell\n for(int i =0 ; i < grid.size() ; i++){\n for(int j =0 ; j < grid.get(0).size() ; j++){\n ans= Math.max(helper(i,j,grid,dp),ans);\n }\n }\n return ans;\n }\n int helper(int i , int j, List<List<Integer>> grid , Integer [][]dp){\n if(i==grid.size()-1 && j==grid.get(0).size()-1){\n return (int)(-1e9);\n }\n if(dp[i][j]!=null) return dp[i][j];\n int right = (int)(-1e9),down =(int)(-1e9);\n if(j<grid.get(0).size()-1){\n right = (grid.get(i).get(j+1) - grid.get(i).get(j)) + Math.max(0,helper(i,j+1,grid,dp));\n }\n if(i<grid.size()-1){\n down = (grid.get(i+1).get(j) - grid.get(i).get(j)) + Math.max(0,helper(i+1,j,grid,dp));\n }\n return dp[i][j]=Math.max(right ,down );\n }\n}\n``` | 3 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Java'] | 2 |
maximum-difference-score-in-a-grid | Python (Simple DP) | python-simple-dp-by-rnotappl-yda9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2024-05-12T09:18:39.103860+00:00 | 2024-05-12T09:18:39.103912+00:00 | 226 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, grid):\n m, n = len(grid), len(grid[0])\n\n @lru_cache(None)\n def dfs(i,j):\n if i >= m or j >= n:\n return 0 \n\n max_val = float("-inf")\n\n if i+1 < m:\n max_val = max(max_val,grid[i+1][j]-grid[i][j]+dfs(i+1,j))\n\n if j+1 < n:\n max_val = max(max_val,grid[i][j+1]-grid[i][j]+dfs(i,j+1))\n\n return max(0,max_val)\n\n mx_val, mx_val1 = float("-inf"), float("-inf")\n\n for i in range(m):\n for j in range(n):\n mx_val = max(mx_val,dfs(i,j))\n if (i+1 < m):\n mx_val1 = max(mx_val1,grid[i+1][j]-grid[i][j])\n if (j+1 < n):\n mx_val1 = max(mx_val1,grid[i][j+1]-grid[i][j])\n\n if mx_val == 0:\n return mx_val1\n\n return mx_val \n``` | 3 | 0 | ['Python3'] | 1 |
maximum-difference-score-in-a-grid | Easiest Python solution | easiest-python-solution-by-edwards310-wpq0 | Intuition\n\n\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- T | Edwards310 | NORMAL | 2024-05-12T04:07:57.199623+00:00 | 2024-05-12T04:07:57.199642+00:00 | 234 | false | # Intuition\n\n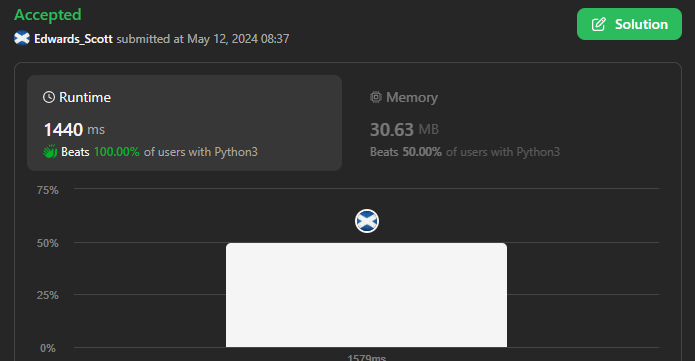\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n rows, cols = len(grid), len(grid[0])\n max_gain = float(\'-inf\')\n\n dp = [[float(\'-inf\')] * cols for _ in range(rows)]\n\n for i in range(rows - 1, -1, -1):\n for j in range(cols - 1, -1, -1):\n if j < cols - 1:\n dp[i][j] = max(dp[i][j], grid[i][j+1] - grid[i][j])\n if i < rows - 1:\n dp[i][j] = max(dp[i][j], grid[i+1][j] - grid[i][j])\n\n if j < cols - 1:\n dp[i][j] = max(dp[i][j], dp[i][j+1] + grid[i][j+1] - grid[i][j])\n\n if i < rows - 1:\n dp[i][j] = max(dp[i][j], dp[i+1][j] + grid[i+1][j] - grid[i][j])\n max_gain = max(max_gain, dp[i][j])\n\n return max_gain if max_gain > float(\'-inf\') else -1\n``` | 3 | 1 | ['Python3'] | 4 |
maximum-difference-score-in-a-grid | ✅✅Beats 100% Users ✅ Easy Solution ✅ Best Approaches✅ | beats-100-users-easy-solution-best-appro-sz4s | Intuition\nThe problem involves finding the maximum score possible while moving from the top-left corner to the bottom-right corner of the grid. You can move ei | arslanarsal | NORMAL | 2024-05-12T04:04:03.504243+00:00 | 2024-05-12T04:04:03.504279+00:00 | 243 | false | # Intuition\nThe problem involves finding the maximum score possible while moving from the top-left corner to the bottom-right corner of the grid. You can move either right or down at each step. The score of the path is determined by the difference between the values of the cells along the path. \n\n# Approach\n1. **Dynamic Programming**: The solution uses dynamic programming to efficiently compute the maximum score for each cell in the grid.\n2. **Backward Propagation**: The algorithm starts from the bottom-right corner and iteratively computes the maximum score for each cell by propagating backward.\n\nThe approach involves the following steps:\n- Initialize a 2D DP array to store intermediate results. Initialize each cell with a value of `INT_MIN`.\n- Propagate backward from the bottom-right corner to the top-left corner of the grid.\n- For each cell, calculate the maximum score by considering both the rightward and downward paths.\n- Store the maximum score for each cell in the DP array.\n- After completing the DP array, iterate through it to find the maximum score.\n\n## Complexity\n- **Time complexity**: $$O(n \\cdot m)$$, where \\( n \\) is the number of rows and \\( m \\) is the number of columns in the grid. This complexity arises from iterating through each cell of the grid once and performing some operations in each cell.\n- **Space complexity**: $$O(n \\cdot m)$$, as the algorithm uses a 2D DP array of size \\( n \\times m \\) to store intermediate results.\n\nThis approach efficiently computes the maximum score for the given grid.\n# Code\n```\n#include <vector>\n#include <algorithm>\n#include <climits>\n\nusing namespace std;\n\nclass Solution\n{\n int solveop(vector<vector<int>> &grid, vector<vector<int>> &dp, int i, int j)\n {\n int n = grid.size();\n int m = grid[0].size();\n\n for (int o = j + 1; o < m; o++)\n {\n int k = grid[i][o] - grid[i][j];\n dp[i][j] = max(dp[i][j], max(k + dp[i][o], k));\n }\n for (int o = i + 1; o < n; o++)\n {\n int k = grid[o][j] - grid[i][j];\n dp[i][j] = max(dp[i][j], max(k + dp[o][j], k));\n }\n return dp[i][j]; // Added return statement\n }\n \n int solvedp(vector<vector<int>> &grid, vector<vector<int>> &dp)\n {\n int n = grid.size();\n int m = grid[0].size();\n\n for (int i = m - 2; i >= 0; i--)\n {\n for (int j = i + 1; j < m; j++)\n {\n if (j != m - 1)\n {\n int k = grid[n - 1][j] - grid[n - 1][i];\n dp[n - 1][i] = max(dp[n - 1][i], max(k + dp[n - 1][j], k));\n }\n else\n {\n int k = grid[n - 1][j] - grid[n - 1][i];\n dp[n - 1][i] = max(dp[n - 1][i], k);\n }\n }\n }\n\n for (int i = n - 2; i >= 0; i--)\n {\n for (int j = i + 1; j < n; j++)\n {\n if (j != n - 1)\n {\n int k = grid[j][m - 1] - grid[i][m - 1];\n dp[i][m - 1] = max(dp[i][m - 1], max(k + dp[j][m - 1], k));\n }\n else\n {\n int k = grid[j][m - 1] - grid[i][m - 1];\n dp[i][m - 1] = max(dp[i][m - 1], k);\n }\n }\n }\n\n for (int i = n - 2; i >= 0; i--)\n {\n for (int j = m - 2; j >= 0; j--)\n {\n solveop(grid, dp, i, j);\n }\n }\n int ans = INT_MIN;\n for (int i = n - 2; i >= 0; i--)\n {\n ans = max(ans, dp[i][m - 1]);\n }\n for (int i = m - 2; i >= 0; i--)\n {\n ans = max(ans, dp[n - 1][i]);\n }\n for (int i = n - 2; i >= 0; i--)\n {\n for (int j = m - 2; j >= 0; j--)\n {\n ans = max(ans, dp[i][j]);\n }\n }\n return ans;\n }\n\npublic:\n int maxScore(vector<vector<int>> &grid)\n {\n int n = grid.size();\n int m = grid[0].size();\n vector<vector<int>> dp(n, vector<int>(m, INT_MIN));\n return solvedp(grid, dp);\n }\n};\n\n``` | 3 | 0 | ['C++'] | 1 |
maximum-difference-score-in-a-grid | 2D-DP,Memoization, Easy to understand C++ | 2d-dpmemoization-easy-to-understand-c-by-kh32 | \n\n# Complexity\n- Time complexity: O(mn)\n\n- Space complexity: O(mn)\n\n\n# Code\n\nclass Solution {\npublic:\n int f(vector<vector<int>>&dp,vector<vector | raj_g1729 | NORMAL | 2024-05-19T08:53:55.812223+00:00 | 2024-05-19T08:55:40.159552+00:00 | 75 | false | \n\n# Complexity\n- Time complexity: O(m*n)\n\n- Space complexity: O(m*n)\n\n\n# Code\n```\nclass Solution {\npublic:\n int f(vector<vector<int>>&dp,vector<vector<int>>&grid,int i,int j)\n {\n if(i>=grid.size() || j>=grid[0].size()) return 0;\n if(dp[i][j]!=-1) return dp[i][j];\n int rowTake=INT_MIN, colTake=INT_MIN;\n if(i<grid.size()-1)rowTake=grid[i+1][j]-grid[i][j]+f(dp,grid,i+1,j);\n if(j<grid[0].size()-1)colTake=grid[i][j+1]-grid[i][j]+f(dp,grid,i,j+1);\n return dp[i][j]=max(0,max(colTake,rowTake));\n }\n int maxScore(vector<vector<int>>& grid) {\n int m=grid.size();\n int n=grid[0].size();\n vector<vector<int>>dp(m+1,vector<int>(n+1,-1));\n int ans=INT_MIN;\n for(int i=0;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(i<m-1) ans=max(ans,grid[i+1][j]-grid[i][j]+f(dp,grid,i+1,j));\n if(j<n-1) ans=max(ans,grid[i][j+1]-grid[i][j]+f(dp,grid,i,j+1)); \n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-difference-score-in-a-grid | Memoized Version of Lee's Solution | memoized-version-of-lees-solution-by-nik-ffm4 | Intuition\n Describe your first thoughts on how to solve this problem. \nFor those whose intuition works by recursion and memoization, this solution is the simp | nik_07 | NORMAL | 2024-05-14T13:34:19.260344+00:00 | 2024-05-14T13:35:22.683562+00:00 | 144 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor those whose intuition works by recursion and memoization, this solution is the simplest way to solve this problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLee\'s solution explains the intuition as follows,\n1. Maintain the top-left min value among the elements. Note that, this problem boils down to one start and end point as in-between cancels out everything. Note this is not the answer,\n2. Maintain a max element of (c2-c1) i.e., for each element checks its subtraction to a memoized min so far for it\'s top-left. This would be the final answer as max can occur anywhere in-between.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N^2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N^2). Note we can use the same input array in memoization and reduce it to O(1)\n\n# Code\n```\nclass Solution {\n int res=-1e6;\npublic:\n int maxScore(vector<vector<int>>& grid) {\n vector<vector<int>> m(grid.size(),vector<int>(grid[0].size(),-1e6));\n dp(grid.size()-1,grid[0].size()-1,grid,m);\n return res;\n }\n //https://leetcode.com/problems/maximum-difference-score-in-a-grid/solutions/5145704/java-c-python-dp-minimum-on-top-left/\n int dp(int i,int j,vector<vector<int>>& grid,vector<vector<int>>& memo){\n if(i<0||j<0){\n return 1e6;\n }\n //cout<<i<<" "<<j<<endl;\n if(memo[i][j]!=-1e6){\n return memo[i][j];\n }\n int pre=min(dp(i-1,j,grid,memo),dp(i,j-1,grid,memo));\n res=max(res,grid[i][j]-pre);\n return memo[i][j]=min(grid[i][j],pre);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 0 |
maximum-difference-score-in-a-grid | Simple recursive solution with Memoization | simple-recursive-solution-with-memoizati-o643 | Intuition\nRecursively go in the bottom and right direction making a note of max. Use memoization to optimize.\n\n# Approach\n- Start from top left (0, 0)\n- Fi | sadanandpai | NORMAL | 2024-05-13T19:13:00.351527+00:00 | 2024-05-13T19:13:00.351552+00:00 | 225 | false | # Intuition\nRecursively go in the bottom and right direction making a note of max. Use memoization to optimize.\n\n# Approach\n- Start from top left (0, 0)\n- Find the max of bottomMax and rightMax\n- Update if max at the current cell is greater\n- Update the memoized cell and return\n\n# Complexity\n- Time complexity:\nO(m * n)\n\n- Space complexity:\nO(m * n)\n\n# Code\n```\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar maxScore = function (grid) {\n const m = grid.length, n = grid[0].length;\n const dp = Array.from({ length: m }, () => []);\n let max = -Infinity;\n getMaxScore(0, 0);\n return max;\n\n function getMaxScore(row, col) {\n if (row >= m || col >= n) {\n return -Infinity;\n }\n\n if (dp[row][col] !== undefined) {\n return dp[row][col];\n }\n\n const bottom = getMaxScore(row + 1, col);\n const right = getMaxScore(row, col + 1);\n const currentMax = Math.max(bottom, right);\n max = Math.max(max, currentMax - grid[row][col]); // update max\n return dp[row][col] = Math.max(grid[row][col], currentMax);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'JavaScript'] | 0 |
maximum-difference-score-in-a-grid | O(N*M) Time Complexity, Simple DP Solution | onm-time-complexity-simple-dp-solution-b-rfo7 | The key idea is to find the minimum element in the top left region and then take the maximum among the difference of grid and the minimum array constructed.\n\n | N0V1C3 | NORMAL | 2024-05-13T08:29:40.421184+00:00 | 2024-05-13T08:39:23.588296+00:00 | 62 | false | The key idea is to find the minimum element in the top left region and then take the maximum among the difference of grid and the minimum array constructed.\n\nThis is because going from a->b->c gives the answer as (b-a)+(c-b) which is essentially (c-a).\n\n\n**Python:**\n\n```\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n n = len(grid)\n m = len(grid[0])\n arr =[[0]*(m) for _ in range(n)]\n \n for i in range(n):\n \n arr[i][0] = grid[i][0]\n if i>0:\n arr[i][0] = min(grid[i-1][0],arr[i-1][0])\n \n for j in range(m):\n arr[0][j] = grid[0][j]\n if j>0:\n arr[0][j] = min(grid[0][j-1],arr[0][j-1])\n \n for i in range(1,n):\n for j in range(1,m):\n arr[i][j] = min(arr[i-1][j], arr[i][j-1], arr[i-1][j-1], grid[i-1][j-1], grid[i][j-1], grid[i-1][j])\n print(arr)\n ans = -1e9\n for i in range(n):\n for j in range(m):\n if i==0 and j==0:\n continue\n ans = max(ans, grid[i][j]-arr[i][j])\n return ans\n\n\n```\n\n**C++:**\n\n```\n\nclass Solution {\npublic:\n int maxScore(vector<vector<int>>& grid) {\n int n = grid.size();\n int m=grid[0].size();\n \n vector<vector<int>> arr(n,vector<int>(m,0));\n \n for(int i=0;i<n;i++){\n arr[i][0] = grid[i][0];\n if (i>0){\n arr[i][0] = min(arr[i-1][0],grid[i-1][0]);\n }\n }\n \n for(int j=0;j<m;j++){\n arr[0][j] = grid[0][j];\n if (j>0){\n arr[0][j] = min(arr[0][j-1],grid[0][j-1]);\n }\n }\n \n for(int i=1;i<n;i++){\n for(int j=1;j<m;j++){\n arr[i][j] = min({arr[i-1][j],arr[i-1][j-1],arr[i][j-1],grid[i-1][j],grid[i-1][j-1],grid[i][j-1]});\n }\n }\n int ans = INT_MIN;\n \n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(i==0 && j==0) continue;\n ans = max(ans, grid[i][j] -arr[i][j]);\n }\n }\n return ans;\n }\n};\n\n\n``` | 2 | 0 | ['Dynamic Programming', 'Python'] | 3 |
maximum-difference-score-in-a-grid | Easy C++ Solution || (Recursion + Memoization) ✅✅ | easy-c-solution-recursion-memoization-by-1ggm | Code\n\nclass Solution {\npublic:\n int helper(vector<vector<int>>& grid,int i,int j,int n,int m,vector<vector<int>> &dp){\n if(i==(n-1) && j==(m-1)){ | Abhi242 | NORMAL | 2024-05-13T08:18:37.155373+00:00 | 2024-05-13T08:18:37.155394+00:00 | 309 | false | # Code\n```\nclass Solution {\npublic:\n int helper(vector<vector<int>>& grid,int i,int j,int n,int m,vector<vector<int>> &dp){\n if(i==(n-1) && j==(m-1)){\n return dp[i][j]=0;\n }\n int ans=-1e6;\n if(dp[i][j]!=-1e6){\n return dp[i][j];\n }\n if((i+1)<n){\n ans=max(ans,grid[i+1][j]-grid[i][j]+helper(grid,i+1,j,n,m,dp));\n ans=max(ans,grid[i+1][j]-grid[i][j]+helper(grid,n-1,m-1,n,m,dp));\n }\n if((j+1)<m){\n ans=max(ans,grid[i][j+1]-grid[i][j]+helper(grid,i,j+1,n,m,dp));\n ans=max(ans,grid[i][j+1]-grid[i][j]+helper(grid,n-1,m-1,n,m,dp));\n }\n return dp[i][j]=ans;\n }\n int maxScore(vector<vector<int>>& grid) {\n int n=grid.size();\n int m=grid[0].size();\n vector<vector<int>> dp(n,vector<int>(m,-1e6));\n helper(grid,0,0,n,m,dp);\n int ans=INT_MIN;\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(i==(n-1) && j==(m-1)){\n continue;\n }\n ans=max(ans,dp[i][j]);\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 0 |
maximum-difference-score-in-a-grid | [python3] easy dp solution + explanation/contest comentary | python3-easy-dp-solution-explanationcont-gv7e | Intuition and Thoughts\n you\'re just looking for the maximum cell that\'s further to the right or further down from the cell you\'re looking at. \n Gonna be si | horseshoecrab | NORMAL | 2024-05-12T22:31:33.888666+00:00 | 2024-05-12T22:42:39.533686+00:00 | 9 | false | #### Intuition and Thoughts\n* you\'re just looking for the maximum cell that\'s further to the right or further down from the cell you\'re looking at. \n* Gonna be size of O(grid) time for each cell if we iterate to get max cell (box with top left at (i,j) and bottom right at (m-1,n-1)), that sucks. \n* If we know the max of one box, can we construct the max for other boxes? hmmm....yes, well just cache them then and use them when we need them.\n* how to traverse the box to get these maxes (so I imagined going from bottom right, and working to the cells neighboring it and then building up these max cells)\n\n#### Contest Solution\n```\nclass Solution:\n def maxScore(self, grid: List[List[int]]) -> int:\n \n @cache\n def dp(i,j): # largest from top left (i,j) to (M-1,N-1)\n if i >= M or j >= N:\n return -inf\n return max(grid[i][j], dp(i+1,j), dp(i,j+1))\n \n M = len(grid)\n N = len(grid[0])\n \n res = -inf\n for i in range(M):\n for j in range(N):\n n = grid[i][j]\n res = max(res, dp(i+1,j)-n, dp(i,j+1)-n)\n return res\n``` | 2 | 0 | [] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.