question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
count-number-of-nice-subarrays | [C++][O(N) Prefix Sum] | con-prefix-sum-by-emli-asgz | \nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n vector<int> prefixSum(nums.size());\n \n for(int i = 0 | emli | NORMAL | 2019-11-03T04:09:13.103668+00:00 | 2019-11-03T04:10:11.114978+00:00 | 1,681 | false | ```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n vector<int> prefixSum(nums.size());\n \n for(int i = 0; i < nums.size(); i++){\n if (nums[i] % 2 == 1){\n prefixSum[i] = 1;\n }\n }\n \n for(int i = 1; i < nums.size(); i++){\n prefixSum[i] += prefixSum[i - 1];\n }\n \n unordered_map<int,int> map;\n \n map[0] = 1;\n \n int ans = 0;\n for(int i = 0; i < nums.size(); i++){\n if (prefixSum[i] - k >= 0){\n ans += map[prefixSum[i] - k];\n }\n map[prefixSum[i]]++;\n }\n \n\n return ans;\n }\n};\n``` | 12 | 1 | [] | 2 |
count-number-of-nice-subarrays | Python - 2 Sliding Window Solutions | python-2-sliding-window-solutions-by-its-pd9z | \n# APPROACH 1- NOT O(1) SPACE\n\nThere are some things to take care of in this problem. We cannot simply consider one window to be valid and just increment cou | itsarvindhere | NORMAL | 2022-09-14T15:35:31.467039+00:00 | 2022-09-16T06:09:39.908099+00:00 | 1,526 | false | \n# **APPROACH 1- NOT O(1) SPACE**\n\nThere are some things to take care of in this problem. We cannot simply consider one window to be valid and just increment count by 1.\n\nConsider this ->\n\n\t\tnums = [2,2,2,1,2,2,1,2,2,2] and k = 2\n\t\t\t\t0 1 2 3 4 5 6 7 8 9\n\t\t\nSo, if we use the sliding window approach, then we will start from index 0 and until the count of odd numbers does not become k, we will keep increasing window size. Now just by looking at the array you will see that when index is 6 then it will have two odd numbers from 0th index to 6th index.\n\nSo we will have a valid window with k odd numbers -\n\n\t\t\t[2,2,2,1,2,2,1]\n\nBut, at this moment, we cannot simply do count += 1. Just think about it. If [2,2,2,1,2,2,1] is a valid subarray with k odd numbers, then how many subarrays of this are also valid?\n\n\tThese are all valid subarrays with k odd numbers\n\t[2,2,2,1,2,2,1]\n\t[2,2,1,2,2,1]\n\t[2,1,2,2,1]\n\t[1,2,2,1]\n\t\nThis means, we cannot do count += 1 only. We have to check for a particular nice subarray, how many total nice subarrays are possible.\n\nAnd to find that, just see above what is the smallest possible subarray. It is [1,2,2,1]. Why we were not able to get more subarrays smaller than it? Because we would\'ve lost one odd number and that would\'ve violated the condition of k odd numbers.\n\nSo this means, just see how many numbers are there between the beginning of the window and the first odd number in the window i.e., the leftmost odd number.\n\nFinally, we will get a general formula as \n\t\n\t\t(index of leftmost odd number in current window - index of beginning of window) + 1\n\t\t\nSo basically, we want to keep track of not just the odd numbers but also their indices. \n\nAnd so I used a queue here to keep all the indices in it from left to right as we encounter odd numbers so that to calculate the count, we can simply get the first item in the queue as that will always be the leftmost odd number index of current window.\n\nAnd as we shrink the window, we will keep checking if the item we are removing from window is an odd number or not. If yes, that means we need to remove the leftmost item from queue as well. \n\n\n```\ndef numberOfSubarrays(self, nums: List[int], k: int) -> int:\n subarrayCount = 0\n \n i,j = 0,0\n\n queue = deque()\n \n\n while( j < len(nums) ):\n # If we encounter an odd number push the index of this odd number to queue\n if(nums[j] % 2 != 0): queue.append(j)\n \n #If the number of odd numbers in this window exceeds k, then shrink the window from left until the count of odds is not greater than k\n if(len(queue) > k):\n while(len(queue) > k):\n #If the number at ith index is odd, that means we have to remove this odd number\'s index from queue\n if(nums[i] % 2 != 0): queue.popleft()\n #Shrink the window from left by incrementing i\n i += 1\n \n # If number of odd numbers in current window = k\n # Then total subarrays we can get out of this current window with k odd numbers => (leftmost odd number index - starting of window + 1)\n if(len(queue) == k): subarrayCount += queue[0] - i + 1\n \n #Increase window size from right side\n j += 1\n \n \n return subarrayCount\n```\n\n# **APPROACH 2 - O(1) SPACE**\nJust remember one thing for such problems where we have to find how many subarrays have "exactly" K something. \n\n\tSubarrays with K something = Subarrays with at most K something - Subarrays with at most K-1 something\n\t\nAt most K means that a subarray should have something <= K. \n\t\nFor this problem, since we have to find subarrays with exactly K odd numbers. That means, \n\t\n\tSubarrays with exactly K odd numbers = Subarrays with at most K odd numbers - Subarrays with at most K-1 odd numbers\n\t\nLet me prove it with an example.\n\n\t\tnums = [1,1,2,1,1], k = 3\n\t\t\nSo here, what are the subarrays with <= 3 odd number ? i.e., how many subarrays have at most 3 odd numbers?\n\n\t[1], [1, 1], [1], [1, 1, 2], [1, 2], [2], [1, 1, 2, 1], [1, 2, 1], [2, 1], [1], [1, 2, 1, 1], [2, 1, 1], [1, 1], [1] => 14 Subarrays\n\nNow, lets see how many subarrays have <= 2 odd numbers i.e., <= K- 1 odd numbers\n\t\n\t[1], [1, 1], [1], [1, 1, 2], [1, 2], [2], [1, 2, 1], [2, 1], [1], [2, 1, 1], [1, 1], [1] => 12 Subarrays\n\t\nSo that means, Subarrays with exactly 3 odd numbers are => 14 - 12 => 2\n\nAnd to prove this, here are all the subarrays with exactly 3 odd numbers\n\t\n\t\t[1,1,2,1] and [1,2,1,1].\n\t\t\nAnd these are the only ones that are not in the list of subarrays with <= 2 odd numbers. \n\nYou can use this template in many similar problems where we are asked to find how many subarrays have exactly K sum, exactly K odd numbers and so on. And there is little to no change you have to make which makes this solution so damn useful.\n\n```\nclass Solution:\n \n def atMost(self, nums: List[int], k: int) -> int:\n \n countOfSubarrays = 0\n \n i,j = 0,0\n n = len(nums)\n \n countOfOdds = 0\n \n while j < n:\n if nums[j] % 2 != 0 : countOfOdds += 1\n \n if countOfOdds > k:\n while countOfOdds > k:\n if nums[i] % 2 != 0: countOfOdds -= 1\n i += 1\n \n countOfSubarrays += j - i + 1\n j += 1\n \n return countOfSubarrays\n \n \n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n return self.atMost(nums, k) - self.atMost(nums, k-1)\n\n\n```\n | 11 | 0 | ['Sliding Window', 'Python'] | 3 |
count-number-of-nice-subarrays | 🔥2 Approaches || ⚡Easiest & Best Code in C++ with explanation ✅ | 2-approaches-easiest-best-code-in-c-with-jxz6 | Please Upvote if u liked my Solution\uD83D\uDE42\n# Using PrefixSum with HashMap(O(n) SC):-\n\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& | aDish_21 | NORMAL | 2022-09-12T16:32:22.742499+00:00 | 2024-06-25T14:32:20.952741+00:00 | 1,169 | false | ## **Please Upvote if u liked my Solution**\uD83D\uDE42\n# Using PrefixSum with HashMap(O(n) SC):-\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int size=nums.size(),i=0,j=0;\n for(auto &it:nums){\n if((it & 1)==0)\n it=0;\n else //Replacing all the even nos. with 0 & odd nos. with 1 \n it=1;\n }\n //Now simply to get the ans we have to return the no of subarrays with sum = k\n unordered_map<int,int> mp;\n int prefixSum=0,ans=0;\n for(auto it:nums){\n prefixSum+=it;\n if(prefixSum==k)\n ans++;\n if(mp.find(prefixSum-k)!=mp.end())\n ans+=mp[prefixSum-k];\n mp[prefixSum]++;\n }\n return ans;\n }\n};\n```\n## Using Three Pointers(O(1) SC):-\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int n = nums.size(), i = 0, j = 0, h = -1, ans = 0, cnt_odd = 0;\n while(j < n){\n if(nums[j] & 1){\n i = j;\n break;\n }\n j++;\n }\n while(j < n){\n if (nums[j] & 1)\n cnt_odd++;\n if (cnt_odd > k){\n h = i;\n while(cnt_odd > k || !(nums[i] & 1)){\n if(nums[i] & 1)\n cnt_odd--;\n i++;\n } \n }\n if(cnt_odd == k)\n ans += i - h;\n j++;\n }\n return ans;\n }\n};\n```\n**Happy LeetCoding\uD83D\uDCAF\nPlease Upvote**\uD83D\uDE42 | 11 | 0 | ['Array', 'Hash Table', 'Math', 'C', 'Sliding Window', 'Prefix Sum'] | 0 |
count-number-of-nice-subarrays | JAVA solution | Current problem transformed to Problem 560 | HashMap | java-solution-current-problem-transforme-hjv3 | Please Upvote !!! (\u25E0\u203F\u25E0)\nWe traverse the whole array and put 0 in place of even elements and 1 in place of odd elements. \nSo instead of finding | sourin_bruh | NORMAL | 2022-09-24T18:09:51.437156+00:00 | 2022-09-24T18:09:51.437198+00:00 | 1,084 | false | #### *Please Upvote !!!* **(\u25E0\u203F\u25E0)**\nWe traverse the whole array and put 0 in place of even elements and 1 in place of odd elements. \nSo instead of finding k odd numbers, we now find subarrays whose sum will be equal to k (Because the odd numbers are all 1 and k odd numbers will give a sum of k now).\n\nThis takes us to the problem [**560. Subarray Sum Equals K**](https://leetcode.com/problems/subarray-sum-equals-k/).\n\nWe can put 0s and 1s in place of even and odd number by simply iterating through the array. \n```\nfor (int i = 0; i < nums.length; i++) {\n\tnums[i] = (nums[i] % 2 == 0) ? 0 : 1;\n}\n```\nBut that would take an extra O(n) time complexity. \n\nSo we won\'t do that. In Problem 560, we add ```nums[i]``` to ```sum``` at each iteration. So why not decide there itself whether to add 0 or 1 to sum!\n\nBelow is the solution, exactly similar to Problem 560.\n```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int total = 0, sum = 0;\n Map<Integer, Integer> map = new HashMap<>();\n map.put(0, 1);\n\n for (int i = 0; i < nums.length; i++) {\n sum += (nums[i] % 2 == 0) ? 0 : 1;\n int rem = sum - k;\n\n if (map.containsKey(rem)) {\n total += map.get(rem);\n }\n\n map.put(sum, map.getOrDefault(sum, 0) + 1);\n }\n\n return total;\n }\n}\n\n// TC: O(n), SC: O(n)\n``` | 10 | 0 | ['Java'] | 1 |
count-number-of-nice-subarrays | beats 100% | beats-100-by-vigneshreddy06-okea | Intuition\nC++\n\nPython3\n\n\n\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nSimply Use the queue to store the indexes of odd el | vigneshreddy06 | NORMAL | 2024-06-22T11:25:26.046829+00:00 | 2024-06-22T11:25:26.046853+00:00 | 186 | false | # Intuition\nC++\n\nPython3\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSimply Use the queue to store the indexes of odd elements.\nStart counting the subarrays when the Queue is of K size.\nMaintain two variables end and last to count the values that can be added to next index.\n# Complexity\n- Time complexity:\nOnly one iterations, e.g. O(n)\n- Space complexity:\nA Queue with max of k elements, e.g. O(k)\n\n# Code C++\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n queue<int> Q;\n int lst = 0, end = -1, ans = 0;\n for (int i = 0; i < nums.size(); i++) {\n if(nums[i]&1){\n Q.push(i);\n }\n if(Q.size() == k){\n lst = end;\n end = Q.front();\n Q.pop();\n }\n if(end != -1){\n ans += end - lst;\n }\n }\n return ans;\n }\n};\n//if you upvote this you will hear good news in 10mins\n```\n# Code Python3\n```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n odd_count = 0\n res = 0\n i = 0\n count = 0\n for ele in nums:\n if ele % 2 == 1:\n odd_count += 1\n count = 0\n\n while odd_count==k:\n if nums[i] % 2 == 1:\n odd_count -= 1\n i += 1\n count += 1\n \n res += count\n return res\n#if you upvote this you will hear good news in 10mins\n``` | 9 | 0 | ['C++', 'Python3'] | 3 |
count-number-of-nice-subarrays | Prefix sum+Sliding window vs at most k odds||35ms Beats 99.99% | prefix-sumsliding-window-vs-at-most-k-od-38ou | Intuition\n Describe your first thoughts on how to solve this problem. \nThe concept is to use sliding window. With the help of prefix sum, it made an acceptibl | anwendeng | NORMAL | 2024-06-22T01:33:39.888292+00:00 | 2024-06-22T02:08:18.435189+00:00 | 618 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe concept is to use sliding window. With the help of prefix sum, it made an acceptible solution.\n\n2nd approach usse at most k odds argument which is applied to solve the hard question [992. Subarrays with K Different Integers](https://leetcode.com/problems/subarrays-with-k-different-integers/solutions/4944461/sliding-window-count-subarrays-with-at-most-k-distinct-elements-15ms-beats-99-87/)\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Build an 1-indexed prefix sum array `cntOdds` for counting odd numbers in subarrays `nums[0:i]`\n2. Use sliding window pattern to solve like the following. It\'s to see that `cntOdds(nums[l..r])` can be easily computed by using prefix sums\n```\nfor (r=0, l=0; r < n; r++) {\n // Ensure the current window [l, r] has at least k odd numbers\n while (l<=r and cntOdds(nums[l..r]) > k) \n l++;\n\n // If the current window [l, r] has exactly k odd numbers\n if (cntOdds(nums[l..r]) == k) {\n l0 = l;\n // Count nice subarrays ending at r\n while (l0 <= r && cntOdds(nums[l0..r]) == k) {\n cnt++;\n l0++;\n }\n }\n}\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code Prefix sum+Sliding window||C++ 35ms Beats 99.99%\n```\nclass Solution {\npublic:\n static int numberOfSubarrays(vector<int>& nums, int k) {\n const int n = nums.size();\n vector<int> cntOdds(n+1, 0); // 1-indexed prefix sum count of odds\n\n // Create the prefix sum array\n for (int i = 0; i < n; i++) \n cntOdds[i+1] = cntOdds[i] + (nums[i] & 1);\n\n int l=0, cnt=0;\n for (int r=0; r < n; r++) {\n // Ensure the current window [l, r] has at least k odd numbers\n while (l<=r && cntOdds[r+1] - cntOdds[l] > k) \n l++;\n\n // If the current window [l, r] has exactly k odd numbers\n if (cntOdds[r+1]-cntOdds[l] == k) {\n int l0 = l;\n // Count nice subarrays ending at r\n while (l0 <= r && cntOdds[r+1]-cntOdds[l0] == k) {\n cnt++;\n l0++;\n }\n }\n }\n return cnt;\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n\n```\n# Solution using at most k odds\n\nThe solution is a slight modifition for [992. Subarrays with K Different Integers](https://leetcode.com/problems/subarrays-with-k-different-integers/solutions/4944461/sliding-window-count-subarrays-with-at-most-k-distinct-elements-15ms-beats-99-87/) \ncount subarrays with at most K odd elements. it makes problem much easier!\n[Please turn on English subtitles if necessary]\n[https://youtu.be/Z113uN6sKDc?si=QvC_REca7V0vt6tW](https://youtu.be/Z113uN6sKDc?si=QvC_REca7V0vt6tW)\nThe following questions can be solved sliding window:\n[713. Subarray Product Less Than K](https://leetcode.com/problems/subarray-product-less-than-k/solutions/4930759/2c-sliding-windows30ms-beats-9992/)\n[2302. Count Subarrays With Score Less Than K](https://leetcode.com/problems/count-subarrays-with-score-less-than-k/solutions/4932340/sliding-windows-like-leetcode-713-44ms-beats-100/)\n[2958. Length of Longest Subarray With at Most K Frequency](https://leetcode.com/problems/length-of-longest-subarray-with-at-most-k-frequency/solutions/4935191/sliding-window-hash-map128ms-beats-9978/)\n[2962. Count Subarrays Where Max Element Appears at Least K Times\n](https://leetcode.com/problems/count-subarrays-where-max-element-appears-at-least-k-times/solutions/4939830/sliding-window-vs-combinatorical-formula-59ms-beats-100/)\n\n\nThese problems can be solved by the following pattern:\n```\nfor(int l,r=0; r<n; r++){\n do_something_by_adding(nums[r]);\n while (!check_condition(k)){\n do_something_by_removing(nums[l]);\n l++;\n }\n update_the_answer();\n}\n```\n# C++ code\n```\nclass Solution {\npublic:\n int n;\n\n // Helper function to count subarrays with at most k odd numbers\n int niceLessEqualK(vector<int>& nums, int k){\n int odds=0, cnt=0;\n for(int l=0, r=0; r<n; r++){\n int x=nums[r];\n odds+=(x&1);\n while(odds>k){\n int y=nums[l];\n odds-=(y&1);\n l++;\n }\n cnt+=(r-l+1); // # of subarrays ending at r with at most k odd numbers\n }\n return cnt;\n }\n\n int numberOfSubarrays(vector<int>& nums, int k) {\n n = nums.size();\n return niceLessEqualK(nums, k)-niceLessEqualK(nums, k-1);\n }\n};\n\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n | 9 | 3 | ['Array', 'Sliding Window', 'Prefix Sum', 'C++'] | 2 |
count-number-of-nice-subarrays | ✅Beats 100% | Variable Size Sliding Window | Easy Explaination | beats-100-variable-size-sliding-window-e-ourv | Intuition\r\n Describe your first thoughts on how to solve this problem. \r\nThe task is to find the number of subarrays with exactly k odd numbers. To achieve | Fidio99 | NORMAL | 2024-06-22T00:06:38.952447+00:00 | 2024-06-22T00:11:16.283450+00:00 | 2,299 | false | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nThe task is to find the number of subarrays with exactly k odd numbers. To achieve this, we use a helper function to count the number of subarrays with at most k odd numbers. The difference between the number of subarrays with at most k odd numbers and the number of subarrays with at most k-1 odd numbers gives us the number of subarrays with exactly k odd numbers.\r\n\r\nExactly `K` times = at most `K` times - at most `K - 1` times\r\n\r\n# Java Code\r\n```\r\nclass Solution {\r\n public int numberOfSubarrays(int[] nums, int k) {\r\n \r\n //SubArrays which have exactly k odd numbers = total subArrays with k odd - totalSubArray with k-1 odd\r\n return findTotalSubArrays(nums, k) - findTotalSubArrays(nums, k - 1);\r\n }\r\n //this will find all the subarrays till k odd numbers\r\n public int findTotalSubArrays(int[] nums, int k){\r\n\r\n int i = 0;\r\n int j = 0;\r\n int subArrays = 0;\r\n int countOdd = 0;\r\n\r\n while(j < nums.length){\r\n\r\n if(nums[j] % 2 != 0){ //calculation part\r\n countOdd++;\r\n }\r\n\r\n while(countOdd > k){ //if !condition \r\n\r\n if(nums[i] % 2 != 0){ //remove the calculation part using i\r\n countOdd--;\r\n }\r\n i++; \r\n }\r\n subArrays += j - i + 1; //find all subarrays\r\n j++;\r\n } \r\n return subArrays;\r\n }\r\n}\r\n```\r\n# C++ Code\r\n```\r\nclass Solution {\r\npublic:\r\n int numberOfSubarrays(vector<int>& nums, int k) {\r\n return findTotalSubArrays(nums, k) - findTotalSubArrays(nums, k - 1);\r\n }\r\n\r\n int findTotalSubArrays(vector<int>& nums, int k) {\r\n int i = 0, j = 0, subArrays = 0, countOdd = 0;\r\n\r\n while (j < nums.size()) {\r\n if (nums[j] % 2 != 0) { // Calculation part\r\n countOdd++;\r\n }\r\n\r\n while (countOdd > k) { // if condition fails\r\n if (nums[i] % 2 != 0) { // Remove the calculation part using i\r\n countOdd--;\r\n }\r\n i++;\r\n }\r\n\r\n subArrays += j - i + 1; // Find all subarrays\r\n j++;\r\n }\r\n return subArrays;\r\n }\r\n};\r\n\r\n```\r\n# Python Code\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n return self.findTotalSubArrays(nums, k) - self.findTotalSubArrays(nums, k - 1)\r\n \r\n def findTotalSubArrays(self, nums: List[int], k: int) -> int:\r\n i = 0\r\n j = 0\r\n subArrays = 0\r\n countOdd = 0\r\n \r\n while j < len(nums):\r\n if nums[j] % 2 != 0: # Calculation part\r\n countOdd += 1\r\n \r\n while countOdd > k: # if condition fails\r\n if nums[i] % 2 != 0: # Remove the calculation part using i\r\n countOdd -= 1\r\n i += 1\r\n \r\n subArrays += j - i + 1 # Find all subarrays\r\n j += 1\r\n \r\n return subArrays\r\n\r\n``` | 9 | 0 | ['Array', 'Hash Table', 'Math', 'Sliding Window', 'Python', 'C++', 'Java'] | 5 |
count-number-of-nice-subarrays | Hash Maps to Find Nice Subarrays. | hash-maps-to-find-nice-subarrays-by-iama-vcgv | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves counting the number of subarrays that contain exactly \uD835\uDC58 | iamanrajput | NORMAL | 2024-06-22T14:22:28.321791+00:00 | 2024-06-22T14:22:28.321813+00:00 | 274 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves counting the number of subarrays that contain exactly \uD835\uDC58.\n\nk odd numbers. Initially, this may seem complex due to the need to evaluate every possible subarray. However, leveraging prefix sums and hash maps can simplify this task significantly. The key observation is that the number of subarrays with exactly \uD835\uDC58.\n\nk odd numbers can be efficiently tracked using a sliding window approach or prefix sums to avoid recomputing sums repeatedly.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPrefix Sum with Odd Counts: Transform the problem into one of counting prefix sums. Keep a running count of the number of odd numbers encountered so far. Use a hash map to store the frequency of each odd count encountered.\nHash Map for Efficient Counting: For each position in the array, check if the count of odd numbers minus \uD835\uDC58.\n\nk exists in the hash map. If it does, it means there exists a subarray ending at the current position with exactly \uD835\uDC58.\n\nIterate and Update Hash Map: As we iterate through the array, we update the hash map with the current count of odd numbers. This allows us to efficiently find the number of subarrays that end at the current position and contain exactly \uD835\uDC58.\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int n = nums.length;\n int[] cnt = new int[n + 1];\n cnt[0] = 1;\n int ans = 0, t = 0;\n for (int v : nums) {\n t += v & 1;\n if (t - k >= 0) {\n ans += cnt[t - k];\n }\n cnt[t]++;\n }\n return ans;\n }\n}\n``` | 8 | 0 | ['Array', 'Hash Table', 'Math', 'Sliding Window', 'C++', 'Java'] | 0 |
count-number-of-nice-subarrays | Python easy prefix sum solution | python-easy-prefix-sum-solution-by-berth-fy0y | Hi guys,\n\nHere is a simple solution using the prefix sum of an array where each element is equal to 1 if nums[i]%2==1 and 0 if nums[i]%2==0. \n\nWe initialize | Berthouille | NORMAL | 2022-09-20T10:10:19.569672+00:00 | 2022-09-20T10:10:19.569715+00:00 | 1,492 | false | Hi guys,\n\nHere is a simple solution using the prefix sum of an array where each element is equal to 1 if nums[i]%2==1 and 0 if nums[i]%2==0. \n\nWe initialize the dictionary so that we take into account the arrays with k odd numbers starting at index 0.\n\n\t\tpref=list(accumulate([0 if num%2==0 else 1 for num in nums]))\n dico=defaultdict(int)\n res=0\n dico[0]=1\n for num in pref:\n if num-k in dico:\n res+=dico[num-k]\n dico[num]+=1\n return res\n\t\t\nThen if pref[i]==j it means we have j odd numbers from index 0 to index j. Hence if j-k is in our hash table, it means that for dico[j-k] indices, we had j-k odd numbers. So between these indices and index i, we have a total k odd numbers : j-(j-k)=k.\n\nPlease upvote if you liked!\n\nCheers,\nBerthouille | 8 | 0 | ['Prefix Sum', 'Python'] | 4 |
count-number-of-nice-subarrays | WELL-EXPLAINED🧠 EASIEST SOLUTION🧐 SLIDING WINDOW🪟TWO-POINTERS | well-explained-easiest-solution-sliding-q4pce | UPVOTE IF YOU FIND THE SOLUTION HELPFUL\uD83D\uDCA1\n\n# Intuition\nThe problem requires us to find the number of continuous subarrays with exactly k odd number | __aayush_01 | NORMAL | 2024-06-22T08:56:27.411969+00:00 | 2024-06-22T08:56:44.036557+00:00 | 610 | false | # ***UPVOTE IF YOU FIND THE SOLUTION HELPFUL\uD83D\uDCA1***\n\n# Intuition\nThe problem requires us to find the number of continuous subarrays with exactly k odd numbers. This can be efficiently solved using a `sliding window` with `two-pointer` approach.\n\n\n# Approach\n1. **Initialization:**\n - Initialize two pointers, `i` and `j`, both set to the start of the array. These pointers define the current window of elements being considered.\n - `oddCount` keeps track of the number of odd numbers within the current window.\n - `subArrayCount` keeps the count of nice subarrays.\n - `temp` temporarily stores the number of valid subarrays ending at the current position `j`.\n\n2. **Sliding Window Expansion:**\n - Traverse the array using pointer `j`. For each element, check if it is odd (`nums[j] % 2 == 1`). If it is odd, increment `oddCount` and reset `temp` to 0.\n - If `oddCount` equals `k`, it means the current window has exactly `k` odd numbers. Start shrinking the window from the left to explore the further possible **Nice sub-arrays**, so (increment `i`) while `oddCount` remains `k`:\n - Increment `temp` for each valid subarray found by moving `i`.\n - If the element at `i` is odd, decrement `oddCount` as it will be excluded from the window.\n - Add `temp` to `subArrayCount` for each valid subarray found ending at the current `j`. In this way, we can find all the possible **Nice sub-arrays** ending at the index `j`\n\n3. **Return Result:**\n - After processing all elements, `subArrayCount` will contain the total number of nice subarrays.\n\n# Code\n``` Java []\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int i = 0, j = 0;\n int oddCount = 0;\n int subArrayCount = 0;\n int temp = 0;\n\n while(j < nums.length){\n if(nums[j] % 2 == 1){\n oddCount++;\n temp = 0;\n }\n\n while(oddCount == k){\n temp++;\n if(nums[i] % 2 == 1){\n oddCount--;\n }\n i++;\n }\n subArrayCount += temp;\n j++;\n }\n return subArrayCount;\n }\n}\n```\n``` Python []\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n i = 0\n j = 0\n odd_count = 0\n sub_array_count = 0\n temp = 0\n\n while j < len(nums):\n if nums[j] % 2 == 1:\n odd_count += 1\n temp = 0\n \n while odd_count == k:\n temp += 1\n if nums[i] % 2 == 1:\n odd_count -= 1\n i += 1\n \n sub_array_count += temp\n j += 1\n \n return sub_array_count\n```\n``` C++ []\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int i = 0, j = 0;\n int oddCount = 0;\n int subArrayCount = 0;\n int temp = 0;\n\n while (j < nums.size()) {\n if (nums[j] % 2 == 1) {\n oddCount++;\n temp = 0;\n }\n\n while (oddCount == k) {\n temp++;\n if (nums[i] % 2 == 1) {\n oddCount--;\n }\n i++;\n }\n subArrayCount += temp;\n j++;\n }\n return subArrayCount;\n }\n};\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar numberOfSubarrays = function(nums, k) {\n let i = 0, j = 0;\n let oddCount = 0;\n let subArrayCount = 0;\n let temp = 0;\n\n while(j < nums.length) {\n if(nums[j] % 2 === 1) {\n oddCount++;\n temp = 0;\n }\n\n while(oddCount === k) {\n temp++;\n if(nums[i] % 2 === 1) {\n oddCount--;\n }\n i++;\n }\n subArrayCount += temp;\n j++;\n }\n return subArrayCount;\n};\n\n```\n\n\n | 7 | 0 | ['Array', 'Hash Table', 'Math', 'Two Pointers', 'Sliding Window', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
count-number-of-nice-subarrays | 🗓️ Daily LeetCoding Challenge Day 185|| 🔥 JAVA SOL | daily-leetcoding-challenge-day-185-java-yli6e | \n# Code\n\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int n = nums.length;\n int[] count = new int[n + 1];\n | DoaaOsamaK | NORMAL | 2024-06-22T03:04:12.672063+00:00 | 2024-06-22T03:04:12.672092+00:00 | 1,344 | false | \n# Code\n```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int n = nums.length;\n int[] count = new int[n + 1];\n count[0] = 1;\n int result = 0, oddCount = 0;\n for (int num : nums) {\n oddCount += num & 1;\n if (oddCount - k >= 0) {\n result += count[oddCount - k];\n }\n count[oddCount]++;\n }\n return result;\n }\n}\n\n``` | 7 | 0 | ['Java'] | 1 |
count-number-of-nice-subarrays | Python3 Solution | python3-solution-by-motaharozzaman1996-dor5 | \n\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n n=len(nums)\n i=0\n count=0\n ans=0\n | Motaharozzaman1996 | NORMAL | 2024-06-22T00:46:48.612302+00:00 | 2024-06-22T00:46:48.612321+00:00 | 1,287 | false | \n```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n n=len(nums)\n i=0\n count=0\n ans=0\n for j in range(n):\n if nums[j] & 1:\n k-=1\n count=0\n while k==0:\n k+= nums[i] & 1\n i+=1\n count+=1\n ans+=count\n return ans \n``` | 7 | 0 | ['Python', 'Python3'] | 3 |
count-number-of-nice-subarrays | C solution using "at least k" approach | c-solution-using-at-least-k-approach-by-zen14 | Algorithm\nMaintain two pointers i and j. If the number of odd numbers between i and j inclusive (i >= j) is exactly k then the number of subarrays with "at lea | psionl0 | NORMAL | 2024-06-22T00:22:10.059238+00:00 | 2024-06-22T02:32:49.809123+00:00 | 260 | false | # Algorithm\nMaintain two pointers `i` and `j`. If the number of odd numbers between `i` and `j` inclusive (`i >= j`) is exactly `k` then the number of subarrays with "at least `k`" odd numbers from `j` onwards will be given as `numsSize - i`.\n\nReturn the difference between the number of subarrays with "at least `k`" odd numbers and the number of subarrays with "at least `k + 1`" odd numbers".\n# Code\n```\nint subArrayAtLeastK(int *nums, int numsSize, int k) {\n int i, j=0, count=0, odds=0;\n for (i = 0; i < numsSize; ++i) {\n odds += (nums[i] & 1);\n while(odds == k) {\n count += numsSize - i;\n odds -= (nums[j++] & 1);\n }\n }\n return count;\n}\n\nint numberOfSubarrays(int* nums, int numsSize, int k) {\n return subArrayAtLeastK(nums, numsSize, k) - \n subArrayAtLeastK(nums, numsSize, k+1);\n}\n``` | 7 | 0 | ['C'] | 1 |
count-number-of-nice-subarrays | Sliding Window,PrefixSum Approach | sliding-windowprefixsum-approach-by-ganj-set4 | \nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n prefixsum=0\n dic=defaultdict(int)\n dic[0]=1\n | GANJINAVEEN | NORMAL | 2023-08-21T08:51:46.348874+00:00 | 2023-08-21T08:51:46.348907+00:00 | 1,115 | false | ```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n prefixsum=0\n dic=defaultdict(int)\n dic[0]=1\n ans=0\n for i in nums:\n if i%2==1:\n prefixsum+=1\n ans+=dic[prefixsum-k]\n dic[prefixsum]+=1\n return ans\n```\n# please upvote me it would encourage me alot\n | 7 | 0 | ['Python3'] | 2 |
count-number-of-nice-subarrays | Easy solution | easy-solution-by-wtfcoder-4djp | Intuition\r\n Describe your first thoughts on how to solve this problem. \r\nConsider the window with k prime numbers, the number of evens on either side are va | wtfcoder | NORMAL | 2023-07-02T10:14:27.922307+00:00 | 2023-07-02T10:14:27.922328+00:00 | 2,152 | false | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nConsider the window with k prime numbers, the number of evens on either side are variables, Maintain evens on left and right of every odd numbers, ans is sum of (evens on left of first number + 1 * evens on right of last number + 1). \r\n\r\n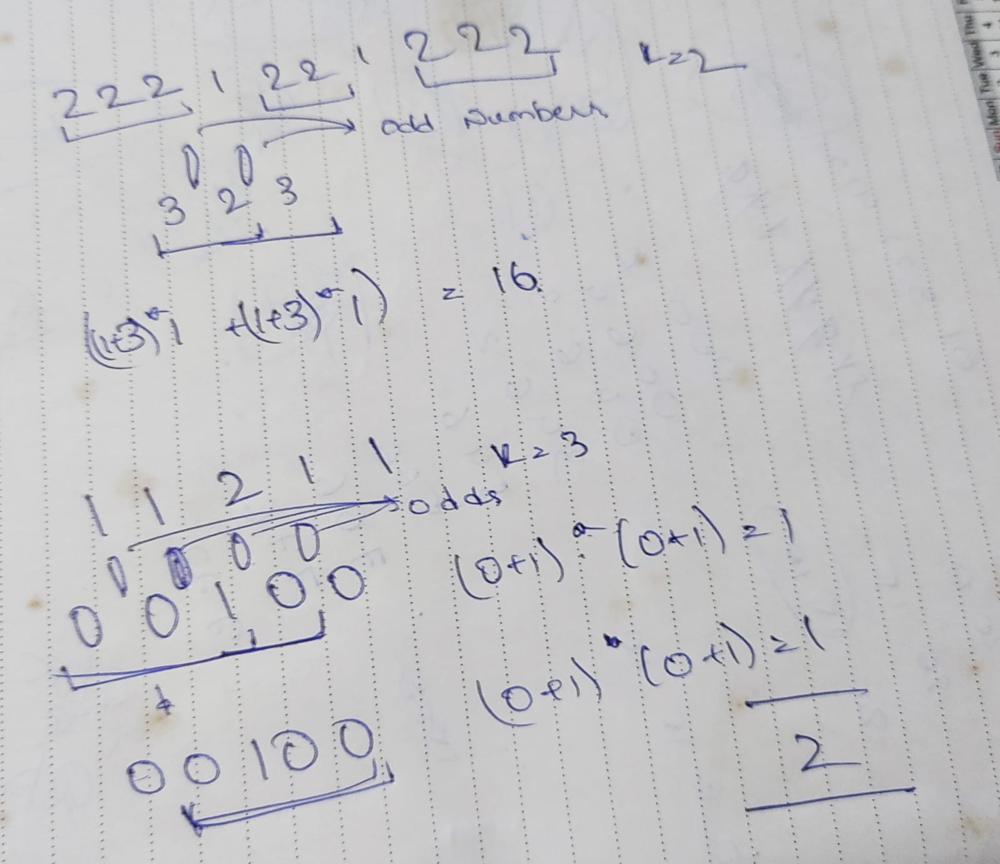\r\n\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\nStore the evens on left of every number in a vector and evens on the right of last element in last. Slide a window of size k , add (s[i]+1 * s[i+k]+1 ) to the sum. \r\n\r\n# Complexity\r\n- Time complexity:O(N)\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:O(N)\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\nPlease upvote if you find it helpful \r\n\r\n# Code\r\n```\r\nclass Solution {\r\npublic:\r\n int numberOfSubarrays(vector<int>& nums, int k) {\r\n // Vector to store the evens between odd numbers\r\n vector<int> t;\r\n int temp = 0, ans = 0; \r\n // Store Evens between odds\r\n for(int i=0; i<nums.size(); i++) {\r\n if(nums[i]%2 == 0) temp++; \r\n else {\r\n t.push_back(temp); temp = 0; \r\n }\r\n }\r\n t.push_back(temp); \r\n int ind = 0; \r\n //sliding window to count number of subarrays\r\n while(ind + k < t.size()){ ans += (t[ind]+1) * (t[ind+k]+1); ind++; }\r\n\r\n return ans; \r\n\r\n }\r\n};\r\n``` | 7 | 0 | ['Sliding Window', 'C++'] | 1 |
count-number-of-nice-subarrays | Easy sliding window solution with O(N) time complexity | easy-sliding-window-solution-with-on-tim-9tz6 | Intuition\r\n Describe your first thoughts on how to solve this problem. \r\nThis Problem is talking about subarrays so the first thought that should come in yo | shivansh_p7 | NORMAL | 2023-03-08T03:39:16.505195+00:00 | 2023-03-08T03:39:16.505241+00:00 | 1,732 | false | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nThis Problem is talking about subarrays so the first thought that should come in your mind -> sliding window\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n1. first take two pointer on index 0\r\n2. now the second pointer will diverse from start , until the number of odds are not equals to k\r\n3. when the number of equal to k start increasing the second pointer until it eliminates the odd from start and makes number of odds less than k, along with it increase the prefix \r\n4.add the prefix in count until the next odd are not found \r\n5. Repeat the steps again\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\nO(n)\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\nO(1)\r\n# Code\r\n```\r\n/**\r\n * @param {number[]} nums\r\n * @param {number} k\r\n * @return {number}\r\n */\r\nvar numberOfSubarrays = function(nums, k) {\r\n let odds=0;\r\n let count=0;\r\n let prefix=0\r\n\r\n let i=0;\r\n\r\n for(let j=0;j<nums.length;j++){\r\n if(nums[j]%2!=0){ \r\n odds+=1\r\n prefix=0\r\n }\r\n\r\n while(odds==k && i<=j){\r\n if(nums[i]%2!=0) odds-=1\r\n i++\r\n prefix++\r\n \r\n }\r\n \r\n count+=prefix\r\n\r\n }\r\n return count\r\n};\r\n``` | 7 | 0 | ['JavaScript'] | 0 |
count-number-of-nice-subarrays | JAVA Easy Consise O(n) | java-easy-consise-on-by-bharat194-z0ji | \nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n return count(nums,k) - count(nums,k-1); \n\t\t// number of subarrays with k o | bharat194 | NORMAL | 2022-04-05T06:18:26.887907+00:00 | 2022-04-06T04:56:53.048073+00:00 | 671 | false | ```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n return count(nums,k) - count(nums,k-1); \n\t\t// number of subarrays with k odd integers = number of subarrays with atmost k odd integer - number of subarrays with atmost k-1 odd integers\n }\n public int count(int[] nums,int k){\n int res = 0,start = 0,end = 0, count =0;\n while(end < nums.length){\n if(nums[end] % 2 == 1) count++;\n while(start <= end && count > k){\n if(nums[start] % 2 == 1) count--;\n start++;\n }\n res += (end - start + 1);\n end++;\n }\n return res;\n }\n}\n``` | 7 | 0 | ['Java'] | 2 |
count-number-of-nice-subarrays | Dont fall into the Two pointer/Sliding Window trap | dont-fall-into-the-two-pointersliding-wi-oesk | This question is a direct variation of running subarray sum. This approach is simple and highly intuitive compared to sliding window and 2 pointers.\n\nThe map | siddhantchimankar | NORMAL | 2021-10-22T07:56:02.502794+00:00 | 2021-11-30T05:35:42.419402+00:00 | 561 | false | This question is a direct variation of running subarray sum. This approach is simple and highly intuitive compared to sliding window and 2 pointers.\n\nThe map is storing {key, val} == {num of odds in subarray, num of subarray with these many odds that have been encountered till now}\n\nKey insight --> The map only stores subarrays starting from the first element of the array. All the other subarrays are are taken care of using the below logic.\n\nSay we want to find all 2 odd num size subarrays. And now we are at a point where we have 5 odd nums with us, we want to look into the map for all the subarrays with 3 odd nums that have been encountered yet(map). This is because if we have a 5 odd num subarray and we know of previous 3 odd num subarrays. All of those 3 odd num sized subarrays when removed out of the 5 sized subarray will give us 2 odd num sized subarrays. Hence add it to result.\n\n----------------------\n```\n int numberOfSubarrays(vector<int>& nums, int k) {\n \n int res = 0; int cnt = 0;\n unordered_map<int, int> mp; mp[0] = 1;\n \n for(auto n : nums) {\n \n if(n % 2) cnt++;\n res += mp[cnt - k];\n mp[cnt]++;\n }\n \n return res;\n }\n``` | 7 | 0 | [] | 1 |
count-number-of-nice-subarrays | [C++] Sliding Window | c-sliding-window-by-thegateway-328v | Exactly = atMostK(k) - atMostK(k-1)\n\nint atMostK(vector<int>& a, int k) {\n int i=0,count = 0,res =0;\n for(int j=0;j<a.size();j++){\n | theGateway | NORMAL | 2021-09-26T17:23:21.648287+00:00 | 2021-09-26T17:23:53.419324+00:00 | 1,645 | false | **Exactly = atMostK(k) - atMostK(k-1)**\n```\nint atMostK(vector<int>& a, int k) {\n int i=0,count = 0,res =0;\n for(int j=0;j<a.size();j++){\n if(a[j]%2==1) count++;\n if(count > k){\n while(count>k){\n if(a[i]%2==1) count--;\n i++;\n }\n }\n res += j-i+1;\n }\n return res;\n }\n \n int numberOfSubarrays(vector<int>& a, int k) {\n return atMostK(a,k) - atMostK(a,k-1);\n }\n``` | 7 | 0 | ['C', 'Sliding Window', 'C++'] | 4 |
count-number-of-nice-subarrays | [C++] Two Pointer O(n) Solution | c-two-pointer-on-solution-by-khushboogup-ia88 | For finding a subarray with exactly k odd elements = count(subarray with at most k odd elements) - count(subarray with at most k-1 odd elements). This solution | khushboogupta13 | NORMAL | 2021-07-20T11:47:18.754762+00:00 | 2021-07-20T11:47:18.754801+00:00 | 495 | false | For finding a subarray with **exactly k odd elements = count(subarray with at most k odd elements) - count(subarray with at most k-1 odd elements)**. This solution consists of passing through the arrays twice (once for k odd elements and once for k-1 odd elements)\n\n```\nclass Solution {\n \n int atMostK(vector<int> &nums, int k){\n \n int len = nums.size();\n int result = 0;\n int start = 0;\n int currOddCnt = 0;\n \n for(int end=0; end<len; end++){\n //if the current element is odd\n if(nums[end]&1) currOddCnt++;\n \n //if the number of odd elements in the window exceeds k -> start contarcting the window\n while(start<=end && currOddCnt>k){\n //reducing the count of odd numbers if the start of window is odd\n if(nums[start]&1) currOddCnt--;\n start++;\n }\n \n //number of subarrays with at most k odd elements\n result += end-start+1;\n }\n \n return result;\n }\n \npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n return atMostK(nums, k) - atMostK(nums, k-1);\n }\n};\n```\n | 7 | 0 | [] | 3 |
count-number-of-nice-subarrays | Solution using hashmap and some math | solution-using-hashmap-and-some-math-by-uqnft | Intuition\n Describe your first thoughts on how to solve this problem. \nInitially thought sliding window but it is a complex one. After a bit of thinking I cam | mahdir246 | NORMAL | 2024-06-22T02:10:35.209132+00:00 | 2024-06-22T02:10:35.209159+00:00 | 402 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nInitially thought sliding window but it is a complex one. After a bit of thinking I came up with this mathy approach which is hopefully easier to understand.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nConvert the nums array to a prefix count of how many odds seen so far\nFor example:\n nums = [2,2,2,1,2,2,1,2,2,2]\nwill convert to \n\nnums = [0 0 0 1 1 1 2 2 2 2]\n\nwhere nums[i] now represents number of odds seen up until index i\n\nNow we can count how many odds seen, for example\n\nodds_seen : count\n0:3\n1:3\n2:4\n\ngo through each odds_seen and see if you can create a subarray with k odds seen\n\nFor example for each odds_seen of 0 we have a count of 4 for (odd_seen+k = 0+2 = 2)\n\nTherefore we can make 3 (count of 0s) x 4 (count of 2s) = 12\nAnd we have odds_seen of 4 from the full array \nSo 4 + 12 = 16\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n count_map = defaultdict(int)\n\n odd_count = 0\n for i in range(len(nums)):\n if nums[i] % 2 == 1:\n odd_count += 1\n nums[i] = odd_count\n count_map[odd_count] += 1\n\n res = count_map[k]\n for cnt in count_map:\n if (cnt + k) in count_map:\n res += count_map[cnt] * count_map[cnt+k]\n \n return res\n``` | 6 | 0 | ['Python3'] | 0 |
count-number-of-nice-subarrays | (C++) A Different Way To Solve This Problem. | c-a-different-way-to-solve-this-problem-x2kty | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | cookie_33 | NORMAL | 2024-06-22T01:36:46.182819+00:00 | 2024-06-22T01:43:48.441473+00:00 | 2,208 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(K)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& v, int k) {\n std::ios_base::sync_with_stdio(false);\n std::cout.tie(nullptr);\n std::cin.tie(nullptr);\n queue<int> q;\n int ans=0,c=0,j=0;\n for(int i=0;i<v.size();i++)\n {\n if(v[i]%2!=0){ \n c++;\n q.push(i);\n }\n while(c>k)\n {\n if(v[j]%2!=0) c--;\n j++;\n if(q.front()<j) q.pop();\n }\n if(c==k)\n ans+=(q.front()-j+1);\n }\n return ans;\n }\n};\n``` | 6 | 0 | ['Queue', 'Sliding Window', 'C++'] | 3 |
count-number-of-nice-subarrays | Editorial solution... #Perfectly Beats all 100% | editorial-solution-perfectly-beats-all-1-h0di | \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) - | Aim_High_212 | NORMAL | 2024-06-22T01:28:39.100394+00:00 | 2024-06-22T01:28:39.100419+00:00 | 103 | false | \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n curr_sum = 0\n subarrays = 0\n prefix_sum = {curr_sum: 1}\n\n for i in range(len(nums)):\n curr_sum += nums[i] % 2\n # Find subarrays with sum k ending at i\n if curr_sum - k in prefix_sum:\n subarrays = subarrays + prefix_sum[curr_sum - k]\n # Increment the current prefix sum in hashmap\n prefix_sum[curr_sum] = prefix_sum.get(curr_sum, 0) + 1\n\n return subarrays\n``` | 6 | 0 | ['Array', 'Hash Table', 'Math', 'C', 'Sliding Window', 'Python', 'C++', 'Java', 'Python3'] | 0 |
count-number-of-nice-subarrays | C++ O(N) Solution (Beats 100% of Users) | c-on-solution-beats-100-of-users-by-cook-szlu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | cookie_33 | NORMAL | 2024-06-22T01:24:31.579665+00:00 | 2024-06-22T01:24:31.579685+00:00 | 1,440 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int solve(vector<int>& v, int k)\n {\n int i=0,j=0;\n int odd=0,ans=0;\n while(j<v.size())\n {\n if(v[j]%2==1) odd++;\n while(odd>k)\n {\n if(v[i++]%2==1) odd--;\n }\n ans+=(j-i+1);\n j++;\n }\n return ans;\n }\n int numberOfSubarrays(vector<int>& v, int k) {\n std::ios_base::sync_with_stdio(false);\n std::cout.tie(nullptr);\n std::cin.tie(nullptr);\n return solve(v,k)-solve(v,k-1);\n }\n};\n``` | 6 | 0 | ['Sliding Window', 'C++'] | 7 |
count-number-of-nice-subarrays | ✅ Easy C++ Solution | easy-c-solution-by-moheat-af98 | Code\n\nclass Solution {\npublic:\n int subarray(vector<int> nums, int k)\n {\n if(k < 0)\n {\n return 0;\n }\n int | moheat | NORMAL | 2024-06-22T00:16:17.141171+00:00 | 2024-06-22T00:16:17.141194+00:00 | 2,112 | false | # Code\n```\nclass Solution {\npublic:\n int subarray(vector<int> nums, int k)\n {\n if(k < 0)\n {\n return 0;\n }\n int n = nums.size();\n\n int l = 0;\n int r = 0;\n int odd = 0;\n int count = 0;\n\n while(r < n)\n {\n if(nums[r] % 2)\n {\n odd++;\n }\n while(odd > k)\n {\n if(nums[l] % 2)\n {\n odd--;\n }\n l++;\n }\n count = count + (r-l+1);\n r++;\n }\n return count;\n }\n\n int numberOfSubarrays(vector<int>& nums, int k) {\n return subarray(nums,k) - subarray(nums, k-1);\n }\n};\n``` | 6 | 0 | ['C++'] | 4 |
count-number-of-nice-subarrays | Very Easy C++ Solution in O(n) - beats 99.48% submissions | very-easy-c-solution-in-on-beats-9948-su-zo94 | To achieve good time complexity we need to use bit munpulation for checking odd number\n\nTime Complexity: O(n)\nSpace Complexity: O(1)\n\n#pragma GCC optimize( | vatsalkesarwani | NORMAL | 2021-06-19T22:11:35.952424+00:00 | 2021-06-19T22:11:35.952454+00:00 | 583 | false | To achieve good time complexity we need to use bit munpulation for checking odd number\n\nTime Complexity: O(n)\nSpace Complexity: O(1)\n```\n#pragma GCC optimize("Ofast") \n#pragma GCC target("avx,avx2,fma") \nstatic auto _ = [] ()\n{ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);return 0;}();\n\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int j = 0, odd = 0, ctr = 0, ans = 0;\n for (int i = 0; i < nums.size(); i++) \n {\n if (nums[i] & 1)\n {\n odd++;\n if (odd >= k) \n {\n ctr = 1;\n while (!(nums[j++] & 1))\n ctr++;\n ans += ctr;\n }\n \n } else if (odd >=k) \n ans += ctr;\n }\n return ans;\n }\n};\n``` | 6 | 2 | ['Two Pointers', 'C++'] | 0 |
count-number-of-nice-subarrays | Easy || Commented || O(N) Time and O(1) Space || Window Sliding | easy-commented-on-time-and-o1-space-wind-0yyd | \nclass Solution {\n public:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int l = 0, r = 0, n = nums.size(), kCount = 0, count = 0, prefix | faltu_admi | NORMAL | 2021-05-26T16:16:41.446848+00:00 | 2021-05-26T16:16:41.446890+00:00 | 528 | false | ```\nclass Solution {\n public:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int l = 0, r = 0, n = nums.size(), kCount = 0, count = 0, prefix = 0;\n while (r < n) {\n // increase odd count\n kCount += (nums[r++] & 1);\n if (kCount > k) {\n l++;\n kCount--;\n prefix = 0;\n }\n\n // Count the number of prefix which is even because either we include them or not still we get the nice one\n while (l < r && (nums[l] % 2 == 0)) prefix++, l++;\n if (kCount == k) {\n count += (1 + prefix);\n }\n }\n return count;\n }\n};\n``` | 6 | 0 | [] | 2 |
count-number-of-nice-subarrays | JavaScript sliding window | javascript-sliding-window-by-zckpp1992-z27u | Move right pointer until odd number reach k, then count even number towards right until reach next odd number or the end, count even number towards left untill | zckpp1992 | NORMAL | 2020-08-07T02:10:19.118364+00:00 | 2020-08-07T02:10:19.118400+00:00 | 344 | false | Move right pointer until odd number reach k, then count even number towards right until reach next odd number or the end, count even number towards left untill left pointer is sitting on an odd number, the product of left and right is the answer for this window, at last move left pointer and reduce odd number for 1 for next window.\n\n```\nvar numberOfSubarrays = function(nums, k) {\n let count = 0;\n let odd = 0;\n let l = 0, r = -1;\n while(r < nums.length-1) {\n r++;\n if (nums[r]%2 !== 0) odd++;\n if (odd === k) {\n let right = 1;\n let left = 1;\n // move r if next element is even\n while(r < nums.length-1 && nums[r+1]%2 === 0) {\n r++;\n right++;\n }\n // move l if current element for l is even\n while(l < r && nums[l]%2 === 0) {\n l++;\n left++;\n }\n count += left*right;\n l++;\n odd--;\n }\n }\n return count;\n};\n``` | 6 | 0 | [] | 0 |
count-number-of-nice-subarrays | Easy Solution Using Sliding Window! | easy-solution-using-sliding-window-by-sa-yngz | \nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int n=nums.size();\n int odd=0,l=0,res=0;\n for(int r= | sanjaygarg | NORMAL | 2019-11-11T07:11:31.848956+00:00 | 2019-11-11T07:11:31.849003+00:00 | 1,180 | false | ```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int n=nums.size();\n int odd=0,l=0,res=0;\n for(int r=0;r<n;r++)\n {\n if(nums[r]%2==1)\n odd++;\n while(l<r && odd>k)\n {\n if(nums[l]%2==1)\n odd--;\n l++;\n }\n if(odd==k)\n res++;\n for(int i=l; odd==k && i<r && nums[i]%2==0;i++)\n res++;\n }\n return res;\n }\n};\n```\nA problem similar to this:\nhttps://leetcode.com/problems/binary-subarrays-with-sum/description/\nsolution:\nhttps://leetcode.com/problems/binary-subarrays-with-sum/discuss/426284/Easy-Solution-Using-Sliding-Window! | 6 | 1 | [] | 2 |
count-number-of-nice-subarrays | Easy C++ solution | no sliding window | O(N) | easy-c-solution-no-sliding-window-on-by-prd1e | IntuitionWe store the indices of odd numbers and use basic math to calculate nice subarrays.Approach1]Store Indices of Odd numbers:
We traverse the array and st | mithilesh_19 | NORMAL | 2025-02-19T12:03:57.189128+00:00 | 2025-03-19T20:13:20.635674+00:00 | 278 | false | # Intuition
We store the indices of odd numbers and use basic math to calculate nice subarrays.
# Approach
***1]Store Indices of Odd numbers:***
- We traverse the array and store the positions (indices) of all odd numbers.
- To handle boundaries, we add ```-1``` at the start and ```n``` (array size) at the end of this list.
***2]Group ```k``` Odd Numbers:***
- For each group of 𝑘 consecutive odd numbers, we want to count how many subarrays contain exactly these 𝑘 odd numbers.
***3]Calculate Gaps:***
- The gap before the first odd number in the group tells us how many even numbers (or positions) we can include at the start.
- The gap after the last odd number tells us how many even numbers (or positions) we can include at the end. We add 1 to each gap because we can also choose not to extend the subarray.
***4]Multiply and Sum:***
- For each group, multiply the two gap values. This multiplication gives the total number of ways to form a subarray that includes exactly ```k``` odd numbers. Finally, add up these values for all groups.
# Complexity
- Time complexity: $$O(n)$$
- We iterate through ```nums``` once to store the indices of odd numbers (O(n)).
- We then iterate over ```index``` (which has at most 𝑂(n) elements) to count subarrays (O(n)).
- Thus, the total time complexity is O(n).
- Space complexity: $$O(n)$$
- We use an auxiliary vector index to store the indices of odd numbers, which takes O(n) space in the worst case (all numbers are odd).
# Code
```cpp []
class Solution {
public:
int numberOfSubarrays(vector<int>& nums, int k) {
// declare ans as 0
int ans = 0;
// declare vector name index for storing indicies
vector<int> index;
// store indices of all odd numbers
int n = nums.size();
index.push_back(-1);
for (int i = 0; i < n; i++) {
// for checking odd numbers
if (nums[i] % 2 != 0)
index.push_back(i);
}
index.push_back(n);
// add for all possible k odd numbers (before gap + 1) * (after gap + 1)
// where gap = index[i]-index[i-1] - 1 (so -1 & +1 get cancel out)
int m = index.size();
for (int i = 1; i < m; i++) {
if (i + k >= m)
break;
ans += (index[i] - index[i - 1]) * (index[i + k] - index[i + k - 1]);
}
return ans;
}
};
``` | 5 | 0 | ['Math', 'C++'] | 0 |
count-number-of-nice-subarrays | Java Solution, Beats 100.00% | java-solution-beats-10000-by-mohit-005-q6er | Intuition\nThe problem requires us to find the number of continuous subarrays that contain exactly k odd numbers. The approach used in the given code leverages | Mohit-005 | NORMAL | 2024-06-22T14:05:01.658170+00:00 | 2024-06-22T14:05:01.658192+00:00 | 1,481 | false | # Intuition\nThe problem requires us to find the number of continuous subarrays that contain exactly `k` odd numbers. The approach used in the given code leverages prefix sums and a hashmap to efficiently count the number of valid subarrays.\n\n# Approach\n1. **Prefix Sum with HashMap**: The idea is to use a prefix sum array where each element in the prefix sum represents the count of odd numbers up to the current index in the `nums` array.\n \n2. **Counting Prefix Sums**: A hashmap (implemented as an array `cnt` in the code) is used to keep track of the number of times each prefix sum has occurred.\n\n3. **Traversing the Array**: As we traverse through the `nums` array:\n - We maintain a running count `t` of the number of odd numbers encountered so far.\n - For each element, we check if there is a prefix sum that is exactly `k` less than the current prefix sum (`t - k`). If it exists, it means there is a subarray ending at the current index that contains exactly `k` odd numbers.\n - We update our result `ans` by adding the count of such prefix sums found in the hashmap.\n - We then update the hashmap to include the current prefix sum.\n\n# Complexity\n- **Time Complexity**: The code runs in `O(n)` time, where `n` is the length of the input array `nums`. This is because we traverse the array once, and all operations inside the loop (including hashmap operations) are `O(1)` on average.\n \n- **Space Complexity**: The space complexity is `O(n)` due to the hashmap (`cnt` array) used to store the count of prefix sums. In the worst case, we might have to store up to `n+1` different prefix sums.\n\n# Detailed Steps in Code\n1. Initialize the hashmap `cnt` with `n+1` size (to handle cases where prefix sums go up to `n`) and set `cnt[0] = 1` because a prefix sum of zero has occurred once before starting.\n2. Traverse through the array and for each element:\n - Update the running total `t` to count odd numbers.\n - Check if `(t - k)` is a valid prefix sum. If so, add the count of this prefix sum to `ans`.\n - Update the hashmap with the current prefix sum.\n\n# Code\n```java\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int n = nums.length;\n int[] cnt = new int[n + 1]; // HashMap to store prefix sums\n cnt[0] = 1; // Base case: prefix sum of 0 occurs once\n int ans = 0, t = 0; // ans: result, t: current prefix sum (count of odd numbers)\n \n for (int v : nums) {\n t += v & 1; // Increment prefix sum if the number is odd\n if (t - k >= 0) {\n ans += cnt[t - k]; // If (t - k) exists in cnt, add its count to ans\n }\n cnt[t]++; // Increment the count of current prefix sum in cnt\n }\n \n return ans; // Return the total number of valid subarrays\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
count-number-of-nice-subarrays | JAVA Solution Explained in HINDI(2 Approaches) | java-solution-explained-in-hindi2-approa-ck8q | https://youtu.be/xufUS2MRAZw\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote | The_elite | NORMAL | 2024-06-22T09:49:40.390947+00:00 | 2024-06-22T13:09:36.402213+00:00 | 638 | false | ERROR: type should be string, got "https://youtu.be/xufUS2MRAZw\\n\\nFor explanation, please watch the above video and do like, share and subscribe the channel. \\u2764\\uFE0F Also, please do upvote the solution if you liked it.\\n\\n# Subscribe:- [ReelCoding](https://www.youtube.com/@reelcoding?sub_confirmation=1)\\n\\nSubscribe Goal:- 500\\nCurrent Subscriber:- 453\\n# Complexity\\n- Time complexity: O(n)\\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\\n\\n- Space complexity: O(1)\\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\\n\\n# Code\\n```\\nclass Solution {\\n private int numSubarraysLessThanOrEqualToGoal(int[] nums, int goal) {\\n int i = 0, j = 0, n = nums.length, count = 0, ans = 0;\\n\\n while (j < n) {\\n if (nums[j] % 2 == 1) count++;\\n while (i <= j && count > goal) {\\n if (nums[i] % 2 == 1) count--;\\n i++;\\n }\\n ans += j - i + 1;\\n j++;\\n }\\n return ans;\\n }\\n\\n public int numberOfSubarrays(int[] nums, int k) {\\n return numSubarraysLessThanOrEqualToGoal(nums, k) - \\n numSubarraysLessThanOrEqualToGoal(nums, k - 1);\\n }\\n}\\n```\\n\\n# Complexity\\n- Time complexity: O(n)\\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\\n\\n- Space complexity: O(n)\\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\\n\\n# Code\\n```\\nclass Solution {\\n public int numberOfSubarrays(int[] nums, int k) {\\n int n = nums.length;\\n int ans = 0;\\n int prefSum = 0;\\n Map<Integer, Integer> freq = new HashMap<>();\\n freq.put(0, 1);\\n\\n for (int i = 0; i < n; i++) {\\n prefSum += (nums[i] % 2 == 1) ? 1 : 0;\\n ans += freq.getOrDefault(prefSum - k, 0);\\n freq.put(prefSum, freq.getOrDefault(prefSum, 0) + 1);\\n }\\n return ans;\\n }\\n}\\n```" | 5 | 0 | ['Java'] | 0 |
count-number-of-nice-subarrays | O(n) - 8 line of code - short explanation | on-8-line-of-code-short-explanation-by-a-hio4 | Intuition\nChange this question to: count of sub-arrays with sum of elements equal to k\n Describe your first thoughts on how to solve this problem. \n\n# Appro | Assault_Rifle | NORMAL | 2024-06-22T01:32:48.449954+00:00 | 2024-06-22T01:32:48.449979+00:00 | 341 | false | # Intuition\nChange this question to: count of sub-arrays with sum of elements equal to k\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nIf we treat all odd numbers as 1 and all even numbers as 0. This problem changes to count of total number of sub arrays with sum of its elements equal to k. \n\nThis is a standard problem, we generally use HashMap to solve this.\n\nTraverse in the array, store the frequecy of prefix sums in the map.\n\nIf you find a prefix sum for which difference between prefix sum and k has seen before, that means elements between those prefix sum ending indexes make a sub array that has total k odd elements. The frequency of that prefix sum - k will contribute to the answer.\n\nWe want to add all such possibilities, that\'s why we are storing frequencies, and using a hashmap instead of hashset.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) \n {\n int n=nums.size(); int pre=0, count=0;\n\n unordered_map <int,int> mp;\n\n for(int i=0; i<n; i++)\n {\n pre += nums[i]%2;\n\n if(pre==k) count++;\n\n if( mp.count(pre-k) ) count += mp[pre-k];\n\n mp[pre]++;\n }\n\n return count;\n }\n};\n``` | 5 | 0 | ['C++'] | 1 |
count-number-of-nice-subarrays | beats 99 % - Using Queue | beats-99-using-queue-by-youknowwho3737-30ou | Approach\nSimply Use the queue to store the indexes of odd elements.\nStart counting the subarrays when the Queue is of K size.\nMaintain two variables end and | youknowwho3737 | NORMAL | 2024-06-22T01:29:13.571571+00:00 | 2024-06-22T01:29:13.571601+00:00 | 939 | false | # Approach\nSimply Use the queue to store the indexes of odd elements.\nStart counting the subarrays when the Queue is of K size.\nMaintain two variables end and last to count the values that can be added to next index.\n\n# Complexity\n- Time complexity:\nOnly one iterations, e.g. $$O(n)$$\n\n- Space complexity:\nA Queue with max of k elements, e.g. $$O(k)$$\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n queue<int> Q;\n int lst = 0, end = -1, ans = 0;\n for (int i = 0; i < nums.size(); i++) {\n if(nums[i]&1){\n Q.push(i);\n }\n if(Q.size() == k){\n lst = end;\n end = Q.front();\n Q.pop();\n }\n if(end != -1){\n ans += end - lst;\n }\n }\n return ans;\n }\n};\n``` | 5 | 0 | ['Greedy', 'Queue', 'C++'] | 1 |
count-number-of-nice-subarrays | Sliding window + deque. One pass | sliding-window-deque-one-pass-by-xxxxkav-kbdw | \nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n ans, left, que = 0, -1, deque()\n for i in range(len(nums)): | xxxxkav | NORMAL | 2024-06-22T00:35:02.517316+00:00 | 2024-06-22T09:02:13.366990+00:00 | 336 | false | ```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n ans, left, que = 0, -1, deque()\n for i in range(len(nums)):\n if nums[i]%2:\n que.append(i)\n if len(que) > k:\n left = que.popleft()\n if len(que) == k:\n ans += que[0]-left\n return ans\n```\n> Alternative solution without deque (a bit slower)\n```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n ans, left, cnt = 0, 0, 0\n for i in range(len(nums)):\n if nums[i]%2:\n k -= 1\n cnt = 0\n while k <= 0:\n k += nums[left]%2\n left += 1\n cnt += 1\n ans += cnt\n return ans\n``` | 5 | 0 | ['Sliding Window', 'Python3'] | 2 |
count-number-of-nice-subarrays | Sliding Window | C++ | sliding-window-c-by-tusharbhart-1rz2 | \r\nclass Solution {\r\npublic:\r\n int numberOfSubarrays(vector<int>& nums, int k) {\r\n int n = nums.size(), dis = 1, i = 0, cnt = 0, ans = 0;\r\n | TusharBhart | NORMAL | 2023-01-16T13:38:33.745731+00:00 | 2023-01-16T13:38:33.745767+00:00 | 5,234 | false | ```\r\nclass Solution {\r\npublic:\r\n int numberOfSubarrays(vector<int>& nums, int k) {\r\n int n = nums.size(), dis = 1, i = 0, cnt = 0, ans = 0;\r\n vector<int> d(n + 1, 1);\r\n\r\n for(int i=n-1; i>=0; i--) {\r\n nums[i] % 2 ? dis = 1 : dis++;\r\n d[i] = dis;\r\n }\r\n \r\n for(int j=0; j<n; j++) {\r\n if(nums[j] % 2) cnt++;\r\n\r\n while(i <= j && cnt == k) {\r\n ans += d[j + 1];\r\n if(nums[i] % 2) cnt--;\r\n i++;\r\n }\r\n }\r\n return ans;\r\n }\r\n};\r\n``` | 5 | 0 | ['Sliding Window', 'C++'] | 1 |
count-number-of-nice-subarrays | [C++] O(1) Space | c-o1-space-by-simplekind-hofa | \nclass Solution {\npublic:\n \n int atmost (vector<int>& arr, int k){\n if(arr.size()==0)\n return 0 ;\n int ans = 0;\n i | simplekind | NORMAL | 2022-03-24T04:58:00.777505+00:00 | 2022-03-24T04:58:00.777540+00:00 | 919 | false | ```\nclass Solution {\npublic:\n \n int atmost (vector<int>& arr, int k){\n if(arr.size()==0)\n return 0 ;\n int ans = 0;\n int j= 0;\n int count = 0;\n for ( int i =0;i<arr.size();i++){\n if(arr[i]&1){\n count++;\n }\n while(count>k){\n if(arr[j]&1)\n count--;\n j++;\n }\n ans+=i-j+1;\n }\n return ans;\n }\n \n int numberOfSubarrays(vector<int>& v, int k) {\n return atmost(v,k)-atmost(v,k-1);\n }\n};\n``` | 5 | 0 | ['C', 'Sliding Window', 'C++'] | 1 |
count-number-of-nice-subarrays | Java | Two-Pointer & Sliding window | Time: O(N) & Space: O(1) | java-two-pointer-sliding-window-time-on-kq336 | \nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n \n int odds = 0;\n int i = 0, j = 0, flag = 0;\n int n = nu | harshitcode13 | NORMAL | 2021-12-24T07:17:30.720758+00:00 | 2021-12-24T07:17:48.579389+00:00 | 1,169 | false | ```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n \n int odds = 0;\n int i = 0, j = 0, flag = 0;\n int n = nums.length;\n int ans = 0;\n while(j < n){\n if(nums[j]%2!=0){\n odds++;\n }\n while(odds > k){\n if(nums[i++]%2!=0)odds--;\n flag = i;\n }\n if(odds == k){\n ans+=(i+1-flag);\n while(nums[i]%2==0){\n i++;\n ans++;\n }\n }\n j++;\n }\n return ans;\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
count-number-of-nice-subarrays | Count Number of Nice Subarray | count-number-of-nice-subarray-by-abhishe-ux6i | \n\n\n\n\n\n\nDiscuss\n\n1. In this problem , First we will change the odd digit from 1 and even with zero in given array.\n2. calculating the sum from start to | abhishekjha786 | NORMAL | 2021-12-16T19:57:17.210511+00:00 | 2021-12-31T05:33:46.880826+00:00 | 286 | false | \n\n\n\n\n\n\n**Discuss**\n\n1. In this problem , First we will change the odd digit from 1 and even with zero in given array.\n2. calculating the sum from start to end index with comparison k value\ni.e. sum - k == 0\n3. then we find subarray whose array has k odd value and stored in map. after this check again for another subarray because if we got odd value equal to the given k value then we got the subarray which has k odd value.\n\n**Note : this problem basically similar to the find subarray whose sum is equal to 0**\n\nclass Solution {\n\n public int numberOfSubarrays(int[] nums, int k) { \n Map<Integer, Integer> mp = new HashMap<>();\n int res = 0;\n int sum = 0;\n for (int j = 0; j < nums.length; j++) {\n sum += nums[j] % 2;\n if (sum - k == 0) {\n res++;\n }\n if (mp.containsKey(sum - k)) {\n res += mp.get(sum - k);\n }\n mp.put(sum, mp.getOrDefault(sum, 0) + 1);\n }\n return res;\n }\n}\n**Please help to UPVOTE if this post is useful for you.\nIf you have any questions, feel free to comment below.\nHAPPY CODING :)\nLOVE CODING :)** | 5 | 0 | ['Sliding Window'] | 2 |
count-number-of-nice-subarrays | Python solution beats 99% | python-solution-beats-99-by-ruizhang84-ko12 | There is a simple solution, by enumerate list and count the combinations of numbers.\n\n\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: i | ruizhang84 | NORMAL | 2019-11-08T03:23:24.095734+00:00 | 2019-11-08T03:23:24.095778+00:00 | 493 | false | There is a simple solution, by enumerate list and count the combinations of numbers.\n\n```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n # count\n arr = []\n for i, x in enumerate(nums):\n if x % 2 != 0:\n arr.append(i) \n arr.append(len(nums))\n \n # not satisify\n if len(arr) <= k:\n return 0\n \n # calculate\n count = 0\n count += (arr[0] + 1) * (arr[k] - arr[k-1])\n for i in range(k+1, len(arr)):\n count += (arr[i-k] - arr[i-k-1]) * (arr[i] - arr[i-1])\n \n return count \n``` | 5 | 1 | [] | 0 |
count-number-of-nice-subarrays | [JAVA] simple O(n) solution | java-simple-on-solution-by-nandathantsin-mwh3 | \nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n ArrayList<Integer> pos = new ArrayList<>();\n pos.add(0);\n for | nandathantsin | NORMAL | 2019-11-03T04:03:07.289666+00:00 | 2019-11-03T04:03:07.289724+00:00 | 1,061 | false | ```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n ArrayList<Integer> pos = new ArrayList<>();\n pos.add(0);\n for(int i=0;i<nums.length;i++){\n if(nums[i]%2==1){\n pos.add(i+1);\n }\n }\n pos.add(nums.length+1);\n int res=0;\n\n for(int i=1;i<=pos.size()-k-1;i++){\n int start=pos.get(i)-pos.get(i-1);\n int end = pos.get(i+k)-pos.get(i+k-1);\n res+=start*end;\n }\n return res;\n }\n}\n``` | 5 | 0 | ['Java'] | 1 |
count-number-of-nice-subarrays | Simple Java HashMap Solution O(n) by keeping track of count of odd numbers | simple-java-hashmap-solution-on-by-keepi-8xu7 | ```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n \n int n = nums.length;\n \n HashMap map = new HashMa | manrajsingh007 | NORMAL | 2019-11-03T04:02:15.192334+00:00 | 2019-11-03T04:03:38.733562+00:00 | 868 | false | ```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n \n int n = nums.length;\n \n HashMap<Integer, Integer> map = new HashMap<>();\n \n int ans = 0;\n int currCount = 0;\n \n map.put(0, 1);\n \n for(int i = 0; i < n; i++){\n if(nums[i] % 2 == 1) currCount ++;\n if(map.containsKey(currCount - k)) ans += map.get(currCount - k);\n if(!map.containsKey(currCount)) map.put(currCount, 1);\n else map.put(currCount, 1 + map.get(currCount));\n }\n \n return ans;\n \n }\n} | 5 | 0 | [] | 0 |
count-number-of-nice-subarrays | [Java] Sliding window / Two Pointers O(n) | java-sliding-window-two-pointers-on-by-p-yx3l | \nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int start = 0, end = 0, len = nums.length;\n int count = 0, oddCount = | pnimit | NORMAL | 2019-11-03T04:00:59.954306+00:00 | 2019-11-03T04:06:13.465562+00:00 | 2,095 | false | ```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int start = 0, end = 0, len = nums.length;\n int count = 0, oddCount = 0, evenCount = 0;\n \n while(end < len){\n \n while(end < len && oddCount < k){\n if(nums[end++] % 2 != 0) ++oddCount;\n }\n \n evenCount = 1;\n while(end < len && nums[end] % 2 == 0){\n ++evenCount;\n ++end;\n }\n \n while(start < len && oddCount == k){\n count += evenCount;\n if(nums[start++] % 2 != 0) --oddCount;\n }\n }\n \n return count;\n }\n}\n``` | 5 | 0 | ['Two Pointers', 'Sliding Window', 'Java'] | 0 |
count-number-of-nice-subarrays | [C++] ✅ 💯 |Three Approaches | Sliding Window along with Advanced Approach | Prefix Sum | Time: O(n) | c-three-approaches-sliding-window-along-97hy6 | Method 1 : Sliding Window Approach\n# Intuition\n Describe your first thoughts on how to solve this problem. \n\nTo solve the problem of counting the number of | sidharthjain321 | NORMAL | 2024-06-22T10:54:19.532590+00:00 | 2024-06-23T05:35:54.065741+00:00 | 106 | false | # Method 1 : Sliding Window Approach\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nTo solve the problem of counting the number of nice subarrays (subarrays with exactly k odd numbers), we can use a sliding window approach. This technique helps in efficiently counting subarrays by expanding and contracting the window based on the number of odd numbers within the window. However, instead of directly counting subarrays with exactly k odd numbers, we can count subarrays with at most k odd numbers and subtract the count of subarrays with at most k-1 odd numbers.\n\n# Approach\n## Also I have written comments in the second code for better understanding of each step. You can refer to it.\n<!-- Describe your approach to solving the problem. -->\n1.\t**Helper Function solve(nums, k)**:\n\t-\tThis function returns the count of subarrays with at most k odd numbers.\n\t-\tInitialize two pointers (left and right), a counter for odd numbers (cntOdd), and a counter for subarrays (subarrays).\n\t-\tIterate through the array using the right pointer, and for each element, increment the count of odd numbers if the current element is odd.\n\t-\tIf the count of odd numbers exceeds k, increment the left pointer to reduce the count of odd numbers within the window.\n\t-\tFor each position of the right pointer, add the number of valid subarrays ending at right to subarrays.\n\t\n2.\t**Main Function numberOfSubarrays(nums, k)**:\n\t-\tCall solve(nums, k) to get the count of subarrays with at most k odd numbers.\n\t-\tCall solve(nums, k-1) to get the count of subarrays with at most k-1 odd numbers.\n\t-\tThe difference between these two results gives the count of subarrays with exactly k odd numbers.\n\n# Complexity\n- Time complexity: $$O(n)$$ where `n` is the size of the nums array. Here each element, at max can be traversed twice, i.e., 2*n times. It is the order of n.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n---\n> #### **Code without Comments :-**\n# Code\n```\nclass Solution {\npublic:\n int solve(vector<int>& nums, int k) {\n int n = nums.size(), left = 0, right = 0, cntOdd = 0, subarrays = 0;\n while(right < n) {\n cntOdd += nums[right] & 1 ;\n while (cntOdd > k) cntOdd -= nums[left++] & 1;\n subarrays += right - left + 1;\n right++;\n }\n return subarrays;\n }\n int numberOfSubarrays(vector<int>& nums, int k) {\n return solve(nums,k) - solve(nums,k-1);\n }\n};\n```\n> #### **Code with comments :-**\n```\nclass Solution {\npublic:\n // This helper function counts the number of subarrays with at most `k` odd numbers\n int solve(vector<int>& nums, int k) {\n int n = nums.size(); // Size of the input array\n int left = 0; // Left pointer for the sliding window\n int right = 0; // Right pointer for the sliding window\n int cntOdd = 0; // Counter for the number of odd numbers in the current window\n int subarrays = 0; // Counter for the number of valid subarrays\n\n // Iterate over the array with the right pointer\n while (right < n) {\n // If the current element is odd, increment the odd number counter\n cntOdd += (nums[right] & 1);\n \n // If the count of odd numbers exceeds `k`, adjust the left pointer\n // to reduce the number of odd numbers in the current window\n while (cntOdd > k) {\n cntOdd -= (nums[left++] & 1);\n }\n \n // The number of valid subarrays ending at the current right pointer is\n // the size of the current window (right - left + 1)\n subarrays += right - left + 1;\n \n // Move the right pointer to the next element\n right++;\n }\n \n // Return the total count of valid subarrays with at most `k` odd numbers\n return subarrays;\n }\n\n // This function returns the number of subarrays with exactly `k` odd numbers\n int numberOfSubarrays(vector<int>& nums, int k) {\n // The number of subarrays with exactly `k` odd numbers is the difference\n // between the number of subarrays with at most `k` odd numbers and the\n // number of subarrays with at most `k-1` odd numbers\n return solve(nums, k) - solve(nums, k-1);\n }\n};\n```\n\n## Advanced Sliding Window Approach:\n\n- ### **One Pass Sliding Window Approach**:\n\n > #### **Code without comments**:\n ```\n class Solution {\n public:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int n = nums.size(), i = 0, j = 0, prevSubarrayCount = 0, oddNumberCount = 0, totalNiceSubarrays = 0;\n while(j < n) {\n if(nums[j++] & 1) oddNumberCount++, prevSubarrayCount = 0;\n while(oddNumberCount == k) {\n prevSubarrayCount++; \n if(nums[i++] & 1) oddNumberCount--;\n }\n totalNiceSubarrays += prevSubarrayCount;\n }\n return totalNiceSubarrays;\n }\n };\n ```\n > #### **Code with comments**:\n ```\n class Solution {\n public:\n int numberOfSubarrays(vector<int>& nums, int k) {\n // Initialize the size of the array\n int n = nums.size();\n // Initialize the pointers for the sliding window\n int i = 0, j = 0;\n // This variable keeps track of the count of subarrays ending at the current position\n // that contain exactly k odd numbers\n int prevSubarrayCount = 0;\n // This variable keeps track of the number of odd numbers in the current window\n int oddNumberCount = 0;\n // This variable will accumulate the total number of nice subarrays\n int totalNiceSubarrays = 0;\n \n // Traverse the array with the right pointer j\n while (j < n) {\n // If the current number is odd, increment the oddNumberCount\n if (nums[j] & 1) {\n oddNumberCount++;\n // Reset the count of valid subarrays ending at the current position\n prevSubarrayCount = 0;\n }\n \n // While the window contains exactly k odd numbers\n while (oddNumberCount == k) {\n // Increment the count of valid subarrays ending at the current position\n prevSubarrayCount++;\n // If the number at the left pointer is odd, decrement the oddNumberCount\n if (nums[i] & 1) {\n oddNumberCount--;\n }\n // Move the left pointer to shrink the window\n i++;\n }\n \n // Add the count of valid subarrays ending at j to the total count\n totalNiceSubarrays += prevSubarrayCount;\n // Move the right pointer to expand the window\n j++;\n }\n \n // Return the total number of nice subarrays after processing the entire array\n return totalNiceSubarrays;\n }\n };\n ```\n\n---\n# Method 2 : Prefix Sum Approach\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve the problem of counting the number of \u201Cnice\u201D subarrays (continuous subarrays containing exactly k odd numbers), we can utilize a combination of prefix sums and hash maps. The main idea revolves around keeping track of the number of odd numbers encountered so far while traversing the array and leveraging this information to count subarrays with exactly k odd numbers.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\t**Prefix Sum with Hash Map**:\n -\tWe will traverse the array while maintaining a count of the odd numbers encountered so far `oddCount`.\n\t-\tWe\u2019ll use a hash map `freq` to store the frequency of each oddCount.\n\t-\tFor each element in the array, we check if there is a prefix subarray (ending before the current element) that has `oddCount - k` odd numbers. If such a prefix exists, it means there are some subarrays ending at the current element that have exactly `k` odd numbers.\n\t-\tBy summing the frequencies of these prefix subarrays, we can get the count of \u201Cnice\u201D subarrays.\n2.\t**Initialization**:\n\t-\tInitialize a frequency array `freq` to count the occurrences of oddCount. We start with `freq[0] = 1` to handle the case when the first `k` odd numbers are found from the beginning of the array.\n\t-\tTraverse the array, update `oddCount` for each element, and update the result by checking the frequency map.\n\n# Complexity\n- Time complexity: $$O(n)$$ where `n` is the size of nums array.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(50001)$$ = $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(1)$$ -->\n--- \n\n> #### **Code without comments :-**\n# Code\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int freq[50001] = {0};\n freq[0] = 1; \n int n = nums.size(), oddCount = 0, subarrays = 0;\n for(int i = 0; i < n; i++) {\n oddCount += nums[i] & 1;\n if(oddCount - k >= 0) subarrays += freq[oddCount - k];\n freq[oddCount]++;\n }\n return subarrays;\n }\n};\n```\n> #### **Code with comments :-**\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n // Initialize frequency array to count occurrences of oddCount\n int freq[50001] = {0};\n freq[0] = 1; \n \n int n = nums.size(); // Size of the input array\n int oddCount = 0; // Count of odd numbers encountered so far\n int subarrays = 0; // Count of nice subarrays\n \n for(int i = 0; i < n; i++) {\n // Update oddCount if current number is odd\n oddCount += nums[i] & 1;\n \n // If there exists a prefix with oddCount - k, add its frequency to subarrays\n if(oddCount - k >= 0) subarrays += freq[oddCount - k];\n \n // Update frequency array for the current oddCount\n freq[oddCount]++;\n }\n \n return subarrays; // Return the total count of nice subarrays\n }\n};\n```\n\n\n[Instagram](https://www.instagram.com/iamsidharthaa__/)\n[LinkedIn](https://www.linkedin.com/in/sidharth-jain-36b542133)\n**If you find this solution helpful, consider giving it an upvote! Your support is appreciated. Keep coding, stay healthy, and may your programming endeavors be both rewarding and enjoyable!** | 4 | 0 | ['Array', 'Hash Table', 'Math', 'Sliding Window', 'C++'] | 1 |
count-number-of-nice-subarrays | simple and easy || C++ and Python || solution 😍❤️🔥 | simple-and-easy-c-and-python-solution-by-3nbn | if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Python Code\n\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n | shishirRsiam | NORMAL | 2024-06-22T08:31:39.898084+00:00 | 2024-06-22T08:31:39.898109+00:00 | 484 | false | # if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Python Code\n```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n pref_count = defaultdict(int)\n pref_count[0] = 1\n odd_count, ans = 0, 0\n for num in nums:\n odd_count += num%2\n if odd_count - k in pref_count:\n ans += pref_count[odd_count - k]\n pref_count[odd_count] += 1\n return ans\n```\n# C++ Code\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) \n {\n int cnt = 0, ans = 0, odd;\n unordered_map<int,int>mp;\n mp[0] = 1;\n for(auto val:nums)\n {\n if(val%2) cnt++;\n odd = cnt - k;\n if(mp.find(odd) != mp.end())\n ans += mp[odd];\n mp[cnt]++;\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Array', 'Hash Table', 'Math', 'Sliding Window', 'C++', 'Python3'] | 3 |
count-number-of-nice-subarrays | Easy C++ Solution with video Explanation | easy-c-solution-with-video-explanation-b-770c | Video Explanation\nhttps://youtu.be/P9YW8n1GrlI?si=pAfMnzN4w9D7aL7d\n\n# Complexity\n- Time complexity: O(n) \n Add your time complexity here, e.g. O(n) \n\n- S | prajaktakap00r | NORMAL | 2024-06-22T04:31:12.982540+00:00 | 2024-06-22T04:31:12.982567+00:00 | 483 | false | # Video Explanation\nhttps://youtu.be/P9YW8n1GrlI?si=pAfMnzN4w9D7aL7d\n\n# Complexity\n- Time complexity: $$O(n)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n unordered_map<int,int>mpp;\n for(auto &num:nums){\n if(num%2) num=1;\n else num=0;\n }\n mpp[0]=1;\n int count=0;\n int sum=0;\n for(int num:nums){\n sum+=num;\n count+=mpp[sum-k];\n mpp[sum]++;\n }\n return count;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
count-number-of-nice-subarrays | Number of Nice Subarray✨|| Easiest 🤩|| Fastest🚀🚀||Beats 99% 😤😤||Prefix Count🪛 | number-of-nice-subarray-easiest-fastestb-ttqr | \n\n\n# Intuition\nThe problem revolves around identifying subarrays that contain exactly k odd numbers. The intuition is to maintain a running count of odd num | AtrijPaul | NORMAL | 2024-06-22T02:53:57.950658+00:00 | 2024-06-22T02:53:57.950690+00:00 | 286 | false | \n\n\n# Intuition\nThe problem revolves around identifying subarrays that contain exactly k odd numbers. The intuition is to maintain a running count of odd numbers encountered as we iterate through the array. By doing so, we can determine if a valid subarray ends at the current position by checking how many previous subarrays (or prefixes) have a specific number of odd numbers. This approach leverages the concept of prefix sums, commonly used in various subarray problems. In essence, if we know how many subarrays have a certain number of odd numbers up to a given point, we can quickly determine how many subarrays ending at the current position have the desired number of odd numbers.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialization: We start by initializing an array count_odds to keep track of the number of subarrays (prefixes) that contain a certain number of odd numbers. We set count_odds[0] = 1 to handle the case where the current prefix has exactly k odd numbers.\n\n2. Iterating through the array: We use a variable t to maintain the cumulative count of odd numbers encountered so far. For each element in the array, we update t by adding 1 if the element is odd (using num & 1).\n\n3. Counting valid subarrays: For each element, we check if there is a valid subarray ending at the current position by verifying if t - k is non-negative. If it is, it means there are count_odds[t - k] subarrays that can form a "nice" subarray with exactly k odd numbers ending at the current position. We add this count to subarray_count.\n\n4. Updating count_odds: Finally, we increment count_odds[t] to record that there is now one more prefix with t odd numbers.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n### Java \n\n```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int[] count_odds = new int[nums.length + 1];\n count_odds[0] = 1; //For the time when sum - k is 0\n int subarray_count = 0;\n int t = 0;\n for(int num : nums)\n {\n t += num & 1; //If it is odd then num & 1 will be 1 , if even then 0\n if(t - k >= 0)\n subarray_count += count_odds[t - k];\n \n count_odds[t]++;\n }\n return subarray_count;\n }\n}\n```\n\n### Python\n\n```\nclass Solution:\n def numberOfSubarrays(self, nums, k):\n count_odds = [0] * (len(nums) + 1)\n count_odds[0] = 1 # For the case when t - k == 0\n subarray_count = 0\n t = 0\n for num in nums:\n t += num % 2 # If the number is odd, num % 2 will be 1, otherwise 0\n if t - k >= 0:\n subarray_count += count_odds[t - k]\n \n count_odds[t] += 1\n return subarray_count\n```\n\n\n | 4 | 0 | ['Array', 'Hash Table', 'Math', 'Prefix Sum', 'Java'] | 1 |
count-number-of-nice-subarrays | Easy o(n) solution | easy-on-solution-by-vinuaqua4u-hadv | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vinuaqua4u | NORMAL | 2024-06-22T02:09:30.124433+00:00 | 2024-06-22T02:09:30.124465+00:00 | 483 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: o(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: o(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n result, cur, l, cur_sub = 0, 0, 0, 0\n for r, v in enumerate(nums):\n if v % 2 == 1: \n cur += 1\n cur_sub = 0\n\n while cur == k:\n if nums[l] % 2 == 1:\n cur -= 1\n l += 1\n cur_sub += 1\n result += cur_sub\n\n return result\n\n``` | 4 | 1 | ['Python3'] | 1 |
count-number-of-nice-subarrays | 💯✅🔥Easy Java ,Python3 ,C++ Solution|| 15 ms ||≧◠‿◠≦✌ | easy-java-python3-c-solution-15-ms-_-by-jzi27 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe idea is to count the number of subarrays with exactly k odd numbers. This is done b | suyalneeraj09 | NORMAL | 2024-06-22T00:43:33.631488+00:00 | 2024-06-22T00:43:33.631522+00:00 | 53 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea is to count the number of subarrays with exactly k odd numbers. This is done by maintaining a sliding window of odd numbers and incrementing the count whenever the window size is equal to k. The subarray function calculates the total number of subarrays with k or fewer odd numbers, and the numberOfSubarrays function subtracts the number of subarrays with k-1 or fewer odd numbers to get the number of subarrays with exactly k odd numbers.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code uses a two-pointer technique to solve the problem. It maintains two pointers, l and r, which represent the start and end of the current subarray. It also keeps track of the number of odd numbers in the current subarray using the variable odd.\n# Complexity\n- Time complexity:**O(n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:**O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```java []\npublic class Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int n = nums.length;\n int l = 0, r = 0, odd = 0, count = 0;\n\n while (r < n) {\n if (nums[r] % 2 != 0) {\n odd++;\n }\n while (odd > k) {\n if (nums[l] % 2 != 0) {\n odd--;\n }\n l++;\n }\n count += r - l + 1;\n r++;\n }\n return count - subarray(nums, k - 1);\n }\n\n public int subarray(int[] nums, int k) {\n if (k < 0) {\n return 0;\n }\n int n = nums.length;\n\n int l = 0, r = 0, odd = 0, count = 0;\n\n while (r < n) {\n if (nums[r] % 2 != 0) {\n odd++;\n }\n while (odd > k) {\n if (nums[l] % 2 != 0) {\n odd--;\n }\n l++;\n }\n count += r - l + 1;\n r++;\n }\n return count;\n }\n}\n```\n```python3 []\nclass Solution:\n def numberOfSubarrays(self, nums, k):\n n = len(nums)\n l = 0\n r = 0\n odd = 0\n count = 0\n\n while r < n:\n if nums[r] % 2 != 0:\n odd += 1\n while odd > k:\n if nums[l] % 2 != 0:\n odd -= 1\n l += 1\n count += r - l + 1\n r += 1\n return count - self.subarray(nums, k - 1)\n\n def subarray(self, nums, k):\n if k < 0:\n return 0\n n = len(nums)\n\n l = 0\n r = 0\n odd = 0\n count = 0\n\n while r < n:\n if nums[r] % 2 != 0:\n odd += 1\n while odd > k:\n if nums[l] % 2 != 0:\n odd -= 1\n l += 1\n count += r - l + 1\n r += 1\n return count\n```\n```C++ []\nclass Solution {\npublic:\n int numberOfSubarrays(std::vector<int>& nums, int k) {\n int n = nums.size();\n int l = 0, r = 0, odd = 0, count = 0;\n\n while (r < n) {\n if (nums[r] % 2 != 0) {\n odd++;\n }\n while (odd > k) {\n if (nums[l] % 2 != 0) {\n odd--;\n }\n l++;\n }\n count += r - l + 1;\n r++;\n }\n return count - subarray(nums, k - 1);\n }\n\n int subarray(std::vector<int>& nums, int k) {\n if (k < 0) {\n return 0;\n }\n int n = nums.size();\n\n int l = 0, r = 0, odd = 0, count = 0;\n\n while (r < n) {\n if (nums[r] % 2 != 0) {\n odd++;\n }\n while (odd > k) {\n if (nums[l] % 2 != 0) {\n odd--;\n }\n l++;\n }\n count += r - l + 1;\n r++;\n }\n return count;\n }\n};\n```\n\n\n | 4 | 4 | ['Array', 'C++', 'Java', 'Python3'] | 0 |
count-number-of-nice-subarrays | Dig Deep into Sliding window pattern & Two pointers | dig-deep-into-sliding-window-pattern-two-d9eq | two pattern approach to solve these problems\r\n\r\n560. Subarray Sum Equals K\r\n930. Binary Subarrays With Sum\r\n1248. Count Number of Nice Subarrays\r\n\r\n | Dixon_N | NORMAL | 2024-05-18T16:55:15.595017+00:00 | 2024-05-19T17:17:24.170589+00:00 | 415 | false | two pattern approach to solve these problems\r\n\r\n[560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/solutions/4416842/simple-as-that-important-pattern-must-read/)\r\n[930. Binary Subarrays With Sum](https://leetcode.com/problems/binary-subarrays-with-sum/solutions/5180407/deep-understanding-of-two-pointer-and-intuitive-problems/)\r\n[1248. Count Number of Nice Subarrays](https://leetcode.com/problems/count-number-of-nice-subarrays/solutions/5175648/dig-deep-into-sliding-window-pattern-two-pointers/)\r\n\r\n\r\nSliding window and two pointers pattern\r\n1. constant window\r\n2. Longest subarray/subString with condition (variable window)\r\n3. count (Longest) the subArray with given condition\r\n4. Minimum window\r\n\r\n### 2- pattern is mostly used\r\n```\r\n\r\n// Longest Subarray/substring pattern sliding window& two pointer pattern parblem.\r\n/*\r\nThere are 4 sliding window & two pointer pattern\r\n1. Constant window\r\n2. Longest Subarray/substring pattern\r\n3. Number of subArray/SubString pattern\r\n4.Find the minimum/shortest window pattern\r\n\r\nExplanation of 2. Longest Subarray/substring pattern\r\n\r\nThis can be again catagorised into 3\r\n1.Brute\r\n2.Optimal -> which is most used also used for printing the longest subarray/substring\r\n3.Optimsed version of 2 where \'while\' is replaced by \'if\'\r\n\r\n2 template --> 2.Optimal -> which is most used also used for printing the longest subarray/substring\r\n\r\nint left=0; int right=0, max=0,n=nums.length;\r\n\r\n while(right<n){//This line is constant always the \'right\' starts from 0->n\r\n \r\n if(nums[right]==0) k--; //operation "on RIGHT" is based on problem\r\n\r\n while(k<0){//while is constant and the condition inside is based on problem\r\n if(nums[l]==0) k++;\r\n left++; \r\n }\r\n max = Math.max(max,right-left+1);//operation done for result\r\n right++;// finally increment right this is constant\r\n }\r\n\r\n return max;\r\n\r\n*/\r\n\r\n```\r\n\r\n### 3 -Pattern\r\n```java []\r\n//Pattern 3 --> count the No of subArray/subString == (no of subArray with sum k) - (no of subArray with sum k-1)\r\n\r\n//This is the general rule but this can also be solved using the below pattern\r\n\r\npublic class Solution {\r\n public int subarraySum(int[] a, int k) {\r\n int n = a.length; // size of the array.\r\n\r\n Map<Integer, Integer> preSumMap = new HashMap<>();\r\n int count = 0;\r\n int sum = 0;\r\n\r\n for (int i = 0; i < n; i++) {\r\n // Calculate the prefix sum till index i:\r\n sum += a[i];\r\n\r\n // If the sum equals k, update the count:\r\n if (sum == k) {\r\n count++;\r\n }\r\n\r\n // Calculate the sum of the remaining part, i.e., x - k:\r\n int rem = sum - k;\r\n\r\n // Increment count based on the occurrences in the map:\r\n if (preSumMap.containsKey(rem)) {\r\n count += preSumMap.get(rem);\r\n }\r\n\r\n // Update the map with the current prefix sum:\r\n preSumMap.put(sum, preSumMap.getOrDefault(sum, 0) + 1);\r\n }\r\n\r\n return count;\r\n }\r\n}\r\n\r\n```\r\n```java []\r\n// 930. Binary Subarrays With Sum\r\n\r\n//Pattern 3 --> count the No of subArray/subString == (no of subArray with sum k) - (no of subArray with sum k-1)\r\n\r\n\r\n\r\nimport java.util.HashMap;\r\nimport java.util.Map;\r\n\r\npublic class Solution {\r\n public int numSubarraysWithSum(int[] nums, int goal) {\r\n Map<Integer, Integer> preSumMap = new HashMap<>();\r\n int count = 0;\r\n int sum = 0;\r\n\r\n // Initialize map with sum 0 having one occurrence to handle subarrays that start from index 0\r\n preSumMap.put(0, 1);\r\n\r\n for (int num : nums) {\r\n sum += num;\r\n\r\n // Calculate the sum of the remaining part needed to reach the goal\r\n int rem = sum - goal;\r\n\r\n // Increment count based on the occurrences in the map\r\n count += preSumMap.getOrDefault(rem, 0);\r\n\r\n // Update the map with the "current" prefix sum\r\n preSumMap.put(sum, preSumMap.getOrDefault(sum, 0) + 1);\r\n }\r\n\r\n return count;\r\n }\r\n}\r\n\r\n```\r\n```java []\r\n\r\n//pattern 3 Approach\r\n// 930. Binary Subarrays With Sum\r\nclass Solution {\r\n\r\n public int numSubarraysWithSum(int[] nums, int goal) {\r\n return atMost(nums, goal) - atMost(nums, goal - 1);\r\n }\r\n\r\n private int atMost(int[] nums, int goal) {\r\n if (goal < 0) return 0;\r\n int res = 0, left = 0, n = nums.length, right = 0;\r\n int sum = 0;\r\n while (right < n) {\r\n sum += nums[right];\r\n while (sum > goal) {\r\n sum -= nums[left];\r\n left++;\r\n }\r\n res += right - left + 1;\r\n right++;\r\n }\r\n return res;\r\n }\r\n}\r\n// Hope that is clear\r\n```\r\n\r\n# 1248. Count Number of Nice Subarrays\r\n\r\n```javascript []\r\n//Pattern 3 --> count the No of subArray/subString\r\n//Pattern 3 --> count the No of subArray/subString == (no of subArray with sum k) - (no of subArray with sum k-1)\r\n\r\nclass Solution {\r\n public int numberOfSubarrays(int[] nums, int k) {\r\n return atMost(nums, k) - atMost(nums, k - 1);\r\n }\r\n private int atMost(int[] nums, int goal) {\r\n if (goal < 0) return 0;\r\n int res = 0, left = 0, n = nums.length, right = 0;\r\n int sum = 0;\r\n while (right < n) {\r\n sum += nums[right]%2;\r\n while (sum > goal) {\r\n sum -= nums[left]%2;\r\n left++;\r\n }\r\n res += right - left + 1;\r\n right++;\r\n }\r\n return res;\r\n }\r\n}\r\n```\r\n```java []\r\nimport java.util.HashMap;\r\nimport java.util.Map;\r\n\r\npublic class Solution {\r\n public int numberOfSubarrays(int[] nums, int k) {\r\n Map<Integer, Integer> preSumMap = new HashMap<>();\r\n int count = 0;\r\n int sum = 0;\r\n\r\n // Initialize map with sum 0 having one occurrence to handle subarrays that start from index 0\r\n preSumMap.put(0, 1);\r\n\r\n for (int num : nums) {\r\n // Increment sum if the number is odd\r\n sum += num % 2;\r\n\r\n // Calculate the sum of the remaining part needed to reach the goal k\r\n int rem = sum - k;\r\n\r\n // Increment count based on the occurrences in the map\r\n count += preSumMap.getOrDefault(rem, 0);\r\n\r\n // Update the map with the "current" prefix sum\r\n preSumMap.put(sum, preSumMap.getOrDefault(sum, 0) + 1);\r\n }\r\n\r\n return count;\r\n }\r\n}\r\n\r\n```\r\n\r\n | 4 | 0 | ['Java'] | 2 |
count-number-of-nice-subarrays | 1248. Count Number of Nice Subarrays - Brute Force & Sliding Window Approaches | 1248-count-number-of-nice-subarrays-brut-5zuh | Brute Force - Memory Limit Exceeded\r\n\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n def countOdds(arr): # | TrGanesh | NORMAL | 2024-05-11T11:18:07.123689+00:00 | 2024-05-11T11:18:07.123713+00:00 | 332 | false | ## Brute Force - Memory Limit Exceeded\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n def countOdds(arr): # Function to Count Odd Values in Arr.\r\n odds = 0\r\n for i in range(len(arr)):\r\n if arr[i] % 2 != 0:\r\n odds += 1\r\n return odds\r\n\r\n # Main\r\n n = len(nums)\r\n all_subarrs = [] # Stores all SubArrays\r\n for i in range(n):\r\n for j in range(i, n):\r\n all_subarrs.append(nums[i:j+1]) \r\n print(all_subarrs)\r\n\r\n # To check whether all SubArrays are Stored are Not\r\n # if len(all_subarrs) == n * (n + 1) / 2:\r\n # print(\'Correct\')\r\n\r\n ans = 0\r\n # Traversing through each SubArr\r\n for sub_arr in all_subarrs:\r\n if countOdds(sub_arr) == k:\r\n ans += 1\r\n\r\n return ans\r\n```\r\n\r\n---\r\n\r\n## Sliding Window - TC : O(N) , SC : O(1)\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n left = right = 0\r\n ans = 0 # Ans is final Answer\r\n count = 0 # Count is used for Counting all SubArrays when Condition got Satisified\r\n odds = 0 # Counts No. of Odds in Current Window\r\n\r\n while right < len(nums):\r\n if nums[right] % 2 != 0: # Odd\r\n odds += 1\r\n count = 0\r\n \r\n while odds == k: \r\n # Try to Move the Left Pointer \r\n # Also, Increment the Count Variable as We can have One More SubArr, satisfying the Condition\r\n if nums[left] % 2 == 0: # Even\r\n count += 1\r\n \r\n if nums[left] % 2 != 0: # Odd \r\n odds -= 1\r\n count += 1\r\n \r\n left += 1\r\n \r\n ans += count\r\n\r\n right += 1\r\n return ans\r\n```\r\n**Please UpVote** | 4 | 0 | ['Array', 'Sliding Window', 'Python3'] | 0 |
count-number-of-nice-subarrays | The solution you are looking for. | the-solution-you-are-looking-for-by-abhi-6buw | Intuition\r\n Describe your first thoughts on how to solve this problem. \r\n# HEY GUYS UPVOTE \r\nOverall Logic:\r\n\r\n1. The main function (numberOfSubarrays | Abhishekkant135 | NORMAL | 2024-04-23T23:42:35.607043+00:00 | 2024-04-23T23:42:35.607063+00:00 | 568 | false | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n# HEY GUYS UPVOTE \r\n**Overall Logic:**\r\n\r\n1. The main function (`numberOfSubarrays`) finds the difference in the number of subarrays allowed with `k` odd numbers and `k-1` odd numbers.\r\n2. The `atmost` function efficiently counts subarrays with at most `k` odd numbers using a sliding window and keeping track of odd numbers encountered.\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\nThe provided code calculates the number of subarrays in an integer array `nums` that contain at most `k` odd numbers. It leverages two functions:\r\n\r\n**1. `numberOfSubarrays(int[] nums, int k)`:**\r\n\r\n- This is the main function that calculates the final result.\r\n- It calls the `atmost(nums, k)` function twice: once with `k` and once with `k-1`.\r\n- It then subtracts the result from `atmost(nums, k-1)` from `atmost(nums, k)`. This effectively calculates the difference in the number of subarrays allowed with `k` odd numbers and with `k-1` odd numbers. This difference represents the number of subarrays allowed with exactly `k` odd numbers.\r\n\r\n**2. `atmost(int[] nums, int k)`:**\r\n\r\n- This function calculates the number of subarrays in the `nums` array that contain at most `k` odd numbers.\r\n- It uses a sliding window approach with two pointers (`i` and `j`) to explore all possible subarrays.\r\n- `int countOdd = 0`: This variable keeps track of the number of odd numbers encountered within the current window.\r\n- The `while` loop iterates as long as `j` (end of the current window) is less than the array length (`n`).\r\n - `if (nums[j] % 2 != 0)`: Checks if the current element (`nums[j]`) is odd.\r\n - If it\'s odd:\r\n - `countOdd++`: Increments `countOdd` to track the additional odd number.\r\n - The inner `while` loop contracts the window from the left (using `i`) as long as `countOdd` is greater than the allowed limit (`k`).\r\n - `if (nums[i] % 2 != 0)`: Checks if the element at the beginning of the window (`nums[i]`) is odd.\r\n - If it\'s odd:\r\n - `countOdd--`: Decrements `countOdd` as an odd number is being removed from the window.\r\n - `i++`: Increments `i` to move the window one step to the right, effectively removing the element from the current window.\r\n- `ans += j - i + 1`: After potentially contracting the window, this line updates the `ans` variable to count the number of subarrays within the current valid window size (`j - i + 1`).\r\n- `j++`: Increments `j` to move the window one step to the right for exploring the next subarray in the next iteration of the outer `while` loop.\r\n\r\n\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\nThis approach provides a time-efficient solution (O(n)) for finding the desired subarrays.\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\nO(1)\r\n# Code\r\n```\r\nclass Solution {\r\n public int numberOfSubarrays(int[] nums, int k) {\r\n return atmost(nums,k)-atmost(nums,k-1);\r\n }\r\n\r\n public int atmost(int [] nums, int k){\r\n int i=0;\r\n int j=0;\r\n int ans=0;\r\n int countOdd=0;\r\n int n=nums.length;\r\n while(j<n){\r\n if (nums[j]%2!=0){\r\n countOdd++;\r\n }\r\n while(countOdd>k){\r\n if (nums[i]%2!=0){\r\n countOdd--;\r\n }\r\n i++;\r\n }\r\n ans+=j-i+1;\r\n j++;\r\n }\r\n return ans;\r\n }\r\n}\r\n``` | 4 | 0 | ['Sliding Window', 'Java'] | 0 |
count-number-of-nice-subarrays | Beginner-Friendly Solution || Easy Video Explanation in Hindi | beginner-friendly-solution-easy-video-ex-n9xj | Intuition\r\nHashing + PrefixSum\r\n\r\n# Approach\r\n\r\nKindly check the video links given below for understanding both the prefix sum concept + actual soluti | nayankumarjha2 | NORMAL | 2024-02-21T16:44:47.342601+00:00 | 2024-02-21T16:44:47.342647+00:00 | 785 | false | # Intuition\r\nHashing + PrefixSum\r\n\r\n# Approach\r\n\r\nKindly check the video links given below for understanding both the prefix sum concept + actual solution. Detailed explanations are provided in Hindi.\r\n\r\nPrefix-Sum Concept(Pre-requisite) : www.youtube.com/watch?v=PX5uIJC4sXQ\r\n\r\nActual Solution : www.youtube.com/watch?v=C_y2PFLyDp8\r\n\r\n\r\n# Complexity\r\n- Time complexity: O(N)\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity: O(N)\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# C++\r\n```\r\nclass Solution {\r\npublic:\r\n int numberOfSubarrays(vector<int>& nums, int k) {\r\n //Optimal Solution T.C.: O(N), S.C.: O(N)\r\n int n = nums.size();\r\n\r\n int i=0;\r\n\r\n //Updating even to 0 and odd to 1\r\n while(i!=n){\r\n if(nums[i]%2!=0)\r\n nums[i]=1;\r\n else\r\n nums[i]=0;\r\n i++;\r\n }\r\n\r\n\r\n //Simple use count subarray with sum K problem logic.\r\n\r\n int count =0;\r\n unordered_map<int,int> map;\r\n int sum=0;\r\n\r\n i=0;\r\n while(i!=n){\r\n sum+=nums[i];\r\n if(sum==k) count++;\r\n\r\n if(map.find(sum-k)!= map.end()){\r\n count+=map[sum-k];\r\n }\r\n\r\n map[sum]++;\r\n i++;\r\n }\r\n return count;\r\n }\r\n};\r\n\r\n```\r\n# Java\r\n```\r\nclass Solution {\r\n public int numberOfSubarrays(int[] nums, int k) {\r\n //Optimal Solution T.C.: O(N), S.C.: O(N)\r\n int n = nums.length;\r\n\r\n int i=0;\r\n\r\n //Updating even to 0 and odd to 1\r\n while(i!=n){\r\n if(nums[i]%2!=0)\r\n nums[i]=1;\r\n else\r\n nums[i]=0;\r\n i++;\r\n }\r\n\r\n\r\n //Simple use count subarray with sum K problem logic.\r\n\r\n int count =0;\r\n Map<Integer,Integer> map = new HashMap<>();\r\n int sum=0;\r\n\r\n i=0;\r\n while(i!=n){\r\n sum+=nums[i];\r\n if(sum==k) count++;\r\n\r\n if(map.containsKey(sum-k)){\r\n count+=map.get(sum-k);\r\n }\r\n\r\n map.put(sum,map.getOrDefault(sum,0)+1);\r\n i++;\r\n }\r\n return count;\r\n }\r\n}\r\n```\r\n# Python3\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n # Optimal Solution T.C.: O(N), S.C.: O(N)\r\n n = len(nums)\r\n\r\n # Updating even to 0 and odd to 1\r\n i = 0\r\n while i < n:\r\n if nums[i] % 2 != 0:\r\n nums[i] = 1\r\n else:\r\n nums[i] = 0\r\n i += 1\r\n\r\n # Simple use count subarray with sum K problem logic.\r\n count = 0\r\n num_map = {}\r\n curr_sum = 0\r\n\r\n i = 0\r\n while i < n:\r\n curr_sum += nums[i]\r\n\r\n if curr_sum == k:\r\n count += 1\r\n\r\n if curr_sum - k in num_map:\r\n count += num_map[curr_sum - k]\r\n\r\n if curr_sum in num_map:\r\n num_map[curr_sum] += 1\r\n else:\r\n num_map[curr_sum] = 1\r\n\r\n i += 1\r\n\r\n return count\r\n```\r\n\r\n## Please upvote if you like the solution. | 4 | 0 | ['Array', 'Hash Table', 'Prefix Sum', 'C++', 'Java', 'Python3'] | 0 |
count-number-of-nice-subarrays | Modifying the question (Making it much more easier) || Sliding window || Easy to Understand | modifying-the-question-making-it-much-mo-4ou6 | Intuition\r\n Describe your first thoughts on how to solve this problem. \r\nTreat odd numbers as 1 and even numbers as 0, then solve as if you want sum of suba | BihaniManan | NORMAL | 2023-07-05T12:00:27.683940+00:00 | 2023-07-05T12:00:27.683962+00:00 | 2,140 | false | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nTreat odd numbers as 1 and even numbers as 0, then solve as if you want sum of subarray having sum = k.\r\n\r\nSame as this question: [930. Binary Subarrays With Sum\r\n](https://leetcode.com/problems/binary-subarrays-with-sum/)\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n1. Replace all the odd elements with 1 and all the even elements with 0.\r\n2. Now calculate the subarrays with sum = k.\r\n3. This can be done by finding the subarrays with **sum <= k** and finding subarrays with **sum <= k - 1** and subtrack later from the previous one.\r\n\r\n**Feel free to post your doubts in the comments :)**\r\n\r\n# Complexity\r\n- Time complexity: **O(n)**\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity: **O(1)**\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution {\r\npublic:\r\n int atMost(vector<int>& nums, int k)\r\n {\r\n int left = 0;\r\n int right = 0;\r\n int ans = 0;\r\n\r\n for(right = 0; right < nums.size(); right++)\r\n {\r\n k -= nums[right];\r\n while(k < 0)\r\n {\r\n k += nums[left];\r\n left++;\r\n }\r\n ans += right - left + 1;\r\n }\r\n return ans;\r\n }\r\n int numberOfSubarrays(vector<int>& nums, int k) {\r\n for(int i = 0; i < nums.size(); i++)\r\n {\r\n if(nums[i] % 2 == 1) nums[i] = 1;\r\n else nums[i] = 0;\r\n }\r\n return atMost(nums, k) - atMost(nums, k - 1);\r\n }\r\n};\r\n``` | 4 | 0 | ['Sliding Window', 'Python', 'C++', 'Java'] | 5 |
count-number-of-nice-subarrays | Java simple with complete explanation | java-simple-with-complete-explanation-by-icot | Approach\r\nThe provided solution employs a sliding window technique to solve the problem. Let\'s break down the approach step by step:\r\n\r\n- Initialize vari | S_SAYUJ | NORMAL | 2023-05-20T08:13:43.266989+00:00 | 2023-05-22T15:16:13.064805+00:00 | 386 | false | # Approach\r\nThe provided solution employs a sliding window technique to solve the problem. Let\'s break down the approach step by step:\r\n\r\n- Initialize variables left, right, count, max, and temp. Set len as the length of the input array nums. Here, left and right represent the left and right pointers of the sliding window, count keeps track of the number of odd numbers encountered, max stores the total count of nice subarrays, and temp is a temporary variable to count the number of nice subarrays at each position.\r\n\r\n- Start iterating through the array using the right pointer until it reaches the end of the array.\r\n\r\n- At each iteration, check if the current number at position right is odd or even. If it is odd\r\n- (nums[right] % 2 == 1)\r\n- increment the count by 1 to indicate the presence of an odd number in the current subarray. Reset temp to 0 to start counting the number of nice subarrays at the current position.\r\n\r\n- Inside the while loop, check if the condition of having exactly k odd numbers is satisfied \r\n- (count == k). \r\n- If this condition is met, it means we have found a nice subarray.\r\n\r\n- Increment temp by 1 to count the number of nice subarrays starting from the current position right.\r\n\r\n- Move the left pointer inside a nested while loop to shrink the window and find more nice subarrays. We keep moving the left pointer and decrementing the count whenever we encounter an odd number. This step ensures that we maintain exactly k odd numbers in the subarray.\r\n\r\n- After finding all possible nice subarrays starting from the current right position, add temp to max to update the total count of nice subarrays.\r\n\r\n- Finally, increment the right pointer to expand the window and continue the process until we reach the end of the array.\r\n\r\n- Return max, which represents the total number of nice subarrays.- \r\n\r\n# Complexity\r\n- **Time complexity:** \r\n\r\n- O(n)\r\nThe time complexity of this approach is O(N), where N is the length of the input array nums. The algorithm only iterates through the array once using the sliding window technique.\r\n<hr>\r\n\r\n- **Space complexity:**\r\nslid \r\n- O(1)\r\nThe space complexity is O(1) because no extra space is used apart from the input array and a few variables to track indices and counts.\r\n\r\n# Code\r\n```\r\nclass Solution {\r\n public int numberOfSubarrays(int[] nums, int k) {\r\n int len=nums.length;\r\n int left=0,right=0,count=0,max=0,temp=0;\r\n while(right<len)\r\n {\r\n if(nums[right]%2==1)\r\n {\r\n count++;\r\n temp=0;\r\n }\r\n \r\n while(count==k)\r\n {\r\n temp++;\r\n if(nums[left]%2==1)\r\n {\r\n count--;\r\n }\r\n \r\n left++;\r\n }\r\n max=max+temp;\r\n \r\n right++;\r\n }\r\n return max;\r\n \r\n }\r\n}\r\n``` | 4 | 0 | ['Array', 'Two Pointers', 'Sliding Window', 'Java'] | 1 |
count-number-of-nice-subarrays | 2 POINTER SIMPLE APPROACH || PYTHON 3 | 2-pointer-simple-approach-python-3-by-an-ogyx | \r\n# Code\r\n\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n count = 0\r\n i = 0\r\n j = 0\r\n | ankitbisht981 | NORMAL | 2023-05-18T17:46:08.100351+00:00 | 2023-05-18T17:46:08.100390+00:00 | 270 | false | \r\n# Code\r\n```\r\nclass Solution:\r\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\r\n count = 0\r\n i = 0\r\n j = 0\r\n temp = 0\r\n ans = 0\r\n while(j<len(nums)):\r\n\r\n if nums[j]%2!=0:\r\n temp+=1\r\n count = 0\r\n\r\n if temp==k:\r\n while(nums[i]%2==0):\r\n count+=1\r\n i+=1\r\n count+=1\r\n i+=1\r\n temp-=1\r\n \r\n ans +=count\r\n j+=1\r\n\r\n return ans\r\n``` | 4 | 0 | ['Array', 'Two Pointers', 'Sliding Window', 'Python3'] | 0 |
count-number-of-nice-subarrays | 🤗👀JAVA | VERY EASY | java-very-easy-by-dipesh_12-51nr | Intuition\r\n Describe your first thoughts on how to solve this problem. \r\n\r\n# Approach\r\n Describe your approach to solving the problem. \r\n\r\n# Complex | dipesh_12 | NORMAL | 2023-05-05T07:40:06.048246+00:00 | 2023-05-05T07:40:06.048286+00:00 | 1,579 | false | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\n\r\n# Complexity\r\n- Time complexity:\r\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\r\n\r\n- Space complexity:\r\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\r\n\r\n# Code\r\n```\r\nclass Solution {\r\n public int numberOfSubarrays(int[] nums, int k) {\r\n int i=0;\r\n int j=0;\r\n int oddCount=0;\r\n int ans=0;\r\n int count=0;\r\n\r\n while(j<nums.length){\r\n \r\n if(nums[j]%2!=0){\r\n oddCount++;\r\n ans=0;\r\n }\r\n \r\n while(oddCount==k){\r\n ans++;\r\n if(nums[i]%2!=0){ \r\n oddCount--;\r\n \r\n }\r\n i++;\r\n }\r\n count+=ans;\r\n j++;\r\n }\r\n return count;\r\n }\r\n}\r\n``` | 4 | 0 | ['Java'] | 2 |
count-number-of-nice-subarrays | Two Pointer Solution easy | two-pointer-solution-easy-by-tejesh_jain-p7hg | \r\n\r\n# Approach\r\n Describe your approach to solving the problem. \r\nIn this solution we basically take 2 pointers (i and j). If the nums[j] is odd we incr | Tejesh_Jain_0912 | NORMAL | 2023-03-04T03:55:37.575851+00:00 | 2023-03-04T03:55:37.575881+00:00 | 1,117 | false | \r\n\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\nIn this solution we basically take 2 pointers (i and j). If the nums[j] is odd we increase the odd counter. If off is equal to k we count all the subarrays in between i and j by increasing i position till odd == k. We add the result in res.\r\n\r\n\r\n# Code\r\n```\r\nclass Solution {\r\n public int numberOfSubarrays(int[] nums, int k) {\r\n int i=0,j=0,odd=0,count=0,res=0;\r\n while(j<nums.length){\r\n if(nums[j]%2!=0){\r\n odd++;\r\n count=0;\r\n }\r\n while(odd==k){\r\n if(nums[i++]%2!=0){\r\n odd--;\r\n }\r\n count++;\r\n }\r\n res+=count;\r\n j++;\r\n }\r\n return res;\r\n }\r\n}\r\n``` | 4 | 1 | ['Two Pointers', 'Java'] | 0 |
count-number-of-nice-subarrays | C++ easy 6 lines of code 🔥 🔥 | c-easy-6-lines-of-code-by-sakettiwari-b9ug | Intuition\nIf you remember two sum question you can have refrence \uD83D\uDD25 \uD83D\uDD25\nEnjoy !\n\n# UPVOTE IF IT HELPED \n# Code\n\nclass Solution {\npubl | Sakettiwari | NORMAL | 2023-02-09T17:35:33.273164+00:00 | 2023-02-09T17:35:33.273209+00:00 | 1,160 | false | # Intuition\nIf you remember two sum question you can have refrence \uD83D\uDD25 \uD83D\uDD25\nEnjoy !\n\n# UPVOTE IF IT HELPED \n# Code\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int i=0 , sum=0 ,count=0;\n unordered_map<int,int>map;\n while(i<nums.size()){\n if(nums[i]%2 != 0) sum+=1;\n if(sum == k) count++;\n if(map.find(sum-k) != map.end()) count+=map[sum-k];\n map[sum]++;\n i++;\n }\n return count;\n }\n};\n```\n | 4 | 0 | ['C++'] | 1 |
count-number-of-nice-subarrays | java solution | java-solution-by-kjain6_11-bnhy | \nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int i = 0;\n int j = 0;\n int odd = 0;\n int result = 0; | kjain6_11 | NORMAL | 2022-07-26T02:57:38.269917+00:00 | 2022-07-26T02:57:38.269952+00:00 | 538 | false | ```\nclass Solution {\n public int numberOfSubarrays(int[] nums, int k) {\n int i = 0;\n int j = 0;\n int odd = 0;\n int result = 0;\n int temp = 0;\n \n \n /* \n Approach : two pointer + sliding window technique\n \n step 1 : we have fix i and moving j until our count of odd numbers == k\n step 2 : when(odd == count) we are counting every possible subarray by reducing the size of subarray from i\n \n why temp?\n from reducing the size of subarray we will count all the possible subarray from between i and j\n but when i encounter a odd element the odd count will reduce and that while will stop executing\n \n now there are two possible cases\n 1.The leftover elements have a odd number\n 2.The leftover elements do not have any odd number\n \n 1. if our leftover elements have a odd number \n then we cannot include our old possible subarrays into new possible subarrays because now new window for having odd == k is formed\n that\'s why temp = 0;\n \n 2. if out leftover elements do not have any odd element left\n then our leftover elements must also take in consideration becuase they will also contribute in forming subarrays\n */\n while(j< nums.length){\n if(nums[j]%2 != 0)\n {\n odd++;\n //if leftover elements have odd element then new window is formed so we set temp = 0;\n temp = 0;\n }\n while(odd ==k){\n temp++;\n if(nums[i] %2 != 0)\n odd--;\n i++;\n }\n //if no leftover elements is odd, each element will part in forming subarray\n //so include them\n result += temp;\n j++;\n \n }\n return result;\n }\n}\n``` | 4 | 0 | ['Sliding Window', 'Java'] | 2 |
count-number-of-nice-subarrays | [C++] 3 ideas, solution, and explanation for beginners | c-3-ideas-solution-and-explanation-for-b-0a5n | First, the naive solution, we check every possible subarray and increment the count everytime we encounter a nice subarray.\n\nclass Solution {\npublic:\n in | haoran_xu | NORMAL | 2021-07-28T14:12:26.566549+00:00 | 2021-07-28T14:12:26.566611+00:00 | 311 | false | First, the naive solution, we check every possible subarray and increment the count everytime we encounter a nice subarray.\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int n = nums.size();\n int sum = 0;\n for(int i = 0; i < n; i++) {\n int count = 0;\n for(int j = i; j < n; j++) {\n if(nums[j] & 1 != 0) {\n count++;\n }\n \n if(count == k) sum++;\n if(count > k) break;\n }\n }\n \n return sum;\n }\n};\n```\nVery standard, not much to talk about. The time complexity is `O(n^2)`while the space complexity is `O(1)`. Submitting this will cause an TLE...so it is clear we must do better on time complexity.\n\nHere is an observation, given a minimum length nice subarray with even number surrounding it. The total amount of different subarray we can construct is the "left wing" * "right wing". Take a look at the following example:\n```\n2,2,2,2,1,2,2,1,2,2,2,2 k = 2\n```\nHow many nice subarray can we construct? The answer is `5 * 5 = 25`. While we can count everything out, a better way is to notice the following pattern `1,2,2,1 -> 1,2,2,1,2 -> 1,2,2,1,2,2 -> ...`, for every element in the "left wing" we can pair it up with every other element in the "right wing" and vice versa. Simple math tells us the number of such combination is simply `left wing * right wing`. I will sepereate the two wings to make it clearer `2,2,2,2,1 | 2,2 | 1,2,2,2,2` (notice that we include the odd number in the wing). How we can locate a "minimum length nice subarray"? Easy, we can simple store indexs of all odd numbers and create a sliding window of length `k`. For every such window, we will calculate the length of both wing, either terminate at the start or end of an array, or terminate immediate before another odd number. For example, our minimum length nice subarray is from index 7 to index 9. \n`2,2,1 | 2,2,2,2,1| 2 |1,2,2,2,2 | 1,1`\nIf you don\'t get it, stare at it for a while and I\'m sure it will come to you. Time for the implementation:\n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> idx;\n for(int i = 0; i < n; i++) {\n if(nums[i] & 1 != 0) idx.push_back(i);\n }\n \n int sum = 0;\n \n int i = 0;\n for(int j = k - 1; j < idx.size(); j++) {\n int left = idx[i] - (i == 0 ? -1 : idx[i - 1]);\n int right = (j == idx.size() - 1 ? n : idx[j + 1]) - idx[j];\n \n sum += left * right;\n i++;\n }\n \n return sum;\n }\n};\n```\nTime complexity is `O(n)` while space complexity is also `O(n)`. \n\nSubmit and the code runs fine. I always like looking for other solutions even after finishing a question. I find it a good practice and also interesting that 1 problem can have so many different solutions.\n\nThis question might remind you of https://leetcode.com/problems/subarrays-with-k-different-integers/. This is a great question and I would definitely recommend checking out. When we do our standard sliding window solutions we get stuck because there is no easy way to slide the window through all possible subarrays. However, we can actually find all subarray with ATMOST `k` odd numbers pretty easily with sliding window. You should try and do this on your own. Eitherway, simple math tells us that `exactly(k) = atmost(k) - atmost(k - 1)`. This gives us a relatively simple algorithm:\n```\nclass Solution {\n \n int atMost(vector<int>& nums, int k) {\n int n = nums.size();\n int i = 0;\n int sum = 0;\n \n for(int j = 0; j < n; j++) {\n if((nums[j] & 1) != 0) k--;\n while(k < 0) {\n if((nums[i] & 1) != 0) k++;\n i++;\n }\n \n sum += j - i + 1;\n }\n \n return sum;\n }\n \npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n return atMost(nums, k) - atMost(nums, k - 1);\n }\n};\n```\nSame time complexity as the solution above, but space complexity is `O(1)`. | 4 | 0 | [] | 0 |
count-number-of-nice-subarrays | Easy C++ solution | easy-c-solution-by-imran2018wahid-8mbu | \nclass Solution \n{\npublic:\n // Function to calculate the number of subarrays having count of odd numbers lees than or equals to k\n int helper(vector< | imran2018wahid | NORMAL | 2021-06-07T19:21:37.221774+00:00 | 2021-06-07T19:22:40.616497+00:00 | 503 | false | ```\nclass Solution \n{\npublic:\n // Function to calculate the number of subarrays having count of odd numbers lees than or equals to k\n int helper(vector<int>&nums,int k)\n {\n int ans=0,i=0,count=0;\n for(int j=0;j<nums.size();j++)\n {\n if(nums[j]%2!=0)\n {\n count++;\n }\n while(i<=j && count>k)\n {\n if(nums[i]%2!=0)\n {\n count--;\n }\n i++;\n }\n ans+=(j-i+1);\n }\n return ans;\n }\n int numberOfSubarrays(vector<int>& nums, int k) \n {\n // Number of subarrays with count of odd numbers <=k = (Numbers of subarrays with count of odd numbers <k + Numbers of subarrays with count of odd numbers =k)\n // so if we exclude the number of subarrays with odd number count less than k from number of subarrays with odd number count equals to k , we\'ll get our answer.\n return helper(nums,k)-helper(nums,k-1);\n }\n};\n```\n**Please upvote if you have got any help from my code. Thank you.** | 4 | 0 | ['C'] | 1 |
count-number-of-nice-subarrays | c++ O(1) space 97%faster 100 % space efficient | c-o1-space-97faster-100-space-efficient-ms4vg | \nclass Solution {\npublic:\n Solution()\n {\n ios_base::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n }\n int func(vector | naman238 | NORMAL | 2020-05-05T16:06:16.178028+00:00 | 2020-05-05T16:06:16.178079+00:00 | 509 | false | ```\nclass Solution {\npublic:\n Solution()\n {\n ios_base::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n }\n int func(vector<int> &nums,int k)\n {\n int j=0;\n int cnt=0;\n int n=nums.size();\n for(int i=0;i<n;i++)\n {\n if(nums[i]%2)k--;\n while(k<0)\n {\n if(nums[j]%2)k++;\n j++;\n }\n cnt+=i-j+1;\n }\n return cnt;\n }\n int numberOfSubarrays(vector<int>& nums, int k) {\n\t\t\treturn func(nums,k)-func(nums,k-1);//func calculate for atmost case. exact k=atmost k -atmost k-1;\n }\n};\n``` | 4 | 0 | ['C', 'Sliding Window'] | 1 |
count-number-of-nice-subarrays | [C++] Map Solution | Easy Implementation | c-map-solution-easy-implementation-by-ni-qscd | \nint numberOfSubarrays(vector<int>& nums, int k) {\n\tint res = 0, sum = 0, n = nums.size();\n\tunordered_map<int, int> mpp;\n\tfor (int i = 0; i < n; ++i) {\n | ninilo97 | NORMAL | 2020-04-04T05:30:29.698988+00:00 | 2020-04-04T05:30:29.699021+00:00 | 609 | false | ```\nint numberOfSubarrays(vector<int>& nums, int k) {\n\tint res = 0, sum = 0, n = nums.size();\n\tunordered_map<int, int> mpp;\n\tfor (int i = 0; i < n; ++i) {\n\t\tmpp[sum]++;\n\t\tsum += nums[i] & 1;\n\t\tres += mpp[sum - k];\n\t}\n\treturn res;\n}\n``` | 4 | 0 | ['C', 'C++'] | 1 |
count-number-of-nice-subarrays | C++ Sliding Window | c-sliding-window-by-esamokhov-yeuz | \nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int count = 0;\n int l = 0;\n int r = 0;\n int | esamokhov | NORMAL | 2020-03-27T09:27:25.948157+00:00 | 2020-03-27T09:27:25.948193+00:00 | 915 | false | ```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int count = 0;\n int l = 0;\n int r = 0;\n int oddCount = 0;\n int size = nums.size();\n while (r < size) {\n while (oddCount < k && r < size) {\n if (nums[r] % 2 != 0) {\n oddCount++;\n }\n r++;\n }\n int c1 = 1;\n while (r < size && nums[r] % 2 == 0) {\n r++;\n c1++;\n } \n int c2 = 0;\n while (oddCount == k && l < r) {\n if (nums[l] % 2 != 0) {\n oddCount--;\n }\n l++;\n c2++;\n }\n count += c1 * c2;\n }\n \n return count;\n }\n};\n``` | 4 | 1 | ['C', 'Sliding Window'] | 1 |
count-number-of-nice-subarrays | Python straightforward solution | python-straightforward-solution-by-otoc-mtt2 | Straightforward Solution: similar to the idea in the solution for 828. Unique Letter String\n\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\ | otoc | NORMAL | 2019-11-05T00:34:32.417291+00:00 | 2019-11-05T00:34:32.417329+00:00 | 640 | false | Straightforward Solution: similar to the idea in [the solution for 828. Unique Letter String](https://leetcode.com/problems/unique-letter-string/discuss/128952/One-pass-O(N)-Straight-Forward)\n```\n def numberOfSubarrays(self, nums: List[int], k: int) -> int:\n lst = [-1]\n for i in range(len(nums)):\n if nums[i] % 2:\n lst.append(i)\n lst.append(len(nums))\n res = 0\n for i in range(1, len(lst) - k):\n\t\t # plus the number of windows containing [lst[i], lst[i+k-1]]\n res += (lst[i] - lst[i-1]) * (lst[i+k] - lst[i+k-1])\n return res\n``` | 4 | 0 | [] | 0 |
count-number-of-nice-subarrays | [Python] Easy to understand, Sliding window (Left & Right evens), Faster than 100% | python-easy-to-understand-sliding-window-snie | \tclass Solution(object):\n\t\tdef numberOfSubarrays(self, nums, k):\n\t\t\t"""\n\t\t\te.g. k = 2\n\t\t\tnums = [2, 2, 1, 2, 1, 2, 2]\n\t\t\tindex= 0 1 2 3 | d-_-b | NORMAL | 2019-11-03T17:35:09.325171+00:00 | 2019-11-03T17:43:20.568949+00:00 | 798 | false | \tclass Solution(object):\n\t\tdef numberOfSubarrays(self, nums, k):\n\t\t\t"""\n\t\t\te.g. k = 2\n\t\t\tnums = [2, 2, 1, 2, 1, 2, 2]\n\t\t\tindex= 0 1 2 3 4 5 6\n\t\t\t2 even numbers to left of first 1\n\t\t\t2 even numbers to right of last 1\n\t\t\ttotal number of subarrays = pick between 0-2 numbers on left, then, pick between 0-2 numbers on right\n\t\t\ti.e (left+1) (right+1)\n\t\t\tThen slide window to next set of 2 odd numbers\n\t\t\t"""\n\n\t\t\todds = []\n\n\t\t\tfor i in range(len(nums)):\n\t\t\t\tif nums[i] & 1:\n\t\t\t\t\todds.append(i) #\' Find index of all odd numbers \'\n\n\t\t\todds = [-1] + odds + [len(nums)] #\' Handle edge cases \'\n\t\t\tnice = 0\n\n\t\t\tfor i in range(1, len(odds)-k):\n\t\t\t\tleft = odds[i] - odds[i-1] - 1 #\' Number of \'left\' even numbers \'\n\t\t\t\tright = odds[i+k] - odds[i+k-1] - 1 #\' Number of \'right\' even numbers \'\n\t\t\t\tnice += (left+1)*(right+1) #\' Total sub-arrays in current window \'\n\n\t\t\treturn nice\n \n | 4 | 0 | ['Python'] | 0 |
count-number-of-nice-subarrays | C++ Sliding window O(N) | c-sliding-window-on-by-orangezeit-vnkj | \nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int i(0), ans(0), c(0);\n for (int j = 0; j < nums.size(); ++ | orangezeit | NORMAL | 2019-11-03T04:10:32.971513+00:00 | 2019-11-03T04:10:32.971550+00:00 | 285 | false | ```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int i(0), ans(0), c(0);\n for (int j = 0; j < nums.size(); ++j) {\n if (nums[j] % 2) c++;\n if (c == k) {\n int t1(i), t2(j);\n while (nums[i++] % 2 == 0) {};\n while (++j < nums.size() && nums[j] % 2 == 0) {}\n ans += (i - t1) * ((j--) - t2);\n c--;\n }\n }\n \n return ans;\n }\n};\n``` | 4 | 3 | [] | 0 |
count-number-of-nice-subarrays | Sliding window solution | sliding-window-solution-by-yushi_lu-0z2k | The idea is sliding window with minor modification. Here is an example:\n2, 2, 3, 2, 2\nWe want to find 1 odd number. Using sliding window, we can find 2, 2, 1 | yushi_lu | NORMAL | 2019-11-03T04:02:43.061688+00:00 | 2019-11-03T04:03:16.411229+00:00 | 1,105 | false | The idea is sliding window with minor modification. Here is an example:\n```2, 2, 3, 2, 2```\nWe want to find 1 odd number. Using sliding window, we can find `2, 2, 1`. And we delete the first two \'2\', which means that there are 3 sub-arrays that contain one 3. \n\nBut it\'s not over, there are still two 2 left in the end. Thus, for any even number afterwards, we add 3 to the final result, which means that, given an even number, we can find 3 sub-arrays. Since there are two 2, we have 2 extra 3.\n\nThus, there are in total 3 * 3 = 9 sub-arrays that contain 1 odd number. \n```\nclass Solution {\npublic:\n int numberOfSubarrays(vector<int>& nums, int k) {\n int i = 0, j = 0, odd_cnt = 0, tot_res = 0, tmp_res = 0;\n for (i = 0; i < nums.size(); i++) {\n if (nums[i] % 2 == 1) odd_cnt++;\n while (odd_cnt == k) {\n tmp_res++;\n if (nums[j] % 2 == 1) odd_cnt--;\n j++;\n }\n tot_res += tmp_res;\n i++;\n while (i < nums.size() && nums[i] % 2 == 0) {\n tot_res += tmp_res;\n i++;\n }\n i--;\n tmp_res = 0;\n }\n \n return tot_res;\n }\n};\n``` | 4 | 0 | ['Sliding Window', 'C++'] | 1 |
count-number-of-nice-subarrays | O(n) solution | on-solution-by-coder206-jyvl | In the example [2,2,2,1,2,2,1,2,2,2] for k = 2 the first element of a nice subarray can be the first 1 or any 2 before it and the last element can be the second | coder206 | NORMAL | 2019-11-03T04:01:13.281353+00:00 | 2019-11-03T04:01:13.281403+00:00 | 906 | false | In the example [2,2,2,1,2,2,1,2,2,2] for k = 2 the first element of a nice subarray can be the first 1 or any 2 before it and the last element can be the second 1 or any 2 after it. We transform this array to [4,3,4] (every number in the new array is the length of subarray of even numbers plus 1). The answer is 16 = 4 (any of the 3 even numbers + 1 odd number at the right end of subarray of even numbers) * 4 (1 odd number at the left end of subarray + any of the 3 even numbers). In general case the distance between multipliers is k for resulting subarray to contain exactly k odd numbers.\n\n\n```\n int numberOfSubarrays(vector<int>& nums, int k)\n {\n int count = 0;\n vector<int> groups;\n groups.push_back(1);\n for (int i = 0; i < nums.size(); i++) {\n if (nums[i] % 2 == 1) groups.push_back(1);\n else groups.back()++;\n }\n for (int i = k; i < groups.size(); i++)\n count += groups[i - k] * groups[i];\n return count;\n }\n``` | 4 | 1 | [] | 0 |
flatten-deeply-nested-array | ✔️Easy Solution✔️2625. Flatten Deeply Nested Array✔️Level up🚀your JavaScript skills 🚀Day 22 | easy-solution2625-flatten-deeply-nested-lr0u9 | Intuition\n Describe your first thoughts on how to solve this problem. \n>The problem requires us to flatten a multi-dimensional array based on a given depth. W | Vikas-Pathak-123 | NORMAL | 2023-05-26T05:55:26.204234+00:00 | 2023-06-04T05:13:26.645405+00:00 | 13,426 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n>The problem requires us to flatten a multi-dimensional array based on a given depth. We need to maintain the structure of the array up to the given depth and flatten the remaining subarrays.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo solve this problem, we can use an iterative approach with a stack.\n>1. Initialize a stack with the elements of the array along with their\ncorresponding depth levels. Each element is represented as a pair [item,\ndepth].\n>2. Initialize an empty array to store the flattened result.\n>3. Enter a while loop, which continues as long as there are elements in the\nstack.\n>4. Within each iteration of the loop, retrieve the top element [item, depth] from\nthe stack.\n>5. If the item is an array and the current depth `depth` is greater than 0, it\nmeans the element is a subarray that needs to be further flattened.\n>6. Iterate over the subarray, and for each element, push it back to the stack\nalong with a reduced depth level (depth - 1).\n>7. If the item is not an array or the depth is 0, it means the element is a nonarray item that should be directly added to the result array.\n>8. Continue the loop until there are no more elements in the stack.\n>9. Finally, return the flattened result array.\n\n\n \n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n```\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n>The time complexity of this approach is O(N), where N is the total number of elements in the input array. This is because we iterate over each element once, either to push it back to the stack or to add it to the result array.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n>The space complexity is also O(N), where N is the total number of elements in the input array. This is because in the worst case, all elements can be pushed onto the stack before being processed or added to the result array.\n\n# Code\n```JavaScript []\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function(arr, depth) {\n const stack = [...arr.map(item => [item, depth])];\n const result = [];\n\n while (stack.length > 0) {\n const [item, depth] = stack.pop();\n\n if (Array.isArray(item) && depth > 0) {\n stack.push(...item.map(subItem => [subItem, depth - 1]));\n } else {\n result.push(item);\n }\n }\n\n return result.reverse();\n};\n\n\n```\n\n# Important topic to Learn \n\n| Sr No. | Topic | Sr No. | Topic |\n|-----|-----|-----|-----|\n1.|Arrays , Array methods() * |2.|Function programming *|\n3.|Higher-order function|4.|Memoization|\n5.|Currying|6.|Promises, async/await|\n7.|Compare Objects|8.|Prototypes, inheritance|\n\n>[ Note:- * marked is related to today\'s problem ]\n\n# Please Comment\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution comment below if you like it.\uD83D\uDE0A\n``` | 156 | 0 | ['JavaScript'] | 12 |
flatten-deeply-nested-array | 100% Simple and Easy explanation | Faster Recursive Solution | 100-simple-and-easy-explanation-faster-r-egci | Understanding the Problem Statement\n\nWe have given a multi-dimensional array, let\'s suppose,\n\narr = [[1, 2], [3, [4, 5]]].\n\nThis array has two elements, | kartikkukreja | NORMAL | 2023-04-14T06:55:13.608711+00:00 | 2023-04-14T06:55:59.729980+00:00 | 5,888 | false | **Understanding the Problem Statement**\n\nWe have given a multi-dimensional array, let\'s suppose,\n\n`arr = [[1, 2], [3, [4, 5]]]`.\n\nThis array has two elements, each of which is itself an array. The first element **[1, 2]** has a depth of **1**, while the second element **[3, [4, 5]]** has a depth of **2**.\n\nTo flatten this array means to create a new array that contains all the elements of the original array, but with the nested arrays **"flattened out"** so that they no longer exist. For example, if we flatten arr with a depth of **1**, we would get:\n\n`answer = [1, 2, 3, [4, 5]];`\n\nThe sub-array **[4, 5]** was not flattened, since its depth is greater than the specified depth of 1.\n\n\n**Intuition**\n\nWe can divide the problem into **sub-problems** as nested list can have any depth levels. Since we have to check for all the levels and flatten the array if depth is greater than 0, we can use **recursion** to do this.\n\n**Approach**\n\n1. Check if **n is equal to 0**, Simply return the original array as no flattening is required.\n2. Initialize an `answer` array to store the result.\n3. Now, traverse the array using for loop, and for each array check if n is greater than zero and element is instance of the `Array` : \n\t* \tIf both the conditions are true, recursively call the function by passing `arr[i]` and reducing the n by 1 and add the result to answer array using the spread `...` operator.\n\t* \tElse, Push the current array `arr[i]` to the `answer` array.\n4. Return the `answer` array once the traversal is complete.\n\n\n**Code**\n```\nvar flat = function (arr, n) {\n \n // if n is 0, no flattening is required, hence return the original array\n if(n == 0){\n return arr;\n }\n \n // create an answer array to store final result\n let answer = [];\n \n // traverse the array\n for(let i=0; i<arr.length; i++){\n \n // check if element is instance of array and depth is not equal to 0\n if(n>0 && Array.isArray(arr[i])){\n \n // recursively call the function for this array and push the flattened array to the answer array\n answer.push(...flat(arr[i], n-1));\n }\n // else directy push the current array\n else{\n answer.push(arr[i]);\n }\n }\n \n return answer;\n};\n```\n\n**Output**\n\n | 33 | 0 | ['Recursion', 'JavaScript'] | 6 |
flatten-deeply-nested-array | Recursive & Iterative Approach | Detailed Explanation | recursive-iterative-approach-detailed-ex-cv38 | \u2705\u2705 Please Upvote if you find it useful \u2705\u2705\n\n## Recursive Approach:\n\n1. The function flat takes an input array arr and a depth as param | sourasb | NORMAL | 2023-05-26T11:33:01.171367+00:00 | 2023-05-26T11:56:11.570883+00:00 | 2,812 | false | ## \u2705\u2705 Please Upvote if you find it useful \u2705\u2705\n\n## Recursive Approach:\n\n1. The function `flat` takes an input array `arr` and a depth as parameters.\n2. If the current `depth` equals `0`, the function reaches the base case where no further flattening is required. In this case, the function creates a shallow copy of the array using the `slice()` method and returns it as the result.\n3. If the current depth is greater than `0`, the function proceeds with flattening the array.\n4. The function initializes an empty array called `flattened` to store the flattened elements.\n5. It iterates through each element of the input array using a `for` loop.\n6. For each element, it checks if it is an array using` Array.isArray(arr[i])`.\n7. If the element is an array, it recursively calls the `flat` function with the nested array `(arr[i])` and a decreased depth `(depth - 1)`.\n8. The result of the recursive call is stored in a variable called `nested`.\n9. The `...` spread operator is used to concatenate the elements of the `nested` array into the `flattened` array.\n10. If the element is not an array, it is a single value, so it is directly pushed into the `flattened` array.\n11. After iterating through all the elements, the function returns the `flattened` array as the final result.\n\n# Code\n```\n// Recursive Approach\nfunction flat(arr, depth) {\n if (depth === 0) {\n return arr.slice(); // Base case: return a shallow copy of the array\n }\n\n let flattened = [];\n\n for (let i = 0; i < arr.length; i++) {\n if (Array.isArray(arr[i])) {\n const nested = flat(arr[i], depth - 1); // Recursively flatten nested arrays\n flattened.push(...nested); // Concatenate flattened nested arrays to the result\n } else {\n flattened.push(arr[i]); // Push individual elements to the result\n }\n }\n\n return flattened; // Return the flattened array\n}\n\n```\n----\n\n## Iterative Approach: \n\nThe function `flat` takes an array `arr` and a depth `depth` as parameters like before.\n\nwe will use a `while` loop to continue the flattening operation as long as there are nested array elements (i.e. `hasNestedArray` is `true`) and the current depth is less than the specified depth.\n\nWithin each iteration of the loop, we initialize a `queue` array to store the flattened elements and then iterates through each element of the input array `arr`.\n\nFor each element, it checks if it\'s an array using `Array.isArray(arr[i])`. If the element is an array, it spreads its elements into the queue array using the spread operator `(...)`. This adds the nested elements to the `queue` for further flattening. Additionally, it sets the `hasNestedArray` flag to true to indicate the presence of nested array elements.\n\nIf the element is not an array, it is a single value, so it is directly pushed into the `queue`.\n\nAfter iterating through all the elements of the current level, the function replaces the original array `arr` with the elements in the `queue`. This prepares for the next iteration of the loop, where the process continues to flatten nested arrays.\n\nwe increment the `currentDepth` at each iteration to keep track of the current depth of nesting.\n\nOnce there are no more nested array elements or the current depth reaches the specified depth, we exit.\n\n```java\n// iterative approach\nfunction flat (arr, depth) {\n let hasNestedArray = true;\n let queue;\n let currentDepth = 0;\n\n // Continue flattening while there are nested array elements and the current depth is less than the specified depth\n while (hasNestedArray && currentDepth < depth) {\n hasNestedArray = false;\n queue = [];\n\n // Iterate through each element in the array\n for (let i = 0; i < arr.length; i++) {\n if (Array.isArray(arr[i])) {\n queue.push(...arr[i]); // If the element is an array, spread its elements into the queue\n hasNestedArray = true; // Set the flag to indicate the presence of nested array elements\n } else {\n queue.push(arr[i]); // If the element is not an array, push it into the queue\n }\n }\n\n arr = [...queue]; // Replace the original array with the elements in the queue\n currentDepth++; // Increment the depth counter\n }\n\n return arr; // Return the flattened array\n};\n```\n\n## \u2705\u2705 Please Upvote if you find it useful \u2705\u2705 | 21 | 0 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | ✔️ JavaScript solution using Recursion || Easiest Solution !!! | javascript-solution-using-recursion-easi-hfz5 | # Intuition \n\n\n# Approach\n\n1. Write a recursive function that keeps track of the current depth.\n2. If the current depth >= the maximum depth, always jus | ray_aadii | NORMAL | 2023-08-31T07:43:24.105537+00:00 | 2023-08-31T07:43:24.105553+00:00 | 2,109 | false | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Write a recursive function that keeps track of the current depth.\n2. If the current depth >= the maximum depth, always just push the value to the returned array.\n3. Otherwise, recursively call flat on the array.\n\n<!-- # Complexity -->\n\n<!-- - Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n const res = [];\n\n function helper(arr,depth) {\n for(const val of arr) {\n if(typeof(val) === \'object\' && depth < n) {\n helper(val,depth + 1);\n } else {\n res.push(val);\n }\n }\n return res;\n }\n return helper(arr,0);\n};\n```\n\n# Code Efficiency\n\n\n> Do UPVOTE if you liked the solution \uD83D\uDC4D\uD83D\uDC4D | 16 | 0 | ['Recursion', 'JavaScript'] | 4 |
flatten-deeply-nested-array | 🗓️ Daily LeetCoding Challenge Day 26|| 🔥 JS SOL | daily-leetcoding-challenge-day-26-js-sol-41s4 | \n# Code\n\nvar flat = function(arr, depth) {\n const stack = [...arr.map(item => [item, depth])];\n const result = [];\n\n while (stack.length > 0) {\n c | DoaaOsamaK | NORMAL | 2024-06-14T19:06:17.589407+00:00 | 2024-06-14T19:06:17.589428+00:00 | 1,505 | false | \n# Code\n```\nvar flat = function(arr, depth) {\n const stack = [...arr.map(item => [item, depth])];\n const result = [];\n\n while (stack.length > 0) {\n const [item, depth] = stack.pop();\n\n if (Array.isArray(item) && depth > 0) {\n stack.push(...item.map(subItem => [subItem, depth - 1]));\n } else {\n result.push(item);\n }\n }\n\n return result.reverse();\n};\n\n``` | 12 | 0 | ['JavaScript'] | 1 |
flatten-deeply-nested-array | Recursive TypeScript solution | recursive-typescript-solution-by-joshua_-o9im | Approach\nAny time I need to traverse a nested data structure, I reach for recursion.\n\nIntuitively, we need to loop through the array and check if each elemen | Joshua_desjones | NORMAL | 2023-04-12T00:52:11.414925+00:00 | 2023-04-12T00:52:11.414968+00:00 | 1,366 | false | # Approach\nAny time I need to traverse a nested data structure, I reach for recursion.\n\nIntuitively, we need to loop through the array and check if each element is a number. If so, it is already flat, so it can be pushed into our result. If the element is also an array, we need to loop it as well and check each of its elements, etc., until we reach the level requested.\n\nSo we need to create a function that will check each element in an array and recursively flatten it if it is also an array.\n\n# Complexity\n- Time complexity: $$O(n)$$ because in the worst case, we have to check every element of the array.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ because we are using recursion, which means we will be pushing function calls onto the stack. In the worst case, we push a function call for each element of each array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ntype MultiDimensionalArray = (number | MultiDimensionalArray)[];\n\n\nvar flat = function (arr: MultiDimensionalArray, n: number): MultiDimensionalArray {\n\n // base case. If we are on depth 0, we don\'t flatten the element\n if (n === 0) {\n return arr;\n }\n \n // temp array to hold the flattened results for this level of the recursion\n const result: MultiDimensionalArray = [];\n\n // loop the elements of this array. If they are numbers, don\'t need to flatten,\n // just push into the result. If they are arrays, we need to flatten,\n // so recursively call the flat function, then spread the returned value and push into result.\n arr.forEach(el => {\n if (typeof el === \'number\') {\n result.push(el);\n } else {\n result.push(...flat(el, n - 1));\n }\n })\n\n return result;\n};\n\n\n\n``` | 11 | 0 | ['TypeScript'] | 1 |
flatten-deeply-nested-array | Easiest Solution Ever | easiest-solution-ever-by-includerajat-ghuf | Code\n\nvar flat = function (arr, n) {\n // if n = 0 then we return arr or if all the element of array is \n // integer (not an array) we return arr.\n | includerajat | NORMAL | 2023-05-26T04:50:27.055549+00:00 | 2023-05-26T04:50:27.055582+00:00 | 1,307 | false | # Code\n```\nvar flat = function (arr, n) {\n // if n = 0 then we return arr or if all the element of array is \n // integer (not an array) we return arr.\n if(n == 0 || arr.every((item) => !Array.isArray(item))) return arr;\n const result = [];\n for(let i=0;i<arr.length;i++)\n if(Array.isArray(arr[i]))\n result.push(...arr[i]);\n else\n result.push(arr[i]);\n return flat(result,n-1);\n};\n``` | 7 | 0 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | ❇ flatten-deeply-nested-array👌 🏆O(N)❤️ Javascript❤️ Memory👀95.45%🕕 Meaningful Vars✍️ 🔴🔥 ✅ 👉 | flatten-deeply-nested-array-on-javascrip-eqb0 | \nvar flat = function (arr, n, tempArray = [], currentCycle = 0) {\n for (let index = 0; index < arr.length; index++) {\n if (Array.isArray(arr[index] | anurag-sindhu | NORMAL | 2023-10-17T16:11:25.271069+00:00 | 2023-10-17T16:11:25.271087+00:00 | 1,172 | false | ```\nvar flat = function (arr, n, tempArray = [], currentCycle = 0) {\n for (let index = 0; index < arr.length; index++) {\n if (Array.isArray(arr[index]) && currentCycle < n) {\n flat(arr[index], n, tempArray, currentCycle + 1)\n } else {\n tempArray.push(arr[index])\n }\n }\n return tempArray\n};\n``` | 6 | 0 | ['JavaScript'] | 2 |
flatten-deeply-nested-array | 🔥 Fastest & Easiest Solution | Time O(n) > 99% & Extra Space O(n) > 90% ✅ | fastest-easiest-solution-time-on-99-extr-2lxb | Solution from Pro JS Developer\n\nPlease take a look at the code below.\n\n# Approach\n\nNo rocket sciense, no magic, nothing excess.\nresult - returning array, | sahaviev | NORMAL | 2023-06-03T20:24:02.972718+00:00 | 2023-06-04T01:00:09.365883+00:00 | 469 | false | # Solution from Pro JS Developer\n\nPlease take a look at the code below.\n\n# Approach\n\nNo rocket sciense, no magic, nothing excess.\n**result** - returning array, accesed from closure.\n**toFlat** - recursion function with same arguments. On each flattening level just passed **n - 1**.\n\n# Complexity\n- Time complexity: O(n) - Runtime: **86 ms** - beats > 99%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) - Memory: **61.1 MB** - beats > 90%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (source, level) {\n const result = [];\n const toFlat = (arr, n) => {\n for (let i = 0; i < arr.length; i++) {\n if (Array.isArray(arr[i]) && n > 0) {\n toFlat(arr[i], n - 1);\n } else {\n result.push(arr[i]);\n }\n }\n };\n toFlat(source, level);\n return result;\n};\n``` | 6 | 0 | ['JavaScript'] | 2 |
flatten-deeply-nested-array | Constant-space, in-place, fast, iterative solution with early-termination optimization | constant-space-in-place-fast-iterative-s-4sd6 | Intuition\nThe problem statement doesn\'t state that the input array must remain untouched, so we can perform operations in-place on the array to save memory. A | brian717fr | NORMAL | 2023-04-13T18:43:40.514785+00:00 | 2023-04-13T18:43:40.514817+00:00 | 1,021 | false | # Intuition\nThe problem statement doesn\'t state that the input array must remain untouched, so we can perform operations in-place on the array to save memory. Additionally, solving things iteratively saves us from adding *n* recursive function calls to the stack, resulting in O(1) space.\n\n# Approach\nIterate over the array a max of *n* times, flattening one-level of arrays each pass until there are no longer any sub-arrays, or we\'ve done the specified number of passes. \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n // Loop n times, flattening one-level at a time\n for (let k = n; k > 0; k--) {\n let alreadyFlat = true;\n for (let i = 0; i < arr.length; i++) {\n if (Array.isArray(arr[i])) {\n let sal = arr[i].length;\n arr.splice(i, 1, ...arr[i]);\n // Skip to the end of the elements we just added\n i += sal - 1;\n alreadyFlat = false;\n }\n }\n // If the array is already flat, we can return early\n if (alreadyFlat) return arr; \n }\n return arr;\n};\n``` | 6 | 0 | ['JavaScript'] | 2 |
flatten-deeply-nested-array | 100% Simple and Easy Solution | Faster Recursive Solution | 100-simple-and-easy-solution-faster-recu-o0fy | Complexity
Time complexity: O(N * D)
Space complexity: O(N)
Code | ashwin_menghar | NORMAL | 2025-02-13T07:22:26.451922+00:00 | 2025-02-13T07:22:26.451922+00:00 | 660 | false | # Complexity
- Time complexity: O(N * D)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {Array} arr
* @param {number} depth
* @return {Array}
*/
var flat = function (arr, n, res = []) {
for(let i = 0; i < arr.length; i++) {
if(Array.isArray(arr[i]) && n)
flat(arr[i], n - 1, res);
else
res.push(arr[i]);
}
return res;
};
``` | 5 | 0 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | DAY(20*O(1)+2*O(1)) | Commented 👍| Eassiest ✅ | day20o12o1-commented-eassiest-by-drontit-olnv | The given code defines a function called flat using arrow function syntax. This function takes in two parameters: arr, which is an array, and n, which represent | DronTitan | NORMAL | 2023-05-26T04:54:43.616091+00:00 | 2023-05-26T04:54:43.616131+00:00 | 590 | false | The given code defines a function called `flat` using arrow function syntax. This function takes in two parameters: `arr`, which is an array, and `n`, which represents the depth level until which the array should be flattened.\n\nThe code uses a ternary operator to check if the value of `n` is truthy. If `n` is truthy (non-zero), it indicates that the array needs to be flattened to a certain depth. Otherwise, if `n` is falsy (zero or undefined), it indicates that the array should be flattened completely.\n\nThe implementation uses the `reduce` method on the `arr` array to flatten it. Inside the `reduce` callback function, the code checks if the current element (`next`) is an array using the `Array.isArray` method.\n\nIf `next` is an array, it recursively calls the `flat` function with the nested array (`next`) and decreases the value of `n` by 1. The spread operator (`...`) is used to spread the flattened nested array elements into the `temp` array.\n\nIf `next` is not an array, it means it\'s a non-nested element, so the code directly pushes it into the `temp` array.\n\nFinally, the callback function returns the `temp` array, which is the accumulated result at each step of the `reduce` operation.\n\nOutside the ternary operator, if `n` is truthy, the function returns the flattened array generated through the `reduce` operation. Otherwise, it returns the original `arr` without any flattening.\n\nHere\'s an example to illustrate the behavior of the `flat` function:\n\n```javascript\nconst array = [1, [2, [3, 4, [5, 6]]], 7];\n\nconsole.log(flat(array, 0));\n// Output: [1, [2, [3, 4, [5, 6]]], 7]\n\nconsole.log(flat(array, 1));\n// Output: [1, 2, [3, 4, [5, 6]], 7]\n\nconsole.log(flat(array, 2));\n// Output: [1, 2, 3, 4, [5, 6], 7]\n\nconsole.log(flat(array, 3));\n// Output: [1, 2, 3, 4, 5, 6, 7]\n\nconsole.log(flat(array));\n// Output: [1, 2, 3, 4, 5, 6, 7] (complete flattening)\n```\n\nIn the above example, the `array` contains nested arrays. By passing different values of `n` to the `flat` function, you can control the depth of flattening.\n\n***Here is the code to the current problem:-***\n\n```\n\nvar flat = (arr, n) =>\n n ?\n arr.reduce(\n (temp, next) => (\n Array.isArray(next) ?\n temp.push(...flat(next, n - 1)) :\n temp.push(next),\n temp\n ),\n []\n ) :\n arr;\n``` | 5 | 0 | ['Array', 'JavaScript'] | 4 |
flatten-deeply-nested-array | 🔥🔥 Detailed Solution Using Recursion In Javascript || Faster Than 80%✔✔ | detailed-solution-using-recursion-in-jav-0y91 | Intuition\n Describe your first thoughts on how to solve this problem. \n According to the Problem Statement:\n 1. If depth of the current array is less than n | Boolean_Autocrats | NORMAL | 2023-05-18T14:57:46.508634+00:00 | 2023-05-18T14:58:42.597698+00:00 | 843 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n According to the Problem Statement:\n 1. If depth of the current array is less than n then we will flatten it.\n 2. If depth of the current array is equal to n then we will flatten it.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n 1. We will use Recursive Function Flat(arr,depth,n).\n 2. if depth==n then we will simply return array //Base Condition.\n 3. else we will try to flatten array by traversing the array completely.\n ```\n let i=0;\n let Arr=[];\n while(i<arr.length)\n {\n //If current element is integer then no need to flatten it\n if(Number.isInteger(arr[i]))\n {\n Arr.push(arr[i]);\n }\n else\n {\n //we will call Flat(arr[i],depth+1,n) to flatten this arr\n let tempArr=Flat(arr[i],dept1,n);\n tempArr.forEach((ele)=>{\n Arr.push(ele);\n })\n }\n i+=1;\n }\n return Arr;\n```\n\n# Complexity\n- Time complexity: O(n*N)\n- where N max number of ele in particular depth while flatting given array.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(Total number of integer in array)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar Flat=function(arr,depth,n){\n if(depth==n)\n {\n return arr;\n }\n let Arr=[];\n let i=0;\n while(i<arr.length)\n {\n if(Number.isInteger(arr[i]))\n { \n Arr.push(arr[i]);\n }\n else\n {\n const v=Flat(arr[i],depth+1,n); \n v.forEach((x)=>{\n Arr.push(x);\n });\n }\n i+=1; \n }\n return Arr;\n}\nvar flat = function (arr, n) {\n return Flat(arr,0,n);\n};\n```\n``` | 5 | 1 | ['JavaScript'] | 3 |
flatten-deeply-nested-array | Recurcive method | recurcive-method-by-yogiv07-5msr | Code\n\n/**\n * @param {Array} arr\n * @param {number} depth\n * @return {Array}\n */\nvar flat = function (arr, n) {\n if(n==0) return arr;\n var ans = [ | yogiv07 | NORMAL | 2024-06-06T15:48:03.129891+00:00 | 2024-06-06T15:48:03.129933+00:00 | 667 | false | # Code\n```\n/**\n * @param {Array} arr\n * @param {number} depth\n * @return {Array}\n */\nvar flat = function (arr, n) {\n if(n==0) return arr;\n var ans = [];\n for(var i=0; i<arr.length; i++){\n if(Array.isArray(arr[i])){\n ans.push(...flat(arr[i], n-1));\n } else {\n ans.push(arr[i]);\n }\n }\n return ans;\n};\n\n``` | 4 | 0 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | So easy 92%-85%✅🤛🍻 | so-easy-92-85-by-itachi2003-ntte | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n\n# Code\n\n/**\n * @ | itachi2003 | NORMAL | 2024-02-29T08:02:21.214981+00:00 | 2024-03-08T13:38:29.411903+00:00 | 606 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n# Code\n```\n/**\n * @param {Array} arr - The input array to be flattened.\n * @param {number} depth - The depth to which the array should be flattened.\n * @return {Array} - The flattened array.\n */\nvar flat = function (arr, depth, result = [], currentCycle = 0) {\n // Iterate through each element in the array\n for (let index = 0; index < arr.length; index++) {\n // If the current element is an array and the depth hasn\'t been reached\n if (Array.isArray(arr[index]) && currentCycle < depth) {\n // Recursively call flat function with the nested array\n flat(arr[index], depth, result, currentCycle + 1);\n } else {\n // If the element is not an array or the depth limit is reached, push it to tempArray\n result.push(arr[index]);\n }\n }\n // Return the flattened array\n return result;\n};\n\n\n```\n# UPVOTE _ PLEASE\n\n\n\n | 4 | 0 | ['JavaScript'] | 1 |
flatten-deeply-nested-array | Java Script Solution for Flatten Deeply Nested Array Problem | java-script-solution-for-flatten-deeply-6yjvp | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind the solution is to recursively flatten the given multi-dimensional | Aman_Raj_Sinha | NORMAL | 2023-05-26T03:56:06.884355+00:00 | 2023-05-26T03:56:06.884399+00:00 | 416 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the solution is to recursively flatten the given multi-dimensional array while considering the depth constraint.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach used in the code is a depth-first traversal of the input array. For each element in the array, it checks if it is an array and if the current depth is greater than 0. If both conditions are met, the function recursively calls itself with the sub-array and reduces the depth by 1. Otherwise, it pushes the element into the result array.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the solution depends on the size of the input array and the depth. In the worst case, if the depth is equal to the maximum depth of the input array, the algorithm will visit all elements once. Therefore, the time complexity is O(N), where N is the total number of elements in the input array.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is also O(N) because the result array stores all the elements in the flattened array. Additionally, the recursive function calls occupy space on the call stack proportional to the depth of the array.\n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, depth) {\n var result = [];\n \n flatten(arr, depth, result);\n \n return result;\n};\n\nfunction flatten(arr, depth, result) {\n for (var i = 0; i < arr.length; i++) {\n if (Array.isArray(arr[i]) && depth > 0) {\n flatten(arr[i], depth - 1, result);\n } else {\n result.push(arr[i]);\n }\n }\n}\n\n``` | 4 | 1 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | Best JavaScript and TypeScript Solution for Beginner 💛 | best-javascript-and-typescript-solution-0ty2t | Code\njavascript []\nvar flat = function (arr, n) {\n if (n === 0) {\n return arr;\n }\n \n let answer = [];\n \n arr.forEach(element = | Ghauoor | NORMAL | 2023-05-23T16:21:28.416936+00:00 | 2023-05-23T16:21:28.416979+00:00 | 1,461 | false | # Code\n```javascript []\nvar flat = function (arr, n) {\n if (n === 0) {\n return arr;\n }\n \n let answer = [];\n \n arr.forEach(element => {\n if (n > 0 && Array.isArray(element)) {\n answer.push(...flat(element, n - 1));\n } else {\n answer.push(element);\n }\n });\n \n return answer;\n};\n\n```\n```typescript []\nconst flat = function (arr: any[], n: number): any[] {\n if (n === 0) {\n return arr;\n }\n \n let answer: any[] = [];\n \n arr.forEach(element => {\n if (n > 0 && Array.isArray(element)) {\n answer.push(...flat(element, n - 1));\n } else {\n answer.push(element);\n }\n });\n \n return answer;\n};\n\n``` | 4 | 0 | ['TypeScript', 'JavaScript'] | 2 |
flatten-deeply-nested-array | Simple 1 line solution | simple-1-line-solution-by-arnavn101-b9ad | Approach\nRecursively reduce arr by recursing through non-numerical inputs until base case of n === 0. If e is an element, it\'s pushed into acc, otherwise, res | arnavn101 | NORMAL | 2023-04-12T01:24:49.470204+00:00 | 2023-04-12T01:25:22.577494+00:00 | 966 | false | # Approach\nRecursively reduce `arr` by recursing through non-numerical inputs until base case of `n === 0`. If `e` is an element, it\'s pushed into `acc`, otherwise, result of recursive call is unpacked before being pushed. For each case we return `acc` in the `reduce` HOF.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nvar flat = function (arr, n) {\n return n === 0 ? arr : arr.reduce(\n (acc, e) => typeof(e) === "number" ? \n (acc.push(e), acc) : (acc.push(...flat(e, n-1)), acc),\n []);\n};\n``` | 4 | 1 | ['Recursion', 'JavaScript'] | 2 |
flatten-deeply-nested-array | JavaScript Solution | javascript-solution-by-motaharozzaman199-vej7 | \n\n\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n if (n==0){\n return arr;\n }\ | Motaharozzaman1996 | NORMAL | 2023-05-26T14:47:39.201449+00:00 | 2023-05-26T14:47:39.201481+00:00 | 1,353 | false | \n\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n if (n==0){\n return arr;\n }\n let ans=[];\n for (let i=0; i<arr.length; i++){\n if(n>0 && Array.isArray(arr[i])){\n ans.push(...flat(arr[i],n-1));\n }else{\n ans.push(arr[i]);\n }\n }\n return ans \n};\n``` | 3 | 0 | ['JavaScript'] | 1 |
flatten-deeply-nested-array | JavaScript Easy Solution | javascript-easy-solution-by-ankush-kashy-q2ll | \n\n# Code\n\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n let res = [];\n const flatte | Ankush-Kashyap | NORMAL | 2023-05-26T09:03:16.257701+00:00 | 2023-05-26T09:03:16.260438+00:00 | 502 | false | \n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n let res = [];\n const flattening = (nums, l) => {\n for (const num of nums) {\n if (Array.isArray(num) && l > 0 && l <= n) {\n flattening(num, l - 1);\n } else {\n res.push(num);\n }\n }\n }\n\n flattening(arr, n);\n return res;\n};\n```\n\n | 3 | 0 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | "Inorder" DFS Traversal (ft. Generators) | inorder-dfs-traversal-ft-generators-by-j-lbmx | Intuition\nThe nested structure of the array suggests a recursive, tree-like structure. Thinking about how the array is flattened in this structure leads to the | jeffreyhu8 | NORMAL | 2023-04-12T14:01:37.234500+00:00 | 2023-04-12T14:01:37.234542+00:00 | 687 | false | # Intuition\nThe nested structure of the array suggests a recursive, tree-like structure. Thinking about how the array is flattened in this structure leads to the idea of a DFS traversal.\n\n# Approach\nFor some array, we scan the elements left to right.\n\nIf the element is a number, we add it to our answer array.\n\nIf the element is an array, we either add it to our answer array if we have reached our depth limit or recurse on the array.\n\nAs an example, consider `arr = [1, 2, [3, [4, 5], 6], 7], n = 1`. The red arrows in the following image demonstrates what a DFS traversal could look like.\n\n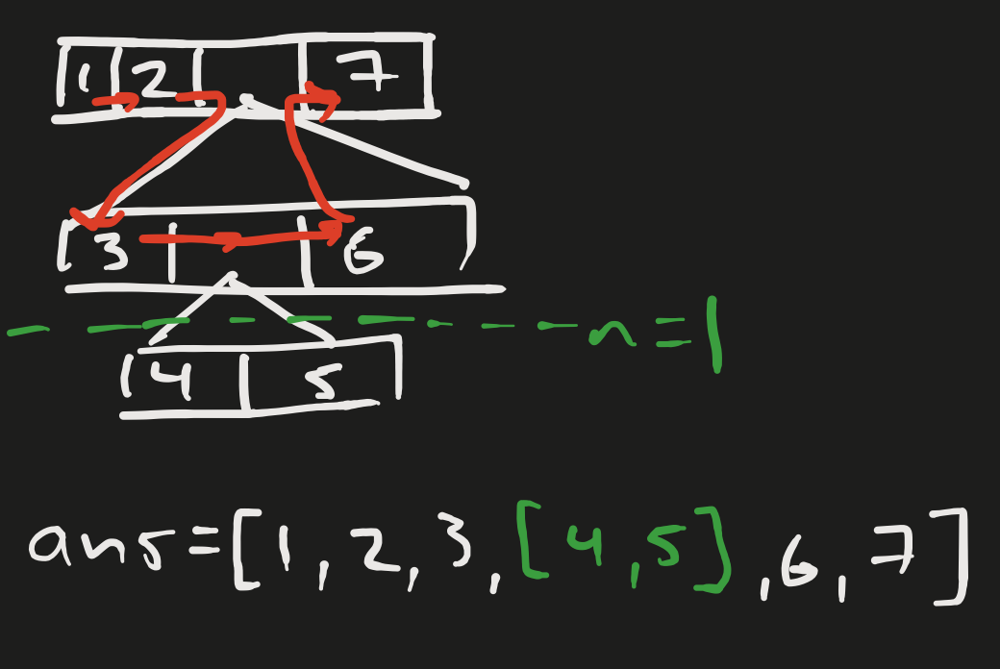\n\nThis "inorder" traversal (and tree traversals in general) can be done nicely with generators.\n\n# Complexity\n- Time complexity: $$O(\\ell)$$, where $\\ell$ is the length of the answer array.\n\n- Space complexity: $$O(\\ell)$$\n\n# Code\n```\ntype MultiDimensionalArray = (number | MultiDimensionalArray)[];\n\nfunction* inorder(arr: MultiDimensionalArray, n: number) {\n // depth limit reached\n if (n < 0) {\n yield arr;\n return;\n }\n\n // recursively DFS\n for (const val of arr) {\n if (typeof val === \'number\') {\n yield val;\n } else {\n yield* inorder(val, n - 1);\n }\n }\n};\n\nvar flat = function (arr: MultiDimensionalArray, n: number): MultiDimensionalArray {\n return [...inorder(arr, n)];\n};\n``` | 3 | 0 | ['Array', 'Depth-First Search', 'Recursion', 'TypeScript'] | 2 |
flatten-deeply-nested-array | [JavaScript] A simple recursive solution | javascript-a-simple-recursive-solution-b-wvpu | Overall Idea\n\nThis problem lends very well for a recursive solution! We iterate through the array, checking for nested arrays within.\n\n1) If the element is | tangj1905 | NORMAL | 2023-04-11T22:47:59.017471+00:00 | 2023-04-12T04:23:41.725424+00:00 | 1,380 | false | # Overall Idea\n\nThis problem lends very well for a recursive solution! We iterate through the array, checking for nested arrays within.\n\n1) If the element is another array, we call it recursively down one level. We can use the spread operator (`...`) to do the flattening for us when appending to our flattened array.\n2) Otherwise, we can simply push the element.\n\nRemember to stop the recursion when `n = 0`!\n\n# Code\n```js\n// A normal, recursive approach.\nconst flat = function (arr, n) {\n if (n === 0)\n return arr;\n let res = [];\n for (let i in arr) {\n if (Array.isArray(arr[i]))\n res.push(...flat(arr[i], n - 1));\n else\n res.push(arr[i]);\n }\n return res;\n}\n```\n\n## Considerations & Optimizations\n\nWe could also get away with not allocating an array at every recursive call! Instead, we can just define an inner recursive function that appends to an outer array for us.\n\nThe rest of the algorithm is more or less the same:\n\n```js\n// An optimization - saves unnecessary\n// array allocations at every call!\nconst flat = function (arr, n) {\n let res = [];\n const recur = (arr, n) => {\n for (let i in arr) {\n if (n > 0 && Array.isArray(arr[i]))\n recur(arr[i], n - 1);\n else\n res.push(arr[i]);\n }\n }\n recur(arr, n);\n return res;\n}\n```\n\n# Complexity\n\n**Time complexity:** $$O(n)$$ - Unless `n = 0`, we wind up checking every element in the input array.\n**Space complexity:** $$O(n)$$ - Besides the space required for the output array, we allocate a function call on the stack for every recursive call. | 3 | 0 | ['Recursion', 'JavaScript'] | 1 |
flatten-deeply-nested-array | using flat() | using-flat-by-joelll-km7i | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Joelll | NORMAL | 2024-03-18T08:44:15.442108+00:00 | 2024-03-18T08:44:15.442143+00:00 | 447 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {Array} arr\n * @param {number} depth\n * @return {Array}\n */\nvar flat = function (arr, n) {\n const doge = arr.flat(n)\nreturn doge\n\n}\n``` | 2 | 0 | ['JavaScript'] | 3 |
flatten-deeply-nested-array | JavaScript | Flatten Deeply Nested Array | javascript-flatten-deeply-nested-array-b-g8qe | Intuition\n Describe your first thoughts on how to solve this problem. \nPre-defined terms:\n\n1. Multi-dimensional array \u2192 a recursive data structure that | samabdullaev | NORMAL | 2023-11-10T20:03:27.526486+00:00 | 2023-11-10T20:03:27.526506+00:00 | 36 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPre-defined terms:\n\n1. `Multi-dimensional array` \u2192 a recursive data structure that contains integers or other multi-dimensional arrays\n\n2. `Flattened array` \u2192 a version of that array with some or all of the sub-arrays removed and replaced with the actual elements in that sub-array\n\nWe need to return a flattened version of the given multi-dimensional array.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. These are comment delimiters for a multi-line comment to help explain and document code while preventing ignored text from executing. These comments are commonly used in formal documentation for better code understanding.\n\n ```\n /**\n * Multi-line comment\n */\n ```\n\n2. This is a special type of comment called a JSDoc comment that explains that the function should take parameters named `arr` and `depth`, which are expected to be an `Array` and a `number`.\n\n ```\n @param {Array} arr\n @param {number} depth\n ```\n\n3. This is a special type of comment called a JSDoc comment that explains what the code should return, which, in this case, is an `Array`. It helps developers and tools like code editors and documentation generators know what the function is supposed to produce.\n\n ```\n @return {Array}\n ```\n\n4. This is how we define a function named `flat` that takes an array `arr` and a number `n` as its arguments.\n\n ```\n var flat = function (arr, n) {\n // code to be executed\n };\n ```\n\n5. This `flat` method flattens the array `arr` up to depth `n`.\n\n ```\n return arr.flat(n)\n ```\n\n# Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`n` is the total number of elements in the input array. This is because the code needs to iterate over each element in the array.\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`n` is the total number of elements in the input array. This is because the function creates a new array with all the elements from the sub-arrays, so the space required is proportional to the number of elements in the input array.\n\n# Code\n```\n/**\n * @param {Array} arr\n * @param {number} depth\n * @return {Array}\n */\nvar flat = function (arr, n) {\n return arr.flat(n)\n};\n``` | 2 | 0 | ['JavaScript'] | 1 |
flatten-deeply-nested-array | Elegant and readable solution | elegant-and-readable-solution-by-arvisix-nici | Code\n\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nconst flat = (arr, n) => {\n if (n === 0) return arr\n\n const flat | arvisix | NORMAL | 2023-08-11T11:44:59.460185+00:00 | 2023-08-11T11:44:59.460211+00:00 | 376 | false | # Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nconst flat = (arr, n) => {\n if (n === 0) return arr\n\n const flatArr = []\n\n arr.forEach(el => \n (Array.isArray(el) && n > 0) ? flatArr.push(...flat(el, n - 1)) : flatArr.push(el)\n )\n\n return flatArr\n};\n``` | 2 | 0 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | JavaScript || Easy to Understand ✅✅ | javascript-easy-to-understand-by-shubham-geo5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Shubhamjain287 | NORMAL | 2023-06-17T05:24:07.096041+00:00 | 2023-06-17T05:24:07.096069+00:00 | 570 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n \n if(n==0){\n return arr.slice();\n }\n \n let newArr = [];\n\n arr.forEach((val) => {\n if(Array.isArray(val)){\n const nested = flat(val, n-1);\n newArr.push(...nested);\n }\n else{\n newArr.push(val);\n }\n });\n\n return newArr;\n};\n``` | 2 | 0 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | JavaScript | Recursive Solution | javascript-recursive-solution-by-foyez-4m3w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | foyez | NORMAL | 2023-05-27T02:44:39.187743+00:00 | 2023-05-27T02:44:39.187780+00:00 | 157 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n return arr.reduce((acc, item) => {\n if(Array.isArray(item) && n > 0) {\n acc.push(...flat(item, n - 1))\n } else {\n acc.push(item)\n }\n\n return acc\n }, [])\n};\n``` | 2 | 0 | ['JavaScript'] | 0 |
flatten-deeply-nested-array | JavaScript | Recursive Solution | javascript-recursive-solution-by-varshar-aym9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | VarshaRani_9 | NORMAL | 2023-05-26T03:05:55.167369+00:00 | 2023-05-26T03:05:55.167410+00:00 | 717 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n if (n === 0) {\n return arr;\n }\n\n let ans = [];\n\n for (let i = 0; i < arr.length; i++) {\n if (Array.isArray(arr[i])) {\n const subArray = flat(arr[i], n - 1);\n ans.push(...subArray);\n } else {\n ans.push(arr[i]);\n }\n }\n return ans; \n};\n``` | 2 | 0 | ['JavaScript'] | 1 |
flatten-deeply-nested-array | Best JavaScript Solution for Beginner 💛 | best-javascript-solution-for-beginner-by-hlfd | Code\n\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n if (n === 0) {\n return arr;\n | Ghauoor | NORMAL | 2023-05-23T16:16:32.509163+00:00 | 2023-05-23T16:16:32.509201+00:00 | 678 | false | # Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n if (n === 0) {\n return arr;\n }\n \n let answer = [];\n \n arr.forEach(element => {\n if (n > 0 && Array.isArray(element)) {\n answer.push(...flat(element, n - 1));\n } else {\n answer.push(element);\n }\n });\n \n return answer;\n};\n\n``` | 2 | 0 | ['JavaScript'] | 1 |
flatten-deeply-nested-array | ✅ JavaScript - recursive solution | javascript-recursive-solution-by-daria_a-i0ce | Approach\n Describe your approach to solving the problem. \nFlatten arrays recursively until n equals 0, then return array itself.\n\n# Code\n\n/**\n * @param { | daria_abdulnasyrova | NORMAL | 2023-04-17T14:37:08.781967+00:00 | 2023-04-17T14:37:08.781996+00:00 | 291 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nFlatten arrays recursively until n equals 0, then return array itself.\n\n# Code\n```\n/**\n * @param {any[]} arr\n * @param {number} depth\n * @return {any[]}\n */\nvar flat = function (arr, n) {\n if (n === 0) return arr;\n\n let result = [];\n\n for (let num of arr) {\n if (Array.isArray(num)) {\n result.push(...flat(num, n - 1));\n } else {\n result.push(num);\n }\n }\n\n return result;\n};\n``` | 2 | 0 | ['JavaScript'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.