question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
sort-an-array | JavaScript MergeSort Solution | javascript-mergesort-solution-by-justbig-6j6f | \nconst sortArray = nums => {\n if(nums.length <= 1) return nums\n \n const middle = Math.floor(nums.length / 2)\n const left = nums.slice(0, middle | justbigmack | NORMAL | 2020-05-30T14:43:26.017553+00:00 | 2020-05-30T14:45:52.321909+00:00 | 1,982 | false | ```\nconst sortArray = nums => {\n if(nums.length <= 1) return nums\n \n const middle = Math.floor(nums.length / 2)\n const left = nums.slice(0, middle)\n const right = nums.slice(middle)\n \n return merge(sortArray(left), sortArray(right))\n};\n\nconst merge = (left, right) => {\n const result = []\n \n while (left.length && right.length) {\n if(left[0] <= right[0]) {\n result.push(left.shift())\n } else {\n result.push(right.shift())\n }\n }\n \n return [...result, ...left, ...right]\n}\n``` | 13 | 0 | ['Merge Sort', 'JavaScript'] | 8 |
sort-an-array | Merge sort - Java | merge-sort-java-by-rakesh_v-sxtx | ```\n public int[] sortArray(int[] nums) {\n mergesort(nums, 0, nums.length-1);\n return nums;\n }\n\t\n public void mergesort(int[] nums, int | Rakesh_v | NORMAL | 2021-04-11T15:45:20.473047+00:00 | 2022-04-28T02:37:36.509067+00:00 | 2,201 | false | ```\n public int[] sortArray(int[] nums) {\n mergesort(nums, 0, nums.length-1);\n return nums;\n }\n\t\n public void mergesort(int[] nums, int start, int end){\n if(start < end){\n int mid = (start + end) / 2;\n mergesort(nums, start, mid);\n mergesort(nums, mid+1, end);\n merge(nums, start, mid, end);\n }\n }\n \n public void merge(int[] nums, int start, int mid, int end){\n int i= start, j= mid+1, k=0;\n int[] temp = new int[end-start+1];\n while( i <= mid && j<= end)\n {\n if (nums[i] < nums[j])\n temp[k++] = nums[i++];\n else\n temp[k++] = nums[j++];\n }\n while (i <= mid) { temp[k++] = nums[i++]; } //copy remaining elements\n while (j <= end) { temp[k++] = nums[j++]; } //copy remaining elements\n for (int pointer = start; pointer <= end; pointer++){\n nums[pointer] = temp[pointer-start];\n }\n } | 12 | 0 | ['Merge Sort', 'Java'] | 3 |
sort-an-array | Javascript Quick Sort faster than 95% | javascript-quick-sort-faster-than-95-by-02zi5 | \tvar sortArray = function(nums) {\n\t\tlet len = nums.length;\n\t\tif(len < 2) return nums;\n\n\t\tquickSort(nums, 0, len-1)\n\t\treturn nums\n\t};\n\n\tvar qu | sindyxin | NORMAL | 2020-06-05T00:00:56.570667+00:00 | 2020-06-05T00:00:56.570714+00:00 | 2,106 | false | \tvar sortArray = function(nums) {\n\t\tlet len = nums.length;\n\t\tif(len < 2) return nums;\n\n\t\tquickSort(nums, 0, len-1)\n\t\treturn nums\n\t};\n\n\tvar quickSort = function(nums, start, end){\n\t\tif(start >= end) return\n\t\tlet left = start, right = end;\n\t\tlet pivot = nums[Math.floor((start+end) / 2)];\n\t\twhile(left <= right) {\n\t\t\twhile(left <= right && nums[left] < pivot){\n\t\t\t\tleft++\n\t\t\t}\n\t\t\twhile(left <= right && nums[right] > pivot){\n\t\t\t\tright--\n\t\t\t}\n\t\t\tif(left <= right){\n\t\t\t\tlet temp = nums[left]\n\t\t\t\tnums[left] = nums[right]\n\t\t\t\tnums[right] = temp\n\t\t\t\tleft++\n\t\t\t\tright--\n\t\t\t}\n\t\t}\n\t\tquickSort(nums, start, right)\n\t\tquickSort(nums, left, end)\n\t} | 12 | 0 | ['Sorting', 'JavaScript'] | 2 |
sort-an-array | Bottom-up iterative merge sort in Python | bottom-up-iterative-merge-sort-in-python-njpe | \nclass Solution(object):\n def sortArray(self, nums):\n """\n :type nums: List[int]\n :rtype: List[int]\n """\n prev = [[ | fluffycoder | NORMAL | 2019-12-20T06:26:08.022772+00:00 | 2019-12-20T06:26:08.022825+00:00 | 977 | false | ```\nclass Solution(object):\n def sortArray(self, nums):\n """\n :type nums: List[int]\n :rtype: List[int]\n """\n prev = [[n] for n in nums]\n while len(prev) > 1:\n cur = []\n for i in range(0, len(prev), 2):\n cur.append(self.merge(prev[i], prev[i+1] if i+1<len(prev) else [])) \n prev = cur\n return prev[0]\n \n \n def merge(self, l1, l2):\n merged = []\n i1 = i2 = 0\n while i1 < len(l1) and i2 < len(l2):\n if l1[i1] < l2[i2]:\n merged.append(l1[i1])\n i1 += 1\n else:\n merged.append(l2[i2])\n i2 += 1\n merged.extend(l1[i1:])\n merged.extend(l2[i2:])\n return merged\n``` | 12 | 1 | ['Merge Sort'] | 3 |
sort-an-array | Quicksort Java | quicksort-java-by-deleted_user-y3ed | java\nint[] A;\nint[] sortArray(int[] A) {\n\tthis.A = A;\n\tsort(0, A.length - 1);\n\treturn A;\n}\nvoid sort(int l, int r) {\n\tif (l >= r) return;\n\tint p = | deleted_user | NORMAL | 2019-04-25T23:10:33.131867+00:00 | 2019-04-25T23:10:33.131899+00:00 | 36,706 | false | ```java\nint[] A;\nint[] sortArray(int[] A) {\n\tthis.A = A;\n\tsort(0, A.length - 1);\n\treturn A;\n}\nvoid sort(int l, int r) {\n\tif (l >= r) return;\n\tint p = part(l, r);\n\tsort(l, p - 1);\n\tsort(p + 1, r);\n}\nint part(int l, int r) {\n\tint p = A[r];\n\tint i = l - 1;\n\tfor (int j = i + 1; j < r; ++j)\n\t\tif (A[j] < p)\n\t\t\tswap(++i, j);\n\tswap(i + 1, r);\n\treturn i + 1;\n}\nvoid swap(int i, int j) {\n\tint t = A[i];\n\tA[i] = A[j];\n\tA[j] = t;\n}\n``` | 12 | 0 | [] | 5 |
sort-an-array | Java. Quick Sort. | java-quick-sort-by-chibug-com5 | \n public int[] sortArray(int[] nums) {\n \tQuickSort(nums, 0, nums.length - 1);\n \tint result[] = new int[nums.length]; \n for (int i = 0; i < | chibug | NORMAL | 2020-03-30T15:51:15.653692+00:00 | 2020-03-30T15:51:15.653722+00:00 | 2,751 | false | ```\n public int[] sortArray(int[] nums) {\n \tQuickSort(nums, 0, nums.length - 1);\n \tint result[] = new int[nums.length]; \n for (int i = 0; i < nums.length; i++) {\n \tresult[i] = nums[i];\n }\n return result;\n }\n \n public static void QuickSort(int nums[], int lhs, int rhs) {\n \tif(lhs >= rhs) return; \n\t\tint mid = Partition(nums, lhs, rhs);\n\t\tQuickSort(nums, lhs, mid);\n\t\tQuickSort(nums, mid + 1, rhs);\n }\n \n public static void Swap(int[] nums, int lhs, int rhs) {\n \tint temp = nums[lhs];\n \tnums[lhs] = nums[rhs]; \n \tnums[rhs] = temp;\n }\n \n public static int Partition(int[] nums, int lhs, int rhs) {\n \tint pivot = nums[lhs];\n \twhile(lhs < rhs) {\n while (lhs < rhs && nums[rhs] >= pivot) rhs--;\n Swap(nums, lhs, rhs);\n while (lhs < rhs && nums[lhs] <= pivot) lhs++;\n Swap(nums, rhs, lhs);\n \t}\n \tnums[lhs] = pivot;\n \treturn lhs;\n }\n``` | 11 | 0 | [] | 1 |
sort-an-array | SORTING USING MERGE SORT ( C++ ) :) | sorting-using-merge-sort-c-by-js0657096-solo | Intuition\n Describe your first thoughts on how to solve this problem. \nin the Given Problem , We have to sort an array.\nTo Sort an array these are the most c | js0657096 | NORMAL | 2023-03-06T09:41:12.798694+00:00 | 2023-03-06T09:42:19.914725+00:00 | 1,613 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nin the Given Problem , We have to sort an array.\nTo Sort an array these are the most common algorithms : \n\n(1) Bubble Sort\n--------------------------------------------------------------\n- Approach : switches neighbouring parts frequently if the wrong order is given. The fundamental principle of Bubble Sort is to iteratively scan the array, compare nearby members, and swap out any that are out of order. Up till the full array is sorted, this procedure is repeated.\n- Time Complexity : O(n^2).\n- Space Complexty : O(1).\n\n(2) Selection Sort \n---------------------------------------------------------------\n- Approach : finding the minimum element from the unsorted part of the array and putting it at the beginning of the sorted part.\n- Time Complexity : O(n^2).\n- Space Complexity : O(1).\n\n(3) Quick Sort \n--------------------------------------------------------------------\n- Approach : divide-and-conquer approach to sort an array. The basic idea of Quick Sort is to divide the array into two smaller sub-arrays around a pivot element, and recursively sort these sub-arrays until the entire array is sorted.\n- Time Complexity :\n(i) Best and Average Case : O(nlogn).\n(ii) Worst Case : O(n^2).\n(iii) Space Complexty : O(n).\n\nThese are the most common sorting algorithms; however, we may also sort an array whose time complexity is "O(nlogn)" directly using the C++ STL "sort()" function.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn the Given Problems , I use Merge Sort Algorithm to Sort an array which uses Divide and Conquer Approach :) \n\nMerge Sort : This algorithms works by dividing an array into smaller subarray , sorting each subarray and then merging the sorted subarray back together to form the final sorted array.\n\n- Pseudo Code\n(1) Declaring the variables "low" and "high," which serve as the array\'s beginning and ending points where low=0 and high=len(array)-1.\n(2) Calculate mid using "(low+high)/2" or "low+(high-low)/2".\n(3) Call the "MergeSort()" function on the part (low,mid) and (mid+1,high).\n(4) The above Call will continue till "low<high" is satisfied.\n(5) Finally Call "Merge" function to merge thse two halves.\n\n# Complexity\n- Time complexity: O(nlogn) { Best , Average and Worst Case }.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n void Merge(vector<int>& arr,int left,int mid,int right){\n\n if(left>=right){\n return;\n }\n\n int len=right-left+1;\n vector<int> temp(len,0);\n int i=left;\n int j=mid+1;\n int k=0;\n\n while(i<=mid && j<=right){\n\n if(arr[i]<arr[j]){\n temp[k++]=arr[i++];\n }\n\n else{\n temp[k++]=arr[j++];\n }\n }\n\n while(i<=mid){\n temp[k++]=arr[i++];\n }\n\n while(j<=right){\n temp[k++]=arr[j++];\n }\n\n for(k=0;k<len;k++){\n arr[k+left]=temp[k];\n }\n\n }\n\n void MergeSort(vector<int>& arr,int left,int right){\n\n if(left>=right){\n return;\n }\n\n int mid=(left+(right-left)/2);\n MergeSort(arr,left,mid);\n MergeSort(arr,mid+1,right);\n Merge(arr,left,mid,right);\n\n }\n\n vector<int> sortArray(vector<int>& nums) {\n // Using Merge Sort to Sort the array \n // Time Complexity --> O(nlogn) \n // Space Complexity --> O(n)\n int left=0;\n int right=nums.size()-1;\n MergeSort(nums,left,right);\n return nums;\n }\n};\n``` | 10 | 0 | ['Sorting', 'Merge Sort', 'C++'] | 2 |
sort-an-array | Accepted Python Quick Sort solution | Beats 93% | accepted-python-quick-sort-solution-beat-8r5t | Have to compromise with space to knock off the leetcode acceptance. \nTime: O(NlogN)\nSpace: O(N^2)\n\n\nclass Solution:\n def sortArray(self, nums: List[int | subconciousCoder | NORMAL | 2022-12-14T03:33:59.729851+00:00 | 2022-12-14T03:51:56.598560+00:00 | 2,528 | false | Have to compromise with space to knock off the leetcode acceptance. \nTime: O(NlogN)\nSpace: O(N^2)\n\n```\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n def quicksort(nums):\n if len(nums) <= 1: return nums\n \n #picking a random pivot\n pivot = random.choice(nums)\n less_than, equal_to, greater_than = [], [], []\n \n for val in nums:\n if val < pivot: less_than.append(val)\n elif val > pivot: greater_than.append(val)\n else: equal_to.append(val)\n return quicksort(less_than) + equal_to + quicksort(greater_than)\n return quicksort(nums)\n``` | 10 | 0 | ['Sorting', 'Python', 'Python3'] | 5 |
sort-an-array | C++ || Easy Merge Sort | c-easy-merge-sort-by-suniti0804-9m6p | \n \n void merge(vector& nums, int l, int m, int r)\n {\n int n1 = m - l + 1;\n int n2 = r - m;\n int A[n1], B[n2];\n \n | suniti0804 | NORMAL | 2021-04-16T06:12:45.936751+00:00 | 2021-04-16T06:12:45.936779+00:00 | 2,006 | false | \n \n void merge(vector<int>& nums, int l, int m, int r)\n {\n int n1 = m - l + 1;\n int n2 = r - m;\n int A[n1], B[n2];\n \n for(int i = 0; i < n1; i++)\n A[i] = nums[l + i];\n \n for(int i = 0; i < n2; i++)\n B[i] = nums[m + 1 + i];\n \n int i = 0, j = 0;\n int k = l;\n \n while(i < n1 && j < n2)\n {\n if(A[i] <= B[j])\n nums[k++] = A[i++];\n else\n nums[k++] = B[j++];\n }\n \n while(i < n1)\n nums[k++] = A[i++];\n while(j < n2)\n nums[k++] = B[j++];\n }\n \n void mergeSort(vector<int>& nums, int l, int r)\n {\n if(l >= r) //remember to put the equal to sign\n return;\n \n int m = l + (r - l)/2;\n mergeSort(nums, l, m);\n mergeSort(nums, m + 1, r);\n merge(nums, l, m, r);\n }\n \n vector<int> sortArray(vector<int>& nums) \n {\n mergeSort(nums, 0, nums.size() - 1);\n return nums;\n } \n \n | 10 | 0 | ['C', 'Merge Sort', 'C++'] | 1 |
sort-an-array | C++ | Quick sort | Merge sort | Visual explanation | c-quick-sort-merge-sort-visual-explanati-1xvc | Quick sort\nThis works just like how a preorder tree traversal does. Here I use Lomuto partition scheme.\n1. For each recursion call, get one element sorted as | yoyotvyoo888 | NORMAL | 2022-08-19T15:35:15.852881+00:00 | 2022-08-20T16:56:56.247050+00:00 | 1,695 | false | **Quick sort**\nThis works just like how a preorder tree traversal does. Here I use Lomuto partition scheme.\n1. For each recursion call, get one element sorted as pivot. \n2. Recurse on the left part and the right part\n\n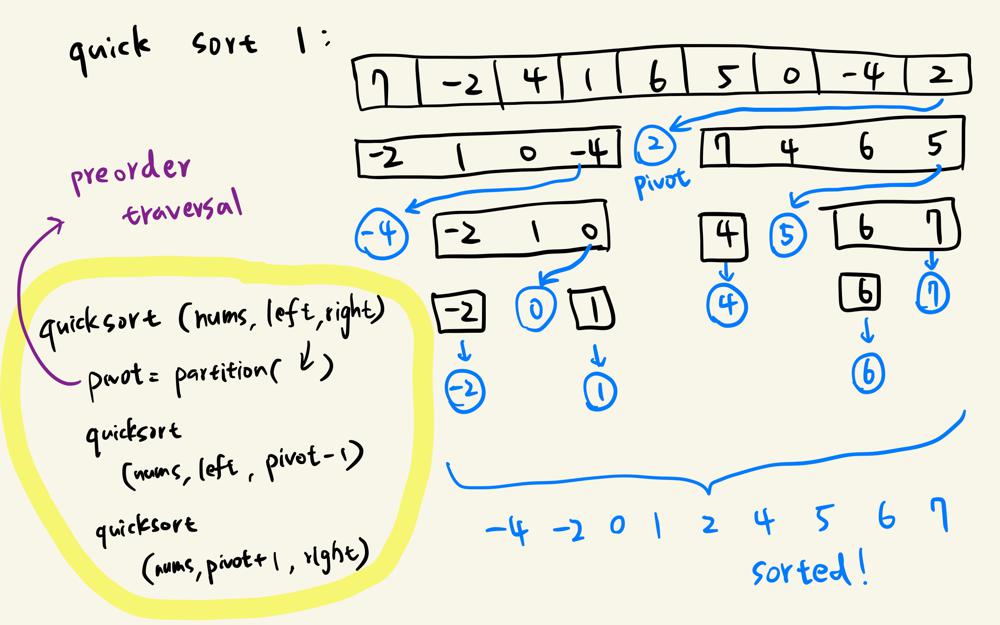\n\n\n\n\n**Code**\n```\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n QuicksortHelper(nums, 0, size(nums) - 1);\n return nums;\n }\nprivate:\n int Partition(vector<int>& nums, int left, int right) {\n\t // To avoid TLE, take the element in the middle as the pivot\n\t\t// Would be even better to use a random element\n int mid = left + (right - left) / 2;\n swap(nums[mid], nums[right]);\n\t\t\n int pivot = nums[right];\n int j = left;\n for (int i = left; i < right; ++i) {\n if (nums[i] < pivot) {\n std::swap(nums[i], nums[j]);\n ++j;\n }\n }\n std::swap(nums[j], nums[right]);\n return j;\n }\n \n void QuicksortHelper(vector<int>& nums, int left, int right) {\n if (left >= right) {\n return;\n }\n int pivot_index = Partition(nums, left, right);\n QuicksortHelper(nums, left, pivot_index - 1);\n QuicksortHelper(nums, pivot_index + 1, right);\n }\n};\n```\n\n\n\n**Merge sort**\nThis works like a postorder tree traversal.\n1. Keep dividing the array in half until only a single element is left.\n2. Start merging pairs of sorted arrays.\n\n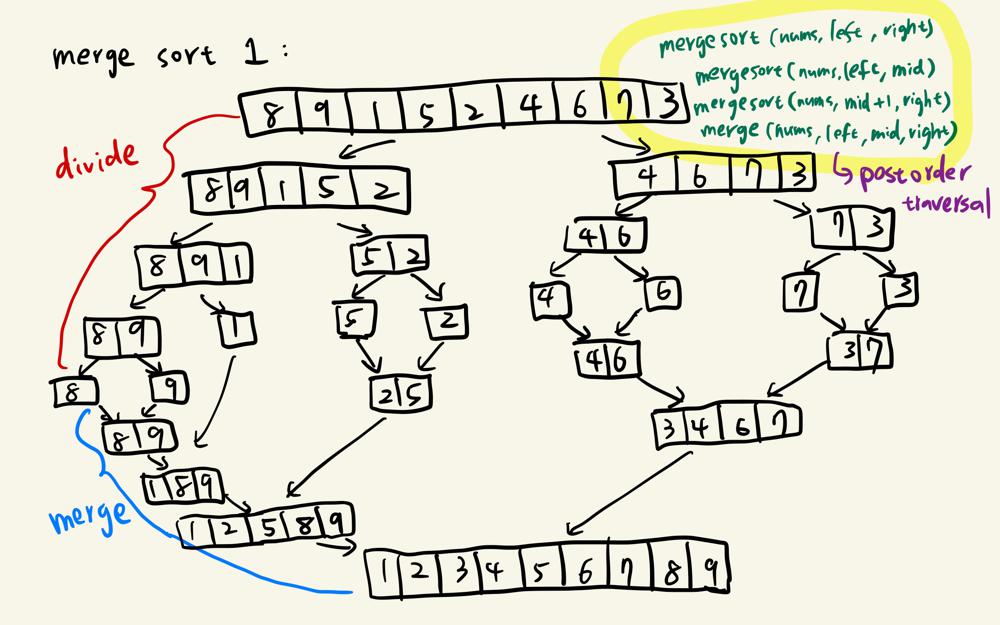\n\n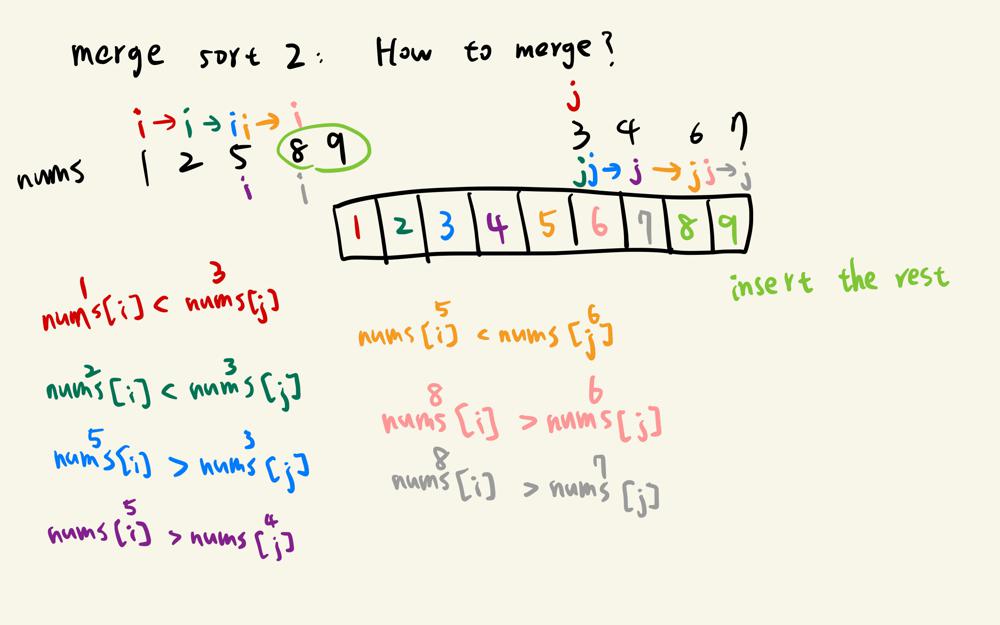\n\n**Code**\n```\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n MergesortHelper(nums, 0, size(nums) - 1);\n return nums;\n }\nprivate:\n void MergeTwoSortedArray(vector<int>& nums, int left, int mid, int right) {\n vector<int> sorted;\n sorted.reserve(right - left + 1);\n \n int k = 0;\n int i = left;\n int j = mid + 1;\n \n while (i <= mid && j <= right) {\n if (nums[i] < nums[j]) {\n sorted[k++] = nums[i++];\n } else {\n sorted[k++] = nums[j++];\n }\n }\n \n while (i <= mid) {\n sorted[k++] = nums[i++];\n }\n \n while (j <= right) {\n sorted[k++] = nums[j++];\n }\n \n while (--k >= 0) {\n nums[right--] = sorted[k];\n }\n }\n \n void MergesortHelper(vector<int>& nums, int left, int right) {\n if (left == right) {\n return;\n }\n int mid = left + (right - left) / 2;\n MergesortHelper(nums, left, mid);\n MergesortHelper(nums, mid + 1, right);\n MergeTwoSortedArray(nums, left, mid, right);\n }\n};\n```\n\nPlease let me know if anything could be improved. Happy coding! | 9 | 0 | ['C', 'C++'] | 3 |
sort-an-array | Java quick sort beat 95% time; time:O(nlogn) | java-quick-sort-beat-95-time-timeonlogn-8zjsf | \nclass Solution {\n public int[] sortArray(int[] nums) {\n \n if (nums.length == 0) { return nums;}\n \n QuickSort(nums, 0, nums | shushujie | NORMAL | 2020-06-24T06:09:02.387607+00:00 | 2020-06-24T06:09:58.815534+00:00 | 2,742 | false | ```\nclass Solution {\n public int[] sortArray(int[] nums) {\n \n if (nums.length == 0) { return nums;}\n \n QuickSort(nums, 0, nums.length - 1);\n return nums;\n \n }\n \n private void QuickSort(int[] nums, int start, int end) {\n \n if(start >= end) return;\n \n int pivot = nums[(start + end)/2];\n int left = start, right = end;\n\n while (left <= right) {\n while (left <= right && nums[left] < pivot ) {\n left++;\n }\n \n while (left <= right && nums[right] > pivot) {\n right--;\n }\n \n if(left <= right) {\n int temp;\n temp = nums[left];\n nums[left] = nums[right];\n nums[right] = temp;\n \n left++;\n right--;\n }\n }\n \n QuickSort(nums, start, right);\n QuickSort(nums, left, end);\n \n \n }\n \n``` | 9 | 2 | ['Java'] | 5 |
sort-an-array | 💯✅🔥Detailed Easy Java ,Python3 ,C++ Solution|| 25 ms ||≧◠‿◠≦✌ | detailed-easy-java-python3-c-solution-25-m4md | Intuition\n\nMerge Sort is a divide-and-conquer algorithm that recursively divides the input array into smaller subarrays until they are small enough to sort. I | suyalneeraj09 | NORMAL | 2024-07-25T02:46:05.357779+00:00 | 2024-07-25T02:46:05.357816+00:00 | 1,039 | false | # Intuition\n\nMerge Sort is a divide-and-conquer algorithm that recursively divides the input array into smaller subarrays until they are small enough to sort. It then merges these sorted subarrays back together to form the final sorted array.\n\n---\n# Approach\n\nThe code consists of three main methods:\n\n1. `sortArray(int[] nums)`: This is the main entry point that takes an unsorted array `nums` as input and returns the sorted array.\n\n2. `mergeSort(int[] arr, int s, int e)`: This method performs the recursive division of the array. It takes an array `arr` and the start and end indices `s` and `e`, respectively. If the subarray has only one element (`e-s == 1`), it returns. Otherwise, it recursively calls `mergeSort` on the left and right halves of the subarray and then merges the sorted subarrays using the `merge` method.\n\n3. `merge(int[] arr, int s, int m, int e)`: This method merges two sorted subarrays `arr[s:m]` and `arr[m:e]` into a single sorted subarray. It uses three pointers `i`, `j`, and `k` to iterate through the left subarray, right subarray, and the merged subarray, respectively. It compares the elements from the left and right subarrays and adds the smaller element to the merged subarray. Finally, it copies the merged subarray back into the original array.\n\n---\n# Time Complexity\n\nThe time complexity of Merge Sort is O(n log n), where n is the size of the input array. This is because the algorithm recursively divides the array into halves and merges the sorted subarrays, which takes O(n) time per merge operation. The number of merge operations is proportional to the height of the recursion tree, which is log n.\n\n---\n# Space Complexity\n\nThe space complexity of Merge Sort is O(n), where n is the size of the input array. This is because the algorithm needs to create a temporary array of size n to store the merged elements during the merge operation.\n\nIn the provided code, the commented line `System.arraycopy(mix, 0, arr, 0, mix.length);` can be used to copy the merged subarray back into the original array. However, the code below it, which uses a for loop to copy the elements, achieves the same result and is more concise.\n\n---\n\nLet\'s walk through the Merge Sort algorithm step by step using the input array `[5, 1, 1, 2, 0, 0]`. We will illustrate how the algorithm divides the array and merges the sorted subarrays.\n\n### Initial Call\n\n1. **Input Array**: `[5, 1, 1, 2, 0, 0]`\n2. **Function Call**: `sortArray(nums)` which calls `mergeSort(nums, 0, nums.length)` or `mergeSort(nums, 0, 6)`.\n\n### Step 1: First Level of Recursion\n\n- **Current Array**: `[5, 1, 1, 2, 0, 0]`\n- **Indices**: `s = 0`, `e = 6`\n- **Middle Index**: `m = 0 + (6 - 0) / 2 = 3`\n\n#### Split into Two Halves\n- Left Half: `[5, 1, 1]` (indices 0 to 3)\n- Right Half: `[2, 0, 0]` (indices 3 to 6)\n\n### Step 2: Second Level of Recursion (Left Half)\n\n- **Current Array**: `[5, 1, 1]`\n- **Indices**: `s = 0`, `e = 3`\n- **Middle Index**: `m = 0 + (3 - 0) / 2 = 1`\n\n#### Split into Two Halves\n- Left Half: `` (indices 0 to 1)\n- Right Half: `[1, 1]` (indices 1 to 3)\n\n### Step 3: Third Level of Recursion (Left Half of Left Half)\n\n- **Current Array**: ``\n- **Indices**: `s = 0`, `e = 1`\n- Since `e - s = 1`, we return without further splitting.\n\n### Step 4: Third Level of Recursion (Right Half of Left Half)\n\n- **Current Array**: `[1, 1]`\n- **Indices**: `s = 1`, `e = 3`\n- **Middle Index**: `m = 1 + (3 - 1) / 2 = 2`\n\n#### Split into Two Halves\n- Left Half: `` (indices 1 to 2)\n- Right Half: `` (indices 2 to 3)\n\n### Step 5: Fourth Level of Recursion (Left Half of Right Half)\n\n- **Current Array**: ``\n- **Indices**: `s = 1`, `e = 2`\n- Since `e - s = 1`, we return.\n\n### Step 6: Fourth Level of Recursion (Right Half of Right Half)\n\n- **Current Array**: ``\n- **Indices**: `s = 2`, `e = 3`\n- Since `e - s = 1`, we return.\n\n### Step 7: Merging the Left Half\n\nNow we merge the two sorted halves `` and `[1, 1]`:\n\n- **Merge Call**: `merge(arr, 0, 1, 3)`\n- **Current State**: \n - Left Array: `` (indices 0 to 1)\n - Right Array: `[1, 1]` (indices 1 to 3)\n- **Merged Result**: \n - Compare `5` and `1`: `1` is smaller, add `1` to the mix.\n - Compare `5` and `1`: `1` is smaller again, add `1` to the mix.\n - Add remaining `5` to the mix.\n- **Merged Array**: `[1, 1, 5]`\n\n### Step 8: Second Level of Recursion (Right Half)\n\nNow we process the right half `[2, 0, 0]`:\n\n- **Current Array**: `[2, 0, 0]`\n- **Indices**: `s = 3`, `e = 6`\n- **Middle Index**: `m = 3 + (6 - 3) / 2 = 4`\n\n#### Split into Two Halves\n- Left Half: `` (indices 3 to 4)\n- Right Half: `[0, 0]` (indices 4 to 6)\n\n### Step 9: Third Level of Recursion (Left Half of Right Half)\n\n- **Current Array**: ``\n- **Indices**: `s = 3`, `e = 4`\n- Since `e - s = 1`, we return.\n\n### Step 10: Third Level of Recursion (Right Half of Right Half)\n\n- **Current Array**: `[0, 0]`\n- **Indices**: `s = 4`, `e = 6`\n- **Middle Index**: `m = 4 + (6 - 4) / 2 = 5`\n\n#### Split into Two Halves\n- Left Half: `` (indices 4 to 5)\n- Right Half: `` (indices 5 to 6)\n\n### Step 11: Fourth Level of Recursion (Left Half of Right Half)\n\n- **Current Array**: ``\n- **Indices**: `s = 4`, `e = 5`\n- Since `e - s = 1`, we return.\n\n### Step 12: Fourth Level of Recursion (Right Half of Right Half)\n\n- **Current Array**: ``\n- **Indices**: `s = 5`, `e = 6`\n- Since `e - s = 1`, we return.\n\n### Step 13: Merging the Right Half\n\nNow we merge the two sorted halves `` and `[0, 0]`:\n\n- **Merge Call**: `merge(arr, 3, 4, 6)`\n- **Current State**: \n - Left Array: `` (indices 3 to 4)\n - Right Array: `[0, 0]` (indices 4 to 6)\n- **Merged Result**: \n - Compare `2` and `0`: `0` is smaller, add `0` to the mix.\n - Compare `2` and `0`: `0` is smaller again, add `0` to the mix.\n - Add remaining `2` to the mix.\n- **Merged Array**: `[0, 0, 2]`\n\n### Step 14: Final Merge\n\nFinally, we merge the two sorted halves `[1, 1, 5]` and `[0, 0, 2]`:\n\n- **Merge Call**: `merge(arr, 0, 3, 6)`\n- **Current State**: \n - Left Array: `[1, 1, 5]` (indices 0 to 3)\n - Right Array: `[0, 0, 2]` (indices 3 to 6)\n- **Merged Result**: \n - Compare `1` and `0`: `0` is smaller, add `0` to the mix.\n - Compare `1` and `0`: `0` is smaller again, add `0` to the mix.\n - Compare `1` and `2`: `1` is smaller, add `1` to the mix.\n - Compare `1` and `2`: `1` is smaller again, add `1` to the mix.\n - Add remaining `5` to the mix.\n- **Final Sorted Array**: `[0, 0, 1, 1, 2, 5]`\n\n### Conclusion\n\nThe Merge Sort algorithm successfully sorts the array `[5, 1, 1, 2, 0, 0]` into `[0, 0, 1, 1, 2, 5]` through a series of recursive splits and merges. This step-by-step breakdown illustrates the power of the divide-and-conquer approach inherent in Merge Sort.\n\n---\n```java []\nclass Solution {\n public int[] sortArray(int[] nums) {\n mergeSort(nums,0,nums.length);\n return nums;\n }\n\n static void mergeSort(int[] arr,int s,int e){\n if(e-s==1){\n return;\n }\n\n int m=s+(e-s)/2;\n\n mergeSort(arr,s,m);\n mergeSort(arr,m,e);\n\n merge(arr,s,m,e);\n }\n\n static void merge(int[] arr,int s,int m,int e){\n int i=s,j=m,k=0;\n int [] mix=new int[e-s];\n\n while(i<m && j<e){\n if(arr[i]<arr[j]){\n mix[k++]=arr[i++];\n }else{\n mix[k++]=arr[j++];\n }\n }\n\n while(i<m){\n mix[k++]=arr[i++];\n }\n while(j<e){\n mix[k++]=arr[j++];\n }\n\n //System.arraycopy(mix,0,arr,0,mix.length);\n for (int l = 0; l < mix.length; l++) {\n arr[s + l] = mix[l];\n }\n }\n}\n\n```\n```python3 []\nclass Solution:\n def sortArray(self, nums):\n self.mergeSort(nums, 0, len(nums))\n return nums\n\n def mergeSort(self, arr, s, e):\n if e - s <= 1:\n return\n\n m = s + (e - s) // 2\n\n self.mergeSort(arr, s, m)\n self.mergeSort(arr, m, e)\n\n self.merge(arr, s, m, e)\n\n def merge(self, arr, s, m, e):\n i, j, k = s, m, 0\n mix = [0] * (e - s)\n\n while i < m and j < e:\n if arr[i] < arr[j]:\n mix[k] = arr[i]\n i += 1\n else:\n mix[k] = arr[j]\n j += 1\n k += 1\n\n while i < m:\n mix[k] = arr[i]\n i += 1\n k += 1\n while j < e:\n mix[k] = arr[j]\n j += 1\n k += 1\n\n for l in range(len(mix)):\n arr[s + l] = mix[l]\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n mergeSort(nums, 0, nums.size());\n return nums;\n }\n\nprivate:\n void mergeSort(vector<int>& arr, int s, int e) {\n if (e - s <= 1) {\n return;\n }\n\n int m = s + (e - s) / 2;\n\n mergeSort(arr, s, m);\n mergeSort(arr, m, e);\n\n merge(arr, s, m, e);\n }\n\n void merge(vector<int>& arr, int s, int m, int e) {\n int i = s, j = m, k = 0;\n vector<int> mix(e - s);\n\n while (i < m && j < e) {\n if (arr[i] < arr[j]) {\n mix[k++] = arr[i++];\n } else {\n mix[k++] = arr[j++];\n }\n }\n\n while (i < m) {\n mix[k++] = arr[i++];\n }\n while (j < e) {\n mix[k++] = arr[j++];\n }\n\n for (int l = 0; l < mix.size(); l++) {\n arr[s + l] = mix[l];\n }\n }\n};\n```\n\n---\n\n\n---\n | 8 | 1 | ['Array', 'Divide and Conquer', 'Sorting', 'Merge Sort', 'C++', 'Java', 'Python3'] | 4 |
sort-an-array | ✅Easy Merge Sort Algorithm with Video Explanation | easy-merge-sort-algorithm-with-video-exp-7htq | Video Explanation\nhttps://youtu.be/lsrEitj-fO8?si=5un2qApRDftE0IyW\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is t | prajaktakap00r | NORMAL | 2024-07-25T00:59:11.226599+00:00 | 2024-07-25T03:54:20.551670+00:00 | 2,222 | false | # Video Explanation\nhttps://youtu.be/lsrEitj-fO8?si=5un2qApRDftE0IyW\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is to sort an array of integers, and we are using the merge sort algorithm to achieve this. Merge sort is a classic divide-and-conquer algorithm that splits the array into halves, sorts each half recursively, and then merges the sorted halves back together.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Divide: Split the array into two halves by finding the middle index.\n2. Conquer: Recursively sort each half of the array.\n3. Combine: Merge the two sorted halves into a single sorted array.\n- The merge operation involves comparing elements from each half and arranging them in the correct order to form a sorted array.\n# Complexity\n- Time complexity:$$O(n*log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n void merge(vector<int>& nums, int low, int mid, int high) {\n vector<int> temp;\n int left = low;\n int right = mid + 1;\n while (left <= mid && right <= high){\n if(nums[left]<=nums[right]){\n temp.push_back(nums[left++]);\n }else{\n temp.push_back(nums[right++]);\n }\n }\n while(left<=mid){\n temp.push_back(nums[left++]);\n }\n while(right<=high){\n temp.push_back(nums[right++]);\n }\n for(int i=low;i<=high;i++){\n nums[i]=temp[i-low];\n }\n }\n void mergeSort(vector<int>& nums, int low, int high) {\n if (low == high)\n return;\n int mid = (low + high) / 2;\n mergeSort(nums, low, mid);\n mergeSort(nums, mid + 1, high);\n merge(nums, low, mid, high);\n }\n\npublic:\n vector<int> sortArray(vector<int>& nums) {\n mergeSort(nums, 0, nums.size() - 1);\n return nums;\n }\n};\n``` | 8 | 0 | ['Array', 'Divide and Conquer', 'Sorting', 'Heap (Priority Queue)', 'Merge Sort', 'Bucket Sort', 'C++'] | 5 |
sort-an-array | Easiest Solution | Python 1-liner | easiest-solution-python-1-liner-by-fromd-0byv | Intuition\nIt\'s not that deep.\n\n# Code\n\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n return sorted(nums)\n | fromdihpout | NORMAL | 2023-03-01T00:48:59.480247+00:00 | 2023-03-01T00:48:59.480288+00:00 | 1,896 | false | # Intuition\nIt\'s not that deep.\n\n# Code\n```\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n return sorted(nums)\n``` | 8 | 7 | ['Python3'] | 5 |
sort-an-array | C++ Easy 1 line Solution | c-easy-1-line-solution-by-anushhhka-pvck | Please upvote, if this helps!! (\u25D4\u203F\u25D4)\n\n\n\nclass Solution {\npublic:\n vector sortArray(vector& nums) {\n\t\n sort(nums.begin(), nums. | anushhhka | NORMAL | 2022-08-27T20:06:36.116285+00:00 | 2022-08-27T20:07:30.712333+00:00 | 1,102 | false | **Please upvote, if this helps!! (\u25D4\u203F\u25D4)**\n\n\n\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n\t\n sort(nums.begin(), nums.end());\n return nums;\n }\n}; | 8 | 1 | ['C', 'C++'] | 0 |
sort-an-array | Just using simple recursion to sort the array | just-using-simple-recursion-to-sort-the-lwvum | Although this will not pass all test cases but still this is the most fundamental way to sort the array using recursion\n\n vector<int> insertAT(vector<int> | chocoTaqo | NORMAL | 2021-08-25T09:55:52.819375+00:00 | 2021-08-25T09:55:52.819412+00:00 | 6,131 | false | Although this will not pass all test cases but still this is the most fundamental way to sort the array using recursion\n```\n vector<int> insertAT(vector<int> &V, int val) {\n int len = V.size(); \n if((len == 0) || (V[len-1] <= val)) {\n V.push_back(val); return V;\n }\n\n int last = V[len-1]; \n V.pop_back(); \n insertAT(V, val);\n V.push_back(last);\n return V;\n }\n\n vector<int> sortArray(vector<int> &V) {\n if(V.size() == 1) return V;\n\n int last = V[V.size() - 1];\n V.pop_back();\n vector<int> temp = sortArray(V);\n vector<int> sorted = insertAT(temp, last);\n return sorted;\n }\n``` | 8 | 0 | ['Recursion', 'Sorting'] | 5 |
sort-an-array | [C++] Sorting an array using recursion | c-sorting-an-array-using-recursion-by-tu-sg8j | Please note that this method will result in a TLE and only pass 10/13 of the test cases.\nI am sharing it because I feel it\'s a good application of recursion t | ihavehiddenmyid | NORMAL | 2021-07-06T06:54:35.177687+00:00 | 2021-07-06T06:57:58.226792+00:00 | 1,878 | false | **Please note that this method will result in a TLE and only pass 10/13 of the test cases.\nI am sharing it because I feel it\'s a good application of recursion to sort an array**\n\n```\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) \n {\n\t\t// Base Condition\n if (nums.size() == 1)\n return nums; \n // Hypothesis\n vector<int> smallerUnsorted(nums.begin() + 1, nums.end());\n vector<int> smallerSorted = sortArray(smallerUnSorted);\n // Induction\n vector<int> originalSorted;\n int i = 0;\n while (i < smallerSorted.size() && smallerSorted[i] <= nums[0])\n originalSorted.push_back(smallerSorted[i++]);\n originalSorted.push_back(nums[0]);\n while (i < smallerSorted.size() && smallerSorted[i] > nums[0])\n originalSorted.push_back(smallerSorted[i++]);\n // Return sorted array\n return originalSorted;\n }\n};\n``` | 8 | 2 | ['Recursion', 'C'] | 2 |
sort-an-array | MergeSort Explained in detail with DIAGRAM 🔥| C++✔️ | Java✔️ | Python✔️ | mergesort-explained-in-detail-with-diagr-f27r | Intuition\n Describe your first thoughts on how to solve this problem. \n- Merge sort is a divide-and-conquer algorithm that splits the array into halves, recu | atharvf14t | NORMAL | 2024-07-25T01:46:07.925712+00:00 | 2024-07-25T01:46:07.925733+00:00 | 2,962 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Merge sort is a divide-and-conquer algorithm that splits the array into halves, recursively sorts each half, and then merges the sorted halves back together. Here\'s a detailed explanation of the code, along with the intuition, approach, and a diagram of the algorithm flow.\n1. Divide: Split the array into two halves.\n2. Conquer: Recursively sort each half.\n3. Combine: Merge the two sorted halves to produce a single sorted array.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. merge Function:\n\n- Parameters: A (original array), start, mid, end (indices), and buff (temporary buffer).\n- Initialization: left points to the start of the left half, right points to the start of the right half, and s is the size of the subarray.\n- Merge Process:\nCompare elements from the left and right subarrays and place the smaller one into the buffer.\nIf one subarray is exhausted, copy the remaining elements from the other subarray.\n- Copy Back: Copy the merged elements from the buffer back to the original array.\n\n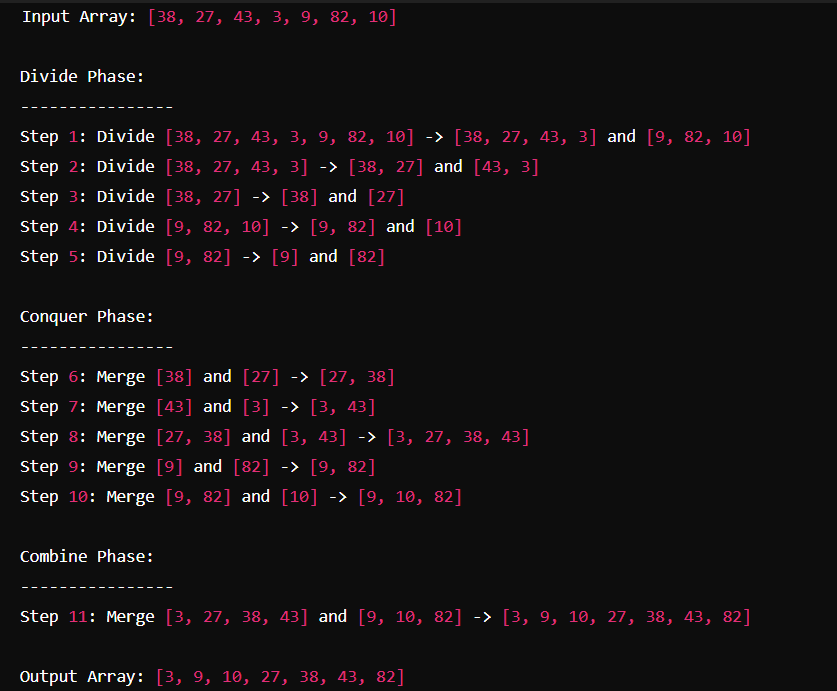\n\n2. mergeSort Function:\n\n- Base Case: If the subarray has one or zero elements, it is already sorted.\n- Recursive Case: Split the array into two halves, sort each half, and merge them.\n- Mid Calculation: mid = start + (end - start) / 2 to avoid overflow.\nsortArray Function:\n\n- Initializes the buffer and calls mergeSort on the entire array.\n- Returns the sorted array.\n\n\n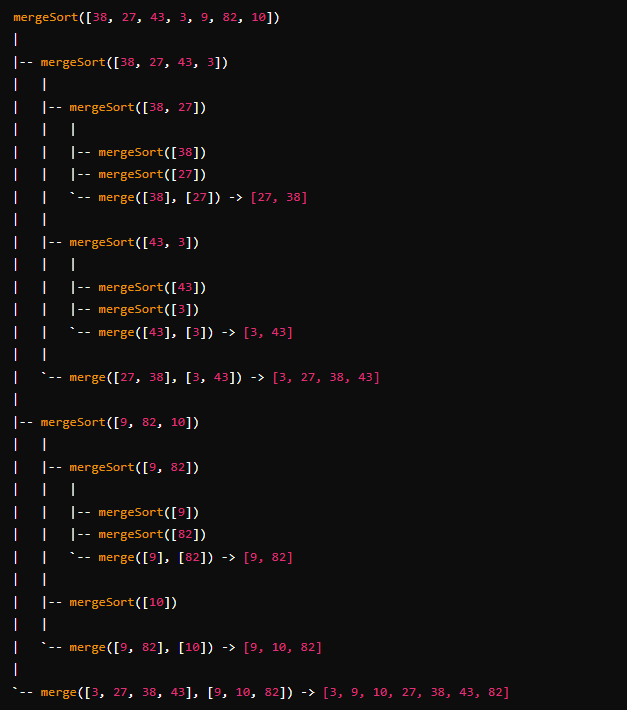\n\n\n\n# Complexity\n1. Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Divide Phase:\nEach recursive call splits the array into two halves. This gives a logarithmic number of levels: O(logn)\n- Conquer Phase:\nAt each level of recursion, the merge function processes the entire array. This involves comparing and copying elements, which takes linear time: O(n).\n\n2. Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- O(n)\n\n\n\n```C++ []\nclass Solution {\npublic:\n void merge(vector<int>& A, int start, int mid, int end, vector<int>& buff)\n {\n int left=start, right=mid+1;\n int s=end-start+1;\n for(int i=0; i<s; i++)\n { \n int i0=start+i;\n if(left>mid){\n buff[i0]=A[right];\n right++;\n } else if (right>end){\n buff[i0]=A[left];\n left++;\n } else if (A[left]<A[right]){\n buff[i0]=A[left];\n left++;\n } else{\n buff[i0]=A[right];\n right++;\n }\n }\n for(int i=start; i<start+s; i++) A[i]=buff[i];\n }\n void mergeSort(vector<int>& A, int start, int end, vector<int>& buff )\n {\n if(end<=start) return;\n int mid=start+(end-start)/2;\n mergeSort(A, start, mid, buff);\n mergeSort(A, mid+1, end, buff);\n merge(A, start, mid, end, buff);\n }\n vector<int> sortArray(vector<int>& nums) {\n vector<int> buff(nums.size());\n mergeSort(nums, 0, nums.size()-1 ,buff);\n return nums;\n }\n};\n```\n```Java []\nclass Solution {\n public void merge(int[] A, int start, int mid, int end, int[] buff) {\n int left = start, right = mid + 1;\n int s = end - start + 1;\n \n for (int i = 0; i < s; i++) {\n int i0 = start + i;\n if (left > mid) {\n buff[i0] = A[right];\n right++;\n } else if (right > end) {\n buff[i0] = A[left];\n left++;\n } else if (A[left] < A[right]) {\n buff[i0] = A[left];\n left++;\n } else {\n buff[i0] = A[right];\n right++;\n }\n }\n \n for (int i = start; i < start + s; i++) {\n A[i] = buff[i];\n }\n }\n\n public void mergeSort(int[] A, int start, int end, int[] buff) {\n if (end <= start) {\n return;\n }\n \n int mid = start + (end - start) / 2;\n mergeSort(A, start, mid, buff);\n mergeSort(A, mid + 1, end, buff);\n merge(A, start, mid, end, buff);\n }\n\n public int[] sortArray(int[] nums) {\n int[] buff = new int[nums.length];\n mergeSort(nums, 0, nums.length - 1, buff);\n return nums;\n }\n\n public static void main(String[] args) {\n Solution solution = new Solution();\n int[] nums = {38, 27, 43, 3, 9, 82, 10};\n int[] sortedNums = solution.sortArray(nums);\n System.out.println(Arrays.toString(sortedNums));\n }\n}\n\n```\n```python []\nclass Solution(object):\n def merge(self, A, start, mid, end, buff):\n left, right = start, mid + 1\n s = end - start + 1\n\n for i in range(s):\n i0 = start + i\n if left > mid:\n buff[i0] = A[right]\n right += 1\n elif right > end:\n buff[i0] = A[left]\n left += 1\n elif A[left] < A[right]:\n buff[i0] = A[left]\n left += 1\n else:\n buff[i0] = A[right]\n right += 1\n\n for i in range(start, start + s):\n A[i] = buff[i]\n\n def mergeSort(self, A, start, end, buff):\n if end <= start:\n return\n\n mid = start + (end - start) // 2\n self.mergeSort(A, start, mid, buff)\n self.mergeSort(A, mid + 1, end, buff)\n self.merge(A, start, mid, end, buff)\n\n def sortArray(self, nums):\n """\n :type nums: List[int]\n :rtype: List[int]\n """\n buff = [0] * len(nums)\n self.mergeSort(nums, 0, len(nums) - 1, buff)\n return nums\n\n\n\n```\n\n | 7 | 0 | ['Array', 'Divide and Conquer', 'Merge Sort', 'Python', 'C++', 'Java'] | 11 |
sort-an-array | [Python] Quick Sort with Optimization | python-quick-sort-with-optimization-by-h-41q7 | Implementation 1: Quick Sort (Using auxiliary space - easy to implement)\n- Firstly, we pick pivot as a random number.\n- We particle nums arrays into 3 section | hiepit | NORMAL | 2023-12-18T23:20:01.208427+00:00 | 2023-12-18T23:22:08.166013+00:00 | 720 | false | **Implementation 1: Quick Sort (Using auxiliary space - easy to implement)**\n- Firstly, we pick pivot as a random number.\n- We particle `nums` arrays into 3 section:\n - Left: All elements < pivot\n - Mid: All elements == pivot\n - Right: All elements > pivot\n```python\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n return self.quickSort(nums)\n\n def quickSort(self, nums):\n if len(nums) <= 1:\n return nums\n\n pivot = random.choice(nums)\n lesser, equal, greater = [], [], []\n for num in nums:\n if num < pivot:\n lesser.append(num)\n elif num == pivot:\n equal.append(num)\n else:\n greater.append(num)\n \n return self.quickSort(lesser) + equal + self.quickSort(greater)\n \n```\nComplexity:\n- Time: `O(NlogN)`, where `N` is length of nums array. `O(N^2)` in the worst case, in case random value always the maximum or the minimum elements in the array, and it\'s impossible!\n- Space: `O(N)`\n---\n**Implementation 2: Quick Sort (in place)**\n- Firstly, we pick pivot as a random number.\n- We particle `nums` arrays into 3 section:\n - Left: All elements < pivot\n - Mid: All elements == pivot\n - Right: All elements > pivot\n```python\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n self.quickSort(nums, 0, len(nums) - 1)\n return nums\n\n def quickSort(self, nums, left, right):\n if left >= right:\n return\n\n pivot = nums[random.randint(left, right)]\n i, j = left, right\n while i <= j:\n while i < right and nums[i] < pivot: # Find first i such that nums[i] >= pivot\n i += 1\n while j > left and nums[j] > pivot: # Find first j such that nums[j] <= pivot\n j -= 1\n if i <= j:\n nums[i], nums[j] = nums[j], nums[i]\n i += 1\n j -= 1\n\n self.quickSort(nums, left, j) # nums[left..j] are elements < pivot\n self.quickSort(nums, i, right) # nums[i..right] are elements > pivot\n```\nComplexity:\n- Time: `O(NlogN)`, where `N` is length of nums array. `O(N^2)` in the worst case, in case random value always the maximum or the minimum elements in the array, and it\'s impossible!\n- Space: `O(logN)`, it\'s the depth of recursion stack memory | 7 | 1 | ['Quickselect', 'Python3'] | 0 |
sort-an-array | JAVA | Quick sort with explaination | java-quick-sort-with-explaination-by-kus-0znz | In-place,Not Stable,Not adaptive,Divide and conquer.\n\nFor primitive it is preferred and for objects merge sort is preferred. As merge sort takes extra o(n) me | kushguptacse | NORMAL | 2022-12-18T07:06:48.497584+00:00 | 2022-12-18T07:16:50.312769+00:00 | 1,308 | false | In-place,Not Stable,Not adaptive,Divide and conquer.\n\nFor primitive it is preferred and for objects merge sort is preferred. As merge sort takes extra o(n) memory it is not preferred for array. But for linked list merge sort does not need extra space.\n\n# Approach\nWe will take one element as pivot(here the last one) and will try to put it in correct position. By correct position we mean that all element to the left of it are small and right to it are greater than pivot. So, basically we fixing pivot position one by one.\n\n\n\n\nSo,now swap high with low. and return low i.e. index 2. So,that we will have two partition {13,6} {17,15} now and index 2 element is fixed.\n\n# Complexity\n- Time complexity:\n $$O(nlogn)$$, but in worst case when data is already sorted it might go to $$O(n2)$$. To avoid worst case we can make pivot as random or mid element always.\n\n- Space complexity:\n$$O(logn)$$ if pivot chosen correctly. else it recursion call might take entire array length and hence will be $$O(n)$$ in worst case.\n\n# Code\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n quickSort(nums, 0, nums.length - 1);\n return nums;\n }\n public void quickSort(int[] arr,int i, int j){\n if (i < j) {\n\t\t\tint p = partition(arr, i, j); \n // p is fixed and call quickSort again for left and right array\n\t\t\tquickSort(arr, i, p-1); \n\t\t\tquickSort(arr, p+1, j); \n\t\t}\n }\n public int partition(int[] arr,int l,int h) {\n // In worst case it will be o(n^2). i.e. if data is already sorted\n\t\t// we can improve it by using middle element as pivot and then before starting\n\t\t// anything just swap it with high. so, that high will remain pivot.\n\n\t\t// Find mid of the array\n\t\tint mid = (low + high) / 2;\n\t\t// swap array element present in mid and high index\n\t\tswapIntArray(arr, mid, high);\n\t\t// now pivot is high again.\n\t\t// we goes from low till high-1 because high is reserved for pivot\n\t\tfor (int j = low; j < high; j++) {\n\t\t\tif (arr[j] < arr[high]) {\n\t\t\t\tswapIntArray(arr, j, low);\n\t\t\t\tlow++;\n\t\t\t}\n\t\t}\n\t\t// when j reached high,we know that low is in pivot position. so we just swap it\n\t\tswapIntArray(arr, high, low);\n\t\treturn low;\n }\n private void swapIntArray(int[] a, int i,int j){\n int temp=a[i];\n a[i]=a[j];\n a[j]=temp;\n }\n}\n``` | 7 | 0 | ['Sorting', 'Java'] | 0 |
sort-an-array | Sort an array using merge sort | sort-an-array-using-merge-sort-by-pavith-ppnm | Intuition\n I thought of solving using merge sort using O(nlogn) complexity \n\n# Approach\n Merge sort \n\n# Complexity\n- Time complexity:\n O(nlogn) \n\n- Sp | pavithra_devi7 | NORMAL | 2022-11-05T09:30:11.482595+00:00 | 2022-11-05T09:33:06.664927+00:00 | 2,019 | false | # Intuition\n<!-- I thought of solving using merge sort using O(nlogn) complexity -->\n\n# Approach\n<!-- Merge sort -->\n\n# Complexity\n- Time complexity:\n<!-- O(nlogn) -->\n\n- Space complexity:\n<!-- O(logn) -->\n\n# Code\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n if(nums.length==1){\n return nums;\n }\n int mid=nums.length/2;\n int[] left=sortArray(Arrays.copyOfRange(nums,0,mid));\n int[] right=sortArray(Arrays.copyOfRange(nums,mid,nums.length));\n return merge(left,right);\n }\n static int[] merge(int[] first,int[] last){\n int[] mix=new int[first.length+last.length];\n int i=0,j=0,k=0;\n while(i<first.length && j<last.length){\n if(first[i]<last[j]){\n mix[k]=first[i];\n i++;\n }else{\n mix[k]=last[j];\n j++;\n }\n k++;\n }\n while(i<first.length){\n mix[k]=first[i];\n i++;\n k++;\n }\n while(j<last.length){\n mix[k]=last[j];\n j++;\n k++;\n }\n return mix;\n } \n}\n``` | 7 | 0 | ['Divide and Conquer', 'Merge Sort', 'Java'] | 1 |
sort-an-array | Classical Sorting Algorithms // JAVA // Some with detailed explanations | classical-sorting-algorithms-java-some-w-9m5w | 1. Quick Sort\n\n\tclass Solution {\n\n\t\tpublic int[] sortArray(int[] nums) {\n\t\t\tquickSort(nums, 0, nums.length - 1);\n\t\t\treturn nums;\n\t\t}\n\n\t\tpu | robinsooooon | NORMAL | 2021-09-27T03:26:07.891936+00:00 | 2021-09-27T07:38:55.397131+00:00 | 1,328 | false | **1. Quick Sort**\n```\n\tclass Solution {\n\n\t\tpublic int[] sortArray(int[] nums) {\n\t\t\tquickSort(nums, 0, nums.length - 1);\n\t\t\treturn nums;\n\t\t}\n\n\t\tpublic void quickSort(int[] nums, int start, int end) {\n\t\t\t// if the start index is larger or equal to the end index, the sort of the subarray is finished\n\t\t\tif (start >= end) {\n\t\t\t\treturn;\n\t\t\t}\n\t\t\tint pivot = partition(nums, start, end);\n\t\t\t// recursively sort the subarray\n\t\t\tquickSort(nums, start, pivot - 1);\n\t\t\tquickSort(nums, pivot + 1, end);\n\t\t}\n\n\t\t/** \n\t\t * This function takes last element as pivot, places the pivot element at its correct position in sorted array,\n\t\t * and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot \n\t\t **/\n\t\tpublic int partition(int[] nums, int start, int end) {\n\t\t\t// choose the number in the middle as the base and swap it with the first number in the subarray\n\t\t\tswap(nums, start, start + (end - start) / 2);\n\t\t\tint base = nums[start];\n\t\t\t// swap every number that is less than the base to the front of the subarray\n\t\t\tint i = start + 1;\n\t\t\tint j = i;\n\t\t\twhile (i <= end) {\n\t\t\t\tif (nums[i] < base) {\n\t\t\t\t\tswap(nums, i, j++);\n\t\t\t\t}\n\t\t\t\ti++;\n\t\t\t}\n\t\t\t// after the iteration the numbers from index start+1 to index j-1 are less than the base\n\t\t\t// swap the number on index j-1 with the base\n\t\t\t// the first j-2 numbers are less than the base\n\t\t\t// the number on index j-1 is the base\n\t\t\t// numbers after index j-1 are larger or equal to the base\n\t\t\tswap(nums, j - 1, start);\n\t\t\treturn j - 1;\n\t\t}\n\n\t\tprivate void swap(int[] nums, int i, int j) {\n\t\t\tint temp = nums[i];\n\t\t\tnums[i] = nums[j];\n\t\t\tnums[j] = temp;\n\t\t}\n\n\t}\n```\n\n**2. Merge Sort**\n```\n\tclass Solution {\n\n\t\tpublic int[] sortArray(int[] nums) {\n\t\t\tmergeSort(nums, 0, nums.length - 1);\n\t\t\treturn nums;\n\t\t}\n\n\t\tpublic void mergeSort(int[] nums, int start, int end) {\n\t\t\t// if the start index is larger or equal to the end index, the sort of the subarray is finished\n\t\t\tif (start >= end) {\n\t\t\t\treturn;\n\t\t\t}\n\t\t\tint mid = start + (end - start) / 2;\n\t\t\tmergeSort(nums, start, mid);\n\t\t\tmergeSort(nums, mid + 1, end);\n\t\t\tmerge(nums, start, end);\n\t\t}\n\n\t\tpublic void merge(int[] nums, int start, int end) {\n\t\t\tint mid = start + (end - start) / 2;\n\t\t\tint[] temp = new int[end - start + 1];\n\t\t\tint leftStart = start;\n\t\t\tint leftEnd = mid;\n\t\t\tint rightStart = mid + 1;\n\t\t\tint rightEnd = end;\n\t\t\tint i = 0;\n\t\t\twhile (leftStart <= leftEnd && rightStart <= rightEnd) {\n\t\t\t\tif (nums[leftStart] <= nums[rightStart]) {\n\t\t\t\t\ttemp[i] = nums[leftStart];\n\t\t\t\t\tleftStart++;\n\t\t\t\t} else {\n\t\t\t\t\ttemp[i] = nums[rightStart];\n\t\t\t\t\trightStart++;\n\t\t\t\t}\n\t\t\t\ti++;\n\t\t\t}\n\t\t\twhile (leftStart <= leftEnd) {\n\t\t\t\ttemp[i] = nums[leftStart];\n\t\t\t\tleftStart++;\n\t\t\t\ti++;\n\t\t\t}\n\t\t\twhile (rightStart <= rightEnd) {\n\t\t\t\ttemp[i] = nums[rightStart];\n\t\t\t\trightStart++;\n\t\t\t\ti++;\n\t\t\t}\n\t\t\tfor (int j = 0; j < i; j++) {\n\t\t\t\tnums[start + j] = temp[j];\n\t\t\t}\n\t\t}\n\n\t\tprivate void swap(int[] nums, int i, int j) {\n\t\t\tint temp = nums[i];\n\t\t\tnums[i] = nums[j];\n\t\t\tnums[j] = temp;\n\t\t}\n\n\t}\n```\n\n**3. Bubble Sort [Time Limit Exceeded]**\n```\n\tclass Solution {\n\n\t\tpublic int[] sortArray(int[] nums) {\n\t\t\tfor (int i = 0; i < nums.length - 1; i++) {\n\t\t\t\tfor (int j = 0; j < nums.length - i - 1; j++) {\n\t\t\t\t\tif (nums[j + 1] < nums[j]) {\n\t\t\t\t\t\tswap(nums, j, j + 1);\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn nums;\n\t\t}\n\n\t\tprivate void swap(int[] nums, int i, int j) {\n\t\t\tnums[i] = nums[i] ^ nums[j];\n\t\t\tnums[j] = nums[i] ^ nums[j];\n\t\t\tnums[i] = nums[i] ^ nums[j];\n\t\t}\n\n\t}\n```\n\n**4. Selection Sort [Time Limit Exceeded]**\n```\n\tpublic class Solution {\n\n\t\tpublic int[] sortArray(int[] nums) {\n\t\t\tif (nums.length <= 1) {\n\t\t\t\treturn nums;\n\t\t\t}\n\t\t\tint[] res = new int[nums.length];\n\t\t\tInteger size = 0;\n\t\t\tfor (int i = 0; i < nums.length; i++) {\n\t\t\t\tint min = nums[size];\n\t\t\t\tint minIndex = size;\n\t\t\t\tfor (int j = nums.length - 1; j > size; j--) {\n\t\t\t\t\tif (nums[j] < min) {\n\t\t\t\t\t\tmin = nums[j];\n\t\t\t\t\t\tminIndex = j;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tres[size] = min;\n\t\t\t\tswap(nums, minIndex, size);\n\t\t\t\tsize++;\n\t\t\t}\n\t\t\treturn res;\n\t\t}\n\n\t\tprivate void swap(int[] nums, int i, int j) {\n\t\t\tnums[i] = nums[i] ^ nums[j];\n\t\t\tnums[j] = nums[i] ^ nums[j];\n\t\t\tnums[i] = nums[i] ^ nums[j];\n\t\t}\n\n\t}\n```\n\n**5. Heap Sort**\n```\n\tclass Solution {\n\t\tpublic int[] sortArray(int[] nums) {\n\t\t\tif (nums == null || nums.length < 2) {\n\t\t\t\treturn nums;\n\t\t\t}\n\t\t\theapSort(nums);\n\t\t\treturn nums;\n\t\t}\n\n\t\tprivate void heapSort(int[] nums) {\n\t\t\tfor (int i = nums.length / 2; i >= 0; i--) {\n\t\t\t\theapify(nums, i, nums.length - 1);\n\t\t\t}\n\t\t\tfor (int i = 0; i < nums.length; i++) {\n\t\t\t\tswap(nums, 0, nums.length - 1 - i);\n\t\t\t\theapify(nums, 0, nums.length - 2 - i);\n\t\t\t}\n\t\t}\n\n\t\tprivate void heapify(int[] nums, int start, int end) {\n\t\t\twhile (start <= end) {\n\t\t\t\tint l = 2 * start + 1;\n\t\t\t\tint r = 2 * start + 2;\n\t\t\t\tint maxIndex = start;\n\t\t\t\tif (l <= end && nums[l] > nums[maxIndex]) {\n\t\t\t\t\tmaxIndex = l;\n\t\t\t\t}\n\t\t\t\tif (r <= end && nums[r] > nums[maxIndex]) {\n\t\t\t\t\tmaxIndex = r;\n\t\t\t\t}\n\t\t\t\tif (maxIndex == start) {\n\t\t\t\t\treturn;\n\t\t\t\t}\n\t\t\t\tswap(nums, start, maxIndex);\n\t\t\t\tstart = maxIndex;\n\t\t\t}\n\t\t}\n\n\t\tprivate void swap(int[] nums, int i, int j) {\n\t\t\tint tmp = nums[i];\n\t\t\tnums[i] = nums[j];\n\t\t\tnums[j] = tmp;\n\t\t}\n\t}\n```\n | 7 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Merge Sort', 'Java'] | 3 |
sort-an-array | Python Merge Sort Easy Implementation | python-merge-sort-easy-implementation-by-w0q2 | \nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]: \n # Length 1 is always sorted\n if len(nums) == 1:\n re | squidimenz | NORMAL | 2020-06-25T15:16:33.957493+00:00 | 2020-06-25T15:16:33.957541+00:00 | 2,985 | false | ```\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]: \n # Length 1 is always sorted\n if len(nums) == 1:\n return nums\n \n # Split array into two subarrays\n half = len(nums) // 2\n left = nums[:half]\n right = nums[half:]\n \n # Recursively break the arrays - O(log n)\n left = self.sortArray(left)\n right = self.sortArray(right)\n \n # O(n) sort\n return sort(left, right)\n \n# Merge sort helper method\ndef sort(a, b):\n out = []\n while a and b:\n if a[0] <= b[0]:\n out.append(a.pop(0))\n else:\n out.append(b.pop(0))\n if a:\n out += a\n else:\n out += b\n return out\n``` | 7 | 1 | [] | 0 |
sort-an-array | 6 Lines Java Solution | Simple Solution | Easy To Understand | Beginner Friendly | 6-lines-java-solution-simple-solution-ea-p3rp | Intuition\n Describe your first thoughts on how to solve this problem. \nUsed PriorityQueue to sort the input array in ascending order. A PriorityQueue is a he | antovincent | NORMAL | 2023-05-12T08:38:03.411003+00:00 | 2023-05-12T08:38:03.411033+00:00 | 1,332 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. --> \nUsed PriorityQueue to sort the input array in ascending order. A PriorityQueue is a heap-based data structure that maintains the order of its elements based on their priority. In this case, we are using a default natural ordering where smaller elements have a higher priority.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- First creates an empty PriorityQueue, and then adds all the elements of the input array to the PriorityQueue using the add() method. Since PriorityQueue maintains the order of its elements, the elements are sorted as they are added to the PriorityQueue.\n\n- Then, iterates over the input array and replaces each element with the smallest element in the PriorityQueue using the poll() method. After iterating over all elements, the input array will be sorted in ascending order.\n\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n PriorityQueue<Integer> pQ = new PriorityQueue<>();\n for(int n:nums)\n pQ.add(n);\n for(int i=0;i<nums.length;i++)\n nums[i]=pQ.poll(); \n return nums;\n }\n \n}\n```\n\n# Brute force(Quick sort)\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n Sort(nums,0,nums.length-1);\n return nums;\n }\n static void Sort(int []nums,int l,int h){\n if(l>=h){\n return ;\n }\n int s=l;\n int e=h;\n int m=s+(e-s)/2;\n int p=nums[m];\n while(s<=e){\n while(nums[s]<p){\n s++;\n }\n while(nums[e] > p){\n e--;\n }\n if(s<=e){\n int t=nums[s];\n nums[s]=nums[e];\n nums[e]=t;\n s++;\n e--;\n }\n }\n Sort(nums,l,e);\n Sort(nums,s,h);\n }\n}\n\n```\n\nUpvotes are Encouraging | 6 | 0 | ['Heap (Priority Queue)', 'Quickselect', 'Java'] | 0 |
sort-an-array | Basic Merge Sort C++|| No In-Built Function Used | basic-merge-sort-c-no-in-built-function-kb8p2 | Complexity\n- Time complexity:\nO(NLOGN)\n\n- Space complexity:\nO(NLOGN)\n\n# Code\n\nclass Solution {\npublic:\n vector<int> mergesorted(vector<int>&arr)\n | Heisenberg2003 | NORMAL | 2023-03-01T00:21:09.767457+00:00 | 2023-03-01T00:46:30.409856+00:00 | 11,474 | false | # Complexity\n- Time complexity:\nO(NLOGN)\n\n- Space complexity:\nO(NLOGN)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> mergesorted(vector<int>&arr)\n {\n if(arr.size()==1)\n {\n return arr;\n }\n int dividesize=arr.size()/2;\n vector<int>merge1,merge2;\n for(int i=0;i<dividesize;i++)\n {\n merge1.push_back(arr[i]);\n }\n for(int i=dividesize;i<arr.size();i++)\n {\n merge2.push_back(arr[i]);\n }\n merge1=mergesorted(merge1);\n merge2=mergesorted(merge2);\n int ptr1=0,ptr2=0,ptr3=0;\n while(ptr3<arr.size())\n {\n if(ptr1==merge1.size())\n {\n arr[ptr3]=merge2[ptr2];\n ptr2++;\n ptr3++;\n continue;\n }\n if(ptr2==merge2.size())\n {\n arr[ptr3]=merge1[ptr1];\n ptr1++;\n ptr3++;\n continue; \n }\n if(merge1[ptr1]<merge2[ptr2])\n {\n arr[ptr3]=merge1[ptr1];\n ptr1++;\n ptr3++;\n }\n else\n {\n arr[ptr3]=merge2[ptr2];\n ptr2++;\n ptr3++;\n }\n }\n return arr;\n }\n vector<int> sortArray(vector<int>&nums) \n {\n return mergesorted(nums);\n }\n};\n``` | 6 | 2 | ['C++'] | 2 |
sort-an-array | Randomize Quick-Sort | worst case Time : O(NlogN) | randomize-quick-sort-worst-case-time-onl-ubn7 | cpp\n int partition(vector<int>&arr,int start,int end){\n int pivot=arr[end];\n int partIdx=start;\n for(int i=start;i<end;i++){\n | shashank9Aug | NORMAL | 2021-09-24T08:45:03.755198+00:00 | 2021-09-24T08:45:03.755233+00:00 | 845 | false | ```cpp\n int partition(vector<int>&arr,int start,int end){\n int pivot=arr[end];\n int partIdx=start;\n for(int i=start;i<end;i++){\n if(arr[i]<=pivot){\n swap(arr[i],arr[partIdx]);\n partIdx++;\n }\n }\n swap(arr[partIdx],arr[end]);\n return partIdx;\n }\n int randompartition(vector<int>&arr,int start,int end){\n\t\t//select random element of array :\n srand(time(NULL));\n int pI = start + rand() % (end - start);\n swap(arr[pI],arr[end]);\n return partition(arr,start,end);\n }\n void quickSort(vector<int>&arr,int start,int end){\n if(start<end){\n int partitionIndex=randompartition(arr,start,end);\n quickSort(arr,start,partitionIndex-1);\n quickSort(arr,partitionIndex+1,end);\n }\n }\n vector<int> sortArray(vector<int>& arr) {\n //Quick sort : time: O(nlogn) and space : O(1)\n quickSort(arr,0,arr.size()-1); \n return arr;\n }\n``` | 6 | 1 | ['C', 'Sorting', 'C++'] | 2 |
sort-an-array | js All Sorting Algorithms | Quick, Merge, Bucket ,Tree, heap and others... | js-all-sorting-algorithms-quick-merge-bu-59r4 | Merge Sort : O(n log n) time O(n) space \n\n\nconst merge = (left, right) => {\n const mergeArr = [];\n let i=0,j=0;\n while(i < left.length && j < rig | brahmavid | NORMAL | 2021-08-11T03:00:18.644601+00:00 | 2021-09-11T12:13:23.943813+00:00 | 963 | false | ## Merge Sort : O(n log n) time O(n) space \n\n```\nconst merge = (left, right) => {\n const mergeArr = [];\n let i=0,j=0;\n while(i < left.length && j < right.length) {\n if (left[i] <right[j]) {\n mergeArr.push(left[i++]);\n } else {\n mergeArr.push(right[j++]);\n }\n }\n while (i < left.length) {\n mergeArr.push(left[i++]);\n }\n while (j < right.length) {\n mergeArr.push(right[j++]);\n }\n \n return mergeArr;\n}\nconst mergeSort = (nums, start,end) => {\n if (end == start) {\n return [nums[start]];\n }\n const mid = start + Math.floor((end-start)/2);\n const left = mergeSort(nums, start, mid);\n const right = mergeSort(nums, mid+1, end);\n const mergeArr = merge(left, right);\n\n return mergeArr;\n}\nvar sortArray = function(nums) {\n return mergeSort(nums, 0, nums.length-1);\n};\n/*\n* Runtime: 140 ms, faster than 73.51% of JavaScript online submissions for Sort an Array.\n* Memory Usage: 54.4 MB, less than 37.99% of JavaScript online submissions for Sort an Array.\n*/\n```\n\n\n\n## Quick Sort :O(n log n) time O(1) space | worst case O(n^2)\n\n```\nconst swap = (nums, start,end) => {\n [nums[start],nums[end]] = [nums[end],nums[start]];\n}\nconst partition = (nums, start, end, pivot) => {\n let left = start, right=end;\n while(left <= right) {\n while(nums[left] < pivot && left <= end) {\n left++;\n }\n while(left <=right && nums[right] > pivot && right >= start) {\n right--;\n }\n if (left <= right) {\n swap(nums, left, right);\n left++;\n right--;\n }\n }\n \n return left;\n}\nconst quickSort = (nums, start, end) => {\n if (start >= end) return ;\n const mid = start + Math.floor((end-start)/2);\n const idx = partition(nums, start, end, nums[mid]);\n quickSort(nums, start, idx-1);\n quickSort(nums, idx, end); \n}\n\nvar sortArray = function(nums) {\n quickSort(nums, 0, nums.length-1);\n return nums;\n \n};\n/*\n*\n* Runtime: 124 ms, faster than 96.80% of JavaScript online submissions for Sort an Array.\n* Memory Usage: 50.2 MB, less than 70.74% of JavaScript online submissions for Sort an Array.\n*\n*/\n\n```\n## Heap Sort : O(n log n) time O(1) space\n```\nconst heapify = (nums, n) => {\n const parent = Math.floor((n-1)/2);\n if (parent < 0) {\n return;\n }\n if (nums[parent] > nums[n]) {\n return;\n }\n [nums[parent],nums[n]] = [nums[n],nums[parent]];\n return heapify(nums, parent)\n}\n\nconst updateHeap = (nums,n, lastIdx) => {\n if (n > lastIdx) return;\n const [left,right] = [2*n+1, 2*n+2];\n \n if (left > lastIdx) {\n return;\n }\n let next = left;\n if (right <= lastIdx && nums[left] < nums[right] ) {\n next = right\n }\n if (nums[next] > nums[n]) {\n [nums[n], nums[next]] = [nums[next],nums[n]];\n updateHeap(nums, next, lastIdx);\n } \n\n}\nconst sortArray = function(nums) {\n for(let i=1; i<nums.length;i++) {\n heapify(nums, i);\n }\n for(let i=nums.length-1;i >0;i--) {\n const max = nums[0];\n nums[0] = nums[i];\n updateHeap(nums, 0, i-1);\n nums[i] = max;\n }\n return nums;\n};\n\n/*\n*\n*Runtime: 168 ms, faster than 52.18% of JavaScript online submissions for Sort an Array.\n*Memory Usage: 49.9 MB, less than 72.85% of JavaScript online submissions for Sort an Array.\n*\n*/\n```\n# Bucket Sort : 0(d*n) t.c O(n) s.c\n`d = number of digits in max number `\n\n```\nconst bucketSort = nums => {\n let place = 1, max = -Infinity;\n for(const num of nums) {\n max = Math.max(max, num);\n }\n const dcount = String(max).length;\n for(let i =0 ;i< dcount; i++) {\n const digits = Array.from(new Array(10), () => []);\n for(const num of nums) {\n const d = Math.floor(num/place) % 10;\n digits[d].push(num);\n }\n let idx = 0;\n for(const digit of digits) {\n for(const num of digit) {\n nums[idx++] = num;\n }\n }\n place *= 10; \n }\n} \n\nvar sortArray = function(nums) {\n const p = [];\n const n = [];\n for(const num of nums) {\n const arr = num < 0 ? n : p;\n arr.push(Math.abs(num));\n }\n bucketSort(p);\n bucketSort(n);\n let idx =0;\n for(let i=n.length-1;i >= 0 ;i--) {\n nums[idx++] = -n[i];\n }\n for(const pnum of p) {\n nums[idx++] = pnum;\n }\n \n return nums;\n};\n\n```\n## Tree Sort : O(n log n) time space O(n) space \nWorst case O(n^2)(unbalanced tree) \nFor balanced tree worst O(n log n) time \n```\nclass Tree {\n constructor(val, left=null, right=null) {\n this.val = val;\n this.count = 1;\n this.left = left;\n this.right = right;\n }\n}\n\nconst find = (root, val) => {\n let node = root;\n while(node !== null) {\n if (node.val == val) {\n return node;\n }\n if (node.val > val) {\n if (!node.left) {\n return node;\n }\n node = node.left;\n } else {\n if (!node.right) {\n return node;\n }\n node = node.right;\n }\n\n }\n}\nconst insert = (root, val) => {\n const node = find(root, val);\n if (node.val == val) {\n node.count += 1;\n return;\n\n }\n if (node.val > val) {\n node.left = new Tree(val);\n } else {\n node.right = new Tree(val);\n }\n}\nconst inorder = (root, nums,idx) => {\n if (!root) return ;\n inorder(root.left, nums, idx);\n const val = root.val;\n for(let i=0;i<root.count;i++) {\n nums[idx.n] = val;\n idx.n += 1;\n }\n \n inorder(root.right,nums,idx);\n}\nvar sortArray = function(nums) {\n const root = new Tree(nums[0]);\n for(let i=1;i<nums.length;i++) {\n insert(root, nums[i]);\n }\n const idx = {n:0};\n inorder(root, nums, idx);\n \n return nums;\n}\n\n/*\nThough Tree sort passes test but is slow, blanced tree will be faster. \nRuntime: 7356 ms, faster than 5.01% of JavaScript online submissions for Sort an Array.\nMemory Usage: 59.1 MB, less than 8.95% of JavaScript online submissions for Sort an Array.\n*/\n```\n\n## Insertion Sort : O(n^2) time O(1) space | best O(n) time [TLE]\n\n```\nvar sortArray = function(nums) { \n for(let i=1;i<nums.length;i++) {\n if(nums[i-1] > nums[i]) {\n let j=i;\n while(j>=0 && nums[j-1] > nums[j]) {\n [nums[j-1], nums[j]] = [nums[j], nums[j-1]];\n j--;\n }\n }\n }\n return nums;\n}\n```\n\n## Bubble Sort : O(n^2) time [TLE]\n\n```\nvar sortArray = function(nums) {\n for(let i=0;i<nums.length;i++) {\n for(let j=0;j<nums.length;j++) {\n if (j <nums.length-1 && nums[j] > nums[j+1]) {\n [nums[j],nums[j+1]] = [nums[j+1], nums[j]];\n }\n }\n }\n \n return nums;\n};\n```\n\n\nI will add more if i feel bored and feel like coding a Sorting algorithm. \uD83D\uDE05 \uD83E\uDD20 | 6 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Merge Sort', 'JavaScript'] | 1 |
sort-an-array | Java iterative/recursive quickSort, mergeSort, 3 ways quickSort, 3 ways mergeSort, max/min heapSort | java-iterativerecursive-quicksort-merges-n6dt | Iterative quick sort\n\nclass Solution {\n public int[] sortArray(int[] nums) {\n return quickIterative(nums, 0, nums.length - 1);\n }\n \n p | lisze1 | NORMAL | 2021-05-22T22:06:06.805718+00:00 | 2021-08-07T00:13:31.483597+00:00 | 1,509 | false | Iterative quick sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n return quickIterative(nums, 0, nums.length - 1);\n }\n \n private int[] quickIterative(int[] nums, int l, int h) {\n if (l >= h) {\n return nums;\n }\n // create a stack to store the low index and high index\n int[] stack = new int[h - l + 1];\n int top = 0;\n // push low index and high index into stack\n stack[top++] = l;\n \n stack[top++] = h;\n \n while (top > 0 ) {\n // pop high and low\n h = stack[--top];\n l = stack[--top];\n // partition, p is at the correct position\n int p = this.partition(nums, l, h);\n // if pivot\'s left side has array left, push into stack;\n if (p - 1 > l) {\n stack[top++] = l;\n stack[top++] = p - 1;\n }\n // if pivot\'s right side has array left, push into stack;\n if (p + 1 < h) {\n stack[top++] = p + 1;\n stack[top++] = h;\n }\n // keep doing this until the stack is empty;\n }\n return nums;\n }\n \n private int partition(int[] nums, int head, int tail) {\n int p_index = this.getMediumValueIndex(nums, head, tail);\n int pivot = nums[p_index];\n nums[p_index] = nums[tail];\n nums[tail] = pivot;\n p_index = tail;\n int i = head - 1;\n for (int j = head; j < tail; ++j) {\n if (nums[j] <= pivot) {\n i++;\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n }\n int temp = nums[i+1];\n nums[i+1] = nums[tail];\n nums[tail] = temp;\n return i + 1;\n }\n \n \n private int getMediumValueIndex(int[] nums, int head, int tail) {\n int mid = head + (tail - head) / 2;\n int l = nums[head];\n int m = nums[mid];\n int r = nums[tail];\n if (l > m) {\n // l > m > r\n if (m > r) return mid;\n // r > l > m\n else if (r > l) return head;\n //l > r > m\n else return tail;\n \n } \n // m > l\n else {\n // r > m > l\n if (r > m) return mid;\n // m > l > r\n else if (l > r) return head;\n // m > r > l\n else return tail;\n }\n }\n}\n```\nStable iterative quick sort(TLE)\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n return quickIterative(nums, 0, nums.length - 1);\n }\n \n private int[] quickIterative(int[] nums, int l, int h) {\n if (l >= h) {\n return nums;\n }\n // create a stack to store the low index and high index\n int[] stack = new int[h - l + 1];\n int top = 0;\n // push low index and high index into stack\n stack[top++] = l;\n \n stack[top++] = h;\n \n while (top > 0 ) {\n // pop high and low\n h = stack[--top];\n l = stack[--top];\n // partition, p is at the correct position\n int p = this.partition(nums, l, h);\n // if pivot\'s left side has array left, push into stack;\n if (p - 1 > l) {\n stack[top++] = l;\n stack[top++] = p - 1;\n }\n // if pivot\'s right side has array left, push into stack;\n if (p + 1 < h) {\n stack[top++] = p + 1;\n stack[top++] = h;\n }\n // keep doing this until the stack is empty;\n }\n return nums;\n }\n \n private int partition(int[] nums, int head, int tail) {\n Queue<Integer> aux = new LinkedList<>();\n Queue<Integer> left = new LinkedList<>();\n Queue<Integer> right = new LinkedList<>();\n for (int i = head + 1; i <= tail; ++i) {\n if (nums[i] < nums[head]) {\n left.add(nums[i]);\n } else {\n right.add(nums[i]);\n }\n }\n aux.addAll(left);\n aux.add(nums[head]);\n aux.addAll(right);\n for (int i = head; i <= tail; ++i) {\n nums[i] = aux.remove();\n }\n return head + left.size();\n }\n \n private int getMediumValueIndex(int[] nums, int head, int tail) {\n int mid = head + (tail - head) / 2;\n int l = nums[head];\n int m = nums[mid];\n int r = nums[tail];\n if (l > m) {\n // l > m > r\n if (m > r) return mid;\n // r > l > m\n else if (r > l) return head;\n //l > r > m\n else return tail;\n \n } \n // m > l\n else {\n // r > m > l\n if (r > m) return mid;\n // m > l > r\n else if (l > r) return head;\n // m > r > l\n else return tail;\n }\n }\n}\n```\n\n\nRecursive quick sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n if (nums.length <= 1) return nums;\n this.qHelper(nums, 0, nums.length - 1);\n return nums;\n }\n \n private void qHelper(int[] nums, int head, int tail) {\n if (head >= tail) return;\n int pivot = this.partition(nums, head, tail);\n this.qHelper(nums, head, pivot-1);\n this.qHelper(nums, pivot+1, tail);\n }\n \n private int partition(int[] nums, int head, int tail) {\n // use the index with medium value as pivot point.\n int pivot_index = this.getMediumValueIndex(nums, head, tail);\n int pivot = nums[pivot_index];\n // int temp = nums[pivot_index];\n nums[pivot_index] = nums[tail];\n nums[tail] = pivot;\n pivot_index = tail;\n int i = head - 1;\n for (int j = head; j < tail; ++j) {\n if (nums[j] < pivot) {\n ++i;\n //swap i and j\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n }\n }\n // swap i+1 and pivot_index\n int temp = nums[i+1];\n nums[i+1] = nums[pivot_index];\n nums[pivot_index] = temp;\n return i+1;\n \n }\n \n private int getMediumValueIndex(int[] nums, int head, int tail) {\n int mid = head + (tail - head) / 2;\n int l = nums[head];\n int m = nums[mid];\n int r = nums[tail];\n if (l > m) {\n // l > m > r\n if (m > r) return mid;\n // r > l > m\n else if (r > l) return head;\n //l > r > m\n else return tail;\n \n } \n // m > l\n else {\n // r > m > l\n if (r > m) return mid;\n // m > l > r\n else if (l > r) return head;\n // m > r > l\n else return tail;\n }\n }\n \n```\nStable recursive quick sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n List<Integer> l = new ArrayList<>();\n for (int i : nums) {\n l.add(i);\n }\n List<Integer> res = this.quickSort(l);\n int size = nums.length;\n for (int i = 0; i < size; ++i) {\n nums[i] = res.get(i);\n }\n return nums;\n }\n public static List<Integer> quickSort(List<Integer> ar) {\n // Base case\n if(ar.size() <= 1) {\n return ar;\n }\n // Let us choose middle element a pivot \n int mid = ar.size() / 2;\n int pivat = ar.get(mid);\n \n // key element is used to break the array\n // into 2 halves according to their values\n List<Integer> smaller = new ArrayList<>();\n List<Integer> greater = new ArrayList<>();\n \n // Put greater elements in greater list,\n // smaller elements in smaller list. Also,\n // compare positions to decide where to put. \n for (int ind = 0; ind < ar.size(); ind++) {\n int val = ar.get(ind);\n if ( ind != mid ) {\n if ( val < pivat ) {\n smaller.add(val);\n } else if (val > pivat) {\n greater.add(val);\n } else {\n // If value is same, then considering\n // position to decide the list. \n if(ind < mid) {\n smaller.add(val);\n } else {\n greater.add(val);\n }\n }\n }\n }\n List<Integer> ans = new ArrayList<Integer>(); \n List<Integer> sa1 = quickSort(smaller);\n List<Integer> sa2 = quickSort(greater);\n // add all elements of smaller list into ans list\n for (Integer val1 : sa1) {\n ans.add(val1);\n } \n // add pivat element into ans list \n ans.add(pivat);\n // add all elements of greater list into ans list\n for(Integer val2 : sa2) {\n ans.add(val2);\n }\n // return ans list\n return ans; \n }\n}\n```\n\n\n3 ways quick sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n this.quick3(nums, 0, nums.length - 1);\n return nums;\n }\n \n private void quick3(int[] nums, int start, int end) {\n if (start >= end) {\n return;\n }\n \n // choose the mid point as the pivot\n int m = this.pickMediumIndex(nums, start, end, (start + (end - start)) / 2);\n int pivot = nums[m];\n \n int temp = nums[start];\n nums[start] = nums[m];\n nums[m] = temp;\n \n int l = start;\n int r = end;\n int i = l + 1;\n // start the process;\n while (i <= r) {\n // if less, move to front\n if (nums[i] < pivot) {\n int tmp = nums[i];\n nums[i] = nums[l];\n nums[l] = tmp;\n ++i;\n ++l;\n }\n // if equal, just keep the same position and move to next index.\n else if (nums[i] == pivot) {\n ++i;\n } \n // if greater, move to end;\n // we do not increment i here because we do not know if the new element in ith position is greater or less than pivot.\n else {\n int tmp = nums[i];\n nums[i] = nums[r];\n nums[r] = tmp;\n --r;\n }\n }\n this.quick3(nums, start, l-1);\n this.quick3(nums, r + 1, end);\n }\n \n private int pickMediumIndex(int[] nums, int head, int tail, int mid) {\n int l = nums[head];\n int m = nums[mid];\n int r = nums[tail];\n if (l > m) {\n // l > m > r\n if (m > r) return mid;\n // r > l > m\n else if (r > l) return head;\n //l > r > m\n else return tail;\n \n } \n // m > l\n else {\n // r > m > l\n if (r > m) return mid;\n // m > l > r\n else if (l > r) return head;\n // m > r > l\n else return tail;\n }\n }\n}\n```\n\nIterative merge sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n mergeSort2(nums);\n return nums;\n }\n private void mergeSort2(int[] nums) {\n for (int size = 1; size < nums.length; size *= 2) {\n for (int i = 0; i < nums.length - size; i += 2 * size) {\n int mid = i + size - 1;\n int end = Math.min(i + 2 * size - 1, nums.length - 1);\n merge2(nums, i, mid, end);\n }\n }\n }\n private void merge2(int[] nums, int l, int mid, int r) {\n int[] tmp = new int[r - l + 1];\n int i = l, j = mid + 1, k = 0;\n while (i <= mid || j <= r) {\n if (i > mid) {\n tmp[k] = nums[j];\n ++k;\n ++j;\n } else if (j > r) {\n tmp[k] = nums[i];\n ++k;\n ++i;\n } else if (nums[i] > nums[j]) {\n tmp[k] = nums[j];\n ++k;\n ++j;\n } else {\n tmp[k] = nums[i];\n ++k;\n ++i;\n }\n }\n for (i = l; i <= r; ++i) {\n nums[i] = tmp[i-l];\n }\n }\n}\n```\n\nRecursive merge sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n return mergeSort(nums);\n \n }\n \n private int[] mergeSort(int[] nums) {\n if (nums.length <= 1) return nums;\n int length = nums.length;\n int mid = nums.length / 2;\n int[] left = new int[mid];\n for (int i = 0; i < mid; ++i) {\n left[i] = nums[i];\n }\n int[] right = new int[nums.length - mid];\n for (int i = mid; i < length; ++i) {\n right[i - mid] = nums[i];\n }\n left = mergeSort(left);\n right = mergeSort(right);\n return merge(left, right);\n }\n private int[] merge(int[] l, int[] r) {\n int[] res = new int[l.length+r.length];\n int lLen = l.length;\n int rLen = r.length;\n int i = 0;\n int li = 0;\n int ri = 0;\n while (lLen > 0 && rLen > 0) {\n if (l[li] <= r[ri]) {\n res[i] = l[li];\n ++i;\n li++;\n --lLen;\n } else {\n res[i] = r[ri];\n ++i;\n ri++;\n --rLen;\n }\n }\n while (lLen > 0) {\n res[i] = l[li];\n --lLen;\n ++i;\n ++li;\n }\n while (rLen > 0) {\n res[i] = r[ri];\n --rLen;\n ++i;\n ++ri;\n }\n return res;\n }\n}\n```\n\nMax Heap Sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n return maxHeapSort(nums);\n }\n \n private int[] maxHeapSort(int[] nums) {\n int[] res = new int[nums.length];\n int size = nums.length;\n // build heap. start from first half because the second half is children.\n for (int i = size / 2 - 1; i >= 0; --i) {\n this.maxHeapify(nums, size, i);\n }\n for (int i = size - 1; i >= 0; --i) {\n // put current node to the end;\n int temp = nums[0];\n nums[0] = nums[i];\n nums[i] = temp;\n // put current largest into ith position.\n this.maxHeapify(nums, i, 0);\n }\n return nums;\n }\n \n private void maxHeapify(int[] nums, int size, int i) {\n int largest = i; \n int left = 2*i + 1;\n int right = 2*i + 2;\n if (left < size) {\n if (nums[left] > nums[largest]) largest = left;\n }\n if (right < size) {\n if (nums[right] > nums[largest]) largest = right;\n }\n if (largest != i) {\n int temp = nums[i];\n nums[i] = nums[largest];\n nums[largest] = temp;\n this.maxHeapify(nums, size, largest);\n }\n }\n}\n```\n\nMin Heap Sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n this.heapSort(nums, nums.length);\n return nums;\n }\n \n // main function to do heap sort\n static void heapSort(int arr[], int n)\n {\n // Build heap (rearrange array)\n for (int i = n / 2 - 1; i >= 0; i--)\n heapify(arr, n, i);\n \n // One by one extract an element from heap\n for (int i = n - 1; i >= 0; i--) {\n \n // Move current root to end\n int temp = arr[0];\n arr[0] = arr[i];\n arr[i] = temp;\n \n // call max heapify on the reduced heap\n heapify(arr, i, 0);\n }\n int l = 0;\n int r = n - 1;\n while (l < r) {\n int temp = arr[l];\n arr[l] = arr[r];\n arr[r] = temp;\n ++l;\n --r;\n }\n }\n \n static void heapify(int arr[], int n, int i)\n {\n int smallest = i; // Initialize smalles as root\n int l = 2 * i + 1; // left = 2*i + 1\n int r = 2 * i + 2; // right = 2*i + 2\n \n // If left child is smaller than root\n if (l < n && arr[l] < arr[smallest])\n smallest = l;\n \n // If right child is smaller than smallest so far\n if (r < n && arr[r] < arr[smallest])\n smallest = r;\n \n // If smallest is not root\n if (smallest != i) {\n int temp = arr[i];\n arr[i] = arr[smallest];\n arr[smallest] = temp;\n \n // Recursively heapify the affected sub-tree\n heapify(arr, n, smallest);\n }\n }\n}\n```\n\n3 way merge sort\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n return this.merge3ways(nums);\n }\n \n private int[] merge3ways(int[] nums) {\n if (nums == null) {\n return nums;\n }\n \n int length = nums.length;\n int[] tar = new int[length];\n for (int i = 0; i < length; ++i) {\n tar[i] = nums[i];\n }\n this.mergeSort(nums, 0, length, tar);\n return nums;\n }\n \n private void mergeSort(int[] ori, int l, int h, int[] tar) {\n if (h - l < 2) {\n return;\n }\n int m1 = l + ((h - l) / 3);\n int m2 = l + 2 * ((h - l) / 3) + 1;\n this.mergeSort(tar, l, m1, ori);\n this.mergeSort(tar, m1, m2, ori);\n this.mergeSort(tar, m2, h, ori);\n this.merge(tar, l, m1, m2, h, ori);\n }\n \n private void merge(int[] ori, int low, int m1, int m2, int h, int[] tar) {\n int i = low;\n int j = m1;\n int k = m2;\n int l = low;\n while ( (i < m1) && (j < m2) && (k < h)) {\n if (ori[i] < ori[j]) {\n if (ori[i] < ori[k]) {\n tar[l++] = ori[i++];\n } else {\n tar[l++] = ori[k++];\n }\n } else {\n if (ori[j] < ori[k]) {\n tar[l++] = ori[j++];\n } else {\n tar[l++] = ori[k++];\n }\n }\n }\n \n while ( (i < m1) && (j < m2)) {\n if (ori[i] < ori[j]) {\n tar[l++] = ori[i++];\n } else {\n tar[l++] = ori[j++];\n }\n }\n \n while ((j < m2) && (k < h)) {\n if (ori[j] < ori[k]) {\n tar[l++] = ori[j++];\n } else {\n tar[l++] = ori[k++];\n }\n }\n \n while ( (i < m1) && (k < h)) {\n if (ori[i] < ori[k]) {\n tar[l++] = ori[i++];\n } else {\n tar[l++] = ori[k++];\n }\n }\n \n while (i < m1) {\n tar[l++] = ori[i++];\n }\n \n while (j < m2) {\n tar[l++] = ori[j++];\n }\n \n while (k < h) {\n tar[l++] = ori[k++];\n }\n }\n}\n``` | 6 | 0 | ['Recursion', 'Sorting', 'Heap (Priority Queue)', 'Merge Sort', 'Iterator', 'Java'] | 0 |
sort-an-array | Iterative merge sort | iterative-merge-sort-by-antrixm-f3tj | \nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n \n nums = [[num] for num in nums]\n\n def merge(l1, l2):\n | antrixm | NORMAL | 2020-05-11T14:28:49.454410+00:00 | 2020-05-11T14:28:49.454460+00:00 | 1,358 | false | ```\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n \n nums = [[num] for num in nums]\n\n def merge(l1, l2):\n i = 0\n j = 0\n new = []\n \n while i < len(l1) and j < len(l2):\n if l1[i] < l2[j]:\n new.append(l1[i])\n i += 1\n else:\n new.append(l2[j])\n j += 1\n \n while i < len(l1):\n new.append(l1[i])\n i += 1\n \n while j < len(l2):\n new.append(l2[j])\n j += 1\n \n return new\n\n \n while len(nums) > 1:\n new = []\n for i in range(0, len(nums), 2):\n if i + 1 < len(nums):\n new_arr = merge(nums[i], nums[i+1])\n new.append(new_arr)\n else:\n new.append(nums[i])\n nums = new\n \n return nums[0]\n``` | 6 | 0 | ['Merge Sort', 'Iterator', 'Python', 'Python3'] | 1 |
sort-an-array | C++ -- Merge sort, Quick sort, Heap sort, Bubble sort, Insert sort, Selection sort. | c-merge-sort-quick-sort-heap-sort-bubble-g1br | \nclass Solution {\npublic:\n /*\n 1. Bubble sort:\n Worstcase time: O(n^2), Bestcase Time: O(n) - list already sorted, Space: O(1)\n */\n vecto | magrawa4 | NORMAL | 2020-03-02T00:19:53.731861+00:00 | 2020-03-02T00:19:53.731908+00:00 | 1,063 | false | ```\nclass Solution {\npublic:\n /*\n 1. Bubble sort:\n Worstcase time: O(n^2), Bestcase Time: O(n) - list already sorted, Space: O(1)\n */\n vector<int> bubbleSort(vector<int>& nums) {\n for(int i=0;i<nums.size()-1;i++){\n bool found = false;\n for (int j=0;j<nums.size()-i-1;j++){\n if (nums[j]>nums[j+1]){\n found = true;\n swap(nums[j],nums[j+1]);\n }\n }\n if (!found)\n return nums;\n }\n return nums;\n }\n \n\t\n /*\n 2. Insertion sort: (Inserting ith element in the proper position)\n Worstcase time: O(n^2), Bestcase Time: O(n) - list already sorted, Space: O(1)\n */\n vector<int> insertionSort(vector<int>& nums) {\n for(int i=0;i<nums.size();i++){\n int j = i;\n while (j>0 && nums[j-1]>nums[j]){\n swap(nums[j],nums[j-1]);\n j--;\n }\n }\n return nums; \n }\n\n\n /*\n 3. Selection sort: (Select the min/max value based on current element and swap it)\n Worstcase time: O(n^2), Bestcase Time: O(n^2), Space: O(1)\n */\n vector<int> selectionSort(vector<int>& nums) {\n for(int i=0;i<nums.size()-1;i++){\n int minIndex = i;\n for (int j=i+1;j<nums.size();j++){\n if (nums[minIndex]>nums[j])\n minIndex = j;\n }\n swap(nums[i], nums[minIndex]);\n }\n return nums;\n }\n\n\n /*\n 4. Merge sort: (divide and concur)\n Worstcase time: O(nlogn), Bestcase Time: O(nlogn), Space: O(n) (not considering recursion call stack space)\n It is a divide and concure technique which \n Divide: Break the given problem into sub-problems of same type.\n Conquer: Recursively solve these sub-problems\n Combine: Appropriately combine the answers\n 1. Base operation: find the mid elemet\n 2. Divide and concure part: divide the array into two halves and recursively solve these sub-problems\n 3. Combine part: appropriately add sorted two halves arrays\n T(n) = 0(1)(Finding mid index -- preprocessing) + 2T(n/2) + O(N) (merging - postprocessing)\n T(n) = 2T(n/2) + O(n) --> O(nlong)\n T(N) = aT(n/b) + f(n) -- > logn(baseb) is the height and max no of leafs is a^heigh and total number a^(height+1)-1 (Here n is the length of the array)\n According to master method:\n T(N) = aT(n/b) + f(n)\n T(n) = \u0398(nloga(baseb)) when f(n) has slower growth that n^loga(baseb)\n T(n) = \u0398(nloga(baseb) log n) when f(n) has equal growth that n^loga(baseb)\n T(n) = \u0398(f(n)) when f(n) has faster growth that n^loga(baseb) \n */\n void merge(vector<int>& nums, int low, int mid, int high) {\n int leftLength = mid-low + 1;\n int rightLength = high -mid; // high-(mid+1)+1\n vector<int> leftList(nums.begin()+low, nums.begin()+mid+1);\n vector<int> rightList(nums.begin()+mid+1, nums.begin()+high+1); \n int i=0,j=0,cur=low;\n while(i<leftLength && j<rightLength){\n if (leftList[i]<rightList[j]){\n nums[cur] = leftList[i];\n i++;\n cur++;\n } else {\n nums[cur] = rightList[j];\n j++;\n cur++; \n } \n }\n while(i<leftLength){\n nums[cur] = leftList[i];\n i++;\n cur++;\n }\n while(j<rightLength){\n nums[cur] = rightList[j];\n j++;\n cur++;\n } \n }\n void mergeSortHelper(vector<int>& nums, int low, int high) {\n if (low<high){\n int mid = (high-low)/2 + low;\n mergeSortHelper(nums, low, mid);\n mergeSortHelper(nums, mid+1, high);\n merge(nums, low, mid, high);\n }\n }\n vector<int> mergeSort(vector<int>& nums) {\n mergeSortHelper(nums, 0, nums.size()-1);\n return nums;\n }\n\n\n /*\n 5. Heapsort (Using heap)\n Worstcase time: O(nlogn), Bestcase Time: O(n)(when all elements are same then heapify will not cost O(logn), it will be O(1)), Space: O(1) (not including recursive function stack space.)\n */ \n // heapify opertaion for max heap\n void heapify(vector<int>& nums, int index, int size){\n int lChildIndex = 2*index +1;\n int rChildIndex = 2*index +2;\n int nextIndex = index;\n if (lChildIndex<size && nums[lChildIndex]>nums[nextIndex])\n nextIndex = lChildIndex;\n if (rChildIndex<size && nums[rChildIndex]>nums[nextIndex])\n nextIndex = rChildIndex;\n if (nextIndex != index){\n swap(nums[index], nums[nextIndex]);\n heapify(nums, nextIndex, size);\n }\n }\n void heapSortHelper(vector<int>& nums){\n // Make the array as max heap. Time complexity is O(n), it is not nlogn because height considered in each call is not the same and decreases.\n for (int i=nums.size()/2;i>=0;i--){ \n heapify(nums, i, nums.size());\n }\n // Swap 0th element with last, as 0 will be the max element and then heapify the 0th element by passing size as last-1. Time complexity is nlogn, and it will be n if all elements are same.\n for (int i=nums.size()-1;i>=0;i--){\n swap(nums[0], nums[i]);\n heapify(nums, 0, i);\n }\n }\n vector<int> heapSort(vector<int>& nums) {\n heapSortHelper(nums);\n return nums;\n }\n\n\n /*\n 6. Quick sort:\n Worstcase time: O(n^2), Bestcase Time: O(nlogn), Ave: O(nlogn), Space: O(1)-- not including recursive function stack space.\n Quicksort uses divide-and-conquer approach.\n 1. Base operation: find pivot element\n 2. Divide and concure art: divide the array into two halves and recursselvy quicksort the array\n 3. Combine part do nothing\n best case and avg case when partition element is around middle and in that case\n T(n) = O(n) + 2T((n-1)/2) + Nothing -- best case \n T(n) = O(n) + T(9n/10)+ T(n/10) -- > O(n logn) -- averge case\n Worstcase when partition element is around start and end every time -- revered sorted input list provided here:\n T(n) = O(n) + T(n-1) + Nothing -- > O(n + n-1 + n-2 + .. ) --> O(n^2)\n We can use randomized quicksort which gives worst case complexity as O(n logn) by picking pivot element randomly. But it can not gurantee, complexity can go to O(n^2) here also.\n */\n \n int partitionIndex(vector<int>& nums, int low, int high){\n int index = low-1;\n for (int j=low;j<=high;j++){\n if (nums[j]<= nums[high]){\n index++;\n swap(nums[index], nums[j]);\n }\n }\n return index;\n }\n void quickSortHelper(vector<int>& nums, int low, int high){\n if (low<high){\n int p = partitionIndex(nums, low, high);\n quickSortHelper(nums, low, p-1);\n quickSortHelper(nums, p+1, high);\n }\n }\n vector<int> quickSort(vector<int>& nums) {\n quickSortHelper(nums, 0, nums.size()-1);\n return nums;\n }\n /*\n Note considering high index for finding partition element gives O(n^2) time complexity in case list is sorted in reverse order. So to increase the probability of getting O(nlogn) complexity, randomized quick sort can be used. \n int partitionIndex(vector<int>& nums, int low, int high){\n int randIndex = low + rand()%(high-low+1);\n swap(nums[randIndex], nums[high]);\n int index = low-1;\n for (int j=low;j<=high;j++){\n if (nums[j]<= nums[high]){\n index++;\n swap(nums[index], nums[j]);\n }\n }\n return index;\n }\n */\n \n vector<int> sortArray(vector<int>& nums) {\n //bubbleSort(nums);\n //insertionSort(nums);\n //selectionSort(nums);\n //heapSort(nums);\n mergeSort(nums);\n //quickSort(nums);\n return nums;\n }\n};\n``` | 6 | 1 | [] | 1 |
sort-an-array | JavaScript Merge Sort and Quick Sort Solution | javascript-merge-sort-and-quick-sort-sol-6llx | Merge Short Solution\n\n\nvar sortArray = function(nums) {\n let len = nums.length;\n if(len < 2) return nums;\n const mid = Math.floor(len / 2);\n | ruzdi | NORMAL | 2019-12-07T19:42:39.363914+00:00 | 2019-12-07T19:42:39.363961+00:00 | 1,171 | false | **Merge Short Solution\n**\n```\nvar sortArray = function(nums) {\n let len = nums.length;\n if(len < 2) return nums;\n const mid = Math.floor(len / 2);\n const left = sortArray(nums.slice(0, mid));\n const right = sortArray(nums.slice(mid, len));\n return merge(left, right);\n \n};\n\nfunction merge(left, right) {\n let res = [];\n while(left.length && right.length) {\n res.push( (left[0] < right[0]) ? left.shift() : right.shift() );\n }\n return res.concat(left, right);\n}\n```\n\n**Quick Sort Solution\n**\n\n```\nvar sortArray = function(nums) {\n let len = nums.length;\n if(len < 2) return nums;\n let pivot = nums[0], left=[], right = [];\n\n\n for(let i=1; i<len; i++) {\n if(nums[i] <= pivot) {\n left.push(nums[i])\n } else {\n right.push(nums[i])\n }\n }\n \n return sortArray(left).concat(pivot, sortArray(right));\n \n};\n``` | 6 | 0 | ['Merge Sort', 'JavaScript'] | 2 |
sort-an-array | golang merge sort | golang-merge-sort-by-craig08-2hrj | Merge sort, O(n) space and O(nlog(n)) time complexity.\ngo\nfunc sortArray(nums []int) []int {\n mergesort(nums, 0, len(nums))\n return nums\n}\n\nfunc me | craig08 | NORMAL | 2019-06-19T14:38:04.697347+00:00 | 2019-06-19T15:11:03.912698+00:00 | 558 | false | Merge sort, O(n) space and O(nlog(n)) time complexity.\n```go\nfunc sortArray(nums []int) []int {\n mergesort(nums, 0, len(nums))\n return nums\n}\n\nfunc mergesort(nums []int, start, end int) {\n if start >= end-1 {\n return\n }\n mergesort(nums, start, (start+end)/2)\n mergesort(nums, (start+end)/2, end)\n merge(nums, start, end)\n}\n\nfunc merge(nums []int, start, end int) {\n arr, mid := make([]int, end-start), (start+end)/2\n for i, j, k := start, mid, 0; k < len(arr); k++ {\n if j == end || (i < mid && nums[i] < nums[j]) {\n arr[k] = nums[i]\n i++\n } else {\n arr[k] = nums[j]\n j++\n }\n }\n copy(nums[start:end], arr)\n}\n``` | 6 | 0 | ['Go'] | 0 |
sort-an-array | O(N) Sort Solution💕🐍 | on-sort-solution-by-jyot_150-cgtd | \n# Complexity\n- Time complexity:\n O(n) \n\n- Space complexity:\n O(n) \n\n# Code\njs\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]: | jyot_150 | NORMAL | 2024-07-25T03:36:41.325804+00:00 | 2024-07-25T03:36:41.325840+00:00 | 789 | false | \n# Complexity\n- Time complexity:\n $$O(n)$$ \n\n- Space complexity:\n $$O(n)$$ \n\n# Code\n```js\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n arr=[0]*(10**5+1)\n for i in nums:\n arr[i+(50000)]+=1\n new=[]\n for i in range(len(arr)):\n if arr[i]:\n for j in range(arr[i]):\n new.append(i-50000)\n return new\n``` | 5 | 0 | ['Python3'] | 3 |
sort-an-array | Using QuickSort(median as a pivot) which works and mergeSort!! | using-quicksortmedian-as-a-pivot-which-w-xphk | Intuition\n Describe your first thoughts on how to solve this problem. \nSince this problem requires O(nlog\u2061n) time complexity, two sorting techniques that | sarahejaz77 | NORMAL | 2024-06-14T18:04:10.931291+00:00 | 2024-06-14T18:59:25.003864+00:00 | 167 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince this problem requires O(nlog\u2061n) time complexity, two sorting techniques that comes to our mind at first is merge and quick sort (without using any built-in functions).\nThe plan wasn\'t to write this post and on that account this is my first such post on LinkedIn but after going through lot of solutions and discussions, I thought my post will make some contribution. \nI saw a lot of folks having doubts like why isn\'t quick sort working on this problem statement? Few months back Quick Sort was working really fine why not now?\nWell, to answer this and showing my approach I am writing this post! However Quick Sort isn\'t the most optimal one, so if you\'re looking for an optimal approach then it isn\'t for you.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach is really simple, plain quicksort and merge sort! However the trick is in the partition function. \n### Quick Sort \nQuick Sort uses a Divide and Conquer approach, We can choose the pivot element. The key process in quicksort is partition(). The target of partition function is to place the pivot element properly, as to the smaller elements than pivot are to the left and greater elements to the right of the pivot. \n\n\nPartition in Quick Sort can be done in multiple ways :\n - Always pick the first element as a pivot.\n - Always pick the last element as a pivot \n - Pick a random element as a pivot.\n - Pick the middle as the pivot.\n\nIn my first approach I was picking the starting element as the pivot element\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n //without using built-in fn in nlogn time complexity -> quick \n //sort\n quickSort(nums,0,nums.length-1);\n return nums;\n }\n private void quickSort(int[] a, int lb , int ub){\n if (lb<ub){\n int loc = partition(a, lb,ub);\n quickSort(a, lb,loc-1);\n quickSort(a, loc+1,ub);\n }\n }\n private int partition(int[] a, int lb, int ub){\n int pivot = a[lb];\n int start=lb;\n int end = ub;\n while(start<end){\n while(start<=end && a[start]<=pivot){\n start++; \n }\n while(start<=end && a[end]>pivot){\n end--;\n }\n if(start<end){\n swap(a, start, end);\n }\n }\n swap(a, lb, end);\n return end;\n }\n private void swap(int[]a , int i, int j){\n int temp = a[i];\n a[i]=a[j];\n a[j]=temp;\n }\n}\n\n```\nBut this approach was giving TLE (Time Limit Exceeded). Why is it so?\nThe time complexity of Quick Sort is generally O(nlog\u2061n) , but this can degrade to O(n^2) in the worst-case scenarios, depending on how the pivot is chosen. \nWorst Case:\nThe Worst case in this problem is the array is nearly sorted and if we choose start or end element as the pivot element complexity could go to O(n^2) as it can lead to unbalanced partition which can result to one subarray of n-1 size and another of 0. To avoid this , we can simply choose the median or randomized partition which reduces the chances of worst case scenario. In my second approach I have chosen the median(middle) element to be the partition which tends to create more balanced partition which reduces the probability of worst case scenario.\n\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n quickSort(nums, 0, nums.length - 1);\n return nums;\n }\n\n private void quickSort(int[] a, int lb, int ub) {\n if (lb < ub) {\n int loc = partition(a, lb, ub);\n quickSort(a, lb, loc - 1);\n quickSort(a, loc + 1, ub);\n }\n }\n\n private int partition(int[] a, int lb, int ub) {\n int mid = lb + (ub - lb) / 2;\n swap(a, mid, lb); \n int pivot = a[lb]; \n int start = lb;\n int end = ub;\n\n while (start < end) {\n while (start <= end && a[start] <= pivot) {\n start++;\n }\n while (start <= end && a[end] > pivot) {\n end--;\n }\n if (start < end) {\n swap(a, start, end);\n }\n }\n swap(a, lb, end);\n return end;\n }\n\n private void swap(int[] a, int i, int j) {\n int temp = a[i];\n a[i] = a[j];\n a[j] = temp;\n }\n}\n\n```\nBetter approach will be simple merge sort which again uses divide and conquer approach and is safe with O(nlogn)\nwhich is mentioned below\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(logn)\n O(n) // for merge sort\n\n# Code\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n mergeSort(nums, 0, nums.length - 1);\n return nums;\n }\n\n private static void mergeSort(int[] A, int lb, int ub) {\n if (lb < ub) {\n int mid = (lb + ub) / 2;\n mergeSort(A, lb, mid);\n mergeSort(A, mid + 1, ub);\n merge(A, lb, mid, ub);\n }\n }\n\n private static void merge(int[] A, int lb, int mid, int ub) {\n int i = lb;\n int j = mid + 1;\n int k = 0; \n int[] b = new int[ub - lb + 1];\n\n while (i <= mid && j <= ub) {\n if (A[i] <= A[j]) {\n b[k++] = A[i++];\n } else {\n b[k++] = A[j++];\n }\n }\n\n while (i <= mid) {\n b[k++] = A[i++];\n }\n while (j <= ub) {\n b[k++] = A[j++];\n }\n for (i = 0; i < b.length; i++) {\n A[lb + i] = b[i];\n }\n }\n}\n\n```\nPlease do upvote my post! | 5 | 0 | ['Java'] | 0 |
sort-an-array | Heap | heap-by-riya_bhadauriya-wwe7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Riya_bhadauriya | NORMAL | 2023-04-21T06:57:29.574571+00:00 | 2023-04-21T06:57:29.574599+00:00 | 571 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n heap=[]\n final=[]\n for i in range(len(nums)):\n heapq.heappush(heap,nums[i])\n while(heap):\n a=heapq.heappop(heap)\n final.append(a)\n return(final)\n\n\n``` | 5 | 0 | ['Heap (Priority Queue)', 'Python3'] | 3 |
sort-an-array | Merge Sort | Most Optimized | merge-sort-most-optimized-by-_aman_gupta-v5m3 | # Intuition \n\n\n\n\n\n# Complexity\n- Time complexity: O(n * log(n))\n\n\n- Space complexity: O(n)\n\n\n# Code\n\nvoid merge(int arr[], int l, int r, int mi | _aman_gupta_ | NORMAL | 2023-03-15T09:51:21.262103+00:00 | 2023-03-15T09:51:21.262131+00:00 | 620 | false | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n * log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nvoid merge(int arr[], int l, int r, int mid) { /* DR167937-ag255126-01 -> */\n int lsize = mid - l + 1, rsize = r - mid;\n int left[lsize];\n int i, j, k;\n int *right = arr + mid + 1;\n for(i = 0; i < lsize; i++)\n left[i] = arr[l + i];\n i = 0, j = 0, k = l;\n while(i < lsize && j < rsize) {\n if(left[i] < right[j])\n arr[k++] = left[i++];\n else\n arr[k++] = right[j++];\n }\n while(i < lsize)\n arr[k++] = left[i++];\n while(j < rsize)\n arr[k++] = right[j++];\n}\nvoid mergesort(int arr[], int l, int r) {\n if(l < r) {\n int mid = l + (r - l) / 2;\n mergesort(arr, l, mid);\n mergesort(arr, mid + 1, r);\n merge(arr, l, r, mid);\n }\n} /* <- DR167937-ag255126-01 -> */\nint* sortArray(int* nums, int numsSize, int* returnSize){\n mergesort(nums, 0, numsSize - 1);\n *returnSize = numsSize;\n return nums;\n}\n``` | 5 | 0 | ['Array', 'C', 'Merge Sort'] | 1 |
sort-an-array | 912. Sort an Array c++solution | 912-sort-an-array-csolution-by-loverdram-jjh3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | loverdrama699 | NORMAL | 2023-03-01T15:09:52.611797+00:00 | 2023-03-01T15:09:52.611832+00:00 | 1,587 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n int n = nums.size();\n mergeSort(nums, n);\n return nums;\n }\n void mergeSort(vector<int> &A, int n)\n {\n if (n < 2)\n return;\n int mid = n / 2;\n vector<int> L;\n vector<int> R;\n\n for (int i = 0; i < n; i++)\n {\n if (i < mid)\n {\n L.push_back(A[i]);\n }\n else\n R.push_back(A[i]);\n }\n mergeSort(L, L.size());\n mergeSort(R, R.size());\n mergeArrays(A, L, R);\n }\n\n void mergeArrays(vector<int> &A, vector<int> &L, vector<int> &R)\n {\n\n int sizeL = L.size();\n int sizeR = R.size();\n int i = 0, j = 0, k = 0;\n\n while (i < sizeL && j < sizeR)\n {\n if (L[i] <= R[j])\n {\n A[k] = L[i];\n i++;\n }\n else\n {\n A[k] = R[j];\n j++;\n }\n k++;\n }\n while (i < sizeL)\n {\n A[k] = L[i];\n i++;\n k++;\n }\n while (j < sizeR)\n {\n A[k] = R[j];\n j++;\n k++;\n }\n }\n};\n``` | 5 | 0 | ['C++'] | 1 |
sort-an-array | HEAP SORT🔄 | O(1) Space Complexity🔥| C++ | heap-sort-o1-space-complexity-c-by-bahni-wwjp | Intuition\nHeap Sort and Merge Sort are such Sorting Algorithms that has the time complexity of O(nlogn). Merge Sort has a Space Complexity of O(n), but Heap so | Bahniman14 | NORMAL | 2023-03-01T11:41:12.755054+00:00 | 2023-06-19T17:47:56.403782+00:00 | 258 | false | # Intuition\nHeap Sort and Merge Sort are such Sorting Algorithms that has the time complexity of O(nlogn). Merge Sort has a Space Complexity of O(n), but Heap sort can be done in O(1), as it doesn\'t take extra space. As the Question suggests to take the **smallest space complexity possible,** it is better to go with Heap Sort.\n\n# Approach\n1. We are converting the given Array to a Max-heap by **Build Heap Algorithm**.\n2. Then We are Sorting the Array by the moving the current Maximum element to the end of the Array and appling **Heapify Algorithm** to the rest of the unsorted array at every iteration.\n\n# Complexity\n- Time complexity: O(nlogn)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n void Max_Heapify(vector<int> &nums, int i, int N){\n int left = 2*i + 1;\n int right = 2 * i + 2;\n int largest = i;\n if(left <= N && nums[left] > nums[largest])\n largest = left;\n if(right <= N && nums[right] > nums[largest])\n largest = right;\n if(largest != i){\n swap(nums[largest], nums[i]);\n Max_Heapify(nums, largest, N);\n }\n \n }\n void Build_Max_Heap(vector<int> &nums, int N){\n for(int i = N/2; i>= 0; i--){\n Max_Heapify(nums, i, N);\n }\n }\n void HeapSort(vector<int> &nums, int N){\n for(int i = N; i > 0; i--){\n swap(nums[0],nums[i]);\n Max_Heapify(nums, 0, i-1);\n }\n }\n vector<int> sortArray(vector<int>& nums) {\n int N = nums.size()-1;\n Build_Max_Heap(nums, N);\n HeapSort(nums, N);\n return nums;\n }\n};\n```\n*Please Upvote if the code and explanation is helpful to you* | 5 | 0 | ['C++'] | 3 |
sort-an-array | [Python][QuickSort] Quick sort with random partition | pythonquicksort-quick-sort-with-random-p-d563 | Quick sort with random parition to make the sorting faster and to handle the worst case (when all elements are already sorted)\n\n\nclass Solution:\n def sor | deafcon | NORMAL | 2022-03-27T00:34:50.955436+00:00 | 2022-03-27T00:34:50.955485+00:00 | 781 | false | Quick sort with random parition to make the sorting faster and to handle the worst case (when all elements are already sorted)\n\n```\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n self.quicksort(nums, 0, len(nums)-1)\n return nums\n \n def quicksort(self, nums, start, end):\n if start >= end:\n return\n \n part = self.part(nums, start, end) # partition the array\n self.quicksort(nums, start, part-1)\n self.quicksort(nums, part+1, end) # dont include the parition idx itself since left..... idx......right\n \n def part(self, nums, left, right):\n idx = left\n ran = randint(left, right)\n nums[right], nums[ran] = nums[ran], nums[right]\n pivot = nums[right]\n \n for i in range(left, right):\n if nums[i] <= pivot:\n nums[idx],nums[i] = nums[i], nums[idx]\n idx+=1\n \n nums[idx],nums[right] = nums[right], nums[idx]\n return idx # return the idx for part\n``` | 5 | 0 | ['Sorting', 'Python'] | 1 |
sort-an-array | SELECTION SORT | selection-sort-by-harsh07khuda-69gu | \n\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n // Selection sort algorithm \n for( int i=0; i <nums.size()-1 ; i++) | harsh07khuda | NORMAL | 2022-03-26T06:18:54.592677+00:00 | 2022-03-26T06:18:54.592711+00:00 | 19,173 | false | ``` \n\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n // Selection sort algorithm \n for( int i=0; i <nums.size()-1 ; i++)\n {\n int min = i;\n for( int j = i+1; j<nums.size(); j++)\n {\n if(nums[j] < nums[min])\n {\n min = j; \n }\n }\n swap(nums[min],nums[i]);\n }\n return nums;\n }\n};\n\n``` | 5 | 0 | [] | 15 |
sort-an-array | Fix if you are getting TLE using Quick Sort | fix-if-you-are-getting-tle-using-quick-s-h18a | I was getting TLE using QuickSort.\nI was always selecting the end element as the pivot. It seems that there are test cases designed to punish you for this, for | kyrixia | NORMAL | 2022-02-26T10:33:31.044351+00:00 | 2022-02-26T10:33:31.044382+00:00 | 237 | false | I was getting TLE using QuickSort.\nI was always selecting the end element as the pivot. It seems that there are test cases designed to punish you for this, for example if the test case is nearly sorted, it will become O(n^2).\n\nA simple solution is to swap the middle element with the end element, before selecting the end element as the pivot.\ne.g.\n```\nvar mid = (start+end)/2;\nSwap(mid, end);\nvar pivot = nums[end];\n```\nOr else you can use a more complicated pivot selection method | 5 | 0 | [] | 1 |
sort-an-array | C++ recursive merge-sort | c-recursive-merge-sort-by-yehudisk-bbgh | \nclass Solution {\npublic:\n vector<int> mergeSorted(vector<int>& a, vector<int>& b)\n {\n vector<int> res;\n int i=0, j=0;\n while | yehudisk | NORMAL | 2020-08-16T06:51:36.198281+00:00 | 2020-08-16T06:51:36.198311+00:00 | 554 | false | ```\nclass Solution {\npublic:\n vector<int> mergeSorted(vector<int>& a, vector<int>& b)\n {\n vector<int> res;\n int i=0, j=0;\n while (i<a.size() && j<b.size())\n {\n if (a[i] < b[j])\n {\n res.push_back(a[i]);\n i++;\n }\n else\n {\n res.push_back(b[j]);\n j++;\n }\n }\n while (i < a.size())\n {\n res.push_back(a[i]);\n i++;\n }\n while (j < b.size())\n {\n res.push_back(b[j]);\n j++;\n }\n return res;\n }\n vector<int> sortArray(vector<int>& nums) {\n if (nums.size() <= 1)\n return nums;\n auto start = nums.begin();\n auto mid = nums.begin() + nums.size()/2;\n auto end = nums.end();\n vector<int> v1(start, mid);\n vector<int> v2(mid, end);\n vector<int> left = sortArray(v1);\n vector<int> right = sortArray(v2);\n return mergeSorted(left, right);\n }\n};\n``` | 5 | 0 | [] | 0 |
sort-an-array | JavaScript - Quicksort | javascript-quicksort-by-ahmedengu-q543 | \n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar sortArray = function(nums) {\n if (nums.length <= 1) return nums;\n const pivot = nums.p | ahmedengu | NORMAL | 2020-07-30T11:10:59.227797+00:00 | 2020-07-30T11:10:59.227844+00:00 | 695 | false | ```\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar sortArray = function(nums) {\n if (nums.length <= 1) return nums;\n const pivot = nums.pop();\n const less = sortArray(nums.filter(n => n <= pivot));\n const more = sortArray(nums.filter(n => n > pivot));\n return less.concat(pivot, more);\n};\n``` | 5 | 1 | ['JavaScript'] | 4 |
sort-an-array | Java LazySort | java-lazysort-by-hobiter-8xdx | \nclass Solution {\n private static final int BBL = 30;\n private static final int SLT = 50;\n private static final int IST = 80;\n private static f | hobiter | NORMAL | 2020-03-10T05:51:20.672396+00:00 | 2020-03-10T06:08:32.215096+00:00 | 867 | false | ```\nclass Solution {\n private static final int BBL = 30;\n private static final int SLT = 50;\n private static final int IST = 80;\n private static final int QCK = 300;\n private static final int LZY = 1000;\n private static final Random rnd = new Random();\n int[] ns;\n int n;\n public List<Integer> sortArray(int[] nums) {\n this.ns = nums;\n n = nums.length;\n if (n < BBL){\n bbl(); \n } else if (n < SLT) {\n slt();\n } else if (n < IST){\n ist();\n } else if (n < QCK){\n quick(0, n - 1);\n } else if (n < LZY) {\n mrg(0, n - 1);\n } else {\n lazySort();\n }\n List<Integer> res = new ArrayList<>();\n for (int i : ns){\n res.add(i);\n }\n return res;\n }\n \n private void ist(){\n for (int i = 0; i < n; i++) {\n for (int j = i; j > 0; j--) {\n if (ns[j] < ns[j - 1]){\n swap(j, j - 1);\n }\n }\n }\n }\n \n private void bbl(){\n for (int i = n - 1; i >= 0; i--){\n for (int j = 0; j < i; j++) {\n if (ns[j] > ns[j + 1]){\n swap(j, j + 1);\n }\n }\n }\n }\n \n private void mrg(int st, int ed) {\n if (st >= ed) return;\n int mid = (st + ed) >> 1;\n mrg(st, mid);\n mrg(mid + 1, ed);\n merge(st, mid, ed);\n }\n \n private void merge(int st, int mid, int ed){\n int[] arr = new int[ed - st + 1];\n int i = st, j = mid + 1, index = 0;\n while(i <= mid && j <= ed) {\n if (ns[i] < ns[j]) {\n arr[index++] = ns[i++];\n } else {\n arr[index++] = ns[j++];\n }\n }\n while(i <= mid) {\n arr[index++] = ns[i++];\n }\n while(j <= ed) {\n arr[index++] = ns[j++];\n }\n index = 0;\n while (st <= ed){\n ns[st++] = arr[index++];\n }\n }\n \n private void quick(int st, int ed){\n if (st >= ed) return;\n int p = st + rnd.nextInt(ed - st + 1);\n int pv = ns[p], idx = st + 1;\n swap(st, p);\n for (int i = st + 1; i <= ed; i++){\n if (ns[i] < pv) {\n swap(i, idx); // remember idx++;\n idx++;\n }\n }\n swap(st, --idx); // bug point\n quick(st, idx - 1);\n quick(idx + 1, ed);\n }\n \n private void slt() {\n for (int i = 0; i < n; i++) {\n int minIdx = i;\n for (int j = i + 1; j < n; j++){\n if (ns[j] < ns[minIdx]){\n minIdx = j;\n }\n }\n swap(i, minIdx);\n }\n }\n \n private void lazySort(){\n Arrays.sort(ns);\n }\n \n private void swap(int i, int j){\n if (i == j) return; // not working ofr i == j\n ns[i] ^= ns[j];\n ns[j] ^= ns[i];\n ns[i] ^= ns[j];\n }\n}\n``` | 5 | 0 | [] | 0 |
sort-an-array | Merge-sort bottom-up Java | merge-sort-bottom-up-java-by-savochkin-u5q7 | Have not found the bottom-up java merge sort solution here.\n\n\nclass Solution {\n\n public int[] sortArray(int[] nums) {\n // starting from nums.len | savochkin | NORMAL | 2019-10-28T06:38:04.893339+00:00 | 2019-10-28T06:38:43.726778+00:00 | 990 | false | Have not found the bottom-up java merge sort solution here.\n\n```\nclass Solution {\n\n public int[] sortArray(int[] nums) {\n // starting from nums.length arrays of size 1 (already sorted)\n // on each step merge two adjacent sorted arrays so that they remain sorted\n // you may notice that sizes of arrays doubles on each step\n for(int currSize = 1; currSize < nums.length; currSize *= 2) {\n // on each step we need to merge/sort two adjacent arrays\n // we calculate the start index of this pair and call merge function\n for(int start = 0; start < nums.length; start += 2*currSize) {\n merge(nums, start, start + currSize, start + 2*currSize);\n }\n }\n \n return nums;\n }\n \n // merge two sorted adjacent arrays\n // first array (start, ..., mid-1) and second array (mid, ..., end-1)\n private void merge(int[] nums, int start, int mid, int end) {\n // need to check for cases when second array do not fully fits in the source array \n if (end > nums.length) end = nums.length;\n // need to check for cases when the first array just partially fits in the source array\n if (mid >= end) return;\n int[] nums2 = new int[end-mid];\n for(int i=0;i<nums2.length;i++) nums2[i] = nums[mid+i];\n \n int i = mid-1, j = nums2.length-1, k = end-1;\n while(i >= start && j >= 0) {\n if (nums[i] > nums2[j]) {\n nums[k--] = nums[i--];\n } else {\n nums[k--] = nums2[j--];\n }\n }\n \n while(i>=start) nums[k--] = nums[i--];\n while(j>=0) nums[k--] = nums2[j--]; \n }\n \n}\n``` | 5 | 2 | ['Merge Sort', 'Java'] | 1 |
sort-an-array | Java HeapSort | java-heapsort-by-pekras-vend | I haven\'t seen any posts here using heapsort, despite it being reasonably good for sorting arrays in-place. A heap is a binary tree where a parent has a value | pekras | NORMAL | 2019-07-19T19:43:45.248131+00:00 | 2019-08-19T15:13:48.670595+00:00 | 2,576 | false | I haven\'t seen any posts here using heapsort, despite it being reasonably good for sorting arrays in-place. A heap is a binary tree where a parent has a value greater than or equal to its children.\n\nBuilding a heap is nlogn. Each value is added as a leaf node, then it bubbles up the heap to its correct location. To turn a heap into a sorted array, remove the root (which is the current max value), replace it with a leaf node, then let the new root sink down to its correct location. This is also nlogn.\n\nedit: Thanks to [RodneyShag](https://leetcode.com/rodneyshag) for suggesting a significant optimization.\nRather than iteratively adding nodes to a heap, we can merge smaller heaps until only one is left. This ends up being O(n) for building the heap.\n\nImproved code: O(n) build heap, O(nlogn) convert heap to sorted array\n\n```Java\npublic static int[] heapSort(int[] nums) {\n\t//build the heap\n\tfor(int i=nums.length-1;i>=0;i--)\n\t\t//merge the 2 sub-heaps below i, by bubbling nums[i] down to the correct location\n\t\tsink(nums,i,nums.length);\n\t//turn it into a sorted list\n\tfor(int i=nums.length-1;i>0;i--){\n\t\t//remove the root, and put the last leaf at the root of the heap\n\t\tint tmp = nums[i];\n\t\tnums[i]=nums[0];\n\t\tnums[0] = tmp;\n\t\t//bubble the new root down to the correct location\n\t\tsink(nums,0,i);\n\t}\n\treturn nums;\n}\nstatic void sink(int[] nums, int start, int end){\n\tint val = nums[start];\n\tint i = start, next = 2*i+1;\n\twhile(next<end){\n\t\tif(next+1<end && nums[next+1]>nums[next])\n\t\t\tnext++;\n\t\tif(nums[next]<=val)\n\t\t\tbreak;\n\t\tnums[i]=nums[next];\n\t\ti=next;\n\t\tnext = 2*i+1; //2*i+1, 2*i+2 are the children of i\n\t}\n\tnums[i]=val;\n}\n```\n\nOriginal code: O(nlogn) build heap\n \n```Java\npublic static int[] heapSort(int[] nums) {\n\t//build the heap\n\tfor(int i=1;i<nums.length;i++){\n\t\tint val = nums[i];\n\t\tint j=i, next = (j-1)/2; //(j-i)/2 is the index of this location\'s parent\n\t\twhile(j>0 && nums[next]<val){\n\t\t\tnums[j]=nums[next];\n\t\t\tj=next;\n\t\t\tnext = (j-1)/2;\n\t\t}\n\t\tnums[j]=val;\n\t}\n\t\n\t//turn it into a sorted list\n\tfor(int i=nums.length-1;i>0;i--){\n\t\tint val = nums[i];\n\t\tnums[i]=nums[0];\n\t\t\n\t\tint j = 0, next = 1;\n\t\twhile(next<i){\n\t\t\tif(next+1<i && nums[next+1]>nums[next])\n\t\t\t\tnext++;\n\t\t\tif(nums[next]<=val)\n\t\t\t\tbreak;\n\t\t\tnums[j]=nums[next];\n\t\t\tj=next;\n\t\t\tnext = 2*j+1; //2*j+1, 2*j+2 are the children of j\n\t\t}\n\t\tnums[j]=val;\n\t}\n\treturn nums;\n}\n``` | 5 | 1 | [] | 0 |
sort-an-array | Swift - Using Quicksort | swift-using-quicksort-by-georrgee-vbq3 | Hey everyone! Did this in swift and used a high order function: filter\n\nclass Solution {\n \n func sortArray(_ nums: [Int]) -> [Int] {\n \n | georrgee | NORMAL | 2019-06-05T19:49:46.013197+00:00 | 2019-06-05T19:49:46.013246+00:00 | 863 | false | Hey everyone! Did this in swift and used a high order function: filter\n```\nclass Solution {\n \n func sortArray(_ nums: [Int]) -> [Int] {\n \n let sortedArray = quickSort(array: nums)\n return sortedArray\n }\n \n func quickSort(array: [Int]) -> [Int] {\n \n if array.count < 1 {\n return array\n }\n \n let pivot = array[array.count / 2]\n let less = array.filter { $0 < pivot }\n let equal = array.filter { $0 == pivot }\n let more = array.filter { $0 > pivot }\n \n return quickSort(array: less) + equal + quickSort(array: more)\n \n }\n}\n```\n\nHappy Coding | 5 | 1 | ['Swift'] | 3 |
sort-an-array | [C++] QuickSort and CountingSort solutions | c-quicksort-and-countingsort-solutions-b-dtqn | Here are two C++ soltuions with different runtimes:\n1. QuickSort: Runtime: 68 ms, Memory Usage: 12.6 MB\n\n void quickSort(vector<int>& V, int from, int to) | todor91 | NORMAL | 2019-04-24T13:28:28.633256+00:00 | 2019-04-24T13:28:28.633349+00:00 | 2,103 | false | Here are two C++ soltuions with different runtimes:\n1. QuickSort: Runtime: 68 ms, Memory Usage: 12.6 MB\n```\n void quickSort(vector<int>& V, int from, int to) {\n if (from + 1 >= to) return;\n // choose random pivot:\n int piv = V[from + rand() % (to - from)];\n \n int i = from - 1, j = to;\n while (true) {\n do i++; while (V[i] < piv);\n do j--; while (V[j] > piv);\n if (i >= j) break;\n swap(V[i], V[j]);\n }\n quickSort(V, from, j + 1);\n quickSort(V, j + 1, to);\n }\n\n vector<int> sortArray(vector<int>& nums) {\n quickSort(nums, 0, nums.size());\n return nums;\n }\n```\n2. CountingSort: Runtime: 44 ms, Memory Usage: 13 MB\n```\nvector<int> sortArray(vector<int>& nums) {\n int n = nums.size();\n int minEl = nums[0], maxEl = nums[0];\n for (int i = 1; i < n; ++i) {\n if (minEl > nums[i]) minEl = nums[i];\n if (maxEl < nums[i]) maxEl = nums[i];\n }\n vector<int> C(maxEl - minEl + 1);\n for (int i : nums) ++C[i - minEl];\n int j = 0;\n for (int i = 0; i < C.size(); ++i) {\n int el = i + minEl;\n int &cnt = C[i];\n while (cnt--) nums[j++] = el;\n }\n return nums;\n}\n``` | 5 | 1 | [] | 2 |
sort-an-array | Sorting Technique🚀 | sorting-technique-by-guhan0907-0sba | Intuition\nThe problem asks us to sort an array of integers. A radix sort seems like a natural fit here since it sorts numbers by processing individual digits.A | Guhan0907 | NORMAL | 2024-10-01T03:37:08.452427+00:00 | 2024-10-01T03:37:08.452454+00:00 | 232 | false | # Intuition\nThe problem asks us to sort an array of integers. A radix sort seems like a natural fit here since it sorts numbers by processing individual digits.Also Radix sort can be used in the places like numbers which having more number of digits. This is an efficient sorting algorithm when the maximum number of digits is small compared to the size of the array.\n\n# Approach\nWe use Radix Sort to sort the numbers in the array. The key steps are:\n\n* First, we determine the maximum number of digits (in decimal) in the array.\n* Then, we sort the array one digit at a time from the least significant to the most significant, using counting sort for each digit position.\n* We store the frequency of each digit in the current position using a hash map and then accumulate those frequencies to determine the sorted positions.\n* Finally, we reconstruct the array based on the sorted positions for the current digit.\n\n# Complexity\n# Time complexity:\nTime complexity:\n\uD835\uDC42(\uD835\uDC5B.\uD835\uDC51)\nO(n\u22C5d) where n is the number of elements in the array and \uD835\uDC51 is the number of digits in the maximum number. Since \n\n# Space complexity:\n\uD835\uDC42(\uD835\uDC5B)\nO(n) because we use extra space for the counting arrays (frq and cumfrq) and the result array (ans)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n int bt = 0, val = INT_MIN,n = 0;\n\n for (auto x : nums) {\n ++n;\n val = max(val,abs(x));\n }\n\n while (val!= 0) {\n ++bt;\n val /= 10;\n // cout<<val<<" ";\n }\n\n for (int i=1; i<=bt; i++) {\n unordered_map<int,int> frq,cumfrq;\n vector<int> ans(n);\n int t = pow(10,i);\n\n for (int x : nums) {\n int v = (x%t)/(t/10);\n frq[v]++;\n }\n\n cumfrq[-9] = frq[-9];\n for (int i=-8; i<=9;i++) {\n cumfrq[i] = cumfrq[i-1] + frq[i];\n }\n\n for (int i=n-1;i>=0;i--) {\n int g = cumfrq[(nums[i]%t) /(t/10)] - 1;\n ans[g] = nums[i];\n cumfrq[(nums[i]%t)/(t/10)]--;\n }\n nums = ans;\n }\n\n return nums;\n }\n};\n``` | 4 | 0 | ['Sorting', 'Radix Sort', 'C++'] | 2 |
sort-an-array | ✅💯🔥Simple Code📌🚀| 🔥✔️Easy to understand🎯 | 🎓🧠Beginner friendly🔥| O(N logN) Time Comp.💀💯 | simple-code-easy-to-understand-beginner-8hlfv | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | atishayj4in | NORMAL | 2024-07-29T19:46:15.971712+00:00 | 2024-08-01T19:35:18.019504+00:00 | 414 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n divide(nums, 0, nums.length - 1);\n return nums;\n }\n\n public void divide(int[] nums, int si, int ei) {\n if (si >= ei) {\n return;\n }\n int mid = si + (ei - si) / 2;\n divide(nums, si, mid);\n divide(nums, mid + 1, ei);\n mergesort(nums, si, ei, mid);\n }\n\n public void mergesort(int[] nums, int si, int ei, int mid) {\n int[] newArr = new int[ei - si + 1];\n int i = si;\n int j = mid + 1;\n int k = 0;\n while (i <= mid && j <= ei) {\n if (nums[i] <= nums[j]) {\n newArr[k] = nums[i];\n i++; k++;\n } else {\n newArr[k] = nums[j];\n j++; k++;\n }\n }\n while (i <= mid) {\n newArr[k] = nums[i];\n i++; k++;\n }\n while (j <= ei) {\n newArr[k] = nums[j];\n j++; k++;\n }\n for (int l = 0; l < newArr.length; l++) {\n nums[si + l] = newArr[l];\n }\n }\n}\n\n```\n | 4 | 0 | ['Array', 'Divide and Conquer', 'C', 'Sorting', 'Heap (Priority Queue)', 'Merge Sort', 'Bucket Sort', 'Python', 'C++', 'Java'] | 0 |
sort-an-array | Very Easy || Easy to understand | very-easy-easy-to-understand-by-abhimany-bc59 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nPriority Queue\nstep 1: Push array elemnt in queue(max heap)\nstep 2: mov | skipper_108 | NORMAL | 2024-07-25T17:56:47.772227+00:00 | 2024-07-25T17:56:47.772257+00:00 | 38 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nPriority Queue\nstep 1: Push array elemnt in queue(max heap)\nstep 2: move queue element in ans array\nstep 3: Now reverse the ans array\n\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(n)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n priority_queue<int>q;\n for(auto x : nums){\n q.push(x);\n }\n int n = nums.size();\n vector<int>ans;\n while(!q.empty()){\n ans.push_back(q.top());\n q.pop();\n }\n reverse(ans.begin(),ans.end());\n return ans;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
sort-an-array | Why Heap Sort is the Ultimate Sorting Solution! 🧠✨ | why-heap-sort-is-the-ultimate-sorting-so-xwl4 | "Code is like humor. When you have to explain it, it\u2019s bad." \u2014 Cory House\n\n# Do upvote if the solution is useful for you <3\n\n\n# Why Heap Sort is | i210844 | NORMAL | 2024-07-25T03:57:23.887257+00:00 | 2024-07-25T03:57:23.887293+00:00 | 572 | false | > **"Code is like humor. When you have to explain it, it\u2019s bad." \u2014 Cory House**\n\n# Do upvote if the solution is useful for you <3\n\n\n# Why Heap Sort is the Best Solution \uD83C\uDF1F\n**Time Complexity \u23F3:**\n\nHeap Sort runs in O(n log n) time in all cases (best, average, and worst), making it consistent and reliable.\n\n**Space Complexity \uD83D\uDCBE:**\n\nIt sorts the array in-place, using only a constant amount of extra space (O(1)), which is beneficial when working with large data sets.\n\n**Performance \uD83D\uDE80:**\n\nHeap Sort does not suffer from the worst-case performance issues like Quick Sort, which can degrade to O(n\xB2) in the worst case. It is a robust choice for sorting arrays with guaranteed performance.\n\n**Versatility \uD83C\uDF0D:**\n\nIt can be easily adapted to find the k-th largest or smallest element in an array, making it a versatile sorting technique.\n\n\n# Approach \uD83D\uDEE0\uFE0F\n**Build the Max-Heap:**\n\n- Start from the last non-leaf node and heapify each node up to the root. This transforms the array into a max-heap.\n\n**Extract Elements from the Heap:**\n\n- Swap the root (largest element) with the last element of the heap. Reduce the heap size by one and heapify the root to maintain the max-heap property.\n\n- Repeat this step until the heap size is reduced to one.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n void heapify(vector<int>& nums, int n, int i) {\n int largest = i;\n int left = 2 * i + 1;\n int right = 2 * i + 2;\n if (left < n && nums[left] > nums[largest]) {\n largest = left;\n }\n if (right < n && nums[right] > nums[largest]) {\n largest = right;\n }\n if (largest != i) {\n swap(nums[i], nums[largest]);\n heapify(nums, n, largest);\n }\n }\n\n void heapSort(vector<int>& nums) {\n int n = nums.size();\n for (int i = n / 2 - 1; i >= 0; i--) {\n heapify(nums, n, i);\n }\n for (int i = n - 1; i > 0; i--) {\n swap(nums[0], nums[i]);\n heapify(nums, i, 0);\n }\n }\n\n vector<int> sortArray(vector<int>& nums) {\n heapSort(nums);\n return nums;\n }\n};\n\n```\n```python []\nclass Solution:\n def heapify(self, nums, n, i):\n largest = i\n left = 2 * i + 1\n right = 2 * i + 2\n\n if left < n and nums[left] > nums[largest]:\n largest = left\n\n if right < n and nums[right] > nums[largest]:\n largest = right\n\n if largest != i:\n nums[i], nums[largest] = nums[largest], nums[i]\n self.heapify(nums, n, largest)\n\n def heapSort(self, nums):\n n = len(nums)\n\n for i in range(n // 2 - 1, -1, -1):\n self.heapify(nums, n, i)\n\n for i in range(n - 1, 0, -1):\n nums[i], nums[0] = nums[0], nums[i]\n self.heapify(nums, i, 0)\n\n def sortArray(self, nums):\n self.heapSort(nums)\n return nums\n\n```\n```C []\n// Helper function to maintain the heap property\nvoid heapify(int nums[], int n, int i) {\n int largest = i;\n int left = 2 * i + 1;\n int right = 2 * i + 2;\n\n if (left < n && nums[left] > nums[largest]) {\n largest = left;\n }\n\n if (right < n && nums[right] > nums[largest]) {\n largest = right;\n }\n\n if (largest != i) {\n int temp = nums[i];\n nums[i] = nums[largest];\n nums[largest] = temp;\n\n heapify(nums, n, largest);\n }\n}\n\n// Helper function to perform heap sort\nvoid heapSort(int nums[], int n) {\n for (int i = n / 2 - 1; i >= 0; i--) {\n heapify(nums, n, i);\n }\n\n for (int i = n - 1; i > 0; i--) {\n int temp = nums[0];\n nums[0] = nums[i];\n nums[i] = temp;\n\n heapify(nums, i, 0);\n }\n}\n\n// Function to sort the array\nint* sortArray(int* nums, int numsSize, int* returnSize) {\n heapSort(nums, numsSize);\n *returnSize = numsSize;\n return nums;\n}\n```\n```C# []\npublic class Solution {\n void Heapify(int[] nums, int n, int i) {\n int largest = i;\n int left = 2 * i + 1;\n int right = 2 * i + 2;\n\n if (left < n && nums[left] > nums[largest]) {\n largest = left;\n }\n\n if (right < n && nums[right] > nums[largest]) {\n largest = right;\n }\n\n if (largest != i) {\n int swap = nums[i];\n nums[i] = nums[largest];\n nums[largest] = swap;\n\n Heapify(nums, n, largest);\n }\n }\n\n void HeapSort(int[] nums) {\n int n = nums.Length;\n\n for (int i = n / 2 - 1; i >= 0; i--) {\n Heapify(nums, n, i);\n }\n\n for (int i = n - 1; i > 0; i--) {\n int temp = nums[0];\n nums[0] = nums[i];\n nums[i] = temp;\n\n Heapify(nums, i, 0);\n }\n }\n\n public int[] SortArray(int[] nums) {\n HeapSort(nums);\n return nums;\n }\n}\n\n```\n```Java []\npublic class Solution {\n void heapify(int[] nums, int n, int i) {\n int largest = i;\n int left = 2 * i + 1;\n int right = 2 * i + 2;\n\n if (left < n && nums[left] > nums[largest]) {\n largest = left;\n }\n\n if (right < n && nums[right] > nums[largest]) {\n largest = right;\n }\n\n if (largest != i) {\n int swap = nums[i];\n nums[i] = nums[largest];\n nums[largest] = swap;\n\n heapify(nums, n, largest);\n }\n }\n\n void heapSort(int[] nums) {\n int n = nums.length;\n\n for (int i = n / 2 - 1; i >= 0; i--) {\n heapify(nums, n, i);\n }\n\n for (int i = n - 1; i > 0; i--) {\n int temp = nums[0];\n nums[0] = nums[i];\n nums[i] = temp;\n\n heapify(nums, i, 0);\n }\n }\n\n public int[] sortArray(int[] nums) {\n heapSort(nums);\n return nums;\n }\n}\n\n```\n```Javascript []\n/**\n * Helper function to maintain the heap property\n * @param {number[]} nums\n * @param {number} n\n * @param {number} i\n */\nfunction heapify(nums, n, i) {\n let largest = i;\n let left = 2 * i + 1;\n let right = 2 * i + 2;\n\n if (left < n && nums[left] > nums[largest]) {\n largest = left;\n }\n\n if (right < n && nums[right] > nums[largest]) {\n largest = right;\n }\n\n if (largest !== i) {\n [nums[i], nums[largest]] = [nums[largest], nums[i]]; // Swap\n heapify(nums, n, largest);\n }\n}\n\n/**\n * Helper function to perform heap sort\n * @param {number[]} nums\n */\nfunction heapSort(nums) {\n let n = nums.length;\n\n for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {\n heapify(nums, n, i);\n }\n\n for (let i = n - 1; i > 0; i--) {\n [nums[0], nums[i]] = [nums[i], nums[0]]; // Swap\n heapify(nums, i, 0);\n }\n}\n\n/**\n * Function to sort the array\n * @param {number[]} nums\n * @return {number[]}\n */\n \nvar sortArray = function(nums) {\n heapSort(nums);\n return nums;\n};\n```\n\n | 4 | 1 | ['C++'] | 2 |
sort-an-array | Efficient Solution for Sorting an Array in 𝑂(𝑛 log 𝑛) Time Complexity | efficient-solution-for-sorting-an-array-ttyhf | If you found this solution helpful, please upvote! \uD83D\uDE0A\n\n# Intuition\nThe problem requires sorting an array in ascending order with optimal time and s | user4612MW | NORMAL | 2024-07-25T03:57:00.715733+00:00 | 2024-07-25T03:57:00.715767+00:00 | 23 | false | # **If you found this solution helpful, please upvote! \uD83D\uDE0A**\n\n# Intuition\nThe problem requires sorting an array in ascending order with optimal time and space complexity. Given the constraints, the Merge Sort algorithm is a suitable choice because it divides the array into smaller subarrays, sorts them, and merges them efficiently. This approach make sures that we maintain a time complexity of \uD835\uDC42(\uD835\uDC5B log \uD835\uDC5B), which is ideal for this problem.\n\n# Approach\nWe use the Merge Sort algorithm to solve this problem. First, we define a **merge** function to combine two sorted subarrays into a single sorted subarray using a temporary array. The **mergeSort** function recursively divides the array into smaller subarrays until each subarray contains a single element. After sorting the subarrays, we merge them back together. Finally, the **sortArray** function initializes the temporary array, invokes **mergeSort** on the entire array, and returns the sorted array.\n\n# Complexity\n- Time complexity - \uD835\uDC42(\uD835\uDC5B log \uD835\uDC5B)\n- Space complexity - \uD835\uDC42(\uD835\uDC5B)\n# Code\n```\nclass Solution {\npublic:\n void merge(vector<int>& nums, int left, int mid, int right, vector<int>& temp) {\n int lSize = mid - left + 1, rSize = right - mid, lIdx = 0, rIdx = 0, k = left;\n for (int i{0}; i < lSize; ++i) {\n temp[i] = nums[left + i];\n }\n while (lIdx < lSize && rIdx < rSize) {\n if (temp[lIdx] <= nums[mid + 1 + rIdx]) nums[k++] = temp[lIdx++];\n else nums[k++] = nums[mid + 1 + rIdx++];\n }\n while (lIdx < lSize) {\n nums[k++] = temp[lIdx++];\n }\n }\n void mergeSort(vector<int>& nums, int left, int right, vector<int>& temp) {\n if (left >= right) return;\n int mid = left + (right - left) / 2;\n mergeSort(nums, left, mid, temp);\n mergeSort(nums, mid + 1, right, temp);\n merge(nums, left, mid, right, temp);\n }\n vector<int> sortArray(vector<int>& nums) {\n vector<int> temp(nums.size());\n mergeSort(nums, 0, nums.size() - 1, temp);\n return nums;\n }\n};\n```\nThis implementation achieves \uD835\uDC42(\uD835\uDC5B log \u2061\uD835\uDC5B)time complexity with \uD835\uDC42(\uD835\uDC5B)auxiliary space due to the temporary arrays used for merging. \nFeel free to ask any questions or provide feedback. | 4 | 0 | ['C++'] | 0 |
sort-an-array | beats 95% of users | beats-95-of-users-by-jatadhara_sai-q2id | Intuition\ncounting sort approach\n\n# Approach\n-50000 is min possible value in array \n50000 is max possible value in array\n\ncreating a new cnt array of siz | Jatadhara_Sai | NORMAL | 2024-06-25T10:24:42.459541+00:00 | 2024-06-25T10:24:42.459569+00:00 | 372 | false | # Intuition\ncounting sort approach\n\n# Approach\n-50000 is min possible value in array \n50000 is max possible value in array\n\ncreating a new cnt array of size 50000+50000+1\nto store all counts of elements\n\nfor(int i=-50000 ; i<=50000 ; i++)\nvalues may be negative also\n \nsorting based on count values\n\n# Complexity\n- Time complexity:\nO(N) where N is range of numbers in array\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums)\n {\n int n = nums.size() ;\n int a = 50000 ;\n int b = -50000 ;\n\n vector<int> cnt(100001,0) ;\n for(int i=0 ; i<n ; i++)\n {\n cnt[nums[i]+50000] ++ ;\n }\n int idx = 0 ;\n for(int i=-50000 ; i<=50000 ; i++)\n { int c = cnt[i+50000] ;\n for(int j=0 ; j < c ; j++)\n {\n nums[idx++] = i ;\n \n }\n }\n return nums ;\n \n }\n};\n``` | 4 | 0 | ['Counting Sort', 'C++'] | 0 |
sort-an-array | C++ and Python3 || Merge Sort || Simple and Optimal | c-and-python3-merge-sort-simple-and-opti-wzma | \n# Complexity\n- Time complexity: O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) | meurudesu | NORMAL | 2024-02-20T16:12:24.445394+00:00 | 2024-02-20T16:12:24.445427+00:00 | 2,193 | false | \n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n void merge(vector<int> &arr, int low, int mid, int high) {\n vector<int> res(high - low + 1);\n int i = low, j = mid + 1, k = 0;\n while(i <= mid && j <= high) {\n if(arr[i] <= arr[j]) res[k++] = arr[i++];\n else res[k++] = arr[j++];\n }\n while(i <= mid) res[k++] = arr[i++];\n while(j <= high) res[k++] = arr[j++];\n for(int x = 0; x < res.size(); x++) {\n arr[low + x] = res[x];\n }\n }\n\n void mergeSort(vector<int> &arr, int low, int high) {\n if(low < high) {\n int mid = low + (high - low) / 2;\n mergeSort(arr, low, mid);\n mergeSort(arr, mid + 1, high);\n merge(arr, low, mid, high);\n }\n }\n\n vector<int> sortArray(vector<int>& nums) {\n mergeSort(nums, 0, nums.size() - 1);\n return nums;\n }\n};\n```\n```Python3 []\nclass Solution:\n def sortArray(self, nums: List[int]) -> List[int]:\n def merge(low, mid, high):\n res = [0] * (high - low + 1)\n i = low\n j = mid + 1\n k = 0\n while i <= mid and j <= high:\n if nums[i] <= nums[j]:\n res[k] = nums[i]\n i += 1\n k += 1\n else:\n res[k] = nums[j]\n j += 1\n k += 1\n while i <= mid:\n res[k] = nums[i]\n i += 1\n k += 1\n while j <= high:\n res[k] = nums[j]\n j += 1\n k += 1\n for x in range(len(res)):\n nums[low + x] = res[x]\n def mergeSort(low, high):\n if low < high:\n mid = low + (high - low) // 2\n mergeSort(low, mid)\n mergeSort(mid + 1, high)\n merge(low, mid, high)\n mergeSort(0, len(nums) - 1)\n return nums\n``` | 4 | 0 | ['Sorting', 'Merge Sort', 'C++', 'Python3'] | 1 |
sort-an-array | Easy Solution || Using Min Heap || C++ | easy-solution-using-min-heap-c-by-007ans-dhgn | \n\n# Code\n\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n \n priority_queue<int,vector <int>,greater<int>> p;\n\n | 007anshuyadav | NORMAL | 2024-02-03T19:35:01.991839+00:00 | 2024-02-03T19:35:01.991864+00:00 | 241 | false | \n\n# Code\n```\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n \n priority_queue<int,vector <int>,greater<int>> p;\n\n for(auto i:nums){\n p.push(i);\n }\n int i=0;\n while(!p.empty()){\n nums[i++]=p.top();\n p.pop();\n }\n return nums;\n }\n};\n``` | 4 | 0 | ['Array', 'Divide and Conquer', 'Heap (Priority Queue)', 'C++'] | 0 |
sort-an-array | O(n) || Counting Sort || 99% beat (4ms) | on-counting-sort-99-beat-4ms-by-priyansh-42ag | Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Tim | Priyanshu_pandey15 | NORMAL | 2024-01-12T04:55:52.746920+00:00 | 2024-01-12T04:55:52.746951+00:00 | 1,227 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(100000)\n# Code\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n int[] arr = new int[100001];\n int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;\n int x = 0;\n for (int i : nums) {\n x = 50000 + i;\n arr[x]++;\n if (min > x)\n min = x;\n if (max < x)\n max = x;\n }\n int k = nums.length - 1, n = k + 1;\n for (int i = max; i >= min; i--) {\n if (arr[i] == 0)\n continue;\n int len = arr[i];\n while (len-- > 0)\n nums[k--] = i - 50000;\n }\n return nums;\n }\n}\n``` | 4 | 0 | ['C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 3 |
sort-an-array | Quick Sort or Count Sort? Why even choose? Let's have both. C++ 47 ms. | quick-sort-or-count-sort-why-even-choose-m77r | Intuition\nOn top of sorting algorithms there are two fundamentally different approaches:\n1. Count sort: O(n + r) time, O(r) space.\n2. Quick sort: O(n \times | sergei99 | NORMAL | 2023-11-03T13:27:57.830111+00:00 | 2024-07-25T04:15:14.809555+00:00 | 141 | false | # Intuition\nOn top of sorting algorithms there are two fundamentally different approaches:\n1. Count sort: $$O(n + r)$$ time, $$O(r)$$ space.\n2. Quick sort: $$O(n \\times log(n))$$ time, $$O(1)$$ space.\nwhere $$n$$ is the number of elements to sort, and $$r$$ is the range between the minimal and the maximal elements.\n\nHere we consider both of them.\n\n# Approach\n## 1. Count Sort\nThe main idea is to use each element as an index to an ordered collection, where the number of that element\'s occurences is accumulated. The simplest approach is to use an array for that.\nConsider the following input data of $$9$$ elements:\n| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |\n|-|-|-|-|-|-|-|-|-|-|\n| Element |10|20|30|1000|-8|-1|20|30|20|\n\nThe range (which corresponds to $$r$$ parameter introduced earlier) is $$(1000-(-8)+1)=1009$$ elements long. So we allocate a `count` array of this size:\n| Index | 0 | 1 | 2 | 3 | ... | 1008 |\n|-|-|-|-|-|-|-|\n\nWe go through the input data and use each element as an index into this array. Since the array indexes are zero-based, and the input values are not, we add a bias which is the negated minimal value ($$-8$$ in this case):\n```\ncounts[10 + bias] += 1;\ncounts[20 + bias] += 1;\ncounts[30 + bias] += 1;\ncounts[1000 + bias] += 1;\n...\n```\nSo we end up with the `count` array populated as follows:\n| Index | 0 | 1 | ... | 7 | ... | 18 | ... | 28 | ... | 38 | ... | 1007 | 1008 |\n|-|-|-|-|-|-|-|-|-|-|-|-|-|-|\n| Value$$^1$$ | -8 | -7 | ... | -1 | ... | 10 | ... | 20 | ... | 30 | ... | 999 | 1000 |\n| Count | 1 | 0 | ... | 1 | ... | 1 | ... | 3 | ... | 2 | ... | 0 | 1 |\n\n$$^1$$"Value" row contains the original unbiased values - these are not stored, but calculated based on index.\n\nHowever, in order to determine the bias this way, we need to scan the entire input array up front. To avoid this, we can use a fixed bias corresponding to the minimal element possible ($$-50000$$ for this task).\n\nThe underlying data type of the `counter` array should be chosen to fit numbers up to `n` (for the worst case of the input array consisting of `n` times a single value). For this particular task $$n$$ does not exceed $$50000$$, so a 16 bit `unsigned short` is just fine. If we knew for sure that the number of duplicates may not exceed a certain value (e.g. $$255$$), then we would be able to choose a smaller data type (in this case, an `unsigned byte`).\n\nFinally, we walk through the `count` array and add elements corresponding to the array indexes to the result array so many times that is the `count` array element\'s value (if it\'s $$0$$ then we don\'t add the element):\n```\nfor (int i = min_value; i <= max_value; i++)\n result.insert(result.end(), count[i], i - bias);\n```\nE.g. each of $$-8$$, $$-1$$, $$10$$ will be added $$1$$ time, $$20$$ will be added $$3$$ times, etc. So we end up with the following result vector:\n| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |\n|-|-|-|-|-|-|-|-|-|-|\n| Element |-8|-1|10|20|20|20|30|30|1000|\n\nThe key advantage of this algorithm is that for range sizes bounded by a linear function of $$n$$ it sorts the array in linear time and space: $$O(n)$$. If the range is less than linear (e.g. constant or logarithmic), then the time stays linear, but the space also decreases to become constant or logarithmic.\n\nThe major disadvantage is that, if the range is too large compared to $$n$$, then the time becomes $$O(r)$$, as is the temporary space required. Consider the input data from the example above. It has only 9 elements, but we have to allocate temporary space for 1009 counters for sorting. There are techniques for dealing with it, but they take us away from the linear time and space anyway.\n\n## 2. Quick Sort\n\nThe main idea of the quick sort (aka Hoare sort) algorithm is divide and conquer. The array is recursively split approximately in halves and each half sorted separately until the size of the chunk becomes $$1$$, which means it is already sorted. This is typically implemented in two parts: partitioning and sorting.\n\nThe sorting part is always simple:\n```\nvoid quicksort(It begin, It end) {\n if (begin + 1 < end) {\n It p = partition(begin, end) + 1;\n quicksort(begin, p);\n quicksort(p, end);\n }\n}\n```\n(where `It` is the iterator type, `begin` points to the first element of the sorted range, and `end` points past the last element of it)\n\nThe complicated part is partitioning, i.e. dividing the range to (preferrably) equal parts. There are a number of partitioning schemes (Lomuto, Hoare, etc), described here to some level of detail: https://en.wikipedia.org/wiki/Quicksort. We are not going to dive deeply into this topic, but just pick the Hoare scheme.\n\nThe partitioning algorithm picks a pivot value from the range and moves elements less than or equal to pivot to the left part of the range and elements greater than pivot to the right part of the array. The index of the pivot value dividing the two parts is then returned. Consider our previous example:\n| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |\n|-|-|-|-|-|-|-|-|-|-|\n| Element |10|20|30|1000|-8|-1|20|30|20|\n\nSuppose we take $$20$$ as the pivot value. Then we move elements as follows:\n| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |\n|-|-|-|-|-|-|-|-|-|-|\n| Element |10|20|20|20|-8|**-1**|1000|30|30|\n\nAnd the index of the last element not exceeding $$20$$ is returned. This is the element $$-1$$ at the index $$5$$. So we see that the partitioning can be unequal, $$6$$ vs $$3$$ elements in this case. And if we took $$-8$$ as pivot, then partitioning would be even worse: $$1$$ vs $$8$$ elements. Whatever the split-up is, we proceed to sorting each part individually.\n\nHoare sort ensures $$O(n^2)$$ complexity in worst case (e.g. when pivot is consistently chosen badly, or if the entire array consists of just one repeated value).\nFor uniformly distributed random data it performs the full scan of the array $$log(n)$$ times, thus giving $$O(n \\times log(n))$$ time complexity. Generally, for more equal partitioning less number of operations is performed, ideally targeting $$n \\times log_2(n)$$. The logarithm base is a constant factor sensitive to the pivot choice and the number of repeating elements in the input data. This dependency is a major disadvantage of the algorithm (remember, the count sort does not care about duplicates or pivot choice at all).\n\nThe advantanges of the quick sort over the count sort are that it does not depend on the range of elements (apart from being sensitive to duplicates), and that it uses a constant space.\n\n## 3. Choice between Algorithms\n\nSo we have two algorithms, each of which is more efficient in certain circumstances than the other. How to we choose between them?\n\nIf we need to minimize the temporary space used, then we obviously go for the Hoare algorithm. But if we aim at the fastest sort possible, then the choice is a bit tricky. Let\'s compare the numbers of operations.\n\n| Count Sort | Quick Sort |\n|-|-|\n| $$n + r$$ | $$n \\times log_2(n)$$ |\n\nIf we try to determine the exact range before making a decision, then we have to take a single pass through the input array any way. If $$n > r$$, then we go for the count sort. Otherwise we compare $$r$$ vs $$n \\times log_2(n)$$. This is an irrational equation for the watermark, and its root can be approximated as follows (considering that $$r > n$$):\n$$n_w \\leq \\frac12(r + \\frac r {log_2(r)})$$\nand\n$$log_2(r) \\leq clz(r)$$\nwhere $$clz(r)$$ (Count Leading Zeroes) is the position of the highest $$1$$ bit in $$r$$.\nSo if $$n < n_w$$, then we go for the quick sort, otherwise we choose the count sort.\n\nHowever, the preliminary scan wastes our valuable CPU cycles, because we don\'t need it if we choose the quick sort. Can we somehow determine $$r$$ without going through the entire array?\n\nIn general, we cannot. But we can get the idea of $$r$$ by picking a random two or more elements from the array, looking at their dispersion and multiplying it by some ratio. We have chosen this approach. The main idea here is to avoid obvious pitfalls like using quick sort for an array of thousands of $$2$$\'s (there is a real test case like this) or count sort for an array of two elements $$-50000$$ and $$50000$$, and not to pay too much attention to the choice when algorithms perform roughly equal.\n\nAlternatively, we could leave the initial array traversal in place, combining it with the first partitioning round for quick sort.\n\n## Micro-optimizations\n\nThese are pretty standard:\n1. Disabling sync with `stdio` (not included here for brevity).\n1. Sorting the input vector in place in both algorithms and returning a reference to it (not its copy as LC suggests).\n1. Using a static array for counting to avoid memory allocation/deallocation.\n1. Unrolling the loop through the `count` array 4 times and aligning its boundaries, so it operates 64-bit aligned integers.\n1. Zeroing the `count` array elements just passed while they are still in cache, and while we know where they are, so we don\'t have to zero the entire array during the next test case execution.\n1. Using STL for element insertions - these might be bundled into faster 64- or 128-bit memory writes.\n\n# Complexity\n- Time complexity: pretending to be $$O(min(n + r, n \\times log_2(n)))$$, but may actually differ because we use heuristics, not the exact information, for the algorithm choice.\n\n- Space complexity: $$O(R)$$ where $$R = 5 \\times 10^4 - (-5 \\times 10^4) + 1 + alignment = $$ since we allocate a static array.\n\n# Measurements\n\n| Language | Time | Beating | Memory | Beating |\n|-|-|-|-|-|\n| C++ | 47 ms | 100% | 67.2 Mb | 69.91% |\n\nThe previous record of the execution time was somewhere below 54 ms (since my less optimized 54 ms attempt wasn\'t showing 100%).\nThe memory usage is high because of the count sorting array ($$200 Kbytes$$ + LC runtime overhead), but that\'s the cost we have to take if we want $$O(n)$$ sorting.\n\nSo we see that the solution outpeforms both the count sort-based and linear-logarithmic sort-based solutions by choosing the most appropriate one for each particular input data set. Probably a faster execution can be achieved by tuning heuristics or applying a different logic for the algorithm choice.\n\n# Code\n``` C++ []\nclass Solution {\nprivate:\n static constexpr int MINV = -50000, MAXV = 50000;\n static constexpr unsigned RANGEV = ((MAXV - MINV) & -4) + 4;\n\n static unsigned short counts[RANGEV];\n\n template <class It>\n static It partition(It begin, It end) {\n end--;\n const auto pivot = *(begin + (end - begin) / 2);\n while (true) {\n while (*begin < pivot) begin++;\n while (*end > pivot) end--;\n if (begin >= end) return end;\n swap(*begin++, *end--);\n }\n }\n\n template <class It>\n static void quicksort(It begin, It end) {\n if (begin + 1 < end) {\n auto p = partition(begin, end) + 1;\n quicksort(begin, p);\n quicksort(p, end);\n }\n }\n\npublic:\n vector<int> &sortArray(vector<int>& nums) {\n const unsigned n = nums.size();\n if (n == 1) return nums;\n int r = min(MAXV - MINV + 1, abs(nums.front() - nums.back()) * 2);\n if (r > 1 && n < (r + r / (31 - __builtin_clz(r))) / 2) {\n quicksort(nums.begin(), nums.end());\n } else {\n int minv = MAXV, maxv = MINV;\n for (int v : nums) {\n counts[v - MINV]++;\n if (minv > v) minv = v;\n if (maxv < v) maxv = v;\n }\n nums.erase(nums.begin(), nums.end());\n const int mina = ((minv - MINV) & -4) + MINV,\n maxa = ((maxv - MINV - 1) & -4) + 4 + MINV;\n for (int i = mina; i <= maxa; i += 4) {\n nums.insert(nums.end(), counts[i - MINV], i);\n nums.insert(nums.end(), counts[i - MINV + 1], i + 1);\n nums.insert(nums.end(), counts[i - MINV + 2], i + 2);\n nums.insert(nums.end(), counts[i - MINV + 3], i + 3);\n *reinterpret_cast<long long*>(counts + (i - MINV)) = 0;\n }\n }\n return nums;\n }\n};\n\nunsigned short Solution::counts[RANGEV];\n``` | 4 | 0 | ['Array', 'Divide and Conquer', 'Sorting', 'Quickselect', 'Counting Sort', 'C++'] | 0 |
sort-an-array | Counting Sort || O(n) Solution || JAVA | counting-sort-on-solution-java-by-kshiti-5nw6 | \n# Approach\n- Create an integer map array integer map Array of size mapRange(max - min +2).//(+2 is just to avoid overflow here in mapRange)\n- Traverse whole | Kshitij_Pandey | NORMAL | 2023-03-01T08:23:49.055818+00:00 | 2023-03-01T08:23:49.055861+00:00 | 31 | false | \n# Approach\n- **Create an integer map array integer map Array of size mapRange(max - min +2).**//(+2 is just to avoid overflow here in mapRange)\n- **Traverse whole array and store the frequency in the map.**\n- **Again traverse the whole map and put the (index + min(offset here)) in the new sorted Array.**\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(max(mapRange, n))\n\n# Code\n```\nclass Solution {\n public int[] sortArray(int[] nums) {\n int n = nums.length;\n int max = Integer.MIN_VALUE;\n int min =Integer.MAX_VALUE;\n\n for(int i: nums){\n max =Math.max(max, i);\n min =Math.min(min, i);\n }\n\n int[] sortedArray = new int[n];\n int mapRange = max -min +2;\n int[] map = new int[mapRange];\n \n for(int i=0; i< n; i++){\n map[nums[i] - min]++;\n }\n int index =0;\n for(int i=0; i< mapRange; i++){\n while(map[i]>0){\n sortedArray[index++] =i+min; \n map[i]--;\n }\n }\n return sortedArray;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
sort-an-array | 🚀Fast | C# & TypeScript Solution | Merge Sort ❇️✅ | fast-c-typescript-solution-merge-sort-by-94k8 | \u2B06\uFE0FLike|\uD83C\uDFAFShare|\u2B50Favourite\n\n# Runtime & Memory\n\n\n\n# Complexity\n- Time complexity:\nO(nlog(n))\n\n- Space complexity:\nO(n)\n\n# C | arafatsabbir | NORMAL | 2023-03-01T06:41:40.763364+00:00 | 2023-03-01T08:46:21.517003+00:00 | 829 | false | # \u2B06\uFE0FLike|\uD83C\uDFAFShare|\u2B50Favourite\n\n# Runtime & Memory\n\n\n\n# Complexity\n- Time complexity:\nO(nlog(n))\n\n- Space complexity:\nO(n)\n\n# C# Code\n```\npublic class Solution\n{\n public int[] SortArray(int[] nums)\n {\n int[] temp = new int[nums.Length];\n MergeSort(nums, temp, 0, nums.Length - 1);\n return nums;\n }\n\n private void MergeSort(int[] nums, int[] temp, int left, int right)\n {\n if (left < right)\n {\n int mid = (left + right) / 2;\n MergeSort(nums, temp, left, mid);\n MergeSort(nums, temp, mid + 1, right);\n Merge(nums, temp, left, mid, right);\n }\n }\n\n private void Merge(int[] nums, int[] temp, int left, int mid, int right)\n {\n int i = left;\n int j = mid + 1;\n int k = left;\n while (i <= mid && j <= right)\n {\n if (nums[i] <= nums[j])\n {\n temp[k++] = nums[i++];\n }\n else\n {\n temp[k++] = nums[j++];\n }\n }\n\n while (i <= mid)\n {\n temp[k++] = nums[i++];\n }\n\n while (j <= right)\n {\n temp[k++] = nums[j++];\n }\n\n for (int m = left; m <= right; m++)\n {\n nums[m] = temp[m];\n }\n }\n}\n```\n\n# TypeScript Code\n```\nfunction sortArray(nums: number[]): number[] {\n let temp: number[] = new Array(nums.length);\n mergeSort(nums, temp, 0, nums.length - 1);\n return nums;\n};\n\nfunction mergeSort(nums: number[], temp: number[], left: number, right: number): void {\n if (left < right) {\n let mid: number = Math.floor((left + right) / 2);\n mergeSort(nums, temp, left, mid);\n mergeSort(nums, temp, mid + 1, right);\n merge(nums, temp, left, mid, right);\n }\n}\n\nfunction merge(nums: number[], temp: number[], left: number, mid: number, right: number): void {\n let i: number = left;\n let j: number = mid + 1;\n let k: number = left;\n while (i <= mid && j <= right) {\n if (nums[i] <= nums[j]) {\n temp[k++] = nums[i++];\n }\n else {\n temp[k++] = nums[j++];\n }\n }\n\n while (i <= mid) {\n temp[k++] = nums[i++];\n }\n\n while (j <= right) {\n temp[k++] = nums[j++];\n }\n\n for (let m: number = left; m <= right; m++) {\n nums[m] = temp[m];\n }\n}\n``` | 4 | 0 | ['Array', 'Divide and Conquer', 'Merge Sort', 'TypeScript', 'C#'] | 0 |
sort-an-array | 🧐Simple way 💻 🔥Merge Sort in Java 📝, Python 🐍, and C++ 🖥️ with Video Explanation 🎥 | simple-way-merge-sort-in-java-python-and-ofwe | Intuition\n Describe your first thoughts on how to solve this problem. \nMerge sort is a sorting algorithm that uses the divide and conquer approach to sort an | Vikas-Pathak-123 | NORMAL | 2023-03-01T01:07:44.131604+00:00 | 2023-03-01T16:18:17.669457+00:00 | 930 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMerge sort is a sorting algorithm that uses the divide and conquer approach to sort an array or a list. In this algorithm, the given array is recursively divided into two halves until the base case of having a single element is reached. The two halves are then merged by comparing and sorting them, thus generating a sorted array\n\n# Approach\nThe merge sort algorithm follows the divide and conquer approach to sort an array. The basic steps involved in the merge sort algorithm are as follows:\n\n1. Divide the array into two halves (left and right).\n2. Recursively apply the merge sort algorithm on the left half until it is sorted.\n3. Recursively apply the merge sort algorithm on the right half until it is sorted.\n5. Merge the left and right halves to obtain a sorted array.\n6. The merging process is performed by comparing and sorting the elements in the left and right halves one by one.\n<!-- Describe your approach to solving the problem. -->\n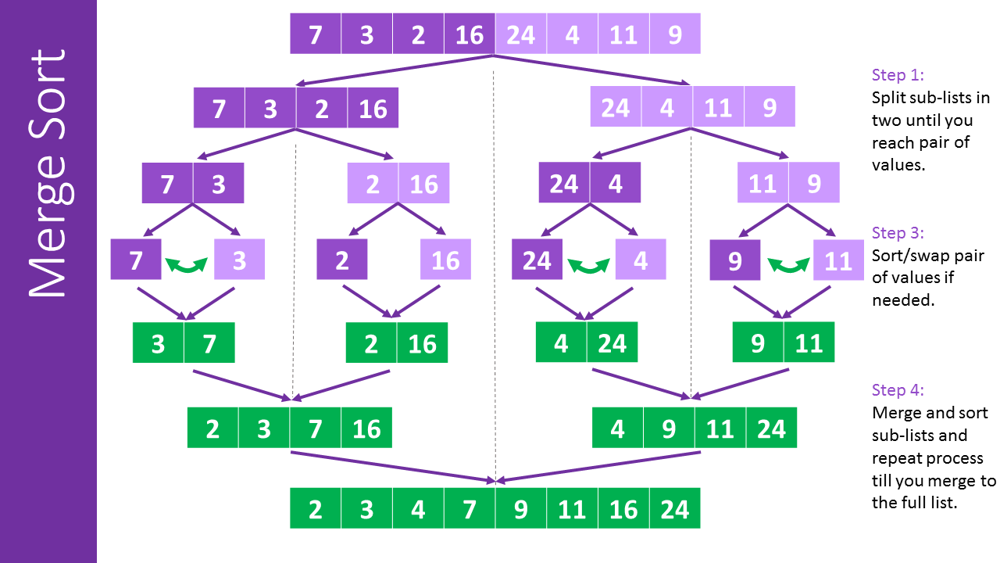\n\n\n\n\n# Video reference\n\n<iframe width="560" height="315" src="https://www.youtube.com/embed/mB5HXBb_HY8" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe>\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\n```\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of the merge sort algorithm is $$O(nlogn)$$ in all cases. This is because the algorithm divides the array into two halves at each recursive call, and the merging process takes $$O(n)$$ time. Therefore, the overall time complexity is given by `T(n) = 2T(n/2) + O(n)`, which results in $$O(nlogn)$$ time complexity.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of the merge sort algorithm is $$O(n)$$. This is because the algorithm creates temporary arrays to store the left and right halves of the array during the merging process. The maximum size of the temporary arrays is` n/2`, which results in $$O(n)$$ space complexity.\n\n# Code\n``` java []\npublic class Solution {\n public int[] sortArray(int[] nums) {\n mergeSort(nums, 0, nums.length - 1); // Call the recursive Merge Sort \n return nums;\n }\nprivate void mergeSort(int[] nums, int start, int end) {\n if (start < end) { // Base case - Check if array has only 1 element\n int mid = (start + end) / 2; // Calculate the middle index\n mergeSort(nums, start, mid); // Recursively call Merge Sort on left subarray\n mergeSort(nums, mid + 1, end); // Recursively call Merge Sort on right subarray\n merge(nums, start, mid, end); // Merge the sorted left and right subarrays\n }\n}\n\nprivate void merge(int[] nums, int start, int mid, int end) {\n int[] temp = new int[end - start + 1]; // Create a temporary array to store the merged subarrays\n int i = start, j = mid + 1, k = 0; // Initialize indices for left subarray, right subarray, and temporary array\n \n // Compare elements in the left and right subarrays, and store the smaller element in the temporary array\n while (i <= mid && j <= end) {\n if (nums[i] < nums[j]) {\n temp[k++] = nums[i++];\n } else {\n temp[k++] = nums[j++];\n }\n }\n \n // Copy any remaining elements in the left subarray to the temporary array\n while (i <= mid) {\n temp[k++] = nums[i++];\n }\n \n // Copy any remaining elements in the right subarray to the temporary array\n while (j <= end) {\n temp[k++] = nums[j++];\n }\n \n // Copy the merged subarray from the temporary array back to the original array\n for (int p = 0; p < temp.length; p++) {\n nums[start + p] = temp[p];\n }\n}\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n void mergeSort(vector<int>& nums, int start, int end) {\n if (start >= end) {\n return;\n }\n int mid = start + (end - start) / 2;\n mergeSort(nums, start, mid);\n mergeSort(nums, mid + 1, end);\n merge(nums, start, mid, end);\n }\n \n void merge(vector<int>& nums, int start, int mid, int end) {\n vector<int> temp(end - start + 1);\n int i = start, j = mid + 1, k = 0;\n while (i <= mid && j <= end) {\n if (nums[i] < nums[j]) {\n temp[k++] = nums[i++];\n } else {\n temp[k++] = nums[j++];\n }\n }\n while (i <= mid) {\n temp[k++] = nums[i++];\n }\n while (j <= end) {\n temp[k++] = nums[j++];\n }\n for (int p = 0; p < temp.size(); p++) {\n nums[start + p] = temp[p];\n }\n }\n \n vector<int> sortArray(vector<int>& nums) {\n mergeSort(nums, 0, nums.size() - 1);\n return nums;\n }\n};\n\n```\n```python []\nclass Solution:\n def mergeSort(self, nums, start, end):\n if start >= end:\n return\n mid = start + (end - start) // 2\n self.mergeSort(nums, start, mid)\n self.mergeSort(nums, mid + 1, end)\n self.merge(nums, start, mid, end)\n \n def merge(self, nums, start, mid, end):\n temp = []\n i, j = start, mid + 1\n while i <= mid and j <= end:\n if nums[i] < nums[j]:\n temp.append(nums[i])\n i += 1\n else:\n temp.append(nums[j])\n j += 1\n while i <= mid:\n temp.append(nums[i])\n i += 1\n while j <= end:\n temp.append(nums[j])\n j += 1\n nums[start:end+1] = temp\n \n def sortArray(self, nums: List[int]) -> List[int]:\n self.mergeSort(nums, 0, len(nums) - 1)\n return nums\n\n```\n# Please Comment\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution comment below if you like it.\uD83D\uDE0A\n```\n | 4 | 0 | ['Divide and Conquer', 'Merge Sort', 'Python', 'C++', 'Java'] | 2 |
sort-an-array | EASIEST SOLUTION, O(1), ONE-LINE SOLUTION, TOURSIT APPROVED | easiest-solution-o1-one-line-solution-to-0lo5 | \nclass Solution {\n public int[] sortArray(int[] nums) {\n Arrays.sort(nums);\n return nums;\n }\n} | nekidaz | NORMAL | 2022-10-26T09:44:19.409259+00:00 | 2022-10-26T09:44:19.409315+00:00 | 583 | false | \nclass Solution {\n public int[] sortArray(int[] nums) {\n Arrays.sort(nums);\n return nums;\n }\n} | 4 | 1 | [] | 1 |
sort-an-array | Quick Sort with explanantion | quick-sort-with-explanantion-by-llu2020-ox3i | Pick the middle number as the pivot.\n2. Set two poiners, left and right, on the start index and end index.\n3. left pointer searches for next number that is bi | LLU2020 | NORMAL | 2022-10-07T01:27:13.662080+00:00 | 2022-10-07T01:44:55.092398+00:00 | 1,594 | false | 1. Pick the middle number as the pivot.\n2. Set two poiners, left and right, on the start index and end index.\n3. left pointer searches for next number that is bigger or equal to pivot.\n4. right pointer searches for next number that is smaller or equal to pivot.\n5. if there exists two numbers as described, swap them. \n**6. So on the left part of the left pointer, all numbers are smaller or equal to pivot. For the right part of right pointer, all numbers are bigger or equal to pivot.**\n7. keep traversing until left pointer > right pointer, which means all numbers have been visited and set to correct positions.\n8. divide into [start, right], [left, end], quick sort the subarray respectively.\n \n```\n public int[] sortArray(int[] nums) {\n if (nums == null || nums.length == 0) {\n return nums;\n }\n \n quickSort(nums, 0, nums.length - 1);\n return nums;\n }\n \n private void quickSort(int[] nums, int start, int end) {\n if (start >= end) return;\n \n int left = start, right = end;\n\t\t// Ideally, numbers are approximately increasing, which means the middle number is most likey the median number. \n\t\t// The closer pivot is to the median number, the less swapping and recursion we need to do.\n int pivot = nums[left + (right - left) / 2];\n // with (left <= right), we can end with: \n\t\t// 1. x, x, x, right, left, x, x, x,\n\t\t// or\n\t\t// 2. x, x, x, right, pivot, left, x, x, x\n\t\t// easy to divide without boundary issues\n while (left <= right) {\n\t\t\t// if we put nums[left] <= pivot, for array like [2, 1], 1 swap with itself and leads to dead loop\n while (left <= right && nums[left] < pivot) left++;\n while (left <= right && nums[right] > pivot) right--;\n if (left <= right) {\n int temp = nums[left];\n nums[left] = nums[right];\n nums[right] = temp;\n left++;\n right--;\n }\n }\n \n quickSort(nums, start, right);\n quickSort(nums, left, end);\n }\n```\n\ntime complexity: \non average O(nlogn); \narray can be divied **O(logn)** times, each time the whole array will be traversed, **O(n) time** every traversal . \nworst case O(n * n): \n[0, 0, 1, 0, 0], if we always choose smallest or biggest number as pivot, then **O(n)** times traverses with **O(n**) time every traversal.\n\t\t\t\t\t\t\t\nspace complexity: \non average O(logn), worst case O(n);\ndecided by the depth of recursion. | 4 | 0 | [] | 0 |
sort-an-array | ✅✅C++ || MERGE SORT | QUICKSORT | INSERTION SORT | HEAP SORT |BUBBLE SORT | c-merge-sort-quicksort-insertion-sort-he-97hf | Bubble sort\n\n\t// bubbleSort(nums);\n\tvoid bubbleSort(vector& nums){\n for(int i = nums.size() - 1; i >= 0; i--)\n for(int j = 0; j < i; j+ | Pianist_01 | NORMAL | 2022-10-01T15:41:50.507215+00:00 | 2022-11-23T21:18:15.858435+00:00 | 336 | false | Bubble sort\n\n\t// bubbleSort(nums);\n\tvoid bubbleSort(vector<int>& nums){\n for(int i = nums.size() - 1; i >= 0; i--)\n for(int j = 0; j < i; j++)\n if(nums[j] > nums[j + 1]) \n swap(nums[j], nums[j + 1]);\n }\nInsertion sort\n\n\t// insertionSort(nums);\n\tvoid insertionSort(vector<int>& nums){\n if(nums.size() == 0 || nums.size() == 1) return;\n for(int i = 1; i < nums.size(); i++){\n int tmp = nums[i];\n int j = i - 1;\n while(j >= 0 && nums[j] > tmp){\n nums[j + 1] = nums[j];\n j--;\n }\n nums[j + 1] = tmp;\n }\n }\nHeap sort\n\nIn terms of heapify stage:\n\nBottom up approach (beginning from bottom + sift down) O(n)\nTop down approach (beginning from top + sift up) O(nlogn)\nBeginning from top + sift down not working\nIn fact, "sift down" of a certain node x works properly only if both of its left subtree and right subtree (if any) already satisfy the heap property.\n\nFor zero-based arrays, for a certain node x:\n\nits parent floor( (x - 1) / 2 )\nits left child 2x + 1\nits right child 2x + 2\nThe index of the last non-leaf node of a n-sized heap is floor( n / 2 ) - 1.\n\n\tvoid siftDown(vector<int>& nums, int n, int i){\n int biggest = i;\n int l = 2 * i + 1;\n int r = 2 * i + 2;\n if(l < n && nums[biggest] < nums[l])\n biggest = l;\n if(r < n && nums[biggest] < nums[r])\n biggest = r;\n if(biggest != i){\n swap(nums[i], nums[biggest]);\n siftDown(nums, n, biggest);\n }\n }\n \n\t// heapSort(nums);\n void heapSort(vector<int>& nums){\n // heapify stage (bottom up approach)\n for(int i = nums.size() / 2 - 1; i >= 0; i--)\n siftDown(nums, nums.size(), i);\n // sorting stage\n for(int i = nums.size() - 1; i > 0; i--){\n swap(nums[0], nums[i]);\n siftDown(nums, i, 0);\n }\n }\nMerge sort (recursive version)\n\n\tvoid merge(vector<int>& nums, int l, int m, int r){\n vector<int> tmp(r - l + 1);\n int i = l; // index for left subarray\n int j = m + 1; // index for right subarray\n int k = 0; // index for temporary array\n while(i <= m && j <= r){\n if(nums[i] <= nums[j]) tmp[k++] = nums[i++]; \n else tmp[k++] = nums[j++];\n }\n while(i <= m) tmp[k++] = nums[i++];\n while(j <= r) tmp[k++] = nums[j++]; \n for(i = 0; i < k; i++) nums[l + i] = tmp[i];\n }\n\t\n\t// mergeSort(nums, 0, nums.size() - 1);\n void mergeSort(vector<int>& nums, int l, int r){\n if(l >= r) return;\n int m = l + (r - l) / 2; //middle index, same as (l+r)/2\n mergeSort(nums, l, m);\n mergeSort(nums, m + 1, r);\n merge(nums, l, m, r);\n }\nQuick sort (recursive version)\n\n\t// quickSort(nums, 0, nums.size() - 1);\n void quickSort(vector<int>& nums, int l, int r){\n if(l >= r) return;\n int i = l; // cursor for final pivot location \n for(int j = l; j <= r - 1; j++){ // nums[r] is chosen as the pivot\n if(nums[j] <= nums[r]){\n swap(nums[i], nums[j]);\n i++; // smaller or equal elements go to the left of i \n }\n }\n swap(nums[i], nums[r]); // after swap, the pivot is nums[i]\n quickSort(nums, l, i - 1);\n quickSort(nums, i + 1, r);\n }\nThe utility function swap is defined as follows\n\n\tvoid swap(int& a, int& b){\n int tmp = a;\n a = b;\n b = tmp;\n } | 4 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Merge Sort'] | 0 |
sort-an-array | merge sort solution | merge-sort-solution-by-abbos99-3nch | \n public int[] sortArray(int[] nums) {\n mergeSort(nums, 0, nums.length - 1);\n return nums;\n }\n\n private void mergeSort(int[] array, in | abbos99 | NORMAL | 2022-08-17T11:03:07.081761+00:00 | 2022-08-17T11:03:07.081798+00:00 | 775 | false | ```\n public int[] sortArray(int[] nums) {\n mergeSort(nums, 0, nums.length - 1);\n return nums;\n }\n\n private void mergeSort(int[] array, int left, int right) {\n if (left < right) {\n var middle = left + (right - left) / 2;\n\n mergeSort(array, left, middle);\n mergeSort(array, middle + 1, right);\n\n merge(array, left, middle, right);\n }\n }\n \n \n private void merge(int[] array, int left, int middle, int right) {\n int n1 = middle - left + 1;\n int n2 = right - middle;\n\n int[] leftArray = new int[n1];\n int[] rightArray = new int[n2];\n\n for (int i = 0; i < n1; ++i)\n leftArray[i] = array[i+left];\n\n for (int j = 0; j < n2; ++j)\n rightArray[j] = array[middle + j + 1];\n\n int i = 0, j = 0, k = left;\n\n while (i < n1 && j < n2) {\n if (leftArray[i] <= rightArray[j]) {\n array[k] = leftArray[i];\n i++;\n }\n else {\n array[k] = rightArray[j];\n j++;\n }\n k++;\n\n }\n\n while (i < n1) {\n array[k] = leftArray[i];\n k++;\n i++;\n }\n\n while (j < n2) {\n array[k] = rightArray[j];\n j++;\n k++;\n\n }\n\n }\n``` | 4 | 0 | ['Java'] | 0 |
sort-an-array | Optimal Javascript Solution | optimal-javascript-solution-by-gautamgun-2h77 | \nOne Liner\n\n\n\nvar sortArray = function(nums) {\n return nums.sort((a, b) => a - b)\n};\n\n\n\nMerge Sort: Time Complexity - O(N Log N) & Space complexit | GautamGunecha | NORMAL | 2022-08-11T06:44:33.845072+00:00 | 2022-08-11T06:59:09.907382+00:00 | 1,176 | false | ```\nOne Liner\n```\n\n```\nvar sortArray = function(nums) {\n return nums.sort((a, b) => a - b)\n};\n```\n\n```\nMerge Sort: Time Complexity - O(N Log N) & Space complexity - O(n)\n```\n\n```\nvar sortArray = function(nums) {\n if(nums.length <= 1) return nums\n \n let midIdx = Math.floor(nums.length / 2)\n let leftArr = sortArray(nums.slice(0, midIdx))\n let rightArr = sortArray(nums.slice(midIdx))\n \n return mergeArr(leftArr, rightArr)\n};\n\nvar mergeArr = function(arr1, arr2) {\n let results = []\n let i = 0\n let j = 0\n \n while(i < arr1.length && j < arr2.length){\n if(arr2[j] > arr1[i]){\n results.push(arr1[i]);\n i++;\n } else {\n results.push(arr2[j])\n j++;\n }\n }\n \n while(i < arr1.length) {\n results.push(arr1[i])\n i++;\n }\n \n while(j < arr2.length) {\n results.push(arr2[j])\n j++;\n }\n \n return results;\n}\n``` | 4 | 0 | ['JavaScript'] | 2 |
sort-an-array | C++ shortest solution | c-shortest-solution-by-easy0peasy1-gnyg | \nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n return nums;\n }\n};\n\n | easy0peasy1 | NORMAL | 2022-07-18T05:18:43.019930+00:00 | 2022-07-18T05:18:43.019996+00:00 | 511 | false | ```\nclass Solution {\npublic:\n vector<int> sortArray(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n return nums;\n }\n};\n```\n | 4 | 0 | ['C', 'C++'] | 0 |
sort-an-array | Java - Beats 99.6% - Count Sort // with comments | java-beats-996-count-sort-with-comments-fh62r | \nclass Solution {\n \n // Count Sort\n public int[] sortArray(int[] arr) {\n int max = Integer.MIN_VALUE;\n int min = Integer.MAX_VALUE; | Samarth-Khatri | NORMAL | 2022-06-22T19:18:05.480109+00:00 | 2022-06-22T19:18:25.481959+00:00 | 486 | false | ```\nclass Solution {\n \n // Count Sort\n public int[] sortArray(int[] arr) {\n int max = Integer.MIN_VALUE;\n int min = Integer.MAX_VALUE;\n for (int i=0;i<arr.length;++i) {\n max = Math.max(max, arr[i]);\n min = Math.min(min, arr[i]);\n }\n \n int []farr = new int[max-min+1];\n int []ans = new int[arr.length];\n\n // collecting the frequencies\n for(int i=0;i<arr.length;++i) \n farr[arr[i]-min]++;\n\n // convert frequencies to prefix sum array\n for(int i=1;i<farr.length;++i) \n farr[i] += farr[i-1];\n\n // fill the ans array from farr\n for(int i=arr.length-1;i>=0;--i) {\n int val = arr[i];\n int pos = farr[val-min];\n ans[pos-1] = val;\n farr[val-min]--;\n }\n \n return ans;\n }\n}\n``` | 4 | 0 | ['Sorting', 'Java'] | 0 |
three-equal-parts | [C++] O(n) time, O(1) space, 12 ms with explanation & comments | c-on-time-o1-space-12-ms-with-explanatio-7mm9 | Algorithm:\n\t1) Count no. of 1\'s in the given array, say countNumberOfOnes.\n\t2) If no 1 is found ie. countNumberOfOnes == 0, just return {0,size-1}\n\t3) If | primenumber | NORMAL | 2018-10-21T03:41:57.127831+00:00 | 2018-10-24T08:53:32.502927+00:00 | 9,567 | false | Algorithm:\n\t1) Count no. of 1\'s in the given array, say ```countNumberOfOnes```.\n\t2) If no 1 is found ie. ```countNumberOfOnes == 0```, just return ```{0,size-1}```\n\t3) If ``` countNumberOfOnes % 3 != 0``` , then we cannot partition the given array for sure. This is because, there is no way to put equal no. of 1\'s in any partition and hence, we will get different binary representations.\n\t4) Let\'s try to find if there is a valid partition possible now. We find the first 1 in the given array and represent it\'s position by ```start```.\n\t5) Also, we know that each partition must have ``` countNumberOfOnes/3 ``` (for same reason as given in step 3). Therefore, after finding the first 1, leave ```k = countNumberOfOnes/3 ``` 1\'s for the first partition.\n\t6) Assign this position as ```mid``` that denotes the beginning of a possible second partition.\n\t7) Further leave ```k = countNumberOfOnes/3 ``` 1\'s for this partition and assign the beginning of last partition as ```end```\n\t8) Now, all we need to do is verify whether all the partitions have same values in them. This can be done by iterating through to the end of the array.\n\t9) If ```end``` doesn\'t reach the end of the array, we find a mismatch and hence, we need to return ```{-1, -1}```\n\t10) Otherwise, we have found our partition, return ```{start-1,mid}```\n\nTime Complexity: ```O(n)```\nSpace Complexity: ```O(1)```\n\n```\nstatic int x=[](){ios::sync_with_stdio(false); cin.tie(NULL); return 0;}();\n\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n\t // Count no of 1\'s in the given array\n int countNumberOfOnes = 0;\n for(int c: A)\n if(c == 1) \n countNumberOfOnes++;\n\t\t\t\t\t\t\t\t\n\t // If no 1 is found, that means we can return ans as {0, size-1}\n if(countNumberOfOnes == 0) \n return {0, A.size()-1};\n\t\t\t\t\t\t\n // If no of 1\'s is not a multiple of 3, then we can never find a possible partition since\n // there will be atkeast one partition that will have different no of 1\'s and hence\n // different binary representation\n // For example,\n // Given :\n // 0000110 110 110 \n // | | |\n // i j\n // Total no of ones = 6\n // 0000110 110 110\n // | | |\n // start mid end\n // Match starting from first 1, and putting 2 more pointers by skipping k 1\'s\n \n if(countNumberOfOnes % 3 != 0) \n return {-1, -1};\n\t\t\t\t\t\t\n // find size of each partition\n int k = countNumberOfOnes/3;\n int i;\n \n // find the first 1 in the array\n for(i=0;i<A.size(); i++)\n if(A[i] == 1)\n break;\n int start = i;\n \n // find (k+1)th 1 in the array\n int count1 = 0;\n for(i=0;i<A.size(); i++)\n {\n if(A[i] == 1)\n count1++;\n if(count1 == k + 1)\n break;\n }\n int mid = i;\n \n //find (2*k +1)th 1 in the array\n count1= 0;\n for(i=0;i<A.size(); i++)\n {\n if(A[i] == 1)\n count1++;\n if(count1 == 2*k + 1)\n break;\n }\n int end = i;\n \n // Match all values till the end of the array\n while(end< A.size() && A[start] == A[mid] && A[mid] == A[end])\n {\n start++; mid++; end++;\n }\n \n // Return appropriate values if all the values have matched till the end\n if(end == A.size()) \n return {start-1, mid};\n \n // otherwise, no such indices found\n return {-1, -1};\n }\n};\n\n```\nCode written during contest, may be optimized further. :-) | 191 | 2 | [] | 13 |
three-equal-parts | Java O(n) simple solution (don't know why official solution is that long) | java-on-simple-solution-dont-know-why-of-90y5 | Key obseration is that three parts must have same number and pattern of 1s except the leading part. My idea is to:\n\n1. count how many ones (if num%3!=0 retu | vincexu | NORMAL | 2019-01-22T19:43:37.132772+00:00 | 2021-01-10T06:15:12.800926+00:00 | 4,531 | false | Key obseration is that three parts must have same number and pattern of 1s except the leading part. My idea is to:\n\n1. count how many ones (if num%3!=0 return [-1,-1])\n2. search from right side to left, until we found num/3 1s. This index is not final answer, but it defines patten of 1s\n3. from feft, ignore leading 0s, and then match the pattern found in step 2, to get the first EndIndex\n4. do another matching to found second EndIndex\n\n\n```\npublic int[] threeEqualParts(int[] A) {\n\t\tint numOne = 0;\n\t\tfor (int i: A){\n\t\t\tif (i==1) numOne++;\n\t\t}\n \n int[] noRes = {-1, -1};\n if (numOne == 0) return new int[]{0,2};\n if (numOne%3 != 0) return noRes;\n \n //find index of starting 1 of third string\n int idxThird=0;\n\t\tint temp = 0;\n for (int i = A.length-1; i>=0; i--){\n if (A[i]==1){\n temp++;\n if (temp == numOne / 3){\n idxThird = i;\n break;\n }\n } \n }\n \n int res1 = findEndIdx(A, 0, idxThird);\n if (res1<0) return noRes;\n \n int res2 = findEndIdx(A, res1+1, idxThird);\n if (res2<0) return noRes;\n \n return new int[]{res1, res2+1};\n }\n \n\t//right is the pattern to compare to. \n\t//return EndIdx of left pattern that matches right side.\n private int findEndIdx(int[] A, int left, int right){\n while (A[left]==0) left++;\n while (right < A.length){\n if (A[left]!=A[right]) return -1;\n left++;\n right++; \n }\n return left-1;\n }\n``` | 78 | 0 | ['Java'] | 9 |
three-equal-parts | [Python] O(n) fast solution, explained | python-on-fast-solution-explained-by-dba-hjkq | In this problem we need to split number into three parts, such that number in each part after removed all zeroes are equal.\n1. Let us check all the places, whe | dbabichev | NORMAL | 2021-07-17T12:58:53.998929+00:00 | 2021-07-17T12:58:53.998973+00:00 | 2,211 | false | In this problem we need to split number into three parts, such that number in each part after removed all zeroes are equal.\n1. Let us check all the places, where we have `1.` Let us have `m` elements such that.\n2. If `m == 0`, it means that we have all zeroes, so we can split in any way, let us split it `[0, 2]`.\n3. If `m` is not divisible by `3`, we can return `[-1, -1]` immedietly, because if we can have three equal parts, number of ones in these parts must be the same.\n4. Let us find now `6` indexes: `p1, p2, p3, p4, p5, p6`, where `p1` is index of first `1`, `p2` is index of last one in first part, `p3` is index of fisrt one in second part, and so on. Then it is necessary that `A[p1:p2+1]` equal to `A[p3:p4+1]` equal to `A[p5:p6+1]`. Note that is is not sufficient though, because we can add some zeroes in the ends. So, if this condition do not holds, we return `[-1, -1]`.\n5. Evaluate lengths of how many zeros we can add in the end: `l1, l2, l3`. For `l3` we do not have any choice: we need to take all there zeroes. For `l1` and `l2` we can put zeroes in the beginning of one number or to the end of the next, so the options we have are: `[0, ..., l1]` for the first, `[0, ..., l2]` for the second and `[l3]` for third. So, if `l3 > l2` or `l3 > l1`, we can not make parts equal and we return `[-1, -1]`.\n6. In the end return `[p2 + l3, p4 + l3 + 1]`, in this way in each part we have `l3` zeroes in the end.\n\n#### Complexity\nTime complexity is `O(n)`, space complexity is `O(n)` as well to keep array of indexes.\n\n#### Code\n```python\nclass Solution:\n def threeEqualParts(self, A):\n n = len(A)\n indexes = [i for i in range(n) if A[i] == 1]\n m = len(indexes)\n \n if m == 0: return [0, 2]\n \n if m % 3 != 0: return [-1, -1]\n p1, p2 = indexes[0], indexes[m//3-1]\n p3, p4 = indexes[m//3], indexes[2*m//3-1]\n p5, p6 = indexes[2*m//3], indexes[-1]\n part1, part2, part3 = A[p1:p2+1], A[p3:p4+1], A[p5:p6+1]\n \n if part1 != part2 or part2 != part3: return [-1, -1]\n \n l1 = p3 - p2 - 1\n l2 = p5 - p4 - 1\n l3 = n - p6 - 1\n \n if l3 > l2 or l3 > l1: return [-1, -1]\n \n return [p2 + l3, p4 + l3 + 1]\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 58 | 2 | [] | 5 |
three-equal-parts | Logical Thinking | logical-thinking-by-gracemeng-tnae | What is \'same binary value\' like? \n> Digits following first 1 in each part should be identical. \n\n> How could we decide which 1 is the first 1 of a divided | gracemeng | NORMAL | 2019-03-06T16:12:14.335513+00:00 | 2019-03-06T16:12:14.335546+00:00 | 2,199 | false | > What is \'same binary value\' like? \n> Digits following first 1 in each part should be identical. \n\n> How could we decide which 1 is the first 1 of a divided part?\n> \n> Assuming `numOnes` is number of 1s in A, each part should be with `numOnesPerPart = numOnes / 3` 1s. \n> So the first \'1\' in left part is `1`st \'1\', first \'1\' in middle part is `numOnesPerPart + 1`th \'1\', first \'1\' in right part is `numOnesPerPart * 2 + 1`th \'1\'.\n>\n> Then we compare the rest part digit by digit. Hopefully, the pointer in right part will reach A.length, which means we can make three equal parts.\n> \n>There is a corner case such as all elements in A are 0s.\n****\n```\nclass Solution {\n public int[] threeEqualParts(int[] A) {\n int numOnes = countOnes(A);\n if (numOnes % 3 != 0) return new int[]{-1, -1};\n else {\n int numOnesPerPart = numOnes / 3;\n \n // Set pointers at first one in each part.\n int leftPtr = locateOne(A, 1), midPtr = locateOne(A, numOnesPerPart + 1), rightPtr = locateOne(A, numOnesPerPart * 2 + 1);\n \n // Compare 3 parts digit by digit.\n while (leftPtr < midPtr && midPtr < rightPtr && rightPtr < A.length) {\n if (A[leftPtr] == A[midPtr] && A[rightPtr] == A[midPtr]) {\n leftPtr++;\n midPtr++;\n rightPtr++;\n } else break;\n }\n \n if (rightPtr == A.length) return new int[]{leftPtr - 1, midPtr};\n else if (rightPtr == 0) return new int[]{0, A.length - 1};\n else return new int[]{-1, -1};\n }\n }\n \n private int countOnes(int[] A) {\n int numOnes = 0;\n for (int i = 0; i < A.length; i++) {\n if (A[i] == 1) {\n numOnes++;\n }\n }\n return numOnes; \n }\n \n private int locateOne(int[] A, int targetOne) {\n int cntOne = 0;\n for (int i = 0; i < A.length; i++) {\n if (A[i] == 1) {\n cntOne++;\n if (cntOne == targetOne) return i;\n }\n }\n return 0; // When all elements in A are 0.\n }\n}\n```\n**(\u4EBA \u2022\u0348\u1D17\u2022\u0348)** Thanks for voting! | 46 | 1 | [] | 6 |
three-equal-parts | ✅ Three Equal Parts || C++ Easy Solution || With Approach | three-equal-parts-c-easy-solution-with-a-3627 | APPROACH\n1. Store every 1\'s position in a vector.\n2. It is easy to know the first 1\'s position of three parts as [x, y, z].\n3. Then verify three parts whet | Maango16 | NORMAL | 2021-07-17T07:13:15.217146+00:00 | 2021-07-17T09:39:19.402239+00:00 | 1,876 | false | # **APPROACH**\n1. Store every 1\'s position in a vector.\n2. It is easy to know the first 1\'s position of three parts as [x, y, z].\n3. Then verify three parts whether equal\n\n***NOTE:***\n* If in cases where number of ones are not a multiple of 3, there will be no case of equal parts so return {-1,-1}\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) \n {\n int n = arr.size() ;\n vector<int> one ;\n for(int i = 0 ; i < n ; i++)\n {\n if(arr[i])\n {\n one.push_back(i) ;\n }\n }\n int cnt = one.size() ;\n if(cnt == 0)\n {\n return {0 , n - 1} ;\n }\n if(cnt%3) //IF NUMBER OF ONES IS NOT A MULTIPLE OF 3\n {\n return {-1 , -1} ;\n }\n int s = one[0] , t = one[cnt/3] , u = one[(cnt/3)*2] ;\n while(u < n && arr[s] == arr[t] && arr[s] == arr[u])\n {\n s++ ;\n t++ ;\n u++ ;\n }\n if(u == n)\n {\n return {s - 1 , t} ;\n }\n return {-1 , -1} ;\n }\n};\n```\n**Time Complexity: O(n)**\n**Space Complexity: O(n)**\n# **Update:**\nThis is the general approach once we know that number of ones are a multiple of three -->\nWe can form intervals for `s , t & u` let\'s say, `[i1, j1], [i2, j2], [i3, j3]` \n__If there is only 3 ones, then this interval length will be one__\nSo the **zeroes after "one, on the position of u"** *let\'s assume z* , must be included in each part (i.e. in s & t)\nMaking the new intervals, `[i1, j1+z] & [i2, j2+z]` for s & t respectively\nIf all this is actually possible, then the final answer is **[j1+z , j2+z+1].**\nHope this helps | 42 | 4 | ['C'] | 6 |
three-equal-parts | C++ | O(N) | Commented Code | easy to understand | c-on-commented-code-easy-to-understand-b-rzcg | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n \n int ones = 0;\n int n = arr.size();\n \n | reetisharma | NORMAL | 2021-07-17T17:24:05.168685+00:00 | 2021-07-17T17:24:19.941404+00:00 | 1,285 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n \n int ones = 0;\n int n = arr.size();\n \n for(int i : arr){\n if(i==1)\n ones++;\n }\n \n //if no ones\n if(ones == 0) return {0,n-1};\n //if irregular ones, that cannot be divided in 3 parts\n if(ones%3!=0) return {-1,-1};\n \n int k = ones/3;\n \n //we find the starting position of 3 parts since leading zeroes does not matter\n int firstOne = -1, secondOne = -1, thirdOne = -1;\n int cnt1 = 0, cnt2 = 0, cnt3 = 0;\n \n //Find first one\n for(int i=0;i<n;i++){\n if(arr[i]==1){\n firstOne = i;\n break;\n }\n }\n //Find second one\n for(int i=firstOne+1;i<n;i++){\n if(arr[i]==1) cnt2++;\n if(arr[i]==1 && cnt2==k){\n secondOne = i;\n break;\n }\n }\n //Find third one\n for(int i=secondOne+1;i<n;i++){\n if(arr[i]==1) cnt3++;\n if(arr[i]==1 && cnt3==k){\n thirdOne = i;\n break;\n }\n }\n \n //checking if they are equal\n int x = firstOne, y = secondOne, z = thirdOne;\n while(x<n && y<n && z<n){\n if(arr[x] == arr[y] && arr[y] == arr[z]){\n x++;y++;z++;\n }\n else\n return {-1,-1};\n }\n \n //after the while loop we\'ll have the\n // | |\n // 1 | 0 1 | 0 1\n // | |\n // ^ ^ ^\n // | | |\n // x y z\n\n return {x-1,y};\n \n }\n};\n``` | 26 | 1 | ['C'] | 3 |
three-equal-parts | [C++] O(N) time O(N) space, 40ms, 14 lines, 2 loops, easy understand with explanation | c-on-time-on-space-40ms-14-lines-2-loops-vpus | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n vector<int> dp;\n for(int i = 0 ; i < A.size(); i++) // this loop | fangzzh | NORMAL | 2018-10-21T05:21:21.834299+00:00 | 2018-10-22T02:41:17.850837+00:00 | 1,434 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n vector<int> dp;\n for(int i = 0 ; i < A.size(); i++) // this loop is used to store the index of all 1s\n if(A[i]) dp.push_back(i);\n if(dp.size() % 3) return {-1, -1}; // if the number of 1s cannot be devided perfectly by 3, the input is invalid\n\tif(dp.empty()) return {0,2}; // if the number of 1 is zero, then it is natually valid, return {0, 2}\n int l1 = 0, l2 = dp.size() / 3, l3 = l2 * 2; //if we want to devide into 3 parts, the distribution pattern of 1s in three parts should be the same\n for(int i = 1; i < l2; i++ ) {\n int diff = dp[i] - dp[i-1];\n if(dp[l2+i] - dp[l2+i-1] != diff || dp[l3+i] - dp[l3+i-1] != diff) //unmatched pattern\n return {-1, -1};\n\t}\n int tail0 = A.size() - dp.back(); // calculate how many 0s tail\n if(dp[l3] - dp[l3-1] < tail0 || dp[l2] - dp[l2-1] < tail0) return {-1,-1};// all three parts should tail with the same number of 0s with that in the last part\n return {dp[l2-1] + tail0 - 1, dp[l3-1] + tail0};\n }\n};\n``` | 20 | 2 | [] | 2 |
three-equal-parts | [Python] O(n) Straightforward Solution | python-on-straightforward-solution-by-wt-ii7e | The solution is inspired by this Logical Thinking.\n\n\nclass Solution:\n def threeEqualParts(self, A: List[int]) -> List[int]:\n \n num_ones = | wt262 | NORMAL | 2020-06-08T19:17:20.398853+00:00 | 2020-06-08T19:21:15.788688+00:00 | 847 | false | The solution is inspired by this [Logical Thinking](https://leetcode.com/problems/three-equal-parts/discuss/250203/Logical-Thinking).\n\n```\nclass Solution:\n def threeEqualParts(self, A: List[int]) -> List[int]:\n \n num_ones = sum(A)\n \n if num_ones == 0:\n return [0, 2]\n \n if num_ones % 3 != 0:\n return [-1, -1]\n \n c = 0\n s1 = s2 = s3 = -1\n for idx,x in enumerate(A):\n\t\t\t# Find the first 1 in each part\n if x == 1:\n c += 1\n \n if c == 1 and s1 < 0:\n s1 = idx\n \n if c == num_ones//3 + 1 and s2 < 0:\n s2 = idx\n \n if c == num_ones*2//3 + 1 and s3 < 0:\n s3 = idx\n break\n \n n = len(A[s3:]) # The length of each part when all the leading 0\'s are removed\n \n if A[s1:s1+n] == A[s2:s2+n] and A[s2:s2+n] == A[s3:]:\n return [s1+n-1, s2+n]\n else:\n return [-1, -1]\n```\n\n | 18 | 0 | [] | 3 |
three-equal-parts | Python Easy Understand Solution With Explanation | python-easy-understand-solution-with-exp-ydrk | The idea is pretty straight forward, you just need some obervation before coding.\n1. If the solution exists, the number of 1 in list should be times of 3.\n2. | xiaozhi1 | NORMAL | 2018-10-21T07:12:48.104035+00:00 | 2018-10-22T17:29:30.776420+00:00 | 1,044 | false | The idea is pretty straight forward, you just need some obervation before coding.\n1. If the solution exists, the number of 1 in list should be times of 3.\n2. Since the ending zeros affect the binary value ([1,1] != [1,1, 0]) and the leading zeros mean nothing, we can find the value of each part (I called potential in the following code) if we scan the list from the end to the beginning.\n3. After we find this number, things become easier. we just need to find the effective points of each part (I mean the position of first 1), we can locate the end of each part. Then the answer is just some calculation.\n```\ndef threeEqualParts(self, A):\n """\n :type A: List[int]\n :rtype: List[int]\n """\n c1 = A.count(1)\n if c1%3: return [-1, -1]\n if c1 == 0: return [0, len(A)-1]\n n1 = c1/3\n potential = []\n count = 0\n\t\t\t\t# find the value of each part\n for a in A[::-1]:\n potential.insert(0, a)\n if a == 1:\n count += 1\n if count == n1:\n break\n lp = len(potential)\n temp = []\n i = 0\n\t\t\t\t# find the effective beginning of each part\n while i < (len(A)-lp):\n if A[i] == 1 and A[i:i+lp] == potential:\n temp.append(i)\n i += lp\n elif A[i] == 0:\n i += 1\n else:\n return [-1, -1]\n ans = [temp[0]+lp-1, temp[1]+lp]\n return ans\n``` | 11 | 1 | [] | 2 |
three-equal-parts | Java O(n) Solution | java-on-solution-by-self_learner-a8hp | ``` // The solution can be optimized to O(1) space, by not using StringBuilder, but only record the index of the first one digit of the right part. class Solut | self_learner | NORMAL | 2018-10-21T03:28:51.600988+00:00 | 2018-10-23T05:35:41.101410+00:00 | 1,945 | false | ```
// The solution can be optimized to O(1) space, by not using StringBuilder, but only record the index of the first one digit of the right part.
class Solution {
public int[] threeEqualParts(int[] A) {
if (A == null || A.length < 3) return new int[] {-1, -1};
int n = A.length;
int cntOneBit = 0;
for (int b : A) {
if (b == 1) cntOneBit++;
}
if (cntOneBit % 3 != 0) return new int[] {-1, -1};
int cnt = cntOneBit / 3;
if (cnt == 0) return new int[] {0, n - 1};
//construct the string using the right most part;
int j = n - 1, cntR = 0;
StringBuilder suffix = new StringBuilder();
for (;j >= 0 && cntR < cnt; j--) {
suffix.append(A[j]);
if (A[j] == 1) cntR++;
}
String target = suffix.reverse().toString();
//matching the left part with target string, omit all leading zero
int i = 0;
while (A[i] == 0) i++;
int k = 0;
while (k < target.length()) {
if (A[i + k] == target.charAt(k) - '0') k++;
else return new int[] {-1, -1};
}
int left = i + k -1;
//matching the middle part with target string, omit all leading zero
i = i + k;
while (A[i] == 0) i++;
k = 0;
while (k < target.length()) {
if (A[i + k] == target.charAt(k) - '0') k++;
else return new int[] {-1, -1};
}
return new int[] {left, i + k};
}
} | 10 | 1 | [] | 3 |
three-equal-parts | Java 10ms solution with O(n) time and O(1)space | java-10ms-solution-with-on-time-and-o1sp-641m | It is obviously that if the array can be divided into three part. The 1\'s number in each should be same. Besides, the 0\'s number in the last part should be th | zhuojiansen | NORMAL | 2018-10-22T19:37:40.934740+00:00 | 2018-10-22T19:37:40.934780+00:00 | 683 | false | It is obviously that if the array can be divided into three part. The 1\'s number in each should be same. Besides, the 0\'s number in the last part should be the true 0\'s number in the end of each part.\nWe get the 1\'s number and divide them into 3 parts. If numOf1 % 3 is not a integer then just return [-1, -1]. Suppose the number of 1 is 3n. The three parts should shart from the first 1, the n + 1th 1 and the 2n + 1th 1. Then we just compare all of them with the last part and can get the answer easily.\n```\nclass Solution {\n public int[] threeEqualParts(int[] A) {\n int[] res = new int[2];\n res[0] = -1;\n res[1] = -1;\n // num Of 1\n int numOf1 = 0;\n for (int a : A) {\n if (a == 1) {\n numOf1++;\n }\n }\n \n if (numOf1 == 0) {\n return new int[]{0, 2};\n }\n \n if (numOf1 % 3 != 0) {\n return res;\n }\n \n int partLength = numOf1 / 3;\n int index0 = -1;\n int index1 = -1;\n int index2 = -1;\n numOf1 = 0;\n for (int i = 0; i < A.length; i ++) {\n if (A[i] == 1) {\n numOf1++;\n if (numOf1 == partLength + 1) {\n index1 = i;\n } else if (numOf1 == 2 * partLength + 1) {\n index2 = i;\n } else if (numOf1 == 1) {\n index0 = i;\n }\n }\n }\n \n while (index2 < A.length) {\n if (A[index2] == A[index0] && A[index2] == A[index1]) {\n index2++;\n index1++;\n index0++;\n } else {\n return res;\n }\n }\n \n return new int[]{index0 - 1, index1};\n }\n}\n``` | 9 | 1 | [] | 2 |
three-equal-parts | 2 clean Python linear solutions | 2-clean-python-linear-solutions-by-cthlo-6u1m | \nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # count number of ones\n ones = sum(arr)\n if ones % 3 != | cthlo | NORMAL | 2021-07-17T13:28:56.593513+00:00 | 2021-07-18T20:37:20.718557+00:00 | 665 | false | ```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # count number of ones\n ones = sum(arr)\n if ones % 3 != 0:\n return [-1, -1]\n elif ones == 0: # special case: all zeros\n return [0, 2]\n \n # find the start index of each group of ones\n c = 0\n starts = []\n for i, d in enumerate(arr):\n if d == 1:\n if c % (ones // 3) == 0:\n starts.append(i)\n c += 1\n\n # scan the groups in parallel to compare digits\n i, j, k = starts\n while k < len(arr): # note that the last/rightmost group must include all digits till the end\n if arr[i] == arr[j] == arr[k]:\n i += 1\n j += 1\n k += 1\n else:\n return [-1, -1]\n return [i-1, j]\n```\nRuntime: *O(n)*\nSpace: *O(1)*\n\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n # gather the indices of the ones\n ones = [i for i, d in enumerate(arr) if d == 1]\n\n if not ones:\n return [0, 2]\n elif len(ones) % 3 != 0:\n return [-1, -1]\n\n # get the start indices of the 3 groups\n i, j, k = ones[0], ones[len(ones)//3], ones[len(ones)//3*2]\n\n # calculate the size/length of what each group should be\n length = len(arr) - k # note that the last/rightmost group must include all digits till the end\n # so we know that the size of each group is `len(arr) - k` (where `k` is start of third group)\n\n # compare the three groups\n if arr[i:i+length] == arr[j:j+length] == arr[k:k+length]:\n return [i+length-1, j+length]\n \n return [-1, -1]\n```\nRuntime: *O(n)*\nSpace: *O(n)* | 8 | 0 | ['Python', 'Python3'] | 0 |
three-equal-parts | ✅ Three Equal Parts | Java | Easy to understand | Detailed approach | three-equal-parts-java-easy-to-understan-0b8m | Intuition\n We can easily see that in order for the array to have equal parts, in each part the number of ones should be equal.\n The above implies that the tot | varunsharma-codes | NORMAL | 2021-07-17T20:41:31.712662+00:00 | 2021-07-17T20:41:48.895980+00:00 | 575 | false | **Intuition**\n* We can easily see that in order for the array to have equal parts, in each part the number of ones should be equal.\n* The above implies that the `totalOnes` should be divisible by 3.\n* Now lets understand of basic cases\n* `totalOnes = 0`: If this is the case any two indices can divide into 3 equal parts since all will be zero\n* `totalOnes%3 !=0 `: Since total ones is not divisble solution is not possible, so we return `[-1,-1]`\n* Next we know that each part will have `k = totalOnes/3` ones. Also if we start from the end the target which we want for each part will start as soon as we have taken `k` ones. So we can keep track of this index from where target starts. ***Note***: This index might not be the index `j` as there can be leading zeroes which will not change the target.\n* Now we have to find if its possible to build the same target from start to the end.\n* Now to get the index `i` we can start from index `0` and move to the index of first `1` (What we do here is ignore leading zeroes). Now we start comparing elements from the target index and index i. If its equal then this part can be equal to target.\n* We do the similar operation for the second part.\n\n```\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int totalOnes = 0;\n for(int e:arr){\n if(e==1){\n totalOnes++;\n }\n }\n \n int l = arr.length;\n if(totalOnes==0){\n return new int[] {0, l-1};\n }\n if(totalOnes%3!=0){\n return new int[] {-1,-1};\n }\n \n int k=totalOnes/3; // Each part will have k number of 1\'s\n int targetIdx = l; // This first index of \'1\' which starts the equal part\n \n while(k>0){\n targetIdx--;\n if(arr[targetIdx]==1){\n k--;\n }\n }\n \n int i = isPartPossible(arr, 0, targetIdx);\n if(i==-1){\n return new int[] {-1,-1};\n }\n int j = isPartPossible(arr, i, targetIdx);\n if(j==-1){\n return new int[] {-1,-1};\n }\n \n return new int[] {i-1,j};\n }\n \n private int isPartPossible(int[] arr, int i, int start) {\n while(arr[i]==0){\n i++;\n }\n while(start<arr.length){\n if(arr[i]!=arr[start]) {\n return -1;\n }\n i++;\n start++;\n }\n return i;\n }\n}\n```\n\nPS: Please upvote if you think it can help others to understand this question. | 7 | 1 | ['Java'] | 0 |
three-equal-parts | Java Solution with detailed Comments & Examples | java-solution-with-detailed-comments-exa-7ruf | \nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int ones = 0;\n for (int i : arr) if (i == 1) ones++;\n\n\t\t/**\n\t\t * The f | gogagubi | NORMAL | 2021-07-17T15:39:07.667699+00:00 | 2021-07-17T17:06:13.299612+00:00 | 439 | false | ```\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int ones = 0;\n for (int i : arr) if (i == 1) ones++;\n\n\t\t/**\n\t\t * The first base case is a hardcoded case when there are only zeros in the array. \n\t\t * Since the array size is at least 3 in the case of only zeros there are still available to cut the array and get three equal binary numbers. \n\t\t * e.g. [0, 0, 0] we can devide into three parts |0, 0, 0| and those numbers are correct binary numbers. \n\t\t * e.g. [0, 0, 0, 0, 0, ...] we can devide into three parts |0, 0, 0...| and those numbers are correct binary numbers. \n\t\t\n\t\t * arr = [0, 0, 0, 0, 0, ...]\n\t\t * ind = [0, 1, 2, 3, 4]\n * i = 0 and j = 2 because first part is 0 - 0(0, i) indexes, second part is 1 - 1(i + 1, j - 1) indexes and third part is 2 - 2(j, n - 1) indexes\n\t\t\n\t\t * So taking into consideration above answer [0, 2] is the first correct answer that we can get in the case of only zeros. \n\t\t*/\n if (ones == 0) return new int[]{0, 2};\n\t\t\n\t\t/**\n\t\t * If there are ones in an array they should be dividable on 3. \n\t\t * This is because we need to divide the array into three parts \n\t\t * and each part should have the same amount of ones \n\t\t * in the case of binary numbers to be equal\n\t\t*/\n if (ones % 3 != 0) return new int[]{-1, -1};\n\n\t\t/**\n\t\t* This is the most trickier part of this solution.\n\t\t* Basically what we are doing here is we are looking for the first occurrence of \'1\' for each chunk. \n\t\t* Let\'s take an example: arr = [0, 1, 1, 0, | 0, 0, 1, 1, 0, | 1, 1, 0]\n\n\t\t* Since the count of ones is 6 and 6 / 3 = 2 it means that after every +2 index we are standing on the next chunk. 0 +, 2 +, 4 + ... \n\t\t* Therefore: \n\t\t* First occurrence of \'1\' for the first chunk is on the index of 1\n\t\t* First occurrence of \'1\' for the second chunk is on the index of 6\n\t\t* First occurrence of \'1\' for the third chunk is on the index of 9\n\t\t*/\n int point1 = 0, point2 = 0, point3 = 0;\n int unit = ones / 3;\n int oneCounter = 0;\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] == 1) {\n if (oneCounter == 0) point1 = i;\n else if (oneCounter == unit) point2 = i;\n else if (oneCounter == 2 * unit) point3 = i;\n\n oneCounter++;\n }\n }\n\n\t\t/**\n\t\t* The last part is pretty straightforward. \n\t\t* We just need to start all pointers from the first occurrences of \'1\' and move three of them simultaneously to the right. \n\t\t* As we know binary numbers are equals if all of their bits are equal. Otherwise we return {-1, -1}\n\t\t*/\n while (point3 < arr.length) {\n if (arr[point1] != arr[point2] || arr[point2] != arr[point3]) return new int[]{-1, -1};\n\n point1++;\n point2++;\n point3++;\n }\n\n return new int[]{point1 - 1, point2};\n }\n}\n``` | 5 | 1 | ['Java'] | 1 |
three-equal-parts | JAVA 50ms with my thinking process | java-50ms-with-my-thinking-process-by-ha-if6c | thinking process is chinese:https://www.jianshu.com/p/c8dbaaf87644\n\npublic int[] threeEqualParts(int[] A) {\n int i = 0, j = A.length-1;\n Deque | happyleetcode | NORMAL | 2018-10-21T03:26:35.896784+00:00 | 2018-10-22T05:09:58.165040+00:00 | 526 | false | thinking process is chinese:https://www.jianshu.com/p/c8dbaaf87644\n```\npublic int[] threeEqualParts(int[] A) {\n int i = 0, j = A.length-1;\n Deque<Integer> pre = new ArrayDeque<>();\n Deque<Integer> mid = new ArrayDeque<>();\n Deque<Integer> last = new ArrayDeque<>();\n if(A[0]!=0) pre.offerLast(1);\n if(A[j]!=0) last.offerLast(1);\n for(int k = 1; k < j; k++){\n if(mid.isEmpty() && A[k] == 0) continue;\n mid.offerLast(A[k]);\n } \n while(i < j){\n int cp = compare(pre,last);\n if(cp<0){\n i++;\n if(A[i] == 0){\n if(!pre.isEmpty()) pre.offerLast(0);\n } \n else{\n if(mid.isEmpty()) break;\n pre.offerLast(mid.pollFirst());\n while(!mid.isEmpty() && mid.peekFirst()==0) mid.pollFirst();\n }\n }else if(cp>0){\n j--;\n if(mid.isEmpty()) break;\n if(A[j] == 0) mid.pollLast();\n else moveMidToLast(A,mid,last,j);\n }else{\n int cp2 = compare(mid,last);\n \n if(cp2 == 0) return new int[]{i,j};\n if(cp2<0) break;\n else{\n j--;\n if(mid.isEmpty()) break;\n if(A[j] == 0) mid.pollLast();\n else moveMidToLast(A,mid,last,j);\n }\n }\n }\n return new int[]{-1,-1};\n }\n private void moveMidToLast(int[] A,Deque<Integer> mid,Deque<Integer> last,int j){\n int idx = j+1;\n while(idx<A.length && A[idx++]==0)\n last.offerFirst(0);\n last.offerFirst(mid.pollLast());\n }\n \n private int compare(Deque<Integer> a, Deque<Integer> b){\n if(a.size() < b.size()) return -1;\n if(a.size() == b.size()){\n Iterator<Integer> itr = a.iterator();\n Iterator<Integer> itr2 = b.iterator();\n while(itr.hasNext()){\n int fa = itr.next();\n int fb = itr2.next();\n if(fa == fb) continue;\n return fa-fb;\n }\n\n return 0;\n }\n return 1;\n }\n``` | 5 | 2 | [] | 2 |
three-equal-parts | [C++] Easy, Clean Solution | c-easy-clean-solution-by-rsgt24-btpl | Solution:\n\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& ar) {\n int cnt0 = 0, cnt1 = 0;\n for(auto i: ar){\n | rsgt24 | NORMAL | 2021-07-17T22:39:33.046182+00:00 | 2021-07-17T22:41:09.259746+00:00 | 368 | false | **Solution:**\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& ar) {\n int cnt0 = 0, cnt1 = 0;\n for(auto i: ar){\n if(i)\n cnt1++;\n else\n cnt0++;\n }\n \n if(cnt1 % 3 != 0)\n return {-1, -1};\n else\n {\n if(cnt1 == 0){\n return {0, 2};\n }\n else{\n int k = cnt1 / 3;\n int one = 0, two = 0, three = 0;\n int cnt = 0;\n for(int i = 0; i < ar.size(); i++){\n if(ar[i]){\n if(cnt == 0)\n one = i;\n cnt++;\n \n if(cnt == k + 1)\n two = i;\n \n if(cnt == 2 * k + 1){\n three = i;\n break;\n }\n }\n }\n \n //now we have 3 indices.......\n //check if each increment in the indices results in similar integer 0/1....\n \n while(1){\n if(ar[one] != ar[two] or ar[two] != ar[three] or three == ar.size())\n break;\n \n one++;\n two++;\n three++;\n }\n \n if(three == ar.size())\n return {one - 1, two};\n else\n return {-1, -1};\n } \n }\n }\n};\n``` | 4 | 0 | ['Bit Manipulation', 'C'] | 0 |
three-equal-parts | 12 lines js solution faster than 100% js solutions | 12-lines-js-solution-faster-than-100-js-g4wkt | First I found out how many ones are in the array. Then I checked if the array is dividable into 3 with the same amount of ones. Then I iterated from the end to | iamawebgeek | NORMAL | 2021-07-17T08:46:04.895325+00:00 | 2021-07-17T08:55:01.153846+00:00 | 320 | false | First I found out how many ones are in the array. Then I checked if the array is dividable into 3 with the same amount of ones. Then I iterated from the end to find out the number. Once I had the number all I had to do is to validate if the sequence of first and second sets match.\n```\n/**\n * @param {number[]} arr\n * @return {number[]}\n */\nvar threeEqualParts = function(arr) {\n const ones = arr.reduce((s, n) => s + n, 0);\n if (ones === 0) return [0, 2];\n if (ones % 3 !== 0) return [-1, -1];\n let onesToFind = ones / 3;\n let k = arr.length;\n while (onesToFind > 0) if (arr[--k] === 1) --onesToFind;\n const iter = arr.length - k;\n const firstOne = arr.indexOf(1);\n const secondOne = arr.indexOf(1, firstOne + iter);\n for (let i = 0; i < iter; i++)\n if (arr[i + firstOne] !== arr[k + i] || arr[i + secondOne] !== arr[k + i]) return [-1, -1];\n return [firstOne + iter - 1, secondOne + iter];\n};\n``` | 4 | 0 | ['JavaScript'] | 1 |
three-equal-parts | [C++] O(n) time, O(n) space, easy to implement | c-on-time-on-space-easy-to-implement-by-5uxti | Store every 1\'s position, easy to know the first 1\'s position of three parts as [x, y, z].\nThen verify three parts whether equal.\n\n\nclass Solution {\npubl | wenpeng2021 | NORMAL | 2020-06-19T01:30:13.237437+00:00 | 2020-06-19T01:30:13.237479+00:00 | 254 | false | Store every 1\'s position, easy to know the first 1\'s position of three parts as [x, y, z].\nThen verify three parts whether equal.\n\n```\nclass Solution {\npublic:\nvector<int> threeEqualParts(vector<int>& v) {\n int n = v.size();\n vector<int> ones;\n for (int i = 0; i < n; ++i) if (v[i]) ones.push_back(i);\n int cnt = ones.size();\n if (!cnt) return {0, n - 1};\n if (cnt % 3) return {-1, -1};\n int x = ones[0], y = ones[cnt/3], z = ones[cnt/3*2];\n while (z < n && v[x] == v[y] && v[x] == v[z]) ++x, ++y, ++z;\n if (z == n) return {x-1, y};\n return {-1, -1};\n}\n};\n``` | 4 | 0 | [] | 1 |
three-equal-parts | python O(n) 108ms | python-on-108ms-by-dashidhy-26ca | ``` class Solution: def threeEqualParts(self, A): """ :type A: List[int] :rtype: List[int] """ N = len(A) if | dashidhy | NORMAL | 2018-10-21T03:15:40.161992+00:00 | 2018-10-21T03:15:40.162044+00:00 | 383 | false | ```
class Solution:
def threeEqualParts(self, A):
"""
:type A: List[int]
:rtype: List[int]
"""
N = len(A)
if N < 3:
return [-1, -1]
num_ones = sum(A)
if num_ones % 3 != 0:
return [-1, -1]
if num_ones == 0:
return [0, 2]
need_ones = num_ones // 3
str_input_reverse = ''.join(map(str, reversed(A)))
count_1 = 0
i = 0
while count_1 != need_ones:
if str_input_reverse[i] == '1':
count_1 += 1
i += 1
second = str_input_reverse.find(str_input_reverse[:i], i)
if(second == -1):
return [-1, -1]
third = str_input_reverse.find(str_input_reverse[:i], second + i)
if(third == -1):
return [-1, -1]
return [N - 1 - third, N - second]
``` | 4 | 0 | [] | 3 |
three-equal-parts | C++ | Detailed Explanation with Proofs | | c-detailed-explanation-with-proofs-by-pr-0ens | Intuition\n Describe your first thoughts on how to solve this problem. \nNot much intuitive as it does not invole any famous algorithm but a bit of observation. | prathamn1 | NORMAL | 2023-01-27T07:08:33.190994+00:00 | 2023-01-27T07:08:33.191026+00:00 | 389 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNot much intuitive as it does not invole any famous algorithm but a bit of observation.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- First and the only thing to notice is that if we have to divide the array into three parts with equal value then ***each part must have equal number of 1 in them.***\nTake your time :) \nProof->\nAs each number must have equal value which means in binary form (After removing leading zeros ) each of them must be equivalent in the position of their bits.\nAnd for all of them to be equivalent , the sufficient condition will be for them to have the equal number of set bits \'1\' in them, we can\'t take zeros \'0\' as it can form leading zeros which will then become unsignificant.\n\n- So calculate the total number of ones and check for it to be a multiple of three. There will be a special case for 0 number of ones ( See the code for it ).\nIf it\'s a multiple of three then, again traverse the array to get the starting point of all the individual parts as\n**First part -> first \'1\' index\nsecond part -> total_one/3+1 th \'1\' index\nthird part -> total_one/3 + total_one/3 + 1 th \'1\' index.**\n\n- Now we have our starting indexes we just have to check if we could actually make them equivalent and for that we simply traverse in our third part till last and correspondingly check the indices in first part and second part.\nIf we reach the end of array ,which means we have the corresponding indices of each part equal, so we could actually divide them and the remaining values will serve as leading zeros for individual parts.\n\n***See the code for more details or try to dry run on any test case for better understanding.***\n \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ Traversing the array three times.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int n=arr.size(),ones=count(arr.begin(),arr.end(),1);\n if(ones==0) return {0,n-1}; // if full array is of zeros\n if(ones%3) return {-1,-1};\n\n ones=ones/3; // calculating the size of each block with equal ones.\n\n\n int curr_one=0,first=-1,second=-1,third=-1;\n for(int i=0;i<n;i++) {\n if(arr[i]==1) curr_one++;\n\n if(curr_one==1 and first==-1) first=i;\n else if(curr_one==ones+1 and second==-1) second=i;\n else if(curr_one==2*ones+1 and third==-1) third=i;\n }\n\n int i,j,k;\n for(i=first,j=second,k=third;k<n;i++,j++,k++) {\n if(not (arr[i]==arr[j] and arr[j]==arr[k])) return {-1,-1};\n }\n return {i-1,j};\n }\n};\n``` | 3 | 0 | ['Array', 'Math', 'C++'] | 2 |
three-equal-parts | 100% TC easy python solution | 100-tc-easy-python-solution-by-nitanshri-ca5w | Hint\nCount the num of ones, and think how they will be split between the 3 segments :)\n\ndef threeEqualParts(self, arr: List[int]) -> List[int]:\n\tn = len(ar | nitanshritulon | NORMAL | 2022-09-04T10:21:06.473422+00:00 | 2022-09-04T10:21:06.473455+00:00 | 260 | false | Hint\nCount the num of ones, and think how they will be split between the 3 segments :)\n```\ndef threeEqualParts(self, arr: List[int]) -> List[int]:\n\tn = len(arr)\n\tpos = [i for i in range(n) if(arr[i])]\n\tl = len(pos)\n\tif(l == 0):\n\t\treturn [0, 2]\n\tif(l % 3):\n\t\treturn [-1, -1]\n\tones = l//3\n\tc = 0\n\tfor i in arr[::-1]:\n\t\tif(i == 1):\n\t\t\tbreak\n\t\tc += 1\n\tans = [-1, -1]\n\t# one hoga pos[ones-1] tak\n\t# uske bad chaiye meko c zeros\n\t# toh index pos[ones-1] + c tak first segment ho jayega\n\tans[0] = pos[ones-1] + c\n\tans[1] = pos[2*ones-1] + c + 1\n\tseg1, seg2, seg3 = arr[pos[0]:ans[0]+1], arr[pos[ones]:ans[1]], arr[pos[2*ones]:]\n\t# without leading zeros\n\tif(seg1 != seg2 or seg1 != seg3):\n\t\treturn [-1, -1]\n\treturn ans\n``` | 3 | 0 | ['Python', 'Python3'] | 0 |
three-equal-parts | [C++/Python] observation leads to solutions & 3-pointer solution | cpython-observation-leads-to-solutions-3-gnfz | Approach 1:\nTrain of thought [1]:\nStep 1: observation: Find 1st 1 of 3rd sub-array\nStep 2: locate the ending of 1st and 2nd sub-arrays\n\nTime Complexity: O( | codedayday | NORMAL | 2021-07-17T19:42:16.647327+00:00 | 2021-07-18T05:18:43.938734+00:00 | 286 | false | Approach 1:\nTrain of thought [1]:\nStep 1: observation: Find 1st 1 of 3rd sub-array\nStep 2: locate the ending of 1st and 2nd sub-arrays\n\nTime Complexity: O(N)\nSpace Complexity: O(1)\n\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n int tot = 0;\n for(auto num: A) tot += num;\n if(tot % 3 != 0) return {-1, -1};\n int n = A.size();\n if(tot == 0) return {0, n - 1};\n \n int seg3_beg_candidate = n - 1;\n for(int i = n - 1, cnt = 0; i >= 0; i--){\n if(A[i]==1){\n cnt++;\n if(cnt == tot / 3){\n seg3_beg_candidate = i;\n break;\n }\n }\n }\n \n int seg1_end = findSegEnd(A, 0, seg3_beg_candidate);\n if(seg1_end == -1) return {-1, -1};\n int seg2_end = findSegEnd(A, seg1_end + 1, seg3_beg_candidate);\n if(seg2_end == -1) return {-1, -1};\n else return {seg1_end, seg2_end + 1};\n }\n \nprivate:\n int findSegEnd(const vector<int>& A, int l, int r){\n while(A[l] == 0) l++;\n while(r < A.size()){\n if(A[l] != A[r]) return -1;\n l++; r++;\n }\n return l - 1;\n }\n};\n```\n\nApproach 2: 3-pointer [2]\nThis might be the only 3-pointer type question out of 1009 questions solved by me.\nThe solution is from [2] with clear step by step illustration.\n```\nstatic int x=[](){ios::sync_with_stdio(false); cin.tie(NULL); return 0;}();\n\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n\t // Count no of 1\'s in the given array\n int countNumberOfOnes = 0;\n for(int c: A)\n if(c == 1) \n countNumberOfOnes++;\n\t\t\t\t\t\t\t\t\n\t // If no 1 is found, that means we can return ans as {0, size-1}\n\t\tint n = A.size();\n if(countNumberOfOnes == 0) \n return {0, n -1};\n\t\t\t\t\t\t\n // If no of 1\'s is not a multiple of 3, then we can never find a possible partition since\n // there will be atkeast one partition that will have different no of 1\'s and hence\n // different binary representation\n // For example,\n // Given :\n // 0000110 110 110 \n // | | |\n // i j\n // Total no of ones = 6\n // 0000110 110 110\n // | | |\n // start mid end\n // Match starting from first 1, and putting 2 more pointers by skipping k 1\'s\n \n if(countNumberOfOnes % 3 != 0) \n return {-1, -1};\n\t\t\t\t\t\t\n // find size of each partition\n int k = countNumberOfOnes/3;\n int i;\n \n // find the first 1 in the array\n for(i=0;i<A.size(); i++)\n if(A[i] == 1)\n break;\n int start = i;\n \n // find (k+1)th 1 in the array\n int count1 = 0;\n for(i=0;i<A.size(); i++)\n {\n if(A[i] == 1)\n count1++;\n if(count1 == k + 1)\n break;\n }\n int mid = i;\n \n //find (2*k +1)th 1 in the array\n count1= 0;\n for(i=0;i<A.size(); i++)\n {\n if(A[i] == 1)\n count1++;\n if(count1 == 2*k + 1)\n break;\n }\n int end = i;\n \n // Match all values till the end of the array\n while(end< A.size() && A[start] == A[mid] && A[mid] == A[end])\n {\n start++; mid++; end++;\n }\n \n // Return appropriate values if all the values have matched till the end\n if(end == A.size()) \n return {start-1, mid};\n \n // otherwise, no such indices found\n return {-1, -1};\n }\n};\n```\n\nApproach 3: Compact version of Approach 2\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n\t // Count no of 1\'s in the given array\n int countNumberOfOnes = 0;\n int n = A.size();\n for(int c: A)\n if(c == 1) \n countNumberOfOnes++;\n\t\t\t\t\t\t\t\t\n\t // If no 1 is found, that means we can return ans as {0, size-1}\n if(countNumberOfOnes == 0) \n return {0, n -1};\n\t\t\t\t\t\t\n // If no of 1\'s is not a multiple of 3, then we can never find a possible partition since\n // there will be atkeast one partition that will have different no of 1\'s and hence\n // different binary representation\n // For example,\n // Given :\n // 0000110 110 110 \n // | | |\n // i j\n // Total no of ones = 6\n // 0000110 110 110\n // | | |\n // start mid end\n // Match starting from first 1, and putting 2 more pointers by skipping k 1\'s\n \n if(countNumberOfOnes % 3 != 0) \n return {-1, -1};\n\t\t\t\t\t\t\n // find size of each partition\n int k = countNumberOfOnes/3;\n int i;\n \n // start: the first 1 in the array\n // mid: the (k+1)th 1 in the array\n // end: the (2k+1)th 1 in the array\n int oneIdx = 0;\n int start, mid, end;\n for(i=0;i<A.size(); i++)\n if(A[i] == 1){\n ++oneIdx;\n if( oneIdx == 1) start = i;\n if( oneIdx == k + 1) mid = i;\n if( oneIdx == 2*k + 1) {end = i;break;}\n }\n \n // Match all values till the end of the array\n while(end< A.size() && A[start] == A[mid] && A[mid] == A[end]){\n start++; mid++; end++;\n }\n \n // Return appropriate values if all the values have matched till the end\n if(end == A.size()) \n return {start-1, mid};\n \n // otherwise, no such indices found\n return {-1, -1};\n }\n};\n```\n\nApproach 4: 8-line python [3]\n```\ndef threeEqualParts(self, nums: List[int]) -> List[int]:\n\tn = nums.count(1)\n\tif n == 0: return [0, 2] # any split would satify\n\tif n % 3 != 0: return [-1, -1]\n\tidx = [i for i, num in enumerate(nums) if num == 1]\n\ts1, e1, s2, e2, s3, e3 = idx[0], idx[n//3-1], idx[n//3], idx[2*n//3-1], idx[2*n//3], idx[n-1]\n\ttracingZeros = len(nums) - 1 - e3\n\tif e1 + tracingZeros >= s2 or e2 + tracingZeros >= s3 or not nums[s1: e1] == nums[s2: e2] == nums[s3: e3]: return [-1, -1]\n\treturn [e1 + tracingZeros, e2 + tracingZeros + 1]\n\n```\nReference:\n[1] https://www.cnblogs.com/grandyang/p/12107091.html\n[2] https://leetcode.com/problems/three-equal-parts/discuss/183922/C%2B%2B-O(n)-time-O(1)-space-12-ms-with-explanation-and-comments\n[3] https://leetcode.com/problems/three-equal-parts/discuss/677626/Python-O(n)-Straightforward-Solution\n | 3 | 0 | ['C', 'Python'] | 0 |
three-equal-parts | [C++] Single Pass Solution Explained, ~100% Time, ~90% Space | c-single-pass-solution-explained-100-tim-z4t9 | Nice problem that becomes much easier once you figure out a few tricks:\n first of all, in order for the problem to be solvable, we need an amount of 1s divisib | ajna | NORMAL | 2021-07-17T19:41:09.101711+00:00 | 2021-07-17T19:52:03.326092+00:00 | 256 | false | Nice problem that becomes much easier once you figure out a few tricks:\n* first of all, in order for the problem to be solvable, we need an amount of `1`s divisible by `3`;\n* with this insight, we can figure out that while we move on checking for the amount of `1`s, we might as well keep track of pointers separating the currently explored portion of the array into `3` parts;\n* to get this pointer in place, we might think of doing something similar to navigating a linked list with the hare-tortoise approach, just this time we would have `3` pointers (`s1`, `s2` and `i`, later in my code), proceeding at 1X, 2X and 3X speed respectively.\n\nFor example, if we started with `{0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0}`, we would initially find all 3 pointers set when we meet the third `1`, so, it would be:\n\n```cpp\ns1 == 1; // position of the first 1\ns2 == 2; // position of the second 1\n i == 5; // position of the third 1\n```\n\nOnce we met the sixth `1` we have:\n\n```cpp\ns1 == 2; // position of the second 1\ns2 == 6; // position of the fourth 1\n i == 13; // position of the sixth 1\n```\n\nAnd so on; with that in mind, then it becomes much easier to figure out the limits of a partition (the position of the last one will dictate the padding `0`s to all the others) and we can proceed from that.\n\nIn order to code it, we will use a few support variables:\n* `tot` is out ongoing total, initialised to `0`;\n* `lastElem` is the position of the last element, initialised to be `arr.size()` (for now, we will fix it in a moment!);\n* `lmt` gives us the upper limit of how many positions for either `s1` or `s2` we are going to store, initalised to be `lastElem / 3` (ie: we will never have more positions than one third of the length, if even if all elements were to be `1`s);\n* `s1`, `s2` and `last` will keep track of where we found the delimiting `1`s for each session discovered so far;\n* `curr1` and `curr2` will be the positions of the `s1` and `s2` pointers we will be using, both set to `0` initially;\n* `pos1` and `pos2`, specularly, will point to where we are going to store them in their respective arrays;\n* `s1s` and `s2s` are the arrays that will store pointers to our dividing points as we go.\n\nDone with the variables, we can now fix `lastElem` to correctly be the index of the last element and loop with `i` through `arr`, and:\n* we will check if the currenlty pointed element `arr[i]` is a `1` and, if so:\n\t* increase `tot` by `1`;\n\t* store the current position in `s1s`, provided we did not do so already for `lmt` elements;\n\t* store the current position in `s2s`, provided we did not do so already for `lmt` elements and that we parsed so far an even number of `1`s;\n\t* it `tot` is divisible by `3`, we will then:\n\t\t* update the `last`, `s1` and `s2` pointers to new values.\n\nWith this out of the way, time to parse for a few edge cases:\n * if no `1`s were found (ie: `!tot`), we will then just `return` `{0, lastElem}` (I think why not any other pointer for the second element was not very clear in the description, but okay);\n * if `tot` is not divisible by `3`, clearly we cannot form `3` parts with the same amount of `1`s, so we will `return` `{-1, -1}`.\n \nOne last condition to check is that the sections have exactly the same binary value and this is a bit trickier.\n \nTo do so, we will use a new variable `diff` computed as the difference between `last` and `lastElem` to get the amount of necessary padding `0`s.\n \n We will then:\n * increase `s1` by `diff` and check if it is still below `s2`, otherwise we will `return` `{-1, -1}`;\n * increase `s2` by `diff` and check if it is still below `last`, otherwise we will `return` `{-1, -1}`;\n * set `curr1` to be `s1`, `curr2` to be `s2`, `last` to `lastElem` and `tot` to one third of its original value;\n * we will loop while `tot > 0` and:\n\t * check if `curr1`, `curr2` and `last` point to the same value (either all point to a `0` or to a `1`), otherwise `return` `{-1, -1}`;\n\t * reduce `tot` by the currently pointed value by any of the pointers;\n\t * decrease all three pointers by `1`.\n\nYou might notice that even if any of the sections still had leading `0`s, in this way we would not care, stopping at the last `1` of each session - assuming no mismatch was detected earlier.\n\nOnce done, we can `return` `{s1, s2 + 1}` (remember that the second pointer is requested to be where the last segment starts) and be done :)\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int tot = 0, lastElem = arr.size(), lmt = lastElem / 3, s1, s2, last,\n curr1 = 0, curr2 = 0, pos1 = 0, pos2 = 0, s1s[lmt], s2s[lmt];\n lastElem--;\n for (int i = 0; i <= lastElem; i++) {\n // finding a `1`\n if (arr[i]) {\n tot++;\n // storing i in s1s if it is not full\n if (pos1 < lmt) s1s[pos1++] = i;\n // storing i in s2s every 2 1s if it is not full\n if (pos2 < lmt && !(tot & 1)) s2s[pos2++] = i;\n // updating pointers every 3 1s\n if (!(tot % 3)) {\n last = i;\n s1 = s1s[curr1++];\n s2 = s2s[curr2++];\n }\n }\n }\n // edge case: no 1s\n if (!tot) return {0, lastElem};\n // exit case: can\'t form 3 groups with the same number of 1s\n if (tot % 3) return {-1, -1};\n // moving the pointer to the last 0 of the sequence\n int diff = lastElem - last;\n // updating s1 and s2, plus exit case: not enough 0s between either s1 and s2 or s2 and last\n s1 += diff;\n if (s1 >= s2) return {-1, -1};\n s2 += diff;\n if (s2 >= last) return {-1, -1};\n // updating curr1, curr2, last and tot to check the segment structure\n curr1 = s1, curr2 = s2, last = lastElem, tot /= 3;\n while (tot) {\n // checking if all the elements match\n if (arr[curr1] != arr[curr2] || arr[curr2] != arr[last]) return {-1, -1};\n // updating variables for the next loop\n tot -= arr[curr1];\n curr1--, curr2--, last--;\n }\n // checking if the segments have the same structure\n return {s1, s2 + 1};\n }\n};\n```\nMicro-optimisation, declaring and assigning `s1` and `s2` at the end and if it might be a proper solution:\n\n```cpp\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int tot = 0, lastElem = arr.size(), lmt = lastElem / 3, last,\n curr1 = -1, curr2 = -1, pos1 = 0, pos2 = 0, s1s[lmt], s2s[lmt];\n lastElem--;\n for (int i = 0; i <= lastElem; i++) {\n // finding a `1`\n if (arr[i]) {\n tot++;\n // storing i in s1s if it is not full\n if (pos1 < lmt) s1s[pos1++] = i;\n // storing i in s2s every 2 1s if it is not full\n if (pos2 < lmt && !(tot & 1)) s2s[pos2++] = i;\n // updating pointers every 3 1s\n if (!(tot % 3)) {\n last = i;\n curr1++;\n curr2++;\n }\n }\n }\n // edge case: no 1s\n if (!tot) return {0, lastElem};\n // exit case: can\'t form 3 groups with the same number of 1s\n if (tot % 3) return {-1, -1};\n // moving the pointer to the last 0 of the sequence\n int diff = lastElem - last, s1 = s1s[curr1], s2 = s2s[curr2];\n // updating s1 and s2, plus exit case: not enough 0s between either s1 and s2 or s2 and last\n s1 += diff;\n if (s1 >= s2) return {-1, -1};\n s2 += diff;\n if (s2 >= last) return {-1, -1};\n // updating curr1, curr2, last and tot to check the segment structure\n curr1 = s1, curr2 = s2, last = lastElem, tot /= 3;\n while (tot) {\n // checking if all the elements match\n if (arr[curr1] != arr[curr2] || arr[curr2] != arr[last]) return {-1, -1};\n // updating variables for the next loop\n tot -= arr[curr1];\n curr1--, curr2--, last--;\n }\n // checking if the segments have the same structure\n return {s1, s2 + 1};\n }\n};\n``` | 3 | 1 | ['C', 'C++'] | 0 |
three-equal-parts | O(n) Java Runtime: 2 ms, faster than 87.50% of Java online submissions | on-java-runtime-2-ms-faster-than-8750-of-1ucl | \npublic int[] threeEqualParts(int[] arr) {\n int oneCount = 0;\n int n = arr.length;\n for(int t : arr){\n if(t == 1) oneCount+ | watermalon | NORMAL | 2021-07-17T12:29:28.926392+00:00 | 2021-07-17T12:29:28.926421+00:00 | 212 | false | ```\npublic int[] threeEqualParts(int[] arr) {\n int oneCount = 0;\n int n = arr.length;\n for(int t : arr){\n if(t == 1) oneCount++;\n }\n if(oneCount == 0) return new int[]{0,n-1};\n if(oneCount % 3 != 0) return new int[]{-1,-1};\n int averageOneCount = oneCount / 3;\n int start = 0;\n int mid = 0;\n int end = 0;\n int cnt = 0;\n for(int i = 0;i<n;i++){\n if(arr[i] == 0) continue;\n if(cnt == 0) {\n start = i;\n }\n cnt++;\n if(cnt == averageOneCount + 1) {\n mid = i;\n }\n if(cnt == 2 * averageOneCount + 1) {\n end = i;\n }\n }\n while(end < n && arr[start] == arr[mid] && arr[mid] == arr[end]){\n start++;\n mid++;\n end++;\n }\n if(end == n) {\n return new int[]{start-1,mid};\n }\n return new int[]{-1,-1};\n }\n``` | 3 | 1 | ['Java'] | 0 |
three-equal-parts | [python 3] brutal force with explanation | python-3-brutal-force-with-explanation-b-oaeq | First, special cases:\n \tIf there is no 1 in list, we can just return [0, len(n)-1].\n \tIf number of 1 cant be divied by 3, return [-1, -1].\n\nThen we find t | Bakerston | NORMAL | 2021-02-05T23:21:31.163448+00:00 | 2021-02-05T23:21:31.163477+00:00 | 120 | false | First, special cases:\n* \tIf there is no 1 in list, we can just return ```[0, len(n)-1]```.\n* \tIf number of 1 cant be divied by 3, return ```[-1, -1]```.\n\nThen we find the valid binary number, since the leading zeros dont matter here, we just need to find the binary start with "1", therefore we traverse the list until we find the ```2 * m / 3 + 1``` th "1", this "1" is the start of the 3rd binary number.\nTherefore we esaily find what this binary number is.\n\nNext, we just need to find the ```1st``` "1" and the ```m / 3 + 1``` th "1", standing for the begining of 1st and 2nd binary number seperatly. Once we find this "1", comparing the array consisting this "1" with the 3rd number we have already found.\n\nReturn the index of ```i``` and ```j``` if both arrays are same with 3rd binary number, otherwise ```[-1, -1]```.\n\n```\ndef threeEqualParts(self, arr: List[int]) -> List[int]:\n m = sum(arr)\n\t\tif m == 0:\n return [0, n - 1]\n if m % 3:\n return [-1, -1]\n\t\t\t\n k = m // 3\n i = 0\n n = len(arr)\n \n \n #start with finding the third (last) binary value in the list\n for idx in range(n):\n if arr[idx] == 1:\n i += 1\n if i == 2 * k + 1:\n res = arr[idx :]\n break\n reslen = len(res)\n \n ans = []\n \n #find the first binary value in list\n for idx in range(n):\n if arr[idx] == 1:\n break\n if arr[idx : idx + reslen] == res:\n ans.append(idx + reslen - 1)\n else:\n return [-1, -1]\n\n #find the second binary in the list\n for idx in range(idx + reslen, n):\n if arr[idx] == 1:\n break\n if arr[idx : idx + reslen] == res:\n ans.append(idx + reslen)\n return ans\n else:\n return [-1, -1]\n``` | 3 | 1 | [] | 0 |
three-equal-parts | Ruby with Regexp | ruby-with-regexp-by-jieqi-bckz | \ndef three_equal_parts(a)\n return [0, a.size-1] if a.all?(&:zero?)\n s = a.join\n tmp = s.match(/^0*(1.*)0*(\\1)0*(\\1)$/)[1]\n i = s.index(tmp) + tmp.siz | jieqi | NORMAL | 2020-06-06T04:50:44.640299+00:00 | 2020-06-06T04:50:44.640335+00:00 | 47 | false | ```\ndef three_equal_parts(a)\n return [0, a.size-1] if a.all?(&:zero?)\n s = a.join\n tmp = s.match(/^0*(1.*)0*(\\1)0*(\\1)$/)[1]\n i = s.index(tmp) + tmp.size - 1\n j = s.index(tmp, i+1) + tmp.size\n [ i , j ]\nrescue => e\n [-1, -1]\nend\n``` | 3 | 0 | [] | 0 |
three-equal-parts | my O( N ) C++ solution | my-o-n-c-solution-by-fish1996-mdwa | At first, we calculate the total number of \'1\', and check if it can be divided by 3. Because each part must contain the same number of \'1\'.\nIf not, we just | fish1996 | NORMAL | 2019-08-16T14:27:52.955030+00:00 | 2019-08-16T14:31:33.277238+00:00 | 285 | false | At first, we calculate the total number of \'1\', and check if it can be divided by 3. Because each part must contain the same number of \'1\'.\nIf not, we just return { -1, -1 }.\nThen, we calculate the number of \'0\' at the end of the array, which means that we won\'t stop until we find the first \'1\' at the end. If the array can be split into 3 parts, each part must has the same number of \'0\' as the end of the array.\nSince we have already got the total number of \'1\' and the number of \'0\' at the end of the array, we can check if the array can be divided into three parts with the exact number of 1 and 0 as we expected, and whether the three parts are equal to each other ( pay attention that we should skip the leading zero ). If we can find the result, we record the index, and return it.\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n vector<int> res; \n int n = A.size();\n int zeros = 0; // number of zero at the end\n int ones = 0; // total number of one\n \n // get number of zero at the end\n for(int i = n - 1; i >= 0;i--)\n {\n if(A[i] == 1) break;\n zeros++;\n }\n // get total number of one\n for(int i = 0;i < n;i++)\n {\n if(A[i] == 1) nums++;\n }\n \n // all data in this array is 0, we can divide the array at every place\n if(nums == 0)\n {\n return {0, n - 1};\n }\n \n // the total number of 1 can\'t be divided by 3. return false.\n if(nums % 3) return {-1, -1};\n\n int count = nums / 3;\n string target;\n \n // check if the array can be split into 3 parts\n // each parts has (ones/3)\'s 1, and has (zeros)\'s 0 at at the end\n int i = 0;\n for(int k = 0; k < 3;k++)\n {\n string str;\n int one_nums = 0;\n int zero_nums = 0;\n for(;i < n; i++)\n {\n if(one_nums == count && zero_nums == zeros) break;\n if(A[i] == 0)\n {\n if(one_nums == count)\n {\n zero_nums++;\n }\n if(!str.empty()) // skip the leading 0.\n str.push_back(A[i]);\n }\n else if(A[i] == 1)\n {\n if(one_nums == count) // the number of 0 at the end is not match\n {\n return {-1, -1};\n }\n one_nums++;\n str.push_back(A[i]);\n } \n }\n\n if(target.empty())\n {\n target = str;\n }\n else\n {\n if(target != str) return {-1, -1}; // current part and last part is not match \n }\n if(k == 0) res.push_back(i - 1); // record the index\n else if(k == 1) res.push_back(i);\n }\n \n return res;\n }\n};\n``` | 3 | 1 | [] | 0 |
three-equal-parts | C++ Easy to Understand O(n) | c-easy-to-understand-on-by-ekaanshgoel-e4yz | If we can divide the number of 1s into 3 equal parts, we can just check the three parts for equality. Dividing 1s into 3 partitions and checking for equality i | ekaanshgoel | NORMAL | 2018-10-21T05:05:38.200501+00:00 | 2018-10-22T07:21:34.582211+00:00 | 604 | false | If we can divide the number of 1s into 3 equal parts, we can just check the three parts for equality.
Dividing 1s into 3 partitions and checking for equality is a necessary and sufficient condition for the answer.
We need to take care of 0s only in the third partition because they will be trailing zeros always and will add to the third binary number representation always.
As long as first and second partition have the same number of trailing zeros as the third representation, we have a solution. We do not care about any other zeros in the first and second partition because trailing zeros of first can add to leading zeros of second and trailing zeros of second can add to leading zeros of third.
```
class Solution {
public:
vector<int> threeEqualParts(vector<int>& A) {
int num1s=0;
for(int i:A) {
if(i==1)
num1s++;
}
if(num1s%3!=0)
return {-1,-1};
if(num1s==0)
return {0,A.size()-1};
int c=num1s/3;
vector<int> nums(3,0);
int count=0;
for(int i=0;i<A.size();i++) {
//If this is the start of the next binary representation(0 or 1 or 2 in vector nums)
if(A[i]==1) {
if(count%c==0) {
nums[count/c]=i; //assign current index to nums[0,1,2]
}
count++;
}
}
//Every other representation should follow Last representation
while(nums[2]!=A.size()) {
if(A[nums[0]]!=A[nums[1]] || A[nums[0]]!=A[nums[2]])
return {-1,-1};
nums[0]++;
nums[1]++;
nums[2]++;
}
return {nums[0]-1, nums[1]};
}
};
``` | 3 | 1 | [] | 1 |
three-equal-parts | [C++] O(n^2) time O(1) space, 96ms, with explanation | c-on2-time-o1-space-96ms-with-explanatio-ana2 | For this problem, we can regarde the string as the type, 000(some zeros)***(a binary number starts with \'1\' and has length k)000(some zeros)***(same binary nu | strange | NORMAL | 2018-10-21T03:18:06.427336+00:00 | 2018-10-21T20:13:52.533655+00:00 | 271 | false | For this problem, we can regarde the string as the type, `000(some zeros)***(a binary number starts with \'1\' and has length k)000(some zeros)***(same binary number)0000(some zeros)***(same binary number)`.\n\nSo what we need to do is try to find the first no-zero bit and iterate the value of k from `1` to `(l-start)/3`.\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n vector<int> ans={-1,-1};\n int sum=0;\n for(int item:A) sum+=item;\n if(sum==0){\n ans={0,A.size()-1};\n return ans;\n }\n int start=0,l=A.size();\n while(A[start]==0) start++;\n for(int k=1;k<=(l-start)/3;++k){\n int start2=k+start;\n while(start2<l && A[start2]==0) start2++;\n if(start2>=l) continue;\n int start3=k+start2;\n while(start3<l && A[start3]==0) start3++;\n if((start3+k)==l){\n if(Compare(A,start,start2,start3,k)){\n ans={start+k-1,start2+k};\n return ans;\n }\n }\n }\n return ans;\n }\n bool Compare(vector<int>& A, int a, int c, int d, int k){\n for(int iter=0;iter<k;++iter)\n if(A[a+iter]!=A[c+iter] || A[d+iter]!=A[c+iter]) return false;\n return true;\n }\n};\n``` | 3 | 3 | [] | 2 |
three-equal-parts | Three Equal Parts | Easiest Approach | O(N) Time complexity and O(1) Space Complexity | | three-equal-parts-easiest-approach-on-ti-pfj0 | Intuition\nThe problem requires us to divide an array of zeros and ones into three parts, each representing the same binary value. At first glance, it might see | nah_man | NORMAL | 2024-05-21T06:59:30.468167+00:00 | 2024-05-21T06:59:30.468201+00:00 | 321 | false | # Intuition\nThe problem requires us to divide an array of zeros and ones into three parts, each representing the same binary value. At first glance, it might seem complex, but by breaking it down into steps, we can solve it systematically. The key insight is to ensure that the count of 1s in each part is equal, which ensures the binary values are identical.\n\n# Approach\n1) Count the total number of 1s in the array. If this number is not divisible by 3, return [-1, -1] as it\'s impossible to split them equally.\n2) Identify the target number of 1s in each part (which will be one-third of the total count of 1s).\n3) Locate the positions of the first, middle, and last groups of 1s that would mark the boundaries of the three parts.\n4) Extract and compare the three parts to ensure they are equal.\n5) Adjust for trailing zeros in each part to ensure valid partition indices.\n\n# Complexity\n- Time complexity:\nO(n) - We traverse the array a few times for counting and extracting parts.\n\n- Space complexity:\nO(1) - We use a constant amount of extra space, not counting the input and output.\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int cnt = 0;\n for(int i = 0 ; i < arr.size() ; i++) if(arr[i] == 1) cnt++;\n if(cnt % 3 != 0) return {-1, -1};\n if(cnt == 0) return {0, 2};\n\n int k = cnt / 3, curr = 0;\n int i1 = -1, i2 = -1, i3 = -1;\n int j1 = -1, j2 = -1, j3 = -1;\n\n for(int i = 0 ; i < arr.size() ; i++)\n {\n if(arr[i] == 1)\n {\n curr++;\n if(curr == 1) i1 = i;\n if(curr == k + 1) i2 = i;\n if(curr == 2*k + 1) i3 = i;\n\n if(curr == k) j1 = i;\n if(curr == 2*k) j2 = i;\n if(curr == 3*k) j3 = i;\n }\n }\n vector < int > a, b, c;\n copy(arr.begin() + i1, arr.begin() + j1 + 1, back_inserter(a));\n copy(arr.begin() + i2, arr.begin() + j2 + 1, back_inserter(b));\n copy(arr.begin() + i3, arr.begin() + j3 + 1, back_inserter(c));\n\n if(a != b || a != c) return {-1, -1};\n\n int first = 0, second = 0, third = 0;\n first = i2 - j1 - 1;\n second = i3 - j2 - 1;\n third = arr.size() - j3 - 1;\n\n if(third > min(first, second)) return {-1, -1};\n \n return {j1 + third, j2 + third + 1};\n }\n};\n```\n\n\n# **Bold** | 2 | 0 | ['Array', 'Math', 'Two Pointers', 'Greedy', 'C++'] | 2 |
three-equal-parts | Simple Python Solution with explanation 🔥 | simple-python-solution-with-explanation-qqnno | Approach\n\n> divide the array into three non-empty parts such that all of these parts represent the same binary value\n\nSame binary value means \n\n each part | wilspi | NORMAL | 2023-01-17T18:13:38.338738+00:00 | 2023-01-17T22:29:18.633711+00:00 | 944 | false | # Approach\n\n> *divide the array into three non-empty parts such that all of these parts represent the same binary value*\n\nSame binary value means \n\n* each part has to have **<ins>equal number of ones<ins>** and zeroes\n* order of ones and zeroes should be same\n\n\n### Part 1: Equal number of ones and ending zeroes\n\n\nLets take below array as an example for understanding:\n\n\n\n\n* These binary values will have equal number of ones, which means the total count of ones should be a multiple of 3\n\n\n 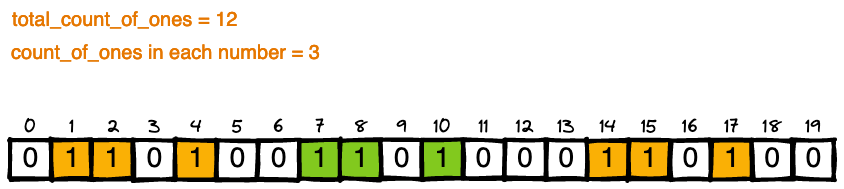\n\n\n\n* We know in a binary number, starting zeroes doesnt matter, however ending zeroes does matter. So I can find the `ending_zeroes` for my binary number using the location of last one:\n\n \n\n\n* We need to add these ending_zeroes count after every `total_count_of_ones // 3` ie in the example after every 3 count of ones\n\n 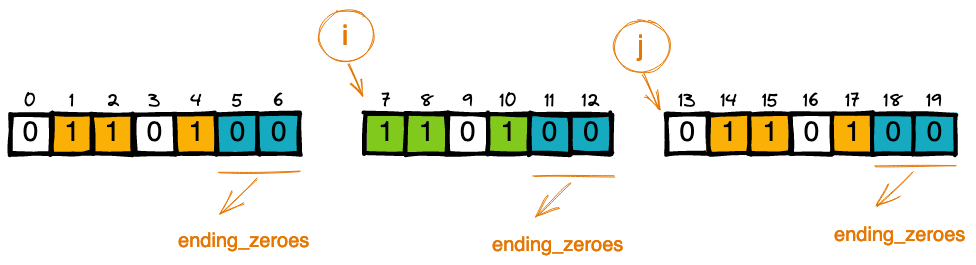\n\n* Now, we know the location of `i` and `j`\n\n\n\nNOTE:\n \n* All above steps can be done by traversing through the loop, \n\n however in my code below I have used prefix sum and binary search --> using modified binary_search to fetch index of the first occurrence in the prefix_sum \n\n for example: \n ```\n ending_zeroes = n - 1 - (index of first occurrence of total_count_of_ones in prefix_sum, ie 9 in this example)\n ```\n \n\n 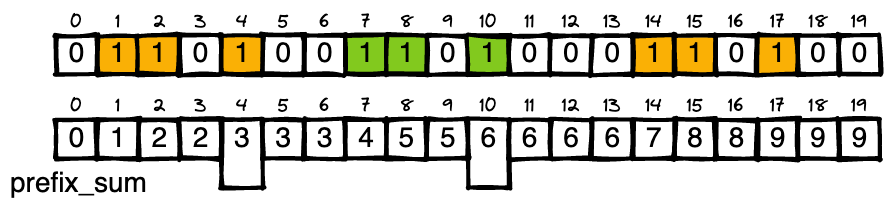\n\n\n Creation of prefix sum takes `O(n)` time, so no major optimisation with this, this just looked clean to me :)\n\n\n\n### Part 2: Order of ones and zeroes\n\nThis is simple, for each identified part\n\n* disregard starting zeroes\n* then, check if order of each ones and zeroes is same\n\n\n\n\n\n\n# Complexity\n- Time complexity:\n$$O(n + log(n))$$ = $$O(n)$$\n\n- Space complexity:\n$$O(n)$$ - for prefix_sum\n\n# Code\n\n```python []\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = len(arr)\n\n # part 1\n\n # get total_count and create prefix_sum\n total_count = 0\n prefix_sum = [0] * n\n for i in range(n):\n total_count += arr[i]\n prefix_sum[i] = total_count\n\n # checking if multiple of 3\n if total_count % 3 != 0:\n return [-1, -1]\n elif total_count == 0:\n return [0, n - 1]\n\n # binary search to get first occurrence of `val` using prefix_sum\n def bin_search(val):\n start = 0\n end = n - 1\n mid = 0\n\n while start <= end:\n mid = (start + end) // 2\n if prefix_sum[mid] >= val:\n if start == end:\n return mid\n end = mid\n else:\n start = mid + 1\n\n return mid\n\n \n # count of ones in each part and count of ending_zeroes\n part_count = total_count // 3\n ending_zeroes = n - 1 - bin_search(total_count)\n\n # value of i and j using binary_search and ending_zeroes\n i = bin_search(part_count) + ending_zeroes + 1\n j = bin_search(total_count - part_count) + ending_zeroes + 1\n\n\n\n # part 2\n\n # disregard starting zeroes in first part\n a = 0\n while a < n and arr[a] == 0:\n a += 1\n\n # disregard starting zeroes in second part\n b = i\n while b < n and arr[b] == 0:\n b += 1\n\n # disregard starting zeroes in third part\n c = j\n while c < n and arr[c] == 0:\n c += 1\n\n # check if indices have same order of ones and zeroes\n while c < n:\n if arr[a] == arr[b] and arr[b] == arr[c]:\n a += 1\n b += 1\n c += 1\n else:\n return [-1, -1]\n\n if a == i and b == j:\n return [i - 1, j]\n else:\n return [-1, -1]\n\n```\n | 2 | 0 | ['Binary Search', 'Prefix Sum', 'Python', 'Python3'] | 0 |
three-equal-parts | Three Pointers || C++ || O(N) time || O(1) space | three-pointers-c-on-time-o1-space-by-aka-n02c | Approach: First of all, it is necessary for the given array to have sufficient count of ones which can be equally divided among three groups. If not, the answer | Aka_YS | NORMAL | 2021-07-18T07:04:50.667653+00:00 | 2021-07-18T07:04:50.667683+00:00 | 105 | false | **Approach:** First of all, it is necessary for the given array to have sufficient count of ones which can be equally divided among three groups. If not, the answer is not possible. If yes, find the occurances of the first ones of each group. Now, simply iterate over these pointers and check whether you can atleast reach to the starting index of other group. If so, return the indexes else answer is not possible. \n**Time complexity:** O(N)\n**Space complexity:** O(1)\n```\nclass Solution {\npublic:\n vector<int> check(vector<int> s, int i, int j, int k) {\n int n=s.size();\n while(i<j && j<k && k<n) {\n if(s[i]!=s[j] || s[j]!=s[k]) return {-1,-1};\n if(i==j || j==k || k==n) break;\n i++;\n j++;\n k++;\n }\n if(i==j || j==k || k==n) return {i-1, j};\n return {-1,-1};\n }\n vector<int> threeEqualParts(vector<int>& arr) {\n int n=arr.size();\n int ctr=count(arr.begin(), arr.end(),1);\n if(ctr % 3 != 0) return {-1,-1};\n \n vector<int> ans(3,-1);\n int k=0, ref=0;\n for(int i=0;i<n;i++) { \n if(arr[i] && !ref) {\n ans[k++]=i;\n }\n if(arr[i]) ref++;\n \n if(ref==ctr/3) {\n ref=0;\n }\n }\n if(ans[0]==ans[1] && ans[1]==ans[2]) return {0, n-1};\n return check(arr, ans[0], ans[1], ans[2]);\n }\n};\n```\n**Upvote if u liked!!** | 2 | 0 | ['C'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.