question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
three-equal-parts | Easy approach using Prefix Sum + 2 Sum [no one is talking about this] | easy-approach-using-prefix-sum-2-sum-no-0hazy | Prefix Sum\nNo post is talking about this apporach, and I came up with this when sleeping.\nTypically, sum of subarray problem can be resovled using prefix sum | jandk | NORMAL | 2021-07-17T23:02:25.231540+00:00 | 2021-07-17T23:02:25.231579+00:00 | 161 | false | ### Prefix Sum\nNo post is talking about this apporach, and I came up with this when sleeping.\nTypically, sum of subarray problem can be resovled using prefix sum array. So is this. Similarly, the `prefix[i]` represents the integer with the binary representation of `nums[:i]`, then `prefix[j] - prefix[i]` is the integer represented by `nums[i:j]`. \n\n```\nprefix[i + 1] = prefix[i] << 1 + num[i]\nprefix[j + 1] - prefix[i + 1] = prefix[j + 1] - (prefix[i] << j - i)\n```\n\nIn order to find out 3 subarrays with the same integer, we just need find out `[i, j]` such that \n\n```prefix[i - 1] == prefix[j] - prefix[i] == prefix[-1] - prefix[j]```\n\nThe naive solution is to iterate each possible pair of `(i, j)`, but we can reduce it to linear using hashmap/dictionary. Recall the 2 sum problem!\nWe iterate each *j* and store the index *i* of `prefix[i]` seen up to *j*, then if `prefix[-1] - prefix[j]` is in the hashmap, then return the pair. Finally, reutrn `[-1, -1]` otherwise.\n\n```python\ndef threeEqualParts(self, arr: List[int]) -> List[int]:\n\tprefix = [0]\n for num in arr:\n\t\tprefix.append((prefix[-1] << 1) + num)\n \n\tseen = {}\n n = len(arr)\n for j in range(n): \n\t\tx = prefix[-1] - (prefix[j + 1] << n - 1 - j)\n if x in seen and prefix[j + 1] == (x << j + 1 - seen[x]) + x:\n\t\t\treturn [seen[x] - 1, j + 1]\n seen[prefix[j + 1]] = j + 1\n\treturn [-1, -1] \n \n```\n*Time Complexity* = **O(N)**\n*Space Complexity* = **O(N)** | 2 | 0 | [] | 1 |
three-equal-parts | easy c++ | O(n) | faster than 99.4% solution | easy-c-on-faster-than-994-solution-by-ra-pqw1 | class Solution {\npublic:\n vector threeEqualParts(vector& arr) {\n int i,j,x=0,n=arr.size();\n for(i=0;iv(2);\n if(x%3!=0){\n | raoprashant61 | NORMAL | 2021-07-17T18:31:45.291885+00:00 | 2021-07-17T18:31:45.291936+00:00 | 42 | false | class Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int i,j,x=0,n=arr.size();\n for(i=0;i<n;i++){\n if(arr[i]==1) x++;\n }\n vector<int>v(2);\n if(x%3!=0){\n v[1]=v[0]=-1;\n return v;\n }\n if(x==0){\n v[0]=0;v[1]=n-1;\n return v;\n }\n int k=0;\n for(i=n-1;i>=0;i--){\n if(arr[i]==1) break;\n k++;\n }\n int z=0;\n vector<int>a;\n for(i=n-1;i>=0;i--){\n if(arr[i]==1) z++;\n a.push_back(arr[i]);\n if(z==x/3){\n v[1]=i;break;\n }\n \n }\n z=0;\n for(i=v[1]-1;i>=0;i--){\n if(arr[i]==1) break;\n z++;\n }\n if(z<k){\n v[1]=v[0]=-1;\n return v;\n }\n z=i+k; v[1]=z+1;\n int sz=a.size();\n for(j=0;j<sz;j++){\n if(arr[z]!=a[j]){\n v[1]=v[0]=-1;\n return v;\n }\n z--;\n }\n v[0]=z;\n z=0;\n for(i=v[0];i>=0;i--){\n if(arr[i]==1) break;\n z++;\n }\n if(z<k){\n v[1]=v[0]=-1;\n return v;\n }\n z=i+k; v[0]=z;\n for(j=0;j<sz;j++){\n if(arr[z]!=a[j]){\n v[1]=v[0]=-1;\n return v;\n }\n z--;\n }\n while(z>=0){\n if(arr[z]==1){\n v[1]=v[0]=-1;\n return v;\n }\n z--;\n }\n return v;\n }\n}; | 2 | 0 | [] | 0 |
three-equal-parts | ✔️ Easy Java O(N) || 100% fast || 1 ms time || count hack approach :) | easy-java-on-100-fast-1-ms-time-count-ha-gbyp | Added comments in java code to explain more deeply\n\n\n// 927. Three Equal Parts\n// Runtime: 1 ms, faster than 100.00% of Java online submissions for Three Eq | hitsa70 | NORMAL | 2021-07-17T17:55:00.686009+00:00 | 2022-02-01T17:35:06.678279+00:00 | 211 | false | **Added comments in java code to explain more deeply**\n```\n\n// 927. Three Equal Parts\n// Runtime: 1 ms, faster than 100.00% of Java online submissions for Three Equal Parts.\n// Memory Usage: 44.9 MB, less than 60.58% of Java online submissions for Three Equal Parts.\n\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int countOne=0,n=arr.length;\n \n //count number of zeroes\n for(int i:arr)\n countOne+=i;\n \n //if all 0 return return (0, length)\n if(countOne==0)\n return new int[]{0,n-1};\n //if not divisible by 3 then return (-1,-1)\n if(countOne%3!=0)\n return new int[]{-1,-1}; \n \n \n \n int start = 0,mid = 0,end = 0;\n int averageOneCount=countOne/3;\n countOne=0;\n \n \n for(int i=0;i<n;i++){\n //skip all zeroes\n if(arr[i]==0)\n continue;\n \n //mark 1st 1 as start\n if(countOne==0)\n start=i;\n \n countOne++; \n //find mid \'1\' element\n if(countOne == averageOneCount + 1) \n mid = i;\n \n //find last \'1\' element\n if(countOne == 2 * averageOneCount + 1) \n end = i;\n \n }\n \n //skip all elements which are same\n while(end < n && arr[start] == arr[mid] && arr[mid] == arr[end]){\n start++;\n mid++;\n end++;\n }\n \n //if we reach end then its possible so return (start-1,end)\n if(end == n) {\n return new int[]{start-1,mid};\n }\n \n //else return as its not possible\n return new int[]{-1,-1}; \n \n }\n}\n\n``` | 2 | 0 | ['Counting', 'Java'] | 0 |
three-equal-parts | [HINTS] If You Look for Observations + Hints + Test Cases Come Over! | hints-if-you-look-for-observations-hints-6qjf | Observations\n1) Number of 1s should be dived by 3 with no remainder\n2) We can skip the leading zeros in the middle except trailing zeros\n3) Number of Middle | shtanriverdi | NORMAL | 2021-07-17T17:49:40.219388+00:00 | 2021-07-17T17:49:57.593039+00:00 | 44 | false | **Observations**\n1) Number of 1s should be dived by 3 with no remainder\n2) We can skip the leading zeros in the middle except trailing zeros\n3) Number of Middle zeros should be at least as num of trailing zeros\n\n**Some Good Test Cases**\n```\n[1,0,0,1,0,0,1,0,0]\n[1,0,0,1,0,0,0,1,0,0]\n[0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0]\n[0,0,1,1,1]\n[1,0,0,1,1]\n[1,1,0,0,1]\n[1,1,1,0,0]\n[1,1,0,0,1,0,0]\n[1,0,0,1,1,0,0]\n[0,0,1,1,1]\n[1,0,0,1,1]\n[1,1,0,0,1]\n[1,1,1,0,0]\n[1,1,1]\n[1,1,1,1]\n[1,1,1,1,1]\n[1,1,1,1,1,1]\n``` | 2 | 0 | [] | 0 |
three-equal-parts | Easy C++ Solution with comments | easy-c-solution-with-comments-by-ashish_-0sf3 | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n // count 1\n int countone=count(arr.begin(),arr.end(),1);\n | ashish_786 | NORMAL | 2021-07-17T12:34:23.923244+00:00 | 2021-07-17T15:49:26.323791+00:00 | 433 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n // count 1\n int countone=count(arr.begin(),arr.end(),1);\n int n=arr.size();\n if(countone%3)\n {\n return {-1,-1};\n }\n if(countone==0)\n {\n return {0,n-1};\n }\n int total=countone/3;\n int p1=0,p2=0,p3=0;\n int count=0;\n // check first occurance of 1 for each part\n // lets take example\n //1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1\n for(int i=0;i<n;i++)\n {\n if(arr[i]==1)\n {\n if(count==0)\n {\n p1=i;\n }\n else if(count==total)\n {\n p2=i;\n }\n else if(count==2*total)\n {\n p3=i;\n }\n count+=1;\n }\n }\n // after this\n // p1 at index 0,p2 at index 6 and p3 at index 13\n // now check all element after of each part\n while(p3<n-1)\n {\n p1+=1;\n p2+=1;\n p3+=1;\n if(arr[p1]!=arr[p2] || arr[p2]!=arr[p3] || arr[p1]!=arr[p3])//if not equal \n {\n return {-1,-1};\n }\n }\n \n return {p1,p2+1};\n \n } \n};\n``` | 2 | 0 | ['C', 'C++'] | 1 |
three-equal-parts | C++ O(n) time and O(1) space | c-on-time-and-o1-space-by-ranjan_1997-182x | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int count = 0;\n for (auto i:arr)\n {\n if(i | ranjan_1997 | NORMAL | 2021-07-17T11:53:53.208062+00:00 | 2021-07-17T11:53:53.208101+00:00 | 289 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int count = 0;\n for (auto i:arr)\n {\n if(i == 1)\n count++;\n }\n if(count == 0)\n return {0,2};\n if(count%3 != 0)\n return {-1,-1};\n int p1 = 0;\n int p2 = 0;\n int p3 = 0;\n count = count/3;\n int temp = 0;\n for(int i = 0;i<arr.size();i++)\n { if(arr[i] == 1)\n { if(temp == 0)\n p1 = i;\n else if(temp == count)\n p2 = i;\n else if(temp == 2*count)\n p3 = i;\n temp++;\n }\n \n }\n\n int oldp2 = p2;\n int oldp3 = p3;\n while(p1<oldp2 and p2<oldp3 and p3<arr.size())\n {\n if(arr[p1] != arr[p2] or arr[p2] != arr[p3])\n return {-1,-1};\n p1++;\n p2++;\n p3++;\n }\n if(p3 == arr.size())\n {\n return {p1-1,p2};\n }\n return {-1,-1};\n }\n};\n``` | 2 | 0 | [] | 0 |
three-equal-parts | [Python] BinarySearch O(nlogn) slow but viable solution | python-binarysearch-onlogn-slow-but-viab-hpyn | \nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = len(arr)\n ps = []\n cur = 0\n for x in arr:\n | samchan0221 | NORMAL | 2021-07-17T10:35:58.347502+00:00 | 2021-07-17T10:35:58.347544+00:00 | 55 | false | ```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n = len(arr)\n ps = []\n cur = 0\n for x in arr:\n cur <<= 1\n cur += x\n ps.append(cur)\n # print(ps[-1])\n for i in range(n-1):\n a = ps[i]\n l,r = i+1,n-1\n cnt = 0\n while l<r:\n cnt += 1\n mid = (l+r)//2\n b = ps[mid]-(ps[i] << (mid-i))\n if b<a:\n l = mid + 1\n elif b>a:\n r = mid\n else:\n c = ps[n-1]-(ps[mid] << (n-1-mid))\n if c==b:\n return [i,mid+1]\n else:\n l = r\n return [-1,-1]\n``` | 2 | 1 | [] | 1 |
three-equal-parts | Python O(N) time /O(1) space | python-on-time-o1-space-by-tonymok97-j2dd | The idea is to count the trailing zero of the last session(must be counted)\nAs the leading zero can be ignored, we can just make sure that each session will ha | tonymok97 | NORMAL | 2021-07-17T09:13:25.499858+00:00 | 2021-07-17T12:54:14.935996+00:00 | 169 | false | The idea is to count the trailing zero of the last session(must be counted)\nAs the leading zero can be ignored, we can just make sure that each session will have enough trailing zeros.\n\nLeading zeros will be ignored automatically by accu sum\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n one_count = sum(arr)\n \n if one_count % 3 != 0: return [-1, -1]\n if one_count == 0: return [0, len(arr)-1]\n \n session_one_count = one_count // 3\n session_trailing_zero = 0 # padding for each session\n for i in range(len(arr)-1, -1, -1):\n if arr[i] == 0:\n session_trailing_zero += 1\n else:\n break\n \n last_accu = -1\n curr_count = 0\n curr_accu = 0\n session_id = []\n \n i = 0\n while(i < len(arr)):\n curr_count += arr[i]\n curr_accu = curr_accu * 2 + arr[i]\n i += 1\n if curr_count == session_one_count:\n curr_trailing = 0\n while(i < len(arr) and curr_trailing < session_trailing_zero):\n # find trailing zeros\n curr = arr[i]\n if curr == 0:\n curr_trailing += 1\n i += 1\n else:\n return [-1, -1] # not enough trailing zeros\n \n if (last_accu != -1) and (curr_accu != last_accu):\n return [-1, -1]\n \n\t\t\t\t# reset\n last_accu = curr_accu\n session_id.append(i)\n curr_count = 0\n curr_accu = 0\n \n return [session_id[0]-1, session_id[1]]\n``` | 2 | 0 | [] | 0 |
three-equal-parts | python O(n) beat 100% 304ms | python-on-beat-100-304ms-by-victerose-6ivh | \nclass Solution(object):\n def threeEqualParts(self, arr):\n N = len(arr)\n \n # ones_number : number of \'1\' in arr\n ones_num | victerose | NORMAL | 2021-07-17T08:44:47.104521+00:00 | 2021-07-17T08:44:47.104561+00:00 | 175 | false | ```\nclass Solution(object):\n def threeEqualParts(self, arr):\n N = len(arr)\n \n # ones_number : number of \'1\' in arr\n ones_number = sum(arr)\n if ones_number % 3 != 0: return [-1,-1]\n if ones_number == 0: return [0,N-1]\n \n # ones_each : number of \'1\' in one part\n ones_each = ones_number // 3\n \n # ones_idx : idx of \'1\', divided in 3 parts\n ones_idx, tmp, count = [], [], 0\n for i in range(len(arr)):\n if arr[i] == 1:\n tmp += [i]\n count += 1\n \n if count == ones_each:\n ones_idx.append(tmp)\n tmp = []\n count = 0\n \n # ones_idx_shift : idx of \'1\', divided in 3 parts, but each subarr is shifted to start with one\n\t\t# used for comparing the pattern\n ones_idx_shift = []\n for ls in ones_idx:\n ones_idx_shift.append([ls[i] - ls[0] for i in range(ones_each)])\n \n # zeros_tail : numbers of \'0\' behind the last \'1\'\n zeros_tail = N - ones_idx[2][-1] -1\n \n # Rule 1: Space for zero\n # no space for zeros for part1 and part2\n if ones_idx[1][0] - ones_idx[0][-1] -1 < zeros_tail or ones_idx[2][0] - ones_idx[1][-1] -1 < zeros_tail:\n return [-1,-1]\n \n # Rule 2: Pattern of three parts\n # compare the pattern of part1, part2, and part3\n if ones_idx_shift[0] == ones_idx_shift[1] and ones_idx_shift[1] == ones_idx_shift[2]:\n return [ones_idx[0][-1] + zeros_tail, ones_idx[1][-1] +1 + zeros_tail]\n \n return [-1,-1]\n```\n### Sum of arr needs to be 3n\nSince the arr is divided into 3 equal parts, the number of \'1\' need to be the multiple of 3.\n\n\n### Need to match two rule\n\n#### Rule 1: Space for zero\nWe need to make sure that there are enough \'0\' between each part.\n\nBecause **the \'0\' behind the last \'1\' is used in part3 for sure**, we can count whether there are enough \'0\' between (part1 ,part2) and between (part2, part3), which meen more than the number of \'0\' behind the last \'1\'.\n\n#### Rule 2: Pattern of three parts\nPattern of three parts need to be the same.\n\nWe divide arr based on the number of \'1\', each part only have 1/3 number of \'1\'.\n\nFor example:\n[1, 0, 0, 1, 0, 1, 0] can be divided into [1,0], [1,0], [1,0] => same\n[1, 1, 0, 1, 0, 1, 1, 0, 0, 1] can be divided into [1, 1, 0], [1, 0, 1], [1, 0, 0, 1] => not the same | 2 | 0 | [] | 1 |
three-equal-parts | Three Equal Parts Python Solution, O(n) | three-equal-parts-python-solution-on-by-4dd4d | python\n\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n ones = []\n for i,num in enumerate(arr):\n if | haotianzhu | NORMAL | 2021-07-17T08:38:09.772802+00:00 | 2021-07-17T08:38:09.772840+00:00 | 87 | false | ```python\n\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n ones = []\n for i,num in enumerate(arr):\n if num == 1:\n ones.append(i)\n \n if len(ones) == 0:\n return [0,len(arr)-1]\n \n if len(ones) < 3 or len(ones)%3 > 0:\n return [-1, -1]\n \n endZeros = len(arr)-ones[-1]-1 \n l1 = ones[0]\n l2 = ones[len(ones)//3 -1]\n m1 = ones[len(ones)//3]\n m2 = ones[2*len(ones)//3-1]\n r1 = ones[2*len(ones)//3]\n r2 = ones[-1]\n \n if arr[l1:l2+1+endZeros] == arr[m1:m2+1+endZeros] and arr[m1:m2+1+endZeros] == arr[r1:]:\n \n return [l2+endZeros,m2+1+endZeros]\n \n \n return [-1,-1]\n``` | 2 | 1 | [] | 1 |
three-equal-parts | scala solution. | scala-solution-by-lyk4411-gu88 | \ndef findEndIdx(arr: Array[Int], i: Int, binary_value: String):Int = {\n if(arr.drop(i).dropWhile(_==0).take(binary_value.length).foldLeft("")((b,a)=> a | lyk4411 | NORMAL | 2021-05-10T03:09:02.880295+00:00 | 2021-05-10T03:09:02.880323+00:00 | 61 | false | ```\ndef findEndIdx(arr: Array[Int], i: Int, binary_value: String):Int = {\n if(arr.drop(i).dropWhile(_==0).take(binary_value.length).foldLeft("")((b,a)=> a + b) != binary_value) return -1\n return arr.drop(i).takeWhile(_==0).length + i + binary_value.length\n }\n def threeEqualParts(arr: Array[Int]): Array[Int] = {\n val cnt = arr.count(_ == 1)\n val n = arr.length\n if (cnt%3 !=0) return Array(-1,-1)\n if(cnt == 0) return Array(0,n - 1)\n val idxThird =arr.zipWithIndex.filter(n=> n._1 == 1).takeRight(cnt/3).take(1)(0)._2\n val binary_value = arr.takeRight(n - idxThird).foldLeft("")((b,a)=>{a + b})\n val res1 = findEndIdx(arr, 0, binary_value)\n if (res1 < 0) return Array(-1,-1)\n val res2 = findEndIdx(arr, res1, binary_value)\n if (res2 < 0) return Array(-1,-1)\n return Array(res1 - 1,res2)\n }\n``` | 2 | 0 | [] | 0 |
three-equal-parts | C++ short clean code | c-short-clean-code-by-soundsoflife-kzac | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int> &A) {\n vector<int> vi;\n for (int i = 0; i < A.size(); ++i) if (A[i] == | soundsoflife | NORMAL | 2020-08-27T15:54:59.805736+00:00 | 2020-08-27T16:02:17.852545+00:00 | 255 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int> &A) {\n vector<int> vi;\n for (int i = 0; i < A.size(); ++i) if (A[i] == 1) vi.push_back(i);\n if (vi.size() == 0) return vector{0, 2};\n if (vi.size() % 3 != 0) return vector{-1, -1};\n int len = A.size() - vi[vi.size() / 3 * 2];\n int a = vi[0], b = vi[vi.size() / 3], c = vi[vi.size() / 3 * 2];\n for (int i = 0; i < len; ++i)\n if (A[a + i] != A[b + i] || A[a + i] != A[c + i]) return vector{-1, -1};\n return vector{a + len - 1, b + len};\n }\n};\n``` | 2 | 1 | [] | 0 |
three-equal-parts | Python simple solution | python-simple-solution-by-gyh75520-4d0a | If the solution exists, the number of 1 in list should be times of 3.\nSearch from right side to left, until we found num/3 1s. This index is not final answer, | gyh75520 | NORMAL | 2019-11-01T07:19:50.358795+00:00 | 2019-11-01T07:19:50.358844+00:00 | 261 | false | If the solution exists, the number of 1 in list should be times of 3.\nSearch from right side to left, until we found num/3 1s. This index is not final answer, but we find the binary value.\nFrom left side to right, find the first 1s and compare whether the first part value equal to bianay value and so on.\n\n```python\n def threeEqualParts(self, A: List[int]) -> List[int]:\n cnt1 = A.count(1)\n if cnt1%3 !=0:\n return [-1,-1]\n if cnt1 == 0:\n return [0,len(A)-1]\n \n cnt, binary_value = 0, 0\n # the binary value has been anchored\n for i in range(len(A)-1,-1,-1):\n if A[i]:\n cnt += 1\n if cnt == cnt1//3:\n binary_value = A[i:]\n length = len(binary_value)\n break\n \n for i in range(0,len(A)):\n if A[i]:\n if A[i:i+length] == binary_value:\n secondPart_startdx = i+length\n for j in range(secondPart_startdx,len(A)):\n if A[j]:\n if A[j:j+length] == binary_value:\n return [secondPart_startdx-1,j+length]\n return [-1,-1]\n return [-1,-1] \n return [-1,-1]\n``` | 2 | 0 | [] | 3 |
three-equal-parts | [C++]O(n) time, simple sol with explaination | con-time-simple-sol-with-explaination-by-96a7 | cpp\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n // check number of 1s\n int oneCount = 0, n = A.size();\n | heyidk | NORMAL | 2019-09-27T13:16:45.607081+00:00 | 2019-09-27T13:16:45.607113+00:00 | 155 | false | ```cpp\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n // check number of 1s\n int oneCount = 0, n = A.size();\n for (int &i: A)\n oneCount += (i == 1);\n if (oneCount % 3 != 0)\n return vector<int> {-1, -1};\n if (oneCount == 0)\n return vector<int> {0, 2};\n \n // find last part\n int count = oneCount / 3, third = n;\n while (count > 0) {\n third--;\n if (A[third] == 1)\n count--;\n }\n \n // find first part\n int first = 0;\n while (first < n && A[first] == 0)\n first++;\n \n // check equalness of 1 and 3\n bool equal = true;\n for (int offset = 0; third + offset < n; offset++)\n if (first + offset >= third || A[first + offset] != A[third + offset])\n return vector<int> {-1, -1};\n \n // check equalness of 2 and 3\n int second = first + n - third;\n while (A[second] == 0)\n second++;\n for (int offset = 0; third + offset < n; offset++)\n if (second + offset >= third || A[second + offset] != A[third + offset])\n return vector<int> {-1, -1};\n\n // okay. return last position of first part and first position of third part.\n return vector<int> {first + n - third - 1, second + n - third};\n }\n};\n``` | 2 | 1 | [] | 0 |
three-equal-parts | Easy java solution | easy-java-solution-by-v2e4lisp-qt9c | \nclass Solution {\n public int[] threeEqualParts(int[] A) {\n List<Integer> plist = new ArrayList<>();\n for (int i = 0; i < A.length; i++) {\ | v2e4lisp | NORMAL | 2019-09-13T16:09:20.524068+00:00 | 2019-09-13T16:09:20.524125+00:00 | 230 | false | ```\nclass Solution {\n public int[] threeEqualParts(int[] A) {\n List<Integer> plist = new ArrayList<>();\n for (int i = 0; i < A.length; i++) {\n if (A[i] == 1) {\n plist.add(i);\n }\n }\n // all zero\n if (plist.size() == 0) {\n return new int[]{0, 2};\n }\n // #1 is not 3x\n if (plist.size() % 3 != 0) {\n return new int[]{-1, -1};\n }\n // check gaps between 1s\n int count = plist.size()/3;\n int s1 = 0;\n int s2 = count;\n int s3 = 2*count;\n for (int i = 0; i < count-1; i++) {\n int gap1 = plist.get(s1+i+1) - plist.get(s1+i);\n int gap2 = plist.get(s2+i+1) - plist.get(s2+i);\n int gap3 = plist.get(s3+i+1) - plist.get(s3+i);\n if (gap1 != gap2 || gap2 != gap3) {\n return new int[]{-1, -1};\n }\n }\n // check right 0-padding for least significant bits\n int rpad1 = plist.get(s2) - plist.get(s2-1) - 1;\n int rpad2 = plist.get(s3) - plist.get(s3-1) - 1;\n int rpad3 = A.length - plist.get(plist.size()-1) - 1;\n if (rpad1 < rpad3 || rpad2 < rpad3) {\n return new int[]{-1, -1};\n }\n \n return new int[]{\n plist.get(s2-1)+rpad3, \n plist.get(s3-1)+rpad3+1\n };\n }\n}\n``` | 2 | 0 | [] | 1 |
three-equal-parts | simple C soultion with detailed analysis | simple-c-soultion-with-detailed-analysis-nut4 | The core idea is:\n1. if we look from backward, the last element must be valid part of the 3-rd number.\n2. we can get how many \'1\' should be in a part by cou | chilauhe | NORMAL | 2019-09-05T12:28:34.993025+00:00 | 2019-09-05T12:28:34.993059+00:00 | 218 | false | The core idea is:\n1. if we look from backward, **the last element must be valid part of the 3-rd number.**\n2. we can get *how many \'1\' should be in a part* by **counting how many one in array** and divde it into 3\n3. if we get a fraction instead an integer, it must **not** equal.\n4. then we just **count how many 1 has seen** to get every part\'s start position\n5. compare 3 parts of the array to ensure they\'re equal.\n\n```\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* threeEqualParts(int* A, int ASize, int* returnSize){\n int n,i;\n int *r = (int *)malloc(sizeof(int)*2);\n r[0]=r[1]=-1;\n *returnSize = 2;\n //count how many ones in array\n for(n = i = 0; i < ASize; i++)\n {\n if(A[i])n++;\n }\n //if it\'s worth trying, it must contain equal ones of each\n if(n && n % 3 == 0)\n {\n uint16_t d = 0; // length of a part\n uint16_t q = 0; // length counter of a part and its forehead\n uint16_t p=0; // counter of \'1\' has read\n uint16_t s=0; // current position record pointer\n uint16_t k[3]={0}; //begin positions of parts\n //every part has this amount of \'1\'\n n /= 3;\n //loop from backward in order to count acutal part size first.\n for(i = ASize - 1;i>=0;i--)\n {\n q++; // count how many chars gone though\n if(A[i] && (++p % n == 0 || n == 1)) // if \'1\' then test if reached a point to do segment\n {\n k[s++]=i; //record and move pointer to next record\n if(d == 0) d = ASize - i; //set corret length of a part\n else if(d < n || d > q) return r; // incorret length found, immediate return\n q = 0; // reset part char counter for next one\n }\n }\n //detect unmatch pattern\n for(i = 0; i < d; i++)\n {\n if(!((A+k[2])[i]==(A+k[0])[i] && (A+k[0])[i] == (A+k[1])[i]))return r;\n }\n //set position to first one\'s last char and second one\'s last char\n r[0] = k[2]+d-1;\n r[1] = k[1]+d;\n }\n else if(n == 0)\n {\n //wired, unwritten rule, even applies to empty input.\n r[0]=0;\n r[1]=ASize-1;\n }\n return r;\n}\n``` | 2 | 0 | ['C'] | 0 |
three-equal-parts | javascript 90ms | javascript-90ms-by-dchamud-game | \nvar threeEqualParts = function(A) {\n const getOneCount = () => {\n const oneCount = A.reduce((acc, bit) => bit == 1 ? acc + 1 : acc, 0)\n if | dchamud | NORMAL | 2019-04-22T16:08:30.833854+00:00 | 2019-04-22T16:08:30.833899+00:00 | 215 | false | ```\nvar threeEqualParts = function(A) {\n const getOneCount = () => {\n const oneCount = A.reduce((acc, bit) => bit == 1 ? acc + 1 : acc, 0)\n if(oneCount % 3 == 0) \n return oneCount / 3\n return -1\n }\n\n const getTail = oneCount => { \n let zeroCount = 0, idx = A.length -1\n let oneRemain = oneCount\n while(oneRemain > 0) {\n if(A[idx] == 1) {\n oneRemain--\n }\n if(A[idx] == 0 && oneRemain == oneCount) {\n zeroCount++\n }\n idx--\n }\n return {zeroCount, tailStart: idx + 1}\n }\n\n const getHead = (oneCount, zeroCount) => {\n let idx = 0\n while(oneCount > 0) {\n if(A[idx] == 1)\n oneCount--\n idx++\n }\n if(zeroCount > 0) {\n while(A[idx] == 0 && zeroCount > 0){\n idx++\n zeroCount--\n }\n }\n return zeroCount == 0 ? idx-1 : -1\n }\n\n const getMiddle = (oneCount, headEnd, tailStart) => {\n let idx = headEnd + 1\n let tailIdx = tailStart\n while(A[idx] != 1) idx++\n while(idx < tailStart && A[idx] == A[tailIdx]) {\n idx++\n tailIdx++\n }\n if(tailIdx != A.length)\n return -1\n return idx\n\n }\n\n const oneCount = getOneCount()\n if(oneCount == -1 || A.length < 3)\n return [-1, -1]\n if(oneCount == 0) return [0, A.length-1]\n const {tailStart, zeroCount} = getTail(oneCount)\n const headEnd = getHead(oneCount, zeroCount)\n if(headEnd == -1)\n return [-1, -1]\n const middleEnd = getMiddle(oneCount, headEnd, tailStart)\n if(middleEnd == -1)\n return [-1, -1]\n return [headEnd, middleEnd]\n};\n``` | 2 | 0 | ['JavaScript'] | 0 |
three-equal-parts | [Java] O(n) time; O(1) space (8 ms) | java-on-time-o1-space-8-ms-by-piroshki-yzh1 | Check if there are enough number of ones for three parts (aka number of ones is a multiple of 3). Iterate the array from the tail and find the spot that marks t | piroshki | NORMAL | 2018-10-21T20:12:49.593872+00:00 | 2018-10-21T20:12:49.593914+00:00 | 129 | false | 1. Check if there are enough number of ones for three parts (aka number of ones is a multiple of 3).
2. Iterate the array from the tail and find the spot that marks the start of a binary number with n/3 1s (n is total number of ones).
3. Lets call the marker in step 2 "part3". We need to check to see if there are 2 more occurences of this part (part3 to end of array) between 0 and part3.
4. In order to lookup the part, start from the beginning of the array, ignoring all the leading zeros (as they don't contribute to the value), try to match with the number formed by part3 - end.
5. Repeat step 4 one more time, this time starting at the end of first match.
```
class Solution {
public int[] threeEqualParts(int[] A) {
int count = 0;
for(int i : A){
count = count+i;
}
if(count==0){
return new int[]{0,A.length-1};
}
if(count%3!=0){
return new int[]{-1,-1};
}
int part3 = A.length;
int soFar = 0;
while(soFar<count/3 && part3>-1){
part3--;
soFar += A[part3];
}
int tracker = match(A, 0, part3);
if(tracker==-1){
return new int[]{-1, -1};
}
int end = match(A, tracker, part3);
if(end==-1){
return new int[]{-1, -1};
}
return new int[]{tracker-1, end};
}
private int match(int[] A, int start, int ref){
while(A[start]==0){
start++;
}
while(ref < A.length){
if(A[ref]!=A[start]){
return -1;
}
ref++;
start++;
}
return start;
}
}
``` | 2 | 0 | [] | 1 |
three-equal-parts | python solution with my thinking process (very simple logic,with extra Chinese explanation) | python-solution-with-my-thinking-process-25i1 | you can get Chinese explanation in \nhttps://buptwc.github.io/2018/10/21/Leetcode-927-Three-Equal-Parts/\n\nI define the three part as a,b,c.\nNotice that the l | bupt_wc | NORMAL | 2018-10-21T15:12:58.549489+00:00 | 2018-10-21T19:44:15.083997+00:00 | 213 | false | you can get Chinese explanation in \nhttps://buptwc.github.io/2018/10/21/Leetcode-927-Three-Equal-Parts/\n\nI define the three part as `a,b,c`.\nNotice that the length of A reaches 30000, so we cannot first determine the value of `a,b` separately and later compare with `c`, it\'s O(n^2) time! We need to find a way to directly determine the remaining two arrays based on the first array.\n\nI propose a definition here called the `effective length`, here it refers to the length of the array without leading `0`.For example, the `effective length` of [0,0,1,1] is `2`\n\nSo, if the value of `a,b,c` is same, the `effective length` of `a,b,c` should also be same.\n\nOK, follow this, I define the index at the end of `a` array is `e1`, and we know the index of first `1` in the array, as `s1`;So we get the `effective length` of `a` array, as `l = e1 - s1 + 1`(assume e1 >= s1)\n\nwe define `s2` as the effective begin index of `b` array, we have `s2 = the index of first 1 after e1`. Because the `effective length` should be same with `a` array. so the end index of `b` array should be `e2 = s2 + l `. We can also use this method to determine the effective index of `c` array(`s3,e3`)\n\nNow we found some termination conditions.\n`if e2 >= n`, we can break\n`if e3 > n`, we can break\n`if e3 < n`, continue to find next `e1`\n`if e3 == n`, we compare `a == b == c`\n\nTo avoid double counting, I define left[i] refers to the index of first `1` before `i`, right[i] refers to the index of first `1` after `i`.\nso we have `s1 = left[e1], s2 = right[e1], e2 = s2 + l, s3 = right[e2], e3 = s3 + l`\n\n```python\n# 120ms\nclass Solution(object):\n def threeEqualParts(self, A):\n # Consider the case where no 0 exists\n if A.count(1) == 0:\n return [0,len(A)-1]\n\n n = len(A)\n # get left and right array\n right = [-1] * n\n index = n\n for i in range(n-1,-1,-1):\n right[i] = index\n if A[i] == 1: index = i\n\n left = [-1] * n\n index = A.index(1)\n for i in range(n):\n if i >= index: left[i] = index\n\n for e1 in range(n-2):\n s1 = left[e1]\n if s1 == -1: continue\n l = e1 - s1 + 1\n\n s2 = right[e1]\n e2 = s2 + l - 1\n if e2 >= n: break\n\n s3 = right[e2]\n if s3 >= n: break\n if n - s3 != l: continue\n\n if A[s1:e1+1] == A[s2:e2+1] == A[s3:n]:\n return [i, e2 + 1]\n return [-1, -1]\n``` | 2 | 2 | [] | 1 |
three-equal-parts | C# It is hard level algorithm and I could not make it in the contest | c-it-is-hard-level-algorithm-and-i-could-p312 | Oct. 20, 2018\n927. Three Equal Parts\n\nIt is the third algorithm in weekly contest 107. I did come out the idea but my code had a few bugs in the contest. It | jianminchen | NORMAL | 2018-10-21T03:36:13.106209+00:00 | 2020-08-20T22:08:41.326656+00:00 | 397 | false | Oct. 20, 2018\n927. Three Equal Parts\n\nIt is the third algorithm in weekly contest 107. I did come out the idea but my code had a few bugs in the contest. It took me more than 30 minutes in the contest and 20 minutes after the contest to make the code work. I also simplify the logic to make it readable. \n\nThe idea is to determine how many one in integer array. So first count how many one\'s in total using one iteration. And then it is true that number of 1 should be divisible by 3. And then the number without considing leading zero can be determined by the map of 1 with its index. \n\n1. Count how many 1 in the integer array, save each 1 and its index to a hashmap\n2. Determine the number in each part using binary string. \n3. Compare three numbers in three parts to make sure they are the same\n4. Considering leading zero, determine the two indexes to return. \n\nI made mistakes when I caculated a few numbers, one is ``` int index2 = map[number1];```, I could not determine second number\'s start index; one is to compare third number with first number and second number. Using string compare is to shorten the time to write my own comparison. ``` var digitsString = string.Join(string.Empty, digits); // look up stackoverflow.com```, I had to learn how to convert integer array to a string using C#. \n\nHere is my C# code to pass online judge after the contest. \n\n```\npublic class Solution {\n public int[] ThreeEqualParts(int[] digits)\n {\n var notFound = new int[] { -1, -1 };\n\n if (digits == null)\n return notFound;\n\n var countof1 = 0;\n var length = digits.Length;\n var map = new Dictionary<int, int>();\n for (int i = 0; i < length; i++)\n {\n if (digits[i] == 1)\n {\n map.Add(countof1, i);\n countof1++;\n }\n }\n\n if (countof1 % 3 != 0)\n return notFound;\n\n if (countof1 == 0)\n return new int[] { 0, 2 };\n\n int number1 = countof1 / 3;\n\n // narrow down the number without considering leading zero\n int thirdNumberStart = map[countof1 - number1];\n\n // constraint\n int minimumLength = length - thirdNumberStart; // substring of number, there are some leading 0s maybe. \n\n // compare the first number with third number \n int index1 = map[0];\n int index2 = map[number1];\n int index3 = map[countof1 - number1]; // test using countof1 = 3, 2 ; 6;\n\n if (length - index1 + 1 < 3 * minimumLength)\n return notFound;\n\n var digitsString = string.Join(string.Empty, digits); // look up stackoverflow.com\n\n var number = digitsString.Substring(thirdNumberStart);\n var firstNumber = digitsString.Substring(index1, minimumLength);\n var secondNumber = digitsString.Substring(index2, minimumLength);\n\n var result = number.CompareTo(firstNumber) == 0 && number.CompareTo(secondNumber) == 0;\n if (!result)\n {\n return notFound;\n }\n // last digit of first number third number\'s first digit\n return new int[] { index1 + minimumLength - 1, index2 + minimumLength };\n }\n}\n```\n | 2 | 1 | [] | 0 |
three-equal-parts | [C++] O(n) Time, O(1) Space. 40ms | c-on-time-o1-space-40ms-by-goddice-hukm | First count the total number of 1s. If it is not a multiple of 3, then it is not possible. Otherwise divide it by 3, we can get the number of 1s should be in ea | goddice | NORMAL | 2018-10-21T03:13:57.287070+00:00 | 2018-10-21T21:53:22.818103+00:00 | 244 | false | First count the total number of 1s. If it is not a multiple of 3, then it is not possible.
Otherwise divide it by 3, we can get the number of 1s should be in each partition. The only uncertain thing now is the number tailing zeros for each partition. However, this can be easily determined by the last partition.
Now, we konw the number of 1s for each partition and the number of tailing zeros for each partition, we can directly calculate the partition positions.
C++ code here [wrote in the contest, maybe can be optimize further]:
```
class Solution {
public:
vector<int> threeEqualParts(vector<int>& A) {
int c = 0; // count the 1
for (auto& x : A) {
if (x == 1) {
++c;
}
}
if (c % 3 != 0) {
return {-1, -1};
}
if (c == 0) {
return {0,2};
}
int n = c / 3;
int nZero = 0;
for (int i = A.size()-1; i >= 0; --i) {
if (A[i] == 0) {
++nZero;
}
else {
break;
}
}
// a and b are the partitioning position
int a, b;
// calculate a
a = 0;
c = 0; // count the 1
while(c < n) {
if (A[a] == 0) {
++a;
}
else {
++a;
++c;
}
}
c = 0; // count the 0
while(c < nZero) {
if (A[a] == 0) {
++c;
++a;
}
else {
return {-1, -1};
}
}
--a;
// calculate b
b = a + 1;
c = 0; // count 1
while(c < n) {
if (A[b] == 0) {
++b;
}
else {
++b;
++c;
}
}
c = 0; // count 0
while(c < nZero) {
if (A[b] == 0) {
++c;
++b;
}
else {
return {-1, -1};
}
}
// verify a, b
if (verify(A, 0, a, a+1, b-1) && verify(A, 0, a, b, A.size()-1)) {
return {a, b};
}
else {
return {-1, -1};
}
}
private:
bool verify(vector<int>& A, int lo1, int hi1, int lo2, int hi2) {
int p1 = lo1;
int p2 = lo2;
while(A[p1] == 0 && p1 <= hi1) ++p1;
while(A[p2] == 0 && p2 <= hi2) ++p2;
if (hi1 - p1 != hi2 - p2) {
return false;
}
while(p1 < hi1) {
if (A[p1] != A[p2]) {
return false;
}
else {
++p1;
++p2;
}
}
return true;
}
};
``` | 2 | 1 | [] | 0 |
three-equal-parts | Solution | solution-by-deleted_user-nudy | C++ []\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n \n int countone=count(arr.begin(),arr.end(),1);\n int | deleted_user | NORMAL | 2023-05-14T03:04:10.618865+00:00 | 2023-05-14T03:26:01.334516+00:00 | 721 | false | ```C++ []\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n \n int countone=count(arr.begin(),arr.end(),1);\n int n=arr.size();\n if(countone%3)\n {\n return {-1,-1};\n }\n if(countone==0)\n {\n return {0,n-1};\n }\n int total=countone/3;\n int p1=0,p2=0,p3=0;\n int count=0;\n \n for(int i=0;i<n;i++)\n {\n if(arr[i]==1)\n {\n if(count==0)\n {\n p1=i;\n }\n else if(count==total)\n {\n p2=i;\n }\n else if(count==2*total)\n {\n p3=i;\n }\n count+=1;\n }\n }\n while(p3<n-1)\n {\n p1+=1;\n p2+=1;\n p3+=1;\n if(arr[p1]!=arr[p2] || arr[p2]!=arr[p3] || arr[p1]!=arr[p3])\n {\n return {-1,-1};\n }\n }\n return {p1,p2+1};\n } \n};\n```\n\n```Python3 []\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n \n ones = [i for i, j in enumerate(arr) if j==1]\n n=len(ones)\n\n if not ones:\n return [0, 2]\n if n%3:\n return [-1, -1]\n \n i,j,k = ones[0], ones[n//3], ones[n//3*2]\n l = len(arr)-k\n\n if arr[i:i+l]==arr[j:j+l]==arr[k:k+l]:\n return [i+l-1, j+l]\n\n return [-1, -1]\n```\n\n```Java []\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int oneSum = 0;\n for(int x : arr) oneSum +=x;\n if(oneSum % 3 !=0)return new int[]{-1,-1};\n if(oneSum == 0)return new int[]{0,2};\n int oneCount = oneSum / 3;\n int i = 0;\n int firstOne = -1;\n int n= arr.length;\n int lastZeroCount = 0;\n i = n-1;\n while(arr[i] ==0){\n lastZeroCount++;\n i--;\n }\n i=0;\n while(oneCount > 0){\n if(arr[i] == 1 && firstOne == -1)firstOne = i;\n oneCount-=arr[i++];\n }\n while(lastZeroCount > 0){\n if(arr[i++] == 1)return new int[]{-1,-1};\n lastZeroCount--;\n }\n int k = i--;\n int t = firstOne;\n while(arr[k] == 0)k++;\n while(firstOne <=i){\n if(arr[firstOne++] != arr[k++])return new int[]{-1,-1};\n }\n int j = k;\n while(arr[k] == 0)k++;\n firstOne = t;\n while(firstOne <=i){\n if(arr[firstOne++] != arr[k++])return new int[]{-1,-1};\n }\n return new int[]{i,j};\n }\n}\n```\n | 1 | 0 | ['C++', 'Java', 'Python3'] | 0 |
three-equal-parts | Easy C++ solution using strings in O(n) time and space complexity | easy-c-solution-using-strings-in-on-time-poo4 | Intuition\nThree Simple observations :-\n1.Total number of ones should be multiple of 3.\n2.Leading zeroes do not contribute\n3.Number of zeroes after the last | dattebayyo | NORMAL | 2023-01-28T19:59:15.490132+00:00 | 2023-01-28T19:59:15.490164+00:00 | 286 | false | # Intuition\nThree Simple observations :-\n1.Total number of ones should be multiple of 3.\n2.Leading zeroes do not contribute\n3.Number of zeroes after the last one of all 3 parts will be equal to the number of zeroes after the last one in 3rd part.\n\n# Approach\n1.Store the indexes of ones in a vector and check if the size is multiple of 3.\n2.Check if the zeroes after the last 1s of first and second part are greater than or equal to zeroes after the last one in 3rd part.\n3.Form strings for all 3 parts ignoring leading zeroes and check if they are equal.\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& v) {\n vector<int> one;\n int n=v.size();\n for(int i=0;i<n;i++){\n if(v[i]==1) one.push_back(i+1);\n }\n if(one.size()==0){\n return {0,2};\n }\n if(one.size()%3) return {-1,-1};\n\n int ext=n-one.back(),sz=one.size();\n int gap1=one[sz/3]-one[sz/3-1]-1,gap2=one[2*sz/3]-one[2*sz/3-1]-1;\n // cout<<gap1<<" "<<gap2<<endl;\n if(gap1<ext || gap2<ext) return {-1,-1};\n\n string s1,s2,s3;\n for(int i=0;i<=one[sz/3-1]+ext-1;i++){\n if(s1.length()>0 || v[i]) s1+=to_string(v[i]);\n }\n\n for(int i=one[sz/3-1]+ext;i<=one[2*sz/3-1]+ext-1;i++){\n if(s2.length()>0 || v[i]) s2+=to_string(v[i]);\n }\n\n for(int i=one[2*sz/3-1]+ext;i<=n-1;i++){\n if(s3.length()>0 || v[i]) s3+=to_string(v[i]);\n }\n //All 3 Numbers in vector v :-\n // num1={0,one[sz/3-1]+ext-1};\n // num2={one[sz/3-1]+ext,one[2*sz/3-1]+ext-1}\n // num3={one[2*sz/3-1]+ext,n-1};\n if(s1==s2 && s2==s3) return {one[sz/3-1]+ext-1,one[2*sz/3-1]+ext};\n return {-1,-1};\n }\n};\n``` | 1 | 0 | ['String', 'C++'] | 0 |
three-equal-parts | C++ | O(N) time complexity solution | c-on-time-complexity-solution-by-virtual-ocr4 | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n // Time complexity - O(N)\n\t\t\n int size = arr.size(), count= | Virtual91 | NORMAL | 2022-11-07T19:39:39.871327+00:00 | 2022-11-07T19:39:39.871375+00:00 | 181 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n // Time complexity - O(N)\n\t\t\n int size = arr.size(), count=0, tcount=0, iptr=0, jptr=2;\n string str = "", t = "", h1 = "", h2 = "";\n vector<int>res(2,-1);\n for(int i=0;i<size;i++){\n str += (arr[i] ? \'1\' : \'0\');\n count += arr[i];\n }\n if(count == 0){\n res[0] = 0, res[1] = size-1;\n return res;\n }\n if(count%3) return res;\n count /= 3;\n reverse(str.begin(), str.end());\n\t\t// reversed the string to easily process ending zeros of 3rd part in unreversed string\n\t\t\n // find first part string for future comparision\n tcount = 0;\n for(int i=0;i<size && tcount < count;i++){\n t += str[i];\n if(str[i] == \'1\') tcount++;\n jptr = i;\n }\n \n // find second string for comparision\n h1 = t, t = "";\n tcount = 0;\n for(int i=jptr+1;i<size && tcount < count;i++){\n t += str[i];\n if(str[i] == \'1\') tcount++;\n iptr = i;\n }\n \n if(t.length() < h1.length()) return res;\n h2 = t.substr( (t.length()-h1.length()), h1.length() );\n \n if(h1 != h2) return res;\n jptr += t.length()-h1.length();\n \n // find last string for comparision\n t = "";\n tcount = 0;\n for(int i=iptr+1;i<size && tcount < count;i++){\n t += str[i];\n if(str[i] == \'1\') tcount++;\n }\n \n if(t.length() < h1.length()) return res;\n h2 = t.substr( (t.length()-h1.length()), h1.length() );\n if(h1 != h2) return res;\n \n iptr += t.length()-h1.length();\n \n res[0] = size-1-(iptr+1);\n res[1] = size-1-jptr;\n return res;\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
three-equal-parts | Python, faster than 100.00% | python-faster-than-10000-by-veanules-urij | \tdef threeEqualParts(self, arr: List[int]) -> List[int]:\n ones = arr.count(1)\n if ones == 0: return [0, 2]\n if ones % 3: return [-1, -1 | Veanules | NORMAL | 2022-04-15T12:25:41.526392+00:00 | 2022-04-15T12:25:41.526432+00:00 | 138 | false | \tdef threeEqualParts(self, arr: List[int]) -> List[int]:\n ones = arr.count(1)\n if ones == 0: return [0, 2]\n if ones % 3: return [-1, -1]\n ones_in_number = ones//3\n \n ones = 0\n start0 = i = arr.index(1)\n while(ones < ones_in_number):\n if arr[i]:\n ones+=1\n i+=1\n \n l = i-start0\n start1 = arr.index(1, start0+l)\n start2 = arr.index(1, start1+l)\n\n l += len(arr)-(start2+l)\n \n if arr[start0:start0+l] == arr[start1:start1+l] == arr[start2:start2+l]:\n return [start0+l-1, start1+l]\n else:\n return [-1, -1] | 1 | 0 | ['Python'] | 0 |
three-equal-parts | Three Equal Parts Solution Java | three-equal-parts-solution-java-by-bhupe-6zvy | class Solution {\n public int[] threeEqualParts(int[] A) {\n int ones = 0;\n\n for (int a : A)\n if (a == 1)\n ++ones;\n\n if (ones == 0)\ | bhupendra786 | NORMAL | 2022-04-12T07:45:03.159460+00:00 | 2022-04-12T07:45:03.159498+00:00 | 62 | false | class Solution {\n public int[] threeEqualParts(int[] A) {\n int ones = 0;\n\n for (int a : A)\n if (a == 1)\n ++ones;\n\n if (ones == 0)\n return new int[] {0, A.length - 1};\n if (ones % 3 != 0)\n return new int[] {-1, -1};\n\n int k = ones / 3;\n int i = 0;\n int j = 0;\n int first = 0;\n int second = 0;\n int third = 0;\n\n for (i = 0; i < A.length; ++i)\n if (A[i] == 1) {\n first = i;\n break;\n }\n\n int gapOnes = k;\n\n for (j = i + 1; j < A.length; ++j)\n if (A[j] == 1 && --gapOnes == 0) {\n second = j;\n break;\n }\n\n gapOnes = k;\n\n for (i = j + 1; i < A.length; ++i)\n if (A[i] == 1 && --gapOnes == 0) {\n third = i;\n break;\n }\n\n while (third < A.length && A[first] == A[second] && A[second] == A[third]) {\n ++first;\n ++second;\n ++third;\n }\n\n if (third == A.length)\n return new int[] {first - 1, second};\n return new int[] {-1, -1};\n }\n}\n | 1 | 0 | ['Array', 'Math'] | 0 |
three-equal-parts | Typescript, documented to be easy-to-understand | typescript-documented-to-be-easy-to-unde-ptvp | \nfunction threeEqualParts(dd: number[]) {\n // Every part has to have the same number of digit 1, and so it must be divisible by 3.\n const countOnes = dd.re | user1145PG | NORMAL | 2022-02-01T22:12:46.423568+00:00 | 2022-02-01T22:12:46.423594+00:00 | 29 | false | ```\nfunction threeEqualParts(dd: number[]) {\n // Every part has to have the same number of digit 1, and so it must be divisible by 3.\n const countOnes = dd.reduce<number>((total, i) => total + (i === 1 ? 1 : 0), 0);\n if (countOnes === 0) return [0, 2];\n if (countOnes % 3 !== 0) return [-1, -1];\n\n // Get inclusive indexes of the middle part, from 1 to 1. So in "1010 101 0101"\n // the indexes would be 4 to 6. Same number of 1s in each third.\n let [i, j] = (() => {\n let indexes = [];\n let ones = 0;\n for (let inx = 0; inx < dd.length && indexes.length < 2; inx++) {\n if (dd[inx] === 1) {\n ones++;\n if (ones === (countOnes * 2) / 3) indexes.push(inx);\n if (ones === countOnes / 3 + 1) indexes.push(inx);\n }\n }\n return [indexes[0], indexes[1]];\n })();\n\n // Every number has to have the same number of zeros on the end as the last number.\n // Otherwise their values won\'t be the same.\n const requiredZerosAtEnd = dd.length - dd.lastIndexOf(1, dd.length - 1) - 1;\n\n // Try to adjust the middle number by incrementing j so it has proper number of 0s on\n // the end.\n const zerosRight = (inx: number) => {\n const nextOne = dd.indexOf(1, inx + 1);\n return nextOne === -1 ? dd.length - inx - 1 : nextOne - inx - 1;\n };\n if (zerosRight(j) >= requiredZerosAtEnd) {\n j += requiredZerosAtEnd;\n } else {\n return [-1, -1];\n }\n\n // Try to adjust the first number by moving i so it has proper number of 0s on the end.\n const lastOneInFirstPart = dd.lastIndexOf(1, i - 1);\n if (zerosRight(lastOneInFirstPart) >= requiredZerosAtEnd) {\n i = lastOneInFirstPart + requiredZerosAtEnd + 1;\n } else {\n return [-1, -1];\n }\n\n // Compare the three numbers, bit by bit, to see if they are the same.\n [i, j] = [i - 1, j + 1];\n let aStart = dd.indexOf(1, 0);\n let bStart = dd.indexOf(1, i + 1);\n let cStart = dd.indexOf(1, j);\n while (cStart !== dd.length) {\n if (dd[aStart] === dd[bStart] && dd[bStart] === dd[cStart]) {\n aStart++;\n bStart++;\n cStart++;\n } else return [-1, -1];\n }\n return [i, j];\n}\n``` | 1 | 0 | [] | 0 |
three-equal-parts | Golang & C++ solution | golang-c-solution-by-tjucoder-3pxh | go\nfunc threeEqualParts(arr []int) []int {\n\t// remove all leading zeros if 1 exist\n\tremovedLeadingZero := 0\n\tfor i := 0; i < len(arr); i++ {\n\t\tif arr[ | tjucoder | NORMAL | 2021-11-13T07:15:40.440667+00:00 | 2021-11-13T08:06:38.855889+00:00 | 101 | false | ```go\nfunc threeEqualParts(arr []int) []int {\n\t// remove all leading zeros if 1 exist\n\tremovedLeadingZero := 0\n\tfor i := 0; i < len(arr); i++ {\n\t\tif arr[i] == 1 {\n\t\t\tremovedLeadingZero = i\n\t\t\tarr = arr[i:]\n\t\t\tbreak\n\t\t}\n\t}\n\t// valid check\n\tif len(arr) < 3 {\n\t\treturn []int{-1, -1}\n\t}\n\t// arr[0] equal to 0 means all value in arr is 0\n\tif arr[0] == 0 {\n\t\treturn []int{0, 2}\n\t}\n\t// first non zero index from current to last index\n\tfirstNonZero := make([]int, len(arr))\n\tnonZeroIndex := math.MaxInt32\n\tfor i := len(arr) - 1; i >= 0; i-- {\n\t\tif arr[i] == 1 {\n\t\t\tnonZeroIndex = i\n\t\t}\n\t\tfirstNonZero[i] = nonZeroIndex\n\t}\nloop:\n\tfor end1 := 0; end1 < len(arr)-2; end1++ {\n\t\tsize := end1 + 1\n\t\tend2 := firstNonZero[end1+1] + end1\n\t\tif end2 >= len(arr)-1 {\n\t\t\tcontinue\n\t\t}\n\t\tend3 := firstNonZero[end2+1] + end1\n\t\tif end3 != len(arr)-1 {\n\t\t\tcontinue\n\t\t}\n\t\tfor i := 0; i < size; i++ {\n\t\t\tif arr[end1-i] != arr[end2-i] {\n\t\t\t\tcontinue loop\n\t\t\t}\n\t\t\tif arr[end1-i] != arr[end3-i] {\n\t\t\t\tcontinue loop\n\t\t\t}\n\t\t}\n\t\treturn []int{end1 + removedLeadingZero, end2 + 1 + removedLeadingZero}\n\t}\n\treturn []int{-1, -1}\n}\n```\n\n```c++\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int sizeOfOne = 0;\n for (auto &i : arr) {\n if (i == 1) {\n sizeOfOne++;\n }\n }\n if (sizeOfOne % 3 != 0) {\n return vector<int>{-1, -1};\n }\n if (sizeOfOne == 0) {\n return vector<int>{0, 2};\n }\n int currentSizeOfOne = 0;\n int end1 = 0;\n int end2 = 0;\n int end3 = 0;\n int prefixZero = -1;\n for (std::vector<int>::size_type i = 0; i < arr.size(); i++) {\n if (arr[i] == 1) {\n currentSizeOfOne++;\n if (prefixZero == -1) {\n prefixZero = i;\n }\n if (currentSizeOfOne == sizeOfOne/3) {\n end1 = i;\n }\n if (currentSizeOfOne == sizeOfOne/3*2) {\n end2 = i;\n }\n if (currentSizeOfOne == sizeOfOne) {\n end3 = i;\n }\n }\n }\n int suffixZero = static_cast<int>(arr.size() - 1) - end3;\n end1 += suffixZero;\n end2 += suffixZero;\n end3 += suffixZero;\n for (auto i = 0; i <= end1-prefixZero; i++) {\n if (arr[end1-i] != arr[end2-i] || arr[end1-i] != arr[end3-i]) {\n return vector<int>{-1, -1};\n }\n }\n return vector<int>{end1, end2+1};\n }\n};\n``` | 1 | 0 | ['C', 'Go'] | 0 |
three-equal-parts | C++ || EASY | c-easy-by-priyanka1230-t6fx | \n\npublic:\n vector threeEqualParts(vector& arr) {\n int i,first,second,third,count=0,one=0;\n for(i=0;i<arr.size();i++)\n {\n | priyanka1230 | NORMAL | 2021-08-31T16:09:25.216817+00:00 | 2021-08-31T16:09:25.216864+00:00 | 111 | false | ```\n\n```public:\n vector<int> threeEqualParts(vector<int>& arr) {\n int i,first,second,third,count=0,one=0;\n for(i=0;i<arr.size();i++)\n {\n if(arr[i]==1)\n {\n count++;\n }\n }\n if(count==0)\n {\n return {0,2};\n }\n if(count%3!=0)\n {\n return {-1,-1};\n }\n int n=count/3;\n for(i=0;i<arr.size();i++)\n {\n if(arr[i]==1)\n {\n one++;\n if(one==1)\n {\n first=i;\n }\n else if(one==n+1)\n {\n second=i;\n }\n else if(one==(2*n)+1)\n {\n third=i;\n }\n }\n }\n while(third<arr.size())\n {\n if(arr[first]==arr[second]&&arr[second]==arr[third])\n {\n first++;\n second++;\n third++;\n }\n else\n {\n return {-1,-1};\n }\n }\n return {first-1,second};\n }\n}; | 1 | 0 | [] | 0 |
three-equal-parts | Java easy O(N), 1ms, with comments | java-easy-on-1ms-with-comments-by-dimitr-kw9h | refactored version :\n\n public int[] threeEqualParts(int[] arr) {\n int len=arr.length, onesCount=0;\n int[] fail = new int[]{-1,-1}; //erro | dimitr | NORMAL | 2021-07-19T10:10:11.917473+00:00 | 2021-07-20T01:42:12.966687+00:00 | 98 | false | refactored version :\n```\n public int[] threeEqualParts(int[] arr) {\n int len=arr.length, onesCount=0;\n int[] fail = new int[]{-1,-1}; //error case return\n \n //every part of tree may have a variable number of zeros due to leading zeros, while\n //number of ones should be the same in all parts;\n //let\'s count overall number of ones\n for(int a : arr) \n onesCount+=a;\n \n //if overall number of ones can\'t be divided equally between all three parts, then we return error\n if(onesCount%3!=0 )\n return fail;\n \n //in case of absence of ones, let\'s return any possible combination\n if(onesCount==0)\n return new int[]{0,2};\n\n int i,j,k,m,l;\n int partOnesCount =onesCount/3; //number of ones in a single part\n \n //let\'s count trailing zeros in the latest part\n for(k=len-1;arr[k]!=1;k--);\n int trailingZeroesCount = len-1-k;\n \n //find beginning of the first part\n l = findBeg(0, partOnesCount, trailingZeroesCount, arr);\n if(l==-1)\n return fail;\n\n //find beginning of the second part\n m = findBeg(l, partOnesCount, trailingZeroesCount, arr);\n if(m==-1)\n return fail; \n \n for(i=--l,j=--m,k=len-1;i>=0 && j>l && k > m; i--,j--,k--)\n if(arr[i]!=arr[j] || arr[j]!=arr[k]) //check item by item in all tree parts, that exact sequence should be the same in all tree parts\n return fail; \n\n return new int[]{l,m+1};\n }\n \n private int findBeg(int i, int partOnesCount, int trailingZeroesCount, int[] arr){\n //shift i to the right by counting ones\n for(;partOnesCount!=0;i++)\n partOnesCount-=arr[i];\n \n //shift i to the right by counting trailing zeros\n for(;trailingZeroesCount>0;i++, trailingZeroesCount--)\n if(arr[i]!=0) //if we face non-zero value in trailing zeros area, the return error\n return -1; \n \n return i; //return potential beginning of the binary representation\n }\n```\n\noriginal version : \n```\n public int[] threeEqualParts(int[] arr) {\n int len=arr.length, onesCount=0;\n int[] fail = new int[]{-1,-1}; //error case return\n \n //every part of tree may have a variable number of zeros due to leading zeros, while\n //number of ones should be the same in all parts;\n //let\'s count overall number of ones\n for(int a : arr) \n onesCount+=a;\n \n //if overall number of ones can\'t be divided equally between all three parts, then we return error\n if(onesCount%3!=0 )\n return fail;\n \n //in case of absence of ones, let\'s return any possible combination\n if(onesCount==0)\n return new int[]{0,2};\n\n int i,j,k;\n int partOnesCount =onesCount/3; //number of ones in a single part\n \n //let\'s count trailing zeros in the latest part\n for(k=len-1;arr[k]!=1;k--);\n int trailingZeroesCount = len-1-k;\n \n //shift i to the right by counting ones\n int leftOnesCount = partOnesCount;\n for(i=0;leftOnesCount!=0;i++)\n leftOnesCount-=arr[i];\n \n //shift i to the right by counting trailing zeros\n int leftTrailingZeros = trailingZeroesCount;\n for(;leftTrailingZeros>0;i++, leftTrailingZeros--)\n if(arr[i]!=0) //if we face non-zero value in trailing zeros area, the return error\n return fail;\n \n int l = i-1, m=i;\n //do the same with the middle part\n int middleOnesCount = onesCount/3;\n for(;middleOnesCount!=0;m++)\n middleOnesCount-=arr[m];\n \n int middleTrailingZeros = trailingZeroesCount;\n for(;middleTrailingZeros>0;m++, middleTrailingZeros--)\n if(arr[m]!=0)\n return fail; \n \n m--; i = l; j = m; k = len-1;\n while(i>=0 && j>l && k > m){\n if(arr[i]!=arr[j] || arr[j]!=arr[k]) //check item by item, that exact sequence is the same in all tree parts\n return fail; \n \n i--; j--; k--;\n }\n return new int[]{l,m+1};\n }\n``` | 1 | 0 | [] | 0 |
three-equal-parts | Simple O(n) logical approach explained with example | simple-on-logical-approach-explained-wit-i41d | Approach \n The array has to contain number of 1\'s that are multiple of 3\n Each of the three parts has to contain equal number of ones\n Now it\'s all abou | 495 | NORMAL | 2021-07-17T20:10:59.375065+00:00 | 2021-07-17T20:11:34.545911+00:00 | 116 | false | ### Approach \n* The array has to contain number of 1\'s that are multiple of 3\n* Each of the three parts has to contain equal number of ones\n* Now it\'s all about locating the beginning of 1s, and comparing the parts\n\n### Example\n```\n 000010101010000101010100001010101 << example\n [0]*1[1,0]*[0]*1[1,0]*[0]*1[1,0]* << pattern\n ^ ^ ^ << beginning of first 1 in each part\n <--n--> <--n--> <--n--> << n = length of the last part \n left middle right << left, middle, right parts whose value is to be compared\n ^ ^ << beginning of each part, having leading 0s\n i j << answer = end of first part, beginning of last part\n```\n\n### Python3 Implementation\n* `O(n)` time\n\t* one pass for counting 1\'s\n\t* one pass for locating the first 1 of each part\n\t* one pass for comparing left, middle and right parts\n* `O(1)` space \n\t* ignores space taken by string splicing\n\t* we can always do that in `O(1)` time with a little bit of extra lines of code\n\n```\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n \n ones = sum(arr) # total count of 1\'s\n \n # early termination conditions\n if ones % 3 != 0: return [-1, -1]\n if ones == 0: return [0, len(arr)-1]\n \n cnt = 0 # running count of 1\'s\n target1 = 1 # first 1 of left part\n target2 = 1 + ones//3 # first 1 of middle part\n target3 = 1 + 2*ones//3 # first 1 of right part\n \n for idx, bit in enumerate(arr):\n if bit == 1:\n cnt += 1\n if cnt == target1: start1 = idx\n if cnt == target2: start2 = idx\n if cnt == target3: start3 = idx\n\n n = len(arr) - start3\n if arr[start1 : start1+n] == arr[start2 : start2+n] == arr[start3 : start3+n]:\n return [start1 + n - 1, start2 + n] \n \n return [-1, -1]\n``` | 1 | 0 | ['Python3'] | 0 |
three-equal-parts | Three Equal Parts | Java solution | three-equal-parts-java-solution-by-arjun-6z3x | ```\n public int[] threeEqualParts(int[] arr) {\n int n = arr.length ;\n List ones=new ArrayList() ;\n for(int i = 0 ; i < n ; i++)\n | arjunagarwal | NORMAL | 2021-07-17T19:39:39.181119+00:00 | 2021-07-17T19:39:39.181155+00:00 | 94 | false | ```\n public int[] threeEqualParts(int[] arr) {\n int n = arr.length ;\n List<Integer> ones=new ArrayList() ;\n for(int i = 0 ; i < n ; i++)\n {\n if(arr[i]>0)\n {\n ones.add(i) ;\n }\n }\n int cnt = ones.size() ;\n if(cnt == 0)\n {\n return new int[]{0 , n - 1} ;\n }\n if(cnt%3!=0) \n {\n return new int[]{-1 , -1} ;\n }\n int f = ones.get(0);\n int s = ones.get(cnt/3);\n int t = ones.get((cnt/3)*2) ;\n while(t < n && arr[f] == arr[s] && arr[f] == arr[t])\n {\n f++ ;\n s++ ;\n t++ ;\n }\n if(t == n)\n {\n return new int[]{f - 1 , s} ;\n }\n return new int[]{-1 , -1} ;\n } | 1 | 0 | [] | 0 |
three-equal-parts | C++ (Clean, Commented for easy understanding) | c-clean-commented-for-easy-understanding-l05a | \n/*\n\tSuch approaches don\'t come to our minds in one go. I had taken help for this solution. Tried to put\n\tcomments so that others can understand well.\n\t | mazhar_mik | NORMAL | 2021-07-17T18:35:46.761876+00:00 | 2021-07-17T18:35:46.761902+00:00 | 42 | false | ```\n/*\n\tSuch approaches don\'t come to our minds in one go. I had taken help for this solution. Tried to put\n\tcomments so that others can understand well.\n\tPersonally, Leetcode\'s solution to this Qn and explanation are not written well. It seems like\n\ta mess and unreadable. I have tried to explain it with comments\n*/\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int n = arr.size();\n int sum = accumulate(begin(arr), end(arr), 0);\n \n if(sum == 0)\n return {0, n-1};\n else if(sum%3 != 0)\n return {-1, -1};\n \n int k = sum/3;\n //So every partition must have k 1\'s\n //So let\'s find three partitions having k 1\'s and compare them bit by bit\n \n int start = -1, mid = -1, end = -1;\n int count = 0;\n\n //[1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1]\n for(int i = 0; i<n; i++) {\n if(arr[i] == 0) continue;\n \n count += arr[i];\n if(count > k) {\n count = 1;\n }\n \n if(count == 1) {\n if(start == -1) start = i;\n else if(mid == -1) mid = i;\n else if(end == -1) end = i;\n else break;\n }\n }\n \n /*\n we have found three sections and we have pointers to starting \'1\' of\n each section.\n we now compare them bit by bit\n */\n \n while(end < n && arr[start] == arr[mid] && arr[mid] == arr[end]) {\n start++; mid++; end++;\n }\n \n //It means we couldn\'t match all sections\n if(end != n) return {-1, -1};\n \n return {start-1, mid};\n }\n};\n``` | 1 | 0 | [] | 0 |
three-equal-parts | Go Solution with a single iteration. Beats 100% | go-solution-with-a-single-iteration-beat-ds8g | \nvar Invalid = []int{-1, -1}\n\nfunc threeEqualParts(arr []int) []int {\n\tones := make([]int, 0, len(arr))\n\tfor i, n := range arr {\n\t\tif n == 1 {\n\t\t\t | evleria | NORMAL | 2021-07-17T17:42:22.192495+00:00 | 2021-07-17T17:42:22.192541+00:00 | 60 | false | ```\nvar Invalid = []int{-1, -1}\n\nfunc threeEqualParts(arr []int) []int {\n\tones := make([]int, 0, len(arr))\n\tfor i, n := range arr {\n\t\tif n == 1 {\n\t\t\tones = append(ones, i)\n\t\t}\n\t}\n\n\tif len(ones) == 0 {\n\t\treturn []int{0, len(arr) - 1}\n\t}\n\tif len(ones)%3 != 0 {\n\t\treturn Invalid\n\t}\n\n\tgr := len(ones) / 3\n\tstart1, start2, start3 := ones[0], ones[gr], ones[2*gr]\n\tgrLen := len(arr) - start3\n\n\tfirst, second, third := arr[start1:start1+grLen], arr[start2:start2+grLen], arr[start3:]\n\tif !equal(first, second, third) {\n\t\treturn Invalid\n\t}\n\n\treturn []int{start1 + grLen - 1, start2 + grLen}\n}\n\nfunc equal(a, b, c []int) bool {\n\tif len(a) != len(b) || len(a) != len(c) {\n\t\treturn false\n\t}\n\n\tfor i := 0; i < len(a); i++ {\n\t\tif a[i] != b[i] || a[i] != c[i] {\n\t\t\treturn false\n\t\t}\n\t}\n\n\treturn true\n}\n``` | 1 | 0 | ['Go'] | 0 |
three-equal-parts | C++ Simple Solution | c-simple-solution-by-alamin-tokee-wth3 | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n vector<int> ans={-1,-1};\n int numOf1s = 0;\n for(int x: | alamin-tokee | NORMAL | 2021-07-17T17:23:33.527217+00:00 | 2021-07-17T17:23:33.527261+00:00 | 39 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n vector<int> ans={-1,-1};\n int numOf1s = 0;\n for(int x:arr){\n numOf1s += x;\n }\n if(numOf1s == 0){\n return {0,2};\n }\n if(numOf1s % 3 != 0){\n return ans;\n } \n int noOfOnesInEachPart = numOf1s / 3;\n int indexOfFirst1InPart0 = -1;\n int indexOfFirst1InPart1 = -1;\n int indexOfFirst1InPart2 = -1;\n numOf1s = 0;\n for(int i = 0; i < arr.size(); i++){\n if(arr[i] == 1){\n numOf1s++;\n if(numOf1s == noOfOnesInEachPart + 1){\n indexOfFirst1InPart1 = i;\n }else if(numOf1s == 2 * noOfOnesInEachPart + 1){\n indexOfFirst1InPart2 = i;\n }else if(numOf1s == 1){\n indexOfFirst1InPart0 = i;\n }\n }\n }\n while(indexOfFirst1InPart2 < arr.size()){\n if(arr[indexOfFirst1InPart0] == arr[indexOfFirst1InPart1] && arr[indexOfFirst1InPart1]==arr[indexOfFirst1InPart2]){\n indexOfFirst1InPart0++;\n indexOfFirst1InPart1++;\n indexOfFirst1InPart2++;\n }else{\n return ans;\n }\n }\n return {indexOfFirst1InPart0-1, indexOfFirst1InPart1};\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
three-equal-parts | Easy C++ Solution || O(n) Time Complexity | easy-c-solution-on-time-complexity-by-pr-uaxg | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) \n {\n int n = arr.size();\n vector<int> res(2);\n res[0] | pragyatewary24 | NORMAL | 2021-07-17T17:20:38.665868+00:00 | 2021-07-17T17:20:38.665911+00:00 | 25 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) \n {\n int n = arr.size();\n vector<int> res(2);\n res[0] = -1;\n res[1] = -1;\n \n int totalCountOne = 0;\n for(auto X: arr)\n {\n totalCountOne += X;\n }\n if(totalCountOne == 0)\n {\n res[0] = 0;\n res[1] = 2;\n return res;\n } \n if((totalCountOne)%3 != 0)\n {\n return res;\n }\n \n int noOfOneInEachPart = totalCountOne/3;\n int idxOfFirstOneInPart0 = -1;\n int idxOfFirstOneInPart1 = -1;\n int idxOfFirstOneInPart2 = -1;\n int NoOfOnes = 0;\n for(int i=0; i<n; i++)\n {\n if(arr[i] == 1)\n {\n NoOfOnes++;\n if(NoOfOnes == 1)\n {\n idxOfFirstOneInPart0 = i;\n }\n else if(NoOfOnes == noOfOneInEachPart + 1)\n {\n idxOfFirstOneInPart1 = i;\n }\n else if(NoOfOnes == 2*noOfOneInEachPart + 1)\n {\n idxOfFirstOneInPart2 = i;\n }\n }\n }\n while(idxOfFirstOneInPart2<n)\n {\n if(arr[idxOfFirstOneInPart2] == arr[idxOfFirstOneInPart1] && arr[idxOfFirstOneInPart2] == arr[idxOfFirstOneInPart0])\n {\n idxOfFirstOneInPart0++;\n idxOfFirstOneInPart2++;\n idxOfFirstOneInPart1++;\n }\n else\n {\n return res;\n }\n \n }\n res[0] = idxOfFirstOneInPart0-1;\n res[1] = idxOfFirstOneInPart1;\n return res;\n }\n};\n``` | 1 | 0 | [] | 0 |
three-equal-parts | C++ Solution | c-solution-by-saurabhvikastekam-b0la | \nclass Solution \n{\n public:\n vector<int> threeEqualParts(vector<int>& arr) \n {\n int count = 0;\n for (auto i:arr)\n {\n | SaurabhVikasTekam | NORMAL | 2021-07-17T16:45:24.733568+00:00 | 2021-07-17T16:45:24.733609+00:00 | 69 | false | ```\nclass Solution \n{\n public:\n vector<int> threeEqualParts(vector<int>& arr) \n {\n int count = 0;\n for (auto i:arr)\n {\n if(i == 1)\n count++;\n }\n if(count == 0)\n return {0,2};\n if(count%3 != 0)\n return {-1,-1};\n int p1 = 0;\n int p2 = 0;\n int p3 = 0;\n count = count/3;\n int temp = 0;\n for(int i = 0;i<arr.size();i++)\n { if(arr[i] == 1)\n { if(temp == 0)\n p1 = i;\n else if(temp == count)\n p2 = i;\n else if(temp == 2*count)\n p3 = i;\n temp++;\n }\n }\n int oldp2 = p2;\n int oldp3 = p3;\n while(p1<oldp2 and p2<oldp3 and p3<arr.size())\n {\n if(arr[p1] != arr[p2] or arr[p2] != arr[p3])\n return {-1,-1};\n p1++;\n p2++;\n p3++;\n }\n if(p3 == arr.size())\n {\n return {p1-1,p2};\n }\n return {-1,-1};\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 0 |
three-equal-parts | Linear times, O(n) Solution in Python [clean] | linear-times-on-solution-in-python-clean-fqqg | \n# Github: Shantanugupta1118\n# DAY 60 of DAY 100\n# 927. Three Equal Parts - Leetcode/July\n# https://leetcode.com/problems/three-equal-parts/\n\n\nclass So | shantanugupta1118 | NORMAL | 2021-07-17T15:46:24.757861+00:00 | 2021-07-17T15:50:48.913690+00:00 | 125 | false | ```\n# Github: Shantanugupta1118\n# DAY 60 of DAY 100\n# 927. Three Equal Parts - Leetcode/July\n# https://leetcode.com/problems/three-equal-parts/\n\n\nclass Solution:\n def threeEqualParts(self, arr):\n ans = [-1,-1]\n numsOf1s = 0\n for i in arr:\n numsOf1s += i\n if numsOf1s == 0:\n return [0,2]\n if numsOf1s%3 != 0:\n return ans\n \n eachPart = numsOf1s//3\n index0, index1, index2 = -1, -1, -1\n numsOf1s = 0\n for i in range(len(arr)):\n if arr[i] == 1:\n numsOf1s += 1\n if numsOf1s == eachPart+1:\n index1 = i\n elif numsOf1s == 2*eachPart+1:\n index2 = i\n elif numsOf1s == 1:\n index0 = i\n while index2 < len(arr):\n if arr[index2] == arr[index0] and arr[index2] == arr[index1]:\n index0 += 1\n index1 += 1\n index2 += 1\n else:\n return ans \n return [index0-1, index1]\n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
three-equal-parts | Pretty short Java solution(~15 lines), explained | pretty-short-java-solution15-lines-expla-lpty | The idea is to count the number of ones numOnes: \n\nIf numOnes isn\'t divisible by 3, then you can\'t divide them into 3 parts so return [-1, -1]. \n\nSecondly | TheJesterKing | NORMAL | 2021-07-17T15:38:58.636259+00:00 | 2021-07-17T15:41:15.186966+00:00 | 76 | false | The idea is to count the number of ones `numOnes`: \n\nIf `numOnes` isn\'t divisible by 3, then you can\'t divide them into 3 parts so return [-1, -1]. \n\nSecondly, if there are only zeroes in the array, you can divide the array arbitrarily.\n\nFinally, if `numOnes` is divisible by 3, we run three pointers `first, second and third` and check whether the division is possible.\n\n`first` points to the First One of the array, `second` points to the `numOnes/3`th One of the array, and `third` points to the `2*numOnes/3`th One of the array.\nAdvance the three pointer, if there is a mismatch at any step, return [-1, -1].\nIf the `third` pointer finally manages to reach the end, we have a valid division, because everything matched!\n\nWhat I said in code:\n```java\nclass Solution {\n public int[] threeEqualParts(int[] arr) {\n int numOnes = 0;\n List<Integer> pos = new ArrayList<>();\n for(int i = 0; i < arr.length; i++){\n numOnes += arr[i];\n if(arr[i] == 1) pos.add(i);\n }\n if(numOnes % 3 != 0) return new int[]{-1, -1};\n if(numOnes == 0) return new int[]{0, arr.length-1};\n int first = pos.get(0), second = pos.get(numOnes/3), third = pos.get(numOnes/3 *2);\n while(first < second && second < third && third < arr.length){\n if(arr[first] != arr[second] || arr[second] != arr[third]) return new int[]{-1, -1};\n first++; second++; third++;\n }\n return third == arr.length ? new int[]{first-1, second} : new int[]{-1, -1};\n }\n}\n```\nOkay, not 15 lines, it\'s 18. You can probably sue me for that ;)\nBut I hope you understand how the solution works. | 1 | 0 | ['Java'] | 0 |
three-equal-parts | O(n) Solution CPP | on-solution-cpp-by-gp1999-chlu | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n vector<int> ans{-1,-1};\n int count=0,ones=0,p1=0,p2=0,p3=0;\n | gp1999 | NORMAL | 2021-07-17T15:06:12.026457+00:00 | 2021-07-17T15:06:12.026486+00:00 | 43 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n vector<int> ans{-1,-1};\n int count=0,ones=0,p1=0,p2=0,p3=0;\n for(int i=0; i<arr.size();i++){\n count+=arr[i];\n }\n if(count%3) return ans;\n if(count==0){\n ans[0] = 0;\n ans[1] = arr.size()-1;\n return ans;\n }\n count/=3;\n for(int i=0; i<arr.size(); i++){\n if(arr[i]==1){\n if(ones==0) p1 = i;\n else if(ones==count) p2 = i;\n else if(ones==2*count) p3 = i;\n ones++;\n }\n }\n int op2=p2,op3=p3;\n while(p1<op2 && p2<op3 && p3<arr.size()){\n if(arr[p1]!= arr[p2] || arr[p2]!=arr[p3]) return ans;\n p1++; p2++; p3++;\n }\n if(p3!=arr.size()) return ans;\n \n ans[0] = p1-1;\n ans[1] = p2;\n return ans;\n }\n};\n```\nInspired from :- https://leetcode.com/problems/three-equal-parts/discuss/1343568/C%2B%2B-O(n)-time-and-O(1)-space | 1 | 0 | [] | 0 |
three-equal-parts | Rust solution | rust-solution-by-sugyan-9evi | rust\nimpl Solution {\n pub fn three_equal_parts(arr: Vec<i32>) -> Vec<i32> {\n let v = arr\n .iter()\n .enumerate()\n | sugyan | NORMAL | 2021-07-17T15:00:48.346334+00:00 | 2021-07-17T15:00:48.346398+00:00 | 70 | false | ```rust\nimpl Solution {\n pub fn three_equal_parts(arr: Vec<i32>) -> Vec<i32> {\n let v = arr\n .iter()\n .enumerate()\n .filter_map(|(i, &a)| if a == 1 { Some(i) } else { None })\n .collect::<Vec<_>>();\n if arr.len() < 3 || v.len() % 3 != 0 {\n return [-1, -1].to_vec();\n }\n if v.is_empty() {\n return [0, 2].to_vec();\n }\n let chunks = v.chunks(v.len() / 3).collect::<Vec<_>>();\n let i = chunks[0][v.len() / 3 - 1] + arr.len() - v[v.len() - 1] - 1;\n let j = chunks[1][v.len() / 3 - 1] + arr.len() - v[v.len() - 1];\n if arr.len() - chunks[2][0] > j - i - 1 || arr.len() - chunks[2][0] > i + 1 {\n return [-1, -1].to_vec();\n }\n for k in 0..(i + 1).min(j - i - 1).min(arr.len() - j) {\n if arr[i - k] != arr[j - 1 - k] || arr[i - k] != arr[arr.len() - 1 - k] {\n return [-1, -1].to_vec();\n }\n }\n [i as i32, j as i32].to_vec()\n }\n}\n``` | 1 | 0 | ['Rust'] | 0 |
three-equal-parts | c++(24ms 99,40%) pointers , three pass (greedy) | c24ms-9940-pointers-three-pass-greedy-by-we0j | Runtime: 24 ms, faster than 99.40% of C++ online submissions for Three Equal Parts.\nMemory Usage: 38.9 MB, less than 55.42% of C++ online submissions for Three | zx007pi | NORMAL | 2021-07-17T10:37:24.422283+00:00 | 2021-07-17T11:19:48.717511+00:00 | 133 | false | Runtime: 24 ms, faster than 99.40% of C++ online submissions for Three Equal Parts.\nMemory Usage: 38.9 MB, less than 55.42% of C++ online submissions for Three Equal Parts.\n**General idea:**\n**1.** If we can split this array for three equal parts we MUST have total number of "ones" is uqual 3* k \n**2.** split our array for three parts with equal numbers of "ones" \n**3.** value of zerous between first and second parts and between second and thrid parts not can be less than value of contigious zerous in end of array. check it.\n**4.** tree parts will be the same\n\n\n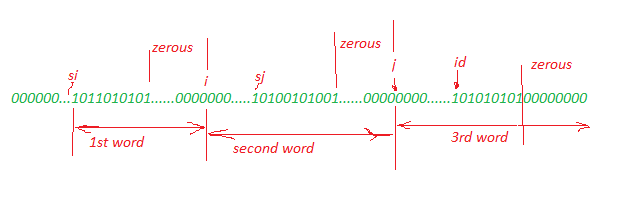\n\n\n\n\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& arr) {\n int ones = 0, N = arr.size();\n for(auto &x: arr) if(x) ones++;\n if(ones%3 != 0) return{-1,-1}; //check ones\n if(ones == 0) return {0,2};\n ones /= 3;\n \n int zeroes = 0, i = N - 1; //last contigious zerous\n while(arr[i--] == 0) zeroes++;\n ///////////////////////////////////////////(splitting) \n int si = -1, sj, j, id = 0, n;\n \n while(arr[id] == 0) si++, id++; //"si"\n \n n = ones;\n while(n) if(arr[id++] == 1) n--; // "i" without zerous\n i = id-1;\n \n int nz = 0;\n while(arr[id] == 0) nz++, id++;\n if(nz < zeroes) return {-1,-1};\n i += zeroes, sj = id; // "i" and "sj" \n \n n = ones;\n while(n) if(arr[id++] == 1) n--; // "j" without zerous\n j = id;\n \n nz = 0;\n while(arr[id] == 0) nz++, id++;\n if(nz < zeroes) return {-1,-1}; // "j" and id\n j += zeroes;\n \n /////////////////////////////////////////////////// second part(if we can split) \n if(i - si != N - id || i - si != j - sj ) return {-1,-1}; //if three word havent the same length\n \n int limit = j - sj - zeroes; //old version -> int limit = j - sj; \n for(int a = si + 1, b = sj, c = id; limit; a++, b++, c++, limit--)\n if(arr[a] != arr[b] || arr[a] != arr[c]) return {-1,-1};\n \n return {i,j};\n }\n};\n``` | 1 | 1 | ['C', 'C++'] | 0 |
three-equal-parts | ✅✅Three Equal Parts || Python || Logic Building | three-equal-parts-python-logic-building-v39z4 | Key obseration is that three parts must have same number and pattern of 1s except the leading 0s part. \nMy idea is to:\n\n1. Count no. of ones, simply taking | code_assassin | NORMAL | 2021-07-17T10:37:10.897268+00:00 | 2021-07-17T10:38:29.883622+00:00 | 163 | false | Key obseration is that three parts must have same number and pattern of 1s except the leading 0s part. \nMy idea is to:\n\n1. Count no. of ones, simply taking sum. (if sum%3!=0 return [-1,-1])\n2. Search from right side to left, until we found sum/3 of 1s. This index defines the pattern of 1s.\n3. From left, ignore leading 0s, and then match the pattern found in step 2, to get the first EndIndex.\n4. Similary, do another matching to found second EndIndex.\n\n```\nclass Solution:\n def threeEqualParts(self, arr: List[int]) -> List[int]:\n n=len(arr)\n x=sum(arr) #gives no. of 1s\n if x==0:\n return [0,2]\n elif x%3!=0:\n return [-1,-1]\n \n # finding index of starting 1 of third string\n idx3=0\n count=0\n for i in range(n-1,-1,-1):\n if arr[i]==1:\n count+=1\n if count==x//3:\n idx3=i\n break\n \n idx1=endIdx(arr,0,idx3)\n if idx1<0:\n return [-1,-1]\n \n idx2=endIdx(arr,idx1+1,idx3)\n if idx2<0:\n return [-1,-1]\n \n return [idx1,idx2+1]\n \n# here, idx3 is index of pattern to compare to.\n# return endIdx of start pattern that matches idx3 side.\ndef endIdx(arr, start, idx3):\n while arr[start]==0:\n start+=1\n while idx3<len(arr):\n if arr[start]!=arr[idx3]:\n return -1\n start+=1\n idx3+=1\n return start-1\n```\n*If case of any doubt or suggestion, do comment.*\n\n***Happy Coding* :)**\n | 1 | 0 | [] | 0 |
three-equal-parts | javascript, 84ms | javascript-84ms-by-momocow-tc2w | Approximately 1.33N operations => O(N).\n\n\n/**\n * @param {number[]} arr\n * @return {number[]}\n */\nvar threeEqualParts = function (arr) {\n const gaps = [ | momocow | NORMAL | 2021-07-17T09:52:57.715231+00:00 | 2021-07-17T09:52:57.715271+00:00 | 145 | false | Approximately 1.33N operations => O(N).\n\n```\n/**\n * @param {number[]} arr\n * @return {number[]}\n */\nvar threeEqualParts = function (arr) {\n const gaps = []\n let head0s = 0\n let prev\n for (let p = 0; p < arr.length; p++) {\n if (arr[p] === 1) {\n if (prev !== undefined) {\n gaps.push(p - prev)\n }\n prev = p\n } else if (prev === undefined) {\n head0s++\n }\n }\n if (head0s === arr.length) {\n return [0, 2]\n }\n if (gaps.length % 3 !== 2) {\n return [-1, -1]\n }\n const groupLen = (gaps.length - 2) / 3\n let groupSum = 0\n for (let q = 0; q < groupLen; q++) {\n if (\n gaps[q] !== gaps[q + groupLen + 1] ||\n gaps[q] !== gaps[q + 2 * groupLen + 2]\n ) {\n return [-1, -1]\n }\n groupSum += gaps[q]\n }\n const tail0s = arr.length -\n head0s -\n groupSum * 3 -\n gaps[groupLen] -\n gaps[2 * groupLen + 1] -\n 1\n if (gaps[groupLen] - 1 < tail0s || gaps[2 * groupLen + 1] - 1 < tail0s) {\n return [-1, -1]\n }\n const i = head0s + groupSum + tail0s\n const j = i + gaps[groupLen] + groupSum + 1\n return [i, j]\n}\n\n``` | 1 | 0 | ['JavaScript'] | 0 |
three-equal-parts | Swift solution | swift-solution-by-yamironov-u3bx | Count ones in arr\n2. If there is no ones in arr, then all parts are zeros\n3. Ones count must be multiple of three, else it is not possible to split arr into t | yamironov | NORMAL | 2021-07-17T08:41:16.093090+00:00 | 2021-07-19T05:54:30.650354+00:00 | 49 | false | 1. Count ones in `arr`\n2. If there is no ones in `arr`, then all parts are zeros\n3. Ones count must be multiple of three, else it is not possible to split `arr` into three parts\n4. Find first significant bit for each part in `arr`\n5. The last part ends at the end of `arr`, it has a reference length. Check that the length of the first two parts is not less than the reference one.\n6. Check the equality of the three parts\n\nTime complexity O(n), space complexity O(1)\n\nUpdate: simplified reduce, as [@Legonaftik](https://leetcode.com/Legonaftik/) suggested\n```\nclass Solution {\n func threeEqualParts(_ arr: [Int]) -> [Int] {\n let n = arr.count, ones = arr.reduce(0, +), partOnes = ones / 3\n guard ones > 0 else { return [0, 2] } // all parts are zeros\n guard ones % 3 == 0 else { return [-1, -1] } // it is not possible to split into three parts\n\n var starts = [Int](repeating: -1, count: 3), runningOnes = 0\n for i in 0..<n where arr[i] == 1 {\n let part = runningOnes / partOnes // 0...2\n if starts[part] == -1 {\n starts[part] = i\n }\n runningOnes += 1\n }\n\n let len = n - starts[2]\n\n guard starts[1] - starts[0] >= len && starts[2] - starts[1] >= len else { return [-1, -1] }\n\n // check if three parts are equal\n for l in 0..<len where arr[starts[0] + l] != arr[starts[1] + l] || arr[starts[0] + l] != arr[starts[2] + l] {\n return [-1, -1]\n }\n \n return [starts[0] + len - 1, starts[1] + len]\n }\n}\n``` | 1 | 0 | ['Swift'] | 1 |
three-equal-parts | Just logic( Super Easy) | just-logic-super-easy-by-sramlax72-whcm | 1) Calculate number of 1\'s , let store it in cnt\n\n2) if cnt is not divisible by 3 return [-1,-1]\n\n\t3) now check in array from right to left and stop when | sramlax72 | NORMAL | 2021-07-17T08:23:05.483602+00:00 | 2021-07-17T08:27:22.323714+00:00 | 71 | false | 1) Calculate number of 1\'s , let store it in cnt\n\n2) if cnt is not divisible by 3 return [-1,-1]\n\n\t3) now check in array from right to left and stop when got cnt/3 ones. the part beyond it must be the number we need. It it is not then no other solution exists.Eg : arr = 01001000100 , so cnt = 3 ,and we got part after first one from right = "100"\n\t\n\t4) Now check it to exist in start as well. skip all trailing zeros and then see if "100" is in start as well. Yes, we it.\n\t\n\t5) Now final step, after that 100 in start, again 100 should exist after start as well. Again skip all trailing zeros after the first "100" and look for another "100", if found, still maybe the it is answer, mayber it is not, therefore check if all the array elements after this middle "100" we got to the "100" that is at the end are all Zeros, only then we get three "100" else return [-1,-1]\n\n 6) Now return { ans = end of first "100" , end of second "100"}\n\n\nCODE :-\n\nvector<int> threeEqualParts(vector<int>& arr) {\n int n = arr.size();\n int l=0,ll=0;\n int cnt = 0;\n for(int i = 0 ; i < n ; i ++ )\n {\n if(arr[i] == 1) cnt++;\n }\n if(cnt == 0) return {0,n-1};\n if(cnt%3 != 0 ) return {-1,-1};\n \n int jj = 0;\n \n int third = n-1;\n\n //while(arr[third] == 0) third--;\n for(int i = n-1 ; i >= 0 ; i--)\n {\n if(arr[i] == 1)\n {\n jj++;\n if(jj==cnt/3)\n {\n third = i;\n break;\n }\n }\n }\n cout<<third<<endl;\n \n int b = 0 , e = third;\n while(arr[b] == 0) b++;\n \n while(e < n)\n {\n cout<<b<<" ---- "<<e<<endl;\n if(arr[b] != arr[e]) \n {\n cout<<b<<" "<<e<<endl;\n return {-1,-1};\n }\n b++;\n e++;\n }\n cout<<b<<" "<<e<<endl;\n int first = 0, sec = b;\n l=b-1;\n \n while(arr[sec] == 0 ) sec++;\n while(arr[first] == 0) first++;\n \n while(first < b && sec < third)\n {\n if(arr[first] != arr[sec])\n {\n cout<<"bye";\n return {-1,-1};\n }\n first++;\n sec++;\n }\n if(sec>=third && first<b) return {-1,-1};\n ll = sec;\n cout<<sec<<" "<<third<<endl;\n while(sec < third)\n {\n if(arr[sec] != 0)\n {\n cout<< "yoyoy";\n return {-1,-1};\n }\n sec++;\n }\n \n \n \n \n return {l,ll};\n }\n\n | 1 | 1 | [] | 0 |
three-equal-parts | Three Equal Parts || Easy C++ Solution | three-equal-parts-easy-c-solution-by-b_u-ylpr | \tclass Solution {\n\tpublic:\n vector threeEqualParts(vector& A) {\n //count number of 1\'s\n int totalOnes=accumulate(A.begin(), A.end(), 0); | B_U_Rafi | NORMAL | 2021-07-17T07:43:24.162080+00:00 | 2021-07-17T07:44:03.740394+00:00 | 86 | false | \tclass Solution {\n\tpublic:\n vector<int> threeEqualParts(vector<int>& A) {\n //count number of 1\'s\n int totalOnes=accumulate(A.begin(), A.end(), 0);\n //if we can not divide into 3 parts then return -1,-1\n if(totalOnes%3!=0){\n return {-1,-1};\n }\n \n int result=totalOnes/3, size=A.size();\n //if sum is zero\n if(result==0){\n return {0, size-1};\n }\n \n int tempSum=0,i1=-1,i2=-1,i3=-1,j1=-1,j2=-1,j3=-1;\n for(int i=0;i<size;i++){\n if(A[i]){\n //count number of 1\'s have occured\n tempSum++;\n //for first 1, initialise the start index of first half\n if(tempSum==1) i1=i;\n //if first half is completed, then initialise the end index of first half\n if(tempSum==result) j1=i;\n //if second half is started, then initialise the start index of second half\n if(tempSum==result+1) i2=i;\n //if second half is completed, then initiliase the end index of second half\n if(tempSum==2*result) j2=i;\n //if third half is started, then initialise the start index of third half\n if(tempSum==2*result+1) i3=i;\n //if third half is completed, then initiliase the end index of third half and break as no need iterator further\n if(tempSum==3*result) { j3=i; break; }\n }\n }\n //verify all three parts are same, if not then they will not generate the same number eg. 101 and 1001 both contains same number of 1\'s but they are not same\n vector<int> firstHalf(A.begin()+i1, A.begin()+j1);\n vector<int> secondHalf(A.begin()+i2, A.begin()+j2);\n vector<int> thirdHalf(A.begin()+i3, A.begin()+j3);\n \n if(firstHalf!=secondHalf or secondHalf!=thirdHalf){\n return {-1,-1};\n }\n \n //now consider the 0\'s between first half and second half or second half and third half or after third half\n int firstZero=i2-j1-1;\n int secondZero=i3-j2-1;\n int thirdZero=A.size()-j3-1;\n //if 0\'s after third half are more than first and second then they will increase the number produced in third Half and the above verification will fail\n //if 0\'s after third half are less than first and second then the extra 0s in first and second will adjust at start of second half and third half and they will not hamper the above verification\n if(thirdZero>firstZero or thirdZero>secondZero){\n return {-1,-1};\n\t\t\t}\n //add those 0\'s found after third at end of firstHalf and secondHalf to make all 3 halfs symmetric\n return {j1+thirdZero, j2+thirdZero+1};\n\t\t}\n\t}; | 1 | 1 | [] | 0 |
three-equal-parts | 1 ms, faster than 100.00% of Java online submissions . O(n) | 1-ms-faster-than-10000-of-java-online-su-5ppt | \nclass Solution {\n public int[] threeEqualParts(int[] A) {\n int l=A.length;\n int ones=0;\n int[] count=new int[l];\n for(int | ashutoshbhardwaj25122000 | NORMAL | 2021-02-18T07:07:27.747159+00:00 | 2021-02-18T07:07:27.747202+00:00 | 125 | false | ```\nclass Solution {\n public int[] threeEqualParts(int[] A) {\n int l=A.length;\n int ones=0;\n int[] count=new int[l];\n for(int i=0;i<l;i++){\n ones=(A[i]==1)?ones+1:ones;\n count[i]=ones;\n }\n \n int[] ans=new int[2];\n ans[0]=-1;\n ans[1]=-1;\n if(ones==0){\n ans[0]=0;\n ans[1]=2;\n return ans;\n }\n if(ones%3!=0){\n return ans;\n }\n int i=l-1;\n while(i>=0 && A[i]!=1){\n i--;\n }\n \n int endzeroes=l-1-i;\n \n i=binarySearch(count,ones/3)+endzeroes;\n int j=binarySearch(count,2*ones/3)+endzeroes+1;\n int firststart=0;\n int secondstart=i+1;\n int thirdstart=j;\n \n while(firststart<=i && A[firststart]==0){\n firststart++;\n }\n while(secondstart<j && A[secondstart]==0){\n secondstart++;\n }\n while(thirdstart<l && A[thirdstart]==0){\n thirdstart++;\n }\n \n boolean possible=true;\n for(int r=firststart,s=secondstart,t=thirdstart;r<=i && s<j && t<l;r++,s++,t++){\n possible=possible && (A[r]==A[s] && A[s]==A[t]);\n }\n if(!possible || i-firststart+1!=j-secondstart || j-secondstart!=l-thirdstart){\n return ans;\n }\n ans[0]=i;\n ans[1]=j;\n return ans;\n }\n public int binarySearch(int[] A,int val){\n int l=0;\n int r=A.length-1;\n while(l<=r){\n int mid=(l+r)/2;\n if((mid==0 || A[mid-1]<val) && A[mid]==val){\n return mid;\n }\n else if(val>A[mid]){\n l=mid+1;\n }\n else{\n r=mid-1;\n }\n }\n return -1;\n }\n}\n``` | 1 | 1 | [] | 0 |
three-equal-parts | Python3 O(n) solution | python3-on-solution-by-owen2-llsc | \nclass Solution:\n def threeEqualParts(self, A: List[int]) -> List[int]:\n """\n 1: (# of 1) mod 3 == 0\n 2: calculate n3 values (start | owen2 | NORMAL | 2021-01-16T07:38:02.587663+00:00 | 2021-01-16T07:38:33.757249+00:00 | 99 | false | ```\nclass Solution:\n def threeEqualParts(self, A: List[int]) -> List[int]:\n """\n 1: (# of 1) mod 3 == 0\n 2: calculate n3 values (start with 0, end to tail)\n 3. check if there exists n1, n2 == n3\n """\n if sum(A) % 3 != 0:\n return [-1, -1]\n \n if sum(A) == 0:\n return [0, len(A) - 1]\n \n tot = sum(A)\n cnt = sum(A) // 3 * 2\n n3 = 0\n for i, n in enumerate(A):\n if cnt > 0:\n cnt -= n\n else:\n n3 = 2 * n3 + n\n \n n1 = 0\n n2 = 0\n i1 = None\n i2 = None\n for i, n in enumerate(A):\n if n1 > n3 or n2 > n3:\n return [-1, -1]\n elif n1 == n3:\n n2 = 2 * n2 + n\n else:\n n1 = 2 * n1 + n\n \n if n1 == n3 and i1 is None:\n i1 = i\n \n if n2 == n3:\n return [i1, i + 1]\n \n return [-1, -1]\n``` | 1 | 0 | [] | 0 |
three-equal-parts | o(n) c++ code with easy explanation | on-c-code-with-easy-explanation-by-mohit-pbdz | Intuition:\nall 3 halfs will have equal no of 1\'s. so find such 3 half\'s start index and end index.\n\nclass Solution {\npublic:\n vector<int> threeEqualPa | mohit_chau | NORMAL | 2020-08-28T20:22:19.394113+00:00 | 2020-08-28T20:22:19.394157+00:00 | 352 | false | **Intuition:**\nall 3 halfs will have equal no of 1\'s. so find such 3 half\'s start index and end index.\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n //count number of 1\'s\n int totalOnes=accumulate(A.begin(), A.end(), 0);\n //if we can not divide into 3 parts then return -1,-1\n if(totalOnes%3!=0){\n return {-1,-1};\n }\n //number 1\'s in 1 half can be possible\n int result=totalOnes/3, size=A.size();\n //if all 0\'s are input\n if(result==0){\n return {0, size-1};\n }\n int tempSum=0,i1=-1,i2=-1,i3=-1,j1=-1,j2=-1,j3=-1;\n for(int i=0;i<size;i++){\n if(A[i]){\n //count number of 1\'s have occured\n tempSum++;\n //for first 1, initialise the start index of first half\n if(tempSum==1) i1=i;\n //if first half is completed, then initialise the end index of first half\n if(tempSum==result) j1=i;\n //if second half is started, then initialise the start index of second half\n if(tempSum==result+1) i2=i;\n //if second half is completed, then initiliase the end index of second half\n if(tempSum==2*result) j2=i;\n //if third half is started, then initialise the start index of third half\n if(tempSum==2*result+1) i3=i;\n //if third half is completed, then initiliase the end index of third half and break as no need iterator further\n if(tempSum==3*result) { j3=i; break; }\n }\n }\n //verify all three parts are same, if not then they will not generate the same number eg. 101 and 1001 both contains same number of 1\'s but they are not same\n vector<int> firstHalf(A.begin()+i1, A.begin()+j1);\n vector<int> secondHalf(A.begin()+i2, A.begin()+j2);\n vector<int> thirdHalf(A.begin()+i3, A.begin()+j3);\n \n if(firstHalf!=secondHalf or secondHalf!=thirdHalf){\n return {-1,-1};\n }\n \n //now consider the 0\'s between first half and second half or second half and third half or after third half\n int firstZero=i2-j1-1;\n int secondZero=i3-j2-1;\n int thirdZero=A.size()-j3-1;\n //if 0\'s after third half are more than first and second then they will increase the number produced in third Half and the above verification will fail\n //if 0\'s after third half are less than first and second then the extra 0s in first and second will adjust at start of second half and third half and they will not hamper the above verification\n if(thirdZero>firstZero or thirdZero>secondZero){\n return {-1,-1};\n }\n //add those 0\'s found after third at end of firstHalf and secondHalf to make all 3 halfs symmetric\n return {j1+thirdZero, j2+thirdZero+1};\n }\n};\n``` | 1 | 1 | ['C'] | 0 |
three-equal-parts | C++ greedy | c-greedy-by-suhailakhtar039-uswo | The only thing horrifying in this problem is its tag hard and its proof which we don\'t have to do by the way.: )\n\nclass Solution {\npublic:\n vector<int> | suhailakhtar039 | NORMAL | 2020-07-05T12:03:15.959942+00:00 | 2020-07-05T12:03:15.959994+00:00 | 286 | false | The only thing horrifying in this problem is its tag hard and its proof which we don\'t have to do by the way.: )\n```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& a) {\n int one=0;\n int n=a.size();\n for(auto it:a)if(it)one++;\n if(one==0)\n return vector<int>{0,n-1};\n if(one%3)\n return vector<int>{-1,-1};\n int k=one/3;\n vector<int> pos;\n int t=0;\n for(int i=0;i<n;i++)\n {\n if(a[i])\n t++;\n if(t==1 and a[i]==1)\n pos.push_back(i);\n if(t==k)t=0;\n }\n int st=pos[0],mid=pos[1],en=pos[2];\n cout<<"st= "<<st<<" mid= "<<mid<<" en= "<<en<<endl;\n while(en<n and a[st]==a[mid] and a[mid]==a[en])\n en++,st++,mid++;\n if(en==n)\n return vector<int>{st-1,mid};\n return vector<int>{-1,-1};\n }\n};\n``` | 1 | 0 | ['C'] | 1 |
three-equal-parts | Python 3 Solution Explained | python-3-solution-explained-by-hsweiner5-bbqe | \nclass Solution:\n def threeEqualParts(self, A):\n """\n Given an array of ones and zeros, this program determines whether\n the array | hsweiner54 | NORMAL | 2020-06-24T00:06:12.511886+00:00 | 2020-06-24T00:08:26.894088+00:00 | 181 | false | ```\nclass Solution:\n def threeEqualParts(self, A):\n """\n Given an array of ones and zeros, this program determines whether\n the array can be partitioned three ways where each partition contains\n the same pattern of ones and zeros beginning with a one. If there\n are no ones, the presence of at least three zeros makes a partition\n possible.\n\n :param A: array of 1\'s and 0\'s\n :type A: list[int]\n :return: pair of integers\n [last location partion 1, first location after partition 2]\n or [-1, -1] if partition is not possible\n :rtype: list[int]\n """\n """\n Initialize:\n - length of A\n - get number of ones in A\n """\n len_A = len(A)\n ones = A.count(1)\n\n """\n If A is all zeros, a valid partition is possible if the length\n of A is 3 or greater.\n """\n if ones == 0:\n if len_A >= 3:\n return [0, len_A - 1]\n else:\n return[-1, -1]\n\n """\n The number of ones must be divisible by 3 in order for it to be\n possible to partition A.\n """\n if ones % 3:\n return [-1, -1]\n\n """\n If we have gotton this far, the number of ones in A is divisible\n by 3. It is now possible to scan A to find the start of each pattern.\n It is also possible to determine the length of the pattern from the\n third pattern.\n """\n ones_in_pattern = ones // 3\n pattern_starts = []\n ones_count = 0\n for k, a in enumerate(A):\n if a:\n ones_count += 1\n if ones_in_pattern == 1 \\\n or ones_count % ones_in_pattern == 1:\n pattern_starts.append(k)\n s1, s2, s3 = pattern_starts\n len_pattern = len(A[s3:])\n\n """\n Compare the patterns and return the result.\n """\n if A[s1:s1 + len_pattern] == A[s2:s2 + len_pattern] == A[s3:]:\n return [s1 + len_pattern - 1, s2 + len_pattern]\n return [-1, -1]\n\n``` | 1 | 0 | ['Python3'] | 0 |
three-equal-parts | Java sol | java-sol-by-cuny-66brother-jzyn | \nclass Solution {\n int t;\n public int[] threeEqualParts(int[] A) {\n int res[]=new int[]{-1,-1};\n int part1=0;int part2=0;int part3=0;in | CUNY-66brother | NORMAL | 2020-04-26T17:38:13.312807+00:00 | 2020-04-26T17:38:13.312855+00:00 | 138 | false | ```\nclass Solution {\n int t;\n public int[] threeEqualParts(int[] A) {\n int res[]=new int[]{-1,-1};\n int part1=0;int part2=0;int part3=0;int cnt=1;\n Map<Integer,Integer>map=new HashMap<>();\n int ones=0;\n for(int n:A)if(n==1)ones++;\n if(ones==0)return new int[]{0,A.length-1};\n if(ones%3!=0)return res;\n t=ones/3;ones=0;\n for(int i=0;i<A.length;i++){\n if(A[i]==1){\n ones++;\n map.put(cnt,i);\n cnt++;\n }\n }\n for(int i=map.get(t)+1;i<=map.get(2*t);i++){\n if(A[i]==0)part1++;\n else break;\n }\n for(int i=map.get(2*t)+1;i<A.length;i++){\n if(A[i]==0)part2++;\n else break;\n }\n for(int i=map.get(ones)+1;i<A.length;i++){\n if(A[i]==0)part3++;\n }\n if(part1<part3||part2<part3)return res;\n List<Integer>l1=getlist(A,map.get(1),map.get(t));\n List<Integer>l2=getlist(A,map.get(t+1),map.get(2*t));\n List<Integer>l3=getlist(A,map.get(2*t+1),map.get(ones));\n if(!compare(l1,l2)||!compare(l2,l3))return res;\n res[0]=map.get(t)+part3;\n res[1]=map.get(2*t)+part3+1;\n return res;\n }\n \n public List<Integer> getlist(int A[],int i1,int i2){\n List<Integer>list=new ArrayList<>();\n for(int i=i1;i<=i2;i++)list.add(A[i]);\n return list;\n }\n public boolean compare(List<Integer>list1,List<Integer>list2){\n if(list1.size()!=list2.size())return false;\n for(int i=0;i<list1.size();i++){\n if(list1.get(i)!=list2.get(i))return false;\n }\n return true;\n }\n}\n``` | 1 | 0 | [] | 0 |
three-equal-parts | simple solution O(N) time complexity O(1) Space | simple-solution-on-time-complexity-o1-sp-oaog | \tclass Solution(object):\n\tdef threeEqualParts(self, A):\n if len(A) < 3:\n return [-1,-1]\n nums = 0\n for i in range(len(A)) | fst-2391 | NORMAL | 2020-04-09T02:30:52.994978+00:00 | 2020-04-09T02:32:17.923014+00:00 | 138 | false | \tclass Solution(object):\n\tdef threeEqualParts(self, A):\n if len(A) < 3:\n return [-1,-1]\n nums = 0\n for i in range(len(A)):\n if A[i] == 1:\n nums += 1\n \n if nums % 3 != 0:\n return [-1,-1]\n \n if nums == 0:\n return [0,len(A) - 1]\n arr = []\n val = 0\n \n\n for i in range(len(A)):\n if A[i] == 1:\n val += 1\n if val == 1 or val == nums/3 or val == nums/3 + 1 or val == 2*nums/3 or val == 2*nums/3 + 1 or val == nums:\n arr.append(i)\n if nums == 3:\n z = len(A) - arr[2] - 1\n x = arr[1] - arr[0] - 1\n y = arr[2] - arr[1] - 1\n if x < z or y < z:\n return [-1,-1]\n \n return [arr[0] + z, arr[1] + z + 1]\n \n if A[arr[0]:arr[1]] != A[arr[2]:arr[3]] or A[arr[0]:arr[1]] != A[arr[4]:arr[5]]:\n return [-1,-1]\n \n z = len(A) - arr[5] - 1\n x = arr[2] - arr[1] - 1\n y = arr[4] - arr[3] - 1\n \n if x < z or y < z:\n return [-1,-1]\n\n return [arr[1] + (len(A) - arr[5]) - 1, arr[3] + (len(A) - arr[5])] | 1 | 0 | [] | 0 |
three-equal-parts | [Python] intuitive solution, less than 100% memory usage | python-intuitive-solution-less-than-100-31pya | \nclass Solution(object):\n def threeEqualParts(self, A):\n """\n :type A: List[int]\n :rtype: List[int]\n """\n N = len(A | lljll | NORMAL | 2020-01-15T19:54:17.732237+00:00 | 2022-10-02T08:24:15.263605+00:00 | 214 | false | ```\nclass Solution(object):\n def threeEqualParts(self, A):\n """\n :type A: List[int]\n :rtype: List[int]\n """\n N = len(A)\n if N < 3:\n return [-1, -1]\n\n count_of_one = A.count(1)\n if count_of_one == 0:\n return [0, N-1]\n if count_of_one % 3 != 0:\n return [-1, -1]\n\n pattern = \'\'\n count = 0\n reversed_str = \'\'.join(map(str, A[::-1]))\n\n for i, digit in enumerate(A[::-1]):\n if digit == 1:\n count += 1\n if count == count_of_one/3:\n break\n pattern = reversed_str[:i+1]\n\n length = len(reversed_str)\n len_pattern = len(pattern)\n\n \'\'\'matching\'\'\'\n index = reversed_str.find(pattern, len_pattern)\n if index == -1:\n return [-1, -1]\n j = length - index\n\n index = reversed_str.find(pattern, len_pattern + index)\n if index == -1:\n return [-1, -1]\n i = length - index - 1\n\n return [i, j]\n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
three-equal-parts | Clean Java solution, with O(1) space and O(n) complexity | clean-java-solution-with-o1-space-and-on-c9dm | \npublic class Solution {\n public int[] threeEqualParts(int[] A) {\n if (A == null || A.length < 3) return new int[]{-1, -1};\n int oneCnt = 0 | sokui | NORMAL | 2019-05-28T00:27:57.072739+00:00 | 2019-05-28T00:27:57.072819+00:00 | 122 | false | ```\npublic class Solution {\n public int[] threeEqualParts(int[] A) {\n if (A == null || A.length < 3) return new int[]{-1, -1};\n int oneCnt = 0;\n for (int i = 0; i < A.length; i++) {\n if (A[i] == 1) oneCnt++;\n }\n if (oneCnt % 3 != 0) return new int[]{-1, -1};\n int oneAvg = oneCnt / 3;\n if (oneAvg == 0) return new int[]{0, A.length - 1};\n\n // find the start index for the 3rd part\n int postOnes = 0, start3 = A.length - 1;\n while (postOnes < oneAvg) {\n if (A[start3--] == 1) postOnes++;\n }\n start3++;\n\n // find the end index for the 1st part\n int l = A.length - start3, i = 0;\n while (A[i] == 0) i++;\n for (int k = 0; k < l; k++) {\n if (A[i + k] != A[start3 + k]) return new int[]{-1, -1};\n }\n int left = i + l - 1, j = left + 1;\n\n // find the end index for the 2nd part\n while (A[j] == 0) j++;\n for (int k = 0; k < l; k++) {\n if (A[k + j] != A[start3 + k]) return new int[]{-1, -1};\n }\n int right = j + l;\n\n return new int[]{left, right};\n }\n}\n``` | 1 | 0 | [] | 0 |
three-equal-parts | python easy solution | python-easy-solution-by-butterfly-777-mwl1 | ```\nclass Solution:\n def threeEqualParts(self, A: List[int]) -> List[int]:\n n = len(A)\n ones = []\n for i in range(n):\n | butterfly-777 | NORMAL | 2019-05-10T15:49:44.115112+00:00 | 2019-05-10T15:49:44.115176+00:00 | 149 | false | ```\nclass Solution:\n def threeEqualParts(self, A: List[int]) -> List[int]:\n n = len(A)\n ones = []\n for i in range(n):\n if A[i]: ones.append(i)\n none = len(ones)\n if none == 0: return [0, n-1]\n if none % 3: return [-1, -1]\n g = none // 3\n i, j = ones[g-1], ones[2*g -1]\n pre_zero = n-1 - ones[-1]\n if ones[g] - ones[g-1]-1 < pre_zero or ones[2*g]-ones[2*g-1]-1 < pre_zero: \n return [-1, -1]\n \n i += pre_zero\n j += pre_zero\n k = n-1\n ans = [i, j+1]\n for _ in range(g):\n if not (A[k]==A[j]==A[i]): return [-1, -1]\n k -=1\n j -= 1\n i -= 1\n return ans\n | 1 | 0 | [] | 0 |
three-equal-parts | O(N) solution in Rust (4ms). | on-solution-in-rust-4ms-by-ttsugrii-cohb | The algorithm proceeds as follows:\n- find the number of 1s that each part must have. This number must be total_number_of_ones/3 sinceo otherwise parts would de | ttsugrii | NORMAL | 2019-01-21T05:09:14.639846+00:00 | 2019-01-21T05:09:14.639906+00:00 | 274 | false | The algorithm proceeds as follows:\n- find the number of `1`s that each part must have. This number must be `total_number_of_ones/3` sinceo otherwise parts would definitely not have same values. Because of this if the total number of `1`s is not a multiple of `3`, we can return `{-1, -1}` immediately. Another simple optimization that can be made at this stage is checking if the total number of `1`s is `0`, since in such case any split would result in equal parts. I use `{0,2}` just because it works for all input sizes, including `3`.\n- find the number of trailing zeros. Since in order to have same values all numbers have to have the exact same number of trailing zeros, we can use the last part to get it, since we know that the end of the thrird part is `A.length-1`.\n- find the end of the first part. To do this we increase the index until we find encounter `part_ones` number of `1`s and then will skip `trailing_zeros` after making sure that there are enough trailing zeros available.\n- find the end of the second part. The procedure is exactly the same as the one used for the first part, but the scan starts with `i+1`.\n- check if all parts are equal and if not return `{-1, -1}`. I\'m relying on iterator `zip` method to stop as soon as one of the ranges is exhausted in order to avoid having to deal with different part lengths.\n- return the end of the first and the start of the third part (one past the end of the second part).\n\n```\nimpl Solution {\n pub fn three_equal_parts(a: Vec<i32>) -> Vec<i32> {\n let ones = a.iter().filter(|&n| *n == 1).count();\n if ones == 0 {\n return vec![0, 2]; // any split works here\n }\n if ones % 3 != 0 {\n return vec![-1, -1];\n }\n let part_ones = ones / 3;\n let trailing_zeros = (0..a.len()).rev().take_while(|&idx| a[idx] == 0).count();\n \n let find_part_end = |start| -> Option<usize> {\n let mut ones = 0;\n let mut i = start;\n while ones < part_ones {\n if a[i] == 1 {\n ones += 1;\n }\n i += 1;\n }\n if !(i..(i+trailing_zeros)).all(|idx| a[idx] == 0) {\n // first part does not have enough trailing zeros\n return None;\n }\n Some(i + trailing_zeros - 1)\n };\n \n let i = match find_part_end(0) { // first part end\n Some(i) => i,\n None => return vec![-1, -1],\n };\n \n let j = match find_part_end(i+1) { // second part end\n Some(j) => j + 1, // j starts after the end of second part\n None => return vec![-1, -1],\n };\n \n if !(0..i+1).rev().zip((i+1..j).rev()).all(|t| a[t.0] == a[t.1]) {\n // first and second parts are different\n return vec![-1, -1];\n }\n \n if !(i+1..j).rev().zip((j..a.len()).rev()).all(|t| a[t.0] == a[t.1]) {\n // second and first parts are different\n return vec![-1, -1];\n }\n \n vec![i as i32, j as i32]\n }\n}\n``` | 1 | 0 | [] | 1 |
three-equal-parts | My concise solution with explanation; beat 100% | my-concise-solution-with-explanation-bea-56uc | Please upvote if you like it.\n\nObservations/algorithm:\n1. Each part must have equal number of 1\'s.\n2. Let nums be the actual binary value of the parts, the | yuxiong | NORMAL | 2019-01-15T23:49:49.859530+00:00 | 2019-01-15T23:49:49.859594+00:00 | 132 | false | *Please upvote if you like it.*\n\n**Observations/algorithm**:\n1. Each part must have equal number of 1\'s.\n2. Let nums be the actual binary value of the parts, then num1 == num2 == num3, and each num starts with a 1. The only exception is when all nums are 0.\n3. Each part can have various number of leading 0\'s.\n Thus, part1/num1 and part2/num2 are more flexible: they can play with the leading 0\'s of the next part.\n\n4. num3 can be certain (if it exists), we find num3 by the following method:\n\t```\n i j k\n 0000[num1]000000[num2]0000000[num3]\n\t```\n\n Let find k first, where k is the first \'1\' we can find in part3 from left to right.\n Then A[k:] is num3, let\'s call it pattern.\n How to find k then? The 1\'s in num3 is one third of the total 1\'s.\n5. There must not be any 1\'s between any two nums.\n So we scan from left to k-1, once we see a 1, it must belong to num1 and num1 must equal to pattern.\n Assume num1 matched, we continue scanning, once we see another 1, it must belong to num2 and num2 must equal to pattern.\n If num2 == pattern, then we are done; there won\'t be any 1\'s between num2 and num3 because the totle 1\'s are all visited in this round.\n\nCode:\n```\nclass Solution:\n def threeEqualParts(self, A):\n N = len(A)\n ones = sum(A)\n if ones == 0: return [0, N-1]\n if ones % 3 > 0: return [-1, -1]\n one_third = ones//3\n k = N-1\n while True:\n if A[k] == 1:\n ones -= 1\n if ones == 2 * one_third: break\n k -= 1\n pattern = A[k:]\n M = len(pattern)\n \n i = j = None\n x = 0\n while x < k:\n if A[x] == 1:\n if A[x:x+M] != pattern: return [-1, -1]\n x += M\n if i is None: i = x - 1\n else: j = x\n else:\n x += 1\n return [i, j]\n```\n\nComplexity Analysis:\n* Running Time: O(N), two passes\n* Space: O(N) for storing and comparing pattern | 1 | 0 | [] | 0 |
three-equal-parts | C++ O(n) time O(1) space with comments. | c-on-time-o1-space-with-comments-by-baba-ufde | If the number at each segment is same, the binary of those segment will also be same. \nThe key thing is to split all the ones into 3 equal parts. Then, the las | babaduredi | NORMAL | 2019-01-10T07:38:24.856308+00:00 | 2019-01-10T07:38:24.856374+00:00 | 184 | false | If the number at each segment is same, the binary of those segment will also be same. \nThe key thing is to split all the ones into 3 equal parts. Then, the last segment is final, it will be the value against which first 2 segments need to be compared.\n```\nvector<int> threeEqualParts(vector<int>& A) {\n int cnt = 0, i, a, b, c, val = 0;\n for (auto x : A)\n cnt += x;\n if (cnt == 0)\n return {0, 2};\n if (cnt % 3) // number of 1\'s are not splittable\n return {-1,-1};\n for (i = A.size() - 1; i >= 0; i--) {\n if (A[i]) {\n val++;\n if (val == cnt/3)\n c = i; // start of 3rd segment\n else if (val == 2 * (cnt/3))\n b = i; // start of 2nd segment\n else if (val == cnt) {\n a = i; // start of 1st segment\n break;\n }\n }\n }\n for (i = 0; i < (int)A.size() - c; i++) {\n if (a+i >= b || b+i >= c) // overlapping regions\n return {-1, -1};\n if (A[c+i] != A[a+i] || A[c+i] != A[b+i]) // mismatch\n return {-1, -1};\n }\n return {a+i-1, b+i};\n }\n\t``` | 1 | 0 | [] | 0 |
three-equal-parts | c++, simple to follow, fast, solution. O(n) time, O(1) space. With description and comments | c-simple-to-follow-fast-solution-on-time-np0z | The problem requires the dividing the input string such that the binary values are equal, so the first thing to do is check that the number of 'bits' set is div | christrompf | NORMAL | 2018-10-23T22:57:45.766723+00:00 | 2018-10-23T22:57:45.766768+00:00 | 178 | false | The problem requires the dividing the input string such that the binary values are equal, so the first thing to do is check that the number of 'bits' set is divisible by 3. If there are no set bits, then the answer is trivial and can be returned now.
If it is divisible by 3, we can relatively easily find the minimum total length of each partition by reading from the back. Why from the back? Well the number of trailing zeros is important, while the leading zeros not. For example, imagine each section has one bit set, an input string must finish with something like [..., 1], [..., 1, 0], [..., 1, 0, 0], ..., [..., 1, <_m_ zeros>]. Once we've encountered the required number of sets bits, we know the _mimimum_ (as there could be 0 or more _leading_ zeros) length of each partition.
From there, the final steps are straight forward.
1. Check that there is at least _m_ zeros before the next set bit is encountered (still reading backwards)
2. Keep moving left until the required number of set bits has been encountered, checking each bit matches the first partition
3. Check that there is at least _m_ zeros before the next set bit is encountered
4. Finally check the last partition matches with a simple `std::equal` (since we know what the distance between the first and last set bits)
5. If it all matches, return the partition indexes
Putting it all together in quite readable code, produces;
```cpp
vector<int> threeEqualParts(vector<int>& A) {
int total_set_bits = std::count(A.begin(), A.end(), 1);
if (3 > A.size() || total_set_bits % 3) {
return {-1, -1};
}
if (!total_set_bits) {
return {0, A.size() - 1};
}
// Number of set bits for each partition
int partition_set_bits = total_set_bits / 3;
// Work from back to front as we need to check trailing zeros and not leading zeros
auto first = std::find(A.rbegin(), A.rend(), 1);
// Number of 0s that must finish each section
int trailing_zeros = first - A.rbegin();
// Jump to the last 1 in the current partition
auto tmp = first;
for (int i = 1; i < partition_set_bits; ++i) {
tmp = std::find(tmp + 1, A.rend(), 1);
}
// Distance between the first set bit and the last for each partition
int distance = tmp - first;
// Check that there is enough trailing zeros in the middle section
auto middle = std::find(++tmp, A.rend(), 1);
if (middle - tmp < trailing_zeros) {
return {-1, -1};
}
// Check the middle partition matches while advancing to the last 1 in the middle
tmp = middle;
for (int i = 0; i < distance; ++i) {
if (*(first + i) != *tmp++) {
return {-1, -1};
}
}
// Check that there is enough trailing zeros in the last section
auto last = std::find(++tmp, A.rend(), 1);
if (last - tmp < trailing_zeros) {
return {-1, -1};
}
// Finally check the last section matches
if (A.rend() - last >= distance && !std::equal(middle, middle + distance, last, last + distance)) {
return {-1, -1};
}
// Finally change the reverse iterators back into a forward index
int break1 = last.base() - A.begin() + trailing_zeros - 1;
int break2 = middle.base() - A.begin() + trailing_zeros;
return {break1, break2};
}
```
| 1 | 1 | [] | 0 |
three-equal-parts | C++ 22 lines ,O(n) time Soluton | c-22-lines-on-time-soluton-by-panghu-ehik | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n int v[30005];\n int cnt = 0,n = A.size();\n for(int i=0;i< | panghu | NORMAL | 2018-10-22T11:38:25.389688+00:00 | 2018-10-22T11:38:25.389728+00:00 | 164 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n int v[30005];\n int cnt = 0,n = A.size();\n for(int i=0;i<n;i++)if(A[i])v[cnt++] = i;\n if (cnt%3!=0) return {-1,-1};\n if (cnt == 0) return {0, n-1};\n int a = v[0];\n int b = v[cnt/3];\n int c = v[cnt/3*2];\n int ed = b,ed2 = c;\n int num = 0;\n while(a<ed && b<ed2 && c<n){\n if(A[a]!= A[b] || A[a]!=A[c] || A[b]!=A[c])return {-1,-1};\n num += A[a];\n if(num==cnt/3 && c==n-1)return {a,b+1};\n a++;b++;c++;\n }\n return {-1,-1};\n }\n};\n``` | 1 | 0 | [] | 0 |
three-equal-parts | Short C++ code | short-c-code-by-yuanjileet-jixh | \nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n int count = std::count(A.begin(), A.end(), 1);\n if(count % 3)\n | yuanjileet | NORMAL | 2018-10-22T02:02:32.731192+00:00 | 2018-10-22T02:02:32.731232+00:00 | 68 | false | ```\nclass Solution {\npublic:\n vector<int> threeEqualParts(vector<int>& A) {\n int count = std::count(A.begin(), A.end(), 1);\n if(count % 3)\n return {-1, -1};\n count /= 3;\n int i = 0,j = 1,k = 2;\n for(int l = 0, cnt = 0; l < A.size(); cnt += A[l], ++l){\n if(cnt == 0 && A[l] == 1)\n i = l;\n if(cnt == count && A[l] == 1)\n j = l;\n if(cnt == 2 * count && A[l] == 1)\n k = l;\n }\n for(; k < A.size(); ++i, ++j, ++k)\n if(A[i] != A[j] || A[i] != A[k])\n return {-1, -1};\n return {i - 1, j};\n }\n};\n``` | 1 | 0 | [] | 0 |
three-equal-parts | C++ solution in O(N), using cumulative sum and binary search | c-solution-in-on-using-cumulative-sum-an-7hoc | ```` class Solution { public: vector threeEqualParts(vector& A) { int ones = 0; vector B = A; for (int i = 0; i < A.size(); i+ | mjzyaad | NORMAL | 2018-10-21T18:25:59.842969+00:00 | 2018-10-21T18:25:59.843011+00:00 | 164 | false | ````
class Solution {
public:
vector<int> threeEqualParts(vector<int>& A) {
int ones = 0;
vector<int> B = A;
for (int i = 0; i < A.size(); i++)
ones += A[i];
if (ones == 0) {
return {0, 2};
}
else {
if (ones % 3 != 0) {
return {-1, -1};
}
else {
ones /= 3;
// Count the number of trailing zeros in part 3
int z3 = 0;
for (int i = A.size() - 1; A[i] == 0; i--)
z3++;
// Cumulate
for (int i = 1; i < A.size(); i++)
A[i] += A[i-1];
int p1 = lower_bound(A.begin(), A.end(), ones) - A.begin();
if (A[p1 + z3] != ones)
return {-1, -1};
int p2 = lower_bound(A.begin(), A.end(), 2 * ones) - A.begin();
if (A[p2 + z3] != 2 * ones)
return {-1, -1};
// Check the content of the 3 arrays
int L = A.size() - 1;
bool ok = true;
for (int i = 0; ones && ok; i++) {
ok &= B[L - i] == B[p2 + z3 - i];
ok &= B[L - i] == B[p1 + z3 - i];
ones -= B[L - i];
}
if (ok)
return {p1 + z3, p2 + z3 + 1};
else
return {-1, -1};
}
}
}
};
````
| 1 | 0 | [] | 0 |
three-equal-parts | Java Solution: with detailed explanation | java-solution-with-detailed-explanation-a46ly | Approach We need to have 3 arrays with binary number represented by them should be all equal. We know that leading '0'(zero) in binary doesn't add value to bin | rkg | NORMAL | 2018-10-21T03:57:33.009799+00:00 | 2018-10-21T03:57:33.009847+00:00 | 131 | false | # Approach
We need to have 3 arrays with binary number represented by them should be all equal. We know that leading '0'(zero) in binary doesn't add value to binary number, but trailiing zero's do. So, if we could first count the trailing zeros in the incoming input first. Then we can try to find 2 other arrays with same number of trailing zeros. If it's not possible to find such 3 arrays, then we can't find solution. Also, since we need to slice array into 3 parts, then we need to make sure the incoming arrays contains '1' which are divisible by 3.
# Algorithm
1. Get the **SUM** of the array. If the **SUM** is not divisible by 3 then we can blindly return [-1,-1] as answer. Otherwise go to step2
2. If sum is 0 then we can split array in many possible ways, we can use [0,A.length-1] as answer. You can hardcode some other value as well, it should work. Otherwise, go to step3
3. Find the trailing zero's in the input. Lets call it **trailingZeros**. **targetSum** is equal to **SUM/3**
4. Now lets iterate through the input and find the 2 split where the running sum of the split array is equal to **targetSum**. We know there are count of **trailingZeros** at the end. So, after we find the **targetSum** store the index with **trailingZeros** count added. Why we add **trailingZeros** count to the first and second split of the array? Reason: If the last array contains those many trailing zeros then other 2 also must contain those, failing to do so means we cannot split the array into 3 parts.
5. Once we find the 2 splits. We can iterate through the split and check whether **splitSum** matches **targetSum**?. Return the [-1,-1] when there is no match.
6. Last part of the algo: We found 3 arrays with equals sum, but it's possible that individual binary number formed by split array may not match. So, lets check the individual bits do they match. Why we need to match? Reason: Matching them gives a clear indication that binary number formed by 3 are actually equal.
Runtime Complexity is O(N) - N is length of input array.
Space Complexity is O(1) - Constant.
My solution took 11 ms.
# Code
```
public int[] threeEqualPartsWorking(int[] A) {
int sum = 0, N = A.length ;
for(int v : A) sum +=v;
if(sum % 3 != 0)
return new int[]{-1, -1};
if(sum == 0){
return new int[]{0, N - 1};
}
int[] ret = new int[]{-1, -1}; // First split and second split index
int trailingZeros = 0;
for(int i= N-1;i >= 0;i--){
if(A[i] == 1){
trailingZeros = N-1-i;
break;
}
}
int runningSum= 0, targetSum = sum /3 ;
for(int i = 0;i < N ;i++){
runningSum += A[i];
if(runningSum == targetSum && ret[0] == -1){
ret[0] = i+trailingZeros;
}
if(runningSum == 2*targetSum && ret[1] == -1){
ret[1] = i+1+trailingZeros;
}
}
if(ret[1] >= N)// if first split has gone beyond the input array length, then we can't split.
return new int[]{-1, -1};
int splitSum = 0 ;
for(int i = 0;i <= ret[0];i++) splitSum += A[i];
if(splitSum != targetSum)return new int[]{-1,-1};
splitSum = 0;
for(int i = ret[0]+1;i < ret[1];i++) splitSum += A[i];
if(splitSum != targetSum)return new int[]{-1,-1};
for(int i = N-1, j = ret[1]-1, k = ret[0]; i >= ret[1] && j >= ret[0]+1 && k >= 0; i--,j--,k--){
int uniqBits = A[i]+A[j]+A[k];
if(!(uniqBits == 3 || uniqBits == 0))return new int[]{-1, -1};
}
return ret;
}
``` | 1 | 0 | [] | 0 |
three-equal-parts | Python3 O(n) in 52ms with explanation | python3-on-in-52ms-with-explanation-by-h-4mk5 | The key observation is that if such a division is possible, then the three parts has to contain equal numbers of 1s. More details are in the comments.\n\ndef t | herbertzou | NORMAL | 2018-10-21T03:56:40.868722+00:00 | 2018-10-21T19:44:30.535026+00:00 | 168 | false | The key observation is that if such a division is possible, then the three parts has to contain equal numbers of 1s. More details are in the comments.\n```\ndef threeEqualParts(self, A):\n """\n :type A: List[int]\n :rtype: List[int]\n """\n one_count=A.count(1)\n if one_count==0:\n return [0,len(A)-1]\n if one_count%3!=0: return [-1,-1]\n\t\t\t\t# waive some impossible instances\n i=0\n count=0\n while count<one_count//3:\n if A[i]==1:\n count+=1\n i+=1\n #count==1_count//3 and A[:i] contains 1/3 of total 1\'s \n j=i\n while count>0:\n if A[j]==1:\n count-=1\n j+=1\n #this takes O(n) time, then final decide where to set i and j such that they can be compared within O(n) time \n tail_count=0#counting how many zeros there are at the tail, and later the number of zeros at the tail of each part have to equal\n pointer=-1\n while A[pointer]==0:\n tail_count+=1\n pointer-=1\n for k in range(tail_count):\n if A[i+k]==1 or A[j+k]==1: return [-1,-1] #If the number of zeros at tails are not equal, then there is a mistake\n i+=tail_count\n j+=tail_count \n a,b,c=0,i,j\n while A[a]==0:\n a+=1\n while A[b]==0:\n b+=1\n while A[c]==0:\n c+=1\n if A[a:i]==A[b:j] and A[b:j]==A[c:]:\n print (i,j)\n return [i-1,j]\n return [-1,-1]\n```\n | 1 | 1 | [] | 1 |
three-equal-parts | O(n) O(1) beat 100% simple count and compare 3 part | on-o1-beat-100-simple-count-and-compare-f5mpq | Approach
count total of arr
separate to 3 part with the same total_part = total/3
compare each index in 3 part, check the same.
return result.
Complexity
Time c | luudanhhieu | NORMAL | 2025-04-08T13:59:05.512140+00:00 | 2025-04-08T13:59:05.512140+00:00 | 2 | false | # Approach
- count total of `arr`
- separate to 3 part with the same `total_part = total/3`
- compare each index in 3 part, check the same.
- return result.
# Complexity
- Time complexity: O(n)
- Space complexity:O(1)
# Code
```golang []
func threeEqualParts(arr []int) []int {
total := 0
for i := range arr {
total += arr[i]
}
if total%3 != 0 {
return []int{-1, -1}
}
if total == 0 {
return []int{0, 2}
}
parts := [3][2]int{{-1, 0}, {-1, 0}, {-1, 0}}
totalPart := 0
for i := range arr {
totalPart += arr[i]
if totalPart == 1 && parts[0][0] == -1 {
parts[0][0] = i
}
if totalPart == total/3+1 && parts[1][0] == -1 {
parts[1][0] = i
}
if totalPart == 2*total/3+1 && parts[2][0] == -1 {
parts[2][0] = i
break
}
}
parts[2][1] = len(arr)
partLength := parts[2][1] - parts[2][0]
parts[0][1] = parts[0][0] + partLength
parts[1][1] = parts[1][0] + partLength
if parts[0][1] > parts[1][0] || parts[1][1] > parts[2][0] {
return []int{-1, -1}
}
for i := 0; i < partLength; i++ {
if arr[parts[0][0]+i] != arr[parts[1][0]+i] || arr[parts[0][0]+i] != arr[parts[2][0]+i] {
return []int{-1, -1}
}
}
return []int{parts[0][1] - 1, parts[1][1]}
}
``` | 0 | 0 | ['Go'] | 0 |
minimum-white-tiles-after-covering-with-carpets | [Java/C++/Python] DP solution | javacpython-dp-solution-by-lee215-vqb5 | Explanation\ndp[i][k] means that,\nusing k tiles to cover the first i tiles\nthe minimum number of white tiles still visible.\n\n\nFor each tile s[i], we heve t | lee215 | NORMAL | 2022-03-19T16:02:23.187495+00:00 | 2022-03-19T16:06:47.176709+00:00 | 6,879 | false | # **Explanation**\n`dp[i][k]` means that,\nusing `k` tiles to cover the first `i` tiles\nthe minimum number of white tiles still visible.\n\n\nFor each tile `s[i]`, we heve two options,\nOne option is doing nothing, `jump` this tile,\n`jump = dp[i - 1][k] + int(s[i - 1])`\nThe other option is covering this tile\n`cover = dp[i - l][k - 1]`\n\nThen we take the minimum result of two options:\n`dp[i][k] = min(jump, cover)`\n\nFinally after explore all combination of `(i,k)`,\nwe return `dp[n][nc]`.\n<br>\n\n# **Complexity**\nTime `O(NC)`\nSpace `O(NC)`\nwhere `N = floor.length` and `C = numCarpets`.\nSpace can be optimized to `O(N)`.\n<br>\n\n**Java**\n```java\n public int minimumWhiteTiles(String s, int nc, int l) {\n int n = s.length(), dp[][] = new int[n + 1][nc + 1];\n for (int i = 1; i <= n; ++i) {\n for (int k = 0; k <= nc; ++k) {\n int jump = dp[i - 1][k] + s.charAt(i - 1) - \'0\';\n int cover = k > 0 ? dp[Math.max(i - l, 0)][k - 1] : 1000;\n dp[i][k] = Math.min(cover, jump);\n }\n }\n return dp[n][nc];\n }\n```\n\n**C++**\n```cpp\n int minimumWhiteTiles(string s, int nc, int l) {\n int n = s.size();\n vector<vector<int>> dp(n + 1, vector<int>(nc + 1));\n for (int i = 1; i <= n; ++i) {\n for (int k = 0; k <= nc; ++k) {\n int jump = dp[i - 1][k] + s[i - 1] - \'0\';\n int cover = k > 0 ? dp[max(i - l, 0)][k - 1] : 1000;\n dp[i][k] = min(cover, jump);\n }\n }\n return dp[n][nc];\n }\n```\n\n**Python3**\n```py\n def minimumWhiteTiles(self, A, k, l):\n\n @lru_cache(None)\n def dp(i, k):\n if i <= 0: return 0\n return min(int(A[i - 1]) + dp(i - 1, k), dp(i - l, k - 1) if k else 1000)\n \n return dp(len(A), k) \n```\n | 117 | 3 | ['C', 'Python', 'Java'] | 18 |
minimum-white-tiles-after-covering-with-carpets | C++ Solution | Top-Down Dynamic Programming | Recursion + Memoization | c-solution-top-down-dynamic-programming-xwtvv | Iterate over string floor:\n\n- At each index pos in the string floor we have two options:\n\n - Use a carpet, that starts from the index pos and ends at pos | invulnerable | NORMAL | 2022-03-19T16:12:04.251920+00:00 | 2022-03-19T16:12:04.251952+00:00 | 3,175 | false | Iterate over string `floor`:\n\n- At each index `pos` in the string `floor` we have two options:\n\n - Use a carpet, that starts from the index `pos` and ends at `pos + carpetLength - 1`. All tiles in this part will change to black, hence move to index `pos + carpetLength`\n - Skip the index and move to next index `pos + 1`. This time the tile at index `pos` will be unchanged, thus add `1` to the answer if it\'s a white tile.\n\n- After either of the options, recursively move to the next index. Return the minimum of the above two options.\n\nBase Case:\n\n- If we have traversed the whole string `floor`, then no white tiles present. Hence return `0`.\n- If we have used all the available carpets, then the remaining string will not change. Hence return the number of `1`\'s in the remaining string. (Store the number of `1`s for the suffix `[i, N]` in the array `suffix` beforehand, instead of finding it again and again).\n\nThere will be repeated subproblems corresponding to index (`pos`) and the number of carpet used (`used`). Hence store the result in the table `dp` and use it to answer repeated problems insetad of going into recursion.\n\n```\nclass Solution {\npublic:\n int dp[1001][1001];\n int suffix[1001];\n\n void findSuffixSum(string& floor) {\n int n = floor.size();\n \n suffix[n - 1] = (floor[n - 1] == \'1\');\n for (int i = n - 2; i >= 0; i--) {\n suffix[i] = suffix[i + 1] + (floor[i] == \'1\');\n }\n }\n \n int solve(string& floor, int numCarpets, int carpetLen, int pos, int used) {\n if (pos >= floor.size()) {\n return 0;\n } else if (used == numCarpets) {\n return suffix[pos];\n }\n \n if (dp[pos][used] != -1) {\n return dp[pos][used];\n }\n\n return dp[pos][used] = min(solve(floor, numCarpets, carpetLen, pos + carpetLen, used + 1),\n (floor[pos] == \'1\') + solve(floor, numCarpets, carpetLen, pos + 1, used));\n }\n \n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n memset(dp, -1, sizeof(dp));\n findSuffixSum(floor);\n \n return solve(floor, numCarpets, carpetLen, 0, 0);\n }\n};\n``` | 58 | 2 | [] | 6 |
minimum-white-tiles-after-covering-with-carpets | [Python] short dp, explained | python-short-dp-explained-by-dbabichev-zuqn | Problem constraints will help you to understand that this problem can be solved with dp. Let the state dp(i, t) be minimum number of white tiles when we allowed | dbabichev | NORMAL | 2022-03-19T16:00:44.001968+00:00 | 2022-03-19T16:00:44.001991+00:00 | 1,552 | false | Problem constraints will help you to understand that this problem can be solved with `dp`. Let the state `dp(i, t)` be minimum number of white tiles when we allowed to use `t` number of carpets such that their right (and hence all carpets) lies in `[0, i]`. Then each moment of time we have option to take carpet or do not take it:\n1. If we take, previous state is `dp(i - L, t - 1)`.\n2. If we do not take it, previous state is `dp(i - 1, t) + `int(floor[i] == "1")`.\n\n#### Complexity\nIt is `O(n^2)` for time and space.\n\n#### Code\n```python\nclass Solution:\n def minimumWhiteTiles(self, floor, k, L):\n @lru_cache(None)\n def dp(i, t):\n if t < 0: return float("inf")\n if i < 0: return 0\n return min(dp(i - L, t - 1), dp(i - 1, t) + int(floor[i] == "1"))\n \n return dp(len(floor) - 1, k)\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 29 | 3 | ['Dynamic Programming'] | 6 |
minimum-white-tiles-after-covering-with-carpets | DP detailed explanation with commented code | dp-detailed-explanation-with-commented-c-0zgr | Imagine we are covering the floor with carpets from left to right. At any point in this exercise, we will be at some point i and have carpetsRemaining carpets r | harmless-potato | NORMAL | 2022-03-19T16:01:33.181933+00:00 | 2022-03-19T16:01:33.181972+00:00 | 1,117 | false | Imagine we are covering the floor with carpets from left to right. At any point in this exercise, we will be at some point i and have carpetsRemaining carpets remaining. At this point we are only concerned with covering the floor from i to n - 1. \nIn other words i can say that the state at any point is fully defined by (current position, carpets remaining)\n\nWhen we are standing at index i, we have 2 choices\n\t* either skip this tile and leave it uncovered\n\t* use one carpet starting from here.\n\nFirst off, If we are currently on a black tile, it makes no sense to start a new carpet here, so we just move one step to the right. (whatever white tiles we cover by starting here, we can cover from i + 1 and possibly more)\nNow that we are on a white tile, \n\t* If we apply option 1 and skip this tile, we would expose 1 white tile and continue the exercise from tile i + 1 with the same number of carpets remaining\n\t* If we apply option 2 and start a new carpet here, we would use one carpet and continue the exercise from tile i + carpetLen.\n\twe would obviously want to take the option which would expose the minumum number of white tiles. \n\nIf f( i , carpetsRemaining ) represents the minimum number if white tiles exposed for the floor from i to n - 1 with carpetsRemaining carpets remaining, \n//base cases\n* if( i >= n) then ans = 0. ( we have fully covered the floor and are standing to the right of it)\n* if( carpetsRemaining == 0 ) then ans = number of zeroes from i to n - 1. (We dont have any more carpets and will expose everything here on out)\n```\n\tif(i >= a.length) {\n\t\treturn 0;\n\t}\n\tif(carpets_left == 0) {\n\t\treturn suffix[i]; //suffix[i] = number of white tiles from index i to n (can be calculated using a simple for loop)\n\t}\n```\n//recursive cases\n* if( floor[i] == BLACK ) then ans = f ( i + 1, carpetsRemaining). (Just ignore this tile, continue from next index)\n* if( floor[i] == WHITE ) then ans = Max of\n\t\t\t\t\t\t\t\t\t* 1 + f( i + 1, carpetsRemaining) (expose this tile, hence + 1, and continue with same number of carpets)\n\t\t\t\t\t\t\t\t\t* f( i + carpetLen, carpetsRemaining - 1 ) (start a new carpet here, skip carpetLen tiles, but have 1 less carpet)\n\n```\n\t // first check if this state has already been visited, if so return the answer already computed\n\tif(dp[i][carpets_left] != UNVISITED) { \n\t\treturn dp[i][carpets_left];\n\t}\n\tif(a[i] == BLACK) {\n\t\t//this tile is black, skip it\n\t\tdp[i][carpets_left] = f(i + 1, carpets_left, a, dp, suffix, carpetLen);\n\t}\n\telse {\n\t\t//start carpet here\n\t\tint start_carpet_here = f(i + carpetLen, carpets_left - 1, a, dp, suffix, carpetLen);\n\t\t//dont start carpet here\n\t\tint dont_start_carpet_here = 1 + f(i + 1, carpets_left, a, dp, suffix, carpetLen);\n\t\tdp[i][carpets_left] = Math.min(start_carpet_here, dont_start_carpet_here);\n\t}\n\n\treturn dp[i][carpets_left];\n```\n\nThere are (n * numCarpets) states, we momoize the result for each state in a 2D array.\nTime Complexity: O(n * numCarpets)\nSpace Complexity: O(n * numCarpets)\n\nFull Code:\n```\nclass Solution {\n private static final int UNVISITED = -1;\n private static final char BLACK = \'0\';\n private static final char WHITE = \'1\';\n\n private int f(int i, int carpets_left, char[] a, int[][] dp, int[] suffix, int carpetLen) {\n if(i >= a.length) {\n return 0;\n }\n if(carpets_left == 0) {\n return suffix[i];\n }\n if(dp[i][carpets_left] != UNVISITED) {\n return dp[i][carpets_left];\n }\n if(a[i] == BLACK) {\n dp[i][carpets_left] = f(i + 1, carpets_left, a, dp, suffix, carpetLen);\n }\n else {\n //start carpet here\n int start = f(i + carpetLen, carpets_left - 1, a, dp, suffix, carpetLen);\n //dont start carpet here\n int dont = 1 + f(i + 1, carpets_left, a, dp, suffix, carpetLen);\n\n dp[i][carpets_left] = Math.min(start, dont);\n }\n\n return dp[i][carpets_left];\n }\n\n public int minimumWhiteTiles(String floor, int numCarpets, int carpetLen) {\n \n int n = floor.length();\n char[] a = floor.toCharArray();\n \n //calculating the suffix array\n int[] suffix = new int[n + 1];\n for(int i = n - 1; i >= 0; i--) {\n suffix[i] = suffix[i + 1];\n if(a[i] == WHITE) {\n suffix[i] ++;\n }\n }\n \n int[][] dp = new int[n + 1][numCarpets + 1];\n for(int[] row : dp) {\n Arrays.fill(row, UNVISITED);\n }\n\n return f(0, numCarpets, a, dp, suffix, carpetLen);\n }\n}\n```\n | 28 | 3 | ['Dynamic Programming'] | 2 |
minimum-white-tiles-after-covering-with-carpets | Memory-Optimized DP | memory-optimized-dp-by-votrubac-hc08 | It feels like there could be some clever way to lay carpets, but there isn\'t. We need to search for an optimal solution.\n\n> Note: problem constrains give it | votrubac | NORMAL | 2022-03-19T16:02:37.149717+00:00 | 2022-03-21T09:24:14.260194+00:00 | 1,578 | false | It feels like there could be some clever way to lay carpets, but there isn\'t. We need to search for an optimal solution.\n\n> Note: problem constrains give it away.\n\nWe start with the top-down approach, and then convert it to the bottom-up one. By analyzing the tabulation, we can reduce the memory usage to O(n). The runtime for the final, memory-optimized bottom-up approach is 120 ms.\n\n#### Top-Down\nFor the search, we can skip positions with black tiles.\n**C++**\n```cpp\nint dp[1001][1001] = {};\nint dfs(string &floor, int i, int n, int len) {\n if (n < 0)\n return floor.size();\n if (floor.size() - i <= n * len)\n return 0;\n if (floor[i] == \'0\')\n return dfs(floor, i + 1, n, len);\n if (dp[i][n] == 0)\n dp[i][n] = 1 + min(1 + dfs(floor, i + 1, n, len), dfs(floor, i + len, n - 1, len)); \n return dp[i][n] - 1;\n}\nint minimumWhiteTiles(string floor, int numCarpets, int len) {\n return dfs(floor, 0, numCarpets, len);\n} \n```\n\n#### Bottom-Up\n**C++**\n```cpp\nint dp[1001][1001] = {};\nint minimumWhiteTiles(string floor, int numCarpets, int len) {\n for (int i = floor.size() - 1; i >= 0; --i) {\n dp[i][0] = dp[i + 1][0] + (floor[i] == \'1\');\n for (int c = 1; c <= numCarpets; ++c)\n dp[i][c] = min(dp[i + 1][c] + (floor[i] == \'1\'), dp[min(1000, i + len)][c - 1]);\n }\n return dp[0][numCarpets];\n} \n```\n\n#### Memory-Optimized Bottom-Up DP\nWe can rearrange loops from the solution above so that the first loop iterates through carpets. That way, we only need to store tabulation values for the current and previous step. \n\n**C++**\n```cpp\nint minimumWhiteTiles(string floor, int numCarpets, int len) {\n int sz = floor.size(), dp[2][1001] = {};\n for (int i = 0; i < sz; ++i)\n dp[0][i + 1] += dp[0][i] + (floor[i] == \'1\'); \n for (int c = 1; c <= numCarpets; ++c)\n for (int i = 0; i < sz; ++i)\n dp[c % 2][i + 1] = min(dp[c % 2][i] + (floor[i] == \'1\'),\n dp[(c + 1) % 2][max(0, i + 1 - len)]);\n return dp[numCarpets % 2][sz];\n} \n``` | 24 | 2 | [] | 4 |
minimum-white-tiles-after-covering-with-carpets | C++ Easy to understand, with explanation and optimizations. DP | c-easy-to-understand-with-explanation-an-bcdy | Hello, while it may seem like a difficult one, the fourth question can be done with an almost bruteforce approach with some optimizations.\n\nLet dp[i][j] denot | dhruvatrejamain | NORMAL | 2022-03-19T16:01:42.163562+00:00 | 2022-03-19T20:21:23.851385+00:00 | 1,295 | false | Hello, while it may seem like a difficult one, the fourth question can be done with an almost bruteforce approach with some optimizations.\n\nLet dp[i][j] denote the maximum number of ones we can cover with i carpets till index j(**with current carpet ending exactly at index j**). Assuming that the current carpet ends at exactly j *greatly simplifies* the problem\n\nNow, dp[i][j]= number of ones in string[j:j-len]+ max(dp[i-1][j-len], dp[i-1][j-len-1],....dp[i-1][0])\n\nOptimizations:\nWe store this max part of previous iteration of i till j-len in a helper variable. (prevmax)\nWe use prefix sum array to calculate number of white blocks in a range in O(1) time\nWe only need the ith and i-1th rows of the dp array, so space can be reduced (didn\'t do it due to time constraints during contest)\n\n```\nclass Solution {\npublic:\n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n int dp[1001][1001]={0};\n int pre[1000]={0};\n if(floor[0]==\'1\')pre[0]=1;\n for(int i=1;i<floor.size();i++){\n pre[i]+=pre[i-1];\n if(floor[i]==\'1\')pre[i]++;\n }\n for(int i=1;i<=numCarpets;i++){\n int prevmax=0;\n for(int j=0;j<floor.size();j++){\n if(j<carpetLen) dp[i][j]=pre[j];\n else{\n prevmax=max(prevmax,dp[i-1][j-carpetLen]);\n dp[i][j]=pre[j]-pre[j-carpetLen]+prevmax;\n }\n }\n }\n int ans=0;\n for(int i=0;i<floor.size();i++)ans=max(ans,dp[numCarpets][i]);\n return pre[floor.size()-1]-ans;\n }\n};\n```\n | 15 | 1 | ['Dynamic Programming', 'C'] | 4 |
minimum-white-tiles-after-covering-with-carpets | Java Knapsack Solution | java-knapsack-solution-by-surajthapliyal-srdj | \nclass Solution {\n int pref[];\n\n public int minimumWhiteTiles(String floor, int tot, int len) {\n char a[] = floor.toCharArray();\n this | surajthapliyal | NORMAL | 2022-03-19T16:50:58.522484+00:00 | 2022-03-19T17:00:20.567291+00:00 | 814 | false | ```\nclass Solution {\n int pref[];\n\n public int minimumWhiteTiles(String floor, int tot, int len) {\n char a[] = floor.toCharArray();\n this.pref = new int[a.length];\n int c = 0;\n this.dp = new int[a.length + 1][tot + 1];\n for (int d[] : dp) Arrays.fill(d, -1);\n for (int i = 0; i < a.length; i++) {\n if (a[i] == \'1\') c++;\n pref[i] = c;\n }\n return pref[a.length - 1] - solve(0, a, tot, len); // total ones - max removed\n }\n\n int dp[][];\n\n private int solve(int index, char a[], int tot, int len) {\n if (index >= a.length || tot == 0) {\n return 0;\n }\n if (dp[index][tot] != -1) return dp[index][tot];\n int ones = pref[Math.min(index + len - 1, a.length - 1)] - (index == 0 ? 0 : pref[index - 1]);\n int take = ones + solve(index + len, a, tot - 1, len); // either take it and add one\'s count in that subsegment\n int dont = solve(index + 1, a, tot, len); // or dont \n return dp[index][tot] = Math.max(take, dont); // return max of both\n }\n}\n``` | 12 | 1 | ['Memoization', 'Java'] | 3 |
minimum-white-tiles-after-covering-with-carpets | C++ Fixed-length Sliding Window + DP | c-fixed-length-sliding-window-dp-by-lzl1-ylwz | See my latest update in repo LeetCode\n\n## Solution 1. Fixed-length Sliding Window + DP\n\nIntuition:\n\n1. Use a sliding window of length carpetLen to compute | lzl124631x | NORMAL | 2022-03-19T16:00:52.804601+00:00 | 2022-03-29T17:14:04.143987+00:00 | 1,261 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Fixed-length Sliding Window + DP\n\n**Intuition**:\n\n1. Use a sliding window of length `carpetLen` to compute a `cover` array where `cover[i]` is the number of white tiles covered by a carpet placed ending at `floor[i]`.\n2. Use DP to calculate the maximum coverable white tiles using `numCarpets` carpets.\n\n**Algorithm**:\n\n**Fixed-length Sliding Window**:\n\nKeep a rolling sum `white` as the number of white tiles within the sliding window.\n\nFor each `i` in range `[0, N)`, we:\n* increment `white` if `s[i] == \'1\'`\n* decrement `white` if `s[i - len] == \'1\'`\n* Set `cover[i] = white`.\n\n**DP**:\n\nLet `dp[i][j + 1]` be the maximum number of coverable white tiles where `1 <= i <= numCarpet` is number of carpets used and `0 <= j < N` is the last index where we can place carpet.\n\nAll `dp` values are initialized as `0`s.\n\nFor each `dp[i][j + 1]`, we have two options:\n1. Don\'t place carpet at index `j`. `dp[i][j+1] = dp[i][j]`\n2. Place carpet ending at index `j` covering `cover[j]` white tiles. And we can place `i-1` carpets at or before `j-carpetLen`. So, `dp[i][j+1] = dp[i-1][j-carpetLen+1] + cover[j]`.\n\n```\ndp[i][j + 1] = max(\n dp[i][j], // don\'t place carpet at index `j`\n (j - carpetLen + 1 >= 0 ? dp[i - 1][j - carpetLen + 1] : 0) + cover[j] // place carpet at index `j`\n )\n```\n\n`dp[numCarpet][N]` is the maximum number of white titles coverable. The answer is the number of total white tiles minus `dp[numCarpet][N]`. \n\n```cpp\n// OJ: https://leetcode.com/problems/minimum-white-tiles-after-covering-with-carpets/\n// Author: github.com/lzl124631x\n// Time: O(N * numCarpet)\n// Space: O(N * numCarpet)\nclass Solution {\npublic:\n int minimumWhiteTiles(string floor, int numCarpet, int carpetLen) {\n int N = floor.size(), sum = 0;\n vector<int> cover(N);\n for (int i = 0, white = 0; i < N; ++i) {\n sum += floor[i] - \'0\';\n white += floor[i] - \'0\';\n if (i - carpetLen >= 0) white -= floor[i - carpetLen] - \'0\'; \n cover[i] = white;\n }\n vector<vector<int>> dp(numCarpet + 1, vector<int>(N + 1));\n for (int i = 1; i <= numCarpet; ++i) {\n for (int j = 0; j < N; ++j) {\n dp[i][j + 1] = max(dp[i][j], (j - carpetLen + 1 >= 0 ? dp[i - 1][j - carpetLen + 1] : 0) + cover[j]);\n }\n }\n return sum - dp[numCarpet][N];\n }\n};\n```\n\nWe can reduce the space complexity to `O(N)` by using rolling arrays.\n\n```cpp\n// OJ: https://leetcode.com/problems/minimum-white-tiles-after-covering-with-carpets/\n// Author: github.com/lzl124631x\n// Time: O(N * numCarpet)\n// Space: O(N)\nclass Solution {\npublic:\n int minimumWhiteTiles(string floor, int numCarpet, int carpetLen) {\n int N = floor.size(), sum = 0;\n vector<int> cover(N);\n for (int i = 0, white = 0; i < N; ++i) {\n sum += floor[i] - \'0\';\n white += floor[i] - \'0\';\n if (i - carpetLen >= 0) white -= floor[i - carpetLen] - \'0\'; \n cover[i] = white;\n }\n vector<int> dp(N + 1);\n for (int i = 1; i <= numCarpet; ++i) {\n vector<int> next(N + 1);\n for (int j = 0; j < N; ++j) {\n next[j + 1] = max(next[j], (j - carpetLen + 1 >= 0 ? dp[j - carpetLen + 1] : 0) + cover[j]);\n }\n swap(dp, next);\n }\n return sum - dp[N];\n }\n};\n``` | 10 | 1 | [] | 3 |
minimum-white-tiles-after-covering-with-carpets | C++ Knapsack Memoization | c-knapsack-memoization-by-kamisamaaaa-fwi5 | \nclass Solution {\n int n;\n vector<int> suffix;\n vector<vector<int>> memo;\npublic:\n \n int doit(string& floor, int carp, int len, int ind) { | kamisamaaaa | NORMAL | 2022-03-19T17:08:43.835082+00:00 | 2022-03-19T18:04:28.281883+00:00 | 740 | false | ```\nclass Solution {\n int n;\n vector<int> suffix;\n vector<vector<int>> memo;\npublic:\n \n int doit(string& floor, int carp, int len, int ind) {\n if (ind >= n) return 0;\n if (carp == 0) return suffix[ind]; // if no carpets are left then all the white tiles from current index to the last will be visible\n if (memo[carp][ind] != -1) return memo[carp][ind];\n int a = doit(floor, carp-1, len, ind+len); // carpet is used\n int b = doit(floor, carp, len, ind+1) + (floor[ind] == \'1\'); // carpet is not used\n return memo[carp][ind] = min(a, b);\n }\n \n int minimumWhiteTiles(string floor, int carp, int len) {\n \n n = size(floor);\n suffix.resize(n+1, 0);\n memo.resize(carp+1, vector<int>(n+1, -1));\n suffix[n-1] = (floor[n-1] == \'1\');\n for (int i=n-2; ~i; i--)\n suffix[i] = suffix[i+1] + (floor[i] == \'1\');\n \n return doit(floor, carp, len, 0);\n }\n};\n``` | 9 | 1 | ['Dynamic Programming', 'Memoization', 'C'] | 0 |
minimum-white-tiles-after-covering-with-carpets | C++| DP | Memoization | c-dp-memoization-by-vaibhavshekhawat-2112 | ```\n\tvector> dp;\n int func(int i,string& s,int car,int len){\n if(i>=s.size()) return 0;\n if(dp[i][car]!=-1) return dp[i][car];\n if | vaibhavshekhawat | NORMAL | 2022-03-19T16:01:01.595632+00:00 | 2022-03-19T16:01:01.595661+00:00 | 632 | false | ```\n\tvector<vector<int>> dp;\n int func(int i,string& s,int car,int len){\n if(i>=s.size()) return 0;\n if(dp[i][car]!=-1) return dp[i][car];\n if(s[i]==\'0\') return dp[i][car]=func(i+1,s,car,len);\n else{ \n int ans=INT_MAX;\n ans=1+func(i+1,s,car,len);\n if(car>0) ans=min(ans,func(i+len,s,car-1,len));\n return dp[i][car]=ans;\n }\n }\n int minimumWhiteTiles(string s, int car, int len) {\n dp=vector<vector<int>>(s.size(),vector<int>(car+1,-1));\n return func(0,s,car,len);\n } | 8 | 1 | ['Memoization', 'C'] | 4 |
minimum-white-tiles-after-covering-with-carpets | [C++] Simple C++ Code | c-simple-c-code-by-prosenjitkundu760-zg94 | If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n int d | _pros_ | NORMAL | 2022-07-25T16:59:39.221759+00:00 | 2022-07-25T16:59:39.221810+00:00 | 518 | false | # **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n int dfs(string &floor, int Carpets, int Len, int idx, vector<vector<int>> &dp)\n {\n if(idx >= floor.size())\n return 0;\n int val = 0;\n if(dp[idx][Carpets] != -1) return dp[idx][Carpets];\n if(Carpets == 0)\n {\n for(int i = idx; i < floor.size(); i++)\n if(floor[i] == \'1\') val++;\n }\n else\n {\n if(floor[idx] == \'0\')\n val = dfs(floor, Carpets, Len, idx+1, dp);\n else\n {\n val = min(1+dfs(floor, Carpets, Len, idx+1, dp), dfs(floor, Carpets-1, Len, idx+Len, dp));\n }\n }\n return dp[idx][Carpets] = val;\n }\npublic:\n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n int n = floor.size();\n vector<vector<int>> dp(n+1, vector<int> (numCarpets+1, -1));\n return dfs(floor, numCarpets, carpetLen, 0, dp);\n }\n};\n``` | 7 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 0 |
minimum-white-tiles-after-covering-with-carpets | ✅ C++ | DP + Memoization | c-dp-memoization-by-chandanagrawal23-hpub | \nclass Solution\n{\n public:\n int recur(string &s, int numCarpets, int len, int i, vector<vector < int>> &dp, vector< int > &sufOnes)\n {\n | chandanagrawal23 | NORMAL | 2022-03-19T16:23:01.068959+00:00 | 2022-03-19T16:25:05.596227+00:00 | 469 | false | ```\nclass Solution\n{\n public:\n int recur(string &s, int numCarpets, int len, int i, vector<vector < int>> &dp, vector< int > &sufOnes)\n {\n if (i >= s.size())\n return 0;\n if (numCarpets == 0)\n return sufOnes[i];\n\n if (dp[i][numCarpets] != -1)\n {\n return dp[i][numCarpets];\n }\n if (s[i] == \'0\')\n {\n dp[i][numCarpets] = recur(s, numCarpets, len, i + 1, dp, sufOnes);\n }\n else\n {\n \t//start carpet here\n int start = recur(s, numCarpets - 1, len, i + len, dp, sufOnes);\n \t//dont start carpet here\n int dont = 1 + recur(s, numCarpets, len, i + 1, dp, sufOnes);\n\n dp[i][numCarpets] = min(start, dont);\n }\n\n return dp[i][numCarpets];\n }\n int minimumWhiteTiles(string s, int n, int len)\n {\n int nn = s.size() + 1, mm = n + 1;\n vector<int> sufOnes(s.size() + 1, 0);\n for (int i = s.size() - 1; i >= 0; i--)\n {\n sufOnes[i] = sufOnes[i + 1];\n if (s[i] == \'1\')\n {\n sufOnes[i]++;\n }\n }\n vector<vector < int>> dp(nn, vector<int> (mm, -1));\n return recur(s, n, len, 0, dp, sufOnes);\n }\n};\n``` | 7 | 0 | ['Memoization'] | 0 |
minimum-white-tiles-after-covering-with-carpets | ✅[Python] Dynamic Programming + Prefix Sum Solution | Explained | python-dynamic-programming-prefix-sum-so-8exn | So this is a dynamic programming question with a trick.\nYou can guess it using the given constraints.\nThe solution can be divided into two parts:\n Recursive | mostlyAditya | NORMAL | 2022-03-19T16:01:33.349825+00:00 | 2022-03-19T16:01:33.349918+00:00 | 497 | false | So this is a dynamic programming question with a trick.\nYou can guess it using the given constraints.\nThe solution can be divided into two parts:\n* Recursively find ways to use carpets to cover the floor \n* Optimize using **Prefix Sum** to find the number of white tiles present between two indices of the floor\n\nPlease read through the comments for better understanding!\n```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n\t\tn = len(floor)\n\t\t#Using memo table to store predefined computations\n memo = [[-1 for x in range(numCarpets+1)] for x in range(len(floor)+1)] \n def solve(N,numCarpets):\n\t\t\t#Base Case\n if N>=n:\n return 0\n\t\t\t#If calculated previously use that solution\n if memo[N][numCarpets]!=-1:\n return memo[N][numCarpets]\n\t\t\t\t\n used = 0 # If you use the carpet\n notused = 0 # If you donot use the carpet\n\t\t\t\n if floor[N]==\'1\': # We might use the carpet in this part\n if numCarpets>0: #Whether we even have some carpets or not\n\t\t\t\t """\n\t\t\t\t\tOptimization Part\n\t\t\t\t\tWe are finding the number of ones present in this part of the floor.\n\t\t\t\t\tprefix[lastInd] - Number of ones till lastInd\n\t\t\t\t\tprefix[N] - Number of ones till Nth Index.\n\t\t\t\t\t\n\t\t\t\t\tTheir difference gives us how many ones present between the two.\n\t\t\t\t """\n lastInd = min(N+carpetLen,len(floor)) \n ans = prefix[lastInd] - prefix[N]\n \n\t\t\t\t\t"""\n\t\t\t\t\tFind the max if we use or donot use carpet at this index\n\t\t\t\t\tIf we do we add --- ans and decrement remaining carpets\n\t\t\t\t\telse we donot\n\t\t\t\t\t"""\n used = max(solve(N+carpetLen,numCarpets-1)+ans,solve(N+1,numCarpets))\n \n else:\n used = 0\n \n else:\n\t\t\t#If we donot use the carpet although I feel this might be redundant code\n notused = solve(N+1,numCarpets)\n \n\t\t\t#Using max function to find the number of white tiles removed\n memo[N][numCarpets] = max(used,notused)\n return memo[N][numCarpets]\n\t\t\n\t\t#Total White tiles\n ones = 0\n for x in floor:\n if x == \'1\':\n ones+=1\n \n\t\t#Using Prefix array to store number of ones till i th index\n prefix = [0]*(n+1)\n for i in range(1,n+1):\n if floor[i-1]==\'1\':\n prefix[i] = prefix[i-1]+1\n else:\n prefix[i] = prefix[i-1]\n\t\t\t\t\n \n removed = solve(0,numCarpets)\n \n return ones-removed\n``` | 6 | 1 | ['Dynamic Programming', 'Prefix Sum', 'Python'] | 3 |
minimum-white-tiles-after-covering-with-carpets | [Python] Readable and Easy understand Bottom-Up DP solution in Python | python-readable-and-easy-understand-bott-qgjh | \nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n n = len(floor)\n if carpetLen*numCarpets | alex391a | NORMAL | 2022-03-22T09:01:13.421497+00:00 | 2022-10-10T17:07:01.641499+00:00 | 298 | false | ```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n n = len(floor)\n if carpetLen*numCarpets >= n:\n return 0\n floorlist = []\n for i in floor:\n if i == \'1\':\n floorlist.append(1)\n else:\n floorlist.append(0)\n dp=[[0] * n for i in range(numCarpets)]\n \n for i in range(carpetLen, n):\n dp[0][i] = min(floorlist[i] + dp[0][i-1], sum(floorlist[:i - carpetLen + 1]))\n for j in range(1, numCarpets):\n for i in range(carpetLen * j, n):\n dp[j][i] = min(floorlist[i] + dp[j][i - 1], dp[j - 1][i - carpetLen])\n return dp[-1][-1]\n``` | 5 | 0 | ['Dynamic Programming', 'Python'] | 1 |
minimum-white-tiles-after-covering-with-carpets | Recursion + memoization + Time-Saver Trick | recursion-memoization-time-saver-trick-b-1zot | \nclass Solution {\npublic: \n int dp[1001][1001];\n int helper(string &floor, int idx, int numCarpets, int len)\n {\n if(idx >= floor.size())\n | ashishdtu007 | NORMAL | 2022-03-19T16:17:51.351087+00:00 | 2022-03-19T18:32:05.166002+00:00 | 327 | false | ```\nclass Solution {\npublic: \n int dp[1001][1001];\n int helper(string &floor, int idx, int numCarpets, int len)\n {\n if(idx >= floor.size())\n return 0;\n\t\t\t\n int &ans = dp[idx][numCarpets]; //reference variable so that we dont have to write this again \n \n if(ans != -1) //if state already calculated no need to calculate again directly return its value\n return ans;\n \n int op1 = INT_MAX, op2 = INT_MAX;\n\t\t//when you dont use a new carpet from the current index\n op1 = (floor[idx] == \'1\') + helper(floor, idx+1, numCarpets, len);\n\t\t//when you use a new carpet from the current index\n if(numCarpets > 0)\n op2 = helper(floor, idx+len, numCarpets-1, len);\n return ans = min(op1, op2);\n }\n int minimumWhiteTiles(string floor, int numCarpets, int carpetlen) {\n memset(dp, -1, sizeof(dp));\n return helper(floor, 0, numCarpets, carpetlen);\n }\n};\n\n```\nThe question could be solved in a recursive manner where you just need to know the index and the number of carpets left, now at any index we have two options either we can use the available carpets or we can leave this index as it is. We can consider both options and return the minimum of both the available options.\n\nI have used a trick that is I used a reference variable to store dp[idx][numCarpets], now imagine those questions where we have 3 or 4 states and we don\'t want those dp[][][] states again and again. We can simply use reference variables and we can use them our code to save sometime in competitions.\n\nPlease upvote if you have learnt anything from this post. | 4 | 0 | ['Recursion', 'Memoization'] | 1 |
minimum-white-tiles-after-covering-with-carpets | Dynamic Programming based solution || Recursion + Memoization || C++ Code | dynamic-programming-based-solution-recur-f2dx | \nclass Solution {\npublic:\n int dp[1002][1002];\n int min(int a, int b)\n {\n if(a<b) return a;\n return b;\n }\n \n int func( | KmIndu | NORMAL | 2022-03-27T17:03:08.949257+00:00 | 2022-03-27T17:03:08.949302+00:00 | 246 | false | ```\nclass Solution {\npublic:\n int dp[1002][1002];\n int min(int a, int b)\n {\n if(a<b) return a;\n return b;\n }\n \n int func(string &floor, int numCarpets, int &carpetLen, int i, vector<int> &prefix)\n {\n //Base Cases\n if(i>=floor.size())\n return 0;\n if(numCarpets==0)\n return 0;\n \n //Memoization\n if(dp[i][numCarpets]!=-1)\n return dp[i][numCarpets];\n \n //Check if current tile is black, if it is then skip it\n if(floor[i]==\'0\')\n return dp[i][numCarpets]=func(floor, numCarpets, carpetLen, i+1, prefix);\n \n //temp stores the value of index where pointer i should point after the carpet covers white tiles \n //sometimes i+len can place you out of scope of prefix array that\'s why floor.size() is also considered\n int temp=min(i+carpetLen, floor.size())-1;\n int white=prefix[temp];\n if(i!=0) // i==0 is not fit for this condition(no elements before index 0)\n white-=prefix[i-1]; // this line gives exact number of white tiles in between(covered by carpet)\n /*Suppose 1 0 1 1 0 1 0 1 is the input floor array and carpetLen =2. Prefix array would be 1 1 2 3 3 4 4 5.\n Let us suppose i=2 then \n temp=i+carpetLen-1 temp=2+2-1 temp=4-1 temp=3 \n white=prefix[temp] white=prefix[3] white=3 \n white=white-prefix[i-1]= white=3-prefix[2-1]= white=3-prefix[1] white=3-1 white=2*/\n \n \n int pick=white+func(floor,numCarpets-1,carpetLen, i+carpetLen, prefix); //when you use a new carpet from the current index\n int notpick=func(floor,numCarpets,carpetLen, i+1, prefix); //when you dont use a new carpet from the current index\n \n return dp[i][numCarpets]=max(pick, notpick); //maximum number of white tiles that can be covered by the carpet\n }\n \n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n //for faster i/p o/p\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n \n memset(dp,-1,sizeof dp);\n \n //prefix array is used to store total number of white tiles till current index\n vector<int>prefix(floor.size()); \n if(floor[0]==\'1\')\n prefix[0]=1;\n else\n prefix[0]=0;\n \n for(int i=1; i<floor.size(); i++)\n {\n prefix[i]=prefix[i-1]+(floor[i]==\'1\');\n }\n \n if(prefix[floor.size()-1]==0)\n return 0;\n \n // minimum number of white tiles still visible = total number of white tiles - maximum number of white tiles that can be covered by the carpet\n return prefix[floor.size()-1]-func(floor, numCarpets, carpetLen, 0, prefix); \n }\n};\n``` | 3 | 0 | ['Dynamic Programming', 'Memoization', 'C'] | 0 |
minimum-white-tiles-after-covering-with-carpets | Java | Top Down Dynamic Programming | Memoization | java-top-down-dynamic-programming-memoiz-74e9 | Solution:\n\nclass Solution {\n Map<String, Integer> cache;\n \n public int minimumWhiteTiles(String floor, int numCarpets, int carpetLen) {\n c | gnaby | NORMAL | 2022-03-24T20:23:18.868026+00:00 | 2022-03-24T20:23:18.868071+00:00 | 223 | false | Solution:\n```\nclass Solution {\n Map<String, Integer> cache;\n \n public int minimumWhiteTiles(String floor, int numCarpets, int carpetLen) {\n cache = new HashMap<>();\n return helper(floor, 0, numCarpets, carpetLen);\n }\n \n public int helper(String floor, int position, int numCarpets, int carpetLen) {\n if (position >= floor.length()) {\n return 0;\n }\n \n if (floor.length() - position <= numCarpets * carpetLen) {\n return 0;\n }\n \n String key = position + ", " + numCarpets;\n if (cache.containsKey(key)) {\n return cache.get(key);\n }\n \n if (numCarpets == 0) {\n int output = floor.charAt(position) - \'0\' + helper(floor, position + 1, 0, carpetLen);\n \n cache.put(key, output);\n return output;\n }\n \n int output = Math.min(floor.charAt(position) - \'0\' + helper(floor, position + 1, numCarpets, carpetLen), helper(floor, position + carpetLen, numCarpets - 1, carpetLen));\n \n cache.put(key, output);\n return output;\n }\n}\n``` | 3 | 0 | ['Dynamic Programming', 'Memoization', 'Java'] | 0 |
minimum-white-tiles-after-covering-with-carpets | Problem Analysis with formula, dynamic programming (tabulation approach) | problem-analysis-with-formula-dynamic-pr-587t | At first glance\n\nLet\'s analyze the problem at hand before writing the code. We are given the following inputs:\n\n - Floor, which is a string of characters 0 | adriandmen | NORMAL | 2022-03-19T16:06:26.671776+00:00 | 2022-03-19T16:22:23.663909+00:00 | 118 | false | ## At first glance\n\nLet\'s analyze the problem at hand before writing the code. We are given the following inputs:\n\n - **Floor**, which is a string of characters `0` and `1` only.\n\t - **0** denotes a black tile.\n\t - **1** denotes a white tile.\n - **Number of Carpets**, the number of carpets we can place.\n - **Length of Carpet**, the range of a carpet to make everything black.\n\nThe problem is about *minimizing* the number of white tiles. Note the keyword \'minimizing\', which already tells us that this is going to be an optimization problem. You might have guessed it, dynamic programming is the answer to this problem. In specific, we will be using the *tabulation* approach.\n\n<br>\n\n## Problem Analysis\n\n*Note*: From this point forward, we will be referring the **Number of Carpets** as **R** (remaining carpets), **Length of Carpet** as **L** and the **Floor** as **F**.\n\nIn order to find minimum number of white tile possible, we need to find the optimal formula for minimizing the white tile count. After further inspection, we can see that at any index ***i***, we have two possible options:\n\n - Place a carpet on index ***i***, if and only if **R > 0**.\n - Skip the current index.\n\nThis gives us the following optimal formula (denoted as ***opt***):\n\n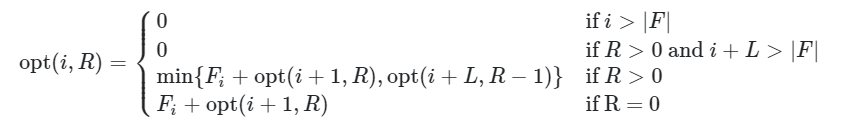\n\n## Implementation\n\nA reference implementation in C++ is given below:\n\n```cpp\nclass Solution {\npublic:\n int minimumWhiteTiles(string floor, int numCarpets, int L) {\n vector<vector<int>> opt(floor.size() + 1, vector<int>(numCarpets + 1, 0));\n\n for (int i = (int) floor.size() - 1; i >= 0; i--) {\n int F_i = floor[i] - \'0\';\n\n for (int R = 0; R <= numCarpets; R++) {\n\n if (R == 0)\n opt[i][R] = F_i + opt[i + 1][R];\n else if (i + L >= floor.size())\n opt[i][R] = 0;\n else\n opt[i][R] = min(F_i + opt[i + 1][R], opt[i + L][R - 1]);\n }\n }\n\n return opt[0][numCarpets];\n }\n};\n```\n\nThis runs in **pseudo-polynomial time O(|F| \xD7 R)** and has a space complexity **O(|F| \xD7 R)**. Note that this is *not polynomial*, but [pseudo-polynomial](https://en.wikipedia.org/wiki/Pseudo-polynomial_time).\n\n\n\n | 3 | 0 | [] | 0 |
minimum-white-tiles-after-covering-with-carpets | Python3 DP Accepted (Is my runtime analysis correct? O(2^N)?) | python3-dp-accepted-is-my-runtime-analys-lf0v | Below is accepted.\n\nI struggle with figuring out runtime for DP problems, can someone help? \nIs it O(2^N)? My reasoning being that at each backtrack calll, y | breadsticks | NORMAL | 2022-03-19T16:00:38.657912+00:00 | 2022-03-19T16:00:38.657953+00:00 | 322 | false | Below is accepted.\n\nI struggle with figuring out runtime for DP problems, can someone help? \nIs it O(2^N)? My reasoning being that at each backtrack calll, you either cover the piano, or you don\'t. That\'s 2 choices with at most N steps/piano tiles.\n\nAlso what would be the best way to manually memoize the results without using @lru_cache here?\n\n```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n if numCarpets * carpetLen >= len(floor):\n return 0\n \n white_to_right = [0] * len(floor)\n for i in range(len(floor)-1, -1, -1):\n if i == len(floor) - 1:\n white_to_right[i] = 1 if floor[i] == \'1\' else 0\n else:\n white_to_right[i] = white_to_right[i+1]\n white_to_right[i] += 1 if floor[i] == \'1\' else 0\n \n @lru_cache(maxsize=None)\n def backtrack(index, remaining):\n if index >= len(floor):\n return 0\n \n if remaining == 0:\n return white_to_right[index]\n \n # cover carpet starting at this index\n cover_now = backtrack(index + carpetLen, remaining - 1)\n\n # no-op, cover at next index\n cover_later = backtrack(index + 1, remaining)\n cover_later += 1 if floor[index] == \'1\' else 0\n \n return min(cover_now, cover_later)\n\n return backtrack(0, numCarpets)\n\n | 3 | 0 | [] | 1 |
minimum-white-tiles-after-covering-with-carpets | C++ || 0/1 knapsack | c-01-knapsack-by-rajput9189-qy9m | \nclass Solution {\nprivate:\n int dp[1001][1001];\n int solve(string& floor,int idx,int n,int car,int len,vector<int>&prefix)\n {\n if(idx==n | | rajput9189 | NORMAL | 2022-04-27T04:48:09.299851+00:00 | 2022-04-27T04:48:09.299883+00:00 | 149 | false | ```\nclass Solution {\nprivate:\n int dp[1001][1001];\n int solve(string& floor,int idx,int n,int car,int len,vector<int>&prefix)\n {\n if(idx==n || car==0)\n return 0;\n \n if(dp[idx][car]!=-1)\n return dp[idx][car];\n \n int range=min(idx+len-1,n-1);\n int cnt=prefix[range];\n \n if(idx>0)\n cnt-=prefix[idx-1];\n \n int pick=cnt+solve(floor,min(idx+len,n),n,car-1,len,prefix);\n int skip=solve(floor,idx+1,n,car,len,prefix);\n return dp[idx][car]=max(pick,skip);\n }\npublic:\n int minimumWhiteTiles(string floor, int Carpet, int carpetLen) { \n \n memset(dp,-1,sizeof dp);\n int n=floor.size();\n vector<int>prefix(n,0);\n int cnt=0;\n for(auto i=0;i<n;++i)\n {\n if(floor[i]==\'1\')\n cnt++;\n \n prefix[i]=cnt;\n \n }\n return cnt-solve(floor,0,floor.size(),Carpet,carpetLen,prefix);\n \n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Memoization', 'C'] | 0 |
minimum-white-tiles-after-covering-with-carpets | Dynamic Programming based solution || Recursion + Memoization || C++ Clean Code | dynamic-programming-based-solution-recur-cdmt | Code :\n\n\n class Solution {\n vector<int> whiteCount; // Stores no. of white tiles from ith index till the end\n \n\t// Count number of white tile from | i_quasar | NORMAL | 2022-03-23T17:44:46.198283+00:00 | 2022-03-23T17:57:23.565561+00:00 | 131 | false | # Code :\n\n```\n class Solution {\n vector<int> whiteCount; // Stores no. of white tiles from ith index till the end\n \n\t// Count number of white tile from index till end \n\t// Suffix sum of no. of white tiles\n void countTiles(string& floor, int n) {\n whiteCount.resize(n+2, 0);\n \n for(int i=n-1; i>=0; i--) {\n whiteCount[i] = whiteCount[i+1] + (floor[i] == \'1\');\n }\n }\n \n int uncoveredWhiteTiles(string& floor, vector<vector<int>>& dp, int numCarpets, int idx, int carpetLen, int n) {\n \n\t\t// If we reach the end, then no white is remaining\n\t\t// Assuming that all previous white tiles are covered already using carpets\n if(idx >= n) {\n return 0;\n }\n\t\t// If no carpet is available, then all the white tiles from current index\n\t\t// Till the end are uncovered. Hence return its count\n if(numCarpets == 0) {\n return whiteCount[idx];\n }\n \n\t\t// If we have some value for current state in DP table, then return it\n if(dp[idx][numCarpets] != -1) return dp[idx][numCarpets];\n \n int countWhites = n;\n \n // We have two choices at this point\n\t\t// Choice 1 : Use a carpet starting from current index till carpetLen\n\t\t// Choice 2 : Do no use any carpet, and move to next index. \n\t\t// But if current tile is white then count it as uncovered\n countWhites = min(\n uncoveredWhiteTiles(floor, dp, numCarpets-1, idx+carpetLen, carpetLen, n),\n uncoveredWhiteTiles(floor, dp, numCarpets, idx+1, carpetLen, n) + (floor[idx] == \'1\')\n );\n \n\t\t// Return minimum count of uncovered white tiles using one of the two choices\n return dp[idx][numCarpets] = countWhites;\n }\n \npublic:\n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n int n = floor.size();\n countTiles(floor, n);\n vector<vector<int>> dp(n+1, vector<int>(numCarpets+1, -1));\n \n return uncoveredWhiteTiles(floor, dp, numCarpets, 0, carpetLen, n);\n }\n};\n```\n\n**Complexity :**\n\n* Time : `O(N*M)` \n* Space : `O(N*M)`\n\t* N : length of `floor` string\n\t* M : number of carpets available\n\n***If you find this helpful, do give it a like :)*** | 2 | 0 | ['Dynamic Programming', 'Memoization', 'C'] | 0 |
minimum-white-tiles-after-covering-with-carpets | ✔ C++ | DP | Heavily Commented | c-dp-heavily-commented-by-jk20-2mqa | \nclass Solution {\n \nprivate:\n int dp[1001][1001];\n int suffix[1001];\npublic:\n int recur(string &floor,int numCarpets,int carpetLen,int idx)\n | jk20 | NORMAL | 2022-03-23T12:21:27.090052+00:00 | 2022-03-23T12:21:27.090128+00:00 | 203 | false | ```\nclass Solution {\n \nprivate:\n int dp[1001][1001];\n int suffix[1001];\npublic:\n int recur(string &floor,int numCarpets,int carpetLen,int idx)\n {\n //Base Cases\n if(idx>=floor.size())\n return 0;\n \n if(numCarpets==0)\n return suffix[idx];\n \n //Memoization\n if(dp[idx][numCarpets]!=-1)\n return dp[idx][numCarpets];\n \n //Check if current tile is white,\n //We need to add 1 because we are skipping\n int op1=(floor[idx]==\'1\')+recur(floor,numCarpets,carpetLen,idx+1);\n //We are using one carpet and hence we jump directly \n //by carpetLen moves\n int op2=recur(floor,numCarpets-1,carpetLen,idx+carpetLen);\n return dp[idx][numCarpets]=min(op1,op2);\n }\n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n \n int n=floor.size();\n memset(dp,-1,sizeof dp);\n \n /*We make a suffix array which will tell \n us count of white tiles after current tile\n (including current tile also), we need to do this step\n else we will get TLE */\n suffix[n - 1] = (floor[n - 1] == \'1\');\n for (int i = n - 2; i >= 0; i--) {\n suffix[i] = suffix[i + 1] + (floor[i] == \'1\');\n }\n return recur(floor,numCarpets,carpetLen,0);\n }\n};\n```\n\n**Pls upvote the solution if you found helpful, it means a lot.\nAlso comment down your doubts.\nHappy Coding : )** | 2 | 0 | ['Dynamic Programming', 'Memoization', 'C', 'C++'] | 1 |
minimum-white-tiles-after-covering-with-carpets | [Python3] dp | python3-dp-by-ye15-80w1 | Please pull this commit for solutions of biweekly 74. \n\n\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int | ye15 | NORMAL | 2022-03-23T01:59:30.885124+00:00 | 2022-03-23T02:18:02.191835+00:00 | 268 | false | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7e91381aab0f51486f380f703245463c99fed635) for solutions of biweekly 74. \n\n```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n \n @cache\n def fn(i, n):\n """Return min while tiles at k with n carpets left."""\n if n < 0: return inf \n if i >= len(floor): return 0 \n if floor[i] == \'1\': return min(fn(i+carpetLen, n-1), 1 + fn(i+1, n))\n return fn(i+1, n)\n \n return fn(0, numCarpets)\n```\n\n```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n dp = [[0]*(1 + numCarpets) for _ in range(len(floor)+1)]\n for i in range(len(floor)-1, -1, -1): \n for j in range(0, numCarpets+1): \n if floor[i] == \'1\': \n dp[i][j] = 1 + dp[i+1][j] \n if j: \n if i+carpetLen >= len(floor): dp[i][j] = 0 \n else: dp[i][j] = min(dp[i+carpetLen][j-1], dp[i][j])\n else: dp[i][j] = dp[i+1][j]\n return dp[0][numCarpets]\n``` | 2 | 0 | ['Python3'] | 0 |
minimum-white-tiles-after-covering-with-carpets | Java solution 100% faster Using DP Tabulation | java-solution-100-faster-using-dp-tabula-xr8b | Explatation in comments.\nPlease Upvote if you undrstand this.\n...\nclass Solution {\n\n\tpublic int minimumWhiteTiles(String floor, int numCarpets, int carpet | harshy736 | NORMAL | 2022-03-20T07:16:35.685013+00:00 | 2022-03-20T07:16:35.685046+00:00 | 199 | false | Explatation in comments.\nPlease **Upvote** if you undrstand this.\n...\nclass Solution {\n\n\tpublic int minimumWhiteTiles(String floor, int numCarpets, int carpetLen) {\n\t\n\t\tchar[] arr = floor.toCharArray();\n\t\t\n\t\tint n = arr.length;\n\t\t//using dp\n\t\t\n\t\tint[][] dp = new int[numCarpets + 1][n + 1];\n\t\t//dp[i][j] -> no of whites in arr(0, i) when j carpet is used\n\t\t//row -> number of carpets\n\t\t//columns -> arr / floor\n \n for(int i = 0; i <= numCarpets; i++){\n for(int j = 1; j <= n; j++){\n if(i == 0)\n dp[i][j] = dp[i][j - 1] + (arr[j - 1] - \'0\');\n else if(j <= carpetLen)//cover all floor\n dp[i][j] = 0;\n else{\n int w = Math.min(dp[i - 1][j - carpetLen], dp[i - 1][j]);\n //minimum no of whites if only j - 1 carpet is used already\n\t\t\t\t\t//we want to minimize whites by using or not using jth carpet\n \n //dp[i][j - 1] -> minimum no of moves if we used i carpets already\n\t\t\t\t\t//arr[j - 1] - \'0\' -> adds white count for j - 1 th char\n\t\t\t\t\t\n int min = Math.min(w, dp[i][j - 1] + (arr[j - 1] - \'0\'));\n //minimum whites in any case\n \n dp[i][j] = min;//update\n }\n }\n }\n \n return dp[numCarpets][n];\n }\n}\n... | 2 | 0 | ['Array', 'Dynamic Programming', 'Java'] | 1 |
minimum-white-tiles-after-covering-with-carpets | Simple Solution in Java || Concise and Elegant || With Memoization | simple-solution-in-java-concise-and-eleg-zttg | \nclass Solution {\n private int[][] dp;\n \n public int minimumWhiteTiles(String floor, int numCarpets, int carpetLen) {\n this.dp = new int[fl | PRANAV_KUMAR99 | NORMAL | 2022-03-20T06:57:05.228654+00:00 | 2022-03-20T06:57:56.243004+00:00 | 49 | false | ```\nclass Solution {\n private int[][] dp;\n \n public int minimumWhiteTiles(String floor, int numCarpets, int carpetLen) {\n this.dp = new int[floor.length()+1][numCarpets+1];\n for(int i=0; i<floor.length(); i++){\n Arrays.fill(dp[i], -1);\n }\n \n char[] str = floor.toCharArray();\n return find(0, str, numCarpets, carpetLen);\n }\n \n // Find the minimum number of white tiles visible\n private int find(int index, char[] floor, int numCarpets, int carpetLen){\n if(numCarpets < 0) return Integer.MAX_VALUE;\n if(index >= floor.length) return 0;\n \n if(dp[index][numCarpets] != -1){\n return dp[index][numCarpets];\n }\n \n int min = Integer.MAX_VALUE;\n // If current tile is black, move to the next\n if(floor[index] == \'0\'){\n min = find(index+1, floor, numCarpets, carpetLen);\n }\n \n // If current tile is white, two options, cover the current white tile or not \n if(floor[index] == \'1\'){\n min = Math.min(min, find(index + carpetLen, floor, numCarpets - 1, carpetLen));\n min = Math.min(min, 1 + find(index + 1, floor, numCarpets, carpetLen));\n }\n \n dp[index][numCarpets] = min;\n return min;\n }\n}\n``` | 2 | 0 | [] | 0 |
minimum-white-tiles-after-covering-with-carpets | Top Down || C++ Solution || Well commented | top-down-c-solution-well-commented-by-sh-ihve | \nclass Solution {\npublic:\n int explore(int i,string &floor,int numCarpets, int &carpetLen, vector<vector<int>> &dp)\n {\n if(i==floor.length())\ | Shishir_Sharma | NORMAL | 2022-03-20T02:23:09.956678+00:00 | 2022-03-20T02:23:09.956708+00:00 | 90 | false | ```\nclass Solution {\npublic:\n int explore(int i,string &floor,int numCarpets, int &carpetLen, vector<vector<int>> &dp)\n {\n if(i==floor.length())\n {\n return 0;\n }\n if(dp[i][numCarpets]!=-1)\n {\n return dp[i][numCarpets];\n }\n \n int ans=0;\n //Put carpet here only if you have 1 or more carpet left\n if(i+carpetLen<=floor.length()&&numCarpets>0)\n {\n ans+=carpetLen+explore(i+carpetLen,floor,numCarpets-1,carpetLen,dp);\n }\n else if(numCarpets>0)\n { //When current index+ carpet length > floor.length\n ans+=floor.length()-i;\n }\n \n \n //Dont put carpert here\n if(floor[i]==\'0\')\n { //If current carpet is black\n ans=max(ans,1+explore(i+1,floor,numCarpets,carpetLen,dp));\n }\n else\n {\n ans=max(ans,explore(i+1,floor,numCarpets,carpetLen,dp));\n }\n \n return dp[i][numCarpets]=ans;\n }\n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n int n=floor.length();\n //Store number of maximum black carpet from index\n vector<vector<int>> dp(n,vector<int>(numCarpets+1,-1));\n //Explore will return maximum number of black carpet \n\t\t//we just subtract it from floor length to get \n\t\t//minimum number of white carpet\n return n-explore(0,floor,numCarpets,carpetLen,dp);\n }\n};\n```\n**Like it? Please Upvote ;-)** | 2 | 0 | ['C', 'C++'] | 0 |
minimum-white-tiles-after-covering-with-carpets | C++ Dynamic Programing Solution | Time-O(n^2), Space- O(n) | c-dynamic-programing-solution-time-on2-s-ss7v | \nclass Solution {\npublic:\n int minimumWhiteTiles(string a, int n, int k) {\n \n int m= a.size();\n \n vector<int> v(m+1,0),h;\ | abhinandan__22 | NORMAL | 2022-03-19T19:16:48.340110+00:00 | 2022-03-19T19:16:48.340152+00:00 | 53 | false | ```\nclass Solution {\npublic:\n int minimumWhiteTiles(string a, int n, int k) {\n \n int m= a.size();\n \n vector<int> v(m+1,0),h;\n \n v[0] = 0;\n \n for(int i=1;i<=m;i++)\n {\n v[i] = v[i-1];\n if(a[i-1]==\'1\')\n v[i]++;\n }\n \n for(int i=1;i<=n;i++)\n {\n h = v;\n v[0] = 0;\n for(int j=1;j<=m;j++)\n {\n if(a[j-1]==\'1\')\n { \n if(j>=k)\n v[j] = min(h[j-k],v[j-1]+1);\n else\n v[j] = 0;\n }\n else\n v[j] = v[j-1];\n }\n } \n \n return v[m];\n \n }\n};\n``` | 2 | 0 | [] | 0 |
minimum-white-tiles-after-covering-with-carpets | [Python][DP] Inspired by kadane algo and buy sell stock IV | pythondp-inspired-by-kadane-algo-and-buy-1033 | I. Intuition:\nThe key idea is that we find the maximum tiles can be covered with one carpet (at a time).\n\nFor the example:\nfloor = "10110101"\nnumCarpets=2\ | hangnguyendieu | NORMAL | 2022-03-19T16:40:52.619374+00:00 | 2022-03-19T16:40:52.619429+00:00 | 140 | false | I. Intuition:\nThe key idea is that we find the maximum tiles can be covered with one carpet (at a time).\n\nFor the example:\n`floor = "10110101"`\n`numCarpets=2`\n`carpetLen=2`\n\nWith numCapets = 2, that means we will have 2 carpets to use. \nFirst, we find the maximum tiles that the first carpet can cover.\n`dp[first_carpet] = [0, 1, 1, 1, 2, 2, 2, 2, 2]`\nWe can say that at the end of 9th floor, with one carpet, we can cover at most 2 tiles. Now we store the maximum tiles can be covered with one carpet in `prev_state`\nSecond, we now need to find the maxmimum tiles that the second carpet can cover. Then we take the sum of max tiles that the first carpet cover with the max tiles that the second carpet can cover. \n`dp[second_carpet] = [0, 1, 1, 2, 3, 3, 3, 3, 3]`\n\nII. Resources:\nhttps://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/solution/627971\n\nIII. Code:\n```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n \n updated_floor = [0]*(len(floor)+1)\n running = 0\n for index, tiles in enumerate(floor):\n if tiles == \'1\':\n running += 1\n updated_floor[index+1] = running\n \n prev_state = [0]*(len(floor)+1)\n for i in range(numCarpets):\n dp = [0]*(len(floor)+1)\n for j in range(len(dp)-1):\n if floor[j] == \'1\':\n \n dp[j+1] = max(prev_state[j+1], prev_state[max(j+1-carpetLen, 0)] + updated_floor[j+1]-updated_floor[max(j+1-carpetLen, 0)], dp[j])\n \n else:\n dp[j+1] = max(prev_state[j+1], dp[j])\n \n prev_state = dp\n \n return updated_floor[-1] - dp[-1]\n``` | 2 | 0 | ['Dynamic Programming', 'Python'] | 0 |
minimum-white-tiles-after-covering-with-carpets | Neat and clean Recursion + Memoization || Easy to understand | neat-and-clean-recursion-memoization-eas-u8cf | ```class Solution {\npublic:\n string s;\n int n;\n int prefix[1001];\n int len;\n int dp[1001][1001];\n int solve(int index, int carpet) {\n | lakshaygrover7 | NORMAL | 2022-03-19T16:21:45.603104+00:00 | 2022-03-19T16:21:45.603140+00:00 | 106 | false | ```class Solution {\npublic:\n string s;\n int n;\n int prefix[1001];\n int len;\n int dp[1001][1001];\n int solve(int index, int carpet) {\n if(carpet <= 0 || index >= n)\n return 0;\n if(dp[index][carpet] != -1)\n return dp[index][carpet];\n int x = 0;\n if(index)\n x = prefix[index - 1];\n int y = prefix[min(index + len - 1, n)];\n return dp[index][carpet] = max(solve(index + 1, carpet), y - x + solve(index + len, carpet - 1));\n }\n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n s = floor;\n n = s.length();\n len = carpetLen;\n memset(dp, -1, sizeof(dp));\n prefix[0] = (s[0] == \'1\');\n for(int i = 1; i < n; ++i)\n prefix[i] = prefix[i-1] + (s[i] == \'1\');\n prefix[n] = prefix[n-1];\n int ans = solve(0, numCarpets);\n return max(0, prefix[n] - ans);\n }\n}; | 2 | 0 | ['Dynamic Programming', 'Memoization'] | 1 |
minimum-white-tiles-after-covering-with-carpets | [Python3] simple bottom-up DP solution | python3-simple-bottom-up-dp-solution-by-9tonu | python\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n n = len(floor)\n dp = [[0]*(numCar | rayhongz | NORMAL | 2022-03-19T16:19:41.573557+00:00 | 2022-03-19T16:19:41.573583+00:00 | 132 | false | ```python\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n n = len(floor)\n dp = [[0]*(numCarpets+1) for _ in range(n+1)]\n for i in range(1, n+1):\n dp[i][0] = dp[i-1][0] + (floor[i-1] == \'1\')\n \n for k in range(1, numCarpets+1):\n for i in range(1, n+1):\n dp[i][k] = min(dp[max(0, i-carpetLen)][k-1], dp[i-1][k]+(floor[i-1] == \'1\'))\n\n return dp[-1][numCarpets]\n```\n | 2 | 0 | ['Dynamic Programming', 'Python'] | 0 |
minimum-white-tiles-after-covering-with-carpets | Classical DP | Memoization | Similiar to 0/1 Knapsack | classical-dp-memoization-similiar-to-01-4cwyr | ```\nclass Solution {\npublic:\n vector pre;\n int n;\n vector> dp;\n int fun(int i,string &f,int nc,int len){\n \n if(i >= n) return | njcoder | NORMAL | 2022-03-19T16:13:15.690377+00:00 | 2022-03-19T16:14:44.177324+00:00 | 158 | false | ```\nclass Solution {\npublic:\n vector<int> pre;\n int n;\n vector<vector<int>> dp;\n int fun(int i,string &f,int nc,int len){\n \n if(i >= n) return 0;\n if(nc == 0){\n return pre[n-1] - (i == 0 ? 0 : pre[i-1]);\n }\n if(dp[i][nc] != -1) return dp[i][nc];\n int left = fun(i+len,f,nc-1,len);\n int right = (f[i] == \'1\' ? 1 : 0) + fun(i+1,f,nc,len);\n \n return dp[i][nc] = min(left,right);\n \n }\n int minimumWhiteTiles(string f, int nc, int len) {\n \n n = f.size();\n pre = vector<int> (n);\n dp = vector<vector<int>> (n,vector<int> (nc+1,-1));\n pre[0] = (f[0] == \'1\' ? 1 : 0);\n for(int i=1;i<n;i++){\n pre[i] = (f[i] == \'1\' ? 1 : 0) + pre[i-1];\n }\n \n return fun(0,f,nc,len);\n }\n}; | 2 | 0 | ['Dynamic Programming', 'Memoization', 'Prefix Sum'] | 0 |
minimum-white-tiles-after-covering-with-carpets | [c++] Simple recursive + memoization | Easy to think | Commented | c-simple-recursive-memoization-easy-to-t-8dj1 | \nclass Solution {\npublic:\n vector<vector<int>> dp;\n int minCover(string& s, int index, int numCarpets, int len){\n if(index >= s.length()) | mohammedismail | NORMAL | 2022-03-19T16:06:08.438489+00:00 | 2022-03-19T16:06:38.583335+00:00 | 73 | false | ```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n int minCover(string& s, int index, int numCarpets, int len){\n if(index >= s.length()) // if index >= s.length(), then there is no tiles present.\n return 0;\n if(dp[index][numCarpets] != -1) // State of the dp is represented by current index and no of Carpets remaining\n return dp[index][numCarpets];\n int res1 = INT_MAX;\n if(numCarpets > 0)\n res1 = minCover(s, index + len, numCarpets-1, len); // If carpet is still remaining, we can try covering tiles in the range [index, index + len - 1]\n int res2 = minCover(s, index+1, numCarpets, len); // finding min no of white tiles visible if we doesn\'t cover the tile on this particular index\n if(s[index] == \'1\') // white tile present at index, so if we don\'t cover those tile, then add corresponding count to res2\n res2++;\n return dp[index][numCarpets] = min(res1, res2); // finally we choose the minimum from the above two case\n }\n \n int minimumWhiteTiles(string floor, int numCarpets, int carpetLen) {\n dp.resize(floor.length(), vector<int>(numCarpets+1, -1));\n return minCover(floor, 0, numCarpets, carpetLen);\n }\n};\n```\n***If you find this helpful, please show some love in the form of upvote*** | 2 | 0 | [] | 0 |
minimum-white-tiles-after-covering-with-carpets | Simple Memoization based solution | simple-memoization-based-solution-by-use-3717 | Approach\nThree choices\n1. Use carpet if available and necessary. In this can case jump to index + carpet length\n2. Do not use carpet even if available and ne | user6337nf | NORMAL | 2023-04-12T05:28:05.008755+00:00 | 2023-04-12T05:28:05.008798+00:00 | 40 | false | # Approach\nThree choices\n1. Use carpet if available and necessary. In this can case jump to index + carpet length\n2. Do not use carpet even if available and necessary. Increase count by 1 and move to next index. Here we save carpt to be used later. \n3. Handle scenarios like no carpet available or carpet not necessary because tile is lready black. \n\n\n# Complexity\n- Time complexity: $$O(floorLength * numberOfCarpets)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(floorLength * numberOfCarpets)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minimumWhiteTiles(String floor, int numCarpets, int carpetLen) {\n int[][] memo = new int[floor.length()][numCarpets+1];\n for(int[] arr : memo) {\n Arrays.fill(arr, -1);\n }\n return solve(floor, numCarpets, carpetLen, 0, memo);\n }\n\n int solve(String floor, int numCarpets, int carpetLen, int index, int[][] memo) {\n if(index >= floor.length()) {\n return 0;\n }\n if(memo[index][numCarpets] != -1) {\n return memo[index][numCarpets];\n }\n if(numCarpets > 0) {\n if(floor.charAt(index) == \'0\') {\n return memo[index][numCarpets] = solve(floor, numCarpets, carpetLen, index+1, memo);\n }\n else {\n int coveredWhite = solve(floor, numCarpets-1, carpetLen, index+carpetLen, memo);\n int unCoveredWhite = 1 + solve(floor, numCarpets, carpetLen, index+1, memo);\n return memo[index][numCarpets] = Math.min(coveredWhite, unCoveredWhite);\n }\n }\n else {\n int count = 0;\n for(int i = index; i < floor.length(); i++) {\n count = floor.charAt(i) == \'1\' ? count + 1 : count;\n }\n return memo[index][numCarpets] = count;\n }\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Java'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.