question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-coins-from-k-consecutive-bags | [Python3] binary search | python3-binary-search-by-ye15-wfz5 | IntuitionThis is essentially a line sweep problem. However, due to the large values, one cannot calcualte the numbers naively. Instead, we could leverage on pre | ye15 | NORMAL | 2025-01-05T04:03:32.996726+00:00 | 2025-01-05T04:16:21.363274+00:00 | 2,177 | false | # Intuition
This is essentially a line sweep problem. However, due to the large values, one cannot calcualte the numbers naively. Instead, we could leverage on prefix sum and binary search to make the calculations more efficiently.
# Approach
We first sort `coins` and calculate the prefix sum of coins. Due to the nature that the coins are constant in a given interval, it is guaranteed that the desired interval of size `k` will have the entire left-most interval or right-most interval unless `k` is not enough to cover an entire interval. As a result, we can collect the right point of the candidate interval. Given an interval `[l, r]`, the points to be considered are `l+k-1` and `r`. The first corresponds to the interval being the left-most one and the second correcsponds to the interval being the right-most one.
In addition, we need a function to calculate the total number of points before a given point (say `x`). Using the prefix sum, this can be calculated in `log(N)` time. See the code for more detail.
# Complexity
- Time complexity: `O(NlogN)`
- Space complexity: `O(N)`
# Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
coins.sort()
ans = 0
prefix = [0]
vals = []
for l, r, c in coins:
prefix.append(prefix[-1] + c*(r-l+1))
vals.extend([l+k-1, r])
def fn(x):
"""Return """
i = bisect_right(coins, x, key=lambda x: x[0])-1
if i < 0: return 0
return prefix[i] + (min(x, coins[i][1]) - coins[i][0] + 1)*coins[i][2]
return max(fn(r) - fn(r-k) for r in sorted(vals))
``` | 19 | 0 | ['Python3'] | 1 |
maximum-coins-from-k-consecutive-bags | Sorting + PrefixSum + Binary Search - O(nlogn) | sorting-prefixsum-binary-search-onlogn-b-82py | IntuitionThe key observation is that the interval we are looking for will always either start with one of the intervals containing coins or end at one of these | aashishrt7 | NORMAL | 2025-01-05T06:46:32.107001+00:00 | 2025-01-05T06:46:32.107001+00:00 | 2,253 | false | # Intuition
The key observation is that the interval we are looking for will always either start with one of the intervals containing coins or end at one of these intervals. Based on this, we can handle the problem in two cases:
1. Starting with a Coin Interval:
For each coin-containing interval, assume it as the starting point of the
𝑘
k-length interval. Then, use binary search to find the end of this interval.
2. Ending with a Coin Interval:
For each coin-containing interval, assume it as the ending point of the
𝑘
k-length interval. Use binary search to find the start of this interval.
In both cases, if the end (or start) falls in the middle of a coin-containing interval, we handle the partial overlap accordingly. Once the start (or end) is determined, we use the prefix sum array to efficiently calculate the total number of coins in the selected interval.
# Approach
1. Sorting and Prefix Sum:
Sort the segments based on their start positions. Create a prefix sum array to quickly calculate the total number of coins in any subarray (interval).
2. Two Loops for Both Cases:
- First Loop (Start with Coin Interval):
For each interval containing coins, treat it as the starting point of the 𝑘-length interval. Use binary search (lower_bound) to find where the interval should end.
- Second Loop (End with Coin Interval):
For each interval containing coins, treat it as the end of the k-length interval. Again, use binary search to find where the interval should start.
3. Handling Partial Overlap:
If the start or end of the interval lies within a coin-containing interval, handle the partial overlap by calculating the contribution of coins in the overlapping portion.
4. Update Maximum Coins:
Track the maximum coins obtained from both scenarios.
# Complexity
- Time complexity:
Sorting the coins takes $$O(nlogn)$$. For each of the two loops, we perform a binary search which takes $$O(logn)$$, leading to an overall time complexity of $$O(nlogn)$$.
- Space complexity:
The space complexity is $$O(n)$$ due to the prefix sum and auxiliary arrays
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
//sort the array and store starts and ends of interval seperately to make binary search easier
int n = coins.size();
sort(coins.begin(), coins.end());
vector<long long> prefix(coins.size()+1, 0);
vector<int> starts(n), ends(n);
//precalculate the prefix sum for calculation of score
for(int i=0; i<n; i++){
starts[i] = coins[i][0];
ends[i] = coins[i][1];
prefix[i+1] = prefix[i] + 1LL*(coins[i][1]-coins[i][0]+1)*coins[i][2];
}
long long ans = 0; //final_score
// First loop: Treat each coin-containing interval as the start of the k-length interval
for(int i=0; i<n; i++){
long long curr = 0; //score for this iteration
int s = coins[i][0], target = s + k - 1;
int j = lower_bound(ends.begin(), ends.end(), target)- ends.begin();
curr += 1LL*(prefix[j] - prefix[i]);
if(j<n) curr += 1LL*max(0, target - coins[j][0] + 1)*coins[j][2]; //handle partial overlap
ans = max(curr, ans);
}
// Second loop: Treat each coin-containing interval as the end of the k-length interval
for(int i=0; i<n; i++){
long long curr = 0;
int s = coins[i][1];
int target = s - k + 1;
int j = lower_bound(starts.begin(), starts.end(), target) - starts.begin();
curr += 1LL*(prefix[i+1] - prefix[j]);
if(j>0) curr += 1LL*max(0, coins[j-1][1] - target + 1)*coins[j-1][2]; //handle partial overlap
ans = max(curr, ans);
}
return ans;
}
};
``` | 18 | 0 | ['C++'] | 2 |
maximum-coins-from-k-consecutive-bags | [Python] Sliding Window | python-sliding-window-by-awice-i1sv | Let the intervals be [li,ri,wi].The final interval I must have Ileft=li or Iright=ri. We can deduce this by imagining we are sliding the interval left o | awice | NORMAL | 2025-01-05T04:29:40.179786+00:00 | 2025-01-05T04:30:05.566235+00:00 | 1,310 | false | Let the intervals be $[l_i, r_i, w_i]$.
The final interval $\bold{I}$ must have $\bold{I}_\text{left} = l_i$ or $\bold{I}_\text{right} = r_i$. We can deduce this by imagining we are sliding the interval left or right. Only the intersection of $\bold{I}$ with the first or last intervals in $A$ will be affected.
To solve for $\bold{I}_\text{left} = l_i$, we can use a sliding window. $\text{window}$ will be the sum of all $A[i:j]$.
To handle the $\bold{I}_\text{right} = r_i$ case, reflect everything and do it again.
# Code
```python3 []
class Solution:
def maximumCoins(self, A: List[List[int]], K: int) -> int:
N = len(A)
# Solve for all I with I.left = A[i].left
def solve(A):
A.sort()
ans = window = j = 0
# We are considering interval I = [l..l+K-1]
for i, (l, r, c) in enumerate(A):
# A[j] is fully in I
while j + 1 < N and A[j + 1][0] < l + K:
lj, rj, cj = A[j]
window += (rj - lj + 1) * cj
j += 1
# A[j] may be partially in I
extra = 0
if j < N and A[j][0] < l + K:
rightmost = min(l + K - 1, A[j][1])
length = rightmost - A[j][0] + 1
extra = length * A[j][2]
ans = max(ans, window + extra)
window -= (r - l + 1) * c
return ans
ans = solve(A)
for i, (l, r, c) in enumerate(A):
A[i] = [-r, -l, c]
ans = max(ans, solve(A))
return ans
``` | 16 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Sliding Window | sliding-window-by-votrubac-fjkq | This problem is tricky to implement due to edge cases.Intuition: the consecutive bags "window" is aligned with either start (left-aligned) or end (right-aligned | votrubac | NORMAL | 2025-01-05T06:42:29.552066+00:00 | 2025-01-05T07:02:25.376830+00:00 | 1,847 | false | This problem is tricky to implement due to edge cases.
**Intuition:** the consecutive bags "window" is aligned with either start (left-aligned) or end (right-aligned) of an interval.
We sort the intervals, and go left-to-right maintaining the total `sum` in the window.
For intervals in the window, we first check the left-aligned case, removing non-covered bags on the right from the sum.
Then, we check the right-aligned case, removing non-covered bags on the left from the sum.
> Note that some intervals on the left could become completely uncovered, so we need to remove those.
# Complexity
- Time: $$O(n)$$
- Space: $$O(1)$$
# Code
```cpp []
long long maximumCoins(vector<vector<int>>& coins, int k) {
long long res = 0, sum = 0;
sort(begin(coins), end(coins));
for (int i = 0, j = 0; i < coins.size(); ++i) {
long long l = coins[i][0], r = coins[i][1], c = coins[i][2];
sum += (r - l + 1) * c;
while(r - k + 1 > coins[j][1]) {
if (coins[j][0] + k - 1 >= l)
res = max(res, sum - (r - (coins[j][0] + k - 1)) * c);
sum -= ((long long)coins[j][1] - coins[j][0] + 1) * coins[j][2];
++j;
}
if (coins[j][0] + k - 1 >= r)
res = max(res, sum);
else {
res = max(res, sum - (r - k + 1 - coins[j][0]) * coins[j][2]);
if (coins[j][0] + k - 1 >= l)
res = max(res, sum - (r - (coins[j][0] + k - 1)) * c);
}
}
return res;
}
``` | 9 | 0 | ['C++'] | 3 |
maximum-coins-from-k-consecutive-bags | Perfectly Explained Code || With Proof || Greedy Approach || O(N logN) Time | perfectly-explained-code-with-proof-gree-q2j7 | IntuitionTake any subarray of length k to maximize coins, I thought either start at l[i] or r[i] but that seemed to be incorrect, later on I thought to also co | Rahul_Gupta07 | NORMAL | 2025-01-05T04:43:59.303186+00:00 | 2025-01-05T19:13:39.839182+00:00 | 1,041 | false | # Intuition
Take any subarray of length k to maximize coins, I thought either start at l[i] or r[i] but that seemed to be incorrect, later on I thought to also consider the fact that either end at l[i] or r[i], then I proved it (check out in code), that it was the approach required.
# Approach
Explained through comments in the code.
# Complexity
- Time complexity:
$$O(NlogN)$$ where N is the number of intervals
Analysis : O(NlogN) for sorting + O(N * 4 * logN) during the iteration
- Space complexity:
$$O(n)$$ for prefix sum array
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& a, int k) {
// l, r, c
sort(a.begin(), a.end()); // sorted by starting point
int n = a.size();
vector<long long> coins(n, 0); // prefix sum of coins till ith interval
for (int i = 0; i < n; ++i) {
long long l = a[i][0], r = a[i][1], c = a[i][2];
coins[i] += (r - l + 1) * c + (i > 0 ? coins[i - 1] : 0);
}
auto sum = [&](int l, int r) -> long long {
// get sum of coins from l-th interval to r-th interval
long long ans = 0;
if (l <= r) {
ans += coins[r];
if (l > 0)
ans -= coins[l - 1];
}
return ans;
};
long long maxScore = 0;
for (int i = 0; i < n; ++i) {
int l = a[i][0], r = a[i][1], c = a[i][2];
// start from l
// l to l+k-1
int index = upper_bound(a.begin(), a.end(), vector<int>({l + k, 0, 0})) - a.begin() - 1; // index of interval in which l+k-1 definitely lies
long long score = 0;
if (index >= 0) {
// take coins from l[index] to l+k-1, but l+k-1 can be > end point of this interval so take min [as l+k-1 can be in a position where no coin is present]
score += (long long)(min(a[index][1], l + k - 1) - a[index][0] + 1) * a[index][2];
}
// we can take all coins from ith interval to (index-1)th interval
score += sum(i, index - 1);
maxScore = max(maxScore, score);
// end at l
// l-k+1 to l
index = lower_bound(a.begin(), a.end(), vector<int>({l - k + 1, 0, 0})) - a.begin() - 1; // index of interval where l-k+1 may lie, we are 100% sure that index+1 interval definitely consist of l-k+1
score = 0;
if (index >= 0) {
// take coins from l-k+1 to r[index], but l-k+1 can be in a position where there is 0 coin, so take max
// we have taken max with 0 too because of the reason that l-k+1 is not in this interval, so we don't have to consider coins of this interval
score += max(0ll, (long long)(a[index][1] - max(l - k + 1, a[index][0]) + 1)) * a[index][2];
}
// take all coins from index+1 to i-1 as it covers the range of l-k+1 to l-1 and for l, we know there are c coins here, so add that
score += sum(index + 1, i - 1) + c;
maxScore = max(maxScore, score);
// start from r
// r to r+k-1
index = upper_bound(a.begin(), a.end(), vector<int>({r + k, 0, 0})) - a.begin() - 1; // interval where r+k-1 lies
score = 0;
if (index > i) {
// this interval must lie ahead of current interval as 'r' is the only point in this interval and we move ahead after this
// take coins from l[index] to r+k-1
score += (long long)(min(a[index][1], r + k - 1) - a[index][0] + 1) * a[index][2];
}
// take all coins from i+1 to index-1 and c coins from ith interval as only 'r' is inside ith interval and we have considered (index)th interval earlier
score += sum(i + 1, index - 1) + c;
maxScore = max(maxScore, score);
// end at r
// l-k+1 to l
index = lower_bound(a.begin(), a.end(), vector<int>({r - k + 1, 0, 0})) - a.begin() - 1; // interval where r-k+1 may lie or in next interval it lies
score = 0;
if (index >= 0) {
// take all coins from r-k+1 to r[index]
score += max(0ll, (long long)(a[index][1] - max(r - k + 1, a[index][0]) + 1)) * a[index][2];
}
// take all coins from index+1 to i interval
score += sum(index + 1, i);
maxScore = max(maxScore, score);
}
// WHY THIS WORKS ?
// Let's prove by contradiction : Suppose there exists two intervals [li, ri] and [lj, rj] (li <= ri < lj <= rj) which give max coins if we start at
// li < x < ri and end at lj < x + k - 1 < rj, here 3 cases arise :
// 1. ci > cj -> its better to shift our range towards [li, ri] as the change would be +ci-cj and stop when we reach x = li
// 2. ci = cj -> take all coins in [li, ri] and take some from [lj, rj]
// 3. ci < cj -> its better to shift our range towards [lj, rj] as the change would be +cj-ci and stop when we reach x+k-1 = rj
// Hence, we should either start at l, end at l, or do same with r for all intervals [l,r]
return maxScore;
}
};
```
# Improved Version
As suggested by @ruhlmarkus02 in the comments that we don't need to take the cases when our range ends at l or starts from r as it won't affect our answer. Proof is similar to what I proved earlier, you can notice there too, we either start at l[i] or end at r[i] and that's it whats needed for solving this problem.
So, just remove the part of code where we end at l and also the part where we start from r.
The time complexity would remain same, but time utilized would be reduced as here will be only 2 upper bound calls (instead of 4).
| 7 | 0 | ['Binary Search', 'Greedy', 'Prefix Sum', 'C++'] | 2 |
maximum-coins-from-k-consecutive-bags | Simple Solution | simple-solution-by-noobiiitian-by86 | Code | noobiiitian | NORMAL | 2025-01-05T09:50:47.647511+00:00 | 2025-01-05T09:50:47.647511+00:00 | 676 | false |
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, long long k) {
// Sort coins intervals by their start time
sort(coins.begin(), coins.end());
queue<vector<long long>> q; // Store intervals: [start, end, coins]
long long sum = 0; // Current sum of coins in the sliding window
long long ans = 0; // Maximum coins collected
int n = coins.size();
for (int i = 0; i < n; i++) {
int start = coins[i][0], end = coins[i][1];
long long value = coins[i][2];
// Remove intervals from the queue that are no longer valid
while (!q.empty() && q.front()[1] + k - 1 < start) {
sum -= (q.front()[1] - q.front()[0] + 1) * q.front()[2];
q.pop();
}
// Adjust the front interval if it overlaps too much with the current interval
while (!q.empty() && end - k + 1 > q.front()[0]) {
long long lastVal = q.front()[0] + k - 1;
ans = max(ans, sum + max(0LL, lastVal - start + 1) * value);
int minVal = end - k + 1;
if (minVal <= q.front()[1]) {
sum -= (minVal - q.front()[0]) * q.front()[2];
q.front()[0] = minVal;
} else {
sum -= (q.front()[1] - q.front()[0] + 1) * q.front()[2];
q.pop();
}
}
// Add the current interval to the queue
int count = end - start + 1;
if (count <= k) {
sum += count * value;
q.push({start, end, value});
} else {
sum += k * value;
q.push({end - k + 1, end, value});
}
// Update the maximum coins collected
ans = max(ans, sum);
}
return ans;
}
};
``` | 6 | 1 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | 1.5hrs after contest ends... | 15hrs-after-contest-ends-by-jmucc314-5c6v | I'm tiredIntuitionI first thought to sort the coins by where they start since that would make iterating through them sensible. Originally I thought to loop thro | jmucc314 | NORMAL | 2025-01-05T05:55:32.387863+00:00 | 2025-01-05T05:55:32.387863+00:00 | 506 | false | I'm tired
# Intuition
I first thought to sort the coins by where they start since that would make iterating through them sensible. Originally I thought to loop through every possibile starting index but that was too slow. Then I thought of course I can just only take ranges that start at the start of a coin range. Except for the end where I would need to check the last k possible spaces as an edge case. But when that wasn't producing the right answer I finally realized that we have to check ranges that start at the start of a coin range AND ranges that end at the end of a coin range.
Suppose a grabbing range did not match either a start index or an end index of a coin range. Then, moving it right will change the value by a number x (gaining a number y on the right and losing a number z on the left) and moving it left will change the value by a number -x (gaining a number z on the left and losing a number y on the right). So, the max possible coins can always be grabbed in a way that involves matching either the start or the end, because if it did not match either, you can always make a nondecreasing coin move.
# Approach
1) Sort coins by left index
2) Now that coins are sorted, loop over them to keep track of the cumulative coins at each index bunch. We can use this later to calculate the amount of coins in between two indices in log(m) time where m is the size of coins
3) Loop through coin ranges and calculate how many coins are grabbed when you start the grabbing at the left index of that coin range. Calculate by subtracting the cumulative amount of coins up to but not including the start from the cumulative amount of coins up to and including the end. We use a binary search to add the coins that are "leftover" when the grabbing range contains only part of a coin range.
4) Repeat above except instead of starting at the left index, we now stop at the right index.
5) Return the highest value calculated in steps 3 and 4.
# Complexity
- Time complexity:
$$O(nlogn)$$ Due to sorting the coins vector and doing binary search inside a loop.
- Space complexity:
$$O(n)$$ due to making the cumCoins vector and also sorting, assuming its not in place
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
// Sort coins by li
// Loop thru coins choosing to start at starts and end at the ends, take max
// If youre grabbing is in the middle of a range on both sides, moving one way or
// the other would at least keep the sum the same (if you lose on way, the other way
// you would gain). From this we conclude it is sufficient to check the edges
sort(coins.begin(), coins.end(), comp);
long long ans = 0;
int n = coins.size();
int wholeStart = coins[0][0];
int wholeEnd = coins[n - 1][1];
int coinsIndex = 0;
// The amount of coins accumulated before ith zone
vector<long long> cumCoins;
cumCoins.push_back(0);
// Loop thru to make and calc cum coins to make it easy to calc range coins later (see getCoins)
for(int i = 0; i < coins.size() - 1; i++) {
cumCoins.push_back((long long) coins[i][2] * (coins[i][1] - coins[i][0] + 1) + cumCoins[cumCoins.size() - 1]);
}
// Check start of ranges
for(int i = 0; i < coins.size(); i++) {
int startIndex = coins[i][0];
int endIndex = startIndex + k - 1;
ans = max(ans, getCoinDiff(coins, cumCoins, endIndex, startIndex));
}
// Check end of ranges
for(int i = 0; i < coins.size(); i++) {
int endIndex = coins[i][1];
int startIndex = endIndex - k + 1;
ans = max(ans, getCoinDiff(coins, cumCoins, endIndex, startIndex));
}
return ans;
}
long long getCoinDiff(vector<vector<int>>& coins, vector<long long>& cumCoins, int e, int s) {
return getCoins(coins, cumCoins, e) - getCoins(coins, cumCoins, s - 1);
}
long long getCoins(vector<vector<int>>& coins, vector<long long>& cumCoins, int index) {
int low = 0;
int high = coins.size() - 1;
int latestI = coins.size();
while(low <= high) {
int mid = (low + high) / 2;
if(index > coins[mid][0]) {
latestI = mid;
low = mid + 1;
}
else if(index < coins[mid][0]) {
high = mid - 1;
}
else {
latestI = mid;
break;
}
}
if(latestI == coins.size()) {
return 0;
}
int totalCoverage = min(coins[latestI][1], index) - coins[latestI][0] + 1;
return cumCoins[latestI] + (long long) totalCoverage * coins[latestI][2];
}
static bool comp(vector<int>& a, vector<int>& b) {
return a[0] < b[0];
}
};
``` | 5 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Java | Fixing Start/End - Prefix | Sliding Window | 2 - Approaches | java-fixing-startend-prefix-sliding-wind-08ak | IntuitionTry to Fix the one position(start/end) and other postion will be ((start+k-1)/end-k+1) and for that postion find the index from coins segment and get t | monukumar012 | NORMAL | 2025-01-05T07:50:38.831006+00:00 | 2025-01-05T07:59:43.307389+00:00 | 766 | false | # Intuition
Try to Fix the one position(start/end) and other postion will be ((start+k-1)/end-k+1) and for that postion find the index from coins segment and get the sum between them using prefix
# Approach 1
For Each Coins Segement fixed start and end if **we fixed the start then our end will be start+k-1** and for reqEnd find highest index in coins which start<=reqEnd and vice versa.
# Complexity
- Time complexity: O(N*log(N))
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maximumCoins(int[][] coins, int k) {
int n = n=coins.length;
Arrays.sort(coins, (a, b)->a[0]-b[0]);
long[] prefix = prefix(coins, n);
//System.out.println(Arrays.toString(prefix));
long maxCoins = 0;
for(int i=0;i<n;i++){
int start = coins[i][0], end = coins[i][1];
int reqEnd = start+k-1, reqStart = end-k+1;
// Cost For start to reqEnd(start+k-1);
// Find highest index which l<=reqEnd
int ub = upperBound(coins, n, reqEnd);
if(ub != -1) {
long totoalCoins1 = prefix[ub+1] - prefix[i];
long extraCoins1 = coins[ub][2] * 1l * Math.max(coins[ub][1]-reqEnd, 0);
maxCoins = Math.max(maxCoins, totoalCoins1 - extraCoins1);
}
// Cost For reqStart(end-k+1) to end;
// Find smallest index which h>=reqStart
int lb = lowerBound(coins, n, reqStart);
if(lb < n) {
long totoalCoins2 = prefix[i+1] - prefix[lb];
long extraCoins2 = coins[lb][2] * 1l * Math.max(reqStart-coins[lb][0], 0);
maxCoins = Math.max(maxCoins, totoalCoins2 - extraCoins2);
}
}
return maxCoins;
}
private long[] prefix(int[][] coins, int n){
long[] pre = new long[n+1];
for(int i=0;i<n;i++){
pre[i+1] = pre[i] + coins[i][2]*1l*(coins[i][1]-coins[i][0]+1);
}
return pre;
}
public int lowerBound(int[][] arr, int n, int x) {
int l = 0, h = n - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (arr[m][1] >= x) {
h = m - 1;
} else
l = m + 1;
}
return l;
}
public int upperBound(int[][] arr, int n, int x) {
int l = 0, h = n - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (arr[m][0] <= x) {
l = m + 1;
} else
h = m - 1;
}
return h;
}
}
```
# Approach 2
Try to Pick Every Segment and if the windowSize exceed the k then we have remove segment from starting and before removing calculate answer for fixing start[left] or end[right].
# Complexity
- Time complexity: O(N*log(N))
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maximumCoins(int[][] coins, int k) {
Arrays.sort(coins, (a, b)->a[0]-b[0]);
long maxCoins = 0, totalCoins=0;
int i = 0, n=coins.length;
for(int j=0;j<n;j++){
// end from jth[end] and start from ith[start]
int windowLen = coins[j][1]-coins[i][0]+1;
int jthCoins = coins[j][1]-coins[j][0]+1;
totalCoins += coins[j][2]*1l*jthCoins;
while(i<=j && windowLen>k){
// fixed starting position
int extraCoin = windowLen - k;
if(jthCoins>=extraCoin) {
maxCoins = Math.max(maxCoins, totalCoins - extraCoin*1l*coins[j][2]);
}
// fixed ending position
int ithCoins = coins[i][1] - coins[i][0]+1;
if(ithCoins>=extraCoin) {
maxCoins = Math.max(maxCoins, totalCoins - extraCoin*1l*coins[i][2]);
}
totalCoins -= coins[i][2]*1l*ithCoins;
i++;
if(i<n) {
windowLen = coins[j][1]-coins[i][0]+1;
}
}
maxCoins = Math.max(maxCoins, totalCoins);
if(i>0){
i--;
totalCoins += coins[i][2]*1l*(coins[i][1]-coins[i][0]+1);
}
}
return maxCoins;
}
}
``` | 4 | 0 | ['Two Pointers', 'Sliding Window', 'Prefix Sum', 'Java'] | 1 |
maximum-coins-from-k-consecutive-bags | Sliding Window | sliding-window-by-dplopez-z4cl | ApproachTechniques Used
The code uses several key techniques to solve the problem efficiently while ensuring all possible valid windows are considered:
Sorting | dplopez | NORMAL | 2025-01-05T05:09:43.053122+00:00 | 2025-01-05T05:09:43.053122+00:00 | 128 | false | # Approach
Techniques Used
The code uses several key techniques to solve the problem efficiently while ensuring all possible valid windows are considered:
1. Sorting the Intervals
The intervals are sorted by their start points (l) to process them in ascending order. This helps in iterating over the intervals and calculating the maximum number of coins in a sliding window.
Example
Input Intervals:
```
coins = [[8, 10, 1], [1, 3, 2], [5, 6, 4]];
```
Sorted Intervals:
```
[[1, 3, 2], [5, 6, 4], [8, 10, 1]];
```
By sorting, we ensure that intervals are processed sequentially, which is crucial for the sliding window technique.
---
2. Sliding Window
A sliding window is used to keep track of the total number of coins within a range of size K. For each interval, we:
Add coins from intervals that are fully within the current window.
Consider coins partially from intervals that partially overlap with the window.
Example
Window of Size K = 4:
We want to calculate the number of coins for a window starting at interval [1, 3] (range [1, 4]).
Interval [1, 3, 2]: Fully inside the window.
Coins = (3 − 1 + 1) × 2 = 6.
Interval [5, 6, 4]: Outside the window, ignored.
Result for this window: 6.
---
3. Handling Partial Overlaps
When an interval partially overlaps the window, we calculate how much of it contributes to the total coins by adjusting its range to fit the window boundaries.
Example
Window of Size K = 4:
Window starting at [8, 10] (range [8, 11]).
Interval [8, 10, 1]: Partially inside the window.
Overlap length = min(10, 11) − 8 + 1 = 3.
Coins = 3 × 1 = 3.
Result for this window: 3.
---
4. Reversing the Intervals
After calculating the maximum coins for windows starting at the beginning of intervals, we reverse the intervals by flipping their start and end points. This allows us to compute windows ending at the end of intervals using the same logic.
Example
Original Intervals:
```
[[1, 3, 2], [5, 6, 4], [8, 10, 1]];
```
Reversed Intervals:
```
[[-3, -1, 2], [-6, -5, 4], [-10, -8, 1]];
```
By reversing, we can now consider windows that terminate at the right endpoint of the intervals.
---
The function calculates the maximum coins for:
Windows that start at the beginning of intervals.
Windows that end at the end of intervals.
The final result is the maximum of these two calculations.
---
# Example
Input
```
coins = [[8, 10, 1], [1, 3, 2], [5, 6, 4]];
k = 4;
```
Step 1: Sort the Intervals
```
coins = [[1, 3, 2], [5, 6, 4], [8, 10, 1]];
```
Step 2: Compute Windows Starting at the Beginning
Window [1, 4]:
Coins = 6 + 0 = 6.
Window [5, 8]:
Coins = 4 + 4 = 8.
Window [8, 11]:
Coins = 3 + 0 = 3.
Maximum = 10.
Step 3: Reverse the Intervals
```
coins = [[-3, -1, 2], [-6, -5, 4], [-10, -8, 1]];
```
Step 4: Compute Windows Ending at the End
Window [-3, -6] (equivalent to [1, 3]):
Coins = 6 + 0 = 6.
Window [-5, -8] (equivalent to [5, 8]):
Coins = 4 + 4 = 8.
Window [-8, -11] (equivalent to [8, 11]):
Coins = 3 + 0 = 3.
Maximum = 10.
Step 5: Compare and Return Result
The maximum coins collected is 10.
# Complexity
- Time complexity: O(nlogn)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
- O(1) additional space if in-place modifications are allowed, otherwise O(n) for reversed intervals.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
function maximumCoins(coins, k) {
const n = coins.length;
function solve(intervals) {
intervals.sort((a, b) => a[0] - b[0]); // Ordenar por inicio del intervalo
let ans = 0, window = 0, j = 0;
for (let i = 0; i < intervals.length; i++) {
const [l, r, c] = intervals[i];
while (j + 1 < n && intervals[j + 1][0] < l + k) {
const [lj, rj, cj] = intervals[j];
window += (rj - lj + 1) * cj;
j++;
}
let extra = 0;
if (j < n && intervals[j][0] < l + k) {
const [lj, rj, cj] = intervals[j];
const rightmost = Math.min(l + k - 1, rj);
const length = rightmost - lj + 1;
extra = length * cj;
}
ans = Math.max(ans, window + extra);
window -= (r - l + 1) * c;
}
return ans;
}
let ans = solve(coins);
for (let i = 0; i < coins.length; i++) {
const [l, r, c] = coins[i];
coins[i] = [-r, -l, c];
}
ans = Math.max(ans, solve(coins));
return ans;
}
``` | 4 | 0 | ['JavaScript'] | 0 |
maximum-coins-from-k-consecutive-bags | General templates for sliding on non-overlapping intervals | general-templates-for-sliding-on-non-ove-qdp2 | Use the following functions for sliding window problems having non-overlapping intervals regardless of whether each interval has a cost(weight) or not.CodeCompl | lokeshwar777 | NORMAL | 2025-01-13T17:01:32.950974+00:00 | 2025-01-13T17:14:20.312138+00:00 | 284 | false | Use the following functions for sliding window problems having non-overlapping intervals regardless of whether each interval has a cost(weight) or not.
# Code
```cpp []
#define ll long long
#define cost(x) ((vec[x].size()>2)?vec[x][2]:1)
class Solution {
public:
ll slide(vector<vector<int>>& vec, int k){ // non-overlapping intervals
sort(vec.begin(),vec.end());
ll curr=0,ans=0,n=vec.size(),partial;
for(int i=0,j=0;i<n;++i){
int l=vec[i][0],r=vec[i][1],windowLen=l+k-1;partial=0;
while(j<n&&vec[j][1]<=windowLen)curr+=1LL*cost(j)*(vec[j][1]-vec[j++][0]+1);
if(j<n)partial=1LL*max(0,windowLen-vec[j][0]+1)*cost(j);
ans=max(ans,curr+partial);
// cout<<i<<" "<<j<<" "<<curr<<" "<<partial<<" "<<ans<<endl;
curr-=1LL*(r-l+1)*cost(i);
}
return ans;
}
ll reverseSlide(vector<vector<int>>& vec, int k){ // non-overlapping intervals
sort(vec.begin(),vec.end());
ll curr=0,ans=0,n=vec.size(),partial;
for(int i=n-1,j=n-1;i>=0;--i){
int l=vec[i][0],r=vec[i][1],windowLen=r-k+1;partial=0;
while(j>=0&&windowLen<=vec[j][0])curr+=1LL*cost(j)*(vec[j][1]-vec[j--][0]+1);
if(j>=0)partial=1LL*max(0,vec[j][1]-windowLen+1)*cost(j);
ans=max(ans,curr+partial);
// // cout<<i<<" "<<j<<" "<<curr<<" "<<partial<<" "<<ans<<endl;
curr-=1LL*(r-l+1)*cost(i);
}
return ans;
}
ll maximumCoins(vector<vector<int>>& coins, int k) {
return max(slide(coins,k),reverseSlide(coins,k));
}
};
```
```python3 []
class Solution:
def slide(self,lst,k):
lst.sort()
n=len(lst)
curr=ans=j=0
def cost(x):return lst[x][2] if len(lst[x])>2 else 1
for i in range(n):
l,r=lst[i][0],lst[i][1]
windowLen=l+k-1
while j<n and lst[j][1]<=windowLen:
curr+=cost(j)*(lst[j][1]-lst[j][0]+1)
j+=1
partial=max(0,windowLen-lst[j][0]+1)*cost(j) if j<n else 0
ans=max(ans,curr+partial)
curr-=(r-l+1)*cost(i)
return ans
def reverseSlide(self,lst,k):
lst.sort()
n=len(lst)
j=n-1
curr=ans=0
def cost(x):return lst[x][2] if len(lst[x])>2 else 1
for i in reversed(range(n)):
l,r=lst[i][0],lst[i][1]
windowLen=r-k+1
while j>=0 and windowLen<=lst[j][0]:
curr+=cost(j)*(lst[j][1]-lst[j][0]+1)
j-=1
partial=max(0,lst[j][1]-windowLen+1)*cost(j) if j>=0 else 0
ans=max(ans,curr+partial)
curr-=(r-l+1)*cost(i)
return ans
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
return max(self.slide(coins,k),self.reverseSlide(coins,k))
```
# Complexity
- Time complexity: $$O(nlogn + n)$$ ~ $$O(nlogn)$$
- slide - $$O(nlogn+2*n)$$
- reverseSlide - $$O(nlogn+2*n)$$
- Space complexity: $$O(1)$$
## Bonus point:
**just use the `slide` function** to solve this problem - [2271. Maximum White Tiles Covered by a Carpet](https://leetcode.com/problems/maximum-white-tiles-covered-by-a-carpet/description/) | 3 | 0 | ['Sliding Window', 'Sorting', 'C++', 'Python3'] | 1 |
maximum-coins-from-k-consecutive-bags | An elegant two-pass sliding window solution with O(n log n) time complexity | an-elegant-two-pass-sliding-window-solut-ptvw | Intuition
The problem involves finding a k-length segment on a number line that collects the maximum possible coins from overlapping segments.
Since we need to | sorenramesh868 | NORMAL | 2025-01-08T11:36:33.764328+00:00 | 2025-01-08T11:36:33.764328+00:00 | 140 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
- The problem involves finding a k-length segment on a number line that collects the maximum possible coins from overlapping segments.
- Since we need to consider how segments overlap with our k-length window, we can use a sliding window approach.
- The key insight is that the optimal k-length segment must either start at the beginning of an existing segment or end at the end of an existing segment.
# Approach
<!-- Describe your approach to solving the problem. -->
1. We consider two cases:
- Case 1: The k-length segment starts at the start of an existing segment
- Case 2: The k-length segment ends at the end of an existing segment
2. For Case 1:
- Sort segments by start position
- For each segment start position, consider a k-length window starting there
- Use a sliding window to track segments that overlap with current k-length window
- Handle partial overlaps at window boundaries
3. For Case 2:
- Sort segments by end position
- For each segment end position, consider a k-length window ending there
- Similar sliding window approach but working backwards
- Handle partial overlaps at window boundaries
4. Track the maximum coins possible across all possible window positions
# Complexity
- Time complexity: $$O(n \log n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Sorting operations require O(n log n)
- Each segment is processed at most twice
- Window pointers traverse the array once
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
- Only constant extra space is used for variables (result, currentSum, pointers)
- The sorting is performed in-place on the input array
- No additional data structures are required
- The algorithm maintains a fixed number of variables regardless of input size
- The temporary variables for window calculations use constant space
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
// Sort the segments based on their start positions
sort(coins.begin(), coins.end(), [&](const vector<int>& a, const vector<int>& b) -> bool {
return a[0] < b[0];
});
int n = coins.size();
long long result = 0;
// -------------------------------
// Case 1: k-length segment starts at coins[i][0]
// -------------------------------
long long currentSum1 = 0;
int j1 = 0; // Pointer for sliding window in Case 1
for(auto& segment : coins){
int windowStart = segment[0];
int windowEnd = windowStart + k - 1;
// Add segments that fully lie within [windowStart, windowEnd]
while(j1 < n && coins[j1][1] < windowEnd){
currentSum1 += 1LL * (coins[j1][1] - coins[j1][0] + 1) * coins[j1][2];
j1++;
}
// Add partial overlap if any
long long partial1 = 0;
if(j1 < n && coins[j1][0] <= windowEnd){
partial1 = 1LL * (windowEnd - coins[j1][0] + 1) * coins[j1][2];
}
// Update the result with the current window's total coins
result = max(result, currentSum1 + partial1);
// Remove the contribution of the current segment as the window slides forward
currentSum1 -= 1LL * (segment[1] - segment[0] + 1) * segment[2];
}
// -------------------------------
// Case 2: k-length segment ends at coins[i][1]
// -------------------------------
// Sort the segments based on their end positions for Case 2
sort(coins.begin(), coins.end(), [&](const vector<int>& a, const vector<int>& b) -> bool {
return a[1] < b[1];
});
long long currentSum2 = 0;
int j2 = n - 1; // Pointer for sliding window in Case 2
for(int i = n - 1; i >= 0; i--){
auto& segment = coins[i];
int windowEnd = segment[1];
int windowStart = windowEnd - k + 1;
// Add segments that fully lie within [windowStart, windowEnd]
while(j2 >=0 && coins[j2][0] > windowStart){
currentSum2 += 1LL * (coins[j2][1] - coins[j2][0] + 1) * coins[j2][2];
j2--;
}
// Add partial overlap if any
long long partial2 = 0;
if(j2 >=0 && coins[j2][1] >= windowStart){
partial2 = 1LL * (coins[j2][1] - windowStart + 1) * coins[j2][2];
}
// Update the result with the current window's total coins
result = max(result, currentSum2 + partial2);
// Remove the contribution of the current segment as the window slides backward
currentSum2 -= 1LL * (segment[1] - segment[0] + 1) * segment[2];
}
return result;
}
};
``` | 3 | 0 | ['Sliding Window', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | 2 Sliding windows || O(n) | 2-sliding-windows-on-by-ayush34513-82n5 | IntuitionThe only fear we all have is the window is using partial ranges in left and right. (left and right denoting index of ranges that we are now considering | Ayush34513 | NORMAL | 2025-01-05T04:44:54.040423+00:00 | 2025-01-05T09:02:30.657210+00:00 | 644 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The only fear we all have is the window is using partial ranges in left and right. (left and right denoting index of ranges that we are now considering )
i.e some complete ranges and at right and left end we arre having some partial values of left-1 and right+1 ranges .
How optimally find this fractions !!
If you care fully observe then you would see that we will never be having partial left and right simultaneously .
as either left-1 is providing best value or right+1 is providing best value.
so there were 2 time sliding window we need to apply , one for considering left partial and one time right partial
# Approach
<!-- Describe your approach to solving the problem. -->
To solve the problem, we sort the intervals by their start positions, then use a sliding window approach to calculate the maximum coins that can be collected from a sub-interval of size k. For each interval, we consider it as the starting point of a valid
k-length sub-interval and calculate the total coins from overlapping intervals that fit within this range. We do this process twice: once iterating from left to right and once from right to left, ensuring we consider all possible sub-intervals. The maximum coins collected in either direction is the final answer.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```cpp []
#define ll long long
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(),coins.end());
int n=coins.size();
ll ans=0;
for(ll i=0,j=0,sum=0,l=1,r=k+1;j<n;j++){
l=coins[j][0],r=coins[j][0]+k-1;
while(i<n&&coins[i][1]<=r){
sum+=((ll)coins[i][1]-coins[i][0]+1)*coins[i][2];
i++;
}
int buff=0;
if(i<n){
if(r>=coins[i][0])buff+=(r-coins[i][0]+1)*coins[i][2];
}
ans=max(ans,sum+buff);
sum-=((ll)coins[j][1]-coins[j][0]+1)*coins[j][2];
}
for(ll i=n-1,j=n-1,sum=0;j>=0;j--){
int r=coins[j][1],l=coins[j][1]-k+1;
while(i>=0&&coins[i][0]>=l){
sum+=((ll)coins[i][1]-coins[i][0]+1)*coins[i][2];
// cout<<sum<<endl;
i--;
}
int buff=0;
if(i>=0&&coins[i][1]>=l)buff+=((ll)coins[i][1]-l+1)*coins[i][2];
// cout<<sum<<" "<<buff<<endl;
ans=max(ans,sum+buff);
sum-=((ll)coins[j][1]-coins[j][0]+ 1)*coins[j][2];
}
return ans;
}
};
``` | 3 | 0 | ['Two Pointers', 'Sliding Window', 'C++'] | 3 |
maximum-coins-from-k-consecutive-bags | C++ Bruteforce-sorta + Binary Search | c-bruteforce-sorta-binary-search-by-bram-bf20 | Complexity
Time complexity: O(n∗log(n))
Space complexity: O(n)
Code | bramar2 | NORMAL | 2025-01-05T04:03:22.466419+00:00 | 2025-01-05T04:03:22.466419+00:00 | 734 | false | # Complexity
- Time complexity: $O(n*log(n))$
- Space complexity: $O(n)$
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(), coins.end());
int n = coins.size();
vector pre(n, 0LL);
// pre[i] = prefix sum of the sum of all bags in coins
pre[0] = (long long) (coins[0][1] - coins[0][0] + 1) * coins[0][2];
for(int i = 1; i < n; i++) {
pre[i] = (long long) (coins[i][1] - coins[i][0] + 1) * coins[i][2];
pre[i] += pre[i - 1];
}
set<int> check;
for(auto& c : coins) {
// consider trying to take all bags of C as the first bag and last bag
check.insert(c[0]);
if(c[1] - k + 1 > 0)
check.insert(c[1] - k + 1);
}
check.insert(1);
long long ans = 0;
for(int x : check) {
// bisect for left and right i
int l = 0, r = n-1;
bool found = false; int mostValid = -1;
while(l <= r) {
int m = (l + r) / 2;
if(coins[m][0] <= x && x <= coins[m][1]) {
l = r = m;
found = true;
break;
}else if(x < coins[m][0]) {
r = m - 1;
mostValid = m;
}else if(coins[m][1] < x) {
l = m + 1;
}
}
int firstBag = found ? l : mostValid;
int end = x + k - 1;
l = 0, r = n-1;
found = false, mostValid = -1;
while(l <= r) {
int m = (l + r) / 2;
if(coins[m][0] <= end && end <= coins[m][1]) {
l = r = m;
found = true;
break;
}else if(end < coins[m][0]) {
r = m - 1;
}else if(coins[m][1] < end) {
l = m + 1;
mostValid = m;
}
}
int lastBag = found ? l : mostValid;
if(firstBag == -1 || lastBag == -1) continue;
if(firstBag == lastBag) {
int y = firstBag;
long long sum = (long long) coins[y][2] * (min(coins[y][1], x + k - 1) - max(coins[y][0], x) + 1);
ans = max(ans, sum);
}else {
int range = coins[lastBag][1] - x + 1;
long long midSum = (firstBag + 1 <= lastBag - 1) ? pre[lastBag - 1] - pre[firstBag] : 0;
// firstBag take from x -> r
// lastBag take from l -> x + k - 1
long long sum = 0;
sum += 1LL * (coins[firstBag][1] - max(x, coins[firstBag][0]) + 1) * coins[firstBag][2];
sum += 1LL * (min(x + k - 1, coins[lastBag][1]) - coins[lastBag][0] + 1) * coins[lastBag][2];
sum += midSum;
ans = max(ans, sum);
}
}
return ans;
}
};
``` | 3 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | AVS | avs-by-vishal1431-necq | null | Vishal1431 | NORMAL | 2025-01-06T17:50:15.324067+00:00 | 2025-01-06T17:50:15.324067+00:00 | 51 | false |
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
long long ret{0};
sort(coins.begin(), coins.end());
long long sum = 0;
for (int i = 0, j = 0; i < coins.size(); ++i) {
int lim = coins[i][0] + k;
for (; j < coins.size() && coins[j][1] < lim; ++j) {
sum += (long long)(coins[j][1] - coins[j][0] + 1) * coins[j][2];
}
int extra = 0;
if (j < coins.size() && coins[j][0] < lim) {
extra = (long long)(lim - coins[j][0]) * coins[j][2];
}
ret = max(ret, sum + extra);
if (j == coins.size())
break;
sum -= (long long)(coins[i][1] - coins[i][0] + 1) * coins[i][2];
}
sum = 0;
for (int i = coins.size() - 1, j = i; i >= 0; --i) {
int lim = coins[i][1] - k;
for (; j >= 0 && coins[j][0] > lim; --j) {
sum += (long long)(coins[j][1] - coins[j][0] + 1) * coins[j][2];
}
int extra = 0;
if (j >= 0 && coins[j][1] > lim) {
extra = (long long)(coins[j][1] - lim) * coins[j][2];
}
ret = max(ret, sum + extra);
if (j < 0)
break;
sum -= (long long)(coins[i][1] - coins[i][0] + 1) * coins[i][2];
}
return ret;
}
};
``` | 2 | 0 | ['Array', 'Greedy', 'Sliding Window', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Well commented code. Sliding window approach | Python | well-commented-code-sliding-window-appro-hhey | Code | tailtit | NORMAL | 2025-01-06T07:08:07.079167+00:00 | 2025-01-06T07:08:07.079167+00:00 | 188 | false | # Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
ans = 0
s = 0
coins.sort() # Sort the coins by the start of each range
j = 0
for i in range(len(coins)):
l, r, c = coins[i] # Extract the left, right, and coin count for the current range
# Add the coins from the current range [l, r] to the total sum
s += (r - l + 1) * c
# Adjust the window from the left side (j) to maintain the size <= k
while r - k + 1 > coins[j][1]:
if coins[j][0] + k - 1 >= l:
# Calculate the new result considering the remaining coins
ans = max(ans, s - (r - (coins[j][0] + k - 1)) * c)
# Subtract the current range from the sum and move `j` to the next
s -= (coins[j][1] - coins[j][0] + 1) * coins[j][2]
j += 1
# Now, process the current range with respect to the window [j, i]
if coins[j][0] + k - 1 >= r:
ans = max(ans, s) # If we can fit all the coins, take the sum
else:
# Adjust the result considering the overlap with the current range
ans = max(ans, s - (r - k + 1 - coins[j][0]) * coins[j][2])
if coins[j][0] + k - 1 >= l:
ans = max(ans, s - (r - (coins[j][0] + k - 1)) * c)
return ans
``` | 2 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Binary Search || Beats 100.00% | binary-search-beats-10000-by-ahmedsayed1-fec1 | ApproachAn optimal starting position for k consecutive bags will be either li or ri - k + 1.Code | AhmedSayed1 | NORMAL | 2025-01-06T00:53:52.459513+00:00 | 2025-01-06T00:53:52.459513+00:00 | 246 | false | # Approach
<h3>An optimal starting position for k consecutive bags will be either li or ri - k + 1.</h3>
# Code
```cpp []
#define ll long long
class Solution {
public:
long long maximumCoins(vector<vector<int>>& x, int k) {
ll ans = 0, n = x.size();
x.insert(x.begin(), {0});
sort(x.begin(), x.end());
vector<ll>pre(n + 1);
for(int i = 1; i <= n; i++)
pre[i] = pre[i - 1] + (x[i][1] - x[i][0] + 1) * (ll)x[i][2];
for(int i = 1; i <= n; i++){
int l = i + 1 , r = n, m, o = x[i][0] + k - 1;
while(l <= r){
m = l + r >> 1;
(o >= x[m][0] ? l = m + 1 : r = m - 1);
}
if(o >= x[r][1]) // if the point is covers all the intervals
ans = max(ans, pre[r] - pre[i - 1]);
else // if the point is not covers all the intervals
ans = max(ans,pre[r-1]-pre[i-1] + (o - x[r][0] + 1) * (ll)x[r][2]);
l = 1 , r = i - 1, o = x[i][1] - k + 1;
while(l <= r){
m = l + r >> 1;
(o <= x[m][1] ? r = m - 1 : l = m + 1);
}
if(o <= x[l][0]) // if the point is covers all the intervals
ans = max(ans, pre[i] - pre[l - 1]);
else // if the point is not covers all the intervals
ans = max(ans, pre[i] - pre[l] + (x[l][1] - o + 1) * (ll)x[l][2]);
}
return ans;
}
};
```
 | 2 | 0 | ['Binary Search', 'Greedy', 'Prefix Sum', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Maximum Coins From K Consecutive Bags | Sliding Window | C++ | maximum-coins-from-k-consecutive-bags-sl-uprn | Code | JeetuGupta | NORMAL | 2025-01-05T10:00:59.022261+00:00 | 2025-01-05T10:00:59.022261+00:00 | 224 | false |
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(), coins.end());
vector<vector<int>> a;
int start = coins[0][0];
if(start > 1){
a.push_back({1, start - 1, 0});
}
int last = start - 1;
for(int i = 0; i<coins.size(); i++){
int cur = coins[i][0];
if(cur != last + 1){
a.push_back({last + 1, cur - 1, 0});
}
a.push_back({cur, coins[i][1], coins[i][2]});
last = coins[i][1];
}
start = a.back()[1];
last = 1e9;
if(start < last){
a.push_back({start + 1, last, 0});
}
long long ans = 0;
int ind = 0, total = 0, till = 0;
for(int i = 0; i<a.size() && total < k; i++){
int size = a[i][1] - a[i][0] + 1;
if(size + total < k){
ans += ((long long)size * (long long)a[i][2]);
total += size;
}else{
int need = k - total;
ans += ((long long)need * (long long)a[i][2]);
total += need;
}
ind = i;
}
till = total;
int from = 0, si = 0;
long long cur = ans;
for(int i = ind; i<a.size(); i++){
int size = a[i][1] - till;
if(size == 0) continue;
else{
update(a, si, i, from, till, ans, cur);
}
}
return ans;
}
void update(vector<vector<int>> &a, int &s, int &e, int &from, int &till, long long &ans, long long &cur){
int size = a[e][1] - till;
while(size > 0){
int mini = min(size, a[s][1] - from);
cur -= ((long long)a[s][2] * (long long)mini);
cur += ((long long)a[e][2] * (long long)mini);
size -= mini;
from += mini;
till += mini;
ans = max(ans, cur);
if(from >= a[s][1]) s++;
if(s == e){
from = a[e][1] - (till - from);
till = a[e][1];
size = 0;
}
}
}
};
``` | 2 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Sliding window. Optimal solution | sliding-window-by-xxxxkav-h1vz | null | xxxxkav | NORMAL | 2025-01-28T21:25:52.453539+00:00 | 2025-01-28T22:55:02.154468+00:00 | 90 | false | ```
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
coins.sort(key = itemgetter(0))
i, total, ans, n = 0, 0, 0, len(coins)
l0, r0, c0 = coins[0]
for l, r, c in coins:
while i < n and r - coins[i][0] + 1 >= k:
l0, r0, c0 = coins[i]
ans = max(total + max(k + l0 - l, 0) * c, ans)
total -= (r0 - l0 + 1) * c0
i += 1
total += (r - l + 1) * c
if i < n and coins[i][0] != l0:
ans = max(total + max(k + r0 - r, 0) * c0, ans)
return max(ans, total)
``` | 1 | 0 | ['Sliding Window', 'Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | For my reference... | for-my-reference-by-user8034yc-wgz1 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | user8034Yc | NORMAL | 2025-01-13T09:20:57.578989+00:00 | 2025-01-13T09:20:57.578989+00:00 | 28 | false | # Intuition
<!-- sort the coins and consider window (L,R C) that are valid (meaning the window size is < k). If added new range of L to R cause window invalid, consider the total obtain by including a much as possible before remove coins from start of window. -->
# Approach
<!-- 1) Sort the coins to obtain the ascending order.
2) Main Loop (extract the left, right and coin values, compute the total number of coins in the current range and adds it into total_accum_points):
for j in range(n):
left, right, coin = coins[j]
total_accum_coins += coin * (right-left+1)
3) Inner While Loop (This inner loop check currange range, which defined by coins[j] and coins[i] exceed k or not. If k is exceeded, it compute the extra, which is the amount by which range exceeds k. Then it update res to be the maximum of its current value with the total_accumulated coins minus the excess coins that cannot be counted, ie the maximum value computed by range of valid k):
while coins[j][1] - coins[i][0] > k-1:
extra = coins[j][1] - coins[i][0] + 1 - k
res = max(res, total_accum_coins - extra * coin)
4) Adjusting the left boundary(retrieve the left, right, coin values for current index i , if the range of the current coin at i exceeds the extra, it reduces the total accumulated coins by the excess and moves the left pointer of the range to the right. If range does not exceed extra, if not exceed extra, it substracts all coins from that range and move left boundary) :
left1, right1, coin1 = coins[i]
if right1 - left1 + 1 > extra:
total_accum_coins -= coin1 * extra
coins[i][0] += extra
else:
total_accum_coins -= coin1 * (right1 - left1 + 1)
i += 1
-->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
coins.sort()
n = len(coins)
total_accum_coins = 0
i = 0
res = 0
for j in range(n):
left, right, coin = coins[j]
total_accum_coins += coin * (right-left+1)
while coins[j][1] - coins[i][0] > k-1:
extra = coins[j][1] - coins[i][0] +1-k
res = max(res, total_accum_coins-extra *coin)
left1, right1, coin1 = coins[i]
if right1-left1 +1 >extra:
total_accum_coins -= coin1 *extra
coins[i][0] +=extra
else:
total_accum_coins -= coin1 * (right1-left1 +1)
i+=1
res = max(res, total_accum_coins)
return res
``` | 1 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | C++ || Sorting + Sliding Window | c-sorting-sliding-window-by-mr_mv-uyzz | Complexity
Time complexity: O(N∗Log(N))
O(N∗Log(N)) For sorting
O(3∗N) For calculating maximum coins
Total : O(N∗Log(N))+O(3∗N)≈O(N∗Log(N))
Space compl | Mr_mv | NORMAL | 2025-01-09T08:57:03.893477+00:00 | 2025-01-09T09:08:53.488084+00:00 | 179 | false | # Complexity
- Time complexity: $$O(N*Log(N))$$
- - $$O(N*Log(N))$$ For sorting
- - $$O(3*N)$$ For calculating maximum coins
Total : $$O(N*Log(N)) + O(3*N) ≈ O(N*Log(N)) $$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
void removeFromBegining(vector<vector<int>>& coins, int& sI,
long long& curCoins, int& k, int& i) {
if (sI == i) {
curCoins = 0;
sI++;
i++;
return;
}
curCoins -= (long long)(coins[sI][1] - coins[sI][0] + 1) * coins[sI][2];
sI++;
}
long long helper(vector<vector<int>>& coins, int k) {
int startIndex = 0;
long long curCoins = 0;
long long ans = 0;
int i = 0;
while (i < coins.size()) {
int s = coins[i][0];
int e = coins[i][1];
int limit = coins[startIndex][0] + k;
if (e <= limit) {
// If the current range is fully within limit, include it entirely
curCoins += ((long long)(e - s + 1) * coins[i][2]);
ans = max(ans, curCoins);
i++;
} else {
// If the current range exceeds the limit, take part of it
ans = max(ans, curCoins + (long long)max(0, limit - s + 1) * coins[i][2]);
// remove range from the begining
removeFromBegining(coins, startIndex, curCoins, k, i);
}
}
return ans;
}
long long maximumCoins(vector<vector<int>>& coins, int k) {
k--;
sort(coins.begin(), coins.end());
// Calculate maximum coins from left to right
long long ans = helper(coins, k);
// reverse the coins array and range for each coins array element
reverse(coins.begin(), coins.end());
int maxi = coins[0][1];
for (int i = 0; i < coins.size(); i++) {
int a = maxi - coins[i][0];
int b = maxi - coins[i][1];
coins[i][0] = b;
coins[i][1] = a;
}
// Calcuate again maximum coins with the reversed range
ans = max(ans, helper(coins, k));
return ans;
}
};
``` | 1 | 0 | ['Array', 'Greedy', 'Sliding Window', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Python Two Pointers | python-two-pointers-by-antrixm-fecy | IntuitionEither start or end of the segment aligns with the start or end of any one interval respectively.Start from the interval which aligns and keep on addin | antrixm | NORMAL | 2025-01-07T05:24:56.452360+00:00 | 2025-01-07T05:24:56.452360+00:00 | 44 | false | # Intuition
Either start or end of the segment aligns with the start or end of any one interval respectively.
Start from the interval which aligns and keep on adding intervals if they are fully in the range and at last, add the partial interval. Do the same in the reversed order too.
# Complexity
- Time complexity:
O(nlogn)
- Space complexity:
Space taken by the sorting algorithm.
# Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
coins.sort(key = lambda coin : coin[0])
ans = 0
curr = 0
#Start from first, start of segment aligns with start of interval
j = 0
for i, (l, r, c) in enumerate(coins):
#Entire interval falls in range
while j < len(coins) and coins[j][1] < l + k:
curr += (coins[j][1] - coins[j][0] + 1) * coins[j][2]
j += 1
#Partial interval falls in range
extra = 0
if j < len(coins) and coins[j][0] < l + k:
extra = (l + k - coins[j][0]) * coins[j][2]
ans = max(ans, curr + extra)
curr -= (r - l + 1) * c
#Start from end, end of segment aligns with end of interval
curr = 0
j = len(coins) - 1
for i in range(len(coins) - 1, -1, -1):
l, r, c = coins[i]
#Entire interval falls in range
while j >= 0 and coins[j][0] > r - k:
curr += (coins[j][1] - coins[j][0] + 1) * coins[j][2]
j -= 1
#Partial interval falls in range
extra = 0
if j >= 0 and coins[j][1] > r - k:
extra = (coins[j][1] - (r - k)) * coins[j][2]
ans = max(ans, curr + extra)
curr -= (r - l + 1) * c
return ans
``` | 1 | 0 | ['Two Pointers', 'Sorting', 'Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Simple Solution - Sliding window [100% runtime] | simple-solution-sliding-window-100-runti-of39 | ApproachIn a subarray, if you have the option to choose between two elements, you would naturally shift the window towards the bag with the maximum weight and a | risky_coder | NORMAL | 2025-01-05T18:24:39.234250+00:00 | 2025-01-05T18:24:39.234250+00:00 | 140 | false | # Approach
In a subarray, if you have the option to choose between two elements, you would naturally shift the window towards the bag with the maximum weight and aim to select elements from that bag.
Therefore, consider all possible starting bags for the subarray in both the forward and reverse arrays.
# Complexity
- Time complexity: O(n)
- Space complexity: S(1)
# Code
```cpp []
class Solution {
public:
long long solve(vector<vector<int>>& coins, int k, bool flip) {
int n = coins.size();
long long cur = 0, len = 0, ans = 0, taken = 0;
int i = 0, j = 0;
while (i < n) {
long long l = coins[i][0], r = coins[i][1], c = coins[i][2];
cur += (r - l + 1) * c;
len += r - l + 1;
if (i > 0) {
if (flip) {
len += coins[i - 1][0] - r - 1;
} else {
len += l - coins[i - 1][1] - 1;
}
}
while (len > k) {
long long l1 = coins[j][0], r1 = coins[j][1], c1 = coins[j][2];
long long remain = r1 - l1 + 1 - taken;
long long mn = min(len - k, remain);
len -= mn;
cur -= mn * c1;
if (mn == remain) {
if (flip) {
len -= coins[j][0] - coins[j + 1][1] - 1;
} else {
len -= coins[j + 1][0] - coins[j][1] - 1;
}
taken = 0;
j++;
} else {
taken += mn;
}
}
ans = max(ans, cur);
i++;
}
return ans;
}
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(), coins.end());
bool flip = false;
long long ans = solve(coins, k, flip);
reverse(coins.begin(), coins.end());
ans = max(ans, solve(coins, k, flip^1));
return ans;
}
};
``` | 1 | 0 | ['Two Pointers', 'Greedy', 'Sliding Window', 'Sorting', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | find Max fromm k consecutive bags | find-max-fromm-k-consecutive-bags-by-sha-i6kp | IntuitionAnalyse that it is better to take start point as either start of interval or end of intervalApproachsort to ensure the intervals are sequential in natu | shashankpant | NORMAL | 2025-01-05T12:39:54.215672+00:00 | 2025-01-05T12:39:54.215672+00:00 | 71 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Analyse that it is better to take start point as either start of interval or end of interval
# Approach
<!-- Describe your approach to solving the problem. -->
sort to ensure the intervals are sequential in nature
sliding window once form i=0 and once from back i=n-1;
# Complexity
- Time complexity:O(nlogn)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define ll long long
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
ll n = coins.size();
sort(coins.begin(), coins.end());
ll ans = 0, sum = 0;
for(ll i = 0, j = 0; i < n; i++) {
ll endingPoint = coins[i][0] + k - 1;
while(j < n && coins[j][1] <= endingPoint) {
ll intervalStart = coins[j][0];
ll intervalEnd = coins[j][1];
ll score = coins[j][2];
sum += (intervalEnd - intervalStart + 1) * score;
j++;
}
ll partialSum;
if(j <= n) {
if(j < n) {
ll intervalStart = coins[j][0];
ll intervalEnd = coins[j][1];
ll score = coins[j][2];
partialSum = max(0LL, endingPoint - intervalStart + 1) * score;
sum += partialSum;
}
ans = max(ans, sum);
if(j < n) sum -= partialSum;
}
ll currentIntervalStart = coins[i][0];
ll currentIntervalEnd = coins[i][1];
ll currentIntervalScore = coins[i][2];
sum -= (currentIntervalEnd - currentIntervalStart + 1) * currentIntervalScore;
}
cout<<sum<<endl;
// Backward pass (same changes as forward pass)
sum = 0;
for(ll i = n-1, j = n-1; i >= 0; i--) {
ll endingPoint = coins[i][1] - k + 1;
//adding contribution of full interval till its possible to do so
while(j >= 0 && coins[j][0] > endingPoint) {
ll intervalStart = coins[j][0];
ll intervalEnd = coins[j][1];
ll score = coins[j][2];
sum += (intervalEnd - intervalStart + 1) * score;
j--;
}
//adding partial sum from the next interval,in case we cant add full interval
ll partialSum;
if(j >= -1) {
if(j >= 0) {
ll intervalStart = coins[j][0];
ll intervalEnd = coins[j][1];
ll score = coins[j][2];
partialSum = max(0LL, intervalEnd - endingPoint + 1) * score;
sum += partialSum;
}
ans = max(ans, sum);
if(j >= 0) sum -= partialSum;
}
//removing the contribution of current start interval before going to next interval start point
ll currentIntervalStart = coins[i][0];
ll currentIntervalEnd = coins[i][1];
ll currentIntervalScore = coins[i][2];
sum -= (currentIntervalEnd - currentIntervalStart + 1) * currentIntervalScore;
}
return ans;
}
};
``` | 1 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | O(n) and O(1) space 2 sliding windows solution in 1 pass | on-and-o1-space-2-sliding-windows-soluti-jfri | IntuitionThe problem gives the hint of sliding window based on that once {l,r} is sorted, any range that lies beyond r, will not have any index to the currentLe | 01DP | NORMAL | 2025-01-05T10:03:00.142564+00:00 | 2025-01-05T10:03:00.142564+00:00 | 60 | false | # Intuition
The problem gives the hint of sliding window based on that once {l,r} is sorted, any range that lies beyond r, will not have any index to the currentLeft, where currentLeft is the leftmost index one can pick to satisfy the range till r.
# Approach
In addition to the above sliding window idea, we need to consider that we can have the current range in 2 ways
1. Have the range starting from l and extending till l + k - 1
2. Have the range ending at r and starting from r - k + 1
Thus, we need 2 sliding windows, one to capture the ranges starting from l, the other to capture ranges ending at l.
# Complexity
- Time complexity:
**O(n)**
- Space complexity:
**O(1)**
# Code
```cpp []
typedef long long ll;
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
ll res = 0;
sort(coins.begin(), coins.end());
ll right = 0, left = 0;
ll curr = 0;
ll curright = 0;
ll total = 0;
for(ll i = 0; i < coins.size(); i++){
ll l = coins[i][0], r = coins[i][1];
ll rightBoundary = l + k - 1, leftBoundary = r - k + 1;
total += (r - l + 1LL) * coins[i][2];
right = max(i, right);
while(right < coins.size() && rightBoundary >= coins[right][0]){
if(rightBoundary <= coins[right][1]){
ll val = (rightBoundary - coins[right][0] + 1) * coins[right][2];
res = max(res, curright + val);
break;
}
else
curright += (1LL * coins[right][1] - coins[right][0] + 1) * coins[right][2];
right++;
res = max(res, curright);
}
while(leftBoundary > coins[left][1]){
total -= (coins[left][1] - coins[left][0] + 1LL) * coins[left][2];
left++;
}
if(coins[left][0] <= leftBoundary){
ll val = (leftBoundary - coins[left][0]) * coins[left][2];
res = max(res, total - val);
}
else
res = max(res, total);
//cout << curright << " " << total << endl;
if(rightBoundary > r)
curright -= (r - l + 1) * coins[i][2];
}
return res;
}
};
``` | 1 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Maximum Coins Collection from Intervals with Fixed Subarray Size | maximum-coins-collection-from-intervals-rlcr5 | IntuitionTo solve the problem of maximizing the number of coins collected from given intervals with a fixed size k, we can leverage sorting, prefix sums, and bi | rthakur2712 | NORMAL | 2025-01-05T09:23:31.612533+00:00 | 2025-01-05T09:23:31.612533+00:00 | 45 | false | ### Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To solve the problem of maximizing the number of coins collected from given intervals with a fixed size `k`, we can leverage sorting, prefix sums, and binary search. Sorting helps structure the intervals in a logical order, prefix sums allow efficient calculation of cumulative sums, and binary search helps identify relevant intervals for computation quickly.
### Approach
<!-- Describe your approach to solving the problem. -->
1. **Sort Intervals**:
Sort the intervals based on their starting points to ensure overlapping intervals are grouped logically.
2. **Prefix Sum Array**:
Compute a prefix sum array where each element holds the cumulative sum of coins up to that interval.
3. **Calculate Maximum Coins from Start Points**:
- For each interval, calculate the start (`start`) and end (`end = start + k - 1`) of the subarray.
- Use `upper_bound` to find the index of the last interval whose start point lies within the range `[start, end]`.
- Use the prefix sum array to calculate the contribution of fully covered intervals.
- Add the contribution of the partially overlapping interval.
4. **Calculate Maximum Coins from End Points**:
- Repeat the same process but start from the end of each interval (`end`) and calculate the start (`start = end - k + 1`) of the subarray.
- Use `lower_bound` to find the first interval whose end point lies within the range `[start, end]`.
5. **Update Maximum**:
Keep track of the maximum coins collected during both iterations.
---
### Complexity
- **Time complexity**:
- Sorting the intervals takes $$O(n \log n)$$.
- Calculating prefix sums and performing binary searches for each interval takes $$O(n \log n)$$.
Overall time complexity is $$O(n \log n)$$.
- **Space complexity**:
- Prefix sum array and auxiliary arrays for starts and ends take $$O(n)$$.
Space complexity is $$O(n)$$.
---
### Code
```cpp
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
long long n = (coins.size());
long long maxi = -1e9;
// Creating the prefix array
vector<long long> pref(n + 1, 0);
vector<long long> start_arr;
vector<long long> end_arr;
long long sum = 0;
// Sort intervals by starting points
sort(coins.begin(), coins.end());
for (long long i = 0; i < n; i++) {
pref[i] = sum;
sum += coins[i][2] * 1LL * (coins[i][1] - coins[i][0] + 1);
}
pref[n] = sum;
for (long long i = 0; i < n; i++) {
start_arr.push_back(coins[i][0]);
end_arr.push_back(coins[i][1]);
}
// Starting from each start point
for (long long i = 0; i < n; i++) {
long long ans = 0;
long long start = coins[i][0];
long long end = start + k - 1;
auto ind = upper_bound(start_arr.begin(), start_arr.end(), end) - start_arr.begin() - 1;
ans += (pref[ind] - pref[i]);
ans += (min(coins[ind][1], int(end)) - coins[ind][0] + 1) * 1LL * coins[ind][2];
maxi = max(maxi, ans);
}
// Starting from each end point
for (long long i = n - 1; i >= 0; i--) {
long long ans = 0;
long long start = coins[i][1];
long long end = start - k + 1;
auto ind = lower_bound(end_arr.begin(), end_arr.end(), end) - end_arr.begin();
ans += pref[i + 1] - pref[ind + 1];
ans += (coins[ind][1] + 1 - max(coins[ind][0], int(end))) * 1LL * coins[ind][2];
maxi = max(maxi, ans);
}
return maxi;
}
};
``` | 1 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Java | Fixing Start/End - Prefix | Sliding Window | 2 - Approaches | java-fixing-startend-prefix-sliding-wind-60v1 | IntuitionTry to Fix the one position(start/end) and other postion will be ((start+k-1)/end-k+1) and for the postion find the index from coins segment and get th | monukumar012 | NORMAL | 2025-01-05T07:50:33.703614+00:00 | 2025-01-05T07:50:33.703614+00:00 | 143 | false | # Intuition
Try to Fix the one position(start/end) and other postion will be ((start+k-1)/end-k+1) and for the postion find the index from coins segment and get the sum between them using prefix
# Approach 1
For Each Coins Segement fixed start and end if **we fixed the start then our end will be start+k-1** and for reqEnd find highest index in coins which start<=reqEnd and vice versa.
# Complexity
- Time complexity: O(N*log(N))
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maximumCoins(int[][] coins, int k) {
int n = n=coins.length;
Arrays.sort(coins, (a, b)->a[0]-b[0]);
long[] prefix = prefix(coins, n);
//System.out.println(Arrays.toString(prefix));
long maxCoins = 0;
for(int i=0;i<n;i++){
int start = coins[i][0], end = coins[i][1];
int reqEnd = start+k-1, reqStart = end-k+1;
// Cost For start to reqEnd(start+k-1);
// Find highest index which l<=reqEnd
int ub = upperBound(coins, n, reqEnd);
if(ub != -1) {
long totoalCoins1 = prefix[ub+1] - prefix[i];
long extraCoins1 = coins[ub][2] * 1l * Math.max(coins[ub][1]-reqEnd, 0);
maxCoins = Math.max(maxCoins, totoalCoins1 - extraCoins1);
}
// Cost For reqStart(end-k+1) to end;
// Find smallest index which h>=reqStart
int lb = lowerBound(coins, n, reqStart);
if(lb < n) {
long totoalCoins2 = prefix[i+1] - prefix[lb];
long extraCoins2 = coins[lb][2] * 1l * Math.max(reqStart-coins[lb][0], 0);
maxCoins = Math.max(maxCoins, totoalCoins2 - extraCoins2);
}
}
return maxCoins;
}
private long[] prefix(int[][] coins, int n){
long[] pre = new long[n+1];
for(int i=0;i<n;i++){
pre[i+1] = pre[i] + coins[i][2]*1l*(coins[i][1]-coins[i][0]+1);
}
return pre;
}
public int lowerBound(int[][] arr, int n, int x) {
int l = 0, h = n - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (arr[m][1] >= x) {
h = m - 1;
} else
l = m + 1;
}
return l;
}
public int upperBound(int[][] arr, int n, int x) {
int l = 0, h = n - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (arr[m][0] <= x) {
l = m + 1;
} else
h = m - 1;
}
return h;
}
}
```
# Approach 2
Try to Pick Every Segment and if the windowSize exceed the k then we have remove segment from starting and before removing calculate answer for fixing start[left] or end[right].
# Complexity
- Time complexity: O(N*log(N))
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maximumCoins(int[][] coins, int k) {
Arrays.sort(coins, (a, b)->a[0]-b[0]);
long maxCoins = 0, totalCoins=0;
int i = 0, n=coins.length;
for(int j=0;j<n;j++){
// end from jth[end] and start from ith[start]
int windowLen = coins[j][1]-coins[i][0]+1;
int jthCoins = coins[j][1]-coins[j][0]+1;
totalCoins += coins[j][2]*1l*jthCoins;
while(i<=j && windowLen>k){
// fixed starting position
int extraCoin = windowLen - k;
if(jthCoins>=extraCoin) {
maxCoins = Math.max(maxCoins, totalCoins - extraCoin*1l*coins[j][2]);
}
// fixed ending position
int ithCoins = coins[i][1] - coins[i][0]+1;
if(ithCoins>=extraCoin) {
maxCoins = Math.max(maxCoins, totalCoins - extraCoin*1l*coins[i][2]);
}
totalCoins -= coins[i][2]*1l*ithCoins;
i++;
if(i<n) {
windowLen = coins[j][1]-coins[i][0]+1;
}
}
maxCoins = Math.max(maxCoins, totalCoins);
if(i>0){
i--;
totalCoins += coins[i][2]*1l*(coins[i][1]-coins[i][0]+1);
}
}
return maxCoins;
}
}
``` | 1 | 0 | ['Two Pointers', 'Sliding Window', 'Prefix Sum', 'Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Python - Binary Search with Prefix Sums [TC: O(n*log(n)) SC: O(n)] | python-binary-search-with-prefix-sums-tc-gppd | Complexity
Time complexity: O(n∗log(n))
Space complexity: O(n)
Code | alexpods | NORMAL | 2025-01-05T04:04:46.585396+00:00 | 2025-01-05T04:04:46.585396+00:00 | 183 | false | # Complexity
- Time complexity: $$O(n*log(n))$$
- Space complexity: $$O(n)$$
# Code
```python3 []
class Solution(object):
def maximumCoins(self, coins, k):
coins.sort(key=lambda x: x[0])
xx = [-int(1e10)]
cc = [0]
ss = 0
for l,r,c in coins:
xx += [l]
cc += [ss]
ss += (r - l + 1) * c
xx += [r+1]
cc += [ss]
xx += [int(1e10)]
cc += [ss]
def left_sum(i):
j = bisect_left(xx, xx[i] - k)
x1 = xx[i]
x2 = xx[j]
x3 = xx[j-1]
c1 = cc[i]
c2 = cc[j]
c3 = cc[j-1]
xd = max(0, k - (x1 - x2))
cd = (c2 - c3) // (x2 - x3)
return (c1 - c2) + xd*cd
def right_sum(i):
j = bisect_left(xx, xx[i] + k)
x1 = xx[i]
x2 = xx[j-1]
x3 = xx[j]
c1 = cc[i]
c2 = cc[j-1]
c3 = cc[j]
xd = max(0, k - (x2 - x1))
cd = (c3 - c2) // (x3 - x2)
return (c2 - c1) + xd*cd
res = 0
for i in range(1,len(xx)-1):
res = max(res, left_sum(i), right_sum(i))
return res
``` | 1 | 0 | ['Binary Search', 'Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Sliding window with a lot of corner cases | sliding-window-with-a-lot-of-corner-case-3jfw | IntuitionConstraints won't let us slide the whole coordinate line. Let's slide intervals instead.ApproachFirst, sort the intervals to process them in order.We h | whoawhoawhoa | NORMAL | 2025-01-05T04:03:14.941873+00:00 | 2025-01-05T04:09:20.830863+00:00 | 658 | false | # Intuition
Constraints won't let us slide the whole coordinate line. Let's slide intervals instead.
# Approach
First, sort the intervals to process them in order.
We have 5 different options in general.
1. Length of an interval is more than `k`.
2. Current window length is less than `k`, but we can fill it with current interval to be equal to `k`.
3. After length of the window extended `k` we can throw leftmost intervals and `k` can be equal to window length.
4. After removal window can become less than `k` in length. We can pick a part of next to leftmost interval.
5. Or we can pick the whole next to leftmost interval and part of current rightmost.
Carefully calculating all these cases - and voila!
# Complexity
- Time complexity:
$$O(n*log(n))$$
- Space complexity:
$$O(1)$$
# Code
```java []
class Solution {
public long maximumCoins(int[][] coins, int k) {
Arrays.sort(coins, (a, b) -> Integer.compare(a[0], b[0]));
long max = 0, curr = 0;
int start = 0;
for (int i = 0; i < coins.length; i++) {
int[] c = coins[i];
int len = c[1] - c[0] + 1, window = c[0] - coins[start][0];
if (len >= k) {
long sum = k * (long) c[2];
max = Math.max(max, sum);
}
if (k >= window && k <= window + len) { // fill to the right
long rSum = curr + (k - window) * (long) c[2];
max = Math.max(max, rSum);
}
// swallow
curr = curr + len * (long) c[2];
window += len;
while (start < i && window > k) {
len = coins[start][1] - coins[start][0] + 1;
long old = len * (long) coins[start][2];
start++;
window = c[1] + 1 - coins[start][0];
curr = curr - old;
}
if (window <= k) {
max = Math.max(curr, max);
}
if (start < i && window == k) { // no need to keep
len = coins[start][1] - coins[start][0] + 1;
long old = len * (long) coins[start][2];
start++;
window = c[1] + 1 - coins[start][0];
curr = curr - old;
} else if (window < k && start != 0 && start <= i) { // can extend back
len = coins[start][0] - coins[start - 1][1] - 1;
if (window + len < k) {
long lSum = curr + (k - window - len) * (long) coins[start - 1][2];
max = Math.max(max, lSum);
}
// and if we swallow left
window = c[0] - coins[start - 1][0];
len = c[1] - c[0] + 1;
if (k >= window && k <= window + len) {
long rSum = curr - (len - k + window) * (long) c[2] + (coins[start - 1][1] - coins[start - 1][0] + 1) * (long) coins[start - 1][2];
max = Math.max(max, rSum);
}
}
}
return max;
}
}
``` | 1 | 0 | ['Sliding Window', 'Line Sweep', 'Sorting', 'Java'] | 0 |
maximum-coins-from-k-consecutive-bags | [C++] binary search, only consider start and end | binary-search-c-by-ziang142019-ficn | Code | ziang142019 | NORMAL | 2025-01-05T04:03:10.832442+00:00 | 2025-01-05T04:08:12.323900+00:00 | 298 | false |
# Code
```cpp []
#define FOR(i,a,b) for(int i = a; i < b.size(); ++i)
#define F(i,a,b) for(int i = a; i < b; ++i)
#define F0(i,b) for(int i = 0; i< b.size();++i)
#define BE(a) a.begin(), a.end()
#define __S(a) a.size()
#define pb(a) push_back(a)
#define pr(a) cout << a << " ";
typedef long long ll;
typedef vector<string> vs;
typedef vector<int> vi;
typedef vector<vector<int>> vvi;
typedef vector <long long> vl;
typedef vector<vector<long long>> vvl;
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
// can only be at the start or the end
// need to find the next number and the previous
// bs
sort(BE(coins));
ll coinPre[100001]; // contain
coinPre[0] = 0;
F(i, 0, __S(coins))
coinPre[i+1] = coinPre[i] + (ll)coins[i][2]*(coins[i][1]-coins[i][0]+1);
ll ans = {};
// need to, find the upper bound the biggest [0] <= i
auto up = [&](int i){
int l = 0, r = __S(coins)-1;
int biggest = -1;
while (l <= r){
int mid = (l+r)/2;
if (coins[mid][0] <= i){
biggest = mid;
l = mid+1;
}else{
r = mid-1;
}
}
return biggest;
};
// need to find the lower bound ,find the smallest [1] >= i
auto lw = [&](int i){
int l = 0, r = __S(coins)-1;
int biggest = -1;
while (l <= r){
int mid = (l+r)/2;
if (coins[mid][1] >= i){
biggest = mid;
r = mid -1;
}else{
l = mid +1;
}
}
return biggest;
};
F0(i, coins){
// from the start +k-1, find the previous one, the biggest [0] <= +k-1
int pre = up(coins[i][0]+k-1);
//cout << pre << " ";
if (coins[i][0]+k-1 >= coins[pre][1]){
ans = max(ans, coinPre[pre+1] - coinPre[i]);
}else{
//take partial
ans = max(ans, coinPre[pre+1] - coinPre[i] - (ll)coins[pre][2]*(coins[pre][1] - (coins[i][0]+k-1)));
}
//cout << ans << endl;
// from the end, -k+1, find the smallest [1] >= -k+1
pre = lw(coins[i][1]-k+1);
//cout << pre << " ";
if (coins[i][1]-k+1 <= coins[pre][0]){
ans = max(ans, coinPre[i+1] - coinPre[pre]);
}else{
//take partial
ans = max(ans, coinPre[i+1] - coinPre[pre] - (ll)coins[pre][2]*((coins[i][1]-k+1)- coins[pre][0]));
}
//cout << ans << endl;
}
return ans;
}
};
``` | 1 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Only consider interval starts and ends for window | only-consider-interval-starts-and-ends-f-vccs | null | theabbie | NORMAL | 2025-01-05T04:01:37.116586+00:00 | 2025-01-05T04:01:37.116586+00:00 | 471 | false | ```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
n = len(coins)
coins.sort()
p = [0] * (n + 1)
for i in range(n):
p[i + 1] = p[i] + coins[i][2] * (coins[i][1] - coins[i][0] + 1)
starts = set()
for l, r, c in coins:
starts.add(l)
starts.add(r - k + 1)
res = 0
starts = sorted(starts)
for s in starts:
l = s
r = s + k - 1
beg = 0
end = n - 1
while beg <= end:
mid = (beg + end) // 2
if coins[mid][0] >= l:
end = mid - 1
else:
beg = mid + 1
first = end + 1
beg = 0
end = n - 1
while beg <= end:
mid = (beg + end) // 2
if coins[mid][1] <= r:
beg = mid + 1
else:
end = mid - 1
last = beg - 1
curr = 0
if first <= last:
curr += p[last + 1] - p[first]
if first - 1 >= 0:
if coins[first - 1][1] >= l:
curr += (coins[first - 1][1] - s + 1) * coins[first - 1][2]
if last + 1 < n and last + 1 != first - 1:
if coins[last + 1][0] <= r:
curr += (r - coins[last + 1][0] + 1) * coins[last + 1][2]
res = max(res, curr)
return res
``` | 1 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Sliding Window using pure C not C++ | sliding-window-using-pure-c-not-c-by-nit-b2ik | IntuitionThere is just one observation/inutition: (whatever)
Either the window is starting at Li or ending at Ri. (optimal)
In those cases you can get more coin | nitish-pattanaik | NORMAL | 2025-03-25T10:30:07.477849+00:00 | 2025-03-25T10:30:07.477849+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
There is just one observation/inutition: (whatever)
- Either the window is starting at `Li` or ending at `Ri`. (optimal)
- In those cases you can get more coins.
- You can't check just `Li` positions. Because each interval have different coins. If they have same coin values then only checking `Li` will be sufficient.
- But, in this case each interval have different values, so you have to check for both `Li` and `Ri`. (starting and ending)
# Approach
<!-- Describe your approach to solving the problem. -->
- Sort 2d array based on increasing interval (intervals are nonoverlapping).
- Forward Pass: checks all `Li`.
- In this pass, for each i, I will find the j and calculate how much coins we can gather.
- remember to count regular intervals and partial intervals separately, otherwise you will be in pain later. (like me.)
- Make sure to shrink window perfectly. In each interval substract whoe left i interval. Because as we move to right.. left most is obsoleted.
- Backward Pass: Checks all `Ri`
- Start i from n -1 to 0 in backward manner. Exact opposite of forward pass.
- for each i we have to find j and calculate corresponding coins that we can collect.
- Like above, make sure to calculate regular intervals and partial intervals separately.
- And shrink window carefully. Like above..
- In each iteration of forward/backward pass we calculate the `max_coins`.
- Remember to calculate `max_coins` before shrinking window. Because `coin_count` will be subtracted after shrinking of the window.
# Complexity
- Time complexity:
nlogn for qsort and almost 2n for two passes.
- Space complexity:
constant space
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# IMP
Please don't post/encourage solutions tagging as C if you're solving it using CPP.
PLEASE...
# Code
```c []
#define ll long long
#define max(a, b) ((a) > (b) ? (a) : (b))
int compare(const void* a, const void* b)
{
//return (*(const int (*)[3])a)[0] - (*(const int (*)[3])b)[0];
return (*(int **)a)[0] - (*(int **)b)[0];
}
long long maximumCoins(int** coins, int coinsSize, int* coinsColSize, int k) {
//sort the array
int n = coinsSize;
qsort(coins, n, sizeof(coins[0]), compare);
ll max_coins = 0, coin_count = 0;
// Forward Pass
for (int i = 0, j = 0; i < n; i++) {
int target = coins[i][0] + k - 1;
while (j < n && coins[j][1] <= target) {
int l = coins[j][0], r = coins[j][1], c =coins[j][2];
int count = r - l + 1;
coin_count += (ll) count * c;
j++;
}
int partial = 0; //make sure to calculate this separate
if (j < n && coins[j][0] <= target) {
partial = (ll)(target-coins[j][0]+1) * coins[j][2];
}
max_coins = max(max_coins, coin_count+partial);
int l = coins[i][0], r = coins[i][1], c = coins[i][2];
coin_count -= (ll)(r-l+1) * c;
}
coin_count = 0;
//Backward Pass
for (int i = n-1, j = i; i >= 0; i--) {
int target = coins[i][1] - k + 1;
while (j >= 0 && coins[j][0] >= target) {
int l = coins[j][0], r = coins[j][1], c = coins[j][2];
int count = (r - l + 1);
coin_count += (ll)count * c;
j--;
}
int partial = 0; //separately calculate
if (j >= 0 && coins[j][1] >= target) {
partial = (ll)(coins[j][1] - target + 1) * coins[j][2];
}
max_coins = max(max_coins, coin_count + partial);
int l = coins[i][0], r = coins[i][1], c = coins[i][2];
coin_count -= (ll)(r-l+1) * c;
}
return max_coins;
}
``` | 0 | 0 | ['C'] | 0 |
maximum-coins-from-k-consecutive-bags | C++ | Prefix sum + Binary Search | c-prefix-sum-binary-search-by-kena7-ksdi | Code | kenA7 | NORMAL | 2025-03-04T09:15:43.989795+00:00 | 2025-03-04T09:15:43.989795+00:00 | 15 | false |
# Code
```cpp []
class Solution {
public:
#define ll long long
int LB(vector<vector<int>>& coins, int x)
{
int n=coins.size();
if(x<coins[0][0])
return -1;
if(x>coins[n-1][1])
return n;
int l=0,h=n-1,res;
while(l<=h)
{
int mid=(l+h)/2;
if(coins[mid][0]>x)
{
res=mid;
h=mid-1;
}
else if(coins[mid][1]<x)
l=mid+1;
else
return mid;
}
return res;
}
int UB(vector<vector<int>>& coins, int x)
{
int n=coins.size();
if(x<coins[0][0])
return -1;
if(x>coins[n-1][1])
return n;
int l=0,h=n-1,res;
while(l<=h)
{
int mid=(l+h)/2;
if(coins[mid][1]<x)
{
res=mid;
l=mid+1;
}
else if(coins[mid][0]>x)
h=mid-1;
else
return mid;
}
return res;
}
long long maximumCoins(vector<vector<int>>& coins, int k)
{
sort(coins.begin(), coins.end());
ll res=0,n=coins.size();
vector<ll>prefix(n+1,0);
for(int i=0;i<n;i++)
{
prefix[i+1]=prefix[i]+(ll)coins[i][2]*(coins[i][1]-coins[i][0]+1LL);
}
for(int i=0;i<n;i++)
{
// Case:1
int start=coins[i][0],end=start+k-1;
int j=LB(coins,end);
ll curr=prefix[j]-prefix[i];
if(j<n)
curr+=1LL*max(0LL,(end-coins[j][0]+1LL))*coins[j][2];
res=max(res,curr);
//Case:2
start=coins[i][1],end=start-k+1;
j=UB(coins,end);
curr=prefix[i+1]-prefix[j+1];
if(j>=0)
curr+=1LL*max((coins[j][1]-end+1LL),0LL)*coins[j][2];
res=max(res,curr);
}
return res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Easy to understand! | easy-to-understand-by-saurabhabd_360-45-4d1y | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Saurabhabd_360-45 | NORMAL | 2025-02-17T06:45:51.721394+00:00 | 2025-02-17T06:45:51.721394+00:00 | 30 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
import java.util.*;
class Solution {
public int bs1(int key, int[][] arr) {
int l = 0, r = arr.length - 1, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (arr[mid][0] <= key) {
l = mid + 1;
ans = mid;
} else {
r = mid - 1;
}
}
return ans;
}
public int bs2(int key, int[][] arr) {
int l = 0, r = arr.length - 1, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (arr[mid][1] >= key) {
r = mid - 1;
ans = mid;
} else {
l = mid + 1;
}
}
return ans;
}
public long maximumCoins(int[][] coins, int k) {
HashMap<Integer, Long> pref = new HashMap<>();
HashMap<Integer, Long> suff = new HashMap<>();
Arrays.sort(coins, (a, b) -> Integer.compare(a[0], b[0]));
int n = coins.length;
long sum = 0;
// Compute prefix sum correctly using long
for (int i = 0; i < n; i++) {
sum += (long) coins[i][2] * (coins[i][1] - coins[i][0] + 1);
pref.put(coins[i][1], sum);
}
sum = 0;
// Compute suffix sum correctly using long
for (int i = n - 1; i >= 0; i--) {
sum += (long) coins[i][2] * (coins[i][1] - coins[i][0] + 1);
suff.put(coins[i][0], sum);
}
long max = 0;
for (int i = 0; i < n; i++) {
int li = coins[i][0];
int idx = bs1(li + k - 1, coins);
long curr = 0;
if (idx >= 1) {
if (i == 0)
curr = pref.getOrDefault(coins[idx - 1][1], 0L);
else
curr = pref.getOrDefault(coins[idx - 1][1], 0L) - pref.getOrDefault(coins[i - 1][1], 0L);
}
if (idx >= 0) {
int rightLim = Math.min(li + k - 1, coins[idx][1]);
curr += (long) (rightLim - coins[idx][0] + 1) * coins[idx][2];
}
max = Math.max(max, curr);
}
for (int i = n - 1; i >= 0; i--) {
int ri = coins[i][1];
int idx = bs2(ri - k + 1, coins);
long curr = 0;
if (idx + 1 < n) {
if (i == n - 1)
curr = suff.getOrDefault(coins[idx + 1][0], 0L);
else
curr = suff.getOrDefault(coins[idx + 1][0], 0L) - suff.getOrDefault(coins[i + 1][0], 0L);
}
if (idx >= 0) {
int leftLim = Math.max(ri - k + 1, coins[idx][0]);
curr += (long) (coins[idx][1] - leftLim + 1) * coins[idx][2];
}
max = Math.max(max, curr);
}
return max;
}
}
``` | 0 | 0 | ['Hash Table', 'Binary Search', 'Sorting', 'Prefix Sum', 'Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Rust Solution | rust-solution-by-abhineetraj1-1xru | IntuitionThe goal of this problem is to maximize the total number of coins we can collect within a range of length k. We are given a list of intervals where eac | abhineetraj1 | NORMAL | 2025-02-13T01:21:34.393910+00:00 | 2025-02-13T01:21:34.393910+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The goal of this problem is to maximize the total number of coins we can collect within a range of length k. We are given a list of intervals where each interval has a start, end, and the number of coins within that interval. To solve this, we need to figure out how to select and accumulate coins from overlapping or adjacent intervals such that the total number of coins is maximized without exceeding a range of length k.
We can approach this problem by sorting the intervals and using two sliding windows or two pointers: one starting from the beginning of the range and another moving as we expand the interval. By maintaining the number of coins within each range and checking when we can maximize it, we can calculate the maximum coins we can collect.
# Approach
<!-- Describe your approach to solving the problem. -->
* Sorting the intervals: First, sort the intervals based on the start of the intervals. This allows us to check and compare each interval in a natural, sequential order.
* Sliding window with two pointers: We use two pointers (i and j) to explore the range of intervals that can fit within the length k. The first pointer (i) iterates over the start of the intervals, while the second pointer (j) moves to include as many intervals as possible that fall within the valid range of length k.
* Accumulate coins: For each interval, we calculate the total coins that can be collected within a range that starts from the first pointer and extends to the second pointer. We maintain a running sum of coins as we slide the window and update the maximum result.
* Edge cases: Handle situations where intervals do not overlap or the range extends beyond the valid length k.
# Complexity
- Time complexity: O(n . logn)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```rust []
impl Solution {
pub fn maximum_coins(coins: Vec<Vec<i32>>, k: i32) -> i64 {
let mut coins = coins;
coins.sort_by_key(|a| a[0]);
let n = coins.len() as i64;
let mut res = 0;
let mut cur = 0;
let mut j = 0;
for i in 0..n {
while j < n && coins[j as usize][1] <= coins[i as usize][0] + k - 1 {
cur += (coins[j as usize][1] - coins[j as usize][0] + 1) as i64 * coins[j as usize][2] as i64;
j += 1;
}
if j < n {
let part = (std::cmp::max(0, coins[i as usize][0] + k - 1 - coins[j as usize][0] + 1)) as i64 * coins[j as usize][2] as i64;
res = std::cmp::max(res, cur + part);
}
cur -= (coins[i as usize][1] - coins[i as usize][0] + 1) as i64 * coins[i as usize][2] as i64;
}
cur = 0;
j = 0;
for i in 0..n {
cur += (coins[i as usize][1] - coins[i as usize][0] + 1) as i64 * coins[i as usize][2] as i64;
while coins[j as usize][1] < coins[i as usize][1] - k + 1 {
cur -= (coins[j as usize][1] - coins[j as usize][0] + 1) as i64 * coins[j as usize][2] as i64;
j += 1;
}
let part = (std::cmp::max(0, coins[i as usize][1] - k - coins[j as usize][0] + 1)) as i64 * coins[j as usize][2] as i64;
res = std::cmp::max(res, cur - part);
}
res
}
}
``` | 0 | 0 | ['Rust'] | 0 |
maximum-coins-from-k-consecutive-bags | O(nlogn) Sliding window solution | onlogn-sliding-window-solution-by-judych-eo5z | IntuitionApproachComplexity
Time complexity: O(nlogn) for sort()
Space complexity: O(1)
Code | JudyCheung | NORMAL | 2025-01-20T22:38:07.259279+00:00 | 2025-01-20T22:38:07.259279+00:00 | 37 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(nlogn) for sort()
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumCoins(self, coins, k):
total = 0
res = 0
i = 0
coins.sort() #O(nlogn)
for j in range(len(coins)): #j和i各自最多移动n次,所以是O(n)
l, r, value = coins[j]
total += (r-l+1)*value #把右指针的bags加入total
while coins[j][1]-coins[i][0]+1 > k: #当窗口超过k,需要缩小
excess = coins[j][1]-coins[i][0]+1-k #超过的长度
res = max(res, total-excess*value) #缩减右边bag,更新结果,没改变total的值
il,ir,ivalue=coins[i]
if ir-il+1 > excess: #如果左边的区间比excess还长,说明可以部分缩减
total -= excess * ivalue #缩减左边的长度,total是原始值
coins[i][0] += excess #调整左指针的左边界
else: #左边不够长的话,需要把整个bag都去掉
total -= ivalue * (ir-il+1)
i+=1
res = max(res, total)
return res
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Easy Java Solution || Sliding Interval Window | easy-java-solution-sliding-interval-wind-1no6 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | ravikumar50 | NORMAL | 2025-01-20T19:10:49.016939+00:00 | 2025-01-20T19:10:49.016939+00:00 | 58 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maximumCoins(int[][] arr, int k) {
Arrays.sort(arr,(a,b)->a[0]-b[0]);
long amount = 0;
int n = arr.length;
long currAmount = 0;
for(int i=0,j=0; i<n; i++){
while(j<n && arr[j][1]<=arr[i][0]+k-1){
currAmount += (long)(arr[j][1]-arr[j][0]+1)*(long)arr[j][2];
j++;
}
long partial = 0;
if(j<n){
int endPart = arr[i][0]+k-1;
if(endPart>=arr[j][0]){
partial = (long)(endPart-arr[j][0]+1)*(long)arr[j][2];
}
}
amount = Math.max(amount,currAmount+partial);
currAmount -= (long)(arr[i][1]-arr[i][0]+1)*(long)arr[i][2];
}
currAmount = 0;
for(int j=n-1,i=n-1; j>=0; j--){
while(i>=0 && arr[i][0]>=arr[j][1]-k+1){
currAmount += (long)(arr[i][1]-arr[i][0]+1)*(long)arr[i][2];
i--;
}
long partial = 0;
if(i>=0){
int endPart = arr[j][1]-k+1;
if(endPart<=arr[i][1]){
partial = (long)(arr[i][1]-endPart+1)*(long)arr[i][2];
}
}
amount = Math.max(amount,currAmount+partial);
currAmount -= (long)(arr[j][1]-arr[j][0]+1)*(long)arr[j][2];
}
return amount;
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Javascript | Sliding Window | O(n) | javascript-sliding-window-on-by-aryonbe-y5gd | Code | aryonbe | NORMAL | 2025-01-17T08:13:13.732655+00:00 | 2025-01-17T08:13:13.732655+00:00 | 9 | false | # Code
```javascript []
/**
* @param {number[][]} coins
* @param {number} k
* @return {number}
*/
var maximumCoins = function(coins, k) {
const n = coins.length;
function solve(A){
A.sort((a,b) => a[0] - b[0]);
let res = 0, cur = 0, i = 0;
for(let j = 0; j < A.length; j++){
const [l,r,c] = A[j];
cur += (r - l + 1)*c;
while(A[j][1] - A[i][1] + 1 > k){
cur -= (A[i][1] - A[i][0] + 1)*A[i][2];
i++;
}
part = Math.max(0, A[j][1] - A[i][0] + 1 - k)*A[i][2];
res = Math.max(res, cur - part);
}
return res;
}
let res = solve(coins);
for(let i = 0; i < coins.length; ++i){
const [l,r,c] = coins[i];
coins[i] = [-r, -l, c];
}
return Math.max(res, solve(coins));
};
``` | 0 | 0 | ['JavaScript'] | 0 |
maximum-coins-from-k-consecutive-bags | Explained sliding window solution [C++/Java/Python/Javascript] || Beats 100% | explained-sliding-window-solution-cjavap-wjqs | IntuitionInput Description:
coins is a list of intervals:
[𝑠𝑡𝑎rt,end,coins]sorted by their starting index.
k is the size of the range (or sliding window) within | be_fighter | NORMAL | 2025-01-16T12:14:21.615107+00:00 | 2025-01-16T12:14:53.099695+00:00 | 93 | false | # Intuition
# Input Description:
1. coins is a list of intervals:
[𝑠𝑡𝑎rt,end,coins]sorted by their starting index.
2. k is the size of the range (or sliding window) within which we can collect coins.
# Overall Goal:
1. For any sliding window of size k, calculate the maximum coins that can be collected.
2. To achieve this, the solution considers two cases:
Case 1: Include the entire current interval and part of the next interval.
Case 2: Include the entire current interval and part of the previous interval.
# Key Observations:
1. The coin intervals can partially or fully overlap the sliding window of size 𝑘
2. The solution leverages a sliding window technique to efficiently calculate the coin sums within any range of 𝑘
# Complexity
- Time complexity:
O(n*logn)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
#define ll long long
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(), coins.end());
int n = coins.size();
ll curr_sum = 0;
ll ans = 0;
// Case 1: Forward partial
for (int i = 0, j = 0; i < n; i++) {
while (j < n && coins[j][1] <= coins[i][0] + k - 1) {
curr_sum += (1ll) * (coins[j][1] - coins[j][0] + 1) * coins[j][2];
j++;
}
if (j < n) {
ll partial = max((1ll) * 0, (1ll) * (coins[i][0] + k - 1 - coins[j][0] + 1) * coins[j][2]);
ans = max(ans, curr_sum + partial);
}
curr_sum -= ((1ll) * (coins[i][1] - coins[i][0] + 1) * coins[i][2]);
}
// Case 2: Back partial sum
curr_sum = 0;
for (int i = 0, j = 0; i < n; i++) {
curr_sum += (1ll) * (coins[i][1] - coins[i][0] + 1) * coins[i][2];
while (coins[j][1] < coins[i][1] - k + 1) {
curr_sum -= (1ll) * (coins[j][1] - coins[j][0] + 1) * coins[j][2];
j++;
}
ll partial = max((1ll) * 0, (1ll) * ((coins[i][1] - k + 1) - coins[j][0]) * coins[j][2]);
ans = max(ans, curr_sum - partial);
}
return ans;
}
};
```
```java []
import java.util.*;
class Solution {
public long maximumCoins(int[][] coins, int k) {
Arrays.sort(coins, (a, b) -> Integer.compare(a[0], b[0]));
int n = coins.length;
long currSum = 0;
long ans = 0;
// Case 1: Forward partial
for (int i = 0, j = 0; i < n; i++) {
while (j < n && coins[j][1] <= coins[i][0] + k - 1) {
currSum += (long) (coins[j][1] - coins[j][0] + 1) * coins[j][2];
j++;
}
if (j < n) {
long partial = Math.max(0, (long) (coins[i][0] + k - 1 - coins[j][0] + 1) * coins[j][2]);
ans = Math.max(ans, currSum + partial);
}
currSum -= (long) (coins[i][1] - coins[i][0] + 1) * coins[i][2];
}
// Case 2: Back partial sum
currSum = 0;
for (int i = 0, j = 0; i < n; i++) {
currSum += (long) (coins[i][1] - coins[i][0] + 1) * coins[i][2];
while (coins[j][1] < coins[i][1] - k + 1) {
currSum -= (long) (coins[j][1] - coins[j][0] + 1) * coins[j][2];
j++;
}
long partial = Math.max(0, (long) ((coins[i][1] - k + 1) - coins[j][0]) * coins[j][2]);
ans = Math.max(ans, currSum - partial);
}
return ans;
}
}
```
```python []
class Solution:
def maximumCoins(self, coins: list[list[int]], k: int) -> int:
coins.sort()
n = len(coins)
curr_sum = 0
ans = 0
# Case 1: Forward partial
j = 0
for i in range(n):
while j < n and coins[j][1] <= coins[i][0] + k - 1:
curr_sum += (coins[j][1] - coins[j][0] + 1) * coins[j][2]
j += 1
if j < n:
partial = max(0, (coins[i][0] + k - 1 - coins[j][0] + 1) * coins[j][2])
ans = max(ans, curr_sum + partial)
curr_sum -= (coins[i][1] - coins[i][0] + 1) * coins[i][2]
# Case 2: Back partial sum
curr_sum = 0
j = 0
for i in range(n):
curr_sum += (coins[i][1] - coins[i][0] + 1) * coins[i][2]
while coins[j][1] < coins[i][1] - k + 1:
curr_sum -= (coins[j][1] - coins[j][0] + 1) * coins[j][2]
j += 1
partial = max(0, ((coins[i][1] - k + 1) - coins[j][0]) * coins[j][2])
ans = max(ans, curr_sum - partial)
return ans
```
```javascript []
class Solution {
maximumCoins(coins, k) {
coins.sort((a, b) => a[0] - b[0]);
const n = coins.length;
let currSum = 0;
let ans = 0;
// Case 1: Forward partial
let j = 0;
for (let i = 0; i < n; i++) {
while (j < n && coins[j][1] <= coins[i][0] + k - 1) {
currSum += (coins[j][1] - coins[j][0] + 1) * coins[j][2];
j++;
}
if (j < n) {
let partial = Math.max(0, (coins[i][0] + k - 1 - coins[j][0] + 1) * coins[j][2]);
ans = Math.max(ans, currSum + partial);
}
currSum -= (coins[i][1] - coins[i][0] + 1) * coins[i][2];
}
// Case 2: Back partial sum
currSum = 0;
j = 0;
for (let i = 0; i < n; i++) {
currSum += (coins[i][1] - coins[i][0] + 1) * coins[i][2];
while (coins[j][1] < coins[i][1] - k + 1) {
currSum -= (coins[j][1] - coins[j][0] + 1) * coins[j][2];
j++;
}
let partial = Math.max(0, ((coins[i][1] - k + 1) - coins[j][0]) * coins[j][2]);
ans = Math.max(ans, currSum - partial);
}
return ans;
}
}
```
| 0 | 0 | ['Array', 'Binary Search', 'Greedy', 'Sliding Window', 'Sorting', 'Prefix Sum', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
maximum-coins-from-k-consecutive-bags | sliding window one pass soln. | sliding-window-one-pass-soln-by-rishiins-3zfo | IntuitionApproachsince the size of the array is 1e9 giving us the idea that computations will not be possible within time thus we pivot to using the intervals f | RishiINSANE | NORMAL | 2025-01-15T19:09:50.258826+00:00 | 2025-01-15T19:09:50.258826+00:00 | 25 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
since the size of the array is 1e9 giving us the idea that computations will not be possible within time thus we pivot to using the intervals for our calculations hence using sliding window approach over intervals completely and not the indexes individually.
there can be a total of 4 cases of window out of which only two of them contribute to our answer because either of the intervals will have a higher value than the other thus it only makes sense of incorporate that interval as much as possible in our window to maximise our answer
thus either taking interval A(starting at A) completely or interval B(ending at B) completely
due to the constraint K there might be an onverlap in an interval which we will handle separately(addition/substraction from our total_sum).
# Complexity
- Time complexity:
O(nlogn + n) ~ O(nlogn).
- Space complexity:
O(1).
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
int n = coins.size();
sort(coins.begin(), coins.end());
long long result = 0, csum = 0, psum = 0;
// intervals that necessarily start from the starting point of a range and taking that complete interval into consideration
for (int i = 0, j = 0; i < n; i++) {
// Expanding the window such that complete intervals are considered(end points of range and not the coordinates in range)
while (j < n && coins[j][1] <= coins[i][0] + k - 1) {
csum += (long long)(coins[j][1] - coins[j][0] + 1) * coins[j][2];
j++;
}
// Handling partial overlap such that an interval ends in the middle of a range and not at the ends of that range due to the CONSTRAINT "K" and thus taking the values of the partial overlap in that interval into consideration and summing it up with the currentsum(sum of complete intervals) thus giving us the total value for the size "K", hence maximising our result.
if (j < n) {
long long val = (long long)(coins[i][0] + k - 1 - coins[j][0] + 1) * coins[j][2];
psum = (val>0)?val:0;
result = max(result, csum + psum);
}
// Shrinking the window in case our window exceeds the given constraint "K" and thus removing the contributions of the intervals being shrinked(the addition and removal is being done of complete intervals and not of indexes individually due to time constraint).
csum -= (long long)(coins[i][1] - coins[i][0] + 1) * coins[i][2];
}
csum = 0, psum = 0;
//doing the same with intervals ending at the range end instead of starting from the range start
for (int i = 0, j = 0; i < n; i++) {
// Expand the window
csum += (long long)(coins[i][1] - coins[i][0] + 1) * coins[i][2];
while (j < n && coins[j][1] < coins[i][1] - k + 1) {
csum -= (long long)(coins[j][1] - coins[j][0] + 1) * coins[j][2];
j++;
}
// Handle partial overlap
if (j < n) {
long long val = (long long)(coins[i][1] - k - coins[j][0] + 1) * coins[j][2];
psum = (val>0)?val:0;
result = max(result, csum - psum);
}
}
return result;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Maximum Coins From K Consecutive Bags | maximum-coins-from-k-consecutive-bags-by-z00k | IntuitionApproachSliding WindowComplexity
Time complexity:O(N log n)
Space complexity:O(1)
Code | Subham_Pujari23 | NORMAL | 2025-01-15T04:46:05.494940+00:00 | 2025-01-15T04:46:05.494940+00:00 | 31 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
Sliding Window
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(N log n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maximumCoins(int[][] A, int k) {
Arrays.sort(A, (a, b) -> a[0] - b[0]);
int n = A.length;
// Start at A[i][0]
long res = 0, cur = 0;
for (int i = 0, j = 0; i < n; ++i) {
while (j < n && A[j][1] <= A[i][0] + k - 1) {
cur += 1L * (A[j][1] - A[j][0] + 1) * A[j][2];
j++;
}
if (j < n) {
long part = 1L * Math.max(0, A[i][0] + k - 1 - A[j][0] + 1) * A[j][2];
res = Math.max(res, cur + part);
}
cur -= 1L * (A[i][1] - A[i][0] + 1) * A[i][2];
}
// End at A[i][1]
cur = 0;
for (int i = 0, j = 0; i < n; ++i) {
cur += 1L * (A[i][1] - A[i][0] + 1) * A[i][2];
while (A[j][1] < A[i][1] - k + 1) {
cur -= 1L * (A[j][1] - A[j][0] + 1) * A[j][2];
j++;
}
long part = 1L * Math.max(0, A[i][1] - k - A[j][0] + 1) * A[j][2];
res = Math.max(res, cur - part);
}
return res;
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Binary Search prefix sum solution | binary-search-prefix-sum-solution-by-ari-d5wo | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Arif2321 | NORMAL | 2025-01-11T19:30:21.436315+00:00 | 2025-01-11T19:30:21.436315+00:00 | 22 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k)
{
long long ans = 0;
int n = coins.size();
sort(coins.begin(),coins.end());
vector<pair<int,int>> v;
map<int,int> mp;
vector<long long> pref(n);
for(int i = 0; i < n; i++)
{
pref[i] = (i ? pref[i-1] : 0LL) + 1LL*(coins[i][1]-coins[i][0]+1)*coins[i][2];
v.push_back({coins[i][0],1});
v.push_back({coins[i][1],-1});
mp[coins[i][0]] = i;
mp[coins[i][1]] = i;
}
for(int i = 0; i < v.size(); i++)
{
if(v[i].second == 1)
{
int tmp = k;
k--;
int idx = lower_bound(v.begin(),v.end(),make_pair(v[i].first + k,-1)) - v.begin();
if(idx == v.size() || v[idx].first > v[i].first + k) idx--;
if(idx < 0) continue;
int r = mp[v[idx].first];
int l = mp[v[i].first];
long long rsum = pref[r]-(l ? pref[l-1] : 0LL);
if(v[idx].second == 1)
{
rsum -= 1LL*(coins[r][1]-coins[r][0]+1)*coins[r][2];
rsum += 1LL*(v[i].first+k-v[idx].first+1)*(coins[r][2]);
}
ans = max(ans,rsum);
k = tmp;
}
else
{
int tmp = k;
k--;
int idx = lower_bound(v.begin(),v.end(),make_pair(v[i].first-k,-1)) - v.begin();
if(idx == v.size()) continue;
int r = mp[v[i].first];
int l = mp[v[idx].first];
long long lsum = pref[r]-(l ? pref[l-1] : 0LL);
if(v[idx].second == -1)
{
lsum -= 1LL*(coins[l][1]-coins[l][0]+1)*coins[l][2];
lsum += 1LL*(v[idx].first-(v[i].first-k)+1)*(coins[l][2]);
}
ans = max(ans,lsum);
k = tmp;
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Simplest Sliding Window after filling the gaps. | simplest-sliding-window-after-filling-th-qpc2 | IntuitionThe problem can become much easier as soon as there is no gaps between intervals.
Once we have some continous intervals, we have to choose a segment of | suri_kumkaran | NORMAL | 2025-01-11T13:14:12.960008+00:00 | 2025-01-11T13:14:12.960008+00:00 | 24 | false | # Intuition
The problem can become much easier as soon as there is no gaps between intervals.
Once we have some continous intervals, we have to choose a segment of intervals such that it's lenght is K.
Now the observation is, every optimal segment selection will either start at some interval or end at some interval.
We can use simple sliding window `left to right` and `right to left` to get final optimal answer.
# Approach
- Sort the coins array to bring segments in sequence.
- Create another array storing the len and coins at each place.
- Make it continous by putting gaps with 0 coins at that place
- Apply sliding window left to right.
- Apply sliding window right to left.
- Return the final answer.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n*log(n))$$ for sorting.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$ for creating another segment array.
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(),coins.end());
vector<vector<long long>> cc;
cc.push_back({coins[0][1]-coins[0][0]+1,coins[0][2]});
int last = coins[0][1];
int n = coins.size();
for(int i=1;i<n;i++)
{
int gapLen = coins[i][0] - last-1;
cc.push_back({gapLen, 0});
cc.push_back({coins[i][1]-coins[i][0]+1, coins[i][2]});
last = coins[i][1];
}
// for(auto x:cc)
// {
// cout<<x[0]<<" "<<x[1]<<endl;
// }
long long int ans = 0;
n = cc.size();
int i = 0, j=0;
long long int tot=0, len=0;
while(i<n)
{
len+=cc[i][0];
tot+=cc[i][1]*cc[i][0];
while(len>k)
{
len-=cc[j][0];
tot-=cc[j][1]*cc[j][0];
j++;
}
if(j-1>=0)
{
long long rem = k-len;
ans = max(ans, tot+rem*cc[j-1][1]);
}
else
ans = max(ans, tot);
i++;
}
j=n-1;
i=n-1;
tot = 0;
len = 0;
while(i>=0)
{
len+=cc[i][0];
tot+=cc[i][1]*cc[i][0];
while(len>k)
{
len-=cc[j][0];
tot-=cc[j][1]*cc[j][0];
j--;
}
if(j+1<n)
{
long long rem = k-len;
ans = max(ans, tot+rem*cc[j+1][1]);
}
else
ans = max(ans, tot);
i--;
}
return ans;
}
};
``` | 0 | 0 | ['Sliding Window', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Clear Detailed Optimal Solution O(nlogn) (Python) | clear-detailed-optimal-solution-onlogn-p-19nr | IntuitionA key observation to solving this problem is as follows: If we only consider windows which start at the left endpoint of a segment or end at the right | carpenoctem | NORMAL | 2025-01-11T09:17:08.639656+00:00 | 2025-01-11T09:17:08.639656+00:00 | 35 | false | # Intuition
A key observation to solving this problem is as follows: If we only consider windows which start at the left endpoint of a segment or end at the right endpoint of a segment, we are guaranteed to find the window with the max number of coins. **This window may not be uniquely optimal (e.g. there may be other windows which yield the same number of coins.**
Proof by contradiction:
- assume the optimal window does not start at the left endpoint of a segment and does not end at the right endpoint of a segment.
- if the window start is not contained in a segment, it can always be moved to the start of the nearest next segment without reducing coins.
- if the window end is not contained in a segment, it can always be moved to the end of the nearest previous segment without reducing coins.
- if both the window start and end are contained in segments but the window start is not at the left endpoint of the its segment and the window end is not at the right endpoint of its segment, we can either shift the window start to the left endpoint of its segment or shift the window end to the right endpoint of its segment without reducing the number of coin containing bags.
- given the above, we can always either improve or maintain the number of coins in the window by making one of those two shifts. we should shift the window to include the bags containing more coins.
# Approach
Given the intuition above, we just need to implement a sliding window algorithm that checks all the relevant windows. We can check all windows that end at the right segment endpoints, and then by symmetry we can negate the number line and reuse the same helper function to check all windows that start at the left segment endpoints (equivalent to checking all windwos that end at the left segment endpoints on the reversed number line).
# Complexity
- Time complexity:
O(nlogn) where n is coins.length, due to sorting. Sliding window is O(n).
- Space complexity:
O(n) additional space to store coins on reversed number line. Possible
to optimize away this additional space to have constant additional space.
# Code
```python3 []
# - Sliding window two passes, ending at right and starting from left (equivalent to ending at left with all indices negated).
# - maintain a start_idx initialized to 0 (refers to coins segment that contains the actual window start).
# - maintain the current max, and current full segment coins.
# - Iterate over coins, take the current interval as
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
reverse_number_line_coins = [[-r, -l, c] for l, r, c in coins]
return max(self.sliding_window(coins, k), self.sliding_window(reverse_number_line_coins, k))
def sliding_window(self, coins, k):
"""Returns the max coins from k bags, considering only windows that end at the right endpoints in coins."""
coins.sort()
max_coins = 0
# full_segment_coins tracks coins in the window considering full segments ONLY! This is done so that
# we can easily remove entire segments from full_segment_coins as we iterate.
full_segment_coins = 0
start_idx = 0
for coin in coins:
l, r, c = coin
# add all coins from current coin segment.
full_segment_coins += (r - l + 1) * c
# remove all coins from previous coin segments that are no longer in the window.
# condition is that right endpoint of previous coin segment is before window start.
ls, rs, cs = coins[start_idx]
while rs <= (r - k):
full_segment_coins -= (rs - ls + 1) * cs
start_idx += 1
ls, rs, cs = coins[start_idx]
# The segment corresponding to the current start_idx may only be partially in the window.
window_start = r - k + 1
segment_coins_before_window = max(0, window_start - ls) * cs
max_coins = max(max_coins, full_segment_coins - segment_coins_before_window)
return max_coins
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | O(n*log(n)) | 2 Pointers | Code Reusebility | onlogn-2-pointers-code-reusebility-by-sa-zofa | IntuitionThe solution will contain atleast "one segment where we take all the bags(at most k) for it"ApproachSort and do 2 pointersComplexity
Time complexity:
O | sagsango | NORMAL | 2025-01-11T08:29:29.680934+00:00 | 2025-01-11T08:29:29.680934+00:00 | 16 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The solution will contain atleast "one segment where we take all the bags(at most k) for it"
# Approach
<!-- Describe your approach to solving the problem. -->
Sort and do 2 pointers
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
/*
The solution will contain atleast "one segment where we take all the bags(at most k) for it"
*/
auto cmp = [&](const vector<int> &a, const vector<int>&b) {
return a[0] < b[0];
};
sort (coins.begin(), coins.end(), cmp);
long long mx = 0;
int n = coins.size();
auto solve = [&]() {
int l = 0, r = 0;
long long have = 0;
while (l<n) {
while (r < n && abs(coins[l][0] - coins[r][0]) + 1 <= k) {
long long took = min(abs(coins[r][1] - coins[r][0])+1, k - (abs(coins[l][0] - coins[r][0])));
mx = max(mx, have + took * coins[r][2]);
if (abs(coins[r][1] - coins[l][0])+1 > k) {
break;
}
have += took * coins[r][2];
r += 1;
}
if (r > l) {
have -= 1ll * (abs(coins[l][0] - coins[l][1]) + 1) * coins[l][2];
assert (have >= 0);
} else {
r = l+1;
have = 0;
}
l += 1;
}
};
solve(); // This will take care when some next one is taken partial
reverse(coins.begin(), coins.end());
for (auto &v: coins){
swap(v[0], v[1]);
}
solve(); // This will take care when some previous one is taken partial
return mx;
}
};
```
```Rust []
impl Solution {
pub fn maximum_coins(coins: Vec<Vec<i32>>, k: i32) -> i64 {
/*
The solution will contain at least "one segment where we take all the bags (at most k) for it."
*/
let mut coins = coins;
// Comparator for sorting by the start position (similar to cmp in C++).
coins.sort_by(|a, b| a[0].cmp(&b[0]));
let mut mx: i64 = 0;
let n = coins.len();
let k = k as i64; // Convert k to i64 for consistency with other operations.
let solve = |coins: &Vec<Vec<i32>>, mx: &mut i64| {
let mut l = 0;
let mut r = 0;
let mut have: i64 = 0;
while l < n {
while r < n && (coins[r][0] - coins[l][0]).abs() as i64 + 1 <= k {
let took = std::cmp::min(
(coins[r][1] - coins[r][0]).abs() as i64 + 1,
k - (coins[r][0] - coins[l][0]).abs() as i64,
);
*mx = std::cmp::max(*mx, have + took * coins[r][2] as i64);
if (coins[r][1] - coins[l][0]).abs() as i64 + 1 > k {
break;
}
have += took * coins[r][2] as i64;
r += 1;
}
if r > l {
have -= ((coins[l][1] - coins[l][0]).abs() as i64 + 1) * coins[l][2] as i64;
assert!(have >= 0);
} else {
r = l + 1;
have = 0;
}
l += 1;
}
};
// First solve pass
solve(&coins, &mut mx);
// Reverse the coins for the second pass
coins.reverse();
for coin in &mut coins {
coin.swap(0, 1);
}
// Second solve pass
solve(&coins, &mut mx);
mx
}
}
```
| 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | lovely_anna | lovely_anna-by-lovely_anna-wrgh | null | lovely_anna | NORMAL | 2025-01-11T04:14:12.678823+00:00 | 2025-01-11T04:14:12.678823+00:00 | 20 | false |
```java []
class Solution {
public long maximumCoins(int[][] a, int k) {
var n = a.length;
var sp = new TreeSet<int[]>((x, y) -> Long.compare(x[0], y[0]));
var ep = new TreeSet<int[]>((x, y) -> Long.compare(x[0], y[0]));
Arrays.sort(a, (x, y) -> x[0] - y[0]);
for (var i = 0; i < n; i++) {
sp.add(new int[] { a[i][0], i });
ep.add(new int[] { a[i][1], i });
}
var pre = new long[n];
pre[0] = (a[0][1] - a[0][0] + 1L) * a[0][2];
for (var i = 1; i < n; i++)
pre[i] = pre[i - 1] + (a[i][1] - a[i][0] + 1L) * a[i][2];
var an = 0L;
for (var i = 0; i < n; i++) {
var l = a[i][1] - k + 1;
var r = a[i][0] + k - 1;
var ll = sp.ceiling(new int[] { l, 0 });
var rr = ep.floor(new int[] { r, 0 });
var lid = (ll != null ? ll[1] : i + 1);
var rid = (rr != null ? rr[1] : i - 1);
var lcom = (lid != i + 1
? pre[i] - (lid != 0 ? pre[lid - 1] : 0)
: 0);
var rcom = (rid != i - 1
? pre[rid] - (i != 0 ? pre[i - 1] : 0)
: 0);
var ladd = (lid != 0 && a[lid - 1][1] >= l
? (a[lid - 1][1] - l + 1L) * a[lid - 1][2]
: 0);
var radd = (rid != n - 1 && a[rid + 1][0] <= r
? (r - a[rid + 1][0] + 1L) * a[rid + 1][2]
: 0);
an = Math.max(an, Math.max(lcom + ladd, rcom + radd));
}
return an;
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Step by Step | Conceptually Good | Binary Search + Prefix Sum | step-by-step-conceptually-good-binary-se-y9wy | Code | Shivam_Kapoor | NORMAL | 2025-01-10T20:35:53.724557+00:00 | 2025-01-10T20:35:53.724557+00:00 | 18 | false | # Code
```cpp []
#define ll long long
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
ll n = coins.size();
sort(coins.begin(), coins.end());
vector<ll> p(n, 0);
p[0] = 1LL * coins[0][2] * (coins[0][1] - coins[0][0] + 1);
for(ll i = 1; i < n; i++){
p[i] = p[i - 1] + ((1LL * coins[i][2]) * (coins[i][1] - coins[i][0] + 1));
}
vector<vector<ll>> v;
for(ll i = 0; i < n; i++){
ll p1 = coins[i][0];
ll p2 = coins[i][1];
v.push_back({p1, p1 + k - 1});
v.push_back({max(p1 - k + 1, 1LL), p1});
v.push_back({p2, p2 + k - 1});
v.push_back({max(1LL, p2 - k + 1), p2});
}
// cout << "# ALL INTERVALS" << endl;
// for(auto &it : v){
// for(auto i : it) cout << i << " ";
// cout << endl;
// }
ll res = 0;
for(auto itv : v){
ll start = itv[0];
ll end = itv[1];
// cout << "# NEW INTERVAL" << endl;
// cout << start << endl;
// cout << end << endl;
ll idx1 = -1, idx2 = -1;
ll lo1 = 0;
ll hi1 = n - 1;
while(lo1 <= hi1){
ll mid = (lo1 + hi1)/2;
if(start <= coins[mid][1]){
idx1 = mid;
hi1 = mid - 1;
}
else{
lo1 = mid + 1;
}
}
ll lo2 = 0;
ll hi2 = n - 1;
while(lo2 <= hi2){
ll mid = (lo2 + hi2)/2;
if(end >= coins[mid][0]){
idx2 = mid;
lo2 = mid + 1;
}
else{
hi2 = mid - 1;
}
}
// idx1, idx1 + 1, ----- , idx2 - 1, idx2 : Prefix sum till this but take care of the boundaries
// complete prefix sum from idx1 + 1 -> idx2 - 1
ll ans = 0;
// cout << idx1 << " : " << idx2 << endl;
if(idx1 + 1 <= idx2 - 1 && (idx2 - 1 >= 0)){
ans += (p[idx2 - 1] - p[idx1]);
}
// cout << ans << endl;
if(idx1 == idx2){
ans += (coins[idx2][2] * (min((ll)coins[idx2][1], end) - max((ll)coins[idx2][0], start) + 1));
}
else {
// cout << "INSIDE" << endl;
ans += (max(min(end, (ll)coins[idx2][1]) - coins[idx2][0] + 1, 0LL))*coins[idx2][2];
// cout << ans << endl;
ans += (max(0LL, coins[idx1][1] - max(start, (ll)coins[idx1][0]) + 1))*coins[idx1][2];
// cout << ans << endl;
}
// cout << "TOTAL COINS : " << ans << endl;
res = max(res, ans);
}
return res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Javascript - Sliding Window | javascript-sliding-window-by-faustaleona-wyex | Code | faustaleonardo | NORMAL | 2025-01-09T23:46:16.023399+00:00 | 2025-01-09T23:46:16.023399+00:00 | 11 | false | # Code
```javascript []
/**
* @param {number[][]} coins
* @param {number} k
* @return {number}
*/
var maximumCoins = function (coins, k) {
coins.sort((a, b) => a[0] - b[0]);
let ans = 0;
let total = 0;
let start = 0;
for (let end = 0; end < coins.length; end++) {
total += (coins[end][1] - coins[end][0] + 1) * coins[end][2];
while (coins[end][1] - coins[start][0] + 1 > k) {
const excess = coins[end][1] - coins[start][0] + 1 - k;
ans = Math.max(ans, total - excess * coins[end][2]);
const [left, right, val] = coins[start];
if (right - left + 1 > excess) {
total -= excess * val;
coins[start][0] += excess;
} else {
total -= (right - left + 1) * val;
start++;
}
}
ans = Math.max(ans, total);
}
return ans;
};
``` | 0 | 0 | ['Sliding Window', 'JavaScript'] | 1 |
maximum-coins-from-k-consecutive-bags | prefix sum on ranges | prefix-sum-on-ranges-by-joshuadlima-rsqw | Intuitionevery valid segment will either start on li and go upto k forward or end at ri and go k backward. We can use prefix sum to calculate the sum between th | joshuadlima | NORMAL | 2025-01-09T21:22:39.263957+00:00 | 2025-01-09T21:22:39.263957+00:00 | 15 | false | # Intuition
every valid segment will either start on li and go upto k forward or end at ri and go k backward. We can use prefix sum to calculate the sum between these ranges and then just bruteforce.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(nlogn)
- Space complexity:
O(n)
# Code
```cpp []
#define ll long long
class Solution {
public:
map<ll, ll> prefix;
map<ll, pair<ll, ll>> mp;
ll getPrefixSum(ll coord){
if(coord < 1)
return 0;
ll ans = 0;
auto it1 = prefix.upper_bound(coord);
if(it1 != prefix.begin())
it1--, ans += it1->second;
auto it2 = mp.upper_bound(coord);
if(it2 != mp.begin()){
it2--;
if(coord < it2->second.first)
ans += (coord - it2->first + 1) * it2->second.second;
}
return ans;
}
ll getLtoR(ll l, ll r){
return getPrefixSum(r) - getPrefixSum(l - 1);
}
ll maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(), coins.end());
ll sum = 0;
for(auto it : coins){
sum += 1ll * it[2] * (it[1] - it[0] + 1);
prefix[it[1]] = sum;
mp[it[0]] = {it[1], it[2]};
}
ll ans = 0;
for(auto it : coins){
// forward
ans = max(ans, getLtoR(it[0], it[0] + k - 1));
cout << getLtoR(it[0], it[0] + k - 1) << "\n";
// backward
if(it[1] >= k)
ans = max(ans, getLtoR(it[1] - k + 1, it[1]));
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | c++() forward & backward prefix sum | c-forward-backward-prefix-sum-by-zx007pi-6dn6 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | zx007pi | NORMAL | 2025-01-09T08:18:49.699332+00:00 | 2025-01-09T08:18:49.699332+00:00 | 14 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(), coins.end());
long ans = 0;
int n = coins.size();
vector<long> ps(n + 1);
ps[0] = 0;
for(int i = 0; i != n; ++i)
ps[i+1] = ps[i] + (long)coins[i][2]*(coins[i][1] - coins[i][0] + 1);
for(int i = 0, j = 0; i != n ; ++i){
while(j != n && coins[j][1] - coins[i][0] + 1 <= k) j++;
long sum = ps[j] - ps[i];
if(j != n && coins[i][0] + k > coins[j][0] )
sum += (long)coins[j][2]*(coins[i][0] + k - coins[j][0]);
ans = max(ans, sum);
}
ps[n] = 0;
for(int i = n-1; i >= 0; --i)
ps[i] = ps[i+1] + (long)coins[i][2]*(coins[i][1] - coins[i][0] + 1);
for(int i = n-1, j = n-1; i >= 0 ; --i){
while(j != -1 && coins[i][1] - coins[j][0] + 1 <= k) j--;
long sum = ps[j+1] - ps[i+1];
if(j != -1 && coins[i][1] - k < coins[j][1] )
sum += (long)coins[j][2]*(coins[j][1] - coins[i][1] + k);
ans = max(ans, sum);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Slide window(to left/right) | slide-windowto-leftright-by-linda2024-kidm | Intuition(Be careful type cast in c#)ApproachComplexity
Time complexity:
Space complexity:
Code | linda2024 | NORMAL | 2025-01-08T22:29:27.626347+00:00 | 2025-01-08T22:29:27.626347+00:00 | 21 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
(Be careful type cast in c#)
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public long MaximumCoins(int[][] coins, int k) {
int len = coins.Length;
long totalScore = 0, curSum = 0;
coins = coins.OrderBy(x => x[0]).ToArray();
// slide window -> to right:
int j = 0;
for (int i = 0; i < len; i++)
{
while (j < len && coins[j][1] - coins[i][0] < k)
{
long nextVal = (long)(coins[j][1] - coins[j][0] + 1) * coins[j][2];
curSum += nextVal;
j++;
}
long rest = 0;
if (j < len)
{
rest = Math.Max(rest, (long)(coins[i][0] + k - 1 - coins[j][0] + 1) * coins[j][2]);
}
totalScore = Math.Max(totalScore, curSum + rest);
curSum -= (long)(coins[i][1] - coins[i][0] + 1) * coins[i][2];
}
// slide window -> to left:
j = len - 1;
curSum = 0;
for (int i = len - 1; i >= 0; i--)
{
while (j >= 0 && coins[i][1] - coins[j][0] < k)
{
curSum += (long)(coins[j][1] - coins[j][0] + 1) * coins[j][2];
j--;
}
long rest = 0;
if (j >= 0)
{
rest = Math.Max(rest, (long)(coins[j][1] - (coins[i][1] - k + 1) + 1) * coins[j][2]);
}
totalScore = Math.Max(totalScore, curSum + rest);
curSum -= (long)coins[i][2] * (coins[i][1] - coins[i][0] + 1);
}
return totalScore;
}
}
``` | 0 | 0 | ['C#'] | 0 |
maximum-coins-from-k-consecutive-bags | Prefix Sum + Binary Search | Intuition Explained | prefix-sum-binary-search-intuition-expla-z93g | Intuition
Maximum coins can be achieved by choosing a starting or ending point of some interval. Hence, we check coins for all starting and ending positions. | adicoder_16 | NORMAL | 2025-01-08T21:09:51.183439+00:00 | 2025-01-08T21:09:51.183439+00:00 | 33 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
- Maximum coins can be achieved by choosing a starting or ending point of some interval. Hence, we check coins for all starting and ending positions.
- For all starting and ending points, we check the reach and calculate number of coins in that reach.
- Also, we maintain a prefix sum array and a suffix sum array to get coins over a range in O(1) time.
- Further, we use binary search to get the index of the interval where we can possibly reach. This reduces the time complexity from O(n) to O(log n).
# Complexity
- Time complexity: O(NlogN)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define ll long long
class Solution {
public:
long long mx(long long a, long b){
if(a>b){
return a;
}
return b;
}
long long maximumCoins(vector<vector<int>>& coins, int k) {
int n=coins.size();
ll ans=0;
sort(coins.begin(), coins.end());
vector<ll> psum(n);
psum[0]=(ll)(coins[0][2])*(ll)((coins[0][1]-coins[0][0]+1));
for(int i=1; i<n; i++){
psum[i]=(ll)psum[i-1]+(ll)coins[i][2]*(ll)(coins[i][1]-coins[i][0]+1);
}
vector<ll> ssum(n);
ssum[n-1]=(ll)coins[n-1][2]*(ll)(coins[n-1][1]-coins[n-1][0]+1);
for(int i=n-2; i>=0; i--){
ssum[i]=(ll)ssum[i+1]+(ll)coins[i][2]*(ll)(coins[i][1]-coins[i][0]+1);
}
vector<int> startTimes, endTimes;
for(int i=0; i<n; i++){
startTimes.push_back(coins[i][0]);
endTimes.push_back(coins[i][1]);
}
//Checking for all starting points
for(int i=0; i<n; i++){
int maxReach=coins[i][0]+k-1;
if(lower_bound(endTimes.begin(), endTimes.end(), maxReach)==endTimes.end()){
if(i==0){
ans=mx(ans, psum[n-1]);
}
else{
ans=mx(ans, psum[n-1]-psum[i-1]);
}
continue;
}
int index=lower_bound(endTimes.begin(), endTimes.end(), maxReach) - endTimes.begin();
long long cur=0;
if(maxReach>=startTimes[index]){
cur+=(ll)(maxReach-startTimes[index]+1)*(ll)coins[index][2];
}
if(index>0){
if(i==0){
cur+=psum[index-1];
}
else{
cur+=psum[index-1]-psum[i-1];
}
}
ans=mx(ans, cur);
}
//Checking for all ending points
for(int i=n-1; i>=0; i--){
int minReach=coins[i][1]-k+1;
if(lower_bound(startTimes.begin(), startTimes.end(), minReach)==startTimes.end()){
ans=mx(ans, (endTimes[i]-minReach+1)*coins[i][2]);
continue;
}
int index=lower_bound(startTimes.begin(), startTimes.end(), minReach)-startTimes.begin();
long long cur=0;
if(index>0 && endTimes[index-1]>=minReach){
cur+=(ll)(endTimes[index-1]-minReach+1)*(ll)coins[index-1][2];
}
if(i==n-1){
cur+=ssum[index];
}
else{
cur+=ssum[index]-ssum[i+1];
}
ans=mx(ans, cur);
}
return ans;
}
};
``` | 0 | 0 | ['Binary Search', 'Greedy', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | [CODE ONLY][DEBUG OUTPUT] PYTHON USING Alex Wice's SLIDING WINDOW SOLUTION | code-onlydebug-output-python-using-alex-tiqgy | Code | greg_savage | NORMAL | 2025-01-08T10:22:49.034272+00:00 | 2025-01-08T10:22:49.034272+00:00 | 23 | false | # Code
```python3 []
# Using Alex Wice's sliding window
# https://leetcode.com/problems/maximum-coins-from-k-consecutive-bags/solutions/6232234/python-sliding-window-by-awice-i1sv
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
n = len(coins)
def helper(h_coins: List[List[int]]) -> int:
h_coins.sort()
local_grab = 0
full_slots = 0
rhs = 0
for i, coin_segment in enumerate(h_coins):
# print(f'Starting at {i}... and {coin_segment}')
start, end, value = coin_segment
while rhs + 1 < n: # Get full windows
peak_next_start = h_coins[rhs + 1][0]
next_start_contained_in_grab = peak_next_start < start + k
if not next_start_contained_in_grab:
# print(f'\tDONE. Retrieved all full windows...')
break
# The next rhs window is fully contained...
adj_start, adj_end, adj_value = h_coins[rhs]
full_slots += (adj_end - adj_start + 1) * adj_value # Add one because inclusive range.
# print(f'\tTAKE full window of {h_coins[rhs]} at {(adj_end - adj_start + 1) * adj_value}')
rhs += 1
partial_slots = 0
partial_segment_start = h_coins[rhs][0]
partial_segment_end = h_coins[rhs][1]
partial_segment_value = h_coins[rhs][2]
if rhs < n and partial_segment_start < start + k:
# print(f'\t\tHANDLE PARTIAL...')
rightmost = min(start + k - 1, partial_segment_end)
# print(f'\t\t...rightmost is {rightmost}')
slots_taken = rightmost - partial_segment_start + 1
# print(f'\t\t......we can take {slots_taken} at {partial_segment_value} each.')
partial_slots += slots_taken * partial_segment_value
# print(f'\tlocal best = max({local_grab}, {full_slots + partial_slots})')
local_grab = max(local_grab, full_slots + partial_slots)
# print(f'\t...finally adjust {full_slots} by taking away {end - start + 1} * {value}')
full_slots -= (end - start + 1) * value # Take curr away
return local_grab
forward_grab = helper(coins)
# print(f'\n...\nREVERSING SLOTS\n...\n')
for i, each_segment in enumerate(coins): # Reverse
start, end, value = each_segment
coins[i] = [end * -1, start * -1, value]
backward_grab = helper(coins)
return max(forward_grab, backward_grab)
# DEBUG OUTPUT
# Input
# coins =
# [[8,10,1],[1,3,2],[5,6,4]]
# k =
# 4
# Stdout
# Starting at 0... and [1, 3, 2]
# DONE. Retrieved all full windows...
# HANDLE PARTIAL...
# ...rightmost is 3
# ......we can take 3 at 2 each.
# local best = max(0, 6)
# ...finally adjust 0 by taking away 3 * 2
# Starting at 1... and [5, 6, 4]
# TAKE full window of [1, 3, 2] at 6
# TAKE full window of [5, 6, 4] at 8
# HANDLE PARTIAL...
# ...rightmost is 8
# ......we can take 1 at 1 each.
# local best = max(6, 9)
# ...finally adjust 8 by taking away 2 * 4
# Starting at 2... and [8, 10, 1]
# HANDLE PARTIAL...
# ...rightmost is 10
# ......we can take 3 at 1 each.
# local best = max(9, 3)
# ...finally adjust 0 by taking away 3 * 1
# ...
# REVERSING SLOTS
# ...
# Starting at 0... and [-10, -8, 1]
# DONE. Retrieved all full windows...
# HANDLE PARTIAL...
# ...rightmost is -8
# ......we can take 3 at 1 each.
# local best = max(0, 3)
# ...finally adjust 0 by taking away 3 * 1
# Starting at 1... and [-6, -5, 4]
# TAKE full window of [-10, -8, 1] at 3
# TAKE full window of [-6, -5, 4] at 8
# HANDLE PARTIAL...
# ...rightmost is -3
# ......we can take 1 at 2 each.
# local best = max(3, 10)
# ...finally adjust 8 by taking away 2 * 4
# Starting at 2... and [-3, -1, 2]
# HANDLE PARTIAL...
# ...rightmost is -1
# ......we can take 3 at 2 each.
# local best = max(10, 6)
# ...finally adjust 0 by taking away 3 * 2
# Greedy Solution... TLE at test case 588...
# coins.sort()
# best_grab = 0
# prev_end = 0
# prev_size = 0
# n = len(coins)
# def grabAndForward(start_index: int) -> int:
# local_grab = 0
# remaining = k
# curr_index = start_index
# # print(f'[FORWARD] STARTING at index {i}')
# curr_segment_start = coins[i][0]
# last_end = curr_segment_start # Begin at start of first segment,
# while remaining > 0 and curr_index < n:
# # print(f'With local_grab={local_grab}, we have remaining={remaining} slots to fill...')
# # print(f'\tassessing coins[{curr_index}]: {coins[curr_index]}')
# curr_start, curr_end, curr_value = coins[curr_index]
# slots_to_get_to_curr_segment = curr_start - last_end
# # print(f'\t\tit took {slots_to_get_to_curr_segment} to get to {curr_start} from {last_end}...')
# remaining -= slots_to_get_to_curr_segment
# # print(f'\t\t\tthat means we have remaining={remaining} slots.')
# if remaining > 0:
# available_slots = (curr_end - curr_start) + 1 # Inclusive range, must add 1 to adjust
# # print(f'\t\t\t\twe have {available_slots} from [{curr_start},{curr_end}]')
# taken_slots = min(available_slots, remaining)
# # print(f'\t\t\t\t\twhich means we can take {taken_slots} for {curr_value} each')
# local_grab += taken_slots * curr_value
# remaining -= taken_slots
# # print(f'\t\t\t\t\t\twe have a new local_grab={local_grab} and new remaining={remaining}')
# # Update last_end
# last_end = curr_end + 1
# curr_index += 1
# continue
# # else:
# # print(f'\t\t\t\t...which means we have filled k.')
# break
# # print(f'\t...return {local_grab}')
# return local_grab
# def grabAndReverse(start_index: int) -> int:
# local_grab = 0
# remaining = k
# curr_index = start_index
# # print(f'[REVERSE] STARTING at index {i}')
# curr_segment_end = coins[i][1]
# last_start = curr_segment_end # Begin at start of first segment,
# while remaining > 0 and curr_index >= 0:
# # print(f'With local_grab={local_grab}, we have remaining={remaining} slots to fill...')
# # print(f'\tassessing coins[{curr_index}]: {coins[curr_index]}')
# curr_start, curr_end, curr_value = coins[curr_index]
# slots_to_get_to_curr_segment = last_start - curr_end
# # print(f'\t\tit took {slots_to_get_to_curr_segment} to get to {curr_end} from {last_start}...')
# remaining -= slots_to_get_to_curr_segment
# # print(f'\t\t\tthat means we have remaining={remaining} slots.')
# if remaining > 0:
# available_slots = (curr_end - curr_start) + 1 # Inclusive range, must add 1 to adjust
# # print(f'\t\t\t\twe have {available_slots} from [{curr_start},{curr_end}]')
# taken_slots = min(available_slots, remaining)
# # print(f'\t\t\t\t\twhich means we can take {taken_slots} for {curr_value} each')
# local_grab += taken_slots * curr_value
# remaining -= taken_slots
# # print(f'\t\t\t\t\t\twe have a new local_grab={local_grab} and new remaining={remaining}')
# # Update last_end
# last_start = curr_start - 1
# curr_index -= 1
# continue
# # else:
# # print(f'\t\t\t\t...which means we have filled k.')
# break
# # print(f'\t...return {local_grab}')
# return local_grab
# for i, _ in enumerate(coins):
# forward_grab = grabAndForward(i)
# reverse_grab = grabAndReverse(i)
# best_local = max(forward_grab, reverse_grab)
# best_grab = max(best_grab, best_local)
# return best_grab
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | My Solutions | my-solutions-by-hope_ma-n0sn | 1. Count the coins of the bags either starting from the left end of every segment or ending with the right end of every segment2. Use the sliding window | hope_ma | NORMAL | 2025-01-07T10:02:11.540824+00:00 | 2025-01-07T10:02:11.540824+00:00 | 13 | false | **1. Count the coins of the bags either starting from the left end of every segment or ending with the right end of every segment**
```
/**
* Time Complexity: O(n * log(n))
* Space Complexity: O(n)
* where `n` is the length of the vector `coins`
*/
class Solution {
private:
static constexpr int l_i = 0;
static constexpr int r_i = 1;
static constexpr int c_i = 2;
public:
long long maximumCoins(vector<vector<int>> &coins, const int k) {
const int n = static_cast<int>(coins.size());
sort(coins.begin(), coins.end());
long long presums[n + 1];
memset(presums, 0, sizeof(presums));
for (int i = 0; i < n; ++i) {
presums[i + 1] = presums[i] + count_coins(coins[i][l_i], coins[i][r_i], coins[i][c_i]);
}
long long ret = 0LL;
for (int i = 0; i < n; ++i) {
const int l = coins[i][l_i];
const int r = coins[i][r_i];
/**
* count the coins from the bags starting from `l` and ending with `right`, both inclusive
*/
const int right = l + k - 1;
const int index_right = find_index(coins, right);
const long long coins_at_index_right = count_coins(coins[index_right][l_i],
min(coins[index_right][r_i], right),
coins[index_right][c_i]);
ret = max(ret, (presums[index_right] - presums[i]) + coins_at_index_right);
/**
* count the coins from the bags starting from `left` and ending with `r`, both inclusive
*/
const int left = r - k + 1;
const int index_left = find_index(coins, left);
const long long coins_at_index_left = count_coins(max(coins[index_left][l_i], left),
coins[index_left][r_i],
coins[index_left][c_i]);
ret = max(ret, (presums[i + 1] - presums[index_left + 1]) + coins_at_index_left);
}
return ret;
}
private:
int find_index(const vector<vector<int>> &coins, const int coordinate) {
int low = 0;
int high = static_cast<int>(coins.size()) - 1;
while (low < high) {
const int mid = low + ((high - low) >> 1);
if (coins[mid][l_i] <= coordinate && coordinate <= coins[mid][r_i]) {
return mid;
}
if (coordinate > coins[mid][r_i]) {
low = mid + 1;
} else {
high = mid;
}
}
return high;
}
long long count_coins(const int l, const int r, const int c) {
return static_cast<long long>(r - l + 1) * c;
}
};
```
**2. Use the sliding window**
```
/**
* Time Complexity: O(n * log(n))
* Space Complexity: O(1)
* where `n` is the length of the vector `coins`
*/
class Solution {
private:
static constexpr int l_i = 0;
static constexpr int r_i = 1;
static constexpr int c_i = 2;
public:
long long maximumCoins(vector<vector<int>> &coins, const int k) {
sort(coins.begin(), coins.end());
long long ret = count_coins(coins, k);
reverse(coins);
ret = max(ret, count_coins(coins, k));
return ret;
}
private:
long long count_coins(const vector<vector<int>> &coins, const int k) {
const int n = static_cast<int>(coins.size());
long long ret = 0LL;
long long covered_coins = 0;
for (int left = numeric_limits<int>::min(), i_left = 0, i_right = 0; i_right < n; ++i_right) {
covered_coins += static_cast<long long>(coins[i_right][r_i] - coins[i_right][l_i] + 1) * coins[i_right][c_i];
for (; coins[i_right][r_i] - coins[i_left][r_i] + 1 > k; ++i_left) {
covered_coins -= static_cast<long long>(coins[i_left][r_i] - max(left, coins[i_left][l_i]) + 1) * coins[i_left][c_i];
}
left = max(left, coins[i_left][l_i]);
const int next_left = coins[i_right][r_i] - k + 1;
covered_coins -= static_cast<long long>(max(0, next_left - left)) * coins[i_left][c_i];
left = next_left;
ret = max(ret, covered_coins);
}
return ret;
}
void reverse(vector<vector<int>> &coins) {
for (vector<int> &coin : coins) {
swap(coin[l_i], coin[r_i]);
coin[l_i] *= -1;
coin[r_i] *= -1;
}
::reverse(coins.begin(), coins.end());
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | 3413. Maximum Coins From K Consecutive Bags(62.88%) | 3413-maximum-coins-from-k-consecutive-ba-ccq5 | Intuition
Represent coin intervals with a difference array-like map.
Flatten the data into positions and their respective coin counts using prefix sums.
Use a s | Nalindalal2004 | NORMAL | 2025-01-07T04:27:04.002085+00:00 | 2025-01-07T04:27:04.002085+00:00 | 32 | false | # Intuition
1. Represent coin intervals with a difference array-like map.
2. Flatten the data into positions and their respective coin counts using prefix sums.
3. Use a sliding window to find the maximum sum of k consecutive positions.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
1. Use a Map for Coin Changes:
- Each interval [li, ri] with ci coins is represented by:
- Adding ci coins to li (coinMap[li] += ci).
- Subtracting ci coins from ri + 1 (coinMap[ri + 1] -= ci).
- This creates a map where each key represents a coordinate, and the value
represents how the number of coins changes at that coordinate.
2. Flatten into Prefix Coins:
- Traverse the map in sorted order of coordinates, maintaining a running
total (currentCoins) of coins at each position.
- Store these positions and their respective currentCoins in a list
prefixCoins.
3. Apply Sliding Window Technique:
- Traverse the prefixCoins list while maintaining a sliding window of size
k.
- For each segment:
- Add the coins in the current interval to windowSum and update the
window size.
- If the window size exceeds k, shrink it from the left by subtracting
coins from the start of the window.
- Keep track of the maximum coins obtained (maxCoins).
# Complexity
- Time complexity: $$O(n+m)$$
- Constructing coinMap: $$O(n)$$, where `n` is the number of intervals in coins.
- Traversing coinMap: $$O(m)$$, where `m` is the number of unique positions.
- Sliding window traversal: $$O(m)$$.
- Space complexity: $$O(m)$$
# Code
```cpp []
#define ll long long
class Solution {
public:
long long maximumCoins(vector<vector<int>>& x, int k) {
ll ans = 0, n = x.size();
x.insert(x.begin(), {0});
sort(x.begin(), x.end());
vector<ll>pre(n + 1);
for(int i = 1; i <= n; i++)
pre[i] = pre[i - 1] + (x[i][1] - x[i][0] + 1) * (ll)x[i][2];
for(int i = 1; i <= n; i++){
int l = i + 1 , r = n, m, o = x[i][0] + k - 1;
while(l <= r){
m = l + r >> 1;
(o >= x[m][0] ? l = m + 1 : r = m - 1);
}
if(o >= x[r][1]) // if the point is covers all the intervals
ans = max(ans, pre[r] - pre[i - 1]);
else // if the point is not covers all the intervals
ans = max(ans,pre[r-1]-pre[i-1] + (o - x[r][0] + 1) * (ll)x[r][2]);
l = 1 , r = i - 1, o = x[i][1] - k + 1;
while(l <= r){
m = l + r >> 1;
(o <= x[m][1] ? r = m - 1 : l = m + 1);
}
if(o <= x[l][0]) // if the point is covers all the intervals
ans = max(ans, pre[i] - pre[l - 1]);
else // if the point is not covers all the intervals
ans = max(ans, pre[i] - pre[l] + (x[l][1] - o + 1) * (ll)x[l][2]);
}
return ans;
}
};
```
```ts []
function maximumCoins(coins: number[][], k: number): number {
let ans = 0n; // Use BigInt for handling large numbers
const n = coins.length;
// Insert a dummy interval at the beginning
coins.unshift([0, 0, 0]);
coins.sort((a, b) => a[0] - b[0]); // Sort intervals by start position
// Prefix sum array
const pre = new Array<bigint>(n + 1).fill(0n);
for (let i = 1; i <= n; i++) {
const [li, ri, ci] = coins[i];
pre[i] = pre[i - 1] + BigInt((ri - li + 1) * ci);
}
for (let i = 1; i <= n; i++) {
// Binary search for right segments
let l = i + 1, r = n, o = coins[i][0] + k - 1;
while (l <= r) {
const m = Math.floor((l + r) / 2);
if (o >= coins[m][0]) {
l = m + 1;
} else {
r = m - 1;
}
}
if (o >= coins[r][1]) {
// Covers all intervals
ans = ans > pre[r] - pre[i - 1] ? ans : pre[r] - pre[i - 1];
} else {
// Partially covers the interval
ans = ans > (pre[r - 1] - pre[i - 1] + BigInt(o - coins[r][0] + 1) * BigInt(coins[r][2]))
? ans
: (pre[r - 1] - pre[i - 1] + BigInt(o - coins[r][0] + 1) * BigInt(coins[r][2]));
}
// Binary search for left segments
l = 1;
r = i - 1;
o = coins[i][1] - k + 1;
while (l <= r) {
const m = Math.floor((l + r) / 2);
if (o <= coins[m][1]) {
r = m - 1;
} else {
l = m + 1;
}
}
if (o <= coins[l][0]) {
// Covers all intervals
ans = ans > pre[i] - pre[l - 1] ? ans : pre[i] - pre[l - 1];
} else {
// Partially covers the interval
ans = ans > (pre[i] - pre[l] + BigInt(coins[l][1] - o + 1) * BigInt(coins[l][2]))
? ans
: (pre[i] - pre[l] + BigInt(coins[l][1] - o + 1) * BigInt(coins[l][2]));
}
}
return Number(ans); // Convert BigInt back to number
}
```
[c++](https://leetcode.com/problems/maximum-coins-from-k-consecutive-bags/submissions/1500253547/)
[ts](https://leetcode.com/problems/maximum-coins-from-k-consecutive-bags/submissions/1500261221/) | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Easy Binary Search New Approach | easy-binary-search-new-approach-by-ankii-2ta0 | Intuitionwe have given to select k consecutive elements and since for 1e9 we cannot traverse on every index and apply sliding window. So we need to check that f | ankii09102003 | NORMAL | 2025-01-06T13:30:30.085720+00:00 | 2025-01-06T13:30:30.085720+00:00 | 48 | false | # Intuition
we have given to select k consecutive elements and since for 1e9 we cannot traverse on every index and apply sliding window. So we need to check that for a particular index given in coins array what is the last element and where it lies.So, directy traverse all the ranges given and find the last element where it lies. Use Binary search.
# Approach
There are two main loops first is that take the starting element and second is to take end element and in them.
Ok SO traversing each and every element and then check that what is the index of element which is k coordinate away basically i want to find that in which range that element lies then consider the coins between index and current index basically we just get the index of range in which it lying now for calculating the actual coins we just add the coins in between these ranges and also + coins left in last index.
suppose 1 2 3 4 is the first range coins(10) and 7 8 9 is the second range coins(4) and 11 12 13 is third range coins(8) so traversing the first element of all range and suppose k=4 now we just go on every range and just check that where the next kth element lie upto.
so here we get index as 0 since all four element lies in first range so add it in ans now go on second range 7 8 9 for 7 just check next indexwhere it lies so for k=4 it would be 10 but having no index so it would also lie in this range so just by doing so we can find the total coins lying in k elements by using prefix sum which we will store initially.so by using prefix sum we can find the total eleemnts lying in between two range.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int binarySearch(const vector<int>& BS, int target,int curr) {
int low = 0, high = BS.size() - 1, ans = curr;
while (low <= high) {
int mid = low + (high - low) / 2;
if (BS[mid] <= target) {
ans = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return ans; // Return the index of the largest element <= target
}
int findGreaterEqualIndex(const vector<int>& BS, int target,int curr) {
int low = 0, high = BS.size() - 1, ans = curr;
while (low <= high) {
int mid = low + (high - low) / 2;
if (BS[mid] >= target) { // Check for greater than or equal to
ans = mid; // Update the answer
high = mid - 1; // Search in the left half
} else {
low = mid + 1; // Search in the right half
}
}
return ans; // Return the index of the smallest element >= target, or -1 if not found
}
long long maximumCoins(vector<vector<int>>& coins, int k) {
// Sort based on the starting index
sort(coins.begin(), coins.end());
int n = coins.size();
long long maxAns = 0;
// Precompute the start indices and total coins for ranges
vector<int> BS(n, 0);
vector<long long> totalCoinsInRange(n, 0);
for (int i = 0; i < n; i++) {
BS[i] = coins[i][0];
}
long long tillNow = 0;
for (int i = 0; i < n; i++) {
totalCoinsInRange[i] = tillNow;
tillNow +=(long long)(coins[i][1] - coins[i][0] + 1) * coins[i][2];
}
// Check maximum coins by taking `i` as the starting index
for (int i = 0; i < n; i++) {
if (BS[i] + k - 1 > coins[n - 1][1]) break; // Early exit if the range exceeds the target
int index = binarySearch(BS, BS[i] + k - 1,i);
int diff = k - (BS[index] - BS[i]);
long long coinsCollected = totalCoinsInRange[index] - totalCoinsInRange[i];
coinsCollected += (long long)(min(diff,coins[index][1]-coins[index][0]+1) *(long long) coins[index][2]);
maxAns = max(maxAns, coinsCollected);
cout<<index<<" "<<maxAns<<endl;
}
// Check maximum coins by taking `i` as the ending index
vector<int>BS2(BS.size(),0);
for(int i=0;i<coins.size();i++){
BS2[i]=coins[i][1];
}
vector<long long> totalCoinsInRange2(n, 0);
tillNow = 0;
for (int i = 0; i < n; i++) {
tillNow +=(long long)(coins[i][1] - coins[i][0] + 1) * coins[i][2];
totalCoinsInRange2[i] = tillNow;
}
for (int i = n - 1; i >= 0; i--) {
// Early exit if the range exceeds the target
int index = findGreaterEqualIndex(BS2, BS2[i] - k + 1,i);
int diff = k - (BS2[i] - BS2[index]);
long long coinsCollected = totalCoinsInRange2[i] - totalCoinsInRange2[index];
cout<<coinsCollected<<endl;
coinsCollected += min((long long)diff,(long long)coins[index][1]-coins[index][0]+1) * coins[index][2];
maxAns = max(maxAns, coinsCollected);
cout<<index<<" "<<maxAns<<endl;
}
return maxAns;
}
};
``` | 0 | 0 | ['Binary Search', 'Sliding Window', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | PrefixSum and BinarySearch Approach | prefixsum-and-binarysearch-approach-by-h-lb9t | IntuitionIt can be proved that in order to collect maximum coins you need to start at leftMostPoint of interval or end at rightMostPoint of a given interval in | harry161998 | NORMAL | 2025-01-06T13:26:20.428836+00:00 | 2025-01-06T13:26:20.428836+00:00 | 37 | false | # Intuition
It can be proved that in order to collect maximum coins you need to start at leftMostPoint of interval or end at rightMostPoint of a given interval in case of distinct division of coins in a given interval.
# Approach
Calculate the prefixSum in order to find totalCoins in O(1) time.
Take two case of starting from leftMost or ending at rightMost for every possible indices.
Maximum of all will give the maxium coins that can be collected.
Example -
```
Sorted Array [[1,3,2], [5,6,4] , [8,10,1]]
PrefixSum [6,14,17]
startpoints [1,5,8] // array creation is not required
endpoints [3,6,10] // array creation is not required
k = 4
```
```
For index 0 [1,3,2]
Start at 1
End = 1+4-1 = 4
lower_bound in endpoints is 6 at index 1
Index = 1
letMostCoins = prefixSum[0] = 6
```
```
For index 0 [1,3,2]
End at 3
Start = 3-4+1 = 0
lower_bound in startpoints is 1 at index 0
rightMostCoins = prefixSum[0] = 6
```
```
For index 1 [5,6,4]
Start at 5
End = 5+4-1 = 8
lower_bound in endpoints is 10 at index 2
leftMostCoins = prefixSum[1] - prefixSum[0] + (8-8+1) * 1 = 14-6+1 = 9
```
```
For index 1 [5,6,4]
End at 6
Start = 6-4+1 = 3
lower_bound in startpoints is 5 at index 1
rightMostCoins = prefixSum[1] - prefixSum[0] + (3-3+1) * 2 = 14-6+2 = 10
```
```
For index 2 [8,10,1]
Start at 8
End = 8+4-1 = 11
lower_bound in endpoints is 11 at index 3
leftMostCoins = prefixSum[2] - prefixSum[1] + 0 = 17-14 = 3
```
```
For index 2 [8,10,1]
End at 10
Start at 10-4+1 = 7
lower_bound in startpoints is 8 at index 2
rightMostCoins = prefixSum[2] - prefixSum[1] + 0 = 17-14 = 3
```
```
Maximum of all cases {6,6,9,10,3,3} is 10
```
# Complexity
- Time complexity:
O(nlogn)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(begin(coins), end(coins));
int n = coins.size();
vector<long long> prefixSum(n,0);
prefixSum[0] = (coins[0][1] - coins[0][0] + 1) * 1LL * coins[0][2];
for(int i=1 ; i<n ;i++)
prefixSum[i] = prefixSum[i-1] + (coins[i][1] - coins[i][0] + 1) * 1LL * coins[i][2];
long long ans = 0;
for(int i=0; i<n ; i++) {
long long leftMostCoins = getLeftMostStartCoins(coins,k,prefixSum,i,n);
long long rightMostCoins = getRightMostEndCoins(coins,k,prefixSum,i,n);
ans = max(ans , max(leftMostCoins,rightMostCoins));
}
return ans;
}
long long getLeftMostStartCoins(vector<vector<int>>& coins, int k, vector<long long> &prefixSum, int i, int n) {
int start = coins[i][0];
int end = start + k - 1;
int index = lower_bound(coins.begin(),coins.end(),end,[&](vector<int> &a,int x){
return a[1] <= x;
}) - coins.begin();
long long leftCoins = 0;
if(index > 0 )
leftCoins += prefixSum[index-1]- (i>0 ? prefixSum[i-1] : 0);
if(index<n && end >= coins[index][0])
leftCoins += (end-coins[index][0]+1) * 1LL * coins[index][2];
return leftCoins;
}
long long getRightMostEndCoins(vector<vector<int>>& coins, int k, vector<long long> &prefixSum, int i, int n) {
int end = coins[i][1];
int start = end - k + 1;
int index = lower_bound(coins.begin(),coins.end(), start,[&](vector<int> &a,int x){
return a[0] <= x;
}) - coins.begin();
long long rightCoins = 0;
rightCoins += prefixSum[i]- (index > 0 ? prefixSum[index-1] : 0);
if(index >0 && coins[index-1][1] >= start)
rightCoins += (coins[index-1][1] - start +1) * 1LL * coins[index-1][2];
return rightCoins;
}
};
``` | 0 | 0 | ['Binary Search', 'Greedy', 'Prefix Sum', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | C++ | Beats 100% | Sliding Window | Clean and Concise | | c-beats-100-sliding-window-clean-and-con-elgv | IntuitionI was not able to solve this in contest i was stuck trying sweepline with map hoping for every window of k i can calculate ans but was very hard to imp | n1kh1l | NORMAL | 2025-01-06T05:51:58.268348+00:00 | 2025-01-06T05:51:58.268348+00:00 | 55 | false | # Intuition
I was not able to solve this in contest i was stuck trying sweepline with map hoping for every window of k i can calculate ans but was very hard to implement eventually it is sliding window only and hint suggests to do it for every interval but how to prove it, I can only think is there is a gap with 0 value in between intervals to minimize gaps take complete intervals either from left or from right of it.
# Approach
Create an array that completes the gaps and slide over the window of size k
check both ways forward and reverse
# Complexity
- Time complexity:
O(N) - 103ms
- Space complexity:
O(N)
# Code
```cpp []
class Solution {
public:
long long window (vector<pair<long long,long long>>& v, int k) {
int n = v.size();
int left = 0, right = 0, len = 0;
long long res = 0ll, ans = 0ll;
while (left < n && right < n) {
if (len + v[right].first <= k) {
len += v[right].first;
ans += v[right].first * v[right].second;
res = max(res, ans);
right++;
}
else {
res = max(res, ans + (abs(len - k) * v[right].second));
ans -= v[left].first * v[left].second;
len -= v[left].first;
left++;
}
}
return res;
}
long long maximumCoins(vector<vector<int>>& coins, int k) {
// check for all start indexes and end indexes
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
sort(coins.begin(), coins.end());
int n = coins.size();
int gap = 0;
vector<pair<long long,long long>> v;
for (int i = 0; i < n; i++) {
int val = coins[i][2];
int dis = coins[i][1] - coins[i][0] + 1;
if (i > 0)
gap = coins[i][0] - coins[i - 1][1] - 1;
if (gap != 0)
v.push_back({gap * 1ll, 0ll});
v.push_back({dis * 1ll, val * 1ll});
}
//forward check
long long res = window(v, k);
//reverse check
reverse(v.begin(), v.end());
res = max(res, window(v, k));
return res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Kotlin || Sliding Window || O(N) | kotlin-sliding-window-on-by-nazmulcuet11-8mkh | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | nazmulcuet11 | NORMAL | 2025-01-06T04:29:17.204091+00:00 | 2025-01-06T04:29:17.204091+00:00 | 16 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```kotlin []
class Solution {
data class Segment(val start: Int, val end: Int, val value: Int) {
val total: Long
get() = (end - start + 1) * value.toLong()
}
fun maximumCoins(coins: Array<IntArray>, k: Int): Long {
val segments = coins.map { Segment(it[0], it[1], it[2]) }.sortedBy { it.start }
var ans = 0L
var i = 0
var j = 0
var sum = 0L
while (i < segments.size) {
val windowStart = segments[i].start
val windowEnd = windowStart + k - 1
while (j < segments.size && windowEnd >= segments[j].end) {
sum += segments[j].total
ans = max(ans, sum)
j++
}
if (j < segments.size && windowEnd >= segments[j].start) {
val diff = windowEnd - segments[j].start + 1
val partial = diff * segments[j].value
ans = max(ans, sum + partial)
}
sum -= segments[i].total
i++
}
sum = 0
i = segments.size - 1
j = segments.size - 1
while (j >= 0) {
val windowEnd = segments[j].end
val windowStart = windowEnd - k + 1
while (i >= 0 && windowStart <= segments[i].start) {
sum += segments[i].total
ans = max(ans, sum)
i--
}
if (i >= 0 && windowStart <= segments[i].end) {
val diff = segments[i].end - windowStart + 1
val partial = diff * segments[i].value
ans = max(ans, sum + partial)
}
sum -= segments[j].total
j--
}
return ans
}
}
``` | 0 | 0 | ['Sliding Window', 'Kotlin'] | 0 |
maximum-coins-from-k-consecutive-bags | two sliding window. python easy solution. | two-sliding-window-python-easy-solution-ovbdh | Code | yuchuehw | NORMAL | 2025-01-06T00:21:05.935618+00:00 | 2025-01-06T00:23:12.922148+00:00 | 50 | false | # Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
def slide():
ans = covers = 0
left = 0 # left index. use for removal
for l,r,c in coins:
covers += (r-l+1)*c # in
while coins[left][1] <= r-k: # out
l2,r2,c2 = coins[left]
covers -= (r2-l2+1)*c2
left += 1
l2,r2,c2=coins[left]
uncover = max((r-k+1-l2)*c2,0) # partially uncover region removal
# uncover is used because we don't want to subtract twice.
ans = max(ans, covers-uncover) # update
return ans
coins.sort()
right_best = slide() # search all right endpoint
coins = [(-r,-l,c) for l,r,c in coins[::-1]] # mirror about origin
left_best = slide() # search all left end point (because of mirror)
return max(left_best, right_best)
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | prefix sum + binary search(es). ~850ms. finished 10m late :/. | prefix-sum-binary-searches-finished-10m-qfha3 | IntuitionThere are two options to make an optimal choice
a) collect bags within range of k starting at a left edge of a coin interval
b) collect bags within ran | hama87 | NORMAL | 2025-01-05T22:06:25.722365+00:00 | 2025-01-06T00:36:20.544124+00:00 | 47 | false | # Intuition
There are two options to make an optimal choice
a) collect bags within range of k starting at a left edge of a coin interval
b) collect bags within range of k ending at a right edge of a coin interval
# Approach
pre-compute a prefix sum over all coin intervals that stores the total number of coins contained up to (including) the current coin interval
then loop over all coin intervals and evalute that total number of coins contained within option a) and option b) when both are anchored at the current coin interval (i.e. range k starting at current left edge and range k ending at current right edge.)
To compute the total number of coins, we need binary searches to obtain the coin interval at which the total range k ends (option a) or at which the total range k starts (option b)
The challenging part is to correctly add the coins from interval that only partly contribute the the solution.
Recommend visualizing on paper to get past the index madness.
# Complexity
- Time complexity:
$$O(n * log(n))$$ where n is the number of coin intervals
- Space complexity:
$$O(n)$$ e.g. storing the prefix sum
# Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
coins.sort()
ls, rs, cs = zip(*coins)
# precompute prefix over all intervals
total_coins_prefix = [0] * len(coins)
curr = 0
for i, (l, r, c) in enumerate(coins):
curr += (r-l+1) * c
total_coins_prefix[i] = curr
ans = 0
for i, (l, r) in enumerate(zip(ls, rs)):
#### case 1: range of length k beginning at each interval's left edge
curr = 0
if i > 0:
# subtract total value of intervals before l
curr -= total_coins_prefix[i-1]
j = bisect_left(ls, l+k+1)-1
# can add value of all intervals up to (but excluding) this potentially partial interval
if j > 0:
curr += total_coins_prefix[j-1]
# now need to handle last partial interval
last_l, last_r = ls[j], rs[j]
curr += (min(last_r, l+k-1) - last_l + 1) * cs[j]
ans = max(ans, curr)
#### case2: range of length k ending at each interval's right edge
curr = 0
# we include up to current box
curr += total_coins_prefix[i]
j = bisect_left(rs, r-k)
# need to subtract intervals up to (and including) this potentially partial interval
curr -= total_coins_prefix[j]
# now need to handle first potentially partial interval
first_l, first_r = ls[j], rs[j]
curr += (first_r - max(first_l, r-k+1) + 1) * cs[j]
ans = max(ans, curr)
return ans
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Sliding Window. Same as 2271, but in both ways | sliding-window-same-as-2271-but-in-both-hpawt | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | srptv | NORMAL | 2025-01-05T21:00:58.674952+00:00 | 2025-01-05T21:00:58.674952+00:00 | 34 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumCoins(self, tiles: List[List[int]], carpetLen: int) -> int:
tiles.sort()
print(tiles)
# return
mx = 0
l = 0
r = 0
cr = 0
cover = carpetLen + tiles[r][0] - 1
while r < len(tiles):
if cover >= tiles[r][1]:
cr += (tiles[r][1] - tiles[r][0] + 1) * tiles[r][2]
mx = max(cr, mx)
r += 1
else:
if cover >= tiles[r][0]:
# cr += (cover - tiles[r][0] + 1)
mx = max(cr + ((cover - tiles[r][0] + 1) * tiles[r][2]), mx)
# else:
cr -= (tiles[l][1] - tiles[l][0] + 1) * tiles[l][2]
l += 1
if l >= len(tiles): break
cover = tiles[l][0] + carpetLen - 1
print
# tiles.sort(reverse=True)
l = len(tiles) - 1
r = len(tiles) - 1
cr = 0
cover = tiles[r][1] - carpetLen + 1
while r >= 0:
if cover <= tiles[r][0]:
cr += (tiles[r][1] - tiles[r][0] + 1) * tiles[r][2]
mx = max(cr, mx)
r -= 1
else:
if cover <= tiles[r][1]:
# cr += (cover - tiles[r][0] + 1)
mx = max(cr + ((tiles[r][1] - cover + 1) * tiles[r][2]), mx)
# else:
cr -= (tiles[l][1] - tiles[l][0] + 1) * tiles[l][2]
l -= 1
if l < 0: break
cover = tiles[l][1] - carpetLen + 1
# print(mx)
# return mx
return mx
# start = []
# end = []
# mxx = 0
# for i, j, c in coins:
# heapq.heappush(start, (i, c))
# heapq.heappush(end, (max(j + 1, i + k), c))
# mxx = max(mxx, j + 1)
# # arr = [0] * (mxx + k)
# print(start, end)
# mx = 0
# cn = 0
# cnt = 0
# # print(arr, mxx)
# for i in range(start[0][0], start[0][0] + k):
# while start and start[0][0] <= i:
# cn += heapq.heappop(start)[1]
# # cnt += 1
# while end and end[0][0] <= i:
# cn = -heapq.heappop(end)[1]
# print(i, cn)
# # arr[i] = cn
# mx += cn
# # print(i)
# print(mx, mxx, i, "----" )
# ans = 0
# ans = max(mx, ans)
# return
# for j in range(i + 1, mxx + 1):
# while start and start[0][0] <= j:
# cn = heapq.heappop(start)[1]
# cnt += 1
# while end and end[0][0] <= j:
# heapq.heappop(end)
# cnt -= 1
# if cnt == 0: cn = 0
# # if cnt - 1 == 0:
# # cn = 0
# # cn = 0
# # arr[j] = cn
# mx += cn - arr[j - k]
# ans = max(ans, mx)
# # print(j, mx, cn, cnt)
# # print(arr, ans)
# return ans
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Easy iterate on array rather than on axis | easy-iterate-on-array-rather-than-on-axi-x4y4 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | VISHAL_REDDY_K | NORMAL | 2025-01-05T18:44:54.698915+00:00 | 2025-01-05T18:44:54.698915+00:00 | 22 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
#define ll long long
long long maximumCoins(vector<vector<int>>& arr, int k){
sort(arr.begin(),arr.end()); int n = arr.size();
ll i = 0; ll j = 0; ll ans = 0; ll curr = 0;
for(int i=0;i<n;i++){
while(j<n && arr[j][1]-arr[i][0]+1<=k){
curr+=((1ll* arr[j][1]-arr[j][0]+1)*arr[j][2]);
j++;
}
ll par = 0;
if(j<n && arr[j][0]<=arr[i][0]+k-1){
par =((1ll* arr[i][0]+k-1-arr[j][0]+1)*arr[j][2]);
curr+=par;
}
ans = max(ans,curr);
curr-=(1ll * arr[i][1]-arr[i][0]+1)*arr[i][2];
curr-=par;
}
j=n-1; curr = 0;
for(int i=n-1;i>=0;i--){
while(j>=0 && arr[i][1]-arr[j][0]+1<=k){
curr+=((1ll* arr[j][1]-arr[j][0]+1)*arr[j][2]);
j--;
}
ll par = 0;
if(j>=0 && arr[i][1]-arr[j][1]+1<=k){
par =((1ll *arr[j][1]-(arr[i][1]-k+1)+1)*arr[j][2]);
curr+=par;
}
ans = max(ans,curr);
curr -= ((1ll *arr[i][1]-arr[i][0]+1)*arr[i][2]);
curr-=par;
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Easy iterate on array rather than on axis | easy-iterate-on-array-rather-than-on-axi-dei9 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | VISHAL_REDDY_K | NORMAL | 2025-01-05T18:44:51.967945+00:00 | 2025-01-05T18:44:51.967945+00:00 | 15 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
#define ll long long
long long maximumCoins(vector<vector<int>>& arr, int k){
sort(arr.begin(),arr.end()); int n = arr.size();
ll i = 0; ll j = 0; ll ans = 0; ll curr = 0;
for(int i=0;i<n;i++){
while(j<n && arr[j][1]-arr[i][0]+1<=k){
curr+=((1ll* arr[j][1]-arr[j][0]+1)*arr[j][2]);
j++;
}
ll par = 0;
if(j<n && arr[j][0]<=arr[i][0]+k-1){
par =((1ll* arr[i][0]+k-1-arr[j][0]+1)*arr[j][2]);
curr+=par;
}
ans = max(ans,curr);
curr-=(1ll * arr[i][1]-arr[i][0]+1)*arr[i][2];
curr-=par;
}
j=n-1; curr = 0;
for(int i=n-1;i>=0;i--){
while(j>=0 && arr[i][1]-arr[j][0]+1<=k){
curr+=((1ll* arr[j][1]-arr[j][0]+1)*arr[j][2]);
j--;
}
ll par = 0;
if(j>=0 && arr[i][1]-arr[j][1]+1<=k){
par =((1ll *arr[j][1]-(arr[i][1]-k+1)+1)*arr[j][2]);
curr+=par;
}
ans = max(ans,curr);
curr -= ((1ll *arr[i][1]-arr[i][0]+1)*arr[i][2]);
curr-=par;
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | ✅ [Java / C++] | 34ms | Beats 100%, super easy sliding window approach. | beats-100-java-sliding-window-solution-b-jjti | IntuitionThe problem is about finding the maximum number of coins we can collect from k consecutive bags. Using a sliding window approach is optimal because it | Only_Night | NORMAL | 2025-01-05T18:21:06.787563+00:00 | 2025-02-02T01:33:17.197684+00:00 | 112 | false | # Intuition
The problem is about finding the maximum number of coins we can collect from k consecutive bags. Using a sliding window approach is optimal because it allows us to efficiently compute and update the sum of coins in the window as it moves across the range.
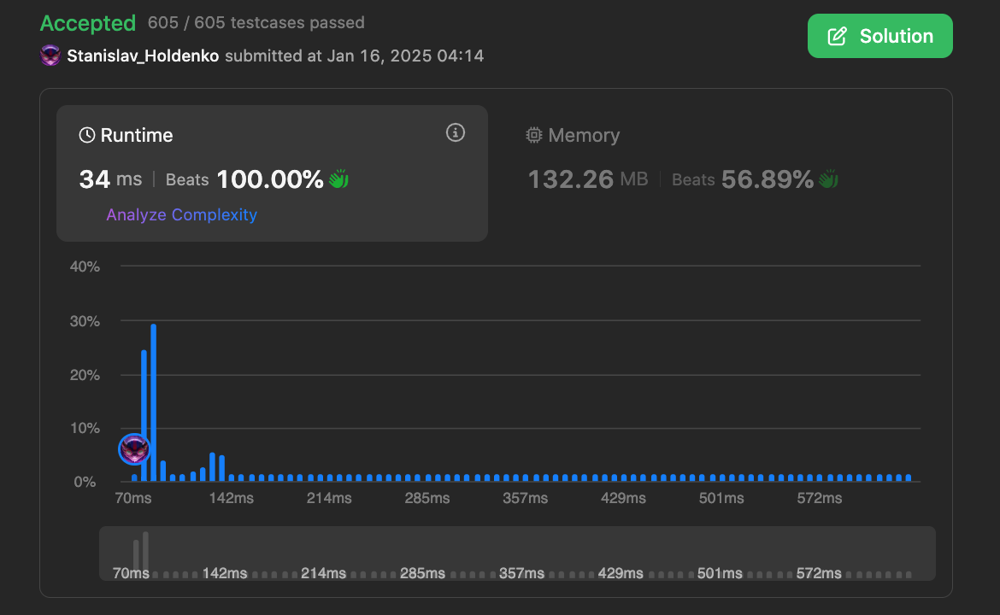
# Approach
1. Sort the Input: Since the coins ranges may be unsorted, start by sorting them based on their starting coordinates.
2. Sliding Window:
- Use two pointers (left and right) to represent the bounds of the current window.
- Maintain a running sum (cur) of coins in the window.
- For each segment, add coins from the right range if it overlaps with the current window.
- Remove coins from the left range if it falls outside the current window.
- Dynamically adjust the start and end of the window based on the constraints of k consecutive bags.
3. Update the Maximum: Track the maximum coins collected during this process.
4. Edge Cases: Handle scenarios where:
- k exceeds the total number of bags in any range.
- Sparse ranges where consecutive bags don't overlap.
# Code
```java []
class Solution {
private static final int S = 32;
public long maximumCoins(int[][] coins, int k) {
int n = coins.length;
// Handle single range case
if (n == 1) {
return (long) Math.min(coins[0][1] - coins[0][0] + 1, k) * coins[0][2];
}
// Sort ranges by starting position.
// For faster sorting we combine start and id in long value.
long[] sorted = new long[n];
for(int i = 0; i < n; i++) {
sorted[i] = (long) coins[i][0] << S | i;
}
Arrays.sort(sorted);
long max = 0, cur = 0;
long start = sorted[0] >> S, end = start + k - 1;
for (int left = 0, right = 0; right < n;) {
int[] r = coins[(int)sorted[right]];
long rs = r[0], re = r[1];
if (end >= re) {
// Add the entire range at `right` if it fits within the window
cur += (re - rs + 1) * r[2];
right++;
continue;
}
// Calculate maximum if the `right` range partially overlaps the window
max = Math.max(max, rs <= end ? (end - rs + 1) * r[2] + cur : cur);
int[] l = coins[(int)sorted[left]];
long le = l[1], newStart = re - k + 1;
if (newStart <= le) {
// Adjust for partial overlap of the new window's start with the `left` range
cur += (re - rs + 1) * r[2] - (newStart - start) * l[2];
end = re;
start = newStart;
right++;
} else {
// Shift the window entirely past the `left` range
left++;
cur -= (le - start + 1) * l[2];
start = sorted[left] >> S;
end = start + k - 1;
}
}
return Math.max(max, cur);
}
}
```
``` C++ []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
const int S = 32;
int n = coins.size();
// Handle single range case
if (n == 1) {
return (long long)min(coins[0][1] - coins[0][0] + 1, k) * coins[0][2];
}
// Using raw array for faster sorting
long long* sorted = new long long[n];
for (int i = 0; i < n; i++) {
sorted[i] = ((long long)coins[i][0] << S) | i;
}
sort(sorted, sorted + n);
long long maxCoins = 0, cur = 0;
long long start = sorted[0] >> S, end = start + k - 1;
for (int left = 0, right = 0; right < n;) {
auto& r = coins[(int)sorted[right]];
long long rs = r[0], re = r[1];
if (end >= re) {
// Add the entire range at `right` if it fits within the window
cur += (re - rs + 1) * r[2];
right++;
continue;
}
// Calculate maximum if the `right` range partially overlaps the window
maxCoins = max(maxCoins, rs <= end ? (end - rs + 1) * r[2] + cur : cur);
auto& l = coins[(int)sorted[left]];
long long le = l[1], newStart = re - k + 1;
if (newStart <= le) {
// Adjust for partial overlap of the new window's start with the `left` range
cur += (re - rs + 1) * r[2] - (newStart - start) * l[2];
end = re;
start = newStart;
right++;
} else {
// Shift the window entirely past the `left` range
left++;
cur -= (le - start + 1) * l[2];
start = sorted[left] >> S;
end = start + k - 1;
}
}
return max(maxCoins, cur);
}
};
```
| 0 | 0 | ['Sliding Window', 'C++', 'Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Python Medium | python-medium-by-lucasschnee-tbtp | null | lucasschnee | NORMAL | 2025-01-05T18:03:26.879296+00:00 | 2025-01-05T18:03:26.879296+00:00 | 39 | false | ```python3 []
class Solution:
def maximumCoins(self, A: List[List[int]], k: int) -> int:
'''
try every l endpoint to the right and r endpoint to the left of exactly k size
prefix sums
(1, 2) (4, 5)
'''
A.sort()
prev_end = 0
for l, r, c in list(A):
if l - 1 != prev_end:
A.append([prev_end + 1, l - 1, 0])
prev_end = r
A.sort()
best = 0
cur_sum = 0
cur_bags = 0
q = deque()
for l, r, c in A:
interval_length = r - l + 1
if interval_length + cur_bags <= k:
cur_bags += interval_length
q.append((l, r, c))
cur_sum += interval_length * c
if cur_bags == k:
best = max(best, cur_sum)
else:
cur_sum += interval_length * c
cur_bags += interval_length
q.append((l, r, c))
while cur_bags > k:
diff = cur_bags - k
tmp_sum = cur_sum
tmp_sum -= diff * c
best = max(best, tmp_sum)
ll, rr, cc = q.popleft()
interval_length_2 = rr - ll + 1
cur_bags -= interval_length_2
cur_sum -= cc * interval_length_2
if cur_bags == k:
best = max(best, cur_sum)
best = max(best, cur_sum)
B = []
for l, r, c in A:
B.append((-r, -l, c))
B.sort()
cur_sum = 0
cur_bags = 0
# print(B)
q = deque()
for r, l, c in B:
r *= -1
l *= -1
interval_length = r - l + 1
if interval_length + cur_bags <= k:
cur_bags += interval_length
q.append((l, r, c))
cur_sum += interval_length * c
best = max(best, cur_sum)
else:
cur_sum += interval_length * c
cur_bags += interval_length
q.append((l, r, c))
while cur_bags > k:
# print(q, cur_sum, cur_bags)
diff = cur_bags - k
tmp_sum = cur_sum
tmp_sum -= diff * c
best = max(best, tmp_sum)
ll, rr, cc = q.popleft()
interval_length_2 = rr - ll + 1
cur_bags -= interval_length_2
cur_sum -= cc * interval_length_2
if cur_bags == k:
best = max(best, cur_sum)
best = max(best, cur_sum)
return best
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | sliding window | sliding-window-by-akbc-80b0 | null | akbc | NORMAL | 2025-01-05T17:05:14.501093+00:00 | 2025-01-05T17:05:14.501093+00:00 | 45 | false | ```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
coins.sort()
n = len(coins)
def _solve(coins):
ans = j = C = 0
for i, (l, r, c) in enumerate(coins):
while j < n and coins[j][1] - l + 1 < k:
C += coins[j][2] * (coins[j][1] - coins[j][0] + 1)
j += 1
if j == n:
ans = max(ans, C)
else:
L = max(0, k - (coins[j][0] - l))
ans = max(ans, C + L * coins[j][2])
C -= c * (r - l + 1)
return ans
M = max(x[1] for x in coins)
coinsReversed = sorted([(M - r, M - l, c) for l, r, c in coins])
return max(_solve(coins), _solve(coinsReversed))
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Simple sliding window | simple-sliding-window-by-risabhuchiha-h1xf | null | risabhuchiha | NORMAL | 2025-01-05T16:40:08.860103+00:00 | 2025-01-05T16:40:08.860103+00:00 | 44 | false |
```java []
class Solution {
public long maximumCoins(int[][] c, int k) {
long ans=0;
Arrays.sort(c,(a,b)->a[0]-b[0]);
int kk=k;
int s=0;
long max=0;
int j=0;
int n=c.length;
for(int i=0;i<n;i++){
while(j<n&&c[j][1]-c[i][0]+1<=k){
ans+=(long)(c[j][1]-c[j][0]+1)*(long)(c[j][2]);
j++;
}
if(j<n){
long p=(long)(c[j][2])*(long)(k-c[j][0]+c[i][0]);
if(p>=0){
max=Math.max(max,p+ans);
}
}
ans-=(long)(c[i][1]-c[i][0]+1)*(long)(c[i][2]);
}
j=0;
ans=0;
for(int i=0;i<n;i++){
ans+=(long)(c[i][1]-c[i][0]+1)*(long)(c[i][2]);
while(k<c[i][1]-c[j][1]+1){
ans-=(long)(c[j][1]-c[j][0]+1)*(long)(c[j][2]);
j++;
}
long p=Math.max(0,-k+c[i][1]-c[j][0]+1)*(long)(c[j][2]);
max=Math.max(max,ans-p);
}
return max;
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-coins-from-k-consecutive-bags | JavaScript O(nlgn): Just test left and right edges of ranges, with binary search | javascript-onlgn-just-test-left-and-righ-80ts | IntuitionThe best outcome can be obtained with the collection starting from some range's left edge, or ending to some range's right edge.Approach
Build two pref | lilongxue | NORMAL | 2025-01-05T15:41:53.395167+00:00 | 2025-01-28T09:40:41.094709+00:00 | 15 | false | # Intuition
The best outcome can be obtained with the collection starting from some range's left edge, or ending to some range's right edge.
# Approach
1. Build two prefix sums.
2. Go from left to right, trying to start the collection from some range's left edge, and see how far it reaches using binary search.
3. Go from right to left, trying to end the collection to some range's right edge, and see how far it reaches using binary search.
4. The result is the maximum outcome.
# Complexity
- Time complexity:
O(nlgn)
- Space complexity:
O(n)
# Code
```javascript []
/**
* @param {number[][]} coins
* @param {number} k
* @return {number}
*/
var maximumCoins = function(coins, k) {
k--
coins.sort((A, B) => A[0] - B[0])
const len = coins.length
const sumFL = new Array(len), sumFR = new Array(1 + len)
sumFL[-1] = sumFR[len] = 0
for (let i = 0; i < len; i++) {
const range = coins[i]
const [l, r, c] = range
const outcome = (1 + r - l) * c
sumFL[i] = outcome + sumFL[i - 1]
range.push(outcome)
}
for (let i = len - 1; i > -1; i--) {
const range = coins[i]
sumFR[i] = range[3] + sumFR[i + 1]
}
let result = 0
const minLeft = coins[0][0], maxRight = coins.at(-1)[1]
for (let i = 0; i < len; i++) {
const range = coins[i]
const edgeLeft = range[0]
let low = i, high = len - 1
if (maxRight - edgeLeft <= k) {
const outcome = sumFL[high] - sumFL[i - 1]
result = Math.max(result, outcome)
break
}
// find latest low where
// coins[low][0] - edgeLeft <= k
while (low < high) {
const mid = Math.ceil((low + high) / 2)
if (coins[mid][0] - edgeLeft <= k)
low = mid
else
high = mid - 1
}
const other = coins[low]
const [otherLeft, otherRight, otherCount] = other
const edgeRight = Math.min(otherRight, edgeLeft + k)
const lastOutcome = (1 + edgeRight - otherLeft) * otherCount
const outcome = sumFL[low - 1] - sumFL[i - 1] + lastOutcome
result = Math.max(result, outcome)
}
for (let i = len - 1; i > -1; i--) {
const range = coins[i]
const edgeRight = range[1]
let low = 0, high = i
if (edgeRight - minLeft <= k) {
const outcome = sumFR[low] - sumFR[i + 1]
result = Math.max(result, outcome)
break
}
// find earliest high where
// edgeRight - coins[high][1] <= k
while (low < high) {
const mid = Math.floor((low + high) / 2)
if (edgeRight - coins[mid][1] <= k)
high = mid
else
low = mid + 1
}
const other = coins[high]
const [otherLeft, otherRight, otherCount] = other
const edgeLeft = Math.max(otherLeft, edgeRight - k)
const lastOutcome = (1 + otherRight - edgeLeft) * otherCount
const outcome = sumFR[high + 1] - sumFR[i + 1] + lastOutcome
result = Math.max(result, outcome)
}
return result
};
``` | 0 | 0 | ['JavaScript'] | 0 |
maximum-coins-from-k-consecutive-bags | Sorting | 2 - Pointer Sliding Window O(nlogn) Time Complexity | sorting-2-pointer-sliding-window-onlogn-ednoy | Intuition
Consider the 2 pointer sliding window.
Now if we check greedily we want to maximize by taking whole interval right, we don't want holes.
We take inter | yash559 | NORMAL | 2025-01-05T15:40:09.483928+00:00 | 2025-01-05T15:40:09.483928+00:00 | 32 | false | # Intuition
- Consider the **2 pointer sliding window.**
- Now if we check greedily we want to maximize by taking whole interval right, we don't want holes.
- We take intervals as whole.
- We consider them either as **start of window or ending at window.**
- so we have to check both possibilities by **2 pointer sliding window.**
# Complexity
- Time complexity: $$O(nlogn)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(nlogn)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
int n = coins.size();
sort(coins.begin(),coins.end());
long long i = 0;
long long original = k;
//forming window
long long cost = 0;
long long size = k + coins[i][0] - 1;
while(i < n && size >= coins[i][1]) {
cost += (long long)(coins[i][1] - coins[i][0] + 1) * coins[i][2];
i++;
}
long long res = cost;
if(i < n && size >= coins[i][0]) {
res = cost + (long long)(size - coins[i][0] + 1) * coins[i][2];
}
//moving window considering the start of the interval
int first = 0,last = i;
while(first <= last) {
cost -= ((long long)coins[first][1] - coins[first][0] + 1) * coins[first][2];
first++;
if(first >= n) break;
long long win_size = k + coins[first][0] - 1;
while(last < n && win_size >= coins[last][1]) {
cost += ((long long)coins[last][1] - coins[last][0] + 1) * coins[last][2];
last++;
}
res = max(res, cost);
if(last < n && win_size >= coins[last][0]) {
res = max(res, cost + ((long long)win_size - coins[last][0] + 1) * coins[last][2]);
}
}
//interchange the coordinates and sort in descending order
for(auto &x : coins) {
swap(x[0],x[1]);
}
sort(coins.begin(),coins.end(),greater<vector<int>>());
//forming window
cost = 0;
i = 0;
k = coins[0][0] - k + 1;
while(i < n && k <= coins[i][1]) {
cost += ((long long)coins[i][0] - coins[i][1] + 1) * coins[i][2];
i++;
}
res = max(res, cost);
if(i < n && k <= coins[i][0]) {
res = max(res, cost + ((long long)coins[i][0] - k + 1) * coins[i][2]);
}
// cout << i << endl;
//moving window
k = original;
first = 0,last = i;
while(first <= last) {
cost -= ((long long)coins[first][0] - coins[first][1] + 1) * coins[first][2];
first++;
// cout << cost << endl;
if(first >= n) break;
// cout << coins[first][0] << endl;
int win_size = coins[first][0] - k + 1;
// cout << win_size << endl;
while(last < n && win_size <= coins[last][1]) {
cost += ((long long)coins[last][0] - coins[last][1] + 1) * coins[last][2];
last++;
}
// cout << cost << endl;
res = max(res, cost);
if(last < n && win_size <= coins[last][0]) {
res = max(res, cost + ((long long)coins[last][0] - win_size + 1) * coins[last][2]);
}
// cout << first << ' ' << last << ' ' << res << endl;
}
return res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | step multiple bags when sliding window | step-multiple-bags-when-sliding-window-b-tulr | IntuitionSliding window with 2 pointers (segment on the left and segment on th right).Step reasonable number of bags instead of step for every single bag, becau | jrmwng | NORMAL | 2025-01-05T15:38:00.635641+00:00 | 2025-01-05T15:38:00.635641+00:00 | 34 | false | # Intuition
Sliding window with 2 pointers (segment on the left and segment on th right).
Step reasonable number of bags instead of step for every single bag, because the problem mentioned many many bags.
# Approach
Replace `std::vector<std::vector<int>> coins` by `std::vector<std::tuple<int, int, int>> vSegment` then sort `vSegment`.
Calculate total coins in the first applicable k-consecutive bags.
Slide the window (k-consecutive bags) from left to right. Step to next bag of interest rather than step at every bag in a segment. The next bag of interest is usually the end of the current segment or the first bag of next segment. While we consider the left-most bag and the right-most bag, step is usually the minimum of "next left bag of interest" and "next right bag of interest". My expression of the minimum may evaluate to zero value, therefore step is `1` when the minimum expression evaluates to zero.
When slide the window,
1. exclude coins in bags on the left
2. include coins in bags on the right
3. update the maximum coins so far
Return the maximum coins as the answer.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define DBG (0)
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k)
{
std::vector<std::tuple<int, int, int>> vSegment; vSegment.reserve(coins.size());
for (std::vector<int> const &c : coins)
{
vSegment.emplace_back(c[0], c[1], c[2]);
}
// 1. sort the segments
std::sort(vSegment.begin(), vSegment.end());
auto itSegmentL = vSegment.begin();
auto itSegmentR = vSegment.begin();
auto const itSegmentEnd = vSegment.end();
int nL = std::get<0>(*itSegmentL);
int nR = nL + k - 1;
long long llCoin_running = 0ll;
// 2. calculate coins in the first k-consecutive bags of interest
for (; itSegmentR != itSegmentEnd && std::get<1>(*itSegmentR) <= nR; ++itSegmentR)
{
int64_t const nCount = std::get<1>(*itSegmentR) + 1 - std::get<0>(*itSegmentR);
llCoin_running += nCount * std::get<2>(*itSegmentR);
}
if (itSegmentR != itSegmentEnd && std::get<0>(*itSegmentR) <= nR)
{
int64_t const nCount = nR + 1 - std::get<0>(*itSegmentR);
llCoin_running += nCount * std::get<2>(*itSegmentR);
}
long long llCoin_max = llCoin_running;
#if DBG
std::cout << '[' << nL << ',' << nR << ']' << std::endl;
std::cout << "\tMax Coin: " << llCoin_max << std::endl;
#endif
// 3. slide k-consecutive bags from left to right
while (itSegmentR != itSegmentEnd && nR < std::get<1>(vSegment.back()))
{
int const nL0 = nL;
int const nR0 = nR;
int const nDelta = std::max(1, std::min
(
(nL0 < std::get<0>(*itSegmentL) ? std::get<0>(*itSegmentL) : std::get<1>(*itSegmentL) + 1) - nL0,
(nR0 < std::get<0>(*itSegmentR) ? std::get<0>(*itSegmentR) : std::get<1>(*itSegmentR)) - nR0
));
int const nL1 = nL0 + nDelta;
int const nR1 = nR0 + nDelta;
#if DBG
std::cout << '[' << nL1 << ',' << nR1 << ']' << std::endl;
#endif
if (std::get<0>(*itSegmentL) <= nL0 && nL0 <= std::get<1>(*itSegmentL))
{
int64_t const nCount = std::min(std::get<1>(*itSegmentL) + 1, nL1) - nL0;
#if DBG
std::cout << "\tExclude " << nCount << " bag(s) from segment {" << std::get<0>(*itSegmentL) << ',' << std::get<1>(*itSegmentL) << ',' << std::get<2>(*itSegmentL) << '}' << std::endl;
#endif
llCoin_running -= nCount * std::get<2>(*itSegmentL);
}
if (std::get<1>(*itSegmentL) < nL1)
{
if (++itSegmentL != itSegmentEnd)
{
if (std::get<0>(*itSegmentL) < nL1)
{
int64_t const nCount = nL1 - std::get<0>(*itSegmentL);
#if DBG
std::cout << "\tExclude " << nCount << " bag(s) from segment {" << std::get<0>(*itSegmentL) << ',' << std::get<1>(*itSegmentL) << ',' << std::get<2>(*itSegmentL) << '}' << std::endl;
#endif
llCoin_running -= nCount * std::get<2>(*itSegmentL);
}
}
}
if ((std::get<0>(*itSegmentR) <= nR0 && nR0 <= std::get<1>(*itSegmentR)) ||
(std::get<0>(*itSegmentR) <= nR1 && nR1 <= std::get<1>(*itSegmentR)))
{
int64_t const nCount = std::min(std::get<1>(*itSegmentR), nR1) - std::max(std::get<0>(*itSegmentR) - 1, nR0);
#if DBG
std::cout << "\tInclude " << nCount << " bag(s) from segment {" << std::get<0>(*itSegmentR) << ',' << std::get<1>(*itSegmentR) << ',' << std::get<2>(*itSegmentR) << '}' << std::endl;
#endif
llCoin_running += nCount * std::get<2>(*itSegmentR);
}
if (std::get<1>(*itSegmentR) < nR1)
{
if (++itSegmentR != itSegmentEnd)
{
if (std::get<0>(*itSegmentR) <= nR1)
{
int64_t const nCount = nR1 - std::get<0>(*itSegmentR) + 1;
#if DBG
std::cout << "\tInclude " << nCount << " bag(s) from segment {" << std::get<0>(*itSegmentR) << ',' << std::get<1>(*itSegmentR) << ',' << std::get<2>(*itSegmentR) << '}' << std::endl;
#endif
llCoin_running += nCount * std::get<2>(*itSegmentR);
}
}
}
nL = nL1;
nR = nR1;
llCoin_max = std::max(llCoin_max, llCoin_running);
#if DBG
std::cout << "\tMax Coin: " << llCoin_max << std::endl;
#endif
}
return llCoin_max;
}
};
static auto _______ = []() {
// turn off sync
std::ios::sync_with_stdio(false);
// untie in/out streams
std::cin.tie(nullptr);
return 0;
}();
``` | 0 | 0 | ['Two Pointers', 'Sliding Window', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | JAVA 100% faster than other codes | Easy to understand | java-100-faster-than-other-codes-easy-to-o7th | Code | rishabhParsec | NORMAL | 2025-01-05T15:24:54.302825+00:00 | 2025-01-05T15:24:54.302825+00:00 | 63 | false |
# Code
```java []
class Solution {
public long maximumCoins(int[][] coins, int k) {
int n = coins.length;
// Sort intervals by start time
Arrays.sort(coins, (a, b) -> a[0] - b[0]);
// Prepare start, end, and sum arrays
int[] start = new int[n];
int[] end = new int[n];
long[] sum = new long[n];
for (int i = 0; i < n; i++) {
start[i] = coins[i][0];
end[i] = coins[i][1];
long total = (end[i] - start[i] + 1L) * coins[i][2];
sum[i] = i > 0 ? sum[i - 1] + total : total;
}
long ans = 0;
// *** From Start ***
for (int i = 0; i < n; i++) {
int ind = start[i] + k - 1; // End index of k-length interval starting from start[i]
if (ind <= end[i]) {
// Entire k-length interval fits within the current interval
ans = Math.max(ans, k * (long) coins[i][2]);
continue;
}
// Find the farthest interval that overlaps or is included
int maxInd = findRangeIndex1(ind, end);
if (maxInd == -1) continue; // No valid range
long totalCoins = sum[maxInd] - (i > 0 ? sum[i - 1] : 0);
// Add partial contribution if next interval starts before `ind`
if (maxInd + 1 < n && ind >= start[maxInd + 1]) {
totalCoins += (ind - start[maxInd + 1] + 1L) * coins[maxInd + 1][2];
}
ans = Math.max(ans, totalCoins);
}
// *** From End ***
for (int i = 0; i < n; i++) {
int ind = end[i] - k + 1; // Start index of k-length interval ending at end[i]
if (ind >= start[i]) {
// Entire k-length interval fits within the current interval
ans = Math.max(ans, k * (long) coins[i][2]);
continue;
}
// Find the nearest interval that overlaps or is included
int maxInd = findRangeIndex2(ind, start);
if (maxInd == -1) continue; // No valid range
long totalCoins = sum[i] - (maxInd > 0 ? sum[maxInd - 1] : 0);
// Add partial contribution if previous interval ends after `ind`
if (maxInd - 1 >= 0 && ind <= end[maxInd - 1]) {
totalCoins += (end[maxInd - 1] - ind + 1L) * coins[maxInd - 1][2];
}
ans = Math.max(ans, totalCoins);
}
return ans;
}
// Find the farthest index where arr[index] <= ind
public int findRangeIndex1(int ind, int[] arr) {
int st = 0, end = arr.length - 1, ans = -1;
while (st <= end) {
int mid = st + (end - st) / 2;
if (arr[mid] <= ind) {
ans = mid;
st = mid + 1;
} else {
end = mid - 1;
}
}
return ans;
}
// Find the nearest index where arr[index] >= ind
public int findRangeIndex2(int ind, int[] arr) {
int st = 0, end = arr.length - 1, ans = -1;
while (st <= end) {
int mid = st + (end - st) / 2;
if (arr[mid] >= ind) {
ans = mid;
end = mid - 1;
} else {
st = mid + 1;
}
}
return ans;
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-coins-from-k-consecutive-bags | 431 | 431-by-itsvijay_y-jlb9 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | itsvijay_y | NORMAL | 2025-01-05T15:17:54.311827+00:00 | 2025-01-05T15:17:54.311827+00:00 | 15 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {number[][]} coins
* @param {number} k
* @return {number}
*/
var maximumCoins = function(coins, k) {
coins.sort((a, b) => a[0] - b[0]);
let intervals = [];
let prev_end = -1;
for (let seg of coins) {
let li = seg[0];
let ri = seg[1];
let ci = seg[2];
if (prev_end !== -1 && li > prev_end + 1) {
intervals.push([prev_end + 1, li - 1, 0]);
}
intervals.push([li, ri, ci]);
prev_end = ri;
}
let parnoktils = coins.slice();
let candidate_starts_set = new Set();
for (let interval of intervals) {
let start = interval[0];
let end = interval[1];
candidate_starts_set.add(start);
let cand_start = end - k + 1;
if (cand_start >= 1) {
candidate_starts_set.add(cand_start);
}
}
let candidates = [];
for (let x of candidate_starts_set) {
if (x <= intervals[intervals.length - 1][1]) {
candidates.push(x);
}
}
candidates.sort((a, b) => a - b);
let n = intervals.length;
let starts = Array(n);
let ends = Array(n);
let sums = Array(n);
for (let i = 0; i < n; ++i) {
starts[i] = intervals[i][0];
ends[i] = intervals[i][1];
sums[i] = intervals[i][2];
}
// Compute prefix sums of coins
let prefix_sum = Array(n).fill(0);
prefix_sum[0] = (ends[0] - starts[0] + 1) * sums[0];
for (let i = 1; i < n; ++i) {
prefix_sum[i] = prefix_sum[i - 1] + (ends[i] - starts[i] + 1) * sums[i];
}
let max_sum = 0;
for (let x of candidates) {
let window_end = x + k - 1;
let l = binarySearch(ends, x);
let r = binarySearch(starts, window_end, true) - 1;
if (l > r || l >= n || r < 0) {
continue;
}
let sum_coins = prefix_sum[r] - (l > 0 ? prefix_sum[l - 1] : 0);
if (starts[l] < x) {
let overlap = Math.min(ends[l], window_end) - x + 1;
sum_coins -= (ends[l] - starts[l] + 1 - overlap) * sums[l];
}
if (ends[r] > window_end) {
let overlap = window_end - starts[r] + 1;
sum_coins -= (ends[r] - starts[r] + 1 - overlap) * sums[r];
}
max_sum = Math.max(max_sum, sum_coins);
}
return max_sum;
};
function binarySearch(arr, target, isUpper = false) {
let low = 0;
let high = arr.length;
while (low < high) {
let mid = Math.floor((low + high) / 2);
if (arr[mid] < target || (isUpper && arr[mid] <= target)) {
low = mid + 1;
} else {
high = mid;
}
}
return low;
}
``` | 0 | 0 | ['JavaScript'] | 0 |
maximum-coins-from-k-consecutive-bags | C Solution | Beats 100% | O(n logn) Time Complexity | Pls Upvote | c-solution-beats-100-on-logn-time-comple-1kkl | Code | Ex1sTzx | NORMAL | 2025-01-05T14:52:13.651470+00:00 | 2025-01-05T14:52:13.651470+00:00 | 11 | false |
# Code
```c []
#define MAX_N 100005
typedef struct {
int l, r, c;
} Segment;
long long prefix[MAX_N];
int cmp(const void* a, const void* b) {
Segment* segA = (Segment*)a;
Segment* segB = (Segment*)b;
if (segA->l < segB->l) {
return -1;
} else if (segA->l > segB->l) {
return 1;
}
return 0;
}
int findLeft(Segment* coins, int n, int val) {
int low = 0, high = n - 1, mid, result = n;
while (low <= high) {
mid = (low + high) / 2;
if (coins[mid].l <= val && coins[mid].r >= val) {
return mid;
} else if (coins[mid].l > val) {
result = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
return result;
}
bool isSatisfied(Segment* coins, int n, long long val, int k) {
long long sum = 0;
int i;
for (i = 0; i < n; i++) {
int r = coins[i].r;
if (r - k < 0) {
if (prefix[i] > sum) {
sum = prefix[i];
}
continue;
}
int idx = findLeft(coins, n, r - k);
if (idx == n || coins[idx].l > r - k) {
long long tempSum = prefix[i];
if (idx > 0) {
tempSum -= prefix[idx - 1];
}
if (tempSum > sum) {
sum = tempSum;
}
} else {
long long tempSum = prefix[i] - prefix[idx];
tempSum += (coins[idx].r - (r - k)) * 1LL * coins[idx].c;
if (tempSum > sum) {
sum = tempSum;
}
}
}
if (sum >= val) {
return true;
}
sum = 0;
for (i = 0; i < n; i++) {
int r = coins[i].l;
int idx = findLeft(coins, n, r + k);
if (idx == n) {
long long tempSum = prefix[n - 1];
if (i > 0) {
tempSum -= prefix[i - 1];
}
if (tempSum > sum) {
sum = tempSum;
}
continue;
}
if (coins[idx].l > r + k) {
long long tempSum = prefix[idx - 1];
if (i > 0) {
tempSum -= prefix[i - 1];
}
if (tempSum > sum) {
sum = tempSum;
}
} else {
long long tempSum = prefix[idx];
if (i > 0) {
tempSum -= prefix[i - 1];
}
tempSum -= (coins[idx].r - (r + k) + 1) * 1LL * coins[idx].c;
if (tempSum > sum) {
sum = tempSum;
}
}
}
return sum >= val;
}
long long maximumCoins(int** coins, int coinsSize, int* coinsColSize, int k) {
Segment* segCoins = (Segment*)malloc(coinsSize * sizeof(Segment));
for (int i = 0; i < coinsSize; i++) {
segCoins[i].l = coins[i][0];
segCoins[i].r = coins[i][1];
segCoins[i].c = coins[i][2];
}
qsort(segCoins, coinsSize, sizeof(Segment), cmp);
prefix[0] = (segCoins[0].r - segCoins[0].l + 1) * 1LL * segCoins[0].c;
for (int i = 1; i < coinsSize; i++) {
prefix[i] = prefix[i - 1] + (segCoins[i].r - segCoins[i].l + 1) * 1LL * segCoins[i].c;
}
long long low = 1, high = 1e12, ans = 0;
while (low <= high) {
long long mid = (low + high) / 2;
if (isSatisfied(segCoins, coinsSize, mid, k)) {
if (mid > ans) {
ans = mid;
}
low = mid + 1;
} else {
high = mid - 1;
}
}
free(segCoins);
return ans;
}
``` | 0 | 0 | ['C'] | 0 |
maximum-coins-from-k-consecutive-bags | C Solution | Beats 100% | O(n logn) Time Complexity | Pls Upvote | c-solution-beats-100-on-logn-time-comple-06oe | Code | Ex1sTzx | NORMAL | 2025-01-05T14:52:11.218700+00:00 | 2025-01-05T14:52:11.218700+00:00 | 13 | false |
# Code
```c []
#define MAX_N 100005
typedef struct {
int l, r, c;
} Segment;
long long prefix[MAX_N];
int cmp(const void* a, const void* b) {
Segment* segA = (Segment*)a;
Segment* segB = (Segment*)b;
if (segA->l < segB->l) {
return -1;
} else if (segA->l > segB->l) {
return 1;
}
return 0;
}
int findLeft(Segment* coins, int n, int val) {
int low = 0, high = n - 1, mid, result = n;
while (low <= high) {
mid = (low + high) / 2;
if (coins[mid].l <= val && coins[mid].r >= val) {
return mid;
} else if (coins[mid].l > val) {
result = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
return result;
}
bool isSatisfied(Segment* coins, int n, long long val, int k) {
long long sum = 0;
int i;
for (i = 0; i < n; i++) {
int r = coins[i].r;
if (r - k < 0) {
if (prefix[i] > sum) {
sum = prefix[i];
}
continue;
}
int idx = findLeft(coins, n, r - k);
if (idx == n || coins[idx].l > r - k) {
long long tempSum = prefix[i];
if (idx > 0) {
tempSum -= prefix[idx - 1];
}
if (tempSum > sum) {
sum = tempSum;
}
} else {
long long tempSum = prefix[i] - prefix[idx];
tempSum += (coins[idx].r - (r - k)) * 1LL * coins[idx].c;
if (tempSum > sum) {
sum = tempSum;
}
}
}
if (sum >= val) {
return true;
}
sum = 0;
for (i = 0; i < n; i++) {
int r = coins[i].l;
int idx = findLeft(coins, n, r + k);
if (idx == n) {
long long tempSum = prefix[n - 1];
if (i > 0) {
tempSum -= prefix[i - 1];
}
if (tempSum > sum) {
sum = tempSum;
}
continue;
}
if (coins[idx].l > r + k) {
long long tempSum = prefix[idx - 1];
if (i > 0) {
tempSum -= prefix[i - 1];
}
if (tempSum > sum) {
sum = tempSum;
}
} else {
long long tempSum = prefix[idx];
if (i > 0) {
tempSum -= prefix[i - 1];
}
tempSum -= (coins[idx].r - (r + k) + 1) * 1LL * coins[idx].c;
if (tempSum > sum) {
sum = tempSum;
}
}
}
return sum >= val;
}
long long maximumCoins(int** coins, int coinsSize, int* coinsColSize, int k) {
Segment* segCoins = (Segment*)malloc(coinsSize * sizeof(Segment));
for (int i = 0; i < coinsSize; i++) {
segCoins[i].l = coins[i][0];
segCoins[i].r = coins[i][1];
segCoins[i].c = coins[i][2];
}
qsort(segCoins, coinsSize, sizeof(Segment), cmp);
prefix[0] = (segCoins[0].r - segCoins[0].l + 1) * 1LL * segCoins[0].c;
for (int i = 1; i < coinsSize; i++) {
prefix[i] = prefix[i - 1] + (segCoins[i].r - segCoins[i].l + 1) * 1LL * segCoins[i].c;
}
long long low = 1, high = 1e12, ans = 0;
while (low <= high) {
long long mid = (low + high) / 2;
if (isSatisfied(segCoins, coinsSize, mid, k)) {
if (mid > ans) {
ans = mid;
}
low = mid + 1;
} else {
high = mid - 1;
}
}
free(segCoins);
return ans;
}
``` | 0 | 0 | ['C'] | 0 |
maximum-coins-from-k-consecutive-bags | Java | 129 ms | Beats 100 % | Binary Search + Prefix Sum | java-129-ms-beats-100-binary-search-pref-i8mt | IntuitionBinary Search + Prefix SumApproachRan two for loops to calculate the sum of coins.
First For loop assumes the ith index to be taken completely and to b | rishit19382 | NORMAL | 2025-01-05T14:48:20.139995+00:00 | 2025-01-05T14:49:27.413124+00:00 | 49 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Binary Search + Prefix Sum
# Approach
<!-- Describe your approach to solving the problem. -->
Ran two for loops to calculate the sum of coins.
First For loop assumes the ith index to be taken completely and to be the first of the sequence. Hence, starts looking to the right of ith index in coins array.
Second For loop assumes the ith index to be taken completely and to be the last of the sequence. Hence, starts looking to the left of ith index in coins array.
Binary Search is used to get upper and lower bounds until where the full coin range is to be considered from the coins array.
To calculate complete range coin sums, Prefix Sum array is used.
And then for the remaining part (partial range), sum is calculated by multiplying the coin value to the number of elements in the partial range.
Now sum up the Complete range sum and the partial range sum.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n*logn)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int getUB(int[][] coins, int end, long t){
int n = coins.length;
int ans = -1;
int low = 0;
int high = end;
while(low <= high){
int mid = (low + high) / 2;
if(t < coins[mid][0]){
ans = mid;
high = mid - 1;
}
else{
low = mid + 1;
}
}
return ans;
}
public int getLB(int[][] coins, int start, long t){
int n = coins.length;
int ans = -1;
int low = start;
int high = n - 1;
while(low <= high){
int mid = (low + high) / 2;
if(coins[mid][1] < t){
ans = mid;
low = mid + 1;
}
else{
high = mid - 1;
}
}
return ans;
}
public long maximumCoins(int[][] coins, int k) {
Arrays.sort(coins, (a, b) -> a[0] - b[0]);
long ans = 0;
int n = coins.length;
long[] prefSum = new long[n + 1];
for(int i = 0; i<n; i++){
prefSum[i + 1] = prefSum[i] + 1L*coins[i][2]*(coins[i][1] - coins[i][0] + 1);
}
//for loop assuming that ith index is the first complete coin range taken in the sequence
// looks to right of ith index to see which all coin ranges need to be taken partial or complete
for(int i = 0; i<n; i++){
int[] curr = coins[i];
int start = curr[0];
int end = curr[1];
int currCoins = curr[2];
int lb = getLB(coins, i, start + k - 1);
long currMax = 0;
if(lb == -1){
currMax = 1L*currCoins*k; // ith partial range taken
}
else{
currMax = prefSum[lb + 1] - prefSum[i]; // complete range taken from ith to lb-th in coins array
}
if(lb != -1 && lb + 1 < n && coins[lb + 1][0] <= start + k - 1){ // adding the last partial range at lb + 1
currMax += 1L*coins[lb + 1][2]*(start + k - 1 - coins[lb + 1][0] + 1);
}
ans = Math.max(currMax, ans);
}
// for loop assuming that ith index is the last complete coin range taken in the sequence
// looks to left of ith index to see which all coin ranges need to be taken partial or complete
for(int i = 0; i<n; i++){
int[] curr = coins[i];
int start = curr[0];
int end = curr[1];
int currCoins = curr[2];
int ub = getUB(coins, i, end - k + 1);
long currMax = 0;
if(ub == -1){
currMax = 1L*currCoins*k; // ith partial range taken
}
else{
currMax = prefSum[i + 1] - prefSum[ub]; // complete range taken from ub-th coin range to ith coin range
}
if(ub - 1 >= 0 && coins[ub - 1][1] >= end - k + 1){ // adding the partial coin range at (ub - 1)th index in coins array
currMax += 1L*coins[ub - 1][2]*(coins[ub - 1][1] - (end - k + 1) + 1);
}
ans = Math.max(ans, currMax);
}
return ans;
}
}
``` | 0 | 0 | ['Binary Search', 'Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Simplest Soln ever possible -> Full Detailed With Comments 🤷♀️✔ | simplest-soln-ever-possible-full-comment-92x8 | IntuitionJust Read the Comments.
U will Get it.ApproachComplexity
Time complexity:
Space complexity:
Code | its-raj3 | NORMAL | 2025-01-05T12:37:57.283447+00:00 | 2025-01-08T15:46:56.874195+00:00 | 76 | false | # Intuition
Just Read the Comments.
U will Get it.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define ll long long
class Solution {
public:
int lower_bound1(vector<vector<int>>& coins, int val){
int n=coins.size();
int l=0,h=n-1,indx=0;
while(l<=h){
int m=l+(h-l)/2;
if(val>=coins[m][0]&&val<=coins[m][1]||coins[m][0]>=val){
indx=m;
h=m-1;
}
else l=m+1;
}
return indx;
}
int higher_bound1(vector<vector<int>>& coins, int val){
int n=coins.size();
int l=0,h=n-1,indx=0;
while(l<=h){
int m=l+(h-l)/2;
if(val>=coins[m][0]&&val<=coins[m][1]||coins[m][1]<=val){
indx=m;
l=m+1;
}
else h=m-1;
}
return indx;
}
long long maximumCoins(vector<vector<int>>& coins, int k) {
// Hey Raj Khud se kiya!
// let's first of all create a prefix array
int n=coins.size();
vector<ll>pre(n);
sort(coins.begin(),coins.end());
for(int i=0;i<n;i++){
ll st=coins[i][0],end=coins[i][1];
if(i==0)pre[i]=(end-st+1)*coins[i][2];
else pre[i]=pre[i-1]+(end-st+1)*coins[i][2];
}
// nnow Traverse all the pairs/ranges and find out the max possible among them
ll ans=0;
for(int i=0;i<n;i++){
// we will try from both ways from l to l+k-1 and from r to r-k+1
// First Way
int st=coins[i][0];
int end=st+k-1;
int lr=lower_bound1(coins,st);
int hr=higher_bound1(coins,end);
// these lr and hr are in respect to the index in the coins vector
// so that we can calculate the sum of the range by subtracting the values before lr
// REMEMBER TO SUBTRACT THE EXTRA SUM ADDED FROM A RANGE WHEN THE LOWER OR HR IS NOT AT THE
// BOUNDARY THAN WE HAVE TO SUBTRACT THE EXTRA
ll csum=pre[hr];
if(lr>0)csum-=pre[lr-1];
// NOW REMOVE THE EXTRA FROM THE HIGHER BOUND AS IN WAY 1 ONLY THIS HAPPENS!
if(end<=coins[hr][1])
csum-=(ll)(coins[hr][1]-end)*(ll)coins[hr][2];
ans=max(ans,csum);
csum=0;
// Second Way
st=coins[i][1]-k+1;
end=coins[i][1];
lr=lower_bound1(coins,st);
hr=higher_bound1(coins,end);
// these lr and hr are in respect to the index in the coins vector
// so that we can calculate the sum of the range by subtracting the values before lr
// REMEMBER TO SUBTRACT THE EXTRA SUM ADDED FROM A RANGE WHEN THE LOWER OR HR IS NOT AT THE
// BOUNDARY THAN WE HAVE TO SUBTRACT THE EXTRA
csum=pre[hr];
if(lr>0)csum-=pre[lr-1];
// NOW REMOVE THE EXTRA FROM THE Lower BOUND AS IN WAY 1 ONLY THIS HAPPENS!
if(st>=coins[lr][0])
csum-=(ll)(st-coins[lr][0])*(ll)coins[lr][2];
ans=max(ans,csum);
}
return ans;
}
};
``` | 0 | 0 | ['Array', 'Binary Search', 'Greedy', 'Sliding Window', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Clean code....looks pretty....nicely commented | clean-codelooks-prettynicely-commented-b-cqc3 | IntuitionThe required answer can only be found if we choose start point of all intervals or the end points of all intervalsApproachUsing sliding window,once fro | niteshsaxena03 | NORMAL | 2025-01-05T11:23:16.314067+00:00 | 2025-01-05T11:23:16.314067+00:00 | 67 | false | # Intuition
The required answer can only be found if we choose start point of all intervals or the end points of all intervals
# Approach
Using sliding window,once from front side and then from back side,taking max of both
# Complexity
- Time complexity:
O(nlogn)
- Space complexity:
O(1)
# Code
```cpp []
#define ll long long
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
ll n = coins.size();
sort(coins.begin(), coins.end());
ll ans = 0, sum = 0;
// Forward pass
for(ll i = 0, j = 0; i < n; i++) {
ll endingPoint = coins[i][0] + k - 1;
//adding contribution of full interval till its possible to do so
while(j < n && coins[j][1] <= endingPoint) {
ll intervalStart = coins[j][0];
ll intervalEnd = coins[j][1];
ll score = coins[j][2];
sum += (intervalEnd - intervalStart + 1) * score;
j++;
}
//adding partial sum from the next interval,in case we cant add full interval
ll partialSum;
if(j <= n) {
if(j < n) {
ll intervalStart = coins[j][0];
ll intervalEnd = coins[j][1];
ll score = coins[j][2];
partialSum = max(0LL, endingPoint - intervalStart + 1) * score;
sum += partialSum;
}
ans = max(ans, sum);
if(j < n) sum -= partialSum;
}
//removing the contribution of current start interval before going to next interval start point
ll currentIntervalStart = coins[i][0];
ll currentIntervalEnd = coins[i][1];
ll currentIntervalScore = coins[i][2];
sum -= (currentIntervalEnd - currentIntervalStart + 1) * currentIntervalScore;
}
// Backward pass (same changes as forward pass)
sum = 0;
for(ll i = n-1, j = n-1; i >= 0; i--) {
ll endingPoint = coins[i][1] - k + 1;
//adding contribution of full interval till its possible to do so
while(j >= 0 && coins[j][0] > endingPoint) {
ll intervalStart = coins[j][0];
ll intervalEnd = coins[j][1];
ll score = coins[j][2];
sum += (intervalEnd - intervalStart + 1) * score;
j--;
}
//adding partial sum from the next interval,in case we cant add full interval
ll partialSum;
if(j >= -1) {
if(j >= 0) {
ll intervalStart = coins[j][0];
ll intervalEnd = coins[j][1];
ll score = coins[j][2];
partialSum = max(0LL, intervalEnd - endingPoint + 1) * score;
sum += partialSum;
}
ans = max(ans, sum);
if(j >= 0) sum -= partialSum;
}
//removing the contribution of current start interval before going to next interval start point
ll currentIntervalStart = coins[i][0];
ll currentIntervalEnd = coins[i][1];
ll currentIntervalScore = coins[i][2];
sum -= (currentIntervalEnd - currentIntervalStart + 1) * currentIntervalScore;
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 1 |
maximum-coins-from-k-consecutive-bags | Clean readable code using HashMaps | implementation-using-hashmaps-by-abhi625-vetm | IntuitionApproachComplexity
Time complexity:O(NLogN)
Space complexity:O(n)
Code :Formatted with ChatGpt | abhi625 | NORMAL | 2025-01-05T10:28:17.848678+00:00 | 2025-01-05T10:30:00.302931+00:00 | 64 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:$$O(NLogN)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code :
Formatted with ChatGpt
```java []
import java.util.*;
class Solution {
public long maximumCoins(int[][] coins, int k) {
Arrays.sort(coins, (a, b) -> a[0] - b[0]);
int n = coins.length;
long[] prefixSum = new long[n]; // Prefix sum array
prefixSum[0] = (coins[0][1] - coins[0][0] + 1) * (long) coins[0][2];
// Build prefix sum array
for (int i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1] + (coins[i][1] - coins[i][0] + 1) * (long) coins[i][2];
}
TreeMap<Integer, int[]> map = new TreeMap<>(); // Key: left, Value: {right, coins, index}
for (int i = 0; i < n; i++) {
map.put(coins[i][0], new int[]{coins[i][1], coins[i][2], i});
}
long max = 0;
// my optimal k window will either end at ith interval or will start from ith interval, the optimal window will never span two intervals paritially
for (int i = 0; i < n; i++) {
max = Math.max(max, Math.max(
value(map, prefixSum, coins[i][1] - k + 1, coins[i][1], false),
value(map, prefixSum, coins[i][0], coins[i][0] + k - 1, true)
));
}
return max;
}
public long value(TreeMap<Integer, int[]> map, long[] prefixSum, int left, int right, boolean forward) {
Map.Entry<Integer, int[]> startEntry = map.floorEntry(left) ;
if (startEntry == null) return 0;
Map.Entry<Integer, int[]> endEntry = map.floorEntry(right);
if (endEntry == null) return 0;
int startIndex = startEntry.getValue()[2];
int endIndex = endEntry.getValue()[2];
long totalCoins = prefixSum[endIndex] - (startIndex > 0 ? prefixSum[startIndex - 1] : 0);
if (forward) {
// Adjust for partial interval at the end
if (endEntry.getValue()[0] > right) {
long excessLength = endEntry.getValue()[0] - right;
totalCoins -= excessLength * (long) endEntry.getValue()[1];
}
} else {
// Adjust for partial interval at the start
if (startEntry.getKey() < left) {
long excessLength = left - startEntry.getKey();
totalCoins -= excessLength * (long) startEntry.getValue()[1];
}
}
return totalCoins;
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Sliding Window C++ | sliding-window-c-by-vaidantjain-snwr | Code | VaidantJain | NORMAL | 2025-01-05T10:26:41.193093+00:00 | 2025-01-05T10:26:41.193093+00:00 | 66 | false |
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(),coins.end());
int n = coins.size();
long long ans = 0;
int j=0;
long long sum=0;
for(int i=0;i<n;i++){
while(j<n && coins[j][1]<=coins[i][0]+k-1){
sum+=(long long)(coins[j][1]-coins[j][0]+1)*coins[j][2];
j++;
}
long long partial = 0;
if(j<n && coins[i][0]+k-1>=coins[j][0])
partial =(long long) (coins[i][0]+k-1-coins[j][0]+1)*coins[j][2];
ans = max(ans,sum+partial);
sum-=(long long)(coins[i][1]-coins[i][0]+1)*coins[i][2];
}
j=n-1;
sum=0;
for(int i=n-1;i>=0;i--){
while(j>=0 && coins[j][0]>=coins[i][1]-k+1){
sum+=(long long)(coins[j][1]-coins[j][0]+1)*coins[j][2];
j--;
}
long long partial = 0;
if(j>=0 && coins[i][1]-k+1<=coins[j][1]){
//cout<<coins[j][1]<<" "<<coins[i][1]-k+1<<" "<<coins[j][2];
long long diff = coins[j][1] - (coins[i][1]-k);
partial = (long long)(diff)*coins[j][2];
}
ans = max(ans,sum+partial);
//cout<<sum<<" "<<partial<<endl;
sum-=(long long)(coins[i][1]-coins[i][0]+1)*coins[i][2];
}
return ans;
}
};
``` | 0 | 0 | ['Sliding Window', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Sorting + PrefixSum + Sliding Window | sorting-prefixsum-sliding-window-by-a_ck-zimq | Intuition
At first, I wanted to solve with sliding window for each position, but I cannot do this because the maximum number of range value is 10^9. This soluti | a_ck | NORMAL | 2025-01-05T10:06:20.647539+00:00 | 2025-01-05T10:06:20.647539+00:00 | 32 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
- At first, I wanted to solve with sliding window for each position, but I cannot do this because the maximum number of range value is 10^9. This solution will get TLE.
- I found that I could either choose the start position of coins[i] or end position of coins[i].
- This works because starting position and end position cannot be placed in the middle of range at the same time. If the value of starting position range is larger than that of end position, then we can shift to left for more coins.
# Approach
<!-- Describe your approach to solving the problem. -->
- To get the total coins in the range of `[i, j]`, I calculated the prefixSum. If the end position is located in the `j`th range, then we can add all of coins within `[i, j-1]`.
- Iterate from the start to fix the starting position and from the end to fix the ending position.
# Complexity
- Time complexity: O(NlogN).
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
const int n = (int)coins.size();
sort(coins.begin(), coins.end());
vector<long long> prefix(n+1, 0LL);
for (int i = 1; i <= n; ++i) {
prefix[i] += prefix[i-1] + (long long)coins[i-1][2] * (coins[i-1][1] - coins[i-1][0] + 1);
}
long long ans = 0LL;
// from the start;
int j = 0;
for (int i = 0; i < n; ++i) {
int s = coins[i][0];
int e = s + k - 1;
while(j < n && coins[j][1] < e) ++j;
long long curr = prefix[j] - prefix[i];
if (j < n && coins[j][0] <= e) {
curr += (long long)coins[j][2] * (e - coins[j][0] + 1);
}
ans = max(ans, curr);
}
// from the end;
j = n-1;
for (int i = n -1; i >= 0; --i) {
int e = coins[i][1];
int s = e - k + 1;
while(j >= 0 && coins[j][0] > s) j--;
long long curr = prefix[i+1] - prefix[j+1];
if (j >= 0 && coins[j][1] >= s) {
curr += (long long)coins[j][2] * (coins[j][1] - s + 1);
}
ans = max(ans, curr);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Java Sliding window Two side | java-sliding-window-two-side-by-vigneshr-pxgc | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | vigneshreddyjulakanti | NORMAL | 2025-01-05T07:56:09.596715+00:00 | 2025-01-05T07:56:09.596715+00:00 | 30 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
coins.sort()
l = 0
temp = 0
ans = 0
print(coins)
for r in range(len(coins)):
temp+=coins[r][2]*(coins[r][1]-coins[r][0]+1)
while coins[r][1] - coins[l][1] + 1 > k:
temp-=coins[l][2]*(coins[l][1]-coins[l][0]+1)
l+=1
extra = max(0,coins[r][1] - coins[l][0] + 1 - k)
ans = max(ans, temp - extra*coins[l][2] )
l = len(coins)-1
temp = 0
for r in range(len(coins)-1,-1,-1):
temp+=coins[r][2]*(coins[r][1]-coins[r][0]+1)
while coins[l][0] - coins[r][0] + 1 > k:
temp-=coins[l][2]*(coins[l][1]-coins[l][0]+1)
l-=1
extra = max(0, coins[l][1] - coins[r][0] + 1 - k)
ans = max(ans, temp - extra*coins[l][2])
return ans
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | ☕ Java solution | java-solution-by-barakamon-3gdd | null | Barakamon | NORMAL | 2025-01-05T07:34:36.373251+00:00 | 2025-01-05T07:34:36.373251+00:00 | 103 | false | 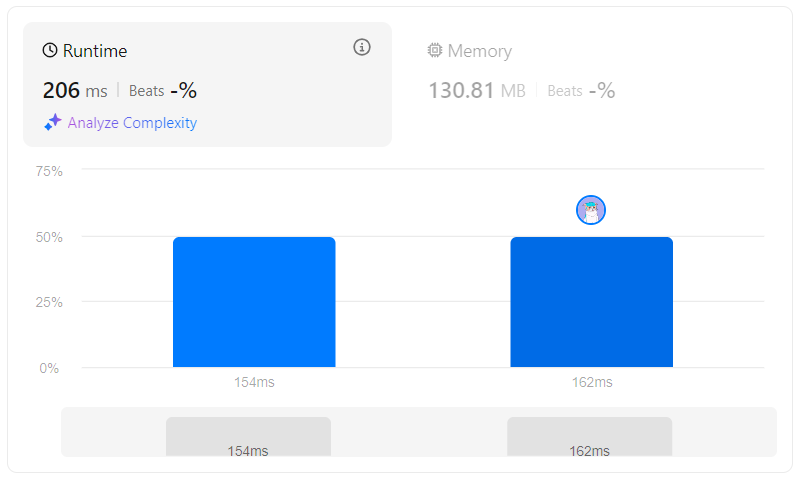
```java []
import java.util.Arrays;
import java.util.Comparator;
class Solution {
public long maximumCoins(int[][] coins, int k) {
Arrays.sort(coins, Comparator.comparingInt(a -> a[0]));
int n = coins.length;
long[] prefixSum = new long[n + 1];
prefixSum[0] = 0;
for (int i = 0; i < n; i++) {
int start = coins[i][0];
int end = coins[i][1];
int value = coins[i][2];
prefixSum[i + 1] = prefixSum[i] + (long) value * (end - start + 1);
}
long maxCoins = 0;
for (int i = 0; i < n; i++) {
int start = coins[i][0];
int end = start + k - 1;
maxCoins = Math.max(maxCoins, calculateRangeCoins(coins, prefixSum, start, end));
}
for (int i = 0; i < n; i++) {
int end = coins[i][1];
int start = end - k + 1;
maxCoins = Math.max(maxCoins, calculateRangeCoins(coins, prefixSum, start, end));
}
return maxCoins;
}
private long calculateRangeCoins(int[][] coins, long[] prefixSum, int start, int end) {
return getCoinsAt(coins, prefixSum, end) - getCoinsAt(coins, prefixSum, start - 1);
}
private long getCoinsAt(int[][] coins, long[] prefixSum, int index) {
if (index < coins[0][0]) {
return 0;
}
int left = 0;
int right = coins.length - 1;
int latest = coins.length;
while (left <= right) {
int mid = (left + right) / 2;
if (index >= coins[mid][0]) {
latest = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
if (latest == coins.length) {
return 0;
}
int coverageStart = coins[latest][0];
int coverageEnd = Math.min(coins[latest][1], index);
int value = coins[latest][2];
return prefixSum[latest] + (long) value * (coverageEnd - coverageStart + 1);
}
}
``` | 0 | 0 | ['Java'] | 1 |
maximum-coins-from-k-consecutive-bags | evulate the interval through two passes | evulate-the-interval-through-two-passes-p8f4m | IntuitionWe should evaluate the windows interval size k through two passes:
interval start with l_i
interval end with r_i
ApproachComplexity
Time complexity:
S | zoneman | NORMAL | 2025-01-05T07:24:37.572460+00:00 | 2025-01-05T07:24:37.572460+00:00 | 32 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We should evaluate the windows interval size k through two passes:
1. interval start with l_i
2. interval end with r_i
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
# Sort the segments based on starting positions
coins.sort()
n = len(coins)
# # Extract separate lists for binary search
starts = [seg[0] for seg in coins]
ends = [seg[1] for seg in coins]
# coin_vals = [seg[2] for seg in coins]
# Compute prefix sums
prefix_sum = [0] * (n + 1)
for i in range(n):
li, ri, ci = coins[i]
prefix_sum[i + 1] = prefix_sum[i] + ci * (ri - li + 1)
# Helper function to find the first segment with ri >= x
def find_left(x):
return bisect.bisect_left(ends, x)
# Helper function to find the last segment with li <= y
def find_right(y):
return bisect.bisect_right(starts, y) - 1
# Helper function to calculate total coins in window [x, y]
def calculate_sum(x, y):
if x > y:
return 0
l = find_left(x)
r = find_right(y)
if l > r:
return 0
total = prefix_sum[r + 1] - prefix_sum[l]
# Adjust for partial overlap on the left
seg_l_start, seg_l_end, seg_l_ci = coins[l]
if seg_l_start < x:
overlap = seg_l_end - x + 1
if overlap > 0:
total -= seg_l_ci * (seg_l_end - seg_l_start + 1)
total += seg_l_ci * overlap
# Adjust for partial overlap on the right
seg_r_start, seg_r_end, seg_r_ci = coins[r]
if seg_r_end > y:
overlap = y - seg_r_start + 1
if overlap > 0:
total -= seg_r_ci * (seg_r_end - seg_r_start + 1)
total += seg_r_ci * overlap
return total
max_total = 0
# Iterate through each segment and consider both window start and end
for seg in coins:
seg_start, seg_end, _ = seg
# 1. Consider seg_start as window start
window_start = seg_start
window_end = window_start + k - 1
total = calculate_sum(window_start, window_end)
if total > max_total:
max_total = total
# 2. Consider seg_end as window end
window_end = seg_end
window_start = window_end - k + 1
if window_start < 1:
window_start = 1
total = calculate_sum(window_start, window_end)
if total > max_total:
max_total = total
return max_total
``` | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | using binary search | using-binary-search-by-shivajich-berv | Intuitionfinding a valid maximum possible coins amountApproachUsing the binary search as maximum possible coins amount following increasing propertyComplexity | shivajich | NORMAL | 2025-01-05T05:59:10.550721+00:00 | 2025-01-05T05:59:10.550721+00:00 | 54 | false | # Intuition
finding a valid maximum possible coins amount
# Approach
Using the binary search as maximum possible coins amount following increasing property
# Complexity
- Time complexity: $$O(nlogn)
- Space complexity:
- $$O(n)
# Code
```cpp []
class Solution {
public:
// bool comp(vector<int> &a, vector<int> &b) {
// return a[]
// }
int findLeft(vector<vector<int>> &c, int val) {
int i=0, j = c.size()-1;
while(i<=j) {
int mid = (i+j)>>1;
int l = c[mid][0];
int r = c[mid][1];
if(val >= l && val <= r)
return mid;
else if(val < l)
j = mid-1;
else
i=mid+1;
}
return i;
}
bool isSatisfied(vector<long long> &pref, vector<vector<int>> &arr, long long val, int k) {
long long sum = 0;
int n = arr.size();
for(int i=0;i<n;i++) {
int r = arr[i][1];
if(r-k <= 0) {
sum = max(sum, pref[i]);
continue;
}
int indx = findLeft(arr, r-k);
if(arr[indx][0] > r-k) {
sum = max(sum, pref[i]-(indx-1>=0?pref[indx-1]:0));
}
else {
// int diff = (r-k)
sum = max(sum, pref[i]-pref[indx]+(arr[indx][1]-(r-k))*1ll*arr[indx][2]);
}
}
// cout << sum << " " << val << " sum value\n";
if(sum >= val)
return true;
sum = 0;
for(int i=0;i<n;i++) {
int r = arr[i][0];
int indx = findLeft(arr, r+k);
// cout << indx << " " << r+k << "\n";
if(indx >= n) {
sum = max(sum, pref[n-1]-(i!=0?pref[i-1]:0));
continue;
}
// if(indx == i)
// sum = max(sum , k*1ll*arr[indx][2]);
// else
if(arr[indx][0] > r+k)
sum = max(sum, pref[indx-1]-(i!=0?pref[i-1]:0));
else
sum = max(sum, pref[indx]-(i==0?0:pref[i-1])-(arr[indx][1]-(r+k)+1)*1ll*arr[indx][2]);
// cout << sum << "\n";
}
return sum>=val;
}
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(), coins.end());
long long high = 1e12;
long long low = 1;
long long ans = 0;
int n = coins.size();
vector<long long> prefix(n);
prefix[0] = (coins[0][1]-coins[0][0]+1)*1ll*coins[0][2];
for(int i=1;i<n;i++) {
prefix[i] = prefix[i-1]+(coins[i][1]-coins[i][0]+1)*1ll*coins[i][2];
}
while(low<=high) {
long long mid = (low+high)>>1;
if(isSatisfied(prefix, coins, mid, k)) {
// cout << mid << "\n";
ans = max(ans, mid);
low = mid+1;
}
else {
high = mid-1;
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | [c++][o(NlogN) solution) | conlogn-solution-by-mumrocks-c1gu | Code | MumRocks | NORMAL | 2025-01-05T05:23:18.656095+00:00 | 2025-01-05T05:23:18.656095+00:00 | 40 | false |
# Code
```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
sort(coins.begin(),coins.end());
int sz=coins.size(), idx=-1;
vector<long long> ps(sz+1);
for (int i=1;i<=sz;i++){
ps[i] = ps[i-1] + 1ll*(coins[i-1][1]-coins[i-1][0]+1)*coins[i-1][2];
}
long long ans=0;
auto l = [](const vector<int>& entry, int v){
return entry[1]<v;
};
long long s1,s2;
for (int i=0;i<sz;i++){
idx = lower_bound(coins.begin()+i,coins.end(),coins[i][0]+k-1, l)-coins.begin();
s1 = ps[idx]-ps[i];
s2 = 0;
if (idx<sz){
s2 = 1ll*max(0,coins[i][0]+k-coins[idx][0])*coins[idx][2];
}
//cout << "postfix " << idx << " " << s1 << " " << s2 << endl;
ans = max(ans, s1+s2);
idx=lower_bound(coins.begin(),coins.end(),coins[i][1]-k+1, l)-coins.begin();
s1 = ps[i+1]-ps[idx+1];
s2 = 1ll*(coins[idx][1]-max(coins[i][1]-k+1,coins[idx][0])+1)*coins[idx][2];
//cout << "prefix " << idx << " " << s1 << " " << s2 << endl;
ans = max(ans,s1+s2);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | The key to this problem | the-key-to-this-problem-by-llcourage123-skbo | It is natural to consider using a sliding window and prefix sum for this problem. The main challenge lies in understanding that the edge of the optimal window w | llcourage123 | NORMAL | 2025-01-05T04:43:29.504142+00:00 | 2025-01-05T04:43:29.504142+00:00 | 83 | false | It is natural to consider using a sliding window and prefix sum for this problem. The main challenge lies in understanding that the edge of the optimal window will always align with either the left or right edge of a segment.
While it is possible for the optimal window to start in the middle of one segment and end in the middle of another, there will always be an equivalent optimal window where one of its edges aligns with a segment boundary.
Everything else is straightforward. | 0 | 0 | ['Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | Easy CPP: Sort, binary search, prefix sum | easy-cpp-by-jpaunikar8-t5eo | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | jpaunikar8 | NORMAL | 2025-01-05T04:43:06.942913+00:00 | 2025-01-05T04:46:28.528152+00:00 | 66 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define ll long long
class Solution {
public:
ll maximumCoins(vector<vector<int>>& coins, int k) {
int n = coins.size();
sort(coins.begin(), coins.end());
vector<pair<int, int>> ends;
for(int i = 0 ; i < n ; i++) {
ends.push_back({coins[i][1], i});
}
vector<ll> ps(n, 0);
ps[0] = 1LL * (coins[0][1] - coins[0][0] + 1) * coins[0][2];
for(int i = 1 ; i < n ; i++) {
ps[i] = ps[i - 1] + 1LL * (coins[i][1] - coins[i][0] + 1) * coins[i][2];
}
ll ans = 0;
for(int i = 0 ; i < n ; i++) {
int l = coins[i][0], r = l + k - 1;
pair<int, int> target = {r, 0};
auto it = upper_bound(ends.begin(), ends.end(), target);
if(it == ends.end()) {
--it;
}
int idx = (*it).second;
ll coinsCollected = idx > 0 ? ps[idx - 1] : 0;
if(i > 0) {
coinsCollected -= ps[i - 1];
}
if(coins[idx][0] <= r) {
coinsCollected += 1LL * (min(r, coins[idx][1]) - coins[idx][0] + 1) * coins[idx][2];
}
ans = max(ans, coinsCollected);
if(i > 0) {
r = coins[i][1], l = r - k + 1;
target = {l, 0};
it = lower_bound(ends.begin(), ends.end(), target);
if(it == ends.end()) {
--it;
}
idx = (*it).second;
if(coins[idx][0] <= l && l <= coins[idx][1]) {
coinsCollected = ps[i];
coinsCollected -= ps[idx];
coinsCollected += 1LL * (coins[idx][1] - max(coins[idx][0], l) + 1) * coins[idx][2];
ans = max(ans, coinsCollected);
}
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | Sorting + greedy + binary search | sorting-greedy-binary-search-by-maxorgus-gofa | Code | MaxOrgus | NORMAL | 2025-01-05T04:38:48.043091+00:00 | 2025-01-05T04:38:48.043091+00:00 | 112 | false |
# Code
```python3 []
class Solution:
def maximumCoins(self, coins: List[List[int]], k: int) -> int:
coins.sort()
starts = [a for a,b,c in coins]
ends = [b for a,b,c in coins]
vals = [c for a,b,c in coins]
pres = [0]
for a,b,c in coins:
pres.append(c*(b-a+1)+pres[-1])
res = 0
N = len(coins)
for i,s in enumerate(starts):
curr = 0
j = bisect.bisect_right(ends,s+k-1)
curr += pres[j]-pres[i]
if j<N and starts[j]<=s+k:
curr += (s+k-starts[j])*vals[j]
res = max(curr,res)
for j,e in enumerate(ends):
curr = 0
i = bisect.bisect_left(starts,e-k+1)
curr += pres[j+1]-pres[i]
if i>0 and ends[i-1]>=e-k:
curr += (ends[i-1]-e+k)*vals[i-1]
res = max(curr,res)
return res
``` | 0 | 0 | ['Binary Search', 'Greedy', 'Sorting', 'Python3'] | 0 |
maximum-coins-from-k-consecutive-bags | C++ sort then iterate left to right and right to left | c-sort-then-iterate-left-to-right-and-ri-pr60 | null | user5976fh | NORMAL | 2025-01-05T04:38:27.974894+00:00 | 2025-01-05T04:38:27.974894+00:00 | 46 | false | ```cpp []
class Solution {
public:
long long maximumCoins(vector<vector<int>>& coins, int k) {
long long ans = 0;
sort(coins.begin(), coins.end());
vector<vector<long long>> p;
long long sum = 0;
for (auto& v : coins){
long long nextSum = v[1] - v[0] + 1;
nextSum *= v[2];
p.push_back({v[0], v[1], sum += nextSum});
}
// from left
k -= 1;
for (int i = 0, r = 0; i < p.size(); ++i){
while (r < p.size() && p[i][0] + k > p[r][1]){
++r;
}
long long topSum = r == p.size() ? p[r - 1][2] : p[r][2],
lSum = i == 0 ? 0 : p[i - 1][2],
tb = r < p.size() ? (p[r][1] - max(p[r][0] - 1, p[i][0] + k)) * coins[r][2] : 0;
ans = max(ans, topSum - lSum - tb);
}
// from right
for (int i = p.size() - 1, l = i; i >= 0; --i){
while (l >= 0 && p[l][0] > p[i][1] - k){
--l;
}
long long topSum = p[i][2];
long long lSum = l == -1 ? 0 : p[l][2];
long long tb = l == -1 ? 0 : max(coins[l][2] * (1 + p[l][1] - max(p[l][0], p[i][1] - k)), 0LL);
ans = max(ans, topSum - lSum + tb);
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-coins-from-k-consecutive-bags | java solution using prefix sum and binary search! | java-solution-using-prefix-sum-and-binar-vq0y | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | abhayrana00018 | NORMAL | 2025-01-05T04:21:43.477046+00:00 | 2025-01-05T04:21:43.477046+00:00 | 133 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
import java.util.*;
class Solution {
public long maximumCoins(int[][] num, int k) {
// Sorting the input 2D array based on the first element of each sub-array
Arrays.sort(num, (a, b) -> Integer.compare(a[0], b[0]));
int n = num.length;
long ans = 0;
// Preparing the x 2D array with same structure as the C++ code
long[][] x = new long[n][3];
for (int i = 0; i < n; i++) {
x[i][0] = num[i][0];
x[i][1] = num[i][1];
x[i][2] = num[i][2];
}
// Arrays for prefix sums, left and right ranges
long[] pref = new long[n];
long[] l = new long[n];
long[] r = new long[n];
// Initialize prefix array
pref[0] = (x[0][1] - x[0][0] + 1) * x[0][2];
for (int i = 1; i < n; i++) {
pref[i] = pref[i - 1] + (x[i][1] - x[i][0] + 1) * x[i][2];
}
// Fill left and right arrays
for (int i = 0; i < n; i++) {
l[i] = x[i][0];
r[i] = x[i][1];
}
// First pass - checking the case where the end range is modified
for (int i = 0; i < n; i++) {
long run = 0;
long c = r[i] - k + 1;
if (c <= 0) continue;
// Binary search for lower bound
int lb = Arrays.binarySearch(r, c);
if (lb < 0) lb = -(lb + 1);
if (lb < n) {
run = (r[lb] - Math.max(c, l[lb]) + 1) * x[lb][2] + pref[i] - pref[lb];
}
ans = Math.max(ans, run);
}
// Second pass - checking the case where the start range is modified
for (int i = 0; i < n; i++) {
long run = 0;
long c = l[i] + k - 1;
// Binary search for upper bound
int lb = Arrays.binarySearch(l, c);
if (lb < 0) lb = -(lb + 1) - 1;
if (lb >= 0) {
run = (Math.min(r[lb], c) - l[lb] + 1) * x[lb][2] + (lb > 0 ? pref[lb - 1] : 0) - (i > 0 ? pref[i - 1] : 0);
}
ans = Math.max(ans, run);
}
return ans;
}
}
``` | 0 | 0 | ['Binary Search', 'Prefix Sum', 'Java'] | 0 |
maximum-coins-from-k-consecutive-bags | C++ | Prefix Sum + Binary Search | prefix-sum-binary-search-by-kizu-x41l | IntuitionApproachComplexity
Time complexity:
O (n log n)
Space complexity:
Code | kizu | NORMAL | 2025-01-05T04:18:48.046851+00:00 | 2025-01-05T04:19:40.467535+00:00 | 154 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O (n log n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
#define ll long long
#define is ==
#define isnt !=
long long maximumCoins(vector<vector<int>>& num, int k) {
sort (num.begin (), num.end ()) ;
vector <vector <ll>> x ;
for (int i = 0 ; i < num.size () ; i ++) {
vector <ll> t ;
t.push_back (num [i][0]) ;
t.push_back (num [i][1]) ;
t.push_back (num [i][2]) ;
x.push_back (t) ;
}
ll n = x.size () ;
for (int i = 0 ; i < n ; i ++) cout << x [i][0] << ' ' << x [i][1] << ' ' << x [i][2] << endl ;
ll ans = 0 ;
vector <ll> pref (n), l (n), r (n) ;
pref [0] = (x [0][1] - x [0][0] + 1) * x [0][2] ;
for (int i = 1 ; i < n ; i ++) pref [i] = pref [i - 1] + (x [i][1] - x [i][0] + 1) * x [i][2] ;
for (int i = 0 ; i < n ; i ++) l [i] = x [i][0], r [i] = x [i][1] ;
for (int i = 0 ; i < n ; i ++) {
ll run = 0 ;
ll c = r [i] - k + 1 ;
if (c <= 0) continue ;
ll lb = lower_bound (r.begin (), r.end (), c) - r.begin () ;
run = (r [lb] - max (c, l [lb]) + 1) * x [lb][2] + pref [i] - pref [lb] ;
ans = max (ans, run) ;
}
for (int i = 0 ; i < n ; i ++) {
ll run = 0 ;
ll c = l [i] + k - 1 ;
ll lb = upper_bound (l.begin (), l.end (), c) - l.begin () ;
lb -- ;
run = (min (r [lb], c) - l [lb] + 1) * (x [lb][2]) + (lb ? pref [lb - 1] : 0) - (i ? pref [i - 1] : 0) ;
ans = max (ans, run) ;
}
return ans ;
}
};
``` | 0 | 0 | ['Binary Search', 'Prefix Sum', 'C++'] | 0 |
maximum-coins-from-k-consecutive-bags | beats 100% java | beats-100-java-by-vishall001-9uba | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Vishall001 | NORMAL | 2025-01-05T04:05:05.458954+00:00 | 2025-01-05T04:05:05.458954+00:00 | 174 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long maximumCoins(int[][] coins, int k) {
Arrays.sort(coins, (a, b) -> Integer.compare(a[0], b[0]));
long max = 0, curr = 0;
int start = 0;
for (int i = 0; i < coins.length; i++) {
int[] c = coins[i];
int len = c[1] - c[0] + 1, window = c[0] - coins[start][0];
if (len >= k) {
long sum = k * (long) c[2];
max = Math.max(max, sum);
}
if (k >= window && k <= window + len) { // fill to the right
long rSum = curr + (k - window) * (long) c[2];
max = Math.max(max, rSum);
}
// swallow
curr = curr + len * (long) c[2];
window += len;
while (start < i && window > k) {
len = coins[start][1] - coins[start][0] + 1;
long old = len * (long) coins[start][2];
start++;
window = c[1] + 1 - coins[start][0];
curr = curr - old;
}
if (window <= k) {
max = Math.max(curr, max);
}
if (start < i && window == k) { // no need to keep
len = coins[start][1] - coins[start][0] + 1;
long old = len * (long) coins[start][2];
start++;
window = c[1] + 1 - coins[start][0];
curr = curr - old;
} else if (window < k && start != 0 && start <= i) { // can extend back
len = coins[start][0] - coins[start - 1][1] - 1;
if (window + len < k) {
long lSum = curr + (k - window - len) * (long) coins[start - 1][2];
max = Math.max(max, lSum);
}
// and if we swallow left
window = c[0] - coins[start - 1][0];
len = c[1] - c[0] + 1;
if (k >= window && k <= window + len) {
long rSum = curr - (len - k + window) * (long) c[2] + (coins[start - 1][1] - coins[start - 1][0] + 1) * (long) coins[start - 1][2];
max = Math.max(max, rSum);
}
}
}
return max;
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-coins-from-k-consecutive-bags | Align with start or end | align-with-start-or-end-by-lyronly-ns16 | IntuitionApproach1 Algin start with each interval
2 ALign end with each interval : here we reverse each interval to make it same as Align with start so we can r | lyronly | NORMAL | 2025-01-05T04:04:18.709254+00:00 | 2025-01-05T04:04:18.709254+00:00 | 137 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
1 Algin start with each interval
2 ALign end with each interval : here we reverse each interval to make it same as Align with start so we can reuse the code.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(nlogn) for sort
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
typedef long long ll;
struct node
{
ll x;
ll y;
ll prefix;
ll coins;
node(int x1, int y1, ll p1, int cs)
{
x = x1;
y = y1;
prefix = p1;
coins = cs;
};
};
class Solution {
public:
long long mxCoins(vector<vector<int>>& cs, int k) {
sort(cs.begin(), cs.end());
// start, prefixsum, end, coins, last start is INT_MAX
// end, prefixsum to end, start, coins
vector<node> prefix;
ll pp = 0;
for (auto c : cs)
{
prefix.push_back(node(c[0], c[1], pp, c[2]));
//cout <<
pp += (ll)(c[1] - c[0] + 1) * (ll)c[2];
}
prefix.push_back(node(INT_MAX, INT_MAX, pp, 0));
auto cmp = [](const node& a, const node& b) { return a.y < b.y; };
sort(prefix.begin(), prefix.end(), cmp);
int n = prefix.size();
ll ans = 0;
int j = 0;
for (int i = 0; i < n - 1; i++)
{
int l = prefix[i].x;
int r = l + k - 1;
ll pre = prefix[i].prefix;
ll v = 0;
node cur = {r, r, 0, 0};
while (j < n && prefix[j].y < r)
{
j++;
}
node* iter = &(prefix[j]);
if (iter->y == INT_MAX)
{
v = iter->prefix - pre;
}
else
{
v = iter->prefix - pre;
if (r >= iter->x)
{
v += (r - iter->x + 1) * iter->coins;
}
}
//cout << l << "," << r << "," << v << "," << pre << "," << iter->prefix << endl;
ans = max(ans, v);
}
//cout << ans << endl;
return ans;
}
long long maximumCoins(vector<vector<int>>& cs, int k) {
ll a = mxCoins(cs, k);
int x = INT_MAX;
int y = INT_MIN;
for (auto& c : cs)
{
x = min(x, c[0]);
y = max(y, c[1]);
}
vector<vector<int>> cs1;
for (auto& c : cs)
{
int a = c[0];
int b = c[1];
int l = y - b;
int r = y - a;
cs1.push_back({l, r, c[2]});
}
ll b = mxCoins(cs1, k);
return max(a, b);
};
};
``` | 0 | 0 | ['C++'] | 1 |
string-without-aaa-or-bbb | Java/C++ (and Python) simple greedy | javac-and-python-simple-greedy-by-votrub-rznk | First, I must note that this problem does not feel like \'Easy\'. The implementation is easy, but the intuition is not. In fact, I spent more time on this probl | votrubac | NORMAL | 2019-01-27T04:01:24.412508+00:00 | 2019-01-27T04:01:24.412629+00:00 | 17,486 | false | First, I must note that this problem does not feel like \'Easy\'. The implementation is easy, but the intuition is not. In fact, I spent more time on this problem then on other \'Medium\' problems in the contest.\n\n- If the initial number of As is greater than Bs, we swap A and B.\n- For each turn, we add \'a\' to our string.\n- If the number of remaining As is greater than Bs, we add one more \'a\'.\n- Finally, we add \'b\'. \n<iframe src="https://leetcode.com/playground/VkpuNFz6/shared" frameBorder="0" width="100%" height="210"></iframe>\n\nIf you feel rather functional, here is a 3-liner (on par with the Python solution, courtesy of [@zengxinhai](https://leetcode.com/zengxinhai)):\n<iframe src="https://leetcode.com/playground/wkpugsHY/shared" frameBorder="0" width="100%" height="150"></iframe> | 189 | 5 | [] | 21 |
string-without-aaa-or-bbb | [Java/Python 3] Two simple logic readable codes, iterative and recursive versions. | javapython-3-two-simple-logic-readable-c-9n47 | If current result ends with aa, next char is b; if ends with bb, next char must be a.\n2. Other cases, if A > B, next char is a; otherwise, next char is b.\n\nj | rock | NORMAL | 2019-01-27T04:22:33.940662+00:00 | 2022-02-07T15:53:34.618374+00:00 | 4,296 | false | 1. If current result ends with `aa`, next char is `b`; if ends with `bb`, next char must be `a`.\n2. Other cases, if A > B, next char is `a`; otherwise, next char is `b`.\n\n```java\n public String strWithout3a3b(int A, int B) {\n StringBuilder sb = new StringBuilder(A + B);\n while (A + B > 0) {\n String s = sb.toString();\n if (s.endsWith("aa")) {\n sb.append("b");\n --B; \n }else if (s.endsWith("bb")){\n sb.append("a");\n --A;\n }else if (A >= B) {\n sb.append("a");\n --A;\n }else {\n sb.append("b");\n --B;\n }\n }\n return sb.toString();\n }\n```\n```python\n def strWithout3a3b(self, a: int, b: int) -> str:\n ans = []\n while a + b > 0:\n if ans[-2 :] == [\'a\', \'a\']:\n b -= 1\n ans.append(\'b\')\n elif ans[-2 :] == [\'b\', \'b\']:\n a -= 1\n ans.append(\'a\') \n elif a >= b:\n a -= 1\n ans.append(\'a\')\n else:\n b -= 1\n ans.append(\'b\')\n return \'\'.join(ans)\n```\n\nRecursive Version, inspired by @lbjlc\n \n```java\n public String strWithout3a3b(int A, int B) {\n if (A == 0 || B == 0) { return String.join("", Collections.nCopies(A + B, A == 0 ? "b" : "a")); } // if A or B is 0, return A \'a\'s or B \'b\'s.\n if (A == B) { return "ab" + strWithout3a3b(A - 1, B - 1); }\n if (A > B) { return "aab" + strWithout3a3b(A - 2, B - 1); }\n return "bba" + strWithout3a3b(A - 1, B - 2);\n }\n```\n```python\n def strWithout3a3b(self, a: int, b: int) -> str:\n if a * b == 0:\n return \'a\' * a + \'b\' * b\n elif a == b:\n return \'ab\' * a\n elif a > b:\n return \'aab\' + self.strWithout3a3b(a - 2, b - 1)\n return self.strWithout3a3b(a - 1, b - 2) + \'abb\'\n``` | 77 | 1 | [] | 14 |
string-without-aaa-or-bbb | APPLES and BANANAS solution (with picture) | apples-and-bananas-solution-with-picture-h56u | Somehow... this weird but fun solution came about:\n\n1. Determine A or B is bigger. "Lay down" the more frequent character in a column of pairs, until we run o | lindyhop | NORMAL | 2020-02-14T06:43:32.132023+00:00 | 2020-06-18T16:14:41.478406+00:00 | 2,830 | false | Somehow... this weird but fun solution came about:\n\n1. Determine A or B is bigger. "Lay down" the more frequent character in a column of pairs, until we run out of the more frequent character.\n2. Row by row, we "top off" each pair of characters with the less frequent character, until we run out of the less frequent character. \n3. String the rows up!\n\n\n\n```\nclass Solution:\n def strWithout3a3b(self, A: int, B: int) -> str:\n if A > B:\n numberToLayDown = A\n numberToTopUp = B\n charToLayDown = "a"\n charToTopUp = "b"\n else:\n numberToLayDown = B\n numberToTopUp = A\n charToLayDown = "b"\n charToTopUp = "a"\n\n \n repetition = int(numberToLayDown / 2)\n remainder = numberToLayDown % 2\n \n stk = []\n for i in range(repetition):\n stk.append(charToLayDown + charToLayDown)\n if remainder:\n stk.append(charToLayDown)\n \n stkSize = len(stk)\n stkIdx = 0\n while numberToTopUp > 0:\n stk[stkIdx] += charToTopUp\n stkIdx = (stkIdx + 1) % stkSize\n numberToTopUp -= 1\n \n return "".join(stk)\n```\n\n\n | 74 | 1 | [] | 5 |
string-without-aaa-or-bbb | Clean C++/python solution | clean-cpython-solution-by-lbjlc-rjc1 | C++:\n\nclass Solution {\npublic:\n string strWithout3a3b(int A, int B) {\n if(A == 0) return string(B, \'b\');\n else if(B == 0) return string | lbjlc | NORMAL | 2019-01-27T04:33:45.076741+00:00 | 2019-01-27T04:33:45.076791+00:00 | 4,335 | false | C++:\n```\nclass Solution {\npublic:\n string strWithout3a3b(int A, int B) {\n if(A == 0) return string(B, \'b\');\n else if(B == 0) return string(A, \'a\');\n else if(A == B) return "ab" + strWithout3a3b(A - 1, B - 1);\n else if(A > B) return "aab" + strWithout3a3b(A - 2, B - 1);\n else return strWithout3a3b(A - 1, B - 2) + "abb";\n }\n};\n```\n\nPython:\n```\nclass Solution(object):\n def strWithout3a3b(self, A, B):\n if A == 0: \n\t\t\treturn \'b\' * B\n elif B == 0: \n\t\t\treturn \'a\' * A\n elif A == B: \n\t\t\treturn \'ab\' * A\n elif A > B: \n\t\t\treturn \'aab\' + self.strWithout3a3b(A - 2, B - 1)\n else: \n\t\t\treturn self.strWithout3a3b(A - 1, B - 2) + \'abb\'\n``` | 63 | 2 | [] | 9 |
string-without-aaa-or-bbb | Java straightforward | java-straightforward-by-wangzi6147-95dn | \nclass Solution {\n public String strWithout3a3b(int A, int B) {\n StringBuilder sb = new StringBuilder();\n while(A + B > 0) {\n i | wangzi6147 | NORMAL | 2019-01-27T04:01:16.460881+00:00 | 2019-01-27T04:01:16.460928+00:00 | 2,929 | false | ```\nclass Solution {\n public String strWithout3a3b(int A, int B) {\n StringBuilder sb = new StringBuilder();\n while(A + B > 0) {\n int l = sb.length();\n if (l > 1 && sb.charAt(l - 2) == sb.charAt(l - 1)) {\n if (sb.charAt(l - 1) == \'a\') {\n sb.append(\'b\');\n B--;\n } else {\n sb.append(\'a\');\n A--;\n }\n } else {\n if (A > B) {\n sb.append(\'a\');\n A--;\n } else {\n sb.append(\'b\');\n B--;\n }\n }\n }\n return sb.toString();\n }\n}\n``` | 35 | 2 | [] | 4 |
string-without-aaa-or-bbb | C++ short and simple solution | c-short-and-simple-solution-by-chrisys-u4y1 | ```\nstring strWithout3a3b(int A, int B) {\n std::string res;\n \n while (A && B) {\n if (A > B) {\n res += "aab" | chrisys | NORMAL | 2019-01-27T14:05:36.027716+00:00 | 2019-01-27T14:05:36.027762+00:00 | 1,849 | false | ```\nstring strWithout3a3b(int A, int B) {\n std::string res;\n \n while (A && B) {\n if (A > B) {\n res += "aab";\n A--;\n } else if (B > A) {\n res += "bba";\n B--;\n } else {\n res += "ab";\n }\n A--;\n B--;\n }\n while (A--) res += "a";\n while (B--) res += "b";\n return res;\n } | 33 | 2 | [] | 2 |
string-without-aaa-or-bbb | my python solution without loop, beat 100% | my-python-solution-without-loop-beat-100-jb2k | \n\nclass Solution(object):\n def strWithout3a3b(self, A, B):\n """\n :type A: int\n :type B: int\n :rtype: str\n """\n | wangyanpeng | NORMAL | 2019-01-28T10:52:45.052790+00:00 | 2019-01-28T10:52:45.052832+00:00 | 1,145 | false | \n```\nclass Solution(object):\n def strWithout3a3b(self, A, B):\n """\n :type A: int\n :type B: int\n :rtype: str\n """\n if A >= 2*B:\n return \'aab\'* B + \'a\'* (A-2*B)\n elif A >= B:\n return \'aab\' * (A-B) + \'ab\' * (2*B - A)\n elif B >= 2*A:\n return \'bba\' * A + \'b\' *(B-2*A)\n else:\n return \'bba\' * (B-A) + \'ab\' * (2*A - B)\n``` | 16 | 0 | [] | 2 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.