question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-erasure-value | JS, Python, Java, C++ | Easy 2-Pointer Sliding Window Solution w/ Explanation | js-python-java-c-easy-2-pointer-sliding-se4c5 | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n | sgallivan | NORMAL | 2021-05-28T07:44:07.250270+00:00 | 2021-05-28T07:57:28.437027+00:00 | 1,677 | false | *(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nLike most problems that ask about a contiguous subarray, this problem naturally calls for a **2-pointer sliding window** approach. There are a few ways we can keep track of the contents of the sliding window, but since the constraint upon **nums[i]** is fairly small, we can use the faster **arraymap** (**nmap**) method, rather than a **hashmap**.\n\nSo as we iterate our sliding window through **nums**, we\'ll move our **right** pointer forward, increasing the counter for the appropriate number in **nmap**. If that bucket in **nmap** goes above **1**, then we know that the newly-added number isn\'t unique in our sliding window, so we need to increase the **left** pointer until the counter is reduced back to **1**.\n\nWe should also, of course, keep track of the sum **total** of the sliding window. At each iteration, once we\'ve confirmed the uniqueness of the contents of the sliding window, we should also update our **best** result so far. Then, once we\'re done, we can just **return best**.\n\n - _**Time Complexity: O(N)** where **N** is the length of **nums**_\n - _**Space Complexity: O(10001)** for **nmap** keeping track of numbers from **0** to **10^4**_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **96ms / 49.4MB** (beats 100% / 100%).\n```javascript\nvar maximumUniqueSubarray = function(nums) {\n let nmap = new Int8Array(10001), total = 0, best = 0\n for (let left = 0, right = 0; right < nums.length; right++) {\n nmap[nums[right]]++, total += nums[right]\n while (nmap[nums[right]] > 1)\n nmap[nums[left]]--, total -= nums[left++]\n best = Math.max(best, total)\n }\n return best\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **1180ms / 28.2MB** (beats 90% / 63%).\n```python\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n nmap, total, best, left = [0] * 10001, 0, 0, 0\n for right in nums:\n nmap[right] += 1\n total += right\n while nmap[right] > 1:\n nmap[nums[left]] -= 1\n total -= nums[left]\n left += 1\n best = max(best, total)\n return best\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **6ms / 47.5MB** (beats 97% / 100%).\n```java\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n short[] nmap = new short[10001];\n int total = 0, best = 0;\n for (int left = 0, right = 0; right < nums.length; right++) {\n nmap[nums[right]]++;\n total += nums[right];\n while (nmap[nums[right]] > 1) {\n nmap[nums[left]]--;\n total -= nums[left++];\n }\n best = Math.max(best, total);\n }\n return best;\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **129ms / 88.9MB** (beats 100% / 100%).\n```c++\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n char nmap[10001]{0};\n int total = 0, best = 0;\n for (int left = 0, right = 0; right < nums.size(); right++) {\n nmap[nums[right]]++, total += nums[right];\n while (nmap[nums[right]] > 1)\n nmap[nums[left]]--, total -= nums[left++];\n best = max(best, total);\n }\n return best;\n }\n};\n``` | 24 | 8 | ['C', 'Python', 'Java', 'JavaScript'] | 1 |
maximum-erasure-value | Python3 O(n) sliding window | python3-on-sliding-window-by-invinciblez-8d31 | \nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n ans = float(\'-inf\')\n cur = 0\n # sliding window; curre | invinciblezz | NORMAL | 2020-12-20T04:22:35.060781+00:00 | 2020-12-20T05:15:21.798189+00:00 | 2,214 | false | ```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n ans = float(\'-inf\')\n cur = 0\n # sliding window; current value = [i, j]\n seen = set()\n i = 0\n for j in range(len(nums)):\n while nums[j] in seen:\n cur -= nums[i]\n seen.remove(nums[i])\n i += 1\n seen.add(nums[j])\n cur += nums[j]\n ans = max(ans, cur)\n \n return ans\n``` | 23 | 2 | [] | 3 |
maximum-erasure-value | Easy C++ Solution using Two Pointers | easy-c-solution-using-two-pointers-by-ha-v428 | The idea here is to keep track of all the elements already visited using a set and deploy two pointers (i&j) to adjust our current window.\nThe flow is as foll | harshit7962 | NORMAL | 2022-06-12T03:39:00.389703+00:00 | 2022-06-12T04:22:57.665144+00:00 | 4,037 | false | The idea here is to keep track of all the elements already visited using a set and deploy two pointers (i&j) to adjust our current window.\nThe flow is as follows:\n* If the current element is not already present in the set we simply add it to our curr_sum and extend the window...\n* If the element is already present in the set, we start removing elements from start of our window until we delete the required element...\n* We keep track of maximum result using another variable...\n\n**Example 1: Lets take this to be our current i and j positions...**\n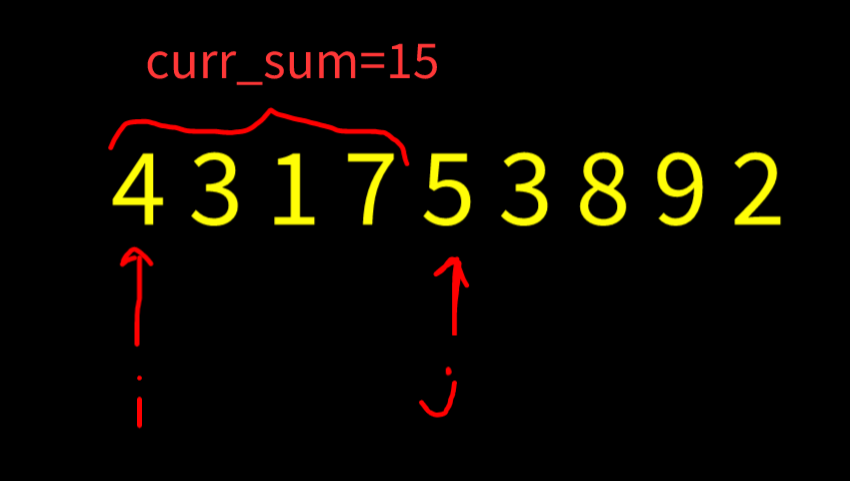\nNow since 5 is not already present in our set, we simply add it to curr_sum variable and increment the j value...\n\n\n**Example 2:**\n\nNow here we are adding 7, which is already present in our set, so we start remove elements of ith index from set and also subtract them from our curr_sum value until we remove the value 7...\n\n**If you found the solution, pls upvote this thread.**\n\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int curr_sum=0, res=0;\n\t\t\n\t\t//set to store the elements\n unordered_set<int> st;\n \n int i=0,j=0;\n while(j<nums.size()) {\n while(st.count(nums[j])>0) {\n\t\t\t\t//Removing the ith element untill we reach the repeating element\n st.erase(nums[i]);\n curr_sum-=nums[i];\n i++;\n }\n\t\t\t//Add the current element to set and curr_sum value\n curr_sum+=nums[j];\n st.insert(nums[j++]);\n\t\t\t\n\t\t\t//res variable to keep track of largest curr_sum encountered till now...\n res = max(res, curr_sum);\n }\n \n return res;\n }\n};\n``` | 22 | 1 | ['Two Pointers', 'C', 'C++'] | 1 |
maximum-erasure-value | ✅ Python Easy 2 approaches | python-easy-2-approaches-by-constantine7-flfm | \u2714\uFE0FSolution I - Two pointers using Counter\n\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n counter=defaultdic | constantine786 | NORMAL | 2022-06-12T00:38:51.416693+00:00 | 2022-06-12T00:39:59.496054+00:00 | 2,823 | false | ## \u2714\uFE0F*Solution I - Two pointers using Counter*\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n counter=defaultdict(int) # track count of elements in the window\n res=i=tot=0\n\t\t\n for j in range(len(nums)):\n x=nums[j] \n tot+=x\n counter[x]+=1\n # adjust the left bound of sliding window until you get all unique elements\n while i < j and counter[x]>1: \n counter[nums[i]]-=1\n tot-=nums[i]\n i+=1\n \n res=max(res, tot) \n return res\n```\n\n## \u2714\uFE0F*Solution II - Two pointers using Visited*\n\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n seen=set() # track visited elements in the window\n res=i=tot=0\n for j in range(len(nums)):\n x=nums[j] \n\t\t\t # adjust the left bound of sliding window until you get all unique elements\n while i < j and x in seen: \n seen.remove(nums[i])\n tot-=nums[i]\n i+=1 \n tot+=x\n seen.add(x)\n res=max(res, tot) \n return res\n```\n\n**Time - O(n)**\n**Space - O(k)** - where` k` is number of unique elements in input `nums`.\n\n\n---\n\n\n***Please upvote if you find it useful*** | 19 | 0 | ['Python', 'Python3'] | 3 |
maximum-erasure-value | C++ Sliding window + hashmap 🥓🥓 | c-sliding-window-hashmap-by-midnightsimo-vo8r | Keep a frequency map of the numbers in the window.\n\nwhile the count of the latest number in the window is greater than 1, shrink the window.\n\nrecord the bes | midnightsimon | NORMAL | 2022-06-12T01:15:18.039801+00:00 | 2022-06-12T01:15:18.039825+00:00 | 3,029 | false | Keep a frequency map of the numbers in the window.\n\nwhile the count of the latest number in the window is greater than 1, shrink the window.\n\nrecord the best answer.\n\n**Solved LIVE ON TWITCH. Link in profile. I stream Everyday at 6pm PT** \n\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int n = nums.size();\n int L = 0;\n int R = 0;\n \n unordered_map<int, int> freqMap;\n int sum = 0;\n int ans = 0;\n while(R < n) {\n int right = nums[R++];\n sum += right;\n freqMap[right]++;\n \n while(freqMap[right] > 1) {\n int left = nums[L++];\n freqMap[left]--;\n sum -= left;\n }\n ans = max(ans, sum);\n }\n return ans;\n }\n};\n``` | 16 | 0 | [] | 3 |
maximum-erasure-value | Maximum Erasure Value | JS, Python, Java, C++ | Easy 2-Pointer Sliding Window Solution w/ Expl. | maximum-erasure-value-js-python-java-c-e-4roh | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n | sgallivan | NORMAL | 2021-05-28T07:44:53.132051+00:00 | 2021-05-28T07:57:42.155194+00:00 | 551 | false | *(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nLike most problems that ask about a contiguous subarray, this problem naturally calls for a **2-pointer sliding window** approach. There are a few ways we can keep track of the contents of the sliding window, but since the constraint upon **nums[i]** is fairly small, we can use the faster **arraymap** (**nmap**) method, rather than a **hashmap**.\n\nSo as we iterate our sliding window through **nums**, we\'ll move our **right** pointer forward, increasing the counter for the appropriate number in **nmap**. If that bucket in **nmap** goes above **1**, then we know that the newly-added number isn\'t unique in our sliding window, so we need to increase the **left** pointer until the counter is reduced back to **1**.\n\nWe should also, of course, keep track of the sum **total** of the sliding window. At each iteration, once we\'ve confirmed the uniqueness of the contents of the sliding window, we should also update our **best** result so far. Then, once we\'re done, we can just **return best**.\n\n - _**Time Complexity: O(N)** where **N** is the length of **nums**_\n - _**Space Complexity: O(10001)** for **nmap** keeping track of numbers from **0** to **10^4**_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **96ms / 49.4MB** (beats 100% / 100%).\n```javascript\nvar maximumUniqueSubarray = function(nums) {\n let nmap = new Int8Array(10001), total = 0, best = 0\n for (let left = 0, right = 0; right < nums.length; right++) {\n nmap[nums[right]]++, total += nums[right]\n while (nmap[nums[right]] > 1)\n nmap[nums[left]]--, total -= nums[left++]\n best = Math.max(best, total)\n }\n return best\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **1180ms / 28.2MB** (beats 90% / 63%).\n```python\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n nmap, total, best, left = [0] * 10001, 0, 0, 0\n for right in nums:\n nmap[right] += 1\n total += right\n while nmap[right] > 1:\n nmap[nums[left]] -= 1\n total -= nums[left]\n left += 1\n best = max(best, total)\n return best\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **6ms / 47.5MB** (beats 97% / 100%).\n```java\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n short[] nmap = new short[10001];\n int total = 0, best = 0;\n for (int left = 0, right = 0; right < nums.length; right++) {\n nmap[nums[right]]++;\n total += nums[right];\n while (nmap[nums[right]] > 1) {\n nmap[nums[left]]--;\n total -= nums[left++];\n }\n best = Math.max(best, total);\n }\n return best;\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **129ms / 88.9MB** (beats 100% / 100%).\n```c++\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n char nmap[10001]{0};\n int total = 0, best = 0;\n for (int left = 0, right = 0; right < nums.size(); right++) {\n nmap[nums[right]]++, total += nums[right];\n while (nmap[nums[right]] > 1)\n nmap[nums[left]]--, total -= nums[left++];\n best = max(best, total);\n }\n return best;\n }\n};\n``` | 16 | 6 | [] | 1 |
maximum-erasure-value | python3 || 9 lines, pref and dict || T/S: 99% / 44% | python3-9-lines-pref-and-dict-ts-99-44-b-t1vy | Here\'s the plan:\n1. We initialize vars and build a prefix array for nums.\n2. We use left to keep track of the starting index of the current subarray.\n3. We | Spaulding_ | NORMAL | 2022-06-12T17:29:04.790146+00:00 | 2024-06-06T21:14:35.772600+00:00 | 214 | false | Here\'s the plan:\n1. We initialize `vars` and build a prefix array for `nums`.\n2. We use `left` to keep track of the starting index of the current subarray.\n3. We use `d` to keep track of the latest indexplus 1 for each value `n` in `nums`. \n4. We iterate through nums, updating `left` (if neccessary), `d`, and `ans`. We return `ans`.\n\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n\n left, d = [0], defaultdict(int)\n pref, ans = 0, 1\n\n for n in nums:\n pref.append(pref[-1]+n)\n\n for idx, n in enumerate(nums):\n if d[n] > left: left = d[n]\n d[n] = idx+1\n\n ans = max(ans, pref[idx+1] - pref[left])\n\n return ans\n```\n[https://leetcode.com/problems/maximum-erasure-value/submissions/1279958488/](https://leetcode.com/problems/maximum-erasure-value/submissions/1279958488/)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ `len(nums)`. | 13 | 0 | ['Python', 'Python3'] | 0 |
maximum-erasure-value | C++ Sliding Window 99% Faster No Library Hash Map O(1) Lookup time | c-sliding-window-99-faster-no-library-ha-4zlm | \nclass Solution {\npublic:\n \n int maximumUniqueSubarray(vector<int>& nums) {\n int res = 0;\n int currSum = 0;\n \n int m[1 | sputnik15963 | NORMAL | 2020-12-23T20:07:11.309855+00:00 | 2020-12-23T20:07:11.309897+00:00 | 1,570 | false | ```\nclass Solution {\npublic:\n \n int maximumUniqueSubarray(vector<int>& nums) {\n int res = 0;\n int currSum = 0;\n \n int m[100001] = {};\n //Value is the index in this map\n int i = 0;\n int j = 0;\n \n while( j < nums.size()){\n \n if( m[nums[j]]){ //We have to contract\n while( m[nums[j]]){\n currSum -= nums[i]; ///Pops it off the tail\n m[nums[i]]--;\n ++i;\n }\n }\n //House keeping comparisons\n m[nums[j]]++;\n currSum += nums[j];\n res = max (res, currSum);\n ++j;\n }\n \n \n return res;\n \n \n }\n};\n\n\n``` | 11 | 0 | ['C', 'Sliding Window'] | 1 |
maximum-erasure-value | ✅ C++ | Sliding Window | Hashmap | O(N) | c-sliding-window-hashmap-on-by-rupam66-jr3r | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int i=0,j=0,sum=0,res=0;\n unordered_map<int,int> mp;\n w | rupam66 | NORMAL | 2022-06-12T04:33:31.831756+00:00 | 2022-06-12T04:48:45.475992+00:00 | 1,448 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int i=0,j=0,sum=0,res=0;\n unordered_map<int,int> mp;\n while(j<nums.size()){\n if(mp[nums[j]]){ // nums[j] is already there in the window\n while(mp[nums[j]]){ // until the occurrence of nums[j] becomes 0, reduce the window from front\n mp[nums[i]]--;\n sum-=nums[i];\n i++;\n }\n }\n else{ // nums[j] is not there in the window, so put it into the window\n sum+=nums[j];\n res=max(res,sum); // update the result with maximum sum value\n mp[nums[j]]++;\n j++;\n }\n }\n return res;\n }\n};\n```\n**If you like this, Do Upvote!** | 10 | 0 | ['Two Pointers', 'C', 'Sliding Window'] | 3 |
maximum-erasure-value | C++ Sliding Window (+Cheat Sheet) | c-sliding-window-cheat-sheet-by-lzl12463-9xsv | See my latest update in repo LeetCode\n## Solution 1. Shrinkable Sliding Window\n\ncpp\n// OJ: https://leetcode.com/problems/maximum-erasure-value/\n// Author: | lzl124631x | NORMAL | 2021-10-05T08:01:46.004151+00:00 | 2021-10-05T08:01:46.004179+00:00 | 3,186 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n## Solution 1. Shrinkable Sliding Window\n\n```cpp\n// OJ: https://leetcode.com/problems/maximum-erasure-value/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(N)\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& A) {\n int i = 0, ans = 0, N = A.size();\n unordered_map<int, int> m; // number -> index of last occurrence.\n vector<int> sum(N + 1);\n partial_sum(begin(A), end(A), begin(sum) + 1);\n for (int j = 0; j < N; ++j) {\n if (m.count(A[j])) i = max(i, m[A[j]] + 1);\n m[A[j]] = j;\n ans = max(ans, sum[j + 1] - sum[i]);\n }\n return ans;\n }\n};\n```\n\n## Solution 2. Shrinkable Sliding Window\n\n```cpp\n// OJ: https://leetcode.com/problems/maximum-erasure-value/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(U) where U is the number of unique elements in `A`\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& A) {\n int ans = 0, N = A.size(), sum = 0;\n unordered_set<int> s;\n for (int i = 0, j = 0; j < N; ++j) {\n while (s.count(A[j])) {\n s.erase(A[i]);\n sum -= A[i++];\n }\n s.insert(A[j]);\n sum += A[j];\n ans = max(ans, sum);\n }\n return ans;\n }\n};\n```\n\n## Solution 3. Shrinkable Sliding Window\n\nCheck out "[C++ Maximum Sliding Window Cheatsheet Template!](https://leetcode.com/problems/frequency-of-the-most-frequent-element/discuss/1175088/C%2B%2B-Maximum-Sliding-Window-Cheatsheet-Template!)"\n\n```cpp\n// OJ: https://leetcode.com/problems/maximum-erasure-value/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(U) where U is the number of unique elements in `A`\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& A) {\n int i = 0, j = 0, N = A.size(), ans = 0, dup = 0, sum = 0;\n unordered_map<int, int> cnt;\n while (j < N) {\n dup += ++cnt[A[j]] == 2;\n sum += A[j++];\n while (dup) {\n dup -= --cnt[A[i]] == 1;\n sum -= A[i++];\n }\n ans = max(ans, sum);\n }\n return ans;\n }\n};\n``` | 9 | 0 | [] | 0 |
maximum-erasure-value | ✔C++|Sliding Window|Hash Table|O(N)🔥 | csliding-windowhash-tableon-by-xahoor72-ulp0 | Intuition\n Describe your first thoughts on how to solve this problem. \nIntuition is simple if u done some sliding window problems I suggest doing in same way | Xahoor72 | NORMAL | 2023-02-12T17:59:12.451327+00:00 | 2023-02-12T17:59:12.451365+00:00 | 780 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIntuition is simple if u done some sliding window problems I suggest doing in same way as u have done those because there are little implementations techniques a liitle different than one another but idea is same or best is what is hitting your mind mostly . So I basically do these problems using a map and checking when there is a duplicate start removing it from map and also decremnt its value form sum. \nU can checkout this problem quite similar to this and many other also : \n- [https://leetcode.com/problems/longest-substring-without-repeating-characters/description/]()\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo using Sliding Window These are the steps:\n- Insert one by one in map and also check a constion along with this .\n- Condition is if mp[arr[i]] is >1 i.e is a duplicate so remove it .\n- Also decrease its value from sum variable.\n- Keep a maxi varaible for maximum window. \n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n**Implementation I**\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& arr) {\n int maxi=0, j=0, n=arr.size(),req=0,sum=0;\n unordered_map<int,int>mp;\n for(int i=0;i<n;i++){\n mp[arr[i]]++;\n sum+=arr[i];\n while(mp[arr[i]]>1){\n sum-=arr[j];\n --mp[arr[j]];\n j++;\n }\n maxi=max(sum,maxi);\n }\n return maxi;\n }\n};\n```\n**Implementation II**\n```\nint maximumUniqueSubarray(vector<int>& arr) {\n int maxi=0, j=0, n=arr.size(),req=0,sum=0;\n unordered_map<int,int>mp;\n for(int i=0;i<n;i++){\n mp[arr[i]]++;\n sum+=arr[i];\n while((i-j+1)>mp.size()){\n sum-=arr[j];\n if(--mp[arr[j]]==0)mp.erase(arr[j]);\n j++;\n }\n maxi=max(sum,maxi);\n }\n return maxi;\n``` | 8 | 0 | ['Array', 'Hash Table', 'Sliding Window', 'C++'] | 0 |
maximum-erasure-value | O(n) Java Sliding Window Solution | on-java-sliding-window-solution-by-admin-q5gw | \n public int maximumUniqueSubarray(int[] nums) {\n int l =0, r = 0, length = nums.length, sum = 0;\n int[] map = new int[10001];\n int | admin007 | NORMAL | 2020-12-20T06:24:28.195001+00:00 | 2020-12-20T06:40:42.807833+00:00 | 938 | false | ```\n public int maximumUniqueSubarray(int[] nums) {\n int l =0, r = 0, length = nums.length, sum = 0;\n int[] map = new int[10001];\n int ans = 0;\n while (r < length) {\n map[nums[r]]++;\n sum += nums[r];\n r++;\n while (map[nums[r - 1]] >= 2) {\n map[nums[l]]--;\n sum -= nums[l];\n l++;\n }\n ans = Math.max(ans, sum);\n }\n return ans;\n }\n``` | 8 | 2 | ['Java'] | 1 |
maximum-erasure-value | Java | Sliding Window | Easy to Understand | java-sliding-window-easy-to-understand-b-48v0 | Use a Sliding window to calculate the maximum sum subarray which has all unique elements. We can use a set to maintain the uniqueness.\n\n\nclass Solution {\n | rajarshi-sarkar | NORMAL | 2020-12-20T04:01:11.257148+00:00 | 2020-12-20T04:02:37.179689+00:00 | 970 | false | Use a Sliding window to calculate the maximum sum subarray which has all unique elements. We can use a set to maintain the uniqueness.\n\n```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n Set<Integer> set = new HashSet<>();\n \n int start = 0, n = nums.length, sum = 0, answer = -1;\n \n for(int end = 0; end < n; end++) {\n // If the window has duplicate elements then shrink the window from the left\n if(set.contains(nums[end])) {\n while(set.contains(nums[end])) {\n sum -= nums[start];\n set.remove(nums[start]);\n start++;\n }\n }\n // Expand the window from the right\n set.add(nums[end]);\n sum += nums[end];\n // Calculate the max window sum\n answer = Math.max(answer, sum);\n }\n \n return answer;\n }\n}\n``` | 8 | 0 | ['Sliding Window', 'Ordered Set', 'Java'] | 1 |
maximum-erasure-value | Maximum Erasure Value | maximum-erasure-value-by-shailu00-ynwd | C++ Code\n\nint maximumUniqueSubarray(vector<int>& nums) {\n int n= nums.size(),psum=0,mx=0,j=0,count=-1; unordered_map<int, pair<int, int>>m;\n f | Shailu00 | NORMAL | 2022-06-13T05:55:03.290109+00:00 | 2022-07-02T19:22:56.317482+00:00 | 124 | false | **C++ Code**\n```\nint maximumUniqueSubarray(vector<int>& nums) {\n int n= nums.size(),psum=0,mx=0,j=0,count=-1; unordered_map<int, pair<int, int>>m;\n for(int i=0; i<n; i++)\n {\n psum+=nums[i];\n if(m.find(nums[i])!=m.end() && m[nums[i]].second >=j )\n {\n mx= max(mx, psum-m[nums[j]].first-nums[i]+nums[j]);\n j = m[nums[i]].second+1; \n } \n m[nums[i]]={psum,i};\n }\n mx=max(mx,psum-m[nums[j]].first + nums[j]);\n return mx;\n }\n``` | 7 | 0 | ['C'] | 2 |
maximum-erasure-value | Maximum Erasure Value Daily June ,Day12,22 | maximum-erasure-value-daily-june-day1222-vfhr | \nSteps:-\n Step 1: Creating prefix sum array\n\t Step 2: Iterating over nums from index 1 and initialized the result with res=nums[0]\n\t Step 3: Usi | omgupta0312 | NORMAL | 2022-06-12T11:05:15.072026+00:00 | 2022-06-12T11:05:15.072055+00:00 | 402 | false | ```\nSteps:-\n Step 1: Creating prefix sum array\n\t Step 2: Iterating over nums from index 1 and initialized the result with res=nums[0]\n\t Step 3: Using unordered_map cheching if element already present or not,\n\t Step 4: If present then checking if the index is greater than the start index. If True then updating the result (res) with max(res,(sum of elements between i th index and start index).\n\t Step 5: Also at last updating the res with max(res,(sum of elements between i th index and start index), because if iterator i have reached at last of nums.\n\t Step 6:return the result (here res).\n\t \nCode:\n int maximumUniqueSubarray(vector<int>& nums) {\n int res=nums[0],s=0,start=0,i=0;\n vector<int>v;unordered_map<int,int>m;\n for (auto x:nums)\n {\n s+=x;\n v.push_back(s);\n }\n \n m[nums[0]]=0;\n for(i=1;i<nums.size();i++)\n {\n if(m.find(nums[i])!=m.end() && m[nums[i]]>=start)\n {\n int ind=m[nums[i]];\n res=max(res,(v[i-1]-v[start]+nums[start]));\n start=ind+1; \n }\n m[nums[i]]=i; \n }\n \n res=max(res,v[i-1]-v[start]+nums[start]);\n return res;\n }\n``` | 6 | 0 | ['C', 'Sliding Window', 'Prefix Sum'] | 3 |
maximum-erasure-value | C++ | O(n) | Single-pass | Map + Prefix Sum | c-on-single-pass-map-prefix-sum-by-shikh-4o23 | The goal of the algorithm to solve this problem was to maximize sum(i,j) such that all elements from i to j are unique (where sum(i,j) for array A is A[i] + A[i | shikhar03Stark | NORMAL | 2022-06-10T12:04:55.053007+00:00 | 2022-06-10T12:05:34.021964+00:00 | 390 | false | The goal of the algorithm to solve this problem was to **maximize** `sum(i,j)` such that all elements from **i** to **j** are **unique** (where `sum(i,j)` for array `A` is `A[i] + A[i+1] + .. A[j-1] + A[j]`).\nWe can think it in terms of **j**, for every **j**, we want to find the **left-most** point in the array such that elements are **unique** between them. The answer would be the **maximum** of all computed **j** values.\n\nWe can create a prefix array to compute `sum(i,j)`.\n\nAlgorithm:\n\n1. Set `left` = -1, `n` = `nums`.size(), create prefix array\n2. For all `j` from `[0...n-1]`\n\t1. If `nums[j]` is **already encountered** && **previous index** of `nums[j]` is greater than `left`\n\t2. Then set `left` = **previous index** of `nums[j]`\n\t3. end if\n\t4. Set index of `nums[j]` to `j`\n\t5. store answer for `j` = `sum(left+1, j)` using **prefix array**\n3. return **maximum** of answer for each `j`.\n\n*Note: We can club creating prefix array in single loop.*\n\nCode:\n```\nint maximumUniqueSubarray(vector<int>& nums) {\n\tunordered_map<int,int> idx;\n\tint n = nums.size();\n\tint ans = 0;\n\tvector<int> prefix(n+1, 0);\n\n\tint left = -1;\n\tfor(int i = 0; i<n; i++){\n\t\t//build prefix on-the-fly\n\t\tprefix[i+1] = prefix[i] + nums[i];\n\n\t\t// pick left index untill elements are unique\n\t\tif(idx.count(nums[i]) > 0 && left < idx[nums[i]]) left = idx[nums[i]];\n\n\t\t//update map with latest index of element\n\t\tidx[nums[i]] = i;\n\t\t\n\t\t//use prefix array to calculate the sum in O(1)\n\t\tans = max(ans, prefix[i+1] - prefix[left+1]);\n\t}\n\n\treturn ans;\n\n}\n```\n\nComplexity analysis:\n\n**Time Complexity (Average Case)**\n| Operation | Upperbound |\n|---------------|------------------|\n| Building Prefix| O(n) |\n|Accessing Map| O(1)|\n|Using prefix| O(1)|\n\nTime complexitity is `O(n * (k1+k2))` = **`O(n)`**, where `k1` and `k2` are constants.\n\n**Space Complexity (Avearage Case)**\n| Operation | Upperbound |\n|---------------|------------------|\n| Prefix | O(n) |\n|Map| O(n)|\n\nSpace complexitity is `O(n + n)` = **`O(n)`**\n\n\n\n*`Shikhar03Stark`*\n\n\n | 6 | 0 | ['Two Pointers', 'C', 'Prefix Sum'] | 1 |
maximum-erasure-value | [Python] Easy PREFIX SUM | python-easy-prefix-sum-by-aatmsaat-n6is | Maximum Erasure Value\n\n\nLets assume for array [1, 2, 5, 2, 5, 1] \n\n Padding :- we add 0 in the beginning of array to prevent Index_Out_Bound error then arr | aatmsaat | NORMAL | 2021-05-28T11:24:29.061736+00:00 | 2021-05-29T05:53:40.083770+00:00 | 444 | false | # Maximum Erasure Value\n\n\nLets assume for array *[1, 2, 5, 2, 5, 1]* \n\n* `Padding :- ` we add 0 in the beginning of array to prevent **Index_Out_Bound** error then array **nums** becomes *[0, 1, 2, 5, 2, 5, 1]*\n* `Index Array :-` we create the index array **Idxarr** which can be formed of the length of maximum element **mx** in the array , since give ```1 <= nums[i] <= 10^4``` \xA0it may reach max at *10^4* so its **time and space complexity is `O(max(10^4, length of array)`** \xA0which is same even if the array length is > 10^5 i.e. `O(N)` , so mx=5 then idxarr becomes *[0,0,0,0,0,0]*(mx+1 i.e. 6)\n* `Prefix sum :- ` Then we form the prefix sum array **pre** becomes *[0, 1, 3, 8, 10, 15, 16]*\n* `Important Variables:- ` Now take **ans=0** to store result and **last=0** to store the index of the last time where *uniqueness* started\n\n So in the final loop **idxarr** keeps on updating index of every element from which update **last** and thus difference between sum untill now and sum till the last index(**last**) gives us sum of unique sub array *(prefix differences at current and last index)*. The max of these differences updated in **ans**.\n \n *Please upvote if you like the solution and comment if have any queries* .\n \n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n nums = [0]+nums#padding\n \n n = len(nums)\n mx = max(nums)\n \n Idxarr = [0]*(mx+1)#Index Array\n \n #prefix sum\n pre = [0]*n\n for i in range(1, n):\n pre[i] = pre[i-1]+nums[i]\n \n ans = last = 0\n for i in range(1, n):\n last = max(last, Idxarr[nums[i]])\n ans = max(ans, pre[i]-pre[last])\n Idxarr[nums[i]]=i\n return ans\n``` | 6 | 2 | ['Prefix Sum', 'Python'] | 1 |
maximum-erasure-value | [C++] Sliding Window - Clear and Concise - O(n) | c-sliding-window-clear-and-concise-on-by-fekx | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int,bool> um;\n int n = nums.size();\n int | morning_coder | NORMAL | 2021-05-28T07:33:46.128379+00:00 | 2021-05-28T07:33:46.128420+00:00 | 688 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int,bool> um;\n int n = nums.size();\n int start = 0;\n int curr_sum = 0;\n int max_sum = 0;\n for(int i = 0; i < n; i++){\n while(um[nums[i]] == true){\n curr_sum -= nums[start];\n um[nums[start]] = false;\n start++;\n }\n um[nums[i]] = true;\n curr_sum += nums[i];\n max_sum = max(max_sum, curr_sum);\n }\n return max_sum;\n }\n};\n``` | 6 | 3 | ['Two Pointers', 'C', 'Sliding Window', 'C++'] | 1 |
maximum-erasure-value | ✅C++ | ✅Use Sliding window and hashing | ✅Simple and efficient solution | 🗓️ DLC June, Day 12 | c-use-sliding-window-and-hashing-simple-jg5ve | Please upvote if it helps \u2764\uFE0F\uD83D\uDE0A\nTC: O(N), SC: O(2N) ~ O(N)\n\nCode:\n\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& | Yash2arma | NORMAL | 2022-06-12T13:55:04.244846+00:00 | 2022-06-12T13:55:04.244881+00:00 | 601 | false | **Please upvote if it helps \u2764\uFE0F\uD83D\uDE0A**\n**TC: O(N), SC: O(2N) ~ O(N)**\n\n**Code:**\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) \n {\n int l=0, r=0; //define left and right pointers for sliding windows approach\n \n vector<int> sum_arr; //sum_arr stores sum of element of nums at index i;\n sum_arr.push_back(0); //initially l and r at 0 so to consider element at index 0 we need to take 0 at index 0\n \n int sum=0, score=nums[0];\n for(auto it:nums) //storing sum into sum_arr\n {\n sum += it;\n sum_arr.push_back(sum);\n }\n \n unordered_map<int, int> mp; //stores element and their index\n \n while(r<nums.size()) //iterate till r pointer is lesser than nums\' size \n {\n if(mp.find(nums[r]) != mp.end()) l=max(l, mp[nums[r]]+1); //when repeated element come we move left pointer of the right of repeated element\n mp[nums[r]] = r; //assigning index to the element\n score = max(score, sum_arr[r+1]-sum_arr[l]); //get max score\n r++; //move r by 1 \n }\n return score;\n \n }\n};\n``` | 5 | 0 | ['C', 'Sliding Window', 'C++'] | 0 |
maximum-erasure-value | cpp solution || hash table || 99.76 % faster and 99.27% space efficient || Two-Pointer | cpp-solution-hash-table-9976-faster-and-8u54m | Thank you for checking out my solution\nDo upvote if it helped :)\n_\n_Approach 1 : Brute Force (Will Fail as per the Constraints)\n__Brute force approach could | TheCodeAlpha | NORMAL | 2022-06-12T13:23:38.028073+00:00 | 2022-06-12T13:24:34.376577+00:00 | 334 | false | __Thank you for checking out my solution\nDo upvote if it helped :)__\n____\n__Approach 1 : Brute Force (Will Fail as per the Constraints)__\n__Brute force approach could be to set a quadratic algorithm\nSet up an answer variable as ans = 0 \nInitialise a new set__\n__Where the outer loop marks a starting position__\n>Sum = value at the current index\n>The inner loop will decide the ending index, based on the first time an element is repeated\n>>If the element is repeated\n>>>__Store the max of the current sum and the ans \n>>>Empty the set\n>>>Add the current element to the set\n>>>Break the loop__\n>>>\n>>Else,\n>>>__Add the elements to the current sum\n>>>insert the element to the set__\n>>>\n__Return the Answer__\n\n__Given below is the Coding implementation for the same__\n\n```\nclass Solution \n{ \npublic:\n int maximumUniqueSubarray(vector<int>& nums) \n {\n ios_base::sync_with_stdio(0);\n unordered_set<int> st;\n int sum = 0, ans = 0;\n for(int i = 0; i < nums.size(); i++)\n {\n st.insert(nums[i]);\n sum = nums[i];\n for(int j = i+1; j < nums.size(); j++)\n {\n if(st.find(nums[j]) != st.end())\n {\n st.clear();\n ans = max(ans, sum);\n break;\n }\n sum += nums[j];\n st.insert(nums[j]);\n ans = max(ans,sum);\n }\n }\n return max(ans,sum);\n }\n};\n```\n__Time Complexity : O(N^2)\nSpace Complexity: O(N)__\n____\n__Approach 2 : Two-Pointers/Sliding Window__\n__Based on the constraints, if you were to try the brute force, you will surely get TLE.\nNow the task at hand is to write an algorithm that works in O(N) time [O(N. log(N)) will also work, if you find one, do comment below]__\n\n__If you closely observe the brute force solution, you will notice that when a running sum is calculated, once an element is repeated, \nall the elements occuring upto its previous occurance can be discarded altogether.\nFor example\nnums = [1,2,3,4,5,6,7,7,8,9]\nNow if start to calculate the sum from any index between 0 to 7, it will always end at 8, because the 7th element repeats\nThat means any element that repeats nullifies the contribution of all the elements that occurred before its previous index.\nLike in our example, the brute force algorithm will sum for all the indices in [0,6], only to break at index 7 everytime for first 7 interations.__\n____\n__Now that we have seen that brute force algorithm is repetitive, we can optimise it to get a better time complexity\nWe already know by now, that we need to keeep a track of indices of the elements, so we will use a frequency array, to do so__\n\n__1. Create a array [mapp] with length = max(in the array) + 1, for simplicity I used the upperbound of the constraints\n2. Create a pointer prev, to store the startingg index of the current sum\n3. Create a sum variable to store the current sum\n4. Create an answer variable to store the maximum of all the running sums__ \n\n__Lets begin with the algorithm__\n>__Iterate from 0 to size of the vector:__\n>>__Store the current element in a variable , say x, this prevents the back to back accessing of the element\n>>Check if the current position has been traversed (If Traversed, then surely there would be an index value at this position)__\n>>>__If traversed\n>>>Store the index stored at the elements position in the map in variable pos( you can name it anything you want);\n>>>Now Iterate from prev to this stored index pos:__\n>>>>Keep Subtracting the elements occuring in the nums from index [prev, pos)\n>>>>\n>>__Store the current index + 1 in mapp[x], mapp[x] = current index + 1\n>>Add the element in x to the sum, sum += x\n>>Store the max of running sum in the answer variable, ans = max(ans, sum)__\n>>\n__Return the answer variable__\n____\n\n__Below Is the coding implementaion for the same__\n```\nclass Solution\n{ // Runtime: 143 ms, faster than 99.76% of C++ online submissions for Maximum Erasure Value.\n // Memory Usage: 89.2 MB, less than 99.27% of C++ online submissions for Maximum Erasure Value.\npublic:\n int maximumUniqueSubarray(vector<int> &nums)\n {\n int a[10001] = {0}; // Creating a hashtable using the array, initialisng all the values to 0\n // Stating that No element has been traversed yet\n int prev = 0, sum = 0, ans = 0; // Using prev to store the index of the last deleted element\n // Sum to calculate the running sum, ans to store the sum of maximum unique subarray\n\n for (int i = 0; i < nums.size(); i++)\n {\n int x = nums[i]; // Storing the current element in the vector nums, prevents the back to back access of elements\n\n if (a[x] != 0) // If the hash value is not 0 for the element, that means it has occurred before\n { // Time to Decrease the available window\n int t = a[x]; // Store the previous index of this element\n while (prev < t) // Subtract (from the sum) all the elements occurring in the vector from [prev, t), notice the brackets, \n // indicating that element at prev is inclusive, but not the one at t is to be excluded\n sum -= nums[prev++]; // The value of sum decreases, \n }\n //Now Our Sliding window is of the size [i - prev + 1]\n a[x] = i + 1; // Storing the occuring index of the current element\n sum += x; // Aadding the value to the sum\n ans = max(ans, sum); // Storing the max sum in the answer variable\n }\n return ans;\n }\n};\n```\n__Time Complexity : O(N)\nSpace Complexity: O(1e4 + 1)__ | 5 | 0 | ['Two Pointers', 'Sliding Window', 'C++'] | 1 |
maximum-erasure-value | ✔Easy 🔥Intuition 🟢Full explanations 🚀 All Lan code | easy-intuition-full-explanations-all-lan-t1t0 | Logic\n This problem is about to find the maximum sum of subarrray (where elements in subarray is unique) in an array.\n This is a classic Sliding Window proble | nitin23rathod | NORMAL | 2022-06-12T09:42:00.467312+00:00 | 2022-06-12T09:42:00.467372+00:00 | 247 | false | **Logic**\n* This problem is about to find the maximum sum of subarrray (where elements in subarray is unique) in an array.\n* This is a classic Sliding Window problem which is simillar to this problem 3. Longest Substring Without Repeating Characters\n* We use seen (HashMap) to keep track of last index of a number.\n* We use sum to keep sum of sub array in range [l..r] so far where elements are unique.\n* While extend right side r if we met an existed number then we move left side l until seen[nums[r]] + 1 and of course, we need to decrease sum corresponding.\n\n**Complexity**\n\n* Time: O(N), where N is number of elements in array nums.\n* Space: O(M), where M <= N is the maximum number of distinct numbers in an subarray.\n\n**Python**\n\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n seen = dict()\n ans = sum = 0\n l = 0\n for r, x in enumerate(nums):\n if x in seen:\n index = seen[x]\n while l <= index: # Move the left side until index + 1\n del seen[nums[l]]\n sum -= nums[l]\n l += 1\n\n seen[x] = r\n sum += x\n ans = max(ans, sum)\n return ans\n```\n\n**C++**\n\n\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int, int> seen;\n int l = 0, sum = 0, ans = 0;\n for (int r = 0; r < nums.size(); r++) {\n int x = nums[r];\n if (seen.find(x) != seen.end()) {\n int index = seen[x];\n while (l <= index) { // Move the left side until index + 1\n seen.erase(nums[l]);\n sum -= nums[l];\n l += 1;\n }\n }\n seen[x] = r;\n sum += x;\n ans = max(ans, sum);\n }\n return ans;\n }\n};\n```\n\n**Java**\n\n```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n Map<Integer, Integer> seen = new HashMap<>();\n int l = 0, sum = 0, ans = 0;\n for (int r = 0; r < nums.length; r++) {\n int x = nums[r];\n if (seen.containsKey(x)) {\n int index = seen.get(x);\n while (l <= index) { // Move the left side until index + 1\n seen.remove(nums[l]);\n sum -= nums[l];\n l += 1;\n }\n }\n seen.put(x, r);\n sum += x;\n ans = Math.max(ans, sum);\n }\n return ans;\n }\n}\nC++\n\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int, int> seen;\n int l = 0, sum = 0, ans = 0;\n for (int r = 0; r < nums.size(); r++) {\n int x = nums[r];\n if (seen.find(x) != seen.end()) {\n int index = seen[x];\n while (l <= index) { // Move the left side until index + 1\n seen.erase(nums[l]);\n sum -= nums[l];\n l += 1;\n }\n }\n seen[x] = r;\n sum += x;\n ans = max(ans, sum);\n }\n return ans;\n }\n};\n``` | 5 | 0 | ['C', 'Python', 'Java'] | 0 |
maximum-erasure-value | Intentionally confusing and short: Tuples and one-letter variable names | intentionally-confusing-and-short-tuples-2h21 | csharp\npublic int MaximumUniqueSubarray(int[] a)\n{\n\tvar (h, m, s, f) = (new HashSet<int>(), 0, 0, 0);\n\tforeach(int n in a)\n\t{\n\t\twhile(!h.Add(n)) (_, | anikit | NORMAL | 2022-06-12T07:05:51.947808+00:00 | 2023-01-03T21:48:05.962148+00:00 | 205 | false | ```csharp\npublic int MaximumUniqueSubarray(int[] a)\n{\n\tvar (h, m, s, f) = (new HashSet<int>(), 0, 0, 0);\n\tforeach(int n in a)\n\t{\n\t\twhile(!h.Add(n)) (_, s, f) = (h.Remove(a[f]), s - a[f], f + 1);\n\t\t(s, m) = (s + n, Math.Max(m, s + n));\n\t}\n\treturn m;\n}\n```\n\nLegend:\n`a` - our input **a**rray\n`h` - **h**ashset, used to determine uniqueness of a number in the sliding subarray\n`m` - the current **m**aximum\n`s` - **s**um of elements in the sliding subarray\n`f` - index of the **f**irst element in the sliding subarray\n`n` - next **n**umber to add to the sliding subarray\n\nCan you make it even shorter and less readable? | 5 | 0 | ['C#'] | 0 |
maximum-erasure-value | C++ || Sliding window || map || 1695. Maximum Erasure Value | c-sliding-window-map-1695-maximum-erasur-k8bu | \t//\tInitially we will keep our i and j pointer at index 0 \n\t//\tkeep moving j and add the current no to sum and \n\t//\talso add the curr no to map \n\t//\t | anubhavsingh11 | NORMAL | 2022-06-12T05:35:43.792151+00:00 | 2022-06-12T05:35:43.792197+00:00 | 232 | false | \t//\tInitially we will keep our i and j pointer at index 0 \n\t//\tkeep moving j and add the current no to sum and \n\t//\talso add the curr no to map \n\t//\tat each step update the ans\n\t// whenever any element comes which is already in map\n\t// then start increasing i pointer and erase nums[i]\n\t// from map and also subtract it from sum\n\n\tclass Solution {\n\tpublic:\n\t\tint maximumUniqueSubarray(vector<int>& nums) {\n\t\t\tunordered_map<int,int>m;\n\t\t\tint sum=0,ans=0;\n\t\t\tint i=0,j=0,n=nums.size();\n\t\t\twhile(j<n)\n\t\t\t{\n\t\t\t\tsum+=nums[j];\n\t\t\t\twhile(m.find(nums[j])!=m.end())\n\t\t\t\t{\n\t\t\t\t\tsum-=nums[i];\n\t\t\t\t\tm.erase(nums[i]);\n\t\t\t\t\ti++;\n\t\t\t\t}\n\t\t\t\tm[nums[j]]++;\n\t\t\t\tans=max(ans,sum);\n\t\t\t\tj++;\n\t\t\t}\n\t\t\treturn ans;\n\t\t}\n\t}; | 5 | 0 | ['C', 'Sliding Window'] | 0 |
maximum-erasure-value | WEEB DOES PYTHON SLIDING WINDOW (BEATS 98.41%) | weeb-does-python-sliding-window-beats-98-y5ne | \n\n\tclass Solution:\n\t\tdef maximumUniqueSubarray(self, nums: List[int]) -> int:\n\t\t\tlow = 0\n\t\t\tvisited = set()\n\t\t\tresult = 0\n\t\t\tcurSum = 0\n\ | Skywalker5423 | NORMAL | 2021-12-25T03:04:40.724919+00:00 | 2021-12-25T03:04:40.724957+00:00 | 671 | false | \n\n\tclass Solution:\n\t\tdef maximumUniqueSubarray(self, nums: List[int]) -> int:\n\t\t\tlow = 0\n\t\t\tvisited = set()\n\t\t\tresult = 0\n\t\t\tcurSum = 0\n\t\t\tfor high in range(len(nums)):\n\t\t\t\twhile nums[high] in visited:\n\t\t\t\t\tvisited.remove(nums[low])\n\t\t\t\t\tcurSum -= nums[low]\n\t\t\t\t\tlow+=1\n\n\t\t\t\tvisited.add(nums[high])\n\t\t\t\tcurSum += nums[high]\n\n\t\t\t\tif curSum > result:\n\t\t\t\t\tresult = curSum\n\n\t\t\treturn result\n\nAlrights, its time to take a break fellow leetcoders\nWatch some anime instead, check out **\u7121\u8077\u8EE2\u751F \uFF5E\u7570\u4E16\u754C\u884C\u3063\u305F\u3089\u672C\u6C17\u3060\u3059\uFF5E (Mushoku Tensei: Jobless Reincarnation)**\n\n# Episodes: 23\n# Genres: Drama, Fantasy, Ecchi\n\nOne of the greatest isekai anime I\'ve watched, give it a go, its pretty good.\n | 5 | 0 | ['Two Pointers', 'Sliding Window', 'Ordered Set', 'Python', 'Python3'] | 2 |
maximum-erasure-value | C++ Sliding Window and Set | c-sliding-window-and-set-by-hmmonotone-hnxe | The idea here is to always have a subarray with no duplicate element. This is where set comes into picture to store the elements from i to j.\nThis will be more | hmmonotone | NORMAL | 2021-05-28T15:31:15.876718+00:00 | 2021-05-28T15:31:15.876762+00:00 | 273 | false | The idea here is to always have a subarray with no duplicate element. This is where `set` comes into picture to store the elements from `i` to `j`.\nThis will be more clear from the code:\n```\n int maximumUniqueSubarray(vector<int>& nums) {\n int sum=0,curr=0;\n unordered_set<int> s;\n int i=0,j=0,n=nums.size();\n while(i<n&&j<n){\n if(s.find(nums[j])==s.end()){\n curr+=nums[j];\n s.insert(nums[j++]);\n sum=max(sum,curr);\n }\n else{\n curr-=nums[i];\n s.erase(nums[i++]);\n }\n }\n return sum;\n }\n```\n | 5 | 0 | ['C', 'Sliding Window', 'Ordered Set'] | 0 |
maximum-erasure-value | Python O(N) solution, 6 lines, use dictionary | python-on-solution-6-lines-use-dictionar-nll4 | use a dictionary to keep the index of each number.\n\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n res, start, dic, sumDic = 0, 0, {}, | wing1001 | NORMAL | 2020-12-20T07:04:26.423481+00:00 | 2021-01-01T06:53:41.670812+00:00 | 441 | false | use a dictionary to keep the index of each number.\n```\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n res, start, dic, sumDic = 0, 0, {}, {-1:0} \n for i in range(len(nums)):\n sumDic[i] = sumDic[i-1] + nums[i]\n if nums[i] not in dic or dic[nums[i]] < start: \n res = max(res, sumDic[i]-sumDic[start-1])\n else: start = dic[nums[i]] + 1\n dic[nums[i]] = i\n return res \n``` | 5 | 3 | [] | 1 |
maximum-erasure-value | simple and easy C++ solution 😍❤️🔥 | simple-and-easy-c-solution-by-shishirrsi-flsl | \n\n# Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n | shishirRsiam | NORMAL | 2024-09-11T01:00:49.369350+00:00 | 2024-09-11T01:00:49.369373+00:00 | 211 | false | \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) \n {\n // Declare a map to keep track of the frequency of each number in the current subarray.\n unordered_map<int, int> mp;\n \n // Initialize variables to store the maximum sum of unique subarray, current sum, and two pointers.\n int maxValue = 0; // Maximum sum of unique subarray found so far.\n int sum = 0; // Current sum of the subarray.\n int i = 0; // Left pointer for the sliding window.\n int j = 0; // Right pointer for the sliding window.\n int n = nums.size(); // Size of the input array.\n\n // Iterate with the right pointer j through the entire array.\n while(j < n)\n {\n // Add the current number to the sum and increment its frequency in the map.\n sum += nums[j];\n mp[nums[j]]++;\n\n // If the frequency of the current number exceeds 1, we have duplicates.\n // We need to adjust the left pointer i to make the subarray unique.\n while(mp[nums[j]] > 1)\n {\n // Decrease the frequency of the number at the left pointer i and subtract its value from the sum.\n mp[nums[i]]--;\n sum -= nums[i++]; // Move the left pointer to the right.\n }\n\n // Update maxValue if the current sum is greater than the previously recorded maximum sum.\n maxValue = max(sum, maxValue);\n \n // Move the right pointer to the next position.\n j++;\n }\n\n // Return the maximum sum of the unique subarray found.\n return maxValue;\n }\n};\n```\n\n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook: www.fb.com/shishirrsiam\n | 4 | 0 | ['Array', 'Hash Table', 'Sliding Window', 'C++'] | 6 |
maximum-erasure-value | TIME & SPACE 99% BEATS || C++ || SLIDING WINDOW | time-space-99-beats-c-sliding-window-by-epqpt | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n vector<int> v(1e4+2);\n int i = 0, j = 0, n = nums.size(),sum = | yash___sharma_ | NORMAL | 2023-02-11T05:37:23.124914+00:00 | 2023-02-11T05:37:23.124945+00:00 | 488 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n vector<int> v(1e4+2);\n int i = 0, j = 0, n = nums.size(),sum = 0,ans = 0;\n while(i<n){\n sum += nums[i];\n v[nums[i]]++;\n while(v[nums[i]]==2){\n sum -= nums[j];\n v[nums[j]]--;\n j++;\n }\n i++;\n ans = max(ans,sum);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Two Pointers', 'C', 'Sliding Window', 'C++'] | 0 |
maximum-erasure-value | Go - Sliding window - O(n) with hashmap | go-sliding-window-on-with-hashmap-by-tua-866t | \nfunc maximumUniqueSubarray(nums []int) int {\n if len(nums) == 0 {return 0}\n if len(nums) == 1 {return nums[0]}\n \n res := -1 << 63\n \n m | tuanbieber | NORMAL | 2022-06-20T15:09:59.547408+00:00 | 2022-06-20T15:09:59.547455+00:00 | 133 | false | ```\nfunc maximumUniqueSubarray(nums []int) int {\n if len(nums) == 0 {return 0}\n if len(nums) == 1 {return nums[0]}\n \n res := -1 << 63\n \n m := make(map[int]int)\n m[nums[0]]++\n l, sum := 0, nums[0]\n \n for i := 1; i < len(nums); i++ {\n sum+= nums[i]\n m[nums[i]]++\n \n for m[nums[i]] > 1 {\n m[nums[l]]--\n sum -= nums[l]\n \n if m[nums[l]] == 0 {\n delete(m, nums[l])\n }\n \n l++\n }\n \n if sum > res {\n res = sum\n }\n }\n \n return res\n}\n``` | 4 | 0 | ['Go'] | 0 |
maximum-erasure-value | C++ Maps + Sum Based Two Pointers | c-maps-sum-based-two-pointers-by-82877ha-u8rd | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n // ekk map banaloooo\n \n // hum ekk map bana lengeeeee | 82877harsh | NORMAL | 2022-06-12T15:26:17.761162+00:00 | 2022-06-12T15:26:17.761199+00:00 | 283 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n // ekk map banaloooo\n \n // hum ekk map bana lengeeeee uske baad max lenge so jo sabse longest side ka map hogaaa wo le lengeeeeeeeee............\n map<int,int>harsh;\n int maxi=INT_MIN;\n int i=0,j=0;\n int sum=0;\n while(i<nums.size())\n {\n while(j<i && harsh[nums[i]] !=0 )\n {\n // ye hum shuru se substring ka size dekh rahe haiiiiii agar humko repetated element dikh raha haiii tohhh hum map se erase kardenge in short uske size ko 0 kardengeeeee\n harsh[nums[j]]=0;\n sum-=nums[j++];\n }\n // normal agar wo repeated nhi haiii bss usme add kardete haiiii substring ke side ko badhate jaooooo matlab sum add karlooooo\n if(harsh[nums[i]]==0)\n {\n harsh[nums[i]]=1;\n sum+=nums[i++];\n }\n maxi=max(maxi,sum);\n }\n return maxi;\n }\n};\n``` | 4 | 0 | ['C'] | 0 |
maximum-erasure-value | Simple, Easy and Faster O(n) solution | simple-easy-and-faster-on-solution-by-un-qbuj | class Solution {\npublic:\n\n int maximumUniqueSubarray(vector& nums) {\n unordered_map m;\n vector arr(vector(nums.size(),0));\n arr[0 | unraveler00 | NORMAL | 2022-06-12T14:32:48.278290+00:00 | 2022-06-12T14:32:48.278340+00:00 | 95 | false | class Solution {\npublic:\n\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int,int> m;\n vector<int> arr(vector<int>(nums.size(),0));\n arr[0] = nums[0];\n \n int max=0, prev=0,sum=0;\n for(int i=0; i<nums.size(); i++) {\n sum+=nums[i];\n if(i!=0) {\n arr[i] = nums[i]+arr[i-1];\n }\n\n if(m.find(nums[i])!=m.end() && m[nums[i]]>=prev) {\n sum = arr[i]-arr[m[nums[i]]];\n prev = m[nums[i]];\n }\n \n m[nums[i]] = i;\n if(sum>max) max=sum;\n }\n \n return max;\n }\n}; | 4 | 0 | ['Two Pointers', 'C', 'Sliding Window'] | 0 |
maximum-erasure-value | Java O(n) Sliding Window With HashSet With Photos and Explanation | java-on-sliding-window-with-hashset-with-hg3o | \n\n\n\n\n\n\n\n\n\n\n\n```\nclass Solution {\n \tpublic static int maximumUniqueSubarray(int[] nums) {\n\n // HashSet to check if the next value is un | mertpinarbasi | NORMAL | 2022-06-12T14:08:16.547549+00:00 | 2022-06-12T14:08:16.547571+00:00 | 764 | false | 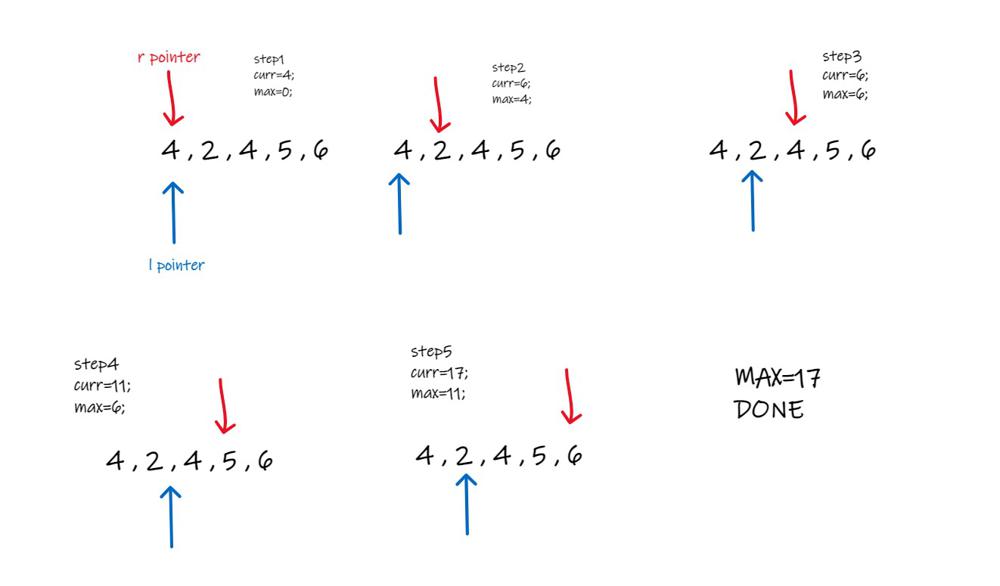\n\n\n\n\n\n\n\n\n\n\n\n```\nclass Solution {\n \tpublic static int maximumUniqueSubarray(int[] nums) {\n\n // HashSet to check if the next value is unique.\n\t\tSet<Integer> set = new HashSet<>();\n \n // maxSum for the maximum score that we can get \n\t\tint maxSum = 0;\n // currSum is used for the current sum of the iteration \n\t\tint currSum = 0;\n\n // We have two pointer left and right \n // r pointer will traverse the array and l will stay to indicate inital \n // value for our current case \n\t\tfor (int l = 0, r = 0; r < nums.length; r++) {\n // let\'s add our next value \n\t\t\tcurrSum += nums[r];\n // if the next element is already in the current set \n // we need to move our l pointer \n \t\t\tif (set.contains(nums[r])) {\n // delete the values until we have found the non-unique value \n\t\t\t\twhile (nums[l] != nums[r]) {\n\t\t\t\t\tcurrSum -= nums[l];\n\t\t\t\t\tset.remove(nums[l]);\n\t\t\t\t\tl++;\n\t\t\t\t}\n // now we have found the non-unique value in our current case \n // lets remove it both currSum and our set \n\t\t\t\tif (nums[l] == nums[r]) {\n\t\t\t\t\tcurrSum -= nums[l];\n\t\t\t\t\tset.remove(nums[l]);\n\t\t\t\t\tl++;\n\t\t\t\t}\n\t\t\t}\n // add current value to the set \n\t\t\tset.add(nums[r]);\n // compare the current case with previous cases to get maximum value .\n\t\t\tmaxSum = Math.max(currSum, maxSum);\n\n\t\t}\n\t\treturn maxSum;\n\t}\n} | 4 | 0 | ['Sliding Window', 'Java'] | 0 |
maximum-erasure-value | C++ || No Hashmap || Simple and easy solution | c-no-hashmap-simple-and-easy-solution-by-rfk4 | \n int maximumUniqueSubarray(vector<int>& nums) {\n vector<int> m(10001); // use this to store frequency as it is faster than map\n int | ashay028 | NORMAL | 2022-06-12T12:16:32.977912+00:00 | 2022-06-12T12:16:32.977946+00:00 | 70 | false | ```\n int maximumUniqueSubarray(vector<int>& nums) {\n vector<int> m(10001); // use this to store frequency as it is faster than map\n int n=nums.size(),ans=0,start=0,end=0,sum=0;\n while(end<n)\n {\n sum+=nums[end];\n m[nums[end]]++;\n while(m[nums[end]]>1) \n {\n sum-=nums[start];\n m[nums[start++]]--;\n }\n ans=max(ans,sum);\n end++;\n }\n return ans;\n }\n``` | 4 | 0 | ['Array', 'Two Pointers'] | 0 |
maximum-erasure-value | ✅C++ || Using Prefix Sum & MAP || 🗓️ Daily LeetCoding Challenge June, Day 12 | c-using-prefix-sum-map-daily-leetcoding-u1tka | Please Upvote If It Helps\n\n\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) \n {\n //finding subarray(with unique eleme | mayanksamadhiya12345 | NORMAL | 2022-06-12T06:11:43.144341+00:00 | 2022-06-12T06:11:43.144370+00:00 | 167 | false | **Please Upvote If It Helps**\n\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) \n {\n //finding subarray(with unique elements) with maximum score\n int score = -1;\n \n //storing index of the elements\n vector<int> map(1e4+1, -1); \n \n \n //make prefix sum to get score\n vector<int> prefixSum;\n int sum = 0;\n for(int it: nums)\n {\n sum+= it;\n prefixSum.push_back(sum);\n }\n \n //finding subarray(with unique elements) with maximum score\n int start = 0;\n for(int i=0; i<nums.size(); i++)\n {\n if(map[nums[i]] != -1)\n { \n //if element repeats in nums, update start\n start = max(start, map[nums[i]]+1);\n }\n \n map[nums[i]] = i; //update index in map\n \n //get max score\n int left = (start==0)? 0: prefixSum[start-1];\n \n score = max(score, prefixSum[i]- left); \n }\n \n return score;\n }\n};\n``` | 4 | 0 | [] | 0 |
maximum-erasure-value | C++ | 106ms[O(n)] & 89 MB[O(|a[i]|)] (100%/99.9%) | two - pointer | explanation | c-106mson-89-mboai-100999-two-pointer-ex-uzx2 | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n bool DP[10001]={};\n int ans=0,r=0,tmp=0;\n for(int i=0;i | SunGod1223 | NORMAL | 2022-06-12T01:54:16.320391+00:00 | 2022-06-15T03:17:02.649342+00:00 | 70 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n bool DP[10001]={};\n int ans=0,r=0,tmp=0;\n for(int i=0;i<nums.size();++i){\n while(r<nums.size()&&!DP[nums[r]]){\n DP[nums[r]]=1;\n tmp+=nums[r++];\n }\n ans=max(ans,tmp);\n if(r>=nums.size()-1)return ans;\n DP[nums[i]]=0;\n tmp-=nums[i];\n }\n return ans;\n }\n};\n```\n1.use boolean array to record nums.\n2.r means the right pointer ,iterating to the rightest point it can be.\n3.tmp means the sum for every i to ri ,ans = max(tmp_i).\n4.when r >= nums.size() - 1 ,the max answer has been found.\n5.left pointer is i. | 4 | 0 | ['Two Pointers', 'C'] | 0 |
maximum-erasure-value | [C++] 76ms, Fastest Solution to Date Explained, 100% Time, ~90% Space | c-76ms-fastest-solution-to-date-explaine-p6sh | This problem is clearly a sliding window problem, with the extra twist of a variable size of the window.\n\nTo solve it, we will need to build a running total o | ajna | NORMAL | 2021-05-29T01:02:19.350400+00:00 | 2021-05-29T01:16:42.714078+00:00 | 285 | false | This problem is clearly a sliding window problem, with the extra twist of a variable size of the window.\n\nTo solve it, we will need to build a running total of all the values in the input, minus the total up to the last repeated element we encountered.\n\nThis would call for a hashmap (or an `unordered_map` in C++), but since hashing does not come for free and not all contant times are equal, not to mention how expensive in terms of space a map might be, it turns out that even justs brutally creating an array of `10001` elements works just fine - faster even when you go to initialise all its cells once and even saves more memory than most implementations!\n\nTo do so we will need a few support variables:\n* `len` will store the length of the initial input;\n* `lastSeenAt` is an array of `10001` elements where we will store the position of were we last saw each value;\n* `sumUpTo` is where we store our ongoing sum;\n* `res` will store our best result so far and will be initialised to be `nums[0]`;\n* `lastRemoved` will store the position of the last element we removed the sum from (and thus be the beginning of our window).\n\nWe will then set all the values in `lastSeen` to be `-1`, and set the first slot in `sumUpto` and `lastSeenAt[nums[0]]` to be `nums[0]` and `0`, respectively, just to avoid an extra check in the upcoming loop where we will always refer to the previous value.\n\nTime then to loop with `i` from `1` to `len` (excluded) and:\n* assign the current value (`nums[i]`) to `n`;\n* compute the current cell of `sumUpTo` as the sum of the previous plus `n`;\n* update `lastRemoved` as the largest between its current value and the last position in which we saw `n` (`lastSeen[n]`);\n* update `res` as the maximum between its current value and the current running sum (`sumUpTo[i]`), minus the sum of all elements up to `lastRemoved`, provided we ever encountered a single duplicated value (`lastRemoved != -1`);\n* update `lastSeen[n]` to be the current position of `n`: `i`.\n\nOnce done, we can return `res` :)\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int len = nums.size(), lastSeenAt[10000 + 1], sumUpTo[len], res = nums[0], lastRemoved = -1;\n // preparing lastSeenAt\n fill_n(lastSeenAt, 10000 + 1, -1);\n // parsing the first value\n sumUpTo[0] = nums[0];\n lastSeenAt[nums[0]] = 0;\n // parsing all the other value\n for (int i = 1, n; i < len; i++) {\n n = nums[i];\n sumUpTo[i] = sumUpTo[i - 1] + n;\n lastRemoved = max(lastRemoved, lastSeenAt[n]);\n res = max(res, sumUpTo[i] - (lastRemoved != -1 ? sumUpTo[lastRemoved] : 0));\n lastSeenAt[n] = i;\n }\n return res;\n }\n};\n```\n\nThe brag:\n\n | 4 | 0 | ['C', 'C++'] | 0 |
maximum-erasure-value | Python, prefix sum O(N) | python-prefix-sum-on-by-warmr0bot-u97e | First calculate the prefix sum, then do a single pass recording last seen positions for each element. \nThese will serve as breaking points for the array.\n\nde | warmr0bot | NORMAL | 2020-12-20T04:20:44.724601+00:00 | 2020-12-20T04:20:44.724640+00:00 | 434 | false | First calculate the prefix sum, then do a single pass recording last seen positions for each element. \nThese will serve as breaking points for the array.\n```\ndef maximumUniqueSubarray(self, nums: List[int]) -> int:\n\tprefix = [0]\n\tfor i in range(len(nums)):\n\t\tprefix += [prefix[-1] + nums[i]]\n\n\tlastpos = {}\n\tmaxsum = 0\n\tleft = 0\n\tfor i, n in enumerate(nums):\n\t\tif n in lastpos:\n\t\t\tleft = max(left, lastpos[n])\n\t\tlastpos[n] = i+1\n\t\tmaxsum = max(maxsum, prefix[i+1] - prefix[left])\n\n\treturn maxsum\n``` | 4 | 0 | ['Prefix Sum', 'Python', 'Python3'] | 0 |
maximum-erasure-value | Sliding window & Two Pointers Pattern | sliding-window-two-pointers-pattern-by-d-dw28 | the sum of unique "subArray" elemets is added\n\n# Code\njava []\nimport java.util.HashMap;\n\nclass Solution {\n public int maximumUniqueSubarray(int[] nums | Dixon_N | NORMAL | 2024-05-20T02:32:40.975575+00:00 | 2024-05-20T15:14:30.526029+00:00 | 246 | false | the sum of unique "subArray" elemets is added\n\n# Code\n```java []\nimport java.util.HashMap;\n\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n HashMap<Integer, Integer> map = new HashMap<>();\n int left = 0, right = 0, sum = 0, maxSum = 0;\n\n while (right < nums.length) {\n sum += nums[right];\n map.put(nums[right], map.getOrDefault(nums[right], 0) + 1);\n\n while (map.get(nums[right]) > 1) {\n sum -= nums[left];\n map.put(nums[left], map.get(nums[left]) - 1);\n if (map.get(nums[left]) == 0) {\n map.remove(nums[left]);\n }\n left++;\n }\n\n maxSum = Math.max(maxSum, sum);\n right++;\n }\n\n return maxSum;\n }\n}\n\n``` | 3 | 0 | ['Java'] | 2 |
maximum-erasure-value | BEST SOLUTION -- 2 POINTERS -- EASIEST TO UNDERSTAND -- BEATS 98% | best-solution-2-pointers-easiest-to-unde-85eu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n Keep SLIDING the " | Skaezr73 | NORMAL | 2023-08-11T16:36:30.131610+00:00 | 2023-08-11T16:36:30.131638+00:00 | 78 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n Keep <b>SLIDING </> the "end" pointer in each iteration. slide the start pointer only when duplicate is found! \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def maximumUniqueSubarray(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n start=0\n end=0\n maxl=0\n cur=0\n dic={}\n while end<len(nums):\n if nums[end] not in dic:\n dic[nums[end]]=-1\n if dic[nums[end]]==-1:\n dic[nums[end]]=end #store index position!\n cur+=nums[end]\n elif dic[nums[end]]!=-1 :\n #repetition found\n if(cur>maxl):\n maxl=cur\n ist=start\n start=dic[nums[end]]+1\n for i in range(ist,dic[nums[end]]+1):\n\n cur-=nums[i]\n \n dic[nums[i]]=-1\n dic[nums[end]]=end\n cur+=nums[end]\n end+=1\n if cur>maxl:\n maxl=cur\n return maxl\n``` | 3 | 0 | ['Python'] | 1 |
maximum-erasure-value | Sliding Window , Easy C++ ✅✅ | sliding-window-easy-c-by-deepak_5910-fy5f | Approach\n Describe your approach to solving the problem. \nUse Sliding Window to find out the maximum Sum of the Subarray With Unique Elements.\n# Complexity\n | Deepak_5910 | NORMAL | 2023-07-10T13:47:03.783021+00:00 | 2023-07-10T13:47:03.783050+00:00 | 147 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nUse **Sliding Window** to find out the **maximum Sum** of the Subarray With **Unique Elements**.\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& arr) {\n int n = arr.size();\n unordered_map<int,int> freq;\n int sum = 0,i = 0,ans = 0,j = 0;\n while(j<n)\n {\n freq[arr[j]]++;\n sum+=arr[j];\n if(freq[arr[j]]>1)\n {\n while(i<j)\n {\n freq[arr[i]]--;\n sum-=arr[i];\n i++;\n if(arr[i-1]==arr[j]) break;\n }\n }\n ans = max(ans,sum);\n j++;\n }\n return ans; \n }\n};\n```\n\n | 3 | 0 | ['Sliding Window', 'C++'] | 0 |
maximum-erasure-value | [Java] Sliding window. O(n) Time. O(1) Space. Clean code with comments and dry run | java-sliding-window-on-time-o1-space-cle-qoc3 | Approach\nUse a sliding window, and keep moving left pointer to get rid of duplicate elements.\nHave a variable to store maxScore.\n\n// Time complexity: O(n) l | new_at_school | NORMAL | 2022-06-12T13:37:18.364482+00:00 | 2022-06-12T14:03:51.244876+00:00 | 309 | false | **Approach**\nUse a sliding window, and keep moving left pointer to get rid of duplicate elements.\nHave a variable to store maxScore.\n```\n// Time complexity: O(n) linear\n// Space complexity: O(1) constant - actually O(100_001)\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n int n = nums.length;\n int[] seen = new int[100_001]; \n \n int left = 0, right = 0;\n int maxScore = 0, currScore = 0;\n \n while (right < n) {\n seen[nums[right]]++;\n currScore += nums[right];\n // Keep moving left pointer until we get rid of duplicate element\n while (right < n && seen[nums[right]] > 1) {\n seen[nums[left]]--;\n currScore -= nums[left];\n left++;\n }\n // Save best score\n maxScore = Math.max(maxScore, currScore);\n right++;\n }\n return maxScore;\n }\n}\n```\n\n**Dry run**\n\n```\n\tnums: [4,2,4,5,6]\n Initially \n left = 0, right = 0, currScore = 0, maxScore = 0\n \n left = 0, right = 1, currScore = 4, maxScore = 4\n \n left = 0, right = 2, currScore = 6, maxScore = 6\n \n left = 1, right = 3, currScore = 6, maxScore = 6\n \n left = 1, right = 4, currScore = 11, maxScore = 11\n \n left = 1, right = 5, currScore = 17, maxScore = 17\n\treturn 17\n``` | 3 | 0 | ['Sliding Window'] | 0 |
maximum-erasure-value | Easy Python Solution | easy-python-solution-by-prernaarora221-r76w | ```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n s = set()\n sum1 = 0\n start = 0\n m = 0\n | prernaarora221 | NORMAL | 2022-06-12T13:35:21.414848+00:00 | 2022-06-12T13:35:21.414886+00:00 | 235 | false | ```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n s = set()\n sum1 = 0\n start = 0\n m = 0\n for i in range(len(nums)):\n while nums[i] in s:\n s.remove(nums[start])\n sum1 -= nums[start]\n start += 1\n s.add(nums[i])\n sum1 += nums[i]\n m = max(m,sum1)\n return m | 3 | 0 | ['Python'] | 0 |
maximum-erasure-value | talks are shit show me code | talks-are-shit-show-me-code-by-fr1nkenst-8kv6 | \nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n int s[]=new int[nums.length];\n s[0]=nums[0];\n for(int i=1;i<nums | fr1nkenstein | NORMAL | 2022-06-12T07:13:23.591821+00:00 | 2022-06-12T07:13:23.591871+00:00 | 101 | false | ```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n int s[]=new int[nums.length];\n s[0]=nums[0];\n for(int i=1;i<nums.length;i++)s[i]+=s[i-1]+nums[i];\n int p[]=new int[1000000];\n Arrays.fill(p,-1);\n int ans=0,b=0;\n for(int i=0;i<nums.length;i++){\n if(p[nums[i]]>=b){\n //System.out.println(i);\n b=p[nums[i]]+1;\n p[nums[i]]=i;\n ans=Math.max(ans,s[i]-s[b]+nums[b]);\n }\n else{\n p[nums[i]]=i;\n ans=Math.max(ans,s[i]-s[b]+nums[b]);\n }\n \n }\n return ans;\n }\n}``` | 3 | 1 | ['Two Pointers'] | 1 |
maximum-erasure-value | [Java] Sliding Window + HashMap | With Explanation | java-sliding-window-hashmap-with-explana-mdmh | the question is similar with 3. Longest Substring Without Repeating Characters\n\n\n### Intuition\nthe goal is to find the max sum subarray with unique elements | visonli | NORMAL | 2022-06-12T07:07:25.932492+00:00 | 2022-06-12T07:14:43.818024+00:00 | 365 | false | > the question is similar with [3. Longest Substring Without Repeating Characters](https://leetcode.com/problems/longest-substring-without-repeating-characters/)\n\n\n### Intuition\nthe goal is to find the max sum subarray with unique elements\nsince the elements are positive numbers, we can use sliding window approach\n\n### Steps\nlet `j`,` i` is the left, right boundary of sliding window\n1. increment `i` to include more elements, and update the sum & element count\n2. if the `element count > 1`, increment `j` and update the sum & element count, until `element count <= 1`\n3. update the result to `max(result, sum)`\n4. repeat step 1-3\n\n### Complexity\ntime: `O(n)`\nspace: `O(n)`\n### Java\n```java\npublic int maximumUniqueSubarray(int[] A) {\n int n = A.length;\n Map<Integer, Integer> map = new HashMap<>(); // element, count\n\n int j = 0, sum = 0, res = 0;\n for (int i = 0; i < n; i++) {\n map.put(A[i], map.getOrDefault(A[i], 0) + 1);\n sum += A[i];\n\n while (map.get(A[i]) > 1) {\n map.put(A[j], map.get(A[j]) - 1);\n sum -= A[j];\n j++;\n }\n res = Math.max(res, sum);\n }\n return res;\n}\n```\n | 3 | 0 | ['Java'] | 0 |
maximum-erasure-value | C++ | Two Pointer | Easy | c-two-pointer-easy-by-victor_knox-9umz | The idea is to have two pointers/sliding window which tracks the sum of the elements inside the window.\nHere\'s how the sliding window works: \n1. To keep trac | Victor_Knox | NORMAL | 2022-06-12T03:44:26.077641+00:00 | 2022-06-12T03:52:14.013470+00:00 | 515 | false | The idea is to have two pointers/sliding window which tracks the sum of the elements inside the window.\nHere\'s how the sliding window works: \n1. To keep track of your unique numbers, initialize a map. \n2. If you see a new number, add it to your window and sum and map(pretty simple).\n3. If you see a repeated number however, keep moving the start pointer until you reach the repeated number. \n4. dont forget to keep updating your max sum :)\n\nThis way your sliding window will always have unique elements.\n\ncode:\n```class Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int start = 0 , end = 0, n = nums.size(), ans = 0, sum = 0;\n \n map<int, int> mp;\n \n while(start < n && end < n){\n \n if(mp[nums[end]] == 0){\n mp[nums[end]] = 1;\n sum += nums[end];\n if(ans < sum){\n ans = sum;\n }\n end++;\n }else{\n sum -= nums[start];\n mp[nums[start]] = 0; \n start++;\n }\n \n }\n \n return ans;\n }\n};\n```\nPlease upvote if you found it useful :) | 3 | 0 | ['Two Pointers', 'C'] | 0 |
maximum-erasure-value | Python3 solution | set | faster than 88% | python3-solution-set-faster-than-88-by-f-n9fv | \'\'\'\nUpvote if you like it\n\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n msf = -9999 # max sum so far\n me | FlorinnC1 | NORMAL | 2021-08-02T13:03:15.998766+00:00 | 2021-08-02T13:04:24.915914+00:00 | 342 | false | \'\'\'\nUpvote if you like it\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n msf = -9999 # max sum so far\n meh = 0 # max sum ending here\n s = set()\n j = 0\n i = 0\n while j < len(nums):\n meh += nums[j]\n while nums[j] in s:\n meh -= nums[i]\n s.remove(nums[i])\n i += 1\n s.add(nums[j])\n if msf < meh:\n msf = meh\n j += 1\n return msf\n```\n\n\'\'\' | 3 | 0 | ['Ordered Set', 'Python', 'Python3'] | 1 |
maximum-erasure-value | Simple C++ Solution using hashset with comments | simple-c-solution-using-hashset-with-com-5i9c | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n // Creating hashset for quick access\n unordered_set<int> set;\n | amratyasaraswat | NORMAL | 2021-05-29T07:08:42.009684+00:00 | 2021-05-29T07:08:42.009724+00:00 | 131 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n // Creating hashset for quick access\n unordered_set<int> set;\n int n = nums.size();\n int i = 0, j = 0, sum = 0, ans =0;\n // Looping until we reach last elemenet\n while (i < n and j < n){\n // Check if we encountered unique element, if yes then increase sum and add to hashset\n if (set.find(nums[j]) == set.end()){\n set.insert(nums[j]);\n sum += nums[j]; \n ans = max(ans, sum);\n j++;\n }\n // If we found a duplicate element then decrement the sum and remove element\n else{\n set.erase(nums[i]);\n sum -= nums[i];\n i++; \n }\n }\n // Return max sum\n return ans;\n }\n};\n```\n\n**Please upvote the solution if this helps you understand better**\n\nThank you! | 3 | 0 | ['Sliding Window'] | 0 |
maximum-erasure-value | Classical Sliding Window problem. | classical-sliding-window-problem-by-sunn-bg1y | This is a classical problem where sliding window technique is used.\n\nSliding window is a technique in which we are interested in looking at a window of consec | sunnygupta | NORMAL | 2021-05-28T12:59:32.627992+00:00 | 2021-05-28T13:02:31.058023+00:00 | 54 | false | This is a classical problem where sliding window technique is used.\n\nSliding window is a technique in which we are interested in looking at a window of consecutive elements, for example:\nIf we have an array arr[]={ 1, 2, 3, 4, 5 }, then the sliding window between 2nd and 4th element would be: { 2, 3, 4 }.\n\nAnother important interview problem where sliding window is used is:\nhttps://leetcode.com/problems/longest-substring-without-repeating-characters/\n\nThese two problems are absolutely similar except for one there are characters and in one there are numbers.\n\nApproach:\n1. In this problem, we have to make sure that our sliding window contains unique numbers only.\n2. To Achieve this, we use a HashSet<> and a variable sum to store sum of unique elements of a particular sliding window and max to store the maximum sum of the sliding window having unique elements.\n3. Let i and j be starting and ending index of the sliding window.\n4. While j is less than length(nums), traverse the array, now there are only two possibilities:\n\t* \tIf set does not contain(nums[j]), it means that it is a new element to be added to the sliding window. Add this element to sliding window by adding it to sum and hash set and increase j by 1. Also, keep updating max.\n\t* \tElse if the set contains(nums[j]), then simply start removing the elements from the start of the sliding window until the set does not contain(nums[j]). Every time you remove an element from the start of sliding window, decrease the sum by nums[i], and decrement i by 1.\n5. Return max. \n\nSolution: JAVA\n```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n \n\t //Length of array\n int n=nums.length;\n\t\t\n\t\t//Sum of unique elements in a particular window\n int sum=0;\n int max=0;\n\t\t\n\t\t//Starting index of the sliding window\n int i=0;\n int j=0;\n Set<Integer> set=new HashSet<Integer>();\n while(j<n){\n if(!set.contains(nums[j])){\n set.add(nums[j]);\n sum+=nums[j];\n j++;\n if(max<sum){\n max=sum;\n }\n }\n else{\n set.remove(nums[i]);\n sum-=nums[i];\n i++;\n }\n }\n return max;\n }\n}\n```\nTime Complexity: O(n), Since the array is traversed only once.\nSpace Complexity: O(n), Since in the worst case all the numbers can be unique.\n\nThanks! Keep coding, keep learning!!! | 3 | 0 | [] | 1 |
maximum-erasure-value | C++ - two pointers, O(n) - faster than 93.5% time and 85% memory | c-two-pointers-on-faster-than-935-time-a-4kx2 | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int l = 0, r = 0, maxSum = 0, tempSum = 0;\n vector<int> occuren | abilda | NORMAL | 2021-05-28T11:32:13.407661+00:00 | 2021-05-28T11:33:28.352374+00:00 | 148 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int l = 0, r = 0, maxSum = 0, tempSum = 0;\n vector<int> occurences(1e4+1, 0);\n while (r < nums.size()) \n\t\t\tif (occurences[nums[r]] == 0) {\n occurences[nums[r]]++;\n tempSum += nums[r];\n maxSum = max(maxSum, tempSum);\n r++;\n } else {\n occurences[nums[l]]--;\n tempSum -= nums[l];\n l++;\n }\n return maxSum;\n }\n};\n```\n | 3 | 0 | ['C'] | 0 |
maximum-erasure-value | ✅ Maximum Erasure Value | Easy Sliding Window Solution | maximum-erasure-value-easy-sliding-windo-avoi | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int,int> mp;\n int i=0;\n int sum=0;\n | shivaye | NORMAL | 2021-05-28T07:41:50.559746+00:00 | 2021-05-28T07:41:50.559795+00:00 | 96 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int,int> mp;\n int i=0;\n int sum=0;\n int ans=0;\n for(int j=0;j<nums.size();j++)\n {\n sum+=nums[j];\n mp[nums[j]]++;\n while(mp[nums[j]]>1)\n {\n mp[nums[i]]--;\n sum-=nums[i];\n i++;\n }\n ans=max(sum,ans);\n \n }\n return ans;\n \n }\n};\n``` | 3 | 3 | ['C'] | 0 |
maximum-erasure-value | Sliding Window || O(N) || HashMap | sliding-window-on-hashmap-by-faltu_admi-yyac | \nclass Solution {\n public:\n int maximumUniqueSubarray(vector<int>& nums) {\n int n = nums.size(), l = 0, r = 0, sum = 0, maxSum = 0;\n uno | faltu_admi | NORMAL | 2021-05-28T07:26:04.651369+00:00 | 2021-05-28T07:26:04.651408+00:00 | 102 | false | ```\nclass Solution {\n public:\n int maximumUniqueSubarray(vector<int>& nums) {\n int n = nums.size(), l = 0, r = 0, sum = 0, maxSum = 0;\n unordered_map<int, int> seen;\n\n while (r < n) {\n if (seen.count(nums[r]) == 0) {\n seen[nums[l]]--;\n sum -= nums[l++];\n } else {\n seen[nums[r]]++;\n sum += nums[r++];\n maxSum = max(maxSum, sum);\n }\n }\n return maxSum;\n }\n};\n``` | 3 | 0 | [] | 0 |
maximum-erasure-value | Javascript | Sliding Window Solution w/ Explanation | 100% / 100% | javascript-sliding-window-solution-w-exp-qjg6 | In order to solve this in O(n) time, we can use a sliding window to evaluate all usable subarrays. For that, we\'ll need to use some data type to keep track of | sgallivan | NORMAL | 2020-12-24T20:24:41.771645+00:00 | 2020-12-24T20:24:41.771679+00:00 | 273 | false | In order to solve this in **O(n)** time, we can use a sliding window to evaluate all usable subarrays. For that, we\'ll need to use some data type to keep track of the numbers in our sliding window. \n\nNormally, I would use a **Map** to keep track of this information, but because we\'re using numbers as keys and because the constraint upon the numbers is so small at **1 <= N[i] <= 10e4**, it is more efficient to use an array. Also, since our array will only need to keep track of three possibilities (**0**, **1**, or **2**), we can use the more lightweight **Int8Array**. As an **Int8Array** is typed, when it is instantiated, it is automatically filled with **0**s.\n\nAs we iterate through **N**, we\'ll also need to keep track of the **sum** of the window and the **max** sum we\'ve seen. The main **for** loop will increase the right end index (**r**) of the window and at each number, we\'ll increase the counter of the current number in our array (**a**) and add its value to our **sum**.\n\nThen, if that number appears more than once in the window (**a[N[r]] > 1**), we\'ll drop numbers out of the sliding window by decreasing the counter for that number in **a**, subtracting its value from our **sum**, and increasing the left index (**l**) until we no longer have the duplicate.\n\nAfter that, we just check to see if we need to update **max**, and when we reach the end return it.\n```\n\nvar maximumUniqueSubarray = function(N) {\n let a = new Int8Array(10001), sum = max = 0, len = N.length\n for (let l = 0, r = 0; r < len; r++) {\n a[N[r]]++, sum += N[r]\n while (a[N[r]] > 1) a[N[l]]--, sum -= N[l++]\n max = sum > max ? sum : max\n }\n return max\n};\n``` | 3 | 0 | ['Sliding Window', 'JavaScript'] | 0 |
maximum-erasure-value | a few solutions | a-few-solutions-by-claytonjwong-kssj | LeetCode Daily: June 12th 2022\n\nUse a sliding window i..j inclusive tracking total t sum of uniquely seen values of the input array A to find and return the b | claytonjwong | NORMAL | 2020-12-20T04:10:46.321900+00:00 | 2022-06-12T16:37:53.530734+00:00 | 205 | false | **LeetCode Daily: June 12<sup>th</sup> 2022**\n\nUse a sliding window `i..j` inclusive tracking total `t` sum of uniquely `seen` values of the input array `A` to find and return the `best` total `t` sum.\n\n*Kotlin*\n```\nclass Solution {\n fun maximumUniqueSubarray(A: IntArray): Int {\n var best = 0\n var (N, i, j) = Triple(A.size, 0, 0)\n var (t, seen) = Pair(0, mutableSetOf<Int>())\n while (j < N) {\n while (seen.contains(A[j])) {\n t -= A[i]; seen.remove(A[i]); ++i\n }\n t += A[j]; seen.add(A[j]); ++j\n best = Math.max(best, t)\n }\n return best\n }\n}\n```\n\n*Javascript*\n```\nlet maximumUniqueSubarray = (A, best = 0) => {\n let [N, i, j] = [A.length, 0, 0];\n let [t, seen] = [0, new Set()];\n while (j < N) {\n while (seen.has(A[j]))\n t -= A[i], seen.delete(A[i]), ++i;\n t += A[j], seen.add(A[j]), ++j;\n best = Math.max(best, t);\n }\n return best;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def maximumUniqueSubarray(self, A: List[int], best = 0) -> int:\n N, i, j = len(A), 0, 0\n t, seen = 0, set()\n while j < N:\n while A[j] in seen:\n t -= A[i]; seen.remove(A[i]); i += 1\n t += A[j]; seen.add(A[j]); j += 1\n best = max(best, t)\n return best\n```\n\n*Rust*\n```\nuse std::cmp::max;\nuse std::collections::HashSet;\nimpl Solution {\n pub fn maximum_unique_subarray(A: Vec<i32>) -> i32 {\n let mut best = 0;\n let (N, mut i, mut j) = (A.len(), 0, 0);\n let (mut t, mut seen) = (0, HashSet::new());\n while j < N {\n while seen.contains(&A[j]) {\n t -= A[i]; seen.remove(&A[i]); i += 1;\n }\n t += A[j]; seen.insert(&A[j]); j += 1;\n best = max(best, t);\n }\n return best;\n }\n}\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using Set = unordered_set<int>;\n int maximumUniqueSubarray(VI& A, int best = 0) {\n auto [N, i, j] = make_tuple(A.size(), 0, 0);\n auto [t, seen] = make_pair(0, Set{});\n while (j < N) {\n while (seen.find(A[j]) != seen.end())\n t -= A[i], seen.erase(A[i]), ++i;\n t += A[j], seen.insert(A[j]), ++j;\n best = max(best, t);\n }\n return best;\n }\n};\n```\n\n---\n\n**Legacy Solutions from May 28, 2021:**\n\nUse a sliding window `i..j` to track the `best` total sum of unique adjacent values of the input array `A`.\n* We shrink the window to exclude each `i`<sup>th</sup> value of `A` to maintain the loop invarant, ie. the `total` sum for each window from `i..j` inclusive is comprised of uniquely `seen` values.\n* We expand the window to include each `j`<sup>th</sup> value of `A`.\n\n\n*Kotlin*\n```\nclass Solution {\n fun maximumUniqueSubarray(A: IntArray): Int {\n var best = 0\n var total = 0\n var seen = mutableSetOf<Int>()\n var N = A.size\n var i = 0\n var j = 0\n while (j < N) {\n if (seen.contains(A[j])) { // \uD83D\uDC49 shrink window to maintain loop invariant A[i..j] \uD83D\uDC40 uniquely seen\n total -= A[i]\n seen.remove(A[i++])\n } else { // \uD83D\uDC49 expand window\n total += A[j]\n seen.add(A[j++])\n }\n best = Math.max(best, total) // \uD83C\uDFAF best total A[i..j]\n }\n return best\n }\n}\n```\n\n*Javascript*\n```\nlet maximumUniqueSubarray = (A, seen = new Set(), total = 0, best = 0) => {\n let N = A.length,\n i = 0,\n j = 0;\n while (j < N) {\n if (seen.has(A[j])) // \uD83D\uDC49 shrink window to maintain loop invariant A[i..j] \uD83D\uDC40 uniquely seen\n total -= A[i],\n seen.delete(A[i++]);\n else // \uD83D\uDC49 expand window\n total += A[j], \n seen.add(A[j++]);\n best = Math.max(best, total); // \uD83C\uDFAF best total A[i..j]\n }\n return best;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def maximumUniqueSubarray(self, A: List[int], total = 0, best = 0) -> int:\n seen = set()\n N = len(A)\n i = 0\n j = 0\n while j < N:\n if A[j] in seen: # \uD83D\uDC49 shrink window to maintain loop invariant A[i..j] \uD83D\uDC40 uniquely seen\n total -= A[i]\n seen.remove(A[i])\n i += 1\n else: # \uD83D\uDC49 expand window\n total += A[j]\n seen.add(A[j])\n j += 1\n best = max(best, total) # \uD83C\uDFAF best total A[i..j]\n return best\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using Set = unordered_set<int>;\n int maximumUniqueSubarray(VI& A, Set seen = {}, int total = 0, int best = 0) {\n int N = A.size(),\n i = 0,\n j = 0;\n while (j < N) {\n if (seen.find(A[j]) != seen.end()) // \uD83D\uDC49 shrink window to maintain loop invariant A[i..j] \uD83D\uDC40 uniquely seen\n total -= A[i],\n seen.erase(A[i++]);\n else // \uD83D\uDC49 expand window\n total += A[j],\n seen.insert(A[j++]);\n best = max(best, total); // \uD83C\uDFAF best total A[i..j]\n }\n return best;\n }\n};\n``` | 3 | 0 | [] | 1 |
maximum-erasure-value | Kotlin - Typical Sliding Window Approach with a HashSet | kotlin-typical-sliding-window-approach-w-n4j5 | Solution - github\n\nProblem List\n#SlidingWindow - github\n#Subarray - github\n\n\n/**\n * @author: Leon\n * https://leetcode.com/problems/maximum-erasure-valu | idiotleon | NORMAL | 2020-12-20T04:10:18.047011+00:00 | 2022-07-06T01:43:30.045678+00:00 | 273 | false | Solution - [github](https://github.com/An7One/leetcode-solutions-kotlin-an7one/tree/main/src/main/kotlin/com/an7one/leetcode/lvl3/lc1695)\n\n<b>Problem List</b>\n#SlidingWindow - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/tree/main/txt/by_technique/n_pointers/by_pointer_amount/2_pointers/sliding_window)\n#Subarray - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/blob/main/txt/by_data_structure/array/by_data_structure/subarray.txt)\n\n```\n/**\n * @author: Leon\n * https://leetcode.com/problems/maximum-erasure-value/\n *\n * Time Complexity: O(`nNums`)\n * Space Complexity: O(`nNums`)\n */\nclass Solution {\n fun maximumUniqueSubarray(nums: IntArray): Int {\n val nNums = nums.size\n \n var lo = 0\n var hi = 0\n var largest = 0\n var sum = 0\n \n val seen = HashSet<Int>()\n \n while(hi < nNums){\n\t\t // to accumulate the running sum\n sum += nums[hi]\n\t\t\t\n // to narrow the sliding window,\n\t\t\t// once any previously visited element has been found,\n\t\t\t// till it has been removed in the current (sliding) window.\n while(seen.contains(nums[hi])){\n sum -= nums[lo]\n seen.remove(nums[lo])\n ++lo\n }\n \n\t\t\t// to mark the element as visited\n seen.add(nums[hi])\n \n\t\t\t// to keep track of the largest running sum ever showing up\n largest = maxOf(largest, sum)\n\t\t\t\n\t\t\t// to enlarge the window\n ++hi\n }\n \n return largest\n }\n}\n``` | 3 | 0 | ['Two Pointers', 'Sliding Window', 'Kotlin'] | 0 |
maximum-erasure-value | Typescript with hashmap + sliding window, O(n) time | typescript-with-hashmap-sliding-window-o-lnra | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | nhat_nguyen123 | NORMAL | 2024-09-22T04:51:32.688940+00:00 | 2024-09-22T04:51:32.688971+00:00 | 15 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```typescript []\nfunction maximumUniqueSubarray(nums: number[]): number {\n const map = new Map<number, number>()\n let sum = 0, max = 0, left = 0\n for (let i=0; i<nums.length; i++) {\n map.set(nums[i], (map.get(nums[i]) || 0) + 1)\n sum += nums[i]\n while (map.get(nums[i]) as number > 1) {\n map.set(nums[left], (map.get(nums[left]) as number) - 1)\n sum -= nums[left]\n left++\n }\n max = Math.max(max, sum)\n }\n return max\n};\n``` | 2 | 0 | ['TypeScript'] | 0 |
maximum-erasure-value | 100% beat sliding window concept | 100-beat-sliding-window-concept-by-somay-ykpz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | somaycoder | NORMAL | 2024-04-27T12:45:11.759641+00:00 | 2024-04-27T12:45:11.759670+00:00 | 177 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int, int> mp;\n int sum = 0;\n int maxi = 0;\n int start = 0; \n for (int i = 0; i < nums.size(); i++) {\n mp[nums[i]]++;\n sum = sum + nums[i];\n while (mp[nums[i]] > 1) {\n mp[nums[start]]--;\n sum = sum - nums[start];\n start++;\n }\n maxi = max(maxi, sum);\n }\n return maxi;\n }\n};\n\n``` | 2 | 0 | ['Array', 'Hash Table', 'Sliding Window', 'C++'] | 1 |
maximum-erasure-value | Two Pointers with HashSet Solution (with step by step explanationTwo) | two-pointers-with-hashset-solution-with-o91cy | Intuition\nWe will use two pointer approach with HashSet to solve this problem\n# Approach\nWe declare HashSet to check for unique in our window, then we iterat | alekseyvy | NORMAL | 2023-09-28T18:15:36.747108+00:00 | 2023-09-28T18:15:36.747138+00:00 | 54 | false | # Intuition\nWe will use two pointer approach with HashSet to solve this problem\n# Approach\nWe declare HashSet to check for unique in our window, then we iterate over nums array, and check if num at right pointer unique to our sub array that we collect in window set, if we found that it\'s not unique then we delete nums from window coming from left pointer, until our window agailn be unique, then we place num at right pointer into window and repeat, on each iteration we support sum of our window by incrementing if num is unique and decrement if not.\n# Complexity\n- Time complexity:\nO(n) -> we iterate with left and right pointers only once\n- Space complexity:\nO(n) -> we use HashSet to store our window\n# Code\n```\nfunction maximumUniqueSubarray(nums: number[]): number {\n // declare window HashSet\n const window = new Set<number>();\n // declare left pointer\n let left = 0;\n // declare max variable that will store result\n let max = 0;\n // declare count variable that will store current window sum\n let count = 0;\n // iterate over nums array:\n for(let right = 0; right < nums.length; right++) {\n // if number at right pointer are not unique to our window:\n while(window.has(nums[right])) {\n // we delete number on left pointer from set\n window.delete(nums[left])\n // we subtract num from window sum\n count -= nums[left]\n // we increment left pointer\n left++;\n }\n // if number unique we add it to our window set\n window.add(nums[right])\n // and add number to window sum\n count += nums[right];\n // check current sum and max and find bigger\n max = Math.max(max, count)\n }\n // return result\n return max\n};\n``` | 2 | 0 | ['Hash Table', 'Two Pointers', 'TypeScript'] | 1 |
maximum-erasure-value | PrefixSum Array + Sliding Window || Easy Solution | prefixsum-array-sliding-window-easy-solu-dwmg | Intuition\n Describe your first thoughts on how to solve this problem. \nPrefixSum Array + Sliding Window \n\n# Approach\n Describe your approach to solving t | ha_vi_ag- | NORMAL | 2023-01-05T07:03:22.960167+00:00 | 2023-01-05T07:05:51.045997+00:00 | 376 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPrefixSum Array + Sliding Window \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use the concept of prefix sum array to currect our current window sum in case of repeating element.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int: \n \n # ans --> final answer\n # cur --> current window sum\n # start --> current window starting position\n \n ans = cur = start = 0 \n d = {} # stores previous(latest) position of element\n\n for i,j in enumerate(nums):\n if i > 0: nums[i] += nums[i-1] # making prefixSum array \n cur += j \n if j in d and d[j] >= start: # if element is present already in our current window \n ind = d[j] \n cur = cur - (nums[ind] - nums[start-1] if start != 0 else nums[ind]) # correction in current window sum\n start = ind + 1 # current window starting position gets changed\n\n d[j] = i \n ans = max(ans,cur)\n\n return ans\n``` | 2 | 0 | ['Python3'] | 1 |
maximum-erasure-value | ✅ C++ ||Simple Solution || Hashmap || Sliding Window | c-simple-solution-hashmap-sliding-window-y49u | Also Try https://leetcode.com/problems/longest-substring-without-repeating-characters/ with same Approach\n\n\nclass Solution {\npublic:\n int maximumUnique | Yogesh02 | NORMAL | 2022-06-16T14:18:05.047437+00:00 | 2022-06-16T14:18:05.047478+00:00 | 165 | false | Also Try https://leetcode.com/problems/longest-substring-without-repeating-characters/ with same Approach\n\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int,int>mp;\n int maxi=0;\n int i=0;\n int j=0;\n int sum=0;\n while(j<nums.size()){\n sum+=nums[j];\n mp[nums[j]]++;\n if(mp.size()<j-i+1){\n while(mp.size()<j-i+1){\n mp[nums[i]]--;\n sum-=nums[i];\n if(mp[nums[i]]==0) mp.erase(nums[i]);\n i++;\n }\n }\n maxi=max(maxi,sum);\n j++; \n }\n return maxi;\n }\n};\n``` | 2 | 0 | ['C', 'Sliding Window', 'C++'] | 0 |
maximum-erasure-value | C++ || Maximum Erasure Value || O(n) | c-maximum-erasure-value-on-by-ronit-khat-0g34 | class Solution {\npublic:\n int maximumUniqueSubarray(vector& nums) {\n \n // Sliding Window Approach\n // Untill duplicate elements we keep o | Ronit-Khatri | NORMAL | 2022-06-16T11:20:52.182043+00:00 | 2022-06-16T11:20:52.182079+00:00 | 163 | false | class Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n \n // Sliding Window Approach\n // Untill duplicate elements we keep on adding and increase our window size\n // hash set -> to keep check for unique elements\n // ans -> storing the maximum sum till now\n // currSum -> storing current sum of the window\n \n unordered_set<int> hashset;\n \n int ans = 0;\n int currSum = 0;\n \n int i = 0;\n int j = 0;\n while(j < nums.size()){\n \n while(hashset.find(nums[j]) != hashset.end()){ // if element present -> remove it\n hashset.erase(nums[i]);\n currSum -= nums[i];\n i++;\n }\n \n hashset.insert(nums[j]); // if element not present -> add it\n currSum += nums[j];\n j++;\n \n ans = max(ans, currSum); \n }\n \n return ans;\n }\n}; | 2 | 0 | ['Array', 'Two Pointers', 'C', 'Sliding Window'] | 0 |
maximum-erasure-value | javascript O(n) | javascript-on-by-apb10016-f6ce | \n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maximumUniqueSubarray = function(nums) {\n const n = nums.length;\n \n const store = ne | apb10016 | NORMAL | 2022-06-13T03:26:44.593253+00:00 | 2022-06-13T03:26:44.593290+00:00 | 132 | false | ```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maximumUniqueSubarray = function(nums) {\n const n = nums.length;\n \n const store = new Set();\n \n let max = 0,\n left = 0,\n sum = 0;\n \n for(let i = 0; i < n; i++) {\n while(store.has(nums[i])) {\n store.delete(nums[left]);\n sum -= nums[left];\n left += 1;\n }\n sum += nums[i];\n store.add(nums[i]);\n max = Math.max(max, sum);\n }\n return max;\n};\n``` | 2 | 0 | ['Sliding Window', 'JavaScript'] | 1 |
maximum-erasure-value | C++ Solution (Variable Sliding Window) | c-solution-variable-sliding-window-by-sh-ncdx | Solution-->\n\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n// Tried acquire ->store and release\n unordered_ma | shubhaamtiwary_01 | NORMAL | 2022-06-12T20:40:40.683025+00:00 | 2022-06-12T20:40:40.683073+00:00 | 51 | false | Solution-->\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n// Tried acquire ->store and release\n unordered_map<int,int> map;\n int i=0;\n int j=0;\n int ans=0;\n int sum=0;\n int count=0;\n while(j<nums.size()){\n// Release\n map[nums[j]]++;\n count++;\n while(count>map.size()){\n map[nums[i]]--;\n sum=sum-nums[i];\n if(map[nums[i]]==0){\n map.erase(nums[i]);\n }\n i++;\n count--;\n }\n\t\t\t//Acquire\n sum=sum+nums[j];\n j++;\n ans=max(ans,sum);\n \n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C', 'Sliding Window'] | 0 |
maximum-erasure-value | Rust - Sliding Window | rust-sliding-window-by-idiotleon-rox4 | Solution - github\n\nProblem List\n#SlidingWindow - github\n#Subarray - github\n\n\nuse std::collections::HashSet;\n/// @author: Leon\n/// https://leetcode.com/ | idiotleon | NORMAL | 2022-06-12T18:49:39.121804+00:00 | 2022-06-12T19:47:25.386280+00:00 | 69 | false | Solution - [github](https://github.com/An7One/lc_soln_rust_leon/tree/main/src/leetcode/lvl2/lc1695)\n\n<b>Problem List</b>\n#SlidingWindow - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/tree/main/txt/by_technique/n_pointers/by_pointer_amount/2_pointers/sliding_window)\n#Subarray - [github](https://github.com/An7One/leetcode-problems-by-tag-an7one/blob/main/txt/by_data_structure/array/by_data_structure/subarray.txt)\n\n```\nuse std::collections::HashSet;\n/// @author: Leon\n/// https://leetcode.com/problems/maximum-erasure-value/\n/// Time Complexity: O(`len_n`)\n/// Space Complexity: O(`len_n`)\n/// Reference:\n/// https://leetcode.com/problems/maximum-erasure-value/discuss/978552/Java-O(n)-Sliding-Window-%2B-HashSet\nimpl Solution {\n pub fn maximum_unique_subarray(nums: Vec<i32>) -> i32 {\n let len_n: usize = nums.len();\n let mut seen: HashSet<i32> = HashSet::new();\n let mut lo: usize = 0;\n let mut hi: usize = 0;\n let mut sum: i32 = 0;\n let mut most: i32 = 0;\n while hi < len_n{\n if seen.insert(nums[hi]){\n sum += nums[hi];\n most = std::cmp::max(most, sum);\n hi += 1;\n }else{\n sum -= nums[lo];\n seen.remove(&nums[lo]);\n lo += 1;\n }\n }\n most\n }\n}\n```\n\n```\nuse std::collections::HashSet;\n/// @author: Leon\n/// https://leetcode.com/problems/maximum-erasure-value/\n/// Time Complexity: O(`len_n`)\n/// Space Complexity: O(`len_n`)\nimpl Solution {\n pub fn maximum_unique_subarray(nums: Vec<i32>) -> i32 {\n let len_n: usize = nums.len();\n let mut seen: HashSet<i32> = HashSet::new();\n let mut lo: usize = 0;\n let mut most: i32 = 0;\n let mut sum: i32 = 0;\n for hi in 0..len_n {\n sum += nums[hi];\n while lo < hi && seen.contains(&nums[hi]) {\n sum -= nums[lo];\n seen.remove(&nums[lo]);\n lo += 1;\n }\n seen.insert(nums[hi]);\n most = std::cmp::max(most, sum);\n }\n most\n }\n}\n```\n\n```\n/// @author: Leon\n/// https://leetcode.com/problems/maximum-erasure-value/\n/// Time Complexity: O(`len_n`)\n/// Space Complexity: O(`RANGE`)\nimpl Solution {\n pub fn maximum_unique_subarray(nums: Vec<i32>) -> i32 {\n const RANGE: usize = 10e4 as usize + 7;\n let len_n: usize = nums.len();\n let mut freqs: Vec<u16> = vec![0; RANGE];\n let mut lo: usize = 0;\n let mut most: i32 = 0;\n let mut sum: i32 = 0;\n for hi in 0..len_n {\n sum += nums[hi];\n freqs[nums[hi] as usize] += 1;\n while lo < hi && freqs[nums[hi] as usize] > 1 {\n sum -= nums[lo];\n freqs[nums[lo] as usize] -= 1;\n lo += 1;\n }\n most = std::cmp::max(most, sum);\n }\n most\n }\n}\n```\n\n```\nuse std::collections::HashMap;\n/// @author: Leon\n/// https://leetcode.com/problems/maximum-erasure-value/\n/// Time Complexity: O(`len_n`)\n/// Space Complexity: O(`len_n`)\nimpl Solution {\n pub fn maximum_unique_subarray(nums: Vec<i32>) -> i32 {\n let len_n: usize = nums.len();\n let mut num_to_freq: HashMap<i32, u16> = HashMap::new();\n let mut lo: usize = 0;\n let mut most: i32 = 0;\n let mut sum: i32 = 0;\n for hi in 0..len_n {\n sum += nums[hi];\n *num_to_freq.entry(nums[hi]).or_default() += 1;\n while lo < hi && *num_to_freq.get(&nums[hi]).unwrap() > 1 {\n sum -= nums[lo];\n *num_to_freq.entry(nums[lo]).or_default() -= 1;\n lo += 1;\n }\n most = std::cmp::max(most, sum);\n }\n most\n }\n}\n```\n\n```\nuse std::collections::HashSet;\n/// @author: Leon\n/// https://leetcode.com/problems/maximum-erasure-value/\n/// Time Complexity: O(`len_n`)\n/// Space Complexity: O(`len_n`)\nimpl Solution {\n pub fn maximum_unique_subarray(nums: Vec<i32>) -> i32 {\n let len_n: usize = nums.len();\n let mut seen: HashSet<i32> = HashSet::new();\n let mut lo: usize = 0;\n let mut hi: usize = 0;\n let mut most: i32 = 0;\n let mut sum: i32 = 0;\n while hi < len_n {\n while hi < len_n && seen.insert(nums[hi]) {\n sum += nums[hi];\n hi += 1;\n }\n most = std::cmp::max(most, sum);\n while hi < len_n && lo < hi && seen.contains(&nums[hi]) {\n seen.remove(&nums[lo]);\n sum -= nums[lo];\n lo += 1;\n }\n if hi < len_n{\n sum += nums[hi];\n seen.insert(nums[hi]);\n }\n hi += 1;\n }\n most\n }\n}\n``` | 2 | 0 | ['Sliding Window', 'Rust'] | 0 |
maximum-erasure-value | This problem is same as Longest Substring Without Repeating Characters (Leetcode Problem No 3) | this-problem-is-same-as-longest-substrin-fi6e | ```\n int maximumUniqueSubarray(vector& nums) {\n int i=0;\n int j=0;\n int sum=0;\n int ans = INT_MIN;\n map mp;\n wh | noErrors | NORMAL | 2022-06-12T17:07:30.299388+00:00 | 2022-06-12T17:07:30.299432+00:00 | 73 | false | ```\n int maximumUniqueSubarray(vector<int>& nums) {\n int i=0;\n int j=0;\n int sum=0;\n int ans = INT_MIN;\n map<int,int> mp;\n while(j<nums.size())\n {\n mp[nums[j]]++;\n sum+=nums[j];\n \n if(mp.size()==j-i+1)\n {\n ans=max(ans,sum);\n j++;\n }\n \n else if(mp.size()<j-i+1)\n {\n while(mp.size()<j-i+1)\n {\n sum-=nums[i];\n mp[nums[i]]--;\n if(mp[nums[i]]==0)\n mp.erase(nums[i]);\n i++;\n }\n j++;\n }\n \n }\n \n return ans;\n } | 2 | 0 | ['C', 'Sliding Window'] | 0 |
maximum-erasure-value | Simple two pointers code ,[O(n) time and memory complexity ] | simple-two-pointers-code-on-time-and-mem-n66w | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int frq[10005]={0};\n int l=0,r=0,mx=0,cur_sum=0;\n while | ma7moud7amdy | NORMAL | 2022-06-12T15:41:56.060900+00:00 | 2022-06-12T15:41:56.060943+00:00 | 28 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int frq[10005]={0};\n int l=0,r=0,mx=0,cur_sum=0;\n while(l<nums.size()){\n while(r<nums.size()&&!frq[nums[r]]){\n cur_sum+=nums[r];\n ++frq[nums[r++]];\n }\n mx=max(mx,cur_sum);\n cur_sum-=nums[l];\n --frq[nums[l++]];\n }\n return mx;\n }\n};\n``` | 2 | 0 | ['Two Pointers'] | 0 |
maximum-erasure-value | Simple java solution | simple-java-solution-by-siddhant_1602-v7l1 | ```\nclass Solution {\n public int maximumUniqueSubarray(int[] n) {\n int i=0,j=0,s=0,p=0,k=n.length;\n Set nm=new HashSet<>();\n while( | Siddhant_1602 | NORMAL | 2022-06-12T14:54:17.492273+00:00 | 2022-06-12T15:02:01.847968+00:00 | 553 | false | ```\nclass Solution {\n public int maximumUniqueSubarray(int[] n) {\n int i=0,j=0,s=0,p=0,k=n.length;\n Set<Integer> nm=new HashSet<>();\n while(i<k&&j<k)\n {\n if(!nm.contains(n[j]))\n {\n s+=n[j];\n p=Math.max(p,s);\n nm.add(n[j++]);\n }\n else\n {\n s-=n[i];\n nm.remove(n[i++]);\n }\n }\n return p;\n }\n} | 2 | 0 | ['Sliding Window', 'Java'] | 0 |
maximum-erasure-value | ✔ C++ ‖ Sliding Window Solution | c-sliding-window-solution-by-_aditya_heg-xixf | Intuition:-\n->We have to find distinct subarray with largest sum\n-> Since we have to find largest sum distinct subarray, I have used unordered map to get uniq | _Aditya_Hegde_ | NORMAL | 2022-06-12T14:12:42.442348+00:00 | 2022-06-12T16:35:46.276193+00:00 | 193 | false | **Intuition:-**\n**->We have to find distinct subarray with largest sum**\n**->** Since we have to find largest sum distinct subarray, I have used unordered map to get unique elements.\n**->** Initially map will be empty and whenever we are traversing we go on adding elements.\n**->** Whenever we find by adding next value subarray will not be distinct,we go on removing the elements from beginning of our subarray.\n**->** We use currsum and maxsum variables to store current window sum and overall max sum.\n**->** For each element\'s insertion we will be calculating maxsum and currsum.\n\n**Complexity:-**\n**Time=O(N)** due to one traversal\n**Space=O(N)** due to additional map.\n\nHoping you understood the solution :)\nPlease upvote if you found it usefull !\nThank you..\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& a) {\n\t\tint n=a.size();\n unordered_map<int,int> mp;\n int mxScore=0,currScore=0;\n int j=0;\n for(int i=0;i<n;i++){\n mp[a[i]]++;\n while(mp[a[i]]>1){\n mp[a[j]]--;\n currScore-=a[j];\n j++;\n }\n currScore+=a[i];\n mxScore=max(mxScore,currScore);\n }\n return mxScore;\n }\n};\n``` | 2 | 0 | ['C', 'Sliding Window', 'C++'] | 1 |
maximum-erasure-value | Java/JavaScript/Python Beginner friendly Solutions | javajavascriptpython-beginner-friendly-s-mvs3 | Java\n\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n Set<Integer> set = new HashSet<>();\n int i = 0, j = 0, sum = 0, ma | HimanshuBhoir | NORMAL | 2022-06-12T13:57:32.107960+00:00 | 2022-06-12T13:57:32.108004+00:00 | 322 | false | **Java**\n```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n Set<Integer> set = new HashSet<>();\n int i = 0, j = 0, sum = 0, max = 0;\n while(i < nums.length && j < nums.length){\n if(!set.contains(nums[j])){\n set.add(nums[j]);\n sum += nums[j++];\n max = Math.max(sum, max);\n } else{\n set.remove(nums[i]);\n sum -= nums[i++];\n }\n }\n return max;\n }\n}\n```\n**JavaScript**\n```\nvar maximumUniqueSubarray = function(nums) {\n let set = new Set()\n let i = 0, j = 0, sum = 0, max = 0\n while(i < nums.length && j < nums.length){\n if(!set.has(nums[j])){\n set.add(nums[j])\n sum += nums[j++]\n max = Math.max(sum, max)\n } else{\n set.delete(nums[i])\n sum -= nums[i++]\n }\n }\n return max\n};\n```\n**Python**\n```\nclass Solution(object):\n def maximumUniqueSubarray(self, nums):\n s = set()\n i, j, summ, maxx = 0, 0, 0, 0\n while i < len(nums) and j < len(nums) :\n if not nums[j] in s:\n s.add(nums[j])\n summ += nums[j]\n maxx = max(summ, maxx)\n j += 1\n else :\n s.remove(nums[i])\n summ -= nums[i]\n i += 1\n return maxx\n``` | 2 | 0 | ['Python', 'Java', 'JavaScript'] | 0 |
maximum-erasure-value | Observation: This ques is same as Longest substring without repeating characters! | observation-this-ques-is-same-as-longest-2tay | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int l=0, r=0, n = nums.size();\n \n unordered_set<int> s; | arpithiside | NORMAL | 2022-06-12T10:06:42.098870+00:00 | 2022-06-12T10:06:42.098917+00:00 | 61 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n int l=0, r=0, n = nums.size();\n \n unordered_set<int> s;\n int sum=0, res=0;\n \n while(r<n) {\n if(s.count(nums[r]) == 0) {\n sum += nums[r];\n res = max(res, sum);\n s.insert(nums[r]);\n r++;\n } \n \n else {\n s.erase(nums[l]);\n sum=sum-nums[l];\n l++;\n }\n }\n \n return res;\n }\n};\n``` | 2 | 0 | ['Sliding Window'] | 0 |
maximum-erasure-value | O(n) CPP Easy Solution | on-cpp-easy-solution-by-abhishek23a-sp9y | ```\n\nint maximumUniqueSubarray(vector& nums) {\n unordered_setst;\n int n=nums.size();\n vectorprefix_sum(n);\n prefix_sum[0]=nums | abhishek23a | NORMAL | 2022-06-12T10:04:13.458793+00:00 | 2022-06-12T10:04:13.458842+00:00 | 40 | false | ```\n\nint maximumUniqueSubarray(vector<int>& nums) {\n unordered_set<int>st;\n int n=nums.size();\n vector<int>prefix_sum(n);\n prefix_sum[0]=nums[0];\n for(int i=1;i<n;i++){\n prefix_sum[i]=prefix_sum[i-1]+nums[i];\n }\n int i=0, max_sum=0;\n for(int j=0;j<n;j++){\n while(st.find(nums[j])!=st.end()){\n st.erase(nums[i]);\n i++;\n }\n st.insert(nums[j]);\n if(i==0)\n max_sum=max(max_sum, prefix_sum[j]);\n else\n max_sum=max(max_sum, prefix_sum[j]-prefix_sum[i-1]);\n \n }\n return max_sum;\n \n } | 2 | 0 | ['Prefix Sum'] | 0 |
maximum-erasure-value | C++ | O(N) | Two pointers & Hash-Set | c-on-two-pointers-hash-set-by-raiaankur1-z6ps | \n\n\nint maximumUniqueSubarray(vector<int>& nums) {\n int ret=0, sum=0, i=0, n=nums.size();\n vector<bool> found(10001,false);\n for(int j | raiaankur1 | NORMAL | 2022-06-12T09:43:14.293017+00:00 | 2022-06-12T09:43:14.293062+00:00 | 35 | false | \n\n```\nint maximumUniqueSubarray(vector<int>& nums) {\n int ret=0, sum=0, i=0, n=nums.size();\n vector<bool> found(10001,false);\n for(int j=0; j<n; j++){\n sum += nums[j];\n if(!found[nums[j]]){\n found[nums[j]] = true;\n }\n else {\n while(nums[i]!=nums[j]){\n sum -= nums[i];\n found[nums[i++]] = false;\n }\n sum-=nums[i];\n i++;\n }\n ret = max(ret, sum);\n }\n return ret;\n }\n``` | 2 | 1 | ['Two Pointers'] | 0 |
maximum-erasure-value | C++ | O(n) | 98.7% faster | Easy to understand | Clean code | c-on-987-faster-easy-to-understand-clean-8156 | Just maintain sum of all the elements between start and end of the subArray - 2 pointers Approach\n\nclass Solution {\npublic:\n\n int getMax(vector &nums){\ | VAIBHAV_SHORAN | NORMAL | 2022-06-12T08:04:30.060127+00:00 | 2022-06-12T08:17:35.405394+00:00 | 102 | false | **Just maintain sum of all the elements between start and end of the subArray - 2 pointers Approach**\n\nclass Solution {\npublic:\n\n int getMax(vector<int> &nums){\n int maxi = nums[0];\n for(int i=1; i<nums.size(); i++){\n if(nums[i] > maxi){\n maxi = nums[i];\n }\n }\n return maxi;\n }\n\n int maximumUniqueSubarray(vector<int>& nums) {\n int start = 0;\n int sum = 0;\n int ans = INT_MIN;\n\n int maxi = getMax(nums);\n vector<int> store(maxi+1, -1);\n\n for(int i=0; i<nums.size(); i++){\n int temp = nums[i];\n\n if(store[temp] != -1){\n ans = max(ans, sum);\n\n int index = store[temp];\n while(start <= index){\n sum = sum - nums[start];\n store[nums[start]] = -1;\n start++;\n }\n }\n\n sum += temp;\n store[temp] = i;\n }\n\n ans = max(ans, sum);\n return ans;\n \n bool like;\n if(like){\n cout << "Hit_upVote" << endl;\n }\n }\n}; | 2 | 0 | [] | 0 |
maximum-erasure-value | Java Solution || Faster than 96% | java-solution-faster-than-96-by-samarth-q3mqf | \nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n int res=0, sum=0;\n boolean[] seen = new boolean[10001];\n for (in | Samarth-Khatri | NORMAL | 2022-06-12T08:03:32.480663+00:00 | 2022-06-12T08:03:32.480705+00:00 | 37 | false | ```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n int res=0, sum=0;\n boolean[] seen = new boolean[10001];\n for (int i=0,j=0;i<nums.length;++i){\n while(seen[nums[i]]){\n seen[nums[j]] = false;\n sum -= nums[j++];\n }\n seen[nums[i]] = true;\n sum += nums[i];\n res = Math.max(sum,res);\n }\n return res;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
maximum-erasure-value | C# Solution | HashSet | Sliding Window | O(N) | c-solution-hashset-sliding-window-on-by-px0lt | \npublic int MaximumUniqueSubarray(int[] nums) {\n int start = 0;\n int end = 0;\n int maxScore = 0;\n int score = 0;\n var h | anshulgarg904 | NORMAL | 2022-06-12T06:41:28.443354+00:00 | 2022-06-12T06:42:20.032997+00:00 | 100 | false | ```\npublic int MaximumUniqueSubarray(int[] nums) {\n int start = 0;\n int end = 0;\n int maxScore = 0;\n int score = 0;\n var hashSet = new HashSet<int>();\n \n while(end < nums.Length){\n if(hashSet.Contains(nums[end])){\n score = score-nums[start];\n hashSet.Remove(nums[start++]);\n }\n else{\n score += nums[end];\n hashSet.Add(nums[end++]);\n }\n \n maxScore = Math.Max(maxScore, score);\n }\n \n return maxScore;\n }\n```\n\nPlease upvote if you like the solution.\n\nImprovements/Suggestions are most welcome.\n\nHappy Coding :) | 2 | 0 | ['C', 'Sliding Window', 'C#'] | 0 |
maximum-erasure-value | EASY AND UNDERSTANDABLE C++ CODE | easy-and-understandable-c-code-by-nayang-dyk5 | \nclass Solution {\npublic:\n int lengthOfLongestSubarray(vector<int>& s) \n {\n int i = 0, j = 0;\n int sum=0;\n int maxsum = 0; | nayangupta143 | NORMAL | 2022-06-12T06:41:18.144422+00:00 | 2022-06-12T06:41:18.144482+00:00 | 271 | false | ```\nclass Solution {\npublic:\n int lengthOfLongestSubarray(vector<int>& s) \n {\n int i = 0, j = 0;\n int sum=0;\n int maxsum = 0; \n unordered_map<int,int> mp;\n \n while(j < s.size())\n {\t\n mp[s[j]]++;\n sum=sum+s[j];\n \n if(mp.size() == j-i+1)\n {\n maxsum = max(maxsum,sum);\n }\n else if(mp.size()< j-i+1)\n {\n while(mp.size() < j-i+1)\n {\n mp[s[i]]--;\n sum= sum-s[i];\n if(mp[s[i]] == 0)\n {\n mp.erase(s[i]);\n }\n i++;\n }\n }\n \n j++;\n }\n\n return maxsum;\n \n } \n int maximumUniqueSubarray(vector<int>& nums) {\n \n return lengthOfLongestSubarray(nums);\n }\n};\n``` | 2 | 0 | ['C', 'Sliding Window'] | 0 |
maximum-erasure-value | Maximum Erasure Value - ✅C++ | Python | O(N) | Easy Solution | maximum-erasure-value-c-python-on-easy-s-xc8d | Maximum Erasure Value\nThis problem is very much similar to Longest Substring Without Repeating Characters. \nI recommend to solve this problem before trying Ma | harish2503 | NORMAL | 2022-06-12T06:38:00.880722+00:00 | 2022-07-06T04:42:37.942084+00:00 | 345 | false | # Maximum Erasure Value\nThis problem is very much similar to Longest Substring Without Repeating Characters. \nI recommend to solve this problem before trying Maximum Erasure Value - https://leetcode.com/problems/longest-substring-without-repeating-characters \n\n**Example:**\n**nums = [4,2,4,5,6]**\nThe output should be maximum subarray with unique elements present in it.\n\n* We take additional space as hashset and use the concept of sliding window.\n* For the sliding window technique, we take two pointers as l(left) and r(right).\n* We use cur to track the current sum in the current window.\n* When there is an duplicate, we move the l untill the current window has no duplicate and at the same time we remove the nums[l] in the hashset.\n* We keep updating the result by taking maximum of result and current sum.\n\nFor the above example,\n1. set={4} maximum =4\n2. set={4,2} maximum= 6\n3. set= {2,4} maximum=6\n4. set={2,4,5} maximum=11\n5. set={2,4,5,6} maximum=17\n\n***So, the output is 17***\n \n**C++ Code**\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_set<int> s;\n int cur = 0, res = 0, l = 0;\n for (int r=0;r<nums.size();r++) {\n while (s.find(nums[r]) != s.end()) {\n cur=cur-nums[l];\n s.erase(nums[l]);\n l=l+1;\n }\n cur=cur+nums[r];\n s.insert(nums[r]);\n res = max(res, cur);\n }\n return res; \n }\n};\n```\n\n**Python Code**\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n res=0\n cur=0\n s=set()\n l=0\n for r in range(len(nums)):\n while nums[r] in s:\n s.remove(nums[l])\n cur=cur-nums[l]\n l=l+1\n s.add(nums[r])\n cur=cur+nums[r]\n res=max(res,cur)\n return res\n```\n\n**Time Complexity - O(N)**\n**Space Complexity - O(N)**\n\n\n\n\n\n | 2 | 0 | ['C', 'Sliding Window', 'Python', 'C++'] | 1 |
maximum-erasure-value | C++ || Easy approach || Sliding Window & Hashmap | c-easy-approach-sliding-window-hashmap-b-qf8u | simply using sliding window technique with map and meanwhile calculatin the sum \nif anywhere found repeated element the slide the window ahead.\n\nupvote if it | Md_Rafiq | NORMAL | 2022-06-12T06:35:09.499526+00:00 | 2022-06-12T06:41:08.538744+00:00 | 35 | false | simply using sliding window technique with map and meanwhile calculatin the sum \nif anywhere found repeated element the slide the window ahead.\n\nupvote if it helped you.\n```\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int ,int> map;\n int i=0,j=0;\n int sum=0;\n int ans=INT_MIN;\n while(j<nums.size())\n {\n sum+=nums[j];\n map[nums[j]]++;\n \n if(map.size()==j-i+1)\n {\n ans=max(sum,ans);\n }\n else if(j-i+1>map.size())\n {\n while(i<=j && j-i+1>map.size())\n {\n sum-=nums[i];\n map[nums[i]]--;\n if(map[nums[i]]==0)\n {\n map.erase(nums[i]);\n }\n i++;\n }\n \n if(j-i+1==map.size())\n {\n ans=max(ans,sum);\n }\n }\n j++;\n }\n return ans;\n \n }``` | 2 | 0 | ['Two Pointers', 'C', 'Sliding Window'] | 0 |
maximum-erasure-value | Java || HashMap || O(N) solution || Single Iteration | java-hashmap-on-solution-single-iteratio-vdrl | \nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n HashMap<Integer,Integer>loc=new HashMap<>(); //stores the index of last occurran | shiv_am | NORMAL | 2022-06-12T05:42:42.447990+00:00 | 2022-06-12T05:42:42.448033+00:00 | 354 | false | ```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n HashMap<Integer,Integer>loc=new HashMap<>(); //stores the index of last occurrance of the number\n HashMap<Integer,Integer>sum=new HashMap<>(); //stores the prefix sum\n int ans=0;//stores the final answer\n int total=0;//stores the sum upto the index\n int idx=-1;//stores the starting index from which the subarray has to be considered\n for(int i=0;i<nums.length;i++)\n {\n total+=nums[i];//calculating total sum\n if(loc.containsKey(nums[i])) //if the number repeats update the starting index of subarray\n idx=Math.max(idx,loc.get(nums[i]));\n if(idx==-1)\n ans=Math.max(ans,total);\n else\n ans=Math.max(ans,total-sum.get(idx));//subtract prefix sum of starting of subarray from total to get sum of subarray\n loc.put(nums[i],i);//update last occurance of the number\n sum.put(i,total);//update prefix sum\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Prefix Sum', 'Java'] | 0 |
maximum-erasure-value | Sliding Window || Set || Clean Code || JAVA | sliding-window-set-clean-code-java-by-ut-ibjx | Time Complexity (Worst) : O(N x K) where K is the range from the starting till we find that duplicate.\n\n\nclass Solution {\n public int maximumUniqueSubar | UttamKumar22 | NORMAL | 2022-06-12T05:35:55.244947+00:00 | 2022-06-12T05:38:19.005041+00:00 | 44 | false | Time Complexity (Worst) : O(N x K) where K is the range from the starting till we find that duplicate.\n\n```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n \n int start = 0, end = 0, sum = 0, max = 0;\n HashSet<Integer> set = new HashSet<>();\n \n while(end < nums.length){\n \n if(set.add(nums[end])){\n\t\t\t// if we don\'t have any duplicate item in our set\n sum += nums[end];\n end++;\n }\n else{\n\t\t\t//remove and substract elements from starting until the duplicate element got removed.\n sum -= nums[start];\n set.remove(nums[start]);\n start++;\n }\n\t\t\t//keeping track of the maximum sum of the subarray we got till now\n max = Math.max(sum, max);\n }\n \n return max;\n }\n}\n``` | 2 | 0 | ['Sliding Window', 'Java'] | 0 |
maximum-erasure-value | ✅C++ | Easy Sliding Window Approach!! | c-easy-sliding-window-approach-by-shm_47-zkgp | This question is similar to: https://leetcode.com/problems/longest-substring-without-repeating-characters/\n\nCode with comments:\n\nclass Solution {\npublic:\n | shm_47 | NORMAL | 2022-06-12T05:22:25.682748+00:00 | 2022-06-12T05:27:12.386029+00:00 | 259 | false | This question is similar to: https://leetcode.com/problems/longest-substring-without-repeating-characters/\n\n**Code with comments:**\n```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n //finding subarray(with unique elements) with maximum score\n int score = -1;\n vector<int> map(1e4+1, -1); //stores index of the elements\n \n \n //make prefix sum to get score\n vector<int> prefixSum;\n int sum = 0;\n for(int it: nums){\n sum+= it;\n // cout<<sum<<endl;\n prefixSum.push_back(sum);\n }\n \n //finding subarray(with unique elements) with maximum score\n int start = 0;\n for(int i=0; i<nums.size(); i++){\n if(map[nums[i]] != -1){ //if element repeats in nums, update start\n start = max(start, map[nums[i]]+1);\n }\n \n map[nums[i]] = i; //update index\n // cout<<nums[i] << " "<< map[nums[i]]<<endl;\n //get max score\n int left = (start==0)? 0: prefixSum[start-1];\n // cout<<left<<endl;\n score = max(score, prefixSum[i]- left); \n }\n \n return score;\n }\n};\n```\n\nTC = O(N)\nSC = O(N)\n\n**Please do upvote if you like the solution:)** | 2 | 0 | ['Two Pointers', 'C', 'Sliding Window'] | 0 |
maximum-erasure-value | Short, Simple and concise | C++ | short-simple-and-concise-c-by-tusharbhar-qas0 | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int, int> m;\n \n int i = 0, j = 0, sum = 0 | TusharBhart | NORMAL | 2022-06-12T04:16:31.321799+00:00 | 2022-06-12T04:16:31.321839+00:00 | 128 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n unordered_map<int, int> m;\n \n int i = 0, j = 0, sum = 0, ans = 0;\n while(j < nums.size()) {\n m[nums[j]]++;\n sum += nums[j];\n \n if(m.size() == j - i + 1) ans = max(ans, sum);\n \n while(m.size() < j - i + 1) {\n m[nums[i]]--;\n sum -= nums[i];\n if(!m[nums[i]]) m.erase(nums[i]);\n i++;\n }\n j++;\n }\n \n return ans;\n }\n};\n``` | 2 | 0 | ['Two Pointers', 'C', 'Sliding Window'] | 0 |
maximum-erasure-value | C++ || sliding window || simple code | c-sliding-window-simple-code-by-priyansh-y1w4 | class Solution {\npublic:\n\n int maximumUniqueSubarray(vector& nums) {\nint n=nums.size();\n unordered_mapmp;\n int sum=0;\n int mx=0;\ | priyanshu2001 | NORMAL | 2022-06-12T03:29:46.380725+00:00 | 2022-06-12T03:29:46.380753+00:00 | 169 | false | class Solution {\npublic:\n\n int maximumUniqueSubarray(vector<int>& nums) {\nint n=nums.size();\n unordered_map<int,int>mp;\n int sum=0;\n int mx=0;\n int i=0;\n int j=0;\n while(j<n)\n {\n sum+=nums[j];\n mp[nums[j]]++;\n \n if(mp.size()==j-i+1)\n {\n mx=max(sum,mx);\n j++;\n }\n \n else if(mp.size()<j-i+1)\n {\n while(mp.size()<j-i+1)\n {\n sum=sum-nums[i];\n mp[nums[i]]--;\n if(mp[nums[i]]==0)\n {\n mp.erase(nums[i]);\n }\n i++;\n }\n \n j++;\n }\n }\n return mx;\n }\n};\n**kindly upvot if it helped** | 2 | 0 | ['C'] | 0 |
maximum-erasure-value | Javascript ||Time: 92 ms (100.00%), Space: 52.6 MB (95.00%) | javascript-time-92-ms-10000-space-526-mb-gps3 | \n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maximumUniqueSubarray = function(nums) {\n let map = new Int8Array(10001), high = 0, sum = 0; | gino23odar | NORMAL | 2022-06-12T02:41:01.728903+00:00 | 2022-06-12T02:41:01.728925+00:00 | 152 | false | ```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maximumUniqueSubarray = function(nums) {\n let map = new Int8Array(10001), high = 0, sum = 0;\n \n for(let left = 0, right = 0; right < nums.length; right++){\n //map the numbers and add to the total sum\n map[nums[right]]++;\n sum += nums[right];\n \n //when a number appears for a second time move the left pointer by one & \n //substract one number from sum until the reapeated number is removed once\n while(map[nums[right]] > 1){\n map[nums[left]]--;\n sum -= nums[left++];\n }\n //highest becomes the top score between this run and the last\n high = Math.max(high, sum);\n }\n return high;\n};\n``` | 2 | 0 | ['Sliding Window', 'JavaScript'] | 0 |
maximum-erasure-value | Python | sliding window (two pointers) + hash set | with comments | python-sliding-window-two-pointers-hash-aoc8j | How I approach this problem:\n1. Use a hash set to track the numbers in the current window. \n2. Use curSum to track the sum of the number in the current window | BoluoUp | NORMAL | 2022-06-12T00:55:09.993195+00:00 | 2022-06-12T00:55:09.993228+00:00 | 185 | false | How I approach this problem:\n1. Use a hash set to track the numbers in the current ```window```. \n2. Use ```curSum``` to track the sum of the number in the current window.\n3. Use two pointers ```l``` and ```r``` to expand and shrink the sliding window.\n4. Move ```r```. When encounter duplicate numbers in the window, move the ```l``` until the current window has no duplicates.\n5. Keep updating hashset ```window``` and ```curSum``` when doing above step.\n\nBelow is my code with comments. Feel free to ask if you have any questions!\n\n```\nclass Solution:\n def maximumUniqueSubarray(self, nums: List[int]) -> int:\n window = set() # a hash set to track the numbers in the current window\n res = 0\n curSum = 0 # track the sum of the numbers in the current window\n l = 0 # initialize the left pointer of the sliding window\n \n for r in range(len(nums)): # move the right pointer of the sliding window\n \n # move the left pointer until the current window has no duplicate numbers\n while nums[r] in window and l < r:\n window.remove(nums[l]) # remove the left-most number\n curSum -= nums[l] # subtract the removed number from curSum \n l += 1\n \n # if no duplicate numbers in the window \n window.add(nums[r]) # add the current number\n curSum += nums[r] # add the number to curSum\n \n res = max(res, curSum) # update the result\n \n return res\n``` | 2 | 0 | ['Two Pointers', 'Sliding Window', 'Python'] | 0 |
maximum-erasure-value | Maximum Erasure Value | Java | Sliding Window | HashMap | maximum-erasure-value-java-sliding-windo-hohu | public int maximumUniqueSubarray(int[] nums) {\n \n int i=0;\n int j=0;\n int max=0;\n int sum=0;\n HashMap map = new HashMap | njyotiprakash189 | NORMAL | 2022-06-10T14:43:41.376898+00:00 | 2022-06-10T14:43:41.376931+00:00 | 131 | false | public int maximumUniqueSubarray(int[] nums) {\n \n int i=0;\n int j=0;\n int max=0;\n int sum=0;\n HashMap<Integer, Integer> map = new HashMap<>();\n while(j<nums.length)\n {\n map.put(nums[j], map.getOrDefault(nums[j],0)+1);\n sum +=nums[j];\n if(map.size()==j-i+1)\n {\n \n max=Math.max(max,sum);\n j++;\n }\n else if(map.size()<j-i+1){\n while(map.size()<j-i+1){\n sum -=nums[i];\n map.put(nums[i], map.get(nums[i])-1);\n if(map.get(nums[i])==0){\n map.remove(nums[i]);\n }\n i++;\n }\n j++;\n }\n \n }\n return max;\n } | 2 | 0 | ['Sliding Window', 'Java'] | 0 |
maximum-erasure-value | Sliding window with unordered_map || c++ || faster | sliding-window-with-unordered_map-c-fast-8vao | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n \n unordered_map<int,int> mp;\n int n = nums.size();\n | binayKr | NORMAL | 2022-02-13T09:17:26.257891+00:00 | 2022-02-13T09:17:26.257942+00:00 | 92 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& nums) {\n \n unordered_map<int,int> mp;\n int n = nums.size();\n int maxi = INT_MIN, sum=0, i =0, j=0;\n while(i<n)\n {\n if(mp.count(nums[i]) and mp[nums[i]]>= j) \n {\n sum -= accumulate(nums.begin() + j ,nums.begin() + mp[nums[i]] +1, 0);\n j = mp[nums[i]]+1;\n }\n else \n {\n sum += nums[i];\n mp[nums[i]]=i;\n i++;\n }\n maxi = max(maxi,sum);\n }\n return maxi;\n }\n};\n``` | 2 | 0 | ['C', 'Sliding Window'] | 0 |
maximum-erasure-value | LinkedIn | Best Solution | Sliding Window | Readable code | C++ | O(N) | linkedin-best-solution-sliding-window-re-c9s6 | \nint maximumUniqueSubarray(vector<int>& nums) {\n int N = nums.size(), left = 0, right = 0;\n int currsum = 0, maxsum = 0;\n bool duplicat | executable16 | NORMAL | 2022-02-12T17:47:54.332720+00:00 | 2022-02-12T17:48:21.542444+00:00 | 83 | false | ```\nint maximumUniqueSubarray(vector<int>& nums) {\n int N = nums.size(), left = 0, right = 0;\n int currsum = 0, maxsum = 0;\n bool duplicateExists = false;\n \n unordered_map <int,int> freq;\n \n while(right < N){\n int num = nums[right];\n freq[num]++;\n currsum = currsum + num;\n \n if(freq[num] > 1) duplicateExists = true;\n \n while(duplicateExists){\n num = nums[left];\n if(freq[num] > 1) duplicateExists = false;\n --freq[num];\n currsum = currsum - num;\n left++;\n }\n maxsum = max(maxsum,currsum);\n right++;\n }\n return maxsum;\n }\n``` | 2 | 0 | ['C', 'Sliding Window'] | 0 |
maximum-erasure-value | Java | Sliding Window | HashMap | java-sliding-window-hashmap-by-user8540k-6gvs | \nclass Solution {\n public int maximumUniqueSubarray(int[] arr) {\n Map<Integer,Integer> mp = new HashMap<>();\n int j = 0;\n int i = 0 | user8540kj | NORMAL | 2021-06-10T11:20:58.418569+00:00 | 2021-06-10T11:20:58.418601+00:00 | 96 | false | ```\nclass Solution {\n public int maximumUniqueSubarray(int[] arr) {\n Map<Integer,Integer> mp = new HashMap<>();\n int j = 0;\n int i = 0;\n int sum = 0;\n int max = Integer.MIN_VALUE;\n while(j < arr.length){\n sum = sum + arr[j];\n //insert into map\n if(mp.containsKey(arr[j])){\n mp.put(arr[j],mp.get(arr[j]) + 1);\n }\n else{\n mp.put(arr[j],1);\n }\n //map size with window size\n if(j - i + 1 == mp.size()){\n max = Math.max(max,sum);\n }\n else if(j - i + 1 > mp.size()){\n //slide your window until you found the unique elements subarray\n while(j - i + 1 > mp.size()){\n sum = sum - arr[i];\n if(mp.containsKey(arr[i])){\n \n int freq = mp.get(arr[i]);\n freq--;\n if(freq == 0) mp.remove(arr[i]);\n else mp.put(arr[i],freq);\n \n }\n i++;\n }\n \n \n \n }\n j++; \n }\n \n return max;\n }\n}\n``` | 2 | 0 | [] | 0 |
maximum-erasure-value | JAVA || Clean & Concise & Optimal Code || Sliding Window Approach || 6ms Time || 95% Faster Solution | java-clean-concise-optimal-code-sliding-w4ix5 | \nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n \n int maxSum = 0;\n int[] sum = new int[nums.length + 1];\n | anii_agrawal | NORMAL | 2021-05-31T04:25:07.082145+00:00 | 2021-05-31T04:25:07.082177+00:00 | 146 | false | ```\nclass Solution {\n public int maximumUniqueSubarray(int[] nums) {\n \n int maxSum = 0;\n int[] sum = new int[nums.length + 1];\n int[] index = new int[10001];\n \n for (int i = 0, j = 0; i < nums.length; i++) {\n j = Math.max (j, index[nums[i]]);\n sum[i + 1] = sum[i] + nums[i];\n maxSum = Math.max (maxSum, sum[i + 1] - sum[j]);\n index[nums[i]] = i + 1;\n }\n \n return maxSum;\n }\n}\n```\n\nPlease help to **UPVOTE** if this post is useful for you.\nIf you have any questions, feel free to comment below.\n\n**LOVE CODING :)\nHAPPY CODING :)\nHAPPY LEARNING :)** | 2 | 1 | ['Sliding Window', 'Java'] | 1 |
maximum-erasure-value | C++| Comments | Clean and small code | 2 pointer | c-comments-clean-and-small-code-2-pointe-bash | \nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& a) {\n int ans=0;\n \n auto it=a.insert(a.begin(),0); //Make 1-base | Coder_Shubham_24 | NORMAL | 2021-05-29T05:54:50.277267+00:00 | 2021-05-29T05:54:50.277300+00:00 | 97 | false | ```\nclass Solution {\npublic:\n int maximumUniqueSubarray(vector<int>& a) {\n int ans=0;\n \n auto it=a.insert(a.begin(),0); //Make 1-based indexing \n \n int st=0, n=a.size()-1, i; //st->is start pointer of each unique window \n \n int vis[10001]={0}; // Maintains last index of each a[i]\n \n int s=0;\n st=1;\n for(i=1;i<=n;i++){\n s+=a[i];\n \n while(st<=vis[a[i]])s-=a[st++]; //shrink window to make it unique again\n \n vis[a[i]]=i;\n ans=max(ans,s);\n \n }\n \n return ans;\n }\n};\n\n/* some testcases \n[4,2,4,5,6]\n[5,2,1,2,5,2,1,2,5]\n[1,2,3,4,5]\n[1,2,2,1,2,3,1,3,5,6,1,7,1]\n[1,2,3,4]\n[1]\n[1,2]\n[3,4]\n*/\n``` | 2 | 0 | [] | 1 |
maximum-erasure-value | C# sliding window solution | c-sliding-window-solution-by-newbiecoder-5rpi | time: O(N)\n- space: O(N)\n\n\npublic class Solution {\n public int MaximumUniqueSubarray(int[] nums) {\n \n if(nums == null || nums.Length == | newbiecoder1 | NORMAL | 2021-05-28T16:05:59.570755+00:00 | 2021-05-28T16:05:59.570800+00:00 | 79 | false | - time: O(N)\n- space: O(N)\n\n```\npublic class Solution {\n public int MaximumUniqueSubarray(int[] nums) {\n \n if(nums == null || nums.Length == 0)\n return 0;\n \n Dictionary<int,int> dic = new Dictionary<int,int>();\n int left = 0, right = 0, sum = 0, max = 0, counter = 0;\n while(right < nums.Length)\n {\n int rightNum = nums[right];\n sum += rightNum;\n if(dic.ContainsKey(rightNum))\n {\n dic[nums[right]]++;\n if(dic[rightNum] > 1)\n counter++;\n }\n else\n dic.Add(rightNum,1);\n right++;\n \n while(counter > 0)\n {\n int leftNum = nums[left];\n dic[leftNum]--;\n if(dic[leftNum] == 1)\n counter--;\n sum -= leftNum;\n left++;\n }\n \n max = Math.Max(max,sum);\n }\n \n return max;\n }\n}\n``` | 2 | 0 | [] | 0 |
maximum-elegance-of-a-k-length-subsequence | [Java/C++/Python] Sort by Profit | javacpython-sort-by-profit-by-lee215-muyg | Intuition\nSort items by decresed profiti,\nand we take k first items.\nThis is biggest total_profit we can have.\n\n\n# Explanation\nContinue to iterate the re | lee215 | NORMAL | 2023-08-06T04:04:37.927859+00:00 | 2023-08-06T04:18:20.394311+00:00 | 3,368 | false | # **Intuition**\nSort `items` by decresed `profiti`,\nand we take `k` first items.\nThis is biggest `total_profit` we can have.\n<br>\n\n# **Explanation**\nContinue to iterate the remaining `n - k` items.\nWe can try to take them,\nif this is a new `category` and not in `seen` set.\n\nBut we already have `k` items,\nso we replace one item with smallest `profit`\nwhich has a duplicate `category`.\n\nWe continue doing this,\nuntil every category has no two items.\n\nFinally return the max result.\n<br>\n\n# **Complexity**\nTime `O(nlogn)`\nSpace `O(n)`\n<br>\n\n**Java**\n```java\n public long findMaximumElegance(int[][] A, int k) {\n Arrays.sort(A, (a, b) -> b[0] - a[0]);\n long res = 0, cur = 0;\n List<Integer> dup = new ArrayList<>();\n Set<Integer> seen = new HashSet<>();\n for (int i = 0; i < A.length; ++i) {\n if (i < k) {\n if (seen.contains(A[i][1])) {\n dup.add(A[i][0]);\n }\n cur += A[i][0];\n } else if (!seen.contains(A[i][1])) {\n if (dup.isEmpty()) break;\n cur += A[i][0] - dup.remove(dup.size() - 1);\n }\n seen.add(A[i][1]);\n res = Math.max(res, cur + 1L * seen.size() * seen.size());\n }\n return res;\n }\n```\n**C++**\n```cpp\n long long findMaximumElegance(vector<vector<int>>& A, int k) {\n sort(A.begin(), A.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] > b[0];\n });\n long long res = 0, cur = 0;\n vector<int> dup;\n unordered_set<int> seen;\n for (int i = 0; i < A.size(); ++i) {\n if (i < k) {\n if (seen.count(A[i][1])) {\n dup.push_back(A[i][0]);\n }\n cur += A[i][0];\n } else if (seen.find(A[i][1]) == seen.end()) {\n if (dup.empty()) break;\n cur += A[i][0] - dup.back();\n dup.pop_back();\n }\n seen.insert(A[i][1]);\n res = fmax(res, cur + 1L * seen.size() * seen.size());\n }\n return res;\n }\n```\n\n**Python**\n```py\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n items = sorted(items, key=lambda v: -v[0])\n res = cur = 0\n A = []\n seen = set()\n for i, (p, c) in enumerate(items):\n if i < k:\n if c in seen:\n A.append(p)\n cur += p\n elif c not in seen:\n if not A: break\n cur += p - A.pop()\n seen.add(c)\n res = max(res, cur + len(seen) * len(seen))\n return res\n```\n | 98 | 0 | ['C', 'Python', 'Java'] | 18 |
maximum-elegance-of-a-k-length-subsequence | Track Dups | track-dups-by-votrubac-whpi | We sort items by profit, and take first k items.\n\nWe also track how many unique categories cats are there. If we see another item in the existing category, we | votrubac | NORMAL | 2023-08-06T05:25:45.040799+00:00 | 2023-08-06T05:40:08.574492+00:00 | 706 | false | We sort items by profit, and take first `k` items.\n\nWe also track how many unique categories `cats` are there. If we see another item in the existing category, we place it into `dups`.\n\nNow, let\'s see if we can improve our result by considering remaining `n - k` items:\n- If the item category already exists in `cats`, we ignore it. We already include items with larger profits from that category.\n- If the category does not exist, we take that item, and remove the smallest profit from `dups`.\n\nWe track and return the largest `res`.\n\n**C++**\n```cpp\nlong long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(begin(items), end(items), greater<>());\n vector<int> dups;\n unordered_set<int> cats;\n for (int i = 0; i < k; ++i)\n if (!cats.insert(items[i][1]).second)\n dups.push_back(items[i][0]);\n long long sum = accumulate(begin(items), begin(items) + k, 0LL, [](long long s, const auto &i) {\n return s + i[0];\n });\n long long res = sum + cats.size() * cats.size();\n for (int i = k, j = dups.size() - 1; i < items.size() && j >= 0; ++i)\n if (cats.insert(items[i][1]).second) {\n sum = sum - dups[j--] + items[i][0];\n res = max(res, sum + (long long)(cats.size() * cats.size()));\n }\n return res;\n}\n``` | 20 | 0 | ['C'] | 3 |
maximum-elegance-of-a-k-length-subsequence | Greedy C++ & Java | greedy-c-java-by-cpcs-yyvg | Btw, the question is excatly the same as the one I published before.\n\n\nhttps://leetcode.com/discuss/interview-question/3624545/GPL-Challenge-Q1\n\n\n# Intuit | cpcs | NORMAL | 2023-08-06T04:01:13.933051+00:00 | 2023-08-06T04:01:13.933074+00:00 | 1,627 | false | Btw, the question is excatly the same as the one I published before.\n\n\n[https://leetcode.com/discuss/interview-question/3624545/GPL-Challenge-Q1](https://leetcode.com/discuss/interview-question/3624545/GPL-Challenge-Q1)\n\n\n# Intuition\nGreedy algorithm\n\n\n(1) sort the items by the profit (items[.][0]) in non increasing order.\n(2) select the first k items according non-increasing sorted profit (items[.][0]).\n(3) For remaining unselected items, try using them one by one (in the non increasing of profit order) to replace the selected ones.\n\nConditions for replacing:\n(a) The items to be replaced\'s category must not be unique in selected items. Namely, removing it doesn\'t reduce the number of categories.\n(b) The items to be replaced must have the minimum profit (items[.][0] value) in the selected items when condition (a) is satisified.\n(c) The new item to replace the original selected one must have a new category. Namely we use an item with lower profit (or equal) to increase the number of categories. \n\nWe can maintain the selected items\'s categories using a hash map.\n\n# Approach\nUse priority queue & hashmap to maintain the profits and categories.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\nC++\n```\nclass Solution {\n long long sqr(long long x) {\n return x * x;\n }\n\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n const int n = items.size();\n vector<int> ind(n);\n for (int i = 0; i < n; ++i) {\n ind[i] = i;\n }\n sort(ind.begin(), ind.end(), [&](const int x, const int y) {\n return items[x][0] > items[y][0];\n });\n unordered_map<int, int> num;\n priority_queue<pair<int, int>> q;\n long long v = 0;\n for (int i = 0; i < k; ++i) {\n v += items[ind[i]][0];\n ++num[items[ind[i]][1]];\n q.push({-items[ind[i]][0], ind[i]});\n }\n long long r = v + sqr(num.size());\n for (int i = k; i < n && !q.empty(); ++i) {\n if (num.count(items[ind[i]][1])) {\n continue;\n }\n const int x = q.top().second;\n q.pop();\n if (num[items[x][1]] == 1) {\n --i;\n continue;\n }\n v += items[ind[i]][0] - items[x][0];\n --num[items[x][1]];\n ++num[items[ind[i]][1]];\n r = max(r, v + sqr(num.size()));\n }\n return r;\n }\n};\n```\nJava:\n```\nclass Solution {\n long sqr(long x) {\n return x * x;\n }\n\n public long findMaximumElegance(int[][] items, int k) {\n final int n = items.length;\n Integer[] ind = new Integer[n];\n for (int i = 0; i < n; ++i) {\n ind[i] = i;\n }\n Arrays.sort(ind, new Comparator<Integer>() {\n @Override\n public int compare(Integer x, Integer y) {\n return Integer.compare(items[y][0], items[x][0]);\n }\n });\n Map<Integer, Integer> num = new HashMap<>();\n PriorityQueue<Pair<Integer, Integer>> q = new PriorityQueue<>(new Comparator<Pair<Integer, Integer>>() {\n @Override\n public int compare(Pair<Integer, Integer> p1, Pair<Integer, Integer> p2) {\n return Integer.compare(p2.getKey(), p1.getKey());\n }\n });\n long v = 0;\n for (int i = 0; i < k; ++i) {\n v += items[ind[i]][0];\n num.put(items[ind[i]][1], num.getOrDefault(items[ind[i]][1], 0) + 1);\n q.add(new Pair<>(-items[ind[i]][0], ind[i]));\n }\n long r = v + sqr(num.size());\n for (int i = k; i < n && !q.isEmpty(); ++i) {\n if (num.containsKey(items[ind[i]][1])) {\n continue;\n }\n int x = q.peek().getValue();\n q.poll();\n if (num.get(items[x][1]) == 1) {\n --i;\n continue;\n }\n v += items[ind[i]][0] - items[x][0];\n num.put(items[x][1], num.get(items[x][1]) - 1);\n num.put(items[ind[i]][1], num.getOrDefault(items[ind[i]][1], 0) + 1);\n r = Math.max(r, v + sqr(num.size()));\n }\n return r;\n }\n}\n``` | 19 | 0 | ['C++', 'Java'] | 5 |
maximum-elegance-of-a-k-length-subsequence | Probably the easiest solution. | probably-the-easiest-solution-by-agnishh-dley | Intuition\nThere is an inclination to go towards DP when you hear subsequences. The constraints made me feel it was greedy.\n\n# Approach\nFirst sort the array | agnishh | NORMAL | 2023-08-06T06:40:28.685585+00:00 | 2023-08-06T10:24:46.290273+00:00 | 555 | false | # Intuition\nThere is an inclination to go towards DP when you hear subsequences. The constraints made me feel it was greedy.\n\n# Approach\nFirst sort the array by profits in descending order.\nSimply take first k elements. Since there is a factor of categories in profit calculation, keep a set with all categories. In case you have a repeated category, push into a vector/stack which stores the values. Next is simple, whichever repeated category has the least profit value is to be replaced by an element whose category hasn\'t been encountered yet.\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) \n {\n sort(items.rbegin(), items.rend());\n stack<int> minAtTop;\n unordered_set<int> s;\n long long sum = 0;\n for(int i=0;i<k;i++)\n {\n sum += items[i][0];\n if(s.count(items[i][1])) minAtTop.push(items[i][0]);\n else s.insert(items[i][1]);\n }\n long long ans = sum + s.size()*1LL*s.size();\n for(int i=k;i<items.size();i++)\n {\n if(!s.count(items[i][1]) && !minAtTop.empty())\n {\n s.insert(items[i][1]);\n sum -= minAtTop.top();\n minAtTop.pop();\n sum += items[i][0];\n int n = s.size();\n ans = max(ans, sum + n*1LL*n);\n }\n }\n return ans;\n }\n};\n``` | 11 | 0 | ['Greedy', 'Sorting', 'C++'] | 3 |
maximum-elegance-of-a-k-length-subsequence | Python 3 || head vs tail || T/S: 99% / 31% | python-3-head-vs-tail-ts-99-31-by-spauld-p3de | \nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n\n items.sort(reverse = True)\n sm, seenCats, dups = | Spaulding_ | NORMAL | 2023-08-08T18:24:18.512146+00:00 | 2024-06-21T18:06:18.161515+00:00 | 283 | false | ```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n\n items.sort(reverse = True)\n sm, seenCats, dups = 0, set(), deque()\n\n for headPrf, headCat in items[:k]:\n \n sm+= headPrf\n\n if headCat in seenCats: dups.append(headPrf)\n else: seenCats.add(headCat)\n\n numCats = len(seenCats) \n\n ans = sm = sm + numCats*numCats\n \n for tailPrf, tailCat in items[k:]:\n\n if not dups or tailCat in seenCats: continue\n numCats+= 1\n diff = tailPrf - dups.pop() + 2 * numCats - 1\n # a**2 - (a-1)**2 - = 2*a - 1\n sm += diff \n if diff > 0: ans = sm\n seenCats.add(tailCat)\n\n return ans\n```\n[https://leetcode.com/problems/maximum-elegance-of-a-k-length-subsequence/submissions/1295907224/](https://leetcode.com/problems/maximum-elegance-of-a-k-length-subsequence/submissions/1295907224/)\n\n\nI could be wrong, but I think that time complexity is *O*(*N* log *N*) and space complexity is *O*(*N*), in which *N* ~ `len(items)`. | 8 | 0 | ['Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | [Python3] Greedy | python3-greedy-by-awice-5b4n | Intuition\n\nSay an item is golden if it has the highest profit in its category.\n\nSuppose we use $C$ categories in our selection. It consists of the most pro | awice | NORMAL | 2023-08-06T14:35:03.804723+00:00 | 2023-08-06T14:35:03.804743+00:00 | 249 | false | **Intuition**\n\nSay an item is *golden* if it has the highest profit in its category.\n\nSuppose we use $C$ categories in our selection. It consists of the most profitable $C$ golden items, and the rest of the items are chosen to be the ones with the highest profit.\n\n**Algorithm**\n\nSort `items` decreasing by profit. When you encounter an item with a new category, it must be golden. Otherwise it is a duplicate.\n\nWe\'re keeping track of `cates`, the set of categories with a golden item, `dupes`, the list of profit of duplicate items, and `cur`, the current total profit.\n\n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items, K):\n items.sort(reverse=True)\n \n dupes = []\n cates = set()\n ans = cur = 0\n for p, c in items:\n cur += p\n if c not in cates:\n cates.add(c)\n else:\n dupes.append(p)\n\n while dupes and len(dupes) + len(cates) > K:\n cur -= dupes.pop()\n if len(dupes) + len(cates) <= K:\n ans = max(ans, cur + len(cates) ** 2)\n \n return ans\n``` | 8 | 0 | ['Python3'] | 1 |
maximum-elegance-of-a-k-length-subsequence | C++ Easy Solution || Best Approach ||✅✅ | c-easy-solution-best-approach-by-abhi_pa-dhdy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | abhi_pandit_18 | NORMAL | 2023-08-06T04:04:37.082117+00:00 | 2023-08-06T04:04:37.082138+00:00 | 540 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n long long sqr(long long x) {\n return x * x;\n }\n\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n const int n = items.size();\n vector<int> ind(n);\n for (int i = 0; i < n; ++i) {\n ind[i] = i;\n }\n sort(ind.begin(), ind.end(), [&](const int x, const int y) {\n return items[x][0] > items[y][0];\n });\n unordered_map<int, int> num;\n priority_queue<pair<int, int>> q;\n long long v = 0;\n for (int i = 0; i < k; ++i) {\n v += items[ind[i]][0];\n ++num[items[ind[i]][1]];\n q.push({-items[ind[i]][0], ind[i]});\n }\n long long r = v + sqr(num.size());\n for (int i = k; i < n && !q.empty(); ++i) {\n if (num.count(items[ind[i]][1])) {\n continue;\n }\n const int x = q.top().second;\n q.pop();\n if (num[items[x][1]] == 1) {\n --i;\n continue;\n }\n v += items[ind[i]][0] - items[x][0];\n --num[items[x][1]];\n ++num[items[ind[i]][1]];\n r = max(r, v + sqr(num.size())); // calling function\n }\n return r;\n }\n};\n``` | 6 | 3 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Greedy Approach | greedy-approach-by-rahulraturi2002-xgg1 | We want to calculate : total_profit + distinct_categories^2\n\n We sort profit in descending order and take first k profits including duplicate categories\n Wh | rahulraturi2002 | NORMAL | 2023-08-06T08:53:30.707699+00:00 | 2023-08-06T08:53:30.707746+00:00 | 303 | false | We want to calculate : **total_profit + distinct_categories^2**\n\n* We sort profit in descending order and take first k profits including duplicate categories\n* When we reach first k items , now we can maximazie distinct_categories by adding them into set and removing lowest duplicate items from set\n\n```\n\n#define ll long long\nclass Solution\n{\n public:\n \n ll max(ll a,ll b)\n {\n return (a>b)?a:b;\n }\n long long findMaximumElegance(vector<vector < int>> &items, int k)\n {\n\n sort(items.begin(), items.end(), [& ](const vector<int> &a, const vector<int> &b)\n {\n return a[0] > b[0];\n\t});\n\n ll res = 0, currSum = 0;\n\n vector<int> duplicate;\n unordered_set<int> seen;\n\n for (int i = 0; i < items.size(); i++)\n {\n if (i < k)\n {\n if (seen.count(items[i][1]))\n {\n duplicate.push_back(items[i][0]);\n }\n currSum += items[i][0];\n }\n else if (seen.find(items[i][1]) == seen.end())\n {\n if (duplicate.empty())\n break;\n\n currSum += items[i][0] - duplicate.back();\n duplicate.pop_back();\n }\n seen.insert(items[i][1]);\n\n res = max(res, currSum + 1ll *seen.size()*seen.size());\n }\n return res;\n }\n};\n``` | 5 | 0 | ['Greedy', 'C'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ Greedy || sorting + map + priority Queue | c-greedy-sorting-map-priority-queue-by-a-5qp8 | \n# Code\n\nclass Solution {\npublic: \n long long findMaximumElegance(vector<vector<int>>&items, int k) {\n sort(items.rbegin(),items.rend());\n | avadhut7969 | NORMAL | 2023-09-01T14:20:53.757758+00:00 | 2023-09-01T14:20:53.757787+00:00 | 62 | false | \n# Code\n```\nclass Solution {\npublic: \n long long findMaximumElegance(vector<vector<int>>&items, int k) {\n sort(items.rbegin(),items.rend());\n long long sum=0;\n map<int,multiset<int>>st;\n priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq;\n for(int i=0;i<k;i++){\n sum+=items[i][0];\n st[items[i][1]].insert(items[i][0]);\n }\n for(int i=1;i<=items.size();i++){\n if(st.find(i)!=st.end() && st[i].size()>1) pq.push({*st[i].begin(),i});\n }\n long long size=st.size();\n long long ans=sum+ size*size;\n for(int i=k;i<items.size();i++){\n if(pq.size()==0) break;\n if(st.find(items[i][1])==st.end()){\n int mini=pq.top().first;\n int minid=pq.top().second;\n pq.pop();\n sum-=mini;\n sum+=items[i][0];\n st[items[i][1]].insert(items[i][0]);\n st[minid].erase(st[minid].find(mini));\n if(st[minid].size()==0) st.erase(minid);\n if(st[minid].size()>1) pq.push({*st[minid].begin(),minid});\n long long size=st.size();\n ans=max(ans,sum + size*size);\n }\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Hash Table', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Ordered Set', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.