question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-elegance-of-a-k-length-subsequence | C++ Greedy in O(NlogN) | c-greedy-in-onlogn-by-yashsinghania-8l4q | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nTaking k elements and trying to maximise the answer by increasing unique | yashsinghania | NORMAL | 2023-08-06T11:26:09.200193+00:00 | 2023-08-06T11:26:09.200217+00:00 | 281 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTaking k elements and trying to maximise the answer by increasing unique elements\n\n# Complexity\n- Time complexity:\n- O(NlogN + N) for sorting and searching\n\n- Space complexity:\n- O(N)\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& v, int k) {\n int n = v.size();\n sort(v.rbegin(), v.rend()); //sort according to profit\n long long ans = 0;\n map<int, int> m;\n for(int i = 0; i < k; i++){\n ans += v[i][0];\n m[v[i][1]]++;\n }\n long long sz = m.size();\n ans += (sz * sz);\n long long res = ans;\n int j = k - 1;\n for(int i = k; i < n; i++){\n if(m.count(v[i][1]) == 0){ //try to increase unique elements\n while(j >= 0 && m[v[j][1]] < 2) j--; //finding smallest number in 0 to k-1 whose frequency is more than 1, and removing it to increasing uniquenes of the subsequence\n if(j < 0) break; //no number found that has frequency more than two\n m[v[j][1]]--;\n m[v[i][1]]++; \n res -= v[j][0];\n res += v[i][0];\n res -= sz*sz;\n sz++;\n res += sz*sz;\n j--;\n ans = max(ans, res); //keep taking max\n }\n }\n return max(ans, res);\n }\n};\n``` | 4 | 0 | ['C++'] | 4 |
maximum-elegance-of-a-k-length-subsequence | Greedy | greedy-by-jeffreyhu8-qhet | Intuition\nAs is often typical with subsequence problems, we may first think of a dynammic programming approach. However, having the state be something like the | jeffreyhu8 | NORMAL | 2023-08-06T04:01:54.390162+00:00 | 2023-08-06T04:05:23.014920+00:00 | 334 | false | # Intuition\nAs is often typical with subsequence problems, we may first think of a dynammic programming approach. However, having the state be something like the current item and the number of distinct values accumulated so far is too large.\n\nWhen there are strict bounds for a dynamic programming approach, a common theme is to optimize that approach using a greedy algorithm.\n\n# Approach\nTo find a greedy algorithm, it is common to make some observations first.\n\nFirst, if we ignore the categories, it is clearly best to choose the `k` items with the highest profit.\n\nSecond, since it seems optimal to choose larger profits, we loop through the items in order of decreasing profit. While looping, let\'s say that we are considering whether or not to swap one of the top `k` items with some other item `item`. We have two cases.\n\na. `item` shares a category with one of the items we already have.\n\nIn this case, it is not optimal to swap the items, since we would have the same categories but decrease our profit if we swapped the items.\n\nb. `item` does not share a category with one of the items we already have.\n\nFirst, note that if we have already `l` distinct categories, then we have already found the optimal solution for `l` distinct categories since any other configuration would result in a lower profit for at least one of the items, meaning a lower profit overall. As such, we should try to swap `item` with some item in our current collection.\n\nSpecifically, we will swap `item` with the lowest profit item that is in a category that already has at least one other item. This ensures the number of distinct categories increases to `l + 1`.\n\nWe can find the lowest profit item using a priority queue.\n\n# Complexity\n- Time complexity: $$O(n\\lg n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n items.sort(key=lambda item: item[0], reverse=True)\n \n grouped = defaultdict(list)\n for profit, category in items[:k]:\n grouped[category].append(profit)\n \n duplicates = []\n for category, group in grouped.items():\n group.sort(reverse=True)\n if len(group) > 1:\n duplicates.extend(grouped[category][1:])\n heapify(duplicates)\n \n curSum = sum(profit for profit, category in items[:k])\n res = curSum + len(grouped) ** 2\n \n for profit, category in items[k:]:\n if category in grouped:\n continue\n \n if not duplicates:\n break\n \n duplicate = heappop(duplicates)\n curSum -= duplicate\n curSum += profit\n grouped[category].append(profit)\n \n res = max(curSum + len(grouped) ** 2, res)\n \n return res\n``` | 4 | 0 | ['Greedy', 'Heap (Priority Queue)', 'Python3'] | 1 |
maximum-elegance-of-a-k-length-subsequence | ✅ Beat 100% | ✨ O(N + k log k) | 🏆 Most Efficient Solution | 💯 Simple Greedy | beat-100-on-k-log-k-most-efficient-solut-ysmx | Intuition\n Describe your first thoughts on how to solve this problem. \n * For each category, we would always pick the items with the largest profits.\n * If | hero080 | NORMAL | 2023-09-04T02:27:42.391526+00:00 | 2023-09-04T02:27:42.391555+00:00 | 122 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n * For each category, we would always pick the items with the largest profits.\n * If we picked any item in a category, we say we "picked this category".\n * The `max_profit` for each category is a key. Assume we sorted categories by this key, we would never pick a "smaller category" when a larger category is not picked.\n * The above intuition tells us that we would always pick the largest $k\'$ categories where $k\' \\le k$.\n * This problem is asking for a balanced between "more total profits" and "more distinct categories".\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe first pick the largest `total_profit`, then gradually\n * remove the smallest item which is in a category that has more than one items picked (so that the `distinct_categories` does not go down)\n * at the same time pick a new category.\n \nThe best answer will be found during this greedy process.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$\\Theta(N + k \\log k)$$\nWe only need to sort the largest k of them.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$\\Theta(N)$$\n\n# Code\n```\nstruct Category {\n int id = 0;\n int max_profit = -1;\n\n bool operator<(const Category& other) const {\n return max_profit < other.max_profit;\n }\n};\n\nstruct Profit {\n int profit;\n int category;\n\n bool operator<(const Profit& other) const {\n return profit < other.profit;\n }\n};\n\ntemplate <typename T>\nvoid SortLastN(vector<T>& data, int n) {\n auto mid = data.end() - n;\n std::nth_element(data.begin(), mid, data.end());\n std::sort(mid, data.end());\n}\n\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n const int N = items.size();\n\n vector<Category> categories(N + 1);\n vector<Profit> profits;\n profits.reserve(N);\n for (const vector<int>& item : items) {\n int profit = item[0];\n int category = item[1];\n categories[category].id = category;\n categories[category].max_profit = max(categories[category].max_profit, profit);\n profits.push_back({.profit = profit, .category = category});\n }\n\n SortLastN(profits, k);\n SortLastN(categories, k);\n\n int64_t total_profit = 0;\n int distinct_categories = 0;\n vector<int> counts(N + 1); // # of items we used for each category.\n for (int i = profits.size() - k; i < profits.size(); ++i) {\n total_profit += profits[i].profit;\n distinct_categories += ++counts[profits[i].category] == 1;\n }\n // Base case: pick the largest k items.\n int64_t answer = total_profit +\n static_cast<int64_t>(distinct_categories) * distinct_categories;\n\n for (int i = profits.size() - k; i < profits.size() && distinct_categories < k; ++i) {\n int& count = counts[profits[i].category];\n if (count == 1) {\n continue;\n }\n total_profit -= profits[i].profit;\n --count;\n\n while (counts[categories.back().id] > 0) { // We need a new category\n categories.pop_back();\n }\n if (categories.back().max_profit < 0) {\n break; // No more new category exists.\n }\n total_profit += categories.back().max_profit;\n ++distinct_categories;\n categories.pop_back();\n\n // Now we removed one item and added one more category.\n // We did this greedily:\n // * Removed the smallest items in use while not reducing `distinct_categories`.\n // * Added a new category with largest single item profit.\n answer = max(answer, total_profit +\n static_cast<int64_t>(distinct_categories) * distinct_categories);\n }\n return answer;\n }\n};\n``` | 3 | 0 | ['Greedy', 'Quickselect', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Video Solution | Complete Contest | C++ | Java | video-solution-complete-contest-c-java-b-7y39 | Intuition, approach, and time complexity discussed in detail in video solution\nhttps://youtu.be/uvF7-rRddzM\n\n# Code\nC++\n\nclass Solution {\npublic:\n lo | Fly_ing__Rhi_no | NORMAL | 2023-08-06T16:07:38.609958+00:00 | 2023-08-06T16:07:38.609981+00:00 | 240 | false | # Intuition, approach, and time complexity discussed in detail in video solution\nhttps://youtu.be/uvF7-rRddzM\n\n# Code\nC++\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(), items.end(), [](const vector<int>&a, const vector<int> & b)->bool{\n return a[0] > b[0];\n });\n unordered_set<int> unqCat;\n vector<int> dupl;\n long long eleg = 0;\n long long netProf = 0;\n for(int indx = 0; indx<items.size(); indx++){\n int curProf = items[indx][0], curCat = items[indx][1];\n if(indx < k){\n if(unqCat.find(curCat) != unqCat.end()){\n dupl.push_back(curProf);\n }\n netProf += curProf;\n }else if(unqCat.find(curCat) == unqCat.end()){\n if(dupl.size() == 0)break; \n //although the k items are already int the bag but increasing the uniquness of the bag will have more positive impact on the eleg of the subseq as compared to decrease in profit by replacing the duplicate item with least profit in the bag which will be present at the end of the bag since we sorted the items accroding to ascending order of the profit.\n int profDec = curProf - dupl[dupl.size()-1];\n dupl.pop_back();\n cout<<profDec<<endl;\n netProf += profDec;\n }\n unqCat.insert(curCat);\n int unqCats = unqCat.size();\n eleg = max(eleg, netProf + 1L * unqCats * unqCats);\n }\n return eleg; \n }\n};\n```\nJava\n```\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n Arrays.sort(items, (a, b)->b[0]-a[0]);\n Set<Integer> unqCat = new HashSet<>();\n List<Integer> dupl = new ArrayList<>();\n long eleg = 0;\n long netProf = 0;\n for(int indx = 0; indx<items.length; indx++){\n int curProf = items[indx][0], curCat = items[indx][1];\n if(indx < k){\n if(unqCat.contains(curCat)){\n dupl.add(curProf);\n }\n netProf += curProf;\n }else if(!unqCat.contains(curCat)){\n if(dupl.size() == 0)break; \n //although the k items are already int the bag but increasing the uniquness of the bag will have more positive impact on the eleg of the subseq as compared to decrease in profit by replacing the duplicate item with least profit in the bag which will be present at the end of the bag since we sorted the items accroding to ascending order of the profit.\n int profDec = curProf - dupl.remove(dupl.size()-1);\n // cout<<profDec<<endl;\n netProf += profDec;\n }\n unqCat.add(curCat);\n int unqCats = unqCat.size();\n eleg = Math.max(eleg, netProf + 1L * unqCats * unqCats);\n }\n return eleg; \n }\n}\n``` | 3 | 0 | ['C++'] | 1 |
maximum-elegance-of-a-k-length-subsequence | [C++/Python] Easy Greedy Solution | beats 100 percent | cpython-easy-greedy-solution-beats-100-p-w2hm | Intuition\n Describe your first thoughts on how to solve this problem. \nTry to optimise between these two\n- Use items with maximum profits\n- Use items of max | UltraSonic | NORMAL | 2023-08-06T05:12:36.624197+00:00 | 2023-08-06T10:30:53.654445+00:00 | 295 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTry to optimise between these two\n- Use items with maximum profits\n- Use items of maximum distinct categories\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStarted with adding all the items with maximum profits in the default elegance.\nUse minheap to Store all the duplicates used\n\nReplace duplicates and use items from categories which are yet to be used in greedy way using priority queue\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# C++ Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(),items.end(),greater<vector<int>>());\n \n int n=items.size(),i;\n vector<int> cat_used(n+1,0);\n \n priority_queue<int,vector<int>,greater<int>> duplicates_min;\n // Include first k items having maximum profit in elegance\n long long elegance=0;\n for(i=0;i<k;i++){\n elegance+=items[i][0];\n if(++cat_used[items[i][1]]>1){\n duplicates_min.push(items[i][0]);\n }\n }\n long long distinct_categories = (k-duplicates_min.size()); \n elegance+=distinct_categories*distinct_categories;\n \n long long ans=elegance;\n \n if(duplicates_min.empty())return ans;\n\n // Finding other categores which are not included in elegance and store maximum of them\n for(;i<n;i++){\n // first occurance of any category will be maximum of them. Since, items are sorted\n if(++cat_used[items[i][1]]==1){\n elegance += (long long)(items[i][0]-duplicates_min.top());\n // elegance += (distinct_categories + 1)^2 - distinct_categories^2\n elegance += (2*distinct_categories + 1); \n ans=max(ans,elegance);\n\n duplicates_min.pop();\n if(duplicates_min.empty())return ans;\n\n distinct_categories++;\n }\n }\n return ans;\n }\n};\n```\n# Python Code\n```\nimport heapq\n\nclass Solution:\n def findMaximumElegance(self, items, k):\n items.sort(reverse=True)\n\n n = len(items)\n cat_used = [0] * (n + 1)\n\n duplicates_min = []\n left_categories_max = []\n elegance = 0\n\n for i in range(k):\n elegance += items[i][0]\n cat_used[items[i][1]] += 1\n if cat_used[items[i][1]] > 1:\n heapq.heappush(duplicates_min, items[i][0])\n\n distinct_categories = k - len(duplicates_min)\n elegance += distinct_categories * distinct_categories\n\n ans = elegance\n\n if not duplicates_min:\n return ans\n\n i = k\n\n while i < n:\n if cat_used[items[i][1]] == 0:\n elegance += items[i][0] - heapq.heappop(duplicates_min)\n elegance += 2 * distinct_categories + 1\n ans = max(ans, elegance)\n\n if not duplicates_min:\n return ans\n\n distinct_categories += 1\n\n cat_used[items[i][1]] += 1\n i += 1\n\n return ans\n\n```\n\n\n | 3 | 0 | ['Greedy', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 1 |
maximum-elegance-of-a-k-length-subsequence | O(n) single pass for adding items and a single pass for removing items | on-single-pass-for-adding-items-and-a-si-9d25 | \nYou first greedily take all top profit values and get the minimal reasonable numCathegories. Then you increase the number of cathegories while removing the wo | Balwierz | NORMAL | 2023-08-17T17:22:25.500021+00:00 | 2023-08-17T17:22:25.500047+00:00 | 62 | false | \nYou first greedily take all top profit values and get the minimal reasonable numCathegories. Then you increase the number of cathegories while removing the worst (lowest) profits.\n\nOnly one structure `cat2count`: number of elements of a given cathegory in the current set.\n\n# Code\n```\ndef findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n items.sort(key = lambda x: -x[0])\n cat2count = defaultdict(lambda: 0)\n nCat = 0\n i = 0\n sumProfit = 0\n while k:\n k -= 1\n prof, cat = items[i]\n if cat not in cat2count:\n nCat += 1\n cat2count[cat] += 1\n sumProfit += prof\n i += 1\n ret = sumProfit + nCat**2\n j = i\n while j<len(items):\n prof, cat = items[j]\n if cat2count[cat] == 0:\n sumProfit += prof\n nCat += 1\n cat2count[cat] = 1\n while i>0:\n i -= 1\n if cat2count[items[i][1]] >= 2:\n sumProfit -= items[i][0]\n cat2count[items[i][1]] -= 1\n break\n if i == 0:\n return ret\n j += 1\n ret = max(ret, sumProfit + nCat**2)\n return ret\n``` | 2 | 0 | ['Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ Solution | c-solution-by-wizard_of_orz-y02p | Approach\n Describe your approach to solving the problem. \nSort all items according to profit from greatest to least.\n\nEnumerate the first K items, and if an | Wizard_of_Orz | NORMAL | 2023-08-06T16:53:22.585069+00:00 | 2023-08-08T01:57:46.703041+00:00 | 112 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nSort all items according to profit from greatest to least.\n\nEnumerate the first K items, and if an item\'s category has already appeared before, push the profit of that item into a priority queue.\n\nYou want to enumerate the rest of the items, and if an item has a category which hasn\'t been seen before, you want to replace the current item with an item in the priority queue, such that you have more distinct category. From the priority queue, you obtain the item with the least profit.\n\n# Complexity\n- Time complexity: $O(n\\log n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nusing ll = long long;\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(), items.end(), [](vector<int>& a, vector<int>& b) {\n return a[0] > b[0];\n });\n unordered_set<int> vis;\n priority_queue<int, vector<int>, greater<int> > heap;\n ll tot = 0;\n for(int i = 0;i<k;++i) {\n auto x = items[i];\n if(vis.count(x[1])) heap.push(x[0]);\n else vis.insert(x[1]);\n tot += x[0];\n }\n ll ans = tot + (ll)vis.size() * (ll)vis.size();\n for(int i = k;i<items.size();++i) if(!heap.empty()) {\n auto x = items[i];\n if(!vis.count(x[1])) {\n vis.insert(x[1]);\n tot -= heap.top(); heap.pop();\n tot += x[0];\n ans = max(ans, tot + (ll)vis.size() * (ll)vis.size());\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ Easy Solution || Sort by Profit || Commented code | c-easy-solution-sort-by-profit-commented-qw5m | Intuition\n Describe your first thoughts on how to solve this problem. \nSort items based on decreasing order of profits and take k elements which leads to maxi | tathagata_roy | NORMAL | 2023-08-06T08:03:53.129431+00:00 | 2023-08-06T08:05:00.202724+00:00 | 109 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSort items based on decreasing order of profits and take k elements which leads to maximize elegance.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n unordered_set<int> s;\n sort(items.begin(), items.end(), [](const vector<int> &A, const vector<int> &B){\n return A[0] > B[0];\n });\n\n long long curr = 0, max_res = 0;\n vector<int> duplicate;\n int n = items.size();\n\n for(int i = 0; i < n; i++)\n {\n if (i < k) // Set is still not reached it\'s capacity, we can take the element\n {\n if(s.find(items[i][1]) != s.end()) // we haven seen this category previously, thus updating duplicate array,\n // this dup array will ensure that if in some later stage we need to remove a \n // duplicate element, we remove the element that has lowest profit.\n // we may need to remove multiple such duplicates thus need to maintain an array\n // instead of some variable that holds last duplicate value.\n {\n duplicate.push_back(items[i][0]);\n }\n curr += items[i][0];\n s.insert(items[i][1]); \n }\n else // We already had reached k elements, we can\'t add a new element without removing an existing element.\n {\n \n if (s.find(items[i][1]) == s.end()) // This is an unique category element, we need to remove a duplicate element, whose profit\n // is the last element of duplicate array and calculate elegance\n {\n if (duplicate.size() == 0) // No duplicate element found, need to break from the for loop\n break;\n curr = curr - duplicate.back(); // Removing the profit from duplicate and subtracting from current profit\n duplicate.pop_back(); \n curr = curr + items[i][0]; // Adding item profit to the current profit.\n \n }\n s.insert(items[i][1]); // Adding the category to the set s.\n\n // But if the category is already been seeing then we can ignore the element\n // since we have an element with same category previously and this element can\'t contribute to maximize the ans.\n // And we can\'t take this element since we already has k elements in the resultant array. \n }\n\n //s.insert(items[i][1]);\n max_res = fmax(max_res, curr + s.size() * s.size()); // calculate elegance\n }\n\n return max_res;\n }\n};\n``` | 2 | 0 | ['Hash Table', 'Sorting', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | [C++] Sorting + Greedy Analysis | c-sorting-greedy-analysis-by-celonymire-ovws | Intuition\n Describe your first thoughts on how to solve this problem. \nWe have two dimensions to this problem at first:\n1. We want to maximize the profit\n2. | CelonyMire | NORMAL | 2023-08-06T04:41:19.975908+00:00 | 2023-08-06T04:41:19.975926+00:00 | 176 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe have two dimensions to this problem at first:\n1. We want to maximize the profit\n2. We want as many distinct categories as possible\n\nSo, we will look for a way to remove one of the dimensions. **We sort the array by non-increasing order of profits (we don\'t need to care about the category in sorting)**. We don\'t have to worry about maximizing the profit because we know **the items in the future will have less or worse than the worst profitable item we have right now.**\n\nWe will look forward to having more distinct categories as we go through the items we haven\'t seen right now.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe start with the first `k` items, so we want to setup the two variables `tot` and `distinct` to calculate the answer. A hash table can be used (in my code I just used a vector of sufficient size) to keep track of how many of the same category items we currently have.\n\nWe also need to keep track of the minimum profit item we have such that **there are other items in the same category**. This is because we want to keep the distinct categories we have **at least the same** (proof of why it works: we have sorted the array in non-increasing order, so if we remove one category, we\'d be adding back a category with a worse profit). We can use a heap to keep track of this.\n\nIMPORTANT: As we add new categories, **we might have a worse answer right now!** (but it may pay off later), so we ensure we don\'t decrease our best answer.\n\n# Complexity\n- Time complexity: $$O(n log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>> &items, int k) {\n int n = items.size();\n\n sort(items.begin(), items.end(), greater<vector<int>>{}); // greater profit to least\n\n long long tot = 0, distinct = 0;\n vector<int> cnt(n + 1);\n priority_queue<pair<int, int>> pq; // current minimum profit item\n for (int i = 0; i < k; i++) {\n tot += items[i][0];\n pq.push({-items[i][0], items[i][1]});\n if (!cnt[items[i][1]]++) distinct++; // first item of a new category\n }\n\n long long ans = tot + distinct * distinct;\n for (int i = k; i < n; i++) {\n if (cnt[items[i][1]]) continue;\n // we don\'t want to decrease the amount of distinct categories\n while (!pq.empty() && cnt[pq.top().second] == 1) pq.pop();\n // we don\'t have any item to replace without reducing distinct categories, break\n // this is correct since we have taken the biggest total profit\n if (pq.empty()) break;\n // update the variables to take the current item\n tot = tot + pq.top().first + items[i][0];\n distinct++;\n ans = max(ans, tot + distinct * distinct);\n cnt[pq.top().second]--;\n pq.pop();\n cnt[items[i][1]]++;\n pq.push({-items[i][0], items[i][1]});\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Hash Table', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 1 |
maximum-elegance-of-a-k-length-subsequence | [Python3] Sorting + Binary search on the number of different categories | python3-sorting-binary-search-on-the-num-5g71 | [Edit : This worked on all testcases during contest but @canlong found a testcase that my algorithm does not work on]\n\n# Intuition\nThe elegance as a function | Berthouille | NORMAL | 2023-08-06T04:07:59.149905+00:00 | 2023-08-08T18:38:15.367454+00:00 | 395 | false | [Edit : This worked on all testcases during contest but @canlong found a testcase that my algorithm does not work on]\n\n# Intuition\nThe elegance as a function of the number of distinct categories should look like a mountain with a peak.\n\n# Approach\nBinary search the number of distinct categories by checking the elegance of p distinct categories and p+1 distinct categories.\n\nFor each number of distinct category p, take the categories with the p highest values, then add the greatest values of these p categories that are not the maximum. If there are not enough elements to reach k elements, we need to take additional categories.\n\n# Complexity\n- Time complexity:\nO(n*log(n))\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n dico=defaultdict(list)\n for profit,category in items:\n dico[category].append(profit)\n categories=[]\n for category in dico:\n categories.append(sorted(dico[category]))\n categories.sort(key=lambda x:x[-1],reverse=True)\n def elegance (distinct):\n res=0\n rest=[]\n for i in range (distinct):\n res+=categories[i][-1]\n for j in range (len(categories[i])-1):\n rest.append(categories[i][j])\n rest.sort(reverse=True)\n if len(rest)<k-distinct:\n return -1\n return res+sum(rest[:k-distinct])+distinct**2\n l,r=1,min(len(categories)-1,k-1)\n mid=(l+r)//2\n while l<r:\n if elegance(mid+1)>elegance(mid) or elegance(mid+1)==-1:\n l=mid+1\n else:\n r=mid\n mid=(l+r)//2\n return max(elegance(mid),elegance(mid+1))\n \n \n \n \n``` | 2 | 0 | ['Binary Search', 'Sorting', 'Python3'] | 5 |
maximum-elegance-of-a-k-length-subsequence | 💥💥 Beats 100% on runtime and memory [EXPLAINED] | beats-100-on-runtime-and-memory-explaine-ccdh | IntuitionThe goal is to pick up to k items that maximize the sum of profits while ensuring we get the most distinct categories. If multiple items belong to the | r9n | NORMAL | 2025-01-07T03:27:31.762591+00:00 | 2025-01-07T03:27:31.762591+00:00 | 12 | false | # Intuition
The goal is to pick up to k items that maximize the sum of profits while ensuring we get the most distinct categories. If multiple items belong to the same category, only one of them can be included. To balance between maximizing the profit and respecting the category constraint, we must carefully manage how we add duplicate profits from the same category.
# Approach
I've started by sorting the items by profit in descending order, then loop through each item, adding its profit to a running total. We keep track of the categories we've seen using a HashSet<int>. If an item belongs to a category we’ve already seen, we add its profit to a list of duplicates (res). If we exceed the allowed number of items (k), we remove the smallest profit from res. When we have exactly k items, we calculate the current elegance, which is the sum of profits plus the square of the number of unique categories.
# Complexity
- Time complexity:
O(n log n) because we need to sort the items by profit. After sorting, we just loop through the items once, which is O(n).
- Space complexity:
O(n) because we use a HashSet<int> to track unique categories and a List<int> to store the duplicate profits for categories.
# Code
```csharp []
public class Solution
{
public long FindMaximumElegance(int[][] items, int k)
{
// Sort items in descending order of profit
Array.Sort(items, (a, b) => b[0].CompareTo(a[0]));
// Initialize variables
long runningVal = 0, maxVal = 0;
HashSet<int> seen = new HashSet<int>(); // To track unique categories
List<int> res = new List<int>(); // To hold profits of duplicate categories
// Iterate through sorted items
foreach (var item in items)
{
int profit = item[0];
int category = item[1];
// Add the current profit to running total
runningVal += profit;
// If category is unique, add it to seen set
if (!seen.Contains(category))
{
seen.Add(category);
}
else
{
// Otherwise, add profit to res (duplicate category profits)
res.Add(profit);
}
// Ensure we do not exceed k items
while (res.Count > 0 && res.Count + seen.Count > k)
{
runningVal -= res[res.Count - 1]; // Remove the last duplicate profit
res.RemoveAt(res.Count - 1); // Pop from the list
}
// Update max elegance when we have exactly k items
if (res.Count + seen.Count == k)
{
maxVal = Math.Max(maxVal, runningVal + (long)seen.Count * seen.Count);
}
}
return maxVal;
}
}
``` | 1 | 0 | ['Array', 'Hash Table', 'Dynamic Programming', 'Stack', 'Greedy', 'Breadth-First Search', 'Sorting', 'Heap (Priority Queue)', 'Quickselect', 'C#'] | 0 |
maximum-elegance-of-a-k-length-subsequence | JS solution | js-solution-by-aastha_b-hlua | \n\n# Code\n\n/**\n * @param {number[][]} items\n * @param {number} k\n * @return {number}\n */\nvar findMaximumElegance = function (items, k) {\n items.sort | aastha_b | NORMAL | 2024-05-18T09:43:41.487832+00:00 | 2024-05-18T09:43:41.487875+00:00 | 3 | false | \n\n# Code\n```\n/**\n * @param {number[][]} items\n * @param {number} k\n * @return {number}\n */\nvar findMaximumElegance = function (items, k) {\n items.sort((a, b) => b[0] - a[0]);\n let minHeap = new MinPriorityQueue();\n let catSet = new Set();\n let maxElegance = 0;\n let totalProfit = 0;\n\n for (let i = 0; i < items.length; i++) {\n if (i >= k) {\n if (catSet.has(items[i][1])) continue;\n if (minHeap.isEmpty()) break;\n totalProfit -= minHeap.dequeue().element;\n }\n\n if (catSet.has(items[i][1])) {\n minHeap.enqueue(items[i][0]);\n }\n catSet.add(items[i][1]);\n totalProfit += items[i][0];\n\n if (i >= k - 1) {\n maxElegance = Math.max(maxElegance, totalProfit + Math.pow(catSet.size, 2));\n }\n }\n\n return maxElegance;\n};\n``` | 1 | 0 | ['JavaScript'] | 1 |
maximum-elegance-of-a-k-length-subsequence | 100% beat || Priority Queue simple solution || O(n.logn) | 100-beat-priority-queue-simple-solution-xlc4c | \n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(n.logn)\n- Space complexity:\n Add your space complexity here, e.g. O(n) \nO | Priyanshu_pandey15 | NORMAL | 2024-05-17T05:31:06.910523+00:00 | 2024-05-17T05:31:06.910554+00:00 | 22 | false | \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n.logn)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass Solution {\n public long findMaximumElegance(int[][] arr, int k) {\n int n = arr.length;\n long s = 0, ms = 0, distinct = 0;\n int[] freq = new int[n + 1];\n Arrays.sort(arr, (a, b) -> b[0] - a[0]);\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);\n for (int i = 0; i < k; i++) {\n s += arr[i][0];\n if (freq[arr[i][1]] == 0)\n distinct++;\n if (freq[arr[i][1]] > 0)\n pq.add(new int[] { arr[i][0], arr[i][1] });\n freq[arr[i][1]]++;\n ms = Math.max(s + distinct * distinct, ms);\n\n }\n for (int i = k; i < n; i++) {\n if (freq[arr[i][1]] == 0) {\n if (!pq.isEmpty()) {\n s -= pq.poll()[0];\n s += arr[i][0];\n distinct++;\n freq[arr[i][1]]--;\n ms = Math.max(s + (distinct) * (distinct), ms);\n }\n }\n }\n return ms;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Just Sort and Take first K || Take remaining non Duplicates | just-sort-and-take-first-k-take-remainin-he19 | Java []\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n Arrays.sort(items, (a,b)-> b[0]-a[0]);\n Stack<Integer> d | Lil_ToeTurtle | NORMAL | 2023-09-20T04:11:28.705333+00:00 | 2023-09-20T04:11:28.705360+00:00 | 59 | false | ```Java []\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n Arrays.sort(items, (a,b)-> b[0]-a[0]);\n Stack<Integer> duplicates=new Stack<>();\n HashSet<Integer> selected_cats=new HashSet<>(k);\n\n long total_profit=0, elegance=0, size;\n for(int i=0;i<items.length;i++) {\n if(i<k){\n total_profit+=items[i][0];\n if(selected_cats.contains(items[i][1])) duplicates.add(items[i][0]);\n } else {\n if(duplicates.isEmpty()) break;\n if(!selected_cats.contains(items[i][1]))\n total_profit+=items[i][0]-duplicates.pop();\n }\n selected_cats.add(items[i][1]);\n elegance=Math.max(elegance, total_profit+(size=selected_cats.size())*size);\n }\n \n return elegance;\n }\n}\n```\nTC: $$O(N*logN)$$ | 1 | 0 | ['Stack', 'Ordered Set', 'Java'] | 1 |
maximum-elegance-of-a-k-length-subsequence | Heap/Priority_queue code with comments easy to understand. | heappriority_queue-code-with-comments-ea-71rq | Intuition\n\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code | vivekkumar1712 | NORMAL | 2023-08-14T13:13:48.236602+00:00 | 2023-08-14T13:13:48.236630+00:00 | 41 | false | # Intuition\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n n=len(items)\n items = sorted(items, key=lambda x : -x[0])\n t_sum=0\n d={}\n heap = []\n #calculating for top k (top k profit, same category element maybe there).\n for i in range(k): \n t_sum+=items[i][0]\n d[items[i][1]]=d.get(items[i][1],0)+1\n heapq.heappush(heap, items[i])\n ans=t_sum+len(d)**2\n\n for i in range(k,n):\n #a bigger profit element of same category is aready in heap.\n if items[i][1] in d: \n continue\n #pop element which is only element of that catgory so dont subtract it from t_sum because it may be part of soluition.\n while heap and d[heap[0][1]]==1:\n heappop(heap)\n #multiple elements belongs to same category so we can remove least of them and add new category element to increate profit.\n if heap:\n profit,idx=heapq.heappop(heap)\n d[idx]-=1\n t_sum+=items[i][0]-profit\n d[items[i][1]]=1\n ans=max(ans,t_sum+len(d)**2)\n # nothing to replace in heap so cant get beter then previous profits\n else: \n break\n return ans\n``` | 1 | 0 | ['Heap (Priority Queue)', 'Python3'] | 1 |
maximum-elegance-of-a-k-length-subsequence | Solution in Swift | solution-in-swift-by-sergeyleschev-hile | Intuition\nThe approach involves sorting the "items" array in descending order based on the "profiti". By selecting the first "k" items, we ensure that we attai | sergeyleschev | NORMAL | 2023-08-12T06:08:16.651514+00:00 | 2023-08-12T06:08:38.680680+00:00 | 3 | false | # Intuition\nThe approach involves sorting the "items" array in descending order based on the "profiti". By selecting the first "k" items, we ensure that we attain the highest possible "total_profit".\n\n# Approach\nUpon the selection of the initial "k" items, attention turns to the remaining "n - k" items. The viability of adding these items depends on whether they belong to an unexplored category (not yet in the "seen" set).\n\nGiven the restriction of maintaining a subsequence size of "k", a pivotal decision arises. To optimize the elegance metric, the algorithm strategically replaces an existing item with the lowest profit when that item shares its category with another.\n\nThis iterative refinement process continually adjusts the subsequence while upholding the imperative of category distinctiveness.\n\nThe final output of the function encapsulates the pinnacle of elegance attained through this intricate process\u2014a union of the cumulative impact of total profit and the singularity of categories.\n\n# Complexity\n- Time complexity: `O(nlogn)`\n- Space complexity: `O(n)`\n\n# Code\n```\nclass Solution {\n func findMaximumElegance(_ items: [[Int]], _ k: Int) -> Int {\n var items = items.sorted(by: { $0[0] > $1[0] })\n var res: Int64 = 0\n var cur: Int64 = 0\n var dup = [Int]()\n var seen = Set<Int>()\n\n for i in 0..<items.count {\n if i < k {\n if seen.contains(items[i][1]) {\n dup.append(items[i][0])\n }\n cur += Int64(items[i][0])\n } else if !seen.contains(items[i][1]) {\n if dup.isEmpty {\n break\n }\n cur += Int64(items[i][0] - dup.removeLast())\n }\n seen.insert(items[i][1])\n res = max(res, cur + Int64(seen.count) * Int64(seen.count))\n }\n\n return Int(res)\n }\n}\n``` | 1 | 0 | ['Swift'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Java | java-by-tetttet-drz9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | tetttet | NORMAL | 2023-08-09T13:42:26.970371+00:00 | 2023-08-09T13:42:26.970393+00:00 | 41 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long findMaximumElegance(int[][] A, int k) {\n Arrays.sort(A, (a, b) -> b[0] - a[0]);\n long res = 0, cur = 0;\n List<Integer> dup = new ArrayList<>();\n Set<Integer> seen = new HashSet<>();\n for (int i = 0; i < A.length; ++i) {\n if (i < k) {\n if (seen.contains(A[i][1])) {\n dup.add(A[i][0]);\n }\n cur += A[i][0];\n } else if (!seen.contains(A[i][1])) {\n if (dup.isEmpty()) break;\n cur += A[i][0] - dup.remove(dup.size() - 1);\n }\n seen.add(A[i][1]);\n res = Math.max(res, cur + 1L * seen.size() * seen.size());\n }\n return res;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Sorting + Traverse + Stack | O(n log n) time, O(n) space | sorting-traverse-stack-on-log-n-time-on-cfipu | Intuition\n Describe your first thoughts on how to solve this problem. \nTo find the maximum elegance of a subsequence with exactly k items, we need to maximize | xun6000 | NORMAL | 2023-08-08T01:35:10.454040+00:00 | 2023-08-08T01:35:10.454067+00:00 | 21 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo find the maximum elegance of a subsequence with exactly **k** items, we need to maximize both the profit and the distinct categories. We can start by selecting the items with the top **k** profits and then explore the possibility of replacing some items to maximize distinct categories.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Sorting**: Sort the items in descending order based on profit. This ensures that the first **k** elements have the top **k** profits.\n2. **Calculate Elegance for Top k Items**: Iterate through the first **k** items, calculating the total profit and identifying distinct categories.\n3. **Identify Replaceable Items**: If there are items with repeated categories, store them in **can_remove**. They might be replaced later to increase the number of distinct categories.\n4. **Explore Replacements**: Iterate from **k** to **n**, checking if any of the remaining items introduce a new category. If yes, replace the item with the smallest profit among the repeated categories. Update the elegance after each replacement.\n5. **Return Maximum Elegance**: Return the maximum elegance after exploring all possible replacements.\n\n# Complexity\n- Time complexity: $$O(n\\log{n})$$. The sorting step takes $$O(n\\log{n})$$ time, and the subsequent operations take $$O(n)$$ time, resulting in a total time complexity of $$O(n\\log{n})$$.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$. The space complexity mainly comes from the space used to store the sorted items and the replaceable items, resulting in $$O(n)$$ space complexity.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n n = len(items)\n items.sort(reverse=True, key=lambda x: x[0]) # Sorting by profit\n tot_profit = 0\n categories = set()\n distinct_categories = 0\n can_remove = []\n for i in range(k):\n tot_profit += items[i][0]\n if items[i][1] in categories:\n can_remove.append(items[i][0]) # The element can be replaced\n else:\n categories.add(items[i][1])\n distinct_categories += 1\n ans = tot_profit + distinct_categories ** 2\n if not can_remove:\n return ans\n \n # A list of results if we replace one of the items\n replace = [ans] * (k - distinct_categories + 1)\n added_categories = 0 \n for i in range(k, n):\n if items[i][1] not in categories: # If we introduce a new category\n added_categories += 1\n distinct_categories += 1\n categories.add(items[i][1])\n tot_profit = tot_profit - can_remove[-1] + items[i][0]\n can_remove.pop()\n ans = tot_profit + distinct_categories ** 2 \n replace[added_categories] = ans # Save the profit after replacement\n if not can_remove: # No way to replace\n break\n return max(replace) # Check the maximum elegance for different replacements.\n``` | 1 | 0 | ['Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Greedy Solution || C++ | greedy-solution-c-by-ayumsh-prtt | Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(n*log(n))\n- Space complexity:\n Add your space complexity here, e.g. O(n) \nO(n)\ | ayumsh | NORMAL | 2023-08-07T20:27:25.964789+00:00 | 2023-08-07T20:27:41.051712+00:00 | 22 | false | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*log(n))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(),items.end());\n reverse(items.begin(),items.end());\n long long sum=0;\n priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;\n map<int,int> mp;\n for(int i=0;i<k;i++)\n { \n sum+=items[i][0];\n mp[items[i][1]]++;\n pq.push({items[i][0],items[i][1]});\n }\n long long maxi=sum+pow(mp.size(),2);\n int index=k;\n while(!pq.empty()&&index<items.size())\n {\n if(mp[items[index][1]]==0)\n {\n int mini=pq.top().first;\n int s=pq.top().second;\n pq.pop();\n if(mp[s]>1)\n {\n mp[s]--;\n sum=sum-mini+items[index][0];\n maxi=max(maxi,(long long)(sum+pow(mp.size(),2)));\n mp[items[index][1]]++;\n index++;\n }\n }\n else\n {\n index++;\n }\n }\n return maxi;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Priority_Queue | C++ | Sorting | priority_queue-c-sorting-by-prabhu_2020-x2cq | Intuition\nWe need the highest profits with unique categories, but there can also be cases where having duplicate categories give us a higher elegance value if | prabhu_2020 | NORMAL | 2023-08-07T07:03:08.395461+00:00 | 2023-08-07T07:03:08.395489+00:00 | 373 | false | # Intuition\nWe need the highest profits with unique categories, but there can also be cases where having duplicate categories give us a higher elegance value if they have big enough profit.\n\n# Approach\nSort by descending order of profits, then take first k elements and after that keep replacing the smallest profit item with the next available highest profit item which has a unique category.\nAll this time, keep taking the maximum in each iteration after k elements.\n\n\n\nU will be having only one option after picking k elements i.e\ndelete from a category with multiple insatance so we try to replace one from the remaining instances.\n\n# Complexity\n- Time complexity: O(nlogn)\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) \n {\n //GREEDY SOLUTION\n unordered_map<int,int> mp;\n priority_queue<pair<int,int>,vector<pair<int,int>>, greater<pair<int,int>>> pq;\n sort(items.begin(),items.end(),greater<vector<int>>());\n long long ele=0,ans=0;\n for(int i=0;i<k;i++)\n {\n ele+=items[i][0];\n mp[items[i][1]]++;\n pq.push({items[i][0],items[i][1]});\n }\n ans=ele+mp.size()*mp.size();\n int n=items.size();\n for(int i=k;i<n && !pq.empty();i++)\n {\n // no need to introduce new category \n if(mp.count(items[i][1]))\n continue;\n // we dont want to delete a unique category\n auto it=pq.top();\n pq.pop();\n while(!pq.empty() && mp[it.second]==1)\n {\n it=pq.top();\n pq.pop();\n }\n if(pq.empty())\n break;\n // a category with multiple insatance so we try to replace one of them\n ele+=items[i][0]-it.first;\n mp[it.second]--;\n mp[items[i][1]]++;\n long long freq=mp.size()*mp.size();\n ans=max(ans,ele+freq);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Greedy', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Easy Java Solution | easy-java-solution-by-prakhar3agrwal-dcq5 | \nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n long ans = 0;\n Arrays.sort(items, (a,b)-> b[0]-a[0]);\n | prakhar3agrwal | NORMAL | 2023-08-06T15:34:04.444758+00:00 | 2023-08-06T15:34:04.444790+00:00 | 33 | false | ```\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n long ans = 0;\n Arrays.sort(items, (a,b)-> b[0]-a[0]);\n Set<Integer> categoriesSeen = new HashSet<>();\n List<Integer> duplicateCategories = new ArrayList<>();\n for(int i=0;i<k;i++){\n ans += items[i][0];\n int currCat = items[i][1];\n if(categoriesSeen.contains(currCat)){\n duplicateCategories.add(items[i][0]);\n }else{\n categoriesSeen.add(currCat);\n }\n }\n long curr = ans;\n ans += 1L*categoriesSeen.size()*categoriesSeen.size();\n \n int n = items.length;\n for(int i=k;i<n;i++){\n int currCat = items[i][1];\n int currVal = items[i][0];\n \n if(categoriesSeen.contains(currCat)){\n continue;\n }\n if(duplicateCategories.size()==0){\n break;\n }\n curr += currVal - duplicateCategories.get(duplicateCategories.size()-1);\n duplicateCategories.remove(duplicateCategories.size()-1);\n categoriesSeen.add(currCat);\n ans = Math.max(ans, curr + 1L*categoriesSeen.size()*categoriesSeen.size());\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Ordered Set', 'Java'] | 1 |
maximum-elegance-of-a-k-length-subsequence | C++| Priority Queue Solution | c-priority-queue-solution-by-coder3484-g4q7 | Code\n\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n = items.size();\n sort(items.beg | coder3484 | NORMAL | 2023-08-06T13:10:51.597592+00:00 | 2023-08-06T13:10:51.597616+00:00 | 40 | false | # Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n = items.size();\n sort(items.begin(), items.end(), greater<vector<int>>{}); // greater profit to least\n\n long long distinct = 0, total = 0;\n vector<int> count(n+1, 0);\n priority_queue<pair<int, int>> pq;\n\n for(int i=0;i<k;i++) {\n total += items[i][0];\n pq.push({-items[i][0], items[i][1]});\n if(!count[items[i][1]]++) distinct++;\n }\n long long ans = total + (distinct * distinct);\n for(int i=k;i<n;i++) {\n if(count[items[i][1]]) continue;\n while(!pq.empty() and count[pq.top().second] == 1) pq.pop();\n if(pq.empty()) break; // we have top k profits\n\n total += (items[i][0] + pq.top().first);\n distinct++;\n ans = max(ans, total + (distinct * distinct));\n count[pq.top().second]--;\n pq.pop();\n count[items[i][1]]++;\n pq.push({-items[i][0], items[i][1]});\n }\n return ans;\n }\n};\n\n``` | 1 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Counting', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | ✅C++ Intuitive solution || ✍️Commented code || | c-intuitive-solution-commented-code-by-j-weet | \n# Code\n\nclass Solution {\npublic:\n bool static cmp(vector<int> &v1,vector<int> &v2){\n return v1[0]>v2[0];\n }\n \n long long findMaximu | JainWinn | NORMAL | 2023-08-06T04:53:19.536365+00:00 | 2023-08-06T04:53:19.536382+00:00 | 247 | false | \n# Code\n```\nclass Solution {\npublic:\n bool static cmp(vector<int> &v1,vector<int> &v2){\n return v1[0]>v2[0];\n }\n \n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n=items.size();\n\n //stores initially taken items\n priority_queue<pair<long long,long long>> pq;\n\n //keeps track of number of categories\n unordered_map<long long,long long> mp;\n\n // sorting array\n sort(items.begin(),items.end(),cmp);\n\n long long ans=0;\n\n //pushing first k items\n for(int i=0 ; i<k ; i++){\n ans+=items[i][0];\n pq.push({-items[i][0],i});\n mp[items[i][1]]++;\n }\n //initial res\n long long res=ans+(long long)mp.size()*(long long)mp.size();\n\n //checking for leftover items if it gives a better result\n int ptr=k;\n while(ptr<n && !pq.empty()){\n //if item category already exists then continue\n if(mp[items[ptr][1]]>0){\n ptr++;\n continue;\n }\n int curr=pq.top().second;\n pq.pop();\n //we cannot remove item if removing item removes existence of a category\n if(mp[items[curr][1]]==1){\n continue;\n }\n\n //we get a new category \n ans+=items[ptr][0]-items[curr][0];\n --mp[items[curr][1]];\n ++mp[items[ptr][1]];\n res=max(res,ans+(long long)mp.size()*(long long)mp.size());\n }\n return res;\n }\n};\n``` | 1 | 0 | ['Sorting', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Python, Hash Table, Sorting with comments | python-hash-table-sorting-with-comments-s32ss | Intuition\nWe separate each item according to their categories.\nWe separete the largest of each category to their own list.\nWe sort the lists to find the smal | FransV | NORMAL | 2023-08-06T04:23:45.078072+00:00 | 2023-08-06T04:23:45.078090+00:00 | 96 | false | # Intuition\nWe separate each item according to their categories.\nWe separete the largest of each category to their own list.\nWe sort the lists to find the smallest items of each list\nWe compare the smallest values of each list to each other removing the smaller until we are left with k items. \nIn these comparisons the unique list will get a \'bonus\' to represent the change in number of categories.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: (O)nlogn\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:(O)n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import defaultdict\n\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n \n #Store items according to their categories\n store = defaultdict(list) \n for val, category in items:\n store[category].append(val)\n \n #Separate largest item of each category from the rest\n unique = []\n double = [] \n for lista in store.values():\n lista.sort()\n unique.append(lista.pop())\n double += lista\n \n #Delete smallest items until we are left with k items\n unique = sorted(unique, reverse=True)[:k]\n double = sorted(double, reverse=True)[:k-1] \n while len(unique) + len(double) > k:\n if double[-1] < unique[-1] + len(unique) ** 2 - (len(unique) - 1) ** 2:\n double.pop()\n else:\n unique.pop()\n \n return sum(unique) + sum(double) + len(unique) ** 2\n\n``` | 1 | 0 | ['Hash Table', 'Greedy', 'Sorting', 'Python3'] | 1 |
maximum-elegance-of-a-k-length-subsequence | Explained Greedy | Clean Code | 19ms | explained-greedy-clean-code-19ms-by-ivan-xwnu | IntuitionBalance between maximizing profit and distinct category count by first prioritizing unique categories, then swapping low-profit unique items with high- | ivangnilomedov | NORMAL | 2025-03-29T14:14:54.153478+00:00 | 2025-03-29T14:14:54.153478+00:00 | 3 | false | # Intuition
Balance between maximizing profit and distinct category count by first prioritizing unique categories, then swapping low-profit unique items with high-profit duplicates.
# Approach
1. **Sort items by profit** (descending) to prioritize high-value items
2. **First phase**: Greedily select items with distinct categories to maximize the distinct_categories² term
- Keep track of used positions, categories, total profit, and distinct category count
3. **Second phase**: Optimize by swapping
- Add high-profit items with duplicate categories to reach k items
- Calculate elegance after each addition
- Remove the lowest-profit distinct category item to make room for more swaps
- Repeat until no more beneficial swaps can be made
4. **Key insight**: Sometimes replacing a low-profit unique category item with a high-profit duplicate can increase overall elegance, despite reducing distinct_categories²
# Complexity
- Time complexity: **O(N log N)**
- Dominated by sorting operation
- The two-phase algorithm runs in O(N) time
# Code
```cpp []
class Solution {
public:
long long findMaximumElegance(vector<vector<int>>& items, int k) {
const int N = items.size();
vector<pair<long long, int>> prof_cat(N);
::transform(items.begin(), items.end(), prof_cat.begin(),
[](const auto& pc) { return make_pair(pc[0], pc[1] - 1); });
// Greedy approach:
::sort(prof_cat.begin(), prof_cat.end(), ::greater<pair<long long, int>>());
vector<bool> pos2used(N);
vector<bool> cat2used(N);
// First phase: Greedily take items with distinct categories
int small_dist_end = 0;
int used_count = 0;
long long sum_profit = 0;
for (; small_dist_end < N && used_count < k; ++small_dist_end) {
if (!cat2used[prof_cat[small_dist_end].second]) {
cat2used[prof_cat[small_dist_end].second] = true;
++used_count;
pos2used[small_dist_end] = true;
sum_profit += prof_cat[small_dist_end].first;
}
}
long long distinct_count = used_count;
long long res = sum_profit + distinct_count * distinct_count;
// Second phase: Try to improve by swapping
// Key insight: We can replace low-profit distinct-category items with
// high-profit duplicate-category items to potentially increase elegance
for (int big_dupl_beg = 0; big_dupl_beg < small_dist_end && small_dist_end > 0; ) {
// Add high-profit items with duplicate categories until we reach k items
for (; big_dupl_beg < small_dist_end && used_count < k; ++big_dupl_beg) {
if (!pos2used[big_dupl_beg]) {
pos2used[big_dupl_beg] = true;
++used_count;
sum_profit += prof_cat[big_dupl_beg].first;
}
}
res = max(res, sum_profit + distinct_count * distinct_count);
// Try removing one lowest-profit distinct-category item
// This frees up space to add another high-profit duplicate-category item
for (--small_dist_end; small_dist_end > big_dupl_beg; --small_dist_end) {
if (pos2used[small_dist_end]) {
pos2used[small_dist_end] = false;
--used_count;
sum_profit -= prof_cat[small_dist_end].first;
--distinct_count;
break;
}
}
}
return res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Python (Simple Maths) | python-simple-maths-by-rnotappl-st1z | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2024-11-28T06:54:20.619042+00:00 | 2024-11-28T06:54:20.619076+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def findMaximumElegance(self, items, k):\n items.sort(reverse = True)\n\n res, seen, max_val, running_val = [], set(), 0, 0\n\n for p,c in items:\n running_val += p\n\n if c not in seen:\n seen.add(c)\n else:\n res.append(p)\n\n while res and len(res) + len(seen) > k:\n running_val -= res.pop()\n\n if len(res) + len(seen) == k:\n max_val = max(max_val,running_val + len(seen)**2)\n\n return max_val\n\n\n\n\n\n\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Sort-greedy-two pointer solution | sort-greedy-two-pointer-solution-by-w100-jjn9 | Intuition\n Describe your first thoughts on how to solve this problem. \nFirst idea was to use a DP approach in O(n^2). Fortunately, by checking the constraints | w100roger | NORMAL | 2024-10-26T09:07:39.627319+00:00 | 2024-10-26T09:07:39.627351+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst idea was to use a DP approach in $$O(n^2)$$. Fortunately, by checking the constraints I hinted at the fact that this might not work and a greedy approach might be more interesting.\nIt is clear that if a number is maximal and its category is not in the solution then we must select it. The issue arises when a number left in our list is maximal but its category has already been selected.\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI iterate over my max_heap and if the element I\'m checking is of a new category I add it to solution, otherwise I save it on a second list (maximal_only).\n\nIf I have selected fewer elements than k, I add the highest values in our maximal list.\n\n\nNext we iterate over our solution and max array and see how many elements we should remove from our solution.\nThis step is a two pointer approach, we will remove from the end of the solution and add from the front of our maximal_values.\n\nAt each step \'removing\' (check code) I compute the gain of removing the smallest value in our solution and adding the highest value in our maximal_values array.\nSuch gain can be computed as:\n$$max\\_num - (min\\_num + 2\\cdot(variety-removing-1) + 1)$$\nTo keep track changes in variety affecting our solution we use this simple equality:\n$$n^2 - (n-1)^2 = n^2 - n^2 - 2n - 1 = -2n - 1$$\n\nWe save which removing index gives the maximal gain and compute the solution as\n```\nsum(solution) + variety^2 + max_gain + sum(maximal_only[:i])\n```\nwhere taken is our set of different values in the solution and i = k - len(taken).\n# Complexity\n- Time complexity:\n$$O(n \\log n)$$ The cost of sorting.\n- Space complexity:\n$$ O(n) $$ The cost of saving our n values.\n\n# Code\n```python []\nclass Solution(object):\n def findMaximumElegance(self, items, k):\n """\n :type items: List[List[int]]\n :type k: int\n :rtype: int\n """\n profits = {}\n taken = set()\n max_values = []\n\n for profit, category in items:\n if category not in profits:\n profits[category] = [-profit]\n else:\n heapq.heappush(profits[category], -profit)\n heapq.heappush(max_values, (-profit, category))\n \n solution = []\n maximal_only = []\n res = 0\n t = k\n while max_values and t > 0:\n prof, cat = max_values[0]\n prof = - prof\n if cat not in taken:\n t -= 1\n taken.add(cat)\n solution.append(prof)\n else:\n maximal_only.append(prof)\n heapq.heappop(max_values)\n\n i = k - len(taken)\n variety = len(taken)\n removing = 0\n gain = 0\n max_rem, max_gain = 0, 0\n n = len(solution)\n\n while i+removing < len(maximal_only):\n gain += maximal_only[i+removing] - (2*(variety-removing-1) + 1 + solution[n-removing-1])\n removing += 1\n if gain > max_gain:\n max_gain = gain\n max_rem = removing\n t -= 1\n \n return sum(solution) + variety**2 + max_gain + sum(maximal_only[:i])\n\n\n\n``` | 0 | 0 | ['Python'] | 0 |
maximum-elegance-of-a-k-length-subsequence | weird sol but works | weird-sol-but-works-by-anikets2002-ecuv | \n\n# Code\ncpp []\nclass Solution {\npublic:\n\n\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n unordered_set<int> cats;\n | anikets2002 | NORMAL | 2024-10-05T13:59:26.143143+00:00 | 2024-10-05T13:59:26.143166+00:00 | 2 | false | \n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n unordered_set<int> cats;\n multimap<int, int, greater<int>> mp;\n for(auto &x : items)\n {\n mp.insert({x[0], x[1]});\n cats.insert(x[1]);\n }\n int cat_len = cats.size();\n int tempk = k;\n auto it = mp.begin();\n unordered_map<int, int> seen, cnt;\n int cycle = 1;\n multiset<pair<long long, int>, greater<pair<long long, int>>> curr_set;\n bool flag = false;\n while(tempk > 0)\n {\n if(seen[it->second] && !flag)\n {\n auto check = next(it);\n if(check == mp.end())\n {\n it = mp.begin();\n flag = true;\n }\n else it = check;\n continue;\n }\n seen[it->second] = 1;\n curr_set.insert({it->first, it->second});\n cnt[it->second]++;\n it = mp.erase(it);\n if(it == mp.end()){\n flag = true;\n it = mp.begin();\n }\n tempk--;\n }\n\n long long curr_sum = 0;\n for(auto x : curr_set)curr_sum += x.first;\n long long len = min((long long)cat_len , (long long)k);\n long long res = curr_sum + len * len;\n\n if(mp.size() == 0)return res;\n it = mp.begin();\n while(len > 0 && cnt[it->second] != 0 && cnt[it->second] < k && it != mp.end())\n {\n if(--cnt[prev(curr_set.end())->second] == 0)len--;\n curr_sum = curr_sum - prev(curr_set.end())->first + it->first;\n res = max(res, curr_sum + len * len);\n curr_set.erase(prev(curr_set.end())); \n it = mp.erase(it);\n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Swift: Beats 100% || TC - O(n * log n) || SC - O(n) | swift-beats-100-tc-on-log-n-sc-on-by-ash-b37a | Approach\n1. Arrange items by profits in decreasing order.\n2. Sum k most profitable items in sorted array.\n3. After kth item check if we have visited any dupl | ashish-badak | NORMAL | 2024-08-30T17:43:02.682443+00:00 | 2024-08-30T17:43:02.682470+00:00 | 0 | false | # Approach\n1. Arrange items by profits in decreasing order.\n2. Sum `k` most profitable items in sorted array.\n3. After `k`th item check if we have visited any duplicate category. If no then we have already visited `k` most profitable items with unique categories. We have found our answer.\n4. If we have visited duplicate categories, then remove least profitable item from duplicate category and current item\'s profit. Then recalculate answer.\n\n# Complexity\n- Time complexity: O(n * log n)\n- Space complexity: O(n)\n\n# Code\n```swift []\nclass Solution {\n func findMaximumElegance(_ items: [[Int]], _ k: Int) -> Int {\n // Sort by profit in decreasing order\n var sortedItems = items.sorted { $0[0] > $1[0] }\n\n var seenCategories: Set<Int> = []\n var duplicateCategoryProfits: [Int] = []\n var currentElegance: Int = 0\n var maxElegance: Int = 0\n\n for (i, item) in sortedItems.enumerated() {\n if i < k { // we have not yet visited minimim k most profitable items, so add them\n\n if seenCategories.contains(item[1]) {\n // we encountered item category from previously visited category\n duplicateCategoryProfits.append(item[0])\n }\n\n currentElegance += item[0]\n } else {\n if duplicateCategoryProfits.isEmpty {\n // we have visited k most profitable items with unique categories\n // following items will yield lower profits so no need to calculate more\n break\n }\n\n if !seenCategories.contains(item[1]) {\n // remove minimum profit from duplicate category\n // as we already sorted the array in decreasing profit\n // minimum one will be last added item;\n currentElegance -= duplicateCategoryProfits.removeLast()\n\n // and then add current item\'s profit\n currentElegance += item[0]\n }\n }\n\n // mark category as visited\n seenCategories.insert(item[1])\n maxElegance = max(\n maxElegance,\n currentElegance + (seenCategories.count * seenCategories.count)\n )\n }\n\n return maxElegance\n }\n}\n``` | 0 | 0 | ['Array', 'Hash Table', 'Swift', 'Sorting'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Simple Hash Table Solution | simple-hash-table-solution-by-rajatktanw-b8ru | Intuition\n Describe your first thoughts on how to solve this problem. \nDp won\'t work with O(n^2) so choose greedy\nMaximize profit and distinct categories\n\ | rajatktanwar | NORMAL | 2024-07-01T07:02:02.971308+00:00 | 2024-07-01T07:02:02.971342+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDp won\'t work with $$O(n^2)$$ so choose greedy\nMaximize profit and distinct categories\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst maximize profit by selecting k max-profit elements, then check if elegance can be maximized by removing max-profit element of same category (within k elements) and including a profit with new category.\n\nYou may keep track of recurring categories and their elements.\n\nSquare of distinct category may overpower maxprofit so you have to check till the end.\n\n# Complexity\n- Time complexity: $$O(nlog n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic: \n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n=items.size();\n long long sum=0;\n unordered_map<int,vector<int>>store;\n\n sort(items.begin(),items.end());\n reverse(items.begin(),items.end());\n\n //maximize profit\n for(int i=0;i<k;i++){\n sum+=items[i][0];\n store[items[i][1]].push_back(i);\n }\n\n //distinct categories\n long long count=store.size();\n\n if(k==n){\n return sum+(count*count);\n }\n\n //to compare new elegance by including distinct category\n int i=k-1,j=k;\n long long tempsum=sum;\n int newcount=count;\n\n //traverse till end\n while(i>=0){\n if(store[items[i][1]].size()==1){\n i--;\n }\n else{\n tempsum-=items[i][0];\n\n //find distinct category\n while(j<n&&store.find(items[j][1])!=store.end()){\n j++;\n }\n if(j==n){\n return sum+(count*count);\n }\n\n //calculate new elegance\n tempsum+=items[j][0];\n newcount+=1;\n\n store[items[j][1]].push_back(j);\n store[items[i][1]].pop_back(); \n j++;i--; \n\n if(tempsum+(newcount*newcount)<=sum+(count*count)){\n //if new elegance is still less than previous\n continue;\n }\n else{\n //new elegance is greater\n sum=tempsum;\n count=newcount; \n }\n }\n \n } \n\n return sum+(count*count); \n }\n};\n``` | 0 | 0 | ['Hash Table', 'Greedy', 'Sorting', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Warning | Don't watch this | 😓 | warning-dont-watch-this-by-anas10005-3gqy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Anas10005 | NORMAL | 2024-06-16T17:04:53.216839+00:00 | 2024-06-16T17:05:51.112621+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:$$O(n*log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.util.*;\n\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n \n int[][] pairs = new int[items.length][2];\n \n // Transform items into pairs with (category, profit)\n for (int i = 0; i < items.length; i++) {\n pairs[i][0] = items[i][1];\n pairs[i][1] = items[i][0];\n }\n \n // Sort pairs by profit in descending order\n Arrays.sort(pairs, (p1, p2) -> p2[1] - p1[1]);\n\n long maxRes = -(long)1e9;\n\n // TreeMap to maintain pairs of (category, profit) with their frequencies, sorted by profit, then category\n TreeMap<int[], Integer> maxProfits = new TreeMap<>((a, b) -> {\n if (a[1] != b[1]) return Integer.compare(a[1], b[1]);\n return Integer.compare(a[0], b[0]);\n });\n\n // Map to store a PriorityQueue of profits for each category\n Map<Integer, PriorityQueue<Integer>> catProfits = new HashMap<>();\n long res = 0;\n Set<Integer> distinctCats = new HashSet<>();\n\n for (int i = 0; i < pairs.length; i++) {\n int[] pair = pairs[i];\n int cat = pair[0];\n int profit = pair[1];\n\n if (distinctCats.size() == k) break;\n\n if (i < k) {\n res += profit;\n distinctCats.add(cat);\n maxRes = Math.max(maxRes, res + (long)distinctCats.size() * distinctCats.size());\n \n } else {\n if (!distinctCats.contains(cat)) {\n\n Map.Entry<int[], Integer> minPairEntry = maxProfits.firstEntry();\n int[] minPair = minPairEntry.getKey();\n int removedCat = minPair[0];\n int removedProfit = minPair[1];\n if (minPairEntry.getValue() == 1) {\n maxProfits.pollFirstEntry();\n } else {\n maxProfits.put(minPair, minPairEntry.getValue() - 1);\n }\n \n distinctCats.add(cat);\n\n res = res - removedProfit + profit;\n maxRes = Math.max(maxRes, res + (long)distinctCats.size() * distinctCats.size());\n\n PriorityQueue<Integer> pq = catProfits.get(removedCat);\n pq.poll();\n if (pq.size() == 1) {\n int remainingProfit = pq.peek();\n maxProfits.put(new int[]{removedCat, remainingProfit}, maxProfits.getOrDefault(new int[]{removedCat, remainingProfit}, 0) - 1);\n if (maxProfits.get(new int[]{removedCat, remainingProfit}) == 0) {\n maxProfits.remove(new int[]{removedCat, remainingProfit});\n }\n }\n catProfits.put(removedCat, pq);\n }\n }\n \n if (i < k || !distinctCats.contains(cat)) {\n PriorityQueue<Integer> pq = catProfits.getOrDefault(cat, new PriorityQueue<>());\n pq.offer(profit);\n catProfits.put(cat, pq);\n PriorityQueue<Integer> updatedPq = catProfits.get(cat);\n \n if (updatedPq.size() == 1) continue;\n\n if (updatedPq.size() == 2) {\n int p1 = updatedPq.poll();\n int p2 = updatedPq.poll();\n maxProfits.put(new int[]{cat, p1}, maxProfits.getOrDefault(new int[]{cat, p1}, 0) + 1);\n maxProfits.put(new int[]{cat, p2}, maxProfits.getOrDefault(new int[]{cat, p2}, 0) + 1);\n updatedPq.offer(p1);\n updatedPq.offer(p2);\n catProfits.put(cat, updatedPq);\n } else {\n maxProfits.put(new int[]{cat, profit}, maxProfits.getOrDefault(new int[]{cat, profit}, 0) + 1);\n }\n }\n }\n\n return maxRes;\n }\n}\n``` | 0 | 0 | ['Hash Table', 'Ordered Map', 'Heap (Priority Queue)', 'Java'] | 0 |
maximum-elegance-of-a-k-length-subsequence | c++ solution | c-solution-by-dilipsuthar60-2r3x | \nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& item, int k) {\n long long ans=0;\n int size=item.size();\n | dilipsuthar17 | NORMAL | 2024-06-15T17:18:58.904371+00:00 | 2024-06-15T17:18:58.904392+00:00 | 2 | false | ```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& item, int k) {\n long long ans=0;\n int size=item.size();\n sort(item.begin(),item.end(),[&](auto &a,auto &b){return a[0]>b[0];});\n unordered_set<int>seen;\n vector<int>duplicateProfit;\n long long profit=0;\n int index=0;\n for(auto &it:item)\n {\n int currentProfit=it[0];\n int currentCategory=it[1];\n if(index++<k){\n if(seen.find(currentCategory)!=seen.end()){\n duplicateProfit.push_back(currentProfit);\n }\n profit+=currentProfit;\n }\n else if (seen.find(currentCategory)==seen.end()){\n if(duplicateProfit.size()==0) return ans;\n profit+=currentProfit-duplicateProfit.back();\n duplicateProfit.pop_back();\n }\n seen.insert(currentCategory);\n long long distint=seen.size()*seen.size();\n ans=max(ans,profit+distint);\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Easy Solution | | Using C++ | easy-solution-using-c-by-arbaz_nitp-ssi4 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Arbaz_nitp | NORMAL | 2024-06-15T09:33:06.975839+00:00 | 2024-06-15T09:33:06.975869+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.rbegin(),items.rend());\n ll n=items.size(),temp=0,ans=0;\n unordered_map<int,int> m;\n for(int i=0;i<k;i++){\n m[items[i][1]]++;\n temp+=items[i][0];\n }\n ll size=m.size(),left=k-1;\n ans=max(ans,temp+(size*size));\n for(int i=k;i<n;i++){\n if(m.count(items[i][1])==0){\n while(left>=0){\n if(m[items[left][1]]>1){\n m[items[left][1]]--;\n m[items[i][1]]++;\n temp-=items[left][0];\n temp+=items[i][0];\n ll o=m.size();\n ans=max(ans,temp+(o*o));\n left--;\n break;\n }\n left--;\n }\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | java solution with time complexity:O(n.logn) Space complexity:O(n) | java-solution-with-time-complexityonlogn-wqih | class Solution {\n public long findMaximumElegance(int[][] arr, int k) {\n int n = arr.length;\n long s = 0, ms = 0, distinct = 0;\n int | sumanth_gonal | NORMAL | 2024-06-15T09:00:02.304468+00:00 | 2024-06-15T09:00:02.304505+00:00 | 0 | false | class Solution {\n public long findMaximumElegance(int[][] arr, int k) {\n int n = arr.length;\n long s = 0, ms = 0, distinct = 0;\n int[] freq = new int[n + 1];\n Arrays.sort(arr, (a, b) -> b[0] - a[0]);\n PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);\n for (int i = 0; i < k; i++) {\n s += arr[i][0];\n if (freq[arr[i][1]] == 0)\n distinct++;\n if (freq[arr[i][1]] > 0)\n pq.add(new int[] { arr[i][0], arr[i][1] });\n freq[arr[i][1]]++;\n ms = Math.max(s + distinct * distinct, ms);\n\n }\n for (int i = k; i < n; i++) {\n if (freq[arr[i][1]] == 0) {\n if (!pq.isEmpty()) {\n s -= pq.poll()[0];\n s += arr[i][0];\n distinct++;\n freq[arr[i][1]]--;\n ms = Math.max(s + (distinct) * (distinct), ms);\n }\n }\n }\n return ms;\n }\n} | 0 | 0 | [] | 0 |
maximum-elegance-of-a-k-length-subsequence | Easy to understand c++ | easy-to-understand-c-by-mahakaal89-2i3w | Intuition\n Describe your first thoughts on how to solve this problem. \nfirst maximum then max no of distinct catagory.\n\n# Approach\n Describe your approach | Mahakaal89 | NORMAL | 2024-06-15T03:53:56.584588+00:00 | 2024-06-15T03:53:56.584615+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfirst maximum then max no of distinct catagory.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.first calculate k max profitable item.and if duplicate catagory found store it in a vector;\n\n2.then traverse if catagory not found then calculate elegance with new profit and after substracting, pop-back() duplicate vector .\n3.if catagory found then countinue because you have already max ele.\n4.if duplicate vector empty return the answer\n \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(NlogN)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(k)\n\n# Code\n```\n bool cmp(vector<int>&a,vector<int>&b){\n return a[0]>b[0];\n }\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(),items.end(),cmp);\n int n=items.size();\n vector<int>dup;\n set<int>s;\n long long totalpro=0;\n for(int i=0;i<k;i++){\n totalpro+=items[i][0];\n if(s.find(items[i][1])!=s.end()) dup.push_back(items[i][0]);\n s.insert(items[i][1]);\n }\n long long ele=totalpro+(s.size()*s.size());\n for(int i=k;i<n;i++){\n if(s.find(items[i][1])!=s.end()) continue;\n else{\n if(!dup.size()) break;\n totalpro-=dup[dup.size()-1];\n dup.pop_back();\n totalpro+=items[i][0];\n s.insert(items[i][1]);\n long long curr=totalpro+(s.size()*s.size());\n ele=max(ele,curr);\n }\n } \n return ele; \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ greedy | c-greedy-by-wufengxuan1230-hviy | \nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(), items.end(), [&](const vector<i | wufengxuan1230 | NORMAL | 2024-06-13T14:55:28.009717+00:00 | 2024-06-13T14:55:28.009784+00:00 | 2 | false | ```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(), items.end(), [&](const vector<int>& a, const vector<int>& b) {\n return a[0] > b[0];\n });\n\n unordered_set<int> m;\n stack<int> s;\n long long maxElegance = 0, sum = 0;\n for (int i = 0; i < items.size(); ++i) {\n auto profit = items[i][0], category = items[i][1];\n if (i < k) {\n sum += profit;\n if (!m.insert(category).second) {\n s.push(i);\n }\n maxElegance = sum + m.size() * m.size();\n } else if (!m.count(category) && !s.empty()) { \n auto p = items[s.top()][0], c = items[s.top()][1];\n long long e = sum - p + profit + (m.size() + 1) * (m.size() + 1);\n s.pop();\n sum = sum - p + profit;\n maxElegance = max(e, maxElegance);\n m.insert(category);\n }\n }\n return maxElegance;\n }\n};\n``` | 0 | 0 | [] | 0 |
maximum-elegance-of-a-k-length-subsequence | Hash and qsort to sovle this issue | hash-and-qsort-to-sovle-this-issue-by-sq-g6y9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | squall1207 | NORMAL | 2024-06-13T14:43:18.193494+00:00 | 2024-06-13T14:43:18.193524+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nint myCmp(const void *p1, const void *p2) {\n int *a = *(int **)p1;\n int *b = *(int **)p2;\n return b[0] - a[0];\n}\n\ntypedef struct {\n int key;\n int val;\n UT_hash_handle hh;\n} hash_t;\n\nhash_t *findhash(hash_t **obj, int key) {\n hash_t *tmp = NULL;\n HASH_FIND_INT(*obj, &key, tmp);\n return tmp;\n}\n\nvoid addhash(hash_t **obj, int key, int val) {\n hash_t *tmp = findhash(obj, key);\n if(tmp == NULL) {\n tmp = malloc(sizeof(hash_t));\n tmp->key = key;\n tmp->val = val;\n HASH_ADD_INT(*obj, key, tmp);\n } else {\n tmp->val = val;\n }\n}\n\nint gethash(hash_t **obj, int key, int defaultVal) {\n hash_t *tmp = findhash(obj, key);\n if(tmp == NULL) {\n return defaultVal;\n }\n return tmp->val;\n}\n\nvoid freehash(hash_t **obj) {\n hash_t *cur = NULL, *next = NULL;\n HASH_ITER(hh, *obj, cur, next) {\n HASH_DEL(*obj, cur);\n free(cur);\n }\n}\n\nlong long findMaximumElegance(int** items, int itemsSize, int* itemsColSize, int k){\n int n = itemsSize;\n hash_t *obj = NULL;\n long long ans = 0, total_profit = 0;\n qsort(items, n, sizeof(int *), myCmp); //\u5229\u6DA6\u4ECE\u5927\u5230\u5C0F\u6392\u5217\n int stack[n];\n int top = 0, val = 0;\n long long len = 0;\n\n for(int i = 0; i < n; i++) {\n int profit = items[i][0], category = items[i][1];\n if(i < k) {\n total_profit += profit; \n val = gethash(&obj, category, 0);\n if(val == 0) {\n addhash(&obj, category, profit);\n len++;\n } else { \n stack[top++] = profit;\n }\n\n } else if((top > 0) && (0 == gethash(&obj, category, 0))) { \n addhash(&obj, category, profit);\n len++;\n total_profit += profit - stack[--top]; \n }\n ans = fmax(ans, total_profit + len * len);\n }\n\n freehash(&obj);\n free(obj);\n\n return ans;\n}\n\n\n\n``` | 0 | 0 | ['Hash Table', 'C', 'Sorting'] | 0 |
maximum-elegance-of-a-k-length-subsequence | 🔥 Go Solution | Greedy | Beat 100% | With Explanation🔥 | go-solution-greedy-beat-100-with-explana-eeca | Intuition\nGreedy with regret.\n\n# Approach\nSort the items by profit in descending order and initially select the first k projects. Then, scan through the rem | ConstantineJin | NORMAL | 2024-06-13T03:24:16.335767+00:00 | 2024-06-13T03:24:16.335807+00:00 | 2 | false | # Intuition\nGreedy with regret.\n\n# Approach\nSort the `items` by profit in descending order and initially select the first `k` projects. Then, scan through the remaining `items` linearly and assess whether selecting `items[i]` can increase the value of `ans`. During the process, we need to deselect a previously selected item. The optimal strategy is to deselect the item from a category that contains more than one item, as this action will increase the count of `len(categories)` even though it may reduce the `totalProfit`.\n\n# Complexity\n- Time complexity: $$O(n\\text{log}n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nfunc findMaximumElegance(items [][]int, k int) int64 {\n\tslices.SortFunc(items, func(a, b []int) int { return b[0] - a[0] })\n\tvar totalProfit int\n\tvisited := make(map[int]bool)\n\tvar duplicate []int\n\tfor _, item := range items[:k] {\n\t\tprofit, category := item[0], item[1]\n\t\ttotalProfit += profit\n\t\tif !visited[category] {\n\t\t\tvisited[category] = true\n\t\t} else {\n\t\t\tduplicate = append(duplicate, profit)\n\t\t}\n\t}\n\tans := totalProfit + len(visited)*len(visited)\n\tfor _, item := range items[k:] {\n\t\tprofit, category := item[0], item[1]\n\t\tif len(duplicate) > 0 && !visited[category] {\n\t\t\tvisited[category] = true\n\t\t\ttotalProfit += profit - duplicate[(len(duplicate)-1)]\n\t\t\tduplicate = duplicate[:(len(duplicate) - 1)]\n\t\t}\n\t\tans = max(ans, totalProfit+len(visited)*len(visited))\n\t}\n\treturn int64(ans)\n}\n``` | 0 | 0 | ['Hash Table', 'Stack', 'Greedy', 'Sorting', 'Go'] | 0 |
maximum-elegance-of-a-k-length-subsequence | greedy Sorting + heap + hashtable python3 | greedy-sorting-heap-hashtable-python3-by-1w8p | \n\n# Code\n\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n items.sort(reverse = True)\n items = [t | MaxOrgus | NORMAL | 2024-06-01T15:11:58.895506+00:00 | 2024-06-01T15:11:58.895534+00:00 | 6 | false | \n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n items.sort(reverse = True)\n items = [tuple(t) for t in items]\n freq = {}\n heap = []\n sumpf = 0\n categories = 0\n res = 0\n for i,(p,c) in enumerate(items):\n if i<k:\n if c not in freq:\n freq[c] = 0\n categories += 1\n freq[c] += 1\n sumpf += p\n if freq[c] > 1:\n heapq.heappush(heap,(p,c))\n if i >= k:\n if c in freq: continue\n while heap and freq[heap[0][1]] <= 1:\n heapq.heappop(heap)\n if heap:\n topp,topc = heapq.heappop(heap)\n freq[topc] -= 1\n freq[c] = 1\n categories += 1\n sumpf += p - topp\n if i >= k-1:\n res = max(res,sumpf+categories*categories)\n return res\n\n\n\n\n\n \n \n \n \n``` | 0 | 0 | ['Hash Table', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | JS MinHeap Clean Solution | js-minheap-clean-solution-by-nanlyn-bs9w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | nanlyn | NORMAL | 2024-05-01T17:37:36.064412+00:00 | 2024-05-01T17:37:36.064436+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[][]} items\n * @param {number} k\n * @return {number}\n */\nvar findMaximumElegance = function (items, k) {\n items.sort((a, b) => b[0] - a[0]);\n let minHeap = new MinPriorityQueue();\n let catSet = new Set();\n let maxElegance = 0;\n let totalProfit = 0;\n\n for (let i = 0; i < items.length; i++) {\n if (i >= k) {\n if (catSet.has(items[i][1])) continue;\n if (minHeap.isEmpty()) break;\n totalProfit -= minHeap.dequeue().element;\n }\n\n if (catSet.has(items[i][1])) {\n minHeap.enqueue(items[i][0]);\n }\n catSet.add(items[i][1]);\n totalProfit += items[i][0];\n\n if (i >= k - 1) {\n maxElegance = Math.max(maxElegance, totalProfit + Math.pow(catSet.size, 2));\n }\n }\n\n return maxElegance;\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Greedy | Stack | No Heap or Priority Queue | greedy-stack-no-heap-or-priority-queue-b-edpw | Approach\nSort by profit from largest to smallest, and take the top k items. If there is already k different categories, we find the best possible profit. Other | popzkk | NORMAL | 2024-04-20T00:58:35.911956+00:00 | 2024-04-20T00:58:35.911981+00:00 | 6 | false | # Approach\nSort by profit from largest to smallest, and take the top $$k$$ items. If there is already $$k$$ different categories, we find the best possible profit. Otherwise, we try to increase the number of categories and record each new total profit as we increase the catrgories.\n\nEvery time when we have a candidate item to swap with some existing item, we want to swap with the item that does not decrease the number of categories. In other words, we want to maintain a collection of items that are not the only item for their categories.\n\nWe don\'t have to use priority queue or heap. Because we have sorted the items beforehand. We only need to know whether this item is free to remove.\n\nFor each category, the first item within that category will never be swapped out. This is important property guaranteed by sorting beforehand.\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n items.sort(reverse=True)\n n = len(items)\n # This stack contains all the items that we should feel\n # free to discard when we want to have a new category.\n stk = []\n s = 0\n # Whether this category has appeared before.\n # When true, that means another item with higher profit\n # and within the same category has been considered.\n visited = [False] * (n + 1)\n diff = 0\n for i in range(k):\n p, c = items[i]\n s += p\n # For each category, first visit == biggest profit\n # within that caregory, and we never discard that item.\n if visited[c]: stk.append(p)\n else: diff += 1\n visited[c] = True\n if diff == k: return s + k * k\n ans = s + diff * diff\n i = k\n while True:\n # Find the next new category.\n while i < n and visited[items[i][1]]:\n i += 1\n if i == n: break\n p, c = items[i]\n visited[c] = True\n s += p - stk.pop()\n diff += 1\n ans = max(ans, s + diff * diff)\n if diff == k: break\n return ans\n``` | 0 | 0 | ['Array', 'Stack', 'Greedy', 'Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Try all but update incrementally | try-all-but-update-incrementally-by-lamb-yxv3 | Intuition\n- Sort items with deceasing profit, and choose the first k items.\n- This gives baseline answer ans, with # categories = c\n- Increase c step by step | lambdacode-dev | NORMAL | 2024-04-11T21:01:06.790523+00:00 | 2024-04-11T21:01:06.790550+00:00 | 0 | false | # Intuition\n- Sort `items` with deceasing profit, and choose the first `k` items.\n- This gives baseline answer `ans`, with `# categories` = `c`\n- Increase `c` step by step up to `c = k`, while updating `ans` incrementally.\n- To do incremental update, replace the worst that is already in `ans` and **replaceable**, by next best in the sorted `items` array, using a min heap.\n \n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n = items.size();\n sort(items.begin(), items.end(), [](auto const& a, auto const& b) { return a[0] > b[0]; });\n long long ans = 0;\n unordered_map<int, int> count;\n struct ValId {\n int val, id;\n bool operator<(ValId const& that) const {\n return val > that.val;\n }\n };\n priority_queue<ValId> pq;\n int i = 0;\n for(; i < k; ++i) {\n int val = items[i][0];\n int id = items[i][1]-1;\n ans += val;\n count[id]++;\n pq.emplace(val, id);\n }\n int sz = count.size();\n long long sz2 = static_cast<long long>(sz) * sz;\n ans += sz2;\n //cout << ans << endl;\n for(long long prev = ans; i < n && sz < k; ++i) {\n //cout << "prev " << prev << \'\\t\';\n long long cur = prev;\n int val = items[i][0];\n int id = items[i][1]-1;\n //cout << "try " << i << " val " << val << " id " << id+1 << " sz " << sz << \'\\t\';\n if(count.contains(id)) continue;\n count[id]++;\n cur -= sz2;\n sz++;\n sz2 = static_cast<long long>(sz) * sz;\n cur += sz2 + val;\n while(! pq.empty() ) {\n auto [val, id] = pq.top();\n //cout << "heap top " << val << ", " << id+1 << \'\\t\';\n pq.pop();\n if(count[id] > 1) {\n cur -= val;\n count[id]--;\n break;\n }\n }\n //cout << "cur " << cur << endl;\n if(cur > ans)\n ans = cur;\n prev = cur;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Python - WITH & WITHOUT A HEAP ✅ | python-with-without-a-heap-by-itsarvindh-56le | The elegance of a subsequence is given as - \n\n\ttotal_profit + distinct_categories^2\n\t\nThis means, for the maximum elegance, we need to maximize not just t | itsarvindhere | NORMAL | 2024-02-09T11:36:58.654115+00:00 | 2024-02-09T11:42:29.232798+00:00 | 4 | false | The elegance of a subsequence is given as - \n\n\ttotal_profit + distinct_categories^2\n\t\nThis means, for the maximum elegance, we need to maximize not just the profit, but also the distinct categories. Ofcourse it is not always possible that both are maximized at the same time so we want to balance them such that the elegance value we get is the maximum.\n\nWhen we have such problems, we can try to maximize one part first, and then try to work on the other part. Here, we will do the same. We can try to maximize the total_profit first. And that is pretty simple. We just need to sort the items by their "profit" values in decreasing order, and then pick the first "k" items for our subsequence. That will be the "k" length subsequence with highest "total_profit".\n\nNow that our profit is maximized, we want to increase the "distinct_categories" in our subsequence. \n\nLet\'s take an example to understand how that will be done.\n\n\tSuppose, we have items = [[3,2],[5,1],[10,1]], k = 2\n\t\n\tWhen we sort items in decreasing order of their profit, we get - \n\t\n\t\titems = [[10,1], [5,1], [3,2]]\n\t\t\n\tSo, the "k" length subsequence with highest total_profit is [[10,1],[5,1]]\n\t\n\tAnd for this, elegance is (10+5) * 1 => 16\n\t\n\tNow, how can we increase this elegance further?\n\t\n\tWe have already maximized "total_profit".\n\t\n\tSo, the other term we can play around with is "distinct_categories"\n\t\n\tCurrently, the distinct_categories is "1"\n\t\n\tBut, what if, we can remove one item and replace it with an item with a different category?\n\t\n\tThat will increase the distinct_categories count to "2"\n\t\n\tWe have [3,2] and we can replace either [10,1] or [5,1]\n\t\n\tWe can replace some item because [3,2] has a category "2" \n\twhich is not already present in the current subsequence.\n\t\n\tIt means, addin this item will increase the distinct_categories.\n\t\n\tNow, which one to replace among [10,1] and [5,1]?\n\t\n\tOfcourse it is the one that has a lower profit value because remember that,\n\twe want to balance "total_profit" and "distinct_categories"\n\t\n\tSo, we replace and the new subsequence we get is [[10,1],[3,2]]\n\tThe new elegance is (10 + 3) + (2*2) => 17\n\t\n\tAnd this is higher than previous elegance value.\n\t\n\tSo, the maximum elegance possible is "17".\n\t\nAnd this is the idea.\n\n# **1. USING A MIN HEAP**\n\nWe first get the "k" length subsequence with the highest total_profit value. When we create that subsequence, if current item has a category that is already present in the subsequence, we also add that item to a minHeap which keeps all the candidates which can be replaced by other items in the range [k,n-1]. This minHeap will order them by their profit values from smallest to largest. So at any time, the item we will replace will always be the one having the smallest profit.\n\nAs we saw in above example, we could replace an item with [3,2] only because the category "2" is not already present in the subsequence. And that\'s the logic we also use in the code. We only do this replacement if the current item\'s category is not already present. And to keep track of this, we can use a Set. If current item\'s category is not present already, it means adding this new item will increase the distincts_count value and might also increase the elegance (not always the case).\n\nSo, we will update the elegance accordingly.\n\n\n```\ndef findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n \n # Length of the list\n n = len(items)\n \n # Sort the items by profit in decreasing order\n items.sort(reverse=True)\n \n # Get the first "k" items for the first subsequence\n # This will ensure that we have the "k" items with maximum profit\n # Also, to keep track of each category we can use a set\n # This will help us to check if a category is already present in current subsequence or not\n categories = set()\n \n # Total profit\n totalProfit = 0\n \n # A Min Heap to keep track of the items based on their profits from smallest to largest\n # This Min Heap will contain those items whose category occurs more than once in the "k" length subsequence\n # Since our motive is to also maximize distinct categories\n minHeap = []\n \n for i in range(k):\n \n # Update the profit so far\n totalProfit += items[i][0]\n \n # if this category already exists in the subsequence so far\n if items[i][1] in categories:\n \n # Put the item into the minHeap\n heappush(minHeap, items[i][0])\n \n # Add to the set\n categories.add(items[i][1])\n \n # Maximum Elegance\n # Initialize it with the current elegance\n maxElegance = totalProfit + (len(categories) ** 2)\n \n # Now, we go over the rest of the values\n for i in range(k,n):\n \n # If the minheap is empty, there is no item left to replace, so we can return the maxElegance here\n if not minHeap: return maxElegance\n \n # If current item has a category that is not already present in the current subsequence\n # Then, we can replace the item on top of the minHeap with this item\n # Since we have sorted the list by the profit initially\n # It also means current item is the item with highest profit among all items of its category\n if items[i][1] not in categories:\n \n # We can replace the item on top of minHeap with current item\n # Hence, pop the top of the minHeap\n top = heappop(minHeap)\n \n # If current item is added to the subsequence, what will be the new total profit\n newTotalProfit = totalProfit - top + items[i][0]\n \n # The count of distincts will increase by 1\n newDistinctCount = len(categories) + 1\n \n # So, what will be the new elegance\n newElegance = newTotalProfit + (newDistinctCount ** 2)\n \n # Add the current category to the set\n categories.add(items[i][1])\n \n # Update the total profit\n totalProfit = newTotalProfit\n\n # If new elegance is higher than maxElegance so far\n maxElegance = max(maxElegance, newElegance)\n \n # Return the maximum elegance\n return maxElegance\n```\n\n# **2. WITHOUT USING A MIN HEAP**\nSince we have already sorted the items by profit in decreasing order, it means, when we get the candidates that can be replaced, they will also be in a sorted order based on their profit values from highest to lowest. So, there is no need to use a Heap. Instead, we can use a simple list and at any time, the item that we should replace will always be at the end of this list.\n\n```\ndef findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n \n # Length of the list\n n = len(items)\n \n # Sort the items by profit in decreasing order\n items.sort(reverse=True)\n \n # Get the first "k" items for the first subsequence\n # This will ensure that we have the "k" items with maximum profit\n # Also, to keep track of each category we can use a set\n # This will help us to check if a category is already present in current subsequence or not\n categories = set()\n \n # Total profit\n totalProfit = 0\n \n # A simple list track of the items based on their profits from smallest to largest\n # There is no need to use a Heap because since the list is sorted based on profits already\n # The candidate list will also be sorted in decreasing order\n # So at any time, the best item to replace will be at the end of the list\n candidates = []\n \n for i in range(k):\n \n # Update the profit so far\n totalProfit += items[i][0]\n \n # if this category already exists in the subsequence so far\n if items[i][1] in categories:\n \n # Put the item into the candidates list\n candidates.append(items[i][0])\n \n # Add to the set\n categories.add(items[i][1])\n \n # Maximum Elegance\n # Initialize it with the current elegance\n maxElegance = totalProfit + (len(categories) ** 2)\n \n # Now, we go over the rest of the values\n for i in range(k,n):\n \n # If the candidates list is empty, there is no item left to replace, so we can return the maxElegance here\n if not candidates: return maxElegance\n \n # If current item has a category that is not already present in the current subsequence\n # Then, we can replace the item at the end of candidates list with this item\n # Since we have sorted the list by the profit initially\n # It also means current item is the item with highest profit among all items of its category\n if items[i][1] not in categories:\n \n # We can replace the item\n # Hence, pop the item at the end of candidates list\n top = candidates.pop()\n \n # If current item is added to the subsequence, what will be the new total profit\n newTotalProfit = totalProfit - top + items[i][0]\n \n # The count of distincts will increase by 1\n newDistinctCount = len(categories) + 1\n \n # So, what will be the new elegance\n newElegance = newTotalProfit + (newDistinctCount ** 2)\n \n # Add the current category to the set\n categories.add(items[i][1])\n \n # Update the total profit\n totalProfit = newTotalProfit\n\n # If new elegance is higher than maxElegance so far\n maxElegance = max(maxElegance, newElegance)\n \n # Return the maximum elegance\n return maxElegance\n``` | 0 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Ordered Set', 'Python'] | 0 |
maximum-elegance-of-a-k-length-subsequence | O(NlogN) greedy solution. | onlogn-greedy-solution-by-leeyongs-uut0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. Sort items by descen | leeyongs | NORMAL | 2024-01-20T18:14:14.691177+00:00 | 2024-01-20T18:14:14.691229+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort items by descending order of profit.\n2. Add top K items. As we add items, keep the minimum profit per category where it has more than one element (since throwing away this element doesn\'t affect the #category)\n3. After K iteration, if adding a new item can increase the number of categories, then do it. Throw away the min element, and add a new one.\n\nTo keep the elements per category -> Category : minHeap (in profit)\nTo keep the min element from all minimum profits in each category -> ordered_set (ascending order in profit).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution\n{\npublic:\n struct Element\n {\n int profit;\n int category;\n };\n long long findMaximumElegance(vector<vector<int>> &items, int k)\n {\n sort(items.begin(), items.end(), [](const vector<int> &a, const vector<int> &b)\n { return a[0] > b[0]; });\n long long ans = 0;\n long long profitSum = 0;\n unordered_map<int, priority_queue<int, vector<int>, greater<int>>> catToProfits; // min heap per cat.\n auto elemComp = [](const Element &a, const Element &b)\n {\n if (a.profit < b.profit)\n return true;\n if (a.profit == b.profit)\n return a.category < b.category;\n return false;\n };\n set<Element, decltype(elemComp)> minProfits(elemComp);\n int seqSize = 0;\n for (int i = 0; i < items.size(); i++) // O(N)\n {\n if (seqSize < k)\n {\n seqSize++;\n profitSum += items[i][0];\n if (catToProfits[items[i][1]].size() > 0)\n {\n Element curMin{catToProfits[items[i][1]].top(), items[i][1]};\n minProfits.erase(curMin); // if we already inserted min, than erase O(logK)\n catToProfits[items[i][1]].push(items[i][0]);\n minProfits.insert({items[i][0], items[i][1]}); // update min to new one. O(logK)\n }\n else\n {\n catToProfits[items[i][1]].push(items[i][0]); // add O(logK)\n }\n }\n else\n {\n // window full. Need to throw away one and add one.\n if (minProfits.empty())\n break; // optimal since we have one elem per category\n if (catToProfits.count(items[i][1]) > 0)\n continue; // cat already exists O(logK)\n\n Element victim = *minProfits.begin();\n minProfits.erase(minProfits.begin()); // erase from the set O(logK)\n catToProfits[victim.category].pop(); // victim gets erased O(logK)\n\n if (catToProfits[victim.category].size() >= 2) // update min\n minProfits.insert({catToProfits[victim.category].top(), victim.category}); // O(logK)\n\n catToProfits[items[i][1]].push(items[i][0]); // always a new one. O(logK)\n\n profitSum -= victim.profit;\n profitSum += items[i][0];\n }\n\n if (seqSize == k)\n ans = max(ans, profitSum + (long long)catToProfits.size() * (long long)catToProfits.size());\n }\n return ans;\n }\n};\n/*\n[[4,5],[4,2],[7,4],[2,3],[5,5],[5,3],[5,11],[6,4],[9,4],[1,7],[6,12],[8,10],[5,14],[8,4]]\n\n*/\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Simple intution based question | simple-intution-based-question-by-sunnyk-z6oa | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sunnykumarbr85 | NORMAL | 2024-01-16T10:57:21.204482+00:00 | 2024-01-16T10:57:21.204509+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) \n {\n Arrays.sort(items, (a,b) -> ( b[0]-a[0]));\n int n = items.length;\n HashSet<Integer> visitedCategory = new HashSet<>();\n ArrayList<Long> duplicatValue = new ArrayList<>();\n long ans = 0;\n\n for(int i=0; i<k; i++)\n {\n int currCat = items[i][1];\n long currVal = items[i][0];\n ans +=currVal;\n\n if(visitedCategory.contains(currCat))\n {\n duplicatValue.add(currVal);\n }\n else\n {\n visitedCategory.add(currCat);\n }\n } \n long curr = ans;\n ans = ans + 1L * visitedCategory.size()*visitedCategory.size();\n for(int i=k; i<n; i++)\n {\n int currCat = items[i][1];\n int currVal = items[i][0];\n\n if(duplicatValue.size()==0) break;\n if(!visitedCategory.contains(currCat))\n {\n visitedCategory.add(currCat);\n curr = curr + currVal - duplicatValue.remove(duplicatValue.size()-1);\n ans = Math.max(ans, curr + 1L * visitedCategory.size()*visitedCategory.size());\n }\n }\n return ans;\n }\n}\n``` | 0 | 0 | ['Sorting', 'Ordered Set', 'Java'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ | c-by-tinachien-uvo8 | \nusing LL = long long;\nusing PII = pair<LL, LL>;\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n s | TinaChien | NORMAL | 2023-12-09T09:31:11.735876+00:00 | 2023-12-09T09:31:11.735905+00:00 | 1 | false | ```\nusing LL = long long;\nusing PII = pair<LL, LL>;\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.rbegin(), items.rend());\n LL sum = 0;\n unordered_map<int, int>Map; //[category, count]\n for(int i = 0; i < k; i++){\n sum += items[i][0];\n Map[items[i][1]]++;\n }\n LL dist_cate = Map.size();\n LL ret = sum + dist_cate*dist_cate;\n cout << ret;\n priority_queue<PII, vector<PII>, greater<>>pq;\n for(int i = 0; i < k; i++){\n pq.push({items[i][0], items[i][1]});\n }\n for(int i = k; i < items.size(); i++){\n if(Map.find(items[i][1]) != Map.end())\n continue;\n while(!pq.empty()){\n auto [profit, category] = pq.top();\n pq.pop();\n if(Map[category] > 1){\n sum -= profit;\n sum += items[i][0];\n dist_cate++;\n Map[category]--;\n Map[items[i][1]]++;\n ret = max(ret, sum + dist_cate*dist_cate);\n break;\n }\n }\n }\n return ret;\n }\n};\n``` | 0 | 0 | [] | 0 |
maximum-elegance-of-a-k-length-subsequence | Solution in C | solution-in-c-by-liamtrudel2008-zony | Intuition\nInitially, one might consider using a dynamic programming approach to solve this problem, as it involves optimizing a certain value (elegance) across | liamtrudel2008 | NORMAL | 2023-11-18T23:24:08.569977+00:00 | 2023-11-18T23:24:08.569996+00:00 | 3 | false | # Intuition\nInitially, one might consider using a dynamic programming approach to solve this problem, as it involves optimizing a certain value (elegance) across a subset of elements (items). However, the key insight is that a greedy approach can be more efficient. We aim to maximize the sum of profits while also maximizing the number of distinct categories, which square in the elegance formula, thus amplifying their impact.\n\n# Approach\nThe solution begins by sorting the items array in non-increasing order based on profits. This ensures we are always considering the most profitable items first for our subsequence of size k. After selecting the initial k items, the algorithm keeps track of the categories using a count array and calculates the initial elegance.\n\nFor the remaining items, the algorithm checks if adding an item would introduce a new category. If so, it finds the least profitable item with a repeated category in the current selection to replace. This step is crucial as it attempts to balance between adding new categories and maximizing profit.\n\nAfter each potential replacement, the elegance is recalculated. The maximum elegance encountered during this process is updated and finally returned.\n# Complexity\n\n- Time complexity:\n\nThe sorting of the items contributes $$O(n \\log n)$$ to the time complexity. The subsequent iteration over the items for potential replacement is $$O(n \\cdot k)$$, where `n` is the total number of items and `k` is the size of the subsequence. Therefore, the total time complexity is $$O(n \\log n + n \\cdot k)$$.\n\n- Space complexity:\n\nThe space complexity is $$O(n)$$, which comes from the use of the `categoryCount` array that keeps track of the counts of categories. The size of this array is proportional to the number of items.\n\n# Code\n```\n#include <stdlib.h>\n#include <string.h>\n#include <limits.h>\n\nint compare(const void *a, const void *b) {\n int *itemA = *(int **)a;\n int *itemB = *(int **)b;\n return itemB[0] - itemA[0]; // Sorting in descending order of profit\n}\n\nlong long findMaximumElegance(int** items, int itemsSize, int* itemsColSize, int k) {\n qsort(items, itemsSize, sizeof(int *), compare);\n\n int categoryCount[itemsSize + 1];\n memset(categoryCount, 0, sizeof(categoryCount));\n\n long long totalProfit = 0;\n int distinctCategories = 0;\n\n // Initial candidate set\n for (int i = 0; i < k; ++i) {\n totalProfit += items[i][0];\n categoryCount[items[i][1]]++;\n if (categoryCount[items[i][1]] == 1) {\n distinctCategories++;\n }\n }\n\n long long maxElegance = totalProfit + (long long)distinctCategories * distinctCategories;\n\n // Iterate over the remaining items\n for (int i = k; i < itemsSize; ++i) {\n if (categoryCount[items[i][1]] == 0) {\n // Identify item to replace\n int minProfit = INT_MAX;\n int replaceIndex = -1;\n for (int j = 0; j < k; ++j) {\n if (categoryCount[items[j][1]] > 1 && items[j][0] < minProfit) {\n minProfit = items[j][0];\n replaceIndex = j;\n }\n }\n\n if (replaceIndex != -1) {\n // Replace item in the candidate set\n totalProfit = totalProfit - items[replaceIndex][0] + items[i][0];\n categoryCount[items[replaceIndex][1]]--;\n categoryCount[items[i][1]]++;\n items[replaceIndex] = items[i];\n\n // Update distinct categories count\n if (categoryCount[items[i][1]] == 1) {\n distinctCategories++;\n }\n\n // Calculate elegance\n long long currentElegance = totalProfit + (long long)distinctCategories * distinctCategories;\n maxElegance = maxElegance > currentElegance ? maxElegance : currentElegance;\n }\n }\n }\n\n return maxElegance;\n}\n\n``` | 0 | 0 | ['C'] | 0 |
maximum-elegance-of-a-k-length-subsequence | 2813. Maximum Elegance of a K-Length Subsequence | 2813-maximum-elegance-of-a-k-length-subs-51kq | ```\nclass Solution {\n public:\n long long findMaximumElegance(vector>& items, int k) {\n long long ans = 0;\n long long totalProfit = 0;\n // Store | abhirajgautam2 | NORMAL | 2023-11-01T13:22:37.170729+00:00 | 2023-11-01T13:22:37.170768+00:00 | 4 | false | ```\nclass Solution {\n public:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n long long ans = 0;\n long long totalProfit = 0;\n // Store seen categories.\n unordered_set<int> seenCategories;\n // Store duplicate profits decreasingly.\n stack<int> decreasingDuplicateProfits;\n\n ranges::sort(items, greater<>());\n\n for (int i = 0; i < k; i++) {\n const int profit = items[i][0];\n const int category = items[i][1];\n totalProfit += profit;\n if (seenCategories.count(category))\n decreasingDuplicateProfits.push(profit);\n else\n seenCategories.insert(category);\n }\n\n ans = totalProfit + 1LL * seenCategories.size() * seenCategories.size();\n\n for (int i = k; i < items.size(); ++i) {\n const int profit = items[i][0];\n const int category = items[i][1];\n if (!seenCategories.count(category) &&\n !decreasingDuplicateProfits.empty()) {\n // If this is a new category we haven\'t seen before, it\'s worth\n // considering taking it and replacing the one with the least profit\n // since it will increase the distinct_categories and potentially result\n // in a larger total_profit + distinct_categories^2.\n totalProfit -= decreasingDuplicateProfits.top(),\n decreasingDuplicateProfits.pop();\n totalProfit += profit;\n seenCategories.insert(category);\n ans = max(ans, static_cast<long long>(totalProfit +\n 1LL * seenCategories.size() *\n seenCategories.size()));\n }\n }\n\n return ans;\n }\n};\n | 0 | 0 | ['Hash Table'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Just a runnable solution | just-a-runnable-solution-by-ssrlive-st3w | \n\nimpl Solution {\n pub fn find_maximum_elegance(items: Vec<Vec<i32>>, k: i32) -> i64 {\n let mut items = items\n .iter()\n .m | ssrlive | NORMAL | 2023-10-17T08:51:40.228246+00:00 | 2023-10-17T09:07:01.634428+00:00 | 3 | false | \n```\nimpl Solution {\n pub fn find_maximum_elegance(items: Vec<Vec<i32>>, k: i32) -> i64 {\n let mut items = items\n .iter()\n .map(|v| v.iter().map(|&x| x as i64).collect::<Vec<_>>())\n .collect::<Vec<_>>();\n let k = k as usize;\n items.sort_unstable_by(|a, b| b[0].cmp(&a[0]));\n let mut vis = std::collections::HashSet::new();\n let mut heap = std::collections::BinaryHeap::new();\n let mut tot = 0;\n for item in items.iter().take(k) {\n if vis.contains(&item[1]) {\n heap.push(std::cmp::Reverse(item[0]));\n } else {\n vis.insert(item[1]);\n }\n tot += item[0];\n }\n let mut ans = tot + vis.len() as i64 * vis.len() as i64;\n for item in items.iter().skip(k) {\n if !heap.is_empty() && !vis.contains(&item[1]) {\n vis.insert(item[1]);\n tot -= heap.pop().unwrap().0;\n tot += item[0];\n ans = ans.max(tot + vis.len() as i64 * vis.len() as i64);\n }\n }\n ans\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
maximum-elegance-of-a-k-length-subsequence | GO || without priority_queue | go-without-priority_queue-by-mohaldarpra-c6pk | \n\nfunc max64(a, b int64) int64 {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\nfunc findMaximumElegance(items [][]int, k int) int64 {\n sort.Slice(items | mohaldarprakash | NORMAL | 2023-08-31T07:12:18.895827+00:00 | 2023-08-31T07:12:18.895849+00:00 | 2 | false | \n```\nfunc max64(a, b int64) int64 {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\nfunc findMaximumElegance(items [][]int, k int) int64 {\n sort.Slice(items, func (i,j int) bool{\n return items[i][0]>items[j][0]\n })\n\n mp := make(map[int]int)\n\n sum := int64(0)\n for i:=0; i<k; i++{\n sum += int64(items[i][0])\n mp[items[i][1]]++\n }\n\n different := len(mp)\n ans := sum + (int64(different)*int64(different))\n\n\n ItemsLeft := k-1 \n for i:= k; i<len(items); i++{\n if mp[items[i][1]] > 0 {\n continue\n }\n\n for ItemsLeft>=0 {\n smallestItem , smallestItemCat := items[ItemsLeft][0], items[ItemsLeft][1]\n ItemsLeft--;\n if mp[smallestItemCat] > 1{\n sum -= int64(smallestItem)\n sum += int64(items[i][0])\n\n mp[smallestItemCat]--\n mp[items[i][1]]++\n\n d := len(mp)\n ans = max64(ans, sum + (int64(d)*int64(d)))\n break\n }\n }\n }\n return ans\n}\n\n``` | 0 | 0 | ['Go'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Golang simple soluation | golang-simple-soluation-by-user8775po-u6fz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | user8775Po | NORMAL | 2023-08-29T17:52:04.382366+00:00 | 2023-08-29T17:52:04.382388+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nfunc findMaximumElegance(items [][]int, k int) int64 {\n\tsort.Slice(items, func(i, j int) bool {\n\t\treturn items[i][0] > items[j][0]\n\t})\n\tcat := make(map[int]int)\n\tsum := int64(0)\n\tfor i := 0; i < k; i++ {\n\t\tcat[items[i][1]]++\n\t\tsum += int64(items[i][0])\n\t}\n\tcats := len(cat)\n\tret := sum + int64(cats)*int64(cats)\n\t// \u521D\u59CB\u6700\u5927\u503C, \u627E\u51FAprofit\u6700\u5927\u7684k\u500B\u5143\u7D20\n\n\n\t// \u627E\u51FA\u6709\u6C92\u6709\u4E00\u7A2E\u7D44\u5408 \u53EF\u4EE5\u640D\u5931 profit\u4F46\u63DB\u5230\u66F4\u591A\u7684category\n\tp := k - 1\n\tfor i := k; i < len(items); i++ {\n\t\t// \u5F9Ek\u500B\u958B\u59CB\u5F80\u5F8C\u627E \u627E\u5230\u66F4\u5C0F\u7684profit\n\t\tif cat[items[i][1]] > 0 {\n\t\t\t// \u5982\u679C\u9019\u500Bcategory\u51FA\u73FE\u904E \u986F\u7136\u4E0D\u662F\u6211\u8981\u7684\n\t\t\tcontinue\n\t\t}\n\t\tfor p >= 0 {\n\t\t\t// k - 1 \u662F\u9078\u4E2D\u7684\u7D44\u5408\u88E1\u9762 profit\u6700\u5C0F\u7684 \u5F9E\u4ED6\u958B\u59CB\u770B\n\t\t\tremove := items[p]\n\t\t\tp--\n\t\t\trProfit, rCat := remove[0], remove[1]\n\t\t\tif cat[rCat] > 1 {\n\t\t\t\tsum -= int64(rProfit)\n\t\t\t\tsum += int64(items[i][0])\n\t\t\t\t// remove from cat\n\t\t\t\tcat[rCat]--\n\t\t\t\t// add to cat\n\t\t\t\tcat[items[i][1]]++\n\t\t\t\tcats++\n\t\t\t\t// update ret\n\t\t\t\tret = max64(ret, sum+int64(cats)*int64(cats))\n\t\t\t\tbreak\n\t\t\t}\n\t\t}\n\t}\n\n\treturn ret\n}\n\nfunc max64(a, b int64) int64 {\n\tif a > b {\n\t\treturn a\n\t}\n\treturn b\n}\n\n``` | 0 | 0 | ['Go'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Sorting + Greedy | sorting-greedy-by-dnitin28-5pgn | \n# Code\n\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& v, int k) {\n int n = v.size();\n sort(v.begin(), v. | gyrFalcon__ | NORMAL | 2023-08-28T05:42:58.681441+00:00 | 2023-08-28T05:42:58.681458+00:00 | 7 | false | \n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& v, int k) {\n int n = v.size();\n sort(v.begin(), v.end(), greater<vector<int>>());\n long long ans = 0, answer = 0;\n vector<int> duplicate;\n set<int> visited;\n for(int i=0;i<n;i++){\n if(i < k){\n ans += v[i][0];\n if(visited.find(v[i][1]) != visited.end()){\n duplicate.push_back(v[i][0]);\n }\n visited.insert(v[i][1]);\n }\n else{\n if(visited.find(v[i][1]) != visited.end()){\n continue;\n }\n else{\n if(((int)duplicate.size()) == 0){\n break;\n }\n ans -= ((duplicate.back()) - v[i][0]);\n duplicate.pop_back();\n visited.insert(v[i][1]);\n }\n }\n int sz = visited.size();\n answer = max(answer, ans + (1ll * sz * sz));\n }\n\n return answer;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | [C/C++/Python] Detailed description and comments. O(nlogn) time, O(n) space | ccpython-detailed-description-and-commen-6z8p | Intuition\nThe problem calls for picking the best of two disconnected values, the number of categories and the total of the profits. My immediate thought was th | christrompf | NORMAL | 2023-08-17T13:18:12.764872+00:00 | 2023-08-18T00:39:03.445191+00:00 | 13 | false | # Intuition\nThe problem calls for picking the best of two disconnected values, the number of categories and the total of the profits. My immediate thought was that starting at one extreme and working towards the other will produced the answer.\n\nStart with maximising the profits by selecting the _k_ most profitable as a base case. Then by definition, swapping out any item by a new item in a as yet unused category, will decrease the total profits, but increase the number of unique categories.\n\n# Approach\nCalculate the initial maximum profit state.\n* Sort _items_ from highest profit to lowest profit\n* Calculate the profits of the first _k_ items while also recording how many of those _k_ items are in each category.\n\nFrom here there is no point swapping one item for a later item unless a new category has been added. Thus the next step is to progressively find the least profitable item in our existing items from a category that has more than one item and swap it with the most profitable item in a new category. This will _decrease_ total profits, but _increase_ the total number of categories.\n\n# Complexity\n- Time complexity: $$O(nlog_2n)$$\n - $$O(nlog_2n)$$ for the sort\n - $$O(n)$$ trying to swap each unused item in\n\n- Space complexity: $$O(n)$$\n - $$O(n)$$ to hold a sorted copy of _items_\n - $$O(n)$$ to hold a count of items in each category.\n\n# Code\n``` python []\ndef findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n sort = sorted(items, key=lambda arr: arr[0], reverse=True)\n \n # Calculate the initial state using the k most profitable items\n curr = 0\n categories = dict()\n for item in sort[:k]:\n curr += item[0]\n if item[1] in categories:\n categories[item[1]] += 1\n else:\n categories[item[1]] = 1\n ret = curr + len(categories) ** 2\n\n # The only way to increase further than this is to increase the number of categories\n # as from above, any other item will have less profits. Thus only swapping an item\n # from a category which we have more than one item for, for an item in a new category\n # will increase the number of unique categories to offset the decrease in total profit.\n option_idx = k\n for item_idx in range(k - 1, 0, -1):\n if 1 == categories[sort[item_idx][1]]:\n # Only one item of this category, swapping it would not increase the number of categories\n continue\n categories[sort[item_idx][1]] -= 1\n\n # Find the first new category if there is one\n while option_idx < len(sort) and sort[option_idx][1] in categories:\n option_idx += 1\n\n if option_idx < len(sort):\n # Try swapping the new item with the least profitable\n curr += -sort[item_idx][0] + sort[option_idx][0]\n categories[sort[option_idx][1]] = 1\n ret = max(ret, curr + len(categories) ** 2)\n\n return ret\n```\n``` cpp []\nlong long findMaximumElegance(vector<vector<int>>& items, int k) {\n // Sort the items from highest profit to lowest\n std::vector<std::reference_wrapper<std::vector<int>>> sorted{std::begin(items), std::end(items)};\n std::sort(\n std::begin(sorted),\n std::end(sorted),\n [] (const std::vector<int>& lhs, const std::vector<int>& rhs) { return lhs[0] > rhs[0]; });\n\n // Calculate the initial state using the k most profitable items\n long long curr = 0;\n std::unordered_map<int, int> categories;\n for (int i = 0; i < k; ++i) {\n const std::vector<int>& item = sorted[i];\n curr += item[0];\n ++categories[item[1]];\n }\n long long ret = curr + categories.size() * categories.size();\n\n // The only way to increase further than this is to increase the number of categories\n // as from above, any other item will have less profits. Thus only swapping an item\n // from a category which we have more than one item for, for an item in a new category\n // will increase the number of unique categories to offset the decrease in total profit.\n auto option_idx = k;\n for (auto item_idx = k - 1; 0 < item_idx; --item_idx) {\n const std::vector<int>& item = sorted[item_idx];\n if (1 == categories[item[1]]) {\n // Only one item of this category, swapping it would not increase the number of categories\n continue;\n }\n --categories[item[1]];\n\n // Find the first new category if there is one\n while (option_idx < sorted.size() && categories.count(sorted[option_idx].get()[1])) {\n ++option_idx;\n }\n\n if (option_idx < sorted.size()) {\n // Try swapping the new item with the least profitable\n const std::vector<int>& option_item = sorted[option_idx++];\n curr += -item[0] + option_item[0];\n ++categories[option_item[1]];\n ret = std::max<long long>(ret, curr + categories.size() * categories.size());\n } \n }\n\n return ret;\n}\n```\n\n``` c []\nstruct category_hash {\n int category;\n int count; /* Number of items included with this category */\n UT_hash_handle hh;\n};\n\nstatic\nint pair_cmp(const void* l, const void* r) {\n const int* lhs = *(const int**) l;\n const int* rhs = *(const int**) r;\n return rhs[0] - lhs[0];\n}\n\nstatic\nlong long llmax(long long a, long long b) { return a > b ? a : b; }\n\nlong long findMaximumElegance(int** items, int itemsSize, int* itemsColSize, int k){\n /* Hashtable to hold a count of the number of items in use by each category */\n struct category_hash* table = NULL;\n struct category_hash entries[itemsSize];\n struct category_hash* pos = entries;\n\n /* Build a set of items sorted from highest profit to lowest */\n int* sorted[itemsSize];\n memcpy(sorted, items, itemsSize * sizeof(*items));\n qsort(sorted, itemsSize, sizeof(*sorted), &pair_cmp);\n\n /* Start by choosing all the highest profit items and building a set of the minimal number of categories */\n long long curr = 0;\n for (int i = 0; i < k; ++i) {\n curr += sorted[i][0];\n struct category_hash* entry;\n HASH_FIND_INT(table, &sorted[i][1], entry);\n if (!entry) {\n entry = pos++;\n entry->category = sorted[i][1];\n entry->count = 0;\n HASH_ADD_INT(table, category, entry);\n }\n ++entry->count;\n }\n\n long long categories = HASH_COUNT(table);\n long long ret = curr + categories * categories;\n\n /*\n The only way to increase further than this is to increase the number of categories\n as from above, any other item will have less profits. Thus only swapping an item\n from a category which we have more than one item for, for an item in a new catefory\n will increase the number of unique categories.\n */\n int idx = k;\n for (int i = k - 1; 0 < i; --i) {\n struct category_hash* entry;\n HASH_FIND_INT(table, &sorted[i][1], entry);\n if (1 == entry->count) {\n /* Only one item of this category, swapping it would not increase the number of categories */\n continue;\n }\n --entry->count;\n\n /* Find the first new category if there is one */\n while (idx < itemsSize) {\n HASH_FIND_INT(table, &sorted[idx][1], entry);\n if (entry) {\n ++idx;\n continue;\n }\n\n /* New category has been found, add it to the set of categories now */\n entry = pos++;\n entry->category = sorted[idx][1];\n entry->count = 1;\n HASH_ADD_INT(table, category, entry);\n break;\n }\n\n if (idx < itemsSize) {\n /* Try swapping the least profitable with our new choice */\n curr += -sorted[i][0] + sorted[idx][0];\n ++categories;\n ret = llmax(ret, curr + categories * categories);\n }\n }\n\n /* Destroy the hashtable and return the final result */\n HASH_CLEAR(hh, table);\n return ret;\n}\n```\n | 0 | 0 | ['C', 'Python', 'C++', 'Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Greedy Algorithm || C++ | greedy-algorithm-c-by-igloo11-zpqp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nGreedy Algorithm\n\n# C | Igloo11 | NORMAL | 2023-08-17T08:26:34.510082+00:00 | 2023-08-17T08:26:34.510105+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy Algorithm\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ntypedef long long ll;\n\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n ll ans = 0;\n \n sort(items.begin(), items.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] > b[0];\n });\n\n set<int> uniq_keys;\n stack<int> seen;\n \n \n ll total = 0;\n for(int i = 0; i < k; i++) {\n total += items[i][0];\n if(uniq_keys.contains(items[i][1]))\n seen.push(items[i][0]);\n uniq_keys.insert(items[i][1]);\n }\n \n ans = total + 1LL * uniq_keys.size() * uniq_keys.size();\n \n for(int i = k; i < items.size(); i++) {\n int p = items[i][0];\n int key = items[i][1];\n \n if(!uniq_keys.contains(key) && seen.size() > 0) {\n total -= seen.top();\n seen.pop();\n total += p;\n uniq_keys.insert(key);\n }\n \n ll tmp = total + 1LL * uniq_keys.size() * uniq_keys.size();\n ans = max(ans, tmp);\n }\n \n return ans;\n }\n};\n``` | 0 | 0 | ['Hash Table', 'Stack', 'Greedy', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Not elegant, but effective | not-elegant-but-effective-by-fredrick_li-5pbs | Code\n\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n cat = {}\n hp = []\n for val,c in item | Fredrick_LI | NORMAL | 2023-08-14T16:10:29.888565+00:00 | 2023-08-14T16:10:29.888593+00:00 | 5 | false | # Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n cat = {}\n hp = []\n for val,c in items:\n if c not in cat:\n cat[c] = val\n elif cat[c] < val:\n heappush(hp,-cat[c])\n cat[c] = val\n else:\n heappush(hp,-val)\n lis = sorted(cat.values(),reverse = True)\n l = min(len(lis),k)\n ans = sum(lis[:k]) + l ** 2\n for _ in range(len(lis), k):\n ans -= heappop(hp)\n res = ans\n while l and hp:\n l -= 1\n a, b = lis[l], -heappop(hp)\n if a < b:\n ans += b - a - 2 * l - 1\n res = max(res,ans)\n else:\n break\n return res\n \n\n\n\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | set + deque solution c++ | set-deque-solution-c-by-dan_zhixu-nbqn | Intuition\nThe elegance is a condition on both profit and category, but to simplify the problem, we can first get the maximum subsequence on profit, and improve | dan_zhixu | NORMAL | 2023-08-13T16:10:08.724628+00:00 | 2023-08-13T16:10:08.724646+00:00 | 5 | false | # Intuition\nThe elegance is a condition on both profit and category, but to simplify the problem, we can first get the maximum subsequence on profit, and improve it on the category. \n\n# Approach\n1. Sort the items by profit. So the first k items are the subsequence with maximum profits. \n2. If the first k items\' categories are all distinct, then problem is solved; however we need to check the rest items, replace the smallest duplicated items with new items on new category. \n3. I use a set to store the existing categories, and a deque to maintain the duplicates. Since the items are sorted on descending order, we should pop front items. \n4. If the deque becomes empty, it means we don\'t have duplicates. Then we break the loop. If the new item\'s category already exists, we ignore this item. \n\n# Complexity\n- Time complexity:\nO(Nlog(N))\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n\n std::sort(items.begin(), items.end(), std::greater<vector<int>>());\n\n long long cumsum = 0;\n std::unordered_set<int> cat_set;\n std::deque<int> duplicates;\n\n for (int i = 0; i < k; ++i)\n {\n int category = items[i][1];\n int profit = items[i][0];\n\n cumsum += profit;\n if (cat_set.find(category) == cat_set.end())\n {\n cat_set.insert(category);\n }\n else\n {\n duplicates.push_front(profit);\n }\n }\n\n long long len = cat_set.size();\n long long res = cumsum + len * len;\n\n int sz = items.size();\n for (int i = k; i < sz; ++i)\n {\n if (duplicates.empty())\n break;\n \n int category = items[i][1];\n int profit = items[i][0];\n\n if (cat_set.find(category) != cat_set.end())\n continue;\n \n int old = duplicates.front();\n duplicates.pop_front();\n cumsum -= old;\n cumsum += profit;\n cat_set.insert(category);\n\n ++len;\n res = std::max(res, cumsum + len * len);\n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ | greedy | c-greedy-by-ouasintheden-u0dv | \n# Code\n\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.rbegin(), items.rend());\n | ouasintheden | NORMAL | 2023-08-13T08:55:09.897896+00:00 | 2023-08-13T08:55:09.897921+00:00 | 8 | false | \n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.rbegin(), items.rend());\n long long profitSum = 0, ans = 0, res = 0;\n unordered_map<int,int> categoreis, dup;\n for(int i = 0 ; i < k;i++){\n profitSum += items[i][0];\n int cat = items[i][1];\n categoreis[cat]++;\n }\n ans = profitSum + 1LL*categoreis.size()*categoreis.size();\n res = ans;\n long long size = categoreis.size();\n int j = k-1;\n int n = items.size();\n for(int i = k; i < n; i++){\n int cat = items[i][1];\n if(categoreis[cat] == 0){\n while(j >= 0 && categoreis[items[j][1]] <= 1){\n j--;\n }\n if(j < 0){\n break;\n }\n categoreis[items[j][1]]--;\n categoreis[cat]++;\n res -= items[j][0];\n res += items[i][0];\n res -= size*size;\n size++;\n res += size*size;\n j--;\n ans = max(ans, res);\n }\n }\n return ans;\n \n }\n};\n``` | 0 | 0 | ['Greedy', 'Sorting', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | c# sort + replace repeated category item one by one | c-sort-replace-repeated-category-item-on-vfov | Intuition and Approach\n To get the result , we need try to select item with larger profit. The best situation is items with first largest profile are with diff | julian_meng_chang | NORMAL | 2023-08-12T20:46:45.670859+00:00 | 2023-08-12T20:46:45.670882+00:00 | 9 | false | # Intuition and Approach\n To get the result , we need try to select item with larger profit. The best situation is items with first largest profile are with different profit.\nThen sort the items according to profit.\nWe start from first k elements, and record all items with repeated category with a Stack. The element with smallest profit will be on the top of the stack, in the later steps, we will replace these items with repeated category one by one with new category in the scan.\n\nfor each step, we calculate the elegance, and record the max.\n \n\n \n# Complexity\n- Time complexity:\n Sort: O(NlogN)\n \n\n- Space complexity:\n we use a stack and hashset , O(N)\n\n# Code\n```\npublic class Solution {\n public long FindMaximumElegance(int[][] items, int k) {\n var sortedItems = items.OrderBy(item=>-item[0]).ToArray();\n HashSet<int> C = new (); \n Stack<int> S = new (); /*index of repeated category*/\n long P = 0; \n for(int i=0; i<k; i++)\n {\n if(C.Contains(sortedItems[i][1]))\n {\n S.Push(i); \n }\n else\n {\n C.Add(sortedItems[i][1]); \n }\n P += sortedItems[i][0];\n }\n \n long E = P + (long)C.Count * C.Count;\n //Console.WriteLine($"{C.Count},{P},{E}");\n if(C.Count==k || k== items.Length)\n return E;\n \n int p = k;\n while(S.Count>0 && p<sortedItems.Length)\n {\n if(C.Contains(sortedItems[p][1]))\n {\n p++;\n continue;\n }\n else\n { \n C.Add(sortedItems[p][1]); \n int idx = S.Pop();\n P = P - sortedItems[idx][0] + sortedItems[p][0];\n E = Math.Max(E,P + (long)C.Count * C.Count); \n p++;\n }\n }\n return E; \n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
maximum-elegance-of-a-k-length-subsequence | [Python3] Sort by profit and use math | python3-sort-by-profit-and-use-math-by-n-ziwu | We can track everything in a single variable current and keep it updated by using the fact that (x^2) - ((x-1)^2) = 2x-1\n\npython\nclass Solution:\n def fin | nottheswimmer | NORMAL | 2023-08-11T11:59:34.114244+00:00 | 2023-08-11T12:00:32.534754+00:00 | 8 | false | We can track everything in a single variable `current` and keep it updated by using the fact that (x^2) - ((x-1)^2) = 2x-1\n\n```python\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n best = current = 0\n seen = set()\n skipped = []\n items.sort(reverse=True)\n for price, category in items:\n if category not in seen:\n seen.add(category)\n current += price + 2 * len(seen) - 1\n if len(skipped) > k - len(seen):\n current -= skipped.pop()\n if len(seen) == k:\n return max(best, current)\n elif len(skipped) < k - len(seen):\n current += price\n skipped.append(price)\n best = max(best, current)\n return best\n``` | 0 | 0 | [] | 0 |
maximum-elegance-of-a-k-length-subsequence | Why the STRIVER approach didn't work ?? | why-the-striver-approach-didnt-work-by-g-gixj | class Solution {\npublic:\n \n long long solve(vector>&items , int n , int i , int k , map&m , int cnt)\n {\n if(i==n || cnt>k) return 0;\n | gauti1309 | NORMAL | 2023-08-11T06:57:58.223449+00:00 | 2023-08-11T06:57:58.223482+00:00 | 68 | false | class Solution {\npublic:\n \n long long solve(vector<vector<int>>&items , int n , int i , int k , map<int,int>&m , int cnt)\n {\n if(i==n || cnt>k) return 0;\n \n m[items[i][1]]++;\n \n long long pick=solve(items , n , i+1 , k , m , cnt+1) + (items[i][0] + pow(m.size() , 2));\n \n m[items[i][1]]--;\n if (m[items[i][1]] == 0) m.erase(items[i][1]);\n \n \n long long nonPick=solve(items , n , i+1 , k , m , cnt);\n\n \n return max(pick , nonPick);\n \n }\n \n \n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n=items.size();\n \n int i=0;\n map<int,int>m;\n int cnt=0;\n \n return solve(items , n , i , k , m , cnt);\n \n }\n}; | 0 | 0 | ['Dynamic Programming', 'Greedy', 'C++'] | 3 |
maximum-elegance-of-a-k-length-subsequence | [C++] 2 Segment Tree Easy to understand | c-2-segment-tree-easy-to-understand-by-c-j0tr | Code\n\nvoid update(vector<long long> &seg, int start, int end, int pos, int node, long long val){\n if(start > pos || end < pos){\n return;\n }\n | caobaohoang03 | NORMAL | 2023-08-10T23:50:59.364106+00:00 | 2023-08-10T23:50:59.364133+00:00 | 10 | false | # Code\n```\nvoid update(vector<long long> &seg, int start, int end, int pos, int node, long long val){\n if(start > pos || end < pos){\n return;\n }\n if(start == end){\n seg[node] += val;\n return;\n }\n int mid = (start+end)/2;\n \n update(seg, start, mid, pos, node*2+1, val);\n update(seg, mid+1, end, pos, node*2+2, val);\n \n seg[node] = seg[node*2+1] + seg[node*2+2];\n}\n\nlong long get(vector<long long> &seg, int start, int end, int left, int right, int node){\n if(start > right || end < left){\n return 0;\n }\n if(left <= start && end <= right){\n return seg[node];\n }\n \n int mid = (start+end)/2;\n return get(seg, start, mid, left, right, node*2+1) + get(seg, mid+1, end, left, right, node*2+2);\n}\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n = items.size();\n \n sort(items.begin(), items.end(), [](vector<int> &a, vector<int> &b){\n return a[0] > b[0];\n });\n \n unordered_map<int, pair<int, int>> maxx;\n \n for(int i=0; i<n; i++){\n if(maxx.find(items[i][1]) == maxx.end() || maxx[items[i][1]].first < items[i][0]){\n maxx[items[i][1]] = {items[i][0], i};\n }\n }\n \n vector<long long> prefix(n, 0);\n \n prefix[0] = items[0][0];\n \n for(int i=1; i<n; i++){\n prefix[i] = prefix[i-1] + items[i][0];\n }\n \n vector<long long> seg1(4*n, 0);\n vector<long long> seg(4*n, 0);\n \n vector<vector<int>> max_cate;\n \n for(auto cate : maxx){\n max_cate.push_back({cate.first, cate.second.first, cate.second.second});\n }\n \n sort(max_cate.begin(), max_cate.end(), [](vector<int> &a, vector<int> &b){\n return a[1] > b[1];\n });\n \n long long res = 0;\n \n for(int i=0; i<max_cate.size(); i++){\n update(seg, 0, n-1, max_cate[i][2], 0, 1);\n update(seg1, 0, n-1, max_cate[i][2], 0, max_cate[i][1]);\n \n \n int low = -1; \n int high = n - 1;\n \n while(low <= high){\n int mid = (low+high)/2;\n if(get(seg, 0, n-1, mid+1, n-1, 0) + mid + 1 <= k){\n low = mid+1;\n }\n else{\n high = mid-1;\n }\n }\n \n if(low == -1){\n continue;\n }\n if(low - 1 < 0){\n res = max(res, 1LL*(get(seg1, 0, n-1, low, n-1, 0) + 1LL*(i+1)*(i+1)));\n }\n else{\n res = max(res, 1LL*(get(seg1, 0, n-1, low, n-1, 0) + prefix[low-1] + 1LL*(i+1)*(i+1)));\n }\n \n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Easy and Intuitive Python soln🔥 | easy-and-intuitive-python-soln-by-ebadd-he61 | Intuition\n Describe your first thoughts on how to solve this problem. \ngreedy\n# Approach\n Describe your approach to solving the problem. \nsort w.r.t profit | ebadd | NORMAL | 2023-08-09T10:45:03.768090+00:00 | 2023-08-09T10:45:03.768111+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ngreedy\n# Approach\n<!-- Describe your approach to solving the problem. -->\nsort w.r.t profit from higher to lower. Take the first K element. \nmake a dp to store the number of times each category occured.\nif all the category are different for first k itself:\nreturn the (sum of profit for first k element) + k**2.\nelse:\nremove the element from last which are having more than one in dp.\nAlso parallely keep an look on ans. \nkeep on doing this either till you reach all distinct category or you go out of range.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n items.sort(reverse=True)\n dp={}\n sm=0\n for i in range(k):\n dp[items[i][1]]=dp.get(items[i][1],0)+1\n sm+=items[i][0]\n ans= sm + (len(dp))**2\n h=[]\n for i in range(k):\n h.append(items[i])\n j=k\n ln=len(dp)\n while h and j<len(items):\n x,y= h.pop()\n if dp[y]==1:\n continue\n else:\n sm-=x\n dp[y]-=1\n while j<len(items) and items[j][1] in dp:\n j+=1\n if j<len(items):\n sm+= items[j][0]\n dp[items[j][1]]=1\n ln+=1\n ans=max(ans,sm+ln**2)\n return ans\n \n \n \n \n``` | 0 | 0 | ['Sorting', 'Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | simple greedy with stack | simple-greedy-with-stack-by-rip-7dzl | Intuition\n\n\n# Approach\nget first k most profitable items, than try to increase numbers of unique catigories by dropping less profitable items.\n\n# Complexi | rip | NORMAL | 2023-08-08T17:13:04.578589+00:00 | 2023-08-08T17:38:33.428281+00:00 | 9 | false | # Intuition\n\n\n# Approach\nget first k most profitable items, than try to increase numbers of unique catigories by dropping less profitable items.\n\n# Complexity\n- Time complexity:\n$$O(log(n)*n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>&X, int k) {\n size_t best=0, current=0;\n unordered_set<int>categories; stack<int>may_drop;\n sort(X.begin(), X.end(), [](auto&l, auto&r){ return l[0] > r[0]; });\n for(auto&x : X){\n if (k) --k;\n else if (may_drop.empty()) break;\n else { current -= may_drop.top(); may_drop.pop(); }\n current += x[0];\n if (!categories.insert(x[1]).second) may_drop.push(x[0]);\n best = max(best, current + categories.size() * categories.size());\n }\n return best;\n }\n};\n``` | 0 | 0 | ['Greedy', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | || CPP || 💡 Track the repeating using stack, Hashing very simple implementaion. | cpp-track-the-repeating-using-stack-hash-zlc4 | Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(nlogn)\n- Space complexity:\n Add your space complexity here, e.g. O(n) \nO(n)\n# | LikeTheSun14 | NORMAL | 2023-08-08T05:30:00.431398+00:00 | 2023-08-08T05:30:00.431425+00:00 | 14 | false | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n // sort according to the non-increasing order of the profit.\n sort(items.begin(), items.end(), []( const vector<int> &x, const vector<int>&y ){return x[0] >y[0];});\n // stack to track repeating element\n stack<int> st;\n // map to track distinct element\n map<int, long long> ans;\n// cur stores the running sum of profit,\n// mx stores the maximum elegence that can be achived using k elements .\n long long cur= 0, mx= 0;\n int n = items.size();\n for(int i =0; i < k; i++)\n {\n if(ans.count(items[i][1]))\n st.push(i);\n ans[items[i][1]]+=1;\n x1+= items[i][0];\n }\n mx = cur;\n mx += ans.size()*ans.size();\n // if answer contains duplicates, try to replace them \n if(ans.size() != k) \n for(int i = k; i < n ; i++)\n {\n if(ans.count(items[i][1]))continue;\n if(st.size() ==0 ) break;\n\n auto last = st.top();\n long long x = ans.size() ;\n st.pop();\n // remove last repeating element and add fresh entry\n ans[items[last][1]]-=1;\n ans[items[i][1]]+=1 ;\n x1 -= items[last][0];\n x1 += items[i][0];\n // update the ans;\n mx = max(x1 + (long long)(ans.size()*1LL*ans.size()) , mx);\n }\n return mx;\n }\n};\n``` | 0 | 0 | ['Array', 'Hash Table', 'Stack', 'Greedy', 'Sorting', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Stack + Sorting | stack-sorting-by-lwy123177-cd48 | \nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n n = len(items)\n items.sort(reverse=True)\n | lwy123177 | NORMAL | 2023-08-08T00:21:49.540623+00:00 | 2023-08-08T00:21:49.540650+00:00 | 14 | false | ```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n n = len(items)\n items.sort(reverse=True)\n seen_category = set()\n stk = []\n ans = 0\n for i in range(k):\n profit, cat = items[i]\n ans += profit\n if cat in seen_category:\n stk.append(profit)\n else:\n seen_category.add(cat) \n i = k\n cur = ans\n for sq in range(1, k + 1):\n if len(seen_category) < sq:\n while i < n and items[i][1] in seen_category:\n i += 1 \n if i == n or len(stk) == 0: break \n p = stk.pop()\n cur = cur - p + items[i][0]\n seen_category.add(items[i][1])\n ans = max(ans, cur + sq * sq)\n return ans\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ solution | Priority queues | sorting | c-solution-priority-queues-sorting-by-ra-1psq | \nclass Solution {\npublic:\n unordered_set<int> on;\n unordered_map<int,vector<int>> v;\n unordered_map<int,int> mp;\n priority_queue<array<int,2>> | rac101ran | NORMAL | 2023-08-07T22:40:12.430856+00:00 | 2023-08-07T22:43:41.672971+00:00 | 11 | false | ```\nclass Solution {\npublic:\n unordered_set<int> on;\n unordered_map<int,vector<int>> v;\n unordered_map<int,int> mp;\n priority_queue<array<int,2>> hq;\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n for(int i=0; i<items.size(); i++) {\n v[items[i][1]].push_back(items[i][0]);\n }\n for(pair<int,vector<int>> p : v) sort(v[p.first].rbegin(),v[p.first].rend());\n \n priority_queue<array<int,2>,vector<array<int,2>>,greater<array<int,2>>> pq;\n \n long long cnt = 0;\n \n for(pair<int,vector<int>> p : v) {\n int d = p.first;\n if(pq.size() < k) {\n cnt+=v[d][0];\n on.insert(d);\n pq.push({v[d][0],d});\n }else if(pq.top()[0] < v[d][0]) {\n on.erase(on.find(pq.top()[1]));\n on.insert(d);\n cnt-=pq.top()[0];\n pq.pop();\n cnt+=v[d][0];\n pq.push({v[d][0],d});\n }\n \n }\n \n for(int pos : on) {\n for(int i = 1; i < v[pos].size(); i++) hq.push({v[pos][i],pos});\n mp[pos]++;\n }\n \n cnt+=((long long) on.size() * on.size()); // one of the possible answer\n \n // we can do better by having a trade off by taking profit , removing category (descreasing distinct count)\n \n long long ans = cnt , len = mp.size();\n while(hq.size()>0) {\n int n = mp.size();\n int highestValue = hq.top()[0] , highestArrayPos = hq.top()[1] , lowestValue = pq.top()[0] , lowestArrayPos = pq.top()[1];\n if(len < k) {\n mp[highestArrayPos]++;\n cnt+=highestValue;\n hq.pop();\n ans = max(ans,cnt);\n len++;\n }else {\n mp[lowestArrayPos]--;\n mp[highestArrayPos]++;\n if(mp[lowestArrayPos] == 0) mp.erase(lowestArrayPos);\n cnt = cnt - ((long long)n * n) + ((long long)mp.size() * mp.size()) + highestValue - lowestValue;\n hq.pop();\n pq.pop();\n ans = max(ans,cnt);\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'Sorting'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Python 3 || Explained in detail | python-3-explained-in-detail-by-mayud-0ldo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\nAs we know we finally | MayuD | NORMAL | 2023-08-07T14:57:50.218542+00:00 | 2023-08-07T14:59:13.468231+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nAs we know we finally want to return a sum of all the first elements in an array and square of different number of categories that are the number of different elements in the array. So write an function that takes the input array and its hashmap of the frequency of the second element in the array.\n\n\nFirst of all sort the items in descending order and create an candidate set that has top k elements.\n\nCreate a hashmap that stores the the frequency of different categories.\n\nIf the length of the hashmap is equal to the length of the candidate set that means all the elements of the candidate set gave unique categories. Anyways we have all the elements having highest value. Thus there cant be any higher elegance value. So return it .\n\nElse find the elegance initially. For all the remaining elements in the original array, we keep on replacing the minimum element in the candidate set having a repeated category with the array element.After every replacement , calculate the elegance and if the new value is higher than the previous then update the elegance value. After all the iterations return the elegance.\n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n \n def find_elegance(arr, freq)->int:\n sum = 0\n for i in arr:\n sum+=i[0]\n\n return sum + len(freq.keys())**2\n\n # items = [[1,1],[2,1],[3,1]]\n # k = 3\n\n # sum = 0\n\n\n items.sort(reverse = True)\n\n candidate_set = items[:k]\n items = items[k:]\n\n # print(candidate_set)\n # print(items)\n\n freq = {}\n\n for i in candidate_set:\n if i[1] in freq:\n freq[i[1]]+=1\n else:\n freq[i[1]] = 1\n\n found = False\n\n # print(freq)\n\n if len(freq.values()) == len(candidate_set):\n return(find_elegance(candidate_set, freq))\n\n else:\n\n ini_elegance= find_elegance(candidate_set, freq)\n # print(candidate_set, items, sep = "|")\n for i in items:\n if i[1] not in freq:\n for j in range(len(candidate_set)-1, -1, -1):\n # print(j)\n if freq[candidate_set[j][1]]>1:\n freq[candidate_set[j][1]] -=1\n candidate_set[j] = i\n if candidate_set[j][1] in freq:\n freq[candidate_set[j][1]] +=1\n else:\n freq[candidate_set[j][1]] = 1\n # print(freq)\n break\n ini_elegance = max(ini_elegance, find_elegance(candidate_set, freq))\n\n return(ini_elegance)\n\n\n\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ || Using Sorting + Map + Stack || Beats 100% || Easiest Code | c-using-sorting-map-stack-beats-100-easi-8hjp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | hector_21 | NORMAL | 2023-08-07T12:31:27.967692+00:00 | 2023-08-07T12:32:27.775883+00:00 | 12 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n*log(n))\n\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int i,j,n=items.size();\n sort(items.rbegin(),items.rend());\n map<int,int> mp;\n stack<int> stk;\n long long sum=0,ans=LLONG_MIN;\n for(i=0;i<k;i++)\n {\n sum+=items[i][0];\n if(mp.find(items[i][1])==mp.end())\n {\n mp[items[i][1]]=1;\n }\n else\n {\n stk.push(items[i][0]);\n }\n }\n ans=max(ans,(long long)sum+(long long)mp.size()*(long long)mp.size());\n for(i=k;i<n;i++)\n {\n if(mp.find(items[i][1])==mp.end()&&stk.size()>0)\n {\n sum-=stk.top();\n stk.pop();\n mp[items[i][1]]=1;\n sum+=items[i][0];\n ans=max(ans,(long long)sum+(long long)mp.size()*(long long)mp.size()); \n }\n }\n return ans; \n }\n};\n``` | 0 | 0 | ['Stack', 'Ordered Map', 'Sorting', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Easy C++ solution | easy-c-solution-by-mridulkaran2021-mj7s | Intuition\n Describe your first thoughts on how to solve this problem. \nThink Greedy. Take top K elements and find the ans. Now, what factors affect the final | mridulkaran2021 | NORMAL | 2023-08-07T08:29:28.860665+00:00 | 2023-08-07T08:29:28.860684+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThink Greedy. Take top K elements and find the ans. Now, what factors affect the final ans? The distinct categories and value of ith element. We just need to optimally choose the elements which increase our ans.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nRemember: `answer = sumOfValues + distinctCategories^2`\nSort the items array in decreasing order of profit.\n\nChoose first K values from items. A variable `currVal` is used to keep the sum of the profit of these values. Here we tried to maximize the `sumOfValues`.\n\nWhenever you encounter a `category` or `items[i][1]` for the first time, just create an instance of it in map. \nIf it has been encountered before, we push the profit of the item associated with category to the stack. The top of this stack denotes "The item with minimum profit value whose category is already present in the subsequence". Why do we need this? Suppose an item comes later on i.e., `i>=k`, then if the category of that item has not been seen before, then it can possibly increase our answer. To maximize our answer, we just need to try to increase `distinctCategories`. On encountering a new category, we will remove the element with minimum profit with a duplicate category i.e, value at top of the stack.\n\nNow run the loop from i>=k and do the above mentioned steps. Note, you cannot add an element in a subsequence of length k if there are no elements with duplicate categoreis., i.e stack is empty. Moreover, you can only add replace a element with a new element only when the category of the new element is unseen. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe sorting taken O(nlogn).\nThe rest operations are O(n).\nInsertions in unorderd_map is on avg O(1) and same with lookup.\nHence the `total time taken : O(nlogn);`\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) for map and for stack it will be maximum of \nO(k-1). So the `total space complexity is O(n)`.\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(),items.end(),[](const auto &a, const auto &b){\n return a[0]>b[0];\n });\n\n unordered_map<int,int> ump;\n stack<int> st;\n long long ans = 0,currVal = 0;\n for(int i=0;i<k;i++){\n currVal += items[i][0];\n if(ump.find(items[i][1])==ump.end()){\n //First encounter\n ump[items[i][1]]++;\n }else{\n //push it into the stack\n st.push(items[i][0]);\n }\n }\n long long sz = ump.size();\n ans = max(ans,currVal + 1LL*sz*sz);\n for(int i=k;i<items.size();i++){\n if(st.empty()){\n continue;\n }\n if(ump.find(items[i][1])!=ump.end()){\n continue;\n }\n //the ith item\'s category should be unseen to add it to the list\n //if it is seen then we have already taken a \n //instance of profit with a greater value\n\n currVal+=(items[i][0]-st.top());\n st.pop();\n ump[items[i][1]]++;\n sz = ump.size();\n ans = max(ans, currVal+1LL*sz*sz);\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ * 400ms * beats 100% * Track Duplicates | c-400ms-beats-100-track-duplicates-by-co-qbio | Intuition\n Describe your first thoughts on how to solve this problem. \nDP won\'t work, look at the constraints once, I got TLE @ 1487 cases.\nThis problem req | coderpriest | NORMAL | 2023-08-07T02:42:14.391533+00:00 | 2023-08-07T02:42:59.214397+00:00 | 18 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDP won\'t work, look at the constraints once, I got TLE @ 1487 cases.\nThis problem requires Greedy approach.\n# Approach\n<!-- Describe your approach to solving the problem. --> \n1. Sort profit in descending order and take first k profits including duplicate categories.\n2. Now we can maximazie distinct_categories by adding them into set and removing lowest duplicate items from set\n# Complexity\n- Time complexity: O( N * log(N) )\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O( N )\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);\n sort(items.begin(), items.end(), [&](vector<int> &a, vector<int> &b){\n return a[0] > b[0];\n });\n long long n = items.size(), ans = 0, curr = 0;\n stack<int> dups;\n unordered_set<int> s;\n for(int i = 0; i < n; i++){\n if(i < k){\n curr += items[i][0];\n if(s.count(items[i][1])) dups.push(items[i][0]);\n else s.insert(items[i][1]);\n }\n else if(!s.count(items[i][1]) && !dups.empty()){\n s.insert(items[i][1]);\n curr -= dups.top();\n dups.pop();\n curr += items[i][0];\n }\n long long t = s.size();\n ans = max(ans, curr + t*t);\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Stack', 'Sorting', 'Ordered Set', 'C++'] | 1 |
maximum-elegance-of-a-k-length-subsequence | [C++] Group by category, add the most profitable and heap for the remaining | c-group-by-category-add-the-most-profita-yi6x | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | phi9t | NORMAL | 2023-08-06T22:33:22.720952+00:00 | 2023-08-06T22:33:22.720982+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n using integer = long long;\npublic:\n integer findMaximumElegance(vector<vector<int>>& items, int k) {\n std::map<int, std::vector<integer>> cat_to_profits;\n for (const auto &item : items) {\n cat_to_profits[item[1]].push_back(item[0]);\n }\n std::vector<std::vector<integer>> profits_by_cat;\n for (auto &&[_, profits] : cat_to_profits) {\n std::sort(profits.begin(), profits.end());\n profits_by_cat.push_back(profits);\n }\n \n // Indices to load profits by values\n std::vector<int> cat_inds_ord(profits_by_cat.size());\n std::iota(cat_inds_ord.begin(), cat_inds_ord.end(), 0);\n std::sort(\n cat_inds_ord.begin(), cat_inds_ord.end(), \n [&](const int i, const int j) -> bool {\n return profits_by_cat[i].back() > profits_by_cat[j].back();\n });\n\n std::priority_queue<integer, std::vector<integer>, std::greater<integer>> vals_ord;\n int remaining = k;\n integer max_sum = 0;\n integer running_sum = 0;\n const auto cleanse_vals_ord = [&]() {\n while (vals_ord.size() > remaining) {\n running_sum -= vals_ord.top();\n vals_ord.pop();\n }\n };\n for (int idx = 0; idx < cat_inds_ord.size(); ++idx) {\n const int cat = cat_inds_ord[idx];\n auto &&profits = profits_by_cat[cat];\n const integer len = idx; \n running_sum += (profits.back() + (len + 1) * (len + 1) - len * len); \n remaining -= 1;\n profits.pop_back();\n cleanse_vals_ord();\n for (; !profits.empty(); profits.pop_back()) {\n vals_ord.push(profits.back());\n running_sum += profits.back();\n cleanse_vals_ord();\n }\n if (idx + 1 + vals_ord.size() == k) {\n max_sum = std::max(running_sum, max_sum);\n }\n }\n return max_sum;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Maximum Elegance | Easy to Understand | Faster than 100% | maximum-elegance-easy-to-understand-fast-im5a | \n\n# Code\n\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n PriorityQueue<int[]>pq=new PriorityQueue<>((a,b)->a[0]-b[0] | Paridhicodes | NORMAL | 2023-08-06T21:56:54.096867+00:00 | 2023-08-06T22:06:32.118861+00:00 | 31 | false | \n\n# Code\n```\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n PriorityQueue<int[]>pq=new PriorityQueue<>((a,b)->a[0]-b[0]);\n HashSet<Integer> hs=new HashSet<>();\n List<int[]>comp=new ArrayList<>();\n\n Arrays.sort(items,(a,b)->b[0]-a[0]);\n\n int n=items.length;\n long sum=0;\n\n for(int i=0;i<n && hs.size()<=k;i++){\n int profit=items[i][0];\n int cat=items[i][1];\n\n if(!hs.contains(cat) && hs.size()<k){\n hs.add(cat);\n sum+=profit;\n pq.add(items[i]);\n }else{\n comp.add(items[i]);\n }\n }\n\n HashSet<Integer> dup=new HashSet<>();\n\n for(int []a:comp){\n\n if(pq.size()<k){\n pq.add(a);\n dup.add(a[1]);\n sum+=a[0];\n continue;\n }\n\n int[] potrem=pq.peek(); //potential element to be removed\n\n //If the new element has the same category \n //as the potential element or\n //if there are 1 or more elements having same category\n //as potential element break because it is irrelevant to \n //check for others\n if(potrem[1]==a[1] || dup.contains(potrem[1])){\n break;\n }else{\n int len=hs.size();\n\n //Check if its actually beneficial to loose a\n //category and gain another profit of the same category\n if((sum+a[0]-potrem[0])+(len-1)*(len-1)>sum+(len*len)){\n sum+=a[0]-potrem[0];\n hs.remove(potrem[1]);\n pq.remove();\n pq.add(a);\n dup.add(a[1]);\n }\n \n }\n }\n return sum+1L*(hs.size())*(hs.size());\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Greedy Python + detailed comments | greedy-python-detailed-comments-by-jrry8-uh0s | Intuition\n Describe your first thoughts on how to solve this problem. \nFirst, compute the elegance of the subseq of k items with maximum total profit. \nThen | jrry8 | NORMAL | 2023-08-06T20:53:10.492426+00:00 | 2023-08-06T20:53:10.492449+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst, compute the elegance of the subseq of k items with maximum total profit. \nThen we iterate by adding items of the highest profit from new categories while removing items of the lowest profit from duplicate categories. \nIn this process we will compute the maximum elegance of k items for every possible number of categories used. \nThe final answer is the maximum of all these values.\n\n# Code\n```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n n = len(items)\n # sort items in descending order of profit\n items.sort(key = lambda item: -item[0])\n # stack of items that can be replaced by an item from a new category\n dupes = []\n # set of categories included in our subseq of k items\n seen = set()\n\n # calculate the elegance of the k items with maximum total profit\n total_profit = 0\n for i in range(k):\n profit, category = items[i]\n total_profit += profit\n # check if item is from a new category; if not, we add it to dupes\n if category not in seen:\n seen.add(category)\n else:\n dupes.append(profit)\n maxElegance = total_profit + len(seen)**2\n \n # while our subseq of k items contains less than k categories\n # pop the lowest profit item of category with multiple items\n # add the highest profit item of a new category\n for i in range(k, n):\n if len(seen) == k:\n break\n profit, category = items[i]\n if category not in seen:\n total_profit -= dupes.pop()\n total_profit += profit\n seen.add(category)\n maxElegance = max(maxElegance, total_profit + len(seen)**2)\n\n return maxElegance\n``` | 0 | 0 | ['Greedy', 'Python', 'Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ solution based on provided hints | c-solution-based-on-provided-hints-by-vv-m4kz | \nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, long long k) {\n long long n = items.size();\n sort(items.begin() | vvhack | NORMAL | 2023-08-06T19:29:58.051140+00:00 | 2023-08-06T19:29:58.051164+00:00 | 4 | false | ```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, long long k) {\n long long n = items.size();\n sort(items.begin(), items.end(), [] (const auto& a, const auto& b) {\n return a[0] > b[0];\n });\n long long totProf = 0;\n int lastMultipleIdx = -1;\n unordered_map<int, int> seen;\n for (int i = 0; i < k; ++i) {\n totProf += items[i][0];\n if (seen[items[i][1]]++ > 0) {\n lastMultipleIdx = i;\n }\n }\n long long maxTot = totProf + ((long long)seen.size() * (long long)seen.size());\n if (lastMultipleIdx == -1) return maxTot;\n for (int i = k; i < n; ++i) {\n if (!seen.count(items[i][1])) {\n long long tot = totProf - (items[lastMultipleIdx][0] - items[i][0]) +\n ((long long)(seen.size() + 1) * (long long)(seen.size() + 1));\n if (tot > maxTot) {\n maxTot = tot;\n }\n totProf -= (items[lastMultipleIdx][0] - items[i][0]);\n //maxTot = tot;\n seen[items[i][1]]++;\n seen[items[lastMultipleIdx][1]]--;\n //swap(items[i], items[lastMultipleIdx]);\n bool foundNew = false;\n for (int j = lastMultipleIdx - 1; j >= 0; --j) {\n if (seen[items[j][1]] > 1) {\n lastMultipleIdx = j;\n foundNew = true;\n break;\n }\n }\n if (!foundNew) break;\n }\n }\n int firstSingleIdx = -1;\n return maxTot;\n }\n};\n``` | 0 | 0 | [] | 0 |
maximum-elegance-of-a-k-length-subsequence | Simple Sorting Solution!!⚡⚡🔥 | simple-sorting-solution-by-yashpadiyar4-pcxr | \n\n# Code\n\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(),items.end(),[&](vect | yashpadiyar4 | NORMAL | 2023-08-06T18:41:24.225890+00:00 | 2023-08-06T18:41:24.225915+00:00 | 7 | false | \n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(),items.end(),[&](vector<int>&a,vector<int>&b){\n return a[0]>b[0];\n });\n unordered_set<int>s;\n long long res=0;\n long long ans=0;\n vector<int>dup;\n for(int i=0;i<items.size();i++){\n if(i<k){\n ans+=(items[i][0]);\n if(s.count(items[i][1])){\n dup.push_back(items[i][0]);\n }\n }\n else if(s.find(items[i][1])==s.end()){\n if(dup.empty())break;\n ans=ans-dup.back()+items[i][0];\n dup.pop_back();\n }\n s.insert(items[i][1]);\n long long v=ans+(s.size()*s.size());\n res=max(res,v);\n }\n return res;\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Beats 100 percent time | beats-100-percent-time-by-abhinav_1820-zdlh | Intuition\n\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n\n- | Abhinav_1820 | NORMAL | 2023-08-06T15:51:00.700648+00:00 | 2023-08-06T15:51:00.700686+00:00 | 6 | false | # Intuition\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& v, int k) {\n sort(v.begin() , v.end());\n reverse(v.begin() , v.end());\n map<long long , long long> mp;\n multiset<pair<long long , long long>> ms;\n long long ans=0;\n for(int i=0 ; i<k ;i++){\n if(mp.find(v[i][1])!=mp.end()){\n ms.insert({v[i][0] , v[i][1]});\n }\n mp[v[i][1]]++;\n \n ans += v[i][0];\n }\n ans += (pow(mp.size() , 2));\n long long ans1 = ans;\n int n = v.size();\n for(int i=(k) ; i<n ;i++){\n if(ms.size()==0)\n break;\n if(mp.find(v[i][1])!=mp.end())\n continue;\n else {\n auto h11 = ms.begin();\n auto h1 = *h11;\n long long h = h1.first;\n long long h2 = h1.second;\n long long l = mp.size();\n auto j = (l+1)*(l+1);\n auto j1 = l*l;\n ms.erase(h11);\n mp[h2]--;\n mp[v[i][1]]++;\n ans = ans-h-(l*l)+((l+1)*(l+1))+v[i][0];\n }\n ans1 = max(ans , ans1);\n }\n ans1 = max(ans , ans1);\n return ans1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Using Priority Queue And Map..................................... | using-priority-queue-and-map-by-kumarrar-blli | Intuition\n Describe your first thoughts on how to solve this problem. \nfor maximum profit how you get?.. taking top k elemetns with higher profit no matter (t | kumarrarya | NORMAL | 2023-08-06T15:21:47.093843+00:00 | 2023-08-06T15:21:47.093873+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfor maximum profit how you get?.. taking top k elemetns with higher profit no matter (they belong to same category or not. think in greedy) after that choose that profit which is from differnt category so that our profit maximize so we can doing thish using min priority queue. first put top k elemetns in priority queue calculate res then iterate over n-k elements and choose that elemetn which from differnt category and remove that elem from queue which has less profit and number of count greater than 1.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution {\npublic:\n static bool compare(vector<int>&p1,vector<int>&p2){\n return p1[0]>p2[0];\n }\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n priority_queue<pair<long long,long long>,vector<pair<long long,long long>>,greater<pair<long long,long long>>>pq;\n sort(items.begin(),items.end(),compare);\n map<long long,long long>mp;\n int n=items.size();\n long long ans=0;\n for(int i=0;i<k;i++){\n ans+=items[i][0];\n mp[items[i][1]]++;\n pq.push({items[i][0],items[i][1]});\n }\n long long res=ans+(mp.size()*mp.size()*1ll);\n int i=k;\n while(i<n&&pq.size()!=0){\n if(mp.count(items[i][1])){\n i++;\n continue;\n }\n auto it=pq.top();\n pq.pop();\n if(mp[it.second]==1){\n continue;\n }\n ans+=items[i][0]-it.first;\n --mp[it.second];\n ++mp[items[i][1]];\n res=max(res,ans+(long long)mp.size()*(long long)mp.size());\n i++;\n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Simple Solution using PriorityQueue | simple-solution-using-priorityqueue-by-n-3myf | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | nikleetcode | NORMAL | 2023-08-06T15:13:25.935901+00:00 | 2023-08-06T15:13:25.935926+00:00 | 22 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n int n = items.length;\n \n TreeMap<Integer, List<Integer>> tm = new TreeMap();\n \n // tm(key, value) -- key = cat, value = list of profits\n for(int i = 0; i < n; i++) {\n if(!tm.containsKey(items[i][1]))\n tm.put(items[i][1], new ArrayList());\n tm.get(items[i][1]).add(items[i][0]);\n }\n \n // Sort profits in desc order\n for(Integer key : tm.keySet()) \n Collections.sort(tm.get(key), (a, b) -> b - a);\n \n // System.out.println(tm);\n \n HashMap<Integer, Integer> hm = new HashMap();\n PriorityQueue<int[]> minHp = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]);\n PriorityQueue<int[]> maxHp = new PriorityQueue<int[]>((a, b) -> b[0] - a[0]);\n \n // put max profit of each category in max heap\n for(Map.Entry<Integer, List<Integer>> map : tm.entrySet()) {\n maxHp.add(new int[] {map.getValue().get(0), map.getKey(), 0});\n }\n \n int cnt = k;\n long sum = 0, sqr = 0, maxEleg = 0;\n List<int[]> list = new ArrayList();\n \n // Get k max profit from all distinct category\n while(cnt-- > 0) {\n int[] top = maxHp.poll();\n sum += top[0];\n hm.put(top[1], hm.getOrDefault(top[1], 0) + 1);\n minHp.add(new int[] {top[0], top[1], top[2]});\n \n if(top[2] + 1 < tm.get(top[1]).size()) {\n top[2]++;\n top[0] = tm.get(top[1]).get(top[2]);\n //maxHp.add(top);\n if(list != null)\n list.add(top);\n else\n maxHp.add(top);\n }\n \n if(maxHp.isEmpty() && list != null) {\n for(int[] a : list)\n maxHp.add(a);\n list = null;\n }\n }\n if(list != null) {\n for(int[] a : list)\n maxHp.add(a);\n }\n \n // System.out.println(Arrays.toString(maxHp.peek())+" "+sum+" "+hm);\n sqr = (long)Math.pow(hm.size(), 2);\n maxEleg = sum + sqr;\n \n while(!maxHp.isEmpty()) {\n int[] next = maxHp.poll();\n int[] top = minHp.poll();\n \n sum -= top[0];\n sum += next[0];\n \n remove(hm, top[1]);\n hm.put(next[1], hm.getOrDefault(next[1], 0) + 1);\n \n sqr = (long)Math.pow(hm.size(), 2);\n maxEleg = Math.max(maxEleg, sum + sqr);\n \n minHp.add(new int[] {next[0], next[1], next[2]});\n if(next[2] + 1 < tm.get(next[1]).size()) {\n next[2]++;\n next[0] = tm.get(next[1]).get(next[2]);\n maxHp.add(next);\n }\n }\n \n return maxEleg;\n }\n \n public void remove(HashMap<Integer, Integer> hm, int x) {\n if(hm.get(x) == 1)\n hm.remove(x);\n else\n hm.put(x, hm.get(x) - 1);\n }\n}\n\n\n\n\n\n\n\n\n\n\n\n\n``` | 0 | 0 | ['Java'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Python Hard | python-hard-by-lucasschnee-306c | \nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n\n categories = set()\n\n count = 0\n\n ans = | lucasschnee | NORMAL | 2023-08-06T14:36:57.767790+00:00 | 2023-08-06T14:36:57.767809+00:00 | 9 | false | ```\nclass Solution:\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n\n categories = set()\n\n count = 0\n\n ans = 0\n\n total_profit = 0\n\n items.sort(key = lambda x: -x[0])\n\n h = []\n\n\n for profit, c in items:\n\n if count < k:\n count += 1\n total_profit += profit\n\n if c not in categories:\n categories.add(c)\n\n else:\n heapq.heappush(h, profit)\n\n \n else:\n if h and c not in categories:\n total_profit -= heapq.heappop(h)\n total_profit += profit\n categories.add(c)\n\n \n ans = max(ans, total_profit + len(categories) ** 2)\n\n \n return ans\n\n\n \n \n \n \n``` | 0 | 0 | ['Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | 100% fastest || Greedy intutive approach complete explanation | 100-fastest-greedy-intutive-approach-com-yy0l | our final goal is to find max profit out of all possible subsequence of k length\nso first thing comes in thought : let\'s sort in decreasing and return sum of | demon_code | NORMAL | 2023-08-06T10:53:41.506375+00:00 | 2023-08-06T10:55:25.455905+00:00 | 10 | false | our final goal is to find max profit out of all possible subsequence of k length\nso first thing comes in thought : let\'s sort in decreasing and return sum of first k elements and in normal condition that would be our best answer but here bcz of addtion of no of squire of unique elements we need to remove some of elemets which present multiple times bcz removing any multiple elements and adding a new unique one may increase our max profit \n\n// SOLUTION\n**first make a multiset with pair<int,int> // profit , catogery**\nwe will only push any element if it\'s count in map is more than one bcz we have sorted the array taking any unique element from start of the array is always goona make more profit as it\'s maximum by price and also adding a new element. and if any elemet occurs multiple time then it may be profitable to remove the lowest price element from the begining of the multi set to add a new unique element\n\n**a map <int, int> // catogery -> count**\nmap will simply keep track of no of unique elemets of array\n\n```\nUPVOTE IF U FIND HELPFUL\n```\n\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>&a, int k) \n {\n \n multiset<pair<int,int>> ms; // price, cat\n map<int,int> m; // cat to count;\n \n sort(a.begin(),a.end(), greater<vector<int>>()); // Decreasing order\n // for(auto i: a) cout<<i[0]<<" "<<i[1]<<endl;\n long long ans=0;\n long long s=0;\n for(int i=0; i<k; i++)// take sum of first k elements\n {\n s+=a[i][0];\n m[a[i][1]]++;\n if(m[a[i][1]]>1)// if present multiple time\n ms.insert({a[i][0],a[i][1]});\n \n }\n \n ans=s+m.size()*m.size();\n int n=a.size();\n for(int i=k; i<n; i++)\n {\n if(m.find(a[i][1])==m.end())// if not present in selection\n {\n \n if(ms.size()) // if their is any dublicate in selection\n {\n\t\t\t\t\tauto it= ms.begin(); \n\t\t\t\t\tint c=it->second;\n\t\t\t\t\tint p=it->first;\n ms.erase(it);// remove the lowest price item\n s-=p;\n s+=a[i][0];\n m[c]--; // update the frequency map\n if(m[c]==0) m.erase(c);\n m[a[i][1]]++;\n if(m[a[i][1]]>1) // won\'t ever happen but still just for logical condition for insertion in ms\n ms.insert({a[i][0],a[i][1]});\n\n ans= max(ans, s+(int)(m.size()*m.size())); // take max of all solutions\n }\n }\n }\n \n return ans;\n \n }\n};\n\n``` | 0 | 0 | ['C', 'Sorting'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Greedy + Heap, Select Profit Top-K Then Replace Duplicate Categories | greedy-heap-select-profit-top-k-then-rep-kop2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | benlegend | NORMAL | 2023-08-06T07:21:43.766184+00:00 | 2023-08-06T07:24:40.360010+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n // simplified code, after contest\n long long findMaximumEleganceSimplified(vector<vector<int>>& items, int k) {\n int n = items.size();\n \n sort(items.begin(), items.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] < b[0] || (a[0] == b[0] && a[1] < b[1]);\n });\n \n long long ans = 0, sum = 0;\n // selected categories\n unordered_set<int> chosen;\n priority_queue<vector<int>, vector<vector<int>>, greater<>> toReplace;\n int i = n - 1;\n for (; i >= n - k; i--) {\n int pro = items[i][0], cat = items[i][1];\n if (chosen.count(cat)) {\n toReplace.push(items[i]);\n } else {\n chosen.insert(cat);\n }\n \n sum += pro;\n }\n \n ans = sum + 1LL * chosen.size() * chosen.size();\n while (i >= 0 && !toReplace.empty()) {\n int pro = items[i][0], cat = items[i][1];\n if (chosen.find(cat) == chosen.end()) {\n sum -= toReplace.top()[0]; toReplace.pop();\n sum += pro;\n\n chosen.insert(cat);\n long long candi = sum + 1LL * chosen.size() * chosen.size();\n ans = max(ans, candi);\n }\n \n i--;\n }\n \n return ans;\n }\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n // return findMaximumEleganceSimplified(items, k);\n\n int n = items.size();\n \n sort(items.begin(), items.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[0] < b[0] || (a[0] == b[0] && a[1] < b[1]);\n });\n \n long long ans = 0, sum = 0;\n // category -> profit in decresing\n unordered_map<int, vector<vector<int>>> table;\n priority_queue<vector<int>, vector<vector<int>>, greater<>> minHeap;\n int i = n - 1;\n for (; i >= n - k; i--) {\n int pro = items[i][0], cat = items[i][1];\n table[cat].push_back(items[i]);\n \n sum += pro;\n }\n \n int keys = table.size(), dup = 0;\n ans = sum + 1LL * keys * keys;\n for (auto it = table.begin(); it != table.end(); it++) {\n if (it->second.size() > 1) {\n // duplicate category items in profit top-k\n dup += it->second.size() - 1;\n minHeap.push(it->second.back());\n it->second.pop_back();\n }\n }\n \n while (i >= 0 && dup > 0) {\n int pro = items[i][0], cat = items[i][1];\n if (table.find(cat) == table.end()) {\n sum -= minHeap.top()[0];\n sum += pro;\n \n int idx = minHeap.top()[1]; minHeap.pop();\n if (table[idx].size() > 1) {\n minHeap.push(table[idx].back());\n table[idx].pop_back();\n }\n \n table[cat].push_back(items[i]);\n keys++;\n \n ans = max(ans, sum + 1LL * keys * keys);\n dup--;\n }\n \n i--;\n }\n \n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ Binary Search + BFS Solution | c-binary-search-bfs-solution-by-solvedor-iz5q | \nclass Solution {\npublic:\n vector<int> delx={-1,1,0,0};\n vector<int> dely={0,0,-1,1};\n bool check(int mid, vector<vector<int>>& dist){\n in | solvedORerror | NORMAL | 2023-08-06T07:15:28.769416+00:00 | 2023-08-06T07:15:28.769439+00:00 | 29 | false | ```\nclass Solution {\npublic:\n vector<int> delx={-1,1,0,0};\n vector<int> dely={0,0,-1,1};\n bool check(int mid, vector<vector<int>>& dist){\n int n=dist.size();\n if(dist[0][0]<mid or dist[n-1][n-1]<mid)return false;\n vector<vector<bool>> vis(n,vector<bool>(n));\n queue<pair<int,int>>q;q.push({0,0});vis[0][0]=true;\n while(!q.empty()){\n int size=q.size();\n while(size--){\n auto [i,j]=q.front();q.pop();\n if(i==(n-1) and j==(n-1))return true;\n for(int k=0;k<4;k++){\n int x=i+delx[k],y=j+dely[k];\n if(x>=0 and y>=0 and x<n and y<n and dist[x][y]>=mid and !vis[x][y]){\n vis[x][y]=true;\n q.push({x,y});\n }\n }\n }\n }\n return false;\n }\n int maximumSafenessFactor(vector<vector<int>>& grid) {\n int n=grid.size();\n if(grid[0][0] or grid[n-1][n-1])return 0;\n queue<pair<int,int>>q;\n vector<vector<int>> dist(n,vector<int>(n,-1));\n for(int i=0;i<n;i++){\n for(int j=0;j<n;j++){\n if(grid[i][j]){\n q.push({i,j});\n dist[i][j]=0;\n }\n }\n }\n int level=1;\n while(!q.empty()){\n int size=q.size();\n while(size--){\n auto [i,j]=q.front();q.pop();\n for(int k=0;k<4;k++){\n int x=i+delx[k],y=j+dely[k];\n if(x>=0 and y>=0 and x<n and y<n and dist[x][y]==-1){\n dist[x][y]=level;\n q.push({x,y});\n }\n }\n }\n level++;\n }\n for(int i=0;i<n;i++){\n for(int j=0;j<n;j++){\n cout<<dist[i][j]<<" ";\n }\n cout<<endl;\n }\n int l=0,r=2*n;int ans=-1;\n while(l<=r){\n int mid=l+(r-l)/2;\n if(check(mid,dist)){\n l=mid+1;\n ans=mid;\n }else{\n r=mid-1;\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Breadth-First Search', 'Binary Tree'] | 1 |
maximum-elegance-of-a-k-length-subsequence | Priority_Queue | C++ | Sorting | priority_queue-c-sorting-by-marcos009-i3o0 | Code\n\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(),items.end());\n rev | marcos009 | NORMAL | 2023-08-06T06:41:21.329549+00:00 | 2023-08-06T06:41:21.329580+00:00 | 45 | false | # Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(),items.end());\n reverse(items.begin(),items.end());\n priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>p;\n if(k==1){\n return items[0][0]+1;\n }\n long long ans=0,sum=0;\n map<int,int>m;\n for(int i=0; i<k; i++){\n p.push({items[i][0],items[i][1]});\n sum+=items[i][0];\n m[items[i][1]]++;\n ans=max(ans,sum+(long long)m.size()*(long long)m.size());\n }\n for(int i=k; i<items.size(); i++){\n if(m.find(items[i][1])!=m.end()) continue;\n while(p.size() && m[p.top().second]==1){\n p.pop();\n }\n if(p.empty()) break;\n sum-=p.top().first;\n m[p.top().second]--;\n if(m[p.top().second]==0) m.erase(p.top().second);\n p.pop();\n sum+=items[i][0];\n p.push({items[i][0],items[i][1]});\n m[items[i][1]]++;\n ans=max(ans,sum+(long long)m.size()*(long long)m.size());\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Heap (Priority Queue)', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Faster but longer solution | faster-but-longer-solution-by-vilmos_pro-jgkp | \n# Complexity\n- Time complexity: O(n\log(n)) due to sorting and the heap.\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n) \n Add your | vilmos_prokaj | NORMAL | 2023-08-06T06:28:35.636689+00:00 | 2023-08-06T06:28:35.636713+00:00 | 18 | false | \n# Complexity\n- Time complexity: $$O(n\\log(n))$$ due to sorting and the heap.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def findMaximumElegance(self, items: List[List[int]], k: int) -> int:\n\n cats = defaultdict(list)\n for profit, cat in items:\n cats[cat].append(profit)\n for cat in cats:\n cats[cat].sort()\n \n sorted_cats = sorted(cats, key=lambda x: -cats[x][-1])\n # print(f"{sorted_cats=}")\n\n base_total = 0\n heap = []\n max_profit = 0\n total_profit = 0\n for i, cat in enumerate(sorted_cats):\n stack = cats[cat]\n profit = stack.pop()+2*i+1\n # print(f"{i=}, {cat=}, {stack=}, {profit=}")\n if i+len(heap) < k:\n total_profit += profit\n elif heap:\n total_profit -= heapq.heappop(heap)\n total_profit += profit\n else:\n break\n\n while stack:\n profit = stack.pop()\n if i + 1 + len(heap) < k:\n total_profit += profit\n heapq.heappush(heap, profit)\n elif heap and profit > heap[0]:\n total_profit += profit-heap[0]\n heapq.heapreplace(heap, profit)\n else:\n break\n\n if total_profit > max_profit:\n max_profit = total_profit\n # print(f"{i=}, {base_total=} {cat=} {heap=}")\n \n return max_profit\n\n\n``` | 0 | 0 | ['Heap (Priority Queue)', 'Python3'] | 0 |
maximum-elegance-of-a-k-length-subsequence | Greedy , take favourable items , well explained Solution✔️✔️✔️✔️ | greedy-take-favourable-items-well-explai-ljod | Approach\n1. The function first sorts the items vector in descending order based on profits. It maintains a set seen to track distinct categories and a vector d | __AKASH_SINGH___ | NORMAL | 2023-08-06T06:28:22.167248+00:00 | 2023-08-06T06:28:22.167274+00:00 | 12 | false | # Approach\n1. The function first sorts the items vector in descending order based on profits. It maintains a set seen to track distinct categories and a vector dup to store duplicate profits encountered in the initial k elements.\n\n2. Then, the function iterates through the sorted items. For the first k elements, it updates the sum of profits and checks if any duplicate profits are present. For subsequent elements, it optimally replaces the duplicate profits in the sum with higher individual profits.\n\n3. The function calculates the current elegance as sum + seen.size() * seen.size() at each step and keeps track of the maximum elegance (res).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(nlog(n))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(n)\n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n \n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n ll n = size(items), sum = 0, res = 0;\n vector<ll> dup;\n unordered_set<ll> seen;\n sort(items.begin(), items.end(), greater<vector<int>>());\n for(int i = 0; i<n; ++i)\n {\n if(i<k)\n {\n if(seen.count(items[i][1])) dup.push_back(items[i][0]);\n sum += items[i][0];\n }\n else if(seen.find(items[i][1]) == seen.end())\n {\n if(!dup.size()) break;\n sum += items[i][0] - dup.back();\n dup.pop_back();\n }\n seen.insert(items[i][1]);\n res = fmax(res, sum + seen.size() * 1ll *seen.size());\n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ Solution | Priority_queue | c-solution-priority_queue-by-juggaljain-0wis | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | juggaljain | NORMAL | 2023-08-06T06:17:38.192151+00:00 | 2023-08-06T06:18:12.528153+00:00 | 19 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long\n\nclass Solution {\npublic:\n\n static bool cmp(vector<int> &a, vector<int> &b) {return a[0]>b[0];}\n \n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n = items.size();\n\n priority_queue<pair<ll,ll>> pq;\n unordered_map<ll,ll> mp;\n sort(items.begin(), items.end(), cmp);\n ll sum = 0;\n for(int i=0; i<k; i++){\n sum += items[i][0];\n pq.push({-items[i][0], i});\n mp[items[i][1]]++;\n }\n ll res = sum + 1ll*mp.size()*mp.size();\n int i=k;\n while(i<n && !pq.empty()){\n if(mp[items[i][1]]>0){\n i++;\n continue;\n }\n int curr = pq.top().second;\n pq.pop();\n if(mp[items[curr][1]]==1) continue;\n sum += items[i][0]-items[curr][0];\n mp[items[curr][1]]--;\n mp[items[i][1]]++;\n res = max(res, sum + (long long)mp.size()*(long long)mp.size());\n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | beats 100%, nlogn sort with explanation | beats-100-nlogn-sort-with-explanation-by-6l6i | Approach\n Describe your approach to solving the problem. \n1) add highest profits with a unique category to a min heap.\n2) if heap is less than k add highest | Id000 | NORMAL | 2023-08-06T06:08:23.150468+00:00 | 2023-08-07T16:31:16.277500+00:00 | 35 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n1) add highest profits with a unique category to a min heap.\n2) if heap is less than k add highest profits that are not unique\n3) loop through remaining values, if any has a profit greater than 2 * (number of unique categories in heap) - 1 + min_profit in heap, replace that profit with looped value and reduce unique categories by one\n4)sum values in heap and mult by square of unique categories\n\nProof it works:\nthe looped values either have a duplicate category or is unique. If it has a unique category, because we placed unique categories with max profit in the heap first these values can be ignored since they are unique items with lowers profits that were not added to the heap therefore the only looped values that matter are high profits with a duplicate category.\nThe min profit in the heap can either have a unique category or is duplicate. If its category is duplicate it means we have added all unique categories of highest profits and ran out of unique values therefor we added duplicate values with highest profits therefore every other value is duplicate with less profit therefore can be skipped. If the min_heap profit is a unique category than the value it adds to the sum is min_profit + (unique_cats)^2 and the profit the looped value with dup category adds is competitor_profit + (unique_cats - 1) ^ 2 =>\ncompetitor_profit + unique_cats^2 - 2 * unique_cats + 1\ntherefore competitor profit must defeat the min_profit + 2 * unique_cats - 1. you must decrement the unique_cats if min_profit was deleted for the next iteration since that cat will be lost in the next calculation\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Code\n```\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n Deque<Integer> pq = new ArrayDeque<>();\n Arrays.sort(items, (a, b) -> b[0] - a[0]);\n Set<Integer> uniq = new HashSet<>();\n int n = items.length;\n for (int i = 0; i < n && pq.size() < k; i++) {\n int cat = items[i][1];\n if (!uniq.contains(cat)) {\n pq.addLast(items[i][0]);\n items[i][0] = -1;\n uniq.add(cat);\n }\n }\n int size = uniq.size();\n long res = 0;\n boolean flag = pq.size() < k;\n for (int i = 0; i < n; i++) {\n if (items[i][0] < 0) continue;\n if (pq.size() < k && flag) {\n pq.addFirst(items[i][0]);\n flag = pq.size() < k;\n continue;\n }\n int min_profit = pq.pollLast();\n int competitor = items[i][0];\n if (competitor > (long)min_profit + 2 * (long)size - 1) {\n res += competitor;\n size--;\n }\n else {\n res += min_profit;\n break;\n }\n }\n while(pq.size() > 0) res += pq.poll();\n res += (long) size * (long) size;\n return res;\n }\n}\n``` | 0 | 0 | ['Java'] | 1 |
maximum-elegance-of-a-k-length-subsequence | Rust/C++ Sorting | rustc-sorting-by-xiaoping3418-rpjx | Intuition\n Describe your first thoughts on how to solve this problem. \n1) Sort the items based on prefit.\n2) Pick one item per category in the descending ord | xiaoping3418 | NORMAL | 2023-08-06T06:05:47.853000+00:00 | 2023-08-06T23:48:40.188026+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1) Sort the items based on prefit.\n2) Pick one item per category in the descending order of profit.\n3) While k > 0, picking additional items in the existing categories.\n4) If k == 0, check to see if the smallest item could be replaced with the cost of reducing one category. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n//Rust\nuse std::collections::BTreeSet;\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn find_maximum_elegance(items: Vec<Vec<i32>>, k: i32) -> i64 {\n let mut used = BTreeSet::new();\n let mut category = HashSet::<i32>::new();\n let (mut items, mut k) = (items, k);\n let (mut ret, mut cnt) = (0, 0);\n \n items.sort();\n for i in (0 .. items.len()).rev() {\n if category.contains(&items[i][1]) { continue }\n \n ret += items[i][0] as i64;\n cnt += 1;\n used.insert(i);\n category.insert(items[i][1]);\n k -= 1;\n if k == 0 { break } \n }\n ret += cnt * cnt;\n\n for i in (0 .. items.len()).rev() {\n if used.contains(&i) { continue }\n \n if k > 0 {\n k -= 1;\n ret += items[i][0] as i64;\n continue; \n }\n\n if let Some(j) = used.iter().next() {\n let j = *j;\n if j >= i { break }\n\n let s = items[i][0] as i64 - items[j][0] as i64;\n let t = cnt * cnt - (cnt - 1) * (cnt - 1);\n \n if s <= t { break }\n ret += s - t;\n cnt -= 1;\n used.remove(&j);\n } \n }\n \n ret\n }\n}\n```\n\n~~~\n// C++\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n sort(items.begin(), items.end());\n set<int> used;\n unordered_set<int> category;\n int cnt = 0, n = items.size();\n long long ret = 0;\n \n for (int i = n - 1; i >= 0; --i) {\n if (category.find(items[i][1]) != category.end()) continue;\n category.insert(items[i][1]);\n ret += items[i][0];\n used.insert(i);\n cnt += 1;\n if (--k == 0) break;\n } \n ret += 1LL * cnt * cnt;\n \n for (int i = n - 1; i >= 0; --i) {\n if (used.find(i) != used.end()) continue;\n \n if (k > 0) {\n ret += items[i][0];\n --k;\n continue;\n } \n \n int j = *used.begin();\n if (j >= i) break;\n long long t = 1LL * cnt * cnt - 1LL * (cnt - 1) * (cnt - 1);\n if (0LL + items[i][0] - items[j][0] <= t) break;\n \n used.erase(j);\n ret -= t;\n cnt -= 1;\n ret += items[i][0] - items[j][0];\n }\n \n return ret;\n }\n};\n~~~ | 0 | 0 | ['Sorting', 'C++', 'Rust'] | 0 |
maximum-elegance-of-a-k-length-subsequence | My Solution | my-solution-by-hope_ma-aqpn | \n/**\n * Time Complexity: O(n * log(n))\n * Space Complexity: O(n)\n * where `n` is the length of the vector `items`\n */\nclass Solution {\n public:\n long l | hope_ma | NORMAL | 2023-08-06T05:57:02.780616+00:00 | 2023-08-11T14:27:22.030468+00:00 | 6 | false | ```\n/**\n * Time Complexity: O(n * log(n))\n * Space Complexity: O(n)\n * where `n` is the length of the vector `items`\n */\nclass Solution {\n public:\n long long findMaximumElegance(vector<vector<int>> &items, const int k) {\n const int n = static_cast<int>(items.size());\n sort(items.begin(), items.end(), [](const vector<int> &lhs, const vector<int> &rhs) -> bool {\n return lhs.front() > rhs.front();\n });\n \n bool occupied_categories[n];\n memset(occupied_categories, 0, sizeof(occupied_categories));\n int categories = 0;\n long long total = 0LL;\n stack<int> removables;\n for (int i = 0; i < k; ++i) {\n const int profit = items[i].front();\n const int category = items[i].back() - 1;\n total += profit;\n if (occupied_categories[category]) {\n // removing the item `items[i]` will not cause the number of the categories to decrease\n removables.emplace(profit);\n } else {\n occupied_categories[category] = true;\n ++categories;\n }\n }\n \n long long ret = total + static_cast<long long>(categories) * categories;\n for (int i = k; i < n && !removables.empty(); ++i) {\n /**\n * some explanations on the condition `!removables.empty()`\n * assume that `removables` is empty,\n * when a new item `items[i]` comes,\n * no matter whether item `items[i]` has a different category\n * among all categories of the owned items, excluding the item `items[i]`,\n * or not, it\'s necessary to remove an existing item to\n * keep the number of owned items `k`,\n * which will cause the number of categories\n * of the owned items, including the item `items[i]`,\n * to unchange or decrease, which can not cause the elegance of the owned\n * items to increase, so when `removables` is empty,\n * it\'s unnecessary to continue\n */\n const int profit = items[i].front();\n const int category = items[i].back() - 1;\n if (occupied_categories[category]) {\n /**\n * 1. adding the item `items[i]` will not cause the number of the categories to increase\n * 2. in order to keep the number of the owned items being `k`,\n * one owned item should be removed, the profit of any owned item is greater than or equal\n * to the profit of the item `items[i]`\n * so adding the item `items[i]` will not increase the elegance of the owned items\n */\n continue;\n }\n \n /**\n * add the item `items[i]`, at the same time one owned item should be removed\n */\n total += profit;\n total -= removables.top();\n removables.pop();\n occupied_categories[category] = true;\n ++categories;\n ret = max(ret, total + static_cast<long long>(categories) * categories);\n }\n return ret;\n }\n};\n``` | 0 | 0 | [] | 0 |
maximum-elegance-of-a-k-length-subsequence | C++ || Sorting || Map || Set | c-sorting-map-set-by-syphenlm12-zolj | Approach\n1. Sort on the basis of profit in decreasing order.\n2. Now take first k elements and also store that which category occurs how many time.\n3. After k | Syphenlm12 | NORMAL | 2023-08-06T05:53:58.374891+00:00 | 2023-08-06T05:53:58.374909+00:00 | 27 | false | # Approach\n1. Sort on the basis of profit in decreasing order.\n2. Now take first k elements and also store that which category occurs how many time.\n3. After k elements you will add any other number other than k elements if any category occurs more than one times in the k size window remove that element that add this current element into that k size and took maximum of all possibilities.\n# Complexity\n- Time complexity:\nnlogn\n\n# Code\n```\nclass Solution {\npublic:\n long long findMaximumElegance(vector<vector<int>>& items, int k) {\n int n = items.size();\n sort(items.rbegin(), items.rend());\n long long ans = 0;\n long long sum = 0;\n map<int, int> mp;\n multiset<pair<int, int>> st;\n for(int i = 0; i < k; i++) {\n sum += items[i][0];\n mp[items[i][1]]++;\n st.insert({items[i][0], items[i][1]});\n }\n sum += ((int) mp.size()) * 1LL * ((int) mp.size());\n ans = max(ans, sum);\n for(int i = k; i < n; i++) {\n if(mp.find(items[i][1]) != mp.end()) {\n continue;\n }\n while(st.size() > 0) {\n auto it = *st.begin();\n int profit = it.first;\n int category = it.second;\n if(mp[category] >= 2) {\n sum -= profit + ((int) mp.size()) * 1LL * ((int) mp.size());\n mp[items[i][1]]++;\n mp[category]--;\n sum += items[i][0] + ((int) mp.size()) * 1LL * ((int) mp.size());\n st.erase(st.begin());\n ans = max(ans, sum);\n break;\n }\n else {\n st.erase(st.begin());\n }\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Ordered Map', 'Sorting', 'Ordered Set', 'C++'] | 0 |
maximum-elegance-of-a-k-length-subsequence | [Java] Greedy solution | java-greedy-solution-by-wddd-8ptj | Intuition\n\nGreedy works here. \n\nIdea: we firstly pick k items with max total profits. Then we gradully/greedily remove some of them and replace with ones in | wddd | NORMAL | 2023-08-06T05:25:25.194199+00:00 | 2023-08-06T05:25:25.194217+00:00 | 28 | false | # Intuition\n\nGreedy works here. \n\nIdea: we firstly pick `k` items with max total profits. Then we gradully/greedily remove some of them and replace with ones in different categories. This way, the `total_profit` decreases, but we are compensated by `distinct_categories^2`, and we may get a bigger elegance value. Above process will be stopped until all categories are used.\n\n\n# Code\n```\nclass Solution {\n public long findMaximumElegance(int[][] items, int k) {\n Set<Integer> distinct = new HashSet<>();\n for (int[] item : items) {\n distinct.add(item[1]);\n }\n\n Arrays.sort(items, Comparator.comparingInt(i -> -i[0]));\n\n long maxElegance = 0;\n Map<Integer, Integer> picked = new HashMap<>();\n\n for (int i = 0; i < k; i++) {\n maxElegance += items[i][0];\n picked.put(items[i][1], picked.getOrDefault(items[i][1], 0) + 1);\n }\n maxElegance += (long) picked.size() * picked.size();\n\n int last = k - 1;\n long runningElegance = maxElegance;\n for (int i = k; i < items.length && picked.size() < distinct.size() && last >= 0; i++) {\n if (picked.containsKey(items[i][1])) {\n continue;\n }\n\n for ( ; last >= 0; last--) {\n if (picked.get(items[last][1]) > 1) {\n break;\n }\n }\n\n if (last < 0) {\n return maxElegance;\n }\n\n runningElegance = runningElegance - items[last][0] + items[i][0];\n long size = picked.size();\n runningElegance += ((size + 1) * (size + 1)) - size * size;\n if (runningElegance > maxElegance) {\n maxElegance = runningElegance;\n }\n picked.put(items[last][1], picked.get(items[last][1]) - 1);\n picked.put(items[i][1], 1);\n last--;\n }\n\n return maxElegance;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
minimum-score-by-changing-two-elements | Explained two solutions - with & without sorting || Very Simple & Easy to Understand | explained-two-solutions-with-without-sor-2ihy | Up Vote if you like the solution \n\n# Approach\n\nFirst of all we can simply replace two numbers with the same value, that results in the lowest difference to | kreakEmp | NORMAL | 2023-02-18T16:02:41.477147+00:00 | 2023-02-18T17:05:22.115952+00:00 | 5,605 | false | Up Vote if you like the solution \n\n# Approach\n\nFirst of all we can simply replace two numbers with the same value, that results in the lowest difference to zero in all cases.\nSo now the problem statement becomes, high (max difference) should be lowest. \nSo to achieve this, we need to decrease the difference between the smallest and largest value. This further can be achieved by doing one out of these three cases :\n1. remove the smallest two numbers\n2. remove the largest two numbers\n3. remove the smallest and largest\n\nso considering above three cases we have to take the minimum value possible.\n\nNote: I have written remove the smallest/largest number, this means => changing the smallest/largest number to any other number in the array.\n\nTo find smallest two and largest two number we can simply sort the array and we will have the value. Another way can be just keep track of two smallest and two largest values in the array which can be done easily using priority queue or just by tracking smallest three and largest three variables.\n \n\n# Solution 1 : with Sorting\n```\n int minimizeSum(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int case1 = nums.back() - nums[2];\n int case2 = nums[nums.size() - 3] - nums[0];\n int case3 = nums[nums.size() - 2] - nums[1];\n return min({case1, case2, case3});\n }\n```\n\n# Solution 2: with out sorting\n```\n/*\nAfter sorting the order of the variables are as follows :\ns1, s2, s3 ......... l3, l2, l1\ns1 is smallest & l1 is largest.\n*/\n\n int minimizeSum(vector<int>& nums) {\n int s1 = INT_MAX, s2 = INT_MAX, s3 = INT_MAX, l1 = 0, l2 = 0, l3 = 0;\n for(auto n: nums){\n if(s1 > n) { s3 = s2; s2 = s1; s1 = n; }\n else if(s2 > n) { s3 = s2; s2 = n; }\n else if(s3 > n) { s3 = n; }\n\n if(l1 < n) { l3 = l2; l2 = l1; l1 = n; }\n else if(l2 < n ) { l3 = l2; l2 = n; }\n else if(l3 < n ) { l3 = n; }\n }\n return min({l1 - s3, l3 - s1, l2 - s2});\n }\n```\n\nHere is an article of my recent interview experience - A Journey to FAANG Company, I recomand you to go through this to know which all resources I have used & how I cracked interview at Amazon:\nhttps://leetcode.com/discuss/interview-experience/3171859/Journey-to-a-FAANG-Company-Amazon-or-SDE2-(L5)-or-Bangalore-or-Oct-2022-Accepted | 75 | 1 | ['C++'] | 9 |
minimum-score-by-changing-two-elements | Simple Diagram Explanation | simple-diagram-explanation-by-l30xl1u-kjaq | Idea\n- Sort nums so that we can easily access maximum and minimum values\n- We will always make the low score 0 by creating duplicate values\n- Now we have cha | L30XL1U | NORMAL | 2023-02-18T20:00:42.079714+00:00 | 2023-02-18T20:04:57.246329+00:00 | 1,780 | false | # Idea\n- Sort `nums` so that we can easily access maximum and minimum values\n- We will always make the low score $$0$$ by creating duplicate values\n- Now we have changed the question to finding the minimum maximum value difference by changing two values\n- We have three options:\n - Change the two largest values to the third largest value. Third largest value now becomes the max value.\n - Change the two smallest values to the third smallest value. Third smallest value now becomes the min value.\n - Change largest value to second largest value and smallest value to second smallest value. Second largest becomes max value and second smallest becomes min value.\n- It must be one of these three options because we have to create duplicates to satisfy the low score constraint and the high score always deals with difference between maximum and minimum.\n\n\n# Example\n\n- Let us use `nums = [1,4,7,8,5]`\n\n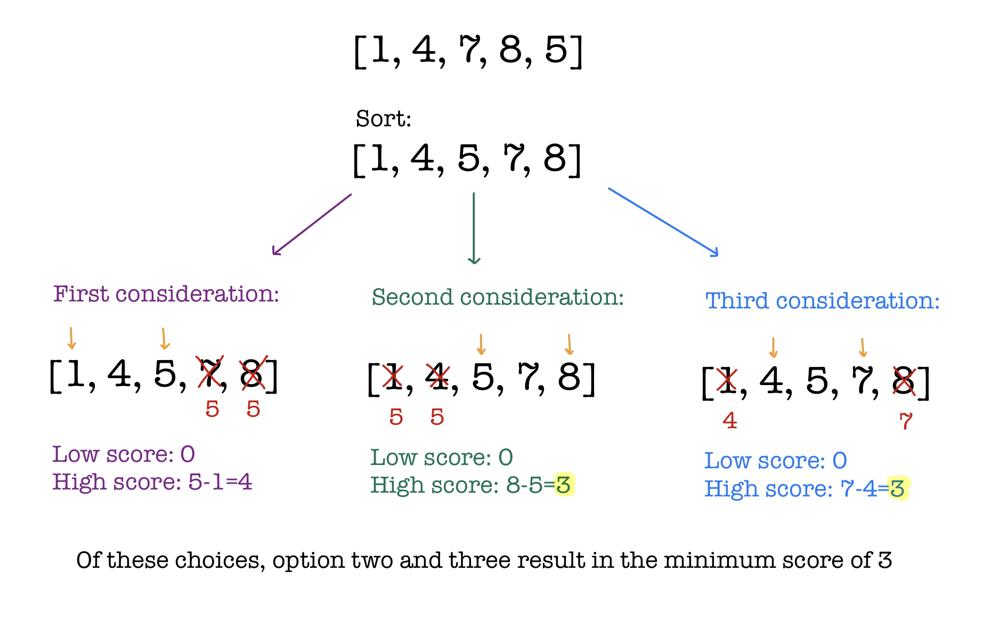\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int minimizeSum(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n return min(nums[n-1]-nums[2], min(nums[n-2]-nums[1], nums[n-3]-nums[0]));\n }\n};\n```\n- Notice from the code that we do not actually need to change the values, we just need to compare the elements of interest by the three options.\n#### If this helped please leave an upvote. Thanks! | 54 | 0 | ['C++', 'Java', 'Python3'] | 3 |
minimum-score-by-changing-two-elements | [Java/C++/Python] Change Biggest or Smallest | javacpython-change-biggest-or-smallest-b-u67s | Intuition\nChange the biggest or the smallest,\nto be other existing number.\n\n\n# Explanation\nChange two biggest,\nthen the high score is A[n-3] - A[0]\n\nCh | lee215 | NORMAL | 2023-02-18T16:10:18.184352+00:00 | 2023-02-19T02:26:13.385137+00:00 | 2,481 | false | # **Intuition**\nChange the biggest or the smallest,\nto be other existing number.\n<br>\n\n# **Explanation**\nChange two biggest,\nthen the high score is `A[n-3] - A[0]`\n\nChange the biggest and the smallest,\nthen the high score is `A[n-2] - A[1]`\n\nChange two smallest,\nthen the high score is `A[n-1] - A[2]`\n\nFor the low score,\nwe can always have 2 same numbers,\nso low score is 0.\n<br>\n\n# **Complexity**\nTime `O(sort)`\nSpace `O(sort)`\n\nAlso we can one pass,\nand find out the 3 biggest and 3 smallest in `O(n)`\n<br>\n\n**Java**\n```java\n public int minimizeSum(int[] A) {\n int n = A.length;\n Arrays.sort(A);\n return Math.min(Math.min(A[n - 1] - A[2], A[n - 3] - A[0]), A[n - 2] - A[1]);\n }\n```\n\n**C++**\n```cpp\n int minimizeSum(vector<int>& A) {\n int n = A.size();\n sort(A.begin(), A.end());\n return min({A[n - 1] - A[2], A[n - 3] - A[0], A[n - 2] - A[1]});\n }\n```\n\n**Python**\n```py\n def minimizeSum(self, A):\n A.sort()\n return min(A[-1] - A[2], A[-2] - A[1], A[-3] - A[0])\n```\n | 30 | 2 | ['C', 'Python', 'Java'] | 7 |
minimum-score-by-changing-two-elements | C++ | Python - Short and easy to understand with sorting | c-python-short-and-easy-to-understand-wi-t15m | Intuition\nWe see that we have to sort the array to easily find low score and high score\n\n# Approach\nAfter sorting the array, we have 3 ways to optimize this | nvthang | NORMAL | 2023-02-18T16:04:48.968039+00:00 | 2023-02-19T09:28:18.543827+00:00 | 2,171 | false | # Intuition\nWe see that we have to sort the array to easily find **low** score and **high** score\n\n# Approach\nAfter sorting the array, we have 3 ways to optimize this problem:\n- Increase `nums[0], nums[1] equal to nums[2]`, now `low=0`, `high=nums[n-1]-nums[2]`\n- Reduce `nums[n-1], nums[n-2] equal to nums[n-3]`, now `low=0`, `high=nums[n-3]-nums[0]`\n- Increase `nums[0] equal to nums[1]`, `nums[n-1] equal to nums[n-2]`, now `low=0`, `high=nums[n-2]-nums[1]`\n\nSo we just need to choose the smallest **high** score\n\n# Complexity\n- Time complexity: O(NlogN)\n\n# Code\n## C++\n```C++\nclass Solution {\npublic:\n int minimizeSum(vector<int> &nums) {\n std::sort(nums.begin(), nums.end());\n int n = nums.size();\n return min({nums[n - 1] - nums[2], nums[n - 3] - nums[0], nums[n - 2] - nums[1]});\n }\n};\n```\n## Python\n```python\nclass Solution:\n def minimizeSum(self, nums: List[int]) -> int:\n nums.sort()\n return min(nums[-1] - nums[2], nums[-3] - nums[0], nums[-2] - nums[1])\n```\n\t\t | 24 | 2 | ['C', 'Sorting'] | 4 |
minimum-score-by-changing-two-elements | 3 Step Logic + Video Solution || c++ solution | 3-step-logic-video-solution-c-solution-b-p4q6 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nhttps://youtu.be/pBJgRVQEDPE\n Describe your approach to solving the prob | u-day | NORMAL | 2023-02-18T16:24:49.764940+00:00 | 2023-02-19T02:00:20.809957+00:00 | 772 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nhttps://youtu.be/pBJgRVQEDPE\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minimizeSum(vector<int>& arr) {\n int n = arr.size();\n \n sort(arr.begin(), arr.end());\n \n int x = arr[n-3]-arr[0];\n int y = arr[n-1]-arr[2];\n int z = arr[n-2]-arr[1];\n \n return min({x, y, z});\n }\n};\n``` | 16 | 0 | ['C++'] | 1 |
minimum-score-by-changing-two-elements | 🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | leetcode-the-hard-way-explained-line-by-5ccpm | \uD83D\uDD34 Check out LeetCode The Hard Way for more solution explanations and tutorials. \n\uD83D\uDFE0 Check out our Discord Study Group for live discussion. | __wkw__ | NORMAL | 2023-02-18T16:15:53.925192+00:00 | 2023-02-18T16:33:17.430075+00:00 | 789 | false | \uD83D\uDD34 Check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \n\uD83D\uDFE0 Check out our [Discord Study Group](https://discord.gg/Nqm4jJcyBf) for live discussion.\n\uD83D\uDFE2 Give a star on [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post if you like it.\n\uD83D\uDD35 Check out [YouTube Channel](https://www.youtube.com/@leetcodethehardway) if you are interested.\n\n---\n\n```cpp\n// the idea is to change two numbers to an existing number \n// so that the low score will be always 0.\n// to minimize the high score, we can either choose \n// - 2 biggest numbers\n// - 2 smallest numbers, or \n// - 1 biggest and 1 smallest\n// we just take the min of them\nclass Solution {\npublic:\n int minimizeSum(vector<int>& nums) {\n int n = nums.size();\n sort(nums.begin(), nums.end());\n return min({\n // choose the biggest 2\n\t\t\t// now nums[n - 3] becomes the biggest\n\t\t\t// and nums[0] is still the smallest\n abs(nums[n - 3] - nums[0]),\n // choose the smallest & the biggest\n\t\t\t// now nums[n - 2] becomes the biggest\n\t\t\t// and nums[1] becomes the smallest\n abs(nums[n - 2] - nums[1]), \n // choose the smallest 2\n\t\t\t// now nums[n - 1] is still the biggest\n\t\t\t// and nums[2] becomes the smallest\n abs(nums[n - 1] - nums[2])\n });\n }\n};\n``` | 13 | 2 | ['C', 'Sorting'] | 1 |
minimum-score-by-changing-two-elements | O(n) | on-by-votrubac-cjcg | We can always make the low score zero. Therefore, we should focus on reducing the high score.\n\nFor that, we can either remove two smallest, one smallest and o | votrubac | NORMAL | 2023-02-18T16:00:58.463566+00:00 | 2023-02-18T16:40:50.031102+00:00 | 792 | false | We can always make the low score zero. Therefore, we should focus on reducing the high score.\n\nFor that, we can either remove two smallest, one smallest and one largest, or two largest elements.\n\nWe use partial sort to find two largest and two smallest elements, so that the time complexity is O(n).\n\n**C++**\n```cpp\nint minimizeSum(vector<int>& n) {\n partial_sort(begin(n), begin(n) + 3, end(n));\n partial_sort(rbegin(n), rbegin(n) + 3, rend(n) - 3, greater{});\n return min({ n[n.size() - 3] - n[0],\n n[n.size() - 2] - n[1], \n n[n.size() - 1] - n[2] });\n}\n``` | 12 | 1 | ['C'] | 1 |
minimum-score-by-changing-two-elements | Python 3 || 2 lines, w/ explanation || T/S: 72% / 81% | python-3-2-lines-w-explanation-ts-72-81-lh1o6 | \nclass Solution:\n def minimizeSum(self, nums: List[int]) -> int:\n\n nums.sort()\n\n return min(nums[-1] - nums[2], # [a,b,c, ..., x,y,z] = | Spaulding_ | NORMAL | 2023-02-20T05:15:38.459839+00:00 | 2024-06-21T20:14:37.361517+00:00 | 196 | false | ```\nclass Solution:\n def minimizeSum(self, nums: List[int]) -> int:\n\n nums.sort()\n\n return min(nums[-1] - nums[2], # [a,b,c, ..., x,y,z] => [c,c,c, ..., x,y,z]\n nums[-2] - nums[1], # [a,b,c, ..., x,y,z] => [b,b,c, ..., x,y,y] \n nums[-3] - nums[0]) # [a,b,c, ..., x,y,z] => [a,b,c, ..., x,x,x]\n\n # Return min((z-c)+(c-c), (x-a)+(x-x), (y-b)+(b-b))\n```\n[https://leetcode.com/problems/minimum-score-by-changing-two-elements/submissions/1296008208/](https://leetcode.com/problems/minimum-score-by-changing-two-elements/submissions/1296008208/)\n\nI could be wrong, but I think that time complexity is *O*(*N* log *N*) and space complexity is *O*(1).\n | 9 | 0 | ['Python3'] | 1 |
minimum-score-by-changing-two-elements | Sorting + Three cases only | sorting-three-cases-only-by-priyanshu_ch-50cp | Approach\n Sort the array\n There can be three cases: \n \n1) pick first two and make them third Example:-[1,2,8,9,11]\n2) pick last two and m | Priyanshu_Chaudhary_ | NORMAL | 2023-02-18T16:05:11.011022+00:00 | 2023-02-18T16:05:11.011068+00:00 | 1,027 | false | # Approach\n* Sort the array\n* There can be three cases: \n \n1) pick first two and make them third **Example:-[1,2,8,9,11]**\n2) pick last two and make it third last element **Example:- [1,2,3,9,11]**\n3) pick first and last and make them second and second last element **Example:- [1,4,5,7,8]**\n\n```\nclass Solution {\npublic:\n int minimizeSum(vector<int>& nums) \n {\n \n int n=nums.size();\n sort(begin(nums),end(nums));\n \n int ans1=abs(nums[n-1]-nums[2]);\n int ans2=abs(nums[1]-nums[n-2]);\n int ans3=abs(nums[0]-nums[n-3]);\n \n return min(ans1,min(ans2,ans3));\n }\n};\n``` | 9 | 0 | ['Sorting', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.