question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-insertion-steps-to-make-a-string-palindrome
|
Image Explanation🏆- [Recursion -> Top Down -> Bottom Up -> Bottom Up O(n)] - C++/Java/Python
|
image-explanation-recursion-top-down-bot-3ywf
|
Video Solution (Aryan Mittal) - Link in LeetCode Profile\nMinimum Insertion Steps to Make a String Palindrome by Aryan Mittal\n\n\n\n# Longest Palindromic Subse
|
aryan_0077
|
NORMAL
|
2023-04-22T01:15:28.090212+00:00
|
2023-04-22T01:30:51.571112+00:00
| 5,554
| false
|
# Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Minimum Insertion Steps to Make a String Palindrome` by `Aryan Mittal`\n\n\n\n# [Longest Palindromic Subsequence - LPS](https://leetcode.com/problems/longest-palindromic-subsequence/solutions/3415577/image-explanation-recursion-top-down-bottom-up-bottom-up-o-n/)\n\n\n# Approach & Intution\n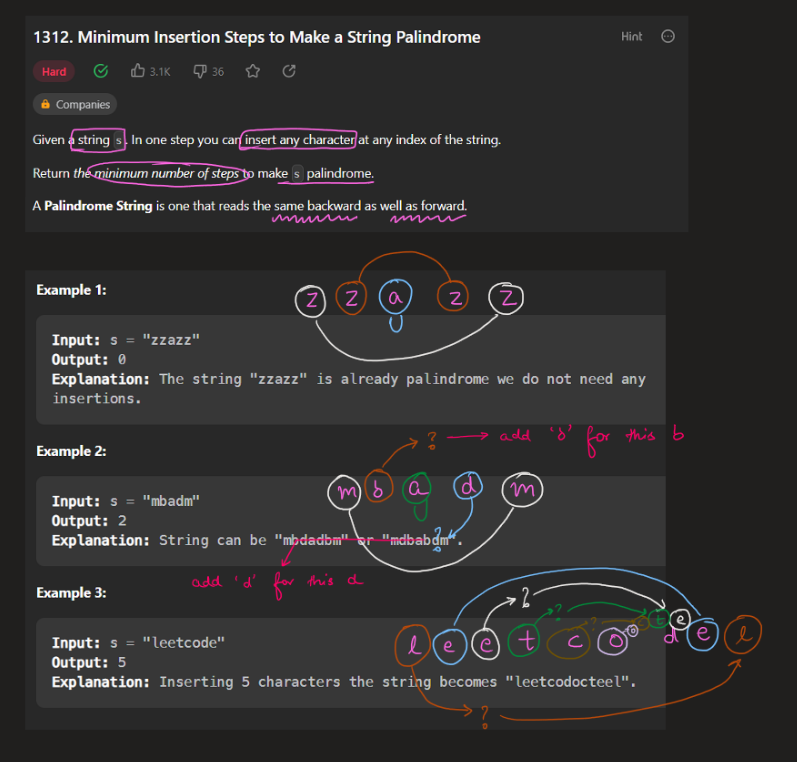\n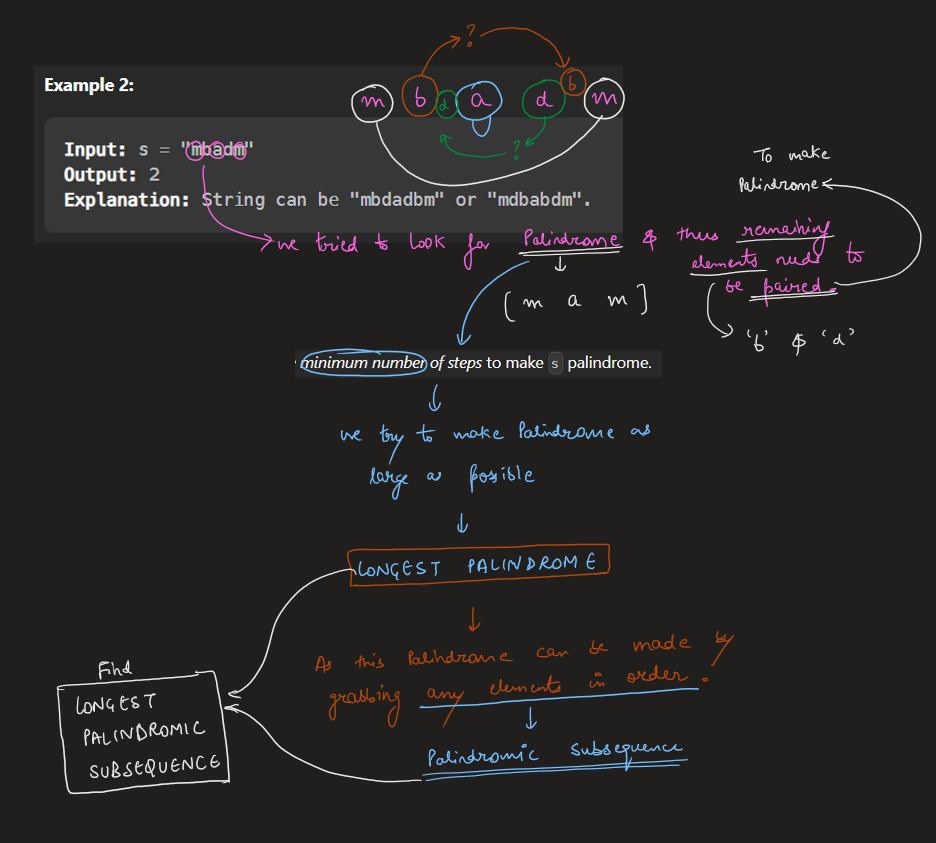\n\n\n\n\n\n# Most Optimized DP Code:\n```C++ []\nclass Solution {\npublic:\n int longestPalindromeSubseq(string& s) {\n int n = s.size();\n vector<int> dp(n), dpPrev(n);\n\n for (int start = n - 1; start >= 0; --start) {\n dp[start] = 1;\n for (int end = start + 1; end < n; ++end) {\n if (s[start] == s[end]) {\n dp[end] = dpPrev[end - 1] + 2;\n } else {\n dp[end] = max(dpPrev[end], dp[end - 1]);\n }\n }\n dpPrev = dp;\n }\n\n return dp[n - 1];\n }\n\n int minInsertions(string s) {\n return s.length() - longestPalindromeSubseq(s);\n }\n};\n```\n```Java []\nclass Solution {\n public int longestPalindromeSubseq(String s) {\n int n = s.length();\n int[] dp = new int[n];\n int[] dpPrev = new int[n];\n\n for (int start = n - 1; start >= 0; --start) {\n dp[start] = 1;\n for (int end = start + 1; end < n; ++end) {\n if (s.charAt(start) == s.charAt(end)) {\n dp[end] = dpPrev[end - 1] + 2;\n } else {\n dp[end] = Math.max(dpPrev[end], dp[end - 1]);\n }\n }\n dpPrev = dp.clone();\n }\n\n return dp[n - 1];\n }\n\n public int minInsertions(String s) {\n return s.length() - longestPalindromeSubseq(s);\n }\n}\n```\n```Python []\nclass Solution:\n def minInsertions(self, s: str) -> int:\n def longestPalindromeSubseq(self, s: str) -> int:\n n = len(s)\n dp = [0] * n\n dpPrev = [0] * n\n\n for start in range(n - 1, -1, -1):\n dp[start] = 1\n for end in range(start + 1, n):\n if s[start] == s[end]:\n dp[end] = dpPrev[end - 1] + 2\n else:\n dp[end] = max(dpPrev[end], dp[end - 1])\n dpPrev = dp[:]\n\n return dp[n - 1]\n\n return len(s) - longestPalindromeSubseq(self, s)\n```\n\n
| 20
| 2
|
['String', 'Dynamic Programming', 'C++', 'Java', 'Python3']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
100% memory efficient and 98% faster solution.[EASY] | [C++] | [DP] | [LCS]
|
100-memory-efficient-and-98-faster-solut-mulc
|
TOP-DOWN DYNAMIC PROGRAMING\nWe need to find if there exist any subsequence of string S1 which is palindrome. \nIf there is such a subsequence sub, then we need
|
sonukumarsaw
|
NORMAL
|
2020-05-15T16:41:58.104929+00:00
|
2020-05-15T16:41:58.104984+00:00
| 2,447
| false
|
**TOP-DOWN DYNAMIC PROGRAMING**\nWe need to find if there exist any subsequence of string **S1** which is palindrome. \nIf there is such a subsequence **sub**, then we need minimum ***len(S1)-len(sub)***\nElse, we need atleast ***len(S1)*** number of insertions to make it palindrome.\n\nTo find the len of subsequence of S1 which is palindrome, we can use [Longest Common Subsequence](https://en.wikipedia.org/wiki/Longest_common_subsequence_problem). \n```\nint minInsertions(string s1) {\n int n = s1.size();\n int DP[n+1][n+1];\n string s2 =s1;\n reverse(s1.begin(),s1.end());\n \n for(int i=0;i<=n;i++){\n for(int j=0;j<=n;j++){\n if(i==0 || j==0){\n DP[i][j] = 0;\n }\n else if(s1[i-1]==s2[j-1]){\n DP[i][j] = DP[i-1][j-1]+1;\n }\n else{\n DP[i][j] = max(DP[i-1][j],DP[i][j-1]);\n }\n }\n }\n \n return n-DP[n][n];\n }\n```\n\nPlease upvote if you liked the post.\nYou can refer to the [this](https://www.youtube.com/watch?v=AEcRW4ylm_c&list=PL_z_8CaSLPWekqhdCPmFohncHwz8TY2Go&index=33&t=0s) link if you want detail explanation.
| 19
| 1
|
['Dynamic Programming', 'C']
| 2
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Python Clean DP
|
python-clean-dp-by-wangqiuc-ru1r
|
dp[i,j] stands for the minimum insertion steps to make s[i:j+1] palindrome.\nIf s[i] == s[j] then dp[i,j] should be equal to dp[i+1,j-1] as no extra cost needed
|
wangqiuc
|
NORMAL
|
2020-01-11T05:11:45.565362+00:00
|
2020-01-11T15:10:43.192848+00:00
| 2,550
| false
|
`dp[i,j]` stands for the minimum insertion steps to make `s[i:j+1]` palindrome.\nIf `s[i] == s[j]` then `dp[i,j]` should be equal to `dp[i+1,j-1]` as no extra cost needed for a palidrome string to include `s[i]` on the left and `s[j]` on the right. \nOtherwise, `dp[i,j]` take an extra 1 cost from the smaller cost between `dp[i+1,j]` and `dp[i,j-1]`.\nThen the recurrence equation would be: \n`dp[i][j] = dp[i+1][j-1] if s[i] == s[j] else min(dp[i+1][j], dp[i][j-1]) + 1`\n\nTo build a bottom-up iteration, we need to iterate all the combination of `(i, j)` where `i < j`. \nThere is no need to check `dp[i,i]` which is `0`. \nAnother base case is `dp[i,i-1]`. This happens only when we are checking a `dp[i,i+1]` and `s[i] == s[i+1]`. This can also be set as `0` so `dp[i,i+1]` will be `0` correctly.\nSo we can savely initialized the entire `dp` array to be filled with `0`.\n```\ndef minInsertions(self, s):\n\tn = len(s)\n\tdp = [[0] * n for _ in range(n)]\n\tfor j in range(n):\n\t\tfor i in range(j-1,-1,-1):\n\t\t\tdp[i][j] = dp[i+1][j-1] if s[i] == s[j] else min(dp[i+1][j], dp[i][j-1]) + 1\n\treturn dp[0][n-1]\n```
| 17
| 0
|
['Python']
| 3
|
minimum-insertion-steps-to-make-a-string-palindrome
|
DP🫡| Simple Java Solution | Longest Palindromic Subsequence
|
dp-simple-java-solution-longest-palindro-5vec
|
Intuition\nIf we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the answer to this problem? It is n - x as we ne
|
Comrade-in-code
|
NORMAL
|
2023-03-19T05:20:25.013710+00:00
|
2023-03-19T05:20:25.013758+00:00
| 1,939
| false
|
# Intuition\nIf we know the **longest palindromic sub-sequence** is x and the length of the string is n then, what is the answer to this problem? It is n - x as we need n - x insertions to make the remaining characters also palindrome.\n\n# Approach\nWe just need to find the length of **longest common subsequence** of the given string and the string obtained by reversing the original string.\n\n# Complexity\n- Time complexity: O(N^2) \n\n- Space complexity: O(N^2)\n\n# Code\n```\nclass Solution {\n public int minInsertions(String a) {\n StringBuilder s = new StringBuilder(a);\n s.reverse();\n // Obtaining the reverse of original string\n String b = s.toString();\n \n int n = a.length();\n int t[][] = new int[n+1][n+1];\n \n // Top-down DP\n for(int i=1; i<=n; i++) \n for(int j=1; j<=n; j++)\n if(a.charAt(i-1)==b.charAt(j-1)) t[i][j] = 1 + t[i-1][j-1];\n else t[i][j] = Math.max(t[i-1][j], t[i][j-1]);\n // Desired answer\n return n-t[n][n];\n }\n}\n```
| 15
| 0
|
['String', 'Dynamic Programming', 'Java']
| 2
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[Javascript] Dynamic Programming Easy and explained
|
javascript-dynamic-programming-easy-and-ao630
|
Explanation : This is the direct implementation of Longest Palindromic Subsequence. \n\nPS: Feel free to ask your questions in comments and do upvote if you lik
|
dhairyabahl
|
NORMAL
|
2021-09-02T13:51:16.547121+00:00
|
2021-09-02T13:51:16.547186+00:00
| 1,117
| false
|
**Explanation** : This is the direct implementation of Longest Palindromic Subsequence. \n\nPS: Feel free to ask your questions in comments and do upvote if you liked my solution.\n\n```\n/**\n * @param {string} s\n * @return {number}\n */\nvar minInsertions = function(s) {\n \n let dp = []\n \n for(let row = 0 ; row <= s.length ; row ++){\n let arr = []\n \n for(let col = 0 ; col <= s.length ; col ++) arr.push(0)\n \n dp.push(arr)\n }\n \n let rev = s.split("")\n \n rev = rev.reverse();\n \n rev = rev.join("");\n \n for(let row = 1 ; row <= s.length ; row ++ )\n for(let col = 1 ; col <= s.length ; col ++) {\n \n if(s[row-1] === rev[col-1])\n dp[row][col] = 1 + dp[row-1][col-1]\n else\n dp[row][col] = Math.max(dp[row-1][col],dp[row][col-1])\n }\n \n return s.length - dp[s.length][s.length];\n \n};\n```
| 14
| 0
|
['Dynamic Programming', 'JavaScript']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
= longest palindrome subsequence
|
longest-palindrome-subsequence-by-hobite-rhbk
|
I know there are a lot of BIG GOD\'s discussions to show how to solve this. \nBut for easy understanding, this problem could be transformed to:\nFinding "longes
|
hobiter
|
NORMAL
|
2020-01-08T06:01:38.794667+00:00
|
2020-01-08T06:12:40.658149+00:00
| 1,668
| false
|
I know there are a lot of BIG GOD\'s discussions to show how to solve this. \nBut for easy understanding, this problem could be transformed to:\n**Finding "longest palindrome subsequence", **\nthen transformed to:\n**Finding "longest common subsequence to his reversed string ".**\n```\ninInsertions(String s) \n= n - longthPalSubSeq(s)\n= n - longthCommonSubSeq(s, reversed(s)) \n```\n\n\n```\nclass Solution {\n //same as find the longest sub palindrome subsequence\n public int minInsertions(String s) {\n int n = s.length();\n int[][] dp = new int[n+1][n+1];\n for(int i = 0; i < n; i++){\n for(int j = 0; j < n; j++){\n if (s.charAt(i) == s.charAt(n - 1 - j)){\n dp[i+1][j+1] = dp[i][j] + 1;\n } else {\n dp[i+1][j+1] = Math.max(dp[i+1][j], dp[i][j+1]);\n }\n }\n }\n return n - dp[n][n];\n }\n}\n```\n\n\n
| 14
| 2
|
[]
| 5
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Easy Solution Of JAVA 🔥C++ 🔥DP 🔥Beginner Friendly
|
easy-solution-of-java-c-dp-beginner-frie-jwyi
|
\n\n# Code\nPLEASE UPVOTE IF YOU LIKE.\n\nclass Solution {\n public int minInsertions(String s) {\n StringBuilder sb = new StringBuilder(s);\n
|
shivrastogi
|
NORMAL
|
2023-04-22T01:02:08.268318+00:00
|
2023-04-22T01:02:08.268341+00:00
| 2,539
| false
|
\n\n# Code\nPLEASE UPVOTE IF YOU LIKE.\n```\nclass Solution {\n public int minInsertions(String s) {\n StringBuilder sb = new StringBuilder(s);\n sb.reverse();\n String rev = sb.toString();\n int n = s.length();\n int[][] dp = new int[n+1][n+1];\n for(int i=1;i<=n;i++) {\n for(int j=1;j<=n;j++) {\n int val = -1;\n if(s.charAt(i-1) == rev.charAt(j-1)) {\n val = 1 + dp[i-1][j-1];\n }\n else {\n val = Math.max(dp[i-1][j], dp[i][j-1]);\n }\n dp[i][j] = val;\n }\n }\n int lcsCount = dp[n][n];\n \n int minInsertion = n - lcsCount; \n return minInsertion;\n }\n}\n```\nC++\n```\nclass Solution {\npublic:\n\tint lcs(string s1, string s2) {\n\t\tint n=s1.size(),m=s2.size();\n\t\tvector<vector<int>> dp(n,vector<int>(m,0));\n\t\tfor(int i=0;i<n;i++){\n\t\t\tfor(int j=0;j<m;j++){\n\t\t\t\tif(!i || !j){\n\t\t\t\t\tif(s1[i]==s2[j]) dp[i][j]=1;\n\t\t\t\t\telse{\n\t\t\t\t\t\tif(!i && !j) dp[0][0]=0;\n\t\t\t\t\t\telse if(!i && j) dp[0][j]=dp[0][j-1];\n\t\t\t\t\t\telse if(i && !j) dp[i][0]=dp[i-1][0];\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\telse{\n\t\t\t\t\tif(s1[i]==s2[j]) dp[i][j]=1+dp[i-1][j-1];\n\t\t\t\t\telse dp[i][j]=max(dp[i-1][j],dp[i][j-1]);\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn dp[n-1][m-1]; \n\t}\n\n\tint minInsertions(string s) {\n\t\treturn s.size()-lcs(s,string(s.rbegin(),s.rend()));\n\t}\n};\n\n```
| 13
| 6
|
['Dynamic Programming', 'C++', 'Java']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
How (len - LPS)??? Explained with images || Recursion to Bottom UP
|
how-len-lps-explained-with-images-recurs-zvh1
|
\n\n\n\n## RECURSION\n\nclass Solution {\npublic:\n int lps(string& s, int start, int end)\n {\n if (start == end) return 1;\n if (start > e
|
mohakharjani
|
NORMAL
|
2023-04-22T00:40:34.354812+00:00
|
2023-04-22T00:42:32.950525+00:00
| 692
| false
|
\n\n\n\n## RECURSION\n```\nclass Solution {\npublic:\n int lps(string& s, int start, int end)\n {\n if (start == end) return 1;\n if (start > end) return 0;\n \n if (s[start] == s[end]) return (2 + lps(s, start + 1, end - 1));\n int leaveLeft = lps(s, start + 1, end);\n int leaveRight = lps(s, start, end - 1);\n return max(leaveLeft, leaveRight);\n }\n int minInsertions(string s) \n {\n int lpsLen = lps(s, 0, s.size() - 1);\n return (s.size() - lpsLen);\n }\n\n};\n```\n//=======================================================================================================================\n## TOP-DOWN\n```\nclass Solution {\npublic:\n int lps(string& s, vector<vector<int>>&dp, int start, int end)\n {\n if (start == end) return 1;\n if (start > end) return 0;\n if (dp[start][end] != -1) return dp[start][end];\n \n if (s[start] == s[end]) return (2 + lps(s, dp, start + 1, end - 1)); //directly return \n \n int leaveLeft = lps(s, dp, start + 1, end);\n int leaveRight = lps(s, dp, start, end - 1);\n return dp[start][end] = max(leaveLeft, leaveRight); //store the ans\n }\n int minInsertions(string s) \n {\n int n = s.size();\n vector<vector<int>>dp(n, vector<int>(n, -1));\n int lpsLen = lps(s, dp, 0, n - 1);\n return (n - lpsLen);\n }\n\n};\n```\n//=======================================================================================================================\n## BOTTOM-UP\n```\nclass Solution {\npublic:\n int lps(string& s)\n {\n int n = s.size();\n vector<vector<int>>dp(n, vector<int>(n, 0));\n //for n length string we need LPS for string with length (n - 1) or (n - 2)\n //We need to already have LPS for smaller lengths before moving to greater lengths\n //so we need to go bottom up \n //Calculating LPS for all strings of length = 1 to length = n\n //================================================================================\n for (int len = 1; len <= n; len++)\n {\n for (int start = 0; start <= (n - len); start++)\n {\n int end = start + len - 1; //[start, end] denotes the string under consideration\n if (len == 1) { dp[start][end] = 1; continue; }\n \n if (s[start] == s[end]) dp[start][end] = 2 + dp[start + 1][end - 1];\n else dp[start][end] = max(dp[start + 1][end], dp[start][end - 1]); \n }\n }\n //=====================================================================================\n return dp[0][n - 1];\n }\n int minInsertions(string s) \n {\n int n = s.size();\n int lpsLen = lps(s);\n return (n - lpsLen);\n }\n\n};\n```
| 12
| 1
|
['Dynamic Programming', 'C', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Day 112 || Recursion > Memoization || Easiest Beginner Friendly Sol
|
day-112-recursion-memoization-easiest-be-77kp
|
NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.\n\n# Intuitio
|
singhabhinash
|
NORMAL
|
2023-04-22T00:39:35.748863+00:00
|
2023-04-22T00:46:53.537589+00:00
| 1,870
| false
|
**NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\n**If you know how to solve Longest palindromic Subsequence then this problem is easy for you. For example s = "acdsddca" then longest palondromic subsequence is "acddca" i.e. of length 6. It means if we insert n - 6 = 8 - 6 = 2 character in this given string then this string is palindromic string. How?\n Earlier we have earlier string s = "acdsddca" now we need to add two more charater to amke this string palindromic i.e. new string s = "acdsddsdca"**\n\n516. Longest Palindromic Subsequence - https://leetcode.com/problems/longest-palindromic-subsequence/\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Code :\n```C++ []\n// Recursive approach - TLE\n//The time complexity of the longestPalindromeSubstring function is O(2^n) where n is the length of the input string s. This is because in the worst case, the function will make two recursive calls at each step, effectively creating a binary tree with 2^n nodes.\n//The space complexity of the algorithm is O(n) due to the recursive calls on the call stack. In the worst case, the call stack can grow to a depth of n, corresponding to the length of the input string s.\nclass Solution {\npublic:\n int longestPalindromeSubstring(string& s, int i, int j) {\n if (i > j)\n return 0;\n else if (i == j)\n return 1;\n else if (s[i] == s[j])\n return 2 + longestPalindromeSubstring(s, i+1, j-1);\n else\n return max(longestPalindromeSubstring(s, i+1, j), longestPalindromeSubstring(s, i, j-1));\n }\n int minInsertions(string s) {\n int n = s.length();\n int minNumSteps = n - longestPalindromeSubstring(s, 0, n-1);\n return minNumSteps;\n }\n};\n```\n```C++ []\n// Memoization (top-down DP) - Accepted\n//The time complexity of the longestPalindromeSubstring function with memoization is O(n^2), where n is the length of the input string s. This is because the function can be visualized as filling in a diagonal strip in a 2D matrix of size n x n, and each entry is computed only once and stored in the memo table.\n//The space complexity of the algorithm is O(n^2) due to the memoization table. It requires a 2D array of size n x n to store the computed results.\nclass Solution {\npublic:\n int longestPalindromeSubstring(string& s, int i, int j, vector<vector<int>>& memo) {\n if (i > j)\n return 0;\n else if (i == j)\n return 1;\n else if (memo[i][j] != -1)\n return memo[i][j];\n else if (s[i] == s[j])\n return memo[i][j] = 2 + longestPalindromeSubstring(s, i+1, j-1, memo);\n else\n return memo[i][j] = max(longestPalindromeSubstring(s, i+1, j, memo), longestPalindromeSubstring(s, i, j-1, memo));\n }\n int minInsertions(string s) {\n int n = s.length();\n vector<vector<int>> memo(n, vector<int>(n, -1));\n int minNumSteps = n - longestPalindromeSubstring(s, 0, n-1, memo);\n return minNumSteps;\n }\n};\n```\n```C++ []\n// Tabulation (bottm-up DP) - coming soon\n```
| 11
| 0
|
['Recursion', 'Memoization', 'C++']
| 3
|
minimum-insertion-steps-to-make-a-string-palindrome
|
JAVA || DP - 1D and 2D || Beats 70% Time & 100% Space || Explanation || Space optimization
|
java-dp-1d-and-2d-beats-70-time-100-spac-i5v6
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo make a given string palindrome, we need to insert some characters at some positions.
|
millenium103
|
NORMAL
|
2023-04-22T05:23:55.286519+00:00
|
2023-04-22T05:23:55.286550+00:00
| 1,660
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo make a given string palindrome, we need to insert some characters at some positions. If we can find out the longest common subsequence between the given string and its reverse, we can find out the characters that don\'t need to be inserted to make the string a palindrome. The number of insertions needed will be equal to the length of the given string minus the length of the longest common subsequence.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can use dynamic programming to find the longest common subsequence between the given string `s` and its reverse. We can define a 2D array `dp` of size `(n+1)x(n+1)`, where `n` is the length of the string `s`. We can then populate the `dp` array using the following recurrence relation:\n\n```\nif s[i-1] == s_reverse[j-1]:\n dp[i][j] = dp[i-1][j-1] + 1\nelse:\n dp[i][j] = max(dp[i-1][j], dp[i][j-1])\n```\nOnce we have filled the `dp` array, we can return the difference between the length of `s` and the length of its longest common subsequence, which will give us the minimum number of insertions required to make `s` a palindrome.\n\nHowever, we can optimize the space complexity of our solution by using only a 1D array instead of a 2D array. We can define a 1D array `dp` of size `(n+1)`, where `n` is the length of the string `s`. We can then populate the `dp` array using the following recurrence relation:\n\n```\nif s[i-1] == s_reverse[j-1]:\n dp[j] = prev + 1\nelse:\n dp[j] = max(dp[j], dp[j-1])\n```\nHere, `prev` represents the value of `dp[j-1]` from the previous iteration of the inner loop.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**O(n^2)** , where `n` is the length of the string `s`. This is because we need to fill the entire `dp` array, which has a size of `(n+1)x(n+1)`.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(n)**, where `n` is the length of the string `s`. This is because we only need to use a 1D array of size `(n+1)` to store our dynamic programming table.\n\n# Code\n```\nclass Solution {\n // Space optimized logic for the below code\n public int minInsertions(String s) {\n int n = s.length();\n int[] dp = new int[n + 1];\n int prev = 0;\n for (int i = 1; i <= n; i++) {\n prev = 0;\n for (int j = 1; j <= n; j++) {\n int temp = dp[j];\n if (s.charAt(i - 1) == s.charAt(n - j)) {\n dp[j] = prev + 1;\n } else {\n dp[j] = Math.max(dp[j], dp[j - 1]);\n }\n prev = temp;\n }\n }\n return n - dp[n];\n }\n /*\n 2D array\n public int minInsertions(String s) {\n return s.length()-helper(s,reverse(s)); \n }\n private String reverse(String s)\n {\n String str = new StringBuilder(s).reverse().toString();\n return str;\n }\n private int helper(String seedha, String ulta)\n {\n // Is function me hum longest common subsequence ka length nikalne wale hai\n int n = seedha.length();\n int[][] dp = new int[n+1][n+1];\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(seedha.charAt(i) == ulta.charAt(j))\n {\n dp[i+1][j+1]= dp[i][j]+1;\n }\n else\n {\n dp[i+1][j+1]= Math.max(dp[i+1][j],dp[i][j+1]);\n }\n }\n }\n return dp[n][n];\n\n }\n\n */\n}\n```\n## If you found this helpful, please don\'t forget to upvote!\n
| 10
| 0
|
['String', 'Dynamic Programming', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Longest Palindromic Subsequence | Aditya Verma's approach
|
longest-palindromic-subsequence-aditya-v-dnt7
|
Just find the length of Longest Palindromic Subsequence and subtract it from the string size (in the same way we can calculate "minimum number of deletions to m
|
iashi_g
|
NORMAL
|
2021-06-29T06:56:52.643842+00:00
|
2021-06-29T06:56:52.643888+00:00
| 928
| false
|
Just find the length of Longest Palindromic Subsequence and subtract it from the string size (in the same way we can calculate "minimum number of deletions to make a string palindrome").\n```\nclass Solution {\npublic:\n int lcs(int x, int y, string s1, string s2)\n {\n int dp[x+1][y+1];\n \n for(int i = 0; i <= x; i++)\n {\n dp[i][0] = 0;\n }\n \n for(int j = 0; j <= y; j++)\n {\n dp[0][j] = 0;\n }\n \n for(int i = 1; i <= x; i++)\n {\n for(int j = 1; j <= y; j++)\n {\n if(s1[i-1] == s2[j-1])\n {\n dp[i][j] = 1 + dp[i-1][j-1];\n }\n else\n {\n dp[i][j] = max(dp[i-1][j], dp[i][j-1]);\n }\n }\n }\n \n return dp[x][y];\n }\n int minInsertions(string A) {\n int n = A.size();\n string B = A;\n reverse(B.begin(),B.end());\n return n - lcs(n,n,A,B);\n }\n};\n```
| 10
| 0
|
['Dynamic Programming', 'C']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
simple python DP solution: longest common subsequence variation.
|
simple-python-dp-solution-longest-common-w8gg
|
Let the first string be a. then take a new string b which is reversed of a.\napply longest common subsequnce on both the strings and subtract the answer from th
|
captain_levi
|
NORMAL
|
2020-08-04T04:42:28.464618+00:00
|
2020-08-04T04:42:28.464653+00:00
| 1,386
| false
|
Let the first string be a. then take a new string b which is reversed of a.\napply longest common subsequnce on both the strings and subtract the answer from the length of the string.\nit works for minimum number of deletion as well as minimum number of insertion to make a string palindrome.\n\n\tclass Solution:\n\t\tdef minInsertions(self, a: str) -> int:\n\t\t\tb = a[::-1]\n\t\t\tn = len(a)\n\n\t\t\tdp = [[0 for x in range(n + 1)] for y in range(n + 1)]\n\n\t\t\tfor i in range(1, n + 1):\n\t\t\t\tfor j in range(1, n + 1):\n\t\t\t\t\tif a[i - 1] == b[j - 1]:\n\t\t\t\t\t\tdp[i][j] = 1 + dp[i - 1][j - 1]\n\n\t\t\t\t\telse:\n\t\t\t\t\t\tdp[i][j] = max(dp[i - 1][j], dp[i][j - 1])\n\n\t\t\treturn n - dp[-1][-1]
| 9
| 0
|
['Dynamic Programming', 'Python', 'Python3']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[JAVA] Simple DP with explanation and very small code
|
java-simple-dp-with-explanation-and-very-ovd1
|
The initution is two pointers (at the beginning and at the end end).\n2. Match the the pointer if the match move the pointers(begin+1 and end-1)\n3. If they don
|
siddhantiitbmittal3
|
NORMAL
|
2020-01-07T14:39:59.251430+00:00
|
2020-01-07T14:39:59.251478+00:00
| 867
| false
|
1. The initution is two pointers (at the beginning and at the end end).\n2. Match the the pointer if the match move the pointers(begin+1 and end-1)\n3. If they dont match either you add character at the end or character at the begin. \n4. Since we have a choice here if have to make the min of the two cases. Thus forming a recursive problem.\n5. Since we will be coming across same begin,end pointer pairs we apply DP.\nThis guarantee min solution as we try to explore all the possible cases\n6. O(n^2 \n\n```\nclass Solution {\n \n Integer[][] dp;\n \n public int helper(int i, int j, String s){\n \n if(i>j)\n return 0;\n \n if(dp[i][j] != null)\n return dp[i][j];\n int val;\n \n if(s.charAt(i) == s.charAt(j))\n val = helper(i+1,j-1,s);\n else\n val = Math.min(helper(i+1,j,s),helper(i,j-1,s)) + 1;\n \n dp[i][j] = val;\n \n return dp[i][j];\n }\n public int minInsertions(String s) {\n dp = new Integer[s.length()][s.length()];\n return helper(0,s.length()-1,s);\n }\n}\n```
| 9
| 0
|
[]
| 2
|
minimum-insertion-steps-to-make-a-string-palindrome
|
"one-liner"
|
one-liner-by-stefanpochmann-q1rr
|
\nfrom functools import lru_cache\n\nclass Solution:\n @lru_cache(None)\n def minInsertions(self, s):\n return(n:=len(s))and 1-(e:=s[0]==s[-1])+min
|
stefanpochmann
|
NORMAL
|
2020-01-05T14:47:07.928109+00:00
|
2020-01-05T14:49:17.825939+00:00
| 660
| false
|
```\nfrom functools import lru_cache\n\nclass Solution:\n @lru_cache(None)\n def minInsertions(self, s):\n return(n:=len(s))and 1-(e:=s[0]==s[-1])+min(map(self.minInsertions,(s[e:-1],s[1:n-e])))\n```
| 9
| 5
|
[]
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Python3 short straight forward DP
|
python3-short-straight-forward-dp-by-kai-mloo
|
\nimport functools\nclass Solution:\n def minInsertions(self, s: str) -> int:\n @functools.lru_cache(None)\n def dp(i, j):\n if j -
|
kaiwensun
|
NORMAL
|
2020-01-05T04:11:21.054250+00:00
|
2020-01-05T04:22:45.655215+00:00
| 1,285
| false
|
```\nimport functools\nclass Solution:\n def minInsertions(self, s: str) -> int:\n @functools.lru_cache(None)\n def dp(i, j):\n if j - i <= 1: return 0\n return dp(i + 1, j - 1) if s[i] == s[j - 1] else min(dp(i + 1, j), dp(i, j - 1)) + 1\n return dp(0, len(s))\n```
| 9
| 1
|
[]
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
C# | Runtime beats 91.07%, Memory beats 82.14% [EXPLAINED]
|
c-runtime-beats-9107-memory-beats-8214-e-0hdy
|
Intuition\nTo make a string a palindrome, you can think of adding characters to balance it out. A palindrome reads the same forwards and backwards. If some char
|
r9n
|
NORMAL
|
2024-09-19T20:20:08.389681+00:00
|
2024-09-19T20:20:08.389700+00:00
| 41
| false
|
# Intuition\nTo make a string a palindrome, you can think of adding characters to balance it out. A palindrome reads the same forwards and backwards. If some characters don\u2019t match, we need to add characters to make them match, which means we need to figure out how many additions are necessary.\n\n# Approach\nDynamic Programming: We use a table to keep track of the minimum insertions needed for each substring of the string.\n\nTwo Pointers: For every substring, if the characters at both ends match, we check the substring inside. If they don\'t match, we decide to insert either character and take the minimum of the two cases.\n\nFill the Table: Start with shorter substrings and build up to the entire string, using previous results to fill in the current one.\n\n# Complexity\n- Time complexity:\nO(n2) because we check all possible substrings.\n\n- Space complexity:\nO(n2) due to the table storing results for each substring.\n\n# Code\n```csharp []\npublic class Solution\n{\n public int MinInsertions(string s)\n {\n int n = s.Length;\n // dp[i][j] will hold the minimum number of insertions needed to make the substring s[i..j] a palindrome\n int[,] dp = new int[n, n];\n\n for (int length = 2; length <= n; length++)\n {\n for (int i = 0; i <= n - length; i++)\n {\n int j = i + length - 1; // End index of the current substring\n if (s[i] == s[j])\n {\n dp[i, j] = dp[i + 1, j - 1]; // Characters match, no insertions needed\n }\n else\n {\n dp[i, j] = Math.Min(dp[i + 1, j], dp[i, j - 1]) + 1; // Insert either character\n }\n }\n }\n \n return dp[0, n - 1]; // The result for the entire string\n }\n}\n\n```
| 8
| 0
|
['Two Pointers', 'Matrix', 'C#']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[Kotlin] Minimum code to solve with DFS + memo
|
kotlin-minimum-code-to-solve-with-dfs-me-2ekm
|
\n fun minInsertions(s: String): Int {\n val cache = Array(s.length) { IntArray(s.length) { -1 } }\n \n fun dfs(l: Int, r: Int): Int {\n
|
dzmtr
|
NORMAL
|
2023-04-22T10:06:37.229523+00:00
|
2023-04-22T10:06:37.229564+00:00
| 34
| false
|
```\n fun minInsertions(s: String): Int {\n val cache = Array(s.length) { IntArray(s.length) { -1 } }\n \n fun dfs(l: Int, r: Int): Int {\n if (l > r) return 0\n if (cache[l][r] != -1) return cache[l][r]\n\n cache[l][r] = if (s[l] == s[r]) {\n dfs(l+1, r-1)\n } else {\n 1 + minOf(dfs(l+1, r), dfs(l, r-1))\n }\n \n return cache[l][r]\n }\n\n return dfs(0, s.lastIndex)\n }\n```
| 8
| 0
|
['Dynamic Programming', 'Kotlin']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
C++ | Clean Code (25 lines) | Easy to understand | Well explained
|
c-clean-code-25-lines-easy-to-understand-srrc
|
\n## Pls upvote the thread if you found it helpful.\n\n# Intuition\n Describe your first thoughts on how to solve this problem.l \nIn order to minimize the ins
|
forkadarshp
|
NORMAL
|
2023-04-22T01:12:10.462849+00:00
|
2023-04-22T15:13:54.662892+00:00
| 3,008
| false
|
\n## **Pls upvote the thread if you found it helpful.**\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem.l --> \nIn order to minimize the insertions, we need to find the **difference** of length of the longest palindromic subsequence and string length. \n\n`Minimum Insertion required = len(string) \u2013 length(lps)`\n\n**This question has a pre req : [Longest Palindromic Subsequence](https://leetcode.com/problems/longest-palindromic-subsequence/)**\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- We are given a string, store its length as n.\n- Find the length of the longest palindromic subsequence (say l) \n- Return n-l as answer.\n\n# Complexity\n- Time complexity: O(N*M) two nested loops\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(M) external array of size \u2018M+1\u2019 to store only two rows\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\nprivate:\n int lcs(string s1, string s2) {\n int n = s1.size();\n int m = s2.size();\n vector<int> prev(m + 1,0), cur(m + 1,0);\n for(int ind1 = 1;ind1 <= n; ind1++){\n for(int ind2 = 1;ind2 <= m;ind2++){\n if(s1[ind1 - 1] == s2[ind2 - 1])\n cur[ind2] = 1 + prev[ind2 - 1];\n else\n cur[ind2] = 0 + max(prev[ind2],cur[ind2 - 1]);\n }\n prev = cur;\n }\n return prev[m];\n}\n int longestPalindromeSubsequence(string s){\n string t = s;\n reverse(s.begin(),s.end());\n return lcs(s,t);\n }\npublic: \n int minInsertions(string s) {\n int n = s.size();\n int k = longestPalindromeSubsequence(s);\n return n-k;\n }\n};\n```
| 8
| 0
|
['String', 'Dynamic Programming', 'C', 'C++']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Top-Down Approach (DP)
|
top-down-approach-dp-by-kunal_kumar_1-pfmm
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThis question is a variation of longest palindromic subsequence(Q.no- 516).\n# Approach
|
Kunal_Kumar_1
|
NORMAL
|
2023-07-09T09:33:48.384152+00:00
|
2023-07-09T09:33:48.384173+00:00
| 37
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis question is a **variation of longest palindromic subsequence**(Q.no- 516).\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind the length of LCS of given string and it\'s reverse. The **difference of the length of string and the LCS will give minimum no. of insertions and deletion** in the string to make it a palindrome\n# Complexity\n- Time complexity: **O(n*n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: **O(n*n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int LCS(string a,string b)\n {\n int n=a.size(),m=b.size();\n int t[n+1][m+1];\n for(int i=0;i<n+1;i++)\n t[i][0]=0;\n for(int j=0;j<m+1;j++)\n t[0][j]=0;\n for(int i=1;i<n+1;i++)\n for(int j=1;j<m+1;j++)\n {\n if(a[i-1]==b[j-1])\n t[i][j]=1+t[i-1][j-1];\n else\n t[i][j]=max(t[i-1][j],t[i][j-1]);\n }\n return t[n][m];\n\n }\n int minInsertions(string s) {\n int l=s.size();\n if(l==1)\n return 0;\n string sr;\n sr.append(s);\n reverse(s.begin(),s.end());\n return l-LCS(s,sr);\n }\n};\n```
| 6
| 0
|
['C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Striver Bhaiya 😎 Chad Approach🦸♂️ | Woh Bhi Space Optimized 🚀
|
striver-bhaiya-chad-approach-woh-bhi-spa-u57y
|
\nclass Solution {\n public int minInsertions(String s1) {\n\t int n =s1.length();\n String s2 ="";\n for(int i=n-1; i>=0; i--) s2 += s1.cha
|
rohits05
|
NORMAL
|
2023-04-25T08:59:53.829270+00:00
|
2023-04-25T09:29:21.201169+00:00
| 206
| false
|
```\nclass Solution {\n public int minInsertions(String s1) {\n\t int n =s1.length();\n String s2 ="";\n for(int i=n-1; i>=0; i--) s2 += s1.charAt(i); // S2 = rev(S1) for L.P.S computation\n \n int dp[] = new int[n+1];\n for(int i=1; i<=n; i++){ // Generating L.C.S ~ Space Optimized!\n int cur[] = new int[n+1];\n for(int j=1; j<=n; j++){\n if(s1.charAt(i-1) == s2.charAt(j-1)) cur[j] = 1 + dp[j-1];\n else cur[j] = Math.max(dp[j], cur[j-1]);\n }\n dp = cur;\n } // Got our L.P.S\n \n // Now, min_operation = n - lps \n return (n - dp[n]); // a c p c a \n }\n}\n```
| 6
| 0
|
['Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
C++ | Extra Small | Dynamic Programming | String
|
c-extra-small-dynamic-programming-string-gn9x
|
Intuition\n Describe your first thoughts on how to solve this problem. \nDynamic programming\n# Approach\n Describe your approach to solving the problem. \n s
|
Rishikeshsahoo_2828
|
NORMAL
|
2023-04-22T18:04:03.761807+00:00
|
2023-04-22T18:04:03.761850+00:00
| 453
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDynamic programming\n# Approach\n<!-- Describe your approach to solving the problem. -->\n size of string - the Longest Palindromic Subsequence\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n*m)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n*m)\n\n# Code\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));\n string t=s;\n reverse(t.begin(),t.end());\n for(int i=0;i<s.size();i++)for(int j=0;j<t.size();j++)\n (s[i]==t[j])?(dp[i][j]= 1+((i-1>=0 && j-1>=0)?dp[i-1][j-1]:0)):( dp[i][j]=max(((i>0)?dp[i-1][j]:0),((j>0)?dp[i][j-1]:0)));\n return s.size()-dp[s.size()-1][t.size()-1];\n }\n};\n```
| 6
| 0
|
['C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Simple Dp solution based on Longest common subsequence (LCS) Pattern
|
simple-dp-solution-based-on-longest-comm-f9uu
|
In lcs code we require 2 string inputs, here we have only 1 string input so we reverse it to get other string. After that we simply write our lcs code.\nFor bet
|
priyesh_raj_singh
|
NORMAL
|
2022-07-30T15:26:51.433944+00:00
|
2022-07-30T15:28:13.626331+00:00
| 393
| false
|
In lcs code we require 2 string inputs, here we have only 1 string input so we reverse it to get other string. After that we simply write our lcs code.\nFor better understanding of patterns in DP you can refer to **Aditya Verma\'s Playlist**:- \nhttps://www.youtube.com/playlist?list=PL_z_8CaSLPWekqhdCPmFohncHwz8TY2Go\n```\n int minInsertions(string s) {\n int n = s.size();\n string b = s;\n reverse(b.begin() , b.end());\n \n vector<vector<int>> dp(n+1 , vector<int>(n+1 , 0));\n \n for(int i = 1 ; i<=n ; i++){\n for(int j = 1 ; j<= n ; j++){\n if(s[i-1]==b[j-1])\n dp[i][j] = 1 + dp[i-1][j-1];\n else\n dp[i][j] = max(dp[i-1][j] , dp[i][j-1]);\n }\n }\n return n - dp[n][n];\n \n }\n```
| 6
| 0
|
[]
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Java/C++ concise solution
|
javac-concise-solution-by-vp-1e07
|
This is a direct implementation of longest palindromic subsequence. \n\n\nclass Solution {\n public String reverseIt(String str)\n {\n int i, le
|
Vp-
|
NORMAL
|
2021-09-02T13:53:33.625999+00:00
|
2021-09-02T13:53:33.626048+00:00
| 670
| false
|
This is a direct implementation of longest palindromic subsequence. \n\n```\nclass Solution {\n public String reverseIt(String str)\n {\n int i, len = str.length();\n \n StringBuilder dest = new StringBuilder(len);\n\n for (i = (len - 1); i >= 0; i--)\n dest.append(str.charAt(i));\n \n return dest.toString();\n }\n \n public int minInsertions(String s) \n {\n String s1 = reverseIt(s);\n\n int dp[][] = new int[s1.length() + 1][s1.length() + 1];\n\n for(int idx = 0; idx < s1.length() + 1; idx++)\n dp[0][idx] = 0;\n\n for(int idx = 0; idx < s.length() + 1; idx++)\n dp[idx][0] = 0;\n\n for(int row = 1; row < s.length() + 1; row++)\n {\n for(int col = 1; col < s1.length() + 1; col++)\n {\n if(s.charAt(row - 1) == s1.charAt(col - 1))\n dp[row][col] = 1 + dp[row - 1][col - 1];\n\n else\n dp[row][col] = Math.max(dp[row - 1][col], dp[row][col - 1]);\n }\n }\n\n return s.length() - dp[s.length()][s1.length()];\n }\n}\n```\n\nSame implementation in Cpp\n```\nclass Solution {\npublic:\n int minInsertions(string s)\n {\n string s1 = s;\n \n reverse(s1.begin(), s1.end());\n \n int dp[s1.size() + 1][s.size() + 1];\n \n for(int idx = 0; idx < s1.size() + 1; idx++)\n dp[0][idx] = 0;\n \n for(int idx = 0; idx < s.size() + 1; idx++)\n dp[idx][0] = 0;\n \n for(int row = 1; row < s.size() + 1; row++)\n {\n for(int col = 1; col < s1.size() + 1; col++)\n {\n if(s[row - 1] == s1[col - 1])\n dp[row][col] = 1 + dp[row - 1][col - 1];\n \n else\n dp[row][col] = max(dp[row - 1][col], dp[row][col - 1]);\n }\n }\n \n return s.size() - dp[s.size()][s1.size()];\n }\n};\n```
| 6
| 0
|
['C++', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Dyanmic Programming Beats 90% solution with detailed explanation
|
dyanmic-programming-beats-90-solution-wi-ae3c
|
The question requires us to breakdown the problem in terms of smaller sub-problem\n\nLet dp be a matrix where dp[i][j] stores the minimum number of insertions r
|
puff_diddy
|
NORMAL
|
2020-09-04T12:15:27.694241+00:00
|
2020-09-04T12:15:27.694277+00:00
| 625
| false
|
The question requires us to breakdown the problem in terms of smaller sub-problem\n\nLet dp be a matrix where dp[i][j] stores the minimum number of insertions required to make subtring [i...j] palindromic \n Case -1 s[i] != s[j]\n in this case we have two choices, add a character equal to s[i] at the position of jth index and now the i and j be will equal ,which will cost us 1 move, the rest can be calculated for smaller subproblem [i+1, ...,j] .\n\t\t\t similarly we can do by adding a character equal to s[j] at the position of ith index and calculate [i,j-1]\n\t\t\t Recurrence Relation -dp[i][j] =min(dp[i+1][j],dp[i][j-1]) +1\n\tCase-2 s[i] ==s[j]\n\t In this case apart from from the above ways we can derive answer, our answer can also be gained by finding out moves to make [i+1,...,j-1] palindromic\n\t Recurrence Relation dp[i][j]=min(dp[i+1][j-1],min(dp[i+1][j],dp[i][j-1])+1)\n\t \n\t \n\t Code ->\n\t int minInsertions(string s) {\n \n int n=s.size();\n int dp[n][n];\n memset(dp,0,sizeof dp);\n \n for(int l=2;l<=n;l++)\n {\n for(int i=0;i<n-l+1;i++)\n {\n int j=i+l-1;\n if(j==(i+1))\n {\n if(s[j]==s[i])\n dp[i][j]=0;\n else\n dp[i][j]=1;\n }\n else\n {\n dp[i][j]=INT_MAX;\n if(s[i]==s[j])\n dp[i][j]=dp[i+1][j-1];\n \n dp[i][j]=min(dp[i][j],min(dp[i+1][j],dp[i][j-1])+1);\n }\n }\n }\n return dp[0][n-1];\n \n }
| 6
| 0
|
[]
| 4
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Java. Minimum Insertion Steps to Make a String Palindrome.
|
java-minimum-insertion-steps-to-make-a-s-i6k9
|
\n\nclass Solution {\n public int longestPalindromeSubseq(String s) {\n char []str = s.toCharArray();\n int [][] answ = new int[s.length() + 1]
|
red_planet
|
NORMAL
|
2023-04-22T16:36:37.018727+00:00
|
2023-04-22T16:36:37.018756+00:00
| 1,183
| false
|
\n```\nclass Solution {\n public int longestPalindromeSubseq(String s) {\n char []str = s.toCharArray();\n int [][] answ = new int[s.length() + 1][s.length() + 1];\n int n = s.length();\n for(int i = 0; i < s.length(); i++)\n {\n for (int j = n - 1; j > -1; j--)\n {\n if (str[i] == str[j]) answ[i + 1][n - j] = answ[i - 1 + 1][n - j - 1 ] + 1;\n else answ[i + 1][n - j ] = Math.max(answ[i - 1 + 1][n - j ], answ[i + 1][n - j - 1]);\n }\n }\n return answ[n][n];\n }\n public int minInsertions(String s) {\n return s.length() - longestPalindromeSubseq(s);\n }\n}\n```
| 5
| 0
|
['Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
C++||Picture Explanation🔥||Recursion-->Memoization 🔥|| With Recursion Tree🔥
|
cpicture-explanationrecursion-memoizatio-kyq4
|
Approach\n Describe your approach to solving the problem. \n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n# Complexity\n- Time complexity: O(n^2
|
kaushikm2k
|
NORMAL
|
2023-04-22T01:47:36.135755+00:00
|
2023-04-22T01:50:53.017829+00:00
| 827
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\n\n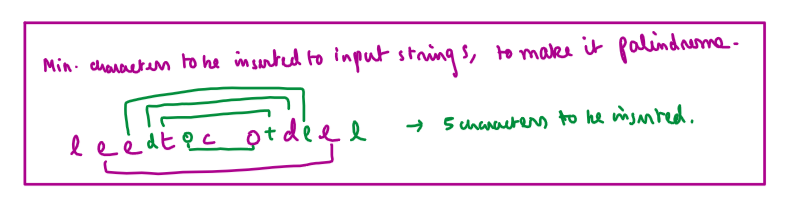\n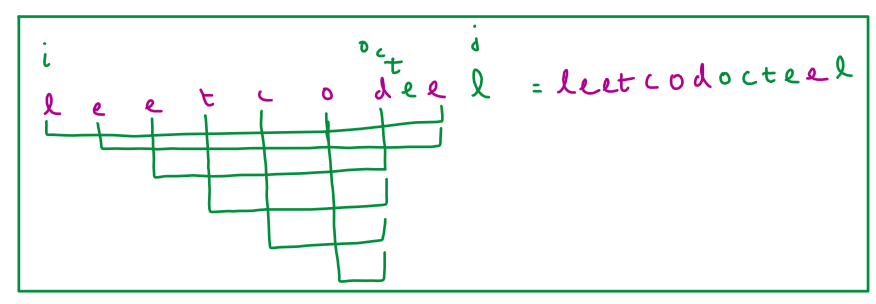\n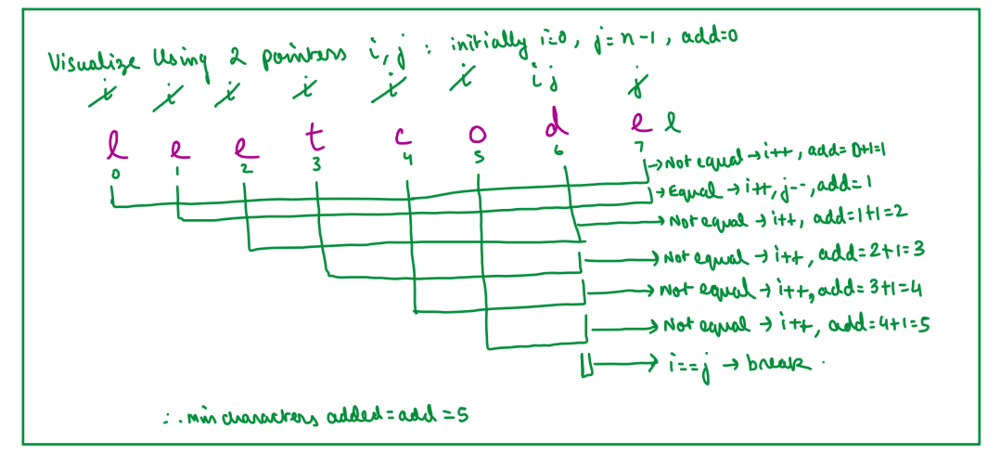\n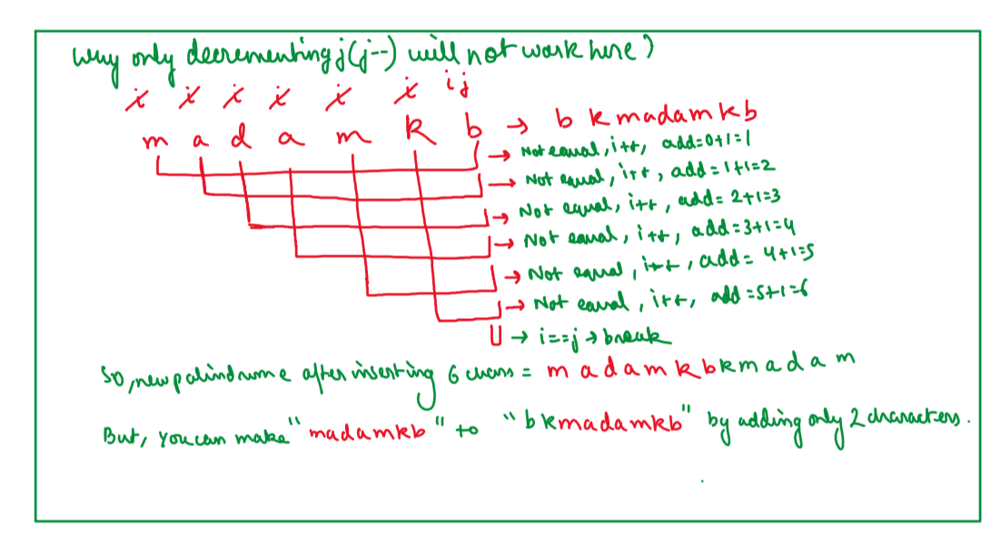\n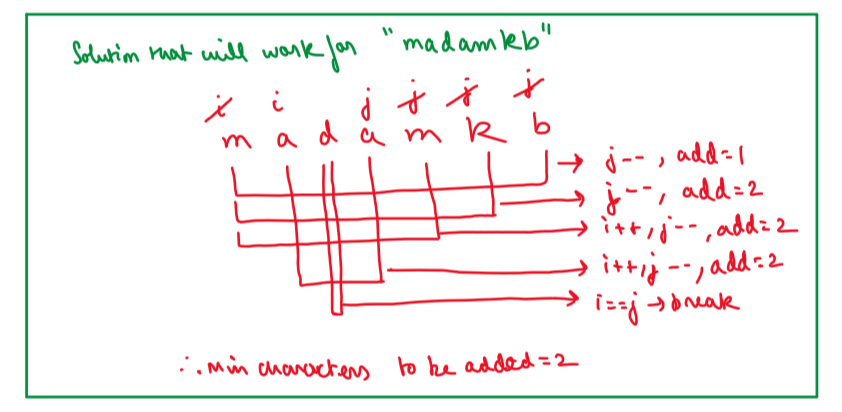\n\n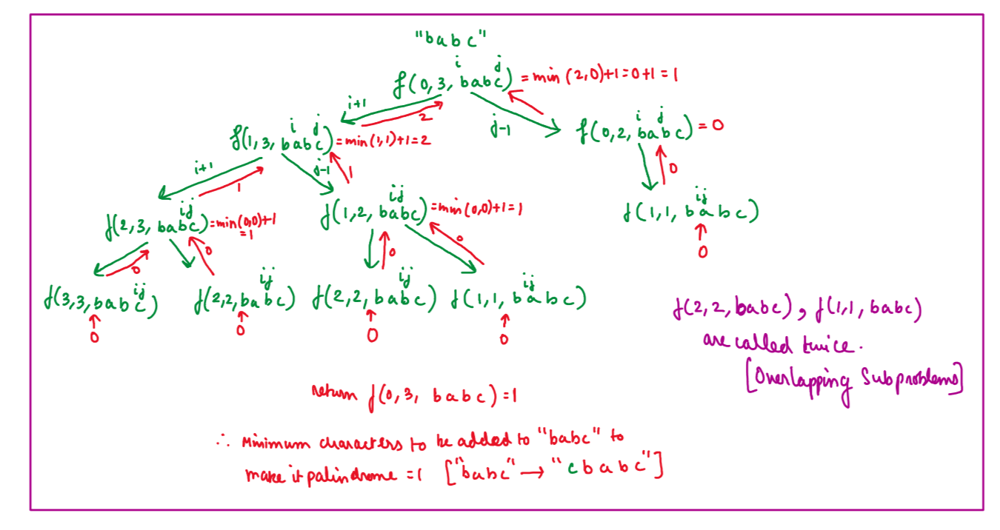\n\n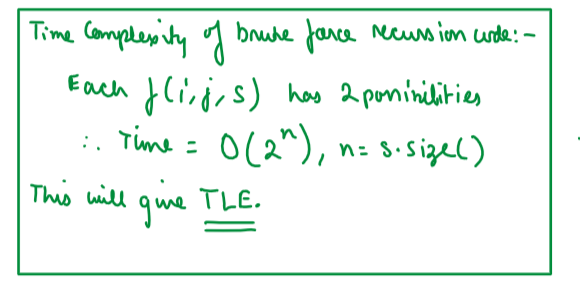\n\n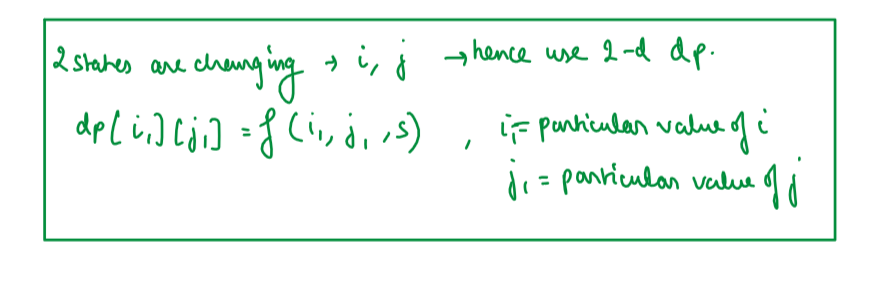\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nPlease UPVOTE if you liked the explanation.\n\n# BRUTE FORCE Code:\n```\nclass Solution {\npublic:\n //BRUTE FORCE= RECURSION\n int makePalindrome(int i, int j, string &s){\n if(i>=j) return 0;\n else if(s[i]==s[j]) return makePalindrome(i+1, j-1, s);\n else{\n int possibility1= makePalindrome(i+1, j, s);\n int possibility2= makePalindrome(i, j-1, s);\n\n return min(possibility1, possibility2)+1;\n }\n }\n int minInsertions(string s) {\n int n= s.size();\n return makePalindrome(0, n-1, s);\n }\n};\n```\n# Memoization Code:\n```\nclass Solution {\npublic:\n int makePalindrome(int i, int j, string &s, vector<vector<int>>&dp){\n if(i>=j) return 0;\n else if(dp[i][j]!=-1) return dp[i][j];\n else if(s[i]==s[j]) return makePalindrome(i+1, j-1, s, dp);\n else{\n int possibility1= makePalindrome(i+1, j, s, dp);\n int possibility2= makePalindrome(i, j-1, s, dp);\n\n dp[i][j]= min(possibility1, possibility2)+1;\n return dp[i][j];\n }\n }\n int minInsertions(string s) {\n int n= s.size();\n vector<vector<int>> dp(n, vector<int>(n,-1));\n return makePalindrome(0, n-1, s, dp);\n }\n};\n```
| 5
| 0
|
['Dynamic Programming', 'Recursion', 'C++']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
✅C++ || DP
|
c-dp-by-chiikuu-vp3h
|
Code\n\nclass Solution {\npublic:\n int minInsertions(string s) {\n string p=s;\n reverse(s.begin(),s.end());\n int n=s.size();\n
|
CHIIKUU
|
NORMAL
|
2023-04-14T08:10:39.792367+00:00
|
2023-04-14T08:10:39.792405+00:00
| 215
| false
|
# Code\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n string p=s;\n reverse(s.begin(),s.end());\n int n=s.size();\n vector<vector<int>>dp(n+1,vector<int>(n+1,0));\n for(int i=1;i<=n;i++){\n for(int j=1;j<=n;j++){\n if(s[j-1]==p[i-1])dp[i][j]=max(dp[i-1][j],max(1+dp[i-1][j-1],dp[i][j-1]));\n else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);\n }\n }\n return n-dp[n][n];\n }\n};\n```\n\n
| 5
| 0
|
['Dynamic Programming', 'C++']
| 3
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Best O(N*M) Solution
|
best-onm-solution-by-kumar21ayush03-xivu
|
Approach\nDP (Bottom Up Approach)\n\n# Complexity\n- Time complexity:\nO(n * m)\n\n- Space complexity:\nO(n * m)\n\n# Code\n\nclass Solution {\nprivate:\n in
|
kumar21ayush03
|
NORMAL
|
2023-03-31T10:14:52.140738+00:00
|
2023-03-31T10:14:52.140775+00:00
| 261
| false
|
# Approach\nDP (Bottom Up Approach)\n\n# Complexity\n- Time complexity:\n$$O(n * m)$$\n\n- Space complexity:\n$$O(n * m)$$\n\n# Code\n```\nclass Solution {\nprivate:\n int longestPalindromeSubseq(string s, string t) { \n int n = s.length(); \n vector<vector<int>> dp(n+1, vector<int>(n+1, 0));\n for (int i = 0; i <= n; i++) {\n dp[i][0] = 0;\n dp[0][i] = 0;\n } \n for (int idx1 = 1; idx1 <= n; idx1++) {\n for (int idx2 = 1; idx2 <= n; idx2++) {\n if (s[idx1-1] == t[idx2-1])\n dp[idx1][idx2] = 1 + dp[idx1-1][idx2-1];\n else\n dp[idx1][idx2] = max (dp[idx1-1][idx2], dp[idx1][idx2-1]);\n }\n } \n return dp[n][n];\n } \npublic:\n int minInsertions(string s) {\n int n = s.length();\n string t = s;\n reverse(t.begin(), t.end());\n int lpsLen = longestPalindromeSubseq(s, t);\n return n - lpsLen;\n }\n};\n```
| 5
| 0
|
['C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
✔3 STEPS DP Sol | Asked by AMAZON-GOOGLE-UBER || EXPLANATION & COMPLEXITIES👈
|
3-steps-dp-sol-asked-by-amazon-google-ub-p3k0
|
EXPLANATION :-\n1. THIS PROBLEM IS MAINLY EXTENSION OF LPS(Longest Palindromic Subsequence).\n2. MOREOVER, THIS IS A DITTO COPY OF A CLASSICAL QUESTION OF DP KN
|
vishi_brownSand
|
NORMAL
|
2021-07-01T10:15:49.849723+00:00
|
2021-07-01T14:54:44.093653+00:00
| 224
| false
|
* ## EXPLANATION :-\n1. **`THIS PROBLEM IS MAINLY EXTENSION OF LPS(Longest Palindromic Subsequence).`**\n2. **`MOREOVER, THIS IS A DITTO COPY OF A CLASSICAL QUESTION OF DP KNOWN AS MINIMUM NUMBER OF DELETION TO MAKE A STRING PALINDROME.`**\n3. **`IDEA : In this problem we just have to find LPS of the given string and subtract the LPS length from given string len !!`\n `BECAUSE, MINIMUM NUMBER OF INSERTIONS IS EQUAL TO MINIMUM NUMBER OF DELETION IN A STRING TO MAKE IT PALINDROME..`\n `ATLAST, HOW THIS QUESTION IS A EXTENSION OF LPS (Longest Palindromic Subsequence). SO, THE BASIC IDEA IS, IF WE FIND OUT LPS OF THE TWO SAME STRING`.\n `AND IF THE LONGEST COMMON(SIMILAR) CHARACTERS ARE MORE \u2B06, THAT MEANS THERE WILL BE LEAST DISIMILAR CHARACTERS \u2B07. HENCE, WE HAVE TO DELETE OR INSERT LEAST`\n `CHARACTERS IN A STRING TO MAKE A STRING PALINDROME!`**\n4. **`IN A SIMPLE WORDS : LONGEST PALINDROMIC SUBSEQUENCE(LPS) IS INVERSELY PROPORTIONAL TO NUMBER OF DELETIONS(OR NUMBER OF INSERTIONS)`**\n```\n\t\t\t\t\t\t 1 \n LPS \u2B06 \u221D -------------------\n\t\t\t\t NO. OF DELETIONS \u2B07\t\n```\t\t\t\n```\nclass Solution {\npublic:\n int minInsertions(string s1) {\n int n = s1.size();\n string s2 = s1;\n reverse(s2.begin(), s2.end());\n vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0));\n for(int i = 1; i <= n; ++i){\n for(int j = 1; j <= n; ++j){\n if(s1[i - 1] == s2[j - 1])\n dp[i][j] = 1 + dp[i - 1][j - 1]; // FIRST STEP\n else\n dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); // SECOND STEP\n }\n }\n int lenLPS = dp[n][n];\n return n - lenLPS; // THIRD STEP\n }\n};\n```\n**TIME COMPLEXITY : `O(n^2) == O(n * n)`, Where, n = size of str1 & str2** \n**SPACE COMPLEXITY : `O(n * n)`, For using 2D array Aux space**\n\nif you find any mistakes pls, drop a comment\nif it makes any sense don\'t forget to **Upvote**
| 5
| 0
|
['Dynamic Programming']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
C++ SIMPLE EASY SOLUTION
|
c-simple-easy-solution-by-chase_master_k-2svh
|
\nvector<vector<int>> memo;\n //code explained below ...\n int dp(string &s,int i,int j)\n {\n if(i>=j)\t\t//Base case.\n return 0;\n
|
chase_master_kohli
|
NORMAL
|
2020-01-11T07:04:25.667825+00:00
|
2020-01-11T07:04:50.987308+00:00
| 606
| false
|
```\nvector<vector<int>> memo;\n //code explained below ...\n int dp(string &s,int i,int j)\n {\n if(i>=j)\t\t//Base case.\n return 0;\n if(memo[i][j]!=-1) //Check if already calculated the value for the pair `i` and `j`.\n return memo[i][j];\n return memo[i][j]=s[i]==s[j]?dp(s,i+1,j-1):1+min(dp(s,i+1,j),dp(s,i,j-1));\t\t//Recursion \n }\n int minInsertions(string s) \n {\n memo.resize(s.length(),vector<int>(s.length(),-1));\n return dp(s,0,s.length()-1);\n }\n```
| 5
| 0
|
[]
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Javascript and C++ solutions
|
javascript-and-c-solutions-by-claytonjwo-fn2c
|
Synopsis:\n\n Recursive Top-Down solutions: let i and j be the indexes corresponding to the substring of s from i to j inclusive (ie. s[i..j])\n\t Base case: if
|
claytonjwong
|
NORMAL
|
2020-01-06T18:14:59.876698+00:00
|
2020-01-07T23:11:30.201651+00:00
| 330
| false
|
**Synopsis:**\n\n* **Recursive Top-Down solutions:** let `i` and `j` be the indexes corresponding to the substring of `s` from `i` to `j` inclusive (ie. `s[i..j]`)\n\t* Base case: if `i >= j` then return `0`\n\t* Recursive cases:\n\t\t* if `s[i] == s[j]` then return the solution for the sub-problem *without* the characters at `i` and `j` (since there\'s a match, there is no "penalty")\n\t\t* if `s[i] != s[j]` then return `1` plus the minimum solution of (the sub-problem *without* the character at `i`) or (the sub-problem *without* the character at `j`)\n\n* **DP Bottom-Up solutions:** Same idea as above, but finding solutions for each substring from right-to-left. Let `dp[i][j]` denote the optimal solution for a substring from `i` to `j` non-inclusive (ie. `s[i..j)`). The bottom-up solution starts with a substring of length `1` (ie. the right-most character) and builds upon itself till length `N`. The answer is `dp[0][N]` (ie. the optimal solution for `s[0..N)`).\n\n**Javascript Solutions: Recursive Top-Down**\n\n*Javascript: TLE without memo*\n```\nlet minInsertions = s => {\n let go = (s, i, j) => {\n if (i >= j)\n return 0;\n if (s[i] == s[j])\n return go(s, i + 1, j - 1);\n return 1 + Math.min(go(s, i + 1, j), go(s, i, j - 1));\n };\n return go(s, 0, s.length - 1);\n};\n```\n\n*Javascript: with memo*\n```\nlet minInsertions = (s, memo = [...Array(501)].map(x => Array(501).fill(-1))) => {\n let go = (s, i, j) => {\n if (memo[i][j] > -1)\n return memo[i][j];\n if (i >= j)\n return memo[i][j] = 0;\n if (s[i] == s[j])\n return memo[i][j] = go(s, i + 1, j - 1);\n return memo[i][j] = 1 + Math.min(go(s, i + 1, j), go(s, i, j - 1));\n };\n return go(s, 0, s.length - 1);\n};\n```\n\n*Javascript: with memo (refactored with a few less lines of code)*\n```\nlet minInsertions = (s, m = [...Array(501)].map(x => Array(501).fill(-1))) => {\n let go = (s, i, j) => {\n return m[i][j] =\n m[i][j] > -1 ? m[i][j] :\n i >= j ? 0 :\n s[i] == s[j] ? go(s, i + 1, j - 1) :\n 1 + Math.min(go(s, i + 1, j), go(s, i, j - 1));\n };\n return go(s, 0, s.length - 1);\n};\n```\n\n**Javascript Solutions: DP Bottom-Up**\n\n*Javascript: full DP matrix (non-optimized for memory)*\n```\nlet minInsertions = (s, dp = [...Array(501)].map(x => Array(501).fill(0))) => {\n let N = s.length;\n for (let i = N - 1; i >= 0; --i)\n for (let j = i + 1; j <= N; ++j)\n if (s[i] == s[j - 1])\n dp[i][j] = dp[i + 1][j - 1];\n else\n dp[i][j] = 1 + Math.min(dp[i + 1][j], dp[i][j - 1]);\n return dp[0][N];\n};\n```\n\n*Javascript: pre/cur row (optimized for memory)*\n```\nlet minInsertions = (s, pre = [...Array(501)].fill(0), cur = [...Array(501)].fill(0)) => {\n let N = s.length;\n for (let i = N - 1; i >= 0; --i, [pre, cur] = [cur, pre])\n for (let j = i + 1; j <= N; ++j)\n if (s[i] == s[j - 1])\n cur[j] = pre[j - 1];\n else\n cur[j] = 1 + Math.min(pre[j], cur[j - 1]);\n return pre[N];\n};\n```\n\n*Javascript: pre/cur row (optimized for memory + more concise code)*\n```\nlet minInsertions = (s, pre = [...Array(501)].fill(0), cur = [...Array(501)].fill(0)) => {\n let N = s.length;\n for (let i = N - 1; i >= 0; --i, [pre, cur] = [cur, pre])\n for (let j = i + 1; j <= N; ++j)\n cur[j] = s[i] == s[j - 1] ? pre[j - 1] : 1 + Math.min(pre[j], cur[j - 1]);\n return pre[N];\n};\n```\n\n**C++ Solutions: Recursive Top-Down**\n\n*C++: TLE without memo*\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n int n = s.size();\n return go(s, 0, n - 1);\n }\nprivate:\n int go(const string& s, int i, int j) {\n if (i >= j)\n return 0;\n if (s[i] == s[j])\n return go(s, i + 1, j - 1);\n return 1 + min(go(s, i + 1, j), go(s, i, j - 1));\n }\n};\n```\n\n*C++: with memo*\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n int n = s.size();\n return go(s, 0, n - 1);\n }\nprivate:\n using VI = vector<int>;\n using VVI = vector<VI>;\n VVI memo = VVI(501, VI(501, -1));\n int go(const string& s, int i, int j) {\n if (memo[i][j] > -1)\n return memo[i][j];\n if (i >= j)\n return memo[i][j] = 0;\n if (s[i] == s[j])\n return memo[i][j] = go(s, i + 1, j - 1);\n return memo[i][j] = 1 + min(go(s, i + 1, j), go(s, i, j - 1));\n }\n};\n```\n\n*C++: with memo (refactored with a few less lines of code)*\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n int n = s.size();\n return go(s, 0, n - 1);\n }\nprivate:\n using VI = vector<int>;\n using VVI = vector<VI>;\n VVI m = VVI(501, VI(501, -1));\n int go(const string& s, int i, int j) {\n return m[i][j] =\n m[i][j] > -1 ? m[i][j] :\n i >= j ? 0 :\n s[i] == s[j] ? go(s, i + 1, j - 1) :\n 1 + min(go(s, i + 1, j), go(s, i, j - 1));\n }\n};\n```\n\n**C++ Solutions: DP Bottom-Up**\n\n*C++: full DP matrix (non-optimized for memory)*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n int minInsertions(string s, VVI dp = VVI(501, VI(501))) {\n int N = s.size();\n for (auto i = N - 1; i >= 0; --i)\n for (auto j = i + 1; j <= N; ++j)\n if (s[i] == s[j - 1])\n dp[i][j] = dp[i + 1][j - 1];\n else\n dp[i][j] = 1 + min(dp[i + 1][j], dp[i][j - 1]);\n return dp[0][N];\n }\n};\n```\n\n*C++: pre/cur row (optimized for memory)*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n int minInsertions(string s, VI pre = VI(501), VI cur = VI(501)) {\n int N = s.size();\n for (auto i = N - 1; i >= 0; --i, swap(pre, cur))\n for (auto j = i + 1; j <= N; ++j)\n if (s[i] == s[j - 1])\n cur[j] = pre[j - 1];\n else\n cur[j] = 1 + min(pre[j], cur[j - 1]);\n return pre[N];\n }\n};\n```\n\n*C++: pre/cur row (optimized for memory + more concise code)*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n int minInsertions(string s, VI pre = VI(501), VI cur = VI(501)) {\n int N = s.size();\n for (auto i = N - 1; i >= 0; --i, swap(pre, cur))\n for (auto j = i + 1; j <= N; ++j)\n cur[j] = s[i] == s[j - 1] ? pre[j - 1] : 1 + min(pre[j], cur[j - 1]);\n return pre[N];\n }\n};\n```
| 5
| 1
|
[]
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
1312. Minimum Insertion Steps to Make a String Palindrome
|
1312-minimum-insertion-steps-to-make-a-s-s6ai
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo make a string palindrome, we need to insert characters in such a way that the result
|
AShukla889012
|
NORMAL
|
2023-05-20T06:36:26.968617+00:00
|
2023-05-20T06:36:26.968660+00:00
| 333
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo make a string palindrome, we need to insert characters in such a way that the resulting string reads the same backward as well as forward. We can approach this problem using dynamic programming. The intuition is to determine the minimum number of insertions required to make substrings of the given string palindrome.\nIf we go for recursion, the Prgram will end in a **Memory Limit Exceeded** issue, which is due to the high no. of recursive calls. So, it is better to use DP.\n\nRecursive Solution: (MEMORY LIMIT EXCEEDED)\n```C++ []\nclass Solution {\npublic:\n int minInsertionsRecursive(string s, int start, int end) {\n // Base cases\n if (start >= end) {\n return 0;\n }\n if (s[start] == s[end]) {\n return minInsertionsRecursive(s, start + 1, end - 1);\n }\n \n // Recursive cases\n int option1 = minInsertionsRecursive(s, start + 1, end) + 1;\n int option2 = minInsertionsRecursive(s, start, end - 1) + 1;\n \n return min(option1, option2);\n }\n\n int minInsertions(string s) {\n return minInsertionsRecursive(s, 0, s.length() - 1);\n }\n};\n```\nTime Complexity of Recurive Approach is exponential -> O(2^n).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Initialize the dp vector**: Create a vector dp of size n (length of the input string). This vector will store the minimum number of insertions required to make the substring from index i to index j a palindrome.\n2. **Iterate through the string**: Start iterating through the string from the second last character to the first character (in reverse order). For each character at index i, iterate through all the characters at indices j greater than i.\n3. **Check if characters at indices i and j are equal**: If the characters at indices i and j are equal, it means that they can form a palindrome without any additional insertions. In this case, set dp[j] to the value of dp[j-1] (which is the value of dp[j] in the previous iteration).\n4. **If characters at indices i and j are not equal**: If the characters at indices i and j are not equal, it means that at least one insertion is required to make the substring from index i to index j a palindrome. In this case, set dp[j] to the minimum of dp[j] and dp[j-1] plus 1.\n5. **Store the previous value of dp[j]**: To use the value of dp[j] in the previous iteration, store it in a variable prev before updating dp[j].\n6. **Return the minimum number of insertions**: After iterating through the entire string, the value of dp[n-1] will store the minimum number of insertions required to make the entire string a palindrome. Return this value as the final result.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n O(n^2), where n is the length of the string.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n), because we use an additional array dp of size n.\n\n# Code\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n int n = s.length();\n vector<int> dp(n);\n for (int i = n - 2; i >= 0; i--) {\n int prev = 0;\n for (int j = i + 1; j < n; j++) {\n int temp = dp[j];\n if (s[i] == s[j]) {\n dp[j] = prev;\n } else {\n dp[j] = min(dp[j], dp[j-1]) + 1;\n }\n prev = temp;\n }\n }\n return dp[n-1];\n }\n};\n```
| 4
| 0
|
['String', 'Dynamic Programming', 'Recursion', 'C++']
| 2
|
minimum-insertion-steps-to-make-a-string-palindrome
|
LPS | [ C++ ] | Recursion -> Memo -> Tabulation -> Space Optimization
|
lps-c-recursion-memo-tabulation-space-op-61wj
|
Approach\nUsing the variant of Longest Common Subsequence, i,e Longest Pallindromic Subsequence find the length of LPS \n\nLPS as the name determine longest sub
|
kshzz24
|
NORMAL
|
2023-04-22T07:31:49.661751+00:00
|
2023-04-22T07:31:49.661785+00:00
| 338
| false
|
# Approach\nUsing the variant of Longest Common Subsequence, i,e Longest Pallindromic Subsequence find the length of LPS \n\nLPS as the name determine longest subsequence in the string which is a pallindrome, so for the answer we just have to add the elements which are not included in the subsequence.\n\nBefore going to Solutions Please Solve these Questions: \n\n## Longest Common Subsequence :-\n https://leetcode.com/problems/longest-common-subsequence/\n## Longest Pallindromic Subsequence :-\n https://leetcode.com/problems/longest-palindromic-subsequence/\n\n# Recursion +MEMO\n```\nclass Solution {\npublic:\n int dp[501][501];\n int lps(string& s, string& t, int i, int j) {\n if(i >= s.size() || j >= t.size())\n return 0;\n if(dp[i][j] != -1)\n return dp[i][j];\n if(s[i] == t[j])\n dp[i][j] = 1 + lps(s, t, i+1, j+1);\n else\n dp[i][j] = max(lps(s, t, i+1, j), lps(s, t, i, j+1));\n return dp[i][j];\n }\n \n int minInsertions(string s) {\n memset(dp, -1, sizeof(dp));\n string t = s;\n reverse(t.begin(), t.end());\n int l = lps(s, t, 0, 0);\n return s.size() - l;\n }\n};\n\n```\n# Tabulation\n```\nclass Solution {\npublic:\n int lps(string s, string t){\n int n = s.size();\n int dp[n+1][n+1];\n for(int i = 0 ;i<=n ; i++){\n dp[0][i] = 0;\n }\n for(int j = 0 ;j<=n ; j++){\n dp[j][0] = 0;\n }\n for(int i = 1;i<=n; i++){\n for(int j = 1; j<=n; j++){\n if(s[i-1] == t[j-1]){\n dp[i][j] = 1+dp[i-1][j-1];\n }\n else{\n dp[i][j] = max(dp[i-1][j], dp[i][j-1]);\n }\n }\n }\n return dp[n][n];\n }\n int minInsertions(string s) {\n string t = s;\n reverse(t.begin(), t.end());\n int l = lps(s,t);\n cout << l << endl;\n return s.size() - l; \n }\n};\n```\n\n# Space Optimization\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n int n = s.size();\n string t = s;\n reverse(t.begin(), t.end());\n int dp[n+1];\n memset(dp, 0, sizeof(dp));\n int prev = 0;\n for(int i = 1; i <= n; i++) {\n prev = dp[0];\n for(int j = 1; j <= n; j++) {\n int temp = dp[j];\n if(s[i-1] == t[j-1])\n dp[j] = 1 + prev;\n else\n dp[j] = max(dp[j-1], dp[j]);\n prev = temp;\n }\n }\n return n - dp[n];\n }\n};\n\n```
| 4
| 0
|
['String', 'Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Longest common Subsequence extension....(Python3)
|
longest-common-subsequence-extensionpyth-g9b4
|
Intuition\n Describe your first thoughts on how to solve this problem. \nI literally donnot have any idea then i came up with brute force and it didnt worked\n#
|
Mohan_66
|
NORMAL
|
2023-01-27T15:08:04.468172+00:00
|
2023-01-27T15:08:04.468206+00:00
| 271
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI literally donnot have any idea then i came up with brute force and it didnt worked\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis is just a longest common subsequence question just reverse the given string and then return the lenght minus the common subsequence length\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n r=s[::-1]\n n=len(r)\n dp=[[0 for i in range(n+1)]for j in range(n+1)]\n for i in range(1,len(dp)):\n for j in range(1,len(dp[0])):\n if(s[i-1]==r[j-1]):\n dp[i][j]=1+dp[i-1][j-1]\n else:\n dp[i][j]=max(dp[i-1][j],dp[i][j-1])\n return n-dp[n][n]\n \n```
| 4
| 0
|
['Python3']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
short and easy to understand
|
short-and-easy-to-understand-by-sushants-ke5h
|
lps(a) = longest common subsequence (a,reverse(a))\nmin no. of deletion = len(a) - lps(a)\n\nclass Solution:\n def minInsertions(self, s: str) -> int:\n
|
sushants007
|
NORMAL
|
2022-05-23T11:56:47.952998+00:00
|
2022-05-23T11:57:20.250779+00:00
| 405
| false
|
lps(a) = longest common subsequence (a,reverse(a))\nmin no. of deletion = len(a) - lps(a)\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n rs= s[::-1]\n n,m = len(s),len(rs)\n t = [[0 for j in range(m+1)]for i in range(n+1)]\n for i in range(1,n+1):\n for j in range(1,m+1):\n if s[i-1] == rs[j-1]:\n t[i][j] = 1+t[i-1][j-1]\n else:\n t[i][j] = max(t[i-1][j],t[i][j-1]) \n return n-t[i][j] \n```
| 4
| 0
|
['Dynamic Programming', 'Python']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Python Simple Recursive DP with Explanation
|
python-simple-recursive-dp-with-explanat-4cd6
|
Define dp(s) as the minimum number of steps to make s palindrome.\nWe\'ll get the recursion below:\ndp(s) = 0 if s == s[::-1]\ndp(s) = dp(s[1:-1]) if s[0] == s[
|
yasufumy
|
NORMAL
|
2020-01-05T05:10:19.272003+00:00
|
2020-03-21T01:37:55.997865+00:00
| 522
| false
|
Define `dp(s)` as the minimum number of steps to make `s` palindrome.\nWe\'ll get the recursion below:\n`dp(s) = 0 if s == s[::-1]`\n`dp(s) = dp(s[1:-1]) if s[0] == s[-1]`\n`dp(s) = 1 + min(dp(s[1:]), dp(s[:-1])) otherwise`\n\n\n```python\nfrom functools import lru_cache\n\n\nclass Solution:\n def minInsertions(self, s: str) -> int:\n @lru_cache(None)\n def dp(s):\n if s == s[::-1]:\n return 0\n elif s[0] == s[-1]:\n return dp(s[1:-1])\n\t\t\telse:\n\t\t\t\treturn 1 + min(dp(s[1:]), dp(s[:-1]))\n \n return dp(s)\n```
| 4
| 0
|
['Dynamic Programming', 'Recursion', 'Python', 'Python3']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[C++] Simple Recursive DP O(N^2)
|
c-simple-recursive-dp-on2-by-nicmit-oigl
|
This hard problem, is not that hard if we try to establish the recurrence relation. \nLet\'s say we start comparing the characters of the string, from both the
|
nicmit
|
NORMAL
|
2020-01-05T04:02:40.907035+00:00
|
2020-01-05T04:08:33.174144+00:00
| 373
| false
|
This hard problem, is not that hard if we try to establish the recurrence relation. \nLet\'s say we start comparing the characters of the string, from both the ends i.e. `i` as starting index of string as `0` and `j` as ending index of string as `n-1`, where `n` is the length of the string.\nSo, the recurrence relation between the indices can be written as : \n\n```\nif s[i] == s[j]\n DP(i, j) = DP(i + 1, j - 1)\notherwise,\n DP(i, j) = 1 + min( DP(i + 1, j), DP(i, j - 1)) //Required to add a character, and see where addition gives minimum characters to insert\n```\nThen you can memoize the results in a matrix, for strings of large length. As here the sub-problems are overlapping. Or you can run an iterative DP length wise.\n\nTime complexity : `O(n^2)`, Space : `O(n^2)`\n```\nclass Solution {\npublic:\n bool isPal(string s)\n {\n if(s.size() <= 1)\n return 1;\n for(int i = 0, j = s.size() - 1; i < j; i++,j--)\n {\n if(s[i] != s[j])\n return 0;\n }\n return 1;\n }\n vector<vector<int>> dp;\n int f(string &s, int i, int j)\n {\n if(i >= j)\n return 0;\n if(dp[i][j] != -1)\n return dp[i][j];\n if(s[i] == s[j])\n {\n dp[i][j] = f(s, i + 1, j - 1); \n }\n else\n dp[i][j] = min(f(s, i , j - 1), f(s, i + 1, j)) + 1;\n \n return dp[i][j];\n }\n \n int minInsertions(string s) {\n if(isPal(s))\n return 0;\n int n = s.size();\n int i = 0, j = n - 1;\n dp = vector<vector<int>> (n, vector<int>(n, - 1));\n return f(s, i, j);\n }\n};\n```
| 4
| 0
|
['Dynamic Programming', 'C']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
LPS Based Approach 💯🔥| LCS Variation DP 🚀✅
|
lps-based-approach-lcs-variation-dp-by-s-hcry
|
IntuitionTo make a string a palindrome, we need to insert characters into the string. The goal is to find the minimum number of insertions required.The key insi
|
sharmanishchay
|
NORMAL
|
2025-02-05T11:19:27.939657+00:00
|
2025-02-05T11:19:27.939657+00:00
| 119
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To make a string a palindrome, we need to insert characters into the string. The goal is to find the minimum number of insertions required.
The key insight here is that the more of the string that is already a palindrome, the fewer insertions are needed. If we can find the Longest Palindromic Subsequence (LPS), then the remaining characters (those not part of the LPS) will need to be inserted in order to form a complete palindrome.
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Reverse the String**:
Given a string `s`, we create a reversed version of the string `t`. The reason we reverse the string is because the **Longest Common Subsequence (LCS)** between the original string `s` and its reversed string `t` will give us the **Longest Palindromic Subsequence (LPS)** of `s`. This works because any sequence of characters that matches in both `s` and `t` is a palindromic subsequence.
2. **Compute the Longest Common Subsequence (LCS)**:
We then compute the **LCS** between `s` and `t`. The **LCS** is the longest subsequence that appears in both strings. In our case, this will be the longest palindromic subsequence of `s`.
3. **Calculate Minimum Insertions**:
After constructing the DP table, the value at `dp[n][n]` (where `n` is the length of `s`) will give us the length of the LPS of `s`
*Formulae :* `Minimum Insertion` = `n` - `LPS`
# Complexity
- Time complexity: $$O(n^2)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n^2)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minInsertions(String s) {
String t = new StringBuilder(s).reverse().toString();
int n = s.length();
int[][]dp = new int[n + 1][n + 1];
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(s.charAt(i - 1) == t.charAt(j - 1)) {
dp[i][j] = 1 + dp[i - 1][j - 1];
}
else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return n - dp[n][n];
}
}
```
| 3
| 0
|
['Dynamic Programming', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
EXPLAINED|| BEGINNER FRIENDLY || DP.
|
explained-beginner-friendly-dp-by-abhish-whw3
|
Understanding the Code: Minimum Insertions to Make a Palindrome ,But before that ! what is your problem ppl? Why dont you shameless guys upvote my posts , I wri
|
Abhishekkant135
|
NORMAL
|
2024-07-27T17:36:29.728808+00:00
|
2024-07-27T17:36:29.728831+00:00
| 47
| false
|
## Understanding the Code: Minimum Insertions to Make a Palindrome ,But before that ! what is your problem ppl? Why dont you shameless guys upvote my posts , I write such long post puttings so much time and you wont wanna give an upvote ;(\n\n### Problem:\nGiven a string, find the minimum number of insertions required to make it a palindrome.\n\n### Solution Approach:\nThe code uses a dynamic programming approach to solve this problem. It calculates the minimum number of insertions needed for every substring of the given string and stores the results in a 2D array `dp`.\n\n### Code Breakdown:\n\n1. **Initialization:**\n - A 2D array `dp` is created to store the minimum number of insertions for each substring. Initially, all values are set to `Integer.MAX_VALUE`.\n\n2. **Recursive Function `solve`:**\n - This function calculates the minimum insertions for a substring defined by indices `i` and `j`.\n - **Base case:** If `i` is greater than or equal to `j`, it means the substring is empty or has only one character, so no insertions are needed, and 0 is returned.\n - **Memoization:** If the result for the current substring is already calculated (stored in `dp[i][j]`), it is returned directly.\n - **Matching Characters:** If the characters at indices `i` and `j` match, the problem reduces to finding the minimum insertions for the substring `i+1` to `j-1`.\n - **Non-matching Characters:** If the characters don\'t match, the minimum insertions are the minimum of two possibilities:\n - Inserting a character at index `i` and solving for the substring `i+1` to `j`.\n - Inserting a character at index `j` and solving for the substring `i` to `j-1`.\n\n3. **Main Function `minInsertions`:**\n - Creates the `dp` array and initializes it with `Integer.MAX_VALUE`.\n - Calls the `solve` function with the entire string and stores the result in `dp[0][str.length()-1]`.\n - Returns the calculated minimum number of insertions.\n\n### Key Points:\n- The code uses a bottom-up approach to populate the `dp` array efficiently.\n- Memoization is used to avoid redundant calculations.\n- The recursive nature of the problem is handled effectively using the `solve` function.\n\n### Time and Space Complexity:\n- Time complexity: O(n^2) due to the nested loops in the `solve` function.\n- Space complexity: O(n^2) for the `dp` array.\n\nThe memoization part is easy but you can make a dp array of half the size , It will work. \n# NOW GO ND UPVOTE.\n\n\n# Code\n```\nclass Solution{\n public int minInsertions(String str){\n int [][] dp=new int [str.length()][str.length()];\n for(int i=0;i<str.length();i++){\n for(int j=0;j<str.length();j++){\n dp[i][j]=Integer.MAX_VALUE;\n }\n }\n return solve(str,0,str.length()-1,dp);\n //return dp[0][str.length()-1];\n }\n public int solve(String str, int i, int j,int [][] dp){\n if(i>=j){\n return 0;\n }\n if(dp[i][j]!=Integer.MAX_VALUE){\n return dp[i][j];\n }\n if(str.charAt(i)==str.charAt(j)){\n return solve(str,i+1,j-1,dp);\n }\n \n return dp[i][j]=1+Math.min(solve(str,i+1,j,dp),solve(str,i,j-1,dp));\n }\n}\n\n\n```
| 3
| 0
|
['Dynamic Programming', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
🔥Java || Dp (tabulation)
|
java-dp-tabulation-by-neel_diyora-m595
|
Code\n\nclass Solution {\n public int minInsertions(String s) {\n String s2 = new StringBuilder(s).reverse().toString();\n int n = s.length();\
|
anjan_diyora
|
NORMAL
|
2023-06-29T16:21:30.839877+00:00
|
2023-06-29T16:21:30.839902+00:00
| 618
| false
|
# Code\n```\nclass Solution {\n public int minInsertions(String s) {\n String s2 = new StringBuilder(s).reverse().toString();\n int n = s.length();\n int[][] dp = new int[n+1][n+1];\n\n for(int i = 1; i <= n; i++) {\n for(int j = 1; j <= n; j++) {\n if(s.charAt(i-1) == s2.charAt(j-1)) dp[i][j] = 1 + dp[i-1][j-1];\n else dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);\n }\n }\n return n - dp[n][n];\n }\n}\n```
| 3
| 0
|
['Java']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
C++ || DP || EASY TO UNDERSTAND
|
c-dp-easy-to-understand-by-ganeshkumawat-a602
|
Code\n\nclass Solution {\npublic:\n int solve(int i,int j,string &s,vector<vector<int>> &dp){\n if(i>=j)return 0;\n if(dp[i][j] != -1)return dp
|
ganeshkumawat8740
|
NORMAL
|
2023-05-26T13:04:21.651864+00:00
|
2023-05-26T13:04:21.651914+00:00
| 718
| false
|
# Code\n```\nclass Solution {\npublic:\n int solve(int i,int j,string &s,vector<vector<int>> &dp){\n if(i>=j)return 0;\n if(dp[i][j] != -1)return dp[i][j];\n if(s[i]==s[j]){\n return dp[i][j] = solve(i+1,j-1,s,dp);\n }else{\n return dp[i][j] = min({solve(i+1,j,s,dp),solve(i,j-1,s,dp)})+1;\n }\n }\n int minInsertions(string s) {\n int n = s.length();\n vector<vector<int>> dp(n,vector<int>(n,-1));\n return solve(0,n-1,s,dp);\n }\n};\n```
| 3
| 0
|
['String', 'Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
✅Without knowing LCS
|
without-knowing-lcs-by-someshrwt-xocw
|
Intuition\nStarted thougth process from checking palindrome.\n\n# Approach\n- Approached from checking palindrome.\n- Added base condition.\n- Checked if charac
|
someshrwt
|
NORMAL
|
2023-04-25T06:13:27.749288+00:00
|
2023-04-25T06:13:27.749322+00:00
| 382
| false
|
# Intuition\nStarted thougth process from checking palindrome.\n\n# Approach\n- Approached from checking palindrome.\n- Added base condition.\n- Checked if character are same or not.\n- If not I just take the minimum of moving from both the ends.\n\nAnalyzed all the possibilities came up with ```recursion``` solution, than converted recursion to ```memoization```.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity:$$O(n^2)$$\n\n# Code\n```\nclass Solution {\npublic:\n int dp[501][501];\n int solve(string &s, int i, int j){\n if(i>=j)\n return 0;\n if(dp[i][j]!=-1)\n return dp[i][j];\n if(s[i]==s[j])\n return dp[i][j]=solve(s, i+1, j-1);\n else\n return dp[i][j]=1+min(solve(s, i+1, j), solve(s, i, j-1));\n return dp[i][j]=0;\n }\n int minInsertions(string s) {\n memset(dp, -1, sizeof(dp));\n return solve(s, 0, s.length()-1);\n }\n};\n```
| 3
| 0
|
['Dynamic Programming', 'C++']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Simple solution using recursion+memoization
|
simple-solution-using-recursionmemoizati-1rhf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
durgapranathi2002
|
NORMAL
|
2023-04-22T16:12:43.825288+00:00
|
2023-04-22T16:12:43.825319+00:00
| 155
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n // min no.of insertions = total length- longest palindromic subsequence \n\n public int minInsertions(String s) {\n \n Integer dp[][]=new Integer[s.length()][s.length()]; //memo\n\n return s.length() - lps(s,rev(s),s.length()-1,s.length()-1,dp);\n\n }\n int lps(String s1,String s2,int i,int j,Integer dp[][]){\n\n if(i<0 || j<0)return 0; //base\n\n if(dp[i][j]!=null)return dp[i][j];\n\n if(s1.charAt(i)==s2.charAt(j)){ //if both characters of string and reversed string matches moe both pointers\n return dp[i][j]=1+lps(s1,s2,i-1,j-1,dp);\n }else{\n return dp[i][j]=Math.max(lps(s1,s2,i-1,j,dp),lps(s1,s2,i,j-1,dp)); //else check moving one pointer at a time \n }\n }\n String rev(String s){\n StringBuilder sb=new StringBuilder(s);\n sb.reverse();\n return sb.toString();\n }\n\n}\n```
| 3
| 0
|
['Recursion', 'Memoization', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Recursion -> Memoization -> DP with explanations using Go
|
recursion-memoization-dp-with-explanatio-8uko
|
Intuition\nDivide the problem into sub problems.\nfor a string s with length n, \n- if s[0]==s[n-1], then f(s) = f(s[1:n-1]) \n- else, f(s) = 1+min(f(s[1:n]), f
|
nacoward
|
NORMAL
|
2023-04-22T13:35:21.255709+00:00
|
2023-04-22T13:44:34.380018+00:00
| 446
| false
|
# Intuition\nDivide the problem into sub problems.\nfor a string s with length n, \n- if s[0]==s[n-1], then f(s) = f(s[1:n-1]) \n- else, f(s) = 1+min(f(s[1:n]), f(s(:n-1)))\n\nSo we can use recursion to solve this problem\n\n# Approach\nRecursion\n\n# Complexity\n- Time complexity:\nO(2^N) for the worst situation\n\n- Space complexity:\nO(Recursion\'s depth) = O(N)\n\n# Code\n```\nfunc minInsertions(s string) int {\n n := len(s)\n if n <= 1 {return 0}\n if s[0]==s[n-1] {return minInsertions(s[1:n-1])}\n return 1+min2(minInsertions(s[1:]), minInsertions(s[:n-1]))\n}\nfunc min2(a, b int) int {if a < b {return a} else {return b}}\n```\n\n# Improve with memorization\nAs we can see, recursion\'s time complexity is O(2^N), a lot of same sub problems are repeatedly computed. \ne.g. for the following equation,\n- else, f(s) = 1+min(f(s[1:n]), f(s(:n-1)))\n\nwe can conclude that f(s[1:n-1]) would be computed in both f(s[1:n]) and f(s[:n-1]), so f(s[1:n-1]) is repeatedly computed. And the same situation for every f(s[i:j]) when i>=1 and j<=n-1 and i<j.\n\nWe can use two variables (l, r) to mark one specific sub problem. Imagine function `f` is what we want, `f(0, n-1)` denotes the original problem. In this way, we need compute every sub problem, which is `f(i, j), for every i<j pair`.\n\nMoreover, use some way to store every sub problem\'s result to avoid repeated computing. This is of vital importance to understand further improvements.\n\nSo what we use and how we use it to store every sub problem\'s result?\nThe answer is easy, use the easiest data structure, which is array. Use the\n2D array, dp[i][j] to denote the answer of sub problem `f(i,j)`, which means the answer of f(s[i:j])\n```\nfunc minInsertions(s string) int {\n n := len(s)\n dp := make([][]int, n)\n for i:=0; i<n; i++ {\n dp[i] = make([]int, n)\n for j:=0; j<n; j++ {dp[i][j] = -1}\n }\n\n var helper func(int, int) int\n helper = func(l, r int) int {\n if r-l<=0 {return 0}\n if dp[l][r] > -1 {return dp[l][r]}\n if s[l] == s[r] {\n dp[l+1][r-1] = helper(l+1, r-1)\n dp[l][r] = dp[l+1][r-1]\n return dp[l][r]\n }\n dp[l][r] = 1 + min2(helper(l+1, r), helper(l, r-1))\n return dp[l][r]\n }\n return helper(0, n-1)\n}\n\nfunc min2(a, b int) int {if a < b {return a} else {return b}}\n```\n\nAt last, we already understand how to use the memoization to solve this\nproblem, we can simplify it one step further.\n\nWe use the bottom-up way, which can help we avoid using recursion.\n\n```\nfunc minInsertions(s string) int {\n n := len(s)\n dp := make([][]int, n)\n for i:=0; i<n; i++ {dp[i] = make([]int, n)}\n\n for d:=1; d<n; d++ { // d means distance\n for i:=0; i+d<n; i++ {\n if s[i]==s[i+d] {\n dp[i][i+d] = dp[i+1][i+d-1]\n } else {\n dp[i][i+d] = 1 + min2(dp[i][i+d-1], dp[i+1][i+d])\n }\n }\n }\n return dp[0][n-1]\n}\nfunc min2(a, b int) int {if a < b {return a} else {return b}}\n```\nWe need pay attention to lots of details here. e.g. dp[i][i] is always equal to 0, because dp[i][i] means the ith character of s, and for one character, it is palindrome itself, so dp[i][i] = 0
| 3
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'Go']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
🎯TLE -> DP approach (Using Two Pointers)✔
|
tle-dp-approach-using-two-pointers-by-ha-buz8
|
Intuition\n Describe your first thoughts on how to solve this problem. \nLet\'s say s="abscsdfa". The longest palindromic subsequence in this string is "ascsa".
|
harsh6176
|
NORMAL
|
2023-04-22T08:54:46.753403+00:00
|
2023-04-22T08:54:46.753443+00:00
| 345
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLet\'s say s="abscsdfa". The longest palindromic subsequence in this string is "ascsa". So, the number of insertions required is `8 - 5 = 3`.\n\nSo we will first find longest palindromic subsequence and then will subtract from total length of string to get the desired answer.\n\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Recursive Solution -- Got TLE\n```\nclass Solution {\n int dfs(string &s, int i, int j){\n if (i>j) \n return 0;\n if (i==j)\n return 1;\n\n if (s[i]==s[j]){\n return 2 + dfs(s, i+1, j-1);\n }\n return max( dfs(s, i+1, j) , dfs(s, i, j-1) );\n }\n\npublic:\n int minInsertions(string s) {\n int n = s.length();\n return n - dfs(s, 0, n-1);\n }\n};\n```\n.\n.\n# Recursive Solution -- With DP\n```C++ []\nclass Solution {\n vector<vector<int>> dp;\n int dfs(string &s, int i, int j){\n if (i>j) \n return 0;\n if (i==j)\n return 1;\n \n if (dp[i][j]^-1) return dp[i][j];\n\n if (s[i]==s[j]){\n return dp[i][j] = 2 + dfs(s, i+1, j-1);\n }\n return dp[i][j] = max( dfs(s, i+1, j) , dfs(s, i, j-1) );\n }\n\npublic:\n int minInsertions(string s) {\n int n = s.length();\n dp.resize(n+1, vector<int> (n+1,-1));\n return n - dfs(s, 0, n-1);\n }\n};\n```\n\n\n\n
| 3
| 0
|
['Two Pointers', 'String', 'Dynamic Programming', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Rust, DP, short and concise solution ✅🔔🚩
|
rust-dp-short-and-concise-solution-by-df-q0s9
|
Intuition\nSimple dynamic programming approach. The subtask is to solve it for substring of length j starting with index i.\ndp[i][j] - the number of insersions
|
dfomin
|
NORMAL
|
2023-04-22T08:05:20.712628+00:00
|
2023-04-22T13:10:38.952167+00:00
| 1,040
| false
|
# Intuition\nSimple dynamic programming approach. The subtask is to solve it for substring of length `j` starting with index `i`.\n`dp[i][j]` - the number of insersions to make palindrome from substring `s[i..=i+j]`.\nEvery time you add one more character to substring you check if it\'s the same as first character, if so, `dp[i][j] = dp[i - 2][j]`, otherwise, to make it palindrome you need to make one insersion to the beginning or the end, so `dp[i][j] = min(dp[i - 1][j], dp[i - 1][j + 1]) + 1`.\n\n# Code\n```\nuse std::cmp::min;\n\nimpl Solution {\n pub fn min_insertions(s: String) -> i32 {\n let chars: Vec<char> = s.chars().collect();\n let mut dp = vec![vec![0; chars.len()]; chars.len() + 1];\n for i in 2..chars.len() + 1 {\n for j in 0..chars.len() - i + 1 {\n if chars[j] == chars[j + i - 1] {\n dp[i][j] = dp[i - 2][j + 1];\n } else {\n dp[i][j] = min(dp[i - 1][j], dp[i - 1][j + 1]) + 1;\n }\n }\n }\n\n return dp[chars.len()][0];\n }\n}\n```
| 3
| 0
|
['Rust']
| 2
|
minimum-insertion-steps-to-make-a-string-palindrome
|
DP || TIME O(m*n),SPACE O(n) || C++
|
dp-time-omnspace-on-c-by-yash___sharma-d94j
|
\nclass Solution {\npublic:\n int minInsertions(string s1) {\n int n = s1.length();\n vector<int> dp1(n+1,0),dp2(n+1,0);\n string s2 = s
|
yash___sharma_
|
NORMAL
|
2023-04-22T03:58:26.224477+00:00
|
2023-04-22T03:58:26.224506+00:00
| 617
| false
|
````\nclass Solution {\npublic:\n int minInsertions(string s1) {\n int n = s1.length();\n vector<int> dp1(n+1,0),dp2(n+1,0);\n string s2 = s1;\n reverse(s1.begin(),s1.end());\n int i,j;\n for(i = 1; i <= n; i++){\n for(j = 1; j <= n; j++){\n if(s1[i-1]==s2[j-1]){\n dp2[j] = dp1[j-1]+1;\n }else{\n dp2[j] = max(dp1[j],dp2[j-1]);\n }\n }\n dp1 = dp2;\n }\n return n-dp1[n];\n }\n};\n````
| 3
| 0
|
['Dynamic Programming', 'C', 'C++']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Python3 clean Solution beats 💯 100% with Proof 🔥
|
python3-clean-solution-beats-100-with-pr-iinb
|
Code\n\nclass Solution:\n def minInsertions(self, s: str) -> int:\n if s == s[::-1]: return 0 \n n = len(s)\n dp = [[0] * n for _ in ran
|
quibler7
|
NORMAL
|
2023-04-22T03:27:48.083651+00:00
|
2023-04-22T03:27:48.083682+00:00
| 1,872
| false
|
# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n if s == s[::-1]: return 0 \n n = len(s)\n dp = [[0] * n for _ in range(n)]\n for i in range(n-1,-1,-1):\n dp[i][i] = 1\n for j in range(i+1,n):\n if s[i] == s[j]:dp[i][j] = dp[i+1][j-1]+2\n else: dp[i][j] = max(dp[i+1][j], dp[i][j-1])\n return n-dp[0][n-1]\n```\n# Proof \n\n
| 3
| 0
|
['Python3']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Java | DP | 10 lines | Clean & simple code
|
java-dp-10-lines-clean-simple-code-by-ju-txak
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIf we figure out the longest palindromic subsequence as per this leetcode problem, the
|
judgementdey
|
NORMAL
|
2023-04-22T01:46:45.789465+00:00
|
2023-04-22T01:50:44.356158+00:00
| 148
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf we figure out the longest palindromic subsequence as per [this leetcode problem](https://leetcode.com/problems/longest-palindromic-subsequence/description/), the answer to the current problem should be the length of the string - the length of the longest palindromic subsequence. The rationale is that we can simply add a matching character for each existing character that is not part of the longest palindromic subsequence and make the entire string a palindrome.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minInsertions(String s) {\n var n = s.length();\n var dp = new int[n];\n var dpPrev = new int[n];\n\n for (var i = n-1; i >= 0; i--) {\n dp[i] = 1;\n\n for (var j = i+1; j < n; j++) {\n dp[j] =\n s.charAt(i) == s.charAt(j)\n ? 2 + dpPrev[j-1]\n : Math.max(dpPrev[j], dp[j-1]); \n }\n dpPrev = dp.clone();\n }\n return n - dp[n-1];\n }\n}\n```\nIf you like my solution, please upvote it!
| 3
| 0
|
['String', 'Dynamic Programming', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
c++ memoization solution (easiest)
|
c-memoization-solution-easiest-by-h_wan8-2kc3
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
h_WaN8H_
|
NORMAL
|
2023-04-22T01:21:11.482816+00:00
|
2023-04-22T01:21:11.482860+00:00
| 472
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int dp[510][510];\n int mininsertions(string&s, int si, int ei){\n if(dp[si][ei]!=-1)return dp[si][ei];\n if(si>=ei)return 0;\n if(s[si]==s[ei]){\n return dp[si][ei]=mininsertions(s,si+1,ei-1);\n }\n return dp[si][ei]=1+min(mininsertions(s,si+1,ei),mininsertions(s,si,ei-1));\n }\n int minInsertions(string s) {\n memset(dp,-1,sizeof(dp));\n return mininsertions(s,0,s.size()-1);\n }\n};\n```
| 3
| 0
|
['String', 'Recursion', 'Memoization', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[ C++ ] [ Dynamic Programming ] [ Longest Palindromic Subsequence ] [ Longest Common Subsequence ]
|
c-dynamic-programming-longest-palindromi-lyea
|
Code\n\nclass Solution {\npublic:\n int lcs(string s,string b){\n int a=s.size();\n int m=b.size();\n int dp[a+1][m+1];\n for(int i=0;i<a+1;i++){
|
Sosuke23
|
NORMAL
|
2023-04-22T00:58:12.256731+00:00
|
2023-04-22T00:58:12.256757+00:00
| 165
| false
|
# Code\n```\nclass Solution {\npublic:\n int lcs(string s,string b){\n int a=s.size();\n int m=b.size();\n int dp[a+1][m+1];\n for(int i=0;i<a+1;i++){\n for(int j=0;j<m+1;j++){\n if(i==0 || j==0)\n dp[i][j]=0;\n }\n }\n for(int i=1;i<a+1;i++){\n for(int j=1;j<m+1;j++){\n if(s[i-1]==b[j-1])\n dp[i][j]=1+dp[i-1][j-1];\n else\n dp[i][j]=max(dp[i-1][j],dp[i][j-1]);\n }\n }\n return dp[a][m];\n}\n int longestPalinSubseq(string A) {\n string s1=A;\n reverse(s1.begin(),s1.end());\n return lcs(A,s1);\n }\n int minInsertions(string s) {\n int a=s.length();\n int b=longestPalinSubseq(s);\n return a-b;\n }\n};\n```
| 3
| 0
|
['Dynamic Programming', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
LONGEST PLINDROMIC SUBSEQUENCE || C++
|
longest-plindromic-subsequence-c-by-yash-47ls
|
\nclass Solution {\npublic:\n int minInsertions(string s1) {\n int n = s1.length();\n vector<int> dp1(n+1,0),dp2(n+1,0);\n string s2 = s
|
yash___sharma_
|
NORMAL
|
2023-04-20T06:02:23.184060+00:00
|
2023-04-20T06:02:23.184104+00:00
| 884
| false
|
````\nclass Solution {\npublic:\n int minInsertions(string s1) {\n int n = s1.length();\n vector<int> dp1(n+1,0),dp2(n+1,0);\n string s2 = s1;\n reverse(s1.begin(),s1.end());\n int i,j;\n for(i = 1; i <= n; i++){\n for(j = 1; j <= n; j++){\n if(s1[i-1]==s2[j-1]){\n dp2[j] = dp1[j-1]+1;\n }else{\n dp2[j] = max(dp1[j],dp2[j-1]);\n }\n }\n dp1 = dp2;\n }\n return n-dp1[n];\n }\n};\n````
| 3
| 0
|
['Dynamic Programming', 'C', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Easy Java Solution| Using Recursion & Dynamic Programming
|
easy-java-solution-using-recursion-dynam-v1hh
|
Code\n\nclass Solution {\n public int minInsertions(String s) {\n int n= s.length();\n int[][] dp= new int[n+1][n+1];\n for(int[] temp:
|
PiyushParmar_28
|
NORMAL
|
2023-02-05T11:54:44.056915+00:00
|
2023-02-05T11:54:44.056958+00:00
| 449
| false
|
# Code\n```\nclass Solution {\n public int minInsertions(String s) {\n int n= s.length();\n int[][] dp= new int[n+1][n+1];\n for(int[] temp: dp){\n Arrays.fill(temp, -1);\n }\n return getCount(s, 0, n-1, dp);\n }\n\n public int getCount(String s, int left, int right, int[][] dp){\n if(dp[left][right] != -1){\n return dp[left][right];\n }\n if(left == right){\n return 0;\n }\n if(left+1 == right){\n if(s.charAt(left) == s.charAt(right)){\n return 0;\n }\n else{\n return 1;\n }\n }\n \n if(s.charAt(left) == s.charAt(right)){\n int ans= getCount(s, left+1, right-1, dp);\n dp[left][right]= ans;\n return ans;\n }\n else{\n int ans1= getCount(s, left, right-1, dp);\n int ans2= getCount(s, left+1, right, dp);\n dp[left][right]= Math.min(ans1, ans2)+1;\n return Math.min(ans1, ans2)+1;\n }\n }\n}\n```\n\n\n
| 3
| 0
|
['String', 'Dynamic Programming', 'Recursion', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
JAVA | SIMPLE EXPLANATION | CODE WITH DETAILED COMMENTS
|
java-simple-explanation-code-with-detail-wom9
|
Simple Explanation of Bottom-up (Tabulation) approach\n\nhttps://www.youtube.com/watch?v=7UpPnWW9GJY\n\nFor more:-\nTelegram group - https://t.me/+IK5-RpKtVWUxM
|
prateekool109
|
NORMAL
|
2022-08-04T06:11:46.227047+00:00
|
2022-08-06T05:16:03.694285+00:00
| 649
| false
|
Simple Explanation of Bottom-up (Tabulation) approach\n\nhttps://www.youtube.com/watch?v=7UpPnWW9GJY\n\nFor more:-\n**Telegram group** - https://t.me/+IK5-RpKtVWUxMDI1\n**Telegram channel**- https://t.me/betterSoftEng\n\n```\nclass LongestPalindromeInAStringSolution{\n static String longestPalin(String S){\n // code here\n if(S.length() == 0) return S;\n if(S.length() == 1) return S;\n\n //Initializing longest Palindromic substring found so far with\n //first letter\n int maxLength = 1;\n int maxPalinStartIndex = 0;\n int maxPalinEndIndex = 0;\n\n int i = 1;\n int n = S.length();\n\n int j; int k;\n\n int currentLength;\n int currentPalinStartIndex;\n int currentPalinEndIndex;\n\n //No use of having last letter as centre. Because, max palindromic\n //substring from there can be of just length = 1.\n\n //One iteration of this loop fixes a centre.\n for(i=0; i<n-1; i++) {\n //Centre length = 1\n //These two are pointers that will move - one to the left\n // one to the right.\n j=i-1;\n k=i+1;\n\n //Below information will keep track of current palindrome we have\n currentLength = 1;\n currentPalinStartIndex = i;\n currentPalinEndIndex = i;\n\n //While no index breaches boundary and we have equal characters\n while(j>=0 && k<n && S.charAt(j) == S.charAt(k)) {\n currentPalinStartIndex = j;\n currentPalinEndIndex = k;\n currentLength = currentLength + 2;\n j--;\n k++;\n }\n\n if(currentLength > maxLength) {\n maxLength = currentLength;\n maxPalinStartIndex = currentPalinStartIndex;\n maxPalinEndIndex = currentPalinEndIndex;\n }\n\n // If Centre length = 2 is possible\n if(S.charAt(i) == S.charAt(i+1)) {\n currentLength = 2;\n currentPalinStartIndex = i;\n currentPalinEndIndex = i+1;\n\n j=i-1;\n k=i+2;\n\n while(j>=0 && k<n && S.charAt(j) == S.charAt(k)) {\n currentPalinStartIndex = j;\n currentPalinEndIndex = k;\n currentLength = currentLength + 2;\n j--;\n k++;\n }\n\n if(currentLength > maxLength) {\n maxLength = currentLength;\n maxPalinStartIndex = currentPalinStartIndex;\n maxPalinEndIndex = currentPalinEndIndex;\n }\n }\n\n }\n\n return S.substring(maxPalinStartIndex, maxPalinEndIndex+1);\n\n }\n}\n```
| 3
| 0
|
['Dynamic Programming', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
JAVA | SIMPLE EXPLANATION | CODE WITH DETAILED COMMENTS
|
java-simple-explanation-code-with-detail-4n6e
|
Simple explanation https://www.youtube.com/watch?v=IWV3wolx13k\n\nAbove video explains Recursion and Top-Down DP approach. Part 2 of the video will have Bottom
|
prateekool109
|
NORMAL
|
2022-08-01T13:37:02.437506+00:00
|
2022-08-06T05:16:16.254036+00:00
| 353
| false
|
Simple explanation https://www.youtube.com/watch?v=IWV3wolx13k\n\nAbove video explains Recursion and Top-Down DP approach. Part 2 of the video will have Bottom up approach as well\n\nFor more:-\n**Telegram group** - https://t.me/+IK5-RpKtVWUxMDI1\n**Telegram channel** - https://t.me/betterSoftEng\n\n```\nclass FormAPalindromeSolution{\n static int countMin(String str)\n {\n // code here\n int n = str.length();\n\n //Each element of the matrix stores the result for substring from i to j\n int[][] matrix = new int[n][n];\n\n //Gap indicates the length of the string for which we are filling the matrix\n //currently\n int gap;\n\n //First we fill size 1 substrings\n //Then we fill size 2 substrings and so on.\n for(gap = 1; gap<=n; gap++) {\n fillMatrix(matrix, gap, str);\n }\n\n return matrix[0][n-1];\n }\n\n private static void fillMatrix(int[][] matrix, int gap, String s) {\n\n int n = s.length();\n //To iterate over string to get a starting position\n int i;\n // j tracks end position\n int j;\n //If gap = 1 => all 1-length strings are already palindromes.\n\n int resultLeft;\n int resultRight;\n int resultMid;\n\n //For gap 1, i and j are same\n if(gap == 1) {\n for(i=0; i<=n-1; i++) {\n j = i;\n matrix[i][j] = 0;\n }\n }\n\n if(gap == 2) {\n //Starting position shouldn\'t reach last character\n for(i=0; i<n-1; i++) {\n //Since length = 2 => j = i+1\n j = i+1;\n if(s.charAt(i) == s.charAt(j)) {\n matrix[i][j] = 0;\n } else {\n matrix[i][j] = 1;\n }\n }\n }\n for(gap=3; gap<=n; gap++) {\n //Loop till Starting position i can reach\n for(i=0; i<=n-gap; i++) {\n //Calculate end position wrt i\n j = i+gap-1;\n //The result for substring except last character + 1\n resultLeft = matrix[i][j-1] + 1;\n // The result for substring except first character + 1\n resultRight = matrix[i+1][j] + 1;\n\n if(s.charAt(i) == s.charAt(j)) {\n //The result if first and last character are same, then\n //how many insertions does it take to make the middle string\n //palindrome\n resultMid = matrix[i+1][j-1];\n //Minimum of all 3\n matrix[i][j] = Math.min(resultMid, Math.min(resultLeft, resultRight));\n } else {\n matrix[i][j] = Math.min(resultLeft, resultRight);\n }\n }\n }\n }\n}\n```
| 3
| 0
|
['Dynamic Programming', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
✅ [C++, Java, Python] Easy to understand | O(n^2) time and O(n) space | bottom up DP
|
c-java-python-easy-to-understand-on2-tim-b2it
|
Minimum Insertion Steps to Make a String Palindrome = Length of string - Length of longest palindromic subsequence. \n\nC++ implementation:\n\nclass Solution {
|
damian_arado
|
NORMAL
|
2022-07-03T14:51:11.915000+00:00
|
2022-07-03T14:52:30.138227+00:00
| 376
| false
|
Minimum Insertion Steps to Make a String Palindrome = Length of string - Length of longest palindromic subsequence. \n\nC++ implementation:\n```\nclass Solution {\nprivate:\n int findLCS(string &s1, string &s2) {\n int n = s1.size();\n vector<int> dp(n + 1, 0);\n for(int i = 1; i <= n; ++i) {\n vector<int> current(n + 1, 0);\n for(int j = 1; j <= n; ++j) {\n // match\n if(s1[i - 1] == s2[j - 1])\n current[j] = 1 + dp[j - 1];\n // not a match\n else \n current[j] = max(dp[j], current[j - 1]);\n }\n dp = current;\n }\n return dp[n];\n }\npublic:\n int minInsertions(string &s1) {\n string s2 = s1;\n reverse(s2.begin(), s2.end());\n return s1.size() - findLCS(s1, s2);\n }\n};\n```\n\nJava implementation:\n\n```\nclass Solution {\n private int findLCS(String s, String reverse) {\n int n = s.length();\n int[] dp = new int[n + 1];\n for(int i = 1; i <= n; ++i) {\n int[] current = new int[n + 1];\n for(int j = 1; j <= n; ++j) {\n if(s.charAt(i - 1) == reverse.charAt(j - 1))\n current[j] = 1 + dp[j - 1];\n else\n current[j] = Math.max(dp[j], current[j - 1]);\n }\n dp = current;\n }\n return dp[n];\n }\n \n public int minInsertions(String s) {\n String reverse = new StringBuilder(s).reverse().toString();\n return s.length() - findLCS(s, reverse);\n }\n}\n```\n\nPython implementation:\n\n```\nclass Solution:\n def findLCS(self, s: str, reverse: str) -> int:\n n = len(s)\n dp = [0] * (n + 1)\n for i in range(1, n + 1):\n current = [0] * (n + 1)\n for j in range(1, n + 1):\n # match\n if s[i - 1] == reverse[j - 1]:\n current[j] = 1 + dp[j - 1]\n else:\n current[j] = max(dp[j], current[j - 1])\n dp = current\n return dp[n]\n \n def minInsertions(self, s: str) -> int:\n # using slicing to reverse a string\n reverse = s[::-1]\n return len(s) - self.findLCS(s, reverse)\n```\n\nTime complexity: O(n^2)\nSpace-complexity: O(n)\n\n\u23E9Thanks for reading! An upvote would be appreciated. ^_^
| 3
| 0
|
['Dynamic Programming', 'C', 'Python', 'C++', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Java brute force using DP. IF anyone knows a better solution please share
|
java-brute-force-using-dp-if-anyone-know-fvzt
|
\nclass Solution {\n public int minInsertions(String s) {\n int len = s.length();\n StringBuilder sb = new StringBuilder();\n sb.append(
|
CosmicLeo
|
NORMAL
|
2022-01-21T14:13:56.171103+00:00
|
2022-01-21T14:13:56.171144+00:00
| 227
| false
|
```\nclass Solution {\n public int minInsertions(String s) {\n int len = s.length();\n StringBuilder sb = new StringBuilder();\n sb.append(s);\n sb.reverse();\n int [][] dp = new int[len+1][len+1];\n \n for(int i =0;i<len+1;i++){\n dp[i][0]=0;\n }\n for(int j =0;j<len+1;j++){\n dp[0][j]=0;\n }\n for(int i =1;i<len+1;i++){\n for(int j=1;j<len+1;j++){\n if(s.charAt(i-1)==sb.charAt(j-1))\n dp[i][j]=1+dp[i-1][j-1];\n else\n dp[i][j] =Math.max(dp[i-1][j], dp[i][j-1]);\n }\n }\n return len-dp[len][len];\n }\n}\n```
| 3
| 0
|
['Dynamic Programming', 'Java']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Why won't the frequency of letters work. Why will LCS work.
|
why-wont-the-frequency-of-letters-work-w-y3ug
|
\ndef minInsertions(self, s: str) -> int:\n if s == s[::-1] or len(s)==1:\n return 0\n t = s[::-1]\n dp = [[0]*(len(s)+1) for _
|
rahulranjan95
|
NORMAL
|
2021-09-15T04:58:12.918313+00:00
|
2021-09-15T04:58:12.918363+00:00
| 332
| false
|
```\ndef minInsertions(self, s: str) -> int:\n if s == s[::-1] or len(s)==1:\n return 0\n t = s[::-1]\n dp = [[0]*(len(s)+1) for _ in range(len(t)+1)]\n for i in range(1,len(s)+1):\n for j in range(1,len(t)+1):\n if s[i-1]==t[j-1]:\n dp[i][j] = 1+dp[i-1][j-1]\n else:\n dp[i][j] = max(dp[i-1][j],dp[i][j-1])\n # print(dp)\n return len(s)-dp[-1][-1]\n```\nAs a noob the first solution that came to my mind was counting the frequency of letters as the minimum requirement to have a string as palindrome is every letter should have even frequency except one. One letter is allowed to have an odd frequency. \nex: **MEMEM**\nIt is a palindrome with E : 2 and M:3. \n Now why wont the capturing of just freq won\'t work? \n It is because in this question we are concerned with the positioning of the letters as well while in freqency capturing technique, we are concerned with any permutation of string which would turn into a plindrome by least insertions.\n EX:\n Lets see a string : "ZJVEIIWVC"\n the freq table will look like this: \n {\n Z:1,\n E:1\n J:1,\n V:2\n I:2\n W:1\n C:1\n }\n So if we just choose any 4 letters among (E,Z,J,W,C) our minimum insertion will be 4 but only one of the permutation of resultant string will be palindrome. \nResultant string can be : Z E W C V I J I V C W E Z\n\nBut with LCS we can find the least insertion we need to do to make the given string a palindrome and not any of its permutations.\n\n**Thanks and Please do let me know if you need any further clarifications**
| 3
| 0
|
['Dynamic Programming', 'Python', 'Python3']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[C++] - Top-down and Bottom-up approaches
|
c-top-down-and-bottom-up-approaches-by-m-e9cc
|
Top Down Approach:\n\nclass Solution {\npublic:\n int solve(string &str,int low,int high,vector<vector<int> > &dp){\n if(low>high)\n return
|
morning_coder
|
NORMAL
|
2021-02-23T16:27:13.257843+00:00
|
2021-02-23T16:27:13.257880+00:00
| 184
| false
|
**Top Down Approach:**\n```\nclass Solution {\npublic:\n int solve(string &str,int low,int high,vector<vector<int> > &dp){\n if(low>high)\n return 0;\n if(dp[low][high]!=-1)\n return dp[low][high];\n if(low==high){\n return dp[low][high]=0;\n }\n if(str[low]==str[high]){\n return dp[low][high]=solve(str,low+1,high-1,dp);\n }\n return dp[low][high]=min(solve(str,low+1,high,dp),solve(str,low,high-1,dp))+1;\n }\n int minInsertions(string s) {\n int n=s.length();\n int index1=0,index2=n-1;\n if(index1>=index2)\n return 0;\n vector<vector<int> > dp(n,vector<int>(n,-1));\n return solve(s,index1,index2,dp);\n }\n};\n```\n**Bottom Up Approach:**\n```\nclass Solution {\npublic:\n int minInsertions(string str) {\n int n=str.length();\n int index1=0,index2=n-1;\n if(index1>=index2)\n return 0;\n vector<vector<int> > dp(n,vector<int>(n,-1));\n //dp[i][j]=no of insertions to make str[i...j] palindrome\n for(int i=0;i<n;i++){\n dp[i][i]=0;\n }\n for(int i=0;i<n-1;i++){\n if(str[i]==str[i+1])\n dp[i][i+1]=0;\n else\n dp[i][i+1]=1;\n }\n for(int i=2;i<n;i++){\n for(int j=0;j<n-i;j++){\n int k=i+j;\n if(str[j]==str[k])\n dp[j][k]=dp[j+1][k-1];\n else\n dp[j][k]=min(dp[j][k-1],dp[j+1][k])+1;\n }\n }\n return dp[0][n-1];\n }\n};\n```
| 3
| 2
|
['Dynamic Programming', 'Memoization', 'C', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[C++] [DP] Heavy Comments on Each Line
|
c-dp-heavy-comments-on-each-line-by-raja-te72
|
\nclass Solution {\npublic:\n // Before reading this, I would highly recommend to take a rought notebook and draw the flow chart of these recursive calls, ch
|
rajatsing
|
NORMAL
|
2020-12-24T18:35:29.893280+00:00
|
2020-12-24T18:36:03.400970+00:00
| 470
| false
|
```\nclass Solution {\npublic:\n // Before reading this, I would highly recommend to take a rought notebook and draw the flow chart of these recursive calls, change the variables values and check for yourself on how all these recursive values are adding up finally and what value is actually getting returned.\n// It would be a little tedious process but it will help u in Visualising the recursion tree.\n// Solve this code for "mbadm"\n int minInsert(string& s,int i,int j,vector<vector<int>>& dp) {\n if(i>=j) { // base case\n return 0;\n }\n if(dp[i][j]!=-1) { // if we have the value already calculated , just return that value\n return dp[i][j];\n }\n if(s[i]==s[j]) { \n dp[i][j]=minInsert(s,i+1,j-1,dp); // call recursion by decreasing j and increasing i and save the result of dp[i][j] which will be calculated recursively\n return dp[i][j]; // return the result that we got above \n }\n // Now if the chars at s[i] and s[j] are not same/palindrome, NOW WE HAVE 2 DECISION, EITHER ADD A CHARACTER ON THE LEFT SIDE(i pointer) OR ADD A CHARCTER on the RIGHT SIDE(j pointer)\n int dec1=minInsert(s,i+1,j,dp)+1; // ADDING ONE CHAR ON THE LEFT AND INCREMENT THE DECISION+1 AND calling recursively ON i+1 and j\n int dec2=minInsert(s,i,j-1,dp)+1; //ADDING ONE CHAR ON THE RIGHT AND INCREMENT THE DECISION+1 AND calling recursively ON i and j+1\n dp[i][j]=min(dec1,dec2); // SAVING THE MINIMUM OF THE 2 DECISION ON dp[i][j]\n return min(dec1,dec2); // RETURNING THE MINIMUM DECISION THAT WE GOT\n } \n int minInsertions(string s) {\n int len=s.length(); // calculating length\n vector<vector<int>>dp(len,vector<int>(len,-1)); // creating 2d vector of size len*len and filling with -1\n return minInsert(s,0,len-1,dp); // calling recursively \n }\n};\n```\n\n`TC will be O(len*len) since we are filling the dp[][] table which is of size len*len`
| 3
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
JAVA | Easy Solution Using Longest Common SubSequence
|
java-easy-solution-using-longest-common-kn0js
|
```\nclass Solution {\n public int minInsertions(String s) {\n StringBuilder S = new StringBuilder();\n S.append(s);\n return S.length()
|
onefineday01
|
NORMAL
|
2020-05-10T05:50:19.684541+00:00
|
2020-05-10T05:50:19.684576+00:00
| 586
| false
|
```\nclass Solution {\n public int minInsertions(String s) {\n StringBuilder S = new StringBuilder();\n S.append(s);\n return S.length() - longestCommonSubsequence(s, S.reverse().toString());\n }\n public int longestCommonSubsequence(String text1, String text2) {\n int m = text1.length(), n = text2.length();\n int[][] dp = new int[m + 1][n + 1];\n for(int i = 1; i <= m; i++)\n for(int j = 1; j <= n; j++)\n if(text1.charAt(i-1) == text2.charAt(j-1)) dp[i][j] = dp[i-1][j-1] + 1;\n else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);\n return dp[m][n];\n }\n}
| 3
| 0
|
['Dynamic Programming', 'Java']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Java DFS with memoization similar to 1216. Valid Palindrome III
|
java-dfs-with-memoization-similar-to-121-b7u5
|
java\nclass Solution {\n public int minInsertions(String s) {\n if (s == null || s.length() == 0) return 0;\n int[][] min = new int[s.length()]
|
dreamyjpl
|
NORMAL
|
2020-01-05T04:01:45.572659+00:00
|
2020-01-07T03:29:23.286663+00:00
| 713
| false
|
```java\nclass Solution {\n public int minInsertions(String s) {\n if (s == null || s.length() == 0) return 0;\n int[][] min = new int[s.length()][s.length()];\n for (int[] row : min) Arrays.fill(row, -1);\n return dp(s, 0, s.length() - 1, min);\n }\n private int dp(String s, int l, int r, int[][] min) {\n if (l >= r) return 0;\n if (min[l][r] >= 0) return min[l][r];\n min[l][r] = s.charAt(l) == s.charAt(r) ? dp(s, l + 1, r - 1, min) : Math.min(dp(s, l + 1, r, min), dp(s, l, r - 1, min)) + 1;\n return min[l][r];\n }\n}\n```
| 3
| 1
|
['Depth-First Search', 'Memoization', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[Java] Small code with Recursion with Memoization
|
java-small-code-with-recursion-with-memo-q30m
|
```\n int[][]dp;\n public int minInsertions(String s) {\n int n = s.length();\n dp = new int[n][n];\n for(int i=0; i=j) return 0;\n
|
tans12
|
NORMAL
|
2020-01-05T04:01:34.038145+00:00
|
2020-01-05T04:01:34.038187+00:00
| 324
| false
|
```\n int[][]dp;\n public int minInsertions(String s) {\n int n = s.length();\n dp = new int[n][n];\n for(int i=0; i<n; i++) {\n Arrays.fill(dp[i], Integer.MAX_VALUE);\n }\n int res = find(s.toCharArray(), 0, s.length()-1);\n return res;\n }\n \n int find(char[] str, int i, int j) {\n if(i>=j) return 0;\n if(dp[i][j] != Integer.MAX_VALUE) return dp[i][j];\n \n if(str[i] == str[j]) {\n dp[i][j] = find(str, i+1, j-1);\n } else {\n dp[i][j] = Math.min(find(str,i+1,j)+1, find(str,i,j-1)+1);\n }\n \n return dp[i][j];\n }
| 3
| 1
|
[]
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Easy to understand cpp solution with space optimization(beats 99.68%)
|
easy-to-understand-cpp-solution-with-spa-zg67
|
Intuition and Approach
The basic idea is to run Longest palindrome sequence on the string and then subtract the value from the string length to find out which a
|
Srikrishna_Kidambi
|
NORMAL
|
2025-04-06T17:46:16.287329+00:00
|
2025-04-06T17:46:16.287329+00:00
| 45
| false
|
# Intuition and Approach
<!-- Describe your first thoughts on how to solve this problem. -->
- The basic idea is to run Longest palindrome sequence on the string and then subtract the value from the string length to find out which are need to duplicated and put in right place to make the string palindrome.
- The longest palindrome sequence can be found by running LCS on string s and it's reverse.
# Complexity
- Time complexity: **O(n<sup>2</sup>)**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: **O(n)**
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minInsertions(string s) {
string s1=s;
reverse(s1.begin(),s1.end());
int m=s.length();
vector<int> prev(m+1),curr(m+1);
for(int i=1;i<=m;i++){
for(int j=1;j<=m;j++){
if(s[i-1]==s1[j-1]){
curr[j]=prev[j-1]+1;
}
else if(prev[j]>curr[j-1]){
curr[j]=prev[j];
}
else {
curr[j]=curr[j-1];
}
}
prev=curr;
}
return s.length()-prev[m];
}
};
```
| 2
| 0
|
['Dynamic Programming', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Java Solution [Beats 97.84%] | LCS Variation | LPS | Minimum Deletions
|
java-solution-beats-9784-lcs-variation-l-02wt
|
ApproachFinding the number of characters need to be deleted and then adding those characters on the opposite side of the string to get total number of insertion
|
neel-thakker
|
NORMAL
|
2025-02-02T18:39:45.291885+00:00
|
2025-02-02T18:39:45.291885+00:00
| 75
| false
|
# Approach
<!-- Describe your approach to solving the problem. -->
Finding the number of characters need to be deleted and then adding those characters on the opposite side of the string to get total number of insertions (minimum)
For minimum # of deletions: find LCS of s with reversed self
# Code
```java []
class Solution {
public int minInsertions(String s) {
return s.length() - lcs(s, new StringBuilder(s).reverse().toString());
}
int lcs(String s1, String s2) {
char[] arr1 = s1.toCharArray(), arr2 = s2.toCharArray();
int m = arr1.length, n = arr2.length, dp[][] = new int[m+1][n+1];
Arrays.fill(dp[0], 0);
for(int i=1; i<=m; i++) {
dp[i][0] = 0;
}
for(int i=1; i<=m; i++) {
for(int j=1; j<=n; j++) {
if(arr1[i-1] == arr2[j-1]) {
dp[i][j] = 1 + dp[i-1][j-1];
} else {
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
return dp[m][n];
}
}
```
| 2
| 0
|
['Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
dp || string c++
|
dp-string-c-by-gaurav_bahukhandi-kj6d
|
IntuitionApproachSAME AS MINIMUM DELECTION REQUIRED TO MAKE STRING PALINDROME .FIRST CALCULATE THE LONGEST COMMAN SUBSEQUENCE OF THE STRING OF ORIGINAL AND REVE
|
Gaurav_bahukhandi
|
NORMAL
|
2025-01-29T13:32:34.839043+00:00
|
2025-01-29T13:32:34.839043+00:00
| 131
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
SAME AS MINIMUM DELECTION REQUIRED TO MAKE STRING PALINDROME .FIRST CALCULATE THE LONGEST COMMAN SUBSEQUENCE OF THE STRING OF ORIGINAL AND REVERSED STRING BY CALCULATING LCS OF BOTH THIS STRING WE GET THE COMMON CHARS THAT ARE ON THE SAME INDEX BEFORE AND AFTER REVERSE STRING SO THIS ARE PALIDROME CHAR..LET ME EXPLAIN YOU THROUGH EXAMPLE
S = ABCBAABA
R(S)ABAABCBA
NOW THE CHARS ARE ON SAME INDEX BEFORE AND AFTER OF REVERSE STRING ARE
ABBBA NOW YOU CAN SEE THAT **ABBA** IS A PALINDROME NOW YOUR TASK IS SIMPLE JUST REMOVE THIS ABBA LENGTH FROM S STRING WHICH IS S-LCS(ABBA)
BY SUBTRACTING WE GET NUMBER OF MORE INSERTION REQUIRED TO MAKE STRING PALINDROME BECAUSE ABBA IS ALREADY PALINDROME
JAI SHREE RAM..HAPPY CODING
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N²)
- Sp2ace complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N²)
# Code
```cpp []
class Solution {
private:
string findLCS(string &s,string&s2,int n)
{
vector<vector<int>>dp(n+1,vector<int>(n+1,0));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(s[i-1]==s2[j-1])
dp[i][j]=1+dp[i-1][j-1];
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
//print lcs
int i=n,j=n;
string res;
while(i!=0 && j!=0)
{
if(s[i-1]==s2[j-1])
{
res.push_back(s[i-1]);
i--;
j--;
}
else if(dp[i-1][j] > dp[i][j-1])
i--;
else
j--;
}
return res;
}
public:
int minInsertions(string s) {
int n=s.length();
string s2=s;
reverse(s2.begin(),s2.end());
return n-findLCS(s,s2,n).length();
}
};
```
| 2
| 0
|
['String', 'Dynamic Programming', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
"Palindrome Perfection: Efficient Dynamic Programming for Minimum Insertions" || Same as 516. LPS✔️
|
palindrome-perfection-efficient-dynamic-0vzah
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires finding the minimum number of insertions needed to make a given st
|
manveet22280
|
NORMAL
|
2024-07-18T17:21:21.592328+00:00
|
2024-07-18T17:21:21.592354+00:00
| 664
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the minimum number of insertions needed to make a given string a palindrome. This can be approached by leveraging the concept of the Longest Common Subsequence (LCS).\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe key idea is to find the length of the Longest Palindromic Subsequence (LPS) in the given string. The difference between the string\'s length and the LPS length gives the minimum number of insertions needed. Here\'s the step-by-step approach:\n\n- Reverse the String:\nCreate a reversed version of the input string. The LCS of the string and its reverse will give the LPS of the string.\n\n- Dynamic Programming Setup:\nCreate a 2D DP array dp where dp[i][j] represents the length of the LCS of the first i characters of the original string and the first j characters of the reversed string.\n\n- DP Array Initialization and Filling:\nInitialize the DP array with zeros.\nIterate through the characters of both the original and reversed strings:\n-If characters match, increment the LCS length by 1.\n-If characters don\'t match, take the maximum LCS length by either excluding the current character of the original string or the reversed string.\n\n- Calculate Result:\nThe length of the LPS is found at dp[s.length()][s.length()].\nThe minimum number of insertions required is the difference between the string length and the LPS length.\n\n# Complexity\n- Time complexity: O(N2)\nWe use nested loops to fill the DP array, where \uD835\uDC41 is the length of the string.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N2)\nThe space is used for the 2D DP array.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minInsertions(String s) {\n String s2 = new StringBuilder(s).reverse().toString();\n int[][] dp = new int[s.length()+1][s.length()+1];\n\n for(int i = 1;i<=s.length();i++){\n for(int j = 1;j<=s.length();j++){\n if(s.charAt(i-1) == s2.charAt(j-1))dp[i][j] = 1 + dp[i-1][j-1];\n else{\n dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);\n }\n }\n }\n return s.length()-dp[s.length()][s.length()];\n }\n}\n```
| 2
| 0
|
['String', 'Dynamic Programming', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Easy || Beginner's Friendly || Easy to Understand || ✅✅
|
easy-beginners-friendly-easy-to-understa-q5wi
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
AadiVerma07
|
NORMAL
|
2024-03-28T00:15:01.810442+00:00
|
2024-03-28T00:15:01.810465+00:00
| 13
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minInsertions(String s) {\n int dp[][]=new int[s.length()+1][s.length()+1];\n for(int i=1;i<dp.length;i++){\n for(int j=1;j<dp[0].length;j++){\n if(s.charAt(i-1)==s.charAt(s.length()-j)){\n dp[i][j]=dp[i-1][j-1]+1;\n }\n else{\n dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);\n }\n }\n }\n return s.length()-dp[dp.length-1][dp[0].length-1];\n }\n}\n```
| 2
| 0
|
['Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Easy to Understand Java Code || Aditya Verma Approach || LPS
|
easy-to-understand-java-code-aditya-verm-ipw5
|
Complexity\n- Time complexity:\nO(mn)\n- Space complexity:\nO(mn)\n# Code\n\nclass Solution {\n public int minInsertions(String s) {\n StringBuilder s
|
Saurabh_Mishra06
|
NORMAL
|
2024-02-20T05:06:14.986822+00:00
|
2024-02-20T05:06:14.986847+00:00
| 101
| false
|
# Complexity\n- Time complexity:\nO(m*n)\n- Space complexity:\nO(m*n)\n# Code\n```\nclass Solution {\n public int minInsertions(String s) {\n StringBuilder s2 = new StringBuilder(s);\n s2.reverse();\n \n int m = s.length();\n int n = s2.length();\n\n int[][] t = new int[m+1][n+1];\n \n // Construct the LCS table\n for(int i=1; i<=m; i++){\n for(int j=1; j<=n; j++){\n if(s.charAt(i-1) == s2.charAt(j-1)){\n t[i][j] = t[i-1][j-1]+1;\n }\n else{\n t[i][j] = Math.max(t[i-1][j], t[i][j-1]);\n }\n }\n }\n\n return m - t[m][n];\n }\n}\n```\n\n
| 2
| 0
|
['Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Minimum Insertion Steps to Make a String Palindrome | 90% Faster | Simplest Approach | DP
|
minimum-insertion-steps-to-make-a-string-yfcj
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe need to find the minimum insertions required to make a string palindrome. Let us kee
|
Utkarsh_mishra0801
|
NORMAL
|
2024-02-12T13:02:00.067428+00:00
|
2024-02-12T13:02:00.067462+00:00
| 51
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to find the minimum insertions required to make a string palindrome. Let us keep the \u201Cminimum\u201D criteria aside and think, how can we make any given string palindrome by inserting characters?\n\nThe easiest way is to add the reverse of the string at the back of the original string. This will make any string palindrome.\n\nHere the number of characters inserted will be equal to n (length of the string). This is the maximum number of characters we can insert to make strings palindrome.\n\nThe problem states us to find the minimum of insertions. Let us try to figure it out:\n\nTo minimize the insertions, we will first try to refrain from adding those characters again which are already making the given string palindrome. For the given example, \u201Caaa\u201D, \u201Caba\u201D,\u201Daca\u201D, any of these are themselves palindromic components of the string. We can take any of them( as all are of equal length) and keep them intact. (let\u2019s say \u201Caaa\u201D).\n\nNow, there are two characters(\u2018b\u2019 and \u2018c\u2019) remaining which prevent the string from being a palindrome. We can reverse their order and add them to the string to make the entire string palindrome.\n\nWe can do this by taking some other components (like \u201Caca\u201D) as well. \n\nIn order to minimize the insertions, we need to find the length of the longest palindromic component or in other words, the longest palindromic subsequence.\n\nMinimum Insertion required = n(length of the string) \u2013 length of longest palindromic subsequence.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nThe algorithm is stated as follows:\n\nWe are given a string (say s), make a copy of it and store it( say string t).\nReverse the original string s.\nFind the longest common subsequence as in problem(1143. Longest Common Subsequence).\n\n\n# Complexity\n- Time complexity:\n- beat 90% of the user\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- beat 98% of the user\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n if s == s[::-1]:\n return 0\n n = len(s)\n return n - self.longestPalindromeSubseq(s)\n \n\n def longestPalindromeSubseq(self, s: str) -> int:\n t = s\n s = s[::-1]\n \n n = len(s)\n \n prev = [0] * (n + 1)\n cur = [0] * (n + 1)\n for ind1 in range(1, n + 1):\n for ind2 in range(1, n + 1):\n if t[ind1 - 1] == s[ind2 - 1]:\n # If the characters match, increment LCS length by 1\n cur[ind2] = 1 + prev[ind2 - 1]\n else:\n # If the characters do not match, take the maximum of LCS\n # by excluding one character from s1 or s2\n cur[ind2] = max(prev[ind2], cur[ind2 - 1])\n \n # Update \'prev\' to be the same as \'cur\' for the next iteration\n prev = cur[:]\n\n # The value in \'prev[m]\' represents the length of the Longest Common Subsequence\n return prev[n]\n \n```
| 2
| 0
|
['Python3']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Using dynamic Programing(Tabulation).
|
using-dynamic-programingtabulation-by-sh-98ta
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIf we find the longest length of the character which are palindrome then we have to do
|
Shrishti007
|
NORMAL
|
2024-02-12T09:13:15.574894+00:00
|
2024-02-12T09:13:15.574932+00:00
| 41
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf we find the longest length of the character which are palindrome then we have to do only insertion for those who are not palindrome.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMin insertions equal the difference in total length of string and length of longest palindrome sequence as we have to only repeat these elements in reversed order to make it a palindrome.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*M) where n is the len of string and m is the len of reversed string.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N*M)\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n n = len(s)\n k = self.longestPalindromeSubseq(s)\n return n -k\n # Helper functions\n def longestPalindromeSubseq(self, s: str) -> int:\n # can find the longest palindrome by reversing the string and and using longest common subsequence\n t = s \n # Reversing the string\n s = s[::-1]\n return self.lcs(s,t)\n def lcs(self, text1: str, text2: str) -> int:\n # Using tabulation\n n = len(text1)\n m = len(text2)\n # Creating the dp matrix with changing variables\n dp = [[-1 for _ in range(m+1)]for _ in range(n+1)]\n # base cases\n # if any of the index is zero means we have nothing left we compare so return 0.\n for j in range(m+1):\n dp[0][j] == 0\n for i in range(n+1):\n dp[i][0] == 0\n # considered the 0 above so start the itereation from 1\n for i in range(1,n+1):\n for j in range(1,m+1):\n # If the character match then add 1 and move 1 step\n if text1[i-1] == text2[j-1]:\n dp[i][j] = 1 + dp[i-1][j-1]\n # If not match then find the max by moving 1 step ahead in string 1 or moving 1 step ahead in string 2\n else:\n dp[i][j] = max(dp[i-1][j],dp[i][j-1])\n return dp[n][m] +1\n \n```
| 2
| 0
|
['Python3']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
C++, DP, tabulation, space optimized, simple
|
c-dp-tabulation-space-optimized-simple-b-jrzc
|
Intuition\n\n\n* Check longest common subsequence between string s and it\'s reverse string t.\n* len(s) - lcs(s, t) will be the number of non-matching characte
|
Arif-Kalluru
|
NORMAL
|
2023-07-19T07:46:36.719481+00:00
|
2023-07-19T07:46:36.719506+00:00
| 284
| false
|
# Intuition\n\n```\n* Check longest common subsequence between string s and it\'s reverse string t.\n* len(s) - lcs(s, t) will be the number of non-matching characters.\n* Hence we need to add those many characters.\n```\n\n# Tabulation (Not space optimized)\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n string t = s; reverse(t.begin(), t.end()); \n int n = s.size();\n return n - lcs(s, t, n);\n }\n\nprivate:\n int lcs(string& s, string& t, int& n) {\n vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0));\n\n for (int i = 1; i <= n; i++) {\n for (int j = 1; j <= n; j++) {\n if (s[i-1] == t[j-1]) dp[i][j] = 1 + dp[i-1][j-1];\n else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);\n }\n }\n\n return dp[n][n];\n }\n};\n```\n\n# Tabulation (Space optimized)\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n int n = s.size();\n return n - lcs(s, n);\n }\n\nprivate:\n int lcs(string& s, int& n) {\n vector<int> prev(n + 1, 0);\n vector<int> curr(n + 1, 0);\n\n for (int i = 1; i <= n; i++) {\n for (int j = 1; j <= n; j++) {\n if (s[i-1] == s[n-j]) curr[j] = 1 + prev[j-1];\n else curr[j] = max(prev[j], curr[j-1]);\n }\n prev = curr;\n }\n\n return prev[n];\n }\n};\n```
| 2
| 0
|
['String', 'Dynamic Programming', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
c++ memoization approach without using LCS
|
c-memoization-approach-without-using-lcs-sn2k
|
Solution without using reverse of the string\n\nclass Solution {\npublic:\n\n int helper(string &s, int i, int j, vector<vector<int>> & dp){\n if(i>
|
ankitkr23
|
NORMAL
|
2023-05-22T08:05:35.447198+00:00
|
2023-05-22T08:05:35.447247+00:00
| 14
| false
|
Solution without using reverse of the string\n```\nclass Solution {\npublic:\n\n int helper(string &s, int i, int j, vector<vector<int>> & dp){\n if(i>j)return 0;\n if(i==j)return 0;\n if(dp[i][j]!=-1)return dp[i][j];\n if(s[i-1]==s[j-1]){\n return dp[i][j]=helper(s, i+1, j-1,dp);\n }\n else{\n return dp[i][j]=min(1+helper(s,i+1, j,dp), 1+helper(s, i, j-1, dp));\n }\n }\n\n int minInsertions(string s) {\n int n=s.size();\n vector<vector<int>> dp(n+1, vector<int>(n+1, 0));\n return helper(s, 1, n, dp);\n \n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++
|
ex-amazon-explains-a-solution-with-a-vid-t9n3
|
My youtube channel - KeetCode(Ex-Amazon)\nI create 155 videos for leetcode questions as of April 24, 2023. I believe my channel helps you prepare for the coming
|
niits
|
NORMAL
|
2023-04-23T21:48:34.796482+00:00
|
2023-04-24T02:59:12.117096+00:00
| 721
| false
|
# My youtube channel - KeetCode(Ex-Amazon)\nI create 155 videos for leetcode questions as of April 24, 2023. I believe my channel helps you prepare for the coming technical interviews. Please subscribe my channel!\n\n### Please subscribe my channel - KeetCode(Ex-Amazon) from here.\n\n**I created a video for this question. I believe you can understand easily with visualization.** \n\n**My youtube channel - KeetCode(Ex-Amazon)**\nThere is my channel link under picture in LeetCode profile.\nhttps://leetcode.com/niits/\n\n\n\n\n# Intuition\nUse 1D dynamic programming to store minimum steps\n\n# Approach\n1. Get the length of the input string s and store it in a variable n.\n\n2. Create a list dp of length n filled with zeros to store the dynamic programming values.\n\n3. Loop through the indices of the string s from n - 2 to 0 in reverse order using for i in range(n - 2, -1, -1):.\n\n4. Inside the outer loop, initialize a variable prev to 0 to keep track of the previous dynamic programming value.\n\n5. Loop through the indices of the string s from i + 1 to n using for j in range(i + 1, n):.\n\n6. Inside the inner loop, store the current dynamic programming value in a temporary variable temp for future reference.\n\n7. Check if the characters at indices i and j in the string s are the same using if s[i] == s[j]:.\n\n8. If the characters are the same, update the dynamic programming value at index j in the dp list with the previous dynamic programming value prev.\n\n9. If the characters are different, update the dynamic programming value at index j in the dp list with the minimum of the dynamic programming values at index j and j-1 in the dp list, incremented by 1.\n\n10. Update the prev variable with the temporary variable temp.\n\n11. After the inner loop completes, the dynamic programming values in the dp list represent the minimum number of insertions needed to make s a palindrome.\n\n12. Return the dynamic programming value at index n-1 in the dp list as the final result. This represents the minimum number of insertions needed to make the entire string s a palindrome.\n\n\n---\n\n\n**If you don\'t understand the algorithm, let\'s check my video solution.\nThere is my channel link under picture in LeetCode profile.**\nhttps://leetcode.com/niits/\n\n\n---\n\n# Complexity\n- Time complexity: O(n^2)\nn is the length of the input string \'s\'. This is because there are two nested loops. The outer loop runs from n-2 to 0, and the inner loop runs from i+1 to n-1. In the worst case, the inner loop iterates n-1 times for each value of i, resulting in a total of (n-2) + (n-3) + ... + 1 = n(n-1)/2 iterations. Therefore, the overall time complexity is O(n^2).\n\n- Space complexity: O(n)\nn is the length of the input string \'s\'. This is because the code uses an array \'dp\' of size n to store the minimum number of insertions required at each position in \'s\'. Hence, the space complexity is linear with respect to the length of the input string.\n\n# Python\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n n = len(s)\n dp = [0] * n\n\n for i in range(n - 2, -1, -1):\n prev = 0\n\n for j in range(i + 1, n):\n temp = dp[j]\n\n if s[i] == s[j]:\n dp[j] = prev\n else:\n dp[j] = min(dp[j], dp[j-1]) + 1\n \n prev = temp\n \n return dp[n-1]\n```\n# JavaScript\n```\n/**\n * @param {string} s\n * @return {number}\n */\nvar minInsertions = function(s) {\n const n = s.length;\n const dp = new Array(n).fill(0);\n\n for (let i = n - 2; i >= 0; i--) {\n let prev = 0;\n\n for (let j = i + 1; j < n; j++) {\n const temp = dp[j];\n\n if (s[i] === s[j]) {\n dp[j] = prev;\n } else {\n dp[j] = Math.min(dp[j], dp[j-1]) + 1;\n }\n\n prev = temp;\n }\n }\n\n return dp[n-1]; \n};\n```\n# Java\n```\nclass Solution {\n public int minInsertions(String s) {\n int n = s.length();\n int[] dp = new int[n];\n\n for (int i = n - 2; i >= 0; i--) {\n int prev = 0;\n\n for (int j = i + 1; j < n; j++) {\n int temp = dp[j];\n\n if (s.charAt(i) == s.charAt(j)) {\n dp[j] = prev;\n } else {\n dp[j] = Math.min(dp[j], dp[j-1]) + 1;\n }\n\n prev = temp;\n }\n }\n\n return dp[n-1]; \n }\n}\n```\n# C++\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n int n = s.length();\n vector<int> dp(n, 0);\n\n for (int i = n - 2; i >= 0; i--) {\n int prev = 0;\n\n for (int j = i + 1; j < n; j++) {\n int temp = dp[j];\n\n if (s[i] == s[j]) {\n dp[j] = prev;\n } else {\n dp[j] = min(dp[j], dp[j-1]) + 1;\n }\n\n prev = temp;\n }\n }\n\n return dp[n-1]; \n }\n};\n```
| 2
| 0
|
['C++', 'Java', 'Python3', 'JavaScript']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
JAVA | DP | Well Explained🔥
|
java-dp-well-explained-by-pavittarkumara-kb38
|
Intuition\n Describe your first thoughts on how to solve this problem. \nMy first intuition was that the no. of insertions needed to make the string palindromic
|
pavittarkumarazad1
|
NORMAL
|
2023-04-23T08:22:31.628259+00:00
|
2023-04-23T08:23:04.759936+00:00
| 103
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy first intuition was that the no. of insertions needed to make the string palindromic would be **same as the no. of deletions** required to make the string palindromic. suppose we have the string ***abbca***. \n\nEither we can add c to make it palindromic ***acbbca*** or we can remove c to make it palindromic ***abba***.\n\nNow the question has reduced to [Find the Longest Palindromic subsequence](https://leetcode.com/problems/longest-palindromic-subsequence/description/). Then subtract the length of LPS from the actual length of the string.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn the above example :\n- length of the LPS -> ***abba*** = 4\n- length of the actual string ***abbca*** = 5\n- ans -> 5 - 4 = 1\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nwe are iterating the string n times for each character. So the time complexity would be $$O(n^2)$$.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe are using 2D array for DP. So the space complexity is $$O(n^2)$$.\nIt can further be reduced to $$O(n)$$ as for a particular moment we are just using the above row to make use to DP. We just need to rows instead of the whole DP array. *For the sake for simplicity I have used 2D array (you can try and further optimise it to $$O(n)$$).*\n\n# Code\n```\nclass Solution {\n\n public int solve(String s) {\n int[][] dp = new int[s.length() + 1][s.length() + 1];\n String sr = (new StringBuilder(s)).reverse().toString();\n\n for(int i = 1; i <= s.length(); i++) {\n for(int j = 1; j <= s.length(); j++) {\n char a = s.charAt(i - 1);\n char b = sr.charAt(j - 1);\n if(a == b) {\n dp[i][j] = dp[i - 1][j - 1] + 1;\n } else {\n dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);\n }\n }\n }\n return dp[s.length()][s.length()];\n }\n\n public int minInsertions(String s) {\n return s.length() - solve(s);\n }\n}\n```
| 2
| 0
|
['Dynamic Programming', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
[ Python ] ✅✅ Simple Python Solution Using Dynamic Programming🥳✌👍
|
python-simple-python-solution-using-dyna-r0yf
|
If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 1317 ms, faster than 27.39% of Python3 online submissi
|
ashok_kumar_meghvanshi
|
NORMAL
|
2023-04-22T16:44:07.756828+00:00
|
2023-04-22T16:44:07.756861+00:00
| 1,008
| false
|
# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 1317 ms, faster than 27.39% of Python3 online submissions for Minimum Insertion Steps to Make a String Palindrome.\n# Memory Usage: 16 MB, less than 67.55% of Python3 online submissions for Minimum Insertion Steps to Make a String Palindrome.\n\n\tclass Solution:\n\t\tdef minInsertions(self, s: str) -> int:\n\n\t\t\tdef LeastCommonSubsequence(string, reverse_string, row, col):\n\n\t\t\t\tdp = [[0 for _ in range(col + 1)] for _ in range(row + 1)]\n\n\t\t\t\tfor r in range(1, row + 1):\n\t\t\t\t\tfor c in range(1, col + 1):\n\n\t\t\t\t\t\tif string[r - 1] == reverse_string[c - 1]:\n\n\t\t\t\t\t\t\tdp[r][c] = dp[r - 1][c - 1] + 1\n\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\tdp[r][c] = max(dp[r - 1][c] , dp[r][c - 1])\n\n\t\t\t\treturn dp[row][col]\n\n\t\t\tlength = len(s)\n\n\t\t\tresult = length - LeastCommonSubsequence(s , s[::-1] , length , length)\n\n\t\t\treturn result\n\t\t\t\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D
| 2
| 0
|
['Dynamic Programming', 'Memoization', 'Python', 'Python3']
| 1
|
minimum-insertion-steps-to-make-a-string-palindrome
|
✅✅ BEST C++ solution DP ( 2 approach ) Memorization vs Tabulation 💯💯 ⬆⬆⬆⬆
|
best-c-solution-dp-2-approach-memorizati-0lr3
|
\n\n# Code\n\n#define vi vector<int>\n#define vvi vector<vi>\n\nclass Solution {\npublic:\n int solveMem(string& a, string& b, int i, int j, vvi& dp) {\n
|
Sandipan58
|
NORMAL
|
2023-04-22T14:33:10.105714+00:00
|
2023-04-22T14:33:10.105739+00:00
| 22
| false
|
\n\n# Code\n```\n#define vi vector<int>\n#define vvi vector<vi>\n\nclass Solution {\npublic:\n int solveMem(string& a, string& b, int i, int j, vvi& dp) {\n if(i == a.length() || j == b.length()) return 0;\n if(dp[i][j] != -1) return dp[i][j];\n if(a[i] == b[j]) dp[i][j] = 1 + solveMem(a, b, i+1, j+1, dp);\n else dp[i][j] = max(solveMem(a, b, i+1, j, dp), solveMem(a, b, i, j+1, dp));\n return dp[i][j];\n }\n\n int solveTab(string& a, string& b) {\n vvi dp(a.length() + 1, vi(a.length() + 1, 0));\n \n for(int i=a.length()-1; i>=0; i--) {\n for(int j=b.length()-1; j>=0; j--) {\n if(a[i] == b[j]) dp[i][j] = 1 + dp[i+1][j+1];\n else dp[i][j] = max(dp[i+1][j], dp[i][j+1]);\n }\n }\n\n return dp[0][0];\n }\n\n\n int minInsertions(string s) {\n string rev = s;\n reverse(rev.begin(), rev.end());\n vvi dp(s.length(), vi(s.length(), -1));\n return s.length() - solveMem(s, rev, 0, 0, dp);\n\n // return s.length() - solveTab(s, rev);\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Very Easy DP Solution | C++ & Java | Fast & Explained
|
very-easy-dp-solution-c-java-fast-explai-yh10
|
Solution\n- Use Dynamic Programming technique to try all possible ways to make the string palindrome.\n- The dp array is a 2D array, where dp[l][r] is the minim
|
Zeyad_Nasef
|
NORMAL
|
2023-04-22T13:19:51.638434+00:00
|
2023-04-22T13:19:51.638466+00:00
| 79
| false
|
# Solution\n- Use `Dynamic Programming` technique to try all possible ways to make the string palindrome.\n- The `dp` array is a 2D array, where `dp[l][r]` is the minimum number of insertions needed to make the substring `s[l..r]` a palindrome.\n- If `s[l] == s[r]`, then you can move the 2 pointers to the inside and calculate the minimum number of insertions needed for the substring `s[l + 1..r - 1]`.\n- If `s[l] != s[r]`, then try the 2 options to move `l` to the right or `r` to the left.\n- For all the combinations return the minimum number needed to convert the string to a palindrome one.\n# Complexity\n- Time Complexity: `O(N ^ 2)`, where `N` is the length of the string.\n- Space Complexity: `O(N ^ 2)`, for the `dp` array.\n\n# Code\n## C++\n```cpp\nclass Solution {\npublic:\n int dp[505][505];\n\n int solve(string &s, int l, int r) {\n if(l >= r) return 0;\n\n auto & ret = dp[l][r];\n if(~ret) return ret;\n\n if(s[l] == s[r]) ret = solve(s, l + 1, r - 1);\n else ret = 1 + min(solve(s, l + 1, r), solve(s, l, r - 1));\n return ret;\n }\n\n int minInsertions(string s) {\n memset(dp, -1, sizeof dp);\n return solve(s, 0, (int) s.size() - 1);\n }\n};\n```\n\n## Java\n```java\nclass Solution {\n int [][] dp = new int[505][505];\n\n int solve(String s, int l, int r) {\n if(l >= r) return 0;\n if(dp[l][r] != -1) return dp[l][r];\n if(s.charAt(l) == s.charAt(r)) return dp[l][r] = solve(s, l + 1, r - 1);\n return dp[l][r] = 1 + Math.min(solve(s, l + 1, r), solve(s, l, r - 1));\n }\n\n public int minInsertions(String s) {\n for (int i = 0; i < 505; i++) {\n for (int j = 0; j < 505; j++) {\n dp[i][j] = -1;\n }\n }\n return solve(s, 0, s.length() - 1);\n }\n}\n```
| 2
| 0
|
['C', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Solution using dp
|
solution-using-dp-by-priyanshu11-l1ad
|
Intuition\nTo solve this problem, we can use dynamic programming (DP). We define dp[i][j] as the minimum number of insertions needed to make the substring s[i..
|
priyanshu11_
|
NORMAL
|
2023-04-22T13:18:22.958226+00:00
|
2023-04-22T13:18:22.958276+00:00
| 51
| false
|
# Intuition\nTo solve this problem, we can use dynamic programming (DP). We define dp[i][j] as the minimum number of insertions needed to make the substring s[i...j] a palindrome.\n\n# Approach\nWe can observe that if the characters s[i] and s[j] are the same, then we don\'t need to do anything and we can just consider the substring s[i+1...j-1]. Otherwise, we have two options:\n\n1. Insert the character s[j] at the end of the substring s[i...j-1], and consider the substring s[i...j-2] for the next step.\n2. Insert the character s[i] at the beginning of the substring s[i+1...j], and consider the substring s[i+1...j-1] for the next step.\nWe can compute the dp values using bottom-up DP. The base case is when i=j, which means that the substring is already a palindrome and we don\'t need any insertions.\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int minInsertions(string s) {\n int n = s.length();\n vector<vector<int>> dp(n, vector<int>(n, 0));\n for (int len = 2; len <= n; len++) {\n for (int i = 0; i < n - len + 1; i++) {\n int j = i + len - 1;\n if (s[i] == s[j]) {\n dp[i][j] = dp[i+1][j-1];\n } else {\n dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1;\n }\n }\n }\n return dp[0][n-1];\n }\n};\n\n```
| 2
| 0
|
['String', 'Dynamic Programming', 'C++', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
python 3 - top down dp
|
python-3-top-down-dp-by-markwongwkh-l70q
|
Intuition\nLogic is straightforward.\n\nstate variable = left, right\nDo all combination of left and right -> DP should be used.\nIf s[left] == s[right], skip b
|
markwongwkh
|
NORMAL
|
2023-04-22T08:30:15.652773+00:00
|
2023-04-22T08:30:15.652817+00:00
| 308
| false
|
# Intuition\nLogic is straightforward.\n\nstate variable = left, right\nDo all combination of left and right -> DP should be used.\nIf s[left] == s[right], skip both left and right. Else, add either s[left] or s[right] and repeat the process.\n\n# Approach\ntop-down dp\n\n# Complexity\n- Time complexity:\nO(n^2) -> dp on all states.\n\n- Space complexity:\nO(n^2) -> cache size\n\n# Code\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n\n @lru_cache(None)\n def dp(l, r): # return min step\n if l >= r:\n return 0\n \n if s[l] == s[r]:\n return dp(l+1, r-1)\n\n else: # add left or right\n t1 = dp(l+1, r) + 1\n t2 = dp(l, r-1) + 1\n return min(t1, t2)\n \n return dp(0, len(s) - 1)\n```
| 2
| 0
|
['Python3']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
⭐✅Clean, Simple & Easy C++ Code💯 || Memoization✅
|
clean-simple-easy-c-code-memoization-by-anrgv
|
Code\n## Please Upvote if u liked my Solution\uD83E\uDD17\n\nclass Solution {\npublic:\n int helper(int i,int j,string& s,vector<vector<int>>& dp){\n
|
aDish_21
|
NORMAL
|
2023-04-22T08:17:05.158152+00:00
|
2023-04-22T08:25:04.523389+00:00
| 190
| false
|
# Code\n## Please Upvote if u liked my Solution\uD83E\uDD17\n```\nclass Solution {\npublic:\n int helper(int i,int j,string& s,vector<vector<int>>& dp){\n if(i >= j)\n return 0;\n if(dp[i][j] != -1)\n return dp[i][j];\n int left = INT_MAX,right = INT_MAX;\n if(s[i] == s[j])\n left = helper(i+1,j-1,s,dp);\n else{\n left = 1 + helper(i+1,j,s,dp);\n right = 1 + helper(i,j-1,s,dp);\n }\n return dp[i][j] = min(left,right);\n }\n int minInsertions(string s) {\n int n = s.size();\n vector<vector<int>> dp(n+1,vector<int>(n+1,-1));\n return helper(0,n-1,s,dp);\n }\n};\n```\n\n
| 2
| 0
|
['String', 'Dynamic Programming', 'Memoization', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Typescript top-down dynamic programming detailed solution. Beats 100%
|
typescript-top-down-dynamic-programming-rj2qr
|
Intuition\n Describe your first thoughts on how to solve this problem. \nA Palindrome string is one that reads the same forward and backward. One way to determi
|
Adetomiwa
|
NORMAL
|
2023-04-22T06:56:20.616707+00:00
|
2023-04-22T13:39:51.857017+00:00
| 407
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA Palindrome string is one that reads the same forward and backward. One way to determine if a string is palindromic is by using a **two-pointer algorithm**. In this case, we use two pointers, one at the start of the string and the other at the end of the string, and then we start comparing the characters at both pointers as we move the pointers.\n\nWe can use this same idea to determine the number of insertions required to make a string a palindrome.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOur approach involves using two pointers, one on the first index `[i]` and the other on the last index `[j]`. We move the pointers based on the following rules:\n\n- If the characters at both pointers are the same (i.e `s[i] === s[j]`), we move both pointers forward `(i++, j--)`, and no insertion operation is necessary.\n- If the characters at both pointers are NOT the same (i.e `s[i] !== s[j]`), we have two options:\n\n - We move the first pointer and leave the second pointer `(i++, j)`, and increment the number of operations by 1. This operation is equivalent to inserting one character before index `j`(i.e `j+1`) that matches the one at index `i`.\n - We move the second pointer and leave the first pointer `(i, j--)`, and increment the number of operations by 1. This operation is equivalent to inserting one character before index `i` (i.e `i-1`) that matches the one at index `j`.\n\n\nTo implement this approach, we wrote a recursive function that keeps track of both pointers and a cache to optimize the solution by storing the results for all pointer pairs to avoid duplicate computations.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\nn = length of string (s.length)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n^2)$$\n\n# Code\n```\nfunction minInsertions(s: string): number {\n const cache: number[][] = new Array(501);\n\n for(let i = 0; i < cache.length; i++){\n cache[i] = new Array(501).fill(-1);\n }\n\n return helper(0, s.length - 1);\n\n function helper(i: number, j: number): number {\n if(i >= j){\n return 0;\n }\n if(cache[i][j] !== -1){\n return cache[i][j];\n }\n\n let min: number = Number.MAX_VALUE;\n\n if(s[i] === s[j]){\n min = Math.min(min, helper(i+1, j-1));\n } else {\n min = Math.min(\n min,\n helper(i+1, j) + 1,\n helper(i, j-1) + 1\n );\n }\n\n cache[i][j] = min;\n return min;\n }\n};\n```
| 2
| 0
|
['Two Pointers', 'Dynamic Programming', 'TypeScript']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
✅ Java | Top Down DP - Memoization Approach
|
java-top-down-dp-memoization-approach-by-uij2
|
\n// Approach 2: Top Down DP (Memoization)\n\n// Time complexity: O(n^2)\n// Space complexity: O(n^2)\n\nclass Solution {\n int[][] memo;\n \n public i
|
prashantkachare
|
NORMAL
|
2023-04-22T06:28:45.237226+00:00
|
2023-04-22T06:28:45.237268+00:00
| 208
| false
|
```\n// Approach 2: Top Down DP (Memoization)\n\n// Time complexity: O(n^2)\n// Space complexity: O(n^2)\n\nclass Solution {\n int[][] memo;\n \n public int minInsertions(String s) {\n int n = s.length();\n memo = new int[n][n];\n return lcs(s, 0, n - 1); \n }\n \n private int lcs(String s, int left, int right) {\n if (left > right)\n return 0;\n \n if (memo[left][right] != 0)\n return memo[left][right];\n \n if (s.charAt(left) == s.charAt(right))\n return memo[left][right] = lcs(s, left + 1, right - 1);\n \n return memo[left][right] = 1 + Math.min(lcs(s, left + 1, right), lcs(s, left, right - 1));\n }\n}\n```\n\n**Please upvote if you find this solution useful. Happy Coding!**
| 2
| 0
|
['Dynamic Programming', 'Memoization', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Python easy 7-liner | DP | Top-down & Bottom-up
|
python-easy-7-liner-dp-top-down-bottom-u-jaf7
|
Code\n\nTop Down\n\nclass Solution:\n def minInsertions(self, s: str) -> int:\n @lru_cache(None)\n def dp(i, j):\n if i >= j:\n
|
atulkoshta
|
NORMAL
|
2023-04-22T05:03:33.568511+00:00
|
2023-04-22T05:35:57.058148+00:00
| 183
| false
|
# Code\n\n***Top Down***\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n @lru_cache(None)\n def dp(i, j):\n if i >= j:\n return 0\n\n if s[i] == s[j]:\n return dp(i+1, j-1)\n else:\n return 1+min(dp(i+1, j), dp(i, j-1))\n\n return dp(0, len(s)-1)\n```\n\n***Bottom-up***\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n n = len(s)\n dp = [[0 for _ in range(n)] for _ in range(2)]\n i = 0\n for i in range(n-2, -1, -1):\n for j in range(i+1, n):\n if s[i] == s[j]:\n dp[i%2][j] = dp[(i+1)%2][j-1]\n else:\n dp[i%2][j] = 1+min(dp[(i+1)%2][j], dp[i%2][j-1])\n\n return dp[i%2][n-1]\n```\nNote: To reduce space complexity, matrix of 2xn is used here. Same can be achieved using nxn matrix which is easy to interpret.\n\nOR (same as above)\n\n```\nclass Solution:\n def minInsertions(self, s: str) -> int:\n n = len(s)\n dp = [[0 for _ in range(n)] for _ in range(2)]\n \n i = 0\n for i in range(n-2, -1, -1):\n for j in range(i+1, n):\n dp[i%2][j] = dp[(i+1)%2][j-1] if s[i] == s[j] else 1+min(dp[(i+1)%2][j], dp[i%2][j-1])\n \n return dp[i%2][n-1]\n```\n
| 2
| 0
|
['Dynamic Programming', 'Python3']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
✅ Java | Naive Recursion - Brute Force Approach
|
java-naive-recursion-brute-force-approac-729t
|
\n// Approach 1: Naive Recursion (Brute Force Approach) - TLE\n\n// Time complexity: O(2^n)\n// Space complexity: O(2^n)\n\nclass Solution {\n public int min
|
prashantkachare
|
NORMAL
|
2023-04-22T04:53:17.093938+00:00
|
2023-04-22T04:53:17.093999+00:00
| 63
| false
|
```\n// Approach 1: Naive Recursion (Brute Force Approach) - TLE\n\n// Time complexity: O(2^n)\n// Space complexity: O(2^n)\n\nclass Solution {\n public int minInsertions(String s) {\n return lcs(s, 0, s.length() - 1); \n }\n \n private int lcs(String s, int left, int right) {\n if (left > right)\n return 0;\n \n if (s.charAt(left) == s.charAt(right))\n return lcs(s, left + 1, right - 1);\n \n return 1 + Math.min(lcs(s, left + 1, right), lcs(s, left, right - 1));\n }\n}\n```\n\n**Please upvote if you find this solution useful. Happy Coding!**
| 2
| 0
|
['Recursion', 'Java']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Python. 2 solutions. Recursive 1-liner DP. Iterative space optimised DP.
|
python-2-solutions-recursive-1-liner-dp-7lcqk
|
Approach 1: Recursive DP with memoization\n\n# Complexity\n- Time complexity: O(n^2)\n\n- Space complexity: O(n^2)\n\nwhere, n is length of s.\n\n# Code\nFormat
|
darshan-as
|
NORMAL
|
2023-04-22T04:51:31.643903+00:00
|
2023-04-22T04:51:31.643945+00:00
| 93
| false
|
# Approach 1: Recursive DP with memoization\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n^2)$$\n\nwhere, `n is length of s`.\n\n# Code\nFormatted to multiline for readability.\n```python\nclass Solution:\n def minInsertions(self, s: str) -> int:\n @cache\n def min_inserts(i: int, j: int) -> int:\n return (\n min_inserts(i + 1, j - 1)\n if s[i] == s[j]\n else 1 + min(min_inserts(i, j - 1), min_inserts(i + 1, j))\n ) if i < j else 0\n \n return min_inserts(0, len(s) - 1)\n\n```\n\n---\n\n# Approach 2: Iterative DP with space optimzation\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n)$$\n\nwhere, `n is length of s`.\n\n# Code\n```python\nclass Solution:\n def minInsertions(self, s: str) -> int:\n n = len(s)\n dp = [0] * (n + 1)\n for i in range(n - 1, -1, -1):\n prev = dp[i]\n for j in range(i + 1, n):\n k = j + 1\n prev, dp[k] = (dp[k], prev if s[i] == s[j] else 1 + min(dp[k - 1], dp[k]))\n return dp[-1]\n\n\n```
| 2
| 1
|
['String', 'Dynamic Programming', 'Recursion', 'Python', 'Python3']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
📌📌 C++ || DP || Memo || Faster || Easy To Understand 🤷♂️🤷♂️
|
c-dp-memo-faster-easy-to-understand-by-_-e4ly
|
Memo\n\n Time Complexity :- O(N * N)\n\n Space Complexity :- O(N * N)\n\n\nclass Solution {\npublic:\n \n // declare a 2D dp array\n \n vector<vecto
|
__KR_SHANU_IITG
|
NORMAL
|
2023-04-22T03:56:22.656076+00:00
|
2023-04-22T03:56:22.656117+00:00
| 120
| false
|
* ***Memo***\n\n* ***Time Complexity :- O(N * N)***\n\n* ***Space Complexity :- O(N * N)***\n\n```\nclass Solution {\npublic:\n \n // declare a 2D dp array\n \n vector<vector<int>> dp;\n \n int helper(string &str, int low, int high)\n {\n // base case\n \n if(low >= high)\n return 0;\n \n // if already calculated\n \n if(dp[low][high] != -1)\n return dp[low][high];\n \n if(str[low] == str[high])\n return dp[low][high] = helper(str, low + 1, high - 1);\n else\n {\n return dp[low][high] = 1 + min(helper(str, low + 1, high), helper(str, low, high - 1));\n }\n \n }\n \n int minInsertions(string str) {\n \n int n = str.size();\n \n int low = 0;\n \n int high = n - 1;\n \n // resize dp\n \n dp.resize(n + 1);\n \n // initialize dp\n \n dp.assign(n + 1, vector<int> (n + 1, -1));\n \n // call helper function\n \n return helper(str, low, high);\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'Memoization', 'C', 'C++']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Easy Explaination 🔥🔥 || Minimum Insertion Steps to make string palimdrome
|
easy-explaination-minimum-insertion-step-0mnc
|
\tclass Solution {\n\tpublic:\n\t\tint vec[501][501];\n\n\t\tint fun(string &s1, string &s2, int n1, int n2)\n\t\t{\n\t\t\tif(n1 == 0 || n2 == 0)\n\t\t\t\tretur
|
ritiktrippathi
|
NORMAL
|
2023-04-22T03:46:52.913350+00:00
|
2023-04-22T03:46:52.913382+00:00
| 15
| false
|
\tclass Solution {\n\tpublic:\n\t\tint vec[501][501];\n\n\t\tint fun(string &s1, string &s2, int n1, int n2)\n\t\t{\n\t\t\tif(n1 == 0 || n2 == 0)\n\t\t\t\treturn 0;\n\n\t\t\tif(vec[n1 - 1][n2 - 1] != -1)\n\t\t\t\treturn vec[n1 - 1][n2 - 1];\n\n\t\t\tif(s1[n1 - 1] == s2[n2 - 1])\n\t\t\t\treturn vec[n1 - 1][n2 - 1] = (1 + fun(s1, s2, n1 - 1, n2 -1));\n\t\t\telse\n\t\t\t\treturn vec[n1 - 1][n2 - 1] = max(fun(s1, s2, n1 - 1, n2), fun(s1, s2, n1, n2 - 1));\n\n\t\t}\n\n\t\tint minInsertions(string s) {\n\t\t\tstring srev = s;\n\t\t\treverse(s.begin(), s.end());\n\n\t\t\tfor(int i = 0; i < 501; i++)\n\t\t\t\tfor(int j = 0; j < 501; j++)\n\t\t\t\t\tvec[i][j] = -1;\n\n\t\t\tfun(srev, s, s.length(), s.length());\n\n\t\t\treturn s.length()- vec[s.length() - 1][s.length() - 1];\n\n\t\t}\n\t};
| 2
| 0
|
['String', 'Dynamic Programming', 'Memoization']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
Easy Golang Solution
|
easy-golang-solution-by-shellpy03-zaae
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shellpy03
|
NORMAL
|
2023-04-22T02:31:35.662627+00:00
|
2023-04-22T02:31:35.662657+00:00
| 42
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\no(n^2) because of (n+1)*(n+1) array.\n\n- Space complexity:\no(n^2) because of (n+1)*(n+1) array.\n\n\n# Code\n```\npackage main\n\nfunc minInsertions(s string) int {\n n := len(s)\n dp := make([][]int, n+1)\n for i := 0; i <= n; i++ {\n dp[i] = make([]int, n+1)\n }\n r := reverse(s)\n for i := 0; i <= n; i++ {\n for j := 0; j <= n; j++ {\n if i == 0 || j == 0 {\n dp[i][j] = 0\n } else if s[i-1] == r[j-1] {\n dp[i][j] = dp[i-1][j-1] + 1\n } else {\n dp[i][j] = max(dp[i-1][j], dp[i][j-1])\n }\n }\n }\n return n - dp[n][n]\n}\n\nfunc reverse(s string) string {\n n := len(s)\n r := make([]byte, n)\n for i := 0; i < n; i++ {\n r[i] = s[n-i-1]\n }\n return string(r)\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n\n```
| 2
| 0
|
['Brainteaser', 'Go']
| 0
|
minimum-insertion-steps-to-make-a-string-palindrome
|
C# Using Longest Palindromic Subsequence
|
c-using-longest-palindromic-subsequence-3jdhy
|
Approach\nUsing 516. Longest Palindromic Subsequence.\nIf we know the longest palindromic sub-sequence is x and the length of the string is n then, what is the
|
dmitriy-maksimov
|
NORMAL
|
2023-04-22T00:43:22.083893+00:00
|
2023-04-22T00:43:22.083920+00:00
| 417
| false
|
# Approach\nUsing [516. Longest Palindromic Subsequence](https://leetcode.com/problems/longest-palindromic-subsequence/).\nIf we know the longest palindromic sub-sequence is x and the length of the string is $$n$$ then, what is the answer to this problem? It is $$n - x$$ as we need $$n - x$$ insertions to make the remaining characters also palindrome.\n\n\n# Complexity\n- Time complexity: $$O(n \\times m)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\npublic class Solution\n{\n private readonly Dictionary<(int i, int j), int> _cache = new();\n\n public int MinInsertions(string s)\n {\n var reversedString = string.Join("", s.Reverse());\n return s.Length - getLCS(s, 0, reversedString, 0);\n }\n \n private int getLCS(string a, int i, string b, int j)\n {\n if (i >= a.Length || j >= b.Length)\n {\n return 0;\n }\n\n if (_cache.TryGetValue((i, j), out var value))\n {\n return value;\n }\n\n if (a[i] == b[j])\n {\n return _cache[(i, j)] = 1 + getLCS(a, i + 1, b, j + 1);\n }\n\n return _cache[(i, j)] = Math.Max(getLCS(a, i + 1, b, j), getLCS(a, i, b, j + 1));\n }\n}\n```
| 2
| 0
|
['C#']
| 0
|
last-stone-weight
|
[Java/C++/Python] Priority Queue
|
javacpython-priority-queue-by-lee215-p4p3
|
Explanation\nPut all elements into a priority queue.\nPop out the two biggest, push back the difference,\nuntil there are no more two elements left.\n\n\n# Comp
|
lee215
|
NORMAL
|
2019-05-19T04:21:18.876547+00:00
|
2020-01-08T15:50:09.007111+00:00
| 59,197
| false
|
# **Explanation**\nPut all elements into a priority queue.\nPop out the two biggest, push back the difference,\nuntil there are no more two elements left.\n<br>\n\n# **Complexity**\nTime `O(NlogN)`\nSpace `O(N)`\n<br>\n\n**Java, PriorityQueue**\n```java\n public int lastStoneWeight(int[] A) {\n PriorityQueue<Integer> pq = new PriorityQueue<>((a, b)-> b - a);\n for (int a : A)\n pq.offer(a);\n while (pq.size() > 1)\n pq.offer(pq.poll() - pq.poll());\n return pq.poll();\n }\n```\n\n**C++, priority_queue**\n```cpp\n int lastStoneWeight(vector<int>& A) {\n priority_queue<int> pq(begin(A), end(A));\n while (pq.size() > 1) {\n int x = pq.top(); pq.pop();\n int y = pq.top(); pq.pop();\n if (x > y) pq.push(x - y);\n }\n return pq.empty() ? 0 : pq.top();\n }\n```\n**Python, using heap, O(NlogN) time**\n```py\n def lastStoneWeight(self, A):\n h = [-x for x in A]\n heapq.heapify(h)\n while len(h) > 1 and h[0] != 0:\n heapq.heappush(h, heapq.heappop(h) - heapq.heappop(h))\n return -h[0]\n```\n\n**Python, using binary insort, O(N^2) time**\n```py\n def lastStoneWeight(self, A):\n A.sort()\n while len(A) > 1:\n bisect.insort(A, A.pop() - A.pop())\n return A[0]\n```
| 364
| 3
|
[]
| 65
|
last-stone-weight
|
✅ Simple easy c++ solution
|
simple-easy-c-solution-by-naman_rathod-eyi1
|
\n\n\n int lastStoneWeight(vector<int>& stones) \n {\n priority_queue<int> pq(stones.begin(),stones.end());\n while(pq.size()>1)\n {\n
|
Naman_Rathod
|
NORMAL
|
2022-04-07T00:42:44.754643+00:00
|
2022-04-07T00:42:44.754677+00:00
| 18,203
| false
|
\n\n```\n int lastStoneWeight(vector<int>& stones) \n {\n priority_queue<int> pq(stones.begin(),stones.end());\n while(pq.size()>1)\n {\n int y=pq.top();\n pq.pop();\n int x=pq.top();\n pq.pop();\n if(x!=y) pq.push(y-x);\n }\n return pq.empty()? 0 : pq.top();\n }\n```
| 193
| 0
|
[]
| 25
|
last-stone-weight
|
[Python] Beginner-friendly Optimisation Process with Explanation
|
python-beginner-friendly-optimisation-pr-27cq
|
Introduction\n\nGiven an array of stones stones, we repeatedly "smash" (i.e., compare) the two heaviest stones together until there is at most one stone left. I
|
zayne-siew
|
NORMAL
|
2022-04-07T01:57:02.104507+00:00
|
2022-04-07T01:57:02.104551+00:00
| 18,567
| false
|
### Introduction\n\nGiven an array of stones `stones`, we repeatedly "smash" (i.e., compare) the two heaviest stones together until there is at most one stone left. If the two heaviest stones are of the same weight, both stones are "destroyed" (i.e., both weights become 0), otherwise, a stone with the absolute weight difference of both stones will remain.\n\nNote that the order in which the stones are "smashed" needs to be followed strictly. Otherwise, we will not end up with the correct weight of the remaining stone, if any.\n\n```text\narr = [2, 7, 4, 1, 8, 1]\n\nCORRECT METHOD\n1) Smash 8 and 7 -> arr = [2, 4, 1, 1, 1]\n2) Smash 4 and 2 -> arr = [2, 1, 1, 1]\n3) Smash 2 and 1 -> arr = [1, 1, 1]\n4) Smash 1 and 1 -> arr = [1]\n\nWRONG METHOD #1 (according to index ordering)\n1) Smash 2 and 7 -> arr = [5, 4, 1, 8, 1]\n2) Smash 5 and 4 -> arr = [1, 1, 8, 1]\n3) Smash 1 and 1 -> arr = [8, 1]\n4) Smash 8 and 1 -> arr = [7]\n\nWRONG METHOD #2 (in ascending order)\n1) Smash 1 and 1 -> arr = [2, 7, 4, 8]\n2) Smash 2 and 4 -> arr = [2, 7, 8]\n3) Smash 2 and 7 -> arr = [5, 8]\n4) Smash 5 and 8 -> arr = [3]\n```\n\n---\n\n### Base Approach - Sort and Insert\n\nSince we are required to "smash" the two heaviest stones, we need to know which two stones are the heaviest, and for all iterations. As such, we will first have to sort the stones in order by weight in order to compare the two heaviest stones.\n\n```python\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n stones.sort()\n while stones:\n s1 = stones.pop() # the heaviest stone\n if not stones: # s1 is the remaining stone\n return s1\n s2 = stones.pop() # the second-heaviest stone; s2 <= s1\n if s1 > s2:\n # we need to insert the remaining stone (s1-s2) into the list\n pass\n # else s1 == s2; both stones are destroyed\n return 0 # if no more stones remain\n```\n\nAll that remains now is how we can insert the stone from the "smashing" of the two heaviest stones back into `stones`. The simplest method is to loop through `stones` and insert the stone in the correct index.\n\n```python\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n stones.sort()\n while stones:\n s1 = stones.pop() # the heaviest stone\n if not stones: # s1 is the remaining stone\n return s1\n s2 = stones.pop() # the second-heaviest stone; s2 <= s1\n if s1 > s2:\n # the remaining stone will be s1-s2\n # loop through stones to find the index to insert the stone\n for i in range(len(stones)+1):\n if i == len(stones) or stones[i] >= s1-s2:\n stones.insert(i, s1-s2)\n break\n # else s1 == s2; both stones are destroyed\n return 0 # if no more stones remain\n```\n\n**TC: O(n<sup>2</sup>)**, where `n` is the length of `stones`, due to the nested inserts.\n**SC: O(1)**, no additonal data structures are used.\n\n---\n\n### Slight Optimisation - Binary Search Insert\n\nAn "optimisation" from the above method to find the index to insert the remaining stone is to binary search for the index to insert to instead of looping through `stones` manually. This involves Python\'s [bisect library](https://docs.python.org/3/library/bisect.html) which has a pre-written function to help us do just that.\n\nNote that we only need to change one portion of the code; the remaining code logic is the same.\n\n```python\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n stones.sort()\n while stones:\n s1 = stones.pop() # the heaviest stone\n if not stones: # s1 is the remaining stone\n return s1\n s2 = stones.pop() # the second-heaviest stone; s2 <= s1\n if s1 > s2:\n # the remaining stone will be s1-s2\n # binary-insert the remaining stone into stones\n insort_left(stones, s1-s2)\n # else s1 == s2; both stones are destroyed\n return 0 # if no more stones remain\n```\n\n**TC: O(n<sup>2</sup>)**. Even though binary searching for the index to insert to takes O(logn) time, the insert function alone takes O(n) time because it needs to shift all the elements after the index to the right by 1. As such, the overall time complexity for `insort_left()` is O(n).\n**SC: O(1)**, as discussed above.\n\n---\n\n### Data Structure - Heap Implementation\n\nUnfortunately, due to the implementation of the list data structure, even the binary search optimisation cannot break free of the O(n) insert. If only there was a data structure that could help us sort and insert automatically without having to rely on a heavier insert function...\n\nPython has an in-built [heap library](https://docs.python.org/3/library/heapq.html) that is perfect for this task. Essentially, all we need to do is insert the elements, and the heap will settle the sorting order for us. Unfortunately, Python\'s heap library implements a min-heap instead of a max-heap, whereby popping will give us the lightest stone instead of the heaviest stone.\n\nA standard (very common!) workaround is to **negate all the weight values of the stones**. This way, the heaviest stone has the most negative value, and hence becomes the smallest value in the heap. Then, all we have to do after obtaining the value from the heap is to un-negate the value to use it in our calculations.\n\n```python\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n # first, negate all weight values in-place\n for i, s in enumerate(stones):\n stones[i] = -s\n heapify(stones) # pass all negated values into the min-heap\n while stones:\n s1 = -heappop(stones) # the heaviest stone\n if not stones: # s1 is the remaining stone\n return s1\n s2 = -heappop(stones) # the second-heaviest stone; s2 <= s1\n if s1 > s2:\n heappush(stones, s2-s1) # push the NEGATED value of s1-s2; i.e., s2-s1\n # else s1 == s2; both stones are destroyed\n return 0 # if no more stones remain\n```\n\n**TC: O(nlogn)**; `heappush()` and `heappop()` both have O(logn) time complexity, and are both nested in the while loop. Note: `heapify()` runs in O(n) time, hence the time complexity is not affected.\n**SC: O(1)**; both the negation and the heapify are done in-place.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :)
| 166
| 3
|
['Heap (Priority Queue)', 'Python', 'Python3']
| 14
|
last-stone-weight
|
C++ Explained 🔥 Easy Solution 🔥Priority Queue 🔥
|
c-explained-easy-solution-priority-queue-3953
|
PLEASE UPVOTE \uD83D\uDC4D\n# Intuition\n- #### To solve this problem, we can use a priority queue to keep track of the heaviest stones. \n- #### At each turn,
|
ribhav_32
|
NORMAL
|
2023-04-24T02:08:23.569056+00:00
|
2023-04-24T02:08:23.569092+00:00
| 12,973
| false
|
# **PLEASE UPVOTE \uD83D\uDC4D**\n# Intuition\n- #### To solve this problem, we can use a priority queue to keep track of the heaviest stones. \n- #### At each turn, we can pop the two heaviest stones from the heap, smash them together according to the given rules, and then push the resulting stone (if any) back onto the heap. \n- #### We repeat this process until there is at most one stone left in the heap.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- #### In this code, we first create the priority queue by negating the values of the stones. \n- #### We then loop until there is at most one stone left in the heap. Inside the loop, we pop the two heaviest stones from the queue and check whether they are equal or not.\n 1. #### If they are not equal, we calculate the weight of the resulting stone and push it back onto the Queue (priority queue heapify itself after every push operation).\n- #### Finally, we return the weight of the last remaining stone (or 0 if there are no stones left).\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(NLogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# **PLEASE UPVOTE \uD83D\uDC4D**\n# Code\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& a) {\n priority_queue<int>pq(a.begin(),a.end());\n\n while(pq.size() > 1)\n {\n int a = pq.top();\n pq.pop();\n int b = pq.top();\n pq.pop();\n\n if(a != b)\n pq.push(abs(a-b));\n }\n return pq.empty() ? 0 : pq.top();\n }\n};\n```\n\n
| 117
| 2
|
['Array', 'Queue', 'Heap (Priority Queue)', 'C++']
| 3
|
last-stone-weight
|
Java simple to complex solutions explained -- 0 ms top 100% time 100% memory 2 lines of code only!
|
java-simple-to-complex-solutions-explain-fcd7
|
At every step of the algorithm, we need to know the top heaviest stone.\nThe most efficient way to retrieve the max for large input sizes is to use a max heap,
|
tiagodsilva
|
NORMAL
|
2020-04-12T10:57:33.478815+00:00
|
2020-04-14T08:19:18.648027+00:00
| 9,972
| false
|
At every step of the algorithm, we need to know the top heaviest stone.\nThe most efficient way to retrieve the max for large input sizes is to use a max heap, which in Java is a PriorityQueue (min heap) with a reverse comparator:\n\nO(n log (n)) time O(n) space \n1 ms time 37.5 MB space\n91% time 100% space\n\n```\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> queue = new PriorityQueue<>(Collections.reverseOrder());\n for(int i : stones) {\n queue.add(i);\n }\n int x;\n int y;\n while(queue.size() > 1) {\n y = queue.poll();\n x = queue.poll();\n if(y > x) {\n queue.offer(y-x); \n }\n }\n return queue.isEmpty() ? 0 : queue.poll();\n }\n```\n\nBut we can do better, right? If you have done a few of these problems you might know to use BucketSort with has constant access and no typical "sorting", we can do O(n) time. \n\nHowever, it is more accurate to say the time would be O(n + maxStoneWeight) because we will build a bucket for every possible weight. And usually a O(n + 1000) would be a great solution, but the test cases here have a very short input size. the number of stones goes only from 0 to 30, so this solution actually performs worse than O(n) since n is at most 30! O(30) == O(1030) but 30 < 1030. Both have the same complexity, but the first runs faster, and you might have not noticed why unless you check the inputs given in the tests.\n\n```\n int[] buckets = new int[1001];\n for(int stone: stones)\n buckets[stone]++;\n int i = 1000;\n int j;\n while(i > 0) {\n if(buckets[i] == 0) {\n i--;\n } else {\n buckets[i] = buckets[i] % 2;\n if(buckets[i] != 0) {\n j = i-1;\n while(j > 0 && buckets[j] == 0)\n j--;\n if(j == 0)\n return i;\n buckets[i - j]++;\n buckets[j]--;\n i--;\n }\n }\n }\n return 0;\n```\n\nRuns even slower! Remember to not always apply a solution that seems faster because you didn\'t consider your context or use cases. here the number of stones is much smaller than the weight of the stones.\n\nSo if we know that the number of stones is quite small, can we do even better than the PriorityQueue? What is a very fast sorting algorithm for small sets, better than building a heap? Sort in place in the array! Don\'t waste time building new objects or copies of the input.\n\nO( n^2 log(n) ) because for every stone n, we sort the array O(nlog(n))\nO(1) space, no extra space, sort in place\n**0 ms time 36.9 MB\tspace\nfaster than 100% and less space used than 100% of other solutions**\n\n```\n public static int lastStoneWeight(int[] stones) {\n Arrays.sort(stones);\n for(int i=stones.length-1; i>0; i--) {\n stones[i-1] = stones[i] - stones[i-1];\n Arrays.sort(stones);\n }\n return stones[0];\n }\n```\n\nAnd just for fun, let\'s mangle it into **2 lines**:\n```\n for(int i=stones.length; i>0; stones[i-1] = i==stones.length? stones[i-1] : stones[i] - stones[i-1], Arrays.sort(stones), i--);\n return stones[0];\n```\n\nEDIT: \nTo be completely clear, if the input size was unrestricted and not less than 30 stones, BucketSort would be the best solution because it runs in O(maxStoneWeight). If the stones weight is not unrestricted, then BucketSort cannot work as you would need 2,147,483,647 buckets. In that case, PriorityQueue would be the best solution.\n\n**In an interview, you should only discuss either BucketSort or PriorityQueue (max head) solutions**. The only reason I mentioned the sorting solution, which is much worse than the two other solutions, is because the input size in the tests of this challenge are so small that this solution is faster.
| 103
| 0
|
[]
| 13
|
last-stone-weight
|
A solid EXPLANATION
|
a-solid-explanation-by-hi-malik-002g
|
How\'s going Ladies - n - Gentlemen, today we are going to solve another coolest problem i.e. Last Stone Weight \n\nOkay, so first of all let\'s understand the
|
hi-malik
|
NORMAL
|
2022-04-07T02:03:53.258617+00:00
|
2022-04-07T07:37:18.185859+00:00
| 4,521
| false
|
How\'s going Ladies - n - Gentlemen, today we are going to solve another coolest problem i.e. **Last Stone Weight** \n\nOkay, so first of all let\'s understand the problem\n\n**We have 2 stones x & y**\n\n\n\nAnd There could be 2 Possiblities :\n* If both the stones x & y have same weight, then **` x == y, both stones are destroyed`**\n\n\n* If they are not equal, then stone y always be greater then stone x, therefore **`x != y, the stone of weight x is destroyed, and the stone of weight y has new weight y - x.`** \n\n```\nAt the end of the game, there is at most one stone left.\n\nReturn the smallest possible weight of the left stone. If there are no stones left, return 0.\n```\n\nI hope problem statement is absolute clear, now let\'s talk about how we gonna solve this problem.\n\n**Let\'s take an example,**\n\n**Input**: stones = [2,7,4,1,8,1]\n**Output**: 1\n\nThe very Brute force Idea came in our mind is, why don;t we just sort that array, such that we will have bigger values in the end, and to maintain that highest value in the end, we always gonna sort them once both of the stones will collide. \n\nWhat I mean is, let\'s take our input array:\n```\n[2,7,4,1,8,1]\n\nLet\'s sort it:\n\n[1,1,2,4,7,8]\n```\n\nNow what we gonna do is, collide the 2 stones and get their difference i.e. `y - x`\n```\n[1,1,2,4,7,8] --> y = 8 & x = 7\n\nThus,\ny - x --> 8 - 7 = 1\n```\nNow we gonna put that one in our array & maintain the order by sorting it back again\n```\n[1,1,2,4] add => 1 in our array\n\n[1,1,2,4,1] now again sort it,\n\n[1,1,1,2,4]\n```\nSo, we gonna perform the same step for all. Well it\'s not a great approach to go with, as our Time Complexity will be much higher.\n\nLet\'s code it up, then we gonna analysis it\'s space & time complexity:-\n\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n Arrays.sort(stones);\n \n for(int i = stones.length - 1; i > 0; i--){\n stones[i - 1] = stones[i] - stones[i - 1];\n Arrays.sort(stones);\n }\n return stones[0];\n }\n}\n```\n\nANALYSIS :-\n* **Time Complexity :-** BigO(NlogN) * BigO(N) => BigO(N^2logN)\n\n* **Space Complexity :-** BigO(1)\n\nWell, now you say. Dude, let;s optimise it. \nYes, we just goona do that stuff now!!\n```\nFor Optimising it, we gonna use the help of Heap\n```\n\nOkay, so we gonna take the same example & now you\'ll ask which heap do we have to use??\n**minHeap OR maxHeap??**\n\nAs, you can see we want highest value at the first & lowest value in the last. So, we gonna use **maxHeap**\n\nLet\'s create our maxHeap and use the same example i.e. **`[2,7,4,1,8,1]`** to fill our heap.\n\nSo, our first job is, let\'s fill our heap.\n```\n Array [2,7,4,1,8,1]\n| |\n|\t |\t\t\n| | \n| |\n| |\n| |\n--------\nmaxHeap\n```\n\nNow let\'s fill our heap,\n```\n Array [2,7,4,1,8,1]\n\t\t\t\t ^\n| |\n|\t |\t\t\n| | \n| |\n| |\n| 2 |\n--------\nmaxHeap\n```\n```\n Array [2,7,4,1,8,1]\n\t\t\t\t ^\n| |\n|\t |\t\t\n| | \n| |\n| 7 |\n| 2 |\n--------\nmaxHeap\n```\n```\n Array [2,7,4,1,8,1]\n\t\t\t\t ^\n| |\n|\t |\t\t\n| | \n| 7 |\n| 4 |\n| 2 |\n--------\nmaxHeap\n```\n```\n Array [2,7,4,1,8,1]\n\t\t\t\t ^\n| |\n|\t |\t\t\n| 7 | \n| 4 |\n| 2 |\n| 1 |\n--------\nmaxHeap\n```\n```\n Array [2,7,4,1,8,1]\n\t\t\t\t ^\n| |\n| 8 |\t\t\n| 7 | \n| 4 |\n| 2 |\n| 1 |\n--------\nmaxHeap\n```\n```\n Array [2,7,4,1,8,1]\n\t\t\t\t ^\n| 8 |\n| 7 |\t\t\n| 4 | \n| 2 |\n| 1 |\n| 1 |\n--------\nmaxHeap\n```\n\nNow it\'s time to get the stone x & y using our heap & after calculating **`y - x`** put the new difference in our stack\n```\n Array [2,7,4,1,8,1]\n\t\t\t\t \n| | y = 8\n| |\t\t x = 7\n| 4 | \n| 2 | and their result will be y - x => 8 - 7 = 1\n| 1 |\n| 1 |\n--------\nmaxHeap\n```\nNow put that **1** into our heap & again calculate the result of stone x & y\n```\n Array [2,7,4,1,8,1]\n\t\t\t\t \n| | y = 4\n| |\t\t x = 2\n| | \n| 1 | and their result will be y - x => 4 - 2 = 2\n| 1 |\n| 1 |\n--------\nmaxHeap\n```\nSo, we gonna perform the same step until & unless only 1 elemnent left in our stack.\n\nI hope so, ladies - n - gentlemen, approach is absolute clear, **then let\'s code it up:**\n\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());\n for(int v : stones){\n maxHeap.offer(v);\n }\n int x;\n int y;\n while(maxHeap.size() > 1){\n y = maxHeap.poll();\n x = maxHeap.poll();\n if(y > x){\n maxHeap.offer(y - x);\n }\n }\n if(maxHeap.size() == 0) return 0;\n return maxHeap.poll();\n }\n}\n```\nANALYSIS :-\n* **Time Complexity :-** BigO(NlogN)\n\n* **Space Complexity :-** BigO(N)\n```\nTime Complexity Explanation\'s may be still if I\'m wrong, correct me then, THANKS <^^>\n```\n\n*Heap is a specialized tree-based data structure* that is essentially almost *complete binary tree.* There are so many operations possible with **max and min heaps like -**\n\n`insert(), delete(), update(), findMinElement(), findMaxElement(), etc`\n\nAnd time complexity depends on the operation you perform on the heap.\n\n**`Heap Sort has O(nlog n) time complexities for all the cases ( best case, average case, and worst case).`**\n\n**Let us understand the reason why.** The height of a complete binary tree containing n elements is **log n**\n\nIn the worst case scenario, we will need to move an element from the root to the leaf node making a multiple of **log(n)** comparisons and swaps.\n\nDuring the `build_max_heap` stage, we do that for **n/2** elements so the worst case complexity of the `build_heap` step is **n/2xlog n ~ nlog n**.\n\nDuring the sorting step, we exchange the root element with the last element and heapify the root element. For each element, this again takes **log n** worst time because we might have to bring the element all the way from the root to the leaf. Since we repeat this n times, the `heap_sort` step is also **nlog n.**\n\nAlso since the `build_max_heap` and `heap_sort` steps are executed one after another, the algorithmic complexity is not multiplied and it remains in the order of **nlog n**.
| 90
| 4
|
[]
| 19
|
last-stone-weight
|
[Java/Python 3] easy code using PriorityQueue/heapq w/ brief explanation and analysis.
|
javapython-3-easy-code-using-priorityque-b46h
|
Sort stones descendingly in PriorityQueue, then pop out pair by pair, compute the difference between them and add back to PriorityQueue.\n\nNote: since we alrea
|
rock
|
NORMAL
|
2019-05-19T04:35:25.806338+00:00
|
2022-04-07T16:31:42.578315+00:00
| 7,409
| false
|
Sort stones descendingly in PriorityQueue, then pop out pair by pair, compute the difference between them and add back to PriorityQueue.\n\nNote: since we already know the first poped out is not smaller, it is not necessary to use Math.abs().\n\n```java\n public int lastStoneWeight(int[] stones) {\n // PriorityQueue<Integer> pq = new PriorityQueue<>(stones.length, Comparator.reverseOrder());\n var q = new PriorityQueue<Integer>(stones.length, Comparator.reverseOrder()); // Credit to @YaoFrankie.\n for (int st : stones) { \n q.offer(st); \n }\n while (q.size() > 1) {\n q.offer(q.poll() - q.poll());\n }\n return q.peek();\n }\n```\n```\n def lastStoneWeight(self, stones: List[int]) -> int:\n q = [-stone for stone in stones]\n heapq.heapify(q)\n while (len(q)) > 1:\n heapq.heappush(q, heapq.heappop(q) - heapq.heappop(q))\n return -q[0]\n```\n\nIn case you want to optimize the time performance, refer to the following version, which does NOT put `0` into the PriorityQueue:\n```java\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> pq = new PriorityQueue<>(stones.length, Comparator.reverseOrder());\n IntStream.of(stones).forEach(pq::offer);\n while (pq.size() > 1) {\n int diff = pq.poll() - pq.poll();\n if (diff > 0) {\n pq.offer(diff);\n }\n }\n return pq.isEmpty() ? 0 : pq.poll();\n }\n```\n```python\n def lastStoneWeight(self, stones: List[int]) -> int:\n heapify(hp := [-s for s in stones])\n while len(hp) > 1:\n if (diff := heappop(hp) - heappop(hp)) != 0:\n heappush(hp, diff)\n return -heappop(hp) if hp else 0\n```\n\n**Analysis:**\n\nTime: O(nlogn), space: O(n), where n = stones.length.\n\n----\n\n**Q & A:**\n\nQ: If not adding zeroes in the queue when polling out two elements are equal, is the result same as the above code?\n\nA: Yes. 0s are always at the end of the PriorityQueue. No matter a positive deduct 0 or 0 deduct 0, the result is same as NOT adding 0s into the PriorityQueue.
| 48
| 2
|
['Heap (Priority Queue)']
| 8
|
last-stone-weight
|
C++ Multiset and Priority Queue
|
c-multiset-and-priority-queue-by-votruba-ektu
|
Approach 1: Multiset\n\nint lastStoneWeight(vector<int>& st) {\n multiset<int> s(begin(st), end(st));\n while (s.size() > 1) {\n auto w1 = *prev(s.end());\
|
votrubac
|
NORMAL
|
2019-05-19T04:12:26.519812+00:00
|
2019-11-10T18:29:28.829732+00:00
| 6,376
| false
|
#### Approach 1: Multiset\n```\nint lastStoneWeight(vector<int>& st) {\n multiset<int> s(begin(st), end(st));\n while (s.size() > 1) {\n auto w1 = *prev(s.end());\n s.erase(prev(s.end()));\n auto w2 = *prev(s.end());\n s.erase(prev(s.end()));\n if (w1 - w2 > 0) s.insert(w1 - w2);\n }\n return s.empty() ? 0 : *s.begin();\n}\n```\n#### Approach 2: Priority Queue\n```\nint lastStoneWeight(vector<int>& st) {\n priority_queue<int> q(begin(st), end(st));\n while (q.size() > 1) {\n auto w1 = q.top(); q.pop();\n auto w2 = q.top(); q.pop();\n if (w1 - w2 > 0) q.push(w1 - w2);\n }\n return q.empty() ? 0 : q.top();\n}\n```\n#### Complexity Analysys\n- Time: O(n log n) to sort stones.\n- Memory: O(n) for the multiset/queue.
| 44
| 3
|
[]
| 8
|
last-stone-weight
|
Super Simple O(N) Java Solution using bucket sort and two pointers
|
super-simple-on-java-solution-using-buck-7dzo
|
```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n int[] buckets = new int[1001];\n for (int i = 0; i < stones.length; i++) {
|
laiyinlg
|
NORMAL
|
2019-08-16T18:31:31.838392+00:00
|
2019-08-30T06:02:20.695862+00:00
| 5,107
| false
|
```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n int[] buckets = new int[1001];\n for (int i = 0; i < stones.length; i++) {\n buckets[stones[i]]++;\n }\n\n int slow = buckets.length - 1; //start from the big to small\n while (slow > 0) {\n\t\t// If the number of stones with the same size is even or zero, \n\t\t// these stones can be totally destroyed pair by pair or there is no such size stone existing, \n\t\t// we can just ignore this situation.\n\t\t\n // When the number of stones with the same size is odd, \n\t\t// there should leave one stone which is to smash with the smaller size one.\n if (buckets[slow]%2 != 0) {\n int fast = slow - 1;\n while (fast > 0 && buckets[fast] == 0) {\n fast--;\n }\n if (fast == 0) break;\n buckets[fast]--;\n buckets[slow - fast]++;\n }\n slow--;\n }\n return slow;\n }\n}\n
| 42
| 5
|
[]
| 16
|
last-stone-weight
|
JavaScript || Faster than 95% ||Easy to understand ||With comments
|
javascript-faster-than-95-easy-to-unders-qw0x
|
\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n while(stones.length>1){\n stones.sort((a,b)=>
|
VaishnaviRachakonda
|
NORMAL
|
2022-04-07T13:41:20.908884+00:00
|
2022-04-07T13:41:20.908989+00:00
| 4,121
| false
|
```\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n while(stones.length>1){\n stones.sort((a,b)=>b-a); //sort the remaining stones in decending order;\n stones[1]=stones[0]-stones[1]; //smash the first and second stones ie the stones with largest weight ans assign the remaining stone weight to 1st index\n stones.shift();//shift the array to get rid of the 0 index\n }\n return stones[0] //return the 0 index value ie the resultl\n};\n```\n\nIts okay if you did not get the solution in the first try, don\'t give up!\nPlease do UPVOTE if you find it helpfull.... I know this is not the best solution to this problem but this is what I came up with.\nHappy C0d1ng!! Cheers!
| 38
| 0
|
['JavaScript']
| 4
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.