question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
last-stone-weight
|
✅ Java | Easy Solution Explained 📝 | Similar Questions | Beginner friendly
|
java-easy-solution-explained-similar-que-54vt
|
Intuition\nSince we need to choose heaviest two stones everytime, this is a clear hint to go for heap data structure. In java we implement heap via priority que
|
nikeMafia
|
NORMAL
|
2023-04-24T05:52:06.381408+00:00
|
2023-05-01T06:28:29.176763+00:00
| 5,492
| false
|
# Intuition\nSince we need to choose heaviest two stones everytime, this is a clear hint to go for heap data structure. In java we implement heap via priority queue.\n\nSimilar questions for heap i faced in interviews.\nLC 347[ Top K Frequent Elements](https://leetcode.com/problems/top-k-frequent-elements/)\nLC 215[ Kth Largest Element in an Array](https://leetcode.com/problems/kth-largest-element-in-an-array/)\nLC 23 [Merge k Sorted Lists](https://leetcode.com/problems/merge-k-sorted-lists/)\n\n\n---\n# Approach\n1) Make a heap via priority queue, we need to make a max heap as we need heaviest stone collision first.\n2) Add stones[] to heap\n3) Now run a while loop till there are two elements remaining in the hea[] i.e ```while(heap.size()>1)``` Two elements because each collision needs two stones atleast. \n- pick top 2 stones and calculate their difference\n- if difference!=0 we need back to heap other both stones are destroyed.\n4) Once outside the loop, check for size!=0 i.e once stone remains return that or return zero.\n\n---\n# Complexity\n- Time complexity:\nO(nlogn) : Building of heap intially nlogn, Then since we poll and push again to the heap, it needs to rebuild which takes logn(heapify) everytime.\n\n- Space complexity:\nO(n) at max we will have n elements in heap.\n\n---\n\nHope it is easy to understand.\nLet me know if there is something unclear and i can fix it.\n\nOtherwise, please upvote if you like the solution, it would be encouraging\n\n\n---\n# Code\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n //setting decreasing order of the heap or max heap\n PriorityQueue<Integer> heap = new PriorityQueue<>((a,b) -> b-a);\n for(int each: stones)\n heap.add(each);\n\n while(heap.size()>1){\n int top1 = heap.poll();\n int top2 = heap.poll();\n int diff = Math.abs(top1-top2);\n\n if(diff!=0){\n heap.add(diff);\n }\n }\n\n if(heap.size()!=0){\n return heap.poll();\n }else{\n return 0;\n }\n }\n}\n```
| 35
| 0
|
['Heap (Priority Queue)', 'Java']
| 5
|
last-stone-weight
|
C++/Java/Python 6 Line Approach, Question Clarifications & Heap Cheatsheet
|
cjavapython-6-line-approach-question-cla-9ysd
|
If you are already familiar with priority_queue in C++ skip to the Approach section at the end\n### C++ Heap Guide/Cheatsheet\nIn C++ priority_queue is the impl
|
numbart
|
NORMAL
|
2022-04-07T10:14:15.087870+00:00
|
2022-04-09T09:53:23.900659+00:00
| 4,452
| false
|
If you are already familiar with priority_queue in C++ skip to the Approach section at the end\n### C++ Heap Guide/Cheatsheet\nIn C++ [priority_queue](https://www.cplusplus.com/reference/queue/priority_queue/) is the implementation for heaps. If you have never used priority_queue before, you can get started by reading this cheatsheet and solving this problem. However, you still should read about [heaps](https://ocw.mit.edu/courses/6-006-introduction-to-algorithms-fall-2011/resources/lecture-4-heaps-and-heap-sort/) and how they work so that you know when and where to use them.\n\n1. **Introduction**\n* Why heaps?\nHeap as a container gives you fast insertion of any element as well as reads and deletion of either the minimum-most or maximum-most element. Also it does not provide random access to any other element in the heap\n* Where to use?\nBased on this advantage, some major use cases for heaps are BFS, Djikstra, Current median of stream of elements\n\n2. **Initialising**\n\t```cpp\n\t// 1. max heap -> for popping largest element\n\t\tpriority_queue<int> pq; // replace int with any other type or a struct based on need\n\t// 2. min heap -> for popping minimum element\n\t\tpriority_queue<int, vector<int>, greater<int>> pq;\n\t// 3. custom heaps in case of custom ordering (here we are creating min heap based on second property)\n\t\tstruct comp {\n\t\t\tbool operator()(pair<int, int> a, pair<int, int> b) {\n\t\t\t\treturn a.second > b.second;\n\t\t\t}\n\t\t};\n\t\tpriority_queue<int, vector<int>, comp> pq;\n\t// 4. If you already have an array and want to initialise using it\n\t\tpriority_queue<int, vector<int>, greater<int>> pq(a.begin(), a.end());\n\t```\n\tThis last operation takes O(n) time where n is size of array a.\n\n3. **Important operations**\n\t```cpp\n\tpq.push(10); // adds element to heap\n\tint cur = pq.top(); // returns top element, does NOT pop though\n\tpq.pop() // pops top element, does NOT return the value of top element though\n\tpq.size() // return size of heap\n\tpq.empty() // returns true if heap is empty else false\n\t```\n - Always make sure that heap is not empty prior to top() and pop() methods\n - *Time* - push() and pop() takes O(logn) time, the other three require O(1) time.\n___\n</br>\n\n### Question Clarifications\nSome people have misinterpreted the question a bit, for example [here](https://leetcode.com/problems/last-stone-weight/discuss/1922217)\nNote, the question states that you always have to pick the two largest stones and then find the minimum-most stone. Its however not necessary that if you had the freedom to pick any two stones, that picking the largest would give you smallest stone at the end. It actually wont, consider the following example -\n> [25, 23, 16, 16, 16]\n\n* If you picked the largest two every time you would end up with 14.\n* However with freedom to pick any stone you can end with 0. By picking following stones at each step -\n\t```text\n\t(25, 16) -> (23, 16) -> (16, 9) -> (7, 7)\n\tleaves 9 -> leaves 7 -> leaves 7 -> leaves 0\n\t```\n\nAnother clarification, is the question states find the minimum most possible stone after only one stone remains. Since there can be only one pair of largest stones possible at each step and you do not have the element of choice, you can only have one way of smashing the stones and hence only one possibility of last stone remaining, which being the only candidate for being the minimum-most will also be the answer.\n___\n</br>\n\n### Approach\nOnce we are aware of how to use the priority queue and the above facts the approach is straightforward as the question instructs us what to do. We need the two largest elements at each step for our operation, since heaps give the fastest access to the extremes its our go to here. The pseudo-code is as follows -\n```text\n\tInitialise heap using the array (use 4th option above)\n\tKeep smashing as long as there is 2 or more stones (use size() method)\n\t\tPick the two largest and remove them from heap (use top() and pop())\n\t\tif their difference is positive add new stone to our heap (use push())\n\t\n\tIf there is a stone remaining in heap return it or else return 0 (use empty() and top())\n```\n\nC++/Java/Python code based on above pseudo code\n\n<iframe src="https://leetcode.com/playground/kocCUYy5/shared" frameBorder="0" width="800" height="370"></iframe>\n\nComplexity - Time: O(nlogn), Space: O(n)\n\nWould also like to add the common heap operations and code for Java and Python along with complexity to this cheatsheet, please mention them if you are familiar with them.\n
| 33
| 0
|
['C', 'Heap (Priority Queue)', 'Python', 'Java']
| 5
|
last-stone-weight
|
Easy to Understand | Heap Based | Faster | Simple | Python Solution
|
easy-to-understand-heap-based-faster-sim-bzkm
|
\ndef lastStoneWeight(self, stones: List[int]) -> int:\n stones = [-i for i in stones]\n heapq.heapify(stones)\n while len(stones)>1:\n
|
mrmagician
|
NORMAL
|
2020-04-04T21:08:05.466078+00:00
|
2020-04-04T21:08:05.466132+00:00
| 3,548
| false
|
```\ndef lastStoneWeight(self, stones: List[int]) -> int:\n stones = [-i for i in stones]\n heapq.heapify(stones)\n while len(stones)>1:\n first = abs(heapq.heappop(stones))\n second = abs(heapq.heappop(stones))\n if first != second:\n heapq.heappush(stones, -abs(first - second))\n \n # this compact return statement way is great ^_^\n return abs(stones[0]) if len(stones) else 0\n \n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38
| 33
| 3
|
['Heap (Priority Queue)', 'Python', 'Python3']
| 2
|
last-stone-weight
|
✅ Java best intuitive solution || Priority Queue || 1ms 99% faster
|
java-best-intuitive-solution-priority-qu-bv1t
|
Code\njava\npublic int lastStoneWeight(int[] stones) {\n\tPriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder());\n\tfor(int st: stones)\n\
|
Chaitanya31612
|
NORMAL
|
2022-04-07T05:06:09.170025+00:00
|
2022-04-07T05:19:06.123504+00:00
| 2,823
| false
|
**Code**\n```java\npublic int lastStoneWeight(int[] stones) {\n\tPriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder());\n\tfor(int st: stones)\n\t\tpq.offer(st);\n\n\twhile(pq.size() > 1) {\n\t\tint f = pq.poll();\n\t\tint s = pq.poll();\n\t\tif(f != s) \n\t\t\tpq.offer(f-s);\n\t}\n\n\treturn pq.isEmpty() ? 0 : pq.peek();\n}\n```\n\n**Explanation**\nWe were required to do operations each time on largest elements, and for that we can use max heap which can use used by reverting the order of priority queue available in Collections framework in java.\n- Push all elements in priority queue.\n- Iterate while the size of priority queue becomes equal to or less than 1.\n- Pop two largest element from top and perform following checks\n\t- if both are equal then we don\'t need to do anything.\n\t- else we add the difference of `f` and `s` to the priority queue.\n- Now return 0 if size of `pq` is 0 otherwise return top element.\n\nHere\'s how it works:-\n\n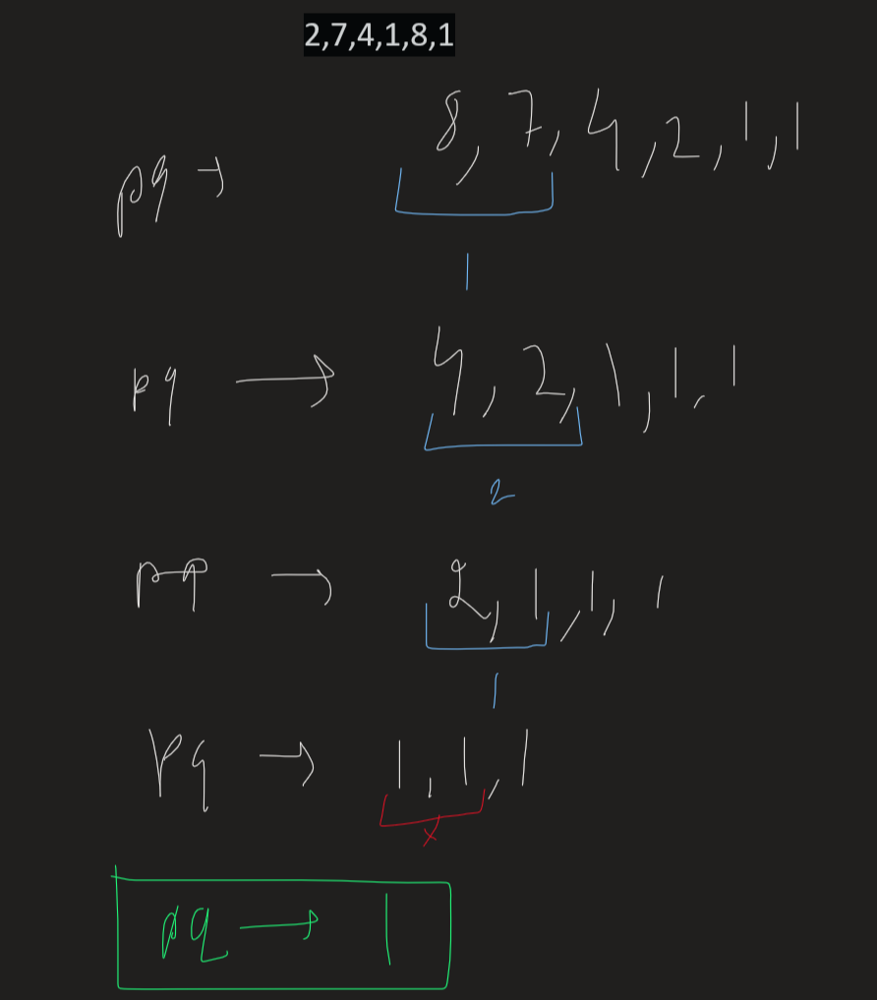\n\n\nHope it helps,\nIf it does do upvote\nThanks
| 31
| 1
|
['Heap (Priority Queue)', 'Java']
| 3
|
last-stone-weight
|
✔️ [C++] SIMULATION 100% ໒( ͡ᵔ ▾ ͡ᵔ )७, Explained
|
c-simulation-100-2-v-7-explained-by-arto-szuu
|
UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.\n\nTo solve this problem, we can conduct an actual simulation o
|
artod
|
NORMAL
|
2022-04-07T01:49:42.246076+00:00
|
2022-04-07T17:04:53.293720+00:00
| 4,898
| false
|
**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nTo solve this problem, we can conduct an actual simulation of the described process. Since we always need to use the heaviest stones, we can use a heap data structure for easy access to max elements.\n\nTime: **O(nlogn)** - for the heap\nSpace: **O(1)** - nothing stored\n\nRuntime: 0 ms, faster than **100.00%** of C++ online submissions for Last Stone Weight.\nMemory Usage: 7.6 MB, less than **34.27%** of C++ online submissions for Last Stone Weight.\n\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& s) {\n make_heap(s.begin(), s.end());\n \n while (s.size() > 1) {\n int x = s.front();\n pop_heap(s.begin(), s.end());\n s.pop_back();\n \n int y = s.front();\n pop_heap(s.begin(), s.end());\n s.pop_back();\n \n if (x == y) continue;\n \n s.push_back(x - y);\n push_heap(s.begin(), s.end());\n }\n \n return s.size() ? s.front() : 0;\n }\n};\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**
| 31
| 1
|
['C']
| 8
|
last-stone-weight
|
[Python3] Heapq (Priority Queue)
|
python3-heapq-priority-queue-by-pinkspid-36fw
|
Since we want the two largest stones each time, and heapq.pop() gives us the smallest each time, we just need to make every value of stones negative at the begi
|
pinkspider
|
NORMAL
|
2020-04-12T07:15:09.709589+00:00
|
2020-04-15T05:54:36.244775+00:00
| 4,003
| false
|
Since we want the two largest stones each time, and heapq.pop() gives us the smallest each time, we just need to make every value of stones negative at the beginning.\n```\nimport heapq\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n stones = [-val for val in stones]\n heapq.heapify(stones)\n while len(stones) > 1:\n x1 = heapq.heappop(stones)\n x2 = heapq.heappop(stones)\n if x1 != x2:\n heapq.heappush(stones,x1-x2)\n if len(stones) == 0:\n return 0\n return -stones[0]\n```
| 31
| 0
|
[]
| 9
|
last-stone-weight
|
Easy Solution Of JAVA 🔥C++🔥Beginner Friendly 🔥ArrayList
|
easy-solution-of-java-cbeginner-friendly-b1cp
|
\n\n# Code\nPLEASE UPVOTE IF YOU LIKE.\n\nclass Solution {\n public int lastStoneWeight(int[] stones)\n{\n\t\tArrayList<Integer> listStones = new ArrayList<>(
|
shivrastogi
|
NORMAL
|
2023-04-24T00:46:26.025631+00:00
|
2023-04-24T00:46:26.025677+00:00
| 6,037
| false
|
\n\n# Code\nPLEASE UPVOTE IF YOU LIKE.\n```\nclass Solution {\n public int lastStoneWeight(int[] stones)\n{\n\t\tArrayList<Integer> listStones = new ArrayList<>();\n\t\tfor (int a : stones)\n\t\t\tlistStones.add(a);\n\n\t\twhile (true)\n\t\t{\n\t\t\tint min = Integer.MAX_VALUE;\n\t\t\tint max = Integer.MIN_VALUE;\n\t\t\tint len = listStones.size();\n\n\t\t\tif (len == 1 || len == 0)\n\t\t\t{\n\t\t\t\tbreak;\n\t\t\t}\n\n\t\t\tCollections.sort(listStones);\n\t\t\tmin = listStones.get(len - 2);\n\t\t\tmax = listStones.get(len - 1);\n\n\t\t\tif (min < max)\n\t\t\t{\n\t\t\t\tmax = max - min;\n\t\t\t\tlistStones.remove(listStones.size()-1);\n\t\t\t\tlistStones.remove(listStones.size()-1);\n\t\t\t\tlistStones.add(max);\n\n\t\t\t}\n\t\t\telse if (min == max)\n\t\t\t{\n\t\t\t\tlistStones.remove(listStones.size()-1);\n\t\t\t\tlistStones.remove(listStones.size()-1);\n\t\t\t}\n\t\t}\n\t\t\n if(listStones.size()==1)\n return listStones.get(0);\n return 0;\n\t}\n}\n```\nC++\n```\n int lastStoneWeight(vector<int>& s) {\n int n = s.size();\n if(n == 1) return s[0];\n sort(s.begin(), s.end());\n int i = n-1;\n while(i >= 1){\n if(s[i-1] == s[i])\n i = i - 2;\n else{\n s[i-1] = s[i] - s[i-1];\n i = i -1;\n int j = i;\n while( j > 0 and s[j-1] > s[j] ){\n swap( s[j-1] , s[j] );\n j--;\n }\n }\n }\n if( i == 0 )\n return s[i];\n else \n return 0;\n }\n\n```
| 28
| 6
|
['Array', 'C++', 'Java']
| 0
|
last-stone-weight
|
☕ Java Solution | Let's learn when to use Heap (Priority Queue) 🔺
|
java-solution-lets-learn-when-to-use-hea-htqg
|
Intuition\nAs soon as we understand that we need to repeatedly get a maximum/minimum value from an array, we can use Heap (Priority Queue).\n\nYou can use Minim
|
B10nicle
|
NORMAL
|
2023-02-23T15:39:11.390879+00:00
|
2023-03-02T11:23:04.093264+00:00
| 1,659
| false
|
# Intuition\nAs soon as we understand that we need to repeatedly get a maximum/minimum value from an array, we can use Heap (Priority Queue).\n\nYou can use Minimum Heap like this:\n***PriorityQueue<Integer> minHeap = new PriorityQueue<>();***\n\nOr you can use Maximum Heap this way:\n***PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());***\n\nAs you can see, if you want to change your heap from min to max you can simply reverse it by adding ***Comparator.reverseOrder()***;\n\nGiven this knowledge we can start implementing our solution.\n\n# Approach\n1. Initialize max heap, because we need the biggest stones.\n2. Add all stones from our initial array to the heap.\n3. While size of our heap is not equal to one we need to remove two stones and confirm if they are equal (then we will add 0 to our heap) or x != y (then we will add y - x to the heap (the biggest stone minus second one)).\n4. The last element from the heap will be our answer.\n\n# Complexity\n- Time complexity: $$O(n\\text{ }log \\text{ } n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());\n for (int stone : stones) {\n maxHeap.add(stone);\n }\n while (maxHeap.size() != 1) {\n int y = maxHeap.remove();\n int x = maxHeap.remove();\n if (x == y) maxHeap.add(0);\n if (x != y) maxHeap.add(y - x);\n }\n return maxHeap.peek();\n }\n}\n```\n\n
| 25
| 0
|
['Heap (Priority Queue)', 'Java']
| 2
|
last-stone-weight
|
[Python] Heap Explained with Easy Code
|
python-heap-explained-with-easy-code-by-dx58p
|
Naive Approach\nThe naive approach to solve the question, would be:\n\n1. Sort the array in decreasing order\n2. Pop the first two elements, subtract them.\n3.
|
satyam_mishra13
|
NORMAL
|
2022-11-27T16:06:42.955252+00:00
|
2023-05-16T18:52:51.285542+00:00
| 1,358
| false
|
# Naive Approach\nThe naive approach to solve the question, would be:\n\n1. Sort the array in decreasing order\n2. Pop the first two elements, subtract them.\n3. If the difference is 0, then do nothing. Else, append the difference in the array\n4. Repeat the step 1, 2 and 3 until there is only one item left in the array\n5. The only item left in the array is the answer\n\nHowever, the time complexity would be high because sorting is performed (N-1) times. The time complexity would be O(N<sup>2</sup>).\n\n---\n\n\n# Optimal Approach\nThe optimal approach uses a very important Data Structure, Heap. Heap is a Complete Binary Tree.\nFirst, let\'s understand what is a <b>Complete Binary Tree</b>. \n*[Skip if you know that already]*\n\n### Complete Binary Tree\n1. <b>Definition 1</b>\nA complete binary tree is a binary tree where all the levels, except the last level must be completely filled. The last level may or may not be filled completely. The last level MUST be filled from left to right.\n2. <b>Definition 2</b>\nA Complete Binary Tree is a Tree, where every level in the tree is required to be filled with maximum nodes, except the last level. The last level may not be completely filled but all the nodes in the last level must be towards the left of the tree.\n\n## Heap\nHeap Data Strucutre, is a Complete Binary Tree, which satisfies the <b>Heap Property</b>. We are going to discuss the heap properties in a moment. There are two types of Heaps: <b>MaxHeap</b> and <b>MinHeap</b>.\n\n## MaxHeap\nProperty for a MaxHeap is "<b>The value of every node is less than or equal to its parent</b>". Therefore, in a MaxHeap, the maximum value resides as the root node. Here is a valid MaxHeap:\n<table width = "100%">\n<tr>\n<td><img src = "https://assets.leetcode.com/users/images/22cb76cb-8d54-4e4a-8947-d500f0c7c0f3_1669561918.8131528.png" style ="text-align: center; margin: 0; width: 100%;" /></td>\n</tr>\n<tr>\n<td>This is a valid MaxHeap Tree because:\n<ol>\n<li>It is a complete binary tree. Every level is completely filled except the last level which is completely left aligned.</li>\n<li>Every Node is less than or equal to its parent node.</li>\n</ol>\n</td>\n</tr>\n</table>\n\n## MinHeap\nMinHeap is just opposite of MaxHeap. The Heap Property for a MinHeap is "<b>The value of every node is greater than or equal to its parent</b>". Therefore, in a MinHeap, the minimum value resides as the root node.\n\n---\n\n# Why Heap?\n\nAs you just saw, in a MaxHeap, the maximum element is guaranteed to be on the top of the tree, or in a MinHeap, the minimum element is guaranteed to be on the top of the tree. In an sorted array, each time, we inserted, removed or updated an element in the array, the whole array needs to be sorted again to keep the array in order. It was a very time costly operation. In heaps, we can remove, insert or update an element in the heap in `log N`.\n\n### How is it so fast?\nThis high performace is achieved because a Heap Tree can be written in an array (list) in such a way that, the traversals are easy as compared to that in a normal array. \nFor example, let\'s write the above mentioned MaxHeap in the array.:\n<table>\n<tr>\n<td>100</td>\n<td>17</td>\n<td>39</td>\n<td>15</td>\n<td>13</td>\n<td>36</td>\n<td>25</td>\n<td>14</td>\n<td>9</td>\n</tr>\n</table>\n\nLet the indices be 1, 2, 3, 4... and so on. If, I ask you to look at the array and tell me the parent of 36 in the Heap, how would you do it?\nWell, there\'s a simple trick. Get the index of 36, which is 6. Floored Division of the index by 2 would give the index of its parent. Hence, its parent is at index 3, i.e. 39. You can try that for other elements as well.... You can also do the opposite, i.e. multiply and index by 2 to get the index of left child, and add 1 to it to get the index of right child.\nThis holds true, as long as the tree is a Complete Binary Tree.\n\nNow, how things work is... say you want to insert an element 19 in the array (or heap). The algorithm goes like:\n1. Add 19 to the next available position in the heap, i.e. 19 would be added as the left child of 13 (Consider the tree diagram above). \n**Important:** Note that, in the array notation of the heap, the element would be added to the last of the array. Actually, there is no data structure like Complete Binary Tree getting involved here, it\'s just for visualisation. All the operations we do are on the array.\n2. Find the parent of 19 and compare both the numbers. Here, the parent is 13 and 13 < 19. Since, it is a Max Heap, larger number remains on top. So, we swap 13 with 19.\n3. Now, again we find the parent of 19, which would be 17 this time. Again, 17 < 19. So, 17 and 19 are swapped.\n4. Again the parent of 19 is 100, but 100 > 19, so no more swapping is done, and we have our element inserted.\n\nSimilarily there are deletion operations, which can also be performed in `log N` time. But, we are not going deeper into this.\n\n---\n\n# Heap in Python\nPython provides an inbuilt module for dealing with heap data structure, namely \'heapq\'. It has various functions which are going to help us throughout the program. Thus, we need to import it to use it. The library can be used to create MinHeap. But, we can use the properties of MaxHeap if we multiply every value in the MinHeap with -1. Then, the negative value of every node acts as a MaxHeap.\nLet\'s code:\n\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n \n\t\t# First, import the heapq module. Specifically the functions heapify, heappop and heappush\n from heapq import heapify, heappop, heappush\n \n\t\t# Initialize an empty array, which we would use as heap\n heap = []\n for stone in stones:\n\t\t\n\t\t# We would add the negative values of the given list in the Heap\n heap.append(-stone)\n \n\t\t# heapify function from the heapq module, takes an array as parameter, arranges the contents\n\t\t# of the array in such a way that the array becomes a minheap\n heapify(heap)\n \n while len(heap) > 1:\n\t\t\n\t\t# heappop function from the heapq module, takes an array (heap) as parameter, and removes\n\t\t# the root of the minheap, returns the value, and then makes the necessary arrangement so\n\t\t# that the heap does not lose its properties.\n x = heappop(heap)\n y = heappop(heap)\n \n\t\t# if the two minimum values from the heap are not equal, then subtract the larger value (smaller\n\t\t# magnitude) from the smaller value (larger magnitude). Add the difference back to the heap\n if x != y:\n\t\t\t\n\t\t# heappush function, from the heapq module, takes an array (heap) as parameter, and adds\n\t\t# the second parameter to the array, maintaining the heap properties of the array.\n heappush(heap, x - y)\n \n\t\t# if heap is not empty then, return the first item in the heap multiplied by -1\n if heap:\n return -heap[0]\n\t\t\t\n\t\t# if heap was empty, then return 0\n return 0\n```\n\nIt took sweats to create this post. Please upvote, if you found it helpful. Happy Leetcoding!
| 24
| 0
|
['Heap (Priority Queue)', 'Python', 'Python3']
| 1
|
last-stone-weight
|
Simple Javascript Soluton ---> Recursion
|
simple-javascript-soluton-recursion-by-n-99ju
|
\nvar lastStoneWeight = function(stones) {\n if(stones.length < 2) return stones;\n stones.sort((a,b) => a-b);\n let a = stones.pop();\n let b = sto
|
nileshsaini_99
|
NORMAL
|
2021-09-18T08:32:00.195763+00:00
|
2021-09-18T08:32:00.195806+00:00
| 2,434
| false
|
```\nvar lastStoneWeight = function(stones) {\n if(stones.length < 2) return stones;\n stones.sort((a,b) => a-b);\n let a = stones.pop();\n let b = stones.pop();\n stones.push(Math.abs(a-b));\n return lastStoneWeight(stones);\n};\n```
| 24
| 0
|
['Recursion', 'JavaScript']
| 3
|
last-stone-weight
|
[Javascript] Simple Priority Queue
|
javascript-simple-priority-queue-by-theh-ysp1
|
\nvar lastStoneWeight = function(stones) {\n const queue = new MaxPriorityQueue();\n \n for (stone of stones) queue.enqueue(stone)\n \n while (qu
|
TheHankLee
|
NORMAL
|
2022-06-07T19:25:16.065594+00:00
|
2022-06-07T19:25:56.135327+00:00
| 2,249
| false
|
```\nvar lastStoneWeight = function(stones) {\n const queue = new MaxPriorityQueue();\n \n for (stone of stones) queue.enqueue(stone)\n \n while (queue.size() > 1) {\n let first = queue.dequeue().element;\n let second = queue.dequeue().element;\n if (first !== second) queue.enqueue(first-second)\n }\n \n return queue.size() === 0 ? 0 : queue.front().element\n};\n```
| 23
| 0
|
['Heap (Priority Queue)', 'JavaScript']
| 3
|
last-stone-weight
|
Shortest solution using Min Heap (PriorityQueue)
|
shortest-solution-using-min-heap-priorit-fuef
|
Step 1: Put the array into a min heap. To avoid creating a custom comparer, let\'s just revert priorities (-x).\nStep 2: Get the two "heaviest" stones from the
|
anikit
|
NORMAL
|
2022-04-07T07:49:10.592302+00:00
|
2023-01-03T22:11:43.862661+00:00
| 1,382
| false
|
**Step 1:** Put the array into a min heap. To avoid creating a custom comparer, let\'s just revert priorities (`-x`).\n**Step 2:** Get the two "heaviest" stones from the heap and smash them together. If there is something left, put it back into the heap.\n\n```csharp\npublic int LastStoneWeight(int[] stones)\n{\n var q = new PriorityQueue<int, int>(stones.Select(x => (x, -x)));\n \n while (q.Count > 1)\n {\n int a = q.Dequeue() - q.Dequeue();\n if (a != 0) q.Enqueue(a, -a);\n }\n \n return (q.Count == 0) ? 0 : q.Peek();\n}\n```
| 19
| 0
|
['Heap (Priority Queue)', 'C#']
| 3
|
last-stone-weight
|
✅2 approaches: Sorting & Max Heap with explanations!
|
2-approaches-sorting-max-heap-with-expla-gg00
|
If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistakes please let me know. Thank you!\u2
|
dhruba-datta
|
NORMAL
|
2022-04-07T07:37:28.153660+00:00
|
2022-04-07T07:39:32.273176+00:00
| 1,768
| false
|
> **If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistakes please let me know. Thank you!\u2764\uFE0F**\n> \n\n\n---\n\n## Explanation:\n\n### Solution 01\n\n- ***Brute force solution*** //not recommended.\n- Here every iteration we\u2019re sorting the array & changing the last 2 values.\n- As the last 2 are the max elements, so ***x=stones[n-2]*** & ***y=stones[n-1].***\n- We\u2019ll replace x with 0 (as all elements will be greater than 0), and y with y-x.\n- Return the last element after n iteration.\n- **Time complexity:** O(n^2logn).\n\n### Solution 02\n\n- Using ***Max Heap.***\n- Max heap keeps the maximum element on top.\n- First, we\u2019ll push all the elements of stones to our max heap.\n- Now until the size of our heap won\u2019t became 1 we\u2019ll continue this operation:\n - Take the top element to y & pop that element. `y = q.top(); q.pop();`\n - Similarly, put the next element to x & pop it. `x = q.top(); q.pop();`\n - Now smallest element will destroy & we\u2019ll push y-x to our heap again. In the case of same weight elements, it will automatically push 0. `q.push(y-x);`\n - When the size of the heap became 1 we\u2019ll break the loop and return top element.\n- **Time complexity:** O(nlogn).\n\n---\n\n## Code:\n\n```cpp\n//Solution 01:\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n int n = stones.size(), ans, count = 0;\n \n if(n == 1) return stones[0];\n \n while(count != n-1){\n sort(stones.begin(), stones.end());\n stones[n-1] = stones[n-1] - stones[n-2];\n stones[n-2] = 0;\n count++;\n }\n return stones[n-1];\n }\n};\n\n//Solution 02:\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n priority_queue<int, vector<int>> q;\n int x, y;\n \n for(auto x:stones)\n q.push(x);\n \n while(q.size() != 1){\n y = q.top();\n q.pop();\n x = q.top();\n q.pop();\n\n q.push(y-x);\n }\n \n return q.top();\n }\n};\n```\n\n---\n\n> **Please upvote this solution**\n>
| 19
| 0
|
['C', 'Sorting', 'Heap (Priority Queue)', 'C++']
| 1
|
last-stone-weight
|
Java 100% time 100% space
|
java-100-time-100-space-by-robsalcedo-z5yj
|
````\npublic int lastStoneWeight(int[] stones) {\n if(stones.length==1)return stones[0];\n Arrays.sort(stones);\n int y = stones.length-1;\
|
robsalcedo
|
NORMAL
|
2020-01-30T07:08:05.371240+00:00
|
2020-01-30T07:08:05.371273+00:00
| 1,804
| false
|
````\npublic int lastStoneWeight(int[] stones) {\n if(stones.length==1)return stones[0];\n Arrays.sort(stones);\n int y = stones.length-1;\n int x = stones.length-2;\n while(x>=0){\n if(stones[x]==stones[y]){\n stones[x] = 0;\n stones[y] = 0;\n }else{\n stones[y] -= stones[x];\n stones[x] = 0;\n }\n Arrays.sort(stones);\n if(stones[x]==0)break;\n }\n return stones[y];\n }
| 19
| 1
|
['Java']
| 6
|
last-stone-weight
|
c++ priority_queue 100% time, short easy to understand
|
c-priority_queue-100-time-short-easy-to-d5v8r
|
\npriority_queue<int> pq(v.begin(),v.end());\n \n while(true)\n {\n if(pq.size() ==0) return 0;\n if(pq.size() ==1)
|
yuganhumyogi
|
NORMAL
|
2019-08-24T15:09:16.467399+00:00
|
2019-08-24T15:09:16.467432+00:00
| 1,449
| false
|
```\npriority_queue<int> pq(v.begin(),v.end());\n \n while(true)\n {\n if(pq.size() ==0) return 0;\n if(pq.size() ==1) return pq.top();\n int a = pq.top();\n pq.pop();\n int b = pq.top();\n pq.pop();\n if(a!=b) pq.push(abs(a-b));\n }\n```
| 18
| 2
|
['C', 'Heap (Priority Queue)']
| 1
|
last-stone-weight
|
✅ [Python] 6 Lines || SortedList || Clean
|
python-6-lines-sortedlist-clean-by-linfq-6nzf
|
Please UPVOTE if you LIKE! \uD83D\uDE01\n\n\nfrom sortedcontainers import SortedList\n\n\nclass Solution(object):\n def lastStoneWeight(self, stones):\n
|
linfq
|
NORMAL
|
2022-04-07T01:39:27.024715+00:00
|
2022-04-07T08:05:44.013651+00:00
| 1,913
| false
|
**Please UPVOTE if you LIKE!** \uD83D\uDE01\n\n```\nfrom sortedcontainers import SortedList\n\n\nclass Solution(object):\n def lastStoneWeight(self, stones):\n sl = SortedList(stones)\n while len(sl) >= 2:\n y = sl.pop()\n x = sl.pop()\n if y > x: sl.add(y - x) # Note that sl is a SortedList\n return sl.pop() if len(sl) else 0\n```\n**If you have any question, feel free to ask. If you like the solution or the explanation, Please UPVOTE!**
| 16
| 0
|
['Python']
| 5
|
last-stone-weight
|
Easy C++ Solution using Priority Queue
|
easy-c-solution-using-priority-queue-by-85wr2
|
Create a Priority queue (pq)\n2. as long as size of pq > 1:\n every time pop two elements \n subtract second from first\n* if res of subtractions is non-zero pu
|
chronoviser
|
NORMAL
|
2020-04-12T07:13:42.690129+00:00
|
2020-04-12T07:13:42.690182+00:00
| 2,179
| false
|
1. Create a Priority queue (pq)\n2. as long as size of pq > 1:\n* every time pop two elements \n* subtract second from first\n* if res of subtractions is non-zero push this result back into pq\nCODE:\n```\nint lastStoneWeight(vector<int>& stones) {\n priority_queue<int> pq;\n for(auto i : stones) pq.push(i);\n while(pq.size() > 1)\n {\n int a = pq.top(); pq.pop();\n int b = pq.top(); pq.pop();\n if(a - b > 0)\n pq.push(a-b);\n }\n return pq.empty()?0:pq.top(); \n }\n
| 16
| 3
|
[]
| 4
|
last-stone-weight
|
Priority Queue | Max Heap | Clean Code | Easy Explaination |
|
priority-queue-max-heap-clean-code-easy-1jbu7
|
Intuition\nIf you reached here it\'s for sure you not able to get to the solution in the first place dont worry I did the same mistake. \n\nJust read the questi
|
yashagrawal20
|
NORMAL
|
2023-04-24T00:28:41.165448+00:00
|
2023-04-24T00:28:41.165495+00:00
| 1,291
| false
|
# Intuition\nIf you reached here it\'s for sure you not able to get to the solution in the first place dont worry I did the same mistake. \n\nJust read the question nicely, It says every time you have to pick the stones with largest weight, so for sure you might have sorted the Array and applied a greedy approach,but you\'ll have to perform sort operation everytime you perform a operation. \n\nSo priority queue uses a Data structure called Max heap for the implemenation where the top node is always the maximum and we can get it in 0(1) time.\n\nYou can see the code we just pop two top stones with heigest weight and put a stone again in it.\n\n# Approach\nSimple thinking, Heap Data structure greedy.\n\n# Complexity\n- Time complexity:\nCreation of priority-0(nlogn)\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n int n = stones.size();\n priority_queue<int> pq;\n for(int i=0;i<n;i++) pq.push(stones[i]);\n while(pq.size()>=2)\n {\n int x = pq.top(); pq.pop();\n int y = pq.top(); pq.pop();\n if(x!=y) pq.push(abs(x-y));\n\n }if(pq.size()==0) return 0;\n return pq.top();\n\n\n }\n};\n```
| 15
| 0
|
['Array', 'Greedy', 'Heap (Priority Queue)', 'C++']
| 3
|
last-stone-weight
|
Python Solution [4 lines]
|
python-solution-4-lines-by-shubhamthrill-srdk
|
\n\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n for i in range(len(stones) - 1):\n stones.sort()\n
|
shubhamthrills
|
NORMAL
|
2020-04-12T07:21:44.859956+00:00
|
2020-04-13T05:34:39.270630+00:00
| 2,637
| false
|
```\n\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n for i in range(len(stones) - 1):\n stones.sort()\n stones.append(stones.pop() - stones.pop()) \n return stones[0]\n\t\t\n\t\t\n\t\tFollow me for more intresting programming questions :\n\t\t\t\t\t\t\thttps://www.github.com/shubhamthrills\n\t\t\t\t\t\t\thttps://www.instagaram.com/shubhamthrills\n\t\t\t\t\t\t\thttps://www.linkedin.com/in/shubhamsagar\n\t\t\t\t\t\t\t\n\t\t\t\t\t\t\t\n#Another Possible approch [If you don\'t want to decrease the length of loop every time]\n\n```\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n #stones=[2,7,4,1,8,1]\n for i in range(len(stones) - 1):\n stones.sort()\n temp=stones[-1] - stones[-2]\n stones[-2]=-1\n stones[-1]=temp\n return (stones[-1])\n```
| 15
| 4
|
['Python']
| 7
|
last-stone-weight
|
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line
|
leetcode-the-hard-way-explained-line-by-g2afw
|
We can see that after two stones break we need to replace them back in the array. Where depends on how much they broke down, and it isn\'t always guaranteed to
|
__wkw__
|
NORMAL
|
2023-04-24T03:55:37.955063+00:00
|
2023-04-26T15:20:32.267021+00:00
| 1,427
| false
|
We can see that after two stones break we need to replace them back in the array. Where depends on how much they broke down, and it isn\'t always guaranteed to be the end. This points toward a data structure that allows us to restructure efficiently, and that would be a Max Heap.\n\nA max heap is a tree structure that keeps the largest value on top, and for each child the same holds true. When we pop from a heap, the heap will restructure itself to maintain the same dynamics. So 2 pops from a max heap will result in us receiving the 2 largest stones. Pushing back on the heap will place the stones in their correct spot.\n\nNote: A lot of built-in heaps are min heap implementations, to utilize them, we must push the negative weights of the stones on the heap to maintain a max heap structure.\n\nTime Complexity: $$O(nlogn)$$. Where $$n$$ is the size of the heap/stones array. It will take $$n*log(n)$$ time to create the initial heap, then up to $$log(n)$$ time to place the broken-down stones back into the heap.\n\nSpace Complexity: $$O(n)$$. Where $$n$$ is the size of the stones array, to maintain our heap data structure with up to $$n$$ stones inside.\n\n\n```py\n# written by ColeB2\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n # initialize an empty array to hold our heap, python uses\n # arrays, and the heapq module to handle min Heaps. We will\n # use negative values of the stones to convert to a max heap.\n heap = []\n # loop through each stone in our stones array\n for stone in stones:\n # push the negative value of the stone onto the heap.\n # heappush takes the heap array, and the value to push\n # onto the heap. -stone will allow the min heap to act\n # as a max heap instead.\n heapq.heappush(heap, -stone)\n # We need at least 2 stones to smash together, so we loop while\n # our heap has at least 2 stones inside.\n while len(heap) >= 2:\n # pop both stones off, the 1st is the largest stone.\n stone1 = heapq.heappop(heap)\n stone2 = heapq.heappop(heap)\n # if the second stone is bigger, since we are using negative\n # values, the second being bigger, means they are not\n # the same size, and the first is larger. This means\n # the stone won\'t be completely destroyed, so we need\n # co calculate the difference to add onto the heap.\n if stone2 > stone1:\n # Add onto the heap the difference of stones 1 and 2.\n heapq.heappush(heap, stone1 - stone2)\n # remembering that we used negative values of the stones, we \n # must return the absolute value of the remaining stone if it\n # exists, else 0 as the question asks.\n return abs(heap[0]) if heap else 0\n```\n\n```cpp\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n // initialize a priority_queue in c++\n priority_queue<int> pq;\n // push the positive value of the stone onto the priority_queue\n for (int x : stones) pq.push(x); \n // We need at least 2 stones to smash together, so we loop while\n // our heap has at least 2 stones inside.\n while (pq.size() >= 2) {\n // pop both stones off, the 1st is the largest stone.\n int y = pq.top(); pq.pop();\n int x = pq.top(); pq.pop();\n // if the stones are not same, then the stone of weight x is detroyed\n // and the stone of weight y has new weight y - x.\n if (x != y) pq.push(y - x);\n }\n // if there are no stones left, return 0\n if (pq.size() == 0) return 0;\n // return the weight of the last remaining stone\n return pq.top();\n }\n};\n```
| 14
| 1
|
['Heap (Priority Queue)', 'Python', 'C++']
| 0
|
last-stone-weight
|
1046 | JavaScript Recursive One-Liner
|
1046-javascript-recursive-one-liner-by-s-gegs
|
Runtime: 64 ms, faster than 52.83% of JavaScript online submissions\n> Memory Usage: 35.2 MB, less than 100.00% of JavaScript online submissions\n\n\nconst last
|
sporkyy
|
NORMAL
|
2020-02-03T14:31:14.075293+00:00
|
2022-07-14T13:40:02.593086+00:00
| 1,720
| false
|
> Runtime: **64 ms**, faster than *52.83%* of JavaScript online submissions\n> Memory Usage: **35.2 MB**, less than *100.00%* of JavaScript online submissions\n\n```\nconst lastStoneWeight = s =>\n 1 === s.length\n ? s[0]\n : lastStoneWeight(s.sort((a, b) => a - b).concat(s.pop() - s.pop()));\n```\n
| 14
| 3
|
['Recursion', 'JavaScript']
| 1
|
last-stone-weight
|
Rust heap and matching
|
rust-heap-and-matching-by-minamikaze392-q9wu
|
Code is short thanks to Rust\'s pattern matching:\nrust\nuse std::collections::BinaryHeap;\n\nimpl Solution {\n pub fn last_stone_weight(stones: Vec<i32>) ->
|
Minamikaze392
|
NORMAL
|
2022-04-07T04:58:10.259900+00:00
|
2022-04-07T04:58:10.259949+00:00
| 288
| false
|
Code is short thanks to Rust\'s pattern matching:\n```rust\nuse std::collections::BinaryHeap;\n\nimpl Solution {\n pub fn last_stone_weight(stones: Vec<i32>) -> i32 {\n let mut heap = BinaryHeap::from(stones);\n loop {\n match (heap.pop(), heap.pop()) {\n (Some(a), Some(b)) => if a > b {\n heap.push(a - b);\n }\n (Some(a), None) => return a,\n (None, _) => return 0,\n };\n }\n }\n}\n```
| 12
| 0
|
['Rust']
| 0
|
last-stone-weight
|
Python solution. Simplest .2 line
|
python-solution-simplest-2-line-by-shawn-ynyt
|
\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n while len(stones) > 1: stones.append(stones.pop(stones.index(max(stones)))
|
shawnzhangxinyao
|
NORMAL
|
2020-04-12T19:28:55.673817+00:00
|
2020-07-18T07:25:22.046286+00:00
| 1,995
| false
|
```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n while len(stones) > 1: stones.append(stones.pop(stones.index(max(stones))) - stones.pop(stones.index(max(stones))))\n return stones[0]\n```\n\n
| 12
| 0
|
['Python', 'Python3']
| 4
|
last-stone-weight
|
C++ CountSort / BucketSort solution
|
c-countsort-bucketsort-solution-by-babhi-z2w1
|
Since range of the elements is limited to integers between 1 and 1000, we can easily extend a bucket sort / count sort technique to this problem.\n\n1. Keep cou
|
babhishek21
|
NORMAL
|
2020-04-12T08:45:31.596382+00:00
|
2020-04-12T08:45:31.596435+00:00
| 1,118
| false
|
Since range of the elements is limited to integers between 1 and 1000, we can easily extend a bucket sort / count sort technique to this problem.\n\n1. Keep count of elements (in say array `arr`) against the indexes derived from their values. So, if we see a value `x`, we increment `arr[x]`. Thus each index is marking the bucket of the index value.\n2. Start from the highest index 1000 and gradually come down to the lowest index 1, smashing rocks along the way. I use two pointers `lo` and `hi` to point to the two rocks that will be smashed in the current iteration. If there are multiple occurrences of a rock, `lo` and `hi` might point to the same index / bucket.\n\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n int arr[1010] = {0};\n \n for(auto num: stones)\n arr[num]++;\n \n int hi = 1000, lo = hi;\n while(lo > 0 && hi > 0) {\n while(hi > 0 && arr[hi] < 1)\n hi--;\n \n if(hi < 1)\n break;\n \n lo = arr[hi] > 1 ? hi : hi-1;\n while(lo > 0 && arr[lo] < 1)\n lo--;\n \n if(lo < 1)\n break;\n \n // smash!\n arr[hi-lo]++;\n arr[hi]--;\n arr[lo]--;\n }\n \n return hi * (arr[hi] > 0);\n }\n};\n```\n\n+ Uses extra linear space in the order of the range of elements.\n+ Runs in linear time in the order of the number of elements.
| 12
| 2
|
[]
| 3
|
last-stone-weight
|
Java | 4 liner | Explained
|
java-4-liner-explained-by-prashant404-1i79
|
Idea:\n Push all stones in a max-heap\n Poll two stones, and push their difference back into the heap\n Do this till there\'s only 1 stone left\n\n>T/S: O(n lg
|
prashant404
|
NORMAL
|
2019-08-08T21:08:47.687835+00:00
|
2022-04-07T01:33:15.873909+00:00
| 1,190
| false
|
**Idea:**\n* Push all stones in a max-heap\n* Poll two stones, and push their difference back into the heap\n* Do this till there\'s only 1 stone left\n\n>**T/S:** O(n lg n)/O(n), where n = size(stones)\n```\npublic int lastStoneWeight(int[] stones) {\n\tvar maxHeap = new PriorityQueue<Integer>(Collections.reverseOrder());\n\t\n\tfor (var stone : stones)\n\t\tmaxHeap.add(stone);\n\n\twhile (maxHeap.size() > 1)\n\t\tmaxHeap.offer(maxHeap.poll() - maxHeap.poll());\n\t\t\n\treturn maxHeap.poll();\n}\n```\n***Please upvote if this helps***
| 12
| 0
|
['Heap (Priority Queue)', 'Java']
| 0
|
last-stone-weight
|
🔥Easy 🔥Java 🔥Soluton using 🔥PriorityQueue with 🔥Explanation/Intuition
|
easy-java-soluton-using-priorityqueue-wi-wy71
|
PLEASE UPVOTE\n\n\n\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nUsing Priority Queue to sort at every operation.\n\n# Approach
|
shahscript
|
NORMAL
|
2023-04-24T01:06:35.165472+00:00
|
2023-04-24T01:06:35.165496+00:00
| 1,931
| false
|
# PLEASE UPVOTE\n\n\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing Priority Queue to sort at every operation.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Inserting the whole array to Priorty Queue,\n2. Popping the first two elements from the pq (MAX and second MAX),\n3. adding the difference back to pq,\n4. repeating 2 & 3.\n5. return max when loop completes.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(NlogN)\n*sorting at every input and operation.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n\n# Code\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> pq = new PriorityQueue<>(Comparator.reverseOrder());\n for(int i=0;i<stones.length;i++){\n pq.add(stones[i]);\n }\n int p,q;\n while(pq.size()>1){\n p=pq.poll();\n q=pq.poll();\n // System.out.println(\xF7p+" "+q);\n pq.add(p-q);\n }\n return pq.poll();\n \n }\n}\n```
| 11
| 3
|
['Java']
| 0
|
last-stone-weight
|
Easy JS Solution
|
easy-js-solution-by-hbjorbj-5p57
|
\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n while (stones.length > 1) {\n let max1 = Math
|
hbjorbj
|
NORMAL
|
2020-07-01T09:17:51.179658+00:00
|
2020-07-01T09:17:51.179699+00:00
| 1,095
| false
|
```\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n while (stones.length > 1) {\n let max1 = Math.max(...stones);\n stones.splice(stones.indexOf(max1),1);\n let max2 = Math.max(...stones);\n stones.splice(stones.indexOf(max2),1);\n if (max1 !== max2) stones.push(Math.abs(max1-max2)); \n }\n return stones[0] || 0;\n};\n```
| 11
| 1
|
['JavaScript']
| 3
|
last-stone-weight
|
O(nlogn) and O(n) algo
|
onlogn-and-on-algo-by-nits2010-epso
|
O(n*log(n)) Using Priority Queue\nO(n) bucket sort\n\n# Code\n\n# Approach : Builtin Priorith Queue:\n\n\n/**\n * O(n*log(n))\n * Runtime: 1 ms, faster than 97.
|
nits2010
|
NORMAL
|
2019-08-16T17:49:50.294939+00:00
|
2024-08-30T20:54:33.111898+00:00
| 2,485
| false
|
$$O(n*log(n))$$ Using Priority Queue\n$$O(n)$$ bucket sort\n\n# Code\n\n# Approach : Builtin Priorith Queue:\n```\n\n/**\n * O(n*log(n))\n * Runtime: 1 ms, faster than 97.26% of Java online submissions for Last Stone Weight.\n * Memory Usage: 34.1 MB, less than 100.00% of Java online submissions for Last Stone Weight.\n */\nclass LastStoneWeightPriorityQueue {\n\n public int lastStoneWeight(int[] stones) {\n if (null == stones || stones.length == 0)\n return 0;\n\n System.out.println(Printer.toString(stones));\n\n PriorityQueue<Integer> pq = new PriorityQueue<>(Comparator.reverseOrder());\n\n for (int i = 0; i < stones.length; i++)\n pq.offer(stones[i]);\n\n while (pq.size() >= 2) {\n\n int s1 = pq.poll();\n int s2 = pq.poll();\n\n if (s1 != s2)\n pq.offer(s1 - s2);\n\n }\n\n /*\n for (int i = 0; i < stones.length - 1; ++i)\n pq.offer(pq.poll() - pq.poll());\n return pq.poll();\n */\n\n return pq.isEmpty() ? 0 : pq.poll();\n }\n}\n```\n\n# Approach Self made Heap (100% beat)\n\n# code\n```\n public int lastStoneWeight(int[] stones) {\n if (stones == null || stones.length == 0)\n return 0;\n\n if (stones.length == 1)\n return stones[0];\n\n MaxHeap pq = new MaxHeap(stones);\n\n while (pq.size() >= 2) {\n\n int x = pq.poll();\n int y = pq.isEmpty() ? 0 : pq.poll();\n\n if (x != y) {\n // x is the first element, hence always greater or equal to the next element\n pq.offer(x - y);\n }\n\n }\n\n return pq.isEmpty() ? 0 : pq.poll();\n\n\n }\n\n\npublic class MaxHeap {\n\n int[] heap;\n int size;\n\n public MaxHeap(int[] elements) {\n heap = elements;\n size = heap.length;\n\n buildHeap((size - 1) / 2); //last element parent\n }\n\n private void buildHeap(int index) {\n for (int i = index; i >= 0; i--)\n heapify(i);\n }\n\n private void heapify(int index) {\n if (index < 0 || index >= size)\n return;\n\n\n int left = 2 * index + 1;\n int right = 2 * index + 2;\n int largest = index;\n\n if (left < size && heap[left] > heap[largest])\n largest = left;\n\n if (right < size && heap[right] > heap[largest])\n largest = right;\n\n if (largest != index) {\n //swap\n int temp = heap[index];\n heap[index] = heap[largest];\n heap[largest] = temp;\n\n heapify(largest);\n }\n\n }\n\n public int peek() {\n if (heap != null && size > 0)\n return heap[0];\n return Integer.MIN_VALUE;\n }\n\n public int poll() {\n\n if (heap != null && size > 0) {\n int max = heap[0];\n heap[0] = heap[size - 1];\n\n heapify(0);\n size--;//decrease heap size\n return max;\n }\n return Integer.MIN_VALUE;\n }\n\n public void offer(int element) {\n\n if (heap != null && size >= 0) {\n size++; //increase heap size\n int i = size - 1;\n\n //find its position to be placed\n while (i > 0 && element > heap[(i - 1) / 2]) {\n heap[i] = heap[(i - 1) / 2];\n i = (i - 1) / 2;\n\n }\n heap[i] = element;\n\n }\n\n }\n\n public int size() {\n return size;\n }\n\n public boolean isEmpty() {\n return size == 0;\n }\n}\n```\n\n# Approach Bucket Sort: $$O(n)$$\nWe can apply bucket sort to achieve linear time complexity.\n\n Given:\n\n 1 <= stones.length <= 30\n 1 <= stones[i] <= 1000\n Algorithm:\n\n 1. Find the maximum value in the stones array.\n 2. Create an array of buckets with size equal to the maximum value.\n 3. Count the frequency of each stone in the corresponding bucket.\n 4. Iterate backward through the buckets from the maximum value to 0:\n a. If a bucket has an even frequency, the stones will destroy each other; move to the next bucket.\n b. If a bucket has an odd frequency, find another bucket to pair with and update the frequency of the resulting bucket. Decrease the frequency of both buckets as the stones are used.\n 5. Continue this process. At the end, the bucket with a frequency greater than 0 and odd is the result.\n\n Complexity:\n\n Space: (O(max)); since 1 <= stones[i] <= 1000, (O(1000)) is constant, thus (O(1)).\n Time: (O(n)) for counting bucket frequencies + (O(1000)) for iterating through the maximum value of stones. Given the maximum length of stones is 30,\n in the worst case (all stones are duplicates or unique), the loop runs at most 1000 times, which is constant.\n Therefore, the overall complexity is:\n\n Space: (O(1))\n Time: (O(n + 1000) => approx O(n))\n\n\n# Code\n```\n public int lastStoneWeight(int[] stones) {\n\n if (stones == null || stones.length == 0)\n return 0;\n\n if (stones.length == 1)\n return stones[0];\n\n int max = 0;\n for (int stone : stones) max = Math.max(max, stone);\n final int[] buckets = new int[max + 1];\n\n\n for (int stone : stones) buckets[stone]++;\n\n\n int i = max, lastJ = max;\n\n while (i > 0) {\n\n //skip invalid buckets, for the first run it will be the valid buckets\n if (buckets[i] == 0) {\n i--;\n } else {\n\n //if current max element has even frequency, then they will be pop up together and destroy each other\n if (buckets[i] % 2 == 0) {\n buckets[i] = 0; //destroy\n i--;\n } else {\n //means the max element and the next max element diff.\n int j = Math.min(i - 1, lastJ);\n while (j > 0 && buckets[j] == 0) {\n j--;\n }\n\n if (j == 0) {\n // no more element left to fight against i, hence i is the answer\n return i;\n } else {\n\n //they will fight each other and destroy each other\n buckets[i]--;\n buckets[j]--;\n\n //if they have different weight, which should be in this case, then we need to update i-j frequency by 1\n buckets[i - j]++;\n lastJ = j; //cache it\n\n //reset i to maximum value in buckets\n //max value could be at i-j (due to above diff update, assume i=1000, j=1 => i-j = 999\n // max value could be at j, because it was the second last max element in the buckets.\n i = Math.max(i - j, j);\n\n }\n }\n\n\n }\n\n\n }\n\n return 0;\n\n\n }\n\n```\n\nworst case like \n[1,1,1,1,1,1000] in this case the while(i>0) will run 1000^2 times if we don\'t cache lastJ otherwise 1000 times and if (j==0) then i will be surely that last element where >0 frequency is there \n
| 11
| 2
|
['Heap (Priority Queue)', 'Bucket Sort', 'Java']
| 4
|
last-stone-weight
|
Python3 easy Solution with Explanation || quibler7
|
python3-easy-solution-with-explanation-q-dvri
|
Code\n\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n #first sort the list\n stones.sort()\n\n while stones:\
|
quibler7
|
NORMAL
|
2023-04-24T03:16:03.362593+00:00
|
2023-04-24T03:16:03.362632+00:00
| 4,488
| false
|
# Code\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n #first sort the list\n stones.sort()\n\n while stones:\n #most heaviest stone\n s1 = stones.pop()\n\n #if list is empty after removing one stone i.e s1 then \n #return s1\n if not stones: return s1\n\n #second heaviest stone s2 where s2 <= s1\n s2 = stones.pop()\n\n #if s1 > s2 then element to be inserted is s1-s2 as given in the \n #problem statement\n if s1 > s2:\n\n #using Insort_left Function Of Bisect Module\n #we will insert s1-s2 at correct position \n insort_left(stones, s1-s2)\n\n #else s1 == s2 and as we are continously popping elements \n #both the stones are destroyed if they are same\n\n #if no more stones remaining return 0 \n return 0 \n\n```
| 10
| 0
|
['Python3']
| 0
|
last-stone-weight
|
JS | Heap | Easy Understanding
|
js-heap-easy-understanding-by-gurubalanh-1ov5
|
Solution 1 - O(n^2logn)\n\n\nvar lastStoneWeight = function(stones) {\n\n while(stones.length > 1) {\n stones.sort((a, b) => a - b);\n let x =
|
gurubalanh
|
NORMAL
|
2022-09-18T16:23:12.945665+00:00
|
2022-09-18T16:23:12.945704+00:00
| 1,188
| false
|
Solution 1 - O(n^2*logn)\n\n```\nvar lastStoneWeight = function(stones) {\n\n while(stones.length > 1) {\n stones.sort((a, b) => a - b);\n let x = stones.pop();\n let y = stones.pop();\n \n if(x === y) continue;\n else stones.push(Math.abs(x - y));\n }\n \n return stones;\n}\n```\n\nSolution 2 - O(n*logn)\n\n```\nclass Heap {\n constructor(stones) {\n this.heap = stones;\n this.size = stones.length;\n this.heapify(0);\n }\n right(pos) {\n return 2 * pos + 2;\n }\n left(pos) {\n return 2 * pos + 1;\n }\n isleaf(pos) {\n if (2 * pos + 1 >= this.size) return true;\n return false;\n }\n swap(a, b) {\n let temp = this.heap[a];\n this.heap[a] = this.heap[b];\n this.heap[b] = temp;\n }\n fix(pos) {\n if (this.isleaf(pos)) return;\n let left = this.left(pos);\n let right = this.right(pos);\n let bigger = left;\n if (right < this.size)\n bigger = this.heap[left] > this.heap[right] ? left : right;\n if (this.heap[pos] < this.heap[bigger]) {\n this.swap(pos, bigger);\n this.fix(bigger);\n }\n }\n heapify(pos) {\n if (this.isleaf(pos)) return;\n this.heapify(this.left(pos));\n this.heapify(this.right(pos));\n this.fix(pos);\n }\n delete() {\n this.swap(0, --this.size);\n this.fix(0);\n return this.heap[0];\n }\n insert(val) {\n this.size++;\n this.heap[this.size - 1] = val;\n this.heapify(0);\n }\n peek() {\n return this.heap[0];\n }\n}\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function (stones) {\n const heap = new Heap(stones);\n while (heap.size > 1) {\n let x = heap.peek();\n heap.delete();\n let y = heap.peek();\n heap.delete();\n const res = x - y;\n if (res > 0) heap.insert(res);\n }\n if (heap.size) return heap.peek();\n return 0;\n}\n```
| 10
| 0
|
['Heap (Priority Queue)', 'JavaScript']
| 0
|
last-stone-weight
|
Simple solution using ArrayList Java. Self explanatory
|
simple-solution-using-arraylist-java-sel-f4zh
|
class Solution {\n\n public int lastStoneWeight(int[] stones) {\n \n ArrayList ar = new ArrayList<>();\n \n for(int i=0;i1){\n
|
RUPESHYADAV120
|
NORMAL
|
2022-04-07T04:41:52.555640+00:00
|
2022-04-07T06:27:41.001272+00:00
| 748
| false
|
class Solution {\n\n public int lastStoneWeight(int[] stones) {\n \n ArrayList<Integer> ar = new ArrayList<>();\n \n for(int i=0;i<stones.length;i++){\n ar.add(stones[i]);\n }\n \n \n \n while(ar.size()>1){\n \n Collections.sort(ar);\n \n int y = ar.get(ar.size()-1);\n ar.remove(new Integer(y));\n \n int x = ar.get(ar.size()-1);\n ar.remove(new Integer(x));\n \n if(x!=y){\n ar.add(y-x);\n }\n \n \n }\n \n if(ar.isEmpty()){\n return 0;\n }else{\n return ar.get(0);\n }\n \n }\n}
| 10
| 0
|
['Array', 'Java']
| 3
|
last-stone-weight
|
|Java| Easy and Fast Solution
|
java-easy-and-fast-solution-by-khalidcod-gesv
|
\n\n\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n Arrays.sort(stones);\n int count = stones.length-1;\n while(count!
|
Khalidcodes19
|
NORMAL
|
2022-04-07T00:22:43.631001+00:00
|
2022-04-07T08:39:52.041638+00:00
| 1,621
| false
|
\n\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n Arrays.sort(stones);\n int count = stones.length-1;\n while(count!=0)\n {\n if(stones[stones.length-1]==stones[stones.length-2])\n {\n stones[stones.length-1]=0;\n stones[stones.length-2]=0;\n }\n if(stones[stones.length-1]!=stones[stones.length-2])\n {\n stones[stones.length-1]=stones[stones.length-1] - stones[stones.length-2];\n stones[stones.length-2]=0;\n }\n Arrays.sort(stones);\n count--;\n }\xA0 \xA0 \xA0 \xA0 \xA0 \xA0\n \xA0 \xA0return stones[stones.length-1]\n\t}\n}\n```
| 10
| 1
|
['Java']
| 3
|
last-stone-weight
|
Go heap solution
|
go-heap-solution-by-casd82-5f1u
|
Cause all I do is dance.\n\ntype IntHeap []int\n\nfunc (h IntHeap) Len() int {return len(h)}\nfunc (h IntHeap) Less(i, j int) bool {return h[i] > h[j]}\nfunc (h
|
casd82
|
NORMAL
|
2020-08-04T13:02:57.613847+00:00
|
2020-08-04T13:02:57.613895+00:00
| 819
| false
|
Cause all I do is dance.\n```\ntype IntHeap []int\n\nfunc (h IntHeap) Len() int {return len(h)}\nfunc (h IntHeap) Less(i, j int) bool {return h[i] > h[j]}\nfunc (h IntHeap) Swap(i, j int) {h[i], h[j] = h[j], h[i]}\nfunc (h *IntHeap) Push(x interface{}) {*h = append(*h, x.(int))}\nfunc (h *IntHeap) Pop() interface{} {\n n := len(*h)\n x := (*h)[n-1]\n *h = (*h)[0:n-1]\n return x\n}\n\nfunc lastStoneWeight(stones []int) int {\n pq := IntHeap(stones)\n heap.Init(&pq)\n for pq.Len() > 1 {\n x, y := heap.Pop(&pq).(int), heap.Pop(&pq).(int)\n if x != y {\n heap.Push(&pq, x-y)\n }\n }\n \n if pq.Len() == 0 {\n return 0\n }\n \n return heap.Pop(&pq).(int)\n}\n```
| 10
| 0
|
['Go']
| 1
|
last-stone-weight
|
[Rust] Binary Heap
|
rust-binary-heap-by-kichooo-7bql
|
\nuse std::collections::BinaryHeap;\n\nimpl Solution {\n pub fn last_stone_weight(stones: Vec<i32>) -> i32 {\n let mut heap = BinaryHeap::from(stones)
|
kichooo
|
NORMAL
|
2020-01-31T12:20:52.692389+00:00
|
2020-01-31T12:20:52.692423+00:00
| 222
| false
|
```\nuse std::collections::BinaryHeap;\n\nimpl Solution {\n pub fn last_stone_weight(stones: Vec<i32>) -> i32 {\n let mut heap = BinaryHeap::from(stones);\n while let Some(stone) = heap.pop() {\n match heap.pop() {\n Some(val) => heap.push(stone - val),\n None => return stone,\n } \n }\n return 0\n }\n}\n```
| 10
| 2
|
[]
| 0
|
last-stone-weight
|
Easy Python Solution❤
|
easy-python-solution-by-meet_10-wo1q
|
\n\n# Code\n\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n while True:\n stones = sorted(stones,reverse = True)
|
Meet_10
|
NORMAL
|
2023-04-24T05:05:14.738963+00:00
|
2023-04-24T05:05:14.739004+00:00
| 1,307
| false
|
\n\n# Code\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n while True:\n stones = sorted(stones,reverse = True)\n if len(stones) == 1:\n return stones[0]\n elif len(stones) == 0:\n return 0\n first = stones.pop(0)\n sec = stones.pop(0)\n if first == sec:\n continue\n else:\n stones.append(first-sec)\n```
| 9
| 0
|
['Python3']
| 2
|
last-stone-weight
|
C++ || 100% || SHORTEST AND EASIEST || Without using any data structure
|
c-100-shortest-and-easiest-without-using-g5ul
|
\n\u2714without using priority_queue\n\u2714all you need to do is sorting the array each time you modify it.\nclass Solution {\npublic:\n int lastStoneWeight
|
rab8it
|
NORMAL
|
2022-04-07T03:05:51.103506+00:00
|
2022-04-07T03:05:51.103542+00:00
| 916
| false
|
```\n\u2714without using priority_queue\n\u2714all you need to do is sorting the array each time you modify it.\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>&s) {\n sort(s.begin(),s.end());\n while(s.size()>1){\n int i=s.size()-1;\n int x=s[i],y=s[i-1];\n s.pop_back();\n s.pop_back();\n if(x!=y)s.push_back(x-y);\n sort(s.begin(),s.end());\n }\n if(s.size()==0)return 0;\n return s[0];\n }\n};\n```\nUPVOTE IF YOU LIKE IT!!\uD83D\uDC4D\uD83D\uDC4D
| 9
| 0
|
['Array', 'Sorting']
| 1
|
last-stone-weight
|
Simple Binary Search based Solution - O(nlogn)
|
simple-binary-search-based-solution-onlo-wseb
|
csharp\npublic class Solution {\n public int LastStoneWeight(int[] stones)\n {\n if (stones.Length == 2)\n {\n retu
|
christris
|
NORMAL
|
2019-05-19T04:13:13.665218+00:00
|
2019-05-19T04:13:13.665398+00:00
| 864
| false
|
``` csharp\npublic class Solution {\n public int LastStoneWeight(int[] stones)\n {\n if (stones.Length == 2)\n {\n return Math.Abs(stones[1] - stones[0]);\n }\n\n Array.Sort(stones);\n List<int> s = new List<int>(stones);\n\n while (s.Count > 1)\n {\n int first = s.ElementAt(s.Count - 1);\n int second = s.ElementAt(s.Count - 2);\n int smash = first - second;\n s.RemoveAt(s.Count - 1);\n s.RemoveAt(s.Count - 1);\n\n if (smash != 0)\n {\n int index = s.BinarySearch(smash);\n if (index < 0)\n {\n index = ~index;\n }\n s.Insert(index, smash);\n }\n }\n\n return s.FirstOrDefault();\n }\n}\n```
| 9
| 4
|
['Binary Search']
| 2
|
last-stone-weight
|
Easy Python Solution
|
easy-python-solution-by-vistrit-nfq1
|
Code\n\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n stones.sort()\n while len(stones)>1:\n y=stones.pop
|
vistrit
|
NORMAL
|
2023-04-24T12:47:19.471735+00:00
|
2023-04-24T12:47:19.471771+00:00
| 1,297
| false
|
# Code\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n stones.sort()\n while len(stones)>1:\n y=stones.pop(-1)\n x=stones.pop(-1)\n if x!=y:\n stones.append(y-x)\n stones.sort()\n return stones[0] if len(stones)>=1 else 0\n```
| 8
| 0
|
['Python3']
| 1
|
last-stone-weight
|
Python Elegant & Short | Max Heap
|
python-elegant-short-max-heap-by-kyrylo-w132k
|
Complexity\n- Time complexity: O(n * \log_2 {n})\n- Space complexity: O(n)\n\n# Maximum heap code\n\nclass MaxHeap:\n def __init__(self, data: List[int]):\n
|
Kyrylo-Ktl
|
NORMAL
|
2023-04-24T07:39:53.926455+00:00
|
2023-04-24T07:39:53.926491+00:00
| 2,531
| false
|
# Complexity\n- Time complexity: $$O(n * \\log_2 {n})$$\n- Space complexity: $$O(n)$$\n\n# Maximum heap code\n```\nclass MaxHeap:\n def __init__(self, data: List[int]):\n self.data = [-num for num in data]\n heapq.heapify(self.data)\n\n def push(self, item: int):\n heapq.heappush(self.data, -item)\n\n def pop(self) -> int:\n return -heapq.heappop(self.data)\n\n def __len__(self) -> int:\n return len(self.data)\n\n def __bool__(self) -> bool:\n return len(self) != 0\n```\n\n# Solution code\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n heap = MaxHeap(stones)\n\n while len(heap) > 1:\n first, second = heap.pop(), heap.pop()\n if first != second:\n heap.push(abs(first - second))\n\n return heap.pop() if heap else 0\n```
| 8
| 0
|
['Heap (Priority Queue)', 'Python', 'Python3']
| 1
|
last-stone-weight
|
Python - Solution using recursion
|
python-solution-using-recursion-by-cppyg-huth
|
\nclass Solution:\n def lastStoneWeight(self, nums: List[int]) -> int: \n if not nums:\n return 0\n \n elif len(nums)
|
cppygod
|
NORMAL
|
2020-04-12T19:25:44.694971+00:00
|
2020-04-12T19:25:57.868110+00:00
| 975
| false
|
```\nclass Solution:\n def lastStoneWeight(self, nums: List[int]) -> int: \n if not nums:\n return 0\n \n elif len(nums) == 1:\n return nums[0]\n \n elif len(nums) == 2:\n return abs(nums[0] - nums[1])\n \n else:\n max1 = max(nums)\n nums.remove(max1)\n max2 = max(nums)\n nums.remove(max2)\n \n if max1 != max2:\n val = abs(max1-max2)\n nums.append(val)\n\n val = self.lastStoneWeight(nums)\n return val\n```
| 8
| 0
|
['Recursion', 'Python', 'Python3']
| 1
|
last-stone-weight
|
Two Appraoches :Heapq and Sorting
|
two-appraoches-heapq-and-sorting-by-ganj-zzco
|
Heap Approach : TC : (NLogN)\n\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n list1=[-x for x in stones]\n while le
|
GANJINAVEEN
|
NORMAL
|
2023-04-24T09:45:47.816441+00:00
|
2023-04-24T09:45:47.816471+00:00
| 1,201
| false
|
# Heap Approach : TC : (NLogN)\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n list1=[-x for x in stones]\n while len(list1)>1:\n heapq.heapify(list1)\n a,b=heapq.heappop(list1),heapq.heappop(list1)\n heapq.heappush(list1,-(abs(a-b)))\n return abs(list1[0])\n```\n# Sorting Approach ,TC:---->N*(N*LogN)\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n while len(stones)>1:\n stones.sort()\n a,b=stones.pop(),stones.pop()\n stones.append(abs(a-b))\n return stones[0]\n````\n# please upvote me it would encourage me alot\n
| 7
| 0
|
['Python']
| 0
|
last-stone-weight
|
100% Beats || Easy C++ Solution || Just see for yourself
|
100-beats-easy-c-solution-just-see-for-y-lei6
|
Intuition\n Describe your first thoughts on how to solve this problem. \nsort in descending order and going through the first two elements and repeating the pro
|
isundeep0
|
NORMAL
|
2023-04-24T04:37:49.628558+00:00
|
2023-05-21T16:07:36.036258+00:00
| 2,018
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nsort in descending order and going through the first two elements and repeating the process.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is very simple. Follow the following steps to understand the approach.\n\n1)Sort the stones vector in descending order.\n2)store the difference of first two numbers(stones[0] and stones[1]) in res.\n3)If res is 0 then remove stones[0] and stones[1]. If res is not equal to zero which is a positve integer, then remove the front element in the vector and replace the res value with front element in the vector. (Since we need to remove 1st two elements and push the positve integer, instead of that am removing one element and replacing the other).\n4)Repeat the steps until stones vector is having atleast 2 elements.\n5)If there is an element in the stones vector, then that is our answer else return 0.\n\n# Complexity\n- Time complexity: O(N*NLogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n sort(stones.begin(), stones.end(), greater<int>());\n int i = 0;\n while (i<stones.size() && (i+1)<stones.size()){\n int res = stones[i] - stones[i+1];\n if (res != 0){\n stones.erase(stones.begin());\n stones[0] = res;\n sort(stones.begin(), stones.end(), greater<int>());\n }\n else{\n stones.erase(stones.begin(), stones.begin()+2);\n }\n }\n if (stones.size()){\n return stones[0];\n }\n return 0;\n }\n};\n\n// (sorted) (updated vector)\n//[2, 7, 4, 1, 8, 1] = [8, 7, 4, 2, 1, 1] -> [1, 4, 2, 1, 1] = [4, 2, 1, 1, 1] ->\n// [2, 1, 1, 1] -> [1, 1, 1] -> \n```
| 7
| 0
|
['C++']
| 2
|
last-stone-weight
|
[Golang] MaxHeap
|
golang-maxheap-by-vasakris-ut6k
|
Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(N)\n\n# Code\n\nfunc lastStoneWeight(stones []int) int {\n maxHeap := &MaxHeap{}\n\n fo
|
vasakris
|
NORMAL
|
2023-02-15T11:22:14.821527+00:00
|
2023-02-15T11:22:14.821554+00:00
| 773
| false
|
# Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nfunc lastStoneWeight(stones []int) int {\n maxHeap := &MaxHeap{}\n\n for _, stone := range stones {\n heap.Push(maxHeap, stone)\n }\n\n for maxHeap.Len() > 1 {\n stone1 := heap.Pop(maxHeap).(int)\n stone2 := heap.Pop(maxHeap).(int)\n\n if stone1 != stone2 {\n heap.Push(maxHeap, stone1 - stone2)\n }\n }\n\n res := 0\n if maxHeap.Len() == 1 {\n res = (*maxHeap)[0]\n }\n return res\n}\n\ntype MaxHeap []int\n\nfunc (h MaxHeap) Len() int { return len(h) }\nfunc (h MaxHeap) Less(i, j int) bool { return h[i] > h[j] }\nfunc (h MaxHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *MaxHeap) Push(x interface{}) {\n *h = append(*h, x.(int))\n}\n\nfunc (h *MaxHeap) Pop() interface{} {\n x := (*h)[len(*h)-1]\n\t*h = (*h)[:len(*h)-1]\n\treturn x\n}\n```
| 7
| 0
|
['Go']
| 1
|
last-stone-weight
|
c# PriorityQueue .NET6
|
c-priorityqueue-net6-by-yokee06-zej9
|
Use c# PriorityQueue\n\n\npublic class Solution {\n public int LastStoneWeight(int[] stones) {\n PriorityQueue<int, int> queue = new();\n forea
|
yokee06
|
NORMAL
|
2022-07-21T20:05:01.583485+00:00
|
2022-07-21T20:05:33.713668+00:00
| 334
| false
|
Use c# PriorityQueue\n\n```\npublic class Solution {\n public int LastStoneWeight(int[] stones) {\n PriorityQueue<int, int> queue = new();\n foreach(int s in stones)\n {\n queue.Enqueue(s,-s);\n }\n while(queue.Count >1)\n {\n int stone1 = queue.Dequeue();\n int stone2 = queue.Dequeue();\n if(stone1 != stone2)\n {\n int newStone = stone1 - stone2;\n newStone = newStone > 0 ? newStone : newStone * -1;\n queue.Enqueue(newStone, -newStone);\n }\n }\n if(queue.Count ==0)\n {\n return 0;\n }\n return queue.Dequeue();\n }\n}\n```
| 7
| 0
|
['Heap (Priority Queue)']
| 2
|
last-stone-weight
|
C# 88%
|
c-88-by-rudymiked-ee5y
|
\npublic class Solution {\n public int LastStoneWeight(int[] stones) {\n List<int> stoneList = new List<int>(stones);\n return stoneHelper(ston
|
rudymiked
|
NORMAL
|
2020-05-30T21:58:10.531853+00:00
|
2020-05-30T21:58:10.531903+00:00
| 295
| false
|
```\npublic class Solution {\n public int LastStoneWeight(int[] stones) {\n List<int> stoneList = new List<int>(stones);\n return stoneHelper(stoneList);\n }\n \n public int stoneHelper(List<int> stones) {\n \n if(stones.Count == 0 )\n return 0;\n else if (stones.Count == 1)\n return stones[0];\n else {\n int max = stones.Max();\n stones.Remove(max);\n \n int sMax = stones.Max();\n stones.Remove(sMax);\n\n if (sMax < max) {\n stones.Add(max-sMax);\n }\n return stoneHelper(stones); \n }\n }\n}\n```
| 7
| 0
|
[]
| 0
|
last-stone-weight
|
JavaScript Priority Queue Solution O(N)
|
javascript-priority-queue-solution-on-by-y9qc
|
javascript\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n const heap = new MaxHeap(stones);\n while (
|
shengdade
|
NORMAL
|
2020-02-24T03:30:10.574670+00:00
|
2020-02-24T03:30:10.574701+00:00
| 1,678
| false
|
```javascript\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n const heap = new MaxHeap(stones);\n while (heap.size() > 1) {\n const max1 = heap.poll();\n const max2 = heap.poll();\n if (max1 > max2) heap.offer(max1 - max2);\n }\n return heap.size() === 1 ? heap.poll() : 0;\n};\n\nclass MaxHeap {\n constructor(data = []) {\n this.data = data;\n this.comparator = (a, b) => b - a;\n this.heapify();\n }\n\n // O(nlog(n)). In fact, O(n)\n heapify() {\n if (this.size() < 2) return;\n for (let i = 1; i < this.size(); i++) {\n this.bubbleUp(i);\n }\n }\n\n // O(1)\n peek() {\n if (this.size() === 0) return null;\n return this.data[0];\n }\n\n // O(log(n))\n offer(value) {\n this.data.push(value);\n this.bubbleUp(this.size() - 1);\n }\n\n // O(log(n))\n poll() {\n if (this.size() === 0) return null;\n const result = this.data[0];\n const last = this.data.pop();\n if (this.size() !== 0) {\n this.data[0] = last;\n this.bubbleDown(0);\n }\n return result;\n }\n\n // O(log(n))\n bubbleUp(index) {\n while (index > 0) {\n const parentIndex = (index - 1) >> 1;\n if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {\n this.swap(index, parentIndex);\n index = parentIndex;\n } else {\n break;\n }\n }\n }\n\n // O(log(n))\n bubbleDown(index) {\n const lastIndex = this.size() - 1;\n while (true) {\n const leftIndex = index * 2 + 1;\n const rightIndex = index * 2 + 2;\n let findIndex = index;\n if (\n leftIndex <= lastIndex &&\n this.comparator(this.data[leftIndex], this.data[findIndex]) < 0\n ) {\n findIndex = leftIndex;\n }\n if (\n rightIndex <= lastIndex &&\n this.comparator(this.data[rightIndex], this.data[findIndex]) < 0\n ) {\n findIndex = rightIndex;\n }\n if (index !== findIndex) {\n this.swap(index, findIndex);\n index = findIndex;\n } else {\n break;\n }\n }\n }\n\n // O(1)\n swap(index1, index2) {\n [this.data[index1], this.data[index2]] = [\n this.data[index2],\n this.data[index1]\n ];\n }\n\n // O(1)\n size() {\n return this.data.length;\n }\n}\n```\n\n* 70/70 cases passed (56 ms)\n* Your runtime beats 84.25 % of javascript submissions\n* Your memory usage beats 100 % of javascript submissions (35 MB)
| 7
| 0
|
['JavaScript']
| 3
|
last-stone-weight
|
C++ vector 100% time and space
|
c-vector-100-time-and-space-by-codily-fyuj
|
\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n while(stones.size() > 1){\n sort(stones.begin(),stones.end(),gre
|
codily
|
NORMAL
|
2020-01-24T11:30:17.071182+00:00
|
2020-01-24T11:30:38.435438+00:00
| 783
| false
|
```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n while(stones.size() > 1){\n sort(stones.begin(),stones.end(),greater<int>());\n if(stones[0] == stones[1])\n stones.erase(stones.begin(),stones.begin()+2);\n else{\n stones.push_back(abs(stones[0] - stones[1]));\n stones.erase(stones.begin(),stones.begin()+2); \n }\n }\n if(!stones.empty())\n return stones[0];\n return 0;\n }\n};\n```
| 7
| 1
|
['C', 'C++']
| 3
|
last-stone-weight
|
Javascript
|
javascript-by-fs2329-8e09
|
\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n if(stones.length < 2) return stones;\n while(ston
|
fs2329
|
NORMAL
|
2019-12-30T01:54:48.828211+00:00
|
2019-12-30T01:54:48.828313+00:00
| 556
| false
|
```\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n if(stones.length < 2) return stones;\n while(stones.length > 1){\n let index1 = stones.indexOf(Math.max(...stones));\n let stone1 = stones.splice(index1,1);\n let index2 = stones.indexOf(Math.max(...stones));\n let stone2 = stones.splice(index2,1);\n stones.push(stone1-stone2); \n }\n return stones;\n};\n```
| 7
| 2
|
[]
| 4
|
last-stone-weight
|
Java Solution using PriorityQueue
|
java-solution-using-priorityqueue-by-mak-03dw
|
Store all elements in the Priority Queue in decreasing order.\n Each time, poll 2 elements from the Priority Queue until its size is 1 and add the absolute diff
|
makubex74
|
NORMAL
|
2019-05-19T07:19:16.297388+00:00
|
2019-05-19T07:19:16.297460+00:00
| 431
| false
|
* Store all elements in the Priority Queue in decreasing order.\n* Each time, poll 2 elements from the Priority Queue until its size is 1 and add the absolute difference between the 2 elements back to the queue.\n* Return 0 if the PriorityQueue is empty or return the last element remaining in the PriorityQueue\n```\npublic int lastStoneWeight(int[] stones) {\n if(stones == null || stones.length == 0)\n return 0;\n PriorityQueue<Integer> pq = new PriorityQueue<Integer>(Collections.reverseOrder());\n for(int i = 0; i < stones.length; i++)\n pq.add(stones[i]);\n while(pq.size() > 1) {\n int a = pq.poll();\n int b = pq.poll();\n if(a - b != 0)\n pq.add(Math.abs(a - b));\n }\n if(pq.size() == 1)\n return pq.poll();\n else\n return 0;\n }\n```\n
| 7
| 2
|
[]
| 0
|
last-stone-weight
|
Java || Don't worry My Solution is Best || 100% || 92% || 39,6 MB
|
java-dont-worry-my-solution-is-best-100-n9stk
|
\t* class Solution {\n\t\t\tpublic int lastStoneWeight(int[] stones) {\n\t\t\t\tArrayList list = new ArrayList<>();\n\t\t\t\tfor (int a : stones) {\n\t\t\t\t
|
sardor_user
|
NORMAL
|
2023-01-11T16:44:45.933918+00:00
|
2023-07-21T09:16:15.963645+00:00
| 46
| false
|
\t* class Solution {\n\t\t\tpublic int lastStoneWeight(int[] stones) {\n\t\t\t\tArrayList<Integer> list = new ArrayList<>();\n\t\t\t\tfor (int a : stones) {\n\t\t\t\t\tlist.add(a);\n\t\t\t\t}\n\t\t\t\tCollections.sort(list);\n\t\t\t\twhile (list.size() > 1) {\n\t\t\t\t\tint a = list.size();\n\t\t\t\t\tif (list.get(a - 1) > list.get(a - 2)) {\n\t\t\t\t\t\tlist.add(( list.get(a - 1) -list.get(a - 2)));\n\t\t\t\t\t\tlist.remove(a-2);\n\t\t\t\t\t\tlist.remove(a-2);\n\t\t\t\t\t\tCollections.sort(list);\n\t\t\t\t\t} else {\n\t\t\t\t\t\tlist.remove(a - 1);\n\t\t\t\t\t\tlist.remove(a -2);\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tif (list.size()==1){\n\t\t\t\t\treturn list.get(0);\n\t\t\t\t}\n\t\t\t\telse {\n\t\t\t\t\treturn 0;\n\t\t\t\t}\n\t\t\t}\n}
| 6
| 0
|
['Array', 'Java']
| 0
|
last-stone-weight
|
[Java] Runtime: 1ms, faster than 99.49% || Queue and Iterative Solutions
|
java-runtime-1ms-faster-than-9949-queue-8miuf
|
PriorityQueue solution:\n\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n Queue<Integer> queue = new PriorityQueue<>(Collections.reve
|
decentos
|
NORMAL
|
2022-11-18T03:47:39.208820+00:00
|
2022-11-18T03:47:39.208872+00:00
| 1,159
| false
|
PriorityQueue solution:\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n Queue<Integer> queue = new PriorityQueue<>(Collections.reverseOrder());\n for (int i : stones) queue.offer(i);\n\n while (queue.size() > 1) {\n int first = queue.poll();\n int next = queue.poll();\n if (first != next) {\n queue.offer(first - next);\n }\n }\n return queue.isEmpty() ? 0 : queue.poll();\n }\n}\n```\n\nWithout extra space solution:\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n if (stones.length == 1) return stones[0];\n Arrays.sort(stones);\n int last = stones.length - 1;\n int prev = stones.length - 2;\n while (stones[last] != 0) {\n if (stones[prev] == 0) return stones[last];\n stones[last] = stones[last] - stones[prev];\n stones[prev] = 0;\n Arrays.sort(stones);\n }\n return 0;\n }\n}\n```\n\n\n
| 6
| 0
|
['Java']
| 1
|
last-stone-weight
|
C++ easy Priority queue solution || 100% time
|
c-easy-priority-queue-solution-100-time-1k4ip
|
\nint lastStoneWeight(vector<int>& stones) {\n\n\tpriority_queue<int>pq;\n\tfor(auto x: stones)\n\t{\n\t\tpq.push(x);\n\t}\n\n\twhile(!p.empty())\n\t{\n\t\tint
|
rajsaurabh
|
NORMAL
|
2021-11-26T05:23:48.192395+00:00
|
2021-11-26T05:27:09.445947+00:00
| 622
| false
|
```\nint lastStoneWeight(vector<int>& stones) {\n\n\tpriority_queue<int>pq;\n\tfor(auto x: stones)\n\t{\n\t\tpq.push(x);\n\t}\n\n\twhile(!p.empty())\n\t{\n\t\tint y = pq.top();\n\t\tif(pq.size()==1)return y;\n\t\tpq.pop();\n\t\tint rem = abs(y - pq.top());\n\t\tpq.pop();\n\t\tpq.push(rem);\n\n }\n return 0;\n }\n\t\n```
| 6
| 0
|
['C', 'Heap (Priority Queue)', 'C++']
| 4
|
last-stone-weight
|
Rust solution
|
rust-solution-by-bigmih-jopx
|
\nimpl Solution {\n pub fn last_stone_weight(stones: Vec<i32>) -> i32 {\n use std::collections::BinaryHeap;\n\n let mut h = BinaryHeap::from(st
|
BigMih
|
NORMAL
|
2021-10-16T19:12:25.279186+00:00
|
2021-10-16T19:14:34.723943+00:00
| 222
| false
|
```\nimpl Solution {\n pub fn last_stone_weight(stones: Vec<i32>) -> i32 {\n use std::collections::BinaryHeap;\n\n let mut h = BinaryHeap::from(stones);\n while h.len() > 1 {\n let s1 = h.pop().unwrap();\n let s2 = h.pop().unwrap();\n h.push(s1 - s2)\n }\n h.pop().unwrap_or(0)\n }\n}\n```
| 6
| 0
|
['Rust']
| 0
|
last-stone-weight
|
python heapq
|
python-heapq-by-dpark068-19wl
|
\n"""\nChoose two heaviest stones and smash them together\n\nx==y: destroyed\nx != y, new weight is difference, return weight of stome\n\nApproach:\nuse max hea
|
dpark068
|
NORMAL
|
2020-09-06T19:24:41.566306+00:00
|
2020-09-06T19:24:41.566368+00:00
| 670
| false
|
```\n"""\nChoose two heaviest stones and smash them together\n\nx==y: destroyed\nx != y, new weight is difference, return weight of stome\n\nApproach:\nuse max heap, get difference\n"""\nimport heapq\n\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n stones = [-x for x in stones]\n heapq.heapify(stones)\n \n while len(stones) > 1:\n stone1 = -(heapq.heappop(stones))\n stone2 = -(heapq.heappop(stones))\n \n if stone1 == stone2: continue\n heapq.heappush(stones,-(abs(stone1-stone2)))\n \n if len(stones) == 0: return 0\n return -(heapq.heappop(stones))\n```
| 6
| 0
|
['Heap (Priority Queue)', 'Python', 'Python3']
| 0
|
last-stone-weight
|
C++ Solution With Explanation
|
c-solution-with-explanation-by-monga_anm-ujd1
|
Priority Queue Implementation\n Make a priority queue(binary max heap) which automatically arrange the element in sorted order.\n Then pick the first element (
|
monga_anmol123
|
NORMAL
|
2020-04-12T07:26:16.547828+00:00
|
2020-04-12T07:26:16.547886+00:00
| 1,525
| false
|
**Priority Queue Implementation**\n* Make a priority queue(binary max heap) which automatically arrange the element in sorted order.\n* Then pick the first element (which is maximum) and 2nd element(2nd max) , if both are equal we dont have to push anything , if not equal push difference of both in queue.\n* Do the above steps till queue size is equal to 1, then return last element. If queue becomes empty before reaching size==1 then return 0.\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n priority_queue<int> pq;\n for(int i=0;i<stones.size();i++)\n {\n pq.push(stones[i]);\n }\n int m1,m2;\n while(!pq.empty())\n {\n if(pq.size()==1)\n return pq.top();\n m1=pq.top();\n pq.pop();\n m2=pq.top();\n pq.pop();\n \n if(m1!=m2)\n pq.push(m1-m2);\n }\n return 0;\n \n }\n};\n```
| 6
| 1
|
['C', 'Heap (Priority Queue)', 'C++']
| 2
|
last-stone-weight
|
Intuitive C++ solution. 100% run time, 100% memory.
|
intuitive-c-solution-100-run-time-100-me-4cli
|
```class Solution {\npublic:\n int lastStoneWeight(vector& stones) { \n while(stones.size() > 1)\n {\n sort(stones.begin(),st
|
coolbassist
|
NORMAL
|
2019-05-27T12:01:09.116282+00:00
|
2019-05-27T12:01:25.200496+00:00
| 1,091
| false
|
```class Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) { \n while(stones.size() > 1)\n {\n sort(stones.begin(),stones.end());\n int y = stones[stones.size()-1];\n int x = stones[stones.size()-2];\n \n if(x == y)\n {\n stones.erase(stones.begin() + stones.size()-1);\n stones.erase(stones.begin() + stones.size()-1); // removes the two biggest numbers.\n }\n else\n {\n stones[stones.size()-2] = stones[stones.size()-1] - stones[stones.size()-2];\n \n stones.erase(stones.begin() + stones.size()-1); \n }\n }\n \n if(stones.size() == 1)\n return stones[0];\n \n return 0;\n }\n};
| 6
| 2
|
[]
| 2
|
last-stone-weight
|
Java Simplest Easiest Priority Queue
|
java-simplest-easiest-priority-queue-by-oznoy
|
\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> queue = new PriorityQueue<Integer>(Collections.reverseOrder()
|
Ordinary-Coder
|
NORMAL
|
2019-05-19T04:44:49.401451+00:00
|
2023-03-08T21:25:33.025788+00:00
| 924
| false
|
```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> queue = new PriorityQueue<Integer>(Collections.reverseOrder());\n for (int s : stones) {\n queue.add(s);\n }\n while (queue.size() > 1) {\n int weight1 = queue.poll();\n int weight2 = queue.poll();\n queue.add(weight1 - weight2);\n }\n return queue.size() == 0? 0 : queue.poll();\n }\n}\n```
| 6
| 3
|
['Java']
| 2
|
last-stone-weight
|
Hank Schrader's Rock Collection
|
heap-solution-no-bull-by-qimprch6bn-l4mb
|
IntuitionYo, dude, like, okay—so we gotta smash the biggest rocks first, right? But how the heck do we always grab the heaviest ones without checkin’ the whole
|
QIMPRCh6bN
|
NORMAL
|
2025-01-30T22:05:15.006438+00:00
|
2025-02-20T17:55:39.985139+00:00
| 167
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Yo, dude, like, okay—so we gotta smash the biggest rocks first, right? But how the heck do we always grab the heaviest ones without checkin’ the whole list every time? Oh snap, a max-heap! But wait, Python’s like, “Nah, bro, I only got min-heaps.” No sweat, yo—just flip the numbers to negatives. Genius, right? Now the “smallest” negative is actually the biggest stone. Science, b****!
# Approach
<!-- Describe your approach to solving the problem. -->
Alright, check it:
1. One rock? Just roll with it, man. If there’s only one stone left, that’s your answer. No brainer.
2. Flippin’ negatives for that max-heap vibe. Turn all stones negative so Python’s min-heap acts like a max-heap. Sneaky, sneaky.
3. Smash ’em till there’s nothin’ left. Keep poppin’ the two biggest (well, the “smallest” negatives, but whatever). If they ain’t equal, chuck the leftover (y - x) back into the heap. Rinse and repeat.
4. What’s left? If there’s a stone chillin’ at the end, that’s your guy. Otherwise, peace out with a 0.
# Complexity
- **Time: O(n log n)**, yo. ‘Cause every pop and push is like O(log n), and we’re doin’ that for all the stones. Math, man.
- **Space: O(n)**, ‘cause the heap’s gotta hold all them stones. Simple enough.
# Code
```python3 []
class Solution:
def lastStoneWeight(self, stones: List[int]) -> int:
heapify(stones := [-s for s in stones])
while len(stones) > 1:
L, S = -heappop(stones), -heappop(stones)
if L != S: heappush(stones, -(L - S))
return -stones[0] if stones else 0
```
```python3 [FOR EXPLANATION CLICK HERE]
class Solution:
def lastStoneWeight(self, stones: List[int]) -> int:
# Only one rock? Yeah, we done here.
if len(stones) == 1:
return stones[0]
# Flip 'em negatives to trick the heap, yo
stones = [-stone for stone in stones]
heapq.heapify(stones) # Boom, max-heap vibes
# Smash rocks like it’s a Breaking Bad montage
while len(stones) > 1:
y = -heapq.heappop(stones) # Biggest rock (but negative, so shhh)
x = -heapq.heappop(stones) # Second biggest
if x != y:
new_stone = y - x
heapq.heappush(stones, -new_stone) # Toss the leftover back in
# What’s left? A hero or zero.
return -stones[0] if stones else 0
```
---
***Stay cookin’***

| 5
| 0
|
['Heap (Priority Queue)', 'Python3']
| 1
|
last-stone-weight
|
C# simple solution with PriorityQueue
|
c-simple-solution-with-priorityqueue-by-pu1d4
|
Code\n\npublic class Solution {\n public int LastStoneWeight(int[] stones) {\n\n var heap = new PriorityQueue<int, int>();\n \n foreach
|
evkobak
|
NORMAL
|
2023-04-17T02:03:18.949041+00:00
|
2023-04-17T02:33:56.755450+00:00
| 540
| false
|
# Code\n```\npublic class Solution {\n public int LastStoneWeight(int[] stones) {\n\n var heap = new PriorityQueue<int, int>();\n \n foreach (var stone in stones)\n heap.Enqueue(stone, 0 - stone);\n\n while (heap.Count > 1)\n {\n var newStone = heap.Dequeue() - heap.Dequeue();\n if (newStone > 0)\n heap.Enqueue(newStone, 0 - newStone);\n }\n \n return heap.Count > 0 ? heap.Dequeue() : 0;\n }\n}\n```
| 5
| 0
|
['C#']
| 0
|
last-stone-weight
|
Kotlin: Priority Queue
|
kotlin-priority-queue-by-artemasoyan-w3uw
|
Code\n\nclass Solution {\n fun lastStoneWeight(stones: IntArray): Int {\n val h = PriorityQueue<Int> { a, b -> b.compareTo(a) }\n stones.forEac
|
artemasoyan
|
NORMAL
|
2022-12-13T15:29:24.345995+00:00
|
2022-12-13T15:29:24.346028+00:00
| 182
| false
|
# Code\n```\nclass Solution {\n fun lastStoneWeight(stones: IntArray): Int {\n val h = PriorityQueue<Int> { a, b -> b.compareTo(a) }\n stones.forEach { h.add(it) }\n\n while (h.size > 1) { \n h.add(h.poll() - h.poll())\n }\n \n return h.poll()\n }\n}\n```
| 5
| 0
|
['Heap (Priority Queue)', 'Kotlin']
| 0
|
last-stone-weight
|
✅C++ ||EASY && SHORT|| Faster than 100% || Priority_queue
|
c-easy-short-faster-than-100-priority_qu-wpsm
|
\n\nT->O(n) && S->O(n)\n\n\tclass Solution {\n\t\tpublic:\n\t\t\tint lastStoneWeight(vector& st) {\n\t\t\t\tint n=st.size();\n\t\t\t\tpriority_queueq;\n\t\t\t\t
|
abhinav_0107
|
NORMAL
|
2022-10-02T07:35:49.814847+00:00
|
2022-10-02T07:35:49.814880+00:00
| 1,794
| false
|
\n\n**T->O(n) && S->O(n)**\n\n\tclass Solution {\n\t\tpublic:\n\t\t\tint lastStoneWeight(vector<int>& st) {\n\t\t\t\tint n=st.size();\n\t\t\t\tpriority_queue<int>q;\n\t\t\t\tfor(auto i: st) q.push(i);\n\t\t\t\twhile(q.size()!=1){\n\t\t\t\t\tint x=q.top();\n\t\t\t\t\tq.pop();\n\t\t\t\t\tint y=q.top();\n\t\t\t\t\tq.pop();\n\t\t\t\t\tq.push(max(x,y)-min(x,y));\n\t\t\t\t}\n\t\t\t\treturn q.top();\n\t\t\t}\n\t\t};
| 5
| 0
|
['C', 'Heap (Priority Queue)', 'C++']
| 0
|
last-stone-weight
|
C++ naive solution
|
c-naive-solution-by-raunak_01-szz5
|
\nint lastStoneWeight(vector<int>& stones) {\n sort(stones.begin(),stones.end());\n int a=stones.size()-1;\n if(a==0){\n return
|
Raunak_01
|
NORMAL
|
2022-04-07T11:46:30.636087+00:00
|
2022-04-07T11:46:30.636119+00:00
| 132
| false
|
```\nint lastStoneWeight(vector<int>& stones) {\n sort(stones.begin(),stones.end());\n int a=stones.size()-1;\n if(a==0){\n return stones[a];\n }\n for(int i=0;i<stones.size();i++){\n sort(stones.begin(),stones.end());\n if(stones[a]>0 && stones[a-1]>0){\n stones[a]=stones[a]-stones[a-1];\n stones[a-1]=0;\n }\n else{\n break;\n }\n }\n return stones[a];\n }\n\t```
| 5
| 0
|
[]
| 1
|
last-stone-weight
|
Java Priority Queue
|
java-priority-queue-by-fllght-i8tj
|
\npublic int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> queue = new PriorityQueue<>(Comparator.reverseOrder());\n for (int stone : s
|
FLlGHT
|
NORMAL
|
2022-04-07T07:21:23.643849+00:00
|
2022-04-07T07:21:23.643893+00:00
| 207
| false
|
```\npublic int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> queue = new PriorityQueue<>(Comparator.reverseOrder());\n for (int stone : stones) {\n queue.offer(stone);\n }\n\n while (queue.size() > 1) {\n queue.offer(queue.poll() - queue.poll());\n }\n\n return queue.isEmpty() ? 0 : queue.peek();\n }\n```
| 5
| 0
|
['Java']
| 0
|
last-stone-weight
|
very easy code with explanation
|
very-easy-code-with-explanation-by-mamta-mie2
|
step 1 create a priority queue\nstep 2 Put all elements into a priority queue.\nstep 3 take two bigest element \npush the difference into queue until\ntwo more
|
Mamtachahal
|
NORMAL
|
2022-04-07T00:54:04.014773+00:00
|
2022-04-07T01:09:00.689752+00:00
| 281
| false
|
**step 1 create a priority queue\nstep 2 Put all elements into a priority queue.\nstep 3 take two bigest element \npush the difference into queue until\ntwo more element left.**\n\n**Complexity\nTime O(NlogN)\nSpace O(N)**\n\n\n\n\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& nums) {\n priority_queue<int> pq;\n for(auto i : nums) \n pq.push(i);\n while(pq.size() > 1)\n {\n int a = pq.top();\n pq.pop();\n int b = pq.top(); \n pq.pop();\n if(a>b)\n pq.push(a-b);\n }\n return pq.empty()?0:pq.top(); \n \n }\n};\n\nif(ishelpfull)\n(upvote);\n\n
| 5
| 0
|
[]
| 0
|
last-stone-weight
|
Last Stone Weight || Python || Easy || 48 ms
|
last-stone-weight-python-easy-48-ms-by-w-c11z
|
\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n while(len(stones)>1):\n p = max(stones)\n pi= stones.
|
workingpayload
|
NORMAL
|
2022-04-07T00:52:24.142939+00:00
|
2022-04-07T00:52:24.142972+00:00
| 153
| false
|
```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n while(len(stones)>1):\n p = max(stones)\n pi= stones.index(p)\n stones.pop(pi)\n q = max(stones)\n qi = stones.index(q)\n stones.pop(qi)\n stones.append(p-q)\n return stones[0] \n ```
| 5
| 0
|
['Python']
| 0
|
last-stone-weight
|
Java Easy Solution | o(nlogn) Time Complexity | Priority Queue
|
java-easy-solution-onlogn-time-complexit-6ego
|
The efficient way to retrieve the max from array is to use a max heap, which in Java is a PriorityQueue (min heap) with a reverse comparator.\n\n Follow 4 Easy
|
sparkle_30
|
NORMAL
|
2021-08-02T13:25:35.014740+00:00
|
2021-08-02T13:25:35.014783+00:00
| 449
| false
|
The efficient way to retrieve the max from array is to use a max heap, which in Java is a PriorityQueue (min heap) with a reverse comparator.\n\n Follow 4 Easy steps-\n**Step1** : Create a max priority queue.\n**Step2** : Add all the elements to queue.\n**Step3** : Remove two max element at a time, find the difference and then add into the queue.\n**Step4** : Check if queue is empty return 0, else return the element\n\n\n```\n public int lastStoneWeight(int[] stones) {\n \n // Create a max priority queue \n PriorityQueue<Integer> queue = new PriorityQueue<>(Collections.reverseOrder());\n \n // Add all the elements to queue \n for(int i : stones) {\n \tqueue.add(i);\n }\n \n // Remove two max element at a time, find the difference and then add into the queue \n while(queue.size() > 1) {\n int num1 = queue.poll();\n int num2 = queue.poll();\n int num = num1 - num2;\n queue.add(num);\n }\n \n // Check if queue is empty return 0, else return the element \n if(queue.isEmpty()) {\n \treturn 0;\n }\n return queue.poll();\n }\n```\n\nTime Complexity - ```o(nlogn)```\nSpace Complexity - ```o(n)```
| 5
| 0
|
[]
| 1
|
last-stone-weight
|
Javascript 99% time
|
javascript-99-time-by-warkanlock-wg9z
|
It\'s not optimal but it\'s efficient without using a priority queue. Just array manipulation \n\n```/*\n * @param {number[]} stones\n * @return {number}\n /\nv
|
warkanlock
|
NORMAL
|
2020-04-23T22:50:49.406672+00:00
|
2020-04-23T22:51:02.124500+00:00
| 298
| false
|
It\'s not optimal but it\'s efficient without using a priority queue. Just array manipulation \n\n```/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n let size = stones.length;\n \n while(size >= 2){\n stones.sort((a,b)=> { return a-b })\n \n x = stones.pop(); \n y = stones.pop();\n \n if(x == y){\n size -= 2;\n }else{\n size -= 1; \n stones.unshift(x - y); \n }\n }\n \n return stones;\n};\n
| 5
| 0
|
[]
| 1
|
last-stone-weight
|
Golang using container/heap
|
golang-using-containerheap-by-ylz-at-byes
|
\npackage main\n\nimport (\n\t"container/heap"\n)\n\nfunc lastStoneWeight(stones []int) int {\n\tpq := IntHeap(stones)\n\theap.Init(&pq)\n\tfor pq.Len() > 1 {\n
|
ylz-at
|
NORMAL
|
2020-03-24T08:10:14.258364+00:00
|
2020-03-24T08:10:14.258400+00:00
| 1,305
| false
|
```\npackage main\n\nimport (\n\t"container/heap"\n)\n\nfunc lastStoneWeight(stones []int) int {\n\tpq := IntHeap(stones)\n\theap.Init(&pq)\n\tfor pq.Len() > 1 {\n\t\theap.Push(&pq, heap.Pop(&pq).(int)-heap.Pop(&pq).(int))\n\n\t}\n\treturn heap.Pop(&pq).(int)\n}\n\ntype IntHeap []int\n\nfunc (h IntHeap) Len() int { return len(h) }\nfunc (h IntHeap) Less(i, j int) bool { return h[i] > h[j] }\nfunc (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }\n\nfunc (h *IntHeap) Push(x interface{}) {\n\t// Push and Pop use pointer receivers because they modify the slice\'s length,\n\t// not just its contents.\n\t*h = append(*h, x.(int))\n}\n\nfunc (h *IntHeap) Pop() interface{} {\n\told := *h\n\tn := len(old)\n\tx := old[n-1]\n\t*h = old[0 : n-1]\n\treturn x\n}\n```
| 5
| 0
|
['Heap (Priority Queue)', 'Go']
| 4
|
last-stone-weight
|
python very simple solution 95% fast
|
python-very-simple-solution-95-fast-by-g-h6lp
|
```\nclass Solution(object):\n def lastStoneWeight(self, stones):\n """\n :type stones: List[int]\n :rtype: int\n """\n \n
|
gyohogo
|
NORMAL
|
2020-01-01T23:27:08.315532+00:00
|
2020-01-01T23:29:09.264974+00:00
| 603
| false
|
```\nclass Solution(object):\n def lastStoneWeight(self, stones):\n """\n :type stones: List[int]\n :rtype: int\n """\n \n while len(stones) > 1:\n stones.sort()\n x, y = stones[-2], stones[-1]\n stones = stones[:-2]\n \n if x != y:\n stones.append(y - x)\n \n return stones[0] if stones else 0
| 5
| 0
|
['Python']
| 1
|
last-stone-weight
|
[Java] easy solution
|
java-easy-solution-by-olsh-mrfl
|
\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer>queue = new PriorityQueue<>(Comparator.reverseOrder());\n
|
olsh
|
NORMAL
|
2019-12-30T21:43:28.339785+00:00
|
2019-12-30T21:43:28.339832+00:00
| 394
| false
|
```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer>queue = new PriorityQueue<>(Comparator.reverseOrder());\n for (int item : stones)queue.add(item);\n while (queue.size()>1){\n int i1 = queue.poll();\n int i2 = queue.poll();\n if (i1!=i2)queue.add(Math.abs(i1-i2));\n }\n return queue.isEmpty()?0:queue.poll();\n }\n}\n```
| 5
| 2
|
['Java']
| 1
|
last-stone-weight
|
Python Simple Solution
|
python-simple-solution-by-saffi-1o7d
|
\tclass Solution:\n\t\tdef lastStoneWeight(self, stones: List[int]) -> int:\n\t\t\tstones.sort()\n\t\t\twhile len(stones)>1:\n\t\t\t\tt = stones.pop()\n\t\t\t\t
|
saffi
|
NORMAL
|
2019-11-25T17:25:08.246373+00:00
|
2019-11-25T17:25:21.836780+00:00
| 532
| false
|
\tclass Solution:\n\t\tdef lastStoneWeight(self, stones: List[int]) -> int:\n\t\t\tstones.sort()\n\t\t\twhile len(stones)>1:\n\t\t\t\tt = stones.pop()\n\t\t\t\tu = stones.pop()\n\t\t\t\tif t==u:\n\t\t\t\t\tcontinue\n\t\t\t\telse:\n\t\t\t\t\tstones.append(t-u)\n\t\t\t\t\tstones.sort()\n\t\t\treturn stones[0] if stones else 0\n
| 5
| 0
|
['Python', 'Python3']
| 0
|
last-stone-weight
|
Javascript simple O(nlogn) solution
|
javascript-simple-onlogn-solution-by-dav-th9t
|
\nvar lastStoneWeight = function(stones) {\n if(!stones || stones.length == 0) return 0\n \n while(stones.length > 1) {\n stones.sort((a, b) =>
|
davidhiggins1712
|
NORMAL
|
2019-05-23T07:25:00.389314+00:00
|
2019-05-23T07:25:00.389380+00:00
| 749
| false
|
```\nvar lastStoneWeight = function(stones) {\n if(!stones || stones.length == 0) return 0\n \n while(stones.length > 1) {\n stones.sort((a, b) => b - a)\n let x = stones.shift() - stones.shift()\n stones.push(x)\n }\n \n return stones[0]\n};\n```
| 5
| 3
|
['Sorting', 'JavaScript']
| 2
|
last-stone-weight
|
C++ 0ms faster than 100% (using priority_queue)
|
c-0ms-faster-than-100-using-priority_que-jd14
|
\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n priority_queue<int> qu(stones.begin(),stones.end());\n \n whi
|
liut2016
|
NORMAL
|
2019-05-22T09:35:57.736100+00:00
|
2019-05-22T09:35:57.736142+00:00
| 702
| false
|
```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n priority_queue<int> qu(stones.begin(),stones.end());\n \n while(qu.size() != 0 && qu.size() != 1){\n int temp1 = qu.top();\n qu.pop();\n int temp2 = qu.top();\n qu.pop();\n \n if(temp2 != temp1) qu.push(temp1 - temp2); \n }\n \n if(!qu.size()) return 0;\n else return qu.top();\n }\n};\n```
| 5
| 2
|
[]
| 2
|
last-stone-weight
|
Simple C++ 100/100
|
simple-c-100100-by-rathnavels-1f5j
|
\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) \n {\n for(int i=stones.size()-1; i>=1;)\n { \n sort(stone
|
rathnavels
|
NORMAL
|
2019-05-19T20:40:46.012135+00:00
|
2019-05-19T20:44:40.312458+00:00
| 262
| false
|
```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) \n {\n for(int i=stones.size()-1; i>=1;)\n { \n sort(stones.begin(),stones.end());\n \n auto iNum = stones[i];\n auto iM1Num = stones[i-1];\n auto temp = iNum - iM1Num;\n\n stones.pop_back();\n stones.pop_back();\n\n if(iNum != iM1Num)\n stones.push_back(temp);\n\n i = stones.size()-1;\n }\n return stones.size() > 0 ? stones[0] : 0;\n }\n};\n```
| 5
| 2
|
[]
| 0
|
last-stone-weight
|
learn heap(max)
|
learn-heapmax-by-izer-v73u
|
Intuition\n Describe your first thoughts on how to solve this problem. \nconcept maching with heap:\n\n# Approach\n Describe your approach to solving the proble
|
izer
|
NORMAL
|
2024-10-13T06:11:45.715531+00:00
|
2024-10-13T06:11:45.715561+00:00
| 71
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nconcept maching with heap:\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfirst, find max and second max\nif same then pop both else change larger elem as diff.\nat the end print ele. remaining on heap\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(NlogN)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n priority_queue<int>pq;\n for(auto ele:stones){\n pq.push(ele);\n }\n while(pq.size()>1){\n int x=pq.top();\n pq.pop();\n int y=pq.top();\n pq.pop();\n if(x-y) pq.push(x-y);\n }\n return pq.size()==0?0:pq.top();\n\n \n }\n};\n```
| 4
| 0
|
['C++']
| 0
|
last-stone-weight
|
Better than 100% in runtime. Simple C++ approach
|
better-than-100-in-runtime-simple-c-appr-k2s8
|
Approach\nAlright, in this I am using Priority Queue. In this first I am adding all elements of the vector "stones" in the priority queue called "pq". Now I am
|
green_day
|
NORMAL
|
2023-04-24T08:19:36.285684+00:00
|
2023-04-24T08:19:36.285725+00:00
| 1,644
| false
|
# Approach\nAlright, in this I am using Priority Queue. In this first I am adding all elements of the vector "stones" in the priority queue called "pq". Now I am initializing a while loop, setting the condition that, the size of "pq" must be greater than 1. I am simply checking the top 2 elements and doing the required manipulations in the question. In the end, if size of "pq" is 0, return 0; else we should return the top element of the same.\n\n# Code\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n int n=stones.size();\n priority_queue<int> pq;\n for(int i=0;i<n;i++)\n {\n pq.push(stones[i]);\n } \n while(pq.size()>1)\n {\n int a=pq.top();\n pq.pop();\n int b=pq.top();\n pq.pop();\n if(a!=b)\n {\n int c=a-b;\n pq.push(c);\n }\n }\n if(pq.size()==0)\n {\n return 0;\n }\n else\n {\n int l=pq.top();\n return l;\n }\n }\n};\n```
| 4
| 0
|
['Array', 'Heap (Priority Queue)', 'C++']
| 3
|
last-stone-weight
|
✅Java Easy Solution|lBeginner Friendly🔥
|
java-easy-solutionlbeginner-friendly-by-83lb9
|
Code\n\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n //creating a heap to store elements in descending order\n PriorityQueue
|
deepVashisth
|
NORMAL
|
2023-04-24T06:45:36.307519+00:00
|
2023-04-24T06:45:36.307559+00:00
| 880
| false
|
# Code\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n //creating a heap to store elements in descending order\n PriorityQueue<Integer> q = new PriorityQueue<>(Comparator.reverseOrder());\n for(int i = 0 ; i < stones.length; i ++){\n q.add(stones[i]);\n }\n while(q.size() > 1){\n int x = q.poll();\n int y = q.poll();\n if(x == y){\n continue;\n }else{\n q.add(Math.abs(y - x));\n }\n }\n if(q.size() == 1){\n return q.poll();\n }\n return 0;\n }\n}\n```\n**Please UpVote If you like it Happy Coding :)\nIf you really found my solution helpful please upvote it, as it motivates me to post such kind of codes and help the coding community, if you have some queries or some improvements please feel free to comment and share your views.**
| 4
| 0
|
['Heap (Priority Queue)', 'Java']
| 2
|
last-stone-weight
|
Ex-Amazon explains a solution with a video, Python, JavaScript, Java and C++
|
ex-amazon-explains-a-solution-with-a-vid-t8oy
|
My youtube channel - KeetCode(Ex-Amazon)\nI create 155 videos for leetcode questions as of April 24, 2023. I believe my channel helps you prepare for the coming
|
niits
|
NORMAL
|
2023-04-24T03:02:26.129374+00:00
|
2023-04-24T03:02:26.129416+00:00
| 1,496
| false
|
# My youtube channel - KeetCode(Ex-Amazon)\nI create 155 videos for leetcode questions as of April 24, 2023. I believe my channel helps you prepare for the coming technical interviews. Please subscribe my channel!\n\n### Please subscribe my channel - KeetCode(Ex-Amazon) from here.\n\n**I created a video for this question. I believe you can understand easily with visualization.** \n\n**My youtube channel - KeetCode(Ex-Amazon)**\nThere is my channel link under picture in LeetCode profile.\nhttps://leetcode.com/niits/\n\n\n\n\n# Intuition\nUse heap to store stones.\n\n# Approach\n- This is Python algorithm. Other languages might be different.\n\n1. Initialize a variable stones as a heap of negative values of the input stones list using list comprehension. This is done to create a min heap where the most negative value (i.e., the largest absolute value) will be at the root of the heap.\n\n2. Convert the stones list into a heap using the heapify function from the heapq module.\n\n3. While the length of stones is greater than 1, perform the following steps in a loop:\n\n - Pop the two smallest (most negative) values from the heap and store them in variables s1 and s2.\n - Check if s1 and s2 are not equal. If they are not equal, calculate the difference between s1 and s2 and negate it (to maintain the negative value) before pushing it back to the heap using the heappush function.\n\n4. After the loop, if the stones heap is not empty, return the negation of the root value (the only remaining value in the heap), which represents the last stone weight. Otherwise, return 0 to indicate that all stones have been destroyed.\n\n---\n\n\n**If you don\'t understand the algorithm, let\'s check my video solution.\nThere is my channel link under picture in LeetCode profile.**\nhttps://leetcode.com/niits/\n\n\n---\n\n# Complexity\n- Time complexity: O(n log n)\nn is the number of elements in the input stones list. This is because the heapify function has a time complexity of O(n) and the while loop iterates n/2 times at most (since two elements are popped from the heap in each iteration), and each iteration involves push and pop operations on the heap which take O(log n) time. Therefore, the overall time complexity is dominated by the heapify function, resulting in O(n log n) time complexity.\n\n- Space complexity: O(n)\nThe stones list is modified in place by converting it into a heap using heapify. No additional data structures are used, and the variables used in the code have constant space requirements. Therefore, the space complexity is proportional to the size of the input stones list, i.e., O(n).\n\n# Python\n```\nclass Solution:\n def lastStoneWeight(self, stones: List[int]) -> int:\n if len(stones) == 1:\n return stones[0]\n \n stones = [-s for s in stones]\n heapq.heapify(stones)\n\n while len(stones) > 1:\n s1 = -(heapq.heappop(stones))\n s2 = -(heapq.heappop(stones))\n\n if s1 != s2:\n heapq.heappush(stones, -(s1-s2))\n \n return -(stones[0]) if stones else 0\n```\n# JavaScript\n```\n/**\n * @param {number[]} stones\n * @return {number}\n */\nvar lastStoneWeight = function(stones) {\n const queue = new MaxPriorityQueue();\n \n for (stone of stones) queue.enqueue(stone)\n \n while (queue.size() > 1) {\n let first = queue.dequeue().element;\n let second = queue.dequeue().element;\n if (first !== second) queue.enqueue(first-second)\n }\n \n return queue.size() === 0 ? 0 : queue.front().element \n};\n```\n# Java\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> queue = new PriorityQueue<>(Comparator.reverseOrder());\n \n for (int stone : stones) {\n queue.offer(stone);\n }\n \n while (queue.size() > 1) {\n int first = queue.poll();\n int second = queue.poll();\n \n if (first != second) {\n queue.offer(first - second);\n }\n }\n \n return queue.size() == 0 ? 0 : queue.peek();\n }\n}\n```\n# C++\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n priority_queue<int, vector<int>> queue;\n int s1, s2;\n \n for(auto s1:stones)\n queue.push(s1);\n \n while(queue.size() != 1){\n s2 = queue.top();\n queue.pop();\n s1 = queue.top();\n queue.pop();\n\n queue.push(s2-s1);\n }\n \n return queue.top();\n }\n};\n```
| 4
| 0
|
['C++', 'Java', 'Python3', 'JavaScript']
| 1
|
last-stone-weight
|
Typescript || Array || Heap
|
typescript-array-heap-by-webdot-0d9x
|
Approach\n Describe your approach to solving the problem. \nWe initialize a maximum priority queue which ensures the element we call each time has the maximum w
|
webdot
|
NORMAL
|
2023-04-24T01:24:15.993361+00:00
|
2023-04-24T01:24:15.993395+00:00
| 454
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nWe initialize a maximum priority queue which ensures the element we call each time has the maximum weight. \n\nWe then insert all stones into this queue. As far as we have at least 2 stones, we pop out the two stones, if they are equal in weight we do nothing, else we get the difference and push back into the queue.\n\nWe then return the weight of the last stone left or 0 if none.\n\n# Complexity\n- Time complexity: $$O(n . logn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunction lastStoneWeight(stones: number[]): number {\n const maxPQueue = new MaxPriorityQueue();\n\n stones.map(stone => maxPQueue.enqueue(stone));\n\n while(maxPQueue.size() > 1) {\n let first: number = maxPQueue.dequeue().element;\n let second: number = maxPQueue.dequeue().element;\n\n if(first !== second) {\n maxPQueue.enqueue(first - second);\n }\n }\n\n return maxPQueue.dequeue()?.element ?? 0;\n};\n```
| 4
| 0
|
['Array', 'Heap (Priority Queue)', 'TypeScript']
| 1
|
last-stone-weight
|
✅ Easy Java solution || using maxHeap 🏆 || Beginner Friendly 🔥
|
easy-java-solution-using-maxheap-beginne-naj7
|
Intuition\nNeed to maitain a DS to get top-2 stone, PriorityQueue is best for this\n\n# Approach\n1. Push all elments in prioriyQueue as MaxHeap.\n2. Pick top 2
|
yshrini
|
NORMAL
|
2023-04-24T00:16:25.382547+00:00
|
2023-04-24T00:16:25.382583+00:00
| 861
| false
|
# Intuition\nNeed to maitain a DS to get top-2 stone, PriorityQueue is best for this\n\n# Approach\n1. Push all elments in prioriyQueue as MaxHeap.\n2. Pick top 2 elements form maxHeap, if there is only one element left then that is answer.\n3. If both element are same, no action needed and continue the process.\n4. If both element are different, push the differece again.\n5. Answer will be if only one stone is left or no stone is left, **In case of only one stone is left, that is the answer, if no stoner are left, 0 is the answer.**\n# Complexity\n- Time complexity: $$O(n)$$ \n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>((stone1, stone2) -> stone2 - stone1);\n\n for(int stone: stones) {\n maxHeap.add(stone);\n }\n\n while(!maxHeap.isEmpty()) {\n // take haviest stone\n int y = maxHeap.poll();\n if(maxHeap.isEmpty()) {\n // if the was only one stone left, so that is answer\n return y;\n } else {\n // take second haviest stone\n int x = maxHeap.poll();\n // if both are no equal then push the difference, no action needed for equal\n if(x != y) {\n maxHeap.add(y - x);\n }\n }\n }\n\n // if no stone left in heap\n return 0;\n\n }\n}\n```
| 4
| 0
|
['Heap (Priority Queue)', 'Java']
| 1
|
last-stone-weight
|
🗓️ Daily LeetCoding Challenge April, Day 24
|
daily-leetcoding-challenge-april-day-24-qd1r8
|
This problem is the Daily LeetCoding Challenge for April, Day 24. Feel free to share anything related to this problem here! You can ask questions, discuss what
|
leetcode
|
OFFICIAL
|
2023-04-24T00:00:20.445404+00:00
|
2023-04-24T00:00:20.445495+00:00
| 4,213
| false
|
This problem is the Daily LeetCoding Challenge for April, Day 24.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/last-stone-weight/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain these 4 approaches in the official solution</summary>
**Approach 1:** Array-Based Simulation
**Approach 2:** Sorted Array-Based Simulation
**Approach 3:** Heap-Based Simulation
**Approach 4:** Bucket Sort
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 4
| 0
|
[]
| 16
|
last-stone-weight
|
Java. Heap. Fight of the stones
|
java-heap-fight-of-the-stones-by-red_pla-in5n
|
\n\nclass Heap\n{\n int [] heap;\n int size;\n Heap(int[] stones)\n {\n heap = new int[stones.length];\n size = 0;\n for (int i
|
red_planet
|
NORMAL
|
2023-04-03T16:59:53.734665+00:00
|
2023-04-03T16:59:53.734710+00:00
| 817
| false
|
\n```\nclass Heap\n{\n int [] heap;\n int size;\n Heap(int[] stones)\n {\n heap = new int[stones.length];\n size = 0;\n for (int i = 0; i < stones.length; i++)\n addStone(stones[i]);\n }\n public int removeMax() //size--\n {\n int answ = heap[0];\n if (size > 0) {\n heap[0] = heap[size - 1];\n size--;\n }\n siftDown();\n return answ;\n }\n public void addStone(int stone) //size++\n {\n size++;\n heap[size - 1] = stone;\n siftUp();\n }\n\n public int[] changePlace(int child, int[] start)\n {\n int tmp;\n\n tmp = heap[child];\n heap[child] = heap[start[0]];\n heap[start[0]] = tmp;\n start[0] = child;\n return new int[]{getLeftChild(start[0]), getRightChild(start[0])};\n }\n\n public void siftDown()\n {\n int []start = new int[]{0};\n int []leftAndRight = new int[2];\n leftAndRight[0] = getLeftChild(start[0]);\n leftAndRight[1] = getRightChild(start[0]);\n int tmp;\n while (true)\n {\n if (leftAndRight[0] < size && leftAndRight[1] < size)\n {\n if(heap[leftAndRight[0]] >= heap[leftAndRight[1]] && heap[start[0]] <= heap[leftAndRight[0]])\n leftAndRight = changePlace(leftAndRight[0], start);\n else if(heap[leftAndRight[1]] > heap[leftAndRight[0]] && heap[start[0]] <= heap[leftAndRight[1]])\n leftAndRight = changePlace(leftAndRight[1], start);\n else\n break;\n }\n else if (leftAndRight[0] < size && heap[start[0]] <= heap[leftAndRight[0]])\n leftAndRight = changePlace(leftAndRight[0], start);\n else if (leftAndRight[1] < size && heap[start[0]] <= heap[leftAndRight[1]])\n leftAndRight = changePlace(leftAndRight[1], start);\n else\n break;\n }\n }\n\n public void siftUp()\n {\n int child = size - 1;\n int parent = getParent(child);\n int tmp;\n while (parent > -1 && heap[parent] < heap[child])\n {\n tmp = heap[child];\n heap[child] = heap[parent];\n heap[parent] = tmp;\n child = parent;\n parent = getParent(child);\n }\n }\n\n public int getParent(int child)\n {\n return (child - 1) / 2;\n }\n\n public int getLeftChild(int parent)\n {\n return parent * 2 + 1;\n }\n\n public int getRightChild(int parent)\n {\n return parent * 2 + 2;\n }\n}\n\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n Heap heap = new Heap(stones);\n int diff;\n while (heap.size > 1)\n {\n diff = Math.abs(heap.removeMax() - heap.removeMax());\n if (diff != 0)\n heap.addStone(diff);\n }\n if (heap.size > 0)\n return heap.removeMax();\n return 0;\n }\n}\n```
| 4
| 0
|
['Java']
| 2
|
last-stone-weight
|
Using Heap- 1ms | JAVA ✅ | beat 💯
|
using-heap-1ms-java-beat-by-sourabh-jadh-xopo
|
\n# Complexity\n- Time complexity:\nO(log n)\n\n# Code\n\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> pq=ne
|
sourabh-jadhav
|
NORMAL
|
2023-02-24T09:13:29.977972+00:00
|
2023-02-24T09:13:29.978023+00:00
| 302
| false
|
\n# Complexity\n- Time complexity:\nO(log n)\n\n# Code\n```\nclass Solution {\n public int lastStoneWeight(int[] stones) {\n PriorityQueue<Integer> pq=new PriorityQueue<>(Collections.reverseOrder());\n for(int i:stones)\n pq.add(i);\n\n int x;\n int y;\n\n while(pq.size()>1){\n\n x=pq.poll();\n y=pq.poll();\n\n if(x>y)\n pq.add(x-y);\n\n }\n \n return pq.isEmpty()?0:pq.poll();\n }\n}\n```\n\n
| 4
| 0
|
['Array', 'Queue', 'Heap (Priority Queue)', 'Java']
| 0
|
last-stone-weight
|
Simple solution on Swift / Beats 100%
|
simple-solution-on-swift-beats-100-by-bl-gp1e
|
Please upvote if the solution was useful!\n\nfunc lastStoneWeight(_ stones: [Int]) -> Int {\n var stones = stones.sorted(by: >)\n while stones.count != 1
|
blackbirdNG
|
NORMAL
|
2023-01-13T13:26:16.269697+00:00
|
2023-01-13T13:26:16.269735+00:00
| 410
| false
|
### Please upvote if the solution was useful!\n```\nfunc lastStoneWeight(_ stones: [Int]) -> Int {\n var stones = stones.sorted(by: >)\n while stones.count != 1 {\n let secondItem = stones.remove(at: 1)\n stones[0] -= secondItem\n stones = stones.sorted(by: >)\n }\n return stones[0]\n}\n```\n\n
| 4
| 0
|
['Swift']
| 3
|
last-stone-weight
|
python, heapq (min) with negative values (equivalent to heap max)
|
python-heapq-min-with-negative-values-eq-ofu7
| ERROR: type should be string, got "https://leetcode.com/submissions/detail/875123729/ \\nRuntime: 29 ms, faster than 94.25% of Python3 online submissions for Last Stone Weight. \\nMemory Usage: 1"
|
nov05
|
NORMAL
|
2023-01-10T02:13:28.407525+00:00
|
2023-01-10T02:14:48.841749+00:00
| 1,375
| false
| ERROR: type should be string, got "https://leetcode.com/submissions/detail/875123729/ \\nRuntime: **29 ms**, faster than 94.25% of Python3 online submissions for Last Stone Weight. \\nMemory Usage: 13.8 MB, less than 61.08% of Python3 online submissions for Last Stone Weight. \\n```\\nclass Solution:\\n def lastStoneWeight(self, stones: List[int]) -> int:\\n s = [-s for s in stones]\\n heapify(s)\\n while len(s)>1:\\n heapq.heappush(s, -abs(heappop(s) - heappop(s)))\\n return -s[0]\\n```"
| 4
| 0
|
['Heap (Priority Queue)', 'Python', 'Python3']
| 1
|
last-stone-weight
|
JavaScript using MaxPriorityQueue
|
javascript-using-maxpriorityqueue-by-yup-c9kn
|
Finally, there\'s a Max/MinPriorityQueue for JavaScript!\n\nadd -> enqueue( )\nremove -> dequeue( )\nhighest number (peek) -> front( )\n.element -> actual value
|
yupdduk
|
NORMAL
|
2022-06-19T03:14:31.384139+00:00
|
2022-06-19T03:14:31.384186+00:00
| 560
| false
|
Finally, there\'s a Max/MinPriorityQueue for JavaScript!\n\nadd -> enqueue( )\nremove -> dequeue( )\nhighest number (peek) -> front( )\n.element -> actual value\n\n```\nvar lastStoneWeight = function(stones) {\n const m = new MaxPriorityQueue()\n for(const w of stones) m.enqueue(w)\n \n while(m.size() > 1){\n const diff = m.dequeue().element - m.dequeue().element\n if(diff > 0) m.enqueue(diff)\n }\n \n return m.size() === 0 ? 0 : m.front().element\n};\n```
| 4
| 0
|
['JavaScript']
| 3
|
last-stone-weight
|
C++ solution with image explanation | No extra space
|
c-solution-with-image-explanation-no-ext-5dwo
|
\n\n\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n while(stones.size() > 1) {\n sort(stones.begin(), stones.end
|
Progra_marauder
|
NORMAL
|
2022-04-07T12:21:38.108364+00:00
|
2022-04-07T12:22:18.529631+00:00
| 179
| false
|
\n\n```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n while(stones.size() > 1) {\n sort(stones.begin(), stones.end());\n int n = stones.size();\n \n if(stones[n - 2] == stones[n - 1]) {\n stones.pop_back();\n stones.pop_back();\n }\n else {\n stones[n - 2] = stones[n - 1] - stones[n - 2];\n stones.pop_back();\n }\n }\n return stones.empty() ? 0:stones[0];\n }\n};\n\n```\n
| 4
| 0
|
[]
| 1
|
last-stone-weight
|
[ Python ] ✅✅ Simple Python Solution Using Three Approach 🥳✌👍
|
python-simple-python-solution-using-thre-d5z6
|
If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Apporach 1 Using Priority Queue :-\n# Runtime: 39 ms, faster th
|
ashok_kumar_meghvanshi
|
NORMAL
|
2022-04-07T10:25:02.699874+00:00
|
2023-04-24T07:20:51.484202+00:00
| 579
| false
|
# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Apporach 1 Using Priority Queue :-\n# Runtime: 39 ms, faster than 55.89% of Python3 online submissions for Last Stone Weight.\n# Memory Usage: 14.1 MB, less than 13.28% of Python3 online submissions for Last Stone Weight.\n\n\tfrom queue import PriorityQueue\n\n\tclass Solution:\n\t\tdef lastStoneWeight(self, stones: List[int]) -> int:\n\n\t\t\tpq = PriorityQueue()\n\n\t\t\tfor stone in stones:\n\t\t\t\tpq.put(-stone)\n\n\t\t\twhile pq.qsize() >= 2:\n\t\t\t\tfirst_heavy = -(pq.get())\n\t\t\t\tsecond_heavy = -(pq.get())\n\n\t\t\t\tif first_heavy == second_heavy:\n\t\t\t\t\tcontinue\n\t\t\t\telse:\n\t\t\t\t\tpq.put(-(first_heavy - second_heavy))\n\n\t\t\tif pq.qsize() == 1:\n\t\t\t\treturn -pq.get()\n\t\t\telse:\n\t\t\t\treturn 0\n\n# Approach 2 Using Sorting :-\n\n\tclass Solution:\n\t\tdef lastStoneWeight(self, stones: List[int]) -> int:\n\n\t\t\twhile len(stones)>1:\n\n\t\t\t\tsort_stones = sorted(stones)\n\n\t\t\t\tsmall_num, large_num = sort_stones[-2], sort_stones[-1]\n\n\t\t\t\tif small_num == large_num :\n\n\t\t\t\t\tstones = sort_stones[:-2]\n\t\t\t\telse:\n\n\t\t\t\t\tsort_stones.remove(small_num)\n\n\t\t\t\t\tsort_stones.remove(large_num)\n\n\t\t\t\t\tsort_stones.append(large_num - small_num)\n\n\t\t\t\t\tstones = sort_stones\n\n\t\t\tif len(stones)==1:\n\n\t\t\t\treturn stones[0]\n\n\t\t\telse:\n\n\t\t\t\treturn 0\n\n# Approach 3 Using SortedList:\n# Runtime: 47 ms, faster than 7.84% of Python3 online submissions for Last Stone Weight.\n# Memory Usage: 14.2 MB, less than 8.03% of Python3 online submissions for Last Stone Weight.\nfrom sortedcontainers import SortedList\n\n\tclass Solution:\n\t\tdef lastStoneWeight(self, stones: List[int]) -> int:\n\n\t\t\tstones = SortedList(stones)\n\n\t\t\twhile len(stones) > 1:\n\n\t\t\t\tlast = stones.pop(-1)\n\t\t\t\tsecond_last = stones.pop(-1)\n\n\t\t\t\tif last == second_last:\n\t\t\t\t\tcontinue\n\t\t\t\telse:\n\t\t\t\t\tstones.add(last - second_last)\n\n\t\t\tif len(stones) > 0:\n\t\t\t\treturn stones[0]\n\t\t\telse:\n\t\t\t\treturn 0\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D\n
| 4
| 0
|
['Sorting', 'Heap (Priority Queue)', 'Python', 'Python3']
| 0
|
last-stone-weight
|
simplest c++ solution with comments
|
simplest-c-solution-with-comments-by-abh-s1jv
|
\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n priority_queue<int> pq; //create max heap having maximum element at top\n
|
abhijeetnishal
|
NORMAL
|
2022-04-07T09:16:49.948500+00:00
|
2022-04-07T09:17:38.567275+00:00
| 36
| false
|
```\nclass Solution {\npublic:\n int lastStoneWeight(vector<int>& stones) {\n priority_queue<int> pq; //create max heap having maximum element at top\n for(int x:stones) //insert all elements into priority queue \n pq.push(x);\n while(pq.size()>1){ //iterate until size is equal to 1\n int fval=pq.top(); //fval is first max val\n pq.pop();\n int sval=pq.top(); //sval is second max val\n pq.pop();\n if(fval==sval){ //if both equal simply push 0 since both stones destroyed\n pq.push(0);\n }\n else if(fval>sval){ //if both not equal substract small val to larger one and insert \n pq.push(fval-sval);\n }\n }\n return pq.top(); //finally return top value\n }\n};\n```\nTC : O(nlogn) \nSC : O(N)\nIf you like the solution please upvote. :)
| 4
| 0
|
['Heap (Priority Queue)']
| 0
|
nearest-exit-from-entrance-in-maze
|
An analysis on Time Limit Exceeded (TLE)
|
an-analysis-on-time-limit-exceeded-tle-b-rn4q
|
If you are facing TLE you probably made the same mistake as me.\n\nCorrect Way: When pushing a coordinate to the queue immediately mark it + or add it to your v
|
b_clodius
|
NORMAL
|
2021-07-10T18:09:25.571299+00:00
|
2021-07-10T18:09:25.571330+00:00
| 8,489
| false
|
If you are facing TLE you probably made the same mistake as me.\n\n**Correct Way**: When pushing a coordinate to the queue immediately mark it ```+``` or add it to your visited hashset.\n\n```\n for path in range(size):\n row, col = queue.popleft()\n if moves > 0 and (row == len(maze) - 1 or row == 0 or col == 0 or col == len(maze[row]) - 1):\n return moves\n\n if row + 1 < len(maze) and maze[row + 1][col] == ".":\n queue.append((row + 1, col))\n maze[row + 1][col] = "+" # Important\n if row - 1 >= 0 and maze[row - 1][col] == ".":\n queue.append((row - 1, col))\n maze[row - 1][col] = "+" # Important\n if col + 1 < len(maze[row]) and maze[row][col + 1] == ".":\n queue.append((row, col + 1))\n maze[row][col + 1] = "+" # Important\n if col - 1 >= 0 and maze[row][col - 1] == ".":\n queue.append((row, col - 1))\n maze[row][col - 1] = "+" # Important\n moves += 1\n```\n\n**Incorrect Way**: Mark ```+``` or add to visited hashset after popping from queue. If we implement this way we mistakenly add many duplicate coordinates to the queue.\n\n```\n for path in range(size):\n row, col = queue.popleft()\n maze[row][col] = "+" # Wrong\n if moves > 0 and (row == len(maze) - 1 or row == 0 or col == 0 or col == len(maze[row]) - 1):\n return moves\n\n if row + 1 < len(maze) and maze[row + 1][col] == ".":\n queue.append((row + 1, col))\n if row - 1 >= 0 and maze[row - 1][col] == ".":\n queue.append((row - 1, col))\n if col + 1 < len(maze[row]) and maze[row][col + 1] == ".":\n queue.append((row, col + 1))\n if col - 1 >= 0 and maze[row][col - 1] == ".":\n queue.append((row, col - 1))\n moves += 1\n```\n\nFascinated by this mistake I decided to profile the mistake using a large test case that gave me my original TLE. This test case used a 100 x 100 graph with all edges being blocked by ```+``` except one exit on the first row and an entrance of ```[82,19]```. All points inside edges are ```.```. For this particular test case the optimal result requires 131 moves.\n\nWith an incorrect implementation we not only have horrible runtime but we eventually run out of memory. My machine was at 12.97 GB after a few minutes before I had to force kill it.\n\n```\nQueue Unique Size | Queue Total Size | Total Moves in\n4 4 1\n8 12 2\n12 28 3\n16 60 4\n20 124 5\n24 252 6\n28 508 7\n32 1020 8\n36 2044 9\n40 4092 10\n44 8188 11\n48 16380 12\n52 32764 13\n56 65532 14\n60 131068 15\n64 262140 16\n67 524283 17\n69 1048535 18\n70 2096766 19\n```\n
| 319
| 2
|
[]
| 26
|
nearest-exit-from-entrance-in-maze
|
C++ BFS solution || commented
|
c-bfs-solution-commented-by-saiteja_ball-3olw
|
A similar problem -\n1765. Map of highest peak\n\nclass Solution {\npublic:\n int nearestExit(vector<vector<char>>& maze, vector<int>& e) {\n queue<pa
|
saiteja_balla0413
|
NORMAL
|
2021-07-10T16:17:24.455915+00:00
|
2021-07-11T02:21:17.217807+00:00
| 12,155
| false
|
A similar problem -\n[1765. Map of highest peak](https://leetcode.com/problems/map-of-highest-peak/)\n```\nclass Solution {\npublic:\n int nearestExit(vector<vector<char>>& maze, vector<int>& e) {\n queue<pair<int,int>> q;\n q.push({e[0],e[1]});\n\t\t\n\t\t//current moves\n int moves=1;\n int rows=maze.size();\n int cols=maze[0].size();\n \n\t\t//to move in all directions\n vector<vector<int>> offsets={{0,1},{1,0},{0,-1},{-1,0}};\n\t\t\n //mark the entrance as visited\n maze[e[0]][e[1]]=\'+\';\n while(!q.empty())\n {\n int l=q.size();\n\t\t\t//for every node in the queue visit all of it\'s adjacent nodes which are not visited yet\n for(int k=0;k<l;k++)\n {\n auto [i,j]=q.front();\n q.pop();\n \n\t\t\t\t//try all 4 directions from the current cell\n for(int l=0;l<4;l++)\n {\n int x=i+offsets[l][0];\n int y=j+offsets[l][1];\n\t\t\t\t\t//a invalid move\n if(x<0 || y<0 || x>=rows || y>=cols || maze[x][y]==\'+\')\n continue;\n\t\t\t\t\t//if we have reached the exit then current moves are the min moves to reach the exit\n if(x==0 || y==0 || x==rows-1 || y==cols-1)\n return moves;\n\t\t\t\t\t//block the cell as we have visited\n maze[x][y]=\'+\';\n q.push({x,y});\n }\n }\n\t\t\t//increment the moves\n moves++;\n \n }\n return -1;\n }\n};\n```\n**Upvote if this helps you :)**
| 136
| 4
|
[]
| 22
|
nearest-exit-from-entrance-in-maze
|
Java || 👍Explained in Detail👍|| Simple & Fast Solution✅|| BFS
|
java-explained-in-detail-simple-fast-sol-19z2
|
I do my best everyday to give a clear explanation, so to help everyone improve their skills.\n\nIf you find this helpful, please \uD83D\uDC4D upvote this post a
|
cheehwatang
|
NORMAL
|
2022-11-21T01:09:21.023581+00:00
|
2022-11-21T01:37:26.639206+00:00
| 8,037
| false
|
I do my best everyday to give a clear explanation, so to help everyone improve their skills.\n\nIf you find this **helpful**, please \uD83D\uDC4D **upvote** this post and watch my [Github Repository](https://github.com/cheehwatang/leetcode-java).\n\nThank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.\n\n---\n\n## Approach\nA classic breadth first search problem, we use slowly expanding from the starting node.\n\nWe can imagine every position in the \'maze\' as a node with the \'maze\' being a directional graph, since we cannot visit the same node twice to find the shortest path to the exit.\n\nAs such, we take one step at a time to all directions to a new valid position.\n\nNote to check for invalid moves, either that direction is out of bound or towards a wall.\n\nIf that direction leads to a border space, it means it is the exit.\nWith breadth first search, we use Queue store the nodes for the next step.\n\nTo mark the visited node, we can either use an additional 2D boolean array to record, or mark the visited node as a wall \'+\' in \'maze\', latter which is implemented here.\n\n## Complexity\nTime Complexity : O(m * n),\nwhere \'m\' is the number of rows, and \'n\' is the number of columns.\nWith the worst case being that we check every position in the \'maze\'.\n\nSpace Complexity : O(m + n),\nwhere \'m\' is the number of rows, and \'n\' is the number of columns.\nThe queue grows linearly with the rows and columns of the matrix, as we are constantly removing nodes from the queue at each step, with the max queue size being the distance from the center to the edge of the \'maze\'.\n\nIf we use a 2D boolean array for the visited nodes, then the space complexity is O(m * n).\n\n---\n### Java - With Explanation\n```\nclass Solution {\n public int nearestExit(char[][] maze, int[] entrance) {\n int rows = maze.length;\n int columns = maze[0].length;\n\n // For breadth first search, offer the first node (\'entrance\').\n // Note that we immediately mark the node as visited when putting into the queue as to\n // prevent other nodes from visiting it. Otherwise, we will be trapped in an infinite loop.\n // Credit: @b_clodius for the detailed explanation and test.\n Queue<int[]> queue = new LinkedList<>();\n queue.offer(entrance);\n maze[entrance[0]][entrance[1]] = \'+\';\n\n // As simple 2D array to keep track of the directions to take.\n // We can use 4 separate operation, but it is more efficient to use a for-loop to go through the four directions.\n int[][] directions = new int[][] {{0,1},{0,-1},{1,0},{-1,0}};\n\n int steps = 0;\n int x, y;\n while (!queue.isEmpty()) {\n // We take a step before checking the directions for the nodes that we are at (in the queue).\n steps++;\n\n // Make sure to use a variable to keep track of the queue.size(),\n // because the queue size continuously changes as we check for the other nodes,\n // which can lead to infinite loops or undue termination of the for-loop.\n int n = queue.size();\n\n // Check every node at the current step.\n for (int i = 0; i < n; i++) {\n int[] current = queue.poll();\n // For each node, check every direction.\n for (int[] direction : directions) {\n x = current[0] + direction[0];\n y = current[1] + direction[1];\n\n // Check if this direction out of bound.\n if (x < 0 || x >= rows || y < 0 || y >= columns) continue;\n // Check if this direction is the wall.\n if (maze[x][y] == \'+\') continue;\n\n // If this direction is empty, not visited and is at the boundary, we have arrived at the exit.\n if (x == 0 || x == rows - 1 || y == 0 || y == columns - 1) return steps;\n\n // Otherwise, we change this direction as visited and put into the queue to check at the next step.\n maze[x][y] = \'+\';\n queue.offer(new int[]{x, y});\n }\n }\n\n }\n // If all the possible nodes and directions checked but no exits found, return -1.\n return -1;\n }\n}\n```\n\n### Java - Clean Code\n```\nclass Solution {\n public int nearestExit(char[][] maze, int[] entrance) {\n int rows = maze.length;\n int columns = maze[0].length;\n\n Queue<int[]> queue = new LinkedList<>();\n queue.offer(entrance);\n maze[entrance[0]][entrance[1]] = \'+\';\n\n int[][] directions = new int[][] {{0,1},{0,-1},{1,0},{-1,0}};\n\n int steps = 0;\n int x, y;\n while (!queue.isEmpty()) {\n steps++;\n\n int n = queue.size();\n for (int i = 0; i < n; i++) {\n int[] current = queue.poll();\n\n for (int[] direction : directions) {\n x = current[0] + direction[0];\n y = current[1] + direction[1];\n\n if (x < 0 || x >= rows || y < 0 || y >= columns) continue;\n if (maze[x][y] == \'+\') continue;\n\n if (x == 0 || x == rows - 1 || y == 0 || y == columns - 1) return steps;\n\n maze[x][y] = \'+\';\n queue.offer(new int[]{x, y});\n }\n }\n }\n return -1;\n }\n}\n```
| 83
| 4
|
['Array', 'Breadth-First Search', 'Matrix', 'Java']
| 9
|
nearest-exit-from-entrance-in-maze
|
BFS
|
bfs-by-votrubac-yi4p
|
C++\ncpp\nint dir[5] = {0, -1, 0, 1, 0};\nint nearestExit(vector<vector<char>>& m, vector<int>& ent) {\n queue<array<int, 3>> q; // i, j, steps\n q.push({
|
votrubac
|
NORMAL
|
2021-07-10T16:25:42.359381+00:00
|
2021-07-10T16:53:35.641305+00:00
| 6,549
| false
|
**C++**\n```cpp\nint dir[5] = {0, -1, 0, 1, 0};\nint nearestExit(vector<vector<char>>& m, vector<int>& ent) {\n queue<array<int, 3>> q; // i, j, steps\n q.push({ent[0], ent[1], 0});\n while(!q.empty()) {\n auto [i, j, steps] = q.front(); q.pop();\n if ((i != ent[0] || j != ent[1]) && (i == 0 || j == 0 || i == m.size() - 1 || j == m[i].size() - 1))\n return steps;\n for (int d = 0; d < 4; ++d) {\n int di = i + dir[d], dj = j + dir[d + 1];\n if (di >= 0 && dj >= 0 && di < m.size() && dj < m[di].size() && m[di][dj] == \'.\') {\n m[di][dj] = \'+\';\n q.push({di, dj, steps + 1});\n }\n }\n }\n return -1;\n}\n```
| 62
| 3
|
[]
| 19
|
nearest-exit-from-entrance-in-maze
|
[python3] BFS (2 styles) with line by line comments O(m*n)
|
python3-bfs-2-styles-with-line-by-line-c-uqex
|
BFS is more suitable for searching vertices closer to the given source. BFS is optimal for finding the shortest path.\n- DFS is more suitable when there are sol
|
MeidaChen
|
NORMAL
|
2022-11-21T06:55:25.294321+00:00
|
2024-01-04T19:21:42.589249+00:00
| 3,600
| false
|
- BFS is more suitable for searching vertices closer to the given source. BFS is optimal for finding the shortest path.\n- DFS is more suitable when there are solutions away from the source. DFS is not optimal for finding the shortest path.\n\nSo we chose BFS over DFS for this problem of finding the shortest path.\n\n**Style 1** Using ```maze``` to track visited positions and store the steps for each position inside the q.\n```python\nclass Solution:\n def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:\n ### Get the maze size, used later to check whether the neighbor is valid.\n m,n = len(maze),len(maze[0])\n \n ### The directions that we can go at each position.\n directions = [[0,1],[1,0],[0,-1],[-1,0]]\n \n ### We use deque to make the pop more efficient\n ### We also have the steps stored at each position, and at any time, \n ### if we see an exit, we simply return the steps.\n ### Note that if you don\'t put the steps along with the positions, \n ### you will need to keep track of the levels you are at during the search (see style2).\n q = deque([[entrance[0],entrance[1],0]])\n \n ### We don\'t need to use extra space to store the visited positions, \n ### since we can directly change the empty position in the maze to a wall.\n maze[entrance[0]][entrance[1]] = \'+\'\n \n ### Doing a regular BFS search using deque; if there is anything left in the q, we will keep doing the search\n while q:\n ### Pop form left of the q,\n ### Since we have steps stored at each position, we don\'t need to make a loop here (see style2 for the loop version).\n xo,yo,steps = q.popleft()\n \n ### Check if the current location is an exit, and make sure it is not the entrance.\n if (0 in [xo,yo] or xo==m-1 or yo==n-1) and [xo,yo]!=entrance:\n return steps\n \n ### We go in four directions.\n for xn,yn in directions:\n x,y = xo+xn,yo+yn\n ### Make sure the new location is still inside the maze and empty.\n if 0<=x<m and 0<=y<n and maze[x][y]==\'.\':\n ### We make the empty space into a wall, so we don\'t visit it in the future.\n maze[x][y] = \'+\'\n ### We need to increase the steps.\n q.append([x,y,steps+1])\n \n ### If we don\'t find the result in BFS, we need to return -1\n return -1\n```\n\n**Style 2** Using extra space for the visited positions and tracking steps using an extra variable (level by level search)\n```python\nclass Solution:\n def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:\n \n m,n = len(maze),len(maze[0])\n directions = [[0,1],[1,0],[0,-1],[-1,0]]\n q = deque([entrance])\n \n ### Using extra space to keep track of the visited positions.\n visited = {tuple(entrance)}\n \n ### Use steps to keep track of the level of the BFS.\n steps = 0\n while q:\n \n ### Since we are tracking the steps using a variable, \n ### we need to pop all elements at each level, then increase the steps.\n for _ in range(len(q)):\n xo,yo = q.popleft()\n if (0 in [xo,yo] or xo==m-1 or yo==n-1) and [xo,yo]!=entrance:\n return steps\n for xn,yn in directions:\n x,y = xo+xn,yo+yn\n ### Check if the new position has been visited or not., and only go into the unvisited ones.\n if 0<=x<m and 0<=y<n and maze[x][y]==\'.\' and (x,y) not in visited:\n visited.add((x,y))\n q.append([x,y])\n ### Increase the steps since we finished one level.\n steps += 1\n \n return -1\n```\n\nBoth styles work fine for this problem, but I prefer the first style for this problem, or more generally, I prefer to use the first one if I need to find some distance, e.g., **[The Maze](https://leetcode.com/problems/the-maze/)**. Style1 can be easily converted into **DFS** or **Dijkstra\'s algorithm**. So it is good to know this style!\n\nThe second style is more preferred, or you have to use it when you are asked to do something at each level during the search, such as this problem **[Reverse Odd Levels of Binary Tree](https://leetcode.com/problems/reverse-odd-levels-of-binary-tree/discuss/2590130/python3-bfs-and-dfs-with-line-by-line-comments)**. Give them a try if you want to practice more on BFS. \n\nThese are just my opinion; leave a comment below to let me know if you agree or disagree.\n\n**Upvote** if you like this post.\n\n**Connect with me on [LinkedIn](https://www.linkedin.com/in/meida-chen-938a265b/)** if you\'d like to discuss other related topics\n\n\uD83C\uDF1F If you are interested in **Machine Learning** || **Deep Learning** || **Computer Vision** || **Computer Graphics** related projects and topics, check out my **[YouTube Channel](https://www.youtube.com/@meidachen8489)**! Subscribe for regular updates and be part of our growing community.
| 48
| 2
|
[]
| 3
|
nearest-exit-from-entrance-in-maze
|
✅ [Python/C++] DFS sucks here, go BFS (explained)
|
pythonc-dfs-sucks-here-go-bfs-explained-uv3po
|
\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.\n*\nThis solution employs Breadth First Search* approach to explore the maze. Time complexity is linear: O(m\n)
|
stanislav-iablokov
|
NORMAL
|
2022-11-21T01:17:48.145458+00:00
|
2022-11-21T04:21:57.676831+00:00
| 4,736
| false
|
**\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n****\nThis solution employs *Breadth First Search* approach to explore the maze. Time complexity is linear: **O(m\\*n)**. Space complexity is linear: **O(m\\*n)**. \n****\n\n**Comment.** This problem can be solved by using both BFS and DFS, however, the latter seems to be a significantly slower approach. It is also important to mark visited cells when they are added to (and not popped from) the queue, check this [**explanation**](https://leetcode.com/problems/nearest-exit-from-entrance-in-maze/discuss/1329445/An-analysis-on-Time-Limit-Exceeded-(TLE)).\n\n**Python #1.** Fast BFS solution.\n```\nclass Solution:\n def nearestExit(self, maze: List[List[str]], e: List[int]) -> int:\n \n m, n = len(maze), len(maze[0])\n x, y = e\n \n # this lambda checks the exit condition \n is_exit = lambda i, j : i*j==0 or i==m-1 or j==n-1\n \n # this generator yields (!) allowed directions\n def adj(i,j, dirs=[1, 0, -1, 0, 1]):\n for d in range(4):\n ii, jj = i + dirs[d], j + dirs[d+1]\n if 0 <= ii < m and 0 <= jj < n and maze[ii][jj] != "+":\n yield ii,jj\n \n dq = deque([(x,y,0)]) # [1] start from the entrance...\n maze[x][y] = \'+\' # ...and mark it as visited\n while dq: # [2] while there are still places to go...\n i, j, s = dq.popleft() # ...try going there (don\'t try, do it!)\n for ii,jj in adj(i,j): # [3] look around, make a step...\n maze[ii][jj] = "+" # ...and mark it as visited\n if is_exit(ii,jj) : return s+1 # [4] great, it\'s the exit!\n dq.append((ii,jj,s+1)) # [5] or maybe not, continue searching\n \n return -1 # [6] BFS failed, there is no escape\n```\n\n**Python #2.** Crappy DFS solution that gives TLE.\n```\nclass Solution:\n def nearestExit(self, maze: List[List[str]], e: List[int]) -> int:\n \n m, n = len(maze), len(maze[0])\n \n is_exit = lambda i, j : (i!=e[0] or j!=e[1]) and (i*j==0 or i==m-1 or j==n-1)\n\n def adj(i,j, dirs=[1, 0, -1, 0, 1]):\n for d in range(4):\n ii, jj = i + dirs[d], j + dirs[d+1]\n if 0 <= ii < m and 0 <= jj < n and maze[ii][jj] != "+":\n yield ii,jj\n \n @lru_cache(None)\n def dfs(i, j, s = 0):\n if is_exit(i,j) : return s\n maze[i][j] = "+"\n dp = [dfs(ii, jj, s+1) for ii,jj in adj(i,j)] or [inf]\n maze[i][j] = "."\n return min(dp)\n \n return s if (s:=dfs(e[0], e[1])) < inf else -1\n```\n\nBFS solution in other languages.\n\n<iframe src="https://leetcode.com/playground/knSTh8vg/shared" frameBorder="0" width="800" height="650"></iframe>
| 34
| 3
|
[]
| 8
|
nearest-exit-from-entrance-in-maze
|
[Python] Easy DFS MEMOIZATION & BFS
|
python-easy-dfs-memoization-bfs-by-aatms-p34v
|
Nearest Exit from Entrance in Maze\n## DFS Idea\n We search from entrance cell for the nearest boundary cell in all four directions and after getting the distan
|
aatmsaat
|
NORMAL
|
2021-07-10T19:35:59.426878+00:00
|
2021-07-12T06:07:42.669353+00:00
| 4,643
| false
|
# **Nearest Exit from Entrance in Maze**\n## DFS Idea\n* We search from entrance cell for the nearest boundary cell in all four directions and after getting the distance from all direction, it returns *minimum* of them.\n* Function `reached` checks if currect cell is boundary and not the entrance cell\n* Here `@lru_cache(None)` is used for top-down memoization approach\n\n**Complexity**\n* Time Complexity :- `O(m*n)`\n* Space Complexity :- `O(m*n)` because of `@lru_cache(None)`\n\n```\nclass Solution:\n def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:\n x, y = entrance\n m, n, infi = len(maze), len(maze[0]), int(1e5)\n reached = lambda p, q: (not p==x or not q==y) and (p==0 or q==0 or p==m-1 or q==n-1)\n @lru_cache(None)\n def dfs(i, j):\n if i<0 or j<0 or i==m or j==n or maze[i][j]==\'+\':\n return infi\n if reached(i, j):\n return 0\n maze[i][j] = \'+\'\n ans = 1+min(dfs(i+1, j), dfs(i-1, j), dfs(i, j+1), dfs(i, j-1))\n maze[i][j] = \'.\'\n return ans\n ans = dfs(x, y)\n return -1 if ans>=infi else ans\n```\n*why DFS with dp sometimes give WA explained in the end*.\n\n## BFS Idea\n* We search from entrance cell for the nearest boundary cell in all four directions level by level i.e. 0, 1.... until we get boundary\n* Function `reached` checks if currect cell is boundary and not the entrance cell\n\n**Complexity**\n* Time Complexity :- `O(m*n)`\n* Space Complexity :- `O(m*n)`\n\n```\nclass Solution:\n def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:\n x, y = entrance\n m, n, infi = len(maze), len(maze[0]), int(1e5)\n reached = lambda p, q: (not p==x or not q==y) and (p==0 or q==0 or p==m-1 or q==n-1)\n q, ans = deque(), 0\n q.append((x, y, ans))\n directions = [1, 0, -1, 0, 1]\n while q:\n row, col, ans = q.popleft()\n for i in range(4):\n r, c = row+directions[i], col+directions [i+1]\n if r<0 or c<0 or r==m or c==n or maze[r][c]==\'+\':\n continue\n if reached(r, c):\n return ans+1\n maze[r][c] = \'+\'\n q.append((r, c, ans+1))\n return -1\n```\n\n**Why DFS with Memoization sometimes gives WA**:-.\n\nFor **DFS without memoization** all test case will give correct answer as it search every path but may give **TLE**, and for **DFS with dp** it totally depends on luck , what you search first.\nFor better understanding let\'s take example:-\n\n**e** denotes Entrance\n```\n++++\n.e.+\n.+.+\n...+\n++++\n```\n`Condition -> 1+min((i, j+1), .............)`\nAfter operations it will look like\n```\n++++\n7e1+\n6+2+\n543+\n++++\n```\n`ans = 1+min(7, 7, infinite, infinite)`\ninstead of \n`ans = 1+min(7, 1, infinite, infinite)`\n\n[Note] => *This example is just for intuition. For real example please see https://github.com/LeetCode-Feedback/LeetCode-Feedback/issues/4115*\n\n**Conclusion**:-\n* DFS without memoization works fine but gives TLE\n* DFS with memoization may give correct but not necessary\n* BFS searches level wise and gives result as soon as finds exit which is best for this problem\n\n*Please upvote if you like the solution and comment if have queries*
| 33
| 1
|
['Depth-First Search', 'Breadth-First Search', 'Memoization', 'Python']
| 6
|
nearest-exit-from-entrance-in-maze
|
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line
|
leetcode-the-hard-way-explained-line-by-ix6u6
|
\uD83D\uDD34 Check out LeetCode The Hard Way for more solution explanations and tutorials. \n\uD83D\uDFE0 Check out our Discord for live discussion.\n\uD83D\uDF
|
__wkw__
|
NORMAL
|
2022-11-21T03:14:21.029749+00:00
|
2022-11-21T03:14:21.029801+00:00
| 3,114
| false
|
\uD83D\uDD34 Check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \n\uD83D\uDFE0 Check out our [Discord](https://discord.gg/Nqm4jJcyBf) for live discussion.\n\uD83D\uDFE2 Give a star on [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post if you like it.\n\n---\n\n<iframe src="https://leetcode.com/playground/9GjRQFxZ/shared" frameBorder="0" width="100%" height="500"></iframe>
| 28
| 3
|
['Breadth-First Search', 'Graph', 'C', 'C++']
| 6
|
nearest-exit-from-entrance-in-maze
|
📌[C++] Most Intuitive | 🔥BFS
|
c-most-intuitive-bfs-by-divyamrai-mgbb
|
Consider looking at some additional BFS-related questions.\n 542. 01 Matrix\n 994. Rotting Oranges\n 1091. Shortest Path in Binary Matrix\n\n-------------------
|
divyamRai
|
NORMAL
|
2022-11-21T01:48:34.716394+00:00
|
2022-11-21T06:13:04.464937+00:00
| 3,310
| false
|
# Consider looking at some additional BFS-related questions.\n* [542. 01 Matrix](https://leetcode.com/problems/01-matrix/)\n* [994. Rotting Oranges](https://leetcode.com/problems/rotting-oranges/)\n* [1091. Shortest Path in Binary Matrix](https://leetcode.com/problems/shortest-path-in-binary-matrix/)\n\n----------------------------------------\n\n**C++**\n\n```\nclass Solution {\npublic:\n int dx[4] = {1 , -1 , 0 , 0};\n int dy[4] = {0 , 0 , -1 , 1};\n \n int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {\n \n queue<pair<int, int>> q;\n int n = maze.size() , m = maze[0].size();\n vector<vector<bool>> visited(n , vector<bool>(m, 0)); // keeping a visited matrix of the same size as that of the maze to keep track of visited cells\n \n visited[entrance[0]][entrance[1]] = 1; // The beginning point should be noted as visited.\n q.push({entrance[0] , entrance[1]}); // now add it to our queue for a subsequent BFS traversal.\n \n int level = 0;\n \n while( !q.empty() ) {\n \n int size = q.size();\n level++;\n \n while( size-- ) {\n \n pair<int, int> p = q.front();\n q.pop();\n \n for( int i = 0; i < 4; i++ ){\n \n int new_row = p.first+dx[i], new_col = p.second+dy[i];\n \n if( new_row >= 0 and new_col >= 0 and new_row < n and new_col < m){\n \n if(maze[new_row][new_col] != \'.\') continue;\n if(visited[new_row][new_col]) continue; // if this cell is already visited, don\'t check further \n \n if( new_row == 0 or new_col==0 or new_row == n-1 or new_col == m-1) return level; // if we reached a boundary, return the level\n \n visited[new_row][new_col] = 1;\n q.push({new_row, new_col});\n }\n }\n }\n }\n return -1;\n }\n};\n```\n\n-----------------------\n------------------------\n
| 20
| 5
|
[]
| 6
|
nearest-exit-from-entrance-in-maze
|
Simple BFS (Java) | 7ms | Beats 100%
|
simple-bfs-java-7ms-beats-100-by-ankitr4-jmfs
|
The idea is to perform simple breadth first search using a queue. While adding new elements, we perform a simple operation to check if the element being offered
|
ankitr459
|
NORMAL
|
2021-07-11T05:49:05.303634+00:00
|
2021-07-11T05:49:54.355472+00:00
| 3,702
| false
|
The idea is to perform simple breadth first search using a queue. While adding new elements, we perform a simple operation to check if the element being offered exists in first or last row **OR** first or last column.\n\n\n```\nclass Solution {\n public int nearestExit(char[][] maze, int[] entrance) {\n int rows = maze.length, cols = maze[0].length, queueSize;\n Queue<int[]> queue = new LinkedList<>();\n boolean[][] visited = new boolean[rows][cols];\n int[] curr;\n int[][] dirs = {{0,1},{0,-1},{1,0},{-1,0}};\n int x, y, steps = 0;\n \n queue.offer(entrance);\n visited[entrance[0]][entrance[1]] = true;\n \n while (!queue.isEmpty()) {\n queueSize = queue.size();\n steps++;\n \n for (int i=0;i<queueSize;i++) {\n curr = queue.poll();\n \n for (int[] dir: dirs) {\n x = dir[0]+curr[0]; \n y = dir[1]+curr[1];\n \n if (x<0||x>=rows||y<0||y>=cols) continue;\n if (visited[x][y] || maze[x][y] == \'+\') continue;\n \n\t\t\t\t\t// check if we have reached boundary\n if (x==0||x==rows-1||y==0||y==cols-1) return steps;\n \n queue.offer(new int[]{x, y});\n visited[x][y] = true;\n }\n }\n }\n \n return -1;\n }\n}\n```\n\nSpace - O(mn)\nTime - O(mn)\nwhere m = number of rows and n = number of columns\n
| 20
| 0
|
['Breadth-First Search', 'Queue', 'Java']
| 6
|
nearest-exit-from-entrance-in-maze
|
Python3 BFS with comments
|
python3-bfs-with-comments-by-brusht-lgy1
|
Idea: use BFS to return shortest path. Since we start BFS from the entrance and iterate level by level, one of our chosen paths will be the minimum (if it exist
|
brushT
|
NORMAL
|
2021-07-10T16:43:55.507335+00:00
|
2021-07-10T16:43:55.507363+00:00
| 4,235
| false
|
Idea: use BFS to return shortest path. Since we start BFS from the entrance and iterate level by level, one of our chosen paths will be the minimum (if it exists)\n```\ndef nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:\n dirs = [(0,1),(0,-1),(1,0),(-1,0)]\n entrance = (entrance[0],entrance[1])\n q = deque([entrance])\n visited = set()\n visited.add(entrance)\n step = 0\n while q:\n stepLength = len(q)\n for i in range(stepLength): # here, we can use length of the deque to iterate through level by level\n node = q.popleft()\n if node[0] == 0 or node[0] == len(maze) -1 or node[1] == 0 or node[1] == len(maze[0]) -1 :\n if maze[node[0]][node[1]] == \'.\' and (node[0],node[1]) != entrance:\n return step\n for d in dirs:\n newD = (node[0] + d[0], node[1] + d[1])\n if newD not in visited and 0<=newD[0]<len(maze) and 0<=newD[1]<len(maze[0]) and maze[newD[0]][newD[1]] == \'.\': # only add valid nodes to the queue!\n visited.add(newD) # mark it as visited, so we don\'t loop forever\n q.append(newD)\n step += 1 # after we finish with a level, increment step by one\n return -1\n\n```
| 19
| 0
|
['Breadth-First Search', 'Python', 'Python3']
| 1
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.