question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
complement-of-base-10-integer
|
C++| 100% faster| EASY TO UNDERSTAND | clean and efficient
|
c-100-faster-easy-to-understand-clean-an-2chc
|
Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome\n```\nclass
|
aarindey
|
NORMAL
|
2021-06-14T16:12:09.733173+00:00
|
2021-06-14T16:12:09.733213+00:00
| 863
| false
|
***Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome***\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int sum=0,i=0;\n if(n==0)\n return 1; \n while(n>0)\n {\n if(n%2==0)\n {\n sum+=1*pow(2,i);\n i++;\n n=n/2;\n }\n else\n {\n i++;\n n=n/2;\n }\n }\n return sum;\n }\n};
| 13
| 1
|
['C']
| 0
|
complement-of-base-10-integer
|
✅Java - One Line Code, Easy Explanation!!!
|
java-one-line-code-easy-explanation-by-p-osuh
|
Idea\n\nBInary Complement of 5(101) is 2(010)\n\nSee,\nConvert all bits of 5(101) to ones i.e 111(5)\nNow we know the answer i.e 7(111)-5(101) =2(010) \n\nSo, f
|
pgthebigshot
|
NORMAL
|
2022-01-04T05:39:57.020944+00:00
|
2022-01-04T06:29:50.739857+00:00
| 590
| false
|
**Idea**\n\nBInary Complement of 5(101) is 2(010)\n\nSee,\nConvert all bits of 5(101) to ones i.e 111(5)\nNow we know the answer i.e 7(111)-5(101) =2(010) \n\nSo, first find the size of bits of n i.e 3 in this case and pow(2,3)= 8 \nTherefore the answer be like 8-1-5=2\n\n````\nclass Solution {\n public int bitwiseComplement(int n) {\n \n return (int)(Math.pow(2,Integer.toBinaryString(n).length())-1-n);\n\t\t//return (int)(Math.pow(2,Integer.toBinaryString(n).length())-1-n) also work\n\t\t//return ((2 << (int)(Math.log(Math.max(n, 1)) / Math.log(2))) - 1) - n; also work(0 ms)\n }\n}\n````\n\nI hope you get it!!!\nPlease **upvote** if you liked the solution :))\n\nAll discussion are most welcomed!!!
| 9
| 4
|
['Java']
| 3
|
complement-of-base-10-integer
|
✅ [Solution] Swift: Complement of Base 10 Integer (+ test cases)
|
solution-swift-complement-of-base-10-int-a29l
|
swift\nclass Solution {\n func bitwiseComplement(_ n: Int) -> Int {\n var s: Int = 1\n while s < n { s = (s << 1) | 1 }\n return s - n\n
|
AsahiOcean
|
NORMAL
|
2021-05-27T19:47:22.671946+00:00
|
2022-01-04T03:38:02.915771+00:00
| 1,187
| false
|
```swift\nclass Solution {\n func bitwiseComplement(_ n: Int) -> Int {\n var s: Int = 1\n while s < n { s = (s << 1) | 1 }\n return s - n\n }\n}\n```\n\n---\n\n<p>\n<details>\n<summary>\n<img src="https://git.io/JDblm" height="24">\n<b>TEST CASES</b>\n</summary>\n\n<p><pre>\n<b>Result:</b> Executed 3 tests, with 0 failures (0 unexpected) in 0.005 (0.006) seconds\n</pre></p>\n\n```swift\nimport XCTest\n\nclass Tests: XCTestCase {\n \n private let solution = Solution()\n \n /// 5 is "101" in binary, with complement "010" in binary, which is 2 in base-10.\n func test1() {\n let value = solution.bitwiseComplement(5)\n XCTAssertEqual(value, 2)\n }\n \n /// 7 is "111" in binary, with complement "000" in binary, which is 0 in base-10.\n func test2() {\n let value = solution.bitwiseComplement(7)\n XCTAssertEqual(value, 0)\n }\n \n /// 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10.\n func test3() {\n let value = solution.bitwiseComplement(10)\n XCTAssertEqual(value, 5)\n }\n}\n\nTests.defaultTestSuite.run()\n```\n\n</details>\n</p>
| 9
| 0
|
['Swift']
| 0
|
complement-of-base-10-integer
|
Idiots solution for Python 3 (100%) no loops/bit manipulation
|
idiots-solution-for-python-3-100-no-loop-dwxd
|
Take the next power of 2 that is bigger than N, then subtract 1 from it to get the number that has the same leftmost bit, but with all of the bits to the right
|
fatmoron
|
NORMAL
|
2020-05-04T10:23:12.100848+00:00
|
2020-05-04T10:23:12.100898+00:00
| 1,117
| false
|
Take the next power of 2 that is bigger than N, then subtract 1 from it to get the number that has the same leftmost bit, but with all of the bits to the right filled. \n\nSubtract N from this number and you will get the bits to the right that are 0 converted to 1, which is what you are looking for, e.g. 010 as input, 011 as the number you calculate, 011-010 = 001. There is only one edge case for this solution at N == 0. \n\n def bitwiseComplement(self, N: int) -> int:\n if N == 0: \n return 1\n else:\n return 2**(int(log2(N))+1)-1 - N
| 9
| 1
|
[]
| 1
|
complement-of-base-10-integer
|
Java, simple 1 line bit manipulation (left & right shifts), 0ms
|
java-simple-1-line-bit-manipulation-left-c920
|
Just actually do the complement operation ~, after first shifting away all the leading zeroes, and then shift away all the trailing ones.\n\n public int bitw
|
jpv
|
NORMAL
|
2019-03-17T11:52:37.636362+00:00
|
2019-03-17T11:52:37.636405+00:00
| 944
| false
|
Just actually do the complement operation ~, after first shifting away all the leading zeroes, and then shift away all the trailing ones.\n```\n public int bitwiseComplement(int N) {\n return (N==0) ? 1 : (~(N<<(N=Integer.numberOfLeadingZeros(N))))>>N;\n }\n```
| 9
| 1
|
[]
| 3
|
complement-of-base-10-integer
|
Easy Python solution
|
easy-python-solution-by-vistrit-z5xa
|
\ndef bitwiseComplement(self, n: int) -> int:\n x=""\n for i in bin(n)[2:]:\n if i=="1":\n x+="0"\n else:\n
|
vistrit
|
NORMAL
|
2022-01-04T01:20:47.226730+00:00
|
2022-01-04T01:20:47.226777+00:00
| 1,099
| false
|
```\ndef bitwiseComplement(self, n: int) -> int:\n x=""\n for i in bin(n)[2:]:\n if i=="1":\n x+="0"\n else:\n x+="1"\n return int(x,2)\n```
| 8
| 1
|
['Python', 'Python3']
| 1
|
complement-of-base-10-integer
|
JAVA One Liner 100% Faster Solution || Explaination
|
java-one-liner-100-faster-solution-expla-8vcf
|
\n\nn = 10 decimal \nn = ...001010\n~n = ...110101\nIntege
|
abhishekpatel_
|
NORMAL
|
2021-07-06T04:14:03.448704+00:00
|
2021-07-06T04:31:36.993608+00:00
| 419
| false
|
\n```\nn = 10 decimal \nn = ...001010\n~n = ...110101\nInteger.highestOneBit(n) = ...001000\nInteger.highestOneBit(n)-1 = ...000111\n~n & Integer.highestOneBit(n)-1 = ...000101\n\n```\n\n\n\n\n**SOLUTION:**\n```\nclass Solution {\n public int bitwiseComplement(int n) {\n return n==0?1: ~n & Integer.highestOneBit(n)-1;\n }\n}\n```
| 8
| 0
|
['Java']
| 1
|
complement-of-base-10-integer
|
[Java/Python] Straightforward Bit Manipulation - Clean code - O(logN)
|
javapython-straightforward-bit-manipulat-3l6w
|
Complexity\n- Time: O(logN)\n- Space: O(1)\n\nPython\npython\nclass Solution(object):\n def bitwiseComplement(self, N):\n def setBit(x, k):\n
|
hiepit
|
NORMAL
|
2020-10-05T07:38:59.097292+00:00
|
2020-10-05T07:58:41.582500+00:00
| 485
| false
|
**Complexity**\n- Time: `O(logN)`\n- Space: `O(1)`\n\n**Python**\n```python\nclass Solution(object):\n def bitwiseComplement(self, N):\n def setBit(x, k):\n return (1 << k) | x\n \n if N == 0: return 1\n i, ans = 0, 0\n while N > 0:\n if N % 2 == 0:\n ans = setBit(ans, i)\n i += 1\n N /= 2\n return ans\n```\n\n**Java**\n```java\nclass Solution {\n public int bitwiseComplement(int N) {\n if (N == 0) return 1;\n int ans = 0, i = 0;\n while (N > 0) {\n if (N % 2 == 0) \n ans = setBit(ans, i);\n i += 1;\n N /= 2;\n }\n return ans;\n }\n \n int setBit(int x, int k) {\n return (1 << k) | x;\n }\n}\n```\n\nFeel free to ask your question in the comments, help to **vote** if this post is useful to you.
| 8
| 6
|
[]
| 1
|
complement-of-base-10-integer
|
[Python] XOR masking explained
|
python-xor-masking-explained-by-sidheshw-4lal
|
For easy writing num is written as n\n\nSo the agenda of the question is to flip all the bits of given number. i.e., \nn = 4 (100) => 3 (011)\n\nOne way of ache
|
sidheshwar_s
|
NORMAL
|
2022-01-04T04:14:45.557875+00:00
|
2022-01-04T04:14:45.557923+00:00
| 680
| false
|
*For easy writing num is written as n*\n\nSo the agenda of the question is to flip all the bits of given number. i.e., \n` n = 4 (100) => 3 (011)`\n\nOne way of acheving it is **xor between the number and its mask**, i.e., `100 ^ 111 == 011`\n\n* **So now how to get its mask ?**\n\t* A simple way would be to initialize mask = 0 and keep flipping bits of it to 1 starting from the rightmost bit (LSB) till we reach the leftmost set bit of num.\n\n* **Now, how do we know that we reached the leftmost set bit in num?**\n\t* We use another variable temp = n. Each time, we will rightshift temp essentially removing the rightmost bit. When we remove the leftmost set bit from it, it will become 0. Thus, we loop till temp is not 0.\n\n* **What if initially n = 0?**\n\t* We handle that case in the start itself, so that there wont be any uncertainity.\n\n```\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n if not n: return 1\n mask = 0\n temp = n\n while temp:\n mask = (mask << 1) | 1\n temp >>= 1\n return n ^ mask\n```\n*Time complexity : O(N) where N = length of bits\nSpace complexity: O(1)*\n\n ***Upvote, if this helped.***\n\n\n\n
| 7
| 1
|
['Bit Manipulation', 'Python']
| 2
|
complement-of-base-10-integer
|
C++, 1-liner, 9 CPU instructions, and future (C++20) solution
|
c-1-liner-9-cpu-instructions-and-future-d7b1p
|
This is a complement of the other "standard solutions". If you haven\'t yet, go read the solution or other posts first, please.\n\nSince this solution uses eith
|
alvin-777
|
NORMAL
|
2020-10-06T05:39:41.404460+00:00
|
2020-10-06T05:39:41.404514+00:00
| 648
| false
|
> This is a complement of the other "standard solutions". If you haven\'t yet, go read the solution or other posts first, please.\n\nSince this solution uses either a C++20 function `std::countl_zero()` (at this point of time, it seems even the latest GCC (10.2) hasn\'t implement it, Microsoft added it in VS2019 version 16.8 preview 2 just last month!) or a built-in function, please read this post just for fun. Or maybe come back in two years :)\n\n----\n### Version 1\n\nIf we have C++20:\n```cpp\n return N ? ((1 << (32 - countl_zero(N))) - 1) ^ N : 1;\n```\nFor now (gcc9), below will work:\n```cpp\n return N ? ((1 << (32 - __builtin_clz(N))) - 1) ^ N : 1;\n```\n\nThis version was inspired by the approach 3 from the [solution](https://leetcode.com/problems/complement-of-base-10-integer/solution/):\n```java\n// Java\nclass Solution {\n public int bitwiseComplement(int N) {\n return N == 0 ? 1 : (Integer.highestOneBit(N) << 1) - N - 1;\n }\n}\n```\n\nLater I realised that it can be better!\n\n### Version 2\n\n```cpp\n // C++20\n return N ? (0xFFFFFFFF >> countl_zero(N)) ^ N : 1;\n // GCC9\n return N ? (0xFFFFFFFF >> __builtin_clz(N)) ^ N : 1;\n```\n\n### Version 3-beta\n\nNow, are we able to eliminate the `ifelse`/`?:` branching?\nWhy not? We can just make the least significant/right most bit of the mask always 1. Easy!\n```cpp\n // C++20\n return ((0xFFFFFFFF >> countl_zero(N)) | 1) ^ N;\n // GCC9 (won\'t work on Leetcode! See note below)\n return ((0xFFFFFFFF >> __builtin_clz(N)) | 1) ^ N;\n```\nNote since LeetCode OJ compiles C++ with the `-fsanitize=undefined` flag, it will throw runtime error if passing 0 to `__builtin_clz()`\nBut don\'t worry! We can tweak the input!\n\n### Version 3\n\n```cpp\n // C++20\n return (0xFFFFFFFF >> countl_zero(N | 1)) ^ N;\n // GCC9\n return (0xFFFFFFFF >> __builtin_clz(N | 1)) ^ N;\n```\nExplain: for N > 1, changing the last bit will not effect the number of leading 0s, and for both 1 and 0 we use the same mask `0x1` (ie, `0xFFFFFFFF >> 31`).\n\n----\n### Performance\n\nSo how much have we improved?\nWe know approach 4 from the solution (for non-premium users who can\'t read the solution, see reference below) is faster than any other approaches since it doesn\'t have any loop or call any other functions like `log()` (Note `__builtin_clz()` is a builtin function that translates to **one single CPU instruction** `BSR` (bit scan reverse))\nI counted number of lines in assembly code and CPU instructions the code compiled into (GCC 10.2):\n\n| | # Lines of assembly code | # CPU instructions |\n| ------------- | ---------------------------- | -------------------- |\n| Approach 4 | 25 | 23 |\n| Version 1 | 16 | 14 |\n| Version 2 | 14 | 12 |\n| Version 3 | 9 | 9 |\n\nReference:\nApproach 4:\n```cpp\nint bitwiseComplement(int N) {\n if (N == 0) return 1;\n int bitmask = N;\n bitmask |= (bitmask >> 1);\n bitmask |= (bitmask >> 2);\n bitmask |= (bitmask >> 4);\n bitmask |= (bitmask >> 8);\n bitmask |= (bitmask >> 16);\n return bitmask ^ N;\n}\n```\n\n----\n## Further thoughts\n\nSince `std::countl_zero()` is a template, which can handle any type of integral values, can we do that as well?\nBelow will do:\n\n```cpp\ntemplate <class T>\nint bitwiseComplement(T N) {\n return (numeric_limits<make_unsigned<T>::type>::max() >> countl_zero(N | 1)) ^ N;\n}\n```\nNote this requires C++20.\nSince `__builtin_clz()` is only for `int` (`__builtin__clzl()` for `long` and `__builtin__clzll()` for `long long`), it\'ll be trickier to make it happen. That\'ll be too far from the scope of this problem, so I\'m stopping here.\n\nEnjoy :)\n
| 7
| 0
|
['C']
| 2
|
complement-of-base-10-integer
|
Best Solution
|
best-solution-by-kumar21ayush03-rvf4
|
Approach\nUsing Bitwise Operator\n\n# Complexity\n- Time complexity:\nO(logn)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int bitwi
|
kumar21ayush03
|
NORMAL
|
2023-05-19T06:04:38.343732+00:00
|
2023-05-19T06:04:38.343774+00:00
| 689
| false
|
# Approach\nUsing Bitwise Operator\n\n# Complexity\n- Time complexity:\n$$O(logn)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int num = n;\n int mask = 0;\n if (n == 0)\n return 1;\n while (num != 0) {\n mask = (mask << 1) | 1;\n num = num >> 1; \n }\n int ans = (~n) & mask;\n return ans;\n }\n};\n```
| 6
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
C++ XOR, simple solution
|
c-xor-simple-solution-by-apoorvtyagi10-onjg
|
Approach: \n\n- Find the first number which is greater than "num" and have all 1s (Eg: 1, 3(11), 7(111), 15(1111), ...)\n- The relation b/w numbers with all 1s
|
apoorvtyagi10
|
NORMAL
|
2021-12-27T13:16:47.371181+00:00
|
2021-12-29T19:20:21.640112+00:00
| 351
| false
|
Approach: \n\n- Find the first number which is greater than "num" and have all 1s (Eg: 1, 3(11), 7(111), 15(1111), ...)\n- The relation b/w numbers with all 1s is 2x + 1, starting from x=1\n- Finally xor the num with x.\n- If num = 5(binary 101), x evaluates as 7 (binary 111) and (num^x) evaluates as 010 which is compliment of 5\n\n\t\n```\nint bitwiseComplement(int num) {\n\tint x = 1;\n\twhile(x<num) x = 2*x + 1;\n\treturn num^x;\n}\n```
| 6
| 0
|
['C', 'C++']
| 1
|
complement-of-base-10-integer
|
Java O(1) | 1 line Solution
|
java-o1-1-line-solution-by-tbekpro-a4qn
|
I find the length of binary representation. For example, for 5 it will base-2 is "101" and length of this String is 3. \n2. Then by doing 1 << 3, I will have "1
|
tbekpro
|
NORMAL
|
2022-12-12T07:05:37.725087+00:00
|
2022-12-12T07:05:37.725125+00:00
| 726
| false
|
1. I find the length of binary representation. For example, for 5 it will base-2 is "101" and length of this String is 3. \n2. Then by doing 1 << 3, I will have "1000" which 8 in base-10. \n3. Then I do 8 - 1 = 7, which is "111" in base-2.\n4. By applying XOR operation I will have "101" XOR "111" = "010", which is 2 in base-10.\n\n# Code\n```\nclass Solution {\n public int bitwiseComplement(int n) {\n return n ^ ((1 << Integer.toBinaryString(n).length()) - 1);\n }\n}\n```
| 5
| 0
|
['Java']
| 1
|
complement-of-base-10-integer
|
Python Simple Solution with Detail Explanation : O(log n)
|
python-simple-solution-with-detail-expla-qjml
|
There are 3 steps to be performed in this question:\n1. Convert Decimal (Base 10) number into to binary (Base 2)\n\t(We divide the number by 2 and write the rem
|
yashitanamdeo
|
NORMAL
|
2022-01-04T15:55:55.214819+00:00
|
2022-01-12T14:53:33.183197+00:00
| 627
| false
|
There are 3 steps to be performed in this question:\n1. Convert Decimal (Base 10) number into to binary (Base 2)\n\t(We divide the number by `2` and write the remainders from bottom to top order)\n\t**Example:**\n\t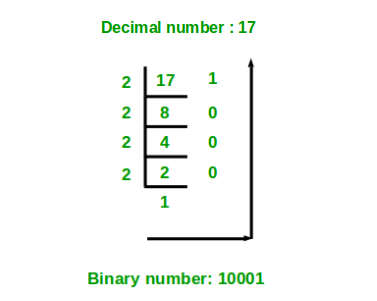\n(Picture credit gfg)\n\n2. Take the complement of the binary number\n\t(Convert all **0 -> 1** and **1 -> 0**)\n\n3. Convert the complement number back into decimal (Base 10)\n\tEvery place in a number has its factors eg: one\'s place(**2^0**), ten\'s place(**2^1**) and so on.\n\t**Example:**\n\t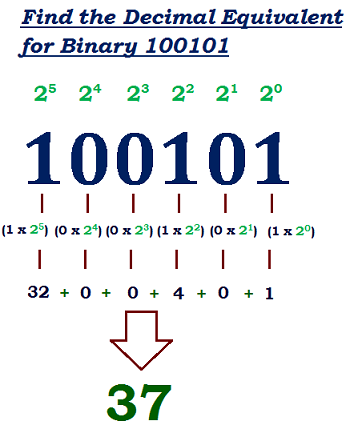\n(Picture credit ncalculators)\t\n\t\n**Base case:**\nIf number (in decimal format) is `0` then it will be `0` (in binary format) and it\'s complement will be `1`(in binary) and converting it again will be `1` (in decimal) \n\tSo we can directly **return `1` if n is `0`**\n\t\n**Else part:**\n We take 2 variables, `result` which will store the final output and, \n\t`factor` which is basically every place factors **(2^0 = 1, 2^1 = 2, 2^2 = 4)** which is inshort multiplied by `2 `in every step.\n \n`(1 if n%2 == 0 else 0) `\nThis part is a mixture of step 1 and 2.\n* If `n % 2` is `0` that means in division(step1) the remainder will come `0` and its complement is `1` so we return the complement (which is `1`) \n* And similarly, is `n % 2` is `1` that means in division(step1) the remainder is `1` and its complement is `0` so we return the complement(which is `0`)\n\t\nLet us understand how the code works with an example:\n\n\n\n**Code:**\n```\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n if n == 0:\n return 1\n else:\n result = 0\n factor = 1\n \n while(n > 0):\n result += factor * (1 if n%2 == 0 else 0)\n factor *= 2\n n //= 2\n return result\n```
| 5
| 0
|
['Python', 'Python3']
| 1
|
complement-of-base-10-integer
|
[C++] Simple Bitwise Solution Explained, 100% Time, ~25% Space
|
c-simple-bitwise-solution-explained-100-9o0ow
|
A rather simple problem to tackle and the way to do it is rather straightforward itself, where you might just decide to do things differently mostly in terms of
|
ajna
|
NORMAL
|
2020-10-05T10:19:35.146489+00:00
|
2020-10-05T10:19:35.146519+00:00
| 574
| false
|
A rather simple problem to tackle and the way to do it is rather straightforward itself, where you might just decide to do things differently mostly in terms of which bitwise trick to employ or not here.\n\nTo solve this challenge, I first of all created 2 support variables:\n* `res` to store our own result;\n* `i` to store the current power of 2 we are working with.\n\nWe are going to loop until we reach `n == 0` and please note that this approach is more efficient than a few others, constantly using 31 bits even for smaller numbers.\n\nAlso notice that we are using a `do`... `while` loop, since we want it to run at least once, in order to handle the edge case when we initially already have `n == 0`.\n\nInside the loop we will keep shaving off the right most (ie: less significant) bit with `2 & 1`, then reverse it with `^ 1` (althought you might just go for other tricks here, like using boolean negation: `!(n % 2)`, for example) and finally we multiply it by the current power of 2 we are treating at the moment.\n\nAfter that, we prepare the ground for the next iteration, specularly multiplying `i` by `2` (with the shift assignment operator `<<=`, because bitwise!) and dividing `n` by `2`.\n\nOnce we are done looping, time to return `res` :)\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n // support variables\n int res = 0, i = 1;\n // shaving off the least significant bit from n and adding its complement to res\n do {\n // updating res\n\t\t\tres += ((n & 1) ^ 1) * i;\n // preparing for the next iteration\n\t\t\ti <<= 1;\n n >>= 1;\n } while (n);\n return res;\n }\n};\n```
| 5
| 0
|
['Bit Manipulation', 'C', 'C++']
| 0
|
complement-of-base-10-integer
|
x86 assembly, six instructions, no branches or loops
|
x86-assembly-six-instructions-no-branche-qszx
|
Assuming input in %edi, output in %eax.\n\n\nmovl $31, %ecx\nlzcntl %edi, %eax\ncmovbl %ecx, %eax\nnotl %edi\nshlxl %eax, %edi, %ecx\nshrxl %eax, %ecx,
|
coder_xyzzy
|
NORMAL
|
2019-03-18T17:43:21.042037+00:00
|
2019-03-18T17:43:21.042067+00:00
| 1,031
| false
|
Assuming input in `%edi`, output in `%eax`.\n\n```\nmovl $31, %ecx\nlzcntl %edi, %eax\ncmovbl %ecx, %eax\nnotl %edi\nshlxl %eax, %edi, %ecx\nshrxl %eax, %ecx, %eax\n```
| 5
| 0
|
[]
| 1
|
complement-of-base-10-integer
|
Simple Java Sol (XOR)
|
simple-java-sol-xor-by-poorvank-bf9z
|
\npublic class ComplementBase10 {\n\n public int bitwiseComplement(int N) {\n // Find number of bits in the given integer\n int bitCount = (int
|
poorvank
|
NORMAL
|
2019-03-17T04:02:29.011313+00:00
|
2019-03-17T04:02:29.011371+00:00
| 881
| false
|
```\npublic class ComplementBase10 {\n\n public int bitwiseComplement(int N) {\n // Find number of bits in the given integer\n int bitCount = (int) Math.floor(Math.log(N)/Math.log(2))+1;\n\n // XOR the given integer with math.pow(2,bitCount-1)\n return ((1 << bitCount) - 1) ^ N;\n }\n\n}\n```
| 5
| 2
|
[]
| 1
|
complement-of-base-10-integer
|
🚀🔥 Beating 100% 🚀 | ⚡ Ultimate Bitwise Complement Solution in Java! 💯✅
|
beating-100-ultimate-bitwise-complement-a1eqy
|
🧠 Intuition
The goal is to find the bitwise complement of a given number n.The bitwise complement flips all bits:
0 ➝ 1 ✅
1 ➝ 0 ❌
Instead of flipping each bit d
|
DanishaDS
|
NORMAL
|
2025-02-15T04:36:32.735113+00:00
|
2025-02-15T04:36:32.735113+00:00
| 144
| false
|
🧠 Intuition
The goal is to find the bitwise complement of a given number n.
The bitwise complement flips all bits:
0 ➝ 1 ✅
1 ➝ 0 ❌
Instead of flipping each bit directly, your approach reconstructs the complement by summing the powers of 2 corresponding to 0 bits. 🛠️
💡 Approach
1️⃣ Edge Cases:
If n == 0, return 1 (since 0 flips to 1). 🟢
If n == 1, return 0 (since 1 flips to 0). ❌
2️⃣ Convert n to Binary & Flip Bits:
Iterate through each bit of n from right to left. 🔄
If the current bit is 0, add the corresponding power of 2 to t. ⚡
Keep dividing n by 2 to process the next bit.
3️⃣ Return the Result 🎯
📊 Complexity Analysis
Time Complexity: 🕒 O(log n)
The loop runs while n > 1, which is approximately log₂(n) iterations. 📉
Space Complexity: 🏗 O(1)
Only a few variables (i, t, n) are used, making it constant space. ✅
🎯 Example Walkthrough
Input: n = 5
Binary Representation: 101 🔢
Complement Calculation:
1st bit: 1 → Skip
2nd bit: 0 → Add 2^1 = 2
3rd bit: 1 → Skip
Complement Result: 2 🎉
Output: 2 🚀
# Code
```java []
class Solution {
public int bitwiseComplement(int n) {
int i=0;
double t=0;
if(n==0)
{
return 1;
}
if(n==1)
{
return 0;
}
while(n>1)
{
if(n%2==0)
{
t=t+Math.pow(2,i);
}
i++;
n/=2;
}
return (int)t;
}
}
```
| 4
| 0
|
['Java']
| 0
|
complement-of-base-10-integer
|
💢☠💫Easiest👾Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅C#✅💥🔥💫Explained☠💥🔥 Beats 100
|
easiestfaster-lesser-cpython3javacpython-jq5r
|
Intuition\n\n\n\n\n\n Describe your first thoughts on how to solve this problem. \njavascript []\n//JavaScript Code\n/**\n * @param {number} n\n * @return {numb
|
Edwards310
|
NORMAL
|
2024-08-22T13:27:44.618342+00:00
|
2024-08-22T13:27:44.618369+00:00
| 568
| false
|
# Intuition\n\n\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n```javascript []\n//JavaScript Code\n/**\n * @param {number} n\n * @return {number}\n */\nvar bitwiseComplement = function(n) {\n if(n === 0)\n return 1\n let i\n for(i = 1; i <= n; i *= 2)\n n = n ^ i\n return n\n};\n```\n```C++ []\n//C++ Code\nclass Solution {\npublic:\n int bitwiseComplement(int num) {\n int m = num;\n int mask = 0;\n if(num == 0)\n return 1;\n \n while(m != 0){\n mask = (mask << 1) | 1;\n m = m >> 1;\n }\n int ans = (~num) & mask;\n return ans;\n }\n};\n```\n```Python3 []\n#Python3 Code\nclass Solution:\n def bitwiseComplement(self, num: int) -> int:\n if num == 0: return 1\n mask = 0\n temp = num\n while temp:\n mask = (mask << 1) | 1\n temp >>= 1\n return num ^ mask\n```\n```Java []\n//Java Code\nclass Solution {\n public int bitwiseComplement(int n) {\n StringBuilder res = new StringBuilder("");\n String t = Integer.toBinaryString(n);\n for(char x : t.toCharArray()){\n if(x == \'1\')\n res.append(\'0\');\n else\n res.append(\'1\');\n }\n\n return Integer.parseInt(res.toString(), 2);\n }\n}\n```\n```C []\n//C Code\nint bitwiseComplement(int num) {\n int m = num;\n int mask = 0;\n if(num == 0)\n return 1;\n \n while(m != 0){\n mask = (mask << 1) | 1;\n m = m >> 1;\n }\n int ans = (~num) & mask;\n return ans;\n}\n```\n```Python []\n#Python Code\nclass Solution(object):\n def bitwiseComplement(self, num):\n """\n :type n: int\n :rtype: int\n """\n if num == 0: return 1\n mask = 0\n temp = num\n while temp:\n mask = (mask << 1) | 1\n temp >>= 1\n return num ^ mask\n```\n```C# []\n//C# Code\npublic class Solution {\n public int BitwiseComplement(int num) {\n int m = num;\n int mask = 0;\n if(num == 0)\n return 1;\n \n while(m != 0){\n mask = (mask << 1) | 1;\n m = m >> 1;\n }\n int ans = (~num) & mask;\n return ans;\n }\n}\n```\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n
| 4
| 0
|
['Bit Manipulation', 'C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript', 'C#']
| 1
|
complement-of-base-10-integer
|
XOR mask method that beats 100% of users
|
xor-mask-method-that-beats-100-of-users-88isv
|
Intuition\nUse XOR to flip the bits.\n\n# Approach\nMake a 111... mask with number n\'s bits length.\nXOR number n with the 111... mask to flip the bits.\n\n# C
|
Josephood7
|
NORMAL
|
2024-06-01T06:54:21.529518+00:00
|
2024-06-01T06:54:21.529583+00:00
| 228
| false
|
# Intuition\nUse XOR to flip the bits.\n\n# Approach\nMake a 111... mask with number n\'s bits length.\nXOR number n with the 111... mask to flip the bits.\n\n# Complexity\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if(n == 0) return 1;\n\n int flip = 0;\n int ans = n;\n while(n){\n n >>= 1; // divided by 2 until it\'s zero\n flip = flip << 1 | 1; // make a n.length 111... mask\n }\n ans ^= flip; // XOR 111... mask to flip the bits\n return ans;\n }\n};\n```
| 4
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
BITWISE OPERATORS SOLUTIONS
|
bitwise-operators-solutions-by-2005115-xkga
|
PLEASE UPVOTE MY SOLUTION IF YOU LIKE IT\n# CONNECT WITH ME\n### https://www.linkedin.com/in/pratay-nandy-9ba57b229/\n#### https://www.instagram.com/pratay_nand
|
2005115
|
NORMAL
|
2023-10-13T05:16:29.125296+00:00
|
2023-10-13T05:16:29.125319+00:00
| 479
| false
|
# **PLEASE UPVOTE MY SOLUTION IF YOU LIKE IT**\n# **CONNECT WITH ME**\n### **[https://www.linkedin.com/in/pratay-nandy-9ba57b229/]()**\n#### **[https://www.instagram.com/pratay_nandy/]()**\n\n# Approach\nHere\'s a step-by-step explanation of the approach used in this code:\n\n1. Initialize `m` to the value of `n`. `m` will be used to calculate the length of the binary representation of `n`.\n\n2. Check if `m` is equal to 0. If `n` is 0, its bitwise complement is 1. In this case, the function directly returns 1.\n\n3. Initialize a variable `mask` to 0. The `mask` variable is used to create a bit mask of 1s with the same length as the binary representation of `n`.\n\n4. Use a `while` loop to calculate the `mask`:\n - In each iteration, `mask` is left-shifted by 1 bit and then bitwise ORed with 1. This effectively adds a \'1\' to the `mask`.\n - The loop continues until `m` becomes 0. This loop calculates a bit mask with all 1s, and the length of the mask is equal to the number of bits required to represent `n`.\n\n5. Calculate the bitwise complement of `n`:\n - `(~n)` computes the bitwise negation of `n`, changing all 0s to 1s and all 1s to 0s.\n - `& mask` performs a bitwise AND operation between the negated value and the mask. This operation sets all bits in `n` to 0 except for the least significant bits that are part of the binary representation of `n`.\n\n6. Return the result, which is the bitwise complement of the input integer `n`.\n\nThis code successfully calculates the bitwise complement of an integer `n` by creating a mask with the same length as the binary representation of `n` and then applying the negation and bitwise AND operations.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:**0(N)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:**0(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int m = n;\n if(m==0)return 1;\n int mask = 0 ;\n while(m!=0)\n {\n mask = (mask << 1) | 1;\n m = m >> 1;\n }\n int ans = (~n) & mask; \n return ans;\n }\n};\n```
| 4
| 0
|
['Bit Manipulation', 'C', 'C++']
| 0
|
complement-of-base-10-integer
|
Python Simple Solution Faster Than 99.49%
|
python-simple-solution-faster-than-9949-l0wb5
|
\t\n\tclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n s=bin(n).replace(\'0b\',\'\')\n t=\'\'\n for i in s:\n
|
pulkit_uppal
|
NORMAL
|
2022-10-26T00:11:44.089132+00:00
|
2022-10-26T00:11:44.089174+00:00
| 616
| false
|
\t```\n\tclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n s=bin(n).replace(\'0b\',\'\')\n t=\'\'\n for i in s:\n if i==\'0\':\n t+=\'1\'\n else:\n t+=\'0\'\n return int(t,2)\n```
| 4
| 0
|
['Python']
| 0
|
complement-of-base-10-integer
|
Easy Python Solution | O(1)T, O(1)S | Explanation
|
easy-python-solution-o1t-o1s-explanation-08y9
|
The idea is to XOR the number with a mask. The mask should contain all 1\'s in it\'s rightmost bits. Here, the number of 1\'s is important. For example: for the
|
mohd_mustufa
|
NORMAL
|
2022-01-04T18:08:31.833021+00:00
|
2022-01-04T18:08:31.833073+00:00
| 76
| false
|
The idea is to XOR the number with a mask. The mask should contain all 1\'s in it\'s rightmost bits. Here, the number of 1\'s is important. For example: for the number 5 (101), the mask should be 7 (111) which contains only 3 1\'s because the number 5 uses only 3 rightmost bits. Now when we XOR 5 and 7, we get 2:\n101 -> 5\n111 -> 7\n---- (XOR)\n010 -> 2\n\nIn positive integers, the rightmost bit is always set to 1. The idea is to use this bit to set all the other bits to 1. For example, if we take an 8-bit number 10000000, we can perform the following operations to generate the mask:\n\nStep 1 : mask |= mask >> 1\n10000000\n 1000000 (OR)\n\\------------\n11000000\n\nStep 2 : mask |= mask >> 2\n11000000\n 110000(OR)\n\\------------\n11110000\n\nStep 3 : mask |= mask >> 4\n11110000\n 1111(OR)\n\\------------\n11111111\n\nThe number (11111111) generated above is the mask. Now all we have to do is XOR this mask with the original number. This operation will invert all the bits in the original number.\n\nThe above number was 8 bit integer, therefore we got the mask in 3 steps. If the number was 32 bit, we would get the mask in the 5th step where we right-shift the number by 16.\n\n```\ndef bitwiseComplement(self, N: int) -> int:\n if N == 0:\n return 1\n \n mask = N\n mask |= mask >> 1\n mask |= mask >> 2\n mask |= mask >> 4\n mask |= mask >> 8\n mask |= mask >> 16\n \n return N ^ mask\n```
| 4
| 0
|
['Bitmask']
| 0
|
complement-of-base-10-integer
|
C++ using vector
|
c-using-vector-by-ayush_srivastava02-ybw6
|
```\n#define ull unsigned long long\nclass Solution {\npublic:\n vector binary(int n){\n vector bin;\n int temp=0;\n while(n>0){\n
|
ayush_srivastava02
|
NORMAL
|
2022-01-04T08:38:33.977673+00:00
|
2022-07-28T18:56:40.398615+00:00
| 214
| false
|
```\n#define ull unsigned long long\nclass Solution {\npublic:\n vector<int> binary(int n){\n vector<int> bin;\n int temp=0;\n while(n>0){\n int rem = n%2;\n bin.push_back(rem);\n n/=2;\n }\n reverse(bin.begin(),bin.end());\n return bin;\n }\n \n int bitwiseComplement(int n) {\n if(n==0) return 1;\n vector<int> bin = binary(n);\n for(auto &it:bin){\n if(it==0) it=1;\n else it=0;\n }\n int k = bin.size();\n ull sum=0;\n int l=k;\n for(int i=0;i<k;i++){\n sum+=pow(2,(l-1))*bin[i];\n l--;\n }\n return sum;\n }\n};
| 4
| 0
|
['C', 'C++']
| 0
|
complement-of-base-10-integer
|
C++ || Easy to Understand || Xor || Masking
|
c-easy-to-understand-xor-masking-by-luci-7fof
|
class Solution {\npublic:\n\n int bitwiseComplement(int n) {\n if(n==0){\n return 1;\n }\n int copy=n;\n int i=0;\n
|
luciferraturi
|
NORMAL
|
2022-01-04T05:12:16.417699+00:00
|
2022-01-04T05:12:16.417769+00:00
| 165
| false
|
class Solution {\npublic:\n\n int bitwiseComplement(int n) {\n if(n==0){\n return 1;\n }\n int copy=n;\n int i=0;\n while(copy!=0){\n copy>>=1;\n n^=(1<<i);\n i++;\n }\n return n;\n }\n};
| 4
| 0
|
['Bit Manipulation', 'C', 'Bitmask', 'C++']
| 0
|
complement-of-base-10-integer
|
Simple Java solution | 0 ms beats 100% submissions
|
simple-java-solution-0-ms-beats-100-subm-srr5
|
```\n public int bitwiseComplement(int N) {\n if(N==0)\n return 1;\n int count = 0;\n int oldnum= N;\n \n //coun
|
yogidalal90
|
NORMAL
|
2020-10-05T12:42:37.926265+00:00
|
2020-10-05T14:05:07.258993+00:00
| 439
| false
|
```\n public int bitwiseComplement(int N) {\n if(N==0)\n return 1;\n int count = 0;\n int oldnum= N;\n \n //count the num of digits in binary form for the given number\n while(N > 0){\n N >>=1;\n count++;\n }\n \n // generate a number with all digits as 1\n int num =0;\n while(count>0){\n num = num <<1;\n num = num|1;\n count--;\n }\n // XOR will reverse the bits (e.g. 1010 ^ 1111 = 0101)\n return num ^ oldnum;\n }\n\t
| 4
| 3
|
['Bit Manipulation', 'Java']
| 1
|
complement-of-base-10-integer
|
Python simplest one-liner solution
|
python-simplest-one-liner-solution-by-ye-e01z
|
\nclass Solution:\n def bitwiseComplement(self, N: int) -> int:\n return (2**len(bin(N)[2:]))-1-N if N != 0 else 1\n\nLike it? please upvote...
|
yehudisk
|
NORMAL
|
2020-10-05T08:43:52.488894+00:00
|
2020-10-05T08:43:52.488940+00:00
| 440
| false
|
```\nclass Solution:\n def bitwiseComplement(self, N: int) -> int:\n return (2**len(bin(N)[2:]))-1-N if N != 0 else 1\n```\n**Like it? please upvote...**
| 4
| 1
|
['Python3']
| 2
|
complement-of-base-10-integer
|
Java simple, short and easy solution, 0 ms - faster than 100%
|
java-simple-short-and-easy-solution-0-ms-a143
|
\nclass Solution {\n int countDigits(int n) {\n if (n == 0)\n return 0;\n return 1 + countDigits(n>>1);\n }\n \n public int
|
yehudisk
|
NORMAL
|
2020-10-05T08:35:11.656575+00:00
|
2020-10-05T08:35:11.656621+00:00
| 300
| false
|
```\nclass Solution {\n int countDigits(int n) {\n if (n == 0)\n return 0;\n return 1 + countDigits(n>>1);\n }\n \n public int bitwiseComplement(int N) {\n if (N == 0) return 1;\n return (int)Math.pow(2, countDigits(N)) - 1 - N;\n }\n}\n```\n**Like it? please upvote...**
| 4
| 0
|
['Java']
| 0
|
complement-of-base-10-integer
|
C++ super-simple, short and easy solution, 0 ms, fatser than 100%
|
c-super-simple-short-and-easy-solution-0-ki3y
|
\nclass Solution {\npublic:\n int countDigits(int n) {\n if (n == 0)\n return 0;\n return 1 + countDigits(n>>1);\n }\n \n i
|
yehudisk
|
NORMAL
|
2020-10-05T08:32:28.494161+00:00
|
2020-10-05T08:32:28.494192+00:00
| 239
| false
|
```\nclass Solution {\npublic:\n int countDigits(int n) {\n if (n == 0)\n return 0;\n return 1 + countDigits(n>>1);\n }\n \n int bitwiseComplement(int N) {\n if (N == 0) return 1;\n return pow(2, countDigits(N)) - 1 - N;\n }\n};\n```\n**Like it? please upvote...**
| 4
| 0
|
['C']
| 1
|
complement-of-base-10-integer
|
[Python, C++] LEGENDARY INNOVATIVE MAVERICK GENIUS SOLUTION; beats 100%, O(1)
|
python-c-legendary-innovative-maverick-g-rkwn
|
We need to XOR the number with a mask having as many 1s as the minimum no. of bits needed to represent the original number.\n\nFor instance:\n\n10 in binary wou
|
hipsuy
|
NORMAL
|
2020-09-20T11:42:29.060128+00:00
|
2020-09-20T11:43:07.500278+00:00
| 294
| false
|
We need to XOR the number with a mask having as many 1s as the minimum no. of bits needed to represent the original number.\n\nFor instance:\n\n10 in binary would be -> 1010\nnotice that the no. of bits is "log2(10) + 1" \n\nThis holds true in general, for any decimal number x, number of bits needed to represent it in binary would be log2(x) + 1.\n\nNow we know how long our mask needs to be, next up we need to create one with all bits set as 1, how do we do it???\n\nObserve!\n\nfor 10, mask needs to be 1111 (decimal 15) which is one less than 10000 (decimal 16), again, this holds in general.\n\nso we can simply create an integer mask = 2^(p+1) - 1, where p = log2(N) \n\nPython:\n```\nclass Solution:\n def bitwiseComplement(self, N: int) -> int:\n if N==0:\n return 1\n p = int(log2(N))\n mask = int(2**(p+1) - 1)\n return N^mask\n```\n\nC++:\n```\nclass Solution {\npublic:\n int bitwiseComplement(int N) {\n if(N ==0 ){\n return 1;\n }\n int p = log2(N);\n int mask = pow(2,p+1) - 1;\n return N^mask;\n }\n};\n```\n\nTime Complexity: O(1)\nSpace Complexity: O(1)\n
| 4
| 0
|
['C', 'Python3']
| 0
|
complement-of-base-10-integer
|
[faster than 100.00%][c++][easy understanding]
|
faster-than-10000ceasy-understanding-by-zqzbj
|
\n//1.\nclass Solution {\npublic:\n int bitwiseComplement(int N) {\n if(N==0) \n\t\t return 1;\n int res=0,k=1;\n while(N){\n
|
rajat_gupta_
|
NORMAL
|
2020-09-15T18:14:14.516981+00:00
|
2020-09-15T18:14:14.517035+00:00
| 119
| false
|
```\n//1.\nclass Solution {\npublic:\n int bitwiseComplement(int N) {\n if(N==0) \n\t\t return 1;\n int res=0,k=1;\n while(N){\n int d=N%2; //finding a bit\n res+=(d==1?0:1)*k; //complement of bit and complement\n N/=2; \n k*=2;\n }\n return res;\n \n }\n};\n//2.\nclass Solution {\npublic:\n int bitwiseComplement(int N) {\n if(N==0)\n return 1;\n int x=N;\n int highval=0;\n\t\t// finding highest value of bit size of N\n while(N){\n highval=highval*2+1;\n N/=2;\n }\n return highval-x;\n }\n};\n```
| 4
| 0
|
['C', 'C++']
| 0
|
complement-of-base-10-integer
|
c++ Solution using Bitwise ^ (Beats 100%)
|
c-solution-using-bitwise-beats-100-by-ra-0mx7
|
XOR of any Number with a number having all bit 1 gives Binary complemented number.\nEg- 101 ^ 111 = 010 \n\n\nclass Solution {\npublic:\n int bitwiseCompleme
|
raven_13
|
NORMAL
|
2020-04-29T07:24:15.484825+00:00
|
2020-04-29T07:24:39.934420+00:00
| 182
| false
|
XOR of any Number with a number having all bit 1 gives Binary complemented number.\nEg- 101 ^ 111 = 010 \n\n```\nclass Solution {\npublic:\n int bitwiseComplement(int N) {\n \n if(N==0)\n return 1;\n int p=log2(N);\n\t\t\t\tlong num=pow(2,p+1)-1; // num has all bit 1;\n \n return N^num;\n }\n};\n\n\n```
| 4
| 0
|
[]
| 0
|
complement-of-base-10-integer
|
PYTHON 5 lines, no need bit manipulation, just math
|
python-5-lines-no-need-bit-manipulation-0jkfv
|
\ndigit, num = 1, N\nwhile N > 1:\n\tdigit += 1\n\tN = N//2\nreturn 2**digit - 1 - num\n
|
kop_fyf
|
NORMAL
|
2019-03-18T18:19:53.605860+00:00
|
2019-03-18T18:19:53.605902+00:00
| 623
| false
|
```\ndigit, num = 1, N\nwhile N > 1:\n\tdigit += 1\n\tN = N//2\nreturn 2**digit - 1 - num\n```
| 4
| 0
|
[]
| 2
|
complement-of-base-10-integer
|
💯Easy Solution | Mastering Complement of Base 10 | Beats 100% Solution | Bit Shifting 🚀
|
mastering-complement-of-base-10-beats-10-fqv8
|
IntuitionThe bitwise complement of a number n means flipping all its bits (0s become 1s and 1s become 0s). Instead of directly flipping the bits, we iterate thr
|
Shivam_Tyagii
|
NORMAL
|
2025-02-15T13:34:54.021626+00:00
|
2025-02-16T03:57:27.966295+00:00
| 152
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The bitwise complement of a number n means flipping all its bits (0s become 1s and 1s become 0s). Instead of directly flipping the bits, we iterate through each bit of n and construct the complement number step by step.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Handle Edge Case: If n=0, return 1 because the complement of 0 (which is just 0000...0000 in binary) is 1.
2. Iterate Through Bits:
- Start with ans = 0 and mul = 1 (representing the least significant bit position).
- If the current bit of n is 0, add mul to ans.
- Shift n right (n = n >> 1) to process the next bit.
- Double mul (mul *= 2) to move to the next binary position.
3. Return Result: The final value of ans is the bitwise complement
# Complexity
- Time complexity:
- The number of bits in n is at most O(logn), so the while loop runs at most O(logn) times
- Space complexity:
- We use only a few integer variables (ans, mul, and n), so extra space usage is constant.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int bitwiseComplement(int n) {
if(n==0) return 1;
int ans = 0;
int mul = 1;
while(n){
if(!(n&1)){
ans += mul;
}
mul*=2;
n=n>>1;
}
return ans;
}
};
```
| 3
| 0
|
['Bit Manipulation', 'C++']
| 1
|
complement-of-base-10-integer
|
100.00% | 3 line easy short | c++ code | math | O(log2(n))
|
10000-3-line-easy-short-c-code-math-olog-rlxd
|
Approach\n Describe your approach to solving the problem. \nJust find the just greater number than n which is power of 2 then subtact 1 from it.\nThen return xo
|
amanraox
|
NORMAL
|
2024-08-22T15:56:49.306020+00:00
|
2024-08-22T15:56:49.306055+00:00
| 34
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nJust find the just greater number than n which is power of 2 then subtact 1 from it.\nThen return xor of both\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n unsigned int b=0,k=0;\n while(k<=n)b++,k=pow(2,b);\n return (k-1)^n;\n }\n};\n```\n# Complexity\n- Time complexity: O(log2(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n
| 3
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
3 line easy short | c++ code | math | O(log2(n))
|
3-line-easy-short-c-code-math-olog2n-by-7jmys
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \njust find the just grea
|
amanraox
|
NORMAL
|
2024-08-22T15:52:14.596454+00:00
|
2024-08-22T15:52:14.596480+00:00
| 27
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\njust find the just greater number than **n** which is power of 2 then subtact 1 from it.\nthen return xor of both\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n unsigned int b=0,k=0;\n while(k<=n)b++,k=pow(2,b);\n return (k-1)^n;\n }\n};\n```\n# Complexity\n- Time complexity: O(log2(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n
| 3
| 0
|
['Bit Manipulation', 'C++']
| 0
|
complement-of-base-10-integer
|
🌟 Efficient Solution for "Complement of Base 10 Integer" | C++ | 0ms Beats 100.00% | O(log n)
|
efficient-solution-for-complement-of-bas-ymzq
|
\n\n---\n\n# Intuition\n\nTo find the complement of an integer, we need to flip all bits in its binary representation. For this, determine the number of bits re
|
user4612MW
|
NORMAL
|
2024-08-22T04:40:30.353658+00:00
|
2024-08-22T04:41:07.730704+00:00
| 30
| false
|
##\n\n---\n\n# **Intuition**\n\nTo find the complement of an integer, we need to flip all bits in its binary representation. For this, determine the number of bits required to represent the integer, create a bitmask with all bits set to 1 for this length, and then apply a bitwise XOR operation with the integer to get its complement.\n\n# **Approach**\n\nTo compute the complement of an integer **n**, first determine the number of bits required to represent **n** in binary. Create a **bitmask** with all bits set to 1 by shifting 1 left by the number of bits and then subtracting 1. Finally, use bitwise XOR between **n** and the **bitmask** to obtain the complement. This method is efficient with time complexity **O(log n)** and space complexity **O(1)**.\n\n# **Complexity**\n\n- **Time Complexity** $$O(\\log n)$$ The operations are proportional to the number of bits in the integer, which is $$\\log_2 n$$.\n- **Space Complexity** $$O(1)$$ The algorithm uses a constant amount of extra space for variables.\n# **Code**\n\n```cpp\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if (n == 0) return 1; \n int bitmask{1}, temp{n};\n while (temp > 0) {\n bitmask <<= 1;\n temp >>= 1;\n }\n bitmask -= 1;\n return bitmask ^ n;\n }\n};\n```\n\n---\n\n## **If you found this solution helpful, please upvote! \uD83D\uDE0A**\n\n---\n\n\n---
| 3
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
Easy and Simple C++ Approach ✅ | Beginner Friendly 🔥🔥🔥
|
easy-and-simple-c-approach-beginner-frie-bqnn
|
Intuition\nTo find the bitwise complement of a number n, we need to flip all the bits of n. For example, if n is 5 (binary 101), its bitwise complement should b
|
AyushBansalCodes
|
NORMAL
|
2024-08-03T07:19:43.063390+00:00
|
2024-08-03T07:19:43.063441+00:00
| 184
| false
|
# Intuition\nTo find the bitwise complement of a number `n`, we need to flip all the bits of `n`. For example, if `n` is `5` (binary `101`), its bitwise complement should be `2` (binary `010`).\n\n# Approach\n1. If `n` is `0`, directly return `1` because the complement of `0` is `1`.\n1. Create a mask that has the same number of bits as `n` but all set to `1`.\n1. XOR `n` with this mask to get the bitwise complement.\n\n# Detailed Steps:\n- Initialize `mask` to `0`.\n- If `n` is `0`, return `1`.\n- Copy `n` to `m`.\n- Create the mask by left shifting `mask` and OR\'ing it with `1` until `m` becomes `0`.\n- XOR `n` with `mask` to get the result.\n\n# Complexity\n- Time complexity: O(logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`Upvote! It only takes 1 click\uD83D\uDE09`\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int m = n ;\n int mask = 0;\n if (n == 0)\n return 1;\n\n while(m!=0){\n mask = (mask<<1)|1;\n m=(m>>1);\n }\n int ans = n^mask;\n //or ans = (~n) & mask;\n return ans;\n\n }\n};\n```\n
| 3
| 0
|
['Bit Manipulation', 'C++']
| 0
|
complement-of-base-10-integer
|
C++ | 0 ms | Beats 100%
|
c-0-ms-beats-100-by-djwhocodes_5-o4ea
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe code handles the base case where num is 0 by returning 1, as the bitwise complement
|
DJwhoCODES_5
|
NORMAL
|
2024-03-17T05:18:37.110942+00:00
|
2024-03-17T05:18:37.110965+00:00
| 222
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code handles the base case where num is 0 by returning 1, as the bitwise complement of 0 is 1.\n\nIt iterates through each bit of num to compute its bitwise complement by flipping each bit individually.\n\nIt does this by extracting each bit (0 or 1) of num, flipping it using XOR with 1, and then accumulating the result by shifting it to the appropriate position.\n\nThe process continues until all bits of num are processed, resulting in the complete bitwise complement of num.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Base Case Handling: If num is 0, its bitwise complement is 1. Therefore, the function returns 1 for this case.\n\n2. Bitwise Complement Calculation: The code iterates through each bit of the input number num by continuously dividing num by 2 until it becomes zero. In each iteration:\n\n3. It computes the remainder when num is divided by 2, which gives the least significant bit (LSB) of num.\n - It flips the LSB using the XOR operator (rem = rem ^ 1), which effectively computes the bitwise complement of the LSB.\n - It then updates the answer by multiplying the complemented bit (rem) with a multiplier (mul) and adding it to the result (ans).\n - It updates the multiplier (mul) by doubling it, which effectively shifts it to the left.\n - Finally, it updates num by integer division (num = num / 2), effectively shifting it to the right.\n\n4. Return Result: After completing the bitwise complement calculation, the function returns the computed result ans.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this approach is O(log n), where n is the value of the input integer num. \n\nThis is because the while loop iterates through the bits of num, and the number of iterations required is proportional to the number of bits in num, which is logarithmic with respect to num.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1), constant space complexity, as the space used by variables (num, ans, mul, rem) does not depend on the size of the input integer num.\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int num) {\n if(num==0) return 1;\n // if(num==1) return 0;\n int ans=0;\n int mul = 1;\n while(num){\n int rem = num%2;\n rem = rem^1;\n ans = rem*mul + ans;\n mul = mul*2;\n num = num/2;\n }\n return ans;\n }\n};\n\n\n```
| 3
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
Simple Python Solution || O(logN)
|
simple-python-solution-ologn-by-dodda_sa-bq3y
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Dodda_Sai_Sachin
|
NORMAL
|
2024-02-27T07:11:57.386786+00:00
|
2024-02-27T07:11:57.386844+00:00
| 519
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n s=bin(n)[2:]\n arr=\'\'\n for i in s:\n if i==\'0\':\n arr+=\'1\'\n else:\n arr+=\'0\' \n res=0\n for i in range(len(arr)-1,-1,-1):\n res=res+(int(arr[i])* 2**(len(arr)-i-1))\n return res\n```
| 3
| 0
|
['Python3']
| 0
|
complement-of-base-10-integer
|
Easy Solution || C++
|
easy-solution-c-by-japneet001-tmb8
|
Intuition\nThe problem requires finding the bitwise complement of a given integer. Bitwise complement is the operation of flipping the bits of a binary represen
|
Japneet001
|
NORMAL
|
2024-02-01T04:08:04.797488+00:00
|
2024-02-01T04:08:04.797519+00:00
| 107
| false
|
# Intuition\nThe problem requires finding the bitwise complement of a given integer. Bitwise complement is the operation of flipping the bits of a binary representation of a number (changing 0s to 1s and vice versa).\n\n# Approach\nThe provided code uses a bitwise operation to iterate through the bits of the input number `n`, flip each bit, and then construct the complemented number. The variable `dec_ans` is used to accumulate the result, and `multiplier` is used to keep track of the position of the current bit in the binary representation.\n\n1. Check if `n` is 0. If it is, return 1 as the bitwise complement of 0 is 1.\n\n2. Iterate through each bit of `n`:\n - Extract the least significant bit using `n & 1`.\n - Compute the complement of the bit using `bit ^ 1`.\n - Update `dec_ans` by adding the complemented bit multiplied by the current position (`multiplier`).\n - Right shift `n` to move to the next bit.\n - Update the `multiplier` to move to the next position.\n\n3. Return the computed `dec_ans`.\n\n# Complexity\n- Time complexity: $$O(log(n))$$ where n is the input number. The while loop iterates through the bits of the number, and the number of bits in a number is log(n).\n- Space complexity: $$O(1)$$ as only a constant amount of additional space is used.\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int bit;\n int comp;\n int multiplier = 1;\n int dec_ans = 0;\n\n if (n == 0) {\n return 1;\n } \n\n while (n != 0) {\n bit = n & 1;\n comp = bit ^ 1;\n dec_ans = comp * multiplier + dec_ans;\n n = n >> 1;\n multiplier *= 2;\n }\n\n return dec_ans;\n }\n};\n```
| 3
| 0
|
['Bit Manipulation', 'C++']
| 0
|
complement-of-base-10-integer
|
100% Beats Solution || Using Bit Manipulation || Step by Step Explain || Easy to Understand ||
|
100-beats-solution-using-bit-manipulatio-h2f7
|
Abhiraj Pratap Singh\n\n---\n\n# UPVOTE IT....\n\n---\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n\n- The goal of the function
|
abhirajpratapsingh
|
NORMAL
|
2023-09-27T17:35:41.072440+00:00
|
2024-01-16T16:06:48.836779+00:00
| 7
| false
|
# Abhiraj Pratap Singh\n\n---\n\n# UPVOTE IT....\n\n---\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n- The goal of the function is to find the bitwise complement of a given integer n. The bitwise complement of a binary number is obtained by flipping each bit (changing 0s to 1s and vice versa).\n\n---\n\n\n\n\n\n---\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. The code initializes a variable mask to 0. This variable will be used to create a bitmask with all bits set to 1 up to the most significant bit of the given number.\n2. It also initializes a copy of the input number n as copyNum and another variable ans to store the final result.\n3. There is a check for the edge case where n is 0. If n is 0, the function returns 1 because the bitwise complement of 0 is 1.\n4. The code then enters a loop where it right shifts copyNum until it becomes 0. Meanwhile, it left shifts mask and sets the least significant bit to 1 in each iteration. This process creates a bitmask with all bits set to 1 up to the most significant bit of the original n.\n5. After constructing the bitmask, the code negates the input number n using the bitwise NOT operator (~), effectively flipping all its bits.\n6. Finally, the code applies the bitmask to the negated n using bitwise AND (&) and stores the result in ans. This step ensures that only the bits up to the most significant bit of the original n are considered in the final answer.\n\n---\n\n\n# Complexity\n\n- **Time complexity :** The time complexity of the solution is determined by the number of bits in the input number n. In the worst case, where n has k bits, the loop will run k times. Therefore, the **time complexity is O(k).**\n\n- **Space complexity:** The **space complexity is O(1)** as the algorithm uses a constant amount of extra space (for variables like mask, copyNum, and ans) that does not depend on the input size.\n\n\n---\n\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) \n {\n int mask=0;\n int copyNum=n;\n int ans=0;\n if(n==0)\n return 1;\n while(copyNum!=0)\n {\n copyNum=copyNum>>1;\n mask = mask <<1;\n mask = mask | 1;\n }\n n = ~n;\n ans = mask & n;\n return ans;\n }\n};\n```\n\n---\n\n# if you like the solution please UPVOTE it....\n\n\n\n\n\n---\n\n\n\n\n---\n
| 3
| 0
|
['Bit Manipulation', 'C++']
| 0
|
complement-of-base-10-integer
|
Python 2 Approach 97.96% beats
|
python-2-approach-9796-beats-by-vvivekya-zofy
|
If you got help from this,... Plz Upvote .. it encourage me\n# EXAMPLE , \n # N = 101 (5)\n # MASK WILL BE 111 (7)\n # COMPLEMENT MASK -
|
vvivekyadav
|
NORMAL
|
2023-09-22T13:00:10.518194+00:00
|
2023-09-23T05:53:42.464679+00:00
| 182
| false
|
**If you got help from this,... Plz Upvote .. it encourage me**\n# EXAMPLE , \n # N = 101 (5)\n # MASK WILL BE 111 (7)\n # COMPLEMENT MASK - N = 7-5 = 2 (010)\n# Code\n```\n<!-- 1ST APPROACH -->\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n \n if n == 0:\n return 1\n\n mask = 0\n m = n\n while m != 0:\n mask = mask << 1 | 1\n m = m >> 1\n \n return mask - n\n # OR\n #return (~n) & mask \n\n<!-- ============================================================ -->\n<!-- 2ND APPROACH -->\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n x = 1\n while n > x:\n x = x * 2 + 1\n return x - n\n```
| 3
| 0
|
['Bit Manipulation', 'Python', 'Python3']
| 1
|
complement-of-base-10-integer
|
C++ Solution || Runtime 0ms || Beats 100% ||
|
c-solution-runtime-0ms-beats-100-by-asad-7lfa
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Asad_Sarwar
|
NORMAL
|
2023-02-18T21:02:40.618487+00:00
|
2023-02-18T21:02:40.618529+00:00
| 726
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n \n int temp=n;\n int mask=0;\n int ans;\n if(n==0)\n {\n ans=1;\n }\n else\n {\n while(temp!=0)\n {\n mask= (mask<<1) | 1;\n temp=temp>>1;\n }\n ans=(~n) & mask;\n }\n return ans;\n\n\n }\n};\n```
| 3
| 0
|
['C++']
| 1
|
complement-of-base-10-integer
|
Easy C++ solution || Beats 100% || 0ms solution || O(log(n)) solution
|
easy-c-solution-beats-100-0ms-solution-o-tx8t
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
umangrathi110
|
NORMAL
|
2022-10-19T13:24:23.971348+00:00
|
2022-10-19T13:24:23.971388+00:00
| 604
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(log(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if (n == 0)\n return 1;\n int num = n;\n int mask = 0;\n while(num)\n {\n mask = mask<<1 | 1;\n num >>= 1;\n }\n return n ^ mask;\n }\n};\n```
| 3
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
3ms || C++ || EASY || SIMPLE || TIME O(position of mst) || SPACE O(1)
|
3ms-c-easy-simple-time-oposition-of-mst-cuh8f
|
\nclass Solution {\npublic:\n int bitwiseComplement(int &n) {\n if(n==0)return 1;\n int ans = 0;\n int i = 0;\n while(n){\n
|
abhay_12345
|
NORMAL
|
2022-09-08T07:38:58.188371+00:00
|
2022-09-08T07:38:58.188409+00:00
| 532
| false
|
```\nclass Solution {\npublic:\n int bitwiseComplement(int &n) {\n if(n==0)return 1;\n int ans = 0;\n int i = 0;\n while(n){\n ans += ((n%2)^1)<<i;\n i++;\n n = n >> 1;\n }\n return ans;\n }\n};\n```
| 3
| 0
|
['Bit Manipulation', 'C', 'C++']
| 1
|
complement-of-base-10-integer
|
(newest approach) c++ 100% 0 ms without converting number into binary
|
newest-approach-c-100-0-ms-without-conve-nnst
|
\nclass Solution {\npublic:\n int power_floor( int n)\n {\n \n if((n!=0) &&!(n & (n-1)))\n {\n return n;\n }\n
|
avani_baheti_59_70
|
NORMAL
|
2022-05-27T07:26:35.006305+00:00
|
2023-02-28T10:18:22.542618+00:00
| 135
| false
|
```\nclass Solution {\npublic:\n int power_floor( int n)\n {\n \n if((n!=0) &&!(n & (n-1)))\n {\n return n;\n }\n int count=0;\n while(n!=0)\n {\n n>>=1;\n count+=1;\n }\n return 1<<count;\n }\n int bitwiseComplement(int n) {\n if(n==0)\n {\n return 1;\n }\n if(n==1)\n {\n return 0;\n }\n int k = power_floor(n);\n if(k-n==0)\n {\n return k-1;\n }\n else\n {\n return k-n-1;\n }\n }\n};\n```
| 3
| 0
|
['Bit Manipulation']
| 0
|
complement-of-base-10-integer
|
C++ | 0 ms | One Line Solution using XOR
|
c-0-ms-one-line-solution-using-xor-by-mu-khci
|
\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if(n==0) return 1;\n \n return (int)(pow(2,(int)log2(n) + 1) - 1) ^ n ;\n
|
mukulnayak
|
NORMAL
|
2022-04-10T07:04:20.431161+00:00
|
2022-04-10T07:05:57.405300+00:00
| 176
| false
|
```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if(n==0) return 1;\n \n return (int)(pow(2,(int)log2(n) + 1) - 1) ^ n ;\n }\n};\n```\n\nExplanation: we have to make ***0101*** from 1010.\nwe observe, 1010 ^ *0101* = 1111\nHence,\nXOR with 1010 on both sides we get (we know that a^a = 0 and a^0 = a),\n1010^*0101*^1010 = 1111^1010\n=> ***0101*** = 1010^1111
| 3
| 0
|
['Bit Manipulation', 'C']
| 0
|
complement-of-base-10-integer
|
Easy Solution, Faster than 100%, Observation Based
|
easy-solution-faster-than-100-observatio-chyk
|
\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if(n==0)\n return 1;\n int i=1;\n while(i<=32){\n i
|
vasu_2006
|
NORMAL
|
2022-02-14T14:36:33.352584+00:00
|
2022-02-14T14:36:33.352626+00:00
| 48
| false
|
```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if(n==0)\n return 1;\n int i=1;\n while(i<=32){\n if(n-pow(2,i)<0)\n break;\n i++;\n }\n return pow(2,i)-n-1;\n }\n};\n```
| 3
| 0
|
['Bit Manipulation']
| 0
|
complement-of-base-10-integer
|
Python 3 (50ms) | Beginner Naive Approach | String, Join & Replace
|
python-3-50ms-beginner-naive-approach-st-njt9
|
\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n t=(str(bin(n).replace("0b", "")))\n a="".join("1" if x==\'0\' else \'0\' for
|
MrShobhit
|
NORMAL
|
2022-01-19T09:18:41.913334+00:00
|
2022-01-19T09:18:41.913370+00:00
| 207
| false
|
```\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n t=(str(bin(n).replace("0b", "")))\n a="".join("1" if x==\'0\' else \'0\' for x in t)\n return int(a,2)\n```
| 3
| 0
|
['String', 'Python']
| 2
|
complement-of-base-10-integer
|
Java Soln if you don't know Bit Manipulation(Just like me)
|
java-soln-if-you-dont-know-bit-manipulat-50fa
|
\nclass Solution {\n public int bitwiseComplement(int n) {\n \n if(n ==0) return 1 ; //If we have 0, the complement will be 1\n \n
|
vbhv_sxn
|
NORMAL
|
2022-01-04T17:41:05.731708+00:00
|
2022-01-05T18:23:41.081074+00:00
| 85
| false
|
```\nclass Solution {\n public int bitwiseComplement(int n) {\n \n if(n ==0) return 1 ; //If we have 0, the complement will be 1\n \n // next = Just greater no. which is Power of 2\n //Using the formulae\'loga b = log10 b / log10 a\' we can calculate log to any base\n int next = (int)(Math.log(n)/Math.log(2)) ;\n \n /* Next now hold the just greater no. which is a power of 2 of te given no.\n * Eg: if n = 14 than next = 16 which is 2^4 which is a power of 2 */ \n next = (int)Math.pow(2,next+1); \n \n /* Now next = 16 and by OBSERVATION** we can say that the compliment of a no. \n * is the difference between next and n. But we need to substract 1 from the\n * result to get the ans */\n return next - n - 1;\n \n }\n}\n```\n**OBSERVATION :**** If a binary no. is subtracted from a no. which has all digits as 1\'s for eg: 111, 1111, 111111 etc it will give the complement of the no. So to get 111 (7 in decimal) we need to substract 1 from 1000 (8 in decimal) wich gives the previous all 1\'s digit binary no. . Thus we are substracting 1 in the ans to get a no. just before the 2^n containing all 1\'s digit.
| 3
| 0
|
['Java']
| 0
|
complement-of-base-10-integer
|
Faster than 100%
|
faster-than-100-by-vasu_2006-bw1c
|
class Solution {\npublic:\n int bitwiseComplement(int n) {\n if(n==0)\n return 1;\n int i=1;\n while(i<=32){\n if(
|
vasu_2006
|
NORMAL
|
2022-01-04T13:51:18.346752+00:00
|
2022-01-04T13:51:18.346789+00:00
| 33
| false
|
class Solution {\npublic:\n int bitwiseComplement(int n) {\n if(n==0)\n return 1;\n int i=1;\n while(i<=32){\n if(n-pow(2,i)<0)\n break;\n i++;\n }\n return pow(2,i)-n-1;\n }\n};
| 3
| 0
|
[]
| 0
|
complement-of-base-10-integer
|
Easy to understand JavaScript solution
|
easy-to-understand-javascript-solution-b-esav
|
How to find an answer without the knowledge of bitwise operators?\n\nThe hint lies here: to find the complement number, we need to find the 111..111 number of N
|
besLisbeth
|
NORMAL
|
2022-01-04T09:34:12.975469+00:00
|
2022-01-04T09:34:12.975499+00:00
| 215
| false
|
How to find an answer without the knowledge of bitwise operators?\n\nThe hint lies here: to find the complement number, we need to find the 111..111 number of N length, where N is the length of the input number in binary representation. That\'s our sum of `n` and complement number. Then convert it to decimal and subtract between `sum` and input number `n`. \nThat\'s it! It will be easier to understand if we\'ll go to the examples.\n\n***Example 1:***\n**Input**: n = 5\n**Explanation**: 5 is "101" in binary, so we create the number "111", find it decimal representation - that\'s 7, and find out the subtract\n**Output**: 7 - 5 = 2. The answer is **2**\n\n***Example 2:***\n**Input**: n = 6435\n**Explanation**: 6435 is "\'1100100100011\'" in binary, the length of the binary is 13 so we create the number "1111111111111", find it decimal representation - that\'s 8191, and find out the subtract\n**Output**: 8191 - 6435 = 1756. The answer is **1756**\n\n***Example 3:***\n**Input**: n = 0\n**Explanation**: 0 is "0" in binary, the length of the binary is 1 so we create the number "1", find it decimal representation - that\'s 1, and find out the subtract\n**Output**: 1 - 0 = 1. The answer is **1**\n\n\n***Easy-to-read code:***\n```\nfunction bitwiseComplement(n: number): number {\n\tlet binary = n.toString(2); // we find our input in binary representation\n\tlet sum = parseInt(\'1\'.repeat(binary.length), 2); // we find the sum in binary and convert in to decimal \n return sum - n; //get the result in decimal \n};\n```\n\n***Good-looking oneliner:***\n```\nfunction bitwiseComplement(n: number): number {\n return parseInt(\'1\'.repeat((n >>> 0).toString(2).length), 2) - n;\n};\n```\n\nMemory Usage: 40.1 MB, less than 100.00% of TypeScript online submissions for Complement of Base 10 Integer.
| 3
| 0
|
['TypeScript', 'JavaScript']
| 0
|
complement-of-base-10-integer
|
The sum of a number and it's complement is all 111's.
|
the-sum-of-a-number-and-its-complement-i-jeir
|
\'\'\'\nclass Solution {\npublic:\n int bitwiseComplement(int N)\n {\n if(N==0)return 1; \n int sum = (int)pow(2,1+(int)log2(N))-1;\n
|
varchirag
|
NORMAL
|
2022-01-04T05:09:55.114961+00:00
|
2022-01-04T05:09:55.115014+00:00
| 91
| false
|
\'\'\'\nclass Solution {\npublic:\n int bitwiseComplement(int N)\n {\n if(N==0)return 1; \n int sum = (int)pow(2,1+(int)log2(N))-1;\n return sum-N;\n }\n};
| 3
| 0
|
['Math', 'C', 'C++']
| 1
|
complement-of-base-10-integer
|
✔️ [Python3] SHIFT AND XOR (ᕗ ͠° ਊ ͠° )ᕗ, Explained
|
python3-shift-and-xor-fo-deg-uu-deg-fo-e-f5z1
|
We create a mask=1 and shift its bit to the left until it gets greater than n. Example: n=101 => mask=1000. After, we substruct 1 from the mask which gives us a
|
artod
|
NORMAL
|
2022-01-04T00:30:39.815823+00:00
|
2022-01-04T00:30:39.815854+00:00
| 277
| false
|
We create a mask=`1` and shift its bit to the left until it gets greater than `n`. Example: `n=101` => `mask=1000`. After, we substruct `1` from the mask which gives us all `1`\'s: `mask=111`. And the last step, we simply return xor between `n` and our mask: `n ^ mask` = `101 ^ 111` = `010`.\n\nTime: **O(1)** - since number of bits to scan are limited\nSpace: **O(1)** - nothing stored\n\nRuntime: 24 ms, faster than **94.01%** of Python3 online submissions for Complement of Base 10 Integer.\nMemory Usage: 14.1 MB, less than **89.54%** of Python3 online submissions for Complement of Base 10 Integer.\n\n```\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n if not n: return 1\n \n mask = 1\n while n >= mask:\n mask <<= 1\n \n return (mask - 1) ^ n\n```
| 3
| 3
|
['Python3']
| 1
|
complement-of-base-10-integer
|
Go solution faster than 100% bit manuplation
|
go-solution-faster-than-100-bit-manuplat-1si2
|
\nfunc bitwiseComplement(N int) int {\n\tif N == 0 {\n\t\treturn 1\n\t}\n\tres := 0\n\tg := 1\n\tfor N > 0 {\n\t\tif N&1 == 0 {\n\t\t\tres += g\n\t\t}\n\t\tg <<
|
nathannaveen
|
NORMAL
|
2021-02-10T16:48:53.033527+00:00
|
2021-02-10T16:48:53.033555+00:00
| 194
| false
|
```\nfunc bitwiseComplement(N int) int {\n\tif N == 0 {\n\t\treturn 1\n\t}\n\tres := 0\n\tg := 1\n\tfor N > 0 {\n\t\tif N&1 == 0 {\n\t\t\tres += g\n\t\t}\n\t\tg <<= 1\n\t\tN >>= 1\n\t}\n\treturn res\n}\n```
| 3
| 0
|
['Bit Manipulation', 'Go']
| 0
|
complement-of-base-10-integer
|
[C++] Math based 3 line no loop
|
c-math-based-3-line-no-loop-by-sameerp98-uaam
|
Math approach\nThe sum of a number and it\'s complement is all 111\'s. For example :\n4 + 3 = 7 (100 + 011= 111)\nNow if we want to find complement we can simpl
|
sameerp98
|
NORMAL
|
2020-10-05T18:56:28.374514+00:00
|
2022-01-20T20:46:24.811957+00:00
| 256
| false
|
# Math approach\nThe sum of a number and it\'s complement is all 111\'s. For example :\n4 + 3 = 7 (100 + 011= 111)\nNow if we want to find complement we can simply subract our number from a number which has all 1\'s from Most significant bit (MSB) to Least significant bit (LSB).\nTo find the most significant bit of a binary number we can simply take log2() of the number. We need to construct a number such that it\'s binary is all 1\'s starting from the most significant bit to least of the number for which we are finding the complement. Consider this example:\n4 in binary is 100\nIn order to get compliment we have to get 111 (all 1\'s from Most significant bit to least) and subract 100 (our number):\n111-100=011 (3)-> Answer\nlog2(4) is 2 in order to get all 1\'s from MSB to LSB we can raise 2 to one power higher than Log2(our number) which would result in 8 for our example and subract 1 from it. Eg:\n2^(log2(4)+1)= 8 in Binary is 1000\nSubtract 1 from it 1000-1 = 0111 (Hence all 1\'s from MSB to LSB)\nNow to get compliment we just have to subtract our number from this and return it.\n```cpp\nclass Solution {\npublic:\n int bitwiseComplement(int N)\n {\n if(N==0)return 1; //As Log(0) is -ve Infinity\n //calculate left-most-1 in binary number\n //create Binary number with all ones and subract N from it\n int sum = (int)pow(2, 1+(int)log2(N))-1;\n return sum - N;\n }\n};\n```
| 3
| 0
|
['Math', 'C', 'C++']
| 0
|
complement-of-base-10-integer
|
C++ One Line Solution 100% faster 0ms
|
c-one-line-solution-100-faster-0ms-by-de-8nue
|
\nclass Solution {\npublic:\n int bitwiseComplement(int N) \n {\n return N == 0 ? 1 : N ^ (int)(pow(2, floor(log2(N)) + 1) - 1);\n }\n};\n
|
debbiealter
|
NORMAL
|
2020-10-05T08:59:59.904898+00:00
|
2020-10-05T10:32:02.258255+00:00
| 494
| false
|
```\nclass Solution {\npublic:\n int bitwiseComplement(int N) \n {\n return N == 0 ? 1 : N ^ (int)(pow(2, floor(log2(N)) + 1) - 1);\n }\n};\n```
| 3
| 1
|
['C', 'C++']
| 0
|
complement-of-base-10-integer
|
Python super-simple short & clean solution
|
python-super-simple-short-clean-solution-dnmt
|
\nclass Solution:\n def bitwiseComplement(self, N: int) -> int:\n if N==0:\n return 1\n \n def countDigits(n):\n i
|
yehudisk
|
NORMAL
|
2020-10-05T08:27:56.134752+00:00
|
2020-10-05T08:27:56.134788+00:00
| 303
| false
|
```\nclass Solution:\n def bitwiseComplement(self, N: int) -> int:\n if N==0:\n return 1\n \n def countDigits(n):\n if n == 0:\n return 0\n return 1 + countDigits(n>>1)\n \n return (2**countDigits(N))-1-N\n```\n**Like it? please upvote...**
| 3
| 0
|
['Python3']
| 1
|
complement-of-base-10-integer
|
c++ solution ,beats 100%(0ms, 5MB)
|
c-solution-beats-1000ms-5mb-by-goyalansh-anbd
|
class Solution {\npublic:\n int bitwiseComplement(int n) {\n \n if(n==0)\n return 1;\n int countbits = floor(log2(n)) + 1;\n
|
goyalanshul809
|
NORMAL
|
2020-08-17T05:56:24.935367+00:00
|
2020-08-17T05:56:24.935400+00:00
| 82
| false
|
class Solution {\npublic:\n int bitwiseComplement(int n) {\n \n if(n==0)\n return 1;\n int countbits = floor(log2(n)) + 1;\n long long int temp = pow(2,countbits);\n temp--;\n long long int ans = n^temp;\n return ans;\n }\n};
| 3
| 0
|
[]
| 0
|
complement-of-base-10-integer
|
Java 0ms, No bitwise, Easy to understand
|
java-0ms-no-bitwise-easy-to-understand-b-7md9
|
```\npublic int findComplement(int num) {\n\n\tint i = 0;\n\tint res = 0;\n\t\n\twhile (num > 0) {\n\t\n\t\tif (num % 2 == 0)\n\t\t\tres += Math.pow(2, i);\n\t\
|
nive00
|
NORMAL
|
2020-05-05T04:52:42.066576+00:00
|
2020-05-05T04:54:56.727056+00:00
| 322
| false
|
```\npublic int findComplement(int num) {\n\n\tint i = 0;\n\tint res = 0;\n\t\n\twhile (num > 0) {\n\t\n\t\tif (num % 2 == 0)\n\t\t\tres += Math.pow(2, i);\n\t\ti++;\n\t\tnum /= 2;\n\t}\n\treturn res;\n}\n\t
| 3
| 1
|
[]
| 0
|
complement-of-base-10-integer
|
C++ : Beats 100% time and 100% space
|
c-beats-100-time-and-100-space-by-metacr-nqgk
|
My approach invloves working from the rightmost bit of the given number.\nIf the rightmost bit is 1, we add 0. Otherwise, we add the power of two correspoding t
|
metacresol
|
NORMAL
|
2020-05-04T11:30:36.809481+00:00
|
2020-05-04T11:31:17.216126+00:00
| 675
| false
|
My approach invloves working from the rightmost bit of the given number.\nIf the rightmost bit is 1, we add 0. Otherwise, we add the power of two correspoding to the bit, which we keep track here using the variable \'pow\'. After each check we rightshift the number.\n```\nclass Solution {\npublic:\n int bitwiseComplement(int N) {\n int sum = 0;\n long pow=1;\n\t\t// Do, while is used because if N is 0, then it has to add 1 and not go directly out of the loop.\n do{\n if(N%2==0) sum+=pow;\n N = (N>>1);\n pow*=2;\n }while(N);\n return sum;\n }\n};\n```\n
| 3
| 0
|
['C++']
| 1
|
complement-of-base-10-integer
|
Javascript solution
|
javascript-solution-by-mmartire-15q5
|
```\n/*\n * @param {number} N\n * @return {number}\n /\nvar bitwiseComplement = function(N) {\n return ((1 << (N.toString(2).length)) - 1) ^ N;\n};
|
mmartire
|
NORMAL
|
2019-09-07T01:55:40.798371+00:00
|
2019-09-07T01:55:40.798430+00:00
| 420
| false
|
```\n/**\n * @param {number} N\n * @return {number}\n */\nvar bitwiseComplement = function(N) {\n return ((1 << (N.toString(2).length)) - 1) ^ N;\n};
| 3
| 0
|
['JavaScript']
| 1
|
complement-of-base-10-integer
|
Java || Beats 100% || Bit Manipulation
|
java-beats-100-bit-manipulation-by-shikh-aoyh
|
Complexity
Time complexity: O(log N)
Space complexity:O(1)
Code
|
shikhargupta0645
|
NORMAL
|
2025-02-11T06:19:13.675462+00:00
|
2025-02-11T06:19:13.675462+00:00
| 75
| false
|
# Complexity
- Time complexity: O(log N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int bitwiseComplement(int n) {
if(n==0){
return 1;
}
int ans = 0;
int i = 0;
while(n>0){
if((n&1) != 1){
ans = (ans ^ (1<<i));
}
n >>= 1;
i++;
}
return ans;
}
}
```
| 2
| 0
|
['Java']
| 0
|
complement-of-base-10-integer
|
Easily Understandable solution || 100% T.C ||CPP
|
easily-understandable-solution-100-tc-cp-lv49
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Ganesh_ag10
|
NORMAL
|
2024-07-03T15:23:28.817315+00:00
|
2024-07-03T15:23:28.817346+00:00
| 104
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if(n==0) return 1;\n vector<int> v;\n int num=n;\n while(num!=0){\n int r=num%2;\n v.push_back(r);\n num/=2;\n }\n for(int i=0;i<v.size();i++){\n if(v[i]==1) v[i]=0;\n else v[i]=1;\n }\n // reverse(v.begin(),v.end());\n int j=0;\n int ans=0;\n for(int i=0;i<v.size();i++){\n int ag=pow(2,j);\n j++;\n ans+=v[i]*ag;\n }\n return ans;\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
Finding the bitwise complement
|
finding-the-bitwise-complement-by-theath-swnq
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires finding the bitwise complement of a given integer. One way to appr
|
theatharvv
|
NORMAL
|
2024-04-17T14:40:43.037151+00:00
|
2024-04-17T14:40:43.037185+00:00
| 13
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the bitwise complement of a given integer. One way to approach this is to iterate through each bit of the integer, flip it, and construct the complement.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI\'ll iterate through each bit of the integer using a while loop. Within each iteration, I\'ll extract the least significant bit using a bitwise AND operation. Then, I\'ll flip the bit using a bitwise XOR operation with 1. After that, I\'ll construct the complement integer by adding the flipped bit to the answer, which is calculated as 2 raised to the power of the position of the bit. Finally, I\'ll increment the position counter.\n\n# Complexity\n- Time complexity: O(log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int num) {\n\n if(num == 0) \n {\n return 1;\n }\n else\n {\n int i = 0, ans = 0;\n while(num!=0)\n {\n int bit = num&1;\n num = num>>1;\n int complement_bit = bit ^ 1;\n if(complement_bit == 1)\n {\n ans += pow(2,i) ;\n }\n i++;\n }\n return ans;\n }\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
easy solution | beats 100%
|
easy-solution-beats-100-by-leet1101-w7h3
|
Approach\n1. If the input number is 0, return 1 as the bitwise complement of 0 is 1.\n2. Determine the number of bits required to represent the input number by
|
leet1101
|
NORMAL
|
2024-04-12T15:47:51.038989+00:00
|
2024-04-12T19:08:37.461518+00:00
| 380
| false
|
# Approach\n1. If the input number is 0, return 1 as the bitwise complement of 0 is 1.\n2. Determine the number of bits required to represent the input number by counting the number of shifts needed until the number becomes 0.\n3. Create a mask with all bits set to 1 using the formula \\(2^i - 1\\), where \\(i\\) is the number of bits.\n4. Compute the bitwise complement by performing a bitwise NOT operation on the input number and applying the mask.\n\n# Complexity\n- Time complexity: $$O(\\log n)$$, where \\(n\\) is the input number.\n- Space complexity: $$O(1)$$\n\n# Code\n```cpp\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n if (n == 0) return 1;\n int i = 0, num = n;\n while (num) {\n i++;\n num >>= 1;\n }\n int mask = pow(2, i) - 1;\n return ((~n) & mask);\n }\n};\n```
| 2
| 0
|
['Bit Manipulation', 'C++']
| 1
|
complement-of-base-10-integer
|
Code to find complement of Base 10 integer
|
code-to-find-complement-of-base-10-integ-uj9o
|
Intuition\nIn this question we have to find the complement of the given number. So we will simply do bitwise complement of the given number.\nFor eg., let x=100
|
Parul_Awasthi
|
NORMAL
|
2024-03-16T06:17:18.555211+00:00
|
2024-03-16T06:17:18.555244+00:00
| 23
| false
|
# Intuition\nIn this question we have to find the complement of the given number. So we will simply do bitwise complement of the given number.\nFor eg., let x=10011 so it\'s complement would be 01100.\n\n# Approach\nWe wil initialize few variables in the starting that are mul and sum for storing the power of 2\'s and the resultant number respectively.\n\nNow, we will iterate the loop untill it is less than 0 .\n\nAnd inside the while loop we will simply find the remainder when the given number is divided by 2.\n\nThen, change the digit to 0 and 1 if it would be 1 and 0 respectively.\n\nThen, reduce the number by n/2 and store it in sum variable after performing some calculations.\n\nAnd we also have to change the mul variable as it is used for 2^0 , 2^1..........2^n. \n\nfor eg., Let x=101 so 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 4 + 0 + 1 = 5\n\n# Complexity\n- Time complexity:\nO(log N) because while loop will iterate till the n becomes less than 0 . And it will jump in N/2 manner.\n\n- Space complexity:\nO(1) as only constant space is used in the code.\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int rem,ans=0,mul=1;\n if(n==0)\n return 1;\n while(n)\n {\n rem=n%2;\n // rem=rem^1;\n rem =!rem;\n n/=2;\n ans=ans+rem*mul;\n mul*=2;\n }\n return ans;\n \n \n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
Simple Java Code || Beats 100%
|
simple-java-code-beats-100-by-saurabh_mi-wesy
|
Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n# Code\n\nclass Solution {\n public int bitwiseComplement(int n) {\n int allOne = 1;\
|
Saurabh_Mishra06
|
NORMAL
|
2024-02-22T10:05:20.215016+00:00
|
2024-02-22T10:05:20.215050+00:00
| 253
| false
|
# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution {\n public int bitwiseComplement(int n) {\n int allOne = 1;\n while(allOne < n){\n allOne = allOne*2+1;\n }\n return allOne - n;\n }\n}\n```
| 2
| 0
|
['Java']
| 0
|
complement-of-base-10-integer
|
100% efficient and easy
|
100-efficient-and-easy-by-desalgentamira-5sdw
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
DesalgenTamirat
|
NORMAL
|
2024-01-13T18:34:38.884222+00:00
|
2024-01-13T18:34:38.884244+00:00
| 1,180
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n bits = list(bin(n))[2:]\n for i, value in enumerate(bits):\n bits[i] = "1" if value == "0" else "0"\n \n return int("".join(bits), 2)\n```
| 2
| 0
|
['Python3']
| 1
|
complement-of-base-10-integer
|
🚀Beats 100%🔥🤩||Super Clean✅||Easy code with explanation..
|
beats-100super-cleaneasy-code-with-expla-kkfa
|
Intuition & Approach\n Describe your approach to solving the problem. \n1. The code constructs a bitmask that has all bits set up to the most significant bit of
|
Saurav_Kr_Singh
|
NORMAL
|
2024-01-02T15:34:02.729469+00:00
|
2024-01-02T15:34:02.729492+00:00
| 49
| false
|
# Intuition & Approach\n<!-- Describe your approach to solving the problem. -->\n1. The code constructs a bitmask that has all bits set up to the most significant bit of n by shifting and OR operations.\n2. It then uses bitwise NOT (~) on n to flip all bits.\n3. Finally, it performs a bitwise AND with the bitmask to get the complement.\n\n# Complexity\n- **Time complexity: O(logN)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity: O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# ***PS - Please upvote (bottom left) if this solution was helpful :) It motivates me to write more solutions***\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int mask = 0;\n int temp = n;\n if(temp==0)\n return 1;//edge case\n while(temp>0){\n mask = (mask<<1)|1;\n temp = temp>>1;\n }\n int ans = (~n) & mask;\n return ans;\n }\n};\n```
| 2
| 0
|
['Bit Manipulation', 'Bitmask', 'C++']
| 0
|
complement-of-base-10-integer
|
Using Bit Masking || Beats 100% || JAVA
|
using-bit-masking-beats-100-java-by-ramu-b42l
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ramuyadav90597
|
NORMAL
|
2023-12-25T14:31:37.592888+00:00
|
2023-12-25T14:31:37.592924+00:00
| 327
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int bitwiseComplement(int n) {\n if(n==0)\n return 1;\n int mask = 0,temp = n;\n while(n!=0){\n mask=mask<<1;\n mask = mask | 1;\n n=n>>1;\n }\n return (~temp) & mask;\n }\n}\n```
| 2
| 0
|
['Java']
| 0
|
complement-of-base-10-integer
|
Easy intuition, approach and code in C++
|
easy-intuition-approach-and-code-in-c-by-uu2x
|
Intuition\nThe basic logic is that we will make a mask and make it bits 1 , equal to the number of bits in the given number and then take bitwise AND with the c
|
arpit123boss
|
NORMAL
|
2023-10-31T17:33:48.918683+00:00
|
2023-10-31T17:33:48.918714+00:00
| 1,174
| false
|
# Intuition\nThe basic logic is that we will make a mask and make it bits 1 , equal to the number of bits in the given number and then take bitwise AND with the compliment of the given number. \n\n# Approach\n- First of all, we will make a mask variable and initialize it with 0.\n- Then store the given number to another variable arp to count the number of bits in the given number.\n- After counting the number of bits by right shifting, we will take bitwise OR of mask variable with 1.\n- Then, run a loop till (number of digits - 1) and inside it left shift the mask variable by 1 and again take bitwise OR with 1.\n- By doing so we will store 1\'s at the positions of the given number.\n- Then, take compliment of the given number and return the bitwise AND of mask and complimented number.\n\n\n# Complexity\n- Time complexity:\n$$O(number of bits)$$\n\n- Space complexity:\n$$O(1)$$\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int mask=0;\n int arp=n;\n int c=0;\n while (arp) {\n c++;\n arp>>=1;\n }\n mask=mask|1;\n for (int i=0;i<c-1;i++) {\n mask<<=1;\n mask|=1;\n }\n n=~n;\n return mask&n;\n }\n};\n\n```
| 2
| 0
|
['C++']
| 1
|
complement-of-base-10-integer
|
Best Java Solution || Beats 100%
|
best-java-solution-beats-100-by-ravikuma-iz0f
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ravikumar50
|
NORMAL
|
2023-09-24T07:55:01.140457+00:00
|
2023-09-24T07:55:01.140482+00:00
| 285
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int bitwiseComplement(int n) {\n if(n==0) return 1;\n int x = 0;\n int ans = 0;\n\n while(n>0){\n int r = n%2;\n if(r==1){\n x++;\n }else{\n ans = ans + (int)Math.pow(2,x);\n x++;\n }\n n=n/2;\n }\n return ans;\n }\n}\n```
| 2
| 0
|
['Java']
| 0
|
complement-of-base-10-integer
|
C++ | Bit Manipulation | O(N)
|
c-bit-manipulation-on-by-omjadhav007-rzmh
|
Intuition\n\n\n# Approach\nBit Manipulation\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n\nclass Solution {\npublic:\n int
|
omjadhav007
|
NORMAL
|
2023-09-16T18:11:19.786438+00:00
|
2023-09-16T18:11:19.786464+00:00
| 0
| false
|
# Intuition\n\n\n# Approach\nBit Manipulation\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int x=0,m=1;\n if(n==0) return 1;\n while(n){\n if(!(n&1)) x+=m;\n m*=2;\n n>>=1;\n }\n return x;\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
Beginner Friendly Python || Beats 91%
|
beginner-friendly-python-beats-91-by-ana-azwx
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nLet\'s assume a number,
|
anakamboj
|
NORMAL
|
2023-09-15T17:38:07.242830+00:00
|
2023-09-15T17:38:07.242856+00:00
| 173
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet\'s assume a number, say 10. \n\n```\nBinary version = 1010\nComplement = 0101\nInteger compelement = 5\n```\n\n```\nmask is initially 0,\nTill m = 10 (1010) is not 0,\n1. add a 1 (left shift 0 at the end + OR with 1), mask = 1\n2. divide 10 by 2 or right shift by 1\n3. now m = 5(101)\n- Iteration 2: mask = 11, m = 2 (10)\n- Iteration 3: mask = 111, m = 1 (1)\n- Iteration 4: mask = 1111, m = 0\n```\n\n\n\nTo do this using code, we follow these steps:\n\n1. First, we check if the given number is 0. If it is, the complement is 1, because flipping 0 gives us 1.\n```\nif n == 0:\n return 1\n```\n\n2. To find the complement for any other number, we need to figure out how many bits it has. \n\n\n3. Now, we create a "mask," which is a pattern of bits. We set as many bits as our number has to 1. So, for 10, our mask is \'1111\' (4 ones in binary).\n\n```\nmask is basically all ones. \nfor example: \nmask for 10 (1010) = 1111\nmask for 5 (101) = 111\nmask for 11 (1011) = 1111\n```\n```\nmask is initially 0,\nTill m = 10 (1010) is not 0,\n- add a 1 (left shift 0 at the end + OR with 1), mask = 1\n- divide 10 by 2 or right shift by 1\n- now m = 5(101)\n- Iteration 2: mask = 11, m = 2 (10)\n- Iteration 3: mask = 111, m = 1 (1)\n- Iteration 4: mask = 1111, m = 0\n\n```\n\n4. Take the complement of the original number (flipping the bits using \'~\' in code) and apply the mask to it (using \'&\' in code). This gives us the complement of the number.\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n #generate a new number\n if n == 0:\n return 1\n m = n\n mask = 0\n while (m!=0):\n #generate a mask\n mask = (mask << 1) | 1\n m = m >> 1\n answer = (~n) & mask\n \n return answer\n \n \n\n \n \n```
| 2
| 0
|
['Python3']
| 1
|
complement-of-base-10-integer
|
Java Code with Explanation
|
java-code-with-explanation-by-athravmeht-nts3
|
Code\n\nclass Solution {\n public int bitwiseComplement(int n) {\n // edge Case \n if(n == 0) return 1;\n\n // ~n or can be said as NOT
|
athravmehta06
|
NORMAL
|
2023-07-17T06:55:53.392072+00:00
|
2023-07-17T06:55:53.392092+00:00
| 200
| false
|
# Code\n```\nclass Solution {\n public int bitwiseComplement(int n) {\n // edge Case \n if(n == 0) return 1;\n\n // ~n or can be said as NOT of n reverses all the bits of the number\n // we will write shift until our no. is not equal to zero so that we can find how many bits have our answer\n // to create mask so that all the 0 bits in left side which got 1 when we NOT them, must be done 0 again \n // and if we know how many bits have our answer than remaining bits can be AND with 0\n // Example:- 5 :- (representing in 16 bit) 0000000000000101\n // mask:- 3 digits, how to calculate:- use right shift until number is zero like\n // 0000000000000010 >> 1\n // 0000000000000001 >> 1\n // 0000000000000000\n\n // so to make our final answer starting bit as zero we need\n // mask right most 3 bits to be 1 and remaining zero\n // 000000000000000 << 1 OR 1\n // 000000000000001 << 1 OR 1\n // 000000000000011 << 1 OR 1\n // 000000000000111, 3 time because we calculated masked digit to be 3 \n \n // and in last do AND with mask;\n\n int m = n;\n int mask = 0;\n\n while(m != 0){\n mask = (mask << 1) | 1; // calculating mask \n m = m >> 1; \n }\n int ans = ~n & mask;\n return ans;\n }\n}\n```
| 2
| 0
|
['Bit Manipulation', 'Java']
| 0
|
complement-of-base-10-integer
|
easiest solution begineer friendly c++
|
easiest-solution-begineer-friendly-c-by-691nm
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
gouravsaroha
|
NORMAL
|
2023-04-27T03:37:09.338070+00:00
|
2023-04-27T03:37:09.338107+00:00
| 237
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n // int ans=0;\n if(n==0) return 1;\n for(int i=1;i<=n;i=i*2){\n n=n^i;\n }\n return n;\n }\n};\n```
| 2
| 0
|
['C++']
| 1
|
complement-of-base-10-integer
|
Simple Soluion
|
simple-soluion-by-arunarunarun7354-rl77
|
\n\n# Code\n\nclass Solution {\n public int bitwiseComplement(int n) {\n String bin = Integer.toBinaryString(n);\n String res = "";\n fo
|
arunarunarun7354
|
NORMAL
|
2023-04-03T23:01:22.117875+00:00
|
2023-04-03T23:01:22.117927+00:00
| 539
| false
|
\n\n# Code\n```\nclass Solution {\n public int bitwiseComplement(int n) {\n String bin = Integer.toBinaryString(n);\n String res = "";\n for(char c :bin.toCharArray())\n {\n if( c == \'1\')\n res += "0";\n else\n res += "1";\n }\n return Integer.parseInt(res, 2);\n }\n}\n```
| 2
| 0
|
['Java']
| 0
|
complement-of-base-10-integer
|
✅ [C++] EASY and Shorter Solution || Intuitive Approach || 100% Accepted
|
c-easy-and-shorter-solution-intuitive-ap-l4n3
|
Intuition\n1. Straight formula based question.\n\n# Approach\n1. Count the number of digits in the number.\n2. Use the formula :- one complement of x is 2^n-x-1
|
akh1465
|
NORMAL
|
2023-03-17T06:22:21.470253+00:00
|
2023-03-17T06:22:21.470280+00:00
| 1,106
| false
|
# Intuition\n1. Straight formula based question.\n\n# Approach\n1. Count the number of digits in the number.\n2. Use the formula :- one complement of x is 2^n-x-1\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n\n //one complement of x is 2^n-x-1\n\n if(n==0)\n return 1;\n\n int count=0;\n int d;\n int m=n;\n while(n!=0)\n {\n // d=n%10;\n count++;\n n=n>>1;\n }\n int res = pow(2,count)-m-1;\n return res;\n }\n};\n```
| 2
| 0
|
['C++']
| 2
|
complement-of-base-10-integer
|
C++ solution faster than 100% of the solutions
|
c-solution-faster-than-100-of-the-soluti-8yqk
|
\n# Code\n\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int m = n ; \n int mask = 0 ; \n \n while(m==0){\n
|
ackerman217
|
NORMAL
|
2023-01-04T11:03:59.716283+00:00
|
2023-01-04T11:03:59.716324+00:00
| 1,204
| false
|
\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int m = n ; \n int mask = 0 ; \n \n while(m==0){\n return 1 ; \n }\n while(m!=0){\n mask = ( mask << 1 ) | 1 ;\n m = m >> 1 ; \n }\n int ans = (~n) & mask;\n return ans ; \n }\n};\n```
| 2
| 0
|
['C++']
| 1
|
complement-of-base-10-integer
|
C++ easy solution beats 100%
|
c-easy-solution-beats-100-by-ackerman217-saz4
|
Intuition\nMake a mask \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g
|
ackerman217
|
NORMAL
|
2022-12-30T20:58:01.592485+00:00
|
2022-12-30T20:58:01.592517+00:00
| 631
| false
|
# Intuition\nMake a mask \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int bitwiseComplement(int n) {\n int m = n ; \n int mask = 0 ; \n \n while(m==0){\n return 1 ; \n }\n while(m!=0){\n mask = ( mask << 1 ) | 1 ;\n m = m >> 1 ; \n }\n int ans = (~n) & mask;\n return ans ; \n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
complement-of-base-10-integer
|
Easy Java Solution Using Bit Manipulation ( Beats : 100 %)
|
easy-java-solution-using-bit-manipulatio-ojbv
|
\n# Approach\n Describe your approach to solving the problem. \nBit Manipulation\n\nHope this helps.\nDo Upvote if you like it !!\n\nThanks :)\n\n# Code\n\nclas
|
aishi535
|
NORMAL
|
2022-12-28T04:09:33.289839+00:00
|
2023-01-06T02:21:42.331950+00:00
| 616
| false
|
\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBit Manipulation\n\nHope this helps.\nDo Upvote if you like it !!\n\nThanks :)\n\n# Code\n```\nclass Solution {\n public int bitwiseComplement(int num) {\n if(num==0){\n return 1;\n }\n int c=0;\n c=(int)(Math.log(num)/Math.log(2));\n num=~num;\n num =num & (int)((Math.pow(2,c))-1);\n return(num);\n }\n}\n```
| 2
| 0
|
['Bit Manipulation', 'Java']
| 0
|
complement-of-base-10-integer
|
Python ✅✅✅ || 5-line Faster than 98.91% || Memory Beats 96.46%
|
python-5-line-faster-than-9891-memory-be-w7vy
|
Code\n\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n b = bin(n)[2:]\n b = b.replace(\'1\', \'_\')\n b = b.replace(\'0
|
a-fr0stbite
|
NORMAL
|
2022-12-16T05:12:12.643542+00:00
|
2022-12-16T05:12:12.643578+00:00
| 179
| false
|
# Code\n```\nclass Solution:\n def bitwiseComplement(self, n: int) -> int:\n b = bin(n)[2:]\n b = b.replace(\'1\', \'_\')\n b = b.replace(\'0\', \'1\')\n b = b.replace(\'_\', \'0\')\n return int(b, 2)\n```\n\n\n
| 2
| 0
|
['Python3']
| 0
|
get-the-size-of-a-dataframe
|
Easy Solution Beginner Friendly || Pandas || Beats 90%
|
easy-solution-beginner-friendly-pandas-b-a36p
|
Intuition\nThe problem asks us to find the size (number of rows and columns) of a given DataFrame.\n\n# Approach\nTo solve this problem, we can use the Pandas l
|
vaish_1929
|
NORMAL
|
2023-10-07T08:20:45.627372+00:00
|
2023-10-07T08:20:45.627400+00:00
| 8,848
| false
|
# Intuition\nThe problem asks us to find the size (number of rows and columns) of a given DataFrame.\n\n# Approach\nTo solve this problem, we can use the Pandas library in Python. We can directly use the `.shape` attribute of the DataFrame to get the number of rows and columns. We return the result as an array containing the number of rows and columns.\n\n# Complexity\n- Time complexity: The time complexity is O(1) because accessing the `.shape` attribute of a DataFrame is a constant-time operation.\n- Space complexity: The space complexity is O(1) as we only return a small array containing two integers.\n\n# Code\n```python\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n return [players.shape[0], players.shape[1]]\n # OR\n return list(players.shape)\n
| 33
| 0
|
['Pandas']
| 0
|
get-the-size-of-a-dataframe
|
Pandas 1-Line | Elegant & Short | And more Pandas solutions ✅
|
pandas-1-line-elegant-short-and-more-pan-tztu
|
Complexity\n- Time complexity: O(1)\n- Space complexity: O(1)\n\n# Code\nPython []\ndef getDataframeSize(players: pd.DataFrame) -> list[int]:\n return list(p
|
Kyrylo-Ktl
|
NORMAL
|
2023-10-06T09:06:45.451797+00:00
|
2023-10-06T09:06:45.451818+00:00
| 2,077
| false
|
# Complexity\n- Time complexity: $$O(1)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```Python []\ndef getDataframeSize(players: pd.DataFrame) -> list[int]:\n return list(players.shape)\n```\n\n# Important!\n###### If you like the solution or find it useful, feel free to **upvote** for it, it will support me in creating high quality solutions)\n\n# 30 Days of Pandas solutions\n\n### Data Filtering \u2705\n- [Big Countries](https://leetcode.com/problems/big-countries/solutions/3848474/pandas-elegant-short-1-line/)\n- [Recyclable and Low Fat Products](https://leetcode.com/problems/recyclable-and-low-fat-products/solutions/3848500/pandas-elegant-short-1-line/)\n- [Customers Who Never Order](https://leetcode.com/problems/customers-who-never-order/solutions/3848527/pandas-elegant-short-1-line/)\n- [Article Views I](https://leetcode.com/problems/article-views-i/solutions/3867192/pandas-elegant-short-1-line/)\n\n\n### String Methods \u2705\n- [Invalid Tweets](https://leetcode.com/problems/invalid-tweets/solutions/3849121/pandas-elegant-short-1-line/)\n- [Calculate Special Bonus](https://leetcode.com/problems/calculate-special-bonus/solutions/3867209/pandas-elegant-short-1-line/)\n- [Fix Names in a Table](https://leetcode.com/problems/fix-names-in-a-table/solutions/3849167/pandas-elegant-short-1-line/)\n- [Find Users With Valid E-Mails](https://leetcode.com/problems/find-users-with-valid-e-mails/solutions/3849177/pandas-elegant-short-1-line/)\n- [Patients With a Condition](https://leetcode.com/problems/patients-with-a-condition/solutions/3849196/pandas-elegant-short-1-line-regex/)\n\n\n### Data Manipulation \u2705\n- [Nth Highest Salary](https://leetcode.com/problems/nth-highest-salary/solutions/3867257/pandas-elegant-short-1-line/)\n- [Second Highest Salary](https://leetcode.com/problems/second-highest-salary/solutions/3867278/pandas-elegant-short/)\n- [Department Highest Salary](https://leetcode.com/problems/department-highest-salary/solutions/3867312/pandas-elegant-short-1-line/)\n- [Rank Scores](https://leetcode.com/problems/rank-scores/solutions/3872817/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Delete Duplicate Emails](https://leetcode.com/problems/delete-duplicate-emails/solutions/3849211/pandas-elegant-short/)\n- [Rearrange Products Table](https://leetcode.com/problems/rearrange-products-table/solutions/3849226/pandas-elegant-short-1-line/)\n\n\n### Statistics \u2705\n- [The Number of Rich Customers](https://leetcode.com/problems/the-number-of-rich-customers/solutions/3849251/pandas-elegant-short-1-line/)\n- [Immediate Food Delivery I](https://leetcode.com/problems/immediate-food-delivery-i/solutions/3872719/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Count Salary Categories](https://leetcode.com/problems/count-salary-categories/solutions/3872801/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n### Data Aggregation \u2705\n- [Find Total Time Spent by Each Employee](https://leetcode.com/problems/find-total-time-spent-by-each-employee/solutions/3872715/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Game Play Analysis I](https://leetcode.com/problems/game-play-analysis-i/solutions/3863223/pandas-elegant-short-1-line/)\n- [Number of Unique Subjects Taught by Each Teacher](https://leetcode.com/problems/number-of-unique-subjects-taught-by-each-teacher/solutions/3863239/pandas-elegant-short-1-line/)\n- [Classes More Than 5 Students](https://leetcode.com/problems/classes-more-than-5-students/solutions/3863249/pandas-elegant-short/)\n- [Customer Placing the Largest Number of Orders](https://leetcode.com/problems/customer-placing-the-largest-number-of-orders/solutions/3863257/pandas-elegant-short-1-line/)\n- [Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/solutions/3863267/pandas-elegant-short-1-line/)\n- [Daily Leads and Partners](https://leetcode.com/problems/daily-leads-and-partners/solutions/3863279/pandas-elegant-short-1-line/)\n\n\n### Data Aggregation \u2705\n- [Actors and Directors Who Cooperated At Least Three Times](https://leetcode.com/problems/actors-and-directors-who-cooperated-at-least-three-times/solutions/3863309/pandas-elegant-short/)\n- [Replace Employee ID With The Unique Identifier](https://leetcode.com/problems/replace-employee-id-with-the-unique-identifier/solutions/3872822/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Students and Examinations](https://leetcode.com/problems/students-and-examinations/solutions/3872699/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n- [Managers with at Least 5 Direct Reports](https://leetcode.com/problems/managers-with-at-least-5-direct-reports/solutions/3872861/pandas-elegant-short/)\n- [Sales Person](https://leetcode.com/problems/sales-person/solutions/3872712/pandas-elegant-short-1-line-all-30-days-of-pandas-solutions/)\n\n\n
| 16
| 0
|
['Python', 'Python3', 'Pandas']
| 0
|
get-the-size-of-a-dataframe
|
✅Easy And Simple Solution With EXPLANATION✅
|
easy-and-simple-solution-with-explanatio-vevr
|
\n\n### Explanation\n\nThis code defines a function named getDataframeSize that takes a pandas DataFrame as input and returns its dimensions (number of rows and
|
deleted_user
|
NORMAL
|
2024-06-07T07:29:52.795139+00:00
|
2024-06-07T07:29:52.795167+00:00
| 3,922
| false
|
\n\n### Explanation\n\nThis code defines a function named `getDataframeSize` that takes a pandas DataFrame as input and returns its dimensions (number of rows and columns) as a list.\n\n#### Step-by-step Explanation:\n\n1. **Import pandas**:\n ```python\n import pandas as pd\n ```\n - This line imports the pandas library, which is used for data manipulation and analysis in Python.\n\n2. **Define the function**:\n ```python\n def getDataframeSize(players: pd.DataFrame) -> List[int]:\n ```\n - The function `getDataframeSize` is defined with one parameter `players`. The type hint suggests that `players` should be a pandas DataFrame.\n - The function returns a list of integers, as indicated by the type hint `-> List[int]`.\n\n3. **Get the shape of the DataFrame**:\n ```python\n [r, c] = players.shape\n ```\n - The `shape` attribute of the DataFrame `players` is accessed to get its dimensions.\n - `players.shape` returns a tuple containing the number of rows and columns in the DataFrame.\n - The tuple is unpacked into two variables: `r` for the number of rows and `c` for the number of columns.\n\n4. **Return the dimensions**:\n ```python\n return [r, c]\n ```\n - The function returns a list containing the number of rows `r` and the number of columns `c`.\n\n\n#### Summary:\n\n- The function takes a pandas DataFrame and returns its dimensions as a list.\n- The `shape` attribute of the DataFrame is used to get the number of rows and columns.\n- The result is returned as a list containing the number of rows and columns.\n\n\n\n---\n\n# Code\n```\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n [r,c] = players.shape\n return [r,c]\n```
| 11
| 0
|
['Pandas']
| 2
|
get-the-size-of-a-dataframe
|
1 line code || Simple code|| (use shape property)
|
1-line-code-simple-code-use-shape-proper-6l4j
|
If you got help from this,... Plz Upvote .. it encourage me\n# Code\n\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n ret
|
vvivekyadav
|
NORMAL
|
2023-10-06T00:43:39.188977+00:00
|
2023-10-06T16:08:48.770081+00:00
| 887
| false
|
**If you got help from this,... Plz Upvote .. it encourage me**\n# Code\n```\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n return [players.shape[0], players.shape[1]]\n # OR\n return list(players.shape)\n```
| 8
| 0
|
['Python', 'Python3', 'Pandas']
| 0
|
get-the-size-of-a-dataframe
|
🔥Best Solution in Pandas || With explanation ||🔥
|
best-solution-in-pandas-with-explanation-qdpo
|
Explanation\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\nThis line defines a function called "getDataframeSize". It takes one argument players, w
|
deleted_user
|
NORMAL
|
2024-03-16T23:07:45.112508+00:00
|
2024-03-16T23:07:45.112541+00:00
| 1,756
| false
|
# Explanation\n`def getDataframeSize(players: pd.DataFrame) -> List[int]:`\nThis line defines a function called "getDataframeSize". It takes one argument players, which is expected to be a pandas DataFrame. The function is annotated to indicate that players should be a DataFrame, and the return type of the function is specified as a list of integers.\n\n\n`row, col = players.shape`\nThis line retrieves the number of rows and columns in the DataFrame players using the .shape attribute of DataFrames in pandas. The .shape attribute returns a tuple containing the number of rows and columns, respectively. Here, we unpack this tuple into the variables "row" and "col".\n\n\n`return [row, col]`\nThis line returns a list containing the number of rows and columns of the DataFrame players. The list [row, col] represents the number of rows in the first element and the number of columns in the second element.\n\nOverall, this function takes a pandas DataFrame as input, retrieves the number of rows and columns in that DataFrame, and returns these values as a list of integers.\n\n\n# Complexity\n- Time complexity: Retrieving the shape of a DataFrame in pandas using the .shape attribute has a time complexity of $$O(1)$$. This is because pandas internally maintains metadata about the DataFrame, including its shape, so accessing this information is a constant-time operation.\n\n- Space complexity: Assigning the values of row and col from the shape tuple to variables has a time complexity of $$O(1)$$ as well, since it\'s just unpacking a tuple.\n\n# Code\n```\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n row, col = players.shape\n return [row, col]\n```\n\n
| 6
| 0
|
['Python', 'Python3', 'Pandas']
| 1
|
get-the-size-of-a-dataframe
|
Pandas 1-Line | Elegant & Short | And more Pandas solutions
|
pandas-1-line-elegant-short-and-more-pan-oh92
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Ankita2905
|
NORMAL
|
2023-11-08T17:07:33.838972+00:00
|
2023-11-08T17:07:33.839005+00:00
| 1,400
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndef getDataframeSize(players: pd.DataFrame) -> list[int]:\n return list(players.shape)\n \n```
| 5
| 0
|
['Pandas']
| 1
|
get-the-size-of-a-dataframe
|
Easy Solution with simple explanation
|
easy-solution-with-simple-explanation-by-8zgc
|
Intuition\nWe need to determine the dimensions of the given DataFrame, which in pandas are easily accessible through built-in attributes.\n\n# Approach\nUse the
|
Swayam248
|
NORMAL
|
2024-09-27T15:42:17.225660+00:00
|
2024-09-27T15:42:17.225691+00:00
| 2,346
| false
|
# Intuition\nWe need to determine the dimensions of the given DataFrame, which in pandas are easily accessible through built-in attributes.\n\n# Approach\nUse the shape attribute of the DataFrame, which returns a tuple containing the number of rows and columns.\nConvert the tuple to a list to match the required output format.\n\n# Complexity\nTime complexity: O(1)\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is constant O(1) because accessing the shape attribute of a pandas DataFrame is an instantaneous operation that doesn\'t depend on the size of the DataFrame.\n\nSpace complexity: O(1)\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is also constant O(1) because we\'re only creating a small list with two integer values, regardless of the size of the input DataFrame.\nThis solution efficiently calculates the number of rows and columns in the DataFrame without iterating through the data, making it both fast and memory-efficient.\n\n# Code\n```pythondata []\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n #shape attribute of DataFrame player is accessed to get its dimensions\n [r,c] = players.shape #returns a tuple\n return[r,c]\n```
| 4
| 0
|
['Pandas']
| 6
|
get-the-size-of-a-dataframe
|
easy program
|
easy-program-by-pranov_raaj__30-lmko
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
pranov_raaj__30
|
NORMAL
|
2024-08-19T06:55:07.932119+00:00
|
2024-08-19T06:55:07.932155+00:00
| 2,095
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n [r,c] = players.shape\n return [r,c]\n```
| 4
| 0
|
['Pandas']
| 2
|
get-the-size-of-a-dataframe
|
easy to learn
|
easy-to-learn-by-yogesh_12-734h
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Yogesh_12__
|
NORMAL
|
2024-08-19T07:15:33.569474+00:00
|
2024-08-19T07:15:33.569501+00:00
| 513
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n [r,c] = players.shape\n return [r,c]\n \n```
| 3
| 0
|
['Pandas']
| 0
|
get-the-size-of-a-dataframe
|
✅EASY SOLUTION
|
easy-solution-by-swayam28-4edq
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
swayam28
|
NORMAL
|
2024-08-09T10:36:57.816018+00:00
|
2024-08-09T10:36:57.816056+00:00
| 876
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n rows = len(players.axes[0])\n cols = len(players.axes[1])\n return [rows,cols]\n```
| 3
| 0
|
['Pandas']
| 0
|
get-the-size-of-a-dataframe
|
✔️✔️✔️easy 3 word solution - shape - PANDAS - beats 90%⚡⚡⚡
|
easy-3-word-solution-shape-pandas-beats-m63pe
|
Code\n\nimport pandas as pd\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n return list(players.shape)\n
|
anish_sule
|
NORMAL
|
2024-04-10T05:23:03.540834+00:00
|
2024-04-10T05:23:03.540868+00:00
| 1,099
| false
|
# Code\n```\nimport pandas as pd\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n return list(players.shape)\n```
| 3
| 0
|
['Pandas']
| 0
|
get-the-size-of-a-dataframe
|
Get the Size of a DataFrame - <PANDAS>
|
get-the-size-of-a-dataframe-pandas-by-pr-nxvb
|
Code
|
PreeOm
|
NORMAL
|
2025-03-15T16:05:39.510839+00:00
|
2025-03-15T16:05:39.510839+00:00
| 630
| false
|
# Code
```pythondata []
import pandas as pd
def getDataframeSize(players: pd.DataFrame) -> List:
return [players.shape[0], players.shape[1]]
```
| 2
| 0
|
['Pandas']
| 0
|
get-the-size-of-a-dataframe
|
Easy Explanation for Beginners ✨
|
easy-explanation-for-beginners-by-amogha-eh9p
|
Intuitionshape is an attribute in pandas that returns a tuple (m,n).
where m is number of rows and n is number of columns.but the question asks us to return a l
|
AmoghaMayya
|
NORMAL
|
2025-03-05T05:54:35.154897+00:00
|
2025-03-05T05:54:35.154897+00:00
| 590
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
**shape** is an attribute in pandas that returns a **tuple (m,n)**.
where **m** is number of rows and **n** is number of columns.
but the question asks us to return a list therefore we use **list()**.
we return a list in this way by making use of inbuilt python method.
# Code
```pythondata []
import pandas as pd
def getDataframeSize(players: pd.DataFrame) -> List[int]:
return list(players.shape)
```
| 2
| 0
|
['Pandas']
| 0
|
get-the-size-of-a-dataframe
|
🚀1-row solution that beats 99999999,99%🚀
|
1-row-solution-that-beats-9999999999-by-0cwxi
|
ApproachTo solve this problem I read the pandas.DataFrame.shape documentation
df.shape return a tuple that consider the number of rows and number of columns (nr
|
cesar4ik
|
NORMAL
|
2025-01-13T09:32:59.989202+00:00
|
2025-01-13T09:32:59.989202+00:00
| 1,323
| false
|
# Approach
To solve this problem I read the pandas.DataFrame.shape documentation
df.shape return a tuple that consider the number of rows and number of columns (nrows, ncols)
But we need to convert it to list to complete the problem condition
Goodbye, my firends!
<3
# Code
```pythondata []
import pandas as pd
def getDataframeSize(players: pd.DataFrame) -> List[int]:
return list(players.shape)
```
| 2
| 0
|
['Pandas']
| 0
|
get-the-size-of-a-dataframe
|
🏆 Shape | 🥇 Beats 99.46% | ✨ Most Efficient | ✔ Explained | Python
|
shape-beats-9946-most-efficient-explaine-n7uc
|
Proof of 99.46%:\n\n\n# Code:\nPython\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n return list(players.shape)\n \n\
|
shlok_t
|
NORMAL
|
2024-11-29T14:10:47.902550+00:00
|
2024-11-29T14:11:31.667977+00:00
| 317
| false
|
# Proof of 99.46%:\n\n\n# Code:\n```Python\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n return list(players.shape)\n \n```\n# Approach:\n\n1. **Importing Pandas:**\n ```python\n import pandas as pd\n ```\n This line imports the Pandas library, which is essential for data manipulation and analysis in Python.\n\n2. **Defining the Function:**\n ```python\n def getDataframeSize(players: pd.DataFrame) -> List[int]:\n ```\n This defines a function called `getDataframeSize`. It takes one argument `players`, which is expected to be a Pandas DataFrame. The function\'s return type is a list of integers (`List[int]`).\n\n3. **Returning the DataFrame\'s Shape:**\n ```python\n return list(players.shape)\n ```\n `players.shape` returns a tuple containing the dimensions of the DataFrame, where the first element is the number of rows and the second element is the number of columns. The `list()` function converts this tuple into a list. So, for example, if the DataFrame has 100 rows and 4 columns, `players.shape` would be `(100, 4)`, and `list(players.shape)` would be `[100, 4]`.\n\nIn summary, this function, `getDataframeSize`, returns a list that represents the size (number of rows and columns) of the given DataFrame.\n\n# Complexity:\nThe code you provided has very simple operations, so the time and space complexities are straightforward:\n\n### Time Complexity:\n- **Importing the library**: `import pandas as pd` happens once and is a constant-time operation, so its complexity is \\( O(1) \\).\n- **Defining the function**: This is also a constant-time operation and doesn\'t depend on the size of the data, so its complexity is \\( O(1) \\).\n- **Calling `players.shape`**: Accessing the shape attribute of a DataFrame is done in constant time, \\( O(1) \\).\n- **Converting to a list**: Converting the tuple `(n, m)` (where `n` is the number of rows and `m` is the number of columns) to a list is a constant-time operation, \\( O(1) \\).\n\nSo, the overall **time complexity** of the function `getDataframeSize` is \\( O(1) \\), which means it runs in constant time regardless of the size of the DataFrame.\n\n### Space Complexity:\n- The function only returns a list of two integers, which occupies a fixed amount of space.\n- The space used by the function is independent of the size of the DataFrame.\n\nThus, the **space complexity** of the function is \\( O(1) \\), meaning it uses a constant amount of space regardless of the input size.\n\nIn summary, both the time and space complexities of your code are \\( O(1) \\). This function is very efficient, as it performs a simple, constant-time operation.\n\n\n
| 2
| 0
|
['Python', 'Python3', 'Pandas']
| 1
|
get-the-size-of-a-dataframe
|
Easy 1-line solution using .shape
|
easy-1-line-solution-using-shape-by-hiya-atfv
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Hiya99
|
NORMAL
|
2024-09-29T05:01:31.143533+00:00
|
2024-09-29T05:01:31.143556+00:00
| 1,411
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```pythondata []\nimport pandas as pd\n\ndef getDataframeSize(players: pd.DataFrame) -> List[int]:\n return list(players.shape)\n \n```
| 2
| 0
|
['Pandas']
| 0
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.