question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
adding-two-negabinary-numbers
|
Add two numbers, then convert with negative base
|
add-two-numbers-then-convert-with-negati-t43t
|
Runtime: 64 ms, faster than 56.20%\nMemory Usage: 14.6 MB, less than 25.62%\n\nclass Solution:\n def addNegabinary(self, arr1, arr2):\n n = (sum(pow(-
|
evgenysh
|
NORMAL
|
2021-06-20T16:19:03.718582+00:00
|
2021-06-20T16:20:33.862635+00:00
| 538
| false
|
Runtime: 64 ms, faster than 56.20%\nMemory Usage: 14.6 MB, less than 25.62%\n```\nclass Solution:\n def addNegabinary(self, arr1, arr2):\n n = (sum(pow(-2, i) for i, v in enumerate(arr1[::-1]) if v) +\n sum(pow(-2, i) for i, v in enumerate(arr2[::-1]) if v))\n res = [] if n else [0]\n while n:\n n, rem = divmod(n, -2)\n if rem < 0:\n n += 1\n res.append(abs(rem))\n res.reverse()\n return res\n```
| 2
| 0
|
['Python', 'Python3']
| 1
|
adding-two-negabinary-numbers
|
[C++] with detailed explanation, easy to understand
|
c-with-detailed-explanation-easy-to-unde-2gvb
|
There are four scenarios, a+b=0/1/2/3/4, \nafter summing up the current digit, carry is set to second carry while second carry is set to 0, this is like shiftin
|
cwpui
|
NORMAL
|
2020-11-06T17:39:13.820626+00:00
|
2020-11-06T17:39:13.820671+00:00
| 344
| false
|
There are four scenarios, a+b=0/1/2/3/4, \nafter summing up the current digit, carry is set to second carry while second carry is set to 0, this is like shifting the carry\n* 0/1: there is no need to update carry, \n* 2/3: their secondCarry is set to 1 while carry is increased by 1, since 2*(-2)^i = (-2)^(i+1) + (-2)^(i+2) = -2*(-2)^i+4*(-2)^i\n* 4: secondCarry is set to 1\n\nOne special case to notice is that when secondCarry=1 and carry=2, they are cancel to 0\n\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n vector<int> res;\n int carry=0; // the carry to the next digit,\n int secondCarry=0; // the carry to the digit after next digit.\n int i=arr1.size()-1,j=arr2.size()-1;\n \n auto helper = [&](int cur) {\n carry=secondCarry;\n secondCarry=0;\n if (cur>=2) {\n if (cur<4) carry++; // case 2,3\n if (carry == 2) {\n carry = 0; // special case\n } else {\n secondCarry = 1; // case 2,3,4\n }\n }\n res.push_back(cur%2);\n };\n \n for (;i>=0 && j>=0; i--,j--) helper(arr1[i]+arr2[j]+carry); // calc the share digits\n while (i>=0) helper(arr1[i--]+carry); // calc the remain digit of arr1\n while (j>=0) helper(arr2[j--]+carry); // calc the remain digit of arr2\n while (secondCarry!=0 || carry!=0) helper(carry); // calc the remain carry\n \n\t\t// remove the leading zero\n while (res.size()>=2) {\n if (res.back()==0) res.pop_back();\n else break;\n }\n reverse(res.begin(),res.end());\n \n return res;\n }\n};
| 2
| 1
|
[]
| 0
|
adding-two-negabinary-numbers
|
Simple C++ solution
|
simple-c-solution-by-caspar-chen-hku-z823
|
\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n if (arr1.size() > arr2.size()) swap(arr1,arr2);\n
|
caspar-chen-hku
|
NORMAL
|
2020-05-23T06:38:02.742148+00:00
|
2020-05-23T06:38:02.742192+00:00
| 533
| false
|
```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n if (arr1.size() > arr2.size()) swap(arr1,arr2);\n arr2.insert(arr2.begin(), 3, 0);\n for (int i = arr1.size()-1, j = arr2.size()-1; j>=0; i--, j--) {\n if (i>=0) arr2[j]+=arr1[i];\n if (arr2[j] == -1) {\n arr2[j] = 1;\n arr2[j-1]++;\n } else if (arr2[j] == 2) {\n arr2[j] = 0;\n arr2[j-1]--;\n } else if (arr2[j] == 3) {\n arr2[j] = 1;\n arr2[j-1]--;\n }\n }\n while (arr2.front() == 0 && arr2.size()>1) arr2.erase(arr2.begin());\n return arr2;\n }\n};\n```
| 2
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
C++ | Similar to Base 2 except carry divided by -2
|
c-similar-to-base-2-except-carry-divided-rdvm
|
\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n \n int n = arr1.size();\n int m = arr2
|
wh0ami
|
NORMAL
|
2020-05-22T19:04:45.603052+00:00
|
2020-05-22T19:04:45.603103+00:00
| 410
| false
|
```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n \n int n = arr1.size();\n int m = arr2.size();\n \n int i = n-1, j = m-1, carry = 0;\n vector<int>res;\n int c = 0;\n \n while (i >= 0 || j >= 0 || carry) {\n if (i >= 0) carry += arr1[i--];\n if (j >= 0) carry += arr2[j--];\n res.push_back(carry & 1);\n carry = -(carry >> 1);\n }\n \n while (res.size() > 1 && res.back() == 0)\n res.pop_back();\n \n reverse(res.begin(), res.end());\n \n return res;\n }\n};\n```
| 2
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
Java solution O(n) & 1ms
|
java-solution-on-1ms-by-colinwei-b1nb
|
\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n int len1 = arr1.length;\n int len2 = arr2.length;\n\n if (le
|
colinwei
|
NORMAL
|
2020-03-01T09:47:51.927223+00:00
|
2020-03-01T09:52:49.134757+00:00
| 322
| false
|
```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n int len1 = arr1.length;\n int len2 = arr2.length;\n\n if (len1 == 0) {\n return arr2;\n }\n if (len2 == 0) {\n return arr1;\n }\n int maxLen = (len1 > len2 ? len1 : len2) + 2;\n int[] result = new int[maxLen];\n int carry = 0;\n int i = 0;\n\t\t// deal with the common part where both the arrays has numbers\n while (len1 - 1 - i >= 0 && len2 - 1 - i >= 0) {\n int sum = arr1[len1 - 1 - i] + arr2[len2 - 1 - i] + carry;\n result[maxLen - 1 - i] = getBit(sum);\n carry = getCarry(sum);\n ++i;\n }\n\t\t// deal with the rest part\n while (len1 - 1 - i >= 0 && maxLen - 1 - i >= 0) {\n int sum = arr1[len1 - 1 - i] + carry;\n result[maxLen - 1 - i] = getBit(sum);\n carry = getCarry(sum);\n ++i;\n }\n while (len2 - 1 - i >= 0 && maxLen - 1 - i >= 0) {\n int sum = arr2[len2 - 1 - i] + carry;\n result[maxLen - 1 - i] = getBit(sum);\n carry = getCarry(sum);\n ++i;\n }\n\t\t// deal with the remaining carry\n while (maxLen - 1 - i >= 0 && carry != 0) {\n result[maxLen - 1 - i] = getBit(carry);\n carry = getCarry(carry);\n ++i;\n }\n\t\t\n\t\t// remove the lead zeros\n int zeroLeadCount = 0;\n while (zeroLeadCount < maxLen && result[zeroLeadCount] == 0) {\n zeroLeadCount++;\n }\n if (zeroLeadCount == maxLen) {\n return new int[] {0};\n }\n int[] res = new int[maxLen - zeroLeadCount];\n for (int k = 0; k + zeroLeadCount < maxLen; k++) {\n res[k] = result[k + zeroLeadCount];\n }\n return res;\n }\n \n\t// get carry according to the addition result number\n private int getCarry(int num) {\n if (num == 2 || num == 3) {\n return -1;\n }\n if (num == -1) {\n return 1;\n }\n return 0;\n }\n\n // get bit according to the addition result number\n private int getBit(int num) {\n if (num == 2) {\n return 0;\n }\n if (num == 3 || num == -1 || num == 1) {\n return 1;\n }\n return 0;\n }\n}\n```
| 2
| 1
|
[]
| 0
|
adding-two-negabinary-numbers
|
[Python] I HATE BIT OPERATION
|
python-i-hate-bit-operation-by-zeyuuuuuu-9mb9
|
\nclass Solution:\n\t# Time Omax(m,n)\n\t# Space O1\n def addBinary(self,arr1,arr2):\n carry = 0\n ans = []\n \n while arr1 or ar
|
zeyuuuuuuu
|
NORMAL
|
2019-07-03T05:57:43.057484+00:00
|
2019-07-03T08:28:16.831205+00:00
| 174
| false
|
```\nclass Solution:\n\t# Time Omax(m,n)\n\t# Space O1\n def addBinary(self,arr1,arr2):\n carry = 0\n ans = []\n \n while arr1 or arr2 or carry:\n carry += (arr1 or [0]).pop() + (arr2 or [0]).pop()\n ans.append(carry & 1)\n carry = carry >> 1\n return ans[::-1]\n \n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n carry = 0\n ans = []\n while arr1 or arr2 or carry:\n carry += (arr1 or [0]).pop() + (arr2 or [0]).pop()\n ans.append(carry & 1)\n carry = -(carry >> 1)\n while len(ans) > 1 and ans[-1] == 0:\n ans.pop()\n return ans[::-1]\n```
| 2
| 1
|
[]
| 2
|
adding-two-negabinary-numbers
|
C++ O(N) Time with Explanation (carry = -(sum >> 1))
|
c-on-time-with-explanation-carry-sum-1-b-2sbq
|
See more code in my repo LeetCode\n\nWhen adding two numbers in base 2 I use a variable carry to store the carryover.\n\nAssume we are adding two bits a, b and
|
lzl124631x
|
NORMAL
|
2019-06-02T04:55:18.224053+00:00
|
2019-06-02T06:08:25.360919+00:00
| 420
| false
|
*See more code in my repo [LeetCode](https://github.com/lzl124631x/LeetCode)*\n\nWhen adding two numbers in base `2` I use a variable `carry` to store the carryover.\n\nAssume we are adding two bits `a`, `b` and `carry`. The `sum` can be `0, 1, 2, 3`, and the leftover bit value is `sum % 2` and the new value of `carry` is `sum / 2`.\n\n\nLet\'s try the same approach for this problem.\n\nAssume the current bit represents `k = (-2)^n`, (`n >= 0`).\n\n* Consider `carry = 0`, `sum` can be `0, 1, 2`.\n * When `sum = 0` or `1`, `leftover = sum`, `carry = 0`.\n * When `sum = 2`, the value is `2k = -1 * (-2k)`, so it\'s the same as `leftover = 1, carry = -1`\n* Consider `carry = -1`, `sum` can be `-1, 0, 1`.\n * For the new case `sum = -1`, the value is `-k = -2k + k`, so it\'s the same as `leftover = 1, carry = 1`.\n* Consider `carry = 1`, `sum` can be `1, 2, 3`.\n * For the new case `sum = 3`, the value is `3k = -1 * (-2k) + k`, so it\'s the same as `leftover = 1, carry = -1`.\n\nNow we\'ve considerred all cases. In sum:\n\nsum|leftover|carry|\n---|---|---\n-1|1|1\n0|0|0\n1|1|0\n2|0|-1\n3|1|-1\n\nThe pattern is:\n```\nleftover = (sum + 2) % 2\ncarry = 1 - (sum + 2) / 2\n```\nOr\n```\nleftover = sum & 1\ncarry = -(sum >> 1)\n```\n\n```cpp\n// OJ: https://leetcode.com/problems/adding-two-negabinary-numbers/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(N)\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& A, vector<int>& B) {\n vector<int> ans;\n for (int i = A.size() - 1, j = B.size() - 1, carry = 0; i >= 0 || j >= 0 || carry;) {\n if (i >= 0) carry += A[i--];\n if (j >= 0) carry += B[j--];\n ans.push_back(carry & 1);\n carry = -(carry >> 1);\n }\n while (ans.size() > 1 && ans.back() == 0) ans.pop_back();\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```
| 2
| 0
|
[]
| 1
|
adding-two-negabinary-numbers
|
Ordinary add and carry works just fine!
|
ordinary-add-and-carry-works-just-fine-b-ahc0
|
Ordinary add and carry works just fine! You just need to realize that carry could be some number other than zero or one and that you only have to subtract the r
|
sladkey
|
NORMAL
|
2019-06-02T04:18:13.369019+00:00
|
2019-06-02T04:22:09.789451+00:00
| 423
| false
|
Ordinary add and carry works just fine! You just need to realize that carry could be some number other than zero or one and that you only have to subtract the right signed bit if it\'s not even before dividing by 2.\n\n```csharp\npublic class Solution {\n public int[] AddNegabinary(int[] arr1, int[] arr2) {\n arr1 = arr1.Reverse().ToArray();\n arr2 = arr2.Reverse().ToArray();\n var arr3 = new int[Math.Max(arr1.Length, arr2.Length) + 4];\n var carry = 0;\n for (var i = 0; i < arr3.Length; i++) {\n var sign = i % 2 == 0 ? 1 : -1;\n var bit1 = i < arr1.Length ? sign * arr1[i] : 0;\n var bit2 = i < arr2.Length ? sign * arr2[i] : 0;\n var sum = bit1 + bit2 + carry;\n var bit3 = sum % 2 == 0 ? 0 : 1;\n arr3[i] = bit3;\n sum -= sign * bit3;\n carry = sum / 2;\n }\n var len = arr3.Length;\n while (len > 1 && arr3[len - 1] == 0) len -= 1;\n arr3 = arr3.Take(len).Reverse().ToArray();\n return arr3;\n }\n}```
| 2
| 1
|
[]
| 0
|
adding-two-negabinary-numbers
|
Just observation
|
just-observation-by-sohailalamx-643o
|
IntuitionApproachComplexity
Time complexity: O(n);
Space complexity: O(1)
Code
|
sohailalamx
|
NORMAL
|
2025-02-08T19:10:47.551388+00:00
|
2025-02-08T19:10:47.551388+00:00
| 41
| false
|
# Intuition
observation
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n);
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {
vector<int> ans;
reverse(arr1.begin(), arr1.end());
reverse(arr2.begin(), arr2.end());
int carry = 0;
int i = 0;
while(i < arr1.size() && i < arr2.size()) {
int a = arr1[i] + carry;
int b = arr2[i];
int c = a+b;
if(c == 2) {
carry = -1;
ans.push_back(0);
} else if(c == 0) {
carry = 0;
ans.push_back(0);
} else if(c == -1){
carry = 1;
ans.push_back(1);
} else if(c == 1) {
carry = 0;
ans.push_back(1);
}
else {
carry = -1;
ans.push_back(1);
}
i++;
}
while(i < arr1.size()) {
int c = arr1[i] + carry;
if(c == 2) {
carry = -1;
ans.push_back(0);
} else if(c == 0) {
carry = 0;
ans.push_back(0);
} else if(c == -1){
carry = 1;
ans.push_back(1);
}else if(c == 1) {
carry = 0;
ans.push_back(1);
} else {
carry = -1;
ans.push_back(1);
}
i++;
}
while(i < arr2.size()) {
int c = arr2[i] + carry;
if(c == 2) {
carry = -1;
ans.push_back(0);
} else if(c == 0) {
carry = 0;
ans.push_back(0);
} else if(c == -1){
carry = 1;
ans.push_back(1);
}else if(c == 1) {
carry = 0;
ans.push_back(1);
} else {
carry = -1;
ans.push_back(1);
}
i++;
}
while(carry) {
int c = carry;
if(c == 2) {
carry = -1;
ans.push_back(0);
} else if(c == 0) {
carry = 0;
ans.push_back(0);
} else if(c == -1){
carry = 1;
ans.push_back(1);
}else if(c == 1) {
carry = 0;
ans.push_back(1);
} else {
carry = -1;
ans.push_back(1);
}
}
while(ans.size() > 1 && ans.back() == 0) {
ans.pop_back();
}
reverse(ans.begin(), ans.end());
return ans;
}
};
```
| 1
| 0
|
['C++']
| 0
|
adding-two-negabinary-numbers
|
Bit Operation with little trick - Beat 100%
|
bit-operation-with-little-trick-beat-100-74zz
|
Intuition\n Describe your first thoughts on how to solve this problem. \nthe list of binary will be different with usual binary, the negabinary representation w
|
muzakkiy
|
NORMAL
|
2024-01-31T07:53:32.142248+00:00
|
2024-01-31T07:53:32.142277+00:00
| 316
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthe list of binary will be different with usual binary, the negabinary representation will be like this:\n[...,64,-32,16,-8,4,-2,1]\n\nif there is 1 + 1 (base 10), the result will be 2. on negabinary will be [1,1,0] = 4 + (-2) + 0 = 2\nso the answer of 1 + 1 = 110\n\nOR\n\nthe next bit is (- prevbit*2), we we have carry over and there is >= 1 bit on the next bit, we just substract it\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\ncalculate arr1 & arr2, iterating it from most left to the most right, if there is carry bit, we check on the next, if next bit is > 0, decrease it by -1, if not, adding next bit and next 2 bit by 1\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nfunc addNegabinary(arr1 []int, arr2 []int) []int {\n if len(arr1) < len(arr2) {\n arr1, arr2 = arr2, arr1\n }\n \n for i := 0; i < len(arr2); i++ {\n arr1[len(arr1)-i-1] += arr2[len(arr2)-i-1]\n }\n\n res := []int{}\n\n for i := 0; i < len(arr1); i++ {\n index := len(arr1)-i-1\n curr := arr1[index]\n arr1[index] %= 2\n if curr <= 1 {continue}\n if index-1 >= 0 && arr1[index-1] > 0 {\n arr1[index-1]--\n } else if index-2 >= 0 {\n arr1[index-1]++\n arr1[index-2]++\n } else {\n res = []int{1,1}\n }\n }\n\n res = append(res, arr1...)\n var i int\n for i = 0; i < len(res); i++ {\n if res[i] == 1 {break} \n }\n if len(res) == i {return []int{0}}\n return res[i:]\n}\n```
| 1
| 0
|
['Go']
| 1
|
adding-two-negabinary-numbers
|
Clean Python | High Speed | O(n) time, O(1) space | Beats 98.9%
|
clean-python-high-speed-on-time-o1-space-q5nh
|
Code\n\nclass Solution:\n def addBinary(self, A, B):\n res = []\n carry = 0\n while A or B or carry:\n carry += (A or [0]).po
|
avs-abhishek123
|
NORMAL
|
2023-01-26T10:02:35.976903+00:00
|
2023-01-26T10:02:35.976955+00:00
| 389
| false
|
# Code\n```\nclass Solution:\n def addBinary(self, A, B):\n res = []\n carry = 0\n while A or B or carry:\n carry += (A or [0]).pop() + (B or [0]).pop()\n res.append(carry & 1)\n carry = carry >> 1\n return res[::-1]\n\n def addNegabinary(self, A, B):\n res = []\n carry = 0\n while A or B or carry:\n carry += (A or [0]).pop() + (B or [0]).pop()\n res.append(carry & 1)\n carry = -(carry >> 1)\n while len(res) > 1 and res[-1] == 0:\n res.pop()\n return res[::-1]\n```
| 1
| 0
|
['Python3']
| 1
|
adding-two-negabinary-numbers
|
Java Solution easy to understand.
|
java-solution-easy-to-understand-by-hsds-9j2n
|
At first, \n0+0=1, 1+0=1, 1+1=110.\nSo you have to calculate with carry over 11.\n11+0+0=11, 11+0+1=0, 11+1+1=1.\nThen you have to to calculate with carry over
|
hsdsh
|
NORMAL
|
2022-11-13T11:59:54.635173+00:00
|
2022-11-13T11:59:54.635218+00:00
| 182
| false
|
At first, \n0+0=1, 1+0=1, 1+1=110.\nSo you have to calculate with carry over 11.\n11+0+0=11, 11+0+1=0, 11+1+1=1.\nThen you have to to calculate with carry over 1.\n1+0+0=1, 1+0+1=110, 1+1+1 = 111.\nThat\'s all you have to calculate and these are implemented in add.\n```\nclass Solution {\n public void add(int[] r, int b){ //r.length == 3\n r[2] += b;\n if(r[2]>1){\n r[2] = 0;\n if(r[1]==1){\n r[1] = 0;\n } else {\n r[0] = 1;\n r[1] = 1;\n }\n } \n }\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n List<Integer> ret = new ArrayList<>();\n int[] w = new int[3];\n for(int i = 0; i < arr1.length || i < arr2.length; i ++){\n if(i < arr1.length){ \n add(w, arr1[arr1.length - 1 - i]);\n }\n if(i < arr2.length){ \n\t\t\t\tadd(w, arr2[arr2.length - 1 - i]);\n }\n ret.add(w[2]);\n w[2] = w[1];\n w[1] = w[0];\n w[0] = 0;\n \n }\n if(w[2]>0 || w[1]>0){\n ret.add(w[2]);\n if(w[1]>0){ret.add(w[2]);}\n } \n while(ret.get(ret.size() - 1 ) == 0 && ret.size()>1){\n ret.remove(ret.size() - 1);\n }\n int[] reta= new int[ret.size()];\n for(int i = 0; i < ret.size(); i ++){\n reta[i] = ret.get(ret.size()-1-i);\n }\n return reta;\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
🔥 Simple Javascript Solution - Easy to Understand
|
simple-javascript-solution-easy-to-under-liod
|
\nfunction addNegabinary(a, b) {\n // reverse first\n a = a.reverse(), b = b.reverse();\n\n // set c as third array, get max as number of loops\n le
|
joenix
|
NORMAL
|
2022-05-25T11:27:15.891085+00:00
|
2022-05-25T11:27:15.891121+00:00
| 178
| false
|
```\nfunction addNegabinary(a, b) {\n // reverse first\n a = a.reverse(), b = b.reverse();\n\n // set c as third array, get max as number of loops\n let c = dp(Math.max(a.length, b.length));\n\n // remove 0\n while (c.length > 1 && c[0] == 0) {\n c.shift();\n }\n\n // result\n return c;\n\n // dp\n function dp(max, r = []) {\n for (let i = 0; i <= max; i++) {\n // fault-tolerant\n r[i] = (a[i] || 0) + (b[i] || 0) + (r[i] || 0);\n\n if (r[i] == -1) {\n r[i] = 1;\n r[i + 1] = 1;\n continue;\n }\n\n if (r[i] == 2) {\n r[i] = 0;\n r[i + 1] = -1;\n continue;\n }\n\n if (r[i] == 3) {\n r[i] = 1;\n r[i + 1] = -1;\n continue;\n }\n }\n return r.reverse();\n }\n};\n```
| 1
| 0
|
['JavaScript']
| 0
|
adding-two-negabinary-numbers
|
C++ Solution O(N)
|
c-solution-on-by-ahsan83-zw14
|
Runtime: 4 ms, faster than 96.48% of C++ online submissions for Adding Two Negabinary Numbers.\nMemory Usage: 19.4 MB, less than 87.32% of C++ online submission
|
ahsan83
|
NORMAL
|
2022-05-14T04:53:37.305122+00:00
|
2022-05-14T04:53:37.305162+00:00
| 315
| false
|
Runtime: 4 ms, faster than 96.48% of C++ online submissions for Adding Two Negabinary Numbers.\nMemory Usage: 19.4 MB, less than 87.32% of C++ online submissions for Adding Two Negabinary Numbers.\n\n\n```\nWe can add 2 negabinary number same way we add 2 binary number.\n\nIn case of Base 2 binary number addition we get the Bit and Carry from Sum \n\nSum = Carry + 1st number Bit + 2nd number Bit\n\nNow the current Bit and Carry comes from the binary representation of the Base 2 Sum \n\nValue => Carry | Bit (Binary Representation in Base 2)\n0 => 0 | 0\n1 => 0 | 1\n2 => 1 | 0\n3 => 1 | 1\n\nSame way in case of Base -2 binary number addition we get Bit and Carry from the binary representation of Sum\n\nValue => Carry | Bit (Binary Representation in Base -2) \n-2 => 1 | 0\n-1 => 1 | 1\n0 => 0 | 0\n1 => 0 | 1\n2 => 1 1 | 0 => Carry 11 is actually binary representation of -1\n3 => 1 1 | 1 => Carry 11 is actually binary representation of -1\n\nSo we prestore these Bit and Carry in array for -2 to 3 Sum values in vector and perform binary addition.\n```\n\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n \n int i = arr1.size()-1;\n int j = arr2.size()-1;\n\n // prestore bits and carry for different sum values\n vector<int>bits = {0,1,0,1,0,1};\n vector<int>carries = {1,1,0,0,-1,-1};\n \n vector<int>res;\n \n int sum;\n int carry = 0;\n \n // perform binary addition using sum and prestored bit and carry values\n while(i>=0 || j>=0 || carry)\n {\n sum = carry + (i>=0 ? arr1[i--] : 0) + (j>=0 ? arr2[j--] : 0);\n \n carry = carries[sum+2];\n\n res.push_back(bits[sum+2]);\n }\n \n // remove leading zeroes\n while(res.size() > 1 && res.back()==0)res.pop_back();\n \n reverse(res.begin(),res.end());\n \n return res;\n }\n};\n```\n\n\n\n\n
| 1
| 0
|
['Math', 'C']
| 0
|
adding-two-negabinary-numbers
|
Python 100% fastest with comments
|
python-100-fastest-with-comments-by-blak-hmvx
|
\nclass Solution(object):\n def addNegabinary(self, arr1, arr2):\n """\n :type arr1: List[int]\n :type arr2: List[int]\n :rtype:
|
blakejmas
|
NORMAL
|
2022-04-14T16:43:25.189814+00:00
|
2022-04-14T16:43:25.189856+00:00
| 237
| false
|
```\nclass Solution(object):\n def addNegabinary(self, arr1, arr2):\n """\n :type arr1: List[int]\n :type arr2: List[int]\n :rtype: List[int]\n """\n # get lengths\n m, n = len(arr1), len(arr2)\n \n # carry for positive and negative places\n c_pos, c_neg = 0, 0 \n \n # reverse arrays for easier indexing\n arr1[:], arr2[:] = arr1[::-1], arr2[::-1]\n \n # define starting place and output variables\n i, out = 0, []\n \n # loop over all indices and sum\n while i < max(m, n) or c_pos or c_neg: \n # extract number at each place handing indexing\n n1 = 0 if i >= m else arr1[i]\n n2 = 0 if i >= n else arr2[i]\n \n # handle case of even bases\n if not i % 2: \n res = c_pos + n1 + n2\n if res in [0, 1]:\n out.append(res)\n c_pos = 0\n elif res > 1:\n out.append(res % 2)\n c_pos = 1\n c_neg = 1\n else:\n out.append(-res)\n c_pos = 0\n c_neg = 1\n \n # handle case of odd bases\n else:\n res = c_neg + n1 + n2\n if res in [0, 1]:\n out.append(res)\n c_neg = 0\n else:\n out.append(res % 2)\n c_pos -= 1\n c_neg = 0\n i += 1\n \n # remove any leading 0\'s due to handling carries:\n while len(out) > 1 and not out[-1]:\n out.pop()\n \n # reverse and return out array\n out[:] = out[::-1]\n return out\n \n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
Java, Easy solution
|
java-easy-solution-by-tanujatammireddy21-eq3i
|
```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n \n List result = new ArrayList();\n int pointer_1 = arr1.
|
tanujatammireddy21
|
NORMAL
|
2022-04-03T01:53:55.955941+00:00
|
2022-04-03T01:53:55.955991+00:00
| 384
| false
|
```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n \n List<Integer> result = new ArrayList();\n int pointer_1 = arr1.length-1;\n int pointer_2 = arr2.length-1;\n\n int carry = 0;\n int current = 0;\n int sum = 0;\n \n while(pointer_1 >= 0 || pointer_2 >= 0){\n \n int a = (pointer_1 >=0)? arr1[pointer_1]: 0;\n int b = (pointer_2 >=0)? arr2[pointer_2]: 0;\n \n sum = a+b+carry;\n if(sum == 3){\n current = 1; carry = -1;\n }\n else if(sum == 2){\n current = 0; carry = -1;\n }\n else if(sum == 1){\n current = 1; carry = 0;\n }\n else if(sum == 0){\n current = 0; carry = 0;\n }\n else if(sum == -1)\n {\n current = 1; carry = 1;\n }\n \n result.add(current);\n pointer_1--;\n pointer_2--;\n }\n \n if(carry != 0)\n result.add(1);\n if(carry == -1)\n result.add(1);\n \n // Removing leading zeros\n int idx = result.size()-1;\n while(idx > 0 && result.get(idx) == 0)\n idx--;\n \n // reversing the list and adding the result to an array\n int len = idx+1;\n int[] negaBinary = new int[len];\n for(int i=0; i<len; i++){\n negaBinary[i] = result.get(idx);\n idx--;\n }\n \n return negaBinary;\n \n }\n}
| 1
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
Java Clean Code
|
java-clean-code-by-shiweiwong-cvlz
|
\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n LinkedList<Integer> res = new LinkedList<>();\n int i = 1, carry =
|
shiweiwong
|
NORMAL
|
2022-03-08T10:37:34.284004+00:00
|
2022-03-08T10:37:34.284045+00:00
| 313
| false
|
```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n LinkedList<Integer> res = new LinkedList<>();\n int i = 1, carry = 0;\n while( i <= arr1.length || i <= arr2.length || carry != 0){\n int a = arr1.length - i > -1 ? arr1[arr1.length - i] : 0;\n int b = arr2.length - i > -1 ? arr2[arr2.length - i] : 0;\n if( a + b - carry >= 0){\n res.addFirst((a + b - carry) % 2);\n carry = ( a + b - carry) / 2;\n }else{\n res.addFirst(1);\n carry = -1;\n }\n i++;\n }\n int[] arr = res.stream().dropWhile(x->x == 0).mapToInt(x->x).toArray();\n return arr.length > 0 ? arr : new int[]{0};\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
[Python] iterative
|
python-iterative-by-artod-5boy
|
Here I just sum corresponding bits from the input arrays starting from the right and carry the leftover to the next bit using the rule from lookup dictionary. A
|
artod
|
NORMAL
|
2021-11-15T04:33:49.279519+00:00
|
2021-11-15T04:33:49.279567+00:00
| 388
| false
|
Here I just sum corresponding bits from the input arrays starting from the right and carry the leftover to the next bit using the rule from `lookup` dictionary. At the end do not forrget remove leading zeros from the answer.\n\nTime: **O(n)** for iteration\nSpace: **O(1)** if the resulting array is not taken into account\n\nRuntime: 48 ms, faster than **42.11%** of Python online submissions for Adding Two Negabinary Numbers.\nMemory Usage: 13.9 MB, less than **10.53%** of Python online submissions for Adding Two Negabinary Numbers.\n\n```\nclass Solution(object):\n def addNegabinary(self, arr1, arr2):\n l1, l2 = len(arr1), len(arr2)\n i, j = l1 - 1, l2 - 1\n carry = 0\n res = deque()\n \n lookup = {\n -1: (1, 1),\n 0: (0, 0),\n 1: (1, 0),\n 2: (0, -1),\n 3: (1, -1),\n }\n \n while i > -1 or j > -1 or carry:\n cur = (arr1[i] if i > -1 else 0) + (arr2[j] if j > -1 else 0) + carry\n \n bit, carry = lookup[cur]\n res.appendleft(bit)\n \n i, j = i - 1, j - 1\n \n while len(res) > 1 and res[0] == 0: # remove leading 0s\n res.popleft()\n \n return list(res)\n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
Python solution (base negative-two conversion)
|
python-solution-base-negative-two-conver-fp9m
|
The tricky part might be how to convert a number to base negative-two representation.\n\nclass Solution:\n def addNegabinary(self, arr1, arr2):\n n =
|
jinghuayao
|
NORMAL
|
2021-10-27T21:02:06.115301+00:00
|
2021-10-27T21:02:06.115360+00:00
| 501
| false
|
The tricky part might be how to convert a number to base negative-two representation.\n```\nclass Solution:\n def addNegabinary(self, arr1, arr2):\n n = (sum(pow(-2, i) for i, v in enumerate(arr1[::-1]) if v) +\n sum(pow(-2, i) for i, v in enumerate(arr2[::-1]) if v))\n res = self.get_base_negative_two(n)\n return res if res else [0]\n \n \n def get_base_negative_two(self, n):\n """\n q, r = divmod(a, b): here a, b can be any non-complex number with abs(b) nonzero. The return r has the same sign as b and 0 <= abs(r) < abs(b).\n A special case is when a, b are positive integers, then q, r are the usual\n quotient and remainder.\n \n """\n res = []\n while n:\n n, rem = divmod(n, -2)\n print(n, rem)\n if rem < 0:\n n += 1\n res.append(abs(rem))\n res.reverse()\n return res\n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
C++, 100 %, Standard negative base addition rules from Wikipedia
|
c-100-standard-negative-base-addition-ru-7n7x
|
\n\nclass Solution {\npublic:\n #define pii pair<int,int>\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n unordered_map<int,
|
aditya_trips
|
NORMAL
|
2021-06-27T06:25:15.799383+00:00
|
2021-06-27T06:25:15.799414+00:00
| 640
| false
|
\n```\nclass Solution {\npublic:\n #define pii pair<int,int>\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n unordered_map<int, pii> mp ;\n mp[-2] = {0,1}, mp[-1] = {1,1}, mp[0] = {0,0}, mp[1] = {1,0}, mp[2] = {0,-1}, mp[3] = {1,-1}; \n vector<int> res ; \n int n = arr1.size(), m = arr2.size();\n int i = n-1, j = m-1, carry = 0, currbit = 0; \n while(i>= 0 || j >= 0 || carry){\n int currSum = carry; \n if(i >=0 ) currSum += arr1[i--];\n if(j >= 0) currSum += arr2[j--]; \n currbit = mp[currSum].first; \n carry = mp[currSum].second; \n res.push_back(currbit); \n }\n reverse(res.begin(), res.end());\n auto it = res.begin(); \n while(it!= res.end() && *it == 0) it ++; \n if(it == res.end()) return {0}; \n res = vector<int> (it, res.end()); \n return res ; \n }\n};\n```
| 1
| 1
|
['C']
| 0
|
adding-two-negabinary-numbers
|
Java O(N)
|
java-on-by-brucezu-pxsl
|
\n /*\n Idea:\n "Given two numbers arr1 and arr2 in base -2."\n So:\n - for any column it s possible to have -1,0,1.\n - For 2 neighbor columns:\n
|
brucezu
|
NORMAL
|
2021-03-20T05:01:28.586741+00:00
|
2021-03-20T05:01:28.586785+00:00
| 258
| false
|
```\n /*\n Idea:\n "Given two numbers arr1 and arr2 in base -2."\n So:\n - for any column it s possible to have -1,0,1.\n - For 2 neighbor columns:\n left:-2^i | right:2^{i-1}:\n -------------------------\n x y\n 1 1\n 0 0\n -1 -1\n -------------------------\n x= y*(-2)\n\n */\n // O(N)\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n int M = arr1.length, N = arr2.length;\n int i = M - 1, j = N - 1;\n Stack<Integer> res = new Stack();\n int carry = 0;\n while (i >= 0 || j >= 0 || carry != 0) {\n if (i >= 0) carry += arr1[i--];\n if (j >= 0) carry += arr2[j--];\n\n res.push(carry & 1);\n carry = (-1) * (carry >> 1);\n }\n\n while (res.size() > 1 && res.peek() == 0) res.pop();\n int[] r = new int[res.size()];\n i = 0;\n while (!res.isEmpty()) {\n r[i++] = res.pop();\n }\n return r;\n }\n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
[Python] Easy to understand solution
|
python-easy-to-understand-solution-by-tg-77o9
|
\tarr1[i] + arr2[i] + carry[i] == -1\n\t\t\t\t-> ans.append(1)\n\t\t\t\t-> carry[i+1] = 1\n \tarr1[i] + arr2[i] + carry[i] == 0\n\t\t\t\t-> ans.append(0)\n\t\t\
|
tgh20
|
NORMAL
|
2021-02-20T01:50:51.803894+00:00
|
2021-02-20T01:50:51.803927+00:00
| 299
| false
|
* \tarr1[i] + arr2[i] + carry[i] == -1\n\t\t\t\t-> ans.append(1)\n\t\t\t\t-> carry[i+1] = 1\n* \tarr1[i] + arr2[i] + carry[i] == 0\n\t\t\t\t-> ans.append(0)\n\t\t\t\t-> carry[i+1] = 0\n* \tarr1[i] + arr2[i] + carry[i] == 1\n\t\t\t\t-> ans.append(1)\n\t\t\t\t-> carry[i+1] = 0\n* \tarr1[i] + arr2[i] + carry[i] == 2\n\t\t\t\t-> ans.append(0)\n\t\t\t\t-> carry[i+1] = -1\n* \tarr1[i] + arr2[i] + carry[i] == 3\n\t\t\t\t-> ans.append(1)\n\t\t\t\t-> carry[i+1] = -1\n\t\t\t\t\n\t\t\t\t\t\t\t---------------------------\n\t\t\t\t\t\t\tcarry | 0 |-1 | 0 |-1 | 0 | \n\t\t\t\t\t\t\tarr1 | 1 | 1 | 1 | 1 | 1 |\n\t\t\t\t\t\t\tarr2 | | | 1 | 0 | 1 |\n\t\t\t\t\t\t\tans | 1 | 0 | 0 | 0 | 0 |\n\t\t\t\t\t\t\t---------------------------\n\n```\nclass Solution(object):\n def addNegabinary(self, arr1, arr2):\n """\n :type arr1: List[int]\n :type arr2: List[int]\n :rtype: List[int]\n """\n ans = []\n carry = 0\n while arr1 or arr2 or carry:\n val1, val2 = (arr1 or [0]).pop(), (arr2 or [0]).pop()\n if val1 + val2 + carry == -1:\n ans.append(1)\n carry = 1\n elif val1 + val2 + carry == 0:\n ans.append(0)\n carry = 0\n elif val1 + val2 + carry == 1:\n ans.append(1)\n carry = 0\n elif val1 + val2 + carry == 2:\n ans.append(0)\n carry = -1\n else:\n ans.append(1)\n carry = -1\n \n while len(ans) > 1 and ans[-1] == 0:\n ans.pop()\n \n return ans[::-1]\n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
C++ solution using 2 carry
|
c-solution-using-2-carry-by-belaid-ektb
|
\nMy solution using two carry: \n\n\n2* (-2)^i = (-2)^(i+1) + (-2)^(i+2); // current = 0, carry1 = 1 and carry2 = 1\n3* (-2)^i = (-2)^i + (-2)^(i+1) + (-2)^(i+2
|
belaid
|
NORMAL
|
2020-10-16T13:39:12.136176+00:00
|
2020-10-16T13:39:12.136210+00:00
| 236
| false
|
\nMy solution using two carry: \n\n```\n2* (-2)^i = (-2)^(i+1) + (-2)^(i+2); // current = 0, carry1 = 1 and carry2 = 1\n3* (-2)^i = (-2)^i + (-2)^(i+1) + (-2)^(i+2) // current = 1, carry1 = 1 and carry2 = 1\n4* (-2)^i = (-2)^(i+2); // current = 0, carry1 = 0 and carry2 = 1\n```\n```\nvector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n\tvector<int> ret;\n\tdeque<int> res(max(arr1.size(), arr2.size()));\n\tunordered_map<int, int> carry;\n\tint i, j;\n\tfor (i = arr1.size() - 1, j = arr2.size() - 1; i >= 0 || j >= 0; i--, j--){\n\t\tint idx = max(i, j);\n\t\tint sum = carry[idx];\n\t\tif (i >= 0) sum += arr1[i];\n\t\tif (j >= 0) sum += arr2[j];\n\t\tif (sum == 0) res[idx] = 0;\n\t\telse if (sum == 1) res[idx] = 1;\n\t\telse if (sum == 2) res[idx] = 0, carry[idx - 1]++, carry[idx - 2]++;\n\t\telse if (sum == 3) res[idx] = 1, carry[idx - 1]++, carry[idx - 2]++;\n\t\telse res[idx] = 0, carry[idx - 2]++;\n\t}\n\tif (carry[-1] != 2 || carry[-2] != 1){\n\t\tif (carry[-1] == 1)res.push_front(1);\n\t\tif (carry[-2] == 1)res.push_front(1);\n\t}\n\tfor (auto e : res) {\n\t\tif (!e) res.pop_front();\n\t\telse break;\n\t}\n\tif (res.size() == 0) return{ 0 };\n\tstd::copy(res.begin(), res.end(), std::back_inserter(ret));\n\treturn ret;\n}\n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
simple java 100%
|
simple-java-100-by-jjyz-rn0l
|
\nthe only thing we need to know is that the carry populates to two digits to the left\n [1]\n+ [1]\n--------\n[1,1,0]\n\n\n```\nclass Solution {\n publ
|
JJYZ
|
NORMAL
|
2020-08-18T03:03:16.473023+00:00
|
2020-08-18T03:32:03.791632+00:00
| 212
| false
|
```\nthe only thing we need to know is that the carry populates to two digits to the left\n [1]\n+ [1]\n--------\n[1,1,0]\n```\n\n```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n int carry = 0;\n int l1 = arr1.length-1;\n int l2 = arr2.length-1;\n int[] res = l1>=l2 ? arr1 : arr2;\n int idx = l1>=l2 ? l1 : l2;\n while(l1>=0 || l2>=0){\n int val1 = l1>=0 ? arr1[l1] : 0;\n int val2 = l2>=0 ? arr2[l2] : 0;\n int val = val1 + val2;\n if(carry > 0){\n if(carry == 2){\n carry = val > 0 ? 0 : 1;\n val = val > 0 ? val-1 : 1;\n }else{\n carry = val > 0 ? 2 : 0;\n val = val > 0 ? val-1 : 1;\n }\n }else{\n if(val == 2){\n val = 0;\n carry = 2;\n }\n }\n res[idx--] = val;\n l1--;\n l2--;\n }\n int start = 0;\n if(carry > 0){\n int[] resExt = new int[res.length+2];\n resExt[0] = 1;\n resExt[1] = 1;\n start += 2;\n for(int i : res)\n resExt[start++] = i;\n return resExt;\n }else{\n while(res[start]==0 && start != res.length-1)\n start++;\n return Arrays.copyOfRange(res, start, res.length);\n }\n }\n}
| 1
| 1
|
[]
| 0
|
adding-two-negabinary-numbers
|
C ++ From Wikipedia & Some explaination
|
c-from-wikipedia-some-explaination-by-ma-4gba
|
The base algorithm is derived from wikipedia, basically, the majority of bit sum is the same. The main difference is to understand that the sum at each bit loca
|
marzio
|
NORMAL
|
2020-06-12T04:03:56.944545+00:00
|
2020-06-12T04:08:15.294984+00:00
| 349
| false
|
The base algorithm is derived from wikipedia, basically, the majority of bit sum is the same. The main difference is to understand that the sum at each bit location, will be decompose to carry, and the bit at current location. So from the wikipedia chart, for example, when bit sum equals to 2, it should be decomposed to current bit = 0, carry = -1. (because 0 * 2^0 + (-1)*(-2) = 2)\n\n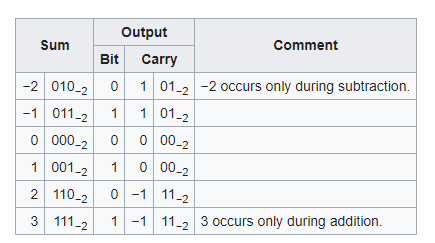\n\nTherefore, we know that we can mostly perform bit additions, and simply addressing the carry based on the total sum.\n\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n int carry = 0;\n vector<int> res;\n int p1 = (int)arr1.size() - 1, p2 = (int)arr2.size() - 1;\n while( p1 >=0 || p2 >=0 || carry!= 0) {\n if(p1 >= 0) carry += arr1[p1--];\n if(p2 >= 0) carry += arr2[p2--];\n res.push_back(abs(carry) & 1);\n carry = carry > 1 ? -1 : carry < 0 ? 1 : 0;\n }\n \n while(res.size() > 1 &&res.back() == 0) \n res.pop_back();\n reverse(res.begin(), res.end());\n return res;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
javascript O(n) solution
|
javascript-on-solution-by-tajinder89-ggtm
|
\n/**\n * @param {number[]} arr1\n * @param {number[]} arr2\n * @return {number[]}\n */\nvar addNegabinary = function(arr1, arr2) {\n // making array size e
|
tajinder89
|
NORMAL
|
2020-02-09T14:39:16.770808+00:00
|
2020-02-09T14:40:43.032242+00:00
| 176
| false
|
```\n/**\n * @param {number[]} arr1\n * @param {number[]} arr2\n * @return {number[]}\n */\nvar addNegabinary = function(arr1, arr2) {\n // making array size equal\n if(arr1.length > arr2.length) {\n arr2 = new Array(arr1.length - arr2.length).fill(0).concat(arr2);\n }\n else {\n arr1 = new Array(arr2.length - arr1.length).fill(0).concat(arr1);\n }\n let carry = 0;\n let result = [];\n\t // carry 1 + 1 = -1 \n for(let i = arr2.length - 1; i >= 0; i--) {\n sum = carry + arr2[i] + arr1[i];\n carry = 0;\n if(sum > 1){\n carry = -1;\n }\n else if(sum < 0){\n carry = 1;\n sum = 1;\n }\n result.push(sum %2);\n }\n \n if( carry == -1) {\n result.push(1,1)\n }\n \n if( carry == 1) {\n result.push(1)\n }\n let t = 0;\n for(let i = result.length-1; i >= 0; i--) {\n if(result[i] === 1)\n break;\n t++;\n }\n if(t === result.length) {\n return [0];\n }\n return result.reverse().slice(t);\n};\n\n```\n
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
Simple Python Solution With Comment
|
simple-python-solution-with-comment-by-5-s3z1
|
\nclass Solution:\n def addNegabinary(self, arr1: [int], arr2: [int]) -> [int]:\n result_len = max(len(arr1), len(arr2)) + 2\n\t\t# reverse both array
|
599hypan
|
NORMAL
|
2019-10-06T20:42:37.003948+00:00
|
2019-10-06T20:42:37.003990+00:00
| 366
| false
|
```\nclass Solution:\n def addNegabinary(self, arr1: [int], arr2: [int]) -> [int]:\n result_len = max(len(arr1), len(arr2)) + 2\n\t\t# reverse both array\n arr1 = arr1[::-1] + [0] * (result_len - len(arr1))\n arr2 = arr2[::-1] + [0] * (result_len - len(arr2))\n\t\t# simply sum, then deal with 2s\n result = [arr1[i] + arr2[i] for i in range(result_len)]\n\n\t\t# note [2, 1] becomes [0, 0]\n\t\t# and [2, 0] becomes [0, 1, 1]\n for i in range(result_len-2):\n if result[i] >= 2:\n if result[i + 1]:\n result[i] -= 2\n result[i + 1] -= 1\n else:\n result[i] -= 2\n result[i + 1] += 1\n result[i + 2] += 1\n\t\t\n\t\t# remove extra 0s\n while result != [0] and result[-1] == 0:\n result = result[:-1]\n\n\t\t# reverse again\n return result[::-1]\n```
| 1
| 0
|
['Python']
| 0
|
adding-two-negabinary-numbers
|
My python solution (Vertical Addition with Explanation)
|
my-python-solution-vertical-addition-wit-or0s
|
Let say we have two number d1 d2 d3 ... dm, and q1 q2 q3... qm (if the two number have different number of digits, we can always left pad the shorter one with a
|
dragonrider
|
NORMAL
|
2019-06-08T09:50:21.703674+00:00
|
2019-06-08T09:56:11.152608+00:00
| 354
| false
|
Let say we have two number d<sub>1</sub> d<sub>2</sub> d<sub>3</sub> ... d<sub>m</sub>, and q<sub>1</sub> q<sub>2</sub> q<sub>3</sub>... q<sub>m</sub> (if the two number have different number of digits, we can always left pad the shorter one with all zeros)\n\nFor k<sup>th</sup> digit d<sub>k</sub> and q<sub>k</sub> there are two scenarios for addition\n\n1. If d<sub>k</sub> + q<sub>k</sub> + carry < 2, then the digit p<sub>k</sub> = d<sub>k</sub> + q<sub>k</sub> + carry, and carry = 0. We move to the next digit position. k = k + 1.\n2. If d<sub>k</sub> + q<sub>k</sub> + carry >= 2, then the digit p<sub>k</sub> = d<sub>k</sub> + q<sub>k</sub> + carry - 2. But we can NOT simply set carry = 1, because position k and position k + 1 has sign difference, since 2*(2<sup>k</sup>) != (-2)<sup>k</sup>. Notice 2*(2<sup>k</sup>) = (-1)*(-2)<sup>k+1</sup> and 2*(2<sup>k</sup>) = (-2)<sup>k+2</sup> + (-2)<sup>k+1</sup>, we can either carry = -1 on k+1<sup>th</sup> position or carry = 1 and carry = 1 for both position k + 1<sup>th</sup> and k + 2<sup>th</sup>. Therefore,\n\t1. If d<sub>k+1</sub> + q<sub>k+1</sub> = 0, the k + 1<sup>th</sup> position is 1 and carry = 1 to position k + 2. We then increase the position k by 2. k = k + 2\n\t2. If d<sub>k +1</sub>+ q<sub>k+1</sub> > 0, then k+1<sup>th</sup> position is d<sub>k+1</sub>+q<sub>k+1</sub> - 1, and carry = 0 to posotion k + 2, because 1<= d<sub>k +1</sub>+ q<sub>k+1</sub> <=2 and 0<= d<sub>k +1</sub>+ q<sub>k+1</sub> - 1 <= 1. We then also increase the position k by 2. k = k + 2.\n\t\nNotice, for the final answer we mush remove all the prevailing zeros. We do the vertical addition by first reverse all the digit and align the two number on the lowest significant digit, so we will remove all the traling zeros. After that, we can reverse the array to get the answer. If the array is empty, we return [0].\n\nAn Example\n```\n 5 4 3 2 1 carry\n\t\t1 1 1 1 1 \n\t\t0 0 1 0 1\n -------------\n\t\t\t 0 0 0\n\t -------------\n\t 0 0 0 0 0\n\t -------------\n\t 1 0 0 0 0 0\n\t -------------\n\t 1 0 0 0 0\n```\nso, 11111 (11)+ 101(5)=10000(16). That is what we want.\n\nAnother example,\n```\n 5 4 3 2 1 carry\n\t\t1 1 1 0 1 \n\t\t0 0 1 0 1\n -------------\n\t\t\t 1 0 1\n\t -------------\n\t 0 1 1 0 0\n\t -------------\n\t 1 0 1 1 0 0\n\t -------------\n\t 1 0 1 1 0\n```\nso, 11101(13)+101(5)=10110(18).\n\nBelow is my python implementation\n```python\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n arr1 = arr1[::-1]\n arr2 = arr2[::-1]\n m = len(arr1)\n n = len(arr2)\n if m > n:\n arr2.extend([0]*(m - n))\n if m < n:\n arr1.extend([0]*(n - m))\n l = len(arr1)\n arr = []\n carry = 0\n i = 0\n while i < l:\n d = arr1[i] + arr2[i] + carry\n if d >= 2:\n d -= 2\n arr.append(d)\n carry = 1\n if i + 1 < l and arr1[i + 1] + arr2[i + 1] == 0:\n arr.append(1)\n carry = 1\n i += 1\n elif i + 1 < l and arr1[i + 1] + arr2[i + 1] != 0:\n arr.append(arr1[i + 1] + arr2[i + 1] - 1)\n carry = 0\n i += 1\n else:\n arr.append(d)\n carry = 0\n i += 1\n \n if carry:\n arr.append(carry)\n arr.append(carry)\n #remove trailing zeros\n i = len(arr) - 1\n while i >= 0:\n if arr[i] == 0:\n i -= 1\n else:\n break\n if i >= 0:\n return arr[:i + 1][::-1]\n else:\n return [0]\n\t\t\t\n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
Standard addition of lists with tricky carry
|
standard-addition-of-lists-with-tricky-c-mmh7
|
Here we use the same technique as for adding two lists with carry\nbut the tricky part is the calculation of the carry.\nIf the sum is positive then just take t
|
todor91
|
NORMAL
|
2019-06-07T10:28:45.007599+00:00
|
2019-06-07T10:28:45.007657+00:00
| 176
| false
|
Here we use the same technique as for adding two lists with carry\nbut the tricky part is the calculation of the carry.\nIf the sum is positive then just take the remainer as carry and multiply it to -1.\nIf the sum is -1 then the carry becomes 1.\n```\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n reverse(arr1.begin(), arr1.end());\n reverse(arr2.begin(), arr2.end());\n int n = arr1.size();\n int m = arr2.size();\n int carry = 0;\n int i = 0, j = 0;\n vector<int> res;\n // Add to res while there is something to add\n while (true) {\n // When ther is no more to add break\n if (carry == 0 && i == n && j == m) break;\n int x1 = i < n ? arr1[i++] : 0;\n int x2 = j < m ? arr2[j++] : 0;\n int sm = x1 + x2 + carry;\n res.push_back(abs(sm % 2));\n // This is the tricky part\n carry = sm >= 0 ? -sm / 2 : 1;\n }\n while (res.size() > 1 && res.back() == 0) \n res.pop_back();\n reverse(res.begin(), res.end());\n return res;\n }\n```
| 1
| 0
|
[]
| 1
|
adding-two-negabinary-numbers
|
simple python solution beats 100%
|
simple-python-solution-beats-100-by-mrde-63hl
|
\n def addNegabinary(self, arr1, arr2):\n """\n :type arr1: List[int]\n :type arr2: List[int]\n :rtype: List[int]\n """\n
|
mrdelhi
|
NORMAL
|
2019-06-02T15:46:41.301141+00:00
|
2019-06-02T15:46:41.301175+00:00
| 91
| false
|
```\n def addNegabinary(self, arr1, arr2):\n """\n :type arr1: List[int]\n :type arr2: List[int]\n :rtype: List[int]\n """\n def num2dec(arr):\n n = 0\n for i, num in enumerate(arr[::-1]):\n n+= ((-2)**i)*num\n return n\n num = num2dec(arr1)+num2dec(arr2)\n \n \n if num == 0:\n digits = [\'0\']\n else:\n digits = []\n while num != 0:\n num, remainder = divmod(num, -2)\n if remainder < 0:\n num, remainder = num + 1, remainder + 2\n digits.append(str(remainder))\n return \'\'.join(digits[::-1])\n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
Java Add (allow overflow) then adjust
|
java-add-allow-overflow-then-adjust-by-b-3kv0
|
Add directly, each digit will be between 0-2\n2. Adjust if overflow, for digit[i] if it\'s >=2\na) if digit[i-1]>=1, digit[i-1]--;\nb) else digit[i - 1]++; digi
|
bluesky999
|
NORMAL
|
2019-06-02T05:48:41.349974+00:00
|
2019-06-02T05:48:41.350021+00:00
| 123
| false
|
1. Add directly, each digit will be between 0-2\n2. Adjust if overflow, for digit[i] if it\'s >=2\na) if digit[i-1]>=1, digit[i-1]--;\nb) else digit[i - 1]++; digit[i - 2]++;\n\n```\n\tpublic int[] addNegabinary(int[] arr1, int[] arr2) {\n\t\tint[] ret = new int[1020];\n\t\tfor (int i = 0; i < ret.length; i++) {\n\t\t\tint i1 = arr1.length - 1 - i;\n\t\t\tint a = (i1 >= 0 ? arr1[i1] : 0);\n\t\t\tint i2 = arr2.length - 1 - i;\n\t\t\tint b = (i2 >= 0 ? arr2[i2] : 0);\n\t\t\tint i3 = ret.length - 1 - i;\n\t\t\tret[i3] = a + b;\n\t\t}\n\t\tfor (int i = ret.length - 1; i > 2; i--) {\n\t\t\tif (ret[i] >= 2) {\n\t\t\t\tret[i] -= 2;\n\t\t\t\tif (ret[i - 1] >= 1)\n\t\t\t\t\tret[i - 1]--;\n\t\t\t\telse {\n\t\t\t\t\tret[i - 1]++;\n\t\t\t\t\tret[i - 2]++;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\tfor (int i = 0; i < ret.length; i++)\n\t\t\tif (ret[i] != 0)\n\t\t\t\treturn Arrays.copyOfRange(ret, i, ret.length);\n\n\t\treturn new int[] { 0 };\n\t}\n\n```
| 1
| 1
|
[]
| 0
|
adding-two-negabinary-numbers
|
Adjust or Carry method ( C++, with explanation )
|
adjust-or-carry-method-c-with-explanatio-a87g
|
Intitution:\nLet\'s just add elements of both numbers in any array to get sum of arr1 and arr2 ( I took result ).\n\nIf an elem of result vector is greater than
|
amitnsky
|
NORMAL
|
2019-06-02T05:33:28.212173+00:00
|
2019-06-03T12:06:57.970971+00:00
| 244
| false
|
# Intitution:\nLet\'s just add elements of both numbers in any array to get sum of arr1 and arr2 ( I took result ).\n\nIf an elem of result vector is greater than 2, it can be balanced in two ways:\n(assuming here that leftmost place is highest bit and rightmost place is lowest bit)\n1. By cancelling values of next place in res if available.\ne.g. If res is [1,2] = ( 1*(-2^1) + 2 * (2^0 ) = 0, can be written as [0,0].\n\n\tThis works because numbers are written on base of -2 so next place value will be in -ve if current value is +ve and vice-versa.\n\n\tconsider another example:\n\tIf result is [0,0,3,4,1,1] it will go as following:\n\t\n\t [0,0,3,4,1,1] -> [0,0,2,2,1,1]\n\t since result[2] = 3 => place value is 3 * (-8) = -24\n\t and result[3] = 4 => place value is 4 * 4 = 16\n\t so if we cancel result[3] by 2 * 4 ( two place values) the result will be \n\t 3 * (-8) + 4 * 4 = 8 = 2 * (-8) + 2 * 4 = 8\n\t \n\t [0,0,2,2,1,1] -> [0,0,1,0,1,1] same as above step.\n\t [0,0,1,0,1,1] will be final answer (ignore or pop two zeros at result[0] and result[1]).\n\n2. By putting a carry if it can not be cancelled with next decimal place value.\ne.g. [0,2] can be written as [1,1,0].\nNote that carry always goes to next two places\nbecause ( as here) 2 = 4 + (-2) + 0 = [1,1,0].\n\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n reverse(arr1.begin(), arr1.end());\n reverse(arr2.begin(), arr2.end());\n \n vector<int> result(1002, 0);\n \n for(int i=0; i<arr1.size(); i++) \n result[i] += arr1[i];\n for(int i=0; i<arr2.size(); i++) \n result[i] += arr2[i];\n \n for(int i=0; i<result.size(); i++){\n while(result[i]>=2){\n result[i] -= 2;\n if(result[i+1]>0) \n\t\t\t\t\t// balance using next digit.\n result[i+1] -= 1; \n else{\n\t\t\t\t\t// no next digit so post a carry.\n result[i+1]++;\n result[i+2]++;\n }\n }\n }\n \n while(result.size() > 1 && result.back()==0) \n result.pop_back();\n reverse(result.begin(), result.end());\n return result;\n }\n};\n```\n\n
| 1
| 1
|
[]
| 1
|
adding-two-negabinary-numbers
|
Simple python solution
|
simple-python-solution-by-merciless-e1mm
|
```\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n\t\t#convert Negabinary Numbers to int\n def helper(ar
|
merciless
|
NORMAL
|
2019-06-02T05:11:09.784892+00:00
|
2019-06-02T06:47:02.892699+00:00
| 160
| false
|
```\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n\t\t#convert Negabinary Numbers to int\n def helper(arr):\n ans = j = 0\n for i in arr[::-1]:\n ans += i * (-2) ** j\n j += 1\n return ans\n \n\t\t#convert an integer to Negabinary Numbers (See No.1017 for more detail)\n def h(N):\n if N == 0 or N == 1: return str(N)\n return h(-(N >> 1)) + str(N & 1)\n \n return [int(i) for i in h(helper(arr1) + helper(arr2))]
| 1
| 1
|
[]
| 0
|
adding-two-negabinary-numbers
|
Java O(n), straight forward,
|
java-on-straight-forward-by-ansonluo-rtja
|
\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n int length1 = arr1.length;\n int length2 = arr2.length;\n in
|
ansonluo
|
NORMAL
|
2019-06-02T04:27:11.865151+00:00
|
2019-06-02T04:27:11.865196+00:00
| 267
| false
|
```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n int length1 = arr1.length;\n int length2 = arr2.length;\n int length = Math.max(length1, length2);\n int[] result = new int[length + 2]; // the result \n for (int i = 0; i < length; i++) {\n int forward = 0;\n int i1 = length1 - i - 1;\n int i2 = length2 -i - 1;\n if (i1 >= 0) {\n forward += arr1[i1];\n }\n if (i2 >= 0) {\n forward += arr2[i2];\n }\n forward += result[length + 1 - i];\n if (forward >= 0) {\n int tmp = forward % 2;\n result[length + 1 - i] = tmp;\n result[length - i] = -(forward / 2);\n } else { // if forward less than 0, update the futher position\n result[length + 1 - i] = 1;\n result[length - i] = 1;\n }\n }\n\t\t// edit the result \n if (result[1] < 0) { \n result[0] = 1;\n result[1] = 1;\n return result;\n } else {\n int index = 0; //remove the zero postion\n while (index < length + 2 && result[index] == 0) {\n index++;\n }\n if (index >= length + 2) {\n return new int[]{0};\n }\n return Arrays.copyOfRange(result, index, length + 2);\n }\n }\n}\n```
| 1
| 1
|
[]
| 0
|
adding-two-negabinary-numbers
|
Python Easy Understand - Convert 2 times
|
python-easy-understand-convert-2-times-b-gwy6
|
\nclass Solution:\n def addNegabinary(self, arr1, arr2):\n num1 = self.convert_to_int(arr1)\n num2 = self.convert_to_int(arr2)\n num = s
|
zt586
|
NORMAL
|
2019-06-02T04:15:23.882336+00:00
|
2019-06-02T04:15:23.882380+00:00
| 168
| false
|
```\nclass Solution:\n def addNegabinary(self, arr1, arr2):\n num1 = self.convert_to_int(arr1)\n num2 = self.convert_to_int(arr2)\n num = self.convert_to_neg(num1+num2)\n return [int(d) for d in str(num)]\n \n def convert_to_int(self, arr):\n ans = i = 0\n for j in range(len(arr)-1, -1, -1):\n num = (-2)**i * arr[j]\n ans += num\n i += 1\n return ans\n \n def convert_to_neg(self, num):\n ans = \'\'\n if num == 0:\n return \'0\'\n while num != 0:\n rmd = num % (-2)\n n = num // (-2)\n \n if rmd < 0:\n rmd += 2\n n += 1\n \n num = n\n ans += str(rmd)\n return ans[::-1] \n```
| 1
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
PHP Solution
|
php-solution-by-neilchavez-dqv5
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Neilchavez
|
NORMAL
|
2025-03-04T00:21:26.427096+00:00
|
2025-03-04T00:21:26.427096+00:00
| 2
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```php []
class Solution {
/**
* @param Integer[] $arr1
* @param Integer[] $arr2
* @return Integer[]
*/
function addNegabinary($arr1, $arr2) {
$res = [];
$i = count($arr1) - 1;
$j = count($arr2) - 1;
$carry = 0;
while ( $i >= 0 || $j >= 0 || $carry != 0)
{
$sum = $carry;
$carry = 0;
if ($i >= 0)
{
$sum += $arr1[$i];
}
if ($j >= 0)
{
$sum += $arr2[$j];
}
if ($sum === 2)
{
$sum = 0;
$carry = -1;
}
if ($sum >= 3)
{
$sum = 1;
$carry = -1;
}
if ($sum < 0)
{
$sum = 1;
$carry = 1;
}
$res[] = $sum;
$i--;
$j--;
}
$res = array_reverse($res);
$k = 0;
while ($res[$k] === 0 && $k < count($res) - 1)
{
array_shift($res);
}
if ( $arr1[0] === 0
&& $arr2[0] === 0
&& count($arr1) === 1
&& count($arr2) === 1)
{
return [0];
}
return $res;
}
}
```
| 0
| 0
|
['PHP']
| 0
|
adding-two-negabinary-numbers
|
great
|
great-by-ivan_1999-v92t
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
ivan_1999
|
NORMAL
|
2025-02-18T12:01:08.396303+00:00
|
2025-02-18T12:01:08.396303+00:00
| 2
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```golang []
func addNegabinary(arr1 []int, arr2 []int) []int {
// Выравниваем длины массивов, дополняя более короткий нулями слева
maxLen := max(len(arr1), len(arr2))
if len(arr1) < maxLen {
arr1 = append(make([]int, maxLen-len(arr1)), arr1...)
}
if len(arr2) < maxLen {
arr2 = append(make([]int, maxLen-len(arr2)), arr2...)
}
// Результат и перенос
result := make([]int, 0)
carry := 0
// Проходим по массивам с конца
for i := maxLen - 1; i >= 0; i-- {
sum := arr1[i] + arr2[i] + carry
// Определяем текущий бит и новый перенос
if sum >= 2 {
result = append([]int{sum - 2}, result...)
carry = -1
} else if sum < 0 {
result = append([]int{sum + 2}, result...)
carry = 1
} else {
result = append([]int{sum}, result...)
carry = 0
}
}
// Обрабатываем оставшийся перенос
if carry != 0 {
result = append([]int{1, 1}, result...)
}
// Удаляем ведущие нули
for len(result) > 1 && result[0] == 0 {
result = result[1:]
}
return result
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
```
| 0
| 0
|
['Go']
| 0
|
adding-two-negabinary-numbers
|
Easy solution
|
easy-solution-by-koushik_55_koushik-46ng
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Koushik_55_Koushik
|
NORMAL
|
2025-02-04T14:24:28.258502+00:00
|
2025-02-04T14:24:28.258502+00:00
| 17
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
from typing import List
class Solution:
def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:
l = []
l1 = []
for i in arr1:
l.append(str(i))
for i in arr2:
l1.append(str(i))
k = "".join(l)
k1 = "".join(l1)
def btd(f):
f = f[::-1]
d = 0
b = -2
for i, j in enumerate(f):
if j == "1":
d += b**i
return d
m = btd(k) + btd(k1)
if m == 0:
return [0]
q = []
while m != 0:
remainder = m % -2
m //= -2
if remainder < 0:
remainder += 2
m += 1
q.append(remainder)
return q[::-1]
```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
easiest solution in c++
|
easiest-solution-in-c-by-prateek_verma14-fkdt
|
IntuitionAs length of array are too big so we cannot convert it to decimal , so we need to think direct additionApproachComplexityO(n)
Time complexity: O(n)
Sp
|
prateek_verma145
|
NORMAL
|
2025-01-14T06:35:34.567678+00:00
|
2025-01-14T06:35:34.567678+00:00
| 14
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
As length of array are too big so we cannot convert it to decimal , so we need to think direct addition
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity$$O(n)$$
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. -->
- Space complexity:$$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {
int i = arr1.size() - 1;
int j = arr2.size() - 1;
int carry = 0;
vector<int> res;
while (i >= 0 || j >= 0 || carry != 0) {
int x = (i >= 0) ? arr1[i] : 0;
int y = (j >= 0) ? arr2[j] : 0;
int sum = x + y + carry;
int remainder = sum % -2;
if (remainder < 0) {
remainder += 2;
carry = (sum / -2) +1;
} else {
carry = sum / -2;
}
res.push_back(remainder);
i--;
j--;
}
while (res.size() > 1 && res.back() == 0) {
res.pop_back();
}
reverse(res.begin(), res.end());
return res;
}
};
```
| 0
| 0
|
['Array', 'Math', 'C++']
| 0
|
adding-two-negabinary-numbers
|
Simple(Optimized) Java Solution
|
simpleoptimized-java-solution-by-angaria-0aac
|
Code
|
angaria_vansh
|
NORMAL
|
2025-01-11T17:34:51.887514+00:00
|
2025-01-11T17:34:51.887514+00:00
| 7
| false
|
# Code
```java []
class Solution {
public int[] addNegabinary(int[] arr1, int[] arr2) {
int i1 = arr1.length - 1, i2 = arr2.length - 1, carry = 0;
List<Integer> resultList = new ArrayList<Integer>();
// 1. calculate sum of arr1 and arr2
while (i1 >= 0 || i2 >= 0 || carry != 0) {
int n1 = i1 >= 0 ? arr1[i1--] : 0;
int n2 = i2 >= 0 ? arr2[i2--] : 0;
int sum = n1 + n2 + carry;
int result = sum & 1;
carry = -1 * (sum >> 1) ;
resultList.add(0, result);
}
// 2. remove leading zero
int beginIndex = 0;
while (beginIndex < resultList.size() && resultList.get(beginIndex) == 0)
beginIndex++;
if (beginIndex == resultList.size())
return new int[]{0};
int resultArray[] = new int[resultList.size() - beginIndex];
for (int i = 0; i < resultArray.length; i++)
resultArray[i] = resultList.get(i + beginIndex);
return resultArray;
}
}
```
| 0
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
1073. Adding Two Negabinary Numbers
|
1073-adding-two-negabinary-numbers-by-g8-i3lw
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-11T16:39:26.711264+00:00
|
2025-01-11T16:39:26.711264+00:00
| 13
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:
def to_decimal(arr):
return sum(val * (-2) ** idx for idx, val in enumerate(arr[::-1]))
def to_negabinary(num):
if num == 0:
return [0]
result = []
while num != 0:
num, remainder = divmod(num, -2)
if remainder < 0:
remainder += 2
num += 1
result.append(remainder)
return result[::-1]
return to_negabinary(to_decimal(arr1) + to_decimal(arr2))
```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
My solution
|
my-solution-by-huyle010504-zjy8
|
IntuitionWe simply add the numbers in the same pattern as binary, but now, instead of multiplying by 1, we multiply by -2.
To add two negabinary numbers, you ca
|
huyle010504
|
NORMAL
|
2025-01-03T22:45:30.254265+00:00
|
2025-01-03T22:45:30.254265+00:00
| 7
| false
|
# Intuition
We simply add the numbers in the same pattern as binary, but now, instead of multiplying by 1, we multiply by -2.
To add two negabinary numbers, you can use the following formula: at each digit position (from least significant bit/rightmost bit), sum the corresponding bits from both numbers along with the carry from the previous position, then **modulo 2 to get the current digit**; if the sum is greater than 1, set the carry to -1 and set current digit of result to be 0, otherwise set the carry to 0 and current digit of result to be sum; repeat this process until all digits are processed, remembering to adjust the final result based on the remaining carry.
# Approach
First, I create an empty list, and an integer n as 2 plus length of the larger array.
Then, I reverse 2 arrays.
Next, I create a pointer i at the beginning and carry as 0.
Then, I loop until i equals n. During the loop, I create the first bit as i-th element of first array, and 2nd bit as ith element of 2nd array, as long as i is smaller than the length of each. If i is at least equal to length of 1st array, I set first bit to be 0. The same for 2nd bit. Then I add 2 bits together with the carry, and create an integer r as sum modulo by 2. Then, I divide carry by -2. If r is negative, I add 2 to r (make sure it's just between 0 and 1), and increase carry by 1. Then, I add r to res. Finally, I increase i by 1 to go to the next position.
Whereupon, I remove all trailing 0s from the list, reverse it, and finally return it.
# Complexity
- Time complexity:
O(n*n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
private:
public:
vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {
vector<int>res;
int n=max(arr1.size(),arr2.size())+2;
reverse(arr1.begin(),arr1.end());
reverse(arr2.begin(),arr2.end());
int i=0,carry=0;
while(i<n){
int bit_1=(i<arr1.size())?arr1[i]:0;
int bit_2=(i<arr2.size())?arr2[i]:0;
int sum=bit_1+bit_2+carry;
int r=sum%2;
carry=sum/(-2);
if(r<0){
r+=2;
carry++;
}
res.push_back(r);
i++;
}
while(res.size()>1 && res.back()==0){
res.pop_back();
}
reverse(res.begin(),res.end());
return res;
}
};
```
| 0
| 0
|
['Array', 'Math', 'C++']
| 0
|
adding-two-negabinary-numbers
|
Just like regular binary addition, except carry can be -1
|
just-like-regular-binary-addition-except-b4xk
|
Intuition
Just like regular binary addition, except carry can be -1 or 1.
Add current two digits, and carry c, the sum can be 0,1,2,3,-1
if 0,2, the resulting d
|
lambdacode-dev
|
NORMAL
|
2024-12-24T20:11:01.686397+00:00
|
2024-12-24T20:11:01.686397+00:00
| 8
| false
|
# Intuition
- Just like regular binary addition, except carry can be -1 or 1.
- Add current two digits, and carry `c`, the sum can be `0,1,2,3,-1`
- if `0,2`, the resulting digit will be `0`, and `1` if `1, 3`.
- next carry `c` will be `-1` if `2,3`.
- if the sum is `-1`, convert it to `-1 = -2 + 1`, so current sum digit will be `1`, and next `c` will be `1`.
# Approach
- reverse `arr1` and `arr2`, and make them same size by filling `0`s.
- iteratively add digits from left to right
- append `1` if final `c = 1`, and `11` if final `c = -1`.
- reverse result to return.
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {
reverse(arr1.begin(), arr1.end());
reverse(arr2.begin(), arr2.end());
int sz = max(arr1.size(), arr2.size());
arr1.resize(sz);
arr2.resize(sz);
int c = 0;
vector<int> sum;
for(int i = 0; i < arr1.size() && i < arr2.size(); ++i) {
int val = arr1[i] + arr2[i] + c;
if(val == -1) {
sum.push_back(1);
c = 1;
}
else {
sum.push_back(val % 2);
c = val/2 ? -1 : 0;
}
}
if(c) {
sum.push_back(1);
if(c == -1)
sum.push_back(1);
}
while(sum.size() > 1 && !sum.back()) sum.pop_back();
reverse(sum.begin(), sum.end());
return sum;
}
};
```
| 0
| 0
|
['C++']
| 0
|
adding-two-negabinary-numbers
|
Time: Beats %100, Memory: Beats 82.76%
|
time-beats-100-memory-beats-8276-by-sobe-5tm0
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sobeitfk
|
NORMAL
|
2024-11-21T00:00:12.184656+00:00
|
2024-11-21T00:00:12.184694+00:00
| 4
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n Stack<Byte> rets = new Stack<>();\n int i = arr1.length - 1;\n int j = arr2.length - 1;\n // \u8FDB\u4F4D\u503C\u3002 \u4E24\u4E2A\u6570\u7EC4\u4E2D\u7684\u5143\u7D20\uFF0C\u5747\u4E3A 0,1, \u6240\u4EE5\u52A0\u4E00\u5757\u7684\u503C\u6709 0,1,2 \u4E09\u79CD\u53EF\u80FD\u3002 \u5982\u679C\u518D\u52A0\u4E0A\u8FDB\u4F4D\uFF0C\u6700\u7EC8\u53EF\u80FD\u4E3A 3\n // \u5F53\u524D\u4F4D\u5E94\u8BE5\u4FDD\u7559\u7684\u503C\u53EF\u4EE5\u7528 current&1 \u8BA1\u7B97, \u663E\u7136 0&1=0\uFF0C 2&1=0, \u800C 1&1=1, 3&1=1\n // \u8FDB\u4F4D\u503C\u8BA1\u7B97\u53EF\u4EE5 \u4F7F\u7528 current>>1 \u8BA1\u7B97, 0>>1=0, 1>>1=0, 2>>1=1, 3>>1=1\uFF0C\u663E\u7136\u53EA\u6709\u548C\u4E3A 2\u30013\u65F6\u624D\u9700\u8981\u8FDB\u4F4D\n // \u8FDB\u4F4D\u4E3A\u4EC0\u4E48\u8981\u8F6C\u6210 \u8D1F\u6570\uFF1F\n byte carry = 0;\n byte current = 0;\n\n while (i >= 0 || j >= 0 || carry != 0) {\n current = carry;\n\n if (i >= 0) {\n current += arr1[i];\n }\n\n if (j >= 0) {\n current += arr2[j];\n }\n\n rets.push( (byte)(current&1));\n carry = (byte) -(current >> 1);\n --i;\n --j;\n }\n\n while (rets.size() > 1 && rets.peek() == 0) {\n rets.pop();\n }\n\n int[] nums = new int[rets.size()];\n int p = 0;\n while(!rets.isEmpty()) {\n nums[p++] = rets.pop();\n }\n return nums;\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
scala solution
|
scala-solution-by-vititov-bwuv
|
https://en.wikipedia.org/wiki/Negative_base#Addition\nscala []\nobject Solution {\n val nMap = Map(\n -2 -> (0,1), -1 -> (1,1), 0 -> (0,0),\n 1 -> (1,0),
|
vititov
|
NORMAL
|
2024-11-02T18:52:17.405157+00:00
|
2024-11-02T18:52:17.405186+00:00
| 0
| false
|
https://en.wikipedia.org/wiki/Negative_base#Addition\n```scala []\nobject Solution {\n val nMap = Map(\n -2 -> (0,1), -1 -> (1,1), 0 -> (0,0),\n 1 -> (1,0), 2 -> (0,-1), 3 -> (1,-1)\n )\n def addNegabinary(arr1: Array[Int], arr2: Array[Int]): Array[Int] = {\n def f(seq:Seq[(Int,Int)], c: Int = 0, \n zero:Boolean=true, acc:Seq[Int] = Nil):Seq[Int] = {\n lazy val (a,b) = seq.headOption.getOrElse((0,0))\n lazy val (bit, carry) = nMap(a+b+c)\n if(seq.isEmpty && c==0) if(zero) List(0) else acc.dropWhile(_ == 0)\n else f(seq.drop(1), carry, zero&(bit==0), bit +: acc)\n }\n f(arr1.reverseIterator.toList zipAll (arr2.reverseIterator.toList,0,0)).toArray\n \n }\n}\n```
| 0
| 0
|
['Scala']
| 0
|
adding-two-negabinary-numbers
|
Beats 99% Cases Python
|
beats-99-cases-python-by-elenazzhao-iryt
|
Intuition\nWe can break down the numbers mathematically and see what happens to each digit at each stage. For example, adding [1] and [1] is performing \n\n$(-2
|
elenazzhao
|
NORMAL
|
2024-10-20T16:24:00.497421+00:00
|
2024-10-20T16:24:00.497465+00:00
| 24
| false
|
# Intuition\nWe can break down the numbers mathematically and see what happens to each digit at each stage. For example, adding [1] and [1] is performing \n\n$(-2)^0 + (-2)^0 = (2)(-2)^0 = (-2)^1 + (4-2)(-2)^0 = (-2)^2 + (-2)^1$\n\nwhich encoded in negabinary as [1, 1, 0].\n\nWe apply this arithmetic knowledge to all cases at each digit $$n $$, and can prove that we only ever need to hold on to two "carry-ons": one for digit $$n+1$$ and one for digit $$n+2$$\n# Approach\n**Cases:**\n **0.** $$0 * (-2)^n + 0 * (-2)^n = 0 * (-2)^n$$\n **1.** $$1 * (-2)^n + 0 * (-2)^n = 1 * (-2)^n = (-2)^n$$\n **2.** $$1 * (-2)^n + 1 * (-2)^n = 2 * (-2)^n = (4-2) * (-2)^n = (-2)^{n+2} + (-2)^{n+1}$$\n\n*You can have a maximum of num 1 + num 1 + carry-on 1 + carry-on 1 so 4, which is two more cases*\n **3.** $$1 * (-2)^n + 1 * (-2)^n + 1 * (-2)^n = (4-2+1) * (-2)^n = (-2)^{n+2} + (-2)^{n+1} + (-2)^n$$\n **4.** $$1 * (-2)^n + 1 * (-2)^n + 1 * (-2)^n + 1 * (-2)^n = (4) * (-2)^n = (-2)^{n+2}$$\n These are all the cases since you can at most impose a carry on two digits forward\n\n**Summarizing the conditions, we have, if the digit sum is:**\n **0.** Make this digit as 0\n **1.** Make this digit as 1\n **2.** Make this digit 0, carry_on 1 += 1, carry_on 2 is 1\n **3.** Make this digit 1, carry_on 1 += 1, carry_on 2 is 1\n **4.** Make this digit 0, carry_on 2 is 1\n\n\n**Special Condition**: If ever carry_on_two is 1, carry_on is 2, they need to cancel out, so add that as a check or else we risk infinite loop\n\nLastly, at the end we pop off any leading zeroes just in case\n\n# Complexity\n- Time complexity:\nO(n) $\\rightarrow$ we just traverse both arrays once\n\n- Space complexity:\nO(n) $\\rightarrow$ we build the new number, keep track of some carry_on values too but that\'s it\n\n# Code\n```python3 []\n\nfrom collections import deque\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n arr1_index = len(arr1) - 1\n arr2_index = len(arr2) - 1\n carry_on = 0\n carry_on_two = 0\n final = deque([])\n while arr1_index >= 0 or arr2_index >= 0 or carry_on > 0 or carry_on_two > 0:\n print(arr1_index, arr2_index)\n digit_sum = carry_on\n if arr1_index >= 0:\n digit_sum += arr1[arr1_index]\n arr1_index -= 1\n if arr2_index >= 0:\n digit_sum += arr2[arr2_index]\n arr2_index -= 1\n carry_on = carry_on_two\n carry_on_two = 0\n if digit_sum == 0:\n digit_value = 0\n elif digit_sum == 1:\n digit_value = 1\n elif digit_sum == 2:\n digit_value = 0\n carry_on += 1\n carry_on_two += 1\n elif digit_sum == 3:\n digit_value = 1\n carry_on += 1\n carry_on_two += 1\n elif digit_sum == 4:\n digit_value = 0\n carry_on_two += 1\n\n if carry_on == 2 and carry_on_two == 1:\n carry_on = 0\n carry_on_two = 0\n\n final.appendleft(digit_value)\n while (len(final) > 1 and final[0] == 0):\n final.popleft()\n return list(final)\n\n \n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
0ms Runtime - Beats 100% in terms of Runtime
|
0ms-runtime-beats-100-in-terms-of-runtim-yw5n
|
Intuition\nWe observe that 1+1 in this context is not 10 but 110 (4-2+0=2) as the base is -2. So we can do it if we maintain two carries for each bit addition.\
|
guptakushagra343
|
NORMAL
|
2024-10-11T07:13:26.357710+00:00
|
2024-10-11T07:13:26.357743+00:00
| 3
| false
|
# Intuition\nWe observe that 1+1 in this context is not 10 but 110 (4-2+0=2) as the base is -2. So we can do it if we maintain two carries for each bit addition.\n\n# Approach\nWe start with initialising the two carries c1, c3 to 0. (c2 stores the value of c3 for the next iteration). Then we do bit addition updating the carries accordingly until one of the numbers is finished. So, 2 has c2=1,c1=1, s=0, 3 has c2 = 1, c1=1, s=1, and 4 has c2 = 1, c1=0, s=0.\n\nWe now do this process until the longer number is finished.\nWe finally do it until the carries are over - to avoid getting stuck in an infinite loop, we break in instances like c1 = 1, c2 = 1, c3 = 1 as `((-2)*1+1*(2))*(2^k)=0`.\n\n# Complexity\n- Time complexity:\nO(m+n)\n\n- Space complexity:\nO(m+n)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n reverse(arr1.begin(), arr1.end());\n reverse(arr2.begin(), arr2.end());\n int i = 0;\n int j = 0;\n int c1 = 0;\n int c2 = 0;\n int c3 = 0;\n vector<int> arr3;\n while (i<arr1.size() && j<arr2.size()){\n int s = arr1[i]+arr2[j]+c1+c3;\n if (s==1 || s==0){\n arr3.push_back(s);\n c3 = c2;\n c1 = 0;\n c2 = 0;\n }\n else if (s==2){\n arr3.push_back(0);\n c3 = c2;\n c1 = 1;\n c2 = 1;\n }\n else if (s==3){\n arr3.push_back(1);\n c3 = c2;\n c1 = 1;\n c2 = 1;\n }\n else{\n arr3.push_back(0);\n c3 = c2;\n c1 = 0;\n c2 = 1;\n }\n j++;\n i++;\n }\n while (i<arr1.size()){\n int s = arr1[i]+c1+c3;\n if (s==1 || s==0){\n arr3.push_back(s);\n c3 = c2;\n c1 = 0;\n c2 = 0;\n }\n else if (s==2){\n arr3.push_back(0);\n c3 = c2;\n c1 = 1;\n c2 = 1;\n }\n else if (s==3){\n arr3.push_back(1);\n c3 = c2;\n c1 = 1;\n c2 = 1;\n }\n else{\n arr3.push_back(0);\n c3 = c2;\n c1 = 0;\n c2 = 1;\n }\n i++;\n }\n while (j<arr2.size()){\n int s = arr2[j]+c1+c3;\n if (s==1 || s==0){\n arr3.push_back(s);\n c3 = c2;\n c1 = 0;\n c2 = 0;\n }\n else if (s==2){\n arr3.push_back(0);\n c3 = c2;\n c1 = 1;\n c2 = 1;\n }\n else if (s==3){\n arr3.push_back(1);\n c3 = c2;\n c1 = 1;\n c2 = 1;\n }\n else{\n arr3.push_back(0);\n c3 = c2;\n c1 = 0;\n c2 = 1;\n }\n j++;\n }\n while (c1!=0 || c3!=0){\n if (c1==1 && c2==1 && c3==1) break;\n int s = c1+c3;\n if (s==1 || s==0){\n arr3.push_back(s);\n c3 = c2;\n c1 = 0;\n c2 = 0;\n }\n else if (s==2){\n arr3.push_back(0);\n c3 = c2;\n c1 = 1;\n c2 = 1;\n }\n else if (s==3){\n arr3.push_back(1);\n c3 = c2;\n c1 = 1;\n c2 = 1;\n }\n else{\n arr3.push_back(0);\n c3 = c2;\n c1 = 0;\n c2 = 1;\n }\n }\n reverse(arr3.begin(),arr3.end());\n i = 0;\n while (arr3[i]==0 && i < arr3.size()-1){\n i++;\n }\n vector<int> arr4;\n arr4 = vector<int> (arr3.begin()+i, arr3.end());\n return arr4;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
adding-two-negabinary-numbers
|
Python. Time: O(n), Space: O(1)
|
python-time-on-space-o1-by-iitjsagar-s38h
|
Approach\n Describe your approach to solving the problem. \nFor any index/bit in two arrays, following scenarios apply:\n1. Sum of their coefficients [0,1], the
|
iitjsagar
|
NORMAL
|
2024-08-28T06:12:59.725878+00:00
|
2024-08-28T06:12:59.725914+00:00
| 2
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nFor any index/bit in two arrays, following scenarios apply:\n1. Sum of their coefficients [0,1], then leave it as is in result.\n2. Sum of their coefficients is > 1. In this situation, next higher bit can have coefficient contribution of -(current coefficient sum)//2.\n3. Sum of their coefficients is < 0. In this situation, next higher bit can have coefficient contribution of +(current coefficient sum)//2. \n\n# Complexity\n- Time complexity: $$O(n)$$ - Three traversals at worst - One traversal to calculate bit coefficients, second to remove leading zeros, and third for reversing the list.\n\n- Space complexity: $$O(1)$$ - Bit coefficients are calculated and stored in the result array which is returned.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution(object):\n def addNegabinary(self, arr1, arr2):\n """\n :type arr1: List[int]\n :type arr2: List[int]\n :rtype: List[int]\n """\n \n l1 = len(arr1)\n l2 = len(arr2)\n\n res = [0]\n i3 = 0\n\n i1 = l1-1\n i2 = l2-1\n\n while i1 >= 0 or i2 >= 0:\n if i3 >= len(res):\n res.append(0)\n \n cur = res[i3]\n if i1 >= 0:\n cur += arr1[i1]\n i1 -= 1\n if i2 >= 0:\n cur += arr2[i2]\n i2 -= 1\n \n if cur > 1:\n carry = cur//2\n if cur & 1:\n res[i3] = 1\n else:\n res[i3] = 0\n \n if i3 + 1 >= len(res):\n res.append(0)\n res[i3+1] -= carry\n elif 0 <= cur <= 1:\n res[i3] = cur\n else:\n if (-cur) & 1 == 0:\n res[i3] = 0\n if i3 + 1 >= len(res):\n res.append(0)\n res.append((-cur)//2)\n else:\n res[i3] = 1\n if i3 + 1 >= len(res):\n res.append(0)\n \n carry = (-cur+1)//2\n res[i3+1] += carry\n \n i3 += 1\n \n while res[-1] != 0 and res[-1] != 1:\n if res[-1] > 1:\n cur = res[-1]\n if cur & 1:\n res[-1] = 1\n else:\n res[-1] = 0\n \n res.append(-(cur//2))\n else:\n cur = -res[-1]\n\n if cur & 1:\n res[-1] = 1\n res.append((cur+1)//2)\n else:\n res[-1] = 0\n res.append(cur//2)\n \n\n while len(res) > 1:\n if res[-1] == 0:\n res.pop(-1)\n else:\n break\n \n #print res\n res.reverse()\n return res\n\n \n \n```
| 0
| 0
|
['Python']
| 0
|
adding-two-negabinary-numbers
|
Not a clear solution C#
|
not-a-clear-solution-c-by-bogdanonline44-hfep
|
\n# Complexity\n- Time complexity: O(max(n, m))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(max(n, m)\n Add your space complexity here,
|
bogdanonline444
|
NORMAL
|
2024-07-05T11:24:58.195275+00:00
|
2024-07-05T11:24:58.195297+00:00
| 3
| false
|
\n# Complexity\n- Time complexity: O(max(n, m))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(max(n, m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int[] AddNegabinary(int[] arr1, int[] arr2) {\n List<int> result = new List<int>();\n int carry = 0;\n int i = arr1.Length - 1, j = arr2.Length - 1;\n\n while (i >= 0 || j >= 0 || carry != 0) \n {\n int x = (i >= 0) ? arr1[i] : 0;\n int y = (j >= 0) ? arr2[j] : 0;\n\n int sum = x + y + carry;\n result.Add(sum & 1); \n carry = -(sum >> 1); \n\n i--;\n j--;\n }\n\n while (result.Count > 1 && result[result.Count - 1] == 0) \n {\n result.RemoveAt(result.Count - 1);\n }\n\n result.Reverse();\n return result.ToArray();\n }\n}\n```\n\n
| 0
| 0
|
['Array', 'Math', 'C#']
| 0
|
adding-two-negabinary-numbers
|
Beats 100%, negabinary to decimal then decimal to negabinary
|
beats-100-negabinary-to-decimal-then-dec-ewus
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vsrfiles
|
NORMAL
|
2024-06-09T07:06:06.717094+00:00
|
2024-06-09T07:06:06.717131+00:00
| 6
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# @param {Integer[]} arr1\n# @param {Integer[]} arr2\n# @return {Integer[]}\ndef add_negabinary(arr1, arr2)\n num1 = find_value(arr1)\n num2 = find_value(arr2)\n to_base_neg2(num1 + num2)\nend\n\ndef find_value(arr)\n sum = 0\n arr.each_with_index do |el, i|\n pos = arr.size - 1 - i\n sum = sum + (el *(-2) ** pos)\n end\n sum\nend\n\ndef to_base_neg2(num)\n return [0] if num == 0\n\n result = []\n while num != 0\n remainder = num % -2\n num = num / -2\n\n if remainder < 0\n remainder += 2\n num += 1\n end\n\n result << remainder\n end\n\n result.reverse\nend\n```
| 0
| 0
|
['Ruby']
| 0
|
adding-two-negabinary-numbers
|
Scala version
|
scala-version-by-igstan-w63e
|
Scala\n\n\nobject Solution {\n def addNegabinary(a: Array[Int], b: Array[Int]): Array[Int] = {\n var large: Array[Int] = a\n var small: Array[Int] = b\n\
|
igstan
|
NORMAL
|
2024-05-09T18:32:16.213681+00:00
|
2024-05-09T18:32:16.213716+00:00
| 4
| false
|
# Scala\n\n```\nobject Solution {\n def addNegabinary(a: Array[Int], b: Array[Int]): Array[Int] = {\n var large: Array[Int] = a\n var small: Array[Int] = b\n\n if (a.length < b.length) {\n large = b\n small = a\n }\n\n val result = Array.ofDim[Int](large.length + 2)\n var carry0 = 0\n var carry1 = 0\n var i = 0\n var lastWrittenIndex = -1\n\n while (i < large.length) {\n val largeElem = large(large.length - 1 - i)\n val smallElem = if (small.length - 1 - i < 0) 0 else small(small.length - 1 - i)\n\n val res = smallElem + largeElem + carry0\n\n if ((res % 2) > 0) {\n lastWrittenIndex = result.length - 1 - i\n result(result.length - 1 - i) = 1\n }\n\n if (res / 2 == 0) {\n carry0 = carry1\n carry1 = 0\n } else {\n if (carry1 == 1) {\n carry0 = 0\n carry1 = 0\n } else {\n carry0 = 1\n carry1 = 1\n }\n }\n\n i += 1\n }\n\n if (carry0 == 1) {\n result(1) = 1\n lastWrittenIndex = 1\n }\n\n if (carry1 == 1) {\n result(0) = 1\n lastWrittenIndex = 0\n }\n\n if (lastWrittenIndex < 0) {\n Array(0)\n } else {\n if (lastWrittenIndex == 0) {\n result\n } else {\n java.util.Arrays.copyOfRange(result, lastWrittenIndex, result.length)\n }\n }\n }\n}\n\n```
| 0
| 0
|
['Scala']
| 0
|
adding-two-negabinary-numbers
|
1073. Adding Two Negabinary Numbers.cpp
|
1073-adding-two-negabinary-numberscpp-by-tkdy
|
Code\n\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) { \n int i = arr1.size()-1;\n int j
|
202021ganesh
|
NORMAL
|
2024-04-30T09:51:56.684574+00:00
|
2024-04-30T09:51:56.684628+00:00
| 6
| false
|
**Code**\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) { \n int i = arr1.size()-1;\n int j = arr2.size()-1;\n vector<int>bits = {0,1,0,1,0,1};\n vector<int>carries = {1,1,0,0,-1,-1}; \n vector<int>res; \n int sum;\n int carry = 0;\n while(i>=0 || j>=0 || carry)\n {\n sum = carry + (i>=0 ? arr1[i--] : 0) + (j>=0 ? arr2[j--] : 0); \n carry = carries[sum+2];\n res.push_back(bits[sum+2]);\n }\n while(res.size() > 1 && res.back()==0)res.pop_back(); \n reverse(res.begin(),res.end()); \n return res;\n }\n};\n```
| 0
| 0
|
['C']
| 0
|
adding-two-negabinary-numbers
|
BEST C++ SOLUTION WITH 7MS OF RUNTIME !
|
best-c-solution-with-7ms-of-runtime-by-r-mjsj
|
\n# Code\n\nclass Solution {\n public:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n deque<int> ans;\n int carry = 0;\n int i
|
rishabnotfound
|
NORMAL
|
2024-04-28T09:11:21.099676+00:00
|
2024-04-28T09:11:21.099706+00:00
| 60
| false
|
\n# Code\n```\nclass Solution {\n public:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n deque<int> ans;\n int carry = 0;\n int i = arr1.size() - 1;\n int j = arr2.size() - 1;\n\n while (carry || i >= 0 || j >= 0) {\n if (i >= 0)\n carry += arr1[i--];\n if (j >= 0)\n carry += arr2[j--];\n ans.push_front(carry & 1);\n carry = -(carry >> 1);\n }\n\n while (ans.size() > 1 && ans.front() == 0)\n ans.pop_front();\n\n return {ans.begin(), ans.end()};\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
adding-two-negabinary-numbers
|
Column Addition
|
column-addition-by-che011-y43h
|
Intuition\n Describe your first thoughts on how to solve this problem. \nBased on concept of Column Addition. \n\n# Approach\n Describe your approach to solving
|
che011
|
NORMAL
|
2024-03-30T10:33:23.102084+00:00
|
2024-03-30T10:33:23.102122+00:00
| 92
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBased on concept of Column Addition. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFrom right to left, add along the column. If the added value exceeds 1, add to the next columns. \n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n arr1_len = len(arr1)\n arr2_len = len(arr2)\n longest_len = max([arr1_len, arr2_len])\n # Allocate memory space for answer\n answer_len = arr1_len + arr2_len + 3\n answer = [0] * answer_len\n\n for i in range(longest_len):\n index = -1 * (i+1)\n value = answer[index]\n # Sum the column\n if (i<arr1_len) and arr1[index]:\n value += 1\n if (i<arr2_len) and arr2[index]:\n value += 1\n if value in [0,1]:\n answer[index] = value\n elif value >= 2:\n # Add to the next columns\n if answer[index-1] > 0:\n answer[index-1] -= 1\n answer[index] = value - 2\n else:\n answer[index-1] = 1\n answer[index-2] = 1\n answer[index] = value - 2\n if 1 not in answer:\n answer = [0]\n else:\n answer = answer[answer.index(1):]\n return answer\n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
Solution for 1073. Adding Two Negabinary Numbers
|
solution-for-1073-adding-two-negabinary-e7a8a
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo me, Key thing is to understand mechanism of base -2 operation. Note to handle the sp
|
user2988N
|
NORMAL
|
2024-03-28T11:14:28.996423+00:00
|
2024-03-28T11:14:28.996457+00:00
| 3
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo me, Key thing is to understand mechanism of base -2 operation. Note to handle the special cases \n1. -1 carry at the end\n2. handling -1 as sum of digits. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInitializes variables for processing the vectors and storing the result.\nIterates through both input vectors from the right end simultaneously.\n\nAdds the corresponding elements of the vectors along with the residue multiplied by the multiplier.\n\nCalls the calculate method to update the digit, residue, and multiplier for the current calculation.\n\nInserts the calculated digit at the beginning of the result vector.\n\nHandles scenarios where one input vector is longer than the other by processing the remaining elements.\n\nInserts additional 1\'s at the beginning of the result if there is remaining residue.\n\nTrims any leading zeros from the result.\n\nReturns the final result vector.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(max(arr1.size, arr2.size))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n/*\nRef: Logic mentioned at https://math.stackexchange.com/questions/3251605/how-to-add-negabinary-numbers\nThis method calculates the digit, residue, and multiplier based on the input value.\nIf the input value is -1, sets digit to 1, residue to 1, and multiplier to 1.\nOtherwise, calculates digit as the modulus of the input value divided by 2, residue as the input value divided by 2, and multiplier as -1.\n*/\n void calculate(int val, int& digit, int& residue, int& multiplier){\n if(val == -1){\n digit = 1;\n residue = 1;\n multiplier = 1;\n }else{\n digit = val % 2;\n residue = val / 2;\n multiplier = -1;\n }\n\n }\n\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n int size1 = arr1.size();\n int size2 = arr2.size();\n int i;\n int j;\n int residue = 0;\n int val;\n vector<int> res;\n int digit;\n int multiplier = -1;\n for(i = size1-1, j=size2-1; i >=0 && j>=0; --i, --j){\n val = arr1[i] + arr2[j] + residue * multiplier;\n //multiplier *= -1;\n calculate(val, digit, residue, multiplier);\n //cout<<" "<<val<<" "<<digit<<" "<<residue<<endl;\n res.insert(res.begin(), digit);\n }\n\n //cout<<" "<<i<<" "<<j<<endl;\n while(i >= 0){\n val = arr1[i] + residue * multiplier;\n calculate(val, digit, residue, multiplier);\n\n res.insert(res.begin(), digit);\n //multiplier *= -1;\n cout<<" "<<val<<" "<<digit<<" "<<residue<<endl;\n --i;\n }\n\n //cout<<" "<<i<<" "<<j<<endl;\n while(j >= 0){\n val = arr2[j] + residue * multiplier;\n calculate(val, digit, residue, multiplier);\n\n res.insert(res.begin(), digit);\n cout<<" "<<val<<" "<<digit<<" "<<residue<<endl;\n //multiplier *= -1;\n --j;\n }\n\n if(residue){\n res.insert(res.begin(), 1);\n res.insert(res.begin(), 1);\n }\n //remove leading zeros\n while(res.size() > 1 && res[0] == 0){\n res.erase(res.begin());\n }\n return res;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
adding-two-negabinary-numbers
|
Solution Adding Two Negabinary Numbers
|
solution-adding-two-negabinary-numbers-b-5y9t
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Suyono-Sukorame
|
NORMAL
|
2024-03-16T02:28:01.777397+00:00
|
2024-03-16T02:28:01.777422+00:00
| 5
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n /**\n * @param Integer[] $arr1\n * @param Integer[] $arr2\n * @return Integer[]\n */\n function addNegabinary($arr1, $arr2) {\n $result = [];\n $carry = 0;\n $i = count($arr1) - 1;\n $j = count($arr2) - 1;\n \n while ($i >= 0 || $j >= 0 || $carry != 0) {\n if ($i >= 0) {\n $carry += $arr1[$i--];\n }\n if ($j >= 0) {\n $carry += $arr2[$j--];\n }\n array_unshift($result, $carry & 1);\n $carry = -(int)($carry >> 1);\n }\n \n // Remove leading zeros\n $index = 0;\n while ($index < count($result) - 1 && $result[$index] == 0) {\n $index++;\n }\n \n return array_slice($result, $index);\n }\n}\n\n```
| 0
| 0
|
['PHP']
| 0
|
adding-two-negabinary-numbers
|
Python beats 98%
|
python-beats-98-by-axxeny-ub6f
|
Intuition\nSimple long addition. Go through digits from right to left, remember to carry. Take special care with carry, which can be both +1 and -1, and remembe
|
axxeny
|
NORMAL
|
2024-02-25T15:55:45.416562+00:00
|
2024-02-25T15:55:45.416600+00:00
| 77
| false
|
# Intuition\nSimple long addition. Go through digits from right to left, remember to carry. Take special care with carry, which can be both +1 and -1, and remember to flip carry sign.\n\n# Complexity\n- Time complexity: $O(n)$\n\n- Space complexity: $O(1)$\n\n# Code\n```\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n mem = 0\n arr3 = []\n for j in range(max(len(arr1), len(arr2))):\n arr1i = len(arr1) - 1 - j\n arr2i = len(arr2) - 1 - j\n\n arr3v = (\n (arr1[arr1i] if arr1i >= 0 else 0)\n + (arr2[arr2i] if arr2i >= 0 else 0)\n + mem\n )\n \n if arr3v == -1:\n arr3.append(1)\n mem = 1\n else:\n mem = -(arr3v // 2)\n arr3.append(arr3v % 2)\n if mem == -1:\n arr3.append(1)\n arr3.append(1)\n if mem == 1:\n arr3.append(1)\n while len(arr3) >= 2 and arr3[-1] == 0:\n arr3.pop()\n return reversed(arr3)\n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
Python (Simple Maths)
|
python-simple-maths-by-rnotappl-i5ad
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rnotappl
|
NORMAL
|
2024-02-24T16:23:37.047553+00:00
|
2024-02-24T16:23:37.047578+00:00
| 67
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addNegabinary(self, arr1, arr2):\n def dfs(nums):\n n, total = len(nums), 0 \n\n for i in range(n):\n if nums[i]:\n total += (-2)**(n-1-i)\n\n return total \n\n def bfs(num):\n result = []\n\n if num == 0:\n return [0]\n\n while num:\n num, rem = divmod(num,-2)\n if rem < 0:\n rem += 2 \n num += 1 \n result.append(rem)\n\n return result[::-1]\n\n return bfs(dfs(arr1)+dfs(arr2))\n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
💎Python3 | Beats 93% | Detailed Explanation💎
|
python3-beats-93-detailed-explanation-by-zj1d
|
Intuition\nSo in normal binary addition, we have the concept of carrying if we overflow the current slot. However, we need to represent the overflow correctly i
|
jessicawyn
|
NORMAL
|
2024-01-30T05:34:22.295737+00:00
|
2024-01-30T05:42:47.176556+00:00
| 63
| false
|
# Intuition\nSo in normal binary addition, we have the concept of carrying if we overflow the current slot. However, we need to represent the overflow correctly in this problem... One key insight: overflow works here is THE OPPOSITE of how it works in normal binary. If we overflow the bit, it means we are actually eliminating the next bit after this one. Think about that for a second. If we add 1 + 1, we get 2. But arithmetically, and in negabinary terms, **the addition operation of these two positive 1\'s are effectively eliminating a -2 from the solution**. It works the other way, too. Say I need to add -2 to -2. The overflow in this bit means we need to eliminate a **positive 4** from our solution. Here we reach the first rule / key observation - **we need to carry a -1 anytime we overflow**. That\'s easy then, we just use that as our carry. But what if we end up in a situation where we have a -1 all by itself? Just an example of 5 + 5- \n- step 1\n 1 0 1 = 5\n 1 0 1 = 5 \n ? -1 0 = 10\n- step 2 \n ???\n\nTo answer this, we need to reason about what this -1 means and how we can represent it in negabinary. Remember what we said earlier, the -1 means we need to negate this number. And how can we do that? Recall that in normal binary, the number after the current one is always twice the value. So, if we want to get the negative representation of our current number, we need to to **add twice its negative to itself**. And how do we get twice its negative? Well, by carrying a 1! Now let\'s complete the addition of 5+5 per step 2 (broken into steps 2a and 2b for clarity):\n\n- step 2a\n 1 0 1 = 5\n1 0 1 = 5\n(-1) 1 1 0 = 10\n\n- step 2b\n1 0 1 = 5\n1 0 1 = 5\n1 1 1 1 0 = 10 \n\nWe just need to translate this to code now. Our rules are simple, we carry -1 if there\'s an overflow (to negate the next power of -2) and represent any lone -1 as a 1 and a carry of 1 to the next (to get the negative equivalent of X as -2X + X).\n\n# Approach\n\n- Do normal addition on the bit if no overflow, set carry to 0 (if 0+0 - new bit is 0, if 1+0 - new bit is 1, etc.)\n- If overflowed, set carry to -1. Do addition with this carry as usual in the next step.\n- If end up with -1 as current bit, set bit = 1 and carry = 1 to negate value.\n\n# Complexity\nM = len(arr1), N = len(arr2)\n- Time complexity: O(max(M, N))\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n carry = 0\n M, N = len(arr1), len(arr2)\n output = []\n for i in range(max(M, N)):\n idx1, idx2 = M - 1 - i, N - 1 - i\n b1, b2 = 0 if idx1 < 0 else arr1[idx1], 0 if idx2 < 0 else arr2[idx2]\n s = b1 + b2 + carry\n if s == -1:\n output.append(1)\n carry = 1\n elif s == 0:\n output.append(0)\n carry = 0\n elif s == 1:\n output.append(1)\n carry = 0\n elif s == 2:\n output.append(0)\n carry = -1\n elif s == 3:\n output.append(1)\n carry = -1\n if carry == -1:\n output.append(1)\n output.append(1)\n elif carry == 1:\n output.append(1)\n \n while True:\n if len(output) == 1:\n break\n if output[-1] == 0:\n output.pop()\n else:\n break\n\n return reversed(output)\n\n\n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
Beats 97.86% of solution With C++ ||*****JAI PEER DATNA******
|
beats-9786-of-solution-with-c-jai-peer-d-kwy0
|
Bold# Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n-
|
Hi_coders786
|
NORMAL
|
2024-01-18T06:39:27.620973+00:00
|
2024-01-18T06:39:27.620999+00:00
| 66
| false
|
***Bold***# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) { \n vector<int> result; \n int carry = 0;\n int i = arr1.size() - 1;\n int j = arr2.size() - 1; \n while (i >= 0 || j >= 0 || carry != 0) { \n int bitSum = carry;\n if (i >= 0) bitSum += arr1[i--];\n if (j >= 0) bitSum += arr2[j--]; \n result.insert(result.begin(), bitSum & 1); \n carry = -(bitSum >> 1);\n } \n while (result.size() > 1 && result[0] == 0) {\n result.erase(result.begin());\n } \n return result;\n}\n};\n```
| 0
| 0
|
['Array', 'Math', 'Divide and Conquer', 'Recursion', 'Sorting', 'Counting', 'Shortest Path', 'C++', 'Ruby', 'JavaScript']
| 0
|
adding-two-negabinary-numbers
|
best Approach 100% beat
|
best-approach-100-beat-by-manish_patil05-bs3m
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Manish_patil05
|
NORMAL
|
2023-12-27T10:15:28.723404+00:00
|
2023-12-27T10:15:28.723461+00:00
| 41
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution{\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n \n int[] arr = new int[arr1.length>arr2.length?arr1.length+2:arr2.length+2];\n\t\tint len = (arr1.length<arr2.length?arr1.length:arr2.length) - 1;\n\n\t\t for(int i = 0; i<arr.length-2; i++){\n\t\t int sum = 0;\n\t\t if((arr1.length-i-1)>= 0){\n\t\t sum = sum + arr1[arr1.length-i-1];\n\t\t } \n\t\t if(arr2.length-i-1 >= 0){\n\t\t sum = sum + arr2[arr2.length-1-i];\n\t\t }\n\t\t \n\t\t int newArr = sum + arr[arr.length-1-i];\n\t\t \n\t\t if(newArr % 2 ==0){\n\t\t arr[arr.length-1-i] = 0;\n\t\t arr[arr.length-2-i] = arr[arr.length-2-i]+ (newArr/2);\n\t\t arr[arr.length-3-i] = arr[arr.length-3-i] + (newArr/ 2);\n\t\t }\n\t\t else{\n\t\t arr[arr.length-1-i] = 1;\n\t\t arr[arr.length-2-i] = arr[arr.length-2-i]+ (newArr/2);\n\t\t\t arr[arr.length-3-i] = arr[arr.length-3-i] +(newArr/2);\n\t\t }\n\t\t }\n\t\t if(arr[1]%2 == 0) {\n\t\t \t arr[0] = arr[0]+ arr[1] /2;\n\t\t \t arr[1] = 0;\n\t arr[0] = arr[0]%2;\n\t\t }\n\t\t else if(arr[1]%2 !=0){\n\t\t \t arr[0] = arr[0] + arr[1]/2;\n\t\t \t arr[1] = 1;\n\t\t \t arr[0] = arr[0] % 2;\n\t\t }\n\t\t for(int i = 0;i<arr.length; i++) {\n\t\t \t if(arr[i] == 1) {\n\t\t \t\t return Arrays.copyOfRange(arr, i, arr.length);\n\t\t \t }\n\t\t }\n\t\t return new int[]{0};\n\t\t }\n\t\t\n\t}\n\n```
| 0
| 0
|
['Bit Manipulation', 'Java']
| 0
|
adding-two-negabinary-numbers
|
Unique Approach 100% beat
|
unique-approach-100-beat-by-vijay_patil-nxc2
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Vijay_patil
|
NORMAL
|
2023-12-27T10:07:53.070735+00:00
|
2023-12-27T10:07:53.070764+00:00
| 18
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n\t int max=Math.max(arr1.length,arr2.length);\n\t int arr[]=new int [max+2];\n\t int div=0;\n\t for (int i=0;i<max;i++){\n\t \t int index1=arr.length-i-1,index2=arr.length-i-2,index3=arr.length-i-3; \n\t \t int sum=0;\n\t int leng1=arr1.length-i-1;\n\t int leng2=arr2.length-i-1;\n\t if(leng1>=0){\n\t sum+=arr1[leng1]; \n\t }if(leng2>=0){\n\t sum+=arr2[leng2]; \n\t }\n\t sum=sum+arr[arr.length-i-1];\n if(sum % 2==0){\n\t arr[index1]=0;\n\t arr[index2]+=sum/2;\n\t arr[index3]+=sum/2;\n }\n else{\n arr[index1]=1;\n\t arr[index2]+=sum/2;\n\t arr[index3]+=sum/2; \n }\n\t }\n\n if(arr[1] % 2 == 0){\n arr[0] = arr[0]+(arr[1] /2);\n arr[1] = 0;\n arr[0] = arr[0]%2;\n }\n else{\n arr[0] = arr[0]+arr[1]/2;\n arr[1] = 1;\n arr[0] = arr[0] % 2; \n }\n\t for(int i=0;i<arr.length;i++){\n\t if(arr[i]==1){\n\t return Arrays.copyOfRange(arr,i,arr.length);\n\t }\n\t \n\t }\n return new int[]{0};\n\t}\n}\n\n```
| 0
| 0
|
['Bit Manipulation', 'Java']
| 0
|
adding-two-negabinary-numbers
|
Python O(n) space and time solution 2 approaches
|
python-on-space-and-time-solution-2-appr-t17o
|
First, I tried to solve the problem a simple way:\n\n1. Convert the negabinary numbers to a decimal\n2. Sum the decimal numbers \n3. Convert the decimal number
|
GrishaZohrabyan
|
NORMAL
|
2023-12-21T12:23:17.579244+00:00
|
2023-12-21T12:23:17.579267+00:00
| 27
| false
|
First, I tried to solve the problem a simple way:\n\n1. Convert the negabinary numbers to a decimal\n2. Sum the decimal numbers \n3. Convert the decimal number back to a negabinary number\n\n```\nn1 = self.toDecimal(arr1)\nn2 = self.toDecimal(arr2)\nn = n1 + n2\nres = self.toNegabinary(n)\n```\n\n**The most important part is `toNegabinary` function because there is a difference in how we divide a number to 2 and -2, and how we treat negative remainders.**\n\n```\nwhile n != 0:\n n, remainder = divmod(n, -2)\n if remainder < 0:\n n, remainder = n + 1, remainder + 2\n arr.append(remainder)\n```\n\nLets devide -5 to -2. We should notice that a remainder should be positive; hence, n is 3 not 2, and remider is 1 not -1. We going to use this property in the second approach too. **The problem of this solution is that it only pass 257 cases from 267 cases**. I think it is becasue of the n is big and it returns 0s.\n\nThe second approach is to sum two numbers element by element. The solution is not so different from summing two binary numbers. We should keep in mind the division to -2.\n\n```\ncarry, s = divmod(s, -2)\nif s < 0:\n carry, s = carry + 1, s + 2\n```\n\nIf we sum 17 and 5 in the decimal system, what do we do? \n1. 7 + 5 = 12, then we 12 % 10 = 2, carry becomes 1\n2. 1 + 0 + carry = 2\n3. so, the sum is 22. \n\nWe do the same here remembering how we shoud do it for -2. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> \n$$O(n)$$\n\n# Code\n```\nclass Solution:\n\n # def toDecimal(self, arr: List[int]) -> int:\n # arr.reverse()\n # r = 0\n # for i, x in enumerate(arr):\n # r += math.pow(-2, i) * x\n\n # return int(r)\n\n # def toNegabinary(self, n: int) -> List[int]:\n # if n == 0:\n # return [0]\n # else:\n # arr = []\n # while n != 0:\n # n, remainder = divmod(n, -2)\n # if remainder < 0:\n # n, remainder = n + 1, remainder + 2\n # arr.append(remainder)\n \n # arr.reverse()\n # return arr\n\n # def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n # n1 = self.toDecimal(arr1)\n # n2 = self.toDecimal(arr2)\n # n = n1 + n2\n # res = self.toNegabinary(n)\n # return res\n # it passes 257/267 tests\n\n def removeZeros(self, arr):\n while len(arr) > 1 and arr[0] == 0:\n _ = arr.pop(0)\n \n return arr\n\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n carry = 0\n result = []\n\n while arr1 or arr2:\n x = 0 if not arr1 else arr1.pop() \n y = 0 if not arr2 else arr2.pop()\n\n s = x + y + carry\n carry, s = divmod(s, -2)\n if s < 0:\n carry, s = carry + 1, s + 2\n result.append(s)\n \n while carry != 0:\n carry, s = divmod(carry, -2)\n if s < 0:\n carry, s = carry + 1, s + 2\n result.append(s)\n \n return self.removeZeros(result[::-1])\n\n\n\n\n \n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
Adding Two Negabinary Numbers || JAVASCRIPT || Solution by Bharadwaj
|
adding-two-negabinary-numbers-javascript-gafv
|
Approach\nSimulating Negabinary Addition\n\n# Complexity\n- Time complexity:\nO(max(n, m))\n\n- Space complexity:\nO(max(n, m))\n\n# Code\n\nvar addNegabinary =
|
Manu-Bharadwaj-BN
|
NORMAL
|
2023-12-21T07:55:49.522898+00:00
|
2023-12-21T07:55:49.522928+00:00
| 21
| false
|
# Approach\nSimulating Negabinary Addition\n\n# Complexity\n- Time complexity:\nO(max(n, m))\n\n- Space complexity:\nO(max(n, m))\n\n# Code\n```\nvar addNegabinary = function(arr1, arr2) {\n // Initialize variables for carry, result, and array indices\n let carry = 0;\n let ans = [];\n let x = arr1.length - 1;\n let y = arr2.length - 1;\n\n // Iterate through arrays and handle addition\n while (x >= 0 || y >= 0 || carry) {\n // Add current elements and carry\n if (x >= 0) carry += arr1[x];\n if (y >= 0) carry += arr2[y];\n\n // Push the least significant bit of the sum to the result\n ans.push(carry & 1);\n\n // Update carry for the next bit\n carry = -(carry >> 1);\n\n // Move to the next elements in the arrays\n x--;\n y--;\n }\n\n // Remove leading zeros in the result\n while (ans.length > 1 && ans[ans.length - 1] === 0) {\n ans.pop();\n }\n\n // Reverse the result array to get the final answer\n return ans.reverse();\n};\n```
| 0
| 0
|
['JavaScript']
| 0
|
adding-two-negabinary-numbers
|
ee
|
ee-by-user3043sb-tdp5
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
user3043SB
|
NORMAL
|
2023-12-16T13:08:25.272372+00:00
|
2023-12-16T13:08:25.272394+00:00
| 11
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.util.*;\n\nclass Solution {\n\n // positive base => max(n1,n2) <= len of sum <= max(n1,n2) + 1\n // negative base => 0 <= len of sum <= max(n1,n2) + 2\n // can be subtraction so any len up to (max(n1,n2) + 2)\n // because the real number might need (max(n1,n2) + 1) but because of negative powers\n // we might have to use 1 more bit to skip the negative power at the front\n\n\n // -2^1 -2^0\n // [1,1,1,1,1] = 11\n // [1,0,1] = 5\n // [1,0,0,0,0] = 16\n // [4,3,2,1,0] powers\n\n // [1,1,1,1,1] = 11\n // [1,0,1] = 5\n // [1,0,0,0,0] = 16\n\n // [1] = 1\n // [1] = 1\n // [1,1,0] = 2\n public int[] addNegabinary(int[] A1, int[] A2) {\n int n1 = A1.length;\n int n2 = A2.length;\n int biggerN = Math.max(n1, n2);\n int maxLen = biggerN + 2;\n ArrayList<Integer> reversed = new ArrayList<>(maxLen);\n\n int carry = 0;\n int base = -2;\n int loopsRemaining = maxLen;\n int i = 1; // how much to subtract from N, to get id\n while (loopsRemaining-- > 0) {\n int a = n1 - i < 0 ? 0 : A1[n1 - i];\n int b = n2 - i < 0 ? 0 : A2[n2 - i];\n int sum = a + b + carry;\n int r = sum % base; // bits we put here = residual of current power\n carry = sum / base; // carryover bits; carry over main part for higher power\n\n if (r < 0) {\n r += Math.abs(base);// r < 0 !! handle!!!\n carry++;\n }\n reversed.add(r);\n i++;\n }\n\n int j = reversed.size() - 1;\n while (j > 0 && reversed.get(j) == 0) j--;\n\n int k = 0;\n int[] ans = new int[j + 1];\n while (j >= 0) ans[k++] = reversed.get(j--);\n return ans;\n }\n\n\n}\n```
| 0
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
[JavaScript] 1073. Adding Two Negabinary Numbers
|
javascript-1073-adding-two-negabinary-nu-5sae
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nTrial & error to get below:\n-1 => reminder is 1 and carry is 1\n\n# Comp
|
pgmreddy
|
NORMAL
|
2023-12-05T10:56:11.320171+00:00
|
2023-12-05T10:56:11.320201+00:00
| 10
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTrial & error to get below:\n`-1 => reminder is 1 and carry is 1`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nvar addNegabinary = function (a1, a2) {\n const ans = []\n ans.push_front = ans.unshift\n ans.pop_front = ans.shift\n const m = a1.length\n const n = a2.length\n var carry = 0\n for (var i = m - 1, j = n - 1; i >= 0 || j >= 0; i--, j--) {\n const sum = (a1[i] || 0) + (a2[j] || 0) + carry\n let reminder = sum % -2\n carry = Math.trunc(sum / -2)\n if (reminder === -1) {\n reminder = 1\n carry = 1\n }\n ans.push_front(reminder)\n }\n if (carry === 1) {\n ans.push_front(carry)\n } else if (carry === -1) {\n ans.push_front(1, 1)\n }\n while (ans[0] === 0 && ans.length > 1) {\n ans.pop_front()\n }\n return ans\n}\n\n```
| 0
| 0
|
['JavaScript']
| 0
|
adding-two-negabinary-numbers
|
Handle sum for different case
|
handle-sum-for-different-case-by-marcust-wyic
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe solution to this problem is to figure out the math behind it, once that is done it
|
marcustut
|
NORMAL
|
2023-11-05T11:37:42.998091+00:00
|
2023-11-05T11:37:42.998113+00:00
| 22
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe solution to this problem is to figure out the math behind it, once that is done it is simple to solve.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIf you think about it, there\'s only a few cases for the bit addition with the carryover, the solution is basically just handle the different cases.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n\tpair<int, int> handleSum(int sum) {\n\t\tint bit = 0;\n\t\tint carry = 0;\n\n\t\tswitch (sum) {\n\t\t\tcase 0:\n\t\t\t\tbit = 0;\n\t\t\t\tcarry = 0;\n\t\t\t\tbreak;\n\t\t\tcase 1:\n\t\t\t\tbit = 1;\n\t\t\t\tcarry = 0;\n\t\t\t\tbreak;\n\t\t\tcase 2:\n\t\t\t\tbit = 0;\n\t\t\t\tcarry = -1;\n\t\t\t\tbreak;\n\t\t\tcase 3:\n\t\t\t\tbit = 1;\n\t\t\t\tcarry = -1;\n\t\t\t\tbreak;\n\t\t\tcase -1:\n\t\t\t\tbit = 1;\n\t\t\t\tcarry = 1;\n\t\t\t\tbreak;\n\t\t\tdefault:\n\t\t\t\tthrow runtime_error("Should not have sum not in range [-1,3]");\n\t\t}\n\n\t\treturn make_pair(bit, carry);\n\t}\n\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n\t\tvector<int> bits;\n int i = (int)arr1.size() - 1;\n int j = (int)arr2.size() - 1;\n\t\tint idx = max(i, j);\n\n\t\tint bit = 0;\n\t\tint carry = 0;\n\n\t\t// Process the arithmetic for all given bits\n\t\twhile (idx >= 0) {\n\t\t\tint x1 = i >= 0 ? arr1[i] : 0;\n\t\t\tint x2 = j >= 0 ? arr2[j] : 0;\n\n\t\t\ttie(bit, carry) = handleSum(x1 + x2 + carry);\n\n\t\t\tbits.push_back(bit);\n\t\t\ti--;\n\t\t\tj--;\n\t\t\tidx--;\n\t\t}\n\n\t\t// Process the leftovers\n\t\twhile (bit != 0 || carry != 0) {\n\t\t\ttie(bit, carry) = handleSum(carry);\n\t\t\tbits.push_back(bit);\n\t\t}\n\n\t\t// Reverse the bits (because we\'re insert at the back)\n\t\treverse(bits.begin(), bits.end());\n\n\t\t// Clean up the leading zeroes\n\t\twhile (bits[0] == 0 && bits.size() > 1)\n\t\t\tbits.erase(bits.begin());\n\n\t\treturn bits;\n }\n};\n\n// [1,1,1,1,1]\n// [1,0,1]\n// 0\n\n// [0]\n// [0]\n// ---\n// [0] = 0 (bit = 0, carry = 0)\n\n// [0]\n// [1]\n// ---\n// [1] = 1 (bit = 1, carry = 0)\n\n// [1]\n// [1]\n// -------\n// [1,1,0] = 4 - 2 = 2 (bit = 0, carry = -1) \n\n// [1]\n// [1]\n// [1]\n// -------\n// [1,1,1] = 4 - 2 + 1 = 3 (bit = 1, carry = -1) \n\n// [-1]\n// -------\n// [1, 1] (bit = 1, carry = 1)\n```
| 0
| 0
|
['C++']
| 0
|
adding-two-negabinary-numbers
|
Best Java Solution || Beats 80%
|
best-java-solution-beats-80-by-ravikumar-4iqk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ravikumar50
|
NORMAL
|
2023-09-26T08:35:57.891350+00:00
|
2023-09-26T08:35:57.891382+00:00
| 37
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n // taken help\n \n public int[] addNegabinary(int[] arr1, int[] arr2) {\n List<Integer> list = new ArrayList<>();\n int n = arr1.length;\n int m = arr2.length;\n int carry = 0;\n int i = n - 1, j = m - 1;\n while(i >= 0 && j >= 0) {\n int val = arr1[i] + arr2[j] + carry; // calculate current value\n int digit = 0;\n if (val < 0) {\n\n carry = 1;\n digit = 1;\n } \n else {\n carry = -(val / 2);\n digit = val % 2;\n }\n list.add(0, digit);\n --i;\n --j;\n }\n while(i >= 0) {\n int val = arr1[i] + carry;\n int digit = 0;\n if (val < 0) {\n carry = 1;\n digit = 1;\n } \n else {\n carry = -(val / 2);\n digit = val % 2;\n }\n list.add(0, digit);\n --i;\n }\n while(j >= 0) {\n int val = arr2[j] + carry;\n int digit = 0;\n if (val < 0) {\n carry = 1;\n digit = 1;\n } \n else {\n carry = -(val / 2);\n digit = val % 2;\n }\n list.add(0, digit);\n --j;\n }\n if (carry != 0) {\n if (carry == -1) {\n list.add(0, 1);\n list.add(0, 1);\n }\n else {\n //carry == 1\n list.add(0, carry);\n }\n }\n // remove leading zeros\n while(list.size() > 1 && list.get(0) == 0) {\n list.remove(0);\n }\n int[] ans = new int[list.size()];\n for (int k = 0; k < list.size(); ++k) {\n ans[k] = list.get(k);\n }\n return ans;\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
Rust Solution
|
rust-solution-by-rchaser53-kljl
|
Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n\nimpl Solution {\n pub fn add_negabinary(mut arr1: Vec<i32>, mut arr2: Vec<i32>)
|
rchaser53
|
NORMAL
|
2023-09-05T13:45:30.513662+00:00
|
2023-09-05T13:45:30.513685+00:00
| 20
| false
|
# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nimpl Solution {\n pub fn add_negabinary(mut arr1: Vec<i32>, mut arr2: Vec<i32>) -> Vec<i32> {\n arr1.reverse();\n arr2.reverse();\n let n = arr1.len();\n let m = arr2.len();\n let mut result = vec![0;n.max(m)+5];\n for i in 0..n.max(m)+2 {\n let mut v = result[i];\n if i < n {\n v += arr1[i];\n }\n if i < m {\n v += arr2[i];\n }\n\n if v == 3 {\n result[i+1] -= 1;\n result[i] = 1;\n } else if v == 2 {\n result[i+1] -= 1;\n result[i] = 0;\n } else if v >= 0 {\n result[i] = v;\n } else if v == -1 {\n result[i+1] += 1;\n result[i] = 1;\n }\n }\n\n while result.len() > 1 && result[result.len()-1] == 0 {\n result.pop();\n }\n result.reverse();\n result\n }\n}\n```
| 0
| 0
|
['Rust']
| 0
|
adding-two-negabinary-numbers
|
Rule based
|
rule-based-by-vegetabird-y6z3
|
Intuition\n Describe your first thoughts on how to solve this problem. \nRule based solution\n\n\n\n\n# Complexity\n- Time complexity: O(n)\n Add your time comp
|
vegetabird
|
NORMAL
|
2023-08-26T10:23:19.087083+00:00
|
2023-08-26T10:23:19.087103+00:00
| 44
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nRule based solution\n\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n l = max(len(arr1), len(arr2)) + 2\n arr1 = [0] * (l - len(arr1)) + arr1\n arr2 = [0] * (l - len(arr2)) + arr2\n\n res = [0] * l\n for i in range(l-1, -1, -1):\n if arr1[i] + arr2[i] + res[i] == 3:\n res[i] = 1\n res[i-1] -= 1\n elif arr1[i] + arr2[i] + res[i] == 2:\n res[i] = 0\n res[i-1] -= 1\n elif arr1[i] + arr2[i] + res[i] == 1:\n res[i] = 1\n elif arr1[i] + arr2[i] + res[i] == 0:\n res[i] = 0\n elif arr1[i] + arr2[i] + res[i] == -1:\n res[i] = 1\n res[i-1] = 1\n \n for i in range(l):\n if res[i] != 0:\n return(res[i:])\n return([0])\n\n\n\n\n\n\n\n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
C++ 4ms solution
|
c-4ms-solution-by-vegabird-6gcw
|
\n# Code\n\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) { \n std::reverse(arr1.begin(), arr1.en
|
vegabird
|
NORMAL
|
2023-08-16T15:13:35.843997+00:00
|
2023-08-16T15:13:35.844020+00:00
| 78
| false
|
\n# Code\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) { \n std::reverse(arr1.begin(), arr1.end());\n std::reverse(arr2.begin(), arr2.end());\n const int dataSize = std::max(arr1.size(), arr2.size());\n const int ansSize = dataSize + 2;\n vector<int> ans(ansSize, 0);\n for (int i = 0; i < ansSize; i ++) {\n const int a1 = (arr1.size() > i) ? arr1[i] : 0;\n const int a2 = (arr2.size() > i) ? arr2[i] : 0;\n const int sum = a1 + a2 + ans[i];\n ans[i] = (sum % 2 == 0) ? 0 : 1;\n if (sum < 0) {\n ans[i + 1] ++;\n } else if (sum > 1) {\n ans[i + 1] --;\n }\n }\n\n while (ans.size() > 1 && ans.back() == 0) {\n ans.pop_back();\n }\n\n std::reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n\n// 16 -8 4 -2 1 = 21 - 10 = 11\n// 5\n// 16\n\n// 16, -8, 4, -2, 1\n// 1. 1. 1. 1. 1\n// 0. 0. 1. 0. 1\n// 1 0 0 0 0\n\n// 1. 1. 1. 0. 1 ==> 13\n// 0. 0. 1. 0. 1 ==> 5 = 18 \n\n// 1. 0. 1. 1. 0 ==> 18 \n\n\n/*\n\n-10 (1010)\n-9 (1011)\n-8 (1000)\n-7 (1001)\n-6 (1110)\n-5 (1111)\n-4 (1100)\n-3 (1101)\n-2 (010)\n-1 (011)\n0 (000)\n1 (001)\n2 (110)\n3 (111)\n4 (100)\n5 (101)\n\n*/\n```
| 0
| 0
|
['C++']
| 0
|
adding-two-negabinary-numbers
|
Fast and Easy O(n) Solution
|
fast-and-easy-on-solution-by-hitesh22ran-92l3
|
Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\npublic:\n pair<int, int> calculateBitAndCarry(int num) {\n
|
hitesh22rana
|
NORMAL
|
2023-08-15T17:54:58.228951+00:00
|
2023-08-15T17:54:58.228984+00:00
| 63
| false
|
# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n pair<int, int> calculateBitAndCarry(int num) {\n int bit = 0;\n int carry = 0;\n\n switch(num) {\n case 1:\n bit = 1;\n carry = 0;\n break;\n\n case 2:\n bit = 0;\n carry = -1;\n break;\n\n case 3:\n bit = 1;\n carry = -1;\n break;\n\n case 0:\n bit = 0;\n carry = 0;\n break;\n\n case -1:\n bit = 1;\n carry = 1;\n break;\n\n default:\n bit = 0;\n carry = 0;\n break;\n }\n\n return {bit, carry};\n }\n\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n int n = arr1.size();\n int m = arr2.size();\n\n if(n < m) \n return addNegabinary(arr2, arr1);\n\n vector<int> vals;\n\n int carry = 0;\n for(int i = 0 ; i < m ; i++) {\n int index1 = n - i - 1;\n int index2 = m - i - 1;\n\n int num = arr1[index1] + arr2[index2] + carry;\n\n pair<int, int> bitAndCarry = calculateBitAndCarry(num);\n\n int bit = bitAndCarry.first;\n carry = bitAndCarry.second;\n\n vals.push_back(bit);\n }\n\n for(int i = n - m - 1 ; i >= 0 ; i--) {\n pair<int, int> bitAndCarry = calculateBitAndCarry(arr1[i] + carry);\n\n int bit = bitAndCarry.first;\n carry = bitAndCarry.second;\n\n vals.push_back(bit);\n }\n\n switch(carry) {\n case 1:\n vals.push_back(1);\n break;\n \n case 2:\n vals.push_back(0);\n vals.push_back(1);\n break;\n\n case -1:\n vals.push_back(1);\n vals.push_back(1);\n break;\n\n default:\n break;\n }\n\n while(vals.size() > 1 && vals.back() == 0)\n vals.pop_back();\n\n reverse(vals.begin(), vals.end());\n\n return vals;\n }\n};\n```
| 0
| 0
|
['Array', 'Math', 'C++']
| 0
|
adding-two-negabinary-numbers
|
C# Solution Run time beat 100%
|
c-solution-run-time-beat-100-by-jack0001-4w7t
|
Intuition\nIn such case, we observe\n1 + 1 = 110\n11 + 01 = 00\n\nAlso we can prove that any bits with a carryforward value will never greater than 3(sum <= 3 h
|
jack0001
|
NORMAL
|
2023-07-29T21:06:22.595149+00:00
|
2023-07-30T17:07:14.911198+00:00
| 16
| false
|
# Intuition\nIn such case, we observe\n1 + 1 = 110\n11 + 01 = 00\n\nAlso we can prove that any bits with a carryforward value will never greater than 3(sum <= 3 holds true)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(k), k = Max(m, n);\n- k is the maximum length of two arrays\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int[] AddNegabinary(int[] arr1, int[] arr2) {\n int carrfor = 0;\n int n1 = arr1.Length, n2 = arr2.Length;\n int n = Math.Max(n1, n2);\n\n int[] ans = new int[n+2];\n int i = n1-1;\n int j = n2-1;\n int k = n-1+2;\n int e1,e2;\n while(i>=0 || j>=0){\n e1 = i >= 0 ? arr1[i] : 0;\n e2 = j >= 0 ? arr2[j] : 0;\n\n var tot = ans[k] + e1 + e2;\n if(tot > 1){\n tot -= 2;\n if(i-1>=0 && arr1[i-1]==1){\n arr1[i-1] = 0;\n }\n else if(j-1>=0 && arr2[j-1]==1){\n arr2[j-1] = 0;\n }\n else if(ans[k-1]>0){\n ans[k-1]--;\n }\n else{\n ans[k-1] = 1;\n ans[k-2] = 1;\n }\n }\n ans[k] = tot;\n\n i--;\n j--;\n k--;\n }\n\n int idx = 0;\n while(idx<n+2 && ans[idx]==0){\n idx++;\n }\n if(idx == n+2){\n return new int[]{0};\n }\n\n int[] res = new int[n+2-idx];\n Array.Copy(ans, idx, res, 0, n+2-idx);\n\n return res;\n }\n}\n```
| 0
| 0
|
['C#']
| 0
|
adding-two-negabinary-numbers
|
My Solutions
|
my-solutions-by-hope_ma-su4r
|
Solution I\n\n/**\n * Time Complexity: O(max(n1, n2))\n * Space Complexity: O(1)\n * where `n1` is the length of the vector `arr1`\n * `n2` is the length
|
hope_ma
|
NORMAL
|
2023-07-17T15:38:51.605684+00:00
|
2023-07-19T00:57:23.848688+00:00
| 22
| false
|
**Solution I**\n```\n/**\n * Time Complexity: O(max(n1, n2))\n * Space Complexity: O(1)\n * where `n1` is the length of the vector `arr1`\n * `n2` is the length of the vector `arr2`\n */\nclass Solution {\n public:\n vector<int> addNegabinary(const vector<int> &arr1, const vector<int> &arr2) {\n constexpr int binary = 2;\n const int n1 = static_cast<int>(arr1.size());\n const int n2 = static_cast<int>(arr2.size());\n vector<int> ret;\n for (int carry = 0, i = 0, i1 = n1 - 1, i2 = n2 - 1; i1 > -1 || i2 > -1 || carry != 0; ++i, --i1, --i2) {\n const int coefficient = (i & 0b1) == 0b1 ? -1 : 1;\n const int d1 = (i1 > -1 ? arr1[i1] : 0) * coefficient;\n const int d2 = (i2 > -1 ? arr2[i2] : 0) * coefficient;\n const int d = d1 + d2 + carry;\n carry = d / binary;\n ret.emplace_back(d & 1);\n if ((d & 0b1) == 0b1 && d * coefficient < 0) {\n carry += -1 * coefficient;\n }\n }\n while (ret.size() > 1 && ret.back() == 0) {\n ret.pop_back();\n }\n reverse(ret.begin(), ret.end());\n return ret;\n }\n};\n```\n**Solution II**\n```\n/**\n * Time Complexity: O(max(n1, n2))\n * Space Complexity: O(1)\n * where `n1` is the length of the vector `arr1`\n * `n2` is the length of the vector `arr2`\n */\nclass Solution {\n public:\n vector<int> addNegabinary(const vector<int> &arr1, const vector<int> &arr2) {\n const int n1 = static_cast<int>(arr1.size());\n const int n2 = static_cast<int>(arr2.size());\n vector<int> ret;\n for (int carry = 0, i1 = n1 - 1, i2 = n2 - 1; i1 > -1 || i2 > -1 || carry != 0; --i1, --i2) {\n const int d1 = i1 > -1 ? arr1[i1] : 0;\n const int d2 = i2 > -1 ? arr2[i2] : 0;\n const int d = d1 + d2 + carry;\n carry = -(d >> 1);\n ret.emplace_back(d & 1);\n }\n while (ret.size() > 1 && ret.back() == 0) {\n ret.pop_back();\n }\n reverse(ret.begin(), ret.end());\n return ret;\n }\n};\n```
| 0
| 0
|
[]
| 0
|
adding-two-negabinary-numbers
|
Java solution - 2ms
|
java-solution-2ms-by-goldrushkl168-3qmz
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
goldrushkl168
|
NORMAL
|
2023-07-17T09:56:31.384604+00:00
|
2023-07-17T09:56:31.384634+00:00
| 49
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n List<Integer> list = new ArrayList<>();\n int m = arr1.length - 1;\n int n = arr2.length - 1;\n int carry = 0;\n while (m >= 0 || n >= 0 || carry != 0) {\n int sum = carry;\n if (m >= 0) {\n sum += arr1[m--];\n }\n if (n >= 0) {\n sum += arr2[n--];\n }\n list.add(0, sum & 1);\n carry = -(sum >> 1);\n }\n while (list.size() > 1 && list.get(0) == 0) {\n list.remove(0);\n }\n int[] res = new int[list.size()];\n for (int i = 0; i < list.size(); i++) {\n res[i] = list.get(i);\n }\n return res;\n }\n}\n\n```
| 0
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
[C++] - Beats 100%, While Loop
|
c-beats-100-while-loop-by-leetcodegrindt-zd0n
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
leetcodegrindtt
|
NORMAL
|
2023-07-02T19:53:17.496011+00:00
|
2023-07-02T19:53:17.496037+00:00
| 60
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n int arr1_length = arr1.size(), arr2_length = arr2.size();\n int maximum_length = max(arr1_length, arr2_length) + 2;\n int minimum_length = max(arr1_length, arr2_length);\n vector<int> result(maximum_length);\n\n reverse(arr1.begin(), arr1.end());\n reverse(arr2.begin(), arr2.end());\n\n for (int i{}; i < arr1.size(); ++i)\n result.at(i) += arr1.at(i);\n\n for (int i{}; i < arr2.size(); ++i)\n result.at(i) += arr2.at(i);\n\n int carry = 0;\n int i = 0;\n while (i < maximum_length)\n {\n auto& number = result.at(i);\n if (number == 0 && carry == -1)\n {\n result.at(i) += 1;\n result.at(i + 1) += 1;\n carry = 0;\n }\n else if (number == 3)\n {\n result.at(i) = 1;\n carry = -1;\n }\n else if (number == 1 && carry == -1)\n {\n number = 0;\n carry = 0;\n }\n else if (number == 2 && carry == -1)\n {\n number = 1;\n carry = 0;\n }\n else if (number == 2)\n {\n number = 0;\n carry = -1;\n }\n i++;\n }\n\n while (result.size() > minimum_length && result.back() == 0)\n result.pop_back();\n\n if (all_of(result.begin(), result.end(), [](auto number) { return number == 0; }))\n return { 0 };\n\n reverse(result.begin(), result.end());\n\n auto one = find(result.begin(), result.end(), 1);\n if (one != result.begin())\n {\n result = {one, result.end()};\n }\n\n return result;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
adding-two-negabinary-numbers
|
[C++] Observation that (1 + 1) == (4 + -2) and (-2 + -2) == (-8 + 4)
|
c-observation-that-1-1-4-2-and-2-2-8-4-b-d0hb
|
(1 + 1) == (4 + -2) \n2. (-2 + -2) == (-8 + 4)\n3. 001 + 001 == 110\n4. Add carry for bit + 1 and bit + 2.\n\nJust do a normal bit addition for base 2. But if
|
pr0d1g4ls0n
|
NORMAL
|
2023-06-29T15:48:57.681458+00:00
|
2023-07-02T05:26:27.596064+00:00
| 45
| false
|
1. `(1 + 1) == (4 + -2)` \n2. `(-2 + -2) == (-8 + 4)`\n3. `001` + `001` == `110`\n4. Add carry for bit + 1 and bit + 2.\n\nJust do a normal bit addition for base 2. But if there is a carry, carry applies for ith + 1 and ith + 2 position.\n\n```\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {\n /*\n carry lhs rhs\n 0 0 0 0\n 0 0 1 1\n 0 1 0 1\n 0 1 1 0 + (1 + 1)\n 1 0 0 1\n 1 0 1 0 + (1 + 1)\n 1 1 0 0 + (1 + 1)\n 1 1 1 1 + (1 + 1)\n */\n int n = arr1.size(), m = arr2.size();\n int lhs = n - 1, rhs = m - 1;\n vector<int> ans(max(n,m)+2);\n for (int i = ans.size() - 1; i >= 0 && lhs >= 0; --i) {\n ans[i] += arr1[lhs--];\n }\n for (int i = ans.size() - 1; i >= 0 && rhs >= 0; --i) {\n ans[i] += arr2[rhs--];\n }\n for (int i = ans.size() - 1; i >= 0; --i) {\n int newval = ans[i] % 2;\n int carry = ans[i] / 2;\n if (i - 1 >= 0) ans[i-1] += carry;\n if (i - 2 >= 0) ans[i-2] += carry; \n ans[i] = newval;\n }\n\t\t// Remove leading zeros\n int i = 0;\n for (; i < ans.size() && ans[i] != 1; ++i) {\n \n }\n int diff = i;\n vector<int> cans(ans.size() - i);\n for (; i < ans.size(); ++i) {\n cans[i - diff] = ans[i];\n }\n if (cans.size() == 0) return {0};\n return cans;\n \n }\n};\n```
| 0
| 0
|
['Bit Manipulation']
| 1
|
adding-two-negabinary-numbers
|
Java no stack
|
java-no-stack-by-yuhui4-nb6i
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nHandle the carryover by
|
yuhui4
|
NORMAL
|
2023-06-29T13:02:07.873549+00:00
|
2023-06-29T13:02:07.873573+00:00
| 97
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHandle the carryover by positive/negative\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n int i = arr1.length - 1, j = arr2.length - 1;\n List<Integer> res = new ArrayList<>();\n int carry = 0;\n while (i >= 0 || j >= 0 || carry != 0) {\n int sum = 0;\n if (i >= 0) sum += arr1[i--];\n if (j >= 0) sum += arr2[j--];\n\n if (sum - carry >= 0) {\n res.add((sum - carry) % 2);\n carry = (sum - carry) / 2 ;\n } else {\n res.add(1);\n carry = -1;\n } \n }\n while (res.size() > 1 && res.get(res.size() - 1) == 0) {\n res.remove(res.size() - 1);\n }\n int[] ret = new int[res.size()];\n for (int k = res.size() - 1; k >= 0; k--) \n ret[res.size()-k-1] = res.get(k);\n return ret; \n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
Solution
|
solution-by-deleted_user-mu8f
|
C++ []\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int> &arr1, vector<int> &arr2)\n {\n reverse(arr1.begin(), arr1.end());\n
|
deleted_user
|
NORMAL
|
2023-05-29T12:36:07.150184+00:00
|
2023-05-29T13:33:07.212198+00:00
| 143
| false
|
```C++ []\nclass Solution {\npublic:\n vector<int> addNegabinary(vector<int> &arr1, vector<int> &arr2)\n {\n reverse(arr1.begin(), arr1.end());\n reverse(arr2.begin(), arr2.end());\n if (arr1.size() < arr2.size())\n swap(arr1, arr2);\n int carry = 0;\n for (int i = 0; i < arr1.size(); i++)\n {\n int cur = arr1[i];\n if (i < arr2.size())\n cur += arr2[i];\n if (cur == 0 && carry == -1)\n {\n arr1[i] = 1;\n carry = 1;\n }\n else\n {\n arr1[i] = (cur + carry) % 2;\n carry = -(cur + carry >= 2);\n }\n }\n if (carry != 0)\n arr1.push_back(1);\n if (carry == -1)\n arr1.push_back(1);\n while (arr1.size() > 1 && arr1.back() == 0)\n arr1.pop_back();\n reverse(arr1.begin(), arr1.end());\n return arr1;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def addBinary(self, A, B):\n res = []\n carry = 0\n while A or B or carry:\n carry += (A or [0]).pop() + (B or [0]).pop()\n res.append(carry & 1)\n carry = carry >> 1\n return res[::-1]\n\n def addNegabinary(self, A, B):\n res = []\n carry = 0\n while A or B or carry:\n carry += (A or [0]).pop() + (B or [0]).pop()\n res.append(carry & 1)\n carry = -(carry >> 1)\n while len(res) > 1 and res[-1] == 0:\n res.pop()\n return res[::-1]\n```\n\n```Java []\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n \n List<Integer> result = new ArrayList();\n int pointer_1 = arr1.length-1;\n int pointer_2 = arr2.length-1;\n\n int carry = 0;\n int current = 0;\n int sum = 0;\n \n while(pointer_1 >= 0 || pointer_2 >= 0){\n \n int a = (pointer_1 >=0)? arr1[pointer_1]: 0;\n int b = (pointer_2 >=0)? arr2[pointer_2]: 0;\n \n sum = a+b+carry;\n if(sum == 3){\n current = 1; carry = -1;\n }\n else if(sum == 2){\n current = 0; carry = -1;\n }\n else if(sum == 1){\n current = 1; carry = 0;\n }\n else if(sum == 0){\n current = 0; carry = 0;\n }\n else if(sum == -1)\n {\n current = 1; carry = 1;\n }\n result.add(current);\n pointer_1--;\n pointer_2--;\n }\n if(carry != 0)\n result.add(1);\n if(carry == -1)\n result.add(1);\n \n int idx = result.size()-1;\n while(idx > 0 && result.get(idx) == 0)\n idx--;\n \n int len = idx+1;\n int[] negaBinary = new int[len];\n for(int i=0; i<len; i++){\n negaBinary[i] = result.get(idx);\n idx--;\n }\n return negaBinary;\n }\n}\n```
| 0
| 0
|
['C++', 'Java', 'Python3']
| 0
|
adding-two-negabinary-numbers
|
[LC-1073-M | Python3] A Plain Solution
|
lc-1073-m-python3-a-plain-solution-by-dr-trb7
|
It can be treated as a direct follow-up of LC-1017.\n\nPython3 []\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\
|
drsv
|
NORMAL
|
2023-05-18T13:12:35.171024+00:00
|
2023-05-18T13:12:35.171067+00:00
| 95
| false
|
It can be treated as a direct follow-up of [LC-1017](https://leetcode.cn/problems/convert-to-base-2/).\n\n```Python3 []\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n v1 = v2 = 0\n i1 = i2 = 0\n for num1 in arr1[::-1]:\n v1 += num1 * (-2)**i1\n i1 += 1\n for num2 in arr2[::-1]:\n v2 += num2 * (-2)**i2\n i2 += 1\n v = v1 + v2\n\n res = [] if v else [0]\n while v:\n res.append(rem := v & 1)\n v = (v - rem) // -2\n \n return res[::-1]\n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
SIMPLE TO UNDERSTAND
|
simple-to-understand-by-anshumanraj252-uf6j
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
anshumanraj252
|
NORMAL
|
2023-04-17T17:43:25.823594+00:00
|
2023-04-17T17:43:25.823630+00:00
| 98
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] addNegabinary(int[] arr1, int[] arr2) {\n// int num1 = first(arr1);\n// int num2 = first(arr2);\n// int sum = num1 +num2;\n// String bin = Integer.tobinaryString(sum);\n// int [] ans = new int[bin.length()];\n// for(int i = 0;i<ans.length();i++){\n// ans[i]=bin.charAt(i)-\'0\';\n// }\n// return ans;\n// }\n// }\n// public int first(int[] arr){\n// //int ans = 0;\n// int j = 0\n// for(int i = arr.length-1;i>0;i--){\n// int ans = ans + (arr[i])*(2)^j;\n// j++;\n\nList<Integer> digits = new ArrayList<>();\n int carry = 0;\n for (int i = 0; i < Math.max(arr1.length, arr2.length) || carry != 0; i++){\n int d1 = 0;\n if (i < arr1.length){\n d1 = arr1[arr1.length - 1 - i];\n }\n int d2 = 0;\n if (i < arr2.length){\n d2 = arr2[arr2.length - 1 - i];\n }\n digits.add(Math.abs(d1 + d2 + carry) % 2);\n if (d1 + d2 + carry < 0){\n carry = (Math.abs(d1 + d2 + carry) + 1) / 2;\n }else{\n carry = -(d1 + d2 + carry) / 2;\n }\n }\n Collections.reverse(digits);\n while(digits.size() > 1 && digits.get(0) == 0){\n digits.remove(0);\n }\n return digits.stream().mapToInt(i -> i).toArray();\n\n }\n\n}\n```
| 0
| 0
|
['Java']
| 0
|
adding-two-negabinary-numbers
|
python basic math
|
python-basic-math-by-achildxd-grtb
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAssumption from basic math\n\n9 = a * (-2) ** x + b * (-2) ** (x-1) + c * (-2) ** (x-2)
|
achildxd
|
NORMAL
|
2023-04-17T06:40:26.249715+00:00
|
2023-04-17T06:40:26.249738+00:00
| 112
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAssumption from basic math\n\n9 = a * (-2) ** x + b * (-2) ** (x-1) + c * (-2) ** (x-2) + ... + 1 \n=> do mod 2 to find last digit => will get 1\n=> new total will be 9 // 2 = 4\n4 = a ** (-2) ** (x-1) + b ** (-2) ** (x-2) + ... + -k => -1 time 2 sides\nfind k by mod2 both side\n-4 = .... + k\n=> repeat the process until total == 0\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n n1 = 0\n power = 0\n for i in range(len(arr1)-1, -1, -1):\n n1 += arr1[i] * (-2) ** power\n power += 1\n\n n2 = 0\n power = 0\n for i in range(len(arr2)-1, -1, -1):\n n2 += arr2[i] * (-2) ** power\n power += 1\n\n total = n1 + n2\n ans = []\n while total != 0:\n rem = abs(total % 2)\n total = total // 2\n ans.append(rem)\n total *= -1\n\n if not ans:\n return [0]\n\n return ans[::-1]\n\n"""\nAssumption from basic math\n\n9 = a * (-2) ** x + b * (-2) ** (x-1) + c * (-2) ** (x-2) + ... + 1 \n=> do mod 2 to find last digit => will get 1\n=> new total will be 9 // 2 = 4\n4 = a ** (-2) ** (x-1) + b ** (-2) ** (x-2) + ... + -k => -1 time 2 sides\nfind k by mod2 both side\n-4 = .... + k\n=> repeat the process until total == 0\n"""\n```
| 0
| 0
|
['Python3']
| 0
|
adding-two-negabinary-numbers
|
2s complement | Commented and Explained | Convert from -2 base then convert back
|
2s-complement-commented-and-explained-co-tfs1
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe want to first know what values we have \nThen, we want to know what we sum up to \nT
|
laichbr
|
NORMAL
|
2023-03-28T20:36:45.436278+00:00
|
2023-03-28T20:36:45.436322+00:00
| 134
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe want to first know what values we have \nThen, we want to know what we sum up to \nThen, we want to convert from where we are to where we want to go \nWe can do this with two functions and a few calls as detailed below. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we build our convert from negative form function \nThis function takes in an array to convert that is assumed to be in base -2. We have no way to check that in the current problem, so we take it on faith. Then, the following occurs \n- Our place value starts in the 1s place for any base (as anything to the power of 0, even a negative base, is 0) \n- Our return valuation starts at 0, and we will adjust from there \n- Then, we reverse our array (could also chose to read from the back, but good to call it when it occurs for readability) \n- Then, for bit in array to convert \n - return valuation is incremented by the product of the bit with the place value \n - place value is incremented as the product of itself with -2 \nWhen done, return return valuation \n\nNow that we have that, we get the array valuations \nDo this for array 1 and array 2 and make sure they match by hand. I have removed the print statements, but you could print these out after and then check. Once this is working correctly, we sum these valuations up as sum of arrays. \n\nNow we build our convert to negative form function which is given a value to convert and returns an array in base -2. To do so, we do the following\n- if value to convert is 0, return [0]\n- otherwise, set a negative form array as a deque\n- while your value to convert is not zero (meaning we are out of material)\n - update value to convert and get the remainder from the update as the result of a call to divmod, passing in value to convert and -2 as arguments\n - if our remainder is less than 0, it must be -1. \n - if our remainder is negative 1 \n - our value to convert is 1 greater than before (carry operation)\n - remainder then is set to 1 \n - append the remainder to the front of the negative form array \n- when done, we have our array, return it \n\n# Complexity\n- Time complexity: O(N) \n - each array is converted \n - the summation is converted back \n - both take linear time \n\n\n- Space complexity: O(N) \n - we end up creating an array to store the solution of size O(N) \n\n# Code\n```\n"""\n array valuation example walkthrough \n for the first problem, we are given \n [1, 1, 1, 1, 1]\n and \n [1, 0, 1]\n\n If we evaluate the converted form of these, the first is 11 and the second is 5 \n This gives a form of 16 in base of -2 \n in base of -2, 16 is -2^4 \n Remembering that we start at power 0, this as an array is then \n [1, 0, 0, 0, 0]\n\n Where we can notice that even powers of -2 will be the same as the regular powers of positive 2 \n This should come as no surprise if you have studied 2\'s complement which the problem is based on\n Learn more here : https://www.cs.cornell.edu/~tomf/notes/cps104/twoscomp.html \n\n"""\n\nclass Solution:\n def addNegabinary(self, arr1: List[int], arr2: List[int]) -> List[int]:\n # converts from negative binary form array to a valuation\n def convert_from_negative_form(array_to_convert) : \n place_value = 1\n return_valuation = 0\n array_to_convert.reverse()\n for bit in array_to_convert : \n return_valuation += bit * place_value \n place_value *= -2\n return return_valuation\n\n # get array valuations \n array_1_valuation = convert_from_negative_form(arr1)\n array_2_valuation = convert_from_negative_form(arr2)\n # sum them \n sum_of_arrays = array_1_valuation + array_2_valuation\n \n # converts from value to convert to array form in 2s complement form \n def convert_to_negative_form(value_to_convert) : \n # base case \n if value_to_convert == 0 : \n return [0]\n # set up for return \n negative_form_array = collections.deque()\n # build negative_form_array while not 0 \n while value_to_convert != 0 : \n # update value to convert \n value_to_convert, remainder = divmod(value_to_convert, -2)\n # remainder is either -1 or 0 \n # if it is 0 we\'re good, \n # but if not we need to account for overflow \n if remainder < 0 : \n # shift value to convert forward on remainder -1 \n value_to_convert += 1 \n # cannot place -1 in binary array, but can place 1\n remainder = 1\n # append remainder as this is the 2s complement left over \n negative_form_array.appendleft(remainder)\n # return when done \n return negative_form_array \n\n # get valuation \n negative_array = convert_to_negative_form(sum_of_arrays)\n # return negative array \n return negative_array \n```
| 0
| 0
|
['Python3']
| 0
|
sales-analysis-iii
|
simple MySQL solution
|
simple-mysql-solution-by-henryz14-vur4
|
\nSELECT s.product_id, product_name\nFROM Sales s\nLEFT JOIN Product p\nON s.product_id = p.product_id\nGROUP BY s.product_id\nHAVING MIN(sale_date) >= CAST(\'2
|
henryz14
|
NORMAL
|
2019-06-20T15:28:35.145827+00:00
|
2019-06-23T00:05:35.282009+00:00
| 30,892
| false
|
```\nSELECT s.product_id, product_name\nFROM Sales s\nLEFT JOIN Product p\nON s.product_id = p.product_id\nGROUP BY s.product_id\nHAVING MIN(sale_date) >= CAST(\'2019-01-01\' AS DATE) AND\n MAX(sale_date) <= CAST(\'2019-03-31\' AS DATE)\n```
| 158
| 1
|
[]
| 28
|
sales-analysis-iii
|
✔️EASIEST solution EVER!
|
easiest-solution-ever-by-namratanwani-1u0r
|
\n# Wherever you are given a range, keep MIN() and MAX() in mind\nSELECT Product.product_id, Product.product_name FROM Product \nJOIN Sales \nON Product.product
|
namratanwani
|
NORMAL
|
2022-06-22T23:39:20.863483+00:00
|
2022-06-24T19:16:00.322769+00:00
| 24,642
| false
|
```\n# Wherever you are given a range, keep MIN() and MAX() in mind\nSELECT Product.product_id, Product.product_name FROM Product \nJOIN Sales \nON Product.product_id = Sales.product_id \nGROUP BY Sales.product_id \nHAVING MIN(Sales.sale_date) >= "2019-01-01" AND MAX(Sales.sale_date) <= "2019-03-31";\n```
| 119
| 0
|
[]
| 24
|
sales-analysis-iii
|
Beat 95% Simple subquery
|
beat-95-simple-subquery-by-zzzzhu-nfrx
|
\nSELECT product_id, product_name \nFROM Product \nWHERE product_id IN\n(SELECT product_id\nFROM Sales\nGROUP BY product_id\nHAVING MIN(sale_date) >= \'2019-01-
|
zzzzhu
|
NORMAL
|
2019-10-05T00:58:11.521965+00:00
|
2019-10-05T00:58:11.522002+00:00
| 9,927
| false
|
```\nSELECT product_id, product_name \nFROM Product \nWHERE product_id IN\n(SELECT product_id\nFROM Sales\nGROUP BY product_id\nHAVING MIN(sale_date) >= \'2019-01-01\' AND MAX(sale_date) <= \'2019-03-31\')\n```
| 63
| 0
|
[]
| 6
|
sales-analysis-iii
|
Superb Logic with Min and Max
|
superb-logic-with-min-and-max-by-ganjina-orsa
|
\n# Logic min and max\n\nselect product_id,product_name\nfrom product natural join sales\ngroup by product_id\nhaving min(sale_date)>=\'2019-01-01\' and max(sal
|
GANJINAVEEN
|
NORMAL
|
2023-04-23T16:15:01.874026+00:00
|
2023-04-23T16:15:01.874065+00:00
| 7,215
| false
|
\n# Logic min and max\n```\nselect product_id,product_name\nfrom product natural join sales\ngroup by product_id\nhaving min(sale_date)>=\'2019-01-01\' and max(sale_date)<=\'2019-03-31\'\n\n```\n# please upvote me it would encourage me alot\n
| 38
| 0
|
['MySQL']
| 4
|
sales-analysis-iii
|
✅MySQL || Beginner level || Faster than 98%||Simple-Short -Solution✅
|
mysql-beginner-level-faster-than-98simpl-d6uc
|
Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome.\n==========
|
Anos
|
NORMAL
|
2022-08-31T19:50:56.737440+00:00
|
2022-08-31T19:50:56.737468+00:00
| 5,708
| false
|
**Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome.***\n*====================================================================*\n\u2705 **MySQL Code :**\n Your runtime beats 98.65 % of mysql submissions.\n```\nSELECT product_id, product_name\nFROM Sales \nJOIN Product \nUsing(product_id)\nGROUP BY product_id\nHAVING MIN(sale_date) >= \'2019-01-01\' AND MAX(sale_date) <= \'2019-03-31\' \n```\n**Runtime:** 980 ms\n**Memory Usage:** 0B\n________________________________\n__________________________________\n\nIf you like the solution, please upvote \uD83D\uDD3C\nFor any questions, or discussions, comment below. \uD83D\uDC47\uFE0F
| 37
| 0
|
['MySQL']
| 4
|
sales-analysis-iii
|
MS SQL + 99.01% faster + Group by + Having
|
ms-sql-9901-faster-group-by-having-by-dd-y746
|
\nselect s.product_id, p.product_name\nfrom sales s, product p\nwhere s.product_id = p.product_id\ngroup by s.product_id, p.product_name\nhaving min(s.sale_date
|
ddeeps2610
|
NORMAL
|
2020-06-25T19:42:31.211291+00:00
|
2020-06-25T19:42:31.211338+00:00
| 5,580
| false
|
```\nselect s.product_id, p.product_name\nfrom sales s, product p\nwhere s.product_id = p.product_id\ngroup by s.product_id, p.product_name\nhaving min(s.sale_date) >= \'2019-01-01\' \n and max(s.sale_date) <= \'2019-03-31\'\n```
| 37
| 0
|
[]
| 6
|
sales-analysis-iii
|
1084. Sales Analysis III
|
1084-sales-analysis-iii-by-spaulding-s8em
|
```\nSELECT product_id, product_name FROM Sales \nJOIN Product USING(product_id)\nGROUP BY product_id\nHAVING MIN(sale_date) >= \'2019-01-01\' AND MAX(sale_date
|
Spaulding_
|
NORMAL
|
2022-09-07T18:46:19.522886+00:00
|
2022-09-07T18:46:19.522927+00:00
| 3,204
| false
|
```\nSELECT product_id, product_name FROM Sales \nJOIN Product USING(product_id)\nGROUP BY product_id\nHAVING MIN(sale_date) >= \'2019-01-01\' AND MAX(sale_date) <= \'2019-03-31\' ;
| 21
| 0
|
['MySQL']
| 0
|
sales-analysis-iii
|
MySQL solution | | Easy solution
|
mysql-solution-easy-solution-by-im_obid-yhfj
|
\n# Code\n\nselect product_id,product_name \nfrom Product where product_id not \nin \n(\n select p.product_id from Product p left join Sales s \n on p.pro
|
im_obid
|
NORMAL
|
2023-01-06T08:03:13.844296+00:00
|
2023-01-06T08:03:13.844340+00:00
| 6,335
| false
|
\n# Code\n```\nselect product_id,product_name \nfrom Product where product_id not \nin \n(\n select p.product_id from Product p left join Sales s \n on p.product_id=s.product_id \n where s.sale_date <date(\'2019-01-01\') \n or\n s.sale_date >date(\'2019-03-31\') \n or\n s.seller_id is null \n);\n```
| 20
| 0
|
['MySQL']
| 3
|
sales-analysis-iii
|
✅ 100% EASY || FAST 🔥|| CLEAN SOLUTION 🌟
|
100-easy-fast-clean-solution-by-kartik_k-cz62
|
\n\n# Code\n\nSELECT product_id, product_name FROM Product \n\nWHERE product_id IN(SELECT product_id FROM Sales \n\nGROUP BY product_id HAVING MIN(sale_date) >=
|
kartik_ksk7
|
NORMAL
|
2024-06-03T12:35:26.146669+00:00
|
2024-06-03T12:35:55.577222+00:00
| 1,625
| false
|
\n\n# Code\n```\nSELECT product_id, product_name FROM Product \n\nWHERE product_id IN(SELECT product_id FROM Sales \n\nGROUP BY product_id HAVING MIN(sale_date) >= \'2019-01-01\'\n \nAND MAX(sale_date) <= \'2019-03-31\')\n```\n\n
| 19
| 0
|
['Oracle']
| 0
|
sales-analysis-iii
|
simple mysql solution
|
simple-mysql-solution-by-merciless-shck
|
\nSELECT product_id, product_name\nFROM product\nJOIN SALES\nUSING(product_id)\nGROUP BY product_id\nHAVING sum(CASE WHEN sale_date between \'2019-01-01\' and \
|
merciless
|
NORMAL
|
2019-06-14T03:55:12.517323+00:00
|
2019-06-14T03:55:12.517358+00:00
| 4,370
| false
|
```\nSELECT product_id, product_name\nFROM product\nJOIN SALES\nUSING(product_id)\nGROUP BY product_id\nHAVING sum(CASE WHEN sale_date between \'2019-01-01\' and \'2019-03-31\' THEN 1 ELSE 0 end) > 0\nAND sum(CASE WHEN sale_date between \'2019-01-01\' and \'2019-03-31\' THEN 0 else 1 end) = 0\n```
| 14
| 0
|
[]
| 5
|
sales-analysis-iii
|
pandas || 2 lines, groupby and merge || T/S: 99% / 99%
|
pandas-2-lines-groupby-and-merge-ts-99-9-3rds
|
\nimport pandas as pd\n\ndef sales_analysis(product: pd.DataFrame, \n sales: pd.DataFrame) -> pd.DataFrame:\n\n df = sales.groupby([\'produ
|
Spaulding_
|
NORMAL
|
2024-05-15T23:33:09.487498+00:00
|
2024-05-22T16:16:33.681611+00:00
| 1,024
| false
|
```\nimport pandas as pd\n\ndef sales_analysis(product: pd.DataFrame, \n sales: pd.DataFrame) -> pd.DataFrame:\n\n df = sales.groupby([\'product_id\'], as_index = False\n ).agg(min=(\'sale_date\', \'min\'), max=(\'sale_date\', \'max\'))\n\n return df[(df[\'min\'] >=\'2019-01-01\') &\n (df[\'max\'] <=\'2019-03-31\')].merge(product).iloc[:,[0,3]]\n```\n[https://leetcode.com/problems/sales-analysis-iii/submissions/1079605385/](https://leetcode.com/problems/sales-analysis-iii/submissions/1079605385/)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ `len(sales)`.
| 13
| 0
|
['Pandas']
| 0
|
sales-analysis-iii
|
Absolutely the simplest solution
|
absolutely-the-simplest-solution-by-zcae-r8gp
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Zcaelum
|
NORMAL
|
2023-01-12T06:42:02.420857+00:00
|
2023-01-12T06:42:02.420930+00:00
| 4,164
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Write your MySQL query statement below\nselect product_id,product_name\nfrom product p join sales s \nusing(product_id)\ngroup by product_id\nhaving sum(sale_date<"2019-01-01")=0\nand sum(sale_date>"2019-03-31")=0\n```
| 13
| 0
|
['MySQL']
| 3
|
sales-analysis-iii
|
Solution without JOIN using NOT IN and NOT BETWEEN
|
solution-without-join-using-not-in-and-n-ldvl
|
\nSELECT Product.product_id, Product.product_name\nFROM Product\nWHERE product_id NOT IN (SELECT product_id FROM Sales WHERE sale_date NOT BETWEEN \'2019-01-01\
|
tresmegistos
|
NORMAL
|
2019-10-29T23:48:39.621406+00:00
|
2019-10-29T23:48:39.621459+00:00
| 2,187
| false
|
```\nSELECT Product.product_id, Product.product_name\nFROM Product\nWHERE product_id NOT IN (SELECT product_id FROM Sales WHERE sale_date NOT BETWEEN \'2019-01-01\' AND \'2019-03-31\');\n```
| 13
| 0
|
[]
| 6
|
sales-analysis-iii
|
[MySQL] || SubQuery || LEFT JOIN
|
mysql-subquery-left-join-by-comauro7511-2w65
|
Write your MySQL query statement below\n\n\nWITH cte AS\n(SELECT product_id FROM Sales\nWHERE sale_date > \'2019-03-31\'\nOR sale_date < \'2019-01-01\')\n\nSELE
|
comauro7511
|
NORMAL
|
2022-10-13T19:28:15.712648+00:00
|
2022-10-14T15:56:18.841752+00:00
| 3,013
| false
|
# Write your MySQL query statement below\n```\n\nWITH cte AS\n(SELECT product_id FROM Sales\nWHERE sale_date > \'2019-03-31\'\nOR sale_date < \'2019-01-01\')\n\nSELECT DISTINCT s.product_id , p.product_name\nFROM Sales s\nLEFT JOIN Product p\nON s.product_id=p.product_id \nWHERE s.product_id NOT \nIN(SELECT product_id FROM cte); \n```\n
| 10
| 0
|
['MySQL']
| 1
|
sales-analysis-iii
|
[ MYSQL ] ✅✅ Simple MYSQL Solution Using Having Clause || Group By 🥳✌👍
|
mysql-simple-mysql-solution-using-having-qxki
|
If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 998 ms, faster than 87.37% of MySQL online submissions
|
ashok_kumar_meghvanshi
|
NORMAL
|
2022-07-16T18:35:07.274533+00:00
|
2022-07-16T18:35:07.274576+00:00
| 942
| false
|
# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 998 ms, faster than 87.37% of MySQL online submissions for Sales Analysis III.\n# Memory Usage: 0B, less than 100.00% of MySQL online submissions for Sales Analysis III.\n\n\tselect p.product_id, p.product_name\n\tfrom Product p\n\tinner join Sales s on p.product_id = s.product_id\n\tgroup by s.product_id\n\thaving min(sale_date) >= \'2019-01-01\'\n\tand max(sale_date) <= \'2019-03-31\';
| 10
| 0
|
['MySQL']
| 0
|
sales-analysis-iii
|
MSSQL Solution
|
mssql-solution-by-vdmhunter-r8jn
|
\nSELECT\n product_id,\n product_name\nFROM\n Product\nWHERE\n product_id IN\n (\n SELECT\n product_id\n FROM\n
|
vdmhunter
|
NORMAL
|
2022-06-14T22:47:03.748351+00:00
|
2022-06-14T22:47:03.748387+00:00
| 1,236
| false
|
```\nSELECT\n product_id,\n product_name\nFROM\n Product\nWHERE\n product_id IN\n (\n SELECT\n product_id\n FROM\n Sales\n GROUP BY\n product_id\n HAVING\n MAX(sale_date) <= \'2019-03-31\'\n AND MIN(sale_date) >= \'2019-01-01\'\n )\n```
| 9
| 0
|
['MySQL', 'MS SQL Server']
| 0
|
sales-analysis-iii
|
mysql +having
|
mysql-having-by-meskaj-292c
|
```\nSELECT \n p.product_id, p.product_name\nFROM \n product p\nJOIN \n Sales s\nON \n p.product_id = s.product_id \n\nGROUP BY s.pr
|
Meskaj
|
NORMAL
|
2021-08-20T04:43:33.283345+00:00
|
2021-08-20T04:48:51.954309+00:00
| 1,576
| false
|
```\nSELECT \n p.product_id, p.product_name\nFROM \n product p\nJOIN \n Sales s\nON \n p.product_id = s.product_id \n\nGROUP BY s.product_id\n \n HAVING max(s.sale_date)<= \'2019-03-31\'\n AND MIN(s.sale_date)>=\'2019-01-01\';
| 9
| 0
|
['MySQL']
| 2
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.