question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
insertion-sort-list | JAVA 2ms insertion sort | java-2ms-insertion-sort-by-kushguptacse-9qh0 | \npublic ListNode insertionSortList(ListNode head) {\n ListNode dummy = new ListNode(Integer.MIN_VALUE);\n\t\tListNode curr = head;\n ListNode pre | kushguptacse | NORMAL | 2020-02-26T08:11:07.854287+00:00 | 2020-02-26T08:11:07.854333+00:00 | 502 | false | ```\npublic ListNode insertionSortList(ListNode head) {\n ListNode dummy = new ListNode(Integer.MIN_VALUE);\n\t\tListNode curr = head;\n ListNode prev = dummy;\n\t\twhile (curr != null) {\n //to save checking from start below condition is used\n if(prev.val > curr.val)\n prev = dummy;\n\t\t\t\n\t\t\twhile (prev.next != null && prev.next.val<curr.val) {\n\t\t\t\tprev = prev.next;\n\t\t\t}\n\t\t\t//insert current node between prev and prev.next \n\t\t\tListNode nextNode=curr.next;\n\t\t\tcurr.next=(prev.next);\n\t\t\tprev.next=(curr);\n\t\t\tcurr=nextNode;\n\t\t}\n\t\treturn dummy.next;\n\t}\n \n\n``` | 3 | 0 | ['Linked List', 'Iterator', 'Java'] | 0 |
insertion-sort-list | Python solution | python-solution-by-zitaowang-5t82 | Time complexity: O(n^2), space complexity: O(1).\n\n\nclass Solution:\n def insertionSortList(self, head):\n """\n :type head: ListNode\n | zitaowang | NORMAL | 2018-12-28T05:59:17.993744+00:00 | 2018-12-28T05:59:17.993796+00:00 | 559 | false | Time complexity: `O(n^2)`, space complexity: `O(1)`.\n\n```\nclass Solution:\n def insertionSortList(self, head):\n """\n :type head: ListNode\n :rtype: ListNode\n """\n if not head or not head.next:\n return head\n dummy = ListNode(float(\'inf\'))\n dummy.next = head\n pre1 = head\n ptr1 = head.next\n while ptr1: # keep the loop invariant that nodes between dummy and ptr1 are sorted\n pre2 = dummy\n ptr2 = dummy.next\n while ptr2 != ptr1 and ptr2.val <= ptr1.val: # ptr2 searches for the right place to insert ptr1\n pre2 = ptr2\n ptr2 = ptr2.next\n if ptr2 == ptr1:\n pre1 = ptr1\n ptr1 = ptr1.next\n else:\n pre2.next = ptr1\n tmp = ptr1.next\n ptr1.next = ptr2\n ptr2 = ptr1\n ptr1 = tmp\n pre1.next = ptr1\n return dummy.next\n``` | 3 | 0 | [] | 0 |
insertion-sort-list | 5ms, O(1) space: 5 small steps that easy to follow | 5ms-o1-space-5-small-steps-that-easy-to-uyouc | Preparation: * Order in LinkedList will be changed, extra variable required -> ListNode n. * LinkedList needs to be divided in sorted and unsorted parts -> List | akquard | NORMAL | 2018-10-20T03:19:27.086650+00:00 | 2018-10-22T22:43:06.674300+00:00 | 290 | false | **Preparation:**
* Order in LinkedList will be changed, extra variable required -> `ListNode n`.
* LinkedList needs to be divided in sorted and unsorted parts -> `ListNode pivot `.
* Iteration of sorted part starting from head -> `ListNode current = head`.
**Implementation:**
1. Iterate LinkedList.
2. Special case: `pivot` smaller than current element:
* Update pivot : `pivot = n`.
* Next iteration -> **step1**.
2. Save link to next element: `n = pivot.next.`
3. Unattach element from list: `pivot.next = n.next`.
4. Insert element into sorted part.
```
public ListNode insertionSortList(ListNode head) {
if( head == null || head.next == null ) return head;
ListNode pivot = head;
ListNode n = null;
while( pivot.next != null){
n = pivot.next;
if( n.val >= pivot.val) {
pivot = n;
continue;
}
pivot.next = n.next;
if( n.val <= head.val) {
n.next = head;
head = n;
continue;
}
ListNode current = head;
while( current.next != n && n.val > current.next.val) current = current.next;
n.next = current.next;
current.next = n;
}
return head;
}
``` | 3 | 0 | [] | 0 |
insertion-sort-list | 15 Lines Java Solution Using DummyHead | 15-lines-java-solution-using-dummyhead-b-wcw0 | \n public ListNode insertionSortList(ListNode head) {\n ListNode dummy = new ListNode(0); // use dummyHead\n ListNode cur = head;\n whil | meganlee | NORMAL | 2018-07-19T03:41:56.832961+00:00 | 2018-07-19T03:41:56.832961+00:00 | 269 | false | ```\n public ListNode insertionSortList(ListNode head) {\n ListNode dummy = new ListNode(0); // use dummyHead\n ListNode cur = head;\n while (cur != null) {\n ListNode iter = dummy; // find the correct insertion point\n while (iter.next != null && iter.next.val < cur.val) {\n iter = iter.next;\n }\n ListNode next = cur.next;\n cur.next = iter.next;\n iter.next = cur;\n cur = next;\n }\n return dummy.next; \n }\n``` | 3 | 0 | [] | 0 |
insertion-sort-list | TLE for Python? | tle-for-python-by-ice4026-2g85 | I have a Time Limit Exceeded when input a list of 5000 numbers.\n\n class Solution:\n # @param head, a ListNode\n # @return a ListNode\n def insertS | ice4026 | NORMAL | 2014-04-24T11:45:35+00:00 | 2014-04-24T11:45:35+00:00 | 2,235 | false | I have a Time Limit Exceeded when input a list of 5000 numbers.\n\n class Solution:\n # @param head, a ListNode\n # @return a ListNode\n def insertSort(self, head):\n if head==None or head.next==None:\n return head\n self.insertSort(head.next)\n l=head\n r=head.next\n while r!=None:\n if l.val>r.val:\n l.val,r.val=r.val,l.val\n l=r\n r=r.next\n else:\n return head\n return head\n def insertionSortList(self, head):\n return self.insertSort(head)\nis there any solution for the problem? | 3 | 0 | ['Python'] | 3 |
insertion-sort-list | Python accepted iterative solution (Another solution is about 330ms). | python-accepted-iterative-solution-anoth-esnl | suppose already sorted the part from the second node, then just need to merge the first node with the second part, if head.val is smaller, then the second can b | oldcodingfarmer | NORMAL | 2015-08-15T12:29:48+00:00 | 2015-08-15T12:29:48+00:00 | 740 | false | suppose already sorted the part from the second node, then just need to merge the first node with the second part, if head.val is smaller, then the second can be connected behind head node, if head.val is larger than the value of the returned node, then we need to find the position to insert head, and return the returned node. The iterative method is quite easy to follow, when we find the node's value is smaller than that of the previous node, we need to find an insertion position for that node in positions ahead.\n \n # Recursively, TLE (Why?)\n def insertionSortList1(self, head):\n if not head or not head.next:\n return head\n second = self.insertionSortList(head.next)\n if head.val <= second.val:\n head.next = second\n return head\n else:\n tmp = pre = second\n while second and second.val < head.val:\n pre = second\n second = second.next\n head.next = second\n pre.next = head\n return tmp\n \n # Iteratively \n def insertionSortList(self, head):\n if not head or not head.next:\n return head\n dummy = ListNode(0)\n dummy.next = node = head\n while node.next:\n if node.val <= node.next.val:\n node = node.next\n else:\n pre = dummy\n while pre.next.val < node.next.val:\n pre = pre.next\n tmp = node.next\n node.next = tmp.next\n tmp.next = pre.next\n pre.next = tmp\n return dummy.next | 3 | 1 | ['Recursion', 'Iterator', 'Python'] | 2 |
insertion-sort-list | Java 34ms solution, clear logic with separate insert method | java-34ms-solution-clear-logic-with-sepa-3o4q | using insertion sort logic. Insert each new node into a sorted linked list with dummy head.\n \n\n public class Solution {\n public ListNode ins | yanggao | NORMAL | 2015-11-23T21:25:29+00:00 | 2015-11-23T21:25:29+00:00 | 886 | false | using insertion sort logic. Insert each new node into a sorted linked list with dummy head.\n \n\n public class Solution {\n public ListNode insertionSortList(ListNode head) {\n ListNode sortedHeadDummy = new ListNode(0);\n ListNode curr = head;\n while (curr != null) {\n ListNode next = curr.next;\n insert(sortedHeadDummy, curr);\n curr = next;\n }\n return sortedHeadDummy.next;\n }\n \n private void insert(ListNode dummyHead, ListNode target) {\n // left to right scan to insert the target node\n ListNode curr = dummyHead;\n while (curr.next != null && curr.next.val < target.val) {\n curr = curr.next;\n }\n target.next = curr.next;\n curr.next = target;\n }\n } | 3 | 0 | [] | 1 |
insertion-sort-list | Insertion sort python solution | insertion-sort-python-solution-by-lime66-tt5r | class Solution(object):\n def insertionSortList(self, head):\n if not head or not head.next:\n return head\n \n d | lime66 | NORMAL | 2016-02-25T05:11:56+00:00 | 2016-02-25T05:11:56+00:00 | 888 | false | class Solution(object):\n def insertionSortList(self, head):\n if not head or not head.next:\n return head\n \n dummy = ListNode(None)\n dummy.next, tail = head, head.next\n dummy.next.next = None\n \n while tail:\n pre, current, next = dummy, dummy.next, tail.next\n while current:\n if tail.val <= current.val:\n pre.next, tail.next = tail, current\n break\n pre, current = current, current.next\n else:\n pre.next, tail.next = tail, None\n tail = next\n \n return dummy.next | 3 | 0 | ['Python'] | 0 |
insertion-sort-list | Easy and Concise C++ | easy-and-concise-c-by-darkhorse007d-1yvh | \n# Code\ncpp []\nclass Solution {\npublic:\n ListNode* insertionSortList(ListNode* head) {\n ListNode* ans = new ListNode(-6000);\n while(head | darkhorse007d | NORMAL | 2024-10-15T19:08:29.189134+00:00 | 2024-10-15T19:08:29.189162+00:00 | 113 | false | \n# Code\n```cpp []\nclass Solution {\npublic:\n ListNode* insertionSortList(ListNode* head) {\n ListNode* ans = new ListNode(-6000);\n while(head){\n ListNode* curr = ans , *prev = ans;\n while(curr and curr -> val < head -> val){\n prev = curr;\n curr = curr -> next;\n }\n prev -> next = head; \n head = head -> next; // go to next node before linking the two parts.\n prev -> next -> next = curr; // curr points to the node whose value is just greater than head -> val\n } \n return ans -> next;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
insertion-sort-list | Best C++ Code (Beats 80%) | best-c-code-beats-80-by-souravsinghal200-qj1e | Intuition\n Describe your first thoughts on how to solve this problem. \nplzz upvote\n# Approach\n Describe your approach to solving the problem. \nplzz upvote\ | souravsinghal2004 | NORMAL | 2024-09-08T12:27:44.428099+00:00 | 2024-09-08T12:27:44.428120+00:00 | 461 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nplzz upvote\n# Approach\n<!-- Describe your approach to solving the problem. -->\nplzz upvote\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nplzz upvote\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nplzz upvote\n# Code\n```cpp []\n\nclass Solution {\npublic:\n ListNode* sortedInsert(ListNode* head, ListNode* node) {\n if (head == nullptr || head->val >= node->val) {\n node->next = head;\n return node;\n }\n ListNode* current = head;\n while (current->next != nullptr && current->next->val < node->val) {\n current = current->next;\n }\n node->next = current->next;\n current->next = node;\n return head;\n }\n ListNode* insertionSortList(ListNode* head) {\n ListNode* sorted = nullptr; \n ListNode* current = head;\n while (current != nullptr) {\n ListNode* next = current->next; \n sorted = sortedInsert(sorted, current);\n current = next; \n }\n return sorted;\n }\n};\n\n``` Thank U for Your Kind Attention | 2 | 0 | ['C++'] | 1 |
insertion-sort-list | Solution By Dare2Solve | Detailed Explanation | Clean Code | solution-by-dare2solve-detailed-explanat-2qjy | Explanation []\nauthorslog.com/blog/cRT2Uc7vvh\n\n# Code\n\ncpp []\nclass Solution {\npublic:\n ListNode* insertionSortList(ListNode* head) {\n if (!h | Dare2Solve | NORMAL | 2024-08-14T17:55:38.861224+00:00 | 2024-08-14T17:55:38.861259+00:00 | 2,610 | false | ```Explanation []\nauthorslog.com/blog/cRT2Uc7vvh\n```\n# Code\n\n```cpp []\nclass Solution {\npublic:\n ListNode* insertionSortList(ListNode* head) {\n if (!head)\n return nullptr;\n\n std::vector<int> arr;\n ListNode* current = head;\n\n while (current) {\n arr.push_back(current->val);\n current = current->next;\n }\n\n for (int i = 1; i < arr.size(); i++) {\n int currVal = arr[i];\n int j = i - 1;\n while (j >= 0 && arr[j] > currVal) {\n arr[j + 1] = arr[j];\n j--;\n }\n arr[j + 1] = currVal;\n }\n\n current = head;\n for (int i = 0; i < arr.size(); i++) {\n current->val = arr[i];\n current = current->next;\n }\n\n return head;\n }\n};\n```\n\n```python []\nclass Solution:\n def insertionSortList(self, head: ListNode) -> ListNode:\n if not head:\n return None\n\n arr = []\n current = head\n\n while current:\n arr.append(current.val)\n current = current.next\n\n for i in range(1, len(arr)):\n curr_val = arr[i]\n j = i - 1\n while j >= 0 and arr[j] > curr_val:\n arr[j + 1] = arr[j]\n j -= 1\n arr[j + 1] = curr_val\n\n current = head\n for i in range(len(arr)):\n current.val = arr[i]\n current = current.next\n\n return head\n\n```\n\n```java []\nclass Solution {\n public ListNode insertionSortList(ListNode head) {\n if (head == null) return null;\n\n List<Integer> arr = new ArrayList<>();\n ListNode current = head;\n\n while (current != null) {\n arr.add(current.val);\n current = current.next;\n }\n\n for (int i = 1; i < arr.size(); i++) {\n int currVal = arr.get(i);\n int j = i - 1;\n while (j >= 0 && arr.get(j) > currVal) {\n arr.set(j + 1, arr.get(j));\n j--;\n }\n arr.set(j + 1, currVal);\n }\n\n current = head;\n for (int i = 0; i < arr.size(); i++) {\n current.val = arr.get(i);\n current = current.next;\n }\n\n return head;\n }\n}\n```\n\n```javascript []\nvar insertionSortList = function (head) {\n let current = head;\n const arr = [];\n while (current) {\n arr.push(current.val);\n current = current.next;\n }\n\n for (let i = 1; i < arr.length; i++) {\n let currVal = arr[i];\n let j = i - 1\n for (; j >= 0 && arr[j] > currVal; j--) {\n arr[j + 1] = arr[j];\n }\n arr[j + 1] = currVal;\n }\n\n current = head;\n for (let i = 0; i < arr.length; i++) {\n current.val = arr[i];\n current = current.next;\n }\n\n return head\n};\n``` | 2 | 0 | ['Linked List', 'Sorting', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 1 |
insertion-sort-list | Clear cpp solution using insertion sort | beats 99.3% | O(1) space | clear-cpp-solution-using-insertion-sort-h25sk | Approach\n Describe your approach to solving the problem. \n\n##### We will follow the procedure of insertion sort as we do for array.\nFor the solution I have | ReNY_1011 | NORMAL | 2024-06-14T18:09:25.486973+00:00 | 2024-06-14T18:09:25.487006+00:00 | 106 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n\n##### We will follow the procedure of insertion sort as we do for array.\nFor the solution I have defined some helper functions namely-\n\n1. `insertNode` which is vanilla insertion in a linked list where the pointer of node after which toinsert is known. Note that it assumes that the next attribute of toinsert node is nullptr.\n2. `insertInSorted` which inserts the toinsert node to a linked list which is given as sorted and its head pointer is given. I have used linear search to first locate the suitable position and then have used the `insertNode` function to insert the toinsert node. After insertion it returns the head of the new linkedlist obtained.Note that here also the next pointer of toinsert node must be nullptr initially.\n\nIn the actual `insertionSortList` function we know that linked list with only one node will be sorted in itself so we start from head->next.\n- We will initialize two pointers `curr` and `prev`. \n`prev` will keep track of last node of the sorted linkedlist that we will constructively build starting from the head node.\n`curr` will the current node that we want to add to the sorted list that we are building in each iteration.\n- In each iteration untill `curr != nullptr`, we first check that if `curr->val>=prev->val` which is to say that curr is already larger than the sorted list, we do nothing and advance both pointers by one node.\nelse we crucially first isolate the node curr by connecting prev to `curr->next` and the setting `curr->next = null` then we use the `insertInSorted` function to insert the curr node to the sorted array build.\n- Finally we return the head.\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$ $$n : number-of-nodes$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n void insertNode(ListNode* node, ListNode* toinsert){\n if(node->next == nullptr){\n node->next = toinsert;\n return;\n }\n toinsert->next = node->next;\n node->next = toinsert;\n return;\n }\n ListNode* insertInSorted(ListNode* head, ListNode* toinsert){\n if(toinsert->val <= head->val){\n toinsert->next = head;\n head = toinsert;\n return head;\n }\n ListNode* curr = head;\n bool flag = false;\n while(curr->next != nullptr){\n if(curr->val <= toinsert->val && curr->next->val >= toinsert->val){\n insertNode(curr, toinsert);\n flag = true;\n break;\n }\n curr = curr->next;\n }\n if(!flag) insertNode(curr, toinsert);\n return head;\n }\n ListNode* insertionSortList(ListNode* head) {\n ListNode* prev = head;\n ListNode* curr = head->next;\n while(curr != nullptr){\n if(prev->val <= curr->val){\n prev = curr;\n curr = curr->next;\n }\n else{\n prev->next = curr->next;\n curr->next = nullptr;\n head = insertInSorted(head, curr);\n curr = prev->next;\n }\n }\n return head;\n }\n\n};\n``` | 2 | 0 | ['Linked List', 'C++'] | 0 |
insertion-sort-list | Using insertion sort | using-insertion-sort-by-abhish010102-x2bv | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | abhish010102 | NORMAL | 2024-06-12T06:38:37.760238+00:00 | 2024-06-12T06:38:37.760273+00:00 | 510 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* insertionSortList(ListNode* head) {\n if(head==NULL || head->next==NULL)\n return head;\n ListNode* dummy=new ListNode(0);\n ListNode* cur=head;\n\n while(cur!=NULL){\n ListNode* pre=dummy;\n ListNode* next=cur->next;\n\n while(pre->next!=NULL && pre->next->val<cur->val)\n pre=pre->next;\n \n cur->next=pre->next;\n pre->next=cur;\n cur=next;\n }\n\n return dummy->next;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
insertion-sort-list | Insertion Sort List | insertion-sort-list-by-khushbu_143-8to5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | khushbu_143 | NORMAL | 2024-05-14T14:18:40.018265+00:00 | 2024-05-14T14:18:40.018293+00:00 | 1,368 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode insertionSortList(ListNode head) {\n ListNode dummy= new ListNode(0);\n ListNode current=head;\n\n while(current != null){\n ListNode prev=dummy;\n ListNode nextNode=current.next;\n\n while(prev.next!=null && prev.next.val < current.val){\n prev=prev.next;\n }\n\n current.next=prev.next;\n prev.next=current;\n current=nextNode;\n }\n return dummy.next;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
sum-of-floored-pairs | ✅ C++ Short & Easy | Frequency Prefix Sum Solution w/ Explanation | c-short-easy-frequency-prefix-sum-soluti-thet | \u2714\uFE0F Solution (Frequency Prefix Sum)\n\nWe can\'t iterate sum up for all the possible pairs since the given constraints would lead to TLE. \n\nWe need t | archit91 | NORMAL | 2021-05-15T16:02:57.803850+00:00 | 2021-05-15T16:43:30.509864+00:00 | 7,478 | false | \u2714\uFE0F ***Solution (Frequency Prefix Sum)***\n\nWe can\'t iterate sum up for all the possible pairs since the given constraints would lead to TLE. \n\nWe need to observe that the result of *`floor(nums[i] / nums[j])`*, will be - \n\n* **`0`** if `nums[i] < nums[j]`\n* **`1`** if `nums[j] <= nums[i] < (2 * nums[j])`\n* **`2`** if `2 * nums[j] <= nums[i] < (3 * nums[j])`\n* and so on...\n\nWe can use this to build a **frequency array** and then **calculate the prefix sum of it**. \n\nAfter this, for every *`num`* in *`nums`*, we will add the answer into *`sum`* as per the above observation. \n\n* All the numbers in the range `[0, num - 1]` will contribute **0** to the sum each. The **frequency of numbers in this range** will be given by *`freq[num - 1] - freq[0]`*.\n* All the numbers in the range `[num, 2*num - 1]` will contribute **1** to the sum each. **Frequency:** *`freq[num] - freq[2num - 1]`*.\n* Numbers in `[2*num, 3*num - 1]` will contribute **3** each. **Frequency:** *`freq[2num] - freq[3num - 1]`*.\n* And so on till our range covers the maximum element of the *`nums`* array...\n\n**C++**\n```\nconst int MAXN = 1e5 + 1, MOD = 1e9 + 7;\nint sumOfFlooredPairs(vector<int>& nums) {\n\tvector<long> freq(2*MAXN+1); \n\tlong mx = 0, sum = 0;\n\tfor(auto num : nums) ++freq[num], mx = max((int)mx, num); // counting frequency of each element in nums\n\tfor(int i = 1; i <= 2*MAXN; ++i) freq[i] += freq[i - 1]; // building prefix sum array of freq. Now freq[i] will hold the frequency of numbers less than or equal to i\n\t// Each num will be assumed in the denominator as floor(nums[i] / num) and \n\t// using freq array, we can calculate the number of terms contributing 1, 2, 3... to the sum each.\n\tfor(auto num : nums) { \n\t\tlong l = num, r = 2 * num - 1, divResult = 1;\n\t\twhile(l <= mx) { \n\t\t\tsum = (sum + divResult * (freq[r] - freq[l - 1])) % MOD;\n\t\t\tl += num, r += num;\n\t\t\t++divResult;\n\t\t}\n\t}\n\treturn sum;\n}\n```\n\n---\n---\n\n\uD83D\uDCBB\uD83D\uDC31\u200D\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, please do comment below \uD83D\uDC47 \n\n---\n--- | 115 | 30 | ['C'] | 13 |
sum-of-floored-pairs | Prefix Sum, Fenwick Tree, Sort and Sieve | prefix-sum-fenwick-tree-sort-and-sieve-b-oi6y | Let max_n be the maximum number in our array. For each number n, we consider all possible factors f in [1, max_n / n].\n\nWe start from the largest factor, and | votrubac | NORMAL | 2021-05-15T16:00:41.269949+00:00 | 2021-05-15T18:29:09.770698+00:00 | 5,330 | false | Let `max_n` be the maximum number in our array. For each number `n`, we consider all possible factors `f` in `[1, max_n / n]`.\n\nWe start from the largest factor, and count how many numbers in our array are greater or equal than `f * n`. Then, we multiply this count by `f` and add it to our result. We then count elements greater or equal than `(f - 1) * n`, but smaller than `f * n`. And so on.\n\nTo count elements in efficiently, we can use a prefix sum array. However, population of that array requires a quadratic time. We have a few options here:\n\n- Use a line sweep approach to compute the prefix sum in linear time.\n- Use a Fenwick Tree, that can do the same in the logarithmic time.\n- Alternativelly, we can sort our array and binary-search for `f * n`. See solution 3.\n\n> There is a different way to look at this, proposed by [Ceay](https://leetcode.com/problems/sum-of-floored-pairs/discuss/1210057/Python-Five-lines-O(-n-log-n)). His solution reminds me Sieve of Eratosthenes, where we add the count of `n` to `[n, 2 * n, 3 * n...]` elements in our sieve. I provided a C++ version of his solution below.\n\n#### Solution 1: Prefix Sum + Line Sweep\nThe code can be simplified if we do not have to deal with duplicates (e.g. `[1, 1, 1, .... 1, 100000]` test case, which is missing from OJ).\n\n**C++ (188 ms)**\n```cpp\nint ps[100001] = {};\nint sumOfFlooredPairs(vector<int>& nums) {\n long res = 0, max_n = *max_element(begin(nums), end(nums));\n for (auto n : nums)\n ++ps[n];\n vector<pair<int, int>> n_cnt;\n for (auto i = 1; i <= max_n; ++i) {\n if (ps[i])\n n_cnt.push_back({i, ps[i]});\n ps[i] += ps[i - 1];\n }\n for (auto &[n, cnt] : n_cnt)\n for (long f = max_n / n; f > 0; --f)\n res = (res + cnt * f * (ps[min(max_n, (f + 1) * n - 1)] - ps[f * n - 1])) % 1000000007;\n return res;\n}\n```\n#### Solution 2: Fenwick Tree\nWe do not have to use `m` for this solution to get accepted, but it would fail for `[1, 1, 1, .... 1, 100000]` test case.\n\n**C++ (456 ms)**\n```cpp\nint bt[100002] = {};\nint bitSum(int i)\n{\n int sum = 0;\n for (i = i + 1; i > 0; i -= i & (-i))\n sum += bt[i];\n return sum;\n}\nvoid bitUpdate(int n, int i, int val)\n{\n for (i = i + 1; i <= n; i += i & (-i))\n bt[i] += val;\n} \nint sumOfFlooredPairs(vector<int>& nums) {\n long res = 0, max_n = *max_element(begin(nums), end(nums));\n unordered_map<int, int> m;\n for (auto n : nums) {\n ++m[n];\n bitUpdate(max_n + 1, n, 1);\n }\n for (auto [n, cnt] : m)\n for (long f = max_n / n; f > 0; --f)\n res = (res + cnt * f * ((bitSum(min(max_n, (f + 1) * n - 1)) - bitSum(f * n - 1)))) % 1000000007;\n return res;\n}\n```\n#### Solution 3: Sort\nSame idea, but we sort the array and binary-search for `f * n`. When we find that element, we can easily tell how many elements are after it. The code below is optimized to deal with test cases with many repeating elements.\n\n**C++ (956 ms)**\n```cpp\nint sumOfFlooredPairs(vector<int>& nums) {\n sort(begin(nums), end(nums));\n long res = 0, max_n = nums.back();\n for (int i = 0, k = 1; i < nums.size(); i += k) {\n k = 1;\n while (i + k < nums.size() && nums[i] == nums[i + k])\n ++k;\n auto prev = end(nums);\n for (long f = max_n / nums[i]; f > 0; --f) {\n auto it = lower_bound(begin(nums) + i, prev, f * nums[i]);\n res = (res + k * f * (prev - it)) % 1000000007;\n prev = it;\n }\n }\n return res;\n}\n```\n#### Solution 4: Sieve\nSimilar aproach but flipped to quickly compute sums for all elements `[1.. n]`. It was proposed by [Ceay](https://leetcode.com/problems/sum-of-floored-pairs/discuss/1210057/Python-Five-lines-O(-n-log-n)). \n\n**C++ (160 ms)**\n```cpp\nint cnt[100001] = {}, sieve[100001] = {};\nint sumOfFlooredPairs(vector<int>& nums) {\n int max_n = *max_element(begin(nums), end(nums));\n for (auto n : nums)\n ++cnt[n];\n for (auto n = 1; n <= max_n; ++n)\n if (cnt[n])\n for (auto f = 1; n * f <= max_n; ++f)\n sieve[f * n] += cnt[n];\n partial_sum(begin(sieve), end(sieve), begin(sieve));\n return accumulate(begin(nums), end(nums), 0, [&](int sum, int n) { return (sum + sieve[n]) % 1000000007; });\n}\n``` | 57 | 2 | ['C'] | 13 |
sum-of-floored-pairs | [Java] O(n log(n)) Straightforward brute force with explanation, 76 ms | java-on-logn-straightforward-brute-force-l7fa | Intuition\n\nThe simplest method that everyone would come up with is to calculate floor(nums[i] / nums[j]) for each pair and add them up.\n\njava\n// Omitted mo | maristie | NORMAL | 2021-05-15T16:25:42.554708+00:00 | 2021-05-21T11:20:32.926015+00:00 | 2,987 | false | ## Intuition\n\nThe simplest method that everyone would come up with is to calculate `floor(nums[i] / nums[j])` for each pair and add them up.\n\n```java\n// Omitted modulo operations\nint m = nums.length;\nint sum = 0;\nfor (int i = 0; i < m; ++i) {\n for (int j = 0; j < m; ++j) {\n sum += nums[i] / nums[j];\n }\n}\n```\n\nHowever, since there\'re at most 10^5 elements in total, such an `O(m^2)` (`m = nums.length, m <= 10^5`) solution would surely get TLE for large inputs. But the idea itself is not bad. In fact, we only need to slightly modify the above naive approach to get it to work.\n\nThe key idea is simple: **consider elements in groups rather than individually**.\n\nObserve that the problem description kindly restricts the value of array elements to the range [1, 10^5]. Hence the quotient of any pair of elements can never exceed 10^5 as well.\n\nWe want to sum the floored quotients of paired elements. For any integer `x` between `k * a <= x < (k + 1) * a` where `a` and `k` are positive intergers, `floor(x / a) = k` holds. Thus given the divisor `a`, what really matters is **to which interval** an integer `x` belongs.\n\nFor an integer `a`, the following intervals `[0, a), [a, 2a), [2a, 3a), ...` correspond to floored quotients `0, 1, 2, ...` respectively. Since the dividend, divisor and quotient all fall into [1, 10^5], the number of intervals is bounded by `10^5 / a`. There can be multiple `a`\'s, but they should be identical for our purpose and can be simply counted together.\n\nTherefore, we can use counting sort to store the count of each value in the original array. Then we consider each value one by one as a *divisor*. Now we only need to compute how many elements fall into the intervals above separately. If there\'re `m` elements that fall into `[k * a, (k + 1) * a)`, we add `m * k` to our result.\n\nThe only problem left is *how to count the numbers in an interval efficiently*. Again notice that all values fall into [1, 10^5] and we already count them using counting sort. As in the output phase in counting sort, let `counts[i] += counts[i - 1]` for each value from `i = 1 to 10^5`. In this way, `counts` array stores the number of elements `j` such that `j <= i`, and thus the number of elements that fall into `[a, b)` can be represented by `counts[b - 1] - counts[a - 1]`.\n\n## Running time analysis\n\nFor each divisor `a` between `1 <= a <= n`, we consider `n/a` intervals, and we can retrieve the number of elements falling into specific interval in `O(1)` time. Therefore the running time is\n\n```\nT(n) <= n/1 + n/2 + n/3 + ... + n/n\n = n * (1/1 + 1/2 + 1/3 + ... + 1/n)\n < n * (ln(n) + 1) (by 1/x < ln(x) - ln(x-1) for all x > 1)\n```\n\nSo the time complexity is `O(n log(n))`.\n\n*Note*: To be precise, we must perform a linear scan to count the elements in the array, which takes linear `O(m)` time (`m = nums.length`). Thus `O(m + n log(n))` would be a more accurate expression.\n\n## Implementation\n*Note*: (credited to @yubad2000) the constant declaration of `MAX` can be further replaced by the actual maximum value in the array through a linear scan, which could bound the running time more tightly.\n\n```java\nclass Solution {\n static final int MAX = (int)1e5;\n static final int MODULUS = (int)1e9 + 7;\n \n public int sumOfFlooredPairs(int[] nums) {\n int[] counts = new int[MAX + 1];\n for (int num : nums) {\n ++counts[num];\n }\n for (int i = 1; i <= MAX; ++i) {\n counts[i] += counts[i - 1];\n }\n \n long total = 0;\n for (int i = 1; i <= MAX; ++i) {\n if (counts[i] > counts[i - 1]) {\n long sum = 0;\n // [i * j, i * (j + 1)) would derive a quotient of j\n for (int j = 1; i * j <= MAX; ++j) {\n int lower = i * j - 1;\n int upper = i * (j + 1) - 1;\n sum += (counts[Math.min(upper, MAX)] - counts[lower]) * (long)j;\n }\n total = (total + (sum % MODULUS) * (counts[i] - counts[i - 1])) % MODULUS;\n }\n }\n return (int)total;\n }\n}\n```\n\n---\n\n*Update1*: fix the skip logic in code\n*Update2*: add further improvements and supplements to running time analysis\n*Update3*: correct and refine running time analysis | 54 | 5 | [] | 6 |
sum-of-floored-pairs | Python - Five lines, O( n log n) | python-five-lines-o-n-log-n-by-ceay-3ciq | For every dividend in the list nums, we need to calculate the sum of all quotients for all the divisors from the same list nums. To do so, we calculate the sum | ceay | NORMAL | 2021-05-15T16:02:02.820551+00:00 | 2021-05-15T21:36:03.258887+00:00 | 3,323 | false | For every dividend in the list *nums*, we need to calculate the sum of all quotients for all the divisors from the same list *nums*. To do so, we calculate the sum of quotients for each possible number until the maximum number of the list and store it in *quots*. Then, we will sum up all sums of the quotients for all the dividends in the list. It probably sounds quite confusing - the script can help. \n\nTake any divisor, say 3. Then the quotient for this divisor increases by 1 at dividends 3, 6, 9, etc. Thus, we can first calculate the increases of quotients for all the divisors. Once we calculate the increases for all the quotiensts (which are the numbers of the list), we can accumulate these increases into *quots* to get the sum of all the quotients for the divisors from the list.\n\nFor a faster solution, we utilize counter of *nums*. \n\n**Complexity is O(*n* log *n*)**, where *n* is the largest number. The loop is over all the numbers that are smaller or equal than n, with n/i operations of the inner loop. Thus, we have sum(*n*/*i*) operations where *i* is up to *n*. This sum is O(*n* log *n*), because 1 + 1/2 + 1/3 +... + 1/n is logarithic - [see harmonic series](https://en.wikipedia.org/wiki/Harmonic_series_(mathematics)).\n\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n \n incs, counter=[0]*(max(nums)+1), Counter(nums) # To store all the quotients increases; counter\n for num in counter: # Loop over all the divisors\n for j in range(num, len(incs), num): # Loop over all the possible dividends where the quotient increases\n incs[j] += counter[num] # Increment the increases in quotients\n quots=list(accumulate(incs)) # Accumulate the increases to get the sum of quotients\n return sum([quots[num] for num in nums]) % 1_000_000_007 # Sum up all the quotients for all the numbers in the list.\n```\n\nNotes. The first solution that was posted here was not utilizing the counter. After the comments from @yaroslav-repeta and @MrGhasita, the solution was updated (I dropped the solution without the counter all together - it was causing quite some confusion).\n\n \n | 52 | 14 | ['Python'] | 9 |
sum-of-floored-pairs | C++ Binary Search | c-binary-search-by-lzl124631x-jknc | See my latest update in repo LeetCode\n\n## Solution 1. Binary Search\n\nIntuition: Sort the array A. For each A[i], we can binary search A[p] >= (k - 1) * A[i] | lzl124631x | NORMAL | 2021-05-15T16:02:16.155258+00:00 | 2021-05-15T16:53:19.320415+00:00 | 2,867 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Binary Search\n\n**Intuition**: Sort the array `A`. For each `A[i]`, we can binary search `A[p] >= (k - 1) * A[i]` and `A[q] >= k * A[i]`, then all numbers `A[j]` with index in range `[p, q)` has `floor(A[j] / A[i]) = k - 1`.\n\n**Algorithm**: \n\n1. Sort the array `A`. \n1. For each `A[i]`, first count the duplicate of `A[i]`. If we have `dup` duplicates, then they will add `dup^2` to the answer.\n1. For the first `A[j] > A[i]`, let `div = A[j] / A[i]`, we use binary search to find the first `A[next] >= A[i] * (div + 1)`, then numbers `A[t]` where `t` is in `[j, next)` will have `floor(A[t] / A[i]) = div`. These numbers will add `(next - j) * div * dup` to the answer.\n\n```cpp\n// OJ: https://leetcode.com/problems/sum-of-floored-pairs/\n// Author: github.com/lzl124631x\n// Time: O(?)\n// Space: O(1)\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& A) {\n long mod = 1e9 + 7, N = A.size(), ans = 0;\n sort(begin(A), end(A));\n for (int i = 0; i < N; ) {\n long j = i + 1;\n while (j < N && A[j] == A[j - 1]) ++j; // skip the duplicates of `A[i]`\n long dup = j - i;\n ans = (ans + dup * dup % mod) % mod; // the `dup` duplicates add `dup * dup` to the answer\n while (j < N) {\n long div = A[j] / A[i], bound = A[i] * (div + 1);\n long next = lower_bound(begin(A) + j, end(A), bound) - begin(A); // find the first number `A[next] >= A[i] * (div + 1)`\n ans = (ans + (next - j) * div % mod * dup % mod) % mod; // Each A[t] (j <= t < next) will add `div * dup` to the answer.\n j = next;\n }\n i += dup;\n }\n return ans;\n }\n};\n``` | 35 | 4 | [] | 5 |
sum-of-floored-pairs | C++|Engaging Explanation and comments | SIEVE kind of logic | image | O(nlog(log(max))) | plz Upvote | cengaging-explanation-and-comments-sieve-sxbm | \n\nWhen we first encounter this question it seems like we need to do it for all pairs \nthat is Nc2 PAIRS or n(n-1)/2 which will give TLE\n\n1. For each a[i] | Coder_Shubham_24 | NORMAL | 2021-05-17T05:22:29.851890+00:00 | 2021-05-18T06:04:25.038058+00:00 | 937 | false | 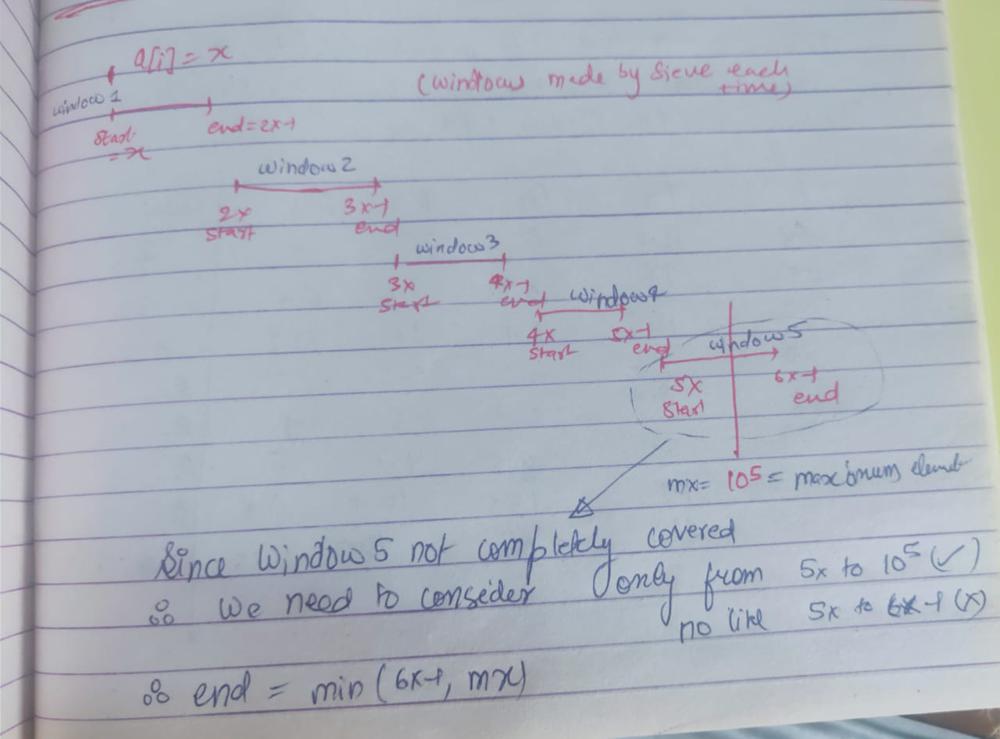\n\nWhen we first encounter this question it seems like we need to do it for all pairs \nthat is Nc2 PAIRS or n*(n-1)/2 which will give TLE\n\n1. For each a[i] we need to consider only numbers greater than a[i] , (This is where SIEVE comes into picture)\n\n2. For eg a=[2,2,2,2,3,3,3,3,4,4,4,5,5,5,7,7,8,8,9,9]\n \n\t For a[i]=2 we need to consider intervals like [2,3], [4,5], [6,7], [8,9] and so on \n\t For a[i]=3 we need to consider intervals like [3,5], [6,8], [9,11] and so on\n\t For a[i]=4 we need to consider intervals like [4,7] , [8,11] and so on\n\t \n\t So generalising for all into interavals in format [start,end] (CRUX of SIEVE)\n\t For a[i]=x we need to consider [x, 2*x-1] , [2*x, 3*x-1] , [3*x, 4*x-1] and so on\n\t \n3. for each interval [start,end] we need to consider no of elements in [start,end] and its floor value like \n for eg a[i] =x \n\t 1. for interval containing elements v= [x, 2*x-1] we get floor_val = v[j]/a[x] (0<=j<=v.size) **( which is same for all elements of v[] )**\n\t\t \n\t\t \n\t\t2. and frequency of no of elements between x to 2*x-1 we make a prefix array \n\t\t where pref [i] = no of elements smaller than i\n\t\t we get frequency = pref[2*x-1]-pref[x-1]\n\t\t\t or frequency = pref[end]-pref[start-1]\n \n 4. So we need to do step 3 for all a[i]\n\n **Corner case**\n 5. Each time u have to select a window of [start , end] **the last window will not come completely so we change our end pointer like refer the picture**\n **end=min(mx,start+num-1); ** \n \n \n \n**plz Upvote if it helps**\n\n```\nclass Solution {\npublic:\n \n int mod=1e9+7;\n \n int add(int a,int b){\n \n return (mod + (a%mod) + (b%mod))%mod;\n }\n \n int sumOfFlooredPairs(vector<int>& a) {\n \n \n int ans=0,i,n=a.size(),mx=-1,num,start,end;\n \n const int N=1e5+1;\n int pref[N]={0};\n \n // store frequency of each number\n for(i=0;i<n;i++){\n pref[a[i]]++;\n mx=max(mx,a[i]);\n }\n \n \n // make prefix array storing frequency of all numbers<=nums in pref[num]\n for(i=1;i<=100000;i++){\n pref[i]=add(pref[i],pref[i-1]); //pref[num]=pref[num]+pref[num-1]; \n \n }\n \n \n \n // For each num check how many valid-pairs(non-zero value of floor) we can get ie numbers>=num will make a valid pair ie floor(number/num)>=1\n for(i=0;i<n;i++){ \n \n num=a[i];\n \n for(start=num; start<=mx; start=start+num){ // now check for ranges of numbers [start,end] such that it is like [x,2*x-1], \n // [2*x, 3*x-1], \n \n end=min(mx,start+num-1); // for last window we have to consider partial part only refer picture \n \n \n int floor_val=start/num;\n \n int fre=(pref[end]-pref[start-1] + mod)%mod;\n \n int contri=((floor_val%mod)*(fre%mod))%mod;\n \n \n \n ans=add(ans,contri);\n }\n \n \n }\n \n \n \n \n return ans;\n \n \n }\n};\n\n\n/*\ntestcase\n[2,2,2,3,3,3,3,5,6,7,7,7,7,7,7,7,1,3]\n*/\n``` | 17 | 3 | [] | 4 |
sum-of-floored-pairs | Python3. Sort + binary search | python3-sort-binary-search-by-yaroslav-r-bakt | \nclass Solution:\n # idea:\n # first thing is that we can easily cache in this problem:\n # if we know result of `sum(nums[i] // nums[k] for k in ra | yaroslav-repeta | NORMAL | 2021-05-15T16:01:09.426267+00:00 | 2021-05-15T16:49:34.113042+00:00 | 1,341 | false | ```\nclass Solution:\n # idea:\n # first thing is that we can easily cache in this problem:\n # if we know result of `sum(nums[i] // nums[k] for k in range(N))`,\n # then we know result for any `j` that `nums[j] = nums[i]`\n #\n # second. if we sort "nums", we can use binary search:\n # let `nums[i] = P` then we can search for `2 * P` that will be position `j`\n # then for all k in `i..j`, `nums[k] // nums[i] = 2`\n # then we can search for `3 * P` that will be `t` and for all k in range `j..t`, `nums[k] // nums[i] = 3` and so on\n \n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n nums.sort()\n res = 0\n mod = 10 ** 9 + 7\n cache = {}\n for i, x in enumerate(nums):\n if x in cache:\n res += cache[x]\n else:\n current_res = 0\n j = i # initialize with `i` because `nums[i] // nums[j]` when `i < j` in sorted array is always 0\n\t\t\t\t # (except cases when `nums[i] = nums[j]`, but duplicates will use cache in this problem)\n while j < len(nums):\n multiplier = nums[j] // x # define multiplier by first element in range\n last_position = bisect_left(nums, x * (multiplier + 1), j) # find all numbers with such multiplier\n current_res += (last_position - j) * multiplier # add result of `sum(nums[k] // nums[i] for k in range(j, last_position))` to `current_res`\n j = last_position\n \n cache[x] = current_res # update cache\n res += current_res\n res %= mod\n return res\n \n``` | 17 | 2 | [] | 3 |
sum-of-floored-pairs | No Advanced DSA| Lower_Bound + Basic Maths | no-advanced-dsa-lower_bound-basic-maths-axwv7 | \n\n#define mod 1000000007\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n \n int n = nums.size();\n unsigned | its_gupta_ananya | NORMAL | 2021-05-15T16:40:55.809171+00:00 | 2021-05-22T11:26:14.621465+00:00 | 1,317 | false | \n```\n#define mod 1000000007\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n \n int n = nums.size();\n unsigned long long int ans =0;\n \n sort(nums.begin(), nums.end());\n \n for(int i=0;i<n;++i){\n int ind = 0;\n\t\t\t//k denotes the next multiple of nums[i] \n for(unsigned long long int k = nums[i]; k <= nums[n-1]; k += nums[i]){\n ind = lower_bound(nums.begin() + ind, nums.end(), k) - nums.begin();\n // Add 1 for every value greater than or equal to k\n\t\t\t\tans = (ans + n - ind)%mod; \n\t\t\t\t//(n-ind) denotes the number of elements greater than equal to k\n }\n }\n return ans;\n }\n};\n```\n\n**Update:- The test cases have been updated and the code gives TLE for bigger test cases like [1,1,1,1,11,........,10^5]. Optimisations for the same are welcome, Thank you!** | 11 | 5 | ['Math', 'Binary Tree', 'C++'] | 6 |
sum-of-floored-pairs | Python/Python3 solution BruteForce & Optimized solution using Dictionary | pythonpython3-solution-bruteforce-optimi-zhyv | Brute Foce Solution(Time Limit Exceeded)\n\nThis solution will work if the length of the elements in the testcase is <50000(5 * 10^4).\nIf it exceeds 50000 it w | prasanthksp1009 | NORMAL | 2021-05-19T17:22:31.306850+00:00 | 2021-05-19T17:22:31.306896+00:00 | 983 | false | **Brute Foce Solution(Time Limit Exceeded)**\n\nThis solution will work if the length of the elements in the testcase is <50000(5 * 10^4).\nIf it exceeds 50000 it will throw TLE error.\n**Code:**\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n sumP = 0 #To store the value of Sum of floor values\n for i in nums: #Traverse every element in nums\n for j in nums: #Traverse every element in nums\n sumP += (j//i) #Simply do floor division and add the number to sumP\n return sumP % (10**9 +7)#return the sumof the pairs\n```\n\n**Optimized Solution**\n\nThe solution is built by using frequency of the prefix elements(freqency prefix sum).\n1. Take the frequency of the elements given in the nums and store ir in dictionary.\n2. After storing calculate the prefix frequency of the nums according to the frequency present in the dictionary.\n3. After computing prefix Frequency just calculate the sum of the floor division.\n* If you need to futher understanding the code kindly watch Part by Part Implementation. \n\n**Code:**\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n maxi = max(nums) + 1\n dic = {}\n prefix=[0]*maxi\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n #print(prefix,dic)\n sumP = 0\n for i in set(nums):\n for j in range(i,maxi,i):\n sumP += dic[i]*(prefix[-1]-prefix[j-1])\n\t\t\t\t#print(sumP,end = " ")\n return sumP % (10**9 +7)\n```\n**Part by Part Implementation**\n```\n#Part - 1 : Calculating the frequency of the elements in nums to dictionary.\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n dic = {}\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n print(dic)\n```\n**Output:\n{2: 1, 5: 1, 9: 1}**\n\n```\n#Part - 2 : Calculation of Prefix frequency according to the frequency of the nums in dictionary.\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n dic = {}\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n maxi = max(nums) + 1\n prefix=[0]*maxi\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n print(prefix)\n```\n**Output:\n[0, 0, 1, 1, 1, 2, 2, 2, 2, 3]**\n\n```\n#Part - 3 : Calculation of sum of floor division \nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n maxi = max(nums) + 1\n dic = {}\n prefix=[0]*maxi\n for i in nums:\n if i in dic:\n dic[i] += 1\n else:\n dic[i] = 1\n #print(dic)\n for i in range(1,maxi):\n if i not in dic:\n prefix[i] = prefix[i-1]\n else:\n prefix[i] = prefix[i-1]+dic[i]\n #print(prefix,dic)\n sumP = 0\n for i in set(nums):\n for j in range(i,maxi,i):\n sumP += dic[i]*(prefix[-1]-prefix[j-1])\n print(sumP,end = " ")\n```\n**Output:\n1 4 6 7 8 10**\n\n***We rise by lifting others*** | 10 | 0 | ['Counting', 'Python', 'Python3'] | 0 |
sum-of-floored-pairs | [Java] Count all frequencies, then enumerate all floor values, O((distinct value count) * max) | java-count-all-frequencies-then-enumerat-hv0f | We don\'t know the value of nums[i] / nums[j], but we can fix the value of nums[i] / nums[j], then find how many times will this value occurs.\njava\nclass Solu | toffeelu | NORMAL | 2021-05-15T16:01:55.388747+00:00 | 2021-05-16T02:01:06.574134+00:00 | 934 | false | We don\'t know the value of `nums[i] / nums[j]`, but we can fix the value of `nums[i] / nums[j]`, then find how many times will this value occurs.\n```java\nclass Solution {\n public int sumOfFlooredPairs(int[] nums) {\n int MOD = 1_000_000_000 + 7;\n int n = nums.length;\n long res = 0;\n int[] count = new int[100_000+1];\n for(int num : nums){\n count[num]++;\n }\n //preSum of counts, for getting range count\n int[] preSum = new int[100_000 + 2];\n for(int i = 1; i < preSum.length; i++){\n preSum[i] = preSum[i-1] + count[i-1];\n }\n for(int i = 0; i < count.length; i++){\n if(count[i] == 0){\n continue;\n }\n int num = i;\n for(int p = 1; p * num <= 100_000; p++){\n int max = num * (p+1)-1;\n int min = num * p;\n //how many nums in the range\n int c = preSum[Math.min(max+1, preSum.length-1)] - preSum[Math.min(min, preSum.length-1)];\n long add = (long)c * p * count[num];\n res += add;\n res %= MOD;\n }\n }\n return (int)res;\n }\n}\n``` | 7 | 0 | [] | 2 |
sum-of-floored-pairs | 💥💥 C# | 100% beats runtime AND memory [EXPLAINED] | c-100-beats-runtime-and-memory-explained-isrc | \n# Intuition\nThe goal is to find the sum of floor divisions for all possible pairs in the array, where one number divides the other. Directly computing this f | r9n | NORMAL | 2024-09-18T20:50:23.267561+00:00 | 2024-09-18T20:50:23.267581+00:00 | 69 | false | \n# Intuition\nThe goal is to find the sum of floor divisions for all possible pairs in the array, where one number divides the other. Directly computing this for every pair would be too slow, so we use a more efficient approach. By leveraging frequency counts and prefix sums, we avoid redundant calculations and speed up the process.\n\n\n# Approach\nCount Frequencies: First, count how many times each number appears in the array. This helps us quickly know how many times a number can contribute to the result.\n\n\nPrefix Sum Array: Build a prefix sum array from these counts to quickly compute how many numbers fall within certain ranges.\n\n\nCalculate Contributions: For each number, determine how many multiples of it exist and compute their contributions using the frequency and prefix sum arrays.\n\n\nSum Up Results: Accumulate these contributions, making sure to handle large numbers with modulo 10(and factor of 9) +7.\n\n\n# Complexity\n- Time complexity:\nO(n + maxVal log maxVal): Efficient due to counting and prefix sums.\n\n\n- Space complexity:\nO(maxVal): Space for frequency and prefix sums, manageable given constraints.\n\n\n# Code\n```csharp []\npublic class Solution {\n private const int MOD = 1000000007;\n\n public int SumOfFlooredPairs(int[] nums) {\n int maxVal = 100000;\n int[] freq = new int[maxVal + 1];\n \n // Count the frequency of each number in the input array\n foreach (int num in nums) {\n freq[num]++;\n }\n \n // Build the prefix sum of the frequency array\n int[] prefixSum = new int[maxVal + 1];\n for (int i = 1; i <= maxVal; i++) {\n prefixSum[i] = prefixSum[i - 1] + freq[i];\n }\n \n long result = 0;\n \n // For each number i, calculate its contribution to the result\n for (int i = 1; i <= maxVal; i++) {\n if (freq[i] == 0) continue; // Skip numbers that don\'t appear in the input\n\n // For each multiple of i, sum the floor divisions\n for (int multiple = i; multiple <= maxVal; multiple += i) {\n int low = multiple;\n int high = Math.Min(maxVal, multiple + i - 1);\n int countInRange = prefixSum[high] - prefixSum[low - 1];\n\n result = (result + (long)freq[i] * countInRange * (multiple / i)) % MOD;\n }\n }\n \n return (int)result;\n }\n}\n\n``` | 6 | 0 | ['C#'] | 0 |
sum-of-floored-pairs | JAVA Readable Code | java-readable-code-by-himanshuchhikara-0qyh | IDEA:\n Basic idea is for every number let say x . I am not going to check for [1,2,...x) . I know the answer of this range that is 0. Similarly for range [x,x+ | himanshuchhikara | NORMAL | 2021-05-17T17:40:18.463021+00:00 | 2021-05-17T17:40:18.463072+00:00 | 805 | false | **IDEA:**\n Basic idea is for every number let say x . I am not going to check for [1,2,...x) . I know the answer of this range that is 0. Similarly for range [x,x+1...2x) If we take floor of x with any value in this answer will be this. keeping this in mind have a eye on code and things will get clear to you .\n \n**CODE:**\n```\n public int sumOfFlooredPairs(int[] nums) {\n int N=(int)1e5;\n int mod=(int)1e9 + 7;\n \n\t\t\n int[] frequencyMap=new int[N+1];\n for(int num:nums) frequencyMap[num]++;\n \n int[] prefixFreq=new int[N+1];\n for(int i=1;i<=N;i++) prefixFreq[i]=prefixFreq[i-1] + frequencyMap[i];\n \n long total=0;\n \n for(int i=1;i<=N;i++){\n if(frequencyMap[i]==0) continue;\n \n // [i * j, i * (j + 1)) \n long sum=0;\n for(int j=1; i*j<=N;j++){\n int lower=i*j-1;\n int upper=i*(j+1)-1;\n \n int count= prefixFreq[Math.min(N,upper)] - prefixFreq[lower]; \n \n sum+=count*j;;\n }\n total=(total + (sum%mod)*frequencyMap[i])%mod;\n }\n return (int)total;\n }\n```\n\n**TimeComplexity:**\n```\n\nFor each divisor i we are considering N/i intervals. where 1<=i<=N\n T(n) <= N/1 + N/2 + N/3 + .... N/N\n <=N(1/1 + 1/2 + ... 1/N)\n\t\t <=N*(logN)\n\t\t \nIts a worse case because if freq is 0 we are just continuing.. \t\t\n``` \n\nPlease upvote if found it helpful :)\n | 6 | 1 | ['Counting', 'Prefix Sum', 'Java'] | 1 |
sum-of-floored-pairs | [Python] Suffix sums detailed explanation | python-suffix-sums-detailed-explanation-3kip6 | \ndef sumOfFlooredPairs(self, nums: List[int]) -> int:\n maxn = 10**5 + 7\n MOD = 10**9 + 7\n f = [0 for i in range(maxn + 1)] # keep a | prasanna648 | NORMAL | 2021-05-15T16:00:54.333723+00:00 | 2021-05-15T16:00:54.333746+00:00 | 681 | false | ```\ndef sumOfFlooredPairs(self, nums: List[int]) -> int:\n maxn = 10**5 + 7\n MOD = 10**9 + 7\n f = [0 for i in range(maxn + 1)] # keep a count of the frequency of each element in the array\n sf = [0 for i in range(maxn + 1)] # suffix array of the frequencies, sf[i] represents frequency of elements greater than equal to i\n n = len(nums)\n \n #create frequency array\n for i in range(n):\n f[nums[i]] += 1\n \n #create suffix array of frequencies\n for i in range(maxn-1, 0, -1):\n sf[i] = sf[i + 1] + f[i]\n \n ans = 0\n """\n for a element x consider all pairs such that x is the denominator\n all numbers less than x will result in 0(float division)\n now for elements greater than x, \n numbers from x to 2*x - 1 will result in 1\n numbers from 2*x to 3*x - 1 will result in 2 and so on \n \n so each number from x to 2*x - 1 will add 1 to the answer\n each number from 2*x to 3*x - 1 will add 2 to the answer \n each number from 3*x to 4*x - 1 will add 3 to the answer and so on\n \n """\n for i in range(1, maxn + 1):\n if f[i] == 0:\n continue\n res = 1\n for j in range(i, maxn + 1, i):\n #number of elements which add res to the answer are sf[j] - sf[j+i]\n #multiply by f[i] to handle duplicate elements, as there are f[i] number of elements equal to i\n ans += (sf[j] - sf[min(j + i, maxn - 1)]) * res * f[i] \n ans = ans % MOD\n res += 1\n \n return ans % MOD\n``` | 5 | 0 | [] | 2 |
sum-of-floored-pairs | >90%, >45%, c++ solution with explanation | 90-45-c-solution-with-explanation-by-sja-z3ez | According to the hints, my idea is the following :\n\n 1. Iterate over nums in order to find the maximum value max_n.\n 2. Create an array of occurences occs of | sjaubain | NORMAL | 2021-11-02T15:00:14.401600+00:00 | 2021-11-02T15:00:14.401649+00:00 | 700 | false | According to the hints, my idea is the following :\n\n* 1. Iterate over `nums` in order to find the maximum value `max_n`.\n* 2. Create an array of occurences `occs` of size `max_n + 1` (no need to have it of size 10<sup>5</sup> if we only have numbers in range `0` to `max_n`.\n* 3. Iterate over `occs` to create the array of cumulated occurences according to prefix sum algorithm.\n\nFor example, if we have the following input : `[4,2,3,5,6,5,7,4]`, with max value `7`, we will obtain :\n\n||0|1|2|3|4|5|6|7|\n|:-| :-: |:-:| :-:| :-:| :-:| :-:| :-:|-:|\n| occs |0|0|1|1|2|2|1|1|\n|occs_acc|0|0|1|2|4|6|7|8\n\nThe sorted arry of our input is `[2,3,4,4,5,5,6,7]`. Having noticed that `floor(i/j) = 0` if `j>i`,brute force solution would still be O(n<sup>2</sup>) cause we would have to test all couples `(i, j)` with `j <= i`, which is easy in a sorted array. With the solution explained above, we can optimize this complexity. We proceed by checking only the multiples of a given value. The array `occs_acc` allow us to know how many numbers are between two different multiples. For example, if we deal from left to right in sorted array (which is in a way already made with a bucket sort in `occs`) and are treating the value `3` with the first multiple `k = 1`, there will be 5 values that will give a floor of 1 :\n\n`3/3, 4/3, 4/3, 5/3, 5/3`\n\nWe can know that number by looking in `occs_acc` at indices `5 = ((k+1)*3 - 1)` and `2 = (k*3 - 1)`. This is because `occs_acc[5]` is the total numbers in input array that are less than `6`, which is the next multiple of `3` and same for `occs_acc[2]`. So, by subtracting those values, we have the exact total occurences of numbers which give a floor of `1` by dividing `3`. To update the sum correctly, we still have to multiply this difference by the number of occurences of number `3`, because it applies for each one of them. In our case, this number is `1`.\n\nWe then iterate this procedure with the multiple `2` and so on, until we have reached the end of the array...\n\nThis solution is satisfying but not perfect, because we may have a lot of `0` in the array of occurences, which could cause extra computations in the last loop. Maybe a map or another data structure could be better but I don\'t know...\n\nThank you for reading \n\n```\nclass Solution {\n \nprivate:\n \n int MOD = 1e9 + 7;\n \npublic:\n \n int sumOfFlooredPairs(vector<int>& nums) {\n\n // first of all, we record the max value\n int max_n = INT_MIN;\n for(int n : nums) max_n = max(max_n, n);\n \n // then the occurences for each number in [0, max]\n vector<int> occs(max_n + 1, 0);\n for(int n : nums) occs[n]++;\n \n // prefix sum algorithm to accumulate the occurences\n vector<int> occs_acc(max_n + 1, 0);\n for(int i = 1; i < max_n + 1; ++i) {\n occs_acc[i] = occs[i] + occs_acc[i - 1]; \n }\n \n // long long needed to prevent overflows\n long long ans = 0; \n for(int i = 0; i < max_n + 1; ++i) {\n \n // just handle numbers that occur at least once\n if(occs[i] != 0) {\n \n int k = 1;\n int k_next;\n \n // for each multiple of i\n do {\n \n k_next = k + 1;\n\n // "right and left" multipliers in occs_acc \n int r = min(k_next * i - 1, max_n);\n int l = k * i - 1;\n \n ans += ((long long) occs_acc[r] - (long long) occs_acc[l]) * (long long) occs[i] * k++;\n \n \n } while(k_next * i - 1 < max_n);\n }\n }\n \n return ans % MOD;\n }\n};\n``` | 4 | 0 | ['C', 'Bucket Sort', 'Prefix Sum'] | 1 |
sum-of-floored-pairs | Python - 8 lines frequency prefix sum | python-8-lines-frequency-prefix-sum-by-l-q7vp | \nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n ans, hi, n, c = 0, max(nums)+1, len(nums), Counter(nums)\n pre = [0] | leetcoder289 | NORMAL | 2021-05-15T23:29:13.511183+00:00 | 2021-05-15T23:29:20.844169+00:00 | 404 | false | ```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n ans, hi, n, c = 0, max(nums)+1, len(nums), Counter(nums)\n pre = [0] * hi\n for i in range(1, hi):\n pre[i] = pre[i-1] + c[i]\n for num in set(nums):\n for i in range(num, hi, num):\n ans += c[num] * (pre[-1] - pre[i-1])\n return ans % (10**9 + 7)\n``` | 4 | 0 | ['Python', 'Python3'] | 2 |
sum-of-floored-pairs | Easy To Understand || C++ Solution | easy-to-understand-c-solution-by-aayushe-b34m | Code\n\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n long long ans=0;\n int | aayushee_123 | NORMAL | 2023-02-08T17:00:48.374202+00:00 | 2023-02-08T17:00:48.374251+00:00 | 191 | false | # Code\n```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n long long ans=0;\n int mx=nums[nums.size()-1];\n\n // Finding the frequency of all elements in the array.\n unordered_map<int,int> mp;\n for(int i=0;i<nums.size();i++) {\n mp[nums[i]]++;\n }\n\n // For each element iterating through its multiples and multiplying frequencies to find the answer.\n for(auto x: mp) {\n int val = x.first;\n long long k = 0;\n while(val<=mx) {\n int idx = lower_bound(nums.begin(), nums.end(), val) - nums.begin();\n // adding all the elements which are greater and equal to val;\n k+=(nums.size()-idx);\n val+=x.first;\n }\n ans += k*x.second;\n }\n return ans%1000000007;\n }\n};\n``` | 3 | 0 | ['Binary Search', 'Sorting', 'C++'] | 0 |
sum-of-floored-pairs | Python | Simple algorithm similar to prime number generators | python-simple-algorithm-similar-to-prime-gbzp | \n\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n freq = Counter(nums)\n maxVal = max(nums)\n cache = [0 fo | satendrapandey | NORMAL | 2022-05-18T05:41:54.571810+00:00 | 2022-05-18T05:41:54.571837+00:00 | 466 | false | ```\n\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n freq = Counter(nums)\n maxVal = max(nums)\n cache = [0 for i in range(maxVal + 1)]\n for key in freq:\n num = freq[key]\n count = 1\n while count*key <= maxVal:\n cache[count*key] += num\n count += 1\n \n count = 0\n result = 0\n for i in range(len(cache)):\n count += cache[i]\n if i in freq:\n result += freq[i] * count\n \n return result % (10**9 + 7)\n``` | 3 | 0 | ['Python'] | 0 |
sum-of-floored-pairs | C++ | O(Nlog(N)) | c-onlogn-by-m-abhi-va35 | \n int sumOfFlooredPairs(vector<int>& nums) {\n int N = 1e5 + 100, MOD = 1e9 + 7;\n\n vector<int> frq(N, 0), preFrq(N, 0);\n\n for (int | m-abhi | NORMAL | 2021-05-15T20:06:13.447032+00:00 | 2021-05-15T20:06:13.447066+00:00 | 243 | false | ```\n int sumOfFlooredPairs(vector<int>& nums) {\n int N = 1e5 + 100, MOD = 1e9 + 7;\n\n vector<int> frq(N, 0), preFrq(N, 0);\n\n for (int i : nums)\n frq[i]++;\n\n for (int i = 1; i < N; ++i)\n preFrq[i] = preFrq[i - 1] + frq[i];\n\n int ans = 0 ;\n\n for (int i = 1; i < N; ++i)\n {\n if (frq[i] == 0)\n continue;\n\n for (int j = i; j < N; j += i)\n {\n\n int numOfElements = preFrq[ min(N-1, j + i - 1) ] - preFrq[ j - 1];\n ans = ( ans ) % MOD + (numOfElements * (j / i) * frq[i] ) % MOD;\n }\n }\n\n return ans % MOD;\n }\n```\n\n | 3 | 2 | [] | 0 |
sum-of-floored-pairs | C++ Prefix Sums + Iterate over Element Values | c-prefix-sums-iterate-over-element-value-9idp | The naive solution to this problem would have a runtime complexity of O(n^2), which results in a TLE for an array size of at most 1e5. However, note the other p | jiaxiangwu | NORMAL | 2021-05-15T16:01:34.373863+00:00 | 2021-05-15T16:02:09.836670+00:00 | 416 | false | The naive solution to this problem would have a runtime complexity of O(n^2), which results in a TLE for an array size of at most 1e5. However, note the other problem size constraint: 1 <= nums[i] <= 1e5. The range of element value is limited, giving us the idea of iterating all possible element values and sum up their their contributions to the result, instead of summing up the results of elements. Note floor(m/n) takes the value of 1 when n <= m < 2*n, 2 when 2*n <=\nm < 3 * n, etc. So to calculate the sum of all floor pair floor(m/n)s where n is known, we only need to find out the number of elements n <= m < 2 *n, 2*n <=m\n< 3*n, etc. From these observations, we can form a rough idea of the problem\'s solution:\n\n1. Find out the number of elements in nums with values 1, 2, 3, ....\n2. Implement a data structure to quickly retrieve the number of element in a certain range. A prefix sum array would suffice.\n3. For each possible *value* n of the elements, find out sum of all floor pair floor(m/n)s. We can use the prefix sum array to find out the number of ms that are between n and 2n, 2n and 3n, 3n and 4n, etc, and add their contributions together.\n\n```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n // freq[i] = number of elements with value i\n vector<int> freq(100001, 0);\n // prefix_freq[i] = number of elements whose values are between 1 to i inclusive\n vector<int> prefix_freq(100002, 0); \n // mx = maximum element\n int mx = -1;\n for(int n : nums) {\n freq[n]++;\n mx = max(mx, n);\n }\n // build prefix sum array\n prefix_freq[1] = freq[1];\n for(int i = 2; i < freq.size(); i++) {\n prefix_freq[i] = freq[i] + prefix_freq[i-1];\n }\n // cnt_sum(start, end) = number of elements between start and end\n auto cnt_sum = [&](int start, int end) {\n if(start == 1) return prefix_freq[end];\n else return prefix_freq[end] - prefix_freq[start - 1];\n };\n int res = 0;\n for(int i = 1; i <= mx; i++) {\n // contribution of sum of floor(m/i)\n int val = 1;\n while(true) {\n int start = val * i;\n int end = (val + 1) * i - 1;\n if(end >= mx) end = mx;\n res += (val * freq[i] * cnt_sum(start, end));\n res %= 1000000007;\n if(end == mx) break;\n val++;\n }\n }\n return res;\n }\n};\n```\n\n | 3 | 0 | [] | 0 |
sum-of-floored-pairs | Python3/C++ Fenwick Tree Solution | python3-fenwick-tree-solution-by-stefan1-lt1c | ApproachFor each possible i<100000, we have the fact that:
numbers between i∗k and i∗(k+1)−1 gives k when divided by i
numbers between i∗(k+1) and i∗(k+2)−1 giv | onceACoder_ | NORMAL | 2025-02-05T17:41:01.587104+00:00 | 2025-02-12T15:42:12.252911+00:00 | 67 | false | # Approach
For each possible $i<100000$, we have the fact that:
- numbers between $i*k$ and $i*(k+1)-1$ gives $k$ when divided by $i$
- numbers between $i*(k+1)$ and $i*(k+2)-1$ gives $k+1$ when divided by $i$
- and so on
We can use this fact to find each interval $[left,right]$ in which all numbers give k when divided by i. To find how many numbers is presenet in the interval $[left,right]$, we can use fenwick tree.
# Complexity
- Time complexity: $O(n*sqrt(n)*log(n))$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $O(n)$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Python3
```
mod=10**9+7
class Solution:
def sumOfFlooredPairs(self, nums: List[int]) -> int:
mx,res=max(nums),0
tree=[0]*4*mx
cnt=Counter(nums)
def addVal(idx,val):
idx+=1
while idx<len(tree):
tree[idx]+=val
idx+=idx&(-idx)
def getVal(idx):
res,idx=0,idx+1
while idx>0:
res+=tree[idx]
idx-=idx&(-idx)
return res
for i in nums:
addVal(i,1)
for i in range(1,mx+1):
freq=cnt[i]
if not freq:continue
for j in range(i,mx+1,i):
d=j//i
left,right=max(0,j),min(mx,j+i-1)
tot=getVal(right)-getVal(left-1)
res+=freq*tot*d
res%=mod
return res
```
# C++
```
class Solution {
public:
static constexpr int mod = 1'000'000'007;
int sumOfFlooredPairs(vector<int>& nums) {
int mx = *max_element(nums.begin(), nums.end());
long long res = 0;
vector<int> tree(4 * mx, 0);
unordered_map<int, int> cnt;
for (int num : nums) {
cnt[num]++;
}
auto addVal = [&](int idx, int val) {
idx++;
while (idx < tree.size()) {
tree[idx] += val;
idx += idx & (-idx);
}
};
auto getVal = [&](int idx) {
long long sum = 0;
idx++;
while (idx > 0) {
sum += tree[idx];
idx -= idx & (-idx);
}
return sum;
};
for (int num : nums) {
addVal(num, 1);
}
for (int i = 1; i <= mx; i++) {
int freq = cnt[i];
if (freq == 0) continue;
for (int j = i; j <= mx; j += i) {
int d = j / i;
int left = max(0, j);
int right = min(mx, j + i - 1);
long long tot = getVal(right) - getVal(left - 1);
res = (res + (long long)freq * tot * d) % mod;
}
}
return res;
}
};
``` | 2 | 0 | ['Python3'] | 0 |
sum-of-floored-pairs | C++ || Sieve || prefix sum || easy Swap27 solution | c-sieve-prefix-sum-easy-swap27-solution-w6zd3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n-sieve\n-prefix sum\n Describe your approach to solving the problem. \n\n | adsulswapnil27 | NORMAL | 2024-05-18T07:55:13.340920+00:00 | 2024-05-18T07:55:13.340956+00:00 | 303 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n-sieve\n-prefix sum\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:n*log(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int n=nums.size();\n vector<int>arr(200005,0);\n map<int,int>mp;\n for(auto it:nums){\n arr[it]++;\n mp[it]++;\n }\n for(int i=1;i<200005;i++)arr[i]+=arr[i-1];\n long long ans=0;\n for(auto it:mp){\n int j=1;\n long long sum=0;\n for(int i=it.first+it.first;i<200005;i+=it.first){\n sum+=(arr[i-1]-arr[i-it.first-1])*j;\n sum%=1000000007;\n j++;\n }\n ans+=(sum*it.second);\n ans%=1000000007;\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
sum-of-floored-pairs | [Python] Sorting + Binary Search with thought process when being asked during interviews | python-sorting-binary-search-with-though-vs88 | Sorting + Binary Search\nMy strategy of resolving hard problems is to start with brute-force solution, and then improve it to sub/optimal approachs by identifyi | jandk | NORMAL | 2021-10-16T20:04:01.439073+00:00 | 2021-10-16T20:06:07.789442+00:00 | 341 | false | ### Sorting + Binary Search\nMy strategy of resolving hard problems is to start with brute-force solution, and then improve it to sub/optimal approachs by identifying and fixing bottleneck.\nSo the brute-force approach for this problem is quite simple, we try out each possible pair of `nums[i], nums[j]` and calculate the total sum of floor, which obviously leads to TLE. Then we start to improve it by observations.\n\n**First Improvement**\nThe first observation is that the value of `floor(i, j) where i < j`is always `0`. So we can only care about the pair of `(i, j) where i > j`, which indicates that we need sort `nums` first. By sorting `nums`, for each `nums[i]`, we can get the floor value by `floor(nums[i], nums[j]) for j < i`. \n\n**Second Improvement**\nBut with this improvement, the time complexity is still *O(N^2)*, how we can improve it further? The reason that we still have *O(N^2)* time complexity is that we still check `floor(nums[i], nums[j])` for each `j` that is smaller than `i`. Can we speed up this process? yes, because we have sorted the `nums` already, we can get the index of number `nums[index]` that divided by `nums[i]` equals to `1`, `2`, `3` ... so on using binary search.\nFor example, we have checked `nums` as `[1,4,5,8,9]`, and we are at index `3` (8). So we can know that the index for `8` that divided by `8` equals to `1` is 3, and the index for `4` that divided by 8 equals to `2` is 1. Then all of numbers in the range `[index + 1:i]` have the same quotient, `[5, 8]` in this case. Then we can find the numbers in next quotient range of `[2: 3]`, `[3: 4]` and so on. \nWhat\'s more, we can achieve better implementation by doing it in reverse way, multiplication instead of division. With the same example, we can check multiples for `4`, which are `[4, 8, 12]`.\n\n**Third Improvment**\nSo far, it seems a working solution, but it might still cause LTE because of duplicates. Then using counter is a common way to reduce complexity with duplicates. However, if we are doing this, the range counting we used in previous binary search doesn\'t work. We have to get the sum of numbers count in that range by checking the count for each number, which is still linear complexity. \nHow we can resolve problem of getting sum of subarray? It\'s prefix sum array.\n\n******\nThen put all together. \n1. Convert `nums` to `counter` (frequency)\n2. Sort the unique keys of `counter`.\n3. Create the prefix sum for the frequency.\n4. For interation of each key `i`, \n 1. We get the index for each multiple using binary search.\n 2. Get the sum of frequency of all numbers in `[index: i]` using prefix sum array\n 3. Increase the `total` by multiplying the `counter[nums[i]]` with the sum\n5. Return the result.\n\n```python\ndef sumOfFlooredPairs(self, nums: List[int]) -> int:\n\tcounter = Counter(nums)\n nums = sorted(counter.keys())\n prefix = [0]\n n = len(nums)\n for i in range(n):\n\t\tprefix.append(prefix[-1] + counter[nums[i]])\n\n\ttotal = 0\n for num in nums:\n\t\tfor mult in range(num, nums[-1] + 1, num):\n\t\t\tindex = bisect.bisect_left(nums, mult)\n total += (prefix[-1] - prefix[index]) * counter[num]\n\treturn total % (10 ** 9 + 7)\n \n``` | 2 | 0 | [] | 0 |
sum-of-floored-pairs | (C++) 1862. Sum of Floored Pairs | c-1862-sum-of-floored-pairs-by-qeetcode-ptv0 | \n\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n int m = *max_element(nums.begin(), nums.end()); \n vector<long> va | qeetcode | NORMAL | 2021-05-16T15:41:23.624726+00:00 | 2021-05-21T16:15:12.939979+00:00 | 364 | false | \n```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n int m = *max_element(nums.begin(), nums.end()); \n vector<long> vals(m+1); \n for (auto x : nums) \n ++vals[x]; \n \n for (int x = m; x > 0; --x) \n for (int xx = 2*x; xx <= m; xx += x) \n vals[xx] += vals[x]; \n \n for (int i = 1; i < vals.size(); ++i) \n vals[i] += vals[i-1]; \n \n int ans = 0; \n for (auto x : nums) \n ans = (ans + vals[x]) % 1\'000\'000\'007; \n return ans; \n }\n};\n``` | 2 | 0 | ['C'] | 1 |
sum-of-floored-pairs | C++ ON2 solution Using Frequency Array | c-on2-solution-using-frequency-array-by-jg2zk | \nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n int A[200005]={0};\n\t int M[200005]={0};\n int N = *max_element( | kartikeya72001 | NORMAL | 2021-05-15T16:29:25.848297+00:00 | 2021-05-15T16:33:22.647681+00:00 | 396 | false | ```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n int A[200005]={0};\n\t int M[200005]={0};\n int N = *max_element(nums.begin(), nums.end())*2+1;\n \n for(int i=0;i<nums.size();i++)\n A[nums[i]]++;\n \n for(int i=1;i<N;i++)\n\t\t M[i]=M[i-1]+A[i];\n \n long long ans = 0;\n for(int i=1;i<N;i++){\n if(A[i]!=0)\n for(int j=2*i;j<N;j+=i)\n ans += (M[j-1] - M[j-i-1]) * 1LL * (j / i - 1) * A[i];\n }\n \n return ans%1000000007;\n }\n};\n```\n\nThe Time Complexity is On2 and The Space Complexity is On | 2 | 0 | ['C', 'Counting'] | 2 |
sum-of-floored-pairs | Reverse Logic Count Prefix Sum with Sieve method O(nlogn) Complexity | reverse-logic-count-prefix-sum-with-siev-fm9d | Intuition\n Describe your first thoughts on how to solve this problem. \n- Here we are going to think in reverse order\n- we are going to fix denominator and fl | yash559 | NORMAL | 2024-08-16T13:56:42.293234+00:00 | 2024-08-16T13:56:42.293277+00:00 | 60 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Here we are going to think in reverse order\n- we are going to fix denominator and floor fractional result and we are going to find how many numerators satisfy this condition.\n- we need **prefix count sum(sieve method)**\n\n***Main Intuition***\n- for ex: **[2,5,9]** we if we fix **2** as denominator and we calculate prefix count sum which is **[1->0,2->1,3->1,4->1,5->2,6->2,7->2,8->2,9->3..]**\n- for ranges if we fix as numerator \n[0,1] res = 0\n[2,3] res = 1\n[3,4] res = 2\n...\nas we can observe that if we iterate for res i.e 0,1,2.. till 1e5 then we can go on fixing ranges\n- **formula for ranges result as j = [j * denominator,j * (denominator+1)-1]** for this interval the res = j so we just need count in this range which can be obtained by **count prefix sum**\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int MOD = 1e9+7;\n long long N = 100000;\n int sumOfFlooredPairs(vector<int>& nums) {\n vector<long long> count(N+1,0);\n //This is the count Prefic sum(Method is Sieve Method)\n unordered_set<long long> se;\n //initially store all the counts in vector count also store in set\n for(auto &x : nums) {\n count[x]++;\n se.insert(x);\n }\n\n //now Get the prefix sum of all the count\n //we are doing this becoz we need count in between range [left,right] \n //for that we are doing this\n for(int i=1;i<=N;i++) {\n count[i] += count[i-1];\n }\n\n //we need to fix denominator and check for each number \n //this is reverse thinking we are getting numerator for given ans of fraction\n long long ans = 0;\n for(auto &i : se) {\n //i is denominator\n long long val = 0;\n for(int j = 1; i*j <= N; j++) {\n //j denotes the floor fraction result\n //for range [left,right] = [i*j, i*(j+1)-1] we get j as fractional result try it \n long long left = i*j;\n long long right = i*(j+1) - 1;\n right = min(right,N); // for not exceeding 1e5\n long long cnt = count[right] - count[left-1]; //getting number of elements in this range \n //why? becoz for that many elements if we fix them as numerator we are gonna get "j" as floor fractional result\n\n //after that store all the results sum in val which means for that particular denominator this is result\n val = (val + (cnt*j) % MOD) % MOD;\n }\n //there might be more than 1 frequency if denominator\n //we can get by count[i] - count[i-1] which gives frequency of i\n long long c = count[i] - count[i-1];\n //multiply and store the result\n ans = (ans + (val*c) % MOD) % MOD;\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
sum-of-floored-pairs | Python 3 best N log(N) solution with 98.78% beats. | python-3-best-n-logn-solution-with-9878-9vv2c | Intuition\n Describe your first thoughts on how to solve this problem. \nThink about frequencies and multiples!\n\n# Approach\n Describe your approach to solvin | MAS5236 | NORMAL | 2024-04-19T01:42:36.853376+00:00 | 2024-04-19T01:42:36.853412+00:00 | 301 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThink about frequencies and multiples!\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFrequencies and multiples.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nN log(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution:\n \n MOD = 10**9 + 7\n \n def sumOfFlooredPairs(self, nums):\n # Initialize an array to keep track of count for each number\n N = max(nums)\n count = [0] * (N + 1)\n \n # Count occurrences of each number in the input list\n for num in nums:\n count[num] += 1\n \n # Calculate cumulative count for each number\n for i in range(1, N + 1):\n count[i] += count[i - 1]\n \n ans = 0\n for i in range(1, N + 1):\n if count[i] - count[i - 1] > 0:\n sum_val = 0\n # Iterate over multiples of i (i * j) up to N\n for j in range(1, (N // i) + 1):\n low = i * j\n high = min(i * (j + 1) - 1, N)\n \n # Calculate the count of numbers in the range [low, high]\n cnt = count[high] - count[low - 1]\n \n \n # Update the sum_val\n sum_val = (sum_val + (cnt * j) % self.MOD) % self.MOD\n \n # Calculate the contribution of the current number\n curr = count[i] - count[i - 1]\n \n ans = (ans + (curr * sum_val) % self.MOD) % self.MOD\n \n return ans\n\n\n``` | 1 | 0 | ['Python3'] | 1 |
sum-of-floored-pairs | Best Java Solution || Beats 80% | best-java-solution-beats-80-by-ravikumar-g2qm | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2023-10-12T19:55:51.519754+00:00 | 2023-10-12T19:55:51.519779+00:00 | 353 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n // T.C = N+N/2+N/3+.....\n // = O(NlogN)\n\n // we do the brute force approach which has the T.C O(n^2)\n \n public int sumOfFlooredPairs(int[] arr) {\n int n = arr.length;\n long ans = 0;\n long mod = 1000000007;\n\n int max = Integer.MIN_VALUE;\n\n for(int i=0; i<n; i++){\n max = Math.max(arr[i],max);\n }\n\n int freq[] = new int[max+1];\n\n for(int i=0; i<n; i++){\n freq[arr[i]]++;\n }\n\n int pre[] = new int[max+1];\n\n for(int i=1; i<=max; i++){\n pre[i] = pre[i-1]+freq[i];\n }\n\n for(int i=1; i<=max; i++){\n \n if(freq[i]==0) continue;\n\n long sum = 0;\n for(int j=1; j*i<=max; j++){\n int left = j*i;\n int right = i*(j+1)-1;\n right = Math.min(right,max);\n int count = pre[right]-pre[left-1];\n sum = (sum+(j*count)%mod)%mod;\n }\n ans = (ans + (long)(freq[i]*sum)%mod)%mod;\n }\n return (int)(ans%mod);\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
sum-of-floored-pairs | [PYTHON] | ALGORITHM | python-algorithm-by-omkarxpatel-bzie | \nRuntime: 3561 ms, faster than 73.68% of Python3 online submissions for Sum of Floored Pairs.\nMemory Usage: 32.6 MB, less than 56.84% of Python3 online submis | omkarxpatel | NORMAL | 2022-07-13T14:40:28.246118+00:00 | 2022-07-13T14:40:28.246146+00:00 | 415 | false | \nRuntime: **3561 ms, faster than 73.68%** of Python3 online submissions for Sum of Floored Pairs.\nMemory Usage: **32.6 MB, less than 56.84%** of Python3 online submissions for Sum of Floored Pairs.\n```\n\nclass Solution:\n def sumOfFlooredPairs(self, n: List[int]) -> int:\n f, m, c = Counter(n), max(n), [0]*(max(n)+1)\n for k in f:\n d, r = f[k], 1\n while r*k <= m: c[r*k] += d; r += 1\n r, j = 0, 0\n for i in range(m+1):\n r += c[i]\n if i in f: j += f[i]*r\n return j%(10**9+7)\n\t\t\n```\n**BTW: THIS IS NOT MY COMPLETE IDEA, I MADE `@satendrapandey`\'s VERSION A BIT FASTER** | 1 | 0 | ['Python', 'Python3'] | 0 |
sum-of-floored-pairs | Segment Tree & prefix sum Solution || Very slow but unique || C++ | segment-tree-prefix-sum-solution-very-sl-2105 | As most of the solutions posted here is highly dependent on prefix array sum and other techniques, I thought that solving using segment tree is a pretty unique | NAHDI51 | NORMAL | 2021-08-11T13:02:33.118043+00:00 | 2021-08-11T13:02:33.118076+00:00 | 287 | false | As most of the solutions posted here is highly dependent on prefix array sum and other techniques, I thought that solving using segment tree is a pretty unique idea.\n\nThis is a materialized idea of the HINTS 1 & 2 provided there.\n\n```\nclass segment_tree {\nvector<int> seg;\nint size;\npublic:\nsegment_tree(vector<int>& a) {\n size = a.size();\n seg.resize(2*size+5);\n for(int i = 0; i < a.size(); i++) \n update(i, a[i]);\n}\nvoid update(int i, int val) {\n i += size;\n seg[i] += val;\n for(i /= 2; i >= 1; i /= 2) \n seg[i] = seg[i*2] + seg[i*2+1];\n}\nint query(int l, int r) {\n l += size, r += size;\n int sm = 0;\n while(l <= r) {\n if(l % 2 == 1) sm += seg[l++];\n if(r % 2 == 0) sm += seg[r--];\n l /= 2, r /= 2;\n }\n return sm;\n}\n};\n\nint sumOfFlooredPairs(vector<int>& a) {\n int mod = (int)1e9+7;\n int mx = 0;\n unordered_map<int, long long> mp;\n\n for(int i = 0; i < a.size(); i++) mx = max(mx, a[i]);\n vector<int> pref(mx+1);\n for(int i = 0; i < a.size(); i++) pref[a[i]]++, mp[a[i]]++;\n segment_tree seg(pref);\n \n\n long long ans = 0;\n for(auto x : mp) {\n int occ = 0;\n int j;\n for(j = x.first; j <= pref.size(); j += x.first) {\n ans += (seg.query(j - x.first, j-1) * occ) * x.second;\n ans %= mod;\n occ++;\n }\n if(j > pref.size()) ans += ((seg.query(j - x.first, pref.size()-1) * occ) * x.second), ans %= mod;\n }\n return ans % mod;\n}\n```\n | 1 | 0 | ['Tree', 'C', 'Prefix Sum'] | 0 |
sum-of-floored-pairs | C++ | c-by-wzypangpang-yqb1 | \nclass Solution {\n typedef long long ll;\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n const int len = 100002;\n ll eg[len] = {} | wzypangpang | NORMAL | 2021-05-29T03:53:09.175816+00:00 | 2021-05-29T03:53:09.175842+00:00 | 338 | false | ```\nclass Solution {\n typedef long long ll;\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n const int len = 100002;\n ll eg[len] = {}; // eg[i] means # of elements equal or greater than i.\n int cnt[len] = {}; // cnt[i] means of elements equal to i.\n int maxnum = 0;\n for(const auto& a : nums) {\n cnt[a]++;\n maxnum = max(maxnum, a);\n }\n \n for(int i=maxnum; i>0; --i) {\n eg[i] += eg[i+1];\n if(cnt[i] > 0) eg[i] += cnt[i]; \n }\n \n ll ans = 0;\n for(int n=maxnum; n>0; n--) {\n if(cnt[n] > 0) {\n for(int f = maxnum / n; f > 0; f--) {\n // Find the # of elements that is >= f * n && < (f + 1) * n. Note that (f + 1) * n may overflow. \n ans += f * (eg[f * n] - eg[min((f+1) * n, maxnum+1)]) * cnt[n];\n }\n }\n }\n \n ll big = 1e9 + 7;\n return ans % big;\n }\n};\n``` | 1 | 0 | [] | 0 |
sum-of-floored-pairs | Java: Sorting with Divide and Conquer | java-sorting-with-divide-and-conquer-by-mmgpr | This solution is not the fastest. It takes 1141ms but uses a different approach than what is mentioned in other posts that utilize a frequency and prefix array. | amitghattimare | NORMAL | 2021-05-28T19:31:03.185872+00:00 | 2021-05-28T19:37:04.953240+00:00 | 271 | false | This solution is not the fastest. It takes 1141ms but uses a different approach than what is mentioned in other posts that utilize a frequency and prefix array.\n\nFirst, we sort the array because that doesn\'t change the answer or time complexity and lets us use previous computations for repeated elements. Then starting from the leftmost element `a_i`, we find `a_i/a_i + a_i+1/a_i + ... + a_n/a_i` for all `a_i`. We solve this recursively by breaking into smaller sub problems. See `findSum()` method to see how the recursion works.\n\nSpace: Due to recursion the space is `O(n)` in the recursion stack when numbers are `[1,2,3, ... , n]`.\nTime: The worst case is achieved when numbers are again `[1,2,3, ... , n]`. In this case, it is `O(n + n-1/2 + n-2/3 + ... + 1/n) = O(nlogn)` Sorting in the beginning doesn\'t change this.\n\n```\nclass Solution {\n final int mod = 1_000_000_007;\n \n // Returns sum of nums[i]/div for from<=i<=to.\n private int findSum(int[] nums, int from, int to, int div) {\n if (from > to) return 0;\n if (from == to) return nums[from] / div;\n if (nums[to] / div == nums[from] / div) {\n return (int)(((to - from + 1) * (long)(nums[to] / div)) % mod);\n }\n int mid = from + (to - from)/2;\n return (findSum(nums, from, mid, div) + findSum(nums, mid + 1, to, div)) % mod;\n }\n \n public int sumOfFlooredPairs(int[] nums) {\n int len = nums.length;\n if (len == 0) return 0;\n \n // Sorting makes the problem simple.\n Arrays.sort(nums);\n \n int total = 0;\n // Duplicates should be handled separately. We cannot ignore the previous numbers that are same.\n int prevNum = -1;\n int prevTotal = -1;\n for (int i=0 ; i<len ; ++i) {\n if (nums[i] == prevNum) {\n total += prevTotal;\n } else {\n prevTotal = findSum(nums, i, len-1, nums[i]);\n prevNum = nums[i];\n total += prevTotal;\n }\n total %= mod;\n }\n return total;\n }\n}\n``` | 1 | 0 | [] | 0 |
sum-of-floored-pairs | [C++, 240ms] Prefix sum * frequency with explanation | c-240ms-prefix-sum-frequency-with-explan-1dts | Basic idea: ranges for the numerators. E.g. 4/4..7/4=1, 8/4..11/4=2. Multiply by count(4..7)*count(4) for the first, count(8..11)*count(4) for the second, etc.\ | nauful | NORMAL | 2021-05-26T18:38:01.180059+00:00 | 2021-05-26T18:38:01.180103+00:00 | 337 | false | Basic idea: ranges for the numerators. E.g. 4/4..7/4=1, 8/4..11/4=2. Multiply by `count(4..7)*count(4)` for the first, `count(8..11)*count(4)` for the second, etc.\n\n```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n const int M = 1e9 + 7;\n const int N = 1e5 + 1;\n \n\t\t// Frequency of nums\n std::vector<int> freq(N + 1, 0);\n \n int max_num = 0;\n for (auto i : nums) {\n max_num = std::max(i, max_num);\n ++freq[i];\n }\n \n\t\t// Prefix sum of frequencies\n std::vector<int> prefix_freq(max_num + 1, 0); \n prefix_freq[0] = freq[0];\n for (int i = 1; i <= max_num; i++)\n prefix_freq[i] = prefix_freq[i - 1] + freq[i];\n\n long res = 0;\n\t\t// Check denominators in nums\n for (int den = 1; den <= max_num; ++den) {\n if (!freq[den])\n continue;\n \n long mul = 1;\n int n0 = den;\n int n1 = 2 * den - 1;\n\t\t\t// (n0 to n1)/d = mul, (n1+1)/d = mul + 1\n while (n0 <= max_num) { \n int f0 = prefix_freq[n0 - 1];\n int f1 = prefix_freq[std::min(max_num, n1)];\n \n\t\t\t\t// res += (n0 to n1)/d * freq(den) * freq(n0..n1-1)\n res += mul * freq[den] * (f1 - f0);\n res %= M;\n \n ++mul;\n n0 += den;\n n1 += den;\n }\n }\n \n return res;\n }\n};\n``` | 1 | 1 | [] | 0 |
sum-of-floored-pairs | JavaScript DP | javascript-dp-by-ektegjetost-uw9b | The idea:\nFor each number, we have x other numbers that are at least as large as it, then some subset that are 2x larger, 3x larger, etc until you go over MAX. | ektegjetost | NORMAL | 2021-05-16T19:35:12.815575+00:00 | 2021-05-16T19:35:27.274843+00:00 | 171 | false | The idea:\nFor each number, we have ```x``` other numbers that are at least as large as it, then some subset that are 2x larger, 3x larger, etc until you go over MAX.\n- Any number that\'s between sizes of ```1 x n``` to ```1.99999... x n``` count once\n- numbers between ```2 x n``` to ```2.99999... x n``` count twice, etc.\n```\n n * 4 L M\n n * 3 I J K L M\nnum n * 2 D E F G H I J K L M\n n * 1 A B C D E F G H I J K L M\n\t\t\t\tnums greater\n```\nSo we can build a table that shows how many numbers are >= any number up to the max of nums. Then, for each num, we\'ll multiply it by 1, 2, 3, etc until we get to max, and look up how many numbers fall into each range.\n\nAn edge case would be, what if we have 99,999 1s and 1 100,000. We can deal with that by using a frequency counter of each num instead of looking at literally every num, so our worst case scenario is if we have all the numbers in the range ```1...100,000```, which is a lot better than if we did ```99,999 x 100,000``` comparisons for all those ones.\n\nGiven the example nums ```[2, 5, 9]```, we get a table that looks like\n```\n[3, 3, 3, 2, 2, 2, 1, 1, 1, 1]\n```\nWe find:\n```\nnum: 2\n3 nums >= 2 * 1\n2 nums >= 2 * 2\n1 nums >= 2 * 3\n1 nums >= 2 * 4\n0 nums >= 2 * 5\n\nnum: 5\n2 nums >= 5 * 1\n0 nums >= 5 * 2\n\nnum: 9\n1 nums >= 9 * 1\n0 nums >= 9 * 2\n```\nSum the first column to get 10, and you\'re done.\n\n**The Code**\n\n```javascript\nvar sumOfFlooredPairs = function(nums) {\n const MAX = Math.max(...nums);\n \n const countsGreaterOrEqualTo = new Array(MAX+1).fill(0);\n \n nums.forEach((num) => countsGreaterOrEqualTo[num] += 1 );\n \n for (let num = MAX - 1; num >= 0; num -= 1) {\n countsGreaterOrEqualTo[num] += countsGreaterOrEqualTo[num + 1];\n }\n\n const numCounts = nums.reduce((counts, num) => {\n counts.set(num, (counts.get(num) || 0) + 1);\n return counts;\n }, new Map())\n \n const MOD = 10 ** 9 + 7;\n let totalCount = 0;\n\n numCounts.forEach((count, num) => {\n let current = num;\n \n while (current <= MAX) {\n totalCount = (totalCount + countsGreaterOrEqualTo[current] * count) % MOD;\n current += num;\n }\n });\n \n return totalCount;\n};\n``` | 1 | 0 | ['Dynamic Programming', 'JavaScript'] | 0 |
sum-of-floored-pairs | [C++] | Prefix Sum | c-prefix-sum-by-avishubht762-a4mo | \nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) \n {\n long long mod = 1e9+7;\n long long h[200002]={0};\n int mx=INT_M | avishubht762 | NORMAL | 2021-05-16T11:58:51.397630+00:00 | 2021-05-16T13:09:08.452390+00:00 | 189 | false | ```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) \n {\n long long mod = 1e9+7;\n long long h[200002]={0};\n int mx=INT_MIN;\n for(auto x: nums)\n {\n h[x]++;\n mx=max(mx,x);\n }\n vector<int> pfx(2*mx+1,0);\n for(int i=1;i<=2*mx;i++)\n {\n pfx[i]=pfx[i-1]+h[i];\n }\n sort(nums.begin(), nums.end());\n long long s = 0;\n for(int i=0;i<nums.size();i++)\n {\n int l=nums[i], r=2*nums[i]-1, fact=1;\n while(l<=mx)\n {\n s=(s+fact*(pfx[r]-pfx[l-1]))%mod;\n l=l+nums[i];\n r=r+nums[i];\n fact++;\n }\n }\n return s;\n }\n};\n``` | 1 | 1 | ['C', 'Sorting', 'Prefix Sum'] | 0 |
sum-of-floored-pairs | C++ Solution using Lower bound + Optimization | c-solution-using-lower-bound-optimizatio-01pr | ```\nint sumOfFlooredPairs(vector& nums) {\n long long ans=0,mod=1000000007,p=0;\n sort(nums.begin(),nums.end());\n int n=nums.size();\n | nonymous | NORMAL | 2021-05-16T05:48:31.347662+00:00 | 2021-05-16T05:50:28.576077+00:00 | 70 | false | ```\nint sumOfFlooredPairs(vector<int>& nums) {\n long long ans=0,mod=1000000007,p=0;\n sort(nums.begin(),nums.end());\n int n=nums.size();\n for(int i=0;i<n;i++)\n {\n if(i>0 && nums[i]==nums[i-1])\n {\n ans=(ans+p)%mod;\n continue;\n }\n int k=1;\n p=0;\n while(nums[i]*k<=nums[n-1])\n {\n int l=lower_bound(nums.begin()+i,nums.end(),nums[i]*k)-nums.begin();\n int r=lower_bound(nums.begin()+l,nums.end(),nums[i]*(k+1))-nums.begin();\n p=(p+ (long long) k*(r-l) )%mod;\n if(r==n)\n break;\n k=nums[r]/nums[i];\n }\n ans=(ans+p)%mod;\n }\n return ans;\n } | 1 | 0 | [] | 0 |
sum-of-floored-pairs | Java - Simple Brute approach, Using memorization, 100% faster!!! | java-simple-brute-approach-using-memoriz-358a | \nimport java.util.Arrays;\n\nclass Solution {\n public int sumOfFlooredPairs(int[] arr) {\n \n \tint i,j,k,max,n=arr.length;\n \tlong sum=0,tot | pgthebigshot | NORMAL | 2021-05-15T18:02:28.880190+00:00 | 2021-05-15T20:47:24.095008+00:00 | 513 | false | ```\nimport java.util.Arrays;\n\nclass Solution {\n public int sumOfFlooredPairs(int[] arr) {\n \n \tint i,j,k,max,n=arr.length;\n \tlong sum=0,tot=0;\n \tArrays.sort(arr);\n \tmax=arr[n-1];\n \tint count[]=new int[max+1];\n \tfor(i=0;i<n;i++)\n \t\tcount[arr[i]]++;\n \tfor(i=1;i<=max;i++)\n \t\tcount[i]+=count[i-1];\n \tfor(k=0;k<n;k++)\n \t{\n if(k>0&&arr[k]-arr[k-1]==0)\n continue;\n i=arr[k];\n \t\tfor(j=2;j<=max/i+1;j++)\n \t\t{\n \t\t\tint lower=i*(j-1)-1;\n \t\t\tint upper=i*(j)-1;\n \t\t\tsum+=(count[Math.min(max, upper)]-count[lower])*(j-1);\n \t\t}\n \t\ttot+=sum*(count[i]-count[i-1]);\n sum=0;\n \t}\n return (int)(tot%1000000007);\n }\n}\n``` | 1 | 0 | ['Java'] | 3 |
sum-of-floored-pairs | Simple C++ solution | Prefix Sum | simple-c-solution-prefix-sum-by-nayakash-sath | \n#define ll long long\n#define mod 1000000007\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& a) {\n ll n=a.size(),s=0,mx=0;\n | nayakashutosh9 | NORMAL | 2021-05-15T16:57:01.800014+00:00 | 2021-05-15T16:57:01.800048+00:00 | 122 | false | ```\n#define ll long long\n#define mod 1000000007\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& a) {\n ll n=a.size(),s=0,mx=0;\n for(int i=0;i<n;i++){\n s+=a[i];mx=max(mx,a[i]*1LL);\n }\n vector<int> p(4*mx+1,0);\n for(int i=0;i<n;i++) p[a[i]]++;\n for(int i=1;i<=4*mx;i++) p[i]+=p[i-1];\n ll ans=0;\n unordered_map<int,int> f;\n for(int i=0;i<n;i++){\n if(a[i]==1){\n ans=(ans+s)%mod;\n ans%=mod;\n continue;\n }\n if(f.count(a[i])){\n ans=(ans+f[a[i]])%mod;\n ans%=mod;\n continue;\n }\n ll cur=0;\n for(ll j=2;a[i]*(j-1)<=mx;j++){\n ll cnt=p[j*a[i]-1];\n cnt-=p[(j-1)*a[i]-1];\n cur=(cur+(j-1)*cnt)%mod;\n cur%=mod;\n }\n f[a[i]]=cur%mod;\n ans=(ans+cur)%mod;\n ans%=mod;\n }\n return ans%mod;\n }\n};\n``` | 1 | 1 | [] | 0 |
sum-of-floored-pairs | C++ | easy to understand sol | c-easy-to-understand-sol-by-kena7-bg30 | \nclass Solution {\npublic:\n int mod=1000000007;\n int sumOfFlooredPairs(vector<int>& nums) \n {\n vector<int>v(200002,0);\n for(auto x: | kenA7 | NORMAL | 2021-05-15T16:10:36.488395+00:00 | 2021-05-15T16:10:36.488427+00:00 | 215 | false | ```\nclass Solution {\npublic:\n int mod=1000000007;\n int sumOfFlooredPairs(vector<int>& nums) \n {\n vector<int>v(200002,0);\n for(auto x:nums)\n v[x+1]++;\n for(int i=1;i<=200001;i++)\n v[i]+=v[i-1];\n int res=0;\n for(auto x:nums)\n {\n for(int s=x;s<=100000;s+=x)\n {\n int k=s/x;\n int l=v[s+x]-v[s];\n res=(res+k*l)%mod;\n }\n }\n return res;\n }\n};\n``` | 1 | 2 | [] | 0 |
sum-of-floored-pairs | C++ | c-by-user5976fh-iqfo | null | user5976fh | NORMAL | 2025-04-10T07:50:26.878297+00:00 | 2025-04-10T07:50:26.878297+00:00 | 4 | false | ```cpp []
class Solution {
public:
int s = 100001, MOD = 1e9 + 7;
int p[100001] = {};
int sumOfFlooredPairs(vector<int>& nums) {
for (auto& n : nums) ++p[n];
for (int i = 1; i < s; ++i)
p[i] += p[i - 1];
long long ans = 0;
for (int i = 1; i < s; ++i) {
int freq = p[i] - p[i - 1];
if (freq > 0) {
for (int f = 1; f * f <= i; ++f) {
int rf = i / f;
int right = i / f;
int left = i / (f + 1);
long long add1 = 1LL * freq * (p[right] - p[left]) % MOD * f % MOD;
ans = (ans + add1) % MOD;
if (rf != f) {
int left2 = i / (rf + 1);
int right2 = i / rf;
long long add2 = 1LL * freq * (p[right2] - p[left2]) % MOD * rf % MOD;
ans = (ans + add2) % MOD;
}
}
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
sum-of-floored-pairs | JAVA | java-by-karthi_saravanan_t-iycj | Code | KARTHI_SARAVANAN_T | NORMAL | 2025-02-01T06:11:50.946237+00:00 | 2025-02-01T06:11:50.946237+00:00 | 9 | false |
# Code
```java []
public class Solution {
public int sumOfFlooredPairs(int[] nums) {
int N = (int) 1e5; // Maximum possible value in nums
int mod = (int) 1e9 + 7; // Modulo value
// Step 1: Create a frequency map to count occurrences of each number
int[] frequencyMap = new int[N + 1];
for (int num : nums) {
frequencyMap[num]++;
}
// Step 2: Create a prefix sum array for the frequency map
int[] prefixFreq = new int[N + 1];
for (int i = 1; i <= N; i++) {
prefixFreq[i] = prefixFreq[i - 1] + frequencyMap[i];
}
long total = 0; // Variable to store the final result
// Step 3: Iterate through all possible numbers in the frequency map
for (int i = 1; i <= N; i++) {
if (frequencyMap[i] == 0) continue; // Skip if the number doesn't exist in nums
long sum = 0; // Variable to store the sum of floor divisions for the current number i
// Step 4: Iterate through all multiples of i
for (int j = 1; i * j <= N; j++) {
int lower = i * j - 1; // Lower bound of the range
int upper = i * (j + 1) - 1; // Upper bound of the range
// Step 5: Calculate the count of numbers in the range [lower + 1, upper]
int count = prefixFreq[Math.min(N, upper)] - prefixFreq[lower];
// Step 6: Add the contribution of this range to the sum
sum += (long) count * j;
}
// Step 7: Multiply the sum by the frequency of i and add it to the total
total = (total + (sum % mod) * frequencyMap[i]) % mod;
}
return (int) total; // Return the result modulo 1e9 + 7
}
}
``` | 0 | 0 | ['Java'] | 0 |
sum-of-floored-pairs | Explained Clean Code | Beats 100% 23ms | explained-clean-code-beats-100-23ms-by-i-mg3o | IntuitionSimilar to the Sieve of Eratosthenes, this solution uses a frequency-based counting approach to compute floor division contributions across all array p | ivangnilomedov | NORMAL | 2025-01-31T15:10:09.821267+00:00 | 2025-01-31T15:10:09.821267+00:00 | 11 | false | # Intuition
Similar to the Sieve of Eratosthenes, this solution uses a frequency-based counting approach to compute floor division contributions across all array pairs.
# Approach
The key insight is transforming the problem from pair-wise computation to a frequency-based counting strategy:
1. **Frequency Accumulation**:
- Count occurrences of each number
- Create a prefix sum of frequencies from right to left
- This allows O(1) access to count of numbers ≥ a given value
2. **Incremental Contribution**:
- Iterate through numbers from maximum to minimum
- For each number, compute its contribution to floor division
- Use accumulated frequencies to quickly calculate multiples impact
# Intuitive Explanation
Imagine you want to count how many times you can divide different numbers in your array by a specific number. Instead of checking every single pair (which would take forever), we:
1. First count how many of each number we have
2. Then calculate how many times we can divide by each possible divisor
3. Accumulate these results step by step
# Complexity
- **Time Complexity**: $$O(M \log M)$$, where M is maximum array value
- Frequency computation: O(N)
- Multiples computation: O(M log M)
- **Space Complexity**: $$O(M)$$
# Code
```cpp []
class Solution {
public:
int sumOfFlooredPairs(vector<int>& nums) {
// 1. Pure count: O(M*log(M)) - best for dense, small-range inputs
return sumOfFlooredPairs_pure_count(nums); // 23ms
// 2. Multiples sliding: O(N*log(N)) - flexible for sparse inputs
return sumOfFlooredPairs_multiples_fw_slide(nums); // 700ms
return sumOfFlooredPairs_seg_end_slide(nums); // TL
}
int sumOfFlooredPairs_pure_count(const vector<int>& nums) {
// Compute accumulated count per value
long long* acc_count = buf.data();
long long M = nums[0];
for (long long n : nums) {
++acc_count[n];
M = max(M, n);
}
for (int i = M - 1; ~i; --i)
acc_count[i] += acc_count[i + 1];
long long res = 0;
for (long long i = M; ~i; --i) {
const long long count = acc_count[i] - acc_count[i + 1]; // De-accumulate
if (count) {
long long sum = 0;
for (long long m = i; m <= M; m += i)
sum += acc_count[m];
// NB: Theoretically the above m=i*k contributes k = i*k / i but all
// lower [k-1..1] we have handled before because we use acc_count not count
// So this is incremental contribution
res = (res + sum * count) % kMod;
}
}
memset(acc_count, 0, sizeof(long long) * (M + 1)); // Reset buffer for next computation
return res;
}
int sumOfFlooredPairs_multiples_fw_slide(vector<int>& nums) {
// Derive pairs: value and accumulated count in value descend order
sort(nums.begin(), nums.end());
vector<pair<long long, long long>> val_acc_count(nums.size());
val_acc_count.clear();
for (int end = nums.size() - 1, i = nums.size() - 2; i > -2; --i) {
if (i < 0 || nums[i] < nums[i + 1]) {
val_acc_count.emplace_back(
nums[i + 1],
(end - i + (val_acc_count.empty() ? 0LL : val_acc_count.back().second)) % kMod);
end = i;
}
}
long long res = 0;
for (auto rit = val_acc_count.rbegin(); rit != val_acc_count.rend(); ++rit) {
long long seg_len = rit->second;
auto pr = next(rit);
if (pr != val_acc_count.rend())
seg_len -= pr->second;
// Find multiples and compute sums
for (long long m = rit->first; ; m += rit->first) {
auto rseg_end = lower_bound(
rit, val_acc_count.rend(), m,
[](const auto& elem, long long tgt) { return elem.first < tgt; });
if (rseg_end == val_acc_count.rend()) break;
// NB: Theoretically the above m=rit->first*k contributes
// k = rit->first*k / rit->first but all lower [k-1..1] we have handled before
// because we use rseg_end->second = accumulated count
res += seg_len * rseg_end->second;
}
res %= kMod;
}
return res;
}
int sumOfFlooredPairs_seg_end_slide(vector<int>& nums) {
sort(nums.begin(), nums.end());
long long res = 0;
for (auto seg_beg = nums.begin(); seg_beg != nums.end(); ) {
// End of segment with same value
auto seg_end = upper_bound(seg_beg, nums.end(), *seg_beg);
long long seg_len = distance(seg_beg, seg_end);
res += seg_len * seg_len; // Self-division contributions
// Floor divisions with previous segments
auto p = nums.begin();
while (p != seg_beg) {
long long r = *seg_beg / *p;
auto q = upper_bound( // The same r will be on whole range [p..q)
p, seg_beg, r, [sb = *seg_beg](int r, int e) { return r > sb / e; });
long long len = distance(p, q);
res += len * r * seg_len;
p = q;
}
res %= kMod;
seg_beg = seg_end;
}
return res;
}
private:
static constexpr long long kMod = 1e9 + 7;
static constexpr int kMaxNum = 1e5;
static array<long long, kMaxNum + 2> buf;
};
array<long long, Solution::kMaxNum + 2> Solution::buf{};
``` | 0 | 0 | ['C++'] | 0 |
sum-of-floored-pairs | 1862. Sum of Floored Pairs | 1862-sum-of-floored-pairs-by-g8xd0qpqty-escg | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-15T14:45:41.397929+00:00 | 2025-01-15T14:45:41.397929+00:00 | 12 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
static final int MAX_LIMIT = 100000;
static final int MOD_CONST = 1000000007;
public int sumOfFlooredPairs(int[] nums) {
int[] freqArray = new int[MAX_LIMIT + 1];
for (int num : nums) {
freqArray[num]++;
}
for (int idx = 1; idx <= MAX_LIMIT; idx++) {
freqArray[idx] += freqArray[idx - 1];
}
long finalSum = 0;
for (int base = 1; base <= MAX_LIMIT; base++) {
if (freqArray[base] > freqArray[base - 1]) {
long quotientTotal = 0;
for (int factor = 1; base * factor <= MAX_LIMIT; factor++) {
int lowerLimit = base * factor - 1;
int upperLimit = base * (factor + 1) - 1;
quotientTotal += (freqArray[Math.min(upperLimit, MAX_LIMIT)] - freqArray[lowerLimit]) * (long) factor;
}
finalSum = (finalSum + (quotientTotal % MOD_CONST) * (freqArray[base] - freqArray[base - 1])) % MOD_CONST;
}
}
return (int) finalSum;
}
}
``` | 0 | 0 | ['Java'] | 0 |
sum-of-floored-pairs | Easy O(nlogn) Solution || Easy to understand || Beats 99% || C++ | easy-onlogn-solution-easy-to-understand-pxll3 | Complexity
Time complexity:O(max(nums)∗log(max(nums)))
Space complexity:O(max(nums))
Code | dubeyad2003 | NORMAL | 2024-12-25T13:06:35.761725+00:00 | 2024-12-25T13:06:35.761725+00:00 | 22 | false | # Complexity
- Time complexity:$$O(max(nums) * log(max(nums)))$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(max(nums))$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int sumOfFlooredPairs(vector<int>& nums) {
int mx = *max_element(nums.begin(), nums.end());
vector<int> freq(mx + 1);
for(auto &it: nums) freq[it]++;
for(int i=1; i<=mx; i++) freq[i] += freq[i-1];
long long ans = 0, mod = 1e9 + 7;
for(int it=1; it<=mx; it++){
int occ = freq[it] - freq[it - 1];
// let's consider each values as the denominator
for(int j=it; j <=mx && occ; j += it){
int el = freq[min(mx, j + it - 1)] - freq[j - 1];
ans = (ans + 1LL * occ * (j / it) * el) % mod;
}
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
sum-of-floored-pairs | ⚡| python | highly optimized | O(n + m. logm)| Beats 100%| ⚡ | python-highly-optimized-on-m-logm-beats-bwpn2 | Intuition\nRather than checking every pair (i, j), we use the frequency of each number and cumulative sums to compute the result in a more efficient way, reduci | bhoomika1005 | NORMAL | 2024-11-23T17:54:56.110878+00:00 | 2024-11-23T17:54:56.110901+00:00 | 3 | false | # Intuition\nRather than checking every pair (i, j), we use the frequency of each number and cumulative sums to compute the result in a more efficient way, reducing the need for nested loops.\n# Approach\nWe optimize the problem using frequency counting and prefix sums. Instead of checking every pair, we first count how many times each number appears in nums using a frequency array. Then, we create a prefix sum array to store cumulative counts up to each number. This helps us efficiently calculate the sum of floored divisions without iterating over all pairs directly.\n\n# Complexity\n- Time complexity:\nO(n+m\u22C5logm), where n is the size of nums, and \uD835\uDC5A is the maximum number in nums. This is because we build the frequency and prefix arrays and then use them to calculate the floored sums.\n\n- Space complexity:\nO(m), where \uD835\uDC5A is the maximum value in nums. We need space for the frequency and prefix sum arrays, each of size \uD835\uDC5A + 1\n\n# Code\n```python []\nclass Solution:\n def sumOfFlooredPairs(self, nums):\n MOD = 10**9 + 7\n max_val = max(nums)\n \n # Step 1: Create a frequency array\n freq = [0] * (max_val + 1)\n for num in nums:\n freq[num] += 1\n \n # Step 2: Create a prefix sum of the frequency array\n prefix = [0] * (max_val + 1)\n for i in range(1, max_val + 1):\n prefix[i] = prefix[i - 1] + freq[i]\n \n # Step 3: Calculate the sum of floored pairs\n result = 0\n for x in range(1, max_val + 1):\n if freq[x] > 0: # Only process if x exists in nums\n for k in range(1, (max_val // x) + 1):\n lower = k * x\n upper = min(max_val, (k + 1) * x - 1)\n result += freq[x] * k * (prefix[upper] - prefix[lower - 1])\n result %= MOD\n \n return result\n\n``` | 0 | 0 | ['Python'] | 0 |
sum-of-floored-pairs | c++ solution | c-solution-by-dilipsuthar60-mffa | \nclass Solution {\npublic:\n const int MAX=1e5+5;\n const int mod= 1e9+7;\n int sumOfFlooredPairs(vector<int>& nums) {\n vector<long long>prefi | dilipsuthar17 | NORMAL | 2024-11-08T12:25:16.964114+00:00 | 2024-11-08T12:25:16.964144+00:00 | 8 | false | ```\nclass Solution {\npublic:\n const int MAX=1e5+5;\n const int mod= 1e9+7;\n int sumOfFlooredPairs(vector<int>& nums) {\n vector<long long>prefix(MAX,0);\n unordered_map<int,int>mp;\n int n=nums.size();\n for(auto &it:nums){\n prefix[it]++;\n mp[it]++;\n }\n for(int i=1;i<MAX;i++){\n prefix[i]+=prefix[i-1];\n prefix[i]%=mod;\n }\n long long ans=0;\n \n for(auto &[key,value]:mp){\n int num=key;\n long long result=0;\n for(int start=num;start<MAX;start+=num){\n int end=min(MAX-1,start+num-1);\n long long rangeSum = (prefix[end]-prefix[start-1])%mod;\n long long floorValue = start/num;\n result+=floorValue*rangeSum;\n result%=mod;\n }\n ans+=result*value;\n ans%=mod;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'C++'] | 0 |
sum-of-floored-pairs | Intuition | intuition-by-singh_avi-ink9 | Intuition\nThis problem seems simple but is tricky. The key idea is as follows:\n\n1. The nums array contains a maximum number m. \n2. For each number from 0 to | singh_avi | NORMAL | 2024-10-23T09:47:37.332112+00:00 | 2024-10-23T09:47:37.332132+00:00 | 8 | false | # Intuition\nThis problem seems simple but is tricky. The key idea is as follows:\n\n1. The nums array contains a maximum number m. \n2. For each number from 0 to m, we keep a track of the frequency of each one of them\n3. For any number n and p where p > n, the number of elements between n and p (inclusive) can be found in constant time using the prefix array approach on the frequency of elements\n4. The main idea is thus for for all the elements from 0 to m, if the frequency of the element is 0, we continue. Else, go for another loop where we multiply the number from 1 to max. Now for each multiplication, all the elements between max*k and max*(k+1) - 1 will have the same quotient k. We multiply the number of elements in the range by k to get the sum. We then multiply the sum with the frequency of the current number and add it to the result. We do this for all the numbers to get the result.\n\nEx: the current number is 2. All the numbers from 2 -3 will give 1, from 4-5 will give 2, from 6-7 will give 4 and so on\n\n\n# Approach\n\n# Complexity\n- Time complexity:\n$$O(N+Max)$$\n\n- Space complexity:\n$$O(Max)$$\n\n# Code\n```golang []\nvar MOD = 1_000_000_007\n\nfunc sumOfFlooredPairs(nums []int) int {\n\tn := len(nums)\n\n\tmax := -1\n\n\tfor i := 0; i < n; i++ {\n\t\tif nums[i] > max {\n\t\t\tmax = nums[i]\n\t\t}\n\t}\n\n\tfreqArr := make([]int, max+1)\n\n\tfor i := 0; i < n; i++ {\n\t\tfreqArr[nums[i]]++\n\t}\n\n\tprefixArr := make([]int, max+1)\n\n\tfor i := 1; i <= max; i++ {\n\t\tprefixArr[i] = prefixArr[i-1] + freqArr[i]\n\t}\n\n\tresult := 0\n\n\tfor j := 0; j <= max; j++ {\n\n if freqArr[j] == 0 {\n continue\n }\n\n sum := 0\n\t\tfor k := 1; k*j <= max; k++ {\n\t\t\tleft := k * j\n\t\t\tright := (k+1)*j - 1\n\n\t\t\tif right > max {\n\t\t\t\tright = max\n\t\t\t}\n\n\t\t\tnumNodes := prefixArr[right] - prefixArr[left-1]\n\n\t\t\tsum = (sum + (k * numNodes)) % MOD\n\t\t}\n\n result = (result + freqArr[j] * sum) % MOD\n\t}\n\n\treturn result\n}\n``` | 0 | 0 | ['Go'] | 0 |
sum-of-floored-pairs | 1862. Sum of Floored Pairs.cpp | 1862-sum-of-floored-pairscpp-by-202021ga-fwds | Code\n\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n int m = *max_element(nums.begin(), nums.end()); \n vector<long | 202021ganesh | NORMAL | 2024-10-18T10:20:37.341632+00:00 | 2024-10-18T10:20:37.341672+00:00 | 1 | false | **Code**\n```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n int m = *max_element(nums.begin(), nums.end()); \n vector<long> vals(m+1); \n for (auto x : nums) \n ++vals[x]; \n for (int x = m; x > 0; --x) \n for (int xx = 2*x; xx <= m; xx += x) \n vals[xx] += vals[x]; \n for (int i = 1; i < vals.size(); ++i) \n vals[i] += vals[i-1]; \n int ans = 0; \n for (auto x : nums) \n ans = (ans + vals[x]) % 1\'000\'000\'007; \n return ans; \n }\n};\n``` | 0 | 0 | ['C'] | 0 |
sum-of-floored-pairs | Sum of Floored Pairs | sum-of-floored-pairs-by-ansh1707-30ph | \n\n# Code\npython []\nfrom collections import Counter\n\nclass Solution(object):\n def sumOfFlooredPairs(self, nums):\n # Create a list to store the | Ansh1707 | NORMAL | 2024-10-14T02:12:36.413006+00:00 | 2024-10-14T02:12:36.413044+00:00 | 0 | false | \n\n# Code\n```python []\nfrom collections import Counter\n\nclass Solution(object):\n def sumOfFlooredPairs(self, nums):\n # Create a list to store the increases and a counter for the frequencies of nums\n incs, counter = [0] * (max(nums) + 1), Counter(nums) \n \n # Loop over all the divisors\n for num in counter: \n # Loop over all the possible dividends where the quotient increases\n for j in range(num, len(incs), num): \n incs[j] += counter[num] # Increment the increases in quotients\n \n # Manually calculate the accumulated sums\n quots = [0] * len(incs) # Initialize the list for accumulated sums\n current_sum = 0 # Variable to hold the running total\n for i in range(len(incs)):\n current_sum += incs[i] # Accumulate the sums\n quots[i] = current_sum # Store the accumulated value\n \n total_sum = 0 # Initialize a variable to store the total sum\n for num in nums:\n total_sum += quots[num] # Sum up all the quotients for all the numbers in the list.\n \n return total_sum % 1000000007 # Return the result modulo 10^9 + 7\n\n``` | 0 | 0 | ['Python'] | 0 |
sum-of-floored-pairs | Typescript | typescript-by-ggnohope-2hkn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ggnohope | NORMAL | 2024-09-18T14:00:49.360878+00:00 | 2024-09-18T14:00:49.360902+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```typescript []\nfunction sumOfFlooredPairs(nums: number[]): number {\n const MOD = 10**9 + 7;\n const maxNum = Math.max(...nums); \n\n const freq = new Array(maxNum + 1).fill(0);\n for (const num of nums) {\n freq[num] += 1;\n }\n\n const prefixSum = new Array(maxNum + 1).fill(0);\n for (let i = 1; i <= maxNum; i++) {\n prefixSum[i] = prefixSum[i - 1] + freq[i];\n }\n\n let result = 0;\n for (let num = 1; num <= maxNum; num++) {\n if (freq[num] > 0) {\n for (let multiple = 1; multiple * num <= maxNum; multiple++) {\n const left = num * multiple;\n const right = Math.min(num * (multiple + 1) - 1, maxNum);\n const countInRange = prefixSum[right] - prefixSum[left - 1];\n result = (result + freq[num] * countInRange * multiple) % MOD;\n }\n }\n }\n\n return result;\n}\n\n``` | 0 | 0 | ['TypeScript'] | 0 |
sum-of-floored-pairs | Python || binary search || Memoization | python-binary-search-memoization-by-vila-k9lz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vilaparthibhaskar | NORMAL | 2024-09-07T22:38:35.170184+00:00 | 2024-09-07T23:04:02.982220+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(Nlog(N))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(N)\n\n# Code\n```python3 []\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n c = Counter(nums)\n m = (10 ** 9) + 7\n nums.sort()\n l = len(nums)\n ans = 0\n self.memo = {}\n for i in range(l - 1, -1, -1):\n if nums[i] in self.memo:\n ans = (ans + self.memo[nums[i]]) % m\n continue\n l = i + 1\n j = 1\n count = 0\n while nums[i] * j <= nums[-1]:\n val = (nums[i] * (j + 1)) - 1\n r = bisect_right(nums, val) - 1\n ln = r - l + 1\n count = (count + (ln * j)) % m\n l = r + 1\n j += 1\n self.memo[nums[i]] = count\n ans = (ans + count) % m\n for i in c.values():\n ans = (ans + (i ** 2)) % m \n return ans\n\n``` | 0 | 0 | ['Array', 'Math', 'Binary Search', 'Memoization', 'Python3'] | 0 |
sum-of-floored-pairs | Fenwick Tree Solution || Explained | fenwick-tree-solution-explained-by-rasto-gibd | Complexity\n- Time complexity: O(n*log(n)) \n\n- Space complexity: O(n) \n\n# Code\n\n#define mod 1000000007\nclass FenwickTree\n{\n vector<int> BIT;\n pu | coder_rastogi_21 | NORMAL | 2024-06-26T09:54:46.237136+00:00 | 2024-06-26T09:54:46.237184+00:00 | 26 | false | # Complexity\n- Time complexity: $$O(n*log(n))$$ \n\n- Space complexity: $$O(n)$$ \n\n# Code\n```\n#define mod 1000000007\nclass FenwickTree\n{\n vector<int> BIT;\n public:\n FenwickTree(int n) {\n BIT.resize(n+1);\n }\n\n void update(int i, int delta)\n {\n for(; i<int(BIT.size()); i += (i&-i)) {\n BIT[i] += delta;\n }\n }\n\n long long query(int i)\n {\n long long sum = 0;\n for(; i>0; i -= (i&-i)) {\n sum += BIT[i];\n }\n return sum;\n }\n};\n\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n FenwickTree ft(100001);\n long long maxi = 0, ans = 0;\n unordered_map<int,int> mpp;\n\n for(auto it : nums) {\n mpp[it]++;\n maxi = max(maxi,1LL*it);\n ft.update(it,1); //update number in Fenwick Tree\n }\n\n for(auto it : mpp) { //for each unique number\n int x = it.first;\n for(long long k = 1; k<=maxi/x; k++) {\n //all numbers \'num\' in range [l,r] will give floor(x/num) = k\n long long r = (k+1)*x-1, l = k*x-1; \n ans = (ans + mpp[x] * k * (ft.query(min(maxi,r)) - ft.query(l))) % mod; \n } //since every occurence of x will give same ans, we multiply by mpp[x]\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Binary Indexed Tree', 'C++'] | 0 |
sum-of-floored-pairs | Two counters | two-counters-by-yoongyeom-av6s | Code\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n c = Counter(nums)\n mx= max(nums)\n muls = defaultdict | YoonGyeom | NORMAL | 2024-04-29T14:00:32.314876+00:00 | 2024-04-29T14:00:32.314912+00:00 | 15 | false | # Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n c = Counter(nums)\n mx= max(nums)\n muls = defaultdict(int)\n for key in c:\n t = 1\n while t*key <= mx:\n muls[t*key]+=c[key]\n t+=1\n t = sorted(muls.keys(), reverse = True)\n cnt = 0\n res = 0\n for key in sorted(c.keys()):\n while t and t[-1] <= key:\n cnt += muls[t.pop()] \n res += cnt* c[key]\n return res%(10**9+7)\n``` | 0 | 0 | ['Python3'] | 0 |
sum-of-floored-pairs | This problem is very hard! | this-problem-is-very-hard-by-heiseshandi-p2u1 | Intuition\n\nThis problem involves finding the sum of all pairs (nums[i], nums[j]) in an array such that for each pair, the result is the quotient of nums[j] / | heiseshandian | NORMAL | 2024-03-31T15:42:24.921983+00:00 | 2024-03-31T15:42:24.922015+00:00 | 7 | false | ## Intuition\n\nThis problem involves finding the sum of all pairs `(nums[i], nums[j])` in an array such that for each pair, the result is the quotient of `nums[j] / nums[i]` floored (i.e., the integer part of the division). The challenge lies in efficiently calculating this sum for all pairs without directly simulating each division, which would be prohibitively slow for large arrays.\n\n## Approach\n\n1. **Precompute Prefix Sums for Counts**: Calculate and store the count of numbers greater than or equal to each number up to the maximum number in `nums`. This allows us to quickly find out how many numbers in `nums` can be divided by a given number `num` with a quotient `q` (where `q > 0`).\n\n2. **Map Counts of Unique Numbers**: Count the occurrences of each unique number in `nums`. This step is crucial for avoiding redundant calculations for repeated numbers.\n\n3. **Iterate Through Unique Numbers**: For each unique number `num`, iterate through its multiples up to the maximum number in `nums`. For each multiple, add to the total count the product of the count of numbers greater than or equal to the current multiple and the count of `num` itself. This effectively calculates the contribution of `num` to the final answer, taking advantage of the precomputed prefix sums for quick lookup.\n\n4. **Modulo Operation**: Since the answer could be very large, take the modulo of the total count with `10^9 + 7` at each step to keep the number within integer limits.\n\n## Complexity\n\n- **Time Complexity**: `O(n + k*log(k))`, where `n` is the size of the input array and `k` is the maximum value in the array. This is because we iterate over the array multiple times (to fill the prefix sums and to count occurrences), and for each unique number, we potentially iterate through its multiples up to `k`.\n\n- **Space Complexity**: `O(k)`, where `k` is the maximum value in the array. The space is mainly used by the array to store counts of numbers greater than or equal to each number up to `k`, and a map to store counts of unique numbers in the input array.\n\n# Code\n```ts\nfunction sumOfFlooredPairs(nums: number[]) {\n const MAX = Math.max(...nums);\n\n const countsGreaterOrEqualTo = new Array(MAX + 1).fill(0);\n\n nums.forEach((num) => (countsGreaterOrEqualTo[num] += 1));\n\n for (let num = MAX - 1; num >= 0; num -= 1) {\n countsGreaterOrEqualTo[num] += countsGreaterOrEqualTo[num + 1];\n }\n\n const numCounts = nums.reduce((counts, num) => {\n counts.set(num, (counts.get(num) || 0) + 1);\n return counts;\n }, new Map());\n\n const MOD = 10 ** 9 + 7;\n let totalCount = 0;\n\n numCounts.forEach((count, num) => {\n let current = num;\n\n while (current <= MAX) {\n totalCount =\n (totalCount + countsGreaterOrEqualTo[current] * count) % MOD;\n current += num;\n }\n });\n\n return totalCount;\n}\n\n``` | 0 | 0 | ['TypeScript'] | 0 |
sum-of-floored-pairs | 😆Runtime 160 ms Beats 100.00% of users with Go | runtime-160-ms-beats-10000-of-users-with-9x3n | Code\n\nfunc sumOfFlooredPairs(arr []int) int {\n const mod = int(1e9 + 7)\n\t// n := len(arr)\n\tvar ans int64\n\tmax := -1\n\n\tfor _, num := range arr {\n | pvt2024 | NORMAL | 2024-02-27T06:21:16.985867+00:00 | 2024-02-27T06:21:16.985900+00:00 | 7 | false | # Code\n```\nfunc sumOfFlooredPairs(arr []int) int {\n const mod = int(1e9 + 7)\n\t// n := len(arr)\n\tvar ans int64\n\tmax := -1\n\n\tfor _, num := range arr {\n\t\tif num > max {\n\t\t\tmax = num\n\t\t}\n\t}\n\n\tfreq := make([]int, max+1)\n\tfor _, num := range arr {\n\t\tfreq[num]++\n\t}\n\n\tpre := make([]int, max+1)\n\tfor i := 1; i <= max; i++ {\n\t\tpre[i] = pre[i-1] + freq[i]\n\t}\n\n\tfor i := 1; i <= max; i++ {\n\t\tif freq[i] == 0 {\n\t\t\tcontinue\n\t\t}\n\t\tvar sum int64\n\t\tfor j := 1; i*j <= max; j++ {\n\t\t\tleft := j * i\n\t\t\tright := i * (j + 1) - 1\n\t\t\tif right > max {\n\t\t\t\tright = max\n\t\t\t}\n\t\t\tcount := pre[right] - pre[left-1]\n\t\t\tsum = (sum + int64(j*count)) % int64(mod) \n\t\t}\n\t\tans = (ans + (int64(freq[i]) * sum) % int64(mod)) % int64(mod) \n\t}\n\treturn int(ans)\n}\n``` | 0 | 0 | ['Go'] | 0 |
sum-of-floored-pairs | just an example | just-an-example-by-igormsc-8umi | Code\n\nclass Solution {\n \n fun sumOfFlooredPairs(nums: IntArray): Int {\n val maxN = nums.max()\n val v = nums.fold(IntArray(N+1)) { a, n | igormsc | NORMAL | 2024-01-07T17:54:13.623580+00:00 | 2024-01-07T17:54:13.623617+00:00 | 2 | false | # Code\n```\nclass Solution {\n \n fun sumOfFlooredPairs(nums: IntArray): Int {\n val maxN = nums.max()\n val v = nums.fold(IntArray(N+1)) { a, n -> a.also{ a[n]++ } }.apply {(1..N).forEach { i -> this[i] += this[i-1] }}\n return nums.toSet().fold(0.toLong()){ sum, x ->\n (sum + generateSequence(D(x, x*2-1, 1, 0)) { d ->\n D(d.l + x, d.r + x, d.acc + 1, (d.sum + d.acc*(v[d.r]-v[d.l-1]))%MOD)\n }.find { it.l > maxN }!!.sum.let { (it*(v[x]-v[x-1]))%MOD } ) % MOD }.toInt()\n }\n\n private val N = 200002\n private val MOD = 1_000_000_007\n private data class D(val l: Int, val r: Int, val acc: Long, val sum: Long)\n}\n``` | 0 | 0 | ['Kotlin'] | 0 |
sum-of-floored-pairs | nlogn solution | nlogn-solution-by-13ethand-seyl | //the main part of the solution is to notice that for a fixed k, there are only so many value floor(n/k) can have\n //so lets ask the question, for a denomin | 13ethand | NORMAL | 2023-12-14T01:11:01.190385+00:00 | 2023-12-14T01:11:01.190407+00:00 | 73 | false | //the main part of the solution is to notice that for a fixed k, there are only so many value floor(n/k) can have\n //so lets ask the question, for a denominator aj how many indices exist such that floor(ai/aj)=some value q\n //if we want to find some target value then we sum up number of indices that have value nums[i] in range [q*aj,q*(aj+1)-1]\n //we also keep a frequency element freq[i] and multiply this result by freq[i] to avoid recalculation\n //now does this satisfy the time complexity?, well time complexity is floor(n/1)+floor(n/2)...floor(n/n) which is approx. nlogn\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n //the main part of the solution is to notice that for a fixed k, there are only so many value floor(n/k) can have\n //so lets ask the question, for a denominator aj how many indices exist such that floor(ai/aj)=some value q\n //if we want to find some target value then we sum up number of indices that have value nums[i] in range [q*aj,q*(aj+1)-1]\n //we also keep a frequency element freq[i] and multiply this result by freq[i] to avoid recalculation\n //now does this satisfy the time complexity?, well time complexity is floor(n/1)+floor(n/2)...floor(n/n) which is approx. nlogn\n long long llmin(long long i,long long j){\n return i>j?j:i;\n }\n int sumOfFlooredPairs(vector<int>& nums) {\n long long n=nums.size();\n long long mod=1e9+7;\n long long res=0;\n vector<long long>freq(1e5+1);\n vector<long long>p(1e5+1);\n vector<long long>vals(1e5+1);\n for(int i=0;i<n;++i){\n freq[nums[i]]++;\n p[nums[i]]++;\n }\n for(int i=1;i<=1e5;++i){\n p[i]+=p[i-1];\n }\n for(long long i=1;i<=1e5;++i){\n for(long long j=1;j*i<=1e5;++j){\n vals[i]+=(p[llmin(100000,i*(j+1)-1)]-p[i*j-1])*j;\n }\n res=(res+vals[i]*freq[i])%mod;\n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
sum-of-floored-pairs | Python most optimized solution | python-most-optimized-solution-by-taco-m-hxic | Intuition\n Describe your first thoughts on how to solve this problem. \n[[2//2, 2//5, 2//9],\n [5//2, 5//5, 5//9],\n [9//2, 9//5, 9//9]]\n\n let\'s take 9//2 w | taco-man | NORMAL | 2023-10-17T16:32:46.276786+00:00 | 2023-10-17T16:32:46.276805+00:00 | 36 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n[[2//2, 2//5, 2//9],\n [5//2, 5//5, 5//9],\n [9//2, 9//5, 9//9]]\n\n let\'s take 9//2 what it represents, it represents that there are total\n of 4 number (2,4,6,8) before 9 that are multiple of 2. so its value \n would be 4. same goes for others like 9//5 its just 1 (5).[next would be\n 10 but its greater than 9 so we cant take that into consideration.]\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwith that knowledege we just have to know for each number how lets say 5 \n how many numbers have its multiple of less than equal to 5 for all number\n smaller than equal to 5[which is in original array nums].\n\n for 5 its just 5\n for 2 its 2, 4 \n\n so there are in total 3 number which gives sum of quotient for all fraction \n that has numerator 5. similarly we can find for all element in array. and \n return its sum.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n \n ls, counter=[0]*(max(nums)+1), Counter(nums)\n for num in counter:\n for j in range(num, len(ls), num):\n ls[j] += counter[num]\n prefix = [ls[0]]\n for i, n in enumerate(ls):\n if i > 0:\n prefix.append(prefix[-1] + n)\n return sum([prefix[num] for num in nums]) % (10**9 + 7)\n``` | 0 | 0 | ['Hash Table', 'Math', 'Prefix Sum', 'Python3'] | 0 |
sum-of-floored-pairs | nlogn solution using maths | nlogn-solution-using-maths-by-culer2024-a249 | \n\n# Code\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n n,ans = 2*max(nums) + 11,0\n p,arr = [0 for _ in range(n)],[ | culer2024 | NORMAL | 2023-08-17T18:13:37.750104+00:00 | 2023-08-17T18:13:37.750137+00:00 | 29 | false | \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n n,ans = 2*max(nums) + 11,0\n p,arr = [0 for _ in range(n)],[]\n for i in nums:\n p[i] += 1 \n if p[i] == 1 : arr.append(i)\n arr.sort()\n for i in range(1,n): p[i] += p[i-1] \n for x in arr : \n i, j, curr = x, x, 0 \n for i in range(x,n,x):\n ans += (p[x] - p[x-1]) * (i//x -1) * (p[i-1]-p[j-1]) \n ans, j = ans%1000000007, i\n \n return ans\n \n``` | 0 | 0 | ['Python3'] | 0 |
sum-of-floored-pairs | 🔥O(1) SC || ✅Easy & Clean Code✅ || 🌟Binary Search💯 | o1-sc-easy-clean-code-binary-search-by-a-gx5g | Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n## Please Upvote if u found my Solution useful\uD83E\uDD17\n\nclass Solution {\ | aDish_21 | NORMAL | 2023-08-01T20:11:08.642334+00:00 | 2023-08-01T20:11:08.642358+00:00 | 129 | false | # Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n## Please Upvote if u found my Solution useful\uD83E\uDD17\n```\nclass Solution {\npublic:\n int mod = 1e9 + 7;\n int sumOfFlooredPairs(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int n = nums.size(), i = 0;\n long sum = 0;\n while(i < n){\n auto x = upper_bound(nums.begin(),nums.end(),nums[i]);\n int j = x - nums.begin(), k = i, c = 2;\n long tmp_sum = 0, duplicates = x - (nums.begin() + i);\n i = j;\n while(j < n){\n int y = nums[k] * c;\n int ind = upper_bound(nums.begin(),nums.end(),y - 1) - nums.begin();\n tmp_sum = (tmp_sum + (ind - j) * (c - 1)) % mod;\n j = ind;\n c++;\n }\n tmp_sum = tmp_sum * duplicates + (duplicates * duplicates);\n sum = (sum + tmp_sum) % mod;\n }\n return sum;\n }\n};\n``` | 0 | 0 | ['Array', 'Math', 'Binary Search', 'C++'] | 0 |
sum-of-floored-pairs | Counting I guesssss | counting-i-guesssss-by-stolenfuture-lnoi | Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(n + max_num * log(max_num))\n- Space complexity:\n Add your space complexity here, | StolenFuture | NORMAL | 2023-06-11T21:58:45.042290+00:00 | 2023-06-11T21:58:45.042319+00:00 | 34 | false | # Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n + max_num * log(max_num))$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(maxnum)$$\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n MOD = 10**9 + 7\n max_num = max(nums)\n freq = [0] * (max_num + 1)\n\n # Count the occurrences of each number\n for num in nums:\n freq[num] += 1\n\n # Calculate prefix sum of frequencies\n prefix_sum = [0] * (max_num + 1)\n for i in range(1, max_num + 1):\n prefix_sum[i] = prefix_sum[i-1] + freq[i]\n\n result = 0\n\n # Calculate the sum of floor divisions\n for i in range(1, max_num + 1):\n if freq[i] == 0:\n continue\n\n # Iterate over all multiples of i\n for j in range(i, max_num + 1, i):\n result += (prefix_sum[min(j + i - 1, max_num)] - prefix_sum[j-1]) * (j // i) * freq[i]\n result %= MOD\n\n return result\n\n``` | 0 | 0 | ['Python3'] | 0 |
sum-of-floored-pairs | Factor Frequency Prefix Sum w/Num Frequency Product | Commented and Explained | O(N) T/S | factor-frequency-prefix-sum-wnum-frequen-uwrr | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem description is deceptively simple and at first a brute force even seems a l | laichbr | NORMAL | 2023-05-31T12:57:18.839045+00:00 | 2023-05-31T12:57:18.839074+00:00 | 18 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem description is deceptively simple and at first a brute force even seems a likely and doable option, for which I got 19/51 and then 25/51 with first Time and then Memory limit expired. From this, it becomes more obvious that we need a more clever solution. \n\nThe first part in any good brute force to get that far was the reduction in time afforded by considering only unique values in nums and using the frequency of those values. \n\nThe second trick was when I considered the contribution of a specific value to a specific total sum. Take 9 and 2. 9 / 2 in floor form gives 4. This can be seen as the statement that there are 4 factors of 2 in 9 (2, 4, 6, 8). This is the key to the second speed up. \n\nIf we keep a number range from 0 to the maximum of nums, then we can account for this contribution exactly. \n\n- For each unique factor in nums \n - for each next factor of this unique factor up to max nums \n - store the frequency of this factor at a point next factor in our number range \n\n- Then, get the prefix sum of the factor frequencies as a list \n- Then, for each actual num in our num frequencies, multiply the prefix sum of the factor frequencies by the frequency of that num. This then gets the other half of the question. \n\nTo simplify, first find out how much and how many items utilize each factor in nums. Then, find out for each of those utilizations what their summed contribution is. Then, sum only the given unique factor contributions present by the frequency of that factor. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIntuitition describes much of the approach, but for completeness, steps outlined here. \n\nGet the frequency of nums \nSet up modulo value as needed \nGet the maximum key in frequency of nums \nSet up a factor frequencies of 0 in range of max key inclusive \n\nFor num and frequency in frequency of nums \n- for factor in range num, max key + 1, num \n - factor frequencies at factor += frequency \n\nGet the prefix sum of factor frequencies \n\nreturn the sum of the product of the prefix sum of factor frequencies for each factor in num frequency with the frequency of that factor \n\n# Complexity\n- Time complexity : O(N) \n - O(N) to get num frequency \n - O(n) to get unique max value \n - O(n * floor(max value / avg other nums)) \n - O(max value) to get prefix sums \n - O(n) to get final value \n - At worst one might think O(N) == O(n) == O(max value) \n - However, when that occurs avg of other nums ~ N \n - Due to this, we can see that the floor mechanism limits \n - Worst would be when n ~ N/2 and n is composed of all values up to N/2 - 1 and N \n - This would give a run time of N/2 * 2 for the loop and shows the value of the floor limit on the run time for the inner loop \n - Thus we can say at worst O(N) \n\n- Space complexity : O(N) \n - As above, at worst is O(N) \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int :\n # uncomment print statements to see in test cases \n # floor nums[i] / nums[j]\n # if nums[i] occurrs multiple times, doing multiple work \n # frequency is first reduction \n num_frequency = collections.Counter(nums)\n mod = 10**9 + 7 \n # second reduction involves consideration of factorization processes \n # for each value in nums, that number will have a number of contributions based on its frequency for its value \n # in relation to all other values. For example, 9 / 2 causes 2 to contribute 4 due to the presence of 9\n # this can be seen as the number of factors of 2 that fit within the value of 9. Due to this, we want to find \n # first the largest value of our num frequency (don\'t search nums! Already did that once to set up num frequency) \n # then we want to find the frequencies related to the factors of a value that fit within range up to that max value \n # this will give us our second reduction, since we can now do loops limited to only unique nums in num frequency \n # as the outer loop and do inner loops over only the factor range for each value, which processes in logarithmic\n # time rather than linear time due to size of steps utilized in advancing towards a set max value \n max_key = max(num_frequency.keys())\n # then, for each factor in range of a num to the max key plus 1 so that the max value is included \n # we will record the frequency that a given factor for any num of nums is found in range and increment \n # by the frequency of the associated base num, as that will denote the contribution frequency times it makes \n # towards the total summation value \n factor_frequencies = [0] * (max_key + 1) \n # loop over num frequency items \n for num, frequency in num_frequency.items() : \n # print(f\'Considering number {num} with frequency {frequency}\')\n # factor values in range of num to max key + 1 in steps of num \n # represents reduction in time by use of multiples of num that are found in floor pairings \n for factor in range(num, max_key + 1, num) : \n # print(f\'Considering factor value {factor} and updating factor frequencies current : {factor_frequencies}\')\n # for which you will have at least frequency occurrences of this value for that partner \n factor_frequencies[factor] += frequency\n # print(f\'New factor_frequencies is {factor_frequencies}\\n\')\n # print(f\'Total factor_frequencies are {factor_frequencies}\')\n # this is the prefix sum of the factors of num frequencies in range of max, accounting for \n # the possible multiple divisions of certain nums by certain other values (i.e. 9 / 2 -> 4)\n prefix_sum_of_factor_frequencies = list(accumulate(factor_frequencies))\n # print(f\'Prefix sum of factor frequencies are {prefix_sum_of_factor_frequencies}\')\n # return the sum of the prefix sum of factor frequencies for each num actually in num frequency multiplied \n # by the frequency of that num. This is because the prefix sum accounts for the number of times it is utilized by others, and now we count by self \n return sum(prefix_sum_of_factor_frequencies[num] * frequency for num, frequency in num_frequency.items()) % mod \n``` | 0 | 0 | ['Python3'] | 0 |
sum-of-floored-pairs | C# version that minimizes the number of iterations in loops. | c-version-that-minimizes-the-number-of-i-q21b | Intuition\nInitial thought was nested loops, however that was inefficient.\n\n# Approach\nCreate an array that contains the frequency, or count, of each number | TwistedStem | NORMAL | 2023-05-31T02:24:47.082083+00:00 | 2023-05-31T02:24:47.082119+00:00 | 17 | false | # Intuition\nInitial thought was nested loops, however that was inefficient.\n\n# Approach\nCreate an array that contains the frequency, or count, of each number in the given array. Create a second array that contains the prepared summation counts.\n\nLooping through the frequency map, determine the count by taking the upper summation count minus the lower summation count. Multiply that count number by the loop counter and the frequency count.\n\n# Code\n```\nclass Solution {\n\n private const int Mod = 1000000007;\n private const int MaxNumber = 100000;\n\n public int SumOfFlooredPairs(int[] nums)\n {\n var total = 0L;\n var min = nums.Min();\n var max = Math.Min(MaxNumber, nums.Max());\n var frequencies = new int[max + 1];\n var preparedSummations = new long[max + 2];\n \n foreach (var num in nums)\n {\n ++frequencies[num];\n }\n \n for (var i = min; i < frequencies.Length; i++)\n {\n preparedSummations[i + 1] = preparedSummations[i] + frequencies[i];\n }\n \n for (var i = min; i < frequencies.Length; i++)\n {\n if (frequencies[i] == 0)\n {\n continue;\n }\n \n for (var j = 1; j * i <= frequencies.Length; j++)\n {\n var lower = i * j;\n var upper = i * (j + 1) - 1;\n var count = preparedSummations[Math.Min(upper + 1, frequencies.Length)] - preparedSummations[Math.Min(lower, frequencies.Length)];\n total += count * j * frequencies[i];\n }\n }\n \n return (int)(total % Mod);\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
sum-of-floored-pairs | C++ | c-by-tinachien-kgmo | \nusing LL = long long ;\nclass Solution {\n int maxN = 1e5 ;\n int M = 1e9 + 7 ;\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n int n | TinaChien | NORMAL | 2023-05-01T06:57:23.758509+00:00 | 2023-05-01T06:57:23.758540+00:00 | 27 | false | ```\nusing LL = long long ;\nclass Solution {\n int maxN = 1e5 ;\n int M = 1e9 + 7 ;\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n int n = nums.size() ;\n vector<int>count(maxN + 1) ;\n vector<LL>presum(maxN + 1) ;\n for(auto& x : nums)\n count[x]++ ;\n for(int i = 1; i <= maxN; i++)\n presum[i] = presum[i-1] + count[i] ;\n \n LL ret = 0 ;\n unordered_set<int>visited ;\n for(auto& x : nums){\n if(visited.count(x))\n continue ;\n visited.insert(x) ;\n LL ans = 0 ;\n int k = 0;\n for(k = 1; x*k+x-1 <= maxN; k++){\n ans = ans + (presum[x*k+x-1] - presum[x*k-1])*k%M ;\n ans %= M ;\n }\n if(x*k-1<=maxN){\n ans = ans + (presum[maxN] - presum[x*k-1])*k % M ;\n ans %= M ;\n }\n ret = ret + ans * count[x] % M ;\n ret %= M ;\n }\n return ret ;\n }\n};\n``` | 0 | 0 | [] | 0 |
sum-of-floored-pairs | C++ implementation | SOE and Prefix SUM | c-implementation-soe-and-prefix-sum-by-k-13gn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. calculate sieve arra | kumarsubham373 | NORMAL | 2023-04-23T09:29:29.460420+00:00 | 2023-04-23T09:29:29.460465+00:00 | 122 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. calculate sieve array\n2. calculate prefix sum of sieve array\n3. iterate a loop to find the value and update the sum value.\n\n# Complexity\n- Time complexity:\n- O(N logN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long int\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n ll mx = 1e5;\n vector<ll>sieve(mx+2,0),prefix(mx+2,0);\n for(auto i : nums)\n sieve[i]++;\n for(ll i=1;i<=mx;i++){\n prefix[i] = prefix[i-1]+sieve[i];\n }\n ll ans = 0;\n ll mod = 1e9+7;\n for(ll i=1;i<=mx;i++){\n ll count =1;\n for(ll j=i;j<=mx;j+=i){\n ll start = j;\n ll end = j+i-1;\n end = min(mx,end);\n ll sum = ((prefix[end]-prefix[start-1])*count)%mod;\n sum = (sum*sieve[i])%mod;\n ans+=sum;\n ans%=mod;\n count++;\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
sum-of-floored-pairs | concept of map, freq and SOE | concept-of-map-freq-and-soe-by-yashsharm-a32h | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | YashSharma2210 | NORMAL | 2023-04-23T09:25:46.107406+00:00 | 2023-04-23T09:25:46.107456+00:00 | 73 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long int\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n ll mx = 1e5;\n vector<ll> freq(mx+2, 0), pref(mx+2, 0);\n for(auto itr : nums) freq[itr]++;\n for(ll i=1;i<=mx;i++) pref[i]=pref[i-1]+freq[i];\n\n ll ans = 0;\n ll MOD = 1e9+7;\n for(ll i=1;i<=mx;i++){\n ll cnt = 1;\n for(ll j=i;j<=mx;j+=i){\n ll st = j;\n ll en = j+i-1;\n en = min(mx, en);\n ll sx = ((pref[en]-pref[st-1])*cnt)%MOD;\n sx = (sx*freq[i])%MOD;\n ans+=sx;\n ans%=MOD;\n cnt++;\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
sum-of-floored-pairs | Algorithm for Integer Arrays | algorithm-for-integer-arrays-by-setunico-l3vu | \n\nfunction sumOfFlooredPairs(nums) {\n const MOD = 1000000007;\n const maxNum = Math.max(...nums);\n const freq = new Array(maxNum + 1).fill(0);\n for (le | setunicode | NORMAL | 2023-04-04T15:28:51.218172+00:00 | 2023-04-04T15:28:51.218213+00:00 | 36 | false | \n```\nfunction sumOfFlooredPairs(nums) {\n const MOD = 1000000007;\n const maxNum = Math.max(...nums);\n const freq = new Array(maxNum + 1).fill(0);\n for (let num of nums) {\n freq[num]++;\n }\n for (let i = 1; i <= maxNum; i++) {\n freq[i] += freq[i - 1];\n }\n let res = 0;\n for (let i = 1; i <= maxNum; i++) {\n if (freq[i] - freq[i - 1] === 0) {\n continue;\n }\n let sum = 0;\n for (let j = 1; i * j <= maxNum; j++) {\n let l = i * j - 1, r = Math.min(maxNum, i * j + i - 1);\n sum += (freq[r] - freq[l]) * j;\n sum %= MOD;\n }\n res += (sum * (freq[i] - freq[i - 1])) % MOD;\n res %= MOD;\n }\n return res;\n}\n\n```\n\n> This is the most difficult thing I have solved | 0 | 0 | ['JavaScript'] | 0 |
sum-of-floored-pairs | Best java 35ms | best-java-35ms-by-ht38nhatphan-srnp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ht38nhatphan | NORMAL | 2023-04-02T20:52:23.156345+00:00 | 2023-04-02T20:52:23.156384+00:00 | 138 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int sumOfFlooredPairs(int[] nums) {\n int MOD = 1000000007;\n int maxNum = Arrays.stream(nums).max().getAsInt();\n int[] count = new int[maxNum + 1];\n for (int num : nums) {\n count[num]++;\n }\n for (int i = 1; i <= maxNum; i++) {\n count[i] += count[i - 1];\n }\n long result = 0;\n for (int i = 1; i <= maxNum; i++) {\n if (count[i] == count[i - 1]) {\n continue;\n }\n long sum = 0;\n for (int j = 1; j * i <= maxNum; j++) {\n int l = j * i - 1;\n int r = Math.min(j * i + i - 1, maxNum);\n sum += (long) j * (count[r] - count[l]);\n }\n result += sum * (count[i] - count[i - 1]);\n }\n return (int) (result % MOD); \n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
sum-of-floored-pairs | 3 Solutions Python | 3-solutions-python-by-sarthakbhandari-r5pp | Harmonic Series: 1/1 + 1/2 + 1/3 + .... + 1/n is logarithmic https://en.wikipedia.org/wiki/Harmonic_series_(mathematics)\nThis fact is used in deriving time co | sarthakBhandari | NORMAL | 2023-03-16T23:50:58.136424+00:00 | 2023-03-16T23:56:50.178982+00:00 | 38 | false | Harmonic Series: `1/1 + 1/2 + 1/3 + .... + 1/n` is logarithmic https://en.wikipedia.org/wiki/Harmonic_series_(mathematics)\nThis fact is used in deriving time complexities\n\n**Binary Search Approach\nTime: O(n * logn * logn)\nSpace: O(n)**\n```\ndef sumOfFlooredPairs(self, nums: List[int]) -> int:\n mx = max(nums)\n nums.sort()\n count = Counter(nums)\n res = 0\n for i in count:\n for factor in range(1, mx//i + 1):\n res += count[i]*factor*(bisect_right(nums, (factor+1)*i - 1) - bisect_left(nums, factor*i))\n \n return res % (10**9 + 7)\n```\n\n**Prefix Sum Approach** - get rid of extra logarithmic factor\n**Time: O(n * log n)\nSpace: O(n)**\n```\ndef sumOfFlooredPairs(self, nums: List[int]) -> int:\n mx = max(nums)\n count = Counter(nums)\n prefix = list(accumulate([count[i] if i in count else 0 for i in range(mx + 1)]))\n res = 0\n for i in count:\n for factor in range(1, mx//i + 1):\n res += factor*count[i]*(prefix[min(i*(factor+1) - 1, mx)] - prefix[i*factor - 1])\n \n return res % (10**9 + 7)\n```\n\nSimilar to **Sieve Eratosthenes** Approach\n**Time: O(n * logn)\nSpace: O(n)**\n```\ndef sumOfFlooredPairs(self, nums: List[int]) -> int:\n mx = max(nums)\n factorCount = [0]*(mx + 1)\n\n for num, count in Counter(nums).items():\n for multiple in range(num, mx + 1, num):\n factorCount[multiple] += count\n \n quotientSum = list(accumulate(factorCount))\n return sum(map(lambda num: quotientSum[num], nums))%(10**9 + 7)\n``` | 0 | 0 | ['Math', 'Binary Search', 'Prefix Sum'] | 0 |
sum-of-floored-pairs | Python (Simple Hashmap + Prefix Sum) | python-simple-hashmap-prefix-sum-by-rnot-u79c | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2023-03-06T13:07:24.845886+00:00 | 2023-03-06T13:07:24.845932+00:00 | 50 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums):\n ans, dict1, mod = [0]*(max(nums)+1), collections.Counter(nums), 10**9 + 7\n\n for num in dict1:\n for j in range(num,len(ans),num):\n ans[j] += dict1[num]\n\n res = [ans[0]]\n\n for i in ans[1:]:\n res.append(res[-1] + i)\n\n return sum([res[i] for i in nums])%mod\n\n\n\n\n\n \n\n \n``` | 0 | 0 | ['Python3'] | 0 |
sum-of-floored-pairs | Python3 Solution With Prefix Sum | python3-solution-with-prefix-sum-by-ixuh-0e8i | \nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n \n num_max = max(nums) + 1\n counter = [0]*(num_max)\n | ixuhangyi | NORMAL | 2022-12-31T12:53:05.583149+00:00 | 2022-12-31T12:55:09.023358+00:00 | 101 | false | ```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n \n num_max = max(nums) + 1\n counter = [0]*(num_max)\n \n for n in nums:\n counter[n] += 1\n \n counter_prefix = [0] * (num_max)\n counter_prefix[0] = counter[0]\n # get prefix sum for each number\n\n for i in range(1, len(counter)):\n counter_prefix[i] = counter_prefix[i - 1] + counter[i]\n result = 0\n for i in range(1, num_max):\n\t\t\t# iterate through numbers in array\n if counter[i] == 0:\n continue\n t = 1\n\t\t\t# count all numbers in the array, where y/i == t, range is [i * t inclusive, i * (t + 1) exclusive]\n while i * t < num_max:\n left = i * t - 1\n right = i * (t + 1) - 1\n if right >= num_max:\n right = num_max - 1\n # count of all "y"\n count = counter_prefix[right] - counter_prefix[left]\n result = result + count * counter[i] * t\n \n t += 1\n \n \n return result % (10**9 + 7)\n``` | 0 | 0 | ['Python'] | 0 |
sum-of-floored-pairs | Python Easy to Understand Solution | Sorting | Binary Search | python-easy-to-understand-solution-sorti-ycph | \n\n# Code\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n nums.sort()\n res, mod, cache = 0, 1000000007, {}\n | hemantdhamija | NORMAL | 2022-12-08T11:01:28.171565+00:00 | 2022-12-08T11:01:28.171613+00:00 | 174 | false | \n\n# Code\n```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n nums.sort()\n res, mod, cache = 0, 1000000007, {}\n for idx, num in enumerate(nums):\n if num in cache:\n res += cache[num]\n else:\n currentRes, j = 0, idx\n while j < len(nums):\n multiplier = nums[j] // num\n lastPosition = bisect_left(nums, num * (multiplier + 1), j)\n currentRes += (lastPosition - j) * multiplier\n j = lastPosition\n cache[num] = currentRes\n res += currentRes\n res %= mod\n return res\n``` | 0 | 0 | ['Binary Search', 'Sorting', 'Python', 'Python3'] | 0 |
sum-of-floored-pairs | sort and count values in range using binary search | sort-and-count-values-in-range-using-bin-piyb | \nfrom collections import Counter\nimport bisect\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n n = len(nums)\n ct | theabbie | NORMAL | 2022-11-27T06:17:19.286732+00:00 | 2022-11-27T06:17:19.286768+00:00 | 109 | false | ```\nfrom collections import Counter\nimport bisect\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n n = len(nums)\n ctr = Counter(nums)\n nums.sort()\n res = 0\n for el in ctr:\n mul = 1\n while el * mul <= nums[-1]:\n res += ctr[el] * (bisect.bisect_left(nums, el * (mul + 1)) - bisect.bisect_left(nums, el * mul)) * mul\n mul += 1\n return res % (10 ** 9 + 7)\n``` | 0 | 0 | ['Python'] | 0 |
sum-of-floored-pairs | Easy C++ solution || commented | easy-c-solution-commented-by-saiteja_bal-xsgb | \nclass Solution {\npublic:\n #define ll long long\n #define MOD 1000000007;\n int sumOfFlooredPairs(vector<int>& nums) {\n ll ans=0;\n l | saiteja_balla0413 | NORMAL | 2022-10-29T14:27:11.171513+00:00 | 2022-10-29T14:27:11.171542+00:00 | 65 | false | ```\nclass Solution {\npublic:\n #define ll long long\n #define MOD 1000000007;\n int sumOfFlooredPairs(vector<int>& nums) {\n ll ans=0;\n long long last=1e5;\n //store the frequencies as a prefix sum\n vector<ll> pref(1e5+1,0);\n for(int i=0;i<nums.size();i++)\n pref[nums[i]]++;\n for(int i=1;i<=1e5;i++)\n pref[i]+=pref[i-1];\n \n //now for every num in [1,1e5] calculate its value towards the sum\n for(ll i=1;i<=1e5;i++)\n {\n if(pref[i]-pref[i-1])\n {\n ll curr=0;\n //if this has a count in nums\n for(ll j=1;i*j<=last;j++)\n {\n ll p=i*j;\n ll q=min(i*(j+1) -1,last);\n ll cnt=pref[q]-pref[p-1];\n curr+=(cnt*j);\n curr%=MOD;\n }\n ll cnt=pref[i]-pref[i-1];\n ans+=(curr*cnt);\n ans%=MOD;\n }\n }\n return (int)ans;\n }\n};\n``` | 0 | 0 | [] | 0 |
sum-of-floored-pairs | ✔️ Java solution: faster than 98.7% of other submissions | java-solution-faster-than-987-of-other-s-w5vg | This Github repository, https://github.com/AnasImloul/Leetcode-solutions, have all the solutions I was looking for.\nIt is extremely beneficial to have every so | Kagoot | NORMAL | 2022-08-21T21:53:02.836091+00:00 | 2022-08-21T21:53:02.836123+00:00 | 223 | false | This Github repository, https://github.com/AnasImloul/Leetcode-solutions, have all the solutions I was looking for.\nIt is extremely beneficial to have every solution available in one place. I hope it is useful to you as well.\n```\nclass Solution {\n public int sumOfFlooredPairs(int[] nums) {\n Arrays.sort(nums);\n int n=nums.length;\n long cnt[]=new long[nums[n-1]+2];\n for(int num:nums){\n cnt[num+1]++;\n }\n for(int i=1;i<cnt.length;i++){\n cnt[i]+=cnt[i-1];\n }\n long res=0;\n long mod=1000000007;\n long dp[]=new long[cnt.length];\n for(int num:nums){\n if(dp[num]!=0){\n res=(res+dp[num])%mod;\n continue;\n }\n long tot=0;\n for(int j=num;j<cnt.length-1;j+=num){\n tot=(tot+(j/num)*(cnt[Math.min(j+num-1,nums[n-1])+1]-cnt[j]))%mod;\n }\n dp[num]=tot;\n res=(res+tot)%mod;\n }\n return (int)res;\n }\n}\n\n``` | 0 | 0 | ['Java'] | 0 |
sum-of-floored-pairs | Java | O(nlogn) | Number theory | java-onlogn-number-theory-by-utsav_deep-e1t5 | \nclass Solution {\n public int sumOfFlooredPairs(int[] nums) {\n Arrays.sort(nums);\n int n=nums.length;\n long cnt[]=new long[nums[n-1 | utsav_deep | NORMAL | 2022-06-15T06:25:15.100258+00:00 | 2022-06-15T06:27:30.129486+00:00 | 296 | false | ```\nclass Solution {\n public int sumOfFlooredPairs(int[] nums) {\n Arrays.sort(nums);\n int n=nums.length;\n long cnt[]=new long[nums[n-1]+2];\n for(int num:nums){\n cnt[num+1]++;\n }\n for(int i=1;i<cnt.length;i++){\n cnt[i]+=cnt[i-1];\n }\n long res=0;\n long mod=1000000007;\n long dp[]=new long[cnt.length];\n for(int num:nums){\n if(dp[num]!=0){\n res=(res+dp[num])%mod;\n continue;\n }\n long tot=0;\n for(int j=num;j<cnt.length-1;j+=num){\n tot=(tot+(j/num)*(cnt[Math.min(j+num-1,nums[n-1])+1]-cnt[j]))%mod;\n }\n dp[num]=tot;\n res=(res+tot)%mod;\n }\n return (int)res;\n }\n}\n``` | 0 | 0 | ['Math', 'Java'] | 0 |
sum-of-floored-pairs | prefix sum for couting frequency otherwise brute force | prefix-sum-for-couting-frequency-otherwi-akrm | \nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& a) \n {\n int n=a.size();\n int fre[200005]; memset(fre,0,sizeof(fre));\n | diyora13 | NORMAL | 2022-06-09T10:44:31.140203+00:00 | 2022-06-09T10:44:31.140249+00:00 | 226 | false | ```\nclass Solution {\npublic:\n int sumOfFlooredPairs(vector<int>& a) \n {\n int n=a.size();\n int fre[200005]; memset(fre,0,sizeof(fre));\n map<int,int> mp;\n for(int i=0;i<n;i++)\n mp[a[i]]++,fre[a[i]]++;\n for(int i=1;i<200005;i++)\n fre[i]+=fre[i-1];\n long long ans=0,mod=1e9+7;\n for(auto i:mp)\n {\n long long cnt=0;\n for(int j=2*i.first-1,div=1;j<200005;j+=i.first,div++)\n cnt+=div*(fre[j]-fre[j-i.first]);\n ans=(ans+cnt*i.second)%mod;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'Prefix Sum', 'C++'] | 0 |
sum-of-floored-pairs | C++ NUMBER THEORY || SEIVE LIKE SOLUTION | c-number-theory-seive-like-solution-by-z-bfz1 | \n int sumOfFlooredPairs(vector<int>& A ) {\n \n int mod = 1e9;\n mod += 7 ;\n\n int mx = *max_element(A.begin(),A.end());\n | zerojude | NORMAL | 2022-05-31T03:12:08.135447+00:00 | 2022-05-31T03:12:08.135488+00:00 | 231 | false | ```\n int sumOfFlooredPairs(vector<int>& A ) {\n \n int mod = 1e9;\n mod += 7 ;\n\n int mx = *max_element(A.begin(),A.end());\n mx = 2*mx+1 ;\n \n vector<int>t(mx,0);\n \n for( auto x : A )\n t[x]++;\n \n vector<int>P(mx+1,0);\n int res = 0 ;\n \n for( int i = 0 ; i < mx ; i++ )\n P[i+1] = (P[i] + t[i])%mod ;\n \n \n\n int temp = 0 ;\n for( int i = 1 ; i < mx ; i++ )\n {\n if(t[i])\n {\n for( int j = 2*i ; j < mx ; j += i )\n {\n int a = (j-i)/i; \n int b = P[j]-P[j-i];\n int c = t[i];\n \n a %= mod ;\n b %= mod ;\n c %= mod ;\n \n res += (1LL*a*b*c)%mod ;\n res %= mod ;\n }\n }\n }\n \n return res%mod; \n }\n``` | 0 | 0 | ['C'] | 0 |
sum-of-floored-pairs | [Python] nln(n) time complexity. Count, sort and enumerate | python-nlnn-time-complexity-count-sort-a-0o2m | First count nums and sort, we mark largerst value + 1 as n, use presum to calculate how many numbers are less or equeal to v in array precnt. Then we iterate al | cava | NORMAL | 2022-05-26T07:57:07.909937+00:00 | 2022-05-26T07:57:07.909970+00:00 | 160 | false | First count nums and sort, we mark largerst value + 1 as n, use presum to calculate how many numbers are less or equeal to v in array *precnt*. Then we iterate all *k, v* pair in *cnt*, *v (precnt[min((t + 1) k - 1, n - 1)] - precnt[t k - 1]) t* will contribute to answer. For example nums = [2,3,4,5,6,7,8], k = 2, v = 1, when t = 3, we will have ans += v * t * 2, where 2 is the size of [6, 7]. In worst case, time cost is (n / 1 + n /2 + .. . + n / n) = n * (1 /1 + 1 / 2 + ... + 1/n)=nln(n).\n```\nfrom collections import Counter\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n cnt = sorted(Counter(nums).items())\n n = cnt[-1][0] + 1\n precnt, idx = [0] * n, 0\n for k in range(1, n):\n precnt[k] = precnt[k - 1]\n if cnt[idx][0] == k:\n precnt[k] += cnt[idx][1]\n idx += 1\n ans, MOD = 0, 10 ** 9 + 7\n for k, v in cnt:\n t = 1\n while t <= n // k:\n ans += v * (precnt[min((t + 1) * k - 1, n - 1)] - precnt[t * k - 1]) * t\n t += 1\n ans %= MOD\n return ans\n``` | 0 | 0 | [] | 0 |
sum-of-floored-pairs | Rust Solution | rust-solution-by-rchaser53-j07d | \nuse std::collections::*;\n\ntype Target = usize;\ntype UseValue = usize;\nfn upper_bound(arr: &Vec<Target>, x: &UseValue) -> usize {\n let mut low = 0;\n le | rchaser53 | NORMAL | 2022-05-25T13:55:39.380864+00:00 | 2022-05-25T13:55:39.380901+00:00 | 79 | false | ```\nuse std::collections::*;\n\ntype Target = usize;\ntype UseValue = usize;\nfn upper_bound(arr: &Vec<Target>, x: &UseValue) -> usize {\n let mut low = 0;\n let mut high = arr.len();\n while low != high {\n let mid = (low + high) / 2;\n match arr[mid].cmp(x) {\n std::cmp::Ordering::Less | std::cmp::Ordering::Equal => {\n low = mid + 1;\n }\n std::cmp::Ordering::Greater => {\n high = mid;\n }\n }\n }\n low\n}\n\nfn lower_bound(arr: &Vec<Target>, x: &UseValue) -> usize {\n let mut low = 0;\n let mut high = arr.len();\n while low != high {\n let mid = (low + high) / 2;\n match arr[mid].cmp(x) {\n std::cmp::Ordering::Less => {\n low = mid + 1;\n }\n std::cmp::Ordering::Equal | std::cmp::Ordering::Greater => {\n high = mid;\n }\n }\n }\n low\n}\n\nconst MOD:usize = 1_000_000_007;\n\nimpl Solution {\n pub fn sum_of_floored_pairs(nums: Vec<i32>) -> i32 {\n let mut map = HashMap::new();\n for &v in &nums {\n *map.entry(v as usize).or_insert(0) += 1;\n }\n \n let mut nums = nums.into_iter().map(|v| v as usize).collect::<Vec<usize>>();\n nums.sort();\n let n = nums.len();\n let mut result = 0;\n\n let mut memo: HashMap<usize, usize> = HashMap::new();\n for i in 0..n {\n let base = nums[i];\n if let Some(v) = memo.get(&base) {\n result += v;\n result %= MOD;\n continue\n }\n\n let mut li = upper_bound(&nums, &base);\n let mut tot = 0;\n while li < n {\n let a = nums[li] / base;\n let v = (a+1) * base;\n let ri = lower_bound(&nums, &v);\n\n let nv = ((ri - li) * a) % MOD;\n tot += nv;\n tot %= MOD;\n\n li = ri;\n }\n result += tot;\n result %= MOD;\n memo.insert(base, tot);\n }\n \n for (_, num) in map {\n result += num * num;\n result %= MOD;\n }\n\n result as i32\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
sum-of-floored-pairs | Python | Binary Search with bisect_right After Sorting | O(nlogn) | Clean Code | python-binary-search-with-bisect_right-a-kmpw | ```\nfrom bisect import bisect_right\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n M = 109 + 7\n nums.sort()\n | aryonbe | NORMAL | 2022-04-15T03:15:59.535475+00:00 | 2022-04-22T10:44:31.119543+00:00 | 159 | false | ```\nfrom bisect import bisect_right\n\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n M = 10**9 + 7\n nums.sort()\n i = 0\n n = len(nums)\n res = 0\n while i < n:\n cur = nums[i]\n l = bisect_right(nums, cur)\n #number of cur element\n curn = (l-i)\n res += curn**2\n i = l\n while l < n:\n q = nums[l]//cur\n r = bisect_right(nums, cur*q+cur-1)\n res = (res+curn*q*(r-l))%M\n l = r\n return res | 0 | 0 | ['Binary Search', 'Python'] | 0 |
sum-of-floored-pairs | C++ Solution (Got 376 ms runtime) | c-solution-got-376-ms-runtime-by-alamsah-cqoa | Will love to hear the improvements for this code in terms of performance as well as code quality .\n\n\nclass Solution {\n int MOD=1e9+7;\npublic:\n int s | alamsahil939 | NORMAL | 2022-04-03T19:20:48.324877+00:00 | 2022-04-04T21:36:57.434803+00:00 | 198 | false | Will love to hear the improvements for this code in terms of performance as well as code quality .\n\n```\nclass Solution {\n int MOD=1e9+7;\npublic:\n int sumOfFlooredPairs(vector<int>& nums) {\n vector<int> freq(1e5+1,0);\n vector<int> validNums;\n int maxNum=INT_MIN;\n for(int i=0;i<nums.size();i++)\n {\n if(!freq[nums[i]])\n {\n validNums.push_back(nums[i]);\n }\n freq[nums[i]]++;\n maxNum=max(maxNum,nums[i]);\n }\n int prevSum=0;\n for(int i=1;i<=maxNum;i++)\n {\n freq[i]+=prevSum;\n prevSum=freq[i];\n }\n int ans=0;\n for(int i=0;i<validNums.size();i++)\n {\n int num=validNums[i];\n int prevNum=0;\n int quotient=0;\n int currAns=0;\n for(int j=num;j<=maxNum;j=j+num)\n {\n if(prevNum)\n {\n int currQuotient=j/num;\n int currNum=j;\n if(currQuotient!=quotient)\n {\n currNum=j-1;\n }\n int count=freq[currNum]-freq[prevNum-1];\n currAns=(currAns%MOD+(quotient%MOD*count%MOD)%MOD)%MOD;\n }\n quotient=(j/num);\n prevNum=j;\n }\n int count=freq[maxNum]-freq[prevNum-1];\n int currNumFreq=freq[num]-freq[num-1];\n currAns=(currAns%MOD+(count%MOD*quotient%MOD)%MOD)%MOD;\n ans=(ans%MOD+((long long)currAns%MOD*currNumFreq%MOD)%MOD)%MOD;\n }\n return ans;\n \n }\n};\n``` | 0 | 0 | [] | 0 |
sum-of-floored-pairs | Binary Search Python | binary-search-python-by-saianirudh_me-6w2r | \nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n nums.sort()\n r,x=0,len(nums)\n for i in range(len(nums)):\n | saianirudh_me | NORMAL | 2022-03-15T11:27:47.435163+00:00 | 2022-03-15T11:27:47.435193+00:00 | 113 | false | ```\nclass Solution:\n def sumOfFlooredPairs(self, nums: List[int]) -> int:\n nums.sort()\n r,x=0,len(nums)\n for i in range(len(nums)):\n if i>0 and nums[i]==nums[i-1]:\n r+=tmp\n continue\n tmp,n,l=0,nums[-1]//nums[i],x\n while n>0:\n b=bisect.bisect_left(nums,nums[i]*n)\n tmp+=(l-b)*(n) \n l,n=b,n-1\n r+=tmp\n return r%(10**9+7)\n``` | 0 | 0 | [] | 0 |
sum-of-floored-pairs | Java|SimpleSolution:165ms|with|Explanation | javasimplesolution165mswithexplanation-b-o5vs | \n\n/*\nHow did you solve it \n 1. its math solution , we bascailly count the quotient for each number \n \n example if we have 2,5,9 in input \n \n our range w | victordey2007 | NORMAL | 2022-03-09T20:37:32.560268+00:00 | 2022-03-09T20:37:32.560311+00:00 | 123 | false | ```\n\n/*\nHow did you solve it \n 1. its math solution , we bascailly count the quotient for each number \n \n example if we have 2,5,9 in input \n \n our range will be till 9\n \n 0 1 2 3 4 5 6 7 8 9 \n 2 1 1 1 1\n 5 1\n 9 1\n -------------------------\n 0 0 1 2 3 4 5 6 \n\nonce we have this acculmutaed array which gives us count of quotient till one number , \nnow i loop over number and add the count on each number and return the sum \n\nexample in this example i will take ( 1 from 2 position, 3 from 5 position , 6 from 9th position ), return 10 as result \n*/\n\n\nclass Solution {\n\tpublic int sumOfFlooredPairs(int[] nums) {\n\t\tlong mod = 1000000007;\n\t\tArrays.sort(nums);\n\t\tint max = nums[nums.length - 1];\n\t\tint[] counts = new int[max + 1];\n\t\tlong[] qnts = new long[max + 1];\n\t\tfor (int k : nums)\n\t\t\tcounts[k]++;\n\t\tfor (int i = 1; i < max + 1; i++) {\n\t\t\tif (counts[i] == 0)\n\t\t\t\tcontinue;\n\t\t\tint j = i;\n\t\t\twhile (j <= max) {\n\t\t\t\tqnts[j] += counts[i];\n\t\t\t\tj = j + i;\n\t\t\t}\n\t\t}\n\t\tfor (int i = 1; i < max + 1; i++)\n\t\t\tqnts[i] = (qnts[i] + qnts[i - 1]) % mod;\n\t\tlong sum = 0;\n\t\tfor (int k : nums)\n\t\t\tsum = (sum + qnts[k]) % mod;\n\t\treturn (int) sum;\n\t}\n}\n``` | 0 | 0 | [] | 0 |
sum-of-floored-pairs | Java prefix sum | java-prefix-sum-by-mi1-a6af | \nclass Solution {\n public int sumOfFlooredPairs(int[] nums) {\n int mod = (int) Math.pow(10,9)+7;\n HashMap<Integer,Integer> map = new HashMa | mi1 | NORMAL | 2022-02-18T19:48:44.868746+00:00 | 2022-02-18T19:48:44.868787+00:00 | 108 | false | ```\nclass Solution {\n public int sumOfFlooredPairs(int[] nums) {\n int mod = (int) Math.pow(10,9)+7;\n HashMap<Integer,Integer> map = new HashMap<>();\n int max = Arrays.stream(nums).max().getAsInt();\n int [] arr = new int[2*max];\n for(int num : nums){\n arr[num]++;\n map.put(num,map.getOrDefault(num,0)+1);\n }\n for(int i = 1;i<arr.length;i++){\n arr[i]+=arr[i-1];\n }\n long total = 0;\n for(int key : map.keySet()){\n for(int i = key,j=1;i<arr.length;i+=key,j++){\n if(i+key-1<arr.length){\n int countNums = arr[i+key-1]-arr[i-1];\n long val = j*countNums;\n val%=mod;\n val = (val*map.get(key))%mod;\n total+=val;\n total%=mod; \n }\n }\n }\n return (int) total;\n }\n}\n``` | 0 | 0 | [] | 0 |
sum-of-floored-pairs | What is wrong with this solution for TLE? | what-is-wrong-with-this-solution-for-tle-jp57 | ```class Solution {\n public int sumOfFlooredPairs(int[] nums) {\n int sum = 0;\n \n\n ArrayDeque q = new ArrayDeque();\n for(i | nexant9 | NORMAL | 2022-02-10T04:01:33.550070+00:00 | 2022-02-10T04:01:33.550095+00:00 | 92 | false | ```class Solution {\n public int sumOfFlooredPairs(int[] nums) {\n int sum = 0;\n \n\n ArrayDeque<Integer> q = new ArrayDeque<Integer>();\n for(int i : nums)\n q.offer(i);\n\n while(!q.isEmpty()) {\n int top = q.poll();\n for(int i = 0; i < nums.length; i++) {\n sum += top / nums[i];\n }\n }\n\n return sum;\n }\n} | 0 | 1 | ['Queue'] | 1 |
sum-of-floored-pairs | Floored pair | floored-pair-by-yadavanuj109-zpsp | Explanation : \n Sort the array\n Find the prefix sum (ps) where the ith element contains number of elements <= i. \n For eg. sorted arr -> 1, 1, 2, 5 | yadavanuj109 | NORMAL | 2022-02-01T03:47:58.787241+00:00 | 2022-02-01T03:47:58.787284+00:00 | 143 | false | **Explanation** : \n* Sort the array\n* Find the prefix sum (ps) where the ith element contains number of elements <= i. \n For eg. sorted arr -> 1, 1, 2, 5\n\t prefix sum -> 0, 2, 2, 3, 3, 4\n* Since the array is sorted. Time complexity for finding the floored sum will be O(n)\n **Reason** : \n\t\t\t\t\tLet\'s take a sorted array : 2, 5, 10, 17, 20, 25, 26, 35\n\t\t\t\t\tFloored sum for (i, j) : Math.floor(arr[j]/arr[i])\n\t\t\t\tfor i = 1 -> | (2/2) <= (5/2) <= (10/2) <= (17/2) <= ..... <= (35/2)\n\t\t\t\tfor i = 2 -> | (5/5) <= (10/5) <= (17/5) <= ...... <= (35/5)\n\t\t\t\t....\n\t\t\t\tfor i = 1 -> minimum floored value is 1 and maximum 17\n\t\t\t\tfor i = 2 -> minimum floored value is 1 and maximum 7\n\t\t\t\t....\n\t\t\t\thence for worst time complexity where the sorted array is 1,2,3,4,5,...,n\n\t\t\t\tfor i = 1 -> minimum floored value is 1 and maximum n\n\t\t\t\tfor i = 2 -> minimum floored value is 1 and maximum (n/2)\n\t\t\t\tfor i = 2 -> minimum floored value is 1 and maximum (n/3)\n\t\t\t\t\n **Hence**, if we iterate for every i, from minimum floored value to maximum floored value\n Time complexity will be ->\n n + (n/2) + (n/3) + .... + (n/n-1) + 1 = 1 + n * ((1/2) + (1/3) + (1/4) + .... + (1/(n-1))\n\t\t\tfor n = 10^5 \n\t\t\t\t<= 1 + 13n = O(n)\n\t\t\t\t\n\tThus, finding the floored sum follows,\n\t\t\t\tfor any floored value x and arr[i].. find the number of elements in between \n\t\t\t\t arr[i] * (x + 1) - 1 and arr[i] * x (which we\'ll get using the ps array)\n\t\t\t\tupdate the sum with the above value multiplied with x\n\t\t\t\t\n\tDo this for all arr[i] and the respective floored sum!!\n\t\n\t\n\tTime complexity -> O(nlogn) (sorting) + O(n) (as discussed above) = O(nlogn)\n\t\t\t\t\n \t\t\t \n```\nvar sumOfFlooredPairs = function(nums) {\n let p = Math.pow(10, 9) + 7;\n nums.sort((a, b) => (a - b));\n\n let ps = [0];\n let sum = 0;\n\n for (let i = 1; i <= nums[nums.length - 1]; i++) {\n ps[i] = 0;\n }\n for (let i = 0; i < nums.length; i++) {\n ps[nums[i]]++;\n }\n for (let i = 1; i <= nums[nums.length - 1]; i++) {\n ps[i] = ps[i] + ps[i - 1];\n }\n\n let prevSum = 0;\n for (let i = 0; i < nums.length; i++) {\n\n if (i > 0 && nums[i] === nums[i - 1]) sum += prevSum;\n else {\n prevSum = 0;\n let flooredValue = Math.floor(nums[nums.length - 1] / nums[i]);\n for (let j = 1; j <= flooredValue; j++) {\n let lastIndex = ((nums[i] * (j + 1) - 1) > nums[nums.length - 1] ? nums[nums.length - 1] : (nums[i] * (j + 1) - 1));\n prevSum += (ps[lastIndex] - ps[(j * nums[i] - 1)]) * j;\n prevSum %= p;\n }\n sum += prevSum;\n }\n\n sum %= p;\n }\n return sum; \n};\n``` | 0 | 0 | ['Math', 'Prefix Sum'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.