question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-number-of-fish-in-a-grid | 695. Max Area of Island | 695-max-area-of-island-by-votrubac-lngk | This is similar to 695. Max Area of Island.\n\nFor each "island" of water, it does not matter where fisherman starts. We just need to mark a visited cell by set | votrubac | NORMAL | 2023-04-29T16:01:01.057026+00:00 | 2023-04-29T16:10:20.218358+00:00 | 2,004 | false | This is similar to [695. Max Area of Island](https://leetcode.com/problems/max-area-of-island/).\n\nFor each "island" of water, it does not matter where fisherman starts. We just need to mark a visited cell by setting it to zero.\n\n```cpp \nint dfs(int r, int c, vector<vector<int>>& g) {\n if (min(r, c) < 0 || r == g.size() || c == g[r].size() || g[r][c] == 0)\n return 0;\n return exchange(g[r][c], 0) + dfs(r + 1, c, g) + dfs(r, c + 1, g) + dfs(r - 1, c, g) + dfs(r, c - 1, g);\n}\nint findMaxFish(vector<vector<int>>& g) {\n int res = 0;\n for (int r = 0; r < g.size(); ++r)\n for (int c = 0; c < g[r].size(); ++c)\n res = max(res, dfs(r, c, g));\n return res;\n}\n``` | 19 | 3 | [] | 1 |
maximum-number-of-fish-in-a-grid | ez DFS, BFS vs UnionFind||C++ beats 100% | ez-dfsc-beats-100-by-anwendeng-nd07 | Intuition1st approach uses DFS.
2nd approach uses BFS.
3rd approach uses UnionFind
This problem has the identical solution with 695. Max Area of Island
thanks | anwendeng | NORMAL | 2025-01-28T00:20:30.749362+00:00 | 2025-01-28T14:14:17.278432+00:00 | 1,622 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1st approach uses DFS.
2nd approach uses BFS.
3rd approach uses UnionFind
This problem has the identical solution with [695. Max Area of Island
](https://leetcode.com/problems/max-area-of-island/solutions/3548861/easy-c-solution-using-dfs-recursion/) thanks to comments by @Sergei.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Declare `d[5]={0, 1, 0, -1, 0}` as a memeber variable for 4 directions
2. let `n, m` be member variables
3. Define the recursive dfs function as follows
```
int dfs(int i, int j, vector<vector<int>>& grid){
int fish=grid[i][j];//obtain the fish in cell (i, j)
grid[i][j]=0;// visited
for (int a=0; a<4; a++){// 4 adjacent cells
int r=i+d[a], c=j+d[a+1]; //adjacent cell (r,c)
if (r<0 || r>=n || c<0 || c>=m || grid[r][c]==0)
continue; // outside or visited
fish+=dfs(r, c, grid);// recursive call
}
return fish;
}
```
4. in `int findMaxFish(vector<vector<int>>& grid)` let `n=|grid|, m=|m=grid[0]` by the matrix convention
5. Proceed the double loop
`if (grid[i][j]>0)
ans=max(ans, dfs(i, j, grid)) for i, j`
6. return `ans`
7. BFS is done.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(nm)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(nm)$$
# Code DFS||C++ 0ms beats 100%
```cpp []
class Solution {
public:
const int d[5]={0, 1, 0, -1, 0};
int n, m;
int dfs(int i, int j, vector<vector<int>>& grid){
int fish=grid[i][j];
grid[i][j]=0;// visited
for (int a=0; a<4; a++){
int r=i+d[a], c=j+d[a+1];
if (r<0 || r>=n || c<0 || c>=m || grid[r][c]==0)
continue;
fish+=dfs(r, c, grid);
}
return fish;
}
int findMaxFish(vector<vector<int>>& grid) {
n=grid.size(), m=grid[0].size();
int ans=0;
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
if (grid[i][j]>0)
ans=max(ans, dfs(i, j, grid));
}
}
return ans;
}
};
```
# Standard Grid/Matrix/Graph problems can solved with DFS/BFS
There are many such kinds of such problem in Leetcode. The fastest way to implement is DFS, & then BFS. If the graph is undirected, some of them can be solved even by UnionFind; but some of them needs more tricks.
The question [1992. Find All Groups of Farmland](https://leetcode.com/problems/find-all-groups-of-farmland/solutions/5047793/dfs-bfs-vs-find-rectangle-corner-74ms-beats-99-64/) is solved by DFS& BFS.
[Please turn on English titles]
[https://youtu.be/v-w9EF67it8?si=Tjqli8PvGjYh0t8X](https://youtu.be/v-w9EF67it8?si=Tjqli8PvGjYh0t8X)
# 2nd Approach uses BFS & sets grid[r][c]=0 as visited
```
// the bfs is called in the same way in dfs solution
int bfs(int i, int j, vector<vector<int>>& grid){
int fish=grid[i][j];
queue<uint8_t> q; // 10*10<256
grid[i][j]=0;// visited
q.push((i<<4)+j); // push packed (i, j) to q
while(!q.empty()){
int idx=q.front(), s=idx>>4, t=idx&15;// get (r, s)
q.pop();
for (int a=0; a<4; a++){// adjacent cells
int r=s+d[a], c=t+d[a+1];
if (r<0 || r>=n || c<0 || c>=m || grid[r][c]==0)
continue;// ouside or visited
fish+=grid[r][c]; // add it to fish
q.push((r<<4)+c); // push the packed (r, c) to q
grid[r][c]=0;// visited
}
}
return fish;
}
```
# UnionFind is good for Undirected Graph
Time complexity for UnionFind: $$O(\alpha(nm)nm)$$ where $\alpha(\cdot)$ is the inverse Ackermann function.
Use UnionFind, one can also solve [959. Regions Cut By Slashes](https://leetcode.com/problems/regions-cut-by-slashes/solutions/5614770/unionfind-dfs-euler-theorem-v-e-f-2-beats-100/)
[https://youtu.be/cR_D4uA3g3s?si=7mIs9wQ0ifN_GoGA](https://youtu.be/cR_D4uA3g3s?si=7mIs9wQ0ifN_GoGA)
1. UnionFind uses Size optimization which has similar performance like rank optimization
2. Since the matrix is small, say at most `10x10` Unionfind brings no benefit over DFS/BFS.
3. To transvere the grids, it needs only 2 directions, i.e. righttward & downwards; for large matrix, this can save much time.
4. The implemented Union method in UnionFind will return true when 2 disjoint components are really connected by this edge, other return false.
5. The crucial part for using Union is as follow:
```
sum2=sum[rA]+sum[rB];
if (G.Union(a, b)){// connect 2 components
rA=G.Find(a);// rA=new root for a & b
sum[rA]=sum2;// Put fish for root rA
ans=max(ans, sum2);// update ans
}
```
# Code for UnionFind
```
// union find class with size
class UnionFind {
vector<int> root, Size;
public:
int components;
UnionFind(int N) : root(N), Size(N, 1), components(N) {
iota(root.begin(), root.end(), 0);
}
int Find(int x) {
if (x == root[x])
return x;
return root[x] = Find(root[x]); // Path compression
}
bool Union(int x, int y) {
x = Find(x), y = Find(y);
if (x == y) return 0;
if (Size[x] > Size[y]) {
Size[x] += Size[y];
root[y] = x;
} else {
Size[y] += Size[x];
root[x] = y;
}
components--;
return 1;
}
};
class Solution {
public:
int n, m;
int idx(int i, int j){ return i*m+j; }
int findMaxFish(vector<vector<int>>& grid) {
n=grid.size(), m=grid[0].size();
const int N=n*m;
vector<int> sum(N, 0);
for(int i=0; i<n; i++)
copy(grid[i].begin(), grid[i].end(), sum.begin()+(i*m));
UnionFind G(N);
int ans=0, sum2;
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
if (grid[i][j]>0){
ans=max(ans, grid[i][j]);// for 1-cell components
int a=idx(i, j), rA, rB, b;
int D=(i<n-1)?grid[i+1][j]:0, R=(j<m-1)?grid[i][j+1]:0;
if (D>0){// down
b=a+m;
rA=G.Find(a), rB=G.Find(b);
sum2=sum[rA]+sum[rB];
if (G.Union(a, b)){ // connect 2 components
rA=G.Find(a);// new root for a
sum[rA]=sum2;
ans=max(ans, sum2);
}
}
if (R>0){// right
b=a+1;
rA=G.Find(a), rB=G.Find(b);
sum2=sum[rA]+sum[rB];
if (G.Union(a, b)){// connect 2 components
rA=G.Find(a);// new root for a
sum[rA]=sum2;
ans=max(ans, sum2);
}
}
}
}
}
return ans;
}
};
```
| 18 | 4 | ['Depth-First Search', 'Breadth-First Search', 'Union Find', 'C++'] | 4 |
maximum-number-of-fish-in-a-grid | It is fishing time🎣 Maximum Fish Catcher! 🐟 | it-is-fishing-time-maximum-fish-catcher-uuoaj | 🧠 IntuitionThe problem involves exploring all possible paths from any starting water cell (r, c) to maximize the number of fish caught. This can be visualized a | lasheenwael9 | NORMAL | 2025-01-28T06:32:40.000931+00:00 | 2025-01-28T06:32:40.000931+00:00 | 557 | false | # 🧠 Intuition
The problem involves exploring all possible paths from any starting water cell `(r, c)` to maximize the number of fish caught. This can be visualized as a **graph traversal problem**, where cells are nodes, and adjacency defines edges.
We will simulate the fisher's movement using **Breadth-First Search (BFS)** to collect fish in all reachable water cells.
---
# 🚀 Approach
1. Traverse the grid to identify potential starting water cells `(r, c)`.
2. Use BFS from each starting cell to collect all fish in connected water cells.
3. Track the **maximum fish count** among all possible starting cells.
4. Mark cells as visited (by setting `grid[r][c] = 0`) during BFS to avoid revisiting them.
---
# 💻 Complexity Analysis
- **Time Complexity:** $$\ O(m \times n)$$
We iterate over all cells in the grid and perform BFS from each water cell. Each cell is visited at most once during BFS.
- **Space Complexity:** $$\ O(m \times n)$$
The BFS queue can grow to the size of the grid in the worst case.
---

# 🧑💻 Code
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int res = 0;
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (grid[i][j] > 0) { // Water cell with fish
res = max(res, bfs(grid, i, j));
}
}
}
return res;
}
private:
int bfs(vector<vector<int>>& grid, int i, int j) {
int res = 0;
queue<pair<int, int>> q;
q.push({i, j});
while (!q.empty()) {
auto [r, c] = q.front(); q.pop();
if (grid[r][c] == 0) continue;
res += grid[r][c];
grid[r][c] = 0; // Mark cell as visited
vector<pair<int, int>> directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (auto [dr, dc] : directions) {
int nr = r + dr, nc = c + dc;
if (nr >= 0 && nr < grid.size() && nc >= 0 && nc < grid[0].size() && grid[nr][nc] > 0) {
q.push({nr, nc});
}
}
}
return res;
}
};
```
```python []
from collections import deque
class Solution:
def findMaxFish(self, grid):
def bfs(grid, i, j):
q = deque([(i, j)])
total_fish = 0
while q:
r, c = q.popleft()
if grid[r][c] == 0:
continue
total_fish += grid[r][c]
grid[r][c] = 0 # Mark cell as visited
for dr, dc in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
nr, nc = r + dr, c + dc
if 0 <= nr < len(grid) and 0 <= nc < len(grid[0]) and grid[nr][nc] > 0:
q.append((nr, nc))
return total_fish
max_fish = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] > 0: # Water cell with fish
max_fish = max(max_fish, bfs(grid, i, j))
return max_fish
```
---
# 🔍 Examples
### Example 1
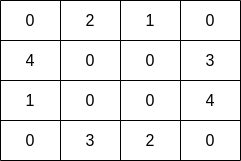
**Input:**
```python
grid = [[0, 2, 1, 0], [4, 0, 0, 3], [1, 0, 0, 4], [0, 3, 2, 0]]
```
**Output:**
```python
7
```
**Explanation:**
- Start at cell `(1, 3)` and catch `3` fish.
- Move to cell `(2, 3)` and catch `4` fish.
- Total = `7`.
> > > > > > >> > > > > > >> > > > > > >> > > > > > > ---
### Example 2
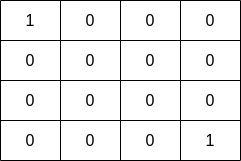
**Input:**
```python
grid = [[1, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 1]]
```
**Output:**
```python
1
```
**Explanation:**
- Start at cell `(0, 0)` or `(3, 3)` to catch `1` fish.
---
# Takeaway 🚀
**Thank you for reading! 😊 I hope this solution helps you understand and solve the problem effectively. Happy coding! 🚀**

| 14 | 3 | ['Array', 'Breadth-First Search', 'Matrix', 'Python', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | 2 Approaches 😈😈|| Beats 💯% with proof 📜 || Easy DFS 🌲 || Recursion 🔄 | 2-approaches-beats-with-proof-easy-dfs-r-n7tt | Approach - 1Complexity
Time complexity: O(M∗N)
Space complexity: O(M∗N)
CodeApproach - 2Complexity
Time complexity: O(M∗N)
Space complexity: O(1)
Code
Please | Garv_Virmani | NORMAL | 2025-01-28T06:29:04.021886+00:00 | 2025-01-28T06:29:04.021886+00:00 | 1,633 | false | 
```
Plzzz... Upvote!!
```
# Approach - 1
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(M*N)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(M*N)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int m,n;
int solve(int i,int j,vector<vector<int>>&grid,vector<vector<bool>>&vis){
if(i<0 || i>=m || j<0 || j>=n || vis[i][j] || !grid[i][j]){
return 0;
}
int temp=grid[i][j];
vis[i][j]=1;
temp+=solve(i+1,j,grid,vis);
temp+=solve(i-1,j,grid,vis);
temp+=solve(i,j+1,grid,vis);
temp+=solve(i,j-1,grid,vis);
return temp;
}
int findMaxFish(vector<vector<int>>& grid) {
m=grid.size(),n=grid[0].size();
int ans=0;
vector<vector<bool>>vis(m,vector<bool>(n,0));
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j] && !vis[i][j]){
ans=max(ans,solve(i,j,grid,vis));
}
}
}
return ans;
}
};
```
```java []
class Solution {
int m, n;
public int solve(int i, int j, int[][] grid, boolean[][] vis) {
if (i < 0 || i >= m || j < 0 || j >= n || vis[i][j] || grid[i][j] == 0) return 0;
int temp = grid[i][j];
vis[i][j] = true;
temp += solve(i + 1, j, grid, vis);
temp += solve(i - 1, j, grid, vis);
temp += solve(i, j + 1, grid, vis);
temp += solve(i, j - 1, grid, vis);
return temp;
}
public int findMaxFish(int[][] grid) {
m = grid.length;
n = grid[0].length;
int ans = 0;
boolean[][] vis = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] != 0 && !vis[i][j]) {
ans = Math.max(ans, solve(i, j, grid, vis));
}
}
}
return ans;
}
}
```
```javascript []
var m, n;
var solve = function(i, j, grid, vis) {
if (i < 0 || i >= m || j < 0 || j >= n || vis[i][j] || grid[i][j] === 0) return 0;
let temp = grid[i][j];
vis[i][j] = true;
temp += solve(i + 1, j, grid, vis);
temp += solve(i - 1, j, grid, vis);
temp += solve(i, j + 1, grid, vis);
temp += solve(i, j - 1, grid, vis);
return temp;
};
var findMaxFish = function(grid) {
m = grid.length;
n = grid[0].length;
let ans = 0;
let vis = Array.from({ length: m }, () => Array(n).fill(false));
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] !== 0 && !vis[i][j]) {
ans = Math.max(ans, solve(i, j, grid, vis));
}
}
}
return ans;
};
```
```python []
class Solution:
def solve(self, i, j, grid, vis):
if i < 0 or i >= self.m or j < 0 or j >= self.n or vis[i][j] or grid[i][j] == 0:
return 0
temp = grid[i][j]
vis[i][j] = True
temp += self.solve(i + 1, j, grid, vis)
temp += self.solve(i - 1, j, grid, vis)
temp += self.solve(i, j + 1, grid, vis)
temp += self.solve(i, j - 1, grid, vis)
return temp
def findMaxFish(self, grid):
self.m, self.n = len(grid), len(grid[0])
ans = 0
vis = [[False] * self.n for _ in range(self.m)]
for i in range(self.m):
for j in range(self.n):
if grid[i][j] != 0 and not vis[i][j]:
ans = max(ans, self.solve(i, j, grid, vis))
return ans
```
---
# Approach - 2
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(M*N)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int m,n;
int solve(int i,int j,vector<vector<int>>&grid){
if(i<0 || i>=m || j<0 || j>=n || !grid[i][j]){
return 0;
}
int temp=grid[i][j];
grid[i][j]=0;
temp+=solve(i+1,j,grid);
temp+=solve(i-1,j,grid);
temp+=solve(i,j+1,grid);
temp+=solve(i,j-1,grid);
return temp;
}
int findMaxFish(vector<vector<int>>& grid) {
m=grid.size(),n=grid[0].size();
int ans=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]){
ans=max(ans,solve(i,j,grid));
}
}
}
return ans;
}
};
```
```java []
class Solution {
int m, n;
public int solve(int i, int j, int[][] grid) {
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == 0) return 0;
int temp = grid[i][j];
grid[i][j] = 0;
temp += solve(i + 1, j, grid);
temp += solve(i - 1, j, grid);
temp += solve(i, j + 1, grid);
temp += solve(i, j - 1, grid);
return temp;
}
public int findMaxFish(int[][] grid) {
m = grid.length;
n = grid[0].length;
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] != 0) {
ans = Math.max(ans, solve(i, j, grid));
}
}
}
return ans;
}
}
```
```javascript []
var m, n;
var solve = function(i, j, grid) {
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] === 0) return 0;
let temp = grid[i][j];
grid[i][j] = 0;
temp += solve(i + 1, j, grid);
temp += solve(i - 1, j, grid);
temp += solve(i, j + 1, grid);
temp += solve(i, j - 1, grid);
return temp;
};
var findMaxFish = function(grid) {
m = grid.length;
n = grid[0].length;
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] !== 0) {
ans = Math.max(ans, solve(i, j, grid));
}
}
}
return ans;
};
```
```python []
class Solution:
def solve(self, i, j, grid):
if i < 0 or i >= self.m or j < 0 or j >= self.n or grid[i][j] == 0:
return 0
temp = grid[i][j]
grid[i][j] = 0
temp += self.solve(i + 1, j, grid)
temp += self.solve(i - 1, j, grid)
temp += self.solve(i, j + 1, grid)
temp += self.solve(i, j - 1, grid)
return temp
def findMaxFish(self, grid):
self.m, self.n = len(grid), len(grid[0])
ans = 0
for i in range(self.m):
for j in range(self.n):
if grid[i][j] != 0:
ans = max(ans, self.solve(i, j, grid))
return ans
```
---
> Please Upvote !!

| 13 | 0 | ['Array', 'Math', 'Depth-First Search', 'Recursion', 'Matrix', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
maximum-number-of-fish-in-a-grid | Explained | C++ | Java | DFS | BFS | Beginner Friendly Code | | explained-c-java-dfs-bfs-beginner-friend-qhnz | DFS Approach\n\n\n1. Define a helper function dfs that takes the grid, the row index r, and the column index c as arguments. The function returns the total numb | Rishabhsinghal12 | NORMAL | 2023-04-29T16:01:28.853373+00:00 | 2023-04-29T16:16:01.545185+00:00 | 1,678 | false | **DFS Approach**\n\n```\n1. Define a helper function dfs that takes the grid, the row index r, and the column index c as arguments. The function returns the total number of fish caught starting from the cell (r, c).\n2. In the dfs function, check if the current cell is out of bounds or a land cell. If so, return 0 (base case).\n3. Otherwise, catch the fish at the current cell by storing its value in a variable fishCaught.\n4. Mark the current cell as caught by setting its value to 0 in the grid.\n5. Define an array moves that contains the possible movements of the fisherman. Each movement is defined as an array of two integers, representing the change in row and column indices, respectively.\n6. For each possible movement in moves, calculate the new cell coordinates by adding the movement to the current cell coordinates.\n7. Recursively call the dfs function with the new cell coordinates, and add the result to fishCaught.\n8. Return fishCaught.\n9. In the findMaxFish function, initialize a variable maxFish to 0 to keep track of the maximum number of fish caught by the fisherman.\n10. Iterate over every cell in the grid.\n11. For each water cell (i.e., cells with a positive value), start a DFS search using the dfs function to find the maximum number of fish that can be caught starting from this cell.\n12. Update maxFish to the maximum value between maxFish and the number of fish caught starting from the current water cell.\n13. Return maxFish.\n```\n\n**C++ Code For DFS Approach**\n```\nint dfs(vector<vector<int>>& grid, int r, int c) {\n if (r < 0 || r >= grid.size() || c < 0 || c >= grid[0].size() || grid[r][c] == 0) {\n return 0; // Base case: out of bounds or land cell\n }\n int fishCaught = grid[r][c]; // Catch fish at current cell\n grid[r][c] = 0; // Mark cell as caught\n int moves[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // Possible movements\n for (int i = 0; i < 4; i++) {\n int newR = r + moves[i][0];\n int newC = c + moves[i][1];\n fishCaught += dfs(grid, newR, newC); // Recursively search adjacent cells\n }\n return fishCaught;\n}\n\nint findMaxFish(vector<vector<int>>& grid) {\n int maxFish = 0;\n for (int i = 0; i < grid.size(); i++) {\n for (int j = 0; j < grid[0].size(); j++) {\n if (grid[i][j] > 0) { // Start DFS search from water cell\n int fishCaught = dfs(grid, i, j);\n maxFish = max(maxFish, fishCaught);\n }\n }\n }\n return maxFish;\n}\n```\n\n**Java Code For DFS Approach**\n```\npublic int dfs(int[][] grid, int r, int c) {\n if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length || grid[r][c] == 0) {\n return 0; // Base case: out of bounds or land cell\n }\n int fishCaught = grid[r][c]; // Catch fish at current cell\n grid[r][c] = 0; // Mark cell as caught\n int[][] moves = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // Possible movements\n for (int[] move : moves) {\n int newR = r + move[0];\n int newC = c + move[1];\n fishCaught += dfs(grid, newR, newC); // Recursively search adjacent cells\n }\n return fishCaught;\n}\n\npublic int findMaxFish(int[][] grid) {\n int maxFish = 0;\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n if (grid[i][j] > 0) { // Start DFS search from water cell\n int fishCaught = dfs(grid, i, j);\n maxFish = Math.max(maxFish, fishCaught);\n }\n }\n }\n return maxFish;\n}\n```\n\n**BFS Approach:**\n```\n1. Initialize a variable maxFish to 0 to keep track of the maximum number of fish caught by the fisherman.\n2. Get the size of the grid m x n.\n3. Define a 2D array moves that contains the possible movements of the fisherman. Each movement is defined as an array of two integers, representing the change in row and column indices, respectively.\n4. Iterate over every cell in the grid.\n5. For each water cell (i.e., cells with a positive value), start a BFS search to find the maximum number of fish that can be caught starting from this cell.\n6. Initialize a queue and add the current water cell coordinates to the queue.\n7. Initialize a variable fishCaught to 0 to keep track of the number of fish caught starting from the current water cell.\n8. While the queue is not empty, do the following:\n\ta. Dequeue the front element of the queue, representing the current water cell coordinates.\n\tb. If the current cell contains fish (i.e., has a positive value), catch the fish and add its value to fishCaught. Set the cell value to 0 to mark it as caught.\n\tc. Iterate over every possible movement in the moves array.\n\td. Calculate the new cell coordinates by adding the movement to the current cell coordinates.\n\te. If the new cell is within the bounds of the grid and is a water cell (i.e., has a positive value), add its coordinates to the queue.\n9. Update maxFish to the maximum value between maxFish and fishCaught.\n10. Return maxFish.\n```\n\n**C++ Code For BFS Approach**\n```\nint findMaxFish(vector<vector<int>>& grid) {\n int maxFish = 0;\n int m = grid.size();\n int n = grid[0].size();\n \n vector<vector<int>> moves = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // Possible moves\n \n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] > 0) { // Start at a water cell\n queue<pair<int, int>> q;\n q.push({i, j});\n int fishCaught = 0;\n while (!q.empty()) {\n int r = q.front().first;\n int c = q.front().second;\n q.pop();\n if (grid[r][c] > 0) { // Catch fish at current cell\n fishCaught += grid[r][c];\n grid[r][c] = 0; // Mark cell as caught\n }\n for (auto& move : moves) { // Iterate over possible moves\n int newR = r + move[0];\n int newC = c + move[1];\n if (newR >= 0 && newR < m && newC >= 0 && newC < n && grid[newR][newC] > 0) {\n q.push({newR, newC}); // Add new water cell to queue\n }\n }\n }\n maxFish = max(maxFish, fishCaught);\n }\n }\n }\n \n return maxFish;\n}\n```\n\n**Java Code For BFS Approach**\n\n```\npublic int findMaxFish(int[][] grid) {\n int maxFish = 0;\n int[][] moves = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // Possible movements\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n if (grid[i][j] > 0) { // Start BFS search from water cell\n int fishCaught = 0;\n Queue<int[]> queue = new LinkedList<>(); // Queue for BFS\n queue.offer(new int[]{i, j}); // Enqueue current cell\n while (!queue.isEmpty()) {\n int[] curr = queue.poll(); // Dequeue first cell\n int r = curr[0];\n int c = curr[1];\n if (grid[r][c] > 0) { // Catch fish at current cell\n fishCaught += grid[r][c];\n grid[r][c] = 0; // Mark cell as caught\n }\n for (int[] move : moves) {\n int newR = r + move[0];\n int newC = c + move[1];\n if (newR >= 0 && newR < grid.length && newC >= 0 && newC < grid[0].length && grid[newR][newC] > 0) {\n queue.offer(new int[]{newR, newC}); // Enqueue adjacent water cell\n }\n }\n }\n maxFish = Math.max(maxFish, fishCaught);\n }\n }\n }\n return maxFish;\n}\n```\n\n**PLEASE DO UPVOTE** | 12 | 2 | ['Depth-First Search', 'Breadth-First Search', 'C', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | [C++] DFS | BFS | Union Find | Maximum of Water Components | c-dfs-bfs-union-find-maximum-of-water-co-9uat | Intuition\nWe can traverse only one complete component of water cells and catch all the fishes in it. Do a DFS/BFS traversal on every water component and count | shivamaggarwal513 | NORMAL | 2023-04-29T16:02:20.721468+00:00 | 2023-05-14T11:25:54.866452+00:00 | 839 | false | # Intuition\nWe can traverse only one complete component of water cells and catch all the fishes in it. Do a DFS/BFS traversal on every water component and count total number of fishes in that component. Take maximum of all possible water components.\n\n# Recursive DFS\n```\nclass Solution {\nprivate:\n int countFishes(vector<vector<int>>& grid, vector<vector<bool>>& visited, int r, int c) {\n if (r == -1 || r == grid.size() || c == -1 || c == grid[0].size() || !grid[r][c] || visited[r][c]) {\n return 0;\n }\n visited[r][c] = true;\n return grid[r][c] +\n countFishes(grid, visited, r, c + 1) +\n countFishes(grid, visited, r, c - 1) +\n countFishes(grid, visited, r + 1, c) +\n countFishes(grid, visited, r - 1, c);\n }\n \npublic:\n int findMaxFish(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size(), result = 0;\n vector visited(m, vector<bool>(n));\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] && !visited[i][j]) {\n result = max(result, countFishes(grid, visited, i, j));\n }\n }\n }\n return result;\n }\n};\n```\n\n# Iterative DFS\n```\nclass Solution {\nprivate:\n vector<int> dr, dc;\n\n int countFishes(vector<vector<int>>& grid, vector<vector<bool>>& visited, int r, int c) {\n int m = grid.size(), n = grid[0].size(), count = 0;\n stack<pair<int, int>> s;\n s.push({r, c});\n visited[r][c] = true;\n while (!s.empty()) {\n r = s.top().first, c = s.top().second; s.pop();\n count += grid[r][c];\n for (int i = 0; i < 4; i++) {\n int r1 = r + dr[i], c1 = c + dc[i];\n if (0 <= r1 && r1 < m && 0 <= c1 && c1 < n && grid[r1][c1] && !visited[r1][c1]) {\n s.push({r1, c1});\n visited[r1][c1] = true;\n }\n }\n }\n return count;\n }\n \npublic:\n int findMaxFish(vector<vector<int>>& grid) {\n dr = vector<int>{0, 0, 1, -1};\n dc = vector<int>{1, -1, 0, 0};\n int m = grid.size(), n = grid[0].size(), result = 0;\n vector visited(m, vector<bool>(n));\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] && !visited[i][j]) {\n result = max(result, countFishes(grid, visited, i, j));\n }\n }\n }\n return result;\n }\n};\n```\n\n# Iterative BFS\n```\nclass Solution {\nprivate:\n vector<int> dr, dc;\n\n int countFishes(vector<vector<int>>& grid, vector<vector<bool>>& visited, int r, int c) {\n int m = grid.size(), n = grid[0].size(), count = 0;\n queue<pair<int, int>> q;\n q.push({r, c});\n visited[r][c] = true;\n while (!q.empty()) {\n r = q.front().first, c = q.front().second; q.pop();\n count += grid[r][c];\n for (int i = 0; i < 4; i++) {\n int r1 = r + dr[i], c1 = c + dc[i];\n if (0 <= r1 && r1 < m && 0 <= c1 && c1 < n && grid[r1][c1] && !visited[r1][c1]) {\n q.push({r1, c1});\n visited[r1][c1] = true;\n }\n }\n }\n return count;\n }\n \npublic:\n int findMaxFish(vector<vector<int>>& grid) {\n dr = vector<int>{0, 0, 1, -1};\n dc = vector<int>{1, -1, 0, 0};\n int m = grid.size(), n = grid[0].size(), result = 0;\n vector visited(m, vector<bool>(n));\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] && !visited[i][j]) {\n result = max(result, countFishes(grid, visited, i, j));\n }\n }\n }\n return result;\n }\n};\n```\n\n# Union Find\n```\nclass UnionFind {\nprivate:\n vector<int> parent, compSize, fishes;\n\npublic:\n UnionFind(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size(), mn = m * n;\n parent.resize(mn);\n compSize.resize(mn, 1);\n fishes.resize(mn);\n iota(parent.begin(), parent.end(), 0);\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n fishes[n * i + j] = grid[i][j];\n }\n }\n }\n\n int getParent(int x) {\n if (x == parent[x]) {\n return x;\n }\n return parent[x] = getParent(parent[x]);\n }\n\n void unionSet(int x, int y) {\n int parx = getParent(x), pary = getParent(y);\n if (parx != pary) {\n if (compSize[parx] < compSize[pary]) {\n swap(parx, pary);\n }\n parent[pary] = parx;\n compSize[parx] += compSize[pary];\n fishes[parx] += fishes[pary];\n }\n }\n\n int getFishes(int x) {\n return fishes[getParent(x)];\n }\n};\n\nclass Solution {\npublic:\n int findMaxFish(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size(), result = 0;\n vector<int> dr{0, 0, 1, -1}, dc{1, -1, 0, 0};\n UnionFind dsu(grid);\n for (int r = 0; r < m; r++) {\n for (int c = 0; c < n; c++) {\n if (grid[r][c]) {\n for (int k = 0; k < 4; k++) {\n int r1 = r + dr[k], c1 = c + dc[k];\n if (0 <= r1 && r1 < m && 0 <= c1 && c1 < n && grid[r1][c1]) {\n dsu.unionSet(n * r + c, n * r1 + c1);\n }\n }\n result = max(result, dsu.getFishes(n * r + c));\n }\n }\n }\n return result;\n }\n};\n```\n\n\n# Complexity\n- Time complexity: $O(mn)$\n- Space complexity: $O(mn)$ | 11 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Union Find', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | Simple java solution | simple-java-solution-by-siddhant_1602-s3ru | Complexity\n- Time complexity: O(mn)\n\n- Space complexity: O(mn)\n\n# Code\n\nclass Solution {\n public int findMaxFish(int[][] grid) {\n int sum=0;\ | Siddhant_1602 | NORMAL | 2023-04-29T16:01:00.126974+00:00 | 2023-04-30T04:08:04.512473+00:00 | 856 | false | # Complexity\n- Time complexity: $$O(m*n)$$\n\n- Space complexity: $$O(m*n)$$\n\n# Code\n```\nclass Solution {\n public int findMaxFish(int[][] grid) {\n int sum=0;\n for(int i=0;i<grid.length;i++)\n {\n for(int j=0;j<grid[0].length;j++)\n {\n if(grid[i][j]!=0)\n {\n int a[]=new int[1];\n task(grid,i,j,a);\n sum=Math.max(sum,a[0]);\n }\n }\n }\n return sum;\n }\n public void task(int grid[][], int i, int j, int a[])\n {\n if(i<0 || j<0 || i>=grid.length || j>=grid[0].length || grid[i][j]==0)\n {\n return;\n }\n a[0]+=grid[i][j];\n grid[i][j]=0;\n task(grid,i+1,j,a);\n task(grid,i-1,j,a);\n task(grid,i,j+1,a);\n task(grid,i,j-1,a);\n }\n}\n``` | 11 | 2 | ['Java'] | 1 |
maximum-number-of-fish-in-a-grid | (BFS +DFS) Simple Solution ✅ | C++| Java | Python | JavaScript | bfs-dfs-simple-solution-c-java-python-ja-9gjq | ⬆️Upvote if it helps ⬆️Connect with me on Linkedin [Bijoy Sing]BFS solutionDFS SolutionIntuition 🧠When exploring grid-based problems with connected components, | BijoySingh7 | NORMAL | 2025-01-28T05:04:46.820108+00:00 | 2025-01-28T05:04:46.820108+00:00 | 1,248 | false | # ⬆️Upvote if it helps ⬆️
---
## Connect with me on Linkedin [Bijoy Sing]
---
# BFS solution
---
```cpp []
class Solution {
public:
int bfs(int i, int j, vector<vector<int>>& grid) {
vector<vector<int>> dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
queue<pair<int, int>> q;
int n = grid.size(), m = grid[0].size();
q.push({i, j});
int fish = grid[i][j];
grid[i][j] = 0;
while (!q.empty()) {
int x = q.front().first, y = q.front().second;
q.pop();
for (auto d : dir) {
int a = x + d[0], b = y + d[1];
if (a >= 0 && a < n && b >= 0 && b < m && grid[a][b]) {
q.push({a, b});
fish += grid[a][b];
grid[a][b] = 0;
}
}
}
return fish;
}
int findMaxFish(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size(), mxFish = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (grid[i][j])
mxFish = max(mxFish, bfs(i, j, grid));
return mxFish;
}
};
```
```python []
class Solution:
def bfs(self, i, j, grid):
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
n, m = len(grid), len(grid[0])
queue = [(i, j)]
fish = grid[i][j]
grid[i][j] = 0
while queue:
x, y = queue.pop(0)
for dx, dy in directions:
a, b = x + dx, y + dy
if 0 <= a < n and 0 <= b < m and grid[a][b] > 0:
queue.append((a, b))
fish += grid[a][b]
grid[a][b] = 0
return fish
def findMaxFish(self, grid):
n, m = len(grid), len(grid[0])
mxFish = 0
for i in range(n):
for j in range(m):
if grid[i][j] > 0:
mxFish = max(mxFish, self.bfs(i, j, grid))
return mxFish
```
```java []
class Solution {
public int bfs(int i, int j, int[][] grid) {
int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int n = grid.length, m = grid[0].length;
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{i, j});
int fish = grid[i][j];
grid[i][j] = 0;
while (!queue.isEmpty()) {
int[] cell = queue.poll();
int x = cell[0], y = cell[1];
for (int[] d : directions) {
int a = x + d[0], b = y + d[1];
if (a >= 0 && a < n && b >= 0 && b < m && grid[a][b] > 0) {
queue.add(new int[]{a, b});
fish += grid[a][b];
grid[a][b] = 0;
}
}
}
return fish;
}
public int findMaxFish(int[][] grid) {
int n = grid.length, m = grid[0].length, mxFish = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] > 0) {
mxFish = Math.max(mxFish, bfs(i, j, grid));
}
}
}
return mxFish;
}
}
```
```javascript []
class Solution {
bfs(i, j, grid) {
const directions = [[-1, 0], [1, 0], [0, -1], [0, 1]];
const n = grid.length, m = grid[0].length;
const queue = [[i, j]];
let fish = grid[i][j];
grid[i][j] = 0;
while (queue.length > 0) {
const [x, y] = queue.shift();
for (const [dx, dy] of directions) {
const a = x + dx, b = y + dy;
if (a >= 0 && a < n && b >= 0 && b < m && grid[a][b] > 0) {
queue.push([a, b]);
fish += grid[a][b];
grid[a][b] = 0;
}
}
}
return fish;
}
findMaxFish(grid) {
const n = grid.length, m = grid[0].length;
let mxFish = 0;
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
if (grid[i][j] > 0) {
mxFish = Math.max(mxFish, this.bfs(i, j, grid));
}
}
}
return mxFish;
}
}
```
---
## DFS Solution
```cpp []
class Solution {
public:
int dfs(int i, int j, vector<vector<int>>& grid) {
if (i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size() || grid[i][j] == 0)
return 0;
int fish = grid[i][j];
grid[i][j] = 0; // Mark visited
vector<vector<int>> dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (auto d : dir)
fish += dfs(i + d[0], j + d[1], grid);
return fish;
}
int findMaxFish(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size(), mxFish = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] > 0)
mxFish = max(mxFish, dfs(i, j, grid));
}
}
return mxFish;
}
};
```
```python []
class Solution:
def dfs(self, i, j, grid):
if i < 0 or i >= len(grid) or j < 0 or j >= len(grid[0]) or grid[i][j] == 0:
return 0
fish = grid[i][j]
grid[i][j] = 0 # Mark visited
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
for dx, dy in directions:
fish += self.dfs(i + dx, j + dy, grid)
return fish
def findMaxFish(self, grid):
n, m = len(grid), len(grid[0])
mxFish = 0
for i in range(n):
for j in range(m):
if grid[i][j] > 0:
mxFish = max(mxFish, self.dfs(i, j, grid))
return mxFish
```
```java []
class Solution {
public int dfs(int i, int j, int[][] grid) {
if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == 0)
return 0;
int fish = grid[i][j];
grid[i][j] = 0; // Mark visited
int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (int[] d : directions)
fish += dfs(i + d[0], j + d[1], grid);
return fish;
}
public int findMaxFish(int[][] grid) {
int n = grid.length, m = grid[0].length, mxFish = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] > 0) {
mxFish = Math.max(mxFish, dfs(i, j, grid));
}
}
}
return mxFish;
}
}
```
```javascript []
class Solution {
dfs(i, j, grid) {
if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] === 0)
return 0;
let fish = grid[i][j];
grid[i][j] = 0; // Mark visited
const directions = [[-1, 0], [1, 0], [0, -1], [0, 1]];
for (const [dx, dy] of directions) {
fish += this.dfs(i + dx, j + dy, grid);
}
return fish;
}
findMaxFish(grid) {
const n = grid.length, m = grid[0].length;
let mxFish = 0;
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
if (grid[i][j] > 0) {
mxFish = Math.max(mxFish, this.dfs(i, j, grid));
}
}
}
return mxFish;
}
}
```
# Intuition 🧠
When exploring grid-based problems with connected components, both DFS and BFS are powerful approaches. Here's why:
- 🔍 DFS dives deep into each connected region of fish
- 🌊 Perfect for finding isolated groups of fish
- 📊 Helps track total fish count in each connected area
- 🎯 Naturally handles the recursive nature of connected components
# Approach Step by Step 🎯
### Grid Traversal 🔄
1. 🔍 Systematically scan grid cells (i, j)
2. 🎣 When finding fish (grid[i][j] > 0):
- Initialize fish count
- Mark cell as visited (set to 0)
- Start DFS/BFS exploration
### DFS Implementation Details 📝
```cpp
Key Components:
- Direction arrays: {-1,0}, {1,0}, {0,-1}, {0,1}
- Visit marking: grid[i][j] = 0
- Fish counting: sum += grid[i][j]
```
### BFS Alternative 🌊
```cpp
Queue based approach:
- Push start cell (i,j)
- Process neighbors level by level
- Track running sum of fish
```
### Optimization Techniques 🚀
1. In-place modification (grid[i][j] = 0)
- Saves space
- Avoids visited array
2. Early termination
- Skip water cells (0)
- Boundary checks first
# Complexity Analysis 📈
### Time Complexity ⏱️
- O(n × m) where:
- n = number of rows
- m = number of columns
- Each cell visited exactly once
- Direction checking: O(1) per cell
### Space Complexity 💾
1. Recursive DFS:
- O(n × m) worst case
- Stack depth = size of largest fish region
2. Iterative BFS:
- O(n × m) worst case
- Queue size = width of fish region
### *If you have questions about implementation details or optimization strategies, feel free to ask! 😊* 💭
| 10 | 2 | ['Array', 'Depth-First Search', 'Breadth-First Search', 'Matrix', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
maximum-number-of-fish-in-a-grid | Easy Peasy DFS | easy-peasy-dfs-by-sky09-vm5p | \nclass Solution {\n \n private int solve(int i, int j, int m, int n, int[][] grid, boolean[][] vis){\n // return if wrong position\n\t if(i < 0 | | Sky09 | NORMAL | 2023-04-29T16:06:40.797820+00:00 | 2023-04-29T16:29:04.543260+00:00 | 1,083 | false | ```\nclass Solution {\n \n private int solve(int i, int j, int m, int n, int[][] grid, boolean[][] vis){\n // return if wrong position\n\t if(i < 0 || j < 0 || i == m || j == n || vis[i][j] || grid[i][j] == 0){\n return 0;\n }\n\t\t\n\t\t// mark visited\n vis[i][j] = true;\n\t\t\n // call 4 directions\n int total = grid[i][j];\n total += solve(i+1, j, m, n, grid, vis);\n total += solve(i, j+1, m, n, grid, vis);\n total += solve(i, j-1, m, n, grid, vis);\n total += solve(i-1, j, m, n, grid, vis);\n return total;\n } \n\t\n public int findMaxFish(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int max = 0;\n boolean[][] vis = new boolean[m][n];\n\t\t\n for(int i = 0; i < m; i++){\n for(int j = 0; j < n; j++){\n if(!vis[i][j] && grid[i][j] > 0){\n max = Math.max(max, solve(i, j, m, n, grid, vis));\n }\n }\n }\n \n return max;\n }\n}\n```\n\n\n | 10 | 1 | ['Java'] | 3 |
maximum-number-of-fish-in-a-grid | Python 3 || 8 lines, dfs || T/S: 72% / 48% | python-3-8-lines-dfs-ts-72-48-by-spauldi-rui3 | \nclass Solution:\n def findMaxFish(self, grid: List[List[int]]) -> int:\n\n def dfs(r: int,c: int) -> int:\n\n if (r,c) not in unseen:retu | Spaulding_ | NORMAL | 2023-04-29T23:38:54.041406+00:00 | 2024-06-19T01:16:25.373816+00:00 | 593 | false | ```\nclass Solution:\n def findMaxFish(self, grid: List[List[int]]) -> int:\n\n def dfs(r: int,c: int) -> int:\n\n if (r,c) not in unseen:return 0\n\n unseen.remove((r,c))\n return grid[r][c] + dfs(r+1,c)+dfs(r,c+1)+dfs(r-1,c)+dfs(r,c-1)\n \n\n m, n, ans = len(grid), len(grid[0]), 0\n unseen = {(i,j) for i,j in product(range(m),range(n))\n if grid[i][j]}\n while unseen: ans = max(ans,dfs(*min(unseen)))\n\n return ans \n```\n[https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1292976476/](https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1292976476/)\n\nI could be wrong, but I think that time complexity is *O*(*MN*) and space complexity is *O*(*MN*), in which *M*, *N* ~ `m`,`n`. | 9 | 0 | ['Python3'] | 2 |
maximum-number-of-fish-in-a-grid | **Java** BFS Code || With Explanation | java-bfs-code-with-explanation-by-mjashw-vf1a | * Please upvote if it is helpful *\n\n# Explanation\n- Given that we have to choose optimal cell i.e grid[r][c] > 0 { water cell } in order to find the maximum | Mjashwanth | NORMAL | 2023-04-29T16:51:59.762801+00:00 | 2023-04-29T16:52:10.987743+00:00 | 1,027 | false | # ********** Please upvote if it is helpful **********\n\n# Explanation\n- Given that we have to choose optimal cell i.e grid[r][c] > 0 { water cell } in order to find the maximum fishes we can get.\n- Traverse the given grid and apply **BFS** on grid[r][c] > 0\n- We have to calculate the maximum fishes using bfs function.\n- # BFS function explanation\n- First of all add the cell into a queue and mark the cell as visited.\n- Since you are on the cell which have water that consists of fishes so add grid[r][c] to your collection of fishes.\n- Now check all adjacent sides of current cell whose value should not be \'0\' i.e it should be a water cell since if grid[r][c] = 0 it is land and you cant caught fish from land. \n- If it is water cell then it consists of fishes so, add grid[r][c] it to your collection of fishes.\n- Now add the adjacent cell to queue if not visited yet.\n- Lastly **BFS** function returns the number of fishes that you are collected from present cell.\n- And each time the max fishes that are collected from each cell{grid[r][c] > 0} calculated in main function.\n\n# Complexity\n- Time complexity: O(N + M) \n- Space Complexity : O(N)\n\n# Code\n```\nclass Solution {\n int[] x = {-1,0,1,0};\n int[] y = {0,1,0,-1};\n class Pair {\n int first;\n int second;\n public Pair(int first,int second) {\n this.first = first;\n this.second = second;\n }\n }\n \n \n \n public int bfs(int i,int j,boolean[][] vis,int[][] grid) {\n \n int sum = 0;\n Queue<Pair> q = new LinkedList<>();\n q.add(new Pair(i,j));\n vis[i][j] = true;\n sum += grid[i][j];\n while(!q.isEmpty()) {\n Pair p = q.poll();\n int first = p.first;\n int second = p.second;\n \n \n \n for(int k = 0;k<4;k++) {\n \n int ind1 = x[k] + first;\n int ind2 = y[k] + second;\n \n if(ind1 >=0 && ind2 >=0 && ind1 < grid.length && ind2 < grid[0].length && !vis[ind1][ind2] ){\n \n \n if(grid[ind1][ind2] > 0) {\n \n sum += grid[ind1][ind2];\n q.add(new Pair(ind1,ind2));\n vis[ind1][ind2] = true;\n }\n \n \n }\n \n }\n \n }\n return sum;\n }\n\n public int findMaxFish(int[][] grid) {\n int ans= 0;\n boolean[][] vis = new boolean[grid.length][grid[0].length];\n \n for(int i = 0;i<grid.length;i++) {\n for(int j = 0;j<grid[i].length;j++) {\n if(!vis[i][j] && grid[i][j] != 0) {\n ans = Math.max(ans,bfs(i,j,vis,grid));\n \n }\n }\n }\n \n return ans;\n }\n}\n``` | 7 | 1 | ['Stack', 'Java'] | 2 |
maximum-number-of-fish-in-a-grid | Easy to understand || Simple DFS | easy-to-understand-simple-dfs-by-mohakha-q54q | Given : We can start at any water cell \n#So why not do the same\n#For a given water cell, collect all the fishes from the cells which are \u2018connected\u2019 | mohakharjani | NORMAL | 2023-04-29T16:02:05.584026+00:00 | 2023-04-29T16:18:11.196654+00:00 | 862 | false | #Given : We can start at any water cell \n#So why not do the same\n#For a given water cell, collect all the fishes from the cells which are **\u2018connected\u2019 [directly/indirectly]** from that cell\n#So **get the count of fishes for each connected component, and then take the maximum**\n\n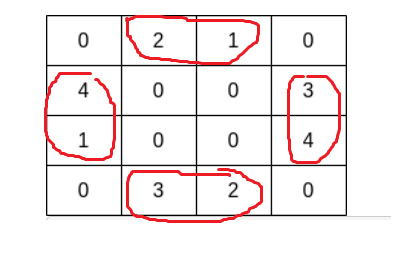\n\n\n```\nclass Solution {\npublic:\n vector<int>rowDir = {-1, 1, 0, 0}; //top, bottom, left, right\n vector<int>colDir = {0, 0, -1, 1};\n int dfs(vector<vector<int>>&grid, int row, int col)\n {\n if (row < 0 || col < 0 || row == grid.size() || col == grid[0].size()) return 0;\n if (grid[row][col] == 0) return 0;\n \n int sum = grid[row][col]; //include fish count of current cell\n grid[row][col] = 0; //mark curr cell as visited [make it a water cell]\n for (int dirIdx = 0; dirIdx < 4; dirIdx++)\n {\n int newRow = row + rowDir[dirIdx];\n int newCol = col + colDir[dirIdx];\n sum += dfs(grid, newRow, newCol); //add fish count of all connected cells to sum\n }\n return sum;\n }\n int findMaxFish(vector<vector<int>>& grid)\n {\n int m = grid.size(), n = grid[0].size();\n int maxCount = 0;\n for (int i = 0; i < m; i++)\n {\n for (int j = 0; j < n; j++)\n {\n if (grid[i][j] == 0) continue; //if it is a water cell \n \n int collectedCount = dfs(grid, i, j);\n maxCount = max(maxCount, collectedCount);\n }\n }\n return maxCount;\n \n }\n};\n``` | 7 | 1 | ['Depth-First Search', 'C', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | JAVA || BEATS 100% 💯 || BACKTRACK ✅|| 3MS 🤘|| EASY TO UNDERSTAND🌟🌟 | java-beats-100-backtrack-3ms-easy-to-und-l3gu | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kavi_k | NORMAL | 2025-01-28T04:29:15.153500+00:00 | 2025-01-28T06:35:30.124481+00:00 | 530 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
private static int max = 0;
private static int sum = 0;
public int findMaxFish(int[][] arr) {
max = 0;
for(int i = 0; i < arr.length; i++)
{
for(int j = 0; j < arr[0].length;j++)
{
if(arr[i][j] > 0)
{
sum = 0;
check(arr, i, j);
}
}
}
return max;
}
private static void check(int[][] arr, int row, int col) {
if(row < 0 || col < 0 || row >= arr.length || col >= arr[0].length || arr[row][col] == 0 || arr[row][col] == -1)
{
return;
}
sum += arr[row][col];
arr[row][col] = -1;
max = Math.max(sum, max);
check(arr, row + 1, col);
check(arr, row - 1, col);
check(arr, row, col + 1);
check(arr, row, col - 1);
}
}
``` | 6 | 0 | ['Java'] | 1 |
maximum-number-of-fish-in-a-grid | Simple Java solution (2 methods) | simple-java-solution-2-methods-by-siddha-ktyk | Method 1Visisted and non Visited array conceptComplexity
Time complexity: O(m∗n)
Space complexity: O(m∗n)
CodeMethod 2Adding values of a matrix conceptCompl | siddhant_2002 | NORMAL | 2025-01-28T04:20:23.215226+00:00 | 2025-01-28T04:20:23.215226+00:00 | 267 | false | # Method 1
# Visisted and non Visited array concept
# Complexity
- Time complexity: $$O(m*n)$$
- Space complexity: $$O(m*n)$$
# Code
```java []
class Solution {
public int findMaxFish(int[][] grid) {
int m = grid.length, n = grid[0].length;
int maxi = 0;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(grid[i][j] != 0)
{
boolean vis[][] = new boolean[m][n];
int a[] = new int[1];
dfs(grid, i, j, m, n, a, vis);
maxi = Math.max(maxi, a[0]);
}
}
}
return maxi;
}
private void dfs(int grid[][], int i, int j, int m, int n, int a[], boolean vis[][])
{
if(i < 0 || j < 0 || i >= m || j >= n || grid[i][j] == 0 || vis[i][j])
{
return;
}
vis[i][j] = true;
a[0] += grid[i][j];
dfs(grid, i+1, j, m, n, a, vis);
dfs(grid, i, j+1, m, n, a, vis);
dfs(grid, i, j-1, m, n, a, vis);
dfs(grid, i-1, j, m, n, a, vis);
}
}
```
# Method 2
# Adding values of a matrix concept
# Complexity
- Time complexity: $$O(m*n)$$
- Space complexity: $$O(m*n)$$ recursive stack space
# Code
```java []
class Solution {
public int findMaxFish(int[][] grid) {
int m = grid.length, n = grid[0].length;
int maxi = 0;
for(int i = 0; i < m; i++)
{
for(int j = 0; j < n; j++)
{
if(grid[i][j] != 0)
{
maxi = Math.max(maxi, dfs(grid, i, j, m, n));
}
}
}
return maxi;
}
private int dfs(int grid[][], int i, int j, int m, int n)
{
if(i < 0 || j < 0 || i >= m || j >= n || grid[i][j] == 0)
{
return 0;
}
int sum = grid[i][j];
grid[i][j] = 0;
sum += dfs(grid, i+1, j, m, n);
sum += dfs(grid, i, j+1, m, n);
sum += dfs(grid, i, j-1, m, n);
sum += dfs(grid, i-1, j, m, n);
return sum;
}
}
``` | 6 | 0 | ['Array', 'Depth-First Search', 'Union Find', 'Matrix', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | ✅✅Beats 100%🔥C++🔥Python|| 🚀🚀Super Simple and Efficient Solution🚀🚀||🔥Python🔥C++✅✅ | beats-100cpython-super-simple-and-effici-gt1v | Complexity
Time complexity: O(mn)
Space complexity: O(mn)
⬆️👇⬆️UPVOTE it⬆️👇⬆️Code⬆️👇⬆️UPVOTE it⬆️👇⬆️ | shobhit_yadav | NORMAL | 2025-01-28T03:18:38.146816+00:00 | 2025-01-28T03:18:38.146816+00:00 | 492 | false | # Complexity
- Time complexity: $$O(mn)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(mn)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
⬆️👇⬆️UPVOTE it⬆️👇⬆️
# Code
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int ans = 0;
for (int i = 0; i < grid.size(); ++i){
for (int j = 0; j < grid[0].size(); ++j){
if (grid[i][j] > 0)
ans = max(ans, dfs(grid, i, j));
}
}
return ans;
}
private:
int dfs(vector<vector<int>>& grid, int i, int j) {
if (i < 0 || i == grid.size() || j < 0 || j == grid[0].size())
return 0;
if (grid[i][j] == 0)
return 0;
int caughtFish = grid[i][j];
grid[i][j] = 0;
return caughtFish +
dfs(grid, i + 1, j) + dfs(grid, i - 1, j) +
dfs(grid, i, j + 1) + dfs(grid, i, j - 1);
}
};
```
```python3 []
class Solution:
def findMaxFish(self, grid: list[list[int]]) -> int:
def dfs(i: int, j: int) -> int:
if i < 0 or i == len(grid) or j < 0 or j == len(grid[0]):
return 0
if grid[i][j] == 0:
return 0
caughtFish = grid[i][j]
grid[i][j] = 0
return (caughtFish +
dfs(i + 1, j) + dfs(i - 1, j) +
dfs(i, j + 1) + dfs(i, j - 1))
return max(dfs(i, j)
for i in range(len(grid))
for j in range(len(grid[0])))
```
⬆️👇⬆️UPVOTE it⬆️👇⬆️
| 6 | 0 | ['Array', 'Depth-First Search', 'Breadth-First Search', 'Union Find', 'Matrix', 'C++', 'Python3'] | 0 |
maximum-number-of-fish-in-a-grid | 🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏| JAVA | C | C++ | PYTHON| JAVASCRIPT | DART | beats-super-easy-beginners-java-c-c-pyth-5m78 | IntuitionThe problem requires us to find the maximum number of fish that can be caught in a grid, where each cell can contain a certain number of fish. The goal | CodeWithSparsh | NORMAL | 2025-01-28T15:52:36.449521+00:00 | 2025-01-28T15:55:21.168436+00:00 | 189 | false | 
---

---
## Intuition
The problem requires us to find the maximum number of fish that can be caught in a grid, where each cell can contain a certain number of fish. The goal is to explore connected cells (up, down, left, right) starting from any cell that contains fish, and sum up the total number of fish in that connected component. My initial thought is to use depth-first search (DFS) to traverse the grid and keep track of the total fish caught from each starting cell.
## Approach
1. **Grid Traversal**:
- Initialize variables to store the dimensions of the grid (`m` for rows and `n` for columns) and a variable (`maxFish`) to keep track of the maximum number of fish caught.
- Define possible movement directions (up, right, down, left) in a list.
2. **Depth-First Search (DFS)**:
- Implement a recursive DFS function that takes the current cell's coordinates and the grid as parameters.
- In the DFS function:
- Check if the current cell is out of bounds or has no fish (i.e., value is 0 or less). If so, return 0.
- Capture the number of fish in the current cell and mark it as visited by setting its value to 0.
- Recursively call DFS for all four possible directions from the current cell, summing up the total fish caught.
3. **Finding Maximum Fish**:
- Iterate through each cell in the grid. If a cell contains fish (greater than 0), call the DFS function from that cell to calculate the total fish caught in that connected component.
- Update `maxFish` with the maximum value found during these calls.
4. **Return Result**:
- After checking all cells, return `maxFish`, which represents the maximum number of fish that can be caught from any connected component.
### Code Examples
```cpp []
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
int maxFish = 0;
vector<vector<int>> directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
function<int(int, int)> dfs = [&](int r, int c) {
if (r < 0 || c < 0 || r >= m || c >= n || grid[r][c] <= 0) return 0;
int fishCaught = grid[r][c];
grid[r][c] = 0; // Mark as visited
for (const auto& dir : directions) {
fishCaught += dfs(r + dir[0], c + dir[1]);
}
return fishCaught;
};
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > 0) {
maxFish = max(maxFish, dfs(i, j));
}
}
}
return maxFish;
}
};
```
```java []
class Solution {
public int findMaxFish(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int maxFish = 0;
int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
// Helper method for DFS
int dfs(int r, int c) {
if (r < 0 || c < 0 || r >= m || c >= n || grid[r][c] <= 0) return 0;
int fishCaught = grid[r][c];
grid[r][c] = 0; // Mark as visited
for (int[] dir : directions) {
fishCaught += dfs(r + dir[0], c + dir[1]);
}
return fishCaught;
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > 0) {
maxFish = Math.max(maxFish, dfs(i, j));
}
}
}
return maxFish;
}
}
```
```javascript []
class Solution {
findMaxFish(grid) {
const m = grid.length;
const n = grid[0].length;
let maxFish = 0;
const directions = [[-1, 0], [0, 1], [1, 0], [0, -1]];
const dfs = (r, c) => {
if (r < 0 || c < 0 || r >= m || c >= n || grid[r][c] <= 0) return 0;
let fishCaught = grid[r][c];
grid[r][c] = 0; // Mark as visited
for (const [dr, dc] of directions) {
fishCaught += dfs(r + dr, c + dc);
}
return fishCaught;
};
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] > 0) {
maxFish = Math.max(maxFish, dfs(i, j));
}
}
}
return maxFish;
}
}
```
```python []
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
m = len(grid)
n = len(grid[0])
max_fish = 0
directions = [(-1, 0), (0, 1), (1, 0), (0, -1)]
def dfs(r: int, c: int) -> int:
if r < 0 or c < 0 or r >= m or c >= n or grid[r][c] <= 0:
return 0
fish_caught = grid[r][c]
grid[r][c] = 0 # Mark as visited
for dr, dc in directions:
fish_caught += dfs(r + dr, c + dc)
return fish_caught
for i in range(m):
for j in range(n):
if grid[i][j] > 0:
max_fish = max(max_fish, dfs(i, j))
return max_fish
```
```dart []
class Solution {
int findMaxFish(List<List<int>> grid) {
int m = grid.length;
int n = grid[0].length;
int maxFish = 0;
List<List<int>> directions = [
[-1, 0],
[0, 1],
[1, 0],
[0, -1],
];
int dfs(int r, int c) {
if (r < 0 || c < 0 || r >= m || c >= n || grid[r][c] <= 0) return 0;
int fishCaught = grid[r][c];
grid[r][c] = 0; // Mark as visited
for (int i = 0; i < directions.length; i++) {
fishCaught += dfs(r + directions[i][0], c + directions[i][1]);
}
return fishCaught;
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > 0) {
maxFish = max(maxFish, dfs(i,j));
}
}
}
return maxFish;
}
}
```
## Complexity
- **Time complexity**: $$O(n \times m)$$ where $$n$$ is the number of rows and $$m$$ is the number of columns in `grid`. This accounts for visiting each cell at most once during DFS traversal.
- **Space complexity**: $$O(n \times m)$$ due to recursion stack space used by DFS. In the worst case where all cells are connected and need to be visited recursively.
---
 {:style='width:250px'} | 5 | 0 | ['Array', 'Depth-First Search', 'C', 'Matrix', 'C++', 'Java', 'Python3', 'JavaScript', 'Dart'] | 2 |
maximum-number-of-fish-in-a-grid | Maximum Number of Fish in a Grid [C++] | maximum-number-of-fish-in-a-grid-c-by-mo-yl4y | Intuition:The approach uses DFS to traverse connected non-zero cells, treating them as a single component (or "pond"). Each DFS call sums the fish count for all | moveeeax | NORMAL | 2025-01-28T02:54:22.855211+00:00 | 2025-01-28T02:54:22.855211+00:00 | 26 | false | ### Intuition:
The approach uses DFS to traverse connected non-zero cells, treating them as a single component (or "pond"). Each DFS call sums the fish count for all connected cells and updates the maximum count found.
### Approach:
1. **DFS Traversal**: Each cell with non-zero fish count acts as a starting point. The DFS explores all connected cells in four directions (up, down, left, right).
2. **Marking Visited Cells**: During traversal, visited cells are set to zero to avoid revisiting and ensure correct component-based counting.
3. **Finding Maximum Fish**: Iterate through all cells in the grid, invoking DFS for each non-zero cell to calculate the total fish in that pond.
### Complexity:
- **Time Complexity**: \(O(n \times m)\), where \(n\) and \(m\) are the dimensions of the grid. Each cell is visited once during the DFS, and the grid is iterated over once.
- **Space Complexity**: \(O(n \times m)\) in the worst case due to the recursion stack in DFS for a fully connected grid.
### Code:
The code is well-structured and handles the problem efficiently:
```cpp
class Solution {
public:
int dfs(int i, int j, vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
if (i < 0 || j < 0 || i >= n || j >= m || grid[i][j] == 0)
return 0;
int cur = grid[i][j];
grid[i][j] = 0; // Mark as visited
cur += dfs(i + 1, j, grid);
cur += dfs(i - 1, j, grid);
cur += dfs(i, j + 1, grid);
cur += dfs(i, j - 1, grid);
return cur;
}
int findMaxFish(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size(), ans = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] != 0) {
ans = max(ans, dfs(i, j, grid));
}
}
}
return ans;
}
};
``` | 5 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | Maximum Number of Fish in a Grid - Solution Explanation and Code (Video Solution Available) | maximum-number-of-fish-in-a-grid-solutio-7mwj | Video SolutionIntuitionThe problem involves finding the maximum number of fishes that can be collected from connected cells in a grid. My initial thought was to | CodeCrack7 | NORMAL | 2025-01-28T02:21:21.184469+00:00 | 2025-01-28T02:21:21.184469+00:00 | 387 | false | # Video Solution
[https://youtu.be/yOZ5-C8XFm4?si=hBbCvNYVg-WNPCY-]()
# Intuition
The problem involves finding the maximum number of fishes that can be collected from connected cells in a grid. My initial thought was to treat this as a graph traversal problem, where each cell in the grid represents a node, and edges connect adjacent non-zero cells. This led to using a Breadth-First Search (BFS) approach to explore connected regions.
# Approach
1. Iterate through all cells in the grid.
2. If a cell contains fish (`grid[i][j] != 0`) and has not been visited, perform a BFS to explore the entire connected region starting from that cell.
3. During BFS, maintain a count of the total number of fishes in the connected region.
4. Keep track of the maximum fish count encountered during the traversal.
5. Return the maximum fish count.
# Complexity
- **Time complexity**:
$$O(m \times n)$$, where $$m$$ is the number of rows and $$n$$ is the number of columns. Each cell is visited once during the traversal.
- **Space complexity**:
$$O(m \times n)$$, due to the `visited` array and the queue used in BFS.
# Code
```java
class Solution {
public int findMaxFish(int[][] grid) {
int numRows = grid.length, numCols = grid[0].length, result = 0;
boolean[][] visited = new boolean[numRows][numCols];
for (int i = 0; i < numRows; i++) {
for (int j = 0; j < numCols; j++) {
if (grid[i][j] != 0 && !visited[i][j]) {
result = Math.max(result, countFishes(grid, visited, i, j));
}
}
}
return result;
}
private int countFishes(int[][] grid, boolean[][] visited, int row, int col) {
int numRows = grid.length, numCols = grid[0].length, fishCount = 0;
Queue<int[]> q = new LinkedList<>();
q.add(new int[] { row, col });
visited[row][col] = true;
int[] rowDirections = { 0, 0, 1, -1 };
int[] colDirections = { 1, -1, 0, 0 };
while (!q.isEmpty()) {
int[] cell = q.poll();
row = cell[0];
col = cell[1];
fishCount += grid[row][col];
for (int i = 0; i < 4; i++) {
int newRow = row + rowDirections[i];
int newCol = col + colDirections[i];
if (
0 <= newRow &&
newRow < numRows &&
0 <= newCol &&
newCol < numCols &&
grid[newRow][newCol] != 0 &&
!visited[newRow][newCol]
) {
q.add(new int[] { newRow, newCol });
visited[newRow][newCol] = true;
}
}
}
return fishCount;
}
} | 5 | 0 | ['Java'] | 0 |
maximum-number-of-fish-in-a-grid | BFS || C++ || ✅Easy Solution | bfs-c-easy-solution-by-vamosabhinav-ehhh | Approach\nSimple BFS approach.\nEnter in a cell when grid[r][c]!=0 and search in neighbours cell using bfs whenever leaving that particular cell add this to our | VamosAbhinav | NORMAL | 2023-04-29T17:04:41.718226+00:00 | 2023-04-29T17:04:41.718269+00:00 | 479 | false | # Approach\nSimple BFS approach.\nEnter in a cell when grid[r][c]!=0 and search in neighbours cell using bfs whenever leaving that particular cell add this to our fish variable and put it equal to 0 that is grid[r][c]=0.\n\n# Complexity\n- Time complexity:\n O(n*m)\n\n- Space complexity:\n O(min(n,m))\n\n# Code\n```\nclass Solution {\npublic:\n int findMaxFish(vector<vector<int>>& grid) {\n int n=grid.size(),m=grid[0].size();\n vector<int> v={0,-1,0,1,0};\n int ans=0,mx=0;\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n ans=0;\n if(grid[i][j]!=0)\n {\n queue<pair<int,int>> q;\n q.push({i,j});\n ans+=grid[i][j];\n grid[i][j]=0;\n while(!q.empty())\n {\n for(int k=0;k<4;k++)\n {\n int r1=q.front().first+v[k];\n int c1=q.front().second+v[k+1];\n if(r1>=0 && r1<n && c1>=0 && c1<m && grid[r1][c1]!=0)\n {\n ans+=grid[r1][c1];\n q.push({r1,c1});\n grid[r1][c1]=0;\n }\n }\n q.pop();\n }\n }\n mx=max(mx,ans);\n }\n }\n return mx;\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | 🔥C++ ✅✅ Best Solution ( 🔥 DFS 🔥 ) Easy to Understand💯💯 ⬆⬆⬆ | c-best-solution-dfs-easy-to-understand-b-7q5l | Intuition\n Describe your first thoughts on how to solve this problem. \nDFS\n\n\n# Code\n\nclass Solution {\npublic:\n \n int solve(vector<vector<int>>& | Sandipan58 | NORMAL | 2023-04-29T16:04:34.816620+00:00 | 2023-04-29T16:04:34.816683+00:00 | 306 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDFS\n\n\n# Code\n```\nclass Solution {\npublic:\n \n int solve(vector<vector<int>>& grid, vector<vector<bool>>& visited, int r, int c) {\n visited[r][c] = true;\n int cnt = grid[r][c], n = grid.size(), m = grid[0].size();\n \n if(c+1<m && grid[r][c+1] && !visited[r][c+1]) {\n cnt += solve(grid, visited, r, c+1);\n }\n \n if(c-1>=0 && grid[r][c-1] && !visited[r][c-1]) {\n cnt += solve(grid, visited, r, c-1);\n }\n \n if(r+1<n && grid[r+1][c] && !visited[r+1][c]) {\n cnt += solve(grid, visited, r+1, c);\n }\n \n if(r-1>=0 && grid[r-1][c] && !visited[r-1][c]) {\n cnt += solve(grid, visited, r-1, c);\n }\n \n return cnt;\n }\n \n int findMaxFish(vector<vector<int>>& grid) {\n int maxi = 0, n = grid.size(), m = grid[0].size();\n vector<vector<bool>> visited(n, vector<bool>(m, false));\n \n for(int i=0; i<n; i++) for(int j=0; j<m; j++) \n // if it is water cell and not visited the call the dfs function to calculate the total fish and compare with the maximum\n if(grid[i][j] && !visited[i][j]) {\n int x = solve(grid, visited, i, j);\n maxi = max(maxi, x);\n }\n return maxi;\n }\n};\n``` | 5 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Graph', 'Recursion', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | My first DFS solution 🚀 || No reference Needed just follow the sol. explanation || 100 % TC || C++ | my-first-dfs-solution-no-reference-neede-thy6 | Intuition 💡The problem involves finding the maximum number of fish that can be collected in a connected component of a grid. Each cell with a non-zero value rep | brijesh03032001 | NORMAL | 2025-01-28T22:30:10.970656+00:00 | 2025-01-28T22:30:10.970656+00:00 | 26 | false |
### Intuition 💡
The problem involves finding the maximum number of fish that can be collected in a connected component of a grid. Each cell with a non-zero value represents a pond, and we can "collect fish" by exploring all adjacent cells in the same connected component. This is a classic **grid traversal problem** solvable using **Depth First Search (DFS)**.
---
### Approach 🛠️
1. **Grid Representation**: Treat the grid as a matrix where each cell either has fish (`grid[i][j] > 0`) or is empty (`grid[i][j] == 0`).
2. **DFS Traversal**:
- Start from an unvisited cell containing fish.
- Use DFS to traverse the connected component and calculate the total number of fish.
- Mark the cells as visited during traversal.
3. **Track Maximum Fish**: Keep a running maximum of fish collected for each connected component.
---
### Complexity 📊
- **Time Complexity**:
$$O(r \times c)$$
Every cell is visited at most once during DFS, where \(r\) and \(c\) are the grid dimensions.
- **Space Complexity**:
$$O(r \times c)$$
Due to the `visited` matrix and the recursion stack in the worst case.
---
### Stylish Code ✨
```cpp
class Solution {
public:
// Directions for moving up, down, left, and right ➡️⬅️⬇️⬆️
vector<pair<int, int>> directions{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
// Helper function: Perform DFS to calculate the total fish in a connected component
int dfs(int i, int j, int rows, int cols, vector<vector<int>>& grid, vector<vector<bool>>& visited) {
// Base conditions: Out of bounds or invalid cell
if (i < 0 || j < 0 || i >= rows || j >= cols || grid[i][j] == 0 || visited[i][j]) {
return 0;
}
// Mark the current cell as visited and start with the current cell's fish count
visited[i][j] = true;
int totalFish = grid[i][j];
// Explore all four directions recursively
for (auto dir : directions) {
totalFish += dfs(i + dir.first, j + dir.second, rows, cols, grid, visited);
}
return totalFish;
}
// Main function to find the maximum fish
int findMaxFish(vector<vector<int>>& grid) {
int rows = grid.size();
int cols = grid[0].size();
// Visited matrix to keep track of explored cells
vector<vector<bool>> visited(rows, vector<bool>(cols, false));
int maxFish = 0; // Variable to track the maximum fish in a connected component
// Iterate through each cell in the grid
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
// If the cell contains fish and hasn't been visited, perform DFS
if (grid[i][j] > 0 && !visited[i][j]) {
maxFish = max(maxFish, dfs(i, j, rows, cols, grid, visited));
}
}
}
return maxFish; // Return the maximum fish collected
}
};
```
---
### Explanation 🔍
1. **Directions Array**: Encodes the 4 possible moves (right, left, down, up).
2. **DFS Function**:
- Checks for valid cells (within bounds, not visited, and contains fish).
- Recursively explores all connected cells to accumulate the total fish.
3. **Main Function**:
- Iterates over the grid and starts a DFS traversal for each unvisited cell with fish.
- Updates the maximum fish collected after each DFS traversal.
---
### Why Upvote This Solution? 🙌
- **Clarity**: Well-structured and easy-to-read code with intuitive variable names.
- **Efficiency**: Optimized traversal logic with minimal overhead.
- **Scalability**: Handles grids of any size while ensuring correctness.
- **Style**: Clean and modular with comments and emojis for better understanding. 😎
If this solution helped you, **please upvote**! 👍✨ | 4 | 0 | ['Array', 'Depth-First Search', 'Graph', 'Matrix', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | 💢Faster✅💯 Lesser C++✅Python3🐍✅Java✅C✅Python🐍✅C#✅💥🔥💫Explained☠💥🔥 Beats 💯 | faster-lesser-cpython3javacpythoncexplai-ky97 | IntuitionThis is a reference vedio for the Solution. I tried to explain the solution in best way i can, please watch out the solution.
Approach
JavaScript Code | Edwards310 | NORMAL | 2025-01-28T12:19:52.845079+00:00 | 2025-01-28T12:19:52.845079+00:00 | 221 | false | 
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
***This is a reference vedio for the Solution. I tried to explain the solution in best way i can, please watch out the solution.***
https://youtu.be/O28LEGXwUlU?si=rUWy3B3cgRvuZfPV
# Approach
<!-- Describe your first thoughts on how to solve this problem. -->
- ***JavaScript Code -->*** https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1523197294
- ***C++ Code -->*** https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1523169681
- ***Python3 Code -->*** https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1523174355
- ***Java Code -->*** https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1523170261
- ***C Code -->*** https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1523188212
- ***Python Code -->*** https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1523173472
- ***C# Code -->*** https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1523193344
- ***Go Code -->*** https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/submissions/1523209117
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N * M)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N * M)
# Code!
 | 4 | 1 | ['Depth-First Search', 'Breadth-First Search', 'C', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#'] | 1 |
maximum-number-of-fish-in-a-grid | DFS || Java || Easy Solution || Beat 100% || | dfs-java-easy-solution-beat-100-by-mmohm-fjwc | To do this, we can use Depth-First Search (DFS), to explores all connected parts of a region recursivelyApproach
Walk Through the Grid:
Look at each cell in t | mmohmedjasim2005 | NORMAL | 2025-01-28T10:24:52.862051+00:00 | 2025-01-28T10:29:20.089088+00:00 | 9 | false | **To do this, we can use Depth-First Search (DFS), to explores all connected parts of a region recursively**
---
# Approach
1. **Walk Through the Grid**:
- Look at each cell in the grid. If the cell contains fish (not zero)...Start a **DFS search** from that cell to find all the fish from neighbor cell
2. **Explore the Pond Using DFS**:
- When DFS starts at a cell, it will look at the four neighboring cells (up, down, left, right)
- If a neighbor also contains (Non zero number)fish, the DFS will move to that neighbor and continue exploring
- Each time DFS visits a cell, it adds the number to the total count (`res`) and marks the cell as visited by setting it to `0`(`grid[r][c]=0`;) (to avoid counting it again)
3. **Keep Track of the Maximum count**:
- After the DFS finishes exploring a grid, compare its count with the current maximum. If it's larger, update the maximum
(It is done inside For loop,once dfs method return counnt)
4. **Repeat for All Cells**:
- Continue this process for all cells(which is not zero) in the grid until you've checked every part
---
# Code
```java
class Solution {
public int findMaxFish(int[][] grid) {
int max=0;
for(int r=0;r<grid.length;r++){
for(int c=0;c<grid[0].length;c++){
if(grid[r][c]!=0){
max=Math.max(dfs(r,c,grid),max);
// System.out.println(max);
}
}
}
return max;
}
public static int dfs(int r,int c,int[][] grid){
if(r<0 || c<0 || r>grid.length-1 || c>grid[0].length-1 || grid[r][c]==0){
return 0;
}
int res=grid[r][c];
grid[r][c]=0;
res+=dfs(r,c+1,grid)+dfs(r,c-1,grid)+dfs(r+1,c,grid)+dfs(r-1,c,grid);
// System.out.println(res);
return res;
}
}
```
| 4 | 0 | ['Java'] | 1 |
maximum-number-of-fish-in-a-grid | ✅ Maximum Number of Fish in a Grid | JS🔥 | beats 99%🚀 | 🚀highly optimised & easy to understand ✅ | maximum-number-of-fish-in-a-grid-js-beat-kt7l | Intuition
To solve the Maximum Number of Fish in a Grid problem, we can use Depth-First Search (DFS) to explore the grid.
Approach
Start from every water cell ( | Naveen_sachan | NORMAL | 2025-01-28T03:34:33.236032+00:00 | 2025-01-28T03:34:33.236032+00:00 | 200 | false | # Intuition
- To solve the Maximum Number of Fish in a Grid problem, we can use Depth-First Search (DFS) to explore the grid.
# Approach
- Start from every water cell (grid[i][j] > 0).
- Use DFS to traverse all reachable water cells and collect the fish.
- Keep track of the maximum number of fish collected starting from any cell.
> **DFS Traversal:**
- Starting from any water cell (grid[r][c] > 0), recursively visit all adjacent water cells, collecting the fish and marking the cells as visited (grid[r][c] = 0).
> **Iterate Through Grid:**
- For every water cell in the grid, start a DFS and calculate the total fish collected. Update the maxFish if this value is greater than the current maximum.
# Complexity
> **Time complexity:**
- O(m×n), where m and n are the dimensions of the grid. Each cell is visited at most once.
> **Space complexity:**
- O(m×n), due to the recursive stack in DFS.
# Code
```javascript []
/**
* @param {number[][]} grid
* @return {number}
*/
var findMaxFish = function (grid) {
const rows = grid.length;
const cols = grid[0].length;
let maxFish = 0;
// Directions for adjacent cells: right, left, down, up
const directions = [
[0, 1], [0, -1], [1, 0], [-1, 0]
];
// Helper function for DFS
function dfs(r, c) {
// Base case: if the cell is out of bounds or is land
if (r < 0 || c < 0 || r >= rows || c >= cols || grid[r][c] === 0) {
return 0;
}
// Collect the fish at the current cell
let fish = grid[r][c];
grid[r][c] = 0; // Mark the cell as visited
// Explore all adjacent cells
for (const [dr, dc] of directions) {
fish += dfs(r + dr, c + dc);
}
return fish;
}
// Iterate over every cell in the grid
for (let r = 0; r < rows; r++) {
for (let c = 0; c < cols; c++) {
if (grid[r][c] > 0) { // Start DFS from every water cell
maxFish = Math.max(maxFish, dfs(r, c));
}
}
}
return maxFish;
};
```

| 4 | 0 | ['JavaScript'] | 1 |
maximum-number-of-fish-in-a-grid | Python | Simple DFS | O(m*n), O(m*n) | Beats 95% | python-simple-dfs-beats-95-by-2pillows-8om0 | CodeComplexity
Time complexity: O(m∗n). Visit each cell once, m*n total cells.
Space complexity: O(m∗n). Based on maximum recursion depth of m*n total cells. | 2pillows | NORMAL | 2025-01-28T00:52:46.160087+00:00 | 2025-01-28T05:01:07.964396+00:00 | 140 | false | # Code
```python3 []
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
def collect_fish(i, j):
num_fish = grid[i][j] # collect fish from current cell
grid[i][j] = 0 # caught fish in current cell, no more remaining
for di, dj in [(0, 1), (0, -1), (1, 0), (-1, 0)]: # explore adjacent cells
ni, nj = i + di, j + dj
if 0 <= ni < m and 0 <= nj < n and grid[ni][nj] != 0:
num_fish += collect_fish(ni, nj) # if cell in bounds and has fish, collect
return num_fish
m = len(grid)
n = len(grid[0])
max_fish = 0
for i in range(m): # loop through each cell and update max fish if cell's section has more
for j in range(n):
if grid[i][j] == 0: continue # skip if cell has no fish
max_fish = max(max_fish, collect_fish(i, j))
return max_fish
```
# Complexity
- Time complexity: $$O(m*n)$$. Visit each cell once, m*n total cells.
- Space complexity: $$O(m*n)$$. Based on maximum recursion depth of m*n total cells.
# Performance
 | 4 | 0 | ['Array', 'Depth-First Search', 'Matrix', 'Python3'] | 1 |
maximum-number-of-fish-in-a-grid | Five Lines Only - According to the Hints | five-lines-only-according-to-the-hints-b-svd5 | IntuitionJust use the Hints from the Problem description:💡Hint 1
Run DFS from each non-zero cell.💡Hint 2
Each time you pick a cell to start from, add up the num | charnavoki | NORMAL | 2025-01-28T00:21:42.744769+00:00 | 2025-01-28T10:05:15.685925+00:00 | 382 | false | # Intuition
Just use the Hints from the Problem description:
💡Hint 1
Run DFS from each non-zero cell.
💡Hint 2
Each time you pick a cell to start from, add up the number of fish contained in the cells you visit.
```javascript []
const deltas = [[1, 0], [-1, 0], [0, 1], [0, -1]];
var findMaxFish = function(grid) {
const f = (i, j, v = grid[i]?.[j]) =>
v ? (grid[i][j] = 0, deltas.reduce((s, [x, y]) => s + f(i + x, j + y), v)) : 0;
return Math.max(...grid.map((row, i) => row.map((c, j) => c && f(i, j))).flat());
};
```
| 4 | 0 | ['JavaScript'] | 1 |
maximum-number-of-fish-in-a-grid | Python DFS Solution - O(m + n) | python-dfs-solution-om-n-by-richyrich200-ftpf | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | RichyRich2004 | NORMAL | 2025-01-28T00:14:19.344220+00:00 | 2025-01-28T00:14:19.344220+00:00 | 712 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
rows, cols = len(grid), len(grid[0])
visited = set()
def dfs(row, col):
if row < 0 or row >= rows or col < 0 or col >= cols or grid[row][col] == 0 or (row, col) in visited:
return 0
visited.add((row, col))
res = 0
for direction in [(0, 1), (1, 0), (-1, 0), (0, -1)]:
res += dfs(row + direction[0], col + direction[1])
return res + grid[row][col]
res = 0
for i in range(rows):
for j in range(cols):
if grid[i][j] > 0 and (i, j) not in visited:
res = max(res, dfs(i, j))
return res
``` | 4 | 0 | ['Python3'] | 0 |
maximum-number-of-fish-in-a-grid | Best O(M*N) Solution | best-omn-solution-by-kumar21ayush03-3xn0 | Approach\nBFS Traversal\n\n# Complexity\n- Time complexity:\nO(mn)\n\n- Space complexity:\nO(mn) \n\n# Code\n\nclass Solution {\npublic:\n int traversal(int | kumar21ayush03 | NORMAL | 2023-08-23T11:02:32.852782+00:00 | 2023-08-23T11:02:32.852814+00:00 | 38 | false | # Approach\nBFS Traversal\n\n# Complexity\n- Time complexity:\n$$O(m*n)$$\n\n- Space complexity:\n$$O(m*n)$$ \n\n# Code\n```\nclass Solution {\npublic:\n int traversal(int i, int j, vector<vector<int>>& grid, vector<vector<int>>& vis) {\n int m = grid.size(), n = grid[0].size();\n int fish = 0;\n queue <pair<int, int>> q;\n q.push({i, j});\n vis[i][j] = 1;\n int drow[] = {-1, 0, 1, 0};\n int dcol[] = {0, 1, 0, -1};\n while (!q.empty()) {\n int r = q.front().first;\n int c = q.front().second;\n q.pop();\n fish += grid[r][c];\n for (int i = 0; i < 4; i++) {\n int nr = r + drow[i];\n int nc = c + dcol[i];\n if (nr >= 0 && nr < m && nc >= 0 && nc < n\n && grid[nr][nc] > 0 && !vis[nr][nc]) {\n q.push({nr, nc});\n vis[nr][nc] = 1;\n }\n }\n }\n return fish;\n }\n\n int findMaxFish(vector<vector<int>>& grid) {\n int m = grid.size(), n = grid[0].size();\n vector<vector<int>> vis(m, vector<int>(n, 0));\n int maxFish = 0;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] > 0 && !vis[i][j]) {\n int fish = traversal(i, j, grid, vis);\n maxFish = max (maxFish, fish);\n }\n }\n }\n return maxFish;\n }\n};\n``` | 4 | 0 | ['C++'] | 1 |
maximum-number-of-fish-in-a-grid | C++ || DFS | c-dfs-by-ganeshkumawat8740-jwuk | Approach\nAPPLE DFS\n\n# Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n void solve(int i,int j, | ganeshkumawat8740 | NORMAL | 2023-05-06T07:37:33.231173+00:00 | 2023-05-06T07:37:33.231216+00:00 | 218 | false | # Approach\nAPPLE DFS\n\n# Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n void solve(int i,int j,int &m,int &n,vector<vector<int>> &g,int &k){\n if(i<0||j<0||i>=m||j>=n||g[i][j]==0)return;\n k += g[i][j];\n g[i][j] = 0;\n solve(i+1,j,m,n,g,k);\n solve(i,j+1,m,n,g,k);\n solve(i-1,j,m,n,g,k);\n solve(i,j-1,m,n,g,k);\n }\n int findMaxFish(vector<vector<int>>& grid) {\n int ans = 0;\n int i,j,m=grid.size(),n=grid[0].size(),k;\n for(i = 0; i < m; i++){\n for(j = 0; j < n; j++){\n if(grid[i][j]){\n k = 0;\n solve(i,j,m,n,grid,k);\n cout<<k<<" ";\n ans = max(ans,k);\n }\n }\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Depth-First Search', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | Easy Solution | JAVA | DFS | easy-solution-java-dfs-by-tracey432-hgq0 | Intuition\nTo find the maximum fish a fisherman can obtain. The zero represent the land and the numbers represent the number of available fish.\n\n# Approach\n | tracey432 | NORMAL | 2023-04-30T06:17:05.727787+00:00 | 2023-04-30T15:16:44.096234+00:00 | 91 | false | # Intuition\nTo find the maximum fish a fisherman can obtain. The zero represent the land and the numbers represent the number of available fish.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize the maximum variable as global\n- Create a boolean matrix called visited to keep track on the visited grid.\n- Create a function dfs, it helps to move to adjacent cells in deep and stop if the grid is already visted or the land is reached.\n- Increase the max for eachs recursive call.\n- Update the maximum vairalbe for each dfs call from the findMaxFish() function.\n> Upvote\n---\n\n\n\n# Code\n```\nclass Solution {\n public int max;\n public int findMaxFish(int[][] grid) {\n int rlen = grid.length;\n int clen = grid[0].length;\n int answer = 0;\n boolean visited[][] = new boolean[rlen][clen];\n for(int i=0;i<rlen;i++){\n for(int j=0;j<clen;j++){\n if(grid[i][j]!=0 && !visited[i][j]){\n max = 0;\n dfs(grid, rlen, clen,visited, i, j);\n answer = Math.max(max, answer );\n }\n }\n }\n return answer;\n }\n \n public void dfs(int[][] grid, int rlen, int clen, boolean[][] visited, int i, int j){\n if(i<0||i>=rlen||j<0||j>=clen||visited[i][j]||grid[i][j] == 0){\n return;\n }\n visited[i][j] = true;\n max +=grid[i][j];\n dfs(grid, rlen, clen, visited, i+1, j);\n dfs(grid, rlen, clen, visited, i-1, j);\n dfs(grid, rlen, clen, visited, i, j+1);\n dfs(grid, rlen, clen, visited, i, j-1);\n }\n}\n``` | 4 | 0 | ['Depth-First Search', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | c++ DFS | c-dfs-by-augus7-bewf | \n# Code\n\nclass Solution {\n void dfs(int row, int col, vector<vector<int>>& grid, vector<vector<int>>& vis, int &fish) {\n int n = grid.size(), m = | Augus7 | NORMAL | 2023-04-29T17:21:00.513373+00:00 | 2023-04-29T17:21:00.513418+00:00 | 1,185 | false | \n# Code\n```\nclass Solution {\n void dfs(int row, int col, vector<vector<int>>& grid, vector<vector<int>>& vis, int &fish) {\n int n = grid.size(), m = grid[0].size(); \n vis[row][col] = 1;\n fish += grid[row][col];\n int r_dir[4] = {-1, 0, 1, 0};\n int c_dir[4] = {0, 1, 0, -1};\n for(int i = 0; i < 4; i++) {\n int r = row + r_dir[i];\n int c = col + c_dir[i];\n if(r >= 0 && r < n && c >= 0 && c < m && grid[r][c] && !vis[r][c]) {\n dfs(r, c, grid, vis, fish);\n }\n }\n }\npublic:\n int findMaxFish(vector<vector<int>>& grid) {\n int n = grid.size(), m = grid[0].size();\n vector<vector<int>> vis(n, vector<int>(m, 0));\n int max_fish = 0;\n for(int i = 0; i < n; i++) {\n for(int j = 0; j < m; j++) {\n if(grid[i][j] > 0 && !vis[i][j]) {\n int fish = 0;\n dfs(i, j, grid, vis, fish);\n max_fish = max(max_fish, fish);\n }\n }\n }\n return max_fish;\n }\n};\n``` | 4 | 0 | ['Depth-First Search', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | PYTHON 3 | EASY SOLUTION | python-3-easy-solution-by-honejzy-y8fw | The function then defines an inner function called dfs that performs a depth-first search on the grid starting from a given position (i,j) and returns the sum o | honejzy | NORMAL | 2023-04-29T16:51:34.138701+00:00 | 2023-04-29T16:52:21.547335+00:00 | 392 | false | The function then defines an inner function called **dfs** that performs a depth-first search on the grid starting from a given position (i,j) and returns the sum of fish in the connected region.\n\nThe dfs function first checks if the **current** position is **outside the bounds** of the grid or if the position corresponds to a cell with value **0 or -1** (0 - water, -1 - visited). If any of these conditions is true, the function returns 0 (**no fish here**).\nOtherwise, the function retrieves the number of fish fish in the current cell, sets the cell value to -1 (*to mark it as visited*), and recursively calls itself on the four adjacent cells (up, left, down, and right), accumulating the fish counts in a variable temp.\n\n```\n def findMaxFish(self, grid: List[List[int]]) -> int:\n N, M = len(grid), len(grid[0])\n \n def dfs(i, j, temp):\n if i < 0 or j < 0 or i >= N or j >= M or grid[i][j] in [0, -1]:\n return 0\n \n fish = grid[i][j]\n grid[i][j] = -1 # visited\n temp += (fish + dfs(i-1, j, temp) + dfs(i, j-1, temp) + dfs(i+1, j, temp) + dfs(i, j+1, temp))\n\n return temp \n \n maxi = 0\n for i in range(N):\n for j in range(M):\n if grid[i][j] > 0:\n maxi = max(maxi, dfs(i, j, 0))\n \n return maxi\n``` | 4 | 0 | ['Depth-First Search', 'Python3'] | 0 |
maximum-number-of-fish-in-a-grid | simple java bfs | simple-java-bfs-by-flyroko123-bts6 | \nclass pair{\n int x;int y;\n pair(int x1,int y1){\n x=x1;\n y=y1;\n }\n}\nclass Solution {\n public int findMaxFish(int[][] grid) {\ | flyRoko123 | NORMAL | 2023-04-29T16:01:27.714809+00:00 | 2023-04-29T16:01:27.714860+00:00 | 367 | false | ```\nclass pair{\n int x;int y;\n pair(int x1,int y1){\n x=x1;\n y=y1;\n }\n}\nclass Solution {\n public int findMaxFish(int[][] grid) {\n int m=grid.length;\n int n=grid[0].length;\n int max=0;\n // System.out.print(bfs(0,1,grid,m,n)+" ");\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(grid[i][j]>0){\n // System.out.print(bfs(i,j,grid,m,n)+" ");\n \n max=Math.max(max,bfs(i,j,grid,m,n));\n }\n }\n }\n return max;\n \n }\n public int bfs(int i,int j,int grid[][],int m,int n){\n Queue<pair> q=new LinkedList<>();\n q.add(new pair(i,j));\n int dx[]={-1,1,0,0};\n int dy[]={0,0,-1,1};\n // int max=0;\n int sum=grid[i][j];\n grid[i][j]=0;\n while(!q.isEmpty()){\n pair it=q.poll();\n int x=it.x;\n int y=it.y;\n // System.out.print(x+" "+y);\n for(int p=0;p<4;p++){\n int newx=x+dx[p];\n int newy=y+dy[p];\n if(newx<0 || newy<0 || newx>=m || newy>=n || grid[newx][newy]==0)continue;\n q.add(new pair(newx,newy));\n \n sum+=grid[newx][newy];\n grid[newx][newy]=0;\n }\n }\n return sum;\n }\n}\n``` | 4 | 0 | ['Breadth-First Search'] | 0 |
maximum-number-of-fish-in-a-grid | JAVA CODE | java-code-by-aysha3211-543e | ApproachUsing DFSComplexity
Time complexity: O(m*n)
Space complexity: O(1)
Code | Aysha3211 | NORMAL | 2025-01-28T14:41:25.024552+00:00 | 2025-01-28T14:41:25.024552+00:00 | 71 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
Using DFS
# Complexity
- Time complexity: O(m*n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
private int m, n;
private final int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
private int dfs(int i, int j, int[][] grid) {
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == 0) {
return 0;
}
int fishCount = grid[i][j];
grid[i][j] = 0; // Mark this cell as visited (fish collected)
for (int[] dir : directions) {
int i_ = i + dir[0];
int j_ = j + dir[1];
fishCount += dfs(i_, j_, grid);
}
return fishCount;
}
public int findMaxFish(int[][] grid) {
m = grid.length;
n = grid[0].length;
int maxFish = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > 0) { // Fish cell found
maxFish = Math.max(maxFish, dfs(i, j, grid));
}
}
}
return maxFish;
}
}
``` | 3 | 0 | ['Java'] | 0 |
maximum-number-of-fish-in-a-grid | Easy to Understand, Beginner C++ | DFS | easy-to-understand-beginner-c-dfs-by-nik-qznw | IntuitionApproachComplexity
Time complexity: O(m*n)
Space complexity:
Code | Nikhilk18 | NORMAL | 2025-01-28T10:26:05.170925+00:00 | 2025-01-28T10:26:05.170925+00:00 | 220 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(m*n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int dfs(vector<vector<int>>& grid, int i, int j, int m, int n, vector<vector<bool>>& vis) {
// Base case: Out of bounds or invalid cell
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == 0 || vis[i][j]) {
return 0;
}
// Mark the cell as visited
vis[i][j] = true;
// Start with the current cell's fish count
int total = grid[i][j];
// Explore all 4 directions
total += dfs(grid, i - 1, j, m, n, vis); // Up
total += dfs(grid, i + 1, j, m, n, vis); // Down
total += dfs(grid, i, j - 1, m, n, vis); // Left
total += dfs(grid, i, j + 1, m, n, vis); // Right
return total;
}
int findMaxFish(vector<vector<int>>& grid) {
int ans = 0;
int m = grid.size();
int n = grid[0].size();
vector<vector<bool>> vis(m, vector<bool>(n, false)); // Visited array
// Iterate over all cells in the grid
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] != 0 && !vis[i][j]) { // Start DFS for each new component
ans = max(ans, dfs(grid, i, j, m, n, vis));
}
}
}
return ans;
}
};
``` | 3 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | ✅ Easy to Understand | Graph Theory | DFS | Connected Components | Detailed Video Explanation 🔥 | easy-to-understand-graph-theory-dfs-conn-upk2 | IntuitionThe problem can be visualized as finding the maximum sum of fish in connected regions of a grid, where each region is defined by non-zero cells that ar | sahilpcs | NORMAL | 2025-01-28T08:50:51.467787+00:00 | 2025-01-28T08:50:51.467787+00:00 | 94 | false | # Intuition
The problem can be visualized as finding the maximum sum of fish in connected regions of a grid, where each region is defined by non-zero cells that are adjacent (either vertically or horizontally). A depth-first search (DFS) is well-suited for exploring such connected regions, as it allows us to traverse all reachable cells in a region systematically while marking them as visited.
# Approach
1. **Grid Traversal**: Iterate through each cell in the grid.
2. **DFS for Connected Regions**: For each cell with a non-zero value, initiate a DFS to calculate the total fish in the connected region.
- During the DFS, add the value of the current cell to a temporary variable (`temp`) and mark the cell as visited by setting its value to `0`.
- Recursively explore all adjacent cells (up, down, left, right) that are within bounds and not yet visited.
3. **Track Maximum Fish**: After completing the DFS for a region, compare the collected fish (`temp`) with the current maximum (`max`) and update `max` if necessary.
4. **Return Result**: After processing all cells, return the maximum fish collected (`max`).
# Complexity
- **Time complexity**:
$$O(m \times n)$$
- Each cell in the grid is visited exactly once during the traversal and DFS. Thus, the total time complexity is proportional to the number of cells in the grid.
- **Space complexity**:
$$O(m \times n)$$ (in the worst case, for the recursion stack)
- In the worst-case scenario, where the grid forms a single large connected region, the recursion stack may grow to contain all cells in the grid.
# Code
```java []
class Solution {
// Variables to store the maximum number of fish collected and temporary fish count for a region
int max;
int temp;
// Dimensions of the grid
int m, n;
// Directions for moving up, down, left, and right
int[][] dir = {{1,0}, {0,1}, {-1,0}, {0,-1}};
// Grid to represent the fishing area
int[][] grid;
// Method to find the maximum fish that can be collected
public int findMaxFish(int[][] grid) {
this.grid = grid; // Initialize the grid
max = 0; // Initialize the maximum fish count to 0
m = grid.length; // Number of rows
n = grid[0].length; // Number of columns
// Iterate through each cell in the grid
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// If the cell has fish, start a DFS from there
if (grid[i][j] != 0) {
temp = 0; // Reset the temporary fish count for the current region
dfs(i, j); // Perform a DFS to collect all fish in the connected region
// Update the maximum fish count if the current region has more fish
if (temp > max)
max = temp;
}
}
}
return max; // Return the maximum fish count
}
// Depth-First Search (DFS) to collect fish in a connected region
private void dfs(int i, int j) {
// Base case: If out of bounds or the cell is empty, return
if (i < 0 || j < 0 || i >= m || j >= n || grid[i][j] == 0)
return;
temp += grid[i][j]; // Add the fish in the current cell to the temporary count
grid[i][j] = 0; // Mark the cell as visited by setting it to 0
// Explore all 4 possible directions
for (int[] d : dir) {
int ii = i + d[0]; // Calculate the new row index
int jj = j + d[1]; // Calculate the new column index
dfs(ii, jj); // Recursively perform DFS in the new direction
}
}
}
```
LeetCode 2658 Maximum Number of Fish in a Grid | Graph Theory | Easy | DFS | Asked in Adobe
https://youtu.be/NK71iQVoPO4
| 3 | 0 | ['Array', 'Depth-First Search', 'Breadth-First Search', 'Matrix', 'Java'] | 1 |
maximum-number-of-fish-in-a-grid | C++ Solution || Simple BFS | c-solution-simple-bfs-by-rohit_raj01-tqux | IntuitionThe problem can be approached by treating the grid as a graph where:
Each cell is a node.
Edges exist between adjacent cells that are non-zero.
The tas | Rohit_Raj01 | NORMAL | 2025-01-28T07:48:37.409941+00:00 | 2025-01-28T07:48:37.409941+00:00 | 170 | false | # Intuition
The problem can be approached by treating the grid as a graph where:
- Each cell is a node.
- Edges exist between adjacent cells that are non-zero.
The task is to find all connected components (regions) of the grid and calculate the sum of fish in each component. The largest sum is the desired answer.
# Algorithm
1. Use Breadth-First Search (BFS) to traverse each region of connected cells starting from a non-zero cell.
2. For each region:
- Add up the number of fish.
- Mark cells as visited by setting them to `0` (water) to avoid revisiting.
3. Track the maximum sum of fish collected across all regions.
---
# Complexity
- **Time Complexity**:
$$O(m \cdot n)$$
Each cell is visited at most once during the BFS traversal.
- **Space Complexity**:
$$O(m \cdot n)$$
In the worst case, the BFS queue could store all cells in the grid.
---
# Code
```cpp
class Solution {
public:
int bfs(vector<vector<int>>& grid, int r, int c) {
int m = grid.size(), n = grid[0].size();
queue<pair<int, int>> q;
q.push({r, c});
int totalFish = 0;
int dr[] = {-1, 0, 0, 1};
int dc[] = {0, -1, 1, 0};
while (!q.empty()) {
int row = q.front().first, col = q.front().second;
q.pop();
totalFish += grid[row][col];
grid[row][col] = 0;
for (int i = 0; i < 4; i++) {
int nr = row + dr[i], nc = col + dc[i];
if (nr >= 0 && nr < m && nc >= 0 && nc < n && grid[nr][nc] > 0) {
q.push({nr, nc});
}
}
}
return totalFish;
}
int findMaxFish(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int maxFish = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > 0) {
maxFish = max(maxFish, bfs(grid, i, j));
}
}
}
return maxFish;
}
};
````

| 3 | 0 | ['Array', 'Breadth-First Search', 'Matrix', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | 🐟 Maximum Fish Catch 🚀 | Easy DFS Solution | Python 🧠 | Dive Into the Grid 🌊 | maximum-fish-catch-easy-dfs-solution-pyt-ca9j | IntuitionThe problem can be thought of as finding the largest connected "pool" of fish in the grid, where we traverse all possible water cells (non-zero values) | Hardikjp7 | NORMAL | 2025-01-28T05:06:16.009449+00:00 | 2025-01-28T05:06:16.009449+00:00 | 53 | false | # Intuition
The problem can be thought of as finding the largest connected "pool" of fish in the grid, where we traverse all possible water cells (non-zero values) starting from each cell. Depth First Search (DFS) is a suitable approach to explore connected components in the grid.
# Approach
1. Use DFS to explore all connected water cells starting from a given water cell `(r, c)`.
2. While visiting each cell, sum up the fish in the cell and mark it as visited by setting its value to `0` (to avoid revisiting).
3. Repeat this process for every cell in the grid. For each starting cell, compute the total fish collected and track the maximum.
4. If no water cells exist, return `0`.
### If you find this explanation helpful, please consider upvoting! 😊
# Complexity
- **Time complexity**:
$$O(m \times n)$$
Each cell is visited once during the DFS traversal.
- **Space complexity**:
$$O(m \times n)$$
For the recursion stack in the worst case.
# Code
```python
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
def dfs(i: int, j: int) -> int:
if i < 0 or i == len(grid) or j < 0 or j == len(grid[0]):
return 0
if grid[i][j] == 0:
return 0
caughtfish = grid[i][j]
grid[i][j] = 0
return (caughtfish + dfs(i+1, j) + dfs(i-1, j) + dfs(i, j+1) + dfs(i, j-1))
return max(dfs(i, j) for i in range(len(grid)) for j in range(len(grid[0])))
``` | 3 | 0 | ['Depth-First Search', 'Python3'] | 0 |
maximum-number-of-fish-in-a-grid | 🚀 Simple Approach Using Backtracking 🚀 [Step by Step Explanation] | simple-approach-using-backtracking-step-29bq4 | 🚀 Approach
We first run a traversal through the grid to find water cells.
When we find a water cell we need to go to all possible directions
left , right , up a | LeadingTheAbyss | NORMAL | 2025-01-28T04:21:11.712200+00:00 | 2025-01-28T04:21:11.712200+00:00 | 14 | false | # 🚀 Approach
- We first run a traversal through the grid to find water cells.
- When we find a water cell we need to go to all possible directions
`left` , `right` , `up` and `down`.
- Until we keep finding water cells we keep adding them in our fishes count.
- Lastly we use `maximumFishes` to count the maximum number of fishes from a cell.
# 💻 Implementation
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int maximumFishes = 0;
for (int row = 0; row < grid.size(); row++) {
for (int col = 0; col < grid[row].size(); col++) {
if (grid[row][col] > 0) {
int fishes = backtrack(grid, row, col);
maximumFishes = max(fishes, maximumFishes);
}
}
}
return maximumFishes;
}
int backtrack(vector<vector<int>>& grid, int row, int col) {
if (row < 0 || row >= grid.size() || col < 0 || col >= grid[row].size() || grid[row][col] == 0) {
return 0;
}
int cnt = grid[row][col];
grid[row][col] = 0;
cnt += backtrack(grid, row + 1, col); // Up
cnt += backtrack(grid, row - 1, col); // Down
cnt += backtrack(grid, row, col + 1); // Right
cnt += backtrack(grid, row, col - 1); // Left
return cnt;
}
};
``` | 3 | 0 | ['Array', 'Backtracking', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | 100% BEATS IN JAVA USING DFS O(M*N) SOLUTION | 100-beats-in-java-using-dfs-omn-solution-mlro | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | shyam4KB | NORMAL | 2025-01-28T03:50:44.423745+00:00 | 2025-01-28T03:50:44.423745+00:00 | 99 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int findMaxFish(int[][] grid) {
int res = 0;
int m = grid.length, n = grid[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] != 0) {
res = Math.max(res, dfs(i,j, grid, m, n));
}
}
}
return res;
}
private int dfs(int r, int c, int[][] grid, int m, int n) {
if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == 0) return 0;
int sum = 0,temp = grid[r][c];
grid[r][c] = 0;
sum += dfs(r, c+1, grid, m, n);
sum += dfs(r+1, c, grid, m, n) ;
sum += dfs(r, c-1, grid, m, n) ;
sum += dfs(r-1, c, grid, m, n);
return sum + temp;
}
}
``` | 3 | 0 | ['Java'] | 1 |
maximum-number-of-fish-in-a-grid | DFS | BFS | 0ms - 100% | 8.04MB - 100% | dfs-bfs-0ms-100-804mb-100-by-dipak__pati-xe7b | DFSBFS | dipak__patil | NORMAL | 2025-01-28T02:14:38.081008+00:00 | 2025-01-28T02:14:38.081008+00:00 | 120 | false | 
# DFS
```golang []
func findMaxFish(grid [][]int) int {
var (
dfs func(int, int) int
maxCatch int
)
dfs = func(row, col int) int {
if row < 0 || col < 0 || row == len(grid) || col == len(grid[0]) || grid[row][col] == 0 {
return 0
}
fish := grid[row][col]
grid[row][col] = 0
return fish + dfs(row, col+1) + dfs(row+1, col) + dfs(row-1, col) + dfs(row, col-1)
}
for row := 0; row < len(grid); row++ {
for col := 0; col < len(grid[0]); col++ {
maxCatch = max(maxCatch, dfs(row, col))
}
}
return maxCatch
}
```
# BFS
```
func findMaxFish(grid [][]int) int {
var (
maxCatch int
q [][2]int
currSum, r, c, cell = 0, 0, 0, [2]int{}
)
for row := 0; row < len(grid); row++ {
for col := 0; col < len(grid[0]); col++ {
if grid[row][col] == 0 {
continue
}
q = q[:0]
q = append(q, [2]int{row, col})
currSum = 0
for len(q) > 0 {
cell = q[len(q)-1]
q = q[:len(q)-1]
r = cell[0]
c = cell[1]
if r < 0 || c < 0 || r == len(grid) || c == len(grid[0]) || grid[r][c] == 0 {
continue
}
currSum += grid[r][c]
grid[r][c] = 0
q = append(q, [2]int{r, c + 1})
q = append(q, [2]int{r + 1, c})
q = append(q, [2]int{r - 1, c})
q = append(q, [2]int{r, c - 1})
}
maxCatch = max(maxCatch, currSum)
}
}
return maxCatch
}
``` | 3 | 0 | ['Depth-First Search', 'Go'] | 1 |
maximum-number-of-fish-in-a-grid | Easy & Detailed Approch 💡 | Simple BFS ✅ | All Languages 🔥 | easy-detailed-approch-simple-bfs-all-lan-c5sb | IntuitionThe problem requires finding the maximum number of fish that can be collected from any connected group of cells in a grid. Each cell may contain some f | himanshu_dhage | NORMAL | 2025-01-28T02:12:19.731633+00:00 | 2025-01-28T02:12:19.731633+00:00 | 290 | false | # Intuition
The problem requires finding the maximum number of fish that can be collected from any connected group of cells in a grid. Each cell may contain some fish, and we can move to adjacent cells (up, down, left, right) to collect fish from connected components. The intuition is to explore each connected component using a Breadth-First Search (BFS) or Depth-First Search (DFS) and calculate the total fish count in that component. The goal is to find the maximum fish count among all such components.
# Approach
1. **Initialization**:
- Create a `vis` array of the same size as the grid to track visited cells.
- Define directions for moving up, down, left, and right.
2. **BFS for Connected Components**:
- For every cell in the grid:
- If the cell contains fish (`grid[i][j] > 0`) and is not visited, start a BFS traversal from that cell.
- Use a queue to explore all connected cells, marking them as visited.
- Accumulate the total fish count for the connected component.
3. **Update Maximum Fish Count**:
- After completing the BFS for a connected component, update the `maxi` variable to store the maximum fish count seen so far.
4. **Return Result**:
- After traversing the entire grid, return the value of `maxi`.
# Complexity
- **Time Complexity**:
$$O(m \times n)$$
Each cell in the grid is visited once during the BFS traversal, where \(m\) is the number of rows and \(n\) is the number of columns.
- **Space Complexity**:
$$O(m \times n)$$
Space is used for the `vis` array and the BFS queue, both of which require space proportional to the number of cells in the grid.
# Code
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int m = grid.size(); // Number of rows
int n = grid[0].size(); // Number of columns
vector<vector<int>> vis(m, vector<int>(n, 0)); // Visited array
int row[4] = {-1, 0, 0, +1}; // Directions for rows
int col[4] = {0, +1, -1, 0}; // Directions for columns
int maxi = 0; // Maximum fish count in a connected component
// Helper function to perform BFS and calculate the total fish in a component
auto bfs = [&](int i, int j) {
queue<pair<int, int>> q;
q.push({i, j});
vis[i][j] = 1; // Mark the starting cell as visited
int sum = grid[i][j]; // Initialize the sum with the fish count of the starting cell
while (!q.empty()) {
auto [r, c] = q.front();
q.pop();
for (int k = 0; k < 4; k++) {
int nrow = r + row[k];
int ncol = c + col[k];
// Check if the new cell is valid, within bounds, unvisited, and has fish
if (nrow >= 0 && nrow < m && ncol >= 0 && ncol < n && !vis[nrow][ncol] && grid[nrow][ncol] > 0) {
vis[nrow][ncol] = 1; // Mark as visited
q.push({nrow, ncol}); // Add to the queue for further exploration
sum += grid[nrow][ncol]; // Add the fish count from the new cell
}
}
}
return sum; // Return the total fish in the connected component
};
// Iterate through all cells in the grid
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// If the cell has fish and is not visited, start BFS from this cell
if (grid[i][j] > 0 && !vis[i][j]) {
maxi = max(maxi, bfs(i, j)); // Update the maximum fish count
}
}
}
return maxi; // Return the maximum fish count from all connected components
}
};
```
```javascript []
class Solution {
findMaxFish(grid) {
const m = grid.length; // Number of rows
const n = grid[0].length; // Number of columns
const vis = Array.from({ length: m }, () => Array(n).fill(0)); // Visited matrix
const directions = [[-1, 0], [0, 1], [0, -1], [1, 0]]; // Directions (up, right, left, down)
let maxi = 0; // Maximum fish count in any connected component
// Helper function to perform BFS
const bfs = (i, j) => {
const queue = [[i, j]]; // Initialize the queue
vis[i][j] = 1; // Mark the starting cell as visited
let totalFish = grid[i][j]; // Initialize the fish count
while (queue.length > 0) {
const [r, c] = queue.shift(); // Dequeue the front cell
// Explore all 4 possible directions
for (const [dr, dc] of directions) {
const nr = r + dr; // Next row
const nc = c + dc; // Next column
// Check if the next cell is valid, unvisited, and has fish
if (nr >= 0 && nr < m && nc >= 0 && nc < n && vis[nr][nc] === 0 && grid[nr][nc] > 0) {
vis[nr][nc] = 1; // Mark the cell as visited
queue.push([nr, nc]); // Add the cell to the queue
totalFish += grid[nr][nc]; // Add the fish count to the total
}
}
}
return totalFish; // Return the total fish count
};
// Iterate through all cells in the grid
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
// If the cell contains fish and is unvisited, start a BFS
if (grid[i][j] > 0 && vis[i][j] === 0) {
maxi = Math.max(maxi, bfs(i, j)); // Update the maximum fish count
}
}
}
return maxi; // Return the largest fish count
}
}
```
```python []
from collections import deque
class Solution:
def findMaxFish(self, grid):
m, n = len(grid), len(grid[0]) # Dimensions of the grid
vis = [[0] * n for _ in range(m)] # Visited matrix
directions = [(-1, 0), (0, 1), (0, -1), (1, 0)] # Directions (up, right, left, down)
maxi = 0 # To store the maximum fish count in any connected component
# Helper function to perform BFS
def bfs(i, j):
q = deque()
q.append((i, j))
vis[i][j] = 1 # Mark the starting cell as visited
total_fish = grid[i][j] # Initialize the fish count from the starting cell
while q:
r, c = q.popleft() # Get the current cell from the queue
# Explore all 4 possible directions
for dr, dc in directions:
nr, nc = r + dr, c + dc # Compute the next cell's coordinates
# Check if the next cell is valid, unvisited, and contains fish
if 0 <= nr < m and 0 <= nc < n and not vis[nr][nc] and grid[nr][nc] > 0:
vis[nr][nc] = 1 # Mark the cell as visited
q.append((nr, nc)) # Add the cell to the queue
total_fish += grid[nr][nc] # Add its fish count to the total
return total_fish # Return the total fish count in this component
# Iterate through all cells in the grid
for i in range(m):
for j in range(n):
# If the cell contains fish and is unvisited, start a BFS
if grid[i][j] > 0 and not vis[i][j]:
maxi = max(maxi, bfs(i, j)) # Update the maximum fish count
return maxi # Return the largest fish count among all connected components
```
```java []
import java.util.*;
class Solution {
public int findMaxFish(int[][] grid) {
int m = grid.length; // Number of rows
int n = grid[0].length; // Number of columns
int[][] vis = new int[m][n]; // Visited array
int[] row = {-1, 0, 0, 1}; // Directions for rows
int[] col = {0, 1, -1, 0}; // Directions for columns
int maxi = 0; // Maximum fish count in a connected component
// BFS helper function
int bfs(int i, int j) {
Queue<int[]> q = new LinkedList<>();
q.add(new int[] {i, j});
vis[i][j] = 1; // Mark the starting cell as visited
int sum = grid[i][j]; // Initialize the sum with the fish count
while (!q.isEmpty()) {
int[] curr = q.poll();
int r = curr[0];
int c = curr[1];
for (int k = 0; k < 4; k++) {
int nr = r + row[k];
int nc = c + col[k];
// Check if the next cell is valid, unvisited, and has fish
if (nr >= 0 && nr < m && nc >= 0 && nc < n && vis[nr][nc] == 0 && grid[nr][nc] > 0) {
vis[nr][nc] = 1; // Mark the cell as visited
q.add(new int[] {nr, nc}); // Add the cell to the queue
sum += grid[nr][nc]; // Add the fish count to the sum
}
}
}
return sum; // Return the total fish count
}
// Iterate through all cells in the grid
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// If the cell contains fish and is unvisited, start BFS
if (grid[i][j] > 0 && vis[i][j] == 0) {
maxi = Math.max(maxi, bfs(i, j)); // Update the maximum fish count
}
}
}
return maxi; // Return the largest fish count
}
}
```

| 3 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Graph', 'Queue', 'Matrix', 'C++', 'Java', 'Python3'] | 0 |
maximum-number-of-fish-in-a-grid | DFS Solution for 'Maximum Number of Fish in a Grid' | Intuitive & Clean Code 💡 | dfs-solution-for-maximum-number-of-fish-eyq0s | IntuitionThe problem is like finding the biggest group of fish in a grid. Think of each cell in the grid as a pond. If two ponds (cells) are next to each other | atharva_kalbande | NORMAL | 2025-01-28T00:56:11.284733+00:00 | 2025-01-28T00:56:11.284733+00:00 | 9 | false | # Intuition
The problem is like finding the biggest group of fish in a grid. Think of each cell in the grid as a pond. If two ponds (cells) are next to each other and have fish, we can treat them as part of the same group. Our goal is to figure out the total number of fish in the biggest group. To do this, we can explore all connected ponds using a technique called DFS (Depth-First Search).
# Approach
- Use DFS to explore connected cells with fish, summing up their values.
- Keep track of visited cells to avoid re-processing.
- For each unvisited cell with fish, calculate the total fish in its connected component and update the maximum.
- Return the largest fish count found.
# Complexity
- Time complexity:
O ( r * c)
- Space complexity:
O ( r * c)
# Code
```python []
class Solution(object):
def findMaxFish(self, grid):
def dfs(r,c):
if( r<0 or c<0 or
r == rows or c == cols or
grid[r][c] == 0 or visit[r][c]):
return 0
visit[r][c] = True
res = grid[r][c]
neigh = [[r+1,c],[r-1,c],[r,c+1],[r,c-1]]
for nr, nc in neigh:
res += dfs(nr,nc)
return res
rows, cols = len(grid),len(grid[0])
res = 0
visit=[[False] * cols for _ in range(rows)]
for r in range(rows):
for c in range(cols):
if grid[r][c] or not visit[r][c]:
res =max(res,dfs(r,c))
return res
``` | 3 | 0 | ['Depth-First Search', 'Python'] | 0 |
maximum-number-of-fish-in-a-grid | Easy Approach C++ | Depth First Search | Maximum Number of Fishes in a Grid | easy-approach-c-depth-first-search-maxim-twgi | Approach\nDepth first Search.\n- Converted each traversed path to land cell so that a separate visited array is not required.\n\n# Code\ncpp []\nclass Solution | pegasus1801 | NORMAL | 2023-06-23T10:30:41.146173+00:00 | 2023-06-23T10:30:41.146191+00:00 | 51 | false | # Approach\nDepth first Search.\n- Converted each traversed path to land cell so that a separate `visited` array is not required.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n bool isValid(int i, int j, int n, int m){\n return i>=0 && i<n && j>=0 && j<m;\n }\n int dfs(vector<vector<int>>& grid, int row, int col){\n int n = grid.size(), m = grid[0].size();\n if(!isValid(row, col, n, m) || grid[row][col] == 0) return 0;\n int direc[5] = {0, 1, 0, -1, 0};\n int res = grid[row][col];\n grid[row][col] = 0;\n for(int k=0; k<4; k++) { \n res += dfs(grid, row+direc[k], col+direc[k+1]);\n }\n return res;\n }\n int findMaxFish(vector<vector<int>>& grid) {\n int ans = 0;\n for(int i = 0; i< grid.size(); ++i){\n for(int j =0; j < grid[0].size(); ++j){\n ans = max(ans, dfs(grid, i, j));\n }\n }\n return ans;\n }\n};\n```\n | 3 | 0 | ['Depth-First Search', 'Graph', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | C++ || DFS || Similar to Number of Islands | c-dfs-similar-to-number-of-islands-by-te-gilo | Intuition\nSimple DFS involves calculating the sum of different islands and taking the maximum one.\nSimilar to Number of Islands problem (https://leetcode.com/ | TESLA_6447 | NORMAL | 2023-04-30T18:25:19.140570+00:00 | 2023-04-30T18:25:19.140609+00:00 | 298 | false | # Intuition\nSimple DFS involves calculating the sum of different islands and taking the maximum one.\nSimilar to Number of Islands problem (https://leetcode.com/problems/number-of-islands/).\n# Approach\nDepth First Search\n\n## Don\'t forget to upvote and give a like \uD83D\uDE43\n\n# Code\n```\nclass Solution {\npublic:\n int dx[4] = {0,0,-1,1};\n int dy[4] = {1,-1,0,0};\n void dfs(int x,int y,vector<vector<int>>& grid,int* ans){\n for(int next = 0;next<4;next++){\n int x1 = x + dx[next];\n int y1 = y + dy[next];\n if(x1>=0 and y1>=0 and y1<grid[0].size() and x1<grid.size() and grid[x1][y1]!=0){\n *ans += grid[x1][y1];\n grid[x1][y1] = 0;\n dfs(x1,y1,grid,ans);\n }\n }\n }\n int findMaxFish(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n //vector<vector<int>> vis(m,vector<int>(m,0));\n int ans = 0;\n for(int i = 0;i<m;i++){\n for(int j = 0;j<n;j++){\n if(grid[i][j] != 0){\n int count = grid[i][j];\n grid[i][j] = 0;\n dfs(i,j,grid,&count);\n ans = max(ans,count);\n }\n }\n }\n return ans;\n }\n};\n```\n### I hope the solution is clear; use the comment section regarding any doubt. | 3 | 0 | ['Depth-First Search', 'Counting', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | Fully explained Java solution | fully-explained-java-solution-by-codehun-a6jh | \n# Code\n\nclass Solution {\n public int findMaxFish(int[][] grid) {\n int max=0;\n\t\t// Loop over the Entire Grid\n for(int i=0;i< grid.leng | codeHunter01 | NORMAL | 2023-04-30T01:05:05.023546+00:00 | 2023-04-30T01:05:05.023592+00:00 | 445 | false | \n# Code\n```\nclass Solution {\n public int findMaxFish(int[][] grid) {\n int max=0;\n\t\t// Loop over the Entire Grid\n for(int i=0;i< grid.length; i++){\n for(int j=0; j<grid[0].length; j++){\n\t\t\t // only call the dfs call when we encounter a value>0, then find the number of connected land and calculate value and compare it with the previous max\n if(grid[i][j]>0){\n max= Math.max(max, dfs(grid, i, j));\n }\n }\n }\n return max;\n }\n \n public int dfs(int[][] grid, int i, int j){\n\t\t// if we gets out of bound or its a 0 i.e. water then return 0\n if(i<0 || i>=grid.length || j<0 || j>=grid[0].length || grid[i][j]==0) return 0;\n\t\t// if not then mark the grid value to 0 to make sure we do not come back to the same piece of land and cause infinite recursion i.e. stack over flow\n int val = grid[i][j];\n grid[i][j]=0;\n\t\t// now just go to all 4 direction get the respective counts and add it all together and return it\n return val+ dfs(grid, i-1, j)+ dfs(grid, i+1, j)+ dfs(grid, i, j-1)+ dfs(grid, i, j+1);\n }\n \n \n}\n``` | 3 | 0 | ['Depth-First Search', 'Graph', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | Easy DFS Solution | O(n) | Rust | easy-dfs-solution-on-rust-by-prog_jacob-7xza | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co | Prog_Jacob | NORMAL | 2023-04-29T16:12:11.729574+00:00 | 2023-04-29T16:12:11.729621+00:00 | 52 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimpl Solution {\n pub fn find_max_fish(mut grid: Vec<Vec<i32>>) -> i32 {\n let mut ans = 0;\n\n for i in 0..grid.len() {\n for j in 0..grid[0].len() {\n if grid[i][j] > 0 {\n ans = ans.max(dfs(&mut grid, i, j));\n }\n }\n }\n \n ans\n }\n}\n\nfn dfs(grid: &mut Vec<Vec<i32>>, i: usize, j: usize) -> i32 {\n if i >= grid.len() || j >= grid[0].len() || grid[i][j] == 0 { return 0 };\n let val = grid[i][j];\n grid[i][j] = 0;\n\n dfs(grid, i + 1, j) +\n dfs(grid, i - 1, j) +\n dfs(grid, i, j + 1) +\n dfs(grid, i, j - 1) + val\n}\n``` | 3 | 0 | ['Rust'] | 0 |
maximum-number-of-fish-in-a-grid | Simple || Clean || Java Solution | simple-clean-java-solution-by-himanshubh-om2v | \njava []\npublic class Solution {\n int max = 0, cur = 0;\n public int findMaxFish(int[][] grid) {\n for(int i=0; i<grid.length; i++){\n | HimanshuBhoir | NORMAL | 2023-04-29T16:04:58.536861+00:00 | 2023-04-29T16:04:58.536903+00:00 | 227 | false | \n```java []\npublic class Solution {\n int max = 0, cur = 0;\n public int findMaxFish(int[][] grid) {\n for(int i=0; i<grid.length; i++){\n for(int j=0; j<grid[0].length; j++){\n if(grid[i][j] == 0) continue;\n pass(grid, i, j);\n cur = 0;\n }\n }\n return max;\n }\n void pass(int[][] grid, int i, int j){\n if(i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] == 0) return;\n cur += grid[i][j];\n grid[i][j] = 0;\n max = Math.max(max,cur);\n pass(grid, i+1, j);\n pass(grid, i-1, j);\n pass(grid, i, j+1);\n pass(grid, i, j-1);\n }\n}\n\n``` | 3 | 0 | ['Java'] | 0 |
maximum-number-of-fish-in-a-grid | Easy to understand [ Clean Solution ] DFS -> (python + java) | easy-to-understand-clean-solution-dfs-py-ws4e | T.C : O(n^2)\n\nPython\n\nclass Solution:\n def findMaxFish(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n fishes = 0\ | KmrVikas | NORMAL | 2023-04-29T16:01:52.651015+00:00 | 2023-04-29T16:05:01.428232+00:00 | 406 | false | **T.C : O(n^2)**\n\n**Python**\n```\nclass Solution:\n def findMaxFish(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n fishes = 0\n\n def catchFish(r, c):\n nonlocal fish\n if 0 <= r < m and 0 <= c < n and grid[r][c] > 0:\n fish += grid[r][c]\n grid[r][c] = 0 # mark cell as visited\n catchFish(r+1, c)\n catchFish(r-1, c)\n catchFish(r, c+1)\n catchFish(r, c-1)\n\n for r in range(m):\n for c in range(n):\n if grid[r][c] > 0:\n fish = 0\n catchFish(r, c)\n fishes = max(fishes, fish)\n\n return fishes\n```\n\n**Java**\n\n```\npublic class Solution {\n public int findMaxFish(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int fishes = 0;\n\n // Helper function to catch fish recursively\n // Updates the \'fishes\' variable as it catches fish\n void catchFish(int r, int c) {\n if (r >= 0 && r < m && c >= 0 && c < n && grid[r][c] > 0) {\n fishes += grid[r][c];\n grid[r][c] = 0; // mark cell as visited\n catchFish(r+1, c);\n catchFish(r-1, c);\n catchFish(r, c+1);\n catchFish(r, c-1);\n }\n }\n\n for (int r = 0; r < m; r++) {\n for (int c = 0; c < n; c++) {\n if (grid[r][c] > 0) {\n int fish = 0;\n catchFish(r, c);\n fishes = Math.max(fishes, fish);\n }\n }\n }\n\n return fishes;\n }\n}\n | 3 | 0 | ['Python', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | C++ Easy and Clean DFS Solution, Explained, 0 ms Beats 100% | c-easy-and-clean-dfs-solution-explained-mzf08 | Algorithm Explanation:This algorithm uses Depth-First Search (DFS) to explore connected regions of non-zero fish values in a grid and finds the largest "lake" o | yehudisk | NORMAL | 2025-02-16T22:24:16.886846+00:00 | 2025-02-16T22:24:16.886846+00:00 | 4 | false | # Algorithm Explanation:
This algorithm uses Depth-First Search (DFS) to explore connected regions of non-zero fish values in a grid and finds the largest "lake" of fish.
##### Initialization:
We iterate over the entire grid to find unvisited cells with fish (grid[i][j] > 0).
We use a `visited` matrix to track which cells have already been explored.
When we find a cell with fish, we start a DFS to explore all connected cells (up, down, left, right).
We mark the cell as visited to avoid counting it multiple times.
We recursively call DFS on neighboring cells and sum up all fish in the connected region.
The DFS function returns the total fish count for that connected region.
Each DFS call gives us the total fish in a connected component (lake).
We update the maximum fish count found so far.
Time Complexity:
# Complexity
- Time complexity: O(n*m)
- Space complexity: O(n*m)
# Code
```cpp []
class Solution {
public:
vector<int> dir_x = {-1,1,0,0}, dir_y = {0,0,-1,1};
bool isValid(vector<vector<int>>& grid, int i, int j) {
return i < grid.size() && i >= 0 && j < grid[0].size() && j >= 0;
}
int dfs(vector<vector<int>>& grid, vector<vector<int>>& visited, int i, int j) {
if (isValid(grid, i, j) == false || grid[i][j] == 0 || visited[i][j] == 1) return 0;
visited[i][j] = 1;
int sum = grid[i][j];
for (int dir = 0; dir < 4; dir++) {
int curr_i = i + dir_x[dir], curr_j = j + dir_y[dir];
sum += dfs(grid, visited, curr_i, curr_j);
}
return sum;
}
int findMaxFish(vector<vector<int>>& grid) {
int res = 0;
vector<vector<int>> visited(grid.size(), vector<int>(grid[0].size(), 0));
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
if (visited[i][j] == 0 && grid[i][j] > 0) {
res = max(res, dfs(grid, visited, i, j));
}
}
}
return res;
}
};
```
## Like it? please upvote! | 2 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | DFS intuitive solution | dfs-intuitive-solution-by-kashyap_lokesh-cudx | IntuitionThink of this problem in terms of connected Components. We can catch all the fish in One connected component of the matrix. If we run a dfs on a cell w | kashyap_lokesh | NORMAL | 2025-01-28T18:11:29.979925+00:00 | 2025-01-28T18:11:29.979925+00:00 | 29 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Think of this problem in terms of connected Components. We can catch all the fish in One connected component of the matrix. If we run a dfs on a cell which is not visited, it will give us the count of all the fishes in that component. We can maintain a visited matrix and whenever we find a cell which is not land and has not been visited before, that means it is a new component of the graph and we run dfs on that cell. We take the answer as max of current answer so far and the fishCount returned by current call.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
int dx[] = {0, -1, 0, 1};
int dy[] = {-1, 0, 1, 0};
class Solution {
public:
int n, m;
int dfs(int x, int y, vector<vector<bool>>& vis,
vector<vector<int>>& grid) {
vis[x][y] = true;
int cnt = grid[x][y];
for (int i = 0; i < 4; i++) {
int nrow = x + dx[i], ncol = y + dy[i];
if (nrow >= 0 && nrow < n && ncol >= 0 && ncol < m &&
!vis[nrow][ncol] && grid[nrow][ncol] > 0) {
cnt += dfs(nrow, ncol, vis, grid);
}
}
return cnt;
}
int findMaxFish(vector<vector<int>>& grid) {
n = grid.size(), m = grid[0].size();
int ans = 0;
vector<vector<bool>> vis(n, vector<bool>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] > 0 && !vis[i][j])
ans = max(ans, dfs(i, j, vis, grid));
}
}
return ans;
}
};
``` | 2 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | Max Number in RUBY! | max-number-in-ruby-by-quantummaniac609-x15j | IntuitionWhen I first saw this problem, I realized that since the fisher can move to any adjacent water cell and collect fish multiple times, we need to find co | quantummaniac609 | NORMAL | 2025-01-28T17:43:28.344802+00:00 | 2025-01-28T17:43:28.344802+00:00 | 10 | false | # Intuition
When I first saw this problem, I realized that since the fisher can move to any adjacent water cell and collect fish multiple times, we need to find connected components of water cells and sum up all fish in each component. The answer would be the maximum sum among all components.
# Approach
1. **Iterate Through Grid**:
- For each cell that contains fish (value > 0)
- Start a DFS to explore all connected water cells
2. **DFS Implementation**:
- Keep track of visited cells to avoid counting twice
- Add current cell's fish to total
- Explore all 4 adjacent cells recursively
- Return total fish collected in this component
3. **Track Maximum**:
- Keep track of maximum fish found across all starting positions
- Return final maximum
# Complexity
- Time complexity: $$O(m * n * 4^{m*n})$$
- For each cell, we might explore entire grid
- Each cell has 4 possible directions
- In practice, much faster due to visited array
- Space complexity: $$O(m * n)$$
- Visited array for each DFS
- Recursion stack depth
# Code
```ruby
# @param {Integer[][]} grid
# @return {Integer}
def find_max_fish(grid)
m, n = grid.length, grid[0].length
max_fish = 0
# For each water cell
(0...m).each do |i|
(0...n).each do |j|
next if grid[i][j] == 0
# Start DFS from this cell
visited = Array.new(m) { Array.new(n, false) }
max_fish = [max_fish, dfs(grid, i, j, visited)].max
end
end
max_fish
end
def dfs(grid, row, col, visited)
return 0 if row < 0 || row >= grid.length ||
col < 0 || col >= grid[0].length ||
visited[row][col] || grid[row][col] == 0
visited[row][col] = true
total = grid[row][col]
# Try all 4 directions
dirs = [[0,1], [1,0], [0,-1], [-1,0]]
dirs.each do |dx, dy|
new_row = row + dx
new_col = col + dy
total += dfs(grid, new_row, new_col, visited)
end
total
end
``` | 2 | 0 | ['Ruby'] | 0 |
maximum-number-of-fish-in-a-grid | Simple py,JAVA code explained in detail!! BFS!! | simple-pyjava-code-explained-in-detail-b-1u1l | Probelm statement
Given m*n matrix named grid
If grid[i][j]>0 then we have a fish in it.
we have to maximise the collection of fish such that we can either
Tak | arjunprabhakar1910 | NORMAL | 2025-01-28T16:19:57.635838+00:00 | 2025-01-29T15:33:55.741512+00:00 | 48 | false | ## Probelm statement
- Given `m*n` matrix named `grid`
- If `grid[i][j]>0` then we have a *fish* in it.
- we have to maximise the collection of fish such that we can either
- Take the fish in `grid[i][j]`.
- Move to water cell which is `grid[i][j]=0`.
---
# Approach:BFS
<!-- Describe your approach to solving the problem. -->
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
- This question is equivalent of finding ***maximum area of given islands***.
- `count` is used to record the maximum fishes in a given water surrounded region.
- Have applied `BFS` to calculate `fish`.
# Complexity
- Time complexity:$O(n^2)$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$O(n^2)$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```Python3 []
#12:31
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
row,col=len(grid),len(grid[0])
count=0
visited=[[False]*col for _ in range(row)]
directions=[(0,1),(1,0),(-1,0),(0,-1)]
def BFS(r,c):
visited[r][c]=True
q=deque([(r,c)])
fish=0
while q:
x,y=q.popleft()
fish+=grid[x][y]
for dx,dy in directions:
nx,ny=x+dx,y+dy
if nx<0 or ny<0 or nx>=row or ny>=col or visited[nx][ny]:
continue
else:
if grid[nx][ny]>0:
#fish+=grid[nx][ny]
q.append((nx,ny))
visited[nx][ny]=True
#print(i,j,fish)
#print('------------------------')
return fish
for i in range(row):
for j in range(col):
if grid[i][j]>0 and not visited[i][j]:
count=max(count,BFS(i,j))
#print(i,j,count)
return count
```
```java []
class Solution {
int row,col;
boolean visited[][];
int directions[][];
int grid[][];
private int BFS(int r,int c){
visited[r][c]=true;
int fish=0;
Queue<int[]> q=new LinkedList<>();
q.add(new int[]{r,c});
while(!q.isEmpty()){
int[] n=q.poll();
int x=n[0];
int y=n[1];
fish+=grid[x][y];
for(int pt=0;pt<directions.length;pt++){
int nx=x+directions[pt][0];
int ny=y+directions[pt][1];
if(nx<0||ny<0||nx>=row||ny>=col||visited[nx][ny]){
continue;
}
else{
if(grid[nx][ny]>0){
visited[nx][ny]=true;
q.add(new int[]{nx,ny});
}
}
}
}
return fish;
}
public int findMaxFish(int[][] grid) {
this.grid=grid;
row=grid.length;
col=grid[0].length;
visited=new boolean[row][col];
directions=new int[][]{{0,1},{1,0},{-1,0},{0,-1}};
int count=0;
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
if(grid[i][j]>0 && !visited[i][j]){
count=Math.max(count,BFS(i,j));
}
}
}
return count;
}
}
``` | 2 | 0 | ['Breadth-First Search', 'Matrix', 'Java', 'Python3'] | 0 |
maximum-number-of-fish-in-a-grid | Maximum fish using DFS | maximum-fish-using-dfs-by-poornasri-aiy5 | IntuitionThe problem can be thought of as finding the connected components in a 2D grid where the grid cells represent fish counts in a pond. The goal is to fin | Poornasri | NORMAL | 2025-01-28T12:34:17.212090+00:00 | 2025-01-28T12:34:17.212090+00:00 | 24 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem can be thought of as finding the connected components in a 2D grid where the grid cells represent fish counts in a pond. The goal is to find the maximum sum of fish in any connected component (group of cells). This is a classic grid traversal problem that can be solved using Depth First Search (DFS).
# Approach
<!-- Describe your approach to solving the problem. -->
### Initialization:
1. **Determine the dimensions of the grid**:
- Let `m` represent the number of rows and `n` represent the number of columns in the grid.
2. **Create a `vis` array**:
- Use a boolean `vis` array of size `m x n` to track visited cells and avoid revisiting them during the DFS.
---
### Depth First Search (DFS):
1. **Condition to initiate DFS**:
- For a given cell `(i, j)`, if:
- `grid[i][j] != 0` (cell contains fish), and
- `vis[i][j] == false` (cell is not visited),
- Then initiate a DFS from that cell.
2. **DFS traversal**:
- Accumulate the total fish count for the connected component by recursively exploring its 4 neighboring cells (up, down, left, right).
3. **Mark cell as visited**:
- During each step, mark the current cell `(i, j)` as visited by setting `vis[i][j] = true`.
---
### Iterate Through the Grid:
1. Traverse every cell in the grid:
- For each cell `(i, j)` that satisfies the DFS initiation condition, compute the fish count for its connected component using the `solve` (DFS) function.
2. Keep track of the maximum fish count:
- Compare the fish count of the current connected component with the maximum fish count encountered so far, and update the maximum.
---
### Return the Result:
- After iterating through all cells in the grid, return the maximum fish count as the result.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Each cell is visited at most once during the DFS traversal, so the total time complexity is **O(m×n)**, where m is the number of rows and n is the number of columns in the grid.
# Code
```java []
class Solution {
int m, n;
public int solve(int i, int j, int[][] grid, boolean[][] vis) {
if (i < 0 || i >= m || j < 0 || j >= n || vis[i][j] || grid[i][j] == 0) return 0;
int temp = grid[i][j];
vis[i][j] = true;
temp += solve(i + 1, j, grid, vis);
temp += solve(i - 1, j, grid, vis);
temp += solve(i, j + 1, grid, vis);
temp += solve(i, j - 1, grid, vis);
return temp;
}
public int findMaxFish(int[][] grid) {
m = grid.length;
n = grid[0].length;
int ans = 0;
boolean[][] vis = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] != 0 && !vis[i][j]) {
ans = Math.max(ans, solve(i, j, grid, vis));
}
}
}
return ans;
}
}
``` | 2 | 0 | ['Array', 'Depth-First Search', 'Matrix', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | Simple C++ Approach ✅ | Beats 100%🔥 | simple-c-approach-beats-100-by-ztvorcaln-5xk5 | Intuition 🧐The problem can be visualized as finding the maximum sum of connected components in a 2D grid where each cell represents the number of fish. A BFS or | its-pratik21 | NORMAL | 2025-01-28T09:55:28.468521+00:00 | 2025-01-28T09:55:28.468521+00:00 | 48 | false | # Intuition 🧐
The problem can be visualized as finding the maximum sum of connected components in a 2D grid where each cell represents the number of fish. A BFS or DFS traversal allows us to explore all connected cells efficiently, while keeping track of the sum for each connected region.
# Approach 🚀
1) Initialization:
- Define direction vectors to navigate the grid in 4 directions (up, down, left, right).
- Create a helper function valid to check if a given cell is within bounds.
2) Traversal:
- Iterate through each cell in the grid.
- If a cell contains fish (grid[i][j] != 0), perform a BFS to explore the connected component:
----> Add the current cell’s fish count to a running sum.
----> Use a queue to process all reachable cells, marking visited cells as 0 to avoid revisiting.
- Compare the sum of the current component with the global maxSum and update it if necessary.
3) Output:
Return the maximum fish sum found across all connected components.
# Complexity ⌛
- Time complexity:
**O(r⋅c)**,
where 𝑟 is the number of rows and 𝑐 is the number of columns. Each cell is visited once during the BFS/DFS.
- Space complexity:
**O(min(r,c))**,
due to the BFS queue storing at most one layer of the grid (worst-case linear space usage).
# Code 📝
```cpp []
class Solution {
public:
int row[4] = {0,0,1,-1};
int col[4] = {1,-1,0,0};
bool valid(int x,int y,int r,int c)
{
return x>=0&&x<r&&y>=0&&y<c;
}
int findMaxFish(vector<vector<int>>& grid) {
int r = grid.size();
int c = grid[0].size();
queue<pair<int,int>> q;
int sum = 0;
int maxSum = 0;
for(int i=0;i<r;i++)
{
for(int j=0;j<c;j++)
{
if(grid[i][j] != 0)
{
sum=0; //**reset sum for each BFS
sum+=grid[i][j];
grid[i][j] = 0;
q.push({i,j});
while(!q.empty())
{
int r1 = q.front().first;
int c1 = q.front().second;
q.pop();
//check all 4 directions
for(int k=0;k<4;k++)
{
if(valid(r1+row[k],c1+col[k],r,c) && grid[r1+row[k]][c1+col[k]] != 0)
{
sum+=grid[r1+row[k]][c1+col[k]];
grid[r1+row[k]][c1+col[k]] = 0;
q.push({r1+row[k],c1+col[k]});
}
}
}
}
maxSum = max(sum,maxSum);
}
}
return maxSum;
}
};
```
 | 2 | 0 | ['Breadth-First Search', 'Graph', 'Matrix', 'C++'] | 1 |
maximum-number-of-fish-in-a-grid | ❄️Simple Recursion to solve easily- C++ || beats 100% 🔥 | simple-recursion-to-solve-easily-c-beats-x0a7 | IntuitionUsing Recursion to traverse each cell where there is fish and counting them. After Finishing I realised it's actually called DFS for searching like thi | Neerajdec2005 | NORMAL | 2025-01-28T07:11:41.156509+00:00 | 2025-01-28T07:11:41.156509+00:00 | 63 | false | # Intuition
Using Recursion to traverse each cell where there is fish and counting them. After Finishing I realised it's actually called DFS for searching like this. So this is a simple recursive DFS code.
# Approach
Traverse Each element from top right to botton left
```
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
rec(i,j,cnt,v);
x=max(cnt,x);
cnt=0;
}
}
```
The recursive call "rec" calls each element and the recursion function moves to each cell where there is fish and also assign v[i][j]=0, which is important, so that the already searched cell won't be searched again!!
> Think again does the already searched element need to be searched?
`Recursive Code`
```
void rec(int i,int j,int& cnt,vector<vector<int>>& v){
cnt+=v[i][j];
if(v[i][j]==0) return;
v[i][j]=0;
if(i>0 && v[i-1][j]>0 && j>=0 && j<n) rec(i-1,j,cnt,v);
if(j>0 && v[i][j-1]>0 && i>=0 && i<m) rec(i,j-1,cnt,v);
if(j<n-1 && v[i][j+1] && i>=0 && i<m) rec(i,j+1,cnt,v);
if(i<m-1 && v[i+1][j] && j>=0 && j<n) rec(i+1,j,cnt,v);
else{
return;
}
}
```
And of course to find the largest among the count taken we have to print the max. So...
`Line: 26`
```
x=max(cnt,x);
cnt=0;
```
# Complexity
- Time complexity:
$$O(n*m)$$
- Space complexity:
$$O(n*m)$$
# Code
```cpp []
class Solution {
public:
int m,n;
void rec(int i,int j,int& cnt,vector<vector<int>>& v){
cnt+=v[i][j];
if(v[i][j]==0) return;
v[i][j]=0;
if(i>0 && v[i-1][j]>0 && j>=0 && j<n) rec(i-1,j,cnt,v);
if(j>0 && v[i][j-1]>0 && i>=0 && i<m) rec(i,j-1,cnt,v);
if(j<n-1 && v[i][j+1] && i>=0 && i<m) rec(i,j+1,cnt,v);
if(i<m-1 && v[i+1][j] && j>=0 && j<n) rec(i+1,j,cnt,v);
else{
return;
}
}
int findMaxFish(vector<vector<int>>& v) {
m=v.size();
n=v[0].size();
int cnt=0;
int x=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
rec(i,j,cnt,v);
x=max(cnt,x);
cnt=0;
}
}
return x;
}
};
``` | 2 | 0 | ['Array', 'Depth-First Search', 'Matrix', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | Simple solution Python3 | simple-solution-python3-by-flyer_51-e4kh | IntuitionThe problem requires finding the maximum number of fish in any connected component of a 2D grid. A connected component is defined by adjacent (up, down | flyer_51 | NORMAL | 2025-01-28T07:04:19.054104+00:00 | 2025-01-28T07:04:19.054104+00:00 | 7 | false | # Intuition
The problem requires finding the maximum number of fish in any connected component of a 2D grid. A connected component is defined by adjacent (up, down, left, right) cells with positive values. The goal is to traverse the grid and calculate the total fish count for each connected component, keeping track of the maximum value encountered.
# Approach
1. **Depth-First Search (DFS)**:
- Use DFS to explore connected components in the grid.
- For each unvisited cell containing fish (`grid[row][col] > 0`), traverse all connected cells to calculate the total fish count.
2. **Tracking Visited Cells**:
- Maintain a `visited` matrix to ensure cells are not counted multiple times.
- Mark a cell as visited during the DFS to avoid revisiting it.
3. **Iterate Through the Grid**:
- For each cell in the grid, if it contains fish and has not been visited, initiate a DFS to compute the total fish count for the connected component starting from that cell.
- Update the maximum fish count if the current component's total fish is greater.
# Complexity
- **Time Complexity**:
$$O(m \times n)$$, where $$m$$ is the number of rows and $$n$$ is the number of columns in the grid.
Each cell is visited at most once, and the DFS explores all connected cells in linear time relative to the total number of cells.
- **Space Complexity**:
$$O(m \times n)$$ for the `visited` matrix. Additionally, the recursive DFS stack may use up to $$O(m \times n)$$ space in the worst case (if the entire grid is a single connected component).
# Code
```python
class Solution:
# Helper function to count the number of fishes in a connected component
def calculate_fishes(self, grid, visited, row, col):
# Check boundary conditions, water cells, or already visited cells
if (
row < 0
or row >= len(grid)
or col < 0
or col >= len(grid[0])
or grid[row][col] == 0
or visited[row][col]
):
return 0
# Mark the current cell as visited
visited[row][col] = True
# Accumulate the fish count from the current cell and its neighbors
return (
grid[row][col]
+ self.calculate_fishes(grid, visited, row, col + 1)
+ self.calculate_fishes(grid, visited, row, col - 1)
+ self.calculate_fishes(grid, visited, row + 1, col)
+ self.calculate_fishes(grid, visited, row - 1, col)
)
def findMaxFish(self, grid):
rows, cols = len(grid), len(grid[0])
max_fish_count = 0
# A 2D list to track visited cells
visited = [[False] * cols for _ in range(rows)]
# Iterate through all cells in the grid
for row in range(rows):
for col in range(cols):
# Start a DFS for unvisited land cells (fish available)
if grid[row][col] > 0 and not visited[row][col]:
max_fish_count = max(
max_fish_count,
self.calculate_fishes(grid, visited, row, col),
)
# Return the maximum fish count found
return max_fish_count
```
# Example
**Input:**
```python
grid = [
[4, 0, 2],
[0, 3, 0],
[1, 0, 5]
]
```
**Output:**
`9`
**Explanation:**
- The first connected component has 4 fish (at `(0, 0)`).
- The second connected component has 9 fish (at `(0, 2)` and `(2, 2)` connected diagonally via `(1, 1)`).
- The third connected component has 1 fish (at `(2, 0)`).
- The maximum fish count is `9`.
This solution is efficient and well-suited for handling grid-based problems. | 2 | 0 | ['Python3'] | 1 |
maximum-number-of-fish-in-a-grid | 🌟BFS for Beginners 💡 | 🎉 Effortless grid exploration with BFS 🧩. | bfs-for-beginners-effortless-grid-explor-mdry | Intuition 🧠
Find the largest group of connected cells with fish using BFS to calculate the total fish in each group. Track the maximum fish among all groups.
Ap | shubhamrajpoot_ | NORMAL | 2025-01-28T06:53:31.555049+00:00 | 2025-01-28T06:53:31.555049+00:00 | 216 | false | # Intuition 🧠
- Find the largest group of connected cells with fish using `BFS` to calculate the `total` fish in each group. Track the maximum fish among all groups.
# Approach 🚀
1. **Traverse Grid:** For each unvisited cell with fish, `start a BFS`.
2. **BFS Exploration:** Use a queue to explore all connected fish cells, summing their values. Mark visited cells in a `vis matrix`.
3. **Update Maximum:** Compare the current group's fish total (currentfish) with the global max (ans).
4. **Return Result:** After checking all cells, return the `largest fish total.`
# Complexity 📊
Time: -> O(m * n)
(Each cell is processed once).
Space: -> O(m * n)
(Visited matrix + BFS queue).
# Code
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
int ans = 0;
vector<vector<int>> vis(m, vector<int>(n, 0));
queue<pair<int, int>> q;
int delrow[] = {-1, 0, 1, 0};
int delcol[] = {0, 1, 0, -1};
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > 0 && vis[i][j] == 0) {
int currentfish = 0;
q.push({i, j});
vis[i][j] = 1;
while (!q.empty()) {
int row = q.front().first;
int col = q.front().second;
currentfish += grid[row][col];
q.pop();
for (int d = 0; d < 4; d++) {
int nrow = row + delrow[d];
int ncol = col + delcol[d];
if (nrow >= 0 && nrow < m && ncol >= 0 && ncol < n)
if (vis[nrow][ncol] == 0 &&
grid[nrow][ncol] > 0) {
vis[nrow][ncol] = 1;
q.push({nrow, ncol});
}
}
}
ans = max(currentfish, ans);
}
}
}
return ans;
}
};
```
```java []
import java.util.*;
class Solution {
public int findMaxFish(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int ans = 0;
boolean[][] vis = new boolean[m][n];
int[] delrow = {-1, 0, 1, 0};
int[] delcol = {0, 1, 0, -1};
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > 0 && !vis[i][j]) {
int currentFish = 0;
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{i, j});
vis[i][j] = true;
while (!q.isEmpty()) {
int[] cell = q.poll();
int row = cell[0], col = cell[1];
currentFish += grid[row][col];
for (int d = 0; d < 4; d++) {
int nrow = row + delrow[d], ncol = col + delcol[d];
if (nrow >= 0 && nrow < m && ncol >= 0 && ncol < n && !vis[nrow][ncol] && grid[nrow][ncol] > 0) {
vis[nrow][ncol] = true;
q.offer(new int[]{nrow, ncol});
}
}
}
ans = Math.max(currentFish, ans);
}
}
}
return ans;
}
}
```
```python []
from collections import deque
class Solution:
def findMaxFish(self, grid):
m, n = len(grid), len(grid[0])
ans = 0
vis = [[False] * n for _ in range(m)]
delrow = [-1, 0, 1, 0]
delcol = [0, 1, 0, -1]
for i in range(m):
for j in range(n):
if grid[i][j] > 0 and not vis[i][j]:
current_fish = 0
q = deque([(i, j)])
vis[i][j] = True
while q:
row, col = q.popleft()
current_fish += grid[row][col]
for d in range(4):
nrow, ncol = row + delrow[d], col + delcol[d]
if 0 <= nrow < m and 0 <= ncol < n and not vis[nrow][ncol] and grid[nrow][ncol] > 0:
vis[nrow][ncol] = True
q.append((nrow, ncol))
ans = max(current_fish, ans)
return ans
```
```ruby []
class Solution
def findMaxFish(grid)
m, n = grid.length, grid[0].length
ans = 0
vis = Array.new(m) { Array.new(n, false) }
delrow = [-1, 0, 1, 0]
delcol = [0, 1, 0, -1]
for i in 0...m
for j in 0...n
if grid[i][j] > 0 && !vis[i][j]
current_fish = 0
q = [[i, j]]
vis[i][j] = true
while !q.empty?
row, col = q.shift
current_fish += grid[row][col]
for d in 0...4
nrow, ncol = row + delrow[d], col + delcol[d]
if nrow >= 0 && nrow < m && ncol >= 0 && ncol < n && !vis[nrow][ncol] && grid[nrow][ncol] > 0
vis[nrow][ncol] = true
q.push([nrow, ncol])
end
end
end
ans = [current_fish, ans].max
end
end
end
return ans
end
end
```
```javascript []
var findMaxFish = function(grid) {
const m = grid.length, n = grid[0].length;
let ans = 0;
const vis = Array.from({length: m}, () => Array(n).fill(false));
const delrow = [-1, 0, 1, 0];
const delcol = [0, 1, 0, -1];
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] > 0 && !vis[i][j]) {
let currentFish = 0;
let q = [[i, j]];
vis[i][j] = true;
while (q.length) {
const [row, col] = q.shift();
currentFish += grid[row][col];
for (let d = 0; d < 4; d++) {
const nrow = row + delrow[d], ncol = col + delcol[d];
if (nrow >= 0 && nrow < m && ncol >= 0 && ncol < n && !vis[nrow][ncol] && grid[nrow][ncol] > 0) {
vis[nrow][ncol] = true;
q.push([nrow, ncol]);
}
}
}
ans = Math.max(currentFish, ans);
}
}
}
return ans;
};
```
```rust []
use std::collections::VecDeque;
impl Solution {
pub fn find_max_fish(grid: Vec<Vec<i32>>) -> i32 {
let m = grid.len();
let n = grid[0].len();
let mut ans = 0;
let mut vis = vec![vec![false; n]; m];
let delrow = [-1, 0, 1, 0];
let delcol = [0, 1, 0, -1];
for i in 0..m {
for j in 0..n {
if grid[i][j] > 0 && !vis[i][j] {
let mut current_fish = 0;
let mut q = VecDeque::new();
q.push_back((i, j));
vis[i][j] = true;
while let Some((row, col)) = q.pop_front() {
current_fish += grid[row][col];
for d in 0..4 {
let nrow = row as i32 + delrow[d];
let ncol = col as i32 + delcol[d];
if nrow >= 0 && nrow < m as i32 && ncol >= 0 && ncol < n as i32
&& !vis[nrow as usize][ncol as usize] && grid[nrow as usize][ncol as usize] > 0 {
vis[nrow as usize][ncol as usize] = true;
q.push_back((nrow as usize, ncol as usize));
}
}
}
ans = ans.max(current_fish);
}
}
}
ans
}
}
```
```typescript []
function findMaxFish(grid: number[][]): number {
const m = grid.length, n = grid[0].length;
let ans = 0;
const vis = Array.from({ length: m }, () => Array(n).fill(false));
const delrow = [-1, 0, 1, 0];
const delcol = [0, 1, 0, -1];
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] > 0 && !vis[i][j]) {
let currentFish = 0;
let q: [number, number][] = [[i, j]];
vis[i][j] = true;
while (q.length) {
const [row, col] = q.shift()!;
currentFish += grid[row][col];
for (let d = 0; d < 4; d++) {
const nrow = row + delrow[d], ncol = col + delcol[d];
if (nrow >= 0 && nrow < m && ncol >= 0 && ncol < n && !vis[nrow][ncol] && grid[nrow][ncol] > 0) {
vis[nrow][ncol] = true;
q.push([nrow, ncol]);
}
}
}
ans = Math.max(currentFish, ans);
}
}
}
return ans;
}
```
| 2 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Matrix', 'Python', 'C++', 'Java', 'TypeScript', 'Rust', 'Ruby', 'JavaScript'] | 1 |
maximum-number-of-fish-in-a-grid | Maximum Number of Fish in a Grid (DFS ) | maximum-number-of-fish-in-a-grid-dfs-by-yu2wj | Code | wjq9YLqfKX | NORMAL | 2025-01-28T06:01:25.559803+00:00 | 2025-01-28T06:01:25.559803+00:00 | 23 | false | # Code
```javascript []
/**
* @param {number[][]} grid
* @return {number}
*/
var findMaxFish = function(grid) {
if (!grid || grid.length === 0) return 0;
let rows = grid.length
let cols = grid[0].length
let max = 0;
function dfs(i, j){
if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] === 0) {
return 0;
}
const fishCount = grid[i][j];
grid[i][j] = 0;
return fishCount + dfs(i + 1, j) + dfs(i - 1, j) + dfs(i, j + 1) + dfs(i, j - 1);
}
for(let i = 0; i < rows; i++){
for(let j = 0; j < cols; j++){
const currentFishCount = dfs(i, j)
max = Math.max(max, currentFishCount)
}
}
return max
};
``` | 2 | 0 | ['Depth-First Search', 'JavaScript'] | 0 |
maximum-number-of-fish-in-a-grid | CPP || !00% beats || easy to understand || BFS | cpp-00-beats-easy-to-understand-bfs-by-a-rx64 | New achievement unlocked-------->
Complexity
Time complexity: O(N*M)
Space complexity: O(N*M)
Code | apoorvjain7222 | NORMAL | 2025-01-28T05:55:13.685723+00:00 | 2025-01-28T05:55:13.685723+00:00 | 52 | false | New achievement unlocked-------->
# Complexity
- Time complexity: O(N*M)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N*M)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
queue<pair<int,int>>q;
set<pair<int,int>>s;
int n = grid.size();
int m = grid[0].size();
int maxa = 0;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
int count =0;
if(grid[i][j] > 0 && !s.count(make_pair(i,j))){
s.insert(make_pair(i,j));
q.push(make_pair(i,j));
// count += grid[i][j];
while(!q.empty()){
auto curr = q.front();
q.pop();
count += grid[curr.first][curr.second];
if(curr.first-1>=0 && grid[curr.first-1][curr.second]>0 && !s.count(make_pair(curr.first-1,curr.second))){
q.push(make_pair(curr.first-1,curr.second));
s.insert(make_pair(curr.first-1,curr.second));
}
if(curr.second-1>=0 && grid[curr.first][curr.second-1]>0 && !s.count(make_pair(curr.first,curr.second-1))){
q.push(make_pair(curr.first,curr.second-1));
s.insert(make_pair(curr.first,curr.second-1));
}
if(curr.first+1<n && grid[curr.first+1][curr.second]>0 && !s.count(make_pair(curr.first+1,curr.second))){
q.push(make_pair(curr.first+1,curr.second));
s.insert(make_pair(curr.first+1,curr.second));
}
if(curr.second+1<m && grid[curr.first][curr.second+1]>0 && !s.count(make_pair(curr.first,curr.second+1))){
q.push(make_pair(curr.first,curr.second+1));
s.insert(make_pair(curr.first,curr.second+1));
}
}
maxa = max(maxa,count);
}
}
}
return maxa;
}
};
``` | 2 | 0 | ['Array', 'Breadth-First Search', 'Union Find', 'Matrix', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | Easy to understand C++ Solution | easy-to-understand-c-solution-by-khushia-6m86 | IntuitionThis problem is similar to: https://leetcode.com/problems/number-of-islands/description/Start a DFS from every water node to find how many fishes can b | khushiagrwl | NORMAL | 2025-01-28T05:51:37.364912+00:00 | 2025-01-28T05:51:52.600581+00:00 | 86 | false | # Intuition
This problem is similar to: https://leetcode.com/problems/number-of-islands/description/
Start a DFS from every water node to find how many fishes can be caught starting from current node.
Once fishes from current index(i, j) are caught - it can be marked visited to avoid recomputation.
Note that one water node can be part of at max one water body. Hence, if we start a dfs from current node, we will explore all the water nodes adjacent to it such that it form a water body surrounded by land in all direction or visit the entire grid.
# Approach
DFS to find the largest number of fishes in one water body.
maximum number of fishes caught from any of the water body will be our answer.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
vector<pair<int, int>> direction = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};
int n, m;
int dfs(vector<vector<int>> & grid, int i, int j) {
if (i < 0 || i == n || j < 0 || j == m) return 0;
if (grid[i][j] == 0) return 0;
int ans = grid[i][j];
grid[i][j] = 0;
for (auto dir: direction) {
ans += dfs(grid, i + dir.first, j + dir.second);
}
return ans;
}
int findMaxFish(vector<vector<int>>& grid) {
n = grid.size(), m = grid[0].size();
int maxfish = 0;
for (int i = 0; i < n; i ++) {
for (int j = 0; j < m; j ++) {
if (grid[i][j] != 0) {
int fish = dfs(grid, i, j);
maxfish = max(fish, maxfish);
}
}
}
return maxfish;
}
};
``` | 2 | 0 | ['Depth-First Search', 'Matrix', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | DFS Concept✅|| ⚡Runtime 5 ms || Java Approach 👍 | dfs-concept-runtime-5-ms-java-approach-b-0v6j | IntuitionThe problem involves finding the maximum number of fish in connected regions of a grid. Each cell in the grid represents water, and the value in the ce | i_dm | NORMAL | 2025-01-28T05:44:03.263309+00:00 | 2025-01-28T05:44:03.263309+00:00 | 21 | false | 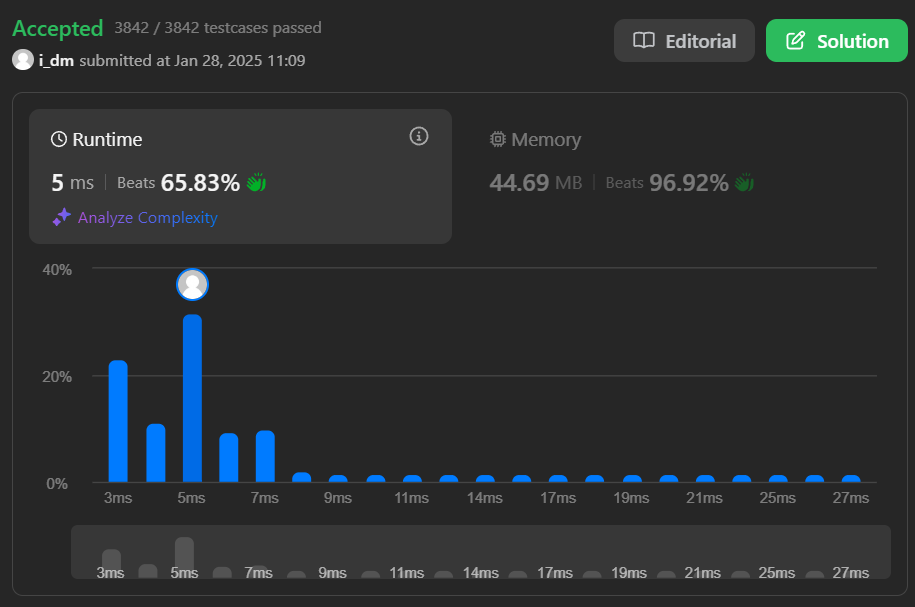
# Intuition
The problem involves finding the maximum number of fish in connected regions of a grid. Each cell in the grid represents water, and the value in the cell represents the number of fish. Connected regions are formed by adjacent cells (up, down, left, right) that contain fish. The goal is to explore all such regions and find the one with the maximum total fish.
My first thought is to use a graph traversal algorithm (either DFS or BFS) to explore all connected cells starting from each unvisited cell that contains fish. By keeping track of visited cells, we can ensure that each region is processed only once.
---
# Approach
1. **Initialization**:
- Store the grid and its dimensions.
- Use a `visited` matrix to keep track of cells that have already been processed.
- Initialize a variable `maxFish` to store the maximum fish count found so far.
2. **Grid Traversal**:
- Iterate through each cell in the grid.
- If a cell contains fish (`grid[r][c] > 0`) and has not been visited, start a DFS or BFS from that cell to explore the entire connected region.
3. **DFS/BFS Exploration**:
- During the traversal, mark cells as visited and accumulate the total fish in the current region.
- Update `maxFish` if the current region's fish count is greater than the previously recorded maximum.
4. **Return Result**:
- After processing all cells, return the value of `maxFish`.
---
# Implementation
Here is the step-by-step implementation of the solution using **DFS**:
1. **Class and Variables**:
- Define the `Solution` class.
- Declare instance variables for the grid, visited matrix, and grid dimensions (`m` and `n`).
2. **Main Method (`findMaxFish`)**:
- Initialize the grid, dimensions, and `visited` matrix.
- Iterate through each cell in the grid.
- If a cell contains fish and is unvisited, call the `dfs` method to explore the connected region and update `maxFish`.
3. **DFS Method**:
- Check if the current cell is out of bounds, has no fish, or has already been visited. If so, return `0`.
- Mark the current cell as visited.
- Accumulate the fish count in the current cell.
- Recursively call `dfs` for all four neighboring cells (up, down, left, right).
- Return the total fish count for the current region.
---
# Complexity
- **Time Complexity**:
- The algorithm visits each cell in the grid exactly once. For each cell, it performs a constant amount of work (checking boundaries, marking as visited, and exploring neighbors).
- Therefore, the time complexity is **O(m × n)**, where `m` is the number of rows and `n` is the number of columns in the grid.
- **Space Complexity**:
- The `visited` matrix requires **O(m × n)** space.
- The recursion stack for DFS can go up to **O(m × n)** in the worst case (e.g., when the entire grid is one connected region).
- Therefore, the space complexity is **O(m × n)**.
# Code
```java []
class Solution {
private int[][] grid;
private boolean[][] visited;
private int m, n;
public int findMaxFish(int[][] grid) {
this.grid = grid;
this.m = grid.length;
this.n = grid[0].length;
this.visited = new boolean[m][n];
int maxFish = 0;
for (int r = 0; r < m; r++) {
for (int c = 0; c < n; c++) {
if (grid[r][c] > 0 && !visited[r][c]) {
int currentFish = dfs(r, c);
maxFish = Math.max(maxFish, currentFish);
}
}
}
return maxFish;
}
private int dfs(int r, int c) {
if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == 0 || visited[r][c]) {
return 0;
}
visited[r][c] = true;
int fish = grid[r][c];
// Explore all four directions
fish += dfs(r + 1, c);
fish += dfs(r - 1, c);
fish += dfs(r, c + 1);
fish += dfs(r, c - 1);
return fish;
}
}
```
# Upvote, if you liked the approach | 2 | 0 | ['Array', 'Math', 'Depth-First Search', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | EASY SOLUTION | JAVA | (Clean Code) | Explained with Comments !! | easy-solution-java-clean-code-explained-zaxhk | Code | Siddharth_Bahuguna | NORMAL | 2025-01-28T05:04:55.593103+00:00 | 2025-01-28T05:04:55.593103+00:00 | 67 | false |
# Code
```java []
class Solution {
int rows;
int cols;
public int findMaxFish(int[][] grid) {
// Store the number of rows and columns in the grid
rows=grid.length;
cols=grid[0].length;
int maxFishes=0;
for(int i=0;i<rows;i++){
for(int j=0;j<cols;j++){
// If the cell contains fish (grid[i][j] > 0), start a DFS search
if(grid[i][j]!=0){
// Update maxFishes with the maximum number of fish caught from the current cell
maxFishes=Math.max(maxFishes,dfs(i,j,grid));
}
}
}
return maxFishes;
}
public int dfs(int r,int c,int grid[][]){
//if current cell is out of bound
if(r<0 || r>=rows || c<0 || c>=cols || grid[r][c]==0){
return 0;
}
// Mark the current cell as visited by setting grid[r][c] to 0 (to avoid revisiting it)
int ans=grid[r][c];
grid[r][c]=0;
ans+=dfs(r-1,c,grid) // Move up
+dfs(r,c+1,grid) // Move right
+dfs(r+1,c,grid) // Move down
+dfs(r,c-1,grid); // Move left
return ans;
}
}
``` | 2 | 0 | ['Java'] | 0 |
maximum-number-of-fish-in-a-grid | Finding Maximum Fish with DFS 🐟💡 | finding-maximum-fish-with-dfs-by-rshohru-j6ms | To solve this problem, we can use Depth-First Search (DFS) to explore connected regions of the grid. Here's the step-by-step approach:
Iterate Through the Grid | rshohruh | NORMAL | 2025-01-28T04:37:27.043374+00:00 | 2025-01-28T04:37:27.043374+00:00 | 166 | false | To solve this problem, we can use **Depth-First Search (DFS)** to explore connected regions of the grid. Here's the step-by-step approach:
1. **Iterate Through the Grid**: Loop through all cells in the grid. If a cell contains fish (`grid[i][j] > 0`), it is the starting point for a new connected region.
2. **Use DFS for Region Exploration**:
- From the starting cell, recursively explore all its valid neighbors (up, down, left, right).
- Add up the fish from all connected cells in the region.
- Mark visited cells by setting them to `0` to prevent revisiting.
3. **Track Maximum Fish**:
- After each DFS, compare the fish count from the current region to the maximum fish count found so far.
4. **Return the Result**: The largest fish count across all connected regions is the answer.
---
#### **Pseudocode**
```
1. Initialize `maxFish = 0`.
2. Define DFS function:
- Take coordinates `x, y` as input.
- If cell is out of bounds or contains `0`, return 0.
- Otherwise:
- Collect the fish from the cell.
- Mark the cell as visited (set it to 0).
- Recursively explore all 4 neighbors and add their fish to the current total.
- Return the total fish collected from this region.
3. Iterate through all cells in the grid:
- If cell contains fish, call DFS and update `maxFish`.
4. Return `maxFish`.
```
---
#### **Code Implementations**
```python []
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
n, m = len(grid), len(grid[0])
directions = [(-1, 0), (0, 1), (1, 0), (0, -1)]
def dfs(x, y):
if x < 0 or x >= n or y < 0 or y >= m or grid[x][y] == 0:
return 0
fish = grid[x][y]
grid[x][y] = 0 # Mark as visited
for dx, dy in directions:
fish += dfs(x + dx, y + dy)
return fish
max_fish = 0
for i in range(n):
for j in range(m):
if grid[i][j] > 0:
max_fish = max(max_fish, dfs(i, j))
return max_fish
```
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<int> dx = {-1, 0, 1, 0};
vector<int> dy = {0, 1, 0, -1};
auto dfs = [&](int x, int y, auto& dfs) -> int {
if (x < 0 || x >= n || y < 0 || y >= m || grid[x][y] == 0) return 0;
int fish = grid[x][y];
grid[x][y] = 0;
for (int d = 0; d < 4; ++d) {
fish += dfs(x + dx[d], y + dy[d], dfs);
}
return fish;
};
int maxFish = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (grid[i][j] > 0) {
maxFish = max(maxFish, dfs(i, j, dfs));
}
}
}
return maxFish;
}
};
```
```golang []
func findMaxFish(grid [][]int) int {
n := len(grid)
m := len(grid[0])
dx := []int{-1, 0, 1, 0}
dy := []int{0, 1, 0, -1}
var dfs func(x, y int) int
dfs = func(x, y int) int {
if x < 0 || x >= n || y < 0 || y >= m || grid[x][y] == 0 {
return 0
}
fish := grid[x][y]
grid[x][y] = 0
for d := 0; d < 4; d++ {
fish += dfs(x+dx[d], y+dy[d])
}
return fish
}
maxFish := 0
for i := 0; i < n; i++ {
for j := 0; j < m; j++ {
if grid[i][j] > 0 {
maxFish = max(maxFish, dfs(i, j))
}
}
}
return maxFish
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
```
```csharp []
public class Solution {
public int FindMaxFish(int[][] grid) {
int n = grid.Length, m = grid[0].Length;
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};
int Dfs(int x, int y) {
if (x < 0 || x >= n || y < 0 || y >= m || grid[x][y] == 0) return 0;
int fish = grid[x][y];
grid[x][y] = 0;
for (int d = 0; d < 4; d++) {
fish += Dfs(x + dx[d], y + dy[d]);
}
return fish;
}
int maxFish = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] > 0) {
maxFish = Math.Max(maxFish, Dfs(i, j));
}
}
}
return maxFish;
}
}
```
```java []
class Solution {
public int findMaxFish(int[][] grid) {
int n = grid.length, m = grid[0].length;
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};
// DFS function
int dfs(int x, int y) {
if (x < 0 || x >= n || y < 0 || y >= m || grid[x][y] == 0) return 0;
int fish = grid[x][y];
grid[x][y] = 0;
for (int d = 0; d < 4; d++) {
fish += dfs(x + dx[d], y + dy[d]);
}
return fish;
}
// Main logic
int maxFish = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] > 0) {
maxFish = Math.max(maxFish, dfs(i, j));
}
}
}
return maxFish;
}
}
```
---
#### **Complexity Analysis**
- **Time Complexity**:
Each cell is visited **once** during DFS and marked as visited. Thus, the time complexity is $$ O(n \times m) $$, where $$ n $$ and $$ m $$ are the dimensions of the grid.
- **Space Complexity**:
The space complexity is $$ O(n \times m) $$ for the recursion stack in the worst case (if the entire grid is one connected region).
---
#### **Example Walkthrough**
**Input**:
```
grid = [[0, 2, 0],
[4, 0, 5],
[0, 3, 0]]
```
**Steps**:
1. Start at cell (1, 0) (value 4). Perform DFS:
- Collect fish: 4.
- Stop DFS as no valid neighbors exist.
Region total = 4.
2. Move to cell (0, 1) (value 2). Perform DFS:
- Collect fish: 2.
- Stop DFS as no valid neighbors exist.
Region total = 2.
3. Move to cell (1, 2) (value 5). Perform DFS:
- Collect fish: 5.
- Stop DFS as no valid neighbors exist.
Region total = 5.
4. Move to cell (2, 1) (value 3). Perform DFS:
- Collect fish: 3.
- Stop DFS as no valid neighbors exist.
Region total = 3.
**Output**:
The largest region has 5 fish, so the result is **5**.
---
| 2 | 0 | ['Array', 'Depth-First Search', 'Matrix', 'C++', 'Java', 'Go', 'Python3', 'C#'] | 0 |
maximum-number-of-fish-in-a-grid | DSU Solution || Path Compression and Ackermann Concept Explained || Time And Space Explained || | dsu-solution-path-compression-and-ackerm-6giw | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Heisenberg_wc | NORMAL | 2025-01-28T04:21:07.374559+00:00 | 2025-01-28T04:21:07.374559+00:00 | 49 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
//Data Set Union to check connected Components
class DSU {
public:
vector<int> parent;//To keep a track of which component the element is
vector<int> rank;//To create a dynamically changing graph
DSU(int n) {//Initializing the DSU
parent.resize(n);
rank.resize(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
rank[i] = 0;
}
}
int find_parent(int n) {//Using Find Parent we can acess whether a elemnt is from certain component or not
if (parent[n] == n) {
return n;
} else {
return parent[n] = find_parent(parent[n]);//Path Compression
}
}
void merge(int a, int b) {//Merging By Rank
int u = find_parent(a);
int v = find_parent(b);
if (u == v)
return;
if (rank[u] > rank[v]) {
parent[v] = u;
} else if (rank[v] > rank[u]) {
parent[u] = v;
} else {
parent[u] = v;
rank[v]++;
}
}
};
class Solution {
public:
//Direction vector to easily navigate the alternate neighbours
vector<int> x = {1, -1, 0, 0};
vector<int> y = {0, 0, 1, -1};
int findMaxFish(vector<vector<int>>& grid) {
if (grid.empty() || grid[0].empty()){//Edge Case
return 0;
}
int n = grid.size();
int m = grid[0].size();
DSU dsu(n * m);//Inittializing the DSU Object
bool flag = true;//To check if there exists water cell
for (int i = 0; i < n; i++) {//O(Row*Col)
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) {
continue;
} else {
flag = false;
int a = i * m + j;
for (int k = 0; k < 4; k++) {//Traversing the neighbor elemnts
if (i + x[k] >= 0 && i + x[k] < n && j + y[k] >= 0 &&
j + y[k] < m && grid[i + x[k]][j + y[k]] != 0) {
int b = (i + x[k]) * m + (j + y[k]);
dsu.merge(a, b);//merging who are part of dame componets
}
}
}
}
}
if (flag) {//When no water cell is present
return 0;
}
unordered_map<int, int> mp;//To track all elemts and find therir sum
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
int p = dsu.find_parent(i * m + j);
mp[p] += grid[i][j];
}
}
int ans = INT_MIN;
for (auto i : mp) {
ans = max(i.second, ans);
}
return ans;
//Time Complexity :O(Row*Col*4)+O(αn)≈O(Row*col*4)
//where α is Ackermann Constant
//Space Complexity :O(M*N)
//Other Ideas : Can be used using a normal Bfs or Dfs Search ....
}
};
``` | 2 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | DFS solution || C++ || Python | dfs-solution-c-python-by-anurag_basuri-ibpn | IntuitionThe problem involves identifying connected components in a grid where each cell represents either a body of water (0) or a cluster of fish (non-zero po | Anurag_Basuri | NORMAL | 2025-01-28T04:11:17.130053+00:00 | 2025-01-28T04:11:17.130053+00:00 | 85 | false | # Intuition
The problem involves identifying connected components in a grid where each cell represents either a body of water (0) or a cluster of fish (non-zero positive integers). The goal is to calculate the maximum number of fish in any connected cluster, where connectivity is defined as adjacency in the 4 cardinal directions (up, down, left, right). This can be solved using Depth First Search (DFS) to traverse and count the fish in each cluster.
# Approach
1. **Initialization**:
Create a `visited` matrix of the same size as the grid to track the cells that have been processed.
2. **DFS Traversal**:
- Use DFS to explore all connected cells starting from an unvisited cell containing fish.
- For each cell visited during the DFS, add its fish count to a running total.
- Mark the cell as visited to prevent revisiting it.
3. **Iterate Through the Grid**:
- Loop through all cells in the grid.
- If a cell contains fish (value > 0) and hasn't been visited, initiate a DFS from that cell and calculate the total fish count for the connected component.
4. **Track the Maximum**:
Keep track of the maximum fish count found during the traversal.
5. **Return the Result**:
After processing the entire grid, return the maximum fish count.
# Complexity
- **Time Complexity**: $$O(m \times n)$$
- Each cell in the grid is visited exactly once during the DFS traversal.
- For a grid with dimensions $$m \times n$$, the total time complexity is proportional to the number of cells.
- **Space Complexity**: $$O(m \times n)$$
- The `visited` matrix requires $$O(m \times n)$$ space.
- The recursion stack for the DFS can hold up to $$O(m \times n)$$ calls in the worst case (e.g., a fully connected grid with fish).
# Why This Works
1. **DFS Correctly Identifies Connected Components**:
The DFS explores all adjacent cells recursively, ensuring that each cluster of connected fish is fully traversed.
2. **Marking Cells as Visited Prevents Reprocessing**:
This avoids redundant calculations and ensures that each cell is processed exactly once.
3. **Iterating Over the Grid Ensures Full Coverage**:
By starting a new DFS for every unvisited cell with fish, all clusters are discovered.
# Code
```cpp []
class Solution {
public:
int dfs(vector<vector<int>>& grid, vector<vector<int>>& visited, int row, int col) {
int n = grid.size();
int m = grid[0].size();
if (row < 0 || col < 0 || row >= n || col >= m || grid[row][col] == 0 || visited[row][col] == 1) {
return 0;
}
visited[row][col] = 1;
int total_fishes = grid[row][col];
total_fishes += dfs(grid, visited, row + 1, col); // Down
total_fishes += dfs(grid, visited, row - 1, col); // Up
total_fishes += dfs(grid, visited, row, col + 1); // Right
total_fishes += dfs(grid, visited, row, col - 1); // Left
return total_fishes;
}
int findMaxFish(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
int max_fish = 0;
vector<vector<int>> visited(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] > 0 && visited[i][j] == 0) {
max_fish = max(max_fish, dfs(grid, visited, i, j));
}
}
}
return max_fish;
}
};
```
``` python []
class Solution:
def dfs(self, grid, visited, row, col):
n = len(grid)
m = len(grid[0])
# Boundary checks and already visited or water cell checks
if row < 0 or col < 0 or row >= n or col >= m or grid[row][col] == 0 or visited[row][col]:
return 0
# Mark the cell as visited
visited[row][col] = True
# Collect fish from the current cell
total_fishes = grid[row][col]
# Perform DFS in all 4 directions
total_fishes += self.dfs(grid, visited, row + 1, col) # Down
total_fishes += self.dfs(grid, visited, row - 1, col) # Up
total_fishes += self.dfs(grid, visited, row, col + 1) # Right
total_fishes += self.dfs(grid, visited, row, col - 1) # Left
return total_fishes
def findMaxFish(self, grid):
n = len(grid)
m = len(grid[0])
max_fish = 0
# Visited matrix to track which cells have been processed
visited = [[False for _ in range(m)] for _ in range(n)]
for i in range(n):
for j in range(m):
# Start a DFS for each unvisited cell containing fish
if grid[i][j] > 0 and not visited[i][j]:
max_fish = max(max_fish, self.dfs(grid, visited, i, j))
return max_fish
``` | 2 | 0 | ['Array', 'Depth-First Search', 'Matrix', 'C++', 'Python3'] | 0 |
maximum-number-of-fish-in-a-grid | leetcodedaybyday - Beats 84.06% with C++ and Beats 73.41% with Python3 | leetcodedaybyday-beats-8406-with-c-and-b-ryk7 | IntuitionTo solve the problem, we can leverage a Depth-First Search (DFS) approach. The idea is to explore all connected cells in the grid that contain non-zero | tuanlong1106 | NORMAL | 2025-01-28T03:58:45.710574+00:00 | 2025-01-28T03:58:45.710574+00:00 | 102 | false | # Intuition
To solve the problem, we can leverage a Depth-First Search (DFS) approach. The idea is to explore all connected cells in the grid that contain non-zero values, as they represent the regions containing fish. By performing DFS for each cell in the grid, we can calculate the total number of fish in connected components and track the maximum fish count.
# Approach
1. **DFS Traversal**:
- Use a helper function `DFS` that takes the current cell and recursively explores all adjacent cells in the four cardinal directions (up, down, left, right).
- Accumulate the fish count for the connected component and mark the cell as visited by setting its value to `0`.
2. **Iterate Over All Cells**:
- For each cell in the grid, check if it contains a positive value (indicating fish).
- If so, call the `DFS` function and update the maximum fish count based on the result.
3. **Edge Cases**:
- Handle cases where the grid is empty or has only one row/column.
- Ensure boundary conditions are respected during DFS traversal.
# Complexity
- **Time Complexity**:
O(r * c), where r is the number of rows and c is the number of columns.
Each cell is visited once during the DFS traversal.
- **Space Complexity**:
O(r * c) in the worst case due to the recursive stack during DFS, if the grid contains a single connected component.
# Code
```cpp []
class Solution {
public:
const int d[5] = {0, 1, 0, -1, 0};
int r, c;
int DFS(int i, int j, vector<vector<int>>& grid){
int fish = grid[i][j];
grid[i][j] = 0;
for (int a = 0; a < 4; a++){
int row = i + d[a];
int col = j + d[a + 1];
if (row < 0 || row >= r || col < 0 || col >= c || grid[row][col] == 0){
continue;
}
fish += DFS(row, col, grid);
}
return fish;
}
int findMaxFish(vector<vector<int>>& grid) {
r = grid.size();
c = grid[0].size();
int ans = 0;
for (int i = 0; i < r; i++){
for (int j = 0; j < c; j++){
if (grid[i][j] > 0){
ans = max(ans, DFS(i, j, grid));
}
}
}
return ans;
}
};
```
```python3 []
class Solution:
def __init__(self):
self.d = [0, 1, 0, -1, 0]
self.r = 0
self.c = 0
def DFS(self, i, j, grid):
fish = grid[i][j]
grid[i][j] = 0
for a in range(4):
row = i + self.d[a]
col = j + self.d[a + 1]
if row < 0 or row >= self.r or col < 0 or col >= self.c or grid[row][col] == 0:
continue
fish += self.DFS(row, col, grid)
return fish
def findMaxFish(self, grid: List[List[int]]) -> int:
self.r = len(grid)
self.c = len(grid[0])
ans = 0
for i in range(self.r):
for j in range(self.c):
if grid[i][j] > 0:
ans = max(ans, self.DFS(i, j, grid))
return ans
```
| 2 | 0 | ['Depth-First Search', 'Matrix', 'C++', 'Python3'] | 1 |
maximum-number-of-fish-in-a-grid | ✅ ⟣ Java Solution ⟢ | java-solution-by-harsh__005-8tzi | Code | Harsh__005 | NORMAL | 2025-01-28T02:40:49.089420+00:00 | 2025-01-28T02:40:49.089420+00:00 | 52 | false | # Code
```java []
class Solution {
int dirs[][] = {{-1,0}, {1,0}, {0,-1}, {0,1}};
private int solve(boolean[][] vis, int i, int j, int r, int c, int[][] grid) {
vis[i][j] = true;
int sum = grid[i][j];
for(int dir[]: dirs) {
int nr = i + dir[0], nc = j + dir[1];
if(nr<0 || nc<0 || nr==r || nc==c || grid[nr][nc]==0 || vis[nr][nc]) continue;
sum += solve(vis, nr, nc, r, c, grid);
}
return sum;
}
public int findMaxFish(int[][] grid) {
int r = grid.length, c = grid[0].length;
boolean vis[][] = new boolean[r][c];
int ans = 0;
for(int i=0; i<r; i++) {
for(int j=0; j<c; j++) {
if(grid[i][j] > 0 && !vis[i][j]) {
ans = Math.max(ans, solve(vis, i, j, r, c, grid));
}
}
}
return ans;
}
}
``` | 2 | 0 | ['Java'] | 1 |
maximum-number-of-fish-in-a-grid | Maximum Number Of Fish In the grid - Easy Solution - Nice Explanation ‼️💯 | maximum-number-of-fish-in-the-grid-easy-ibu7w | Intuition
We can use bfs to keep track of the adjacent cells and once the cell is visited,it's marked as 0 in-place.
At each bfs,we'll obtain max number of f | RAJESWARI_P | NORMAL | 2025-01-28T02:40:36.959367+00:00 | 2025-01-28T02:40:36.959367+00:00 | 32 | false | # Intuition
1. We can use bfs to keep track of the adjacent cells and once the cell is visited,it's marked as 0 in-place.
1. At each bfs,we'll obtain max number of fishes, so that we'll get the maximum of the fishes that can be obtained in the grid.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
**findMaxFish**:
**parameter**: grid (2-D integer array).
**return value**: int
**Initialization**:
Initialize row to be the length of the grid ,col to be the length of each row and maxFish is set to 0 initially.
int row=grid.length;
int col=grid[0].length;
int maxFish=0;
**Perform bfs**:
Iterate through all the cells in the grid 2-D array.
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
Perform bfs on the grid 2-D array if it is not the land cell and obtain the maximum number of fishes possible.
if(grid[i][j]>0){
int fishReg=bfs(grid,row,col,i,j);
Each bfs will return the fish in that region, compare that at each iteration and return the maximum number of fishes.
maxFish=Math.max(maxFish,fishReg);
**Returning the result**:
Return maxFish which contains maximum number of fishes that can be obtained from the given grid.
return maxFish;
**bfs**:
**parameter**: grid (2-D integer array), row, col, i and j of integer.
**return value**: int.
**Base Condition**:
If i is not within the range of 0 to row or j is not within the range of 0 to col or the cell is the land,then stop recursion and return 0.
if(i<0 || i>=row || j<0 || j>=col || grid[i][j]==0)
{
return 0;
}
**Perform bfs for fish count**:
Initialize fish to be the fishes in the particular cell of grid at index i and j.
int fish=grid[i][j];
If used, mark the cell as 0.
grid[i][j]=0;
Visit the adjacent cells of the grid by bfs and increment the fish count.
fish+=bfs(grid,row,col,i+1,j);
fish+=bfs(grid,row,col,i-1,j);
fish+=bfs(grid,row,col,i,j+1);
fish+=bfs(grid,row,col,i,j-1);
**Returning the result**:
Return fish which contains the fish at the region of the grid at index i and j.
return fish;
<!-- Describe your approach to solving the problem. -->
# Complexity
- ***Time complexity***: **O(mxn)**.
m -> number of rows in the grid.
n -> number of columns in the grid.
**Outer Loops**: **O(mxn)**.
The two nested for loops in the findMaxFish function iterate over all cells of the grid.
For grid size mxn, the total time complexity of these loops are **O(mxn)**.
**bfs function**: **O(mxn)**.
Each cell is visited once during the DFS traversal. When a cell is visited, it is marked as 0 (visited), so it is not revisited.
In the worst case, all cells are part of one large connected component. Here, the DFS would visit every cell in the grid.Hence it takes **O(mxn) time**.
**Total Time Complexity**: **O(mxn)**.
The bfs function is called for every unvisited cell that has a positive value. Since each cell is visited exactly once, the total work done is proportional to the number of cells in the grid.
Thus the total time complexity is **O(mxn)**.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- ***Space complexity***: **O(mxn)**.
m -> number of rows in the grid.
n -> number of columns in the grid.
**Recursive Depth**: **O(mxn)**.
The bfs function uses recursion to perform DFS. The recursion depth corresponds to the **size of the largest connected component** of non-zero cells.
In the worst case, all cells are part of one large connected component, resulting in a recursion depth of O(mxn).Hence it consumes **O(mxn) space**.
**Auxillary Space**: **O(1)**.
No additional data structures are used, and the grid itself is modified in-place to mark visited cells.
Hence, the **auxiliary space is negligible** (O(1)).
**Total Space Complexity**: **O(mxn)**.
Total Space Complexity is **dominated by the recursive depth**.Hence the total Space Complexity is **O(mxn)**.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
int max;
private int bfs(int[][] grid,int row,int col,int i,int j)
{
if(i<0 || i>=row || j<0 || j>=col || grid[i][j]==0)
{
return 0;
}
int fish=grid[i][j];
grid[i][j]=0;
fish+=bfs(grid,row,col,i+1,j);
fish+=bfs(grid,row,col,i-1,j);
fish+=bfs(grid,row,col,i,j+1);
fish+=bfs(grid,row,col,i,j-1);
return fish;
}
public int findMaxFish(int[][] grid) {
int row=grid.length;
int col=grid[0].length;
int maxFish=0;
for(int i=0;i<row;i++)
{
for(int j=0;j<col;j++)
{
if(grid[i][j]>0)
{
int fishReg=bfs(grid,row,col,i,j);
maxFish=Math.max(maxFish,fishReg);
}
}
}
return maxFish;
}
}
``` | 2 | 0 | ['Array', 'Breadth-First Search', 'Matrix', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | BFS & DFS Approach Python Solution | bfs-dfs-approach-python-solution-by-feni-orii | DFS Solution# IntuitionThe problem involves finding the maximum number of fish that can be collected in a grid by moving in 4 possible directions (up, down, lef | fenilpatel61 | NORMAL | 2025-01-28T02:33:38.632970+00:00 | 2025-01-28T02:36:07.357092+00:00 | 19 | false | ### DFS Solution
---
#### **# Intuition**
The problem involves finding the maximum number of fish that can be collected in a grid by moving in 4 possible directions (up, down, left, right). Since connected components of non-zero cells represent a valid path to collect fish, the goal is to explore all such components and track the maximum sum. A **depth-first search (DFS)** is suitable because it allows us to recursively explore each connected component efficiently.
---
#### **# Approach**
1. **Initialize Variables**:
- Create a DFS function that will explore all connected non-zero cells starting from a given cell.
- Track visited cells by marking them as \(0\) in the grid after processing.
2. **DFS Traversal**:
- Recursively visit each valid neighbor (within bounds and non-zero).
- Accumulate the fish count from the current cell and neighbors.
3. **Iterate Over the Grid**:
- For each cell in the grid, if it is non-zero, invoke the DFS function to calculate the total fish in that connected component.
- Update the maximum fish count.
4. **Return the Result**:
- After visiting all cells, return the maximum fish count.
---
# Code
```python3 []
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
def dfs(x,y):
maxi = 0
if x < 0 or x >= len(grid) or y < 0 or y >= len(grid[0]) or grid[x][y] == 0:
return maxi
maxi += grid[x][y]
grid[x][y] = 0
return dfs(x+1,y) + dfs(x-1,y) + dfs(x,y+1) + dfs(x,y-1) + maxi
maximum = 0
for x in range(len(grid)):
for y in range(len(grid[0])):
if grid[x][y] != 0:
maximum = max(maximum, dfs(x,y))
return maximum
```
#### **# Complexity**
- **Time Complexity**:
\(O(m * n)\), where \(m\) and \(n\) are the dimensions of the grid.
- Each cell is visited exactly once during the DFS traversal.
- Each recursive call processes up to 4 directions (a constant factor).
- **Space Complexity**:
\(O(m * n)\) in the worst case (if the grid is one large connected component), due to the recursion stack.
---
### BFS Solution
---
#### **# Intuition**
The problem can also be solved using a **breadth-first search (BFS)**, which explores a connected component level by level. BFS uses a queue to manage the exploration of valid neighbors. This approach allows systematic exploration and accumulation of fish counts, ensuring every component is processed.
---
#### **# Approach**
1. **Initialize Variables**:
- Use a queue (`deque`) to manage cells to visit.
- Implement a BFS function to explore all valid neighbors for a given starting cell.
2. **BFS Traversal**:
- Start from a cell with non-zero fish.
- Add the current cell's fish count to the total, mark it as visited by setting its value to \(0\), and enqueue all valid neighbors.
3. **Iterate Over the Grid**:
- For each cell in the grid, if it is non-zero, invoke the BFS function to calculate the total fish in that connected component.
- Update the maximum fish count.
4. **Return the Result**:
- After visiting all cells, return the maximum fish count.
---
# Code
```
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
def bfs():
maxi = 0
while queue:
x,y = queue.popleft()
maxi += grid[x][y]
grid[x][y] = 0
directions = [(x+1,y),(x-1,y),(x,y+1),(x,y-1)]
for r,c in directions:
if 0<=r< len(grid) and 0<=c < len(grid[0]) and grid[r][c] !=0:
queue.append((r,c))
return maxi
queue = deque()
maxFish = 0
for x in range(len(grid)):
for y in range(len(grid[0])):
if grid[x][y] !=0:
queue.append((x,y))
maxFish = max(maxFish,bfs())
return maxFish
```
#### **# Complexity**
- **Time Complexity**:
\(O(m * n)\), where \(m\) and \(n\) are the dimensions of the grid.
- Each cell is visited exactly once during the BFS traversal.
- Each cell's neighbors are processed up to 4 times (constant factor).
- **Space Complexity**:
\(O(m * n)\) in the worst case, for the queue (if all cells are part of the same connected component).
---
### Comparison
- **DFS** is often faster in practice due to lower overhead, as it uses the call stack for traversal instead of explicit queue management.
- **BFS** might be preferred for grids with very large components, as it avoids potential stack overflow issues in DFS.
| 2 | 0 | ['Python3'] | 0 |
maximum-number-of-fish-in-a-grid | Easy C++ solution | easy-c-solution-by-harsh_indoria-g81q | IntuitionThe problem involves finding the maximum sum of connected non-zero cells in a grid. This suggests a graph traversal problem, where each non-zero cell i | HARSH_INDORIA | NORMAL | 2025-01-28T02:18:26.334091+00:00 | 2025-01-28T02:18:26.334091+00:00 | 105 | false | # Intuition
The problem involves finding the maximum sum of connected non-zero cells in a grid. This suggests a **graph traversal problem**, where each non-zero cell is a node, and edges exist between adjacent non-zero cells (up, down, left, right). We can treat the problem as finding the largest **connected component** in the grid.
Depth-First Search (DFS) is well-suited for exploring connected components in a grid-based problem.
---
# Approach
1. **DFS Traversal**:
- Start DFS from each unvisited non-zero cell.
- Explore all four possible directions (up, down, left, right).
- Mark cells as visited to prevent revisiting.
- Sum the values of all connected non-zero cells.
2. **Iterate Over the Grid**:
- For each unvisited non-zero cell, initiate DFS to compute the sum of connected non-zero values.
- Keep track of the maximum sum encountered.
---
# Complexity
- **Time Complexity**:
Each cell is visited once, and each DFS call processes up to 4 directions. In the worst case, all cells are part of one large connected component, leading to an $$O(m \times n)$$ complexity.
- **Space Complexity**:
- **Recursive Stack**: In the worst case, the DFS recursion depth could reach $$O(m \times n)$$ in the case of a single large connected component.
- **Visited Array**: Requires $$O(m \times n)$$ space.
- **Total Space Complexity**: $$O(m \times n)$$
---
# Code
```cpp
class Solution {
public:
int dfs(int r, int c, vector<vector<int>> &grid, vector<vector<bool>> &visited) {
int m = grid.size(), n = grid[0].size();
if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == 0 || visited[r][c])
return 0;
visited[r][c] = true;
int sum = grid[r][c]; // Collect fish from the current cell
// Explore all 4 possible directions
sum += dfs(r + 1, c, grid, visited);
sum += dfs(r - 1, c, grid, visited);
sum += dfs(r, c + 1, grid, visited);
sum += dfs(r, c - 1, grid, visited);
return sum;
}
int findMaxFish(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<bool>> visited(m, vector<bool>(n, false));
int maxFish = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > 0 && !visited[i][j]) {
maxFish = max(maxFish, dfs(i, j, grid, visited));
}
}
}
return maxFish;
}
};
``` | 2 | 0 | ['Depth-First Search', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | DFS from Water Cells | C++, Python, Java | dfs-from-water-cells-c-python-java-by-no-2z8e | ApproachPerform a DFS starting from every unmarked water cell where you visit every 4-directionally adjacent cells (up, down, left, right). When you visit an ad | not_yl3 | NORMAL | 2025-01-28T00:50:14.611269+00:00 | 2025-01-28T00:50:14.611269+00:00 | 245 | false | # Approach
<!-- Describe your approach to solving the problem. -->
Perform a DFS starting from every unmarked water cell where you visit every 4-directionally adjacent cells (up, down, left, right). When you visit an adjacent water cell, mark it as visited by setting it to zero so that we don't visit it again. After each dfs return the amount of fish we got from every nearby water cell.
# Complexity
- Time complexity: $$O(m \cdot n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(m \cdot n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size(), res = 0;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (grid[i][j] > 0)
res = max(res, dfs(i, j, grid));
return res;
}
private:
int dfs(int r, int c, vector<vector<int>>& grid){
if (r < 0 || c < 0 || r == grid.size() || c == grid[0].size() || grid[r][c] == 0)
return 0;
int res = grid[r][c];
grid[r][c] = 0;
return res + dfs(r + 1, c, grid) + dfs(r - 1, c, grid) + dfs(r, c + 1, grid) + dfs(r, c - 1, grid);
}
};
```
```python []
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
def dfs(r, c):
if r < 0 or r == m or c < 0 or c == n or grid[r][c] == 0:
return 0
total = grid[r][c]
grid[r][c] = 0
return total + dfs(r + 1, c) + dfs(r - 1, c) + dfs(r, c + 1) + dfs(r, c - 1)
return max(dfs(r, c) if grid[r][c] > 0 else 0 for r in range(m) for c in range(n))
```
```java []
class Solution {
public int findMaxFish(int[][] grid) {
int res = 0, m = grid.length, n = grid[0].length;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (grid[i][j] > 0)
res = Math.max(res, dfs(i, j, grid));
return res;
}
private int dfs(int r, int c, int[][] grid){
if (r < 0 || c < 0 || r == grid.length || c == grid[0].length || grid[r][c] == 0)
return 0;
int res = grid[r][c];
grid[r][c] = 0;
return res + dfs(r + 1, c, grid) + dfs(r - 1, c, grid) + dfs(r, c + 1, grid) + dfs(r, c - 1, grid);
}
}
``` | 2 | 0 | ['Array', 'Depth-First Search', 'Breadth-First Search', 'Union Find', 'C', 'Matrix', 'Python', 'C++', 'Java', 'Python3'] | 0 |
maximum-number-of-fish-in-a-grid | Swift💯DFS | swiftdfs-by-upvotethispls-2uo8 | DFS Flood Fill (accepted answer) | UpvoteThisPls | NORMAL | 2025-01-28T00:26:23.025864+00:00 | 2025-01-28T00:26:23.025864+00:00 | 69 | false | **DFS Flood Fill (accepted answer)**
```
class Solution {
func findMaxFish(_ grid: consuming [[Int]]) -> Int {
let (rows,cols) = (grid.indices, grid[0].indices)
func dfs(_ x:Int, _ y:Int) -> Int {
guard rows ~= y, cols ~= x, grid[y][x] > 0 else { return 0 }
var fish = grid[y][x]
grid[y][x] = 0
for (dx,dy) in [0,1,0,-1,0].adjacentPairs() {
fish += dfs(x+dx, y+dy)
}
return fish
}
return product(cols, rows).lazy.map(dfs).reduce(0, max)
}
}
``` | 2 | 0 | ['Depth-First Search', 'Recursion', 'Swift'] | 0 |
maximum-number-of-fish-in-a-grid | C++ | DFS | c-dfs-by-ahmedsayed1-nr1s | Code | AhmedSayed1 | NORMAL | 2025-01-28T00:19:59.841607+00:00 | 2025-01-28T00:19:59.841607+00:00 | 145 | false | # Code
```cpp []
class Solution {
public:
int dx[4]{1, -1 , 0 ,0}, dy[4]{0, 0 , 1 , -1};
int dfs(int i, int j, vector<vector<int>>& grid){
int ret = grid[i][j];
grid[i][j] = 0;
for(int k = 0 ;k < 4 ;k++){
int a = i + dx[k], b = j + dy[k];
if(min(a, b) >= 0 && a < grid.size() && b < grid[0].size() && grid[a][b])
ret += dfs(a, b , grid);
}
return ret;
}
int findMaxFish(vector<vector<int>>& grid) {
int ans = 0;
for(int i = 0 ; i < grid.size() ;i++)
for(int j = 0; j < grid[0].size() ;j++)
if(grid[i][j])ans = max(ans, dfs(i, j , grid));
return ans;
}
};
``` | 2 | 0 | ['Depth-First Search', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | "🚀🚀Maximize Fish Catch🔥🔥|| ✅Efficient Solution by Kanishka✅|| 🔥🔥Beginner Friendly Solution🚀🚀 | maximize-fish-catch-efficient-solution-b-loef | 🧠 IntuitionThe first thought is to traverse the grid and explore each possible connected component of non-zero fish values using Depth-First Search (DFS). The g | kanishka21535 | NORMAL | 2025-01-28T00:12:13.765672+00:00 | 2025-01-28T00:12:13.765672+00:00 | 30 | false | # 🧠 Intuition
The first thought is to traverse the grid and explore each possible connected component of non-zero fish values using Depth-First Search (DFS). The goal is to find the maximum fish count in any connected component.
# 🔍 Approach
Here's the approach step-by-step:
1. **Initialize Variables**: Set up a `visited` array to keep track of visited cells and an `answer` variable to store the maximum fish count found.
2. **Traverse the Grid**: For each cell in the grid, if it is not visited and contains a non-zero value, use DFS to explore the connected component.
3. **DFS Exploration**: For each unvisited cell in the connected component, mark it as visited and accumulate the fish count.
4. **Update Maximum**: After exploring each connected component, update the `answer` with the maximum fish count found.
# ⏳ Complexity
- **Time Complexity**: $$O(n \times m)$$
- We traverse each cell in the grid once.
- **Space Complexity**: $$O(n \times m)$$
- We use additional space for the `visited` array and recursion stack.
# 📜 Code
```java
class Solution {
public int max;
public int findMaxFish(int[][] grid) {
int rlen = grid.length;
int clen = grid[0].length;
int answer = 0;
boolean visited[][] = new boolean[rlen][clen];
for(int i=0;i<rlen;i++){
for(int j=0;j<clen;j++){
if(grid[i][j]!=0 && !visited[i][j]){
max = 0;
dfs(grid, rlen, clen, visited, i, j);
answer = Math.max(max, answer );
}
}
}
return answer;
}
public void dfs(int[][] grid, int rlen, int clen, boolean[][] visited, int i, int j){
if(i<0 || i>=rlen || j<0 || j>=clen || visited[i][j] || grid[i][j] == 0){
return;
}
visited[i][j] = true;
max += grid[i][j];
dfs(grid, rlen, clen, visited, i+1, j);
dfs(grid, rlen, clen, visited, i-1, j);
dfs(grid, rlen, clen, visited, i, j+1);
dfs(grid, rlen, clen, visited, i, j-1);
}
}
| 2 | 0 | ['Depth-First Search', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | "🚀🚀Maximize Fish Catch🔥🔥|| ✅Efficient Solution by Dhandapani✅|| 🔥🔥Beats 100% in Java🚀🚀 | maximize-fish-catch-efficient-solution-b-qqal | 🧠 IntuitionThe first thought is to traverse the grid and explore each possible connected component of non-zero fish values using Depth-First Search (DFS). The g | Dhandapanimaruthasalam | NORMAL | 2025-01-28T00:06:43.309262+00:00 | 2025-01-28T00:06:43.309262+00:00 | 134 | false | # 🧠 Intuition
The first thought is to traverse the grid and explore each possible connected component of non-zero fish values using Depth-First Search (DFS). The goal is to find the maximum fish count in any connected component.
# 🔍 Approach
Here's the approach step-by-step:
1. **Initialize Variables**: Set up a `visited` array to keep track of visited cells and an `answer` variable to store the maximum fish count found.
2. **Traverse the Grid**: For each cell in the grid, if it is not visited and contains a non-zero value, use DFS to explore the connected component.
3. **DFS Exploration**: For each unvisited cell in the connected component, mark it as visited and accumulate the fish count.
4. **Update Maximum**: After exploring each connected component, update the `answer` with the maximum fish count found.
# ⏳ Complexity
- **Time Complexity**: $$O(n \times m)$$
- We traverse each cell in the grid once.
- **Space Complexity**: $$O(n \times m)$$
- We use additional space for the `visited` array and recursion stack.
# 📜 Code (Java)
```
class Solution {
public int max;
public int findMaxFish(int[][] grid) {
int rlen = grid.length;
int clen = grid[0].length;
int answer = 0;
boolean visited[][] = new boolean[rlen][clen];
for(int i=0;i<rlen;i++){
for(int j=0;j<clen;j++){
if(grid[i][j]!=0 && !visited[i][j]){
max = 0;
dfs(grid, rlen, clen, visited, i, j);
answer = Math.max(max, answer );
}
}
}
return answer;
}
public void dfs(int[][] grid, int rlen, int clen, boolean[][] visited, int i, int j){
if(i<0 || i>=rlen || j<0 || j>=clen || visited[i][j] || grid[i][j] == 0){
return;
}
visited[i][j] = true;
max += grid[i][j];
dfs(grid, rlen, clen, visited, i+1, j);
dfs(grid, rlen, clen, visited, i-1, j);
dfs(grid, rlen, clen, visited, i, j+1);
dfs(grid, rlen, clen, visited, i, j-1);
}
}
```
##### I hope this helps! Feel free to reach out if you need more assistance. Happy coding! 🚀✨
| 2 | 0 | ['Depth-First Search', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | Rust 0ms 🔥 2.15Mb ☄️ One Function Solution 🦀 | rust-0ms-215mb-one-function-solution-by-x14xn | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | rony0000013 | NORMAL | 2024-06-01T13:30:42.946992+00:00 | 2024-06-01T13:30:42.947025+00:00 | 22 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimpl Solution {\n pub fn find_max_fish(mut grid: Vec<Vec<i32>>) -> i32 {\n fn dfs(v: &mut Vec<Vec<i32>>, i: usize, j: usize) -> i32 {\n if i>=v.len() || j>=v[0].len() || v[i][j] == 0 {return 0;}\n let x = v[i][j];\n v[i][j] = 0;\n x + dfs(v, i+1, j) + dfs(v, i, j+1)\n + dfs(v, i.saturating_sub(1), j)\n + dfs(v, i, j.saturating_sub(1))\n }\n\n (0..grid.len())\n .map(|i| {\n (0..grid[0].len())\n .map(|j| {\n dfs(&mut grid, i, j)\n })\n .max()\n .unwrap() \n })\n .max()\n .unwrap()\n }\n}\n``` | 2 | 0 | ['Rust'] | 1 |
maximum-number-of-fish-in-a-grid | Easy DFS || Beats 70% || Java | easy-dfs-beats-70-java-by-youssef1998-nlw0 | Complexity\n- Time complexity: O(nm)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(nm) , stack space.\n Add your space complexity here, e | youssef1998 | NORMAL | 2023-07-31T14:20:28.396890+00:00 | 2023-07-31T14:20:28.396916+00:00 | 17 | false | # Complexity\n- Time complexity: $$O(n*m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n*m)$$ , stack space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private final List<Integer[]> directions = List.of(\n new Integer[]{1, 0}, new Integer[]{-1, 0}, new Integer[]{0, 1}, new Integer[]{0, -1}\n );\n\n public int findMaxFish(int[][] grid) {\n int maxFish = 0;\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n if (grid[i][j] != 0) maxFish = Math.max(maxFish, dfs(i, j, grid));\n }\n }\n return maxFish;\n }\n\n private int dfs(int i, int j, int[][] grid) {\n if (notValid(i, j, grid) || grid[i][j] == 0) return 0;\n int fish = grid[i][j];\n grid[i][j] = 0;\n for (Integer[] direction: directions) {\n int x = i + direction[0], y = j + direction[1];\n fish += dfs(x, y, grid);\n }\n return fish;\n }\n\n private boolean notValid(int i, int j, int[][] grid) {\n return i < 0 || i >= grid.length || j < 0 || j >= grid[0].length;\n }\n}\n``` | 2 | 0 | ['Depth-First Search', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | ✅✅DFS Approach || Easy to understand || Standard method || C++ || beats 100% | dfs-approach-easy-to-understand-standard-z68e | Intuition\n Describe your first thoughts on how to solve this problem. \nThis is a standard traversal problem where we will traverse each component, find the su | 2uringTested | NORMAL | 2023-05-11T09:22:58.377087+00:00 | 2023-05-11T09:22:58.377119+00:00 | 30 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a standard traversal problem where we will traverse each component, find the sum of fishes on each component and find out the maximum of all the sums.\n\n# Complexity\n- Time complexity: O(M*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n using vvi = vector<vector<int>>;\n void dfs(vvi& grid, int i,int j, int& sum){\n int m = grid.size();\n int n = grid[0].size();\n if(i>=m || i<0 || j<0 || j>=n){\n return;\n }\n if(grid[i][j]!=0 && grid[i][j]!=-1){\n sum += grid[i][j];\n grid[i][j]=-1;\n dfs(grid,i+1,j,sum);\n dfs(grid,i,j+1,sum);\n dfs(grid,i-1,j,sum);\n dfs(grid,i,j-1,sum);\n }\n }\n int findMaxFish(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n int ans = INT_MIN;\n int sum=0;\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(grid[i][j]>0){\n dfs(grid,i,j,sum);\n ans = max(ans,sum);\n sum=0;\n }\n }\n }\n \n return ans==INT_MIN?0:ans;\n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'Graph', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | ✅ C++ BFS Solution ✅ | c-bfs-solution-by-akshay_ar_2002-pxq5 | Intuition\n Describe your first thoughts on how to solve this problem. \n- BFS traversal on the Connected Components. Just a variation of LC #200[Number Of Isla | akshay_AR_2002 | NORMAL | 2023-05-07T17:22:33.411067+00:00 | 2023-05-07T17:23:12.948030+00:00 | 47 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- BFS traversal on the Connected Components. Just a variation of LC #200[Number Of Islands]\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The code uses a breadth-first search (BFS) approach to traverse the water cells in the given grid and calculate the maximum number of fish that can be caught.\n\n- For each water cell in the grid, the BFS is applied to find out all the connected water cells and count the total number of fish in those cells.\n\n- The maximum fish count obtained from all the BFS traversals is then returned as the result.\n\n# Complexity\nTime complexity: O(m * n(m + n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- where m and n are the number of rows and columns in the input grid. In the worst case, we may have to traverse all the water cells in the grid, and each BFS traversal takes O(m + n) time.\n\nSpace complexity: O(m * n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- since we are using a 2D visited matrix to keep track of the visited water cells. In the worst case, all the water cells may need to be visited, requiring a visited matrix of size mn. Additionally, the queue used in BFS will hold a maximum of O(m*n) water cell positions at any point in time.\n\n# Code\n```\nclass Solution {\npublic:\n\n int maxFishes = INT_MIN;\n\n void bfs(int row, int col, vector <vector<int>> &grid, vector <vector<int>> &vis, int dx[], int dy[])\n {\n int n = grid.size();\n int m = grid[0].size();\n \n vis[row][col] = 1;\n queue <pair<int, int>> q;\n q.push({row, col});\n\n int fishes = 0;\n while(!q.empty())\n {\n int x = q.front().first;\n int y = q.front().second;\n\n //adding the count of the number of fishes in the current cell\n fishes += grid[x][y];\n q.pop();\n\n //finding out the current cell neighbours\n for(int i = 0; i < 4; i++)\n {\n int nRow = x + dx[i];\n int nCol = y + dy[i];\n \n //check for the validity of neighbouring row & col\n if(nRow >= 0 && nRow < n && nCol >= 0 && nCol < m && grid[nRow][nCol] > 0 && !vis[nRow][nCol])\n {\n vis[nRow][nCol] = 1;\n q.push({nRow, nCol});\n }\n }\n }\n\n maxFishes = max(maxFishes, fishes);\n return;\n }\n \n int findMaxFish(vector<vector<int>>& grid) \n {\n //no of rows\n int n = grid.size();\n \n //no of cols\n int m = grid[0].size();\n \n //create the visited matrix to keep track of the water cell\n vector <vector <int>> vis(n, vector <int> (m, 0));\n \n //can move only in 4-directions\n int dx[] = {0, 0, 1, -1};\n int dy[] = {1, -1, 0, 0}; \n \n for(int i = 0; i < n; i++)\n {\n for(int j = 0; j < m; j++)\n {\n if(grid[i][j] > 0 && !vis[i][j])\n bfs(i, j, grid, vis, dx, dy);\n }\n }\n \n return maxFishes == INT_MIN ? 0 : maxFishes;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | C++|| Simple BFS Approach | c-simple-bfs-approach-by-arko-816-al13 | \nclass Solution {\npublic:\n int maxi=INT_MIN;\n int dx[4]={0,1,0,-1};\n int dy[4]={1,0,-1,0};\n void f(int i,int j,int m,int n,vector<vector<int>> | Arko-816 | NORMAL | 2023-04-29T16:54:18.931353+00:00 | 2023-04-29T16:54:18.931392+00:00 | 233 | false | ```\nclass Solution {\npublic:\n int maxi=INT_MIN;\n int dx[4]={0,1,0,-1};\n int dy[4]={1,0,-1,0};\n void f(int i,int j,int m,int n,vector<vector<int>> &grid,vector<vector<int>> &vis)\n {\n queue<pair<int,int>> q;\n q.push({i,j});\n vis[i][j]=1;\n int s=0;\n while(!q.empty())\n {\n int x=q.front().first;\n int y=q.front().second;\n s+=grid[x][y];\n q.pop();\n for(int k=0;k<4;k++)\n {\n int newx=x+dx[k];\n int newy=y+dy[k];\n if(newx<0 or newy<0 or newx>=m or newy>=n or vis[newx][newy]==1 or grid[newx][newy]==0)\n continue;\n q.push({newx,newy});\n vis[newx][newy]=1;\n }\n }\n maxi=max(maxi,s);\n }\n int findMaxFish(vector<vector<int>>& grid) {\n int m=grid.size();\n int n=grid[0].size();\n vector<vector<int>> vis(m,vector<int>(n,0));\n for(int i=0;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(grid[i][j]>0 and !vis[i][j])\n {\n f(i,j,m,n,grid,vis);\n }\n }\n }\n return (maxi==INT_MIN)?0:maxi;\n }\n};\n``` | 2 | 0 | [] | 0 |
maximum-number-of-fish-in-a-grid | C++ Solution | c-solution-by-pranto1209-33ud | Approach\n Describe your approach to solving the problem. \n DFS 2D\n\n# Code\n\nclass Solution {\npublic:\n vector<vector<int>> grids;\n int n, m, cnt | pranto1209 | NORMAL | 2023-04-29T16:52:26.026606+00:00 | 2023-04-29T16:52:26.026648+00:00 | 340 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n DFS 2D\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> grids;\n int n, m, cnt, vis[11][11];\n \n bool valid(int x, int y) {\n if(x >= 0 and x < n and y >= 0 and y < m and !vis[x][y] and grids[x][y]) return true;\n else return false;\n }\n \n void dfs(int x, int y) {\n if(valid(x, y)) {\n vis[x][y] = 1;\n cnt += grids[x][y];\n dfs(x, y+1);\n dfs(x, y-1);\n dfs(x+1, y);\n dfs(x-1, y);\n }\n }\n \n int findMaxFish(vector<vector<int>>& grid) {\n n = grid.size();\n m = grid[0].size();\n grids = grid;\n int ans = 0;\n for(int i = 0; i < n; i++) {\n for(int j = 0; j < m; j++) {\n if(!vis[i][j] and grid[i][j]) {\n cnt = 0;\n dfs(i, j);\n ans = max(ans, cnt);\n }\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | ✔💯 DFS || MOST SIMPLE SOLUTION|| C++ | dfs-most-simple-solution-c-by-yash___sha-t3fb | \n\nclass Solution {\npublic:\n void solve(int i,int j,int &a,int &b,int &sum,int &ans,vector<vector<int>> &g){\n ans = max(ans,sum);\n if(i<0| | yash___sharma_ | NORMAL | 2023-04-29T16:11:14.497722+00:00 | 2023-04-29T16:11:14.497782+00:00 | 365 | false | \n````\nclass Solution {\npublic:\n void solve(int i,int j,int &a,int &b,int &sum,int &ans,vector<vector<int>> &g){\n ans = max(ans,sum);\n if(i<0||j<0||i>=a||j>=b||g[i][j]==0){\n return;\n }\n sum += g[i][j];\n g[i][j] = 0;\n solve(i+1,j,a,b,sum,ans,g);\n solve(i,j+1,a,b,sum,ans,g);\n solve(i-1,j,a,b,sum,ans,g);\n solve(i,j-1,a,b,sum,ans,g);\n }\n int findMaxFish(vector<vector<int>>& grid) {\n int ans = 0;\n int i,j,a = grid.size(),b = grid[0].size();\n int sum = 0;\n for(i = 0; i < a; i++){\n for(j = 0; j < b; j++){\n if(grid[i][j]){\n sum = 0;\n solve(i,j,a,b,sum,ans,grid);\n }\n }\n }\n return ans;\n }\n};\n````\n\n | 2 | 0 | ['Depth-First Search', 'Graph', 'C', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | Intuitive JavaScript solution using DFS | intuitive-javascript-solution-using-dfs-xqr8q | Approach\n Describe your approach to solving the problem. \nDFS\n\n# Complexity\n- Time complexity: O(M * N)\n Add your time complexity here, e.g. O(n) \n\n- Sp | deleted_user | NORMAL | 2023-04-29T16:08:24.975609+00:00 | 2023-04-29T16:09:08.747372+00:00 | 193 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nDFS\n\n# Complexity\n- Time complexity: O(M * N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(M * N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[][]} grid\n * @return {number}\n */\nvar findMaxFish = function(grid) {\n let max_fishes = 0;\n let ROW = grid.length;\n let COL = grid[0].length;\n \n // returns the sum of fishes possible\n const DFS = (r, c, visit) => {\n \n // base cases returns 0; \n if( r < 0 || r >= ROW ||\n c < 0 || c >= COL || \n visit.has(`${r}_${c}`) ||\n grid[r][c] == 0 \n ){\n return 0;\n }\n \n // set visted\n visit.add(`${r}_${c}`);\n \n let sum = grid[r][c]; // add current value to sum\n \n // check the surrounding nodes\n sum += DFS(r, c + 1, visit);\n sum += DFS(r, c - 1, visit);\n sum += DFS(r + 1, c, visit);\n sum += DFS(r - 1, c, visit);\n \n return sum;\n }\n \n let set = new Set(); // to record all visted nodes\n \n // go through each cell\n for(let r = 0; r < ROW; r++){\n for(let c = 0; c < COL; c++){\n // if the cell is water\n if(grid[r][c] != 0){ \n let res = DFS(r, c, set);\n\n //compare the result from DFS to main global variable \n max_fishes = Math.max(res, max_fishes);\n }\n }\n }\n \n return max_fishes; \n};\n``` | 2 | 0 | ['Depth-First Search', 'JavaScript'] | 1 |
maximum-number-of-fish-in-a-grid | SIMPLE BFS solution | | Connected Components | | C++ | simple-bfs-solution-connected-components-fhmx | \n# Approach\nSame as island problem connected component. Using BFS traverse all the components and return the maximum sum of the the components.\n Describe you | yashpal_97 | NORMAL | 2023-04-29T16:04:30.105457+00:00 | 2023-04-29T16:04:30.105526+00:00 | 202 | false | \n# Approach\nSame as island problem connected component. Using BFS traverse all the components and return the maximum sum of the the components.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: o(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N*M)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n /* dfs(int row,int col,vector<vector<int>>&vis,cnt){\n vis[row][col]=1;\n cnt+=grid[row][col];\n \n }*/\n int findMaxFish(vector<vector<int>>& grid) {\n int cnt = 0;\n int m = grid.size();\n int n = grid[0].size();\nvector<vector<int>>vis;\n for (int i = 0; i < m; i++)\n {\n for (int j = 0; j < n; j++)\n {\n if (grid[i][j] > 0)\n {\n queue<pair<int, int>> q;\n q.push({i, j});\n int fish = grid[i][j];\n grid[i][j] = 0;\n\n while (!q.empty())\n {\n int row = q.front().first;\n int col = q.front().second;\n q.pop();\n\n if (row > 0 && grid[row - 1][col] > 0)\n {\n fish += grid[row - 1][col];\n q.push({row - 1, col});\n grid[row - 1][col] = 0;\n }\n if (row < m - 1 && grid[row + 1][col] > 0)\n {\n fish += grid[row + 1][col];\n q.push({row + 1, col});\n grid[row + 1][col] = 0;\n }\n if (col > 0 && grid[row][col - 1] > 0)\n {\n fish += grid[row][col - 1];\n q.push({row, col - 1});\n grid[row][col - 1] = 0;\n }\n if (col < n - 1 && grid[row][col + 1] > 0)\n {\n fish += grid[row][col + 1];\n q.push({row, col + 1});\n grid[row][col + 1] = 0;\n }\n }\n\n cnt = max(cnt, fish);\n grid[i][j] = fish;\n }\n }\n }\n\n return cnt;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | Concise DFS | C++ | concise-dfs-c-by-tusharbhart-bz3q | \nclass Solution {\n vector<int> dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};\n int dfs(int i, int j, vector<vector<int>>& grid, vector<vector<int>>& vis, int | TusharBhart | NORMAL | 2023-04-29T16:01:55.740463+00:00 | 2023-04-29T16:01:55.740515+00:00 | 191 | false | ```\nclass Solution {\n vector<int> dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};\n int dfs(int i, int j, vector<vector<int>>& grid, vector<vector<int>>& vis, int n, int m) {\n vis[i][j] = 1;\n int cnt = grid[i][j];\n \n for(int k=0; k<4; k++) {\n int x = i + dx[k], y = j + dy[k];\n if(x >= 0 && x < n && y >= 0 && y < m && grid[x][y] > 0 && !vis[x][y]) {\n cnt += dfs(x, y, grid, vis, n, m);\n }\n }\n return cnt;\n }\npublic:\n int findMaxFish(vector<vector<int>>& grid) {\n int n = grid.size(), m = grid[0].size(), ans = 0;\n vector<vector<int>> vis(n, vector<int>(m));\n \n for(int i=0; i<n; i++) {\n for(int j=0; j<m; j++) {\n if(grid[i][j] > 0 && !vis[i][j]) {\n ans = max(ans, dfs(i, j, grid, vis, n, m));\n }\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Depth-First Search', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | Starting is hard ,Flow is tough and end is beauty given by God. | starting-is-hard-flow-is-tough-and-end-i-ey5p | IntuitionNothing but just Dfs.Approachcheck the water count the fish and then give it back the problem is similar to the number of island.Complexity
Time compl | Madhavendrasinh44 | NORMAL | 2025-03-30T15:30:03.020114+00:00 | 2025-03-30T15:30:03.020114+00:00 | 6 | false | # Intuition
Nothing but just Dfs.
# Approach
check the water count the fish and then give it back the problem is similar to the number of island.
# Complexity
- Time complexity: $$O(n*m)$$
- Space complexity: $$O(n*m)$$
# Code
```java []
class Solution {
public int findMaxFish(int[][] grid1) {
int ans=0;
int r=grid1.length;
int c=grid1[0].length;
for(int i=0;i<r;i++){
for(int j=0;j<c;j++){
if(grid1[i][j]>0){
ans=Math.max(ans,dfs(i,j,grid1));
}
}
}
return ans;
}
private int dfs(int r ,int c, int[][]grid1){
if(r<0 || c<0 ||r>=grid1.length||c >= grid1[0].length || grid1[r][c] == 0){
return 0;
}
int res = grid1[r][c];
grid1[r][c] = 0;
res +=dfs(r-1,c,grid1);
res +=dfs(r,c-1,grid1);
res +=dfs(r+1,c,grid1);
res +=dfs(r,c+1,grid1);
return res;
}
}
``` | 1 | 0 | ['Depth-First Search', 'Matrix', 'Java'] | 0 |
maximum-number-of-fish-in-a-grid | C# | c-by-adchoudhary-f094 | Code | adchoudhary | NORMAL | 2025-02-27T04:31:41.955822+00:00 | 2025-02-27T04:31:41.955822+00:00 | 4 | false | # Code
```csharp []
public class Solution {
public int FindMaxFish(int[][] grid) {
int m = grid.Length;
int n = grid[0].Length;
int maxFish = 0;
// Directions for moving up, down, left, right
int[][] directions = new int[][] {
new int[] { 1, 0 }, // down
new int[] { -1, 0 }, // up
new int[] { 0, 1 }, // right
new int[] { 0, -1 } // left
};
// Helper function for DFS
int Dfs(int r, int c)
{
// Check for out of bounds or land cell
if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == 0)
{
return 0;
}
// Count fish in the current cell
int fish = grid[r][c];
// Mark the cell as visited by setting it to 0
grid[r][c] = 0;
int totalFish = fish; // Start with the fish in the current cell
// Explore all four directions
foreach (var dir in directions)
{
totalFish += Dfs(r + dir[0], c + dir[1]);
}
return totalFish;
}
// Iterate through the grid
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (grid[i][j] > 0)
{ // If it's a water cell
maxFish = Math.Max(maxFish, Dfs(i, j)); // Perform DFS and update maxFish
}
}
}
return maxFish;
}
}
``` | 1 | 0 | ['C#'] | 0 |
maximum-number-of-fish-in-a-grid | Can't get easier than that | cant-get-easier-than-that-by-lucifer_fa1-s0uy | IntuitionApproachComplexity
Time complexity:
Space complexity:
BFSDFS | Lucifer_Fa11in | NORMAL | 2025-02-02T07:54:07.429807+00:00 | 2025-02-02T07:54:07.429807+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# BFS
```cpp []
class Solution {
public:
int dfs(int r,int c,vector<vector<int>>& grid)
{
int rsize=grid.size(),csize=grid[0].size();
if(r<0 || c<0 || r>=rsize || c>=csize || grid[r][c]==0)return 0;
vector<pair<int,int>> directions = {{1,0},{0,1},{-1,0},{0,-1}};
int maxhere=grid[r][c];
grid[r][c]=0;
for(auto [dr,dc] : directions)
{
maxhere += dfs(r+dr,c+dc,grid);
}
return maxhere;
}
int findMaxFish(vector<vector<int>>& grid) {
int rsize=grid.size(),csize=grid[0].size();
int maxfish=0;
for(int i=0;i<rsize;i++)
{
for(int j=0;j<csize;j++)
{
if(grid[i][j]!=0)
{
maxfish = max(maxfish, dfs(i,j,grid));
}
}
}
return maxfish;
}
};
```
# DFS
```cpp []
class Solution {
public:
int findMaxFish(vector<vector<int>>& grid) {
int rsize = grid.size(), csize = grid[0].size();
vector<pair<int, int>> direction = {{1,0},{0,1},{-1,0},{0,-1}};
vector<vector<bool>> visited(rsize, vector<bool>(csize,false));
int maxfish=0;
auto bfs = [&](int r,int c) -> int
{
queue<pair<int, int>> q;
visited[r][c] = true;
q.push({r,c});
int maxHere=grid[r][c];
while(!q.empty())
{
auto [Rpos,Cpos] = q.front();
q.pop();
for(auto [dr,dc] : direction)
{
int curR=Rpos+dr,curC=Cpos+dc;
if(curR>=0 && curR<rsize && curC>=0 && curC<csize && !visited[curR][curC] && grid[curR][curC]!=0)
{
q.push({curR,curC});
visited[curR][curC]=true;
maxHere+=grid[curR][curC];
}
}
}
return maxHere;
};
for(int i=0; i<rsize; i++)
{
for(int j=0; j<csize; j++)
{
if(grid[i][j]!=0 && !visited[i][j])
{
maxfish = max(maxfish, bfs(i,j));
}
}
}
return maxfish;
}
};
``` | 1 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Queue', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | simple py sol - dfs | simple-py-sol-dfs-by-noam971-le5l | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | noam971 | NORMAL | 2025-01-28T22:51:42.870901+00:00 | 2025-01-28T22:53:23.432184+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
def dfs(i, j):
curr = grid[i][j]
grid[i][j] = 0
directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
for dx, dy in directions:
x, y = i + dx, j + dy
if -1 < x < m and -1 < y < n and grid[x][y] != 0:
curr += dfs(x, y)
return curr
res = float('-inf')
for i in range(m):
for j in range(n):
if grid[i][j] != 0:
res = max(res, dfs(i, j))
return max(res, 0)
``` | 1 | 0 | ['Python3'] | 0 |
maximum-number-of-fish-in-a-grid | easy c++ sol | easy-c-sol-by-shivesh977-rrpe | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Shivesh977 | NORMAL | 2025-01-28T22:27:13.420473+00:00 | 2025-01-28T22:27:13.420473+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<vector<int>> visited;
vector<vector<int>> dir = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int count = 0;
int bfs(int i, int j, vector<vector<int>>& grid) {
queue<pair<int, int>> q;
q.push({i, j});
int ans = 0;
while (q.size()) {
int a = q.front().first;
int b = q.front().second;
q.pop();
visited[a][b] = 1;
ans += grid[a][b];
cout<<"value : "<<grid[a][b]<<" ";
for (int k = 0; k < 4; k++) {
int x = a + dir[k][0];
int y = b + dir[k][1];
if (x < 0 || y < 0 || x >= grid.size() || y >= grid[0].size() ||
grid[x][y] == 0 || visited[x][y] == 1)
continue;
else
cout<<x<<" "<<y<<" "<<endl;
visited[x][y]=1;
q.push({x, y});
}
}
return ans;
}
int findMaxFish(vector<vector<int>>& grid) {
visited.clear();
visited.resize(grid.size(), vector<int>(grid[0].size(), 0));
for (int i = 0; i < grid.size(); i++) {
for (int j = 0; j < grid[0].size(); j++) {
// 0 means land else water
if (grid[i][j] != 0 and visited[i][j] == 0) count = max(count, bfs(i, j, grid));
}
}
return count;
}
};
``` | 1 | 0 | ['C++'] | 0 |
maximum-number-of-fish-in-a-grid | Python, classic solution with stack | python-classic-solution-with-stack-by-de-h326 | IntuitionFew steps:
determind cells with water
for next available cell in water do explore with counting fish
compute max per "pond"
ApproachComplexity
Time co | dev_lvl_80 | NORMAL | 2025-01-28T21:50:06.812452+00:00 | 2025-01-28T21:50:06.812452+00:00 | 5 | false | # Intuition
Few steps:
- determind cells with water
- for next available cell in water do explore with counting fish
- compute max per "pond"
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(N)
- Space complexity:
O(N)
# Code
```python3 []
class Solution:
def findMaxFish(self, grid: List[List[int]]) -> int:
water = set()
m = len(grid)
n = len(grid[0])
for row_id, r in enumerate(grid):
for col_id, v in enumerate(r):
if v:
water.add((row_id, col_id))
def catch(r,c)->int:
cnt_fish = 0
Q = [[r,c]]
while Q:
r,c = Q.pop()
cnt_fish +=grid[r][c]
grid[r][c] = 0
if (r,c) in water:
water.remove((r,c))
#print("",r,c, cnt_fish, grid)
for r, c in [[r-1, c], [r+1, c], [r, c-1], [r, c+1]]:
if 0<=r<m and 0<=c<n and grid[r][c]:
Q.append([r, c])
return cnt_fish
max_catch = 0
while water:
r,c = water.pop()
cnt_fish = catch(r,c)
max_catch = max(cnt_fish, max_catch)
return max_catch
``` | 1 | 0 | ['Python3'] | 0 |
maximum-number-of-fish-in-a-grid | Exploring Connected Waters | c++ | Easy | DFS 🚀🚀 | exploring-connected-waters-c-easy-dfs-by-yp4n | IntuitionThe problem can be viewed as finding the maximum sum of connected components in a grid, where each cell represents a node, and its value represents the | kirigaya07 | NORMAL | 2025-01-28T20:18:58.180991+00:00 | 2025-01-28T20:18:58.180991+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem can be viewed as finding the maximum sum of connected components in a grid, where each cell represents a node, and its value represents the number of fish present. The goal is to explore all connected cells with non-zero values and sum their values to determine the maximum fish that can be collected in a single connected component.
# Approach
<!-- Describe your approach to solving the problem. -->
We use Depth-First Search (DFS) to traverse the grid and calculate the total number of fish in each connected component:
1. Iterate over all cells in the grid. If a cell has a value greater than 0 and has not been visited, start a DFS from that cell.
2. During the DFS:
- Mark the current cell as visited.
- Add the value of the current cell to the total fish count.
- Recursively visit all valid neighboring cells (up, down, left, right) that have not been visited and contain fish.
3. Keep track of the maximum fish count encountered across all connected components.
4. Return the maximum fish count as the result.
To ensure we do not revisit cells during DFS, we maintain a visited set to track the cells that have already been processed.
# Complexity
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Time complexity: O(m×n)
- Each cell is visited at most once during the DFS.
- Here, mm and nn are the number of rows and columns in the grid.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(m×n)
- The visited set may store up to m×nm×n cells in the worst case.
- The recursion stack for DFS can also go as deep as m×nm×n in the worst case (when the entire grid is a single connected component).
# Code
```cpp []
class Solution {
public:
// DFS to calculate total fish in a connected component
int dfs(vector<vector<int>>& grid, set<pair<int, int>> &visited, int r,
int c) {
// Out of bounds, no fish, or already visited
if (r < 0 || c < 0 || r >= grid.size() || c >= grid[0].size() ||
grid[r][c] == 0 || visited.count({r, c}) > 0)
return 0;
visited.insert({r, c}); // Mark current cell as visited
int res = grid[r][c]; // Add fish at the current cell
// Explore all four directions
res += dfs(grid, visited, r + 1, c);
res += dfs(grid, visited, r - 1, c);
res += dfs(grid, visited, r, c + 1);
res += dfs(grid, visited, r, c - 1);
return res;
}
int findMaxFish(vector<vector<int>>& grid) {
int row = grid.size(), col = grid[0].size();
set<pair<int, int>> visited; // Tracks visited cells
int res = 0;
// Start DFS from each cell with fish
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
res =
max(res, dfs(grid, visited, i, j)); // Find the maximum fish
}
}
return res;
}
};
``` | 1 | 0 | ['Depth-First Search', 'Graph', 'Ordered Set', 'C++'] | 0 |
maximum-number-of-fish-in-a-grid | DFS solytion | dfs-solytion-by-ishaan_p-2r2q | Code | Ishaan_P | NORMAL | 2025-01-28T20:11:30.883693+00:00 | 2025-01-28T20:11:30.883693+00:00 | 7 | false |
# Code
```java []
class Solution {
public int findMaxFish(int[][] grid) {
int maxFishyFishies = 0;
boolean[][] visited = new boolean[grid.length][grid[0].length]; //dont modify input
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(visited[i][j] || grid[i][j] == 0)
continue;
maxFishyFishies = Math.max(maxFishyFishies, howManyFishyFishies(grid,i,j, visited));
}
}
return maxFishyFishies;
}
public int howManyFishyFishies(int[][] grid, int i, int j, boolean[][] visited){
if(i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] == 0 || visited[i][j])
return 0;
visited[i][j] = true;
int total = grid[i][j];
total += howManyFishyFishies(grid, i+1,j,visited);
total += howManyFishyFishies(grid, i-1,j,visited);
total += howManyFishyFishies(grid, i,j+1,visited);
total += howManyFishyFishies(grid, i,j-1,visited);
return total;
}
}
``` | 1 | 0 | ['Java'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [Python] BFS * BFS | 130ms | beats 95% | Explained & Commented | python-bfs-bfs-130ms-beats-95-explained-lyius | Lets break the question into simple parts:\n\n1. Lets think that we have no person and we have to find the minimum path between box and the target. Easy right? | zypher27 | NORMAL | 2020-06-18T15:36:35.676154+00:00 | 2021-10-05T05:51:03.254347+00:00 | 12,990 | false | Lets break the question into simple parts:\n\n1. Lets think that we have no person and we have to find the minimum path between box and the target. Easy right? Simple BFS.\n\n2. If you know how to solve the first part, what I actually do is modify first part with few constraints. \n\t* \tI just check whether the box can be shifted to the new position(up, down, left, right)\n\t* \tFor it to be shifted to the new position the person has to be in a corresponding position right?\n\t* \tSo we check if the person can travel from his old position to his corresponding new position(using another BFS). \n\t* \tIf the person can travel to his new position than the box can be shifted, otherwise the box cannot be shifted.\n\n3. We keep repeating step 2 until we reach the target or it is not possible to move the box anymore.\n\nNOTE : If you know A* algorithm, you can use Euclidean distance as heuristic and use a priority queue instead of normal queue, the worst case time might increase but average case will get better.\n\n\n```\nclass Solution:\ndef minPushBox(self, grid: List[List[str]]) -> int:\n\n # this loop is to get the coordinates of target, box and person. Nothing else is gained here\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == "T":\n target = (i,j)\n if grid[i][j] == "B":\n box = (i,j)\n if grid[i][j] == "S":\n person = (i,j)\n\n # this function checks whether the given coordinates/indices are valid to go\n def valid(x,y):\n return 0<=x<len(grid) and 0<=y<len(grid[0]) and grid[x][y]!=\'#\'\n\n # this function checks whether the person can travel from current position to the destination position.\n # used simple bfs(dfs can also be used here), should be self explainatory if you know BFS.\n def check(curr,dest,box):\n que = deque([curr])\n v = set()\n while que:\n pos = que.popleft()\n if pos == dest: return True\n new_pos = [(pos[0]+1,pos[1]),(pos[0]-1,pos[1]),(pos[0],pos[1]+1),(pos[0],pos[1]-1)]\n for x,y in new_pos:\n if valid(x,y) and (x,y) not in v and (x,y)!=box:\n v.add((x,y))\n que.append((x,y))\n return False\n\n q = deque([(0,box,person)])\n vis = {box+person}\n # this is the main bfs which gives us the answer\n while q :\n dist, box, person = q.popleft()\n if box == target: # return the distance if box is at the target\n return dist\n\n #these are the new possible coordinates/indices box can be placed in (up, down, right, left).\n b_coord = [(box[0]+1,box[1]),(box[0]-1,box[1]),(box[0],box[1]+1),(box[0],box[1]-1)]\n #these are the corresponding coordinates the person has to be in to push .. the box into the new coordinates\n p_coord = [(box[0]-1,box[1]),(box[0]+1,box[1]),(box[0],box[1]-1),(box[0],box[1]+1)]\n\n for new_box,new_person in zip(b_coord,p_coord): \n # we check if the new box coordinates are valid and our current state is not in vis\n if valid(*new_box) and new_box+box not in vis:\n # we check corresponding person coordinates are valid and if it is possible for the person to reach the new coordinates\n if valid(*new_person) and check(person,new_person,box):\n vis.add(new_box+box)\n q.append((dist+1,new_box,box))\n\n return -1\n```\n\nTime = Space = O((rows*cols)^2) | 200 | 2 | ['Breadth-First Search', 'Python'] | 22 |
minimum-moves-to-move-a-box-to-their-target-location | A-star search | a-star-search-by-yorkshire-2bnc | Heuristic (an under-estimate of the remaining moves required) is the Manhattan distance between box and target.\nA state consist of box and person locations tog | yorkshire | NORMAL | 2019-11-17T04:01:39.968224+00:00 | 2019-11-17T04:28:13.952575+00:00 | 15,903 | false | Heuristic (an under-estimate of the remaining moves required) is the Manhattan distance between box and target.\nA state consist of box and person locations together.\n\nRepeatedly pop the state with the lowest heuristic + previous moves off the heap.\nAttempt to move the person in all 4 directions.\nIf any direction moves the person to the box, check if the box can move to the nex position in the grid.\n\n```\n rows, cols = len(grid), len(grid[0])\n for r in range(rows):\n for c in range(cols):\n if grid[r][c] == "T":\n target = (r, c)\n if grid[r][c] == "B":\n start_box = (r, c)\n if grid[r][c] == "S":\n start_person = (r, c)\n \n def heuristic(box):\n return abs(target[0] - box[0]) + abs(target[1] - box[1])\n \n def out_bounds(location): # return whether the location is in the grid and not a wall\n r, c = location\n if r < 0 or r >= rows:\n return True\n if c < 0 or c >= cols:\n return True\n return grid[r][c] == "#"\n \n heap = [[heuristic(start_box), 0, start_person, start_box]]\n visited = set()\n \n while heap:\n _, moves, person, box = heapq.heappop(heap)\n if box == target:\n return moves\n if (person, box) in visited: # do not visit same state again\n continue\n visited.add((person, box))\n \n for dr, dc in [[0, 1], [1, 0], [-1, 0], [0, -1]]:\n new_person = (person[0] + dr, person[1] + dc)\n if out_bounds(new_person):\n continue\n \n if new_person == box:\n new_box = (box[0] + dr, box[1] + dc)\n if out_bounds(new_box):\n continue\n heapq.heappush(heap, [heuristic(new_box) + moves + 1, moves + 1, new_person, new_box])\n else:\n heapq.heappush(heap, [heuristic(box) + moves, moves, new_person, box]) # box remains same\n \n return -1\n``` | 104 | 2 | [] | 23 |
minimum-moves-to-move-a-box-to-their-target-location | Java straightforward BFS solution | java-straightforward-bfs-solution-by-cod-3d6b | For me, this is a typical bfs question to find the minimum step, so the key point is to find out the state. For this problem, I choose the coordinates of box an | codejoker | NORMAL | 2019-11-17T10:53:27.726916+00:00 | 2019-11-22T07:14:41.730605+00:00 | 11,891 | false | For me, this is a typical bfs question to find the minimum step, so the key point is to find out the state. For this problem, I choose the coordinates of box and storekeeper as the state. Because the grid length is from 1 to 20, we can use one 32 bit integer to present all the coordinates.\nEvery step, move storekeeper 1 step, if it meet the box, then the box move 1 step in the same direction. Because it want to know the minimum step the box move, so when the first time box on the target pocision, it may not be the minimum anwser. So we compare every one and find the minimum step.\n\n```java\nclass Solution {\n int[][] moves = new int[][]{{0,-1}, {0,1}, {-1,0}, {1,0}};\n public int minPushBox(char[][] grid) {\n int[] box = null, target = null, storekeeper = null;\n int n = grid.length, m = grid[0].length;\n for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) {\n if (grid[i][j] == \'B\') box = new int[]{i, j};\n else if (grid[i][j] == \'T\') target = new int[]{i, j};\n else if (grid[i][j] == \'S\') storekeeper = new int[]{i, j};\n }\n Queue<Integer> q = new LinkedList<>();\n Map<Integer, Integer> dis = new HashMap<>();\n int start = encode(box[0], box[1], storekeeper[0], storekeeper[1]);\n dis.put(start, 0);\n q.offer(start);\n int ret = Integer.MAX_VALUE;\n while (!q.isEmpty()) {\n int u = q.poll();\n int[] du = decode(u);\n if (dis.get(u) >= ret) continue;\n if (du[0] == target[0] && du[1] == target[1]) {\n ret = Math.min(ret, dis.get(u));\n continue;\n }\n int[] b = new int[]{du[0], du[1]};\n int[] s = new int[]{du[2], du[3]};\n\t\t\t// move the storekeeper for 1 step\n for (int[] move : moves) {\n int nsx = s[0] + move[0];\n int nsy = s[1] + move[1];\n if (nsx < 0 || nsx >= n || nsy < 0 || nsy >= m || grid[nsx][nsy] == \'#\') continue;\n\t\t\t\t// if it meet the box, then the box move in the same direction\n if (nsx == b[0] && nsy == b[1]) {\n int nbx = b[0] + move[0];\n int nby = b[1] + move[1];\n if (nbx < 0 || nbx >= n || nby < 0 || nby >= m || grid[nbx][nby] == \'#\') continue;\n int v = encode(nbx, nby, nsx, nsy);\n if (dis.containsKey(v) && dis.get(v) <= dis.get(u) + 1) continue;\n dis.put(v, dis.get(u) + 1);\n q.offer(v);\n } else { // if the storekeeper doesn\'t meet the box, the position of the box do not change\n int v = encode(b[0], b[1], nsx, nsy);\n if (dis.containsKey(v) && dis.get(v) <= dis.get(u)) continue;\n dis.put(v, dis.get(u));\n q.offer(v);\n }\n }\n }\n return ret == Integer.MAX_VALUE ? -1 : ret;\n }\n int encode(int bx, int by, int sx, int sy) {\n return (bx << 24) | (by << 16) | (sx << 8) | sy;\n }\n int[] decode(int num) {\n int[] ret = new int[4];\n ret[0] = (num >>> 24) & 0xff;\n ret[1] = (num >>> 16) & 0xff;\n ret[2] = (num >>> 8) & 0xff;\n ret[3] = num & 0xff;\n return ret;\n }\n}\n``` | 95 | 6 | [] | 20 |
minimum-moves-to-move-a-box-to-their-target-location | Java use 2 level BFS, beat 99% | java-use-2-level-bfs-beat-99-by-hobiter-nejs | It will be easy coming up with BFS. But some key point:\n1, you need to make sure Storekeeper:\na has room to push the box;\nb has a way to go to the room to pu | hobiter | NORMAL | 2020-06-28T05:53:19.973855+00:00 | 2020-06-28T05:53:40.245418+00:00 | 4,904 | false | It will be easy coming up with BFS. But some key point:\n1, you need to make sure Storekeeper:\na has room to push the box;\nb has a way to go to the room to push the box. \nTherefore you need another bfs to find if the path exist;\n\n2 Make sure to set box as a blocker during bfs;\n\n3, Visited boolean array is tricky:\n2-d is not enough, some corner case:\nSenario 1, some push room is reachable if Storekeeper stands right, where another Senario 2, push room not reachable if Storekeeper stands right, though the postion of box are the same;\ntherefore, you need a 3-d array to mark box\' postion and another num to represents Storekeeper\'s postion compared to box(left, right, up, down);\n\n```\nclass Solution {\n char[][] g;\n int m, n;\n int[][] dir = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};\n public int minPushBox(char[][] grid) {\n g = grid;\n m = g.length; \n n = g[0].length;\n int step = 0;\n boolean[][][] vs = new boolean[m][n][4];\n \n Queue<int[]> q = new LinkedList<>();\n int[] st = new int[]{-1, -1}, ed = new int[]{-1, -1}, pl = new int[]{-1, -1};\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (g[i][j] == \'B\') st = new int[]{i, j};\n if (g[i][j] == \'T\') ed = new int[]{i, j};\n if (g[i][j] == \'S\') pl = new int[]{i, j};\n }\n }\n q.offer(new int[]{st[0], st[1], pl[0], pl[1]});\n while (!q.isEmpty()) {\n for (int i = 0, l = q.size(); i < l; i++) {\n int[] curr = q.poll();\n if (curr[0] == ed[0] && curr[1] == ed[1]) return step;\n for (int j = 0; j < dir.length; j++) {\n if (vs[curr[0]][curr[1]][j]) continue;\n int[] d = dir[j];\n int r0 = curr[0] + d[0], c0 = curr[1] + d[1]; // where pl stands, have room to push;\n if (r0 < 0 || r0 >= m || c0 < 0 || c0 >= n || g[r0][c0] == \'#\') continue;\n int r = curr[0] - d[0], c = curr[1] - d[1]; // box next spots;\n if (r < 0 || r >= m || c < 0 || c >= n || g[r][c] == \'#\') continue;\n if (!reachable(r0, c0, curr)) continue;\n vs[curr[0]][curr[1]][j] = true;\n q.offer(new int[]{r, c, curr[0], curr[1]});\n }\n }\n step++;\n }\n return -1;\n }\n \n private boolean reachable(int i, int j, int[] curr) {\n Queue<int[]> q = new LinkedList<>();\n q.offer(new int[]{curr[2], curr[3]});\n boolean[][] vs = new boolean[m][n];\n vs[curr[0]][curr[1]] = true;\n while (!q.isEmpty()) {\n int[] cur = q.poll();\n if (cur[0] == i && cur[1] == j) return true;\n for (int[] d : dir) {\n int r = cur[0] - d[0], c = cur[1] - d[1]; // box next spots;\n if (r < 0 || r >= m || c < 0 || c >= n || vs[r][c] || g[r][c] == \'#\') continue;\n vs[r][c] = true;\n q.offer(new int[]{r, c});\n }\n }\n return false;\n }\n}\n``` | 50 | 3 | [] | 11 |
minimum-moves-to-move-a-box-to-their-target-location | cpp two bfs solution, 8ms beat 100% | cpp-two-bfs-solution-8ms-beat-100-by-sgu-1c3b | typical bfs problem for shortest distance.\nThe person shall be able to move to the location behind the box to make a move.\nwe can use dfs/bfs to check if pers | sguo-lq | NORMAL | 2019-11-19T00:01:28.037145+00:00 | 2019-11-19T00:01:28.037199+00:00 | 3,866 | false | typical bfs problem for shortest distance.\nThe person shall be able to move to the location behind the box to make a move.\nwe can use dfs/bfs to check if person can move to desired location.\nhowever dfs will get TLE since dfs is one direction forward until failure, hence dfs will use more time in average.\n\ncheck if person can move a position is a conventional bfs.\ncheck box can be moved to a position is a bit tricky, it needs both the person and box position, so we use a pair of position in the queue\nand the visited shall also use combined information, I used the string combination of the two positions.\n\n```cpp\n int minPushBox(vector<vector<char>>& grid) {\n //bfs with person and box, the person can move in the free cells\n //person must be able to walk to the box.\n int m=grid.size(),n=grid[0].size();\n queue<pair<int,int>> q; //store the next valid box position: it shall store: player,box,\n unordered_set<string> v;\n int src=0,dst=0,player=0;\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(grid[i][j]==\'S\') {player=i*n+j;grid[i][j]=\'.\';}\n if(grid[i][j]==\'B\') {src=i*n+j;grid[i][j]=\'.\';}\n if(grid[i][j]==\'T\') {dst=i*n+j;grid[i][j]=\'.\';}\n }\n }\n if(src==dst) return 0;\n q.push({src,player});\n int step=0;\n int dir[][4]={{-1,0},{1,0},{0,-1},{0,1}};\n while(q.size()){\n int sz=q.size();\n while(sz--){\n auto pos=q.front();\n q.pop();\n int box=pos.first,player=pos.second;\n if(box==dst) return step;\n int xb=box/n,yb=box%n;\n for(auto d: dir){\n int x=xb+d[0],y=yb+d[1]; //new box position\n int xp=xb-d[0],yp=yb-d[1];\n if(x<0||y<0||x>=m||y>=n||grid[x][y]==\'#\') continue;\n if(xp<0||yp<0||xp>=m||yp>=n||grid[xp][yp]==\'#\') continue;\n string s=to_string(box)+","+to_string(xp*n+yp);//box pos+person pos\n if(v.count(s)) continue;\n if(can_access(grid,player,xp*n+yp,box)){\n q.push({x*n+y,box});//make a push, box move to new, p moves to box\n v.insert(s);\n }\n }\n }\n step++;\n }\n return -1;\n }\n bool can_access(vector<vector<char>>& g,int src,int dst,int box){\n int m=g.size(),n=g[0].size();\n //bfs shall be better than dfs\n queue<int> q;\n vector<bool> v(m*n);\n q.push(src);\n v[src]=1;\n int dir[][2]={{-1,0},{1,0},{0,-1},{0,1}};\n g[box/n][box%n]=\'#\';\n while(q.size()){\n int sz=q.size();\n while(sz--){\n int p=q.front();\n q.pop();\n if(p==dst) {g[box/n][box%n]=\'.\';return 1;}\n int x0=p/n,y0=p%n;\n for(auto d: dir){\n int x=x0+d[0],y=y0+d[1];\n if(x<0||y<0||x>=m||y>=n||g[x][y]!=\'.\'||v[x*n+y]) continue;\n v[x*n+y]=1;\n q.push(x*n+y);\n }\n }\n }\n g[box/n][box%n]=\'.\';\n return 0;\n }\n```\n\t\n | 38 | 1 | [] | 4 |
minimum-moves-to-move-a-box-to-their-target-location | Python Dijkstra Short | python-dijkstra-short-by-dylan20-0rjf | edit: added an explanation below\nedit2: fixed a bug found by StefanPochmann@\n\n\ndef minPushBox(self, grid: List[List[str]]) -> int:\n free = set((i, j) fo | dylan20 | NORMAL | 2019-11-17T15:38:37.842010+00:00 | 2019-12-01T19:45:41.835144+00:00 | 2,834 | false | edit: added an explanation below\nedit2: fixed a bug found by StefanPochmann@\n\n```\ndef minPushBox(self, grid: List[List[str]]) -> int:\n free = set((i, j) for i, row in enumerate(grid) for j, cell in enumerate(row) if cell != \'#\')\n target = next((i, j) for i, row in enumerate(grid) for j, cell in enumerate(row) if cell == \'T\')\n boxi, boxj = next((i, j) for i, row in enumerate(grid) for j, cell in enumerate(row) if cell == \'B\')\n si, sj = next((i, j) for i, row in enumerate(grid) for j, cell in enumerate(row) if cell == \'S\')\n visited = set()\n heap = [(0, si, sj, boxi, boxj)]\n while heap:\n moves, si, sj, boxi, boxj = heapq.heappop(heap)\n if (boxi, boxj) == target:\n return moves\n if (si, sj, boxi, boxj) in visited:\n continue\n visited.add((si, sj, boxi, boxj))\n for dx, dy in [(1, 0), (-1, 0), (0, 1), (0, -1)]:\n ni, nj = si + dx, dy + sj\n if (ni, nj) == (boxi, boxj) and (boxi + dx, boxj + dy) in free and (ni, nj, boxi + dx, boxj + dy) not in visited:\n heapq.heappush(heap, (moves + 1, ni, nj, boxi + dx, boxj + dy))\n elif (ni, nj) in free and (ni, nj) != (boxi, boxj) and (ni, nj, boxi, boxj) not in visited:\n heapq.heappush(heap, (moves, ni, nj, boxi, boxj))\n return -1\n```\n\nIn this solution, a Node is represented by the position of the box, and the position of the person i.e. ```(si, sj, boxi, boxj)```.\n\nTo find a Node\'s neighbors we add ```UP/DOWN/LEFT/RIGHT``` to the person\'s position and if the persons position ```==``` the boxes position, we also add this direction to the boxes position. The weight of the edge is ```1``` if the box moved,```0``` if not.\n\nWe could explicitly define ```Node, Edge, and Graph``` in the code, and even construct the whole graph prior to running Dijkstra, but it\'s easier and quicker to determine edge weights / neighbors by doing calculations on the ```(si, sj, boxi, boxj)``` tuple.\n\nNow we have our representations in place, just run Dijkstra in the normal way. I don\'t want to explain Dijkstra here, there are already really good explanations elsewhere. | 37 | 0 | [] | 10 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.